question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
minimum-moves-to-move-a-box-to-their-target-location | [C++] Accepted, Clear solution to understand for this long problem with proper variable names | c-accepted-clear-solution-to-understand-cvlcr | \nclass Solution {\npublic:\n int n , m;\n int dx[4] = {1, 0, -1, 0};\n int dy[4] = {0, 1, 0, -1};\n\t\n bool inside(int x, int y) {\n return | vaibhav15 | NORMAL | 2021-06-11T14:52:55.699047+00:00 | 2021-06-11T14:52:55.699094+00:00 | 2,154 | false | ```\nclass Solution {\npublic:\n int n , m;\n int dx[4] = {1, 0, -1, 0};\n int dy[4] = {0, 1, 0, -1};\n\t\n bool inside(int x, int y) {\n return (x >= 0 && x < n && y >= 0 && y < m);\n }\n\n bool canWalk(int srcX, int srcY, int destX, int destY, vector<vector<char>>&grid, vector<vector<int>>&visited)\n {\n if(srcX == destX && srcY == destY) return true;\n visited[srcX][srcY] = 1;\n for(int i = 0; i < 4; i++)\n {\n int x = srcX + dx[i];\n int y = srcY + dy[i];\n if(inside(x, y) && grid[x][y] != \'#\' && !visited[x][y])\n {\n if(canWalk(x, y, destX, destY, grid, visited))\n return true;\n }\n }\n return false;\n }\n int minPushBox(vector<vector<char>>& grid) {\n n = grid.size();\n m = grid[0].size();\n int boxX, boxY, targetX, targetY, personX, personY; \n for(int i = 0; i < n; i++)\n {\n for(int j = 0; j < m; j++)\n {\n if(grid[i][j] == \'S\')\n {\n personX = i;\n personY = j;\n }\n else if(grid[i][j] == \'T\')\n {\n targetX = i;\n targetY = j;\n }\n else if(grid[i][j] == \'B\')\n {\n boxX = i;\n boxY = j;\n }\n }\n }\n\t\t \n queue<vector<int>>q;\n set<vector<int>> seen;\n q.push({boxX, boxY,personX, personY});\n int ans = 0;\n\t\t \n while(!q.empty())\n {\n int sz = q.size();\n while(sz--)\n {\n auto p = q.front();\n q.pop();\n boxX = p[0]; boxY = p[1];\n personX = p[2]; personY = p[3];\n\t\t\t\t\n if(boxX == targetX && boxY == targetY)\n return ans;\n\t\t\t\t\t\n grid[boxX][boxY] = \'#\';\n\t\t\t\t\n for(int i = 0; i < 4; i++)\n {\n int new_boxX = boxX + dx[i];\n int new_boxY = boxY + dy[i];\n int new_personX = boxX - dx[i];\n int new_personY = boxY - dy[i];\n vector<int>curPos({new_boxX,new_boxY,new_personX,new_personY});\n vector<vector<int>> visited(n, vector<int>(m, 0));\n if(inside(new_boxX, new_boxY) && grid[new_boxX][new_boxY]!=\'#\' && !seen.count(curPos) && canWalk(personX, personY, new_personX, new_personY, grid, visited))\n {\n seen.insert(curPos);\n q.push(curPos);\n }\n }\n grid[boxX][boxY] = \'.\';\n }\n ans++;\n }\n return -1;\n }\n};\n``` | 34 | 2 | [] | 7 |
minimum-moves-to-move-a-box-to-their-target-location | Python Straightforward 2-stage BFS, Explained | python-straightforward-2-stage-bfs-expla-vw2l | First define a function to check from current state, what are the possible neighbouring states (use BFS to check if we can move the player to required location) | davyjing | NORMAL | 2019-11-17T04:04:05.043235+00:00 | 2019-11-18T19:45:52.408779+00:00 | 4,672 | false | First define a function to check from current state, what are the possible neighbouring states (use BFS to check if we can move the player to required location). Notice that the state includes both the location of the box and the player.\nSecond BFS to see if we can reach the target location.\n```\nclass Solution:\n def minPushBox(self, grid: List[List[str]]) -> int:\n dire = [(1,0),(0,1),(-1,0),(0,-1)]\n\t\t\n def can_get(cur_b,cur_p,tar):\n seen,cur = set([cur_p]),set([cur_p])\n while cur:\n tmp = []\n for loc in cur:\n for x,y in dire:\n if 0<= loc[0]+x < len(grid) and 0 <= loc[1] + y < len(grid[0]) and (loc[0]+x,loc[1] +y) != cur_b and grid[loc[0] +x][loc[1] +y] != \'#\' and (loc[0]+x,loc[1] +y) not in seen:\n tmp += [(loc[0]+x,loc[1] +y)]\n cur = set(tmp)\n seen |= cur\n if tar in seen:\n return True\n return False\n\t\t\t\n for i in range(len(grid)):\n for j in range(len(grid[0])):\n if grid[i][j] == \'B\': box = (i,j)\n if grid[i][j] == \'S\': player = (i,j)\n if grid[i][j] == \'T\': target = (i,j)\n\t\t\t\t\n seen,cur,res = set([(box,player)]), set([(box,player)]), 0\n while cur:\n tmp = []\n res += 1\n for b,p in cur:\n for x,y in dire:\n if 0<= b[0]+x < len(grid) and 0 <= b[1] + y < len(grid[0]) and grid[b[0]+x][b[1]+y] != \'#\' and can_get(b,p,(b[0]-x,b[1]-y)) and ((b[0]+x,b[1]+y),b) not in seen:\n tmp += [((b[0]+x,b[1]+y),b)]\n cur = set(tmp)\n seen |= cur\n for x,y in dire:\n if (target,(target[0]+x,target[1]+y)) in seen:\n return res\n return -1\n``` | 25 | 1 | [] | 5 |
minimum-moves-to-move-a-box-to-their-target-location | Fast easy to understand solution using 2 BFSs [intuition+diagram+explanation] | fast-easy-to-understand-solution-using-2-9mro | Little improvisation of the solution provided by sguo-lq, and also explaining every step and the intuition for the approach.\n\nDon\'t panic by seeing the lengt | coderangshu | NORMAL | 2021-09-18T20:31:33.928147+00:00 | 2022-10-12T04:43:53.920935+00:00 | 1,232 | false | Little improvisation of the solution provided by [sguo-lq](https://leetcode.com/problems/minimum-moves-to-move-a-box-to-their-target-location/discuss/432593/cpp-two-bfs-solution-8ms-beat-100), and also explaining every step and the intuition for the approach.\n\n**Don\'t panic by seeing the length of the solution it is actually the implementation of 2 BFSs that makes it long.**\nP.S - You know the no. of lines required for implementing a single BFS \uD83D\uDE1C.\n\nOur goal is that the box reaches the target and for that we need a BFS to get the shortest distance between the source and destination of it.\nNow the twist is we need to use the storekeeper to push it to the destination and thus here our goal is to bring him to the position adjacent to the box from where he can push the box towards the direction that would led the box\'s travelling in the shortest path given by the box\'s BFS.\n\nTo achieve the above objective we need to maintain a BFS of the box and also for each step taken by the box we need to align the storekeeper to the required adjacent cell so that the box can be pushed in the required direction provided by the box\'s BFS. \nFrom above we can infer that the storekeeper needs to be just behind the box w.r.t the direction in which it is to be pushed.\n\nLet\'s Understand pictorially:\nInitial condition (the empty cells are marked by there coresponding cell numbers): \n```\n#\t1\t2\t#\t#\t#\t#\t#\t\n#\t9\t10\tT\t#\t13\t14\t#\t\n#\t17\t18\t19\t#\tB\t22\t#\t\n#\t25\t26\t27\t28\t29\t30\t#\t\n#\t33\t34\t35\t#\t37\tS\t#\t\n#\t41\t42\t#\t#\t#\t#\t#\t\n```\nFrom above the shortest route for the box would be B -> 29 -> 28 -> 27 -> 19 -> T,\nbut the storekeeper needs to push the block to T, for the above path when the box is at 27 the person cannot be anywhere but in the right part of the maze with the only opening being at 28. So for pushing the box the storekeeper must be at 35 which isn\'t possible, thus to accomodate this the shortest route for the box is modified\nB -> 29 -> 28 -> 27 -> 26 -> 18 -> 10 -> T\nTo achieve this intuitive behaviour just need to make the storekeeper to reach the correct oriented position to push the box in its shortest path.\n\nFor 1st iteration B available options are 29, 22, 13 (according to box\'s BFS, here 20 is not suitable next stop for the box as it is a wall), thus we need to check if S ```canAccess()``` 13, 20, 29 respectively, for this a second BFS is done(can use DFS too but that would check each route individually thus increasing the search time) for the storekeeper with ```src=S(i.e. 38)``` and ```dest=13```, ```dest=20```, ```dest=29```, from the 3 dests 20 isn\'t accessable as it is a wall, thus only 2 options are left 13 or 29 this ```canAccesss```.\n\nHope you got the idea how the 2 BFS traversals are done for box and storekeeper, the basic idea is very simple get the possible next stops for the box from the box\'s BFS and for each of this stops check whether the accordingly oriented cells where the storekeeper must be present to push it forward is accessible by the storekeeper from his current location using the storekeeper\'s BFS.\nTo simplify further explanation we follow the answer path of the box.\n\n13 is to be the dest of the storekeeper,\nThus now the scenario is :\n```\n#\t1\t2\t#\t#\t#\t#\t#\t\n#\t9\t10\tT\t#\tS\t14\t#\t\n#\t17\t18\t19\t#\tB\t22\t#\t\n#\t25\t26\t27\t28\t29\t30\t#\t\n#\t33\t34\t35\t#\t37\t38\t#\t\n#\t41\t42\t#\t#\t#\t#\t#\t\n```\nNow push box to new location and storekeeper occupies the boxes old position\nPushes = 1\n```\n#\t1\t2\t#\t#\t#\t#\t#\t\n#\t9\t10\tT\t#\t13\t14\t#\t\n#\t17\t18\t19\t#\tS\t22\t#\t\n#\t25\t26\t27\t28\tB\t30\t#\t\n#\t33\t34\t35\t#\t37\t38\t#\t\n#\t41\t42\t#\t#\t#\t#\t#\t\n```\nNow check S ```canAccess``` 30 as box is to be pushed to 28\n```\n#\t1\t2\t#\t#\t#\t#\t#\t\n#\t9\t10\tT\t#\t13\t14\t#\t\n#\t17\t18\t19\t#\t21\t22\t#\t\n#\t25\t26\t27\t28\tB\tS\t#\t\n#\t33\t34\t35\t#\t37\t38\t#\t\n#\t41\t42\t#\t#\t#\t#\t#\t\n```\nNow push box to new location and storekeeper occupies the boxes old position\nPushes = 2\n```\n#\t1\t2\t#\t#\t#\t#\t#\t\n#\t9\t10\tT\t#\t13\t14\t#\t\n#\t17\t18\t19\t#\t21\t22\t#\t\n#\t25\t26\t27\tB\tS\t30\t#\t\n#\t33\t34\t35\t#\t37\t38\t#\t\n#\t41\t42\t#\t#\t#\t#\t#\t\n```\nNow check S ```canAccess``` 29 as box is to be pushed to 27, push box to new location\nPushes = 3\n```\n#\t1\t2\t#\t#\t#\t#\t#\t\n#\t9\t10\tT\t#\t13\t14\t#\t\n#\t17\t18\t19\t#\t21\t22\t#\t\n#\t25\t26\tB\tS\t29\t30\t#\t\n#\t33\t34\t35\t#\t37\t38\t#\t\n#\t41\t42\t#\t#\t#\t#\t#\t\n```\nNow for B possible next choices are 35, 19, 26. For these the storekeeper should be at 19, 35, 28 respectively. Using the ```canAccess``` the only option is to shift box to 26 as storekeeper can only access 28\nPushes = 4\n```\n#\t1\t2\t#\t#\t#\t#\t#\t\n#\t9\t10\tT\t#\t13\t14\t#\t\n#\t17\t18\t19\t#\t21\t22\t#\t\n#\t25\tB\tS\t28\t29\t30\t#\t\n#\t33\t34\t35\t#\t37\t38\t#\t\n#\t41\t42\t#\t#\t#\t#\t#\t\n```\nNow box has choice 34, 27, 18, 25 correspondingly the respective locations for the storekeeper to be present are 18, 25, 34, 27, we take the shortest path for the box (notice here choosing either 27 or 18 as next stop for box would lead to shortest answer we continue with 18)\nPushes = 5\n```\n#\t1\t2\t#\t#\t#\t#\t#\t\n#\t9\t10\tT\t#\t13\t14\t#\t\n#\t17\tB\t19\t#\t21\t22\t#\t\n#\t25\tS\t27\t28\t29\t30\t#\t\n#\t33\t34\t35\t#\t37\t38\t#\t\n#\t41\t42\t#\t#\t#\t#\t#\t\n```\nSkipping the last 2 steps as these are visible from the above state.\nThus Pushes = 7 (answer)\n\nHope the dry run helped understand the complete logic.\n\nSee through the inline comments to understand the reason for line\n```\nclass Solution {\npublic:\n \n vector<vector<int>> dir = {{1,0},{0,1},{-1,0},{0,-1}};\n \n bool isValid(vector<vector<char>>&grid, int x, int y){\n int m = grid.size(), n = grid[0].size();\n return (x>=0 and y>=0 and x<m and y<n and grid[x][y]!=\'#\');\n }\n \n bool canAccess(vector<vector<char>>&grid, int dest, int src, int box){\n int m = grid.size(), n = grid[0].size();\n \n vector<bool> visited(m*n,false);\n visited[src] = true;\n \n // mark the location of box as blocked as stkp can\'t travel there\n grid[box/n][box%n] = \'#\';\n \n queue<int> q;\n q.push(src);\n while(!q.empty()){\n int cp = q.front();\n q.pop();\n if(dest==cp){grid[box/n][box%n] = \'.\';return true;}\n for(auto e:dir){\n int nx = cp/n+e[0], ny = cp%n+e[1];\n int np = nx*n+ny;\n if(np>=0 and np<m*n){\n if(visited[np]) continue;\n visited[np] = true;\n if(!isValid(grid,nx,ny)) continue;\n q.push(np);\n }\n }\n }\n grid[box/n][box%n] = \'.\';\n return false;\n }\n \n int minPushBox(vector<vector<char>>& grid) {\n int m = grid.size(), n = grid[0].size();\n // get position of storekeeper, box and target\n // and mark those points as open path, i.e. \'.\'\n int stkp, box, tar;\n for(int i=0;i<m;i++){\n for(int j=0;j<n;j++){\n if(grid[i][j]==\'S\') {stkp = i*n+j;grid[i][j]=\'.\';}\n else if(grid[i][j]==\'B\') {box = i*n+j;grid[i][j]=\'.\';}\n else if(grid[i][j]==\'T\') {tar = i*n+j;;grid[i][j]=\'.\';}\n }\n }\n if(box==tar) return 0;\n \n // BFSing for box to target\n \n // queue stores the stkp and the box locations\n // as both needs to be kept track of while traversing\n // for each location of the box\n queue<pair<int,int>> q;\n q.push({box,stkp});\n \n // keeping track of visited nodes for the stkp and \n // the box simultaneously using a string\n unordered_set<string> visited;\n visited.insert(to_string(stkp)+" "+to_string(box));\n \n int pushes = 0;\n while(!q.empty()){\n int len = q.size();\n while(len--){\n auto [bo,stkpo] = q.front();\n q.pop();\n if(bo==tar) return pushes;\n for(auto e:dir){\n int nbx = bo/n+e[0], nby = bo%n+e[1];\n int nstkpx = bo/n-e[0], nstkpy = bo%n-e[1];\n int nstkp = nstkpx*n+nstkpy, nb = nbx*n+nby;\n if(nstkp>=0 and nb>=0 and nstkp<m*n and nb<m*n){\n string key = to_string(nstkp)+" "+to_string(nb);\n if(visited.find(key)!=visited.end()) continue;\n if(!isValid(grid,nbx,nby) or !isValid(grid,nstkpx,nstkpy)) continue;\n \n // if stkp can get to the position from where he can push the box\n // push new position of box and new position of stkp (old position of box)\n // into the queue\n if(canAccess(grid,nstkp,stkpo,bo)){\n visited.insert(key);\n q.push({nb,bo});\n }\n }\n }\n }\n // if reached this point means 1 push has been performed\n // and the box is 1 step closer to the target\n pushes++;\n }\n return -1;\n }\n};\n```\n\nUpvote please if understood my explantion, devoted quite a bit of effort to put up this explanation, as I found it necessary as there\'s no proper explanation along with the intution behind the logic anywhere.\nThanks\nCheers\nHappy Coding | 22 | 0 | [] | 3 |
minimum-moves-to-move-a-box-to-their-target-location | [Java] BFS (17ms), Explained with comments | java-bfs-17ms-explained-with-comments-by-9fy4 | Two things need to pay attention:\n While trying to recorded to visited position of Box, we need to include an additional dimension to record which direction th | lucas_zhc | NORMAL | 2019-11-18T00:37:57.776201+00:00 | 2019-12-03T18:24:27.323563+00:00 | 2,967 | false | Two things need to pay attention:\n* While trying to recorded to **visited position of Box**, we need to include an additional dimension to record which direction the Player pushed the box from. For example, there are 4 previous positions that the Box can arrive position (x, y). We have to treat those 4 states separately.\n* While checking if the Player is able to reach the correct position to make a valid push, we need to **set the Box position as an obstacle(#)** since the Player cannot walk pass Box. Also, we need to keep track of **the previous position of the Player** after making the push.\n\nI have included comments in my code. Hope this helps.\n\n```\nclass Solution {\n private char[][] G;\n private int rows;\n private int cols;\n private int[] dir = new int[]{-1,0,1,0,-1};\n public int minPushBox(char[][] grid) {\n // Sanity check\n if(grid == null || grid.length == 0 || grid[0].length == 0) \n return-1;\n \n rows = grid.length;\n cols = grid[0].length;\n G = grid;\n \n // Find the location of the Target, the Box and the Player.\n int[] tLoc = new int[2];\n int[] pLoc = new int[2];\n int[] bLoc = new int[2];\n for(int r = 0; r < rows; r++) {\n for(int c = 0; c < cols; c++) {\n if(G[r][c] == \'S\')\n pLoc = new int[]{r,c};\n \n if(G[r][c] == \'T\') \n tLoc = new int[]{r,c};\n \n if(G[r][c] == \'B\') \n bLoc = new int[]{r,c};\n \n // Set those location to be Floor so we can BFS easier\n if(G[r][c] != \'#\') \n G[r][c] = \'.\';\n }\n }\n \n // BFS on Box\n return bfs(pLoc, bLoc, tLoc);\n }\n \n // BFS for Box\n private int bfs(int[] p, int[] b, int[] t) {\n Queue<int[]> queue = new LinkedList<>();\n // Keep a record of the Player position along with the Box positon\n int[] L = new int[]{b[0],b[1],p[0],p[1]};\n \n // An extra dimension to keep track of where the Box is pushed from\n boolean[][][] visited = new boolean[rows][cols][4];\n queue.offer(L);\n int step = 0;\n \n // Standard BFS\n while(!queue.isEmpty()) {\n int len = queue.size();\n while(len > 0) {\n int[] loc = queue.poll();\n // Mark the current Box position as an obstacle\n G[loc[0]][loc[1]] = \'#\';\n \n // Use directional array to check 4 directions\n for(int i = 0; i < 4; i++) {\n int deltaR = dir[i];\n int deltaC = dir[i+1];\n int newR = loc[0] + deltaR;\n int newC = loc[1] + deltaC;\n \n // If the new Box position is in bound \n // && the Play can reach that position\n // && that position is a Floor\n // && that position is visited with the current push direction "i"\n if(inBound(newR,newC) \n && reachable(loc[2],loc[3],loc[0]-deltaR,loc[1]-deltaC)\n && G[newR][newC] != \'#\' \n && !visited[newR][newC][i]) {\n \n // If the Target is reached\n if(t[0] == newR && t[1] == newC) return step+1;\n \n // Put the new Box position into the queue along with the Player position\n queue.offer(new int[]{newR, newC,loc[0],loc[1]});\n visited[newR][newC][i] = true;\n }\n }\n \n // Mark the Box position back to Floor\n G[loc[0]][loc[1]] = \'.\';\n \n len--;\n }\n step++;\n }\n \n // If the program reaches here, it means no solution.\n return -1;\n }\n \n // BFS for Plahyer\n // This is just standard BFS, return true if Player can reach that position\n private boolean reachable(int pR, int pC, int r, int c) {\n // If the Play is on that position to start with, return true\n if(pR == r && pC == c) \n return true;\n Queue<int[]> queue = new LinkedList<>();\n boolean[][] visited = new boolean[rows][cols];\n queue.offer(new int[]{pR, pC});\n \n while(!queue.isEmpty()) {\n int len = queue.size();\n while(len > 0) {\n int[] loc = queue.poll();\n if(!visited[loc[0]][loc[1]]) {\n visited[loc[0]][loc[1]] = true;\n for(int i = 0; i < 4; i++) {\n int newR = loc[0] + dir[i];\n int newC = loc[1] + dir[i+1];\n if(inBound(newR,newC) \n && G[newR][newC] != \'#\' \n && !visited[newR][newC]) {\n if(r == newR && c == newC) return true;\n queue.offer(new int[]{newR, newC});\n }\n }\n }\n len--;\n }\n }\n return false;\n }\n \n // Check if the coordinate is out of bound\n private boolean inBound(int r, int c) {\n return r >= 0 && c >= 0 && r < rows && c < cols;\n }\n}\n```\n\nTime complexity: O((nm)^2)\nIn worse case, the Box has to traverse through the entire matrix which has nm vertices. We also need to do the same thing for the Play with each vertice. That makes the total iteration to be (nm)^2. But, in practice, it will be way lower than that.\n\nSpace complexity: O(nm)\nMemory needed for Queue in BFS.\n | 20 | 0 | ['Breadth-First Search', 'Java'] | 1 |
minimum-moves-to-move-a-box-to-their-target-location | [cpp] BFS + DFS solution | cpp-bfs-dfs-solution-by-insomniacat-v6xr | Use BFS to solve the problem:\nFor each state [person, box], use dfs to find if the person can walk to the \'back\' of the box and push the box. Once the box | insomniacat | NORMAL | 2019-11-17T04:25:54.905143+00:00 | 2020-09-06T05:55:47.230992+00:00 | 2,089 | false | Use BFS to solve the problem:\nFor each state `[person, box]`, use dfs to find if the person can walk to the \'back\' of the box and push the box. Once the box reaches the destination, bfs guarantees to find the optimal solution.\nBe careful with the box position since we may be obstructed by the box after we push it.\n\n(grid size `M` x `N`)\n**Time Complexity**: `O((MN)^2)` \nIt may look like `O((MN)^3)` at the first glance, we have `O((MN)^2)` person-box states and each canReach() takes `O(MN)` time. However, for each box location, the person must be adjacent to him, so there\'re total `O(MN)` state for this bfs solution and the all time is `O((MN)^2)`.\n\n**Space complexity**: `O(M*N)`\n\nUpdate 09/05/2020: code refactored for a better view.\n```\nclass Solution {\n int m, n;\n vector<vector<int>> dir = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};\n bool valid(vector<vector<char>>& g, int x, int y) {\n if(x < 0 || x >= m || y < 0 || y >= n || g[x][y] == \'#\') {\n return false;\n }\n return true;\n }\n \n bool canReach(vector<vector<char>>& g, vector<vector<bool>>& pplLoc, int x, int y, int bx, int by) {\n if(!valid(g, x, y) || pplLoc[x][y]) {\n return false;\n }\n if(bx == x && by == y) {\n return true;\n }\n pplLoc[x][y] = true;\n for(auto& d : dir) {\n if(canReach(g, pplLoc, x + d[0], y + d[1], bx, by)) {\n return true;\n }\n }\n return false;\n }\n \n \npublic:\n typedef pair<int, int> PI;\n typedef pair<PI, PI> PII;\n \n int minPushBox(vector<vector<char>>& g) {\n m = g.size(), n = g[0].size();\n int px, py, bx, by, gx, gy;\n for(int x = 0; x < m; ++x) {\n for(int y = 0; y < n; ++y) {\n if(g[x][y] == \'S\') {\n px = x, py = y;\n }else if(g[x][y] == \'B\') {\n bx = x, by = y;\n }else if(g[x][y] == \'T\') {\n gx = x, gy = y;\n }\n }\n }\n queue<PII> q;\n set<PII> visited;\n q.push({{px, py}, {bx, by}});\n visited.insert({{px, py}, {bx, by}});\n int ans = 0;\n while(q.size()) {\n ans++;\n for(int l = q.size(); l > 0; --l) {\n auto f = q.front();\n q.pop();\n auto [px, py] = f.first;\n auto [bx, by] = f.second;\n g[bx][by] = \'#\';\n for(auto& d : dir) {\n vector<vector<bool>> pplLoc(m, vector<bool>(n, false));\n if(canReach(g, pplLoc, px, py, bx - d[0], by - d[1])) {\n int nbx = bx + d[0], nby = by + d[1];\n if(nbx == gx && nby == gy) {\n return ans;\n }\n if(valid(g, nbx, nby)) {\n PII newState = {{bx, by}, {nbx, nby}};\n if(!visited.count(newState)) {\n visited.insert(newState);\n q.push(newState);\n }\n }\n }\n }\n g[bx][by] = \'.\';\n }\n }\n return -1;\n }\n};\n``` | 15 | 1 | [] | 7 |
minimum-moves-to-move-a-box-to-their-target-location | [C++ 16ms/12MB]Pictures to show step-by-step problem solving | c-16ms12mbpictures-to-show-step-by-step-ltho3 | At the first sight of this problem, I was trying to use backtracking or recursion to solve until I reread the question and examples: even there is a valid path | dennysun | NORMAL | 2021-09-29T09:08:35.896119+00:00 | 2021-09-29T09:08:35.896160+00:00 | 990 | false | At the first sight of this problem, I was trying to use backtracking or recursion to solve until I reread the question and examples: even there is a valid path from box position to target position the player could still be not able to make it. Then I gave up recursion also considering it can end up with O(4^(mn)) in worst cases.\n\nBacktracking or recursion is actually depth-first-search, though breadth-first-search seems to be more suitable for this problem (we can know the number of moves easier).\n\nThen I know at least I need two queues to do breadth-first-search, one is for box, another is for player.\n\nThen the problem comes to be how to record the path, one thing off the top of my head is using "**visit[row][col]**" to keep a record of the positions that has been visited.\n\nI started to write code based on the analysis above until failed at this test case: \n\nwhere the player has to revisit a cell to get through when the box is blocking the way to the target.\n\n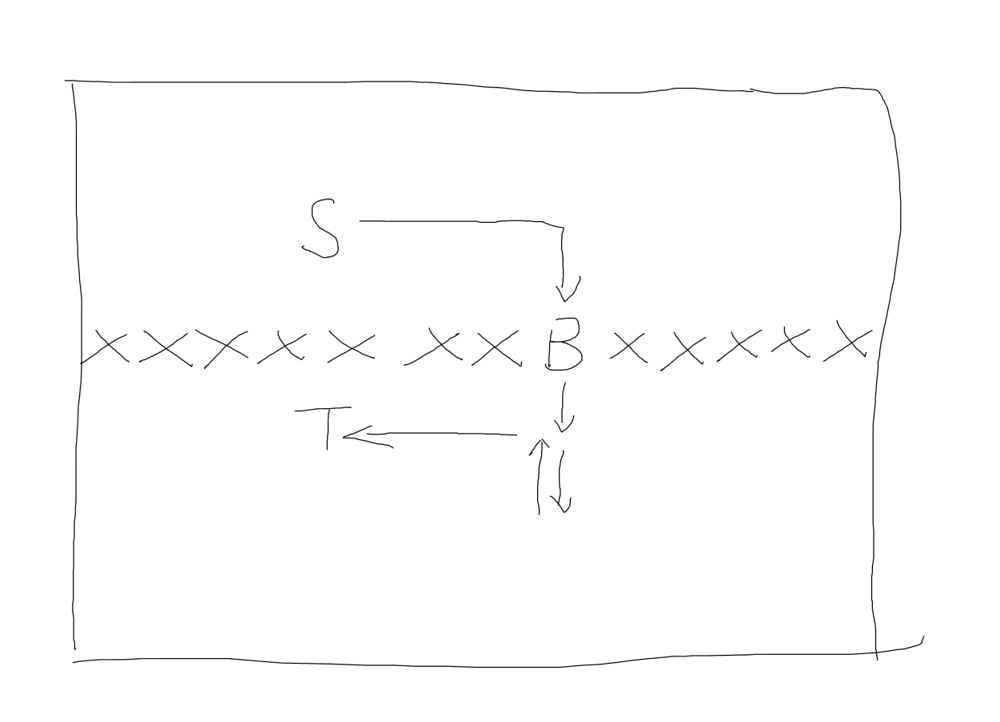\n\nApparently just using **visit[row][col]** cannot cover this type of cases, we need to take player\'s position into account, maybe **visit[box_row][box_col][player_row][player_col]**. \n\nWhat does it mean? **It represents the minimal moves that the player needs to do when the box is at (box_row, box_col) and the player is at (player_row, player_col).**\n\nThe box can be anywhere in the grid, but do we need to know all the doable position of the player for each positon of the box?\n\nThe answer is NO, because we only care the position that is next to the box, which is up/right/down/left. For example, when the player is up the box, the box will be pushed down by the player, when the player is on the right side of the box, the box will be pushed towards the left by the player.\n\nThis suggests us to simplify from **visit[box_row][box_col][player_row][player_col]** to **visit[box_row][box_col][direction]** to bring the space complexity from n^4 down to 4*(n^2). 0<= box_row < n, 0<= box_col < n, direction = 4 (up/right/down/left).\n \n**visit[box_row][box_col][direction]** means the minimal moves when the player pushes the box from that direction.\n\nYou can walk through an example in the picture below, if you can understand how the numbers get calculated, it will be easy to understand the code at the end of this post.\n\n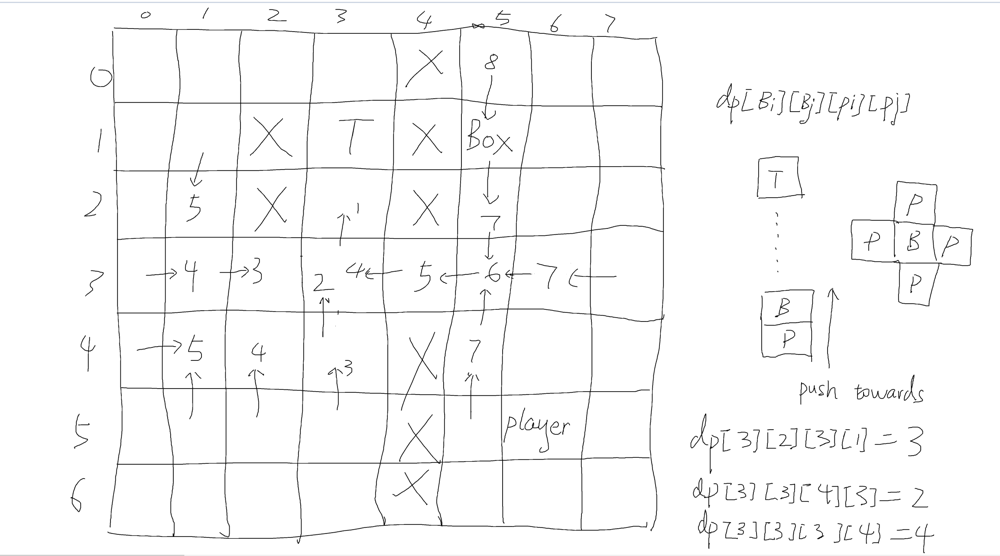\n\n\n```\nclass Solution {\npublic:\n \n// check if the player can get to (pi1, pj1) from (pi2, pj2) when the box is in (bi, bj)\n bool canPlayerDoIt(vector<vector<char>>& grid, vector<vector<int>>& directions, int bi, int bj, int pi1, int pj1, int pi2, int pj2) {\n if (pi1 == pi2 && pj1 == pj2)\n return true;\n\n vector<vector<int>> visit(grid.size(), vector<int>(grid[0].size(), 0));\n queue<pair<int, int>> qp;\n qp.push(pair<int, int>(pi1, pj1));\n visit[pi1][pj1] = 1;\n\n while (!qp.empty()) {\n int row = qp.front().first, col = qp.front().second;\n for (int idx = 0; idx < directions.size(); idx++) {\n int r = row + directions[idx][0], c = col + directions[idx][1];\n if (r<0 || c<0 || r>grid.size() - 1 || c>grid[0].size() - 1 || visit[r][c] != 0) continue;\n if (r == pi2 && c == pj2) return true;\n else if (grid[r][c] != \'#\' && (r != bi || c != bj))\n qp.push(pair<int, int>(r, c)), visit[r][c] = 1;\n }\n qp.pop();\n }\n return false;\n }\n\n int minPushBox(vector<vector<char>>& grid) {\n int m = grid.size(), n = grid[0].size();\n int dp[20][20][4] = { 0 }; // (box_row, box_col, up/right/down/left)\n vector<vector<int>> directions = { {-1, 0}, {0, 1}, {1, 0}, {0, -1} }; // up, right, down, left\n queue<pair<int, int>> qb; // queue for box\n int ti = 0, tj = 0, pi = 0, pj = 0, bi = 0, bj = 0; //target, player, box\n\n // find target, player, box\n for (int i = 0; i < m; i++)\n for (int j = 0; j < n; j++)\n if (grid[i][j] == \'T\')\n ti = i, tj = j;\n else if (grid[i][j] == \'S\')\n pi = i, pj = j;\n else if (grid[i][j] == \'B\')\n bi = i, bj = j;\n\n // Trying to get the minimum pushes \n qb.push(pair<int, int>(ti, tj));\n for (int idx = 0; idx < directions.size(); idx++) {\n int pr = ti + 2 * directions[idx][0], pc = tj + 2 * directions[idx][1], br = ti + directions[idx][0], bc = tj + directions[idx][1];\n if (pr >= 0 && pr < m && pc >= 0 && pc < n && grid[pr][pc] != \'#\' && grid[br][bc] != \'#\'){\n dp[br][bc][idx] = 1;\n if (grid[br][bc] == \'B\'){ // find the box\n if (canPlayerDoIt(grid, directions, br, bc, br + directions[idx][0], bc + directions[idx][1], pi, pj))\n return dp[br][bc][idx];\n }\n qb.push(pair<int, int>(br, bc));\n }\n }\n qb.pop();\n\n while (!qb.empty()){\n int row = qb.front().first, col = qb.front().second, current = 0, move = 0;\n for (int idx = 0; idx < directions.size(); idx++)\n if (dp[row][col][idx] > move)\n move = dp[row][col][idx], current = idx; // what if there are 1+ max values , 1+ current\n\n for (int idx = 0; idx < directions.size(); idx++){\n int pr = row + 2 * directions[idx][0], pc = col + 2 * directions[idx][1], br = row + directions[idx][0], bc = col + directions[idx][1];\n if (pr >= 0 && pr < m && pc >= 0 && pc < n && grid[pr][pc] != \'#\' && grid[br][bc] != \'#\') { //&& grid[pr][pc] != \'T\' && grid[br][bc] != \'T\')\n if (current == idx || (dp[br][bc][idx] == 0 &&\n canPlayerDoIt(grid, directions, row, col, row + directions[idx][0], col + directions[idx][1], row + directions[current][0], col + directions[current][1])))\n {\n dp[br][bc][idx] = 1 + move;\n if (grid[br][bc] == \'B\') // FIND THE BOX\n if (canPlayerDoIt(grid, directions, br, bc, br + directions[idx][0], bc + directions[idx][1], pi, pj))\n return dp[br][bc][idx];\n if (dp[br][bc][idx] > dp[br][bc][(idx + 1) % 4] && dp[br][bc][idx] > dp[br][bc][(idx + 2) % 4] && dp[br][bc][idx] > dp[br][bc][(idx + 3) % 4])\n qb.push(pair<int, int>(br, bc));\n }\n }\n }\n qb.pop();\n }\n\n return -1;\n }\n};\n``` | 14 | 1 | [] | 3 |
minimum-moves-to-move-a-box-to-their-target-location | c++, 2 * BFS with explanations | c-2-bfs-with-explanations-by-savvadia-1jq2 | Intuition and observations:\n we need to count only the box moves, so let\'s kick around the box and count the moves\n for the person we need to check if he can | savvadia | NORMAL | 2019-11-27T07:49:21.607184+00:00 | 2019-11-27T07:50:18.150334+00:00 | 1,139 | false | Intuition and observations:\n* we need to count only the box moves, so let\'s kick around the box and count the moves\n* for the person we need to check if he can walk to the place in front of the box\n* to move the box, the person have to stand in front of it:\n```\n[[".",".","."], [[".",".","."], [[".","S","."], [[".","T","."],\n ["S","B","T"], ["T","B","S"], [".","B","."], [".","B","."],\n [".",".","."]] [".",".","."]] [".","T","."]] [".","S","."]]\n```\n* When the person moves the box, he will take the place of the box\n* Usually the person will hang around the box so BFS is preferrable\n* The box itself is an obstacle so we need to check if a person can walk separately for each box position. As a consequence, we need to track person+box positions as visited\n* The same position of the person and the box can be walkable or not depending on where the person starts. So we should mark the person+box position as visited only when it is reachable.\n* To navigate properly always use rows and cols (and never x and y) because it matches the intuition: ```grid[r][c]```. For x and y it would be ```grid[y][x]``` so don\'t do that\n\nSteps:\n* find the positions of person, box and target\n* iterate all positions reachable with one more move (and add next moves to the same list)\n* for each position try to move the box in all 4 directions (BFS #1)\n* check if the person can walk to stand in front of the box (BFS #2)\n\n```\nclass Solution {\n int rows, cols;\n vector<vector<int>> dirs={{1,0},{0,1},{-1,0},{0,-1}};\n \n\t// positions: person, new_person, box\n bool isReachable(int pr, int pc, int npr, int npc, int br, int bc, vector<vector<char>>& grid)\n {\n vector<int> visited(rows*cols,0);\n visited[pr*cols+pc]=1;\n list<vector<int>> togo; togo.push_back({pr,pc});\n while(togo.size())\n {\n int r=togo.front()[0], c=togo.front()[1];\n togo.pop_front();\n if(r==npr && c==npc) return true;\n for(auto& d:dirs)\n {\n int nr=r+d[0], nc=c+d[1], key=nr*cols+nc;\n if(nr<0||nc<0||nr>=rows||nc>=cols||grid[nr][nc]==\'#\'||(nr==br&&nc==bc)) continue;\n if(visited[key]) continue;\n visited[key]=1;\n togo.push_back({nr,nc});\n }\n }\n return false;\n }\npublic:\n int minPushBox(vector<vector<char>>& grid) {\n rows = grid.size(), cols=grid[0].size();\n int pr,pc,br,bc,tr,tc; // person, box, target\n for(int r=0;r<rows;r++)\n for(int c=0;c<cols;c++)\n if( grid[r][c]==\'S\') pr=r, pc=c;\n else if(grid[r][c]==\'B\') br=r, bc=c;\n else if(grid[r][c]==\'T\') tr=r, tc=c;\n \n vector<vector<int>> visited(rows*cols,vector<int>(rows*cols,0));\n int pkey=pr*cols+pc, bkey=br*cols+bc;\n visited[pkey][bkey]=1;\n queue<vector<int>> q;\n q.push({pr,pc,br,bc}); // person.r, person.c, box.r, box.c\n\n int moves=0;\n while(q.size())\n {\n int len = q.size();\n moves++;\n for(int i=0; i<len; i++) // iterate throuh all positions reachable within 1 move\n {\n vector<int>& pos = q.front();\n int pr=pos[0], pc=pos[1], br=pos[2], bc=pos[3];\n q.pop();\n for(auto& d:dirs) // try to move the box\n {\n // person stands in front of the box to move it \n int nbr=br+d[0], nbc=bc+d[1], npr=br-d[0], npc=bc-d[1];\n if(nbr<0||nbc<0||nbr>=rows||nbc>=cols||grid[nbr][nbc]==\'#\') continue;\n if(npr<0||npc<0||npr>=rows||npc>=cols||grid[npr][npc]==\'#\') continue;\n\n pkey=npr*cols+npc, bkey=br*cols+bc;\n if(visited[pkey][bkey]==1) continue;\n \n // try to walk to the new position and consider where is the box now\n if(!isReachable(pr,pc,npr,npc,br,bc,grid)) continue;\n visited[pkey][bkey]=1; // trick: mark as visited only if we managed to get there\n if(nbr==tr && nbc==tc) return moves;\n \n q.push({br,bc,nbr,nbc}); // the person takes the place of the box\n }\n }\n }\n return -1;\n }\n};\n```\n\nThis test case is the most advanced since the same position of the box and person have to be checked twice (```grid[3][4]``` to move the box up):\n```\n[["#",".",".","#","T","#","#","#","#"],["#",".",".","#",".","#",".",".","#"],["#",".",".","#",".","#","B",".","#"],["#",".",".",".",".",".",".",".","#"],["#",".",".",".",".","#",".","S","#"],["#",".",".","#",".","#","#","#","#"]]\n\n[\n["#",".",".","#","T","#","#","#","#"], 0\n["#",".",".","#",".","#",".",".","#"], 1\n["#",".",".","#",".","#","B",".","#"], 2\n["#",".",".",".",".",".",".",".","#"], 3\n["#",".",".",".",".","#",".","S","#"], 4\n["#",".",".","#",".","#","#","#","#"]] 5\n 0 1 2 3 4 5 6 7 8\n``` | 11 | 1 | ['Breadth-First Search'] | 2 |
minimum-moves-to-move-a-box-to-their-target-location | [Python] Level-by-level BFS solution (similar problems listed) | python-level-by-level-bfs-solution-simil-9nog | Level-by-level BFS visit can be used to solve a lot of problems of finding discrete shortest distance.\nPlease see and vote for my solutions for these similar p | otoc | NORMAL | 2019-11-17T04:22:58.930413+00:00 | 2022-07-30T23:59:49.103044+00:00 | 1,826 | false | Level-by-level BFS visit can be used to solve a lot of problems of finding discrete shortest distance.\nPlease see and vote for my solutions for these similar problems\n[102. Binary Tree Level Order Traversal](https://leetcode.com/problems/binary-tree-level-order-traversal/discuss/1651394/Python-level-by-level-BFS-Solution)\n[127. Word Ladder](https://leetcode.com/problems/word-ladder/discuss/352659/Simple-Python-BFS-solution)\n[126. Word Ladder II](https://leetcode.com/problems/word-ladder-ii/discuss/352661/Simple-Python-BFS-solution)\n[301. Remove Invalid Parentheses](https://leetcode.com/problems/remove-invalid-parentheses/discuss/327481/Python-DFS-solution-with-pruning-(28-ms-beat-99.56)-%2B-BFS-solution)\n[317. Shortest Distance from All Buildings](https://leetcode.com/problems/shortest-distance-from-all-buildings/discuss/331983/Python-BFS-solution-(52-ms-beat-98.27))\n[529. Minesweeper](https://leetcode.com/problems/minesweeper/discuss/1651414/python-level-by-level-bfs-solution)\n[773. Sliding Puzzle](https://leetcode.com/problems/sliding-puzzle/discuss/412586/Standard-Python-BFS-solution-(level-by-level-traversal))\n[815. Bus Routes](https://leetcode.com/problems/bus-routes/discuss/1651399/Python-Level-by-level-BFS-solution)\n[854. K-Similar Strings](https://leetcode.com/problems/k-similar-strings/discuss/420506/Python-BFS-solution)\n[864. Shortest Path to Get All Keys](https://leetcode.com/problems/shortest-path-to-get-all-keys/discuss/364604/Simple-Python-BFS-Solution-(292-ms-beat-97.78))\n[1091. Shortest Path in Binary Matrix](https://leetcode.com/problems/shortest-path-in-binary-matrix/discuss/313229/Python-BFS-solution)\n[1210. Minimum Moves to Reach Target with Rotations](https://leetcode.com/problems/minimum-moves-to-reach-target-with-rotations/discuss/392940/Standard-Python-BFS-solution)\n[1263. Minimum Moves to Move a Box to Their Target Location](https://leetcode.com/problems/minimum-moves-to-move-a-box-to-their-target-location/discuss/431138/Python-straightforward-BFS-solution)\n[1293. Shortest Path in a Grid with Obstacles Elimination](https://leetcode.com/problems/shortest-path-in-a-grid-with-obstacles-elimination/discuss/1651383/Python-level-by-level-BFS-Solution)\n\n\n\n```\nStraightforward BFS:\n(1) find the positions of the box and player (x_B, y_B, x_S, y_S), reset the cells to be \'.\'\n(2) use (x_B, y_B, x_S, y_S) to represent the state\n (i) find the valid next steps to move the box (x_B, y_B) to its possible neighbors: \n\t one move is valid if one neighbor is empty and the opposite neighbor is connected to (x_S, y_S)\n\t (ii) use BFS to to check the opposite neighbor is connected to (x_S, y_S) or not\n(3) traverse all possible states level-by-level\n```\n \n\n```\n def minPushBox(self, grid: List[List[str]]) -> int: \n def bfs_to_reach_S(r, c, x_B, y_B, x_S, y_S):\n curr_level = {(r, c)}\n visited = set()\n while curr_level:\n next_level = set()\n for i, j in curr_level:\n visited.add((i, j))\n if i == x_S and j == y_S:\n return True\n for di, dj in [(0, 1), (0, -1), (1, 0), (-1, 0)]:\n i1, j1 = i + di, j + dj\n if 0 <= i1 < n and 0 <= j1 < m and (i1, j1) not in visited and (i1, j1) != (x_B, y_B) and grid[i1][j1] != \'#\':\n next_level.add((i1, j1))\n curr_level = next_level\n return False\n \n def valid_moves(grid, x_B, y_B, x_S, y_S):\n next_moves = []\n for dx, dy in [(0, 1), (1, 0), (-1, 0), (0, -1)]:\n r1, c1 = x_B + dx, y_B + dy\n r2, c2 = x_B - dx, y_B - dy\n if 0 <= r1 < n and 0 <= c1 < m and grid[r1][c1] != \'#\' and 0 <= r2 < n and 0 <= c2 < m and grid[r2][c2] != \'#\':\n if bfs_to_reach_S(r1, c1, x_B, y_B, x_S, y_S):\n next_moves.append((r2, c2, x_B, y_B))\n return next_moves\n \n n, m = len(grid), len(grid[0])\n for i in range(n):\n for j in range(m):\n if grid[i][j] == \'B\':\n x_B, y_B = i, j\n elif grid[i][j] == \'S\':\n x_S, y_S = i, j\n grid[x_B][y_B], grid[x_S][y_S] = \'.\', \'.\'\n curr_level = {(x_B, y_B, x_S, y_S)}\n visited = set()\n moves = 0\n while curr_level:\n next_level = set()\n for i_B, j_B, i_S, j_S in curr_level:\n visited.add((i_B, j_B, i_S, j_S))\n if grid[i_B][j_B] == \'T\':\n return moves\n for i_B1, j_B1, i_S1, j_S1 in valid_moves(grid, i_B, j_B, i_S, j_S):\n if (i_B1, j_B1, i_S1, j_S1) not in visited:\n next_level.add((i_B1, j_B1, i_S1, j_S1))\n curr_level = next_level\n moves += 1\n return -1\n``` | 10 | 1 | [] | 2 |
minimum-moves-to-move-a-box-to-their-target-location | Two BFS for player and box - beats 100 % | two-bfs-for-player-and-box-beats-100-by-7r83o | \npublic class Solution \n{\n private int[] x = new int[4] { 0, 0, 1, -1 };\n private int[] y = new int[4] { 1, -1, 0, 0 };\n \n public int MinPushB | srithar | NORMAL | 2020-02-05T02:21:02.178427+00:00 | 2020-02-05T02:21:02.178513+00:00 | 1,139 | false | ```\npublic class Solution \n{\n private int[] x = new int[4] { 0, 0, 1, -1 };\n private int[] y = new int[4] { 1, -1, 0, 0 };\n \n public int MinPushBox(char[][] grid) \n {\n int bx = 0, by = 0, px = 0, py = 0, tx = 0, ty = 0;\n \n int m = grid.Length;\n int n = grid[0].Length;\n \n // Set to maintain the visited positions of the player and box\n HashSet<int> boxSet = new HashSet<int>();\n HashSet<int> playerSet = new HashSet<int>();\n \n for(int i = 0; i < m; i++)\n {\n for(int j = 0; j < n; j++)\n {\n if(grid[i][j] == \'B\')\n {\n bx = i;\n by = j;\n }\n else if(grid[i][j] == \'S\')\n {\n px = i;\n py = j;\n }\n else if(grid[i][j] == \'T\')\n {\n tx = i;\n ty = j;\n }\n }\n }\n \n Queue<Position> queue = new Queue<Position>();\n \n Position pos = new Position(px, py, bx, by);\n \n queue.Enqueue(pos);\n \n boxSet.Add(bx * n + by);\n \n for(int step = 0; queue.Count > 0; step++)\n {\n for(int size = queue.Count; size > 0; size--)\n {\n pos = queue.Dequeue();\n \n // Box has reached the target location\n if(pos.bx == tx && pos.by == ty)\n return step;\n \n for(int i = 0; i < 4; i++)\n {\n // Compute box position\n bx = pos.bx + x[i];\n by = pos.by + y[i];\n \n // Compute player position to move the box\n px = pos.bx - x[i];\n py = pos.by - y[i];\n \n if(bx < 0 || bx > m - 1 || by < 0 || by > n - 1)\n continue;\n \n if(px < 0 || px > m - 1 || py < 0 || py > n - 1)\n continue;\n \n if(grid[px][py] != \'#\' && grid[bx][by] != \'#\' && (boxSet.Add(bx * n + by) || playerSet.Add(px * n + py)) && CanReachThePosition(grid, pos.px, pos.py, px, py, pos.bx, pos.by, m, n))\n {\n queue.Enqueue(new Position(pos.bx, pos.by, bx, by));\n }\n }\n }\n }\n \n return -1;\n }\n \n // Check whether the player can reach the required position to move the box in a particular direction\n private bool CanReachThePosition(char[][] grid, int x1, int y1, int x2, int y2, int bx, int by, int m, int n)\n {\n Queue<Position> queue = new Queue<Position>();\n queue.Enqueue(new Position(x1, y1, x2, y2));\n \n HashSet<int> set = new HashSet<int>();\n \n set.Add(x1 * n + y1);\n set.Add(bx * n + by);\n \n while(queue.Count > 0)\n {\n Position pos = queue.Dequeue();\n \n if(pos.px == x2 && pos.py == y2)\n return true;\n\n for(int i = 0; i < 4; i++)\n {\n int px = pos.px + x[i];\n int py = pos.py + y[i];\n\n if(px < 0 || px > m - 1 || py < 0 || py > n - 1)\n continue;\n \n if(grid[px][py] != \'#\' && set.Add(px * n + py))\n {\n queue.Enqueue(new Position(px, py, x2, y2));\n }\n }\n }\n \n return false;\n }\n}\n\npublic class Position\n{\n // Player\'s position in the grid\n public int px;\n public int py;\n \n // Box position in the grid\n public int bx;\n public int by;\n \n public Position(int px, int py, int bx, int by)\n {\n this.px = px;\n this.py = py;\n this.bx = bx;\n this.by = by;\n }\n}\n``` | 8 | 1 | [] | 5 |
minimum-moves-to-move-a-box-to-their-target-location | Python 3 - 2 BFS clean code | python-3-2-bfs-clean-code-by-yunqu-8kaz | For each push, make sure the person can stand at the required location that is reachable from a previous standing location.\n\npython\nclass Solution:\n def | yunqu | NORMAL | 2021-03-26T22:35:48.154537+00:00 | 2021-03-26T22:35:48.154567+00:00 | 425 | false | For each push, make sure the person can stand at the required location that is reachable from a previous standing location.\n\n```python\nclass Solution:\n def minPushBox(self, grid: List[List[str]]) -> int:\n m, n = len(grid), len(grid[0])\n for i in range(m):\n for j in range(n):\n if grid[i][j] == "T":\n target = (i,j)\n if grid[i][j] == "B":\n box = (i,j)\n if grid[i][j] == "S":\n person = (i,j)\n\n def valid(x, y):\n return 0<=x<m and 0<=y<n and grid[x][y]!=\'#\'\n \n def get_neighbor(i, j):\n for dx,dy in [(-1,0),(1,0),(0,-1),(0,1)]:\n x, y = i + dx, j + dy\n if valid(x, y):\n yield x, y\n \n def get_box_neighbor(i, j):\n for dx,dy in [(-1,0),(0,-1)]:\n x, y = i + dx, j + dy\n px, py = i - dx, j - dy\n if valid(x, y) and valid(px, py):\n yield (x, y), (px, py)\n yield (px, py), (x, y)\n\n def check(curr, dest, box):\n queue = deque([curr])\n v = set()\n while queue:\n i, j = queue.popleft()\n if (i, j) == dest: \n return True\n for x, y in get_neighbor(i, j):\n if (x,y) not in v and (x,y) != box:\n v.add((x,y))\n queue.append((x,y))\n return False\n\n q = deque([(box, person)])\n seen = set()\n seen.add(box + person)\n steps = 0\n while q:\n size = len(q)\n for _ in range(size):\n box, person = q.popleft()\n if box == target:\n return steps\n for new_box, new_person in get_box_neighbor(*box):\n if new_box + box not in seen and \\\n check(person, new_person, box):\n seen.add(new_box + box)\n q.append((new_box, box))\n steps += 1\n return -1\n``` | 5 | 0 | [] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | [55 Lines] [challenge me] Possible shortest C++ solution | 55-lines-challenge-me-possible-shortest-59zwu | Python is always my envy to be able to write short code.\nAfter I picked up some more knolwedge about C++, I can also write some code comparable with python in | codedayday | NORMAL | 2020-05-13T06:37:48.475542+00:00 | 2020-05-14T03:36:33.617135+00:00 | 742 | false | Python is always my envy to be able to write short code.\nAfter I picked up some more knolwedge about C++, I can also write some code comparable with python in terms of length.\nIf you can help me make it shorter, I will highly apprecitate. \n\nActually, in terms of space cost, this solution is also competitive. But I am sure there are always lots of people can do much better than me.\nSo I will be waiting for the comments from you.\n```\nRuntime: 84 ms, faster than 59.21% of C++ online submissions for Minimum Moves to Move a Box to Their Target Location.\nMemory Usage: 8.5 MB, less than 100.00% of C++ online submissions for Minimum Moves to Move a Box to Their Target Location.\n```\n\n```\nstruct Node{\n pair<int, int> b, p;\n int key() const {return ( (b.first*20 + b.second) << 16 ) | (p.first*20 + p.second); };\n};\n\nclass Solution {\npublic:\n int minPushBox(vector<vector<char>>& grid) { \n const int m = grid.size(), n = grid[0].size(); \n Node start, end;\n for(int i = 0; i < m; i++)\n for(int j = 0; j < n; j++)\n if(grid[i][j] == \'B\') start.b = {i, j};\n else if(grid[i][j] == \'S\') start.p = {i, j};\n else if(grid[i][j] == \'T\') end.b = {i, j}; \n \n auto hasPath = [&](const Node& cur, int p_i, int p_j){ // hasPath: can move behind box \n int seen[400]={}; \n function <bool(int, int)> dfs = [&](int i, int j){\n if(i < 0 || i >= m || j < 0 || j >= n || grid[i][j] == \'#\') return false;\n if(i== cur.b.first && j == cur.b.second ) return false; \n if(seen[i*m+j]++) return false; \n if(i== p_i && j == p_j ) return true;\n return dfs(i-1, j) || dfs(i+1, j) || dfs(i, j-1) || dfs(i, j+1);\n };\n \n return dfs(cur.p.first, cur.p.second); \n }; \n //canMove is true means 2 things: front cell is valid & free; back cell is accessible from mover\'s current position\n auto canMove= [&](const Node& cur, int delta_i, int delta_j, Node& nxt){ \n int i = cur.b.first + delta_i, j = cur.b.second + delta_j;\n if(i < 0 || i >= m || j <0 || j >= n || grid[i][j] == \'#\') return false; \n if(!hasPath(cur, cur.b.first - delta_i, cur.b.second - delta_j) ) return false;\n nxt.b={i,j};\n nxt.p = cur.b;\n return true; \n }; \n \n queue<Node> q{{start}}; \n unordered_set<int> seen{start.key()}; \n int dirs[5]={0, -1, 0, 1, 0};\n for(int step = 0; !q.empty(); ++step)\n for(int sz = q.size(); sz > 0; sz--){\n auto cur = q.front(); q.pop();\n Node nxt;\n for(int i = 0; i < 4; i++){ \n if(!canMove(cur, dirs[i], dirs[i+1], nxt) || seen.count(nxt.key()) ) continue; \n if(nxt.b == end.b) return step+1;\n seen.insert(nxt.key());\n q.emplace(nxt);\n }\n }\n return -1;\n }\n};\n``` | 5 | 1 | ['Depth-First Search', 'Breadth-First Search', 'C'] | 2 |
minimum-moves-to-move-a-box-to-their-target-location | [Java] BFS + DFS with explanation | java-bfs-dfs-with-explanation-by-lnbyk-o7rd | The idea is using BFS find the shortest path from the box location to the destination.\nHowever, each time we check if the box can be moved we need to check 2 p | lnbyk | NORMAL | 2019-11-24T02:44:06.183407+00:00 | 2019-11-24T02:44:06.183464+00:00 | 903 | false | The idea is using BFS find the shortest path from the box location to the destination.\nHowever, each time we check if the box can be moved we need to check 2 position\n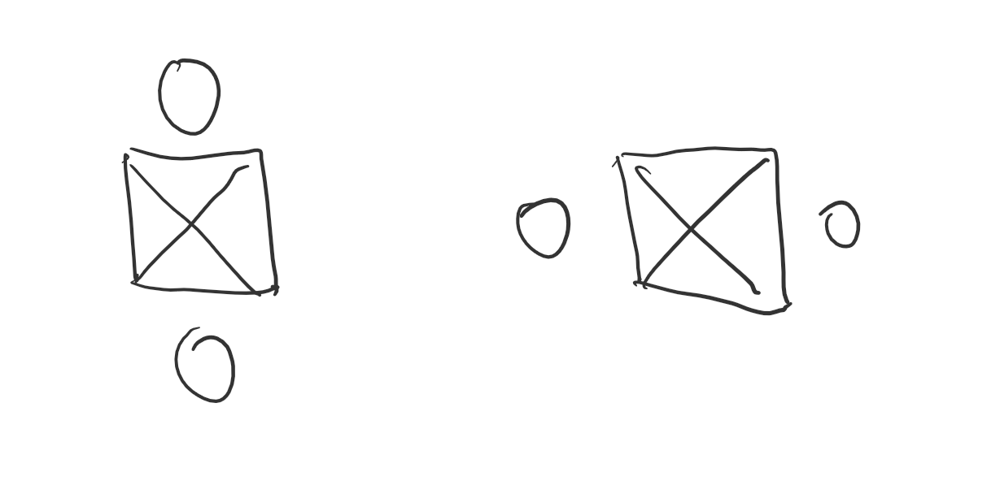\n\nThe Box is just the box and the cycle is the position we need check\nWhen we want to move box to left we need check if the position both the cell at the left of the box and right of the box is ok. And we need to do the same thing for four directions.\n\nDFS:\n\tThe reason use DFS is to check if the person can move to the position where he can move the box.\n\tSuch as below \n\t\n\tThe green arrow is just the one of the path we need to check if person can move.\n\n\n```\nclass Solution {\n private class Sugarcane{\n int box;\n int person;\n public Sugarcane(int box, int person){\n this.box = box;\n this.person = person;\n }\n public String toString(){\n return this.box + " " + this.person;\n }\n }\n \n Set<Integer> set = new HashSet<>();\n int[] dir = {0, 1, 0, -1, 0};\n int m, n;\n public int minPushBox(char[][] grid) {\n int res = -1;\n m = grid.length; n = grid[0].length;\n int d = 0, p = 0;\n Queue<Sugarcane> queue = new LinkedList<>();\n Set<String> visited = new HashSet<>();\n \n for(int i = 0; i < m; i++){\n for(int j = 0; j < n; j++){\n if(grid[i][j] == \'B\'){\n d = i * n + j;\n }\n else if(grid[i][j] == \'S\'){\n p = i * n + j; \n }\n }\n }\n Sugarcane sugarcane = new Sugarcane(d, p);\n queue.offer(sugarcane);\n visited.add(sugarcane.toString());\n \n while(!queue.isEmpty()){\n int size = queue.size();\n res++;\n for(int i = 0; i < size; i++){\n Sugarcane sugar = queue.poll();\n int bp = sugar.box, pp = sugar.person;\n int x = bp / n, y = bp % n;\n if(grid[x][y] == \'T\')\n return res;\n \n grid[x][y] = \'#\';\n for(int j = 0; j < 4; j++){\n int bx = x + dir[j], by = y + dir[j + 1];\n int px = x - dir[j], py = y - dir[j + 1];\n Sugarcane nextSugar = new Sugarcane(bx * n + by, px * n + py);\n String nV = nextSugar.toString();\n set = new HashSet<>();\n if(isVaild(bx, by, grid) && !visited.contains(nV) && dfs(pp / n, pp % n, grid, px, py)){\n queue.offer(nextSugar);\n visited.add(nV);\n }\n }\n grid[x][y] = \'.\';\n }\n }\n return -1;\n }\n \n \n public boolean isVaild(int x, int y, char[][] grid){\n return x >= 0 && x < m && y >= 0 && y < n && grid[x][y] != \'#\';\n }\n \n public boolean dfs(int x, int y, char[][] grid, int dx, int dy){\n if(x == dx && y == dy)\n return true;\n for(int i = 0; i < 4; i++){\n int nx = x + dir[i], ny = y + dir[i + 1];\n if(isVaild(nx, ny, grid) && set.add(nx * n + ny))\n if(dfs(nx, ny, grid, dx, dy))\n return true;\n }\n return false;\n }\n}\n``` | 5 | 1 | [] | 3 |
minimum-moves-to-move-a-box-to-their-target-location | Java Deque bfs | java-deque-bfs-by-gcl272633743-bc20 | \nclass Solution {\n /**\n \u8FD9\u4E2A\u9898\u76EE\u4E0D\u540C\u4E8E\u4EE5\u524D\u7684bfs, \u56E0\u4E3A\u4EBA\u8981\u63A8\u7740\u7BB1\u5B50\u8D70\uFF0C\ | gcl272633743 | NORMAL | 2021-06-14T03:30:26.387652+00:00 | 2021-06-14T03:30:26.387682+00:00 | 476 | false | ```\nclass Solution {\n /**\n \u8FD9\u4E2A\u9898\u76EE\u4E0D\u540C\u4E8E\u4EE5\u524D\u7684bfs, \u56E0\u4E3A\u4EBA\u8981\u63A8\u7740\u7BB1\u5B50\u8D70\uFF0C\u6240\u6709\u4EBA\u548C\u7BB1\u5B50\u7684\u5750\u6807\u8054\u5408\u8D77\u6765\u4F5C\u4E3Abfs\u7684\u5750\u6807\n [bx][by][px][py]\n\n \u884D\u751F\u51FA\u6765\u7684\u4E0B\u4E00\u4E2A\u72B6\u6001\u5E94\u8BE5\u6709:\n 1 \u4EBA\u52A8\uFF0C\u7BB1\u5B50\u4E0D\u52A8\uFF0C\u6B64\u65F6\u63A8\u52A8\u7BB1\u5B50\u7684\u6B21\u6570\u4E0D\u53D8\n [bx][by][px-1][py] , [bx][by][px+1][py] , [bx][by][px][py-1] , [bx][by][px][py+1]\n\n 2 \u4EBA\u548C\u7BB1\u5B50\u4E00\u8D77\u52A8\uFF0C\u6B64\u65F6\u63A8\u52A8\u7BB1\u5B50\u7684\u6B21\u6570\u52A01\n [bx-1][by][px-1][py] , [bx+1][by][px+1][py] , [bx][by-1][px][py-1] , [bx][by+1][px][py+1]\n\n \u5BF9\u4E8E\u7B2C\u4E00\u79CD\u60C5\u51B5\uFF0C\u8FDB\u884Cbfs\u904D\u5386\u7684\u65F6\u5019\uFF0C\u9700\u8981\u52A0\u5165\u961F\u5217\u7684\u5934\u90E8\n\n \u5BF9\u4E8E\u7B2C\u4E8C\u79CD\u60C5\u51B5\uFF0C\u8FDB\u884Cbfs\u904D\u5386\u7684\u65F6\u5019\uFF0C\u9700\u8981\u52A0\u5165\u961F\u5217\u7684\u5C3E\u90E8\n */\n int[][] dir ={{-1,0},{1,0},{0,1},{0,-1}};\n public int minPushBox(char[][] grid) {\n int m=grid.length, n=grid[0].length;\n int bx=-1, by=-1, px=-1, py=0, tx=-1, ty=-1;\n for(int i=0; i<m; i++){\n for(int j=0; j<n; j++){\n if(grid[i][j]==\'B\'){\n bx=i;\n by=j;\n }\n if(grid[i][j]==\'T\'){\n tx=i;\n ty=j;\n }\n if(grid[i][j]==\'S\'){\n px=i;\n py=j;\n }\n }\n }\n\n //\u8BB0\u5F55\u79FB\u52A8\u5230\u5F53\u524D\u72B6\u6001\u9700\u8981\u63A8\u52A8\u76D2\u5B50\u7684\u6B65\u9AA4\n int[][][][] memo = new int[m][n][m][n];\n for(int i=0; i<m; i++){\n for(int j=0; j<n; j++){\n for(int k=0; k<m; k++){\n Arrays.fill(memo[i][j][k], -1);\n }\n }\n }\n memo[bx][by][px][py] = 0;\n\n //\u53CC\u7AEF\u961F\u5217\u505ABFS\n Deque<int[]> queue = new LinkedList<>();\n queue.add(new int[]{bx, by, px, py});\n\n while(!queue.isEmpty()){\n int[] cur = queue.poll();\n //\u63A8\u5230\u4E86\u6700\u7EC8\u4F4D\u7F6E\n if(cur[0]==tx && cur[1]==ty){\n return memo[cur[0]][cur[1]][cur[2]][cur[3]];\n }\n\n //\u4EBA\u5728\u52A8\uFF0C\u76D2\u5B50\u4E0D\u52A8\u7684\u60C5\u51B5\uFF0C\u63A8\u52A8\u6B21\u6570\u4E0D\u53D8\uFF0C\u5C06\u65B0\u7684\u5750\u6807\u52A0\u5165\u52A0\u5165\u961F\u9996\n for(int k=0; k<dir.length; k++){\n int npx = cur[2] + dir[k][0], npy = cur[3] + dir[k][1];\n if(npx<0 || npx>=m || npy<0 || npy>=n) continue; //\u8D8A\u754C\n if(grid[npx][npy]==\'#\') continue; //\u649E\u5899\n if(npx==cur[0] && npy==cur[1]) continue; //\u4E0E\u76D2\u5B50\u91CD\u5408\n if(memo[cur[0]][cur[1]][npx][npy] >= 0) continue; //\u5DF2\u7ECF\u8BBF\u95EE\u8FC7\u4E86\n queue.addFirst(new int[]{cur[0], cur[1], npx, npy});\n memo[cur[0]][cur[1]][npx][npy] = memo[cur[0]][cur[1]][cur[2]][cur[3]]; //\u63A8\u52A8\u6B21\u6570\u4E0D\u53D8\n }\n\n //\u4EBA\u63A8\u52A8\u7BB1\u5B50\uFF0C\u8981\u6C42\uFF1A1 \u4EFB\u4F55\u7BB1\u5B50\u76F8\u90BB 2 \u63A8\u52A8\u7684\u65B9\u5411\u4E0D\u662F\u5899\n if(Math.abs(cur[0]-cur[2]) + Math.abs(cur[1]-cur[3])==1){ //\u76F8\u90BB\n //\u627E\u5230\u63A8\u52A8\u7684\u65B9\u5411,\u4EBA\u6309\u7167\u67D0\u4E2A\u65B9\u5411\u79FB\u52A8\u4E4B\u540E\uFF0C\u5C31\u662Fbox,\u5219\u5F53\u524D\u65B9\u5411\u5C31\u662F\u8981\u627E\u7684\u65B9\u5411\n for(int k=0; k<dir.length; k++){\n int npx = cur[2] + dir[k][0], npy = cur[3] + dir[k][1];\n if(npx==cur[0] && npy==cur[1]){ //\u5F53\u524Dk\u6307\u5411\u7684\u65B9\u5411\u5C31\u662F\u8981\u627E\u7684\u65B9\u5411\n //\u5224\u65ADbox\u662F\u5426\u80FD\u671D\u8FD9\u4E2A\u65B9\u5411\u79FB\u52A8\n int nbx = cur[0] + dir[k][0], nby = cur[1] + dir[k][1];\n if(nbx<0 || nbx>=m || nby<0 || nby>=n) continue;\n if(grid[nbx][nby] == \'#\') continue;//\u5899\n if(memo[nbx][nby][cur[2]][cur[3]] >= 0) continue; //\u5DF2\u7ECF\u8BBF\u95EE\u8FC7\u4E86\n queue.addLast(new int[]{nbx, nby, cur[2], cur[3]});\n memo[nbx][nby][cur[2]][cur[3]] = memo[cur[0]][cur[1]][cur[2]][cur[3]]+1; //\u63A8\u52A8\u6B21\u6570\u52A0\u4E00\n }\n }\n }\n }\n return -1;\n }\n}\n``` | 4 | 0 | ['Breadth-First Search', 'Queue', 'Java'] | 2 |
minimum-moves-to-move-a-box-to-their-target-location | [Python] 0-1 BFS with comments and explanation | python-0-1-bfs-with-comments-and-explana-p65c | Each node in our graph will contain state of box, person and the minimum cost to reach it.\n- We do a 0-1 BFS where 0 is the cost between vertices where a perso | bharadwaj6 | NORMAL | 2020-03-02T10:22:10.811261+00:00 | 2020-03-02T10:39:25.884507+00:00 | 795 | false | - Each node in our graph will contain state of box, person and the minimum cost to reach it.\n- We do a 0-1 BFS where 0 is the cost between vertices where a person can reach without having to move the box, and 1 is the cost between vertices where box moved.\n- For more explanation on 0-1 BFS, watch [this video](https://www.youtube.com/watch?v=2RDQVW7RspM), or read [this article](https://cp-algorithms.com/graph/01_bfs.html)\n- By nature of BFS we reach the target with minimum cost path first, or we return not possible.\n- Time complexity is `O(M*N*M*N)` as we go through all the vertices in the worst case.\n\n```Python\nclass Solution:\n def minPushBox(self, grid: List[List[str]]) -> int:\n m, n = len(grid), len(grid[0])\n is_valid = lambda x, y: 0 <= x < m and 0 <= y < n and grid[x][y] != \'#\'\n reached = lambda x, y: (x, y) == target\n\t\t# we use these to move to the neighboring states\n dist_row, dist_col = [0, 0, 1, -1], [1, -1, 0, 0]\n\n def get_neighbors(state):\n bx, by, mx, my = state\n new_states = []\n \n # generate all possible states you can move to\n for i in range(4):\n X, Y = mx + dist_row[i], my + dist_col[i]\n # ignore out of bounds and walls\n if not is_valid(X, Y): continue\n if (X, Y) == (bx, by):\n if is_valid(bx + dist_row[i], by + dist_col[i]):\n # move box if current person state is neighbor of box and valid move exists\n # the cost for move in this case would be 1\n new_states.append((bx + dist_row[i], by + dist_col[i], X, Y, 1))\n else:\n # move the person keeping box intact. Cost will be 0.\n new_states.append((bx, by, X, Y, 0))\n return new_states\n\n # go through the grid and take a note of starting positions of box, man and target\n for r, row in enumerate(grid):\n for c, col in enumerate(row):\n if grid[r][c] == \'S\':\n start = (r, c)\n elif grid[r][c] == \'B\':\n box_start = (r, c)\n elif grid[r][c] == \'T\':\n target = (r, c)\n\n # each node of our graph will contain (box_row, box_column, man_row, man_column, cost_so_far)\n start_state = (*box_start, *start, 0)\n\n # we can use double ended queue for 0/1 BFS. Append to left if distance is 0, else to the right.\n queue = collections.deque([start_state])\n\n # keep note of already visited (box_row, box_col, man_row, man_col) positions.\n # By nature of BFS, we visit them with lower cost path first,\n # so we can ignore if they appear again on our path as cost would be higher.\n visited = set()\n while queue:\n current = queue.popleft()\n bx, by, mx, my, d = current\n visited.add((bx, by, mx, my))\n if reached(bx, by): return d # reached target return the distance\n for nb_details in get_neighbors((bx, by, mx, my)):\n *neigh, dist = nb_details\n if tuple(neigh) not in visited:\n if dist:\n queue.append((*neigh, dist + d)) # edge of weight 1\n else:\n queue.appendleft((*neigh, dist + d)) # edge of weight 0\n\n # target can\'t be reached\n return -1\n```\n\n\n | 4 | 0 | ['Breadth-First Search', 'Python3'] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | [Python3] A* - Simple | python3-a-simple-by-dolong2110-h9fo | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | dolong2110 | NORMAL | 2024-03-24T16:22:17.206200+00:00 | 2024-03-24T16:22:17.206233+00:00 | 240 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minPushBox(self, grid: List[List[str]]) -> int:\n m, n = len(grid), len(grid[0])\n for r in range(m):\n for c in range(n):\n if grid[r][c] == "T": target = (r, c)\n if grid[r][c] == "B": start_box = (r, c)\n if grid[r][c] == "S": start_person = (r, c)\n \n def heuristic(box: tuple) -> int:\n return abs(target[0] - box[0]) + abs(target[1] - box[1])\n \n def out_bounds(location: tuple) -> bool:\n r, c = location\n return not (0 <= r < m and 0 <= c < n and grid[r][c] != "#")\n \n pq = [(heuristic(start_box), 0, start_person, start_box)]\n visited = set()\n while pq:\n _, moves, person, box = heapq.heappop(pq)\n if box == target: return moves\n if (person, box) in visited: continue\n visited.add((person, box))\n for dr, dc in [(0, 1), (1, 0), (-1, 0), (0, -1)]:\n new_person = (person[0] + dr, person[1] + dc)\n if out_bounds(new_person): continue\n if new_person == box:\n new_box = (box[0] + dr, box[1] + dc)\n if out_bounds(new_box): continue\n heapq.heappush(pq, (heuristic(new_box) + moves + 1, moves + 1, new_person, new_box))\n else: heapq.heappush(pq, (heuristic(box) + moves, moves, new_person, box))\n return -1\n``` | 3 | 0 | ['Breadth-First Search', 'Heap (Priority Queue)', 'Python3'] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | JAVE intuitive BFS solution | jave-intuitive-bfs-solution-by-guiguia-jbsc | Two BFS. \n1st BFS to push box as regular BFS. \n2nd BFS to check if the person can reach the box inside 1st BFS\n\nBFS to push box. For each positon of box, ch | guiguia | NORMAL | 2021-08-22T00:08:43.708854+00:00 | 2021-08-22T00:08:43.708891+00:00 | 367 | false | Two BFS. \n1st BFS to push box as regular BFS. \n*2nd BFS to check if the person can reach the box inside 1st BFS\n\nBFS to push box. For each positon of box, check if player can push it.\nBox can be pushed only when it has two opposite adajacent grids are empty\n\t1. traverse the grid to find the location of player, box, target, and set their grid value to \'.\'\n\t2. Use 4d boolean array visited (boolean[box_x][box_y][player_x][player_y]) to record visited box\n\t3. In the BFS Queue, it is an array of box_x, box_y, player_x, player_y, step\n\t4. During BFS, check the 2 adajcent grids for the box in x and y direction. \nIf both they are within grid and have \'.\', do second BFS to see if the player can reach the position \n\nTime complexity: O(n^2*m^2)\nSpace complexity: O(n*m)\nn, m is the grid width and length\n\n```\nclass Solution {\n public int minPushBox(char[][] grid) {\n int m = grid.length;\n int n = grid[0].length;\n int[] box = {-1, -1};\n int[] player = {-1, -1};\n int[] target = {-1, -1};\n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n if (grid[i][j] == \'S\') {\n player = new int[]{i, j};\n } else if (grid[i][j] == \'B\') {\n box = new int[]{i, j};\n } else if (grid[i][j] == \'T\') {\n target = new int[]{i, j};\n }\n }\n }\n grid[player[0]][player[1]] = \'.\';\n grid[box[0]][box[1]] = \'.\';\n grid[target[0]][target[1]] = \'.\';\n boolean[][][][] visited = new boolean[m][n][m][n];\n Queue<int[]> queue = new ArrayDeque<>();\n queue.offer(new int[]{box[0], box[1], player[0], player[1], 0});\n visited[box[0]][box[1]][player[0]][player[1]] = true;\n int[][] dirs = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};\n while(!queue.isEmpty()) {\n int[] cur = queue.poll();\n for (int i = 0; i < 4; i += 2) {\n int x1 = cur[0] + dirs[i][0];\n int y1 = cur[1] + dirs[i][1];\n int x2 = cur[0] + dirs[i + 1][0];\n int y2 = cur[1] + dirs[i + 1][1];\n if (inGrid(m, n, x1, y1, grid) && inGrid(m, n, x2, y2, grid)) {\n if (!visited[x1][y1][x2][y2] && canReach(grid, cur[2], cur[3], x2, y2, new int[]{cur[0], cur[1]})) {\n if (x1 == target[0] && y1 == target[1]) {\n return cur[4] + 1;\n }\n visited[x1][y1][x2][y2] = true;\n queue.offer(new int[]{x1, y1, x2, y2, cur[4] + 1});\n }\n if (!visited[x2][y2][x1][y1] && canReach(grid, cur[2], cur[3], x1, y1, new int[]{cur[0], cur[1]})) {\n if (x2 == target[0] && y2 == target[1]) {\n return cur[4] + 1;\n }\n visited[x2][y2][x1][y1] = true;\n queue.offer(new int[]{x2, y2, x1, y1, cur[4] + 1});\n }\n }\n\n }\n }\n return -1;\n }\n private boolean canReach(char[][]grid, int px, int py, int tx, int ty, int[] box) {\n int m = grid.length;\n int n = grid[0].length;\n Queue<int[]> queue = new ArrayDeque<>();\n boolean[][] visited = new boolean[grid.length][grid[0].length];\n queue.offer(new int[]{px, py});\n int[][] dirs = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};\n while(!queue.isEmpty()) {\n int[] cur = queue.poll();\n if (cur[0] == tx && cur[1] == ty) {\n return true;\n }\n for (int[] dir : dirs) {\n int x = cur[0] + dir[0];\n int y = cur[1] + dir[1];\n if (inGrid(m, n, x, y, grid) && !visited[x][y]) {\n if (x == tx && y == ty) {\n return true;\n }\n if (x == box[0] && y == box[1]) {\n continue;\n }\n queue.offer(new int[]{x, y});\n visited[x][y] = true;\n }\n }\n }\n return false;\n }\n\n\n private boolean inGrid(int m, int n, int x, int y, char[][]grid) {\n return x >= 0 && y >= 0 && x < m && y < n && grid[x][y] != \'#\'; // can be target\n }\n}\n``` | 3 | 0 | [] | 1 |
minimum-moves-to-move-a-box-to-their-target-location | Java | BFS + BFS | java-bfs-bfs-by-smartyvibhuse-cdru | \nclass Solution {\n // Up, Right, Bottom & Left\n private int[][] dir = new int[][]{{0, 1}, {1, 0}, {0, -1}, {-1, 0 | smartyvibhuse | NORMAL | 2021-06-28T12:44:26.454163+00:00 | 2021-06-28T12:44:26.454248+00:00 | 454 | false | ```\nclass Solution {\n // Up, Right, Bottom & Left\n private int[][] dir = new int[][]{{0, 1}, {1, 0}, {0, -1}, {-1, 0}};\n \n public int minPushBox(char[][] grid) {\n int step = 0;\n int m = grid.length;\n int n = grid[0].length;\n Queue<int[]> q = new LinkedList<>();\n int[] box,target,player;\n box = target = player = null;\n \n // TO Store Already Processed Node.\n // Box coordinates with respect to Player\'s Moves\n boolean[][][] visited = new boolean[m][n][4];\n\n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n if (grid[i][j] == \'B\') box = new int[]{i, j};\n else if (grid[i][j] == \'T\') target = new int[]{i, j};\n else if (grid[i][j] == \'S\') player = new int[]{i, j};\n }\n }\n \n q.offer(new int[]{box[0], box[1], player[0], player[1]});\n while (!q.isEmpty()) {\n int size = q.size();\n // Process Each Level Nodes of Queue\n while(size!=0) {\n int[] curr = q.poll();\n // Box reached Target Location Return steps...\n if (curr[0] == target[0] && curr[1] == target[1]) \n return step;\n // Explore 4 directions at this point ...\n for (int j = 0; j < dir.length; j++) {\n \n if (visited[curr[0]][curr[1]][j]) \n continue;\n \n int[] d = dir[j];\n \n int r0 = curr[0] + d[0];\n int c0 = curr[1] + d[1]; \n int r = curr[0] - d[0];\n int c = curr[1] - d[1];\n if (!isValid(r0,c0,grid) || !isValid(r,c,grid)) \n continue;\n if (!isReachable(r0, c0, curr, grid)) \n continue;\n \n visited[curr[0]][curr[1]][j] = true;\n q.offer(new int[]{r, c, curr[0], curr[1]});\n }\n size--;\n }\n step++;\n }\n return -1;\n \n }\n \n // can player reach a position to push ?\n private boolean isReachable(int x, int y, int[] curr, char[][] grid) {\n int m = grid.length;\n int n = grid[0].length;\n Queue<int[]> q = new LinkedList<>();\n int playerStartR = curr[2];\n int playerStartC = curr[3];\n q.offer(new int[]{playerStartR, playerStartC});\n boolean[][] visited = new boolean[m][n];\n // mark the box current position as visited // [0:1] ==> Box Pos\n visited[curr[0]][curr[1]] = true;\n while (!q.isEmpty()) {\n int[] temp = q.poll();\n if (temp[0] == x && temp[1] == y) \n return true;\n for (int[] d : dir) {\n int r = temp[0] + d[0];\n int c = temp[1] + d[1]; \n if (!isValid(r,c,grid) || visited[r][c]) \n continue;\n visited[r][c] = true;\n q.offer(new int[]{r, c});\n }\n }\n return false;\n }\n \n private boolean isValid(int x, int y,char[][] grid){\n int r = grid.length;\n int c = grid[0].length;\n return x>=0 && x<r && y>=0 && y<c && grid[x][y] != \'#\';\n }\n \n}\n``` | 3 | 0 | [] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | Simple to Understand Java solution | simple-to-understand-java-solution-by-us-qh6z | \nclass Solution {\n \n /**\n \n 1. Find the start , box and target cordinate .\n \n 2. Then using Start Cordinate start BFS . Create No | user5958h | NORMAL | 2021-06-11T15:08:31.301454+00:00 | 2021-06-11T15:08:31.301501+00:00 | 918 | false | ```\nclass Solution {\n \n /**\n \n 1. Find the start , box and target cordinate .\n \n 2. Then using Start Cordinate start BFS . Create Normal Visted set \n \n 3. There will be 3 Possibilities :\n \n 3.1 You find the Target , return whateevr No of Moves you have done till now .\n 3.2 You find the Box , increase the Moves by 1, distance + moves +1 .\n 3.2 You dont find Box , so move On without increasing Moves \n \n \n NOTE : Use PriotityQueue to sort Next value by Distance to get MIN diustnace \n \n **/\n \n \n \n private static final int [][] DIRS = {{1,0},{-1,0},{0,1},{0,-1}};\n \n public int minPushBox(char[][] grid) {\n \n // STEP-1 Find the start , Box and Target Cordinate \n \n int start [] = new int[2];\n int box [] = new int[2];\n int target[] = new int[2];\n \n int rows = grid.length;\n int cols = grid[0].length;\n boolean startFound = false; \n boolean boxFound = false;\n boolean targetFound = false;\n boolean found =false;\n \n for( int row =0; row < rows ; row++){\n for( int col =0; col< cols ; col++){\n char curValue = grid[row][col];\n switch(curValue){\n case \'S\':\n startFound=true;\n start[0] = row;\n start[1] = col; \n break;\n case \'B\' :\n boxFound = true;\n box[0] = row;\n box[1] = col; \n break;\n case \'T\':\n targetFound = true; \n target[0] = row;\n target[1] = col;\n break;\n }\n if(startFound && boxFound && targetFound){\n found = true;\n break;\n }\n }\n if( found){\n break;\n }\n }\n \n // STEP-2 STart BFS starting from start Cordinate\n PriorityQueue<int[]> pq = new PriorityQueue<>((pq1,pq2)->new Integer(pq1[0]).compareTo(pq2[0]));\n pq.offer(new int[]{dist(box[0],box[1], target[0],target[1]) + 0,\n 0 ,\n start[0],\n start[1], \n box[0],\n box[1]});\n \n Set<String> visited = new HashSet<>();\n while(!pq.isEmpty()){\n int size = pq.size();\n for( int i=0; i < size ; i++){\n int [] node = pq.poll();\n int dist = node[0];\n int moves = node[1];\n int row = node[2];\n int col = node[3];\n int bxX = node[4];\n int bxY = node[5];\n \n // if box equals to target return \n if(bxX == target[0] && bxY== target[1]){\n return moves;\n }\n String key = row + "-" + col +"-"+ bxX +"-"+ bxY;\n if(visited.contains(key)){\n continue;\n }\n visited.add(key);\n // EXplore \n for(int dir []: DIRS){\n int nRow = row + dir[0];\n int nCol = col + dir[1];\n if(!isValid(nRow,nCol, rows, cols, grid)){\n continue;\n }\n // if its equal to Box \n if(bxX == nRow && bxY == nCol) {\n int nBxX = nRow + dir[0];\n int nBxY = nCol + dir[1];\n if(!isValid(nBxX,nBxY, rows, cols, grid)){\n continue;\n }\n pq.offer( new int[]{dist(nBxX,nBxY,target[0],target[1]) + moves + 1 , moves +1 , nRow,nCol,nBxX,nBxY} );\n }else {\n // If the new cordinate not equal to Box \n pq.offer( new int[]{dist,moves,nRow,nCol,bxX, bxY} );\n }\n }\n }\n }\n return -1;\n \n }\n \n private boolean isValid(int row , int col , int rows , int cols, char grid[][]){\n if(row < 0 || row > rows-1 || col < 0 || col > cols-1 || grid [row][col] == \'#\'){\n return false;\n }\n return true;\n }\n \n private int dist(int x, int y, int tx, int ty){\n return Math.abs(x-tx)+Math.abs(y-ty);\n }\n}\n``` | 3 | 0 | ['Java'] | 5 |
minimum-moves-to-move-a-box-to-their-target-location | python bfs code with explanation | python-bfs-code-with-explanation-by-yiyu-qbii | To push a box, we need two steps\n- Check whether we could go to the neighbor cell of the box. Also the opposite side of this neighbor cell should be empty. Oth | yiyue15 | NORMAL | 2019-11-20T11:01:49.428428+00:00 | 2019-11-20T11:01:49.428459+00:00 | 394 | false | To push a box, we need two steps\n- Check whether we could go to the neighbor cell of the box. Also the opposite side of this neighbor cell should be empty. Otherwise there is no point moving there.\n\t- E.g. `.B.` has two neighbor cells which we could check whether we could move there\n\t- `#B.` won\'t be checked. Although there is an empty cell, however there is wall on the other side of the box. Even if the player could move there, he couldn\'t push the box\n- Push the box by one step. Here, our player is moved to the place where the original box is.\n\nIn the above two steps, we both use breadth first search to implement.\n\n```\ndef minPushBox(self, grid):\n\tplayer = None\n\tbox = None\n\ttarget = None\n\n\tn = len(grid)\n\tif n == 0:\n\t\treturn -1\n\tm = len(grid[0])\n\tif m == 0:\n\t\treturn -1\n\tfor i in range(n):\n\t\tfor j in range(m):\n\t\t\tif grid[i][j] == \'S\':\n\t\t\t\tplayer = (i, j)\n\t\t\tif grid[i][j] == \'T\':\n\t\t\t\ttarget = (i, j)\n\t\t\tif grid[i][j] == \'B\':\n\t\t\t\tbox = (i, j)\n\t\t\tif player != None and target != None and box != None:\n\t\t\t\tbreak\n\t\tif player != None and target != None and box != None:\n\t\t\tbreak\n\n\tqueue = [(box, target, player, 0)]\n\tvisited = set([(box, player)])\n\twhile len(queue) > 0:\n\t\tbox, target, player, steps = queue.pop()\n\t\tif target == box:\n\t\t\treturn steps\n\t\ti, j = box\n\t\tif i > 0 and i < (n-1) and grid[i-1][j] != \'#\' and grid[i+1][j] != \'#\':\n\t\t\tif ((i+1, j), (i, j)) not in visited:\n\t\t\t\tif self.canGoToBox(grid, (i-1, j), player, box):\n\t\t\t\t\tqueue.insert(0, ((i+1, j), target, (i, j), steps + 1))\n\t\t\t\t\tvisited.add(((i+1, j), (i, j)))\n\t\t\tif ((i-1, j), (i, j)) not in visited:\n\t\t\t\tif self.canGoToBox(grid, (i+1, j), player, box):\n\t\t\t\t\tqueue.insert(0, ((i-1, j), target, (i, j), steps + 1))\n\t\t\t\t\tvisited.add(((i-1, j), (i, j)))\n\n\t\tif j > 0 and j < (m-1) and grid[i][j-1] != \'#\' and grid[i][j+1] != \'#\':\n\t\t\tif ((i, j-1), (i, j)) not in visited:\n\t\t\t\tif self.canGoToBox(grid, (i, j+1), player, box):\n\t\t\t\t\tqueue.insert(0, ((i, j-1), target, (i, j), steps + 1))\n\t\t\t\t\tvisited.add(((i, j-1), (i, j)))\n\t\t\tif ((i, j+1), (i, j)) not in visited:\n\t\t\t\tif self.canGoToBox(grid, (i, j-1), player, box):\n\t\t\t\t\tqueue.insert(0, ((i, j+1), target, (i, j), steps + 1))\n\t\t\t\t\tvisited.add(((i, j+1), (i, j)))\n\treturn -1\n\ndef canGoToBox(self, grid, loc, player, box):\n\tif loc == player:\n\t\treturn True\n\trows = len(grid)\n\tcols = len(grid[0])\n\tqueue = [player]\n\tvisited = [player]\n\n\twhile len(queue) != 0:\n\t\ti, j = queue.pop()\n\t\tif (i, j) == loc:\n\t\t\treturn True\n\t\tneighbors = [(i-1, j), (i+1, j), (i, j-1), (i, j+1)]\n\t\tfor x, y in neighbors:\n\t\t\tif x >= 0 and x < rows and y >= 0 and y < cols:\n\t\t\t\tif (x, y) != box and grid[x][y] != "#" and (x, y) not in visited:\n\t\t\t\t\tqueue.append((x, y))\n\t\t\t\t\tvisited.append((x, y))\n\treturn False\n``` | 3 | 0 | [] | 1 |
minimum-moves-to-move-a-box-to-their-target-location | C++ Solution. Using Dijkstra's Algorithm | c-solution-using-dijkstras-algorithm-by-ql4a1 | Intuition\nUse Dijkstra\'s Algorithm\n\n# Code\n\nclass Solution {\npublic:\n // 0 - distance\n // 1 - BoxX\n // 2 - BoxY\n // 3 - ManX\n // 4 - | pulkitgupta38 | NORMAL | 2023-08-02T12:41:52.078266+00:00 | 2023-08-02T12:47:41.202430+00:00 | 556 | false | # Intuition\nUse Dijkstra\'s Algorithm\n\n# Code\n```\nclass Solution {\npublic:\n // 0 - distance\n // 1 - BoxX\n // 2 - BoxY\n // 3 - ManX\n // 4 - ManY\n\n int dx[4] = {0, 0, -1, 1};\n int dy[4] = {-1, 1, 0, 0};\n\n bool isValid(int x, int y, int n, int m, vector<vector<char>> &grid){\n if(x >= 0 && y >= 0 && x < n && y < m && grid[x][y] != \'#\'){\n return true;\n }\n return false;\n }\n\n int minPushBox(vector<vector<char>>& grid) {\n int n = grid.size(), m = grid[0].size();\n priority_queue<vector<int>, vector<vector<int>>, greater<vector<int>>> pq;\n vector<int> init(5, 0);\n for(int i = 0; i < n; i++){\n for(int j = 0; j < m; j++){\n if(grid[i][j] == \'B\'){\n init[1] = i;\n init[2] = j;\n }\n else if(grid[i][j] == \'S\'){\n init[3] = i;\n init[4] = j;\n }\n }\n }\n\n pq.push(init);\n map<vector<int>, int> dist;\n dist[{init[1], init[2], init[3], init[4]}] = 0;\n\n while(!pq.empty()) {\n int distance = pq.top()[0], boxX = pq.top()[1], boxY = pq.top()[2], manX = pq.top()[3], manY = pq.top()[4];\n pq.pop();\n // cout << "MAN: " << manX << " " << manY << " BOX: " << boxX << " " << boxY << "\\n";\n\n if(grid[boxX][boxY] == \'T\'){\n return distance;\n }\n\n for(int i = 0; i < 4; i++){\n if(isValid(manX + dx[i], manY + dy[i], n, m, grid)){\n if(manX + dx[i] == boxX && manY + dy[i] == boxY){\n if(isValid(boxX + dx[i], boxY + dy[i], n, m, grid) && (dist.find({boxX + dx[i], boxY + dy[i], manX + dx[i], manY + dy[i]}) == dist.end()) || (dist[{boxX + dx[i], boxY + dy[i], manX + dx[i], manY + dy[i]}] > distance + 1)) {\n if(manX + dx[i] == boxX + dx[i] && manY + dy[i] == boxY + dy[i]){\n cout << "hello\\n";\n }\n pq.push({distance + 1, boxX + dx[i], boxY + dy[i], manX + dx[i], manY + dy[i]});\n dist[{boxX + dx[i], boxY + dy[i], manX + dx[i], manY + dy[i]}] = distance + 1;\n }\n }\n else{\n if((dist.find({boxX, boxY, manX + dx[i], manY + dy[i]}) == dist.end()) || (dist[{boxX, boxY, manX + dx[i], manY + dy[i]}] > distance)) {\n pq.push({distance, boxX, boxY, manX + dx[i], manY + dy[i]});\n dist[{boxX, boxY, manX + dx[i], manY + dy[i]}] = distance;\n } \n }\n }\n }\n }\n\n return -1;\n }\n};\n``` | 2 | 0 | ['Array', 'Breadth-First Search', 'Graph', 'Heap (Priority Queue)', 'Matrix', 'Shortest Path', 'C++'] | 1 |
minimum-moves-to-move-a-box-to-their-target-location | c++ | easy | short | c-easy-short-by-venomhighs7-w14t | \n# Code\n\nclass Solution {\npublic:\n int n , m;\n int dx[4] = {1, 0, -1, 0};\n int dy[4] = {0, 1, 0, -1};\n\t\n bool inside(int x, int y) {\n | venomhighs7 | NORMAL | 2022-10-19T01:49:14.877486+00:00 | 2022-10-19T01:49:14.877521+00:00 | 732 | false | \n# Code\n```\nclass Solution {\npublic:\n int n , m;\n int dx[4] = {1, 0, -1, 0};\n int dy[4] = {0, 1, 0, -1};\n\t\n bool inside(int x, int y) {\n return (x >= 0 && x < n && y >= 0 && y < m);\n }\n\n bool canWalk(int srcX, int srcY, int destX, int destY, vector<vector<char>>&grid, vector<vector<int>>&visited)\n {\n if(srcX == destX && srcY == destY) return true;\n visited[srcX][srcY] = 1;\n for(int i = 0; i < 4; i++)\n {\n int x = srcX + dx[i];\n int y = srcY + dy[i];\n if(inside(x, y) && grid[x][y] != \'#\' && !visited[x][y])\n {\n if(canWalk(x, y, destX, destY, grid, visited))\n return true;\n }\n }\n return false;\n }\n int minPushBox(vector<vector<char>>& grid) {\n n = grid.size();\n m = grid[0].size();\n int boxX, boxY, targetX, targetY, personX, personY; \n for(int i = 0; i < n; i++)\n {\n for(int j = 0; j < m; j++)\n {\n if(grid[i][j] == \'S\')\n {\n personX = i;\n personY = j;\n }\n else if(grid[i][j] == \'T\')\n {\n targetX = i;\n targetY = j;\n }\n else if(grid[i][j] == \'B\')\n {\n boxX = i;\n boxY = j;\n }\n }\n }\n\t\t \n queue<vector<int>>q;\n set<vector<int>> seen;\n q.push({boxX, boxY,personX, personY});\n int ans = 0;\n\t\t \n while(!q.empty())\n {\n int sz = q.size();\n while(sz--)\n {\n auto p = q.front();\n q.pop();\n boxX = p[0]; boxY = p[1];\n personX = p[2]; personY = p[3];\n\t\t\t\t\n if(boxX == targetX && boxY == targetY)\n return ans;\n\t\t\t\t\t\n grid[boxX][boxY] = \'#\';\n\t\t\t\t\n for(int i = 0; i < 4; i++)\n {\n int new_boxX = boxX + dx[i];\n int new_boxY = boxY + dy[i];\n int new_personX = boxX - dx[i];\n int new_personY = boxY - dy[i];\n vector<int>curPos({new_boxX,new_boxY,new_personX,new_personY});\n vector<vector<int>> visited(n, vector<int>(m, 0));\n if(inside(new_boxX, new_boxY) && grid[new_boxX][new_boxY]!=\'#\' && !seen.count(curPos) && canWalk(personX, personY, new_personX, new_personY, grid, visited))\n {\n seen.insert(curPos);\n q.push(curPos);\n }\n }\n grid[boxX][boxY] = \'.\';\n }\n ans++;\n }\n return -1;\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | [Golang] A-Star | golang-a-star-by-vasakris-h3z7 | \ntype State struct {\n Box []int\n Person []int\n TotalDistanceToTarget int\n DistanceToBox int\n Moves int\n}\n\nfunc minPushBox(grid [][]byte) | vasakris | NORMAL | 2022-10-01T20:33:25.327055+00:00 | 2022-11-29T17:17:25.703714+00:00 | 185 | false | ```\ntype State struct {\n Box []int\n Person []int\n TotalDistanceToTarget int\n DistanceToBox int\n Moves int\n}\n\nfunc minPushBox(grid [][]byte) int {\n m := len(grid)\n n := len(grid[0])\n \n visited := make(map[string]bool)\n var target, box, person []int\n for r := 0; r < m; r++ {\n for c := 0; c < n; c++ {\n if grid[r][c] == \'S\' {\n person = []int{r, c}\n } else if grid[r][c] == \'B\' {\n box = []int{r, c}\n } else if grid[r][c] == \'T\' {\n target = []int{r, c}\n }\n }\n }\n \n minHeap := &MinHeap{}\n heap.Push(minHeap, State{box, person, calculateDistance(box, target), calculateDistance(box, person), 0})\n \n for minHeap.Len() > 0 {\n state := heap.Pop(minHeap).(State)\n currBox := state.Box\n currPerson := state.Person\n \n if currBox[0] == target[0] && currBox[1] == target[1] {\n return state.Moves\n }\n \n key := fmt.Sprintf("%d-%d-%d-%d", currBox[0], currBox[1], currPerson[0], currPerson[1])\n\n if visited[key] {\n continue\n }\n visited[key] = true\n \n for _, dir := range [][]int{{-1, 0}, {1, 0}, {0, -1}, {0, 1}} {\n newPerson := []int{currPerson[0] + dir[0], currPerson[1] + dir[1]}\n if !ValidMove(newPerson, grid) {\n continue\n }\n \n // Now person may come on Box Cell, which is like pushing Box\n if currBox[0] == newPerson[0] && currBox[1] == newPerson[1] {\n newBox := []int{currBox[0] + dir[0], currBox[1] + dir[1]}\n if !ValidMove(newBox, grid) {\n continue\n }\n heap.Push(minHeap, State{newBox, newPerson, calculateDistance(newBox, target)+state.Moves+1, calculateDistance(newBox, newPerson), state.Moves+1})\n } else {\n heap.Push(minHeap, State{currBox, newPerson, state.TotalDistanceToTarget, calculateDistance(currBox, newPerson), state.Moves})\n }\n }\n }\n \n return -1\n}\n\nfunc calculateDistance(start, end []int) int {\n return abs(start[0]-end[0]) + abs(start[1]-end[1])\n}\n\nfunc ValidMove(cell []int, grid [][]byte) bool {\n r := cell[0]\n c := cell[1]\n if r < 0 || r == len(grid) || c < 0 || c == len(grid[0]) || grid[r][c] == \'#\' {\n return false\n }\n return true\n}\n\nfunc abs(a int) int {\n if a < 0 {\n return -a\n }\n return a\n}\n\ntype MinHeap []State\n\nfunc (h MinHeap) Len() int {\n return len(h)\n}\n\nfunc (h MinHeap) Less(i int, j int) bool {\n if h[i].TotalDistanceToTarget == h[j].TotalDistanceToTarget {\n return h[i].DistanceToBox < h[j].DistanceToBox\n }\n return h[i].TotalDistanceToTarget < h[j].TotalDistanceToTarget\n}\n \nfunc (h MinHeap) Swap(i int, j int) {\n h[i], h[j] = h[j], h[i]\n} \n \nfunc (h *MinHeap) Push(a interface{}) {\n *h = append(*h, a.(State))\n}\n\nfunc (h *MinHeap) Pop() interface{} {\n l := len(*h)\n res := (*h)[l - 1]\n *h = (*h)[:l - 1]\n return res\n}\n``` | 2 | 0 | ['Go'] | 1 |
minimum-moves-to-move-a-box-to-their-target-location | C++| BFS | O((m*n)^2) | c-bfs-omn2-by-kumarabhi98-0yad | This problem, is not too Hard. Just Think of brute force solution and apply BFS.\nWhat are the conditions to move from one cell to Another?\nLet\'s assume that | kumarabhi98 | NORMAL | 2022-04-12T15:08:52.807666+00:00 | 2022-04-12T15:08:52.807706+00:00 | 175 | false | This problem, is not too Hard. Just Think of brute force solution and apply BFS.\n**What are the conditions to move from one cell to Another?**\nLet\'s assume that current position of Box is **[i,j]**.\n* If We want to move box to [i+1,j] then this cell should\'nt contain any wall and player should be able to come to cell [i-1,j] from it\'s curr position.\n* If We want to move box to [i-1,j] then this cell should\'nt contain any wall and player should be able to come to cell [i+1,j] from it\'s curr position.\n* If We want to move box to [i,j+1] then this cell should\'nt contain any wall and player should be able to come to cell [i,j-1] from it\'s curr position.\n* If We want to move box to [i,j-1] then this cell should\'nt contain any wall and player should be able to come to cell [i,j+1] from it\'s curr position.\n\nChecking the Condition of player to move from one cell to another can be Done using BFS by applying the current position of Box and player. I have used BFS because of simpler implementation, you guys can use DSU also.\nUsing These extra conditions, apply simple BFS.\n```\nclass Solution {\npublic:\n string stringigy(int x,int t,int a,int b){\n return to_string(x)+"_"+to_string(t)+"_"+\n to_string(a)+"_"+to_string(b);\n }\n bool check(vector<vector<char>>& nums,int ni,int nj,int i,int j,int x,int y){\n vector<vector<bool>> vis(nums.size(),vector<bool>(nums[0].size(),0));\n vis[i][j] = 1;\n queue<pair<int,int>> q; \n q.push({i,j});\n while(!q.empty()){\n int s = q.size();\n while(s--){\n auto [i,j] = q.front(); q.pop();\n if(i==ni && j==nj) continue;\n if(i==x && j==y) return 1;\n if(i+1<nums.size() && !vis[i+1][j] && nums[i+1][j]!=\'#\' ){\n q.push({i+1,j}); vis[i+1][j] = 1;\n }\n if(i-1>=0 && !vis[i-1][j] && nums[i-1][j]!=\'#\' ){\n q.push({i-1,j}); vis[i-1][j] = 1;\n }\n if(j+1<nums[0].size() && !vis[i][j+1] && nums[i][j+1]!=\'#\' ){\n q.push({i,j+1}); vis[i][j+1] = 1;\n }\n if(j-1>=0 && !vis[i][j-1] && nums[i][j-1]!=\'#\' ){\n q.push({i,j-1}); vis[i][j-1] = 1;\n }}\n }\n return 0;\n }\n int minPushBox(vector<vector<char>>& nums) {\n int bi,bj,si,sj,ti,tj;\n for(int i = 0; i<nums.size();++i){\n for(int j = 0;j<nums[0].size();++j){\n if(nums[i][j]==\'B\'){ bi = i,bj = j; }\n if(nums[i][j]==\'S\'){ si = i,sj = j; }\n if(nums[i][j]==\'T\'){ ti = i,tj = j; }\n }\n }\n unordered_map<string,int> mp;\n queue<vector<int>> q;\n q.push({bi,bj,si,sj});\n mp[stringigy(bi,bj,si,sj)]++;\n int n = nums.size(),m=nums[0].size(),l=0;\n while(!q.empty()){\n int s = q.size();\n while(s--){\n vector<int> temp = q.front(); q.pop();\n int i=temp[0],j=temp[1],si=temp[2],sj=temp[3];\n if(i==ti && j==tj) return l;\n if(j-1>=0 && nums[i][j-1]!=\'#\'){\n if(j+1<m && nums[i][j+1]!=\'#\' && mp.find(stringigy(i,j-1,i,j))==mp.end() &&\n check(nums,i,j,si,sj,i,j+1)){\n q.push({i,j-1,i,j});\n mp[stringigy(i,j-1,i,j)]++;\n }\n }\n if(j+1<m && nums[i][j+1]!=\'#\'){\n if(j-1>=0 && nums[i][j-1]!=\'#\' && mp.find(stringigy(i,j+1,i,j))==mp.end() &&\n check(nums,i,j,si,sj,i,j-1)){\n q.push({i,j+1,i,j});\n mp[stringigy(i,j+1,i,j)]++;\n }\n }\n if(i+1<n && nums[i+1][j]!=\'#\'){\n if(i-1>=0 && nums[i-1][j]!=\'#\' && mp.find(stringigy(i+1,j,i,j))==mp.end() &&\n check(nums,i,j,si,sj,i-1,j)){\n q.push({i+1,j,i,j});\n mp[stringigy(i+1,j,i,j)]++;\n }\n }\n if(i-1>=0 && nums[i-1][j]!=\'#\'){\n if(i+1<n && nums[i+1][j]!=\'#\' && mp.find(stringigy(i-1,j,i,j))==mp.end() &&\n check(nums,i,j,si,sj,i+1,j)){\n q.push({i-1,j,i,j});\n mp[stringigy(i-1,j,i,j)]++;\n }\n }\n }\n l++;\n }\n return -1;\n }\n};\n```\n | 2 | 0 | ['Breadth-First Search', 'C'] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | Python Dijkstra (player and box coordinates - state space) | python-dijkstra-player-and-box-coordinat-u54l | If state space (vertices of a graph) represented as player and box coordinates, and the edges have value 1 if during state transition we pushed the box, 0 other | 404akhan | NORMAL | 2021-11-10T13:45:09.751738+00:00 | 2021-11-10T13:45:09.751770+00:00 | 254 | false | If state space (vertices of a graph) represented as player and box coordinates, and the edges have value 1 if during state transition we pushed the box, 0 otherwise. Given this formulation we can run Dijkstra algorithm to find minimum number of pushes to get box to the target.\n\n```\nfrom sortedcontainers import SortedList\n\nclass Solution:\n def minPushBox(self, grid):\n n = len(grid)\n m = len(grid[0])\n\n player, box, target = (0, 0), (0, 0), (0, 0)\n for i in range(n):\n for j in range(m):\n if grid[i][j] == \'S\':\n player = (i, j)\n if grid[i][j] == \'T\':\n target = (i, j)\n if grid[i][j] == \'B\':\n box = (i, j)\n\n def get_nbs(p):\n x, y = p\n return [(dx, dy) for dx, dy in [(x + 1, y), (x - 1, y), (x, y + 1), (x, y - 1)]\n if 0 <= dx < n and 0 <= dy < m and grid[dx][dy] != \'#\']\n\n def get_next_state(state):\n p, b = state\n\n next_states = []\n for dp in get_nbs(p):\n if dp != b:\n next_states.append((0, dp, b))\n else:\n dx = dp[0] - p[0]\n dy = dp[1] - p[1]\n db = (b[0] + dx, b[1] + dy)\n if 0 <= db[0] < n and 0 <= db[1] < m and grid[db[0]][db[1]] != \'#\':\n next_states.append((1, dp, db))\n return next_states\n\n start = (player, box)\n q = SortedList([(0, start)])\n attended = set()\n\n while len(q):\n d, state = q.pop(0)\n if state in attended: continue\n attended.add(state)\n if state[1] == target:\n return d\n\n for ns in get_next_state(state):\n if ns[1:] not in attended:\n q.add((d + ns[0], ns[1:]))\n return -1\n``` | 2 | 0 | [] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | 10 ms solution, BFS with some comments | 10-ms-solution-bfs-with-some-comments-by-3u52 | \nclass Solution {\n public int minPushBox(char[][] grid) {\n if(grid == null)\n return 0;\n \n int row = grid.length;\n | ssgurpreetsingh | NORMAL | 2021-10-08T05:33:18.772085+00:00 | 2021-10-08T05:33:18.772132+00:00 | 498 | false | ```\nclass Solution {\n public int minPushBox(char[][] grid) {\n if(grid == null)\n return 0;\n \n int row = grid.length;\n int col = grid[0].length;\n int[] target = null;\n int[] box = null;\n int[] player = null;\n \n for(int i=0; i < row; i++) {\n for(int j=0; j < col; j++) {\n if(grid[i][j] == \'T\')\n target = new int[] {i, j};\n if(grid[i][j] == \'S\')\n player = new int[] {i, j};\n if(grid[i][j] == \'B\')\n box = new int[] {i, j}; \n }\n }\n \n Queue<int[]> q = new ArrayDeque<>();\n Set<List<Integer>> visited = new HashSet<>();\n\n //Add player and box current location to queue as state\n q.offer(new int[] {player[0], player[1], box[0], box[1]});\n visited.add(new ArrayList<>(Arrays.asList(player[0], player[1], box[0], box[1]))); \n \n int[][] dirs = new int[][] {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};\n int push = 0;\n \n while(!q.isEmpty()) {\n int size = q.size();\n \n for(int i=0; i < size; i++) {\n int[] state = q.poll();\n if(state[2] == target[0] && state[3] == target[1])\n return push;\n \n for(int[] dir: dirs) {\n //player need to be here\n int pX = state[2] - dir[0];\n int pY = state[3] - dir[1];\n \n //To push box in this direction\n int bX = state[2] + dir[0];\n int bY = state[3] + dir[1];\n if(pX < 0 || pX >= row || pY < 0 || pY >= col || \n bX < 0 || bX >= row || bY < 0 || bY >= col ||\n grid[bX][bY] == \'#\' || grid[pX][pY] == \'#\' ||\n visited.contains(new ArrayList<>(Arrays.asList(state[2], state[3], bX, bY))) || \n //player can reach the push location given current box location\n !canReach(state[0], state[1], grid, pX, pY, state[2], state[3])) \n continue;\n \n //box location updated and player location updated to last box location \n q.offer(new int[] {state[2], state[3], bX, bY}); \n visited.add(new ArrayList<>(Arrays.asList(state[2], state[3], bX, bY))); \n }\n }\n push++;\n \n }\n \n return -1;\n \n }\n \n \n public boolean canReach(int x, int y, char[][] grid, int tX, int tY, int bX, int bY) {\n Queue<int[]> q = new ArrayDeque<>();\n \n q.offer(new int [] {x, y});\n int[][] dirs = new int[][] {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};\n boolean visited[][] = new boolean[grid.length][grid[0].length];\n while(!q.isEmpty()) {\n int size = q.size();\n \n for(int i=0; i < size; i++){\n int[] state = q.poll();\n \n if(state[0] == tX && state[1] == tY)\n return true;\n \n for(int[] dir: dirs) {\n int newX = state[0] + dir[0];\n int newY = state[1] + dir[1];\n \n if(newX < 0 || newY < 0 || \n newX >= grid.length || newY >= grid[0].length || \n visited[newX][newY] || grid[newX][newY] == \'#\' || \n (newX == bX && newY == bY))\n continue;\n q.offer(new int[] {newX, newY});\n visited[newX][newY] = true;\n }\n \n \n }\n \n }\n \n return false;\n\n }\n \n}\n\n``` | 2 | 0 | [] | 2 |
minimum-moves-to-move-a-box-to-their-target-location | Super clean Java code | super-clean-java-code-by-kshittiz-hjce | \nclass Solution {\n int n, m;\n char[][] grid;\n int[][] dirs = new int[][] {\n {1, 0}, {0, 1}, {-1, 0}, {0, -1}\n };\n public int minPus | kshittiz | NORMAL | 2021-09-19T08:11:07.897554+00:00 | 2021-09-19T08:11:07.897581+00:00 | 343 | false | ```\nclass Solution {\n int n, m;\n char[][] grid;\n int[][] dirs = new int[][] {\n {1, 0}, {0, 1}, {-1, 0}, {0, -1}\n };\n public int minPushBox(char[][] grid) {\n n = grid.length;\n m = grid[0].length;\n this.grid = grid;\n int[] box = new int[2], target = new int[2], player = new int[2];\n findLocations(box, target, player);\n\n Queue<int[]> q = new LinkedList();\n q.offer(new int[]{box[0], box[1], player[0], player[1]});\n boolean[][][] visited = new boolean[n][m][4]; // for 4 directions\n int steps = 0;\n while(!q.isEmpty()) {\n int size = q.size();\n while(size-- > 0) {\n int[] cur = q.poll();\n if(cur[0] == target[0] && cur[1] == target[1]) return steps;\n for(int i = 0; i < 4; i++) {\n int[] newPlayerLoc = new int[]{cur[0] + dirs[i][0], cur[1] + dirs[i][1]};\n int[] newBoxLoc = new int[]{cur[0] - dirs[i][0], cur[1] - dirs[i][1]};\n if(visited[cur[0]][cur[1]][i] || isOutOfBounds(newPlayerLoc, newBoxLoc) || !isReachable(newPlayerLoc, cur)) continue;\n visited[cur[0]][cur[1]][i] = true;\n q.offer(new int[]{newBoxLoc[0], newBoxLoc[1], cur[0], cur[1]});\n }\n }\n steps++;\n }\n \n return -1;\n \n }\n \n public boolean isReachable(int[] targetPlayerLoc, int[] cur) {\n boolean[][] visited = new boolean[n][m];\n visited[cur[0]][cur[1]] = true;\n visited[cur[2]][cur[3]] = true;\n\n Queue<int[]> q = new LinkedList();\n q.offer(new int[]{cur[2], cur[3]});\n while(!q.isEmpty()) {\n int[] playerLoc = q.poll();\n if(playerLoc[0] == targetPlayerLoc[0] && playerLoc[1] == targetPlayerLoc[1]) return true;\n for(int[] d: dirs) {\n int x = playerLoc[0] + d[0];\n int y = playerLoc[1] + d[1];\n if(isOutOfBounds(x, y) || visited[x][y]) continue;\n visited[x][y] = true;\n q.offer(new int[]{x, y});\n } \n }\n return false;\n }\n \n public boolean isOutOfBounds(int[] player, int[] box) {\n return isOutOfBounds(player[0], player[1]) || isOutOfBounds(box[0], box[1]);\n }\n \n public boolean isOutOfBounds(int x, int y) {\n return (x < 0 || y < 0 || x == n || y == m || grid[x][y] == \'#\');\n }\n \n public void findLocations(int[] box, int[] target, int[] player) {\n boolean p = false, t = false, b = false;\n for(int i = 0; i < n; i++) {\n for(int j = 0; j < m; j++) {\n if(grid[i][j] == \'S\') {\n player[0] = i;\n player[1] = j;\n p = true;\n } else if(grid[i][j] == \'T\') {\n target[0] = i;\n target[1] = j;\n t = true;\n } else if(grid[i][j] == \'B\') {\n box[0] = i;\n box[1] = j;\n b = true;\n }\n \n if(p && b && t) return; // found all\n }\n }\n }\n}\n``` | 2 | 0 | [] | 1 |
minimum-moves-to-move-a-box-to-their-target-location | C# clean & easy to understand | c-clean-easy-to-understand-by-showwhite-xfot | \n //{\'#\',\'.\',\'.\',\'.\'}\n //{\'.\',\'.\',\'S\',\'.\'}\n //{\'.\',\'B\',\'.\',\'T\'}\n //{\'.\',\'.\',\'.\',\'#\'}\n //We can start from th | showwhite | NORMAL | 2021-07-30T06:14:55.268162+00:00 | 2021-07-30T06:14:55.268201+00:00 | 186 | false | \n //{\'#\',\'.\',\'.\',\'.\'}\n //{\'.\',\'.\',\'S\',\'.\'}\n //{\'.\',\'B\',\'.\',\'T\'}\n //{\'.\',\'.\',\'.\',\'#\'}\n //We can start from the current Box location & do a BFS.\n //We don\'t really need to move player, we can just simulate it.\n //In each level, we can try to find valid positions for box in all 4 directions around it\n //& if those positions have a valid position around it for player then,\n //we can push those positions to Q.\n //Box & player new positions valid if: valid boundary/no wall/player can move to the pos.\n //In each step, we can try finding all valid player positions in grid using DFS before hand.\n //The level where we reach the target will be our minimum moves.\n //*********Key is\n //if we want to push box to left, player must stand at right, to simulate this \n //we can just use box position & current direction & add current direction to box position\n //& subtract current direction from box position to get new box & player positions. \n //we can ignore the player position to simulate the player can move to any position\n //int bxNew = boxPos.X + d[0], byNew = boxPos.Y + d[1];\n //int pxNew = boxPos.X - d[0], pyNew = boxPos.Y - d[1];\n //D[1,0] B[1,1] P[0,1] =>move box left[0,-1]\n //=> D[1,0] B[1,0(1-1)] P[1(1+0),2(1-(-1)]\n public class MBM2\n {\n static readonly List<int[]> Dirs = new List<int[]>\n {new[] { -1, 0 }, new[] { 1, 0 }, new[] { 0, 1 }, new[] { 0, -1 }};\n public static int MinPushBox(char[][] grid)\n {\n Position box = null, target = null, player = null;\n #region Get the box, player & target positions\n int rows = grid.Length, cols = grid[0].Length;\n for (var row = 0; row < rows; row++)\n {\n for (var col = 0; col < cols; col++)\n {\n if (grid[row][col] == \'B\')\n box = new Position(row, col);\n else if (grid[row][col] == \'T\')\n target = new Position(row, col);\n else if (grid[row][col] == \'S\')\n player = new Position(row, col);\n }\n }\n #endregion\n\n //Do BFS to find the min moves\n //we can save block & player encoded positions int the Q\n var startPos = Position.GetPositionsAsString(box, player);\n var q = new Queue<string>();\n q.Enqueue(startPos);\n //We use a set to record all the positions we have visited\n //(including the position of the player)\n var visitedSet = new HashSet<string>();\n visitedSet.Add(startPos);\n\n var res = 0;\n while (q.Any())\n {\n res++;\n var size = q.Count();\n while (size > 0)\n {\n size--;\n var decodedPositions = Position.GetPositions(q.Dequeue());\n var boxPos = decodedPositions.Key;\n var playerPos = decodedPositions.Value;\n var canVisit = new bool[rows, cols];\n\n //Use dfs to find all the positions that the player can reach at this moment. \n UpdatePlayerReachablePositions(grid, canVisit, playerPos, boxPos);\n\n //Move the box and update the set\n foreach (var d in Dirs)\n {\n //if we want to push box to right, storekeeper must stand at left\n int bxNew = boxPos.X + d[0], byNew = boxPos.Y + d[1];\n int pxNew = boxPos.X - d[0], pyNew = boxPos.Y - d[1];\n var newBoxPos = new Position(bxNew, byNew);\n var newPlayerPos = new Position(pxNew, pyNew);\n\n //Box cannot move to this direction in any of the following condition \n if (!newPlayerPos.IsValid(grid) || !newBoxPos.IsValid(grid) ||\n newBoxPos.IsWall(grid) || !canVisit[pxNew, pyNew])\n continue;\n\n //If we have reached destination return\n if (newBoxPos.Equals(target))\n return res;\n\n //Now we can move the box, also record the new position(including the original position of the box)\n var newPosition = Position.GetPositionsAsString(newBoxPos, newPlayerPos);\n //Make sure the newPosition has never been visited before\n if (visitedSet.Add(newPosition))\n {\n q.Enqueue(newPosition);\n }\n }\n }\n }\n return -1;\n }\n //DFS to find locations the player can reach\n public static void UpdatePlayerReachablePositions(char[][] grid, bool[,] canVisit, Position playerPosition, Position boxPosition)\n {\n if (!playerPosition.IsValid(grid) ||\n playerPosition.IsWall(grid) ||\n playerPosition.Equals(boxPosition) ||\n canVisit[playerPosition.X, playerPosition.Y])\n return;\n canVisit[playerPosition.X, playerPosition.Y] = true;\n foreach (var d in Dirs)\n {\n var newPlayerPos = new Position(playerPosition.X + d[0], playerPosition.Y + d[1]);\n UpdatePlayerReachablePositions(grid, canVisit, newPlayerPos, boxPosition);\n }\n }\n\n public class Position\n {\n public int X { get; set; }\n public int Y { get; set; }\n public Position(int x, int y)\n {\n X = x;\n Y = y;\n }\n public static string GetPositionsAsString(Position box, Position storeKeeper)\n {\n return box.ToString() + "|" + storeKeeper.ToString();\n }\n\n public static KeyValuePair<Position, Position> GetPositions(string num)\n {\n var pos = num.Split(\'|\');\n var res = new KeyValuePair<Position, Position>(new Position(pos[0], pos[1]), new Position(pos[2], pos[3]));\n return res;\n }\n public Position(string x, string y)\n {\n int.TryParse(x, out var x1);\n X = x1;\n int.TryParse(y, out var y1);\n Y = y1;\n }\n public override string ToString()\n {\n return X + "|" + Y;\n }\n\n public bool IsValid(char[][] grid)\n {\n return X >= 0 && Y >= 0 && X < grid.Length && Y < grid[0].Length;\n }\n\n public bool IsWall(char[][] grid)\n {\n return grid[X][Y] == \'#\';\n }\n\n public bool Equals(Position position)\n {\n return X == position.X && Y == position.Y;\n }\n }\n } | 2 | 0 | [] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | Can player walk through target cell because its an empty cell? | can-player-walk-through-target-cell-beca-hyfc | The following is possible only if the player can walk through Target. Why doesn\'t the problem mention this? Is this a test of something in an actual interview? | RockyTheAlienSpider | NORMAL | 2021-07-21T12:26:22.496512+00:00 | 2021-07-21T12:26:22.496554+00:00 | 119 | false | The following is possible only if the player can walk through Target. Why doesn\'t the problem mention this? Is this a test of *something* in an actual interview? \n\n```\n\nExample 3:\n\nInput: grid = [["#","#","#","#","#","#"],\n ["#","T",".",".","#","#"],\n ["#",".","#","B",".","#"],\n ["#",".",".",".",".","#"],\n ["#",".",".",".","S","#"],\n ["#","#","#","#","#","#"]]\nOutput: 5\nExplanation: push the box down, left, left, up and up.\n\n```` | 2 | 0 | [] | 1 |
minimum-moves-to-move-a-box-to-their-target-location | [C++] BFS with deque | c-bfs-with-deque-by-tianchunh97-rhvm | 0-1 BFS implemented by deque: when the new state pushes the box, push it to the back of the deque; otherwise push front. In this way, every node we pop from the | tianchunh97 | NORMAL | 2020-09-13T04:02:36.706607+00:00 | 2020-09-13T04:02:36.706647+00:00 | 231 | false | 0-1 BFS implemented by deque: when the new state pushes the box, push it to the back of the deque; otherwise push front. In this way, every node we pop from the deque has the smallest number of pushes in the deque.\n\nPriority queue can also be used instead of deque. My results for both methods:\ndeque: 120ms 16MB\npriority queue: 760ms 8MB\n\n```\nclass Solution {\n typedef pair<int, pair<int, int>> PIII;\npublic:\n int minPushBox(vector<vector<char>>& grid) {\n int M = grid.size();\n int N = grid[0].size();\n deque<PIII> dq;\n int box = -1, start = -1;\n for (int i = 0; i < M; i++) {\n for (int j = 0; j < N; j++) {\n if (grid[i][j] == \'B\') box = i*N+j;\n if (grid[i][j] == \'S\') start = i*N+j; \n }\n }\n dq.push_back({0, {box, start}});\n vector<vector<bool>> visited(M*N, vector<bool>(M*N, false));\n int dir1[] = {0, 0, -1, 1};\n int dir2[] = {-1, 1, 0, 0};\n while (!dq.empty()) {\n int push = dq.front().first;\n int b_pos = dq.front().second.first;\n int p_pos = dq.front().second.second;\n dq.pop_front();\n if (visited[b_pos][p_pos]) continue;\n visited[b_pos][p_pos] = true;\n int rb = b_pos/N, cb = b_pos%N;\n int rp = p_pos/N, cp = p_pos%N;\n for (int i = 0; i < 4; i++) {\n int nr = rp + dir1[i];\n int nc = cp + dir2[i];\n if (nr < 0 || nc < 0 || nr >= M || nc >= N || grid[nr][nc] == \'#\') continue;\n if (nr*N+nc != b_pos) {\n dq.push_front({push, {b_pos, nr*N+nc}});\n }\n else { // move box\n int nrb = rb + dir1[i], ncb = cb+dir2[i];\n if (nrb < 0 || ncb < 0 || nrb >= M || ncb >= N || grid[nrb][ncb] == \'#\') continue;\n if (grid[nrb][ncb] == \'T\') return push+1;\n dq.push_back({push+1, {nrb*N+ncb, b_pos}});\n }\n }\n }\n return -1;\n }\n};\n``` | 2 | 0 | [] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | [JAVA] BFS with comments | java-bfs-with-comments-by-magiciendecode-jbrr | visited array is 3 dimentional, box x,y index and last move direction.\n2. as we have 4 direcitons, when ierate, just use index as direction.\n3. for each next | magiciendecode | NORMAL | 2020-08-15T23:38:19.871615+00:00 | 2020-08-15T23:38:19.871646+00:00 | 498 | false | 1. visited array is 3 dimentional, box x,y index and last move direction.\n2. as we have 4 direcitons, when ierate, just use index as direction.\n3. for each next move, we need to check next box position and next player position is in bound.\n4. an additional bfs function to check the player can mvoe the target player postion or not.\n```\nclass Solution {\n public int minPushBox(char[][] grid) {\n final Queue<int[]> queue = new LinkedList<>();\n final boolean[][][] visited =\n new boolean[grid.length][grid[0].length][4];\n final int[] target = new int[2];\n final int[] player = new int[2];\n final int[] box = new int[2];\n for (int i = 0; i < grid.length; i++) {\n for (int j = 0; j < grid[0].length; j++) {\n if (grid[i][j] == \'T\') {\n target[0] = i;\n target[1] = j;\n grid[i][j] = \'.\';\n }\n if (grid[i][j] == \'S\') {\n player[0] = i;\n player[1] = j;\n grid[i][j] = \'.\';\n }\n if (grid[i][j] == \'B\') {\n box[0] = i;\n box[1] = j;\n grid[i][j] = \'.\';\n }\n }\n }\n queue.offer(new int[]{\n box[0], box[1], player[0], player[1]\n });\n int level = 0;\n while (!queue.isEmpty()) {\n final int currentSize = queue.size();\n // iterate by level\n for (int size = 0; size < currentSize; size++) {\n final int[] current = queue.poll();\n if (current[0] == target[0] &&\n current[1] == target[1]\n ) {\n return level;\n }\n for (int index = 0; index < 4; index++) {\n // next box position\n final int nextX = current[0] + deltaX[index];\n final int nextY = current[1] + deltaY[index];\n // next player position is opposite to box\n final int playerX = current[0] - deltaX[index];\n final int playerY = current[1] - deltaY[index];\n // next box player should be in bound, equals to \'.\'\n // player can move from current player position to (playerX,playerY)\n if (inBound(grid, nextX, nextY) &&\n inBound(grid, playerX, playerY) &&\n !visited[nextX][nextY][index] &&\n grid[nextX][nextY] == \'.\' &&\n grid[playerX][playerY] == \'.\' &&\n canPush(grid, playerX, playerY, current[2], current[3], current[0], current[1])\n ) {\n queue.offer(new int[]{nextX, nextY, playerX, playerY});\n visited[nextX][nextY][index] = true;\n }\n }\n }\n ++level;\n }\n return -1;\n }\n\n // as we mark box as \'.\', so we need its position to block player\'s moves\n private boolean canPush(\n char[][] grid,\n int targetX,\n int targetY,\n int x,\n int y,\n int boxX,\n int boxY) {\n final Queue<int[]> queue = new LinkedList<>();\n final boolean[][] visited =\n new boolean[grid.length][grid[0].length];\n queue.offer(new int[]{x, y});\n visited[x][y] = true;\n while (!queue.isEmpty()) {\n final int[] current = queue.poll();\n if (current[0] == targetX && current[1] == targetY) {\n return true;\n }\n for (int index = 0; index < 4; index++) {\n final int nextX = current[0] + deltaX[index];\n final int nextY = current[1] + deltaY[index];\n if (inBound(grid, nextX, nextY) &&\n !visited[nextX][nextY] &&\n grid[nextX][nextY] == \'.\' &&\n (nextX != boxX || nextY != boxY)\n ) {\n queue.offer(new int[]{nextX, nextY});\n visited[nextX][nextY] = true;\n }\n }\n }\n return false;\n }\n\n\n private final int[] deltaX = {0, 0, -1, 1};\n private final int[] deltaY = {-1, 1, 0, 0};\n\n private boolean inBound(\n char[][] grid,\n int x,\n int y\n ) {\n return x >= 0 && y >= 0 && x < grid.length && y < grid[0].length;\n }\n}\n``` | 2 | 0 | ['Breadth-First Search', 'Java'] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | Simple Java Solution -- Union Find & BFS | simple-java-solution-union-find-bfs-by-r-qhh5 | \nclass Solution {\n //1. \u5E76\u67E5\u96C6\u5224\u65AD\u80FD\u5426\u5230\u8FBE\n //2. BFS \u7BB1\u5B50\n int[][] dir = new int[][]{{-1, 0}, {1, 0}, { | renyajie | NORMAL | 2020-01-23T06:58:01.269329+00:00 | 2020-01-23T06:58:01.269362+00:00 | 244 | false | ```\nclass Solution {\n //1. \u5E76\u67E5\u96C6\u5224\u65AD\u80FD\u5426\u5230\u8FBE\n //2. BFS \u7BB1\u5B50\n int[][] dir = new int[][]{{-1, 0}, {1, 0}, {0, 1}, {0, -1}};\n public int minPushBox(char[][] grid) {\n int m = grid.length, n = grid[0].length;\n int px = 0, py = 0, tx = 0, ty = 0, bx = 0, by = 0;\n for(int i = 0; i < m; i++) {\n for(int j = 0; j < n; j++) {\n if(grid[i][j] == \'B\') {\n bx = i;\n by = j;\n } else if(grid[i][j] == \'S\') {\n px = i;\n py = j;\n } else if(grid[i][j] == \'T\') {\n tx = i;\n ty = j;\n }\n }\n }\n int[] parent = buildSet(grid, m, n);\n int sp = find(parent, px * n + py);\n int st = find(parent, tx * n + ty);\n int sb = find(parent, bx * n + by);\n if(!(sp == st && st == sb)) return -1;\n \n Queue<int[]> que = new LinkedList<>();\n Set<String> visited = new HashSet<>();\n que.offer(new int[]{bx * n + by, px * n + py});\n visited.add((bx * n + by) + "," + (px * n + py));\n \n int res = 0;\n while(!que.isEmpty()) {\n for(int size = que.size(); size > 0; size--) {\n int[] p = que.poll();\n if(p[0] == tx * n + ty) return res;\n int r = p[0] / n, c = p[0] % n;\n \n char ch = grid[r][c];\n grid[r][c] = \'#\';\n parent = buildSet(grid, m, n);\n for(int[] d : dir) {\n int x = r + d[0], y = c + d[1];\n int rx = r - d[0], ry = c - d[1];\n \n if(x >= 0 && x < m && y >= 0 && y < n && grid[x][y] != \'#\' && rx >= 0 && rx < m && ry >= 0 && ry < n && grid[rx][ry] != \'#\') {\n \n if(find(parent, rx * n + ry) == find(parent, p[1]) && visited.add((x * n + y) + "," + p[0])) {\n que.offer(new int[]{x * n + y, p[0]});\n }\n }\n }\n grid[r][c] = (char)(res + \'0\');\n }\n res++;\n }\n return -1;\n }\n \n private int[] buildSet(char[][] grid, int m, int n) {\n int[] parent = new int[m * n];\n for(int i = 0; i < m * n; i++) parent[i] = i;\n for(int i = 0; i < m; i ++) {\n for(int j = 0; j < n; j++) {\n if(grid[i][j] != \'#\') {\n if(i > 0 && grid[i-1][j] != \'#\') union(parent, (i-1)*n+j, i*n+j);\n if(i < m-1 && grid[i+1][j] != \'#\') union(parent, (i+1)*n+j, i*n+j);\n if(j > 0 && grid[i][j-1] != \'#\') union(parent, i*n+j-1, i*n+j);\n if(j < n-1 && grid[i][j+1] != \'#\') union(parent, i*n+j+1, i*n+j);\n }\n }\n }\n return parent;\n }\n \n private void union(int[] p, int a, int b) {\n int pa = find(p, a), pb = find(p, b);\n if(pa != pb) p[pa] = pb;\n }\n \n private int find(int[] p, int a) {\n return p[a] = p[a] == a ? a : find(p, p[a]);\n }\n}\n``` | 2 | 0 | [] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | C# Readable BFS + BFS with inline comments | c-readable-bfs-bfs-with-inline-comments-8wzkm | \npublic class Solution {\n private char[][] grid;\n private Position boxPosition;\n private int[] directions = new int[] {0, 1, 0, -1, 0};\n \n | mmikhail | NORMAL | 2019-11-25T20:29:47.926142+00:00 | 2019-11-25T20:29:47.926193+00:00 | 215 | false | ```\npublic class Solution {\n private char[][] grid;\n private Position boxPosition;\n private int[] directions = new int[] {0, 1, 0, -1, 0};\n \n // Represents coordinate with Equals() implemented by default for Queues\n public struct Position\n {\n public int X;\n public int Y;\n \n public Position(int x, int y)\n {\n X = x;\n Y = y;\n }\n \n public override string ToString()\n {\n return $"[{Y},{X}]";\n }\n }\n \n // State, what we will store in BFS for the box\n public struct BoxAndPlayerPosition\n {\n public Position boxPosition;\n public Position playerPosition;\n \n public BoxAndPlayerPosition(Position boxPosition, Position playerPosition)\n {\n this.boxPosition = boxPosition;\n this.playerPosition = playerPosition;\n }\n \n // where the box will be moved along with player. Player will fill in the box spot, box will be moved 1 cell in corresponding direction\n public BoxAndPlayerPosition NextPosition()\n {\n if (boxPosition.X == playerPosition.X)\n {\n if (playerPosition.Y < boxPosition.Y)\n return new BoxAndPlayerPosition(new Position(boxPosition.X, boxPosition.Y + 1), new Position(playerPosition.X, playerPosition.Y + 1));\n return new BoxAndPlayerPosition(new Position(boxPosition.X, boxPosition.Y - 1), new Position(playerPosition.X, playerPosition.Y - 1));\n }\n \n if (playerPosition.X < boxPosition.X)\n return new BoxAndPlayerPosition(new Position(boxPosition.X + 1, boxPosition.Y), new Position(playerPosition.X + 1, playerPosition.Y));\n return new BoxAndPlayerPosition(new Position(boxPosition.X - 1, boxPosition.Y), new Position(playerPosition.X - 1, playerPosition.Y));\n }\n \n public override string ToString()\n {\n return $"b:{boxPosition};p:{playerPosition}";\n }\n }\n \n // BFS for player, can player move to the position, assuming box is just another \'wall\' for the sake of this method\n private bool PlayerCanMove(BoxAndPlayerPosition current, Position target)\n {\n Queue<Position> queue = new Queue<Position>();\n boxPosition = current.boxPosition;\n \n queue.Enqueue(current.playerPosition);\n HashSet<Position> visited = new HashSet<Position>();\n visited.Add(current.playerPosition);\n \n while (queue.Count > 0)\n {\n Position currPos = queue.Dequeue();\n if (currPos.Equals(target))\n {\n return true;\n }\n \n for (int i = 0; i < 4; i++)\n {\n int newX = currPos.X + directions[i];\n int newY = currPos.Y + directions[i+1];\n Position newPos = new Position(newX, newY);\n \n if (CanMoveTo(newPos, visited))\n {\n visited.Add(newPos);\n queue.Enqueue(newPos);\n }\n }\n }\n \n return false;\n }\n \n private bool CanMoveTo(Position pos, HashSet<Position> visited)\n {\n return (IsValidAndEmpty(pos) && !visited.Contains(pos) &&\n !pos.Equals(boxPosition));\n }\n \n private bool IsValidAndEmpty(Position pos)\n {\n int x = pos.X;\n int y = pos.Y;\n \n return x >= 0 && x < grid[0].Length && y >= 0 && y < grid.Length && grid[y][x] == \'.\';\n }\n \n public int MinPushBox(char[][] grid) {\n this.grid = grid;\n \n Position boxPosition = FindBox(grid);\n Position playerPosition = FindPlayer(grid);\n Position targetPosition = FindTarget(grid);\n \n // since we captured box, player, and target positions, we change it to \'.\' so it would be easier to check whether we can move in a cell\n grid[boxPosition.Y][boxPosition.X] = \'.\';\n grid[playerPosition.Y][playerPosition.X] = \'.\';\n grid[targetPosition.Y][targetPosition.X] = \'.\';\n \n int pushes = 0;\n Queue<BoxAndPlayerPosition> queue = new Queue<BoxAndPlayerPosition>();\n HashSet<BoxAndPlayerPosition> visited = new HashSet<BoxAndPlayerPosition>();\n \n BoxAndPlayerPosition initial = new BoxAndPlayerPosition(boxPosition, playerPosition);\n \n // adding all possible starting points: box and positions to the left, right, top, bottom to the box.\n for (int i = 0; i < 4; i++)\n {\n int newX = boxPosition.X + directions[i];\n int newY = boxPosition.Y + directions[i+1];\n Position target = new Position(newX, newY);\n \n if (!IsValidAndEmpty(target) || !PlayerCanMove(initial, target))\n continue;\n \n var start = new BoxAndPlayerPosition(boxPosition, target);\n queue.Enqueue(start);\n visited.Add(start);\n }\n \n // BFS for player and the box\n while (queue.Count > 0)\n {\n var length = queue.Count;\n \n for (int j = 0; j < length; j++)\n {\n BoxAndPlayerPosition current = queue.Dequeue();\n if (current.boxPosition.Equals(targetPosition))\n return pushes;\n\n var next = current.NextPosition();\n var nextBox = next.boxPosition;\n\n if (!visited.Contains(next) && IsValidAndEmpty(nextBox)) \n {\n queue.Enqueue(next);\n visited.Add(next);\n\n // when we add another position \'next\' for the player and the box, we need to try to add all possible positions for the player if the box is fixed. So whenever we move the box, always add all positions for the player as well around the box to the queue.\n for (int i = 0; i < 4; i++)\n {\n int newX = nextBox.X + directions[i];\n int newY = nextBox.Y + directions[i+1];\n Position newPosition = new Position(newX, newY);\n\n if (!next.playerPosition.Equals(newPosition) && IsValidAndEmpty(newPosition) && PlayerCanMove(next, newPosition))\n {\n var start = new BoxAndPlayerPosition(nextBox, newPosition);\n if (!visited.Contains(start))\n {\n queue.Enqueue(start);\n visited.Add(start);\n }\n }\n }\n }\n }\n pushes++;\n }\n\n return -1;\n }\n \n private Position FindBox(char[][] grid)\n {\n return Find(grid, \'B\');\n }\n private Position FindPlayer(char[][] grid)\n {\n return Find(grid, \'S\');\n }\n private Position FindTarget(char[][] grid)\n {\n return Find(grid, \'T\');\n }\n \n private Position Find(char[][] grid, char c)\n {\n for (int i = 0; i < grid.Length; i++)\n for (int j = 0; j < grid[0].Length; j++)\n if (grid[i][j] == c)\n return new Position(j, i);\n \n throw new Exception();\n } \n}\n``` | 2 | 0 | [] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | non-nested BFS with O(1) connectivity check | non-nested-bfs-with-o1-connectivity-chec-g0c0 | Up to now all these solutions here contain nested BFS/DFS/Union inside the outer BFS to check if the person can reach certain position. However, this can be don | 617280219 | NORMAL | 2019-11-20T11:10:08.970486+00:00 | 2019-11-20T11:10:08.970516+00:00 | 200 | false | Up to now all these solutions here contain nested BFS/DFS/Union inside the outer BFS to check if the person can reach certain position. However, this can be done in O(1) time with some preprocessing.\nNotice that after the first push, we only need to consider states with the person next to the box. In that case, we only check connnectivity between two cells both adjacent to the box with the box cell treated as a wall. Now we can see that under this circumstance the two cells are connected if and only if they are in a loop, or more generally, a 2-connected component. With a DFS we can get all the 2-connected components, and given that a cell can be in no more than 4 components, we can check connectivity in O(1) time.\nFinally we get an algorithm of one-pass DFS and one-pass BFS, with complexity O(nm) rather than O((nm)^2) for nested algorithms. The result is python3 48ms, faster than 99.70%, and the rest 0.3% is a cheater. It should be able to deal with n,m~500 cases.\n```\nclass Solution:\n def minPushBox(self, grid: List[List[str]]) -> int:\n n,m=len(grid),len(grid[0])\n bcc=[[set() for j in range(m)] for i in range(n)]\n low=[[0]*m for i in range(n)]\n dfn=[[0]*m for i in range(n)]\n T,cnt,st=0,0,[]\n def dfs(i,j):\n nonlocal T,cnt\n if not (0<=i<n and 0<=j<m) or grid[i][j]==\'#\':\n return -1\n elif dfn[i][j]>0:\n return 0\n st.append((i,j))\n T+=1\n low[i][j]=dfn[i][j]=T\n for x,y in [(i+1,j),(i-1,j),(i,j+1),(i,j-1)]:\n temp=dfs(x,y)\n if temp==-1:\n continue\n elif temp==0:\n low[i][j]=min(low[i][j],dfn[x][y])\n continue\n if low[x][y]>=dfn[i][j]:\n cnt+=1\n while True:\n a,b=st.pop()\n bcc[a][b].add(cnt)\n if (a,b)==(x,y):\n break\n bcc[i][j].add(cnt)\n low[i][j]=min(low[i][j],low[x][y])\n for i in range(n):\n for j in range(m):\n if grid[i][j]!=\'#\' and dfn[i][j]==0:\n dfs(i,j)\n if grid[i][j]==\'S\':\n sx,sy=i,j\n elif grid[i][j]==\'T\':\n tx,ty=i,j\n elif grid[i][j]==\'B\':\n bx,by=i,j\n q0,visited=[(sx,sy)],[[0]*m for i in range(n)]\n visited[sx][sy]=1\n while q0:\n temp=[]\n for x,y in q0:\n for px,py in [(x+1,y),(x-1,y),(x,y+1),(x,y-1)]:\n if 0<=px<n and 0<=py<m and grid[px][py] in \'.T\' and visited[px][py]==0:\n visited[px][py]=1\n temp.append((px,py))\n q0=temp\n q=[(bx,by,x,y) for x,y in [(bx+1,by),(bx-1,by),(bx,by+1),(bx,by-1)] if visited[x][y]]\n visited,ans=set(q),0\n while q:\n temp=[]\n for x1,y1,x2,y2 in q:\n #print(x1,y1,x2,y2)\n if (x1,y1)==(tx,ty):\n return ans\n x1,y1,x2,y2=x1*2-x2,y1*2-y2,x1,y1\n if not (0<=x1<n and 0<=y1<m) or grid[x1][y1]==\'#\':\n continue\n for px,py in [(x1+1,y1),(x1-1,y1),(x1,y1+1),(x1,y1-1)]:\n #print(px,py)\n if (0<=px<n and 0<=py<m) and (grid[px][py]!=\'#\') and (bcc[px][py]&bcc[x2][y2]) and ((x1,y1,px,py) not in visited):\n nxt=x1,y1,px,py\n visited.add(nxt)\n temp.append(nxt)\n q,ans=temp,ans+1\n return -1\n``` | 2 | 0 | [] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | ✅ 2 BFS | Easy to understand | 75% TC | 80% SC | 2-bfs-easy-to-understand-75-tc-80-sc-by-5hyh0 | Intuition\n1. If the box is just sitting with robotic wheels, if we want to move to target, it is a simple problem, we can just use BFS to find the shortest rou | gregor_98 | NORMAL | 2024-12-01T17:13:26.651216+00:00 | 2024-12-01T17:13:26.651244+00:00 | 49 | false | # Intuition\n1. If the box is just sitting with robotic wheels, if we want to move to target, it is a simple problem, we can just use BFS to find the shortest route to the target (simple right, we should work on robotic wheels \uD83D\uDE1B)\n2. Now lets introduce the constraint that the person need to be standing behind the box to push it, so while verifying if the box can travel to the next position we also need to verify if the person can travel and come stand behind the box. To verify this we need another BFS.\n3. Now one additional change we need is that we cannot simply say that we are not going to reach a pos where box has already been placed, because there can be some cases where person needs to just move the box to unblock himself and get to the right position, now for this we are using a set to store the position of box and position of person.\n\n# Code\n```cpp []\nclass Solution {\npublic:\n bool isValid(pair<int, int> pos, vector<vector<char>>& grid) {\n int m = grid.size(), n = grid[0].size();\n int ni = pos.first, nj = pos.second;\n return ni >= 0 && ni < m && nj >= 0 && nj < n && grid[ni][nj] != \'#\';\n }\n bool canTravel(vector<vector<char>>& grid, pair<int, int> box,\n pair<int, int> per, pair<int, int> tar) {\n int m = grid.size(), n = grid[0].size();\n grid[box.first][box.second] = \'#\';\n queue<pair<int, int>> q;\n vector<vector<bool>> vis(m, vector<bool>(n, false));\n q.push(per);\n int dir[5] = {0, 1, 0, -1, 0};\n while (!q.empty()) {\n auto [i, j] = q.front();q.pop();\n if(make_pair(i, j) == tar) {\n grid[box.first][box.second] = \'.\';\n return true;\n }\n if(vis[i][j]) continue;\n vis[i][j] = true;\n for (int x = 0; x < 4; x++) {\n int ni = i + dir[x], nj = j + dir[x + 1];\n if (ni >= 0 && ni < m && nj >= 0 && nj < n &&\n grid[ni][nj] != \'#\' &&\n !vis[ni][nj]) {\n q.push(make_pair(ni, nj));\n }\n }\n }\n grid[box.first][box.second] = \'.\';\n return false;\n }\n int minPushBox(vector<vector<char>>& grid) {\n int m = grid.size(), n = grid[0].size();\n pair<int, int> box, per, tar;\n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n if (grid[i][j] == \'S\') {\n per = make_pair(i, j);\n grid[i][j] = \'.\';\n } else if (grid[i][j] == \'T\') {\n tar = make_pair(i, j);\n grid[i][j] = \'.\';\n } else if (grid[i][j] == \'B\') {\n box = make_pair(i, j);\n grid[i][j] = \'.\';\n }\n }\n }\n\n queue<pair<pair<int, int>, pair<int, int>>> q;\n set<vector<int>> vis;\n int dir[5] = {0, 1, 0, -1, 0};\n\n q.push(make_pair(box, per));\n int pushes = 0;\n while (!q.empty()) {\n for (int i = q.size(); i > 0; i--) {\n auto [bpos, ppos] = q.front();\n q.pop();\n if (bpos == tar)\n return pushes;\n\n if (vis.contains(\n {bpos.first, bpos.second, ppos.first, ppos.second}))\n continue;\n vis.insert({bpos.first, bpos.second, ppos.first, ppos.second});\n\n for (int x = 0; x < 4; x++) {\n int nbi = bpos.first + dir[x],\n nbj = bpos.second + dir[x + 1];\n int npi = bpos.first + (dir[x] * -1),\n npj = bpos.second + (dir[x + 1] * -1);\n if (isValid({nbi, nbj}, grid) &&\n isValid({npi, npj}, grid) && \n canTravel(grid, bpos, ppos, {npi,npj}) &&\n !vis.contains({nbi, nbj, npi, npj})) {\n q.push({{nbi, nbj}, bpos});\n vis.insert({bpos.first, bpos.second, npi, npj});\n }\n }\n }\n pushes++;\n }\n\n return -1;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | BFS with a heap | bfs-with-a-heap-by-maxorgus-2i5g | Note normal bfs can lead to wrong answers, since the number of pushes of which we wish to find the minimum is not necessarily increasing in the normal queue whe | MaxOrgus | NORMAL | 2024-01-15T02:09:26.988387+00:00 | 2024-01-15T02:09:26.988405+00:00 | 102 | false | Note normal bfs can lead to wrong answers, since the number of pushes of which we wish to find the minimum is not necessarily increasing in the normal queue where the step counts corresponds to, rather, the moves of the player, which include steps that are not pushes. So we need to restructure the queue using a heap to keep the step of the minimum pushes atop the heap.\n\n# Code\n```\nclass Solution:\n def minPushBox(self, grid: List[List[str]]) -> int:\n m = len(grid)\n n = len(grid[0])\n for i in range(m):\n for j in range(n):\n if grid[i][j] == \'S\':\n player = (i,j)\n if grid[i][j] == \'B\':\n box = (i,j)\n if grid[i][j] == \'T\':\n target = (i,j)\n seen = set([(player,box)])\n queue = [(0,player,box)]\n heapq.heapify(queue)\n while queue:\n s,p,b = heapq.heappop(queue)\n if b == target:\n return s\n pi,pj = p\n bi,bj = b\n for di,dj in [(0,1),(1,0),(-1,0),(0,-1)]:\n ni,nj = pi+di,pj+dj\n if (ni,nj)==(bi,bj):\n nbi,nbj = bi+di,bj+dj\n if 0<=ni<m and 0<=nj<n and 0<=nbi<m and 0<=nbj<n and grid[nbi][nbj] != \'#\' and ((ni,nj),(nbi,nbj)) not in seen:\n heapq.heappush(queue,(s+1,(ni,nj),(nbi,nbj)))\n seen.add(((ni,nj),(nbi,nbj)))\n else:\n if 0<=ni<m and 0<=nj<n and grid[ni][nj] != \'#\' and ((ni,nj),(bi,bj)) not in seen:\n heapq.heappush(queue,(s,(ni,nj),(bi,bj)))\n seen.add(((ni,nj),(bi,bj)))\n return -1\n\n\n\n \n``` | 1 | 0 | ['Breadth-First Search', 'Heap (Priority Queue)', 'Python3'] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | Single BFS || Priority queue || Intuitive Solution | single-bfs-priority-queue-intuitive-solu-s85z | \n\nclass Solution {\npublic:\n\nint dx[4] = {1,0,-1,0}, dy[4] = {0,1,0,-1};\nint dp[22][22][22][22],vis[22][22][22][22];\nint ti,tj;\nbool check(int i,int j,ve | princegup678 | NORMAL | 2023-10-04T17:20:09.645089+00:00 | 2023-10-04T17:20:31.001008+00:00 | 39 | false | \n```\nclass Solution {\npublic:\n\nint dx[4] = {1,0,-1,0}, dy[4] = {0,1,0,-1};\nint dp[22][22][22][22],vis[22][22][22][22];\nint ti,tj;\nbool check(int i,int j,vector<vector<char>>& grid){\n int n=grid.size(),m=grid[0].size();\n if(i<0 || i>=n ||j<0|| j>=m || grid[i][j]==\'#\') return false;\n return true;\n}\n\n int minPushBox(vector<vector<char>>& grid) {\n int si,sj,bi,bj;\n int n=grid.size(),m=grid[0].size();\n memset(dp,-1,sizeof(dp));\n memset(vis,0,sizeof(vis));\n for(int i=0;i<n;i++)\n for(int j=0;j<m;j++){\n if(grid[i][j] == \'S\')\n si=i,sj=j;\n if(grid[i][j] == \'B\')\n bi=i,bj=j;\n if(grid[i][j] == \'T\')\n ti=i,tj=j;\n }\n \nint ans = 0;\n\n\n\npriority_queue<vector<int>> q;\nq.push({0,si,sj,bi,bj});\nvis[si][sj][bi][bj] = 1;\n\nwhile(!q.empty()){\n int sz = q.size();\n while(sz--){\n auto p = q.top(); q.pop();\n int d=p[0];\n si = p[1], sj=p[2],bi=p[3],bj=p[4];\n\n if(bi==ti && bj==tj) return -d;\n\n for(int i=0;i<4;i++){\n int x = si + dx[i], y=sj+dy[i];\n\n if(check(x,y,grid) && (!(x==bi && y==bj) || check(x+dx[i],y+dy[i],grid))){\n if(x==bi && y==bj){\n if(vis[x][y][dx[i]+x][dy[i]+y] == 0)\n q.push({d-1,x,y,dx[i]+x,dy[i]+y});\n vis[x][y][dx[i]+x][dy[i]+y]=1;\n }\n else{\n if(vis[x][y][bi][bj] == 0)\n q.push({d,x,y,bi,bj});\n vis[x][y][bi][bj]=1;\n }\n }\n }\n }\n\n ans++;\n}\nreturn -1;\n\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | O(n*m) solution using Tarjan to precauculate biconnected component | onm-solution-using-tarjan-to-precauculat-ye33 | Approach\nBefore we start, I need to mention, this is definately not an answer interviewer expects you to implement. Feel free to ignore this solution if you ar | t3cmax | NORMAL | 2023-06-22T10:02:36.920596+00:00 | 2023-06-22T11:01:10.995969+00:00 | 100 | false | # Approach\nBefore we start, I need to mention, this is definately not an answer interviewer expects you to implement. Feel free to ignore this solution if you are just preparing for interview. They are not hiring you to paticipate coding competition.\n\nI shared this solution just want to give some inspiration to those people who have a little coding competition experience. O(n*m) is possible! Not just O(bfs*bfs).\n\nSteps:\n1. we consider each cell as vertex, 4 direction as edge, build a graph.\n2. calculate [biconnected component](https://en.wikipedia.org/wiki/Biconnected_component) for this graph.\n3. When box is at any cell, it can be considered as: removing one vertex in graph, we know the removed vertex is a cut vertex or not, thus we can use O(1) time to know if 4 cells next to it can reach each other.\n4. dp[i][j][k], mean the minimal push we need to use to reach a situation that box is at [i][j], and person is at direction[k] to the box.\n5. BFS to calculate the dp to get dp[target_x][target_y][0-4].\n\n# Complexity\n- Time complexity:\nO(n*m)\n\n- Space complexity:\nO(n*m)\n\n# Code\n```\nstruct node\n{\n int x,y;\n node(int xx,int yy)\n {\n x=xx;y=yy;\n }\n};\n\nstruct node2\n{\n int x,y,dir;\n node2(int xx,int yy,int dd)\n {\n x=xx;y=yy;dir=dd;\n }\n};\n\nclass Solution {\n vector<vector<int>>dfn;\n vector<vector<vector<int>>>color;\n vector<vector<vector<bool>>>cover;\n vector<vector<int>>mi;\n vector<vector<char>>grid;\n int dir[4][2]={{0,1},{0,-1},{1,0},{-1,0}};\n int id;\n int sid;\n vector<vector<bool>>ins;\n stack<node2>st;\n int n,m;\n \n void dfs(int x,int y,int last_dir)\n {\n dfn[x][y]=mi[x][y]=++id;\n int i;\n\n for(i=0;i<4;i++)\n {\n if((last_dir^1)==i)\n {\n continue;\n }\n int nx,ny;\n nx=x+dir[i][0];\n ny=y+dir[i][1];\n\n if(nx>=0 && nx<n && ny>=0 && ny<m && grid[nx][ny]!=\'#\')\n {\n if(cover[x][y][i]==0 && cover[nx][ny][i^1]==0)\n {\n st.push(node2(x,y,i));\n cover[x][y][i]=cover[nx][ny][i^1]=1;\n }\n if(dfn[nx][ny]==0)\n {\n dfs(nx,ny,i);\n if(dfn[x][y]<=mi[nx][ny])\n {\n node2 now(0,0,0);\n do\n {\n now=st.top();\n st.pop();\n color[now.x][now.y][now.dir]=sid;\n color[now.x+dir[now.dir][0]][now.y+dir[now.dir][1]][now.dir^1]=sid;\n }while(now.x!=x || now.y!=y || now.dir!=i);\n sid++;\n }\n mi[x][y]=min(mi[x][y],mi[nx][ny]);\n }\n else // if(ins[nx][ny]==1)\n {\n mi[x][y]=min(mi[x][y],dfn[nx][ny]);\n }\n }\n }\n return;\n }\n\npublic:\n int minPushBox(vector<vector<char>>& grid) {\n this->grid=grid;\n n=grid.size();\n m=grid[0].size();\n int i,j,k;\n dfn=vector<vector<int>>(n,vector<int>(m,0));\n color=vector<vector<vector<int>>>(n,vector<vector<int>>(m,vector<int>(4,0)));\n cover=vector<vector<vector<bool>>>(n,vector<vector<bool>>(m,vector<bool>(4,0)));\n mi=vector<vector<int>>(n,vector<int>(m,INT_MAX));\n ins=vector<vector<bool>>(n,vector<bool>(m,0));\n id=0;\n sid=1;\n for(i=0;i<n;i++)\n {\n for(j=0;j<m;j++)\n {\n if(grid[i][j]!=\'#\' && dfn[i][j]==0)\n {\n dfs(i,j,-1);\n }\n }\n }\n\n int sx,sy,ex,ey,bx,by;\n for(i=0;i<n;i++)\n {\n for(j=0;j<m;j++)\n {\n if(grid[i][j]==\'S\')\n {\n sx=i;sy=j;\n }\n\n if(grid[i][j]==\'T\')\n {\n ex=i;ey=j;\n }\n\n if(grid[i][j]==\'B\')\n {\n bx=i;by=j;\n }\n }\n }\n\n ins=vector<vector<bool>>(n,vector<bool>(m,0));\n queue<node>q;\n queue<node2>q2;\n q.push(node(sx,sy));\n ins[sx][sy]=1;\n int dp[n][m][4];\n memset(dp,-1,sizeof(dp));\n\n while(!q.empty())\n {\n node now=q.front();\n q.pop();\n for(i=0;i<4;i++)\n {\n int nx,ny;\n nx=now.x+dir[i][0];\n ny=now.y+dir[i][1];\n if(nx>=0 && nx<n && ny>=0 && ny<m)\n {\n if(nx==bx && ny==by)\n {\n dp[bx][by][i^1]=0;\n q2.push(node2(bx,by,i^1));\n }\n else if(grid[nx][ny]!=\'#\' && ins[nx][ny]==0)\n {\n ins[nx][ny]=1;\n q.push(node(nx,ny));\n }\n }\n }\n }\n\n while(!q2.empty())\n {\n node2 now=q2.front();\n q2.pop();\n\n if(now.x==ex && now.y==ey)\n {\n return dp[now.x][now.y][now.dir];\n }\n \n int nx,ny;\n \n\n for(i=0;i<4;i++)\n {\n if(i==now.dir)\n {\n continue;\n }\n\n nx=now.x+dir[i][0];\n ny=now.y+dir[i][1];\n if(nx>=0 && nx<n && ny>=0 && ny<m && grid[nx][ny]!=\'#\' && dp[now.x][now.y][i]==-1 && color[now.x][now.y][now.dir]==color[now.x][now.y][i])\n {\n dp[now.x][now.y][i]=dp[now.x][now.y][now.dir];\n q2.push(node2(now.x,now.y,i));\n }\n }\n\n int d=(now.dir^1);\n nx=now.x+dir[d][0];\n ny=now.y+dir[d][1];\n if(nx>=0 && nx<n && ny>=0 && ny<m && grid[nx][ny]!=\'#\' && dp[nx][ny][now.dir]==-1)\n {\n dp[nx][ny][now.dir]=dp[now.x][now.y][now.dir]+1;\n q2.push(node2(nx,ny,now.dir));\n }\n }\n\n return -1;\n }\n};\n``` | 1 | 0 | ['Biconnected Component', 'C++'] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | standard BFS Approach solution ,clean Code ,BFS*BFS | standard-bfs-approach-solution-clean-cod-sfeg | Intuition\nwe use BFS to find minimum distance \n\n# Approach\nBFS * BFS\n# Complexity\n- Time complexity:\nO(n^2 * m^2) \n\n- Space complexity:\n O(n^2 * m^2) | latecoder001 | NORMAL | 2023-04-04T15:31:37.218812+00:00 | 2023-04-04T15:31:37.218850+00:00 | 99 | false | # Intuition\nwe use BFS to find minimum distance \n\n# Approach\nBFS * BFS\n# Complexity\n- Time complexity:\n$$O(n^2 * m^2)$$ \n\n- Space complexity:\n $$O(n^2 * m^2)$$ \n\n# Code\n```\nclass Solution {\npublic:\nint dx[4]={0,0,1,-1};\nint dy[4]={1,-1,0,0};\nint m,n;\n\nbool check(int x,int y,vector<vector<char>>& grid ){\nreturn (x>=0 && x<m ) && (y>=0 && y<n) && (grid[x][y]!=\'#\');\n}\n\n\nbool possible(int px,int py,int npx,int npy,int bx,int by,vector<vector<char>>& grid){\n queue<vector<int>>q;\n vector<vector<bool>>vis(m,vector<bool>(n,false));\n vis[px][py]=true;\n q.push({px,py});\n while(!q.empty()){\n auto it=q.front();\n q.pop();\n if(it[0]==npx && it[1]==npy){\n return true;\n }\n for(int i=0;i<4;i++){\n int x=it[0]+dx[i],y=it[1]+dy[i];\n if(check(x,y,grid) && !(x==bx && y==by) && vis[x][y]==false){\n vis[x][y]=true;\n q.push({x,y});\n }\n }\n \n }\n return false;\n\n}\n int minPushBox(vector<vector<char>>& grid) {\n m=grid.size(),n=grid[0].size();\n int bx,by,tx,ty,px,py;\n for(int i=0;i<m;i++){\n for(int j=0;j<n;j++){\n if(grid[i][j]==\'T\'){\n tx=i;\n ty=j;\n }\n if(grid[i][j]==\'B\'){\n bx=i ;\n by=j;\n } \n if(grid[i][j]==\'S\'){\n px=i;\n py=j;\n }\n }\n }\n\n \n int seen[20][20][20][20]={0};\n queue<vector<int>>q;\n q.push({bx,by,px,py});\n seen[bx][by][px][py];\n int ans=0;\n while(!q.empty()){\n int sz=q.size();\n while(sz--){\n auto vec=q.front();\n q.pop();\n bx=vec[0],by=vec[1],px=vec[2],py=vec[3];\n if(bx==tx && by==ty)\n return ans;\n for(int i=0;i<4;i++){\n int nbx=bx+dx[i],nby=by+dy[i],npx=bx-dx[i],npy=by-dy[i];\n if(check(nbx,nby,grid) && possible(px,py,npx,npy,bx,by,grid) && seen[nbx][nby][bx][by]==0){\n seen[nbx][nby][bx][by]=1;\n q.push({nbx,nby,bx,by});\n } \n }\n }\n ans++;\n\n }\n return -1; \n } \n \n};\n``` | 1 | 0 | ['C++'] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | [C#] BFS + Top-down DP (explained) | c-bfs-top-down-dp-explained-by-sh0wmet3h-enz1 | Intuition\nPorted from C++: [1] https://leetcode.com/problems/minimum-moves-to-move-a-box-to-their-target-location/solutions/431144/cpp-bfs-dfs-solution/\n# BFS | sh0wMet3hC0de | NORMAL | 2022-12-03T02:47:39.692643+00:00 | 2022-12-03T02:48:10.671137+00:00 | 65 | false | # Intuition\nPorted from C++: [1] https://leetcode.com/problems/minimum-moves-to-move-a-box-to-their-target-location/solutions/431144/cpp-bfs-dfs-solution/\n# BFS\nFirst we sweep the given grid for finding and storing the locations of the person, the box and the target.\nNext we initialize a queue and a hashSet with the locations of the person and of the box.\n```\nQueue<PII> q = new();\nHashSet<PII> visited = new();\nq.Enqueue(new PII(new PI(px, py), new PI(bx, by)));\nvisited.Add(new PII(new PI(px, py), new PI(bx, by)))\n```\nNext, we use that queue to do BFS traversal of the 2d grid. \nEach queue element will have new box and person locations. Once an element is dequeued, the box location is updated on the grid to be maked as #.\n```\nvar f = q.Dequeue();\n(px, py) = f.Item1;\n(bx, by) = f.Item2;\ngrid[bx][by] = \'#\';\n```\nBFS will find the shortest distance simply because of its radial-search pattern which considers nodes in order of their distance from the starting point [2]. It can be shown that, for unweighted graphs, the BFS is equivalent to Dijkstra\'s algorithm and thus finds the shortest path in this circumstance. Thus the first path found will be the shortest path.\n```\nif(nbx == gx && nby == gy) {\n return ans;\n}\n```\nValid() is used for validating a person location or a box location.\n\nOne smart feature of this implementation is the use of a HashSet for keeping track of visited cells. The HashSet keeps track of "states", not of visits. The HashSet has the location of a box and of person by the time the an element got into the queue, not simply if the grid cell was visited. That allows us to re-visit a certain cell if the "state" is different. \n```\nif(Valid(grid, nbx, nby)) {\n PII newState = new PII(new PI(bx, by), new PI(nbx, nby));\n if(!visited.Contains(newState)) {\n visited.Add(newState);\n q.Enqueue(newState);\n }\n}\n```\n# Top-Down DP\nCanReach() is the DFS part of this solution. It will find if a person can get to the "back" of the box. pplLoc is our memoization array (turning this into top-down dp).\n```\n bool CanReach(char[][] g, bool[,] pplLoc, int x, int y, int bx, int by) {\n if(!Valid(g, x, y) || pplLoc[x,y]) {\n return false;\n }\n if(bx == x && by == y) {\n return true;\n }\n pplLoc[x,y] = true;\n foreach(var d in Dirs) {\n if(CanReach(g, pplLoc, x + d[0], y + d[1], bx, by)) {\n return true;\n }\n }\n return false;\n }\n```\n# Code\n```\npublic class Solution {\n public record class PI(int Item1, int Item2);\n public record class PII(PI Item1, PI Item2);\n public static int[][] Dirs = new int[][]{new int[]{0,1},\n new int[]{1,0}, new int[]{-1,0}, new int[]{0,-1}};\n public static int m,n;\n public int MinPushBox(char[][] grid) {\n m = grid.Length;\n n = grid[0].Length;\n int px=0, py=0, bx=0, by=0, gx=0, gy=0;\n for(int x = 0; x < m; ++x) \n {\n for(int y = 0; y < n; ++y) \n {\n if(grid[x][y] == \'S\') {\n px = x; \n py = y;\n }else if(grid[x][y] == \'B\') {\n bx = x; \n by = y;\n }else if(grid[x][y] == \'T\') {\n gx = x; \n gy = y;\n }\n }\n }\n Queue<PII> q = new();\n HashSet<PII> visited = new();\n q.Enqueue(new PII(new PI(px, py), new PI(bx, by)));\n visited.Add(new PII(new PI(px, py), new PI(bx, by)));\n int ans = 0;\n while(q.Count > 0) {\n ans++;\n for(int l = q.Count; l > 0; --l) {\n var f = q.Dequeue();\n (px, py) = f.Item1;\n (bx, by) = f.Item2;\n grid[bx][by] = \'#\';\n foreach(var d in Dirs) {\n var pplLoc = new bool[m,n];\n if(CanReach(grid, pplLoc, px, py, bx - d[0], by - d[1])) {\n int nbx = bx + d[0], nby = by + d[1];\n if(nbx == gx && nby == gy) {\n return ans;\n }\n if(Valid(grid, nbx, nby)) {\n PII newState = new PII(new PI(bx, by), new PI(nbx, nby));\n if(!visited.Contains(newState)) {\n visited.Add(newState);\n q.Enqueue(newState);\n }\n }\n }\n }\n grid[bx][by] = \'.\';\n }\n }\n return -1;\n }\n bool CanReach(char[][] g, bool[,] pplLoc, int x, int y, int bx, int by) {\n if(!Valid(g, x, y) || pplLoc[x,y]) {\n return false;\n }\n if(bx == x && by == y) {\n return true;\n }\n pplLoc[x,y] = true;\n foreach(var d in Dirs) {\n if(CanReach(g, pplLoc, x + d[0], y + d[1], bx, by)) {\n return true;\n }\n }\n return false;\n }\n bool Valid(char[][] g, int x, int y) {\n if(x < 0 || x >= m || y < 0 || y >= n || g[x][y] == \'#\') {\n return false;\n }\n return true;\n }\n}\n```\n# References\n[1] https://leetcode.com/problems/minimum-moves-to-move-a-box-to-their-target-location/solutions/431144/cpp-bfs-dfs-solution/\n[2] https://stackoverflow.com/questions/8379785/how-does-a-breadth-first-search-work-when-looking-for-shortest-path | 1 | 0 | ['Depth-First Search', 'Breadth-First Search', 'C#'] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | All edge cases: | all-edge-cases-by-anujjadhav-2knc | There are many great solutions available for this post, here I will only focus on the edge cases where your code may go wrong.\n\nI will highly suggest to give | AnujJadhav | NORMAL | 2022-09-06T21:11:55.788893+00:00 | 2022-09-06T21:12:41.161684+00:00 | 163 | false | There are many great solutions available for this post, here I will only focus on the edge cases where your code may go wrong.\n\nI will highly suggest to give it a try first otherwise this will ruin your experience \u2639\uFE0F.\n\nImp edge cases:\n\n1. Check whether there exists a path from person till the pos from which we are pushing the box.\nTC:\n```\n [["#","#","#","#","#","#","#"],\n ["#","S","#",".","B","T","#"],\n ["#","#","#","#","#","#","#"]]\n\tans = -1\n```\nHere out person S in blocked by obstacles so he can\'t reach the box only hence ans will be -1\n\n2. We can\'t pass through the box so mark the box as wall before starting a path search to the pos from where you are going to push the box then unmark it after the path search.\nTC:\n```\n [["#",".",".","#","#","#","#","#"],\n ["#",".",".","T","#",".",".","#"],\n ["#",".",".",".","#","B",".","#"],\n ["#",".",".","_",".",".",".","#"], <-\n ["#",".",".",".","#",".","S","#"],\n ["#",".",".","#","#","#","#","#"]]\n\t ^\n\tans = 7\n```\ne.g.: pushing box (pos = [row][col]) up so we need to reach below the box (pos = [row+1][col]) \n```\n\t\tchar prev = grid[box_i][box_j];\n\t\tgrid[box_i][box_j] = \'#\';\n\t\tbool path = checkPath(person_i, person_j, box_i+1, box_j, grid);\n\t\tgrid[box_i][box_j] = prev;\n```\n\nWhile pushing when the box reached the pos represented by "_" then we can\'t directly go to left part without pushing the box again to left.\n\n3. We may have to do extra push (like above) so visited vector with only i, j is not sufficient so we also maintain dir from which it is pushed.\nWhat this means is you might push a box to left and then push it back to right to reach target, we need to do this if there is a case when we want to go right but its not possible without pushing the box further and then back to its original start.\nTC:\n```\n [["#",".",".","#","T","#","#","#","#"],\n ["#",".",".","#",".","#",".",".","#"],\n ["#",".",".","#",".","#","B",".","#"],\n ["#",".",".",".",".",".",".",".","#"],\n ["#",".",".",".",".","#",".","S","#"],\n ["#",".",".","#",".","#","#","#","#"]]\n\t ans = 8\n```\nIf you use a visited array of i, j then you won\'t be able to push it back to the same place it was before. So we also maintain one more parameter dir. vis with i, j, and dir where dir represents from which dir it was pushed.\n```\nbool vis[rows][cols][dir]; \nor\nbool vis[n][m][4] // 4 directions\n```\n\nMy code:\n```\n\nclass Solution {\npublic:\n bool isValid(int box_i, int box_j, int person_i, int person_j, vector<vector<char>>& grid) {\n int n = grid.size();\n int m = grid[0].size();\n\n if (box_i >= 0 && person_i >= 0 && box_j >= 0 && person_j >= 0 && box_i < n && person_i < n && box_j < m && person_j < m && grid[box_i][box_j] != \'#\' && grid[person_i][person_j] != \'#\') {\n return true;\n }\n return false;\n }\n\n class Node {\n public:\n int box_i;\n int box_j;\n int person_i;\n int person_j;\n\n Node() {\n\n }\n\n Node(int boxi, int boxj, int personi, int personj) {\n box_i = boxi;\n box_j = boxj;\n person_i = personi;\n person_j = personj;\n }\n };\n\n bool checkPath(int start_i, int start_j, int target_i, int target_j, vector<vector<char>>& grid) {\n int n = grid.size();\n int m = grid[0].size();\n vector<vector<int>> vis(n, vector<int>(m, false));\n vector<pair<int, int>> dir = { {-1,0},{1,0},{0,-1},{0,1} };\n\n queue<pair<int, int>> q;\n q.push({ start_i, start_j });\n vis[start_i][start_j] = true;\n\n while (q.empty() == false) {\n auto t = q.front();\n q.pop();\n start_i = t.first;\n start_j = t.second;\n\n if (start_i == target_i && start_j == target_j) {\n return true;\n }\n\n for (auto it : dir) {\n int ni = start_i + it.first;\n int nj = start_j + it.second;\n\n if (ni >= 0 && ni < n && nj >= 0 && nj < m && grid[ni][nj] != \'#\' && vis[ni][nj] == false) {\n q.push({ ni, nj });\n vis[ni][nj] = true;\n }\n }\n }\n\n return false;\n }\n\n int getPush(int box_i, int box_j, int person_i, int person_j, vector<vector<char>>& grid) {\n int n = grid.size();\n int m = grid[0].size();\n\n vector<vector<vector<int>>> vis(n, vector<vector<int>>(m, vector<int>(5, false)));\n\n int count = 0;\n Node curr(box_i, box_j, person_i, person_j);\n queue<Node> q;\n q.push(curr);\n vis[box_i][box_j][0] = true;\n\n bool reached = false;\n while (q.empty() == false) {\n int sz = q.size();\n\n for (int r = 0; r < sz; r++) {\n curr = q.front();\n q.pop();\n\n box_i = curr.box_i;\n box_j = curr.box_j;\n person_i = curr.person_i;\n person_j = curr.person_j;\n\n if (grid[box_i][box_j] == \'T\') {\n reached = true;\n break;\n }\n\n // boxi, boxj, personi, personj\n\n // push box up\n if (isValid(box_i - 1, box_j, box_i + 1, box_j, grid) && vis[box_i - 1][box_j][1] == false) {\n char prev = grid[box_i][box_j];\n grid[box_i][box_j] = \'#\';\n bool path = checkPath(person_i, person_j, box_i + 1, box_j, grid);\n grid[box_i][box_j] = prev;\n if (path) {\n q.push(Node(box_i - 1, box_j, box_i, box_j));\n vis[box_i - 1][box_j][1] = true;\n }\n }\n // push box left\n if (isValid(box_i, box_j - 1, box_i, box_j + 1, grid) && vis[box_i][box_j - 1][2] == false) {\n char prev = grid[box_i][box_j];\n grid[box_i][box_j] = \'#\';\n bool path = checkPath(person_i, person_j, box_i, box_j + 1, grid);\n grid[box_i][box_j] = prev;\n if (path) {\n q.push(Node(box_i, box_j - 1, box_i, box_j));\n vis[box_i][box_j - 1][2] = true;\n }\n }\n // push box right\n if (isValid(box_i, box_j + 1, box_i, box_j - 1, grid) && vis[box_i][box_j + 1][3] == false) {\n char prev = grid[box_i][box_j];\n grid[box_i][box_j] = \'#\';\n bool path = checkPath(person_i, person_j, box_i, box_j - 1, grid);\n grid[box_i][box_j] = prev;\n if (path) {\n q.push(Node(box_i, box_j + 1, box_i, box_j));\n vis[box_i][box_j + 1][3] = true;\n }\n }\n // push box down\n if (isValid(box_i + 1, box_j, box_i - 1, box_j, grid) && vis[box_i + 1][box_j][4] == false) {\n char prev = grid[box_i][box_j];\n grid[box_i][box_j] = \'#\';\n bool path = checkPath(person_i, person_j, box_i - 1, box_j, grid);\n grid[box_i][box_j] = prev;\n if (path) {\n q.push(Node(box_i + 1, box_j, box_i, box_j));\n vis[box_i + 1][box_j][4] = true;\n }\n }\n }\n if (reached) {\n break;\n }\n count++;\n }\n if (reached == false) return -1;\n return count;\n }\n\n int minPushBox(vector<vector<char>>& grid) {\n int n = grid.size();\n int m = grid[0].size();\n\n int person_i, person_j;\n int box_i, box_j;\n for (int i = 0; i < n; i++) for (int j = 0; j < m; j++) {\n if (grid[i][j] == \'S\') {\n person_i = i;\n person_j = j;\n }\n if (grid[i][j] == \'B\') {\n box_i = i;\n box_j = j;\n }\n }\n\n return getPush(box_i, box_j, person_i, person_j, grid);\n }\n};\n\n``` | 1 | 0 | [] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | [Python 3] 0-1 BFS clean code | python-3-0-1-bfs-clean-code-by-gabhay-aa2q | \tclass Solution:\n\t\tdef minPushBox(self, grid: List[List[str]]) -> int:\n\t\t\tn,m=len(grid),len(grid[0])\n\t\t\tfor i in range(n):\n\t\t\t\tfor j in range(m | gabhay | NORMAL | 2022-08-08T12:53:53.939096+00:00 | 2022-08-08T12:56:32.211336+00:00 | 332 | false | \tclass Solution:\n\t\tdef minPushBox(self, grid: List[List[str]]) -> int:\n\t\t\tn,m=len(grid),len(grid[0])\n\t\t\tfor i in range(n):\n\t\t\t\tfor j in range(m):\n\t\t\t\t\tif grid[i][j]==\'S\':\n\t\t\t\t\t\tplayer=[i,j]\n\t\t\t\t\telif grid[i][j]==\'T\':\n\t\t\t\t\t\ttarget=[i,j]\n\t\t\t\t\telif grid[i][j]==\'B\':\n\t\t\t\t\t\tbox=[i,j]\n\t\t\tq=deque([[player[0],player[1],box[0],box[1],0]])\n\t\t\tvis=set([(player[0],player[1],box[0],box[1])])\n\t\t\twhile q:\n\t\t\t\ti,j,bi,bj,steps=q.pop()\n\t\t\t\tif [bi,bj]==target:\n\t\t\t\t\treturn steps\n\t\t\t\tfor dx,dy in [(0,1),(1,0),(-1,0),(0,-1)]:\n\t\t\t\t\tx,y=i+dx,j+dy\n\t\t\t\t\tif 0<=x<n and 0<=y<m and grid[x][y]!=\'#\':\n\t\t\t\t\t\tif (x,y)==(bi,bj):\n\t\t\t\t\t\t\tif 0<=bi+dx<n and 0<=bj+dy<m and grid[bi+dx][bj+dy]!=\'#\':\n\t\t\t\t\t\t\t\tif not (x,y,bi+dx,bj+dy) in vis:\n\t\t\t\t\t\t\t\t\tvis.add((x,y,bi+dx,bj+dy))\n\t\t\t\t\t\t\t\t\tq.appendleft([x,y,bi+dx,bj+dy,steps+1])\n\t\t\t\t\t\telif (x,y,bi,bj) not in vis:\n\t\t\t\t\t\t\tvis.add((x,y,bi,bj))\n\t\t\t\t\t\t\tq.append([x,y,bi,bj,steps])\n\t\t\treturn -1 | 1 | 0 | ['Breadth-First Search', 'Python3'] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | Python Double BFS | python-double-bfs-by-akli64-pmqi | \nfrom collections import deque\n\nclass Solution:\n def minPushBox(self, grid: List[List[str]]) -> int:\n \n in_bounds = lambda grid, i, j : 0 | akli64 | NORMAL | 2022-04-20T06:49:38.981260+00:00 | 2022-04-20T06:49:38.981298+00:00 | 121 | false | ```\nfrom collections import deque\n\nclass Solution:\n def minPushBox(self, grid: List[List[str]]) -> int:\n \n in_bounds = lambda grid, i, j : 0 <= i < len(grid) and 0 <= j < len(grid[0])\n \n dirs = [\n (1, 0),\n (-1, 0),\n (0, 1),\n (0, -1)\n ]\n\n def mover_bfs(grid, mover, behind_box, box):\n \n queue = deque([mover])\n visited = set()\n \n while queue:\n move_pos = queue.popleft()\n \n if move_pos in visited:\n continue\n \n visited.add(move_pos)\n \n if move_pos == behind_box:\n return True\n x, y = move_pos\n for d in dirs:\n r, c = x + d[0], y + d[1]\n \n if not in_bounds(grid, r, c) or (r, c) == box or grid[r][c] == \'#\':\n continue\n \n queue.append((r, c))\n return False\n\n def box_bfs(grid, box, start, dest):\n queue = deque([ (box, start, 0) ])\n visited = set()\n while queue:\n box_pos, mover_pos, moves = queue.popleft()\n if box_pos == dest:\n return moves\n \n if (box_pos, mover_pos) in visited:\n continue\n \n visited.add((box_pos, mover_pos))\n\n x, y = box_pos\n x1, y1 = mover_pos\n\n for d in dirs:\n r, c = x + d[0], y + d[1]\n \n if not in_bounds(grid, r, c) or grid[r][c] == \'#\' or (r, c) in visited:\n continue\n \n next_mover_pos = x + (-1) * d[0], y + (-1) * d[1]\n if not mover_bfs(grid, mover_pos, next_mover_pos, box_pos):\n continue\n queue.append(((r, c), next_mover_pos, moves + 1))\n return -1\n\n start = None\n box = None\n target = None\n \n rows = len(grid)\n cols = len(grid[0])\n \n for r in range(rows):\n for c in range(cols):\n if grid[r][c] == \'S\':\n start = (r, c)\n elif grid[r][c] == \'T\':\n target = (r, c)\n elif grid[r][c] == \'B\':\n box = (r, c)\n \n return box_bfs(grid, box, start, target)\n``` | 1 | 0 | [] | 1 |
minimum-moves-to-move-a-box-to-their-target-location | C++ | Easy implementation | BFS*BFS | Clean code | c-easy-implementation-bfsbfs-clean-code-rxfkz | \nclass Solution {\npublic:\n int arr[4]= {0,0,1,-1};\n int brr[4]={1,-1,0,0};\n bool chk (vector<vector<char>>& grid, int reachx,int reachy,int bx,in | coz_its_raunak | NORMAL | 2022-02-01T17:38:39.603587+00:00 | 2022-02-01T17:38:39.603632+00:00 | 236 | false | ```\nclass Solution {\npublic:\n int arr[4]= {0,0,1,-1};\n int brr[4]={1,-1,0,0};\n bool chk (vector<vector<char>>& grid, int reachx,int reachy,int bx,int by,int sx,int sy)\n {\n \n int r = grid.size();\n int c = grid[0].size();\n vector<vector<int>>vis(r,vector<int>(c,-1));\n queue<pair<int,int>>qq;\n qq.push({sx,sy});\n vis[sx][sy] =1;\n \n while(qq.size()>0)\n {\n auto it = qq.front();\n qq.pop();\n int x = it.first;\n int y= it.second;\n if(x==reachx && y==reachy)\n { \n return true;\n }\n for(int i=0;i<4;i++)\n {\n int xx = x + arr[i];\n int yy = y+brr[i];\n if(xx>=0 && xx<r && yy>=0 && yy<c && vis[xx][yy]==-1 && grid[xx][yy]!=\'#\'&& !(xx==bx&& yy==by))\n {\n vis[xx][yy] = 1;\n qq.push({xx,yy});\n }\n }\n }\n return false;\n }\n int minPushBox(vector<vector<char>>& grid) \n {\n int r = grid.size();\n int c = grid[0].size();\n int box_x ;\n int box_y;\n int t_x;\n int t_y;\n int s_x;\n int s_y;\n for(int i=0;i<r;i++)\n {\n for(int j=0;j<c;j++)\n {\n if(grid[i][j]==\'S\')\n {\n s_x = i;\n s_y = j;\n }\n else if(grid[i][j]==\'B\')\n {\n box_x = i;\n box_y=j;\n }\n else if(grid[i][j]==\'T\')\n {\n t_x = i;\n t_y = j;\n }\n }\n }\n grid[t_x][t_y]=\'.\';\n grid[s_x][s_y]=\'.\';\n \n queue<vector<int>>q;\n q.push({box_x,box_y,s_x,s_y});\n set<vector<int>>stt;\n int ans = 0;\n \n while(q.size()>0)\n {\n int si = q.size();\n while(si--)\n {\n auto it = q.front();\n q.pop();\n int x = it[0];\n int y = it[1];\n int ssx = it[2];\n int ssy = it[3];\n if(x==t_x && y==t_y)\n {\n return ans;\n }\n for(int i=0;i<4;i++)\n {\n int xx_new = x + arr[i];\n int yy_new = y +brr[i];\n int sx = x-arr[i];\n int sy = y-brr[i];\n if(xx_new>=0 && xx_new<r && sx>=0 && sx<r && yy_new>=0 && yy_new<c && sy>=0 && sy<c && grid[xx_new][yy_new]!=\'#\' && !stt.count({xx_new,yy_new,sx,sy}) )\n { \n bool chkk = chk(grid,sx,sy,x,y,ssx,ssy);\n if(chkk)\n {\n stt.insert({xx_new,yy_new,sx,sy}); \n q.push({xx_new,yy_new,sx,sy});\n }\n }\n }\n \n }\n ans++;\n \n }\n \n return -1;\n }\n};\n``` | 1 | 0 | [] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | [Python] Solution with detailed thinking | python-solution-with-detailed-thinking-b-b1e1 | Background\nIn this problem, we are given a grid, there\'re 4 types of element:\n player - \'S\'\n box - \'B\'\n obstacle - \'#\'\n floor - \'.\'\n\nplayer need | bestbowenzhao | NORMAL | 2022-01-08T20:15:57.765618+00:00 | 2022-01-08T20:15:57.765652+00:00 | 531 | false | ### Background\nIn this problem, we are given a grid, there\'re 4 types of element:\n* player - \'S\'\n* box - \'B\'\n* obstacle - \'#\'\n* floor - \'.\'\n\nplayer need to push the box to the final target position, our target is to find the mininum push.\n\nThis is a variant of finding the shortest path from start to the end in a 2-D grid. In general, this is a unweighted graph search problem. \n* We start from the begining\n* at each position, we search at 4 direction\n* before goes to each position, we need to check if the next position\n\t* out of boundary\n\t* is an obstacle or not\n\t* if visited or not\n* we should stop when reaching to the target position\n\n#### BFS \n\n```\ndirs = {(1,0), (0,1), (-1,0), (0,-1)}\nqueue = collections.deque([(start, 0)])\nvisited = {start}\n\nwhile queue:\n\t(i, j), step = queue.popleft()\n\tif (i,j) == target:\n\t\treturn step\n\tfor dx, dy in dirs:\n\t\tx, y = i+dx, j+dy\n\t\tif isValid(x,y,visited) is False:\n\t\t\tcontinue\n\t\tvisited.add((x,y))\n\t\tqueue.append((x,y,step+1))\nreturn -1\n```\n\n#### DFS\n* i, j the current position\n* visited: from the start to the end, which position are visited\n\n```\ndef dfs(i, j, visited):\n\tif (i,j) == target:\n\t\treturn 0\n\tif isValid(i,j,visited) is False:\n\t\treturn float(\'inf\')\n\tstep = float(\'inf\')\n\tfor dx, dy in dirs:\n\t\tx, y = i+dx, j+dy\n\t\tvisited.add((x,y))\n\t\tstep = min(step, dfs(x,y,visited))\n\t\tvisisted.remove((x,y))\n\treturn step\n```\n\n#### helper function\n```\ndef isValid(i,j,visisted)\n\tif i < 0 or j < 0 or i >= len(grid) or j >= len(grid[0]):\n\t\treturn False\n\tif (i,j) in visited:\n\t\treturn False\n\tif grid[i][j] == \'#\':\n\t\treturn False\n\treturn True\n```\n\n### Analysis\nThe difference of this problem is that\n* there\'s a player, if the player wants to move the box, he/she needs\n\t* be able to be on another side of the box\n\nSo for the box, at each position, it can move to 4 directions, but for each directions, the player should be able to reach to another position, so our target is to find if the player can be able to reach to that position. How to do so? This is also a traditional graph search problem. But the only problem is player could not cross the box.That\'s say, box is also an obstacle.\n\nSo the basic structure of the solution is two BFS/DFS. \nThe status of the search be be described by \n* player position\n* box position\n\n```\nclass Solution:\n def minPushBox(self, grid: List[List[str]]) -> int:\n \'\'\'\n find start pos of box, start pos of player, and the pos of target \n for box start from the begining, do the graph search\n if reach to the target, return step\n else: for each 4 dires, also find the player\'s next pos\n check if next box and next player pos is valid or not\n also check if next box and next player pos has been recorded before\n then push the info for the next move\n\n \'\'\'\n m, n = len(grid), len(grid[0])\n dirs = {(0,1), (1,0), (0,-1), (-1,0)}\n \n def get_initials():\n box, player, target = None, None, None\n for i in range(m):\n for j in range(n):\n if grid[i][j] == \'S\':\n player = (i,j)\n if grid[i][j] == \'B\':\n box = (i,j)\n if grid[i][j] == \'T\':\n target = (i,j)\n \n return box, player, target\n \n def isReacheable(box_i, box_j, player_i, player_j, nxt_player_i, nxt_player_j):\n tmp = grid[box_i][box_j]\n grid[box_i][box_j] = \'#\'\n res = _isReacheable(player_i, player_j, nxt_player_i, nxt_player_j)\n grid[box_i][box_j] = tmp\n return res\n \n def _isReacheable(start_i, start_j, end_i, end_j):\n queue = collections.deque([(start_i, start_j)])\n visited = {(start_i, start_j)}\n while queue:\n i, j = queue.popleft()\n if (i,j) == (end_i, end_j):\n return True\n for dx, dy in dirs:\n x, y = i+dx, j+dy\n if _isValidPos(x, y, visited):\n queue.append((x,y))\n visited.add((x,y))\n return False\n \n def _isValidPos(x,y,visited):\n return 0<=x<m and 0<=y<n and (x,y) not in visited and grid[x][y] != \'#\'\n \n def isValidPos(box_i, box_j, player_i, player_j, visited):\n def isInBoundary(i,j):\n return 0<=i<m and 0<=j<n\n \n return isInBoundary(box_i, box_j) and isInBoundary(player_i, player_j)\\\n and (box_i, box_j, player_i, player_j) not in visited\\\n and grid[box_i][box_j] != \'#\' and grid[player_i][player_j] != \'#\'\n \n \n (box_i, box_j), (player_i, player_j), target = get_initials()\n grid[box_i][box_j] = \'.\'\n grid[player_i][player_j] = \'.\'\n \n queue = collections.deque([(box_i, box_j, player_i, player_j, 0)])\n visited = {(box_i, box_j, player_i, player_j)}\n while queue:\n b_i, b_j, p_i, p_j, step = queue.popleft()\n if (b_i, b_j) == target:\n return step\n for dx, dy in dirs:\n nxt_b_i, nxt_b_j, nxt_p_i, nxt_p_j = b_i+dx, b_j+dy, b_i-dx, b_j-dy\n if isValidPos(nxt_b_i, nxt_b_j, nxt_p_i, nxt_p_j, visited) is False:\n continue\n if isReacheable(b_i, b_j, p_i, p_j, nxt_p_i, nxt_p_j) is False:\n continue\n queue.append((nxt_b_i, nxt_b_j, nxt_p_i, nxt_p_j, step+1))\n visited.add((nxt_b_i, nxt_b_j, nxt_p_i, nxt_p_j))\n return -1\n``` | 1 | 0 | ['Depth-First Search', 'Breadth-First Search', 'Python'] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | Java - BFS easy to understand solution | java-bfs-easy-to-understand-solution-by-u6zc7 | \nclass Solution {\n public int minPushBox(char[][] grid) {\n if (grid == null || grid.length == 0 || grid[0].length == 0) {\n return -1;\n | code_newbie | NORMAL | 2021-11-13T10:34:52.788894+00:00 | 2021-11-13T10:34:52.788934+00:00 | 423 | false | ```\nclass Solution {\n public int minPushBox(char[][] grid) {\n if (grid == null || grid.length == 0 || grid[0].length == 0) {\n return -1;\n }\n int[] box = new int[2];\n int[] player = new int[2];\n int[] target = new int[2];\n Map<String, Integer> steps = new HashMap<>();\n for (int i = 0; i < grid.length; i++) {\n for (int j = 0; j < grid[0].length; j++) {\n if (grid[i][j] == \'B\') {\n box = new int[] {i, j};\n } else if (grid[i][j] == \'S\') {\n player = new int[] {i, j};\n } else if (grid[i][j] == \'T\') {\n target = new int[] {i, j};\n }\n }\n }\n int[] dx = new int[] {0, 0, 1, -1};\n int[] dy = new int[] {1, -1, 0, 0};\n // so in BFS, instead of save a single point, save both box and player together\n String start = encode(box[0], box[1], player[0], player[1]);\n int res = Integer.MAX_VALUE;\n Queue<String> queue = new LinkedList<>();\n queue.offer(start);\n steps.put(start, 0);\n while (!queue.isEmpty()) {\n String curr = queue.poll();\n if (steps.getOrDefault(curr, 0) > res) {\n continue;\n }\n int[] currBox = new int[] {Integer.parseInt(curr.split(":")[0]), Integer.parseInt(curr.split(":")[1])};\n int[] currPlayer = new int[] {Integer.parseInt(curr.split(":")[2]), Integer.parseInt(curr.split(":")[3])};\n if (currBox[0] == target[0] && currBox[1] == target[1]) {\n res = Math.min(res, steps.get(curr));\n continue;\n }\n for (int i = 0; i < 4; i++) {\n // every step, move player, if player meet the box, push the box.\n int[] newP = new int[] {currPlayer[0] + dx[i], currPlayer[1] + dy[i]};\n if (newP[0] < 0 || newP[1] < 0 || newP[0] >= grid.length \n || newP[1] >= grid[0].length || grid[newP[0]][newP[1]] == \'#\') {\n continue;\n }\n if (newP[0] == currBox[0] && newP[1] == currBox[1]) {\n int[] newB = new int[] {currBox[0] + dx[i], currBox[1] + dy[i]};\n if (newB[0] < 0 || newB[1] < 0 || newB[0] >= grid.length \n || newB[1] >= grid[0].length || grid[newB[0]][newB[1]] == \'#\') {\n continue;\n }\n String temp = encode(newB[0], newB[1], newP[0], newP[1]);\n if (steps.containsKey(temp) && steps.get(temp) <= steps.get(curr) + 1) {\n continue;\n }\n steps.put(temp, steps.get(curr) + 1);\n queue.offer(temp);\n } else {\n // if not meet box, just save it to the queue.\n String temp = encode(currBox[0], currBox[1], newP[0], newP[1]);\n if (steps.containsKey(temp) && steps.get(temp) <= steps.get(curr) + 1) {\n continue;\n }\n steps.put(temp, steps.get(curr));\n queue.offer(temp);\n }\n } \n }\n return res == Integer.MAX_VALUE ? -1 : res;\n }\n \n private String encode(int i1, int i2, int i3, int i4) {\n return i1 + ":" + i2 + ":" + i3 + ":" + i4;\n }\n}\n``` | 1 | 0 | [] | 2 |
minimum-moves-to-move-a-box-to-their-target-location | Why the output is 5? | why-the-output-is-5-by-swetha96-zirg | grid = [["#","#","#","#","#","#"],\n ["#","T",".",".","#","#"],\n ["#",".","#","B",".","#"],\n ["#",".",".",".",".","# | swetha96 | NORMAL | 2021-11-11T04:43:02.414250+00:00 | 2021-11-11T04:43:02.414281+00:00 | 87 | false | grid = [["#","#","#","#","#","#"],\n ["#","T",".",".","#","#"],\n ["#",".","#","B",".","#"],\n ["#",".",".",".",".","#"],\n ["#",".",".",".","S","#"],\n ["#","#","#","#","#","#"]]\nOutput: 5\n\nFor the above testcase, why the output is 5, instead of 3?\nThe player can go up to (2, 3) and then push the box Up, Left and Left to reach the target.\n\nWhat am I missing here? | 1 | 0 | [] | 1 |
minimum-moves-to-move-a-box-to-their-target-location | c++ dijkstra + union find solution | c-dijkstra-union-find-solution-by-hanzho-2hqe | \nclass Solution {\npublic:\n int find(vector<int>& a, int i) {\n if(a[i] == i) {\n return i;\n }\n return a[i] = find(a, a[i | hanzhoutang | NORMAL | 2021-11-01T06:26:02.978465+00:00 | 2021-11-01T06:26:02.978516+00:00 | 216 | false | ```\nclass Solution {\npublic:\n int find(vector<int>& a, int i) {\n if(a[i] == i) {\n return i;\n }\n return a[i] = find(a, a[i]);\n }\n \n void merge(vector<int>& a, vector<int>& r, int i, int j) {\n int i_ = find(a,i);\n int j_ = find(a,j);\n if(i_ == j_) {\n return; \n }\n if(r[i_] > r[j_]) {\n a[j_] = i_;\n } else {\n a[i_] = j_; \n if(r[i_] == r[j_]) {\n r[j_]++;\n }\n }\n }\n \n bool same(vector<int>& a, int i, int j) {\n return find(a,i) == find(a,j);\n }\n \n typedef pair<int,pair<int,int>> pipii;\n const int INF = INT_MAX / 2; \n int minPushBox(vector<vector<char>>& grid) {\n const int m = grid.size();\n const int n = grid[0].size();\n vector<vector<int>> dp(m*n,vector<int>(m*n, INF));\n int p = -1; \n int b = -1; \n int target = -1; \n for(int i = 0;i<m;i++) {\n for(int j = 0;j<n;j++) {\n if(grid[i][j] == \'S\') {\n p = i * n + j; \n grid[i][j] = \'.\';\n } else if(grid[i][j] == \'B\') {\n b = i * n + j;\n grid[i][j] = \'.\';\n } else if(grid[i][j] == \'T\') {\n target = i * n + j; \n grid[i][j] = \'.\';\n }\n }\n }\n priority_queue<pipii,vector<pipii>,greater<pipii>> q; \n q.push({0,{p,b}});\n while(q.size()) {\n auto value = q.top();\n q.pop();\n int w = value.first; \n p = value.second.first; \n b = value.second.second; \n if(b == target) {\n return w; \n }\n if(dp[b][p] <= w) {\n continue; \n }\n dp[b][p] = w;\n int x = b/n; \n int y = b%n; \n grid[x][y] = \'#\';\n vector<int> a(m*n);\n vector<int> rank(m*n);\n for(int i = 0;i<a.size();i++) {\n a[i] = i; \n }\n for(int i = 0;i<m;i++) {\n for(int j = 0;j<n;j++) {\n if(grid[i][j] != \'.\') {\n continue; \n } \n int t = i * n + j; \n if(i+1<m && grid[i+1][j] == \'.\') {\n merge(a,rank,t,t+n);\n }\n if(j+1<n && grid[i][j+1] == \'.\') {\n merge(a,rank,t,t+1);\n }\n }\n }\n int p_x = p / n; \n int p_y = p % n; \n if(x+1<m && x - 1>=0 && same(a,b-n,p) && grid[x+1][y] == \'.\') {\n q.push({w+1,{b,b+n}});\n }\n if(x-1>=0 && x + 1 < m && same(a,p,b+n) && grid[x-1][y] == \'.\') {\n q.push({w+1,{b,b-n}});\n }\n if(y+1<n && y-1>=0 && same(a,p,b-1) && grid[x][y+1] == \'.\') {\n q.push({w+1,{b,b+1}});\n }\n if(y-1>=0 && y + 1 < n && same(a,p,b+1) && grid[x][y-1] == \'.\') {\n q.push({w+1,{b,b-1}});\n }\n grid[x][y] = \'.\';\n }\n return -1; \n }\n};\n``` | 1 | 0 | [] | 1 |
minimum-moves-to-move-a-box-to-their-target-location | BFS without using priority queue | O(m^2n^2) | clear explaination | Python | bfs-without-using-priority-queue-om2n2-c-kiq2 | We could reduce this problem to a shortest distance problem in graph:\n\nConstruct graph G = (V, E) as follows:\nLet vertice v denotes game state, a.k.a (player | flyneopolitan | NORMAL | 2021-10-02T20:43:45.861236+00:00 | 2021-10-02T20:46:10.798870+00:00 | 274 | false | We could reduce this problem to a shortest distance problem in graph:\n\nConstruct graph G = (V, E) as follows:\nLet vertice v denotes game state, a.k.a (player position, box position).\nLet edge e denotes change from one game state to another, so there are at most 4 edges for a vertex: player has at most 4 choices to move right, left, up, down and if there\'s box on the way while he could push it then he could push the box. If he doesn\'t push the box to make change, the according edge weight is 0; If he pushes the box to make change, the according edge weight is 1.\n\nThen we need to calculate shortest distance from start vertex to a set of target vertices in this graph. The brute force is to use dijkstra directly; But we could do better: since edge weight can only be 0 or 1, we could use BFS with a tiny change: everytime we want to insert a neighbor we insert it at the front if the edge to the neighbor is 0 and insert it at the back if the edge to the neighbor is 1. (Think about why!) Thanks for my friend, zpt, who tells me this method when we are taking CS374 together.\n\nHere\'s the actual code:\n```\n # method to get start position of player, box and target position\n def get_pos(self, grid):\n m, n = len(grid), len(grid[0])\n player, B, T = None, None, None\n for i in range(m):\n for j in range(n):\n if grid[i][j] == \'S\':\n player = (i, j)\n elif grid[i][j] == \'B\':\n B = (i, j)\n elif grid[i][j] == \'T\':\n T = (i, j)\n return player, B, T\n \n\t# return true if (i,j) is in range\n def valid(self, i, j, grid):\n m, n = len(grid), len(grid[0])\n return 0 <= i < m and 0 <= j < n\n \n\t# Given current vertex (playerPos, boxPos), get its neighbors who have not been visited yet\n def neighbors(self, playerPos, boxPos, grid, visited):\n res = []\n i, j = playerPos\n bi, bj = boxPos\n for di, dj in {(0, 1), (0, -1), (1, 0), (-1, 0)}:\n nextI, nextJ = i + di, j + dj\n if Solution.valid(self, nextI, nextJ, grid) and grid[nextI][nextJ] != \'#\':\n if (nextI, nextJ) != boxPos and ((nextI, nextJ), boxPos) not in visited:\n res.append((0, (nextI, nextJ), boxPos))\n elif (nextI, nextJ) == boxPos:\n box_nextI, box_nextJ = bi + di, bj + dj\n if Solution.valid(self, box_nextI, box_nextJ, grid) and grid[box_nextI][box_nextJ] != \'#\' and ((nextI, nextJ), (box_nextI, box_nextJ)) not in visited:\n res.append((1, (nextI, nextJ), (box_nextI, box_nextJ)))\n return res\n \n\t# the main method\n def minPushBox(self, grid: List[List[str]]) -> int:\n m, n = len(grid), len(grid[0])\n player, B, T = Solution.get_pos(self, grid)\n visited = {(player, B)}\n queue = [(0, player, B)]\n while queue:\n currDis, playerPos, boxPos = queue.pop(0)\n if boxPos == T:\n return currDis\n for w, nextPos, nextBox in Solution.neighbors(self, playerPos, boxPos, grid, visited):\n if w == 0:\n queue.insert(0, (currDis, nextPos, nextBox))\n else:\n queue.append((1 + currDis, nextPos, nextBox))\n visited.add((nextPos, nextBox))\n return -1\n```\n\n | 1 | 0 | [] | 1 |
minimum-moves-to-move-a-box-to-their-target-location | Apply BFS twice - with some helpful hints | apply-bfs-twice-with-some-helpful-hints-9ppos | Algorithm:\n1. Choose the location of the box, \n2. Then, new person location should be opposite to that of the box.\n3. Then ask the algorithm - (can_reach def | ikna | NORMAL | 2021-08-22T19:16:25.142926+00:00 | 2021-08-22T19:16:25.142972+00:00 | 302 | false | **Algorithm**:\n1. Choose the location of the box, \n2. Then, new person location should be opposite to that of the box.\n3. Then ask the algorithm - (can_reach def) Can I reach to new_person from current person location? Only if the answer is \'yes\', consider that new box location.\n\n```\nclass Solution:\n def minPushBox(self, grid: List[List[str]]) -> int:\n self.nRow, self.nCol = len(grid), len(grid[0])\n DIR = [-1,0,1,0,-1]\n \n # find out the location of box and the person and the target\n for i in range(self.nRow):\n for j in range(self.nCol):\n if grid[i][j] == \'S\':\n person = (i,j)\n if grid[i][j] == \'B\':\n box = (i,j)\n if grid[i][j] == \'T\':\n target = (i,j)\n \n def is_valid(pos):\n pos_x, pos_y = pos\n if pos_x < 0 or pos_y < 0 or pos_x >= self.nRow or pos_y >= self.nCol or grid[pos_x][pos_y] == \'#\':\n return False\n return True\n \n def can_reach(curr_loc, new_loc, box_loc):\n \'\'\'\n Can I reach to new location from the current location?\n \'\'\'\n _q = deque()\n _v = set()\n _q.append(curr_loc)\n _v.add(curr_loc)\n \n while _q:\n curr_loc = _q.popleft()\n if curr_loc == new_loc:\n return True\n curr_loc_x, curr_loc_y = curr_loc\n for d in range(4):\n ncurr_loc_x, ncurr_loc_y = curr_loc_x + DIR[d], curr_loc_y + DIR[d+1]\n ncurr_loc = (ncurr_loc_x, ncurr_loc_y)\n if is_valid(ncurr_loc) and ncurr_loc != box_loc and ncurr_loc not in _v:\n _q.append(ncurr_loc)\n _v.add(ncurr_loc)\n return False\n \n q = deque()\n visited = set()\n q.append((0, box, person)) # start location\n visited.add((box, person))\n \n while q:\n dist, box, person = q.popleft()\n box_x, box_y = box\n person_x, person_y = person\n \n if box == target:\n return dist\n \n for d in range(4):\n new_box_x, new_box_y = box_x + DIR[d] , box_y + DIR[d+1]\n # now new person location should be opposite to that of the box\n new_person_x, new_person_y = box_x - DIR[d] , box_y - DIR[d+1]\n \n new_box = (new_box_x, new_box_y)\n new_person = (new_person_x, new_person_y)\n \n if is_valid(new_box) and is_valid(new_person) and can_reach(person, new_person, box) and grid[new_box_x][new_box_y] != \'#\' and (new_box, new_person) not in visited:\n q.append((dist+1, new_box, new_person)) \n visited.add((new_box, new_person))\n \n return -1 \n \n```\n\nComplexity O(M*N*M*N) | 1 | 0 | [] | 1 |
minimum-moves-to-move-a-box-to-their-target-location | BFS with (box,player) as state | bfs-with-boxplayer-as-state-by-simd_mmx-o2ad | This problem involves regular BFS with a few important distinctions.\n1. We cannot just directly look for shortest path from box to target. An additional condit | simd_mmx | NORMAL | 2021-07-20T16:17:33.272316+00:00 | 2021-07-20T16:22:36.163895+00:00 | 249 | false | This problem involves regular BFS with a few important distinctions.\n1. We cannot just directly look for shortest path from box to target. An additional condition is that the player should be able to reach the push_spot from where the box can be pushed. This extra condition needs to be checked at each step before considering a box in our BFS traversal.\n2. The way we consider visited set changes slightly. It is not just the posiiton of the box that matters but also the player. There are some cases where a box needs to be pushed past a position and then pushed back into it to allow the player to reach the push spots. \n3. In terms of implementation, it is easier if we maintain the positions of box and player outside the grid, in two variables. This is because we evaluate several options, and maintaing the box and player within the grid can get messy\n\nSo overall, this problem can be solved by taking(box, player) as state and checking if player can reach the push_spot\n```\nfrom collections import deque\nclass Solution:\n def minPushBox(self, grid: List[List[str]]) -> int:\n box, player = None, None\n for r in range(len(grid)):\n for c in range(len(grid[0])):\n if grid[r][c] == "S":\n player = (r,c)\n grid[r][c] = "."\n elif grid[r][c] == "B":\n box = (r, c)\n grid[r][c] = "."\n \n def get_neighbours_for_box(box, grid):\n moves = [(0,-1),(0,1),(-1,0),(1,0)]\n r,c = box[0], box[1]\n neighbours = []\n for m in moves:\n n_r, n_c = r + m[0], c + m[1]\n push_spot = r - m[0], c - m[1]\n if 0 <= n_r < len(grid) and 0 <= n_c < len(grid[0]) and grid[n_r][n_c] not in ["#"] and 0 <= push_spot[0] < len(grid) and 0 <= push_spot[1] < len(grid[0]) and grid[push_spot[0]][push_spot[1]] not in ["#"]:\n neighbours.append(((n_r, n_c), push_spot))\n return neighbours\n \n def get_neighbours_for_player(player, box, grid):\n moves = [(0,-1),(0,1),(-1,0),(1,0)]\n r,c = player[0], player[1]\n neighbours = []\n for m in moves:\n n_r, n_c = r + m[0], c + m[1]\n if 0 <= n_r < len(grid) and 0 <= n_c < len(grid[0]) and grid[n_r][n_c] not in ["#"] and (n_r,n_c) != box:\n neighbours.append((n_r, n_c))\n return neighbours\n \n def player_can_reach(player, push_spot, box, grid):\n queue = deque()\n queue.append(player)\n visited = set()\n visited.add(player)\n while queue:\n p = queue.popleft()\n if p == push_spot:\n return True\n for n in get_neighbours_for_player(p, box, grid):\n if n not in visited:\n visited.add(n)\n queue.append(n)\n return False\n \n queue = deque()\n visited = set()\n visited.add((box,player))\n queue.append((box, player, 0))\n while queue:\n box,player,d = queue.popleft()\n if grid[box[0]][box[1]] == "T":\n return d\n neighbours = get_neighbours_for_box(box, grid)\n for n, ps in neighbours:\n if (n,box) not in visited and player_can_reach(player, ps, box, grid):\n visited.add((n,box))\n queue.append((n,box,d+1))\n return -1\n\t\t``` | 1 | 0 | [] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | Python BFS x 2 | python-bfs-x-2-by-fftnim-4xbt | ```py\nclass Solution:\n \n offsets = ((1, 0), (-1, 0), (0, 1), (0, -1))\n \n def minPushBox(self, grid: List[List[str]]) -> int:\n\n # check | fftnim | NORMAL | 2021-07-16T00:29:48.256995+00:00 | 2021-07-16T00:29:48.257034+00:00 | 142 | false | ```py\nclass Solution:\n \n offsets = ((1, 0), (-1, 0), (0, 1), (0, -1))\n \n def minPushBox(self, grid: List[List[str]]) -> int:\n\n # check if player can move from start to end given the ball\'s position\n def can_move(start, end, ball):\n if not (0 <= end[0] < rows and 0 <= end[1] < cols):\n return False\n q = collections.deque([start])\n seen = {start}\n while q:\n row, col = q.popleft()\n if (row, col) == end:\n return True\n for r_offset, c_offset in self.offsets:\n r, c = row + r_offset, col + c_offset\n if 0 <= r < rows and 0 <= c < cols and grid[r][c] != \'#\' and (r, c) != ball and (r, c) not in seen:\n seen.add((r, c))\n q.append((r, c))\n return False\n\n rows, cols = len(grid), len(grid[0])\n\n # find source, target, ball\n for r in range(rows):\n for c in range(cols):\n if grid[r][c] == \'T\':\n target = (r, c)\n elif grid[r][c] == \'S\':\n source = (r, c)\n elif grid[r][c] == \'B\':\n ball = (r, c)\n\n # dfs starting from source, ball\n seen = {(source, ball)}\n q = collections.deque([(0, source, ball)])\n\n while q:\n dist, source, ball = q.popleft()\n\n if ball == target:\n return dist\n\n for r_offset, c_offset in self.offsets:\n r, c = ball[0] + r_offset, ball[1] + c_offset\n\n if 0 <= r < rows and 0 <= c < cols and grid[r][c] != \'#\':\n push_pos = (ball[0] - r_offset, ball[1] - c_offset)\n\n if (ball, (r, c)) not in seen and can_move(source, push_pos, ball):\n seen.add((ball, (r, c)))\n q.append((dist + 1, ball, (r, c)))\n\n return -1\n | 1 | 0 | [] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | [C++] BFS and DFS 80 lines | c-bfs-and-dfs-80-lines-by-yunqu-wc0b | I am trying to be as "clean-code" as possible.\n\ncpp\nclass Solution {\npublic:\n int dx[4] = {0, -1, 0, 1};\n int dy[4] = {-1, 0, 1, 0};\n int m, n;\ | yunqu | NORMAL | 2021-07-14T13:21:01.063812+00:00 | 2021-07-14T13:21:01.063855+00:00 | 210 | false | I am trying to be as "clean-code" as possible.\n\n```cpp\nclass Solution {\npublic:\n int dx[4] = {0, -1, 0, 1};\n int dy[4] = {-1, 0, 1, 0};\n int m, n;\n queue<vector<int>> q;\n unordered_set<string> seen1; // book-keeping worker and box locations\n unordered_set<string> seen2; // book-keeping for hasPath() DFS\n \n int minPushBox(vector<vector<char>>& grid) {\n m = grid.size();\n n = grid[0].size();\n int bx, by, sx, sy, tx, ty;\n for (int i = 0; i < m; i++){\n for (int j = 0; j < n; ++j){\n if (grid[i][j] == \'B\')\n bx = i, by = j;\n else if (grid[i][j] == \'S\')\n sx = i, sy = j;\n else if (grid[i][j] == \'T\')\n tx = i, ty = j;\n }\n }\n \n q.push({sx, sy, bx, by, 0});\n seen1.insert(getKey4(sx, sy, bx, by));\n\n int w1, w2, b1, b2;\n int x1, x2, y1, y2;\n while (!q.empty()){\n w1 = q.front()[0], w2 = q.front()[1]; // worker location\n b1 = q.front()[2], b2 = q.front()[3]; // box location\n int steps = q.front()[4];\n q.pop();\n \n if (b1 == tx and b2 == ty) return steps;\n \n for (int d = 0; d < 4; ++d){\n x1 = b1 + dx[d], y1 = b2 + dy[d]; // worker push from this\n x2 = b1 - dx[d], y2 = b2 - dy[d]; // box will move to this\n\n if (seen1.count(getKey4(b1, b2, x2, y2))) continue;\n if (canMove(grid, x1, y1, x2, y2, w1, w2, b1, b2)){\n q.push({b1, b2, x2, y2, steps + 1});\n seen1.insert(getKey4(b1, b2, x2, y2));\n }\n }\n }\n return -1;\n }\n \n string getKey4(int a, int b, int c, int d){\n return to_string(a) + "#" + to_string(b) + "#" + to_string(c) + "#" + to_string(d);\n }\n \n string getKey2(int a, int b){\n return to_string(a) + "#" + to_string(b);\n }\n\n bool canMove(vector<vector<char>>& grid, int x1, int y1, int x2, int y2, int sx, int sy, int bx, int by){\n if (0 > x1 or x1 >= m or 0 > y1 or y1 >= n or grid[x1][y1] == \'#\') return false;\n if (0 > x2 or x2 >= m or 0 > y2 or y2 >= n or grid[x2][y2] == \'#\') return false;\n seen2.clear();\n return hasPath(grid, sx, sy, x1, y1, bx, by);\n }\n \n bool hasPath(vector<vector<char>>& grid, int sx, int sy, \n int px, int py, int bx, int by){\n if (sx == px and sy == py) return true;\n for (int d = 0; d < 4; ++d){\n int x = sx + dx[d], y = sy + dy[d];\n if (0 <= x and x < m and 0 <= y and y < n and grid[x][y] != \'#\'\n and !seen2.count(getKey2(x, y)) and !(x == bx and y == by)){\n seen2.insert(getKey2(x, y));\n if (hasPath(grid, x, y, px, py, bx, by)) {\n return true;\n }\n }\n }\n return false;\n }\n};\n``` | 1 | 1 | [] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | Java A* Search | java-a-search-by-brucezu-xjk8 | \n /*\n \n Idea:\n concern:\n 1> how to avoid repeat or endless loop of person walking and box moving\n answer: S can repeat location when B is in di | brucezu | NORMAL | 2021-06-26T23:39:53.926018+00:00 | 2021-06-26T23:42:06.901788+00:00 | 190 | false | ```\n /*\n \n Idea:\n concern:\n 1> how to avoid repeat or endless loop of person walking and box moving\n answer: S can repeat location when B is in different location,\n but for a given fix B location, S should not repeat walking\n B should not repeat moving.\n need a visited variable to keep the visited status using box and person location\n 2> if failed to move to any direction should restore the B to one of original location?\n answer: yeah, only when there is not any direction is possible to move on.\n the one of original location is decided by the priority value of heuristic\n So should keep Box and person location in status.\n heuristic decided by moved steps and manhattan distance.\n so the status include: manhattan distance, moved steps, Box and person location\n\n Solution:\n find the initial location of B, S, T\n A * search: BFS + priority queue.\n a priority queue keeping status and heuristic ( manhattan + steps)\n avoid repeating visited status: locations of person and box\n initial status in priority queue\n loop while queue is not empty\n 1> if current B is T then return moved steps\n 2> if current B is visited return, stop trying from this status\n 3> make person + B location as visited\n try a step toward 4 direction of person.\n effective: try to move box a step toward 4 directions if box\n have space to move & person can walk to the place to push\n details:\n from current status: person try walk a step toward 4 directions if\n person can walk: in grid and no # at next cell\n if the next cell for person to walk is box location and box\'s next cell\n is allow it to move:\n it is move box\n else\n it is only person walk.\n update related status and add to priority queue.\n\n out of loop return -1\n Variables:\n target T location [A,B],\n person S location [c,r] or [column, row]\n box B location [a,b]\n */\n int A = 0, B = 0;\n int[][] d4 = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};\n\n public int minPushBox(char[][] grid) {\n int R = grid.length, C = grid[0].length;\n // searching initial location T[A,B], B[ia,ib],S[ix,iy]\n int ia = 0, ib = 0, ix = 0, iy = 0;\n for (int i = 0; i < R; i++) {\n for (int j = 0; j < C; j++) {\n char c = grid[i][j];\n if (c == \'T\') {\n A = j;\n B = i;\n }\n if (c == \'B\') {\n ia = j;\n ib = i;\n }\n if (c == \'S\') {\n ix = j;\n iy = i;\n }\n }\n }\n\n Set<String> v = new HashSet();\n Queue<int[]> q = new PriorityQueue<>((o, o2) -> o[0] + o[1] - o2[0] - o2[1]);\n q.offer(new int[] {Math.abs(ia - A) + Math.abs(ib - B), 0, ix, iy, ia, ib});\n while (!q.isEmpty()) {\n int[] c = q.poll();\n int a = c[4], b = c[5], steps = c[1];\n if (a == A && b == B) return steps;\n\n int x = c[2], y = c[3];\n String k = x + "" + y + "" + a + "" + b;\n if (v.contains(k)) continue;\n v.add(k);\n\n for (int[] d : d4) {\n int nx = x + d[0], ny = y + d[1];\n if (!canWalk(nx, ny, R, C, grid)) continue;\n if (nx == a && ny == b) {\n int na = a + d[0], nb = b + d[1];\n if (!canWalk(na, nb, R, C, grid)) continue;\n q.offer(new int[] {Math.abs(na - A) + Math.abs(nb - B), steps + 1, nx, ny, na, nb});\n } else q.offer(new int[] {c[0], steps, nx, ny, a, b});\n }\n }\n return -1;\n }\n\n private boolean canWalk(int x, int y, int R, int C, char[][] grid) {\n if (x < 0 || x >= C || y < 0 || y >= R || grid[y][x] == \'#\') return false;\n return true;\n } \n``` | 1 | 0 | [] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | Don't step on the Box! | dont-step-on-the-box-by-liamdaburke-gc5u | ```\n def minPushBox(self, grid: List[List[str]]) -> int:\n for i, row in enumerate(grid):\n for j, col in enumerate(row):\n | liamdaburke | NORMAL | 2021-06-15T14:30:37.288868+00:00 | 2021-06-15T14:30:37.288935+00:00 | 357 | false | ```\n def minPushBox(self, grid: List[List[str]]) -> int:\n for i, row in enumerate(grid):\n for j, col in enumerate(row):\n if col == \'S\':\n si,sj = i,j\n elif col == \'B\':\n bi,bj = i,j\n elif col == \'T\':\n ti,tj = i,j\n \n H, W = len(grid), len(grid[0])\n dirs = [(-1,0), (0, -1), (1,0),(0,1)]\n def playerreach(standi, standj, pli, plj, nbi, nbj):\n q = deque([(pli, plj)])\n seenpr = set()\n while q:\n ppi, ppj = q.popleft()\n \n for di, dj in dirs:\n newpi, newpj = di + ppi, dj + ppj\n\t\t\t\t\t#Don\'t step on the Box!\n if 0 <= newpi < H and 0 <= newpj < W and grid[newpi][newpj] != \'#\' and (newpi, newpj) != (nbi, nbj):\n if (newpi, newpj) == (standi, standj):\n return True\n if (newpi, newpj) not in seenpr:\n seenpr.add((newpi, newpj))\n q.append((newpi, newpj))\n \n return False\n \n seen = {(bi, bj, si, sj)}\n \n q = deque([(bi, bj, si, sj, 0)])\n best = float(\'inf\')\n while q:\n bxi, bxj, pli, plj, pushes = q.popleft()\n \n for di, dj in dirs:\n newi, newj = di + bxi, dj + bxj\n \n if 0 <= newi < H and 0 <= newj < W and grid[newi][newj] != \'#\':\n \n if (newi, newj, pli, plj) not in seen:\n seen.add((newi, newj, pli, plj))\n standi, standj = di*-1 + bxi, dj*-1 + bxj\n \n if playerreach(standi, standj, pli, plj, bxi, bxj):\n \n if (newi, newj) == (ti, tj):\n best = min(best, pushes+1)\n else:\n q.append((newi, newj, standi+di, standj+dj, pushes+1))\n \n \n return -1 if best == float(\'inf\') else best | 1 | 0 | ['Python'] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | Java - Dual BFS | java-dual-bfs-by-rv777-vyu8 | \n// We need to track the min number of steps that the box needs to be pushed to the target\n// We don\'t care how many steps the player takes\n// We will track | rv777 | NORMAL | 2021-06-10T04:48:11.051195+00:00 | 2021-08-12T17:00:07.510842+00:00 | 278 | false | ```\n// We need to track the min number of steps that the box needs to be pushed to the target\n// We don\'t care how many steps the player takes\n// We will track the state of the box and the player\n// For every box position we consider each possible next box position\n// - The usual checks, is the box position in bounds, visited, not a wall, etc. plus...\n// - Can the player be moved into position to move the box to the new position? Use separate BFS\n// We track the visited position and direction of the box\n// 4 ms, faster than 99.60%\nclass State {\n int pRow;\n int pCol;\n int bRow;\n int bCol;\n State() {}\n State(int pRow, int pCol, int bRow, int bCol) {\n this.pRow = pRow;\n this.pCol = pCol;\n this.bRow = bRow;\n this.bCol = bCol;\n }\n}\nclass Solution {\n private static final int[][] DIRS = new int[][]{{0,1},{1,0},{0,-1},{-1,0}};\n public int minPushBox(char[][] grid) {\n int rows = grid.length;\n int cols = grid[0].length;\n State initState = new State();\n for (int row = 0; row < rows; row++) {\n for (int col = 0; col < cols; col++) {\n if (grid[row][col] == \'S\') {\n initState.pRow = row;\n initState.pCol = col;\n } else if (grid[row][col] == \'B\') {\n initState.bRow = row;\n initState.bCol = col;\n }\n }\n }\n boolean[][][] visited = new boolean[rows][cols][4];\n Deque<State> deque = new ArrayDeque<>();\n deque.add(initState);\n int steps = 1;\n while (!deque.isEmpty()) {\n int size = deque.size();\n for (int i = 0; i < size; i++) {\n State curr = deque.remove();\n for (int dir = 0; dir < 4; dir++) {\n int adjBRow = curr.bRow + DIRS[dir][0];\n int adjBCol = curr.bCol + DIRS[dir][1];\n // player must have been in this position to push box to new adj position\n int adjPRow = curr.bRow - DIRS[dir][0]; \n int adjPCol = curr.bCol - DIRS[dir][1];\n if (adjBRow < 0 || adjBRow > rows - 1 || adjBCol < 0 || adjBCol > cols - 1 || \n adjPRow < 0 || adjPRow > rows - 1 || adjPCol < 0 || adjPCol > cols - 1 ||\n visited[adjBRow][adjBCol][dir] || \n grid[adjBRow][adjBCol] == \'#\' || grid[adjPRow][adjPCol] == \'#\' || \n !playerCanReachBox(grid, curr.pRow, curr.pCol, adjPRow, adjPCol, curr.bRow, curr.bCol))\n continue;\n if (grid[adjBRow][adjBCol] == \'T\')\n return steps;\n visited[adjBRow][adjBCol][dir] = true;\n deque.add(new State(curr.bRow, curr.bCol, adjBRow, adjBCol));\n }\n }\n steps++;\n }\n return -1;\n }\n private boolean playerCanReachBox(char[][] grid, int pRow1, int pCol1, int pRow2, int pCol2, int bRow, int bCol) {\n int rows = grid.length;\n int cols = grid[0].length;\n if (pRow1 == pRow2 && pCol1 == pCol2)\n return true;\n Deque<Integer> deque = new ArrayDeque<>();\n deque.add(pRow1 * cols + pCol1);\n boolean[][] visited = new boolean[rows][cols];\n visited[pRow1][pCol1] = true;\n visited[bRow][bCol] = true;\n while (!deque.isEmpty()) {\n int index = deque.remove();\n int row = index / cols;\n int col = index % cols;\n for (int[] dir : DIRS) {\n int adjRow = row + dir[0];\n int adjCol = col + dir[1];\n if (adjRow < 0 || adjRow > rows - 1 || adjCol < 0 || adjCol > cols - 1 ||\n visited[adjRow][adjCol] || grid[adjRow][adjCol] == \'#\')\n continue;\n if (adjRow == pRow2 && adjCol == pCol2)\n return true;\n deque.add(adjRow * cols + adjCol);\n visited[adjRow][adjCol] = true;\n }\n }\n return false;\n }\n}\n``` | 1 | 0 | [] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | c# A* | c-a-by-cpp0x-o96j | Using custom Heap and A* algorithm from https://www.redblobgames.com/pathfinding/a-star/implementation.html#python-astar\n\n\npublic class Solution \n{\n\tpubli | cpp0x | NORMAL | 2021-01-12T10:15:43.525231+00:00 | 2021-01-12T10:51:19.633722+00:00 | 254 | false | Using custom Heap and A* algorithm from https://www.redblobgames.com/pathfinding/a-star/implementation.html#python-astar\n\n```\npublic class Solution \n{\n\tpublic int MinPushBox(char[][] grid)\n\t{\n\t\tPoint target = new Point();\n\t\tPoint startBox = new Point();\n\t\tPoint startPerson = new Point();\n\t\tfor (int r = 0; r < grid.Length; ++r)\n\t\t{\n\t\t\tfor (int c = 0; c < grid[r].Length; ++c)\n\t\t\t{\n\t\t\t\tif (grid[r][c] == \'T\')\n\t\t\t\t\ttarget = new Point(r, c);\n\t\t\t\telse if (grid[r][c] == \'S\')\n\t\t\t\t\tstartPerson = new Point(r, c);\n\t\t\t\telse if (grid[r][c] == \'B\')\n\t\t\t\t\tstartBox = new Point(r, c);\n\t\t\t}\n\t\t}\n\n\t\tvar heap = new Heap<State>((n1, n2) => n1.Priority.CompareTo(n2.Priority));\n\t\tvar costSoFar = new Dictionary<(Point, Point), int>();\n\n\t\theap.Insert(new State { Priority = this.Heurestic(startBox, target), Box = startBox, Person = startPerson });\n\t\tcostSoFar[(startBox, startPerson)] = 0;\n\n\t\twhile (heap.Count > 0)\n\t\t{\n\t\t\tvar state = heap.RemoveMin();\n\n\t\t\tif (state.Box == target)\n\t\t\t\treturn state.Moves;\n\n\t\t\tfor (int dr = -1; dr <= 1; dr++)\n\t\t\t{\n\t\t\t\tfor (int dc = -1; dc <= 1; dc++)\n\t\t\t\t{\n\t\t\t\t\tif ((dr == 0 && dc == 0) || (dr != 0 && dc != 0))\n\t\t\t\t\t\tcontinue;\n\n\t\t\t\t\tvar newPersonLocation = new Point(state.Person.Row + dr, state.Person.Col + dc);\n\t\t\t\t\tif (!this.CanMove(newPersonLocation, grid))\n\t\t\t\t\t\tcontinue;\n\n\t\t\t\t\tvar currentState = (state.Box, state.Person);\n\n\t\t\t\t\tif (newPersonLocation == state.Box)\n\t\t\t\t\t{\n\t\t\t\t\t\tvar newBoxLocation = new Point(state.Box.Row + dr, state.Box.Col + dc);\n\t\t\t\t\t\tif (!this.CanMove(newBoxLocation, grid))\n\t\t\t\t\t\t\tcontinue;\n\n\t\t\t\t\t\tvar nextState = (newBoxLocation, newPersonLocation);\n\t\t\t\t\t\tvar newCost = costSoFar[currentState] + 1;\n\t\t\t\t\t\tif (!costSoFar.ContainsKey(nextState) || newCost < costSoFar[nextState])\n\t\t\t\t\t\t{\n\t\t\t\t\t\t\tcostSoFar[nextState] = newCost;\n\t\t\t\t\t\t\tint priority = newCost + this.Heurestic(newBoxLocation, target);\n\t\t\t\t\t\t\theap.Insert(new State { Box = newBoxLocation, Person = newPersonLocation, Moves = state.Moves + 1, Priority = priority });\n\t\t\t\t\t\t}\n\t\t\t\t\t}\n\t\t\t\t\telse\n\t\t\t\t\t{\n\t\t\t\t\t\tvar nextState = (state.Box, newPersonLocation);\n\t\t\t\t\t\tvar newCost = costSoFar[currentState];\n\t\t\t\t\t\tif (!costSoFar.ContainsKey(nextState) || newCost < costSoFar[nextState])\n\t\t\t\t\t\t{\n\t\t\t\t\t\t\tcostSoFar[nextState] = newCost;\n\t\t\t\t\t\t\tint priority = newCost + this.Heurestic(state.Box, target);\n\t\t\t\t\t\t\theap.Insert(new State { Box = state.Box, Person = newPersonLocation, Moves = state.Moves, Priority = priority });\n\t\t\t\t\t\t}\n\t\t\t\t\t}\n\t\t\t\t}\n\t\t\t}\n\t\t}\n\n\t\treturn -1;\n\t}\n\n\tprivate bool CanMove(Point point, char[][] grid)\n\t{\n\t\tbool invalidLocation =\n\t\t\tpoint.Row < 0 ||\n\t\t\tpoint.Row >= grid.Length ||\n\t\t\tpoint.Col < 0 ||\n\t\t\tpoint.Col >= grid[0].Length ||\n\t\t\tgrid[point.Row][point.Col] == \'#\';\n\n\t\treturn !invalidLocation;\n\t}\n\n\tprivate int Heurestic(Point box, Point target) => Math.Abs(box.Row - target.Row) + Math.Abs(box.Col - target.Col);\n\n\tpublic struct Point : IEquatable<Point>\n\t{\n\t\tpublic Point(int row, int col) => (this.Row, this.Col) = (row, col);\n\n\t\tpublic int Row { get; set; }\n\n\t\tpublic int Col { get; set; }\n\n\t\tpublic static bool operator ==(Point p1, Point p2) => p1.Equals(p2);\n\n\t\tpublic static bool operator !=(Point p1, Point p2) => !p1.Equals(p2);\n\n\t\tpublic bool Equals(Point other) => this.Row == other.Row && this.Col == other.Col;\n\n\t\tpublic override bool Equals(object obj) => base.Equals(obj);\n\n\t\tpublic override int GetHashCode() => HashCode.Combine(Row, Col);\n\t}\n\n\tpublic class State : IComparable<State>\n\t{\n\t\tpublic int Priority { get; set; }\n\t\tpublic int Moves { get; set; }\n\t\tpublic Point Box { get; set; }\n\t\tpublic Point Person { get; set; }\n\n\t\tpublic int CompareTo(State other) => this.Priority.CompareTo(other.Priority);\n\t}\n\t\t\n public class Heap<T>\n {\n private readonly List<T> list = new List<T>();\n\n private readonly Comparison<T> compare;\n\n public Heap(Comparison<T> compare) => this.compare = compare;\n\n public T Min\n {\n get => this.list[0];\n }\n\n public int Count\n {\n get => this.list.Count;\n }\n\n public void Insert(T item)\n {\n this.list.Add(item);\n this.FixHeapUp();\n }\n\n public void Build(IList<T> items)\n {\n this.list.Clear();\n this.list.AddRange(items);\n\n int parentIndex = this.GetParentIndex(items.Count - 1);\n int index;\n for (index = items.Count - 1; index >= 0; --index)\n {\n if (index != parentIndex)\n break;\n }\n\n for (int i = index; i >= 0; --i)\n this.FixHeapDown(i);\n }\n\n public T RemoveMin()\n {\n T min = this.list[0];\n\n if (this.list.Count == 1)\n {\n this.list.Clear();\n }\n else\n {\n this.list[0] = this.list[this.list.Count - 1];\n this.list.RemoveAt(this.list.Count - 1);\n this.FixHeapDown(0);\n }\n\n return min;\n }\n\n private int GetParentIndex(int index) => (index - 1) / 2;\n\n private int GetLeftChildIndex(int index)\n {\n int leftIndex = 2 * index + 1;\n if (leftIndex >= this.list.Count)\n leftIndex = -1;\n return leftIndex;\n }\n\n private int GetRightChildIndex(int index)\n {\n int rightIndex = 2 * index + 2;\n if (rightIndex >= this.list.Count)\n rightIndex = -1;\n return rightIndex;\n }\n\n private void Swap(int i1, int i2)\n {\n T tmp = this.list[i1];\n this.list[i1] = this.list[i2];\n this.list[i2] = tmp;\n }\n\n private void FixHeapUp()\n {\n int i = this.list.Count - 1;\n int parentIndex = this.GetParentIndex(i);\n\n while (i != 0 && this.compare(this.list[parentIndex], this.list[i]) > 0)\n {\n this.Swap(parentIndex, i);\n i = this.GetParentIndex(i);\n parentIndex = this.GetParentIndex(i);\n }\n }\n\n private void FixHeapDown(int rootIndex)\n {\n int leftChildIndex = this.GetLeftChildIndex(rootIndex);\n int rightChildIndex = this.GetRightChildIndex(rootIndex);\n\n int smallestIndex = rootIndex;\n\n if (leftChildIndex != -1 && rightChildIndex != -1)\n {\n smallestIndex = this.compare(this.list[leftChildIndex], this.list[rightChildIndex]) < 0\n ? leftChildIndex\n : rightChildIndex;\n }\n else if (leftChildIndex != -1)\n smallestIndex = leftChildIndex;\n else if (rightChildIndex != -1)\n smallestIndex = rightChildIndex;\n\n smallestIndex = this.compare(this.list[smallestIndex], this.list[rootIndex]) < 0\n ? smallestIndex\n : rootIndex;\n\n if (smallestIndex == rootIndex)\n return;\n\n this.Swap(smallestIndex, rootIndex);\n this.FixHeapDown(smallestIndex);\n }\n } \n}\n``` | 1 | 0 | [] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | C++ BFS - DFS solution [32ms] | c-bfs-dfs-solution-32ms-by-varkey98-26fm | \nvector<int> dx={1,0,-1,0};\nvector<int> dy={0,1,0,-1};\nint memo[20][20];\nbool dfs(int i1,int j1,int i2,int j2,int b1,int b2,vector<vector<char>>& grid)\n{\n | varkey98 | NORMAL | 2020-08-18T11:48:28.170029+00:00 | 2020-08-18T11:48:28.170061+00:00 | 487 | false | ```\nvector<int> dx={1,0,-1,0};\nvector<int> dy={0,1,0,-1};\nint memo[20][20];\nbool dfs(int i1,int j1,int i2,int j2,int b1,int b2,vector<vector<char>>& grid)\n{\n memset(memo,0,sizeof(memo)); \n return hasPath(i1,j1,i2,j2,b1,b2,grid);\n}\nbool hasPath(int i1,int j1,int i2,int j2,int b1,int b2,vector<vector<char>>& grid)\n{\n if(grid[i1][j1]==\'#\'||(i1==b1&&j1==b2))\n return false;\n memo[i1][j1]=1;\n if(i1==i2&&j1==j2)\n return true;\n else\n {\n bool q=false;\n for(int k=0;k<4;++k)\n if(i1+dx[k]<0||j1+dy[k]<0||i1+dx[k]>=grid.size()||j1+dy[k]>=grid[0].size()||memo[i1+dx[k]][j1+dy[k]])\n continue;\n else\n q=q||hasPath(i1+dx[k],j1+dy[k],i2,j2,b1,b2,grid);\n return q;\n }\n \n}\nint minPushBox(vector<vector<char>>& grid) \n{\n int grey[20][20][20][20];\n memset(grey,0,sizeof(grey));\n queue<vector<int>> q;\n int n=grid.size(),m=grid[0].size();\n int i1,j1,i2,j2,e1,e2;\n for(int i=0;i<n;++i)\n for(int j=0;j<m;++j)\n if(grid[i][j]!=\'#\')\n {\n if(grid[i][j]==\'S\')\n {\n i2=i;\n j2=j;\n }\n else if(grid[i][j]==\'B\')\n {\n i1=i;\n j1=j;\n }\n else if(grid[i][j]==\'T\')\n {\n e1=i;\n e2=j;\n }\n }\n q.push({i1,j1,i2,j2,0});\n grey[i1][j1][i2][j2]=1;\n while(!q.empty())\n {\n vector<int> temp=q.front();\n q.pop();\n i1=temp[0],j1=temp[1],i2=temp[2],j2=temp[3];\n int d=temp[4];\n if(i1==e1&&j1==e2)\n return d;\n else\n {\n if(i1+1<n&&grid[i1+1][j1]!=\'#\'&&i1>0&&grid[i1-1][j1]!=\'#\'&&dfs(i2,j2,i1-1,j1,i1,j1,grid)&&!grey[i1+1][j1][i1][j1])\n {\n q.push({i1+1,j1,i1,j1,d+1});\n grey[i1+1][j1][i1][j1]=1;\n }\n if(j1+1<m&&grid[i1][j1+1]!=\'#\'&&j1>0&&grid[i1][j1-1]!=\'#\'&&dfs(i2,j2,i1,j1-1,i1,j1,grid)&&!grey[i1][j1+1][i1][j1])\n {\n q.push({i1,j1+1,i1,j1,d+1});\n grey[i1][j1+1][i1][j1]=1;\n }\n if(i1>0&&grid[i1-1][j1]!=\'#\'&&i1+1<n&&grid[i1+1][j1]!=\'#\'&&dfs(i2,j2,i1+1,j1,i1,j1,grid)&&!grey[i1-1][j1][i1][j1])\n {\n q.push({i1-1,j1,i1,j1,d+1});\n grey[i1-1][j1][i1][j1]=1;\n }\n if(j1>0&&grid[i1][j1-1]!=\'#\'&&j1+1<m&&grid[i1][j1+1]!=\'#\'&&dfs(i2,j2,i1,j1+1,i1,j1,grid)&&!grey[i1][j1-1][i1][j1])\n {\n q.push({i1,j1-1,i1,j1,d+1});\n grey[i1][j1-1][i1][j1]=1;\n }\n }\n \n }\n return -1;\n}\n``` | 1 | 0 | ['Depth-First Search', 'Breadth-First Search', 'C'] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | Idiomatic Rust using BFS | idiomatic-rust-using-bfs-by-yeetcoder473-tnrq | Long but idiomatic solution in Rust.\n\n\nuse std::collections::{HashSet, VecDeque};\n\n#[derive(PartialEq, Eq, Hash, Debug, Clone, Copy)]\nenum Tile {\n Wal | yeetcoder4736 | NORMAL | 2020-07-23T23:41:25.516204+00:00 | 2020-07-23T23:41:25.516254+00:00 | 57 | false | Long but idiomatic solution in Rust.\n\n```\nuse std::collections::{HashSet, VecDeque};\n\n#[derive(PartialEq, Eq, Hash, Debug, Clone, Copy)]\nenum Tile {\n Wall,\n Empty,\n}\n\n#[derive(PartialEq, Eq, Hash, Debug, Clone, Copy)]\nstruct Position {\n i: usize,\n j: usize,\n}\n\nimpl Position {\n pub fn new(i: usize, j: usize) -> Position {\n Position { i, j }\n }\n\n pub fn pos_in_dir(&self, d: Direction, grid_sizes: Position) -> Option<Position> {\n let adj_pos = match d {\n Direction::Right => Position::new(self.i, self.j + 1),\n Direction::Left => Position::new(self.i, self.j.checked_sub(1)?),\n Direction::Down => Position::new(self.i + 1, self.j),\n Direction::Up => Position::new(self.i.checked_sub(1)?, self.j),\n };\n\n if adj_pos.i < grid_sizes.i && adj_pos.j < grid_sizes.j {\n Some(adj_pos)\n } else {\n None\n }\n }\n}\n\n#[derive(PartialEq, Eq, Hash, Debug, Clone, Copy)]\nstruct State {\n box_pos: Position,\n player_pos: Position,\n}\n\nimpl State {\n pub fn new(box_pos: Position, player_pos: Position) -> State {\n State {\n box_pos,\n player_pos,\n }\n }\n}\n\n#[derive(PartialEq, Eq, Hash, Debug, Clone, Copy)]\nenum Direction {\n Right,\n Left,\n Down,\n Up,\n}\n\nimpl Direction {\n pub fn opposite(&self) -> Direction {\n match self {\n Direction::Right => Direction::Left,\n Direction::Left => Direction::Right,\n Direction::Down => Direction::Up,\n Direction::Up => Direction::Down,\n }\n }\n}\n\nlazy_static! {\n static ref DIRECTIONS: Vec<Direction> = vec![\n Direction::Right,\n Direction::Left,\n Direction::Down,\n Direction::Up,\n ];\n}\n\n/// Returns a list of tuples of `(expected_player_position, moved_box_position)`.\n/// If the player were to reach `expected_player_position`, the box could be moved to `moved_box_position`.\nfn push_positions(grid: &Vec<Vec<Tile>>, box_pos: Position) -> Vec<(Position, Position)> {\n let mut res = vec![];\n\n let grid_sizes = Position::new(grid.len(), grid[0].len());\n for direction in &*DIRECTIONS {\n let new_player_pos = box_pos.pos_in_dir(direction.opposite(), grid_sizes);\n let new_box_pos = box_pos.pos_in_dir(*direction, grid_sizes);\n if let (Some(new_player_pos), Some(new_box_pos)) = (new_player_pos, new_box_pos) {\n if grid[new_player_pos.i][new_player_pos.j] == Tile::Empty\n && grid[new_box_pos.i][new_box_pos.j] == Tile::Empty\n {\n res.push((new_player_pos, new_box_pos))\n }\n }\n }\n\n res\n}\n\n/// Returns whether the player can move from `state.player_pos` to `new_player_pos`.\n/// Player cannot move through `Tile::Wall` or `state.box_pos`.\nfn can_move_player(grid: &Vec<Vec<Tile>>, state: State, new_player_pos: Position) -> bool {\n let mut worklist = vec![state.player_pos];\n\n let grid_sizes = Position::new(grid.len(), grid[0].len());\n let mut visited = HashSet::new();\n visited.insert(state.player_pos);\n while let Some(player_pos) = worklist.pop() {\n if player_pos == new_player_pos {\n return true;\n }\n\n for direction in &*DIRECTIONS {\n if let Some(adj_pos) = player_pos.pos_in_dir(*direction, grid_sizes) {\n if grid[adj_pos.i][adj_pos.j] == Tile::Empty\n && adj_pos != state.box_pos\n && visited.insert(adj_pos)\n {\n worklist.push(adj_pos);\n }\n }\n }\n }\n\n false\n}\n\n/// Returns the minimum number of pushes to get the box from `start` to `end` given\n/// the player position `player`.\nfn num_pushes(\n grid: &Vec<Vec<Tile>>,\n box_pos: Position,\n end: Position,\n player_pos: Position,\n) -> Option<usize> {\n let mut q = VecDeque::new();\n let init_state = State::new(box_pos, player_pos);\n q.push_back((0, init_state));\n\n let mut visited = HashSet::new();\n visited.insert(init_state);\n while let Some((cur_dist, state)) = q.pop_front() {\n if state.box_pos == end {\n return Some(cur_dist);\n }\n\n // let mut s = vec!["".to_string(); grid.len()];\n // for (i, row) in grid.iter().enumerate() {\n // for (j, tile) in row.iter().enumerate() {\n // if *tile == Tile::Empty {\n // s[i].push(\'.\');\n // } else {\n // s[i].push(\'#\');\n // }\n\n // if Position::new(i, j) == state.box_pos {\n // s[i].pop();\n // s[i].push(\'B\');\n // } else if Position::new(i, j) == state.player_pos {\n // s[i].pop();\n // s[i].push(\'P\');\n // }\n // }\n // println!("{:?}", s[i]);\n // }\n // println!("------");\n\n // For each position the box can be pushed into, check if the player can move behind the box.\n for (expected_player_pos, new_box_pos) in push_positions(grid, state.box_pos) {\n let new_state = State::new(new_box_pos, expected_player_pos);\n // Order is important here! If we insert before moving, we can discount some possibilities early.\n if can_move_player(grid, state, expected_player_pos) && visited.insert(new_state) {\n q.push_back((cur_dist + 1, new_state));\n }\n }\n }\n\n None\n}\n\npub fn min_push_box(grid: Vec<Vec<char>>) -> i32 {\n let mut box_pos = None;\n let mut end = None;\n let mut player_pos = None;\n let mut grid_tile = vec![vec![]; grid.len()];\n for (i, row) in grid.into_iter().enumerate() {\n for (j, ch) in row.into_iter().enumerate() {\n match &ch {\n \'#\' => grid_tile[i].push(Tile::Wall),\n _ => grid_tile[i].push(Tile::Empty),\n }\n\n match ch {\n \'B\' => box_pos = Some(Position::new(i, j)),\n \'T\' => end = Some(Position::new(i, j)),\n \'S\' => player_pos = Some(Position::new(i, j)),\n _ => {}\n }\n }\n }\n\n match num_pushes(\n &grid_tile,\n box_pos.unwrap(),\n end.unwrap(),\n player_pos.unwrap(),\n ) {\n Some(x) => x as i32,\n None => -1,\n }\n}\n\n#[cfg(test)]\nmod test {\n use super::*;\n\n #[test]\n fn test_num_box_pushes() {\n let grid = vec![\n vec![\'#\', \'#\', \'#\', \'#\', \'#\', \'#\'],\n vec![\'#\', \'T\', \'#\', \'#\', \'#\', \'#\'],\n vec![\'#\', \'.\', \'.\', \'B\', \'.\', \'#\'],\n vec![\'#\', \'.\', \'#\', \'#\', \'.\', \'#\'],\n vec![\'#\', \'.\', \'.\', \'.\', \'S\', \'#\'],\n vec![\'#\', \'#\', \'#\', \'#\', \'#\', \'#\'],\n ];\n\n assert_eq!(min_push_box(grid), 3);\n }\n\n #[test]\n fn test_num_box_pushes_five_pushes() {\n let grid = vec![\n vec![\'#\', \'#\', \'#\', \'#\', \'#\', \'#\'],\n vec![\'#\', \'T\', \'.\', \'.\', \'#\', \'#\'],\n vec![\'#\', \'.\', \'#\', \'B\', \'.\', \'#\'],\n vec![\'#\', \'.\', \'.\', \'.\', \'.\', \'#\'],\n vec![\'#\', \'.\', \'.\', \'.\', \'S\', \'#\'],\n vec![\'#\', \'#\', \'#\', \'#\', \'#\', \'#\'],\n ];\n\n assert_eq!(min_push_box(grid), 5);\n }\n\n #[test]\n fn test_num_box_pushes_difficult() {\n let grid = vec![\n vec![\'#\', \'.\', \'.\', \'#\', \'T\', \'#\', \'#\', \'#\', \'#\'],\n vec![\'#\', \'.\', \'.\', \'#\', \'.\', \'#\', \'.\', \'.\', \'#\'],\n vec![\'#\', \'.\', \'.\', \'#\', \'.\', \'#\', \'B\', \'.\', \'#\'],\n vec![\'#\', \'.\', \'.\', \'.\', \'.\', \'.\', \'.\', \'.\', \'#\'],\n vec![\'#\', \'.\', \'.\', \'.\', \'.\', \'#\', \'.\', \'S\', \'#\'],\n vec![\'#\', \'.\', \'.\', \'#\', \'.\', \'#\', \'#\', \'#\', \'#\'],\n ];\n\n assert_eq!(min_push_box(grid), 8);\n }\n}\n\n``` | 1 | 0 | [] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | Need help for one test case | need-help-for-one-test-case-by-rralex-z205 | In my opinion, for the test case below, the answer should be 5 instead of 7\n\n\n{\n{\'#\',\'.\',\'.\',\'#\',\'#\',\'#\',\'#\',\'#\'},\n{\'#\',\'.\',\'.\',\'T\' | rralex | NORMAL | 2020-03-10T14:33:35.698559+00:00 | 2020-03-10T14:35:59.529143+00:00 | 120 | false | In my opinion, for the test case below, the answer should be 5 instead of 7\n\n```\n{\n{\'#\',\'.\',\'.\',\'#\',\'#\',\'#\',\'#\',\'#\'},\n{\'#\',\'.\',\'.\',\'T\',\'#\',\'.\',\'.\',\'#\'},\n{\'#\',\'.\',\'.\',\'.\',\'#\',\'B\',\'.\',\'#\'},\n{\'#\',\'.\',\'.\',\'.\',\'.\',\'.\',\'.\',\'#\'},\n{\'#\',\'.\',\'.\',\'.\',\'#\',\'.\',\'S\',\'#\'},\n{\'#\',\'.\',\'.\',\'#\',\'#\',\'#\',\'#\',\'#\'}\n}\n```\n\nhere is the path of moving block:\n\n\n | 1 | 0 | [] | 1 |
minimum-moves-to-move-a-box-to-their-target-location | Javascript A* search implementation | javascript-a-search-implementation-by-de-5m9l | 168 ms, 45.9MB\n\nAn ugly implementation, but since didn\'t see a javascript implementation of this yet decided to post mine up to see if it helps someone. The | dejeckt | NORMAL | 2020-02-03T08:17:04.956212+00:00 | 2020-02-03T08:17:04.956268+00:00 | 222 | false | 168 ms, 45.9MB\n\nAn ugly implementation, but since didn\'t see a javascript implementation of this yet decided to post mine up to see if it helps someone. The priorityqueue implementation was straight lifted from a stack overflow post. Basically a* search is bfs + heuristics + priorityqueue. Used the same heuristic that many other users are using which is just the manhattan distance + number of moves thus far.\n\nOriginally I try to just solve this without using a priorityqueue and just sorting the array at every loop, but the time penalty was too great (I naively thought time complexity will remain the same assuming that nlogn of sort is equivalent to heapifying n moves, but I realized that at each instance you are only really considering 5 new states to push in to the queue so it\'s not the same). Also, now looking at it using Map for states was probably not necessary, probably would\'ve been better to use a Set and use...\n((block[0]*grid[0].length)+block[1])*(grid[0].length*grid.length) +((character[0]*grid[0].length)+character[1])\n\n```\n/**\n * @param {character[][]} grid\n * @return {number}\n */\nconst top = 0;\nconst parent = i => ((i + 1) >>> 1) - 1;\nconst left = i => (i << 1) + 1;\nconst right = i => (i + 1) << 1;\n\nclass PriorityQueue {\n constructor(comparator = (a, b) => a > b) {\n this._heap = [];\n this._comparator = comparator;\n }\n size() {\n return this._heap.length;\n }\n isEmpty() {\n return this.size() == 0;\n }\n peek() {\n return this._heap[top];\n }\n push(...values) {\n values.forEach(value => {\n this._heap.push(value);\n this._siftUp();\n });\n return this.size();\n }\n pop() {\n const poppedValue = this.peek();\n const bottom = this.size() - 1;\n if (bottom > top) {\n this._swap(top, bottom);\n }\n this._heap.pop();\n this._siftDown();\n return poppedValue;\n }\n replace(value) {\n const replacedValue = this.peek();\n this._heap[top] = value;\n this._siftDown();\n return replacedValue;\n }\n _greater(i, j) {\n return this._comparator(this._heap[i], this._heap[j]);\n }\n _swap(i, j) {\n [this._heap[i], this._heap[j]] = [this._heap[j], this._heap[i]];\n }\n _siftUp() {\n let node = this.size() - 1;\n while (node > top && this._greater(node, parent(node))) {\n this._swap(node, parent(node));\n node = parent(node);\n }\n }\n _siftDown() {\n let node = top;\n while (\n (left(node) < this.size() && this._greater(left(node), node)) ||\n (right(node) < this.size() && this._greater(right(node), node))\n ) {\n let maxChild = (right(node) < this.size() && this._greater(right(node), left(node))) ? right(node) : left(node);\n this._swap(node, maxChild);\n node = maxChild;\n }\n }\n}\n\nvar minPushBox = function(grid) {\n if(typeof(grid)===\'undefined\' || grid===null\n || grid.length===0 || grid[0].length===0){\n return -1;\n }\n \n let TARGET = null;\n let startBlk = null;\n let startPer = null;\n const DIR = [\n [0,1], [1,0], [0,-1], [-1,0]\n ];\n \n for(let i = 0; i<grid.length; i++){\n for(let j = 0; j<grid[0].length; j++){\n if(grid[i][j]===\'S\'){\n startPer = [i,j];\n grid[i][j]=\'.\';\n }\n if(grid[i][j]===\'T\'){\n TARGET = [i,j];\n }\n if(grid[i][j]===\'B\'){\n startBlk = [i,j];\n grid[i][j]=\'.\';\n }\n }\n }\n \n let queue = new PriorityQueue((a,b)=>a.weight<b.weight);\n let states = new Map();\n queue.push({weight: manDist(startBlk), block: startBlk, character: startPer, move: 0});\n while(!queue.isEmpty()){\n let {weight,block,character,move} = queue.pop();\n if(TARGET[0]===block[0] && TARGET[1]===block[1]){\n return move;\n }\n let key = (block[0]*grid[0].length)+block[1];\n let val = (character[0]*grid[0].length)+character[1];\n if(!states.has(key)){\n states.set(key,new Set());\n }\n states.get(key).add(val);\n DIR.forEach(d=>{\n let i = d[0]+character[0];\n let j = d[1]+character[1];\n let curV = (i*grid[0].length)+j;\n if(validMove(i,j,block[0],block[1]) && !states.get(key).has(curV)){\n queue.push({weight: manDist(block)+move, block: block, character: [i,j], move: move});\n }\n });\n let pushDir = tryPush(character,block);\n if(pushDir!==null){\n let newBlk = [block[0]+pushDir[0],block[1]+pushDir[1]];\n let newCha = [character[0]+pushDir[0],character[1]+pushDir[1]];\n let nBK = (newBlk[0]*grid[0].length)+newBlk[1];\n let nVal = (newCha[0]*grid[0].length)+newCha[1];\n if(!states.has(nBK) || !states.get(nBK).has(nVal)){\n queue.push({weight: manDist(newBlk)+(move+1), block: newBlk, character: newCha, move: move+1}); \n }\n }\n }\n \n return -1;\n \n \n function manDist(block){\n let [x,y] = TARGET;\n let [i,j] = block;\n return Math.abs(x-i) + Math.abs(y-j);\n }\n function validMove(i,j,x=null,y=null){\n if(i<0 || j<0 || i>=grid.length || \n j>=grid[0].length){\n return false;\n }\n if(((x!==null&&(i===x)) && (y!==null&&(j===y))) || grid[i][j]===\'#\'){\n return false;\n }\n return true;\n }\n function tryPush(c,b){\n let [i,j] = c;\n let [x,y] = b;\n for(let u = 0; u<DIR.length; u++){\n let [v,w] = DIR[u];\n if(((Math.abs(x-i)===1 && y===j) || (Math.abs(y-j)===1 && x===i)) && validMove(i+v,j+w) && validMove(x+v,y+w) && (i+v)===x && (j+w)===y){\n return [v,w];\n }\n }\n return null;\n }\n};\n``` | 1 | 0 | [] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | C++ two BFS solution | c-two-bfs-solution-by-jake1900-9hkg | ```\nclass Solution {\npublic:\n \n vector dx = {0, 1, 0, -1};\n vector dy = {1, 0, -1, 0};\n pair B;\n pair P;\n pair T;\n \n struct no | jake1900 | NORMAL | 2020-01-29T11:54:31.285040+00:00 | 2020-01-29T11:54:31.285075+00:00 | 442 | false | ```\nclass Solution {\npublic:\n \n vector<int> dx = {0, 1, 0, -1};\n vector<int> dy = {1, 0, -1, 0};\n pair<int, int> B;\n pair<int, int> P;\n pair<int, int> T;\n \n struct node {\n int x;\n int y;\n int px;\n int py;\n node(int x, int y, int px, int py) : x(x), y(y), px(px), py(py) {\n \n };\n string to_string() {\n return std::to_string(x) + "-" + \n std::to_string(y) + "-" + \n std::to_string(px) + "-" + \n std::to_string(py);\n \n }\n };\n \n bool inside(vector<vector<char>>& grid, int x, int y) {\n return x >= 0 && y >= 0 && x < grid.size() && y < grid[0].size();\n }\n\n bool canReachPosition(vector<vector<char>>& grid, \n int px, int py,\n int tx, int ty, \n int bx, int by) {\n if(!inside(grid, tx, ty)) return false;\n if(grid[tx][ty] == \'#\') return false;\n \n int m = grid.size(), n = grid[0].size();\n \n vector<vector<bool>> seen(m, vector<bool>(n, false));\n queue<pair<int, int>> q;\n q.push({px, py}); \n seen[px][py] = true;\n seen[bx][by] = true;\n \n while(!q.empty()) {\n int x = q.front().first, y = q.front().second; q.pop();\n if(x == tx && y == ty) return true;\n \n for(int k = 0; k < 4; k++) {\n int nx = x + dx[k], ny = y + dy[k];\n if(!inside(grid, nx, ny)) continue;\n if(seen[nx][ny] || grid[nx][ny] == \'#\') continue;\n q.push({nx, ny});\n seen[nx][ny] = true;\n }\n }\n return false;\n }\n \n vector<node> expand(vector<vector<char>>& grid, node n) {\n vector<node> nodes;\n int bx = n.x, by = n.y;\n int px = n.px, py = n.py;\n \n for(int k = 0; k < 4; k++) {\n int nbx = bx + dx[k], nby = by + dy[k];\n int tx = bx - dx[k], ty = by - dy[k];\n \n if(!inside(grid, nbx, nby)) continue;\n if(grid[nbx][nby] == \'#\') continue;\n \n if(canReachPosition(grid, px, py, tx, ty, bx, by))\n nodes.push_back(node(nbx, nby, bx, by));\n }\n return nodes;\n }\n bool canReachBox(vector<vector<char>>& grid) {\n int px = P.first, py = P.second;\n int bx = B.first, by = B.second;\n for(int k = 0; k < 4; k++) {\n int tx = bx + dx[k];\n int ty = by + dy[k];\n if(!inside(grid, tx, ty)) continue;\n if(grid[tx][ty] == \'#\') continue;\n if(canReachPosition(grid, px, py, tx, ty, bx, by)) return true;\n }\n return false;\n }\n \n int minPushBox(vector<vector<char>>& grid) {\n int m = grid.size(), n = grid[0].size();\n \n for(int i = 0; i < m; i++) {\n for(int j = 0; j < n; j++) {\n if(grid[i][j] == \'B\') {\n B = make_pair(i, j);\n grid[i][j] = \'.\';\n } \n else if(grid[i][j] == \'S\') {\n P = make_pair(i, j);\n grid[i][j] = \'.\';\n } else if(grid[i][j] == \'T\') {\n T = make_pair(i, j);\n grid[i][j] = \'.\';\n } \n }\n }\n if(!canReachBox(grid)) return -1;\n \n \n queue<node> q;\n unordered_set<string> seen;\n for(int k = 0; k < 4; k++) {\n int tx = B.first + dx[k];\n int ty = B.second + dy[k];\n if(!canReachPosition(grid, P.first, P.second, tx, ty, B.first, B.second)) \n continue;\n auto nd = node(B.first, B.second, tx, ty);\n q.push(nd);\n seen.insert(nd.to_string());\n }\n int steps = 0;\n while(!q.empty()) {\n for(int t = q.size(); t > 0; t--) {\n auto node = q.front(); q.pop();\n int x = node.x, y = node.y;\n if(x == T.first && y == T.second) return steps;\n auto nodes = expand(grid, node);\n \n for(auto &node : nodes) {\n if(seen.count(node.to_string())) continue;\n q.push(node);\n seen.insert(node.to_string());\n } \n }\n steps++;\n }\n return -1;\n }\n}; | 1 | 0 | ['Breadth-First Search', 'C'] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | Python Dijkstra solution | python-dijkstra-solution-by-merciless-gir8 | ```\nclass Solution:\n def minPushBox(self, m: List[List[str]]) -> int:\n de = ((1,0),(0,1),(-1,0),(0,-1))\n rl,cl = len(m),len(m[0])\n | merciless | NORMAL | 2019-12-06T21:45:27.694143+00:00 | 2019-12-06T21:45:27.694177+00:00 | 302 | false | ```\nclass Solution:\n def minPushBox(self, m: List[List[str]]) -> int:\n de = ((1,0),(0,1),(-1,0),(0,-1))\n rl,cl = len(m),len(m[0])\n memo, q = set(), []\n for i in range(rl):\n for j in range(cl):\n if m[i][j] == "T":\n tx,ty = i,j\n elif m[i][j] == "S":\n a,b = i,j\n elif m[i][j] == "B":\n c,d = i,j\n memo.add((a, b, c, d))\n q += (0,a,b,c,d),\n while q:\n t, x, y, bx, by = heapq.heappop(q)\n for d in de:\n nx, ny = x + d[0], y + d[1]\n if 0 <= nx < rl and 0 <= ny < cl:\n nbx, nby = bx + d[0], by + d[1]\n if nx == bx and ny == by and 0 <= nbx < rl and 0 <= nby < cl and m[nbx][nby] != "#" and (nx, ny, nbx, nby) not in memo:\n if nbx == tx and nby == ty:\n return t + 1\n memo.add((nx, ny, nbx, nby))\n heapq.heappush(q, (t + 1, nx, ny, nbx, nby))\n elif m[nx][ny] != "#" and (nx, ny, bx, by) not in memo:\n memo.add((nx, ny, bx, by))\n heapq.heappush(q, (t, nx, ny, bx, by))\n return -1 | 1 | 0 | [] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | Golang BFS Solution | golang-bfs-solution-by-shuoyan-b5dj | Inspired by : https://leetcode.com/problems/minimum-moves-to-move-a-box-to-their-target-location/discuss/431431/Java-straightforward-BFS-solution\n\ngolang\nfun | shuoyan | NORMAL | 2019-12-05T06:21:39.782382+00:00 | 2019-12-05T06:22:22.281353+00:00 | 108 | false | Inspired by : https://leetcode.com/problems/minimum-moves-to-move-a-box-to-their-target-location/discuss/431431/Java-straightforward-BFS-solution\n\n```golang\nfunc minPushBox(grid [][]byte) int {\n\tmv := [5]int{0, 1, 0, -1, 0}\n\tres := math.MaxInt32\n\tm := len(grid)\n\tn := len(grid[0])\n\tqueue := make([]int, 0, m*n)\n\tmem := make(map[int]int)\n\ttarget, st, box := [2]int{}, [2]int{}, [2]int{}\n\tfor i := 0; i < m; i++ {\n\t\tfor j := 0; j < n; j++ {\n\t\t\tswitch grid[i][j] {\n\t\t\tcase \'B\':\n\t\t\t\tbox = [2]int{i, j}\n\t\t\tcase \'T\':\n\t\t\t\ttarget = [2]int{i, j}\n\t\t\tcase \'S\':\n\t\t\t\tst = [2]int{i, j}\n\t\t\t}\n\t\t}\n\t}\n\tstart := encode(box[0], box[1], st[0], st[1])\n\tqueue = append(queue, start)\n\tmem[start] = 0\n\tfor len(queue) > 0 {\n\t\tcur := queue[0]\n\t\tqueue = queue[1:]\n\t\tif mem[cur] > res {\n\t\t\tcontinue\n\t\t}\n\t\tpos := decode(cur)\n\t\tif pos[0] == target[0] && pos[1] == target[1] {\n\t\t\tif mem[cur] < res {\n\t\t\t\tres = mem[cur]\n\t\t\t}\n\t\t\tcontinue\n\t\t}\n\t\tb := [2]int{pos[0], pos[1]}\n\t\ts := [2]int{pos[2], pos[3]}\n\t\tfor i := 0; i < 4; i++ {\n\t\t\tsx := s[0] + mv[i]\n\t\t\tsy := s[1] + mv[i+1]\n\t\t\tif sx >= 0 && sx < m && sy >= 0 && sy < n && grid[sx][sy] != \'#\' {\n\t\t\t\tif sx == b[0] && sy == b[1] {\n\t\t\t\t\t//if the store keeper can move to the box position, check if the box can move one step further\n\t\t\t\t\tnbx := b[0] + mv[i]\n\t\t\t\t\tnby := b[1] + mv[i+1]\n\t\t\t\t\tif nbx >= 0 && nby >= 0 && nbx < m && nby < n && grid[nbx][nby] != \'#\' {\n\t\t\t\t\t\tnewpos := encode(nbx, nby, sx, sy)\n\t\t\t\t\t\tif val, ok := mem[newpos]; ok && val <= mem[cur]+1 {\n\t\t\t\t\t\t\tcontinue\n\t\t\t\t\t\t}\n\t\t\t\t\t\tqueue = append(queue, newpos)\n\t\t\t\t\t\tmem[newpos] = mem[cur] + 1\n\t\t\t\t\t}\n\t\t\t\t} else {\n\t\t\t\t\t//the store keeper move to other position, the number of steps shall not change\n\t\t\t\t\tnewpos := encode(b[0], b[1], sx, sy)\n\t\t\t\t\tif val, ok := mem[newpos]; ok && val <= mem[cur] {\n\t\t\t\t\t\tcontinue\n\t\t\t\t\t}\n\t\t\t\t\tmem[newpos] = mem[cur]\n\t\t\t\t\tqueue = append(queue, newpos)\n\t\t\t\t}\n\t\t\t}\n\t\t}\n\t}\n\tif res == math.MaxInt32 {\n\t\treturn -1\n\t} else {\n\t\treturn res\n\t}\n}\n\nfunc encode(bx int, by int, sx int, sy int) int {\n\tres := bx<<24 | by<<16 | sx<<8 | sy\n\treturn res\n}\n\nfunc decode(state int) [4]int {\n\tres := [4]int{}\n\tres[0] = (state >> 24) & 0xff\n\tres[1] = (state >> 16) & 0xff\n\tres[2] = (state >> 8) & 0xff\n\tres[3] = (state) & 0xff\n\treturn res\n}\n```\n\nMy other solutions in Golang: https://github.com/yinfirefire/LeetCode-GoSol | 1 | 0 | [] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | python3, 32ms, 100%, tarjan+A* | python3-32ms-100-tarjana-by-typingmonkey-toyf | python []\nclass Solution:\n def minPushBox(self, grid: List[List[str]]) -> int:\n m, n, g = len(grid), len(grid[0]), collections.defaultdict(list)\n | typingmonkeyli | NORMAL | 2019-12-02T17:33:19.002426+00:00 | 2019-12-12T15:24:35.870387+00:00 | 254 | false | ```python []\nclass Solution:\n def minPushBox(self, grid: List[List[str]]) -> int:\n m, n, g = len(grid), len(grid[0]), collections.defaultdict(list)\n for i in range(m):\n for j in range(n):\n g[grid[i][j]] += [complex(i, j)]\n def f(b, s): \n nonlocal time\n time += 1\n\t\t\tboxToTarget = b - target\n return (abs((boxToTarget).real) + abs((boxToTarget).imag) + s, abs(boxToTarget), time)\n player, box, target, time = *g[\'S\'], *g[\'B\'], *g[\'T\'], 1\n floor = {player, target, box, *g[\'.\']}\n alphaStarQueue = [(f(box, 1), 1, player, box)]\n directions, visited = (1, 1j, -1, -1j), set()\n low = dict.fromkeys(floor, 0)\n dfn = low.copy()\n count = 0\n index = {}\n def tarjan(currIndex, parentIndex):\n nonlocal count\n count += 1\n dfn[currIndex] = low[currIndex] = count\n index[count] = currIndex\n for direction in directions:\n nextIndex = currIndex + direction\n if nextIndex in floor and nextIndex != parentIndex:\n if not low[nextIndex]:\n tarjan(nextIndex, currIndex)\n low[currIndex] = min(low[currIndex], low[nextIndex])\n tarjan(box, -1)\n for currIndex in floor:\n connect = [currIndex]\n while dfn[connect[-1]] != low[connect[-1]]:\n connect.append(index[low[connect[-1]]])\n for w in connect[: -2]:\n low[w] = low[connect[-1]]\n while alphaStarQueue:\n _, steps, currPlayer, currBox = heapq.heappop(alphaStarQueue)\n for direction in directions:\n nextPlayer, nextBox = currBox - direction, currBox + direction\n if nextBox in floor \\\n and nextPlayer in floor \\\n and (nextPlayer, currBox) not in visited \\\n and low[currPlayer] == low[nextPlayer]:\n if nextBox == target:\n return steps\n heapq.heappush( alphaStarQueue, (f(nextBox, steps + 1), steps + 1, currBox, nextBox))\n visited.add((nextPlayer, currBox))\n return -1\n``` | 1 | 0 | [] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | Java | java-by-jzyz-v34k | \nimport java.util.*;\n\nclass Solution {\n int m, n;\n char[][] grid;\n private static final int[][] DIRECTIONS = {{1, 0}, {0, 1}, {-1, 0}, {0, -1}};\ | jzyz | NORMAL | 2019-11-24T01:43:52.662710+00:00 | 2019-11-24T01:43:52.662745+00:00 | 245 | false | ```\nimport java.util.*;\n\nclass Solution {\n int m, n;\n char[][] grid;\n private static final int[][] DIRECTIONS = {{1, 0}, {0, 1}, {-1, 0}, {0, -1}};\n\n public int minPushBox(char[][] grid) {\n Queue<int[]> q1 = new ArrayDeque<>();\n int[] man = null, box = null, destination = null;\n m = grid.length;\n n = grid[0].length;\n this.grid = grid;\n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n if (grid[i][j] == \'T\') {\n grid[i][j] = \'.\';\n destination = new int[]{i, j};\n } else if (grid[i][j] == \'S\') {\n man = new int[]{i, j};\n grid[i][j] = \'.\';\n } else if (grid[i][j] == \'B\') {\n box = new int[]{i, j};\n grid[i][j] = \'.\';\n }\n }\n }\n Set<String> set = new HashSet<>();\n if (goUp(man, box)) {\n set.add(box[0] - 1 + " " + box[1] + " " + box[0] + " " + box[1]);\n q1.add(new int[]{box[0] - 1, box[1], box[0], box[1]});\n }\n if (goDown(man, box)) {\n set.add(box[0] + 1 + " " + box[1] + " " + box[0] + " " + box[1]);\n q1.add(new int[]{box[0] + 1, box[1], box[0], box[1]});\n }\n if (goLeft(man, box)) {\n set.add(box[0] + " " + (box[1] - 1) + " " + box[0] + " " + box[1]);\n q1.add(new int[]{box[0], box[1] - 1, box[0], box[1]});\n }\n if (goRight(man, box)) {\n set.add(box[0] + " " + (box[1] + 1) + " " + box[0] + " " + box[1]);\n q1.add(new int[]{box[0], box[1] + 1, box[0], box[1]});\n }\n if (q1.isEmpty()) return -1;\n int step = 0;\n while (!q1.isEmpty()) {\n int size = q1.size();\n for (int z = 0; z < size; z++) {\n int[] node = q1.poll();\n box = new int[]{node[2], node[3]};\n man = new int[]{node[0], node[1]};\n if (node[2] == destination[0] && node[3] == destination[1]) {\n return step;\n }\n if (goRight(man, box)) {\n goFromRight(box, set, q1);\n }\n if (goUp(man, box)) {\n goFromUp(box, set, q1);\n }\n if (goDown(man, box)) {\n goFromDown(box, set, q1);\n }\n if (goLeft(man, box)) {\n goFromLeft(box, set, q1);\n }\n }\n step++;\n }\n return -1;\n }\n\n private void goFromRight(int[] box, Set<String> set, Queue<int[]> q1) {\n String next = box[0] + " " + box[1] + " " + box[0] + " " + (box[1] - 1);\n if (box[1] - 1 >= 0 && !set.contains(next) && grid[box[0]][box[1] - 1] == \'.\') {\n set.add(next);\n q1.add(new int[]{box[0], box[1], box[0], box[1] - 1});\n }\n }\n\n private void goFromLeft(int[] box, Set<String> set, Queue<int[]> q1) {\n String next = box[0] + " " + box[1] + " " + box[0] + " " + box[1] + 1;\n if (box[1] + 1 < n && !set.contains(next) && grid[box[0]][box[1] + 1] == \'.\') {\n set.add(next);\n q1.add(new int[]{box[0], box[1], box[0], box[1] + 1});\n }\n }\n\n private void goFromDown(int[] box, Set<String> set, Queue<int[]> q1) {\n String next = box[0] + " " + box[1] + " " + (box[0] - 1) + " " + box[1];\n if (box[0] - 1 >= 0 && !set.contains(next) && grid[box[0] - 1][box[1]] == \'.\') {\n set.add(next);\n q1.add(new int[]{box[0], box[1], box[0] - 1, box[1]});\n }\n }\n\n private void goFromUp(int[] box, Set<String> set, Queue<int[]> q1) {\n String next = box[0] + " " + box[1] + " " + (box[0] + 1) + " " + box[1];\n if (box[0] + 1 < m && !set.contains(next) && grid[box[0] + 1][box[1]] == \'.\') {\n set.add(next);\n q1.add(new int[]{box[0], box[1], box[0] + 1, box[1]});\n }\n }\n\n private boolean goUp(int[] man, int[] box) {\n return bfs(man, box[0] - 1, box[1], box);\n }\n\n private boolean goDown(int[] man, int[] box) {\n return bfs(man, box[0] + 1, box[1], box);\n }\n\n private boolean goLeft(int[] man, int[] box) {\n return bfs(man, box[0], box[1] - 1, box);\n }\n\n private boolean goRight(int[] man, int[] box) {\n return bfs(man, box[0], box[1] + 1, box);\n }\n\n private boolean bfs(int[] man, int iEnd, int jEnd, int[] box) {\n if (iEnd < 0 || iEnd >= m || jEnd < 0 || jEnd >= n) {\n return false;\n }\n Queue<int[]> q = new ArrayDeque<>();\n q.add(man);\n boolean[][] visited = new boolean[m][n];\n visited[man[0]][man[1]] = true;\n while (!q.isEmpty()) {\n int[] node = q.poll();\n if (node[0] == iEnd && node[1] == jEnd) {\n return true;\n }\n for (int[] dir : DIRECTIONS) {\n int x = dir[0] + node[0];\n int y = dir[1] + node[1];\n if (Arrays.equals(new int[]{x, y}, box)) continue;\n if (x >= 0 && y >= 0 && x < m && y < n && grid[x][y] == \'.\' && !visited[x][y]) {\n q.add(new int[]{x, y});\n visited[x][y] = true;\n }\n }\n }\n return false;\n }\n}\n``` | 1 | 0 | [] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | BFS + DFS Simple C++ solution | Easy to understand with Explanation | bfs-dfs-simple-c-solution-easy-to-unders-i0zu | Intuition:\n\n1. For a moment lets forget about the player and reduce our problem to what is the minimum push that is required to place the box to it\'s target? | himsingh11 | NORMAL | 2019-11-21T18:31:17.945247+00:00 | 2019-12-02T03:06:42.955283+00:00 | 646 | false | Intuition:\n\n1. For a moment lets forget about the player and reduce our problem to `what is the minimum push that is required to place the box to it\'s target?` , the obvious answer come to our mind is to use BFS to get this answer.\n2. Now we can assume what if someone has to push the box to place it to target and we have given the player position in matrix. It is also given that player can move in all 4 directions, it means same movement is also allowed to box if we are pushing it along the way.\n3. Then we can ask ourselves.. ohh how do we do that? How can we reach box, then only we can push. We can simply use dfs to get the answer. Like if box is reachable then we might push it along the way if push is valid.\n4. Now for a moment just ignore constraint and ask ourselves what if player is doing same push again? Like if we are doing same push again then it is of no use to us. So we can store this information in a set using pair. [You can think it is as a loop in a graph]\n\nConsider below example, assume we pushed B to its right when player stands left to B. But `current` player\'s position `S\'` can be reached via different path in this matrix. So this push we save in a set and for next same push we can ignore as result will be same.\n\n\t\t\t [["#","#","#","#","#","#"],\n ["#","T",".",".","#","#"],\n ["#",".","S\'","B",".","#"],\n ["#",".",".",".",".","#"],\n ["#",".",".",".","S","#"],\n ["#","#","#","#","#","#"]]\n\n5. So final Idea is to first do dfs to reach box with given constraint and then add all possible push to queue [basically all its neighbor push]. \n6. To handle case where we cannot pass through the box, before we start visiting all the neighbors of current Box position , we set the value in grid to `#` and then revert it back to `.` \n\n```cpp\nclass Solution {\npublic:\n //direction vector\n vector<vector<int>> dir {{0,1},{0,-1},{1,0},{-1,0}};\n \n int minPushBox(vector<vector<char>>& grid) {\n //rows, cols\n int N = grid.size();\n int M = grid[0].size();\n \n //intitial position\n int target=-1, box =-1, player = -1;\n \n //calcluate distance of target, box, player in grid\n for(int i=0; i<N;i++){\n for(int j=0;j <M;j++){\n if(grid[i][j]==\'S\'){\n player = i * M + j;\n }\n if(grid[i][j]==\'B\'){\n box = i*M + j;\n } \n if(grid[i][j]==\'T\'){\n target = i*M + j;\n }\n }\n }\n //set stl to track player-box movement\n //if already visited same path, ignore it\n set<pair<int, int>> visited;\n visited.insert({player, box});\n \n //declare queue for BFS\n //move box to all it\'s eligible neighbor\n queue<pair<int,int>> q;\n q.push({player, box});\n \n int ans =0;\n while(!q.empty()){\n \n ans++;\n \n //size of neighbor to be visited\n int size = q.size();\n \n while(size--){\n \n auto f = q.front();\n q.pop();\n \n //current box position \n int box_curr = f.second;\n //get box position in matrix\n int box_x = box_curr/ M;\n int box_y = box_curr % M;\n //palyer position\n int p = f.first;\n \n //make grid with box as obstacle \n grid[box_x][box_y] = \'#\';\n \n for(auto &d : dir){\n \n int new_box_x = box_x + d[0];\n int new_box_y = box_y + d[1];\n \n int px = box_x - d[0];\n int py = box_y - d[1];\n \n //to be used in dfs walk by player to reach box\n vector<vector<int>> walk(N, vector<int>(M, 0));\n \n if(isValid(grid, new_box_x, new_box_y) && canWalk(grid, p/M, p %M, px, py, walk) && visited.count({px * M + py, new_box_x*M + new_box_y})==0){\n \n if(new_box_x == target/M && new_box_y==target%M)\n return ans;\n \n visited.insert({px * M + py, new_box_x * M + new_box_y});\n q.push({px * M + py, new_box_x * M + new_box_y});\n }\n } \n grid[box_x][box_y] = \'.\';\n }\n \n }\n \n return -1;\n }\n \n bool isValid(vector<vector<char>>& grid, int i, int j){\n if(i < 0 || i>=grid.size() || j <0 || j>=grid[0].size() || grid[i][j]==\'#\')\n return false;\n \n return true;\n }\n \n bool canWalk(vector<vector<char>>& grid, int x, int y, int i, int j, vector<vector<int>>& walk){\n if(x==i && y==j)\n return true;\n \n for(auto &d: dir){\n int nx = x + d[0], ny = y+d[1]; \n if(isValid(grid, nx, ny) && walk[nx][ny] == 0){\n walk[nx][ny] = 1;\n if(canWalk(grid, nx, ny, i, j, walk))\n return true;\n }\n }\n return false;\n }\n};\n```\n\nCredit : https://leetcode.com/problems/minimum-moves-to-move-a-box-to-their-target-location/discuss/431144/cpp-BFS-%2B-DFS-solution | 1 | 0 | ['Depth-First Search', 'Breadth-First Search', 'C++'] | 1 |
minimum-moves-to-move-a-box-to-their-target-location | Python3 nested BFS (95.82%) | python3-nested-bfs-9582-by-ye15-q7aj | Outer BFS - move box to next place \nInner BFS - check if player can be placed to move box to next place \n\n\nfrom itertools import product\n\nclass Solution:\ | ye15 | NORMAL | 2019-11-20T06:12:49.658819+00:00 | 2019-11-20T06:12:49.658851+00:00 | 164 | false | Outer BFS - move box to next place \nInner BFS - check if player can be placed to move box to next place \n\n```\nfrom itertools import product\n\nclass Solution:\n def minPushBox(self, grid: List[List[str]]) -> int:\n #constants\n m, n = len(grid), len(grid[0]) #dimensions\n neighbors = ((-1,0), (1,0), (0,-1), (0,1)) \n \n #initial values\n for i, j in product(range(m), range(n)):\n if grid[i][j] == "B": box = i, j\n elif grid[i][j] == "S": player = i, j\n elif grid[i][j] == "T": target = i, j\n \n #helper functions\n not_wall = lambda i, j: 0 <= i < m and 0 <= j < n and grid[i][j] !="#" #true if not wall\n \n def connected(s, d):\n """bfs to check if s and d are connected"""\n queue = [s]\n seen = set(queue)\n for i, j in queue: #okay to change size\n for di, dj in neighbors:\n ii, jj = i + di, j + dj\n if not_wall(ii, jj) and (ii, jj) != box and (ii, jj) not in seen: \n queue.append((ii, jj))\n seen.add((ii, jj))\n if d in seen: return True\n return False \n \n #logic -- nested bfs \n final = set((target, (target[0]+di, target[1]+dj)) for di, dj in neighbors)\n \n moves = 0 \n queue = [(box, player)] #initial position\n seen = set(queue)\n while queue: #bfs by level \n temp = []\n for box, player in queue:\n i, j = box\n for di, dj in neighbors:\n if not_wall(i+di, j+dj) and ((i+di, j+dj), (i, j)) not in seen and not_wall(i-di, j-dj) and connected(player, (i-di, j-dj)):\n temp.append(((i+di, j+dj), (i, j)))\n seen.add(((i+di, j+dj), (i, j)))\n queue = temp\n moves += 1\n if seen & final: return moves #final configuration => arrive at target\n return -1 \n``` | 1 | 0 | ['Python3'] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | The reason of adding person location in seen or visited set. | the-reason-of-adding-person-location-in-74k1u | If BFS is used, if we do not add the location of the person to the seen set, we will get an error for the following test case. It is supposed to get 8, however, | liketheflower | NORMAL | 2019-11-19T04:36:29.212027+00:00 | 2019-11-19T04:37:06.750465+00:00 | 114 | false | If BFS is used, if we do not add the location of the person to the seen set, we will get an error for the following test case. It is supposed to get 8, however, without the person add in the seen set, we will get -1.\nThe @ location is critical. When the box is pushed to the location of "@", it has to be moved to the left of @ then the person can go to the left region throught the only entry which is the right of the @. If only box location not the person location is added in the seen. As the first time when the box is moved to @ location, it will be added to seen, and since it is in the seen, box can not be pushed back to the @ location again. This explains why it will get -1. If we add person location also, we will get rid of the problem.\n```python\n#["#",".",".","#","T","#","#","#","#"],\n#["#",".",".","#",".","#",".",".","#"],\n#["#",".",".","#",".","#","B",".","#"],\n#["#",".",".",".","@",".",".",".","#"],\n#["#",".",".",".",".","#",".","S","#"], \n#["#",".",".","#",".","#","#","#","#"]]\n```\nHope it is helpful. | 1 | 0 | [] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | Summary of BFS+BFS, BFS+DFS, BFS+UnionFind and other possible ways. | summary-of-bfsbfs-bfsdfs-bfsunionfind-an-qxi1 | The solution to this problem can be: BFS + BFS or BFS + DFS or BFS + Union Find\nIn the code\nbi, bj, pi, pj mean the box location and person location. ti, tj m | liketheflower | NORMAL | 2019-11-19T04:14:35.373565+00:00 | 2019-11-19T04:39:59.760735+00:00 | 237 | false | The solution to this problem can be: BFS + BFS or BFS + DFS or BFS + Union Find\nIn the code\nbi, bj, pi, pj mean the box location and person location. ti, tj mean the target location of the person in order to push the box.\nSolution 1(BFS + BFS, runtime 160ms)\n```python\nclass Solution:\n def minPushBox(self, grid: List[List[str]]) -> int:\n R, C = len(grid), len(grid[0])\n for i in range(R):\n for j in range(C):\n if grid[i][j] == \'S\':\n pi, pj = i, j\n elif grid[i][j] == \'B\':\n bi, bj = i, j\n \n def bfs_person(i, j, ti, tj, bi, bj):\n seen = set()\n if ti>=R or tj>=C or grid[ti][tj]==\'#\':return False\n cur_level = {(i,j)}\n while cur_level:\n nxt_level = set()\n for i,j in cur_level:\n if (i,j)==(ti,tj):return True\n seen.add((i, j))\n for di, dj in [(1, 0),(-1, 0), (0, 1), (0, -1)]:\n r, c = i+di, j+dj\n if 0<=r<R and 0<=c<C and (r,c)!=(bi,bj) and (r,c) not in seen and grid[r][c]!=\'#\':\n nxt_level.add((r,c))\n cur_level = nxt_level\n return False \n \n def bfs(i, j, pi, pj):\n b_seen = set()\n cur_level = {(i,j, pi, pj, 0)}\n while cur_level:\n nxt_level = set()\n for i, j, pi, pj, d in cur_level:\n b_seen.add((i,j, pi, pj))\n if grid[i][j] == \'T\':return d\n for di, dj in [(1, 0),(-1, 0), (0, 1), (0, -1)]:\n r, c = i+di, j+dj\n if 0<=r<R and 0<=c<C and grid[r][c]!=\'#\' and (r,c, i, j) not in b_seen:\n ti, tj = i-di, j-dj\n if bfs_person(pi, pj, ti, tj, i, j):\n nxt_level.add((r,c,i, j, d+1))\n cur_level = nxt_level \n return -1\n return bfs(bi, bj, pi, pj)\n```\nSolution 2(BFS + DFS runtime 632 ms)\n```python\nclass Solution:\n def minPushBox(self, grid: List[List[str]]) -> int:\n R, C = len(grid), len(grid[0])\n for i in range(R):\n for j in range(C):\n if grid[i][j] == \'S\':\n pi, pj = i, j\n elif grid[i][j] == \'B\':\n bi, bj = i, j\n \n def dfs_person(i, j, ti, tj, bi, bj):\n seen = set()\n if ti>=R or tj>=C or grid[ti][tj]==\'#\':return False\n open_list = [(i,j)]\n while open_list:\n i,j = open_list.pop()\n if (i,j)==(ti,tj):return True\n seen.add((i, j))\n for di, dj in [(1, 0),(-1, 0), (0, 1), (0, -1)]:\n r, c = i+di, j+dj\n if 0<=r<R and 0<=c<C and (r,c)!=(bi,bj) and (r,c) not in seen and grid[r][c]!=\'#\':\n open_list.append((r,c))\n return False\n \n \n def bfs(i, j, pi, pj):\n b_seen = set()\n cur_level = {(i,j, pi, pj, 0)}\n while cur_level:\n nxt_level = set()\n for i, j, pi, pj, d in cur_level:\n b_seen.add((i,j, pi, pj))\n if grid[i][j] == \'T\':return d\n for di, dj in [(1, 0),(-1, 0), (0, 1), (0, -1)]:\n r, c = i+di, j+dj\n if 0<=r<R and 0<=c<C and grid[r][c]!=\'#\' and (r,c, i, j) not in b_seen:\n ti, tj = i-di, j-dj\n if dfs_person(pi, pj, ti, tj, i, j):\n nxt_level.add((r,c,i, j, d+1))\n cur_level = nxt_level \n return -1\n return bfs(bi, bj, pi, pj)\n```\nSolution 3(BFS + Union Find runtime1608 ms)\n```python\nclass Solution:\n def minPushBox(self, grid: List[List[str]]) -> int:\n R, C = len(grid), len(grid[0])\n self.uf = {}\n for i in range(R):\n for j in range(C):\n if grid[i][j] == \'S\':\n pi, pj = i, j\n elif grid[i][j] == \'B\':\n bi, bj = i, j\n def find(x):\n self.uf.setdefault(x, x)\n if self.uf[x] != x:\n self.uf[x] = find(self.uf[x])\n return self.uf[x]\n \n def union(x, y):\n self.uf[find(y)] = find(x)\n \n def union_find(i, j, bi, bj):\n open_list = [(i,j)]\n seen = set()\n while open_list:\n i,j = open_list.pop()\n seen.add((i, j))\n for di, dj in [(1, 0),(-1, 0), (0, 1), (0, -1)]:\n r, c = i+di, j+dj\n if 0<=r<R and 0<=c<C and (r,c)!=(bi,bj) and (r,c) not in seen and grid[r][c]!=\'#\':\n union((i, j), (r, c))\n open_list.append((r, c)) \n \n def bfs(i, j, pi, pj):\n b_seen = set()\n cur_level = {(i,j, pi, pj, 0)}\n while cur_level:\n nxt_level = set()\n for i, j, pi, pj, d in cur_level:\n b_seen.add((i,j, pi, pj))\n if grid[i][j] == \'T\':return d\n children = [(i+di, j+dj, i-di, j-dj) \n for di, dj in [(1, 0),(-1, 0), (0, 1), (0, -1)]\n if 0<=i+di<R and 0<=j+dj<C and grid[i+di][j+dj]!=\'#\' and (i+di, j+dj, i, j) not in b_seen]\n if children:\n self.uf = {}\n union_find(pi, pj , i, j)\n for r, c, ti, tj in children:\n if find((ti, tj)) == find((pi, pj)):\n nxt_level.add((r,c,i, j, d+1))\n cur_level = nxt_level \n return -1\n return bfs(bi, bj, pi, pj)\n```\nSolution 4(BFS + DFS TLE) The reason that this solution is TLE might be the open_list size is too large if we keep all levels elements in the whole list. Solution 2 compares with this solution, only the open_list part is changed to only maintain the current level and next level. The speed of solution 2 is much faster and can get accepted.\n```python\nclass Solution:\n def minPushBox(self, grid: List[List[str]]) -> int:\n R, C = len(grid), len(grid[0])\n for i in range(R):\n for j in range(C):\n if grid[i][j] == \'S\':\n pi, pj = i, j\n elif grid[i][j] == \'B\':\n bi, bj = i, j\n \n def dfs_person(i, j, ti, tj, bi, bj):\n seen = set()\n if ti>=R or tj>=C or grid[ti][tj]==\'#\':return False\n open_list = [(i,j)]\n while open_list:\n i,j = open_list.pop()\n if (i,j)==(ti,tj):return True\n seen.add((i, j))\n for di, dj in [(1, 0),(-1, 0), (0, 1), (0, -1)]:\n r, c = i+di, j+dj\n if 0<=r<R and 0<=c<C and (r,c)!=(bi,bj) and (r,c) not in seen and grid[r][c]!=\'#\':\n open_list.append((r,c))\n return False \n \n def bfs(i, j, pi, pj):\n b_seen = set()\n open_list = [(i,j, pi, pj, 0)]\n for i, j, pi, pj, d in open_list:\n b_seen.add((i,j, pi, pj))\n if grid[i][j] == \'T\':return d\n for di, dj in [(1, 0),(-1, 0), (0, 1), (0, -1)]:\n r, c = i+di, j+dj\n if 0<=r<R and 0<=c<C and grid[r][c]!=\'#\' and (r,c, i, j) not in b_seen:\n ti, tj = i-di, j-dj\n if dfs_person(pi, pj, ti, tj, i, j):\n open_list.append((r,c,i, j, d+1)) \n return -1\n return bfs(bi, bj, pi, pj)\n```\nSolution 5 (BFS + DFS return a seen set 788 ms) It seems in this case union find is slower than DFS.\n```python\nclass Solution:\n def minPushBox(self, grid: List[List[str]]) -> int:\n R, C = len(grid), len(grid[0])\n for i in range(R):\n for j in range(C):\n if grid[i][j] == \'S\':\n pi, pj = i, j\n elif grid[i][j] == \'B\':\n bi, bj = i, j\n \n def dfs_person(i, j, bi, bj):\n seen = set()\n open_list = [(i,j)]\n while open_list:\n i,j = open_list.pop()\n seen.add((i, j))\n for di, dj in [(1, 0),(-1, 0), (0, 1), (0, -1)]:\n r, c = i+di, j+dj\n if 0<=r<R and 0<=c<C and (r,c)!=(bi,bj) and (r,c) not in seen and grid[r][c]!=\'#\':\n open_list.append((r,c))\n return seen \n \n def bfs(i, j, pi, pj):\n b_seen = set()\n cur_level = {(i,j, pi, pj, 0)}\n while cur_level:\n nxt_level = set()\n for i, j, pi, pj, d in cur_level:\n b_seen.add((i,j, pi, pj))\n if grid[i][j] == \'T\':return d\n children = [(i+di, j+dj, i-di, j-dj) \n for di, dj in [(1, 0),(-1, 0), (0, 1), (0, -1)]\n if 0<=i+di<R and 0<=j+dj<C and grid[i+di][j+dj]!=\'#\' and (i+di, j+dj, i, j) not in b_seen]\n if children:\n seen = dfs_person(pi, pj , i, j)\n for r, c, ti, tj in children:\n if (pi, pj) in seen and (ti, tj ) in seen:\n nxt_level.add((r,c,i, j, d+1))\n cur_level = nxt_level \n return -1\n return bfs(bi, bj, pi, pj)\n```\nSolution 6 (BFS + DFS change data type of open_list for DFS from list to set runtime 192 ms) No idea why it can have such a significant speedup. The appending, traversing and pop speed between list and set should not be that much. Still unclear about this part.\n```python\nclass Solution:\n def minPushBox(self, grid: List[List[str]]) -> int:\n R, C = len(grid), len(grid[0])\n for i in range(R):\n for j in range(C):\n if grid[i][j] == \'S\':\n pi, pj = i, j\n elif grid[i][j] == \'B\':\n bi, bj = i, j\n \n def dfs_person(i, j, ti, tj, bi, bj):\n seen = set()\n if ti>=R or tj>=C or grid[ti][tj]==\'#\':return False\n open_list = {(i,j)}\n while open_list:\n i,j = open_list.pop()\n if (i,j)==(ti,tj):return True\n seen.add((i, j))\n for di, dj in [(1, 0),(-1, 0), (0, 1), (0, -1)]:\n r, c = i+di, j+dj\n if 0<=r<R and 0<=c<C and (r,c)!=(bi,bj) and (r,c) not in seen and grid[r][c]!=\'#\':\n open_list.add((r,c))\n return False\n \n \n def bfs(i, j, pi, pj):\n b_seen = set()\n cur_level = {(i,j, pi, pj, 0)}\n while cur_level:\n nxt_level = set()\n for i, j, pi, pj, d in cur_level:\n b_seen.add((i,j, pi, pj))\n if grid[i][j] == \'T\':return d\n for di, dj in [(1, 0),(-1, 0), (0, 1), (0, -1)]:\n r, c = i+di, j+dj\n if 0<=r<R and 0<=c<C and grid[r][c]!=\'#\' and (r,c, i, j) not in b_seen:\n ti, tj = i-di, j-dj\n if dfs_person(pi, pj, ti, tj, i, j):\n nxt_level.add((r,c,i, j, d+1))\n cur_level = nxt_level \n return -1\n return bfs(bi, bj, pi, pj)\n```\nFrom this post, hope it can be helpful for a better understanding about the difference and connections between BFS, DFS, and union-find.\n\nReference\nhttps://leetcode.com/problems/minimum-moves-to-move-a-box-to-their-target-location/discuss/431138/Python-straightforward-BFS-solution | 1 | 0 | [] | 1 |
minimum-moves-to-move-a-box-to-their-target-location | Python [for newbie] BFS, borrowed from @davyjing | python-for-newbie-bfs-borrowed-from-davy-emxf | I cleaned a bit the excellent code of @davyjing for new comers. \n\nclass Solution:\n def minPushBox(self, grid: List[List[str]]) -> int:\n m, n = len | bos | NORMAL | 2019-11-17T19:37:50.576501+00:00 | 2019-11-18T17:39:58.237015+00:00 | 233 | false | I cleaned a bit the excellent code of @davyjing for new comers. \n```\nclass Solution:\n def minPushBox(self, grid: List[List[str]]) -> int:\n m, n = len(grid), len(grid[0])\n for i in range(m):\n for j in range(n):\n if grid[i][j] == \'B\': box = (i, j)\n if grid[i][j] == \'T\': target = (i, j)\n if grid[i][j] == \'S\': player = (i, j)\n \n if target == box: return 0\n \n def can_get(cur_b, cur_p, pos): # can player get to a certain position pos\n if cur_p == pos: return True\n seen = {cur_p}\n q = [cur_p]\n for x, y in q:\n for X, Y in ([(x-1, y), (x+1, y), (x, y-1), (x, y+1)]):\n if 0 <= X < m and 0 <= Y < n and (X, Y) not in seen and grid[X][Y] != \'#\' and (X, Y) != cur_b:\n if (X, Y) == pos:\n return True\n seen.add((X, Y))\n q.append((X, Y))\n return False\n \n q, seen, ans = {(box, player)}, {(box, player)}, 0\n dire = [(-1, 0), (1, 0), (0, -1), (0, 1)]\n while q:\n tmp = []\n ans += 1\n for b, p in q:\n for d in dire:\n nb = (b[0] + d[0], b[1] + d[1])\n oppo = (b[0] - d[0], b[1] - d[1]) # player is required to be the opposite side of the box to push\n if 0 <= nb[0] < m and 0 <= nb[1] < n and grid[nb[0]][nb[1]] != \'#\' and can_get(b, p, oppo) and (nb, b) not in seen:\n tmp.append((nb, b))\n q = set(tmp)\n seen |= q\n for d in dire:\n if (target, (target[0]+d[0], target[1]+d[1])) in seen:\n return ans\n \n return -1\n``` | 1 | 0 | [] | 1 |
minimum-moves-to-move-a-box-to-their-target-location | BFS with (box pos+ direction) as the state | bfs-with-box-pos-direction-as-the-state-y21jl | \n\nclass Solution {\n int m=0,n=0;\n public int minPushBox(char[][] grid) {\n m=grid.length;\n n=grid[0].length;\n int sx=0,sy=0,bx= | leon123 | NORMAL | 2019-11-17T06:09:49.925487+00:00 | 2019-11-17T06:09:49.925535+00:00 | 151 | false | ```\n\nclass Solution {\n int m=0,n=0;\n public int minPushBox(char[][] grid) {\n m=grid.length;\n n=grid[0].length;\n int sx=0,sy=0,bx=0,by=0,tx=0,ty=0;\n for(int i=0;i<m;i++) for(int j=0;j<n;j++){\n if(grid[i][j]==\'S\'){sx=i;sy=j;grid[i][j]=\'.\';}\n if(grid[i][j]==\'T\'){tx=i;ty=j;grid[i][j]=\'.\';}\n if(grid[i][j]==\'B\'){bx=i;by=j;grid[i][j]=\'.\';}\n }\n \n Queue<int[]> q=new LinkedList();\n boolean[][][] visited=new boolean[m][n][4];\n if(valid(grid,sx,sy,bx-1,by,bx,by)) {q.offer(new int[]{bx,by,0});visited[bx][by][0]=true;}\n if(valid(grid,sx,sy,bx+1,by,bx,by)) {q.offer(new int[]{bx,by,1});visited[bx][by][1]=true;}\n if(valid(grid,sx,sy,bx,by+1,bx,by)) {q.offer(new int[]{bx,by,2});visited[bx][by][2]=true;}\n if(valid(grid,sx,sy,bx,by-1,bx,by)) {q.offer(new int[]{bx,by,3});visited[bx][by][3]=true;}\n int depth=0;\n while(!q.isEmpty()){\n int size=q.size();\n for(int i=0;i<size;i++){\n int[] v=q.poll();\n int[] d=trans(v[2]);\n int x=v[0]-d[0],y=v[1]-d[1];//move one step x,y is new box position\n //System.out.println(v[0]+"-"+v[1]+"##"+x+"-"+y+"");\n if(x<0||x>m-1||y<0||y>n-1) continue;\n if(grid[x][y]!=\'.\') continue;\n if(x==tx&&y==ty) return depth+1;\n //grid[v[0]][v[1]]=\'.\';\n //grid[x][y]=\'B\';\n for(int[] dir:dirs){\n if(valid(grid,v[0],v[1],x+dir[0],y+dir[1],x,y)) {\n int dd=transv(dir);\n if(visited[x][y][dd]) continue;\n visited[x][y][dd]=true;\n q.offer(new int[]{x,y,dd});\n }\n }\n //grid[x][y]=\'.\';\n //grid[v[0]][v[1]]=\'B\';\n }\n depth++;\n }\n return -1;\n }\n \n private boolean valid(char[][] graph,int sx,int sy,int tx,int ty,int bx,int by){\n if(tx<0||tx>m-1||ty<0||ty>n-1) return false;\n if(graph[tx][ty]!=\'.\') return false;\n Queue<int[]> q=new LinkedList();\n boolean[][] visited=new boolean[m][n];\n q.offer(new int[]{sx,sy});visited[sx][sy]=true;\n \n while(!q.isEmpty()){\n int size=q.size();\n for(int i=0;i<size;i++){\n int[] v=q.poll();\n if(v[0]==tx&&v[1]==ty) return true;\n for(int[] dir:dirs){\n int x=v[0]+dir[0],y=v[1]+dir[1];\n if(x<0||x>m-1||y<0||y>n-1) continue;\n if(graph[x][y]!=\'.\') continue;\n if(x==bx&&y==by) continue;\n if(visited[x][y]) continue;\n visited[x][y]=true;\n q.offer(new int[]{x,y});\n }\n }\n \n }\n return false;\n }\n \n \n private int[][] dirs={{-1,0},{1,0},{0,1},{0,-1}};\n private int[] trans(int dir){\n int[] res=new int[2];\n if(dir==0) res[0]=-1;\n else if(dir==1) res[0]=1;\n else if(dir==2) res[1]=1;\n else res[1]=-1;\n return res;\n }\n \n private int transv(int[] dir){\n if(dir[0]==-1) return 0;\n else if(dir[0]==1) return 1;\n else if(dir[1]==1) return 2;\n else if(dir[1]==-1) return 3;\n return -1;\n }\n \n}\n\n``` | 1 | 0 | [] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | Python3 2-level BFS, a few notes | python3-2-level-bfs-a-few-notes-by-hello-nql0 | A few key points that distinguishes this problem from your typical BFS:\n\n1. To push the box to a specific direction, player has to be at the opposite directio | helloterran | NORMAL | 2019-11-17T05:09:59.178280+00:00 | 2019-11-17T05:10:19.453873+00:00 | 231 | false | A few key points that distinguishes this problem from your typical BFS:\n\n1. To push the box to a specific direction, player has to be at the opposite direction. So there needs be empty space on both sides\n\n2. Player has to be able to find a path from previous position to the needed position described in point 1 above\n\n3. Box position changes everytime players moves it, which affects point 2 above\n\n4, Box can return to a previous location if coming from different direction.\n\n```\nclass Solution:\n def minPushBox(self, grid: List[List[str]]) -> int:\n h = len(grid)\n w = len(grid[0])\n \n target, box, player = (0,0), (0,0), (0,0)\n for row in range(h):\n for col in range(w):\n if grid[row][col] == \'B\':\n cur = (row, col)\n if grid[row][col] == \'T\':\n target = (row, col)\n if grid[row][col] == \'S\':\n player = (row, col)\n\n dirs = [(0, 1), (0, -1), (1, 0), (-1 ,0)]\n \n def has_path(pos, target):\n # print(grid)\n myq = [pos]\n visited = set()\n while myq:\n cur = myq.pop(0)\n if cur == target:\n return True\n for dir in dirs:\n new_pos = (cur[0] + dir[0], cur[1] + dir[1])\n if new_pos[0] >= 0 and new_pos[0] < h and new_pos[1] >= 0 and new_pos[1] < w:\n if grid[new_pos[0]][new_pos[1]] != \'#\' and grid[new_pos[0]][new_pos[1]] != \'B\' and new_pos not in visited:\n myq.append(new_pos)\n visited.add(new_pos)\n return False\n\n myq = [(cur, player, 0)]\n visited = set()\n grid[box[0]][box[1]] = \'.\' \n \n while myq:\n box, player, cur_round = myq.pop(0)\n if box == target:\n return cur_round\n grid[box[0]][box[1]] = \'B\' # \u83B7\u5F97\u5F53\u524D\u7BB1\u5B50\u7684\u4F4D\u7F6E\n for dir in dirs:\n new_pos = (box[0] + dir[0], box[1] + dir[1])\n oppo_pos = (box[0] - dir[0], box[1] - dir[1])\n if new_pos[0] >= 0 and new_pos[0] < h and new_pos[1] >= 0 and new_pos[1] < w:\n if oppo_pos[0] >= 0 and oppo_pos[0] < h and oppo_pos[1] >= 0 and oppo_pos[1] < w:\n # \u5982\u679C\u6765\u7684\u65B9\u5411\u4E0D\u540C\uFF0C\u90A3\u4E48\u7BB1\u5B50\u53EF\u4EE5\u56DE\u5230\u4E4B\u524D\u7ECF\u8FC7\u5230\u8FC7\u7684\u4F4D\u7F6E\n if grid[new_pos[0]][new_pos[1]] != \'#\' and grid[oppo_pos[0]][oppo_pos[1]] != \'#\' and (new_pos, box) not in visited: \n if has_path(player, oppo_pos): # player \u80FD\u5426\u5230\u8FBE\u9700\u8981\u5230\u8FBE\u7684\u4F4D\u7F6E\n myq.append((new_pos, box, cur_round + 1))# \u63A8\u5B8C\u7BB1\u5B50\u540Eplayer\u5904\u4E8Ebox\u539F\u672C\u7684\u4F4D\u7F6E\n # print(box, \'->\', new_pos)\n visited.add((new_pos, box))\n grid[box[0]][box[1]] = \'.\'\n return -1\n \n \n \n \n \n \n``` | 1 | 0 | [] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | one time bfs + priority_queue c++ (explaination included) | one-time-bfs-priority_queue-c-explainati-6tc9 | when we mark as visit we need two coords, box and keeper.\nbecause they all <= 20, so I just use 100 , and easy for debug,\nmy algorith first work on keeper min | 0xffffffff | NORMAL | 2019-11-17T04:28:59.858902+00:00 | 2019-11-17T04:38:07.925709+00:00 | 327 | false | when we mark as visit we need two coords, box and keeper.\nbecause they all <= 20, so I just use 100 , and easy for debug,\nmy algorith first work on keeper minimized moves, but the mini push is asked so have to use pq to pop min pushes.\n\n```\nclass Solution {\npublic:\n int minPushBox(vector<vector<char>>& grid) {\n\t // remember three coords, and retore them to not \'#\' it is road not wall\n int row = grid.size(), col = grid.front().size();\n pair<int, int> t, b, s;\n for (int r = 0; r < row; ++r) {\n for (int c = 0; c < col; ++c) {\n if (grid[r][c] == \'T\') {\n t = make_pair(r, c);\n grid[r][c] = \'.\';\n }\n if (grid[r][c] == \'B\') {\n b = make_pair(r, c);\n grid[r][c] = \'.\';\n }\n if (grid[r][c] == \'S\') {\n s = make_pair(r, c);\n grid[r][c] = \'.\';\n }\n }\n }\n priority_queue<pair<int, int>, vector<pair<int,int>>, greater<pair<int,int>>> q;\n unordered_set<int> vi;\n\t\t// step is pushes, and key contains two coords\n q.emplace(0, b.first * 1000000 + b.second * 10000 + s.first * 100 + s.second);\n vi.emplace(b.first * 1000000 + b.second * 10000 + s.first * 100 + s.second);\n\n\t\t// just helper function to get cell\n auto g = [&](int r, int c) {\n if (r < 0 || r >= row || c < 0 || c >= col) return \'#\';\n return grid[r][c];\n };\n\n\t\t// if keeper possible moves\n auto check = [&](int step, int br, int bc, int r, int c) {\n if (g(r, c) != \'.\') return;\n if (br == r && bc == c) return;\n int key = br * 1000000 + bc * 10000 + r * 100 + c;\n if (vi.count(key)) return;\n vi.emplace(key);\n q.emplace(step, key);\n };\n\n\t\t// if push is possible, we need +1 on steps if possible\n auto push = [&](int step, int br, int bc, int r, int c) {\n int key = -1;\n if (make_pair(r + 1, c) == make_pair(br, bc) && g(r + 2, c) == \'.\') {\n key = (br + 1) * 1000000 + bc * 10000 + (r + 1) * 100 + c;\n } else if (make_pair(r - 1, c) == make_pair(br, bc) && g(r - 2, c) == \'.\') {\n key = (br - 1) * 1000000 + bc * 10000 + (r - 1) * 100 + c;\n } else if (make_pair(r, c + 1) == make_pair(br, bc) && g(r, c + 2) == \'.\') {\n key = br * 1000000 + (bc + 1) * 10000 + r * 100 + c + 1;\n } else if (make_pair(r, c - 1) == make_pair(br, bc) && g(r, c - 2) == \'.\') {\n key = br * 1000000 + (bc - 1) * 10000 + r * 100 + c - 1;\n }\n if (key == -1) return;\n if (vi.count(key)) return;\n vi.emplace(key);\n q.emplace(step + 1, key);\n };\n\t\t// here is just simple bfs\n while (q.size()) {\n int step = q.top().first;\n int cbr = q.top().second / 1000000 % 100;\n int cbc = q.top().second / 10000 % 100;\n int csr = q.top().second / 100 % 100;\n int csc = q.top().second / 1 % 100;\n q.pop();\n if (cbr == t.first && cbc == t.second) return step;\n check(step, cbr, cbc, csr + 1, csc);\n check(step, cbr, cbc, csr, csc + 1);\n check(step, cbr, cbc, csr - 1, csc);\n check(step, cbr, cbc, csr, csc - 1);\n push(step, cbr, cbc, csr, csc);\n }\n return -1;\n }\n}; | 1 | 0 | [] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | 2-stage DFS solution using java | 2-stage-dfs-solution-using-java-by-hunte-cezf | I used minReach array to record minimal reach steps from 4 directions, then using dfs to walk step by step, finally return minReach of target position.\n\nclass | huntersjm | NORMAL | 2019-11-17T04:20:22.798494+00:00 | 2019-11-17T04:20:22.798548+00:00 | 464 | false | I used minReach array to record minimal reach steps from 4 directions, then using dfs to walk step by step, finally return minReach of target position.\n```\nclass Solution {\n public int minPushBox(char[][] grid) {\n int[][][] minReach = new int[grid.length][grid[0].length][4];\n for (int i = 0; i < minReach.length; i++) {\n for (int j = 0; j < minReach[0].length; j++) {\n for (int k = 0; k < minReach[0][0].length; k++) {\n minReach[i][j][k] = -1;\n }\n }\n }\n int px = 0, py = 0, bx = 0, by = 0, tx = 0, ty = 0;\n for (int i = 0; i < grid.length; i++) {\n for (int j = 0; j < grid[i].length; j++) {\n if (grid[i][j] == \'B\') {\n minReach[i][j][0] = 0;\n minReach[i][j][1] = 0;\n minReach[i][j][2] = 0;\n minReach[i][j][3] = 0;\n bx = i;\n by = j;\n } else if (grid[i][j] == \'T\') {\n tx = i;\n ty = j;\n } else if (grid[i][j] == \'S\') {\n px = i;\n py = j;\n }\n }\n }\n dfs(grid, minReach, bx, by, px, py, 0);\n int result = -1;\n for (int i = 0; i < 4; i++) {\n if (minReach[tx][ty][i] != -1) {\n if (result == -1) {\n result = minReach[tx][ty][i];\n } else {\n result = Math.min(result, minReach[tx][ty][i]);\n }\n }\n }\n return result;\n }\n\n private void dfs(char[][] grid, int[][][] minReach, int bx, int by, int px, int py, int current) {\n current++;\n if (bx + 1 < grid.length && grid[bx + 1][by] != \'#\' && (minReach[bx + 1][by][0] == -1 || current < minReach[bx + 1][by][0]) && canReach(grid, bx - 1, by, px, py)) {\n minReach[bx + 1][by][0] = current;\n grid[bx + 1][by] = \'B\';\n grid[bx][by] = \'.\';\n dfs(grid, minReach, bx + 1, by, bx - 1, by, current);\n grid[bx][by] = \'B\';\n grid[bx + 1][by] = \'.\';\n }\n\n if (bx - 1 >= 0 && grid[bx - 1][by] != \'#\' && (minReach[bx - 1][by][1] == -1 || current < minReach[bx - 1][by][1]) && canReach(grid, bx + 1, by, px, py)) {\n minReach[bx - 1][by][1] = current;\n grid[bx - 1][by] = \'B\';\n grid[bx][by] = \'.\';\n dfs(grid, minReach, bx - 1, by, bx + 1, by, current);\n grid[bx - 1][by] = \'.\';\n grid[bx][by] = \'B\';\n }\n\n if (by + 1 < grid[0].length && grid[bx][by + 1] != \'#\' && (minReach[bx][by + 1][2] == -1 || current < minReach[bx][by + 1][2]) && canReach(grid, bx, by - 1, px, py)) {\n minReach[bx][by + 1][2] = current;\n grid[bx][by + 1] = \'B\';\n grid[bx][by] = \'.\';\n dfs(grid, minReach, bx, by + 1, bx, by - 1, current);\n grid[bx][by + 1] = \'.\';\n grid[bx][by] = \'B\';\n }\n\n if (by - 1 >= 0 && grid[bx][by - 1] != \'#\' && (minReach[bx][by - 1][3] == -1 || current < minReach[bx][by - 1][3]) && canReach(grid, bx, by + 1, px, py)) {\n minReach[bx][by - 1][3] = current;\n grid[bx][by - 1] = \'B\';\n grid[bx][by] = \'.\';\n dfs(grid, minReach, bx, by - 1, bx, by + 1, current);\n grid[bx][by - 1] = \'.\';\n grid[bx][by] = \'B\';\n }\n }\n\n private boolean canReach(char[][] grid, int x, int y, int px, int py) {\n if (x < 0 || x >= grid.length || y < 0 || y >= grid[0].length || grid[x][y] == \'#\') {\n return false;\n }\n boolean[][] visit = new boolean[grid.length][grid[0].length];\n travel(grid, px, py, visit);\n return visit[x][y];\n }\n\n private void travel(char[][] grid, int px, int py, boolean[][] visit) {\n if (px >= 0 && px < grid.length && py >= 0 && py < grid[0].length && !visit[px][py] && grid[px][py] != \'#\' && grid[px][py] != \'B\') {\n visit[px][py] = true;\n travel(grid, px - 1, py, visit);\n travel(grid, px + 1, py, visit);\n travel(grid, px, py - 1, visit);\n travel(grid, px, py + 1, visit);\n }\n }\n\n public static void main(String[] args) {\n System.out.println(new Solution().minPushBox(new char[][]{{\'#\', \'#\', \'#\', \'#\', \'#\', \'#\'}, {\'#\', \'T\', \'#\', \'#\', \'#\', \'#\'}, {\'#\', \'.\', \'.\', \'B\', \'.\', \'#\'}, {\'#\', \'#\', \'#\', \'#\', \'.\', \'#\'}, {\'#\', \'.\', \'.\', \'.\', \'S\', \'#\'}, {\'#\', \'#\', \'#\', \'#\', \'#\', \'#\'}}));\n }\n}\n``` | 1 | 0 | [] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | Python - Very Upset. Finish 20 seconds after the contest end! | python-very-upset-finish-20-seconds-afte-ozgs | \nclass Solution:\n def minPushBox(self, grid: List[List[str]]) -> int:\n m, n = len(grid), len(grid[0])\n for i in range(m):\n for | llcourage123 | NORMAL | 2019-11-17T04:08:05.921839+00:00 | 2019-11-17T04:08:24.553104+00:00 | 262 | false | ```\nclass Solution:\n def minPushBox(self, grid: List[List[str]]) -> int:\n m, n = len(grid), len(grid[0])\n for i in range(m):\n for j in range(n):\n if grid[i][j] == "S":\n people = [i, j]\n if grid[i][j] == "T":\n end = [i, j]\n if grid[i][j] == "B":\n box = [i, j]\n if box == end: return 0\n dict1 = collections.defaultdict(int)\n dict1[tuple(box)] = 1\n queue = collections.deque()\n queue.append(box + [0] + people)\n cnt = 0\n while queue:\n x, y, step, nx, ny = queue.pop()\n if [x, y] == end:\n return step\n neighs = [[x+1, y, x-1, y], [x-1, y, x+1, y], [x, y-1, x, y+1], [x, y+1,x, y-1]]\n for dx, dy, sx, sy in neighs:\n if 0 <= dx < m and 0 <= dy < n:\n if dict1[(dx, dy)] < 4 and grid[dx][dy] != "#":\n if 0 <= sx < m and 0 <= sy < n and grid[sx][sy] != "#":\n if [sx, sy] == [x,y] or self.dfs([sx, sy], [nx, ny], grid, [x, y], set([(sx, sy)])):\n dict1[(dx, dy)] += 1\n queue.appendleft([dx, dy, step+1, x, y])\n cnt += 1\n return -1\n \n def dfs(self, start, end, grid, box, visited):\n m, n = len(grid), len(grid[0])\n if start == end: return True\n i, j = start\n neighs = [[i+1, j], [i-1, j], [i, j-1], [i, j+1]]\n tmp = False\n for di, dj in neighs:\n if 0 <= di < m and 0 <= dj < n:\n if grid[di][dj] != "#" and (di, dj) not in visited and [di, dj] != box:\n visited.add((di, dj))\n tmp = tmp or self.dfs([di, dj], end, grid, box, visited)\n if tmp:\n break\n return tmp\n \n``` | 1 | 1 | [] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | ✅✅✅Easiest Solution || Beats 76.69% || BFS Solution for LeetCode#1263✅✅✅✅ | easiest-solution-beats-7669-bfs-solution-kd2y | IntuitionThe problem requires pushing a box ('B') to a target ('T') while controlling a player ('S') in a grid with obstacles ('#'). The challenge is that the p | subhu04012003 | NORMAL | 2025-02-19T17:20:25.135698+00:00 | 2025-02-19T17:20:25.135698+00:00 | 5 | false | 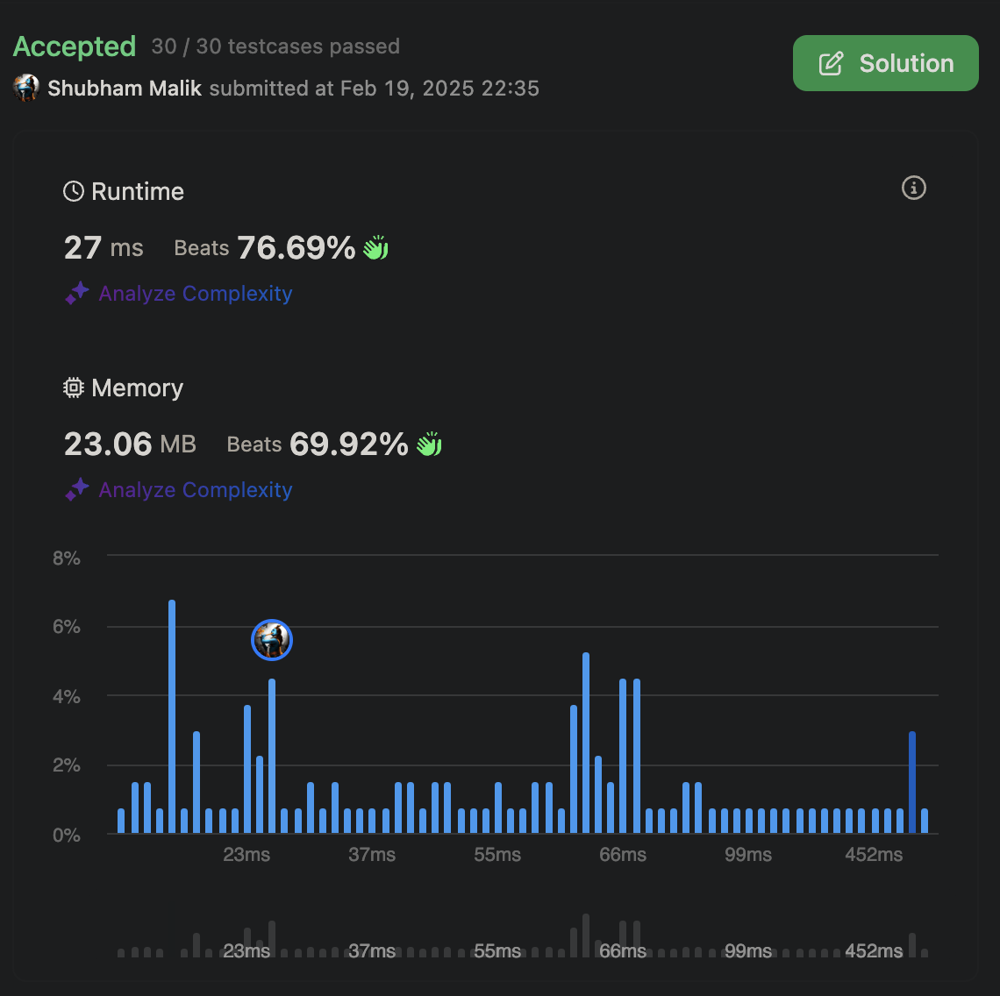
# Intuition
The problem requires pushing a box ('B') to a target ('T') while controlling a player ('S') in a grid with obstacles ('#'). The challenge is that the player must be in the correct position to push the box, and movement is constrained by walls.
Since we want to minimize the number of pushes, we need a shortest-path approach that prioritizes states with fewer pushes. This suggests using Dijkstra’s algorithm (priority queue / min-heap) to always expand the most promising state first.
# Approach
State Representation
Each state is represented as (boxX, boxY, playerX, playerY, pushes).
We track the box position, the player position, and the number of pushes made so far.
The goal is to move the box to the target (T) with the fewest pushes.
Priority Queue (Min-Heap)
We use a min-heap (priority_queue) to always process states with fewer pushes first.
This ensures we find the shortest push sequence optimally.
Valid Moves
The box moves only when pushed by the player.
The player must reach the correct pushing position before each move.
The box cannot move into walls ('#') or go out of bounds.
Algorithm (Dijkstra-like BFS with Priority Queue)
Initialize the priority queue with the starting state (boxX, boxY, playerX, playerY, 0 pushes).
Use BFS with a priority queue:
Extract the state with the least pushes.
Try all four possible box moves (right, left, down, up):
Compute the new box position.
Compute the required player position to push the box.
Check if the player can reach the required position (using BFS).
If valid, add the new state to the priority queue.
Return the minimum number of pushes when the box reaches the target.
If the box cannot reach the target, return -1.
# Complexity
- Time complexity: O( m^2 * n^2 )
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O( m^2 * n^2 )
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
bool isValid(const vector<vector<char>>& grid, int x, int y) {
return x >= 0 && y >= 0 && x < grid.size() && y < grid[0].size() &&
grid[x][y] != '#';
}
bool canReach(const vector<vector<char>>& grid, int startX, int startY,
int targetX, int targetY, int boxX, int boxY) {
queue<pair<int, int>> q;
q.push({startX, startY});
vector<vector<bool>> visited(grid.size(),
vector<bool>(grid[0].size(), false));
visited[startX][startY] = true;
vector<pair<int, int>> directions = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
while (!q.empty()) {
auto [x, y] = q.front();
q.pop();
if (x == targetX && y == targetY)
return true;
for (auto [dx, dy] : directions) {
int newX = x + dx, newY = y + dy;
if (isValid(grid, newX, newY) && !visited[newX][newY] &&
!(newX == boxX && newY == boxY)) {
visited[newX][newY] = true;
q.push({newX, newY});
}
}
}
return false;
}
int minPushBox(vector<vector<char>>& grid) {
int m = grid.size(), n = grid[0].size();
vector<int> box, player, target;
for (int i = 0; i < m; ++i)
for (int j = 0; j < n; ++j) {
if (grid[i][j] == 'B')
box = {i, j};
if (grid[i][j] == 'S')
player = {i, j};
if (grid[i][j] == 'T')
target = {i, j};
}
queue<tuple<int, int, int, int, int>> q;
q.push({box[0], box[1], player[0], player[1], 0});
vector<vector<vector<vector<bool>>>> visited(
m, vector<vector<vector<bool>>>(
n, vector<vector<bool>>(m, vector<bool>(n, false))));
visited[box[0]][box[1]][player[0]][player[1]] = true;
vector<pair<int, int>> directions = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
while (!q.empty()) {
auto [boxX, boxY, playerX, playerY, pushes] = q.front();
q.pop();
if (boxX == target[0] && boxY == target[1])
return pushes;
for (auto [dx, dy] : directions) {
int newBoxX = boxX + dx, newBoxY = boxY + dy;
int pushPosX = boxX - dx, pushPosY = boxY - dy;
if (!isValid(grid, newBoxX, newBoxY) ||
!isValid(grid, pushPosX, pushPosY))
continue;
if (visited[newBoxX][newBoxY][boxX][boxY])
continue;
if (canReach(grid, playerX, playerY, pushPosX, pushPosY, boxX, boxY)) {
visited[newBoxX][newBoxY][boxX][boxY] = true;
q.push({newBoxX, newBoxY, boxX, boxY, pushes + 1});
}
}
}
return -1;
}
};
``` | 0 | 0 | ['Array', 'Breadth-First Search', 'Heap (Priority Queue)', 'Matrix', 'C++'] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | Python Hard | python-hard-by-lucasschnee-2ush | null | lucasschnee | NORMAL | 2025-01-24T15:59:01.886349+00:00 | 2025-01-24T15:59:01.886349+00:00 | 8 | false | ```python3 []
class Solution:
def minPushBox(self, grid: List[List[str]]) -> int:
'''
m and n are very small
m * n * m * n is 20 ** 4 = 160000
so thats all we have to do
'''
directions = [(0, 1), (1, 0), (-1, 0), (0, -1)]
M, N = len(grid), len(grid[0])
INF = 10 ** 5
seen = [[[[INF for _ in range(N)] for _ in range(M)] for _ in range(N)] for _ in range(M)]
s = [0, 0, 0, 0, 0]
for i in range(M):
for j in range(N):
if grid[i][j] == "B":
s[3] = i
s[4] = j
grid[i][j] = "."
if grid[i][j] == "S":
s[1] = i
s[2] = j
grid[i][j] = "."
seen[s[1]][s[2]][s[3]][s[4]] = 0
h = []
heapq.heappush(h, tuple(s))
while h:
val, i, j, ii, jj = heapq.heappop(h)
# print(i, j, ii, jj)
# print(0, 4)
if seen[i][j][ii][jj] < val:
continue
# print(i, j, ii, jj)
if grid[ii][jj] == "T":
return val
# moving the character
for dx, dy in directions:
nx, ny = i + dx, j + dy
if (nx, ny) == (ii, jj):
continue
if not (0 <= nx < M) or not (0 <= ny < N):
continue
if grid[nx][ny] == "#":
continue
if seen[nx][ny][ii][jj] <= val:
continue
seen[nx][ny][ii][jj] = val
heapq.heappush(h, (val, nx, ny, ii, jj))
'''
box is at (1, 1)
o o o
o x o
o o o
4 cases
person at (0, 1) -> down or add 1 to ii
person at (1, 0) -> right or add 1 to jj
person at (2, 1) -> up or sub 1 to ii
person at (1, 2) -> left or sub 1 to jj
'''
if (i + 1, j) == (ii, jj):
nx, ny = i + 1, j
nxx, nyy = ii + 1, jj
if (0 <= nxx < M) and (0 <= nyy < N):
if grid[nxx][nyy] != "#":
nxt_val = val + 1
if seen[nx][ny][nxx][nyy] > nxt_val:
seen[nx][ny][nxx][nyy] = nxt_val
heapq.heappush(h, (nxt_val, nx, ny, nxx, nyy))
if (i, j + 1) == (ii, jj):
nx, ny = i, j + 1
nxx, nyy = ii, jj + 1
if (0 <= nxx < M) and (0 <= nyy < N):
if grid[nxx][nyy] != "#":
nxt_val = val + 1
if seen[nx][ny][nxx][nyy] > nxt_val:
seen[nx][ny][nxx][nyy] = nxt_val
heapq.heappush(h, (nxt_val, nx, ny, nxx, nyy))
if (i - 1, j) == (ii, jj):
nx, ny = i - 1, j
nxx, nyy = ii - 1, jj
if (0 <= nxx < M) and (0 <= nyy < N):
if grid[nxx][nyy] != "#":
nxt_val = val + 1
if seen[nx][ny][nxx][nyy] > nxt_val:
seen[nx][ny][nxx][nyy] = nxt_val
heapq.heappush(h, (nxt_val, nx, ny, nxx, nyy))
if (i, j - 1) == (ii, jj):
nx, ny = i, j - 1
nxx, nyy = ii, jj - 1
if (0 <= nxx < M) and (0 <= nyy < N):
if grid[nxx][nyy] != "#":
nxt_val = val + 1
if seen[nx][ny][nxx][nyy] > nxt_val:
seen[nx][ny][nxx][nyy] = nxt_val
heapq.heappush(h, (nxt_val, nx, ny, nxx, nyy))
return -1
``` | 0 | 0 | ['Python3'] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | 1263. Minimum Moves to Move a Box to Their Target Location | 1263-minimum-moves-to-move-a-box-to-thei-5l86 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | G8xd0QPqTy | NORMAL | 2025-01-04T04:33:45.005281+00:00 | 2025-01-04T04:33:45.005281+00:00 | 10 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int minPushBox(char[][] grid) {
int m = grid.length, n = grid[0].length;
int[][] directions = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
int[] box = new int[2], target = new int[2], player = new int[2];
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++) {
if (grid[i][j] == 'B') box = new int[]{i, j};
else if (grid[i][j] == 'T') target = new int[]{i, j};
else if (grid[i][j] == 'S') player = new int[]{i, j};
}
Queue<int[]> queue = new LinkedList<>();
queue.add(new int[]{box[0], box[1], player[0], player[1], 0});
boolean[][][][] visited = new boolean[m][n][m][n];
visited[box[0]][box[1]][player[0]][player[1]] = true;
while (!queue.isEmpty()) {
int[] curr = queue.poll();
int bx = curr[0], by = curr[1], px = curr[2], py = curr[3], pushes = curr[4];
if (bx == target[0] && by == target[1]) return pushes;
for (int[] dir : directions) {
int nx = bx + dir[0], ny = by + dir[1];
int pxNew = bx - dir[0], pyNew = by - dir[1];
if (nx >= 0 && nx < m && ny >= 0 && ny < n && pxNew >= 0 && pxNew < m && pyNew >= 0 && pyNew < n &&
grid[nx][ny] != '#' && grid[pxNew][pyNew] != '#' &&
!visited[nx][ny][bx][by] && canReach(grid, px, py, pxNew, pyNew, bx, by)) {
visited[nx][ny][bx][by] = true;
queue.add(new int[]{nx, ny, bx, by, pushes + 1});
}
}
}
return -1;
}
private boolean canReach(char[][] grid, int sx, int sy, int tx, int ty, int bx, int by) {
int m = grid.length, n = grid[0].length;
Queue<int[]> queue = new LinkedList<>();
queue.add(new int[]{sx, sy});
boolean[][] visited = new boolean[m][n];
visited[sx][sy] = true;
while (!queue.isEmpty()) {
int[] curr = queue.poll();
int x = curr[0], y = curr[1];
if (x == tx && y == ty) return true;
for (int[] dir : new int[][]{{0, 1}, {1, 0}, {0, -1}, {-1, 0}}) {
int nx = x + dir[0], ny = y + dir[1];
if (nx >= 0 && nx < m && ny >= 0 && ny < n && grid[nx][ny] != '#' && !visited[nx][ny] && (nx != bx || ny != by)) {
visited[nx][ny] = true;
queue.add(new int[]{nx, ny});
}
}
}
return false;
}
}
``` | 0 | 0 | ['Java'] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | My java 8ms solution 87% faster | my-java-8ms-solution-87-faster-by-raghav-6luz | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | raghavrathore7415 | NORMAL | 2024-10-20T13:55:11.361188+00:00 | 2024-10-20T13:57:35.206919+00:00 | 7 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int minPushBox(char[][] grid) {\n int sr = 0, sc = 0;\n int er = 0, ec = 0, r = 0, c = 0;\n for(int i = 0; i < grid.length; i++){\n for(int j = 0; j < grid[0].length; j++){\n if(grid[i][j] == \'T\'){\n er = i;\n ec = j;\n }\n if(grid[i][j] == \'B\'){\n sr = i;\n sc = j;\n }\n if(grid[i][j] == \'S\'){\n r = i;\n c = j;\n }\n }\n }\n boolean[][][][] vis = new boolean[grid.length][grid[0].length][grid.length][grid[0].length];\n ArrayDeque<int[]> q = new ArrayDeque<>();\n dfs(r, c, sr, sc, grid, vis, q);\n grid[sr][sc] = \'.\';\n int lvl = 1;\n while(!q.isEmpty()){\n int size = q.size();\n for(int i = 0; i < size; i++){\n int[] curr = q.poll();\n if(curr[2] == er && curr[3] == ec){\n return lvl - 1;\n }\n int nextR = curr[2] + curr[4];\n int nextC = curr[3] + curr[5];\n if(valid(nextR, nextC, grid)){\n curr[0] += curr[4];\n curr[1] += curr[5];\n curr[2] = nextR;\n curr[3] = nextC;\n }\n grid[curr[2]][curr[3]] = \'B\'; // putting block in the path and trying all the ways a person can stand near the box\n dfs(curr[0], curr[1], curr[2], curr[3], grid, vis, q);\n grid[curr[2]][curr[3]] = \'.\'; // remove block again\n }\n lvl++;\n }\n return -1;\n }\n\n public boolean valid(int r, int c, char[][] grid){\n if(r < 0 || r == grid.length || c < 0 || c == grid[0].length || grid[r][c] == \'#\'){\n return false;\n }\n return true;\n }\n\n public void dfs(int r, int c, int er, int ec, char[][] grid, boolean[][][][] vis, ArrayDeque<int[]> q){\n if(r < 0 || r == grid.length || c < 0 || c == grid[0].length || grid[r][c] == \'#\' || \n grid[r][c] == \'B\' || vis[r][c][er][ec]){\n return;\n }\n check(r, c, er, ec, grid, q);\n vis[r][c][er][ec] = true;\n dfs(r + 1, c, er, ec, grid, vis, q);\n dfs(r - 1, c, er, ec, grid, vis, q);\n dfs(r, c + 1, er, ec, grid, vis, q);\n dfs(r, c - 1, er, ec, grid, vis, q);\n }\n\n public void check(int r, int c, int er, int ec, char[][] grid, ArrayDeque<int[]> q){\n if(r == er){\n if(c + 1 == ec){\n q.offer(new int[]{r, c, er, ec, 0, 1});\n }else if(c - 1 == ec){\n q.offer(new int[]{r, c, er, ec, 0, -1});\n }\n }else if(c == ec){\n if(r + 1 == er){\n q.offer(new int[]{r, c, er, ec, 1, 0});\n }else if(r - 1 == er){\n q.offer(new int[]{r, c, er, ec, -1, 0});\n }\n }\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | Python3 | Modified BFS and Heap | python3-modified-bfs-and-heap-by-tigprog-99rv | Complexity\n- Time complexity: O(m^2 \cdot n^2 \cdot \log(m^2 \cdot n^2))\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(m^2 \cdot n^2)\n | tigprog | NORMAL | 2024-10-07T16:45:33.308088+00:00 | 2024-10-07T16:46:06.487942+00:00 | 7 | false | # Complexity\n- Time complexity: $$O(m^2 \\cdot n^2 \\cdot \\log(m^2 \\cdot n^2))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(m^2 \\cdot n^2)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nimport heapq\n\nclass Solution:\n def minPushBox(self, grid: List[List[str]]) -> int:\n table = set()\n p = b = target = None\n for i, line in enumerate(grid):\n for j, elem in enumerate(line):\n if elem == \'#\':\n continue\n table.add((i, j))\n if elem == \'S\': # player\n p = (i, j)\n elif elem == \'B\': # box\n b = (i, j)\n elif elem == \'T\': # target\n target = (i, j)\n \n h = [(0, p, b)]\n in_progress = set()\n\n while h:\n dist, p, b = heapq.heappop(h)\n if (p, b) in in_progress:\n continue\n in_progress.add((p, b))\n\n if b == target:\n return dist\n \n dx = b[0] - p[0]\n dy = b[1] - p[1]\n if (\n (abs(dx) == 1 and dy == 0)\n or (abs(dy) == 1 and dx == 0)\n ):\n new_b = (b[0] + dx, b[1] + dy)\n if new_b in table:\n heapq.heappush(h, (dist + 1, b, new_b))\n \n for dx, dy in ((-1, 0), (1, 0), (0, -1), (0, 1)):\n new_p = (p[0] + dx, p[1] + dy)\n if new_p in table and new_p != b:\n heapq.heappush(h, (dist, new_p, b))\n \n return -1\n``` | 0 | 0 | ['Breadth-First Search', 'Heap (Priority Queue)', 'Matrix', 'Python3'] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | 1263. Minimum Moves to Move a Box to Their Target Location.cpp | 1263-minimum-moves-to-move-a-box-to-thei-owkf | Code\n\nclass Solution {\nprivate:\n int m, n;\n vector<pair<int, int>> dir;\n struct Hash {\n size_t operator()(const vector<int> &v) const {\n | 202021ganesh | NORMAL | 2024-09-20T09:46:11.727143+00:00 | 2024-09-20T09:46:11.727171+00:00 | 0 | false | **Code**\n```\nclass Solution {\nprivate:\n int m, n;\n vector<pair<int, int>> dir;\n struct Hash {\n size_t operator()(const vector<int> &v) const {\n return v[0] * 20 + v[1] + v[2] * 20 + v[3];\n }\n };\n unordered_set<vector<int>, Hash> visited;\n struct Hash2 {\n size_t operator()(const vector<int> &v) const {\n return v[0] * 20 + v[1];\n }\n }; \npublic:\n int minPushBox(vector<vector<char>>& grid) {\n m = grid.size();\n n = grid[0].size();\n dir = vector<pair<int, int>>{{-1, 0}, {1, 0}, {0, -1}, {0, 1}};\n vector<int> target, box, person;\n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n if (grid[i][j] == \'S\') {\n person = vector<int>{i, j};\n } else if (grid[i][j] == \'B\') {\n box = vector<int>{i, j};\n } else if (grid[i][j] == \'T\') {\n target = vector<int>{i, j};\n }\n }\n }\n queue<vector<int>> q;\n q.push(vector<int>{box[0], box[1], person[0], person[1]});\n visited.insert(vector<int>{box[0], box[1], person[0], person[1]});\n int res = 0;\n while (!q.empty()) {\n int N = q.size();\n while (N--) {\n vector<int> cur = q.front();\n q.pop();\n if (cur[0] == target[0] && cur[1] == target[1])\n return res;\n for (auto &d : dir) {\n int b_row_nex = cur[0] + d.first;\n int b_col_nex = cur[1] + d.second;\n int p_row_nex = cur[0] - d.first;\n int p_col_nex = cur[1] - d.second;\n if (valid(grid, b_row_nex, b_col_nex) && valid(grid, p_row_nex, p_col_nex)) {\n if (canReach(grid, cur, p_row_nex, p_col_nex) &&\n visited.find(vector<int>{b_row_nex, b_col_nex, cur[0], cur[1]}) == visited.end()) {\n q.push(vector<int>{b_row_nex, b_col_nex, cur[0], cur[1]});\n visited.insert(vector<int>{b_row_nex, b_col_nex, cur[0], cur[1]});\n }\n }\n }\n }\n res += 1;\n }\n return -1;\n } \n bool canReach(vector<vector<char>> &grid, vector<int> &start, int &p_row, int &p_col) {\n queue<vector<int>> q;\n unordered_set<vector<int>, Hash2> visited2;\n q.push(vector<int>{start[2], start[3]});\n visited2.insert(vector<int>{start[2], start[3]});\n while (!q.empty()) {\n vector<int> cur = q.front();\n q.pop();\n if (cur[0] == p_row && cur[1] == p_col)\n return true;\n for (auto &d : dir) {\n int row_nex = cur[0] + d.first;\n int col_nex = cur[1] + d.second;\n if (valid(grid, row_nex, col_nex) && !(row_nex == start[0] && col_nex == start[1]) &&\n visited2.find(vector<int>{row_nex, col_nex}) == visited2.end()) {\n q.push(vector<int>{row_nex, col_nex});\n visited2.insert(vector<int>{row_nex, col_nex});\n }\n }\n }\n return false;\n } \n bool valid(vector<vector<char>> &grid, int row, int col) {\n return row >= 0 && row < m && col >= 0 && col < n && grid[row][col] != \'#\';\n }\n};\n``` | 0 | 0 | ['C'] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | C++ - Double BFS | c-double-bfs-by-a4yan1-ksuc | Code\n\nclass Solution {\npublic:\n static constexpr int drow[4] = {-1,0,1,0};\n static constexpr int dcol[4] = {0,1,0,-1};\n bool isPossible(int box_r | a4yan1 | NORMAL | 2024-08-18T04:04:18.198933+00:00 | 2024-08-18T04:04:18.198965+00:00 | 25 | false | # Code\n```\nclass Solution {\npublic:\n static constexpr int drow[4] = {-1,0,1,0};\n static constexpr int dcol[4] = {0,1,0,-1};\n bool isPossible(int box_row,int box_col,int dest_row,int dest_col,int row,int col,vector<vector<char>> &grid){\n int n = grid.size(); int m = grid[0].size();\n if(dest_row < 0 || dest_col < 0 || dest_row >=n || dest_col >=m || grid[dest_row][dest_col] == \'#\') return false;\n vector<vector<int>> vis(grid.size(),vector<int> (grid[0].size(),0));\n vis[row][col] = 1;\n queue<pair<int,int>> q;\n q.push({row,col});\n while(!q.empty()){\n auto it = q.front();\n int r = it.first;\n int c = it.second;\n q.pop();\n if(r == dest_row && c == dest_col) return true;\n for(int i=0;i<4;i++){\n int nrow = r + drow[i];\n int ncol = c + dcol[i];\n if(nrow >=0 && ncol>=0 && nrow < n && ncol < m && !vis[nrow][ncol] && grid[nrow][ncol] == \'.\'){\n if(nrow == box_row && ncol == box_col) continue;\n q.push({nrow,ncol});\n vis[nrow][ncol] = 1;\n }\n }\n }\n return false;\n }\n int minPushBox(vector<vector<char>>& grid) {\n int n = grid.size(); int m = grid[0].size();\n pair<int,int> target = {-1,-1};\n pair<int,int> man = {-1,-1};\n pair<int,int> block = {-1,-1};\n for(int i=0;i<n;i++){\n for(int j=0;j<m;j++){\n if(grid[i][j] == \'T\') target = {i,j};\n else if(grid[i][j] == \'B\') block = {i,j};\n else if(grid[i][j] == \'S\') man = {i,j};\n else continue;\n }\n if(target.first != -1 && man.first != -1 && block.first!=-1) break;\n }\n map<pair<int,int>,pair<int,int>> mpp;\n mpp[{0,-1}] = {0,1};\n mpp[{0,1}] = {0,-1};\n mpp[{-1,0}] = {1,0};\n mpp[{1,0}] = {-1,0};\n grid[target.first][target.second] = \'.\';\n grid[block.first][block.second] = \'.\';\n grid[man.first][man.second] = \'.\';\n queue<vector<int>> q; // {dis,block_row,block_col,man_row,man_col}\n set<vector<int>> vis; // block,man\n q.push({0,block.first,block.second,man.first,man.second});\n while(!q.empty()){\n auto it = q.front();\n q.pop();\n int dis = it[0];\n int row = it[1];\n int col = it[2];\n int man_row = it[3];\n int man_col = it[4];\n if(row == target.first && col == target.second) return dis;\n for(int i=0;i<4;i++){\n int nrow = row + drow[i];\n int ncol = col + dcol[i];\n int opp_row = row + mpp[{drow[i],dcol[i]}].first;\n int opp_col = col + mpp[{drow[i],dcol[i]}].second;\n if(nrow >=0 && ncol >=0 && nrow < n && ncol < m && !vis.contains({nrow,ncol,row,col}) && grid[nrow][ncol] == \'.\' && isPossible(row,col,opp_row,opp_col,man_row,man_col,grid)){\n q.push({dis+1,nrow,ncol,row,col});\n vis.insert({nrow,ncol,row,col});\n }\n }\n }\n return -1;\n }\n};\n``` | 0 | 0 | ['Breadth-First Search', 'Matrix', 'C++'] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | C++ Solution || BFS || Easy to Understand || Fully Explanation | c-solution-bfs-easy-to-understand-fully-9dyq8 | Approach\n\nThis problem has two sub-problems:\n - Find the path from box to target, using BFS\n - Find the path from player to the position which is posi | dnanper | NORMAL | 2024-08-02T11:25:10.488476+00:00 | 2024-08-02T11:25:10.488498+00:00 | 13 | false | # Approach\n\nThis problem has two sub-problems:\n - Find the path from box to target, using BFS\n - Find the path from player to the position which is posible to push the box, using BFS\n \nBFS state is the position of the box and the player\n\nAfter push the box, the position of player is in the box\'s previous position\n\nA 2D-Map is used to memorize the position of the box and player \n\n\n# Complexity\n- Time complexity:\nO((n*m)^2)\n\n- Space complexity:\nO((n*m)^2)\n\n# Code\n```\nclass Solution {\npublic:\n int m, n;\n // up: 1 , down: 2, right: 3, left: 4\n bool valid(int x, int y, vector<vector<char>>& grid)\n {\n return x>=0 && x<m && y>=0 && y<n && grid[x][y]!=\'#\';\n }\n bool check(int x, int y, int box_x, int box_y, int t_x, int t_y, vector<vector<char>>& grid)\n {\n map<pair<int,int>, bool> visited;\n queue<pair<int,int>> mem;\n mem.push(make_pair(x,y));\n visited[make_pair(x,y)] = true;\n while ( !mem.empty() )\n {\n auto cur = mem.front();\n int cur_x = cur.first, cur_y = cur.second;\n if ( cur_x == t_x && cur_y == t_y ) return true;\n mem.pop();\n pair<int,int> new_pos[] = {{cur_x+1, cur_y}, {cur_x-1, cur_y}, {cur_x, cur_y-1},\n {cur_x, cur_y+1} };\n for ( auto u : new_pos )\n {\n if ( valid(u.first, u.second, grid) && !(u.first==box_x && u.second==box_y) && !visited[make_pair(u.first,u.second)] )\n {\n visited[make_pair(u.first,u.second)] = true;\n mem.push(make_pair(u.first,u.second));\n }\n }\n }\n return false;\n }\n \n int minPushBox(vector<vector<char>>& grid) \n {\n int b_x, b_y, t_x, t_y, s_x, s_y;\n m = grid.size(), n = grid[0].size();\n for ( int i = 0; i < m; i ++)\n for ( int j = 0; j < n; j++)\n {\n if ( grid[i][j] == \'B\' )\n {\n b_x = i;\n b_y = j;\n }\n if ( grid[i][j] == \'T\' )\n {\n t_x = i;\n t_y = j;\n }\n if ( grid[i][j] == \'S\' )\n {\n s_x = i;\n s_y = j;\n }\n } \n queue<tuple<int,int,int,int>> mem;\n mem.push(make_tuple(b_x,b_y,s_x,s_y));\n map<pair<int,int>, map<pair<int,int>, bool>> visited;\n visited[make_pair(b_x, b_y)][make_pair(s_x, s_y)] = true;\n int res = 0;\n while( !mem.empty() )\n {\n int k = mem.size();\n while ( k-- )\n {\n auto [x, y, p_x, p_y] = mem.front();\n mem.pop();\n\n if ( x == t_x && y == t_y ) return res;\n pair<int,int> step[] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};\n for (int i = 0; i < 4; i++)\n {\n int dx = step[i].first, dy = step[i].second;\n int new_x = x+dx, new_y = y+dy, p_new_x = x-dx, p_new_y = y-dy;\n if ( valid(new_x, new_y, grid) && valid(p_new_x, p_new_y, grid) &&\n check(p_x, p_y, x, y, p_new_x, p_new_y, grid) &&\n !visited[make_pair(new_x, new_y)][make_pair(x, y)] )\n {\n visited[make_pair(new_x, new_y)][make_pair(x, y)] = true;\n mem.push(make_tuple(new_x, new_y, x, y));\n }\n }\n }\n res++;\n }\n return -1;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | A* short C++ version | a-short-c-version-by-rsysz-pvhi | https://leetcode.com/problems/minimum-moves-to-move-a-box-to-their-target-location/solutions/431061/a-star-search/\n\n# Code\n\nstruct Node {\n int playerX, | rsysz | NORMAL | 2024-07-27T07:55:09.221778+00:00 | 2024-07-27T07:55:09.221800+00:00 | 0 | false | https://leetcode.com/problems/minimum-moves-to-move-a-box-to-their-target-location/solutions/431061/a-star-search/\n\n# Code\n```\nstruct Node {\n int playerX, playerY;\n int boxX, boxY;\n int g, h, f; // f = g + h\n\n bool operator < (const Node& n) const {\n return n.f < f;\n }\n};\n\nclass Solution {\npublic:\n vector<pair<int, int>> dirs{{0, -1}, {0, 1}, {-1, 0}, {1, 0}};\n int heuristic(Node& src, Node& dst) {\n return abs(src.boxX - dst.boxX) + abs(src.boxY - dst.boxY);\n }\n bool isValid(vector<vector<char>>& grid, int i, int j) {\n return i >= 0 && j >= 0 && i < grid.size() && j < grid[0].size() && grid[i][j] != \'#\';\n }\n int minPushBox(vector<vector<char>>& grid) {\n int m = grid.size(), n = grid[0].size();\n Node src, dst;\n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n if (grid[i][j] == \'S\') {\n src.playerX = i;\n src.playerY = j;\n }\n if (grid[i][j] == \'B\') {\n src.boxX = i;\n src.boxY = j;\n }\n if (grid[i][j] == \'T\') {\n dst.boxX = i;\n dst.boxY = j;\n }\n }\n }\n\n src.g = 0;\n src.h = heuristic(src, dst);\n src.f = src.g + src.h;\n\n priority_queue<Node> pq;\n pq.push(src);\n set<vector<int>> visited;\n \n\n while (!pq.empty()) {\n Node curr = pq.top();\n pq.pop();\n\n if (curr.boxX == dst.boxX && curr.boxY == dst.boxY)\n return curr.g;\n if (visited.count({curr.playerX, curr.playerY, curr.boxX, curr.boxY}))\n continue;\n visited.insert({curr.playerX, curr.playerY, curr.boxX, curr.boxY});\n\n for (auto& [dx, dy] : dirs) {\n Node next = curr;\n next.playerX = curr.playerX + dx;\n next.playerY = curr.playerY + dy;\n\n if (!isValid(grid, next.playerX, next.playerY))\n continue;\n \n if (next.playerX == curr.boxX && next.playerY == curr.boxY) {\n next.boxX = curr.boxX + dx;\n next.boxY = curr.boxY + dy;\n if (!isValid(grid, next.boxX, next.boxY))\n continue;\n \n next.g = curr.g + 1;\n next.h = heuristic(next, dst);\n next.f = next.g + next.h;\n }\n pq.push(next);\n }\n }\n return -1;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | Standard BFS with Twist - Expand on Pushes, not Steps | standard-bfs-with-twist-expand-on-pushes-kwlo | Intuition\n Describe your first thoughts on how to solve this problem. \nA very conventional BFS algorithm with a small twist. Instead of always adding to the e | matt_scott | NORMAL | 2024-07-26T03:36:12.069605+00:00 | 2024-07-26T03:36:12.069639+00:00 | 5 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nA very conventional BFS algorithm with a small twist. Instead of always adding to the end of the queue, we should prioritise nodes (greedily) with less steps and expand them first\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nAdd a state transition function: this generates the next shopkeep and box state from the current shopkeep and box state. \n\nIf the shopkeep moves in direction (x, y), and this movement coincides with the box, then it must be next to the box, and therefore will result in the box moving. In the latter case, we need to check if the box is OOB/hitting a `#`, otherwise we just check if the shopkeep is in a valid position.\n\nThen, just use a queue (Q) for the standard BFS, but append to the $$left$$ of the Q when we don\'t push the box, and append to the $right$ when we do. We then expand the least-pushed nodes first.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$O(n^4)$ - each state can hold the shopkeep in any position ($n^2$ positions) and the box in any position ($n^2$) positions, giving $n^2*n^2=n^4$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nSame as time complexity - we may need to store all states\n\n# Code\n```\nclass Solution:\n def minPushBox(self, grid: List[List[str]]) -> int:\n dirs = [[-1, 0], [0, -1], [1, 0], [0, 1]]\n M, N = len(grid), len(grid[0])\n\n q = deque()\n vis = set([(None, None)])\n\n initMan, initBox = None, None\n\n for i, r in enumerate(grid):\n for j, c in enumerate(r): \n if c == "S":\n initMan = (i, j)\n elif c == "B":\n initBox = (i, j)\n\n q.append((initMan, initBox, 0))\n \n // returns newManPos, newBoxPos, numPushes\n def getCoordChange(currMan, currBox, dirr):\n mX, mY = currMan\n bX, bY = currBox\n dx, dy = dirr\n\n nmX, nmY = mX + dx, mY + dy\n if nmX == bX and nmY == bY: // man facing box\n nbX, nbY = bX + dx, bY + dy // can box move??\n if 0 <= nbX < M and 0 <= nbY < N and grid[nbX][nbY] != "#":\n return ((nmX, nmY), (nbX, nbY)), 1\n\n elif 0 <= nmX < M and 0 <= nmY < N and grid[nmX][nmY] != "#":\n return ((nmX, nmY), (bX, bY)), 0\n\n // shopkeep neither in bounds nor facing box\n return (None, None), -1\n\n\n while q:\n for _ in range(len(q)):\n currMan, currBox, steps = q.popleft()\n\n if grid[currBox[0]][currBox[1]] == "T":\n return steps\n \n for d in dirs:\n newState, push = getCoordChange(currMan, currBox, d)\n if newState in vis:\n continue\n vis.add(newState)\n nextState = (*newState, steps + push)\n // if we pushed, expand later\n if push == 1:\n q.append(nextState)\n // if we didn\'t push, expand sooner\n else:\n q.appendleft(nextState)\n\n return -1\n\n``` | 0 | 0 | ['Python3'] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | Python 0-1 BFS, Straightforward | python-0-1-bfs-straightforward-by-brando-edyl | Intuition / Approach\nWe can view this problem is a state-space single source shortest path (SSSP) problem.\n\nWe formulate each state as a tuple $(r, c, x, y)$ | BrandonTang89 | NORMAL | 2024-07-21T07:43:18.764554+00:00 | 2024-07-21T07:43:50.994243+00:00 | 5 | false | # Intuition / Approach\nWe can view this problem is a state-space single source shortest path (SSSP) problem.\n\nWe formulate each state as a tuple $(r, c, x, y)$ where $(r,c)$ is the position of the player and $(x, y)$ is the position of the box.\n- The initial state is $(r, c, x, y)$ where `grid[r][c] = "S"` and `grid[x][y] = "B"`\n- The initial state is any $(r, c, x, y)$ where `grid[x][y] = "T"`\n\nThe edges of the graph between each state correspond to the character walking in one of the NSEW directions. \n- If the player doesn\'t push the box, cost 0\n- If the player pushes the box, cost 1\n\nSince the costs are 0 and 1, we can just do 0-1 BFS rather than Dijkstra. We maintain a deque of frontier nodes to explore and expand.\n- If the step cost 0, we push to the front of the deque\n- If the step cost 1, we push to the back of the deque\n- This ensures that the deque is always sorted by the cost of state and that we will exhaust all the states of distance $i$ before moving to states of distance $i+1$, ensuring correctness\n\n\n# Complexity\n- Time complexity: $O(H^2 W^2)$\n\n- Space complexity: $O(H^2 W^2)$\n\n# Code\n```\nfrom collections import deque \nclass Solution:\n def minPushBox(self, grid: List[List[str]]) -> int:\n h = len(grid)\n w = len(grid[0])\n\n sr, sc = -1, -1\n tr, tc = -1, -1\n pr, pc = -1, -1\n for r in range(h):\n for c in range(w):\n if grid[r][c] == \'S\':\n pr, pc = r, c\n grid[r][c] = \'.\'\n elif grid[r][c] == \'B\':\n sr, sc = r, c\n grid[r][c] = \'.\'\n elif grid[r][c] == \'T\':\n tr, tc = r, c\n grid[r][c] == \'.\'\n\n assert -1 not in {tr, tc, sr, sc, pr, pc}\n\n q = deque([(pr, pc, sr, sc)]) # (player row, player col, box row, box col)\n \n dist = {(pr, pc, sr, sc): 0}\n dr = [-1, 1, 0, 0]\n dc = [0, 0, 1, -1]\n\n def valid(r, c):\n if r >= h or r < 0 or c >= w or c < 0: return False # out of grid\n if grid[r][c] == "#": return False # impossible\n return True\n\n while len(q) > 0:\n state = q[0]\n q.popleft()\n\n r, c, br, bc = state\n print(state)\n if br == tr and bc == tc:\n return dist[state]\n\n for i in range(4):\n nr, nc = r + dr[i], c + dc[i]\n\n if not valid(nr, nc): continue\n if (nr, nc) == (br, bc):\n # check if box can be moved\n nbr, nbc = br + dr[i], bc + dc[i]\n if not valid(nbr, nbc): continue\n push = True\n else:\n nbr, nbc = br, bc\n push = False\n \n newState = (nr, nc, nbr, nbc)\n if newState in dist: continue\n \n if push:\n dist[newState] = dist[state] + 1\n q.append(newState)\n else:\n dist[newState] = dist[state]\n q.appendleft(newState)\n\n return -1\n``` | 0 | 0 | ['Python3'] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | Both Dijkstra and A star. Easy for comparison | both-dijkstra-and-a-star-easy-for-compar-tdk0 | \n# Dijkstra: \nAlgorithm for shortest path from origin. Only consider the distance from origin.\n\nIn essence: dijkstra is advanced BFS(breadth-first search). | mythsky | NORMAL | 2024-05-27T05:52:28.443570+00:00 | 2024-10-22T05:34:09.048715+00:00 | 17 | false | \n# Dijkstra: \nAlgorithm for shortest path from origin. Only consider the distance from origin.\n\n**In essence**: dijkstra is advanced BFS(breadth-first search). The only difference is Dijkstra search through the shorter path first. The idea is the future step of shorter path has potential to replace the current longer path.\n\n**E.g.** Imagine we have a BFS tree with next step option:1,7\nFor this conditon, if we go through 1 first, there will be chance we don\'t need to go through 7.\nMore clear: the next step of 1 is 2, 1+2=3 which is smaller than 7. And suppose it points to the same node as 7 does, we don\'t need to go through 7 at all.\n\n start\n | | \n 1 7\n | |\n 2 |\n \\ |\n goal\n\n\n# Dijkstra code\n```\nclass Solution:\n def minPushBox(self, grid: List[List[str]]) -> int:\n direction=[[1,0],[-1,0],[0,1],[0,-1]]\n def dijkstra(start,end,box): # a-star modification\n if end[0]<0 or end[0]>=len(grid) or end[1]<0 or end[1]>=len(grid[0]) or grid[end[0]][end[1]]=="#":\n return False\n heap=[(0,start[0],start[1])]\n visited={(start[0],start[1]):0}\n while heap:\n k,i,j=heappop(heap)\n if [i,j]==end:\n return True\n if visited[(i,j)]==k:\n for q,p in direction:\n q+=i\n p+=j\n if 0<=q<len(grid) and 0<=p<len(grid[0]) and grid[q][p]!="#" and [q,p]!=box:\n if (q,p) not in visited or k+1<visited[(q,p)]:\n visited[(q,p)]=k+1\n heappush(heap,(k+1,q,p))\n return False\n\n\n for i in range(len(grid)):\n for j in range(len(grid[0])):\n if grid[i][j]=="#" or grid[i][j]==".":\n continue\n elif grid[i][j]==\'S\':\n start=[i,j]\n elif grid[i][j]==\'B\':\n box=[i,j]\n elif grid[i][j]==\'T\':\n end=[i,j]\n\n heap=[(0,box[0],box[1],start[0],start[1])]\n visit={(box[0],box[1],start[0],start[1]):0}\n while heap:\n k,i,j,s,t=heappop(heap)\n if [i,j]==end:\n return k\n if visit[(i,j,s,t)]==k:\n for q,p in direction:\n u=i+q\n v=j+p\n if 0<=u<len(grid) and 0<=v<len(grid[0]) and grid[u][v]!="#":\n if dijkstra([s,t],[i-q,j-p],[i,j]):#set i-q,j-p as target to check if the position of push is available.\n if (u,v,i,j) not in visit or k+1<visit[(u,v,i,j)]:\n visit[(u,v,i,j)]=k+1\n heappush(heap,(k+1,u,v,i,j))\n \n return -1\n\n```\n# A star\n**In essence**: It is advanced Dijkstra. \nAs mentioned, "Dijkstra only considers the distance to origin". This time we consider both distance to origin as well as distance to goal. The idea is with only distance to origin, we may go to the opposite direction from correct one. \n\n**E.g.** imagine now I am at origin, there are four directions I can choose. Up down left right. The goal is on the left, however I only consider the distance to origin so the 4 directions have the same cost which leads into inefficiency.\n\nIn short, A star just introduces the idea of direction compares to Dijkstra. \n**In code**, just replace the **\'distance to origin\'** in dijkstra to **\'distance to origin + distance to goal\'**\n\n# A star code\n```\nimport math\nclass Solution:\n def minPushBox(self, grid: List[List[str]]) -> int:\n direction=[[1,0],[-1,0],[0,1],[0,-1]]\n def dijkstra(start,end,box): # a-star modification\n if end[0]<0 or end[0]>=len(grid) or end[1]<0 or end[1]>=len(grid[0]) or grid[end[0]][end[1]]=="#":\n return False\n heap=[(hypot(start[0]-end[0],start[1]-end[1]),start[0],start[1])]\n visited={(start[0],start[1]):[0,hypot(start[0]-end[0],start[1]-end[1])]}\n while heap:\n k,i,j=heappop(heap)\n if [i,j]==end:\n return True\n \n #Need following if statement, if the state of visited[(i,j)] will be updated. \n #However, different from normal dijkstra, steps are guaranteed to be equal(because it is matrix). There will be no update.\n # if sum(visited[(i,j)])==k: \n d=visited[(i,j)][0] #dijkstra distance\n for q,p in direction:\n q+=i#new pos\n p+=j\n if 0<=q<len(grid) and 0<=p<len(grid[0]) and grid[q][p]!="#" and [q,p]!=box:\n hyp=hypot(q-end[0],p-end[1])\n if (q,p) not in visited or d+1+hyp<sum(visited[(q,p)]):\n visited[(q,p)]=[d+1,hyp]\n heappush(heap,(d+1+hyp,q,p))\n return False\n\n\n for i in range(len(grid)):\n for j in range(len(grid[0])):\n if grid[i][j]=="#" or grid[i][j]==".":\n continue\n elif grid[i][j]==\'S\':\n start=[i,j]\n elif grid[i][j]==\'B\':\n box=[i,j]\n elif grid[i][j]==\'T\':\n end=[i,j]\n\n heap=[(hypot(box[0]-end[0],box[1]-end[1]),box[0],box[1],start[0],start[1])]\n visit={(box[0],box[1],start[0],start[1]):[0,hypot(box[0]-end[0],box[1]-end[1])]}#Only want the movement of box\n while heap:\n k,i,j,s,t=heappop(heap)\n if [i,j]==end:\n return visit[(i,j,s,t)][0]\n\n #Need following if statement, if the state of visited[(i,j)] will be updated. \n #However, different from normal dijkstra, steps are guaranteed to be equal(because it is matrix). There will be no update.\n # if sum(visit[(i,j,s,t)])==k:\n d=visit[(i,j,s,t)][0]\n for q,p in direction:\n u=i+q\n v=j+p\n if 0<=u<len(grid) and 0<=v<len(grid[0]) and grid[u][v]!="#":\n if dijkstra([s,t],[i-q,j-p],[i,j]):#set i-q,j-p as target to check if the position of push is available.\n hyp=hypot(u-end[0],v-end[1])\n if (u,v,i,j) not in visit or d+1+hyp<sum(visit[(u,v,i,j)]):\n visit[(u,v,i,j)]=[d+1,hyp]\n heappush(heap,(d+1+hyp,u,v,i,j))\n return -1\n\n```\nHope it helps :) | 0 | 0 | ['Python3'] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | Dijkstra solution | dijkstra-solution-by-mythsky-ghyy | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | mythsky | NORMAL | 2024-05-27T04:27:04.825623+00:00 | 2024-05-27T04:27:04.825641+00:00 | 6 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minPushBox(self, grid: List[List[str]]) -> int:\n direction=[[1,0],[-1,0],[0,1],[0,-1]]\n def dijkstra(start,end,box):\n if end[0]<0 or end[0]>=len(grid) or end[1]<0 or end[1]>=len(grid[0]) or grid[end[0]][end[1]]=="#":\n return False\n heap=[(0,start[0],start[1])]\n visited={(start[0],start[1]):0}\n while heap:\n k,i,j=heappop(heap)\n if [i,j]==end:\n return True\n if visited[(i,j)]==k:\n for q,p in direction:\n q+=i\n p+=j\n if 0<=q<len(grid) and 0<=p<len(grid[0]) and grid[q][p]!="#" and [q,p]!=box:\n if (q,p) not in visited or k+1<visited[(q,p)]:\n visited[(q,p)]=k+1\n heappush(heap,(k+1,q,p))\n return False\n\n\n for i in range(len(grid)):\n for j in range(len(grid[0])):\n if grid[i][j]=="#" or grid[i][j]==".":\n continue\n elif grid[i][j]==\'S\':\n start=[i,j]\n elif grid[i][j]==\'B\':\n box=[i,j]\n elif grid[i][j]==\'T\':\n end=[i,j]\n\n heap=[(0,box[0],box[1],start[0],start[1])]\n visit={(box[0],box[1],start[0],start[1]):0}\n while heap:\n k,i,j,s,t=heappop(heap)\n if [i,j]==end:\n return k\n if visit[(i,j,s,t)]==k:\n for q,p in direction:\n u=i+q\n v=j+p\n if 0<=u<len(grid) and 0<=v<len(grid[0]) and grid[u][v]!="#":\n if dijkstra([s,t],[i-q,j-p],[i,j]):\n if (u,v,i,j) not in visit or k+1<visit[(u,v,i,j)]:\n visit[(u,v,i,j)]=k+1\n heappush(heap,(k+1,u,v,i,j))\n \n\n return -1\n \n\n``` | 0 | 0 | ['Python3'] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | Djikstra | djikstra-by-muzakkiy-ad4u | Intuition\nThe Box Movement will follow the person movement, if the person movement to the left, box should move also to the left. this means, if our next move | muzakkiy | NORMAL | 2024-05-10T14:04:27.808015+00:00 | 2024-05-10T14:04:27.808062+00:00 | 6 | false | # Intuition\nThe Box Movement will follow the person movement, if the person movement to the left, box should move also to the left. this means, if our next move is a current box state, we need to push the box the same direction with us. for example, if we move 1 point to left, the box also need to move 1 point. but should check possibility if we move to those direction also with the box. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nprioritize the movement with priority queue to get the minimum movement each steps\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO((m\xD7n)^2log(m\xD7n))\n\n\n# Code\n```\ntype PQ []State\n\nfunc (pq *PQ) Push(i interface{}) {(*pq) = append((*pq), i.(State))}\nfunc (pq *PQ) Pop() (val interface{}) {\n val = (*pq)[pq.Len()-1]\n (*pq) = (*pq)[:pq.Len()-1]\n return \n}\nfunc (pq PQ) Less(i, j int) bool {return pq[i].Move < pq[j].Move}\nfunc (pq PQ) Swap(i, j int) {pq[i], pq[j] = pq[j], pq[i]}\nfunc (pq PQ) Len() int {return len(pq)}\n\ntype State struct {\n Visit\n Move int\n}\n\ntype Visit struct {\n Box [2]int\n Player [2]int\n}\n\nfunc minPushBox(grid [][]byte) int {\n visit := make(map[Visit]bool)\n var queue PQ\n var player, target, box [2]int\n\n heap.Init(&queue)\n\n for y := range grid {\n for x := range grid[y] {\n if grid[y][x] == \'S\' {\n player = [2]int{y, x}\n } else if grid[y][x] == \'B\' {\n box = [2]int{y, x}\n } else if grid[y][x] == \'T\' {\n target = [2]int{y, x}\n }\n } \n }\n\n queue = append(queue, State{Visit{Box: box, Player: player}, 0})\n dirs := [][2]int{\n [2]int{0, -1},\n [2]int{0, 1},\n [2]int{-1, 0},\n [2]int{1, 0},\n }\n\n for queue.Len() > 0 {\n curr := heap.Pop(&queue).(State)\n if visit[curr.Visit] {continue}\n visit[curr.Visit] = true\n if curr.Box == target {return curr.Move}\n for _, dir := range dirs {\n next := [2]int{curr.Player[0]+dir[0], curr.Player[1]+dir[1]}\n nextBox := [2]int{curr.Player[0]+2*dir[0], curr.Player[1]+2*dir[1]}\n if !Allow(grid, next[0], next[1]) {continue}\n if next == curr.Box && !Allow(grid, nextBox[0], nextBox[1]){continue}\n if next == curr.Box {\n queue = append(queue, State{\n Move: curr.Move+1,\n Visit: Visit{\n Box: nextBox,\n Player: next,\n },\n })\n } else {\n queue = append(queue, State{\n Visit: Visit{\n Box: curr.Box,\n Player: next,\n },\n Move: curr.Move,\n })\n }\n }\n }\n\n return 0-1\n}\n\nfunc Allow(grid [][]byte, y, x int) bool {\n if y < 0 || x < 0 || y == len(grid) || x == len(grid[y]) || grid[y][x] == \'#\' {return false}\n return true\n}\n``` | 0 | 0 | ['Go'] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | Djikstra | djikstra-by-muzakkiy-aalb | Intuition\nThe Box Movement will follow the person movement, if the person movement to the left, box should move also to the left. this means, if our next move | muzakkiy | NORMAL | 2024-05-10T14:04:21.639125+00:00 | 2024-05-10T14:04:21.639159+00:00 | 1 | false | # Intuition\nThe Box Movement will follow the person movement, if the person movement to the left, box should move also to the left. this means, if our next move is a current box state, we need to push the box the same direction with us. for example, if we move 1 point to left, the box also need to move 1 point. but should check possibility if we move to those direction also with the box. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nprioritize the movement with priority queue to get the minimum movement each steps\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO((m\xD7n)^2log(m\xD7n))\n\n\n# Code\n```\ntype PQ []State\n\nfunc (pq *PQ) Push(i interface{}) {(*pq) = append((*pq), i.(State))}\nfunc (pq *PQ) Pop() (val interface{}) {\n val = (*pq)[pq.Len()-1]\n (*pq) = (*pq)[:pq.Len()-1]\n return \n}\nfunc (pq PQ) Less(i, j int) bool {return pq[i].Move < pq[j].Move}\nfunc (pq PQ) Swap(i, j int) {pq[i], pq[j] = pq[j], pq[i]}\nfunc (pq PQ) Len() int {return len(pq)}\n\ntype State struct {\n Visit\n Move int\n}\n\ntype Visit struct {\n Box [2]int\n Player [2]int\n}\n\nfunc minPushBox(grid [][]byte) int {\n visit := make(map[Visit]bool)\n var queue PQ\n var player, target, box [2]int\n\n heap.Init(&queue)\n\n for y := range grid {\n for x := range grid[y] {\n if grid[y][x] == \'S\' {\n player = [2]int{y, x}\n } else if grid[y][x] == \'B\' {\n box = [2]int{y, x}\n } else if grid[y][x] == \'T\' {\n target = [2]int{y, x}\n }\n } \n }\n\n queue = append(queue, State{Visit{Box: box, Player: player}, 0})\n dirs := [][2]int{\n [2]int{0, -1},\n [2]int{0, 1},\n [2]int{-1, 0},\n [2]int{1, 0},\n }\n\n for queue.Len() > 0 {\n curr := heap.Pop(&queue).(State)\n if visit[curr.Visit] {continue}\n visit[curr.Visit] = true\n if curr.Box == target {return curr.Move}\n for _, dir := range dirs {\n next := [2]int{curr.Player[0]+dir[0], curr.Player[1]+dir[1]}\n nextBox := [2]int{curr.Player[0]+2*dir[0], curr.Player[1]+2*dir[1]}\n if !Allow(grid, next[0], next[1]) {continue}\n if next == curr.Box && !Allow(grid, nextBox[0], nextBox[1]){continue}\n if next == curr.Box {\n queue = append(queue, State{\n Move: curr.Move+1,\n Visit: Visit{\n Box: nextBox,\n Player: next,\n },\n })\n } else {\n queue = append(queue, State{\n Visit: Visit{\n Box: curr.Box,\n Player: next,\n },\n Move: curr.Move,\n })\n }\n }\n }\n\n return 0-1\n}\n\nfunc Allow(grid [][]byte, y, x int) bool {\n if y < 0 || x < 0 || y == len(grid) || x == len(grid[y]) || grid[y][x] == \'#\' {return false}\n return true\n}\n``` | 0 | 0 | ['Go'] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | Bidirectional Search+ A* Search (70 ms Beats 100%) | bidirectional-search-a-search-70-ms-beat-pbb9 | \nclass Solution:\n def minPushBox(self, grid: List[List[str]]) -> int:\n m = len(grid)\n n = len(grid[0])\n directions = [(0,-1), (0,1) | laxelee1 | NORMAL | 2024-04-19T16:27:21.762123+00:00 | 2024-04-19T16:27:21.762158+00:00 | 4 | false | ```\nclass Solution:\n def minPushBox(self, grid: List[List[str]]) -> int:\n m = len(grid)\n n = len(grid[0])\n directions = [(0,-1), (0,1), (-1,0), (1,0)] # left, right, up, down\n\n found = 0\n for i in range(m):\n for j in range(n):\n if grid[i][j] in (\'#\',\'.\'):\n continue\n if grid[i][j] == \'S\':\n mi, mj = i, j\n found += 1\n if found == 3:\n break\n elif grid[i][j] == \'B\':\n bi, bj = i, j\n found += 1\n if found == 3:\n break\n else:\n ti, tj = i, j\n found += 1\n if found == 3:\n break\n if found == 3:\n break\n\n def can_push(mi, mj, bi, bj):\n \'\'\'Uses a bidirectional search\'\'\'\n res = [False] * 4\n\n banned = set()\n for i in range(4):\n di, dj = directions[i]\n bii, bjj = bi + di, bj + dj\n if bii < 0 or bjj < 0 or bii >= m or bjj >= n or grid[bii][bjj] == \'#\':\n banned.add(i//2)\n\n targets = {}\n for i in range(4):\n if i//2 in banned:\n continue\n di, dj = directions[i]\n ti, tj = bi - di, bj - dj\n targets[(ti, tj)] = i\n\n if not targets:\n return res\n\n stop = len(targets)\n found = 0\n q = deque([(mi, mj)])\n visited = {(mi, mj)}\n while q:\n i, j = q.popleft()\n\n if (i, j) in targets:\n res[targets[(i, j)]] = True\n found += 1\n if found == stop:\n break\n \n for di, dj in directions:\n ii, jj = i + di, j + dj\n if ii < 0 or jj < 0 or ii >= m or jj >= n or grid[ii][jj] == \'#\':\n continue\n if (ii, jj) == (bi, bj):\n continue\n if (ii, jj) in visited:\n continue\n visited.add((ii, jj))\n q.append((ii, jj))\n return res\n\n q = deque()\n visited = set()\n pushes = can_push(mi, mj, bi, bj)\n for k in range(4):\n di, dj = directions[k]\n if pushes[k]:\n ii, jj, bii, bjj = bi - di, bj - dj, bi, bj\n q.append((ii, jj, bii, bjj))\n visited.add((ii, jj, bii, bjj))\n\n def h(bi, bj):\n \'\'\'Heuristic function\'\'\'\n return abs(bi - ti) + abs(bj - tj)\n\n minHeap = []\n visited = set()\n pushes = can_push(mi, mj, bi, bj)\n for k in range(4):\n di, dj = directions[k]\n if pushes[k]:\n ii, jj, bii, bjj = bi - di, bj - dj, bi, bj\n minHeap.append( (h(bii, bjj), 0, ii, jj, bii, bjj) ) # f, d, i, j, bi, bj\n\n while minHeap:\n f, d, i, j, bi, bj = heapq.heappop(minHeap)\n if (bi, bj) == (ti, tj):\n return d\n \n if (i, j, bi, bj) in visited:\n continue\n visited.add((i, j, bi, bj))\n\n pushes = can_push(i, j, bi, bj)\n for k in range(4):\n di, dj = directions[k]\n if pushes[k]:\n ii, jj, bii, bjj = bi, bj, bi + di, bj + dj\n if (ii, jj, bii, bjj) in visited:\n continue\n heapq.heappush(minHeap, (d + 1 + h(bii, bjj), d + 1, ii, jj, bii, bjj))\n return -1\n``` | 0 | 0 | ['Python3'] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | BFS with composite encoded key for visited | bfs-with-composite-encoded-key-for-visit-3n9d | Intuition\nBecause this is a grid, edge weights are equal,\nso we can use BFS instead of UCS or A.\n\nA BFS search can be done from the box to the target,\nbut | _nichole_ | NORMAL | 2024-04-18T23:42:34.173873+00:00 | 2024-04-18T23:42:34.173918+00:00 | 5 | false | # Intuition\nBecause this is a grid, edge weights are equal,\nso we can use BFS instead of UCS or A*.\n\nA BFS search can be done from the box to the target,\nbut each move of the box must have a free space\non the opposite side of move,\nand that free space must be reachable by S at its current position.\n\n\n# Approach\nI used BFS to perform a search from the box B to the target T, checking at each move that S could get to the free space needed for the push.\n\nOne important detail was to use a composite key for the visited data structure which is used to avoid never ending cycles of actions. The composite key is composed of the box position and the direction of its motion.\n\nAnother detail of the BFS search is to enqueu the box position and the person position.\n\n\n# Complexity\n- Time complexity:\n$$O((m*n)^2)$$ in the worst case where m and n are the dimensions of the grid.\nThe extra factor of m*n is due to needing to check that the push position is reachable by the person.\n\n- Space complexity:\n$$O(m*n)$$\n\n# Code\n```\nclass Solution {\n\n protected static int[][] offsets = new int[4][];\n static {\n offsets[0] = new int[]{0, 1};\n offsets[1] = new int[]{0, -1};\n offsets[2] = new int[]{-1, 0};\n offsets[3] = new int[]{1, 0};\n }\n\n public int minPushBox(char[][] grid) {\n\n /*\n m x n grid of characters grid where each element \n is a wall, floor, or box.\n\n only the box moves are counted.\n\n Because this is a grid, edge weights are equal,\n so we can use BFS instead of UCS or A*.\n\n BFS of the box to the target,\n but each move of the box must have a free space\n on opposite side of move,\n and that free space must be reachable by S at its current position.\n\n A box needs to be able to revisit a cell, so the\n visited array which helps constrain repeated visits\n to a cell, needs to have a key that is a composite key\n of position and other information unique to the action.\n We can use the box position and push direction as a composite\n key, or alternatively, we could\n use the push position and direction as a composite key.\n \n The box position value range is [0, m*n] where m and n are\n have max value constraints of 20.\n The box position range = [0, 400] so position needs 9 bits.\n The direction needs 2 numbers which are both 2 bits.\n So, the composite index uses 13 bits of an integer.\n \n Note, that the visited state should not be set until all checks that\n the box is pushable by person are done, so that we are only\n restricting revisits of truly visitable states.\n\n The runtime complexity at worst is O((n*m)^2).\n The space complexity is O(n*m).\n */\n\n return useBFS(grid);\n }\n\n /*\n 9 bits for box position,\n 2 bits for offset[0]\n 2 bits for offset[2]\n */\n protected int encodeCompositeIndex(int idx, int[] offset) {\n int a = idx;\n // offset range is -1 to 1, so we add 1 to make range [0,2]\n a |= ((offset[0]+1) << 9);\n a |= ((offset[1]+1) << 11);\n return a;\n }\n\n protected int useBFS(char[][] grid) {\n int m = grid.length;\n int n = grid[0].length;\n\n int bIdx = -1;\n int sIdx = -1;\n int tIdx = -1;\n // find the box, person, and target\n int r, c;\n char cell;\n for (r = 0; r < m; ++r) {\n for (c = 0; c < n; ++c) {\n cell = grid[r][c];\n switch(cell) {\n case \'B\':\n bIdx = (r*n) + c;\n break;\n case \'S\':\n sIdx = (r*n) + c;\n break;\n case \'T\':\n tIdx = (r*n) + c;\n break;\n default:\n break;\n }\n }\n }\n assert(sIdx > -1);\n assert(bIdx > -1);\n assert(tIdx > -1);\n\n // index is composite key of box position and direction of motion\n Set<Integer> visited = new HashSet<>();\n\n int r2, c2, bIdx2, sIdx2;\n char cell2;\n int bIdx1, sIdx1;\n\n Queue<Integer> q = new ArrayDeque<>();\n Queue<Integer> qS = new ArrayDeque<>();\n q.offer(bIdx);\n qS.offer(sIdx);\n\n int len = -1;\n while (!q.isEmpty()) {\n ++len;\n \n int qSz = q.size();\n\n while (qSz > 0) {\n --qSz;\n\n bIdx1 = q.poll();\n sIdx1 = qS.poll();\n\n r = bIdx1 / n;\n c = bIdx1 % n;\n\n if (grid[r][c] == \'T\') return len;\n\n // candidate moves:\n for (int[] offset : offsets) {\n r2 = r + offset[0];\n c2 = c + offset[1];\n if (r2 < 0 || r2 == m || c2 < 0 || c2 == n) continue; \n\n if (grid[r2][c2] == \'#\') continue;\n\n bIdx2 = (r2*n) + c2;\n\n int ec = encodeCompositeIndex(bIdx2, offset);\n \n if (visited.contains(ec)) continue;\n \n int pushR2 = r - offset[0];\n int pushC2 = c - offset[1];\n\n if (pushR2 < 0 || pushR2 == m || pushC2 < 0 || pushC2 == n) continue; \n\n // Example 3 shows that a person can step on T\n if (grid[pushR2][pushC2] == \'#\') continue;\n\n sIdx2 = (pushR2 * n) + pushC2;\n\n // O(N) at worst\n boolean isReachable = isReachable(grid, sIdx1, sIdx2, bIdx1);\n\n if (!isReachable) continue;\n\n visited.add(ec); \n\n q.offer(bIdx2);\n qS.offer(sIdx2);\n }\n\n } // end single layer\n } // end q while\n\n return -1;\n }\n\n protected boolean isReachable(char[][] grid, int srcIdx, int destIdx,\n final int boxIdx) {\n\n int m = grid.length;\n int n = grid[0].length;\n\n int[] visited = new int[m*n];\n visited[srcIdx] = 1;\n\n int r2, c2, idx2;\n char cell2;\n int r1, c1, idx1;\n\n Queue<Integer> q = new ArrayDeque<>();\n q.offer(srcIdx);\n\n int len = -1;\n while (!q.isEmpty()) {\n ++len;\n \n int qSz = q.size();\n\n while (qSz > 0) {\n --qSz;\n idx1 = q.poll();\n\n if (idx1 == boxIdx) continue;\n\n if (idx1 == destIdx) return true;\n\n r1 = idx1/n;\n c1 = idx1 % n;\n\n // candidate moves:\n for (int[] offset : offsets) {\n r2 = r1 + offset[0];\n c2 = c1 + offset[1];\n if (r2 < 0 || r2 == m || c2 < 0 || c2 == n) continue;\n \n // example 3 implies can step on . or T\n if (grid[r2][c2] == boxIdx \n || grid[r2][c2] == \'#\') continue;\n\n idx2 = (r2*n) + c2;\n\n if (visited[idx2] != 0) continue;\n visited[idx2] = 1;\n\n q.offer(idx2);\n }\n\n } // end single layer\n } // end q while\n\n return false;\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | Ugly solution | ugly-solution-by-yoongyeom-l2g3 | Code\n\nclass Solution:\n def minPushBox(self, grid: List[List[str]]) -> int:\n def canvisit(r1, c1, r2, c2, r3, c3):\n if (r1, c1) == (r2, | YoonGyeom | NORMAL | 2024-04-05T13:32:18.407783+00:00 | 2024-04-05T13:32:18.407817+00:00 | 2 | false | # Code\n```\nclass Solution:\n def minPushBox(self, grid: List[List[str]]) -> int:\n def canvisit(r1, c1, r2, c2, r3, c3):\n if (r1, c1) == (r2, c2): return True\n grid[r3][c3] = \'R\'\n q = [(r1, c1)]\n seen = set([(r1, c1)])\n while q:\n r, c = q.pop()\n for dr, dc in [[-1, 0], [1, 0], [0, 1], [0, -1]]:\n if 0<=r+dr<R and 0<=c+dc<C and grid[r+dr][c+dc] == \'.\' and (r+dr, c+dc) not in seen:\n if (r+dr, c+dc)==(r2, c2):\n grid[r3][c3] = \'.\'\n return True\n seen.add((r+dr, c+dc))\n q.append((r+dr, c+dc))\n grid[r3][c3] = \'.\'\n return False\n @cache\n def solve(r1, c1, r2, c2):\n if (r2, c2) == goal: return 0\n hsh = (r1, c1, r2, c2)\n if hsh in memo: return memo[hsh]\n memo[hsh] = res = 10**8\n for dr, dc in [[1, 0], [0, 1]]:\n if 0<=r2+dr<R and 0<=c2+dc<C and grid[r2+dr][c2+dc] == \'.\' and\\\n 0<=r2-dr<R and 0<=c2-dc<C and grid[r2-dr][c2-dc] == \'.\':\n if canvisit(r1, c1, r2+dr, c2+dc, r2, c2):\n res = min(res, solve(r2, c2, r2-dr, c2-dc)+1)\n if canvisit(r1, c1, r2-dr, c2-dc, r2, c2):\n res = min(res, solve(r2, c2, r2+dr, c2+dc)+1)\n grid[r2][c2] = \'.\'\n memo[hsh] = res\n return res\n \n memo = {}\n R, C = len(grid), len(grid[0])\n for i in range(R):\n for j in range(C):\n if grid[i][j] ==\'T\': \n goal = (i, j)\n grid[i][j] = \'.\'\n if grid[i][j] == \'B\': \n r2, c2 = i, j\n grid[i][j] = \'.\'\n if grid[i][j] == \'S\': \n r1, c1 = i, j\n grid[i][j] = \'.\'\n return solve(r1, c1, r2, c2) if solve(r1, c1, r2, c2) != 10**8 else -1\n``` | 0 | 0 | ['Python3'] | 0 |
minimum-moves-to-move-a-box-to-their-target-location | Beats 100% users | beats-100-users-by-aim_high_212-bvdl | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Aim_High_212 | NORMAL | 2024-03-11T15:00:04.920886+00:00 | 2024-03-11T15:00:04.920907+00:00 | 7 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minPushBox(self, grid: List[List[str]]) -> int:\n m = len(grid)\n n = len(grid[0])\n\n def neighbours(x,y):\n res = []\n cand = [(x+1,y),(x-1,y),(x,y+1),(x,y-1)]\n for e in cand:\n x_cand,y_cand = e\n if 0 <= x_cand < n and 0 <= y_cand < m and grid[y_cand][x_cand] != "#":\n res.append(e)\n return(res)\n\n def find(car):\n for x in range(n):\n for y in range(m):\n if grid[y][x] == car:\n return(x,y)\n\n def oppose(neighbour,boite):\n nx,ny = neighbour\n bx,by = boite\n candx,candy = 2*bx-nx,2*by-ny\n return(candx,candy)\n\n def is_accessible(P,O,B):\n visited = set()\n to_visit = [P]\n while to_visit:\n current_P = to_visit.pop(0)\n if current_P == O:\n return(True)\n if not current_P in visited:\n visited.add(current_P)\n px,py = current_P\n neighs = neighbours(px,py)\n for neigh in neighs:\n if neigh != B:\n to_visit.append(neigh)\n\n return(False)\n\n P = find(\'S\')\n B = find(\'B\')\n\n seen_set = set()\n seen_set.add((P,B))\n\n state_stack = [(P,B,0)]\n while state_stack:\n P,B,count = state_stack.pop(0)\n bx,by = B\n if grid[by][bx] == \'T\':\n return(count)\n neighs = neighbours(bx,by)\n for neigh in neighs:\n if (B,neigh) not in seen_set: # nouvel etat\n oppx,oppy = oppose(neigh,B)\n O = oppx,oppy \n if 0 <= oppx < n and 0 <= oppy < m and grid[oppy][oppx] != "#":\n if is_accessible(P,O,B):\n seen_set.add((B,neigh))\n state_stack.append((B,neigh,count+1))\n return(-1)\n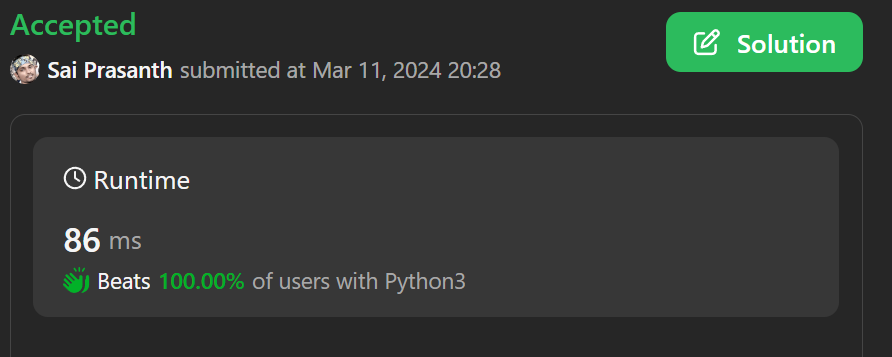\n\n\n\n \n``` | 0 | 0 | ['Python', 'Python3'] | 0 |
minimum-deletions-to-make-array-beautiful | ✅ Best and Most Easy Explanantion || 3 line of code | best-and-most-easy-explanantion-3-line-o-wa13 | \uD83D\uDC68\u200D\uD83D\uDCBB Friend\'s if you find this solution helpful \uD83D\uDE0A, PLEASE do UPVOTE. By doing that motivates me to create a better post li | intellisense | NORMAL | 2022-03-27T05:11:07.462749+00:00 | 2022-03-27T05:27:02.504074+00:00 | 6,377 | false | \uD83D\uDC68\u200D\uD83D\uDCBB Friend\'s if you find this solution helpful \uD83D\uDE0A, PLEASE do UPVOTE. By doing that motivates me to create a better post like this \u270D\uFE0F\n____________________________________________________________________________________________________________\n____________________________________________________________________________________________________________\n\n#### \u2714\uFE0F **Question Conclusion**\n* there must be no repetitive value next to even index\n* if we found any element for the above point we have to delete the element and shift every right element to its left by 1.\n#### \u2714\uFE0F **Solution - I (Best Approach)**\n##### **Intuition :-**\n* we will fly the vector.\n* every time we find a duplicate we will increment ans by 1.\n* thus to check the second condition we will subtract the ans value from the index as we are shifting the element to the left.\n* for the last edge case we will check the remaining size after removing ans element from the vector if the result is odd we have to remove 1 more element else just return the ans.\n##### **Code :-**\n```\nclass Solution {\npublic:\n int minDeletion(vector<int> &nums) {\n int ans = 0;\n for (int i = 0; i < nums.size() - 1; i++)\n if (nums[i] == nums[i + 1] and (i - ans) % 2 == 0) ans++;\n return ans + (nums.size() - ans) % 2;\n }\n};\n```\n**Time Complexity** : `O(N)` time to fly the vector, \n**Space Complexity** : `O(1)` no extra space is used, \n \n_____________________________________________________________________________________________________________\n_____________________________________________________________________________________________________________\n\n\uD83D\uDCBBIf there are any suggestions/questions in my post, comment below \uD83D\uDC47 | 168 | 2 | ['C'] | 11 |
minimum-deletions-to-make-array-beautiful | [Java/C++/Python] O(1) Greedy Solution with Explanation | javacpython-o1-greedy-solution-with-expl-qouv | Solution 1\nGreedily add all element to a result array.\n\nAnyway, greedy solution is not obvious to be right.\nTo handle every continuous elements pair, we act | lee215 | NORMAL | 2022-03-27T04:04:57.613754+00:00 | 2022-03-27T04:40:17.221625+00:00 | 7,423 | false | # **Solution 1**\nGreedily add all element to a result array.\n\nAnyway, greedy solution is not obvious to be right.\nTo handle every continuous elements pair, we actually only care if the number of deleted numbers is even or single.\n\nWe never need to delete a number when not necessary to optimize the deleting in future, because the benefit is at most 1.\nIt doesn\'t worth an early deletion.\n\nTime `O(n)`\nSpace `O(n)`\n<br>\n\n**Python**\n```py\n def minDeletion(self, A):\n res = []\n for a in A:\n if len(res) % 2 == 0 or a != res[-1]:\n res.append(a)\n return len(A) - (len(res) - len(res) % 2)\n```\n<br>\n\n# **Solution 2: Space O(1)**\nUsing a variable `pre` to record the last element with even index.\n\n**Java**\n```java\n public int minDeletion(int[] A) {\n int res = 0, pre = -1;\n for (int a : A) {\n if (a == pre)\n res++;\n else\n pre = pre < 0 ? a : -1;\n }\n return pre < 0 ? res : res + 1;\n }\n```\n\n**C++**\n```cpp\n int minDeletion(vector<int>& A) {\n int res = 0, pre = -1;\n for (int& a: A) { \n if (a == pre)\n res++;\n else\n pre = pre < 0 ? a : -1;\n }\n return res + (pre >= 0);\n }\n```\n**Python**\n```py\n def minDeletion(self, A):\n res, pre = 0, -1\n for a in A:\n if a == pre:\n res += 1\n else:\n pre = a if pre < 0 else -1\n return res + (pre >= 0)\n```\n | 61 | 4 | ['C', 'Python', 'Java'] | 15 |
minimum-deletions-to-make-array-beautiful | ✅ C++ | Easy | c-easy-by-chandanagrawal23-fmfy | \nclass Solution\n{\n public:\n int minDeletion(vector<int> &nums)\n {\n int shift = 0;\n for (int i = 0; i < nums.size() | chandanagrawal23 | NORMAL | 2022-03-27T04:02:12.309238+00:00 | 2022-03-27T04:41:04.548760+00:00 | 2,577 | false | ```\nclass Solution\n{\n public:\n int minDeletion(vector<int> &nums)\n {\n int shift = 0;\n for (int i = 0; i < nums.size() - 1; i++)\n {\n if ((i + shift) % 2 == 0)\n {\n if (nums[i] == nums[i + 1])\n {\n shift++;\n }\n }\n }\n if ((nums.size() - shift) % 2 == 1)\n {\n shift++;\n }\n return shift;\n }\n};\n``` | 37 | 2 | [] | 5 |
minimum-deletions-to-make-array-beautiful | Java/C++ | O(N) time O(1) space | javac-on-time-o1-space-by-surajthapliyal-v2im | JAVA\n\nclass Solution {\n\n public int minDeletion(int[] nums) {\n boolean even = true;\n int size = 0, c = 0;\n for (int i = 0; i < nu | surajthapliyal | NORMAL | 2022-03-27T04:02:16.596387+00:00 | 2022-03-28T06:41:21.403842+00:00 | 2,898 | false | **JAVA**\n```\nclass Solution {\n\n public int minDeletion(int[] nums) {\n boolean even = true;\n int size = 0, c = 0;\n for (int i = 0; i < nums.length; i++) {\n\t\t\t//current index is even and i+1 is same \n while (i + 1 < nums.length && even && nums[i] == nums[i + 1]) {\n i++;\n c++;\n }\n\t\t\t//change index parity\n\t\t\teven = !even;\n size++;\n }\n return c + size % 2; // as even number of elements needed\n }\n}\n```\n**CPP**\n```\nclass Solution {\n public:\n int minDeletion(vector < int > & nums) {\n bool even = true;\n int size = 0, c = 0;\n for (int i = 0; i < nums.size(); i++) {\n while (i + 1 < nums.size() && even && nums[i] == nums[i + 1]) i++, c++;\n size++;\n even = !even;\n }\n return c + size % 2;\n }\n};\n``` | 30 | 0 | [] | 10 |
minimum-deletions-to-make-array-beautiful | [JAVA]Simple Detailed Solution with O(N) time O(1) space!! | javasimple-detailed-solution-with-on-tim-o46y | The idea is simple go through the array along with checking the conditions!!\n\n\n\n int counter = 0;\n for (int i = 0; i < nums.length - 1; i += | sadriddin17 | NORMAL | 2022-03-27T04:03:19.572463+00:00 | 2022-03-27T05:04:00.417313+00:00 | 1,179 | false | The idea is simple go through the array along with checking the conditions!!\n\n\n```\n int counter = 0;\n for (int i = 0; i < nums.length - 1; i += 2) { // the second condition given\n if (nums[i] == nums[i + 1]) {\n counter++;\n i--;\n }\n }\n\t\treturn (nums.length - counter) % 2 == 1?++counter: counter; //checking if the array is even\n``` | 25 | 0 | ['Java'] | 3 |
minimum-deletions-to-make-array-beautiful | Two Pointers | two-pointers-by-votrubac-w5me | This problem may look harder than it is. We just need to realize that we always have to delete if two consecutive elements (after the shift) are equal.\n\nWe ca | votrubac | NORMAL | 2022-03-27T04:01:43.323112+00:00 | 2022-03-27T04:10:29.534674+00:00 | 2,076 | false | This problem may look harder than it is. We just need to realize that we always have to delete if two consecutive elements (after the shift) are equal.\n\nWe can use the two-pointer approach to track the shift (`j`).\n\n**C++**\n```cpp\nint minDeletion(vector<int>& nums) {\n int j = 0, sz = nums.size();\n for(int i = 0; i - j + 1 < sz; i += 2)\n j += nums[i - j] == nums[i - j + 1];\n return j + (sz - j) % 2;\n}\n``` | 22 | 1 | ['C'] | 4 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.