question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
abbreviating-the-product-of-a-range | C++ Solution | Using logarithm property | c-solution-using-logarithm-property-by-k-gtaa | Approach\n1. remove all 2\'s and 5\'s while multiplying numbers and count how many times 2\'s and 5\'s appear\n2. number of zeros will be equal to min(two,five) | Kartikey_1109 | NORMAL | 2021-12-25T20:57:46.251712+00:00 | 2021-12-26T14:26:08.895574+00:00 | 556 | false | **Approach**\n1. remove all 2\'s and 5\'s while multiplying numbers and count how many times 2\'s and 5\'s appear\n2. number of zeros will be equal to ```min(two,five)```\n3. get original number back by multiplying extra occurence of two or five\n4. we maintain two numbers ```original``` and ```suffix``` by taking modulus with different numbers. If our final product has 10 or less digits then ```original``` value is equal to the ```suffix``` value otherwise we take last five digits of ```suffix```.\n5. to get first 5 digits we take ```log``` of all values from ```left``` to ```right``` and add them all. Coz we need only first five digits of number we take ```10^(4+fraction part)```\n\n**Time Complexity :** **O(n),** **where n=(right-left)**\n\n```\nclass Solution\n{\n public:\n void reduceNumber(unsigned long long& val,unsigned long long x,unsigned long long& count)\n {\n while (val%x==0)\n {\n val/=x;\n count++;\n }\n }\n void getBackOriginal(unsigned long long& val,unsigned long long two,unsigned long long five,unsigned long long& mod)\n {\n if (two<five)\n {\n five-=two;\n while (five--)\n val=(val*5)%mod;\n }\n else if (five<two)\n {\n two-=five;\n while (two--)\n val=(val*2)%mod;\n }\n }\n string abbreviateProduct(int left, int right)\n {\n unsigned long long original=1,suffix=1,two=0,five=0,mod1=1e10,mod2=1e13;\n double power=0;\n for (long long i=left;i<=right;i++)\n {\n unsigned long long val=i;\n power=power+(double)(log10(i));\n \n //Reduce number by removing multiple of 2 and 5 from them and count them\n reduceNumber(val,2,two);\n reduceNumber(val,5,five);\n \n //Maintain two number suffix and original by taking modulus with different numbers\n suffix=(suffix*val)%mod1;\n original=(original*val)%mod2;\n }\n \n //Get original number back by multiplying extra two or five\n getBackOriginal(suffix,two,five,mod1);\n getBackOriginal(original,two,five,mod2);\n \n string ans="";\n //If suffix is equal to original it means final product has 10 or maybe less digits\n if (original==suffix)\n ans=to_string(original)+\'e\'+to_string(min(two,five));\n else\n {\n power=power-(int)(power)+4.0;\n long long prefix=pow(10,power);\n string temp=to_string(suffix);\n for (int i=temp.length()-1;i>temp.length()-6;i--)\n ans=temp[i]+ans;\n ans=to_string(prefix)+"..."+ans+\'e\'+to_string(min(two,five));\n }\n return ans;\n }\n};\n``` | 6 | 0 | [] | 3 |
abbreviating-the-product-of-a-range | Java Solution - Brute Force | java-solution-brute-force-by-extremania-i283 | \nclass Solution {\n public String abbreviateProduct(int left, int right) {\n double a = 1L; // for first 5 digits\n long b = 1L; // for last 5 | extremania | NORMAL | 2021-12-28T03:46:23.786595+00:00 | 2021-12-28T03:46:23.786628+00:00 | 250 | false | ```\nclass Solution {\n public String abbreviateProduct(int left, int right) {\n double a = 1L; // for first 5 digits\n long b = 1L; // for last 5 digits\n long c = 1L; // for small result\n int zn = 0; // zero count\n for(int i=left; i<=right; i++){\n a*=i;\n b*=i;\n while(b%10==0){\n b/=10;\n zn++;\n }\n if(a>1000000000000L) a/=1000000;\n if(b>1000000000000L) b%=1000000;\n if(c<10000000000L) c*=i;\n while(c%10==0) c/=10;\n }\n if(c<10000000000L) return c+"e"+zn;\n String astr = String.valueOf(a).replace(".", "");\n String bstr = String.valueOf(b);\n while(bstr.length()<5) bstr="0"+bstr;\n return astr.substring(0,5)+"..."+bstr.substring(bstr.length()-5)+"e"+zn;\n }\n}\n``` | 4 | 2 | [] | 1 |
abbreviating-the-product-of-a-range | C++ | Pure math, no algorithm | c-pure-math-no-algorithm-by-changkunli-h1mi | \nclass Solution {\npublic:\n string abbreviateProduct(int left, int right) {\n int num_2 = 0, num_5 = 0;\n vector<int> arr;\n for(int i | changkunli | NORMAL | 2021-12-25T17:12:00.148927+00:00 | 2021-12-25T17:12:00.148965+00:00 | 723 | false | ```\nclass Solution {\npublic:\n string abbreviateProduct(int left, int right) {\n int num_2 = 0, num_5 = 0;\n vector<int> arr;\n for(int i=left; i<=right; i++) {\n int num = i;\n while(!(num % 2)) {\n num_2 += 1;\n num /= 2;\n }\n while(!(num % 5)) {\n num_5 += 1;\n num /= 5;\n }\n arr.push_back(num);\n }\n int C = min(num_2, num_5);\n long M = 1e5;\n long suf = 1;\n for(auto& num : arr) {\n suf *= long(num);\n suf %= M;\n }\n for(int i=C+1; i<=num_2; i++) {\n suf *= 2;\n suf %= M;\n }\n for(int i=C+1; i<=num_5; i++) {\n suf *= 5;\n suf %= M;\n }\n double log = 0.0;\n for(int i=left; i<=right; i++) log += log10(double(i));\n log -= double(C);\n if(log < 10.0) {\n suf = 1;\n for(auto& num : arr) suf *= long(num);\n for(int i=C+1; i<=num_2; i++) suf *= 2;\n for(int i=C+1; i<=num_5; i++) suf *= 5;\n return to_string(suf) + "e" + to_string(C);\n }\n log -= floor(log);\n log += 4.0;\n int prev = int(pow(10.0, log));\n char p[30];\n snprintf(p, 30, "%5d...%05de%d", prev, suf, C);\n return string(p);\n }\n};\n``` | 4 | 1 | ['C'] | 2 |
abbreviating-the-product-of-a-range | [Java] Keep track of the product start and end | java-keep-track-of-the-product-start-and-sh8e | We can separately compute the start and end part of the number (as well as the number of trailing zeros).\nExample (with smaller numbers):\n\n 999[999]999 * | tobias2code | NORMAL | 2021-12-25T16:30:57.789873+00:00 | 2022-01-11T07:34:51.158654+00:00 | 722 | false | We can separately compute the start and end part of the number (as well as the number of trailing zeros).\nExample (with smaller numbers):\n```\n 999[999]999 * 99 // start = 999, end = 999\n = 989[99999]901 // start = 989, end = 901 => same as computing separately with 999 * 99 = 98901\n```\n\nUsing `long` provides enough precision to pass the tests (though I don\'t have a formal proof yet).\nGiven that input numbers are smaller than 10^6 and the max value of a long is (roughly) 9 * 10^18, we need to keep start and end smaller than 9 * 10^12.\n\nEdit: we actually need to use `double` for start, to have enough precision to pass new tests. Thanks @DIMITR for the comment!\n\n```\npublic static final long LIMIT = 1_000_000_000_000l; // keep start/end smaller than 10^12\n \npublic String abbreviateProduct(int left, int right) {\n long end = 1; // end part of the product (or the whole number if small enough)\n long nZeros = 0; // trailing zeros\n boolean usedModulo = false;\n for (int n = left; n <= right; n++) {\n end *= n;\n\n while (end % 10 == 0) { // extract trailing zeros into nZeros\n end /= 10;\n nZeros++;\n }\n\n if (end >= LIMIT) { // truncate if needed\n end %= LIMIT;\n usedModulo = true;\n }\n }\n\n if (!usedModulo && end < 10_000_000_000l) { // doesn\'t need abbreviation below 10^10\n return String.format("%de%d", end, nZeros);\n }\n\n double start = 1; // start part of the product\n for (int n = left; n <= right; n++) {\n start *= n;\n\n while (start >= LIMIT) { // truncate if needed\n start /= 10;\n }\n }\n\n return buildAbbreviation(usedModulo, start, end, nZeros);\n}\n\nprivate String buildAbbreviation(boolean usedModulo, double start, long end, long nZeros) {\n while (start >= 100_000) { // keep the 5 first digits\n start /= 10;\n }\n\n end %= 100_000; // keep the last 5 digits\n\n return String.format("%d...%05de%d", (int) start, end, nZeros); // zero-padding of the end\n}\n```\n\nQuestions and comments welcome! | 4 | 0 | ['Math', 'Java'] | 3 |
abbreviating-the-product-of-a-range | Python Straightforward | python-straightforward-by-lz2657-bsg9 | Track the head, tail and trailing zero when passing through the range.\nFor trailing zero, we need to count the number of 2 and 5 within the range.\nFor the hea | lz2657 | NORMAL | 2021-12-25T16:01:44.516125+00:00 | 2021-12-25T16:01:44.516167+00:00 | 366 | false | Track the head, tail and trailing zero when passing through the range.\nFor trailing zero, we need to count the number of 2 and 5 within the range.\nFor the head, as 1 <= left <= right <= 10^6, the top 5 digits can be calculated with the 1st ~ 12th digits, so we track top 12 digits.\nFor the tail, if we track the last 5 digits, when a new trailing zero pops up, we may get 4 effective digits left. \nSo I remove all the 2 and 5 in each step and multiply the remaining ones in the end.\n\n```\nclass Solution:\n def abbreviateProduct(self, left: int, right: int) -> str:\n c2 = c5 = 0\n top12 = tail5 = 1\n\n for i in range(left, right+1):\n # count and remove all 2 and 5\n while i % 2 == 0:\n i //= 2\n c2 += 1\n while i % 5 == 0:\n i //= 5\n c5 += 1\n\n # track top 12 and last 5\n top12 = int(str(top12 * i)[:12])\n tail5 = tail5 * i % 100000\n \n # multiply the remained 2 or 5\n if c2 > c5:\n for _ in range(c2 - c5):\n top12 = int(str(top12 * 2)[:12])\n tail5 = tail5 * 2 % 100000\n elif c2 < c5:\n for _ in range(c5 - c2):\n top12 = int(str(top12 * 5)[:12])\n tail5 = tail5 * 5 % 100000\n\n zero = min(c2, c5)\n\n # as is included in top 12, it\'s easy to tell when d<=10\n if len(str(top12))<=10:\n return str(top12)+\'e\'+str(zero)\n \n return str(top12)[:5] + \'.\'*3 + \'0\'*(5-len(str(tail5)))+str(tail5)+\'e\'+str(zero)\n``` | 4 | 1 | ['Python'] | 1 |
abbreviating-the-product-of-a-range | Basic Maths Shortest C++ Cleanest Solution | Easy to Understand | | basic-maths-shortest-c-cleanest-solution-x93n | The Solution basically consists of 3 things \n\n1. Counting Zeroes \n2. Getting Suffix\n3. Getting Prefix\n\nCounting Zeroes and Suffix can be done easily by | 1806manan | NORMAL | 2023-05-11T14:19:08.231793+00:00 | 2023-05-11T14:28:37.930469+00:00 | 322 | false | The Solution basically consists of 3 things \n\n1. Counting Zeroes \n2. Getting Suffix\n3. Getting Prefix\n\nCounting Zeroes and Suffix can be done easily by extracting only last 10-12 digits of the answer after every multiplication and counting and removing zeroes as soon as we found them.\n\nNow is the time tricky part :- How to get the first 5 digits ??\nHere comes the Logarithmic property : To get the start 5 digits \n1. Take sum of log(base10)(number) of all the numbers from left to right.\n2. Once the sum is calculated extract the decimal part by ```Decimal(Sum) - long(Sum)```.\n3. Then Add 4 to it since we want first 5 numbers.\n4. After that lets say you get result Res , Take ```floor(10 power Res)``` and that will be the first 5 digits.\n\nCode Snippet for the above tricky Part\n```\n long double SumLog= 0;\n for(int i=left;i<=right;i++)\n SumLog += log10(i);\n string P =to_string(floor(pow(10,4.0+(SumLog-long(SumLog)))));\n```\n\nNote : ``` long double ``` is used to get more precision avoid the round off errors which comes with float/double. \n\n```\nclass Solution {\npublic:\n\n string abbreviateProduct(int left, int right) {\n \n string Ans = "1",Prefix ="1";\n int count = 0;\n for(int i=left;i<=right;i++)\n {\n Ans = to_string(i*stol(Ans));\n while(Ans.back()==\'0\') Ans.pop_back() , count++;\n if(Ans.size()>12)\n Ans =Ans.substr(Ans.size()-12); \n }\n \n long double SumLog= 0;\n for(int i=left;i<=right;i++)\n SumLog += log10(i);\n string P =to_string(floor(pow(10,4.0+(SumLog-long(SumLog)))));\n \n if(Ans.size()>10)\n Ans = (P.size()>5?P.substr(0,5):P) +"..." + Ans.substr(Ans.size()-5);\n \n return Ans+"e"+to_string(count);\n }\n};\n``` | 3 | 0 | ['Math', 'C'] | 0 |
abbreviating-the-product-of-a-range | (C++) 2117. Abbreviating the Product of a Range | c-2117-abbreviating-the-product-of-a-ran-gqph | \n\nclass Solution {\npublic:\n string abbreviateProduct(int left, int right) {\n int highest = 0, trailing = 0; \n long prefix = 1, suffix = 1 | qeetcode | NORMAL | 2021-12-25T17:57:57.562419+00:00 | 2021-12-25T17:57:57.562480+00:00 | 537 | false | \n```\nclass Solution {\npublic:\n string abbreviateProduct(int left, int right) {\n int highest = 0, trailing = 0; \n long prefix = 1, suffix = 1; \n \n for (int x = left; x <= right; ++x) {\n prefix *= x; \n suffix *= x; \n for (; prefix >= 1e12; ++highest, prefix /= 10); \n for (; suffix % 10 == 0; ++trailing, suffix /= 10); \n if (suffix >= 1e10) suffix %= 10\'000\'000\'000; \n }\n \n for (; prefix >= 1e5; ++highest, prefix /= 10); \n highest += log10(prefix); \n if (highest - trailing < 10) return to_string(suffix) + "e" + to_string(trailing); \n suffix %= 100\'000; \n return to_string(prefix) + "..." + string(5-to_string(suffix).size(), \'0\') + to_string(suffix) + "e" + to_string(trailing); \n }\n};\n``` | 3 | 0 | ['C'] | 1 |
abbreviating-the-product-of-a-range | Python (Simple Maths) | python-simple-maths-by-rnotappl-hz8h | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | rnotappl | NORMAL | 2023-04-14T18:00:38.535025+00:00 | 2023-04-14T18:00:38.535070+00:00 | 242 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def abbreviateProduct(self, left, right):\n string = str(prod(list(range(left,right+1))))\n n_string = string.rstrip("0")\n zeros = len(string) - len(n_string)\n\n if len(n_string) <= 10:\n return n_string + "e" + str(zeros)\n else:\n return n_string[:5] + "..." + n_string[-5:] + "e" + str(zeros)\n\n \n \n``` | 2 | 1 | ['Python3'] | 1 |
abbreviating-the-product-of-a-range | Java : precision... precision... precision... | java-precision-precision-precision-by-di-fz2s | \n public String abbreviateProduct(int left, int right) {\n final long threshold0 = 100_000_000_000_000L,threshold1 = 10_000_000_000L,threshold2 = 100 | dimitr | NORMAL | 2022-01-11T07:15:54.722118+00:00 | 2022-01-11T07:45:31.896513+00:00 | 268 | false | ```\n public String abbreviateProduct(int left, int right) {\n final long threshold0 = 100_000_000_000_000L,threshold1 = 10_000_000_000L,threshold2 = 100_000;\n long curr=1;\n int i, zerosCount = 0;\n for(i=left;i<=right && curr<threshold0;i++){\n curr *= i;\n while(curr%10==0){\n curr/=10;\n zerosCount++;\n }\n }\n if(curr<threshold1)\n return String.format("%de%d",curr,zerosCount);\n\n long low=curr%threshold1;\n double high = curr; //double precision is more accurate than long when we need to divide by 10 by 10 and multiply again\n while(high>threshold1)\n high/=10;\n \n for(;i<=right;i++){\n low *=i;\n high *=i;\n while(low%10==0){\n low/=10;\n zerosCount++;\n }\n if(low>=threshold1)\n low %= threshold1;\n while(high>threshold1)\n high/=10;\n }\n\n while(high>=threshold2)\n high/=10;\n low %= threshold2;\n return String.format("%d...%05de%d",(int)high,low,zerosCount);\n }\n``` | 2 | 0 | [] | 1 |
abbreviating-the-product-of-a-range | straight forward, brute force | straight-forward-brute-force-by-platinum-ufg5 | \nclass Solution:\n def abbreviateProduct(self, left: int, right: int) -> str:\n num = 1\n while left<=right:\n num *= left\n | platinum_s | NORMAL | 2021-12-30T19:32:42.231150+00:00 | 2022-01-03T05:40:38.842272+00:00 | 211 | false | ```\nclass Solution:\n def abbreviateProduct(self, left: int, right: int) -> str:\n num = 1\n while left<=right:\n num *= left\n left+= 1\n a = str(num)\n b = a.rstrip("0")\n e = len(a)-len(b)\n if len(b) > 10:\n b = b[:5]+"..."+b[-5:]\n return b+"e"+str(e)\n \n``` | 2 | 0 | ['Python'] | 2 |
abbreviating-the-product-of-a-range | Python, almost brute force | python-almost-brute-force-by-kryuki-hq7d | There are 2 steps:\nStep1: Calculate the number of trailing zeros\nStep2: Multiply & Keep track of the first 12 numbers and the last 5 numbers\n\nFor step1, we | kryuki | NORMAL | 2021-12-25T16:40:21.747835+00:00 | 2021-12-25T16:51:03.583773+00:00 | 278 | false | There are 2 steps:\nStep1: Calculate the number of trailing zeros\nStep2: Multiply & Keep track of the first 12 numbers and the last 5 numbers\n\nFor step1, we need to know the number of factors 2 and 5 in [right, left], because 10 = 2 * 5. The minimum of the two will be the number of trailing zeros.\n\nFor step2, If the final number is less than 10 ** 10, I just output the number without abbreviation, but if the number exceeds 10 ** 10, then I switch to the calculation of the "big" number which needs abbreviation. For each, step, I only keep track of the first and last few numbers because they don\'t change by multiplication. \n\n```\nclass Solution:\n def abbreviateProduct(self, left: int, right: int) -> str:\n #Step1: count the num of trailing zeros\n factor_two, factor_five = 0, 0\n curr_factor = 2\n while curr_factor <= right:\n factor_two += (right // curr_factor) - ((left - 1) // curr_factor)\n curr_factor *= 2\n curr_factor = 5\n while curr_factor <= right:\n factor_five += (right // curr_factor) - ((left - 1) // curr_factor)\n curr_factor *= 5\n trailing_zeros = min(factor_two, factor_five)\n \n #Step2: Multiply until it gets too big, while dividing 2 and 5\n\t\tdivide_two_so_far, divide_five_so_far = 0, 0\n curr_num = 1\n for i in range(left, right + 1):\n multiply = i\n while multiply % 2 == 0 and divide_two_so_far < trailing_zeros:\n multiply //= 2\n divide_two_so_far += 1\n while multiply % 5 == 0 and divide_five_so_far < trailing_zeros:\n multiply //= 5\n divide_five_so_far += 1\n curr_num *= multiply\n if curr_num >= 10 ** 10:\n break\n \n #if the number doesn\'t get too large (less than or equal to 10 digits)\n if curr_num < 10 ** 10:\n return str(curr_num) + \'e\' + str(trailing_zeros)\n \n #Step2: if the number exceeds 10 ** 10, then keep track of the first and last digits\n first_digits, last_digits = int(str(curr_num)[:12]), int(str(curr_num)[-5:])\n start = i + 1\n for i in range(start, right + 1):\n multiply = i\n while multiply % 2 == 0 and divide_two_so_far < trailing_zeros:\n multiply //= 2\n divide_two_so_far += 1\n while multiply % 5 == 0 and divide_five_so_far < trailing_zeros:\n multiply //= 5\n divide_five_so_far += 1\n first_digits = int(str(first_digits * multiply)[:12])\n last_digits = int(str(last_digits * multiply)[-5:])\n \n\t\t#output\n return str(first_digits)[:5] + \'...\' + \'{:>05d}\'.format(last_digits) + \'e\' + str(trailing_zeros)\n``` | 2 | 0 | ['Python', 'Python3'] | 0 |
abbreviating-the-product-of-a-range | [Python] Short, contest-oriented solution | python-short-contest-oriented-solution-b-2z7f | Multiply all the numbers within the range but only keep track of the # of trailing zeros and the last 10 digits before that. Set the flag if the product ever gr | chuan-chih | NORMAL | 2021-12-25T16:26:36.402304+00:00 | 2021-12-27T22:02:31.891311+00:00 | 226 | false | Multiply all the numbers within the range but only keep track of the # of trailing zeros and the last 10 digits before that. Set the flag if the product ever grows above what `mod` can express. If it does, use the sum of `math.log10()` to calculate the leading 5 digits.\n\nI can probably use the sum of `math.log10()` to estimate whether I need the last 10 digits or just the last 5, but it wouldn\'t be much faster.\n```\nclass Solution:\n def abbreviateProduct(self, left: int, right: int) -> str:\n mod = 1\n zeros = 0\n div = False\n for x in range(left, right + 1):\n mod *= x\n while not mod % 10:\n mod //= 10\n zeros += 1\n d, mod = divmod(mod, 10000000000)\n if d:\n div = True\n if not div:\n return f\'{str(mod)}e{zeros}\'\n else:\n log_sum = sum(math.log10(i) for i in range(left, right + 1))\n s = str(10 ** (log_sum % 1))\n leading = s[0] + s[2:6]\n return f\'{leading}...{str(mod % 10 ** 5).zfill(5)}e{zeros}\'\n```\n**A note on floating point precision**\nWe only need to get the first 5 leading digits right so we never come close to the limit of floating point precision, but it\'s interesting to note how many leading digits we can get right and by what implementation. The largest exact product `functools.reduce(operator.mul, range(1, 10 ** 6 + 1))` is\n```\n826393168833124006237...\n```\nThe simplest implementation `10 ** (sum(math.log10(i) for i in range(1, 10 ** 6 + 1)) % 1)` gives\n```\n8.263930516641858\n```\n, correct up to 6 digits. `math.fsum()` is more precise than `sum()`: `10 ** (math.fsum(math.log10(i) for i in range(1, 10 ** 6 + 1)) % 1)` gives\n```\n8.263931686266318\n```\n, correct up to 9 digits. However, it\'s more important not to sum up a large number if we only want the mantissa. `10 ** functools.reduce(lambda a, b: (a + b) % 1, (math.log10(i) for i in range(1, 10 ** 6 + 1)))` gives\n```\n8.26393168831949\n```\nwhich is correct up to 11 digits.\n\n**Addendum**\nApparently [the standard solution failed for `left=184, right=70145`](https://github.com/LeetCode-Feedback/LeetCode-Feedback/issues/5657) and the most precise implementation above somehow [gives different answers on my computer vs. on LC](https://github.com/LeetCode-Feedback/LeetCode-Feedback/issues/5657#issuecomment-1001244092). The correct leading digits for `left=184, right=70145` are\n```\n391180000000002366...\n```\n`10 ** functools.reduce(lambda a, b: (a + b) % 1,...)` on my computer gives\n```\n3.9118000000001816\n```\n`10 ** (math.fsum(...) % 1)` gives\n```\n3.9117999998468442\n```\nbut `10 ** (sum(...) % 1)` gives\n```\n3.911800002992591\n```\nSo the ordering of the implementations in terms of precision doesn\'t change, but ironically in this case more precise implementation may fail to give the correct answer\uD83E\uDD37\uD83C\uDFFB\u200D\u2642\uFE0F\n\n**Addendum 2**\nUsing `np.longdouble` and vectorized `np.log10()` yields the most precise estimate so far, but it still takes some luck to err on the "right side" for the case `left=184, right=70145`:\n\n```\nimport numpy as np\n\nlog_sum = functools.reduce(lambda a, b: (a + b) % 1, np.log10(np.arange(left, right + 1, dtype=np.longdouble)))\nestimate = 10 ** (log_sum + 4)\nprint(estimate)\n```\nThe stdout:\n```\n39118.00000000122791\n```\nSolution doing this is slower and takes more memory but still fast enough to get AC. | 2 | 0 | ['Python'] | 0 |
abbreviating-the-product-of-a-range | [Python3] Just Working Code - 27.09.2024 | python3-just-working-code-27092024-by-pi-9407 | \npython3 []\nimport math\n\nclass Solution:\n def abbreviateProduct(self, left: int, right: int) -> str:\n last = 1\n modulo = 10 ** 5\n\n | Piotr_Maminski | NORMAL | 2024-09-27T14:39:54.844775+00:00 | 2024-09-27T14:40:32.379676+00:00 | 37 | false | \n```python3 []\nimport math\n\nclass Solution:\n def abbreviateProduct(self, left: int, right: int) -> str:\n last = 1\n modulo = 10 ** 5\n\n twosCount = 0\n fivesCount = 0\n\n sumLog10 = 0\n maxBufferValue = 10 ** 1200\n bufferProduct = 1\n \n for x in range(left, right + 1):\n bufferProduct *= x\n\n if bufferProduct > maxBufferValue:\n sumLog10 += math.log10(bufferProduct)\n bufferProduct = 1\n\n while x % 2 == 0:\n twosCount += 1\n x //= 2\n \n while x % 5 == 0:\n fivesCount += 1\n x //= 5\n \n last = (last * x) % modulo \n\n sumLog10 += math.log10(bufferProduct)\n zerosCount = min(twosCount, fivesCount)\n\n if sumLog10 < 10 + zerosCount:\n productString = str(bufferProduct)\n return productString[:len(productString) - zerosCount] + \'e\' + str(zerosCount)\n \n twosCount -= zerosCount\n fivesCount -= zerosCount \n \n last = (last * pow(2, twosCount, modulo)) % modulo\n last = (last * pow(5, fivesCount, modulo)) % modulo\n first = int(pow(10, sumLog10 % 1 + 4.0))\n \n return str(first) + \'...\' + str(last).zfill(5) + \'e\' + str(zerosCount)\n``` | 1 | 0 | ['Python3'] | 0 |
abbreviating-the-product-of-a-range | Simple (5-line) Python solution beats 100% || 5 line solution || beats 100% | simple-5-line-python-solution-beats-100-ya0zy | \n Describe your first thoughts on how to solve this problem. \n\n# Approach: Simple and step by step approach as mentiones in problem description \nstep 1: cal | s1ttu | NORMAL | 2023-01-03T14:47:16.517580+00:00 | 2023-01-03T14:47:16.517628+00:00 | 221 | false | \n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach: Simple and step by step approach as mentiones in problem description \nstep 1: calculate the product of the given range (left, right)\nrange(left, right+1) will give us a range object or the range which is converted into list by list() function and then to calculate the product of whole list we use prod() function \nso till here the 1st line is explained \n**prod(list(range(left, right+1)))** and converting the result into string with the help of str() function as we have to print our solution in string format and for later opertions\n\nstep 2: removing the trailing zeros form the end of the calculated product with the help of rstrip() method which removes the white space in case of no string is given to it (i.e. "hii ".rstrip() will become "hii" if we give it any string/parameter it will remove all occurence till any other charater apper for example- "hii00000000000000".rstrip("0") will become "hii")\n\nstep 3: count of traling zeros of the string \nthe experssion goes like this **lenght of string with zeros - length of string without zeros**\n\nstep 4: as there is 2 way to output the result if the lenght of string (without zeros) is less then or equal to 10 the we will output it as it is string (without zeros)+"e"+ count of zeros\n\nstep 5: if the lenght of string after removing zeros is greater then > 10 then we have to print the it in 2 parts the starting 5 digits and the last 5 digits \nexample 123456789987654 consider this as our non zero string \nso we have to print the starting 5 digits which is 12345 and the last 5 digits if it which is 87654 in the given format \nstarting 5 digits + "..." + last 5 digits + "e" + count of zeros\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(1) \n- as we have not used any loops or recursion call so i think the TC will be O(1) **correct me if i\'m wrong** \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1) \n- as for space complexity, we are not doing any recursion and using only 3 veriables to store our calculation so i think this solution uses constant space \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def abbreviateProduct(self, left: int, right: int) -> str:\n summ = str(prod(list(range(left, right+1))))\n su = summ.rstrip("0")\n zeros = len(summ)-len(su)\n if len(su)<=10: return (su+"e"+str(zeros))\n else: return (su[:5]+"..."+su[-5:]+"e"+str(zeros))\n``` | 1 | 0 | ['Python3'] | 1 |
abbreviating-the-product-of-a-range | python soln | python-soln-by-kumarambuj-0br7 | \nclass Solution:\n def abbreviateProduct(self, l: int, r: int) -> str:\n \n num=1\n for i in range(l,r+1):\n num=num*i\n | kumarambuj | NORMAL | 2022-06-10T07:42:00.997809+00:00 | 2022-06-10T07:42:00.997851+00:00 | 110 | false | ```\nclass Solution:\n def abbreviateProduct(self, l: int, r: int) -> str:\n \n num=1\n for i in range(l,r+1):\n num=num*i\n \n c=0\n while(num>0 and num%10==0):\n c+=1\n num=num//10\n \n s=str(num)\n res=s\n if len(s)>10:\n res=s[:5]+\'...\'+s[-5:]\n res=res+\'e\'+str(c)\n return res\n \n``` | 1 | 0 | [] | 0 |
abbreviating-the-product-of-a-range | C++ Math Solution | c-math-solution-by-ahsan83-02bl | \n1. We can always store first 12 digits of and last 12 digits of the multiplication as upper and lower\n2. We can count the number of digits in final product u | ahsan83 | NORMAL | 2022-05-18T08:59:01.376688+00:00 | 2022-05-18T08:59:01.376728+00:00 | 267 | false | ```\n1. We can always store first 12 digits of and last 12 digits of the multiplication as upper and lower\n2. We can count the number of digits in final product using Log formula\n3. We can count number of trailing zero by incrementing counter when lower digit is 0\n4. We can get first and last 5 digits of upper and lower from their 12 digit\n```\n\n```\nclass Solution {\npublic:\n string abbreviateProduct(int left, int right) {\n \n // upper 12 digit of product\n double upper = 1;\n \n // lower 12 digit of product\n long long lower = 1L;\n \n // offset to make 12 digit in upper and lower\n long long Offset = 1e12;\n \n // offset to make 5 digit in upper and lower\n long long cutOffset = 1e5;\n \n // store log value of the product \n double product = 0.0;\n \n // count trailing zero in the product\n int trailing = 0;\n \n for(int i=left;i<=right;i++)\n {\n // update log value of product\n product += log10(i);\n \n // multiple value with upper and lower 12 digit\n upper *= i;\n lower *= i;\n \n // keep 12 digit in upper\n while(upper>=Offset)upper/=10;\n \n // remove trailing zeroes\n while(lower%10==0)lower/=10,trailing++;\n \n // keep 12 digits in lower\n lower %= Offset;\n }\n \n // count total digits in product except trailing zeroes\n int digitLength = (int)product + 1 - trailing;\n \n // keep 5 digit in upper and lower\n while(upper>=cutOffset)upper/=10;\n lower %= cutOffset;\n \n int upperInt = upper;\n \n // take digit length digits from upper and lower when digit length <= 10\n if(digitLength<=10)\n {\n // make all digit 0 to tackle missing MSB zeroes in lower\n string result(digitLength,\'0\');\n string upperStr = to_string(upperInt);\n string lowerStr = to_string(lower);\n \n for(int i=0;i<upperStr.length() && digitLength >0; i++,digitLength--)\n result[i] = upperStr[i];\n \n for(int k=1;!lowerStr.empty() && digitLength >0; digitLength--,k++)\n {\n result[result.length()-k] = lowerStr.back();\n lowerStr.pop_back();\n }\n\n \n return result + "e" + to_string(trailing);\n } \n else\n { \n // take upper and lower 5 digits \n string result = to_string(lower);\n return to_string(upperInt) + "..." + string(5-result.size(),\'0\') + result + "e" + to_string(trailing);\n }\n }\n};\n``` | 1 | 0 | ['Math', 'C'] | 0 |
abbreviating-the-product-of-a-range | Python Solution Brute Force | python-solution-brute-force-by-reahaansh-jpvt | Upvote if you like the solution\n\n\nclass Solution:\n def abbreviateProduct(self, left: int, right: int) -> str:\n value = 1\n count = 0\n | ReahaanSheriff | NORMAL | 2022-01-18T13:57:49.786503+00:00 | 2022-01-18T13:57:49.786531+00:00 | 130 | false | **Upvote if you like the solution**\n```\n\nclass Solution:\n def abbreviateProduct(self, left: int, right: int) -> str:\n value = 1\n count = 0\n for i in range(left,right+1):\n value*=i # calculation of product value from left to right\n string = str(value)\n for j in string[::-1]:\n if(j == \'0\'):\n count+=1 # counting suffix zeros(trailing zeros)\n else:\n break\n length = len(string) # Total length of product\n len_digit = length-count # Length of product neglecting trailing zeros\n if(\'0\' in string and len(string[0:len_digit]) <= 10): # If length without zeros less than 10\n return string[0:len_digit]+\'e\'+str(count)\n elif(\'0\' in str(value) and len(string[0:len_digit]) > 10): # If length without zeros greater than 10\n return str(value)[0:5]+\'...\'+str(value)[0:len_digit][-5:]+\'e\'+str(count)\n else:\n return str(value)+\'e0\' # If no trailing zeros\n\n```\n\n**Thank You** | 1 | 0 | ['Python'] | 0 |
abbreviating-the-product-of-a-range | Brute Force (Python) | brute-force-python-by-rishav_1999-f1ap | \tclass Solution:\n\t\tdef abbreviateProduct(self, left: int, right: int) -> str:\n\t\t\tans=1\n\t\t\tfor i in range(left,right+1):\n\t\t\t\tans*=i\n\t\t\tst=st | Rishav_1999 | NORMAL | 2021-12-31T08:57:50.479897+00:00 | 2021-12-31T08:57:50.479925+00:00 | 98 | false | \tclass Solution:\n\t\tdef abbreviateProduct(self, left: int, right: int) -> str:\n\t\t\tans=1\n\t\t\tfor i in range(left,right+1):\n\t\t\t\tans*=i\n\t\t\tst=str(ans)\n\t\t\tcnt=0\n\t\t\ti=len(st)-1\n\t\t\twhile st[i]=="0":\n\t\t\t\tcnt+=1\n\t\t\t\ti-=1\n\t\t\tst=st[:i+1]+"e"+str(cnt)\n\t\t\tif len(st)-cnt>10:\n\t\t\t\te_idx=st.index("e")\n\t\t\t\ts_idx=e_idx-5\n\t\t\t\tans=st[:5]+"..."+st[s_idx:e_idx]+st[e_idx:]\n\t\t\t\treturn ans\n\t\t\telse:\n\t\t\t\treturn st | 1 | 0 | [] | 0 |
abbreviating-the-product-of-a-range | Two working solutions, easy python solution. | two-working-solutions-easy-python-soluti-humg | Intuitionjust obtain the product of range value and convert it into string, check number of '0' in the string , and return the output as per condition.Complexit | ukmh02 | NORMAL | 2025-03-25T06:20:23.903369+00:00 | 2025-03-25T06:20:23.903369+00:00 | 2 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
just obtain the product of range value and convert it into string, check number of '0' in the string , and return the output as per condition.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(Right−Left)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(1)
# Code
```python3 []
import sys
sys.set_int_max_str_digits(100000)
class Solution:
def abbreviateProduct(self, left: int, right: int) -> str:
#this logic also works but it takes a time a lot --1530ms
# x,k = 1,0
# for i in range(left, right+1):
# x*=i
# x = str(x)
# n = len(x)
# for j in x:
# if j == '0':
# k+=1
# else:
# k = 0
# x = x[:n-k]
# if len(x)<=10: return x+'e'+str(k)
# else: return (x[:5]+'...'+x[-5:]+'e'+str(k))
#**************************************************************************************
k = str(prod(list(range(left, right+1)))) #1524ms
i = k.rstrip('0')
zeros = len(k) - len(i)
if len(i)<=10: return (i+'e'+str(zeros))
else: return (i[:5]+'...'+i[-5:]+'e'+str(zeros))
``` | 0 | 0 | ['Python3'] | 0 |
abbreviating-the-product-of-a-range | Abbreviate Product | O(B−A) | 100% Optimized C# | abbreviate-product-ob-a-100-optimized-c-7o1kf | IntuitionThe product grows too large for direct computation, so we track only the leading and trailing digits while counting trailing zeros.Approach
Leading dig | Gustavo_Mariano | NORMAL | 2025-02-10T13:08:53.285676+00:00 | 2025-02-10T13:08:53.285676+00:00 | 6 | false | # Intuition
The product grows too large for direct computation, so we track only the leading and trailing digits while counting trailing zeros.
# Approach
1. Leading digits (value): Multiply and normalize to keep only the first few significant digits while counting shifts (digitShift).
2. Trailing digits (remainder): Multiply, remove trailing zeros (countZeros), and keep only the last 14 digits to avoid overflow.
3. Result construction:
- If the product has ≤10 significant digits, return it normally.
- Otherwise, return "prefix...suffixeC" format.
# Complexity
- Time complexity:
O(B−A), since we iterate through the range once.
- Space complexity:
O(1), using only a few variables.
# Code
```csharp []
public class Solution {
public string AbbreviateProduct(int a, int b) {
double value = 1.0;
int countZeros = 0, digitShift = 0;
long remainder = 1;
for (int num = a; num <= b; num++) {
value *= num;
while (value >= 1)
{
value /= 10;
digitShift++;
}
remainder *= num;
while (remainder % 10 == 0)
{
countZeros++;
remainder /= 10;
}
if (remainder > (long)Math.Pow(10, 14))
remainder %= (long)Math.Pow(10, 14);
}
if (digitShift - countZeros <= 10)
return ((long)(value * Math.Pow(10, digitShift - countZeros) + 0.5)).ToString() + "e" + countZeros;
else
{
string prefix = ((long)(value * 100000)).ToString();
string suffix = (remainder % 100000).ToString().PadLeft(5, '0');
return prefix + "..." + suffix + "e" + countZeros;
}
}
}
```
# Explanation
1. Initialize value, remainder, digitShift, and countZeros.
2. Loop through [a, b], updating value and remainder, counting shifts and trailing zeros.
3. Format the result based on digit length. | 0 | 0 | ['Math', 'C#'] | 0 |
abbreviating-the-product-of-a-range | 2117. Abbreviating the Product of a Range | 2117-abbreviating-the-product-of-a-range-a37p | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | G8xd0QPqTy | NORMAL | 2025-01-18T02:59:29.993096+00:00 | 2025-01-18T02:59:29.993096+00:00 | 6 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution(object):
def abbreviateProduct(self, a, b):
value, count_zeros, digit_shift = 1.0, 0, 0
remainder = 1
for num in range(a, b + 1):
value *= num
while value >= 1:
value /= 10
digit_shift += 1
remainder *= num
while remainder % 10 == 0:
count_zeros += 1
remainder //= 10
if remainder > 10 ** 14:
remainder %= 10 ** 14
if digit_shift - count_zeros <= 10:
return str(int(value * (10 ** (digit_shift - count_zeros)) + 0.5)) + 'e' + str(count_zeros)
else:
return str(int(value * 100000)) + '...' + ('0000' + str(remainder))[-5:] + 'e' + str(count_zeros)
``` | 0 | 0 | ['Python3'] | 0 |
abbreviating-the-product-of-a-range | C++ mini BigInt implementation | c-mini-bigint-implementation-by-ivangnil-5s38 | IntuitionThe key is to handle large products by tracking both leading and trailing digits separately while counting trailing zeros.Approach
Use BigInt class to | ivangnilomedov | NORMAL | 2025-01-17T13:17:37.273834+00:00 | 2025-01-17T13:17:37.273834+00:00 | 20 | false | # Intuition
The key is to handle large products by tracking both leading and trailing digits separately while counting trailing zeros.
# Approach
1. Use BigInt class to store large numbers in base 10^13 chunks for leading digits
2. Track trailing digits separately modulo 10^10 to prevent overflow
3. Count trailing zeros by dividing out factors of 10
# Code
```cpp []
class BigInt {
public:
BigInt(long long val, int keep_lead_digs = -1) : keep_lead_digs(keep_lead_digs) {
for (; val > 0 || data.empty(); val /= kDig)
data.push_back(val % kDig);
reverse(data.begin(), data.end());
}
void operator*=(long long m) {
long long inherit = 0;
for (int i = beg; i < data.size() || inherit > 0; ++i) {
if (i == data.size())
data.resize(i + 1);
long long r = m * data[i] + inherit;
inherit = r / kDig;
data[i] = r % kDig;
}
if (keep_lead_digs > 0)
beg = max<int>(0, data.size() - keep_lead_digs);
}
string to_string() const {
ostringstream oss;
int i = data.size() - 1;
oss << data[i] << ::setfill('0') << ::setw(kDecCount);
for (--i; i >= beg; --i)
oss << data[i];
return oss.str();
}
private:
static constexpr int kDecCount = 13;
static const long long kDig;
static const string kLeadZeroFmt;
vector<long long> data;
int beg = 0;
int keep_lead_digs = -1;
static long long calculate_kdig() {
long long val = 1;
for (int i = 0; i < kDecCount; ++i)
val *= 10;
return val;
}
};
const long long BigInt::kDig = calculate_kdig();
const string BigInt::kLeadZeroFmt = "%0" + ::to_string(kDecCount) + "lld";
class Solution {
public:
string abbreviateProduct(int left, int right) {
BigInt bint(left, 5);
int tzc = 0;
long long trail = left;
for (int i = left + 1; i <= right; ++i) {
bint *= i;
trail *= i;
for (; trail % 10 == 0; trail /= 10)
++tzc;
trail %= kTrailAccMod;
}
trail %= kTrailResMod;
string s = bint.to_string();
for (; !s.empty() && s.back() == '0'; s.pop_back());
ostringstream oss;
if (s.length() > 10)
oss << string_view(s.c_str(), 5) << "..." << ::setfill('0') << ::setw(5) << trail;
else
oss << s;
oss << "e" << tzc;
return oss.str();
}
private:
static constexpr long long kTrailAccMod = 1e10;
static constexpr long long kTrailResMod = 1e5;
};
``` | 0 | 0 | ['C++'] | 0 |
abbreviating-the-product-of-a-range | Python (Simple Maths) | python-simple-maths-by-rnotappl-bphz | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | rnotappl | NORMAL | 2024-11-01T16:54:07.647437+00:00 | 2024-11-01T16:54:07.647471+00:00 | 4 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def abbreviateProduct(self, left, right):\n sys.set_int_max_str_digits(100000)\n string = str(prod(list(range(left,right+1))))\n n_string = string.rstrip("0")\n zeros = len(string) - len(n_string) \n\n if len(n_string) <= 10:\n return n_string + "e" + str(zeros)\n else:\n return n_string[:5] + "..." + n_string[-5:] + "e" + str(zeros)\n``` | 0 | 0 | ['Python3'] | 0 |
abbreviating-the-product-of-a-range | 2117. Abbreviating the Product of a Range.cpp | 2117-abbreviating-the-product-of-a-range-x0o1 | Code\n\nclass Solution {\npublic:\n string abbreviateProduct(int left, int right) {\n double upper = 1;\n long long lower = 1L;\n long l | 202021ganesh | NORMAL | 2024-11-01T10:52:15.216026+00:00 | 2024-11-01T10:52:15.216056+00:00 | 1 | false | **Code**\n```\nclass Solution {\npublic:\n string abbreviateProduct(int left, int right) {\n double upper = 1;\n long long lower = 1L;\n long long Offset = 1e12;\n long long cutOffset = 1e5; \n double product = 0.0;\n int trailing = 0;\n \n for(int i=left;i<=right;i++)\n {\n product += log10(i);\n upper *= i;\n lower *= i;\n while(upper>=Offset)upper/=10;\n while(lower%10==0)lower/=10,trailing++;\n lower %= Offset;\n }\n int digitLength = (int)product + 1 - trailing;\n while(upper>=cutOffset)upper/=10;\n lower %= cutOffset;\n \n int upperInt = upper;\n if(digitLength<=10)\n {\n string result(digitLength,\'0\');\n string upperStr = to_string(upperInt);\n string lowerStr = to_string(lower);\n \n for(int i=0;i<upperStr.length() && digitLength >0; i++,digitLength--)\n result[i] = upperStr[i];\n \n for(int k=1;!lowerStr.empty() && digitLength >0; digitLength--,k++)\n {\n result[result.length()-k] = lowerStr.back();\n lowerStr.pop_back();\n }\n\n \n return result + "e" + to_string(trailing);\n } \n else\n { \n string result = to_string(lower);\n return to_string(upperInt) + "..." + string(5-result.size(),\'0\') + result + "e" + to_string(trailing);\n }\n }\n};\n``` | 0 | 0 | ['C'] | 0 |
abbreviating-the-product-of-a-range | Python 3: TC O((right-left)*log(right)) SC O(1): Tricks for First and Last Five Digits | python-3-tc-oright-leftlogright-sc-o1-tr-kpfw | Intuition\n\nThe easy case is when the explicit product is less than a few thousand digits, in which case we can use Python\'s arbitrary precision math. Unfortu | biggestchungus | NORMAL | 2024-09-09T02:06:05.297854+00:00 | 2024-09-09T02:06:05.297878+00:00 | 2 | false | # Intuition\n\nThe easy case is when the explicit product is less than a few thousand digits, in which case we can use Python\'s arbitrary precision math. Unfortunately there\'s a limit of 4300 digits and we can easily hit that because we\'re basically computing factorials.\n\n## Counting Trailing Zeros\n\nIf there\'s a trailing zero then the product is divisible by `10 == 2*5`.\n\nThat means if we have `twos` factors of `2` and `fives` factors of `5` then we will have `min(twos, fives)` tailing zeros.\n\n## Last Five Digits\n\nThe last five is a bit easier to get. We know that the resulting number is something like this:\n```a\n................ ABCDE 0000000..00000\n---------------- ----- --------------\nfirst D-1 digits last C trailing zeros\n five\n```\n\nThe whole product is `left * ... * right = 2**twos * 5**fives * rest` where `rest` are all prime factors that are not `2` or `5`.\n\nThe trailing zeros account for `2**C * 5**C`.\n\nTherefore we need the last five digits of `rest * 2**(twos-C) * 5**(fives-C)`.\n\nTo get this is easier than it might look:\n* we can get the last five digits of `rest` by brute-force\n * for each `x` divide out the `2` and `5` factors\n * then include `x` in the product and take the residue mod `1e5`\n* then we have `twos-C` factors of two, multiply those in and take the residue each time\n* and we have `fives-C` factors of five, same thing\n\nEither `twos-C` or `fives-C` will be zero so we won\'t get any additional trailing zeros.\n\nWe only need the last five digits of `rest` becauase we know the last five digits of `lhs * rhs` only depend on the last five digits of both. And we know none of them will be zero because we divided out all the factors that can possibly give us zero.\n\n## First Five Digits\n\nThe insight we need here is that if we get `log10(product)` then it can be written as\n\n```a\nlog10(first * 10**(digits-1) + second * 10**(digits-2) + ...)`\n = log10(10**(digits-1)) + log10(first + second/10 + ... + fifth/1e4)\n --------------------- ------------------------------------------\n integer < 10: decimal\n```\n\nSo if we get the `log10` of the product (floating point), then the decimal part gives us the digits. We only need the first five so if we\'re careful with floating-point math we can extract them from the log10.\n\n**Tricky part:** if we add up the log10 of each `x` in `left..right` then we lose some precision because the sum can be order `1e4` (see Stirling\'s approximation). This means we\'ll lose about four digits of precision when adding log10s, e.g. `4000.<lhs_digits> + 0.<rhs_digits>` will drop some digits of precision from `rhs_digits`. **We need all the digits we can get to maximum precision or else we\'ll get off-by-one errors.**\n\nTo avoid this we do the following:\n* for each `x`, divide out the factors of 10\n* **then** take the log10 and add to `l10`\n* **remove the integer part of `l10` aggressively**\n\nThis minimizes precison loss in the floating point math, gaining us a few precious digits at the end.\n\n**Without these tricks to improve precision we get off-by-one errors.**\n\n# Approach\n\nSee code and the docs for details.\n\n# Complexity\n- Time complexity: `O((right-left)*log(right))` for each value `x` in `left..right` we need to divde out factors of 2 and 5 in some of the loops, `O(log(x))` operations. The rest are floating-point math operations and machine-precision integer multiplications that can be done in `O(1)`\n\n- Space complexity: `O(1)`\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def abbreviateProduct(self, left: int, right: int) -> str:\n # calc prod of l..r\n\n # abbreviate as follows:\n # > count trailing zeros == C and remove them\n # > let remainder be d\n # > if d > 10 then report first and last five digits\n\n # then print either (<=10 digits)eC\n # or (first5..last5)eC\n\n # last five pretty easy, mod 1e5\n # first five more interesting\n\n # if we have Ae10 + Be9 + Ce8 + ...\n # and we multiply by x\n # we get Axe10 + Bxe9 + ...\n # and the carry from D, E, F can roll up through A, B\n\n # solutions include:\n # Python, Java: brute-force with arb. prec. ints\n # C++: roll your own\n \n # is there a clever way to get the first several digits?\n # e.g. 1999 * 3 = 5997 via (2000-1)*3\n\n # maybe groups of 10?\n # if we know the product of a..b\n # then a+10..b+10 would be\n # (a+10)(a+1+10)..(b+10)\n # a..b + 10*(a+1..b + a,a+2..b + ... + a..b-1) + 100*(all ways to drop 2) + 1000*(all ways to drop 3) + ...\n # YIKES\n\n # so manual multiply is probably the way to go barring some other innovations\n\n # except manual multiply takes an order n*log10(n) digit number, does 3 mults on it, then sum\n # for four passes over n*log10(n) digits O(n) times, yikes\n # TOO EXPENSIVE\n\n # so we need a math trick for this\n # last five digits are EZ\n\n # first five digits are hard\n # ... we\'re not expected to do the FFT multiply right? that would be very mean\n\n # is there a faster way to get just a specific digit? For example what\'s the first digit?\n # or can we get the number of digits?\n # yes, from log10 of the numbers summed\n #\n # we can get log10 of the number, and the floating point might give us what we need\n\n twos = 0\n fives = 0\n for x in range(left, right+1):\n while x % 2 == 0:\n twos += 1\n x //= 2\n while x % 5 == 0:\n fives += 1\n x //= 5\n\n C = min(twos, fives)\n\n l10 = sum(log10(x) for x in range(left, right+1))\n digits = int(l10 + 1)\n \n if digits - C <= 10:\n # at most 10 digits besides trailing zeros: find the number via explicit multiply and divide-out-10s\n p = 1\n for x in range(left, right+1):\n p *= x\n while p % 10 == 0:\n p //= 10\n\n return f"{p}e{C}"\n\n # FIXED: lost some essential precision when the product is huge, e.g. l10 is 5000.something\n # which means we dropped 3 digits from some of the values. So aggressively remove the integer\n # part of the log10 so we retain as many digits as possible\n l10 = 0\n for x in range(left, right+1):\n while x % 10 == 0: x //= 10\n l10 += log10(x)\n l10 -= int(l10)\n\n # separate calculation of first and last 5 digits,\n # potentially too many digits to divide out\n\n # for first five:\n # log10(p) = log10(first*10**(digits-1) + second*10**(digits-2) + ...)\n # digits-1 + log10(first + second/10 + third/100 + ...)\n #\n # so 10**(l10-int(l10)) == first+second/10 + ... fifth/1e4\n # (.................) * 1e4 is first*1e4 + .. + fifth <- this is the number we want\n\n firstFive = int(10**l10*1e4)\n\n # fixed: last 5 are tricky\n # we know that the last five are from factors that are not 2 or 5\n # so what we need to do is get the digits other than 2 and 5\n # multiply in excess factors of 2 and 5 to get all of them\n # then mod 1e5\n lastFive = right\n for x in range(left, right):\n # get last five digits if we drop all powers of 2 and 5\n lastFive *= x\n while lastFive % 2 == 0: lastFive //= 2\n while lastFive % 5 == 0: lastFive //= 5\n\n lastFive %= 100_000\n\n # C handles 2**C and 5**C\n # if we have excess 2s and 5s we need to add them in\n lastFive = (lastFive * pow(2, twos-C, 100_000)) % 100_000\n lastFive = (lastFive * pow(5, fives-C, 100_000)) % 100_000\n\n # FIXED: must print leading zeros in lastFive % 1e5\n return f"{firstFive}...{lastFive:05d}e{C}"\n``` | 0 | 0 | ['Python3'] | 0 |
abbreviating-the-product-of-a-range | Python3 Easy || O(N) | python3-easy-on-by-yangzen09-gjyd | Intuition:- Computing the product of all integers in a specified range and in a compact format, handling large numbers by using scientific notation and suppress | YangZen09 | NORMAL | 2024-08-08T05:22:55.956559+00:00 | 2024-08-08T05:22:55.956591+00:00 | 12 | false | **Intuition:-** *Computing the product of all integers in a specified range and in a compact format, handling large numbers by using scientific notation and suppressing trailing zeros.*\n**It also provides utility functions for calculating factorials and checking if a product exceeds a given threshold.**\n\n# Approach-\n**1- Iteration Through Range:-** *Loop through all integers from left to right, calculating their cumulative product.*\n\n**2- Normalization:-** *Normalize the product to keep it within a manageable range (0.1 to <1) by continuously dividing by 10, while tracking the number of digits removed.*\n\n**3- Suffix Calculation:-** *Maintain a separate variable (suffix) to compute the product of the integers while also counting and removing trailing zeros.*\n\n**4- Abbreviation Logic:-** *Depending on the number of original digits and the count of zeros, format the final product either in scientific notation or a more condensed string if the product is too large.*\n\n**5- Utility Function:-** *Provide additional functionalities through helper functions (factorial and is_product_large) for further mathematical operations and checks related to the product calculated.*\n\n# Complexity\n**Time complexity:-**\n *O(n) for each of the three functions.*\n\n**Space complexity:-**\n *O(1) for each of the three functions.*\n\n# Code\n```\nclass Solution(object): \n def abbreviateProduct(self, left: int, right: int) -> str: \n product, suffix, zeros, org_digits = 1.0, 1, 0, 0 \n for n in range(left, right + 1): \n product *= n \n while product >= 1: \n product /= 10 \n org_digits += 1 \n suffix *= n \n while suffix % 10 == 0: \n zeros += 1 \n suffix //= 10 \n if suffix > 10 ** 14: \n suffix %= 10 ** 14 \n if org_digits - zeros <= 10: \n return str(int(product * (10 ** (org_digits - zeros)) + 0.5)) + \'e\' + str(zeros) \n else: \n return str(int(product * 100000)) + \'...\' + (\'0000\' + str(suffix))[-5:] + \'e\' + str(zeros) \n\n def factorial(self, n): \n """Returns the factorial of n.""" \n if n < 0: \n raise ValueError("Factorial is not defined for negative numbers") \n if n == 0 or n == 1: \n return 1 \n result = 1 \n for i in range(2, n + 1): \n result *= i \n return result \n\n def is_product_large(self, left, right, threshold=10**14): \n """Checks if the product of the range left to right exceeds the given threshold.""" \n product = 1 \n for n in range(left, right + 1): \n product *= n \n if product > threshold: \n return True \n return False\n``` | 0 | 0 | ['Math', 'Python3'] | 0 |
abbreviating-the-product-of-a-range | Best Performing Solution | Simple Python | Math | Very Detailed Explanation | Scientific Notation ✨ | best-performing-solution-simple-python-m-8cpf | UPVOTE is Highly Appreciated\n\n# Intuition\nUsing float or double to record prefix, inspired by scientific notation\n\n# Approach\n1. keep 0.1 <= prod < 1.0, s | Sci-fi-vy | NORMAL | 2024-05-25T10:40:24.762427+00:00 | 2024-05-25T10:40:24.762463+00:00 | 9 | false | **UPVOTE is Highly Appreciated**\n\n# Intuition\nUsing float or double to record prefix, inspired by scientific notation\n\n# Approach\n1. keep `0.1 <= prod < 1.0`, so len(str`(int(product * 100000))) == 5`, just like scientific notation\n\n2. so we can easily get `prefix` via `prefix = str(int(product * 100000))`\n\n3. `org_digits` is the number of digits of the original very very large product number, `zeros` is the number of its trailing zeros, so that `org_digits - zeros` is the number of its actual non-zero digits.\n\n4. The error of `suffix` can only come from the trailing zeros.\n\n5. Although we remove all of the trailing zeros every time and then take the modulus, but 2 and 5 as the division of `suffix` may squeeze the effective digit length.\n\n6. so if we want to keep the exactly accurate last 5 Digits, we need to increase the digit length.\n\n7. Since `n` is less than or equal to `10 ** 4`, there are no more than 5 trailing zeros that can be eliminated at one time. So to not waste memory we asiign `suffix %= 10 ** 14` is large enough to keep accurate 5 digits of `suffix`.\n\n8. Another reason we chose `10 ** 14` is that `(10 ** 14) * (10 ** 4) = 10 ** 18` is in the range of int64, so it can be easily migrated to other programming languages as well.\n\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(1)$$\n\n# Code\n```\nclass Solution(object):\n\tdef abbreviateProduct(self, left, right):\n\t\tproduct, suffix, zeros, org_digits = 1.0, 1, 0, 0\n\t\tfor n in range(left, right + 1):\n\t\t\tproduct *= n\n\t\t\twhile product >= 1: # keep 0.1 <= prod < 1.0, so len(str(int(prod * 100000))) == 5\n\t\t\t\tproduct /= 10\n\t\t\t\torg_digits += 1 # add 1 while remove 1 digit\n\t\t\tsuffix *= n\n\t\t\twhile suffix % 10 == 0: # count and remove the trailing zeros\n\t\t\t\tzeros += 1\n\t\t\t\tsuffix //= 10\n\t\t\tif suffix > 10 ** 14:\n\t\t\t\tsuffix %= 10 ** 14\n\t\tif org_digits - zeros <= 10:\n\t\t\treturn str(int(product * (10 ** (org_digits - zeros)) + 0.5)) + \'e\' + str(zeros)\n\t\telse:\n\t\t\treturn str(int(product * 100000)) + \'...\' + (\'0000\' + str(suffix))[-5:] + \'e\' + str(zeros)\n``` | 0 | 0 | ['Math', 'Brainteaser', 'Python', 'Python3'] | 0 |
abbreviating-the-product-of-a-range | The worst solution I've ever written (this is horrible). | the-worst-solution-ive-ever-written-this-1858 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | NickUlman | NORMAL | 2024-03-25T17:55:39.817465+00:00 | 2024-03-25T17:55:39.817531+00:00 | 28 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public static final double NATURAL_LOG_10 = Math.log(10);\n public static final double NATURAL_LOG_2 = Math.log(2);\n public static final double NATURAL_LOG_17 = Math.log(17);\n public static final double NATURAL_LOG_3 = Math.log(3);\n double ERR = 0.00000012;\n public String abbreviateProduct(int left, int right) {\n //for 0s, find number of 5 and 2 factors.\n //for last 5 digits, after taking out 5 and 2 factors, the product mod 100000 should get the last five digits\n //log(product) = log(left) + log(left+1) +.... log(right)\n //e^(sum(k = left to right )(ln(k))) -> approx first 5 digits with \n \n double logSum = 0;\n double logSumB10 = 0;\n double logSumB2 = 0;\n double logSumB17 = 0;\n double logSumB3 = 0;\n for(int i = left; i <= right; i++) {\n double log = Math.log(i);\n logSum += log;\n logSumB10 += log/NATURAL_LOG_10;\n logSumB2 += log/NATURAL_LOG_2;\n logSumB17 += log/NATURAL_LOG_17;\n logSumB3 += log/NATURAL_LOG_3;\n }\n logSumB10 = (logSumB10 + logSum/NATURAL_LOG_10)/2;\n logSumB2 = (logSumB2 + logSum/NATURAL_LOG_2)/2;\n logSumB17 = (logSumB17 + logSum/NATURAL_LOG_17)/2;\n logSumB3 = (logSumB3 + logSum/NATURAL_LOG_3)/2;\n int twoFactors = 0;\n int fiveFactors = 0;\n\n for(int i = left; i <= right; i++) {\n int curr = i;\n while(curr % 2 == 0) {\n curr /= 2;\n twoFactors++;\n } \n while(curr % 5 == 0) {\n curr /= 5;\n fiveFactors++;\n }\n }\n\n //each 10 needs 1 five and 1 two factor, so the amount of 10s = min(fiveFactors, twoFactors) \n \n int trailingZeros = Math.min(fiveFactors, twoFactors);\n //for each trailiing zero, string number loses 1 place in length to abbrev, this is equivalent to the e^(logSum)/(10*trailingZeros) = e^(logSum - trailingZeros*ln(10)) -> so do logSum -= trailingZeros*ln(10)\n double log2Of10 = NATURAL_LOG_10/NATURAL_LOG_2;\n double log17of10 = NATURAL_LOG_10/NATURAL_LOG_17;\n double log3of10 = NATURAL_LOG_10/NATURAL_LOG_3;\n\n logSumB10 -= trailingZeros;\n logSum -= NATURAL_LOG_10*trailingZeros;\n logSumB2 -= trailingZeros*log2Of10;\n logSumB17 -= trailingZeros*log17of10;\n\n int fivesToIgnore = trailingZeros;\n int twosToIgnore = trailingZeros;\n\n //this means that the total product is < max for long values\n if(logSum <= 43.668) {\n long product = 1;\n for(long i = left; i <= right; i++) {\n long curr = i;\n while(curr % 5 == 0 && fivesToIgnore > 0) {\n curr /= 5;\n fivesToIgnore--;\n }\n while(curr % 2 == 0 && twosToIgnore > 0) {\n curr /= 2;\n twosToIgnore--;\n }\n product *= curr;\n }\n\n String num = String.valueOf(product);\n \n return (num.length() > 10 ? num.substring(0, 5) + "..." + num.substring(num.length()-5) : num) + "e" + trailingZeros;\n }\n\n \n\n /*e^logSum = product\n divide product by 10 until product is 5 digits, those are highest 5 digits\n e^(logSum)/(10^n) = 5 digits of product and following decimals\n 10^n = e^(n*ln(10)) -> e^(logSum)/(10^n) = e^(logSum)/e^(n*ln(10)) = e^(logSum-n*ln(10))\n n is the integer that forces five digits.\n e^x is 5 digits when 10000 <= e^x < 100000 -> 10^4 <= e^x < 10^5 -> 4*ln(10) <= x < 5*ln(10)\n e^(logSum-n*ln(10)) -> where 4*ln(10) <= logSum-n*ln(10) < 5*ln(10) -> since only subtracting integer multiples of ln(10), exp should stay the same % ln(10)\n e^(logSum - n*ln(10)) = e^((logSum % ln(10)) + 4*ln(10))\n\n */\n double expTest = Math.exp((logSum % NATURAL_LOG_10) + 4.0*NATURAL_LOG_10);\n double expTestB10 = Math.pow(10, (logSumB10 % 1) + 4);\n double expTestB2 = Math.pow(2, (logSumB2 % log2Of10) + 4.0 * log2Of10);\n double expTestB17 = Math.pow(17, (logSumB17 % log17of10) + 4.0 * log17of10);\n double expTestB3 = Math.pow(3, (logSumB3 % log3of10) + 4.0*log3of10);\n\n int freq = 0;\n int val = Math.max(Math.max(Math.max((int)expTest, (int)expTestB10), Math.max((int)expTestB2, (int)expTestB17)), (int)expTestB3);\n if((int)expTest == val) freq++;\n if((int)expTestB10 == val) freq++;\n if((int)expTestB2 == val) freq++;\n if((int)expTestB17 == val) freq++;\n if((int)expTestB3 == val) freq++;\n freq %= 5; //if all of them are max, none surpass to next integer barrier, so freq is equivalent to 0\n\n //take average of both to make lessen the error of either base\n double expAVG = (expTest + expTestB10 + expTestB2 + expTestB17 + expTestB3)/5.0;\n\n String firstFiveDigits = String.valueOf((int)(ERR*freq + expAVG));\n \n long prodTest = 1l;\n \n\n long modProduct = 1l;\n long MOD = 100000l;\n\n for(int i = left; i <= right; i++) {\n int curr = i;\n while(curr % 5 == 0 && fivesToIgnore > 0) {\n curr /= 5;\n fivesToIgnore--;\n }\n while(curr % 2 == 0 && twosToIgnore > 0) {\n curr /= 2;\n twosToIgnore--;\n }\n modProduct = (modProduct * curr) % MOD;\n prodTest *= curr; \n while(prodTest > MOD *10 * i) {\n prodTest /= 10;\n }\n }\n /*\n System.out.println(prodTest);\n System.out.println(expTest);\n System.out.println(expTestB10);\n System.out.println(expTestB2);\n System.out.println(expTestB17);\n System.out.println(expTestB3);\n System.out.println(expAVG);\n\n*/\n String lastFiveDigits = String.valueOf(modProduct);\n while(lastFiveDigits.length() < 5) {//if leading zeros were cut off in string conversion, add them back\n lastFiveDigits = "0" + lastFiveDigits;\n }\n return firstFiveDigits + "..." + lastFiveDigits + "e" + trailingZeros;\n\n \n \n \n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
abbreviating-the-product-of-a-range | Python optimized long arithmetics (beats 96%) | python-optimized-long-arithmetics-beats-706ie | Intuition\nLet Product=L\cdot(L+1)\cdot...\cdot R.\nWhen the Product is small, we can handle it easily.\nOtherwise, the problems of finding first digits, last d | kapart | NORMAL | 2024-03-10T21:44:00.764922+00:00 | 2024-03-11T15:10:33.702790+00:00 | 19 | false | # Intuition\nLet $$Product=L\\cdot(L+1)\\cdot...\\cdot R$$.\nWhen the $$Product$$ is small, we can handle it easily.\nOtherwise, the problems of finding first digits, last digits and zeros count are solved independently.\n\n# Approach\n\n\n1. Represent the $$Product$$ in exponential form:\n$$Product=\\overline{a_1,a_2a_3a_4a_5a_6a_7...}\\cdot 10^p=M\\cdot 10^p$$,\nwhere $$a_i$$ is $$i$$-th digit from left,\n$$M$$ - mantissa, the fractional part of the base-10 logarithm ($$1\\leq M<10$$):\n$$log_{10}Product=log_{10}M+p$$\n$$\\{log_{10}Product\\}=log_{10}M$$\n$$10^{\\{log_{10}Product\\}}=M$$\n ##### So we can find the first digits from mantissa:\n $$\\overline{a_1,a_2a_3a_4a_5a_6a_7...}=M$$\n$$\\overline{a_1a_2a_3a_4a_5,a_6a_7...}=M\\cdot10^4$$\n$$\\overline{a_1a_2a_3a_4a_5}=\u230AM\\cdot10^4\u230B$$\n\n Because \n$$log_{10}M=\\{log_{10}Product\\}=\\{log_{10}(L\\cdot(L+1)\\cdot...\\cdot R)\\}=\\{ \\sum_{i=L}^{R} log_{10}i\\}$$,\n ##### we can get a cumulative floating point error due to calling the logarithm function many times.\n So it is better to minimize the number of calls to the logarithm function.\n Using Python long arithmetic you need to call the logarithm function only once.\n Second approach is keeping product of numbers on a segment ($$bufferProduct$$ in code) and calling the logarithm function when the product becomes greater than the threshold ($$maxBufferValue$$ in code).\n I got AC with $$maxBufferValue=10^{1200}$$.\n\n1. We can find the last digits using modulo operation:\n$$LastNdigits=Product \\% 10^N$$\n\n1. Trailing zeros count is $$min(pow_2, pow_5)$$, where $$pow_2$$ and $$pow_5$$ are powers of 2 and 5 respectively from prime factorization of $$Product$$.\n \n\n# Complexity\n- Time complexity\n$$O(n)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n``` Python_call_log10_with_threshold []\n# Runtime: 343ms, beats 96.15% of users with Python3\n# Memory Usage: 16.83MB, beats 40.38% of users with Python3\n\nclass Solution:\n def abbreviateProduct(self, left: int, right: int) -> str: \n last = 1\n modulo = 10 ** 5\n\n twosCount = 0\n fivesCount = 0\n\n sumLog10 = 0\n maxBufferValue = 10 ** 1200\n bufferProduct = 1\n \n for x in range(left, right + 1):\n bufferProduct *= x\n\n if bufferProduct > maxBufferValue:\n sumLog10 += math.log10(bufferProduct)\n bufferProduct = 1\n\n while x % 2 == 0:\n twosCount += 1\n x //= 2\n \n while x % 5 == 0:\n fivesCount += 1\n x //= 5\n \n last = (last * x) % modulo \n\n sumLog10 += math.log10(bufferProduct)\n zerosCount = min(twosCount, fivesCount)\n\n if sumLog10 < 10 + zerosCount:\n productString = str(bufferProduct)\n return productString[:len(productString) - zerosCount] + \'e\' + str(zerosCount)\n \n twosCount -= zerosCount\n fivesCount -= zerosCount \n \n last = (last * pow(2, twosCount, modulo)) % modulo\n last = (last * pow(5, fivesCount, modulo)) % modulo\n \n first = int(pow(10, sumLog10 % 1 + 4.0))\n \n return str(first) + \'...\' + str(last).zfill(5) + \'e\' + str(zerosCount) \n \n```\n``` Python_single_log10_call []\n# Runtime: 6085 ms, beats 19.23% of users with Python3\n# Memory Usage: 16.80 MB, beats 40.38% of users with Python3\n\nclass Solution:\n def abbreviateProduct(self, left: int, right: int) -> str: \n modulo = 10 ** 5\n product = 1\n\n for i in range(left, right + 1):\n product *= i\n\n zerosCount = 0\n\n while product % 10 == 0:\n product //= 10\n zerosCount += 1\n \n prodLog10 = math.log10(product)\n\n if prodLog10 < 10:\n productString = str(product)\n return productString + \'e\' + str(zerosCount)\n\n first = int(pow(10, prodLog10 % 1 + 4))\n last = product % modulo\n \n return str(first) + \'...\' + str(last).zfill(5) + \'e\' + str(zerosCount) \n``` | 0 | 0 | ['Number Theory', 'Python3'] | 0 |
abbreviating-the-product-of-a-range | Abbreviation of Product of a Range with Trailing Zeros | abbreviation-of-product-of-a-range-with-04zpq | Intuition\nThe code calculates the product of integers in a given range while removing trailing zeros. It then abbreviates the product and counts the number of | Gheshu | NORMAL | 2023-10-19T13:58:15.786601+00:00 | 2023-10-19T13:58:15.786626+00:00 | 12 | false | # Intuition\nThe code calculates the product of integers in a given range while removing trailing zeros. It then abbreviates the product and counts the number of removed zeros if the product is greater than a certain length. The goal is to make the code more efficient and optimized\n\n# Approach\n1. Initialize a count variable to keep track of the number of trailing zeros.\n2. Initialize a product variable to store the product of integers in the given range.\n3. Iterate through the range from \'left\' to \'right\' and calculate the product, simultaneously removing trailing zeros. This is done by dividing the product by 10 until it\'s not divisible by 10 anymore.\n4. Convert the product to a string once to avoid unnecessary conversions.\n5. If the length of the product string is greater than 10, abbreviate the product by taking the first 5 and last 5 characters and add \'...\' in between. Append \'e\' followed by the count of removed trailing zeros.\n6. If the length of the product string is not greater than 10, simply append \'e\' followed by the count of removed trailing zeros.\n\n\n# Code\n```\n/**\n * @param {number} left\n * @param {number} right\n * @return {string}\n */\nvar abbreviateProduct = function(left, right) {\n let product = 1n\n let count = 0\n for(let i = left; i <= right; i++){\n product *= BigInt(i)\n }\n while(product % 10n === 0n){\n product /= 10n\n count++\n }\n \n product = product.toString()\n if(product.length > 10){\n const first = product.slice(0,5)\n const last = product.slice(-5)\n\n return first + \'...\' + last + \'e\' + count\n\n }\n return product + \'e\' + count\n \n \n};\n``` | 0 | 0 | ['Math', 'JavaScript'] | 0 |
abbreviating-the-product-of-a-range | [Python] 5 lines- only by '0' count for beginner | python-5-lines-only-by-0-count-for-begin-94cy | Time complexity: O(n)\n- Space complexity: O(1)\n\nclass Solution(object):\n def abbreviateProduct(self, left, right):\n t, k = str(reduce(operator.mu | hanifvub | NORMAL | 2023-09-10T13:16:20.414089+00:00 | 2023-09-10T13:16:20.414110+00:00 | 5 | false | - Time complexity: $$O(n)$$\n- Space complexity: $$O(1)$$\n```\nclass Solution(object):\n def abbreviateProduct(self, left, right):\n t, k = str(reduce(operator.mul,range(left,right+1))), 0\n while t[-k-1]==\'0\': k +=1\n if k: t=t[:-k]\n if len(t)>10: t=t[:5]+\'...\'+t[-5:]\n return t+\'e\'+str(k)\n``` | 0 | 0 | ['Python'] | 0 |
abbreviating-the-product-of-a-range | Very straightforward completely beginner friendly Python solution | very-straightforward-completely-beginner-171u | Intuition\n Describe your first thoughts on how to solve this problem. \nFairly easy. Just find the product and convert it to str\n\n# Approach\n Describe your | farhad_zada | NORMAL | 2023-08-27T11:40:14.555344+00:00 | 2023-08-27T11:40:14.555366+00:00 | 17 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFairly easy. Just find the product and convert it to str\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nYou just find the product and convert to string to slice it\n\n# Complexity\n- Time complexity: 51%\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: 70%\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport sys \nclass Solution:\n def abbreviateProduct(self, left: int, right: int) -> str:\n sys.set_int_max_str_digits(20000000)\n p = 1\n for i in range(left, right+1):\n p *= i\n s = str(p)\n c = len(s) \n s = s.rstrip(\'0\')\n c = c - len(s)\n if len(s) > 10:\n return \'%s...%se%s\' % (s[:5], s[-5:], str(c))\n return \'%se%s\' % (s, str(c))\n``` | 0 | 0 | ['Python3'] | 0 |
abbreviating-the-product-of-a-range | Easy to understand Python solution for Abbreviating the Product of a Range , | easy-to-understand-python-solution-for-a-imel | Intuition\n Describe your first thoughts on how to solve this problem. \nGood challenging problem \n\n# Approach\n Describe your approach to solving the problem | amaroww_0603 | NORMAL | 2023-06-16T16:48:04.466053+00:00 | 2023-06-16T16:48:04.466073+00:00 | 30 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nGood challenging problem \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nnormal method , solution is easy to understand just used simple string slicing methods to solve it \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->O(right-left+logN) \nN = value of product of all numbers between left and right\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->O(1)\n\n# Code\n```\nclass Solution(object):\n def abbreviateProduct(self, left, right):\n """\n :type left: int\n :type right: int\n :rtype: str\n """\n prod=1\n for i in range(left,right+1):\n prod*=i\n str_prod = str(prod)\n count_digit=0\n count_zeros=0\n str5=str_prod\n while (str5[-1] == \'0\'):\n str5 = str5[:-1]\n count_zeros = count_zeros+1\n count_digit = len(str5)\n res=""\n if count_digit<=10:\n str2="e"+str(count_zeros)\n if(count_zeros==0):\n res = str_prod+str2\n else:\n res = str_prod[:-count_zeros]\n res = res+str2\n #print(res)\n else:\n str4 = str_prod[:-count_zeros]\n str3 = "e"+str(count_zeros)\n pre = str5[:5]\n suf = str5[len(str5)-5:]\n res = pre+"..."+suf+str3\n #print("res = ",res)\n return res\n``` | 0 | 0 | ['Python'] | 0 |
abbreviating-the-product-of-a-range | Just a runnable solution | just-a-runnable-solution-by-ssrlive-dk63 | Code\n\nimpl Solution {\n pub fn abbreviate_product(left: i32, right: i32) -> String {\n let (mut suff, mut c, mut total, max_suff) = (1, 0, 0, 100_00 | ssrlive | NORMAL | 2023-03-04T02:26:54.393425+00:00 | 2023-03-04T02:26:54.393458+00:00 | 19 | false | # Code\n```\nimpl Solution {\n pub fn abbreviate_product(left: i32, right: i32) -> String {\n let (mut suff, mut c, mut total, max_suff) = (1, 0, 0, 100_000_000_000);\n let mut pref = 1.0;\n for i in left..=right {\n pref *= i as f64;\n suff *= i as i64;\n while pref >= 100_000.0 {\n pref /= 10.0;\n total = if total == 0 { 6 } else { total + 1 };\n }\n while suff % 10 == 0 {\n suff /= 10;\n c += 1;\n }\n suff %= max_suff;\n }\n let s = suff.to_string();\n format!(\n "{}{}{}e{}",\n pref as i32,\n if total - c <= 10 { "" } else { "..." },\n if total - c < 5 {\n ""\n } else {\n &s[s.len() - (total - c - 5).min(5) as usize..]\n },\n c\n )\n }\n}\n``` | 0 | 0 | ['Rust'] | 0 |
abbreviating-the-product-of-a-range | Understandable Python Solution with linear time complexity | understandable-python-solution-with-line-blk7 | Intuition\n Describe your first thoughts on how to solve this problem. \nThe intuition behind the above code is to efficiently calculate and represent the produ | udaykiran_3 | NORMAL | 2023-01-11T14:06:13.861139+00:00 | 2023-01-11T14:06:13.861184+00:00 | 89 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition behind the above code is to efficiently calculate and represent the product of all integers in the given range in a human-readable format. The product can be very large and contain many trailing zeros, which can make it difficult to read and understand. So this code aims to simplify the representation of the product by removing trailing zeros and truncating the number to the first 5 and last 5 digits, if it has more than 10 digits.\n\n# Approach\n1. Initialize a variable \'product\' to 1 and a variable \'trailing_zeros\' to 0.\n2. Use a for loop to iterate over all integers in the range [left, right]. For each integer in the range, multiply it with the current value of \'product\'\n3. While the last digit of product is zero, count number of trailing zeros and divide product by 10\n4. Convert product to a string, store the number of digits of product in a variable \'digits\'\n5. If the number of digits of the product is greater than 10, return the first 5 digits followed by \'...\' and the last 5 digits, followed by \'e\' and the number of trailing zeros.\n6. If the number of digits of the product is less than or equal to 10, return the original number followed by \'e\' and the number of trailing zeros.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def abbreviateProduct(self, left: int, right: int) -> str:\n product = 1\n for i in range(left, right + 1):\n product *= i\n trailing_zeros = 0\n while product % 10 == 0:\n trailing_zeros += 1\n product //= 10\n product_str = str(product)\n digits = len(product_str)\n if digits > 10:\n pre = product_str[:5]\n suf = product_str[-5:]\n return f"{pre}...{suf}e{trailing_zeros}"\n else:\n return f"{product_str}e{trailing_zeros}"\n``` | 0 | 0 | ['Python3'] | 0 |
abbreviating-the-product-of-a-range | I strive for the simple things LOL | Python TRULY SIMPLE solution | i-strive-for-the-simple-things-lol-pytho-gbr9 | The longest it took for me: https://leetcode.com/submissions/detail/852714885/\n\n\nclass Solution:\n def abbreviateProduct(self, left: int, right: int) -> s | hemantdhamija | NORMAL | 2022-12-01T06:49:43.390152+00:00 | 2022-12-01T06:49:43.390189+00:00 | 111 | false | The longest it took for me: https://leetcode.com/submissions/detail/852714885/\n\n```\nclass Solution:\n def abbreviateProduct(self, left: int, right: int) -> str:\n product, numZeros = factorial(right) // factorial(left - 1), 0\n while not product % 10:\n product //= 10\n numZeros += 1\n product = str(product)\n if len(product) > 10:\n return product[:5] + \'...\' + product[-5:] + \'e\' + str(numZeros)\n return product + \'e\' + str(numZeros)\n``` | 0 | 0 | ['Math', 'Python'] | 0 |
abbreviating-the-product-of-a-range | Python Easy Solution | python-easy-solution-by-user7457rv-e3z0 | \nclass Solution:\n def abbreviateProduct(self, left: int, right: int) -> str:\n prod = left\n for i in range(prod+1,right+1):\n pro | user7457RV | NORMAL | 2022-10-28T18:41:19.129955+00:00 | 2022-10-28T18:41:19.129988+00:00 | 69 | false | ```\nclass Solution:\n def abbreviateProduct(self, left: int, right: int) -> str:\n prod = left\n for i in range(prod+1,right+1):\n prod *= i\n \n prod = str(prod)\n prod = [prod[i] for i in range(len(prod))]\n pos = len(prod)-1\n count = 0\n for j in range(pos,-1,-1):\n if prod[j] == "0":\n count += 1\n else:\n break\n \n start = pos-count\n prod = prod[:start+1]\n if len(prod) > 10:\n first_five = "".join(prod[:5])\n last_five = "".join(prod[len(prod)-5:])\n return first_five + "..." + last_five + "e" + str(count)\n else:\n string = "".join(prod)\n return string + "e" + str(count)\n \n \n\n``` | 0 | 0 | ['Python'] | 0 |
abbreviating-the-product-of-a-range | python solution (faster 90%) | python-solution-faster-90-by-dugu0607-w6gm | \tclass Solution:\n\t\tdef abbreviateProduct(self, l: int, r: int) -> str:\n\n\t\t\tnum=1\n\t\t\tfor i in range(l,r+1):\n\t\t\t\tnum=num*i\n\n\t\t\tc=0\n\t\t\tw | Dugu0607 | NORMAL | 2022-10-05T07:10:41.814533+00:00 | 2022-10-05T07:10:41.814573+00:00 | 39 | false | \tclass Solution:\n\t\tdef abbreviateProduct(self, l: int, r: int) -> str:\n\n\t\t\tnum=1\n\t\t\tfor i in range(l,r+1):\n\t\t\t\tnum=num*i\n\n\t\t\tc=0\n\t\t\twhile(num>0 and num%10==0):\n\t\t\t\tc+=1\n\t\t\t\tnum=num//10\n\n\t\t\ts=str(num)\n\t\t\tres=s\n\t\t\tif len(s)>10:\n\t\t\t\tres=s[:5]+\'...\'+s[-5:]\n\t\t\tres=res+\'e\'+str(c)\n\t\t\treturn res | 0 | 0 | [] | 0 |
abbreviating-the-product-of-a-range | Non-bruteforce algorithm in Python3 with numpy | non-bruteforce-algorithm-in-python3-with-xjc4 | As suggested in the hints, the three parts are calculated separately. The precision issue in the Python built-in floating numbers happen, so I use numpy.float1 | metaphysicalist | NORMAL | 2022-07-23T19:18:30.310585+00:00 | 2022-07-23T19:18:30.310618+00:00 | 100 | false | As suggested in the hints, the three parts are calculated separately. The precision issue in the Python built-in floating numbers happen, so I use numpy.float128 instead of the built-in floats. \n\n```\nimport numpy\n\nclass Solution:\n def abbreviateProduct(self, left: int, right: int) -> str:\n log_prod = numpy.float128(0)\n last = 1\n num_zeros = 0\n for x in range(left, right+1):\n log_prod += numpy.log10(x)\n last *= x\n while last % 10 == 0:\n last //= 10\n num_zeros += 1\n last %= 1000000000000\n x = floor(log_prod)\n if x - num_zeros < 10:\n return "%de%d" % (last % 10000000000, num_zeros)\n return "%.0f...%05de%d" % (floor(numpy.power(10, (4 + log_prod - x))), last % 100000, num_zeros)\n \n | 0 | 0 | ['Python', 'Python3'] | 0 |
abbreviating-the-product-of-a-range | fast O(polylog n) time algorithm, C++ 0ms 100% | fast-opolylog-n-time-algorithm-c-0ms-100-kd5d | An algorithmic math problem.\nFirst 5 digits: numerical analysis.\nLast 5 digits: number theory.\n\n#define double long double\nconst double PI=atan((double)1)* | hqztrue | NORMAL | 2022-07-04T10:21:33.489804+00:00 | 2022-07-17T08:42:32.760413+00:00 | 112 | false | An algorithmic math problem.\nFirst 5 digits: numerical analysis.\nLast 5 digits: number theory.\n```\n#define double long double\nconst double PI=atan((double)1)*4,E=exp((double)1),\n B[]={1,1./2,1./6,0,-1./30,0,1./42,0,-1./30,0,5./66,0,-691./2730,0,7./6,0,-3617./510,0,43867./798,0,-174611./330};\nconst int M=10;\ndouble log_fac(double n){\n\tdouble ans=n*log(n/E)+log(n)/2+log(sqrt(PI*2));\n\tfor (int i=2;i<=M;++i)ans+=pow(-1,i)*B[i]/(i*(i-1)*pow(n,i-1));\n\tif (n<20){\n\t\tans=0;\n\t\tfor (int i=1;i<=n;++i)ans+=log(i);\n\t}\n\treturn ans;\n}\nint leading(int l,int r){\n\tdouble t=log_fac(r)-log_fac(l-1);\n\tt/=log((double)10); t-=int(t)-4;\n\treturn pow(10,t);\n}\n\nconst int P=3125;\ntemplate<class T> T extend_gcd(T a,T b,T &x,T &y){\n\tif (!b){x=1;y=0;return a;}\n\tT res=extend_gcd(b,a%b,y,x); y-=x*(a/b);\n\treturn res;\n}\ntemplate<class T>\ninline T inv(T a,T M){\n\tT x,y; extend_gcd(a,M,x,y);\n\treturn (x%M+M)%M;\n}\nconst int inv2=inv(2,P);\nint exp(int x,int y,int z){\n\tint ans=1;\n\twhile (y){\n\t\tif (y&1)ans=ans*x%z;\n\t\tx=x*x%z;y>>=1;\n\t}\n\treturn ans;\n}\nint Chinese_Remainder_Theorem(int A[],int M[],int n){\n\tfor (int i=1;i<n;++i){\n\t\tint x,y,P=M[0]*M[i];\n\t\textend_gcd(M[0],M[i],x,y);\n\t\tx=(x*(A[i]-A[0])%P+P)%P;\n\t\tA[0]=(x*M[0]+A[0])%P; M[0]=P;\n\t}\n\treturn A[0];\n}\n// PolynomialMod[Product[If[Mod[i,5]>0,5^4*x+i,1],{i,1,5^4}],3125]\nint calc(int x,int d){\n\tswitch(d){\n\t\tcase 0: return x%5?x%P:1;\n\t\tcase 1: return (24+250*x+875*x%P*x+1250*x%P*x%P*x+625*x%P*x%P*x%P*x)%P;\n\t\tcase 2: return 124;\n\t\tcase 3: return 624;\n\t\tcase 4:\n\t\tcase 5: return 3124;\n\t}\n\treturn 0;\n}\nint get(int l,int r,int d){\n\tif (l>r||d<0)return 1;\n\tint mod=pow(5,d),l0=(l-1)/mod+1,r0=(r+1)/mod,res=1;\n\tfor (int i=l0;i<r0;++i)res=res*calc(i,d)%P;\n\tif (l0<r0)return res*get(l,l0*mod-1,d-1)%P*get(r0*mod,r,d-1)%P;\n\telse return get(l,r,d-1);\n}\nstring abbreviateProduct1(int left, int right) { // brute force\n long long suff = 1, c = 0, total = 0, max_suff = 100000000000LL;\n double pref = 1.0;\n for (int i = left; i <= right; ++i) {\n pref *= i;\n suff *= i;\n while (pref >= 100000) {\n pref /= 10;\n total = total == 0 ? 6 : total + 1; \n }\n while (suff % 10 == 0) {\n suff /= 10;\n ++c;\n }\n suff %= max_suff;\n }\n string s = to_string(suff);\n return to_string((int)pref) + (total - c <= 10 ? "" : "...") \n \t+ (total - c < 5 ? "" : s.substr(s.size() - min(5LL, total - c - 5))) + "e" + to_string(c);\n}\nclass Solution {\npublic:\n\tstring abbreviateProduct(int l, int r) {\n\t\tif (r-l<20)return abbreviateProduct1(l,r);\n\t\tint last=1,l0=l,r0=r,zeros=0;\n\t\twhile (l0<=r0){\n\t\t\tlast=last*get(l0,r0,5)%P;\n\t\t\tl0=(l0-1)/5+1; r0/=5;\n\t\t\tzeros+=r0-l0+1;\n\t\t}\n\t\tlast=last*exp(inv2,zeros,P)%P;\n\t\tint A[]={0,last},M[]={32,3125};\n\t\tlast=Chinese_Remainder_Theorem(A,M,2);\n\t\tchar str1[15]; sprintf(str1,"%05d",last);\n\t\treturn to_string(leading(l,r))+"..."+string(str1)+"e"+to_string(zeros);\n\t}\n};\n``` | 0 | 0 | ['Math'] | 0 |
abbreviating-the-product-of-a-range | Go | Golang | Prefix | Suffix | TotalDigits Count | TrailingZeroes | Math | go-golang-prefix-suffix-totaldigits-coun-sssk | ```\nfunc abbreviateProduct(left int, right int) string {\n product, trailingZeros, totalDigitsInProduct := 1, 0, 0.0\n maxSuffix:=100000000000\n maxPr | camusabsurdo | NORMAL | 2022-06-18T16:21:48.573395+00:00 | 2022-06-18T16:34:18.329026+00:00 | 106 | false | ```\nfunc abbreviateProduct(left int, right int) string {\n product, trailingZeros, totalDigitsInProduct := 1, 0, 0.0\n maxSuffix:=100000000000\n maxPrefix:=100000\n\tprefix := 1.0\n\n\tfor i := left; i <= right; i++ {\n\t\tproduct *= i\n totalDigitsInProduct += math.Log10(float64(i))\n prefix *= float64(i)\n for prefix >= float64(maxPrefix) {\n\t\t\tprefix /= 10\n\t\t}\n \n\t\tfor product%10 == 0 {\n\t\t\tproduct /= 10\n\t\t\ttrailingZeros++\n\t\t}\n\n\t\tproduct %= maxSuffix\n\t}\n totalDigitsInProduct+=1\n totalDigitsInProduct=math.Floor(totalDigitsInProduct)\n workingDigits:= int(totalDigitsInProduct) - trailingZeros\n \n\tsuffix := fmt.Sprintf("%v",product)\n if workingDigits > 10 {\n return fmt.Sprintf("%v...%se%v",int(prefix),suffix[len(suffix)-5:],trailingZeros)\n\t}\n\tif workingDigits >= 5 {\n return fmt.Sprintf("%v%se%v",int(prefix),suffix[len(suffix)-(workingDigits-5):],trailingZeros)\n\t}\n return fmt.Sprintf("%ve%v",int(prefix),trailingZeros)\n} | 0 | 0 | ['Math', 'Go'] | 0 |
abbreviating-the-product-of-a-range | Modulo and Double. | modulo-and-double-by-baba_dro-u5eq | Go version of the solution:\nhttps://leetcode.com/problems/abbreviating-the-product-of-a-range/discuss/1647115/Modulo-and-Double\n\n\nfunc abbreviateProduct(lef | baba_dro | NORMAL | 2022-03-22T05:50:25.446849+00:00 | 2022-03-22T05:50:25.446889+00:00 | 105 | false | Go version of the solution:\nhttps://leetcode.com/problems/abbreviating-the-product-of-a-range/discuss/1647115/Modulo-and-Double\n\n```\nfunc abbreviateProduct(left int, right int) string {\n\tstuff, c, total, maxStuff := 1, 0, 0, 100000000000\n\tpref := 1.0\n\n\tfor i := left; i <= right; i++ {\n\t\tpref *= float64(i)\n\t\tstuff *= i\n\n\t\tfor pref >= 100000 {\n\t\t\tpref /= 10\n\t\t\tif total == 0 {\n\t\t\t\ttotal = 6\n\t\t\t} else {\n\t\t\t\ttotal++\n\t\t\t}\n\t\t}\n\n\t\tfor stuff%10 == 0 {\n\t\t\tstuff /= 10\n\t\t\tc++\n\t\t}\n\n\t\tstuff %= maxStuff\n\t}\n\n\ts := strconv.Itoa(stuff)\n\n\tres := strconv.Itoa(int(pref))\n\tif total-c > 10 {\n\t\tres += "..."\n\t}\n\tif total-c >= 5 {\n\t\tres += s[len(s)-min(5, total-c-5):]\n\t}\n\n\tres += "e" + strconv.Itoa(c)\n\n\treturn res\n}\n\nfunc min(a, b int) int {\n\tif a < b {\n\t\treturn a\n\t}\n\n\treturn b\n}\n``` | 0 | 0 | ['Go'] | 0 |
abbreviating-the-product-of-a-range | Python3 accepted solution (using rstrip) | python3-accepted-solution-using-rstrip-b-0y91 | \n class Solution:\n def abbreviateProduct(self, left: int, right: int) -> str:\n product=1\n for i in range(left,right+1):\n produ | sreeleetcode19 | NORMAL | 2022-02-22T16:14:56.426812+00:00 | 2022-02-22T16:18:04.047106+00:00 | 182 | false | ```\n class Solution:\n def abbreviateProduct(self, left: int, right: int) -> str:\n product=1\n for i in range(left,right+1):\n product *= i\n if(len(str(product).rstrip("0"))<=10):\n return str(product).rstrip("0") + "e" + str(len(str(product)) - len(str(product).rstrip("0")))\n else:\n return str(product).rstrip("0")[:5] +"..."+ str(product).rstrip("0")[-5:]+"e" + str(len(str(product)) - len(str(product).rstrip("0")))\n \n ``` | 0 | 0 | ['String', 'Python3'] | 0 |
abbreviating-the-product-of-a-range | Straightforward Python 3 solution (beats 98.29% on memory) | straightforward-python-3-solution-beats-y18rr | Hope this helps...\n\n\'\'\'\nclass Solution:\n def abbreviateProduct(self, left: int, right: int) -> str:\n\t\n product = 1\n \n #Since | tianxiaozhang | NORMAL | 2022-02-02T05:20:34.370438+00:00 | 2022-02-02T05:20:34.370473+00:00 | 125 | false | Hope this helps...\n\n\'\'\'\nclass Solution:\n def abbreviateProduct(self, left: int, right: int) -> str:\n\t\n product = 1\n \n #Since trailing zeros come from 2*5 ultimately...\n two_count = 0\n five_count = 0\n\n for i in range(left, right+1):\n \n #Filter all 2s and 5s:\n while i%2 == 0:\n i = i//2\n two_count += 1\n while i%5 == 0:\n i = i//5\n five_count += 1\n \n #Do the math on the rest\n product *= i\n\n #Whichever smaller is the pairs of 2*5 we have\n trailing_zeros = min(two_count, five_count)\n\n two_count -= trailing_zeros\n five_count -= trailing_zeros\n \n #Multiply the "unused 2s or 5s"\n if two_count > 0:\n product *= 2 ** two_count\n elif five_count > 0:\n product *= 5 ** five_count\n \n #Format as instructed\n if product > 9999999999:\n product = str(product)[:5] +"..."+ str(product)[-5:]\n\n product = str(product)+"e"+str(trailing_zeros)\n\n return(product)\n\'\'\' | 0 | 0 | [] | 0 |
abbreviating-the-product-of-a-range | C math solution | c-math-solution-by-oryliavner-rrdr | See problem hints for why this works.\n\n#define MAX_CONTIGUOUS 10000000000ULL\n\nchar *abbreviateProduct(int left, int right){\n // Max size: #####...#####e | oryliavner | NORMAL | 2022-01-13T08:26:21.851937+00:00 | 2022-01-13T08:29:57.372868+00:00 | 151 | false | See problem hints for why this works.\n```\n#define MAX_CONTIGUOUS 10000000000ULL\n\nchar *abbreviateProduct(int left, int right){\n // Max size: #####...#####e####\n char* ret = calloc(19, sizeof(char));\n \n uint64_t product = 0;\n uint32_t top = 0;\n uint32_t bottom = 0;\n // 10000! has 2499 trailing zeros\n uint16_t numZeros = 0;\n \n { // Num zeros\n uint16_t numTwos = 0;\n uint16_t numFives = 0;\n\n for (uint16_t m = left; m <= right; m++) {\n uint16_t cur = m;\n \n for(; (cur % 2) == 0; cur /= 2, numTwos++);\n for(; (cur % 5) == 0; cur /= 5, numFives++);\n }\n \n numZeros = (numTwos < numFives) ? numTwos : numFives;\n }\n \n { // Bottom 5 digits\n uint16_t numTwos = numZeros;\n uint16_t numFives = numZeros;\n\n bottom = 1;\n product = 1;\n for (uint16_t m = left; m <= right; m++) {\n uint16_t cur = m;\n \n for(; (cur % 2) == 0 && numTwos > 0; cur /= 2, numTwos--);\n for(; (cur % 5) == 0 && numFives > 0; cur /= 5, numFives--);\n \n bottom *= cur;\n bottom %= 100000;\n \n if (product < MAX_CONTIGUOUS) {\n product *= cur;\n }\n }\n }\n \n // Top 5 digits\n if (product >= MAX_CONTIGUOUS) { \n // \'long double\' precision is required for all tests to pass.\n long double sum = 0;\n double temp = 0;\n \n for (double m = left; m <= right; m++) {\n sum += log10(m);\n }\n \n\t\t// Set sum to fraction part of the double\n sum = modf(sum, &temp);\n top = floor(pow(10.0, 4.0 + sum));\n }\n \n if (product < MAX_CONTIGUOUS) {\n sprintf(ret, "%llue%lu", product, numZeros);\n } else {\n sprintf(ret, "%lu...%05lue%lu", top, bottom, numZeros);\n }\n \n return ret;\n}\n``` | 0 | 0 | ['Math', 'C'] | 0 |
abbreviating-the-product-of-a-range | Clean and fast Java solution | clean-and-fast-java-solution-by-programw-f9j9 | \n\tprivate static final long MAX_SUFFIX = 1000000000000L;\n private static final int MAX_PREFIX = 100000;\n \n public String abbreviateProduct(int lef | programwithsai | NORMAL | 2022-01-06T11:46:27.611183+00:00 | 2022-01-06T11:46:27.611230+00:00 | 178 | false | ```\n\tprivate static final long MAX_SUFFIX = 1000000000000L;\n private static final int MAX_PREFIX = 100000;\n \n public String abbreviateProduct(int left, int right) {\n long product = 1;\n int trailingZeros = 0;\n double prefix = 1.0;\n \n for (int num = left; num <= right; num++) {\n product *= num;\n while (product % 10 == 0) {\n product /= 10;\n trailingZeros++;\n }\n \n if (product >= MAX_SUFFIX) {\n product %= MAX_SUFFIX;\n }\n \n prefix *= num;\n \n while (prefix >= MAX_PREFIX) {\n prefix /= 10;\n }\n }\n return buildAbbreviation(prefix, product, trailingZeros);\n }\n \n private String buildAbbreviation(double prefix, long product, int trailingZeros) {\n String suffix = String.valueOf(product);\n if (suffix.length() > 10) {\n suffix = (int)prefix + "..." + suffix.substring(suffix.length() - 5);\n }\n \n return String.format("%se%d", suffix, trailingZeros);\n }\n```\n\nHopefully code is self explanatory. But if you need explanation, reply below and I\'ll send the video link. \nThank you!\n | 0 | 0 | [] | 1 |
abbreviating-the-product-of-a-range | [Python] easy to read | python-easy-to-read-by-gusghrlrl101-1vde | \n\ndef abbreviateProduct(self, left: int, right: int) -> str:\n\tpre, suf, cnt = 1, 1, 0\n\tthreshold, pre_precision, suf_precision = int(1e14), int(1e5), (1e1 | gusghrlrl101 | NORMAL | 2022-01-01T16:57:14.343597+00:00 | 2022-01-01T16:57:14.343635+00:00 | 154 | false | \n```\ndef abbreviateProduct(self, left: int, right: int) -> str:\n\tpre, suf, cnt = 1, 1, 0\n\tthreshold, pre_precision, suf_precision = int(1e14), int(1e5), (1e10)\n\n\tfor num in range(left, right + 1):\n\t\tpre *= num\n\t\tsuf *= num\n\n\t\twhile pre >= pre_precision:\n\t\t\tpre /= 10\n\n\t\twhile suf % 10 == 0:\n\t\t\tsuf //= 10\n\t\t\tcnt += 1\n\n\t\tsuf %= threshold\n\n\tif suf // suf_precision == 0:\n\t\treturn f"{suf}e{cnt}"\n\telse:\n\t\treturn f"{int(pre)}...{suf % pre_precision:05}e{cnt}"\n``` | 0 | 0 | ['Python'] | 0 |
abbreviating-the-product-of-a-range | Brute Force Approach Python3 (Accepted) (Commented) | brute-force-approach-python3-accepted-co-eex5 | \nclass Solution:\n def abbreviateProduct(self, left: int, right: int) -> str:\n ans = 1 | sdasstriver9 | NORMAL | 2021-12-30T07:48:40.537649+00:00 | 2021-12-30T07:48:40.537705+00:00 | 108 | false | ```\nclass Solution:\n def abbreviateProduct(self, left: int, right: int) -> str:\n ans = 1 //Initialise the product with 1\n while left <= right: // Start the multiplying numbers in\n if left == right: // Exception case when left is right else the number will be multiplied 2 times\n ans *= left //then only multiply either left or right\n else:\n ans *= left * right // Else multiply left and right numbers and multiply with ans\n left += 1 // Increment left by one\n right -= 1 //Decrement right by 1\n count = 0 // Initialise count of trailing zeroes\n ans = str(ans) // Converting integer to string\n i = len(ans) - 1 // Start the pointer with end of string\n while i >= 0 and ans[i] == \'0\': // Decrement pointer by one while the value at pointer is 0\n count += 1 //and increase the count of trailing zeroes\n i -= 1\n fans = \'\' //Empty string which will store the number without the trailing zeroes\n for j in range(i+1): // will use the i pointer which stored the last location of the trailing zero\n fans += ans[j] //store each character until the trailing zero isn\'t reached\n final = \'\' //Final ans which will give the required result \n if len(fans) > 10: //If the length of the number without the trailing zeroes has a length greater than 10\n temp1 = \'\' //Will store the first 5 character of the number\n for j in range(5): // Adding the first 5 characters\n temp1 += fans[j]\n temp2 = \'\' //Will store the last 5 characters of the number\n for j in range(-5,0): // Add the last 5 characters\n temp2 += fans[j]\n final = temp1 + \'...\' + temp2 + \'e\' + str(count) //Final ans with first 5 character, last 5 characters + e + count of trailing zeroes\n else: //If length of the number is less than 10\n final = fans + \'e\' + str(count) // Final ans with number without trailing zeroes + e + count of trailing zeroes\n return final //Return the final string\n \n``` | 0 | 0 | ['Python', 'Python3'] | 0 |
abbreviating-the-product-of-a-range | Python 3, math solution that follows hints | python-3-math-solution-that-follows-hint-box0 | Hints followed\n\n\nclass Solution:\n def abbreviateProduct(self, left: int, right: int) -> str:\n # hints followed\n left = max(2, left)\n | huangshan01 | NORMAL | 2021-12-28T16:07:50.867212+00:00 | 2021-12-28T17:36:45.959773+00:00 | 123 | false | Hints followed\n\n```\nclass Solution:\n def abbreviateProduct(self, left: int, right: int) -> str:\n # hints followed\n left = max(2, left)\n mod = 10 ** 5\n p = 1 # 10**5 modulo of the product to represent the lowest 5 digits\n lg = 0 # cumulates log10 of each number left to right, for the highest 5 digits\n c2 = 0 # occurrences of prime factor 2\n c5 = 0 # occurrences of prime factor 5\n \n for i in range(left, right + 1):\n lg += log10(i)\n while i > 1 and not (i % 2):\n c2 += 1\n i //= 2\n while i > 1 and not (i % 5):\n c5 += 1\n i //= 5\n p *= i\n if p > mod:\n p %= mod\n \n e = min(c2, c5)\n es = \'e\' + str(e)\n c2 -= e\n c5 -= e\n if not c2:\n p *= pow(5, c5, mod)\n else:\n p *= pow(2, c2, mod)\n if p > mod:\n p %= mod\n ps = str(p)\n \n lg = lg - e\n if lg <= 5:\n return ps + es\n \n # more than 5 digits to display, fill ps with leading 0s as need\n if len(ps) < 5:\n ps = \'0\' * (5 - len(ps)) + ps\n \n # digits to display <= 10\n lg -= 5\n if lg < 5:\n return str(10**lg)[:ceil(lg)] + ps + es\n \n # digits to display > 10, abbreviate the middle\n lg -= (ceil(lg) - 5)\n return str(10**lg)[:5] + \'...\' + ps + es\n``` | 0 | 0 | [] | 0 |
abbreviating-the-product-of-a-range | Java | Handwritten Illustrations | Very Easy to understand | java-handwritten-illustrations-very-easy-8km5 | \nAny corrections, suggestions or optimizations to code are welcomed. :)\nIf you found this post helpful then please like and comment to increase it\'s reach. : | Fly_ing__Rhi_no | NORMAL | 2021-12-28T09:51:05.878967+00:00 | 2021-12-28T09:51:05.879014+00:00 | 136 | false | \nAny corrections, suggestions or optimizations to code are welcomed. :)\nIf you found this post helpful then please like and comment to increase it\'s reach. :) | 0 | 0 | [] | 0 |
abbreviating-the-product-of-a-range | [Java] Follow hints 275ms Two-Pass Solution | java-follow-hints-275ms-two-pass-solutio-vqdg | Use module to get last 5 digits in first pass\n* Use log10 to get first 5 digits in second pass\n\n\nclass Solution {\n public String abbreviateProduct(int l | 1v9n418vn51 | NORMAL | 2021-12-27T15:39:38.397861+00:00 | 2021-12-27T15:41:55.488610+00:00 | 255 | false | * Use module to get last 5 digits in first pass\n* Use log10 to get first 5 digits in second pass\n\n```\nclass Solution {\n public String abbreviateProduct(int left, int right) {\n int zero = 0;\n boolean mod = false;\n \n long val = 1L;\n for (int i = left; i <= right; i++) {\n val *= i;\n while (val % 10 == 0) {\n val /= 10;\n zero++;\n }\n if (val > 10_000_000_000L) {\n val %= 10_000_000_000L;\n mod = true;\n }\n }\n if (!mod) {\n return String.format("%de%d", val, zero);\n }\n long end = val % 100_000L;\n double s = 0.0;\n for (int i = left; i <= right; i++) {\n s += Math.log10(i);\n }\n s -= (int)s;\n double start = Math.pow(10.0, (s + 4));\n return String.format("%d...%05de%d", (int)start, end, zero);\n }\n}\n``` | 0 | 0 | ['Java'] | 1 |
abbreviating-the-product-of-a-range | I just followed the hints | i-just-followed-the-hints-by-relentless1-etfw | https://anothercasualcoder.blogspot.com/2021/12/lc-hard-problem-follow-hints.html | relentless123 | NORMAL | 2021-12-27T06:47:21.444553+00:00 | 2021-12-27T06:47:21.444583+00:00 | 86 | false | [https://anothercasualcoder.blogspot.com/2021/12/lc-hard-problem-follow-hints.html](http://) | 0 | 2 | [] | 0 |
abbreviating-the-product-of-a-range | [C++] solution | c-solution-by-lovejavaee-7a8z | \npublic:\n int calcBas(int x, int y, int bas){\n int ret = 0;\n -- x;\n while(x)\n ret -= (x /= bas);\n while(y)\n | lovejavaee | NORMAL | 2021-12-25T22:55:08.948641+00:00 | 2021-12-26T05:42:31.167364+00:00 | 141 | false | ```\npublic:\n int calcBas(int x, int y, int bas){\n int ret = 0;\n -- x;\n while(x)\n ret -= (x /= bas);\n while(y)\n ret += (y /= bas);\n return ret;\n }\n int calcZeros(int x, int y){\n return min(calcBas(x, y, 2), calcBas(x, y, 5));\n }\n string toFixedString(int x){\n string ret = "";\n for(int i=0; i<5; i++){\n ret = (char)((x % 10) + \'0\') + ret;\n x /= 10;\n }\n return ret;\n }\n string abbreviateProduct(int left, int right) {\n int Z = calcZeros(left, right);\n long long x = 1;\n bool sCalc = true;\n int eZ = Z, fZ = Z;\n for(int i=left; i<=right; i++){\n int X = i;\n while(X % 2 == 0 && eZ)\n X /= 2, -- eZ;\n while(X % 5 == 0 && fZ)\n X /= 5, -- fZ;\n x *= X;\n if(x >= 1e10){\n sCalc = false;\n break;\n }\n }\n if(sCalc)\n return to_string(x) + \'e\' + to_string(Z);\n long long las = 1;\n eZ = Z, fZ = Z;\n for(int i=left; i<=right; i++){\n int X = i;\n while(X % 2 == 0 && eZ)\n X /= 2, -- eZ;\n while(X % 5 == 0 && fZ)\n X /= 5, -- fZ;\n las *= X;\n las %= 100000;\n }\n long long fir = 1;\n eZ = Z, fZ = Z;\n for(int i=left; i<=right; i++){\n int X = i;\n while(X % 2 == 0 && eZ)\n X /= 2, -- eZ;\n while(X % 5 == 0 && fZ)\n X /= 5, -- fZ;\n fir *= X;\n while(fir >= 1e12)\n fir /= 10;\n }\n while(fir >= 1e5)\n fir /= 10;\n return to_string(fir) + "..." + toFixedString(las) + \'e\' + to_string(Z);\n }\n};\n``` | 0 | 0 | ['C'] | 0 |
abbreviating-the-product-of-a-range | [C++] Linear scan, modulo, trailing zero counting, log10, etc... | c-linear-scan-modulo-trailing-zero-count-cvzo | \nclass Solution {\npublic:\n string abbreviateProduct(int left, int right) {\n // Find trailing zeros.\n int five_cnts = 0, two_cnts = 0;\n | phi9t | NORMAL | 2021-12-25T22:53:07.236785+00:00 | 2021-12-25T22:53:36.681903+00:00 | 73 | false | ```\nclass Solution {\npublic:\n string abbreviateProduct(int left, int right) {\n // Find trailing zeros.\n int five_cnts = 0, two_cnts = 0;\n for (int d = left; d <= right; ++d) {\n int val = d; \n while ((val % 5) == 0) {\n val /= 5;\n ++five_cnts;\n }\n two_cnts += __builtin_popcount((d - 1) & (d ^ (d - 1)));\n }\n const int zero_cnts = std::min(five_cnts, two_cnts);\n \n // Compute trailing digits and the full version when we have no more than 10 digits.\n int64_t trailing = 1, full = 1;\n constexpr int64_t kModTrailing = 1E5;\n constexpr int64_t kModFull = 1E10;\n five_cnts = two_cnts = zero_cnts;\n for (int64_t d = left; d <= right; ++d) {\n auto val = d;\n while ((five_cnts > 0) && (val % 5 == 0)) {\n val /= 5;\n --five_cnts;\n }\n while ((two_cnts > 0) && (val % 2 == 0)) {\n val /= 2;\n --two_cnts;\n }\n trailing = (trailing * val) % kModTrailing;\n full = (full * val) % kModFull;\n }\n \n // Find how many digits the result has (after removing trailing zeros).\n double log_prod = 0;\n for (double d = left; d <= right; ++d) {\n log_prod += std::log10(d);\n } \n constexpr double kPrec = 1E-9;\n const int num_digits = 1 + std::floor(log_prod + kPrec) - zero_cnts; \n\n std::ostringstream sout;\n if (num_digits > 10) {\n const auto frac = log_prod - std::floor(log_prod + kPrec);\n auto base = std::pow(10, frac);\n for (int k = 1; k < 5; ++k) {\n base *= 10;\n }\n const int64_t leading = std::floor(base + kPrec);\n sout << leading << "..." << setw(5) << setfill(\'0\') << trailing;\n } else {\n sout << full;\n }\n sout << "e" << zero_cnts; \n return sout.str();\n }\n};\n``` | 0 | 0 | [] | 0 |
abbreviating-the-product-of-a-range | javascript math 1948ms | javascript-math-1948ms-by-henrychen222-1g7j | \nconst ll = BigInt;\n\nconst abbreviateProduct = (l, r) => {\n let p = 1n, e = 0, over10 = false, prePow = 1;\n for (let x = l; x <= r; x++) {\n p | henrychen222 | NORMAL | 2021-12-25T21:21:42.728999+00:00 | 2021-12-25T21:21:42.729024+00:00 | 128 | false | ```\nconst ll = BigInt;\n\nconst abbreviateProduct = (l, r) => {\n let p = 1n, e = 0, over10 = false, prePow = 1;\n for (let x = l; x <= r; x++) {\n p *= ll(x);\n while (p % 10n == 0) {\n p /= 10n;\n e++;\n }\n prePow += Math.log10(x);\n while (prePow > 100) prePow--;\n if (p > 1e10) {\n over10 = true;\n p %= ll(1e10);\n }\n }\n p = Number(p);\n if (!over10) return p + \'e\' + e;\n let pre = (10 ** prePow) + \'\', suf = p + \'\';\n pre.indexOf(\'e\') == -1 ? pre = pre.slice(0, 5) : pre = pre[0] + pre.slice(2, 6);\n suf = \'...\' + suf.slice(-5) + \'e\' + e;\n return pre + suf;\n};\n``` | 0 | 0 | ['Math', 'JavaScript'] | 0 |
abbreviating-the-product-of-a-range | [Kotlin] 200 ms. One pass | kotlin-200-ms-one-pass-by-atrubin-shgh | \nclass Solution {\n fun abbreviateProduct(left: Int, right: Int): String {\n val eps = 1_000_000_000_000L\n\n var pre = 1L\n var suf = | atrubin | NORMAL | 2021-12-25T17:21:47.357793+00:00 | 2021-12-25T17:25:16.380486+00:00 | 91 | false | ```\nclass Solution {\n fun abbreviateProduct(left: Int, right: Int): String {\n val eps = 1_000_000_000_000L\n\n var pre = 1L\n var suf = 1L\n\n var zeroCount = 0\n\n (left.toLong()..right.toLong()).forEach {\n pre *= it\n suf *= it\n\n while (pre > eps) pre /= 10\n\n while (suf % 10L == 0L) {\n suf /= 10L\n zeroCount++\n }\n\n if (suf > eps) suf %= eps\n }\n\n return if (suf.toString().run { length <= 10 && pre.toString().indexOf(this) >= 0 }) {\n "${suf}e$zeroCount"\n } else {\n pre.toString().padStart(5, \'0\').substring(0, 5) +\n "..." +\n suf.toString().padStart(5, \'0\').let {\n it.substring(it.length - 5, it.length)\n } +\n "e$zeroCount"\n }\n }\n}\n``` | 0 | 0 | ['Kotlin'] | 0 |
abbreviating-the-product-of-a-range | c++, 56ms | c-56ms-by-jamieyang-9asa | \nclass Solution {\npublic:\n string abbreviateProduct(int left, int right) {\n long long t1=1; // 5 digits, <100000\n long long t2=0; // 5+6 | jamieyang | NORMAL | 2021-12-25T17:02:40.386190+00:00 | 2021-12-25T17:03:49.102537+00:00 | 108 | false | ```\nclass Solution {\npublic:\n string abbreviateProduct(int left, int right) {\n long long t1=1; // 5 digits, <100000\n long long t2=0; // 5+6 digits, <100000000000\n // t1,t2 ... t3\n unsigned long long e=0;\n int i;\n // very small\n for(i=right; i>=left; i--) {\n //cout<<i<<endl;\n t1*=i;\n while(t1%10==0) {\n t1/=10;\n e++;\n }\n if(t1>=1000000000000ll) // >=12 digits \n break;\n }\n string ret;\n \n if(i!=left-1) {// bigger\n t2 = t1;\n t1 %=10000000000ll;\n while(t2>=1000000000000ll)\n t2/=10;\n for(i--; i>=left; i--) {\n t1*=i;\n while(t1%10==0) {\n e++;\n t1/=10;\n }\n t2*=i;\n t1%=10000000000ll;\n while(t2>=1000000000000ll)\n t2/=10;\n }\n }\n \n if(t2==0) {\n if(t1<10000000000ll) {\n ret = to_string(t1)+"e"+to_string(e);\n } else {\n t2 = t1;\n while(t2>=100000000000ll)\n t2 /=10;\n }\n }\n \n if(t2>0) {\n while(t2>=100000)\n t2/=10;\n t1 %=100000; \n ret = to_string(t2)+"...";\n if(t1<10)\n ret += "0000";\n else if(t1<100)\n ret += "000";\n else if(t1<1000)\n ret += "00";\n else if(t1<10000)\n ret += "0";\n \n ret = ret+to_string(t1)+"e"+to_string(e);\n }\n \n return ret;\n }\n};\n``` | 0 | 0 | ['Math'] | 0 |
abbreviating-the-product-of-a-range | [C++] Brute Force | c-brute-force-by-ericyxing-ksys | Thanks for @linfq\'s solution, here is the C++ version. \n\n\nclass Solution {\npublic:\n string abbreviateProduct(int left, int right) {\n int c = 0; | EricYXing | NORMAL | 2021-12-25T16:59:07.982143+00:00 | 2021-12-25T17:03:16.743761+00:00 | 133 | false | Thanks for <code>@linfq</code>\'s solution, here is the C++ version. \n\n```\nclass Solution {\npublic:\n string abbreviateProduct(int left, int right) {\n int c = 0;\n long long pre = 1, suf = 1, mod = 1e12;\n for (int i = left; i <= right; i++)\n {\n long long cur(i);\n pre *= cur;\n while (pre > mod)\n pre /= 10;\n suf *= cur;\n while (suf % 10 == 0)\n {\n suf /= 10;\n c++;\n }\n suf %= mod;\n }\n string pres = to_string(pre), sufs = to_string(suf), ans = "";\n if (sufs.length() <= 10)\n ans = sufs + "e" + to_string(c);\n else\n {\n if (sufs.length() < 5)\n sufs = string(5 - sufs.length(), \'0\') + sufs;\n ans = pres.substr(0, 5) + "..." + sufs.substr(sufs.length() - 5) + "e" + to_string(c);\n }\n return ans;\n }\n};\n```\n\nDuring the contest, I used the similar method but converted the solution to string for each step, so I got TLE.\n```\nclass Solution {\npublic:\n string abbreviateProduct(int left, int right) {\n string ans = convert(left);\n for (int i = left + 1; i <= right; i++)\n ans = prod(ans, i);\n int p = ans.find(\'.\');\n int q = ans.find(\'e\');\n if (q > 10)\n ans = ans.substr(0, 5) + "..." + ans.substr(q - 5);\n return ans;\n }\n \nprivate: \n string prod(string a, int i)\n {\n string b = convert(i);\n int p = a.find(\'e\'), q = b.find(\'e\');\n int c = stoi(a.substr(p + 1)) + stoi(b.substr(q + 1));\n a = a.substr(0, p);\n b = b.substr(0, q);\n p = a.find(\'.\');\n if (p == -1)\n {\n long long a1 = stoll(a.substr(0, p)), b1 = stoll(b), c1 = a1 * b1;\n while (c1 % 10 == 0)\n {\n c++;\n c1 /= 10;\n }\n string cs = to_string(c1);\n if (cs.length() > 12)\n {\n string cs1 = cs.substr(0, 12);\n string cs2 = cs.substr(cs.length() - 12);\n cs = cs1 + "..." + cs2;\n }\n return (cs + "e" + to_string(c));\n }\n else\n {\n long long a1 = stoll(a.substr(0, p)), b1 = stoll(b), c1 = a1 * b1;\n p = a.find_last_of(\'.\');\n long long a2 = stoll(a.substr(p + 1)), c2 = a2 * b1;\n while (c2 % 10 == 0)\n {\n c++;\n c2 /= 10;\n }\n while (c1 % 10 == 0)\n c1 /= 10;\n string cs1 = to_string(c1);\n if (cs1.length() >= 12)\n cs1 = cs1.substr(0, 12);\n string cs2 = to_string(c2);\n if (cs2.length() >= 12)\n cs2 = cs2.substr(cs2.length() - 12);\n else\n cs2 = string(12 - cs2.length(), \'0\') + cs2;\n string cs = cs1 + "..." + cs2;\n return (cs + "e" + to_string(c));\n }\n }\n \n string convert(int i)\n {\n int c = 0;\n while (i % 10 == 0)\n {\n i /= 10;\n c++;\n }\n string s = to_string(i) + "e" + to_string(c);\n return s;\n }\n};\n``` | 0 | 1 | ['C'] | 0 |
abbreviating-the-product-of-a-range | C++ | Getting Runtime Error | Same Code working in VS | c-getting-runtime-error-same-code-workin-ivt0 | Can anyone help me - why i\'m getting runtime error in this one\nLine no - if i\'m commenting from \nint m = up.length() to st.pop();\nMy code is running on LC | kumarvoman | NORMAL | 2021-12-25T16:45:38.634709+00:00 | 2021-12-25T16:45:38.634734+00:00 | 181 | false | Can anyone help me - why i\'m getting runtime error in this one\nLine no - if i\'m commenting from \nint m = up.length() to st.pop();\nMy code is running on LC... and without commenting that part i\'m getting correct ouput in VS.\nAny suggestions ?\n\n```\nstring abbreviateProduct(int left, int right) {\n long long int prod = 1;\n for(int i =left; i<=right;i++)\n {\n prod = prod*i;\n }\n \n string word = std::to_string(prod);\n \n int n = word.length();\n string prefix = word.substr(0,5);\n int zero =0, k;\n for(int i = n-1;i>=0;i--)\n {\n if(word[i] == \'0\')\n zero++;\n else\n {\n k = i;\n break;\n }\n }\n \n string up = word.substr(0, k+1);\n \n string suffix;\n\n int m = up.length();\n queue<char> st;\n for(int i = m-5;i<m;i++)\n {\n st.push(up[i]);\n }\n while(!st.empty())\n {\n suffix+=st.front();\n st.pop();\n }\n\n up = up + "e" + std::to_string(zero);\n\n if (up.length() > 10)\n {\n up.clear();\n up+=prefix;\n up.push_back(\'.\');\n up.push_back(\'.\');\n up.push_back(\'.\');\n up+=suffix;\n up = up + "e" + std::to_string(zero);\n }\n return up;\n }\n``` | 0 | 0 | ['C'] | 2 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | [Java/C++/Python] Straight Forward | javacpython-straight-forward-by-lee215-j11s | Intuition\nIf we can do 0 move, return max(A) - min(A)\nIf we can do 1 move, return min(the second max(A) - min(A), the max(A) - second min(A))\nand so on.\n\n | lee215 | NORMAL | 2020-07-11T16:04:35.062467+00:00 | 2020-07-16T16:46:56.090842+00:00 | 48,630 | false | # Intuition\nIf we can do 0 move, return max(A) - min(A)\nIf we can do 1 move, return min(the second max(A) - min(A), the max(A) - second min(A))\nand so on.\n<br>\n\n# **Explanation**\nWe have 4 plans:\n1. kill 3 biggest elements\n2. kill 2 biggest elements + 1 smallest elements\n3. kill 1 biggest elements + 2 smallest elements\n3. kill 3 smallest elements\n<br>\n\nExample from @himanshusingh11:\n\n`A = [1,5,6,13,14,15,16,17]`\n`n = 8`\n\nCase 1: kill 3 biggest elements\n\nAll three biggest elements can be replaced with 14\n[1,5,6,13,14,`15,16,17`] -> [1,5,6,13,14,`14,14,14`] == can be written as `A[n-4] - A[0] == (14-1 = 13)`\n\nCase 2: kill 2 biggest elements + 1 smallest elements\n\n[`1`,5,6,13,14,15,`16,17`] -> [`5`,5,6,13,14,15,`15,15`] == can be written as `A[n-3] - A[1] == (15-5 = 10)`\n\nCase 3: kill 1 biggest elements + 2 smallest elements\n\n[`1,5`,6,13,14,15,16,`17`] -> [`6,6`,6,13,14,15,16,`16`] == can be written as `A[n-2] - A[2] == (16-6 = 10)`\n\nCase 4: kill 3 smallest elements\n\n[`1,5,6`,13,14,15,16,17] -> [`13,13,13`,13,14,15,16,17] == can be written as `A[n-1] - A[3] == (17-13 = 4)`\n\nAnswer is minimum of all these cases!\n<br>\n\n# Solution 1: Quick Sort\nI used quick sort to find out the biggest and smallest\nSo time and space are `O(quick sort)`\n<br>\n\n**C++**\n```cpp\n int minDifference(vector<int>& A) {\n int n = A.size();\n if (n < 5) return 0;\n sort(A.begin(), A.end());\n return min({A[n - 1] - A[3], A[n - 2] - A[2], A[n - 3] - A[1], A[n - 4] - A[0]});\n }\n```\n**Java**\n```java\n public int minDifference(int[] A) {\n int n = A.length, res = Integer.MAX_VALUE;\n if (n < 5) return 0;\n Arrays.sort(A);\n for (int i = 0; i < 4; ++i) {\n res = Math.min(res, A[n - 4 + i] - A[i]);\n }\n return res;\n }\n```\n**Python:**\n```py\n def minDifference(self, A):\n A.sort()\n return min(b - a for a, b in zip(A[:4], A[-4:]))\n```\n<br>\n\n# Solution 2: Partial Sorting\nChanged from @Sklert\nReference https://en.cppreference.com/w/cpp/algorithm/partial_sort\n\nTime `O(NlogK)`\nSpace `O(logK)`\n\n**C++**\n```cpp\n int minDifference(vector<int>& A) {\n int n = A.size();\n if (n < 5)\n return 0;\n partial_sort(A.begin(), A.begin() + 4, A.end());\n nth_element(A.begin() + 4, A.end() - 4, A.end());\n sort(A.end() - 4, A.end());\n return min({A[n - 1] - A[3], A[n - 2] - A[2], A[n - 3] - A[1], A[n - 4] - A[0]});\n }\n```\n**Python**\n```py\n def minDifference(self, A):\n return min(a - b for a,b in zip(heapq.nlargest(4, A), heapq.nsmallest(4, A)[::-1]))\n``` | 597 | 7 | [] | 58 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | a few solutions | a-few-solutions-by-claytonjwong-gdn7 | Sort A, then perform a brute-force search of all posibilities using a sliding window of size 3 similar to 1423. Maximum Points You Can Obtain from Cards. Initi | claytonjwong | NORMAL | 2020-07-11T22:18:02.852116+00:00 | 2022-03-20T00:04:52.694278+00:00 | 10,313 | false | Sort `A`, then perform a brute-force search of all posibilities using a sliding window of size 3 similar to [1423. Maximum Points You Can Obtain from Cards](https://leetcode.com/problems/maximum-points-you-can-obtain-from-cards/discuss/597883/Javascript-and-C%2B%2B-solutions). Initially set the disclude window of size 3 to the last 3 elements of `A`, then slide the disclude window by 3. Since `A` is sorted, we know the element at the `i`<sup>th</sup> index is the minimum element under consideration and the element at the `j`<sup>th</sup> index is the maximum element under consideration. Below is a picture of this sliding disclude window for example 4. In this example, `i` and `j` are adjacent to eachother, however, for larger inputs there exists an arbitrary and irrelevant amount of monotonically non-decreasing values in between `i` and `j`.\n\n---\n\n**Example 4:**\n\n**Input:** A = [1,5,6,14,15]\n**Output:** 1\n\n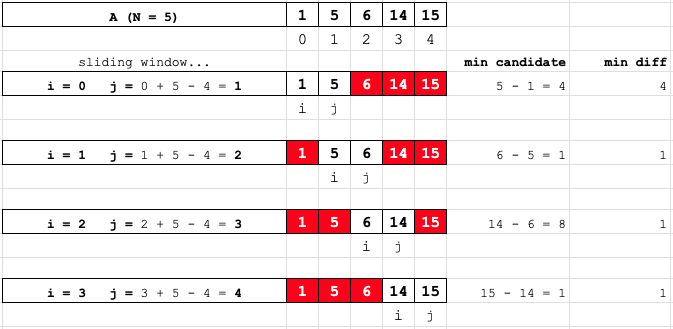\n\n---\n\n*Kotlin*\n```\nclass Solution {\n fun minDifference(A: IntArray, INF: Int = (2e9 + 1).toInt()): Int {\n A.sort()\n var lo = INF\n var N = A.size\n var (i, j) = Pair(0, N - 4) // \u2B50\uFE0F -4 because N - 1 is the last element and we want to disclude 3 elements, thus N - 1 - 3 == N - 4\n while (0 <= j && j < N) {\n lo = Math.min(lo, A[j++] - A[i++]) // slide window by 3 \uD83D\uDC49\n }\n return if (lo < INF) lo else 0\n }\n}\n```\n\n*Javascript*\n```\nlet minDifference = (A, min = Infinity) => {\n A.sort((a, b) => a - b);\n let N = A.length,\n i = 0,\n j = N - 4; // \u2B50\uFE0F -4 because N - 1 is the last element and we want to disclude 3 elements, thus N - 1 - 3 == N - 4\n while (0 <= j && j < N)\n\t\tmin = Math.min(min, A[j++] - A[i++]); // slide window by 3 \uD83D\uDC49\n return min < Infinity ? min : 0;\n};\n```\n\n*Python3*\n```\nclass Solution:\n def minDifference(self, A: List[int], lo = float(\'inf\')) -> int:\n A.sort()\n N = len(A)\n i = 0\n j = N - 4 # \u2B50\uFE0F -4 because N - 1 is the last element and we want to disclude 3 elements, thus N - 1 - 3 == N - 4\n while 0 <= j and j < N:\n lo = min(lo, A[j] - A[i]); j += 1; i += 1 # slide window by 3 \uD83D\uDC49\n return lo if lo < float(\'inf\') else 0\n```\n\n*Rust*\n```\ntype VI = Vec<i32>;\nuse std::cmp::min;\nuse std::cmp::max;\nimpl Solution {\n pub fn min_difference(A_: VI) -> i32 {\n let mut lo = 100000007;\n let mut A = A_.clone(); A.sort();\n let N = A.len();\n let (mut i, mut j) = (0, N - 4); // \u2B50\uFE0F -4 because N - 1 is the last element and we want to disclude 3 elements, thus N - 1 - 3 == N - 4\n while 0 <= j && j < N {\n lo = min(lo, A[j] - A[i]); j += 1; i += 1; // slide window by 3 \uD83D\uDC49\n }\n return if lo < 100000007 { lo } else { 0 };\n }\n}\n```\n\n*C++*\n```\nclass Solution {\npublic:\n using VI = vector<int>;\n static constexpr int INF = 2e9 + 7;\n int minDifference(VI& A, int min = INF) {\n sort(A.begin(), A.end());\n int N = A.size(),\n i = 0,\n j = N - 4;// \u2B50\uFE0F -4 because N - 1 is the last element and we want to disclude 3 elements, thus N - 1 - 3 == N - 4\n while (0 <= j && j < N)\n\t\t\tmin = std::min(min, A[j++] - A[i++]); // slide window by 3 \uD83D\uDC49\n return min < INF ? min : 0;\n }\n};\n``` | 124 | 1 | ['Sliding Window'] | 16 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | [3 Solutions Tutorial O(n) Included] Minimum Difference Between Largest and Smallest Value | 3-solutions-tutorial-on-included-minimum-co78 | Topic : Greedy, Sort\n\nI remember solving this Google OA problem three years ago.\n___\n\n## Solution 1\nIf the length of the input array is 4 or fewer, the a | never_get_piped | NORMAL | 2024-07-03T00:19:17.307711+00:00 | 2024-07-03T20:12:40.894727+00:00 | 29,495 | false | **Topic** : Greedy, Sort\n\n**I remember solving this Google OA problem three years ago.**\n___\n\n## Solution 1\nIf the length of the input array is 4 or fewer, the answer is 0 because we can make all numbers equal with up to 3 moves.\n\nThree moves means that **we can remove 3 numbers from the input array to make the remaining numbers equal to any number in the array**.\n\nIf we have more than 4 numbers, the **greedy intuition** suggests that excluding a total of 3 elements from both the leftmost and rightmost ends of the sorted array minimizes the difference between the maximum and minimum values remaining in the array. \n\nThis can simply be proven by contradiction. If we do not remove such numbers (three from both the leftmost and rightmost sides), then either the maximum or minimum of the array might be among the first three or last three numbers after sorting, potentially increasing the difference between them.\n\nThe solution involves iterating through the number of elements removed from the leftmost side. If we choose `i` elements from the leftmost side, then we must choose `3 - i` elements from the right side to remove.\n\n\n```c++ []\nclass Solution {\npublic:\n int minDifference(vector<int>& nums) {\n if(nums.size() <= 4) {\n return 0;\n }\n sort(nums.begin(), nums.end());\n int ans = nums.back() - nums[0];\n for(int i = 0; i <= 3; i++) {\n ans = min(ans, nums[nums.size() - (3 - i) - 1] - nums[i]);\n }\n return ans;\n }\n};\n```\n```java []\nclass Solution {\n public int minDifference(int[] nums) {\n if(nums.length <= 4) {\n return 0;\n }\n Arrays.sort(nums);\n int ans = nums[nums.length - 1] - nums[0];\n for(int i = 0; i <= 3; i++) {\n ans = Math.min(ans, nums[nums.length - (3 - i) - 1] - nums[i]);\n }\n return ans;\n }\n}\n```\n```python []\nclass Solution:\n def minDifference(self, nums: List[int]) -> int:\n if len(nums) <= 4:\n return 0\n nums.sort()\n ans = nums[-1] - nums[0]\n for i in range(4):\n ans = min(ans, nums[-(4 - i)] - nums[i])\n return ans\n```\n```Go []\nfunc minDifference(nums []int) int {\n if len(nums) <= 4 {\n return 0\n }\n sort.Ints(nums)\n ans := nums[len(nums)-1] - nums[0]\n for i := 0; i <= 3; i++ {\n ans = min(ans, nums[len(nums) - (3 - i) - 1] - nums[i])\n }\n return ans\n}\n```\n```PHP []\nclass Solution {\n\n /**\n * @param Integer[] $nums\n * @return Integer\n */\n function minDifference($nums) {\n if (count($nums) <= 4) {\n return 0;\n }\n sort($nums);\n $ans = $nums[count($nums) - 1] - $nums[0];\n for ($i = 0; $i <= 3; $i++) {\n $ans = min($ans, $nums[count($nums) - (3 - $i) - 1] - $nums[$i]);\n }\n return $ans;\n }\n}\n```\n```javascript []\n/**\n * @param {number[]} nums\n * @return {number}\n */\nvar minDifference = function(nums) {\n if (nums.length <= 4) {\n return 0;\n }\n nums.sort((a, b) => a - b);\n let ans = nums[nums.length - 1] - nums[0];\n for (let i = 0; i <= 3; i++) {\n ans = Math.min(ans, nums[nums.length - (3 - i) - 1] - nums[i]);\n }\n return ans;\n};\n```\n\n**Complexity**:\n* Time Complexity : `O(n log n)`\n* Space Complexity : `O(1)`\n\n<br/><br/>\n## Solution 2\nAnother approach involves computing the difference between the maximum and minimum values within each sliding window of size `len(nums) - 3`. This approach simplifies the implementation and enhances readability compared to the previous method.\n\n```c++ []\nclass Solution {\npublic:\n int minDifference(vector<int>& nums) {\n if(nums.size() <= 4) {\n return 0;\n }\n sort(nums.begin(), nums.end());\n int k = nums.size() - 3;\n int ans = nums.back() - nums[0];\n for(int i = k - 1; i < nums.size(); i++) {\n ans = min(ans, nums[i] - nums[i - k + 1]);\n }\n return ans;\n }\n};\n```\n```java []\nclass Solution {\n public int minDifference(int[] nums) {\n if (nums.length <= 4) {\n return 0;\n }\n Arrays.sort(nums);\n int k = nums.length - 3;\n int ans = nums[nums.length - 1] - nums[0];\n for (int i = k - 1; i < nums.length; i++) {\n ans = Math.min(ans, nums[i] - nums[i - k + 1]);\n }\n return ans;\n }\n}\n```\n```python []\nclass Solution:\n def minDifference(self, nums: List[int]) -> int:\n if len(nums) <= 4:\n return 0\n nums.sort()\n k = len(nums) - 3\n ans = nums[-1] - nums[0]\n for i in range(k - 1, len(nums)):\n ans = min(ans, nums[i] - nums[i - k + 1])\n return ans\n```\n```Go []\nfunc minDifference(nums []int) int {\n if len(nums) <= 4 {\n return 0\n }\n sort.Ints(nums)\n k := len(nums) - 3\n ans := nums[len(nums)-1] - nums[0]\n for i := k - 1; i < len(nums); i++ {\n ans = min(ans, nums[i] - nums[i - k + 1])\n }\n return ans\n}\n```\n```PHP []\nclass Solution {\n\n /**\n * @param Integer[] $nums\n * @return Integer\n */\n function minDifference($nums) {\n if (count($nums) <= 4) {\n return 0;\n }\n sort($nums);\n $k = count($nums) - 3;\n $ans = $nums[count($nums) - 1] - $nums[0];\n for ($i = $k - 1; $i < count($nums); $i++) {\n $ans = min($ans, $nums[$i] - $nums[$i - $k + 1]);\n }\n return $ans;\n }\n}\n```\n```javascript []\n/**\n * @param {number[]} nums\n * @return {number}\n */\nvar minDifference = function(nums) {\n if (nums.length <= 4) {\n return 0;\n }\n nums.sort((a, b) => a - b);\n let k = nums.length - 3;\n let ans = nums[nums.length - 1] - nums[0];\n for (let i = k - 1; i < nums.length; i++) {\n ans = Math.min(ans, nums[i] - nums[i - k + 1]);\n }\n return ans;\n};\n```\n\n**Complexity**:\n* Time Complexity : `O(n log n)`\n* Space Complexity : `O(1)`\n\n<br/>\n\n## Bonus\nWe only need the first four numbers and the last four numbers, so there\'s no need to sort the entire array. We can use an array of size 4 to keep track of both the top 4 largest and the top 4 smallest elements.\n\nHere is the simple and clean implementation:\n\n```c++ []\nclass Solution {\npublic:\n int minDifference(vector<int>& nums) {\n if(nums.size() <= 4) {\n return 0;\n }\n \n vector<int> min4, max4;\n \n for(int i = 0; i < nums.size(); i++) {\n bool add = false;\n for(int j = 0; j < min4.size(); j++) {\n if(nums[i] < min4[j]) {\n shift(min4, j);\n min4[j] = nums[i];\n add = true;\n break;\n }\n } \n if(!add && min4.size() < 4) {\n min4.push_back(nums[i]);\n }\n }\n \n for(int i = 0; i < nums.size(); i++) {\n bool add = false;\n for(int j = 0; j < max4.size(); j++) {\n if(nums[i] > max4[j]) {\n shift(max4, j);\n max4[j] = nums[i];\n add = true;\n break;\n }\n } \n if(!add && max4.size() < 4) {\n max4.push_back(nums[i]);\n }\n }\n \n int ans = max4[0] - min4[0];\n for(int i = 0; i <= 3; i++) {\n ans = min(ans, max4[3 - i] - min4[i]);\n }\n return ans;\n }\n \n void shift(vector<int>& a, int start) { //[1 2 3] \n int last = a.back();\n for(int j = a.size() - 1; j > start; j--) {\n a[j] = a[j - 1];\n }\n if(a.size() < 4) a.push_back(last);\n }\n};\n```\n```java []\nclass Solution {\n public int minDifference(int[] nums) {\n if (nums.length <= 4) {\n return 0;\n }\n \n int[] min4 = new int[4];\n int[] max4 = new int[4];\n \n Arrays.fill(min4, Integer.MAX_VALUE);\n Arrays.fill(max4, Integer.MIN_VALUE);\n \n for (int num : nums) {\n boolean added = false;\n for (int j = 0; j < min4.length; j++) {\n if (num < min4[j]) {\n shift(min4, j);\n min4[j] = num;\n added = true;\n break;\n }\n }\n if (!added && min4[min4.length - 1] == Integer.MAX_VALUE) {\n min4[min4.length - 1] = num;\n }\n }\n \n for (int num : nums) {\n boolean added = false;\n for (int j = 0; j < max4.length; j++) {\n if (num > max4[j]) {\n shift(max4, j);\n max4[j] = num;\n added = true;\n break;\n }\n }\n if (!added && max4[max4.length - 1] == Integer.MIN_VALUE) {\n max4[max4.length - 1] = num;\n }\n }\n \n int ans = max4[0] - min4[0];\n for (int i = 0; i <= 3; i++) {\n ans = Math.min(ans, max4[3 - i] - min4[i]);\n }\n return ans;\n }\n private void shift(int[] a, int start) {\n int last = a[a.length - 1];\n for (int j = a.length - 1; j > start; j--) {\n a[j] = a[j - 1];\n }\n if (a.length < 4) {\n a[a.length - 1] = last;\n }\n }\n}\n```\n```python []\nclass Solution:\n def shift(self, a: List[int], start: int) -> None:\n last = a[-1]\n for j in range(len(a) - 1, start, -1):\n a[j] = a[j - 1]\n if len(a) < 4:\n a.append(last)\n \n def minDifference(self, nums: List[int]) -> int:\n if len(nums) <= 4:\n return 0\n \n min4 = [float(\'inf\')] * 4\n max4 = [float(\'-inf\')] * 4\n \n for num in nums:\n added = False\n for j in range(4):\n if num < min4[j]:\n self.shift(min4, j)\n min4[j] = num\n added = True\n break\n if not added and min4[-1] == float(\'inf\'):\n min4[-1] = num\n \n for num in nums:\n added = False\n for j in range(4):\n if num > max4[j]:\n self.shift(max4, j)\n max4[j] = num\n added = True\n break\n if not added and max4[-1] == float(\'-inf\'):\n max4[-1] = num\n \n ans = max4[0] - min4[0]\n for i in range(4):\n ans = min(ans, max4[3 - i] - min4[i])\n \n return ans\n```\n```PHP []\nclass Solution {\n\n /**\n * @param Integer[] $nums\n * @return Integer\n */\n function minDifference($nums) {\n if (count($nums) <= 4) {\n return 0;\n }\n \n $min4 = array_fill(0, 4, PHP_INT_MAX);\n $max4 = array_fill(0, 4, PHP_INT_MIN);\n \n foreach ($nums as $num) {\n $added = false;\n for ($j = 0; $j < 4; $j++) {\n if ($num < $min4[$j]) {\n $this->shift($min4, $j);\n $min4[$j] = $num;\n $added = true;\n break;\n }\n }\n if (!$added && end($min4) == PHP_INT_MAX) {\n $min4[3] = $num;\n }\n }\n \n foreach ($nums as $num) {\n $added = false;\n for ($j = 0; $j < 4; $j++) {\n if ($num > $max4[$j]) {\n $this->shift($max4, $j);\n $max4[$j] = $num;\n $added = true;\n break;\n }\n }\n if (!$added && end($max4) == PHP_INT_MIN) {\n $max4[3] = $num;\n }\n }\n \n $ans = $max4[0] - $min4[0];\n for ($i = 0; $i < 4; $i++) {\n $ans = min($ans, $max4[3 - $i] - $min4[$i]);\n }\n \n return $ans;\n }\n \n function shift(&$a, $start) {\n $last = end($a);\n for ($j = count($a) - 1; $j > $start; $j--) {\n $a[$j] = $a[$j - 1];\n }\n if (count($a) < 4) {\n $a[] = $last;\n }\n }\n}\n```\n```Go []\nfunc shift(a []int, start int) {\n\tlast := a[len(a)-1]\n\tfor j := len(a)-1; j > start; j-- {\n\t\ta[j] = a[j-1]\n\t}\n\tif len(a) < 4 {\n\t\ta = append(a, last)\n\t}\n}\n\nfunc minDifference(nums []int) int {\n if len(nums) <= 4 {\n\t\treturn 0\n\t}\n\t\n\tmin4 := make([]int, 4)\n\tmax4 := make([]int, 4)\n\t\n\tfor i := 0; i < 4; i++ {\n\t\tmin4[i] = math.MaxInt32\n\t\tmax4[i] = math.MinInt32\n\t}\n\t\n\tfor _, num := range nums {\n\t\tadded := false\n\t\tfor j := 0; j < 4; j++ {\n\t\t\tif num < min4[j] {\n\t\t\t\tshift(min4, j)\n\t\t\t\tmin4[j] = num\n\t\t\t\tadded = true\n\t\t\t\tbreak\n\t\t\t}\n\t\t}\n\t\tif !added && min4[3] == math.MaxInt32 {\n\t\t\tmin4[3] = num\n\t\t}\n\t}\n\t\n\tfor _, num := range nums {\n\t\tadded := false\n\t\tfor j := 0; j < 4; j++ {\n\t\t\tif num > max4[j] {\n\t\t\t\tshift(max4, j)\n\t\t\t\tmax4[j] = num\n\t\t\t\tadded = true\n\t\t\t\tbreak\n\t\t\t}\n\t\t}\n\t\tif !added && max4[3] == math.MinInt32 {\n\t\t\tmax4[3] = num\n\t\t}\n\t}\n\t\n\tans := max4[0] - min4[0]\n\tfor i := 0; i < 4; i++ {\n\t\tans = min(ans, max4[3-i] - min4[i])\n\t}\n\t\n\treturn ans\n}\n```\n```javascript []\n/**\n * @param {number[]} nums\n * @return {number}\n */\nvar minDifference = function(nums) {\n function shift(a, start) {\n let last = a[a.length - 1];\n for (let j = a.length - 1; j > start; j--) {\n a[j] = a[j - 1];\n }\n if (a.length < 4) {\n a[a.length] = last;\n }\n }\n if (nums.length <= 4) {\n return 0;\n }\n \n let min4 = Array(4).fill(Number.MAX_SAFE_INTEGER);\n let max4 = Array(4).fill(Number.MIN_SAFE_INTEGER);\n \n for (let num of nums) {\n let added = false;\n for (let j = 0; j < 4; j++) {\n if (num < min4[j]) {\n shift(min4, j);\n min4[j] = num;\n added = true;\n break;\n }\n }\n if (!added && min4[3] === Number.MAX_SAFE_INTEGER) {\n min4[3] = num;\n }\n }\n \n for (let num of nums) {\n let added = false;\n for (let j = 0; j < 4; j++) {\n if (num > max4[j]) {\n shift(max4, j);\n max4[j] = num;\n added = true;\n break;\n }\n }\n if (!added && max4[3] === Number.MIN_SAFE_INTEGER) {\n max4[3] = num;\n }\n }\n \n let ans = max4[0] - min4[0];\n for (let i = 0; i < 4; i++) {\n ans = Math.min(ans, max4[3 - i] - min4[i]);\n }\n \n return ans;\n};\n```\n\nIllustration of the above logic : \n\n```\nSuppose we want to find the top4 minimum numbers (the logic is the same for maximum) and we have the following array : [1, 3, 5, 4, 6, 2]\n\nSteps:\n* Inialized an array with size 4 [INF, INF, INF, INF] with max int value.\n* Add 1 to min4 : [1, INF, INF, INF]\n* Add 3 to min4 : [1, 3, INF, INF]\n* Add 5 to min4 : [1, 3, 5, INF]\n* Add 4 to min4:\n\t* First, find the position where we need to insert 4 and shift all elements after it one place to the right. [1, 3, 5, 5] \n\t* Insert 4 => [1, 3, 4, 5]\n* Add 6 to min4 : [1, 3, 4, 5]\n* Add 2 to min4:\n\t* First, find the position where we need to insert 2 and shift all elements after it one place to the right. [1, 3, 3, 4]\n\t* Insert 2 => [1, 2, 3, 4]\n\n```\n\n\n\n**Complexity**:\n* Time Complexity : `O(n)`\n* Space Complexity : `O(1)`\n\n**Feel free to leave a comment if something is confusing, or if you have any suggestions on how I can improve the post.** | 106 | 1 | ['C', 'PHP', 'Python', 'Java', 'Go', 'JavaScript'] | 26 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | Python, 3 lines, well explained, Greedy O(nlogn) | python-3-lines-well-explained-greedy-onl-qk1j | If the size <= 4, then just delete all the elements and either no or one element would be left giving the answer 0.\nelse sort the array\nthere are 4 possibilit | abhinavbajpai2012 | NORMAL | 2020-08-20T14:58:26.490133+00:00 | 2020-08-20T14:58:26.490182+00:00 | 9,434 | false | If the size <= 4, then just delete all the elements and either no or one element would be left giving the answer 0.\nelse sort the array\nthere are 4 possibilities now:-\n1. delete 3 elements from left and none from right\n2. delete 2 elements from left and one from right\nand so on.. now just print the minima.\n```\nclass Solution:\n def minDifference(self, nums: List[int]) -> int:\n \n if len(nums) <= 4: return 0\n nums.sort()\n return min(nums[-1] - nums[3], nums[-2] - nums[2], nums[-3] - nums[1], nums[-4] - nums[0])\n``` | 89 | 1 | ['Python', 'Python3'] | 10 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | Optimal + Easy sol | Time - o(nlogn) | Easy Vid Explanation also | optimal-easy-sol-time-onlogn-easy-vid-ex-ei0i | https://youtu.be/wQUB0lhYK6Y\n# Intuition\n Describe your first thoughts on how to solve this problem. \nThe goal is to minimize the difference between the maxi | Atharav_s | NORMAL | 2024-07-03T01:48:07.208417+00:00 | 2024-07-03T01:48:07.208436+00:00 | 15,868 | false | https://youtu.be/wQUB0lhYK6Y\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe goal is to minimize the difference between the maximum and minimum values in the array after making at most 3 moves. Since we can make up to 3 changes, effectively we can remove up to 3 elements from either end (start or end) of the sorted array to minimize the difference. The main insight is to try out the combinations of removing elements from both ends and find the minimum possible difference.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Sort the array nums.\n2. If the size of the array n is less than or equal to 4, return 0 since we can remove all elements to get an empty array which results in a difference of 0.\n3. Calculate the minimum difference by removing elements in these combinations:\n- Remove the last 3 elements.\n- Remove the first 3 elements.\n- Remove the first 1 and last 2 elements.\n- Remove the first 2 and last 1 elements.\n\nThe result will be the minimum of these differences.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n- \uD835\uDC42(\uD835\uDC5Blog\uD835\uDC5B)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n- O(1)\n\n# Code\n```\nclass Solution {\npublic:\n int minDifference(vector<int>& nums) {\n\n sort(nums.begin(),nums.end());\n\n int minVal = INT_MAX;\n\n int n = nums.size();\n\n if(n <= 4) return 0;\n\n minVal = min(minVal, nums[n-4] - nums[0]);\n minVal = min(minVal, nums[n-1] - nums[3]);\n minVal = min(minVal, nums[n-2] - nums[2]);\n minVal = min(minVal, nums[n-3] - nums[1]);\n\n return minVal;\n \n }\n};\n``` | 53 | 3 | ['C++'] | 13 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | Java straightforward heap O(N) | java-straightforward-heap-on-by-hobiter-93u1 | Time: \nO(N * lg4 * 2) == O(N), if N > 8;\nO(NlgN) if N <= 8;\nspace: O(1);\nJust calculate smallest 4 numbers and largest 4 numbers, and compare the difference | hobiter | NORMAL | 2020-07-11T20:27:50.862984+00:00 | 2020-07-12T21:07:39.697939+00:00 | 7,378 | false | Time: \nO(N * lg4 * 2) == O(N), if N > 8;\nO(NlgN) if N <= 8;\nspace: O(1);\nJust calculate smallest 4 numbers and largest 4 numbers, and compare the differences (see getDiff for detail.\n```\nclass Solution {\n public int minDifference(int[] nums) {\n if (nums.length < 5) return 0;\n if (nums.length <= 8) return getDiff(nums, true);\n PriorityQueue<Integer> top4 = new PriorityQueue<>(), bot4 = new PriorityQueue<>((a, b) -> b - a);\n for (int n : nums) {\n top4.offer(n);\n bot4.offer(n);\n if (top4.size() > 4) top4.poll();\n if (bot4.size() > 4) bot4.poll();\n }\n int[] arr = new int[8];\n for (int l = 3, r = 4; l >= 0 && r < 8; l--, r++) {\n arr[l] = bot4.poll();\n arr[r] = top4.poll();\n } \n return getDiff(arr, false);\n }\n \n private int getDiff(int[] arr, boolean needSort) {\n if (needSort) Arrays.sort(arr);\n int res = Integer.MAX_VALUE, n = arr.length;\n for (int i = 0; i < 4; i++) {\n res = Math.min(res, arr[n - (4 - i)] - arr[i]);\n }\n return res;\n }\n}\n``` | 41 | 4 | [] | 8 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | Simple Greedy Approach | My screen recording | simple-greedy-approach-my-screen-recordi-vh04 | \nclass Solution {\npublic:\n int minDifference(vector<int>& nums) {\n \n // if the size is smaller than 4 than we can easily make each of them | rachilies | NORMAL | 2020-07-11T16:02:16.680934+00:00 | 2020-07-11T22:58:06.777710+00:00 | 3,574 | false | ```\nclass Solution {\npublic:\n int minDifference(vector<int>& nums) {\n \n // if the size is smaller than 4 than we can easily make each of them equal and hence min possible difference is zero\n if(nums.size() <= 3)\n return 0;\n \n int n = nums.size();\n \n // sort the array in increasing order because we want to consider few of the largest and smallest numbers.\n sort(nums.begin(), nums.end());\n \n \n \n // Now idea is to try greedy. First of all we must agree that the values \n\t\t// which we will be changing should be either from left end or right end, \n\t\t// As there is no gain if we start changing values from middle of the array. \n\t\t// And hence we can try to make these 3 moves in all following possible \n\t\t// ways and choose the one which gives the best answer. \n // And because there are only 3 moves so total possibilities will be exactly 4.\n \n int ans = INT_MAX; // initialize the answer with INT_MAX.\n \n // CASE 1: when changing only from beg\n ans = min(ans, abs(nums[3] - nums[n - 1]));\n \n // CASE 2: when change two from beg and one from last\n ans = min(ans, abs(nums[2] - nums[n - 2]));\n \n // CASE 3: when change only from beg and two from last\n ans = min(ans, abs(nums[1] - nums[n - 3]));\n \n // CASE 4: when change all the values from last\n ans = min(ans, abs(nums[0] - nums[n - 4]));\n \n return ans;\n }\n};\n```\n\nIncase if you\'re interested in watching a boring recording \n\nhttps://youtu.be/8TgT77Ijei8\n | 33 | 2 | [] | 6 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | ✅Easiest 3 Step Cpp / Java / Py / JS Solution | Beginner Level 🏆| No Advance | easiest-3-step-cpp-java-py-js-solution-b-ihkh | \n### C++\n\nclass Solution {\npublic:\n int minDifference(vector<int>& nums) {\n //step 1\n int n = nums.size();\n if (n <= 4) return 0 | dev_yash_ | NORMAL | 2024-07-03T01:11:28.565627+00:00 | 2024-07-03T07:07:39.399973+00:00 | 7,075 | false | \n### C++\n```\nclass Solution {\npublic:\n int minDifference(vector<int>& nums) {\n //step 1\n int n = nums.size();\n if (n <= 4) return 0;\n\n // step 2: Sort the array\n sort(nums.begin(), nums.end());\n\n // step 3: Evaluate the minimum difference possible with at most 3 moves\n int minDiff = min({ \n nums[n-1] - nums[3], // Change 3 smallest elements\n nums[n-2] - nums[2], // Change 2 smallest and 1 largest element\n nums[n-3] - nums[1], // Change 1 smallest and 2 largest elements\n nums[n-4] - nums[0] // Change 3 largest elements\n });\n\n return minDiff;\n }\n};\n\n```\n### Java\n```\nclass Solution {\n public int minDifference(int[] nums) {\n int n = nums.length;\n if (n <= 4) return 0;\n\n // Sort the array\n Arrays.sort(nums);\n\n // Evaluate the minimum difference possible with at most 3 moves\n int minDiff = Math.min(\n Math.min(nums[n - 1] - nums[3], nums[n - 2] - nums[2]),\n Math.min(nums[n - 3] - nums[1], nums[n - 4] - nums[0])\n );\n\n return minDiff;\n }\n}\n```\n\n### Python3\n```\nclass Solution:\n def minDifference(self, nums: List[int]) -> int:\n n = len(nums)\n if n <= 4:\n return 0\n\n # Sort the array\n nums.sort()\n\n # Evaluate the minimum difference possible with at most 3 moves\n min_diff = min(\n nums[n-1] - nums[3], # Change 3 smallest elements\n nums[n-2] - nums[2], # Change 2 smallest and 1 largest element\n nums[n-3] - nums[1], # Change 1 smallest and 2 largest elements\n nums[n-4] - nums[0] # Change 3 largest elements\n )\n\n return min_diff\n```\n### JavaScript\n```\n/**\n * @param {number[]} nums\n * @return {number}\n */\nvar minDifference = function(nums) {\n let n = nums.length;\n if (n <= 4) return 0;\n\n // Sort the array\n nums.sort((a, b) => a - b);\n\n // Evaluate the minimum difference possible with at most 3 moves\n let minDiff = Math.min(\n nums[n - 1] - nums[3], // Change 3 smallest elements\n nums[n - 2] - nums[2], // Change 2 smallest and 1 largest element\n nums[n - 3] - nums[1], // Change 1 smallest and 2 largest elements\n nums[n - 4] - nums[0] // Change 3 largest elements\n );\n\n return minDiff;\n};\n\n```\n#### STAY COOL STAY DISCIPLINED..\n\n | 32 | 0 | ['Array', 'Greedy', 'C', 'Sorting', 'Python', 'Java', 'Python3', 'JavaScript'] | 13 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | Help understanding the question? | help-understanding-the-question-by-pytho-vrur | As of 7/28/2021, this is the description of the problem. \n\nGiven an array nums, you are allowed to choose one element of nums and change it by any value in on | python-rocks | NORMAL | 2021-07-29T02:45:49.763875+00:00 | 2021-07-29T02:45:49.763919+00:00 | 1,716 | false | As of 7/28/2021, this is the description of the problem. \n```\nGiven an array nums, you are allowed to choose one element of nums and change it by any value in one move.\n\nReturn the minimum difference between the largest and smallest value of nums after perfoming at most 3 moves.\n```\nAm I missing something here? \n\nIf I can take any element of nums and change it to anything, why wouldn\'t I just change max(nums) to min(nums) in very first move and always return the difference of 0? \n\nDid nobody else have a problem understanding the question? | 31 | 0 | [] | 9 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | nth_element & sort 4 smallest, biggest vs 2 heaps vs 1-liner||17ms Beats 100% | nth_element-sort-4-smallest-biggest-vs-2-u6ym | Intuition\n Describe your first thoughts on how to solve this problem. \nGreedy algorithm.\n\nSorting the whole array nums is easy, but the time complexity is r | anwendeng | NORMAL | 2024-07-03T02:30:46.054631+00:00 | 2024-07-03T12:07:31.028584+00:00 | 6,921 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nGreedy algorithm.\n\nSorting the whole array nums is easy, but the time complexity is raised up to $O(n\\log n)$.\n\nTry nth_element to find the 4 smallest & 4 biggest ints, then sort.\n\nPython solution is 1-liner using sorting the whole nums.\n\n3rd approach uses maxheap & minheap to hold 4 smallest, biggest elements. This solution is linear & run in 26ms Beats 99.74%.\n\nAn optimized version is done as a variant for the 1st C++ code by adopting the suggestion of @Sergei avoiding of using extra space. That code has runtime 17ms & beats 100%.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. When n<=4, just return 0\n2. Use `nth_element` to find the 4 smallest ints & store them in a 4 elemented array `small`; then sort\n3. Use `nth_element` to find the 4 biggest ints & store them in a 4 elemented array `big`; then sort\n4. Consider 4 scenarios min(big[i]-small[i] for i=0...3) which is the answer.\n5. Python 1 liner uses usual sort.\n6. 3rd approach uses maxheap `small` & minheap `big` to hold 4 smallest, biggest elements. This solution is linear & run in 26ms Beats 99.74%\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(8)=O(1)$$\n# Code C++ 28ms Beats 99.61%\n```\nclass Solution {\npublic:\n static int minDifference(vector<int>& nums) {\n const int n=nums.size();\n if (n<=4) return 0;\n\n //nth_element & sort find 4 smallest elements\n nth_element(nums.begin(), nums.begin()+4, nums.end());\n vector<int> small(nums.begin(), nums.begin()+4);\n sort(small.begin(), small.end());\n\n //nth_element & sort find 4 biggest elements\n nth_element(nums.begin(), nums.begin()+4, nums.end(), greater<int>());\n vector<int> big(nums.begin(), nums.begin()+4);\n sort(big.begin(), big.end());\n\n // difference by considering 4 scenarios\n int min_diff=INT_MAX;\n for (int i=0; i<=3; ++i) \n min_diff = min(min_diff, big[i]-small[i]);\n \n\n return min_diff;\n }\n};\n\n\n\n\n\nauto init = []() {\n ios::sync_with_stdio(false);\n cin.tie(nullptr);\n cout.tie(nullptr);\n return \'c\';\n}();\n```\n# Python 1-liner\n```\nclass Solution:\n def minDifference(self, nums: List[int]) -> int:\n return 0 if len(nums)<=4 else nums.sort() or min(nums[len(nums)-4+i]-nums[i] for i in range(4))\n \n```\n# C++ using maxheap & min heap ||26ms Beats 99.74%\n```\nclass Solution {\npublic:\n static int minDifference(vector<int>& nums) {\n const int n=nums.size();\n if (n<=4) return 0;\n priority_queue<int> small;\n priority_queue<int, vector<int>, greater<int>> big;\n for (int x :nums){\n if (small.size()>3){\n if (x<small.top()){\n small.pop();\n small.push(x);\n }\n }\n else small.push(x);\n if (big.size()>3){\n if (x>big.top()){\n big.pop();\n big.push(x);\n }\n }\n else big.push(x);\n }\n \n int Big[4];\n for(int i=3; i>=0; i--){\n Big[i]=big.top();\n big.pop();\n }\n\n // difference by considering 4 scenarios\n int min_diff=INT_MAX;\n for (int i=0; i<=3; i++){ \n int Small=small.top();\n small.pop();\n min_diff=min(min_diff, Big[i]-Small);\n }\n\n return min_diff;\n }\n};\n\n\n\n\n\nauto init = []() {\n ios::sync_with_stdio(false);\n cin.tie(nullptr);\n cout.tie(nullptr);\n return \'c\';\n}();\n```\n# C++ using nth_element & sort 4 smallest, biggest ints||17ms beats 100%\n\nThanks to @Serger, no extra space for `small` & `big` in use. The use for nth_element & sort is also optimized.\n```\nclass Solution {\npublic:\n static int minDifference(vector<int>& nums) {\n const int n = nums.size();\n if (n<=4) return 0;\n\n //nth_element & sort find 4 smallest elements\n nth_element(nums.begin(), nums.begin()+3, nums.end());\n sort(nums.begin(), nums.begin()+3);\n\n //nth_element & sort find 4 biggest elements\n nth_element(nums.begin()+4, nums.end()-4, nums.end());\n sort(nums.end()-3, nums.end());\n\n // difference by considering 4 scenarios\n int min_diff=INT_MAX;\n for (int i=0; i<=3; ++i) \n min_diff = min(min_diff, nums[n-4+i]-nums[i]);\n \n\n return min_diff;\n }\n};\n\n\n\n\n\nauto init = []() {\n ios::sync_with_stdio(false);\n cin.tie(nullptr);\n cout.tie(nullptr);\n return \'c\';\n}();\n```\nSince the std::sort is used for sorting 3 elements twice, it can replaced by the following very easy function\n```\n static void sort3(int& x, int& y, int& z){\n if (y > z) swap(y, z); // Ensure y <= z\n if (x > z) swap(x, z); // Ensure x <= z\n if (x > y) swap(x, y); // Ensure x <= y\n }\n``` | 30 | 0 | ['Array', 'Greedy', 'Sorting', 'Heap (Priority Queue)', 'C++', 'Python3'] | 14 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | C++ Simple Solution with Explanation | 100% Faster | c-simple-solution-with-explanation-100-f-iyom | kill 3 smallest elements\n2. kill 3 biggest elements\n3. kill 1 biggest elements + 2 smallest elements\n4. kill 2 biggest elements + 1 smallest elements\n\ncla | chiragjain77 | NORMAL | 2021-05-25T16:48:51.686423+00:00 | 2021-05-25T16:48:51.686468+00:00 | 2,986 | false | 1. kill 3 smallest elements\n2. kill 3 biggest elements\n3. kill 1 biggest elements + 2 smallest elements\n4. kill 2 biggest elements + 1 smallest elements\n```\nclass Solution {\npublic:\n int minDifference(vector<int>& nums) {\n sort(nums.begin(),nums.end());\n int n=nums.size();\n if(n<=4){\n return 0;\n }\n //1st\n int res=nums[n-1]-nums[3];\n //2nd\n res=min(res,nums[n-4]-nums[0]);\n //3rd\n res=min(res,nums[n-2]-nums[2]);\n //4th\n res=min(res,nums[n-3]-nums[1]);\n return res;\n \n }\n};\n```\n | 25 | 0 | ['C', 'Sorting'] | 4 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | Simple O(N) | C++ | Partial Sort | Detailed explaination | simple-on-c-partial-sort-detailed-explai-ma79 | We need to minimize the amplitude range (max_ele - min_ele) by changing at most 3 elements. \n\nIn order to do this, first we can sort the elements and then eit | joyful_bytes | NORMAL | 2022-03-15T06:47:18.638789+00:00 | 2022-03-15T06:55:05.026839+00:00 | 1,626 | false | We need to minimize the amplitude range (max_ele - min_ele) by changing at most 3 elements. \n\nIn order to do this, first we can **sort** the elements and then either\n**1. Kill last 3 elements\n2. Kill last 2 elements and first 1 element\n3. Kill last 1 element and first 2 element\n4. Kill first 3 elements**\nHere, killing would mean either changing it to new max_ele or new min_ele\n\nexample: \nnums: [1, 3, 5, 7, 8, 9, 10, 12, 13]\n1. Kill last 3 elements\n\ti.e. change last three elements to either 1 or 9 so whether we update it or forget about them at all won\'t matter. All we need is new_max_ele and new_min_ele\n\tnums: [1, 3, 5, 7, 8, 9, **9**, **9**, **9**]\n\tdiff = 9 - 1 = 8\n\t\n2. Kill last 2 elements and first 1 element\n\tnums: [**3**, 3, 5, 7, 8, 9, 10, **10**,**10**]\n\tdiff = 10 - 3 = 7\n\t\n3. Kill last 1 element and first 2 element\n\tnums: [**5**, **5**, 5, 7, 8, 9, 10, 12, **12**]\n\tdiff = 12 - 5 = 7\n\t\n4. Kill first 3 elements\n\tnums: [**7**, **7**, **7**, 7, 8, 9, 10, 12, 13]\n\tdiff = 13 - 7 = 6\nThus, min_diff = min(8, 7, 7, 6) = 6\n\nSorting will require **O(N logN)** time.\nBut wait!! Can we do better? Do we need to sort the whole array? (Observe: Does number 8 have any role in the above example?)\nNo, right? We only need to **sort the first 4 elements and the last 4 elements** and it would always lead to an optimal answer. \n\nIn C++, we can do this using [Partial Sorting](http://en.wikipedia.org/wiki/Partial_sorting).\nTime Complexity of Partial Sort: **O(N logK)** where\nN = total number of elements \nK = number of elements from start to middle. \nHence, this works best when K <<<< N as compared to normal sort function. \nIn this problem, K = 4 and N can be as high as 10^5. (1 <= N <= 10^5)\n\nCode: \n```\nint minDifference(vector<int>& nums) {\n\tint n = nums.size();\n\t// for 1 <= n <= 4 we can always change all the numbers to equal numbers\n\tif(n < 5)\n\t\treturn 0;\n\t\n\t// first 4 elements\n\tpartial_sort(nums.begin(), nums.begin() + 4, nums.end());\n\t// last 4 elements\n partial_sort(nums.rbegin(), nums.rbegin() + 4, nums.rend(), greater<int>());\n\t\n\tint min_diff = INT_MAX;\n\tfor(int i = 0, j = n - 4; i < 4; ++i, ++j)\n\t\tmin_diff = min(min_diff, nums[j] - nums[i]);\n \n\treturn min_diff;\n}\n```\n\nTime Complexity: O(N * log(4) * 2) = **O(N)** \n\nHope this helps!! :D | 22 | 0 | ['C', 'C++'] | 2 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | Python Solution 🚀 | python-solution-by-a_bs-uan5 | Intuition\nThe problem requires minimizing the difference between the largest and smallest values in an array after at most three moves. By changing up to three | 20250406.A_BS | NORMAL | 2024-07-03T01:41:21.887081+00:00 | 2024-07-03T01:41:21.887099+00:00 | 2,168 | false | ### Intuition\nThe problem requires minimizing the difference between the largest and smallest values in an array after at most three moves. By changing up to three elements to any value, we can effectively remove up to three outliers. Thus, the core insight is that we can minimize the range by focusing on changing either the smallest or the largest elements.\n\n### Approach\n1. **Sort the Array:** Sorting helps us quickly access the smallest and largest elements in a structured manner.\n2. **Consider Edge Case:** If the array has 4 or fewer elements, we can make all elements the same with three moves, resulting in a difference of 0.\n3. **Analyze Scenarios:** Post sorting, consider four scenarios:\n - Change the three smallest elements to the fourth smallest element.\n - Change the two smallest elements and the largest element.\n - Change the smallest element and the two largest elements.\n - Change the three largest elements to the fourth largest element.\n4. **Compute Differences:** Calculate the differences for these scenarios.\n5. **Return Minimum Difference:** The result is the minimum difference computed from the above scenarios.\n\n### Complexity\n- **Time complexity:** \\(O(n \\log n)\\) due to sorting the array.\n- **Space complexity:** \\(O(1)\\) as we are using a constant amount of extra space for computation, aside from the input array.\n\n# Code\n```\nclass Solution:\n def minDifference(self, nums: List[int]) -> int:\n if len(nums) <= 4:\n return 0\n \n nums.sort()\n \n # Possible scenarios to consider after sorting\n return min(\n nums[-1] - nums[3], # Remove the three smallest\n nums[-2] - nums[2], # Remove the two smallest and the largest\n nums[-3] - nums[1], # Remove the smallest and the two largest\n nums[-4] - nums[0] # Remove the three largest\n )\n\n``` | 19 | 0 | ['Python3'] | 4 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | Easy understanding, Commented C++ solution with sort and sliding window | easy-understanding-commented-c-solution-n0oo1 | \n// Idea: \n// 1. Chaning a number to any value is the same as removing them from array,\n// in the sense of calculating min difference.\n// 2. Try | tinfu330 | NORMAL | 2021-11-06T01:13:42.786515+00:00 | 2021-11-08T00:53:18.212059+00:00 | 1,528 | false | ```\n// Idea: \n// 1. Chaning a number to any value is the same as removing them from array,\n// in the sense of calculating min difference.\n// 2. Try to simplify the question, what if you were asked to change one value\n// from a sorted array and get the min difference of largest and smallest value of a sorted array?\n// 3. You will probably get the answer of removing either the front or the end.\n// 4. How about changing 2 numbers? You will either need to remove the first 2, last 2 or 1 from each end.\n// 5. Notice the pattern here, it is a sliding window. This can also be applied in our case.\n\n// Sliding window for changing 3 elements\n// [x, x, x, 4, 5, 6] -> diff = 6 - 4 = 2\n// [x, x, 3, 4, 5, x] -> diff = 5 - 3 = 2\n// [x, 2, 3, 4, x, x] -> diff = 4 - 2 = 2\n// [1, 2, 3, x, x, x] -> diff = 3 - 1 = 2\n// Ans: 2\n\nclass Solution {\npublic:\n // Time: O(nlogn), n = nums.size()\n // Space: O(1)\n int minDifference(vector<int>& nums) {\n int i = 0;\n int j = nums.size() - 1;\n \n int k = 3;\n \n if (nums.size() <= k + 1) {\n return 0;\n }\n \n sort(nums.begin(), nums.end()); // time: O(nlogn)\n \n int diff = nums.back() - nums[k];\n int res = diff;\n \n for (int i = 1; i <= k; i++) { // time: O(k), k = 3, since k is bounded, thus O(1)\n diff = nums[nums.size() - 1 - i] - nums[k - i];\n res = min(diff, res);\n }\n \n return res;\n }\n};\n``` | 19 | 0 | ['C', 'Sliding Window', 'Sorting', 'C++'] | 3 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | Java | With Explanation | java-with-explanation-by-surajthapliyal-25jv | Let say arr : \n[2,3,1,9,8,6,4]\n\nAfter sort :\n[1,2,3,4,6,8,9]\n\nwe\'ll replace 3 max/min elements with the min/max respectively\nobviously to make the diff | surajthapliyal | NORMAL | 2021-09-16T07:18:26.244639+00:00 | 2021-09-16T07:20:52.730631+00:00 | 1,102 | false | Let say arr : \n`[2,3,1,9,8,6,4]`\n\nAfter sort :\n`[1,2,3,4,6,8,9]`\n\nwe\'ll replace 3 max/min elements with the min/max respectively\nobviously to make the diff smaller.\n\n**case1** - [1,2,3,4,changed,changed,changed] => `res = Min(res,4-1) = 3`\n**case2** - [changed,2,3,4,5,changed,changed] => `res = Min(res,5-2) = 3`\n**case3** - [changed,changed,3,4,5,6,changed] => `res = Min(res,6-3) = 3`\n**case4** - [changed,changed,changed,4,5,6,7] => `res = Min(res,7-4) = 3`\n\n```\nclass Solution {\n public int minDifference(int[] nums) {\n int n = nums.length;\n if(n <= 3) return 0;\n Arrays.sort(nums);\n int res = Integer.MAX_VALUE;\n for(int i=0;i<=3;i++)\n res = Math.min(res,nums[n-4+i]-nums[i]);\n return res;\n }\n}\n``` | 19 | 0 | [] | 5 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | [C++] Partial sort; O(n); with explanation | c-partial-sort-on-with-explanation-by-mh-l6lz | We just need to know the four smallest numbers and the four largest to choose our optimal strategy. We could sort the entire array, but we don\'t have to. We ca | mhelvens | NORMAL | 2020-07-11T16:02:25.025212+00:00 | 2020-07-11T16:02:25.025262+00:00 | 1,221 | false | We just need to know the four smallest numbers and the four largest to choose our optimal strategy. We could sort the entire array, but we don\'t have to. We can use [partial sort](https://en.cppreference.com/w/cpp/algorithm/partial_sort).\n\n```C++\nint minDifference(vector<int>& nums) {\n int const N = nums.size();\n\n // For up to four numbers, we can always make them all equal.\n if (N <= 4) return 0;\n\n // Shift the four smallest numbers to the beginning\n // and the four largest numbers to the end.\n std::partial_sort(nums.begin(), nums.begin() + 4, nums.end());\n std::partial_sort(nums.rbegin(), nums.rbegin() + 4, nums.rend(), std::greater<int>());\n\n // Try all four possible ways to pick our 3 moves.\n int result = INT_MAX;\n for (int l = 0; l <= 3; ++l)\n result = std::min(result, nums[N-4+l] - nums[l]);\n return result;\n}\n``` | 19 | 0 | ['C'] | 6 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | ✅💯🔥Explanations No One Will Give You🎓🧠2 Detailed Approaches🎯🔥Extremely Simple And Effective🔥 | explanations-no-one-will-give-you2-detai-38vk | \n \n \n Nothing is impossible. The word itself says \'I\'m possible!\'"\n \n \n \n | heir-of-god | NORMAL | 2024-07-03T14:16:06.338019+00:00 | 2024-07-03T14:21:36.363492+00:00 | 773 | false | <blockquote>\n <p>\n <b>\n Nothing is impossible. The word itself says \'I\'m possible!\'"\n </b> \n </p>\n <p>\n --- Audrey Hepburn ---\n </p>\n</blockquote>\n\n# \uD83D\uDC51Problem Explanation and Understanding:\n\n## \uD83C\uDFAF Problem Description\nYou are given a list of integers ```nums``` and three moves. On each move you can choose any number in list and turn it into any nubmer you want. You want to return the minimum difference between the maximum and the minimum elements in ```nums``` after perfoming up to 3 moves.\n\n## \uD83D\uDCE5\u2935\uFE0F Input:\n- Integer array ```nums```\n\n## \uD83D\uDCE4\u2934\uFE0F Output:\nThe minimum possible difference after after perfomin up to 3 moves.\n\n---\n\n# 1\uFE0F\u20E3\u2728 Approach 1: Greedy + Sorting\n\n# \uD83E\uDD14 Intuition\nIn fact, both approaches are pretty simillar, so once you understand this approach the second will be trivial\n- Okay, let\'s think, if we have <= 4 elements in array, then we always can make all elements equal and make the minimum possible difference 0 (we can\'t achieve any lower difference because difference between something bigger or equal to something else is always >= 0)\n- Do we interested in every element in ```nums```? Obviously not, we want to keep difference between maximum and minimum as small as possible, so on every step we want either to decrease maximum or increase minimum so ```maximum - minimum``` will become smaller. \n- So, considering that we have only 3 moves, we can either move maximum three times to left or minimum three times to right. We always want to perform exactly 3 moves because doing lesser doesn\'t have sense because if we can try to achieve smaller difference why we wouldn\'t? \n- To make it easier to find the "next minimum/maximum" element of the list, we will sort the list and check all possible options for moving these values \u200B\u200Bto achieve the minimum difference.\n\n# \uD83D\uDC69\uD83C\uDFFB\u200D\uD83D\uDCBB Coding \n- As was said if ```len(nums)<=4``` then minimum difference is 0. \n- Sort ```nums``` to easily find next minimum/maximum\n- Find minimum difference between 4 options: move minimum 2 times and maximum 1, minimum 1 and maximum 2, minimum 3 and maximum 0, minimum 0 and maximum 3\n\n# \uD83D\uDCD5 Complexity Analysis\n- \u23F0 Time complexity: O(n*log n), since we sort whole array \n- \uD83E\uDDFA Space complexity: O(n), since sorting takes extra space in most languages\n\n# \uD83D\uDCBB Code\n``` python []\nclass Solution:\n def minDifference(self, nums: list[int]) -> int:\n if len(nums) <= 4:\n return 0\n nums.sort()\n return min(\n nums[-4] - nums[0],\n nums[-1] - nums[3],\n nums[-3] - nums[1],\n nums[-2] - nums[2],\n )\n```\n``` C++ []\nclass Solution {\npublic:\n int minDifference(vector<int>& nums) {\n if (nums.size() <= 4) {\n return 0;\n }\n sort(nums.begin(), nums.end());\n return min({\n nums[nums.size() - 4] - nums[0],\n nums[nums.size() - 1] - nums[3],\n nums[nums.size() - 3] - nums[1],\n nums[nums.size() - 2] - nums[2]\n });\n }\n};\n```\n``` JavaScript []\nvar minDifference = function(nums) {\n if (nums.length <= 4) {\n return 0;\n }\n nums.sort((a, b) => a - b);\n return Math.min(\n nums[nums.length - 4] - nums[0],\n nums[nums.length - 1] - nums[3],\n nums[nums.length - 3] - nums[1],\n nums[nums.length - 2] - nums[2]\n );\n};\n```\n``` Java []\nclass Solution {\n public int minDifference(int[] nums) {\n if (nums.length <= 4) {\n return 0;\n }\n Arrays.sort(nums);\n return Math.min(\n Math.min(nums[nums.length - 4] - nums[0], nums[nums.length - 1] - nums[3]),\n Math.min(nums[nums.length - 3] - nums[1], nums[nums.length - 2] - nums[2])\n );\n }\n}\n```\n``` C []\nint compare(const void* a, const void* b) {\n return (*(int*)a - *(int*)b);\n}\n\nint min(int a, int b) {\n return a < b ? a : b;\n}\n\nint minDifference(int* nums, int numsSize) {\n if (numsSize <= 4) {\n return 0;\n }\n qsort(nums, numsSize, sizeof(int), compare);\n return min(\n min(nums[numsSize - 4] - nums[0], nums[numsSize - 1] - nums[3]),\n min(nums[numsSize - 3] - nums[1], nums[numsSize - 2] - nums[2])\n );\n}\n```\n\n\n# 2\uFE0F\u20E3\uD83D\uDE0E Approach 2: Greedy + Smart Sorting\n\n# \uD83E\uDD14 Intuition\n- To be honest, I\'ve thinked about this but this is first time I learnt about partial sort. We need only four maximum and four minimum elements, so why would we sort whole array for this? \n\n# \uD83D\uDC69\uD83C\uDFFB\u200D\uD83D\uDCBB Coding \n- All the same as before, but now if we have more than 4 elements we want to sort just maximums and minimums\n\n# \uD83D\uDCD7 Complexity Analysis\n- \u23F0 Time complexity: O(n), since we sort up to 8 elements (partial sort time complexity)\n- \uD83E\uDDFA Space complexity: O(1), since partial sort algorithms don\'t use extra memory\n\n# \uD83D\uDCBB Code\n``` python []\nclass Solution:\n def minDifference(self, nums: list[int]) -> int:\n n: int = len(nums)\n if n <= 4:\n return 0\n elif n < 8:\n nums.sort()\n else:\n nums = sorted(heapq.nsmallest(4, nums)) + sorted(heapq.nlargest(4, nums))\n\n return min(\n nums[-4] - nums[0],\n nums[-1] - nums[3],\n nums[-3] - nums[1],\n nums[-2] - nums[2],\n )\n```\n``` C++ []\nclass Solution {\npublic:\n int minDifference(vector<int>& nums) {\n int n = nums.size();\n if (n <= 4) {\n return 0;\n } else if (n < 8) {\n sort(nums.begin(), nums.end());\n } else {\n vector<int> smallest(nums.begin(), nums.end());\n vector<int> largest(nums.begin(), nums.end());\n\n partial_sort(smallest.begin(), smallest.begin() + 4, smallest.end());\n partial_sort(largest.rbegin(), largest.rbegin() + 4, largest.rend());\n \n nums = vector<int>(smallest.begin(), smallest.begin() + 4);\n nums.insert(nums.end(), largest.rbegin(), largest.rbegin() + 4);\n }\n \n return min({\n nums[nums.size() - 4] - nums[0],\n nums[nums.size() - 1] - nums[3],\n nums[nums.size() - 3] - nums[1],\n nums[nums.size() - 2] - nums[2]\n });\n }\n};\n```\n``` JavaScript []\nvar minDifference = function(nums) {\n const n = nums.length;\n if (n <= 4) {\n return 0;\n } else if (n < 8) {\n nums.sort((a, b) => a - b);\n } else {\n let smallest = nums.slice().sort((a, b) => a - b).slice(0, 4);\n let largest = nums.slice().sort((a, b) => b - a).slice(0, 4);\n nums = smallest.concat(largest.reverse());\n }\n return Math.min(\n nums[nums.length - 4] - nums[0],\n nums[nums.length - 1] - nums[3],\n nums[nums.length - 3] - nums[1],\n nums[nums.length - 2] - nums[2]\n );\n};\n```\n``` Java []\nclass Solution {\n public int minDifference(int[] nums) {\n int n = nums.length;\n if (n <= 4) {\n return 0;\n } else if (n < 8) {\n Arrays.sort(nums);\n } else {\n PriorityQueue<Integer> smallest = new PriorityQueue<>(4);\n PriorityQueue<Integer> largest = new PriorityQueue<>(4, Collections.reverseOrder());\n\n for (int num : nums) {\n smallest.offer(num);\n if (smallest.size() > 4) {\n smallest.poll();\n }\n largest.offer(num);\n if (largest.size() > 4) {\n largest.poll();\n }\n }\n \n int[] combined = new int[8];\n for (int i = 0; i < 4; ++i) {\n combined[i] = smallest.poll();\n }\n for (int i = 4; i < 8; ++i) {\n combined[i] = largest.poll();\n }\n nums = combined;\n Arrays.sort(nums);\n }\n return Math.min(\n Math.min(nums[n - 4] - nums[0], nums[n - 1] - nums[3]),\n Math.min(nums[n - 3] - nums[1], nums[n - 2] - nums[2])\n );\n }\n}\n```\n``` C []\nint compare(const void* a, const void* b) {\n return (*(int*)a - *(int*)b);\n}\n\nvoid partial_sort(int* nums, int numsSize, int k) {\n qsort(nums, numsSize, sizeof(int), compare);\n}\n\nint min(int a, int b) {\n return a < b ? a : b;\n}\n\nint minDifference(int* nums, int numsSize) {\n if (numsSize <= 4) {\n return 0;\n } else if (numsSize < 8) {\n qsort(nums, numsSize, sizeof(int), compare);\n } else {\n int smallest[4];\n int largest[4];\n int smallestSize = 0;\n int largestSize = 0;\n int i;\n\n for (i = 0; i < numsSize; i++) {\n if (smallestSize < 4) {\n smallest[smallestSize++] = nums[i];\n if (smallestSize == 4) {\n partial_sort(smallest, 4, 4);\n }\n } else if (nums[i] < smallest[3]) {\n smallest[3] = nums[i];\n partial_sort(smallest, 4, 4);\n }\n\n if (largestSize < 4) {\n largest[largestSize++] = nums[i];\n if (largestSize == 4) {\n partial_sort(largest, 4, 4);\n }\n } else if (nums[i] > largest[3]) {\n largest[3] = nums[i];\n partial_sort(largest, 4, 4);\n }\n }\n\n for (i = 0; i < 4; i++) {\n nums[i] = smallest[i];\n nums[4 + i] = largest[i];\n }\n qsort(nums, 8, sizeof(int), compare);\n }\n return min(\n min(nums[numsSize - 4] - nums[0], nums[numsSize - 1] - nums[3]),\n min(nums[numsSize - 3] - nums[1], nums[numsSize - 2] - nums[2])\n );\n}\n```\n\n## \uD83D\uDCA1\uD83D\uDCA1\uD83D\uDCA1I encourage you to check out [my profile](https://leetcode.com/heir-of-god/) and [Project-S](https://github.com/Heir-of-God/Project-S) project for detailed explanations and code for different problems (not only Leetcode). Happy coding and learning!\uD83D\uDCDA\n\n### Please consider *upvote*\u2B06\uFE0F\u2B06\uFE0F\u2B06\uFE0F because I try really hard not just to put here my code and rewrite testcase to show that it works but explain you WHY it works and HOW. Thank you\u2764\uFE0F\n\n## If you have any doubts or questions feel free to ask them in comments. I will be glad to help you with understanding\u2764\uFE0F\u2764\uFE0F\u2764\uFE0F\n\n\n | 17 | 9 | ['Array', 'Greedy', 'C', 'Sorting', 'Python', 'C++', 'Java', 'Python3', 'JavaScript'] | 10 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | JAVA - sorting O(nLog(n)) - only 4 choices | java-sorting-onlogn-only-4-choices-by-ru-5phh | Once we have array sorted, we can cut down this problem to selecting among only 4 choices for making 3 moves. \n\nConsider below example:\na b c d e f g h i j ( | rupesh25127 | NORMAL | 2021-07-05T06:32:14.257572+00:00 | 2021-07-05T06:32:33.976175+00:00 | 1,579 | false | Once we have array sorted, we can cut down this problem to selecting among only 4 choices for making 3 moves. \n\nConsider below example:\na b c d e f g h i j (say, this array is sorted)\n\n1. Will it matter if you change d, e, f, g to anything? No. You can set them all to a or j, and result will still be same.\n2. This means our focus can be concentrated on only changing either first three or last three elements.\n3. We can make following moves \n\ta. 3 from last, 0 from start. Set h, i, j to anything else between a - g. Diff: g - a\n\tb. 2 from last, 1 from start. Set i,j to anything between b - h, same for a. Diff: h - b\n\tc. 1 from last, 2 from start. Set j to anything between c - i, same for a,b. Diff: i - c\n\td. 0 from last, 3 from start. Set a,b,c to anything between d - j. Diff: j - d\n4. We can take minimum of these 4 scenarios and there goes our answer.\n5. Also, if array length is <= 4, you can set other three elements same as 4th one, making the difference 0.\n\n```\nclass Solution {\n public int minDifference(int[] nums) {\n if(nums.length <= 4)\n return 0;\n \n int n = nums.length;\n Arrays.sort(nums);\n return Math.min(\n Math.min(nums[n-1] - nums[3], nums[n-2] - nums[2]),\n Math.min(nums[n-3] - nums[1], nums[n-4] - nums[0])\n );\n }\n}\n```\n\nTime complexity: O(n Log(n) ) (for sorting)\nspace complexity: O(1) | 17 | 0 | ['Sorting', 'Java'] | 3 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | Full Detailed Explanation 🏆🏆 | full-detailed-explanation-by-shivakumar1-sitd | Intuition\nGiven the array 0 1 5 10 14, we need to remove 3 numbers to make the difference between the maximum and minimum values as small as possible. There ar | shivakumar1 | NORMAL | 2024-07-03T06:34:13.898644+00:00 | 2024-07-03T06:34:13.898701+00:00 | 706 | false | # Intuition\nGiven the array `0 1 5 10 14`, we need to remove 3 numbers to make the difference between the maximum and minimum values as small as possible. There are four possible ways to achieve this:\n\n1. Remove the first 3 elements: `? ? ? 10 14`. The difference between the maximum and minimum is `14 - 10 = 4`.\n2. Remove the last 3 elements: `0 1 ? ? ?`. The difference between the maximum and minimum is `1 - 0 = 1`.\n3. Remove the first 2 and the last 1 elements: `? ? 5 10 ?`. The difference between the maximum and minimum is `10 - 5 = 5`.\n4. Remove the first 1 and the last 2 elements: `? 1 5 ? ?`. The difference between the maximum and minimum is `5 - 1 = 4`.\n\nThe smallest difference among these scenarios is `1`. \n\n# Code Explanation \n- The variable `n` is assigned the length of the array `nums`.\n- A conditional check is performed: if the length of the array `n` is less than or equal to 4, the method returns 0 because any array with 4 or fewer elements can be made identical with at most three moves, resulting in a difference of 0.\n- The array `nums` is sorted in ascending order using `Arrays.sort(nums)`.\n- The variable `res` is initialized to `Integer.MAX_VALUE` to store the minimum difference.\n- Four potential minimum differences are calculated:\n - The difference between the element at index `n-4` (fourth last element) and the element at index 0 (first element).\n - The difference between the element at index `n-1` (last element) and the element at index 3 (fourth element).\n - The difference between the element at index `n-3` (third last element) and the element at index 1 (second element).\n - The difference between the element at index `n-2` (second last element) and the element at index 2 (third element).\n- For each of these differences, the method updates `res` with the minimum value using `Math.min`.\n- Finally, the method returns the value of `res`, which is the minimum difference between the largest and smallest values of `nums` after performing at most three moves.\n# Complexity\n- Time complexity: $$O(nlogn)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(logn)$$ because of sorting\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int minDifference(int[] nums) {\n int n = nums.length;\n if (n <= 4) return 0;\n\n Arrays.sort(nums);\n\n int res = Integer.MAX_VALUE;\n res = Math.min(res, nums[n-4]-nums[0]);\n res = Math.min(res, nums[n-1]-nums[3]);\n res = Math.min(res, nums[n-3]-nums[1]);\n res = Math.min(res, nums[n-2]-nums[2]);\n return res;\n }\n}\n\n\n```\n\n\n# Follow me on LinkedIn https://www.linkedin.com/in/shivakumar139/\n# If you found this helpful, Please Upvote it \u2764\uFE0F\n\n\n | 15 | 0 | ['Array', 'Greedy', 'Sorting', 'Java'] | 3 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | Java | Greedy | Easy Solution | java-greedy-easy-solution-by-rishabh255-6rri | \nclass Solution {\n public int minDifference(int[] nums) {\n int n = nums.length; \n if(n <= 4) return 0;\n Arrays.sort(nums);\n | rishabh255 | NORMAL | 2021-10-06T18:05:13.455221+00:00 | 2021-10-06T18:05:13.455267+00:00 | 1,489 | false | ```\nclass Solution {\n public int minDifference(int[] nums) {\n int n = nums.length; \n if(n <= 4) return 0;\n Arrays.sort(nums);\n \n int minv = Integer.MAX_VALUE;\n \n // Case 1 : converting last three values\n minv = Math.min(minv, nums[n-4] - nums[0]);\n \n // Case 2: Converting first three values\n minv = Math.min(minv, nums[n-1] - nums[3]);\n \n // Case 3: Converting 2 left vaules and 1 right value\n minv = Math.min(minv, nums[n-3]-nums[1]);\n \n // Case 4 : Converting 1 left value and 2 right values\n minv = Math.min(minv, nums[n-2] - nums[2]);\n \n // returning min value\n return minv;\n }\n}\n``` | 15 | 0 | ['Greedy', 'Sorting', 'Java'] | 5 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | Nth_element and Single Pass| C++ 11 ms 100% | Java 2 ms 100% | Python3 241 ms 99% | nth_element-and-single-pass-c-11-ms-100-rzkhp | Intuition\nUsing no more than 3 element removals, we need to minimize the array diameter, which is the max difference between its elements (the task statement s | sergei99 | NORMAL | 2024-07-03T07:53:26.614034+00:00 | 2024-07-03T18:04:13.658529+00:00 | 771 | false | # Intuition\nUsing no more than 3 element removals, we need to minimize the array diameter, which is the max difference between its elements (the task statement says "change element to any value", but from the target function perspective it\'s effectively the same as the element removal).\n\nObviously we are going to choose among minimal and maximal elements, specifically from these cases:\n* Remove 3 minimums\n* Remove 2 minimums and 1 maximum\n* Remove 1 minimum and 2 maximums\n* Remove 3 maximums\n\nThe first case requires access to the 4-th minimum, and the last case requires access to the 4-th maximum. Once we have these, we can simply pick the minimal diameter from the following expressions:\n* Ultimate maximum - 4-th minimum\n* 2-nd maximum - 3-rd minimum\n* 3-rd maximum - 2-nd minimum\n* 4-th maximum - ultimate minimum\n\nConsidering the limitations (up to $10^5$ array elements and their values in the range of $[-10^9; 10^9]$), the main performance-affecting matter is how to pick those 4 minimums and 4 maximums.\n\n# Approach\n\nFor 4-element or shorter arrays the result is 0 since the set degrades to 1 point after 3 or fewer element removals.\n\nIf we have 8 or fewer elements, we can sort the array using a standard library sort routine, and this will give us the smallest 4 elements at the beginning of the array and the largest 4 elements at the end of the array, in ascending order. We can take this route for slightly larger sizes, e.g. 16 or 32, but for $n=10^3$ we are going to have an average of $n \\times log_2(n) = 10^4$ element swaps to achieve full ordering, which we actually don\'t need; we only need min 4 and max 4 elements. For the maximal length of $10^5$ the standard library sort would give us an average of $1.7 \\times 10^6$ element comparisons, which is too slow.\n\nThe element value range is too wide for a Count sort. Radix sort might be a better choice, but it has too high constant multiplier. It might be more practical to use a quick selection algorithm.\n\n## Quick Select\n\nC++ has a nice STL function `nth_element`, which does all the magic. We pick the 4 smallest elements with one call and the 4 largest elements with another call. We can even exclude the first 4 elements from the second call\'s range since we know they are minimal. Then we sort 4-element subarrays on both ends (even bubble sort would do).\n\nJDK is not generous enough, so we have to implement our own `nth_element`. It\'s similar to Quicksort with the main distinction of recursion going to just one half of the array. Subarrays small enough are sorted using a JDK function.\n\nThe number of swaps in `nth_element` would be $C \\times (n + \\frac n k + \\frac n {k^2} + ...) = C \\times n \\times \\frac {1 - \\frac 1 k} {1 - \\frac 1 {k^{log_2(n)}}} = C \\times n \\times {k^{log_2(\\frac n 2)}} \\frac {k - 1} {k^{log_2(n)} - 1}$ where $1 \\le k \\le 2 $ depends on the quality of the pivot choice, and $C$ is a constant. So the algorithm time complexity becomes linear except the wost case with $k$ degenerating to $1$ and making the series diverge. This can be countered by picking a median-3 pivot or some other techniques, but we don\'t use those here to minimize expensive array accesses in Java.\n\nAs for Python, its main rule is "never implement algorithms in Python". Enormously high cost of interpreted language and its data structures often nullifies asymptotic complexity advantage. Whatever we program in Python, we should seek for out-of-the-box implementations of algorithms in C libraries. A quick selection implementation is available in _numpy_, but copying all the list data to a _numpy_ array would degrade the memory complexity to $O(n)$.\n\n## Multi-Value Accumulation\n\nAn alternative way to find minimums and maximums is to collect them in a separate accumulator during a single pass.\n\nFor C++ we could use local variables (4 for min and 4 for max, maintaining sorted lists in them). The advantage of this approach is that if the CPU has enough named registers, the entire calculation can go without memory accesses (apart from reading the input array). We could even use binary search to determine the insertion point. E.g. if we had maximums `10 5 1 0`, and we need to insert `14`, we could first compare it to the second element (`5`) and depending on the result, seek the insertion point to the left or to the right of it. For 5 possible insertion points there would be no more than 3 comparisons in total, resulting in $O(n \\times \\lceil log_2(m+1) \\rceil)$ comparisons and $2 \\times n$ swaps where $m$ is the number of extremums to track.\n\nA heap-based accumulation in $4 \\times 2$ variables is also possible for C++, giving the same asymptotic complexity and potentially better execution time (for moving fewer elements on average insertions).\n\nA Python implementation, as mentioned above, should look for a library function to do the algorithm. We could use a builtin `sort` for smaller arrays and heap-based n-minimum and n-maximum search from `heapq`. Different watermarks have been tried, and we have chosen 64.\n\n# Complexity\n- Time complexity: $O(n)$\n- Space complexity: $O(1)$\n\n# Code\n\n## Quick Select\n\n``` C++ []\nclass Solution {\npublic:\n static int minDifference(vector<int>& nums) {\n const uint n = nums.size();\n if (n <= 4) return 0;\n const auto beg = nums.begin(), end = nums.end();\n if (n <= 16)\n sort(beg, end);\n else {\n nth_element(beg, beg + 3u, end);\n sort(beg, beg + 4u);\n nth_element(beg + 4u, end - 4u, end);\n sort(end - 4u, end);\n }\n return min(min(nums[n-4u]-nums[0], nums[n-3u]-nums[1]), min(nums[n-2u]-nums[2], nums[n-1u]-nums[3]));\n }\n};\n```\n``` Java []\nclass Solution {\n private static void nth_element(final int[] arr, final int ibeg, final int pos, final int iend) {\n if (ibeg + 8 >= iend) {\n Arrays.sort(arr, ibeg, iend);\n return;\n }\n int beg = ibeg, end = iend;\n final var pivot = arr[(beg+end)/2];\n\n // Divide the values about the pivot\n while (true) {\n while (beg + 1 < end && arr[beg] < pivot)\n beg++;\n while (end > beg + 1 && arr[end-1] > pivot)\n end--;\n if (beg + 1 >= end)\n break;\n\n final var t = arr[beg];\n arr[beg] = arr[end-1];\n arr[end-1] = t;\n beg++;\n end--;\n }\n if (arr[beg] < pivot)\n beg++;\n\n // Recurse on one of the two sides\n nth_element(arr, pos < beg ? ibeg : beg, pos, pos < beg ? beg : iend);\n }\n\n public static int minDifference(final int[] nums) {\n final int n = nums.length;\n if (n <= 4) return 0;\n if (n <= 16)\n Arrays.sort(nums);\n else {\n nth_element(nums, 0, 3, n);\n Arrays.sort(nums, 0, 4);\n nth_element(nums, 4, n - 4, n);\n Arrays.sort(nums, n - 4, n);\n }\n return Math.min(Math.min(nums[n-4]-nums[0], nums[n-3]-nums[1]), Math.min(nums[n-2]-nums[2], nums[n-1]-nums[3]));\n }\n}\n```\n\n## Multi-Value Accumulation - Sorted List\n\n``` C++ []\nclass Solution {\npublic:\n static int minDifference(vector<int>& nums) {\n const uint n = nums.size();\n if (n <= 4) return 0;\n const auto beg = nums.begin(), end = nums.end();\n int a = INT_MAX, b = INT_MAX, c = INT_MAX, d = INT_MAX,\n w = INT_MIN, x = INT_MIN, y = INT_MIN, z = INT_MIN;\n for (const int v : nums) {\n if (v < b) {\n d = c, c = b;\n if (v < a) b = a, a = v;\n else b = v;\n }\n else if (v < c) d = c, c = v;\n else if (v < d) d = v;\n if (v > x) {\n z = y, y = x;\n if (v > w) x = w, w = v;\n else x = v;\n }\n else if (v > y) z = y, y = v;\n else if (v > z) z = v;\n }\n return min(min(z - a, y - b), min(x - c, w - d));\n }\n};\n```\n\n## Multi-Value Accumulation - Heap\n\n``` C++ []\nclass Solution {\npublic:\n static int minDifference(vector<int>& nums) {\n const uint n = nums.size();\n if (n <= 4) return 0;\n const auto beg = nums.begin(), end = nums.end();\n int a = INT_MAX, b = INT_MAX, c = INT_MAX, d = INT_MAX, // max-heap for mins: a > b a > c b > d\n w = INT_MIN, x = INT_MIN, y = INT_MIN, z = INT_MIN; // min-heap for maxes: w < x w < y x < z\n for (const int v : nums) {\n if (v < a) {\n // push v\n int e;\n if (v > b) e = b, b = v;\n else e = v;\n // pop\n if (b > c) {\n a = b;\n if (d > e) b = d, d = e;\n else b = e;\n }\n else a = c, c = e;\n }\n if (v > w) {\n // push v\n int t;\n if (v < x) t = x, x = v;\n else t = v;\n // pop\n if (x < y) {\n w = x;\n if (z < t) x = z, z = t;\n else x = t;\n }\n else w = y, y = t;\n }\n }\n // Convert heaps to sorted lists\n if (b < c) swap(b, c);\n else if (c < d) swap(c, d);\n if (x > y) swap(x, y);\n else if (y > z) swap(y, z);\n return min(min(z - a, y - b), min(x - c, w - d));\n }\n};\n```\n``` Python3 []\nclass Solution:\n def minDifference(self, nums: List[int]) -> int:\n # 3 cases depending on length\n n = len(nums)\n if n <= 4: return 0\n if n <= 64:\n nums.sort()\n ns = nums[:4]\n nl = nums[:-5:-1]\n else:\n ns = heapq.nsmallest(4, nums)\n nl = heapq.nlargest(4, nums)\n return min(nl[3]-ns[0], nl[2]-ns[1], nl[1]-ns[2], nl[0]-ns[3])\n```\n\n# Measurements\n\n|Language|Algorithm|Time, ms|Beating|Memory, Mb|Beating|Submission Link|\n|-|-|-|-|-|-|-|\n|C++|Quick Select|11|100%|37.62|97.67%|https://leetcode.com/problems/minimum-difference-between-largest-and-smallest-value-in-three-moves/submissions/1307832772|\n|C++|Sorted List|14|100%|37.81|94.31%|https://leetcode.com/problems/minimum-difference-between-largest-and-smallest-value-in-three-moves/submissions/1308231423|\n|C++|Heap|15|100%|37.8|95.34%|https://leetcode.com/problems/minimum-difference-between-largest-and-smallest-value-in-three-moves/submissions/1308571539|\n|Java|Quick Select|2|100%|56.73|83.99%|https://leetcode.com/problems/minimum-difference-between-largest-and-smallest-value-in-three-moves/submissions/1307928224|\n|Python3|Heap|241|99.06%|27.89|19.81%|https://leetcode.com/problems/minimum-difference-between-largest-and-smallest-value-in-three-moves/submissions/1308101213| | 14 | 0 | ['Array', 'Sorting', 'Quickselect', 'C++', 'Java', 'Python3'] | 3 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | simple and easy C++ solution with explanation 😍❤️🔥 | simple-and-easy-c-solution-with-explanat-hgcr | if it\'s help, please up \u2B06 vote! \u2764\uFE0F\n\n\n# Code\n\nclass Solution {\npublic:\n int minDifference(vector<int>& nums) \n {\n if(nums.s | shishirRsiam | NORMAL | 2024-07-03T01:25:03.138779+00:00 | 2024-07-03T01:25:03.138804+00:00 | 1,517 | false | # if it\'s help, please up \u2B06 vote! \u2764\uFE0F\n\n\n# Code\n```\nclass Solution {\npublic:\n int minDifference(vector<int>& nums) \n {\n if(nums.size() <= 3) return 0;\n sort(begin(nums), end(nums));\n\n int ans = INT_MAX, n = nums.size();\n\n // frist three remove\n ans = min(ans, nums.back() - nums[3]);\n\n // last three remove\n ans = min(ans, nums[n-4] - nums[0]);\n\n // first 2 remove, last 1 remove\n ans = min(ans, nums[n-2] - nums[2]);\n\n // first 1 remove, last 2 remove\n ans = min(ans, nums[n-3] - nums[1]);\n\n return ans;\n }\n};\n``` | 14 | 0 | ['Array', 'Greedy', 'Sorting', 'C++'] | 8 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | [Python3] 1-line O(N) | python3-1-line-on-by-ye15-dl8m | Algo\nHere, at most 8 numbers are relevant, i.e. the 4 smallest and the 4 largest. Suppose they are labeled as \n\nm1, m2, m3, m4, ... M4, M3, M2, M1 \n\nthen m | ye15 | NORMAL | 2020-07-11T16:23:20.376828+00:00 | 2020-07-11T16:50:18.515880+00:00 | 1,873 | false | Algo\nHere, at most 8 numbers are relevant, i.e. the 4 smallest and the 4 largest. Suppose they are labeled as \n\n`m1, m2, m3, m4, ... M4, M3, M2, M1` \n\nthen `min(M4-m1, M3-m2, M2-m3, M1-m4)` gives the solution. It is linear `O(N)` to find `m1-m4` and `M1-M4` like below. \n\n`O(N)` time & `O(1)` space leveraging on the `heapq` module \n\n```\nclass Solution:\n def minDifference(self, nums: List[int]) -> int:\n return min(x-y for x, y in zip(nlargest(4, nums), reversed(nsmallest(4, nums))))\n```\n\nA more readable version is below \n```\nclass Solution:\n def minDifference(self, nums: List[int]) -> int:\n small = nsmallest(4, nums)\n large = nlargest(4, nums)\n return min(x-y for x, y in zip(large, reversed(small)))\n``` | 14 | 2 | ['Python3'] | 4 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | One-pass solution with intuition | No sorting | Beats 99% | Python3 | one-pass-solution-with-intuition-no-sort-w54d | Intuition\nObserve that when making a move, there is no point in introducing a new number in the array - it is better to replace a number with something already | reas0ner | NORMAL | 2024-07-03T07:14:04.201511+00:00 | 2024-07-03T07:17:09.281718+00:00 | 806 | false | # Intuition\nObserve that when making a move, there is no point in introducing a new number in the array - it is better to replace a number with something already present elsewhere in the array, so as to not introduce a new max-min difference. This is equivalent to removing a number from the array.\n\nSo how do we remove 3 numbers from the array such that the new max-min difference is minimal? If we had to remove one number, clearly it would have to be the max or the min, else it makes no difference. We can extend this logic to considering a few largest and few smallest numbers and make a decision on which numbers to remove. These numbers can be found by simply iterating over the array. \n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def minDifference(self, nums: List[int]) -> int:\n if len(nums) < 5:\n return 0\n \n a, b, c, d, x, y, z, t = inf, inf, inf, inf, -inf, -inf, -inf, -inf\n for num in nums:\n if num < a:\n d, c, b, a = c, b, a, num\n elif num < b:\n d, c, b = c, b, num\n elif num < c:\n d, c = c, num\n elif num < d:\n d = num\n\n if num > t:\n x, y, z, t = y, z, t, num\n elif num > z:\n x, y, z = y, z, num\n elif num > y:\n x, y = y, num\n elif num > x:\n x = num\n\n return min(x - a, y - b, z - c, t - d)\n``` | 13 | 1 | ['Array', 'Greedy', 'Python3'] | 6 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | kya O(N) possible hain !? Lets Solve || C++, Beats 100% ?? | kya-on-possible-hain-lets-solve-c-beats-au3w2 | Check Out My New Channel : https://www.youtube.com/@Intuit_and_Code\n> if you came for O(N) approach then skip the first part\n# Intuition\n\n\n Describe your f | Rarma | NORMAL | 2024-07-03T04:54:05.463489+00:00 | 2024-09-11T11:57:12.589183+00:00 | 1,619 | false | **Check Out My New Channel : https://www.youtube.com/@Intuit_and_Code**\n> if you came for O(N) approach then skip the first part\n# Intuition\n\n\n<!-- Describe your first thoughts on how to solve this problem. -->\nMera pehla thought yeh tha ki agar main array ko sort kar doon, toh mujhe easily smallest aur largest elements mil jayenge. Phir main different combinations ko check kar sakta hoon taaki minimum difference find kar saku after removing up to 3 elements.\n\nIsko ese bhi soch sakte hain ki prefix suffix sliding window on an array and size hme upto 3 tk rkhna hain \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Agar array size 4 ya usse kam hai, toh return 0.\n2. Array ko sort karo.\n3. Ek loop chalao jo 4 combinations ko check kare (0 se 3 tak loop).\n4. Har combination mein, sabse chhota aur sabse bada element choose karo aur unka difference nikaalo.\n5. Minimum difference ko update karo aur return karo.\n\n# Image Visualization [ dont have table-pen so notebook me smjh lo]\n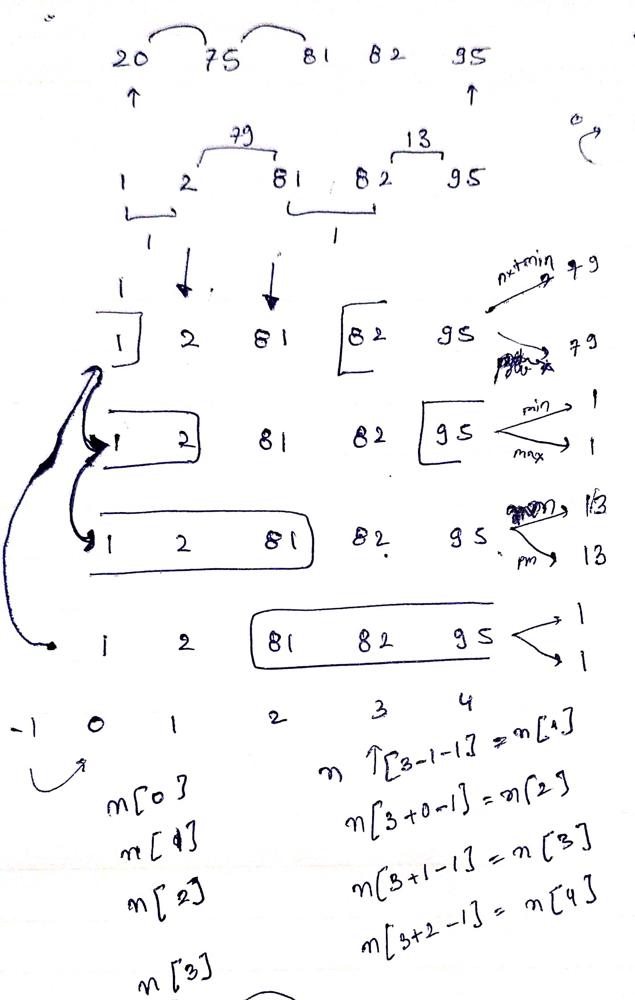\n\n\n# Complexity\n- Time complexity: O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int minDifference(vector<int>& n) {\n if(n.size()<=4){\n return 0;\n }\n int ans=INT_MAX;\n sort(n.begin(),n.end());\n\n int w=-1,siz=n.size()-2;\n for(int i=0;i<=3;i++){\n // nxtmin\n int nxtmin = n[w+1];\n // prevmax\n int prevmax = n[siz+w-1];\n\n ans = min(ans,prevmax-nxtmin);\n w++;\n }\n \n return ans;\n }\n};\n```\n\n\n# Intuition & Approach\n\nToh ghum firake baat aa rhi thi ki we need atleast 4 minimum element and then 4 maximum element jisse hamara computation possible ho\ntoh without sorting finding 4 max and 4 min is possible\nbs thoda code bada likhna pda \uD83E\uDD75\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int minDifference(vector<int>& n) {\n if (n.size() <= 4) {\n return 0;\n }\n\n // Initialize variables to store the four smallest and four largest values\n int min1 = INT_MAX, min2 = INT_MAX;\n int min3 = INT_MAX, min4 = INT_MAX;\n int max1 = INT_MIN, max2 = INT_MIN;\n int max3 = INT_MIN, max4 = INT_MIN;\n\n // Traverse the array once to find the four smallest and four largest elements\n for (int num : n) {\n if (num < min1) {\n min4 = min3;\n min3 = min2;\n min2 = min1;\n min1 = num;\n } else if (num < min2) {\n min4 = min3;\n min3 = min2;\n min2 = num;\n } else if (num < min3) {\n min4 = min3;\n min3 = num;\n } else if (num < min4) {\n min4 = num;\n }\n\n if (num > max1) {\n max4 = max3;\n max3 = max2;\n max2 = max1;\n max1 = num;\n } else if (num > max2) {\n max4 = max3;\n max3 = max2;\n max2 = num;\n } else if (num > max3) {\n max4 = max3;\n max3 = num;\n } else if (num > max4) {\n max4 = num;\n }\n }\n\n // Compute the minimum difference by considering different removal strategies\n vector<int> smallest = {min1, min2, min3, min4};\n vector<int> largest = {max1, max2, max3, max4};\n int ans = INT_MAX;\n \n for (int i = 0; i < 4; ++i) {\n ans = min(ans, largest[3-i] - smallest[i]);\n }\n\n return ans;\n }\n};\n```\n | 13 | 0 | ['Array', 'Greedy', 'Sliding Window', 'Sorting', 'C++'] | 5 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | 💯✅🔥Detailed Easy Java ,Python3 ,C++ Solution|| 15 ms ||≧◠‿◠≦✌ | detailed-easy-java-python3-c-solution-15-hro1 | Intuition\n Describe your first thoughts on how to solve this problem. \nThe key insights behind this intution is:\n1. If the array has less than 5 elements, th | suyalneeraj09 | NORMAL | 2024-07-03T02:24:28.803877+00:00 | 2024-07-03T02:24:49.228509+00:00 | 3,542 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe key insights behind this intution is:\n1. If the array has less than 5 elements, the minimum difference will be 0, as we can\'t form two groups of 4 elements.\n1. Sorting the array in ascending order allows us to easily identify the 4 smallest and 4 largest elements.\n1. By calculating the difference between the sum of the 4 largest elements and the sum of the 4 smallest elements, we can find the minimum difference.\n\n---\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe approach used in the provided code is to find the minimum difference between the sum of the largest 4 elements and the sum of the smallest 4 elements in the given array A.\nThe intuition behind this approach is that the minimum difference will be achieved by either:\n- Removing the 4 smallest elements and keeping the 4 largest elements.\n- Removing the 4 largest elements and keeping the 4 smallest elements.\n---\n# Complexity\n- Time complexity:O(n log n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n---\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n---\n# Step By Step Explanation\n**Let\'s go through the step-by-step explanation of how the code works using the array [5, 3, 2, 4].**\n\n- **Check if the array has less than 5 elements:**\n1. The given array A has 4 elements, which is less than 5.\n1. Therefore, the function returns 0, as per the problem statement.\n\n- **Sort the array in ascending order**:\n1. The sorted array is [2, 3, 4, 5].\n\n**Calculate the minimum difference:**\n1. The function calculates the minimum difference between the sum of the largest 4 elements and the sum of the smallest 4 elements.\n**The possible differences are:**\n- A[-1] - A: 5 - 3 = 2\n- A[-2] - A: 4 - 2 = 2\n- A[-3] - A: 3 - 3 = 0\n- A[-4] - A: 2 - 2 = 0\n\n**The minimum of these differences is 0, which is returned as the final result.**\n\n---\n# Code\n```java []\nclass Solution {\n public int minDifference(int[] A) {\n int n = A.length, res = Integer.MAX_VALUE;\n if (n < 5) return 0;\n Arrays.sort(A);\n for (int i = 0; i < 4; ++i) {\n res = Math.min(res, A[n - 4 + i] - A[i]);\n }\n return res;\n }\n}\n```\n```python3 []\nclass Solution:\n def minDifference(self, A: List[int]) -> int:\n n = len(A)\n if n < 5:\n return 0\n A.sort()\n return min(A[-1] - A[3], A[-2] - A[2], A[-3] - A[1], A[-4] - A[0])\n```\n```C++ []\nclass Solution {\npublic:\n int minDifference(vector<int>& A) {\n int n = A.size();\n if (n < 5) return 0;\n sort(A.begin(), A.end());\n return min({A[n - 1] - A[3], A[n - 2] - A[2], A[n - 3] - A[1], A[n - 4] - A[0]});\n }\n};\n```\n---\n\n\n\n\n | 13 | 0 | ['Array', 'Greedy', 'Sorting', 'C++', 'Java', 'Python3'] | 6 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | JAVA Solution Explained in HINDI(2 Approaches) | java-solution-explained-in-hindi2-approa-hyx0 | https://youtu.be/eb4vwq4BBxI\n\nFor explanation, please watch the above video and do like, share and subscribe the channel. \u2764\uFE0F Also, please do upvote | The_elite | NORMAL | 2024-07-03T08:54:53.771686+00:00 | 2024-07-03T08:56:29.590098+00:00 | 413 | false | https://youtu.be/eb4vwq4BBxI\n\nFor explanation, please watch the above video and do like, share and subscribe the channel. \u2764\uFE0F Also, please do upvote the solution if you liked it.\n\n# Subscribe:- [ReelCoding](https://www.youtube.com/@reelcoding?sub_confirmation=1)\n\nSubscribe Goal:- 500\nCurrent Subscriber:- 473\n# Complexity\n- Time complexity: O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n private int minDiff(List<Integer> nums) {\n int n = nums.size();\n return Math.min(\n Math.min(nums.get(n - 1) - nums.get(3), nums.get(n - 2) - nums.get(2)),\n Math.min(nums.get(n - 3) - nums.get(1), nums.get(n - 4) - nums.get(0))\n );\n }\n\n public int minDifference(int[] nums) {\n if (nums.length <= 4) return 0;\n \n Arrays.sort(nums);\n \n List<Integer> numsList = new ArrayList<>();\n for (int num : nums) {\n numsList.add(num);\n }\n\n return minDiff(numsList);\n }\n}\n```\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n private int minDiff(List<Integer> nums) {\n int n = nums.size();\n return Math.min(\n Math.min(nums.get(n - 1) - nums.get(3), nums.get(n - 2) - nums.get(2)),\n Math.min(nums.get(n - 3) - nums.get(1), nums.get(n - 4) - nums.get(0))\n );\n }\n\n private int minDiffViaPq(List<Integer> nums) {\n PriorityQueue<Integer> maxHeap = new PriorityQueue<>(Collections.reverseOrder());\n PriorityQueue<Integer> minHeap = new PriorityQueue<>();\n\n for (int el : nums) {\n maxHeap.add(el);\n minHeap.add(el);\n\n if (maxHeap.size() > 4) maxHeap.poll();\n if (minHeap.size() > 4) minHeap.poll();\n }\n\n int l = 3;\n int r = nums.size() - 4;\n while (!maxHeap.isEmpty()) {\n nums.set(l--, maxHeap.poll());\n nums.set(r++, minHeap.poll());\n }\n return minDiff(nums);\n }\n\n public int minDifference(int[] nums) {\n if (nums.length <= 4) return 0;\n \n List<Integer> ans = new ArrayList<>();\n for (int num : nums) {\n ans.add(num);\n }\n\n return minDiffViaPq(ans);\n }\n}\n``` | 10 | 0 | ['Java'] | 1 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | [C++] Try 4 Possible Choices After Sorting | c-try-4-possible-choices-after-sorting-b-y2lo | Intuition\n Describe your first thoughts on how to solve this problem. \n- There are only 4 possible choices after sorting the integer array\n\n# Approach\n Des | pepe-the-frog | NORMAL | 2024-07-03T00:35:36.378157+00:00 | 2024-07-03T01:08:11.259121+00:00 | 1,342 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- There are only 4 possible choices after sorting the integer array\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Handle the base case\n - when `nums.size() <= 4`, we can make all the elements to the same value in the array\n- Sort the integer array\n- Try 4 possible choices\n\n# Complexity\n- Time complexity: $$O(n\\log n)$$ for sorting\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(\\log n)$$ for sorting\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int minDifference(vector<int>& nums) {\n // base case: we can make all the elements to the same value in the array\n int n = nums.size();\n if (n <= 4) return 0;\n\n // sort the integer array\n sort(nums.begin(), nums.end());\n\n // there are 4 possible choices\n return min({\n nums[n - 1] - nums[3], // discard 0 biggest and 3 smallest\n nums[n - 2] - nums[2], // discard 1 biggest and 2 smallest\n nums[n - 3] - nums[1], // discard 2 biggest and 1 smallest\n nums[n - 4] - nums[0], // discard 3 biggest and 0 smallest\n });\n }\n};\n```\n\n# Future Work\n- Use 2 priority queues (min. and max. heap) to record the 4 biggest and 4 smallest integers\n- The Time/Space complexity can be improved to $$O(n)$$/$$O(1)$$ | 10 | 0 | ['Greedy', 'Sorting', 'C++'] | 6 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | [Python3/Python] Easy readable solution with comments. | python3python-easy-readable-solution-wit-2hbb | \nclass Solution:\n \n def minDifference(self, nums: List[int]) -> int:\n \n n = len(nums)\n # If nums are less than 3 all can be rep | ssshukla26 | NORMAL | 2021-08-30T00:25:35.986528+00:00 | 2021-08-30T00:26:25.606995+00:00 | 1,921 | false | ```\nclass Solution:\n \n def minDifference(self, nums: List[int]) -> int:\n \n n = len(nums)\n # If nums are less than 3 all can be replace,\n # so min diff will be 0, which is default condition\n if n > 3:\n \n # Init min difference\n min_diff = float("inf")\n \n # sort the array\n nums = sorted(nums)\n \n # Get the window size, this indicates, if we\n # remove 3 element in an array how many element\n # are left, consider 0 as the index, window\n # size should be (n-3), but for array starting\n # with 0 it should be ((n-1)-3)\n window = (n-1)-3\n \n # Run through the entire array slinding the\n # window and calculating minimum difference\n # between the first and the last element of\n # that window\n for i in range(n):\n if i+window >= n:\n break\n else:\n min_diff = min(nums[i+window]-nums[i], min_diff)\n \n # return calculated minimum difference\n return min_diff\n \n return 0 # default condition\n``` | 10 | 0 | ['Sorting', 'Python', 'Python3'] | 4 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | ✅ One Line Solution | one-line-solution-by-mikposp-647m | Code #1\nTime complexity: O(n). Space complexity: O(1).\n\nclass Solution:\n def minDifference(self, a: List[int]) -> int:\n return min(map(sub,nlarge | MikPosp | NORMAL | 2024-07-03T08:16:28.444307+00:00 | 2024-07-03T08:45:27.174699+00:00 | 670 | false | # Code #1\nTime complexity: $$O(n)$$. Space complexity: $$O(1)$$.\n```\nclass Solution:\n def minDifference(self, a: List[int]) -> int:\n return min(map(sub,nlargest(4,a)[::-1],nsmallest(4,a)))\n```\n\n# Code #2\nTime complexity: $$O(n*log(n))$$. Space complexity: $$O(n)$$.\n```\nclass Solution:\n def minDifference(self, a: List[int]) -> int:\n return min(map(sub,(a:=sorted(a))[-4:],a[:4]))\n```\n[Ref](https://leetcode.com/problems/minimum-difference-between-largest-and-smallest-value-in-three-moves/solutions/730567/java-c-python-straight-forward) | 9 | 0 | ['Array', 'Sorting', 'Python', 'Python3'] | 2 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | Easy 3 liner code beats 97.8% users... | easy-3-liner-code-beats-978-users-by-aim-lvqy | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Aim_High_212 | NORMAL | 2024-07-03T02:26:28.682546+00:00 | 2024-07-03T02:26:28.682569+00:00 | 105 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minDifference(self, A):\n A.sort()\n return min(b - a for a, b in zip(A[:4], A[-4:]))\n \n \n \n\n \n\n``` | 9 | 0 | ['Array', 'Greedy', 'C', 'Sorting', 'Python', 'C++', 'Python3'] | 0 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | Well Explained || 2 Approaches || Easy for mind to Accept it | well-explained-2-approaches-easy-for-min-s8nx | BRUTE APPROACH\n\nclass Solution {\n public int minDifference(int[] nums) {\n int n = nums.length;\n if(n <= 4) return 0;\n Arrays.sort( | hi-malik | NORMAL | 2022-01-03T07:18:12.895501+00:00 | 2022-01-03T07:18:12.895550+00:00 | 811 | false | **BRUTE APPROACH**\n```\nclass Solution {\n public int minDifference(int[] nums) {\n int n = nums.length;\n if(n <= 4) return 0;\n Arrays.sort(nums);\n int res = Integer.MAX_VALUE;\n for(int i = 0; i < 4; i++){\n res = Math.min(res, nums[n - 1 - 3 + i] - nums[i]);\n }\n return res;\n }\n}\n// T.C = O(nlogn) as sorting and loop is constant of 4\n```\nANALYSIS:-\n* **Time Complexity** :- O(NlogN) as sorting and loop is constant of 4\n\n\n* **Space Complexity** :- O(1)\n\n\n**GREEDY APPROACH**\n```\nclass Solution {\n public int minDifference(int[] nums) {\n \n // if the size is smaller than 4 than we can easily make each of them equal and hence min possible difference is zero\n if(nums.length <= 3) return 0;\n \n int n = nums.length;\n \n // sort the array in increasing order because we want to consider few of the largest and smallest numbers.\n Arrays.sort(nums);\n \n int res = Integer.MAX_VALUE; // initialize the result with INT_MAX.\n \n \n // Now idea is to try greedy. First of all we must agree that the values \n\t\t// which we will be changing should be either from left end or right end, \n\t\t// As there is no gain if we start changing values from middle of the array. \n\t\t// And hence we can try to make these 3 moves in all following possible \n\t\t// ways and choose the one which gives the best answer. \n // And because there are only 3 moves so total possibilities will be exactly 4.\n \n \n // CASE 1: when changing only from beg\n res = Math.min(res, Math.abs(nums[3] - nums[n - 1]));\n \n // CASE 2: when change two from beg and one from last\n res = Math.min(res, Math.abs(nums[2] - nums[n - 2]));\n \n // CASE 3: when change only from beg and two from last\n res = Math.min(res, Math.abs(nums[1] - nums[n - 3]));\n \n // CASE 4: when change all the values from last\n res = Math.min(res, Math.abs(nums[0] - nums[n - 4]));\n \n return res;\n }\n}\n// Time Complexity :- O(NlogN)\n// Space Complexity :- O(1)\n```\nANALYSIS:-\n* **Time Complexity** :- O(NlogN) as sorting\n\n\n* **Space Complexity** :- O(1) | 9 | 0 | ['Java'] | 2 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | Simple JAVA code with detailed explanation | simple-java-code-with-detailed-explanati-g532 | To minimize the diff between the max and min values, we need to alter either the values in the min range or the value in the max range. Here min range means the | prakhar3agrwal | NORMAL | 2021-07-10T15:53:39.001444+00:00 | 2021-07-10T15:59:17.965710+00:00 | 658 | false | To minimize the diff between the max and min values, we need to alter either the values in the min range or the value in the max range. Here min range means the minimum value and the values present close to it, and the max range means the maximum value and the values present close to it in the array. So, we just need to deal with the smallest and largest 4 values of the array. To do this, we sort our array and explore the 4 possibilities (and find the diff of the extreme values in each case):\n1. Alter the 3 values on the left and 0 values on the right.\n2. Alter the 2 values on the left and 1 value on the right.\n3. Alter the 1 value on the left and 2 values on the right.\n4. Alter the 0 values on the left and 3 values on the right.\n\nThe minimum of these 4 values is our answer. \n**Time complexity**: O(nlogn) because of sorting.\n\n```\nclass Solution {\n public int minDifference(int[] nums) {\n int n = nums.length;\n if(n<5){\n return 0;\n }\n Arrays.sort(nums);\n int ans = Integer.MAX_VALUE;\n \n int left = 0;\n int right = n-4;\n int i = 0;\n while(i<4){\n ans = Math.min(ans,nums[right]-nums[left]);\n left++;\n right++;\n i++;\n }\n return ans;\n }\n}\n | 8 | 0 | [] | 0 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | [Python] O(N) Time, O(1) Space, beats 100 % without sorting | python-on-time-o1-space-beats-100-withou-9wlm | We only need to find the max 4 and min 4 elements in nums, and It could be done by O(n) time without sorting (O(nlogn)).\n\nclass Solution:\n def minDifferen | licpotis | NORMAL | 2020-11-03T07:27:38.037396+00:00 | 2020-11-03T07:29:05.764096+00:00 | 1,316 | false | We only need to find the max 4 and min 4 elements in nums, and It could be done by O(n) time without sorting (O(nlogn)).\n```\nclass Solution:\n def minDifference(self, nums: List[int]) -> int:\n if len(nums) < 5:\n return 0\n \n maxV, minV = [-float(\'inf\')] * 4, [float(\'inf\')] * 4\n for n in nums:\n if n > maxV[0]:\n maxV[0] = n\n for i in range(0, 3):\n if maxV[i] > maxV[i + 1]:\n maxV[i], maxV[i + 1] = maxV[i + 1], maxV[i] \n if n < minV[0]:\n minV[0] = n\n for i in range(0, 3):\n if minV[i] < minV[i + 1]:\n minV[i], minV[i + 1] = minV[i + 1], minV[i]\n \n return min(maxV[i] - minV[3 - i] for i in range(4)) \n``` | 8 | 1 | ['Python', 'Python3'] | 1 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | [Python] O(n) time O(1) space - Two heaps solution | python-on-time-o1-space-two-heaps-soluti-5fvr | Explanation:\n First, handle the case for n<=4 is easy as it means the diff will be 0 always. so let\'s assume n >= 5.\n Basically the max | theleetman | NORMAL | 2020-07-11T16:08:00.448526+00:00 | 2020-07-11T16:08:15.284534+00:00 | 1,038 | false | Explanation:\n First, handle the case for n<=4 is easy as it means the diff will be 0 always. so let\'s assume n >= 5.\n Basically the max diff is determined by the diff between the biggest and smallest element.\n Our options to remove elements are only to remove 3 elements between the combined list of first 3 and last 3.\n Why remove? because removing is the same as changing value to some median value (easy to prove).\n Look at the sorted array:\n a0, a1, ...., a_(n-1)\n\n And actually we have less options than previously stated. only 4 options:\n - remove 0 from left and 3 from right\n - remove 1 from left and 2 from right\n - remove 2 from left and 1 from right\n - remove 3 from left and 0 from right\n\n My code checks exactly these 4 options.\n\n All I need for these options calculations is the first and last 4 members of the sorted array.\n I get them with min heap and max heap (implemented by negative min heap in my python code) with size at most 4.\n\n Time: O(n)\n Space: O(1)\n\nCode:\n\n```\nfrom heapq import *\nfrom typing import *\n\nclass Solution:\n def minDifference(self, A: List[int]) -> int:\n if len(A) <= 4: return 0\n\n largestH, smallestH = [], []\n for a in A:\n heappush(largestH, a)\n heappush(smallestH, -1 * a)\n for H in [largestH, smallestH]:\n if len(H) > 4:\n heappop(H)\n\n smallest = sorted([-1 * h for h in smallestH])\n largest = sorted(largestH, reverse=True)\n res = float(\'inf\')\n for i in range(3, -1, -1):\n res = min(res, largest[i] - smallest[3 - i])\n return res\n\n``` | 8 | 3 | [] | 6 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | ✔️ 100% Fastest TypeScript Solution | 100-fastest-typescript-solution-by-serge-v7eo | \nfunction minDifference(nums: number[]): number {\n if (nums.length <= 4) return 0\n\n nums.sort((a, b) => a - b)\n\n let opts = [\n nums[nums.length - 4 | sergeyleschev | NORMAL | 2022-03-29T05:05:41.138936+00:00 | 2022-03-30T16:40:53.703998+00:00 | 479 | false | ```\nfunction minDifference(nums: number[]): number {\n if (nums.length <= 4) return 0\n\n nums.sort((a, b) => a - b)\n\n let opts = [\n nums[nums.length - 4] - nums[0],\n nums[nums.length - 3] - nums[1],\n nums[nums.length - 2] - nums[2],\n nums[nums.length - 1] - nums[3],\n ]\n\n return Math.min(...opts)\n}\n```\n\nLet me know in comments if you have any doubts. I will be happy to answer.\n\nPlease upvote if you found the solution useful. | 7 | 0 | ['TypeScript', 'JavaScript'] | 1 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | O(n) time and O(1) space solution Python | on-time-and-o1-space-solution-python-by-ng1qr | The hardest part of this problem is recognizing the trick. The value you change the numbers in the array to need not be calculated, so changed values can be tre | ck7aj | NORMAL | 2021-10-19T16:38:26.550881+00:00 | 2021-10-19T16:38:26.550920+00:00 | 982 | false | The hardest part of this problem is recognizing the trick. The value you change the numbers in the array to need not be calculated, so changed values can be treated as though they are removed entirely. Also, notice that removing elements will never increase the spread of the numbers in an array, so we will use all 3 of our changes every time. The spread of numbers can be calculated as the largest value minus the smallest. If we remove the three smallest numbers, then we must subtract the 4th smallest from the largest number to get the spread. There are 4 other possible combinations of removals we must check (2 removed from front, 1 from back; 1 removed from front, 2 from back; 0 removed from front, 3 from back).\n\nIf we sort, then our solution is nlogn time. However, because we only really need to sort the first 4 and last 4 elements, we can just iterate over the loop in linear time, and eject elements from our min and max heaps when they\'re within the 4 largest or smallest elements encountered so far. Whether the array is 5 elements or 500, we iterate over it once, find the 4 smallest and largest, and put them in data structures that will never exceed length 4, so our time in O(n) and our space is constant.\n"""\n\n if len(nums) < 5: #4 elements and 3 changes mean we can make all elements the same\n return 0\n s, l = [], []\n mx, mn = [], []\n h = heapq\n\t\t\n for i in range(4):\n h.heappush(s,-1*nums[i]) #max heap for 4 smallest values\n h.heappush(l,nums[i]) #min heap for 4 largest values\n \n for i in nums[4:]:\n if i > l[0]:\n h.heappushpop(l,i)\n if -1*i > s[0]:\n h.heappushpop(s,-1*i)\n for i in range(4):\n mn.append(-1*h.heappop(s))\n mx.append(h.heappop(l))\n return min([mx[i]-mn[3-i] for i in range(4)])\n \n""" | 7 | 0 | ['Heap (Priority Queue)', 'Python'] | 2 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | JAVA beats 100% | Clear Explanation | java-beats-100-clear-explanation-by-shah-6rj3 | Its actually pretty simple. If you think, we dont need to change any values, it is just that we need to remove any 3 numbers, such that max - min is the least. | shahrukhitsme | NORMAL | 2021-07-10T09:55:05.637110+00:00 | 2021-07-10T14:12:39.237014+00:00 | 545 | false | Its actually pretty simple. If you think, we dont need to change any values, it is just that we need to remove any 3 numbers, such that max - min is the least. Now if you sort the array, the best ways to remove the numbers are at the ends, becuase then only you would be able to lessen the range. So you can remove the numbers from the end in 4 ways.\n1. 3 on left, 0 on right\n2. 2 on left, 1 on right\n3. 1 on left, 2 on right\n4. 0 on left, 3 on right\nAnd by finding which of these yields the minimum range, we get our final answer.\nComplexity is O(nlog n) becasue of sorting.\n```\nclass Solution {\n public int minDifference(int[] nums) {\n if(nums.length<=3) return 0;\n Arrays.sort(nums);\n int lastIndex = nums.length-1;\n return Math.min(Math.min(nums[lastIndex]-nums[3], nums[lastIndex-3]-nums[0]), Math.min(nums[lastIndex-2]-nums[1],nums[lastIndex-1]-nums[2]));\n }\n}\n``` | 7 | 1 | [] | 3 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | Beats 100%|| Simple and Easy Solution||Properly explained||T.C:O(n log n)|| | beats-100-simple-and-easy-solutionproper-b84j | Intuition\nIf the array has fewer than 5 elements (n < 5), it returns 0.\nBy sorting the array first, we can easily access the smallest and largest values.\nFor | twaritagrawal | NORMAL | 2024-07-03T04:28:11.815262+00:00 | 2024-07-03T04:28:11.815317+00:00 | 459 | false | # Intuition\nIf the array has fewer than 5 elements (n < 5), it returns 0.\nBy sorting the array first, we can easily access the smallest and largest values.\nFor arrays with 5 or more elements, the strategy to minimize the range would be to either raise the value of the smallest numbers or lower the value of the largest numbers. Since we can make at most three moves, it leaves us with a few scenarios on which numbers to change:\n1.Change the three smallest numbers..\n2.Change the two smallest numbers and the largest number.\n3.Change the smallest number and the two largest numbers.\n4.Change the three largest numbers.\n\n# Approach\nAfter sorting, the algorithm checks the length of the array.If the array has fewer than 5 elements (n < 5), it returns 0 immediately.\nIf there are 5 or more elements, the algorithm considers four possible scenarios for amending the array using at most three moves:\n1.Change the three smallest numbers (nums[n-1] - nums[3]).\n2.Change the two smallest numbers and the largest number (nums[n - 2] - nums[2]).\n3.Change the smallest number and the two largest numbers (nums[n - 3] - nums[1]).\n4.Change the three largest numbers (nums[n - 4] - nums[0]).\n\n# Complexity\n- Time complexity:\nO(nlog n).\n\n- Space complexity:\nO(1).\n\n# Code\n```\nclass Solution {\npublic:\n int minDifference(vector<int>& nums) {\n /*there are total four cases which can arise\n 1.Change the three smallest numbers (nums[n-1] - nums[3]). \n 2.Change the two smallest numbers and the largest number (nums[n - 2] - nums[2]).\n 3.Change the smallest number and the two largest numbers (nums[n - 3] - nums[1]).\n 4.Change the three largest numbers (nums[n - 4] - nums[0]).*/\n int n=nums.size();\n if(n<=4){\n return 0;\n }\n int ans=INT_MAX;\n sort(nums.begin(),nums.end());\n for(int i=0;i<4;i++){\n int j=3-i;\n ans=min(ans,nums[n-1-j]-nums[i]);\n }\n return ans;\n }\n};\n``` | 6 | 0 | ['Array', 'Math', 'Greedy', 'Brainteaser', 'Sorting', 'C++'] | 1 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | try all combos | solution for generic k moves | try-all-combos-solution-for-generic-k-mo-8w8r | Intuition & Approach\n\nFirst note that instead of "changing" the elements, we can simply remove them instead, since we\'re allowed to change them to any value, | jyscao | NORMAL | 2024-07-03T03:48:20.009662+00:00 | 2024-07-03T04:17:20.736814+00:00 | 1,495 | false | # Intuition & Approach\n\nFirst note that instead of "changing" the elements, we can simply remove them instead, since we\'re allowed to change them to any value, which means we can always change the chosen elements to the median of the input, thereby making their remaining presence in the array inconsequential.\n\nNow we first sort the input array, then try all possible combinations of `k`-removals: i.e. remove the first `k` elements from the left end of the sorted array (the `k`-smallest elements), and get the difference between the `k+1`-th (1-indexed) element (the new minimum) and the last element (the maximum); then try removing the smallest `k-1`-smallest elements plus the largest element, and get the difference between the `k`-th element (the new minimum) with the second last element (the new maximum); and so on, in the end we can just return the minimum difference found in all of those combinations of removals.\n\n# Code\n```\nclass Solution:\n def minDifference(self, nums: List[int]) -> int:\n k = 3 # maximum of 3 moves considered for this question\n\n if len(nums) <= k + 1:\n return 0\n\n res, _ = math.inf, nums.sort()\n for (a, b) in [(k - i, -(1 + i)) for i in range(k + 1)]:\n # (a, b) will take on index values of: {(k, -1), (k-1, -2),\n # (k-2, -3), ..., (2, -(k-1)) , (1, -k), (0, -(k+1))}; for\n # k = 3, these are: {(3, -1), (2, -2), (1, -3), (0, -4)}\n res = min(res, nums[b] - nums[a])\n\n return res\n```\n\n# Complexity\n- Time complexity: $$O(nlogn)$$ for sorting `nums`\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(k)$$, where $k$ is the max number of moves allowed\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> | 6 | 0 | ['Sorting', 'Python3'] | 5 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | A concise solution | a-concise-solution-by-jaihindh-u5ox | If there are 4 or less elements in it, we\'re going to be left with 1 element at most, making the difference b/w min and max 0.\nIf there are more elements, the | jaihindh | NORMAL | 2021-04-22T16:32:01.304971+00:00 | 2021-04-22T16:39:52.128672+00:00 | 425 | false | If there are 4 or less elements in it, we\'re going to be left with 1 element at most, making the difference b/w min and max 0.\nIf there are more elements, then we have one of these four choices:\n1. get rid of the 3 biggest elements.\n2. get rid of 2 biggest elements, and the smallest.\n3. get rid of the biggest element, and 2 smallest.\n4. get rid of the 3 smallest elements.\n\nAnd in these four choices respectively, the min and the max will be the following:\n1. 1st element, and 4th from the last\n2. 2nd element, and 3rd from the last\n3. 3rd element, and 2nd from the last\n4. 4th element, and (1st from) the last.\n\nIn other words, we simply need to take the pairwise difference b/w the 4 smallest elements in the array, and the 4 largest elements in the array (in reverse order). Sorting the entire array for this is inefficient. A more efficient way is provided by the `heapq` module.\n\nAnd of course, we can use this for any number of moves, not just 3. At a large number of moves though, it would be faster to sort the entire array.\n```python\nimport heapq\n\nclass Solution:\n def minDifference(self, nums: List[int]) -> int:\n return 0 if len(nums) <= 4 else min(y-x for x, y in zip(heapq.nsmallest(4, nums), reversed(heapq.nlargest(4, nums))))\n``` | 6 | 0 | ['Heap (Priority Queue)', 'Python'] | 1 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.