question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
split-message-based-on-limit | C# || Solution | c-solution-by-vdmhunter-1gzx | Code\n\npublic class Solution\n{\n public string[] SplitMessage(string message, int limit)\n {\n var cur = 0;\n var k = 0;\n var i = | vdmhunter | NORMAL | 2022-11-13T01:03:45.320135+00:00 | 2022-11-13T01:03:45.320182+00:00 | 99 | false | # Code\n```\npublic class Solution\n{\n public string[] SplitMessage(string message, int limit)\n {\n var cur = 0;\n var k = 0;\n var i = 0;\n\n while (3 + k.ToString().Length * 2 < limit && cur + message.Length + (3 + k.ToString().Length) * k > limit * k)\n {\n k += 1;\n cur += k.ToString().Length;\n }\n\n var result = new List<string>();\n\n if (3 + k.ToString().Length * 2 < limit)\n foreach (var j in Enumerable.Range(1, k))\n {\n var l = limit - (j.ToString().Length + 3 + k.ToString().Length);\n var r = i + l > message.Length ? message.Length : i + l;\n result.Add($"{message[i..r]}<{j}/{k}>");\n i += l;\n }\n\n return result.ToArray();\n }\n}\n``` | 1 | 0 | ['C#'] | 0 |
split-message-based-on-limit | Binary search | binary-search-by-changkunli-3xbp | Approach\n Describe your approach to solving the problem. \n\nBinary search the number of parts\n\n# Complexity\n- Time complexity: O(log n + n), binary search | changkunli | NORMAL | 2022-11-12T18:39:15.157761+00:00 | 2022-11-13T02:10:02.419897+00:00 | 703 | false | # Approach\n<!-- Describe your approach to solving the problem. -->\n\nBinary search the number of parts\n\n# Complexity\n- Time complexity: O(log n + n), binary search + answer construction\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int isLargerOrFit(int n, int sz, int limit) {\n string b = to_string(sz);\n int b_sz = b.size();\n if (2 * b_sz + 3 > limit) return true;\n int total = (limit - b_sz - 3) * (sz - 1);\n if (sz <= 10) total -= (sz - 1);\n else if (sz <= 100) total -= 9 + 2 * (sz - 10);\n else if (sz <= 1000) total -= 9 + 2 * 90 + 3 * (sz - 100);\n else if (sz <= 10000) total -= 9 + 2 * 90 + 3 * 900 + 4 * (sz - 1000);\n int res = n - total; // residual or remained characters\n if (res >= 0 && res + 2 * b_sz + 3 <= limit) { // fit\n return 0;\n } else if (res < 0) { // larger\n return 1;\n }\n return -1; // smaller\n }\n \n vector<string> splitMessage(string message, int limit) {\n if (limit <= 5) return vector<string>(); // unrealistic limit\n int n = message.size();\n int low = 0, high = n + 1;\n while (low + 1 < high) {\n int mid = low + (high - low) / 2;\n if (isLargerOrFit(n, mid, limit) >= 0) high = mid;\n else low = mid;\n }\n if (isLargerOrFit(n, high, limit) == 1) return vector<string>();\n vector<string> ans(high);\n string b = to_string(high);\n for (int a = 1, l = 0; a <= high; a++) {\n string suffix = "<" + to_string(a) + "/" + b + ">";\n int sz = limit - suffix.size();\n ans[a - 1] += message.substr(l, sz) + suffix;\n l += sz;\n }\n return ans;\n }\n};\n``` | 1 | 0 | ['C++'] | 1 |
split-message-based-on-limit | C++ Binary Search || Easy Implementation || Video Solution || prashar32 | c-binary-search-easy-implementation-vide-cjp8 | Myself Adarsh Prashar\n\nI am top 0.02% (Globally) Candidate Master(2048) at Codeforces, Guardian (top 0.8%) at Leetcode and 6 Star (2208) at Codechef\n\nAbout | prashar32 | NORMAL | 2022-11-12T17:20:51.697134+00:00 | 2022-11-12T17:20:51.697172+00:00 | 276 | false | Myself Adarsh Prashar\n\n**I am top 0.02% (Globally) Candidate Master(2048) at Codeforces, Guardian (top 0.8%) at Leetcode and 6 Star (2208) at Codechef**\n\n**About Me -** I have a youtube channel in which I upload editorials of leetcode, codeforces and codechef contest.\n\nYou can understand my method to solve that.\n\n**Split Message Based on Limit (Video Editorial Link) -** https://youtu.be/t98PMWpd-yU\n**My channel Link -** https://www.youtube.com/@prashar32\n\n**If you like my video kindly like share and subscribe to my channel** | 1 | 1 | ['Binary Tree'] | 0 |
split-message-based-on-limit | Fast, Tricky Python3 Explained | fast-tricky-python3-explained-by-ryangra-v9hw | The idea here is to iterate through all possible numbers of parts we could split into, and for each one check if it is possible to split into that many parts. W | ryangrayson | NORMAL | 2022-11-12T16:40:45.959510+00:00 | 2022-11-12T16:41:45.851193+00:00 | 195 | false | The idea here is to iterate through all possible numbers of parts we could split into, and for each one check if it is possible to split into that many parts. We can do this efficiently in O(log10(N)) time where N is the length of the message - (note that log10(N) <= 4 given the constraint of N <= 1000). Thus, worst case we are doing about 4N operations so we can say the overall time complexity is O(N).\n\nNotice that we can determine how much of the message we can add for a certain number of parts based on the prefix and suffix sizes for each iteration of the inner while loop. For example, in parts 1 - 9, we know that the a term in `<a/b>` is one digit, so the length of the suffix starts at simply `len(str(parts)) + 3 + 1`. if parts was 100, we would start out with a suffix length would start at 7, i.e `<1/100>`. Then, we can increment the suffix length for part numbers 10-99, and increment it again for 100-999, and so on. The prefix length will of course be `limit - suffix`. We continue this while loop until we have either expended all of the parts, or expended all of the characters in the message, or the prefix length is 0 (in which case we couldn\'t add any more of the message). Once this while loop is complete, if we used the right number of parts, used the full message, and didn\'t break any of the rules, then it must be possible to construct a valid split and we can simply build one using the simple logic in the `split` method.\n\nPlease upvote if it helps!\n```\nclass Solution:\n def split(self, message, limit, parts):\n i, res = 0, []\n for part in range(1, parts+1):\n suffix = \'<\' + str(part) + \'/\' + str(parts) + \'>\'\n prefix_len = limit - len(suffix)\n res.append(message[i:i+prefix_len] + suffix)\n i += prefix_len\n return res\n \n def splitMessage(self, message: str, limit: int) -> List[str]:\n if limit < 6:\n return []\n n = len(message)\n for parts in range(1, n+1):\n \n tot_parts = parts\n cur_parts = 9\n suffix = len(str(parts)) + 4\n prefix = limit - suffix\n mess = n\n \n while tot_parts > 0 and mess > 0 and prefix > 0:\n max_take = cur_parts * prefix\n if mess > max_take:\n tot_parts -= cur_parts\n mess -= max_take\n else:\n full_parts = mess // prefix\n tot_parts -= full_parts\n mess -= full_parts * prefix\n if mess > 0:\n tot_parts -= 1\n mess = 0\n \n cur_parts *= 10\n prefix -= 1\n suffix += 1\n \n if tot_parts == mess == 0:\n return self.split(message, limit, parts)\n \n return [] | 1 | 0 | ['Python3'] | 0 |
split-message-based-on-limit | [C++] Brute Force, O(n) | c-brute-force-on-by-kevin1010607-m28e | Search how many chunks from 1 to n.\n\nIn each iteration:\nspace is the number of total capacity to fill message.\nlast is the capacity of last chunk.\nramain i | kevin1010607 | NORMAL | 2022-11-12T16:09:08.212429+00:00 | 2022-11-12T16:13:01.894337+00:00 | 356 | false | Search how many chunks from 1 to n.\n\nIn each iteration:\n`space` is the number of total capacity to fill message.\n`last` is the capacity of last chunk.\n`ramain` is the number of reamining character after filling the first i-1 chunks.\n\nFunction:\n`digit` is the length of a number.\n`all_len` is the sum of the length of each number from 1 to n.\n```\nclass Solution {\nprivate:\n int digit(int n){\n if(n >= 10000) return 5;\n else if(n >= 1000) return 4;\n else if(n >= 100) return 3;\n else if(n >= 10) return 2;\n else return 1;\n }\n int all_len(int n){\n if(n >= 10000) return 9+2*90+3*900+4*9000+5*(n-9999);\n else if(n >= 1000) return 9+2*90+3*900+4*(n-999);\n else if(n >= 100) return 9+2*90+3*(n-99);\n else if(n >= 10) return 9+2*(n-9);\n else return n;\n }\npublic:\n vector<string> splitMessage(string m, int limit) {\n if(limit <= 5) return {};\n int n = m.size();\n for(int i = 1; i <= n; i++){\n int space = limit*i-3*i-digit(i)*i-all_len(i);\n int last = limit-3-digit(i)*2;\n int remain = n-(space-last);\n if(remain<0 || remain>last) continue;\n int idx = 0;\n vector<string> res(i);\n for(int j = 1; j < i; j++){\n int k = limit-3-digit(i)-digit(j);\n res[j-1] = m.substr(idx, k)+"<"+to_string(j)+"/"+to_string(i)+">";\n idx += k;\n }\n res[i-1] = m.substr(idx)+"<"+to_string(i)+"/"+to_string(i)+">";\n return res;\n }\n return {};\n }\n};\n``` | 1 | 0 | ['C++'] | 1 |
split-message-based-on-limit | Leveraging Ranged Approach: Beats 80+ % | leveraging-ranged-approach-beats-80-by-a-qerk | IntuitionOver specific ranges of part numbers, overhead is predictable. Use a piece-wise buildupApproachGiven that the suffix length is subtracted from the avai | aleetlf | NORMAL | 2025-04-10T02:12:24.667708+00:00 | 2025-04-10T02:12:24.667708+00:00 | 1 | false | # Intuition
Over specific ranges of part numbers, overhead is predictable. Use a piece-wise buildup
# Approach
Given that the suffix length is subtracted from the available space per part, and that suffix length is both dependent on the current part number's width in digit and dependent on width of the total part count, use a piece-wise subtraction.
Here, I have deduced that a single digit part number (1-9) will add 4 to the overhead for the suffix. The remaining overhead is taken by the number of total parts' digit count.
Rather than trying to calculate what's required, I instead throw ranges of digits at a test to see what will work. A range from 100 parts to 999 parts will use the same overhead per part. Likewise a range from 1 to 9 parts uses the same overhead as each other. So you do not have to know in advance that 687 parts are needed; you only need to guess that <= 999 parts are needed. The algorithm tells the exact number.
Note that this solution is not DRY. There is an opportunity to use another function or two to eliminate some redundant code.
# Complexity
- Time complexity:
O(N) - one thrip through the string message to build the outputs.
- Space complexity:
O(N) - output size is a duplicate of input size.
# Code
```java []
class Solution {
public String[] splitMessage(String message, int limit) {
if (limit < 5) {
return new String[] {};
}
int mlen = message.length();
int partsRequired = -1;
int powerOfTen = 1;
while (0 > (partsRequired = partsRequired(limit, powerOfTen, mlen))) {
powerOfTen ++;
if (powerOfTen > 5) {
break;
}
}
if (partsRequired == -1) {
return new String[] {};
}
// Part Two: build all the parts.
String[] rtnVal = new String[partsRequired];
int sOffset = 0;
int arrOffset = 0;
String ending = "/" + partsRequired + ">";
while (sOffset < mlen) {
String suffix = "<" + (arrOffset+1) + ending;
int endPt = Math.min(sOffset + (limit - suffix.length()), mlen);
rtnVal[arrOffset] = message.substring(sOffset, endPt) + suffix;
sOffset = endPt;
arrOffset ++;
}
return rtnVal;
}
/**
* Settle the range based on powers of ten.
* Assume 10,000, for example. This provides a wide range of values
* that will all behave in the same way w.r.t. use of suffixes.
*/
private int partsRequired(int limit, int powerOfTen, int msgSize) {
int remainingChars = msgSize;
int requiredParts = -1;
if (powerOfTen == 1) {
int perFragment = limit - overheadAtRegion(1, powerOfTen); // <n/n>
if (perFragment < 0) {
return -1;
}
return checkRequired(remainingChars, perFragment, 9);
}
requiredParts = 9;
// Reduce by how many we can get above.
remainingChars -= availableAtRegion(limit, 1, powerOfTen) * 9;
if (powerOfTen == 2) {
int perFragment = limit - overheadAtRegion(powerOfTen, powerOfTen); // <nn/nn>
if (perFragment < 0) {
return -1;
}
int atLevel = checkRequired(remainingChars, perFragment, 90);
if (atLevel == -1) {
return -1;
}
return requiredParts + atLevel;
}
requiredParts = 99;
remainingChars -= availableAtRegion(limit, 2, powerOfTen) * 90;
if (powerOfTen == 3) {
int perFragment = limit - overheadAtRegion(powerOfTen, powerOfTen); // <nnn/nnn>
if (perFragment < 0) {
return -1;
}
int atLevel = checkRequired(remainingChars, perFragment, 900);
if (atLevel == -1) {
return -1;
}
return requiredParts + atLevel;
}
requiredParts = 999;
remainingChars -= availableAtRegion(limit, 3, powerOfTen) * 900;
if (powerOfTen == 4) {
int perFragment = limit - overheadAtRegion(powerOfTen, powerOfTen); // <nnnn/nnnn>
if (perFragment < 0) {
return -1;
}
int atLevel = checkRequired(remainingChars, perFragment, 9000);
if (atLevel == -1) {
return -1;
}
return requiredParts + atLevel;
}
remainingChars -= availableAtRegion(limit, 4, powerOfTen) * 9000;
// Not going above 10^5
int perFragment = limit - overheadAtRegion(powerOfTen, powerOfTen); // <nnnnn/nnnnn>
if (perFragment < 0) {
return -1;
}
int atLevel = checkRequired(remainingChars, perFragment, 90000);
if (atLevel == -1) {
return -1;
}
return requiredParts + atLevel;
}
private int checkRequired(int remainingChars, int perFragment, int maxAtLevel) {
int requiredParts = (int)Math.ceil((double)remainingChars / (double)perFragment);
if (requiredParts > maxAtLevel) {
return -1;
} else {
return (int)requiredParts;
}
}
private int availableAtRegion(int limit, int countSize, int powerOfTen) {
return limit - overheadAtRegion(countSize, powerOfTen);
}
private int overheadAtRegion(int countSize, int powerOfTen) {
return 3 + countSize + powerOfTen;
}
}
``` | 0 | 0 | ['Java'] | 0 |
split-message-based-on-limit | Find the denominator first | find-the-denominator-first-by-kchetan-2qkp | IntuitionHardest part of the problem is finding the denominator. We do this itertively checking if denomminator is 1 digit,.. 2 digit, .. n digit.Added some che | kchetan | NORMAL | 2025-04-04T06:38:20.058282+00:00 | 2025-04-04T06:38:20.058282+00:00 | 4 | false | # Intuition
Hardest part of the problem is finding the denominator. We do this itertively checking if denomminator is 1 digit,.. 2 digit, .. n digit.
Added some checks to return early.
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
O(log(length(n))) - almost O(1)
- Space complexity:
O(1) if result is excluded
# Code
```python3 []
class Solution:
def splitMessage(self, message: str, limit: int) -> list[str]:
if limit <= 5:
return []
l = len(message)
def messageSizeLog10() -> int:
possibleSegments = [9]
while True:
strLen = l
possibleSegmentsLessThan = possibleSegments[-1]
if possibleSegmentsLessThan > strLen * 10:
return 0
denominatorSize = len(str(possibleSegmentsLessThan))
syntaxLength = 3
for s in possibleSegments:
numeratorSize = len(str(s))
strLen -= (
limit - numeratorSize - denominatorSize - syntaxLength
) * s
if strLen <= 0:
return denominatorSize
possibleSegments.append(possibleSegments[-1] * 10)
denominatorSize = messageSizeLog10()
if denominatorSize == 0:
return []
messageList = []
numerator = 1
cursor = 0
while cursor < l:
numeratorSize = len(str(numerator))
syntaxSize = numeratorSize + denominatorSize + 3
messageSize = limit - syntaxSize
thisMessage = message[cursor : cursor + messageSize]
messageList.append((thisMessage, numerator))
cursor = cursor + messageSize
numerator += 1
denominator = str(numerator - 1)
res = []
for m in messageList:
[message, thisNumerator] = m
formattedMessage = f"{message}<{thisNumerator}/{denominator}>"
res.append(formattedMessage)
return res
``` | 0 | 0 | ['Python3'] | 0 |
split-message-based-on-limit | C# Soluction with Binary Search | c-soluction-with-binary-search-by-icecof-m6cy | Code | IceCoffeeY | NORMAL | 2025-03-20T22:08:42.888886+00:00 | 2025-03-20T22:08:42.888886+00:00 | 2 | false | # Code
```csharp []
public class Solution {
public string[] SplitMessage(string message, int limit)
{
var n = message.Length;
var digit = 1;
while (true)
{
// 1 - 9, 10 - 99, 100 - 999, 1000, 9999....
var count = 0;
var x = 1;
for (var i = 0; i < digit; ++i)
{
var labelSize = 3 + digit + x.ToString().Length;
var wordSize = limit - labelSize;
if (wordSize <= 0 && count < n)
return [];
count += 9 * x * wordSize;
if (count >= n) break;
x *= 10;
}
if (count >= n) break;
digit += 1;
}
int CalculateSize(int parts)
{
var remains = parts;
var x = 1;
var count = 0;
while (remains > 0)
{
var labelSize = 3 + digit + x.ToString().Length;
var wordSize = limit - labelSize;
var wordsCnt = Math.Min(9 * x, remains);
count += wordSize * wordsCnt;
remains -= wordsCnt;
x *= 10;
}
return count;
}
int l = (int)Math.Pow(10, digit - 1), r = (int)Math.Pow(10, digit);
while (l < r)
{
var mid = l + (r - l) / 2;
if (CalculateSize(mid) < n)
l = mid + 1;
else
r = mid;
}
var size = l;
var idx = 0;
var res = new List<string>();
for (var i = 1; i <= size; ++i)
{
var label = $"<{i}/{size}>";
var wordSize = limit - label.Length;
if (idx + wordSize >= n) wordSize = n - idx;
var word = message.Substring(idx, wordSize);
var part = word + label;
res.Add(part);
idx += wordSize;
}
return res.ToArray();
}
}
``` | 0 | 0 | ['C#'] | 0 |
split-message-based-on-limit | Homegrown Pythonic Simple Solution (28 Lines) | homegrown-pythonic-simple-solution-28-li-l2ep | IntuitionTake advantage of the static message trailer length per digit range.ApproachUse the ranges for number of available digits in 1-9, 10-99, 100-999, 1000- | baninja6 | NORMAL | 2025-03-05T01:14:55.791081+00:00 | 2025-03-05T01:14:55.791081+00:00 | 9 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Take advantage of the static message trailer length per digit range.
# Approach
<!-- Describe your approach to solving the problem. -->
Use the ranges for number of available digits in 1-9, 10-99, 100-999, 1000-9999, etc to find the right order of packets and then backfill the trailer
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(n * log(n))
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(n)
# Code
```python3 []
class Solution:
def splitMessage(self, message: str, limit: int) -> List[str]:
def gen(b, message):
a = 1
B = len(str(b))
out = []
while message:
A = len(str(a))
if a > b:
return ([], False)
overhead = 3 + A + B
N = limit - overhead
frag = message[0:N]
message = message[N:]
out.append(frag)
a += 1
a -= 1
for i in range(a, 0, -1):
out[i - 1] = out[i - 1] + f'<{i}/{a}>'
return (out, True)
base = 1
test, ok = gen(base ** 10 - 1, message)
while not ok:
base *= 10
if 3 + 1 + 2 * len(str(base - 1)) > limit:
return []
test, ok = gen(base - 1, message)
return test
``` | 0 | 0 | ['String', 'Python3'] | 0 |
split-message-based-on-limit | [Java] Binary Search for Message Partitioning. Beats 92.48% runtime and 96.08% memory | java-binary-search-for-message-partition-8dwb | IntuitionYou can use binary search to determine the optimal number of parts, initially ranging from 1 to message.length(). Additionally, you can calculate the l | fleum | NORMAL | 2025-02-17T03:56:24.472468+00:00 | 2025-02-17T03:56:24.472468+00:00 | 19 | false | # Intuition
You can use binary search to determine the optimal number of parts, initially ranging from 1 to message.length(). Additionally, you can calculate the length of the first segment to extract, given that each part has a fixed length:
```
int x = limit - 4 - l;
```
Here, 4 accounts for the characters '<', '1', '/', and '>', which are always present in the first part. The variable l represents the length of the total number of parts in digits (e.g., if there are 367 parts, then l = 3).
# Approach
First, determine the number of parts using binary search, similar to Leetcode 1891: Cutting Ribbons. Note that if an m-part partition is not feasible, you won’t know which side contains the valid answer, so both halves must still be explored.
Once the number of parts is determined, split the message accordingly.
# Complexity
- Time complexity:
$$O(n)$$
- Space complexity:
$$O(n)$$
# Code
```java []
class Solution {
private String message;
private int limit;
private int res = Integer.MAX_VALUE;
public String[] splitMessage(String message, int limit) {
if (limit <= 5) {
return new String[0];
}
this.message = message;
this.limit = limit;
bs(1, message.length());
return res != Integer.MAX_VALUE ? split(res) : new String[0];
}
private void bs(int l, int r) {
if (l > r) {
return;
}
int m = (l + r) / 2;
if (possible(m)) {
res = Math.min(res, m);
bs(l, m - 1);
} else {
bs(l, m - 1);
bs(m + 1, r);
}
}
private boolean possible(int m) {
int l = Integer.toString(m).length();
int p = message.length();
int x = limit - 4 - l;
if (1 <= m && m <= 9) {
p -= (m - 1) * x;
} else if (10 <= m && m <= 99) {
p -= (m - 1) * x - m + 10;
} else if (100 <= m && m <= 999) {
p -= (m - 1) * x - 2 * m + 110;
} else if (1000 <= m && m <= 9999) {
p -= (m - 1) * x - 3 * m + 1110;
} else {
p -= (m - 1) * x - 4 * m + 11110;
}
return p + 2 * l + 3 <= limit;
}
private String[] split(int m) {
int l = Integer.toString(m).length();
int x = limit - 4 - l;
String[] res = new String[m];
int i = 0;
for (int k = 1; k < m; k++) {
StringBuilder sb = new StringBuilder();
int t = x;
if (10 <= k && k <= 99) {
t -= 1;
} else if (100 <= k && k <= 999) {
t -= 2;
} else if (1000 <= k && k <= 9999) {
t -= 3;
}
sb.append(message.substring(i, i + t));
sb.append("<");
sb.append(k);
sb.append("/");
sb.append(m);
sb.append(">");
res[k - 1] = sb.toString();
i = i + t;
}
StringBuilder sb = new StringBuilder();
sb.append(message.substring(i));
sb.append("<");
sb.append(m);
sb.append("/");
sb.append(m);
sb.append(">");
res[m - 1] = sb.toString();
return res;
}
}
``` | 0 | 0 | ['Java'] | 1 |
split-message-based-on-limit | C++, binary search, hopefully a good explanation | c-binary-search-hopefully-a-good-explana-nuz0 | IntuitionI wanted to describe what tripped me up on this problem.I stumbled upon this problem because I wanted to practice binary search problems, so I knew goi | mklose | NORMAL | 2025-02-13T08:33:40.308029+00:00 | 2025-02-13T08:33:40.308029+00:00 | 26 | false | # Intuition
I wanted to describe what tripped me up on this problem.
I stumbled upon this problem because I wanted to practice binary search problems, so I knew going in that binary search had to be used somehow.
Initially I thought I could create a function that would create a kind of step function that goes from not possible to possible (ie a step function) and I would just need to find the transition from zero to 1 (which a binary search is great at).
However, after implementing a function that just returned a bool, I saw that it was false for a long time, then true, then false for a long time, so I knew that this wasn't it.
I then looked at the left over message bytes after trying to encode it into p parts and this gave me more hope. With the examples given, it ran from positive to negative (negative meaning we used more message than we actually have available), much better for binary search!
One caveat is that the last message is allowed to have between 1 and `limit-suffix` chars. So if the suffix size of the last part is 7 but we have a limit of 9, we can have a value of -1 (one less than maximum used) and it still be OK. (0 left means all 9-7 = 2 slots used, it is ok to leave one slot unoccupied, but not two. So if it is still valid, the function adjusts the message left over size to 0.
I experimented a bit with the messages and found that the message "this is really a very awesome messag" (note the missing "e") actually has two solutions. One with 9 parts, and one with 14 parts.
Looking at the leftover message lengths, it looked like this (first number is 1 part, the zeros are at 9 and 14 parts):
`32, 28, 24, 20, 16, 12, 8, 4, 0, 7, 5, 3, 1, 0, -3, -5, -7, -9, -11`
This tripped me up because I can't use binary search in this.
Then I realized that the issue is that I need to look at each number of part digits individually: Find if I have a solution between 1 and 9, then see if I have a solution between 10 and 99, between 100 and 999, etc...
With a constant part number length, the values are always decreasing values, so binary search can be used!
The rest is just mechanical coding.
# Complexity
- Time complexity:
- We do a logarithmic (base 10) number of binary searches, each of which does log message size operations (worst case). Each operation is also logarithmic in regards to the message size.
- I hard coded 10^6 in the outer loop just because (and only requires 6 loop iterations), but it could have used the length of the string as the minimum should be one message for each character. Let's say I used message size instead of 10^6
Then the final time complexity should be O((log message_size)^3)
# Code
```cpp []
class Solution {
public:
vector<string> splitMessage(string message, int limit) {
int prev_ten_power = 1;
while (prev_ten_power < 1000000) {
int l = prev_ten_power;
int next_ten_power = prev_ten_power * 10;
int r = next_ten_power - 1;
prev_ten_power = next_ten_power;
while (l <= r) {
int mid = (r - l) / 2 + l;
int message_left_over =
LeftOverMessage(message.size(), limit, mid);
if (message_left_over == 0)
return CalculateResult(message, limit, mid);
if (message_left_over > 0) {
// we are too far left. Go right.
l = mid + 1;
} else {
r = mid - 1;
}
}
}
return {};
}
std::vector<std::string> CalculateResult(std::string_view message,
int limit, int parts) {
std::vector<std::string> result;
for (int i = 1; i <= parts; ++i) {
std::string suffix = "<";
suffix += std::to_string(i);
suffix += "/";
suffix += std::to_string(parts);
suffix += ">";
int num_chars = limit - suffix.size();
std::string s = std::string(message.substr(0, num_chars));
s += suffix;
message.remove_prefix(num_chars);
result.push_back(s);
}
return result;
}
int LeftOverMessage(int message_size, int limit, int parts) {
int suffix_size = 0;
int p = parts;
while (p > 0) {
++suffix_size;
p = p / 10;
}
suffix_size += 4; /// <1/9> (single digit included)
int prev_ten_power = 1;
while (parts > 0) {
int next_ten_power = prev_ten_power * 10;
int parts_with_digit =
std::min(next_ten_power - prev_ten_power, parts);
message_size -= parts_with_digit * (limit - suffix_size);
parts -= parts_with_digit;
suffix_size += 1;
prev_ten_power = next_ten_power;
}
suffix_size = suffix_size - 1; // undo
// The last block is allowed to have less characters, but not zero
if (message_size < 0 && message_size + limit - suffix_size > 0) {
return 0;
}
return message_size;
}
};
``` | 0 | 0 | ['C++'] | 0 |
split-message-based-on-limit | Javascript solution | javascript-solution-by-kancerezeroglu-uycl | Example:Step 1: Finding kksasbscAvailable Space (limit * k - (sumOfDigits + totalLenOfIndicies + totalLenOfFormat))Can Fit?11139 * 1 - (1 + 1 + 3) = 4❌22269 * 2 | kancerezeroglu | NORMAL | 2025-02-07T16:01:24.881759+00:00 | 2025-02-07T16:05:59.098762+00:00 | 11 | false | # Example:
### **Step 1: Finding `k`**
| `k` | `sa` | `sb` | `sc` | Available Space (`limit * k - (sumOfDigits + totalLenOfIndicies + totalLenOfFormat)`) | Can Fit? |
|----|----|----|----|--------------------------------|---------|
| 1 | 1 | 1 | 3 | `9 * 1 - (1 + 1 + 3) = 4` | ❌ |
| 2 | 2 | 2 | 6 | `9 * 2 - (2 + 4 + 6) = 5` | ❌ |
| 3 | 3 | 3 | 9 | `9 * 3 - (3 + 9 + 9) = 6` | ❌ |
| ... | ... | ... | ... | ... | ... |
| 14 | 15 | 28 | 42 | `9 * 14 - (15 + 28 + 42) = 37` | ✅ **Found!** |
✅ **Final `k = 14`**
# Complexity
### **Step 1: Finding the correct `k`**
- The loop runs **at most `O(log N)`** times because:
- The value of `k` grows gradually, increasing when suffix lengths change (`9 → 10`, `99 → 100`, etc.).
- The length of `k` increases logarithmically (`log N` digits for `N`).
- Inside the loop, we perform:
- **String operations** (`String(k).length`) → `O(log k)`, but `k` is small (`≤ N`).
- **Mathematical operations** → `O(1)`.
- **Total complexity for this step:** `O(log N)`.
---
### **Step 2: Constructing the parts**
- The second loop **iterates `k` times**, where `k` is the number of parts.
- Each iteration **creates a substring (`message.slice()`)**, which is `O(1)`.
- **Total complexity for this step:** `O(N)`, since the message is fully traversed.
---
### **Overall Time Complexity**
| Step | Complexity |
|------|------------|
| Finding `k` (Number of Parts) | `O(log N)` |
| Splitting Message (`O(N)`) | `O(N)` |
| **Total Complexity** | **`O(N log N)`** |
---
## **Space Complexity**
- **`result` stores `k` substrings**, which is proportional to `O(k)`.
- **`String(k).length` and suffix calculations use `O(1)` extra space.**
- **The input `message` is not modified in-place**, so the new array takes `O(N)`.
### **Overall Space Complexity**
| Memory Usage | Complexity |
|-------------|------------|
| Output list (`k` substrings) | `O(N)` |
| Extra variables (`i`, `j`) | `O(1)` |
| **Total Complexity** | **`O(N)`** |
---
## **Complexity Summary**
| Complexity Type | Complexity |
|----------------|------------|
| **Time Complexity** | **`O(N log N)`** |
| **Space Complexity** | **`O(N)`** |
# Code
```javascript []
/**
* @param {string} message
* @param {number} limit
* @return {string[]}
*/
var splitMessage = function (message, limit) {
let n = message.length;
let sumOfDigits = 0; // Sum of digits of each part index
for (let k = 1; k <= n; k++) {
sumOfDigits += String(k).length;
let totalLenOfIndicies = String(k).length * k; // Total length of k indices
let totalLenOfFormat = 3 * k; // Total length of '<' + '/' + '>'
// Check if the message can fit into `k` parts
if (limit * k - (sumOfDigits + totalLenOfIndicies + totalLenOfFormat) >= n) {
let result = [];
let i = 0;
for (let j = 1; j <= k; j++) {
let suffix = `<${j}/${k}>`;
let maxPartLen = limit - suffix.length;
let t = message.slice(i, i + maxPartLen) + suffix;
result.push(t);
i += maxPartLen;
}
return result;
}
}
return [];
};
``` | 0 | 0 | ['JavaScript'] | 0 |
split-message-based-on-limit | [Java] Two binary search faster than 100% | java-two-binary-search-faster-than-100-b-8kx4 | Intuition
First binary search searching the minimum digits we need.
Second binary search searching the minimum 'b' based on the digitswe got in the first binary | raywang945 | NORMAL | 2025-01-19T20:06:49.354245+00:00 | 2025-01-19T20:06:49.354245+00:00 | 23 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
- First binary search searching the minimum digits we need.
- Second binary search searching the minimum 'b' based on the digitswe got in the first binary search.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
$$O(log(n))$$ for binary sesarch and $$O(n)$$ to construct the output. Overall $$O(n)$$.
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
$$O(1)$$ for binary search and $$O(n)$$ to construct the output. Overall $$O(n)$$.
# Code
```java []
class Solution {
public String[] splitMessage(String message, int limit) {
int n = message.length();
int left = 1;
int right = getIntLen(n);
while (left < right) {
int mid = left + (right - left) / 2;
if (3 + mid * 2 >= limit) {
right = mid - 1;
continue;
}
int count = 0;
for (int i = 1; i <= mid; ++i) {
count += (limit - (3 + mid + i)) * 9 * (int)Math.pow(10, i - 1);
}
if (count < n) {
left = mid + 1;
} else {
right = mid;
}
}
if (left > right || (3 + left * 2) >= limit) {
return new String[0];
}
int digits = left;
left = (int)Math.pow(10, digits - 1);
right = left * 10 - 1;
while (left < right) {
int mid = left + (right - left) / 2;
int count = 0;
for (int i = 1; i < digits; ++i) {
count += (limit - (3 + digits + i)) * 9 * (int)Math.pow(10, i - 1);
}
count += (limit - (3 + digits * 2)) * (mid - (int)Math.pow(10, digits - 1) + 1);
if (count < n) {
left = mid + 1;
} else {
right = mid;
}
}
String[] result = new String[left];
char[] cArray = message.toCharArray();
int idx = 0;
for (int i = 1; i <= left; ++i) {
StringBuilder sb = new StringBuilder();
int len = limit - 3 - digits - getIntLen(i);
while (len > 0 && idx < n) {
sb.append(cArray[idx]);
++idx;
--len;
}
sb.append('<').append(i).append('/').append(left).append('>');
result[i - 1] = sb.toString();
}
return result;
}
private int getIntLen(int num) {
int result = 0;
while (num > 0) {
++result;
num /= 10;
}
return result;
}
}
``` | 0 | 0 | ['Java'] | 0 |
split-message-based-on-limit | 2468. Split Message Based on Limit | 2468-split-message-based-on-limit-by-g8x-brqr | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | G8xd0QPqTy | NORMAL | 2025-01-18T16:22:30.251901+00:00 | 2025-01-18T16:22:30.251901+00:00 | 24 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def splitMessage(self, s: str, limit: int) -> List[str]:
cursor = part_count = pointer = 0
while 3 + len(str(part_count)) * 2 < limit and cursor + len(s) + (3 + len(str(part_count))) * part_count > limit * part_count:
part_count += 1
cursor += len(str(part_count))
segments = []
if 3 + len(str(part_count)) * 2 < limit:
for i in range(1, part_count + 1):
remaining_space = limit - (len(str(i)) + 3 + len(str(part_count)))
segments.append(f'{s[pointer:pointer + remaining_space]}<{i}/{part_count}>')
pointer += remaining_space
return segments
``` | 0 | 0 | ['Python3'] | 0 |
split-message-based-on-limit | Simple Easy Approach | simple-easy-approach-by-umerwajih-hmzx | IntuitionThe problem requires splitting a message into parts such that each part includes a suffix in the format <part/total> and the total length of each part | umerwajih | NORMAL | 2025-01-17T22:20:33.078314+00:00 | 2025-01-17T22:20:33.078314+00:00 | 19 | false | # Intuition
The problem requires splitting a message into parts such that each part includes a suffix in the format <part/total> and the total length of each part does not exceed the given limit. The challenge lies in dynamically adjusting the number of characters available for the message as the suffix grows in length when the number of parts crosses thresholds (e.g., from 9 to 10, or 99 to 100). This necessitates a two-step approach: first, determine the total number of parts required, and then construct the output while respecting the constraints.
# Approach
**Initialization:**
- Start with the smallest suffix length (<1/1>, 5 characters) and calculate the available characters for the message in each part.
- If the available characters are less than zero (limit too small for any message), return an empty array.
**Determine Total Parts:**
- Iterate through the message, consuming available characters per part and incrementing the part count.
- When the part count reaches a threshold (e.g., 10, 100), adjust the suffix length by adding 2 characters and recalculate the available characters.
- If the limit becomes too small for any part due to increased suffix length, return an empty array.
**Construct the Output:**
- Use the total number of parts calculated in the previous step to split the message.
- For each part, append the appropriate suffix in the <part/total> format and adjust the number of characters taken from the message accordingly.
- Ensure no part exceeds the limit and properly concatenate the suffix to each substring.
**Return the Result:**
- Return an array containing all the parts with the message segments and their respective suffixes.
This approach ensures the message is split efficiently while accounting for the dynamic changes in suffix length. It also handles edge cases, such as when the message is too long to fit even with minimal suffix adjustments.
# Code
```java []
class Solution {
public String[] splitMessage(String message, int limit) {
// Calculate the total number of parts needed and handle dynamic suffix length
int parts = 0; // Total number of parts needed for the message
int suffixLen = 5; // Minimum suffix length for "<1/1>" format
int index = 0; // Current index of the message
int target = 10; // Threshold for increasing suffix length (e.g., from 9 to 10, 99 to 100)
int available = limit - suffixLen; // Characters available in each part after accounting for suffix
// If the limit is too small to fit even the minimum suffix, return an empty array
if (available <= 0) return new String[] {};
// Step 1: Determine the total number of parts required
while (index < message.length()) {
index += available; // Move the index forward by the number of available characters
parts++; // Increment the number of parts
// Check if we've hit a target threshold where the suffix length increases
if (parts == target) {
// Adjust the index to account for extra characters required due to the increased suffix length
index = index - target - 1;
// Update the target for the next threshold (e.g., 10 -> 100)
target *= 10;
// Increase the suffix length by 2 as it grows with the number of digits in "total parts"
suffixLen += 2;
// Recalculate the available characters per part
available = limit - suffixLen;
// If the available characters become zero, splitting is not possible
if (available <= 0) return new String[] {};
}
}
// Reset the index for the next loop
index = 0;
// Step 2: Split the message into parts and construct the output
String[] output = new String[parts]; // Initialize the array to hold all parts
for (int part = 1; part <= parts; part++) {
// Construct the suffix for the current part (e.g., "<1/3>", "<2/3>")
StringBuilder builder = new StringBuilder();
builder.append("<");
builder.append(part);
builder.append("/");
builder.append(parts);
builder.append(">");
// Recalculate the available characters per part after appending the suffix
available = limit - builder.length();
// If the remaining part of the message fits in the current part, take it
if (index + available > message.length()) {
output[part - 1] = message.substring(index).concat(builder.toString());
} else {
// Otherwise, take the available characters and move the index forward
output[part - 1] = message.substring(index, index += available).concat(builder.toString());
}
}
// Return the array of split message parts
return output;
}
}
``` | 0 | 0 | ['Java'] | 1 |
split-message-based-on-limit | Python beats 91%, cheap calculation of number of iterations without fancy data structures | python-beats-91-cheap-calculation-of-num-2g8l | IntuitionThe intuition here is that we can easily calculate the number of iterations without traversing the message, by estimating the number of digits of the t | passadore | NORMAL | 2024-12-30T14:35:32.535958+00:00 | 2024-12-30T14:35:32.535958+00:00 | 22 | false | # Intuition
The intuition here is that we can easily calculate the number of iterations without traversing the message, by estimating the number of digits of the total number of chunks. Once we have that value, it is easy to return the result by travesing the message.
# Approach
Since the size of each chunk depends on the number of digits of the chunk index and the number of digits of total chunks, we first need to find the number of digits of the total chunks.
But that number is limited by the size of input. If len(message)==100,
worst case is less than 100 chuks, which means 3 digits max.
If we assume the number of digits is 1, this means we can split the message in 9 chunks of size (limit-5) where 5 is len("<x/y>")
if 9* (limit-5)>= len(message), we found the number of digits.
If we assume the number of digits is 2, this means we can split the message in 9 chunks of size (limit-6) where 6 is len("<x/yz>") and 90 chunks of size (limit-7) where 7 is len("<xl/yz>")
if 9* (limit-6)+90*(limit-7)>= len(message), we found the number of digits.
Essentially, we are evaluating the following sum:
$$\sum_{i=0}^{d} 9*10^i*(k-5-i-d)$$
Where d is the total digits, until this is larger than len(message)
Given input maximum size, we only need to try d in range(1,6)
# Complexity
- Time complexity:
I'm not sure about this. Definetely less or equal to $$O(n)$$
- Space complexity:
$$O(n)$$
# Code
```python3 []
class Solution:
def splitMessage(self, message: str, limit: int) -> List[str]:
if limit<=3: # escape edge case
return []
n = len(message)
found = False
for i in range(1,6): # estimating number of digits
l=0
for j in range(i):
actualLimit = limit-4-i-j # how many chars in each chunk
if l+actualLimit * 9 * (10**j)>=n:
found = True
# stop searching. Keep values calculated until
# last digit to calculate actual number of chunks later
break
if l+s<n and actualLimit ==0:
return []
l+=actualLimit * 9 * (10**j)
if found:
break
# num of chunks is calculated by how many chars
# we still need to distribute in the last iteration
# since l+actualLimit * 9 * (10**j) can be larger than n
rest = ((n-l)//actualLimit)
if (n-l)%actualLimit!=0:
rest+=1
numPages = rest+ 10**(i-1) -1
result = []
c= 0
it = 1
ptr=0
actualLimit = limit - 4 - i
turningPts = set([10,100,1000,10000,100000])
while c+actualLimit<n:
if it in turningPts:
actualLimit-=1
result.append((message[ptr:ptr+actualLimit])+f"<{it}/{numPages}>")
ptr+=actualLimit
c+=actualLimit
it+=1
result.append((message[ptr:])+f"<{it}/{numPages}>")
return result
``` | 0 | 0 | ['Python3'] | 0 |
split-message-based-on-limit | Simple Cpp Solution. TC - O(len(message)) | simple-cpp-solution-tc-olenmessage-by-re-nua5 | Code | reet-bhaati | NORMAL | 2024-12-26T17:31:05.125195+00:00 | 2024-12-26T17:31:05.125195+00:00 | 15 | false | # Code
```cpp []
class Solution {
public:
vector<string> solve(string message, int limit, int digit){
int k;
if(digit == 1){
k = 9;
}else if(digit == 2){
k = 99;
}else if(digit == 3){
k = 999;
}else{
k = 9999;
}
vector<string> ans;
int idx = 0;
for(int i=1;i<=k;i++){
string str = "<" + to_string(i) + "/" + to_string(k) + ">";
int len = limit - str.size();
if(len <= 0){
return {};
}
if(idx + len < message.size()){
str = message.substr(idx, len) + str;
idx += len;
ans.push_back(str);
}else{
str = message.substr(idx) + str;
idx = message.size();
ans.push_back(str);
break;
}
}
if(idx < message.size()){
return {};
}
int replace = ans.size();
vector<string> finalString;
for(int i=0;i<ans.size();i++){
string str = "";
for(int j=0;j<ans[i].size();j++){
if(ans[i][j] != '/'){
str += ans[i][j];
}else{
break;
}
}
str += "/";
str += to_string(replace);
str += ">";
finalString.push_back(str);
}
return finalString;
}
vector<string> splitMessage(string message, int limit) {
for(int i=1;i<=4;i++){
vector<string> ans = solve(message, limit, i);
if(ans.size() > 0){
return ans;
}
}
return {};
}
};
``` | 0 | 0 | ['C++'] | 0 |
split-message-based-on-limit | Python solution | python-solution-by-sabyasachim999-z6tn | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | sabyasachim999 | NORMAL | 2024-12-26T07:05:02.829705+00:00 | 2024-12-26T07:05:02.829705+00:00 | 10 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def splitMessage(self, message: str, limit: int) -> List[str]:
N = len(message)
min_suf_len = max_suf_len = 5
while True:
if max_suf_len >= limit:
return []
i = 9
n = N
parts = 0
for l in range(min_suf_len, max_suf_len):
part_len = limit - l
n = n - (i * part_len)
parts += i
i *= 10
part_len = limit - max_suf_len
parts += ceil(n / part_len)
if i * part_len >= n:
break
min_suf_len += 1
max_suf_len += 2
# print(parts)
i = 0
res = []
for p in range(parts):
suffix = '<' + str(p + 1) + '/' + str(parts) + '>'
l = limit - len(suffix)
tmp = message[i : i+l] + suffix
i = i + l
res.append(tmp)
return res
``` | 0 | 0 | ['Python3'] | 0 |
split-message-based-on-limit | JAVA O(N) time complexity, beat 100% | java-on-time-complexity-beat-100-by-zwan-lqc3 | IntuitionTry to find the number of element in the array, and make the new string in the array with stringbuilderApproachfirst start from 1, to find the proper l | zwang3184 | NORMAL | 2024-12-20T03:18:25.469298+00:00 | 2024-12-20T03:18:25.469298+00:00 | 23 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Try to find the number of element in the array, and make the new string in the array with stringbuilder
# Approach
<!-- Describe your approach to solving the problem. -->
first start from 1, to find the proper length of array, to make the last element of array can be filled, and remaining any char in the string, then use stringbuilder to form every element in the array.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
$$O(n)$$
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
$$O(n)$$
# Code
```java []
class Solution {
public String[] splitMessage(String message, int limit) {
int num = 0;
int numL=0;
if (message.length() == 0)
return new String[0];
for (int i = 1; i <= 9999; i++) {
if (i < 10) {
int newlen = 5 * i + message.length();
numL=1;
if (newlen >= (limit * (i - 1) + 1) && newlen <= (limit * i)) {
num = i;
break;
}
} else if (i >= 10 && i < 100) {
numL=2;
int newlen = 6 * 9 + 7 * (i - 9) + message.length();
if (newlen >= (limit * (i - 1) + 1) && newlen <= (limit * i)) {
num = i;
break;
}
} else if (i >= 100 && i < 1000) {
numL=3;
int newlen = 7 * 9 + 8 * 90+9*(i-99) + message.length();
if (newlen >= (limit * (i - 1) + 1) && newlen <= (limit * i)) {
num = i;
break;
}
}else if (i >= 1000 && i < 10000) {
numL=4;
int newlen = 8 * 9 + 9 * 90+10*900 + 11*(i-999) +message.length();
if (newlen >= (limit * (i - 1) + 1) && newlen <= (limit * i)) {
num = i;
break;
}
}
}
String[] res=new String[num];
int start=0;
int end=0;
//System.out.println(num);
for(int i=1;i<=num;i++){
StringBuilder sb=new StringBuilder();
int textLen=0;
if(i<10){
textLen=limit-3-numL-1;
}else if(i<100){
textLen=limit-3-numL-2;
}else if(i<1000){
textLen=limit-3-numL-3;
}else{
textLen=limit-3-numL-4;
}
end=Math.min(start+textLen,message.length());
sb.append(message.substring(start,end));
sb.append('<');
sb.append(i);
sb.append('/');
sb.append(num);
sb.append('>');
res[i-1]=sb.toString();
start=end;
}
return res;
}
}
``` | 0 | 0 | ['Java'] | 0 |
split-message-based-on-limit | scala solution | scala-solution-by-vititov-oh0w | scala []\nobject Solution {\n def splitMessage(message: String, limit: Int): Array[String] = {\n LazyList.range(1,6).flatMap { len =>\n lazy val x0 = L | vititov | NORMAL | 2024-12-08T20:51:51.303823+00:00 | 2024-12-08T20:51:51.303875+00:00 | 3 | false | ```scala []\nobject Solution {\n def splitMessage(message: String, limit: Int): Array[String] = {\n LazyList.range(1,6).flatMap { len =>\n lazy val x0 = List.unfold((0, 1)) { case (i, j) => Option.when(i < message.length) {\n lazy val i1 = ((i + limit - 3 - len - j.toString.length) max i + 1) min message.length\n ((i, i1), (i1, j + 1))\n }}\n Option.when(limit>len*2+3 && (x0.length).toString.length == len)(x0)\n }.headOption.map{x0 =>\n x0.zipWithIndex.map{case ((i0,i1),j) => message.substring(i0,i1) + s"<${j+1}/${x0.length}>" }.toArray\n }.getOrElse(Array())\n }\n}\n``` | 0 | 0 | ['Scala'] | 0 |
split-message-based-on-limit | Modified Binary Search to Avoid Problem | modified-binary-search-to-avoid-problem-lszbd | Explanation\n Describe your first thoughts on how to solve this problem. \nSince the length of the message that can be expressed as a function of the number of | dddwww | NORMAL | 2024-11-12T07:10:21.900088+00:00 | 2024-11-12T07:10:21.900123+00:00 | 18 | false | # Explanation\n<!-- Describe your first thoughts on how to solve this problem. -->\nSince the length of the message that can be expressed as a function of the number of suffix is not monotonic, it creates a trouble for using Binary search. (e.g. 100 suffix will likely be able to express a message shorter than 99 messages.)\n\nTo solve this problem, we just need to first find what is the least number of digits needed for the number of suffix. Then use this as the upper bound for the number of suffix in binary search. (set it as the r pointer at the beginning) \n\nThis should solve the problem with using Binary Search.\n\n# Code\n```python3 []\nclass Solution:\n def splitMessage(self, message: str, limit: int) -> List[str]:\n \n def message_len(num_suffix):\n num_suffix_str = str(int(num_suffix))\n num_digits = len(num_suffix_str)\n out = 0\n for digit in range(num_digits):\n num_message_char = limit - 3 - num_digits - digit-1\n if num_message_char <= 0:\n return out\n else:\n if digit != num_digits-1:\n out += num_message_char * 9 * 10**digit\n else: # last digit\n out += num_message_char * (num_suffix - (int("9"*(num_digits-1)) if num_digits>1 else 0))\n return out\n\n possible = False\n for num_digits in range(1, 10):\n if message_len(int("9"*num_digits)) >= len(message):\n num_digits_ub = num_digits\n possible = True\n break\n if not possible:\n return []\n\n # binary search, find least num_suffix\n l,r = 1, int("9"*num_digits_ub)\n while l<r:\n mid = (l+r) // 2\n if message_len(mid) >= len(message):\n r = mid\n else:\n l = mid + 1\n \n out = []\n i = 0 # ptr on the message string\n num_digits = len(str(l))\n for suffix_ind in range(1, l+1):\n digits = len(str(suffix_ind))\n num_message_char = limit - 3 - num_digits - digits\n out.append(message[i:i+num_message_char] + "<"+str(suffix_ind)+"/"+str(l)+">")\n i += num_message_char\n\n return out\n\n\n\n\n\n\n\n\n\n``` | 0 | 0 | ['Python3'] | 0 |
split-message-based-on-limit | C++ soln with comments and clear code beats 85% soln time. | c-soln-with-comments-and-clear-code-beat-6p15 | Intuition\nFirst compute number of digits of denominator and then compute the denominator itself and then actual answer i.e. vector.\n\n# Approach\nOnce we know | ayusverma | NORMAL | 2024-11-09T18:44:56.274582+00:00 | 2024-11-09T18:44:56.274622+00:00 | 15 | false | # Intuition\nFirst compute number of digits of denominator and then compute the denominator itself and then actual answer i.e. vector<string>.\n\n# Approach\nOnce we know the denominator it\'s just travesal over original string to compute the final answer.\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int NoDigits(int no) {\n if (no == 0)\n return 0;\n int ans = 0;\n while (no > 0) {\n ++ans;\n no /= 10;\n }\n return ans;\n }\n\n // Check if the message can be split into x number of parts where number of digits in x is given. Also computes x and populate it in den.\n bool IsPossible(const std::string& message, const int limit,\n const int overhead, const int digit, int& den) {\n int i,j,k;\n if (overhead >= limit)\n return false;\n j = 0;\n const int n = message.size();\n int cnt = 1;\n\n while (j < n) {\n if (NoDigits(cnt) > digit)\n return false;\n if (limit <= (overhead + NoDigits(cnt)))\n return false;\n j = j + (limit-overhead-NoDigits(cnt));\n ++cnt;\n }\n --cnt;\n den = cnt;\n return (NoDigits(cnt) == digit);\n }\n\n vector<string> Compute(const std::string& message, const int limit,\n const int overhead, const int den) {\n const int den_digit = NoDigits(den);\n std::string den_part = "/" + std::to_string(den) + ">";\n vector<string> ans;\n std::string temp;\n int j = 0;\n const int n = message.size();\n int mn;\n\n for (int cnt = 1; cnt <= den && j < n; ++cnt) {\n temp = "<" + std::to_string(cnt) + den_part;\n mn = min(n-j, limit-(int)(temp.size()));\n temp = message.substr(j, mn) + temp;\n j += mn;\n ans.push_back(std::move(temp));\n }\n return ans;\n }\n\n vector<string> splitMessage(string message, int limit) {\n int overhead;\n std::vector<string> ans;\n int den;\n\n for (int digit = 1; digit <= 7; ++digit) {\n overhead = 3 + digit;\n if (overhead + digit >= limit)\n break;\n if (IsPossible(message, limit, overhead, digit, den)) {\n return Compute(message, limit, overhead, den);\n }\n }\n return {};\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
split-message-based-on-limit | Simple beats 94% (self documenting) | simple-beats-94-self-documenting-by-rang-t1z9 | Intuition\nFind out the max suffix length for your inputs. \n\n# Approach\nBrute force first time to determine the buckets and then hard code the same. \n\n# Co | rangareddy | NORMAL | 2024-11-06T15:24:59.953936+00:00 | 2024-11-06T15:24:59.953970+00:00 | 21 | false | # Intuition\nFind out the max suffix length for your inputs. \n\n# Approach\nBrute force first time to determine the buckets and then hard code the same. \n\n# Complexity\n- Time complexity: O(n)\n- Space complexity: O(n)\n\n# Code\n```python3 []\nclass Solution:\n def _get_suffix_size_blocks(self):\n blocks = OrderedDict()\n # for max_val in [9, 99, 999, 9999, 99999]:\n # total_suffix_len = sum([len(f\'<{i}/{max_val}>\') for i in range(1, max_val + 1)])\n # blocks[max_val] = total_suffix_len\n blocks[9] = 45\n blocks[99] = 684\n blocks[999] = 8883\n blocks[9999] = 108882\n blocks[99999] = 1288881\n return blocks\n\n\n def _determine_max_suffix_val(self, suffix_size_blocks: Dict[int,int], message: str, limit: int):\n message_len = len(message)\n for max_suffix_val, total_suffix_len in suffix_size_blocks.items():\n if (limit * max_suffix_val) - total_suffix_len - message_len >= 0:\n return max_suffix_val\n\n return None\n\n\n def splitMessage(self, message: str, limit: int) -> List[str]:\n suffix_size_blocks = self._get_suffix_size_blocks()\n max_suffix_val = self._determine_max_suffix_val(suffix_size_blocks, message, limit)\n if max_suffix_val is None:\n return []\n\n message_chunks, suffix_chunks = [], []\n i, j = 0, 1\n suffix_total_placeholder = \'_\' * len(str(max_suffix_val))\n while i < len(message):\n suffix = f\'<{j}/{suffix_total_placeholder}>\'\n j += 1\n suffix_chunks.append(suffix)\n\n n = limit - len(suffix)\n partial_message = message[i:i+n]\n i += n\n message_chunks.append(partial_message)\n\n answer, total_parts = [], str(len(suffix_chunks))\n for i, (msg, suffix) in enumerate(zip(message_chunks, suffix_chunks), 1):\n line = msg + suffix.replace(suffix_total_placeholder, total_parts)\n answer.append(line)\n\n return answer\n\n``` | 0 | 0 | ['Python3'] | 0 |
split-message-based-on-limit | simple o(n) linear search | simple-on-linear-search-by-ashishkumanar-3lx4 | Intuition\n Describe your first thoughts on how to solve this problem. \nAt max there can be n partitions.we iterate from 1 to n and check whether it is possibl | Ashishkumanar | NORMAL | 2024-11-02T08:05:26.202417+00:00 | 2024-11-02T08:05:26.202448+00:00 | 9 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAt max there can be n partitions.we iterate from 1 to n and check whether it is possible to split in o(1). then once we found ideal partiton size we partition the string in linear search.\n# Approach\nlets say we have m partiton.total *size* = n(size of actual string) + m * 3(each partiton have </>)+ m * lengthof(m) [each partiton should have total partion length] + totalsumof(digit from 1 to m)[we increment at each index making it o(1)];\n\nNOW, we got final size of string now we have to partition to mtimes\nlet psize=(size/m),bias=(size%k>1);\nNow we have make sure every partition have atleast onecharacter and psize+bias<= limit\n\n# Complexity\n- Time complexity:\no(n)\n\n- Space complexity:\no(n)\n\n# Code\n```cpp []\nclass Solution {\npublic:\n vector<int> inc={10,100,1000,10000};\n vector<string> splitMessage(string s, int limit) {\n int n=s.size();\n //there can be at max n parts;\n int j=-1;\n long long prev=0,i0=0,size=1;\n for(int i=1;i<=n;i++){\n if(i==inc[i0]){\n size++;\n i0++;\n }\n long long br=i*3+size*i;//</size> used in each part\n prev+=size; //add new i length\n br+=prev+n; //additional lenght;\n int bias=br%i?1:0;\n br=br/i;\n int last=3+2*size+1; //at min this should be size of last element\n if(br+bias>limit || br<last) continue;\n j=i;\n break;\n }\n if(j==-1) return {}; //we got our required ith path\n string lb="/"+to_string(j)+">";\n vector<string> ans;\n i0=0;\n for(int i=1;i<=j;i++){\n string ind="<"+to_string(i)+lb;\n int bias=ind.size(),l=1;\n string str="";\n str+=s[i0];\n while(i0+1<s.size() && l+1+bias<=limit){\n str+=s[i0+1];\n i0++;\n l++;\n }\n i0++;\n ans.push_back(str+ind);\n }\n return ans;\n \n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
split-message-based-on-limit | beats 100%, 16 line with explanations | beats-100-16-line-with-explanations-by-a-g9fo | Intuition\n\n# Approach\n1. Find the number of digits for the number messages required (3 digits if number of messages required is 100<= #messages <= 999)\n2. F | afamsmith | NORMAL | 2024-10-23T18:06:47.640217+00:00 | 2024-10-23T18:06:47.640272+00:00 | 22 | false | # Intuition\n\n# Approach\n1. Find the number of digits for the number messages required (3 digits if number of messages required is 100<= #messages <= 999)\n2. Find exact number of messages\n3. Construct the result \n\nFor step 1:\n#### Assuming limit -= 5 (not counting already required characters)\n#### 1 digit enough if\n N <= 9 * limit\n\n#### 2 digit enough if \n N <= (limit-1) * 9 + (limit -2) * 90\n#### 3 digit enough if \n N <= (limit-2) * 9 + (limit -3) * 90 + (limit-4)*900 \n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```python3 []\nclass Solution:\n def splitMessage(self, message: str, limit: int) -> List[str]:\n limit -= 5\n N = len(message)\n for d in range(1,100): # find the number of digits of the required number of messages\n arr = [9*(limit-d+1-i)*10**i for i in range(d)] # max num of msg with varying digits num of messages\n if arr[0] < 0: return []\n if N <= sum(arr):\n break\n\n remaining_num_chars = N-sum(arr[:-1])\n msg_count = math.ceil(remaining_num_chars/(limit-2*d+2)) + 10**(d-1) - 1\n\n total, result = 0, []\n for m in range(1, msg_count+1):\n suffix = f\'<{m}/{msg_count}>\'\n c = limit + 5 - len(suffix)\n result.append(message[total:total+c] + suffix)\n total += c\n return result\n \n \n``` | 0 | 0 | ['Python3'] | 0 |
split-message-based-on-limit | Do binary search 4 times | do-binary-search-4-times-by-andreashzz-ox6e | Intuition\n Describe your first thoughts on how to solve this problem. \nAt first, I thought I only need to do one binary search, but then I realized that for d | AndreasHzz | NORMAL | 2024-10-22T17:49:09.888107+00:00 | 2024-10-22T17:49:09.888144+00:00 | 10 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAt first, I thought I only need to do one binary search, but then I realized that for different post length( the length of "/#number of parts>") it is not monotonic. There are at most 4 post length, since the max length is 10^4, so we do binary search for times.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n int limit;\n String message;\n public String[] splitMessage(String message, int limit) {\n this.limit = limit;\n this.message = message;\n int max = 10;\n int min = 1;\n \n for(int i = 1; i<=4; i++) {\n max = Math.min(message.length(), max);\n int m = max;\n int mi = min;\n if(max!=message.length()) max = max-1;\n if(min>message.length()) break;\n if(i == 2) System.out.println(max);\n while(min+1<max) {\n int mid = (max+min)/2;\n int val = helper(mid);\n \n if(val == Integer.MAX_VALUE) max = mid - 1;\n else if(val == Integer.MIN_VALUE) min = mid+1;\n else if(val == message.length()) min = mid;\n else min = mid;\n }\n \n if(helper(min) != message.length()) {\n if(helper(max) == message.length()){\n String[] res = new String[max];\n helper2(res);\n return res;\n }\n } else {\n String[] res = new String[min];\n helper2(res);\n return res;\n }\n max = m;\n min = mi;\n \n max*=10;\n min*=10;\n }\n return new String[0];\n\n }\n \n \n\n public int helper(int count) {\n String s = Integer.toString(count);\n int len = s.length()+3;\n int cur = 1;\n int res = 0;\n while(cur*10-1<count) {\n len+=1;\n res+=(limit-len) * (cur*10-cur);\n cur*=10;\n }\n \n if(len>limit)return Integer.MAX_VALUE;\n \n cur-=1;\n //if(count == 11) System.out.println(count);\n int original = count;\n \n count-=cur;\n \n res+=(limit-(len+1)) * (count - 1);\n if(message.length() - res <= 0) return Integer.MAX_VALUE;\n if(message.length() - res > limit - (len+1)) return Integer.MIN_VALUE;\n return message.length();\n }\n\n public void helper2(String[] res) {\n String post = "/" + Integer.toString(res.length) + ">";\n int start = 0;\n for(int i = 1; i<=res.length-1; i++) {\n String postString = "<" + Integer.toString(i) + post;\n int len = limit - postString.length();\n String sub = message.substring(start, start+len) + postString;\n //System.out.println(sub);\n res[i-1] = sub;\n start+=len;\n }\n String postString = "<" + Integer.toString(res.length) + post;\n res[res.length-1] = message.substring(start, message.length()) + postString;\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
split-message-based-on-limit | Python3 beats 100% | python3-beats-100-by-l33twarrior-5b4i | Approach\n1. reduce limit for 3 chars () and calculate number of parts based on it to get initial number of parts\n2. calculate how many digits we will need for | L33tWarrior | NORMAL | 2024-10-22T16:09:31.351463+00:00 | 2024-10-22T16:09:31.351491+00:00 | 17 | false | # Approach\n1. reduce limit for 3 chars (</>) and calculate number of parts based on it to get initial number of parts\n2. calculate how many digits we will need for total number of parts X in the message (<Y/X>) and adjust limit based on that\n3. calculate how many more spaces we will need for Y (<Y/X>)\n4. if total spaces needed is larger than what we can send with current value of parts, we increase parts and re-adjust limit if needed\n5. check again if number of parts will provide enough space for Y\n6. otherwise we have number of parts and starting limit\n\n# Code\n```python3 []\nclass Solution:\n def splitMessage(self, message: str, limit: int) -> List[str]:\n if limit <= 5:\n return []\n \n n = len(message)\n\n if n == 0:\n return []\n\n og_limit = limit\n limit -= 3 # </>\n parts = n // limit\n parts += 1 if (n % limit) > 0 else 0\n\n d = 1\n while parts >= d:\n limit -= 1\n parts = n // limit\n parts += 1 if (n % limit) > 0 else 0\n d *= 10\n\n while True:\n\n d = 1\n more_spaces_needed = 0\n while parts >= d:\n more_spaces_needed += parts - d + 1\n d *= 10\n\n total_needed = n + more_spaces_needed + parts * (og_limit - limit)\n total_space = parts * og_limit\n if total_space >= total_needed:\n break\n else:\n prev_parts = parts\n parts_to_add = (total_needed - total_space) // limit\n parts += parts_to_add if parts_to_add > 0 else 1\n print(prev_parts, parts)\n if len(str(parts)) > len(str(prev_parts)):\n limit -= 1\n if limit == 0:\n return []\n potential_new_parts = n // limit\n potential_new_parts += 1 if (n % limit) > 0 else 0\n if potential_new_parts > parts:\n parts = potential_new_parts\n \n lst = []\n i = 0\n part_cnt = 1\n parts_str = str(parts)\n d = 1\n while i < n:\n if part_cnt >= d:\n limit -= 1\n d *= 10\n msg_part = message[i:(i + limit)]\n lst.append(msg_part + "<" + str(part_cnt) + "/" + parts_str + ">")\n part_cnt += 1\n i += limit\n return lst\n\n\n \n``` | 0 | 0 | ['Python3'] | 0 |
split-message-based-on-limit | Easy Greedy Solution | easy-greedy-solution-by-kvivekcodes-mppp | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | kvivekcodes | NORMAL | 2024-10-10T10:24:23.282432+00:00 | 2024-10-10T10:24:23.282467+00:00 | 17 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int find_len(int num){\n int ret = 0;\n while(num > 0){\n ret++;\n num /= 10;\n }\n\n return ret;\n }\n vector<string> splitMessage(string s, int limit) {\n if(limit <= 4) return {};\n int n = s.size();\n for(int i = 1; i <= 4; i++){\n int k = 1;\n int ind = 0;\n while(ind < n){\n int len = find_len(k);\n if(len > i) break;\n int rem = limit - i - len - 3;\n ind += rem;\n k++;\n }\n if(ind >= n){\n vector<string> ans;\n int ind = 0;\n for(int i = 1; i < k; i++){\n int len = limit - find_len(i) - find_len(k-1) - 3;\n len = min(len, n - ind);\n string str = s.substr(ind, len);\n str += \'<\';\n str += to_string(i);\n str += \'/\';\n str += to_string(k-1);\n str += \'>\';\n ans.push_back(str);\n\n ind += len;\n }\n return ans;\n }\n }\n\n return {};\n }\n};\n``` | 0 | 0 | ['String', 'Greedy', 'C++'] | 0 |
split-message-based-on-limit | Calculate parts needed based on suffix sizes up to 9999 parts | calculate-parts-needed-based-on-suffix-s-44sy | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | calvitronic | NORMAL | 2024-10-09T21:24:15.231091+00:00 | 2024-10-09T21:27:34.856882+00:00 | 3 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python []\nimport math\nclass Solution(object):\n def splitMessage(self, message, limit):\n """\n :type message: str\n :type limit: int\n :rtype: List[str]\n """\n n = len(message)\n if limit <= 5:\n return []\n \n parts = 0\n if (limit-5) * 9 >= n:\n parts = math.ceil(n / float(limit-5))\n elif (limit-6) * 9 + (limit-7) * 90 >= n:\n parts = 9 + math.ceil((n - (limit-6) * 9) / float(limit-7))\n elif (limit-7) * 9 + (limit-8) * 90 + (limit-9) * 900 >= n:\n parts = 99 + math.ceil((n - (limit-7) * 9 - (limit-8) * 90) / float(limit-9))\n elif (limit-8) * 9 + (limit-9) * 90 + (limit-10) * 900 + (limit-11) * 9000 >= n:\n parts = 999 + math.ceil((n - (limit-8) * 9 - (limit-9) * 90 - (limit-10) * 900) / float(limit-11))\n else:\n return []\n\n parts = int(parts)\n idx = 0\n out = []\n for p in range(1,parts+1):\n chars = limit - 3 - len(str(parts)) - len(str(p))\n prefix = ""\n if p < parts:\n prefix = message[idx:idx+chars]\n else:\n prefix = message[idx:]\n suffix = "<{}/{}>".format(p, parts)\n out.append(prefix+suffix)\n idx = idx+chars\n \n return out\n``` | 0 | 0 | ['Python'] | 0 |
split-message-based-on-limit | Python3 Intuitive: Assume Message Count < 9, Update as Needed O(n) O(n) | python3-intuitive-assume-message-count-9-j7be | Intuition\nAs others noted, problem reduces to finding total number of messages. Let ml=message length. While ml>0, assume total number of messages is <9, now y | jbradleyglenn | NORMAL | 2024-10-05T23:51:09.166551+00:00 | 2024-10-05T23:53:30.474487+00:00 | 15 | false | # Intuition\nAs others noted, problem reduces to finding total number of messages. Let ml=message length. While ml>0, assume total number of messages is <9, now you know how big each message is. After processing message 9, if you still have message length to send, then assume total number of messages <99 instead, and keep sending. Since the suffix for previous messages is off (was /9, now needs to be /99), we sent one (1) too many characters of content in every message we\'ve done so far, so we increase the message length to send (ml) by num messages sent so far. It is impossible when the suffix length >= message length.\n\nThe O(n) from processing each message in the first step doesn\'t matter since we have to do O(n) to create the messages anyway.\n\n# Code\n```python3 []\nclass Solution:\n def splitMessage(self, m: str, pl: int) -> List[str]:\n # guess: O(n), O(n)\n\n # for the a in <a/b>, there are \n # 9-0 = 9 parts of length 1,\n # 99-9 = 90 parts of length 2\n # 999-99 = 900 parts of length 3\n # 9999-999 = 9000 parts of length 4\n # ..\n ml=len(m)\n np,npl=0,0\n while 0<ml:\n npl+=1\n ml+=np \n # stop if can\'t make progress by sending message\n if pl<=3+2*npl:\n return []\n for _ in range(9*(10**(npl-1))):\n if ml<=0:\n break\n np+=1\n ml-=(pl-(3+2*npl))\n ml=len(m)\n i,pi=0,1\n out=[]\n while pi<=np:\n tag=f"<{pi}/{np}>"\n out.append(m[i:i+pl-len(tag)]+tag)\n pi+=1\n i+=(pl-len(tag))\n return out\n``` | 0 | 0 | ['Python3'] | 0 |
split-message-based-on-limit | Two Sub Problems - Find Number of Splits and Split Message | two-sub-problems-find-number-of-splits-a-lpl5 | Intuition\n Describe your first thoughts on how to solve this problem. \nTo split the messages, we need to know the total split, we can get out of the message. | ned1m | NORMAL | 2024-10-05T16:27:35.855949+00:00 | 2024-10-05T16:27:35.855975+00:00 | 9 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo split the messages, we need to know the total split, we can get out of the message. This breaks down the problem into 2 simpler problems.\n- Find number of split\n- Split the message\n# Approach\n<!-- Describe your approach to solving the problem. -->\n## Find Number of Message Split\nDepending on the length of the messages, and the limit, our last suffix could be in the range:\n- <1/1>, ..., <9/9>\n- <10/10>, ..., <99,99>\n- <100/100>, ..., <999/999>\n- ...\n\nLets assume that our last suffix is going t0 be <9/9>.\nThen we calculate number of possible characters all message splits from <1/1> to <9/9> can take as follows:\n```\nnum_chars = limit - 5 // 5 is the length of the suffix <9/9>\nused_chars = 9 * num_chars\ntotal_splits += 9\n```\nif we exhausted all the characters in the message, we know this is our band but we need to determine the actual number of splits.\nFirst we assume our total split is 9. Then we remove any overflow splits from it.\n```\ntotal_splits -= (used_chars - msg_len) / num_chars // 9 is the number of possible splits in this band.\n```\n\nIf we did not exhaust all the message characters, we move to the next suffix band <99/99>.\nfirst we need to determine the remaining message length by subtracting the number of characters we used in the previous band. Notice also that if we used this band to calculate number of characters in the previous band, we could have used 9 characters less than our previous calculation. so we update our remaining message length as follows:\n```\nmsg_len += (prev_used_chars - total_splits)\n```\n\nNext we need to calculate number characters we can use in this band and use it to determine the total used characters in the band.\n```\nnum_chars = limit - 7\nused_chars = 90 * num_chars // 90 because we have already used 9 out of the 99 possible splits in this band.\ntotal_splits += 90\n```\n\nAgain, if we exhausted all the characters in the message, we know this is our band but we need to determine the actual number of splits.\nFirst we assume our total split is 90. Then we remove any overflow splits from it.\ntotal_splits -= (used_chars - msg_len) / num_chars\n\nWe need to repeat this process for every band until we have exhausted all the message characters\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def get_total_splits(self, msg_len: int, limit: int) -> int:\n total_splits: int = 0\n suffix_len: int = 5\n curr_split: int = 9\n\n while msg_len > 0:\n num_chars: int = limit - suffix_len\n if num_chars <= 0:\n return 0\n\n msg_len += total_splits\n total_splits += curr_split\n used_chars: int = num_chars * curr_split\n if used_chars >= msg_len:\n total_splits -= (used_chars - msg_len) // num_chars\n\n msg_len -= used_chars\n curr_split *= 10\n suffix_len += 2\n return total_splits\n\n\n def splitMessage(self, message: str, limit: int) -> List[str]:\n total_splits: int = self.get_total_splits(len(message), limit)\n if total_splits == 0:\n return []\n\n msg_splits: List[str] = []\n total_splits_len: int = len(str(total_splits))\n start_index: int = 0\n for split_index in range(1, total_splits + 1):\n num_chars: int = limit - 3 - len(str(split_index)) - total_splits_len\n curr_msg = message[start_index:start_index+num_chars]\n msg_splits.append(f"{curr_msg}<{split_index}/{total_splits}>")\n start_index += num_chars\n\n return msg_splits\n``` | 0 | 0 | ['Python3'] | 0 |
split-message-based-on-limit | [Python3] Search lowers, if needed binary search | python3-search-lowers-if-needed-binary-s-gdd3 | python3 []\nclass Solution:\n def splitMessage(self, message: str, limit: int) -> List[str]:\n def cnt(x):\n mdig_num = len(str(x))\n | timetoai | NORMAL | 2024-09-29T15:39:57.778842+00:00 | 2024-09-29T15:39:57.778868+00:00 | 23 | false | ```python3 []\nclass Solution:\n def splitMessage(self, message: str, limit: int) -> List[str]:\n def cnt(x):\n mdig_num = len(str(x))\n res = sum(dig_num * (9 * 10 ** (dig_num - 1)) for dig_num in range(1, mdig_num))\n lst = mdig_num * ((9 * 10 ** (mdig_num - 1)) - (10 ** mdig_num - x) + 1)\n return res + lst\n\n n = len(message)\n # print([(x, cnt(x)) for x in range(1, 20)], (99, cnt(99)), (100, cnt(100)), (101, cnt(101)))\n # print([(x, limit - len(str(x)) * 2 + 3 > 0, cnt(x) + n + len(str(x)) * x + 3 * x <= x * limit)\n # for x in (100, 964, 965, 966, 999)])\n for l in range(1, 1001):\n if limit - len(str(l)) * 2 + 3 > 0 and cnt(l) + n + len(str(l)) * l + 3 * l <= l * limit:\n break\n if not (limit - len(str(l)) * 2 + 3 > 0 and cnt(l) + n + len(str(l)) * l + 3 * l <= l * limit):\n l, r = 1, n\n while l < r:\n m = (l + r) // 2\n if limit - len(str(m)) * 2 + 3 > 0 and cnt(m) + n + len(str(m)) * m + 3 * m <= m * limit:\n r = m\n else:\n l = m + 1\n if not (limit - len(str(l)) * 2 + 3 > 0 and cnt(l) + n + len(str(l)) * l + 3 * l <= l * limit):\n return []\n ret = [None] * l\n ll = len(str(l))\n i = 0\n for j in range(l):\n left = limit - (3 + len(str(j + 1)) + ll)\n ret[j] = f"{message[i: i + left]}<{j + 1}/{l}>"\n i += left\n return ret\n \n\n``` | 0 | 0 | ['Python3'] | 0 |
split-message-based-on-limit | My Solution | my-solution-by-vicvictle-v324 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | vicvictle | NORMAL | 2024-09-16T19:02:51.260906+00:00 | 2024-09-16T19:02:51.260933+00:00 | 12 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def splitMessage(self, message: str, limit: int) -> List[str]:\n \n n = len(message)\n\n # First determine the length of thingie\n x = 1\n # Number of msgs needed\n msgCount = 0\n\n # Computes msgCount and its length respectivaly if possible\n while True:\n if (3 + 2 * x) >= limit: # suffix exceeds limit\n # unable to find a number of msgs\n return []\n \n\n # With msgCount of length x, find what msgCount it could be \n def getMsgCount(x):\n msgCount = 0\n total = 0 # max possible msg length\n for i in range(x):\n numMsg = 9 * (10 ** i) # number of messages of length i\n suffixLen = 3 + x + (i + 1) # length of suffix needed\n lenForMsg = limit - suffixLen # available length for actual message\n total += numMsg * lenForMsg\n\n if total >= n: # We know now number of msg has thingie of length x:\n total -= numMsg * lenForMsg # time to figure out min msg needed\n remaining = n - total\n extraNeeded = remaining // lenForMsg + (remaining % lenForMsg > 0) # extra msgs of thingie length i\n msgCount += extraNeeded # We now have number of msgsNeeded, can break\n return msgCount\n else:\n msgCount += numMsg # Otherwise we continue to keep track of numMsg\n \n return 0\n \n msgCount = getMsgCount(x)\n if msgCount != 0:\n break\n\n x += 1 # increase length needed\n\n # print(x)\n # print(msgCount)\n\n # Build output\n output = []\n a = 0 # pointer for string\n currMsgCount = 1\n\n for i in range(x - 1):\n numMsg = 9 * (10 ** i) # number of messages of length i\n suffixLen = 3 + x + (i + 1) # length of suffix needed\n lenForMsg = limit - suffixLen # available length for actual message\n\n for _ in range(numMsg):\n output.append(message[a:a + lenForMsg] + f"<{currMsgCount}/{msgCount}>")\n currMsgCount += 1\n a += lenForMsg\n \n # Finally, rest of messages\n\n while currMsgCount <= msgCount:\n suffixLen = 3 + 2 * x # length of suffix needed\n lenForMsg = limit - suffixLen # available length for actual message\n output.append(message[a:a + lenForMsg] + f"<{currMsgCount}/{msgCount}>")\n a += lenForMsg\n currMsgCount += 1\n\n return output\n\n \n \n``` | 0 | 0 | ['Python3'] | 0 |
split-message-based-on-limit | Python binary search solution | python-binary-search-solution-by-sreejag-epw2 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | sreejagov | NORMAL | 2024-09-13T03:02:49.900654+00:00 | 2024-09-13T03:02:49.900681+00:00 | 42 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution(object):\n def splitMessage(self, message, limit):\n """\n :type message: str\n :type limit: int\n :rtype: List[str]\n """\n\n def can_split_with_parts(num_parts: int) -> list[str]:\n parts = []\n idx = 0\n \n # Loop through each part from 1 to num_parts and build the message parts\n for i in range(1, num_parts + 1):\n suffix = f"<{i}/{num_parts}>"\n suffix_len = len(suffix)\n available_len = limit - suffix_len # Available space for message\n \n if available_len <= 0:\n return [] # Invalid, no space left for the message content\n \n # Cut the message up to the available length\n part = message[idx:idx + available_len]\n \n # If the part + suffix exceeds the limit, return an empty list\n if len(part) + suffix_len > limit:\n return []\n \n parts.append(part + suffix)\n idx += len(part)\n \n # If all characters in the message were used, return the parts\n return parts if idx == len(message) else []\n\n # Perform binary search over the number of parts\n low, high = 1, len(message)\n result = []\n cache_9 = defaultdict(bool)\n while low <= high:\n mid = (low + high) // 2\n candidate = can_split_with_parts(mid)\n \n if candidate:\n result = candidate # Found a valid solution, try fewer parts incl 1\n high = mid - 1\n low = 1\n else:\n #if you dont find a candidate, maybe the number just below its 10**numdigits ie 9 or 99 or 999 or 9999... etc could be a candidate and we might miss the left space if we dont consider those\n num_digits = len(str(abs(mid)))\n if num_digits in cache_9 :\n high = 10**(num_digits-1)-1\n else:\n candidate = can_split_with_parts(10**(num_digits-1)-1)\n if candidate:\n high = 10**(num_digits-1)-1\n cache_9[num_digits] = True\n else:\n low = mid + 1 # No valid solution, need more parts\n return result\n\n\n\n\n\n\n \n \n``` | 0 | 0 | ['Python3'] | 0 |
split-message-based-on-limit | python bruteforce | python-bruteforce-by-renolest-t2qr | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Renolest | NORMAL | 2024-09-04T23:04:25.681318+00:00 | 2024-09-04T23:04:25.681350+00:00 | 7 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def splitMessage(self, message: str, limit: int) -> List[str]:\n def helper(length, limit):\n if (limit-5) * 9 >= length:\n return (length + (limit-5)-1) // (limit-5)\n elif ((limit-6) * 9) + ((limit-7) * 90) >= length:\n return ((length - ((limit-6) * 9) + limit-7 - 1) // ((limit-7))) + 9\n elif ((limit-7) * 9) + ((limit-8) * 90) + ((limit-9)* 900) >= length:\n return ((length - ((limit-7) * 9) - ((limit-8) * 90) + (limit-9)-1) // (limit-9)) + 99\n elif ((limit-8) * 9) + ((limit-9) * 90) + ((limit-10)* 900) + ((limit-11)* 9000) >= length:\n return ((length - ((limit-8) * 9) - ((limit-9) * 90) - ((limit-10) * 900) + (limit-11)-1) // (limit-11)) + 999\n else:\n return 0\n lines = helper(len(message), limit)\n start, end = 0, 0\n res = []\n for i in range(1, lines+1):\n suffix = f"<{i}/{lines}>"\n end = start + limit - len(suffix)\n text = message[start: end]\n res.append(text+suffix)\n start = end\n return res\n\n``` | 0 | 0 | ['Python3'] | 0 |
split-message-based-on-limit | ■■■■■■■■■■BINARY TREE APPROACH, BRAND NEW■■■■■■■■■■ | binary-tree-approach-brand-new-by-user58-08ut | Intuition\n Describe your first thoughts on how to solve this problem. \nbinary approacch, nlogn\ninput arange was 100,000\n\n# Approach\n Describe your approac | user5898VA | NORMAL | 2024-08-27T05:15:54.513285+00:00 | 2024-08-27T05:15:54.513308+00:00 | 4 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nbinary approacch, nlogn\ninput arange was 100,000\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nbinary search\n\n# Complexity\n- Time complexity: m * nlogn\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: m * nlogn\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n vector<string> final_ret;\n bool flag = false;\n\n int get_len_of_num(int n) {\n int cnt = 0;\n \n while (n) {\n n = n / 10;\n cnt++;\n }\n\n return cnt;\n }\n\n bool check_validation(string message, int limit, int dividen_cnt) {\n queue<char> q1;\n int ret = 0;\n\n for (int i = 0; i < message.size(); i++) q1.push(message[i]);\n int length_for_dividen_cnt = get_len_of_num(dividen_cnt);\n\n int i = 0;\n vector<string> temp;\n\n for (i = 1; i <= dividen_cnt; i++) {\n // <1/18>\n string cur_temp = "<" + to_string(i) + "/" + to_string(dividen_cnt) + ">";\n int cur = 1 + get_len_of_num(i) + 1 + length_for_dividen_cnt + 1;\n int iteration = limit - cur;\n\n if (iteration <= 0)\n return false;\n\n string cur_temp2 = "";\n while (!q1.empty() && iteration) {\n cur_temp2.push_back(q1.front());\n q1.pop();\n iteration--;\n }\n\n string input_temp = cur_temp2 + cur_temp;\n temp.push_back(input_temp);\n }\n\n if (q1.size() == 0) {\n final_ret = temp;\n flag = true;\n return true;\n } else\n return false;\n }\n\n vector<string> splitMessage(string message, int limit) {\n int left_array[5] = { 0, 9, 99, 999, 9999 };\n int right_array[5] = { 10, 100, 1000, 10000, 10001 };\n\n for (int k = 0; k < 5; k++) {\n int left = left_array[k];\n int right = right_array[k];\n\n int mid = (left + right) / 2;\n\n while (left != mid) {\n if (check_validation(message, limit, mid))\n right = mid;\n else\n left = mid;\n\n mid = (left + right) / 2;\n }\n\n if (flag)\n break;\n }\n\n return final_ret;\n }\n};\n\n``` | 0 | 0 | ['C++'] | 0 |
split-message-based-on-limit | Easy-to-Understand Binary Search Approach in Java | easy-to-understand-binary-search-approac-nkby | Code\njava []\nclass Solution {\n public String[] splitMessage(String message, int limit) {\n int digit = 1;\n\n while (true) {\n in | user2762Pr | NORMAL | 2024-08-20T15:44:06.850797+00:00 | 2024-08-20T15:44:06.850884+00:00 | 73 | false | # Code\n```java []\nclass Solution {\n public String[] splitMessage(String message, int limit) {\n int digit = 1;\n\n while (true) {\n int left = (int) Math.pow(10, digit - 1);\n int right = (int) Math.pow(10, digit) - 1;\n\n if (left > message.length()) {\n break;\n }\n\n while (left + 1 < right) {\n int mid = left + (right - left) / 2;\n if (canSplit(mid, message, limit) <= 0) {\n right = mid;\n } else {\n left = mid;\n }\n }\n\n if (canSplit(left, message, limit) == 0) {\n return split(left, message, limit);\n }\n\n if (canSplit(right, message, limit) == 0) {\n return split(right, message, limit);\n }\n\n ++digit;\n }\n\n return new String[0];\n }\n\n private String[] split(int n, String message, int limit) {\n String[] substrs = new String[n];\n int start = 0;\n int lenN = len(n);\n\n for (int i = 1; i <= n; ++i) {\n StringBuilder sb = new StringBuilder();\n\n int suffix = 3 + len(i) + lenN;\n int last = limit - suffix;\n int end = Math.min(message.length(), start + last);\n sb.append(message.substring(start, end));\n\n sb.append("<");\n sb.append(i);\n sb.append("/");\n sb.append(n);\n sb.append(">");\n\n substrs[i - 1] = sb.toString();\n start += last;\n }\n\n return substrs;\n }\n\n private int canSplit(int n, String message, int limit) {\n if (n > message.length()) {\n return -1;\n }\n\n int lenN = len(n);\n int total = message.length();\n\n for (int i = 1; i <= n; ++i) {\n if (total <= 0) {\n return -1;\n }\n\n // <i/n>\n int suffix = 3 + len(i) + lenN;\n int last = limit - suffix;\n total -= last;\n }\n\n return total > 0 ? 1 : 0;\n }\n\n private int len(int n) {\n int l = 0;\n while (n > 0) {\n n = n / 10;\n ++l;\n }\n return l;\n }\n}\n``` | 0 | 0 | ['Binary Search', 'Java'] | 0 |
split-message-based-on-limit | Python Solution | python-solution-by-rohamghotbi-v7fr | Not my best work tbh but Does the Job\n# Code\npython3 []\nclass Solution:\n def splitMessage(self, message: str, limit: int) -> List[str]:\n if limit | rohamghotbi | NORMAL | 2024-08-20T09:49:24.946535+00:00 | 2024-08-20T09:49:24.946566+00:00 | 17 | false | Not my best work tbh but Does the Job\n# Code\n```python3 []\nclass Solution:\n def splitMessage(self, message: str, limit: int) -> List[str]:\n if limit < 6:\n return ""\n if len(message) < limit - 5:\n return [f"{message}<1/1>"]\n lo = len(message) // (limit - 5)\n hi = len(message)\n results = {}\n\n while lo <= hi:\n num_secs = (lo + hi) // 2\n tot = len(message)\n res = []\n s = 0\n for i in range(num_secs - 1):\n suffix = f"<{i+1}/{num_secs}>"\n num_chars = limit - len(suffix)\n tot -= num_chars\n res.append(message[s:s + num_chars] + suffix)\n s += num_chars\n\n suffix = f"<{num_secs}/{num_secs}>"\n num_chars = limit - len(suffix)\n if message[s:s + num_chars] == "":\n tot = -1\n else:\n tot -= len(message[s:s + num_chars])\n\n res.append(message[s:s + num_chars] + suffix)\n\n if tot == 0:\n hi = num_secs - 1\n results[num_secs] = res\n lo = 1\n elif tot < 0:\n hi = num_secs - 1\n else:\n lo = num_secs + 1\n\n return results[min(results.keys())] if len(results) else ""\n\n``` | 0 | 0 | ['Python3'] | 0 |
split-message-based-on-limit | Java Solution | java-solution-by-lockmyre-m9gf | Intuition\nIntuition is difficult on this one. Since the question involves getting the least number of parts, binary search should be a reasonable answer; i.e., | lockmyre | NORMAL | 2024-08-10T20:33:23.659678+00:00 | 2024-08-10T20:38:42.794706+00:00 | 22 | false | # Intuition\nIntuition is difficult on this one. Since the question involves getting the least number of parts, binary search should be a reasonable answer; i.e., if the current number uses too few parts, go right. If the current number uses too many parts, go left. If the current number uses just the right amount of parts, you have a possible solution.\n\n# Approach\nThe question then becomes, how do you determine when there are too many or too few parts? Well, when the **suffix** grows greater than the **limit**, you need less parts. When you\'re not able to fit the entirety of **message** inside of the given number of parts, you need more parts.\n\n# Complexity\n- Time complexity:\n$$O(n * log n)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\nclass Solution {\n public String[] splitMessage(String message, int limit) {\n int lo = 1, hi = message.length();\n int leastNumParts = hi + 1;\n\n while (lo <= hi) {\n int mid = lo + (hi - lo) / 2;\n char testResult = testSplit(message, mid, limit);\n\n if (testResult == \'L\')\n hi = mid - 1;\n else if (testResult == \'R\')\n lo = mid + 1;\n else {\n leastNumParts = mid;\n hi = mid - 1;\n lo = 1;\n }\n }\n return leastNumParts > message.length() ? new String[0] : buildSplit(message, leastNumParts, limit);\n }\n\n private char testSplit(String message, int numParts, int limit) {\n int totalLength = 0;\n int digits = String.valueOf(numParts).length();\n \n for (int i = 1; i <= numParts; i++) {\n int suffixLength = 3 + digits + String.valueOf(i).length();\n int partLength = Math.min(limit - suffixLength, message.length() - totalLength);\n\n if (suffixLength >= limit) return \'L\';\n\n totalLength += partLength;\n }\n return totalLength < message.length() ? \'R\' : \'-\';\n }\n \n private String[] buildSplit(String message, int numParts, int limit) {\n String[] parts = new String[numParts];\n int messageIndex = 0;\n int partIndex = 1;\n int numPartsDigits = String.valueOf(numParts).length();\n\n while (messageIndex < message.length()) {\n int partIndexDigits = String.valueOf(partIndex).length();\n int suffixLength = 3 + partIndexDigits + numPartsDigits;\n int contentLength = Math.min(limit - suffixLength, message.length() - messageIndex);\n\n String part = message.substring(messageIndex, messageIndex + contentLength);\n parts[partIndex - 1] = part + "<" + partIndex + "/" + numParts + ">";\n partIndex++;\n\n messageIndex += contentLength;\n }\n\n return parts;\n }\n}\n``` | 0 | 0 | ['Binary Search', 'Java'] | 0 |
split-message-based-on-limit | JS approach for this solution with human readable comments | js-approach-for-this-solution-with-human-ge7h | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | perchytheace | NORMAL | 2024-07-13T21:13:54.833647+00:00 | 2024-07-13T21:13:54.833666+00:00 | 20 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * @param {string} message\n * @param {number} limit\n * @return {string[]}\n */\nvar splitMessage = function(message, limit) {\n \n\n const getSuffLen = (a,b) => {\n return `<${a}/${b}>`.length;\n } \n\n\n // Increase the numnber of parts until we have enough capacity to store mesage\n // OR until the suffixes take up the entire limit (meaning each additional part adds no more capacity)\n\n let numParts = 0;\n let prefixLengthSoFar = 0;\n while(\n 3 + (`${numParts}`.length * 2) < limit && // suffix can still fit in limit\n (numParts * limit) - (prefixLengthSoFar) - (numParts * (3+`${numParts}`.length)) < message.length// we dont have enough capacity yet\n ){\n numParts++; // try adding another part\n prefixLengthSoFar += `${numParts}`.length; // keep track of number of chars used to write prefixes\n }\n\n // same conditon as while loop...\n // Do we have enough capacity to transmit this message? \n // if not, return empty array\n if((numParts * limit) - (prefixLengthSoFar) - (numParts * (3+`${numParts}`.length)) < message.length){\n return []\n }\n\n\n //We have enough capacity with "numParts" # of parts \n // construct response and return it\n let arr = [];\n let l = 0;\n for(let i = 1; i <= numParts; i++){\n const dataLength = limit - getSuffLen(i,numParts);\n const token = `${message.slice(l, l+dataLength)}<${i}/${numParts}>`\n l+=dataLength;\n arr.push(token);\n }\n\n return arr;\n};\n``` | 0 | 0 | ['JavaScript'] | 0 |
split-message-based-on-limit | Simple O(N) code, no tricks, no embedded constants and other shits. | simple-on-code-no-tricks-no-embedded-con-7k6f | Intuition - Only the total\'s size is unknown.\n Describe your first thoughts on how to solve this problem. \n\n# Approach - As moving forward, we update a valu | pretrator | NORMAL | 2024-07-07T19:01:51.500603+00:00 | 2024-07-07T19:01:51.500628+00:00 | 79 | false | # Intuition - Only the total\'s size is unknown.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach - As moving forward, we update a value called globalRemover which allows reducing length at back\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def splitMessage(self, message: str, limit: int) -> List[str]:\n globalRemover = 0\n messageList = []\n pointer = 0\n last = 1\n while(pointer < len(message)):\n curNumLength = len(str(len(messageList) + 1))\n if(curNumLength != last):\n globalRemover += 1\n last = curNumLength\n pointer -= len(messageList)\n rem = limit - 3 - (curNumLength * 2)\n if rem <= 0: return []\n messageList.append([rem, 3, curNumLength])\n pointer += rem\n \n result = []\n lastPointer = 0\n lenMess = len(messageList)\n for ind, messLen in enumerate(messageList):\n start = lastPointer\n end = start + (messLen[0] - (globalRemover - len(str(ind + 1)) + 1))\n mess = message[start: end]\n other = "<" + str(ind + 1) + "/" + str(lenMess) + ">"\n result.append(mess+other)\n lastPointer = end\n return result\n\n``` | 0 | 0 | ['Python3'] | 0 |
split-message-based-on-limit | C++ Dividing a Message into Parts with Order-Preserving Suffixes | c-dividing-a-message-into-parts-with-ord-eu99 | Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem requires splitting a message into multiple segments such that each segment, | orel12 | NORMAL | 2024-07-07T13:48:15.874439+00:00 | 2024-07-07T13:48:15.874462+00:00 | 34 | false | ### Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem requires splitting a message into multiple segments such that each segment, including its suffix indicating its order, fits within a specified character limit. The suffix helps in maintaining the order and completeness of the message segments. To solve this, we need to dynamically determine the optimal number of segments and construct each segment accordingly.\n\n### Approach\n<!-- Describe your approach to solving the problem. -->\n1. **Initial Estimation**: Start by estimating the number of segments based on the message length and limit.\n2. **Adjust Segment Count**: Iteratively adjust the number of segments until it stabilizes. This involves:\n - Calculating the maximum suffix length for the current number of segments.\n - If the suffix length exceeds the limit, return an empty result.\n - Recalculating the number of segments based on the total suffix length and message length.\n3. **Create Segments**: Once the number of segments is determined, split the message into these segments. Each segment includes a portion of the message and its corresponding suffix in the format `<current_segment/total_segments>`.\n4. **Return Result**: Collect all segments into a vector and return it.\n\n### Complexity\n- **Time complexity**:\n The time complexity is $$O(n)$$ because we traverse the message to split it into segments and the while loop iterations are logarithmic concerning the number of segments but overall linear in terms of the message length.\n\n- **Space complexity**:\n The space complexity is $$O(n)$$ where \\(n\\) is the length of the message, primarily for storing the result segments.\n\n# Code\n```\n\nclass Solution {\npublic:\n vector<string> splitMessage(string msg, int limit) {\n int n = msg.size();\n int segCount = max(1, n / limit);\n int prevSegCount = 0;\n\n \n while (prevSegCount != segCount) {\n int maxSuffixLen = calcMaxSuffixLen(segCount);\n if (maxSuffixLen > limit) {\n return {}; \n }\n\n prevSegCount = segCount;\n segCount = (calcTotalSuffixLen(prevSegCount) + n + limit - 1) / limit;\n }\n\n string suffixEnd = "/" + to_string(segCount) + ">";\n int idx = 0;\n vector<string> result;\n result.reserve(segCount);\n\n \n for (int i = 1; i <= segCount; ++i) {\n string suffix = "<" + to_string(i) + suffixEnd;\n int segLen = limit - suffix.size();\n string segContent = msg.substr(idx, segLen) + suffix;\n result.push_back(move(segContent));\n idx += segLen;\n }\n\n return result;\n }\n\n int calcMaxSuffixLen(int segCount) {\n int digits = log10(segCount) + 1;\n return 2 * digits + 3;\n }\n\n \n int calcTotalSuffixLen(int segCount) {\n int digits = log10(segCount) + 1;\n int totalLen = (2 * digits + 3) * segCount;\n\n for (int i = 1, factor = 10; i < digits; ++i, factor *= 10) {\n totalLen -= (factor - 1);\n }\n\n return totalLen;\n }\n};\n\n``` | 0 | 0 | ['C++'] | 0 |
split-message-based-on-limit | no binary search, calculate the number of messages directly | no-binary-search-calculate-the-number-of-mtsy | Approach\nCan we use 9 messages to split the original message? If we cannot, can use 99 messages to split the original message?...\nWe only has to try up to 999 | xslpeter | NORMAL | 2024-06-28T20:07:43.098664+00:00 | 2024-06-28T20:07:43.098687+00:00 | 32 | false | # Approach\nCan we use 9 messages to split the original message? If we cannot, can use 99 messages to split the original message?...\nWe only has to try up to 99999 as there\'re only 10000 chars max so max number of messages is 10000. That\'s what function findMessageCountSize() does, which returns the number of digits of the message count.\n\nAfter we get the number of digits, we call findMessageCount() to find out how many exact messages we need. eg. If we find we need 3 digts for the message count, then we calculate how many chars we can send in the first 99 messages. Then the number of rest messages which index has 3 digits can be calculated. That\'s what findMessageCount() does.\n\n\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution {\npublic:\n vector<string> splitMessage(string message, int limit) {\n int len = findMessageCountSize(message.size(), limit);\n vector<string> res;\n if (len == -1) {\n return res;\n }\n int count = findMessageCount(message.size(), limit, len);\n int start = 0;\n int messageCount = 1;\n string suffix = "/"+to_string(count)+">";\n while (start < message.size()) {\n string msgSuffix = "<"+to_string(messageCount)+suffix;\n int length = limit - msgSuffix.size();\n res.push_back(message.substr(start, length)+msgSuffix);\n start += length;\n ++messageCount;\n }\n return res; \n }\n\n int findMessageCountSize(int mesLen, int limit) {\n for (int i = 1; i <=5; ++i) {\n int cost = 0;\n for (int j = 0; j < i; ++j) {\n cost += pow(10, j)*9*(i+4+j);\n }\n int count = ceil((mesLen+cost)/double(limit));\n if (count <= pow(10, i)-1) {\n return i;\n }\n }\n return -1;\n }\n int findMessageCount(int mesLen, int limit, int countLen) {\n int chars = 0;\n for (int i = 1; i < countLen; ++i) {\n chars += pow(10, i-1)*9*(limit-(countLen+i+3));\n }\n int count = ceil((mesLen - chars) / (limit - (3.0+countLen+countLen)));\n return pow(10, countLen-1) + count - 1;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
split-message-based-on-limit | Easy Java Solution! | easy-java-solution-by-srula-4945 | Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem requires us to split a message into multiple parts where each part ends wit | srula | NORMAL | 2024-06-26T07:20:42.359324+00:00 | 2024-06-26T07:22:16.353277+00:00 | 23 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem requires us to split a message into multiple parts where each part ends with a suffix indicating its position. The length of each part including the suffix should not exceed a given limit, and we aim to use as few parts as possible.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initial Setup: Calculate the total length of the message and initialize variables for the number of parts (b) and the total length of the suffixes (aLength).\n2. Determine Number of Parts (b):\n - Use a while loop to determine the minimum number of parts needed such that the total length of the parts including their suffixes does not exceed the allowed limit.\n - In each iteration, check if the suffix length itself exceeds the limit. If so, return an empty array as it\'s impossible to split the message as required.\n - Update the cumulative length of the indices (aLength) as b increases.\n3. Create Resulting Parts:\n - Initialize an array to store the resulting parts.\n - Iterate over the number of parts and form each part by taking the appropriate substring from the message and appending the suffix.\n - Ensure that the combined length of the message portion and the suffix does not exceed the limit.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n - Calculating the number of parts involves a loop that depends on the number of parts, which can be approximated as O(b).\n - Creating the resulting parts involves another loop over the number of parts, which is also O(b).\n - Overall, the time complexity is O(b), where b is the number of parts.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n - The space used to store the resulting parts is O(b).\n - Additional space is used for storing substrings and suffixes, which is linear in relation to the size of the message.\n - Overall, the space complexity is O(n), where n is the length of the message.\n# Code\n```\nclass Solution {\n public String[] splitMessage(String message, int limit) {\n int n = message.length();\n int part = 1;\n int alen = 1;\n\n // Determine the number of parts (b)\n while(part * limit < (String.valueOf(part).length() + 3) * part + n + alen) {\n if(String.valueOf(part).length() * 2 + 3 >= limit)\n return new String[]{};\n alen += String.valueOf(++part).length();\n }\n\n int b = part;\n String[] ans = new String[b];\n\n // Create resulting parts\n for(int a = 1, i = 0; a <= b; a++) {\n int idx = limit - (3 + String.valueOf(a).length() + String.valueOf(b).length());\n ans[a - 1] = message.substring(i, Math.min(i + idx, message.length())) + \n "<" + String.valueOf(a) + "/" + String.valueOf(b) + ">";\n i += idx;\n }\n\n return ans;\n }\n}\n``` | 0 | 0 | ['Math', 'Java'] | 0 |
split-message-based-on-limit | Solution Beats 100% Binary Search | solution-beats-100-binary-search-by-mych-cs68 | Intuition\n Describe your first thoughts on how to solve this problem. \nBeats 100%\n\n# Approach\n Describe your approach to solving the problem. \nBinary sear | mycherryblossomsareinbloomforu | NORMAL | 2024-06-25T04:47:47.235363+00:00 | 2024-06-25T04:47:47.235393+00:00 | 19 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nBeats 100%\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nBinary search\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(logn)\n\n\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n\n# Code\n```\nclass Solution(object):\n def splitMessage(self, message, limit):\n """\n :type message: str\n :type limit: int\n :rtype: List[str]\n """\n if limit < 5:\n return []\n\n def message_length(num):\n min_length = 4 + len(num)\n operand = 1\n size = 0\n for i in range(len(num) - 1):\n size += (limit - min_length) * 9 * operand\n min_length += 1\n operand *= 10\n calculated = \'9\' * (len(num) - 1) if (len(num) - 1) > 0 else 0\n rest = int(num) - int(calculated)\n max_suffix_len = len(num) * 2 + 3\n size += (limit - max_suffix_len) * rest\n return size\n\n max_part = \'9\'\n while message_length(max_part) < len(message):\n max_part += \'9\'\n if limit < len(max_part) * 2 + 3:\n return []\n \n last_suffix_len = len(max_part) * 2 + 3\n shortest_last_part = last_suffix_len + 1\n bias = limit - shortest_last_part\n hi = int(max_part)\n lo = pow(10, len(max_part) - 1)\n mid = (lo + hi) // 2\n while len(message) < message_length(str(mid)) - bias or \\\n len(message) > message_length(str(mid)):\n if message_length(str(mid)) > len(message):\n hi = mid - 1\n else:\n lo = mid + 1\n mid = (lo + hi) // 2\n \n pointer = 0\n result = []\n\n for i in range(mid):\n msg_len = limit - 3 - len(str(i+1)) - len(str(mid))\n s = message[pointer:pointer+msg_len]\n s = s + \'<\' + str(i+1) + \'/\' + str(mid) + \'>\'\n result.append(s)\n pointer += msg_len\n\n return result\n``` | 0 | 0 | ['Python'] | 0 |
split-message-based-on-limit | Wasn't able to BS it, instead linear for pages with skipping to avoid TLE | wasnt-able-to-bs-it-instead-linear-for-p-m2v2 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | murh | NORMAL | 2024-06-15T14:15:51.623399+00:00 | 2024-06-15T14:15:51.623416+00:00 | 8 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\npublic class Solution {\n public string[] SplitMessage(string message, int limit) {\n var M = message.Length;\n \n var P = 0;\n var canFitMessage = false;\n\n // Sped up linear search\n while(!canFitMessage && P < M) {\n P++;\n var m = M;\n for(var i = 1; i <= P; i++) {\n var suffix = 3 + StrLen(i) + StrLen(P);\n if(limit <= suffix) \n break;\n var mUsed = limit - suffix;\n m -= mUsed;\n }\n\n canFitMessage = m <= 0;\n var skipP = m / limit;\n if(skipP > 0) {\n P += (skipP-1); \n }\n }\n\n if(!canFitMessage) {\n return new string[0] {};\n }\n if(P > M) {\n return new string[0] {};\n }\n\n var result = new List<string>();\n var l = 0;\n var cp = 0;\n\n while(l <= M && cp < P) {\n cp++;\n\n var suffix = 3 + StrLen(cp) + StrLen(P);\n var used = limit - suffix;\n \n var part = message.Substring(l, Math.Min(used, message.Length - l));\n result.Add($"{part}<{cp}/{P}>");\n \n l += used;\n }\n\n if(l < M) {\n return new string[0]{};\n }\n\n return result.ToArray();\n }\n\n int StrLen(int i) => i.ToString().Length;\n}\n``` | 0 | 0 | ['C#'] | 0 |
split-message-based-on-limit | Simple Solution | simple-solution-by-gilbert2-9e4y | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | gilbert2 | NORMAL | 2024-05-28T04:48:50.853181+00:00 | 2024-05-28T04:48:50.853206+00:00 | 61 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom typing import List\n\nclass Solution:\n def splitMessage(self, message: str, limit: int) -> List[str]:\n # \u83B7\u53D6\u6570\u5B57\u7684\u5B57\u7B26\u957F\u5EA6\n def getLen(num: int) -> int:\n return len(str(num))\n\n lenOfSign = 3 # \u6807\u8BB0\u7684\u957F\u5EA6\uFF0C\u5305\u542B <, > \u548C /\n cur = 0 # \u5206\u5272\u8FC7\u7A0B\u4E2D\u7D2F\u79EF\u7684\u7D22\u5F15\u957F\u5EA6\n k = 0 # \u90E8\u5206\u6570\n\n # \u8BA1\u7B97\u6700\u5C0F\u7684\u90E8\u5206\u6570\n while lenOfSign + getLen(k) * 2 < limit and cur + len(message) + (lenOfSign + getLen(k)) * k > limit * k:\n k += 1\n cur += getLen(k)\n\n # \u5206\u5272\u6D88\u606F\n parts = []\n idx = 0\n\n if lenOfSign + getLen(k) * 2 < limit:\n for j in range(1, k + 1):\n suf_len = getLen(j) + getLen(k) + lenOfSign\n par_len = limit - suf_len\n if idx + par_len < len(message):\n parts.append(message[idx:idx + par_len] + f"<{j}/{k}>")\n else:\n parts.append(message[idx:] + f"<{j}/{k}>")\n idx += par_len\n \n return parts\n\n``` | 0 | 0 | ['Python3'] | 0 |
split-message-based-on-limit | EASY || Beats 85% | easy-beats-85-by-sam78692-qctw | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \nFirst we divide the tex | Sam78692 | NORMAL | 2024-05-21T17:35:31.378771+00:00 | 2024-05-21T17:35:31.378800+00:00 | 33 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFirst we divide the text into words with max limit "LIMIT - 5" because ["<_/_>" (5 min characters)] then we will see how many characters will the suffix take acc to ans size(WE WILL DO IT TWICE BEACUSE IN SOME CASE THE ANS SIZE MAY CHANGE FROM 2 DIGIT TO 3 DIGIT).\n\nAnd in the last we put the suffix\n\n# Complexity\n- Time complexity:O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<string> splitMessage(string m, int limit) {\n if(limit <= 5){\n return {};\n }\n vector<string> ans;\n int n = m.length(), i = 0;\n\n while(i < n){\n int l = min(limit - 5, n - i);\n ans.push_back(m.substr(i, l));\n i = i + limit - 5;\n }\n\n int s = 1, place = log10(ans.size()) + 1;\n i = 0;\n ans.clear();\n while(i < n){\n int cntr = limit - 4 - place;\n int c = log10(s);\n cntr -= c;\n if(cntr <= 0){\n return {};\n }\n int l = min(cntr, n - i);\n ans.push_back(m.substr(i, l));\n i = i + cntr;\n s++;\n }\n\n int p = log10(ans.size()) + 1;\n if(p != place){\n s = 1;\n place = p;\n i = 0;\n ans.clear();\n while (i < n)\n {\n int cntr = limit - 4 - place;\n int c = log10(s);\n cntr -= c;\n int l = min(cntr, n - i);\n if(cntr <= 0){\n return {};\n }\n ans.push_back(m.substr(i, l));\n i = i + cntr;\n s++;\n }\n }\n\n n = ans.size();\n int t = log10(n) + 1;\n int maxi_ = (2 * t) + 3;\n if(maxi_ >= limit){\n return {};\n }\n string si = to_string(n);\n string suf = "/" + si + ">";\n\n for(int i = 0; i < n; i++){\n string t = "<" + to_string(i + 1) + suf;\n ans[i] = ans[i] + t;\n }\n\n return ans;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
split-message-based-on-limit | c++ solution | c-solution-by-gamer2023-nsp1 | Intuition\nthis solution is based on @lee215\'s solution in https://leetcode.com/problems/split-message-based-on-limit/solutions/2807533/python-find-the-number- | gamer2023 | NORMAL | 2024-05-06T20:36:41.158727+00:00 | 2024-05-06T20:36:41.158779+00:00 | 18 | false | # Intuition\nthis solution is based on @lee215\'s solution in https://leetcode.com/problems/split-message-based-on-limit/solutions/2807533/python-find-the-number-of-substrings\n\nwith small modifications and comments to help to understand.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n// this solution is based on @lee215\'s solution in https://leetcode.com/problems/split-message-based-on-limit/solutions/2807533/python-find-the-number-of-substrings\n\nclass Solution {\npublic:\n vector<string> splitMessage(string message, int limit) {\n int k=0; // number of split parts\n int indexLen=0; // total string len of all digits from 1 to k\n\n /* find k:\n k needs to meet the following standards:\n 1. max len of suffix can fit in limit (k needs to be small enough)-> 3+to_string(k).size()*2<limit \n 2. there is sufficient message to split to k parts with limit (k needs to be large enough) -> (curr + message.size() + \n (3+to_string(curr).size())*k <= limit*k \n */\n while( (3+to_string(k).size()*2<=limit) && \n (indexLen + message.size() + \n (3+to_string(k).size())*k > limit*k)) {\n k+=1;\n indexLen+=to_string(k).size();\n }\n\n vector<string> res;\n if(3+to_string(k).size()*2>limit) return res; // no result, return\n\n int i=0; // pointer of message, starting from 0\n for(int j=1; j<=k; ++j) {\n int len = limit-(to_string(j).size() + to_string(k).size()+3);\n res.emplace_back(message.substr(i, len) + \n "<" + to_string(j) + "/" + to_string(k) + ">");\n i+=len;\n }\n return res;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
split-message-based-on-limit | dp | dp-by-jaikechen2018-zs43 | \n# Code\n\nfunc splitMessage(message string, limit int) []string {\n idxLen := 0\n ok := false\n for i:= 1; i <= len(message); i ++{\n idxLen, | jaikechen2018 | NORMAL | 2024-04-08T14:34:12.835478+00:00 | 2024-04-08T14:34:12.835506+00:00 | 9 | false | \n# Code\n```\nfunc splitMessage(message string, limit int) []string {\n idxLen := 0\n ok := false\n for i:= 1; i <= len(message); i ++{\n idxLen, ok = find(message, limit, i, idxLen)\n if ok {\n return build(message, limit, i)\n }\n }\n return nil\n}\n\nfunc build(message string, limit, parts int) []string{\n ret := []string{}\n for i := 1 ; i <= parts; i ++{\n suffix := fmt.Sprintf("<%v/%v>", i, parts)\n prefixLen := limit - len(suffix)\n if prefixLen > len(message) {\n prefixLen = len(message)\n }\n w := message[:prefixLen] + suffix\n ret = append(ret, w)\n message = message[prefixLen:]\n }\n return ret\n}\n\nfunc find (message string, limit, parts, idxLen int) (int, bool){\n idxLen += nl(parts) // for the new added <14/14>\n if len(message) + idxLen + (nl(parts) + len("</>")) * parts <= limit * parts{\n return idxLen, true\n }\n return idxLen, false\n}\n\nfunc nl (n int) int{\n return len(strconv.Itoa(n))\n}\n``` | 0 | 0 | ['Go'] | 0 |
split-message-based-on-limit | An recursive implementation | an-recursive-implementation-by-jcodefun-vj9a | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | JCodeFun | NORMAL | 2024-04-03T22:25:40.317947+00:00 | 2024-04-03T22:26:03.504026+00:00 | 45 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(log_10 N * N/limit)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n\n# Code\n```\nclass Solution:\n # O(log_10 N * N/limit)\n def splitMessage(self, message: str, limit: int) -> List[str]:\n N = len(message)\n\n # O(N / (limit-tagLen)), roughtly O(N/limit)\n def dfs(bLen, start, count):\n tag = f\'<{count}/>\'\n tagLen = len(tag) + bLen\n if len(str(count)) > bLen or start >= N:\n return -1\n\n if N-start+tagLen <= limit:\n return count\n\n res = dfs(bLen, start+limit-tagLen, count+1)\n return res\n\n count = -1\n # O(log_10 N)\n for i in range(len(str(N))):\n count = dfs(i+1, 0, 1)\n if count > -1:\n break\n \n res = []\n if count == -1:\n return res\n\n start = 0\n # O(N/limit)\n for i in range(count):\n tag = f\'<{i+1}/{count}>\'\n txtLen = limit-len(tag) \n end = start + txtLen\n txt = f\'{message[start : end]}{tag}\'\n res.append(txt)\n start = end\n\n return res\n``` | 0 | 0 | ['Python3'] | 0 |
split-message-based-on-limit | Java solution -> calculate necessary parts first | java-solution-calculate-necessary-parts-ub517 | Intuition\nCalculate the necessary number of parts, then fill in the array.\n\n# Approach\nFirst try to use only one part, then allocate the remaining message e | adamk90 | NORMAL | 2024-03-31T19:34:12.731184+00:00 | 2024-03-31T19:34:12.731230+00:00 | 57 | false | # Intuition\nCalculate the necessary number of parts, then fill in the array.\n\n# Approach\nFirst try to use only one part, then allocate the remaining message evenly respect to the needed suffix size. Keep on trying with increasing number of parts until we find the right number to eliminate all the message (no remainings).\n\nAssembling the array is trivial.\n\n# Complexity\n- Time complexity:\nO(n) - the worst case when you need to allocate the message into parts one character at a time\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution {\n private String message;\n private int limit;\n\n public String[] splitMessage(String message, int limit) {\n /* Not enough space for even smallest suffix */\n if (limit - 5 <= 0) {\n return new String[0];\n }\n this.message = message;\n this.limit = limit - 3;\n \n int n = 1;\n int parts = calcPartsNum(n);\n while (n < parts) {\n n = parts;\n parts = calcPartsNum(n);\n }\n \n /* Suffix hit limit or went above it */\n if (parts <= 0) {\n return new String[0];\n }\n\n return assembleMessageArray(parts);\n }\n\n private int calcPartsNum(int n) {\n int numbers = String.valueOf(n).length();\n int remainingMessageLength = message.length();\n int currentSuffixLength = 1 + numbers;\n int partNum = 0;\n for (int i = 1; i < numbers; ++i) {\n int currParts = (int)(Math.pow(10, i) - Math.pow(10, i - 1));\n partNum += currParts;\n remainingMessageLength -= currParts * (this.limit - currentSuffixLength);\n currentSuffixLength += 1;\n if (this.limit - currentSuffixLength <= 0) {\n return 0;\n }\n }\n remainingMessageLength -= (n - partNum) * (this.limit - currentSuffixLength);\n return n + (int)Math.ceil((double)remainingMessageLength / (this.limit - currentSuffixLength));\n }\n\n private String[] assembleMessageArray(int n) {\n String[] ret = new String[n];\n for (int i = 1, index = 0; i <= n; ++i) {\n int currLength = this.limit - String.valueOf(i).length() - String.valueOf(n).length();\n if (index + currLength >= this.message.length()) {\n currLength = this.message.length() - index;\n }\n ret[i - 1] = this.message.substring(index, index + currLength) + "<" + String.valueOf(i) + "/" + String.valueOf(n) + ">";\n index += currLength;\n }\n return ret;\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
split-message-based-on-limit | Binary search, O(log2(N)), fix regular binary search not working for some cases | binary-search-olog2n-fix-regular-binary-hfs4c | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\nFixed bug in binary search, search from 10, 100, 1000 ... return whenever | fath2012 | NORMAL | 2024-02-24T23:24:21.776431+00:00 | 2024-02-24T23:24:21.776463+00:00 | 29 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nFixed bug in binary search, search from 10, 100, 1000 ... return whenever the parts is too big or correct size\n\n# Complexity\n- Time complexity:\nO(log2(N))\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<string> splitMessage(string message, int limit) {\n\n vector<string> ans;\n\n if(limit>=message.size()+5) {\n ans.push_back(message+"<1/1>");\n }\n\n int sufLen[5];\n sufLen[0] = 0;\n sufLen[1] = 6*9; // first 9 with two digit, 10<= len <100\n sufLen[2] = sufLen[1]+9 + 90*(3+5); // first 99 with 3 digit, 100=<len<1000\n sufLen[3] = sufLen[2]+99 + 900*(3+7); // first 999 with 4 digit, 1000=<len<10000\n sufLen[4] = sufLen[3]+999 + 9000*(3+9); //10^4\n\n int n = message.size();\n int left =n/limit;\n int right = n*(1+3+10)/limit;\n\n int parts, res, minParts = -1;;\n while(left<=right) {\n parts = (left+right)/2;\n res = testSplit(n, limit, parts, sufLen);\n if(res==1) {\n break;\n }\n else if(res==0) {\n left = parts+1;\n } else {\n right = parts-1;\n }\n }\n \n if(res!=1) return ans;\n return splitMessage2(message, limit, parts);\n }\n\nprivate:\n\n int countDigits(int n) {\n int count = 1;\n while(n/10>0) {\n count++;\n n = n/10;\n }\n return count;\n }\n\n int testSplit(int total, int limit, int &parts, int* sufLen) {\n int res;\n int digNum = countDigits(parts);\n int tenpow = 10;\n\n while(parts>=tenpow) {\n res = testSplit2(total, limit, tenpow-1, sufLen); // use 9, 99, 999 as parts first\n if(res>=1) { // too big or fit, don\'t need to go to next digit\n parts = tenpow-1;\n return res;\n }\n tenpow *= 10;\n }\n return testSplit2(total, limit, parts, sufLen);\n }\n \n int testSplit2(int total, int limit, int parts, int* sufLen) {\n \n int digNum = countDigits(parts);\n int i = digNum;\n int tenpow = 1;\n while(i>0) {\n tenpow *= 10;\n i--;\n }\n\n int lastSufSize = (3+2*digNum) ;\n int sufLen2 = sufLen[digNum-1] + (parts-(tenpow/10-1))*lastSufSize;\n\n if(lastSufSize>=limit) return 2; // parts size too big\n if(parts*limit<total+sufLen2) return 0; //too small\n if(parts*limit>=total+sufLen2 && (parts-1)*limit<total+sufLen2-lastSufSize) return 1; // fit\n else return 2; // too big\n }\n\n vector<string> splitMessage2(string message, int limit, int parts) {\n vector<string> res;\n\n string sp2 = "/"+ to_string(parts) + ">";\n int curPos=0;\n for(int i=0;i<parts-1;i++) {\n string sp1 = "<"+ to_string(i+1) + sp2;\n int k = limit - sp1.size();\n string curStr = message.substr(curPos, k);\n res.push_back(curStr+sp1);\n curPos += k;\n }\n\n string sp1 = "<"+ to_string(parts) + sp2;\n int k = message.size()-curPos;\n string curStr = message.substr(curPos, k);\n res.push_back(curStr+sp1);\n return res;\n\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
split-message-based-on-limit | Java Solution | java-solution-by-ck1612-nzsl | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | ck1612 | NORMAL | 2024-02-06T21:40:47.365674+00:00 | 2024-02-06T21:40:47.365706+00:00 | 55 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public String[] splitMessage(String message, int limit) {\n int n = message.length();\n int i = 0;\n long maxPossible =0;\n do {\n i++;\n long max = (long)Math.pow(10, i);\n long a = (max - (long)Math.pow(10L, i-1)) * (i-1);\n long b = (max-1) * (i-1 + 5) ;\n maxPossible = (limit * (max -1)) - (a + b); \n if(maxPossible <=0) return new String[0];\n } while(maxPossible < n);\n\n List<String> parts = new ArrayList<>();\n int j =0;\n int a =1;\n while(j < n ) {\n String aString = Integer.toString(a);\n int countA = aString.length();\n int e = Math.min(n , j + limit - i - countA - 3);\n String s = message.substring(j, e) + "<" + aString + "/";\n parts.add(s);\n j = e;\n a++;\n }\n int m = parts.size();\n String[] res = new String[m];\n String b = Integer.toString(m);\n for(int k =0 ; k < m ; k++) {\n res[k] = parts.get(k) + b + ">";\n }\n\n return res;\n\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
split-message-based-on-limit | [Python3] 99% solution | python3-99-solution-by-zhfang1111-876f | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | zhfang1111 | NORMAL | 2024-01-27T17:22:30.849343+00:00 | 2024-01-27T17:22:30.849368+00:00 | 190 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def splitMessage(self, message: str, limit: int) -> List[str]:\n n = len(message)\n b = self.find_b(n, limit)\n\n if b == -1:\n return []\n\n return self.construct_parts(message, b, limit)\n\n def construct_parts(self, message, b, l):\n parts = []\n nb = len(str(b))\n index = 0\n\n for i in range(1, nb+1):\n a_start = int("1" + "".join(["0" for _ in range(i-1)]))\n a_end = int("".join(["9" for _ in range(i)]))\n for a in range(a_start, a_end+1):\n\n suffix = f"<{a}/{b}>"\n len_mes = l - len(suffix)\n segment = message[index:index+len_mes]\n segment = segment + suffix\n parts.append(segment)\n index += len_mes\n if a >= b:\n return parts\n\n\n\n \n def find_b(self, n, l):\n nb = 1\n\n while True:\n if l - (3 + nb + nb) <= 0:\n break\n\n # compute length of covered message for len(str(a)) < len(str(b))\n covered_mes = 0\n for i in range(1, nb):\n len_suffix = 3 + nb + i\n len_mes = l - len_suffix\n\n num_parts = self.get_num_parts(i)\n covered_mes += num_parts * len_mes\n\n remain = n - covered_mes\n len_suffix = 3 + nb + nb\n len_mes = l - len_suffix\n req_remain_num_parts = math.ceil(remain / len_mes)\n\n if nb == 1:\n req_b = req_remain_num_parts\n else:\n req_b = int("".join(["9" for _ in range(nb - 1)])) + req_remain_num_parts\n max_b = int("".join(["9" for _ in range(nb)]))\n if req_b <= max_b:\n return req_b\n nb += 1\n\n return -1\n\n def get_num_parts(self, i):\n if i == 1:\n return 9\n\n hi = "".join(["9" for _ in range(i)])\n lo = "1" + "".join(["0" for _ in range(i - 1)])\n return int(hi) - int(lo) + 1\n``` | 0 | 0 | ['Python3'] | 0 |
split-message-based-on-limit | Brute Force O(n). Just a Simple Trick.✅✅ | brute-force-on-just-a-simple-trick-by-co-lulg | Intuition\n Describe your first thoughts on how to solve this problem. \nObservation1:\nWhen you observe every suffix will be minimum of length 5. How?\n => of | code__hard | NORMAL | 2024-01-25T20:21:46.853121+00:00 | 2024-01-25T20:21:46.853141+00:00 | 872 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nObservation1:\nWhen you observe every suffix will be minimum of length 5. How?\n<a/b> => </> of length 3 + single_digit_a + single_digit_b.\nSo if your given limit is <=5 then return [].\n\nObservation2:\nWe need to find the no_of_digits in given range from [1,max_part].\nThis is the mathematical part.\nThere are 9 single digit numbers[1,9]\nThere are 90 two digit numbers [10,99]\nThere are 900 three digit numbers [100,999]\nThere are 9000 four digit numbers [1000,9999]\n.........\nUse this concept the calculate number of digits.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nRun for loop from range(math.ceil(n/limit),some_max_number).\nCalulate the total lenght of op string if we take i parts.\nI break down finding this into 4 parts.\ntotal_length=<a_length/b_length>+sum(given_string)\nb_length=len(str(i))\na_length is calculate by using the technique above.\nevery part has 3 lenth i.e; "</>"\nno check if math.ceil(total_length/limit)<= i\nIf true add releavent characters to op.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n# Code\n```\nclass Solution:\n\n def splitMessage(self, message: str, limit: int) -> List[str]:\n if limit<=5:\n return []\n\n n=len(message)\n \n def calculate(val):\n op=0\n if val>9:\n op+=9\n elif val<=9:\n op+=val\n if val>99:\n op+=(90*2)\n elif 10<=val<=99:\n digits=val-10+1\n print(digits)\n op+=(digits*2)\n if val>999:\n op+=(900*3)\n elif 100<=val<=999:\n digits=val-100+1\n op+=(digits*3)\n if val>10000:\n op+=(9000*4)\n elif 1000<=val<=9999:\n digits=val-1000+1\n op+=(digits*4)\n return op\n\n #print(calculate(40))\n op=[]\n \n for no_of_parts in range(math.ceil(n/limit),10000):\n b_length=len(str(no_of_parts))*no_of_parts\n brackets=3*no_of_parts\n a_length=calculate(no_of_parts)\n\n total=n+a_length+brackets+b_length\n\n if math.ceil(total/limit)==no_of_parts:\n #print(no_of_parts)\n \n i=0\n present_part=1\n while(i<n):\n #print(op)\n already_taken=(3+len(str(present_part))+len(str(no_of_parts)))\n remaining=limit-already_taken\n #print(remaining)\n present_string=""\n while(i<n and remaining>0):\n present_string+=message[i]\n i+=1\n remaining-=1\n present_string+=("<"+str(present_part)+"/"+str(no_of_parts)+">")\n op.append(present_string)\n present_part+=1\n break\n\n return op\n``` | 0 | 0 | ['Math', 'Python3'] | 1 |
split-message-based-on-limit | Binary search solution | binary-search-solution-by-haomingw-5fxp | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\nfindLen(9, 8) > findLen(10, 8). Need to define the right bounder of binar | haomingw | NORMAL | 2024-01-23T20:58:50.900305+00:00 | 2024-01-23T20:58:50.900337+00:00 | 51 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nfindLen(9, 8) > findLen(10, 8). Need to define the right bounder of binary search in {9, 99, 999, 999} first.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution {\n public String[] splitMessage(String message, int limit) {\n int len = message.length();\n int part = findPart(len, limit);\n if(part == -1) return new String[0];\n int partIndex = 1;\n StringBuilder sb = new StringBuilder();\n String[] res = new String[part];\n for(int i = 0; i < len; i ++) {\n sb.append(message.charAt(i));\n int suffixLen = 3 + countDigit(part) + countDigit(partIndex);\n if(sb.length() + suffixLen == limit || i == len - 1) {\n sb.append("<" + partIndex + "/" + part + ">");\n res[partIndex - 1] = sb.toString();\n partIndex++;\n sb = new StringBuilder();\n }\n }\n return res;\n }\n\n private int findPart(int len, int limit) { \n int[] partSection = {9, 99, 999, 9999};\n int left = 0;\n int index = 0;\n while(index <= 3 && getLen(partSection[index], limit) < len) {\n index++;\n }\n if(index > 3) return -1;\n int right = partSection[index];\n while(left <= right) {\n int mid = left + (right - left) / 2;\n if(getLen(mid, limit) < len) left = mid + 1;\n else right = mid - 1;\n }\n return left;\n }\n\n private int getLen(int part, int limit) {\n int res = part * (limit - 3 - countDigit(part));\n int cur = 1;\n int digit = 1;\n while(cur * 10 < part) {\n res -= digit * cur * 9;\n cur *= 10;\n digit++;\n }\n res -= (part - cur + 1) * digit;\n return res;\n }\n\n private int countDigit(int num) {\n return Integer.toString(num).length();\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
split-message-based-on-limit | Binary search is wrong | binary-search-is-wrong-by-crazy_y-vnbt | \n Describe your first thoughts on how to solve this problem. \nBinary search only works when the answer is monotonic, which means if you can split it into x pa | crazy_y | NORMAL | 2024-01-16T10:33:17.048390+00:00 | 2024-01-16T10:33:17.048415+00:00 | 21 | false | \n<!-- Describe your first thoughts on how to solve this problem. -->\nBinary search only works when the answer is monotonic, which means if you can split it into x parts, it must can be split into x+1 parts. but it is not true, consider a case where you can split a long message into 999 parts, but you may not split it into 1000 parts, because 1000 is one character more than 999, will take 999 more characters in first 999 parts, but the new 1000th part holds less than 999 characters (when limit is less than 999). | 0 | 0 | ['C++'] | 0 |
merge-in-between-linked-lists | 🔥✅✅ Beat 97.13% | ✅ Full Explanation ✅✅🔥 | beat-9713-full-explanation-by-devogabek-i3u7 | Show your appreciation by clicking the upvote button\n# UPVOTE\n# UPVOTE\n# UPVOTE\n# UPVOTE\n# UPVOTE\n# UPVOTE\n# UPVOTE\n# UPVOTE\n# UPVOTE\n\n\n\n\n\n\n\n\n | DevOgabek | NORMAL | 2024-03-20T00:08:23.602604+00:00 | 2024-03-20T18:04:48.263130+00:00 | 19,216 | false | # Show your appreciation by clicking the upvote button\n# UPVOTE\n# UPVOTE\n# UPVOTE\n# UPVOTE\n# UPVOTE\n# UPVOTE\n# UPVOTE\n# UPVOTE\n# UPVOTE\n\n\n\n[](https://leetcode.com/problems/merge-in-between-linked-lists/submissions/1208633836?envType=daily-question&envId=Invalid%20Date)\n\n\n\n\n\n\n\n\n\n<details>\n<summary><b>Click here to see the text explanation</b></summary>\n<br>\n<br>\n\n1. **Initialization**:\n - `ptr` is initialized to `list1`. This will serve as a pointer to navigate to the node just before the `a`th node in `list1`.\n - `qtr` is initialized to the node after `ptr`. This will serve as a pointer to navigate to the node after the `b`th node in `list1`.\n\n2. **Navigating to the Appropriate Positions**:\n - A loop is used to move `ptr` to the node just before the `a`th node in `list1`. It iterates `a - 1` times.\n - Another loop is used to move `qtr` to the node after the `b`th node in `list1`. It iterates `b - a + 1` times.\n\n3. **Merging `list2` into `list1`**:\n - The `next` pointer of the node pointed by `ptr` is updated to point to the head of `list2`, effectively inserting `list2` into `list1` at position `a`.\n - Then, it traverses through `list2` until it reaches the last node.\n - Finally, it sets the `next` pointer of the last node of `list2` to point to the node pointed by `qtr`, effectively linking `list2` to `list1` after the removed portion.\n\n4. **Return**: \n - It returns `list1`, which now represents the merged linked list.\n</details>\n\n<br>\n<br>\n\n```python []\nclass Solution(object):\n def mergeInBetween(self, list1, a, b, list2):\n ptr = list1\n for _ in range(a - 1):\n ptr = ptr.next\n \n qtr = ptr.next\n for _ in range(b - a + 1):\n qtr = qtr.next\n \n ptr.next = list2\n while list2.next:\n list2 = list2.next\n list2.next = qtr\n \n return list1\n```\n```python3 []\nclass Solution:\n def mergeInBetween(self, list1: ListNode, a: int, b: int, list2: ListNode) -> ListNode:\n ptr = list1\n for _ in range(a - 1):\n ptr = ptr.next\n \n qtr = ptr.next\n for _ in range(b - a + 1):\n qtr = qtr.next\n \n ptr.next = list2\n while list2.next:\n list2 = list2.next\n list2.next = qtr\n \n return list1\n```\n```C++ []\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n ListNode* ptr = list1;\n for (int i = 0; i < a - 1; ++i)\n ptr = ptr->next;\n \n ListNode* qtr = ptr->next;\n for (int i = 0; i < b - a + 1; ++i)\n qtr = qtr->next;\n \n ptr->next = list2;\n while (list2->next)\n list2 = list2->next;\n list2->next = qtr;\n \n return list1;\n }\n};\n```\n```javascript []\nvar mergeInBetween = function(list1, a, b, list2) {\n let ptr = list1;\n for (let i = 0; i < a - 1; ++i)\n ptr = ptr.next;\n \n let qtr = ptr.next;\n for (let i = 0; i < b - a + 1; ++i)\n qtr = qtr.next;\n \n ptr.next = list2;\n while (list2.next)\n list2 = list2.next;\n list2.next = qtr;\n \n return list1;\n};\n```\n\n\n<hr>\n\n*These solutions are sorted from easiest to most challenging problems, tailored to your expertise*\n\n<details>\n<summary><b>Click here to see more of my solutions</b></summary>\n\n## **My solutions**\n\n\uD83D\uDFE2 - easy \n\uD83D\uDFE1 - medium \n\uD83D\uDD34 - hard\n\n**These solutions are sorted from easiest to most challenging problems, tailored to your expertise.**\n\n\uD83D\uDFE2 [9. Palindrome Number](https://leetcode.com/problems/palindrome-number/solutions/4795373/why-not-1-line-of-code-python-python3-c-everyone-can-understand/)\n\uD83D\uDFE2 [1. Two Sum](https://leetcode.com/problems/two-sum/solutions/4791305/5-methods-python-c-python3-from-easy-to-difficult/)\n\uD83D\uDFE2 [35. Search Insert Position](https://leetcode.com/problems/search-insert-position/solutions/4898401/beat-100-full-explanation-binary-search-demystified)\n\uD83D\uDFE2 [543. Diameter of Binary Tree](https://leetcode.com/discuss/topic/4787634/surpassing-9793-memory-magician-excelling-at-9723/)\n\uD83D\uDFE2 [2864. Maximum Odd Binary Number](https://leetcode.com/problems/maximum-odd-binary-number/solutions/4802402/visual-max-odd-binary-solver-python-python3-javascript-c)\n\uD83D\uDFE2 [2864. Maximum Odd Binary Number](https://leetcode.com/problems/maximum-odd-binary-number/solutions/4802402/visual-max-odd-binary-solver-python-python3-javascript-c)\n\uD83D\uDFE2 [977. Squares of a Sorted Array](https://leetcode.com/problems/squares-of-a-sorted-array/solutions/4807704/square-sorter-python-python3-javascript-c/)\n\uD83D\uDFE2 [876. Middle of the Linked List](https://leetcode.com/problems/middle-of-the-linked-list/solutions/4834682/beat-10000-full-explanation-with-pictures)\n\uD83D\uDFE2 [3028. Ant on the Boundary](https://leetcode.com/problems/ant-on-the-boundary/solutions/4837433/full-explanation-with-pictures)\n\uD83D\uDFE2 [3005. Count Elements With Maximum Frequency](https://leetcode.com/problems/count-elements-with-maximum-frequency/solutions/4839796/beat-8369-full-explanation-with-pictures)\n\uD83D\uDFE2 [2540. Minimum Common Value](https://leetcode.com/problems/minimum-common-value/solutions/4845076/beat-9759-full-explanation-with-pictures)\n\uD83D\uDFE2 [101. Symmetric Tree](https://leetcode.com/problems/symmetric-tree/solutions/4848126/beat-100-full-explanation-with-pictures)\n\uD83D\uDFE2 [349. Intersection of Two Arrays](https://leetcode.com/problems/intersection-of-two-arrays/solutions/4850588/beat-100-full-explanation-with-pictures)\n\uD83D\uDFE2 [88. Merge Sorted Array](https://leetcode.com/problems/merge-sorted-array/solutions/4856902/beat-100-full-explanation-with-pictures/)\n\uD83D\uDFE2 [136. Single Number](https://leetcode.com/problems/single-number/solutions/4862807/master-the-xor-trick-beat-9720-with-full-explanation)\n\uD83D\uDFE2 [283. Move Zeroes](https://leetcode.com/problems/move-zeroes/solutions/4864068/mastering-efficiency-beat-9871)\n\uD83D\uDFE2 [108. Convert Sorted Array to Binary Search Tree](https://leetcode.com/problems/convert-sorted-array-to-binary-search-tree/solutions/4864578/mastering-efficiency-beat-8974)\n\uD83D\uDFE2 [2485. Find the Pivot Integer](https://leetcode.com/problems/find-the-pivot-integer/solutions/4866463/beat-100-full-explanation-with-pictures)\n\uD83D\uDFE2 [104. Maximum Depth of Binary Tree](https://leetcode.com/problems/maximum-depth-of-binary-tree/solutions/4876170/beat-100-full-explanation-with-pictures)\n\uD83D\uDFE1 [1669. Merge In Between Linked Lists](https://leetcode.com/problems/merge-in-between-linked-lists/solutions/4898944/beat-97-13-full-explanation)\n\uD83D\uDFE1 [513. Find Bottom Left Tree Value](https://leetcode.com/problems/find-bottom-left-tree-value/solutions/4792022/binary-tree-explorer-mastered-javascript-python-python3-c-10000-efficiency-seeker/)\n\uD83D\uDFE1 [1609. Even Odd Tree](https://leetcode.com/problems/even-odd-tree/solutions/4797529/even-odd-tree-validator-python-python3-javascript-c/)\n\uD83D\uDFE1 [19. Remove Nth Node From End of List](https://leetcode.com/problems/remove-nth-node-from-end-of-list/solutions/4813340/beat-10000-full-explanation-with-pictures/)\n\uD83D\uDFE1 [948. Bag of Tokens](https://leetcode.com/problems/bag-of-tokens/solutions/4818912/beat-10000-full-explanation-with-pictures)\n\uD83D\uDFE1 [1750. Minimum Length of String After Deleting Similar Ends](https://leetcode.com/problems/minimum-length-of-string-after-deleting-similar-ends/solutions/4824224/beat-10000-full-explanation-with-pictures)\n\uD83D\uDFE1 [17. Letter Combinations of a Phone Number](https://leetcode.com/problems/letter-combinations-of-a-phone-number/solutions/4845532/there-is-an-80-chance-of-being-in-the-interview-full-problem-explanation)\n\uD83D\uDFE1 [22. Generate Parentheses](https://leetcode.com/problems/generate-parentheses/solutions/4845742/beat-9334-simple-explanation-with-pictures)\n\uD83D\uDFE1 [39. Combination Sum](https://leetcode.com/problems/combination-sum/solutions/4847482/beat-8292-full-explanation-with-pictures)\n\uD83D\uDFE1 [1171. Remove Zero Sum Consecutive Nodes from Linked List](https://leetcode.com/problems/remove-zero-sum-consecutive-nodes-from-linked-list/solutions/4862064/mastering-efficiency-beat-9231-with-full-explanation-and-visuals)\n\uD83D\uDFE1 [238. Product of Array Except Self](https://leetcode.com/problems/product-of-array-except-self/solutions/4876797/beat-8080-full-explanation-with-pictures)\n\uD83D\uDFE1 [57. Insert Interval](https://leetcode.com/problems/insert-interval/solutions/4885946/beat-9722-full-explanation-with-pictures)\n\uD83D\uDFE1 [452. Minimum Number of Arrows to Burst Balloons](https://leetcode.com/problems/minimum-number-of-arrows-to-burst-balloons/solutions/4890366/beat-9380-full-explanation-with-pictures)\n\uD83D\uDFE1 [131. Palindrome Partitioning](https://leetcode.com/problems/palindrome-partitioning/solutions/4892678/beat-9373-full-explanation-with-pictures)\n\uD83D\uDFE1 [930. Binary Subarrays With Sum](https://leetcode.com/problems/binary-subarrays-with-sum/solutions/4872569/beat-8020-full-explanation-with-pictures)\n\n[More...](https://leetcode.com/DevOgabek/)\n\n</details>\n\n<hr>\n<details>\n<summary><b>Why I do not respond to negative comments</b></summary>\n\n## **Why I do not respond to negative comments**\n\n\n\n</details>\n\n<hr>\n | 98 | 4 | ['Linked List', 'Python', 'C++', 'Python3', 'JavaScript'] | 17 |
merge-in-between-linked-lists | [Java/Python 3] Straight forward codes w/ comments and analysis. | javapython-3-straight-forward-codes-w-co-67li | \n\njava\n public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n ListNode end = list1, start = null;\n for (int i = | rock | NORMAL | 2020-11-28T16:04:08.077420+00:00 | 2020-11-29T14:06:35.337947+00:00 | 9,322 | false | \n\n```java\n public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n ListNode end = list1, start = null;\n for (int i = 0; i < b; ++i, end = end.next) { // locate b upon termination of the loop.\n if (i == a - 1) { // locate the node right before a.\n start = end;\n }\n }\n start.next = list2; // connect the node right before a to the head of list2, hence cut off a from list1.\n while (list2.next != null) { // traverse till the end of list2. \n list2 = list2.next;\n }\n list2.next = end.next; // connect end of list2 to the node right after b.\n end.next = null; // cut off b from list1.\n return list1;\n }\n```\n\n```python\n def mergeInBetween(self, list1: ListNode, a: int, b: int, list2: ListNode) -> ListNode:\n start, end = None, list1\n for i in range(b):\n if i == a - 1:\n start = end\n end = end.next\n start.next = list2\n while list2.next:\n list2 = list2.next\n list2.next = end.next\n end.next = None\n return list1\n```\n**Analysis:**\n\nTime: O(n), space: O(1), where n = size(list1) + size(list2). | 71 | 4 | [] | 13 |
merge-in-between-linked-lists | [C++] easy approch | c-easy-approch-by-sanjeev1709912-2g0q | null | sanjeev1709912 | NORMAL | 2020-11-28T16:05:29.476898+00:00 | 2020-11-28T16:24:22.165231+00:00 | 7,406 | false | <iframe src="https://leetcode.com/playground/aE2EFkMv/shared" frameBorder="0" width="1000" height="400"></iframe> | 62 | 3 | [] | 8 |
merge-in-between-linked-lists | Java easy solution - beats 100% Time O(n) Space - O(1) | java-easy-solution-beats-100-time-on-spa-p3pp | Approach\n Assign left pointer as list1 and traverse till you find a value\n Have middle pointer and traverse till you find b value\n Map the left to list2 and | vinsinin | NORMAL | 2020-12-30T02:13:23.647859+00:00 | 2020-12-30T02:13:23.647919+00:00 | 3,164 | false | **Approach**\n* Assign `left` pointer as `list1` and traverse till you find `a` value\n* Have `middle` pointer and traverse till you find `b` value\n* Map the `left` to `list2` and traverse till the end\n* At last assign the next element of the `list2` as the next element of the `middle` pointer\n```\nclass Solution {\n public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n ListNode left = list1;\n for (int i = 1; i < a; i++)\n left = left.next;\n \n ListNode middle = left;\n for (int i = a; i <= b; i++)\n middle = middle.next;\n \n\t\tleft.next = list2;\n while (list2.next != null)\n list2 = list2.next;\n \n list2.next = middle.next;\n return list1;\n }\n}\n``` | 38 | 1 | ['Java'] | 4 |
merge-in-between-linked-lists | [Java] Straightforward solution in O(N) time | java-straightforward-solution-in-on-time-54zo | \nclass Solution {\n public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n ListNode start = list1;\n for (int i = 1; | roka | NORMAL | 2020-11-28T16:02:36.038062+00:00 | 2020-11-28T16:02:36.038097+00:00 | 3,162 | false | ```\nclass Solution {\n public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n ListNode start = list1;\n for (int i = 1; i < a; i++) {\n start = start.next;\n }\n \n ListNode end = start;\n for (int i = a; i <= b; i++) {\n end = end.next;\n }\n \n start.next = list2;\n while (list2.next != null) {\n list2 = list2.next;\n }\n \n list2.next = end.next;\n return list1;\n }\n}\n``` | 38 | 1 | [] | 3 |
merge-in-between-linked-lists | Basic C++ approach (Clean and Simple with explanation) | basic-c-approach-clean-and-simple-with-e-q3u5 | The basic approach is as follows :-\n\n1. Traverse the linked list to the given elements a and b\n1. Set the next of a to the head of the other given linked lis | Righley | NORMAL | 2020-11-28T22:22:02.047444+00:00 | 2020-12-06T07:18:33.519846+00:00 | 1,981 | false | The basic approach is as follows :-\n\n1. Traverse the linked list to the given elements a and b\n1. Set the next of a to the head of the other given linked list\n1. Set the next of the tail of the other given linked list to the pointer to b\n1. Return the original linked list as the final answer\n\n```\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n \n int jump1 = 1;\n ListNode *temp1 = list1;\n while (jump1 < a){\n temp1 = temp1->next;\n jump1++;\n } //Gets the pointer to a\n \n\t\tint jump2 = 1;\n ListNode *temp2 = list1;\n while(jump2 <= b){\n temp2 = temp2->next;\n jump2++;\n } //Gets the pointer to b\n \n\t\tListNode *temp3=list2;\n while(temp3->next != NULL){\n temp3=temp3->next;\n } //Gets the pointer to the tail of list2\n \n\t\t\n\t\ttemp1->next=list2; //set the next pointer of a to the head of list2\n \n\t\ttemp3->next = temp2->next; //set next of tail of list2 to the pointer to b\n \n\t\treturn list1; //return the original list i.e. list1\n \n }\n};\n```\n\nAuthor: shubham1592\n[https://github.com/shubham1592/LeetCode/blob/main/1669_Merge_In_Between_Linked_Lists.cpp](https://github.com/shubham1592/LeetCode/blob/main/1669_Merge_In_Between_Linked_Lists.cpp) | 18 | 0 | ['C'] | 2 |
merge-in-between-linked-lists | Linked List without memory leaks||154ms Beats 98.13% | linked-list-without-memory-leaks154ms-be-nndz | Intuition\n Describe your first thoughts on how to solve this problem. \nIt is no problem to obtain a solution.\nBut work for a while to remove the possiblity c | anwendeng | NORMAL | 2024-03-20T01:17:09.722269+00:00 | 2024-03-20T09:59:28.584286+00:00 | 2,386 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIt is no problem to obtain a solution.\nBut work for a while to remove the possiblity causing memory leaks.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Transverse the list1 for i=1 to a-1 do `curr=curr->next;`\n2. The crucial part removes the nodes among [a, b] by using 2 pointers `rm_start` & `rm_end` with care on deallocation of memory for each removed node.\n3. Connect `rm_start->next` to `list2`\n4. Transverse the whole `list2`\n5. Connect `curr->next = rm_end;`\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n+m)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n# Code ||154ms Beats 98.13%\n```\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode() : val(0), next(nullptr) {}\n * ListNode(int x) : val(x), next(nullptr) {}\n * ListNode(int x, ListNode *next) : val(x), next(next) {}\n * };\n */\n#pragma GCC optimize("O3", "unroll-loops")\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n ListNode* head=list1, *curr=list1;\n for(int i=1; i<a; i++)\n curr=curr->next;\n\n ListNode* rm_start = curr; // node before the section to be removed\n ListNode* rm_end = curr->next; // first node to be removed\n \n // Move rm_end to the last node of the section to be removed\n for (int i= a; i<=b; i++) {\n ListNode* tmp = rm_end;\n rm_end = rm_end->next;\n delete tmp; // Deallocate memory for each removed node\n }\n\n // Connect the remaining part of list1 to list2\n rm_start->next = list2;\n \n // Move curr to the end of list2\n for (; curr->next; curr=curr->next);\n \n \n // Connect the remaining part of list1 after the removed section\n curr->next = rm_end;\n \n return head;\n }\n};\n\n\nauto init = []() {\n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n```\n | 17 | 0 | ['Linked List', 'C++'] | 2 |
merge-in-between-linked-lists | [Python 3] - 2 pointers approach code with comments - O(m+n) | python-3-2-pointers-approach-code-with-c-y30x | This is my approach to the problem using 2 pointers :\n\nclass Solution:\n def mergeInBetween(self, list1: ListNode, a: int, b: int, list2: ListNode) -> List | sarthak6246 | NORMAL | 2021-01-11T06:05:57.786035+00:00 | 2021-01-11T06:06:34.190646+00:00 | 1,832 | false | This is my approach to the problem using 2 pointers :\n```\nclass Solution:\n def mergeInBetween(self, list1: ListNode, a: int, b: int, list2: ListNode) -> ListNode:\n # Define 2 pointers\n\t\tptr1 = list1\n ptr2 = list1\n i, j = 0, 0\n\t\t\n\t\t# Loop for pointer 1 to reach previous node from a\n while i!=a-1:\n ptr1 = ptr1.next\n i += 1 \n\t\t\t\n\t\t# Loop for pointer 2 to reach node b\n while j!=b:\n ptr2 = ptr2.next\n j += 1\n\t\t\t\n\t\t# Connect list2 to the next of pointer1\n ptr1.next = list2\n\t\t\n\t\t# Traverse the list2 till end node\n while list2.next!=None:\n list2 = list2.next\n\t\t\n\t\t# Assign the next of pointer 2 to the next of list2 i.e connect the remaining part of list1 to list2\n list2.next = ptr2.next\n\t\t\n\t\t# return final list\n return list1\n```\n\nFeel free to comment down your solutions as well :) | 17 | 0 | ['Linked List', 'Python3'] | 7 |
merge-in-between-linked-lists | C++ Straightforward O(N) | c-straightforward-on-by-lzl124631x-uyug | See my latest update in repo LeetCode\n\n## Solution 1.\n\nFind the following pointers:\n p where p->next points to ath node.\n q where p points to bth node.\n\ | lzl124631x | NORMAL | 2020-11-28T16:02:27.753244+00:00 | 2020-11-28T16:29:10.088696+00:00 | 1,723 | false | See my latest update in repo [LeetCode](https://github.com/lzl124631x/LeetCode)\n\n## Solution 1.\n\nFind the following pointers:\n* `p` where `p->next` points to `a`th node.\n* `q` where `p` points to `b`th node.\n\nThen we can stitch them together by assigning:\n* `B` to `p->next`\n* `q->next` to the `next` pointer of `B`\'s tail node.\n\n```cpp\n// OJ: https://leetcode.com/contest/biweekly-contest-40/problems/merge-in-between-linked-lists/\n// Author: github.com/lzl124631x\n// Time: O(N)\n// Space: O(1)\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* A, int a, int b, ListNode* B) {\n ListNode *q = A, *p = NULL;\n for (int i = 0; i < b; ++i) {\n if (i == a - 1) p = q;\n q = q->next;\n }\n p->next = B;\n while (B->next) B = B->next;\n B->next = q->next;\n return A;\n }\n};\n``` | 16 | 2 | [] | 2 |
merge-in-between-linked-lists | Modifying the Links | Java | C++ | modifying-the-links-java-c-by-fly_ing__r-i9dl | Intuition, approach, and complexity dicussed in video solution in detail.\nhttps://youtu.be/sxUXGlvTWt8\n\n# Code\nC++\n\nclass Solution {\npublic:\n ListNod | Fly_ing__Rhi_no | NORMAL | 2024-03-20T02:33:33.106853+00:00 | 2024-03-20T02:33:33.106881+00:00 | 8,657 | false | # Intuition, approach, and complexity dicussed in video solution in detail.\nhttps://youtu.be/sxUXGlvTWt8\n\n# Code\nC++\n```\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n ListNode *currNode = list1;\n int index = 0;\n while(index < a-1){\n currNode = currNode->next;\n index++;\n }\n ListNode *front = currNode;\n while(index < b+1){\n currNode = currNode->next;\n index++;\n }\n ListNode *rear = currNode;\n ListNode *secondListTail = list2, *secondListHead = list2;\n while(secondListTail->next != NULL)secondListTail = secondListTail->next;\n front->next = secondListHead;\n secondListTail->next = rear;\n return list1;\n }\n};\n```\nJava\n```\nclass Solution {\n public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n ListNode currNode = list1;\n int index = 0;\n while (index < a - 1) {\n currNode = currNode.next;\n index++;\n }\n ListNode front = currNode;\n while (index < b + 1) {\n currNode = currNode.next;\n index++;\n }\n ListNode rear = currNode;\n ListNode secondListTail = list2, secondListHead = list2;\n while (secondListTail.next != null) {\n secondListTail = secondListTail.next;\n }\n front.next = secondListHead;\n secondListTail.next = rear;\n return list1;\n }\n}\n\n``` | 15 | 0 | ['Linked List', 'C++', 'Java'] | 4 |
merge-in-between-linked-lists | Python | 99.50 beats | T-O(n) | python-9950-beats-t-on-by-vsahoo-m86n | \n\nclass Solution:\n def mergeInBetween(self, list1: ListNode, a: int, b: int, list2: ListNode) -> ListNode:\n head = list1\n for _ in range(a | vsahoo | NORMAL | 2021-03-07T15:30:08.665072+00:00 | 2021-03-07T15:30:08.665113+00:00 | 1,122 | false | ```\n\nclass Solution:\n def mergeInBetween(self, list1: ListNode, a: int, b: int, list2: ListNode) -> ListNode:\n head = list1\n for _ in range(a-1):\n head = head.next\n cur = head.next\n for _ in range(b-a):\n cur = cur.next\n head.next = list2\n while head.next:\n head = head.next\n if cur.next:\n head.next = cur.next\n return list1\n```\nPlease upvote if you get it. | 15 | 1 | ['Python'] | 5 |
merge-in-between-linked-lists | Basic Approach | | Easy Explanation | | Time O(n) , Space O(1) | | C++ | | Java | | Python3 | | ✅✅🔥 | basic-approach-easy-explanation-time-on-tw6r7 | \n\nIntuition:\n\nTo solve this problem, we need to traverse list1 to find the nodes at positions a and b. Once we locate these nodes, we can splice list2 betwe | Hunter_0718 | NORMAL | 2024-03-20T00:24:43.082595+00:00 | 2024-03-20T00:40:22.778962+00:00 | 4,935 | false | \n\n**Intuition:**\n\nTo solve this problem, we need to traverse `list1` to find the nodes at positions `a` and `b`. Once we locate these nodes, we can splice `list2` between them. We\'ll connect the node before position `a` to the head of `list2`, and the last node of `list2` to the node after position `b`. \n\n**Approach:**\n\n1. Traverse `list1` to find the node at position `a-1`, `a`, and `b+1`.\n2. Attach the last node of `list2` to the node after position `b`.\n3. Attach the node before position `a` to the head of `list2`.\n4. Return the head of `list1`.\n\n**Complexity:**\n- Time complexity: O(n), where n is the size of `list1` since we traverse it once to find the positions.\n- Space complexity: O(1), as we use a constant amount of extra space.\n\n**Code with Story:**\n\n```C++ []\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n ListNode *prev = list1; // Initialize pointers to traverse list1\n ListNode *temp1 = list1; // Modified variable name\n ListNode *curr = list1;\n a--; // Adjust a to match zero-based indexing\n \n // Traverse list1 to find the node at position (a-1)\n while(temp1 != NULL && a--) {\n temp1 = temp1->next;\n prev = temp1;\n }\n \n temp1 = list1; // Reset temp1 to traverse list1 again\n \n // Traverse list1 to find the node at position (b+1)\n while(temp1 != NULL && b--) {\n temp1 = temp1->next;\n curr = temp1;\n }\n \n ListNode *temp2 = list2; // Initialize pointer to traverse list2\n \n // Traverse list2 to find the last node\n while(temp2->next != NULL) {\n temp2 = temp2->next;\n }\n \n prev->next = list2; // Connect the node before position \'a\' to the head of list2\n temp2->next = curr->next; // Connect the last node of list2 to the node after position \'b\'\n \n return list1; // Return the head of list1\n }\n};\n\n```\n```Java []\n/**\n * Definition for singly-linked list.\n * public class ListNode {\n * int val;\n * ListNode next;\n * ListNode() {}\n * ListNode(int val) { this.val = val; }\n * ListNode(int val, ListNode next) { this.val = val; this.next = next; }\n * }\n */\nclass Solution {\n public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n ListNode prev = list1, temp1 = list1, curr = list1;\n a--; // Adjust a to match zero-based indexing\n \n // Traverse list1 to find the node at position (a-1)\n while (temp1 != null && a-- > 0) {\n temp1 = temp1.next;\n prev = temp1;\n }\n \n temp1 = list1; // Reset temp1 to traverse list1 again\n \n // Traverse list1 to find the node at position (b+1)\n while (temp1 != null && b-- > 0) {\n temp1 = temp1.next;\n curr = temp1;\n }\n \n ListNode temp2 = list2; // Initialize pointer to traverse list2\n \n // Traverse list2 to find the last node\n while (temp2.next != null) {\n temp2 = temp2.next;\n }\n \n prev.next = list2; // Connect the node before position \'a\' to the head of list2\n temp2.next = curr.next; // Connect the last node of list2 to the node after position \'b\'\n \n return list1; // Return the head of list1\n }\n}\n\n```\n```Python3 []\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def mergeInBetween(self, list1: ListNode, a: int, b: int, list2: ListNode) -> ListNode:\n prev = list1\n temp1 = list1\n curr = list1\n a -= 1 # Adjust a to match zero-based indexing\n \n # Traverse list1 to find the node at position (a-1)\n while temp1 and a > 0:\n temp1 = temp1.next\n prev = temp1\n a -= 1\n \n temp1 = list1 # Reset temp1 to traverse list1 again\n \n # Traverse list1 to find the node at position (b+1)\n while temp1 and b > 0:\n temp1 = temp1.next\n curr = temp1\n b -= 1\n \n temp2 = list2 # Initialize pointer to traverse list2\n \n # Traverse list2 to find the last node\n while temp2.next:\n temp2 = temp2.next\n \n prev.next = list2 # Connect the node before position \'a\' to the head of list2\n temp2.next = curr.next # Connect the last node of list2 to the node after position \'b\'\n \n return list1 # Return the head of list1\n```\n\n```Kotlin []\n/**\n * Example:\n * var li = ListNode(5)\n * var v = li.`val`\n * Definition for singly-linked list.\n * class ListNode(var `val`: Int) {\n * var next: ListNode? = null\n * }\n */\nclass Solution {\n fun mergeInBetween(list1: ListNode?, a: Int, b: Int, list2: ListNode?): ListNode? {\n var prev = list1\n var temp1 = list1\n var curr = list1\n var aCopy = a - 1 // Adjust a to match zero-based indexing\n \n // Traverse list1 to find the node at position (a-1)\n while (temp1 != null && aCopy > 0) {\n temp1 = temp1.next\n prev = temp1\n aCopy--\n }\n \n temp1 = list1 // Reset temp1 to traverse list1 again\n \n // Traverse list1 to find the node at position (b+1)\n var bCopy = b\n while (temp1 != null && bCopy > 0) {\n temp1 = temp1.next\n curr = temp1\n bCopy--\n }\n \n var temp2 = list2 // Initialize pointer to traverse list2\n \n // Traverse list2 to find the last node\n while (temp2?.next != null) {\n temp2 = temp2.next\n }\n \n prev?.next = list2 // Connect the node before position \'a\' to the head of list2\n temp2?.next = curr?.next // Connect the last node of list2 to the node after position \'b\'\n \n return list1 // Return the head of list1\n }\n}\n```\n```JavaScript []\n/**\n * Definition for singly-linked list.\n * function ListNode(val, next) {\n * this.val = (val===undefined ? 0 : val)\n * this.next = (next===undefined ? null : next)\n * }\n */\n/**\n * @param {ListNode} list1\n * @param {number} a\n * @param {number} b\n * @param {ListNode} list2\n * @return {ListNode}\n */\nvar mergeInBetween = function(list1, a, b, list2) {\n let prev = list1, temp1 = list1, curr = list1;\n a--; // Adjust a to match zero-based indexing\n \n // Traverse list1 to find the node at position (a-1)\n while (temp1 && a-- > 0) {\n temp1 = temp1.next;\n prev = temp1;\n }\n \n temp1 = list1; // Reset temp1 to traverse list1 again\n \n // Traverse list1 to find the node at position (b+1)\n while (temp1 && b-- > 0) {\n temp1 = temp1.next;\n curr = temp1;\n }\n \n let temp2 = list2; // Initialize pointer to traverse list2\n \n // Traverse list2 to find the last node\n while (temp2.next !== null) {\n temp2 = temp2.next;\n }\n \n prev.next = list2; // Connect the node before position \'a\' to the head of list2\n temp2.next = curr.next; // Connect the last node of list2 to the node after position \'b\'\n \n return list1; // Return the head of list1\n};\n```\n\n\n**Dry Run:**\n\n\n**Here\'s a step-by-step execution of the code using the specified input:**\n\n1. **Initialization:**\n - `prev`: points to head of `list1` (node 0).\n - `temp1`: points to head of `list1` (node 0).\n - `curr`: points to head of `list1` (node 0).\n - `a`: decremented to 1 (for zero-based indexing).\n\n2. **Traverse list1 to position (a-1):**\n - Loop iterates once:\n - `temp1` moves to node 1 (value 1).\n - `prev` also moves to node 1 (value 1).\n - After loop:\n - `prev` points to node 1 (value 1).\n - `temp1` points to node 2 (value 2).\n\n3. **Reset temp1 and traverse list1 to position (b+1):**\n - `temp1` is reset back to head of `list1` (node 0).\n - Loop iterates 5 times:\n - `temp1` moves to node 5 (value 5).\n - `curr` also moves to node 5 (value 5).\n - After loop:\n - `curr` points to node 6 (value 6).\n\n4. **Find last node of list2:**\n - `temp2` iterates through `list2` until it reaches the last node (node 1000004).\n\n5. **Merge the lists:**\n - `prev->next` (node 1\'s next pointer) is set to `list2` (connecting node 1 to `list2`).\n - `temp2->next` (last node of `list2`\'s next pointer) is set to `curr->next` (connecting `list2` to node 6).\n\n**Final Output:**\n- The modified `list1` becomes: [0, 1, 1000000, 1000001, 1000002, 1000003, 1000004, 6].\n- Nodes from index 2 to 5 of the original `list1` are effectively replaced with `list2`.\n\n**Edge Cases:**\n- If `list1` is empty.\n- If `list2` is empty.\n- If `a` is 0 (edge case for the beginning of the list).\n- If `b` is the last index of `list1` (edge case for the end of the list). | 14 | 2 | ['Linked List', 'C++', 'Java', 'Python3', 'Kotlin', 'JavaScript'] | 6 |
merge-in-between-linked-lists | Python | Easy | python-easy-by-khosiyat-1xw1 | see the Successfully Accepted Submission\n\n# Code\n\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# | Khosiyat | NORMAL | 2024-03-20T03:07:20.192836+00:00 | 2024-03-20T03:07:20.192862+00:00 | 555 | false | [see the Successfully Accepted Submission](https://leetcode.com/problems/merge-in-between-linked-lists/submissions/1208722799/?envType=daily-question&envId=2024-03-20)\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def mergeInBetween(self, list1: ListNode, a: int, b: int, list2: ListNode) -> ListNode:\n # Find the ath node\n current = list1\n for _ in range(a - 1):\n current = current.next\n \n # Find the bth node\n temp = current\n for _ in range(b - a + 2):\n temp = temp.next\n \n # Connect ath node to the head of list2\n current.next = list2\n \n # Find the end of list2\n while list2.next:\n list2 = list2.next\n \n # Connect the end of list2 to the b+1th node\n list2.next = temp\n \n return list1\n```\n | 11 | 0 | ['Python3'] | 0 |
merge-in-between-linked-lists | Merge Linked Lists In Between Indices | merge-linked-lists-in-between-indices-by-94do | Intuition\nWe need to merge list2 into list1 by removing a portion of list1 specified by indices a and b.\n\n# Approach\nTraverse list1 until reaching the node | Stella_Winx | NORMAL | 2024-02-29T12:03:13.908272+00:00 | 2024-02-29T12:03:13.908301+00:00 | 204 | false | # Intuition\nWe need to merge list2 into list1 by removing a portion of list1 specified by indices a and b.\n\n# Approach\n*Traverse list1 until reaching the node just before index a and store this node in prev.\n\n*Keep track of the node at index a in track.\n\n*Traverse list1 until reaching the node at index b.\n\n*Point track to the head of list2,then traverse list2.\n\n*Connect end of list2 to list1.\n\n*Return the merged list.\n\n# Complexity\n- Time complexity:\n\nThe time complexity of the provided solution is O(n), where n is the number of nodes in list1. \n\n> This is because we iterate through[]() list1 twice:\n*Once to find the nodes at indices a-1 and b.\n*Once to find the end of list2. All other operations are constant time.\n\n- Space complexity:\nThe space complexity is O(1) because we are not using any extra space.\n\n# Code\n```\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode() : val(0), next(nullptr) {}\n * ListNode(int x) : val(x), next(nullptr) {}\n * ListNode(int x, ListNode *next) : val(x), next(next) {}\n * };\n */\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n ListNode* prev=list1;\n\n //prev will point in node one before a\n for(int i=0;i<a-1;i++)\n {\n prev=prev->next;\n }\n\n ListNode* track=prev;\n\n for(int i=a;i<=b;i++)\n {\n prev=prev->next;\n }\n\n //traversing list2\n track->next=list2;\n ListNode* end=list2;\n while(end->next!=NULL)\n {\n end=end->next;\n }\n\n //connnect end to prev of list1\n end->next=prev->next;\n\n return list1;\n }\n};\n``` | 11 | 0 | ['C++'] | 0 |
merge-in-between-linked-lists | Rust | Linear time and no extra space (O(n + m) time and O(1) space) | rust-linear-time-and-no-extra-space-on-m-6v13 | \nuse std::mem;\n\nimpl Solution {\n pub fn merge_in_between(\n list1: Option<Box<ListNode>>, \n a: i32, \n b: i32,\n mut list2: | garciparedes | NORMAL | 2020-12-27T16:43:00.360350+00:00 | 2020-12-27T19:06:02.915082+00:00 | 185 | false | ```\nuse std::mem;\n\nimpl Solution {\n pub fn merge_in_between(\n list1: Option<Box<ListNode>>, \n a: i32, \n b: i32,\n mut list2: Option<Box<ListNode>>,\n ) -> Option<Box<ListNode>> {\n let mut head = list1.unwrap();\n \n let mut current = head.as_mut();\n for _ in 0..(a - 1) {\n current = current.next.as_mut().unwrap();\n }\n\t\t\n mem::swap(&mut current.next, &mut list2);\n \n while current.next.is_some() {\n current = current.next.as_mut().unwrap();\n }\n\n for _ in 0..(b - a + 1) {\n list2 = list2.unwrap().next;\n }\n current.next = list2;\n \n return Some(head);\n }\n}\n```\nYou can see more Leetcode solutions writen in Rust on: https://github.com/garciparedes/leetcode | 11 | 0 | ['Linked List', 'Rust'] | 1 |
merge-in-between-linked-lists | 🗓️ Daily LeetCoding Challenge Day 3|| 🔥 JAVA SOL | daily-leetcoding-challenge-day-3-java-so-4oyp | I hope a good day for u!\n\n# Code\n\nclass Solution {\n public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n ListNode cur | DoaaOsamaK | NORMAL | 2024-03-20T09:14:43.531847+00:00 | 2024-03-20T09:14:43.531878+00:00 | 1,040 | false | I hope a good day for u!\n\n# Code\n```\nclass Solution {\n public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n ListNode currNode = list1; // Start of the first list\n int index = 0; // Variable to track current position\n // Move to the element before index "a"\n while (index < a - 1) {\n currNode = currNode.next;\n index++;\n }\n ListNode front = currNode; // Store current position as "front"\n // Move to the element after index "b"\n while (index < b + 1) {\n currNode = currNode.next;\n index++;\n }\n ListNode rear = currNode; // Store current position as "rear"\n ListNode secondListTail = list2, secondListHead = list2;\n // Finding the tail of the second list\n while (secondListTail.next != null) {\n secondListTail = secondListTail.next;\n }\n // Link the front part of the second list after "front"\n front.next = secondListHead;\n // Link the rear part of the second list before "rear"\n secondListTail.next = rear;\n return list1; // Return the updated list\n }\n}\n\n``` | 9 | 0 | ['Java'] | 1 |
merge-in-between-linked-lists | C++ Solution (Don't forget to free memory for removed nodes) | c-solution-dont-forget-to-free-memory-fo-iynr | \nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n int splitPosition = 0;\n ListNode* c | navan72 | NORMAL | 2020-12-13T17:53:10.075864+00:00 | 2020-12-13T17:54:48.541569+00:00 | 752 | false | ```\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n int splitPosition = 0;\n ListNode* current = list1;\n while(splitPosition != a - 1)\n {\n current = current->next;\n splitPosition++;\n }\n \n ListNode* removeNodes = current->next;\n current->next = list2;\n splitPosition++;\n \n while(splitPosition != b + 1)\n {\n ListNode* deleteNode = removeNodes;\n removeNodes = removeNodes->next;\n delete deleteNode; \n splitPosition++;\n }\n \n ListNode* endNodeOfList2 = list2;\n while(endNodeOfList2->next != NULL)\n endNodeOfList2 = endNodeOfList2->next;\n \n endNodeOfList2->next = removeNodes;\n \n return list1;\n }\n};\n``` | 9 | 0 | ['C'] | 0 |
merge-in-between-linked-lists | 🔥🔥Beats 100% | Easiest Approach 🚀🚀 | Must Watch 😎 | beats-100-easiest-approach-must-watch-by-ayit | \uD83E\uDD14 Intuition:\n- Traverse through list1 to find the nodes at positions a and b and their previous nodes.\n- Identify the end node of list2.\n- Link th | The_Eternal_Soul | NORMAL | 2024-03-20T02:21:11.069240+00:00 | 2024-03-20T02:21:11.069279+00:00 | 1,073 | false | \uD83E\uDD14 **Intuition:**\n- Traverse through `list1` to find the nodes at positions `a` and `b` and their previous nodes.\n- Identify the end node of `list2`.\n- Link the previous node of `a` to the head of `list2`.\n- Link the end node of `list2` to the node following `b`.\n\n\uD83D\uDEE0\uFE0F **Approach:**\n1. Initialize pointers `temp1`, `prev`, and `temp2` to traverse `list1`, where `temp1` points to the node at position `a`, `prev` points to the node before `a`, and `temp2` points to the node at position `b`.\n2. Traverse `list2` to find its end node, `tail`.\n3. Connect `prev` to the head of `list2` and `tail` to the node following `temp2`.\n4. Return the modified `list1`.\n\n\u23F0 **Time Complexity:**\n- Traversing `list1` and `list2` takes O(n + m), where n and m are the lengths of the lists respectively.\n\n\uD83D\uDCBE **Space Complexity:**\n- The space complexity is O(1) since we are using constant extra space.\n\n# Code\n```\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode() : val(0), next(nullptr) {}\n * ListNode(int x) : val(x), next(nullptr) {}\n * ListNode(int x, ListNode *next) : val(x), next(next) {}\n * };\n */\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n ios_base::sync_with_stdio(false);\n cin.tie(0);\n cout.tie(0);\n \n \n ListNode *temp1 = list1;\n ListNode *prev = list1;\n ListNode *temp2 = list1;\n ListNode *tail = list2;\n\n int index = 0;\n while(temp1 != 0 and index < a)\n {\n prev = temp1;\n temp1 = temp1->next;\n index++;\n }\n\n index = 0;\n while(temp2 != 0 and index < b)\n {\n temp2 = temp2->next;\n index++;\n }\n\n while(tail != 0 and tail->next != 0) \n tail = tail->next;\n\n cout << prev->val << " " << temp2->val << endl;\n\n prev->next = list2;\n tail->next = temp2->next;\n\n return list1;\n }\n};\n```\nUPVOTE IF YOU FIND THIS HELPFUL!!\n\n\n | 8 | 1 | ['Linked List', 'C', 'Python', 'C++', 'Java', 'JavaScript'] | 1 |
merge-in-between-linked-lists | C++ || Straight forward code || Simplest Approach | c-straight-forward-code-simplest-approac-sh4a | \nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n ListNode *ptr=list1;\n ListNode *pt | garvit14 | NORMAL | 2022-08-20T18:18:04.012481+00:00 | 2022-08-20T18:18:04.012525+00:00 | 912 | false | ```\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n ListNode *ptr=list1;\n ListNode *ptr2=list1;\n while(a>1)\n {\n a--;\n ptr=ptr->next;\n }\n while(b)\n {\n ptr2=ptr2->next;\n b--;\n }\n ptr->next=list2;\n while(ptr->next)\n {\n ptr=ptr->next;\n }\n ptr->next=ptr2->next;\n return list1;\n }\n};\n```\nPlz upvote, it means a lot. | 8 | 0 | ['Linked List', 'C', 'C++'] | 2 |
merge-in-between-linked-lists | [Java] Two pointer approach | java-two-pointer-approach-by-lucifer1019-85i3 | ```\n public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n if(list1 == null || list2 == null){\n return null;\n | lucifer101998 | NORMAL | 2020-11-28T17:41:47.789855+00:00 | 2020-11-28T17:42:26.335890+00:00 | 989 | false | ```\n public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n if(list1 == null || list2 == null){\n return null;\n }\n ListNode slow,fast;\n slow=list1;\n fast=list1;\n int k=b-a+1;\n for(int i=0;i<k;i++)\n fast=fast.next;\n \n for(int i=1;i<a;i++)\n\t\t{ \n slow=slow.next;\n fast=fast.next;\n }\n slow.next=list2;\n while(list2.next!=null)\n list2=list2.next;\n\t\t\t\n list2.next=fast.next;\n \n return list1;\n }\n | 8 | 0 | ['Two Pointers', 'Java'] | 4 |
merge-in-between-linked-lists | Beats 100%🚀➡️Intuitive Solution Full Explained ➡️[Java/C++/C/C#/JavaScript/Python3/Rust] | beats-100intuitive-solution-full-explain-7j17 | Intuition\n1. We have to get the node before a and node after b.\n2. We will attach the node before a to the start of list2, and add the the end of the list2 to | Shivansu_7 | NORMAL | 2024-03-20T09:57:02.929363+00:00 | 2024-03-20T14:00:21.282395+00:00 | 441 | false | # Intuition\n1. We have to get the node before a and node after b.\n2. We will attach the node before a to the start of list2, and add the the end of the list2 to the node after b.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. **Check for `null` lists:** \n - The method begins by checking if either `list1` or `list2` is null. \n - If either is `null`, it returns `null` immediately, indicating that there\'s nothing to merge.\n\n2. **Initialize pointers and variables:** \n - It initializes several pointers and a counter variable.\n - `curr`, `start`, and end are ListNode pointers initially pointing to `list1`.\n - `count` is an integer variable initialized to `0`.\n3. **Traverse list1 to find start and end points:** \n - It traverses `list1` using the `curr` pointer while counting the number of nodes visited `(count)`.\n - When the `count` equals `a`, it sets `start` to the current node.\n - When the `count` equals `b + 1`, it sets `end` to the current node.\n4. **Merge list2 between start and end points:** \n - After finding the appropriate `start` and `end` points in `list1`, it sets the next pointer of start to `list2`, effectively merging `list2` into `list1`.\n - It then traverses `list2` to find its `end` node `(curr)` and sets the next pointer of `curr` to `end`.\n5. **Return the modified list1:** \n - Finally, it returns the modified `list1`.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```Java []\nclass Solution {\n public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n if(list1==null || list2==null) {\n return null;\n }\n ListNode curr = list1;\n ListNode start = list1;\n ListNode end =list1;\n int count = 0;\n\n while(curr!=null) {\n count++;\n if(count==a) {\n start = curr;\n }\n curr = curr.next;\n if(count==b+1) {\n end = curr;\n }\n }\n\n curr = list2;\n start.next = list2;\n while(curr.next!=null) {\n curr=curr.next;\n }\n\n curr.next = end;\n return list1;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n if (!list1 || !list2) {\n return nullptr;\n }\n ListNode* curr = list1;\n ListNode* start = list1;\n ListNode* end = list1;\n int count = 0;\n\n while (curr) {\n count++;\n if (count == a) {\n start = curr;\n }\n curr = curr->next;\n if (count == b + 1) {\n end = curr;\n }\n }\n\n curr = list2;\n start->next = list2;\n while (curr->next) {\n curr = curr->next;\n }\n\n curr->next = end;\n return list1;\n }\n};\n```\n```Python3 []\nclass Solution:\n def mergeInBetween(self, list1: ListNode, a: int, b: int, list2: ListNode) -> ListNode:\n if not list1 or not list2:\n return None\n curr = list1\n start = list1\n end = list1\n count = 0\n\n while curr:\n count += 1\n if count == a:\n start = curr\n curr = curr.next\n if count == b + 1:\n end = curr\n\n curr = list2\n start.next = list2\n while curr.next:\n curr = curr.next\n\n curr.next = end\n return list1\n```\n```Go []\nfunc mergeInBetween(list1 *ListNode, a int, b int, list2 *ListNode) *ListNode {\n if list1 == nil || list2 == nil {\n return nil\n }\n curr := list1\n start := list1\n end := list1\n count := 0\n\n for curr != nil {\n count++\n if count == a {\n start = curr\n }\n curr = curr.Next\n if count == b+1 {\n end = curr\n }\n }\n\n curr = list2\n start.Next = list2\n for curr.Next != nil {\n curr = curr.Next\n }\n\n curr.Next = end\n return list1\n}\n```\n```C# []\npublic class Solution {\n public ListNode MergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n if (list1 == null || list2 == null) {\n return null;\n }\n ListNode curr = list1;\n ListNode start = list1;\n ListNode end = list1;\n int count = 0;\n\n while (curr != null) {\n count++;\n if (count == a) {\n start = curr;\n }\n curr = curr.next;\n if (count == b + 1) {\n end = curr;\n }\n }\n\n curr = list2;\n start.next = list2;\n while (curr.next != null) {\n curr = curr.next;\n }\n\n curr.next = end;\n return list1;\n }\n}\n```\n```Rust []\nimpl Solution {\n pub fn merge_in_between(list1: Option<Box<ListNode>>, a: i32, b: i32, list2: Option<Box<ListNode>>) -> Option<Box<ListNode>> {\n let mut list1 = list1;\n let mut list2 = list2;\n\n if list1.is_none() || list2.is_none() {\n return None;\n }\n\n let mut curr = list1.as_mut().unwrap().as_mut();\n let mut start = curr;\n let mut end = curr;\n let mut count = 0;\n\n while let Some(node) = curr {\n count += 1;\n if count == a {\n start = node;\n }\n curr = node.next.as_mut().map(|n| n.as_mut());\n if count == b + 1 {\n end = curr.unwrap();\n }\n }\n\n let mut curr = list2.as_mut().unwrap().as_mut();\n start.next = list2;\n while let Some(node) = curr {\n if let Some(next) = &mut node.next {\n curr = next.as_mut();\n } else {\n break;\n }\n }\n\n curr.unwrap().next = end.next;\n list1\n }\n}\n```\n```JavaScript []\n/**\n * Definition for singly-linked list.\n */\nfunction ListNode(val, next) {\n this.val = (val === undefined ? 0 : val);\n this.next = (next === undefined ? null : next);\n}\n\n/**\n * @param {ListNode} list1\n * @param {number} a\n * @param {number} b\n * @param {ListNode} list2\n * @return {ListNode}\n */\nvar mergeInBetween = function(list1, a, b, list2) {\n if (!list1 || !list2) {\n return null;\n }\n let curr = list1;\n let start = list1;\n let end = list1;\n let count = 0;\n\n while (curr) {\n count++;\n if (count === a) {\n start = curr;\n }\n curr = curr.next;\n if (count === b + 1) {\n end = curr;\n }\n }\n\n curr = list2;\n start.next = list2;\n while (curr.next) {\n curr = curr.next;\n }\n\n curr.next = end;\n return list1;\n};\n```\n\n---\n\n\n---\n\n\n\n | 7 | 0 | ['C', 'Python', 'C++', 'Java', 'Python3', 'Rust', 'JavaScript', 'C#'] | 4 |
merge-in-between-linked-lists | ✔️100% Beats ✔️Python ✔️C++ ✔️Java ✔️Js ✔️C# ✔️Go | 100-beats-python-c-java-js-c-go-by-otabe-k3av | \n\n\n# Approach\nThis solution creates a dummy node to handle cases where the removal starts from the head of list1. Then, it traverses to the (a-1)th node to | otabek_kholmirzaev | NORMAL | 2024-03-20T01:05:09.231261+00:00 | 2024-03-21T17:07:01.719873+00:00 | 775 | false | 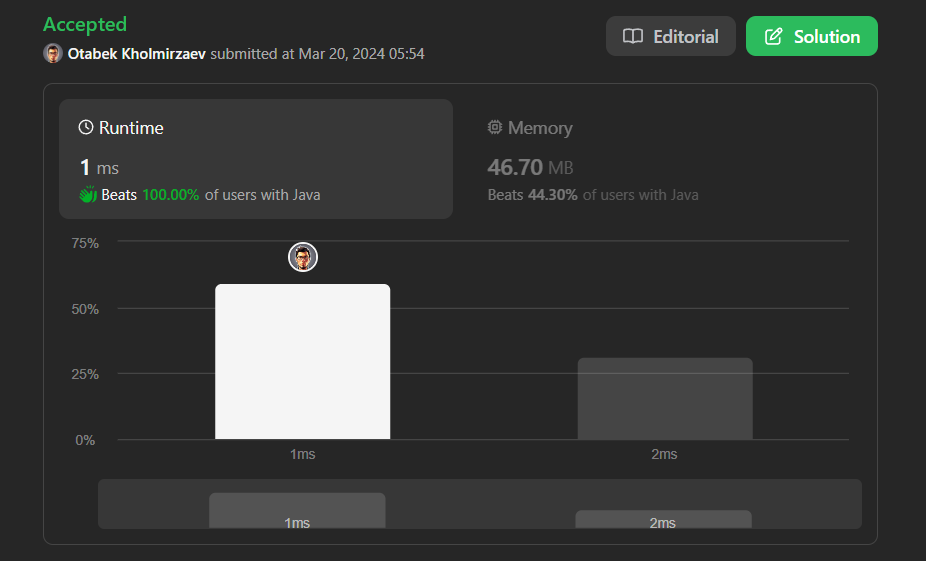\n\n\n# Approach\nThis solution creates a dummy node to handle cases where the removal starts from the head of **list1**. Then, it traverses to the **(a-1)th** node to find the node before the range to be removed. After that, it traverses to the **bth** node to find the node after the range to be removed. It then connects the **(a-1)th** node to the head of **list2**, and traverses to the end of **list2** to connect it with the node after the range to be removed. Finally, it returns the modified **list1**.\n\n# Complexity\n- Time complexity: O(n + m)\n\n- Space complexity: O(1)\n\n# Code\n```python []\nclass Solution:\n def mergeInBetween(self, list1, a, b, list2):\n # Create a dummy node to handle cases where the removal starts from the head of list1\n dummy = ListNode(0)\n dummy.next = list1\n \n # Traverse to the (a-1)th node\n current = dummy\n for i in range(a):\n current = current.next\n \n # Save the reference to the (a-1)th node\n before_a = current\n \n # Traverse to the bth node\n for i in range(a, b + 1):\n current = current.next\n \n # Save the reference to the (b+1)th node\n after_b = current.next\n \n # Connect the (a-1)th node to list2\n before_a.next = list2\n \n # Traverse to the end of list2\n while list2.next:\n list2 = list2.next\n \n # Connect the end of list2 to the (b+1)th node\n list2.next = after_b\n \n return dummy.next\n```\n\n```cpp []\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n // Create a dummy node to handle cases where the removal starts from the head of list1\n ListNode* dummy = new ListNode(0);\n dummy->next = list1;\n \n // Traverse to the (a-1)th node\n ListNode* current = dummy;\n for (int i = 0; i < a; ++i) {\n current = current->next;\n }\n \n // Save the reference to the (a-1)th node\n ListNode* beforeA = current;\n \n // Traverse to the bth node\n for (int i = a; i <= b; ++i) {\n current = current->next;\n }\n \n // Save the reference to the (b+1)th node\n ListNode* afterB = current->next;\n \n // Connect the (a-1)th node to list2\n beforeA->next = list2;\n \n // Traverse to the end of list2\n while (list2->next) {\n list2 = list2->next;\n }\n \n // Connect the end of list2 to the (b+1)th node\n list2->next = afterB;\n \n return dummy->next;\n }\n};\n```\n\n```java []\nclass Solution {\n public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n // Create a dummy node to handle cases where the removal starts from the head of list1\n ListNode dummy = new ListNode(0);\n dummy.next = list1;\n \n // Traverse to the (a-1)th node\n ListNode current = dummy;\n for (int i = 0; i < a; i++) {\n current = current.next;\n }\n \n // Save the reference to the (a-1)th node\n ListNode beforeA = current;\n \n // Traverse to the bth node\n for (int i = a; i <= b; i++) {\n current = current.next;\n }\n \n // Save the reference to the (b+1)th node\n ListNode afterB = current.next;\n \n // Connect the (a-1)th node to list2\n beforeA.next = list2;\n \n // Traverse to the end of list2\n while (list2.next != null) {\n list2 = list2.next;\n }\n \n // Connect the end of list2 to the (b+1)th node\n list2.next = afterB;\n \n return dummy.next;\n }\n}\n```\n```javascript []\nvar mergeInBetween = function(list1, a, b, list2) {\n // Create a dummy node to handle cases where the removal starts from the head of list1\n const dummy = new ListNode(0);\n dummy.next = list1;\n \n // Traverse to the (a-1)th node\n let current = dummy;\n for (let i = 0; i < a; i++) {\n current = current.next;\n }\n \n // Save the reference to the (a-1)th node\n const beforeA = current;\n \n // Traverse to the bth node\n for (let i = a; i <= b; i++) {\n current = current.next;\n }\n \n // Save the reference to the (b+1)th node\n const afterB = current.next;\n \n // Connect the (a-1)th node to list2\n beforeA.next = list2;\n \n // Traverse to the end of list2\n while (list2.next) {\n list2 = list2.next;\n }\n \n // Connect the end of list2 to the (b+1)th node\n list2.next = afterB;\n \n return dummy.next;\n}\n```\n```csharp []\npublic class Solution {\n public ListNode MergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n // Create a dummy node to handle cases where the removal starts from the head of list1\n ListNode dummy = new ListNode(0);\n dummy.next = list1;\n \n // Traverse to the (a-1)th node\n ListNode current = dummy;\n for (int i = 0; i < a; i++) {\n current = current.next;\n }\n \n // Save the reference to the (a-1)th node\n ListNode beforeA = current;\n \n // Traverse to the bth node\n for (int i = a; i <= b; i++) {\n current = current.next;\n }\n \n // Save the reference to the (b+1)th node\n ListNode afterB = current.next;\n \n // Connect the (a-1)th node to list2\n beforeA.next = list2;\n \n // Traverse to the end of list2\n while (list2.next != null) {\n list2 = list2.next;\n }\n \n // Connect the end of list2 to the (b+1)th node\n list2.next = afterB;\n \n return dummy.next;\n }\n}\n```\n```go []\nfunc mergeInBetween(list1 *ListNode, a int, b int, list2 *ListNode) *ListNode {\n // Create a dummy node to handle cases where the removal starts from the head of list1\n dummy := &ListNode{Val: 0, Next: list1}\n \n // Traverse to the (a-1)th node\n current := dummy\n for i := 0; i < a; i++ {\n current = current.Next\n }\n \n // Save the reference to the (a-1)th node\n beforeA := current\n \n // Traverse to the bth node\n for i := a; i <= b; i++ {\n current = current.Next\n }\n \n // Save the reference to the (b+1)th node\n afterB := current.Next\n \n // Connect the (a-1)th node to list2\n beforeA.Next = list2\n \n // Traverse to the end of list2\n for list2.Next != nil {\n list2 = list2.Next\n }\n\n // Connect the end of list2 to the (b+1)th node\n list2.Next = afterB\n\n return dummy.Next;\n}\n```\n\n\n | 7 | 0 | ['C#'] | 3 |
merge-in-between-linked-lists | 🍀🍀 optimized || Neat Solution|| O(1) memory and O(n+m) space complexity | optimized-neat-solution-o1-memory-and-on-p002 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | A9201 | NORMAL | 2024-03-20T00:41:01.666224+00:00 | 2024-03-20T00:41:01.666261+00:00 | 1,156 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` python3 []\nclass Solution:\n def mergeInBetween(self, list1: ListNode, a: int, b: int, list2: ListNode) -> ListNode:\n temp1=list2\n head=list1\n pos=list2\n end=list1\n while list2.next:\n list2=list2.next\n i,j=0,0\n while list1:\n if i==a-1:\n pos=list1\n if j==b:\n end=list1\n i+=1\n j+=1\n list1=list1.next\n pos.next=temp1\n list2.next=end.next\n return head\n```\n``` c++ []\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n ListNode *temp1=list2,*head=list1,*pos=list2,*end=list1;\n while(list2->next)\n {list2=list2->next;}\n int i=0,j=0;\n while(list1||i==a&&j==b)\n {\n if(i==a-1)\n {pos=list1;}\n if(j==b){\n end=list1;\n }\n i++;j++;list1=list1->next;\n }\n pos->next=temp1;\n list2->next=end->next;\n return head;\n }\n};\n``` | 7 | 0 | ['C++', 'Python3'] | 3 |
merge-in-between-linked-lists | [C++] Linked-list to Vector || Easy-Understanding | c-linked-list-to-vector-easy-understandi-8ypm | \nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n vector<int> nums1, nums2, res;\n Lis | vaibhav4859 | NORMAL | 2021-12-17T18:51:29.989314+00:00 | 2021-12-17T18:51:29.989357+00:00 | 587 | false | ```\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n vector<int> nums1, nums2, res;\n ListNode* temp1 = list1, *temp2 = list2;\n while(temp1 != NULL)\n nums1.push_back(temp1->val), temp1 = temp1->next;\n \n while(temp2 != NULL)\n nums2.push_back(temp2->val), temp2 = temp2->next;\n \n \n for(int i = 0; i < a; i++)\n res.push_back(nums1[i]);\n for(int i = 0; i < nums2.size(); i++)\n res.push_back(nums2[i]);\n for(int i = b+1; i < nums1.size(); i++)\n res.push_back(nums1[i]);\n \n ListNode* head = new ListNode(0), *curr = head;\n int i = 0;\n while(i < res.size()){\n curr->next = new ListNode(res[i++]);\n curr = curr->next;\n }\n \n return head->next;\n \n }\n};\n``` | 7 | 2 | ['Linked List', 'C', 'C++'] | 1 |
merge-in-between-linked-lists | 🔥🔥|| Beats 100% , Easy Solution || Traverse || 🔥🔥 | beats-100-easy-solution-traverse-by-hars-a76l | \n\n# Approach\nTraverse till (a-1)th node and till (b+1)th node ,\n(a-1).next= head of list2 \ntail of list2.next =(b+1)th node\n\n\nin the code head1 is nothi | harshchand78 | NORMAL | 2024-03-20T05:38:52.094923+00:00 | 2024-03-20T16:18:27.277181+00:00 | 194 | false | \n\n# Approach\nTraverse till (a-1)th node and till (b+1)th node ,\n(a-1).next= head of list2 \ntail of list2.next =(b+1)th node\n\n\nin the code head1 is nothing but (b+1)th node and (a-1)th node is stored in list1 , rearrange variable names according to your convenience\n\n# Complexity\n- Time complexity: O(b + list2.length)\n\n- Space complexity: O(1)\n\n# Code\n```\n/**\n * Definition for singly-linked list.\n * public class ListNode {\n * int val;\n * ListNode next;\n * ListNode() {}\n * ListNode(int val) { this.val = val; }\n * ListNode(int val, ListNode next) { this.val = val; this.next = next; }\n * }\n */\nclass Solution {\n public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n int c=1;\n int d=1;\n ListNode head1=list1;\n ListNode head=list1;\n while(d<=b){\n head1=head1.next;\n d++;\n }\n if(head1.next!=null) head1=head1.next;\n while(c<a){\n list1=list1.next;\n c++;\n }\n ListNode head2=list2;\n while(list2.next!=null){\n list2=list2.next;\n }\n list1.next=head2;\n list2.next=head1;\n return head;\n }\n}\n``` | 6 | 0 | ['Two Pointers', 'Java'] | 3 |
merge-in-between-linked-lists | c++ || beats 96% | c-beats-96-by-niyander-smx8 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | niyander | NORMAL | 2024-03-24T19:53:34.471588+00:00 | 2024-03-24T19:53:34.471618+00:00 | 803 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode() : val(0), next(nullptr) {}\n * ListNode(int x) : val(x), next(nullptr) {}\n * ListNode(int x, ListNode *next) : val(x), next(next) {}\n * };\n */\n#pragma GCC optimize("O3", "unroll-loops")\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n ListNode* head=list1, *curr=list1;\n for(int i=1; i<a; i++)\n curr=curr->next;\n\n ListNode* rm_start = curr; // node before the section to be removed\n ListNode* rm_end = curr->next; // first node to be removed\n \n // Move rm_end to the last node of the section to be removed\n for (int i= a; i<=b; i++) {\n ListNode* tmp = rm_end;\n rm_end = rm_end->next;\n delete tmp; // Deallocate memory for each removed node\n }\n\n // Connect the remaining part of list1 to list2\n rm_start->next = list2;\n \n // Move curr to the end of list2\n for (; curr->next; curr=curr->next);\n \n \n // Connect the remaining part of list1 after the removed section\n curr->next = rm_end;\n \n return head;\n }\n};\n\n\nauto init = []() {\n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n``` | 5 | 0 | ['C++'] | 0 |
merge-in-between-linked-lists | ✅ BEST C++ SOLUTION ☑️ | best-c-solution-by-2005115-uykb | PLEASE UPVOTE MY SOLUTION IF YOU LIKE IT\n# CONNECT WITH ME\n### https://www.linkedin.com/in/pratay-nandy-9ba57b229/\n#### https://www.instagram.com/pratay_nand | 2005115 | NORMAL | 2024-03-20T17:36:32.054233+00:00 | 2024-03-20T17:36:32.054265+00:00 | 88 | false | # **PLEASE UPVOTE MY SOLUTION IF YOU LIKE IT**\n# **CONNECT WITH ME**\n### **[https://www.linkedin.com/in/pratay-nandy-9ba57b229/]()**\n#### **[https://www.instagram.com/_pratay_nandy_/]()**\n\n# Approach\n\n\n### Let\'s break down the functionality of this function:\n\n1. **Initialization**:\n - It initializes three pointers `p`, `q`, and `r` to the head nodes of `list1`, `list1`, and `list2`, respectively.\n\n2. **Finding the Tail of `list2`**:\n - It iterates through `list2` to find its tail node `r`. This is done to determine where to append the nodes of `list2` to `list1`.\n\n3. **Moving `p` to the Node Before Index `a`**:\n - It decrements the value of `a` by 1 (assuming the indices are 0-based).\n - It then traverses `list1` by moving the pointer `p` to the node just before the node at index `a`.\n\n4. **Moving `q` to the Node After Index `b`**:\n - It increments the value of `b` by 1.\n - It then traverses `list1` by moving the pointer `q` to the node just after the node at index `b`.\n\n5. **Merging `list2` into `list1`**:\n - It updates the `next` pointer of the node pointed to by `p` to point to the head of `list2`, effectively inserting `list2` into `list1`.\n - It updates the `next` pointer of the tail node of `list2` (pointed to by `r`) to point to the node pointed to by `q`, connecting the remainder of `list1` after the removed portion.\n \n6. **Returning the Head of the Merged List**:\n - It returns the head node of `list1`, which now contains the merged list.\n\n\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:**0(N)**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:**0(1)**\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n**Bold**\n# Code\n```\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n ListNode* p = list1;\n ListNode* q = list1;\n ListNode* r = list2;\n while(r->next!=NULL)\n {\n r = r->next;\n }\n a = a-1; \n while(a > 0)\n {\n p = p->next;\n a--;\n }\n b+=1;\n while(b>0)\n {\n q = q->next;\n b--;\n }\n p->next = list2; \n r->next = q; \n return list1;\n }\n};\n``` | 5 | 0 | ['Linked List', 'C++'] | 0 |
merge-in-between-linked-lists | ✅Easy✨ ||C++|| Beats 100% || With Explanation|| | easy-c-beats-100-with-explanation-by-ola-gae1 | Intuition\n Describe your first thoughts on how to solve this problem. \nThe intuition of code is to merge two singly linked lists by replacing a segment of the | olakade33 | NORMAL | 2024-03-20T05:19:01.489487+00:00 | 2024-03-20T05:19:01.489522+00:00 | 467 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition of code is to merge two singly linked lists by replacing a segment of the first list (from position a to b) with the entire second list. The approach involves three main steps: finding the node just before the start of the segment to be replaced in the first list, finding the node just after the end of this segment, and finally linking the second list between these two nodes. The last part of the process connects the end of the second list to the node just after the segment in the first list. This operation effectively splices the second list into the first, between the positions a and b, inclusive.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialize Pointers and Counter: The solution starts by initializing a pointer point1 to the start of list1 and a counter variable count to 1. This setup prepares for traversal through the list.\n\n2. Traverse to the a-1th Node: The loop continues until point1 points to the node just before the ath node (1-indexed) or the a-1th node (0-indexed). This is the node after which list2 will be inserted.\n\n3. Traverse to the b+1th Node: A second pointer point2 starts at the node immediately after point1 and moves forward until it points to the node just after the bth node. This node will be the point where list1 continues after list2 has been inserted.\n\n4. Insert list2 Between a and b: The next pointer of the node at a-1 is updated to point to the start of list2. This effectively inserts list2 at position a.\n\n5. Find the End of list2: A temporary pointer traverses list2 to find its last node. This step is necessary to link the end of list2 back to list1.\n\n6. Link the End of list2 to list1: The next pointer of the last node in list2 is updated to point to point2, the b+1th node of list1. This completes the insertion process.\n\n7. Return list1: The function returns the head of the modified list1, which now includes list2 between the ath and bth positions.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n The algorithm traverses each list at most once. The traversal of list1 to positions a and b takes (O(b)) time, as it stops after reaching the b+1th node. The traversal of list2 to find its end takes (O(n)) time, where (n) is the length of list2. Thus, the total time complexity is (O(b + n)), where (b) is the position in list1 where the merge ends, and (n) is the length of list2.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe algorithm uses a constant amount of extra space for pointers and the counter variable, so the space complexity is (O(1)). Note that the space used by the lists themselves is not considered part of the space complexity for this analysis, as it is not additional space allocated by the algorithm.\n# Code\n```\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode() : val(0), next(nullptr) {}\n * ListNode(int x) : val(x), next(nullptr) {}\n * ListNode(int x, ListNode *next) : val(x), next(next) {}\n * };\n */\n\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n ListNode *point1 = list1;\n int count = 1;\n while (count != a)\n {\n point1 = point1 -> next;\n count++;\n }\n\n ListNode *point2 = point1 -> next;\n while (count != b+1)\n {\n point2 = point2 -> next;\n count++;\n }\n\n point1->next = list2;\n ListNode *temp = list2;\n while (temp -> next != NULL)\n temp = temp -> next;\n\n temp -> next = point2;\n \n return list1;\n\n }\n};\n``` | 5 | 0 | ['C++'] | 1 |
merge-in-between-linked-lists | C++ easy solution || C++ | c-easy-solution-c-by-prashant_71200-hhre | Intuition\nTo solve this problem, we need to find the ath and (b+1)th nodes in the list1 and then adjust the pointers to insert list2 between them.\n# Approach\ | prashant_71200 | NORMAL | 2024-03-20T03:40:49.778904+00:00 | 2024-03-20T03:40:49.778932+00:00 | 432 | false | # Intuition\nTo solve this problem, we need to find the ath and (b+1)th nodes in the list1 and then adjust the pointers to insert list2 between them.\n# Approach\n1) Create a dummy node to simplify handling edge cases.\n2) Traverse list1 to find the ath node and the (b+1)th node.\n3) Traverse list2 to find its tail.\n4) Adjust pointers to insert list2 between the ath and (b+1)th nodes.\n5) Return the modified list1.\n# Complexity\n- Time complexity:\nO(n + m), where n is the size of list1 and m is the size of list2.\n- Space complexity:\nO(1), as we are using constant extra space.\n# Code\n```\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode() : val(0), next(nullptr) {}\n * ListNode(int x) : val(x), next(nullptr) {}\n * ListNode(int x, ListNode *next) : val(x), next(next) {}\n * };\n */\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n ListNode* dummy = new ListNode();\n dummy->next = list1;\n \n ListNode* prevA = dummy;\n for (int i = 0; i < a; ++i) {\n prevA = prevA->next;\n }\n \n ListNode* prevB = prevA;\n for (int i = a; i <= b + 1; ++i) {\n prevB = prevB->next;\n }\n \n ListNode* list2Tail = list2;\n while (list2Tail->next != nullptr) {\n list2Tail = list2Tail->next;\n }\n \n prevA->next = list2;\n list2Tail->next = prevB;\n \n return dummy->next;\n }\n};\n\n```\nUPVOTE IF YOU FINDS IT HELPFULL | 5 | 0 | ['C++'] | 1 |
merge-in-between-linked-lists | Beats 100% of users with C++ || Step by Step Explain || Fast Solution || | beats-100-of-users-with-c-step-by-step-e-0oeo | Abhiraj Pratap Singh\n\n---\n\n# UPVOTE IT....\n\n\n\n---\n\n# Intuition\n Describe your first thoughts on how to solve this problem. \n- The mergeInBetween fun | abhirajpratapsingh | NORMAL | 2024-01-12T16:56:33.258662+00:00 | 2024-01-12T16:56:33.258692+00:00 | 87 | false | # Abhiraj Pratap Singh\n\n---\n\n# UPVOTE IT....\n\n\n\n---\n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- The mergeInBetween function appears to merge two singly-linked lists list1 and list2 by removing a portion of nodes from list1 between the indices a and b (inclusive) and inserting the nodes of list2 in their place.\n\n\n---\n\n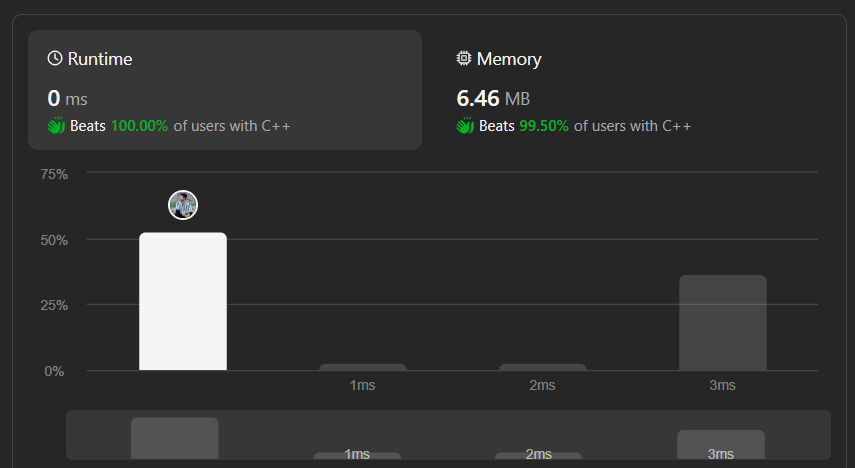\n\n\n---\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n1. Iterate through the nodes of list1 until reaching the node at index a-1. Set a pointer (temp1) to this node.\n2. Iterate through the nodes of list1 until reaching the node at index b+1. Set a pointer (temp2) to this node.\n3. Iterate through the nodes of list2 until reaching the last node. Set a pointer (ptr2) to this node.\n4. Update the next pointer of temp1 to point to the head of list2.\n5. Update the next pointer of the last node of list2 (pointed by ptr2) to point to temp2.\n6. Return the modified list1.\n\n---\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- **Time complexity: O(n+m),** where n is the length of list1 and m is the length of list2. The function iterates through both lists once.\n\n\n---\n\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n- **Space complexity: O(1),** The space required is constant as the function uses a constant number of pointers regardless of the size of the input lists.\n\n\n---\n\n\n# Code\n```\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode() : val(0), next(nullptr) {}\n * ListNode(int x) : val(x), next(nullptr) {}\n * ListNode(int x, ListNode *next) : val(x), next(next) {}\n * };\n */\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) \n {\n int Break_point=2;\n int node_no=0;\n ListNode *ptr1=list1;\n ListNode *ptr2=list2;\n ListNode *temp1=NULL;\n ListNode *temp2=NULL;\n while( Break_point != 0)\n {\n if(node_no==a-1)\n {\n Break_point--;\n temp1=ptr1;\n }\n if( node_no== b+1)\n {\n Break_point--;\n temp2=ptr1;\n }\n node_no++;\n ptr1=ptr1->next;\n } \n while(ptr2!=NULL && ptr2->next!=NULL)\n ptr2=ptr2->next;\n temp1->next=list2;\n ptr2->next=temp2;\n return list1;\n }\n};\n```\n\n---\n\n# if you like the solution please UPVOTE it.....\n\n---\n\n\n---\n\n\n\n---\n--- | 5 | 0 | ['Linked List', 'C++'] | 1 |
merge-in-between-linked-lists | Java || 1000% beats ❤️❤️ || 0(N) || 3 Solution || Easy || ❤️❤️ | java-1000-beats-0n-3-solution-easy-by-sa-3mfy | Intuition\n Describe your first thoughts on how to solve this problem. \nPLEASE UPVOTE ME \u2764\uFE0F\u2764\uFE0F\u2764\uFE0F\u2764\uFE0F\n\n# Approach\n Descr | saurabh_kumar1 | NORMAL | 2023-09-05T08:53:48.387926+00:00 | 2023-09-05T08:53:48.387947+00:00 | 685 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nPLEASE UPVOTE ME \u2764\uFE0F\u2764\uFE0F\u2764\uFE0F\u2764\uFE0F\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:0(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:0(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for singly-linked list.\n * public class ListNode {\n * int val;\n * ListNode next;\n * ListNode() {}\n * ListNode(int val) { this.val = val; }\n * ListNode(int val, ListNode next) { this.val = val; this.next = next; }\n * }\n */\nclass Solution {\n public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n ListNode curr = list1;\n ListNode NewNode1 = list1;\n ListNode NewNode2 = list1;\n \n for(int i=0; i<b; i++){\n if(i==a-1) NewNode1 = curr;\n curr = curr.next;\n }\n NewNode2 = curr.next;\n NewNode1.next = list2;\n while(list2.next!=null){\n list2 = list2.next;\n } \n list2.next = NewNode2;\n return list1;\n \n \n// Another solution\n\n // int count = 0;\n // ListNode curr = list1;\n // ListNode newVal = null;\n // while(curr!=null){\n // if(count==b) newVal = curr.next;\n // count++;\n // curr = curr.next;\n // }\n // curr = list1; count=0;\n // while(curr!=null){\n // count++;\n // if(count==a) curr.next = list2;\n // curr = curr.next; \n // }\n // curr = list1;\n // while(curr.next!=null){\n // curr = curr.next;\n // }\n // curr.next = newVal;\n // return list1;\n }\n}\n// same approach but using for loop\n\n // ListNode head = list1;\n // for(int i = 1; i < a; i++) {\n // head = head.next;\n // }\n // ListNode temp = head;\n // for(int i = 0; i < b-a+2; i++) {\n // temp = temp.next;\n // }\n // ListNode temp2 = list2;\n // while(temp2.next != null) {\n // temp2 = temp2.next;\n // }\n // head.next = list2;\n // temp2.next = temp;\n // return list1;\n\n \n``` | 5 | 0 | ['Java'] | 0 |
merge-in-between-linked-lists | JAVA solution: Easy Explanation | java-solution-easy-explanation-by-mandip-irdb | Intuition\n Describe your first thoughts on how to solve this problem. \nThe naive approach of the solution is that, we declare a new linked list and copy the l | Mandip_Sah | NORMAL | 2023-03-24T18:01:30.480196+00:00 | 2023-03-24T18:01:30.480240+00:00 | 193 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe naive approach of the solution is that, we declare a new linked list and copy the `list1` in new list upto `a` and the further traverse `list2` and copy them in the new linked list and again traverse `list1` upto `b` and start copying and then finally return the head of the new linked list.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe step by step approach to solve this problem is described below:\n1. First traverse list1 upto `a-1` and store its address at `curr1` and again traverse the same `list1` upto position b and store its address at `curr2`.\n2. Set the `curr1 next` address as the starting address of `list2`.\n3. Further traverse `list2` upto the last node and finally set the next of last node of `list2` as `curr2 next.`\n4. Return `list1.`\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$ where n is the length of the `list1`\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n\n***KINDLY UPVOTE THIS SOLUTION.***\n# Code\n```\n/**\n * Definition for singly-linked list.\n * public class ListNode {\n * int val;\n * ListNode next;\n * ListNode() {}\n * ListNode(int val) { this.val = val; }\n * ListNode(int val, ListNode next) { this.val = val; this.next = next; }\n * }\n */\nclass Solution {\n public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n int i=1;\n ListNode curr1=list1, curr2=list1;\n // Traversing list1 to store address of a-1 in curr1\n while(i<a){\n curr1=curr1.next;\n i++;\n }\n i=0;\n //Traversing list2 to store address of b in curr2\n while(i<b){\n curr2=curr2.next;\n i++;\n }\n //curr1\'s next store the starting address of list2\n curr1.next=list2;\n // Traversing list2 to reach the last node\n while(list2.next!=null)\n list2=list2.next;\n // The last node of list2 next value should store the address of curr2.next\n list2.next=curr2.next;\n return list1;\n }\n}\nKINDLY UPVOTE THIS SOLUTION IF YOU FIND IT USEFUL. | 5 | 0 | ['Java'] | 0 |
merge-in-between-linked-lists | Python (Simple Maths) | python-simple-maths-by-rnotappl-h48m | \n def mergeInBetween(self, list1, a, b, list2):\n cur1, cur2, res1, res2 = list1, list2, [], []\n \n while cur1:\n res1.appe | rnotappl | NORMAL | 2022-07-24T17:08:00.583287+00:00 | 2022-07-24T17:33:58.837881+00:00 | 77 | false | \n def mergeInBetween(self, list1, a, b, list2):\n cur1, cur2, res1, res2 = list1, list2, [], []\n \n while cur1:\n res1.append(cur1.val)\n cur1 = cur1.next\n \n while cur2:\n res2.append(cur2.val)\n cur2 = cur2.next\n \n res = res1[:a] + res2 + res1[b+1:]\n \n r1 = r2 = ListNode()\n \n for i in res:\n r1.next = ListNode(i)\n r1 = r1.next\n \n return r2.next | 5 | 0 | [] | 0 |
merge-in-between-linked-lists | Java simple and easy to understand soln, 1 ms, faster than 100.00% , clean code with comment | java-simple-and-easy-to-understand-soln-4sx40 | PLEASE UPVOTE IF YOU LIKE THIS SOLUTION\n\n\n\nclass Solution {\n public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n Lis | satyaDcoder | NORMAL | 2021-03-14T11:02:49.772538+00:00 | 2021-03-14T11:02:49.772566+00:00 | 287 | false | **PLEASE UPVOTE IF YOU LIKE THIS SOLUTION**\n\n\n```\nclass Solution {\n public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n ListNode curr1 = list1;\n \n //find the ath prev node and bth next node of list 1\n ListNode athPrevNode = null;\n ListNode bthNextNode = null;\n int i = 0;\n while(curr1 != null){\n if(i == a - 1){\n athPrevNode = curr1;\n }\n \n if(i == b + 1){\n bthNextNode = curr1;\n break;\n }\n \n curr1 = curr1.next;\n i++;\n }\n \n //find last node of list 2\n ListNode curr2 = list2;\n while(curr2 != null && curr2.next != null){\n curr2 = curr2.next;\n }\n \n //now insert list2 in list 1\n athPrevNode.next = list2;\n curr2.next = bthNextNode;\n \n return list1;\n }\n}\n``` | 5 | 2 | ['Java'] | 0 |
merge-in-between-linked-lists | C++ | 100% Faster and 100% Efficient | Most Efficient | Linear Approach | | c-100-faster-and-100-efficient-most-effi-c8fp | Code -\n\n\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n ListNode *slow = list1, *fast = l | dhruv_73 | NORMAL | 2021-01-14T07:21:48.168881+00:00 | 2021-01-14T07:21:48.168918+00:00 | 612 | false | **Code** -\n\n```\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n ListNode *slow = list1, *fast = list1, *temp = list2;\n while(--a){\n slow = slow -> next;\n }\n b += 2;\n while(--b){\n fast = fast -> next;\n }\n while(list2 -> next != nullptr){\n list2 = list2 -> next;\n }\n \n slow -> next = temp;\n list2 -> next = fast;\n return list1;\n }\n};\n```\n\n**Result**\n\n**Runtime**: **260 ms**, faster than **100.00%** of C++ online submissions for Merge In Between Linked Lists.\n**Memory Usage**: **94.5 MB**, less than **100.00%** of C++ online submissions for Merge In Between Linked Lists. | 5 | 2 | ['Linked List', 'C'] | 3 |
merge-in-between-linked-lists | [easy understanding][c++][explained] | easy-understandingcexplained-by-rajat_gu-c46f | \n//list1 = [0,1,2,3,4,5], a = 3, b = 4, list2 = [1000000,1000001,1000002]\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int | rajat_gupta_ | NORMAL | 2020-11-28T18:16:39.640210+00:00 | 2020-11-28T18:24:56.282960+00:00 | 398 | false | ```\n//list1 = [0,1,2,3,4,5], a = 3, b = 4, list2 = [1000000,1000001,1000002]\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n ListNode* prev,*tail,*head=list1;\n int x=a-1;\n while(x--) head=head->next; \n\t\t//prev and head is at index=3 i.e. val=2 of list1\n prev=head;\n b=b-a+1; //node that we have to delete\n while(b--) head=head->next;\n\t\t//know head is at index=5 i.e. val=4 of list1\n tail=head->next; //tail is at index=6 i.e. val=5 of list1 \n head->next=NULL;\n\t\t//merge list2 in list1 with prev\n prev->next=list2;\n while(prev->next!=NULL){\n prev=prev->next;\n }\n\t\t//prev is the know the last element of list2\n\t\t//join it with list1(tail)\n prev->next=tail;\n return list1;\n }\n};\n```\n**Feel free to ask any question in the comment section.**\nI hope that you\'ve found the solution useful.\nIn that case, **please do upvote and encourage me** to on my quest to document all leetcode problems\uD83D\uDE03\nHappy Coding :)\n | 5 | 1 | ['C', 'C++'] | 0 |
merge-in-between-linked-lists | Best/Easiest Java Code 🔥 | besteasiest-java-code-by-thepriyanshpal-ibmt | Intuition\nWe need to replace nodes from the ath node to the bth node of list1 with the entire list2. To do this, we find the node before ath and the node after | thepriyanshpal | NORMAL | 2024-03-20T08:40:36.873599+00:00 | 2024-03-20T08:40:36.873628+00:00 | 555 | false | # Intuition\nWe need to replace nodes from the ath node to the bth node of list1 with the entire list2. To do this, we find the node before ath and the node after bth in list1. Then, we connect the node before ath to the head of list2 and the tail of list2 to the node after bth.\n\n# Approach\n1. Traverse list1 until the node before ath node and store it.\n2. Traverse list1 from ath node to (b+1)th node and store the node after bth node.\n3. Find the tail of list2.\n4. Connect the node before ath to the head of list2.\n5. Connect the tail of list2 to the node after bth.\n6. Return the modified list1.\n\n# Complexity\n- Time complexity:\nO(a + b + list2.length)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution {\n public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n // Initialize current node to traverse list1\n ListNode currNode = list1;\n // Initialize index to keep track of current position in list1\n int index = 0;\n \n // Traverse list1 until the node before ath node\n while (index < a - 1) {\n currNode = currNode.next;\n index++;\n }\n // Store the node before ath node\n ListNode front = currNode;\n \n // Traverse list1 from ath node to (b+1)th node\n while (index < b + 1) {\n currNode = currNode.next;\n index++;\n }\n // Store the node after bth node\n ListNode rear = currNode;\n \n // Find the tail of list2\n ListNode secondListTail = list2, secondListHead = list2;\n while (secondListTail.next != null) {\n secondListTail = secondListTail.next;\n }\n \n // Connect the front node to the head of list2\n front.next = secondListHead;\n // Connect the tail of list2 to the rear node\n secondListTail.next = rear;\n \n // Return the modified list1\n return list1;\n }\n}\n\n``` | 4 | 0 | ['Java'] | 0 |
merge-in-between-linked-lists | Super simple solution with step by step dry run ✅✅✅ | super-simple-solution-with-step-by-step-psf4c | https://youtu.be/CUHQHKTu51I\n\n# Code\n\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n Lis | priyankachowdhury2002 | NORMAL | 2024-03-20T03:48:42.170255+00:00 | 2024-03-20T03:53:58.124334+00:00 | 248 | false | https://youtu.be/CUHQHKTu51I\n\n# Code\n```\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n ListNode* ath = list1; //pointer to find the ath position \n ListNode* bth = list1; //pointer to find the bth position\n while(a>1){ // i want the a pointer before the ath index\n ath = ath->next;\n a--;\n }\n while(b>0){ // i want b pointer on the bth index\n bth = bth->next;\n b--;\n }\n ath->next = list2; // adding a\'s end to list2\n while(list2->next!=NULL){\n list2 = list2->next; //going till the end\n }\n list2->next = bth->next; //modifying links\n return list1;\n }\n};\n``` | 4 | 0 | ['C++'] | 2 |
merge-in-between-linked-lists | Merge In Between Linked Lists - Java Solution (Beats 100%) | merge-in-between-linked-lists-java-solut-uvrt | Intuition\n Describe your first thoughts on how to solve this problem. \nMy intuition involves identifying the nodes aPrev and bNext in list1, representing the | Naveen-NaS | NORMAL | 2024-01-12T14:26:10.644940+00:00 | 2024-01-12T14:26:10.644969+00:00 | 140 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nMy intuition involves identifying the nodes aPrev and bNext in list1, representing the positions before and after the removal range, and finding the last node of list2. By connecting aPrev to the head of list2 and the last node of list2 to bNext seamlessly replace the specified range in list1 with list2.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nLet\'s break down my approach for solution step by step:\n- **Finding the Node aPrev:** Start by iterating through the list1 until you reach the (a-1)th node, which is the node just before the range you want to remove.\n\n- **Finding the Node bNext:** Similarly, iterate through the list1 until you reach the (b+1)th node, which is the node just after the range you want to remove.\n\n- **Finding the Last Node of list2:** Iterate through list2 to find its last node. This is important for connecting list2 to the remaining part of list1 after removal.\n\n- **Connecting list2 to list1:** After finding aPrev, bNext, and the last node of list2, set aPrev.next to point to the head of list2, effectively connecting the part before the removal range to list2.\nThen, set the next of the last node in list2 to point to bNext, linking the remaining part of list1 after the removal range.\n\nAt last return the head of modified list1.\n# Complexity\n- **Time complexity:** The time complexity of my code is **O(n + m)**, where n is the size of list1, and m is the size of list2. O(n + m) is equivalent to O(n).\n\n- **Space complexity:** The space complexity is **O(1)** as we use a constant amount of extra space to store variables like aPrev, bNext, and temp.\n# Code\n```\nclass Solution {\n public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n ListNode aPrev = list1;\n int i = 0;\n while (i < a-1) {\n aPrev = aPrev.next;\n i++;\n }\n ListNode bNext = list1;\n int j = 0;\n while (j <= b) {\n bNext = bNext.next;\n j++;\n }\n\n ListNode temp = list2;\n while (temp.next != null) {\n temp = temp.next;\n }\n\n aPrev.next = list2;\n temp.next = bNext;\n\n return list1;\n }\n}\n/**\n * Definition for singly-linked list.\n * public class ListNode {\n * int val;\n * ListNode next;\n * ListNode() {}\n * ListNode(int val) { this.val = val; }\n * ListNode(int val, ListNode next) { this.val = val; this.next = next; }\n * }\n */\n``` | 4 | 0 | ['Java'] | 2 |
merge-in-between-linked-lists | C++ solution | c-solution-by-raghavkhandelwal2710-hy14 | ```\nclass Solution {\npublic:\n ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n \n ListNode start;\n ListNode | raghavkhandelwal2710 | NORMAL | 2021-06-07T12:43:10.229928+00:00 | 2021-06-07T12:43:10.229992+00:00 | 197 | false | ```\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n \n ListNode* start;\n ListNode* last;\n ListNode* curr = list1;\n \n int count = 1;\n \n while(curr){\n \n if(count == a) start = curr;\n if(count == b) last = curr->next->next;\n curr = curr->next;\n count++;\n }\n \n start->next = list2;\n curr = list2;\n while(curr->next){\n curr= curr->next;\n }\n curr->next = last;\n \n return list1;\n }\n}; | 4 | 0 | [] | 1 |
merge-in-between-linked-lists | JavaScript Solution | javascript-solution-by-deadication-8ukj | \nvar mergeInBetween = function(list1, a, b, list2) {\n let start = list1;\n let end = list1;\n \n for (let i = 0; i <= b && start != null && end != | Deadication | NORMAL | 2021-03-05T14:54:28.907903+00:00 | 2021-03-05T14:54:28.907947+00:00 | 559 | false | ```\nvar mergeInBetween = function(list1, a, b, list2) {\n let start = list1;\n let end = list1;\n \n for (let i = 0; i <= b && start != null && end != null; i++) {\n if (i < a - 1) start = start.next;\n if (i <= b) end = end.next;\n }\n \n let tail = list2;\n \n while (tail.next != null) {\n tail = tail.next;\n }\n \n start.next = list2;\n tail.next = end;\n \n return list1;\n};\n``` | 4 | 1 | ['JavaScript'] | 1 |
merge-in-between-linked-lists | C# | c-by-mhorskaya-bs0j | \npublic ListNode MergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n\tListNode p1 = list1, p2 = list1;\n\twhile (--a > 0) p1 = p1.next;\n\twhile ( | mhorskaya | NORMAL | 2020-12-02T18:58:32.757303+00:00 | 2020-12-02T18:58:32.757350+00:00 | 166 | false | ```\npublic ListNode MergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n\tListNode p1 = list1, p2 = list1;\n\twhile (--a > 0) p1 = p1.next;\n\twhile (b-- > 0) p2 = p2.next;\n\tp1.next = list2;\n\twhile (p1.next != null) p1 = p1.next;\n\tp1.next = p2.next;\n\treturn list1;\n}\n``` | 4 | 0 | [] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.