question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
merge-in-between-linked-lists | Python, straightforward | python-straightforward-by-warmr0bot-ri7g | Find the node before a and after b in the list1, then fix the next pointers to join prea and postb nodes with list2:\n\ndef mergeInBetween(self, list1: ListNode | warmr0bot | NORMAL | 2020-11-28T16:02:30.748139+00:00 | 2020-11-28T16:22:50.050799+00:00 | 997 | false | Find the node before a and after b in the `list1`, then fix the next pointers to join `prea` and `postb` nodes with `list2`:\n```\ndef mergeInBetween(self, list1: ListNode, a: int, b: int, list2: ListNode) -> ListNode:\n\tprea = postb = None\n\tdummy = cur = ListNode(next=list1)\n\tfor i in range(b+1):\n\t\tif i == a: prea = cur\n\t\tcur = cur.next\n\tpostb = cur.next\n\n\tprea.next = list2\n\twhile list2.next:\n\t\tlist2 = list2.next\n\n\tlist2.next = postb\n\treturn dummy.next\n``` | 4 | 0 | ['Python', 'Python3'] | 0 |
merge-in-between-linked-lists | 🏆 Easy to Understand Python Solution with 99% Running Time 🚀 | easy-to-understand-python-solution-with-12kx1 | Intuition\n Describe your first thoughts on how to solve this problem. \nTo merge list2 into list1 between indices a and b, we need to locate the nodes at posit | LinhNguyen310 | NORMAL | 2024-07-28T14:06:53.879144+00:00 | 2024-07-28T14:06:53.879173+00:00 | 22 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo merge list2 into list1 between indices a and b, we need to locate the nodes at positions a-1 and b+1 in list1, and link them correctly to list2.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTraverse list1 to find the nodes at positions a-1 and b+1.\nTraverse list2 to find the last node.\nLink the node at position a-1 in list1 to the head of list2.\nLink the last node of list2 to the node at position b+1 in list1.\n# Complexity\n- Time complexity:O(n+m) where \nn is the length of list1 and \nm is the length of list2.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: \nO(1) since we are only using a few extra pointers.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode(object):\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution(object):\n def mergeInBetween(self, list1, a, b, list2):\n """\n :type list1: ListNode\n :type a: int\n :type b: int\n :type list2: ListNode\n :rtype: ListNode\n """\n count = 0\n prev, curr = ListNode(None), list1\n ret = list1\n temp2, last2 = list2, list2\n\n while last2 and last2.next:\n last2 = last2.next\n\n found = None\n b += 1\n while curr:\n count += 1\n if count == a:\n prev = curr\n elif count == b + 1:\n found = curr\n prev.next = temp2\n last2.next = curr\n curr = curr.next\n return ret\n```\n\n | 3 | 0 | ['Linked List', 'Python', 'Python3'] | 0 |
merge-in-between-linked-lists | Beats 70% using C++ | easy solution | beats-70-using-c-easy-solution-by-xuankh-q9kk | Intuition\nFind tail of list 2, and link tail of list2 to node b + 1;\n\n\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(1)\n\n# Code\n\n/**\ | xuankhuongw | NORMAL | 2024-03-31T16:03:04.582659+00:00 | 2024-03-31T16:03:04.582692+00:00 | 9 | false | # Intuition\nFind tail of list 2, and link tail of list2 to node b + 1;\n\n\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(1)\n\n# Code\n```\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode() : val(0), next(nullptr) {}\n * ListNode(int x) : val(x), next(nullptr) {}\n * ListNode(int x, ListNode *next) : val(x), next(next) {}\n * };\n */\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n ListNode *tailOfList2 = NULL;\n ListNode *cur1 = list1, *tmp = list1;\n //find tail of list 2\n for (ListNode *p = list2; p ; p = p -> next)\n if (!p -> next) tailOfList2 = p;\n //jump to a - 1\n for (int i = 0; i < a - 1; i++)\n {\n cur1 = cur1 -> next;\n tmp = tmp -> next;\n }\n tmp = tmp->next; // jump to a\n //then jump to b + 1\n for (int i = 0; i < b - a + 1; i++)\n tmp = tmp -> next;\n //link\n tailOfList2 -> next = tmp;\n cur1 -> next = list2;\n return list1;\n }\n};\n``` | 3 | 0 | ['C++'] | 0 |
merge-in-between-linked-lists | 🔥🔥🔥🔥🔥 Beat 99% 🔥🔥🔥🔥🔥 EASY 🔥🔥🔥🔥🔥🔥 | beat-99-easy-by-abdallaellaithy-hu6c | \n\n\n# Code\n\n# Definition for singly-linked list.\n# class ListNode(object):\n# def __init__(self, val=0, next=None):\n# self.val = val\n# | abdallaellaithy | NORMAL | 2024-03-20T17:46:27.610666+00:00 | 2024-03-20T17:47:16.299423+00:00 | 32 | false | \n\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode(object):\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution(object):\n def mergeInBetween(self, list1, a, b, list2):\n """\n :type list1: ListNode\n :type a: int\n :type b: int\n :type list2: ListNode\n :rtype: ListNode\n """\n fast = list1\n slow = list1\n for _ in range(a-1): # Catch first node befor removing\n fast= fast.next\n slow= slow.next\n for _ in range(a, b+2): # Catch first node after removing\n fast = fast.next\n slow.next = list2 # link slow node to list2\n while list2.next is not None: \n list2 = list2.next\n list2.next = fast # link last node of list2 to fast node\n return list1\n``` | 3 | 0 | ['Python', 'Python3'] | 2 |
merge-in-between-linked-lists | Beat 100%%%!!!!! Users | Full Explanation 0(n+m) !!!!!!!| 🔥🔥🔥🔥🔥🔥🔥🔥🔥🔥Java!!!!!!!!!!!!! | beat-100-users-full-explanation-0nm-java-u25k | Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem requires merging two linked lists list1 and list2 by removing a segment of | shuddhi08 | NORMAL | 2024-03-20T16:33:56.640971+00:00 | 2024-03-20T16:42:51.207100+00:00 | 91 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem requires merging two linked lists list1 and list2 by removing a segment of nodes from list1 and replacing them with list2. To solve this, we can traverse list1 to identify the nodes to be removed (from position a to position b), connect the node just before a to the head of list2, and connect the last node of list2 to the node after b.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nIdentifying Nodes to Remove: We traverse list1 to find the node just before position a and the node at position b. This step ensures that we can properly connect list2 without losing track of the nodes in list1.\n\nConnecting list2: Once we have identified the nodes to remove in list1, we connect the node just before a to the head of list2. This effectively places list2 in the segment that needs to be removed from list1.\n\nConnecting the Tail of list2: After connecting the head of list2, we traverse to the end of list2 to find its last node. We then connect this last node to the node after b in list1. This step effectively merges list2 into list1.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nTraversing list1 to find the nodes at positions a and b: This takes linear time, proportional to the size of list1, so it\'s O(n), where n is the size of list1.\nTraversing list2 to find its last node: Similarly, this takes linear time, so it\'s O(m), where m is the size of list2.Overall, the time complexity is O(n+m).\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nWe\'re using constant space for variables, and we\'re not creating any additional data structures proportional to the size of the input lists. Hence, the space complexity is O(1).\n\n# DryRun\nLet\'s dry run the algorithm with an example:\n\nlist1 = [10, 1, 13, 6, 9, 5]\na = 3, b = 4\nlist2 = [1000000, 1000001, 1000002]\nWe start with list1 and traverse to the node just before position a (which is the 2nd node with value 1) and the node at position b (which is the 3rd node with value 6).\n\nWe connect the node just before a to the head of list2, making list1 look like [10, 1, 1000000, 1000001, 1000002, 9, 5].\n\nWe traverse list2 to find its last node, which is the 3rd node with value 1000002. We connect this last node to the node after b in list1, effectively merging list2 into list1.\n\nThe final merged list is [10, 1, 1000000, 1000001, 1000002, 9, 5].\n\n# Code\n```\nclass Solution {\n public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n if (list2 == null) {\n return list1; \n }\n \n ListNode temp = list1;\n \n \n for (int i = 0; i < a - 1; i++) {\n temp = temp.next;\n }\n \n ListNode beforeA = temp;\n \n for (int i = 0; i < b - a + 1; i++) {\n temp = temp.next;\n }\n \n ListNode afterB = temp.next;\n \n beforeA.next = list2;\n \n while (list2.next != null) {\n list2 = list2.next;\n }\n \n list2.next = afterB;\n \n return list1;\n }\n}\n\n\n``` | 3 | 0 | ['Java'] | 0 |
merge-in-between-linked-lists | JAVA Solution Explained in HINDI | java-solution-explained-in-hindi-by-the_-j4i4 | https://youtu.be/clHuUMe0UeM\n\nFor explanation, please watch the above video and do like, share and subscribe the channel. \u2764\uFE0F Also, please do upvote | The_elite | NORMAL | 2024-03-20T07:23:58.847311+00:00 | 2024-03-20T07:23:58.847341+00:00 | 325 | false | https://youtu.be/clHuUMe0UeM\n\nFor explanation, please watch the above video and do like, share and subscribe the channel. \u2764\uFE0F Also, please do upvote the solution if you liked it.\n\nSubscribe link:- https://www.youtube.com/@reelcoding?sub_confirmation=1\n\nSubscribe Goal:- 300\nCurrent Subscriber:- 242\n\n# Complexity\n- Time complexity: O(m+n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for singly-linked list.\n * public class ListNode {\n * int val;\n * ListNode next;\n * ListNode() {}\n * ListNode(int val) { this.val = val; }\n * ListNode(int val, ListNode next) { this.val = val; this.next = next; }\n * }\n */\nclass Solution {\n public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n \n ListNode start = null;\n ListNode end = list1;\n\n for(int i = 0; i < b; i++) {\n if(i == a - 1) {\n start = end;\n }\n end = end.next;\n }\n\n start.next = list2;\n\n while(list2.next != null) {\n list2 = list2.next;\n }\n\n list2.next = end.next;\n end.next = null;\n\n return list1;\n }\n}\n``` | 3 | 0 | ['Java'] | 0 |
merge-in-between-linked-lists | Just simple code | just-simple-code-by-nbekweb-lwdg | \n\n# Code\n\nvar mergeInBetween = function(list1, a, b, list2) {\n let ptr = list1;\n for (let i = 0; i < a - 1; ++i)\n ptr = ptr.next;\n \n | Nbekweb | NORMAL | 2024-03-20T05:11:46.435981+00:00 | 2024-03-20T05:11:46.436014+00:00 | 13 | false | \n\n# Code\n```\nvar mergeInBetween = function(list1, a, b, list2) {\n let ptr = list1;\n for (let i = 0; i < a - 1; ++i)\n ptr = ptr.next;\n \n let qtr = ptr.next;\n for (let i = 0; i < b - a + 1; ++i)\n qtr = qtr.next;\n \n ptr.next = list2;\n while (list2.next)\n list2 = list2.next;\n list2.next = qtr;\n \n return list1;\n};\n``` | 3 | 0 | ['JavaScript'] | 1 |
merge-in-between-linked-lists | ✅✅ Beginner's Friendly || Easy Approach || JAVA || 1s || Beats 100%🔥🔥 | beginners-friendly-easy-approach-java-1s-p43p | Intuition\n Describe your first thoughts on how to solve this problem. \nJust points the required points to new points\n\n# Approach\n Describe your approach to | aadibajaj1502 | NORMAL | 2024-03-20T04:14:33.094518+00:00 | 2024-03-20T04:14:33.094551+00:00 | 37 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nJust points the required points to new points\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for singly-linked list.\n * public class ListNode {\n * int val;\n * ListNode next;\n * ListNode() {}\n * ListNode(int val) { this.val = val; }\n * ListNode(int val, ListNode next) { this.val = val; this.next = next; }\n * }\n */\nclass Solution {\n public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n ListNode temp = list1;\n for(int i = 0 ; i < b ; i++){\n temp = temp.next;\n }\n ListNode temp2 = list2;\n while(temp2.next!=null){\n temp2 = temp2.next;\n }\n temp2.next = temp.next;\n\n ListNode temp3 = list1;\n for(int i = 0 ; i < a-1 ; i++){\n temp3 = temp3.next;\n }\n temp3.next = list2;\n return list1;\n }\n}\n``` | 3 | 0 | ['Java'] | 0 |
merge-in-between-linked-lists | Simple as pie || Effort less :) | simple-as-pie-effort-less-by-jhaainsuhmr-9ya8 | Intuition\nTo solve this question we need to locate the nodes at positions a-1 and b+1 in list1,(Because as we know inorder to connect node next to other node w | jhaainsuhmrainram33 | NORMAL | 2024-03-20T02:03:58.285669+00:00 | 2024-03-20T02:03:58.285701+00:00 | 39 | false | # Intuition\nTo solve this question we need to locate the nodes at positions a-1 and b+1 in list1,(Because as we know inorder to connect node next to other node we need to get the previous node so we acquire the a-1 node,then we have to remove node from a to b so we get the b+1th node and connect to the existing LL) and then connect these nodes to the head and tail of list2, respectively.\n\n# Approach\n1.Traverse list1 to find the nodes at positions a-1 and b+1.\n2.Connect the node at position a-1 to the head of list2.\n3.Traverse list2 to find its last node.\n4.Connect the last node of list2 to the node at position b+1 in list1.\n5.Return list1 after merging list2.\n\n# Complexity\n- Time complexity:O(n)\n\n- Space complexity:O(1)\n\n# Code\n```\n/**\n * Definition for singly-linked list.\n * public class ListNode {\n * int val;\n * ListNode next;\n * ListNode() {}\n * ListNode(int val) { this.val = val; }\n * ListNode(int val, ListNode next) { this.val = val; this.next = next; }\n * }\n */\nclass Solution {\n public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n \n int i=0;\n ListNode an=null,bn=null,temp=list1;\n while(temp!=null)\n {\n if(i==a-1)\n {\n an=temp;\n }\n else if(i==b+1)\n {\n bn=temp;\n }\n temp=temp.next;\n i++;\n }\n //connect a-1 node to the list 2 head\n an.next=list2;\n\n //traversing through the list 2 LL to find end of list2\n\n ListNode temp2=list2;\n while(temp2.next!=null)\n {\n temp2=temp2.next;\n }\n\n //connecting end of list2 to b+1 node of list\n temp2.next=bn;\n\n return list1;\n\n }\n}\n``` | 3 | 0 | ['Java'] | 0 |
merge-in-between-linked-lists | ✅✅ Beginner's Friendly || Easy Approach || JAVA || 3ms || 🔥🔥 | beginners-friendly-easy-approach-java-3m-aqhp | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | AadiVerma07 | NORMAL | 2024-03-20T01:46:25.607543+00:00 | 2024-03-20T01:46:25.607567+00:00 | 109 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for singly-linked list.\n * public class ListNode {\n * int val;\n * ListNode next;\n * ListNode() {}\n * ListNode(int val) { this.val = val; }\n * ListNode(int val, ListNode next) { this.val = val; this.next = next; }\n * }\n */\nclass Solution {\n public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n ListNode ans=new ListNode(-1);\n ListNode temp=ans;\n int index=0;\n while(list1!=null){\n if(index==a){\n while(list2!=null){\n temp.next=list2;\n list2=list2.next;\n temp=temp.next;\n }\n }\n if(index<a || index>b){\n temp.next=list1;\n temp=temp.next;\n }\n list1=list1.next;\n index++;\n }\n return ans.next;\n \n }\n}\n``` | 3 | 0 | ['Linked List', 'Java'] | 1 |
merge-in-between-linked-lists | EASY|| FULLY DETAILED EXPLANATION || MAKE CONNECTIONS | easy-fully-detailed-explanation-make-con-n4v1 | Intuition\n Describe your first thoughts on how to solve this problem. \nThe Intuition is as simple as it says . Just do as directed , there is no catch in the | Abhishekkant135 | NORMAL | 2024-03-20T01:35:40.361857+00:00 | 2024-03-20T01:35:40.361876+00:00 | 118 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe Intuition is as simple as it says . Just do as directed , there is no catch in the question . \n# GET MY LINKEDIN IN THE COMMENTS LETS CONNECT TOGETHER AND MASTER DSA.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n\n**Steps:**\n\n1. **Initialization:**\n - `temp`: A temporary pointer to traverse `list1`.\n - `jointStart`: A pointer to store the node before the insertion point (`a-1`).\n - `jointEnd`: A pointer to store the node after the insertion point (`b+1`).\n - `index`: A counter to track the current position in `list1`.\n\n2. **Finding Insertion Points:**\n - The loop iterates through `list1` using `temp`:\n - If `index == a - 1`: This indicates the node before the insertion point. The code sets `jointStart` to the current node `temp`.\n - If `index == b + 1`: This indicates the node after the insertion point. The code sets `jointEnd` to the current node `temp`.\n - The loop increments `index` for each iteration.\n\n3. **Connecting `list1` and `list2`:**\n - After finding the insertion points:\n - `jointStart.next = list2`: Connects the node before the insertion point (`jointStart`) to the head of `list2`. This effectively inserts `list2` at the beginning of the desired location.\n\n4. **Finding the Tail of `list2`:**\n - `temp2`: A temporary pointer to traverse `list2`.\n - `tail`: A pointer to store the last node of `list2`.\n - The loop iterates through `list2` using `temp2`:\n - It finds the last node (`tail`) by checking for `temp2.next == null`.\n\n5. **Connecting the Tail of `list2` to `list1`:**\n - `tail.next = jointEnd`: Connects the last node of `list2` (`tail`) to the node after the insertion point (`jointEnd`). This completes the insertion of `list2` between nodes `a` and `b` of `list1`.\n\n6. **Returning the Modified List:**\n - The function returns `list1`, which has now been modified with `list2` inserted between the specified nodes.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\n/**\n * Definition for singly-linked list.\n * public class ListNode {\n * int val;\n * ListNode next;\n * ListNode() {}\n * ListNode(int val) { this.val = val; }\n * ListNode(int val, ListNode next) { this.val = val; this.next = next; }\n * }\n */\nclass Solution {\n public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n ListNode temp =list1;\n ListNode jointStart=null;\n ListNode jointEnd=null;\n int index=0;\n while(temp!=null){\n if(index==a-1){\n jointStart=temp;\n }\n else if(index==b+1){\n jointEnd=temp;\n }\n temp=temp.next;\n index++;\n }\n jointStart.next=list2;\n //lets find tail of list 2;\n ListNode temp2 =list2;\n ListNode tail=null;\n while(temp2.next!=null){\n temp2=temp2.next;\n tail=temp2;\n \n }\n tail.next=jointEnd;\n return list1;\n }\n}\n``` | 3 | 0 | ['Linked List', 'Java'] | 1 |
merge-in-between-linked-lists | Simple solution || Explained step by step || Java ✅|| Beats 100% ✌️ | simple-solution-explained-step-by-step-j-whr3 | Intuition\n1. We can solve this by iterating through the first list list1 to find the nodes where we want to insert list2.\n2. Once we find those nodes, we can | prateekrjt14 | NORMAL | 2024-03-20T00:40:42.714765+00:00 | 2024-03-20T00:41:48.215012+00:00 | 138 | false | # Intuition\n1. We can solve this by iterating through the first list `list1` to find the nodes where we want to insert `list2.`\n2. Once we find those nodes, we can manipulate the pointers to detach the segment in `list1` and connect `list2` in its place.\n\n# Approach\n1. **Find Insertion and Removal Points:** *Iterate through* `list1` keeping track of positions. Store the node before position `a` and the node after position `b`.\n2. **Detach Segment:** Set the `next` pointer of the node before `a` to point to the head of `list2`.\n3. **Connect list2 Tail:** Traverse `list2` to find its last node and set its `next` pointer to the node after position `b` in `list1`.\n4. **Return Modified List:** The head of `list1` now points to the merged list, so return it.\n\n# Complexity\n- Time complexity:\n**O(m+n)**\n\n- Space complexity:\n**O(1)**\n\n# Code\n```Java []\n/**\n * Definition for singly-linked list.\n * public class ListNode {\n * int val;\n * ListNode next;\n * ListNode() {}\n * ListNode(int val) { this.val = val; }\n * ListNode(int val, ListNode next) { this.val = val; this.next = next; }\n * }\n */\nclass Solution {\n public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n ListNode current = list1;\n for (int i = 0; i < a - 1; i++) {\n current = current.next;\n }\n \n ListNode startNode = current;\n \n for (int i = a; i <= b + 1; i++) {\n current = current.next;\n }\n \n startNode.next = list2;\n \n while (list2.next != null) {\n list2 = list2.next;\n }\n \n list2.next = current;\n \n return list1;\n }\n}\n\n```\n```C++ []\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode() : val(0), next(nullptr) {}\n * ListNode(int x) : val(x), next(nullptr) {}\n * ListNode(int x, ListNode *next) : val(x), next(next) {}\n * };\n */\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n // Traverse to the node before \'a\'\n ListNode* current = list1;\n for (int i = 0; i < a - 1; i++) {\n current = current->next;\n }\n \n // Mark the node before \'a\'\n ListNode* startNode = current;\n \n // Traverse to the node after \'b\'\n for (int i = a; i <= b + 1; i++) {\n current = current->next;\n }\n \n // Connect list2 at the position of \'a\' to \'b\'\n startNode->next = list2;\n \n // Traverse to the end of list2\n while (list2->next != nullptr) {\n list2 = list2->next;\n }\n \n // Connect the end of list2 to the node after \'b\'\n list2->next = current;\n \n return list1; // Return the head of modified linked list\n }\n};\n\n```\n```javascript []\n/**\n * Definition for singly-linked list.\n */\nfunction ListNode(val, next) {\n this.val = (val === undefined ? 0 : val);\n this.next = (next === undefined ? null : next);\n}\n\n/**\n * @param {ListNode} list1\n * @param {number} a\n * @param {number} b\n * @param {ListNode} list2\n * @return {ListNode}\n */\nvar mergeInBetween = function(list1, a, b, list2) {\n let current = list1;\n \n // Traverse to the node before \'a\'\n for (let i=0; i<a-1; i++) {\n current=current.next;\n }\n \n // Mark the node before \'a\'\n let startNode=current;\n \n // Traverse to the node after \'b\'\n for (let i=a; i<=b+1; i++) {\n current=current.next;\n }\n \n // Connect list2 at the position of \'a\' to \'b\'\n startNode.next=list2;\n \n // Traverse to the end of lis t21\n while(list2.next!=null){\n list2=list2.next;\n }\n\n // Connect the end of list21 to the node after\'b"\n list2.next=current;\n\n return list1//Return the head of modified linkedlist (list1) \n};\n\n```\n```python3 []\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\n\nclass Solution:\n def mergeInBetween(self, list1: ListNode, a: int, b: int, list2: ListNode) -> ListNode:\n # Traverse to the node before \'a\'\n current = list1\n for _ in range(a - 1):\n current = current.next\n \n # Mark the node before \'a\'\n startNode = current\n \n # Traverse to the node after \'b\'\n for _ in range(b - a + 2):\n current = current.next\n \n # Connect list2 at the position of \'a\' to \'b\'\n startNode.next = list2\n \n # Traverse to the end of list2\n while(list2.next != None):\n list2 =list2.next\n \n # Connect the end of list2 to the node after \'b\'\n list2.next = current\n \n return list1 # Return the head of modified linked list\n\n```\n | 3 | 0 | ['Linked List', 'C++', 'Java', 'Python3', 'JavaScript'] | 0 |
merge-in-between-linked-lists | Java | Easy solution | Beats 100% | java-easy-solution-beats-100-by-guinex-nyhg | Intuition\n\n---\n\nJust by iterating list1 we can find out where we need to insert the list2 at appropriate position. \n# Approach\n\n---\n\n*Remember List s | guinex | NORMAL | 2024-03-20T00:31:17.979541+00:00 | 2024-03-20T00:43:35.200299+00:00 | 633 | false | # Intuition\n\n---\n\nJust by iterating list1 we can find out where we need to insert the list2 at appropriate position. \n# Approach\n\n---\n\n*Remember List starts from 0th position, so we need to go till ath, and (b+1)th position * \n- Iterate over list1 and find ListNode at ath, (b+1)th position, as aListNode, bListNode.\n- Then switch the next pointers as follows: \n - aListNode.next = list2 \n - tail_of_list2.next = bListNode.next\n# Complexity\n\n---\n\n- Time complexity:\nO(M+N)\n\n- Space complexity:\nO(1)\n\n# Code\n```\n/**\n * Definition for singly-linked list.\n * public class ListNode {\n * int val;\n * ListNode next;\n * ListNode() {}\n * ListNode(int val) { this.val = val; }\n * ListNode(int val, ListNode next) { this.val = val; this.next = next; }\n * }\n */\nclass Solution {\n public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n ListNode aListNode = null, bListNode = null, dummyNode = null;\n dummyNode = new ListNode(0, list1);\n b++;\n while(dummyNode.next != null) {\n a--;\n b--;\n dummyNode = dummyNode.next;\n if(a==0){\n aListNode = dummyNode;\n }\n if(b==0) {\n bListNode = dummyNode;\n break;\n }\n }\n if(aListNode == null) aListNode = list1;\n aListNode.next = list2;\n // find tail of list2\n while(list2.next!=null){\n list2 = list2.next;\n }\n list2.next=bListNode.next;\n return list1;\n }\n}\n``` | 3 | 0 | ['Java'] | 1 |
merge-in-between-linked-lists | ✅☑ [C || Python3] || 100% Working 🔥🔥 || Easy Method Solution || Please Upvote If Find useful 🔥|| | c-python3-100-working-easy-method-soluti-sgd2 | Code\n\npython3 []\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# se | khakse_0003 | NORMAL | 2024-02-20T11:44:22.638868+00:00 | 2024-02-20T11:44:22.638904+00:00 | 139 | false | # Code\n\n```python3 []\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def mergeInBetween(self, list1: ListNode, a: int, b: int, list2: ListNode) -> ListNode:\n itr = list1\n count = 0\n while itr:\n if count == a-1:\n ptr = itr\n if count == b+1:\n qtr = itr\n count += 1\n itr = itr.next\n itr2 = list2\n while itr2.next:\n itr2 = itr2.next\n ptr.next = list2\n itr2.next = qtr\n return list1\n```\n```C []\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * struct ListNode *next;\n * };\n */\n\n\nstruct ListNode* mergeInBetween(struct ListNode* list1, int a, int b, struct ListNode* list2){\n struct ListNode *itr = list1;\n struct ListNode *ptr;\n struct ListNode *qtr;\n int count = 0;\n while (itr != NULL){\n if (count == a - 1){\n ptr = itr;\n }\n if (count == b + 1){\n qtr = itr;\n }\n count++;\n itr = itr->next;\n }\n struct ListNode *itr2 = list2;\n while (itr2->next != NULL){\n itr2 = itr2->next;\n }\n ptr->next = list2;\n itr2->next = qtr;\n return list1;\n}\n```\n\n | 3 | 0 | ['Linked List', 'C', 'Python3'] | 0 |
merge-in-between-linked-lists | Simple ,Beginner friendly & Dry Run & Advanced Sol, Full Explanation||Time O(n) Space O(1)||Gits✅✅✅ | simple-beginner-friendly-dry-run-advance-d6ew | \n\n# Intuition \uD83D\uDC48\n\nIn the question, we are given two linked lists, List1 and List2, and two numbers, a and b. We have to remove nodes of List1 from | GiteshSK_12 | NORMAL | 2024-02-08T08:39:44.209621+00:00 | 2024-03-09T05:03:23.992443+00:00 | 198 | false | \n\n# Intuition \uD83D\uDC48\n\nIn the question, we are given two linked lists, List1 and List2, and two numbers, a and b. We have to remove nodes of List1 from a to b and insert List2 in their place.\n\n# Approach \uD83D\uDC48\n\nTo solve this question, we will simply create a dummy list with a random value and a `prev` node, which will point to the node previous to `a`. Then, we will create a node `after_idx`, which will point to the node next to `b`. Next, we will set `prev.next` to point to `list2`. We will create a node `last_idx`, which will point to the last node of `list2`. Finally, we will set `last_idx.next` to point to `after_idx`.\n\n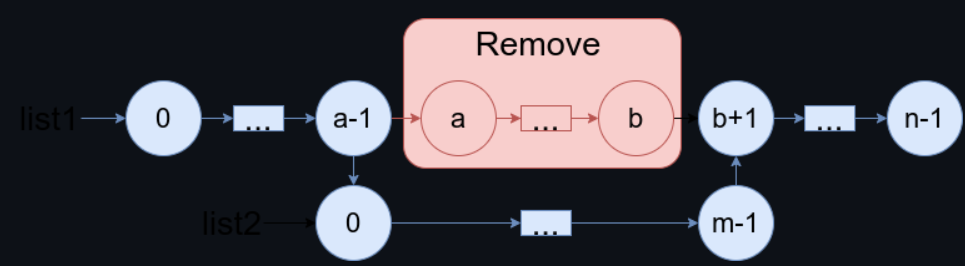\n\n# Code Explanation \uD83D\uDC48\n\n\n* **Creating a Dummy Node**: A new `ListNode` named `dummy` is created with a value of `0`. This node does not actually hold data relevant to the lists being merged but serves as a placeholder to simplify manipulation of the list heads and ensure uniform handling of all nodes during the merge. `dummy.next` is set to point to the head of `list1`, effectively placing the dummy node at the beginning of `list1`.\n \n* **Locating the Insertion Point**: The method starts by finding the node in `list1` immediately before the position `a` where `list2` will be inserted. This is done by advancing a pointer `pre` from the dummy node up to, but not including, the `a`th node. This loop runs `a` times.\n \n* **Skipping Over Nodes to be Replaced**: Another pointer, `last`, is set to the position of `pre` and then advanced to the node immediately after position `b`, effectively locating the part of `list1` that will remain after the nodes from `a` to `b` are replaced by `list2`. This loop runs `(b - a + 1)` times to include both the start and end positions in the count.\n \n* **Inserting `list2` into `list1`**: The `next` pointer of the node just before `a` (now held by `pre`) is set to point to the head of `list2`, beginning the process of insertion by linking the end of the preserved start segment of `list1` to the beginning of `list2`.\n \n* **Finding the End of `list2`**: The code then iterates through `list2` to find its last node, using a pointer `tail2`. This is necessary to connect the end of `list2` back into `list1`.\n \n* **Completing the Merge**: Once the end of `list2` is found, `tail2.next` is set to `last`, which points to the node immediately after position `b` in `list1`. This links the end of `list2` to the remainder of `list1`, completing the merge.\n \n* **Returning the Merged List**: Finally, the method returns `dummy.next`. Since `dummy` was initially set to point to the head of `list1`, and `list1` was modified to include `list2`, `dummy.next` now points to the head of the fully merged list. The use of the dummy node means the head of the merged list is returned correctly, even if `list2` was inserted at the very start of `list1`.\n\n# Complexity \uD83D\uDC48\n- Time complexity: O(n) Where n is the sum of length of the Linked Lists .\n\n- Space complexity: O(1)\n\n# Code \uD83D\uDC48\n\n```C []\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * struct ListNode *next;\n * };\n */\n\n\nstruct ListNode* mergeInBetween(struct ListNode* list1, int a, int b, struct ListNode* list2){\n struct ListNode* dummy = (struct ListNode*)malloc(sizeof(struct ListNode)); // Corrected type casting\n dummy->val = 0;\n dummy->next = list1;\n struct ListNode* prev = dummy;\n\n for(int i = 0; i < a; i++) {\n prev = prev->next;\n }\n\n struct ListNode* after_idx = prev;\n for(int i = a; i <= b + 1; i++) {\n after_idx = after_idx->next;\n }\n\n struct ListNode* last_idx = list2;\n while(last_idx->next != NULL) {\n last_idx = last_idx->next;\n }\n\n last_idx->next = after_idx;\n prev->next = list2;\n\n struct ListNode* result = dummy->next;\n free(dummy); \n return result;\n}\n```\n```C++ []\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode() : val(0), next(nullptr) {}\n * ListNode(int x) : val(x), next(nullptr) {}\n * ListNode(int x, ListNode *next) : val(x), next(next) {}\n * };\n */\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n ListNode* dummy = new ListNode(0);\n dummy->next = list1;\n ListNode* prev = dummy;\n for(int i=0; i<a; i++){\n prev = prev->next;\n }\n ListNode* after_idx = prev;\n for(int i = a; i<= b+1; i++){\n after_idx = after_idx->next;\n }\n ListNode* last_idx = list2;\n while(last_idx->next != NULL){\n last_idx = last_idx->next;\n }\n last_idx->next = after_idx;\n prev->next = list2;\n return dummy->next;\n }\n};\n```\n```Java []\n/**\n * Definition for singly-linked list.\n * public class ListNode {\n * int val;\n * ListNode next;\n * ListNode() {}\n * ListNode(int val) { this.val = val; }\n * ListNode(int val, ListNode next) { this.val = val; this.next = next; }\n * }\n */\nclass Solution {\n public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n ListNode dummy = new ListNode(0);\n dummy.next = list1;\n ListNode prev = dummy;\n for(int i=0; i<a; i++){\n prev = prev.next;\n }\n ListNode after_idx = prev;\n for(int i = a; i<= b+1; i++){\n after_idx = after_idx.next;\n }\n ListNode last_idx = list2;\n while(last_idx.next != null){\n last_idx = last_idx.next;\n }\n last_idx.next = after_idx;\n prev.next = list2;\n return dummy.next;\n }\n}\n```\n```javascript []\n/**\n * Definition for singly-linked list.\n * function ListNode(val, next) {\n * this.val = (val===undefined ? 0 : val)\n * this.next = (next===undefined ? null : next)\n * }\n */\n/**\n * @param {ListNode} list1\n * @param {number} a\n * @param {number} b\n * @param {ListNode} list2\n * @return {ListNode}\n */\nvar mergeInBetween = function(list1, a, b, list2) {\n dummy = new ListNode(0);\n dummy.next = list1;\n prev = dummy;\n for(let i=0; i<a; i++){\n prev = prev.next;\n }\n after_idx = prev;\n for(let i = a; i<= b+1; i++){\n after_idx = after_idx.next;\n }\n last_idx = list2;\n while(last_idx.next != null){\n last_idx = last_idx.next;\n }\n last_idx.next = after_idx;\n prev.next = list2;\n return dummy.next;\n};\n```\n```C# []\n/**\n * Definition for singly-linked list.\n * public class ListNode {\n * public int val;\n * public ListNode next;\n * public ListNode(int val=0, ListNode next=null) {\n * this.val = val;\n * this.next = next;\n * }\n * }\n */\npublic class Solution {\n public ListNode MergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n ListNode dummy = new ListNode(0);\n dummy.next = list1;\n ListNode prev = dummy;\n for(int i=0; i<a; i++){\n prev = prev.next;\n }\n ListNode after_idx = prev;\n for(int i = a; i<= b+1; i++){\n after_idx = after_idx.next;\n }\n ListNode last_idx = list2;\n while(last_idx.next != null){\n last_idx = last_idx.next;\n }\n last_idx.next = after_idx;\n prev.next = list2;\n return dummy.next;\n }\n}\n```\n```python []\n# Definition for singly-linked list.\n# class ListNode(object):\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution(object):\n def mergeInBetween(self, list1, a, b, list2):\n """\n :type list1: ListNode\n :type a: int\n :type b: int\n :type list2: ListNode\n :rtype: ListNode\n """\n dummy = ListNode(0)\n dummy.next = list1\n pre = dummy\n\n for _ in range(0,a):\n pre = pre.next\n\n last = pre\n\n for _ in range(a, b+2):\n last = last.next\n\n pre.next = list2\n tail2 = list2\n\n while tail2.next != None:\n tail2 = tail2.next\n \n tail2.next = last\n return dummy.next\n```\n```ruby []\n# Definition for singly-linked list.\n# class ListNode\n# attr_accessor :val, :next\n# def initialize(val = 0, _next = nil)\n# @val = val\n# @next = _next\n# end\n# end\n# @param {ListNode} list1\n# @param {Integer} a\n# @param {Integer} b\n# @param {ListNode} list2\n# @return {ListNode}\ndef merge_in_between(list1, a, b, list2)\n dummy = ListNode.new(0)\n dummy.next = list1\n pre = dummy\n\n for i in 0..a-1 do\n pre = pre.next\n end\n\n last = pre\n\n for i in a..b+1 do\n last = last.next\n end\n\n pre.next = list2\n tail2 = list2\n\n while tail2.next != nil \n tail2 = tail2.next\n end\n tail2.next = last\n return dummy.next\nend\n```\n\n\n# Dry Run \uD83D\uDC48\n\n1. **Traverse to Node Before `a`**: The loop runs until `i < a`, moving `pre` to point to the node just before the `a`th node in `list1`. For `a = 3`, `pre` ends up pointing to the node with value `2`.\n \n2. **Find Node After `b`**: Another loop runs to move the `last` pointer to the node just after `b`, which for `b = 4`, ends up pointing to the node with value `5`.\n \n3. **Insert `list2` into `list1`**: The `next` of `pre` (which points to `2`) is set to the head of `list2` (`1000000`). This operation effectively begins the process of inserting `list2` between the nodes `2` and `5` of `list1`.\n \n4. **Find Last Node of `list2`**: Iteration through `list2` finds the last node, which has the value `1000002`.\n \n5. **Link the Last Node of `list2` to `list1`**: The `next` of the last node of `list2` (`1000002`) is set to `last`, which points to the node with value `5` in `list1`.\n \n6. **Result**: The `dummy.next` is returned, which now points to the head of the modified `list1`.\n \n\nHere\'s how the lists change at each step:\n\n* **Original list1**: `0 -> 1 -> 2 -> 3 -> 4 -> 5`\n* **list2**: `1000000 -> 1000001 -> 1000002`\n\n**After Step 2**: `pre` points to `2`.\n\n**After Step 3**: `last` points to `5`.\n\n**After Step 4**: `list1` changes to `0 -> 1 -> 2 -> 1000000 -> 1000001 -> 1000002` (temporarily disconnected from the rest of `list1`).\n\n**After Step 6**: The connection is completed as `1000002 -> 5`.\n\n**Final merged list**: `0 -> 1 -> 2 -> 1000000 -> 1000001 -> 1000002 -> 5`\n\nThus, nodes `3` and `4` from `list1` have been replaced by all nodes from `list2`, and the final list after the operation is `[0, 1, 2, 1000000, 1000001, 1000002, 5]`.\n\n# Guys if the explanation and solution is helpful then up vote me.\u2764\uFE0F\u2764\uFE0F\u2764\uFE0F\u2764\uFE0F\u2764\uFE0F\n\n\n | 3 | 0 | ['Linked List', 'C', 'Python', 'C++', 'Java', 'Python3', 'Ruby', 'JavaScript', 'C#'] | 0 |
merge-in-between-linked-lists | Simple Java Solution O(n^2) | simple-java-solution-on2-by-sohaebahmed-5klu | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | sohaebAhmed | NORMAL | 2023-08-30T10:13:33.914842+00:00 | 2023-08-30T10:13:33.914866+00:00 | 49 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for singly-linked list.\n * public class ListNode {\n * int val;\n * ListNode next;\n * ListNode() {}\n * ListNode(int val) { this.val = val; }\n * ListNode(int val, ListNode next) { this.val = val; this.next = next; }\n * }\n */\nclass Solution {\n public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n ListNode head = list1;\n for(int i = 1; i < a; i++) {\n head = head.next;\n }\n ListNode temp = head;\n for(int i = 0; i < b-a+2; i++) {\n temp = temp.next;\n }\n ListNode temp2 = list2;\n while(temp2.next != null) {\n temp2 = temp2.next;\n }\n head.next = list2;\n temp2.next = temp;\n return list1;\n }\n}\n``` | 3 | 0 | ['Linked List', 'Java'] | 0 |
merge-in-between-linked-lists | Simple Java Solution O(n) | simple-java-solution-on-by-sohaebahmed-5440 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | sohaebAhmed | NORMAL | 2023-08-30T10:13:01.279199+00:00 | 2023-08-30T10:13:01.279217+00:00 | 51 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for singly-linked list.\n * public class ListNode {\n * int val;\n * ListNode next;\n * ListNode() {}\n * ListNode(int val) { this.val = val; }\n * ListNode(int val, ListNode next) { this.val = val; this.next = next; }\n * }\n */\nclass Solution {\n public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n ListNode head = list1;\n for(int i = 1; i < a; i++) {\n head = head.next;\n }\n ListNode temp = head;\n for(int i = 0; i < b-a+2; i++) {\n temp = temp.next;\n }\n ListNode temp2 = list2;\n while(temp2.next != null) {\n temp2 = temp2.next;\n }\n head.next = list2;\n temp2.next = temp;\n return list1;\n }\n}\n``` | 3 | 0 | ['Linked List', 'Java'] | 0 |
merge-in-between-linked-lists | Easy C++ Code||O(N)|| fully explained||short code | easy-c-codeon-fully-explainedshort-code-e9gn7 | Intuition\n Describe your first thoughts on how to solve this problem. \ni Have solved merge two list problem on leetcode, so from their this method came in my | Bhaskar_Agrawal | NORMAL | 2023-04-17T19:45:52.625370+00:00 | 2023-04-17T19:45:52.625426+00:00 | 1,285 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\ni Have solved merge two list problem on leetcode, so from their this method came in my mind.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Consider list1 and list2 as a head of the linkedlist.\n2. Traverse the list1 and store the address of (a-1)th node in variable.\n3. Traverse the list1 and store the address of (b+1)th node in another variable.\n4. Traverse the list2 and store the address of last node in variable.\n5. Now link (a-1)th node to list2. list2 last node to (b+1)th node.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->O(M+N)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->O(1)\n\n# Code\n```\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode() : val(0), next(nullptr) {}\n * ListNode(int x) : val(x), next(nullptr) {}\n * ListNode(int x, ListNode *next) : val(x), next(next) {}\n * };\n */\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n ListNode* t1 = list1;\n ListNode* t2 = list1;\n for(int i = 0; i < a-1; i++) // setting t1 at its correct place, that is , at (a-1) nodes from starting\n t1 = t1 -> next;\n for(int i = 0; i < b; i++) // setting t2 at its correct place, that is , at b nodes from starting \n t2 = t2 -> next;\n ListNode* temp = t2 -> next; // storing the track of rest of the list after b nodes\n t1 -> next = list2; // merging list2 in list1.\n ListNode* t3 = list2;\n while(t3 -> next != NULL)\n t3 = t3 -> next;\n\n t3 -> next = temp; // t3->next is NULL, so merging the track of list1 after b nodes.\n return list1;\n }\n};\n``` | 3 | 0 | ['Linked List', 'C++'] | 0 |
merge-in-between-linked-lists | C++ Easy Solution | c-easy-solution-by-techlism-5fdr | \nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n ListNode * l1a = list1;\n ListNode * | techlism | NORMAL | 2023-04-06T03:22:22.797212+00:00 | 2023-04-06T03:23:14.752142+00:00 | 251 | false | ```\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n ListNode * l1a = list1;\n ListNode * l1b = list1;\n ListNode * l2 = list2;\n for(int i=1;i<a;i++){\n if(l1a->next) l1a = l1a->next;\n }\n for(int i=0;i<=b;i++){\n if(l1b) l1b = l1b->next;\n }\n l1a->next = l2;\n while(l2->next) l2=l2->next;\n l2->next = l1b;\n return list1;\n }\n};\n```\n**Time Complexity : O(a+b+no. of nodes in list2)** \n**Worst Case: O(list1+list2)**\n**Space Complexity: O(1)** | 3 | 0 | ['C', 'C++'] | 0 |
merge-in-between-linked-lists | Easy to understand ||Beats 100% O(n)Time complexity java code 🔥🔥🔥 | easy-to-understand-beats-100-ontime-comp-2aqo | \n\n# Complexity\n- Time complexity:\n- O(n+m)\n\n\n- Space complexity:\n- O(1)\n\n\n# Code\n\n/**\n * Definition for singly-linked list.\n * public class ListN | gopal619chouhan | NORMAL | 2023-03-06T09:08:02.734546+00:00 | 2023-03-06T09:08:02.734579+00:00 | 331 | false | \n\n# Complexity\n- Time complexity:\n- O(n+m)\n\n\n- Space complexity:\n- O(1)\n\n\n# Code\n```\n/**\n * Definition for singly-linked list.\n * public class ListNode {\n * int val;\n * ListNode next;\n * ListNode() {}\n * ListNode(int val) { this.val = val; }\n * ListNode(int val, ListNode next) { this.val = val; this.next = next; }\n * }\n */\nclass Solution {\n public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n int i=0;\n // CREATE A TEMPORARY NODE FOR LIST1\n ListNode temp=list1;\n // TRAVERSE TILL A-1 INDEX TO JOIN IT WITH STARTING NODE OF LIST2\n while(i<a-1)\n {\n temp = temp.next;\n i++;\n }\n i=0;\n // CREATE A TEMPORARY NODE FOR LIST2\n ListNode temp2 = list1;\n // TRAVERSE TILL BTH INDEX TO JOIN LAST NODE OF LIST2 WITH BTH INDEX\n while(i<b)\n {\n temp2=temp2.next;\n i++;\n }\n ListNode temp3 = list2;\n // REACH TILL LAST NODE OF LIST2\n while(temp3.next!=null)\n temp3=temp3.next;\n // JOIN RESPECTIVE NODE TO EACH OTHER\n temp.next = list2;\n` temp3.next = temp2.next;\n return list1;\n \n }\n}\n``` | 3 | 0 | ['Linked List', 'Java'] | 1 |
merge-in-between-linked-lists | Python3 || Explanation & Example | python3-explanation-example-by-rushi_jav-u758 | Idea: Given the integer a and integer b we first Traversal a node of list1 then save the pointer suppose in start. Then continue traversal to b node. We point s | rushi_javiya | NORMAL | 2022-03-09T14:02:01.131843+00:00 | 2022-03-09T14:02:01.131880+00:00 | 268 | false | **Idea:** Given the integer a and integer b we first Traversal a node of list1 then save the pointer suppose in `start`. Then continue traversal to b node. We point `start` to list2 and we traversal list2 to the end and point end of list2 to b.\n\n**Example:**\n```\nlist1 = [0,1,2,3,4,5], a = 3, b = 4, list2 = [1000000,1000001,1000002]\n \n(i) First do traversal of a node(3 node). so we travel 0->1->2.\n\tNow save the pointer in start. \n(ii) Continue Traversal of list to b node(4 node). \n\tso 0->1->2->3.\n(iii) Now point start to list2. \n\t so, 0->1->2->1000000->1000001->1000002.\n(iv) Now do travesal of list2. and map end of list2 to b, \n\t so, 0->1->2->1000000->1000001->1000002->5.\n```\n\n**Code:**\n```\nclass Solution:\n def mergeInBetween(self, list1: ListNode, a: int, b: int, list2: ListNode) -> ListNode:\n curr=list1\n for count in range(b):\n if count==a-1: # travel to a node and --> step 1\n start=curr # then save pointer in start\n curr=curr.next # continue travel to b node --> step 2\n start.next=list2 # point start to list2 --> step3\n while list2.next: # travel list2 --> step 4\n list2=list2.next\n list2.next=curr.next # map end of list2 to b\n return list1\n```\nUpvote if you find it helpful :) | 3 | 0 | ['Python3'] | 0 |
merge-in-between-linked-lists | [Java/C#] Single loop minimalistic readable code w/ comments & explanation | javac-single-loop-minimalistic-readable-lgwkn | Example : list1 = [0,1,2,3,4,5], a = 3, b = 4, list2 = [1000000,1000001,1000002]\n\t\n\t- - Pick the previous node where a = 3th . prevStart = 2\n\t- - Pick th | tamimarefinanik | NORMAL | 2021-10-14T07:09:23.341780+00:00 | 2021-10-14T07:10:24.375972+00:00 | 88 | false | **Example : list1 = [0,1,2,3,4,5], a = 3, b = 4, list2 = [1000000,1000001,1000002]**\n\t\n\t- - Pick the previous node where a = 3th . prevStart = 2\n\t- - Pick the after node where b = 4th . postEnd = 4\n\t- - Then assign node 2 -> list2 and find last node of list2\n\t- - Then assign to the last node to rest of the list1. 2 -> list2 ->5\n\t\n```\npublic ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2)\n {\n\t\t\tListNode cur = list1, prevStart = null, postEnd = null;\n\n while (cur.next != null)\n {\n\t\t\t\t// find previous node from where removing start\n if (--a == 0)\n prevStart = cur;\n\t\t\t\t\n if (b-- == 0)\n {\n postEnd = cur.next; // find after the removing node\n cur = prevStart; // cur node assign to the start position of remove\n prevStart.next = list2; // assign list2 from the start position of removing\n }\n cur = cur.next;\n }\n cur.next = postEnd; // assign remain nodes of list1 \n return list1;\n }\n``` | 3 | 0 | ['Linked List', 'Java'] | 0 |
merge-in-between-linked-lists | c++ | clean code | explained | easy to understand | c-clean-code-explained-easy-to-understan-56or | I have used 3 pointers for the soution of this problem one pointer will be one node behind the point of merging in list 1 and second pointer will be on node ahe | crabbyD | NORMAL | 2021-07-14T15:44:58.598522+00:00 | 2021-07-14T15:44:58.598566+00:00 | 295 | false | I have used 3 pointers for the soution of this problem one pointer will be one node behind the point of merging in list 1 and second pointer will be on node ahead of the last point of merging. My 3rd pointer will be at the last point of my list 2 and then after having these 3 pointers we can perform the merge operation like a piece of cake.\n\n\n```\nListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n a=a-1;\n b=b+1;\n ListNode *start=list1;\n ListNode *end=list1;\n ListNode *tail=list2;\n while(a--)\n {\n start=start->next;\n }\n while(b--)\n {\n end=end->next;\n }\n while(tail->next!=NULL)\n {\n tail=tail->next;\n }\n start->next=list2;\n tail->next=end;\n \n \n return list1;\n }\n ``` | 3 | 0 | ['C'] | 0 |
merge-in-between-linked-lists | Python3 two pointers commented | python3-two-pointers-commented-by-mxmb-5cpo | python\ndef mergeInBetween(self, list1: ListNode, a: int, b: int, list2: ListNode) -> ListNode:\n pos, a_node = 0, list1\n while pos < a - 1: | mxmb | NORMAL | 2020-12-13T02:07:56.654355+00:00 | 2020-12-22T18:03:03.908084+00:00 | 395 | false | ```python\ndef mergeInBetween(self, list1: ListNode, a: int, b: int, list2: ListNode) -> ListNode:\n pos, a_node = 0, list1\n while pos < a - 1: # let a_node point to the list1 node at index a - 1\n a_node = a_node.next\n pos += 1\n b_node = a_node\n while pos < b + 1: # let b_node point to the list1 node at index b + 1\n b_node = b_node.next\n pos += 1\n a_node.next = list2 # put list2 after a_node\n while list2.next:\n list2 = list2.next\n list2.next = b_node # put list2 before b_node\n return list1 # return the head\n``` | 3 | 0 | ['Python', 'Python3'] | 0 |
merge-in-between-linked-lists | [Python3] O(M+N) time O(1) space solution | python3-omn-time-o1-space-solution-by-re-prlj | M -> len(list1)\nN -> len(list2)\n\nclass Solution:\n def mergeInBetween(self, list1: ListNode, a: int, b: int, list2: ListNode) -> ListNode:\n list2_ | redsand | NORMAL | 2020-11-28T16:02:02.172828+00:00 | 2021-04-01T22:10:19.234753+00:00 | 610 | false | M -> len(list1)\nN -> len(list2)\n```\nclass Solution:\n def mergeInBetween(self, list1: ListNode, a: int, b: int, list2: ListNode) -> ListNode:\n list2_head = list2_tail = list2\n while list2_tail and list2_tail.next:\n list2_tail = list2_tail.next\n \n list1_head = list1\n for _ in range(a-1):\n list1_head = list1_head.next\n \n nxt = list1_head.next\n list1_head.next = list2_head\n list1_head = nxt\n \n for _ in range(a, b):\n list1_head = list1_head.next\n \n list2_tail.next = list1_head.next\n list1_head.next = None # Not necessary and is just for the sake of completeness and detaching the middle\n \n return list1\n``` | 3 | 0 | ['Linked List', 'Python3'] | 1 |
merge-in-between-linked-lists | c++ - Short Concise -Simple Readable - 15 lines - Explanation - Interview - O(N) | c-short-concise-simple-readable-15-lines-roae | \n/*\n\nc++ - Short Concise -Simple Readable - Beginner - 15 lines - explanation - Interview - O(N)\n\nCreate a listNode pointer, move it till a, then insert li | justcodingandcars | NORMAL | 2020-11-28T16:01:43.096227+00:00 | 2020-11-28T16:04:52.662767+00:00 | 285 | false | ```\n/*\n\nc++ - Short Concise -Simple Readable - Beginner - 15 lines - explanation - Interview - O(N)\n\nCreate a listNode pointer, move it till a, then insert list2 there, then move till the end of list 2. Similarly the same pointer after skipping b-a+1 nodes. Then attach the tail of current list2 there.\n\nThen return the head of list1\n\nBeats 100% Space\n\n*/\n\n\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode() : val(0), next(nullptr) {}\n * ListNode(int x) : val(x), next(nullptr) {}\n * ListNode(int x, ListNode *next) : val(x), next(next) {}\n * };\n */\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n int p1=0;\n ListNode*curr1=list1,*curr2=list1;\n while(p1<a-1 && curr1){\n p1+=1;\n curr1=curr1->next;\n curr2=curr2->next;\n }\n while(p1<b+1){\n p1+=1;\n curr2=curr2->next;\n }\n curr1->next=list2;\n while(curr1->next){\n curr1=curr1->next;\n }\n curr1->next=curr2;\n return list1;\n }\n};\n``` | 3 | 1 | [] | 0 |
merge-in-between-linked-lists | Merge Linked List in Between Another Linked List || Beats 100% | merge-linked-list-in-between-another-lin-ad3a | IntuitionThe problem requires merging a second linked list (list2) into a first linked list (list1) by replacing the segment between indices a and b. The goal i | lokeshthakur8954 | NORMAL | 2025-03-31T16:53:11.102902+00:00 | 2025-03-31T16:53:11.102902+00:00 | 46 | false | # Intuition
The problem requires merging a second linked list (list2) into a first linked list (list1) by replacing the segment between indices a and b. The goal is to identify the nodes before and after this segment, attach list2 in place of the removed nodes, and return the modified list.
# Approach
Find the Tail of list2: Traverse list2 to reach its last node.
Locate the a-1 and b+1 Nodes in list1:
Traverse list1 while keeping track of the node at index a-1 (let’s call it an).
Continue traversing until index b+1 to get the node after b.
Modify Pointers to Merge Lists:
Set an.next = list2 to connect list1 to list2.
Set the last node of list2 to point to the node at index b+1 of list1.
# Complexity
- Time complexity:
$$O(N+M)$$
O(M) for traversing list2 to find its tail.
O(N) for traversing list1 to locate a-1 and b+1.
- Space complexity:
$$O(1)$$
Only a few extra pointers are used, independent of input size.
# Code
```java []
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {
ListNode an=null;
ListNode temp=list2;
while(temp.next!=null){
temp=temp.next;
}
ListNode t=list1;
int i=0;
while(i<b+1){
if(i==a-1){
an=t;
}
t=t.next;
i++;
}
temp.next=t;
an.next=list2;
return list1;
}
}
``` | 2 | 0 | ['Java'] | 0 |
merge-in-between-linked-lists | Beats 50% 🔥|| Smart Solution Easy 😎|| Notes++ || Java,C++,Python | beats-50-smart-solution-easy-notes-javac-imo3 | IntuitionThis problem involves modifying a linked list by removing a portion from indices a to b and replacing it with another linked list. Let's break down the | VIBHU_DIXIT | NORMAL | 2025-03-11T11:39:43.989068+00:00 | 2025-03-11T11:39:43.989068+00:00 | 75 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
This problem involves modifying a linked list by removing a portion from indices a to b and replacing it with another linked list. Let's break down the intuition and approach step by step.
# Approach
<!-- Describe your approach to solving the problem. -->

# NOTES


# Complexity
# Code
```java []
class Solution {
public ListNode mergeInBetween(ListNode l1, int a, int b, ListNode l2) {
ListNode left=null,right=l1;
for(int i=0;i<=b;i++){
if(i==a-1) left=right;
right = right.next;
}
left.next = l2;
ListNode temp = l2;
while(temp!=null && temp.next!=null){
temp = temp.next;
}
temp.next = right;
return l1;
}
}
```
```c++ []
#include <iostream>
using namespace std;
// Definition for singly-linked list.
struct ListNode {
int val;
ListNode* next;
ListNode(int x) : val(x), next(nullptr) {}
};
class Solution {
public:
ListNode* mergeInBetween(ListNode* l1, int a, int b, ListNode* l2) {
ListNode* left = nullptr;
ListNode* right = l1;
// Traverse the list to find 'left' and 'right'
for (int i = 0; i <= b; i++) {
if (i == a - 1) left = right;
right = right->next;
}
// Connect left part to l2
left->next = l2;
// Traverse l2 to find its last node
ListNode* temp = l2;
while (temp->next != nullptr) {
temp = temp->next;
}
// Connect last node of l2 to right
temp->next = right;
return l1;
}
};
```
```python []
class ListNode:
def __init__(self, x):
self.val = x
self.next = None
class Solution:
def mergeInBetween(self, l1: ListNode, a: int, b: int, l2: ListNode) -> ListNode:
left, right = None, l1
# Find the left (a-1) and right (b+1) nodes
for i in range(b + 1):
if i == a - 1:
left = right
right = right.next
# Connect left to l2
left.next = l2
# Traverse l2 to find the last node
temp = l2
while temp.next:
temp = temp.next
# Connect last node of l2 to right
temp.next = right
return l1
```
 | 2 | 0 | ['Linked List', 'Python', 'C++', 'Java', 'JavaScript'] | 0 |
merge-in-between-linked-lists | Merge Two Linked Lists in a Specified Range C++ Solution | merge-two-linked-lists-in-a-specified-ra-x5ho | IntuitionTo merge list2 into list1 between indices a and b, we first need to identify two key positions in list1: the node just before index a (athNode) and the | shakthashetty274 | NORMAL | 2025-01-05T09:07:21.233317+00:00 | 2025-01-05T09:07:21.233317+00:00 | 39 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
To merge **list2** into **list1** between indices `a` and `b`, we first need to identify two key positions in **list1**: the node just before index `a` (`athNode`) and the node at index `b` (`bthNode`). Then, we find the last node of **list2**. After that, we update the pointers: set `athNode->next` to the head of **list2**, and link the last node of **list2** to `bthNode->next` (the node after `b`). This effectively merges **list2** into **list1** within the specified range.
# Approach
<!-- Describe your approach to solving the problem. -->
To solve this problem, we:
1. Traverse list1 to find the nodes at indices a-1 (just before the insertion point) and b (the last node to remove from list1).
2. Traverse list2 to find the last node.
3. Modify the next pointers of these key nodes to merge list2 between the nodes at positions a-1 and b in list1.
This approach ensures an efficient solution with a time complexity of O(b + m).
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(b+m)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(1)
The solution only uses a constant amount of extra space to store pointers (athNode, bthNode, and endNode). These pointers are used to navigate through the two lists, but they do not depend on the size of the input lists.
The solution does not create any new data structures (such as arrays or additional linked lists) that grow with the size of the input.
Thus, the space complexity is O(1), meaning the algorithm uses a constant amount of extra space.
# Code
```cpp []
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {
ListNode *athNode= list1;
ListNode *bthNode = list1;
ListNode *endNode = list2;
for(int i=1;i<b+1;i++ ){
if(i==a-1){
athNode = bthNode->next;
}
bthNode = bthNode->next;
}
while(endNode->next!=NULL){
endNode = endNode->next;
}
athNode->next = list2;
endNode->next = bthNode->next;
return list1;
}
};
``` | 2 | 0 | ['C++'] | 0 |
merge-in-between-linked-lists | Simple to follow Python Code (Beats 98.82%) | simple-to-follow-python-code-beats-9882-5dayz | Intuition\nThis problem is essentially swapping a chunk of list1 with the entirety of list2, so we need to adjust some "next" pointers to create this swap. \n\n | the_KevKev | NORMAL | 2024-07-10T01:39:36.578080+00:00 | 2024-07-10T01:39:36.578109+00:00 | 3 | false | # Intuition\nThis problem is essentially swapping a chunk of `list1` with the entirety of `list2`, so we need to adjust some "next" pointers to create this swap. \n\n# Approach\nWe should record pointers to the last kept node of `list1` before the swap (`pointer`), the first kept node of `list1` after the swap (`pointer2`), and the start and end nodes of `list2` (`newPointer`). Then, we can adjust so that the next pointers are accordingly updated. \n\n# Complexity\n- Time complexity: $$O(n)$$\n\nSince you will have to iterate through each linked list exactly once, the time is proportional to the number of nodes in the two lists. \n\n- Space complexity: $$O(1)$$\n\nSince we only store four pointers (optimized slightly for only storing three) at a time, regardless of how long the list is, this takes **constant** space. \n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def mergeInBetween(self, list1: ListNode, a: int, b: int, list2: ListNode) -> ListNode:\n pointer = list1\n for i in range(a - 1):\n pointer = pointer.next\n \n pointer2 = pointer\n for j in range(b - a + 2):\n pointer2 = pointer2.next\n\n newPointer = list2\n pointer.next = newPointer\n while newPointer.next is not None:\n newPointer = newPointer.next\n\n newPointer.next = pointer2\n\n return list1\n``` | 2 | 0 | ['Linked List', 'Python3'] | 0 |
merge-in-between-linked-lists | Easiest Solution || Linked List || C++ | easiest-solution-linked-list-c-by-sanon2-9nkl | Code\nc++\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode() : val(0), next(nullptr) | sanon2025 | NORMAL | 2024-05-24T17:13:11.109736+00:00 | 2024-05-24T17:13:11.109765+00:00 | 273 | false | # Code\n```c++\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode() : val(0), next(nullptr) {}\n * ListNode(int x) : val(x), next(nullptr) {}\n * ListNode(int x, ListNode *next) : val(x), next(next) {}\n * };\n */\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n \n ListNode* prev=list1;\n ListNode* curr1=list1;\n ListNode* temp=list2;\n int i=1;\n while(i!=a){\n prev=prev->next;\n i++;\n }\n curr1 = prev->next;\n while (i <= b) {\n curr1 = curr1->next;\n i++;\n }\n while(temp->next!=NULL){\n temp=temp->next;\n }\n prev->next=list2;\n temp->next=curr1;\n curr1=NULL;\n\n return list1;\n }\n};\n``` | 2 | 0 | ['C++'] | 1 |
merge-in-between-linked-lists | Merge Portion of One Linked List with Another | merge-portion-of-one-linked-list-with-an-093t | Intuition\n Describe your first thoughts on how to solve this problem. \nWhen approaching this problem, we want to find the portion of the first list that needs | panchalyash | NORMAL | 2024-03-29T07:18:13.114396+00:00 | 2024-03-29T07:18:13.114431+00:00 | 96 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWhen approaching this problem, we want to find the portion of the first list that needs to be replaced with the second list. We\'ll locate the starting and ending points of this portion in the first list and then stitch the second list in between.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nStart by traversing the first list until we find the node at the starting index a.\n\nContinue traversing until we reach the node at the ending index b, while keeping track of the node immediately after this portion to be replaced.\n\nTraverse through the second list to find its last node, which will be the tail.\n\nConnect the beginning of the second list to the node just before the portion to be replaced in the first list.\n\nConnect the end of the second list (its tail) to the node just after the portion to be replaced in the first list.\n\nFinally, return the modified first list.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nTime complexity: We traverse both lists once, so the time complexity is O(n), where n is the total number of nodes in both lists.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nSpace complexity: We use a few extra pointers, but we don\'t use additional data structures that scale with the input size, so the space complexity is O(1)\n\n# Code\n```\n/**\n * Definition for singly-linked list.\n * public class ListNode {\n * int val;\n * ListNode next;\n * ListNode() {}\n * ListNode(int val) { this.val = val; }\n * ListNode(int val, ListNode next) { this.val = val; this.next = next; }\n * }\n */\nclass Solution {\n public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n \n int idx = 1;\n ListNode temp1L1 = list1;\n while(idx < a){\n temp1L1 = temp1L1.next;\n idx++;\n }\n ListNode temp2L1 = temp1L1;\n while(idx <= b+1){\n temp2L1 = temp2L1.next;\n idx++;\n }\n\n ListNode tailL2 = list2;\n ListNode headL2 = list2;\n while(tailL2.next!=null){\n tailL2 = tailL2.next;\n }\n temp1L1.next = headL2;\n tailL2.next = temp2L1;\n return list1;\n\n }\n}\n``` | 2 | 0 | ['Java'] | 0 |
merge-in-between-linked-lists | 🔥One Pass + Start - End Pointer | Clean Code | C++ | | one-pass-start-end-pointer-clean-code-c-hke21 | Code\n\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode() : val(0), next(nullptr) {}\ | Antim_Sankalp | NORMAL | 2024-03-21T12:21:58.830279+00:00 | 2024-03-21T12:21:58.830301+00:00 | 3 | false | # Code\n```\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode() : val(0), next(nullptr) {}\n * ListNode(int x) : val(x), next(nullptr) {}\n * ListNode(int x, ListNode *next) : val(x), next(next) {}\n * };\n */\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n ListNode* start = list1;\n for (int i = 0; i < a - 1; i++)\n {\n start = start->next;\n }\n\n ListNode* end = start->next;\n for (int i = 0; i < b - a + 1; i++)\n {\n end = end->next;\n }\n\n start->next = list2;\n while (list2->next)\n {\n list2 = list2->next;\n }\n\n list2->next = end;\n\n return list1;\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
merge-in-between-linked-lists | Simple Traversal Solution || C++ || JAVA | simple-traversal-solution-c-java-by-saja-zgf2 | Intuition\nThe problem requires merging a sublist of list1 defined by the indices a and b, with another linked list list2. The straightforward approach involves | Sajalgarg10 | NORMAL | 2024-03-20T16:44:56.031800+00:00 | 2024-03-20T16:44:56.031828+00:00 | 6 | false | # Intuition\nThe problem requires merging a sublist of list1 defined by the indices a and b, with another linked list list2. The straightforward approach involves traversing list1 to reach the node just before index a and the node at index b. Then, we point the next of the node at index a - 1 to list2, traverse to the end of list2, and connect it with the node at index b + 1.\n\n# Approach\nTraverse list1 to reach the node just before index a.\nTraverse list1 again to reach the node at index b.\nConnect the next of the node at index a - 1 to list2.\nTraverse list2 to reach its end.\nConnect the last node of list2 to the node at index b + 1.\nReturn list1.\n# Complexity\nTime complexity: $$O(n)$$, where n is the length of list1.\nSpace complexity: $$O(1)$$, as the space used is constant irrespective of the input size.\n\n# Code\n```cpp []\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode() : val(0), next(nullptr) {}\n * ListNode(int x) : val(x), next(nullptr) {}\n * ListNode(int x, ListNode *next) : val(x), next(next) {}\n * };\n */\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n ListNode *temp1 = list1;\n ListNode *temp2 = list1;\n \n // Traverse to the node just before index \'a\'\n for (int i = 0; i < a - 1; i++) {\n temp1 = temp1->next;\n }\n \n // Traverse to the node at index \'b\'\n for (int i = 0; i < b; i++) {\n temp2 = temp2->next;\n }\n \n // Connect the sublist of \'list1\' with \'list2\'\n temp1->next = list2;\n \n // Traverse to the end of \'list2\'\n while (list2->next != nullptr) {\n list2 = list2->next;\n }\n \n // Connect the last node of \'list2\' with the node after index \'b\'\n list2->next = temp2->next;\n \n return list1;\n }\n};\n\n```\n\n```java []\n/**\n * Definition for singly-linked list.\n * public class ListNode {\n * int val;\n * ListNode next;\n * ListNode() {}\n * ListNode(int val) { this.val = val; }\n * ListNode(int val, ListNode next) { this.val = val; this.next = next; }\n * }\n */\nclass Solution {\n public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n ListNode temp1=list1;\n ListNode temp2=list1;\n for(int i=0;i<b+1;i++){\n temp2=temp2.next;\n }\n for(int i=0;i<a-1;i++){\n temp1=temp1.next;\n }\n temp1.next=list2;\n while(temp1.next!=null){\n temp1=temp1.next;\n }\n temp1.next=temp2;\n System.gc();\n return list1;\n }\n}\n``` | 2 | 0 | ['C++', 'Java'] | 0 |
merge-in-between-linked-lists | Easy to Understand C++ O(n) | easy-to-understand-c-on-by-negimanshi696-4fvk | # Intuition\n\n Describe your first thoughts on how to solve this problem. \n\n\n\n# Code\n\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* l | negimanshi696 | NORMAL | 2024-03-20T16:03:16.318563+00:00 | 2024-03-20T16:03:16.318589+00:00 | 13 | false | []()# Intuition\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n\n\n# Code\n```\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n ListNode *p1=list1,*p2=list1,*p3=list2;\n for(int i=0;i<a-1;i++) p1=p1->next;\n for(int i=0;i<=b;i++)p2=p2->next;\n while(p3->next!=NULL)p3=p3->next;\n p1->next=list2;\n p3->next=p2;\n return list1;\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
merge-in-between-linked-lists | easy code in c++ | easy-code-in-c-by-shobhit_panuily-btka | \n\n# Code\n\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode() : val(0), next(nullpt | Shobhit_panuily | NORMAL | 2024-03-20T15:56:12.145515+00:00 | 2024-03-20T15:56:12.145553+00:00 | 137 | false | \n\n# Code\n```\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode() : val(0), next(nullptr) {}\n * ListNode(int x) : val(x), next(nullptr) {}\n * ListNode(int x, ListNode *next) : val(x), next(next) {}\n * };\n */\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n int count=0;\n ListNode* start=nullptr;\n ListNode* tail=nullptr;\n ListNode* result=list1;\n while(count<=b) {\n if(count==a-1) {\n start=list1;\n }\n if(count==b) {\n tail=list1->next;\n }\n count++;\n list1=list1->next;\n }\n ListNode*ptr=list2;\n while(ptr->next != nullptr) {\n ptr=ptr->next;\n }\n ptr->next=tail;\n start->next=list2;\n return result;\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
merge-in-between-linked-lists | Best Approach💯 | best-approach-by-adwxith-xlf5 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | adwxith | NORMAL | 2024-03-20T14:43:14.202608+00:00 | 2024-03-20T14:43:14.202645+00:00 | 94 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(n+m)\n\n- Space complexity:\nO(1)\n\n# Code\n```\n/**\n * Definition for singly-linked list.\n * function ListNode(val, next) {\n * this.val = (val===undefined ? 0 : val)\n * this.next = (next===undefined ? null : next)\n * }\n */\n/**\n * @param {ListNode} list1\n * @param {number} a\n * @param {number} b\n * @param {ListNode} list2\n * @return {ListNode}\n */\nvar mergeInBetween = function(list1, a, b, list2) {\n let cur=list1,pivot=null,pos=0\n while(cur.next){\n if(pos==a-1){\n pivot=cur.next\n cur.next=list2\n }\n pos++\n cur=cur.next\n }\n for(let i=a;i<b+1;i++){\n pivot=pivot.next\n }\n\n cur.next=pivot\n\n\n return list1\n};\n``` | 2 | 0 | ['JavaScript'] | 0 |
merge-in-between-linked-lists | Simple JAVA Solution || Beats 100% | simple-java-solution-beats-100-by-saad_h-a0oi | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | saad_hussain_ | NORMAL | 2024-03-20T14:35:30.095556+00:00 | 2024-03-20T14:35:30.095576+00:00 | 6 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for singly-linked list.\n * public class ListNode {\n * int val;\n * ListNode next;\n * ListNode() {}\n * ListNode(int val) { this.val = val; }\n * ListNode(int val, ListNode next) { this.val = val; this.next = next; }\n * }\n */\nclass Solution {\n public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n ListNode cur=list1;\n\n for(int i=0;i<a-1;i++){\n cur=cur.next;\n } \n\n ListNode start_from_here=cur;\n\n for(int i=a;i<=b+1;i++){\n cur=cur.next;\n // now my linked list pointer is at 5\n }\n \n start_from_here.next=list2;\n while(list2.next!=null){\n list2=list2.next;\n }\n // connect the second list to the first after removing the interval\n list2.next=cur;\n\n return list1;\n\n }\n}\n``` | 2 | 0 | ['Java'] | 0 |
merge-in-between-linked-lists | Easy to follow straight forward solution ✅ || O(n) time and O(1) space ✅ || clean code ✅ | easy-to-follow-straight-forward-solution-yr4e | Intuition\n Describe your first thoughts on how to solve this problem. \n- We only require the addresses of nodes located at indices a and b. \n- We can navigat | yousufmunna143 | NORMAL | 2024-03-20T11:14:16.906197+00:00 | 2024-03-20T11:14:16.906259+00:00 | 4 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- We only require the addresses of nodes located at indices `a` and `b`. \n- We can navigate through the list until we reach the node at position `a`, then connect it with `list2`. \n- After that, we can reconnect it back to its original position using the address of the node at position `b`.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Start by declaring two variables: `addressOfa` and `addressOfb`.\n2. Traverse through `list1` to find the addresses of nodes at positions `a` and `b`.\n3. Begin traversing `list1` using a temporary variable `temp`. If you encounter a node whose address matches `addressOfa`, change its next pointer to point to `list2`.\n4. Traverse through `list2` from this point until the end.\n5. Connect the end of `list2` with the node at address `addressOfb`.\n6. Finally, return `list1`.\n\n# Complexity\n- Time complexity:$$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for singly-linked list.\n * public class ListNode {\n * int val;\n * ListNode next;\n * ListNode() {}\n * ListNode(int val) { this.val = val; }\n * ListNode(int val, ListNode next) { this.val = val; this.next = next; }\n * }\n */\nclass Solution \n{\n public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) \n {\n ListNode addressOfa = null; \n ListNode addressOfb = null;\n ListNode temp = list1;\n int ind = 0;\n // finding addresses of nodes at indices a and b\n while(temp != null)\n {\n if(ind == a)\n {\n addressOfa = temp;\n }\n if(ind == b)\n {\n addressOfb = temp;\n }\n temp = temp.next;\n ind ++;\n }\n // traverse till addressOfa and change address of that node to list 2\n temp = list1;\n while(true)\n {\n if(temp.next == addressOfa)\n {\n temp.next = list2;\n break;\n }\n temp = temp.next;\n }\n // go to end of list 2\n while(temp.next != null)\n {\n temp = temp.next;\n }\n // connect it back to list 1 with help of addressOfb\n temp.next = addressOfb.next;\n return list1;\n }\n}\n``` | 2 | 0 | ['Linked List', 'Java'] | 0 |
merge-in-between-linked-lists | Easy To Understand for Beginners Using Queue data Structure Very easy Approach🔥🔥🔥👍👍 | easy-to-understand-for-beginners-using-q-cpbh | Intuition\n Describe your first thoughts on how to solve this problem. \nTo Solve Question with simple approach by any data Structure\n\n# Approach\n Describe y | RonitTomar | NORMAL | 2024-03-20T09:29:12.750614+00:00 | 2024-03-20T09:29:12.750642+00:00 | 53 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo Solve Question with simple approach by any data Structure\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1.First we have add the element to queue and take variable "num" while we are adding the element , and inc the num then simultaneously we check if num equals to "a" and in between "b" skip those elemnt from the listnode and add another all elemnt to queue.\n2.After that make num = 0 , make a new ListNode of name ans , traverse on queue and make inc to num ans check if num equals to "a" then add the elemnt of Listnode List2 to ans Listnode until it become null and after the remaning elemnt of queue will add to ans Listnode\n\n# Complexity\n- Time complexity: O(n^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for singly-linked list.\n * public class ListNode {\n * int val;\n * ListNode next;\n * ListNode() {}\n * ListNode(int val) { this.val = val; }\n * ListNode(int val, ListNode next) { this.val = val; this.next = next; }\n * }\n */\nclass Solution {\n public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n ListNode temp1 = list1;\n ListNode temp2 = list2;\n Queue<Integer> q1 = new LinkedList<>();\n int num = 0;\n\n while(temp1!=null)\n {\n while(num>=a && num<=b)\n {\n num++;\n temp1=temp1.next;\n continue;\n }\n q1.add(temp1.val);\n temp1=temp1.next;\n num++;\n }\n // System.out.print(q1);\n num=0;\n ListNode ans = new ListNode(-1);\n ListNode temp3 = ans;\n\n while(!q1.isEmpty())\n {\n if(num==a)\n {\n while(temp2!=null)\n {\n temp3.next=temp2;\n temp3=temp2;\n temp2=temp2.next;\n }\n }\n ListNode z = new ListNode(q1.poll());\n temp3.next=z;\n temp3=z;\n num++;\n }\n\n return ans.next;\n }\n}\n``` | 2 | 0 | ['Java'] | 2 |
merge-in-between-linked-lists | Java Solution O(n) Complexity Beats 100% in Runtime | java-solution-on-complexity-beats-100-in-zyti | \n\n# Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem here is to traverse through the linked list to find the a\'th and b\' | ProgrammerAditya36 | NORMAL | 2024-03-20T09:03:07.045499+00:00 | 2024-03-20T09:07:46.510571+00:00 | 101 | false | \n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem here is to traverse through the linked list to find the a\'th and b\'th nodes. Then remove list1\'s nodes from a to b and replace it with l2.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- We begin by declaring to temporary nodes node1 and node2 which help us to find the ath and bth node respectively.\n- Using a for loop we traverse from 1 to b (we will find positions of node1 and node2 using 1 loop itself). Since a<=b we iterate from 1 to b.\n- Till we reach b update node2 to point to its next element by `node2=node2.next;` and also check if the current value of i in the loop is lesser than a (We need to find the node before the ath node that\'s why we check for lesser than not lesser than or equal to.)\n- If true then update node1 to point to its next elemnt by `node1=node1.next`.\n- Now we have node1 pointing to node before the ath element and node2 pointing to bth element.\n- To remove the nodes we simply make node1.next to point to first element of list2 by `node1.next=list2`.\n- Now to make the last item of list2 to point to b+1th node in list1 we simply use node1 iteself and travese using a while loop untill node1.next is not null (Find the last node in list2).\n- Now we use node1 to point to b+1 th element in the list by `node1.next=node2.next` (as node2 is pointing to bth node).\n- Finally we disconnect the bth node by making its next as null by `node2.next=null`\n- Return the head of list1 by `return list1`\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for singly-linked list.\n * public class ListNode {\n * int val;\n * ListNode next;\n * ListNode() {}\n * ListNode(int val) { this.val = val; }\n * ListNode(int val, ListNode next) { this.val = val; this.next = next; }\n * }\n */\nclass Solution {\n public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n ListNode node1 = list1;\n ListNode node2 = list1;\n for(int i=1;i<=b;i++){\n node2 = node2.next;\n if(i<a)\n node1 = node1.next;\n }\n node1.next = list2;\n while(node1.next!=null)node1=node1.next;\n node1.next = node2.next;\n node2.next = null;\n return list1;\n \n }\n}\n``` | 2 | 0 | ['Linked List', 'Java'] | 0 |
merge-in-between-linked-lists | LinkedList Easy Solution | linkedlist-easy-solution-by-aditya0890-32zv | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Aditya0890 | NORMAL | 2024-03-20T07:20:39.156345+00:00 | 2024-03-20T07:20:39.156389+00:00 | 105 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for singly-linked list.\n * public class ListNode {\n * int val;\n * ListNode next;\n * ListNode() {}\n * ListNode(int val) { this.val = val; }\n * ListNode(int val, ListNode next) { this.val = val; this.next = next; }\n * }\n */\nclass Solution {\n public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n ListNode temp1 =list1;\n ListNode temp2 =list1;\n for(int i=0;i<a-1;i++){\n temp1 = temp1.next;\n }\n for(int i=0;i<b+1;i++){\n temp2 = temp2.next;\n }\n //System.out.println(temp1.val+" "+temp2.val);\n // I put pointer temp1 and temp2;\n temp1.next=list2;\n ListNode pointer = list2;\n\n while(pointer.next != null){\n pointer = pointer.next;\n } \n pointer.next = temp2;\n return list1;\n }\n}\n``` | 2 | 0 | ['Java'] | 3 |
merge-in-between-linked-lists | yeah i know not the most optimal solution but iam running late so gtg bye | yeah-i-know-not-the-most-optimal-solutio-alx7 | Intuition\n Describe your first thoughts on how to solve this problem. \njust basic cutting and joining\n# Approach\n Describe your approach to solving the prob | srinivas_bodduru | NORMAL | 2024-03-20T07:12:02.256257+00:00 | 2024-03-20T07:12:02.256275+00:00 | 12 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\njust basic cutting and joining\n# Approach\n<!-- Describe your approach to solving the problem. -->\nwe use dummy linked lists to make copies whenever needed\nwe cut the linked list at the pointer \nwe get the linked list that should be joined \nand attach it to the end of the first linked list \nsee the code youll get it\nif not comment down \n# Complexity\n- Time complexity:O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for singly-linked list.\n * function ListNode(val, next) {\n * this.val = (val===undefined ? 0 : val)\n * this.next = (next===undefined ? null : next)\n * }\n */\n/**\n * @param {ListNode} list1\n * @param {number} a\n * @param {number} b\n * @param {ListNode} list2\n * @return {ListNode}\n */\nvar mergeInBetween = function(list1, a, b, list2) {\n let counter=0\n let dummy = list1\n for(let i=0;i<b+1;i++){\n dummy=dummy.next\n }\n //console.log(dummy)\n let traveladapter = function(ll,p,idx){\n if(p==idx){\n ll.next=list2\n }\n else{\n traveladapter(ll.next,p+1,idx)\n }\n }\n traveladapter(list1,0,a-1)\n //console.log(list1)\n let traveller = function(ll1,ll2){\n if(ll1.next){\n traveller(ll1.next,ll2)\n }\n else{\n ll1.next=ll2\n }\n }\n traveller(list1,dummy)\n return list1\n \n \n\n};\n``` | 2 | 0 | ['JavaScript'] | 2 |
merge-in-between-linked-lists | Kotlin | Rust | kotlin-rust-by-samoylenkodmitry-ywfz | \nhttps://youtu.be/0NU6p7K7INY\n#### Join me on Telegram\n\nhttps://t.me/leetcode_daily_unstoppable/544\n\n#### Problem TLDR\n\nReplace a segment in a LinkedLis | SamoylenkoDmitry | NORMAL | 2024-03-20T06:51:18.731186+00:00 | 2024-03-20T06:51:18.731223+00:00 | 92 | false | \nhttps://youtu.be/0NU6p7K7INY\n#### Join me on Telegram\n\nhttps://t.me/leetcode_daily_unstoppable/544\n\n#### Problem TLDR\n\nReplace a segment in a LinkedList #medium\n\n#### Intuition\n\nJust careful pointers iteration.\n\n#### Approach\n\n* use dummy to handle the first node removal\n* better to write a separate cycles\n* Rust is hard\n\n#### Complexity\n\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(1)$$\n\n#### Code\n\n```kotlin []\n\n fun mergeInBetween(list1: ListNode?, a: Int, b: Int, list2: ListNode?) = \n ListNode(0).run {\n next = list1\n var curr: ListNode? = this\n for (i in 1..a) curr = curr?.next\n var after = curr?.next\n for (i in a..b) after = after?.next\n curr?.next = list2\n while (curr?.next != null) curr = curr?.next\n curr?.next = after\n next\n }\n\n```\n```rust []\n\n pub fn merge_in_between(list1: Option<Box<ListNode>>, a: i32, b: i32, list2: Option<Box<ListNode>>) -> Option<Box<ListNode>> {\n let mut dummy = Box::new(ListNode::new(0));\n dummy.next = list1;\n let mut curr = &mut dummy;\n for _ in 0..a { curr = curr.next.as_mut().unwrap() }\n let mut after = &mut curr.next;\n for _ in a..=b { after = &mut after.as_mut().unwrap().next }\n let after_b = after.take(); // Detach the rest of the list after `b`, this will allow the next line for the borrow checker\n curr.next = list2;\n while let Some(ref mut next) = curr.next { curr = next; }\n curr.next = after_b;\n dummy.next\n }\n\n``` | 2 | 0 | ['Rust', 'Kotlin'] | 1 |
merge-in-between-linked-lists | Merge In Between Linked Lists || Optimal Solution || Java || Easy to understand || 100% beats | merge-in-between-linked-lists-optimal-so-qctl | Merge In Between Linked Lists\n\n## Intuition\nTo solve this problem, we need to remove a range of nodes from the list1 and replace them with the nodes from lis | vanshsehgal08 | NORMAL | 2024-03-20T06:45:23.987649+00:00 | 2024-03-20T06:58:30.561612+00:00 | 555 | false | # Merge In Between Linked Lists\n\n## Intuition\nTo solve this problem, we need to remove a range of nodes from the `list1` and replace them with the nodes from `list2`. This involves finding the nodes at positions `a` and `b` in `list1`, connecting the node before `a` to the head of `list2`, and connecting the last node of `list2` to the node after `b`.\n\n## Approach\n1. Traverse through `list1` to find the ath node and connect the node before `a` to the head of `list2`.\n2. Traverse through `list2` to find the last node.\n3. Traverse through `list1` to find the (b+1)th node and connect the last node of `list2` to it.\n\n## Complexity\n- Time complexity: O(n + m)\n - We traverse through `list1` once to find the ath and (b+1)th nodes, which takes O(n) time.\n - We traverse through `list2` once to find the last node.\n- Space complexity: O(1)\n - We use only a constant amount of extra space.\n\n\n\n## Code\n\n```java []\n/**\n * Definition for singly-linked list.\n * public class ListNode {\n * int val;\n * ListNode next;\n * ListNode() {}\n * ListNode(int val) { this.val = val; }\n * ListNode(int val, ListNode next) { this.val = val; this.next = next; }\n * }\n */\nclass Solution {\n public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n // Find the ath node in list1\n int count = 0;\n ListNode current = list1;\n while (count < a - 1) {\n current = current.next;\n count++;\n }\n\n // Connect the ath node to the head of list2\n ListNode aNode = current;\n while (count < b + 1) {\n current = current.next;\n count++;\n }\n\n // Connect the last node of list2 to the node after b\n ListNode lastNodeOfList2 = list2;\n while (lastNodeOfList2.next != null) {\n lastNodeOfList2 = lastNodeOfList2.next;\n }\n lastNodeOfList2.next = current;\n\n // Connect the node before a to the head of list2\n aNode.next = list2;\n\n return list1;\n }\n}\n\n```\n```python []\n# Definition for singly-linked list.\n# class ListNode(object):\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution(object):\n def mergeInBetween(self, list1, a, b, list2):\n """\n :type list1: ListNode\n :type a: int\n :type b: int\n :type list2: ListNode\n :rtype: ListNode\n """\n # Find the ath node in list1\n count = 0\n current = list1\n while count < a - 1:\n current = current.next\n count += 1\n\n # Connect the ath node to the head of list2\n a_node = current\n while count < b + 1:\n current = current.next\n count += 1\n\n # Connect the last node of list2 to the node after b\n last_node_of_list2 = list2\n while last_node_of_list2.next is not None:\n last_node_of_list2 = last_node_of_list2.next\n last_node_of_list2.next = current\n\n # Connect the node before a to the head of list2\n a_node.next = list2\n\n return list1\n\n```\n```C++ []\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode() : val(0), next(nullptr) {}\n * ListNode(int x) : val(x), next(nullptr) {}\n * ListNode(int x, ListNode *next) : val(x), next(next) {}\n * };\n */\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n // Find the ath node in list1\n int count = 0;\n ListNode* current = list1;\n while (count < a - 1) {\n current = current->next;\n count++;\n }\n\n // Connect the ath node to the head of list2\n ListNode* aNode = current;\n while (count < b + 1) {\n current = current->next;\n count++;\n }\n\n // Connect the last node of list2 to the node after b\n ListNode* lastNodeOfList2 = list2;\n while (lastNodeOfList2->next != nullptr) {\n lastNodeOfList2 = lastNodeOfList2->next;\n }\n lastNodeOfList2->next = current;\n\n // Connect the node before a to the head of list2\n aNode->next = list2;\n\n return list1;\n }\n};\n\n```\n```C []\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * struct ListNode *next;\n * };\n */\n\n\nstruct ListNode* mergeInBetween(struct ListNode* list1, int a, int b, struct ListNode* list2){\n struct ListNode* current = list1;\n int count = 0;\n\n // Find the ath node in list1\n while (count < a - 1) {\n current = current->next;\n count++;\n }\n\n // Connect the ath node to the head of list2\n struct ListNode* aNode = current;\n while (count < b + 1) {\n current = current->next;\n count++;\n }\n\n // Connect the last node of list2 to the node after b\n struct ListNode* lastNodeOfList2 = list2;\n while (lastNodeOfList2->next != NULL) {\n lastNodeOfList2 = lastNodeOfList2->next;\n }\n lastNodeOfList2->next = current;\n\n // Connect the node before a to the head of list2\n aNode->next = list2;\n\n return list1;\n}\n\n```\n```JavaScript []\n/**\n * Definition for singly-linked list.\n * function ListNode(val, next) {\n * this.val = (val===undefined ? 0 : val)\n * this.next = (next===undefined ? null : next)\n * }\n */\n\nvar mergeInBetween = function(list1, a, b, list2) {\n let current = list1;\n let count = 0;\n\n // Find the ath node in list1\n while (count < a - 1) {\n current = current.next;\n count++;\n }\n\n // Connect the ath node to the head of list2\n let aNode = current;\n while (count < b + 1) {\n current = current.next;\n count++;\n }\n\n // Connect the last node of list2 to the node after b\n let lastNodeOfList2 = list2;\n while (lastNodeOfList2.next !== null) {\n lastNodeOfList2 = lastNodeOfList2.next;\n }\n lastNodeOfList2.next = current;\n\n // Connect the node before a to the head of list2\n aNode.next = list2;\n\n return list1;\n};\n\n```\n\n | 2 | 0 | ['Linked List', 'C', 'Python', 'C++', 'Java', 'Python3', 'JavaScript'] | 0 |
merge-in-between-linked-lists | 🔥✅✅ Beat 99.56% | ✅ Full Explanation ✅✅🔥 | beat-9956-full-explanation-by-sidharthja-9v61 | Intuition\n Describe your first thoughts on how to solve this problem. \nFirst,We have to store the refernces to the (a-1)th node and (b+1)th node of the list1 | sidharthjain321 | NORMAL | 2024-03-20T06:14:31.550655+00:00 | 2024-03-20T06:14:31.550688+00:00 | 47 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFirst,We have to store the refernces to the (a-1)th node and (b+1)th node of the list1 so that we can use them later for connections to the other list. We have to connect the (a-1)th node of the list1 to the head of the list2. Then go the end of the list2 and connect the end of the list2 to the (b+1)th node of the list1. After that return the updated `list1`.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- First, make temporary pointer references to the list1 and list2, so that we can use them later for connections to the list2.\n```\nListNode* list1_Ptr1 = list1;\nListNode* list1_Ptr2 = list1; \nListNode* list2_Ptr1 = list2; // temporary pointer references\n```\n- Initialise `int i = 0` for checking the current node index.\n- Now, First we have to connect the (a-1)th node\'s next to the head of the list2. So , We have to go to the (a-1)th Node of the list1 and we are storing the (a-1)th node reference in the `list1_Ptr` Pointer.\n```\n for(i; i < a-1; i++) { \n list1_Ptr1 = list1_Ptr1 -> next; // going to the (a-1)th node of the list1. -\n}\n```\n- Now, we have to connect the end of the list2 to the (b+1)th node of the list1, so first we have to go to the (b+1)th node of the list1.\n\n```\nfor(i = 0; i < b+1; i++) {\n list1_Ptr2 = list1_Ptr2 -> next; // going to the (b+1)th node of the list1. -\n}\n```\n- Now, connect the (a+1)th node of the list1 to the head of the list2.\n```\nlist1_Ptr1 -> next = list2_Ptr1; // connecting the (a-1)th node of the list1 to the head of the list2.\n```\n- Now , go to the End of the list2, so that we can connect its end to the (b+1)th node of the list1.\n```\n while(list2_Ptr1 -> next != NULL) {\n list2_Ptr1 = list2_Ptr1 -> next; // // going to the end of the list2.\n }\n```\n- Connect the end of the list2 to the (b+1)th node of the list1.\n```\nlist2_Ptr1 -> next = list1_Ptr2; // // connecting the end of the list2 to the (b+1)th node of the list1.\n```\n- Now , return the updated list1.\n```\nreturn list1; // returning the updated linked list list1.\n```\n\n\n\n# Complexity\n- Time complexity: O(m+n) , where m and n are the list1 and list2 sizes respectiely.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode() : val(0), next(nullptr) {}\n * ListNode(int x) : val(x), next(nullptr) {}\n * ListNode(int x, ListNode *next) : val(x), next(next) {}\n * };\n */\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n ListNode* list1_Ptr1 = list1; // for connecting the part of this list1 just from (a-1)th node to 1st node of the list2. \n ListNode* list1_Ptr2 = list1; // first reach the (b+1)th node of the list1 and then connect the end of the list2 to this (b+1)th node of the list1.\n ListNode* list2_Ptr1 = list2; // firstly, for connecting the (a-1)th node of the list1 to the head of the list2 and\n // secondly, for going to the end of the list2 and then connect its end to the (b+1)th node of the list1.\n\n int i = 0; // for checking the current node.\n\n for(i; i < a-1; i++) { \n list1_Ptr1 = list1_Ptr1 -> next; // going to the (a-1)th node of the list1.\n }\n\n for(i = 0; i < b+1; i++) {\n list1_Ptr2 = list1_Ptr2 -> next; // going to the (b+1)th node of the list1.\n }\n\n list1_Ptr1 -> next = list2_Ptr1; // connecting the (a-1)th node of the list1 to the head of the list2.\n\n while(list2_Ptr1 -> next != NULL) {\n list2_Ptr1 = list2_Ptr1 -> next; // going to the end of the list2.\n }\n\n list2_Ptr1 -> next = list1_Ptr2; // connecting the end of the list2 to the (b+1)th node of the list1.\n\n return list1; // returning the updated linked list list1.\n }\n};\n```\n\n\n\n\n[Instagram](https://www.instagram.com/iamsidharthaa__/)\n[LinkedIn](https://www.linkedin.com/in/sidharth-jain-36b542133)\n**If you find this solution helpful, consider giving it an upvote! Your support is appreciated. Keep coding, stay healthy, and may your programming endeavors be both rewarding and enjoyable!** | 2 | 1 | ['Linked List', 'C++'] | 2 |
merge-in-between-linked-lists | Easy 3-Pointer Approach in Java | easy-3-pointer-approach-in-java-by-its_n-ricl | Here\'s the algorithm for the code, explained step-by-step:\n\n1. Initialization:\np1: A pointer that traverses the head1 list to reach the node before the inse | its_Nae | NORMAL | 2024-03-20T05:48:57.990898+00:00 | 2024-03-20T05:48:57.990926+00:00 | 20 | false | Here\'s the algorithm for the code, explained step-by-step:\n\n**1. Initialization:**\np1: A pointer that traverses the head1 list to reach the node before the insertion point (a).\np2: A pointer that traverses the head1 list to reach the node at the insertion point (b).\np3: A pointer that traverses the head2 list.\nres: A pointer that stores the head of the original head1 list (used for returning the final result).\n\n**2. Finding Insertion Nodes:**\nThe first loop iterates a-1 times using p1 to reach the node before the insertion point (a).\nThe second loop iterates b times using p2 to reach the node at the insertion point (b).\n\n**3. Insertion:**\nhead1.next: This line connects the node before the insertion point (p1) to the head of the head2 list (head2). This effectively inserts the head2 list between the two nodes in head1.\np3.next: We iterate through the head2 list using p3 until the last node. The last node\'s next pointer is then assigned the node after the insertion point (p2.next). This connects the head2 list back to the original head1 list after the insertion point.\n\n**4. Returning the Result:**\nThe function returns the res pointer, which still points to the original head of the head1 list. The modified list with the inserted head2 list is now accessible through head1.\n\n\n```\nclass Solution {\n public ListNode mergeInBetween(ListNode head1, int a, int b, ListNode head2) {\n \n ListNode p1 = head1;\n \n for(int i=0; i<a-1; i++){\n p1 = p1.next;\n }\n \n ListNode p2 = head1;\n \n for(int i=0; i<b; i++){\n p2 = p2.next;\n }\n \n ListNode p3 = head2;\n \n ListNode res = head1;\n \n while(head1!=p1){\n head1 = head1.next;\n }\n \n head1.next = head2;\n \n while(p3.next!=null){\n p3 = p3.next;\n }\n \n p3.next = p2.next;\n \n return res;\n \n }\n}\n``` | 2 | 0 | ['Linked List', 'Two Pointers', 'Java'] | 0 |
merge-in-between-linked-lists | Easy solution with c++ | easy-solution-with-c-by-adrijchakraborty-two5 | Follow the code along to understand the concept :\n\n\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next; | adrijchakraborty7 | NORMAL | 2024-03-20T05:25:57.013745+00:00 | 2024-03-20T05:25:57.013789+00:00 | 51 | false | Follow the code along to understand the concept :\n\n```\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode() : val(0), next(nullptr) {}\n * ListNode(int x) : val(x), next(nullptr) {}\n * ListNode(int x, ListNode *next) : val(x), next(next) {}\n * };\n */\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n int i = 0;\n ListNode *temp1 = list1;\n //running a loop to find the previous node from where it will join the list with list2\n while(i<a-1){\n temp1 = temp1->next;\n i++;\n }\n \n ListNode *temp2 = temp1->next;\n temp1->next = list2;\n //this loop is for the next node where we have to join the tail of list2\n while(i<b){\n temp1 = temp2;\n temp2 = temp2->next;\n delete(temp1);//free the nodes to be removed\n i++;\n }\n //iterating through list2 to find the tail and joining it with the list1\n while(list2->next!=NULL){\n list2 = list2->next;\n }\n list2->next = temp2;\n \n return list1;\n }\n};\n``` | 2 | 0 | ['Linked List', 'C'] | 0 |
merge-in-between-linked-lists | Easy Java Solution with 1ms runtime | easy-java-solution-with-1ms-runtime-by-k-4v9x | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\nstep1:\n first take tail and head of list2 to attach between list1\n fi | klu_2100032169 | NORMAL | 2024-03-20T05:01:25.305480+00:00 | 2024-03-20T05:01:25.305512+00:00 | 18 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nstep1:\n first take tail and head of list2 to attach between list1\n first loop is used to find tail of list2\n------\nstep2:\n we need to attach list2 at position a-1 and b+1 to make list in between \n2 for loops are used to find ath and bth position \n------\nstep3:\n just we need to attach list2 at ath and bth position\n observe the postion given in digram and attach them\n ath-->head of list2 then tail2-->bth \nthen return the list1\n------\n \n \n\n\n# Complexity\n- Time complexity:\nO(n)+O(a-1)+O(b+1)\nn:size of list 2\n- Space complexity:\n O(1)\n\n# Code\n```\n/**\n * Definition for singly-linked list.\n * public class ListNode {\n * int val;\n * ListNode next;\n * ListNode() {}\n * ListNode(int val) { this.val = val; }\n * ListNode(int val, ListNode next) { this.val = val; this.next = next; }\n * }\n */\nclass Solution {\n public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n ListNode tail2=list2,head2=list2;\n while(tail2.next!=null){\n tail2=tail2.next;\n }\n ListNode ath=list1,bth=list1;\n for(int i=0;i<a-1;i++){\n ath=ath.next;\n }\n for(int i=0;i<b+1;i++){\n bth=bth.next;\n }\n ath.next=head2;\n tail2.next=bth;\n return list1;\n\n \n \n }\n}\n``` | 2 | 0 | ['Java'] | 0 |
merge-in-between-linked-lists | Simple solution in C || Basic approach || using two loops || Two Flags Solutpoion | simple-solution-in-c-basic-approach-usin-263o | Intuition\n Describe your first thoughts on how to solve this problem. \nSimple solution in c. it is a basic approach to solve this problem. \n\n# Approach\n De | yaswanthkarri | NORMAL | 2024-03-20T04:46:24.738357+00:00 | 2024-03-20T04:53:04.476455+00:00 | 313 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSimple solution in c. it is a basic approach to solve this problem. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFor this problem there are three stages:\nstage 1: Traverse the list1 and point a-1 as flag1 and b as flag2 nodes\nstage 2: Now add list 2 to the **flag1->next(a-1)** \nstage 3: Now Traverse to list2 end and add **list2 end->next to flag2** \nnow return the list1.....\n\n# Complexity\n- Time complexity: O(n**2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * struct ListNode *next;\n * };\n */\n\n\nstruct ListNode* mergeInBetween(struct ListNode* list1, int a, int b, struct ListNode* list2){\n // if(list1==NULL)\n // {\n // return list2;\n // }\n // return NULL\n int c=0;\n struct ListNode * temp=list1;\n struct ListNode * t1=NULL,*t2=NULL;\n while(temp)\n {\n \n if(c==a-1)\n {\n t1=temp;\n }\n temp=temp->next;\n c++;\n if (c==b)\n {\n t2=temp;\n break;\n }\n }\n t1->next=list2;\n temp=list2;\n while(temp->next)\n {\n temp=temp->next;\n }\n temp->next=t2->next;\n return list1;\n}\n``` | 2 | 0 | ['Linked List', 'Two Pointers', 'C', 'Counting', 'C++'] | 1 |
merge-in-between-linked-lists | ✅✅ Easy to understand CPP Solution 🚀🚀 | easy-to-understand-cpp-solution-by-barag-eom1 | \n# Complexity\n- Time complexity: O(n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(1)\n Add your space complexity here, e.g. O(n) \n\n | baragemanish6258 | NORMAL | 2024-03-20T03:41:32.829683+00:00 | 2024-03-20T03:41:32.829721+00:00 | 83 | false | \n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode() : val(0), next(nullptr) {}\n * ListNode(int x) : val(x), next(nullptr) {}\n * ListNode(int x, ListNode *next) : val(x), next(next) {}\n * };\n */\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n \n ListNode * temp = list1;\n ListNode *prev = NULL;\n\n while(a--)\n {\n prev = temp;\n temp = temp->next;\n }\n\n ListNode *temp2 = list1;\n ListNode *prev2 = NULL;\n\n while(b--)\n {\n prev2 = temp2;\n temp2 = temp2->next;\n }\n\n ListNode *demo = list2;\n\n while(demo->next != NULL)\n {\n demo=demo->next;\n }\n\n demo->next = temp2->next;\n prev2->next = NULL;\n\n prev->next = list2;\n\n return list1;\n }\n};\n``` | 2 | 0 | ['Linked List', 'C++'] | 0 |
merge-in-between-linked-lists | Simple implementation | TC O(b + m) & SC O(1) | simple-implementation-tc-ob-m-sc-o1-by-i-7uh1 | Intuition\n Describe your first thoughts on how to solve this problem. \nsince we have to remove nodes from a to b. keep note of node just previous to ath node | IIScBLR | NORMAL | 2024-03-20T03:22:11.712613+00:00 | 2024-03-20T03:31:17.873314+00:00 | 53 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nsince we have to remove nodes from a to b. keep note of node just previous to ath node and node next to bth node. point l1_node_prev_to_ath\'s next to head of list2 and next of last node of list2 to l1_node_next_to_bth\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(b + m)$$ \nsince we are iterating on list1 till we get bth node and iterating on list2 till we get the last node.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n# Code\n```\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode() : val(0), next(nullptr) {}\n * ListNode(int x) : val(x), next(nullptr) {}\n * ListNode(int x, ListNode *next) : val(x), next(next) {}\n * };\n */\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n ListNode *l1_node_prev_to_ath, *l1_node_next_to_bth, *ptr;\n ptr = list1; // initializing ptr to head of list1\n int cnt=0;\n while(ptr!=NULL){\n if(cnt == a-1){\n l1_node_prev_to_ath = ptr;\n }\n else if(cnt == b){\n l1_node_next_to_bth = ptr->next;\n break;\n }\n \n cnt++;\n ptr = ptr->next;\n \n }\n\n l1_node_prev_to_ath->next = list2;\n ptr = list2; // re-initializing ptr to head of list2\n while(ptr->next!=NULL){\n ptr=ptr->next;\n }\n ptr->next = l1_node_next_to_bth;\n \n return list1;\n }\n};\n``` | 2 | 0 | ['Linked List', 'C++'] | 0 |
merge-in-between-linked-lists | simple and easy understand solution | simple-and-easy-understand-solution-by-s-v9c5 | if it\'s help, please up \u2B06 vote! \u2764\uFE0F\n\n# Code\n\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* | shishirRsiam | NORMAL | 2024-03-20T03:11:40.746010+00:00 | 2024-03-20T03:11:40.746042+00:00 | 497 | false | # if it\'s help, please up \u2B06 vote! \u2764\uFE0F\n\n# Code\n```\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) \n {\n ListNode* tmp = list1, *tmp2 = list2;\n while(b--) tmp = tmp->next;\n while(tmp2->next) tmp2 = tmp2->next;\n tmp2->next = tmp->next;\n\n a--;\n tmp = list1;\n while(a--) tmp = tmp->next;\n\n tmp->next = list2;\n return list1;\n }\n};\n``` | 2 | 1 | ['Linked List', 'C', 'C++', 'Java', 'TypeScript', 'Rust', 'Ruby', 'Kotlin', 'JavaScript', 'C#'] | 3 |
merge-in-between-linked-lists | C# Solution for Merge In Between Linked Lists Problem | c-solution-for-merge-in-between-linked-l-yevk | Intuition\n Describe your first thoughts on how to solve this problem. \nThe intuition behind the solution is to traverse through the linked list until reaching | Aman_Raj_Sinha | NORMAL | 2024-03-20T02:56:22.375891+00:00 | 2024-03-20T02:56:22.375927+00:00 | 61 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition behind the solution is to traverse through the linked list until reaching the node before the range to be replaced (a-1th node). Then, skip the nodes within the range (ath to bth node) and connect the a-1th node to the start of list2. After that, traverse through list2 to find its end and connect it to the node after the bth node.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1.\tTraverse through the linked list to reach the (a-1)th node and store it in prev.\n2.\tTraverse through the linked list again to reach the bth node and store it in curr.\n3.\tConnect the next of prev to list2.\n4.\tTraverse through list2 to find its end.\n5.\tConnect the next of the last node of list2 to curr.next.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\u2022\tTraversing through the linked list twice: O(n), where n is the number of nodes in list1.\n\u2022\tTraversing through list2 to find its end: O(list2.length)\nOverall, the time complexity is O(n + list2.length).\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(1) because we are using a constant amount of extra space regardless of the input size.\n\n# Code\n```\n/**\n * Definition for singly-linked list.\n * public class ListNode {\n * public int val;\n * public ListNode next;\n * public ListNode(int val=0, ListNode next=null) {\n * this.val = val;\n * this.next = next;\n * }\n * }\n */\npublic class Solution {\n public ListNode MergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n ListNode dummy = new ListNode(0);\n dummy.next = list1;\n ListNode prev = dummy;\n \n // Move prev to the (a-1)th node\n for (int i = 0; i < a; i++) {\n prev = prev.next;\n }\n \n // Move curr to the bth node\n ListNode curr = prev;\n for (int i = a; i <= b; i++) {\n curr = curr.next;\n }\n \n // Connect the (a-1)th node to list2\n prev.next = list2;\n \n // Find the end of list2\n while (list2.next != null) {\n list2 = list2.next;\n }\n \n // Connect the end of list2 to the node after the bth node\n list2.next = curr.next;\n \n return dummy.next;\n }\n}\n``` | 2 | 0 | ['C#'] | 0 |
merge-in-between-linked-lists | Iterative Solution | Python | iterative-solution-python-by-pragya_2305-hids | Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(1)\n\n# Code\n\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, v | pragya_2305 | NORMAL | 2024-03-20T02:51:42.765412+00:00 | 2024-03-20T02:51:42.765452+00:00 | 51 | false | # Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(1)\n\n# Code\n```\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def mergeInBetween(self, list1: ListNode, a: int, b: int, list2: ListNode) -> ListNode:\n tempA = tempB = list1\n\n while a>1:\n tempA=tempA.next\n a-=1\n \n while b>=0:\n tempB = tempB.next\n b-=1\n\n tempA.next = list2\n \n while tempA and tempA.next:\n tempA=tempA.next\n\n tempA.next = tempB\n\n return list1\n\n\n \n``` | 2 | 0 | ['Linked List', 'Python', 'Python3'] | 0 |
merge-in-between-linked-lists | Easiest Fast W/Explanation beats 100% in [ Python3/C++/Python/C#/Java/C ] -- Have a look | easiest-fast-wexplanation-beats-100-in-p-trai | Intuition\n\n\n\nC++ []\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode() : val(0), | Edwards310 | NORMAL | 2024-03-20T02:50:53.744504+00:00 | 2024-03-20T03:05:53.440527+00:00 | 14 | false | # Intuition\n\n\n\n```C++ []\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode() : val(0), next(nullptr) {}\n * ListNode(int x) : val(x), next(nullptr) {}\n * ListNode(int x, ListNode *next) : val(x), next(next) {}\n * };\n */\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n ListNode *f = list1, *s = list1;\n for (int i = 0; i < a - 1; i++)\n f = f->next;\n\n for (int i = 0; i < b; i++)\n s = s->next;\n\n f->next = list2;\n while (list2->next != NULL)\n list2 = list2->next;\n\n list2->next = s->next;\n return list1;\n }\n};\n```\n```python3 []\n# Definition for singly-linked list.\n# class ListNode:\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution:\n def mergeInBetween(\n self, list1: ListNode, a: int, b: int, list2: ListNode) -> ListNode:\n f, s = list1, list1\n for i in range(a - 1):\n f = f.next\n for i in range(b):\n s = s.next\n f.next = list2\n while list2.next is not None:\n list2 = list2.next\n list2.next = s.next\n return list1\n```\n```C# []\n/**\n * Definition for singly-linked list.\n * public class ListNode {\n * public int val;\n * public ListNode next;\n * public ListNode(int val=0, ListNode next=null) {\n * this.val = val;\n * this.next = next;\n * }\n * }\n */\npublic class Solution {\n public ListNode MergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n ListNode f = list1 , s = list1;\n for(var i = 0; i < a - 1; ++i)\n f = f.next;\n for(int j = 0; j < b; j++)\n s = s.next;\n f.next = list2;\n while(list2.next != null)\n list2 = list2.next;\n list2.next = s.next;\n return list1;\n }\n}\n```\n```C []\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * struct ListNode *next;\n * };\n */\n\nstruct ListNode* mergeInBetween(struct ListNode* list1, int a, int b, struct ListNode* list2) {\n struct ListNode *itr = list1, *ptr = NULL, *qtr = NULL, *itr2 = list2;\n int cnt = 0;\n\n while (itr) {\n if (cnt == a - 1)\n ptr = itr;\n if (cnt == b + 1)\n qtr = itr;\n cnt = cnt + 1;\n itr = itr->next;\n }\n\n itr2 = list2;\n while (itr2->next)\n itr2 = itr2->next;\n ptr->next = list2;\n itr2->next = qtr;\n return list1;\n}\n```\n```java []\n/**\n * Definition for singly-linked list.\n * public class ListNode {\n * int val;\n * ListNode next;\n * ListNode() {}\n * ListNode(int val) { this.val = val; }\n * ListNode(int val, ListNode next) { this.val = val; this.next = next; }\n * }\n */\nclass Solution {\n public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n ListNode f = list1;\n ListNode s = list1;\n for (int i = 0; i < a - 1; i++)\n f = f.next;\n\n for (int j = 0; j < b; j++)\n s = s.next;\n f.next = list2;\n while (list2.next != null)\n list2 = list2.next;\n list2.next = s.next;\n return list1;\n }\n}\n```\n```C# []\n/**\n * Definition for singly-linked list.\n * public class ListNode {\n * public int val;\n * public ListNode next;\n * public ListNode(int val=0, ListNode next=null) {\n * this.val = val;\n * this.next = next;\n * }\n * }\n */\npublic class Solution {\n public ListNode MergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n ListNode pointerA = list1;\n ListNode pointerB = list1;\n \n for (var i = 0; i < b; i++) {\n if (i == a - 1) {\n pointerA = pointerB;\n }\n pointerB = pointerB.next;\n }\n ListNode pointerC = list2;\n\n while (pointerC.next != null) {\n pointerC = pointerC.next;\n }\n\n pointerA.next = list2;\n pointerC.next = pointerB.next;\n pointerB.next = null;\n return list1;\n }\n}\n```\n```python []\n# Definition for singly-linked list.\n# class ListNode(object):\n# def __init__(self, val=0, next=None):\n# self.val = val\n# self.next = next\nclass Solution(object):\n def mergeInBetween(self, list1, a, b, list2):\n """\n :type list1: ListNode\n :type a: int\n :type b: int\n :type list2: ListNode\n :rtype: ListNode\n """\n f, s = list1, list1\n for i in range(a - 1):\n f = f.next\n for i in range(b):\n s = s.next\n f.next = list2\n while list2.next is not None:\n list2 = list2.next\n list2.next = s.next\n return list1\n```\n```C []\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * struct ListNode *next;\n * };\n */\n\nstruct ListNode* mergeInBetween(struct ListNode* list1, int a, int b, struct ListNode* list2) {\n struct ListNode *f = list1, *s = list1;\n for (int i = 0; i < a - 1; i++)\n f = f->next;\n\n for (int i = 0; i < b; i++)\n s = s->next;\n\n f->next = list2;\n while (list2->next != NULL)\n list2 = list2->next;\n\n list2->next = s->next;\n return list1;\n}\n```\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n Very Simple approach take two pointers on list1 move them on their desired position (move f to a-1th node && b to bth node) .. Now make the f->next as list2 (join list1 to list2) and then move the list2 head\'s pointer to it\'s last position .. after that make list->next = s->next(joins list2\'s last node to slow\'s next node in list1) .. Then finally return list1 ... Here we are not deleting the nodes of list1 which are not required here but they are now not accessible for us .. still bth node -> next is pointing towards the list1 next nodes..\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(1)\n# Code\n```\n/**\n * Definition for singly-linked list.\n * struct ListNode {\n * int val;\n * ListNode *next;\n * ListNode() : val(0), next(nullptr) {}\n * ListNode(int x) : val(x), next(nullptr) {}\n * ListNode(int x, ListNode *next) : val(x), next(next) {}\n * };\n */\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n ListNode *f = list1, *s = list1;\n for (int i = 0; i < a - 1; i++)\n f = f->next;\n\n for (int i = 0; i < b; i++)\n s = s->next;\n\n f->next = list2;\n while (list2->next != NULL)\n list2 = list2->next;\n\n list2->next = s->next;\n return list1;\n }\n};\n```\n# PLease upvote if it\'s useful for you..\n\n | 2 | 0 | ['Linked List', 'C', 'Python', 'C++', 'Java', 'Python3', 'C#'] | 1 |
merge-in-between-linked-lists | 🔥Beats 100%🔥✅Super Easy (C++/Java/Python) Solution With Detailed Explanation✅ | beats-100super-easy-cjavapython-solution-u1rd | Intuition\nThe intuition of code is to merge two singly linked lists by replacing a segment of the first list (from position a to b) with the entire second list | suyogshete04 | NORMAL | 2024-03-20T01:41:09.641913+00:00 | 2024-03-20T02:20:54.245890+00:00 | 270 | false | # Intuition\nThe intuition of code is to merge two singly linked lists by replacing a segment of the first list (from position a to b) with the entire second list. The approach involves three main steps: finding the node just before the start of the segment to be replaced in the first list, finding the node just after the end of this segment, and finally linking the second list between these two nodes. The last part of the process connects the end of the second list to the node just after the segment in the first list. This operation effectively splices the second list into the first, between the positions a and b, inclusive.\n\n\n\n## Step-by-Step Approach\n\n1. **Initialize Pointers and Counter**: The solution starts by initializing a pointer `point1` to the start of `list1` and a counter variable `count` to 1. This setup prepares for traversal through the list.\n\n2. **Traverse to the `a-1`th Node**: The loop continues until `point1` points to the node just before the `a`th node (1-indexed) or the `a-1`th node (0-indexed). This is the node after which `list2` will be inserted.\n\n3. **Traverse to the `b+1`th Node**: A second pointer `point2` starts at the node immediately after `point1` and moves forward until it points to the node just after the `b`th node. This node will be the point where `list1` continues after `list2` has been inserted.\n\n4. **Insert `list2` Between `a` and `b`**: The `next` pointer of the node at `a-1` is updated to point to the start of `list2`. This effectively inserts `list2` at position `a`.\n\n5. **Find the End of `list2`**: A temporary pointer traverses `list2` to find its last node. This step is necessary to link the end of `list2` back to `list1`.\n\n6. **Link the End of `list2` to `list1`**: The `next` pointer of the last node in `list2` is updated to point to `point2`, the `b+1`th node of `list1`. This completes the insertion process.\n\n7. **Return `list1`**: The function returns the head of the modified `list1`, which now includes `list2` between the `a`th and `b`th positions.\n\n## Complexity Analysis\n\n- **Time Complexity**: The algorithm traverses each list at most once. The traversal of `list1` to positions `a` and `b` takes \\(O(b)\\) time, as it stops after reaching the `b+1`th node. The traversal of `list2` to find its end takes \\(O(n)\\) time, where \\(n\\) is the length of `list2`. Thus, the total time complexity is \\(O(b + n)\\), where \\(b\\) is the position in `list1` where the merge ends, and \\(n\\) is the length of `list2`.\n\n- **Space Complexity**: The algorithm uses a constant amount of extra space for pointers and the counter variable, so the space complexity is \\(O(1)\\). Note that the space used by the lists themselves is not considered part of the space complexity for this analysis, as it is not additional space allocated by the algorithm.\n\n# Code\n```C++ []\n\nclass Solution {\npublic:\n ListNode* mergeInBetween(ListNode* list1, int a, int b, ListNode* list2) {\n ListNode *point1 = list1;\n int count = 1;\n while (count != a)\n {\n point1 = point1 -> next;\n count++;\n }\n\n ListNode *point2 = point1 -> next;\n while (count != b+1)\n {\n point2 = point2 -> next;\n count++;\n }\n\n point1->next = list2;\n ListNode *temp = list2;\n while (temp -> next != NULL)\n temp = temp -> next;\n\n temp -> next = point2;\n \n return list1;\n\n }\n};\n```\n```Java []\nclass Solution {\n public ListNode mergeInBetween(ListNode list1, int a, int b, ListNode list2) {\n ListNode point1 = list1;\n int count = 1;\n while (count != a) {\n point1 = point1.next;\n count++;\n }\n\n ListNode point2 = point1.next;\n while (count != b + 1) {\n point2 = point2.next;\n count++;\n }\n\n point1.next = list2;\n ListNode temp = list2;\n while (temp.next != null)\n temp = temp.next;\n\n temp.next = point2;\n\n return list1;\n }\n};\n```\n```Python []\nclass Solution:\n def mergeInBetween(self, list1, a, b, list2):\n point1 = list1\n count = 1\n while count != a:\n point1 = point1.next\n count += 1\n \n point2 = point1.next\n while count != b + 1:\n point2 = point2.next\n count += 1\n \n point1.next = list2\n temp = list2\n while temp.next is not None:\n temp = temp.next\n \n temp.next = point2\n \n return list1\n\n``` | 2 | 0 | ['Linked List', 'C++', 'Java', 'Python3'] | 0 |
the-earliest-and-latest-rounds-where-players-compete | Recursion, Memo and Optimized Recursion | recursion-memo-and-optimized-recursion-b-319s | We start with the straightforward recursion, then optimize it using memoisation, and finally arrive at the efficient solution using all that insight we gained. | votrubac | NORMAL | 2021-06-13T04:05:11.521803+00:00 | 2021-06-19T20:31:47.003570+00:00 | 5,313 | false | > We start with the straightforward recursion, then optimize it using memoisation, and finally arrive at the efficient solution using all that insight we gained. \n\n#### Recursion\nWe try all combinations, and it should work since `n` is limited to `28`. For the first round, we have no more than 2 ^ 12 choices (14 pairs, and winners are predefined for 2 pairs), second round - 2 ^ 5, then 2 ^ 2, then 1 choice, and finally we will have just two winners left. Therefore, we will have up to 524,288 total combinations and 5 rounds.\n\nThe tricky part is to make it as efficient as possible. For that, I am using `mask` to indicate which players have been eliminated.\n \nWe move `i` and `j` to pick the pairs; when `i >= j`, we start a new round. When `i` and `j` point to our finalists, we update the min and max rounds.\n\n**C++**\n```cpp\nint min_r = INT_MAX, max_r = INT_MIN;\nvoid dfs(int mask, int round, int i, int j, int first, int second) {\n if (i >= j)\n dfs(mask, round + 1, 0, 27, first, second);\n else if ((mask & (1 << i)) == 0)\n dfs(mask, round, i + 1, j, first, second);\n else if ((mask & (1 << j)) == 0)\n dfs(mask, round, i, j - 1, first, second);\n else if (i == first && j == second) {\n min_r = min(min_r, round);\n max_r = max(max_r, round);\n }\n else {\n if (i != first && i != second)\n dfs(mask ^ (1 << i), round, i + 1, j - 1, first, second);\n if (j != first && j != second)\n dfs(mask ^ (1 << j), round, i + 1, j - 1, first, second);\n }\n}\nvector<int> earliestAndLatest(int n, int first, int second) {\n dfs((1 << n) - 1, 1, 0, 27, first - 1, second - 1);\n return { min_r, max_r };\n}\n```\n**Complexity Analysis**\n- Time: O(2 ^ n).\n- Memory: O(log n) for the recursion.\n\n#### Add Memoisation\nI tried to memoise `visited` masks, but it only gave a modest boost. Then I realized that what really matters are the number of players standing before the first (left), in between (mid), and after (right) the second player. So we keep track of `l`, `m`, and `r` - a bit messy but does the job. With this insight, the runtime improved from 500 to 0 ms.\n\n**C++**\n```cpp\nint min_r = INT_MAX, max_r = INT_MIN;\nbool visited[27][27][27] = {};\nvoid dfs(int mask, int round, int i, int j, int first, int second, int l, int m, int r) {\n if (i >= j)\n dfs(mask, round + 1, 0, 27, first, second, l, m, r);\n else if ((mask & (1 << i)) == 0)\n dfs(mask, round, i + 1, j, first, second, l, m, r);\n else if ((mask & (1 << j)) == 0)\n dfs(mask, round, i, j - 1, first, second, l, m, r);\n else if (i == first && j == second) {\n min_r = min(min_r, round);\n max_r = max(max_r, round);\n }\n else if (!visited[l][m][r]) {\n visited[l][m][r] = true;\n if (i != first && i != second)\n dfs(mask ^ (1 << i), round, i + 1, j - 1, first, second, \n l - (i < first), m - (i > first && i < second), r - (i > second));\n if (j != first && j != second)\n dfs(mask ^ (1 << j), round, i + 1, j - 1, first, second,\n l - (j < first), m - (j > first && j < second), r - (j > second));\n }\n}\nvector<int> earliestAndLatest(int n, int first, int second) {\n dfs((1 << n) - 1, 1, 0, 27, first - 1, second - 1, first - 1, second - first - 1, n - second);\n return { min_r, max_r };\n}\n```\n**Complexity Analysis**\n- Time: O(n ^ 3).\n- Memory: O(n ^ 3) for the memoisation.\n\n#### Optimized Recursion\nWith the insight about tracking the number of players between champions, we can simplify the algorithm by computing possible transitions instead of simulating individual competitions. Say, we have 15 total players; 4 players on the left and 5 - on the right (including champions).\n\n\n\nFor the second round, we will have 8 total players, and two possible cases: `[1, 4]` (or `[4, 1]`) and `[2, 3]` (or `[3, 2]`).\n\n\n\nSo, we will track players on the left `l` and right `r`, including champions, and total number of players `n`. If `l == r`, our champions will compete in the current round. \n\nDetermining the valid standings of players `i` and `j` after the round is a bit tricky, but here are ground rules:\n- To simplify the calculation, we always make sure `l < r`. We can do it because reult for `[8, 3]` will be the same as for `[3, 8]`. \n- `i` and `j` should be at least one to account for a champion.\n- Picking `i` players on the left meaning that `l - i` players lose to players on the right.\n\t- So we have to pick `l - i + 1` players on the right or more (`+1` is for the champion).\n- Winers on the left and right (`i + j`) should not exceed the number of players in the next round (`(n + 1) / 2`).\n- Loosers on the left and right (`l - i + r - j`) should not exceed the half of players in the current round.\n\n**C++**\n```cpp\nint min_r = INT_MAX, max_r = INT_MIN;\nvoid dfs(int l, int r, int n, int round) {\n if (l == r) {\n min_r = min(min_r, round);\n max_r = max(max_r, round);\n }\n else\n if (l > r)\n swap(l, r);\n for (int i = 1; i < l + 1; ++i)\n for (int j = l - i + 1; i + j <= min(r, (n + 1) / 2); ++j)\n if (l + r - (i + j) <= n / 2)\n dfs(i, j, (n + 1) / 2, round + 1);\n}\nvector<int> earliestAndLatest(int n, int first, int second) {\n dfs(first, n - second + 1, n, 1);\n return { min_r, max_r };\n}\n``` | 113 | 7 | ['C'] | 27 |
the-earliest-and-latest-rounds-where-players-compete | [Python] 2 Solution: dfs and smart dp, explained | python-2-solution-dfs-and-smart-dp-expla-hzxa | Not very difficult problem, the main problem in python to make it work without TLE. Let us use dfs(pos, i) function, where:\n1. pos is tuple of players we still | dbabichev | NORMAL | 2021-06-13T04:00:52.688169+00:00 | 2021-06-14T12:18:10.954013+00:00 | 2,744 | false | Not very difficult problem, the main problem in python to make it work without TLE. Let us use `dfs(pos, i)` function, where:\n1. `pos` is tuple of players we still have.\n2. `i` is how many matches were already played.\n\nEach time we run recursion, check that pair `(firstPlayer, secondPlayer)` is not here yet (denoted by `F` and `S`), if it is, add number of matches played to set `ans` and return. Also, ignore pairs where one of the two players is `S` or `F`. Finally, use functionality of python `product` function to fastly generate all next positions.\n\n#### Complexity\nWe have `n` players in the beginning, and we have `n//2` pairs, so there is `O(2^(n//2))` options for the first step, then it will be `O(2^(n//4))` and so on, so in the end we can have potentially `O(2^n)` positions, which is our time complexity. However, due to careful prunning, it practice it is much less, like if we have `28`, then on the next step we have not `2^14`, but `2^12` positions, because `S` and `F` always go to the next match or we stop, then we have `2^5` and then we have `2^1`, so it is more like `2^(12 + 5 + 1) = 2^18`, so it is still feasible. Space complexity is `O(n)`.\n\n#### Code\n```python\nclass Solution:\n def earliestAndLatest(self, n, F, S):\n ans = set()\n def dfs(pos, i):\n M, pairs = len(pos), []\n if M < 2: return\n\n for j in range(M//2):\n a, b = pos[j], pos[-1-j]\n if (a, b) == (F, S):\n ans.add(i)\n return\n if a != F and b != F and a != S and b != S:\n pairs.append((a, b))\n\n addon = (F, S) if M%2 == 0 else tuple(set([F, S, pos[M//2]]))\n for elem in product(*pairs):\n dfs(sorted(elem + addon), i + 1)\n\n dfs(list(range(1, n+1)), 1)\n return [min(ans), max(ans)]\n```\n\n#### Solution 2\nThis solution is borrowed from https://leetcode.com/problems/the-earliest-and-latest-rounds-where-players-compete/discuss/1268560/Python-simple-top-down-dp-solution-O(N4*logN), here I just rewrote it a bit and try to add some explanations with examples. Please go and upvote this post, it deserves more upvotes.\n\nDefine by `dp(l, r, m, q)` state with the following parameters:\n\n1. `l` and `r` are positions of our `F` and `S` players from start and from end. For example if we have 1, 2, **3**, 4, 5, 6, **7**, 8, 9, 10, 11, 12, where we denoted by bold elements the first and the second player, and we have `l = 3` and `r = 6`.\n2. `m` is current number of players, we have 12 here and `q` is number of games already played.\n\nWhat can happen on the next step? Let us go through options and see what is going on. Let us denote by underline <u>x</u> the players who loose and by **x** player who win.\nThen at the moment we have the following situation:\n\n1, 2, **3**, 4, 5, <u>6</u>, **7**, 8, 9, <u>10</u>, 11, 12.\n\nWhat can happen that among players `1` and `2` there can be zero, one or two wins, and actually it does not matter which ones. Let us consider the cases:\n\n1. We have zero wins, so we have <u>1</u>, <u>2</u>, **3**, 4, 5, <u>6</u>, **7**, 8, 9, <u>10</u>, **11**, **12**. Then what we know for sure is in new round player **3** will be the first. Player **7** can be either 3, 4 or 5 from the end.\n2. We have one wins, so we have <u>1</u>, **2**, **3**, 4, 5, <u>6</u>, **7**, 8, 9, <u>10</u>, <u>11</u>, **12**. Then what we know for sure is in new round player **3** will be the second. Player **7** can be either 2, 3 or 4 from the end.\n3. We have two wins, so we have **1**, **2**, **3**, 4, 5, <u>6</u>, **7**, 8, 9, <u>10</u>, <u>11</u>, <u>12</u>. Then what we know for sure is in new round player **3** will be the third. Player **7** can be either 1, 2 or 3 from the end.\n\nSo, what we need to do is to carefully understand all the cases we can meet.\n\n#### Complexity\nWe have `O(n^2*log(n)` states: `O(n)` for both `l` and `r` and `log(n)` states for `m`, which will define `q` in unique way. We have `O(n^2)` transactions from one state to others, so time complexity is `O(n^4*log n)`, space complexity is `O(n^2*log n)`. Actually, more detailed analysis shows that log factor can be removed, because say `n = 64`, then we have `O(64*64)` states for `m = 64`, then we have `O(32*32)` states for `m = 32` and so on. So final time complexity is `O(n^4)`, space is `O(n^2)`.\n\n#### Code\n```python\nclass Solution:\n def earliestAndLatest(self, n, F, S):\n @lru_cache(None)\n def dp(l, r, m, q):\n if l > r: dp(r, l, m, q)\n if l == r: ans.add(q)\n \n for i in range(1, l + 1):\n for j in range(l-i+1, r-i+1):\n if not (m+1)//2 >= i + j >= l + r - m//2: continue\n dp(i, j, (m + 1) // 2, q + 1)\n \n ans = set()\n dp(F, n - S + 1, n, 1)\n return [min(ans), max(ans)]\n```\n\nIf you have any questions, feel free to ask. If you like solution and explanations, please **Upvote!** | 56 | 5 | ['Depth-First Search'] | 10 |
the-earliest-and-latest-rounds-where-players-compete | [Python] simple top-down dp solution - O(N^4) | python-simple-top-down-dp-solution-on4-b-eyts | Idea\n\ndp(l, r, m) is the result when firstPlayer is the l-th player from left and secondPlayer is the r-th player from right, and there are m players in total | alanlzl | NORMAL | 2021-06-13T04:06:43.855223+00:00 | 2021-06-18T06:34:17.163226+00:00 | 1,653 | false | **Idea**\n\n`dp(l, r, m)` is the result when firstPlayer is the `l-th` player from left and secondPlayer is the `r-th` player from right, and there are `m` players in total.\n\nThe base case is straight-forward: simply check `l == r`. \n\nBy making sure `l <= r`, the dp transition is also manageable. In the next round, `l` can be `1, ..., l`. The only tricky part is the range of `r` in the next round. This depends on two things:\n1) how many times the players to the left of first player win/lose. \n2) the second player is in the left or right half of the remaining players. \n\nPlease see code below for more details =)\n\n</br>\n\n**Complexity**\n\nFor `dp(l, r, m)`, `l` and `r` are of `O(N)`, and `m` is of `O(logN)`. The loop in `dp` takes `O(M^2)`. \n\nBased on [@DBabichev](https://leetcode.com/DBabichev/)\'s comment, there are in total `n^2 + (n//2)^2 + ...` states, so the total time complexity is `O(N^4)`.\n\n- Time complexity: `O(N^4)`\n- Space complexity: `O(N^2)`\n\n</br>\n\n**Python**\n\n```Python\nclass Solution:\n def earliestAndLatest(self, n: int, firstPlayer: int, secondPlayer: int) -> List[int]:\n @cache\n def dp(l, r, m):\n # make sure l <= r\n if l > r:\n return dp(r, l, m)\n # base case\n if l == r:\n return (1, 1)\n # dp transition\n nxt_m = (m + 1) // 2\n ans = [n, 0]\n for i in range(1, l + 1):\n l_win, l_lose = i - 1, l - i\n for j in range(max(r - (m//2) - 1, 0) + l_lose + 1, min(r - 1 - l_win, nxt_m - i) + 1):\n tmp = dp(i, j, nxt_m)\n ans = min(ans[0], tmp[0]), max(ans[1], tmp[1])\n return (ans[0] + 1, ans[1] + 1)\n \n return dp(firstPlayer, n - secondPlayer + 1, n)\n``` | 43 | 1 | [] | 10 |
the-earliest-and-latest-rounds-where-players-compete | C++ bit mask DFS solution. | c-bit-mask-dfs-solution-by-chejianchao-tb3g | Idea\n- seperate the team to left side and right side, use bit mask to try all the winning status of left side and generate the next round of players and go to | chejianchao | NORMAL | 2021-06-13T04:00:44.143969+00:00 | 2021-06-13T04:00:44.143997+00:00 | 1,665 | false | ### Idea\n- seperate the team to left side and right side, use bit mask to try all the winning status of left side and generate the next round of players and go to the next round.\n- if we can match first player and second player in the current round, then calculate the max and min round.\n- if we can not find first and second player in current array, we can early return.\n\n### Complexity\n- Time: O(2 ^ (n / 2) * n)\n- Space: O(n)\n\n### Solution\n- C++\n```\nclass Solution {\npublic:\n int mn = 10000;\n int mx = 0;\n int first;\n int second;\n void dfs(vector<int> &arr, int round) {\n int size = arr.size() / 2;\n if(arr.size() == 1) return;\n for(int i = 0; i < size; i++) {\n //if we can match first and second in this round.\n if(arr[i] == first && arr[arr.size() - i - 1] == second) {\n mn = min(mn, round);\n mx = max(mx, round);\n return;\n }\n }\n bool f1 = false, f2 = false;\n for(auto n : arr) {\n f1 |= n == first;\n f2 |= n == second;\n }\n if(!f1 || !f2) { //can not find first and second player.\n return;\n }\n vector<int> nextarr(size + (arr.size() % 2));\n int m = (1 << size) - 1;\n for(int i = 0; i <= m; i++) { //try all the winning status for the left side players.\n int left = 0, right = nextarr.size() - 1;\n for(int j = 0; j < size; j++) {\n if((1 << j) & i) { //left side player win, put it to the next array.\n nextarr[left++] = arr[j];\n }else { //right side player win.\n nextarr[right--] = arr[arr.size() - j - 1];\n }\n \n }\n if(arr.size() % 2) { //middle player go to the next round.\n nextarr[left] = arr[arr.size() / 2];\n }\n dfs(nextarr, round + 1);\n }\n }\n vector<int> earliestAndLatest(int n, int firstPlayer, int secondPlayer) {\n vector<int> arr(n);\n for(int i= 1; i <= n; i++) {\n arr[i - 1] = i;\n }\n first = firstPlayer;\n second = secondPlayer;\n dfs(arr, 1);\n return {mn, mx};\n }\n};\n``` | 22 | 1 | [] | 1 |
the-earliest-and-latest-rounds-where-players-compete | Greedy log(N) solution | greedy-logn-solution-by-wisdompeak-u60j | This greedy code can handle n up to 1e18. No iteration over choices, no min() or max() used. \nHowever, the solution is hard to explain. Sorry, have to leave it | wisdompeak | NORMAL | 2021-06-14T08:36:19.708902+00:00 | 2021-06-14T08:55:25.790216+00:00 | 1,703 | false | This greedy code can handle n up to 1e18. No iteration over choices, no min() or max() used. \nHowever, the solution is hard to explain. Sorry, have to leave it for you guys to understand.\n```py\nclass Solution(object):\n def earliestAndLatest(self, n, a, b):\n """\n :type n: int\n :type firstPlayer: int\n :type secondPlayer: int\n :rtype: List[int]\n """\n def simplify(n, a, b):\n # swap\n if a>b: a, b = b, a\n # flip\n if a+b >= n+1:\n a, b = n+1-b, n+1-a\n return n, a, b\n \n def get_info(n,a,b):\n ll, rr = a-1, n-b\n aa = n-ll\n bb = 1+rr\n return ll,rr,aa,bb\n\n def while_loop(n, a, b):\n ans = 1\n while a+b < n+1:\n n = (n+1)/2\n ans += 1\n if b-a-1==0:\n while n%2:\n n = (n+1)/2\n ans += 1\n return ans\n\n def solve_fast(n, a, b):\n n, a, b = simplify(n, a, b)\n if a+b == n+1: \n return 1\n\n # b is on the left, including center\n if b <= (n+1)/2:\n return while_loop(n, a, b)\n \n # b is on the right\n ll, rr, aa, bb = get_info(n, a, b)\n if (ll%2==1 and bb-a-1==0):\n if (n%2==0) and (b == n/2+1): \n return 1 + while_loop((n+1)/2, a, a+1)\n else:\n return 3\n else:\n return 2\n\n def solve_slow(n, a, b):\n n, a, b = simplify(n, a, b)\n if a+b==n+1: \n return 1\n # b is in the left, all can be deleted\n if b <= n+1-b: \n return 1+solve_slow((n+1)/2, 1, 2)\n else:\n # b is in the right\n ll, rr, aa, bb = get_info(n, a, b)\n keep = (b-bb-1)/2 + n%2\n return 1+solve_slow((n+1)/2, 1, 1+keep+1) \n\n return [solve_fast(n,a,b), solve_slow(n,a,b)]\n```\t\t | 20 | 0 | ['Greedy', 'Python'] | 4 |
the-earliest-and-latest-rounds-where-players-compete | 10 lines + 0ms bit counting solution - O(1) time, O(1) space | 10-lines-0ms-bit-counting-solution-o1-ti-iddh | Idea\nI was heavily inspired by @wisdompeak\'s O(log n) greedy recursive solution, and looked for more patterns and how to eliminate all the recursive calls and | kcsquared | NORMAL | 2021-06-14T20:24:56.809966+00:00 | 2021-06-17T21:54:41.382046+00:00 | 1,096 | false | **Idea**\nI was heavily inspired by @wisdompeak\'s [`O(log n)` greedy recursive solution](https://leetcode.com/problems/the-earliest-and-latest-rounds-where-players-compete/discuss/1271531/Greedy-log(N)-solution), and looked for more patterns and how to eliminate all the recursive calls and loops. \n\nThis problem turns out to have a pretty simple solution. A key insight also came from @alanlzl\'s post: we can assume that `first` is closer to the left than `second` is to the right.\n\n1. **Finding Latest**: The optimal strategy for getting the latest round is to push `first` and `second` into positions 1 and 2, so all players left of \'second\' should try to lose. This is always possible to do if `second` is left of or at the middle, after which we return the most significant bit of n (rounds left). If `second` is close to the right edge, we can\'t push it to position 2, and `first` will eliminate at least one player to the right of `second` each round.\n\n2. **Finding Earliest**: It\'s usually possible to win in around 2-3 rounds. This is intuitive by the huge amount of control we have for where `first` and `second` will go in the next round, especially if there are many spaces between `first` and `second`. However, the position of each player only moves left, so we may need to wait some rounds for the midpoint of our player list to fall between `first` and `second`, in which case all players left of `second` should try to win.\n\n**Complexity**\nAssuming that we can read the number of trailing zeroes and leading zeroes from `n` in `O(1)` time, e.g. with the builtin assembly functions, there are a fixed number of operations. There\'s no recursion or loops (and both versions can be done without any function calls), and our only memory usage is 2 or 3 ints. \n* Time complexity: `O(1)` if `n` fits in a machine word / 64 bits\n* Space complexity: `O(1)`\n\t\n\n**C++:**\n\n```c++\nclass Solution {\npublic:\n vector<int> earliestAndLatest(int n, int first, int second) {\n if (first + second == n + 1) return {1, 1};\n if (first + second > n + 1) tie(first, second) = make_tuple(n+1-second, n+1-first);\n \n int ans_earliest = 1, ans_latest = min(32 - __builtin_clz(n-1), n+1-second);\n if (first + second==n){\n if (first % 2 == 0) ans_earliest = first+2 < second? 2: 1 + __builtin_ctz(first);\n }\n else if (first+1 == second){\n ans_earliest = 32 - __builtin_clz((n-1) / (first+second-1));\n ans_earliest += __builtin_ctz((n-1)>>ans_earliest);\n }\n else if (first+second <= (n+1)/2) ans_earliest = 32 - __builtin_clz((n-1) / (first+second-1));\n return {ans_earliest+1, ans_latest};\n }\n};\n```\n\nSome more insight:\n\n* One trick used repeatedly is that the number of players transforms as: `n -> (n+1) / 2` every round. This means that the number of rounds by the time `n` becomes 2 is `ceiling(log_2(n))`, at which point the game ends. `ceiling(log_2(n))` can be computed efficiently as `# of bits in an int (32) - leading zeros(n-1)`. \n* This line requires special attention:\n```python\n# We want to know the number of rounds left until first + second >= n+1. \n# By the game rules, this is the minimum value of \n# k >= 0 such that ceiling(n / 2^k) < first + second.\n# With some rearranging, this becomes \nrounds_left = ceiling_of_log2((n + first + second - 2) // (first + second - 1))\n```\n\n\nMost of the Python code is just the bitwise implementations of C++ builtins/ assembly operations, working for up to 32 bit ints, as well as many comments. If `2**31 < n < 2**64`, a single extra line is required for these functions. These are fairly common; I found these 3 functions in a textbook. If `n` is tiny and needs much fewer than `32` bits, it\'s faster to just loop over the bits.\n\nI wrote out a full proof for each of the cases, but the \'earliest\' case is quite long. The key idea is to treat the problem as having 3 boxes, left, middle, and right, and trying to allocate an equal number of players into the left and right boxes. We get a choice of distributing `first-1` players to either the left or right boxes. If `second` is at or right of the midpoint, we also get `n-first-second` players to place in the middle or right boxes, and so we can make the left and right boxes equal in 2 or 3 rounds, at which point we\'ve won if `first+1 != second`. If `second` is left of the midpoint, we only get `second-first-1` players to place in the middle or right boxes, which means the right box will end up larger than the left box. So we use induction to show that the optimal placement is having all `first-1` players left of `first` win their games, and all players between `first` and `second` try to win their games, minimizing the difference between right and left.\n\n**Python:**\n```python\nclass Solution:\n\tdef earliestAndLatest(self, n: int, first: int, second: int) -> List[int]:\n\t\tdef ceiling_of_log2(x: int) -> int:\n\t\t\t""" Return the ceiling of the integer log 2, i.e. index(MSB) - 1 + (1 if x not pow2) """\n\t\t\tassert 0 < x < 0x100000000\n\t\t\t# Use power of 2 test. offset is 1 iff x is NOT a power of 2\n\t\t\toffset = 1 if (x & (x - 1)) != 0 else 0\n\t\t\tx |= (x >> 1)\n\t\t\tx |= (x >> 2)\n\t\t\tx |= (x >> 4)\n\t\t\tx |= (x >> 8)\n\t\t\tx |= (x >> 16)\n\t\t\t# Remove offset to get floor_of_log2. floor(log2(x)) + 1 == ceil(log2(x)) iff x not a power of 2.\n\t\t\treturn popcount(x) - 1 + offset\n\n\t\tdef popcount(x: int) -> int:\n\t\t\t""" Return the number of set bits in 32 bit unsigned x (Hamming weight) """\n\t\t\tassert 0 <= x < 0x100000000\n\t\t\tx = x - ((x >> 1) & 0x55555555)\n\t\t\tx = (x & 0x33333333) + ((x >> 2) & 0x33333333)\n\t\t\treturn (((x + (x >> 4) & 0xF0F0F0F) * 0x1010101) & 0xffffffff) >> 24\n\n\t\tdef count_trailing_zeroes(x: int) -> int:\n\t\t\t""" Return the number of trailing zeroes in 32 bit unsigned x > 0 (LSB + 1). This method is similar to\n\t\t\t\tbranchless binary search, but there are many other methods using the integer log2"""\n\t\t\tassert 0 < x < 0x100000000\n\t\t\tif x & 0x1: return 0 # odd x, quick break\n\t\t\tc = 1\n\t\t\tif (x & 0xffff) == 0:\n\t\t\t\tx >>= 16\n\t\t\t\tc += 16\n\t\t\tif (x & 0xff) == 0:\n\t\t\t\tx >>= 8\n\t\t\t\tc += 8\n\t\t\tif (x & 0xf) == 0:\n\t\t\t\tx >>= 4\n\t\t\t\tc += 4\n\t\t\tif (x & 0x3) == 0:\n\t\t\t\tx >>= 2\n\t\t\t\tc += 2\n\t\t\treturn c - (x & 0x1)\n\n\t\t# Base case, we can return instantly\n\t\tif first + second == n + 1: return [1, 1]\n\n\t\t# This ensures that \'first\' is closer to the left than \'second\' is to the right.\n\t\t# Also, crucially ensures that the sum of first and second is minimal among equivalent configs.\n\t\tif first + second >= n + 1: first, second = n + 1 - second, n + 1 - first\n\n\t\tfirst_plus_second = first + second\n\n\t\t# Special case if first + 1 == second, since we then need to find which round will have an even # of players\n\t\tif first + 1 != second and first_plus_second >= (n + 1) // 2 + 1:\n\t\t\tif first_plus_second == n:\n\t\t\t\t# If n is 4k + 2, first is 2k, and second is 2k+2, then parity of n also matters.\n\t\t\t\tif n % 4 == 2 and first + 2 == second:\n\t\t\t\t\t# Using n // 4 instead of n//4 + 1 because trailing_zeroes(x-1) = rounds until x is even\n\t\t\t\t\tans_earliest = 3 + count_trailing_zeroes(n // 4)\n\t\t\t\telse:\n\t\t\t\t\tans_earliest = 3 - (first % 2)\n\t\t\telse:\n\t\t\t\tans_earliest = 2\n\n\t\t# If we are in a special case: Players are too far left and close together to meet next round\n\t\telse:\n\t\t\tans_earliest = 1 + ceiling_of_log2((n + first_plus_second - 2) // (first_plus_second - 1))\n\t\t\tif first + 1 == second:\n\t\t\t\tans_earliest += count_trailing_zeroes(((n + (1 << (ans_earliest-1)) - 1) >> (ans_earliest-1)) - 1)\n\n\t\t# ceiling_of_log2 of n is the number of rounds left until there are exactly 2 players remaining, starting at n.\n\t\t# This implicitly assumes that optimal strategy for ans_latest is moving \'first\' and \'second\' to pos. 1 and 2\n\t\tans_latest = min(ceiling_of_log2(n), n + 1 - second)\n\n\t\treturn [ans_earliest, ans_latest]\n``` | 12 | 0 | ['C', 'Python'] | 2 |
the-earliest-and-latest-rounds-where-players-compete | C++ | Recursion | dfs | without using mask | c-recursion-dfs-without-using-mask-by-sh-skd9 | Inspired by Votrubac\'s solution \n1. We make a players string with all 1s\n1. If a player looses we mark it as 0\n1. We maintain l = left and r = right bounds | shourabhpayal | NORMAL | 2021-06-13T13:21:54.202136+00:00 | 2021-06-18T06:55:10.859110+00:00 | 576 | false | **Inspired by [Votrubac\'s solution ](https://leetcode.com/problems/the-earliest-and-latest-rounds-where-players-compete/discuss/1268539/Recursion)**\n1. We make a players string with all 1s\n1. If a player looses we mark it as 0\n1. We maintain l = left and r = right bounds \n1. New round begins when l >= r means either 1 player remains or no player remains\n\n**Approach 1 (500ms)**\n```\nclass Solution {\npublic:\n int f, s, n;\n int maxr = INT_MIN, minr = INT_MAX;\n vector<int> earliestAndLatest(int N, int F, int S) {\n f = F-1, s = S-1, n = N;\n string players = string(n, \'1\');\n\t\tint round = 1, left = 0, right = n-1;\n help(players, left, right, round);\n return {minr, maxr};\n }\n \n //passing players by reference is crucial to avoid tle\n void help(string &players, int l, int r, int round){\n \n //round finished start next round\n if(l >= r){\n help(players, 0, n-1, round+1);\n }\n //left player is already eliminated continue with other players\n else if(players[l] == \'0\'){\n help(players, l+1, r, round);\n }\n //right player is already eliminated continue with other players\n else if(players[r] == \'0\'){\n help(players, l, r-1, round);\n }\n //we have found the place where first and second players come head to head\n else if((l == f and r == s) or (l == s and r == f)){\n minr = min(minr, round);\n maxr = max(maxr, round);\n }\n //the left player will win this match\n else if(l == f || l == s){\n //make the right player loose\n players[r] = \'0\';\n help(players, l+1, r-1, round);\n //reset for more exploration (more exploration happens when an earlier call was made from the last else block)\n players[r] = \'1\';\n }\n //the right player will win this match\n else if(r == f || r == s){\n //make the left player loose\n players[l] = \'0\';\n help(players, l+1, r-1, round);\n //reset for more exploration (more exploration happens when an earlier call was made from the last else block)\n players[l] = \'1\';\n }\n else{\n //both can win or loose, perform both scenarios\n players[r] = \'0\';\n help(players, l+1, r-1, round);\n players[r] = \'1\';\n players[l] = \'0\';\n help(players, l+1, r-1, round);\n players[l] = \'1\';\n }\n }\n};\n```\n\n**Approach 2 (extention of approach 1) (16ms)**\n1. We memoize the state (players) of help function using a key.\n1. key = ```NUMBER_OF_PLAYERS_BEFORE_FIRST_PLAYER + | + NUMBER_OF_PLAYERS_BETWEEN_FIRST_AND_SECOND_PLAYER + | + NUMBER_OF_PLAYERS_AFTER_SECOND_PLAYER```\n1. All these are number of players still left means they have value = 1\n1. This key is stored in visited.\n```\nclass Solution {\npublic:\n int f, s, n;\n int maxr = INT_MIN, minr = INT_MAX;\n unordered_set<string> visited;\n \n vector<int> earliestAndLatest(int N, int F, int S) {\n f = F-1, s = S-1, n = N;\n string players = string(n, \'1\');\n\t\tint round = 1, left = 0, right = n-1;\n help(players, left, right, round);\n return {minr, maxr};\n }\n \n //passing players by reference is crucial to avoid tle\n void help(string &players, int l, int r, int round){\n \n //round finished start next round\n if(l >= r){\n help(players, 0, n-1, round+1);\n }\n //left player is already eliminated continue with other players\n else if(players[l] == \'0\'){\n help(players, l+1, r, round);\n }\n //right player is already eliminated continue with other players\n else if(players[r] == \'0\'){\n help(players, l, r-1, round);\n }\n //we have found the place where first and second players come head to head\n else if((l == f and r == s) or (l == s and r == f)){\n minr = min(minr, round);\n maxr = max(maxr, round);\n }\n //the left player will win this match\n else if(l == f || l == s){\n //make the right player loose\n players[r] = \'0\';\n help(players, l+1, r-1, round);\n //reset for more exploration (more exploration happens when an earlier call was made from the last else block)\n players[r] = \'1\';\n }\n //the right player will win this match\n else if(r == f || r == s){\n //make the left player loose\n players[l] = \'0\';\n help(players, l+1, r-1, round);\n //reset for more exploration (more exploration happens when an earlier call was made from the last else block)\n players[l] = \'1\';\n }\n else if(visited.count(getPlayersBeforeBetweenAndAfterFAndS(players)) == 0){\n visited.insert(getPlayersBeforeBetweenAndAfterFAndS(players));\n \n //both can win or loose, perform both scenarios\n players[r] = \'0\';\n help(players, l+1, r-1, round);\n players[r] = \'1\';\n players[l] = \'0\';\n help(players, l+1, r-1, round);\n players[l] = \'1\';\n }\n }\n \n string getPlayersBeforeBetweenAndAfterFAndS(string &s1){\n int d1 = 0, d2 = 0, d3 = 0;\n for(int i = 0; i < s1.size(); i++){\n if(i < min(f, s) and s1[i] == \'1\'){\n d1++;\n }\n else if(min(f,s) < i and i < max(f,s) and s1[i] == \'1\'){\n d2++;\n }\n else if(i > max(f,s) and s1[i] == \'1\'){\n d3++;\n }\n }\n return to_string(d1) + "|" + to_string(d2) + "|" + to_string(d3) ;\n }\n};\n```\n | 12 | 0 | ['C'] | 2 |
the-earliest-and-latest-rounds-where-players-compete | Java 0ms 100.00% simple recursion for all new positions of two players | java-0ms-10000-simple-recursion-for-all-zoc9g | In current round of n players, these two players with 1-based indexes p1 and p2 will compete if (p1 + p2 == n + 1). Otherwise, the game will enter next round wi | danzhi | NORMAL | 2021-06-13T19:25:25.029932+00:00 | 2021-06-13T22:51:05.998482+00:00 | 863 | false | In current round of n players, these two players with 1-based indexes p1 and p2 will compete if (p1 + p2 == n + 1). Otherwise, the game will enter next round with (n+1)/2 players. Only the new positions (1-based indexes) of the two players matter in next round. We consider all possible such new positions based on their current positions and recursively get and merge into (min,max) as the final answer. \n\nDue to at most O(log(n)) rounds and the likelyhood p1 and p2 compete in earlier round, and the simplicity of the logic, the real runtime is 0ms and beats 100.00% Java submissions.\n\n```\n public int[] earliestAndLatest(int n, int firstPlayer, int secondPlayer) {\n int p1 = Math.min(firstPlayer, secondPlayer);\n int p2 = Math.max(firstPlayer, secondPlayer);\n if (p1 + p2 == n + 1) {\n // p1 and p2 compete in the first round\n return new int[] {1,1};\n }\n if (n == 3 || n == 4) {\n // p1 and p2 must compete in the second round (only two rounds).\n return new int[] {2,2};\n }\n\n // Flip to make p1 be more closer to left than p2 to right end for convenience\n if (p1 - 1 > n - p2) {\n int t = n + 1 - p1;\n p1 = n + 1 - p2;\n p2 = t;\n }\n\n int m = (n + 1) / 2;\n int min = n;\n int max = 1;\n if (p2 * 2 <= n + 1) {\n // p2 is in first half (n odd or even) or exact middle (n odd)\n // 1 2 3 4 5 6 7 8 9 10 11 12 13 14\n // . . * . . * . . . . . . . .\n // ^ ^\n // p1 p2\n\t // Group A are players in front of p1\n\t // Group B are players between p1 and p2\n int a = p1 - 1;\n int b = p2 - p1 - 1;\n // i represents number of front players in A wins\n // j represents number of front players in B wins\n for (int i = 0; i <= a; i++) {\n for (int j = 0; j <= b; j++) {\n int[] ret = earliestAndLatest(m, i + 1, i + j + 2);\n min = Math.min(min, 1 + ret[0]);\n max = Math.max(max, 1 + ret[1]);\n }\n }\n } else {\n // p2 is in the later half (and has >= p1 distance to the end)\n // 1 2 3 4 5 6 7 8 9 10 11 12 13 14\n // . . * . . . . . . * . . . .\n // ^ ^\n // p1 p4 p2 p3\n // ^--------------^\n // ^--------------------------^\n int p4 = n + 1 - p2;\n int a = p1 - 1;\n int b = p4 - p1 - 1;\n\t // Group C are players between p4 and p2, (c+1)/2 will advance to next round.\n int c = p2 - p4 - 1;\n for (int i = 0; i <= a; i++) {\n for (int j = 0; j <= b; j++) {\n int[] ret = earliestAndLatest(m, i + 1, i + j + 1 + (c+1)/2 + 1);\n min = Math.min(min, 1 + ret[0]);\n max = Math.max(max, 1 + ret[1]);\n }\n }\n }\n return new int[] {min, max};\n }\n``` | 11 | 0 | [] | 3 |
the-earliest-and-latest-rounds-where-players-compete | [Python3] bit-mask dp | python3-bit-mask-dp-by-ye15-7bh5 | \n\nclass Solution:\n def earliestAndLatest(self, n: int, firstPlayer: int, secondPlayer: int) -> List[int]:\n firstPlayer, secondPlayer = firstPlayer | ye15 | NORMAL | 2021-06-13T05:25:06.520620+00:00 | 2021-06-13T05:27:39.573346+00:00 | 551 | false | \n```\nclass Solution:\n def earliestAndLatest(self, n: int, firstPlayer: int, secondPlayer: int) -> List[int]:\n firstPlayer, secondPlayer = firstPlayer-1, secondPlayer-1 # 0-indexed\n \n @cache\n def fn(k, mask): \n """Return earliest and latest rounds."""\n can = deque()\n for i in range(n): \n if mask & (1 << i): can.append(i)\n \n cand = [] # eliminated player\n while len(can) > 1: \n p1, p2 = can.popleft(), can.pop()\n if p1 == firstPlayer and p2 == secondPlayer or p1 == secondPlayer and p2 == firstPlayer: return [k, k] # game of interest \n if p1 in (firstPlayer, secondPlayer): cand.append([p2]) # p2 eliminated \n elif p2 in (firstPlayer, secondPlayer): cand.append([p1]) # p1 eliminated \n else: cand.append([p1, p2]) # both could be elimited \n \n minn, maxx = inf, -inf\n for x in product(*cand): \n mask0 = mask\n for i in x: mask0 ^= 1 << i\n mn, mx = fn(k+1, mask0)\n minn = min(minn, mn)\n maxx = max(maxx, mx)\n return minn, maxx\n \n return fn(1, (1<<n)-1)\n``` | 8 | 0 | ['Python3'] | 1 |
the-earliest-and-latest-rounds-where-players-compete | [Python] Simple dp+memo | python-simple-dpmemo-by-colwind-esg5 | there are 4 situations:\n1. [ mid ]\n1. a b \n2. a b\n3. a | colwind | NORMAL | 2021-06-13T05:24:47.840753+00:00 | 2021-06-13T05:42:41.599209+00:00 | 378 | false | there are 4 situations:\n1. [ mid ]\n1. a b \n2. a b\n3. a b\n4. a b\n\nAccording to the principle of symmetry, we can reduce them to these two situations:\n1. [ mid ]\n2. a b \n3. a b\n\nThere for we just need to translate firstPlayer and secondPlayer to these two situations and do operations on them.\n\nEach round, we try to reduce n players into ceil(n/2) players.\n\nFor the first situation, for players before A, No matter how these players are combined, their impact on the entire formation depends only on how many players win on the left and how many players win on the right. For the players who win on the right, we will decrease the indexes of A and B at the same time. There are (n-1) possibilities. In each possibility, we perform the same operation on the players between A and B, and correspondingly decrease the index of b (because the operation is performed on the players between A and B, the index of player A would not be changed.)\n```\nfor i in range(a):\n\tfor j in range(b-a):\n\t\tl = min(l,self.earliestAndLatest(mid,a-i,b-i-j)[0])\n\t\tr = max(r,self.earliestAndLatest(mid,a-i,b-i-j)[1]) \n```\nFor the second situation, the index of B is greater than the index of mid. If all battles are won by the left player, then B\'s position in the next round should be the last of array. Based on this point, we can perform the same operation on them, and we can get the following code.\n```\nfor i in range(a):\n\tfor j in range(c-a):\n\t\tl = min(l,self.earliestAndLatest(mid,a-i,mid-i-j)[0])\n\t\tr = max(r,self.earliestAndLatest(mid,a-i,mid-i-j)[1])\n```\n\nEnumerate and select the smallest earlier round and the largest latest round to get the answer we want.\nTC: \nFor earliestAndLatest( n, firstPlayer, secondPlayer): O(log n*n^2)\nThe loop in function takes O(n^2)\n=> O(n^4 logn)\nSC:\n=> O(n^2 logn)\n\n\n```\nclass Solution:\n @lru_cache(None)\n def earliestAndLatest(self, n: int, firstPlayer: int, secondPlayer: int) -> List[int]:\n if firstPlayer + secondPlayer == n + 1:\n return [1,1]\n a,b = min(firstPlayer, secondPlayer), max(firstPlayer, secondPlayer)\n mid = ceil(n/2)\n l = inf\n r = -inf\n if b<=mid or a>mid:\n if a>mid:\n a,b = n+1-b,n+1-a\n for i in range(a):\n for j in range(b-a):\n l = min(l,self.earliestAndLatest(mid,a-i,b-i-j)[0])\n r = max(r,self.earliestAndLatest(mid,a-i,b-i-j)[1]) \n else:\n if n+1-b < a:\n a,b = n+1-b,n+1-a\n c = n+1-b\n for i in range(a):\n for j in range(c-a):\n l = min(l,self.earliestAndLatest(mid,a-i,mid-i-j)[0])\n r = max(r,self.earliestAndLatest(mid,a-i,mid-i-j)[1])\n return [l+1,r+1]\n``` | 6 | 0 | [] | 1 |
the-earliest-and-latest-rounds-where-players-compete | Java DP with memory | java-dp-with-memory-by-lianglee-ka2n | Use DP with memory\n* Divide players to 3 parts because of the first and second players\n * xFySz, left has x players, middle has y players, right has z player | lianglee | NORMAL | 2021-06-13T04:09:08.418513+00:00 | 2021-06-13T04:15:23.252356+00:00 | 690 | false | * Use DP with memory\n* Divide players to 3 parts because of the first and second players\n * xFySz, left has x players, middle has y players, right has z players\n```\nclass Solution {\n int[][][][] dp = new int[28][28][28][2];\n public int[] earliestAndLatest(int n, int f, int s) {\n return helper(f-1, s-f-1, n-s);\n }\n \n int[] helper(int x, int y, int z) {\n if (x == z)\n return new int[]{1, 1};\n if (x > z) // Make sure z > x\n return helper(z, y, x);\n if (dp[x][y][z][0] > 0)\n return dp[x][y][z];\n int a = x, b = y, c = z;\n c--; // Remove because of the First Player\n if (a+b < c) // Remove because of the Second Player\n c--;\n else if (a+b > c)\n b--;\n dp[x][y][z][0] = 100;\n int n = (a+b+c)/2; // Players to remove\n for (int i = 0; i <= a; i++)\n for (int j = a-i; j <= c-i; j++) {\n int k = a+b+c-n-i-j;\n if (k >= 0 && k <= b) {\n int[] tmp = helper(i, k, j);\n dp[x][y][z][0] = Math.min(dp[x][y][z][0], tmp[0] + 1);\n dp[x][y][z][1] = Math.max(dp[x][y][z][1], tmp[1] + 1);\n }\n }\n return dp[x][y][z];\n }\n}\n``` | 5 | 0 | [] | 3 |
the-earliest-and-latest-rounds-where-players-compete | 💥💥Beats 100% on runtime and memory [EXPLAINED] | beats-100-on-runtime-and-memory-explaine-xfiq | \n\n\n# Intuition\nSimulate a knockout tournament where players face off in pairs, and two special players must be tracked to find out when they compete against | r9n | NORMAL | 2024-10-19T09:48:53.037824+00:00 | 2024-10-19T09:48:53.037856+00:00 | 25 | false | \n\n\n# Intuition\nSimulate a knockout tournament where players face off in pairs, and two special players must be tracked to find out when they compete against each other. The goal is to identify the earliest and latest rounds where these two players can meet based on their winning potential.\n\n# Approach\nUse a recursive function to simulate rounds of the tournament, tracking remaining players, and determine matchups until the two special players face each other, while leveraging bit manipulation to manage player states and ensuring that visited states are stored to avoid unnecessary calculations.\n\n# Complexity\n- Time complexity:\nO(n log n) because each round eliminates half of the players, and we process each player multiple times.\n\n- Space complexity:\nO(n) for storing the visited states and the players array.\n# Code\n```typescript []\n/**\n * @param {number} n - Total number of players\n * @param {number} firstPlayer - First important player\n * @param {number} secondPlayer - Second important player\n * @return {number[]} - Array containing the earliest and latest round where both players meet\n */\nfunction earliestAndLatest(n: number, firstPlayer: number, secondPlayer: number): number[] {\n let earliest: number = n; // Initialize the earliest round to the maximum possible\n let latest: number = 0; // Initialize the latest round to 0\n\n const visited: Set<number> = new Set(); // Track visited game states to avoid repetition\n\n // Recursive function to simulate rounds\n const findRounds = (remain: number, players: number[], currentIndex: number, round: number): void => {\n // If this state has already been visited, return early\n if (visited.has(remain)) return;\n\n const player = players[currentIndex]; // Current player in the matchup\n const opponent = players[players.length - currentIndex]; // Opponent from the other end\n\n // If firstPlayer and secondPlayer face each other, update earliest and latest round numbers\n if ((player === firstPlayer && opponent === secondPlayer) ||\n (player === secondPlayer && opponent === firstPlayer)) {\n earliest = Math.min(earliest, round);\n latest = Math.max(latest, round);\n return;\n }\n\n // If all matchups are completed for this round, move to the next round\n if (opponent <= player) {\n const nextPlayers = players.filter(p => remain & (1 << p)); // Filter advancing players\n findRounds(remain, nextPlayers, 1, round + 1); // Recurse for the next round\n return;\n }\n\n // Simulate both outcomes where player or opponent wins\n const remainIfPlayerWins = remain ^ (1 << opponent); // Player wins, opponent eliminated\n const remainIfOpponentWins = remain ^ (1 << player); // Opponent wins, player eliminated\n const nextIndex = currentIndex + 1;\n\n // Recursion based on which player is important\n if (player === firstPlayer || player === secondPlayer) {\n findRounds(remainIfPlayerWins, players, nextIndex, round);\n return;\n }\n if (opponent === firstPlayer || opponent === secondPlayer) {\n findRounds(remainIfOpponentWins, players, nextIndex, round);\n return;\n }\n\n // Recurse for both outcomes\n findRounds(remainIfPlayerWins, players, nextIndex, round);\n findRounds(remainIfOpponentWins, players, nextIndex, round);\n\n // Mark the current state as visited\n visited.add(remain);\n };\n\n // Create a list of players (1-indexed)\n const players: number[] = Array.from({ length: n + 1 }, (_, i) => i);\n\n // Bitmask to represent all players remaining\n const ALL_PLAYERS_REMAIN = (1 << (n + 1)) - 1;\n\n // Start the search from the first round\n findRounds(ALL_PLAYERS_REMAIN, players, 1, 1);\n\n // Return the earliest and latest round where the two players meet\n return [earliest, latest];\n}\n\n``` | 4 | 0 | ['TypeScript'] | 0 |
the-earliest-and-latest-rounds-where-players-compete | [JavaScript] DFS + Bitwise | javascript-dfs-bitwise-by-stevenkinouye-q3ud | javascript\n var earliestAndLatest = function(numPlayers, firstPlayer, secondPlayer) {\n let minRounds = Infinity;\n let maxRounds = 0;\n const dfs = ( | stevenkinouye | NORMAL | 2021-06-13T06:10:54.532089+00:00 | 2021-06-13T06:20:29.889687+00:00 | 396 | false | ```javascript\n var earliestAndLatest = function(numPlayers, firstPlayer, secondPlayer) {\n let minRounds = Infinity;\n let maxRounds = 0;\n const dfs = (playersEliminated, numRounds) => {\n \n // find all the combinations for this round starting with the\n // current players that are eliminated. We will move the 2 pointers\n // from opposite ends inwards until we find players that aren\'t eliminated\n // and then create new possible results of this current round.\n // Every loop in the while loop will correspond to a competition between player\n // i and j while roundResults will hold all possible round results.\n let roundResults = [playersEliminated];\n let i = 1;\n let j = numPlayers;\n while (true) {\n // find players that aren\'t eliminated\n while (playersEliminated & (1 << i)) i++;\n while (playersEliminated & (1 << j)) j--;\n // if we are at or past the same player, we can stop\n if (i >= j) break;\n // if during this round the first and second player are playing\n // against each other, we can record the results and stop searching.\n if (i === firstPlayer && j === secondPlayer) {\n minRounds = Math.min(minRounds, numRounds);\n maxRounds = Math.max(maxRounds, numRounds);\n return;\n } \n \n // create new round results by eliminating player as long as it isn\'t\n // the first or second player.\n // roundResult | (1 << i) means we eliminated player i (player i lost)\n const newRoundResults = [];\n if (j !== firstPlayer && j !== secondPlayer) {\n for (const roundResult of roundResults) {\n newRoundResults.push(roundResult | (1 << j));\n }\n } \n if (i !== firstPlayer && i !== secondPlayer){\n for (const roundResult of roundResults) {\n newRoundResults.push(roundResult | (1 << i));\n }\n }\n // move the pointers inwards to find next matching players\n i++;\n j--;\n // save the new round results to round results\n roundResults = newRoundResults;\n }\n \n // if we have exhausted all round results return as the base case\n if (!roundResults.length) return;\n \n // add a round for the next round and try each result to see if it will\n // update the max and min number of rounds\n numRounds++;\n roundResults.forEach((roundResult) => dfs(roundResult, numRounds));\n }\n dfs(0,1)\n return [minRounds, maxRounds];\n};\n``` | 4 | 0 | ['Bit Manipulation', 'Depth-First Search', 'JavaScript'] | 1 |
the-earliest-and-latest-rounds-where-players-compete | [Java] straightforward DFS solution, simulation | java-straightforward-dfs-solution-simula-xzio | \tint first;\n int second;\n public int[] earliestAndLatest(int n, int firstPlayer, int secondPlayer) {\n first = firstPlayer;\n second = se | charmingzzz | NORMAL | 2021-06-13T04:13:10.557507+00:00 | 2021-06-13T04:13:10.557556+00:00 | 440 | false | \tint first;\n int second;\n public int[] earliestAndLatest(int n, int firstPlayer, int secondPlayer) {\n first = firstPlayer;\n second = secondPlayer;\n List<Integer> list = new ArrayList<>();\n for (int i = 1; i <= n; i++) {\n list.add(i);\n }\n int[] res = new int[2];\n res[0] = n;\n res[1] = 0;\n dfs(list, new ArrayList<>(), 1, n, res, 0);\n return res;\n }\n \n void dfs(List<Integer> list, List<Integer> temp, int round, int n, int[] res, int i) {\n \n if (i > n - 1- i) {\n List<Integer> next = new ArrayList<>(temp);\n Collections.sort(next);\n dfs(next, new ArrayList<>(), round + 1, next.size(), res, 0);\n return;\n }\n \n if (list.get(i) == first && list.get(n-1-i) == second) {\n res[0] = Math.min(res[0], round);\n res[1] = Math.max(res[1], round);\n return;\n }\n \n if (list.get(i) == first || list.get(i) == second) {\n temp.add(list.get(i));\n dfs(list, temp, round, n, res, i+1);\n temp.remove(temp.size() - 1);\n } else if (list.get(n-1-i) == second || list.get(n-1-i) == first) {\n temp.add(list.get(n-1-i));\n dfs(list, temp, round, n, res, i+1);\n temp.remove(temp.size() - 1);\n } else {\n temp.add(list.get(i));\n dfs(list, temp, round, n, res, i+1);\n temp.remove(temp.size() - 1);\n\n temp.add(list.get(n-1-i));\n dfs(list, temp, round, n, res, i+1);\n temp.remove(temp.size() - 1);\n }\n \n } | 4 | 0 | [] | 2 |
the-earliest-and-latest-rounds-where-players-compete | O(n^3) C++ solution, <200ms for n=900, hard to understand | on3-c-solution-200ms-for-n900-hard-to-un-mv3r | \n#define N 28\nstatic array<array<array<bool, N>, N>, N+1> mem;\nclass Solution {\n int mn, mx;\n void dfs(int n, int p1, int p2, int d) {\n if (n | mzchen | NORMAL | 2021-06-13T10:50:12.998728+00:00 | 2021-06-13T10:56:20.696479+00:00 | 582 | false | ```\n#define N 28\nstatic array<array<array<bool, N>, N>, N+1> mem;\nclass Solution {\n int mn, mx;\n void dfs(int n, int p1, int p2, int d) {\n if (n == 1 || mem[n][p1][p2])\n return;\n mem[n][p1][p2] = true;\n int q1 = n - p1 - 1, q2 = n - p2 - 1;\n if (p1 == q2) {\n mn = min(mn, d);\n mx = max(mx, d);\n return;\n }\n int m = n + 1 >> 1;\n for (int i = max(0, p1 - q1 >> 1);\n i <= p1 - (q1 < p1) - (q2 < p1) - max(0, p1 - q1 - 1 >> 1);\n i++)\n for (int j = max(0, min(q1, p2) - max(q2, p1) >> 1);\n j <= p2 - p1 - 1 - (q1 > p1 && q1 < p2) - (q2 > p1 && q2 < p2) - max(0, min(q1, p2) - max(q2, p1) - 1 >> 1);\n j++)\n if (m - i - j - 2 >= max(0, q2 - p2 >> 1)\n && m - i - j - 2 <= q2 - (q1 > p2) - (q2 > p2) - max(0, q2 - p2 - 1 >> 1))\n dfs(m, i, i + j + 1, d + 1);\n }\npublic:\n vector<int> earliestAndLatest(int n, int first, int second) {\n mn = n, mx = 0, mem = {};\n dfs(n, first - 1, second - 1, 1);\n return {mn, mx};\n }\n};\n``` | 3 | 1 | ['Depth-First Search', 'C'] | 1 |
the-earliest-and-latest-rounds-where-players-compete | DFS + Memoization explanation | dfs-memoization-explanation-by-mahipalke-wrk3 | 1) the only importent thing to remember is the position of first and second player. \n2) if the positions are same than the actual content of array is not impor | mahipalkeizer | NORMAL | 2021-06-13T04:22:09.024768+00:00 | 2021-06-13T04:22:34.867172+00:00 | 496 | false | 1) the only importent thing to remember is the position of first and second player. \n2) if the positions are same than the actual content of array is not importent and can be avoided in recursion.\n3) there will be n*(n-1)/2 pairs of first and second players positions and for each pair recursive fuction will take 2^(n/2) time. Hence the time complexity. \n\nTime Complexity : **( n ^ 2 * ( 2 ^ (n/2) ) )**\nMemory Complexity : **n ^ 2**\n\n\n\'\'\'\n\n\tint mn=1e9,mx=-1;\n\tset<array<int,3>> st; \n\tvoid recur(int n,int fp, int sp,int cnt){\n\n\t\tif(st.find({n,fp,sp})!=st.end()){ //if the state is already processed \n\t\t\treturn ;\n\t\t}\n\t\tst.insert({n,fp,sp});\n\n\t\tif(sp==n-1-fp){ // if first and second are against each other in this round \n\t\t\tmn=min(mn,cnt);\n\t\t\tmx=max(mx,cnt);\n\t\t\treturn ;\n\t\t}\n\t\t\n\t\tfor(int mask=0; mask<(1<<(n/2)); mask++){\n\t\t\tint nfp=fp,nsp=sp; // new positions. \n\t\t\tfor(int i=0;i<(n/2);i++){\n\t\t\t\tint j=i;\n\t\t\t\tif(mask&(1<<i)){\n\t\t\t\t\tj=n-1-i;\n\t\t\t\t}\n\t\t\t\t// handling the case that first and second \n\t\t\t\t// always win before competing each other .\n\t\t\t\tif(j==fp)\n\t\t\t\t\tj=n-1-j;\n\t\t\t\tif(j==sp)\n\t\t\t\t\tj=n-1-j;\n\n\t\t\t\t// finding the new index of first and second player .\n\t\t\t\t// decrease the index if removed element was before it. \n\t\t\t\tif(j<fp )\n\t\t\t\t\tnfp-=1;\n\t\t\t\tif(j<sp )\n\t\t\t\t\tnsp-=1;\n\t\t\t}\n\t\t\t// recursive step \n\t\t\trecur(n/2+n%2, nfp,nsp,cnt+1);\n\t\t}\n\t}\n\n\n\tclass Solution {\n\tpublic:\n\t\tvector<int> earliestAndLatest(int n, int fp, int sp) { \n\t\t\tmn=1e9,mx=-1;\n\t\t\tst.clear(); \n\t\t\tfp-=1;\n\t\t\tsp-=1;\n\t\t\trecur(n,fp,sp,0);\n\t\t\treturn {mn+1,mx+1};\n\t\t}\n\t};\n\n\'\'\' | 3 | 0 | [] | 0 |
the-earliest-and-latest-rounds-where-players-compete | cpp | cpp-by-pankajkumar101-84sj | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | PankajKumar101 | NORMAL | 2024-05-24T02:36:40.377296+00:00 | 2024-05-24T02:36:40.377317+00:00 | 51 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int mn = 10000;\n int mx = 0;\n int first;\n int second;\n void dfs(vector<int> &arr, int round) {\n int size = arr.size() / 2;\n if(arr.size() == 1) return;\n for(int i = 0; i < size; i++) {\n if(arr[i] == first && arr[arr.size() - i - 1] == second) {\n mn = min(mn, round);\n mx = max(mx, round);\n return;\n }\n }\n bool f1 = false, f2 = false;\n for(auto n : arr) {\n f1 |= n == first;\n f2 |= n == second;\n }\n if(!f1 || !f2) { \n return;\n }\n vector<int> nextarr(size + (arr.size() % 2));\n int m = (1 << size) - 1;\n for(int i = 0; i <= m; i++) { \n int left = 0, right = nextarr.size() - 1;\n for(int j = 0; j < size; j++) {\n if((1 << j) & i) { \n nextarr[left++] = arr[j];\n }else { \n nextarr[right--] = arr[arr.size() - j - 1];\n }\n \n }\n if(arr.size() % 2) { \n nextarr[left] = arr[arr.size() / 2];\n }\n dfs(nextarr, round + 1);\n }\n }\n vector<int> earliestAndLatest(int n, int firstPlayer, int secondPlayer) {\n vector<int> arr(n);\n for(int i= 1; i <= n; i++) {\n arr[i - 1] = i;\n }\n first = firstPlayer;\n second = secondPlayer;\n dfs(arr, 1);\n return {mn, mx};\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
the-earliest-and-latest-rounds-where-players-compete | c++ | easy | short | c-easy-short-by-venomhighs7-7j8v | \n\n# Code\n\nclass Solution {\npublic:\n int mn = 10000;\n int mx = 0;\n int first;\n int second;\n void dfs(vector<int> &arr, int round) {\n | venomhighs7 | NORMAL | 2022-11-03T03:49:28.211218+00:00 | 2022-11-03T03:49:28.211263+00:00 | 490 | false | \n\n# Code\n```\nclass Solution {\npublic:\n int mn = 10000;\n int mx = 0;\n int first;\n int second;\n void dfs(vector<int> &arr, int round) {\n int size = arr.size() / 2;\n if(arr.size() == 1) return;\n for(int i = 0; i < size; i++) {\n if(arr[i] == first && arr[arr.size() - i - 1] == second) {\n mn = min(mn, round);\n mx = max(mx, round);\n return;\n }\n }\n bool f1 = false, f2 = false;\n for(auto n : arr) {\n f1 |= n == first;\n f2 |= n == second;\n }\n if(!f1 || !f2) { \n return;\n }\n vector<int> nextarr(size + (arr.size() % 2));\n int m = (1 << size) - 1;\n for(int i = 0; i <= m; i++) { \n int left = 0, right = nextarr.size() - 1;\n for(int j = 0; j < size; j++) {\n if((1 << j) & i) { \n nextarr[left++] = arr[j];\n }else { \n nextarr[right--] = arr[arr.size() - j - 1];\n }\n \n }\n if(arr.size() % 2) { \n nextarr[left] = arr[arr.size() / 2];\n }\n dfs(nextarr, round + 1);\n }\n }\n vector<int> earliestAndLatest(int n, int firstPlayer, int secondPlayer) {\n vector<int> arr(n);\n for(int i= 1; i <= n; i++) {\n arr[i - 1] = i;\n }\n first = firstPlayer;\n second = secondPlayer;\n dfs(arr, 1);\n return {mn, mx};\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
the-earliest-and-latest-rounds-where-players-compete | [Python] Same idea here, maybe a little bit easier to digest | python-same-idea-here-maybe-a-little-bit-cj9j | This is essentially the same idea as other top-voted posts. Not as concise but I think the thought process might be easier to come up with during interview.\n\n | rupertd | NORMAL | 2021-06-17T03:38:20.189085+00:00 | 2021-06-17T03:38:20.189130+00:00 | 170 | false | This is essentially the same idea as other top-voted posts. Not as concise but I think the thought process might be easier to come up with during interview.\n\n```\nclass Solution:\n def earliestAndLatest(self, n: int, firstPlayer: int, secondPlayer: int) -> List[int]:\n \n @lru_cache(None)\n def dp(n, first, second):\n """\n recursion with memorization to calculate [earliest, latest] \n """\n \n # base case: if first and second players have to compete in current round\n if first == n-second+1:\n return (1, 1)\n \n # the number of players going into next round\n nxt_n = (n+1)//2\n \n # preset ealiest and latest\n earliest = float(\'inf\')\n latest = 0\n \n # the positions of first and second players, and their mirrors in the array, in sorted order\n # if first player is right in the middle l2 == r1, but it is trivally covered so no need to treat specially.\n l1, l2, r1, r2 = sorted([first, second, n-first+1, n-second+1])\n \n # essentially, the above 4 positions chop the arr into 5 parts like this: *** l1 *** l2 ****** r1 *** r2 ***\n # name the length of first 3 parts below. The last two parts are the same as part2 and part1 \n part1, part2, part3 = l1-1, l2-l1-1, r1-l2-1\n \n # now lets consider all possible next-round positions of first and second players as nxt_f and nxt_s\n \n # for the middle part (part3), after this round, it will become half and stay in the same position relative to first and second player.\n # so it is simple to calculate the number of players entering next round in this part\n p3 = (part3+1)//2\n \n # for part1 and part2, let\'s name p1 as the number of players win (and stay) in part1, and p2 for part2.\n for p1 in range(part1+1):\n for p2 in range(part2+1):\n \n # now here comes the fun part (or actually not fun at all?) to calculate nxt_f and nxt_s using p1, p2 and p3.\n # total 4 scenarios depending on where first and second players are located in current round\n \n # case1: *** l1 *** l2 ****** first *** second ***\n if first == r1:\n nxt_f = p1 + p2 + p3 + 1\n nxt_s = nxt_f + part2-p2 + 1\n \n # case2: *** l1 *** first ****** r1 *** second ***\n elif first == l2:\n nxt_f = p1 + p2 + 1\n nxt_s = nxt_f + p3 + part2-p2 + 1\n \n # case3: *** first *** l2 ****** second *** r2 ***\n elif first == l1 and second == r1:\n nxt_f = p1+1\n nxt_s = nxt_f + p2 + p3 + 1\n \n # case4: *** first *** second ****** r1 *** r2 ***\n else:\n nxt_f = p1+1\n nxt_s = nxt_f + p2+1\n \n # update earliest and latest based on the answers from next round\n nxt = dp(nxt_n, nxt_f, nxt_s)\n earliest = min(earliest, nxt[0])\n latest = max(latest, nxt[1])\n \n return (earliest+1, latest+1)\n \n return dp(n, firstPlayer, secondPlayer)\n``` | 2 | 0 | [] | 0 |
the-earliest-and-latest-rounds-where-players-compete | Python BFS, easy to understand | python-bfs-easy-to-understand-by-qiuqiul-6jts | Using a deque to carry the (array , #round)\n\nin the array, the struct will looks like [[1,5],[2],[4]] the sub_arr with two elements means two player have equa | qiuqiuli | NORMAL | 2021-06-13T04:13:07.007527+00:00 | 2021-06-13T04:19:20.823077+00:00 | 232 | false | Using a deque to carry the (array , #round)\n\nin the *array*, the struct will looks like [[1,5],[2],[4]] the sub_arr with two elements means two player have equal chance to next round, one elements means that player will go to next round because he/she is the mid of the previous array or he/she is 1st/2nd player.\nand allcombine in my code is designed to get all pair result form previous round, using backtrack. \n\'\'\'\n \n class Solution:\n\t def earliestAndLatest(self, n: int, firstPlayer: int, secondPlayer: int) -> List[int]:\n def allcombin(pair):#try to find all combinations for the next round \n def bt(path,ind): #backtrack similar like LC17\n if ind == len(pair):\n ans.append(path)\n return \n for ele in pair[ind]:\n bt(path+[ele],ind+1)\n ans = []\n bt([],0) \n return ans\n\t\t\t\n seen = set() #To avoid duplicate combinations\n res = []\n q = deque()\n start = [i for i in range(1,n+1)]\n q.append((start,0))\n while q:\n arr,rd = q.popleft()\n pair = []\n flg = True # to check if 1st and 2nd meet\n for i in range(len(arr)//2):\n x,y = arr[i],arr[len(arr)-1-i]\n if (x,y) == (firstPlayer,secondPlayer):\n\t\t\t\t\t#if x,y matched 1st/2nd, put this round to res, and return\n res.append(rd+1)\n flg = False\n break\n elif x in (firstPlayer,secondPlayer):\n\t\t\t\t\t# x win, so in next round only one player in the pair\n pair.append([x])\n elif y in (firstPlayer,secondPlayer):\n pair.append([y])\n else:\n\t\t\t\t\t# put two players to next round with two elements \n pair.append([x,y])\n if len(arr)%2 ==1:\n pair.append([arr[len(arr)//2]])\n if flg: # if 1st/2nd does not in one pair, continue\n for newarr in allcombin(pair):\n sornew = sorted(newarr)\n if len(newarr) > 1 and tuple(sornew) not in seen:\n seen.add(tuple(sornew))\n q.append((sorted(newarr),rd+1))\n return [min(res),max(res)]\n \'\'\' \n \n \n \n \n \n\t\t | 2 | 0 | ['Breadth-First Search', 'Python'] | 0 |
the-earliest-and-latest-rounds-where-players-compete | c++ brute force with memoization solution | c-brute-force-with-memoization-solution-zmmlc | \nclass Solution {\npublic:\n void f(string str, int depth, int& small, int& big, unordered_set<string>& dp) {\n //cout<<str<<endl; \n const in | hanzhoutang | NORMAL | 2021-06-13T04:08:17.489248+00:00 | 2021-06-13T04:08:17.489281+00:00 | 334 | false | ```\nclass Solution {\npublic:\n void f(string str, int depth, int& small, int& big, unordered_set<string>& dp) {\n //cout<<str<<endl; \n const int n = str.size();\n for(int i = 0;i<n/2;i++) {\n if(str[i] == \'1\' && str[str.size()-1-i] == \'1\') {\n small = min(small,depth);\n big = max(big,depth);\n return;\n }\n }\n if(dp.count(str)) {\n return; \n }\n const int total = (1<<(n/2)) - 1; \n for(int i = 0;i<=total;i++) {\n string a;\n string b; \n bool valid = true; \n for(int j = 0;j<n/2;j++) {\n // 1 left win \n // 0 right win\n if(i&(1<<j) && str[str.size()-j-1] == \'1\') {\n valid = false; \n break;\n } \n if(!(i&(1<<j)) && str[j] == \'1\') {\n valid = false; \n break; \n }\n if(i&(1<<j)) {\n a.push_back(str[j]);\n } else {\n b.push_back(str[str.size()-j-1]);\n }\n }\n if(!valid) {\n continue; \n }\n string tmp; \n reverse(b.begin(),b.end());\n if(str.size() % 2 == 1) {\n tmp = a + string(1,str[str.size()/2]) + b; \n } else {\n tmp = a + b; \n }\n f(tmp,depth+1,small,big,dp);\n }\n dp.insert(str);\n }\n vector<int> earliestAndLatest(int n, int fp, int sp) {\n string str; \n for(int i = 1;i<=n;i++) {\n if(i == fp || i == sp) {\n str.push_back(\'1\');\n } else {\n str.push_back(\'0\');\n }\n }\n unordered_set<string> dp; \n //cout<<str<<endl;\n int big = 0; \n int small = INT_MAX; \n f(str,1,small,big,dp);\n return {small,big};\n }\n};\n``` | 2 | 0 | [] | 1 |
the-earliest-and-latest-rounds-where-players-compete | [Python] Consider all possibilities | python-consider-all-possibilities-by-ton-7scw | We consider every possible outcome of the matches.\n\nThe worst case complexity is O(n2^0.75n), which is not too bad.\n\nWe begin with a maximum of 28 players, | tonghuikang | NORMAL | 2021-06-13T04:03:22.780813+00:00 | 2021-06-13T04:14:48.077677+00:00 | 168 | false | We consider every possible outcome of the matches.\n\nThe worst case complexity is O(n*2^0.75n), which is not too bad.\n\nWe begin with a maximum of 28 players, which will have 14, 7, 4, 2, 1 in successive rounds.\n\nLet\'s say we have 2^14 possibilities that will advance the first round. For each of these possibility we consider 2^7 outcomes. The complexity to calculate the possibilites of the next round is 28*2^21=58720256, which is reasonable.\n\nThere are (28-2 choose 7-2)=65780 possibilities for the second round, which makes successive computations even more reasonable. \n\n```\nclass Solution:\n def earliestAndLatest(self, n: int, firstPlayer: int, secondPlayer: int) -> List[int]:\n \n round_num = 0\n valid_rounds = set()\n possibilities = set([tuple(range(1,n+1))])\n \n while possibilities:\n round_num += 1\n\n next_possibilities = set()\n num_players = len(next(iter(possibilities)))\n num_matches = num_players // 2\n \n for possibility in possibilities:\n for a,b in zip(possibility[:num_matches], possibility[::-1]):\n if a == firstPlayer and b == secondPlayer:\n valid_rounds.add(round_num)\n continue\n\n for comb in itertools.product([0,1], repeat=num_matches):\n next_possibility = [possibility[i] if c else possibility[~i] for i,c in enumerate(comb)]\n\n if num_players%2 == 1: # center player automatically advance\n next_possibility.append(possibility[num_matches])\n \n if firstPlayer not in next_possibility or secondPlayer not in next_possibility:\n continue\n \n next_possibilities.add(tuple(sorted(next_possibility)))\n \n possibilities = next_possibilities\n \n return [min(valid_rounds), max(valid_rounds)]\n``` | 2 | 1 | [] | 0 |
the-earliest-and-latest-rounds-where-players-compete | Python: [Intuitive Solution] Simulate rounds using DFS + string map | python-intuitive-solution-simulate-round-ynj8 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | chinmay997 | NORMAL | 2023-01-08T04:53:34.394881+00:00 | 2023-01-08T04:53:34.394918+00:00 | 437 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def earliestAndLatest(self, n: int, firstPlayer: int, secondPlayer: int) -> List[int]:\n minR,maxR=999999,-122\n players=\'\'\n for i in range(1,n+1):\n players+=chr(i+65)\n fp=chr(firstPlayer+65)\n sp=chr(secondPlayer+65)\n\n @cache\n def dfs(s,num_round,winners):\n nonlocal maxR, minR\n if len(s)==0:\n dfs("".join(sorted(winners)),num_round+1,\'\')\n return\n if len(s)==1:\n winners+=s[0]\n dfs("".join(sorted(winners)),num_round+1,\'\')\n return\n if s[0]==fp and s[-1]==sp:\n \n maxR=max(maxR,num_round)\n minR=min(minR,num_round)\n return\n elif s[0]==fp or s[0]==sp:\n winners+=s[0]\n s=s[1:-1]\n dfs(s,num_round,winners)\n elif s[-1]==fp or s[-1]==sp:\n winners+=s[-1]\n s=s[1:-1]\n dfs(s,num_round,winners)\n else:\n l,r=s[0],s[-1]\n dfs(s[1:-1],num_round,winners+l)\n dfs(s[1:-1],num_round,winners+r)\n return\n \n dfs(players, 1, \'\')\n return [minR,maxR]\n\n\n \n``` | 1 | 0 | ['Python3'] | 0 |
the-earliest-and-latest-rounds-where-players-compete | C++ | DP with bit masking | c-dp-with-bit-masking-by-omniphantom-c8ej | \nclass Solution {\npublic:\n vector<int> earliestAndLatest(int n_, int firstPlayer, int secondPlayer) {\n vector<int> v(n_);\n firstPlayer--;\ | omniphantom | NORMAL | 2021-07-03T10:32:51.748930+00:00 | 2021-07-03T10:32:51.748961+00:00 | 285 | false | ```\nclass Solution {\npublic:\n vector<int> earliestAndLatest(int n_, int firstPlayer, int secondPlayer) {\n vector<int> v(n_);\n firstPlayer--;\n secondPlayer--;\n for(int i=0;i<n_;i++)\n v[i]=i;\n map<int,pair<int,int>> my;//min,max\n std::function<pair<int,int>(int,int,int)> minTimes = [&](int hash, int val, int n){\n if(n<=1){\n pair<int,int> p = {1000,0};\n return p;\n }\n if(my.find(hash)!=my.end())\n return my[hash];\n int size = n;\n int w[size];\n int times = n/2;\n int j = 0;\n for(int i=0;i<n_;i++){\n if(!((1<<i)&hash)){\n w[j++]=i;\n }\n }\n int i = 0;\n j = n-1;\n bool check = false;\n while(i<j){\n if((v[w[i]]==firstPlayer && v[w[j]]==secondPlayer) || (v[w[j]]==firstPlayer && v[w[i]]==secondPlayer)){\n check = true;\n break;\n }\n i++;\n j--;\n }\n if(check){\n pair<int,int> p = {val,val};\n return p;\n }\n // L R -> L wins => 1\n // L R -> R wins => 0\n int upto = (1<<times);\n int ans1 = 1000;\n int ans2 = 0;\n for(int k=0;k<upto;k++){\n i=0,j=n-1;\n int track = 0;\n for(int p=0;p<times;p++){\n int t = (1<<p);\n if(v[w[i]]==firstPlayer)\n track^=(1<<v[w[i]]);\n else if(v[w[i]]==secondPlayer)\n track^=(1<<v[w[i]]);\n else if(v[w[j]]==firstPlayer)\n track^=(1<<v[w[j]]);\n else if(v[w[j]]==secondPlayer)\n track^=(1<<v[w[j]]);\n else{\n if(t&k)\n track^=(1<<v[w[i]]);\n else\n track^=(1<<v[w[j]]);\n }\n i++;\n j--;\n }\n if(n&1)\n track^=(1<<v[w[times]]);\n int bit_val = (1<<n_)-1;\n bit_val^=track;\n track=bit_val;\n pair<int,int> p = minTimes(track,val+1,(n+1)/2);\n ans1=min(ans1,p.first);\n ans2=max(ans2,p.second);\n }\n \n return my[hash] = {ans1,ans2};\n };\n auto p = minTimes(0,1,n_);\n vector<int> ret={p.first,p.second};\n return ret;\n }\n};\n\n\n\n\n``` | 1 | 1 | [] | 0 |
the-earliest-and-latest-rounds-where-players-compete | simplicity in code > infinity | simplicity-in-code-infinity-by-kira3018-v7k7 | \'\'\'class Solution {\npublic:\n int earliest = INT_MAX;\n int latest = INT_MIN;\n vector earliestAndLatest(int n, int first, int second) {\n b | kira3018 | NORMAL | 2021-06-13T10:17:30.747858+00:00 | 2021-06-13T14:51:58.100195+00:00 | 56 | false | \'\'\'class Solution {\npublic:\n int earliest = INT_MAX;\n int latest = INT_MIN;\n vector<int> earliestAndLatest(int n, int first, int second) {\n bool visit[n];\n memset(visit,true,sizeof(visit));\n solve(first-1,second-1,1,0,n-1,visit,n);\n vector<int> vec = {earliest,latest};\n return vec;\n }\n void solve(int first,int second,int round,int i,int j,bool visit[],int n)\n {\n while(i < n && visit[i] != true) \n i++;\n while(j >= 0 && visit[j] != true)\n j--;\n if(i >= j){ \n solve(first,second,round+1,0,n-1,visit,n);\n return;\n }\n if(i == first && j == second)\n {\n earliest = min(earliest,round);\n latest = max(latest,round); \n return;\n }\n else if(i == first || i == second)\n {\n visit[j] = false;\n solve(first,second,round,i+1,j-1,visit,n);\n visit[j] = true;\n }\n else if(j == first || j == second)\n {\n visit[i] = false;\n solve(first,second,round,i+1,j-1,visit,n);\n visit[i] = true;\n }\n else\n {\n visit[j] = false;\n solve(first,second,round,i+1,j-1,visit,n);\n visit[j] = true;\n visit[i] = false;\n solve(first,second,round,i+1,j-1,visit,n);\n visit[i] = true;\n } \n }\n \n \n}; | 1 | 3 | [] | 0 |
the-earliest-and-latest-rounds-where-players-compete | Java DFS solution. O(2^N/2 * N/2) | java-dfs-solution-o2n2-n2-by-varkey98-2ygv | First of all, why is this not a DP. Because there are no recurring sub problems. Each state is different.\nBecause, whenever a chosen player plays, they definit | varkey98 | NORMAL | 2021-06-13T08:12:02.436881+00:00 | 2021-06-13T08:12:02.436914+00:00 | 305 | false | First of all, why is this not a DP. Because there are no recurring sub problems. Each state is different.\nBecause, whenever a chosen player plays, they definitely win. For every other player, we have 2 options, they win or they lose. Although this part looks like a DP, these never make us do recurring sub-problems. The reason for that is whenever someone plays, the opposing player\'s choice is already made, which leads to a different part of the decision tree. \n```\nclass Solution \n{\n int firstPlayer,secondPlayer,n;\n boolean enumerate(ArrayList<Integer> ret,int mask,int start,int end)\n {\n if(start>=end)\n {\n ret.add(mask);\n return false;\n }\n else\n {\n while((start<end)&&((mask&(1<<start))!=0))\n start++;\n while((start<end)&&((mask&(1<<end))!=0))\n end--;\n if(start>=end)\n return enumerate(ret,mask,start+1,end-1);\n else if(start==firstPlayer&&end==secondPlayer)\n return true;\n else if(start==firstPlayer||start==secondPlayer)\n return enumerate(ret,mask|1<<end,start+1,end-1);\n else if(end==firstPlayer||end==secondPlayer)\n return enumerate(ret,mask|1<<start,start+1,end-1);\n else return enumerate(ret,mask|1<<start,start+1,end-1)||enumerate(ret,mask|1<<end,start+1,end-1);\n \n }\n }\n int minDFS(int mask)\n {\n int start=0,end=n-1;\n ArrayList<Integer> arr=new ArrayList<Integer>();\n if(enumerate(arr,mask,start,end))\n return 1;\n else\n {\n int q=Integer.MAX_VALUE;\n for(int x:arr)\n q=Math.min(q,1+minDFS(x));\n return q;\n }\n } \n int maxDFS(int mask)\n {\n int start=0,end=n-1;\n ArrayList<Integer> arr=new ArrayList<Integer>();\n if(enumerate(arr,mask,start,end))\n return 1;\n else\n {\n int q=Integer.MIN_VALUE;\n for(int x:arr)\n q=Math.max(q,1+maxDFS(x));\n return q;\n }\n }\n\n public int[] earliestAndLatest(int n, int firstPlayer, int secondPlayer) \n {\n this.n=n;\n this.firstPlayer=firstPlayer-1;\n this.secondPlayer=secondPlayer-1;\n return new int[]{minDFS(0),maxDFS(0)}; \n }\n}\n``` | 1 | 0 | ['Depth-First Search', 'Java'] | 0 |
the-earliest-and-latest-rounds-where-players-compete | [Java] Dfs + memo solution | java-dfs-memo-solution-by-66brother-7rnm | state : remaining people, pos of first player, pos of second player\n2. Simulation : Use bitmask to simulate and get the next round\'s standing\n\n\nclass Solut | 66brother | NORMAL | 2021-06-13T06:13:05.628657+00:00 | 2021-06-13T06:35:31.090809+00:00 | 128 | false | 1. state : remaining people, pos of first player, pos of second player\n2. Simulation : Use bitmask to simulate and get the next round\'s standing\n\n```\nclass Solution {\n int dp1[][][];\n int dp2[][][];\n \n public int[] earliestAndLatest(int n, int a, int b) {\n dp1=new int[n+1][n+1][n+1];\n dp2=new int[n+1][n+1][n+1];\n for(int i=0;i<dp1.length;i++){\n for(int j=0;j<dp1[0].length;j++){\n Arrays.fill(dp1[i][j],-1);\n Arrays.fill(dp2[i][j],-1);\n }\n }\n int res[]=new int[2];\n res[0]=dfs1(n,a,b);\n res[1]=dfs2(n,a,b);\n return res;\n }\n \n public int dfs1(int n,int pos1,int pos2){\n if(pos1+pos2==1+n){\n return 1;//match directly\n }\n if(dp1[n][pos1][pos2]!=-1)return dp1[n][pos1][pos2];\n \n int res=Integer.MAX_VALUE;\n int match=(n+1)/2;\n \n \n for(int state=0;state<(1<<match);state++){\n List<Integer>list=new ArrayList<>();\n boolean a=false,b=false;\n for(int i=0;i<match;i++){\n if((state&(1<<i))!=0){\n list.add(i+1);\n if(i+1==pos1)a=true;\n if(i+1==pos2)b=true;\n }\n else{\n list.add(n-i);\n if(n-i==pos1)a=true;\n if(n-i==pos2)b=true;\n }\n }\n if(a&b){\n int p1=-1,p2=-1;\n Collections.sort(list);\n for(int i=0;i<list.size();i++){\n if(list.get(i)==pos1)p1=i+1;\n if(list.get(i)==pos2)p2=i+1;\n }\n res=Math.min(res,1+dfs1(match,p1,p2));\n }\n \n }\n \n dp1[n][pos1][pos2]=res;\n return res;\n }\n \n \n public int dfs2(int n,int pos1,int pos2){//mn\n if(pos1+pos2==1+n){\n return 1;//match directly\n }\n if(dp2[n][pos1][pos2]!=-1)return dp2[n][pos1][pos2];\n \n int res=Integer.MIN_VALUE;\n int match=(n+1)/2;\n \n \n for(int state=0;state<(1<<match);state++){\n List<Integer>list=new ArrayList<>();\n boolean a=false,b=false;\n for(int i=0;i<match;i++){\n if((state&(1<<i))!=0){\n list.add(i+1);\n if(i+1==pos1)a=true;\n if(i+1==pos2)b=true;\n }\n else{\n list.add(n-i);\n if(n-i==pos1)a=true;\n if(n-i==pos2)b=true;\n }\n }\n if(a&b){\n int p1=-1,p2=-1;\n Collections.sort(list);\n for(int i=0;i<list.size();i++){\n if(list.get(i)==pos1)p1=i+1;\n if(list.get(i)==pos2)p2=i+1;\n }\n res=Math.max(res,1+dfs2(match,p1,p2));\n }\n \n }\n \n dp2[n][pos1][pos2]=res;\n return res;\n }\n}\n\n\n``` | 1 | 0 | [] | 0 |
the-earliest-and-latest-rounds-where-players-compete | C# DFS with memorization | c-dfs-with-memorization-by-leoooooo-r7dd | \npublic class Solution\n{\n public int[] EarliestAndLatest(int n, int firstPlayer, int secondPlayer)\n {\n var res = DFS(n, firstPlayer - 1, secon | leoooooo | NORMAL | 2021-06-13T05:13:24.838334+00:00 | 2021-06-13T05:13:24.838365+00:00 | 75 | false | ```\npublic class Solution\n{\n public int[] EarliestAndLatest(int n, int firstPlayer, int secondPlayer)\n {\n var res = DFS(n, firstPlayer - 1, secondPlayer - 1, new (int Min, int Max)?[n + 1, n + 1, n + 1]);\n return new int[] { res.Min, res.Max };\n }\n\n private (int Min, int Max) DFS(int len, int firstPlayer, int secondPlayer, (int Min, int Max)?[,,] memo)\n {\n if (firstPlayer + secondPlayer + 1 == len)\n return (1, 1);\n\n if (memo[len, firstPlayer, secondPlayer].HasValue)\n return memo[len, firstPlayer, secondPlayer].Value;\n\n int min = len;\n int max = 0;\n int nextLen = (len + 1) / 2;\n for (int mask = 0; mask < (1 << nextLen); mask++)\n {\n int nextFirstPlayer = firstPlayer;\n int nextSecondPlayer = secondPlayer;\n bool valid = true;\n for (int n = 0; n < len / 2; n++)\n {\n int m = (mask & 1 << n) == 0 ? n : len - n - 1;\n if (m == firstPlayer || m == secondPlayer)\n valid = false;\n if (m < firstPlayer)\n nextFirstPlayer--;\n if (m < secondPlayer)\n nextSecondPlayer--;\n }\n\n if (!valid) continue;\n\n var next = DFS(nextLen, nextFirstPlayer, nextSecondPlayer, memo);\n min = Math.Min(min, next.Min + 1);\n max = Math.Max(max, next.Max + 1);\n }\n\n memo[len, firstPlayer, secondPlayer] = (min, max);\n return memo[len, firstPlayer, secondPlayer].Value;\n }\n}\n``` | 1 | 0 | [] | 0 |
the-earliest-and-latest-rounds-where-players-compete | 1900. The Earliest and Latest Rounds Where Players Compete | 1900-the-earliest-and-latest-rounds-wher-l8vb | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | G8xd0QPqTy | NORMAL | 2025-01-05T08:13:19.784505+00:00 | 2025-01-05T08:13:19.784505+00:00 | 12 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def earliestAndLatest(self, n: int, first: int, second: int) -> List[int]:
first -= 1
second -= 1
@cache
def process_round(current_round, remaining_players):
players_in_round = deque()
for player in range(n):
if remaining_players & (1 << player):
players_in_round.append(player)
possible_matchups = []
while len(players_in_round) > 1:
p1, p2 = players_in_round.popleft(), players_in_round.pop()
if (p1 == first and p2 == second) or (p1 == second and p2 == first):
return [current_round, current_round]
if p1 in (first, second):
possible_matchups.append([p2])
elif p2 in (first, second):
possible_matchups.append([p1])
else:
possible_matchups.append([p1, p2])
min_round, max_round = float('inf'), -float('inf')
for match in product(*possible_matchups):
updated_mask = remaining_players
for winner in match:
updated_mask ^= 1 << winner
min_r, max_r = process_round(current_round + 1, updated_mask)
min_round = min(min_round, min_r)
max_round = max(max_round, max_r)
return min_round, max_round
return process_round(1, (1 << n) - 1)
``` | 0 | 0 | ['Python3'] | 0 |
the-earliest-and-latest-rounds-where-players-compete | 1900. The Earliest and Latest Rounds Where Players Compete.cpp | 1900-the-earliest-and-latest-rounds-wher-oe67 | Code\n\nclass Solution {\npublic:\n vector<int> earliestAndLatest(int n, int firstPlayer, int secondPlayer) {\n firstPlayer -= 1, secondPlayer -= 1; | 202021ganesh | NORMAL | 2024-10-20T08:01:58.264374+00:00 | 2024-10-20T08:01:58.264399+00:00 | 5 | false | **Code**\n```\nclass Solution {\npublic:\n vector<int> earliestAndLatest(int n, int firstPlayer, int secondPlayer) {\n firstPlayer -= 1, secondPlayer -= 1; \n map<int, vector<int>> memo; \n function<vector<int>(int, int, int, int)> fn = [&](int r, int mask, int i, int j) {\n if (memo.find(mask) == memo.end()) {\n if (i >= j) return fn(r+1, mask, 0, n-1); \n if (!(mask & (1 << i))) return fn(r, mask, i+1, j); \n if (!(mask & (1 << j))) return fn(r, mask, i, j-1); \n if ((i == firstPlayer && j == secondPlayer) || (i == secondPlayer && j == firstPlayer)) return vector<int>(2, r); \n if (i == firstPlayer || i == secondPlayer) return fn(r, mask^(1<<j), i+1, j-1); \n if (j == firstPlayer || j == secondPlayer) return fn(r, mask^(1<<i), i+1, j-1); \n else {\n vector<int> x = fn(r, mask^(1<<j), i+1, j-1); \n vector<int> y = fn(r, mask^(1<<i), i+1, j-1); \n memo[mask] = {min(x[0], y[0]), max(x[1], y[1])}; \n }\n }\n return memo[mask]; \n }; \n return fn(1, (1<<n)-1, 0, n-1); \n }\n};\n``` | 0 | 0 | ['C'] | 0 |
the-earliest-and-latest-rounds-where-players-compete | Interview Preparation | interview-preparation-by-najnifatima01-s1cs | Let me clarify the question once ...\ntestcase\nconstraints :\n2 <= n <= 28\n1 <= firstPlayer < secondPlayer <= n\nGive me a few minutes to think it through\nco | najnifatima01 | NORMAL | 2024-08-25T14:22:48.692003+00:00 | 2024-08-25T14:22:48.692041+00:00 | 5 | false | Let me clarify the question once ...\ntestcase\nconstraints :\n2 <= n <= 28\n1 <= firstPlayer < secondPlayer <= n\nGive me a few minutes to think it through\ncomment - BF, optimal\ncode\n\n# Intuition\nrecursion -> memoization\n\n# Approach - optimal memoization\n\n# Complexity\n- Time complexity:\n$$O(n^3)$$\n\n- Space complexity:\n$$O(n^3)$$\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int mini=INT_MAX, maxi = INT_MIN; \n bool visited[27][27][27]={};\n void dfs(int mask, int round, int i, int j, int first, int second, int l, int m, int r) {\n if(i>=j) {\n dfs(mask, round+1, 0, 27, first, second, l, m, r);\n } else if ((mask & (1<<i)) == 0) {\n dfs(mask, round, i+1, j, first, second, l, m, r);\n }else if((mask &(1<<j)) == 0) {\n dfs(mask, round, i, j-1, first, second, l, m, r);\n }\n else if( i== first && j == second) {\n mini = min(mini, round);\n maxi = max(maxi, round);\n } else if(!visited[l][m][r]) {\n visited[l][m][r] = true;\n if( i != first && i != second) {\n dfs(mask^(1<<i), round, i+1, j-1, first, second, l-(i<first), m-(i>first && i<second), r-(i>second));\n }\n if(j!=first && j!= second) {\n dfs(mask^(1<<j), round, i+1, j-1, first, second, l-(j<first), m-(j>first && j<second), r-(j>second));\n }\n }\n }\n vector<int> earliestAndLatest(int n, int firstPlayer, int secondPlayer) {\n dfs((1<<n)-1, 1, 0, 27, firstPlayer-1, secondPlayer-1, firstPlayer-1, secondPlayer-firstPlayer-1, n-secondPlayer);\n return {mini, maxi};\n }\n};\n```\n\n# Approach - recursion(brute force)\n\n# Complexity\n- Time complexity:\n$$O(2^n)$$\n\n- Space complexity:\n$$O(log n)$$\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int mini=INT_MAX, maxi = INT_MIN; \n void dfs(int mask, int round, int i, int j, int first, int second) {\n if(i>=j) {\n dfs(mask, round+1, 0, 27, first, second);\n } else if ((mask & (1<<i)) == 0) {\n dfs(mask, round, i+1, j, first, second);\n }else if((mask &(1<<j)) == 0) {\n dfs(mask, round, i, j-1, first, second);\n }\n else if( i== first && j == second) {\n mini = min(mini, round);\n maxi = max(maxi, round);\n } else {\n if( i != first && i != second) {\n dfs(mask^(1<<i), round, i+1, j-1, first, second);\n }\n if(j!=first && j!= second) {\n dfs(mask^(1<<j), round, i+1, j-1, first, second);\n }\n }\n }\n vector<int> earliestAndLatest(int n, int firstPlayer, int secondPlayer) {\n dfs((1<<n)-1, 1, 0, 27, firstPlayer-1, secondPlayer-1);\n return {mini, maxi};\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
the-earliest-and-latest-rounds-where-players-compete | Moduler solution, self explanatory names and methods. | moduler-solution-self-explanatory-names-clv82 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | akshay_gupta_7 | NORMAL | 2024-08-19T15:37:22.013690+00:00 | 2024-08-19T15:37:22.013723+00:00 | 17 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int[] earliestAndLatest(int n, int firstPlayer, int secondPlayer) {\n Finder finder=new Finder(n,firstPlayer,secondPlayer);\n List<Integer> allPlayers=new ArrayList<>();\n for(int i=0;i<n;i++){\n allPlayers.add(i+1);\n }\n NoOfRounds finalRounds = finder.checkNoOfRounds(allPlayers);\n return new int[]{finalRounds.minRound,finalRounds.maxRound};\n }\n}\nclass Finder{\n int firstPlayer,secondPlayer,n;\n Finder(int n,int firstPlayer,int secondPlayer){\n this.n=n;\n this.firstPlayer=firstPlayer;\n this.secondPlayer=secondPlayer;\n }\n NoOfRounds checkNoOfRounds(List<Integer> currPlayers){\n if(theyCompete(currPlayers) || currPlayers.size()==1){\n return new NoOfRounds(1,1);\n }\n List<List<Integer>> nextRounds=new RoundBuilder().buildNextRound(currPlayers,firstPlayer,secondPlayer);\n int currMin=1000, currMax=0;\n for(List<Integer> nextRound:nextRounds){\n NoOfRounds fromThisRound=checkNoOfRounds(nextRound);\n currMin=Math.min(currMin,fromThisRound.minRound);\n currMax=Math.max(currMax,fromThisRound.maxRound);\n // System.out.println(currMin+" "+currMax);\n }\n //System.out.println(currPlayers+" "+nextRounds);\n return new NoOfRounds(currMin+1,currMax+1);\n }\n boolean theyCompete(List<Integer> currPlayers){\n for(int i=0,j=currPlayers.size()-1;i<j;i++,j--){\n if(isWinner(currPlayers.get(i)) && isWinner(currPlayers.get(j))){\n return true;\n }\n }\n return false;\n }\n boolean isWinner(int player){\n return player==firstPlayer || player==secondPlayer;\n }\n}\nclass RoundBuilder{\n List<List<Integer>> allRounds=new ArrayList<>();\n List<Integer> newRound,currPlayers;\n int firstPlayer,secondPlayer;\n List<List<Integer>> buildNextRound(List<Integer> currPlayers,int firstPlayer,int secondPlayer){\n this.newRound=new ArrayList<>();\n this.allRounds=new ArrayList<>();\n this.currPlayers=currPlayers;\n this.firstPlayer=firstPlayer;\n this.secondPlayer=secondPlayer;\n buildNextRound(0);\n return allRounds;\n }\n void buildNextRound(int leftIndex){\n int rightIndex=currPlayers.size()-1-leftIndex;\n if(leftIndex>=rightIndex){\n List<Integer> currRound=new ArrayList<>(newRound);\n if(leftIndex==rightIndex){\n currRound.add(currPlayers.get(leftIndex));\n }\n Collections.sort(currRound);\n allRounds.add(currRound);\n return;\n }\n int leftPlayer=currPlayers.get(leftIndex);\n int rightPlayer=currPlayers.get(rightIndex);\n if(rightPlayer!=firstPlayer && rightPlayer!=secondPlayer){\n newRound.add(leftPlayer);\n buildNextRound(leftIndex+1);\n newRound.remove(newRound.size()-1);\n }\n if(leftPlayer!=firstPlayer && leftPlayer!=secondPlayer){\n newRound.add(rightPlayer);\n buildNextRound(leftIndex+1);\n newRound.remove(newRound.size()-1);\n }\n }\n}\nclass NoOfRounds{\n int minRound,maxRound;\n NoOfRounds(int minRound,int maxRound){\n this.minRound=minRound;\n this.maxRound=maxRound;\n }\n public String toString(){\n return minRound+" "+maxRound;\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
the-earliest-and-latest-rounds-where-players-compete | Python 3: FT 100%: TC O(N**4), SC O(N**2): State Transitions and BFS | python-3-ft-100-tc-on4-sc-on2-state-tran-99o3 | Welcome to my ~11th FT 100%\n\n# Intuition\n\nThe first in the line fights the last in line, then second fights second to last, etc.\n\nNot sure why I keep sayi | biggestchungus | NORMAL | 2024-07-23T23:09:18.007049+00:00 | 2024-07-23T23:09:18.007079+00:00 | 7 | false | Welcome to my ~11th FT 100%\n\n# Intuition\n\nThe first in the line fights the last in line, then second fights second to last, etc.\n\nNot sure why I keep saying "fight." Maybe [I\'m feeling violent](https://www.youtube.com/watch?v=8vx_WqwKb74&t=39s)? idk lol\n\nAnyway after we determine a pattern for who wins and loses, we\'ll have\n* some number of people before `first`\n* then `first`\n* more people\n* `second`\n* and a bunch of people on the right\n\nThe pattern will look like this:\n```a\nL first L-R-2 second R\n```\n\n## Step 1: Indistinct People, Canonical L >= R\n\nWe know that people in front will fight people at the back. If we flip the array then it won\'t change the outcomes because the problem doesn\'t depend on first versus second or vice-versa, and it also doesn\'t depend on who exactly the other people are.\n\nTherefore we can\n* summarize the current state as `L first L-R-2 second R`\n* and also treat all the non-first-or-second people as indistinguishable. Only the number of people relative to first and second matter, not their numbers.\n\nTo simplify logic we\'ll pick `L >= R` as our convention. If not, just flip the array (conceptually).\n\n## Step 2: Find the Pattern\n\nIf we have `L == R` then we know this is the round where first and last will fight, so we\'re done.\n\nThus we continue with `L > R`.\n\nIn this situation the first `R` and last `R` fight each other. There are many possible outcomes. But we only care about the *number* of winners on the left versus right. So let\'s call `wl` the number of these `R` fights that result in the left person winning.\n\nThen that leaves an interior region in the array that looks like this:\n```a\n L-1-R first n-L-R-2\n ML MR\n```\n\nThe first part, `R` people, have been handled with the `wl` stuff. The last part `second R` has been handled with the `wl` stuff as well.\n\nWe now have `ML` elements left of `first` and `MR` elements on the right of `first` as labeled above. There are three cases:\n* `ML < MR`: we have `ML` fights with people left of `first`, which can resolve to `0..ML` people remaining left of first\n* `ML == MR`: same as `ML < MR`: they all fight and `first` continues without fighting anyone\n* `ML > MR`: this time we have `MR` fights with people left of `first`, so there can be `0..MR` winners that stay left. Let\'s call that `wl2`, "winners on the left in the second set of fights we care about." Regardless of those these play out, there are still another `ML-1-MR` pairs of people on the left before first. They will fight each other such that `ceil((ML-1-MR)/2)` of them proceed to the next round, all on the left of `first`\n\n## Simplify Logic\n\nThe last paragraph is pretty nasty.\n\nBut we see there\'s a pattern:\n* if `ML <= MR` then `wl2 = 0..ML`, and those are the only people on the left from the interior of the array\n* if `ML > MR` then `wl2 = 0..MR` and there are an extra `ceil((ML-MR-1)/2)` people on the left\n\nSo we can\n* run `wl2 = 0..min(ML, MR)`\n* set `extraLeft = 0 if ML <= MR else ceil((ML-MR-1)/2)`\n* then use the same loop to handle all `ML, MR` relations\n\nThe new states available have\n* `wl + wl2 + extraLeft` people on the left (see above)\n* then `first`\n* then some number of people (which we don\'t need to calculate!)\n* then `second`\n* then `R-wl` people: if `wl` of the `R` fights were won by left people, then `wl` right people lost\n\nThis keeps the loop code simple... although it\'s not *actually* simple to derive this, takes a lot of detailed thinking to get it all exactly right. Hence the extremely high docs:code ratio as I figured it out!\n\n# Approach\n\nFrom the Intuition section we have a way to start from any current state and get new states.\n\nNow we just use BFS:\n* start with `first-1, n-second` to count the people left and right, `n` is the starting value\n* then in each round of BFS:\n * if `L==R` then this state ends, `first` and `second` fight in this round\n * otherwise find all the possible resulting states, an `O(N**2)` and enqueue them if we haven\'t already seen them *for this current `n`*\n * at the end of each BFS level, we know that there were `n//2` fights and thus `n//2` losers, so `n -= n//2`\n\nFinally we just record the first and last round where we found `L==R`.\n\n# Complexity\n- Time complexity: `O(n**4)`\n - in round one we do `O(n**2)` iterations because we loop over all `wl`, `wl2` combinations and append that order of elements to the queue\n - then in round two we do iterate over `wl, wl2`, `O(n**2)` things, for each of the `O(n**2)` items in the queue. That\'s `O(n**4)`\n - however: the most `L` and `R` can be is `O(n)`, each iteration has about half as many elements because about half the people lose\n - therefore the complexity will look like `O(n**4 + n**4/16 + n**4 / 256 + ...) = O(n**4)`. That\'s because the worst case combinations come from `wl, wl2` both iterating over about half the array size, current n squared over 4, and the current n itself is half of what it used to be\n\n- Space complexity: `O(n**2)` because at worst we have `wl, wl2 ~ O(n)` to start all combinations get pushed to the queue\n\nQuartic scaling is obviously bad. But `n <= 28` is a huge tipoff that we can afford bad scaling and still not get TLE.\n\n# Code\n```\nclass Solution:\n def earliestAndLatest(self, n: int, firstPlayer: int, secondPlayer: int) -> List[int]:\n # row, 1..n\n \n # in each round i from front competes with i from the back, winner advances. if odd, middle advances\n # the winner remains in place, such that they\'re ordered by initial position (so numerically 1..n)\n \n # firstPlayer, secondPlayer are best, they win against all other players and\n # we pick who among those two win head-to-head\n\n # return the first and last possible round they can compete\n\n # first possible round:\n # ....... first ...... second ....\n # ABCDEFG GFEDCBA\n #\n # each match is basically popFront vs popBack\n # then we push the winner to their original side\n #\n # so if we have L first M second R then\n # if L == R then first and second face off in this current turn\n #\n # otherwise suppose L > R, otherwise flip the array\n # R = R + 1 + E, E for "extra"\n #\n # wlog let first be farther from front than second is from back\n\n # then we have R 1 (L-1-R) first (N-2*R-2-(L-1-R)-1) second R\n # N-R-2-L\n # ML MR\n\n # from R vs R: suppose W win on the left. Then we have\n # W x second (R-W)\n # if ML < MR: can choose any up to min(ML, MR) to win left\n # then first defeats one in MR\n # then among the rest we remove half rounded down\n\n # so let\'s do BFS with a seen set\n rounds = 1 # current round\n q = deque()\n q.append((firstPlayer-1, n-secondPlayer))\n earliest = n\n latest = 0\n while q:\n seen = set() # seen only needs to have states for the current round and its number of players\n for _ in range(len(q)):\n L, R = q.popleft()\n\n if L == R:\n earliest = min(earliest, rounds)\n latest = rounds\n continue\n \n if R > L:\n L, R = R, L\n\n # we have R 1 L-R-1 first n-L-R-2 second R\n # R vs R: let WL be number of wins that go to left, in 0..R\n #\n # result WL 0 ??????????????????? second (R-WL)\n \n ML = L-R-1\n MR = n-L-R-2\n\n # really tricky: interior is ML 1/first MR\n #\n # if ML < MR: looks like ... first .............\n # 0..ML can be on the left, then first, rest fight AFTER\n # if ML > MR: looks like ............ first ...\n # 0..MR can be on the right, then ceil((ML-1-MR)/2) ALSO on the left before first\n # we\'ll call the ceil(...) extraLeft, the number of winners that will be on the left no matter what\n # if ML == MR: looks like .... first ....\n # any number on left (same as ML < MR case)\n\n matches = min(ML, MR)\n extraLeft = 0 if ML <= MR else (ML-1-MR+1)//2\n\n lo = min(ML, MR)\n for wl in range(R+1):\n for wl2 in range(matches+1):\n newstate = (wl+wl2+extraLeft, R-wl)\n\n if newstate in seen: continue\n\n seen.add(newstate)\n q.append(newstate)\n\n # prep for next round\n rounds += 1\n n -= n//2 # each of the n//2 battles has a loser that gets knocked out\n\n return [earliest, latest]\n``` | 0 | 0 | ['Python3'] | 0 |
the-earliest-and-latest-rounds-where-players-compete | 👍Runtime 0 ms Beats 100.00% | runtime-0-ms-beats-10000-by-pvt2024-bcgy | Code\n\nclass Solution {\n public int[] earliestAndLatest(int n, int firstPlayer, int secondPlayer) {\n int p1 = Math.min(firstPlayer, secondPlayer);\ | pvt2024 | NORMAL | 2024-07-08T02:59:41.564747+00:00 | 2024-07-08T02:59:41.564777+00:00 | 40 | false | # Code\n```\nclass Solution {\n public int[] earliestAndLatest(int n, int firstPlayer, int secondPlayer) {\n int p1 = Math.min(firstPlayer, secondPlayer);\n int p2 = Math.max(firstPlayer, secondPlayer);\n if (p1 + p2 == n + 1) {\n // p1 and p2 compete in the first round\n return new int[]{1, 1};\n }\n if (n == 3 || n == 4) {\n // p1 and p2 must compete in the second round (only two rounds).\n return new int[]{2, 2};\n }\n\n // Flip to make p1 be more closer to left than p2 to right end for convenience\n if (p1 - 1 > n - p2) {\n int t = n + 1 - p1;\n p1 = n + 1 - p2;\n p2 = t;\n }\n\n int m = (n + 1) / 2;\n int min = n;\n int max = 1;\n if (p2 * 2 <= n + 1) {\n // p2 is in the first half (n odd or even) or exact middle (n odd)\n int a = p1 - 1;\n int b = p2 - p1 - 1;\n // i represents the number of front players in A wins\n // j represents the number of front players in B wins\n for (int i = 0; i <= a; i++) {\n for (int j = 0; j <= b; j++) {\n int[] ret = earliestAndLatest(m, i + 1, i + j + 2);\n min = Math.min(min, 1 + ret[0]);\n max = Math.max(max, 1 + ret[1]);\n }\n }\n } else {\n // p2 is in the later half (and has >= p1 distance to the end)\n int p4 = n + 1 - p2;\n int a = p1 - 1;\n int b = p4 - p1 - 1;\n // Group C are players between p4 and p2, (c+1)/2 will advance to the next round.\n int c = p2 - p4 - 1;\n for (int i = 0; i <= a; i++) {\n for (int j = 0; j <= b; j++) {\n int[] ret = earliestAndLatest(m, i + 1, i + j + 1 + (c + 1) / 2 + 1);\n min = Math.min(min, 1 + ret[0]);\n max = Math.max(max, 1 + ret[1]);\n }\n }\n }\n return new int[]{min, max};\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
the-earliest-and-latest-rounds-where-players-compete | Rust memoization | rust-memoization-by-minamikaze392-31w0 | Approach\n1. Convert first_player and second_player to i and j, which are 0-based and i < j.\n\n2. When a player (let\'s say a) other than i and j advances to n | Minamikaze392 | NORMAL | 2024-06-17T08:01:12.540251+00:00 | 2024-06-17T08:07:39.156581+00:00 | 4 | false | # Approach\n1. Convert `first_player` and `second_player` to `i` and `j`, which are 0-based and `i < j`.\n\n2. When a player (let\'s say `a`) other than `i` and `j` advances to next round, there are 3 cases to consider regarding to `a`\'s position:\n- Region 0 (left -> l): `a < i`.\n- Region 1 (middle -> m): `i < a < j`.\n- Region 2 (right -> r): `j < a`.\n```\n[...i...j...]\n \u2191 \u2191 \u2191\n 0 1 2\n```\n\n3. Considering that when two players compete, there can be different cases of what region the winner can fall into after each match. Some variables (`l`, `m`, `lr`, `lm`, `mr`) are used here to count each possibility. (There is no `r` simply because it is not needed for calculation in step 4.)\n\n4. Use those variables (`l`, `m`, `lr`, `lm`, `mr`) to **iterate through all possibilities** of what **new indices** `i` and `j` can fall into in the next round.\n\n4. Add top-down DP logic to get the answer using the memoized answers of next round.\n# Code\n```\nimpl Solution {\n pub fn earliest_and_latest(n: i32, first_player: i32, second_player: i32) -> Vec<i32> {\n let n = n as usize;\n let i = first_player as usize - 1;\n let j = second_player as usize - 1;;\n let mut dp = vec![vec![vec![vec![-1; 2]; j + 1]; i + 1]; n + 1];\n Self::memo(n, i, j, &mut dp);\n dp[n][i].pop().unwrap()\n }\n\n fn memo(n: usize, i: usize, j: usize, dp: &mut Vec<Vec<Vec<Vec<i32>>>>) {\n if dp[n][i][j][0] != -1 {\n return;\n }\n if i + j + 1 == n {\n dp[n][i][j][0] = 1;\n dp[n][i][j][1] = 1;\n return;\n }\n let n2 = (n + 1) / 2;\n let i_seq = i.min(n - i - 1);\n let j_seq = j.min(n - j - 1);\n let mut l = 0;\n let mut m = 0;\n let mut lr = 0;\n let mut lm = 0;\n let mut mr = 0;\n for a in 0..n2 {\n if a == i_seq || a == j_seq {\n continue;\n }\n let b = n - a - 1;\n match (Self::get_region(a, i, j), Self::get_region(b, i, j)) {\n (0, 0) => l += 1,\n (0, 1) => lm += 1,\n (0, 2) => lr += 1,\n (1, 1) => m += 1,\n (1, 2) => mr += 1,\n (2, 2) => (),\n _ => unreachable!(),\n }\n }\n dp[n][i][j][0] = i32::MAX;\n dp[n][i][j][1] = i32::MIN;\n for lr_i in 0..=lr {\n for lm_i in 0..=lm {\n for mr_i in 0..=mr {\n let i2 = l + lr_i + lm_i;\n let j2 = l + m + lr_i + lm + mr_i + 1;\n Self::memo(n2, i2, j2, dp);\n dp[n][i][j][0] = dp[n][i][j][0].min(dp[n2][i2][j2][0] + 1);\n dp[n][i][j][1] = dp[n][i][j][1].max(dp[n2][i2][j2][1] + 1);\n }\n }\n }\n }\n\n fn get_region(a: usize, i: usize, j: usize) -> i32 {\n if a < i { 0 } else if a < j { 1 } else { 2 }\n }\n}\n``` | 0 | 0 | ['Dynamic Programming', 'Memoization', 'Rust'] | 0 |
the-earliest-and-latest-rounds-where-players-compete | just a variant | just-a-variant-by-igormsc-udix | Code\n\nclass Solution {\n fun earliestAndLatest(n: Int, firstPlayer: Int, secondPlayer: Int): IntArray {\n val res = intArrayOf(Int.MAX_VALUE, Int.MI | igormsc | NORMAL | 2024-02-10T10:06:19.025542+00:00 | 2024-02-10T10:06:19.025575+00:00 | 2 | false | # Code\n```\nclass Solution {\n fun earliestAndLatest(n: Int, firstPlayer: Int, secondPlayer: Int): IntArray {\n val res = intArrayOf(Int.MAX_VALUE, Int.MIN_VALUE)\n\n fun dfs(l: Int, r: Int, n: Int, rn: Int) {\n if (l == r) {\n res[0] = minOf(res[0], rn)\n res[1] = maxOf(res[1], rn)\n }\n val (l,r) = if (l<r) l to r else r to l\n (1..<l + 1).forEach { i ->\n (l - i + 1..minOf(r, (n + 1) / 2) - i).forEach { j ->\n if (l + r - j - i <= n / 2) dfs(i, j, (n + 1) / 2, rn + 1) } }\n }\n\n dfs(firstPlayer, n - secondPlayer + 1, n, 1)\n return res\n }\n}\n``` | 0 | 0 | ['Kotlin'] | 0 |
the-earliest-and-latest-rounds-where-players-compete | full comented solution py3 )) | full-comented-solution-py3-by-borkiss-7xwk | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | borkiss | NORMAL | 2024-01-28T20:48:36.143117+00:00 | 2024-01-28T20:48:36.143141+00:00 | 11 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def earliestAndLatest(self, n: int, firstPlayer: int, secondPlayer: int) -> List[int]:\n # Initialize minR and maxR with extreme values\n minR, maxR = 999999, -122\n players = \'\'\n \n # Generate a string representing all players using uppercase letters\n for i in range(1, n+1):\n players += chr(i + 65)\n fp = chr(firstPlayer + 65)\n sp = chr(secondPlayer + 65)\n\n @cache\n def dfs(s, num_round, winners):\n nonlocal maxR, minR\n # Base case: If no players are left, update minR and maxR\n if len(s) == 0:\n dfs("".join(sorted(winners)), num_round + 1, \'\')\n return\n # Base case: If only one player is left, update winners and continue\n if len(s) == 1:\n winners += s[0]\n dfs("".join(sorted(winners)), num_round + 1, \'\')\n return\n # Case: The first and last players are the target players\n if s[0] == fp and s[-1] == sp:\n maxR = max(maxR, num_round)\n minR = min(minR, num_round)\n return\n # Case: The first player is one of the target players\n elif s[0] == fp or s[0] == sp:\n winners += s[0]\n s = s[1:-1]\n dfs(s, num_round, winners)\n # Case: The last player is one of the target players\n elif s[-1] == fp or s[-1] == sp:\n winners += s[-1]\n s = s[1:-1]\n dfs(s, num_round, winners)\n # Case: Both the first and last players are not the target players\n else:\n l, r = s[0], s[-1]\n dfs(s[1:-1], num_round, winners + l)\n dfs(s[1:-1], num_round, winners + r)\n return\n \n # Start the recursive DFS with initial parameters\n dfs(players, 1, \'\')\n # Return the result as a list [minR, maxR]\n return [minR, maxR]\n\n\n\n \n``` | 0 | 0 | ['Python3'] | 0 |
the-earliest-and-latest-rounds-where-players-compete | a | a-by-user3043sb-pc47 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | user3043SB | NORMAL | 2024-01-17T20:03:29.899967+00:00 | 2024-01-17T20:03:29.899990+00:00 | 5 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport java.util.*;\n\n\npublic class Solution {\n\n // every round we remove N/2 people\n // for A and B to play together the MID must be between them; so they must be at same dist from MID to play\n\n // Input: n = 11, firstPlayer = 2, secondPlayer = 4 // Output: [3,4]\n // Explanation:\n // One possible scenario which leads to the earliest round number:\n // 1 round: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11\n // 2 round: 2, 3, 4, 5, 6, 11\n // 3 round: 2, 3, 4\n\n // 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11\n // 1, 2, 3, 4, 5, 6\n // 1, 2, 3\n\n // One possible scenario which leads to the latest round number:\n // 1 round: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11\n // 2 round: 1, 2, 3, 4, 5, 6\n // 3 round: 1, 2, 4\n // Fourth round: 2, 4\n\n // Step 1: Think of brute-force solution: we can encode the state in 1 INT; 32 bits so we dont do arraylist work\n // Step 2: Simplify the problem !!! Notice: SYMMETRY !!!!!\n // xxxx A xxx B\' xxx M xxx B xxxx A\' ========= xxxx A\' xxx B xxx M xxx B\' xxxx A\n // we can flip left/right sides; we can also flip A and B !!!!!!!! always take A < B\n // so we can always convert the problem into the order ....A......B.....M; BOTH ON LEFT never work with both on RIGHT\n\n // Step 3: solve RECURSIVELY adjusting indexes\n\n // NOTICE: 2 cases for A,B and MID:\n // 1) A,B on same side of MID\n // xxxx A xxx B xxx M xxx B\' xxxx A\'\n // X Y Z\n // dp[n][a][b] -> dp[(n+1)/2][x+1][x+1+y+1]\n\n // 2) A,B on DIFF side of MID; CASE 2:\n // xxxx A xxx B\' xxx M xxx B xxxx A\'\n // X Y Z = 3 groups of people we can retain; enumerate all possible values for those at each step !!!\n // and update the next indexes for A,B e.g.\n // dp[n][a][b] -> dp[(n+1)/2][x+1][x+1+y+1+z]\n\n\n public int[] earliestAndLatest(int n, int a, int b) {\n dp = new int[n + 1][n + 1][n + 1][2];\n return recMemo(n, a, b);\n }\n\n int[] recMemo(int n, int a, int b) {\n if (n == 2 || a + b == n + 1) return new int[]{1, 1}; // they are fighting now\n if (dp[n][a][b][0] != 0) return dp[n][a][b];\n if (a > b) return recMemo(n, b, a); // reverse A,B so A < B always\n if (a + b > n + 1) return recMemo(n, n - b + 1, n - a + 1); // reverse left,right so always A...B..M\n // also remap: 1,A,3,4,B -> B,A,3,4,5 -> A,B,3,4,5\n\n int nextN = (n + 1) / 2; // also mid\n dp[n][a][b][0] = Integer.MAX_VALUE / 2;\n dp[n][a][b][1] = Integer.MIN_VALUE / 2;\n\n if (b <= nextN) { // case 1: xxxx A xxx B xxx M xxx B\' xxxx A\'\n for (int x = 0; x < a; x++) {\n for (int y = 0; y < b - a; y++) {\n int[] case1 = recMemo(nextN, x + 1, x + 1 + y + 1);\n dp[n][a][b][0] = Math.min(dp[n][a][b][0], 1 + case1[0]);\n dp[n][a][b][1] = Math.max(dp[n][a][b][1], 1 + case1[1]);\n }\n }\n } else { // case 2: xxxx A xxx B\' xxx M xxx B xxxx A\'\n int bb = n + 1 - b;\n for (int x = 0; x < a; x++) {\n for (int y = 0; y < bb - a; y++) {\n int bToBb = b - bb - 1;\n int z = (bToBb + 1) / 2;\n int[] case2 = recMemo(nextN, x + 1, x + 1 + y + 1 + z);\n dp[n][a][b][0] = Math.min(dp[n][a][b][0], 1 + case2[0]);\n dp[n][a][b][1] = Math.max(dp[n][a][b][1], 1 + case2[1]);\n }\n }\n }\n\n return dp[n][a][b];\n }\n\n // A B\n // 1,2,3,4,5 --> \n\n int[][][][] dp;\n\n\n}\n\n\n``` | 0 | 0 | ['Java'] | 0 |
the-earliest-and-latest-rounds-where-players-compete | Simple Recursion only, No DP, Beats 100%, 0ms, C++ | simple-recursion-only-no-dp-beats-100-0m-7gp2 | Intuition\n\n\n# Code\n\nclass Solution {\npublic:\n\n vector<int> rec(int left, int mid, int right){\n vector<int> ans = {(int)1e9,-(int)1e9};\n | Samuel-Aktar-Laskar | NORMAL | 2023-11-22T07:36:46.619657+00:00 | 2023-11-22T07:36:46.619675+00:00 | 63 | false | # Intuition\n\n\n# Code\n```\nclass Solution {\npublic:\n\n vector<int> rec(int left, int mid, int right){\n vector<int> ans = {(int)1e9,-(int)1e9};\n if (left == right){\n return {1,1};\n }\n if (left > right) swap(left, right);\n \n int tot = left+1+mid+1+right;\n for(int n_left=0;n_left<=left;n_left++){\n int right_pos = left+1+mid+1;\n if (right_pos > (tot+1)/2){\n for(int right_add=0;right_add <= tot-right_pos-left-1; right_add++){\n int n_right = left-n_left + right_add;\n int n_mid = (tot+1)/2 - n_left-n_right-2 ;\n auto tmp = rec(n_left,n_mid,n_right);\n ans[0] = min(ans[0], tmp[0]+1);\n ans[1] = max(ans[1], tmp[1]+1);\n }\n }\n else {\n for(int n_mid=0;n_mid<= right_pos-1-left-1; n_mid++){\n int n_right= (tot+1)/2 - n_left-n_mid-2;\n auto tmp = rec(n_left,n_mid,n_right);\n ans[0] = min(ans[0], tmp[0]+1); \n ans[1] = max(ans[1], tmp[1]+1); \n }\n }\n }\n return ans;\n\n }\n vector<int> earliestAndLatest(int n, int firstPlayer, int secondPlayer) {\n return rec(firstPlayer-1, secondPlayer-firstPlayer-1, n-secondPlayer);\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
the-earliest-and-latest-rounds-where-players-compete | Golang beginner - DFS + DP | golang-beginner-dfs-dp-by-vegabird-goh8 | Intuition\nThis is a typical resursive DFS search + DP problem\n\nMyy golang is not good, so just see the idea of solving\n\n# Code\n\n\ntype State struct {\n\t | vegabird | NORMAL | 2023-05-23T15:44:32.741653+00:00 | 2023-05-24T08:52:47.992148+00:00 | 11 | false | # Intuition\nThis is a typical resursive DFS search + DP problem\n\nMyy golang is not good, so just see the idea of solving\n\n# Code\n```\n\ntype State struct {\n\tstate []bool\n\tcurRound int\n}\n\ntype Result struct {\n\tearliest int\n\tlatest int\n}\n\nvar visited map[string]Result\n\nfunc (s State) ToString() string {\n\treturn fmt.Sprintf("%v", s.state)\n}\n\nfunc (r *Result) Merge(other Result) {\n\tif other.earliest < r.earliest {\n\t\tr.earliest = other.earliest\n\t}\n\tif other.latest > r.latest {\n\t\tr.latest = other.latest\n\t}\n}\n\nfunc SolveInternal(state State) (result Result) {\n\tif r, ok := visited[state.ToString()]; ok {\n\t\treturn r\n\t}\n\n\tstate.curRound++\n\n\tfmt.Println("SolveInternal", state)\n\n\tmakingQueue := [][]int{\n\t\tmake([]int, 0),\n\t}\n\tcompletedQueue := make([]State, 0)\n\toldState := state.state\n\n\tfor len(makingQueue) > 0 {\n\t\tmakingState := makingQueue[0]\n\t\tmakingQueue = makingQueue[1:]\n\n\t\tcurIndex := len(makingState)\n\n\t\t//fmt.Println("Examining ", makingState, "curIndex", curIndex)\n\n\t\tif curIndex == len(oldState)/2 {\n\t\t\tif len(oldState)%2 == 1 {\n\t\t\t\tmakingState = append(makingState, curIndex)\n\t\t\t}\n\n\t\t\tsort.Ints(makingState)\n\t\t\tcompletedState := State{\n\t\t\t\tstate: make([]bool, len(makingState)),\n\t\t\t\tcurRound: state.curRound,\n\t\t\t}\n\t\t\tfor i := range makingState {\n\t\t\t\tcompletedState.state[i] = oldState[makingState[i]]\n\t\t\t}\n\t\t\tcompletedQueue = append(completedQueue, completedState)\n\t\t} else {\n\t\t\toppIndex := len(oldState) - curIndex - 1\n\n\t\t\tif oldState[curIndex] && oldState[oppIndex] {\n\t\t\t\tfmt.Println("Found terminal condition at ", state)\n\t\t\t\treturn Result{earliest: state.curRound, latest: state.curRound}\n\t\t\t}\n\t\t\tif !oldState[curIndex] {\n\t\t\t\t//fmt.Println("- adding", oppIndex, "to", makingState, "as curIndex", curIndex, "is not true")\n\t\t\t\tmakingQueue = append(makingQueue, append(makingState, oppIndex))\n\t\t\t}\n\t\t\tif !oldState[oppIndex] {\n\t\t\t\t//fmt.Println("- adding", curIndex, "to", makingState, "as curIndex", oppIndex, "is not true")\n\t\t\t\tcopiedState := make([]int, len(makingState))\n\t\t\t\tcopy(copiedState, makingState)\n\t\t\t\tmakingQueue = append(makingQueue, append(copiedState, curIndex))\n\t\t\t}\n\t\t}\n\t}\n\n\tresult = Result{earliest: math.MaxInt, latest: math.MinInt}\n\n\tfor _, newState := range completedQueue {\n\t\tnewState.curRound = state.curRound\n\n\t\toneResult := SolveInternal(newState)\n\t\tresult.Merge(oneResult)\n\t}\n\n\tvisited[state.ToString()] = result\n\treturn\n}\n\nfunc earliestAndLatest(n int, firstPlayer int, secondPlayer int) []int {\n\n\tvisited = make(map[string]Result)\n\n\tfmt.Println("Started to solve", n, firstPlayer, secondPlayer)\n\n\tstate := State{\n\t\tstate: make([]bool, n),\n\t\tcurRound: 0,\n\t}\n\n\tfor i := 0; i < n; i++ {\n\t\tstate.state[i] = (i+1) == firstPlayer || (i+1) == secondPlayer\n\t}\n\n\tresult := SolveInternal(state)\n\n\tfmt.Println("Finished", result)\n\n\treturn []int{result.earliest, result.latest}\n}\n``` | 0 | 0 | ['Go'] | 0 |
the-earliest-and-latest-rounds-where-players-compete | Just a runnable solution | just-a-runnable-solution-by-ssrlive-mitl | Code\n\nimpl Solution {\n pub fn earliest_and_latest(n: i32, first_player: i32, second_player: i32) -> Vec<i32> {\n let mut mn = 10000;\n let m | ssrlive | NORMAL | 2023-02-24T12:43:07.456560+00:00 | 2023-02-24T12:43:07.456590+00:00 | 14 | false | # Code\n```\nimpl Solution {\n pub fn earliest_and_latest(n: i32, first_player: i32, second_player: i32) -> Vec<i32> {\n let mut mn = 10000;\n let mut mx = 0;\n\n let mut arr = vec![0; n as usize];\n for i in 1..=n {\n arr[i as usize - 1] = i;\n }\n Solution::dfs(&arr, 1, &mut mn, &mut mx, first_player, second_player);\n vec![mn, mx]\n }\n\n fn dfs(arr: &Vec<i32>, round: i32, mn: &mut i32, mx: &mut i32, first: i32, second: i32) {\n let size = arr.len() / 2;\n if arr.len() == 1 {\n return;\n }\n for i in 0..size {\n if arr[i] == first && arr[arr.len() - i - 1] == second {\n *mn = (*mn).min(round);\n *mx = (*mx).max(round);\n return;\n }\n }\n let mut f1 = false;\n let mut f2 = false;\n for n in arr {\n f1 |= *n == first;\n f2 |= *n == second;\n }\n if !f1 || !f2 {\n return;\n }\n let mut nextarr = vec![0; size + (arr.len() % 2)];\n let m = (1 << size) - 1;\n for i in 0..=m {\n let mut left = 0_i32;\n let mut right = nextarr.len() as i32 - 1;\n for j in 0..size {\n if (1 << j) & i != 0 {\n nextarr[left as usize] = arr[j];\n left += 1;\n } else {\n nextarr[right as usize] = arr[arr.len() - j - 1];\n right -= 1;\n }\n }\n if arr.len() % 2 != 0 {\n nextarr[left as usize] = arr[arr.len() / 2];\n }\n Solution::dfs(&nextarr, round + 1, mn, mx, first, second);\n }\n }\n}\n``` | 0 | 0 | ['Rust'] | 0 |
the-earliest-and-latest-rounds-where-players-compete | JS | js-by-shaheenparveen-1m8w | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | shaheenparveen | NORMAL | 2022-12-23T16:36:28.731123+00:00 | 2022-12-23T16:36:28.731153+00:00 | 40 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * @param {number} n\n * @param {number} firstPlayer\n * @param {number} secondPlayer\n * @return {number[]}\n */\n\n\nvar earliestAndLatest = function (n, firstPlayer, secondPlayer) {\n let earliest = n;\n let latest = 0;\n\n const visited = new Set();\n\n const findEarliestAndLatest = (remain, players, current, round) => {\n if (visited.has(remain)) return;\n \n const player = players[current];\n const opponent = players[players.length - current]; // since we\'re 1-indexed\n\n if (player === firstPlayer && opponent === secondPlayer) {\n earliest = Math.min(earliest, round);\n latest = Math.max(latest, round);\n return;\n }\n\n if (opponent <= player) {\n\t // we\'ve gone halfway through the list, so everyone has been matched up\n\t // go to the next round\n const nextPlayers = players.filter((p) => remain & (1 << p));\n findEarliestAndLatest(remain, nextPlayers, 1, round + 1);\n return;\n }\n\n const remainIfPlayerWins = remain ^ (1 << opponent);\n const remainIfOpponentWins = remain ^ (1 << player);\n const next = current + 1;\n\n\t// it\'s possible both firstPlayer and secondPlayer are in the first half of the list\n if (player === firstPlayer || player === secondPlayer) {\n findEarliestAndLatest(remainIfPlayerWins, players, next, round);\n return;\n }\n \n\t// it\'s possible both firstPlayer and secondPlayer are in the second half of the list\n if (opponent === firstPlayer || opponent === secondPlayer) {\n findEarliestAndLatest(remainIfOpponentWins, players, next, round);\n return;\n }\n\n // neither player nor opponent are firstPlayer or secondPlayer\n findEarliestAndLatest(remainIfPlayerWins, players, next, round);\n findEarliestAndLatest(remainIfOpponentWins, players, next, round);\n visited.add(remain);\n }\n\n const players = new Array(n + 1).fill(0).map((_, i) => i);\n const ALL_PLAYERS_REMAIN = 2 ** (n + 1) - 1;\n findEarliestAndLatest(ALL_PLAYERS_REMAIN, players, 1, 1);\n\n return [earliest, latest]\n};\n``` | 0 | 0 | ['JavaScript'] | 0 |
the-earliest-and-latest-rounds-where-players-compete | Python DP Solution | Memoization | Easy to understand | python-dp-solution-memoization-easy-to-u-alhm | \n\n# Code\n\nclass Solution:\n def earliestAndLatest(self, n: int, firstPlayer: int, secondPlayer: int) -> List[int]:\n @lru_cache(None)\n def | hemantdhamija | NORMAL | 2022-12-06T11:40:56.536167+00:00 | 2022-12-06T11:40:56.536208+00:00 | 157 | false | \n\n# Code\n```\nclass Solution:\n def earliestAndLatest(self, n: int, firstPlayer: int, secondPlayer: int) -> List[int]:\n @lru_cache(None)\n def dp(left, right, curPlayers, numGamesAlreadyPlayed):\n if left > right: \n dp(right, left, curPlayers, numGamesAlreadyPlayed)\n if left == right: \n ans.add(numGamesAlreadyPlayed)\n for i in range(1, left + 1):\n for j in range(left - i + 1, right - i + 1):\n if not (curPlayers + 1) // 2 >= i + j >= left + right - curPlayers // 2: \n continue\n dp(i, j, (curPlayers + 1) // 2, numGamesAlreadyPlayed + 1)\n\n ans = set()\n dp(firstPlayer, n - secondPlayer + 1, n, 1)\n return [min(ans), max(ans)]\n``` | 0 | 0 | ['Dynamic Programming', 'Memoization', 'Python', 'Python3'] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.