question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
find-the-shortest-superstring | [Python3] travelling sales person (TSP) | python3-travelling-sales-person-tsp-by-y-zmhy | \n\nclass Solution:\n def shortestSuperstring(self, words: List[str]) -> str:\n n = len(words)\n graph = [[0]*n for _ in range(n)] # graph as a | ye15 | NORMAL | 2021-05-26T04:21:13.885708+00:00 | 2021-05-26T04:28:31.105650+00:00 | 884 | false | \n```\nclass Solution:\n def shortestSuperstring(self, words: List[str]) -> str:\n n = len(words)\n graph = [[0]*n for _ in range(n)] # graph as adjacency matrix \n \n for i in range(n):\n for j in range(n): \n if i != j: \n for k in range(len(words[j])): \n if words[i].endswith(words[j][:k]): \n graph[i][j] = len(words[j]) - k \n \n @cache\n def fn(prev, mask): \n """Return length of shortest superstring & current choice of word."""\n if mask == 0: return 0, None\n vv, kk = inf, None\n for k in range(n): \n if mask & 1<<k: \n v, _ = fn(k, mask ^ 1<<k)\n offset = len(words[k]) if prev == -1 else graph[prev][k]\n if v + offset < vv: vv, kk = v + offset, k\n return vv, kk\n \n ans = []\n prev = -1 \n mask = (1<<n) - 1\n while mask: \n _, k = fn(prev, mask)\n if ans: ans.append(words[k][-graph[prev][k]:])\n else: ans.append(words[k])\n prev = k\n mask ^= 1<<k \n return "".join(ans)\n``` | 1 | 0 | ['Python3'] | 0 |
find-the-shortest-superstring | Java Simple and easy to understand solution, clean code with comments | java-simple-and-easy-to-understand-solut-wcj4 | PLEASE UPVOTE IF YOU LIKE THIS SOLUTION\n\n\n\n\nclass Solution {\n public String shortestSuperstring(String[] words) {\n int n = words.length;\n | satyaDcoder | NORMAL | 2021-05-25T04:46:19.314492+00:00 | 2021-05-25T04:46:19.314525+00:00 | 291 | false | **PLEASE UPVOTE IF YOU LIKE THIS SOLUTION**\n\n\n\n```\nclass Solution {\n public String shortestSuperstring(String[] words) {\n int n = words.length;\n \n int[][] overlaps = createOverlapGraph(words);\n \n int maskLen = 1 << n;\n \n //dp[mask][i] : maximum overlap of set of words (which is represented by mask), \n //and ending with words[i]\n int[][] dp = new int[maskLen][n];\n \n //prevWordIndex[mask][i] : Previous word index, after creating the set of words (which is represented by mask),\n //and ending with words[i]\n int[][] prevWordIndex = new int[maskLen][n]; \n \n \n calculateMaximumOverlap(words, dp, prevWordIndex, overlaps);\n \n //correct order of words, which lead to shortest superstring\n int[] orders = getCorrectOrder(dp, prevWordIndex);\n \n return getShortestSuperString(words, overlaps, orders);\n }\n \n \n private int[][] createOverlapGraph(String[] words){\n int n = words.length;\n int[][] overlaps = new int[n][n];\n \n for(int i = 0; i < n; i++){\n for(int j = 0; j < n; j++){\n if(i == j) continue;\n \n overlaps[i][j] = getOverlap(words[i], words[j]);\n }\n }\n \n return overlaps;\n }\n \n private int getOverlap(String word, String nextWord){\n int len = Math.min(word.length(), nextWord.length());\n \n for(int i = len; i >= 0; i--){\n if(word.endsWith(nextWord.substring(0, i))) return i;\n }\n \n return 0;\n }\n \n private void calculateMaximumOverlap(String[] words, int[][] dp, int[][] prevWordIndex, int[][] overlaps){\n int n = words.length;\n int maskLen = 1 << n;\n \n for(int mask = 1; mask < maskLen; mask++){\n Arrays.fill(prevWordIndex[mask], -1);\n \n for(int maskBitPos = 0; maskBitPos < n; maskBitPos++){\n \n //ignore the zero bit of mask[current set of words]\n if(((mask >> maskBitPos) & 1) <= 0) continue;\n \n //set of word which was selected previously for current mask\n int prevMask = (mask ^ (1 << maskBitPos));\n \n //previous mask is zero, it means, first word we are adding\n //ignore this, as there will be 0 overlapping\n if(prevMask == 0) continue;\n \n \n \n for(int prevMaskBitPos = 0; prevMaskBitPos < n; prevMaskBitPos++){\n \n //ignore the zero bit of prevMask[Previous set of words]\n if(((prevMask >> prevMaskBitPos) & 1) <= 0) continue;\n \n //previous set of word overlap, ending with words[prevMaskBitPos]\n int prevOverlap = dp[prevMask][prevMaskBitPos];\n \n //overlap after appending new words[maskBitPos] next to words[prevMaskBitPos]\n prevOverlap += overlaps[prevMaskBitPos][maskBitPos];\n \n \n \n if(prevOverlap >= dp[mask][maskBitPos]){\n //replace with maximum overlap\n dp[mask][maskBitPos] = prevOverlap;\n \n prevWordIndex[mask][maskBitPos] = prevMaskBitPos;\n }\n \n }\n }\n }\n }\n \n private int[] getCorrectOrder(int[][] dp, int[][] prevWordIndex){\n int rows = dp.length;\n int cols = dp[0].length;\n \n \n //last word index\n int lastWordIndex = 0;\n for(int col = 1; col < dp[0].length; col++){\n if(dp[rows - 1][col] > dp[rows - 1][lastWordIndex]){\n lastWordIndex = col;\n }\n }\n \n int[] orders = new int[cols];\n int mask = rows - 1;\n \n for(int i = cols - 1; i >= 0; i--){\n orders[i] = lastWordIndex;\n \n int prev = prevWordIndex[mask][lastWordIndex];\n int prevMask = mask ^ (1 << lastWordIndex);\n \n mask = prevMask;\n lastWordIndex = prev;\n }\n \n return orders;\n }\n \n private String getShortestSuperString(String[] words, int[][] overlaps, int[]orders){\n StringBuilder sb = new StringBuilder(words[orders[0]]);\n \n for(int i = 1; i < orders.length; i++){\n \n int overlap = overlaps[orders[i - 1]][orders[i]];\n \n String word = words[orders[i]].substring(overlap);\n sb.append(word);\n }\n \n return sb.toString();\n }\n}\n``` | 1 | 2 | ['Java'] | 0 |
find-the-shortest-superstring | C++ simple solution using dynamic programming | c-simple-solution-using-dynamic-programm-lmjt | cpp\n#define PSI pair<string, int>\nclass Solution {\npublic:\n int calculateOverlap(string s, string pattern){\n for(int i=min((int)s.size(), (int)pa | sirkp19 | NORMAL | 2021-05-24T11:25:01.270581+00:00 | 2021-05-24T11:25:01.270610+00:00 | 288 | false | ```cpp\n#define PSI pair<string, int>\nclass Solution {\npublic:\n int calculateOverlap(string s, string pattern){\n for(int i=min((int)s.size(), (int)pattern.size()); i>0; i--){\n if(s.substr((int)s.size()-i)==pattern.substr(0, i)){\n return i;\n }\n }\n return 0;\n }\n \n inline bool isPresentInMask(int n, int mask){\n return (((mask>>n)&1)>0);\n }\n\n string intToString(int n){\n ostringstream s;\n s<<n;\n return s.str();\n }\n\n int stringToInt(string s){\n stringstream str(s);\n int x;\n str >> x;\n return x;\n }\n\n string getAns(string s, vector<string> words, vector<vector<int>> overlap){\n string ans = "", temp;\n int i=0, prev = -1, index;\n while(i< (int)s.size()){\n if(s[i]==\',\'){\n index = stringToInt(temp);\n if((int)ans.size()==0){\n ans = words[index];\n }else{\n ans = ans + words[index].substr(overlap[prev][index]);\n }\n prev = index;\n temp = "";\n }else{\n temp.push_back(s[i]);\n }\n i++;\n }\n index = stringToInt(temp);\n if((int)ans.size()==0){\n ans = words[index];\n }else{\n ans = ans + words[index].substr(overlap[prev][index]);\n }\n return ans;\n }\n\n\n string shortestSuperstring(vector<string>& words) {\n int n = (int)words.size();\n vector<vector<int>> overlap(n, vector<int>(n, 0));\n for(int i=0; i<n; i++){\n for(int j=0; j<n; j++){\n if(i!=j){\n overlap[i][j] = calculateOverlap(words[i], words[j]);\n }\n }\n }\n\n int M = 1<<n;\n PSI empt = {"", -1};\n vector<vector<PSI>> dp(M, vector<PSI>(n, empt));\n for(int i=0; i<n; i++){\n dp[1<<i][i] = {intToString(i), 0};\n }\n\n for(int mask=1; mask<M; mask++){\n for(int ennd=0; ennd<n; ennd++){\n if(isPresentInMask(ennd, mask)){\n for(int i=0; i<n; i++){\n if(i!=ennd && isPresentInMask(i, mask)){\n PSI temp = {dp[mask^(1<<ennd)][i].first + "," + intToString(ennd),\n dp[mask^(1<<ennd)][i].second + overlap[i][ennd]};\n\n if(dp[mask][ennd].second == -1 || temp.second>dp[mask][ennd].second){\n dp[mask][ennd] = temp;\n }\n }\n }\n }\n }\n }\n\n int row = M-1;\n PSI ans = dp[row][0];\n for(int j=1; j<n; j++){\n if(dp[row][j].second>ans.second){\n ans = dp[row][j];\n }\n }\n return getAns(ans.first, words, overlap);\n }\n\n};\n\n``` | 1 | 0 | [] | 0 |
find-the-shortest-superstring | Java | the best (Held-Karp ~97%, 17ms) and the worst solution (Greedy backtracking DFS, ~1000ms) | java-the-best-held-karp-97-17ms-and-the-5i1qi | Updated this by adding Solution 2. based on Held-Karp traveling salesman DP algorithm.\n\nSolution 2 - Held-Karp optimized to run for glueable words only (~17ms | prezes | NORMAL | 2021-05-24T03:07:08.167634+00:00 | 2021-05-24T21:10:37.330960+00:00 | 552 | false | Updated this by adding Solution 2. based on Held-Karp traveling salesman DP algorithm.\n\n**Solution 2 - Held-Karp optimized to run for glueable words only (~17ms)**\nThe incrementally improved solution uses Held-Karp-like algorithm (traveling salesman) with bitmask for efficiently iterating subsets of words.\nUnlike in the traveling salesman, my function is max (not min) - but it doesn\'t make a difference (the function maximizes the amount of characters that can be removed by gluing suffixes and prefixes of the word pairs together). Also it needs to run considering all words as the first word, not just one (as the path does not come back to the starting word, like in the traveling salesman). The rest is the same.\nIt also uses the previous idea of removing the non-glueable words from DP (using the remap[] array), but in this case it\'s a smallish improvement for the current set of test cases (20ms->17ms). In addition to the max score array memo[], the next[] array is used to be able to not only find the optimal score, but also reconstruct the optimal solution (order of words). \n```\nclass Solution {\n int n= -1, k= -1, max= 0;\n int[] maxOrder, maxcp= null, maxcs= null, remap= null;\n int[][] lcsps= null; \n \n public String shortestSuperstring(String[] words) {\n this.n= words.length;\n\t\t// first calculate longest common suffix-prefix for all pairs of strings\n\t\t// also keep max common suffix / prefix per string to easily check for strings \n\t\t// that have no commonalities with other strings either as prefix or suffix (maxcp==0 && maxcs==0)\n\t\tthis.lcsps= new int[n][n];\n this.maxcp= new int[n];\n this.maxcs= new int[n];\n for(int i=0; i<n; i++){\n for(int j=0; j<n; j++)\n if(i!=j) {\n lcsps[i][j]= lcsp(words[i], words[j]);\n maxcp[j]= Math.max(maxcp[j], lcsps[i][j]);\n maxcs[i]= Math.max(maxcs[i], lcsps[i][j]);\n }\n }\n\n // reduce the problem if possible, no need to include non-glueable strings in dp\n this.max= 0;\n this.maxOrder= new int[n];\n this.remap= new int[n];\n this.k= 0;\n for(int i=n-1, j=0; i>-1; i--){\n if(maxcp[i]==0 && maxcs[i]==0)\n maxOrder[n-1-k++]= i;\n else\n remap[j++]= i;\n }\n // run DP\n if(k<n) dpts();\n \n\t\t// build the final string from the optimal order found\n\t\tStringBuilder sb= new StringBuilder();\n sb.append(words[maxOrder[0]]);\n for(int i=1; i<n; i++)\n sb.append(words[maxOrder[i]].substring(lcsps[maxOrder[i-1]][maxOrder[i]]));\n return sb.toString();\n }\n\n // dynamic programming traveling salesman-like (Held-Karp algorithm)\n void dpts(){\n int ndp= n-k; \n int[][] memo= new int[ndp][1<<ndp]; // score of optimal order\n int[][] next= new int[ndp][1<<ndp]; // next word in the optimal order\n for(int i=0; i<ndp; i++)\n Arrays.fill(memo[i], -1);\n max= 0;\n int first= 0, mask= (1<<ndp)-1; // 1 means available (unvisited)\n for(int i=0; i<ndp; i++){\n int score= dpts(i, mask^(1<<i), memo, next);\n if(score>max){\n max= score;\n first= i;\n }\n }\n // recover order\n maxOrder[0]= remap[first];\n for(int i=1, j= first, m= mask^(1<<first); i<ndp; i++){\n j= next[j][m];\n maxOrder[i]= remap[j];\n m^= (1<<j);\n }\n } \n\n int dpts(int i, int mask, int[][] memo, int[][] next){\n if(mask==0) return 0;\n int max= memo[i][mask], maxj= -1;\n if(max!=-1) return max;\n for(int m=mask; m!=0;){\n int j= Integer.numberOfTrailingZeros(m);\n int score= lcsps[remap[i]][remap[j]] + dpts(j, mask^(1<<j), memo, next);\n if(score>max){\n max= score;\n maxj= j;\n }\n m^= 1<<j;\n }\n next[i][mask]= maxj;\n return memo[i][mask]= max;\n }\n\n \n\t// longest common suffix-prefix for a pair of strings (which is at most len-1 of either string)\n\t// it looks for s1 suffix, s2 prefix - separately invoked for all pairs, in both orders\n int lcsp(String s1, String s2){\n int n1= s1.length(), n2= s2.length();\n for(int i=Math.max(1, n1-n2+1); i<n1; i++)\n if(s1.endsWith(s2.substring(0,n1-i))) return n1-i;\n return 0;\n } \n}\n```\n**Solution 1 - heuristically optimized brute force ("greedy DFS" across permutations) (~1000ms, Accepted!)**\nStarted with full brute force, for all permutations.\nThe problem has up to 12 strings which is just above the practical boundary for permutation algos (<=11).\nAfter TLE, added two hacks:\n1. reduced the permutations for certain test cases, by removing strings that cannot be "glued" (reducing length) with any other string -- this is good and correct;\n2. the greedy part: first processing only permutations for glueable pairs, unless/until the DFS gets stuck (no more such pairs) - then unstucking it by resuming with all remaining permutations -- no proof that this would result in an exact (always correct) solution.\n\n```\nclass Solution {\n int n= -1, max= 0;\n int[] maxOrder= null;\n int[][] lcsps= null;\n \n public String shortestSuperstring(String[] words) {\n this.n= words.length;\n\t\t// first calculate longest common suffix-prefix for all pairs of strings\n\t\t// also keep max common suffix / prefix per string to easily check for non-glueable strings \n\t\tthis.lcsps= new int[n][n];\n int[] maxcp= new int[n], maxcs= new int[n];\n for(int i=0; i<n; i++)\n for(int j=0; j<n; j++){\n if(i!=j) lcsps[i][j]= lcsp(words[i], words[j]);\n maxcp[j]= Math.max(maxcp[j], lcsps[i][j]);\n maxcs[i]= Math.max(maxcs[i], lcsps[i][j]);\n }\n this.max= 0;\n this.maxOrder= new int[n];\n boolean[] visited= new boolean[n];\n int[] order= new int[n];\n \n // reduce the problem if possible, no need to include non-glueable strings in dfs\n int k= 0;\n for(int i=0; i<n; i++)\n if(maxcp[i]==0 && maxcs[i]==0){\n visited[i]= true;\n order[k++]= i;\n }\n \n // backtracking dfs for optimal permutation search on the remaining unreduced strings (skip if all words are non-glueable)\n if(k==n)\n System.arraycopy(order, 0, maxOrder, 0, n); \n\t\telse\n\t\t\tfor(int i=0; i<n; i++){\n\t\t\t\tif(visited[i]) continue;\n\t\t\t\tvisited[i]= true;\n\t\t\t\torder[k]= i;\n\t\t\t\tdfs(i, k+1, 0, order, visited);\n\t\t\t\tvisited[i]= false;\n\t\t\t}\n\t\t// build the final string from the optimal permutation found\n\t\tStringBuilder sb= new StringBuilder();\n sb.append(words[maxOrder[0]]);\n for(int i=1; i<n; i++)\n sb.append(words[maxOrder[i]].substring(lcsps[maxOrder[i-1]][maxOrder[i]]));\n return sb.toString();\n }\n \n void dfs(int i, int k, int score, int[] order, boolean[] visited){\n if(k==n){\n if(score>max){\n System.arraycopy(order, 0, maxOrder, 0, n);\n max= score;\n }\n return; \n }\n // // the outer loop is a greedy attempt to prune some permutations and beat TLE:\n // // 1. visit only glueable pairs to start with\n // // 2. if we can\'t find any more glueables, brute force the yet unvisited words and hope for the best\n for(boolean visitedAny= false, glueableOnly= true; !visitedAny; glueableOnly= false)\n for(int j=0; j<n; j++){\n if(visited[j] || glueableOnly && lcsps[i][j]==0) continue;\n visited[j]= visitedAny= true;\n order[k]= j;\n dfs(j, k+1, score+lcsps[i][j], order, visited);\n visited[j]= false;\n }\n }\n \n\t// longest common suffix-prefix for a pair of strings (which is at most len-1 of either string)\n\tint lcsp(String s1, String s2){\n int n1= s1.length(), n2= s2.length();\n for(int i=Math.max(1, n1-n2+1); i<n1; i++)\n if(s1.endsWith(s2.substring(0,n1-i))) return n1-i;\n return 0;\n } \n} | 1 | 0 | [] | 0 |
find-the-shortest-superstring | Rust translated DP solution | rust-translated-dp-solution-by-sugyan-6x3x | rust\nimpl Solution {\n pub fn shortest_superstring(words: Vec<String>) -> String {\n let n = words.len();\n let mut graph = vec![vec![0; n]; n | sugyan | NORMAL | 2021-05-24T02:07:40.327670+00:00 | 2021-05-24T02:07:40.327703+00:00 | 212 | false | ```rust\nimpl Solution {\n pub fn shortest_superstring(words: Vec<String>) -> String {\n let n = words.len();\n let mut graph = vec![vec![0; n]; n];\n for i in 0..n {\n for j in 0..n {\n if i != j {\n let mut k = words[j].len();\n while !words[i].ends_with(&words[j][..k]) {\n k -= 1;\n }\n graph[i][j] = k;\n }\n }\n }\n let mut dp = vec![vec![0; n]; 1 << n];\n let mut parent = vec![vec![None; n]; 1 << n];\n for mask in 0..1 << n {\n for b in 0..n {\n if mask >> b & 1 == 0 {\n continue;\n }\n let prev = mask ^ 1 << b;\n for (i, row) in graph.iter().enumerate() {\n if prev >> i & 1 == 0 {\n continue;\n }\n let val = dp[prev][i] + row[b];\n if val > dp[mask][b] {\n dp[mask][b] = val;\n parent[mask][b] = Some(i);\n }\n }\n }\n }\n let mut mask = (1 << n) - 1;\n let mut perm = Vec::with_capacity(n);\n let mut seen = vec![false; n];\n if let Some(mut p) = (0..n).max_by_key(|&i| dp[(1 << n) - 1][i]) {\n loop {\n perm.push(p);\n seen[p] = true;\n if let Some(t) = parent[mask][p] {\n mask ^= 1 << p;\n p = t;\n } else {\n break;\n }\n }\n }\n perm.extend((0..n).filter(|&i| !seen[i]));\n (1..perm.len())\n .rev()\n .fold(words[perm[n - 1]].clone(), |acc, i| {\n let overlap = graph[perm[i]][perm[i - 1]];\n acc + &words[perm[i - 1]][overlap..]\n })\n }\n}\n``` | 1 | 0 | ['Rust'] | 0 |
find-the-shortest-superstring | [C++] Greedy merge 2 strings a time. Pick the 'best' pair according to heuristics. | c-greedy-merge-2-strings-a-time-pick-the-q142 | \nclass Solution {\n static bool cmp(vector<int>& a, vector<int>& b) {\n int ascore = a[0]-a[3]-a[4];\n int bscore = b[0]-b[3]-b[4];\n i | llc5pg | NORMAL | 2021-05-23T21:44:31.796421+00:00 | 2021-05-23T21:44:31.796466+00:00 | 247 | false | ```\nclass Solution {\n static bool cmp(vector<int>& a, vector<int>& b) {\n int ascore = a[0]-a[3]-a[4];\n int bscore = b[0]-b[3]-b[4];\n if (ascore>bscore) return true;\n if (ascore<bscore) return false;\n return (a[0]>b[0]);\n }\n void printvv(const vector<vector<int>>& vv) {\n for (vector<int> row : vv) {\n for (int elem : row)\n cout << elem << ", ";\n cout << endl;\n }\n }\n void printvs(const vector<string>& vs) {\n for (string s : vs)\n cout << s << ", ";\n cout << endl;\n }\npublic:\n string shortestSuperstring(vector<string>& words) {\n while (words.size()>1) {\n int n = words.size();\n vector<vector<int>> vv;\n for (int i=0; i<n; i++) {\n int wordi_len = words[i].length();\n for (int j=0; j<n; j++) {\n if (i==j) continue;\n int min_len = min(wordi_len, (int)words[j].length());\n int common_len = 0;\n for (int k=1; k<=min_len; k++) {\n string t = words[i].substr(wordi_len-k);\n if (0 == words[j].find(t))\n common_len = max(common_len, k);\n }\n vector<int> row{common_len, i, j, 0, 0};\n vv.push_back(row);\n }\n }\n //printvv(vv);\n int m = vv.size();\n for (int i=0; i<m; i++) {\n int maxFrom=0;\n for (int j=0; j<m; j++) {\n if (i==j) continue;\n if (vv[j][1]!=vv[i][1])\n continue;\n maxFrom = max(maxFrom, vv[j][0]);\n }\n vv[i][3] = maxFrom;\n }\n for (int i=0; i<m; i++) {\n int maxTo=0;\n for (int j=0; j<m; j++) {\n if (i==j) continue;\n if (vv[j][2]!=vv[i][2])\n continue;\n maxTo = max(maxTo, vv[j][0]);\n }\n vv[i][4] = maxTo;\n }\n sort(vv.begin(), vv.end(), cmp);\n //printvv(vv);\n int i = vv[0][1];\n int j = vv[0][2];\n string combined_word = words[i] + words[j].substr(vv[0][0]);\n if (i>j) {\n words.erase(words.begin()+i);\n words.erase(words.begin()+j);\n } else {\n words.erase(words.begin()+j);\n words.erase(words.begin()+i);\n }\n words.push_back(combined_word);\n //printvs(words);\n }\n return words[0];\n }\n};\n``` | 1 | 0 | [] | 0 |
find-the-shortest-superstring | Working one-liner bug | working-one-liner-bug-by-leaderboard-dw4l | I normally don\'t like providing percentage metrics, but this is true speed: 100% time (16 ms) and 97.69% space (14.1 MB). Credits for this goes to @DBabichev ( | leaderboard | NORMAL | 2021-05-23T20:30:57.680143+00:00 | 2021-05-23T20:31:44.087412+00:00 | 206 | false | I normally don\'t like providing percentage metrics, but this is true speed: 100% time (16 ms) and 97.69% space (14.1 MB). Credits for this goes to @DBabichev ([reference post](https://leetcode.com/problems/find-the-shortest-superstring/discuss/1225543/Python-dp-on-subsets-solution-3-solutions-%2B-oneliner-explained)). Will *not* work on Java/C++ due to their differing return types, but somehow accepted on Python 2 and 3 for reasons that I do not know.\n\n```python\nclass Solution:\n def shortestSuperstring(self, words: List[str]) -> str:\n return words;\n```\n | 1 | 0 | [] | 1 |
find-the-shortest-superstring | Rust Dynamic Programming | rust-dynamic-programming-by-michielbaird-01kz | The goal here is to covert the problem to the the Travelling Salesman Problem. We define and edge between 2 words as the amount of characters you need to add to | michielbaird | NORMAL | 2021-05-23T19:48:28.072099+00:00 | 2021-05-23T19:48:28.072146+00:00 | 387 | false | The goal here is to covert the problem to the the Travelling Salesman Problem. We define and edge between 2 words as the amount of characters you need to add to go from word1 to word2. Then we use a bitset to define which words are in the set.\n\n```\nuse std::usize;\n\n\nimpl Solution {\n \n fn recurse(\n dp: &mut Vec<Vec<Option<(usize, Option<usize>)> >>, \n edges: &Vec<Vec<usize>>,\n set: usize, \n dest: usize\n ) {\n if dp[set][dest].is_some() {\n return;\n }\n let prev_set = set & ( !(1<<dest) );\n let mut best = usize::MAX;\n let mut best_i = 0; \n \n for i in 0..edges.len() {\n if i == dest { continue };\n if ((1 << i) & prev_set) == 0 { continue };\n Self::recurse(dp, edges, prev_set, i);\n let w = (dp[prev_set][i].as_ref().unwrap().0) + edges[i][dest];\n if w < best {\n best = w;\n best_i = i;\n }\n }\n dp[set][dest] = Some((best, Some(best_i)));\n }\n \n pub fn shortest_superstring(mut words: Vec<String>) -> String {\n\n let mut edges = vec![vec![0; words.len()]; words.len()];\n \n for i in 0..words.len() {\n for j in 0..words.len() {\n if i == j { continue; }\n\n let mut best = 0;\n let w1 = words[i].as_bytes();\n let w2 = words[j].as_bytes();\n let max_overlap = w1.len().min(w2.len());\n\n for k in (1..=max_overlap) {\n if w1[..k] == w2[(w2.len() - k)..] {\n best = k; \n }\n }\n edges[j][i] = w1.len() - best;\n }\n }\n let total_sets = (2i32.pow(words.len() as u32)) as usize;\n let mut dp = vec![vec![None; words.len()]; total_sets];\n let full_set = (2i32.pow((words.len()) as u32) -1) as usize;\n for i in 0..words.len() {\n let set = (1 << i);\n dp[set][i] = Some((words[i].as_bytes().len(), None));\n }\n let mut best = (usize::MAX, None);\n for i in 0..words.len() {\n Self::recurse(&mut dp, &edges, full_set, i);\n let s = (dp[full_set][i].as_ref().unwrap()).0;\n if best.0 > s {\n best = (s, Some(i));\n }\n }\n \n let mut order = vec![];\n let mut cur = Some((best.1.unwrap(), full_set));\n while let Some((index, set)) = cur {\n order.push(index);\n let next_set = set & (!(1<<index));\n if let Some(&(_, o_n)) = dp[set][index].as_ref() {\n if let Some(n) = o_n {\n cur = Some((n, next_set)); \n } else {\n cur = None;\n } \n } else {\n cur = None; \n } \n }\n order.reverse();\n let mut answer = words[order[0]].clone();\n for i in 1..(order.len()) {\n let add = edges[order[i-1]][order[i]];\n let size = words[order[i]].len();\n answer.push_str(&words[order[i]][size-add..]);\n }\n\n \n\n answer\n }\n}\n``` | 1 | 0 | ['Dynamic Programming', 'Rust'] | 0 |
find-the-shortest-superstring | [c++] deep-first search with memorization | c-deep-first-search-with-memorization-by-xrqk | \nclass Solution {\npublic:\n string shortestSuperstring(vector<string>& words) {\n size_t n = words.size();\n vector<vector<int>> overlap(n, v | zonghao_li | NORMAL | 2021-05-23T18:58:38.321694+00:00 | 2021-05-23T18:58:38.321738+00:00 | 228 | false | ```\nclass Solution {\npublic:\n string shortestSuperstring(vector<string>& words) {\n size_t n = words.size();\n vector<vector<int>> overlap(n, vector<int>(n));\n for (size_t i = 0; i < n; ++i) \n for (size_t j = 0; j < n; ++j)\n update(i, j, words, overlap);\n vector<vector<int>> dp(n, vector<int>(1 << n, -1));\n vector<vector<int>> next(n, vector<int>(1 << n, -1));\n int max_length = -1;\n int curr = -1;\n vector<int> max_path;\n for (size_t i = 0; i < n; ++i) {\n dfs(i, overlap, 0, dp, next);\n if (dp[i][0] > max_length) {\n max_length = dp[i][0];\n curr = i;\n }\n }\n vector<size_t> path;\n path.push_back(curr);\n int bitmask = 0;\n while (next[curr][bitmask] >= 0) {\n path.push_back(next[curr][bitmask]);\n bitmask ^= (1 << curr);\n curr = path.back();\n }\n string ans = words[path[0]];\n for (size_t i = 1; i < n; ++i) \n ans += words[path[i]].substr(overlap[path[i-1]][path[i]]);\n return ans;\n }\n \n\t//build the overlap graph\n void update(size_t i, size_t j, vector<string>& words, vector<vector<int>>& overlap) {\n if (i == j) \n return;\n size_t n1 = words[i].size();\n size_t n2 = words[j].size();\n size_t n = min(n1, n2);\n int count = 0;\n for (size_t k = n; k > 0; --k) {\n if (words[i].substr(n1 - k) == words[j].substr(0, k)) {\n overlap[i][j] = k;\n return;\n }\n }\n }\n \n\t\n\t//deep-first search with memerization\n\t//"i" is the current node; "bitmask" saves previously visited nodes; "dp" saves the longest lengh with the remaining nodes\n\t//"next" saves the next node we should go in the current situation, used to recover the path in the end\n void dfs(size_t i, vector<vector<int>>& overlap, int bitmask, vector<vector<int>>& dp, vector<vector<int>>& next) {\n if (dp[i][bitmask] >= 0)\n return;\n size_t n = overlap.size();\n bitmask ^= (1 << i);\n int remain_length = -1;\n int next_node = -1;\n for (size_t j = 0; j < n; ++j) {\n if (!((1 << j) & bitmask)) {\n dfs(j, overlap, bitmask, dp, next);\n if (overlap[i][j] + dp[j][bitmask] > remain_length) {\n remain_length = overlap[i][j] + dp[j][bitmask];\n next_node = j;\n }\n }\n }\n bitmask ^= (1 << i);\n dp[i][bitmask] = max(0, remain_length);\n next[i][bitmask] = next_node;\n return;\n }\n};\n``` | 1 | 0 | [] | 0 |
find-the-shortest-superstring | 97.60% Time | 88.62% Space | C++ | 9760-time-8862-space-c-by-dibyajyotidhar-so3o | \nclass Solution {\npublic:\n \n string GetOverLapping(string a, string b){\n \n int M=0;\n \n int aplusb=0;\n \n | dibyajyotidhar | NORMAL | 2021-01-11T16:27:23.619084+00:00 | 2021-01-11T16:27:23.619132+00:00 | 355 | false | ```\nclass Solution {\npublic:\n \n string GetOverLapping(string a, string b){\n \n int M=0;\n \n int aplusb=0;\n \n int bplusa=0;\n \n //string ans="";\n \n for(int i=1;i<=min(a.length(),b.length());i++){\n if(a.compare(a.length()-i,i,b,0,i)==0){\n if(i>M){\n M=i;\n bplusa=0;\n aplusb=1;\n }\n } \n }\n \n for(int i=1;i<=min(a.length(),b.length());i++){\n if(b.compare(b.length()-i,i,a,0,i)==0){\n if(i>M){\n M=i;\n bplusa=1;\n aplusb=0;\n }\n } \n }\n \n //cout<<aplusb<<" "<<bplusa<<endl;\n if(aplusb){\n //cout<<a.substr(0,a.length()-M)+b.substr(M)<<endl;\n //cout<<a<<" "<<b<<" "<<M<<endl;\n return a+b.substr(M);\n }\n else\n {\n //cout<<b.substr(0,b.length()-M)+a.substr(M)<<endl;\n //cout<<b<<" "<<a<<" "<<M<<endl;\n return b+a.substr(M);\n }\n }\n \n \n string shortestSuperstring(vector<string>& A) {\n \n \n vector <string> collection = A;\n \n while(1){\n \n if(collection.size()==1)\n break;\n \n int maxSize = -1;\n \n int x = -1;\n int y = -1;\n \n string mystr;\n \n for(int i=0;i<collection.size();i++){\n for(int j=i+1;j<collection.size();j++){\n string f = collection[i];\n string s = collection[j];\n \n string ovl = GetOverLapping(f,s);\n \n int saved = f.length()+s.length() - ovl.length();\n \n //maxSize = max(maxSize, saved);\n \n if(saved > maxSize){\n maxSize = saved;\n x=i;\n y=j;\n \n mystr = ovl;\n }\n }\n }\n \n \n \n string str1 = collection[x];\n string str2 = collection[y];\n \n //cout<<str1<<" "<<str2<<endl;\n collection.erase(collection.begin()+min(x,y));\n collection.erase(collection.begin()+(max(x,y)-1));\n \n collection.push_back(mystr);\n /*\n for(auto x: collection)\n cout<<x<<" ";\n cout<<endl;\n */\n \n \n \n \n }\n return collection[0];\n \n }\n};\n``` | 1 | 2 | [] | 1 |
find-the-shortest-superstring | C++ easy to understand backtracking | c-easy-to-understand-backtracking-by-use-jft5 | \n// Time: O(M! * ML)\n// Algo: Backtracking\n// 50/72 tests passed, TLE\n\nclass Solution {\npublic:\n // M: Number of strigs\n // L : combined length o | user8531d | NORMAL | 2020-12-03T01:17:19.426381+00:00 | 2020-12-03T01:17:19.426412+00:00 | 543 | false | ```\n// Time: O(M! * ML)\n// Algo: Backtracking\n// 50/72 tests passed, TLE\n\nclass Solution {\npublic:\n // M: Number of strigs\n // L : combined length of all strings\n // Time: O(ML)\n string strCompress(vector<string>& svec) {\n string current = svec[0];\n \n // Find if the postfix of current string is common with prefix of next string\n for (int i = 0; i < svec.size() - 1; i++) {\n int clen = current.length();\n string next = svec[i + 1]; \n \n int j = 1;\n int max_overlap = 0;\n \n // Test for an overlap for all lengths starting 1\n while (j <= min(current.length(), next.length())) {\n string postfix = next.substr(0, j); \n string prefix = current.substr(clen - j, j);\n \n if (postfix.compare(prefix) != 0) {\n j++;\n continue;\n }\n \n max_overlap = max(max_overlap, j);\n j++;\n }\n \n if (max_overlap == 0) {\n current += next;\n continue;\n }\n \n current += next.substr(max_overlap);\n }\n \n return current;\n } \n\n \n void shortestSuperstringRec(vector<string>& A, string& result, vector<string>& svec, int idx, vector<bool>& visited) {\n if (svec.size() == A.size()) {\n string s = strCompress(svec);\n \n //cout << s << endl;\n \n if (result.length() == 0 || s.length() < result.length())\n result = s;\n \n return;\n }\n\n for (int i = 0; i < A.size(); i++) { \n if (visited[i] == true)\n continue;\n \n svec.push_back(A[i]);\n visited[i] = true;\n shortestSuperstringRec(A, result, svec, idx + 1, visited);\n // Backtrack\n svec.pop_back();\n visited[i] = false;\n }\n }\n \n string shortestSuperstring(vector<string>& A) {\n string result;\n int len = 0;\n vector<string> svec;\n vector<bool> visited(A.size(), false);\n \n if (A.size() == 1)\n result = A[0];\n \n if (A.size() < 2)\n return result;\n\n \n for (int i = 0; i < A.size(); i++)\n len += A[i].length();\n \n shortestSuperstringRec(A, result, svec, 0, visited);\n return result;\n }\n};\n``` | 1 | 0 | [] | 0 |
find-the-shortest-superstring | bla bla bla | bla-bla-bla-by-mrghasita-gy5n | \nWe may assume that no string in A is substring of another string in A.\n\nRead this carefully, or face TLE.\nWhat this means is that, cost of adding current s | mrghasita | NORMAL | 2020-12-02T09:16:13.804855+00:00 | 2020-12-02T09:16:13.804887+00:00 | 291 | false | ```\nWe may assume that no string in A is substring of another string in A.\n```\nRead this carefully, or face TLE.\nWhat this means is that, cost of adding current string only depend on previous string added not whole sequence. i.e previous path doesn\'t matter, only last city matters. | 1 | 1 | [] | 0 |
find-the-shortest-superstring | Python DP solution | python-dp-solution-by-xing_yi-casi | \nclass Solution:\n def shortestSuperstring(self, A: List[str]) -> str:\n \n def overlap_length(a, b):\n for i in range(1, len(a)):\ | xing_yi | NORMAL | 2020-08-08T23:04:57.650402+00:00 | 2020-08-08T23:04:57.650437+00:00 | 387 | false | ```\nclass Solution:\n def shortestSuperstring(self, A: List[str]) -> str:\n \n def overlap_length(a, b):\n for i in range(1, len(a)):\n aa = a[i:]\n ll = len(aa)\n bb = b[:ll]\n if aa == bb:\n return ll\n return 0\n \n N = len(A)\n \n g = collections.defaultdict(list)\n for i in range(N):\n for j in range(N):\n if i == j: continue\n g[i].append([j, overlap_length(A[i], A[j])])\n\n ret = \'a\' * (12 * 20 + 1)\n \n @functools.lru_cache(None)\n def dfs(idx, mask):\n nonlocal ret\n if mask == 2 ** N - 1:\n return A[idx] \n \n # Shortest of all possible strings\n` s = \'a\' * (12 * 20 + 1)\n for neigh, ovlp in g[idx]:\n if mask & (1 << neigh):\n continue\n s2 = dfs(neigh, mask | (1 << neigh))\n if len(s2) + len(A[idx]) - ovlp < len(s):\n s = A[idx][:len(A[idx])-ovlp] + s2\n return s\n\n for i in range(N):\n cur = dfs(i, 0 | (1 << i))\n if len(cur) < len(ret):\n ret = cur\n \n return ret\n``` | 1 | 0 | [] | 0 |
find-the-shortest-superstring | [Python] 80ms A* algorithm | python-80ms-a-algorithm-by-tommmyk253-0mhn | Using ordinary TSP DP solution will try out every possible permutation and this is very time-consuming.\nSo I decided to use A algorithm to achieve some pruning | tommmyk253 | NORMAL | 2020-07-11T00:28:12.865670+00:00 | 2020-07-11T00:28:12.865704+00:00 | 362 | false | Using ordinary TSP DP solution will try out every possible permutation and this is very time-consuming.\nSo I decided to use A* algorithm to achieve some pruning.\n\nModel the directed graph:\n1. node: a pair of state and last inserted string\'s index, as (state, last)\n2. edge: represent the number of characters need to be inserted from (state, last) to (state | new_last, new_last)\n3. goal: find the shortest path from (0, None) to (target, *)\n\nI use state compression to represent the usage of strings. For example, "0b\'1101" means I have used strings of index 0, 2 and 3.\n\nFor A* alogrithm, if the heuristic function is admissible, meaning that it never overestimates the actual cost to get to the goal, A* is guaranteed to return a least-cost path from start to goal. https://en.wikipedia.org/wiki/A*_search_algorithm\nTherefore, if we can come up with an underestimate heuristic function, we can ensure A* algorithm will return the answer we want.\n\nWe first calcualte the discount matrix, M[i][j] means how many more chatacters we need to insert A[j] after A[i]. For example, S[i] = "abcd" and S[j] = "abcdef", we only need to insert 2 more chatacters and M[i][j] = 2.\n\nAfter the calculation, we know the lowest number of chatacters for insertion for each string, and we use them as our heuristic function. More specifically, given a state, if a string has not yet been inserted, we add the lowest number of characters to our guess.\nThis heuristic function is guaranteed to not overestimate.\n\nThe remaining part is just implementing.\n\n```\nclass Solution:\n def calcuclate_discount_matrix(self, A):\n Trie = lambda : collections.defaultdict(Trie)\n M = []\n for i in range(len(A)):\n # construct suffix trie\n row, root = [], Trie()\n for j in range(len(A[i])):\n functools.reduce(dict.__getitem__, A[i][j:], root)[\'#\'] = True\n # calculate the discount\n for j in range(len(A)):\n if i == j:\n row.append(float(\'inf\'))\n continue\n word, discount, cur = A[j], 0, root\n for k in range(len(word)):\n if word[k] not in cur:\n break\n cur = cur[word[k]]\n if \'#\' in cur:\n discount = k + 1\n row.append(len(word) - discount)\n M.append(row)\n M.append(list(map(len, A)))\n return M\n \n def shortestSuperstring(self, A: List[str]) -> str:\n count = len(A)\n target = (1 << count) - 1\n \n M = self.calcuclate_discount_matrix(A)\n\n # an underestimate heuristic function\n # we estimate the cost from current state to the final target:\n # why underestimate? we choose every string\'s shortest version for concatenation.\n min_cost = [min(M[j][i] for j in range(count)) for i in range(count)]\n def heuristic(state):\n return sum(min_cost[i] for i in range(count) if state & (1 << i) == 0)\n\n seen = [[float(\'inf\')] * (1 + count) for _ in range(target + 1)]\n \n mini, sequence = float(\'inf\'), []\n prio = [(0, 0, 0, count, [])]\n while prio and prio[0][0] < mini:\n _, cost, state, last, seq = heapq.heappop(prio)\n \n if seen[state][last] <= cost:\n continue\n seen[state][last] = cost\n \n if state == target:\n if mini > cost:\n mini, sequence = cost, seq\n continue\n \n costs = M[last]\n for i in range(count):\n mask = 1 << i\n if state & mask == 0:\n total = cost + costs[i] + heuristic(state | mask)\n if total < seen[state | mask][i]:\n heapq.heappush(prio, (total, cost + costs[i], state | mask, i, seq + [i]))\n \n # reconstruct the answer\n answer, state, last = [], 0, count\n for nex in sequence:\n answer.append(A[nex][(len(A[nex]) - M[last][nex]):])\n state, last = state | (1 << nex), nex\n \n return \'\'.join(answer)\n\n\t# this part is just the ordinary TSP DP solution, 1100ms\n def shortestSuperstring_DP_TSP(self, A: List[str]) -> str:\n count = len(A)\n target = (1 << count) - 1\n \n M = []\n for i in range(count):\n a, row = A[i], []\n for j in range(count):\n if i == j:\n row.append(float(\'inf\'))\n continue\n b = A[j]\n for k in range(len(b), -1, -1):\n if a.endswith(b[:k]):\n row.append(len(b) - k)\n break\n M.append(row)\n\n M.append(list(map(len, A)))\n path = [[float(\'inf\')] * (1 + count) for _ in range(target + 1)]\n DP = [[float(\'inf\')] * (1 + count) for _ in range(target + 1)]\n DP[-1] = [0] * count\n\n for state in range(target - 1, -1, -1):\n for last in range(count + 1):\n nex, costs = -1, M[last]\n for i in range(count):\n mask = 1 << i\n if state & mask == 0:\n t = costs[i] + DP[state | mask][i]\n if t < DP[state][last]:\n nex, DP[state][last] = i, t\n path[state][last] = nex \n \n# path = {}\n# functools.lru_cache(None)\n# def helper(state, last):\n# if state == target:\n# return 0\n \n# nex, answer, costs = None, float(\'inf\'), M[last]\n# for i in range(count):\n# mask = 1 << i\n# if state & mask == 0:\n# t = costs[i] + helper(state | mask, i)\n# if t < answer:\n# nex, answer = i, t\n# path[(state, last)] = nex\n# return answer\n# helper(0, count)\n \n answer, state, last = [], 0, count\n for _ in range(count):\n nex = path[state][last]\n answer.append(A[nex][(len(A[nex]) - M[last][nex]):])\n state, last = state | (1 << nex), nex\n \n return \'\'.join(answer)\n``` | 1 | 0 | [] | 0 |
find-the-shortest-superstring | (Easy to understand) Python - Recursion + Bitmask cache + overlaps | easy-to-understand-python-recursion-bitm-44wz | There are 3 key ideas in this solution.\n\n1. calculate overlap for each string concatenation, since we don\'t need to merge two full string to make a string co | ecsca | NORMAL | 2020-07-01T02:16:10.248725+00:00 | 2020-07-01T02:17:01.964039+00:00 | 464 | false | There are 3 key ideas in this solution.\n\n1. calculate overlap for each string concatenation, since we don\'t need to merge two full string to make a string contains both as a substring.\n\tex) "abcd", "cde" -> "abcde" contains both as a substring.\n\n2. We are going to use recursion to build every possible cases. What we need for the recursion are, \n\t1. list of remaining words, \n\t2. the index of the last word we used in the last step (to get the overlap)\n\n3. To keep list of remaining words, there are several ways to do so, but we are going to use bitmask. This will make us easy to cache them, and also save our time to build new list in every recursion call\n\tex) If we use "list" as a parameter of recursion, we should use `new_words = words[:i] + words[i+1:] `\n\t we can make it with `new_bits = bits - (1<<i)`\nIn our bit mask, `(bits & (1<<i)) == 1 ` means, A[i] is still remaining\n\n4. We can cache partial result, since our recursion function will calculate the optimized result for (remaining_words, last_word_idx). Since we used bitmask for remaining_words, we can use (bitmask: int, last_word_idx: int) tuple as a key\n\tex) If len(A) == 10, and there are 4 remaining words, ended with A[5], This result will be used 5! times. \n\tBecause available prefix should be made with used 6strings, and must be ended with A[5], still we need to make a line with 5 other used strings, # of cases are 5!\n\n\n\n```class Solution(object):\n def shortestSuperstring(self, A):\n self.overlaps = [[0 for _ in range(len(A))] for _ in range(len(A))]\n for i in range(len(A)):\n for j in range(len(A)):\n if i == j: continue\n x, y = A[i], A[j]\n for count in range(min(len(x), len(y)), -1, -1):\n if x.endswith(y[:count]):\n self.overlaps[i][j] = count\n break\n self.words = A\n self.cache = {}\n wordsbit = (1 << len(A))-1\n return self.helper(wordsbit, -1)\n \n def helper(self, wordsbit, last_word_idx):\n if not wordsbit:\n return \'\'\n key = (wordsbit, last_word_idx)\n if key in self.cache:\n return self.cache[key]\n words = []\n for i in range(len(self.words)):\n if (wordsbit>>i) & 1 == 1:\n words.append((i, self.words[i]))\n \n local_res = None\n for idx, word in words:\n append_idx = 0\n if last_word_idx != -1:\n append_idx = self.overlaps[last_word_idx][idx]\n new_bit = wordsbit - (1 << idx)\n child_res = self.helper(new_bit, idx)\n new_res = word[append_idx:] + child_res\n if not local_res or len(local_res) > len(new_res):\n local_res = new_res\n self.cache[key] = local_res\n return local_res | 1 | 0 | ['Recursion', 'Python'] | 0 |
find-the-shortest-superstring | C++ TSP Solution !!! | c-tsp-solution-by-kylewzk-8wv3 | \n string shortestSuperstring(vector<string>& A) {\n int N = A.size();\n vector<vector<int>> dp(1<<N, vector<int>(N, -1)), parent(1<<N, vector< | kylewzk | NORMAL | 2020-02-29T14:23:53.386305+00:00 | 2020-02-29T14:23:53.386357+00:00 | 421 | false | ```\n string shortestSuperstring(vector<string>& A) {\n int N = A.size();\n vector<vector<int>> dp(1<<N, vector<int>(N, -1)), parent(1<<N, vector<int>(N, -1)) , dist(N, vector<int>(N, 0));\n \n for(int i = 0; i < N; i++) {\n for(int j = 0; j < N; j++) {\n if(i == j) continue;\n for(int k = 0; k < A[i].length(); k++) {\n if(A[j].find(A[i].substr(k)) == 0) {\n dist[i][j] = A[i].length()-k;\n break;\n }\n }\n }\n }\n \n for(int i = 0; i < N; i++) dp[1<<i][i] = 0;\n \n int last = -1, total = -1;\n for(int mask = 0; mask < (1 << N); mask++) {\n for(int i = 0; i < N; i++) {\n if(((mask >> i)&1) == 0) continue;\n int pmask = mask ^ (1 << i);\n for(int j = 0; j < N; j++) {\n if((pmask >> j)&1 == 0) continue;\n \n if(dp[pmask][j] != -1 && dp[mask][i] < dp[pmask][j] + dist[j][i]) {\n dp[mask][i] = dp[pmask][j] + dist[j][i];\n parent[mask][i] = j;\n }\n }\n \n if(mask == (1 << N)-1 && dp[mask][i] > total) {\n total = dp[mask][i];\n last = i;\n }\n }\n }\n\n int cur = (1 << N)-1;\n vector<int> path;\n while(cur != 0) {\n path.push_back(last);\n int prev = cur ^ (1 << last);\n last = parent[cur][last];\n cur = prev;\n }\n \n reverse(path.begin(), path.end());\n string res = A[path[0]];\n for(int i = 1; i < path.size(); i++) {\n res += A[path[i]].substr(dist[path[i-1]][path[i]]);\n }\n return res;\n }\n``` | 1 | 0 | [] | 0 |
find-the-shortest-superstring | Just for whom looking for a C# solution | just-for-whom-looking-for-a-c-solution-b-k6rz | \n\npublic class Solution {\n public string ShortestSuperstring(string[] A) {\n int n = A.Length;\n int[,] graph = new int[n, n];\n \n | flyingingray | NORMAL | 2019-12-14T21:24:17.724772+00:00 | 2019-12-14T21:24:17.724806+00:00 | 182 | false | ```\n\npublic class Solution {\n public string ShortestSuperstring(string[] A) {\n int n = A.Length;\n int[,] graph = new int[n, n];\n \n // build the graph\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < n; j++) {\n graph[i, j] = calc(A[i], A[j]);\n graph[j, i] = calc(A[j], A[i]);\n }\n }\n \n int[,] dp = new int[1 << n, n];\n int[,] path = new int[1 << n, n];\n int last = -1, min = int.MaxValue;\n\t\t\n // start TSP DP\n for (int i = 1; i < (1 << n); i++) {\n for (int j = 0; j < n; j++) {\n dp[i, j] = int.MaxValue;\n if ((i & (1 << j)) > 0) {\n int prev = i - (1 << j);\n if (prev == 0) {\n dp[i, j] = A[j].Length;\n } else {\n for (int k = 0; k < n; k++) {\n if (dp[prev, k] < int.MaxValue && dp[prev, k] + graph[k, j] < dp[i, j]) {\n dp[i, j] = dp[prev, k] + graph[k, j];\n path[i, j] = k;\n }\n }\n }\n }\n if (i == (1 << n) - 1 && dp[i, j] < min) {\n min = dp[i, j];\n last = j;\n }\n }\n }\n \n // build the path\n StringBuilder sb = new StringBuilder();\n int cur = (1 << n) - 1;\n var stack = new Stack<int>();\n while (cur > 0) {\n stack.Push(last);\n int temp = cur;\n cur -= (1 << last);\n last = path[temp, last];\n }\n\t\t\n // build the result\n int l = stack.Pop();\n sb.Append(A[l]);\n while (stack.Any()) {\n int j = stack.Pop();\n sb.Append(A[j].Substring(A[j].Length - graph[l, j]));\n l = j;\n }\n \n return sb.ToString();\n }\n \n private int calc(string a, string b) {\n for (int i = 1; i < a.Length; i++) {\n if (b.StartsWith(a.Substring(i))) {\n return b.Length - a.Length + i;\n }\n }\n return b.Length;\n }\n}\n\n``` | 1 | 0 | [] | 0 |
find-the-shortest-superstring | Python TSP, straightforward DP by using Bellman-Held-Karp algorithm | python-tsp-straightforward-dp-by-using-b-jvzb | Implement a straightforward Bellman\u2013Held\u2013Karp algorithm.\nIf we have A, B, C, D\nall the path contains 4 elements and ends with D can be written as:\n | liketheflower | NORMAL | 2019-11-27T18:28:50.325240+00:00 | 2019-11-27T19:42:18.794870+00:00 | 2,469 | false | Implement a straightforward Bellman\u2013Held\u2013Karp algorithm.\nIf we have A, B, C, D\nall the path contains 4 elements and ends with D can be written as:\n{A,B,C,D} ends with D\nIt can be generated from\n{A,B,C} ends with A + AD\n{A,B,C} ends with B + BD\n{A,B,C} ends with C+ CD\nPick up the path which has the minimum length. This is the critical part of Bellman\u2013Held\u2013Karp algorithm.\nThen comes this solution. I am using (A, B, C) + (A, ) to encode {A,B,C} ends with A\n```python\nfrom functools import lru_cache\nclass Solution:\n def shortestSuperstring(self, A: List[str]) -> str:\n # TSP, DP \n n = len(A)\n w = [[0] * n for _ in range(n)]\n for i in range(n):\n for j in range(n):\n for k in range(min(len(A[i]), len(A[j])), 0, -1):\n if A[j].startswith(A[i][-k:]):\n w[i][j] = k\n break\n @lru_cache(None)\n def dp(nodes):\n if len(nodes) == 2:return A[nodes[0]]\n end = nodes[-1]\n end_idx = nodes.index(end) \n # remove the current ending nodes from nodes[:-1]\n nodes_wo_end = nodes[:end_idx]+nodes[end_idx+1:-1]\n # A[end][w[node][end]:] will remove overlap part from the end node.\n return min((dp(nodes_wo_end +(node, ))+A[end][w[node][end]:]\n for node in nodes_wo_end), key=len)\n return min((dp(tuple(range(n))+(node, )) for node in range(n)), key=len)\n```\nDetail analysis is given here. \nhttps://medium.com/@jim.morris.shen/are-you-read-for-solving-the-traveling-salesman-problem-80e3c4ea45fc?source=friends_link&sk=b28ea8888460935401ae02f800d6ccd8\nPart of the code is using the reference here:\nhttps://leetcode.com/problems/find-the-shortest-superstring/discuss/195077/Clean-python-DP-with-explanations\n\nThanks. | 1 | 0 | [] | 0 |
find-the-shortest-superstring | Modularized Travelling Salesman Problem Solution | modularized-travelling-salesman-problem-2w5r6 | Learned from Travelling Salesman Problem\n\nclass Solution {\n public String shortestSuperstring(String[] A) {\n int n = A.length;\n int[][] gr | lxhq | NORMAL | 2019-09-05T16:36:56.588499+00:00 | 2019-09-05T16:36:56.588536+00:00 | 1,259 | false | Learned from [Travelling Salesman Problem](https://www.youtube.com/watch?v=cY4HiiFHO1o)\n```\nclass Solution {\n public String shortestSuperstring(String[] A) {\n int n = A.length;\n int[][] graph = new int[n][n];\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < n; j++) {\n graph[i][j] = calWordDistance(A[i], A[j]);\n }\n }\n int[][] dp = new int[n][1 << n];\n setUp(graph, dp, n, A);\n solve(graph, dp, n);\n int[] tour = findOptimalTour(graph, dp, n);\n StringBuilder sb = new StringBuilder();\n merage(sb, tour, graph, A);\n return sb.toString();\n }\n \n private void setUp(int[][] graph, int[][] dp, int n, String[] A) {\n for (int start = 0; start < n; start++) {\n dp[start][1 << start] = A[start].length();\n }\n }\n \n private void solve(int[][] graph, int[][] dp, int n) {\n for (int r = 2; r <= n; r++) {\n List<Integer> list = combination(r, n);\n for (int subset : list) {\n for (int next = 0; next < n; next++) {\n if (notIn(next, subset)) continue;\n int state = (1 << next) ^ subset;\n int minDist = Integer.MAX_VALUE;\n for (int end = 0; end < n; end++) {\n if (end == next || notIn(end, subset)) continue;\n int newDist = dp[end][state] + graph[end][next];\n if (newDist < minDist) {\n minDist = newDist;\n }\n }\n dp[next][subset] = minDist;\n }\n }\n }\n }\n \n private int findMinCost(int[][] graph, int[][] dp, int n) {\n int endState = (1 << n) - 1;\n int minTourCost = Integer.MAX_VALUE;\n for (int end = 0; end < n; end++) {\n int tourCost = dp[end][endState];\n if (tourCost < minTourCost) {\n minTourCost = tourCost;\n }\n }\n return minTourCost;\n }\n \n private int[] findOptimalTour(int[][] graph, int[][] dp, int n) {\n int endState = (1 << n) - 1;\n int minTourCost = Integer.MAX_VALUE;\n int lastIndex = -1;\n for (int end = 0; end < n; end++) {\n int tourCost = dp[end][endState];\n if (tourCost < minTourCost) {\n minTourCost = tourCost;\n lastIndex = end;\n }\n }\n int[] tour = new int[n];\n tour[n - 1] = lastIndex;\n int state = ((1 << n) - 1) ^ (1 << lastIndex);\n for (int i = n - 2; i >= 0; i--) {\n int index = -1;\n for (int j = 0; j < n; j++) {\n if (notIn(j, state)) continue;\n if (index == -1) index = j;\n int prevDist = dp[index][state] + graph[index][lastIndex];\n int newDist = dp[j][state] + graph[j][lastIndex];\n if (newDist < prevDist) {\n index = j;\n }\n }\n tour[i] = index;\n state = state ^ (1 << index);\n lastIndex = index;\n }\n return tour;\n }\n \n private List<Integer> combination(int r, int n) {\n List<Integer> res = new ArrayList<>();\n combination(res, r, n, 0, 0);\n return res;\n }\n \n private void combination(List<Integer> res, int r, int n, int pos, int temp) {\n if (r == 0) {\n res.add(temp);\n return;\n }\n for (int i = pos; i < n; i++) {\n temp = temp | (1 << i);\n combination(res, r - 1, n, i + 1, temp);\n temp = temp & ~(1 << i);\n }\n }\n \n private boolean notIn(int i, int subset) {\n return (subset & (1 << i)) == 0;\n }\n private int calWordDistance(String a, String b) {\n for (int i = 0; i < a.length(); i++) {\n if (b.startsWith(a.substring(i))) {\n return b.length() - (a.length() - i); //a == ga b == ab -> gab i == 1 dis = 2 - (2 - 1);\n }\n }\n return b.length();\n }\n\n private void merage(StringBuilder sb, int[] tour, int[][] graph, String[] A) {\n int lastIndex = -1;\n for (int i : tour) {\n if (lastIndex == -1) {\n sb.append(A[i]);\n } else {\n int len = A[i].length();\n int dis = graph[lastIndex][i];\n sb.append(A[i].substring(len - dis));\n }\n lastIndex = i;\n }\n }\n}\n``` | 1 | 0 | [] | 0 |
find-the-shortest-superstring | c++ easy to understand with recursion and greedy approach | c-easy-to-understand-with-recursion-and-98iz1 | ```\nclass Solution {\n std::vector res;\npublic:\n string shortestSuperstring(vector& arr) {\n shortestSuperstringH(arr, arr.size());\n int | afflatus | NORMAL | 2019-02-23T17:57:41.376852+00:00 | 2019-02-23T17:57:41.376918+00:00 | 482 | false | ```\nclass Solution {\n std::vector<string> res;\npublic:\n string shortestSuperstring(vector<string>& arr) {\n shortestSuperstringH(arr, arr.size());\n int m = INT_MAX;\n int ind;\n for(int i=0;i<res.size();i++){\n if(res[i].size() < m){\n ind = i;\n m = res[i].size();\n }\n }\n \n return res[ind];\n \n }\n \n void shortestSuperstringH(vector<string> arr, int n) {\n \t\n if (n == 1)\n {\n res.push_back(arr[0]);\n\n }else{\n // to store maximum overlap\n int max = INT_MIN;\n\n // to store array index of strings involved in maximum overlap\n int p, q;\n\n // to store resultant string after maximum overlap\n vector<string> res_str;\n \n for (int i = 0; i < n; i++)\n {\n for (int j = i + 1; j < n; j++)\n {\n vector<string> str;\n\n // r will store maximum length of the matching prefix and\n // suffix. str is passed by reference and store the result\n // string after maximum overlap of arr[i] and arr[j], if any\n int r = findOverlappingPair(arr[i], arr[j], str);\n\n // check for maximum overlap\n if (max < r)\n {\n max = r;\n res_str = str;\n p = i, q = j;\n }\n else if( max == r){\n if(str.size() < res_str.size()){\n res_str = str;\n p = i, q = j;\n }\n \n }\n\n }\n }\n\n \n // ignore last element in next cycle\n n--;\n\n // if no overlap, append arr[n] to arr[0]\n if (max == INT_MIN){\n arr[0] += arr[n];\n shortestSuperstringH(arr, n);\n }\n else\n {\n for(auto item:res_str){\n // copy resultant string to index p\n \n arr[p] = item;\n // copy string at last index to index q\n arr[q] = arr[n];\n shortestSuperstringH(arr, n);\n }\n }\n }\n \n }\n \n int findOverlappingPair(string& s1, string& s2, vector<string>& str){\n //compare s1 suffic and s2 prefix\n int max = INT_MIN;\n int m = s1.length();\n int n = s2.length();\n\n // check suffix of s1 matches with prefix of s2\n for (int i = 1; i <= min(m, n); i++)\n {\n // compare last i characters in s1 with first i characters in s2\n if (s1.compare(m - i, i, s2, 0, i) == 0)\n {\n if (max < i)\n {\n //update max and str\n max = i;\n str.push_back({s1 + s2.substr(i)});\n }\n }\n }\n\n // check prefix of s1 matches with suffix of s2\n for (int i = 1; i <= min(m, n); i++)\n {\n // compare first i characters in s1 with last i characters in s2\n if (s1.compare(0, i, s2, n - i, i) == 0)\n {\n if (max <= i)\n {\n //update max and str\n max = i;\n str.push_back({s2 + s1.substr(i)});\n }\n }\n }\n\n return max;\n }\n}; | 1 | 1 | [] | 1 |
find-the-shortest-superstring | A slow but easy to understand Python solution | a-slow-but-easy-to-understand-python-sol-1l8d | \nfrom functools import lru_cache\nfrom typing import *\n\nclass Solution:\n def shortestSuperstring(self, strings: List[str]) -> str:\n """\n | senmenty | NORMAL | 2019-02-06T22:58:55.661004+00:00 | 2019-02-06T22:58:55.661047+00:00 | 319 | false | ```\nfrom functools import lru_cache\nfrom typing import *\n\nclass Solution:\n def shortestSuperstring(self, strings: List[str]) -> str:\n """\n Dynamic programming\n \n Reduce the problem of find the best concatenation for [1, 2, 3] to:\n - Choose 1 and recurse on [2, 3], and put 1 at the start or at the end of this sub-solution\n - Choose 2 and recurse on [1, 3], and put 2 at the start or at the end of this sub-solution\n - Etc\n """\n \n def concat(s1, s2):\n l = min(len(s1), len(s2))\n for i in reversed(range(1, l+1)):\n if s1.endswith(s2[:i]):\n return s1 + s2[i:]\n return s1 + s2\n \n @lru_cache(maxsize=None)\n def visit(visited): \n best_score = float(\'inf\')\n best_suffix = ""\n \n for i, s in enumerate(strings):\n if not (1 << i) & visited: \n sub_suffix = visit((1 << i) | visited)\n \n suffix = concat(s, sub_suffix)\n if len(suffix) < best_score:\n best_score = len(suffix)\n best_suffix = suffix\n \n suffix = concat(sub_suffix, s)\n if len(suffix) < best_score:\n best_score = len(suffix)\n best_suffix = suffix\n \n return best_suffix\n \n best_solution = visit(0)\n return best_solution\n``` | 1 | 0 | [] | 0 |
find-the-shortest-superstring | C++ Bottom up DP + KMP 20ms | c-bottom-up-dp-kmp-20ms-by-firejox-1sf5 | \nclass Solution {\n static int dp[4096][12];\n static int failure[12][20];\n static int cost[12][12];\n static int trace_table[4096][12];\n \npu | firejox | NORMAL | 2019-01-28T10:37:20.381051+00:00 | 2019-01-28T10:37:20.381121+00:00 | 354 | false | ```\nclass Solution {\n static int dp[4096][12];\n static int failure[12][20];\n static int cost[12][12];\n static int trace_table[4096][12];\n \npublic:\n string shortestSuperstring(vector<string>& A) {\n const int sz = A.size();\n const int dp_sz = 1 << sz;\n \n std::fill(&dp[0][0], std::next(&dp[0][0], sizeof(dp)), 0);\n \n // compute the failure table for each string\n for (int i = 0; i < sz; i++) {\n const int str_sz = A[i].size();\n \n failure[i][0] = -1;\n \n for (int j = 1, k = -1; j < str_sz; j++) {\n while (k >= 0 && A[i][k + 1] != A[i][j])\n k = failure[i][k];\n \n if (A[i][k + 1] == A[i][j]) k++;\n \n failure[i][j] = k;\n }\n }\n \n // compute the append cost\n for (int i = 0; i < sz; i++) {\n const int i_sz = A[i].size();\n \n for (int j = 0; j < sz; j++) {\n if (i != j) {\n const int j_sz = A[j].size();\n int h = -1;\n \n for (int k = 0; k < j_sz; k++) {\n while (h >= 0 && A[i][h + 1] != A[j][k])\n h = failure[i][h];\n \n if (A[i][h + 1] == A[j][k])\n h++;\n }\n \n cost[j][i] = i_sz - h - 1;\n }\n }\n }\n \n // process bottom-up DP\n for (int i = 0; i < sz; i++)\n dp[1 << i][i] = A[i].size();\n \n for (int state = 1; state < dp_sz; state++) {\n for (int t1 = state, b1 = t1 & (-t1); t1 ; t1 ^= b1 , b1 = t1 & (-t1)) {\n const int state1 = state ^ b1;\n const int i = __builtin_ctz(b1);\n const int i_sz = A[i].size();\n \n for (int t2 = state1, b2 = t2 & (-t2); t2; t2 ^= b2, b2 = t2 & (-t2)) { \n const int j = __builtin_ctz(b2);\n const int tmp = dp[state1][j] + cost[j][i];\n \n if (!dp[state][i] || tmp < dp[state][i]) {\n dp[state][i] = tmp;\n trace_table[state][i] = j;\n }\n }\n }\n }\n \n const auto last = dp[dp_sz - 1];\n string res;\n \n int i = std::distance(last, std::min_element(last, last + sz));\n \n for (int state = dp_sz - 1, j = trace_table[state][i]; state & (state - 1); state ^= (1 << i), i = j, j = trace_table[state][i])\n res = A[i].substr(A[i].size() - cost[j][i]) + res;\n \n return A[i] + res;\n }\n};\n\nint Solution::dp[4096][12];\nint Solution::failure[12][20];\nint Solution::cost[12][12];\nint Solution::trace_table[4096][12];\n``` | 1 | 0 | [] | 0 |
find-the-shortest-superstring | BFS Solution with explanation | bfs-solution-with-explanation-by-zhassan-jzn6 | The problem is just a slight modification of the Find Shortest Path Visiting All Nodes problem. \nBelow are some thoughts that led me to that solution:\n Findin | zhassanb | NORMAL | 2018-11-19T00:42:10.642979+00:00 | 2018-11-19T00:42:10.643022+00:00 | 479 | false | The problem is just a slight modification of the [Find Shortest Path Visiting All Nodes](https://leetcode.com/problems/shortest-path-visiting-all-nodes/) problem. \nBelow are some thoughts that led me to that solution:\n* Finding the worst, but correct, superstring is easy, just concatenate all the strings. \n* Let\'s assume we have just two strings **a** and **b**. What is the shortest superstring containing both of them? It depends on the order in which the strings should be merged. Let\'s call **c_ab** the suffix of **a** which is also a prefix of **b**, and **c_ba** on the contrary the suffix of **b** which is also a prefix of **a**. If **c_ab** is shorter than **c_ba** then the shortest superstring of **a** and **b** is **a+(b - c_ab)**, else it is **b+(a-c_ba)**.\n* The problem is in general about the right order of merging all the strings, so that the total superstring is shortest possible. That idea sounds much like the problem I provided link to above. The only thing left is to define weight, which is straightforward. Referring to the idea above the weight going from string **a** to string **b** would be length of **(b - c_ab)** and so on.\n\n\n```\nclass Solution {\n public String shortestSuperstring(String[] A) {\n if(A == null || A.length == 0) return "";\n \n int weights[][] = new int[A.length][A.length];\n \n for(int i = 0;i<A.length;i++) {\n for(int j = i+1;j<A.length;j++) {\n weights[i][j] = getWeight(A[i], A[j]);\n weights[j][i] = getWeight(A[j], A[i]);\n }\n }\n \n return concatSmart(A, weights);\n }\n \n String concatSmart(String [] A, int [][] weights) {\n \n int memo[][] = new int[A.length][1<<A.length];\n \n Queue<Pair> bfs = new PriorityQueue<>(new Comparator<Pair>() {\n @Override\n public int compare(Pair a, Pair b) {\n return Integer.compare(a.weight, b.weight);\n }\n });\n \n for(int [] row:memo) Arrays.fill(row, Integer.MAX_VALUE);\n \n for(int i = 0;i<A.length;i++) {\n bfs.add(new Pair(A[i], i, A[i].length(), 1<<i));\n memo[i][1<<i] = A[i].length();\n }\n \n while(!bfs.isEmpty()) {\n Pair node = bfs.poll();\n \n if(node.mask == memo[node.index].length-1) return node.str;\n \n for(int i = 0;i<A.length;i++) {\n int newMask = node.mask | (1<<i);\n if(newMask != node.mask && memo[i][newMask] > memo[node.index][node.mask]+weights[node.index][i]) {\n bfs.add(new Pair(concat(node.str, A[i], weights[node.index][i]), i, node.weight+weights[node.index][i], newMask));\n memo[i][newMask] = node.weight+weights[node.index][i];\n }\n }\n }\n \n throw null;\n }\n \n \n \n String concat(String a, String b, int commonPartLength) {\n return a + b.substring(b.length()-commonPartLength, b.length());\n }\n \n int getWeight(String a, String b) {\n String kmpStr = b+"#"+a;\n int kmp [] = new int[kmpStr.length()];\n \n int k = 1;\n for(int i = 1;i<kmpStr.length();i++) {\n int j = kmp[i-1]; \n while(j != 0 && kmpStr.charAt(i) != kmpStr.charAt(j)) {\n j = kmp[j-1];\n }\n if(kmpStr.charAt(i) == kmpStr.charAt(j)) {\n ++j;\n }\n kmp[i] = j;\n }\n \n int x = kmp[kmp.length-1];\n \n return b.length() - x;\n }\n \n String join(String [] A) {\n StringBuilder res = new StringBuilder();\n for(String str:A) res.append(str);\n return res.toString();\n } \n \n class Pair {\n String str;\n int index;\n int weight;\n int mask;\n \n public Pair(String str, int index, int weight, int mask) {\n this.str = str;\n this.index = index;\n this.weight = weight;\n this.mask = mask;\n }\n }\n}\n``` | 1 | 0 | [] | 0 |
find-the-shortest-superstring | JavaScript Greedy Solution with clean explaination | javascript-greedy-solution-with-clean-ex-fq93 | \nvar shortestSuperstring = function(arr) {\n while (arr.length > 1) {\n let maxCommonLength = 0;\n let maxCommonString = arr[0] + arr[1];\n let maxCo | zidianlyu | NORMAL | 2018-11-18T08:10:45.402898+00:00 | 2018-11-18T08:10:45.402971+00:00 | 370 | false | ```\nvar shortestSuperstring = function(arr) {\n while (arr.length > 1) {\n let maxCommonLength = 0;\n let maxCommonString = arr[0] + arr[1];\n let maxCommonWords = [arr[0], arr[1]];\n for (let i = 0; i < arr.length - 1; i++) {\n for (let j = i + 1; j < arr.length; j++) {\n const {commonLength, commonString} = checkCommonPair(arr[i], arr[j])\n /**\n * Updates only when find a common string and the common length is not\n * less than the max common length.\n */\n if (commonString && commonLength >= maxCommonLength) {\n maxCommonLength = commonLength;\n maxCommonString = commonString;\n maxCommonWords = [arr[i], arr[j]];\n }\n }\n }\n /** Removes the checked word. */\n arr = arr.filter(word => word !== maxCommonWords[0] &&\n word !== maxCommonWords[1]);\n /** Adds the ideal common string at the head. */\n arr.unshift(maxCommonString);\n }\n return arr[0];\n};\n\n/** Checks the length and pair string of the pair. */\nvar checkCommonPair = function(s1, s2) {\n let maxCommonLength = 0;\n let commonString = \'\';\n /** Makes sure s1 is always the shorter one. */\n if (s1.length > s2.length) s1, s2 = s2, s1;\n\n /** Checks s1 suffix and s2 prefix. */\n for (let stringLength = 1; stringLength < s1.length; stringLength++) {\n const s1Suffix = s1.substring(s1.length - stringLength);\n const s2Prefix = s2.substring(0, stringLength);\n if (s1Suffix === s2Prefix && stringLength > maxCommonLength) {\n maxCommonLength = stringLength;\n commonString = s1 + s2.substring(stringLength);\n }\n }\n\n /** Checks s1 prefix and s2 suffix. */\n for (let stringLength = 1; stringLength < s1.length; stringLength++) {\n const s1Prefix = s1.substring(0, stringLength);\n const s2Suffix = s2.substring(s2.length - stringLength);\n if (s1Prefix === s2Suffix && stringLength > maxCommonLength) {\n if (stringLength > maxCommonLength) {\n maxCommonLength = stringLength;\n commonString = s2 + s1.substring(stringLength);\n }\n }\n }\n\n return {\n commonLength: maxCommonLength,\n commonString,\n };\n}\n``` | 1 | 0 | [] | 0 |
find-the-shortest-superstring | Complete search (DFS) with simple prunning | complete-search-dfs-with-simple-prunning-y5fe | Straightforward DFS with the following simple prunning strategy: for every string s we pre-calculate the length of the longest possible overlap between s and an | blackskygg | NORMAL | 2018-11-18T08:09:11.289589+00:00 | 2018-11-18T08:09:11.289633+00:00 | 554 | false | Straightforward DFS with the following simple prunning strategy: for every string `s` we pre-calculate the length of the longest possible overlap between `s` and any other strings. Then for every possible subset `A\'`of A, we could use the sum of the precalculated lengths as an upperbound to the total overlaps that can be obtained by combining all the strings in `A\'`. Using this upperbound, we could give up early on many branches. \n```\nclass Solution {\npublic:\n string shortestSuperstring(vector<string>& A) {\n g.assign(A.size(), vector<int>(A.size(), 0));\n max_points.assign(A.size(), 0);\n \n for (int i = 0; i < A.size(); ++i) {\n for (int j = 0; j < A.size(); ++j) {\n if (i == j) {\n continue;\n }\n int max_len = min(A[i].size(), A[j].size());\n for (int t = 1; t <= max_len; ++t) {\n if (std::equal(A[i].begin()+A[i].size()-t, A[i].end(), A[j].begin())) {\n g[i][j] = t;\n }\n }\n max_points[i] = max(max_points[i], g[i][j]);\n max_points[j] = max(max_points[j], g[i][j]);\n }\n }\n \n for (int i = 0; i < A.size(); ++i) {\n unused.insert(i);\n }\n for (int u = 0; u < A.size(); ++u) {\n unused.erase(u);\n path.push_back(u);\n dfs();\n path.pop_back();\n unused.insert(u);\n }\n string res = A[max_path[0]];\n for (int i = 1; i < max_path.size(); ++i) {\n res += A[max_path[i]].substr(g[max_path[i-1]][max_path[i]]); \n }\n return res;\n } \nprivate:\n void dfs() {\n if (unused.size() == 0) {\n if (sum >= max_sum) {\n max_sum = sum;\n max_path = path;\n }\n return;\n }\n \n std::vector<int> un;\n int mp = 0;\n for (auto u : unused) {\n un.push_back(u);\n mp += max_points[u];\n }\n if (mp + sum < max_sum) {\n return; // cut\n }\n \n int prev = path.back();\n for (auto u: un) {\n unused.erase(u);\n path.push_back(u);\n sum += g[prev][u];\n dfs();\n sum -= g[prev][u];\n path.pop_back();\n unused.insert(u);\n }\n }\n \nprivate:\n vector<vector<int>> g;\n \n vector<int> max_points;\n unordered_set<int> unused;\n int sum = 0;\n vector<int> path;\n vector<int> max_path;\n int max_sum = 0;\n};\n``` | 1 | 0 | [] | 0 |
find-the-shortest-superstring | Simple Java Solution Greedy [Approximation Only, DP is the complete solution] | simple-java-solution-greedy-approximatio-x1ql | ```\nimport java.util.*;\n\nclass Solution {\n private Map.Entry maxOverlap(String a, String b) {\n int len = Math.min(a.length(), b.length());\n int max | mo0000 | NORMAL | 2018-11-18T04:38:18.058681+00:00 | 2018-11-18T04:38:18.058726+00:00 | 639 | false | ```\nimport java.util.*;\n\nclass Solution {\n private Map.Entry<Integer, String> maxOverlap(String a, String b) {\n int len = Math.min(a.length(), b.length());\n int max = -1;\n String s = a + b;\n for (int i = len; i > 0; i--) {\n String right = b.substring(0, i);\n if(a.endsWith(right)) {\n max = right.length();\n s = a + b.substring(max);\n break;\n }\n }\n\n for (int i = len; i > 0; i--) {\n String right = a.substring(0, i);\n if(b.endsWith(right)) {\n if(right.length() > max) {\n max = right.length();\n s = b + a.substring(max);\n }\n break;\n }\n }\n return new AbstractMap.SimpleEntry<>(max, s);\n }\n\n public String shortestSuperstring(String[] A) {\n if(A.length == 1) return A[0];\n List<String> list = new ArrayList<>();\n Collections.addAll(list, A);\n while(list.size() > 1) {\n String s = list.get(0) + list.get(1);\n int max = -1;\n int l=0, r=1;\n for (int i = 0; i < list.size(); i++) {\n for (int j = i+1; j < list.size(); j++) {\n String left = list.get(i);\n String right = list.get(j);\n Map.Entry<Integer, String> entry = maxOverlap(list.get(i), list.get(j));\n if(entry.getKey() > max) {\n max = entry.getKey();\n s = entry.getValue();\n l = i;\n r = j;\n }\n }\n }\n list.remove(r);\n list.remove(l);\n list.add(s);\n }\n return list.get(0);\n }\n} | 1 | 1 | [] | 4 |
find-the-shortest-superstring | 943. Find the Shortest Superstring | 943-find-the-shortest-superstring-by-g8x-r8rl | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | G8xd0QPqTy | NORMAL | 2025-01-02T03:39:32.956176+00:00 | 2025-01-02T03:39:32.956176+00:00 | 12 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python []
class Solution:
def shortestSuperstring(self, words):
n = len(words)
overlap = [[0] * n for _ in range(n)]
def calc_overlap(a, b):
max_overlap = 0
for i in range(1, min(len(a), len(b)) + 1):
if a[-i:] == b[:i]:
max_overlap = i
return max_overlap
for i in range(n):
for j in range(n):
if i != j:
overlap[i][j] = calc_overlap(words[i], words[j])
dp = {}
def dfs(mask, last):
if (mask, last) in dp:
return dp[(mask, last)]
if mask == (1 << n) - 1:
return words[last]
best = None
for i in range(n):
if mask & (1 << i) == 0:
new_mask = mask | (1 << i)
candidate = dfs(new_mask, i)
best_candidate = words[last] + candidate[overlap[last][i]:]
if best is None or len(best_candidate) < len(best):
best = best_candidate
dp[(mask, last)] = best
return best
return min((dfs(1 << i, i) for i in range(n)), key=len)
``` | 0 | 0 | ['Python'] | 0 |
find-the-shortest-superstring | Commented bitmasking dp solution beats 99.5% runtime and 90% memory | commented-bitmasking-dp-solution-beats-9-xml9 | ApproachStandard dp approach where states are a bitset representing which indices are included along with the last index and the value is the length of the shor | lovesbumblebees | NORMAL | 2025-01-01T23:53:05.547013+00:00 | 2025-01-01T23:53:05.547013+00:00 | 18 | false | # Approach
Standard dp approach where states are a bitset representing which indices are included along with the last index and the value is the length of the shortest possible string matching the state requirements. We then backtrace the dp to find a minimal sequence of strings that produces the optimal result.
The performance gains come from using 1D arrays to reduce indirection and improve cache locality. We create a lookup table that maps popcount to states so that our dp iterations are efficient. Finally we use some bitmasking tricks to iterate over valid transitions more efficiently (roughly 2x performance increase compared to looping over all combinations and skipping invalid ones)
getOffset method could be improved using a table based string matching algorithm. This would reduce that portion from $O(n^2w^2)$ to $O(n^2w)$ this would actually make an appreciable difference for $n=12$ but I didn't want to focus on that aspect.
# Complexity
- Time complexity: $$O(n2^n + n^2w^2)$$ where $n$ is the number of words and $w$ is the maximal word length.
$$O(\sum_{k = 0}^n k(n-k)2^k) \equiv O(n2^n)$$ For the dynamic programming step. $$O(n^2w^2)$$ to compute the transition matrix between words, $$O(n^2 + nw)$$ to backtrace the dp and determine the minimal string.
- Space complexity: $$O(n2^n + wn)$$
$$O(n2^n)$$ for the states, an additional $$O(2^n)$$ for the state lookup, $$O(n^2)$$ for the offset matrix, and $$O(wn)$$ to construct the minimal string.
# Code
```cpp []
class Solution {
public:
string shortestSuperstring(vector<string>& words) {
size_t sz = words.size();
size_t mask = (1 << sz) - 1;
vector<int> offsets(sz * sz, 0);
for(size_t i = 0; i < sz; i++) {
for(size_t j = 0; j < sz; j++) {
offsets[sz * i + j] = getOffset(words[i], words[j]);
}
}
// distribute states into buckets according to their size
vector<vector<size_t>> popcounts(sz + 1);
for(size_t i = 0; i < (1 << sz); i++) {
popcounts[__builtin_popcount(i)].push_back(i);
}
// prepare the actual dp: combination of mask and last element
vector<int> dp(1 << (sz + 4), INT_MAX);
// seed initial values
for(size_t i = 0; i < sz; i++) {
dp[(1 << (i + 4)) | i] = words[i].size();
}
// perform dp on states
// we need to consider all possible transitions
// j represents the index of a set bit in the state and i is the index of an unset bit in the state
// we iterate over the number of set bits, propagating forward
for(size_t n = 1; n < sz; n++) {
// for each possible bitset
for(size_t state: popcounts[n]) {
// we iterate over the set bits in the complement
// equivalent to iterating over the unset bits
size_t comp_bits = (~state) & mask;
while(comp_bits > 0) {
// bitmasking trick to isolate the least significant set bit
size_t cbit = comp_bits ^ (comp_bits & (comp_bits - 1));
// convert the bit to an index 0b100 -> 2
size_t i = std::countr_zero(cbit);
// here we iterate over the set bits
size_t state_bits = state;
size_t next = state | cbit;
while(state_bits > 0) {
// same bitmasking trick as before
size_t sbit = state_bits ^ (state_bits & (state_bits - 1));
size_t j = std::countr_zero(sbit);
// the transition itself is very simple
// we append string i to a string ending in j, and lengthen it according to the overlap
// we take the minimum over the new value and previous value
dp[(next << 4) | i] = min(dp[(next << 4) | i], dp[(state << 4) | j] + offsets[sz * j + i]);
// unset the bit so we can find the next least significant bit
state_bits ^= sbit;
}
// unset the bit so we can find the next least significant bit
comp_bits ^= cbit;
}
}
}
// in the first pass we find the state that has minimal length and contains every word
size_t backtrack = (1 << sz) - 1;
// for the first pass we do not have a previous word and we don't know the length
size_t prev = -1;
size_t len = 0;
// the output string to be constructed
string output;
// iterate until we have recovered a minimal sequence (there might be more than one!)
while(backtrack > 0) {
// this will hold the index of the optimal word, working from the end towards the beginning
size_t best = 0;
for(size_t i = 0; i < sz; i++) {
if(dp[(backtrack << 4) | i] == INT_MAX) {
continue;
}
if(prev < sz) {
// find the first valid transition during all subsequent iterations
if(dp[(backtrack << 4) | i] + offsets[sz * i + prev] == len) {
best = i;
break;
}
}
// during the first iteration we find the smallest possible value
if(dp[(backtrack << 4) | i] < dp[(backtrack << 4) | best]) {
best = i;
}
}
len = dp[(backtrack << 4) | best];
if(output.size() == 0) {
output.resize(len);
}
copy(words[best].begin(), words[best].end(), output.begin() + len - words[best].size());
// we are now interested states that transition into this state
// this means that the most recent word index will be unset!
backtrack ^= (1 << best);
prev = best;
}
return output;
}
// the rest of the algorithm is sufficiently heavy that I am content writing something suboptimal here
// this function returns how much the string will grow if string first is followed by string second
// we cache these results into a transition matrix
int getOffset(const string& first, const string& second) {
for(int i =0; i < first.size(); i++) {
// in case the second word is a terminal substring of the first word
for(int j = 0; j <= second.size(); j++) {
if(i + j == first.size()) {
return second.size() - first.size() + i;
}
if(second[j] != first[i + j]) {
break;
}
}
}
return second.size();
}
};
```
Questions and feedback are both welcome :) | 0 | 0 | ['Dynamic Programming', 'Bit Manipulation', 'C++'] | 0 |
find-the-shortest-superstring | Dijkstra + Bitmask AC | dijkstra-bitmask-ac-by-kalpit00-ybs1 | If TSP DP is too impossible for anyone to remember, this is a relatively easier approach
It uses Dijkstra with a Custom Node object which stores the index of | kalpit00 | NORMAL | 2024-12-22T23:41:22.961611+00:00 | 2024-12-22T23:41:22.961611+00:00 | 22 | false | If TSP DP is too impossible for anyone to remember, this is a relatively easier approach
It uses Dijkstra with a Custom `Node` object which stores the `index` of the word, a `bitmask` to determine which of the `n` words have been visited/added, a `cost` variable similar to the one used in Official solution and the actual answer `str` computed by appending words/chars to generate superstrings.
The idea is to run dijkstra `N` times, once from each `word`. This computes a TSP like algo itself by trying to visit every other word/node once in the shortest distance (cost) possible. For each `dijsktra` call, we would generate a potential SuperString, we have to find the minimum Length one from these, so just add these to a list `Candidates` and finally iterate the list and return the one with the shortest length
```java []
class Solution {
class Node {
int node, state, cost;
String str;
public Node (int node, int state, int cost, String str) {
this.node = node;
this.state = state;
this.cost = cost;
this.str = str;
}
}
public String shortestSuperstring(String[] words) {
int n = words.length, min = Integer.MAX_VALUE;
List<String> candidates = new ArrayList<>();
List<List<int[]>> adj = new ArrayList<>();
for (int i = 0; i < n; i++) {
adj.add(new ArrayList<>());
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (i == j || words[i].equals(words[j])) {
continue; // skip duplicates and edges to itself
}
adj.get(i).add(new int[]{j, helper(words[i], words[j])});
}
}
for (int i = 0; i < n; i++) {
dijkstra(adj, words, i, n, candidates);
}
String res = "";
for (String candidate : candidates) {
if (min > candidate.length()) {
min = candidate.length();
res = candidate;
}
}
return res;
}
private void dijkstra(List<List<int[]>> adj, String[] words,
int i, int n, List<String> candidates) {
PriorityQueue<Node> pq = new PriorityQueue<>((a, b) -> a.cost - b.cost);
boolean[][] visited = new boolean[n][1 << n];
pq.offer(new Node(i, 1 << i, 0, words[i])); // start with cost = 0
visited[i][1 << i] = true; // each node initially visits itself
while (!pq.isEmpty()) {
Node node = pq.poll();
int parent = node.node, state = node.state, parentDist = node.cost;
String str = node.str;
if (state == (1 << n) - 1) { // all words have been joined
candidates.add(str); // add to the candidate strings
}
for (int[] neighbor : adj.get(parent)) {
int child = neighbor[0], childDist = neighbor[1];
int nextState = state | (1 << child);
if (!visited[child][nextState]) {
visited[child][nextState] = true;
StringBuilder sb = new StringBuilder(str);
sb.append(words[child].substring(words[child].length() - childDist)); // append the suffix of child to parent!
pq.offer(new Node(child, nextState, parentDist + childDist, sb.toString())); // dijkstra will poll minCost childs!
}
}
}
} // compute the minimum chars needed to append to s to make it contain t as a suffix.
private int helper(String s, String t) {
int m = s.length(), n = t.length();
for (int i = 0; i < m; i++) {
if (t.startsWith(s.substring(i))) {
return n - (m - i);
}
}
return n;
}
}
``` | 0 | 0 | ['Java'] | 0 |
find-the-shortest-superstring | Travelling Salesman Problem (TSP) | travelling-salesman-problem-tsp-by-brynn-0cfq | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Brynner | NORMAL | 2024-11-14T12:38:53.090266+00:00 | 2024-11-14T12:38:53.090306+00:00 | 29 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nfrom typing import List\nimport itertools\nimport functools\n\nclass Solution:\n def shortestSuperstring(self, words: List[str]) -> str:\n\n # Function to calculate the overlap between two strings\n @functools.lru_cache(None)\n def overlap(a: str, b: str) -> int:\n max_overlap = 0\n for i in range(1, min(len(a), len(b)) + 1):\n if a[-i:] == b[:i]:\n max_overlap = i\n return max_overlap\n\n # Precompute the overlap between all pairs of words\n n = len(words)\n overlaps = [[0] * n for _ in range(n)]\n for i, j in itertools.product(range(n), repeat=2):\n if i != j:\n overlaps[i][j] = overlap(words[i], words[j])\n\n # dp[mask][i] will be the length of the shortest superstring that contains\n # all words corresponding to the bits in mask, ending with words[i]\n dp = [[float(\'inf\')] * n for _ in range(1 << n)]\n parent = [[None] * n for _ in range(1 << n)]\n for i in range(n):\n dp[1 << i][i] = len(words[i])\n\n # Iterate over all subsets of words\n for mask in range(1 << n):\n for i in range(n):\n if not (mask & (1 << i)):\n continue\n for j in range(n):\n if mask & (1 << j):\n continue\n new_mask = mask | (1 << j)\n new_len = dp[mask][i] + len(words[j]) - overlaps[i][j]\n if new_len < dp[new_mask][j]:\n dp[new_mask][j] = new_len\n parent[new_mask][j] = i\n\n # Reconstruct the shortest superstring\n mask = (1 << n) - 1\n min_len = float(\'inf\')\n last = -1\n for i in range(n):\n if dp[mask][i] < min_len:\n min_len = dp[mask][i]\n last = i\n\n result = []\n while mask:\n result.append(words[last])\n next_last = parent[mask][last]\n mask ^= (1 << last)\n last = next_last\n\n result.reverse()\n superstring = result[0]\n for i in range(1, len(result)):\n overlap_len = overlap(result[i - 1], result[i])\n superstring += result[i][overlap_len:]\n\n return superstring\n\n``` | 0 | 0 | ['Python3'] | 0 |
find-the-shortest-superstring | Bitmasking + DP + KMP | bitmasking-dp-kmp-by-adidala-divishath-r-5xm2 | Intuition\n1) First we need to know which one to pick before what, there 2^n possibilities\n2) Use bit masking so that we will know how many strings are alread | Adidala-Divishath-Reddy | NORMAL | 2024-11-02T14:50:24.389177+00:00 | 2024-11-02T14:50:24.389214+00:00 | 14 | false | # Intuition\n1) First we need to know which one to pick before what, there 2^n possibilities\n2) Use bit masking so that we will know how many strings are already used before we pick current string.\n\n# Approach\n1) First find common substring when we combine two strings into one. which would be suffix of one and prefix of other. KMP will be easier and quicker.\n2) Then just like travelling salesman problem, start from one node and reach all other nodes with minimum cost. Whenever we reach any node, check the path how we reached that node using masking and return minimum cost path from that node.\n\n# Complexity\n- Time complexity:\nO(n^2 * 2^n)\n\n- Space complexity:\n-O(n^2 * 2^n)\n\n# Code\n```cpp []\nclass Solution {\nprivate:\n int findcpslen(string a, string b){\n int maxi = 0;\n string temp = b + "#" + a;\n int j, n = temp.size();\n vector<int> pi(n, 0);\n for(int i = 1; i < n; i++){\n j = pi[i-1];\n while(j>0 && temp[i] != temp[j])\n j = pi[j-1];\n if(temp[i] == temp[j])\n j++;\n pi[i] = j;\n maxi = max(maxi, pi[i]);\n }\n\n return pi[n-1];\n }\n string find(vector<string>& words, int idx, vector<vector<string>> &dp, vector<vector<int>> &req, int mask){\n int n = words.size();\n\n if(dp[idx][mask] != "")\n return dp[idx][mask];\n \n dp[idx][mask] = words[idx];\n int mini = INT_MAX;\n for(int j = 0; j < n; j++){\n if(idx == j || ((mask >> j) & 1))\n continue;\n string temp = find(words, j, dp, req, (mask | (1 << idx)));\n if(temp.size() + n - req[idx][j] < mini){\n mini = temp.size() + n - req[idx][j];\n dp[idx][mask] = words[idx].substr(0, words[idx].size() - req[idx][j]) + temp;\n }\n }\n\n return dp[idx][mask];\n }\npublic:\n string shortestSuperstring(vector<string>& words) {\n int n = words.size();\n vector<vector<string>> dp(n, vector<string>(pow(2, n), ""));\n vector<vector<int>> req(n, vector<int>(n, 0));\n string ans = "";\n for(int i = 0; i < n; i++){\n ans += words[i];\n for(int j = 0; j < n; j++){\n if(i == j)\n continue;\n req[i][j] = findcpslen(words[i], words[j]);\n }\n }\n\n \n for(int i = 0; i < n; i++){\n string temp = find(words, i, dp, req, 0);\n if(temp.size() < ans.size()) ans = temp;\n }\n\n return ans;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
find-the-shortest-superstring | C# DP | c-dp-by-everest911119-y7zk | Intuition\nDP\n\n# Approach\ndp[mask][i] := min distance to visit nodes (represented as a binary state s) once and only once and the path ends with node i.\n\n# | everest911119 | NORMAL | 2024-10-31T21:09:24.364408+00:00 | 2024-10-31T21:09:24.364448+00:00 | 4 | false | # Intuition\nDP\n\n# Approach\ndp[mask][i] := min distance to visit nodes (represented as a binary state s) once and only once and the path ends with node i.\n\n# Complexity\n- Time complexity:\nO(n^2*2^n)\n\n- Space complexity:\nO(n*2^n)\n\n# Code\n```csharp []\nusing System.Runtime.CompilerServices;\nusing System.Runtime.InteropServices;\npublic class Solution {\n public string ShortestSuperstring(string[] words) {\n int n = words.Length;\nint[,] graph = new int[n, n];\nfor (int i = 0; i < n; i++)\n{\n for (int j = 0; j < n; j++)\n {\n graph[i, j] = words[j].Length;\n \n for (int k = 1; k <= Math.Min(words[i].Length, words[j].Length); k++)\n {\n if (words[j].Substring(0, k) == words[i].Substring(words[i].Length - k))\n {\n graph[i, j] = words[j].Length - k;\n }\n }\n }\n}\n\n// path and last index get minlength\nint[,] dp = new int[1 << n, n];\nvar data = MemoryMarshal.CreateSpan(ref Unsafe.As<byte, int>(ref MemoryMarshal.GetArrayDataReference(dp)), dp.Length);\ndata.Fill(21 * 13);\n// path and last index with minLength get next last index\nint[,] paths = new int[1 << n, n];\nvar data2 = MemoryMarshal.CreateSpan(ref Unsafe.As<byte, int>(ref MemoryMarshal.GetArrayDataReference(paths)), paths.Length);\ndata2.Fill(-1);\nfor (int i = 0; i < n; i++)\n{\n dp[1 << i, i] = words[i].Length;\n}\nfor (int mask = 0; mask < (1 << n); mask++)\n{\n for (int i = 0; i < n; i++)\n {\n // mask not include i n\n if ((mask & (1 << i)) == 0) continue;\n int prev = mask ^ (1 << i);\n for (int j = 0; j < n; j++)\n {\n // prev mask not include j\n if ((prev & (1 << j)) == 0) continue;\n if (dp[prev, j] + graph[j, i] < dp[mask, i])\n {\n dp[mask, i] = dp[prev, j] + graph[j, i];\n paths[mask, i] = j;\n }\n }\n }\n \n \n\n}\nint minLength = int.MaxValue;\nint currentIndex = -1;\nfor (int i = 0; (i < n); i++)\n{\n if (dp[(1 << n) - 1, i] < minLength)\n {\n minLength = Math.Min(minLength, dp[(1 << n) - 1, i]);\n currentIndex = i;\n }\n\n}\nstring ans = "";\nint path = (1 << n) - 1;\nwhile (path > 0)\n{\n int prev = paths[path,currentIndex];\n if (prev >= 0)\n {\n ans = words[currentIndex].Substring(words[currentIndex].Length - graph[prev, currentIndex]) + ans;\n }else\n {\n ans = words[currentIndex]+ ans;\n }\n path = path^(1<<currentIndex);\n currentIndex= prev;\n\n}\nreturn ans;\n }\n}\n``` | 0 | 0 | ['Dynamic Programming', 'Bit Manipulation', 'C#'] | 0 |
find-the-shortest-superstring | Python3-459 ms Beats 66.48% | python3-459-ms-beats-6648-by-hassam_472-2fww | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | hassam_472 | NORMAL | 2024-10-19T13:06:39.743662+00:00 | 2024-10-19T13:06:39.743693+00:00 | 20 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def shortestSuperstring(self, words: List[str]) -> str:\n n = len(words)\n \n # Calculate the overlap between two words\n def calculate_overlap(word1, word2):\n max_overlap = 0\n for i in range(1, min(len(word1), len(word2)) + 1):\n if word1.endswith(word2[:i]):\n max_overlap = i\n return max_overlap\n \n # Calculate overlap for all pairs of words\n overlap = [[calculate_overlap(words[i], words[j]) for j in range(n)] for i in range(n)]\n \n # Initialize DP table\n dp = [[\'\'] * n for _ in range(1 << n)]\n \n # Fill DP table\n for mask in range(1, 1 << n):\n for bit in range(n):\n if mask & (1 << bit):\n prev_mask = mask ^ (1 << bit)\n if prev_mask == 0:\n dp[mask][bit] = words[bit]\n else:\n for prev_bit in range(n):\n if prev_mask & (1 << prev_bit):\n current = dp[prev_mask][prev_bit] + words[bit][overlap[prev_bit][bit]:]\n if dp[mask][bit] == \'\' or len(current) < len(dp[mask][bit]):\n dp[mask][bit] = current\n \n # Find the shortest superstring\n full_mask = (1 << n) - 1\n return min(dp[full_mask], key=len)\n\n``` | 0 | 0 | ['Python3'] | 0 |
find-the-shortest-superstring | BackTracking+DP | backtrackingdp-by-linda2024-8tch | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | linda2024 | NORMAL | 2024-10-12T01:07:49.692409+00:00 | 2024-10-12T01:07:49.692436+00:00 | 4 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```csharp []\npublic class Solution {\n \n private int CommonChars(string a, string b)\n {\n int len = a.Length;\n if(len == 0 || b.Length == 0)\n return 0;\n\n int minLen = Math.Min(len, b.Length);\n while(minLen > 0)\n {\n string p1 = a.Substring(len-minLen), p2 = b.Substring(0, minLen);\n if(p1 == p2)\n break;\n\n minLen--;\n }\n\n return minLen;\n }\n private string[,] remains;\n private string BackTracking2(string[] words, int start, int mask, int len, string[,] dp)\n {\n if (dp[start, mask] != "")\n return dp[start, mask];\n\n int minLen = int.MaxValue;\n string res = "";\n for (int i = 0; i < len; i++)\n {\n if ((mask & (1 << i)) == 0)\n {\n string temp = remains[start, i] + BackTracking2(words, i, mask | (1<<i), len, dp);\n if (temp.Length <minLen)\n { \n minLen = temp.Length;\n res = temp;\n }\n }\n }\n\n dp[start, mask] = res;\n return res;\n }\n\n\n public string ShortestSuperstring(string[] words) {\n int len = words.Length, minLen = int.MaxValue;\n if (len == 0)\n return "";\n if (len == 1)\n return words[0];\n string[,] dp = new string[len, (1<< (len+1))];\n\n remains = new string[len, len];\n for (int i = 0; i < len; i++)\n {\n for (int j = 0; j < len; j++)\n {\n remains[i, j] = "";\n }\n\n for (int k = 0; k < dp.GetLength(1); k++)\n {\n dp[i, k] = "";\n }\n }\n\n\n for (int i = 0; i < len - 1; i++)\n {\n for (int j = i + 1; j < len; j++)\n {\n int p1 = CommonChars(words[i], words[j]);\n int p2 = CommonChars(words[j], words[i]);\n remains[i, j] = words[j].Substring(p1);\n remains[j,i] = words[i].Substring(p2);\n }\n }\n int mask = 0;\n\n string res = "";\n\n for (int i = 0; i < len; i++)\n {\n string tmpStr = words[i] + BackTracking2(words, i, mask |(1<<i), len, dp);\n if (tmpStr.Length < minLen)\n {\n res = tmpStr;\n minLen = tmpStr.Length;\n }\n }\n\n return res;\n\n }\n}\n``` | 0 | 0 | ['C#'] | 0 |
find-the-shortest-superstring | C++ Bitmask DP: maintain choice made at each step of the recursion. | c-bitmask-dp-maintain-choice-made-at-eac-uz56 | \n# Code\ncpp []\nint sufPref[12][12];\nint dp[12][1<<12];\nint choice[12][1<<12];\n\nclass Solution {\n private:\n\n int n;\n \n // length of t | pradyumnaym | NORMAL | 2024-10-09T20:22:39.823913+00:00 | 2024-10-09T20:28:31.538579+00:00 | 10 | false | \n# Code\n```cpp []\nint sufPref[12][12];\nint dp[12][1<<12];\nint choice[12][1<<12];\n\nclass Solution {\n private:\n\n int n;\n \n // length of the permutations\n int f(int last, int mask, vector<string> &words) {\n // if all strings added, no extra length\n if (mask == (1<<n) - 1) return 0;\n // if already computed, return\n if (dp[last][mask] != INT_MAX) return dp[last][mask];\n\n // compute the result\n for (int i = 0; i < n; i++) {\n if (mask & (1<<i)) continue;\n int newLen = f(i, mask | (1<<i), words) - sufPref[last][i] + words[i].size();\n if (newLen < dp[last][mask]) {\n dp[last][mask] = newLen;\n choice[last][mask] = i;\n }\n }\n\n return dp[last][mask];\n\n }\n\npublic:\n string shortestSuperstring(vector<string>& words) {\n n = words.size();\n fill_n(&dp[0][0], 12 * (1<<12), INT_MAX);\n fill_n(&choice[0][0], 12 * (1<<12), -1);\n\n // What is the largest suffix of i that is a prefix of j?\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < n; j++) {\n int l1 = words[i].size(), l2 = words[j].size();\n int len = min(l1, l2);\n\n sufPref[i][j] = 0;\n\n for(int k = 1; k <= len; k++) {\n int x = l1 - k, y = 0;\n while (y < k and words[i][x] == words[j][y]) {x++; y++;}\n if (y == k) sufPref[i][j] = k;\n }\n }\n }\n\n // check the prefix matches\n // for (int i = 0; i < n; i++) {\n // for (int j = 0; j < n; j++) cout << sufPref[i][j] << " ";\n // cout << endl;\n // }\n\n int minlen = 10000, minword = 0;\n for (int i = 0; i < n; i++) {\n int len = f(i, 1<<i, words) + words[i].size();\n if (len < minlen) {\n minlen = len;\n minword = i;\n }\n }\n\n string res;\n res.append(words[minword]);\n\n int prev = -1, mask = (1<<minword);\n\n for (int i = 1; i < n; i++) {\n prev = minword;\n // find the next word\n minword = choice[minword][mask];\n // update the mask to indicate that this word has been used now.\n mask = mask | (1<<minword);\n\n int commonPrefix = sufPref[prev][minword];\n\n res.append(words[minword], commonPrefix, words[minword].size() - commonPrefix);\n }\n \n return res;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
find-the-shortest-superstring | String Matching || Bitmask || DP || Beats 100% | string-matching-bitmask-dp-beats-100-by-ow0e3 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\nBitMask and dp\n\n# Complexity\n- Time complexity:\nO((1<<12)(13))\n\n- S | surajnishad930 | NORMAL | 2024-10-09T10:21:35.514290+00:00 | 2024-10-09T10:21:35.514331+00:00 | 9 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nBitMask and dp\n\n# Complexity\n- Time complexity:\nO((1<<12)*(13))\n\n- Space complexity:\nO((1<<12)*(13))\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int overlap[13][13];\n int Max_overlap(string &a,string &b){\n int ans=0;\n for(int i=0;i<a.size();i++){\n int j=0;\n for(j=0;j<b.size() && i+j<a.size();j++){\n if(a[i+j]!=b[j])break;\n }\n if(i+j==a.size())ans=max(ans,j); \n }\n return ans;\n }\n int dp[1<<12][13];\n \n string shortestSuperstring(vector<string>& words) {\n int n=words.size();\n memset(overlap,0,sizeof(overlap));\n for(int i=0;i<n;i++){\n for(int j=0;j<n;j++){\n overlap[i][j]=Max_overlap(words[i],words[j]);\n }\n }\n memset(dp,-1,sizeof(dp));\n int min_length=find(12,n,0,words);\n string ans="";\n shortest_string(12,n,0,words,ans,min_length);\n return ans;\n }\n void shortest_string(int pre,int &n,int mask,vector<string>&words,string &ans,int &l){\n \n for(int i=0;i<n;i++){\n if(mask&(1<<i))continue;\n int p=words[i].size()-overlap[pre][i];\n if(dp[mask^(1<<i)][i]==l-p){\n for(int x=overlap[pre][i];x<words[i].size();x++){\n ans.push_back(words[i][x]);\n }\n l-=p;\n shortest_string(i,n,mask^(1<<i),words,ans,l);\n break;\n }\n }\n\n }\n int find(int pre,int &n,int mask,vector<string>&words){\n if(mask==(1<<n)-1)return dp[mask][pre]=0;\n if(dp[mask][pre]!=-1)return dp[mask][pre];\n int ans=INT_MAX;\n for(int i=0;i<n;i++){\n if(mask&(1<<i))continue;\n int x=words[i].size()-overlap[pre][i];\n ans=min(ans,x+find(i,n,mask^(1<<i),words));\n }\n return dp[mask][pre]=ans;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
patching-array | Solution + explanation | solution-explanation-by-stefanpochmann-89bf | Solution\n\n int minPatches(vector& nums, int n) {\n long miss = 1, added = 0, i = 0;\n while (miss <= n) {\n if (i < nums.size() && | stefanpochmann | NORMAL | 2016-01-27T05:07:57+00:00 | 2018-10-27T00:57:14.137408+00:00 | 64,164 | false | **Solution**\n\n int minPatches(vector<int>& nums, int n) {\n long miss = 1, added = 0, i = 0;\n while (miss <= n) {\n if (i < nums.size() && nums[i] <= miss) {\n miss += nums[i++];\n } else {\n miss += miss;\n added++;\n }\n }\n return added;\n }\n\n---\n\n**Explanation**\n\nLet `miss` be the smallest sum in `[0,n]` that we might be missing. Meaning we already know we can build all sums in `[0,miss)`. Then if we have a number `num <= miss` in the given array, we can add it to those smaller sums to build all sums in `[0,miss+num)`. If we don't, then we must add such a number to the array, and it's best to add `miss` itself, to maximize the reach.\n\n---\n\n**Example:** Let's say the input is `nums = [1, 2, 4, 13, 43]` and `n = 100`. We need to ensure that all sums in the range [1,100] are possible.\n\nUsing the given numbers 1, 2 and 4, we can already build all sums from 0 to 7, i.e., the range [0,8). But we can't build the sum 8, and the next given number (13) is too large. So we insert 8 into the array. Then we can build all sums in [0,16).\n\nDo we need to insert 16 into the array? No! We can already build the sum 3, and adding the given 13 gives us sum 16. We can also add the 13 to the other sums, extending our range to [0,29).\n\nAnd so on. The given 43 is too large to help with sum 29, so we must insert 29 into our array. This extends our range to [0,58). But then the 43 becomes useful and expands our range to [0,101). At which point we're done.\n\n---\n\n**Another implementation**, though I prefer the above one.\n\n int minPatches(vector<int>& nums, int n) {\n int count = 0, i = 0;\n for (long miss=1; miss <= n; count++)\n miss += (i < nums.size() && nums[i] <= miss) ? nums[i++] : miss;\n return count - i;\n } | 1,111 | 6 | [] | 99 |
patching-array | 🔥 🔥 🔥 💯 Easy to understand | Greedy Approach | Detailed Explanation 🔥 🔥 🔥 | easy-to-understand-greedy-approach-detai-ddek | To look into solutions to other problems visit my leetcode profle\n\n# Intuition\n\n- The code works like providing change with limited coin denominations. Supp | bhanu_bhakta | NORMAL | 2024-06-16T00:20:24.821547+00:00 | 2024-06-16T01:53:16.220375+00:00 | 41,216 | false | To look into solutions to other problems visit my [leetcode profle](https://leetcode.com/u/bhanu_bhakta/)\n\n# Intuition\n\n- The code works like providing change with limited coin denominations. Suppose you need to cover every amount up to \uD835\uDC5B cents. If you can\'t make exact change for a particular amount miss, it indicates you lack a coin of value less than or equal to miss. To fill this gap, you add a coin of that exact missing amount. This addition allows you to now cover new amounts up to 2 * miss. Repeat this process until you can provide change for every amount up to \uD835\uDC5B. This method ensures you add the minimum number of new coins needed to cover any shortages.\n\n# Approach\nIf its hard to understand the approach, I have clear explanation [here](https://www.youtube.com/watch?v=vmKXw3lgt7I).\n\n- **Initialize Variables:** Start with miss set to 1, added to 0, and index i at 0 to track the smallest sum that cannot be formed and the number of patches added.\n\n- **Iterate with Condition:** Continue the loop as long as miss (the target sum we need to achieve) is less than or equal to n.\n\n- **Use Existing Numbers:** Check if the current number in the list (nums[i]) can be used to form miss. If yes, add it to miss to extend the range of formable sums and increment the index i.\n\n- **Add Necessary Numbers:** If nums[i] is greater than miss or all numbers are already used, add miss itself to cover the smallest unformable sum, and double the value of miss.\n\n- **Increment Added Count:** Whenever a number is added to cover a gap, increase the added counter.\n\n- **Return Total Patches:** Once miss exceeds n, return the total count of added numbers as the result, representing the minimum patches needed to form every number up to n.\n\n**Example:**\n\n**Input: [1, 5, 10]**\n\n| Step | Current nums | Miss | Action | Reason | New Coverage |\n|------|--------------|------|--------|------------------------------------------|--------------|\n| 1 | [1, 5, 10] | 1 | Use 1 | 1 is available and matches miss | Sums up to 1 |\n| 2 | [1, 5, 10] | 2 | Add 2 | 5 is too large to form sum 2 | Sums up to 3 |\n| 3 | [1, 5, 10] | 4 | Add 4 | 5 is too large to form sum 4 | Sums up to 7 |\n| 4 | [1, 5, 10] | 8 | Use 5 | Can use 5 with existing numbers to form 8| Sums up to 12 |\n| 5 | [1, 5, 10] | 13 | Use 10 | Can use 10 with existing numbers to form 13 | Sums up to 22 |\n\n# Complexity\n- Time complexity:\n**O(N)**\n\n- Space complexity:\n**O(1)**\n\n# Code\n```Python []\nclass Solution:\n def minPatches(self, nums: List[int], n: int) -> int:\n miss = 1\n result = 0\n i = 0\n\n while miss <= n:\n if i < len(nums) and nums[i] <= miss:\n miss += nums[i]\n i += 1\n else:\n miss += miss\n result += 1\n\n return result\n\n```\n```C++ []\nclass Solution {\npublic:\n int minPatches(vector<int>& nums, int n) {\n long long miss = 1;\n int result = 0;\n size_t i = 0;\n\n while (miss <= n) {\n if (i < nums.size() && nums[i] <= miss) {\n miss += nums[i];\n i++;\n } else {\n miss += miss;\n result++;\n }\n }\n\n return result;\n }\n};\n```\n```Java []\nclass Solution {\n public int minPatches(int[] nums, int n) {\n long miss = 1;\n int result = 0;\n int i = 0;\n\n while (miss <= n) {\n if (i < nums.length && nums[i] <= miss) {\n miss += nums[i];\n i++;\n } else {\n miss += miss;\n result++;\n }\n }\n\n return result;\n }\n}\n```\n```Go []\nfunc minPatches(nums []int, n int) int {\n\tmiss := int64(1)\n\tresult := 0\n\ti := 0\n\n\tfor miss <= int64(n) {\n\t\tif i < len(nums) && int64(nums[i]) <= miss {\n\t\t\tmiss += int64(nums[i])\n\t\t\ti++\n\t\t} else {\n\t\t\tmiss += miss\n\t\t\tresult++\n\t\t}\n\t}\n\n\treturn result\n}\n```\n```Kotlin []\nclass Solution {\n fun minPatches(nums: IntArray, n: Int): Int {\n var miss: Long = 1\n var result = 0\n var i = 0\n\n while (miss <= n) {\n if (i < nums.size && nums[i].toLong() <= miss) {\n miss += nums[i]\n i++\n } else {\n miss += miss\n result++\n }\n }\n\n return result\n }\n}\n```\n```Javascript []\n/**\n * @param {number[]} nums\n * @param {number} n\n * @return {number}\n */\nvar minPatches = function (nums, n) {\n let miss = 1; // JavaScript uses let for block scope variables\n let result = 0;\n let i = 0;\n\n while (miss <= n) {\n if (i < nums.length && nums[i] <= miss) {\n miss += nums[i];\n i++;\n } else {\n miss += miss;\n result++;\n }\n }\n\n return result;\n};\n```\n\n**If you like the solution please upvote**\n\n | 251 | 2 | ['C++', 'Java', 'Go', 'Python3', 'Kotlin', 'JavaScript'] | 18 |
patching-array | C++, 8ms, greedy solution with explanation | c-8ms-greedy-solution-with-explanation-b-ht04 | show the algorithm with an example,\n\nlet nums=[1 2 5 6 20], n = 50.\n\nInitial value: with 0 nums, we can only get 0 maximumly.\n\nThen we need to get 1, sinc | dragonpw | NORMAL | 2016-05-14T17:47:35+00:00 | 2018-10-13T02:35:01.199312+00:00 | 13,355 | false | show the algorithm with an example,\n\nlet nums=[1 2 5 6 20], n = 50.\n\nInitial value: with 0 nums, we can only get 0 maximumly.\n\nThen we need to get 1, since nums[0]=1, then we can get 1 using [1]. now the maximum number we can get is 1. (actually, we can get all number no greater than the maximum number)\n\n number used [1], number added []\n can achieve 1~1\n\nThen we need to get 2 (maximum number +1). Since nums[1]=2, we can get 2. Now we can get all number between 1 ~ 3 (3=previous maximum value + the new number 2). and 3 is current maximum number we can get.\n\n number used [1 2], number added []\n can achieve 1~3\n\nThen we need to get 4 (3+1). Since nums[2]=5>4; we need to add a new number to get 4. The optimal solution is to add 4 directly. In this case, we could achieve maximumly 7, using [1,2,4].\n\n number used [1 2], number added [4]\n can achieve 1~7\n\nThen we need to get 8 (7+1). Since nums[2]=5<8, we can first try to use 5. Now the maximum number we can get is 7+5=12. Since 12>8, we successfully get 8.\n\n number used [1 2 5], number added [4]\n can achieve 1~12\n\nThen we need to get 13 (12+1), Since nums[3]=6<13, we can first try to use 6. Now the maximum number we can get is 12+6=18. Since 18>13, we successfully get 13.\n\n number used [1 2 5 6], number added [4]\n can achieve 1~18\n\nThen we need to get 19 (18+1), Since nums[4]=20>19, we need to add a new number to get 19. The optimal solution is to add 19 directly. In this case, we could achieve maximumly 37.\n\n number used [1 2 5 6], number added [4 19]\n can achieve 1~37\n\nThen we need to get 38(37+1), Since nums[4]=20<38, we can first try to use 20. Now the maximum number we can get is 37+20=57. Since 57>38, we successfully get 38.\n\n number used [1 2 5 6 20], number added [4 19]\n can achieve 1~57\n\nSince 57>n=50, we can all number no greater than 50. \n\nThe extra number we added are 4 and 19, so we return 2.\n\n\nThe code is given as follows\n\n class Solution {\n public:\n int minPatches(vector<int>& nums, int n) {\n int cnt=0,i=0;\n long long maxNum=0;\n while (maxNum<n){\n if (i<nums.size() && nums[i]<=maxNum+1)\n maxNum+=nums[i++];\n else{\n maxNum+=maxNum+1;cnt++;\n }\n }\n return cnt;\n }\n }; | 160 | 0 | [] | 16 |
patching-array | ✅LeetCode Hard in 6 mins 💯Beats 100% - Explained with [ Video ] - C++/Java/Python/JS - Arrays | leetcode-hard-in-6-mins-beats-100-explai-ld15 | \n\n\n\n# YouTube Video Explanation:\n\n **If you want a video for this question please write in the comments** \n\n https://www.youtube.com/watch?v=ujU-jeO1v-k | lancertech6 | NORMAL | 2024-06-16T04:51:05.832180+00:00 | 2024-06-16T09:39:10.488614+00:00 | 10,892 | false | \n\n\n\n# YouTube Video Explanation:\n\n<!-- **If you want a video for this question please write in the comments** -->\n\n<!-- https://www.youtube.com/watch?v=ujU-jeO1v-k -->\n\nhttps://youtu.be/igi901q2uv8\n\n**\uD83D\uDD25 Please like, share, and subscribe to support our channel\'s mission of making complex concepts easy to understand.**\n\nSubscribe Link: https://www.youtube.com/@leetlogics/?sub_confirmation=1\n\n*Subscribe Goal: 2000 Subscribers*\n*Current Subscribers: 1976*\n\n---\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem requires ensuring that any number in the range `[1, n]` can be formed by the sum of some elements in the given sorted array `nums`. The key is to identify the smallest number that cannot be formed (`missing`). If `missing` is in the array, we include it and check the next `missing`. If `missing` is not in the array, we need to add it (patch it) to cover that gap and update our `missing` value accordingly. The goal is to minimize the number of patches required.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialize `missing` to 1, which is the smallest number we want to be able to form.\n2. Use a variable `i` to iterate through the array and another variable `patches` to count the number of patches needed.\n3. While `missing` is less than or equal to `n`:\n - If the current array element (`nums[i]`) is less than or equal to `missing`, add this element to `missing` and move to the next element (`i++`).\n - If the current array element is greater than `missing`, patch the `missing` value by adding `missing` itself, and increment the `patches` counter.\n4. Repeat until `missing` exceeds `n`.\n5. Return the number of patches needed.\n\n# Complexity\n- Time complexity: `O(m)`, where `m` is the length of the array `nums`. The while loop iterates through the array at most once, and each patching operation is constant time.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: `O(1)`, as we only use a few extra variables.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n\n\n\n### Explanation with Tables\nLet\'s illustrate the example with `nums = [1, 3]` and `n = 6`.\n\n| Step | Missing Value (`missing`) | Array Element (`nums[index]`) | Action | Updated Missing Value (`missing`) | Patches |\n|------|----------------------------|-------------------------------|-----------------------|-----------------------------------|---------|\n| 1 | 1 | 1 | Add array element | 2 | 0 |\n| 2 | 2 | 3 | Patch (add 2) | 4 | 1 |\n| 3 | 4 | 3 | Add array element | 7 | 1 |\n\n**Detailed Explanation**:\n1. **Step 1**:\n - Initial `missing` is 1.\n - The first element in `nums` is 1, which is less than or equal to `missing`.\n - Add `nums[i]` to `missing`: `missing` becomes 2.\n - Move to the next element in `nums`.\n\n2. **Step 2**:\n - Current `missing` is 2.\n - The next element in `nums` is 3, which is greater than `missing`.\n - Patch the `missing` value by adding `missing` itself: `missing` becomes 4.\n - Increment the `patches` counter to 1.\n\n3. **Step 3**:\n - Current `missing` is 4.\n - The next element in `nums` is 3, which is less than `missing`.\n - Add `nums[i]` to `missing`: `missing` becomes 7.\n - Since `missing` (7) is now greater than `n` (6), we stop.\n\nAfter these steps, the range `[1, 6]` can be formed using the numbers in `nums` and the patches.\n\n### Summary\n- **Initial `missing`**: 1\n- **Patch if `missing` is not covered**.\n- **Update `missing`** and **count patches** until `missing` exceeds `n`.\n\n\nAfter these steps, all numbers in the range `[1, 6]` can be formed.\n\nFor `nums = [1, 5, 10]` and `n = 20`:\n\n| Step | Missing Value (`missing`) | Array Element (`nums[index]`) | Action | Updated Missing Value (`missing`) | Patches |\n|------|----------------------------|-------------------------------|-----------------------|-----------------------------------|---------|\n| 1 | 1 | 1 | Add array element | 2 | 0 |\n| 2 | 2 | 5 | Patch (add 2) | 4 | 1 |\n| 3 | 4 | 5 | Patch (add 4) | 8 | 2 |\n| 4 | 8 | 5 | Add array element | 13 | 2 |\n| 5 | 13 | 10 | Add array element | 23 | 2 |\n\n\nThus, 2 patches are needed to cover the range `[1, 20]`.\n\n\n# Code\n```java []\nclass Solution {\n public int minPatches(int[] nums, int n) {\n long missing = 1;\n int patches = 0;\n int index = 0;\n\n while (missing <= n) {\n if (index < nums.length && nums[index] <= missing) {\n missing += nums[index];\n index++;\n } else {\n missing += missing;\n patches++;\n }\n }\n\n return patches;\n }\n}\n\n```\n```C++ []\nclass Solution {\npublic:\n int minPatches(vector<int>& nums, int n) {\n long missing = 1;\n int patches = 0;\n int index = 0;\n\n while (missing <= n) {\n if (index < nums.size() && nums[index] <= missing) {\n missing += nums[index];\n index++;\n } else {\n missing += missing;\n patches++;\n }\n }\n\n return patches;\n }\n};\n```\n```Python []\nclass Solution(object):\n def minPatches(self, nums, n):\n missing = 1\n patches = 0\n index = 0\n\n while missing <= n:\n if index < len(nums) and nums[index] <= missing:\n missing += nums[index]\n index += 1\n else:\n missing += missing\n patches += 1\n\n return patches\n\n \n```\n```JavaScript []\nvar minPatches = function(nums, n) {\n let missing = 1;\n let patches = 0;\n let index = 0;\n\n while (missing <= n) {\n if (index < nums.length && nums[index] <= missing) {\n missing += nums[index];\n index++;\n } else {\n missing += missing;\n patches++;\n }\n }\n\n return patches;\n};\n```\n\n\n | 91 | 1 | ['Array', 'Binary Search', 'Greedy', 'Python', 'C++', 'Java', 'JavaScript'] | 5 |
patching-array | [Python] 2 solutions: merge intervals + greedy, explained | python-2-solutions-merge-intervals-greed-mm2l | Solution 1\nLet as keep all possible numbers we can get as list of intervals, for example 0, 1, 2, 4, 5, 12 is [[0, 2], [4, 5], [12, 12]]. Then when we add new | dbabichev | NORMAL | 2021-08-29T08:09:58.574034+00:00 | 2021-08-29T08:09:58.574069+00:00 | 3,936 | false | #### Solution 1\nLet as keep all possible numbers we can get as list of intervals, for example `0, 1, 2, 4, 5, 12` is `[[0, 2], [4, 5], [12, 12]]`. Then when we add new number we can merge our intervals, using idea of Problem **0056**. What numbers we need to add next? We need to add number `3` in our example, the smallest possible number, which are not in our array. \n\n#### Complexity\nComplexity is `O(m * log n)`, where `m <= 10000` is the biggest value of `num`. The idea is that in the beginning we can have not more than `m//2` intervals and then on each iteration number of intervals can not increase or increase not too fast (I do not have strict proof at the moment). Also number of iterations can not too big, because it is enough `log n` patches always.\n\n#### Code\n```python\nclass Solution:\n def merge(self, intervals):\n intervals.sort(key=lambda x: x[0])\n merged = []\n \n for interval in intervals:\n if not merged or merged[-1][1] < interval[0] - 1:\n merged.append(interval)\n else:\n merged[-1][1] = max(merged[-1][1], interval[1])\n\n return merged\n\n\n def minPatches(self, nums, n):\n ints, patches = [[0,0]], 0\n for num in nums:\n ints = self.merge(ints + [[i+num, j+num] for i,j in ints])\n\n while ints[0][1] < n:\n ints = self.merge(ints + [[i+ints[0][1]+1, j+ints[0][1]+1] for i,j in ints])\n patches += 1\n\n return patches\n```\n\n#### Solution 2\nWe can improve this solution, if we upgrade the idea of smallest number which we do not have yet. \n\n**Example**: `nums = [1, 2, 4, 13, 43]`. We go form the smallest number add them one by one and always keep the possible range of numbers we can get in the form `[0, k]`, that is, it is not union of intervals, but only one interval. Let us go through this example. \n\n1. We did not choose any numbers yet, so we have interval `[0, 0]`.\n2. Are we missing something if we take next number `1`? No, let us take it, now we have interval `[0, 1]`.\n3. Are we missing something if we take next number `2`? No, let us take it, now we have interval `[0, 3]`.\n4. Are we missing something if we take next number `4`? No, let us take it, now we have interval `[0, 7]`.\n5. Are we missing something if we take next number `13`? Yes, we missing! What we need to take next patch equal to `8`. So now, our interval is `[0, 15]`.\n6. Our next missing number `16` is more, than next number in array: `13`. So if fact, we can create `[0, 28]`.\n7. Our next missing number is `29`, it is less than `43`, so we add `29` as patch. and we have interval `[0, 57]`.\n\n#### Complexity\n\nComplexity of this solution is `O(n)`.\n\n#### Code\n```python\nclass Solution:\n def minPatches(self, nums, n):\n reach, ans, idx = 0, 0, 0\n \n while reach < n:\n if idx < len(nums) and nums[idx] <= reach + 1:\n reach += nums[idx]\n idx += 1\n else:\n ans += 1\n reach = 2*reach + 1 \n \n return ans\n```\n\nIf you have any questions, feel free to ask. If you like solution and explanations, please **Upvote!** | 79 | 5 | ['Greedy'] | 9 |
patching-array | Python O(n) with detailed explanation | python-on-with-detailed-explanation-by-y-2jlo | Initialize an empty list, keep adding new numbers from provided nums into this list, keep updating the coverage range and ensure a continus coverage range. If y | yuanzhi247012 | NORMAL | 2019-07-19T04:44:05.512209+00:00 | 2020-02-06T08:03:53.530327+00:00 | 2,667 | false | Initialize an empty list, keep adding new numbers from provided nums into this list, keep updating the coverage range and ensure a continus coverage range. If you do so, you only need to care about whether the newly added number will break the coverage range or not.\n\nSuppose 1~10 is already covered during this process, (by whatever combinations in the above list, doesn\'t matter), then for the next number added\n1. If the next number is "11", you will have these new sums: \n 11, 11+1, 11+2, ..., 11+10, so your total coverage becomes 1~21, which is "2 x coverage + 1"\n2. If the next numberis smaller than "11", for example "3", then the new coverage becomes: 10+3, 9+3, 8+3-> 1~13, which is "num + coverage"\n3. If the next number is bigger than "11", for example "12", then number "11" is missing forever. There is no way to sum 11 by existing combinations. You have to manually patch "11" before being able to process the next number. Note that Patching number "1~10" can also cover the missing "11", but patching "11" is optimal because it maximizes the total coverage.\n\n```\nclass Solution:\n def minPatches(self, nums: List[int], n: int) -> int:\n covered=0\n res=0\n for num in nums:\n while num>covered+1:\n res+=1\n covered=covered*2+1\n if covered>=n:\n return res\n covered+=num\n if covered>=n:\n return res\n while covered<n:\n res+=1\n covered=covered*2+1 \n return res\n```\n\nShorter version with same logic:\n```\nclass Solution:\n def minPatches(self, nums: List[int], n: int) -> int:\n covered,res,i=0,0,0\n while covered<n:\n num=nums[i] if i<len(nums) else math.inf\n if num>covered+1:\n covered=covered*2+1\n res+=1\n else:\n covered+=num\n i+=1 \n return res\n``` | 57 | 0 | [] | 10 |
patching-array | 详细解释/Detailed Explanation with Example | xiang-xi-jie-shi-detailed-explanation-wi-i9h8 | \u4F8B\u5B50\uFF08Example\uFF09\n\n[1,2,3,5,10,50,70], n=100\n1. Seeing 1, we know [1,1] can be covered\n2. Seeing 2, we know [1,3] can be covered\n3. Similarly | lishichengyan | NORMAL | 2019-04-23T06:41:22.012744+00:00 | 2019-04-23T06:41:22.012815+00:00 | 2,293 | false | **\u4F8B\u5B50\uFF08Example\uFF09**\n\n[1,2,3,5,10,50,70], n=100\n1. Seeing 1, we know [1,1] can be covered\n2. Seeing 2, we know [1,3] can be covered\n3. Similarly for 3, [1,6] can be covered\n4. for 5, [1,11] can be covered\n5. for 10, [1, 21] can be covered\n6. for 50, however, we have to add a patch, if the patch is 1, the range can be extended to [1, 22], if the patch is 2, the range can be extended to [1, 23]...From the observation we know in order to extend the range as longer as possible, we need to add 22, so that we get [1,43]. Why not add 23? Because [1,2,3,5,10,23] can NOT cover 22!\n6. [1,43] does not cover 50 yet. Following a similar way of thinking, we know this time we need to add 44, extending the range to [1, 87]\n7. for 70, it\'s already in [1,87], add 70 would extend the range to [1,157]\n8. 157 > 100, done\n\nIn conclusion, we need 2 patches, i.e., 22 and 44.\nSo the key point is if the current range is [1,m], and the current number > m, we need to add m+1 as a patch, to extend the range to [1, 2m+1].\n\n--------\n\n[1,2,3,5,10,50,70], n=100\n1. \u770B\u5230\u7B2C\u4E00\u4E2A\u65701\uFF0C\u6211\u4EEC\u77E5\u9053[1,1]\u53EF\u4EE5\u88AB\u8986\u76D6\n2. \u770B\u5230\u7B2C\u4E8C\u4E2A\u65702\uFF0C\u6211\u4EEC\u77E5\u9053[1,3]\u53EF\u4EE5\u88AB\u8986\u76D6\n3. 3\u540C\u7406\uFF0C[1,6]\u53EF\u4EE5\u88AB\u8986\u76D6\n4. 5\u540C\u7406\uFF0C[1,11]\u53EF\u4EE5\u88AB\u8986\u76D6\n5. 10\u540C\u7406\uFF0C[1,21]\u53EF\u4EE5\u88AB\u8986\u76D6\n6. \u73B0\u5728\u523050\uFF0C\u53D1\u73B0\u4E0D\u5F97\u4E0D\u6253\u8865\u4E01\u4E86\uFF0C\u5982\u679C\u6253\u8865\u4E011\uFF0C\u53EF\u4EE5\u6269\u5C55\u4E3A[1,22]\uFF0C\u5982\u679C\u6253\u8865\u4E012\uFF0C\u53EF\u4EE5\u6269\u5C55\u4E3A[1,23]...\u53EF\u89C1\uFF0C\u8981\u5F97\u5230\u6700\u5927\u7684\u8303\u56F4\uFF0C\u5E94\u8BE5\u6253\u7684\u8865\u4E01\u662F22\uFF0C\u8FD9\u6837\u80FD\u5F97\u5230[1,43]\uFF0C\u4E3A\u4EC0\u4E48\u4E0D\u80FD\u6253\u8865\u4E0123\u5462\uFF1F\u56E0\u4E3A[1,2,3,5,10,23]\u5F97\u4E0D\u523022\uFF01 \n7. [1,43]\u8FD8\u662F\u6CA1\u6709\u8986\u76D650\uFF0C\u6309\u7167\u7C7B\u4F3C\u7684\u903B\u8F91\uFF0C\u8FD9\u6B21\u5E94\u8BE5\u6253\u7684\u8865\u4E01\u662F44\uFF0C\u5C06\u8303\u56F4\u6269\u5145\u5230[1,87]\n8. \u6700\u540E\u523070\uFF0C\u5728[1,87]\u5185\uFF0C\u8303\u56F4\u88AB\u6269\u5145\u5230[1,157]\n9. 157 > 100\uFF0C\u7ED3\u675F\n\n\u7EFC\u4E0A\uFF0C\u4E00\u5171\u89812\u4E2A\u8865\u4E01\uFF0C\u537322\u548C44\n\u6240\u4EE5\uFF0C\u9898\u76EE\u7684\u8981\u70B9\u5728\u4E8E\uFF0C\u5982\u679C\u5F53\u524D\u7684\u8303\u56F4\u662F[1,m]\uFF0C\u4E14\u5F53\u524D\u7684\u6570\u5B57num > m\uFF0C\u6211\u4EEC\u5E94\u8BE5\u6253\u8865\u4E01m+1\uFF0C\u4F7F\u5F97\u8303\u56F4\u6269\u5145\u5230[1\uFF0C2m+1]\u3002\n\n\n**\u4EE3\u7801\uFF08Code\uFF09**\n```\ndef minPatches(self, nums: List[int], n: int) -> int:\n\tcnt = 0\n\tpatch = 0\n\ttot = len(nums)\n\ti = 0\n\twhile patch < n:\n\t\tif i < tot and patch + 1 >= nums[i]:\n\t\t\tpatch += nums[i]\n\t\t\ti += 1\n\t\telse:\n\t\t\tcnt += 1\n\t\t\t#print(patch+1)\n\t\t\tpatch += patch + 1 # patch + 1 is the new patch to be added\n\treturn cnt\n``` | 42 | 0 | [] | 9 |
patching-array | ✅✅Fastest 💯💯 Efficient 💎💎Simplest Solution 🏃♂️🏃♂️DryRun🔥🔥 | fastest-efficient-simplest-solution-dryr-9ia0 | Thanks for checking out my solution.This post has been made with ❤ by Alok KhansaliDo Upvote if this helped 👍🎯Approach : Greedy 🤑Intuition 🔮Leetcode walo ne wee | TheCodeAlpha | NORMAL | 2024-06-16T08:00:45.565747+00:00 | 2025-01-07T16:58:50.074086+00:00 | 2,267 | false | #### Thanks for checking out my solution.
#### This post has been made with ❤ by [Alok Khansali](https://leetcode.com/u/TheCodeAlpha/)
### Do Upvote if this helped 👍
# 🎯Approach : Greedy 🤑
<!-- Describe your approach to solving the problem. -->
# Intuition 🔮
<!-- Describe your first thoughts on how to solve this problem. -->
##### Leetcode walo ne weekend hi hard bana diya, par agar tumne meri kl wali post dekhi hogi toh shayad itna mushkil nahi raha hoga. Aur aaj wali dekhne ke baad toh din hi set ho jayega.
##### Sawal hard hai, issi liye leetcode ne hint bhi ni di, Easy hota toh shayad 5-6 hint mil jaati, kyuki leetcode ko lagta hai hard toh ye bana hi lenge, seekhane ki jarurat toh easy wale hain.
___
#### 💡Chalo koi ni, mai koshish karta hu samjhaane ki.🤗
##### Maanlo tumhare paas koi bhi rupay💷 nahi hai, toh sabse pehli dikkat kitne rupay banane mai aayegi?
##### Sahi jawab 1✅, tez hote jaare ho nice!
##### Ab tumko 1 rupay dediye, toh ab kitne rupay banane mai dikkat aayegi?
##### Ekdum sahi 2 rupay, kya baat back to back sahi jawab
##### Ab tumko do rupay bhi de diye, fir kis pe dikkat aayegi?
##### Arey gajab bilkul sahi 4rupay banane mai. Dekha samaj rahe ho tum..
##### Oh🤔 agar nahi samjhe toh aisa isiliye kyuki 1 + 2 = 3, toh teen rupay toh ab tum kisi ke bhi muh pe fek ke maar sakte ho.(Maarna mat😂, saamne wale ke paas sikke jyada huye toh....)
##### Ab tumko 4 rupay bhi de diye, ab batao kitne rupay pe agli dikkat aari?
##### Very nice 8 hi hai sahi sawab.
##### Ab jo pattern ban raha hai, usko dekh ke ye mat socho ki 2 ki power mai khel denge aur crazy kar denge. Nahi❌
##### Thoda thoda idea lag gya hain humko ki ho kya raha hai, isko crystal clear💎 karte hain ab.
`nums` = [1,2,2,6,18]
#### Ab batao pehli dikkat kab aayegi?
- 1 ban jayega, kyuki diya hua hai
- 2,6,18 bhi ban jayenge upar wale reason se
- 3 banega 1 + 2 se, 4 banega 2 + 2 se, 5 banega 1+ 2 + 2 se, 7,8,9,10,11 bhi ban jayenge 6 ke saath pichle combinations ko jod kar
- Isse conclude hua ye ki hum 12 nahi bana paare hain abhi, pehla patch humko 12 pe dena hoga
#### Agar ab tumko dikha prefix sum, toh ekdum sahi raah🚉 par ho tum mitra💯. Par manzil tak pahuchne ke liye humko lagani padegi uss sum pe kuch shartein urf conditions
#### Humko values ka tokra sorted mila hai matlab ki jodne wala kaam shuru se aram se karlenge, 🧠dimag ni lagana sort karne mai. Ab agar tumne mere pehle example ko (haan voi jisme tumko power of 2 dikhra tha) dusre ke sath mix kiya hoga toh tum paaoge ki 12 par toh hum seedha aare hain....
**Pehli dikkat thi 1 rupya, humare aaray mai bhi 1 rupya, dikkat khatam, 1 ko jodo current dikkat pe, hogya 2 rupya, array ki dusri value 2 rupya, dikkat khatam, isko jodo current dikkat pe 4 rupya, array mai hai 2 rupya, koi dikkat hi ni....isi silisile ko dikhaya hai neeche maine**
**1 < 1, pehli dikkat
2 < 2, dusri dikkat
4 < 2, teesri dikkat
6 < 6, chauthi dikkat, abke sawal par
12 < 18, yaha par condition hogyi true aur humko mila pehla patch**
<details>
<summary> Sawal ko pese ke terms mai samjhane ka reason </summary>
- Ab maine rupyo ki baat isliye nahi ki kyuki mujhe pasand hain.(matlab hain par, yaha vo reason nahi hai)
- Aisa isliye kyuki ek sawal kiya hua hai maine pehle jisko kehte hain Minimum Sum Coin,
- uss ka saar ye hai ki aapko dediye sikke, aapko batana hai ki aisi konsi sabse choti value hai, jisko hum diye huye sikko se nahi bana payenge.
-
</details>
.
**Ab bas is par ek cheez ka dhyaan rakhna ki jab koi value `x` currentSum se badi hogi, toh humko currentSum ko hi dugna kardena hai, iss se `currentSum` se lekar `currentSum * 2 - 1`, tak sab cover ho jayega, aisa tabtak karte rahein jabtak array ki value `x` se humara `currentSum` bada na ho jaye**
#### Bas issi Soch ke sath aage aap algorithm or dryrun ki sahayata lekar iss sawal ki chutti kar sakte hain. Meri dua lene ke liye mujhe upvote dein, tatha comment karein aur comment mai ek slightly simpler code ko bhi dekhein. Dhanyawaad!
#### Aasha karta hu aap sawal ko samaj gaye honge, aur aage isko code karne mai aapko ko koi kathinayi nahi hogi.
____
# Algorithm 👩💻
### 1. Initialisation:
- `currentSum` ko 1 pe set karo. Yeh track karta hai sabse chhota number jo abhi tak nahi ban sakta.
- `patches` ko 0 pe set karo. Yeh track karta hai kitne patches lagaye gaye hain.
- `index` ko 0 pe set karo. Yeh `nums` array ko iterate karne ke liye hai.
### 2. Array ko Iterate karo:
- Jab tak `currentSum` chhota ya barabar hai `n` ke:
- Agar `index` chhota hai `nums.size()` se aur `nums[index]` chhota ya barabar hai `currentSum` ke:
- `currentSum` mein `nums[index]` ko add karo.
- `index` ko increment karo.
- Agar nahi:
1. __Patch Add karo:__
- `patches` ko increment karo.
- Ek patch add karo (`currentSum` ko) taaki range cover ho jaye `currentSum * 2 - 1` tak.
- `currentSum` ko update karo (`currentSum` + `currentSum`).
### 3. Return karo Answer:
- `patches` ko return karo jo total patches lagaye gaye hain.
___
___
# DryRun Time🏃♂️🏃♂️
<details>
<summary> DRYRUN</summary>
### Let's perform a dry run of the minPatches function with the given inputs:
nums = [1, 2, 31, 33]
n = 250
### Initial Setup:
currentSum = 1 (Tracks the smallest number that cannot be formed)
patches = 0 (Tracks the number of patches added)
index = 0 (Iterator through the nums array)
## Step-by-Step Dry Run:
### Iteration 1:
currentSum = 1
index = 0, nums[index] = 1
Since nums[index] <= currentSum:
Add nums[index] to currentSum: currentSum = 1 + 1 = 2
Increment index: index = 1
### Iteration 2:
currentSum = 2
index = 1, nums[index] = 2
Since nums[index] <= currentSum:
Add nums[index] to currentSum: currentSum = 2 + 2 = 4
Increment index: index = 2
### Iteration 3:
currentSum = 4
index = 2, nums[index] = 31
Since nums[index] > currentSum:
Add a patch: currentSum = 4 + 4 = 8
Increment patches: patches = 1
### Iteration 4:
currentSum = 8
index = 2, nums[index] = 31
Since nums[index] > currentSum:
Add a patch: currentSum = 8 + 8 = 16
Increment patches: patches = 2
### Iteration 5:
currentSum = 16
index = 2, nums[index] = 31
Since nums[index] > currentSum:
Add a patch: currentSum = 16 + 16 = 32
Increment patches: patches = 3
### Iteration 6:
currentSum = 32
index = 2, nums[index] = 31
Since nums[index] <= currentSum:
Add nums[index] to currentSum: currentSum = 32 + 31 = 63
Increment index: index = 3
### Iteration 7:
currentSum = 63
index = 3, nums[index] = 33
Since nums[index] <= currentSum:
Add nums[index] to currentSum: currentSum = 63 + 33 = 96
Increment index: index = 4
### Iteration 8:
currentSum = 96
index = 4, nums has no more elements.
Since index >= nums.size():
Add a patch: currentSum = 96 + 96 = 192
Increment patches: patches = 4
### Iteration 9:
currentSum = 192
index = 4, nums has no more elements.
Since index >= nums.size():
Add a patch: currentSum = 192 + 192 = 384
Increment patches: patches = 5
### Summary:
#### At the end of the iterations, currentSum exceeds n = 250, and we have added 5 patches in total.
### Final State:
currentSum = 384 (Greater than n = 250)
patches = 5
### Thus, the minimum number of patches required to make all numbers up to 250 representable is 5.
</details>
___
# Code
```cpp []
class Solution
{
public:
int minPatches(vector<int> &nums, int n)
{
ios_base::sync_with_stdio(0);
long long int currentSum = 1; // Tracks the smallest number that cannot be formed
int patches = 0, index = 0; // Pathches to keep track of the patch and Index to iterate through the nums array
while (currentSum <= n)
{
// If the current number in nums is within the range and can be added to currentSum
if (index < nums.size() && nums[index] <= currentSum)
{
currentSum += nums[index];; // Include nums[index] in the range
index++;
}
else
{
// Add a patch (currentSum itself) to cover the range up to currentSum * 2 - 1
currentSum += currentSum;
patches++;
}
}
return patches;
}
};
```
```java []
class Solution
{
public
int minPatches(int[] nums, int n)
{
long currentSum = 1; // Tracks the smallest number that cannot be formed
int patches = 0; // Number of patches added
int index = 0; // Index to iterate through the nums array
// Continue until we can form numbers up to n
while (currentSum <= n)
{
// If current index lies in the array
//and the current value is less than equal to the currentSum
if (index < nums.length && nums[index] <= currentSum)
{
// If the current number in nums can be added to currentSum
currentSum += nums[index]; // Include nums[index] in the range
index++;
}
else
{
// Add a patch (currentSum itself) to cover the range up to currentSum * 2 - 1
currentSum += currentSum;
patches++;
}
}
return patches;
}
}
```
```python []
class Solution:
def minPatches(self, nums: List[int], n: int) -> int:
currentSum = 1 # Tracks the smallest number that cannot be formed
patches = 0 # Number of patches added
index = 0 # Index to iterate through the nums array
# Continue until we can form numbers up to n
while currentSum <= n:
if index < len(nums) and nums[index] <= currentSum:
# If the current number in nums can be added to currentSum
currentSum += nums[index] # Include nums[index] in the range
index += 1
else:
# Add a patch (currentSum itself) to cover the range up to currentSum * 2 - 1
currentSum += currentSum
patches += 1
return patches
```
____
# Complexity
- Time complexity: $$O(N)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(1)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
____

| 39 | 0 | ['Array', 'Math', 'Greedy', 'C++', 'Java', 'Python3'] | 4 |
patching-array | C++ Simple and Easy Explained Solution, 7-Short-Lines | c-simple-and-easy-explained-solution-7-s-3x0q | Idea:\nEvery time count reaches a number that the next element in nums is greater than it, we need a patch.\nIf we add the number itself, count can be doubled b | yehudisk | NORMAL | 2021-08-29T12:10:35.212338+00:00 | 2021-08-29T12:10:35.212390+00:00 | 2,653 | false | **Idea:**\nEvery time `count` reaches a number that the next element in `nums` is greater than it, we need a patch.\nIf we add the number itself, `count` can be doubled because we can add the new number to any of the previous numbers.\nSo if `count` = 7, and the next number in `nums` is 10, if we add 7 to `nums` now we have all numbers until 14.\n```\nclass Solution {\npublic:\n int minPatches(vector<int>& nums, int n) {\n long patches = 0, count = 1, i = 0, sz = nums.size();\n while (count <= n) {\n \n if (i < sz && nums[i] <= count) count += nums[i++];\n \n else {\n count *= 2;\n patches++;\n }\n }\n \n return patches;\n }\n};\n```\n**Like it? please upvote!** | 37 | 2 | ['C'] | 5 |
patching-array | Rigorous Mathematical Proof | No Lucky Guess/Intuition | rigorous-mathematical-proof-no-lucky-gue-dtnt | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n\n# Algorithm (with explaination on an example)\n\nAt any point, if the n | prabhatjha26 | NORMAL | 2024-06-16T10:40:20.425486+00:00 | 2024-06-17T08:12:26.697671+00:00 | 840 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n\n# Algorithm (with explaination on an example)\n\nAt any point, if the next item in the array is greater than (sum of all previous elements plus 1), then add (sum of all previous elements plus 1)\nin the array.\n\nInitialization: sum of all previous elements starts at 0.\n\nFor example, in array [1,5,10], target = 20\n\nlet\'s call sum of all previous elements as prevSum:\nInitialization: prevSum = 0\n\nIs 1 > prevSum + 1 = 1 ? No, Good we dont do anything, just update prevSum to 1 and move ahead.\n\nIs 5 > prevSum + 1 = 2? Yes, Add (prevSum + 1) = 2 to the array (array: [1, 2, 5, 10]) update prevSum to prevSum + new_element = (1 + 2 ) = 3 and move ahead. \n\n(Note: next time we again check 5, as we have to check the 3rd element next time which is again 5 after adding 2 in last step.)\n\nIs 5 > prevSum + 1 = 4? Yes, Add (prevSum + 1) = 4 to the array (array: [1, 2, 4, 5, 10]) update prevSum to prevSum + new_element = (3 + 4) = 7 and move ahead.\n\nIs 5 > prevSum + 1 = 8? No, Good we dont do anything, just update prevSum to (prevSum + 5) = 12 and move ahead.\n\nIs 10 > prevSum + 1 = 13? No, Good we dont do anything, just update prevSum to (prevSum + 10) = 22 and move ahead.\n\nAs we already see th target of 20 is achieved, so let\'s stop. We have added two elements to the list so the answer is 2.\n\n# Proof\n\n**Definition:** Let A be an array [x1, x2, x3, . . . , x_r]. Then Span(A)\nis defined as a positive natural number x if all positive natural numbers less than or equal to x can be formed using elements in A and (x + 1) can not be formed using it.\n\nExample: Span([1,2,5]) = 3 as all of 1, 2 and 3 (3 = 1 + 2) can be formed using [1,2,5] but not 4. In other is words, 4 is the smallest positive natural number that can not be formed using [1,2,5] so 3 is the span of [1,2,5].\n\n**Lemma:** Let\'s suppose the first r elements in an array is A_r = [x1, x2, . . . , x_r] and Span(A_r) = x = x1 + x2 + . . . + x_r, then the span of A_(r+1) = [x1, x2, . . . , x_r, x_(r+1)] is x1 + x2 + . . . + x_r + x_(r+1) if and only if x_(r+1) <= x + 1 i.e x1 + x2 + . . . + x_(r+1).\n\nProof: The proof is trivial:\n\nAs we have to prove (A <=> B)\nProving First: \nB => A (i.e if x_(r+1) <= x + 1) => Span(A_(r+1)) = x1 + x2 + . . + x_(r+1)\n\n Easier Part: No number bigger than x1 + x2 + . . . + x_r + x_(r+1) can be formed using [x1, x2, . . . , x_r, x_(r+1)].\n\n Other Part: Let y <= x1 + x2 + . . . + x_r + x_(r+1) = x + x_(r+1). . . (1)\n\n Claim: y can be formed. How? \n\n if y <= x, it can be formed using first r elements itself as Span(A_r) = x = x1 + x2 + . . . + x_r.\n\n else: x < y <= x + x_(r + 1) \n therefore, y = x_(r+1) + z,\n now z <= x ... from(1)\n also z >= 0 (as z = y - x_(r+1) and y >= (x+1) and x_(r+1) <= x+1 (from 1))\n Thus, z can be formed using first r elements, Thus y can be formed, so done.\n\nProving Other Way:\nA => B (i.e Span(A_(r+1)) = x1 + x2 + . . + x_(r+1) => i.e if x_(r+1) <= x + 1))\n\nNow, as we know that A => B is same as proving Not B => Not A:\n\nSo, we prove that if x_(r+1) > x + 1 => Span(A_(r+1)) != x1 + x2 + . . + x_(r+1) = x + x_(r+1).\n\nThis is pretty simple part: If x_(r+1) > x + 1. \nWe can\'t even form x + 1, as fisrt r items can only form upto x, and the next element is greater than (x + 1). So the span would be x itself as we can form all numbers till x and can not form (x + 1). Thus Span(A_(r+1)) can\'t be x + x_(r+1).\n\n Hence Proved \n\n\n**Theorem** Let\'s suppose the first r elements in an array is A_r = [x1, x2, . . . , x_r] and Span(A_r) = x = x1 + x2 + . . . + x_r, and the next element is greater than x + 1. Then there exist an optimal solution (one with minimum number of additions into the array) which would add (x + 1) to the array.\n\nProof: As Span(A_r) is sum of all previous elemnts ie (x = x1 + x2 + . . . + x_r), and next element in the array is greater than (x + 1), so we need to add a number to the array to form the element x + 1. \n\nThere are multiple possibilities which when added can make the sum x + 1. In particular, anything from [1, 2, 3, . . . , x + 1] when added to existing array would do. As A_r can form (x + 1)- k for positive k, so adding extra k would do.\n\nWhich is the best choice, though? Ans: (x + 1), why?\n\nJustification: If i show that the Span([x1, x2, . . . , x_r, k]) is smaller than Span([x1, x2, . . . , x_r, x + 1]) for k < x + 1. Then, this would do, **why**?\n\n\n**{Jutification of Why, you can choose to read it later:** Lets say the optimal solution has array [x1, x2, . . . , x_r, k, y1, y2, .., y_t]\n\nThen [x1, x2, . . . , x_r, x+1, y1, y2, .., y_t] is also an optimal solution. \n\nBeacuse: is z is formed using [x1, x2, . . . , x_r, k, y1, y2, .., y_t], \nz = (elements from [x1, x2, . . . , x_r, k]) + elements from([y1, y2, .., y_t])\n\nNow, given that i show Span([x1, x2, . . . , x_r, k]) <= Span([x1, x2, . . . , x_r, x + 1]), thus the first part can be formed by Span([x1, x2, . . . , x_r, x + 1]) too. Thus z can be formed by [x1, x2, . . . , x_r, x + 1, y1, y2, .., y_t] too. Similarly, if you replace all added elements in the optimal solution by the one produced by this algorithm, you are bind to get an optimal solution.**}**\n\nComing back to the showing:\n\nSpan([x1, x2, . . . , x_r, k]) < Span([x1, x2, . . . , x_r, x + 1]) when \nk < x + 1.\n\nFrom if part of lemma: Span([x1, x2, . . . , x_r, k]) = x1 + x2 + . . . + x_r + k < x1 + x2 + . . . + x_r + (x + 1) = Span([x1, x2, . . . , x_r, x + 1]).\n\n QED\n\n\n\nNow, how does these lemma and theorem helps solve this problem?\n\nIf the first element of the sorted array is not 1, what choice do we have. Nothing rather than adding 1, as we also want to produce 1 and that can not be done using any other number.\n\nNow, lets say we have added 1 as our first element. Does the condition of theorem satisfies which is the span of first r element is sum fo first r element. Yes. As Span([1]) = 1 = sum of first 1 element. From, here ownwards the theorem suggests that, add an element (previous sum of all elements + 1) when next element is greater than (previous sum of all elements + 1) else dont. \n\n\n\n**Hi Guys, it took a lot of time and effort to devise and write the algorithm and its rigorous proof, upvote if it has helped you a bit. Also, feel free to ask questions if you have any, I will reply to them.**\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution(object):\n def minPatches(self, nums, n):\n """\n :type nums: List[int]\n :type n: int\n :rtype: int\n """\n \n l = len(nums)\n d = defaultdict(lambda : float("inf"))\n for i in range(l):\n d[i] = nums[i]\n\n ans = 0 \n baseSum = 0\n\n i = 0\n while True:\n if baseSum >= n:\n return ans \n\n elif d[i] > baseSum + 1:\n ans += 1\n baseSum += baseSum + 1\n\n else:\n baseSum += d[i]\n i+=1\n\n``` | 35 | 0 | ['Python'] | 3 |
patching-array | ✔✔ Patching Array. Simple Solution with Explanation | patching-array-simple-solution-with-expl-ljkb | \nint minPatches(vector<int>& nums, int n) {\n long miss = 1, added = 0, i = 0;\n while (miss <= n) {\n if (i < nums.size() && nums[i] <= miss) {\n | inomag | NORMAL | 2021-08-29T07:16:08.779881+00:00 | 2021-08-29T07:21:10.782490+00:00 | 1,679 | false | ```\nint minPatches(vector<int>& nums, int n) {\n long miss = 1, added = 0, i = 0;\n while (miss <= n) {\n if (i < nums.size() && nums[i] <= miss) {\n miss += nums[i++];\n } else {\n miss += miss;\n added++;\n }\n }\n return added;\n}\n```\n\nLet **miss** be the smallest sum in **[0,n]** that we might be missing. Meaning we already know we can build all sums in **[0,miss)**. Then if we have a number **num <= miss** in the given array, we can add it to those smaller sums to build all sums in **[0,miss+num)**. If we don\'t, then we must add such a number to the array, and it\'s best to add miss itself, to maximize the reach\n\n | 29 | 10 | [] | 6 |
patching-array | Share my greedy solution by Java with simple explanation (time: 1 ms) | share-my-greedy-solution-by-java-with-si-u7uo | public static int minPatches(int[] nums, int n) {\n\t\tlong max = 0;\n\t\tint cnt = 0;\n\t\tfor (int i = 0; max < n;) {\n\t\t\tif (i >= nums.length || max < num | liqiwei | NORMAL | 2016-01-27T09:53:11+00:00 | 2018-10-02T05:40:35.766686+00:00 | 6,917 | false | public static int minPatches(int[] nums, int n) {\n\t\tlong max = 0;\n\t\tint cnt = 0;\n\t\tfor (int i = 0; max < n;) {\n\t\t\tif (i >= nums.length || max < nums[i] - 1) {\n\t\t\t\tmax += max + 1;\n\t\t\t\tcnt++;\n\t\t\t} else {\n\t\t\t\tmax += nums[i];\n\t\t\t\ti++;\n\t\t\t}\n\t\t}\n\t\treturn cnt;\n\t}\n\nThe variable `max` records the maximal value that can be formed by the elements in `nums` and patched numbers. If `max` is less than `nums[i] - 1` which means we need to patch a new number, we then patch `max + 1`. | 27 | 1 | [] | 7 |
patching-array | 100% Beats | Easy to Understand | Detailed Step by Step Explaination | Greedy Approach | 100-beats-easy-to-understand-detailed-st-hdw9 | Problem Statement\nWe are given a sorted integer array nums and an integer n. Our task is to determine the minimum number of patches required to ensure that any | tanishqsingh | NORMAL | 2024-06-16T03:30:37.806551+00:00 | 2024-06-16T04:20:43.666166+00:00 | 4,303 | false | # Problem Statement\nWe are given a sorted integer array `nums` and an integer `n`. Our task is to determine the minimum number of patches required to ensure that any number in the range `[1, n]` can be formed by summing some elements from the array `nums`. Each element in `nums` can only be used once.\n\n# Highly Optimised with 100% beats\n\n\n\n# Intuition\nWhen I first looked at the problem, I understood that we need to ensure every number from 1 to n can be formed using elements in a sorted array `nums`. My initial thought was to use a greedy strategy because it seemed efficient. \n\n# Approach\n### Step 1: **Start with Initialization**:\n - Begin with `missing = 1`. This variable represents the smallest number that we cannot yet form using the elements from `nums`.\n - Also, set `patches = 0` to keep track of how many patches we need to add.\n\n### Step 2: **Traverse through `nums`**:\n - Iterate through the sorted array `nums`.\n - For each number `num` in `nums`, check if it can help in forming the current range up to `missing`.\n\n### Step 3: **Handling the Current Number**:\n - If `num` is less than or equal to `missing`, it means we can extend our coverage using `num`.\n - Update `missing` to `missing + num` to reflect that we can now form sums up to this new value.\n - If `num` is greater than `missing`, there\'s a gap between `missing` and `num - 1` that needs to be covered.\n - To cover this gap, add `missing` to `nums` and increment `patches`.\n - Update `missing` to `missing + missing` because now we can form sums up to `2 * missing`.\n\n### Step 4: **Repeat Until Coverage**:\n - Continue the above steps until `missing` exceeds `n`. This ensures that every number from 1 to n can be formed using elements from `nums` and the patches added.\n\n### Step 5: **Count and Return**:\n - After exiting the loop, `patches` will contain the minimum number of patches required.\n\n### Example\nLet\'s go through an example with `nums = [1, 3]` and `n = 6`:\n\n- **Initialization**: Start with `missing = 1`, `patches = 0`.\n \n- **Step 1**: \n - `num = 1`: `1 <= missing`, so update `missing = 2`.\n \n- **Step 2**:\n - `num = 3`: `3 > missing`, so add `missing = 2` to `nums` and increment `patches`. Now `missing = 4`.\n \n- **Step 3**:\n - Continue the loop until `missing > n`, ensuring all numbers up to `n` can be formed.\n\n# Complexity\n- **Time Complexity**: ``O(m + log n)``\n \n- **Space Complexity**: ``O(1)``\n\n# Code\nThis implementation follows the approach I described, ensuring that every step is clear and understandable in a conversational manner.\n\n```C++ []\nclass Solution {\npublic:\n int minPatches(vector<int>& nums, int n) {\n int patches = 0;\n int index = 0;\n long long nextSum = 1;\n\n while (nextSum <= n) {\n if (index < nums.size() && nums[index] <= nextSum) {\n nextSum += nums[index++];\n } else {\n nextSum += nextSum;\n patches++;\n }\n }\n\n return patches;\n }\n};\n\n```\n\n```Java []\nclass Solution {\n public int minPatches(int[] nums, int n) {\n int count = 0;\n long missing = 1;\n int i = 0;\n \n while (missing <= n) {\n if (i < nums.length && nums[i] <= missing) {\n missing += nums[i++];\n } else {\n missing += missing;\n count++;\n }\n }\n \n return count;\n }\n}\n\n```\n```Python3 []\nclass Solution:\n def minPatches(self, nums: List[int], n: int) -> int:\n count = 0\n missing = 1\n i = 0\n \n while missing <= n:\n if i < len(nums) and nums[i] <= missing:\n missing += nums[i]\n i += 1\n else:\n missing += missing\n count += 1\n \n return count\n\n```\n```JavaScript []\n/**\n * @param {number[]} nums\n * @param {number} n\n * @return {number}\n */\nvar minPatches = function(nums, n) {\n let count = 0;\n let missing = 1;\n let i = 0;\n \n while (missing <= n) {\n if (i < nums.length && nums[i] <= missing) {\n missing += nums[i++];\n } else {\n missing += missing;\n count++;\n }\n }\n \n return count;\n};\n\n```\n\n\nThank you for exploring this solution! I hope it helped clarify the problem. \n### Please feel free to upvote if you found it useful. Happy coding!\n | 17 | 0 | ['Greedy', 'C++', 'Java', 'Python3', 'JavaScript'] | 3 |
patching-array | A concrete example to work down the algorithm | a-concrete-example-to-work-down-the-algo-321o | \nThink it reversely: the maximum value we can form based on a given set of numsers?\nif for a give set [1, ..., k], and anything less or equal to k is already | winkee | NORMAL | 2020-06-12T12:19:11.063444+00:00 | 2020-06-12T12:28:54.994359+00:00 | 825 | false | \nThink it reversely: the maximum value we can form based on a given set of numsers?\nif for a give set [1, ..., k], and anything less or equal to k is already covered. then anything [k+1 .... k + k) must also be covered! In another word, if we have k and all value before k is covered, then the later part [k, 2*k) is also covered.\n**This is the most important observation.** coverage is just symmetric around the largest item in the array! \nthe reason why 2k is not covered is because each element can only be pick only one time.\n\ne.g. [1, 2, 4] , since all value between [1, 4] is covered, this array will also cover [5, 8), the whole coverage is [1, 8).\ntherefore, for this array, if we ask for a target value that is between [8, 16) to be covered, we just need to add 8 to the array.\n\nNow, we want a coverage to N, how should we approach to it?\nwe just need to scan the array and keep increasing our coverage until it >= N.\n\nexample:\n`[1, 2, 4, 13, 43], n = 100`\nprobable missing starts at 1, we encounter first item nums[0] = 1, it can cover `[1, 2)`\nincrease probable missing to nums[0] + missing = 2; next iteration, we encounter second item nums[1] = 2, it can cover `[1, 2 * nums[1])`\nincrease probable missing to nums[1] + missing = 4; next iteration, encounter `nums[2] = 4`, covered, it can cover `[1, 4*nums[2])` = `[1, 8)`\nincrease probable missing to nums[2] + missing = 8, next iteration, encounter `nums[3] = 13`, 13 is not covered!, so we must add 8 to the array!\n when we add 8 to the array, the coverage will become `2*8 = 16` (right open range), and since we have 13, we can extend the coverage to `16 + 13 = 29`. literally, `[1, 29)`\nso the next probable missing number should be 29; next searching iteration, encounter 43, not covered! so we add 29.\nand the coverage is extended to` [1, 43 + 29*2)` = `[1, 101)`, we are done!\n\n\n```cpp\nint minPatches(vector<int>& nums, int n) {\n int missing = 1, patches = 0, int i = 0;\n while (missing <= n) {\n if (i < nums.size() && nums[i] <= missing) {\n missing += nums[i++];\n } else {\n missing += missing;\n patches++;\n }\n }\n return pathces;\n}\n```\n\n | 17 | 0 | [] | 1 |
patching-array | 💯✅🔥Easy Java ,Python3 ,C++ Solution|| 0 ms ||≧◠‿◠≦✌ | easy-java-python3-c-solution-0-ms-_-by-s-urpt | Intuition\n Describe your first thoughts on how to solve this problem. \nThe idea behind this solution is to keep track of the largest number that can be repres | suyalneeraj09 | NORMAL | 2024-06-16T02:01:02.894764+00:00 | 2024-06-16T02:01:02.894789+00:00 | 2,327 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe idea behind this solution is to keep track of the largest number that can be represented using the given numbers and the patches added so far. We start with the first number in the nums array, and if it is greater than the current largest number plus 1, we add a patch to cover the gap. Otherwise, we add the current number to the largest number that can be represented\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Initialize patch to keep track of the largest number that can be represented, count to keep track of the number of patches added, and index to keep track of the current index in the nums array.\n- While patch is less than n, do the following:\n- If index is less than the length of nums and patch + 1 is less than or equal to nums[index], add nums[index] to patch and increment index.\n- Otherwise, add patch + 1 to patch and increment count.\nReturn count.\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\n\nclass Solution {\n public int minPatches(int[] nums, int n) {\n long patch = 0;\n int count = 0;\n int index = 0;\n while (patch < n) {\n if (index < nums.length && patch + 1 >= nums[index]) {\n patch += nums[index];\n index++;\n } else {\n patch += (patch + 1);\n count++;\n }\n }\n\n return count;\n }\n}\n\n```\n```python3 []\nclass Solution:\n def minPatches(self, nums: List[int], n: int) -> int:\n patch = 0\n count = 0\n index = 0\n while patch < n:\n if index < len(nums) and patch + 1 >= nums[index]:\n patch += nums[index]\n index += 1\n else:\n patch += (patch + 1)\n count += 1\n return count\n```\n```C++ []\nclass Solution {\npublic:\n int minPatches(std::vector<int>& nums, int n) {\n long long patch = 0;\n int count = 0;\n int index = 0;\n while (patch < n) {\n if (index < nums.size() && patch + 1 >= nums[index]) {\n patch += nums[index];\n index++;\n } else {\n patch += (patch + 1);\n count++;\n }\n }\n\n return count;\n}\n};\n```\n\n\n\n\n\n\n | 14 | 0 | ['Array', 'C++', 'Java', 'Python3'] | 4 |
patching-array | My simple accepted C++ solution | my-simple-accepted-c-solution-by-violinv-2vqi | Idea: 1. Check the content if the current one is within sum +1, which is the total sum of all previous existing numbers. If yes, we proceed and update sum. If n | violinviolin | NORMAL | 2016-02-03T06:48:41+00:00 | 2016-02-03T06:48:41+00:00 | 3,853 | false | Idea: 1. Check the content if the current one is within sum +1, which is the total sum of all previous existing numbers. If yes, we proceed and update sum. If not, we patch one number that is within sum + 1. \n2. Keep updating the sum until it reaches n.\n \n\n\n\n\n\n int minPatches(vector<int>& nums, int n) {\n \n int len = nums.size();\n int sum = 0;\n int patch = 0;\n int count = 0;\n\n while (sum < n) {\n if (count != len && nums[count] <= sum + 1) {\n sum += nums[count];\n count ++;\n }\n else {\n patch ++;\n if (sum > (INT_MAX - 1) / 2) {\n sum = INT_MAX;\n }\n else {\n sum = sum * 2 + 1;\n }\n }\n }\n \n return patch;\n } | 14 | 0 | ['C++'] | 4 |
patching-array | Simple intuitive and well-explained solution accepted as best in C | simple-intuitive-and-well-explained-solu-d6rc | Before we hack this, we should be generous and think nothing about performance and try to come up with a sub-problem of it and then boot it from the beginning p | lhearen | NORMAL | 2016-02-22T11:39:36+00:00 | 2016-02-22T11:39:36+00:00 | 3,882 | false | Before we hack this, we should be generous and think nothing about performance and try to come up with a sub-problem of it and then boot it from the beginning point.\n\nSo before we truly get started, let's suppose we are in a state where we can reach <font color="#ff0000">**top**</font> by its sub-array nums[0...i] then what should we consider for the next element nums[i+1]? \n\n - now we need to check if `nums[i+1]<=top+1` then update <font color="#ff0000">**top**</font> to **top+nums[i+1]** and move to the next element;\n\n - but if nums[i+1] is greater than top+1, then there is a gap (how many? God knows) between top and nums[i+1]; in this case we need to patch a number to the array, then what number it should be? As we have discussed, it should top+1 which will be the largest we can achieve now **by patching** and then the top will be updated to **2*top+1**, right? Good, let's move on...\n - the generalised case have been discussed, then so what's the start? As we can easily get that the start value should be 1 then the top should be initialized to 0 and then everything just moves around! \n\n> End of the story!\n\nAs for the time cost, the nums array is limited and n is then determined by the **top = 2*top+1** equation, so O(logn) should be better to describe its time cost.\n\n - Space cost O(1)\n - Time cost O(logn)\n\n----------\n\n int minPatches(int* nums, int size, int n)\n {\n int count=0, index=0;\n long long top = 0;\n while(top < n)\n {\n if(index<size && nums[index]<=(top+1))\n top += nums[index++];\n else\n {\n count++;\n top = 2*top+1;\n }\n }\n return count;\n } | 12 | 2 | ['Iterator'] | 7 |
patching-array | Beats 98% users.. efficient and easy to understand solution 🆒 | beats-98-users-efficient-and-easy-to-und-i27v | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Aim_High_212 | NORMAL | 2024-06-16T03:21:52.417711+00:00 | 2024-06-16T03:21:52.417744+00:00 | 64 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minPatches(self, nums: List[int], n: int) -> int:\n ans = 0\n i = 0 # nums\' index\n miss = 1 # the minimum sum in [1, n] we might miss\n\n while miss <= n:\n if i < len(nums) and nums[i] <= miss:\n miss += nums[i]\n i += 1\n else:\n # Greedily add `miss` itself to increase the range from\n # [1, miss) to [1, 2 * miss).\n miss += miss\n ans += 1\n\n return ans\n``` | 11 | 0 | ['C', 'Python', 'C++', 'Java', 'Python3'] | 0 |
patching-array | [Greedy + Formal Proof + Tutorial] Patching Array | greedy-formal-proof-tutorial-patching-ar-agth | Topic : Greedy\nGreedy algorithms are a class of algorithms that make locally optimal choices at each step with the hope of finding a global optimum solution. | never_get_piped | NORMAL | 2024-06-16T01:41:30.228032+00:00 | 2024-06-21T04:51:12.483256+00:00 | 1,533 | false | **Topic** : Greedy\nGreedy algorithms are a class of algorithms that make locally optimal choices at each step with the hope of finding a global optimum solution. In these algorithms, decisions are made based on the information available at the current moment without considering the consequences of these decisions in the future. The key idea is to select the best possible choice at each step, leading to a solution that may not always be the most optimal but is often good enough for many problems. (GFG Reference)\n\n**A thorough proof is essential to demonstrate the correctness of a perfect Greedy solution.**\n\nFeel free to refer back to recent challenge on how I constructed a proof for it :\n* [Minimum Number of Moves to Seat Everyone](https://leetcode.com/problems/minimum-number-of-moves-to-seat-everyone/discuss/5304525/greedy-formal-proof-minimum-number-of-moves-to-seat-everyone)\n* [Minimum Increment to Make Array Unique](https://leetcode.com/problems/minimum-increment-to-make-array-unique/discuss/5309958/greedy-formal-proof-minimum-increment-to-make-array-unique)\n* [IPO](https://leetcode.com/problems/ipo/discuss/5315196/greedy-proof-ipo)\n\n___\n\n## Greedy Solution\nSolving a greedy problem generally involves coming up with a quick idea, but we need to prove its correctness before starting implementation. **Please refer to the section below for the solution walkthrough. This part exclusively focuses on guiding through the solution approach**.\n\nThe **greedy intuition** suggests that if you can already form any number from `0 to n` by using the current set of numbers, then adding a new number `x` such that `0 <= x <= n + 1` to our set allows you to from any number from `1` to `2 * n + 1`.\n\nWe initialize a variable `sum` to `0`, which signifies that with our current set, we can form any number from `0` up to `sum`. Our set starts empty, and we attempt to add elements from the input array or introduce new numbers using one operation.\n\nWe iterate through the `nums` array. If `nums[i]` is less than or equal to `sum + 1`, we add `nums[i]` to our current set, updating `sum` as `sum = sum + nums[i]`. If `nums[i]` is greater than `sum + 1`, our current set can already form any number from 0 to `sum`. In this case, we need to introduce `sum + 1` as the maximum possible number into our set, updating `sum` as `sum = sum * 2 + 1`.\n\nAfter picking all numbers from the input array, if we still cannot form every number from 1 to n, we must manually add new numbers to our current set. Each time, the maximum number we can introduce is `sum + 1`, and we update `sum` as `sum = sum * 2 + 1`.\n\n\n## Proof \nWe need to proof our greedy intuition idea:\nif you can already form any number from `0 to n` by using the current set of numbers, then adding a new number `x` such that `1 <= x <= n + 1` to our set allows you to from any number from `0` to `2 * n + 1`.\n\n```\nLet S denotes the current set you have where S can form any number from 0 to n.\nYou introduce a number x into S where 0 <= x <= 1 + n. \n\nSince you can already form any number from 0 to n using S, you can also form any number from x to x + n by concatenating with x.\n\nBy using all elements without x, you can form any number from 0 to n. By introducing x, you can form any number from x + 0 to x + n. \nNote that since x + 0 <= n + 1, now the new S by introducing x can form any number from 0 to x + n.\n\nIf we take x > n + 1, since x + 0 > n + 1, n + 1 can not be fromed.\n```\n\n## Code\n<iframe src="https://leetcode.com/playground/WvWWjLzy/shared" frameBorder="0" width="800" height="300"></iframe>\n\n**Complexity**:\n* Time Complexity : `O(max(len(nums), log n))`\n* Space Complexity : `O(1)`\n\n**Feel free to leave a comment if something is confusing, or if you have any suggestions on how I can improve the post.** | 11 | 0 | ['C', 'PHP', 'Python', 'Java', 'Go', 'JavaScript'] | 7 |
patching-array | Simple 9-line Python Solution | simple-9-line-python-solution-by-myliu-kgi9 | class Solution(object):\n def minPatches(self, nums, n):\n """\n :type nums: List[int]\n :type n: int\n :rtyp | myliu | NORMAL | 2016-04-18T06:21:29+00:00 | 2016-04-18T06:21:29+00:00 | 1,835 | false | class Solution(object):\n def minPatches(self, nums, n):\n """\n :type nums: List[int]\n :type n: int\n :rtype: int\n """\n miss, i, added = 1, 0, 0\n while miss <= n:\n if i < len(nums) and nums[i] <= miss:\n miss += nums[i]\n i += 1\n else:\n miss += miss\n added += 1\n return added | 10 | 2 | ['Python'] | 2 |
patching-array | Python | Easy | python-easy-by-khosiyat-s12f | see the Successfully Accepted Submission\n\n# Code\n\nclass Solution(object):\n def minPatches(self, nums, n):\n ans = 0\n sum_val = 1\n | Khosiyat | NORMAL | 2024-06-16T05:12:04.634820+00:00 | 2024-06-16T05:12:04.634854+00:00 | 423 | false | [see the Successfully Accepted Submission](https://leetcode.com/problems/patching-array/submissions/1289786216/?envType=daily-question&envId=2024-06-16)\n\n# Code\n```\nclass Solution(object):\n def minPatches(self, nums, n):\n ans = 0\n sum_val = 1\n m = len(nums)\n i = 0\n\n while sum_val <= n:\n if i < m and nums[i] <= sum_val:\n sum_val += nums[i]\n i += 1\n else:\n sum_val += sum_val\n ans += 1\n \n return ans\n```\n\n | 9 | 0 | ['Python3'] | 1 |
patching-array | NOT so hard || Easy to understand || Beginner friendly code || Python 3 | not-so-hard-easy-to-understand-beginner-avk59 | Intuition\n\nThe goal is to ensure that we can form all integers from 1 to n using a given array of positive integers (nums). If certain numbers are missing in | Saksham_chaudhary_2002 | NORMAL | 2024-06-16T01:05:08.810594+00:00 | 2024-06-16T01:05:08.810613+00:00 | 1,262 | false | # Intuition\n\nThe goal is to ensure that we can form all integers from 1 to n using a given array of positive integers (nums). If certain numbers are missing in the array to form the desired range, we need to determine the minimum number of additional integers (patches) required. The key insight here is that to cover the smallest missing number (miss), we can either use an existing number from nums if it is within the range, or we need to add miss itself to the array to extend the range of numbers we can form.\n\n# Approach\n\n1. **Initialization:** Start with miss equal to 1, which represents the smallest number we currently cannot form. Initialize added equal to 0 to keep track of the number of patches added. Use index equal to 0 to iterate through nums.\n\n2. **Iteration:** Continue the process until miss exceeds n:\n\n* If the current number in nums (pointed by index) is less than or equal to miss, it means we can use this number to extend our range. Add this number to miss and move to the next number by incrementing index.\n\n* If the current number in nums is greater than miss or if we have used all numbers in nums, we need to add miss itself to the array. This effectively doubles the range of numbers we can form. Increment added to reflect this patch.\n\n3. **Termination:** The loop terminates once miss exceeds n, meaning we can form all numbers from 1 to n. Return the value of added as the result.\n\n# Code\n```\nclass Solution:\n def minPatches(self, nums: List[int], n: int) -> int:\n miss, added, index = 1, 0, 0\n while miss <= n:\n if index < len(nums) and nums[index] <= miss:\n miss += nums[index]\n index += 1\n else:\n miss += miss\n added += 1\n return added\n\n``` | 9 | 1 | ['Array', 'Greedy', 'Python3'] | 5 |
patching-array | Simple C++ 12ms easy understanding O(n) | simple-c-12ms-easy-understanding-on-by-a-fl5u | class Solution {\n public:\n int minPatches(vector<int>& nums, int n) {\n if (n == 0) return 0;\n int num = nums.size();\n | algoguruz | NORMAL | 2016-01-27T17:12:05+00:00 | 2016-01-27T17:12:05+00:00 | 1,733 | false | class Solution {\n public:\n int minPatches(vector<int>& nums, int n) {\n if (n == 0) return 0;\n int num = nums.size();\n long reach = 0;\n int patch = 0;\n for (int i = 0; i < num; ){\n while (nums[i] > reach + 1){\n reach += (reach + 1);\n ++patch;\n if (reach >= n) return patch;\n }\n reach += nums[i];\n if (reach >= n) return patch;\n ++i;\n }\n while (reach < n){\n reach += (reach + 1);\n ++patch;\n } \n return patch;\n }\n }; | 8 | 1 | [] | 1 |
patching-array | 1ms Java solution with explain | 1ms-java-solution-with-explain-by-codepl-2lne | public int minPatches(int[] nums, int n) {\n int index = 0;\n int addedCount = 0;\n long canReachTo = 0;\n while( canReachTo < n){\n | codeplexer | NORMAL | 2016-04-09T04:44:02+00:00 | 2016-04-09T04:44:02+00:00 | 2,915 | false | public int minPatches(int[] nums, int n) {\n int index = 0;\n int addedCount = 0;\n long canReachTo = 0;\n while( canReachTo < n){\n if( nums.length > index){\n int nextExisting = nums[index];\n if(nextExisting == canReachTo + 1){\n canReachTo = (canReachTo << 1) + 1;\n index++;\n } else if(nextExisting > canReachTo + 1){\n addedCount++;\n canReachTo = (canReachTo << 1) + 1;\n } else {\n canReachTo = nextExisting + canReachTo;\n index++;\n }\n } else {\n addedCount++;\n canReachTo = (canReachTo << 1) + 1;\n }\n }\n return addedCount;\n }\n\nThis solution is based on greedy method. \nFor example, if you have 1, 2, it can reach 2+(2-1) = 3. So when we want to add up to 4, we have to add 4 into the list. And 1,2,4 can reach to 4+(4-1). \nSimilarly, for any added number n, they can add up to n+(n-1) without missing one number. \nIf there is one number x which satisfies n < x < n+(n-1), then we don't have to worry about the numbers until x + n + n - 1. Repeatedly evaluate the next number that the list of numbers can reach to, and add into the list next one when missing.\nSo basically this method is <log(n) time complexity and O(1) space complexity. | 8 | 0 | [] | 4 |
patching-array | beats 100% | beats-100-by-vigneshreddy06-cyk5 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | vigneshreddy06 | NORMAL | 2024-06-16T11:25:02.196442+00:00 | 2024-06-16T11:25:02.196468+00:00 | 48 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int minPatches(int[] nums, int n) {\n int i=0, patches = 0;\n long currRange = 1L;\n \n while (currRange <= n) {\n if (i < nums.length && nums[i] <= currRange) {\n currRange += nums[i];\n i++;\n } else {\n patches++;\n currRange += currRange;\n }\n }\n \n return patches;\n }\n}\n// if you click the upvote button you will get goodnews in 10mins\n[]()\n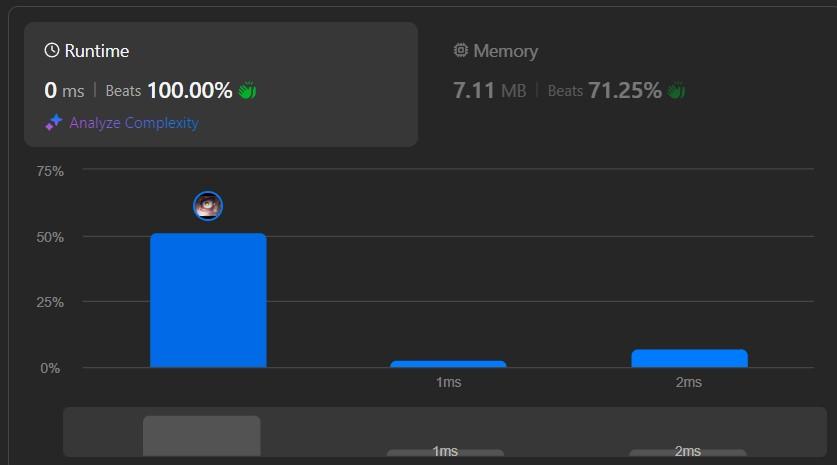\n\n```\n```python []\nclass Solution(object):\n def minPatches(self, nums, n):\n missing = 1\n patches = 0\n index = 0\n\n while missing <= n:\n if index < len(nums) and nums[index] <= missing:\n missing += nums[index]\n index += 1\n else:\n missing += missing\n patches += 1\n\n return patches\n\n \n# if you click the upvote button you will get goodnews in 10mins\n```\n```C++ []\nclass Solution {\npublic:\n int minPatches(vector<int>& nums, int n) {\n long missing = 1;\n int patches = 0;\n int index = 0;\n\n while (missing <= n) {\n if (index < nums.size() && nums[index] <= missing) {\n missing += nums[index];\n index++;\n } else {\n missing += missing;\n patches++;\n }\n }\n\n return patches;\n }\n};\n// if you click the upvote button you will get goodnews in 10mins\n```\n | 7 | 0 | ['C++', 'Python3'] | 0 |
patching-array | Easy to understand C++ solution beats 100% | easy-to-understand-c-solution-beats-100-vdb2c | Intuition\n Describe your first thoughts on how to solve this problem. \nIf the current sum < nums[i]-1, then we cannot create nums[i] using the sum, we need to | anuragkumar2608 | NORMAL | 2024-06-16T00:32:47.199359+00:00 | 2024-06-16T07:03:09.532173+00:00 | 1,129 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIf the current sum < nums[i]-1, then we cannot create nums[i] using the sum, we need to add sum+1 to the array,so next the sum becomes sum += sum + 1.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nEach time while adding a new number to the current sum, we want the sum to cover the number sum + 1, if the number is greater than sum + 1, then sum + 1 cannot be covered, so we need to add that number to the list, so we increment count, we also increment the current sum to sum = sum + sum + 1. We continue this operation until we cover all the elements.\n\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int minPatches(vector<int>& nums, int n) {\n long long count = 0;\n long long sum = 0;\n long long i = 0;\n while(sum < n){\n if(i<nums.size() && nums[i] <= (sum+1)){\n sum += nums[i++];\n }else{\n count++;\n sum += (sum + 1);\n }\n }\n return count;\n }\n};\n``` | 7 | 0 | ['C++'] | 3 |
patching-array | Python solution faster than 97% with explanation | python-solution-faster-than-97-with-expl-vfs2 | \n you just need to figure out one thing:\n if you can sum up from 1 to 10, what happen if you have another number\n suppose this number is 2, then you can sum | flyingspa | NORMAL | 2021-05-20T14:12:36.353830+00:00 | 2021-05-20T14:14:22.299924+00:00 | 579 | false | \n* you just need to figure out one thing:\n* if you can sum up from 1 to 10, what happen if you have another number\n* suppose this number is 2, then you can sum up from 1 to 12\n* suppose this number is 11, then you can sum up from 1 to 21 \n* suppose this number is 12, then you can\'t get 11 and the consecutive sum is broken at 11\n* suppose this number is 100, then you can\'t get the sum from 11 to 99\n* so we know if you can sum up from 1 to k, the next largest number you can have is k+1, otherwise the consecutive sum will be invalid\n* traverse from left, if the current number x is lower than or equal to k+1, let k = k+x, otherwise let k = k+1(k+1 is the largest we can have to keep the sum valid)\n\nclass Solution:\n\n def minPatches(self, nums: List[int], n: int) -> int:\n ans = cum = index = 0 \n while(cum<n):\n if index<len(nums):\n if cum+1<nums[index]:\n cum+=cum+1\n ans+=1\n else:\n cum+=nums[index]\n index+=1 \n else:\n cum += cum+1\n ans+=1\n\n return ans | 7 | 0 | ['Python'] | 2 |
patching-array | [recommend for beginners]clean C++ implementation with detailed explanation | recommend-for-beginnersclean-c-implement-8zmr | we run the code on an example to illustrate the ideas:\n \n [1, miss) : the right miss is open field\n\n nums=[1,5,10] n=20\n\n in | rainbowsecret | NORMAL | 2016-02-04T01:49:53+00:00 | 2016-02-04T01:49:53+00:00 | 1,182 | false | we run the code on an example to illustrate the ideas:\n \n [1, miss) : the right miss is open field\n\n nums=[1,5,10] n=20\n\n initialize state : miss=1 i=0 size=3\n\nmiss=1 : i=0\n\n if find [number<=1] in nums { i++ } else add 1 to nums update miss+=1 [1,2)\n found 1, i++, so added 1 to the nums \n \nmiss=2 : i=1\n\n if find [number<=2] in nums { i++ } else add 2 to nums update miss+=2; [1,4)\n not found , so add 2 to the nums\n\nmiss=4 : i=1\n\n if find [number<=4] in nums { i++ } else add 4 to nums update miss+=2; [1,8)\n not found , so add 4 to the nums\n \nmiss=8: i=1\n\n if find [number<=8] in nums { i++ } else add 8 to nums update miss+=2; [1,13)\n found 5 , so add 5 to the nums \n\nmiss=13:i=2\n\n if find [number<=13] in nums { i++ } else add 13 to nums update miss+=2; [1,23)\n found 10 , so add 10 to the nums \n\nmiss=23 \n\n covers [1,20], done!\n\nreturn added=2\n\n\nCode:\n\n\n class Solution {\n public:\n int minPatches(vector<int>& nums, int n) {\n long miss=1, added=0, i=0;\n while(miss<=n){\n /*** update the miss to the (miss+nums[i]) **/\n if(i<nums.size() && nums[i]<=miss){\n miss+=nums[i++];\n }else{\n /*** update the miss to the miss+miss **/\n miss+=miss;\n added++;\n }\n }\n return added;\n }\n }; | 7 | 3 | [] | 2 |
patching-array | Java Solution, Beats 100.00% | java-solution-beats-10000-by-mohit-005-lz8y | Intuition \n\nThe problem requires adding the minimum number of patches (elements) to an array such that any number from 1 to n can be formed by the sum of some | Mohit-005 | NORMAL | 2024-06-16T02:43:22.704387+00:00 | 2024-06-16T02:43:22.704420+00:00 | 476 | false | # Intuition \n\nThe problem requires adding the minimum number of patches (elements) to an array such that any number from 1 to `n` can be formed by the sum of some elements in the array. The key is to iteratively ensure that every integer up to `n` can be constructed using the existing elements and the patches added so far.\n\n# Approach\n\n1. **Initialization**:\n - Initialize `patches` to count the number of patches needed.\n - Initialize `miss` to track the smallest number that we cannot form yet. Start with `miss = 1`.\n - Use an index `i` to traverse through the `nums` array.\n\n2. **Iterate Until `miss` Exceeds `n`**:\n - While `miss <= n`, do the following:\n - If the current element in `nums` (i.e., `nums[i]`) is less than or equal to `miss`, it means we can extend our range of constructible numbers. Add `nums[i]` to `miss` and move to the next element (`i++`).\n - If `nums[i]` is greater than `miss`, we need to add a patch (i.e., `miss` itself) to the array. This patch will double the current `miss` value (since `miss` is being added to itself), and increment the patch count (`patches++`).\n\n3. **Return the Number of Patches**:\n - Once `miss` exceeds `n`, return the total number of patches added.\n\n# Code\n```java\nclass Solution {\n public int minPatches(int[] nums, int n) {\n int patches = 0;\n int i = 0;\n long miss = 1;\n while(miss <= n) {\n if(i < nums.length && nums[i] <= miss)\n miss += nums[i++];\n else {\n miss += miss;\n patches++;\n }\n }\n return patches;\n }\n}\n```\n\n#### Detailed Explanation\n\n- **Variables**:\n - `patches` counts the number of patches added.\n - `i` is the index for traversing `nums`.\n - `miss` is the smallest number that cannot be formed yet, initialized to 1.\n\n- **Loop**:\n - The loop continues until `miss` exceeds `n`.\n - **Condition**: If the current element in `nums` (`nums[i]`) can be used to form `miss` (i.e., `nums[i] <= miss`), add it to `miss` and move to the next element (`i++`).\n - **Else**: If `nums[i]` cannot form `miss`, add `miss` as a patch, double `miss`, and increment the patch count.\n\n# Complexity\n\n### Time Complexity\n\n- The loop runs while `miss` is less than or equal to `n`.\n- In each iteration, either:\n - We use an element from `nums` (which runs in `O(nums.length)`) or,\n - We double `miss` and increment patches.\n- Since `miss` doubles each time it is patched, the number of iterations in the worst case is `O(log n)`.\n- Thus, the overall time complexity is `O(nums.length + log n)`.\n\n### Space Complexity\n\n- The space complexity is `O(1)` because we are using a constant amount of extra space (i.e., variables `patches`, `i`, and `miss`).\n | 6 | 0 | ['Java'] | 1 |
patching-array | ✅Simple and Easy Solution🔥 | simple-and-easy-solution-by-kg-profile-941u | Code\n\nclass Solution:\n def minPatches(self, nums: List[int], n: int) -> int:\n p = 0\n x = 1\n i = 0\n \n while x <= n: | KG-Profile | NORMAL | 2024-06-16T01:28:51.942305+00:00 | 2024-06-16T01:28:51.942322+00:00 | 35 | false | # Code\n```\nclass Solution:\n def minPatches(self, nums: List[int], n: int) -> int:\n p = 0\n x = 1\n i = 0\n \n while x <= n:\n if i < len(nums) and nums[i] <= x:\n x += nums[i]\n i += 1\n else:\n p += 1\n x *= 2\n \n return p\n``` | 6 | 0 | ['Python3'] | 0 |
patching-array | Simple Easy to Understand Java Solution || Faster than 100% | simple-easy-to-understand-java-solution-go0ci | Logic\n\nIterating the nums[], and keeps adding them up, and we are getting a running sum. At any position, if nums[i] > sum+1, them we are sure we have to patc | rohitkumarsingh369 | NORMAL | 2021-08-29T16:17:57.453194+00:00 | 2021-08-29T16:20:02.049375+00:00 | 1,099 | false | **Logic**\n```\nIterating the nums[], and keeps adding them up, and we are getting a running sum. At any position, if nums[i] > sum+1, them we are sure we have to patch \na sum+1 because all nums before index i can\'t make sum+1 even add all of them up, and all nums after index i are all simply too large.\n```\n\n**Solution**\n```\nclass Solution {\n public int minPatches(int[] nums, int n) {\n long sum = 0;\n int count = 0;\n for (int x : nums) {\n if (sum >= n) break;\n while (sum+1 < x && sum < n) { \n ++count;\n sum += sum+1;\n }\n sum += x;\n }\n while (sum < n) {\n sum += sum+1;\n ++count;\n }\n return count;\n }\n}\n``` | 6 | 0 | ['Java'] | 1 |
patching-array | [C++ | Python3 | JAVA] Easy Approach with simple solution | c-python3-java-easy-approach-with-simple-twi5 | APPROACH\n Let us assume that we are on some ith element of the array.\n We were successfullly able to create each and every number till the range arr[i]-1 by t | Maango16 | NORMAL | 2021-08-29T11:17:58.618318+00:00 | 2021-08-29T11:17:58.618359+00:00 | 502 | false | **APPROACH**\n* Let us assume that we are on some `i`th element of the array.\n* We were successfullly able to create each and every number till the range `arr[i]-1` by taking some numbers from arr in the range `0` to `i-1`. \n* Hence after choosing `arr[i]` we can create numbers from `0` to `arr[i]-1 + arr[i]` . \n\t* Extra `arr[i]+1 to arr[i]+arr[i] -1` can be created by using `some numbers` and `arr[i]`\n* If we are able to create numbers upto `arr[i]-1` \n\t* No need to patch\n* Else \n\t* patch it with whatever numbers we are able to make +1 i.e `sum+1`\n\n\n**SOLUTION**\n`In C++`\n```\nclass Solution {\npublic:\n int minPatches(vector<int>& nums, int n) {\n int m = nums.size() ;\n long long i = 1, sum = 1 ,ans = 0 ;\n if(nums[0] != 1)\n {\n ans++ ;\n i--;\n }\n while(i < m && sum < n)\n {\n while(sum < nums[i]-1 && sum < n)\n {\n ans++ ;\n sum += sum + 1 ;\n }\n sum += nums[i] ;\n i++ ;\n }\n while(sum < n)\n {\n ans++ ;\n sum += sum + 1 ;\n }\n return ans;\n }\n}; \n```\n`In JAVA`\n```\nclass Solution {\n public int minPatches(int[] nums, int n) {\n int m = nums.length ;\n int i = 1 , ans = 0 ;\n long sum = 1 ;\n if(nums[0] != 1)\n {\n ans++ ;\n i-- ;\n }\n while(i < m && sum < n)\n {\n while(sum < nums[i]-1 && sum < n)\n {\n ans++ ;\n sum = (sum<<1) + 1 ;\n }\n sum += nums[i] ;\n i++ ;\n }\n while(sum < n)\n {\n ans++ ;\n sum = (sum<<1) + 1;\n }\n return ans ;\n }\n}\n```\n`In Python3`\n```\nclass Solution:\n def minPatches(self, nums: List[int], n: int) -> int:\n m = len(nums)\n i = 1 \n ans = 0\n summ = 1\n if nums[0] != 1:\n ans+=1\n i -= 1\n while i < m and summ < n:\n while summ < nums[i]-1 and summ < n:\n ans+=1\n summ += summ + 1\n \n summ += nums[i] \n i+=1\n while summ < n:\n ans+=1\n summ += summ + 1\n return ans\n``` | 6 | 2 | [] | 0 |
patching-array | *Java* here is my greedy version with brief explanations (1ms) | java-here-is-my-greedy-version-with-brie-cc91 | Greedy idea: add the maximum possible element whenever there is a gap\n\n public int minPatches(int[] nums, int n) {\n int count = 0;\n long pr | elementnotfoundexception | NORMAL | 2016-01-27T05:44:26+00:00 | 2016-01-27T05:44:26+00:00 | 2,070 | false | Greedy idea: add the maximum possible element whenever there is a gap\n\n public int minPatches(int[] nums, int n) {\n int count = 0;\n long priorSum = 0; // sum of elements prior to current index\n for(int i=0; i<nums.length; i++) {\n \tif(priorSum>=n) return count; // done\n \twhile(priorSum<n && nums[i]>priorSum+1) { // whenever there is a gap between priorSum and current value, add elements in a greedy manner\n \t\t++count;\n \t\tpriorSum = (priorSum<<1) + 1;\n \t}\n \tpriorSum += nums[i];\n }\n while(priorSum<n) {\n \t++count;\n \tpriorSum = (priorSum<<1) + 1;\n }\n return count;\n }\n\nThe above one can be further simplified to one-pass as follows:\n\n public int minPatches(int[] nums, int n) {\n int count = 0, i = 0;\n long priorSum = 0;\n while(priorSum<n) {\n if(i>=nums.length || nums[i]>priorSum+1) {\n ++count;\n priorSum = (priorSum<<1) + 1;\n }\n else priorSum += nums[i++];\n }\n return count;\n } | 6 | 0 | ['Java'] | 1 |
patching-array | Greedy solution in Python | greedy-solution-in-python-by-gavincode-88e5 | I used a greedy algorithm. When traversing through the given number list, consider each number as a goal and resource. When in the for loop for the ith number, | gavincode | NORMAL | 2016-01-27T07:10:22+00:00 | 2016-01-27T07:10:22+00:00 | 1,063 | false | I used a greedy algorithm. When traversing through the given number list, consider each number as a **goal** and **resource**. When in the for loop for the *ith* number, try to add some numbers so that you can represent every number in the range [ 1, nums[i] ). Then, add the *ith* number to your source for further loops. \n\nTo reach the goal, suppose all the resource (the numbers smaller than the goal) sums to a number `sum`, then, `sum+1` is what we don't have. So we need to add a `sum+1` to our resource. And now you can represent all the numbers not bigger than `sum+sum+1`.\n\n class Solution(object):\n\n def minPatches(self, nums, n):\n """\n :type nums: List[int]\n :type n: int\n :rtype: int\n """\n count = 0\n sum = 0\n for x in nums:\n if sum >= n:\n return count\n while sum < x-1: # x-1 is the goal; when reaches the goal, we can represent [1, x)\n count += 1\n sum += sum + 1 # add a resource number\n if sum >= n:\n return count\n sum += x\n while sum + 1 <= n:\n count += 1\n sum += sum + 1\n return count | 6 | 1 | [] | 0 |
patching-array | Patching Array - Solution Explanation and Code (Video Solution Available) | patching-array-solution-explanation-and-hpndr | Video SolutionIntuitionTo cover all numbers in the range [1, n] using the given array nums, we need to ensure that every integer in the range can be formed as t | CodeCrack7 | NORMAL | 2025-01-18T01:34:05.755715+00:00 | 2025-01-18T01:34:05.755715+00:00 | 74 | false | # Video Solution
[https://youtu.be/3XvfM0fOnjc?si=hz58mAXHPF62vVxq]()
# Intuition
To cover all numbers in the range `[1, n]` using the given array `nums`, we need to ensure that every integer in the range can be formed as the sum of one or more elements from `nums`. If `nums` lacks certain values necessary to achieve this, we can "patch" the array by adding new numbers.
The key idea is to track the smallest number `miss` that we cannot form using the current elements of `nums` and any previously added patches. If a number in `nums` can contribute to forming `miss`, we use it. Otherwise, we add `miss` as a patch and update `miss`.
# Approach
1. **Initialize variables**:
- `miss` starts at 1, representing the smallest number we cannot yet form.
- `result` counts the patches added.
- `i` is the index for traversing `nums`.
2. **Iterate while `miss <= n`**:
- If `nums[i] <= miss`, add `nums[i]` to `miss` (i.e., we can now form numbers up to `miss + nums[i]`) and increment `i`.
- Otherwise, add `miss` as a patch. This ensures we can form numbers up to `2 * miss`.
3. **Repeat until `miss > n`**:
- At this point, all numbers in `[1, n]` are covered, and we return the number of patches.
# Complexity
- **Time complexity**:
$$O(m + \log n)$$, where `m` is the length of `nums`. Traversing `nums` takes $$O(m)$$, and each patch approximately doubles `miss`, leading to $$O(\log n)$$ iterations for patches.
- **Space complexity**:
$$O(1)$$, as we use constant extra space.
# Code
```java []
class Solution {
public int minPatches(int[] nums, int n) {
long miss = 1;
int result = 0;
int i = 0;
while (miss <= n) {
if (i < nums.length && nums[i] <= miss) {
miss += nums[i];
i++;
} else {
miss += miss;
result++;
}
}
return result;
}
} | 5 | 0 | ['Java'] | 0 |
patching-array | ✅5 lines only , Fastest Greedy Efficient Simplest Solution with DryRun in C++ | 5-lines-only-fastest-greedy-efficient-si-di9c | Intuition\n Describe your first thoughts on how to solve this problem. \n> First of all, we have to understand what we want.\n\nWe want that nums must have the | sidharthjain321 | NORMAL | 2024-06-16T21:56:29.223810+00:00 | 2024-06-16T22:22:11.258128+00:00 | 121 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n> First of all, we have to understand what we want.\n\nWe want that `nums` must have the required elements, so that there combinations of numbers will sum upto n, i.e., from `[1,n]` both inclusive.\n**At every step we will check , for each `nums[i]`, Is it possible to make all numbers from `[1, (nums[i]+ nums[i+1]....nums[j]) ]` where `0 <= i < nums.size()` and where `i+1 <= j < nums.size()` by combining different combinations of numbers present in nums.**\n*Inside this :-*\n***If yes :- \nIt means we have all the numbers from `[1,nums[i] + nums[i+1] + ... nums[j]]`***\n\n***If No :-\nIt means we have to add some elements so that so that it can generate all elements from `[1,nums[i] + nums[i+1] + ... nums[j] + k]` where k > 0.***\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nInitially, we want that the nums must produce 1 as the minimum sum.\n- Initialise variables :-\n```\nlong nextRequiredMinimumSum = 1; // It means what is the total sum value required to get all numbers from 1 to nextRequiredMinimumSum.\nint patchedElements = 0; // number of added elements in the nums.\nint i = 0; // for iterating the nums vector\n```\n- Start a while loop with condition as, while the nextRequiredMinimumSum is less than equal to n :- \n```\nwhile(nextRequiredMinimumSum <= n) {\n}\n```\n- If the `nextRequiredMinimumSum` is greater than or equal to the current value of `nums[i]`, it means we can generate all numbers from `[1 , nextRequiredMinimumSum]`. It means now we can generate numbers from `[1 , nextRequiredMinimumSum + nums[i]]`. We can iterate to the next number. i.e., `i++`.\n```\n// \nif(i < nums.size() && nextRequiredMinimumSum >= nums[i]) {\n nextRequiredMinimumSum += nums[i];\n i++;\n}\n```\n- Else, this means, we can\'t generate the numbers from `[1 , nextRequiredMinimumSum]`. But we are sure , that we can generate all numbers from `[1 , nextRequiredMinimumSum - 1]`, because in the else case, we are always adding the nextRequiredMinimumSum.\n```\nelse {\n nextRequiredMinimumSum += nextRequiredMinimumSum;\n patchedElements++;\n}\n\n```\n---\nlet me give you an example :-\n**- DRY RUN :-**\nlet nums = {1,2,9,10}, n = 20\n\nWhen i = 0, \n`i = 0`, `nums[i] = 1`, `nextRequiredMinimumSum = 1`, \n**nextRequiredMinimumSum >= nums[i]** , (1 >= 1)\ntherefore, **nextRequiredMinimumSum = 1 + 1 = 2** , **i++.**\n\n---\n\nWhen i = 1, `i = 1`, `nums[i] = 2`, `nextRequiredMinimumSum = 2`, **nextRequiredMinimumSum >= nums[i]** , (2 >= 2)\ntherefore, **nextRequiredMinimumSum = 2 + 2 = 4**, **i++.**\n\n---\n\nWhen i = 2, `i = 2`, `nums[i] = 9`, `nextRequiredMinimumSum = 4`, **nextRequiredMinimumSum < nums[i]** , (4 < 9) , **patchedElements++.**\n\n> but, you can see , previously we were able to generate till 3. i.e., till nextRequiredMinimumSum - 1.\n\n**nextRequiredMinimumSum += 4**, therefore, **nextRequiredMinimumSum = 8**.\n\n---\n\nNow, **nextRequiredMinimumSum <= n** therefore, check again , `i = 2`, `nums[i] = 9`, `nextRequiredMinimumSum = 8`, **nextRequiredMinimumSum < nums[i]** , (8 < 9) , **patchedElements++.**\n> but, you can see , previously we were able to generate till 7. i.e., till nextRequiredMinimumSum - 1;\n\n**nextRequiredMinimumSum += 8**, therefore, **nextRequiredMinimumSum = 16**.\nIt means we are able to make till 15, i.e., nextRequiredMinimumSum - 1.\n\n---\n\nNow, **nextRequiredMinimumSum <= n** therefore, check again , `i = 2`, `nums[i] = 9`, `nextRequiredMinimumSum = 16`, **nextRequiredMinimumSum >= nums[i]** , (16 >= 9)\ntherefore, **nextRequiredMinimumSum = 16 + 9 = 25** , **i++.**\n\n---\n\nNow, **nextRequiredMinimumSum > n** , (25 > 20), therefore, break the while loop. \n\n**return the patchedElement**s.\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int minPatches(vector<int>& nums, int n) {\n long nextRequiredMinimumSumPossible = 1; int patchedElements = 0, i = 0, size = nums.size();\n while(nextRequiredMinimumSumPossible <= n)\n if(i < size && nextRequiredMinimumSumPossible >= nums[i]) nextRequiredMinimumSumPossible += nums[i] , i++;\n else nextRequiredMinimumSumPossible += nextRequiredMinimumSumPossible, patchedElements++;\n return patchedElements;\n }\n};\n```\n\n\n\n\n\n[Instagram](https://www.instagram.com/iamsidharthaa__/)\n[LinkedIn](https://www.linkedin.com/in/sidharth-jain-36b542133)\n**If you find this solution helpful, consider giving it an upvote! Your support is appreciated. Keep coding, stay healthy, and may your programming endeavors be both rewarding and enjoyable!** | 5 | 0 | ['Array', 'Greedy', 'Sorting', 'C++'] | 2 |
patching-array | 💯JAVA Solution Explained in HINDI | java-solution-explained-in-hindi-by-the_-cff7 | https://youtu.be/Qk1elv8QGj0\n\nFor explanation, please watch the above video and do like, share and subscribe the channel. \u2764\uFE0F Also, please do upvote | The_elite | NORMAL | 2024-06-16T13:23:31.906410+00:00 | 2024-06-16T13:23:31.906524+00:00 | 301 | false | https://youtu.be/Qk1elv8QGj0\n\nFor explanation, please watch the above video and do like, share and subscribe the channel. \u2764\uFE0F Also, please do upvote the solution if you liked it.\n\n# Subscribe:- [ReelCoding](https://www.youtube.com/@reelcoding?sub_confirmation=1)\n\nSubscribe Goal:- 500\nCurrent Subscriber:- 440\n\n# Complexity\n- Time complexity: O(m+logn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int minPatches(int[] nums, int n) {\n long minNumberPatches = 0, maxNumber = 0;\n int i = 0, len = nums.length;\n\n while (maxNumber < n) {\n if (i < len && maxNumber + 1 >= nums[i]) {\n maxNumber += nums[i];\n i++;\n } else {\n minNumberPatches++;\n maxNumber += (maxNumber + 1);\n }\n }\n return (int) minNumberPatches;\n }\n}\n``` | 5 | 0 | ['Java'] | 0 |
patching-array | Very Easy C++ Solution with Video Explanation | very-easy-c-solution-with-video-explanat-65ym | Video Explanation\nhttps://youtu.be/YPY6EOfYANY?si=6NQWVso6wi1OiFtU\n# Complexity\n- Time complexity:O(nums.size())\n Add your time complexity here, e.g. O(n) \ | prajaktakap00r | NORMAL | 2024-06-16T04:26:55.934462+00:00 | 2024-06-16T04:26:55.934481+00:00 | 854 | false | # Video Explanation\nhttps://youtu.be/YPY6EOfYANY?si=6NQWVso6wi1OiFtU\n# Complexity\n- Time complexity:$$O(nums.size())$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int minPatches(vector<int>& nums, int n) {\n long long sum=0;\n long long patches=0;\n long long i=0;\n\n while(sum<n){\n if(i<nums.size() && nums[i]<=sum+1){\n sum+=nums[i++];\n }else{\n patches++;\n sum+=sum+1;\n }\n }\n return patches;\n }\n};\n``` | 5 | 0 | ['C++'] | 2 |
patching-array | 💯✅🔥Easy Java ,Python3 ,C++ Solution|| 0 ms ||≧◠‿◠≦✌ | easy-java-python3-c-solution-0-ms-_-by-s-0ocj | Intuition\n Describe your first thoughts on how to solve this problem. \nThe idea behind this solution is to keep track of the largest number that can be repres | suyalneeraj09 | NORMAL | 2024-06-16T00:58:53.434035+00:00 | 2024-06-16T01:58:39.374160+00:00 | 160 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe idea behind this solution is to keep track of the largest number that can be represented using the given numbers and the patches added so far. We start with the first number in the nums array, and if it is greater than the current largest number plus 1, we add a patch to cover the gap. Otherwise, we add the current number to the largest number that can be represented\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Initialize patch to keep track of the largest number that can be represented, count to keep track of the number of patches added, and index to keep track of the current index in the nums array.\n- While patch is less than n, do the following:\n- If index is less than the length of nums and patch + 1 is less than or equal to nums[index], add nums[index] to patch and increment index.\n- Otherwise, add patch + 1 to patch and increment count.\nReturn count.\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\n\nclass Solution {\n public int minPatches(int[] nums, int n) {\n long patch = 0;\n int count = 0;\n int index = 0;\n while (patch < n) {\n if (index < nums.length && patch + 1 >= nums[index]) {\n patch += nums[index];\n index++;\n } else {\n patch += (patch + 1);\n count++;\n }\n }\n\n return count;\n }\n}\n\n```\n```python3 []\nclass Solution:\n def minPatches(self, nums: List[int], n: int) -> int:\n patch = 0\n count = 0\n index = 0\n while patch < n:\n if index < len(nums) and patch + 1 >= nums[index]:\n patch += nums[index]\n index += 1\n else:\n patch += (patch + 1)\n count += 1\n return count\n```\n```C++ []\nclass Solution {\npublic:\n int minPatches(std::vector<int>& nums, int n) {\n long long patch = 0;\n int count = 0;\n int index = 0;\n while (patch < n) {\n if (index < nums.size() && patch + 1 >= nums[index]) {\n patch += nums[index];\n index++;\n } else {\n patch += (patch + 1);\n count++;\n }\n }\n\n return count;\n}\n};\n```\n\n\n\n\n\n\n | 5 | 0 | ['Array', 'C++', 'Java', 'Python3'] | 2 |
patching-array | Python || Math | python-math-by-in_sidious-6c8w | Intuition\nIf sum of all the numbers considered till now is x, we can form all the numbers from 1 to x. This condition is True every time.\n\n# Approach\nKeep a | iN_siDious | NORMAL | 2023-02-05T18:03:01.873190+00:00 | 2023-02-05T18:11:31.213254+00:00 | 537 | false | # Intuition\nIf sum of all the numbers considered till now is x, we can form all the numbers from 1 to x. This condition is True every time.\n\n# Approach\nKeep a variable limit which tracks till what max value we can form which is nothing but sum of all values considered till now.\nIf we encounter any number i.e. num which is greater than limit+1, it means we can\'t get any number between limit+1 to num-1.So we add limit+1 to our limit to extend our current limit and increase our answer count by 1 (Internally we are adding limit+1 to our array).Continue this process untill num is greater than limit+1.Meanwhile if at any moment limit >=ssum break off the loop.\nAfter considering all numbers from array , check if limit is still less than ssum and keep adding limit+1 and incrementing answer count to our limit till limit<ssum.\nNote : We need to necessarily add limit+1 every time and not any number greater than this as we can\'t form limit+1 using any of our previously considered numbers.\n\n# Complexity\n- Time complexity:\nO(n) \n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def minPatches(self, nums: List[int], ssum: int) -> int:\n n=len(nums)\n limit,cnt=0,0\n for i in range(n):\n if nums[i]>limit+1:\n while nums[i]>limit+1:\n limit+=limit+1\n cnt+=1\n if limit>=ssum: break\n limit+=nums[i]\n if limit>=ssum: break\n while limit<ssum:\n limit+=limit+1\n cnt+=1\n return cnt\n\n``` | 5 | 0 | ['Math', 'Python', 'Python3'] | 1 |
patching-array | C++ 4ms 98% greedy solution w/ explanation | c-4ms-98-greedy-solution-w-explanation-b-uv5k | The idea is to greedily add the maximum missing number, and the numbers from nums once we can reach those numbers.\n\nWhy this works\n\nAssume we have nums = [1 | guccigang | NORMAL | 2019-08-21T00:26:46.038193+00:00 | 2020-01-27T19:35:20.495473+00:00 | 457 | false | The idea is to greedily add the maximum missing number, and the numbers from ```nums``` once we can reach those numbers.\n\n**Why this works**\n\nAssume we have ```nums = [1, 5, 10]``` and we want all numbers to 20. To start thing off, we need to look for a 1. We have a 1 in the array, so are we good. Then we look for a 2. We do not have a 2 in the array, and the next element in the array is 5. This means **we must add a patch to get ```2```**. \n\nHow do we decide which patch to add? Well since we already have `1`, we can either add a `1`, or we can add a `2`. However, if we add a `2`, we will be able to make ```2``` _and_ ```3```, but if we add a ```1```, we will only be able to get ```2```. Since we want the minimum number of patches, we should aim to maximize the new numbers we can make from each patch. \n\nNow we can make ```[1, 4)```, and we are missing `4`, so by the previous logic we would add a `4` as the second patch, to get all numbers between ```0``` and ```7```. If we look at the next number in `nums`, we can see that it is a 5, so we have already covered it. But this is a "free" number. We can add it to any of our sums from ```0 ... 7``` and get a new number. The maximum number is now ```12```. This means we are able to increase the numbers we can reach _without having to add a patch_. Thus, we keep this up, and either add mandatory patches that maximizes the numbers we get, or add in free numbers from ```nums``` that extends our maximum range, until we reach the required range.\n\n```\nclass Solution {\npublic:\n int minPatches(vector<int>& nums, int n) {\n uint32_t m = 1, i = 0, p = 0, size = nums.size();\n while(m <= n) {\n if(i < size && nums[i] <= m) m += nums[i++];\n else {\n m += m;\n ++p;\n }\n }\n return p;\n }\n};\n\nauto gucciGang = []() {std::ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);return 0;}();\n``` | 5 | 0 | [] | 2 |
patching-array | 4ms C++ Greedy solution with explanation(极简代码+详细中文注释) | 4ms-c-greedy-solution-with-explanationji-jhza | \n/*\n\u9996\u5148\u53EF\u4EE5\u786E\u5B9A\u7684\u662F\uFF0C\nnums\u4E2D\u5FC5\u7136\u5305\u542B1\uFF0C\u5982\u679C\u4E0D\u5305\u542B1\uFF0C\u90A3\u4E48[1,n]\u8 | leetcoderchen | NORMAL | 2018-11-21T13:51:57.748816+00:00 | 2018-11-21T13:51:57.748856+00:00 | 831 | false | ```\n/*\n\u9996\u5148\u53EF\u4EE5\u786E\u5B9A\u7684\u662F\uFF0C\nnums\u4E2D\u5FC5\u7136\u5305\u542B1\uFF0C\u5982\u679C\u4E0D\u5305\u542B1\uFF0C\u90A3\u4E48[1,n]\u8FD9\u4E2A\u8303\u56F4\u4E2D\u76841\u5C31\u6CA1\u6CD5\u5B9E\u73B0\n\u5176\u6B21\u6570\u7EC4\u4E2D\u7684\u5143\u7D20\u4E0D\u80FD\u91CD\u590D\u4F7F\u7528\uFF0C\u5982\u679C\u5141\u8BB8\u91CD\u590D\u4F7F\u7528\uFF0C\u90A3\u4E48\u628A1\u91CD\u590D\u591A\u6B21\uFF0C\u5C31\u53EF\u4EE5\u7EC4\u6210\u4EFB\u610F\u6574\u6570\u3002\n\u4EE4miss\u4E3A[0,n]\u4E2D\u7F3A\u5C11\u7684\u6700\u5C0F\u6574\u6570\uFF0C\u610F\u5473\u7740\u6211\u4EEC\u53EF\u4EE5\u5B9E\u73B0[0,miss)\u8303\u56F4\u5185\u7684\u4EFB\u610F\u6574\u6570\u3002\n\u5982\u679C\u6570\u7EC4\u4E2D\u6709\u67D0\u4E2A\u6574\u6570x<=miss, \u90A3\u4E48\u6211\u4EEC\u53EF\u4EE5\u628A[0,miss)\u533A\u95F4\u7684\u6240\u6709\u6574\u6570\u52A0\u4E0Ax\uFF0C\u533A\u95F4\u53D8\u6210\u4E86[x, miss+x)\uFF0C\u7531\u4E8E\u533A\u95F4[0,miss)\u548C[x, miss+x)\u91CD\u53E0\uFF0C\u4E24\u4E2A\u533A\u95F4\u53EF\u4EE5\u65E0\u7F1D\u8FDE\u63A5\u8D77\u6765\uFF0C\u610F\u5473\u7740\u6211\u4EEC\u53EF\u4EE5\u628A\u533A\u95F4[0,miss)\u6269\u5C55\u5230[0, miss+x)\u3002\n\u5982\u679C\u6570\u7EC4\u4E2D\u4E0D\u5B58\u5728\u5C0F\u4E8E\u6216\u7B49\u4E8Emiss\u7684\u5143\u7D20\uFF0C\u5219\u533A\u95F4[0,miss)\u548C[x, miss+x) \u8131\u8282\u4E86\uFF0C\u8FDE\u4E0D\u8D77\u6765\u3002\u6B64\u65F6\u6211\u4EEC\u9700\u8981\u6DFB\u52A0\u4E00\u4E2A\u6570\uFF0C\u6700\u5927\u9650\u5EA6\u7684\u6269\u5C55\u533A\u95F4[0, miss)\u3002\u90A3\u6DFB\u52A0\u54EA\u4E2A\u6570\u5462\uFF1F\u5F53\u7136\u662F\u6DFB\u52A0miss\u672C\u8EAB\uFF0C\u8FD9\u6837\u533A\u95F4[0,miss)\u548C[miss, miss+miss)\u6070\u597D\u53EF\u4EE5\u65E0\u7F1D\u62FC\u63A5\u3002\n\u4E3E\u4E2A\u4F8B\u5B50\uFF0C\u4EE4nums=[1, 2, 4, 13, 43], n=100\uFF0C\u6211\u4EEC\u9700\u8981\u8BA9[1,100]\u5185\u7684\u6570\u90FD\u80FD\u591F\u7EC4\u5408\u51FA\u6765\u3002\n\u4F7F\u7528\u6570\u5B571,2,4\uFF0C\u6211\u4EEC\u53EF\u4EE5\u7EC4\u5408\u51FA[0, 8)\u5185\u7684\u6240\u6709\u6570\uFF0C\u4F46\u65E0\u6CD5\u7EC4\u5408\u51FA8\uFF0C\u7531\u4E8E\u4E0B\u4E00\u4E2A\u6570\u662F13\uFF0C\u6BD48\u5927\uFF0C\u6839\u636E\u89C4\u52192\uFF0C\u6211\u4EEC\u6DFB\u52A08\uFF0C\u628A\u533A\u95F4\u4ECE[0,8)\u6269\u5C55\u5230[0,16)\u3002\n\u4E0B\u4E00\u4E2A\u6570\u662F13\uFF0C\u6BD416\u5C0F\uFF0C\u6839\u636E\u89C4\u52191\uFF0C\u6211\u4EEC\u53EF\u4EE5\u628A\u533A\u95F4\u4ECE[0,16)\u6269\u5C55\u5230[0,29)\u3002\n\n\u4E0B\u4E00\u4E2A\u6570\u662F43\uFF0C\u6BD429\u5927\uFF0C\u6839\u636E\u89C4\u52192\uFF0C\u6DFB\u52A029\uFF0C\u628A\u533A\u95F4\u4ECE[0,29)\u6269\u5927\u5230[0,58)\u3002\n\n\u7531\u4E8E43\u6BD458\u5C0F\uFF0C\u6839\u636E\u89C4\u52191\uFF0C\u53EF\u4EE5\u628A\u533A\u95F4\u4ECE[0,58)\u6269\u5C55\u5230[0,101)\uFF0C\u521A\u597D\u8986\u76D6\u4E86[1,100]\u5185\u7684\u6240\u6709\u6570\u3002\n\n\u6700\u7EC8\u7ED3\u679C\u662F\u6DFB\u52A02\u4E2A\u6570\uFF0C8\u548C29\uFF0C\u5C31\u53EF\u4EE5\u7EC4\u5408\u51FA[1,100]\u5185\u7684\u6240\u6709\u6574\u6570\u3002\n*/\n\nclass Solution {\npublic:\n int minPatches(vector<int>& nums, int n) {\n long long r=0;\n int nextn=1;\n int index=0;\n int res=0;\n while(r<n){\n if(index<(int)nums.size()&&r>=(nums[index]-1)){\n r+=nums[index++];\n }else{\n res++;\n r+=(r+1);\n }\n }\n return res;\n }\n};\n\n/*\n\u9700\u8981\u6CE8\u610F\u7684\u6D4B\u8BD5\u7528\u4F8B\uFF1A\n[1,2,31,33]\n2147483647\n\n[1000000]\n1000\n*/\n``` | 5 | 0 | [] | 3 |
patching-array | Share my simple Java code | share-my-simple-java-code-by-mach7-ny9s | public class Solution {\n public int minPatches(int[] nums, int n) {\n int count = 0, i = 0;\n for (long covered=0; covered < n; ) | mach7 | NORMAL | 2016-02-03T08:57:25+00:00 | 2016-02-03T08:57:25+00:00 | 1,707 | false | public class Solution {\n public int minPatches(int[] nums, int n) {\n int count = 0, i = 0;\n for (long covered=0; covered < n; ) {\n if ((i<nums.length && nums[i]>covered+1) || i>=nums.length) { // at this moment, we need (covered+1), patch it.\n covered += covered+1;\n ++count;\n } else { covered += nums[i++]; }\n }\n return count;\n }\n } | 5 | 0 | [] | 2 |
patching-array | C# Solution for Patching Array Problem | c-solution-for-patching-array-problem-by-wybg | Intuition\n Describe your first thoughts on how to solve this problem. \nThe intuition behind this solution is that we aim to cover the range of sums from 1 to | Aman_Raj_Sinha | NORMAL | 2024-06-16T12:28:02.586540+00:00 | 2024-06-16T12:28:02.586572+00:00 | 173 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition behind this solution is that we aim to cover the range of sums from 1 to n using the elements in nums and additional patches if necessary. However, this solution uses a dynamic approach to iteratively extend the maximum sum that can be covered (maxSumCovered). If there is a gap (i.e., a number that cannot be formed with the current set of numbers), we add a patch to bridge that gap.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1.\tInitialization:\n\t\u2022\tpatches is initialized to 0 to count the number of patches added.\n\t\u2022\tmaxSumCovered is initialized to 0, representing the largest sum that can be formed with the current set of numbers.\n\t\u2022\ti is initialized to 0 to iterate through the nums array.\n2.\tIteration:\n\t\u2022\tWhile maxSumCovered is less than n:\n\t\u2022\tIf the current element in nums (i.e., nums[i]) is less than or equal to maxSumCovered + 1, it means we can use nums[i] to extend our range of sums. Update maxSumCovered to maxSumCovered + nums[i] and increment i.\n\t\u2022\tIf nums[i] is greater than maxSumCovered + 1 or there are no more elements left in nums, we add maxSumCovered + 1 as a patch. This new element bridges the gap and extends our coverage to 2 * maxSumCovered + 1, and we increment the patches count.\n3.\tReturn:\n\t\u2022\tThe total number of patches added is returned.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of this solution is O(m + log n), where:\n\n\t\u2022\tm is the length of the array nums.\n\t\u2022\tlog n comes from the fact that each patching operation doubles the value of maxSumCovered, and the number of such operations required to reach n is log n.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity of this solution is O(1) since we are using only a fixed amount of additional space (for variables like maxSumCovered, patches, and i).\n\n# Code\n```\npublic class Solution {\n public int MinPatches(int[] nums, int n) {\n int patches = 0;\n long maxSumCovered = 0;\n int i = 0;\n \n while (maxSumCovered < n) {\n if (i < nums.Length && nums[i] <= maxSumCovered + 1) {\n maxSumCovered += nums[i];\n i++;\n } else {\n maxSumCovered += maxSumCovered + 1;\n patches++;\n }\n }\n \n return patches;\n }\n}\n``` | 4 | 0 | ['C#'] | 1 |
patching-array | BEATS 100% users with java | simple approach | beats-100-users-with-java-simple-approac-gjwt | \n\n\n# Approach\n Describe your approach to solving the problem. \n- The algorithm uses a while loop to iterate from 1 to n (inclusive) and checks if the curre | sukritisinha0717 | NORMAL | 2024-06-16T06:17:48.239514+00:00 | 2024-06-16T06:17:48.239552+00:00 | 58 | false | 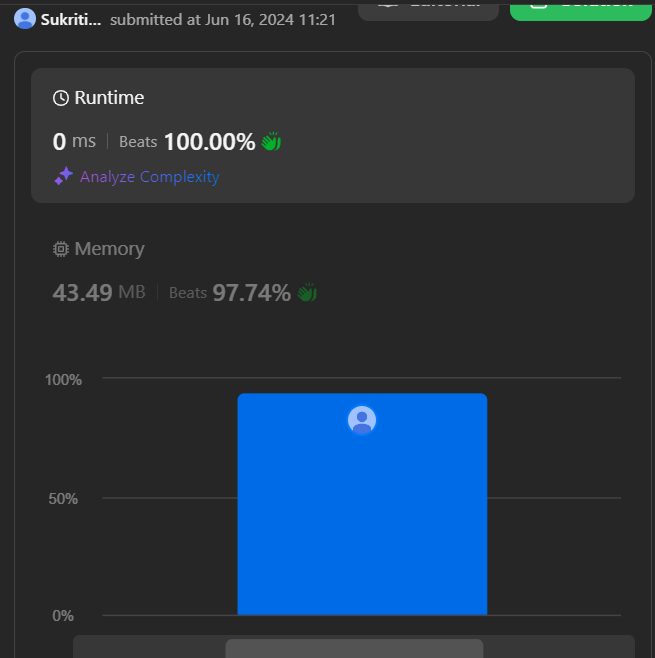\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- The algorithm uses a while loop to iterate from 1 to n (inclusive) and checks if the current miss value can be obtained using the elements in the nums array.\n- If the current number in nums is less than or equal to the miss value, it is added to miss, and the index i is incremented to consider the next element.\n- If the current number in nums is greater than the miss value, it means a patch is required. In this case, the result is incremented, and miss is doubled.\n- This process continues until miss exceeds n, at which point the algorithm returns the final result.\n\n# Complexity\n- Time complexity:o(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int minPatches(int[] nums, int n) {\n long miss = 1;\n int result = 0;\n int i = 0;\n\n while (miss <= n) {\n if (i < nums.length && nums[i] <= miss) {\n miss += nums[i];\n i++;\n } else {\n miss += miss;\n result++;\n }\n }\n\n return result;\n }\n}\n``` | 4 | 0 | ['Java'] | 1 |
patching-array | ✅ Easy C++ Solution | easy-c-solution-by-moheat-y510 | Code\n\nclass Solution {\npublic:\n int minPatches(vector<int>& nums, int n) {\n long long int sum = 0;\n int cnt = 0;\n int i = 0;\n | moheat | NORMAL | 2024-06-16T00:35:40.279309+00:00 | 2024-06-16T00:35:40.279327+00:00 | 613 | false | # Code\n```\nclass Solution {\npublic:\n int minPatches(vector<int>& nums, int n) {\n long long int sum = 0;\n int cnt = 0;\n int i = 0;\n while(sum < n)\n {\n if(i<nums.size() && nums[i] <= sum+1)\n {\n sum = sum + nums[i++];\n }\n else\n {\n cnt++;\n sum = sum * 2 + 1;\n }\n }\n return cnt;\n }\n};\n``` | 4 | 0 | ['C++'] | 2 |
patching-array | 330: Solution with step by step explanation | 330-solution-with-step-by-step-explanati-roue | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n\nTo solve this problem, we can use a greedy approach. We start with a va | Marlen09 | NORMAL | 2023-03-01T05:44:13.323724+00:00 | 2023-03-01T05:44:13.323774+00:00 | 1,320 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n\nTo solve this problem, we can use a greedy approach. We start with a variable miss that represents the smallest number that cannot be formed by summing up any combination of the numbers in the array. Initially, miss is set to 1, since we can always form 1 by taking an empty combination. We also initialize a variable i to 0, which represents the index of the next number that we need to consider adding to the array.\n\nWe then loop while miss is less than or equal to n, which means that we still need to add more numbers to the array. If i is less than the length of the array and the next number in the array is less than or equal to miss, we add that number to the sum and increment i. Otherwise, we add miss to the array and update miss to be the new smallest number that cannot be formed by summing up any combination of the numbers in the array.\n\nThe reason why this greedy approach works is that whenever we add a number to the array, we can form all the numbers up to miss + number - 1. If we then update miss to be miss + number, we can now form all the numbers up to 2 * miss - 1. Therefore, we keep increasing miss until we can form all the numbers up to n.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minPatches(self, nums: List[int], n: int) -> int:\n miss, i, patches = 1, 0, 0\n while miss <= n:\n if i < len(nums) and nums[i] <= miss:\n miss += nums[i]\n i += 1\n else:\n miss *= 2\n patches += 1\n return patches\n\n\n``` | 4 | 0 | ['Array', 'Greedy', 'Python', 'Python3'] | 3 |
patching-array | ✅C++ || Explained in Hinglish || Easy | c-explained-in-hinglish-easy-by-mayank88-yiq3 | \nclass Solution {\npublic:\n // Approach -\n // Ham kya karege ki ek reach variable lenge\n // Reach hame bataega ki kis number tak ham pohoch sakt | mayank888k | NORMAL | 2022-03-12T19:50:38.405919+00:00 | 2022-03-12T19:50:38.405948+00:00 | 461 | false | ```\nclass Solution {\npublic:\n // Approach -\n // Ham kya karege ki ek reach variable lenge\n // Reach hame bataega ki kis number tak ham pohoch sakte he jo hamare pass number he unse\n // Ham kya krege ki jab tak reach < n tab tak lopp chalaege\n \n // Agar reach < nums[i] to matlab abhi ham nums[i] tak number generate nahi kar sakte\n // isliye hame kuch patch add karna hoga, or bo patch reach + 1 hoga kyuki reach tak ke number ham generate kar sakte he\n // Lekin Reach se Jyada nahi isliye ham reach se ek jyada number ko patch kaarege array me jisse reach increase ho jaegi\n // reach += reach + 1 se\n \n \n // Or jab reach nums[i] se jyada ho to matlab ham nums[i] se jyada generate kar sakte nums[i] ke bina \n // or agar nums[i] ko bhi saath le le to reach increase ho jaegi reach + nums[i] kyoki nums[i] ko ham 1 to reach sabke saath\n // add kar sakte he to jisse max reach hamari reach + nums[i] ho jaegi\n \n //Ek case or jab reach nums[i] se ek kam ho tab means (nums[i] == reach + 1) is time ham reach ko nums[i] se increase kar denge\n // kyoki ham nums[i] - 1 tak generate kar sakte agar nums[i] aa jaega to nums[i] + reach ista generate kar paege\n \n // For Ex - 1 5 10\n // reach = 0 nums[i] = 1 nums[i] <= reach + 1 ye last bala case jab nums[i] == reach + 1 to reach me num[i] add karege == > i++ (jab bhi nums[i] add ho jaega tabhi i++ karege)\n // reach = 1 nums[i] = 5 nums[i] > reach array me patch karege reach + 1 (1 + 1 = 2) or reach increase karege\n // reach = 3 (1 +2) nums[i] = 5 nums[i] > reach array me patch karege reach + 1 (3 + 1 = 4) or reach increase karege\n // reach = 7 (3 +4) nums[i] = 5 nums[i] <= reach + 1 reach += nums[i] ==> i++\n // reach = 12(7 +5) nums[i] = 10 nums[i] <= reach + 1 reach += nums[i] ==> i++\n // reach = 22 (12+10) reach > n breack loop return the patch count (we added 2 and 4 so count will be 2)\n \n \n int minPatches(vector<int>& nums, int n) {\n long long reach = 0; \n int patches = 0;\n int i = 0;\n \n while(reach < n)\n {\n if(i < nums.size() && nums[i] <= reach+1) reach += nums[i++];\n else\n {\n reach += reach + 1;\n patches++;\n }\n }\n \n return patches;\n }\n};\n``` | 4 | 0 | ['Greedy', 'C'] | 2 |
patching-array | Concise Java Solution Faster than 100% with in depth explanation | concise-java-solution-faster-than-100-wi-c6y5 | Explaination:\nInput: [1, 5, 10]\n\nInitially, our reach is 0. Let\'s start the process of adding elts step by step:\n1) Adding 1st elt, doesn\'t make us miss e | 1_mohit_1 | NORMAL | 2021-09-13T04:56:52.864330+00:00 | 2021-09-13T04:56:52.864376+00:00 | 178 | false | Explaination:\nInput: [1, 5, 10]\n\nInitially, our **reach is 0**. Let\'s start the process of adding elts step by step:\n1) Adding 1st elt, doesn\'t make us miss elts. Since, reach is 0 and 1st element is 1. So Now **reach=1**.\n2) Now, adding 2nd elt(i.e. 5) makes us miss elts 2,3,4 since reach is only 1 till now. So we add the lowest unreachable elt yet i.e. 2. So, now **reach=reach+(reach+1) i.e. 1 +2 = 3**.\n**Why?**\nSince, reach at any stage means that all elts from 1 to reach are reachable for example if reach is 5, all elements i.e 1, 2, 3, 4, 5 are reachable now suppose if we add 6 to it, then we get 6 more elements which can be reached i.e. [1+6, 2+6, 3+6, 4+6, 5+6]. Hence, reach increases by the element we add.\nSo, in above case previous reach was 1, we added (reach+1) element **hence, reach=reach+(reach+1) i.e. reach = 2 * reach + 1.**\n3) Again 2nd element(i.e. 5) cannot be added since reach is still 3, hence 4 is missing. So we add 4 to the array which makes **reach=reach+4 = 3 + 4 = 7.**\n4) Now, we can add 2nd element because it\'s less than reach, hence we don\'t miss any element. \n**Now, reach = reach + 5 = 7 + 5 = 12.**\n5) Next, we add the 3rd element(i.e. 10) since it\'s less than reach and that means we don\'t miss any element.\n**Now, reach = reach + 10 = 12 + 10 = 22**.\nWhich is greater than n, hence we added 2 and 4 to the array as in step 2 and 3.\n\n**Key Points:**\n**1) From 2nd Point:\n\tif(arr[i]>(reach+1)){\n\t\t// This indicates certain elts are missing and we add lowest elt after reach i.e. (reach+1)\n\t\t// 2nd and 3rd Points indicate this.\n\t\treach=reach+(reach+1)\n\t\telts_added+=1;\n\t}else{\n\t\t// This indicates that no elts are missing - 4th and 5th Points indicates this.\n\t\treach=reach+(arr[i]);\n\t}**\n\t\n\tNow below code should make sense.\n\t`\n\tpublic int minPatches(int[] nums, int n) {\n int ans=0,i=0;\n long reach=0;\n while(reach<n){\n if(i<nums.length && nums[i]<=(reach+1))\n reach+=nums[i++];\n else{\n reach=(reach<<1)+1;\n ans++;\n }\n }\n return ans;\n }\n\t` | 4 | 0 | [] | 1 |
patching-array | My 8 ms O(N) C++ code | my-8-ms-on-c-code-by-lejas-1hcg | The basic idea is to use "bound" to save the maximum number that can be generated with nums[0..i-1] and the added numbers (i.e. using nums[0..i-1] and the added | lejas | NORMAL | 2016-01-28T14:57:33+00:00 | 2016-01-28T14:57:33+00:00 | 803 | false | The basic idea is to use "bound" to save the maximum number that can be generated with nums[0..i-1] and the added numbers (i.e. using nums[0..i-1] and the added numbers, we can generate all the numbers in [1..bound]). If bound is less than n and nums[i] is larger than bound+1, then we need to add bound+1, which extend the maximum number that can be generated to bound*2 +1. If nums[i] is no larger than bound+1, then by add nums[i], we can extend the maximum number that can be generated to bound + nums[i].\n\n class Solution {\n public:\n int minPatches(vector<int>& nums, int n) {\n int len = nums.size(), i=0, res=0;\n long long bound = 0;\n while(bound<n) \n {// if it does not reach to the end\n if(i<len && nums[i]<=(bound+1)) bound+=nums[i++]; // if nums[i] is no larger than bound, then including nums[i] allow us to generate all the numbers [1.. bound+nums[i]]\n else{++res; bound= 2*bound+1;} // we need to add a new number bound+1, and that extend the bound to 2*bound+1\n }\n return res;\n }\n }; | 4 | 0 | [] | 0 |
patching-array | Python solution + clear explanation, o(|nums| + log n) | python-solution-clear-explanation-onums-4mlp5 | We want to form all numbers from 1 to n. Let's assume we already have the solutions for a smaller problem. We have an array to reach all numbers up to k, 1 <= k | pbarrera | NORMAL | 2016-10-28T12:13:31.934000+00:00 | 2016-10-28T12:13:31.934000+00:00 | 380 | false | We want to form all numbers from 1 to n. Let's assume we already have the solutions for a smaller problem. We have an array to reach all numbers up to k, 1 <= k < n, but not more. We have used nums<sub>0</sub> to nums<sub>i</sub> to create that array plus some patches. The next element is k+1. There is no way we can create k+1 with our current array (we defined the array that way), so I need to add a new element to it, nums<sub>i+1</sub>. As my previous array was able to give all elements from 1 to k, adding nums<sub>i+1</sub> will give me all elements between 1 and k+nums<sub>i+1</sub>.\n\nThe trick here is to find those compact arrays that are able to produce all values between 1 and k. We can do that starting in k=1 and adding elements from nums or patching our array. To reach k=1 I need a 1. If nums_0 is 1, I can add it to my array otherwise I need to pad with 1. To reach k=2 I need another 1 or a 2.\n\nAnd so on. So, if you keep track of the highest number you can reach in your current array there could be two possibilities:\n- nums<sub>i</sub> is smaller than k. Just increase k.\n- nums<sub>i</sub> is bigger than k. That means that you can't create any number between k+1 and nums<sub>i</sub>-1. Add k+1 instead. That will move k to 2*k+1.\n\nRepeat until k>=n.\n\n```python\ndef minPatches(self, nums, n):\n i, k, added = 0,0,0\n while k < n:\n if i < len(nums) and nums[i] <= k+1:\n k += nums[i]\n i+=1\n else:\n k += k+1\n added += 1\n return added\n``` | 4 | 0 | [] | 0 |
patching-array | Simple || Easy to Understand || Clear | simple-easy-to-understand-clear-by-kdhak-encw | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | kdhakal | NORMAL | 2024-10-07T04:55:22.529067+00:00 | 2024-10-07T04:55:22.529095+00:00 | 3 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int minPatches(int[] nums, int n) {\n int minPatch = 0, i = 0;\n long max = 1;\n\n while(max <= n) {\n\n if(i < nums.length && nums[i] <= max) max += nums[i++];\n else {\n minPatch++;\n max += max;\n }\n }\n\n return minPatch;\n }\n}\n\n\n``` | 3 | 0 | ['Java'] | 0 |
patching-array | Why not you tried Prefix Sum !!! Greedy Approach O(logN) | why-not-you-tried-prefix-sum-greedy-appr-p06s | Intuition\nIf we have non-descending array [a, ....., b, c, ....., d] and the consecutive numbers formed from subarray [a, ....., b] are k and c >= k-1, then w | k_patil092 | NORMAL | 2024-06-16T11:11:59.465802+00:00 | 2024-06-16T11:11:59.465832+00:00 | 133 | false | # Intuition\nIf we have non-descending array $$[a, ....., b, c, ....., d]$$ and the consecutive numbers formed from subarray $$[a, ....., b]$$ are $$k$$ and $$c >= k-1$$, then we can ensure that the consecutive numbers formed from subarray $$[a, ....., b, c]$$ will be $$k+c$$.\n\nFor example,\nGiven $$nums = [1,2,3,6,13]$$ and for subarray $$[1,2,3]$$ we know that we can form all the numbers from *1 to 6* *({1, 2, 3, 3+1=4, 3+2=5, 3+2+1=6})*. \nNow next number in subarray is 6, which follows the condition $$c >= k-1$$ i.e., $$(6 >= 6 - 1)$$. So, now we can say that the consecutive numbers formed from subarray $$[1,2,3,6]$$ will be $$6 + 6 = 12$$.\nWe can visualize it as, if we can form all the numbers taking numbers from the previous subarray, here then adding 6 to all that numbers, we can get all the other 6 for next subarray.\nviz., \nfor subarray $$[1,2,3]$$ we get all the numbers from *1 to 6* *({1, 2, 3, 3+1=4, 3+2=5, 3+2+1=6})*, then after adding 6 to each number we can get other numbers from *6 to 12* *({6, 1+6=7, 2+6=8, 3+6=9, 1+3+6=10, 2+3+6=11, 1+2+3+6=12})*.\n\nAgain, for the next index which satisfies the condition, numbers formed will be $$12+13=25$$.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nIn the loop, for each index, if the condition gets true, we add it to prefix sum and move to next index. If the condition doesn\'t satisfy, it infers that some of the numbers are missing, that we need to add, so we increases the missing numbers value (answer) and also add up the largest number which will cover all the in between values, i.e. `prefix sum + 1`, to the `prefix sum`.\n\nIn case, if we our numbers form doesn\'t reach to the `n`, we will loop it until we reach there.\n\n# Complexity\n- Time complexity: max(O(len(nums)), O(log n)) = **O(logN)**\n\n- Space complexity: **O(1)**\n\n# Code\n\n### C++ :\n```\nclass Solution {\npublic:\n int minPatches(vector<int>& nums, int n) {\n int ans = 0;\n long int presum = 0;\n for(int i=0; i<nums.size() and presum < n;) {\n if(presum >= nums[i]-1) {presum += nums[i]; i++;}\n else {ans += 1; presum += presum+1;}\n }\n while(presum < n) {presum += presum+1; ans += 1;}\n return ans;\n }\n};\n\n```\n\n### Python3 :\n```\nclass Solution:\n def minPatches(nums, n):\n prefix_sum, res, i = 0, 0, 0\n while i < len(nums) and prefix_sum < n:\n if prefix_sum >= nums[i] - 1:\n prefix_sum += nums[i]\n i += 1\n else:\n prefix_sum += prefix_sum + 1\n res += 1\n while prefix_sum < n:\n prefix_sum += prefix_sum + 1\n res += 1\n return res\n```\n# .\n## .\n### .\n# >>>>>>>>>>**Please Upvote**<<<<<<<<<<<\n### .\n## .\n# . | 3 | 0 | ['Array', 'Greedy', 'C', 'Sorting', 'Prefix Sum', 'C++', 'Python3'] | 1 |
patching-array | Intuitive Approach with Observation and Dry Run ✅💯 | intuitive-approach-with-observation-and-pfw4n | Minimum Number of Patches\n\n## Problem Statement\nGiven a sorted array of positive integers nums and an integer n, you need to add the minimum number of patche | _Rishabh_96 | NORMAL | 2024-06-16T07:25:09.738551+00:00 | 2024-06-16T07:25:09.738570+00:00 | 100 | false | # Minimum Number of Patches\n\n## Problem Statement\nGiven a sorted array of positive integers `nums` and an integer `n`, you need to add the minimum number of patches to the array such that every number in the range `[1, n]` can be formed by the sum of some elements in the array.\n\n## Intuition\nTo solve the problem, we can use a greedy algorithm. The goal is to ensure that for every integer up to `n`, we can form it using the elements of the array `nums` and any additional patches we add.\n\n## Approach\n1. **Initialize Variables**:\n - `patches`: A counter to keep track of the number of patches added.\n - `maxReach`: A variable to track the maximum number we can form using the numbers in `nums` and the patches added so far.\n - `i`: An index to iterate over the array `nums`.\n\n2. **Iterate Until the Range is Covered**:\n - While `maxReach` is less than `n`:\n - If the current element in `nums` can extend the range (`maxReach + 1 >= nums[i]`), use it and update `maxReach`.\n - If the current element in `nums` cannot be used, add a patch (the number `maxReach + 1`) and update `maxReach`.\n\n3. **Return the Result**:\n - Once the loop ends, `patches` will contain the minimum number of patches required to ensure the range from `1` to `n` can be formed.\n## Dry Run\nGiven `nums = [1, 5, 10]` and `n = 20`:\n\n- **Initial State**:\n - `patches = 0`\n - `maxReach = 0`\n - `i = 0`\n\n- **Iteration 1**:\n - `maxReach + 1 = 1`, `nums[i] = 1` (1 can be used)\n - Update `maxReach = maxReach + nums[i] = 0 + 1 = 1`\n - Increment `i = 1`\n - `patches = 0`\n \n- **Iteration 2**:\n - `maxReach + 1 = 2`, `nums[i] = 5` (2 cannot be formed with current `maxReach`)\n - Add patch `2`\n - Update `maxReach = maxReach + (maxReach + 1) = 1 + 2 = 3`\n - `patches = 1`\n\n- **Iteration 3**:\n - `maxReach + 1 = 4`, `nums[i] = 5` (4 cannot be formed with current `maxReach`)\n - Add patch `4`\n - Update `maxReach = maxReach + (maxReach + 1) = 3 + 4 = 7`\n - `patches = 2`\n\n- **Iteration 4**:\n - `maxReach + 1 = 8`, `nums[i] = 5` (5 can be used)\n - Update `maxReach = maxReach + nums[i] = 7 + 5 = 12`\n - Increment `i = 2`\n - `patches = 2`\n\n- **Iteration 5**:\n - `maxReach + 1 = 13`, `nums[i] = 10` (10 can be used)\n - Update `maxReach = maxReach + nums[i] = 12 + 10 = 22`\n - Increment `i = 3`\n - `patches = 2`\n\n- **End Condition**:\n - `maxReach = 22`, which is greater than `n = 20`\n - Total patches added = 2\n\nThus, the minimum number of patches required is `2`.\n\n\n## Complexity\n- **Time Complexity**: \\(O(max(m, lon(n)))\\), where \\(m\\) is the number of elements in the input array `nums`. This is because each element is processed at most once.\n- **Space Complexity**: \\(O(1)\\), as we are using a constant amount of extra space regardless of the input size.\n\n## Code\n```cpp\nclass Solution {\npublic:\n int minPatches(vector<int>& nums, int n) {\n long long patches = 0, maxReach = 0;\n int i = 0;\n\n while (maxReach < n) {\n if (i < nums.size() && maxReach + 1 >= nums[i]) {\n maxReach += nums[i];\n i++;\n } else {\n patches++;\n maxReach += (maxReach + 1);\n }\n }\n\n return patches;\n }\n};\n``` | 3 | 0 | ['Array', 'Greedy', 'C++'] | 1 |
patching-array | Binary Search || Code With Comments || Super Easy | binary-search-code-with-comments-super-e-5aad | Intuition\n\nThe code is well commented. This is the intuition for isPossible function in the code first read the comments in the code to get a better understan | vikalp_07 | NORMAL | 2024-06-16T06:08:06.416999+00:00 | 2024-06-16T06:08:06.417029+00:00 | 362 | false | # Intuition\n\n**The code is well commented. This is the intuition for isPossible function in the code first read the comments in the code to get a better understanding**\n\nThe isPossible Function in my code is based on the fact that if we have n consequtive numbers starting from 1,\nthen we can make each and every sum from 1 to (n)*(n+1)/2 with that numbers only\neg [1,2,3,4,5] we can make sums from [1, 15] both inclusive,\nnow if we have a missing number eg 3 is missing\neg [1,2,4,5] we can make upto [1, 15-missingNumber] ie [1, 15-3] ie [1,12]\n\nwe will take the range variable for counting the range\n\nwe will take totalSum for calculating the totalSum\n\nwhenever we will not find a number that is greater than range+1 we will always add range+1 in our range to maintain that consequtive nature of out sequence\n\nand if range is 10 and we found 9 we ll update our range simply as 19\nbut if we find 12 we will make our range as range = range+range+1\nie 10+10+1 = 21 ie (10+11)\n\nthat simple \n\nif we found range+1 in our nums then no increase in patches\nif we dont please increase the patch by one\n\nif the patches are less than or equal to the required patches\nreturn true else return false\n\nrest will be held by binary search\n\nPlease upvote :)\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n#define ll long long\n\nclass Solution {\npublic:\n\n vector<ll> nums;\n ll TOTALSUM;\n\n bool isPossible(int nop, ll n)\n {\n ll totalSum = TOTALSUM;\n\n int reqPatch = 0;\n ll range = 0;\n int i = 0;\n\n while(i<nums.size())\n {\n if(nums[i]<=(range+1))\n {\n range = range + nums[i];\n i++;\n }\n else\n {\n while(nums[i]>(range+1))\n {\n reqPatch++;\n totalSum = totalSum + range + 1;\n range = range + range + 1;\n }\n }\n }\n\n while(range<n)\n {\n reqPatch++;\n totalSum = totalSum + range + 1;\n range = range + range + 1;\n }\n\n if(totalSum<n)\n {\n reqPatch++;\n }\n\n if(reqPatch<=nop)\n {\n return true;\n }\n else\n {\n return false;\n }\n\n }\n\n int minPatches(vector<int>& N, int n) {\n bool flag = false;\n\n //if one is not present include 1\n if(N[0]!=1)\n {\n nums.push_back(1);\n TOTALSUM+=1;\n flag = true;\n }\n\n //if n==1 then special case\n if(n==1)\n {\n if(flag==true)\n {\n return 1;\n }\n else\n {\n return 0;\n }\n }\n\n //exclude all those numbers which are greater than n\n for(int i=0;i<N.size();i++)\n {\n if(N[i]<n)\n {\n nums.push_back(N[i]);\n TOTALSUM+=N[i];\n }\n }\n\n //initialize the binary search\n int high = n;\n int low = 0;\n\n int ans = high;\n\n //carry out binary search\n while(low<=high)\n {\n int mid = (high+low)/2;\n if(isPossible(mid, n))\n {\n ans = mid;\n high = mid-1;\n }\n else\n {\n low = mid+1;\n }\n }\n\n if(flag==true)\n {\n ans++;\n }\n\n return ans;\n }\n};\n``` | 3 | 0 | ['Binary Search', 'C++'] | 1 |
patching-array | Simple solution in Java!! With dry run ✅✅✅✅ | simple-solution-in-java-with-dry-run-by-qkrbd | Intuition\nTo ensure all numbers from 1 to n can be formed using a given array nums, we can add the smallest missing number that cannot be formed so far. This m | PavanKumarMeesala | NORMAL | 2024-06-16T04:31:03.930446+00:00 | 2024-06-16T04:31:03.930486+00:00 | 66 | false | ## Intuition\nTo ensure all numbers from 1 to `n` can be formed using a given array `nums`, we can add the smallest missing number that cannot be formed so far. This minimizes the number of patches needed.\n\n## Approach\n1. **Initialize**: Start with the smallest missing number `patch` set to 1 and counters for total patches and index.\n2. **Iterate**: \n - If the current number in `nums` can be used to form `patch`, add it to `patch`.\n - If it can\'t, add `patch` itself to form the next number, increment total patches.\n3. **Repeat**: Continue until all numbers up to `n` can be formed.\n\n## Dry Run\nExample:\n- `nums = [1, 3]`, `n = 6`\n\n| Step | `patch` | `index` | `total` | Action | New `patch` |\n|------|---------|---------|---------|---------------------------------|-------------|\n| 1 | 1 | 0 | 0 | Use `nums[0]` | 2 |\n| 2 | 2 | 1 | 0 | Add `patch` itself (missing 2) | 4 |\n| 3 | 4 | 1 | 1 | Use `nums[1]` | 7 |\n\nFinal number of patches required is 1.\n\n# Complexity\n- Time complexity: O(log N) cause array is already sorted.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1), nom extra space.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int minPatches(int[] nums, int n) {\n long patch = 1;\n int total = 0;\n int index = 0;\n\n while(patch <= n)\n {\n if(index < nums.length && patch >= nums[index])\n {\n patch += nums[index];\n index++;\n }\n else\n {\n patch += patch;\n total++;\n }\n }\n\n return total;\n }\n}\n```\n\n\n | 3 | 0 | ['Java'] | 0 |
patching-array | Easy Java Solution | Greedy | Beats 100 💯✅ | easy-java-solution-greedy-beats-100-by-s-ivls | Min Patches Problem\n\n## Problem Description\n\nGiven a sorted integer array nums and a positive integer n, your goal is to compute the minimum number of patch | shobhitkushwaha1406 | NORMAL | 2024-06-16T02:59:42.933390+00:00 | 2024-06-16T02:59:42.933423+00:00 | 440 | false | # Min Patches Problem\n\n## Problem Description\n\nGiven a sorted integer array `nums` and a positive integer `n`, your goal is to compute the minimum number of patches required to ensure that every integer in the range `[1, n]` can be formed as a sum of some elements from `nums`. A patch is an integer that you can add to `nums`.\n\n## Intuition\n\nTo solve this problem efficiently, we need to ensure that we can generate all numbers in the range `[1, n]` using the elements in `nums` and a minimal number of additional patches. The key insight is to track the smallest number that we cannot form (`miss`). Initially, `miss` is `1`, meaning we need to form the number `1` first. If the smallest number in `nums` that we haven\'t used yet is less than or equal to `miss`, we can use it to extend our range of representable sums. If it is greater than `miss`, we must add `miss` itself as a patch to extend our range.\n\nThe approach ensures that at each step, we either extend our range of representable sums using existing elements from `nums` or we add a new patch that extends the range significantly. This greedy strategy minimizes the number of patches needed.\n\n## Approach\n\n1. **Initialize**:\n - `patches` to `0` to count the number of patches added.\n - `i` to `0` to iterate through `nums`.\n - `miss` to `1` which is the smallest number that cannot be formed.\n\n2. **Iterate while `miss` is less than or equal to `n`**:\n - If `i` is within the bounds of `nums` and `nums[i]` is less than or equal to `miss`:\n - Add `nums[i]` to `miss`.\n - Increment `i`.\n - Otherwise, add `miss` itself as a patch.\n - Double `miss` to extend the range significantly.\n - Increment the `patches` count.\n\n3. **Return the total number of patches**.\n\nThis process continues until `miss` exceeds `n`, ensuring that every number up to `n` can be formed.\n\n## Time Complexity\n\nThe time complexity is **O(m)**, where `m` is the length of `nums`. This is because we iterate through the elements of `nums` at most once, and each patch operation is essentially a constant time operation relative to `nums`.\n\n## Space Complexity\n\nThe space complexity is **O(1)**. The algorithm uses a fixed amount of additional space for variables regardless of the size of `nums` or `n`.\n\n\n# Code\n```\nclass Solution {\n public int minPatches(int[] nums, int n) {\n int patches = 0;\n int i = 0;\n long miss = 1;\n while(miss <= n) {\n if(i < nums.length && nums[i] <= miss)\n miss += nums[i++];\n else {\n miss += miss;\n patches++;\n }\n }\n return patches;\n }\n}\n``` | 3 | 0 | ['Array', 'Math', 'Greedy', 'Java'] | 2 |
patching-array | 🔥 🔥 🔥 💯 Easy to understand || Greedy Approach || Detailed Explanation || Python,C++,Java🔥 🔥 🔥 | easy-to-understand-greedy-approach-detai-ysou | Intuition\n Describe your first thoughts on how to solve this problem. \n The code works like providing change with limited coin denominations. Suppose you need | avinash_singh_13 | NORMAL | 2024-06-16T02:04:40.924111+00:00 | 2024-06-16T02:04:40.924139+00:00 | 27 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n* The code works like providing change with limited coin denominations. Suppose you need to cover every amount up to \uD835\uDC5B cents. If you can\'t make exact change for a particular amount miss, it indicates you lack a coin of value less than or equal to miss. To fill this gap, you add a coin of that exact missing amount. This addition allows you to now cover new amounts up to 2 * miss. Repeat this process until you can provide change for every amount up to \uD835\uDC5B. This method ensures you add the minimum number of new coins needed to cover any shortages.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n* **Initialize Variables:** Start with miss set to 1, added to 0, and index i at 0 to track the smallest sum that cannot be formed and the number of patches added.\n\n* **Iterate with Condition:** Continue the loop as long as miss (the target sum we need to achieve) is less than or equal to n.\n\n* **Use Existing Numbers:** Check if the current number in the list (nums[i]) can be used to form miss. If yes, add it to miss to extend the range of formable sums and increment the index i.\n\n* **Add Necessary Numbers:** If nums[i] is greater than miss or all numbers are already used, add miss itself to cover the smallest unformable sum, and double the value of miss.\n\n* **Increment Added Count:** Whenever a number is added to cover a gap, increase the added counter.\n\n* **Return Total Patches:** Once miss exceeds n, return the total count of added numbers as the result, representing the minimum patches needed to form every number up to n.\n\n# Example:\n\n* Input: [1, 5, 10]\n\nStep\tCurrent nums\tMiss\tAction\tReason\tNew Coverage\n1. \t[1, 5, 10]\t1\tUse 1\t1 is available and matches miss\tSums up to 1\n2.\t[1, 5, 10]\t2\tAdd 2\t5 is too large to form sum 2\tSums up to 3\n3.\t[1, 5, 10]\t4\tAdd 4\t5 is too large to form sum 4\tSums up to 7\n4.\t[1, 5, 10]\t8\tUse 5\tCan use 5 with existing numbers to form 8\tSums up to 12\n5.\t[1, 5, 10]\t13\tUse 10\tCan use 10 with existing numbers to form 13\tSums up to 22\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(N)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(1)\n\n```python []\nclass Solution:\n def minPatches(self, nums: List[int], n: int) -> int:\n c=1\n res=0\n i=0\n while c<=n:\n if i<len(nums) and nums[i]<=c:\n c+=nums[i]\n i+=1\n else:\n c+=c\n res+=1\n return res\n```\n```C++ []\nclass Solution {\npublic:\n int minPatches(vector<int>& nums, int n) {\n long long miss = 1;\n int result = 0;\n size_t i = 0;\n\n while (miss <= n) {\n if (i < nums.size() && nums[i] <= miss) {\n miss += nums[i];\n i++;\n } else {\n miss += miss;\n result++;\n }\n }\n\n return result;\n }\n};\n```\n```java []\nclass Solution {\n public int minPatches(int[] nums, int n) {\n long miss = 1;\n int result = 0;\n int i = 0;\n\n while (miss <= n) {\n if (i < nums.length && nums[i] <= miss) {\n miss += nums[i];\n i++;\n } else {\n miss += miss;\n result++;\n }\n }\n\n return result;\n }\n}\n```\n\n | 3 | 0 | ['C++', 'Java', 'Python3'] | 1 |
patching-array | 🔥Explained :🔥 🔥 c++🔥 🔥sorting 🔥 🔥100% faster🔥 🔥Tricky🔥💯💯 ⬆⬆⬆ | explained-c-sorting-100-faster-tricky-by-kycs | Intuition\n Describe your first thoughts on how to solve this problem. \n1. if we can make all number from 1 to n, and nums[i] = 5 => then we can make all numbe | sandipan103 | NORMAL | 2023-12-03T05:41:33.902741+00:00 | 2023-12-03T05:41:33.902771+00:00 | 139 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n1. if we can make all number from 1 to n, and nums[i] = 5 => then we can make all number from 1 to n+5\n\n2. if we can make (1 to n) then we need to make the next number i.e n+1;\n\n3. **Case-1 :** the current number (i.e `nums[i] > required` ) then we need to add the required number in the nums array. \n in this case `count++` and our next required number will be `2*required` . \n\n4. **Case-2 :** the current number is less than required (i.e `nums[i] < required`) then our next required number will be `required + nums[i]`\n\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n log(n))$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n\n# Code\n```\nclass Solution {\npublic:\n int minPatches(vector<int>& nums, int n) {\n long long ans = 0, required = 1;\n sort(nums.begin(), nums.end());\n\n for(int i=0; i<nums.size(); i++) {\n if(required > n) return ans;\n if(required < nums[i]) {\n ans++;\n required *= 2;\n i--;\n }\n else \n required += nums[i];\n }\n\n while(required <= n) {\n ans++;\n required *= 2;\n }\n\n return ans;\n }\n};\n``` | 3 | 0 | ['C++'] | 1 |
patching-array | TIME O(n), SPACE (1) || C++ || EASY TO UNDERSTAND || SHORT & SWEET | time-on-space-1-c-easy-to-understand-sho-ve4c | \n/*\ni E to [1,n]\nreach at ith day if nums[j]<=i+1 than add nums[j] into i else add i+1 in to ith day\n*/\nclass Solution {\npublic:\n int minPatches(vect | yash___sharma_ | NORMAL | 2023-03-28T06:35:29.130752+00:00 | 2023-03-28T06:35:38.188224+00:00 | 1,920 | false | ````\n/*\ni E to [1,n]\nreach at ith day if nums[j]<=i+1 than add nums[j] into i else add i+1 in to ith day\n*/\nclass Solution {\npublic:\n int minPatches(vector<int>& nums, int n) {\n long long sum = 0, cnt = 0, i = 0;\n while(sum<n){\n if(i<nums.size()&&nums[i]<=sum+1){\n sum += nums[i++];\n }else{\n cnt++;\n sum += sum+1;\n }\n }\n return cnt;\n }\n};\n```` | 3 | 0 | ['Array', 'Greedy', 'C', 'C++'] | 1 |
patching-array | Shortest Solution | C++ | greedy | shortest-solution-c-greedy-by-hritik_014-m95v | \nclass Solution {\npublic:\n int minPatches(vector<int>& nums, int n) {\n int patches = 0, i = 0, sz = nums.size();\n long count = 1;\n | hritik_01478 | NORMAL | 2022-10-13T04:28:25.664723+00:00 | 2022-10-13T04:28:25.664752+00:00 | 578 | false | ```\nclass Solution {\npublic:\n int minPatches(vector<int>& nums, int n) {\n int patches = 0, i = 0, sz = nums.size();\n long count = 1;\n while (count <= n) {\n \n if (i < sz && nums[i] <= count) \n count += nums[i++];\n \n else {\n count *= 2;\n patches++;\n }\n }\n \n return patches;\n }\n};\n``` | 3 | 0 | ['Greedy', 'C'] | 2 |
patching-array | Java | Simple solution | java-simple-solution-by-pulkitswami7-dukq | \n\nUPVOTE IF YOU FIND IT USEFUL\n\n\n\nclass Solution {\n public int minPatches(int[] nums, int n) {\n int patches = 0, i = 0;\n long val = 1; | pulkitswami7 | NORMAL | 2022-03-02T14:39:40.260421+00:00 | 2022-03-02T14:40:49.989591+00:00 | 180 | false | <hr>\n\n***UPVOTE IF YOU FIND IT USEFUL***\n<hr>\n\n```\nclass Solution {\n public int minPatches(int[] nums, int n) {\n int patches = 0, i = 0;\n long val = 1;\n \n while(val <= n){\n if(i < nums.length && nums[i] <= val){\n val += nums[i++];\n }\n else{\n val += val;\n patches++;\n }\n \n //System.out.println(val);\n }\n \n return patches;\n }\n}\n``` | 3 | 0 | ['Array'] | 0 |
patching-array | Python, O(n), greedy | python-on-greedy-by-404akhan-trmi | Consider some prefix of our array and say the minimal number it can\'t achieve is minn, if the next number is greater than minn we won\'t be able to achieve min | 404akhan | NORMAL | 2021-11-06T11:18:34.967377+00:00 | 2021-11-06T11:18:34.967411+00:00 | 248 | false | Consider some prefix of our array and say the minimal number it can\'t achieve is `minn`, if the next number is greater than `minn` we won\'t be able to achieve `minn` at all (since all numbers are increasing and greater than `minn`) thus next number must be less or equal than `minn` if not so we need to patch with such a number. Say our next number `k` satisfies being less or equal than `minn` or otherwise we patched it with some number `k`, then in the new prefix minimal number it can\'t achieve will be `minn + k` and so on we keep maintaining our minimal unachievable number until it is greater than `n`. It is better to patch with such `k` that maximizes `minn+k` and satisfies `k<=minn`, such `k` is actually equal to `minn`. (This part is greedy). After performing such linear scan we will achieve what we want.\n\n```\nclass Solution:\n def minPatches(self, nums, n):\n i, ct, minn = 0, 0, 1\n while minn <= n:\n if i < len(nums) and nums[i] <= minn:\n minn += nums[i]\n i += 1\n else:\n minn += minn\n ct += 1\n return ct\n``` | 3 | 0 | [] | 0 |
patching-array | [C++ Solution ] Detailed explanation -- greedy | c-solution-detailed-explanation-greedy-b-plwh | Let\'s start from an example, the given vector input = {1, 4, 6, 10}, n = 20;\n\nSince we are aimed to cover all the numbers in range [1, 20], let\'s consider t | charles1791 | NORMAL | 2021-06-26T08:23:27.788464+00:00 | 2023-02-26T01:16:21.475403+00:00 | 324 | false | Let\'s start from an example, the given vector input = {1, 4, 6, 10}, n = 20;\n\nSince we are aimed to cover all the numbers in range [1, 20], let\'s consider the elements one by one.\nWe may create an aiding vector<int> aid, which is used to contain all the elements that have been covered SO FAR.\nOf course, this "aid" is empty from the begining. What\'s more, use a counter to count how many extra elements should we provide, i.e. the output. \n\nFirstly, we expect the first element "1" to be added into the aid. After check the input vector, we find we have an "1", so just use it add it into our "aid" vector;\naid = {1} so far, count = 0\n\nNext, we expect "2" to be added. Looking at the input vector, since the first element has already been used, we check from the second element, which is "4". Apparently, we need to patch one extra element to get the expected "2". \nNow the problem comes, should we directly give a "2" or we may give an "1" since 1+1 also yeilds "2". The answer is that both ways work, HOWEVER, "2" is a better choice since 1+2 gives 3, adding a "2" expand aid into {1,2,3} while adding an "1" just turns aid = {1,2}. So we patch a "2", and the count++; BTW, this this can be though as "greedy strategy"\naid = {1,2,3} so far, count =1\n\nAfter that, we expect "4". Checking input, we find a 4 and so there\'s no need for extra patching. Add 4 into the aid would expand it into {1, 2, 3 ,4 ,1+4, 2+4, 3+4}. You may have notice that\n\n#### adding an element x would incrase the size of the aid vector by x. \n\naid = {1,2,3,4,5,6,7} so far, count = 1\n\nThen we expect 8, searching the input vector, the next element not used is "6", since we may use the "2" in aid vector to add 6 and get 8, so it meets our needs. What\'s more, as said before, the "6" would expand our aid vector into {1, 2, 3, 4, 5, 6, 7, 2+6, 3+6, 4+6, 5+6, 6+6, 7+6}.\naid = {1,2,3,4,5,6,7,8,9,10,11,12,13} by now, count = 1\n\nThe next expected element is 14, and the next element provided by input is "10", again, this would turn our aid vector into {1,2,3,....,23} and we notice that 23 > 20, which means the task is completed.\n\n\nLooking back the whole process, we could easily draw two conclucions:\n#### 1. We only need to patch when the next element that the input vector offers is bigger that what we expect. When this circumstance occurs, just patch the desired element and add it into aid vector.\n#### 2. Once we add an element x to aid vector, no matter whether it\'s provided by input vector or patching, the aid vector\'s size increase x, which would turn the next "expected value" into "current expected value + x". When the next expected value > n, the task is finished.\n\nActually, why do we need an aid vector? We can just use the "expected value" to indicate the aid vector we have, since aid vector = [1, expected value - 1]. This yeilds my final result:\n\n```\nclass Solution {\npublic:\n int minPatches(vector<int>& nums, int n) {\n int index = 0;\n int count = 0;\n if(nums[0]>1){\n ++count; \n }\n else{\n ++index;\n }\n long long expect = 2;\n while(expect <= n){\n if(index>=nums.size() || nums[index]>expect){\n // need to add this number\n ++count;\n // expect += expect -> expect<<1\n expect = expect<<1; \n }\n else{\n // expand the range\n expect += nums[index];\n ++index;\n }\n }\n return count;\n }\n};\n```\n\n\n | 3 | 1 | ['C++'] | 2 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.