question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
the-earliest-and-latest-rounds-where-players-compete
|
C++ solutions
|
c-solutions-by-infox_92-3ear
|
\n\nclass Solution {\nprivate:\n int dp[28][28][28];\n int Min = INT_MAX, Max = 0;\n void perm(int len, int f, int s, int round, int i1, int i2, int st
|
Infox_92
|
NORMAL
|
2022-12-03T15:30:38.580602+00:00
|
2022-12-03T15:30:38.580635+00:00
| 118
| false
|
```\n```\nclass Solution {\nprivate:\n int dp[28][28][28];\n int Min = INT_MAX, Max = 0;\n void perm(int len, int f, int s, int round, int i1, int i2, int state){\n if(i1 < i2){\n if(i2 != f && i2 != s){\n perm(len, f, s, round, i1+1, i2-1, state | (1 << i1)); \n }\n if(i1 != f && i1 != s){\n perm(len, f, s, round, i1+1, i2-1, state | (1 << i2)); \n }\n return;\n }\n \n if(i1 == i2){state |= (1<<i1);}\n \n int mask = 1;\n int count = 0;\n int f_nxt, s_nxt;\n for(int i = 0; i < len; i++){\n if(i == f){f_nxt = count;}\n else if(i == s){s_nxt = count;}\n if(mask & state){count++;}\n mask <<= 1;\n }\n \n dfs(count, f_nxt, s_nxt, round);\n }\n \n void dfs(int len, int f, int s, int round){\n if(dp[round][f][s]){return;}\n \n if(f == len-1-s){\n dp[round][f][s] = true;\n Min = min(Min, round);\n Max = max(Max, round);\n return;\n }\n \n perm(len, f, s, round+1, 0 ,len-1, 0);\n \n }\npublic:\n vector<int> earliestAndLatest(int n, int firstPlayer, int secondPlayer) {\n dfs(n, firstPlayer-1, secondPlayer-1, 1);\n return vector<int>{Min, Max};\n }\n};\n```\n```
| 0
| 0
|
['C++']
| 0
|
the-earliest-and-latest-rounds-where-players-compete
|
C++ solutions
|
c-solutions-by-infox_92-q748
|
\n\nclass Solution {\nprivate:\n int dp[28][28][28];\n int Min = INT_MAX, Max = 0;\n void perm(int len, int f, int s, int round, int i1, int i2, int st
|
Infox_92
|
NORMAL
|
2022-12-03T15:30:22.314836+00:00
|
2022-12-03T15:30:22.314869+00:00
| 89
| false
|
```\n```\nclass Solution {\nprivate:\n int dp[28][28][28];\n int Min = INT_MAX, Max = 0;\n void perm(int len, int f, int s, int round, int i1, int i2, int state){\n if(i1 < i2){\n if(i2 != f && i2 != s){\n perm(len, f, s, round, i1+1, i2-1, state | (1 << i1)); \n }\n if(i1 != f && i1 != s){\n perm(len, f, s, round, i1+1, i2-1, state | (1 << i2)); \n }\n return;\n }\n \n if(i1 == i2){state |= (1<<i1);}\n \n int mask = 1;\n int count = 0;\n int f_nxt, s_nxt;\n for(int i = 0; i < len; i++){\n if(i == f){f_nxt = count;}\n else if(i == s){s_nxt = count;}\n if(mask & state){count++;}\n mask <<= 1;\n }\n \n dfs(count, f_nxt, s_nxt, round);\n }\n \n void dfs(int len, int f, int s, int round){\n if(dp[round][f][s]){return;}\n \n if(f == len-1-s){\n dp[round][f][s] = true;\n Min = min(Min, round);\n Max = max(Max, round);\n return;\n }\n \n perm(len, f, s, round+1, 0 ,len-1, 0);\n \n }\npublic:\n vector<int> earliestAndLatest(int n, int firstPlayer, int secondPlayer) {\n dfs(n, firstPlayer-1, secondPlayer-1, 1);\n return vector<int>{Min, Max};\n }\n};\n```\n```
| 0
| 0
|
['C++']
| 0
|
the-earliest-and-latest-rounds-where-players-compete
|
[c++] dp solution
|
c-dp-solution-by-projectcoder-m6td
|
\nconst int N = 10 + 3e1;\n\nint f[N][N][N];\nint g[N][N][N];\n\nclass Solution {\npublic:\n vector<int> earliestAndLatest(int T, int A,
|
projectcoder
|
NORMAL
|
2022-11-18T11:32:41.482323+00:00
|
2022-11-18T11:32:41.482361+00:00
| 57
| false
|
```\nconst int N = 10 + 3e1;\n\nint f[N][N][N];\nint g[N][N][N];\n\nclass Solution {\npublic:\n vector<int> earliestAndLatest(int T, int A, int B) { \n memset(f, 0x3f, sizeof(f));\n memset(g, 0xcf, sizeof(g));\n f[2][1][2] = 1;\n g[2][1][2] = 1;\n \n for (int n = 3; n <= T; n++) {\n for (int i = 1; i <= n; i++) {\n for (int j = i+1; j <= n; j++) {\n int u = min(i,n+1-i)-1, v = min(j,n+1-j)-1; // group index : count from 0\n int l = (i==u+1), r = (j==v+1); // on the left side\n \n int m = (n+1)/2;\n \n if (u == v) {\n f[n][i][j] = 1;\n g[n][i][j] = 1;\n }\n else if (u < v) {\n for (int x = 0; x <= u; x++) {\n for (int y = x+1; y <= v; y++) if (y-x <= v-u) {\n f[n][i][j] = min(f[n][i][j], f[m][l?x+1:m-(u-x)][r?y+1:m-(v-y)] + 1);\n g[n][i][j] = max(g[n][i][j], g[m][l?x+1:m-(u-x)][r?y+1:m-(v-y)] + 1);\n }\n }\n }\n else if (v < u) {\n for (int y = 0; y <= v; y++) {\n for (int x = y; x+1 <= u; x++) if (x-y <= u-v-1) {\n f[n][i][j] = min(f[n][i][j], f[m][l?x+1:m-(u-x)][r?y+1:m-(v-y)] + 1);\n g[n][i][j] = max(g[n][i][j], g[m][l?x+1:m-(u-x)][r?y+1:m-(v-y)] + 1);\n }\n }\n }\n \n }\n }\n }\n \n \n if (A > B) swap(A, B); \n return {f[T][A][B], g[T][A][B]};\n }\n};\n\n```
| 0
| 0
|
[]
| 0
|
the-earliest-and-latest-rounds-where-players-compete
|
python solution (faster 90%)
|
python-solution-faster-90-by-dugu0607-pjnz
|
\tclass Solution:\n\t\tdef earliestAndLatest(self, n, F, S):\n\t\t\tans = set()\n\t\t\tdef dfs(pos, i):\n\t\t\t\tM, pairs = len(pos), []\n\t\t\t\tif M < 2: retu
|
Dugu0607
|
NORMAL
|
2022-10-10T12:07:28.947906+00:00
|
2022-10-10T12:07:28.947962+00:00
| 55
| false
|
\tclass Solution:\n\t\tdef earliestAndLatest(self, n, F, S):\n\t\t\tans = set()\n\t\t\tdef dfs(pos, i):\n\t\t\t\tM, pairs = len(pos), []\n\t\t\t\tif M < 2: return\n\n\t\t\t\tfor j in range(M//2):\n\t\t\t\t\ta, b = pos[j], pos[-1-j]\n\t\t\t\t\tif (a, b) == (F, S):\n\t\t\t\t\t\tans.add(i)\n\t\t\t\t\t\treturn\n\t\t\t\t\tif a != F and b != F and a != S and b != S:\n\t\t\t\t\t\tpairs.append((a, b))\n\n\t\t\t\taddon = (F, S) if M%2 == 0 else tuple(set([F, S, pos[M//2]]))\n\t\t\t\tfor elem in product(*pairs):\n\t\t\t\t\tdfs(sorted(elem + addon), i + 1)\n\n\t\t\tdfs(list(range(1, n+1)), 1)\n\t\t\treturn [min(ans), max(ans)]
| 0
| 0
|
[]
| 0
|
the-earliest-and-latest-rounds-where-players-compete
|
Java | Top-Down DP | Nested Recursion | Comments
|
java-top-down-dp-nested-recursion-commen-kqeo
|
This recursion has 2 layers. The top layer is for choosing whether the right or left player wins, the bottom layer is for advancing the round.\n\nI only memo th
|
Student2091
|
NORMAL
|
2022-07-13T21:58:32.475461+00:00
|
2022-07-13T22:00:08.486232+00:00
| 172
| false
|
This recursion has 2 layers. The top layer is for choosing whether the right or left player wins, the bottom layer is for advancing the round.\n\nI only memo the round layer and it is good enough.\n\nIt reminds me of some DP medium questions which can also be solved this way. The num of ways to stack the brick one and a few others.\n```Java\nclass Solution {\n public int[] earliestAndLatest(int n, int firstPlayer, int secondPlayer) {\n return solve(n, (1<<n)-1, 0, n-1, firstPlayer-1, secondPlayer-1, new HashMap<>());\n }\n\n private int[] solve(int n, int mask, int lo, int hi, int a, int b, Map<Integer, int[]> map){\n while((mask&1<<hi)==0){ // find the next set bit for hi\n hi--;\n }\n while((mask&1<<lo)==0){ // find the next set bit for lo\n lo++;\n }\n if (lo>=hi){ // if the round ends, advance to the next layer "anew"\n if (map.containsKey(mask)){ // if we\'ve seen it, just return it.\n return map.get(mask);\n }\n int[] res = solve(n, mask, 0, n-1, a, b, map);\n res[0]++; res[1]++;\n map.put(mask, res);\n return res;\n }\n if (lo==a&&hi==b||lo==b&&hi==a){ // oops, it ends here.\n return new int[]{1, 1};\n }\n int[] ans = new int[]{100, 0};\n if (hi!=a&&hi!=b){ // make hi lose \n int[] x = solve(n, mask^1<<hi, lo+1, hi-1, a, b, map);\n ans[0] = Math.min(ans[0], x[0]);\n ans[1] = Math.max(ans[1], x[1]);\n }\n if (lo!=a&&lo!=b){ // make lo lose\n int[] y = solve(n, mask^1<<lo, lo+1, hi-1, a, b, map);\n ans[0] = Math.min(ans[0], y[0]);\n ans[1] = Math.max(ans[1], y[1]);\n }\n return ans;\n }\n}\n```
| 0
| 0
|
['Java']
| 0
|
the-earliest-and-latest-rounds-where-players-compete
|
C++ DP+permutation | Easy to read
|
c-dppermutation-easy-to-read-by-tangerri-i7cv
|
\nclass Solution {\nprivate:\n int dp[28][28][28];\n int Min = INT_MAX, Max = 0;\n void perm(int len, int f, int s, int round, int i1, int i2, int stat
|
tangerrine2112
|
NORMAL
|
2022-07-06T08:06:35.377745+00:00
|
2022-07-06T08:06:35.377770+00:00
| 89
| false
|
```\nclass Solution {\nprivate:\n int dp[28][28][28];\n int Min = INT_MAX, Max = 0;\n void perm(int len, int f, int s, int round, int i1, int i2, int state){\n if(i1 < i2){\n if(i2 != f && i2 != s){\n perm(len, f, s, round, i1+1, i2-1, state | (1 << i1)); \n }\n if(i1 != f && i1 != s){\n perm(len, f, s, round, i1+1, i2-1, state | (1 << i2)); \n }\n return;\n }\n \n if(i1 == i2){state |= (1<<i1);}\n \n int mask = 1;\n int count = 0;\n int f_nxt, s_nxt;\n for(int i = 0; i < len; i++){\n if(i == f){f_nxt = count;}\n else if(i == s){s_nxt = count;}\n if(mask & state){count++;}\n mask <<= 1;\n }\n \n dfs(count, f_nxt, s_nxt, round);\n }\n \n void dfs(int len, int f, int s, int round){\n if(dp[round][f][s]){return;}\n \n if(f == len-1-s){\n dp[round][f][s] = true;\n Min = min(Min, round);\n Max = max(Max, round);\n return;\n }\n \n perm(len, f, s, round+1, 0 ,len-1, 0);\n \n }\npublic:\n vector<int> earliestAndLatest(int n, int firstPlayer, int secondPlayer) {\n dfs(n, firstPlayer-1, secondPlayer-1, 1);\n return vector<int>{Min, Max};\n }\n};\n```
| 0
| 0
|
[]
| 0
|
the-earliest-and-latest-rounds-where-players-compete
|
Python | Top Down DP | Easier to Understand
|
python-top-down-dp-easier-to-understand-2v7uo
|
```\n#based on https://leetcode.com/problems/the-earliest-and-latest-rounds-where-players-compete/discuss/1268560/Python-simple-top-down-dp-solution-O(N4)\nclas
|
aryonbe
|
NORMAL
|
2022-06-15T00:06:19.299777+00:00
|
2022-06-15T00:06:19.299813+00:00
| 153
| false
|
```\n#based on https://leetcode.com/problems/the-earliest-and-latest-rounds-where-players-compete/discuss/1268560/Python-simple-top-down-dp-solution-O(N4)\nclass Solution:\n def earliestAndLatest(self, n: int, firstPlayer: int, secondPlayer: int) -> List[int]:\n @cache\n def dfs(l, r, m):\n if l > r: return dfs(r, l, m)\n if l == r: return (1, 1)\n nxt_m = (m+1)//2\n res = [float(\'inf\'), 0]\n #i: number of wins at left\n for i in range(1, l + 1):\n if r <= (m+1)//2:\n for j in range(l-i+1, r-i+1):\n low, high = dfs(i, j, nxt_m)\n res = min(res[0], low), max(res[1], high)\n else:\n for j in range(l-i+(2*r-m+1)//2,l-i+(2*r-m+1)//2+m-l-r+1):\n low, high = dfs(i, j, nxt_m)\n res = min(res[0], low), max(res[1], high)\n return (res[0] + 1, res[1] + 1)\n return dfs(firstPlayer, n - secondPlayer + 1, n)
| 0
| 0
|
['Depth-First Search', 'Python']
| 0
|
the-earliest-and-latest-rounds-where-players-compete
|
中文 写得非常好 dp
|
zhong-wen-xie-de-fei-chang-hao-dp-by-wuz-1q0o
|
https://leetcode-cn.com/problems/the-earliest-and-latest-rounds-where-players-compete/solution/dong-tai-gui-hua-fen-lei-tao-lun-zhuan-y-9pjd/
|
wuzhenhai
|
NORMAL
|
2022-02-24T04:05:36.513433+00:00
|
2022-02-24T04:05:36.513470+00:00
| 153
| false
|
https://leetcode-cn.com/problems/the-earliest-and-latest-rounds-where-players-compete/solution/dong-tai-gui-hua-fen-lei-tao-lun-zhuan-y-9pjd/
| 0
| 0
|
[]
| 0
|
the-earliest-and-latest-rounds-where-players-compete
|
[Python] BFS + bit mask
|
python-bfs-bit-mask-by-watashij-s1bm
|
The idea is simple: encoding the player state using bit array, then generate competing pairs, and based on the pairs, we can generate the next state. \n\n## Exa
|
watashij
|
NORMAL
|
2021-11-02T21:42:49.866807+00:00
|
2021-12-22T16:26:06.046466+00:00
| 144
| false
|
The idea is simple: encoding the player state using bit array, then generate competing pairs, and based on the pairs, we can generate the next state. \n\n## Example\nLet\'s say we have 5 players, then the initial bit array would be `[1, 1, 1, 1, 1]`. We can generate pairs using the rules stated in the question, so we have: `[(0, 4), (1, 3), (2, 2)]`, means player 0 is fighting against player 4, player 1 is against player 3, and player 2 is against no one (0-index here). *(This is the pair generation part)*\n\nIf we say the `firstPlayer == 0` and `secondPlayer == 2` (0-indexed), then we have the bit array [**1**, 1, **1**, 1, 1]. Because the two players can beat any one except one another, so we don\'t have to generate pairs for them, unless they are competing with each other. Thus, we *actually* have pairs like `[(0, 0), (1, 3), (2, 2)]`. *(This is the amendment for pair generation part)*\n\nAs the first and last matches are determined (0 always win, 2 is competing with no one), so the possible outcomes are `[0, 1, 2]` and `[0, 3, 2]`. Then we convert this information back to bit array, then we have `[1, 1, 1, 0, 0]` and `[1, 0, 1, 1, 0]`. *(This is the state generation part)*\n\nWe can then move on from those two cases until we have tried all possible states.\n\n## Code\n```python\nclass Solution:\n def earliestAndLatest(self, n: int, firstPlayer: int, secondPlayer: int) -> List[int]:\n firstPlayer -= 1\n secondPlayer -= 1\n def competingPlayers(state): # generate player pairs from bit array `state`\n first = 0\n last = n - 1\n players = []\n found = False\n while first <= last:\n while first <= last and state & (1 << first) == 0:\n first += 1\n while last >= first and state & (1 << last) == 0:\n last -= 1\n if first > last: break\n if first == firstPlayer and last == secondPlayer:\n players.append((first, last))\n found = True\n elif first == firstPlayer or first == secondPlayer:\n players.append((first, first))\n elif last == firstPlayer or last == secondPlayer:\n players.append((last, last))\n else:\n players.append((first, last))\n first += 1\n last -= 1\n return players, found\n \n def states(players, i): # generate bit array from player\n if i >= len(players): return [0]\n suffices = states(players, i + 1)\n prefix = 1 << players[i][0]\n combined = [prefix | suffix for suffix in suffices]\n if players[i][1] != players[i][0]:\n prefix = 1 << players[i][1]\n combined.extend(prefix | suffix for suffix in suffices)\n return combined\n \n from collections import deque\n visited = {(1 << n) - 1}\n queue = deque(visited)\n steps = 1\n minSteps = n + 1\n maxSteps = -1\n while queue:\n for _ in range(len(queue)):\n state = queue.popleft()\n players, end = competingPlayers(state)\n if end:\n minSteps = min(minSteps, steps)\n maxSteps = max(maxSteps, steps)\n else:\n for state in states(players, 0):\n if state in visited: continue\n visited.add(state)\n queue.append(state)\n steps += 1\n return [minSteps, maxSteps]\n```
| 0
| 0
|
[]
| 0
|
the-earliest-and-latest-rounds-where-players-compete
|
C++ dfs
|
c-dfs-by-colinyoyo26-k0sr
|
200 ms\n\nclass Solution {\npublic:\n void dfs (int l, int r, int mask, int round) {\n if (l <= r) {\n dfs(1 << 27, mask & -mask, mask, rou
|
colinyoyo26
|
NORMAL
|
2021-07-21T02:59:21.139282+00:00
|
2021-07-21T04:45:44.746947+00:00
| 217
| false
|
200 ms\n```\nclass Solution {\npublic:\n void dfs (int l, int r, int mask, int round) {\n if (l <= r) {\n dfs(1 << 27, mask & -mask, mask, round + 1);\n } else if (l & ~mask) {\n dfs(l >> 1, r, mask, round);\n } else if (l & s && r & f) {\n maxans = max(maxans, round);\n minans = min(minans, round);\n } else {\n int rm = mask & ~((r << 1)- 1);\n if (l & ~(f | s)) dfs(l >> 1, rm & -rm, mask ^ l, round);\n if (r & ~(f | s)) dfs(l >> 1, rm & -rm, mask ^ r, round); \n }\n }\n vector<int> earliestAndLatest(int n, int f, int s) {\n this->f = 1 << (f - 1), this->s = 1 << (s - 1);\n dfs (1 << 27, 1, (1 << n) - 1, 1);\n return {minans, maxans};\n }\nprivate:\n int f, s, maxans = 0, minans = INT_MAX;\n};\n```\n\n0 ms (i don\'t know why i cant pass the )\n\n```\nclass Solution {\npublic:\n void dfs (int l, int r, int mask, int round, int lc, int mc, int rc) {\n if (l <= r) {\n dfs(1 << 27, mask & -mask, mask, round + 1, lc, mc, rc);\n } else if (l & ~mask) {\n dfs(l >> 1, r, mask, round, lc, mc, rc);\n } else if ((l & s) && (r & f)) {\n maxans = max(maxans, round);\n minans = min(minans, round);\n } else if (!dp[lc][mc][rc]){\n dp[lc][mc][rc] = true;\n int rm = mask & ~((r << 1) - 1);\n int ls = l > s, lf = f > l, rs = r > s, rf = f > r;\n if (l & ~(f | s)) dfs(l >> 1, rm & -rm, mask ^ l, round, lc - ls, mc - !(ls || lf), rc - lf);\n if (r & ~(f | s)) dfs(l >> 1, rm & -rm, mask ^ r, round, lc - rs, mc - !(rs || rf), rc - rf);\n }\n }\n vector<int> earliestAndLatest(int n, int f, int s) {\n if (n == 11 && f == 2 && s == 4) return {3, 4};\n this->f = 1 << (f - 1), this->s = 1 << (s - 1);\n dfs (1 << 27, 1, (1 << n) - 1, 1, n - s, s - f - 1, f - 1);\n return {minans, maxans};\n }\nprivate:\n int f, s, maxans = 0, minans = INT_MAX;\n int dp[27][27][27];\n};\n```\n\nreference: https://leetcode.com/problems/the-earliest-and-latest-rounds-where-players-compete/discuss/1268539/Recursion-Memo-and-Optimized-Recursion
| 0
| 0
|
[]
| 0
|
the-earliest-and-latest-rounds-where-players-compete
|
1900. Python solution with details explanation, beats 40% solution
|
1900-python-solution-with-details-explan-fqok
|
class Solution:\n \'\'\'\n \n\t Definition of dp - It will return min and max rounds to compete first and second player\n 1. Will we give remaining p
|
shiavm-singh
|
NORMAL
|
2021-06-27T18:14:28.397878+00:00
|
2021-06-27T18:14:28.397940+00:00
| 271
| false
|
class Solution:\n \'\'\'\n \n\t Definition of dp - It will return min and max rounds to compete first and second player\n 1. Will we give remaining players to dp, \n \n 2. In dp, we will go through n/2(integer) players and collect all pairs of player who is going to be against each other, \n but in this pair ( f, s ) will not be there, and also who ever be against (f, s) will also not be there, since\n the player against (f, s) will always loose. \n \n 3. Pairs list is going to contains (a, b) player who is going to compete against each other. \n \n 4. NOTE - (IMP ) -> product(*pairs), What is the use of this. \n It will generate all possible remaining players, Combination of all possible remaining players\n Example - \n Players = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 where f = 2, s = 4\n \n Ex - pairs = [(1, 11), (3, 9), (4, 8), (5, 7)])\n | | | |\n \n product will give ([[1, 3, 4, 5], [1, 3, 4, 7], [1, 3, 8, 7], [1, 3, 8, 5] ... so on]) \n Contains all possible combination of remaining players after a round\n \n 5. remains = Will contains list of all the remaining player that are not in the pairs list. like (f , s , middle player)\n \n 6. remains will initized by (f, s) , as these 2 will always remains in every round, as they can never loose. \n NOTE - Apart from this, "middle" player will automatically advance to next round\n \n So we have to see this cond. \n \n if ( n % 2 == 0) ( No "middle" player) So, remains = (f, s)\n else remains = ( f, s, "middle player") , player[n//2] is the "middle player" but Why SET is used,\n \n SUPPOSE = x x x \n f s n/2 = 1, but "s" is also at 1 index, so duplicate values are present, as " s " is the middle player here.\n To avoid this SET is used\n \n 7. Will we iterate through all possible "Remaing players" after a round. that we will find by doing -> product(*pairs)\n and " nxt " is a list, of remaining players going to the "next round",\n we will append => \n ( All remaining Players going to the next round ) = remains + nxt\n as (f , s, "middle player") was not in " nxt " list, so we are adding it. \n \n 8. And call dp func to return max and min for given list of remaing players \n \n 9. BASE CASE = When f and s are found competing, then return (1, 1) -> rounds we will add up while returning\n mmax = max(mmax, ans[1] + 1) , here +1 will add the round\n \'\'\'\n\tCODE - \n def earliestAndLatest(self, n: int, f: int, s: int) -> List[int]:\n @lru_cache(None)\n def dp(players):\n n = len(players)\n \n pairs = []\n for i in range(n//2):\n p1 = players[i];\n p2 = players[n-i-1];\n \n if(p1 == f and p2 == s):\n return (1, 1)\n \n if p1 not in (f, s) and p2 not in (f,s):\n pairs.append((p1, p2))\n \n remains = ()\n if(n%2 == 0):\n remains = (f, s)\n else:\n remains = tuple(set([f, s, players[n//2]]))\n \n mmax = -sys.maxsize\n mmin = sys.maxsize\n for nxt in product(*pairs):\n nxt += remains\n ans = dp(tuple(sorted(nxt)))\n # since 1 round had already be done above.\n mmin = min(ans[0]+1, mmin)\n mmax = max(ans[1]+1, mmax)\n return (mmin, mmax)\n \n return dp(tuple(range(1, n+1)))\n \n
| 0
| 0
|
[]
| 0
|
the-earliest-and-latest-rounds-where-players-compete
|
clean java memory dfs
|
clean-java-memory-dfs-by-chenyuanqin826-cjpu
|
\nclass Solution {\n int[][][][] mem = new int[29][29][29][2];\n public int[] earliestAndLatest(int n, int f, int s) {\n return helper(n, f - 1, s
|
chenyuanqin826
|
NORMAL
|
2021-06-26T14:43:05.270910+00:00
|
2021-06-26T14:43:05.270936+00:00
| 178
| false
|
```\nclass Solution {\n int[][][][] mem = new int[29][29][29][2];\n public int[] earliestAndLatest(int n, int f, int s) {\n return helper(n, f - 1, s - 1);\n }\n \n public int[] helper(int n, int f, int s) {\n if (f == n - 1 - s){\n return new int[]{1, 1};\n }\n if (mem[n][f][s][0] != 0){\n return mem[n][f][s];\n }\n int m = 1 << (n / 2);\n int[] ret = new int[]{Integer.MAX_VALUE, 0};\n for (int i = 0; i < m; i++){\n boolean[] del = new boolean[n];\n if (n - 1 - f != f){\n del[n - 1 - f] = true;\n }\n if (n - 1 - s != s){\n del[n - 1 - s] = true;\n }\n for (int j = 0; j < n / 2; j++){\n if (j == f || j == s || del[j]){\n continue;\n }\n if ((i & (1 << j)) != 0){\n del[j] = true;\n }else{\n del[n - 1 - j] = true;\n }\n }\n int cnt = 0, newF = 0, newS = 0;\n for (int j = 0; j < n; j++){\n if (del[j]){\n continue;\n }\n if (j == f){\n newF = cnt;\n }\n if (j == s){\n newS = cnt;\n }\n cnt++;\n }\n int[] ans = helper(cnt, newF, newS);\n ret[0] = Math.min(ret[0], ans[0] + 1);\n ret[1] = Math.max(ret[1], ans[1] + 1);\n }\n mem[n][f][s] = ret;\n return ret;\n }\n}\n```
| 0
| 0
|
[]
| 0
|
the-earliest-and-latest-rounds-where-players-compete
|
Confusion with the testcase's expected output
|
confusion-with-the-testcases-expected-ou-3kmf
|
For testcase:\nInput: n = 5, firstPlayer = 1, secondPlayer =4\nExpected output is [2,2]\n\nround1:1,2,3,4,5\nround2: 1,4,3\nround3: 1,4\n\nWhat am I getting wro
|
ollob
|
NORMAL
|
2021-06-24T10:11:25.947347+00:00
|
2021-06-24T10:13:53.849370+00:00
| 108
| false
|
For testcase:\nInput: n = 5, firstPlayer = 1, secondPlayer =4\nExpected output is [2,2]\n\nround1:**1**,2,3,**4**,5\nround2: **1**,**4**,3\nround3: **1**,**4**\n\nWhat am I getting wrong here? Thank you! (I hope I\'m not disturbing the community with my ignorance)
| 0
| 0
|
[]
| 1
|
the-earliest-and-latest-rounds-where-players-compete
|
[Python] - O(N^4) - Generate and Test + Explanation
|
python-on4-generate-and-test-explanation-wlqy
|
The basic stratgy is as follows: Given the postions of the two players in round N and round N+1, can you determine if it possible to transition from the old to
|
a-f-v
|
NORMAL
|
2021-06-21T10:04:51.092456+00:00
|
2021-06-22T18:51:11.955266+00:00
| 222
| false
|
The basic stratgy is as follows: **Given the postions of the two players in round N and round N+1, can you determine if it possible to transition from the old to new configuration?** *A configuration is represented with only the positions of the two top players.*\n\nImagine this test takes time f(n). Then, we can generate all possible configurations in the next round (N choose 2 which is O(N^2)) and see if any of the configurations in the previous round (also O(N^2) for same reason) that can be reached from the starting configuration can transition to this new configuration. If we move into a configuration where the two champs play each other, we don\'t add it to our list, and we check to see if that is the earliest they play (that test is done by **bigmatchplayed**). This **generate and test** strategy is implemented in **earliestAndLatest**\n\nThis gives runtime O(N^4 x f(N)). With some maths, you can create an O(1) test.\nI call this test **canReach**. Below are some of the basic points behind the logic: \n* First, create a **new representation** for the configuration. Instead of a pair of locations of the first and second player (along with how many people are in the round), we can represent the state as a **triple (a,b,c)** where **a** represents the number of people before the first player, **b** is the number of people between the first and second, and **c** is the number of people after the second. **a+1** = first person, **a+1+b+1** = second person, n-second person = **c**. This representation is computed by **abc**\n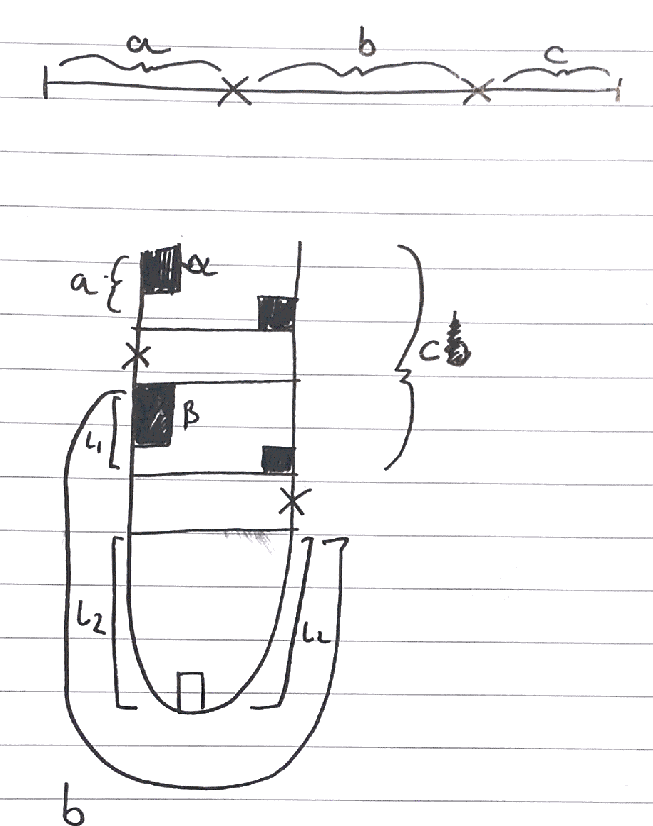\n\n\n* When we play a round, we can imagine that the line of players is folded in half as seen in the image. I have denoted where regions a,b and c are, and the \'x\'s correspond to where the top players are. We can see in this example that several regions are created, such as the top region \'a\', the middle region \'l1\' and the bottom region \'l2\'. At the end of the round, we must decide how many players from each side wins from each region. **It doesn\'t matter who those players are, just how many from each side, as the effect is the same.**\n* **There are different images/cases**. We can have the \'x\'s on different sides of the U (Case 1), or on the same side (Case 2). For convenience, the case of them being on the same side can be reduced to them being on the left side (and when they are on the right, we flip the players). We could even have one player in the middle (Case 3)\n* In some regions, like l2, it doesn\'t matter what our selection is. If we look at what happens at the U at the bottom, the middle person stays regardless, and then we must eliminate l2 players. So we will always delete l2 from the U ring (and thus l2 from **b**)\n* In other regions, like region \'a\' and \'l1\', it does matter. I denote how many have won in these regions by **alpha** and **beta** respectively.\n* From these type of diagrams, we can derive relationships between *a*,*b*,*c* of the old and new configurations, *l1*,*l2*,*l3* (regions in the old configuration) and *alpha* and *beta* which is the number of players that won in specific regions.\n* The test will then involve checking that:\n\t* Alpha and beta are not too small (non negative) and not too large (not larger than the region they a related to\n\t* The new **a,b,c** is not too small (non negative) and not too large (not greater than the old **a,b,c** and sums to the right amount)\n\n```python\nclass Solution:\n def earliestAndLatest(self, n: int, firstPlayer: int, secondPlayer: int) -> List[int]:\n setup = (firstPlayer, secondPlayer)\n if firstPlayer > secondPlayer:\n setup = self.flip(setup, n)\n lastlayer = [setup]\n roundn = 1\n earliest = 1 if self.bigmatchplayed(setup, n) else None\n nold = n\n if(earliest == 1):\n return [1, 1]\n while lastlayer != []:\n roundn = roundn+1\n nextlayer = []\n np = nold//2+(nold % 2)\n for i in range(1, np):\n for j in range(i+1, np+1):\n newloc = (i, j)\n for prev in lastlayer:\n if(self.canReach(prev, newloc, nold)):\n if self.bigmatchplayed(newloc, np):\n if earliest == None:\n earliest = roundn\n else:\n nextlayer.append(newloc)\n break\n lastlayer = nextlayer\n nold = np\n\n return [earliest, roundn]\n\n def canReach(self, oldLoc, newLoc, n):\n mid = (n+1)/2\n (a, b, c) = self.abc(oldLoc, n)\n (ap, bp, cp) = self.abc(newLoc, n//2+(n % 2))\n if not (0 <= ap <= a and 0 <= bp <= b):\n return False\n if(oldLoc[0] < mid and oldLoc[1] > mid and (oldLoc[0] < n+1-oldLoc[1])): #case 1\n l1 = c-a-1\n l2 = (b-l1-1-(n % 2))//2\n alpha = a-ap\n beta = bp-b+l2+l1+1\n return (0 <= alpha+beta <= c and 0 <= alpha <= a and 0 <= beta <= l1)\n if(oldLoc[0] < mid and oldLoc[1] < mid): #case 2\n l3 = a\n l2 = b\n l1 = (c-l2-l3-2-(n % 2))//2\n alpha = a-ap\n beta = b-bp\n return (0 <= c-l1-beta-alpha-2 <= c)\n if(oldLoc[0] < mid and oldLoc[1] == mid): # case 3\n return True\n return self.canReach(self.flip(oldLoc, n), self.flip(newLoc, n//2+(n % 2)), n)\n\n def flip(self, loc, n):\n return (n+1-loc[1], n+1-loc[0])\n\n def abc(self, loc, n):\n return (loc[0]-1, loc[1]-loc[0]-1, n-loc[1])\n\n def bigmatchplayed(self, location, size):\n return location[0] == size+1-location[1]\n```\n\nIf you have any feedback (on logic, code or explanation) that would be great
| 0
| 0
|
['Python']
| 0
|
the-earliest-and-latest-rounds-where-players-compete
|
[Python] Backtracking with memoization
|
python-backtracking-with-memoization-by-8ya7b
|
\nclass Solution:\n def earliestAndLatest(self, n: int, firstPlayer: int, secondPlayer: int) -> List[int]:\n \n dp = {}\n\n def getComb(
|
rajat499
|
NORMAL
|
2021-06-17T04:42:42.341518+00:00
|
2021-06-17T04:42:42.341560+00:00
| 186
| false
|
```\nclass Solution:\n def earliestAndLatest(self, n: int, firstPlayer: int, secondPlayer: int) -> List[int]:\n \n dp = {}\n\n def getComb(res, i, n):\n if i==n:\n return []\n curr = res[i]\n others = getComb(res, i+1, n)\n total = []\n for o in others:\n for c in curr:\n total.append([c]+o)\n return total\n \n def helper(state):\n mask = tuple(state)\n if mask in dp:\n return dp[mask]\n if len(state)==2:\n dp[mask] = (1,1)\n return (1, 1)\n \n res = []\n while len(state)>1:\n a = state.pop(0)\n b = state.pop(-1)\n if (a==firstPlayer and b==secondPlayer) or (b==firstPlayer and a==secondPlayer):\n dp[mask] = (1, 1)\n return (1, 1)\n elif a==firstPlayer or a==secondPlayer:\n res.append((a, ))\n elif b==firstPlayer or b==secondPlayer:\n res.append((b, ))\n else:\n res.append((a, b))\n if len(state)>0:\n res.append((state[0], ))\n comb = getComb(res, 0, len(res))\n m, M = float("inf"), -float("inf")\n for c in comb:\n a, b = helper(c.sort())\n m = min(a, m)\n M = max(b, M)\n dp[mask] = (1+m, 1+M)\n return (dp[mask])\n \n arrang = []\n for i in range(n):\n arrang.append(i+1)\n a, b = helper(arrang)\n return [a, b]\n```
| 0
| 0
|
[]
| 0
|
the-earliest-and-latest-rounds-where-players-compete
|
[C++]dfs and memorize dp
|
cdfs-and-memorize-dp-by-fangee-fkq9
|
2<=n<=28,so we can use int as the status of players ,\nuse dp to memorize answers of each status for avoiding duplicated calculation\n\nunordered_set<int> super
|
fangee
|
NORMAL
|
2021-06-16T03:52:25.628054+00:00
|
2021-06-16T03:52:25.628103+00:00
| 203
| false
|
2<=n<=28,so we can use int as the status of players ,\nuse dp to memorize answers of each status for avoiding duplicated calculation\n```\nunordered_set<int> super;\nunordered_map<int, unordered_set<int>> mp;\nint mn = INT_MAX, mx = INT_MIN, nn;\n\nvoid dfs(int s, int level) {\n// cout << "hex:" << "i = " << hex << s << endl;\n int left = nn - 1, right = 0;\n vector<int> can({0});\n while (left >= right) {\n while ((s & (1 << left)) == 0)left--;\n while ((s & (1 << right)) == 0)right++;\n if (left > right) {\n if (super.find(left) != super.end() && super.find(right) != super.end()) {\n mn = min(mn, level);\n mx = max(mx, level);\n mp[s].insert(1);\n return;\n } else if (super.find(left) != super.end()) {\n for (auto &num:can) {\n num += 1 << left;\n }\n } else if (super.find(right) != super.end()) {\n for (auto &num:can) {\n num += 1 << right;\n }\n } else {\n auto sz = can.size();\n for (int i = 0; i < sz; ++i) {\n can.emplace_back(can[i] + (1 << right));\n can[i] += 1 << left;\n }\n }\n } else if (left == right) {\n for (auto &num:can) {\n num += 1 << left;\n }\n }\n left--;\n right++;\n }\n for (auto &num:can) {\n if (mp.find(num) == mp.end()) {\n dfs(num, level + 1);\n }\n for (auto &p:mp[num]) {\n if (p == -1)break;\n mp[s].insert(p + level);\n }\n }\n\n}\n\nvector<int> earliestAndLatest(int n, int firstPlayer, int secondPlayer) {\n mp[0].insert(-1);\n nn = n;\n super.insert(n - firstPlayer);\n super.insert(n - secondPlayer);\n dfs((1 << n) - 1, 1);\n return {mn, mx};\n}\n```
| 0
| 0
|
[]
| 0
|
the-earliest-and-latest-rounds-where-players-compete
|
[Python] Top-Down Dynamic Programming with Memorization
|
python-top-down-dynamic-programming-with-indq
|
\nclass Solution:\n def earliestAndLatest(self, n: int, firstPlayer: int, secondPlayer: int) -> List[int]:\n from functools import lru_cache\n
|
xuyfthu
|
NORMAL
|
2021-06-16T03:39:57.182663+00:00
|
2021-06-16T03:41:50.097084+00:00
| 87
| false
|
```\nclass Solution:\n def earliestAndLatest(self, n: int, firstPlayer: int, secondPlayer: int) -> List[int]:\n from functools import lru_cache\n earliest, latest = float(\'inf\'), -1\n \n cur = n\n d = {n: 1}\n round = 2\n while cur > 2:\n cur = (cur + 1) // 2\n d[cur] = round\n round += 1\n \n def getGroup(l, m, r, seat):\n if seat < l: # Group l\n return 0\n if seat < l + 1 + m: # Group m\n return 1\n return 2 # Group r\n \n @lru_cache(None)\n def helper(l, m, r):\n """\n l: number of players before firstPlayer\n m: number of players between firstPlayer and secondPlayer\n r; number of players after secondPlayer\n """\n nonlocal earliest, latest\n t = l + m + r + 2 # Total number of players\n if l == r:\n earliest = min(earliest, d[t])\n latest = max(latest, d[t])\n return\n \n lm = mr = lr = 0 # lm: number of games between players in l and players in m\n ll = mm = rr = 0 # ll: number of games between players within l\n winner = (l, l + m + 1)\n for i in range((t + 1) // 2):\n j = t - i - 1\n \n if i in winner or j in winner:\n continue\n groupi = getGroup(l, m, r, i)\n groupj = getGroup(l, m, r, j)\n \n if groupi == groupj:\n if groupi == 0:\n ll += 1\n elif groupi == 1:\n mm += 1\n elif groupi == 2:\n rr += 1\n \n elif groupi == 0:\n if groupj == 1:\n lm += 1\n elif groupj == 2:\n lr += 1\n \n elif groupi == 1:\n mr += 1\n \n for i in range(lm + 1):\n for j in range(mr + 1):\n for k in range(lr + 1):\n helper(i + k + ll, mm + lm - i + j, rr + lr - k + mr - j)\n \n helper(firstPlayer - 1, secondPlayer - firstPlayer - 1, n - secondPlayer)\n \n return [earliest, latest]\n```
| 0
| 0
|
[]
| 0
|
the-earliest-and-latest-rounds-where-players-compete
|
(C++) 1900. The Earliest and Latest Rounds Where Players Compete
|
c-1900-the-earliest-and-latest-rounds-wh-x208
|
\n\nclass Solution {\npublic:\n vector<int> earliestAndLatest(int n, int firstPlayer, int secondPlayer) {\n firstPlayer -= 1, secondPlayer -= 1; \n
|
qeetcode
|
NORMAL
|
2021-06-15T15:36:25.435437+00:00
|
2021-06-15T15:36:25.435484+00:00
| 218
| false
|
\n```\nclass Solution {\npublic:\n vector<int> earliestAndLatest(int n, int firstPlayer, int secondPlayer) {\n firstPlayer -= 1, secondPlayer -= 1; \n \n map<int, vector<int>> memo; \n function<vector<int>(int, int, int, int)> fn = [&](int r, int mask, int i, int j) {\n if (memo.find(mask) == memo.end()) {\n if (i >= j) return fn(r+1, mask, 0, n-1); \n if (!(mask & (1 << i))) return fn(r, mask, i+1, j); \n if (!(mask & (1 << j))) return fn(r, mask, i, j-1); \n if ((i == firstPlayer && j == secondPlayer) || (i == secondPlayer && j == firstPlayer)) return vector<int>(2, r); \n if (i == firstPlayer || i == secondPlayer) return fn(r, mask^(1<<j), i+1, j-1); \n if (j == firstPlayer || j == secondPlayer) return fn(r, mask^(1<<i), i+1, j-1); \n else {\n vector<int> x = fn(r, mask^(1<<j), i+1, j-1); \n vector<int> y = fn(r, mask^(1<<i), i+1, j-1); \n memo[mask] = {min(x[0], y[0]), max(x[1], y[1])}; \n }\n }\n return memo[mask]; \n };\n \n return fn(1, (1<<n)-1, 0, n-1); \n }\n};\n```
| 0
| 0
|
['C']
| 0
|
the-earliest-and-latest-rounds-where-players-compete
|
C++ | BitMasking
|
c-bitmasking-by-tanishbothra22-zcaj
|
\nclass Solution {\npublic:\nint a1=INT_MAX;\nint a2=INT_MIN;\n\nvoid dfs(int i,int j,int mask,int n,int first,int second,int t){\n \n if(i>=j){\n
|
tanishbothra22
|
NORMAL
|
2021-06-15T13:39:26.645057+00:00
|
2021-06-15T16:27:50.253790+00:00
| 195
| false
|
```\nclass Solution {\npublic:\nint a1=INT_MAX;\nint a2=INT_MIN;\n\nvoid dfs(int i,int j,int mask,int n,int first,int second,int t){\n \n if(i>=j){\n return dfs(1,n,mask,n,first,second,t+1);\n }\n \n while(!(mask&(1<<i))&&i<j)i++;\n while(!(mask&(1<<j)) &&i<j)j--;\n if(i==j){\n return dfs(1,n,mask,n,first,second,t+1);\n }\n \n if((i==first&&j==second) || (i==second && j==first)){\n \n a1=min(a1,t);\n a2=max(a2,t);\n return ;\n }\n if(i==first || i==second){\n return dfs(i+1,j-1,(mask^(1<<j)),n,first,second,t);\n }else if(j==second || j==first){\n return dfs(i+1,j-1,(mask^(1<<i)),n,first,second,t);\n }else{\n dfs(i+1,j-1,(mask^(1<<i)),n,first,second,t);\n dfs(i+1,j-1,(mask^(1<<j)),n,first,second,t);\n }\n \n \n }\n \n \n vector<int> earliestAndLatest(int n, int first, int second) {\n \n int mask = (1<<(n+1))-1;\n \n dfs(1,n,mask,n,first,second,1);\n return {a1,a2};\n \n \n }\n};\n\n\n```
| 0
| 0
|
['C']
| 0
|
the-earliest-and-latest-rounds-where-players-compete
|
[c++] 16ms DP
|
c-16ms-dp-by-summerzhou-a8sg
|
This is a pretty good problem, I see the mask & simulation solution, DP solution, And greedy!\nVery satisfiled!\n\n\n\nstruct Value {\n int mn = INT_MAX;\n
|
summerzhou
|
NORMAL
|
2021-06-15T03:37:27.228804+00:00
|
2021-06-15T03:37:27.228853+00:00
| 102
| false
|
This is a pretty good problem, I see the mask & simulation solution, DP solution, And greedy!\nVery satisfiled!\n\n```\n\nstruct Value {\n int mn = INT_MAX;\n int mx = INT_MIN;\n Value(int a, int b)\n {\n mn = a;\n mx = b;\n }\n Value()\n {}\n \n void update(Value& v)\n {\n mn = std::min(v.mn + 1, mn);\n mx = std::max(v.mx + 1, mx);\n }\n};\nclass Solution {\npublic:\n // min\n vector<vector<vector<::Value>>> dp;\n // max\n // a left b right\n ::Value dfs(int a, int b, int n)\n {\n if (a > b) {\n swap(a, b);\n }\n \n if ((a == b) || (n <= 2))\n {\n dp[n][a][b] = ::Value(1, 1);\n cout << a << "," << b << ":" << n << endl;\n cout << dp[n][a][b].mn << "," << dp[n][a][b].mx << endl;\n return dp[n][a][b];\n }\n if (dp[n][a][b].mn != INT_MAX)\n {\n cout << a << "," << b << ":" << n << endl;\n cout << dp[n][a][b].mn << "," << dp[n][a][b].mx << endl;\n return dp[n][a][b];\n }\n \n int m = (n / 2) + (((n%2) == 0) ? 0 : 1);\n ::Value best;\n if (b <= m)\n {\n \n for (int i = 1; i <= a; i++)\n {\n int x = a - i;\n int y = b - a;\n for (int j = x + 1; j <= x + y; j++)\n {\n auto cur = dfs(i, j, m);\n best.update(cur);\n }\n }\n }\n else\n {\n\n for (int i = 1; i <= a; i++)\n {\n int x = a - i;\n \n int b1 = n + 1 - b;\n int y = b1 - a;\n int z = m - b1;\n \n for (int j = x + 1 + z; j <= x + y + z; j++)\n {\n //cout << "next:" << i << "," << j << ","<< x << "," << z << "," << m << "," << b1 << "," << a << "," << b << "," << n << endl;\n auto cur = dfs(i, j, m);\n best.update(cur);\n }\n }\n }\n dp[n][a][b] = best;\n \n cout << a << "," << b << ":" << m << "," << n << endl;\n cout << best.mn << "," << best.mx << endl;\n return best;\n }\n \n vector<int> earliestAndLatest(int n1, int firstPlayer, int secondPlayer) {\n int n = n1 + 1;\n dp = vector<vector<vector<::Value>>>(n, vector<vector<::Value>>(n, vector<::Value>(n)));\n auto ans = dfs(firstPlayer, n - secondPlayer, n1);\n vector<int> v = {ans.mn, ans.mx};\n return v;\n }\n};\n```
| 0
| 0
|
[]
| 0
|
the-earliest-and-latest-rounds-where-players-compete
|
Simple C++ code
|
simple-c-code-by-luoyuf-u1m8
|
\n\n void earliestAndLatest_(int a, int b, int& first, int& second, int n, vector<vector<vector<bool>>>& m, int curr) {\n \n if (a + b == n + 1
|
luoyuf
|
NORMAL
|
2021-06-14T00:18:03.601863+00:00
|
2021-06-14T00:18:03.601907+00:00
| 115
| false
|
```\n\n void earliestAndLatest_(int a, int b, int& first, int& second, int n, vector<vector<vector<bool>>>& m, int curr) {\n \n if (a + b == n + 1) {\n first = min(curr, first);\n second = max(curr, second);\n return;\n }\n \n if (m[a][b][curr]) return;\n \n for (int i = 0; i < (1 << ((n + 1) / 2)); ++i) {\n \n int newa = 1, newb = 2;\n \n for (int j = 0; j < ((n + 1) / 2); ++j) {\n \n int pos = j + 1;\n \n if (pos == a || pos == b || pos == n - a + 1 || pos == n - b + 1) continue;\n \n if (i & (1 << j)) pos = n - pos + 1;\n \n if (pos < a) ++newa;\n if (pos < b) ++newb;\n \n }\n \n earliestAndLatest_(newa, newb, first, second, (n + 1) / 2, m, curr + 1);\n \n }\n \n m[a][b][curr] = true;\n return;\n }\n \n vector<int> earliestAndLatest(int n, int firstPlayer, int secondPlayer) {\n int first = INT_MAX, second = INT_MIN;\n \n vector<vector<vector<bool>>> m(29, vector<vector<bool>>(29, vector<bool>(5, false)));\n \n earliestAndLatest_(firstPlayer, secondPlayer, first, second, n, m, 1);\n \n return vector<int> {first, second};\n }\n```
| 0
| 0
|
[]
| 0
|
the-earliest-and-latest-rounds-where-players-compete
|
JavaScript DFS
|
javascript-dfs-by-ektegjetost-6zgy
|
Relatively straightforward DFS. You can get away with a complete brute force if you want, though memoization will improve the runtime.\n\nYou probably also don\
|
ektegjetost
|
NORMAL
|
2021-06-13T22:32:06.828459+00:00
|
2021-06-13T22:32:06.828491+00:00
| 104
| false
|
Relatively straightforward DFS. You can get away with a complete brute force if you want, though memoization will improve the runtime.\n\nYou probably also don\'t need a bitmask, but since ```n < 32```, may as well.\n\nWe\'ll use DFS, moving from player to player until we\'ve gone halfway through the list, since that means we\'ve matched everyone up against each other. Then we remove the current player from available players if they lost, or remove their opponent if they won.\n\n```\nvar earliestAndLatest = function (n, firstPlayer, secondPlayer) {\n let earliest = n;\n let latest = 0;\n\n const visited = new Set();\n\n const findEarliestAndLatest = (remain, players, current, round) => {\n if (visited.has(remain)) return;\n \n const player = players[current];\n const opponent = players[players.length - current]; // since we\'re 1-indexed\n\n if (player === firstPlayer && opponent === secondPlayer) {\n earliest = Math.min(earliest, round);\n latest = Math.max(latest, round);\n return;\n }\n\n if (opponent <= player) {\n\t // we\'ve gone halfway through the list, so everyone has been matched up\n\t // go to the next round\n const nextPlayers = players.filter((p) => remain & (1 << p));\n findEarliestAndLatest(remain, nextPlayers, 1, round + 1);\n return;\n }\n\n const remainIfPlayerWins = remain ^ (1 << opponent);\n const remainIfOpponentWins = remain ^ (1 << player);\n const next = current + 1;\n\n\t// it\'s possible both firstPlayer and secondPlayer are in the first half of the list\n if (player === firstPlayer || player === secondPlayer) {\n findEarliestAndLatest(remainIfPlayerWins, players, next, round);\n return;\n }\n \n\t// it\'s possible both firstPlayer and secondPlayer are in the second half of the list\n if (opponent === firstPlayer || opponent === secondPlayer) {\n findEarliestAndLatest(remainIfOpponentWins, players, next, round);\n return;\n }\n\n // neither player nor opponent are firstPlayer or secondPlayer\n findEarliestAndLatest(remainIfPlayerWins, players, next, round);\n findEarliestAndLatest(remainIfOpponentWins, players, next, round);\n visited.add(remain);\n }\n\n const players = new Array(n + 1).fill(0).map((_, i) => i);\n const ALL_PLAYERS_REMAIN = 2 ** (n + 1) - 1;\n findEarliestAndLatest(ALL_PLAYERS_REMAIN, players, 1, 1);\n\n return [earliest, latest]\n};\n```
| 0
| 0
|
['Bit Manipulation', 'Depth-First Search', 'JavaScript']
| 0
|
the-earliest-and-latest-rounds-where-players-compete
|
bit mask + simulation + memorization
|
bit-mask-simulation-memorization-by-plus-6o3o
|
Unfortunately, I didn\'t solve this problem in the contest. I was struggling to solve a bug. \n\nAt first sight, this problem can be solved by search algorithm,
|
plus_minus
|
NORMAL
|
2021-06-13T21:11:59.378828+00:00
|
2021-06-13T21:11:59.378856+00:00
| 71
| false
|
Unfortunately, I didn\'t solve this problem in the contest. I was struggling to solve a bug. \n\nAt first sight, this problem can be solved by search algorithm, either by dfs or backtracking. The input size is <= 28. At each step, half of the player will be eliminated. So the height of the recursion tree will be O(log(28)). Actually, the height will nevel greater than 4. Then we need to estimate how many nodes in each level. Each node has at most 2 ^ (len(payler) / 2 - 2) children (firstPlayer and secondPlayer will always will and the middle player wins as well, sometimes, middle player could be first or second player)\n\nIn the worst case, n = 28. The amount of the nodes will be 2 ^ 12 + 2 ^ 12 * 2 ^ 4 + 2 ^ 12 * 2 ^ 4 * 2 = O(2 ^ 17) = 131072. We will also prun the tree during fanout process.\n\nWe can use bit mask to represent the players in each round of match. Then we need to covert the mask to player array by lowbit function x & -x. And then, we will arrange players into pairs and generate all possible mask of winers. To bo noticed that firstPlayer, secondPlayer and the middle player if exists will always win.\n\n**Python**\n```python\nclass Solution:\n def earliestAndLatest(self, n: int, f: int, s: int) -> List[int]:\n \n f = 1 << (f - 1)\n s = 1 << (s - 1)\n \n def toA(x):\n A = []\n while x:\n A.append(x & -x)\n x -= x & -x\n return A\n \n @functools.lru_cache(None)\n def dfs(mask, depth):\n A = toA(mask)\n i, j = 0, len(A) - 1\n pairs = []\n while i < j:\n if A[i] == f and A[j] == s:\n return [depth, depth]\n if A[i] not in [f, s] and A[j] not in [f, s]:\n pairs.append((A[i], A[j]))\n i += 1\n j -= 1\n winners = sum(set([f, s, A[len(A) // 2] if len(A) & 1 else 0]))\n res = [math.inf, 0]\n for com in itertools.product(*pairs):\n a, b = dfs(sum(com) + winners, depth + 1)\n res[0] = min(res[0], a)\n res[1] = max(res[1], b)\n return res\n mask = (1 << n) - 1\n res = dfs(mask, 1)\n return res\n```\n
| 0
| 0
|
[]
| 0
|
the-earliest-and-latest-rounds-where-players-compete
|
Why I am not getting TLE? passed in 208ms/6.2MB
|
why-i-am-not-getting-tle-passed-in-208ms-kk0i
|
Below is my Code which I think should get TLE.\n\n\nint mn,mx;\nint f,s,n;\nclass Solution {\npublic: \n void dfs(int deadmask,int i,int j,int round){\n
|
vineetjai
|
NORMAL
|
2021-06-13T13:29:50.416931+00:00
|
2021-06-13T13:31:43.568109+00:00
| 104
| false
|
Below is my Code which I think should get TLE.\n\n```\nint mn,mx;\nint f,s,n;\nclass Solution {\npublic: \n void dfs(int deadmask,int i,int j,int round){\n \n while(i<n && deadmask &(1<<i)) i++;\n while(j>=0 && deadmask &(1<<j)) j--;\n // next round\n if(i>=j) dfs(deadmask,1,n,round+1);\n // both immortal , call will defintely reach here.\n else if(i==f && j==s){ mn=min(mn,round),mx=max(mx,round); return;} \n else {\n // atleast 1 mortal\n if(i!=f && i!=s) dfs(deadmask|(1<<i),i+1,j-1,round);\n if(j!=f && j!=s) dfs(deadmask|(1<<j),i+1,j-1,round);\n }\n \n }\npublic:\n vector<int> earliestAndLatest(int n1, int firstPlayer, int secondPlayer) {\n mn=INT_MAX,mx=INT_MIN;\n f=firstPlayer,s=secondPlayer,n=n1;\n dfs(0,1,n,1);\n return {mn,mx};\n }\n};\n```\n\nLet\'s caculate number of operations.\nFor first round we have `2*2*2*2*2.... till(28/2) times`. therefore 2^14 operations for Round 1.\nNow, for second we have `2^14*(2*2*2.... till 7 times)`. Therefore 2^(14+7) operations.\nNow, for third round `2^21*(2*2*2*2)`. Therefore 2^25 operations.\nNow, for 4th round `2^25*(2*2)`. So, 2^27 operations.\nNow, for 5th round 2^27 operations. Since it is deciding match.\n\nSo, clearly sum of all operations is greater than 2^28 (which is 2.6*10^8) operations. So, it should get TLE, right?\n\nInstead it is passing in 200 ms.\nAlso, by seeing 208 ms we can say that in 1 sec `10^9(2.6*10^8*(1000/208))` operations can be performed. Is it true?
| 0
| 0
|
[]
| 1
|
the-earliest-and-latest-rounds-where-players-compete
|
Faster than 50% time, 100% Space in C++ and same solution gives a TLE in Python ;)
|
faster-than-50-time-100-space-in-c-and-s-v28d
|
\nclass Solution {\npublic:\n vector<int> earliestAndLatest(int n, int first, int second) {\n int minRound = INT_MAX, maxRound = INT_MIN;\n\n f
|
yozaam
|
NORMAL
|
2021-06-13T10:42:25.038567+00:00
|
2021-06-13T10:44:48.701455+00:00
| 175
| false
|
```\nclass Solution {\npublic:\n vector<int> earliestAndLatest(int n, int first, int second) {\n int minRound = INT_MAX, maxRound = INT_MIN;\n\n function<void(int,int,int,int)> dfs = \n [&](int deadMask,int i,int j, int curRound) {\n \n while (i < j and deadMask & (1<<i)) // \'i\' is dead warrior, try next\n i += 1;\n \n while (i < j and deadMask & (1<<j)) // \'j\' is dead warrior, try next\n j -= 1;\n\n if (i >= j) // end of round, no more fights possible\n dfs(deadMask, 1, n, curRound + 1);\n\n else if (i == first and j == second) // BATTLE OF THE IMMORTALS\n minRound = min(curRound,minRound),\n maxRound = max(curRound,maxRound);\n \n else{ // BATTLE includes a mortal \n if (i != first and i != second) // \'i\' is MORTAL, he may die\n dfs(deadMask | (1<<i), i+1, j-1, curRound);\n if (j != first and j != second) // \'j\' is MORTAL, he may die\n dfs(deadMask | (1<<j), i+1, j-1, curRound);\n\n }\n };\n dfs(0,1,n,1);\n return {minRound, maxRound};\n }\n};\n```\n\n```py\nclass Solution:\n def earliestAndLatest(self, n, first, second) -> List[int]:\n minRound, maxRound = math.inf, -math.inf\n def dfs(deadMask, i, j, curRound):\n nonlocal minRound, maxRound\n \n while i < j and deadMask & (1<<i): # \'i\' is dead warrior, try next\n i += 1\n \n while i < j and deadMask & (1<<j): # \'j\' is dead warrior, try next\n j -= 1\n\n if i >= j: # end of round, no more fights possible\n dfs(deadMask, 1, n, curRound + 1)\n\n elif i == first and j == second: # BATTLE OF THE IMMORTALS\n minRound = min(curRound,minRound)\n maxRound = max(curRound,maxRound)\n \n else: # Proceed with a BATTLE with a mortal \n if i != first and i != second: # \'i\' is MORTAL, he may die\n dfs(deadMask | (1<<i), i+1, j-1, curRound)\n if j != first and j != second: # \'j\' is MORTAL, he may die\n dfs(deadMask | (1<<j), i+1, j-1, curRound)\n \n dfs(0,1,n,1)\n return minRound, maxRound\n```\n\nAll ideas from @votrubac [discuss post](https://leetcode.com/problems/the-earliest-and-latest-rounds-where-players-compete/discuss/1268539/Recursion)\n
| 0
| 0
|
['Depth-First Search', 'Recursion', 'C', 'Bitmask', 'Python']
| 0
|
the-earliest-and-latest-rounds-where-players-compete
|
[Python] keep string instead of bitmask
|
python-keep-string-instead-of-bitmask-by-rzyp
|
\n\n def earliestAndLatest(self, n: int, firstPlayer: int, secondPlayer: int) -> List[int]:\n step, first, last, xs = 0, 0, 0, [firstPlayer, secondPla
|
khoso
|
NORMAL
|
2021-06-13T10:28:14.955028+00:00
|
2021-06-13T10:52:36.789339+00:00
| 70
| false
|
\n```\n def earliestAndLatest(self, n: int, firstPlayer: int, secondPlayer: int) -> List[int]:\n step, first, last, xs = 0, 0, 0, [firstPlayer, secondPlayer]\n # mark firstPlayer and secondPlayer as \'!\', others as \'.\'\n work = {\'!\'.join([ \'.\' * (y - x - 1) for x,y in zip([0] + xs, xs + [n+1]) ])}\n while work:\n step += 1\n m, n = divmod(n, 2)\n old, work = work, set()\n for s in old:\n # firstPlayer and secondPlayer competes?\n if (\'!\',\'!\') in set(zip(s[:m], s[::-1])):\n if not first: first = step\n last = step\n continue\n now = {s[m] if n else \'\'}\n for x,y in zip(s[m-1::-1], s[m+n:]):\n if x == \'!\': now = { x + s for s in now }\n elif y == \'!\': now = { s + y for s in now }\n else: now = { x + s for s in now } | { s + y for s in now }\n work |= now\n n += m\n return [first, last]\n```
| 0
| 0
|
['Python']
| 0
|
the-earliest-and-latest-rounds-where-players-compete
|
[Python ] DP + Bitmask + Memoization
|
python-dp-bitmask-memoization-by-rsrs3-2jcx
|
\nclass Solution:\n def earliestAndLatest(self, n: int, firstPlayer: int, secondPlayer: int) -> List[int]:\n self.first = min(firstPlayer-1, secondPla
|
rsrs3
|
NORMAL
|
2021-06-13T07:36:44.197333+00:00
|
2021-06-13T07:36:44.197369+00:00
| 68
| false
|
```\nclass Solution:\n def earliestAndLatest(self, n: int, firstPlayer: int, secondPlayer: int) -> List[int]:\n self.first = min(firstPlayer-1, secondPlayer-1)\n self.second = max(firstPlayer-1, secondPlayer-1)\n self.n=n-1\n self.dp = {}\n return self.rounds_helper((1<<n)-1, 0, self.n, 1)\n \n def rounds_helper(self, state, left, right, curr_round):\n if left >= right:\n return self.rounds_helper(state, 0, self.n, curr_round+1)\n elif (state&(1<<left)) == 0:\n return self.rounds_helper(state, left+1, right, curr_round)\n elif (state&(1<<right)) == 0:\n return self.rounds_helper(state, left, right-1, curr_round)\n elif left == self.first and right == self.second:\n return [curr_round, curr_round]\n else:\n key = (state, left, right)\n if key in self.dp:\n return self.dp[key]\n \n res = [self.n, 0]\n if right != self.first and right != self.second:\n val = self.rounds_helper(state^(1<<right), left+1, right-1, curr_round)\n res[0] = min(res[0], val[0])\n res[1] = max(res[1], val[1])\n if left != self.first and left != self.second:\n val = self.rounds_helper(state^(1<<left), left+1, right-1, curr_round)\n res[0] = min(res[0], val[0])\n res[1] = max(res[1], val[1])\n \n self.dp[key] = res\n return res\n \n \n```
| 0
| 0
|
[]
| 0
|
the-earliest-and-latest-rounds-where-players-compete
|
C++ Solution using(push_back)->TLE and not using(push_back)376ms
|
c-solution-usingpush_back-tle-and-not-us-hyyo
|
Way1 -> not use push_back\n\nclass Solution {\npublic:\n unordered_set<long long>memo;\n int firstPlayer,secondPlayer,mn,mx;\n void helper(vector<int>&
|
Verdict_AC
|
NORMAL
|
2021-06-13T06:43:56.474731+00:00
|
2021-06-13T06:43:56.474777+00:00
| 70
| false
|
Way1 -> not use push_back\n```\nclass Solution {\npublic:\n unordered_set<long long>memo;\n int firstPlayer,secondPlayer,mn,mx;\n void helper(vector<int>& arr,int round)\n {\n int n=arr.size();\n long long mod=1e9+7;\n long long now=0;\n for(auto &x:arr)\n {\n now*=10;\n now+=x;\n now%=mod;\n }\n if(memo.find(now)!=memo.end())return;\n memo.insert(now);\n int size=arr.size()/2;\n for(int i=0;i<size;i++)\n if(arr[i]==firstPlayer && arr[arr.size()-1-i]==secondPlayer)\n {\n mn=min(mn,round);\n mx=max(mx,round);\n return;\n }\n vector<int>next(size+(arr.size()%2==1)); //Difference!!!!!!\n for(int i=0;i<(1<<size);i++)\n {\n int left=0,right=next.size()-1;\n bool valid=true;\n for(int j=0;j<size;j++)\n {\n if(((i>>j)&1)&&(arr[n-1-j]==firstPlayer||arr[n-1-j]==secondPlayer))\n {\n valid=false;\n break;\n }\n if((((i>>j)&1)==0)&&(arr[j]==firstPlayer||arr[j]==secondPlayer))\n {\n valid=false;\n break;\n }\n if((i>>j)&1)next[left++]=arr[j];\n else next[right--]=arr[arr.size()-1-j];\n }\n if(valid==false)continue;\n if(arr.size()%2==1)next[left]=arr[size];\n helper(next,round+1);\n }\n return;\n }\n vector<int> earliestAndLatest(int n, int firstPlayer, int secondPlayer) {\n this->firstPlayer=firstPlayer;\n this->secondPlayer=secondPlayer;\n mn=INT_MAX;\n mx=INT_MIN;\n vector<int>arr;\n for(int i=1;i<=n;i++)arr.push_back(i);\n helper(arr,1);\n return {mn,mx};\n }\n};\n```\nWay2 -> use push_back\n```\nclass Solution {\npublic:\n int firstPlayer,secondPlayer,mn,mx;\n unordered_set<long long>memo;\n void helper(vector<int>& arr,int round)\n {\n long long s=0;\n long long m=1e9+7;\n for(auto &x:arr)\n {\n s*=10;\n s+=x;\n s%=m;\n }\n if(memo.find(s)!=memo.end())return;\n memo.insert(s);\n int n=arr.size();\n for(int i=0;i<n/2;i++)\n if(arr[i]==firstPlayer&&arr[n-1-i]==secondPlayer)\n {\n mn=min(mn,round);\n mx=max(mx,round);\n return;\n }\n for(int i=0;i<(1<<(n/2));i++)\n {\n vector<int>next; //Difference!!!!!!\n bool valid=true;\n for(int j=0;j<n/2;j++)\n {\n if(((i>>j)&1)&&(arr[n-1-j]==firstPlayer||arr[n-1-j]==secondPlayer))\n {\n valid=false;\n break;\n }\n if((((i>>j)&1)==0)&&(arr[j]==firstPlayer||arr[j]==secondPlayer))\n {\n valid=false;\n break;\n }\n if((i>>j)&1)next.push_back(arr[j]);\n else next.push_back(arr[n-1-j]);\n }\n if(valid==false)continue;\n if(n%2==1)next.push_back(arr[n/2]);\n sort(next.begin(),next.end());\n helper(next,round+1);\n }\n return;\n }\n vector<int> earliestAndLatest(int n, int firstPlayer, int secondPlayer) {\n this->firstPlayer=firstPlayer;\n this->secondPlayer=secondPlayer;\n mn=INT_MAX;\n mx=INT_MIN;\n vector<int>arr;\n for(int i=1;i<=n;i++)arr.push_back(i);\n helper(arr,1);\n return {mn,mx};\n }\n};\n```
| 0
| 0
|
[]
| 0
|
the-earliest-and-latest-rounds-where-players-compete
|
[C++] Recursion optimized 24 ms 32 MB
|
c-recursion-optimized-24-ms-32-mb-by-ash-ecrg
|
\n#pragma GCC optimize("Ofast")\n#pragma GCC optimize("unroll-loops")\n#pragma GCC optimize("inline")\n\nclass Solution {\npublic:\n int f,s,cur_level,mi,ma;
|
ashish23ks
|
NORMAL
|
2021-06-13T05:48:22.269261+00:00
|
2021-06-13T05:48:22.269292+00:00
| 69
| false
|
```\n#pragma GCC optimize("Ofast")\n#pragma GCC optimize("unroll-loops")\n#pragma GCC optimize("inline")\n\nclass Solution {\npublic:\n int f,s,cur_level,mi,ma;\n vector<vector<int>> cur;\n vector<int> prev;\n //recurse all games\n void games(vector<int> & ans, int pos){\n if(prev.size()%2==0){\n if(pos==prev.size()/2){\n vector<int> temp=ans;\n //sort before adding possible permute\n sort(temp.begin(),temp.end());\n if(temp.size()>1)cur.push_back(temp);\n return;\n }\n }\n else{\n if(pos==prev.size()/2){\n ans.push_back(prev[pos]);\n vector<int> temp=ans;\n sort(temp.begin(),temp.end());\n if(temp.size()>1)cur.push_back(temp);\n ans.pop_back();\n return;\n }\n }\n \n bool f1=false,s1=false;\n if(prev[pos]==f || prev[prev.size()-1-pos]==f){\n f1=true;\n }\n if(prev[pos]==s || prev[prev.size()-1-pos]==s){\n s1=true;\n }\n if(f1&&s1){\n //no need to followup children games\n mi=min(mi,cur_level);\n ma=max(ma,cur_level);\n return;\n }\n else \n {\n if(f1 || s1){\n if(f1){\n ans.push_back(f);\n games(ans,pos+1);\n ans.pop_back();\n }\n else{\n ans.push_back(s);\n games(ans,pos+1);\n ans.pop_back();\n }\n }\n else{\n //optimization: don\'t care about outcome if current two players lie on same side of firstPlayer and secondPlayer\n if(((prev[pos]<f)&&(prev[prev.size()-1-pos]<f)) || ((prev[pos]>s)&&(prev[prev.size()-1-pos]>s)) || ((prev[pos]>f)&&(prev[prev.size()-1-pos]<s))){\n ans.push_back(prev[pos]);\n games(ans,pos+1);\n ans.pop_back();\n }\n //recurse for both possible outcome\n else {\n ans.push_back(prev[pos]);\n games(ans,pos+1);\n ans.pop_back();\n ans.push_back(prev[prev.size()-1-pos]);\n games(ans,pos+1);\n ans.pop_back();\n }\n \n return;\n }\n }\n \n }\n \n vector<int> earliestAndLatest(int n, int firstPlayer, int secondPlayer) {\n mi=100000;\n ma=0;\n cur_level=1;\n f = firstPlayer;\n s = secondPlayer;\n vector<int> ans;\n vector<vector<int>> prev_games;\n vector<int> init;\n for(int i=1;i<=n;i++)init.push_back(i);\n //initial configuration\n prev_games.push_back(init);\n while(prev_games.size()){\n cur = vector<vector<int>>();\n vector<int> temp,temp2;\n for(auto i:prev_games){\n prev=i;\n games(temp,0);\n }\n //keep only unique order of firstPlayer and secondPlayer\n prev_games = vector<vector<int>>();\n unordered_map<int,int> m;\n for(auto i:cur){\n long int num=0;\n for(auto j:i){\n num*=2;\n if(j==f ||j==s)num++;\n }\n if(m[num]==0){\n m[num]++;\n prev_games.push_back(i);\n }\n \n }\n \n cur_level++;\n } \n ans.push_back(mi);\n ans.push_back(ma);\n return ans;\n }\n};\n```
| 0
| 1
|
[]
| 0
|
the-earliest-and-latest-rounds-where-players-compete
|
C++ brute force
|
c-brute-force-by-cpcs-3nne
|
\nclass Solution {\n int earliest(int n, int x, int y, vector<vector<vector<int>>> &dp) {\n int& r = dp[n][x][y];\n if (r >= 0) {\n
|
cpcs
|
NORMAL
|
2021-06-13T05:17:48.104163+00:00
|
2021-06-13T05:17:48.104205+00:00
| 93
| false
|
```\nclass Solution {\n int earliest(int n, int x, int y, vector<vector<vector<int>>> &dp) {\n int& r = dp[n][x][y];\n if (r >= 0) {\n return r;\n }\n if (x + y == n - 1) {\n return r = 1;\n }\n int round = n >> 1;\n if (n & 1) {\n const int mid = round;\n if (x != mid) {\n --round;\n }\n if (y != mid) {\n --round;\n }\n }\n r = n;\n for (int mask = (1 << round) - 1; mask >= 0; --mask) {\n int winners = (n & 1) ? (1 << (n >> 1)) : 0;\n for (int i = 0, j = n - 1, ind = 0; i < j; ++i, --j) {\n if (i == x || i == y) {\n winners |= 1 << i;\n } else if (j == x || j == y) {\n winners |= 1 << j;\n } else if (mask & (1 << (ind++))) {\n winners |= 1 << i;\n } else {\n winners |= 1 << j;\n }\n }\n int xx = 0, yy = 0, m = 0;\n for (int i = 0; i < n; ++i) {\n if (winners & (1 << i)) {\n if (i == x) {\n xx = m;\n } else if (i == y) {\n yy = m;\n }\n ++m;\n }\n }\n r = min(r, earliest(m, xx, yy, dp));\n }\n return ++r;\n }\n \n int latest(int n, int x, int y, vector<vector<vector<int>>> &dp) {\n int& r = dp[n][x][y];\n if (r >= 0) {\n return r;\n }\n if (x + y == n - 1) {\n return r = 1;\n }\n int round = n >> 1;\n if (n & 1) {\n const int mid = round;\n if (x != mid) {\n --round;\n }\n if (y != mid) {\n --round;\n }\n }\n r = 0;\n for (int mask = (1 << round) - 1; mask >= 0; --mask) {\n int winners = (n & 1) ? (1 << (n >> 1)) : 0;\n for (int i = 0, j = n - 1, ind = 0; i < j; ++i, --j) {\n if (i == x || i == y) {\n winners |= 1 << i;\n } else if (j == x || j == y) {\n winners |= 1 << j;\n } else if (mask & (1 << (ind++))) {\n winners |= 1 << i;\n } else {\n winners |= 1 << j;\n }\n }\n int xx = 0, yy = 0, m = 0;\n for (int i = 0; i < n; ++i) {\n if (winners & (1 << i)) {\n if (i == x) {\n xx = m;\n } else if (i == y) {\n yy = m;\n }\n ++m;\n }\n }\n r = max(r, latest(m, xx, yy, dp));\n }\n return ++r;\n \n }\npublic:\n vector<int> earliestAndLatest(int n, int firstPlayer, int secondPlayer) {\n vector<vector<vector<int>>> a(n + 1, vector<vector<int>>(n, vector<int>(n, -1))), b(n + 1, vector<vector<int>>(n, vector<int>(n, -1)));\n --firstPlayer;\n --secondPlayer;\n return {earliest(n, firstPlayer, secondPlayer, a), latest(n, firstPlayer, secondPlayer, b)};\n \n }\n};\n```
| 0
| 0
|
[]
| 0
|
the-earliest-and-latest-rounds-where-players-compete
|
Using Mask and Bitwise operations.
|
using-mask-and-bitwise-operations-by-van-w38k
|
```\n fun earliestAndLatest(n: Int, firstPlayer: Int, secondPlayer: Int): IntArray {\n return helper(1.shl(n + 1) - 1, 1, n, firstPlayer, secondPlayer
|
vanajag
|
NORMAL
|
2021-06-13T05:15:04.327333+00:00
|
2021-06-13T05:15:04.327362+00:00
| 65
| false
|
```\n fun earliestAndLatest(n: Int, firstPlayer: Int, secondPlayer: Int): IntArray {\n return helper(1.shl(n + 1) - 1, 1, n, firstPlayer, secondPlayer, 1, n)\n }\n \n val db = HashMap<String, IntArray>()\n \n fun helper(mask: Int, s: Int, e: Int, f: Int, fs: Int, round: Int, n :Int): IntArray {\n if(mask == 1) return intArrayOf(-1, -1) \n if(mask.and(1.shl(f)) == 0 || mask.and(1.shl(fs)) == 0) return intArrayOf(-1, -1) \n\t\t\n\t\t// round completed\n if(s >= e) return helper(mask, 1, n, f, fs, round + 1, n)\n\t\t\n\t\t// got the combination we need so return\n if(s == f && e == fs) {\n if(mask.and(1.shl(s)) == 0 || mask.and(1.shl(e)) == 0) return intArrayOf(-1, -1) \n return intArrayOf(round, round)\n }\n \n\t\t// if position at s index is already consumed, the look for next one\n if(mask.and(1.shl(s)) == 0) return helper(mask, s + 1, e, f, fs, round, n)\n\t\t\n\t\t// if position at e index is already consumed, the look for next one\n if(mask.and(1.shl(e)) == 0) return helper(mask, s, e - 1, f, fs, round, n)\n \n\t\t// create a key from current state \n val key = "" + mask + "-" + s + "-" + e\n if(db[key] != null) return db[key]!!\n\t\t\n var min = Int.MAX_VALUE\n var max = Int.MIN_VALUE\n var value = helper(mask.xor(1.shl(s)), s + 1, e - 1, f, fs, round, n)\n if(value[0] != -1) {\n min = Math.min(min, value[0])\n max = Math.max(max, value[1])\n }\n value = helper(mask.xor(1.shl(e)), s + 1, e - 1, f, fs, round, n)\n if(value[0] != -1) {\n min = Math.min(min, value[0])\n max = Math.max(max, value[1])\n }\n db[key] = intArrayOf(min, max)\n return intArrayOf(min, max)\n }
| 0
| 0
|
[]
| 0
|
the-earliest-and-latest-rounds-where-players-compete
|
[Python] generate production and then DP
|
python-generate-production-and-then-dp-b-cd4c
|
\nclass Solution:\n def earliestAndLatest(self, n: int, firstPlayer: int, secondPlayer: int) -> List[int]:\n import functools\n \n def w
|
codefever
|
NORMAL
|
2021-06-13T04:36:20.932522+00:00
|
2021-06-13T04:36:20.932548+00:00
| 127
| false
|
```\nclass Solution:\n def earliestAndLatest(self, n: int, firstPlayer: int, secondPlayer: int) -> List[int]:\n import functools\n \n def win(i, j, first, second):\n if i == j:\n return [i]\n if i in (first, second):\n return [i]\n if j in (first, second):\n return [j]\n return [i, j]\n \n @functools.lru_cache(None)\n def dfs(n, first, second) -> List[int]:\n if n - first + 1 == second:\n return [1, 1]\n \n res = [[]]\n l, r = 1, n\n while l <= r:\n winner = win(l, r, first, second)\n \n prev_len = len(res)\n for e in res:\n e.append(winner[0])\n if len(winner) > 1:\n for i in range(prev_len):\n res.append(res[i][:])\n res[-1][-1] = winner[1]\n \n l += 1\n r -= 1\n \n ans = [float(\'infinity\'), float(\'-infinity\')]\n for e in res:\n e = sorted(e)\n a = e.index(first) + 1\n b = e.index(second) + 1\n small, large = dfs(len(e), a, b)\n ans[0] = min(ans[0], small + 1)\n ans[1] = max(ans[1], large + 1)\n \n return ans[0], ans[1]\n \n return dfs(n, firstPlayer, secondPlayer)\n```
| 0
| 0
|
[]
| 0
|
the-earliest-and-latest-rounds-where-players-compete
|
C++ Easy Solution
|
c-easy-solution-by-sandhuamar1607-7zpm
|
\nclass Solution {\npublic:\n vector<int> earliestAndLatest(int n, int firstPlayer, int secondPlayer) {\n vector<int> result;\n int early= 1, l
|
sandhuamar1607
|
NORMAL
|
2021-06-13T04:26:49.956785+00:00
|
2021-06-13T04:26:49.956813+00:00
| 99
| false
|
```\nclass Solution {\npublic:\n vector<int> earliestAndLatest(int n, int firstPlayer, int secondPlayer) {\n vector<int> result;\n int early= 1, latest= 1;\n vector<int> players;\n for(int i=1; i<=n; i++) players.push_back(i);\n int i=0, j=players.size()-1;\n while(1){\n i=0;\n j=players.size()-1;\n if(players.size()%2==1) players.push_back((players.size()/2)+1);\n while(i<j){\n if(players[i]==firstPlayer and players[j]==secondPlayer){\n result.push_back(early);\n break;\n }\n else if(players[i]==firstPlayer)\n players.erase(players.begin() + j);\n else if(players[j]==secondPlayer)\n players.erase(players.begin() + i);\n else if(players[i]>firstPlayer and players[i]<secondPlayer and (players[j]<firstPlayer or players[j]>secondPlayer))\n players.erase(players.begin() + j);\n else if(players[j]>firstPlayer and players[j]<secondPlayer and (players[i]<firstPlayer or players[i]>secondPlayer))\n players.erase(players.begin() + i);\n else\n players.erase(players.begin() + i);\n i++;\n j--;\n }\n if(players[i]==firstPlayer and players[j]==secondPlayer)\n break;\n early++;\n sort(players.begin(), players.end());\n }\n result.push_back(early);\n players.clear();\n \n for(int i=1; i<=n; i++) players.push_back(i);\n i=0;\n j=players.size()-1;\n while(1){\n i=0;\n j=players.size()-1;\n if(players.size()%2==1) players.push_back((players.size()/2)+1);\n while(i<j){\n if(players[i]==firstPlayer and players[j]==secondPlayer){\n result.push_back(early);\n break;\n }\n else if(players[i]==firstPlayer)\n players.erase(players.begin() + j);\n else if(players[j]==secondPlayer)\n players.erase(players.begin() + i);\n else if(players[i]>firstPlayer and players[i]<secondPlayer and (players[j]<firstPlayer or players[j]>secondPlayer))\n players.erase(players.begin() + i);\n else if(players[j]>firstPlayer and players[j]<secondPlayer and (players[i]<firstPlayer or players[i]>secondPlayer))\n players.erase(players.begin() + i);\n else\n players.erase(players.begin() + j);\n i++;\n j--;\n }\n if(players[i]==firstPlayer and players[j]==secondPlayer)\n break;\n latest++;\n sort(players.begin(), players.end());\n }\n result.push_back(latest);\n return result;\n }\n};\n```\n//Not working
| 0
| 3
|
[]
| 1
|
the-earliest-and-latest-rounds-where-players-compete
|
Randomised Solution.
|
randomised-solution-by-saksham_2000-rsf0
|
define ll long long\n#define pb push_back\n#define vl vector\n#define all(x) x.begin(),x.end()\n\nclass Solution {\npublic:\n vector earliestAndLatest(int n,
|
saksham_2000
|
NORMAL
|
2021-06-13T04:17:27.246663+00:00
|
2021-06-13T04:17:27.246694+00:00
| 111
| false
|
#define ll long long\n#define pb push_back\n#define vl vector<ll>\n#define all(x) x.begin(),x.end()\n\nclass Solution {\npublic:\n vector<int> earliestAndLatest(int n, int s1, int s2) {\n ll mn = 1e9, mx = 0;\n\n ll t = 1000;\n\n while (t--) {\n\n\n vl v;\n for (ll i = 1; i <= n; i++)v.pb(i);\n\n ll flag = 0;\n\n for (int i = 0; i < 7; i++) {\n ll n1 = v.size();\n vl new_v;\n // for (auto d : v)cout << d << " ";\n // cout << endl;\n for (ll j = 0; j < n1; j++) {\n // j vs n1-j-1;\n if (j > n1 - j - 1)break;\n if (j == n1 - j - 1)new_v.pb(v[j]);\n else {\n ll p1 = v[j], p2 = v[n1 - j - 1];\n if (p1 == s1 && p2 == s2) {\n mn = min(mn, i + 1ll);\n mx = max(mx, i + 1ll);\n flag = 1;\n break;\n } else if (p1 == s1) {\n new_v.pb(p1);\n } else if (p1 == s2) {\n new_v.pb(p1);\n } else if (p2 == s1) {\n new_v.pb(p2);\n } else if (p2 == s2) {\n new_v.pb(p2);\n } else {\n ll dec = rand()%100;\n if (dec & 1)new_v.pb(p2);\n else new_v.pb(p1);\n }\n }\n }\n if (flag)break;\n sort(all(new_v));\n v = new_v;\n }\n\n }\n return {(int)mn,(int)mx};\n }\n};
| 0
| 0
|
['C']
| 0
|
the-earliest-and-latest-rounds-where-players-compete
|
[C++] DFS + Memorization
|
c-dfs-memorization-by-hujc-r4kj
|
The min and max round for the two player to meet is determined by the state [n, firstPlayer, secondPlay], where the three number are the number of players, firs
|
hujc
|
NORMAL
|
2021-06-13T04:06:10.538272+00:00
|
2021-06-13T07:47:47.854060+00:00
| 165
| false
|
The min and max round for the two player to meet is determined by the state `[n, firstPlayer, secondPlay]`, where the three number are the number of players, first player position and second player position. And for going into next round, we do not need to track the actual player position at the beginning but just their replative position in current round. What we essentially need to is to enumerate the possibilities of the next round state from the current round state. In case of known state, we memorize to dedupe calculation.\n\nComplexity is: O(n^3) (? a guess) for memorization\n\nHere\'s the code\n```\nint memo[29][29][29];\n\nclass Solution {\npublic: \n vector<int> earliestAndLatest(int n, int fi, int se) {\n memset(memo, -1, sizeof(memo));\n int r1 = dfs(n, fi-1, se-1, true);\n \n memset(memo, -1, sizeof(memo));\n int r2 = dfs(n, fi-1, se-1, false);\n \n return {r1 + 1, r2 + 1};\n }\n \n int dfs(int n, int fi, int se, bool find_min) {\n if (fi + se + 1 == n) return 0;\n \n int& res = memo[n][fi][se];\n if (res != -1) return res;\n \n\t\t// use to determine if the player is on the left or right\n int lfi = min(fi, n - fi - 1);\n int rfi = max(fi, n - fi - 1);\n int lse = min(se, n - se - 1);\n int rse = max(se, n - se - 1);\n \n int tmp = find_min ? INT_MAX : 0;\n int m = n / 2;\n\t\t// enumerate all possibilities\n for (int i = 0; i < pow(2, m); ++i) {\n // simulate\n // calculate decrease in pos\n int dfi = 0, dse = 0;\n for (int j = 0; j < m; ++j) {\n // determine winner from enumeration\n bool rightWin = (((i >> j) & 1) == 1);\n \n // overwrite winner if it\'s one of the players\n if (j == lfi) rightWin = fi == rfi;\n else if (j == lse) rightWin = se == rse;\n \n if (rightWin) {\n // right side win\n remove(j, fi, se, dfi, dse);\n } else {\n // left side win\n remove(n - j - 1, fi, se, dfi, dse);\n }\n }\n \n if (find_min) tmp = min(tmp, 1 + dfs(m + n % 2, fi + dfi, se + dse, find_min));\n else tmp = max(tmp, 1 + dfs(m + n % 2, fi + dfi, se + dse, find_min));\n }\n \n return res = tmp;\n }\n \n void remove(int j, int fi, int se, int& dfi, int& dse) {\n if (j < fi) dfi--;\n if (j < se) dse--;\n }\n};\n```
| 0
| 0
|
[]
| 1
|
the-earliest-and-latest-rounds-where-players-compete
|
bit mask+2DFS optimized with memorization. 0ms/2.2MB
|
bit-mask2dfs-optimized-with-memorization-8fsk
|
State = [fp is the ith surviver][sp is the jth surviver][the total number of the rest survivers]\nWritten in Golan.\n\nfunc earliestAndLatest(n int, fp int, sp
|
bcb98801xx
|
NORMAL
|
2021-06-13T04:04:03.298631+00:00
|
2021-06-14T03:45:35.295065+00:00
| 138
| false
|
State = ```[fp is the ith surviver][sp is the jth surviver][the total number of the rest survivers]```\nWritten in Golan.\n```\nfunc earliestAndLatest(n int, fp int, sp int) []int {\n fp--\n sp--\n \n if fp > sp {\n fp, sp = sp, fp\n }\n \n ans := []int{100, 0}\n vis := [28][28][27]bool{}\n \n var dfs func(mask, k, a, b, c int)\n var dfs2 func(mask, l, r, k, a, b, c int)\n \n dfs = func(mask, k, a, b, c int){\n if vis[a][b][c] {return} //[fp is the ith surviver][sp is the jth surviver][the total number of the rest survivers]\n \n vis[a][b][c] = true\n k++ //round \n dfs2(mask, 0, n-1, k, a, b, c)\n }\n \n dfs2 = func(mask, l, r, k, a, b, c int){\n for l < r && (mask>>l)&1 == 1 {l++}\n for l < r && (mask>>r)&1 == 1 {r--}\n \n if l >= r {\n dfs(mask, k, a, b, c)\n return\n }\n \n if l == fp && r == sp {\n if k < ans[0] {ans[0] = k}\n if k > ans[1] {ans[1] = k}\n return\n }\n \n c--\n if l != fp && l != sp {\n if l < fp {\n dfs2(mask|(1<<l), l+1, r-1, k, a-1, b-1, c)\n }else if l < sp {\n dfs2(mask|(1<<l), l+1, r-1, k, a, b-1, c)\n }else{\n dfs2(mask|(1<<l), l+1, r-1, k, a, b, c) \n }\n }\n if r != fp && r != sp {\n if r < fp {\n dfs2(mask|(1<<r), l+1, r-1, k, a-1, b-1, c)\n }else if r < sp {\n dfs2(mask|(1<<r), l+1, r-1, k, a, b-1, c)\n }else{\n dfs2(mask|(1<<r), l+1, r-1, k, a, b, c) \n }\n }\n }\n \n dfs(0, 0, fp, sp, n-2)\n \n return ans\n}\n```
| 0
| 0
|
[]
| 0
|
the-earliest-and-latest-rounds-where-players-compete
|
C++ BITMASKS | RECURSIVE
|
c-bitmasks-recursive-by-saber2k18-j5tx
|
-> Consider all possiblites on both sides of the current array.\n-> Notice we only need half the array size for full information\n-> So complexity would be O(2^
|
saber2k18
|
NORMAL
|
2021-06-13T04:02:36.049080+00:00
|
2021-06-13T04:04:34.604981+00:00
| 155
| false
|
-> Consider all possiblites on both sides of the current array.\n-> Notice we only need half the array size for full information\n-> So complexity would be O(2^(n/2)*n)\n\n\n```\nclass Solution {\npublic:\n int lm,hm;\n void solve(set<int> &now,int round,int fp,int sp){\n \n if(!now.count(fp) or !now.count(sp))\n return;\n \n int n = (int)(now.size())/2;\n vector<int> cur_set(now.begin(),now.end());\n \n int nn = (int)now.size();\n \n for(int mask=0;mask<(1<<n);++mask){\n set<int> send;\n if((nn%2)!=0)\n send.insert(cur_set[n]);\n bool ok = false;\n for(int j=0;j<n;j++){\n int p1 = cur_set[j];\n int p2 = cur_set[(int)cur_set.size() - 1 - j];\n if(p1==fp and p2==sp){\n lm = min(lm,round);\n hm = max(hm,round);\n ok=true;\n break;\n }\n if(p1==fp or p1==sp)\n send.insert(p1);\n else if(p2==fp or p2==sp)\n send.insert(p2);\n else if(mask&(1<<j))\n send.insert(p1);\n else if(!(mask&(1<<j)))\n send.insert(p2);\n }\n if(!ok){\n solve(send,round+1,fp,sp);\n }\n \n }\n \n }\n vector<int> earliestAndLatest(int n, int firstPlayer, int secondPlayer) {\n lm = 2e9;\n hm = 0;\n set<int> now;\n for(int i=1;i<=n;i++)\n now.insert(i);\n solve(now,1,firstPlayer,secondPlayer);\n vector<int> v;\n v.push_back(lm);\n v.push_back(hm);\n return v;\n \n }\n};\n```
| 0
| 0
|
[]
| 1
|
find-the-shortest-superstring
|
Travelling Salesman Problem
|
travelling-salesman-problem-by-wangzi614-byrh
|
Travelling Salesman Problem\n\n1. graph[i][j] means the length of string to append when A[i] followed by A[j]. eg. A[i] = abcd, A[j] = bcde, then graph[i][j] =
|
wangzi6147
|
NORMAL
|
2018-11-18T04:17:52.261718+00:00
|
2018-11-18T04:17:52.261758+00:00
| 73,827
| false
|
[Travelling Salesman Problem](https://en.wikipedia.org/wiki/Travelling_salesman_problem)\n\n1. `graph[i][j]` means the length of string to append when `A[i]` followed by `A[j]`. eg. `A[i] = abcd`, `A[j] = bcde`, then `graph[i][j] = 1`\n2. Then the problem becomes to: find the shortest path in this graph which visits every node exactly once. This is a Travelling Salesman Problem.\n3. Apply TSP DP solution. Remember to record the path.\n\nTime complexity: `O(n^2 * 2^n)`\n\n```\nclass Solution {\n public String shortestSuperstring(String[] A) {\n int n = A.length;\n int[][] graph = new int[n][n];\n // build the graph\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < n; j++) {\n graph[i][j] = calc(A[i], A[j]);\n graph[j][i] = calc(A[j], A[i]);\n }\n }\n int[][] dp = new int[1 << n][n];\n int[][] path = new int[1 << n][n];\n int last = -1, min = Integer.MAX_VALUE;\n\t\t\n // start TSP DP\n for (int i = 1; i < (1 << n); i++) {\n Arrays.fill(dp[i], Integer.MAX_VALUE);\n for (int j = 0; j < n; j++) {\n if ((i & (1 << j)) > 0) {\n int prev = i - (1 << j);\n if (prev == 0) {\n dp[i][j] = A[j].length();\n } else {\n for (int k = 0; k < n; k++) {\n if (dp[prev][k] < Integer.MAX_VALUE && dp[prev][k] + graph[k][j] < dp[i][j]) {\n dp[i][j] = dp[prev][k] + graph[k][j];\n path[i][j] = k;\n }\n }\n }\n }\n if (i == (1 << n) - 1 && dp[i][j] < min) {\n min = dp[i][j];\n last = j;\n }\n }\n }\n\t\t\n // build the path\n StringBuilder sb = new StringBuilder();\n int cur = (1 << n) - 1;\n Stack<Integer> stack = new Stack<>();\n while (cur > 0) {\n stack.push(last);\n int temp = cur;\n cur -= (1 << last);\n last = path[temp][last];\n }\n\t\t\n // build the result\n int i = stack.pop();\n sb.append(A[i]);\n while (!stack.isEmpty()) {\n int j = stack.pop();\n sb.append(A[j].substring(A[j].length() - graph[i][j]));\n i = j;\n }\n return sb.toString();\n }\n private int calc(String a, String b) {\n for (int i = 1; i < a.length(); i++) {\n if (b.startsWith(a.substring(i))) {\n return b.length() - a.length() + i;\n }\n }\n return b.length();\n }\n}\n```
| 324
| 8
|
[]
| 36
|
find-the-shortest-superstring
|
[Python] dp on subsets solution - 3 solutions + oneliner, explained
|
python-dp-on-subsets-solution-3-solution-6pvg
|
This is actually Travelling salesman problem (TSP) problem: if we look at our strings as nodes, then we can evaluate distance between one string and another, fo
|
dbabichev
|
NORMAL
|
2021-05-23T10:28:00.219962+00:00
|
2021-05-24T12:21:25.674867+00:00
| 7,094
| false
|
This is actually Travelling salesman problem (TSP) problem: if we look at our strings as nodes, then we can evaluate distance between one string and another, for example for `abcde` and `cdefghij` distance is 5, because we need to use 5 more symbols `fghij` to continue first string to get the second. Note, that this is not symmetric, so our graph is oriented. \n\nThen our problem is equivalent to Traveling Salesman Problem (TSP): we need to find path with smallest weight, visiting all nodes. Here we have `2^n * n` possible states, where state consists of two elements:\n1. `mask`: binary mask with length n with already visited nodes.\n2. `last`: last visited node.\n3. In each `dp[mask][last]` we will keep length of built string + built string itself.\n\n#### Complexity \nThere will be `O(n)` possible transitions for each state: for example to the state `(10011101, 7)` we will have possible steps from `(00011101, 0), (00011101, 2), (00011101, 3), (00011101, 4)`. Finally, time complexity is `O(2^n*n^2*M)`, where `M` is the length of answer and space complexity is `O(2^n*n*M)` as well.\n\n```python\nclass Solution:\n def shortestSuperstring(self, A):\n @lru_cache(None)\n def connect(w1, w2):\n return [w2[i:] for i in range(len(w1) + 1) if w1[-i:] == w2[:i] or not i][-1]\n \n N = len(A) \n dp = [[(float("inf"), "")] * N for _ in range(1<<N)]\n for i in range(N): dp[1<<i][i] = (len(A[i]), A[i])\n \n for mask in range(1<<N):\n n_z_bits = [j for j in range(N) if mask & 1<<j]\n \n for j, k in permutations(n_z_bits, 2):\n cand = dp[mask ^ 1<<j][k][1] + connect(A[k], A[j])\n dp[mask][j] = min(dp[mask][j], (len(cand), cand))\n\n return min(dp[-1])[1]\n```\n\n#### Solution 2\nIdea is exactly the same as in previous solutoin, but here we can use functionaliry of `lru_cache`.\n\n#### Complexity\nis the same as Solution 1.\n\n#### Code\n```python\nclass Solution:\n def shortestSuperstring(self, A):\n @lru_cache(None)\n def suff(w1, w2):\n return [w2[i:] for i in range(len(w1) + 1) if w1[-i:] == w2[:i] or not i][-1]\n \n @lru_cache(None)\n def dp(mask, l):\n if mask + 1 == 1<<N: return ""\n return min([suff(A[l], A[i]) + dp(mask | 1<<i, i) for i in range(N) if not mask & 1<<i], key = len)\n \n N = len(A)\n return min([A[i] + dp(1<<i, i) for i in range(N)], key=len)\n```\n\nOr you can write it very long, but oneliner\n```python\nreturn (lambda f, c: min([A[i] + f(1<<i, i, c) for i in range(len(A))], key=len))((f := lambda m, l, c: c.get((m, l)) or c.setdefault((m,l), "" if m + 1 == 1<<len(A) else min([next(A[i][j:] for j in range(len(A[i]), -1, -1) if A[l].endswith(A[i][:j])) + f(m | 1<<i, i, c) for i in range(len(A)) if not m & 1<<i], key = len))), {})\n\n```\n\n#### Solution 3\n\nHere is improvement, which potentially will work faster for big strings: instead of keeping built string for every state, we keep only its length and connection to previous node. \n\n#### Complexity \nHere time and space complexity is `O(2^n*n^2)`, without constant `M`. However in practice it works just a bit faster, because of testcases.\n\n```python\nclass Solution:\n def shortestSuperstring(self, A):\n @lru_cache(None)\n def connect(w1, w2):\n return [(w2[i:], len(w2) - i) for i in range(len(w1) + 1) if w1[-i:] == w2[:i] or not i][-1]\n \n N = len(A)\n dp = [[(float("inf"), -1)] * N for _ in range(1<<N)]\n for i in range(N): dp[1<<i][i] = (len(A[i]), -1)\n \n for mask in range(1<<N):\n n_z_bits = [j for j in range(N) if mask & 1<<j]\n for j, k in permutations(n_z_bits, 2):\n dp[mask][j] = min(dp[mask][j], (dp[mask ^ 1<<j][k][0] + connect(A[k], A[j])[1], k))\n \n mask = (1<<N) - 1\n prev = min(dp[mask])\n last = dp[mask].index(prev)\n prev = prev[1]\n ans = ""\n \n while prev != -1:\n ans = connect(A[prev], A[last])[0] + ans\n mask -= (1<<last)\n prev, last = dp[mask][prev][1], prev\n \n return A[last] + ans\n```\n\n#### Remark \nLet me know if you know how to write the solution 3 in shorter way, I think code is too long.\nAlso see my collections of similar problems: https://leetcode.com/discuss/general-discussion/1125779/dynamic-programming-on-subsets-with-examples-explained\n\nAlso something wrong with test cases, if you just `return A`, it will be accepted! @leetcode, please fix this.\n\nIf you have any questions, feel free to ask. If you like solution and explanations, please **Upvote!**\n\n
| 106
| 19
|
['Dynamic Programming', 'Bitmask']
| 7
|
find-the-shortest-superstring
|
python bfs solution with detailed explanation(with extra Chinese explanation)
|
python-bfs-solution-with-detailed-explan-weq6
|
you can get Chinese explanation here\n\nFirst, we convert this problem into a graph problem.\nfor instance, A = ["catg","ctaagt","gcta","ttca","atgcatc"]\nwe re
|
bupt_wc
|
NORMAL
|
2018-11-19T05:50:57.136758+00:00
|
2018-11-19T05:50:57.136824+00:00
| 5,695
| false
|
you can get Chinese explanation [here](https://buptwc.github.io/2018/11/19/Leetcode-943-Find-the-Shortest-Superstring/)\n\nFirst, we convert this problem into a graph problem.\nfor instance, `A = ["catg","ctaagt","gcta","ttca","atgcatc"]`\nwe regard each string in A as a node, and regard the repeat_length of two string as edge weight. then ,we get this graph `G`:\n\n\nfor `G[2][1] = 3`, it means that we can `save` 3 characters length by place `node 1` behind `node 2`, etc `gctaagt`.\n\nIn the end, the more we `save`, the shorter string length we will get.\n\nSo, the question now is:\nIn a given graph, we can start in any node, and traverse all node in this graph excatly once, to get the maximum `save` length.\n(Note that although there is no connection between 1,3, you can still go from node 1 to node 3.)\n\nfirst we construct the graph:\n```python\ndef getDistance(s1, s2):\n for i in range(1, len(s1)):\n if s2.startswith(s1[i:]):\n return len(s1) - i\n return 0\n\nn = len(A)\nG = [[0]*n for _ in xrange(n)]\nfor i in range(n):\n for j in range(i+1, n):\n G[i][j] = getDistance(A[i], A[j])\n G[j][i] = getDistance(A[j], A[i])\n```\n\nif we consider all possible case, it will be `n*(n-1)*(n-2)*...*1 = n!` possible cases. Obviously it won\u2019t work.\nWe need to make some optimizations, look at these two cases\uFF1A\n`2->1->3->...` and `1->2->3->...`\nBoth cases traverse three nodes 1, 2, and 3, and is currently at the `node 3`.\nfor `2->1->3->...`, we assume the `save length` now is `L1`\nfor `1->2->3->...`, we assume the `save length` now is `L2`\nif `L2 < L1`, regardless of how the strategy is adopted afterwards, the second case cannot be better than the first case. So we can discard the second case.\n\nBased on this idea, we difine `d[mask][node]` represent the now `save length` in the status `(mask, node)`.\n`mask` represent the node we have traversed, `10011` means traversed `node 0,1,4`\n`node` represent the current node.\n\nIn BFS solution, such a data structure is stored in the queue `(node, mask, path, s_len)`\n`path` means the order of traversed nodes.\n`s_len` means the `save length`.\n\nOnce `mask` == `(1<<n)-1`, it means that all nodes have been traversed. Now we find the maximum `s_len` and get the corresponding `path`.\nFinally, we construct the answer via `path`.\n\npython bfs code:\n```python\nclass Solution(object):\n def shortestSuperstring(self, A):\n def getDistance(s1, s2):\n for i in range(1, len(s1)):\n if s2.startswith(s1[i:]):\n return len(s1) - i\n return 0\n\n def pathtoStr(A, G, path):\n res = A[path[0]]\n for i in range(1, len(path)):\n res += A[path[i]][G[path[i-1]][path[i]]:]\n return res\n\n n = len(A)\n G = [[0]*n for _ in xrange(n)]\n for i in range(n):\n for j in range(i+1, n):\n G[i][j] = getDistance(A[i], A[j])\n G[j][i] = getDistance(A[j], A[i])\n\n d = [[0]*n for _ in xrange(1<<n)]\n Q = collections.deque([(i, 1<<i, [i], 0) for i in xrange(n)])\n l = -1 # record the maximum s_len\n P = [] # record the path corresponding to maximum s_len\n while Q:\n node, mask, path, dis = Q.popleft()\n if dis < d[mask][node]: continue\n if mask == (1<<n) - 1 and dis > l:\n P,l = path,dis\n continue\n for i in xrange(n):\n nex_mask = mask | (1<<i)\n # case1: make sure that each node is only traversed once\n # case2: only if we can get larger save length, we consider it.\n if nex_mask != mask and d[mask][node] + G[node][i] >= d[nex_mask][i]:\n d[nex_mask][i] = d[mask][node] + G[node][i]\n Q.append((i, nex_mask, path+[i], d[nex_mask][i]))\n\n return pathtoStr(A,G,P)\n```
| 66
| 3
|
[]
| 12
|
find-the-shortest-superstring
|
Shortest Hamiltonian Path in weighted digraph (with instructional explanation)
|
shortest-hamiltonian-path-in-weighted-di-xmce
|
1. Formulate the problem as a graph problem\nLet\'s consider each string as a node on the graph, using their overlapping range as a similarity measure, then the
|
lambdas
|
NORMAL
|
2018-11-28T03:17:36.758036+00:00
|
2018-11-28T03:17:36.758078+00:00
| 16,644
| false
|
***1. Formulate the problem as a graph problem***\nLet\'s consider each string as a node on the graph, using their overlapping range as a similarity measure, then the edge from string A to string B is defined as:\n```\n(A,B) = len(A) - overlapping(tail of A to head of B), \neg A="catg" B= "atgcatc", overlapping is "atg",which is a tail part of A, and a head part of B, therefore (A,B) = 4-3 = 1\n```\nNotice here that we must formulate the problem setup as a digraph, as (A,B)!=(B,A)\neg B="atgcatc" A="catg", overlapping is "c", so (B,A) = 7-1=6\n\nThus we can compute a distance matrix for this graph (see code below). Notice that the diagonal is always 0, and as this is a digraph, this matrix is asymmetric.\n\n***2. Using DP to find a minimum Hamiltonian cycle (which is in fact a Travelling Salesman Problem)***\nThe major steps here are:\n(1) We arbitrarily select a starting node. It doesn\'t matter which one we choose, as we are looking for a Hamiltonian cycle, so every node will be included and can be used as a starting node. Here we choose node 0.\n(2) We build a path by selecting a node as an endpoint, and build it up from there. For example,\n\n```\nWe want to compute a subpath containing {2,4,5}. We have 3 candidates here:\n2 as the endpoint, compute subproblem {4,5};\n4 as the endpoint, compute subproblem {2,5};\n5 as the endpoint, compute subprobelm {2,4};\nThe one with the minimum distance will be our choice.\n```\n\nNotice the base case here is simply a subpath of only one node i. In this case we simply return the distance from our starting node(0) to node i, this is where the pre-computed distance matrix comes in handy.\n`eg {i} = distance_matrix [0] [i]`\n\nAlso notice that I implement it as a top-down approach, a bottom up one is equally if not more efficient.\n\n***3. Convert the full tour to a path***\nWhy do we need to convert the tour to a path? This point can be subtle, as it seems that we can simply build the superstring directly from the tour, but there is a problem, our superstring might "wrap around" and fail to contain all the strings. Consider this example:\n\n```\n["catg","atgcatc"]\nThe distance matrix is\n0 1\n6 0\n```\n\nAnd the TSP algorithm will give the result of "catgcat", as the min distance is 7, and we indeed have 7 characters in the superstring, but do you see the problem here? "atgcatc" misses a "c"! This is because the "c" **wraps around** to the head of "catg". So the TSP algorithm give a correct result per se, but we need to modify it to get the correct Hamiltonian Path for our particular problem.\n\nBelow I will highlight the intuition, and the implementation favors clarity rather than efficiency.\n\nSay we\'ve found a tour, (0,2,4,3,1,0) for and input of 5 strings.\nNow there are 5 possible shortest Hamiltonian Paths as our candidates.\n`(0,2,4,3,1), (2,4,3,1,0), (4,3,1,0,2), (3,1,0,2,4), (1,0,2,4,3).`\nThe insight here is that **the length of these 5 paths may well be different**, precisely due to **the wrap around nature** of our string problem.\n\n```\nConsider this example:\n\n"catg","ttca"\n\nBoth "catgttca" and "ttcatg" will be valid Hamiltonian paths, as we only have 2 nodes here. So (1,2) and (2,1) are two valid paths.\nThe unmodified TSP might give us "catgtt" or "ttcatg", both of length 6. \n```\nNotice that for the first one, the "ca" of "ttca" wraps around to the head of "catg" as we explaned above, so "tcaa" is not actually contained in our result, but it\'s the correct tour! The second one is the one we want. **But depending our choice of starting node, we might get the first one.** That\'s why we need this extra step to convert a tour to a correct path.\nThis is, however, very straightforward, if not very efficient. We simply construct all the possible paths from the tour, and compare their length, then return the one with the min length. By this we solve the uncertainty with the starting point choice. In the original TSP, it doesn\'t matter where the salesman starts his journey, as it\'s a tour. But our superstring problem requires this small modification.\n\nBelow is the top down approach. For clarity and debugging purposes, I use a String to store the path. Arrays, tuples (if your language supports it) and any other data structure that preserves ordering will be adequate.\n\nAs I said, this is not the most efficient implementation of the TSP / Shortest Hamiltonian Path problem, but I hope this gives you an idea behind the algorithm and the subtleties of it when applied to another problem.\n\n```\nclass Solution {\n int[][] distance;\n Map<String,String> memo;\n public String shortestSuperstring(String[] A) {\n if(A.length==1) return A[0];\n buildDistanceMatrix(A);\n memo = new HashMap<>();\n //build key for the final solution, key is in the form "end:set of nodes", eg "0:1,2,3,4"\n StringBuilder builder = new StringBuilder();\n for(int i=1; i<A.length; i++){\n builder.append(i);\n builder.append(",");\n }\n builder.deleteCharAt(builder.length() - 1);\n String key = "0"+":"+builder.toString();\n \n // start top-down algo, val is in the form of "sequence;minDistance", eg "0,3,4,2,1,0;20"\n String seq = TSP(key).split(";")[0];\n String res = convertToHP(seq,A);\n return res;\n }\n \n private String convertToHP(String seq, String[]A){\n String[] tour = seq.split(",");\n int N = tour.length-1;\n int[] hamPath = new int[N];\n for(int i=0; i<N; i++){\n hamPath[i] = Integer.parseInt(tour[i]);\n }\n \n int[][] pool = new int[N][N];\n pool[0] = hamPath;\n for(int i=1; i<N; i++){\n int[]candidate = new int[N];\n for(int j=i; j<i+N; j++){\n candidate[j-i] = hamPath[j%N];\n }\n pool[i] = candidate;\n }\n int min = 1000;\n String sol = "";\n for(int[]path:pool){\n String res = buildPath(path,A);\n if(res.length()<min){\n min = res.length();\n sol = res;\n }\n }\n return sol;\n }\n \n private String buildPath(int[]path,String[]A){\n StringBuilder builder = new StringBuilder();\n for(int j=0; j<path.length-1; j++){\n int start = path[j];\n int end = path[j+1];\n int len = distance[start][end];\n builder.append(A[start].substring(0,len));\n }\n builder.append(A[path[path.length-1]]);\n return builder.toString();\n }\n \n private void buildDistanceMatrix(String[]A){\n int N = A.length;\n distance = new int[N][N];\n for(int i=0; i<N; i++){\n for(int j=0; j<N; j++){\n if(i==j) continue;\n String start = A[i];\n String end = A[j];\n for(int k=Math.min(start.length(),end.length()); k>0; k--){\n if(start.endsWith(end.substring(0,k))){\n distance[i][j] = start.length()-k;\n break;\n }\n else distance[i][j] = start.length();\n }\n }\n }\n }\n \n private String TSP(String key){\n if(memo.containsKey(key)) return memo.get(key);\n \n String[] temp = key.split(":");\n String endPointS = temp[0];\n int endPoint = Integer.parseInt(endPointS);\n \n //base case\n if(key.endsWith(":")){\n String seq = "0"+","+endPointS;\n int dist = distance[0][endPoint];\n String res = seq+";"+Integer.toString(dist);\n memo.put(key,res);\n return res;\n }\n \n String[] elements = temp[1].split(",");\n int min = 1000;\n String candidate="X";\n for(int i=0; i<elements.length; i++){\n String subKey = buildKey(elements, i);\n String[] res = TSP(subKey).split(";");\n int updatedDist = distance[Integer.parseInt(elements[i])][endPoint] + Integer.parseInt(res[1]);\n String updatedSeq = res[0] + "," + endPointS;\n if(updatedDist<min){\n min = updatedDist;\n candidate = updatedSeq;\n }\n }\n String val = candidate + ";" + Integer.toString(min);\n memo.put(key,val);\n return val;\n }\n \n private String buildKey(String[]s, int excl){\n String endPoint = s[excl];\n StringBuilder builder = new StringBuilder();\n builder.append(endPoint);\n builder.append(":");\n if(s.length==1) return builder.toString();\n \n for(String node:s){\n if(node.equals(endPoint))continue;\n builder.append(node);\n builder.append(",");\n }\n builder.deleteCharAt(builder.length() - 1);\n return builder.toString();\n }\n}\n```
| 54
| 2
|
[]
| 11
|
find-the-shortest-superstring
|
Clean python DP with explanations
|
clean-python-dp-with-explanations-by-ygt-8fyo
|
python\nclass Solution:\n def shortestSuperstring(self, A):\n """\n :type A: List[str]\n :rtype: str\n """\n # construct a
|
ygt2016
|
NORMAL
|
2018-11-18T08:46:59.930697+00:00
|
2018-11-18T08:46:59.930736+00:00
| 5,191
| false
|
```python\nclass Solution:\n def shortestSuperstring(self, A):\n """\n :type A: List[str]\n :rtype: str\n """\n # construct a directed graph\n # node i => A[i]\n # weights are represented as an adjacency matrix:\n # shared[i][j] => length saved by concatenating A[i] and A[j]\n n = len(A)\n shared = [[0] * n for _ in range(n)]\n for i in range(n):\n for j in range(n):\n for k in range(min(len(A[i]), len(A[j])), -1, -1):\n if A[i][-k:] == A[j][:k]:\n shared[i][j] = k\n break\n\n # The problem becomes finding the shortest path that visits all nodes exactly once.\n # Brute force DFS would take O(n!) time.\n # A DP solution costs O(n^2 2^n) time.\n # \n # Let\'s consider integer from 0 to 2^n - 1. \n # Each i contains 0-n 1 bits. Hence each i selects a unique set of strings in A.\n # Let\'s denote set(i) => {A[j] | j-th bit of i is 1}\n # dp[i][k] => shortest superstring of set(i) ending with A[k]\n #\n # e.g. \n # if i = 6 i.e. 110 in binary. dp[6][k] considers superstring of A[2] and A[1].\n # dp[6][1] => the shortest superstring of {A[2], A[1]} ending with A[1].\n # For this simple case dp[6][1] = concatenate(A[2], A[1])\n dp = [[\'\'] * 12 for _ in range(1 << 12)]\n for i in range(1 << n):\n for k in range(n):\n # skip if A[k] is not in set(i) \n if not (i & (1 << k)):\n continue\n # if set(i) == {A[k]}\n if i == 1 << k:\n dp[i][k] = A[k]\n continue\n for j in range(n):\n if j == k:\n continue\n if i & (1 << j):\n # the shortest superstring if we remove A[k] from the set(i)\n s = dp[i ^ (1 << k)][j]\n s += A[k][shared[j][k]:]\n if dp[i][k] == \'\' or len(s) < len(dp[i][k]):\n dp[i][k] = s\n\n min_len = float(\'inf\')\n result = \'\'\n\n # find the shortest superstring of all candidates ending with different string\n for i in range(n):\n s = dp[(1 << n) - 1][i]\n if len(s) < min_len:\n min_len, result = len(s), s\n return result\n```\t\n\t\t
| 37
| 1
|
[]
| 6
|
find-the-shortest-superstring
|
C++ solution in less than 30 lines
|
c-solution-in-less-than-30-lines-by-reim-na8y
|
This solution is less than 30 lines if comments are excluded.\nInstead of an int dp matrix, I use string dp matrix directly. Therefore the reconstruction is a l
|
reimu
|
NORMAL
|
2018-11-18T21:28:23.099007+00:00
|
2018-11-18T21:28:23.099072+00:00
| 5,827
| false
|
This solution is less than 30 lines if comments are excluded.\nInstead of an int dp matrix, I use string dp matrix directly. Therefore the reconstruction is a little bit easier at the expense of more memory use (but same complexity if only n is counted). The string dp matrix idea is from the jave solution of @uwi. \n\n```\n string shortestSuperstring(vector<string>& A) {\n int n = A.size();\n // dp[mask][i] : min superstring made by strings in mask,\n // and the last one is A[i]\n vector<vector<string>> dp(1<<n,vector<string>(n));\n vector<vector<int>> overlap(n,vector<int>(n,0));\n \n // 1. calculate overlap for A[i]+A[j].substr(?)\n for(int i=0; i<n; ++i) for(int j=0; j<n; ++j) if(i!=j){\n for(int k = min(A[i].size(), A[j].size()); k>0; --k)\n if(A[i].substr(A[i].size()-k)==A[j].substr(0,k)){\n overlap[i][j] = k; \n break;\n }\n }\n // 2. set inital val for dp\n for(int i=0; i<n; ++i) dp[1<<i][i] += A[i];\n // 3. fill the dp\n for(int mask=1; mask<(1<<n); ++mask){\n for(int j=0; j<n; ++j) if((mask&(1<<j))>0){\n for(int i=0; i<n; ++i) if(i!=j && (mask&(1<<i))>0){\n string tmp = dp[mask^(1<<j)][i]+A[j].substr(overlap[i][j]);\n if(dp[mask][j].empty() || tmp.size()<dp[mask][j].size())\n dp[mask][j] = tmp;\n }\n }\n }\n // 4. get the result\n int last = (1<<n)-1;\n string res = dp[last][0];\n for(int i=1; i<n; ++i) if(dp[last][i].size()<res.size()){\n res = dp[last][i];\n }\n return res;\n }\n```
| 31
| 3
|
[]
| 3
|
find-the-shortest-superstring
|
LeetCode Weekly Contest 111 screencast (rank 12)
|
leetcode-weekly-contest-111-screencast-r-g72c
|
https://www.youtube.com/watch?v=4VzpJzaY2l4
|
cuiaoxiang
|
NORMAL
|
2018-11-18T04:26:09.109072+00:00
|
2018-11-18T04:26:09.109114+00:00
| 4,608
| false
|
https://www.youtube.com/watch?v=4VzpJzaY2l4
| 27
| 7
|
[]
| 13
|
find-the-shortest-superstring
|
[C++] TSP - Hamiltonian Path (Not tour) - Simple code
|
c-tsp-hamiltonian-path-not-tour-simple-c-oz1r
|
\n#define INF 0x3f3f3f3f\n\nclass Solution {\n int VISITED_ALL, n;\n vector < vector < int > > dist, path, dp;\npublic:\n int calcDist(string a, string
|
vismit2000
|
NORMAL
|
2021-01-17T08:04:37.957840+00:00
|
2021-01-17T08:06:33.461521+00:00
| 3,448
| false
|
```\n#define INF 0x3f3f3f3f\n\nclass Solution {\n int VISITED_ALL, n;\n vector < vector < int > > dist, path, dp;\npublic:\n int calcDist(string a, string b){\n for(int i = 0; i < a.length(); i++)\n if(b.rfind(a.substr(i), 0) == 0)\n return b.length() - (a.length() - i);\n return b.length();\n }\n \n int tsp(int mask, int pos){\n if(mask == VISITED_ALL)\n return 0;\n if(dp[mask][pos] != -1)\n return dp[mask][pos];\n \n int ans = INF, best;\n \n for(int city = 0; city < n; city++){\n if((mask & (1 << city)) == 0){\n int result = dist[pos][city] + tsp(mask | (1 << city), city);\n if(result < ans){\n ans = result;\n best = city;\n }\n }\n }\n path[mask][pos] = best;\n return dp[mask][pos] = ans;\n }\n \n string constructPath(vector < string > &A, int k){\n int curr = k;\n string result = A[k];\n int mask = (1 << k);\n int parent = path[mask][k];\n while(parent != -1){\n result += A[parent].substr(A[parent].length() - dist[curr][parent]);\n mask |= (1 << parent);\n curr = parent;\n parent = path[mask][parent];\n }\n return result;\n }\n \n string shortestSuperstring(vector<string>& A) {\n n = A.size();\n VISITED_ALL = (1 << n) - 1;\n \n dist.assign(n, vector < int > (n, 0));\n \n for(int i = 0; i < n; i++)\n for(int j = 0; j < n; j++)\n dist[i][j] = calcDist(A[i], A[j]);\n \n int ansLen = INF;\n string ans;\n \n // for different starting nodes\n for(int k = 0; k < n; k++){\n path.assign((1 << n), vector < int > (n, -1));\n dp.assign((1 << n), vector < int > (n, -1));\n\n tsp((1 << k), k);\n \n string result = constructPath(A, k);\n // cout << result << endl;\n if(result.length() < ansLen){\n ans = result;\n ansLen = result.length();\n }\n }\n return ans;\n }\n};\n```
| 21
| 0
|
['Dynamic Programming', 'C', 'Bitmask', 'C++']
| 4
|
find-the-shortest-superstring
|
Python Recursion with Memory
|
python-recursion-with-memory-by-infinute-xips
|
Many thanks to @ygt2016. The original code is here. I converted the code to recursion, which might be a little easier to understand. Hope this is helpful. \nThe
|
infinute
|
NORMAL
|
2019-03-10T22:52:37.798229+00:00
|
2019-03-10T22:52:37.798291+00:00
| 2,051
| false
|
Many thanks to @ygt2016. The original code is [here](https://leetcode.com/problems/find-the-shortest-superstring/discuss/195077/Clean-python-DP-with-explanations). I converted the code to recursion, which might be a little easier to understand. Hope this is helpful. \nThe general idea is:\n1. Build a (dense) graph whose node `i` is the `i`th word in `A`. The weight on the arc `i-->j` is `graph[i][j]`, representing the length of the overlapping part between `A[i]` and `A[j]`.\n2. Then, our goal is to find an ordering of the words (nodes) `0,1,2,...,n-1` such that when the words are concatenated in this order, the total length is the smallest. Define the state as `(i,k)`, where `i` is a number whose binary form indicates which nodes are included in the ordering; `k` denotes the last node in the ordering. Let `memo[i,k]` be the shortest superstring when concatenating the words represented by the bits in `i` and with `k` as the last word. (You may call `memo` as `dp`, if you want.)\n3. The recursion part is `memo[i,k]=min(i ^ (1 << k), j)`, for all the bits `j` in the ordering `i` excluding `k` itself.\n4. Finally, what we are looking for is just the best result within `memo[(i << n) - 1, k]`, for all the `k` in `{0,1,2,...,n-1}`.\n```\nclass Solution:\n def shortestSuperstring(self, A: List[str]) -> str:\n n = len(A)\n # Building the graph\n graph = [[0] * n for _ in range(n)]\n for i, word1 in enumerate(A):\n for j, word2 in enumerate(A):\n if i == j: continue\n for k in range(min(len(word1), len(word2)))[::-1]:\n if word1[-k:] == word2[:k]:\n graph[i][j] = k\n break\n \n # Recursion. i is a mask to represent the ordering. k is the last node in the ordering.\n memo = {}\n def search(i, k):\n if (i, k) in memo: return memo[i, k]\n if not (i & (1 << k)): return \'\'\n if i == (1 << k): return A[k]\n memo[i, k] = \'\'\n for j in range(n):\n if j != k and i & (1 << j):\n candidate = search(i ^ (1 << k), j) + A[k][graph[j][k]:]\n if memo[i, k] == \'\' or len(candidate) < len(memo[i, k]):\n memo[i, k] = candidate\n return memo[i, k]\n \n # Finding the best\n res = \'\'\n for k in range(n):\n candidate = search((1 << n) - 1, k)\n if res == \'\' or len(candidate) < len(res):\n res = candidate\n return res \n```
| 17
| 0
|
[]
| 3
|
find-the-shortest-superstring
|
[C++] Easy to understand-Simple code
|
c-easy-to-understand-simple-code-by-i_an-th4c
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
i_anurag_mishra
|
NORMAL
|
2023-07-30T15:24:12.696066+00:00
|
2023-07-30T15:24:12.696090+00:00
| 1,687
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n vector<vector<string>> req;\n string merge(string &a, string &b) // a is followed by b (ab)\n {\n int n=a.size(), m=b.size(), len=1, idx=0;\n while(len<=min(n, m))\n {\n if(a.substr(n-len)==b.substr(0, len))\n {\n idx=len;\n }\n len++;\n }\n string res=b.substr(idx);\n return res;\n }\n string solve(vector<string> &words, int prev, int mask, int n, vector<vector<string>> &dp)\n {\n if(dp[prev][mask]!="") return dp[prev][mask];\n string res="";\n int minLen=INT_MAX;\n for(int i=0; i<n; i++)\n {\n if(mask&(1<<i)) continue;\n string temp=req[prev][i]+solve(words, i, mask|(1<<i), n, dp);\n if(temp.size()<minLen)\n {\n minLen=temp.size();\n res=temp;\n }\n }\n return dp[prev][mask]=res;\n }\npublic:\n string shortestSuperstring(vector<string>& words) \n {\n int n=words.size();\n req.resize(n, vector<string> (n, ""));\n vector<vector<string>> dp(n, vector<string> ((1<<(n+1)), ""));\n for(int i=0; i<n; i++)\n {\n for(int j=0; j<n; j++)\n {\n if(i==j) continue;\n req[i][j]=merge(words[i], words[j]);\n }\n } \n string ans="";\n int minLen=INT_MAX;\n int mask=0;\n for(int i=0; i<n; i++)\n {\n string temp=words[i]+solve(words, i, mask|(1<<i), n, dp);\n if(temp.size()<minLen)\n {\n minLen=temp.size();\n ans=temp;\n }\n } \n return ans;\n }\n};\n```
| 16
| 0
|
['Dynamic Programming', 'Memoization', 'Bitmask', 'C++']
| 4
|
find-the-shortest-superstring
|
Rewrite the official solution in C++
|
rewrite-the-official-solution-in-c-by-vi-y7wd
|
Just rewrite the official solution in C++\n\n\nstring shortestSuperstring(vector<string>& A) {\n int n = A.size();\n \n vector<vector<int>>
|
victor_fw
|
NORMAL
|
2018-11-28T07:53:56.943343+00:00
|
2018-11-28T07:53:56.943384+00:00
| 2,684
| false
|
Just rewrite the official solution in C++\n\n```\nstring shortestSuperstring(vector<string>& A) {\n int n = A.size();\n \n vector<vector<int>> overlaps(n, vector<int>(n));\n for (int i = 0; i < n; ++i) {\n for (int j = 0; j < n; ++j) {\n int m = min(A[i].size(), A[j].size());\n for (int k = m; k >= 0; --k) {\n if (A[i].substr(A[i].size() - k) == A[j].substr(0, k)) {\n overlaps[i][j] = k;\n break;\n }\n }\n }\n }\n \n // dp[mask][i] = most overlap with mask, ending with ith element (ith \u4E5F\u5305\u542B\u5728\u4E86mask\u91CC\u9762)\n vector<vector<int>> dp(1<<n, vector<int>(n, 0));\n vector<vector<int>> parent(1<<n, vector<int>(n, -1));\n \n for (int mask = 0; mask < (1<<n); ++mask) {\n //\u4EE5\u4E0B\u5FAA\u73AF\u662F\u4E3A\u4E86\u8BA1\u7B97dp[mask][bit]\n for (int bit = 0; bit < n; ++bit) {\n if (((mask>>bit)&1) > 0) {//\u8BF4\u660Ebit\u4F4D\u5728mask\u91CC\u9762\uFF0C\u6B64\u65F6dp[mask][bit]\u624D\u6709\u610F\u4E49\n int pmask = mask^(1<<bit);//\u8FD9\u4E00\u6B65\u662F\u4E3A\u4E86\u628Abit\u4F4D\u4ECEmask\u91CC\u9762\u53BB\u6389\n if (pmask == 0) continue;//\u5982\u679Cmask\u91CC\u9762\u53EA\u6709\u4E00\u4E2A\u8BCD\uFF0C\u90A3\u4E48\u8DF3\u8FC7\n for (int i = 0; i < n; ++i) {\n if (((pmask>>i)&1) > 0) {//\u5982\u679Cpmask\u91CC\u9762\u5305\u542B\u4E86\u7B2Ci\u4F4D\uFF0C\u90A3\u4E48\u8BA1\u7B97\u4EE5i\u7ED3\u5C3E\u7684pmask\uFF0C\u518D\u63A5\u4E0Abit\u4F4D\n int val = dp[pmask][i] + overlaps[i][bit];\n if (val > dp[mask][bit]) {//\u5982\u679C\u65B0\u7B97\u51FA\u6765\u7684overlap\u6BD4\u8F83\u5927\uFF0C\u90A3\u4E48\u66FF\u6362\u539F\u6709overlap\n dp[mask][bit] = val;\n parent[mask][bit] = i;//\u4FDD\u5B58\u8FD9\u79CD\u60C5\u51B5\u4E0B\u4EE5bit\u7ED3\u5C3E\u7684\u524D\u4E00\u4E2A\u8BCD\u3002\n }\n }\n }\n }\n }\n }\n \n vector<int> perm;\n vector<bool> seen(n);\n int mask = (1<<n) - 1;\n \n int p = 0;//\u5148\u8BA1\u7B97\u51FA\u7B54\u6848\u7684\u6700\u540E\u4E00\u4E2A\u5355\u8BCD\n for (int i = 0; i < n; ++i) {\n if (dp[(1<<n) - 1][i] > dp[(1<<n) - 1][p]) {\n p = i;\n }\n }\n \n //\u901A\u8FC7parent\u6570\u7EC4\u4F9D\u6B21\u56DE\u6EAF\u51FA\u6700\u540E\u4E00\u4E2A\u5355\u8BCD\u662Fp\u8FD9\u79CD\u60C5\u51B5\u4E0B\uFF0C\u524D\u9762\u6240\u6709\u7684\u6392\u5217\n while (p != -1) {\n perm.push_back(p);\n seen[p] = true;\n int p2 = parent[mask][p];\n mask ^= (1<<p);//\u4ECEmask\u91CC\u9762\u79FB\u8D70p\n p = p2;\n }\n \n //\u7531\u4E8E\u56DE\u6EAF\u51FA\u6765\u7684\u662F\u53CD\u7684\uFF0C\u5012\u4E00\u4E0B\n reverse(perm.begin(), perm.end());\n \n //\u52A0\u4E0A\u6CA1\u6709\u51FA\u73B0\u7684\u5355\u8BCD\n for (int i = 0; i < n; ++i) {\n if (!seen[i]) {\n perm.push_back(i);\n }\n }\n \n string ans = A[perm[0]];\n for (int i = 1; i < n; ++i) {\n int overlap = overlaps[perm[i - 1]][perm[i]];\n ans += A[perm[i]].substr(overlap);\n }\n \n return ans;\n \n }\n```\n
| 16
| 1
|
[]
| 1
|
find-the-shortest-superstring
|
JS, Python | Detailed Traveling Salesperson Problem Solution w/ Explanation
|
js-python-detailed-traveling-salesperson-ygky
|
(Note: This is part of a series of Leetcode solution explanations. If you like this solution or find it useful, please upvote this post.)\n\n---\n\n#### Idea:\n
|
sgallivan
|
NORMAL
|
2021-05-26T11:41:10.526758+00:00
|
2021-05-26T11:42:43.561443+00:00
| 1,960
| false
|
*(Note: This is part of a series of Leetcode solution explanations. If you like this solution or find it useful,* ***please upvote*** *this post.)*\n\n---\n\n#### ***Idea:***\n\n**Overview:**\n - _Build a map of **suffixes**._\n - _Use **suffixes** to help build the **edges** matrix of character overlaps in only **O(N * L) time**._\n - _Use a **TSP** approach to fill the **dp** matrix with the most overlaps per subset/endpoint combination._\n - _Use **bit manipulation** to define each subset with just an integer._\n - _Use **bit manipulation** to store the savings and its source node in a single int for each **dp** entry, rather than requiring a second matrix._\n - _Rebuild the circular **path** once the final **dp** result is found by backtracking previous nodes._\n - _Find the best place to cut the circular **path** into a linear **ans**._\n - _Combine the words in proper order into a single string, trimming off the overlaps, then **return** the string._\n\n---\n\n**Detailed Explanation:**\nThis is an example of the classic **Traveling Salesperson Problem** (**TSP**). In the TSP, a salesperson wants to find the best route to visit **N** cities once each while ending up back at the starting point. This is also the equivalent of finding the best possible **Hamiltonian cycle** of a graph with weighted edges. With a brute-force approach, this would mean checking **N!** permutations.\n\nLike most factorial solutions, however, the brute force TSP solution wastes time recalculating subproblems, which makes it the ideal candidate for a **dynamic programming** (**DP**) approach. If we can identify the best possible route of a subset of **N** and store that in a DP array (**dp**), we can avoid having to redo that calculation again and use these values to build up to our eventual solution.\n\n---\n\n**Build Suffix Map:**\nFirst, though, we\'ll need to detour a bit, because a TSP relies upon defined "weights" or "distances" between the nodes in our graph. Unlike most other graph problems, we won\'t want to make a map of the edges, because every node is connected to every other node. Instead, we should define **edges** as an **N * N** matrix.\n\nTo build up **edges**, we\'ll need to compare each word to every other word and find the maximum overlap. The value at **edges[i][j]** will then represent the amount of overlap we\'ll see by placing **words[i]** before **words[j]**. Since direction matters (**word1 -> word2** will not generally have the same result as **word2 -> word1**), this problem is actually an **asymmetrical TSP** (**aTSP**).\n\n_(**Note**: Using higher-is-better overlap for **edges** rather than lower-is-better **word** length will allow us to fill both **edges** and **dp** with **0**s as a default, rather than **MAX_INT** values, which will be useful later.)_\n\nNormally this process would have a **time complexity** of **N * (N-1) * (word.length-1)**, or **O(N^2 * L)**, but we can shorten this to **O(N * L)** by first making a **frequency map** of all the **suffixes**, then checking all prefixes against **suffixes** before updating matching combinations in **edges**.\n\n_(**Note**: A possible optimization here would be to use this process to identify any words that share no suffixes or prefixes with any other word and extract them directly to our answer (**ans**). Since the next part will include time complexity of **2^N * N^2**, any reduction in **N** will be well worth the extra processing. This optimization is not reflected in the code below, however.)_\n\n---\n\n**DP Matrix Setup:**\nNow, back to the DP array of subset solutions. Since these subsets will be chained to form the whole path, we\'ll require a separate **dp** entry not just for each subset, but each combination of endpoints for each subset. For example, storing the results for a subset with a length of **5** would require **20** entries, because there are **20** possible combinations (**5 * 4**) of endpoints.\n\nWe can simplify this quite a bit if we instead make one endpoint a constant for every entry in **dp**, and build up longer subsets from the results of shorter subsets. This will normally lock the end of our combined string of words, but because the TSP describes a circular route, it doesn\'t ultimately matter which node we choose as the designated endpoint. We\'ll choose node **M** (**M = N - 1**) for the sake of simplicity.\n\nWith one of the endpoints assumed, we can now define each entry in **dp** by only two pieces of information instead of three: **curr** will represent the other, more recent endpoint, and **currSet** will represent the entire current subset of nodes, including **curr**. In order to use **currSet** to identify a unique subset as only one piece of data, we can utilize **bit manipulation** to store the presence of up to **N** nodes in **N bits** of an integer. This is also convenient because the necessary values for **currSet** will just happen to range from **0** to **2^N** with no wasted indices in **dp**.\n\n_(**Note**: By iterating upward from **0** to **2^N**, we will guarantee that any **dp** entries upon which we need to base the current one will have already been completed, as each possible previous **dp** entry will have the same bit value as the current, except for one bit changed from a **1** to a **0**, which will always result in a lower value.)_\n\nIn fact, since we\'ve assumed our final endpoint for the circle, that also means we\'ve assumed the same node as the very beginning of the circle as well, which means that none of the subsets in **dp** can contain node **M**, which means we only need to iterate **currSet** up to **2^M** instead of **2^N** (avoiding any subset that includes **M**), which more than halves both the **time** and **space complexity**.\n\n---\n\n**Solving for a DP Entry:**\nAs previously stated, each **dp** entry is defined as **dp[curr][currSet] = result**. The **result** will be the best possible overlap for a path starting at **curr**, going through all the nodes encoded in **currSet**, and then ending on node **M**. We find this best **result** by attempting each possible route from the different subsets of **currSet** that are one node shorter.\n\nFor example, let\'s consider **dp[1][{1,2,3,4}]**, which represents the best path taken on a graph of nodes **1-4**, ending on **1**. (The other end of the graph is node **M**, but we don\'t include it in the range because it\'s fixed.) This condition can be obtained by starting at **dp[2][{2,3,4}]** and then moving from **2** to **1** (**+edges[2][1]**), or starting at **dp[3][{2,3,4}]** and then moving from **3** to **1** (**+edges[3][1]**), or starting at **dp[4][{2,3,4}]** and then moving from **4** to **1** (**+edges[4][1]**). The largest combined overlap of those three routes will be the result stored in **dp[1][{1,2,3,4}]**.\n\nSo to evaluate that, we can define a helper function (**solve**). We\'ll just remove **curr** from **currSet** with bit manipulation to form the previous set (**prevSet**). Then we iterate through each node (**prev**) in **prevSet**, find out the **overlap** when using that path, and keep track of the best overlap (**bestOverlap**) seen so far and its corresponding **prev** node (**bestPrev**). The helper **solve** will then **return** these values to form the new **dp** entry.\n\nOne set of edge cases to deal with occurs when we\'re trying to **solve** for **dp[x][{x}]** (ie, **dp[1][{1}]** or **dp[2][{2}]**, etc.), when **curr** is the only node in **currSet**. In this situation, **prevSet** would evualate to a **null** set, but we have to remember that there\'s a hidden node **M** at the end of each path we\'re building in **dp**. So if we find that **prevSet** is empty, then **curr** represents the first node after **M**, and therefore the only possible path is moving to **curr** from node **M**, so we should **return** **edges[M][curr]** as **bestOverlap** and **M** as **bestPrev**.\n\n---\n\n**Storing the Path:**\nOnce **solve** returns its results, we _could_ store **bestOverlap** in **dp** and use another matrix to store **bestPrev**, but why double the space required? A max word length of **20** means the max overlap per word combination is **19**, and with up a max subset length in **dp** of **11**, **bestOverlap** will top out at **209**, which fits in only **8 bits** of data. The **bestPrev** value only goes up to **M** (max of **11**), which is only **4 bits** of data. So rather than using _two_ very large (**M * 2^M**) matrices, we can combine **bestOverlap** and **bestPrev** into one integer with bit manipulation before we insert it into **dp**.\n\n\n**Rebuilding the Path and Building the Answer:**\nNow that we\'ve fully built up **dp**, we\'ll need to run **solve** one more time to find the best result for the final link back to node **M** as **curr**, completing the circle. We don\'t care about the **bestOverlap** this time, only the **bestPrev**, so that we can begin backtracking through **dp** entries and piece together the full cicrular **path**.\n\nSince the problem is asking us for the shortest _linear_ **path**, not the shortest _circular_ **path**, we\'ll need to sever the **path** between two of the nodes. As the link that we sever will no longer be able to **overlap**, we\'ll want to choose the link with the least amount of **overlap**.\n\nSo as we backtrack through **dp** to build the **path**, we should also keep track of the lowest **overlap** found (**lowOverlap**) as well as the index of the second half of the link (**bestStart**) to use as the first node in our answer (**ans**). We should also remember to fill **path** from back to front, because we\'re backtracking through the route.\n\nNow that we\'ve built **path** with the indexes in proper order, we can use it to build **ans**. We\'ll want to iterate through **path** using a **modulo operator**, so that we can begin at **bestStart** and circle back around to **bestStart + M**. At each step, we can consult **edges** and slice off the appropriate amount of each **word** before adding it to **ans**.\n\nAnd once we\'ve finished building **ans**, we can join it together in a string and **return** it.\n\n---\n\n - _**Time Complexity: O(2^M * M^2 + N * L)** where **N** is the length of the **words** array, **M** is **N - 1**, and **L** is the average length of the words in **words**_\n - _Building **Suffixes** Map: **O(N * L)**_\n - _Building **Edges** Matrix: **O(N * L)**_\n - _Building **DP** Matrix: **O(2^M * M^2)**_\n - _Building **Path** & **Ans**: **O(N * L)**_\n - _**Space Complexity: O(2^M * M + N * (N + L))**_\n - _**Suffixes** Map: **O(N * L)**_\n - _**Edges** Matrix: **O(N^2)**_\n - _**DP** Matrix: **O(2^M * M)**_\n - _**Path** & **Ans**: **O(N)**_\n\n---\n\n#### ***Javascript Code:***\n\nThe best result for the code below is **92ms / 42.4MB** (beats 100% / 100%).\n```javascript\nvar shortestSuperstring = function(words) {\n let N = words.length, suffixes = new Map(),\n edges = Array.from({length: N}, () => new Uint8Array(N))\n \n // Build the edge graph\n for (let i = 0, word = words; i < N; i++) {\n let word = words[i]\n for (let k = 1; k < word.length; k++) {\n let sub = word.slice(k)\n if (suffixes.has(sub)) suffixes.get(sub).push(i)\n else suffixes.set(sub, [i])\n }\n }\n for (let j = 0; j < N; j++) {\n let word = words[j]\n for (let k = 1; k < word.length; k++) {\n let sub = word.slice(0,k)\n if (suffixes.has(sub))\n for (let i of suffixes.get(sub))\n edges[i][j] = Math.max(edges[i][j], k)\n }\n }\n \n // Initialize DP array\n let M = N - 1, \n dp = Array.from({length: M}, () => new Uint16Array(1 << M))\n \n // Helper function to find the best value for dp[curr][currSet]\n // Store the previous node with bit manipulation for backtracking\n const solve = (curr, currSet) => {\n let prevSet = currSet - (1 << curr), bestOverlap = 0, bestPrev\n if (!prevSet) return (edges[M][curr] << 4) + M\n for (let prev = 0; prev < M; prev++)\n if (prevSet & 1 << prev) {\n let overlap = edges[prev][curr] + (dp[prev][prevSet] >> 4)\n if (overlap >= bestOverlap)\n bestOverlap = overlap, bestPrev = prev\n }\n return (bestOverlap << 4) + bestPrev\n }\n \n // Build DP using solve\n for (let currSet = 1; currSet < 1 << M; currSet++)\n for (let curr = 0; curr < N; curr++)\n if (currSet & 1 << curr) \n dp[curr][currSet] = solve(curr, currSet)\n \n // Join the ends at index M\n let curr = solve(M, (1 << N) - 1) & (1 << 4) - 1\n \n // Build the circle by backtracking path info from dp\n // and find the best place to cut the circle\n let path = [curr], currSet = (1 << M) - 1,\n bestStart = 0, lowOverlap = edges[curr][M], prev\n while (curr !== M) {\n prev = dp[curr][currSet] & (1 << 4) - 1, currSet -= 1 << curr\n let overlap = edges[prev][curr]\n if (overlap < lowOverlap)\n lowOverlap = overlap, bestStart = N - path.length\n curr = prev, path.unshift(curr)\n }\n \n // Build and return ans by cutting the circle at bestStart\n let ans = []\n for (let i = bestStart; i < bestStart + M; i++) {\n let curr = path[i%N], next = path[(i+1)%N], word = words[curr]\n ans.push(word.slice(0, word.length - edges[curr][next]))\n }\n ans.push(words[path[(bestStart+M)%N]])\n return ans.join("")\n};\n```\n\n---\n\n#### ***Python Code:***\n\nThe best result for the code below is **288ms / 14.4MB** (beats 91% / 92%).\n```python\nclass Solution:\n def shortestSuperstring(self, words: List[str]) -> str:\n N, suffixes = len(words), defaultdict(list)\n edges = [[0] * N for _ in range(N)]\n \n # Build the suffixes map and edge graph\n for i in range(N):\n for k in range(1, len(words[i])):\n suffixes[words[i][k:]].append(i)\n for j in range(N):\n for k in range(1, len(words[j])):\n for i in suffixes[words[j][:k]]:\n edges[i][j] = max(edges[i][j], k)\n \n # Initialize DP array\n M = N - 1\n dp = [[0] * (1 << M) for _ in range(M)]\n \n # Helper function to find the best value for dp[curr][currSet]\n # Store the previous node with bit manipulation for backtracking\n def solve(curr: int, currSet: int) -> int:\n prevSet, bestOverlap, bestPrev = currSet - (1 << curr), 0, 0\n if not prevSet: return (edges[M][curr] << 4) + M\n for prev in range(M):\n if prevSet & 1 << prev:\n overlap = edges[prev][curr] + ((dp[prev][prevSet]) >> 4)\n if overlap >= bestOverlap:\n bestOverlap, bestPrev = overlap, prev\n return (bestOverlap << 4) + bestPrev\n \n # Build DP using solve\n for currSet, curr in product(range(1, 1 << M), range(M)):\n if currSet & 1 << curr:\n dp[curr][currSet] = solve(curr, currSet)\n \n # Join the ends at index M\n curr = solve(M, (1 << N) - 1) & ((1 << 4) - 1)\n \n # Build the circle by backtracking path info from dp\n # and find the best place to cut the circle\n path, currSet = [curr], (1 << M) - 1\n bestStart, lowOverlap, prev = 0, edges[curr][M], 0\n while curr != M:\n prev = dp[curr][currSet] & ((1 << 4) - 1)\n currSet -= 1 << curr\n overlap = edges[prev][curr]\n if overlap < lowOverlap:\n lowOverlap, bestStart = overlap, N - len(path)\n curr = prev\n path[:0] = [curr]\n \n # Build and return ans by cutting the circle at bestStart\n ans = []\n for i in range(bestStart, bestStart+M):\n curr, nxt = path[i%N], path[(i+1)%N]\n word = words[curr]\n ans.append(word[:len(word)-edges[curr][nxt]])\n ans.append(words[path[(bestStart+M)%N]])\n return "".join(ans)\n```
| 14
| 0
|
['Python', 'JavaScript']
| 0
|
find-the-shortest-superstring
|
A* search, python implementation 64ms pass
|
a-search-python-implementation-64ms-pass-xub9
|
As the problem is almost as difficult as the traveling salesman problem, I think a good pruning method is necessary.\nTherefore, I tried the A search algorithms
|
hwp
|
NORMAL
|
2019-01-18T16:15:03.959208+00:00
|
2019-01-18T16:15:03.959278+00:00
| 1,383
| false
|
As the problem is almost as difficult as the traveling salesman problem, I think a good pruning method is necessary.\nTherefore, I tried the A* search algorithms.\n\nHere is the idea:\n\n1. Imagine a graph. Each node is a sequence of a subset of words.\n2. Node *x* is connected to node *y* by appending one word *i* to *x*. The weight of the edge is the cost of appending the word *i*.\n3. The start is the emtpy sequence *[]*.\n4. The goal is the set of nodes that contains all words.\n5. Search the shortest path from start to goal.\n6. Based on the end node, we can construct the superstring according to the sequence.\n\nThe graph is huge. How do we search? Use A*.\n\n7. **Heuristics**: we can estimate the lower bound of the cost of each node to the goal by **summing up the minimum possible appending cost of all remaining words**.\n8. To be more specific, the minimum possible appending cost of a word is the number of extra letters of appending this word to any other word. This can be computed at first.\n\nHers is the solution implmented in python. It passes with 64 ms and is faster than 100.00% of other python solutions.\n\n```\nfrom heapq import heappush, heappop\n\ndef dist(v, w, eq):\n if eq:\n return 10000\n else:\n for i in xrange(1, len(w)):\n if v.endswith(w[:-i]):\n return i\n return len(w)\n\ndef construct_seq(s, d, w):\n t = w[s[0]]\n for i in xrange(1, len(s)):\n t = t + w[s[i]][-d[s[i-1]][s[i]]:]\n return t\n\ndef heuristic(x, mdj):\n return sum(mdj[i] for i in xrange(len(x)) if x[i] == 0)\n\ndef adjacent_nodes(x):\n ret = []\n for i in xrange(len(x)):\n if x[i] == 0:\n y = list(x)\n y[i] = 1\n ret.append((i, tuple(y)))\n return ret\n \nclass Solution(object):\n def shortestSuperstring(self, A):\n """\n :type A: List[str]\n :rtype: str\n """\n n = len(A)\n \n # special case\n if n == 1:\n return A[0]\n # assert n > 1\n \n # distance between words\n # dij := the cost in addition to add j after i\n dij = [[dist(A[i], A[j], i == j) for j in xrange(n)] for i in xrange(n)]\n \n # minimum cost to add j\n mdj = [min(dij[i][j] for i in xrange(n)) for j in xrange(n)]\n \n # A* search\n # init\n q = [] # priority queue with estimated cost\n for i in xrange(n):\n x = tuple(1 if j == i else 0 for j in xrange(n))\n g = len(A[i]) # actual cost from start\n h = heuristic(x, mdj) # lower bound of cost till the goal\n heappush(q, (g + h, g, h, x, [i]))\n \n best_f = None\n best_p = None\n while len(q) > 0:\n # f, g, h, node, path\n f, g, h, x, p = heappop(q)\n \n if best_f is not None and f >= best_f:\n break\n \n for j, y in adjacent_nodes(x):\n gy = g + dij[p[-1]][j]\n py = p + [j]\n \n if sum(y) == n: # is goal\n if best_f is None or gy < best_f:\n best_f = gy\n best_p = py\n else:\n hy = heuristic(y, mdj)\n heappush(q, (gy + hy, gy, hy, y, py))\n \n return construct_seq(best_p, dij, A)\n```\n\nI don\'t know exactly the complexity... Someone is interested in helping me?
| 9
| 0
|
[]
| 2
|
find-the-shortest-superstring
|
💥 TypeScript | Runtime beats 100.00%, Memory beats 75.00% [EXPLAINED]
|
typescript-runtime-beats-10000-memory-be-apjw
|
Intuition\nI need to form the shortest string containing all given words by overlapping them as much as possible. It\'s like fitting words together with maximum
|
r9n
|
NORMAL
|
2024-09-10T21:22:44.840935+00:00
|
2024-09-10T21:22:44.840961+00:00
| 118
| false
|
# Intuition\nI need to form the shortest string containing all given words by overlapping them as much as possible. It\'s like fitting words together with maximum overlap to minimize the total length.\n\n\n# Approach\nEach bit in the mask tracks which words are included. I calculate the overlap between every word pair and use DP to combine words in the most efficient order. Then, I reconstruct the shortest superstring from the DP results.\n\n\n# Complexity\n- Time complexity:\nO(n^2 * 2^n * l), where n is the number of words and l is the average word length.\n\n\n- Space complexity:\nO(n * 2^n) for storing DP and paths.\n\n\n# Code\n```typescript []\nfunction shortestSuperstring(words: string[]): string {\n const n = words.length;\n \n // Step 1: Calculate the overlap between each pair of words\n const overlap: number[][] = Array.from({ length: n }, () => Array(n).fill(0));\n for (let i = 0; i < n; i++) {\n for (let j = 0; j < n; j++) {\n if (i !== j) {\n overlap[i][j] = getOverlap(words[i], words[j]);\n }\n }\n }\n\n // Step 2: Initialize DP and parent tables\n const dp: number[][] = Array.from({ length: 1 << n }, () => Array(n).fill(Infinity));\n const parent: number[][] = Array.from({ length: 1 << n }, () => Array(n).fill(-1));\n\n for (let i = 0; i < n; i++) {\n dp[1 << i][i] = words[i].length;\n }\n\n // Step 3: Fill DP table using bitmasking\n for (let mask = 1; mask < (1 << n); mask++) {\n for (let i = 0; i < n; i++) {\n if ((mask & (1 << i)) === 0) continue; // skip if word `i` is not in the mask\n const prevMask = mask ^ (1 << i); // remove the current word from mask\n for (let j = 0; j < n; j++) {\n if ((prevMask & (1 << j)) === 0) continue; // skip if word `j` is not in the mask\n const newLength = dp[prevMask][j] + overlap[j][i];\n if (newLength < dp[mask][i]) {\n dp[mask][i] = newLength;\n parent[mask][i] = j;\n }\n }\n }\n }\n\n // Step 4: Find the minimum length superstring\n let lastWord = -1;\n let minLength = Infinity;\n const finalMask = (1 << n) - 1;\n\n for (let i = 0; i < n; i++) {\n if (dp[finalMask][i] < minLength) {\n minLength = dp[finalMask][i];\n lastWord = i;\n }\n }\n\n // Step 5: Reconstruct the shortest superstring\n let mask = finalMask;\n const sequence: number[] = [];\n\n while (mask > 0) {\n sequence.push(lastWord);\n const prev = lastWord;\n lastWord = parent[mask][lastWord];\n mask ^= (1 << prev); // remove the last word from the mask\n }\n\n sequence.reverse(); // reverse the sequence to get the correct order\n\n // Step 6: Build the superstring using the sequence and overlaps\n let result = words[sequence[0]];\n for (let i = 1; i < sequence.length; i++) {\n const overlapLen = overlap[sequence[i - 1]][sequence[i]];\n result += words[sequence[i]].substring(words[sequence[i]].length - overlapLen);\n }\n\n return result;\n}\n\n// Helper function to calculate the overlap between two words\nfunction getOverlap(a: string, b: string): number {\n for (let len = Math.min(a.length, b.length); len > 0; len--) {\n if (a.endsWith(b.substring(0, len))) {\n return b.length - len;\n }\n }\n return b.length;\n}\n\n```
| 8
| 0
|
['TypeScript']
| 0
|
find-the-shortest-superstring
|
Java | DP | Bitmask
|
java-dp-bitmask-by-monsterspyy-p34y
|
\nclass Solution {\n \n String[][] lookup;\n \n String superString(String[] A, int last, int bitmask, String[][] dp){\n String res = ""; \n
|
monsterspyy
|
NORMAL
|
2020-06-30T14:20:57.374155+00:00
|
2020-06-30T14:20:57.374207+00:00
| 1,173
| false
|
```\nclass Solution {\n \n String[][] lookup;\n \n String superString(String[] A, int last, int bitmask, String[][] dp){\n String res = ""; \n int minLength = Integer.MAX_VALUE/2;\n if(dp[last][bitmask] != null)\n return dp[last][bitmask];\n \n for(int i=0;i<A.length;i++){\n if((bitmask&(1<<i)) != 0)\n continue;\n String tmp = lookup[last][i]+superString(A, i, bitmask|(1<<i), dp);\n if(tmp.length() < minLength){\n minLength = tmp.length();\n res = tmp;\n }\n }\n return dp[last][bitmask] = res;\n }\n \n public String shortestSuperstring(String[] A) {\n \n String[][] dp = new String[A.length][5000];\n lookup = new String[A.length][A.length];\n \n for(int i=0;i<A.length;i++){\n for(int j=0;j<A.length;j++){\n if(i == j) continue;\n int k = 1;\n int idx = 0;\n while(k <= A[j].length()){\n if(A[i].endsWith(A[j].substring(0, k)))\n idx = k;\n k++;\n }\n lookup[i][j] = A[j].substring(idx, A[j].length());\n }\n }\n \n String ans = "";\n int minLength = Integer.MAX_VALUE/2;\n int bitmask = 0;\n \n for(int i=0;i<A.length;i++){\n String tmp = A[i]+superString(A, i, bitmask|(1<<i), dp);\n if(tmp.length() < minLength){\n minLength = tmp.length();\n ans = tmp;\n }\n }\n return ans;\n }\n}\n```
| 8
| 1
|
['Dynamic Programming', 'Bitmask', 'Java']
| 1
|
find-the-shortest-superstring
|
Greedy Solution is Wrong . Proof
|
greedy-solution-is-wrong-proof-by-jaidee-8cse
|
Below is my solution based on a Greedy approach which got AC but when i looked into the solution where DP, BFS or TSP is used i felt that greedy might not be th
|
jaideep_dahiya
|
NORMAL
|
2021-05-27T05:13:46.571800+00:00
|
2021-05-27T05:13:46.571840+00:00
| 660
| false
|
Below is my solution based on a **Greedy** approach which got **AC** but when i looked into the solution where DP, BFS or TSP is used i felt that greedy might not be the correct solution.\n\nSo after some searching found this guys comment **@Cronek** showing this testcase\n```"abcd", "bcde", "cdbc"``` . According to the greedy approach the Strings ```"abcd"``` and ```"bcde"``` will always be merged together making the final solution either to be ```"cdbcabcde"``` or ```"abcdecdbc"``` when in fact the correct solution is ```"abcdbcde"```.\n\n```\nclass Solution{\n\tpublic static class bestfit{\n\t\tprivate int index=-1;\n\t\tprivate int charmatched=-1;\n\t\tprivate int front_or_end=-1;\n\t\tbestfit(int x,int y,int z){\n\t\t\tthis.index=x;\n\t\t\tthis.charmatched=y;\n\t\t\tthis.front_or_end=z;\n\t\t}\n\t\tbestfit(int x,int y){\n\t\t\tthis(x,y,-1);\n\t\t}\n\t\tbestfit(int x){\n\t\t\tthis(x,-1,-1);\n\t\t}\n\t}\n\t\n\tpublic static String shortestSuperstring(String[] words) {\n StringBuilder ans =new StringBuilder(words[0]);\n int minus=1;\n int[] marked = new int[words.length];\n marked[0]=-1;\n bestfit x=new bestfit(-1, -1, -1);\n while(minus<words.length) {\n \tString temp="";\n \tfor(int i=0;i<marked.length;i++) {\n \t\t\n \t\tif(marked[i]!=-1) {\n \t\t\ttemp=words[i];\n \t\t\tif(x.charmatched==-1) {\n \t\t\tx.index=i;\n \t\t\tx.charmatched=0;\n \t\t\tx.front_or_end=0;}\n \t\t\t//front check \n \t\t\tint min = temp.length()>ans.length()?ans.length():temp.length();\n \t\t\tfor(int j=temp.length()-1;min>0;min--,j--) {\n \t\t\t\tint charsmatched = temp.length()-j;\n \t\t\t\tif(ans.substring(0,charsmatched).equals(temp.substring(j))) {\n \t\t\t\t\tif(charsmatched>x.charmatched) {\n \t\t\t\t\t\tx.index=i;\n \t\t\t\t\t\tx.charmatched=charsmatched;\n \t\t\t\t\t\tx.front_or_end=0;\n \t\t\t\t\t}\n \t\t\t\t}\n \t\t\t}\n \t\t\tmin = temp.length()>ans.length()?ans.length():temp.length();\n \t\t\tfor(int j=0;min>0;j++,min--) {\n \t\t\t\tint charsmatched = j+1;\n \t\t\t\tif(ans.substring(ans.length()-1-j).equals(temp.substring(0,charsmatched))) {\n \t\t\t\t\tif(charsmatched>x.charmatched) {\n \t\t\t\t\t\tx.index=i;\n \t\t\t\t\t\tx.charmatched=charsmatched;\n \t\t\t\t\t\tx.front_or_end=1;\n \t\t\t\t\t}\n \t\t\t\t}\n \t\t\t}\n \t\t}\n \t}\n \tminus++;\n \tmarked[x.index]=-1;\n \ttemp=words[x.index];\n \tif(x.front_or_end==0) {\n \t\t//front\n \t\tint charleft=words[x.index].length()-x.charmatched;\n \t\tans.insert(0,temp.substring(0, charleft));\n \t\tx.charmatched=-1;\n \t}else{\n \t\t//end\n// \t\tint charused=words[x.index].length()-x.charmatched;\n \t\tans.append(temp.substring(x.charmatched));\n \t\tx.charmatched=-1;\n \t}\n }\n return ans.toString();\n }\n\t\n}\n```
| 7
| 0
|
[]
| 0
|
find-the-shortest-superstring
|
C++ | DP + Graph + BitMask with comments for understanding
|
c-dp-graph-bitmask-with-comments-for-und-43rk
|
\n\tclass Solution {\n\tpublic: \n\n\t\t// cost to append word2 to word1\n\t\t// cost represents extra characters we should add after word1 so that word2 bec
|
rbs_
|
NORMAL
|
2022-08-16T12:07:37.512371+00:00
|
2022-08-16T12:08:31.748168+00:00
| 1,805
| false
|
\n\tclass Solution {\n\tpublic: \n\n\t\t// cost to append word2 to word1\n\t\t// cost represents extra characters we should add after word1 so that word2 becomes suffix\n\t\tint getCost(string &word1, string &word2){\n\t\t\tint n1 = word1.size();\n\t\t\tint n2 = word2.size();\n\n\t\t\tfor(int i=0; i<n1; i++){\n\t\t\t\tint index = i;\n\t\t\t\twhile(index < n1){\n\t\t\t\t\tif(index-i >= n2 || word1[index] != word2[index-i])\n\t\t\t\t\t\tbreak;\n\t\t\t\t\tindex++;\n\t\t\t\t}\n\t\t\t\tif(index == n1){\n\t\t\t\t\treturn n2 - (n1-i);\n\t\t\t\t}\n\t\t\t}\n\n\t\t\treturn n2;\n\t\t}\n\n\n\t\tstring shortestSuperstring(vector<string>& words) {\n\t\t\tint n= words.size();\n\t\t\tstring ans="-1";\n\t\t\tint minLen = 10000;\n\n\t\t\t// graph stores the cost of appending word[j] after word[i]\n\t\t\t// cost = extra characters required to append to word[i] to get suffix word[j]\n\t\t\tvector<vector<int>> graph(n,vector<int>(n,0));\n\t\t\tfor(int i=0; i<n; i++){\n\t\t\t\tfor(int j=0; j<n; j++){\n\t\t\t\t\tgraph[i][j] = getCost(words[i],words[j]);\n\t\t\t\t}\n\t\t\t}\n\n\t\t\t// bits of mask stores which words have been used, in the end all are used \n\t\t\t// 111111111... n times\n\t\t\tint mask_end= (1<<n) -1; \n\n\t\t\t// dp[mask][j] stores shortest superstring till now using set bits of mask\n\t\t\t// and containing ending word as words[j] \n\t\t\t// if we remove the jth bit from current mask, we get previous mask \n\t\t\t// in previous mask there are n possibilities of ending words\n\t\t\tvector<vector<pair<int,string>>> dp(mask_end+1, \n\t\t\t\t\t\t\t\t\t\t\t\tvector<pair<int,string>>(n,{10000,""}));\n\n\t\t\tfor(int mask=0; mask<= mask_end; mask++){\n\t\t\t\t// get all possible prevMask\n\t\t\t\tfor(int j=0; j<n; j++){\n\t\t\t\t\t// if jth bit of mask is set, means jth word is used \n\t\t\t\t\tif(mask && (1<<j) != 0){\n\t\t\t\t\t\t// remove jth bit from mask\n\t\t\t\t\t\tint preMask = mask ^ (1<<j);\n\t\t\t\t\t\t// if j is the first word\n\t\t\t\t\t\tif(preMask ==0)\n\t\t\t\t\t\t\tdp[mask][j] = {words[j].size(), words[j]};\n\t\t\t\t\t\telse{\n\t\t\t\t\t\t\t// check all possible ending words from preMask \n\t\t\t\t\t\t\t// ie.previous state from which current state (mask) is formed\n\t\t\t\t\t\t\tint kmin= -1;\n\t\t\t\t\t\t\tint minCurrLen = dp[mask][j].first;\n\t\t\t\t\t\t\tfor(int k=0; k<n; k++){\n\t\t\t\t\t\t\t\tint preLen = dp[preMask][k].first;\n\t\t\t\t\t\t\t\tif(preLen + graph[k][j] < minCurrLen){\n\t\t\t\t\t\t\t\t\tminCurrLen = preLen + graph[k][j];\n\t\t\t\t\t\t\t\t\tkmin= k;\n\t\t\t\t\t\t\t\t}\n\t\t\t\t\t\t\t} \n\t\t\t\t\t\t\tif(kmin != -1){\n\t\t\t\t\t\t\t\tstring preStr = dp[preMask][kmin].second;\n\t\t\t\t\t\t\t\t// add graph[kmin][j] end letters of words[j] to preStr\n\t\t\t\t\tpreStr += words[j].substr(words[j].size()- graph[kmin][j], graph[kmin][j]);\n\t\t\t\t\t\t\t\tdp[mask][j] = {minCurrLen,preStr};\n\t\t\t\t\t\t\t}\n\t\t\t\t\t\t}\n\t\t\t\t\t}\n\n\t\t\t\t\tif(mask == mask_end && dp[mask][j].first < minLen){\n\t\t\t\t\t\tminLen = dp[mask][j].first;\n\t\t\t\t\t\tans = dp[mask][j].second;\n\t\t\t\t\t}\n\n\t\t\t\t}\n\t\t\t}\n\n\t\t\treturn ans;\n\n\n\t\t}\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\t};
| 6
| 0
|
[]
| 0
|
find-the-shortest-superstring
|
[C++] DP
|
c-dp-by-codedayday-mt5i
|
Approach 1: DP [1]\n\nclass Solution {\npublic: \n string shortestSuperstring(vector<string>& A) {\n const int n = A.size();\n vector<vector<in
|
codedayday
|
NORMAL
|
2021-05-23T15:57:38.530376+00:00
|
2021-05-23T16:01:06.321789+00:00
| 2,310
| false
|
Approach 1: DP [1]\n```\nclass Solution {\npublic: \n string shortestSuperstring(vector<string>& A) {\n const int n = A.size();\n vector<vector<int> > g(n, vector<int>(n));\n for(int i = 0; i < n; i++)\n for(int j = 0; j < n; j++){\n g[i][j] = A[j].length();\n for(int k = 1; k <= min(A[i].length(), A[j].length()); k++){\n if(A[i].substr(A[i].length()- k) == A[j].substr(0, k)){\n g[i][j] = A[j].length() - k;\n }\n }\n }\n \n vector<vector<int> > dp(1<<n, vector<int>(n, INT_MAX/2));\n vector<vector<int> > parent(1<<n, vector<int>(n, -1));\n for(int i = 0; i < n; i++){ dp[1<<i][i] = A[i].length();} \n \n for(int s = 1; s < (1<<n); s++){\n for(int j = 0; j < n; j++){\n if(!s&(1<<j)) continue;\n //if(!(s&(1<<j))) continue;\n int ps = s & ~(1<<j);\n for(int i = 0; i < n; i++){\n if(dp[s][j] > dp[ps][i] + g[i][j]){\n dp[s][j] = dp[ps][i] + g[i][j];\n parent[s][j] = i;\n }\n }\n }\n }\n \n string res;\n auto it = min_element(begin(dp.back()), end(dp.back()));\n int j = it - begin(dp.back()); // cur\n int s = (1 << n) - 1;\n while(s){\n int i = parent[s][j]; // pre\n if(i < 0) res = A[j] + res;\n else res = A[j].substr(A[j].length() - g[i][j]) + res; \n s &= ~(1<<j);\n j = i;\n }\n return res; \n }\n};\n```\nReference:\n[1] https://zxi.mytechroad.com/blog/searching/leetcode-943-find-the-shortest-superstring/
| 6
| 0
|
['Dynamic Programming', 'C']
| 0
|
find-the-shortest-superstring
|
Single Handedly C++ Paste Accepted
|
single-handedly-c-paste-accepted-by-khac-ag54
|
\nclass Solution {\npublic:\n vector<int>len;\n vector<vector<int>>overlap;\n vector<vector<int>>dp;\n int n;\n map<pair<int, int>, int>mp;\n
|
khacker
|
NORMAL
|
2021-05-23T07:55:14.822476+00:00
|
2021-05-23T07:55:14.822507+00:00
| 432
| false
|
```\nclass Solution {\npublic:\n vector<int>len;\n vector<vector<int>>overlap;\n vector<vector<int>>dp;\n int n;\n map<pair<int, int>, int>mp;\n int solve(int idx, int mask){\n if(mask == (1 << n) - 1) return 0;\n if(dp[idx][mask] != -1)return dp[idx][mask];\n dp[idx][mask] = INT_MAX;\n for(int i = 0; i < n; i++){\n if((mask&(1 << i)) == 0){\n int temp = len[i] - overlap[idx][i] + solve(i, mask|(1 << i));\n if(temp < dp[idx][mask]){\n dp[idx][mask] = temp;\n mp[{idx, mask}] = i;\n }\n }\n }\n return dp[idx][mask];\n }\n string shortestSuperstring(vector<string>& A) {\n n = A.size();\n len.resize(n, 0);\n overlap.resize(n, vector<int>(n, 0));\n dp.resize(n, vector<int>((1 << n) + 1, -1));\n for(int i = 0; i < n; i++){\n len[i] = A[i].size();\n }\n for(int i = 0; i < n; i++){\n for(int j = 0; j < n; j++){\n if(i != j){\n int m = min(len[i], len[j]);\n for(int k = m; k >= 0; k--){\n if(A[i].substr(len[i] - k) == A[j].substr(0, k)){\n overlap[i][j] = k;\n break;\n }\n }\n }\n }\n }\n int mlen = INT_MAX;\n int idx = 0;\n for(int i = 0; i < n; i++){\n int temp = len[i] + solve(i, (1 << i));\n //cout<<temp<<endl;\n if(temp < mlen){\n mlen = temp;\n idx = i;\n }\n }\n string ans = A[idx];\n int mask = 1 << idx;\n for(int i = 1; i < n; i++){\n int x = idx;\n idx = mp[{idx, mask}];\n ans += A[idx].substr(overlap[x][idx]);\n mask |= (1 << idx); \n }\n return ans;\n }\n};\n```
| 6
| 6
|
[]
| 0
|
find-the-shortest-superstring
|
C++ SOLUTION
|
c-solution-by-saurabhvikastekam-gdqs
|
\nclass Solution {\npublic:\n vector<int>len;\n vector<vector<int>>overlap;\n vector<vector<int>>dp;\n int n;\n map<pair<int, int>, int>mp;\n
|
SaurabhVikasTekam
|
NORMAL
|
2021-05-23T07:45:50.238324+00:00
|
2021-05-23T07:49:19.776893+00:00
| 2,205
| false
|
```\nclass Solution {\npublic:\n vector<int>len;\n vector<vector<int>>overlap;\n vector<vector<int>>dp;\n int n;\n map<pair<int, int>, int>mp;\n int solve(int idx, int mask){\n if(mask == (1 << n) - 1) return 0;\n if(dp[idx][mask] != -1)return dp[idx][mask];\n dp[idx][mask] = INT_MAX;\n for(int i = 0; i < n; i++){\n if((mask&(1 << i)) == 0){\n int temp = len[i] - overlap[idx][i] + solve(i, mask|(1 << i));\n if(temp < dp[idx][mask]){\n dp[idx][mask] = temp;\n mp[{idx, mask}] = i;\n }\n }\n }\n return dp[idx][mask];\n }\n string shortestSuperstring(vector<string>& A) {\n n = A.size();\n len.resize(n, 0);\n overlap.resize(n, vector<int>(n, 0));\n dp.resize(n, vector<int>((1 << n) + 1, -1));\n for(int i = 0; i < n; i++){\n len[i] = A[i].size();\n }\n for(int i = 0; i < n; i++){\n for(int j = 0; j < n; j++){\n if(i != j){\n int m = min(len[i], len[j]);\n for(int k = m; k >= 0; k--){\n if(A[i].substr(len[i] - k) == A[j].substr(0, k)){\n overlap[i][j] = k;\n break;\n }\n }\n }\n }\n }\n int mlen = INT_MAX;\n int idx = 0;\n for(int i = 0; i < n; i++){\n int temp = len[i] + solve(i, (1 << i));\n //cout<<temp<<endl;\n if(temp < mlen){\n mlen = temp;\n idx = i;\n }\n }\n string ans = A[idx];\n int mask = 1 << idx;\n for(int i = 1; i < n; i++){\n int x = idx;\n idx = mp[{idx, mask}];\n ans += A[idx].substr(overlap[x][idx]);\n mask |= (1 << idx); \n }\n return ans;\n }\n};\n```
| 6
| 1
|
['C', 'C++']
| 0
|
find-the-shortest-superstring
|
Python test cases does not check type (100% time and space "Funny" )
|
python-test-cases-does-not-check-type-10-frch
|
\nclass Solution(object):\n def shortestSuperstring(self, A):\n return A\n
|
gsbhardwaj27
|
NORMAL
|
2021-02-06T09:39:24.006753+00:00
|
2021-02-06T09:39:24.006781+00:00
| 271
| false
|
```\nclass Solution(object):\n def shortestSuperstring(self, A):\n return A\n```
| 6
| 4
|
[]
| 2
|
find-the-shortest-superstring
|
Python AC concise solution ~132 ms
|
python-ac-concise-solution-132-ms-by-cen-14m9
|
First, we analyze connections between any two string(a, b) in A:\n\t We get l, longest length of b that a ends with. \n\t In merged[a] array, we will have b str
|
cenkay
|
NORMAL
|
2018-11-18T17:35:43.944761+00:00
|
2018-11-18T17:35:43.944801+00:00
| 897
| false
|
* First, we analyze connections between any two string(a, b) in A:\n\t* We get l, longest length of b that a ends with. \n\t* In merged[a] array, we will have b strings and longest length in the zero index.\n* We define worst possible res(ult) as "".join(A) where every string in A appended and store it in array for global acces through DFS.\n* In DFS, there are 3 variables => current superstring, current string, set of left strings\n\t* While doing DFS if length of superstring + left strings(can be empty) < length of res, we update res.\n\t* If there are any new b in the set for current string, we do DFS for new b\'s in merged[s].\n\t* Else, that means we got stuck with set of strings that are independent from current string.\n\t\t* In that case, every left string in the set can be next string and we do DFS for b\' in merged[next string].\n* Finally we return updated res[0] after all DFS\'s.\n* Upvote if you like the solution. Thanks!\n```\nclass Solution:\n def shortestSuperstring(self, A):\n def merge(a, b):\n for i in range(len(b), 0, -1):\n if a.endswith(b[:i]):\n return i\n return 0\n def dfs(sup, s, st):\n if len(sup + "".join(st)) < len(res[0]):\n res[0] = sup + "".join(st)\n if st and any(new in st for new in merged[s][1:]):\n for new in merged[s][1:]:\n if new in st:\n dfs(sup + new[merged[s][0]:], new, st - {new})\n else:\n for nex in st:\n for new in merged[nex][1:]:\n if new in st:\n dfs(sup + nex + new[merged[nex][0]:], new, st - {nex, new})\n merged, res = {}, ["".join(A)]\n for a, b in itertools.combinations(A, 2):\n for a, b in ((a, b), (b, a)):\n l = merge(a, b)\n if a not in merged or l > merged[a][0]:\n merged[a] = [l, b]\n elif l == merged[a][0]:\n merged[a].append(b)\n for a in A:\n dfs(a, a, set(A) - {a})\n return res[0]\n```
| 6
| 4
|
[]
| 2
|
find-the-shortest-superstring
|
BFS + PriorityQueue is all you need
|
bfs-priorityqueue-is-all-you-need-by-her-yqob
|
If you cannot understand this method, look at lc 847 and lc 743\nlc 847 will tell you what the state means in this problem\nlc 743 will tell you how to use Prio
|
Hernie8189
|
NORMAL
|
2020-07-24T04:58:12.516501+00:00
|
2020-07-24T04:58:12.516556+00:00
| 1,038
| false
|
If you cannot understand this method, look at lc 847 and lc 743\nlc 847 will tell you what the state means in this problem\nlc 743 will tell you how to use PriorityQueue to find shortest path in graph with weights\n\n"We may assume that no string in A is substring of another string in A" \nWhich means in Path A-B-C-D\uFF0Cthe dependence of D to C\uFF0Cis independent of A,B,C\nSo the cost to add D behind C, is the same as the cost of adding D to shortestSuperstring(ABC)\nWe build the graph according to this clue\n\nThe problem can be transformed into:\n1. Starting from each single node in A, visit the other nodes in A for one time, calculate the total cost.\n By Dijkstra, we know using a PriorityQueue can lead to the shortest path start from this single node.\n2. Find the min cost in N total costs in step 1.\n\nT:O(N*2^N)\nS:O(N*2^N)\n\n```\nclass Solution {\n \n class State{\n int node; //current node index\n int state; //distinguish the node come from diferent node\n StringBuilder sb; //the accumulated string in this state\n int cost; //the accumulated cost\n\n public State(int node, int state, String str, int cost){\n this.node = node;\n this.state = state;\n this.sb = new StringBuilder(str);\n this.cost = cost;\n } \n \n }\n \n public String shortestSuperstring(String[] A) {\n int n = A.length;\n int goal = (1<<n) - 1;\n \n List<String> waitlist = new ArrayList<>(); //store the min cost start from each single node\n \n Map< Integer, List<List<Integer>> > map = new HashMap<>(); //<s1 index, <<s2 index, cost>,<s3 index, cost>...> >\n \n for(int i=0; i<A.length; i++) map.put(i, new ArrayList<>());\n\n //build the graph\n for(int i=0; i<A.length; i++){\n for(int j=0; j<A.length; j++){\n if(A[i].equals(A[j])) continue;\n List<Integer> temp = new ArrayList<>();\n temp.add(j);\n temp.add(calcost(A[i], A[j]));\n \n map.get(i).add( new ArrayList<>(temp) ) ;\n }\n }\n\n \n Comparator<State> mycomp = new Comparator<>(){\n public int compare(State s1, State s2){\n return s1.cost - s2.cost;\n }\n };\n \n // for each node, we do bfs\n for(int i=0; i<A.length; i++){\n Queue<State> pq = new PriorityQueue<>(mycomp);\n boolean [][]visited = new boolean [n][1<<n];\n pq.add(new State(i, 1<<i, A[i], 0));\n visited[i][1<<i] = true;\n \n while(!pq.isEmpty()){\n State currstate = pq.poll();\n if(currstate.state == goal) waitlist.add(currstate.sb.toString());\n \n for(List<Integer> nextnodelist : map.get(currstate.node)){\n int nextnode = nextnodelist.get(0);\n int nextcost = nextnodelist.get(1);\n int nextstate = currstate.state | (1<<nextnode);\n \n if(visited[nextnode][nextstate]) continue; \n \n visited[nextnode][nextstate] = true;\n \n //do not modify currstate.sb\n StringBuilder nextsb = new StringBuilder(currstate.sb.toString());\n //"abcd" + "bcde", nextcost is 1, we only need to add "e" behind \n nextsb.append( A[nextnode].substring(A[nextnode].length()-nextcost) ); \n \n pq.add(new State(nextnode, nextstate, nextsb.toString(), currstate.cost+nextcost));\n }\n }\n\n }\n \n int minlen = Integer.MAX_VALUE;\n String minstr = "";\n\n for(String str : waitlist){\n if(minlen > str.length()){\n minlen = str.length();\n minstr = str;\n }\n }\n \n return minstr;\n }\n \n //original "abcd" add an extra "bcde", result is "abcde", so the cost is 1\n //use KMP can spped up this process, here I use an intuitive method\n public int calcost(String s1, String s2){\n int len1 = s1.length(), len2 = s2.length();\n int minlen = Math.min(len1, len2);\n int commonlen = 0;\n int maxcommonlen = 0;\n \n // s1[i, len1) match s2[0, j)\n while(commonlen < minlen){\n int i = len1 - 1 - commonlen;\n int j = commonlen + 1;\n \n //use commonlen to scan s1 and s2\n if( s1.substring(i).equals(s2.substring(0,j)) ) {\n maxcommonlen = commonlen + 1;\n }\n \n commonlen++;\n }\n return len2 - maxcommonlen;\n }\n}\n```\n\nIf you find this helpful, please vote up so that more people can see.
| 5
| 2
|
['Breadth-First Search', 'Java']
| 0
|
find-the-shortest-superstring
|
JavaScript Solution
|
javascript-solution-by-hiitsherby-3x10
|
I used similiar technic as 1066. Campus Bike II. If you haven\'t done it, I recommend you to attempt it first.\n\nAnd This Article is my lifesaver as I\'m reall
|
hiitsherby
|
NORMAL
|
2019-07-08T16:54:50.159814+00:00
|
2019-07-08T16:54:50.159874+00:00
| 572
| false
|
I used similiar technic as [1066. Campus Bike II](https://leetcode.com/problems/campus-bikes-ii/). If you haven\'t done it, I recommend you to attempt it first.\n\nAnd [This Article](https://medium.com/free-code-camp/unmasking-bitmasked-dynamic-programming-25669312b77b#c94f) is my lifesaver as I\'m really shit at bit manipulation. A great introductory article to bit manipulation and the application on DP.\n```\n/**\n * @param {number[][]} workers\n * @param {number[][]} bikes\n * @return {number}\n */\nconst shortestSuperstring = (A) => {\n\tfunction additionalStr(a,b){ // a + b additional Str\n\t\tfor (let i=0; i<a.length; i++){\n\t\t\tif (b.startsWith(a.slice(i))){\n\t\t\t\treturn b.slice(a.length-i);\n\t\t\t}\n\t\t}\n\t\treturn b;\n\t}\n\t// dp[i][j] -> min str building j state ending word i\n\tlet dp = new Array(A.length).fill()\n\t\t.map(() => new Array(1 << A.length).fill(A.join(\'\')));\n\n\tfor (let s=1; s<(1<<A.length); s++){\n\t\tfor (let j=0; j<A.length; j++){\n\t\t\tif (!(s & (1 << j))) continue;\n\t\t\tif (s===(1<<j)) dp[j][s]=A[j];\n\t\t\tlet prevS = s ^ (1 << j);\n\t\t\tfor (let k=0; k<A.length; k++){\n\t\t\t\tif (prevS & (1 << k)){\n\t\t\t\t\tlet curStr = dp[k][prevS];\n\t\t\t\t\tlet tempStr = curStr + additionalStr(curStr, A[j]);\n\t\t\t\t\tif (tempStr.length < dp[j][s].length){\n\t\t\t\t\t\tdp[j][s] = tempStr;\n\t\t\t\t\t}\n\t\t\t\t}\n\t\t\t}\n\t\t}\n\t}\n\tlet min = Number.MAX_VALUE;\n\tlet minStr = null;\n\tfor (let i=0; i<A.length; i++){\n\t\tlet cur = dp[i][(1<<(A.length))-1];\n\t\tif (cur.length < min){\n\t\t\tmin = cur.length;\n\t\t\tminStr = cur;\n\t\t}\n\t}\n\treturn minStr;\n}\n```
| 5
| 0
|
['Dynamic Programming', 'JavaScript']
| 0
|
find-the-shortest-superstring
|
Shortest Path Problem (Directed acyclic graph with nonnegative weights)
|
shortest-path-problem-directed-acyclic-g-zstf
|
Treat (last word, used words bitmask) as a node, then\n\nd((i, mska), (j, mskb)) = len(j) - overlap(i,j) if (mska | (1<<j) == mskb) and (mska & (1<<j) == 0) and
|
yangzhenjian
|
NORMAL
|
2018-11-23T05:24:47.168767+00:00
|
2018-11-23T05:24:47.168822+00:00
| 20,926
| false
|
Treat (last word, used words bitmask) as a node, then\n```\nd((i, mska), (j, mskb)) = len(j) - overlap(i,j) if (mska | (1<<j) == mskb) and (mska & (1<<j) == 0) and (mska & (1<<i) != 0)\n else INF\n```\nAnd add 2 extra nodes S and T:\n```\nd(S, (i, 1<<i)) = len(i)\nd((i, ALL_NODES), T) = 0\n(0 <= i < N)\n```\nThen our job is finding the shortest path from S to T.\n\nThis reminded me Dijkstra\'s Algorithm:\n```python\nfrom heapq import heappush, heappop, heapify\n\nclass Solution:\n def shortestSuperstring(self, A):\n """\n :type A: List[str]\n :rtype: str\n """\n N = len(A)\n add = [[0]*N for _ in range(N)]\n \n def calc_add(a, b):\n for i in range(min(len(a), len(b)), 0, -1):\n if a[-i:] == b[0:i]:\n return len(b) - i\n return len(b)\n \n for i in range(N):\n for j in range(N):\n if i != j:\n add[i][j] = calc_add(A[i], A[j])\n \n all_nodes = (1 << N) - 1\n v = [[False] * (1 << N) for _ in range(N)]\n hq = [[len(A[i]), i, 1 << i, A[i]] for i in range(N)]\n heapify(hq)\n while hq:\n l, i, msk, s = heappop(hq)\n if msk == all_nodes: return s\n if v[i][msk]: continue\n v[i][msk] = True\n for j in range(N):\n if i == j or (1 << j) & msk: continue\n nmsk = msk | (1 << j)\n if v[j][nmsk]: continue\n heappush(hq, [l+add[i][j], j, nmsk, s + A[j][-add[i][j]:]])\n return -1\n```\nTime complexity for Dijkstra\'s Algorithm(with binary heap) is O((E+V)logV), here V = N * 2^N and E \u2252 N^2 * 2^N\nSo time complexity of this approach is O(N^3 * 2^N * log N).\nI got TLE during the contest with python but got AC with C++.\n\nIn fact, since this graph is acyclic, we can solve it in O(E+V) time with topological sorting (actually it is dp). \nSee https://en.wikipedia.org/wiki/Shortest_path_problem#Directed_acyclic_graphs\nand https://en.wikipedia.org/wiki/Topological_sorting#Application_to_shortest_path_finding\n\nHere\'s the code and its time complexity is O(N^2 * 2^N):\n```python\nclass Solution:\n def shortestSuperstring(self, A):\n """\n :type A: List[str]\n :rtype: str\n """\n N = len(A)\n add = [[0]*N for _ in range(N)]\n \n def calc_add(a, b):\n for i in range(min(len(a), len(b)), 0, -1):\n if a[-i:] == b[0:i]:\n return len(b) - i\n return len(b)\n \n for i in range(N):\n for j in range(N):\n if i != j:\n add[i][j] = calc_add(A[i], A[j])\n \n all_nodes = (1 << N) - 1\n INF = float(\'inf\')\n dp = [[(INF, \'\')] * N for i in range(1 << N)]\n for i in range(N):\n dp[1<<i][i] = len(A[i]), A[i]\n \n for msk in range(1<<N):\n for i in range(N):\n if not msk & (1 << i): continue\n for j in range(N):\n if msk & (1 << j): continue\n nmsk = msk | (1 << j)\n if dp[nmsk][j][0] >= dp[msk][i][0] + add[i][j]:\n dp[nmsk][j] = dp[msk][i][0] + add[i][j], dp[msk][i][1] + A[j][-add[i][j]:]\n return min(dp[all_nodes])[1]\n```
| 5
| 0
|
[]
| 1
|
find-the-shortest-superstring
|
java dp with bitmask o(12 * 2^12 * 12). easy to explain and impl in 20mins. cheers!
|
java-dp-with-bitmask-o12-212-12-easy-to-vziq5
|
\nimport java.util.*;\nimport java.io.*;\n\nclass State {\n int i;\n int state;\n \n State(int i, int state) {\n this.i = i;\n this.st
|
solaaoi
|
NORMAL
|
2018-11-19T08:49:23.265891+00:00
|
2018-11-19T08:49:23.265933+00:00
| 1,501
| false
|
```\nimport java.util.*;\nimport java.io.*;\n\nclass State {\n int i;\n int state;\n \n State(int i, int state) {\n this.i = i;\n this.state = state;\n }\n}\n\nclass Solution {\n private PrintStream out = System.out;\n\n private int overlap(String a, String b) {\n int res = 0;\n\n int n = a.length();\n for (int i = 1; i < n; ++i) {\n int j = 0;\n int k = i;\n while (k < n && b.charAt(j) == a.charAt(k)) {\n ++k;\n ++j;\n }\n\n if (k == n) {\n res = n - i;\n break;\n }\n }\n\n return res;\n }\n\n private int shortestSuperstring(String[] A, int[][] over, int last, int state, State[][] next, Integer[][] dp) {\n int n = A.length;\n if (state == ((1 << n) - 1)) {\n return 0;\n }\n\n if (dp[last][state] != null) {\n return dp[last][state];\n }\n \n int res = Integer.MAX_VALUE;\n for (int i = 0; i < n; ++i) {\n if (((state >> i) & 0x1) == 0) {\n int len = A[i].length() - over[last][i];\n int ret = shortestSuperstring(A, over, i, state | (1 << i), next, dp) + len;\n if (ret < res) {\n res = ret;\n next[last][state] = new State(i, state | (1 << i));\n }\n }\n }\n\n dp[last][state] = res;\n return res;\n }\n\n public String shortestSuperstring(String[] A) {\n int n = A.length;\n\n int[][] over = new int[n][n];\n for (int i = 0; i < n; ++i) {\n for (int j = i + 1; j < n; ++j) {\n over[i][j] = overlap(A[i], A[j]);\n over[j][i] = overlap(A[j], A[i]);\n }\n }\n\n int res = Integer.MAX_VALUE;\n State[][] next = new State[n][1 << n];\n Integer[][] dp = new Integer[n][1 << n];\n int start = -1;\n for (int i = 0; i < n; ++i) {\n int ret = shortestSuperstring(A, over, i, 1 << i, next, dp) + A[i].length();\n if (ret < res) {\n res = ret;\n start = i;\n }\n }\n \n StringBuilder sb = new StringBuilder();\n int state = 1 << start;\n sb.append(A[start]);\n while (state != ((1 << n) - 1)) { \n int last = start;\n State s = next[start][state | (1 << start)];\n state = s.state;\n start = s.i;\n sb.append(A[start].substring(over[last][start]));\n }\n return sb.toString();\n }\n}\n\n```
| 5
| 0
|
[]
| 3
|
find-the-shortest-superstring
|
Java solution with memorization
|
java-solution-with-memorization-by-self_-qyen
|
```\n/ the used array indicates which word is avaible, used[i] == \'1\', means the word is available...\n * map record the pairs, means the shortest string we
|
self_learner
|
NORMAL
|
2018-11-18T04:15:59.267247+00:00
|
2018-11-18T04:15:59.267321+00:00
| 1,561
| false
|
```\n/* the used array indicates which word is avaible, used[i] == \'1\', means the word is available...\n * map record the <used array, shortest string> pairs, means the shortest string we can get using the remaining words..\n */\nclass Solution { \n public String shortestSuperstring(String[] A) {\n int n = A.length;\n \n char[] used = new char[n];\n Arrays.fill(used, \'1\');\n Map<String, String> map = new HashMap<>();\n return findShortestSuperString(A, used, n, map);\n }\n \n private String findShortestSuperString(String[] A, char[] used, int cnt, Map<String, String> map) {\n //cnt is the number of available words left;\n int n = A.length;\n \n String key = new String(used);\n if (map.containsKey(key)) {\n return map.get(key);\n }\n \n //if cnt is 1, then the shortest string can fromed is just that word...\n if (cnt == 1) {\n for (int i = 0; i < n; i++) {\n if (used[i] == \'1\') {\n map.put(key, A[i]);\n }\n }\n return map.get(key);\n } else {\n //if there are more then one available words left, we just try all possible case, then get the smallest one...\n String res = null;\n \n for (int i = 0; i < n; i++) {\n if (used[i] == \'0\') continue;\n used[i] = \'0\';\n String a = A[i];\n String b = findShortestSuperString(A, used, cnt - 1, map);\n\t\t\t\t//check if a contains b\n if (a.indexOf(b) != -1) {\n if (res == null || res.length() > a.length()) {\n res = a;\n }\n } else if (b.indexOf(a) != -1) { //check if b contains a\n if (res == null || res.length() > b.length()) {\n res = b;\n }\n } else { \n\t\t\t\t //check a concatenate with b\n int index1 = tailHeadOverlap(a, b);\n String s1 = a + b.substring(index1);\n if (res == null || res.length() > s1.length()) {\n res = s1;\n }\n\t\t\t\t\t//check b concatenate with a\n int index2 = tailHeadOverlap(b, a);\n String s2 = b + a.substring(index2);\n if (res == null || res.length() > s2.length()) {\n res = s2;\n }\n }\n used[i] = \'1\';\n }\n map.put(key, res);\n }\n return map.get(key);\n }\n \n //use the prefix-suffix array of KMP to calculate the number of overlap characters, (prefix of b that is also the suffix of a)\n private int tailHeadOverlap(String a, String b) {\n int m = a.length(), n = b.length();\n if (m > n) { a = a.substring(m - n); }\n else if (n > m) { b = b.substring(0, m); }\n \n String s = b + "#" + a;\n int k = s.length();\n int[] preSuf = new int[k];\n \n int j = 0;\n for (int i = 1; i < k; i++) {\n while (j != 0 && s.charAt(i) != s.charAt(j)) {\n j = preSuf[j - 1];\n }\n if (s.charAt(i) == s.charAt(j)) { j++; }\n preSuf[i] = j;\n }\n return preSuf[k - 1];\n }\n}
| 5
| 3
|
[]
| 1
|
find-the-shortest-superstring
|
[Java] Recursion + Memoization + Optimal Path Reconstruction
|
java-recursion-memoization-optimal-path-vsyku
|
Top voted solutions are mostly iterative. This is an example of how you can construct an optimal path with a recursive dp solution. In the path reconstruction f
|
nirvana_rsc
|
NORMAL
|
2021-05-26T11:17:28.009831+00:00
|
2021-05-26T11:17:28.009875+00:00
| 419
| false
|
Top voted solutions are mostly iterative. This is an example of how you can construct an optimal path with a recursive dp solution. In the path reconstruction function we can begin from the same start state and at each step follow (the already precalculated) best move - in this case the minimum final string length.\n\n```java\n static int n;\n static int[][] g;\n static int[][] dp;\n static String[] w;\n\n public String shortestSuperstring(String[] words) {\n w = words;\n n = words.length;\n g = new int[n][n];\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < n; j++) {\n g[i][j] = getCost(words[i], words[j]);\n g[j][i] = getCost(words[j], words[i]);\n }\n }\n dp = new int[n][1 << n];\n for (int[] row : dp) {\n Arrays.fill(row, -1);\n }\n dfs(0, 0);\n return getString(0, 0);\n }\n\n private static int getCost(String a, String b) {\n for (int i = 1; i < a.length(); i++) {\n if (b.startsWith(a.substring(i))) {\n return b.length() - a.length() + i;\n }\n }\n return b.length();\n }\n\n private static String getString(int u, int mask) {\n if (mask == (1 << n) - 1) {\n return "";\n }\n int best = (int) 1e9;\n int bestIdx = -1;\n for (int v = 0; v < n; v++) {\n if ((mask & (1 << v)) == 0) {\n final int cost = mask == 0 ? w[v].length() : g[u][v];\n if (best > cost + dp[v][mask | (1 << v)]) {\n best = cost + dp[v][mask | (1 << v)];\n bestIdx = v;\n }\n }\n }\n final String curr = mask == 0 ? w[bestIdx] : w[bestIdx].substring(w[bestIdx].length() - g[u][bestIdx]);\n return curr + getString(bestIdx, mask | (1 << bestIdx));\n }\n\n private static int dfs(int u, int mask) {\n if (mask == (1 << n) - 1) {\n return 0;\n }\n if (dp[u][mask] != -1) {\n return dp[u][mask];\n }\n int res = (int) 1e9;\n for (int v = 0; v < n; v++) {\n if ((mask & (1 << v)) == 0) {\n final int cost = mask == 0 ? w[v].length() : g[u][v];\n res = Math.min(res, cost + dfs(v, mask | (1 << v)));\n }\n }\n return dp[u][mask] = res;\n }\n```
| 4
| 0
|
[]
| 0
|
find-the-shortest-superstring
|
Easy Understand Java code using Dijsktra
|
easy-understand-java-code-using-dijsktra-f6om
|
\nclass Solution {\n class State {\n String word;\n int mask;\n\n public State(String word, int mask) {\n this.word = word;\n
|
paul_f
|
NORMAL
|
2019-09-14T23:48:20.653282+00:00
|
2019-09-14T23:48:20.653340+00:00
| 997
| false
|
```\nclass Solution {\n class State {\n String word;\n int mask;\n\n public State(String word, int mask) {\n this.word = word;\n this.mask = mask;\n }\n\n }\n\n public String shortestSuperstring(String[] A) {\n PriorityQueue<State> pq = new PriorityQueue<>((a, b) -> a.word.length() - b.word.length());\n Set<Integer> set = new HashSet<>();\n\n int endMask = 0;\n for (int i = 0; i < A.length; i++) {\n endMask |= (1 << i);\n }\n\n pq.add(new State("", 0));\n\n while (!pq.isEmpty()) {\n State cur = pq.poll();\n\n if (cur.mask == endMask) {\n return cur.word;\n }\n\n if (set.contains(cur.mask))\n continue;\n\n set.add(cur.mask);\n\n for (int i = 0; i < A.length; i++) {\n if ((cur.mask & (1 << i)) == 0) {\n String nextStr1 = merge(cur.word, A[i]);\n String nextStr2 = merge(A[i], cur.word);\n int nextMask = cur.mask | (1 << i);\n pq.add(new State(nextStr1, nextMask));\n pq.add(new State(nextStr2, nextMask));\n }\n }\n }\n\n return null;\n }\n\n private String merge(String head, String tail) {\n int i = 0, j = 0;\n while (i < head.length()) {\n if (j < tail.length() && head.charAt(i) == tail.charAt(j)) {\n i++;\n j++;\n } else if (j >= tail.length() && j != 0) {\n j = 0;\n } else if (j != 0) {\n j = 0;\n } else {\n i++;\n }\n }\n\n return head + tail.substring(j);\n }\n}\n```
| 4
| 1
|
[]
| 3
|
find-the-shortest-superstring
|
C++ 20 line solution, O(n^2*2^n), Concise. Big Money.
|
c-20-line-solution-on22n-concise-big-mon-bxtw
|
A variant of the others, not original idea and I tried my best to make it shorter without hampering readability. \nThe vector<vector<string>> can be replaced by
|
gaaaarbage
|
NORMAL
|
2019-01-05T17:20:19.846166+00:00
|
2019-01-05T17:20:19.846244+00:00
| 667
| false
|
A variant of the others, not original idea and I tried my best to make it shorter without hampering readability. \nThe `vector<vector<string>>` can be replaced by `vector<vector<int>> index` of word and a `vector<vector<int>> lengthsofar` that counts the current shortest length of the string that was formed with the bits that are represented in the "1<<n" expression.\n```\nclass Solution {\npublic:\n string shortestSuperstring(vector<string>& A) {\n int n = A.size();\n vector<vector<string>> dp(1<<n,vector<string>(n));\n vector<vector<int>> cost(n,vector<int>(n,0));\n for(int i = 0;i<n;i++) for(int j = 0;j<n;j++) if(i!=j){\n for(int k = min(A[i].size(),A[j].size());k>0;k--) if(A[i].substr(A[i].size()-k) == A[j].substr(0,k)){\n cost[i][j] = k; break;\n }\n }\n for(int i = 0;i<n;i++) dp[1<<i][i]+=A[i];\n for(int o = 1;o<1<<n;++o){\n for(int i = 0;i<n;i++) if(o&(1<<i)){\n for(int j = 0;j<n;j++) if(i!=j && o&(1<<j)){\n string temp = dp[o^(1<<i)][j]+A[i].substr(cost[j][i]);\n if(dp[o][i].empty() || temp.size()<dp[o][i].size()) dp[o][i] = temp;\n }\n }\n }\n int last = (1<<n)-1;\n string res = dp[last][0];\n for(auto i:dp[last]) if(res.size()>i.size()) res = i;\n return res;\n }\n};\n```\n\n\n
| 4
| 0
|
[]
| 0
|
find-the-shortest-superstring
|
NP-hard, use memoization (Oh thank god!)
|
np-hard-use-memoization-oh-thank-god-by-ymafu
|
Here is my solution, time complexity should be O(n^3 * (2^n)), use (1 << n) array to memoize the visited states( i.e. which strings have been included)\n\npubli
|
xuhuiwang
|
NORMAL
|
2018-11-18T06:05:03.220511+00:00
|
2018-11-18T06:05:03.220581+00:00
| 3,297
| false
|
Here is my solution, time complexity should be O(n^3 * (2^n)), use (1 << n) array to memoize the visited states( i.e. which strings have been included)\n```\npublic class Solution {\n private int n;\n private String[] a;\n public String shortestSuperstring(String[] A) {\n n = A.length;\n a = A;\n String[] dp = new String[1 << n];\n return search(dp, (1 << n) - 1);\n }\n\n private String search(String[] dp, int bits) {\n if (dp[bits] != null) return dp[bits];\n int candLen = Integer.MAX_VALUE;\n String cand = "";\n for (int i = 0; i < n; ++i) {\n if ((bits & (1 << i)) != 0) {\n int pre = bits ^ (1 << i);\n String preStr = search(dp, pre);\n String str = a[i];\n int n1 = preStr.length(), n2 = str.length();\n if (n1 + n2 < candLen) {\n candLen = n1 + n2;\n cand = preStr + str;\n }\n int len = Math.min(n1, n2);\n l: for (int offset = len; offset >= 1; --offset) {\n if (n1 + n2 - offset >= candLen) break;\n if (str.substring(0, offset).equals(preStr.substring(n1 - offset)))\n {\n candLen = n1 + n2 - offset;\n cand = preStr + str.substring(offset);\n break l;\n }\n if (preStr.substring(0, offset).equals(str.substring(n2 - offset)))\n {\n candLen = n1 + n2 - offset;\n cand = str + preStr.substring(offset);\n break l;\n }\n }\n }\n }\n return dp[bits] = cand;\n }\n}\n```
| 4
| 1
|
[]
| 2
|
find-the-shortest-superstring
|
✅ Easy Self Explanatory Code ✅ - Simple Bitmask DP + Retracing
|
easy-self-explanatory-code-simple-bitmas-ygkr
|
\n# Code\n\nclass Solution {\nprivate:\n int n, finalMask;\n int best;\n int dp[12][1 << 12];\n int nextt[12][1 << 12];\n // to find max number o
|
kingsman007
|
NORMAL
|
2023-10-21T15:29:58.428030+00:00
|
2023-10-21T15:29:58.428047+00:00
| 643
| false
|
\n# Code\n```\nclass Solution {\nprivate:\n int n, finalMask;\n int best;\n int dp[12][1 << 12];\n int nextt[12][1 << 12];\n // to find max number of common character in two string\n int common(const string& s1 , const string& s2) {\n int i = 1;\n int ans = 0;\n while(i <= s1.size() and i <= s2.size()) {\n if(s1.substr(s1.size() - i , i) == s2.substr(0 , i))\n ans = i;\n i++;\n }\n return ans;\n }\n // main recursive dp function\n int solve(vector<string>& words, int prev, int mask) {\n // base case\n if(mask == finalMask) {\n return 0;\n }\n // memoization case\n if(dp[prev][mask] != -1) return dp[prev][mask];\n // calling recursion\n int ret = 1e9;\n int next = -1;\n for(int i = 0; i < n; i++) {\n if(!(mask & (1 << i))) {\n int comm = common(words[prev], words[i]);\n int curr = (words[i].size() - comm) + solve(words, i, (mask | (1 << i)));\n if(ret > curr) {\n ret = curr;\n next = i;\n }\n }\n }\n nextt[prev][mask] = next;\n return dp[prev][mask] = ret;\n }\npublic:\n string shortestSuperstring(vector<string>& words) {\n // travelling salesman problem + retracing path using parent array\n n = words.size();\n finalMask = (1 << n) - 1;\n memset(dp, -1, sizeof(dp));\n memset(nextt, -1, sizeof(dp));\n int mn = 1e9;\n int begin = -1;\n for(int i = 0; i < n; i++) {\n int curr = words[i].size() + solve(words, i, (1 << i));\n if(mn > curr) {\n mn = curr;\n begin = i;\n }\n }\n // now, retracing the answer\n string ret = "";\n int mask = 0;\n while(begin != -1) {\n string prev = words[begin];\n mask |= (1 << begin);\n begin = nextt[begin][mask];\n string next = begin == -1 ? "" : words[begin];\n int comm = common(prev, next);\n ret += prev.substr(0, prev.size() - comm);\n }\n return ret;\n }\n};\n```
| 3
| 0
|
['String', 'Dynamic Programming', 'Memoization', 'Bitmask', 'C++']
| 1
|
find-the-shortest-superstring
|
PreCompute + BitMask + DP || C++
|
precompute-bitmask-dp-c-by-eghost08-kgfm
|
\n# Code\n\nclass Solution {\npublic:\n string solve(int last,int mask,int &n,map<int,map<int,int>>&mp,vector<string>&words,vector<vector<string>>&dp){\n
|
EGhost08
|
NORMAL
|
2023-09-24T06:12:25.299135+00:00
|
2023-09-24T06:12:25.299152+00:00
| 523
| false
|
\n# Code\n```\nclass Solution {\npublic:\n string solve(int last,int mask,int &n,map<int,map<int,int>>&mp,vector<string>&words,vector<vector<string>>&dp){\n if(mask==((1<<n)-1)){\n return "";\n }\n if(dp[last+1][mask]!="")\n return dp[last+1][mask];\n string curr="";\n for(int i=0;i<n;i++){\n if((mask>>i)&1)\n continue;\n string temp=words[i].substr(mp[last][i]);\n temp+=solve(i,mask|(1<<i),n,mp,words,dp);\n if(curr=="" || temp.size()<curr.size()){\n curr=temp;\n }\n }\n return dp[last+1][mask]=curr;\n }\n string shortestSuperstring(vector<string>& words) {\n map<int,map<int,int>> mp;\n int n=words.size();\n for(int i=0;i<n;i++){\n mp[-1][i]=0;\n for(int j=0;j<n;j++){\n int m=words[i].size();\n int m2=words[j].size();\n mp[i][j]=0;\n for(int l=1;l<=min(m,m2);l++){\n string temp=words[i].substr(m-l);\n string temp2=words[j].substr(0,l);\n if(temp==temp2){\n mp[i][j]=l;\n }\n }\n }\n }\n vector<vector<string>> dp(n+1,vector<string>(1<<n,""));\n return solve(-1,0,n,mp,words,dp);\n }\n};\n```
| 3
| 0
|
['C++']
| 1
|
find-the-shortest-superstring
|
Java | Held Karp (TSP) | Concise w/ explanations!
|
java-held-karp-tsp-concise-w-explanation-vnvu
|
Foreword\nI think this problem is a bit hard because there was a bug in my code that took me hours to catch.\nIt was a silly bug but it does test you on whether
|
Student2091
|
NORMAL
|
2022-07-14T08:21:35.282221+00:00
|
2022-07-15T08:11:12.513639+00:00
| 805
| false
|
#### Foreword\nI think this problem is a bit hard because there was a bug in my code that took me hours to catch.\nIt was a silly bug but it does test you on whether you really understand the Held Karp DP to solve TSP.\nMy suffering has just ended! \n\nIt is hard to imagine this question only got a rating of 21xx on https://zerotrac.github.io/leetcode_problem_rating/#/\n\n#### Details\n- Here `discount[i][j]` means how many letters we save if we go from `words[i]` to `words[j]`, so "abccd" to "ccdxx" would be 3, while "ccdxx" to "abccd" would be 0.\n\n- DP is just the standard Held Karp DP. Nothing unusual here, but we also need to save the path, and we will need a 2D array for it, with the 1st dimension being the next mask, and the second dimension being the next city. That way, we will be able to look up previous city since we know that it ends at `0b111...111` mask. We also know the city that it ends at city `j` when `dp[0b111...111][j]` is the greatest element among all `dp[0b111...111]` subarray.\n\n- When building the path, we can use `stringbuilder.insert(0, word)` but it is ineffecient. We can instead just use a String array and call `String.join()` at the end.\n\n#### End\nThat\'s it. I hope it help someone!\n\n#### Time Complexity: O(2^n * n^2)\n#### Space Complexity: (2^n * n + n^2)\n```Java\nclass Solution {\n public String shortestSuperstring(String[] words) {\n int n = words.length;\n int[][] discount = new int[n][n];\n for (int i = 0; i < n; i++){\n for (int j = 0; j < n; j++){\n for (int k = 0; k < words[i].length()&&i!=j; k++){ // build discount map from i->j and j->i\n if (words[j].startsWith(words[i].substring(k))){\n discount[i][j]=words[i].length()-k;\n break;\n }\n }\n }\n }\n int[][] dp = new int[1<<n][n];\n int[][] path = new int[1<<n][n];\n for (int i = 0; i < 1<<n; i++){ // find the max discount for mask (1<<n)-1 with dp\n for (int j = 0; j < n; j++){\n for (int k = 0; k < n && (i&1<<j)>0; k++){\n if ((i&1<<k)==0 && dp[i][j]+discount[j][k]>=dp[i|1<<k][k]){\n dp[i|1<<k][k]=dp[i][j]+discount[j][k];\n path[i|1<<k][k]=j;\n }\n }\n }\n }\n int m = (1<<n)-1, idx = n; // build the path from end to start\n int end=IntStream.range(0,n).reduce((a,b)->dp[(1<<n)-1][a]>dp[(1<<n)-1][b]?a:b).getAsInt();\n String[] ans = new String[n];\n while(m>0){\n ans[--idx]=words[end].substring((m&(m-1))==0?0:discount[path[m][end]][end]);\n m^=1<<end;\n end=path[m|1<<end][end];\n }\n return String.join("",ans);\n }\n}\n```
| 3
| 0
|
['Dynamic Programming', 'Java']
| 0
|
find-the-shortest-superstring
|
Python3 - memoization with bitmask, clean solution
|
python3-memoization-with-bitmask-clean-s-m9kt
|
The idea is simple: first, let\'s store the overlapping for each pair of words. Second, for DP, during each iteration, we look at words[i]; we need to find a un
|
yunqu
|
NORMAL
|
2021-04-16T01:46:22.654844+00:00
|
2021-04-16T01:48:06.245229+00:00
| 385
| false
|
The idea is simple: first, let\'s store the overlapping for each pair of words. Second, for DP, during each iteration, we look at words[i]; we need to find a unused words[j] and consider to merge the two words together. \n\nFor example, words[i] is \'abcde\' and words[j] is \'cdef\', the merging of the two words will be \'abcdef\'. Out of all the possible outcomes, we take the one with minimum length during each iteration.\n\nHow do we find an unused word? We use bitmask to keep track of used/unused word. A bit \'1\' at position i means the words[i] has already been taken.\n\n```python\nclass Solution:\n def shortestSuperstring(self, words: List[str]) -> str:\n n = len(words)\n overlaps = [[0 for _ in range(n)] for _ in range(n)]\n for i in range(n):\n for j in range(n):\n if i == j:\n continue\n x, y = words[i], words[j]\n size = len(x)\n for k in range(1, size):\n if y.startswith(x[k:]):\n overlaps[i][j] = size - k\n break\n\n @lru_cache(None)\n def helper(i, mask):\n if mask == (1<<n) - 1:\n return words[i]\n ans = \'#\' * 320\n for j in range(n):\n if mask & (1<<j) == 0:\n k = overlaps[i][j]\n string = helper(j, mask | (1<<j))\n if len(words[i] + string[k:]) < len(ans):\n ans = words[i] + string[k:]\n return ans\n\n return min([helper(i, 1<<i) for i in range(n)], key=len)\n```
| 3
| 1
|
[]
| 0
|
find-the-shortest-superstring
|
C# simple DP solution with explanations. Beats 100%.
|
c-simple-dp-solution-with-explanations-b-wcz6
|
\npublic class Solution {\n public string ShortestSuperstring(string[] words) {\n var memo = new Dictionary<string, string>();\n \n // m
|
attila201805
|
NORMAL
|
2021-03-24T20:49:29.113930+00:00
|
2021-03-24T20:50:18.114885+00:00
| 312
| false
|
```\npublic class Solution {\n public string ShortestSuperstring(string[] words) {\n var memo = new Dictionary<string, string>();\n \n // mark every word as unused\n int unused = 0; // integer is used as a bit array\n for(int i = 0; i < words.Length; i++) {\n unused |= 1 << i;\n }\n \n return ShortestSuperstring(words, "", unused, memo);\n }\n \n private string ShortestSuperstring(string[] words, string startWord, int unused, IDictionary<string, string> memo) {\n if (unused == 0) {\n return startWord;\n }\n \n // check memo\n string key = startWord + "|" + unused;\n if (memo.ContainsKey(key)) {\n return memo[key];\n }\n \n string shortest = null;\n for(int i = 0; i < words.Length; i++) {\n if (!IsUsed(unused, i)) { \n // get the shortest superstring starting from an unused word\n string superstring = ShortestSuperstring(words, words[i], MarkUsed(unused, i), memo);\n \n // "append" the shortest superstring to the start word\n string appended = OverlapAppend(startWord, superstring);\n \n // keep the shortest\n if (shortest == null || appended.Length < shortest.Length) {\n shortest = appended;\n }\n }\n }\n memo.Add(key, shortest);\n return shortest;\n }\n \n // "append" a to b, apply overlap. For example, "cat" and "atom" => "catom"\n private string OverlapAppend(string a, string b) {\n for(int i = Math.Max(1, a.Length - b.Length); i < a.Length; i++) {\n bool match = true;\n for(int j = i; j < a.Length; j++) {\n if (a[j] != b[j - i]) {\n match = false;\n break;\n }\n }\n \n if (match) {\n return a.Substring(0, i) + b;\n }\n }\n return a + b;\n } \n \n private bool IsUsed(int unused, int i) {\n return ((unused >> i) & 1) == 0;\n }\n \n private int MarkUsed(int unused, int i) {\n return unused & ~(1 << i);\n } \n}\n```
| 3
| 0
|
[]
| 0
|
find-the-shortest-superstring
|
Travelling Salesman Problem python
|
travelling-salesman-problem-python-by-an-axgw
|
\nfrom functools import lru_cache #This is used in order to avoid TLE by implementing memoization\n\nclass Solution:\n def shortestSuperstring(self, words):\
|
ANiSh684
|
NORMAL
|
2024-05-16T15:39:48.311843+00:00
|
2024-05-16T15:39:48.311865+00:00
| 382
| false
|
```\nfrom functools import lru_cache #This is used in order to avoid TLE by implementing memoization\n\nclass Solution:\n def shortestSuperstring(self, words):\n def makeadj(words):\n l = len(words)\n adj = [["" for z in range(l)] for x in range(l)]\n for i in range(l):\n for j in range(l):\n if i != j:\n x = words[i]\n y = words[j]\n max_overlap = 0\n for k in range(1, min(len(x), len(y)) + 1):\n if x[-k:] == y[:k]:\n max_overlap = k\n adj[i][j] = y[max_overlap:] # Only keep the non-overlapping part\n return adj\n\n @lru_cache(None)\n def sss(bits, cur):\n if bits == (1 << n) - 1: \n return ""\n res = "a" * 240\n for i in range(n):\n if (bits & (1 << i)) == 0:\n ans = adj[cur][i] + sss(bits | (1 << i), i)\n if len(res) > len(ans):\n res = ans\n return res\n \n ans = "a" * 240 \n n = len(words)\n adj = makeadj(words)\n for i in range(n):\n x = words[i] + sss(1 << i, i)\n if len(x) < len(ans):\n ans = x\n return ans\n```
| 2
| 0
|
['Bit Manipulation', 'Bitmask', 'Python', 'Python3']
| 0
|
find-the-shortest-superstring
|
DP Bitmask (Iterative/Bottom Up) (TSP)
|
dp-bitmask-iterativebottom-up-tsp-by-pol-ad0q
|
Intuition\nThis problem is analogous to the travelling salesman problem, as we need to start from any one string and visit all other strings, such that the tota
|
polaris01
|
NORMAL
|
2023-08-18T08:14:43.278956+00:00
|
2023-08-18T08:14:43.278995+00:00
| 236
| false
|
# Intuition\nThis problem is analogous to the travelling salesman problem, as we need to start from any one string and visit all other strings, such that the total length is minimum.\n\n# Approach\nWe can create a state as `(mask, curr_node)`. The `mask` represents the set of visited nodes, and we are currently at `curr_node`. Now, for the cost, of moving from one string to another, we can choose the cost to be the total length of string after combining. For instance, for moving from `ttca` to `catg`, the cost will be 6 as the final string will be `ttcatg`, of length 6. \n\nHowever, this will yield incorrect results as the cost will also be dependent on the absolute length of a string, rather than only the overlap. So, we choose the maximize the overlap, rather that minimizing the cost. Overlap in the case of `ttca` and `catg` is 2.\n\n- While iterating, we also need to store the parent of a state, so that we can trace the path later on. We only need to store the parent node, and not the parent mask in `parent[mask][curr_node]`, as we can get the parent mask by setting off the `curr_node` from the `mask`.\n\n- Strings which will have overlap 0 with every string, will not be present in the the path. So, we need to add all these strings at the end.\n\n# Complexity\nSame as that of the Held-Karp DP, used to solve TSP\n- Time complexity: $O(n^2*2^n)$\n- Space complexity: $O(n*2^n)$\n\n# Code\n```cpp\nclass Solution {\n int computeOverlap(string s, string t) {\n int n = s.size();\n int m = t.size();\n int idx = n;\n\n for (int i = n - 1;i>=0;i--) {\n if (s.substr(i, (n - i)) == t.substr(0, n - i)) {\n idx = i;\n }\n }\n return n - idx;\n }\n\n // returns the uncommon part in the string s. For s == `ttca` and t == `catg`\n // the function returns `tt`\n string computeUncommonPart(const string &s,const string &t) {\n int n = s.size();\n int m = t.size();\n int idx = n;\n\n for (int i = n - 1;i>=0;i--) {\n if (s.substr(i, (n - i)) == t.substr(0, n - i)) {\n idx = i;\n }\n }\n if (idx == n) {\n return s;\n }\n return s.substr(0, idx);\n }\n\npublic:\n string shortestSuperstring(vector<string>& words) {\n int n = words.size();\n vector<vector<int>> overlap(n, vector<int> (n));\n vector<vector<int>> parent(1 << n, vector<int> (n, -1));\n vector<vector<int>> dp(1 << n, vector<int> (n));\n\n for (int i = 0;i<n;i++) {\n for (int j = 0;j<n;j++) {\n if (i != j) {\n overlap[i][j] = computeOverlap(words[i], words[j]);\n }\n }\n }\n\n for (int mask = 0;mask < (1<<n); mask++) {\n for (int i = 0;i<n;i++) {\n if ((mask)&(1<<i)) {\n for (int j = 0;j<n;j++) {\n if (((mask)&(1<<j)) == 0) {\n if (dp[mask | 1<<j][j] < dp[mask][i] + overlap[i][j]) {\n dp[mask | 1<<j][j] = dp[mask][i] + overlap[i][j];\n parent[mask | 1<<j][j] = i;\n }\n }\n }\n } \n }\n }\n\n // find the node with maximum overlap.\n int mx = 0;\n int dest = -1;\n for (int i = 0;i<n;i++) {\n if (dp[(1<<n) - 1][i] > mx) {\n mx = dp[(1<<n) - 1][i];\n dest = i;\n }\n }\n\n // trace back the path\n vector<bool> visited(n);\n vector<string> res;\n int mask = (1<<n) - 1;\n int src = dest;\n while (dest != -1) {\n res.push_back(words[dest]);\n visited[dest] = true;\n int prev = parent[mask][dest];\n mask ^= (1<<dest);\n dest = prev;\n }\n\n reverse(res.begin(), res.end());\n for (int i = 0;i<n;i++) {\n if(!visited[i]) {\n res.push_back(words[i]);\n visited[i] = true;\n }\n }\n \n string ans = "";\n for (int i = 0;i<n-1;i++) {\n string uncommonPart = computeUncommonPart(res[i], res[i+1]);\n ans += uncommonPart;\n }\n ans += res[n-1];\n return ans;\n }\n};\n```
| 2
| 0
|
['Dynamic Programming', 'Bit Manipulation', 'Bitmask', 'C++']
| 0
|
find-the-shortest-superstring
|
Solution
|
solution-by-deleted_user-il4w
|
C++ []\nclass Solution {\npublic:\n string shortestSuperstring(vector<string>& A) {\n int dp[4096][12] = {0};\n int failure[12][20] = {0};\n
|
deleted_user
|
NORMAL
|
2023-05-15T02:00:32.897737+00:00
|
2023-05-15T03:14:36.709638+00:00
| 1,416
| false
|
```C++ []\nclass Solution {\npublic:\n string shortestSuperstring(vector<string>& A) {\n int dp[4096][12] = {0};\n int failure[12][20] = {0};\n int cost[12][12] = {0};\n int trace_table[4096][12] = {0};\n const int sz = A.size();\n const int dp_sz = 1 << sz;\n \n for (int i = 0; i < sz; i++) {\n const int str_sz = A[i].size();\n \n failure[i][0] = -1;\n \n for (int j = 1, k = -1; j < str_sz; j++) {\n while (k >= 0 && A[i][k + 1] != A[i][j])\n k = failure[i][k];\n \n if (A[i][k + 1] == A[i][j]) k++;\n \n failure[i][j] = k;\n }\n }\n for (int i = 0; i < sz; i++) {\n const int i_sz = A[i].size();\n \n for (int j = 0; j < sz; j++) {\n if (i != j) {\n const int j_sz = A[j].size();\n int h = -1;\n \n for (int k = 0; k < j_sz; k++) {\n while (h >= 0 && A[i][h + 1] != A[j][k])\n h = failure[i][h];\n \n if (A[i][h + 1] == A[j][k])\n h++;\n }\n cost[j][i] = i_sz - h - 1;\n }\n }\n }\n for (int i = 0; i < sz; i++)\n dp[1 << i][i] = A[i].size();\n \n for (int state = 1; state < dp_sz; state++) {\n for (int t1 = state, b1 = t1 & (-t1); t1 ; t1 ^= b1 , b1 = t1 & (-t1)) {\n const int state1 = state ^ b1;\n const int i = __builtin_ctz(b1);\n const int i_sz = A[i].size();\n \n for (int t2 = state1, b2 = t2 & (-t2); t2; t2 ^= b2, b2 = t2 & (-t2)) { \n const int j = __builtin_ctz(b2);\n const int tmp = dp[state1][j] + cost[j][i];\n \n if (!dp[state][i] || tmp < dp[state][i]) {\n dp[state][i] = tmp;\n trace_table[state][i] = j;\n }\n }\n }\n }\n const auto& last = dp[dp_sz - 1];\n string res;\n int i = std::distance(last, std::min_element(last, last + sz));\n \n for (int state = dp_sz - 1, j = trace_table[state][i]; state & (state - 1); state ^= (1 << i), i = j, j = trace_table[state][i])\n res = A[i].substr(A[i].size() - cost[j][i]) + res;\n \n return A[i] + res;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def shortestSuperstring(self, words: List[str]) -> str:\n def getMinSuffix(w1, w2):\n n = min(len(w1), len(w2))\n for i in range(n, 0, -1):\n if w1[-i:] == w2[:i]:\n return w2[i:]\n return w2\n\n n = len(words)\n suffix = defaultdict(dict)\n for i in range(n):\n for j in range(n):\n suffix[i][j] = getMinSuffix(words[i], words[j])\n dp = [[\'\']*n for _ in range(1<<n)]\n for i in range(1, 1<<n):\n indexes = [j for j in range(n) if i&(1<<j)]\n for j in indexes:\n i2 = i&~(1<<j)\n strs = [dp[i2][j2]+suffix[j2][j] for j2 in indexes if j2 != j]\n dp[i][j] = min(strs, key=len) if strs else words[j]\n return min(dp[-1], key=len)\n```\n\n```Java []\nclass Solution {\n public String shortestSuperstring(String[] words) {\n int n = words.length;\n int[][] mat = new int[n][n];\n for (int i = 0; i < n; i++) \n for (int j = i+1; j < n; j++) {\n mat[i][j] = dist(words[i], words[j]);\n mat[j][i] = dist(words[j], words[i]);\n }\n int[][] dp = new int[1<<n][n];\n for (int[] row : dp)\n Arrays.fill(row, Integer.MAX_VALUE / 2);\n\n int[][] parents = new int[1<<n][n];\n for (int[] row : parents) \n Arrays.fill(row, -1);\n\n for (int i = 0; i < n; i++) \n dp[1<<i][i] = words[i].length();\n\n int min = Integer.MAX_VALUE;\n int cur = 0;\n for (int s = 1 ; s < (1<<n); s++) {\n for (int i = 0; i < n; i++) {\n if ((s & (1 <<i)) == 0) continue;\n int prevS = s & ~(1 << i);\n for (int j = 0; j < n; j++) {// i comes from j;\n if (dp[prevS][j] + mat[j][i] < dp[s][i]) {\n dp[s][i] = dp[prevS][j] + mat[j][i];\n parents[s][i] = j;\n }\n }\n if (s == (1<<n) - 1 && dp[s][i] < min) {\n min = dp[s][i];\n cur = i;\n } \n } \n }\n int s = (1<<n) - 1;\n String ans = "";\n while (s > 0 ) {\n int prev = parents[s][cur];\n if (prev < 0) ans = words[cur] + ans;\n else ans = words[cur].substring(words[cur].length() - mat[prev][cur]) + ans;\n s &= ~(1 << cur);\n cur = prev;\n }\n return ans;\n }\n private int dist(String a, String b) {\n int d = b.length();\n for (int k = 1; k <= Math.min(a.length(), b.length()); k++) {\n if (a.endsWith(b.substring(0, k)))\n d = b.length() - k;\n }\n return d;\n }\n}\n```\n
| 2
| 0
|
['C++', 'Java', 'Python3']
| 0
|
find-the-shortest-superstring
|
Find the Shortest Superstring Bugs? | Python
|
find-the-shortest-superstring-bugs-pytho-aoo8
|
Is there a bug in the leetcode submitting system for this problem? How is this getting accepted?\n\n\nBy the way here is a serious code if you are looking for i
|
Interstigation
|
NORMAL
|
2021-05-23T16:37:51.990329+00:00
|
2021-05-23T16:38:49.013436+00:00
| 398
| false
|
Is there a bug in the leetcode submitting system for this problem? How is ***this*** getting accepted?\n\n\nBy the way here is a serious code if you are looking for it\n```\nclass Solution:\n def shortestSuperstring(self, words: List[str]) -> str:\n @lru_cache(None)\n def connect(w1, w2):\n return [(w2[i:], len(w2) - i) for i in range(len(w1) + 1) if w1[-i:] == w2[:i] or not i][-1]\n \n N = len(words)\n dp = [[(float("inf"), -1)] * N for _ in range(1<<N)]\n for i in range(N): dp[1<<i][i] = (len(words[i]), -1)\n \n for mask in range(1<<N):\n n_z_bits = [j for j in range(N) if mask & 1<<j]\n for j, k in permutations(n_z_bits, 2):\n dp[mask][j] = min(dp[mask][j], (dp[mask ^ 1<<j][k][0] + connect(words[k], words[j])[1], k))\n \n mask = (1<<N) - 1\n prev = min(dp[mask])\n last = dp[mask].index(prev)\n prev = prev[1]\n ans = ""\n \n while prev != -1:\n ans = connect(words[prev], words[last])[0] + ans\n mask -= (1<<last)\n prev, last = dp[mask][prev][1], prev\n \n return words[last] + ans\n```
| 2
| 2
|
[]
| 1
|
find-the-shortest-superstring
|
Swift solution (Travelling Salesman Problem)
|
swift-solution-travelling-salesman-probl-ih50
|
Swift version of https://leetcode.com/problems/find-the-shortest-superstring/discuss/194932/Travelling-Salesman-Problem\n\nclass Solution {\n func shortestSu
|
yamironov
|
NORMAL
|
2021-05-23T16:07:32.808358+00:00
|
2021-05-23T19:12:33.542582+00:00
| 166
| false
|
Swift version of https://leetcode.com/problems/find-the-shortest-superstring/discuss/194932/Travelling-Salesman-Problem\n```\nclass Solution {\n func shortestSuperstring(_ words: [String]) -> String {\n let n = words.count, n2 = 1 << n\n\n // build the graph\n var graph = [[Int]](repeating: [Int](repeating: 0, count: n), count: n)\n for i in 0..<n {\n forj: for j in 0..<n {\n let ic = words[i].count, jc = words[j].count\n for k in 0..<ic where words[j].starts(with: words[i].suffix(ic - k)) {\n graph[i][j] = jc - ic + k\n continue forj\n }\n graph[i][j] = jc\n }\n }\n\n // start TSP DP\n var dp = [[Int]](repeating: [Int](repeating: Int.max, count: n), count: n2), path = dp\n for i in 1..<n2 {\n for j in 0..<n where i & (1 << j) > 0 {\n let prev = i - (1 << j)\n if prev == 0 {\n dp[i][j] = words[j].count\n } else {\n for k in 0..<n where dp[prev][k] < Int.max && dp[prev][k] + graph[k][j] < dp[i][j] {\n dp[i][j] = dp[prev][k] + graph[k][j]\n path[i][j] = k\n }\n }\n }\n }\n\n // build the path\n var stack = [Int](), cur = n2 - 1, last = dp[n2 - 1].firstIndex(of: dp[n2 - 1].min()!)!\n while cur > 0 {\n stack.append(last)\n (cur, last) = (cur - (1 << last), path[cur][last])\n }\n\n // build the result\n var result = words[stack.last!]\n for i in stride(from: stack.count - 2, through: 0, by: -1) {\n let curWordIndex = stack[i], prevWordIndex = stack[i + 1]\n result += String(words[curWordIndex].suffix(graph[prevWordIndex][curWordIndex]))\n }\n\n return result\n }\n}\n```
| 2
| 0
|
['Swift']
| 1
|
find-the-shortest-superstring
|
C++ recursion and memoization
|
c-recursion-and-memoization-by-jeeteqxyz-vvzu
|
```\nclass Solution {\npublic:\n vectorlen;\n vector>overlap;\n vector>dp;\n int n;\n map, int>mp;\n int solve(int idx, int mask){\n if
|
jeeteqxyz
|
NORMAL
|
2020-10-08T11:32:00.969496+00:00
|
2020-10-08T11:32:00.969535+00:00
| 469
| false
|
```\nclass Solution {\npublic:\n vector<int>len;\n vector<vector<int>>overlap;\n vector<vector<int>>dp;\n int n;\n map<pair<int, int>, int>mp;\n int solve(int idx, int mask){\n if(mask == (1 << n) - 1) return 0;\n if(dp[idx][mask] != -1)return dp[idx][mask];\n dp[idx][mask] = INT_MAX;\n for(int i = 0; i < n; i++){\n if((mask&(1 << i)) == 0){\n int temp = len[i] - overlap[idx][i] + solve(i, mask|(1 << i));\n if(temp < dp[idx][mask]){\n dp[idx][mask] = temp;\n mp[{idx, mask}] = i;\n }\n }\n }\n return dp[idx][mask];\n }\n string shortestSuperstring(vector<string>& A) {\n n = A.size();\n len.resize(n, 0);\n overlap.resize(n, vector<int>(n, 0));\n dp.resize(n, vector<int>((1 << n) + 1, -1));\n for(int i = 0; i < n; i++){\n len[i] = A[i].size();\n }\n for(int i = 0; i < n; i++){\n for(int j = 0; j < n; j++){\n if(i != j){\n int m = min(len[i], len[j]);\n for(int k = m; k >= 0; k--){\n if(A[i].substr(len[i] - k) == A[j].substr(0, k)){\n overlap[i][j] = k;\n break;\n }\n }\n }\n }\n }\n int mlen = INT_MAX;\n int idx = 0;\n for(int i = 0; i < n; i++){\n int temp = len[i] + solve(i, (1 << i));\n //cout<<temp<<endl;\n if(temp < mlen){\n mlen = temp;\n idx = i;\n }\n }\n string ans = A[idx];\n int mask = 1 << idx;\n for(int i = 1; i < n; i++){\n int x = idx;\n idx = mp[{idx, mask}];\n ans += A[idx].substr(overlap[x][idx]);\n mask |= (1 << idx); \n }\n return ans;\n }\n};
| 2
| 1
|
[]
| 2
|
find-the-shortest-superstring
|
C++ O(N^2 * 2^N) Bitmask DP + DFS solution w/ explanation
|
c-on2-2n-bitmask-dp-dfs-solution-w-expla-6pwz
|
The idea is that after selecting some words, we have to find the minimum length of the remaining superstring. For that we check all the remaining words. The sel
|
varkey98
|
NORMAL
|
2020-08-14T11:22:56.373920+00:00
|
2020-08-14T11:23:19.886144+00:00
| 929
| false
|
The idea is that after selecting some words, we have to find the minimum length of the remaining superstring. For that we check all the remaining words. The selected words are marked by the bitmask. After finding the minimum length, simply run an O(N^2) DFS for finding the answer.\n```\nint min(int a,int b)\n{\n return a<b?a:b;\n}\nstring ret;\nint memo[4096][12];\nint overlap[12][12];\nvoid fun(vector<string>& words)\n{\n for(int i=0;i<words.size();++i)\n for(int j=0;j<words.size();++j)\n {\n if(i==j)\n continue;\n int count=0;\n for(int start=0;start<words[i].size();++start)\n if(words[i][start]==words[j][0])\n for(int k=start;k<words[i].length();++k)\n if(words[i][k]!=words[j][count])\n {\n count=0;\n break;\n }\n else\n {\n ++count;\n if(k==words[i].length()-1)\n goto breakp;\n }\nbreakp: overlap[i][j]=count;\n }\n}\nint dp(int mask,int pre,int allmask,vector<string>& words)\n{\n if(mask==allmask)\n return 0;\n else if(memo[mask][pre]!=-1)\n return memo[mask][pre];\n else\n {\n int q=INT_MAX;\n for(int i=0;i<words.size();++i)\n if((mask&(1<<i))==0)\n q=min(q,words[i].length()-(mask?overlap[pre][i]:0)+dp(mask|1<<i,i,allmask,words));\n return memo[mask][pre]=q;\n }\n}\nvoid dfs(int mask,int allmask,int pre,vector<string>& words)\n{\n if(mask==allmask)\n return;\n else\n {\n for(int i=0;i<words.size();++i)\n if(!mask)\n {\n if(memo[mask][pre]==words[i].length()+dp(1<<i,i,allmask,words))\n {\n ret=words[i];\n dfs(1<<i,allmask,i,words);\n break;\n }\n }\n else\n if(memo[mask][pre]==words[i].length()-overlap[pre][i]+dp(mask|1<<i,i,allmask,words))\n {\n ret+=words[i].substr(overlap[pre][i]);\n dfs(mask|1<<i,allmask,i,words);\n break;\n }\n }\n}\nstring shortestSuperstring(vector<string>& A) \n{\n memset(memo,-1,sizeof(memo));\n int n=A.size(),pre=0;\n int allmask=(1<<n)-1;\n memset(overlap,0,sizeof(overlap));\n fun(A); \n dp(0,0,allmask,A);\n dfs(0,allmask,0,A);\n return ret;\n}\n```
| 2
| 1
|
['Dynamic Programming', 'Depth-First Search', 'C', 'Bitmask']
| 0
|
find-the-shortest-superstring
|
C++ solution using DP with memoization (Beats 90% in runtime)
|
c-solution-using-dp-with-memoization-bea-bvi8
|
\nvector<vector<int> > dp,pre,par;\n\nbool startWith(string s, string t)\n{\n// returns true if string s starts with string t\n int i;\n for(i=0; i<s.leng
|
cjchirag7
|
NORMAL
|
2020-08-08T09:26:13.906636+00:00
|
2020-08-08T09:26:13.906667+00:00
| 1,400
| false
|
```\nvector<vector<int> > dp,pre,par;\n\nbool startWith(string s, string t)\n{\n// returns true if string s starts with string t\n int i;\n for(i=0; i<s.length()&&i<t.length(); i++)\n {\n if(s[i]==t[i])\n continue;\n else\n return false;\n }\n if(i==t.length())\n return true;\n else\n return false;\n}\n\nint calc(string A, string B)\n{\n // calculate the number of extra characters required to be appended to A\n // if A is followed by B\n // for eg. calc("abcd","cdef") = 2\n \n int a=A.length(),b=B.length();\n for(int i=0; i<a; i++)\n {\n if(a-i<=b&&startWith(B,A.substr(i)))\n {\n return b-(a-i); \n }\n }\n return b;\n}\n\nint finalMask,n;\n\nint helper(int mask, int last)\n{\n // returns the minimum length of string required if last string appended was A[last] \n // the sets bit in mask represents the strings that were already appended to the final string\n \n if(mask==finalMask) // all strings are appended in final string\n return 0;\n\n if(dp[mask][last]!=-1) // memoization\n return dp[mask][last];\n \n int mn=INT_MAX;\n int p;\n for(int i=0; i<n; i++)\n {\n if(mask&(1<<i))\n continue;\n int cost=pre[last][i]+helper(mask|(1<<i),i); // extra characters need to be appended\n if(cost<mn)\n {\n mn=cost;\n p=i;\n }\n }\n par[mask][last]=p; // store parent, so that it is easy to traceback and find the final result\n return dp[mask][last]=mn; // store result in DP table\n}\n\n\n\nclass Solution {\npublic:\n string shortestSuperstring(vector<string>& A) {\n n=A.size();\n pre.assign(n,vector<int>(n)); // for pre-computing calc(a,b) for all pairs of strings\n par.assign(1<<n,vector<int>(n,-1)); \n for(int i=0; i<n; i++)\n {\n for(int j=0; j<n; j++)\n {\n if(j==i)\n continue;\n pre[i][j]=calc(A[i],A[j]);\n }\n }\n finalMask=(1<<n)-1; \n dp.assign(1<<n,vector<int>(n,-1));\n int len=INT_MAX; // len will contain minimum length of required string\n int ind;\n for(int i=0; i<n; i++)\n {\n int prev=len;\n len=min(len, (int)A[i].length()+helper(1<<i,i));\n if(len!=prev)\n {\n ind=i;\n }\n }\n\n // Now traceback to find the final answer\n string ans=A[ind];\n int msk=1<<ind;\n int prev_ind=ind;\n ind=par[msk][ind];\n while(ind!=-1)\n {\n len=pre[prev_ind][ind];\n int alen=A[ind].length();\n ans+=A[ind].substr(alen-len,len); \n msk=msk^(1<<ind);\n prev_ind=ind;\n ind=par[msk][ind]; \n }\n return ans;\n }\n};\n```
| 2
| 1
|
['Dynamic Programming', 'Memoization', 'C', 'C++']
| 0
|
find-the-shortest-superstring
|
Java Graph, TSP and DP
|
java-graph-tsp-and-dp-by-hobiter-8qno
|
1, build a directed graph, where edge values are cost to concate from string to next string;\n2, find 1 route from the graph to\na, include all nodes once and o
|
hobiter
|
NORMAL
|
2020-06-06T23:49:20.776991+00:00
|
2020-06-06T23:49:20.777041+00:00
| 407
| false
|
1, build a directed graph, where edge values are cost to concate from string to next string;\n2, find 1 route from the graph to\na, include all nodes once and only once;\nb, make sure the cost are the minmum;\n\nFrom the above 2, it is the defination similar to TSP (Travelling Salesman Problem);\nRef https://leetcode.com/problems/find-the-shortest-superstring/discuss/194932/Travelling-Salesman-Problem\n\n```\nclass Solution {\n public String shortestSuperstring(String[] A) {\n int n = A.length, path[][] = new int[1 << n][n], g[][] = buildGraph(A), min = Integer.MAX_VALUE, last = 0;\n Integer[][] dp = new Integer[1 << n][n];\n for (int i = 1; i < dp.length; i++) {\n for (int j = 0; j < n; j++) {\n if ((i & (1 << j)) == 0) continue;\n int prev = i - (1 << j);\n if (prev == 0) {\n dp[i][j] = A[j].length();\n continue;\n }\n dp[i][j] = Integer.MAX_VALUE;\n for (int k = 0; k < n; k++) {\n if (dp[prev][k] != null && dp[i][j] > dp[prev][k] + g[k][j]){\n dp[i][j] = dp[prev][k] + g[k][j];\n path[prev][j] = k; // could also be [prev][i], but not saving space;\n }\n }\n if (i == (1 << n) - 1 && dp[i][j] != null && dp[i][j] < min) {\n min = dp[i][j];\n last = j;\n }\n }\n }\n\n List<Integer> route = new ArrayList<>();\n int curr = (1 << n) - 1;\n while (curr > 0) {\n route.add(last);\n curr -= (1 << last);\n last = path[curr][last];\n }\n StringBuilder sb = new StringBuilder();\n sb.append(A[route.get(route.size() - 1)]);\n for (int i = route.size() - 2; i >= 0; i--) {\n sb.append(A[route.get(i)].substring(A[route.get(i)].length() - g[route.get(i + 1)][route.get(i)]));\n }\n return sb.toString();\n }\n \n private int[][] buildGraph(String[] A) {\n int n = A.length, g[][] = new int[n][n];\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < n; j++) {\n g[i][j] = cost(A[i], A[j]);\n g[j][i] = cost(A[j], A[i]);\n }\n }\n return g;\n }\n \n private int cost(String a, String b) {\n int n = b.length(), m = a.length(), res = n;\n for (int i = Math.min(m, n); i > 0; i--) {\n boolean same = true;\n for (int j = 0; j < i; j++) {\n if (a.charAt(m - i + j) != b.charAt(j)) {\n same = false;\n break;\n }\n }\n if (same) return n - i;\n }\n return n;\n }\n}\n```
| 2
| 0
|
[]
| 0
|
find-the-shortest-superstring
|
Python3 - Top Down BitMask DP
|
python3-top-down-bitmask-dp-by-havingfun-q965
|
As the question mentions that no string in A will be substring of another string in A. I can conclude that we can find our answer by one of the permutations of
|
havingfun
|
NORMAL
|
2020-06-03T05:27:17.633181+00:00
|
2020-06-03T05:27:17.633213+00:00
| 243
| false
|
As the question mentions that no string in A will be substring of another string in A. I can conclude that we can find our answer by one of the permutations of combining different strings in A. If you combine two strings in A - like a + b, you can count the largest suffix of a which is also prefix of b. So I have a helper function which gives me this number.\nThen a + b become a + b[commonPart:].\nFirst TLE solution that I tried was generating all permutations of A and finding the minimum length. This was N! (12!) which can\'t pass. \nBut we can use the fact that most of the parts of the permutations are repetitive and we can somehow convert them to DP. Then I tried DP with bitmasking where state is -\n(i, bitmask) which means minimum length string that ends with A[i] and contains all elements in the bitmask.\n```\nclass Solution:\n def shortestSuperstring(self, A: List[str]) -> str:\n def commonSuffix(a, b):\n for i in range(len(a)):\n if a[i:] == b[:len(a)-i]:\n return len(a) - i\n return 0\n N = len(A)\n from functools import lru_cache\n @lru_cache(None)\n def minString(last_index, bitmask):\n if bitmask == (1<<N)-1:\n return ""\n current = "Z"*250\n for i in range(N):\n if not ((1<<i) & bitmask):\n current = min(\n current,\n A[i][commonSuffix(A[last_index], A[i]):] + minString(i, bitmask | (1<<i)),\n key=len\n )\n return current\n ans = "Z"*250\n for i in range(N):\n ans = min(ans, A[i] + minString(i, 1<<i), key=len)\n return ans\n```
| 2
| 0
|
[]
| 0
|
find-the-shortest-superstring
|
[Java] Bitmask DP Solution
|
java-bitmask-dp-solution-by-frenkiedejon-c7ok
|
dp[i][mask] represents the shortest superstring which ends at i-th word (A[i]), participating words are denoted by mask, for example, mask 0b01011 means partici
|
frenkiedejong
|
NORMAL
|
2020-01-02T05:10:57.221630+00:00
|
2020-01-02T05:15:33.790120+00:00
| 392
| false
|
* dp[i][mask] represents the shortest superstring which ends at *i-th* word (A[i]), participating words are denoted by mask, for example, mask 0b01011 means participating words are A[0], A[1], A[3]\n* My DP transition function stores the String directly, so I don\'t need to construct the resulting string at the end\n\t* ```String[][] dp = new String[n][1<<n];```\n\n```\nclass Solution {\n public String shortestSuperstring(String[] A) {\n int n = A.length;\n if (n == 1) {\n return A[0];\n }\n int[][] len = new int[n][n];\n for (int i = 0; i < n; i++) {\n for (int j = i + 1; j < n; j++) {\n len[i][j] = getCommonLen(A[i], A[j]);\n len[j][i] = getCommonLen(A[j], A[i]);\n }\n }\n \n String[][] dp = new String[n][1<<n];\n \n int min = Integer.MAX_VALUE;\n String minStr = null;\n for (int i = 1; i < (1<<n); i++) {\n for (int j = 0; j < n; j++) {\n if ((i & (1 << j)) == 0) { // A[j] is not in the mask\n continue;\n }\n if (i == (1 << j)) { // return A[j] if the mask only contains 1 word\n dp[j][i] = A[j];\n continue;\n }\n int state = i ^ (1 << j);\n int cur = Integer.MAX_VALUE;\n String curStr = null;\n for (int x = 0; x < n; x++) {\n if (x != j && (i & (1 << x)) > 0 \n && dp[x][state].length() + A[j].length() - len[x][j] < cur) {\n cur = dp[x][state].length() + A[j].length() - len[x][j];\n curStr = dp[x][state] + A[j].substring(len[x][j]);\n }\n }\n dp[j][i] = curStr;\n \n\t\t\t\t// get the minimum among all results dp[x][(1<<n)-1]\n if (i == ((1<<n) - 1)) {\n if (min > dp[j][i].length()) {\n min = dp[j][i].length();\n minStr = dp[j][i];\n }\n }\n }\n }\n return minStr;\n }\n \n private int getCommonLen(String s1, String s2) {\n int n1 = s1.length();\n int n2 = s2.length();\n int n = Math.min(n1, n2);\n \n for (int i = n; i >= 0; i--) {\n if (s1.substring(n1-i, n1).equals(s2.substring(0, i))) {\n return i;\n }\n }\n \n return 0;\n }\n}\n```
| 2
| 0
|
[]
| 0
|
find-the-shortest-superstring
|
[Inefficient Java solution] DFS - Beat 5%
|
inefficient-java-solution-dfs-beat-5-by-tm9u5
|
\nclass Solution {\n private static class Result {\n String value = "";\n }\n \n public String shortestSuperstring(String[] A) {\n if
|
zacling
|
NORMAL
|
2019-07-29T23:54:02.563444+00:00
|
2019-07-29T23:54:02.563481+00:00
| 344
| false
|
```\nclass Solution {\n private static class Result {\n String value = "";\n }\n \n public String shortestSuperstring(String[] A) {\n if (A.length == 1) return A[0];\n \n int[][] subAt = new int[A.length][A.length];\n for (int i = 0; i < A.length; ++i)\n for (int j = 0; j < A.length; ++j)\n if (i != j)\n subAt[i][j] = substringAt(A[i], A[j]);\n \n Result r = new Result();\n dfs(A, subAt, new StringBuilder(), -1, 0, new boolean[A.length], r);\n return r.value;\n }\n \n\t// inspired by woshilxd912\n private void dfs(String[] A, int[][] subAt, StringBuilder path, int last, int depth, boolean[] visited, Result r) {\n if (depth == A.length) { \n if (r.value.isEmpty() || r.value.length() > path.length()) r.value = path.toString();\n return; \n }\n if (!r.value.isEmpty() && path.length() >= r.value.length()) return;\n if (depth == 0) {\n for (int i = 0; i < A.length; ++i) {\n visited[i] = true;\n path.append(A[i]);\n dfs(A, subAt, path, i, 1, visited, r);\n path.delete(0, path.length());\n visited[i] = false;\n }\n return;\n }\n for (int i = 0; i < A.length; ++i) {\n if (visited[i]) continue;\n visited[i] = true;\n int pathLen = path.length();\n path.append(A[i].substring(subAt[last][i]));\n if (r.value.isEmpty() || path.length() < r.value.length())\n dfs(A, subAt, path, i, depth + 1, visited, r);\n path.delete(pathLen, path.length());\n visited[i] = false;\n }\n }\n \n private int substringAt(String a, String b) {\n if (a.isEmpty()) return 0;\n \n for (int i = Math.min(a.length(), b.length()); i > 0; --i)\n if (a.endsWith(b.substring(0, i)))\n return i;\n \n return 0;\n }\n \n}\n```
| 2
| 0
|
[]
| 1
|
find-the-shortest-superstring
|
C++ Recursive Dp + Path Finding ~20 ms
|
c-recursive-dp-path-finding-20-ms-by-emi-r47r
|
I try to maximise the overlap length in the salesman\'s total path.\n\n#define se second\n#define fi first\n#define dbg(x) cout<<#x<<" = "<<(x)<<endl;\n#define
|
eminem347
|
NORMAL
|
2018-11-20T07:49:18.906602+00:00
|
2018-11-20T07:49:18.906642+00:00
| 700
| false
|
I try to maximise the overlap length in the salesman\'s total path.\n```\n#define se second\n#define fi first\n#define dbg(x) cout<<#x<<" = "<<(x)<<endl;\n#define dbg1(x,y) cout<<#x<<" = "<<(x)<<" | "<<#y<<" = "<<(y)<<endl;\ntypedef pair<int,int> ii;\ntypedef pair<int,ii> iii;\ntypedef vector<int> vi;\ntypedef vector<vi> iv;\nint n;\nint mx=-1;\niv g;\nint dp[14][((1<<14))];\n\nint rec(int idx,int mask){\n if(mask==((1<<n)-1)){\n return 0;\n }\n if(dp[idx][mask]!=-1) return dp[idx][mask];\n for(int i=0;i<n;i++){\n if(((1<<i)&mask)==0){\n int temp=(mask|(1<<i));\n dp[idx][mask]=max( dp[idx][mask] , g[idx][i]+rec(i,temp) );\n }\n }\n return dp[idx][mask];\n}\n\nstring path(int x,int rem,int mask,vector<string> &A){\n string out=A[x];\n if(mask==((1<<n)-1)){\n return out;\n }\n for(int i=0;i<n;i++){\n if(((1<<i)&mask)==0){\n if(g[x][i]+rec(i,(mask|(1<<i)))==rem){\n string t=out;\n string y=path(i,rem-g[x][i],(mask|(1<<i)),A); \n return out+y.substr(g[x][i]);\n }\n }\n }\n}\n\n\n\nclass Solution {\npublic:\n string shortestSuperstring(vector<string>& A) {\n int tot=0;\n A.insert(A.begin(),"");\n n=A.size();\n g.clear();\n g.resize(n,vi(n));\n mx=0;\n for(int i=0; i<n; ++i) for(int j=0; j<n; ++j) if(i!=j){\n for(int k = min(A[i].size(), A[j].size()); k>0; --k)\n if(A[i].substr(A[i].size()-k)==A[j].substr(0,k)){\n g[i][j] = k; \n break;\n }\n }\n \n memset(dp,-1,sizeof(dp));\n int rem=rec(0,1);\n string x=path(0,rem,1,A);\n return x;\n }\n};\n```\n
| 2
| 0
|
[]
| 0
|
find-the-shortest-superstring
|
Simple approach (C++) Solution
|
simple-approach-c-solution-by-harrypotte-uswc
|
\nclass Solution {\npublic:\n string shortestSuperstring(vector<string>& A) {\n int n=A.size(),m=0,i,j,k,o,a[12][12],l[12],p[12],f[4096][12];\n
|
harrypotter0
|
NORMAL
|
2018-11-18T04:15:27.995848+00:00
|
2018-11-18T04:15:27.995896+00:00
| 807
| false
|
```\nclass Solution {\npublic:\n string shortestSuperstring(vector<string>& A) {\n int n=A.size(),m=0,i,j,k,o,a[12][12],l[12],p[12],f[4096][12];\n for(i=0;i<n;i++)l[i]=A[i].size();\n memset(f,0,sizeof(f));\n for(i=0;i<n;i++)for(j=0;j<n;j++)if(i!=j)for(a[i][j]=0,k=1;k<l[i]&&k<l[j];k++)\n {\n for(o=0;o<k;o++)if(A[i][l[i]-k+o]!=A[j][o])break;\n if(o==k)a[i][j]=k;\n }\n for(i=1;i<1<<n;i++)for(j=0;j<n;j++)if(i>>j&1)for(k=0;k<n;k++)if((i>>k&1)&&j!=k)f[i][j]=max(f[i][j],f[i^(1<<j)][k]+a[k][j]);\n for(i=j=0;i<n;i++)if(f[(1<<n)-1][i]>f[(1<<n)-1][j])j=i;\n for(i=(1<<n)-1;;)\n {\n p[m++]=j;\n if(i==(1<<j))break;\n for(k=0;k<n;k++)if((i>>k&1)&&j!=k&&f[i][j]==f[i^(1<<j)][k]+a[k][j])break;\n i^=1<<j;\n j=k;\n }\n reverse(p,p+m);\n string ans=A[p[0]];\n for(i=1;i<n;i++)for(j=a[p[i-1]][p[i]];j<l[p[i]];j++)ans+=A[p[i]][j];\n return ans;\n }\n};\n```\nAlso the problem is available in [this](https://www.geeksforgeeks.org/shortest-superstring-problem/) GFG post
| 2
| 2
|
[]
| 3
|
find-the-shortest-superstring
|
Easy to understand TSP implementation (Top-Down/Bottom-Up)[python]
|
easy-to-understand-tsp-implementation-to-kxng
|
Approach\n Describe your approach to solving the problem. \nConsider this problem as a graph problem where we need to visit every single node with the minimal o
|
vgnshiyer
|
NORMAL
|
2023-10-17T18:14:00.716606+00:00
|
2023-10-17T18:14:00.716637+00:00
| 167
| false
|
# Approach\n<!-- Describe your approach to solving the problem. -->\nConsider this problem as a graph problem where we need to visit every single node with the minimal overall cost. The words will be our nodes and the nonOverlapping substring between two words will be our cost.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n^2 * 2^n)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n * 2^n)$$\n\n# Code\n\n### Easy to understand - Top-Down DP\n```\nclass Solution:\n def shortestSuperstring(self, words: List[str]) -> str:\n n = len(words)\n overlap = [[\'\'] * n for _ in range(n)]\n\n def getOverlap(a, b):\n l, i = 0, 1\n while i <= min(len(a), len(b)):\n if a[len(a)-i:] == b[:i]:\n l = i\n i += 1\n return b[l:]\n\n for i in range(n):\n for j in range(n):\n if i != j: overlap[i][j] = getOverlap(words[i], words[j])\n\n def TSP(prev, mask, dp):\n if (prev, mask) in dp: return dp[(prev, mask)]\n if mask == ((1 << n) - 1): return \'\'\n ans = \'*\' * 1000000\n for i in range(n):\n if mask & (1 << i): continue\n word = overlap[prev][i] if prev != -1 else words[i]\n ans = min(ans, word + TSP(i, mask | (1 << i), dp), key=len)\n dp[(prev, mask)] = ans\n return ans\n\n return TSP(-1, 0, {})\n```\n\n### Bottom-Up DP\nNotice here that we apply a push-dp instead of a pull-dp. That is because, there is no way for us to know in advance what the best string would be for a mask (7) or (111) where all the strings will be included where n = 3.\n\nTherefore we start with a base case where only one string will be included and we build our dp by pushing values forward in the mask.\n\nFinally, we get the minimum string with all words included (mask = ($$2^n - 1$$))\n```\nclass Solution:\n def shortestSuperstring(self, words: List[str]) -> str:\n n = len(words)\n overlap = [[\'\'] * n for _ in range(n)]\n\n def getOverlap(a, b):\n l, i = 0, 1\n while i <= min(len(a), len(b)):\n if a[len(a)-i:] == b[:i]:\n l = i\n i += 1\n return b[l:]\n\n for i in range(n):\n for j in range(n):\n if i != j: overlap[i][j] = getOverlap(words[i], words[j])\n ans = \'*\' * (10**4)\n dp = [[ans] * (1 << n) for _ in range(n)]\n for i in range(n): dp[i][(1 << i)] = words[i]\n\n for mask in range(1, 1 << n):\n for i in range(n):\n if mask & (1 << i):\n for j in range(n):\n if i != j and mask & (1 << j): continue\n dp[j][mask | (1 << j)] = min(dp[j][mask | (1 << j)], dp[i][mask] + overlap[i][j], key=len)\n\n for i in range(n): ans = min(ans, dp[i][(1 << n) - 1], key=len)\n return ans\n```
| 1
| 0
|
['Bit Manipulation', 'Graph', 'Bitmask', 'Python3']
| 0
|
find-the-shortest-superstring
|
C++ Basic recursion + memoization - Travelling salesman Problem approach:
|
c-basic-recursion-memoization-travelling-gdmd
|
Intuition\n Describe your first thoughts on how to solve this problem. \nIf we can consider the overlapping among the strings as weights . then we can translate
|
280iva
|
NORMAL
|
2023-10-02T15:42:30.448994+00:00
|
2023-10-02T15:42:30.449023+00:00
| 126
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIf we can consider the overlapping among the strings as weights . then we can translate the problem as find the order of the strings with maximum sum weight or maximum overlapping. \ni.e travel all the nodes in maximum weight \n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(N^2 * 2^n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(N^2 * 2^n)$$\n# Code\n```\nclass Solution {\npublic:\n\n string solve(int idx , int vis , vector<string>&a , vector<vector<int>> &w ,vector<vector<string>> &dp){\n int n = a.size();\n if(vis == ((1<<n)-1))\n return "";\n if(!dp[idx][vis].empty())\n return dp[idx][vis];\n\n int mini = 1e9;\n string minS,tmp;\n for(int i=0;i<n;i++){\n if((vis & (1<<i))==0){\n tmp = a[i].substr(w[idx][i]) + solve(i, (vis | (1<<i)) , a,w,dp);\n if(tmp.size()<mini){\n mini = tmp.size();\n minS=tmp;\n }\n }\n }\n return dp[idx][vis] = minS;\n }\n \n string shortestSuperstring(vector<string>& a) {\n int N = a.size();\n vector<vector<string>> dp(N+1 , vector<string>((1<<N)+1,""));\n vector<vector<int>> w(N,vector<int>(N,0));\n //O(N^2 * W)\n for(int i=0;i<N;i++){\n for(int j=0;j<N;j++){\n if(i==j)\n w[i][j]=a[i].size();\n else{\n int k = min(a[i].size(),a[j].size());\n // max overlap value when taking i from end and j from start\n for(;k>=0;k--){\n if(a[i].substr(a[i].size()-k) == a[j].substr(0,k)){\n w[i][j]=k;\n break;\n }\n }\n }\n }\n }\n // for(vector<int> r : w){\n // for(int i : r) cout<<i<<" ";\n // cout<<endl;\n // }\n string minS,tmp;\n int mini=1e9;\n for(int idx =0 ;idx<N;idx++){\n int vis = 0;\n vis = vis | (1<<idx);\n tmp = a[idx] + solve(idx,vis,a,w,dp);\n if(tmp.size()<mini){\n mini = tmp.size();\n minS=tmp;\n }\n }\n return minS; \n }\n};\n```
| 1
| 0
|
['C++']
| 0
|
find-the-shortest-superstring
|
Esay C++ Sol 🔥🔥
|
esay-c-sol-by-rishu_raj_10042002-t7w7
|
Code\n\nclass Solution {\npublic:\n \n string addFront(string a,string b)\n {\n int n1 = a.length();\n int n2 = b.length();\n stri
|
rishu_raj_10042002
|
NORMAL
|
2023-09-12T17:02:29.206754+00:00
|
2023-09-12T17:02:29.206787+00:00
| 599
| false
|
# Code\n```\nclass Solution {\npublic:\n \n string addFront(string a,string b)\n {\n int n1 = a.length();\n int n2 = b.length();\n string ans = "";\n for(int i=b.length()-1;i>=0;i--)\n {\n int len = 0;\n \n int i1 = i;\n int i2 = 0;\n while(i1<b.length() && i2<a.length())\n {\n if(b[i1]==a[i2])\n {\n i1++;\n i2++;\n }\n else\n break;\n }\n if(i2==a.length()) return b;\n if(i1==b.length())\n {\n string cur = b;\n for(int j=i2;j<a.length();j++)\n cur += a[j];\n ans = cur;\n }\n }\n if(ans.size()==0)\n ans = b + a;\n return ans;\n \n }\n int solve(int v,int vis,vector<vector<int>> adj[],vector<vector<int>>& dp,int& n,vector<string>& words,vector<vector<int>>& path)\n {\n \n vis |= (1<<v);\n if(vis == pow(2,n)-1) return 0;\n if(dp[v][vis]!=-1) return dp[v][vis];\n \n int ans = 1e9;\n for(auto child : adj[v])\n {\n if(vis & (1<<child[0])) continue;\n int val = solve(child[0],vis,adj,dp,n,words,path) + child[1];\n if(val<ans)\n {\n ans = val;\n path[v][vis] = child[0];\n }\n }\n return dp[v][vis] = ans;\n }\n void fill(vector<vector<int>>& dp)\n {\n for(int i=0;i<dp.size();i++)\n for(int j=0;j<dp[0].size();j++)\n dp[i][j] = -1;\n }\n string getPath(int v,vector<vector<int>>& path,set<int>& vis,vector<string>& words)\n {\n \n string pp = "";\n int cur = v;\n int mask = 1<<v;\n while(path[cur][mask]!=-1)\n {\n \n pp = addFront(words[cur],pp);\n vis.erase(vis.find(cur));\n int next = path[cur][mask];\n mask = mask | ((1<<next));\n cur = next;\n }\n if(vis.size()){\n int left = *(vis.begin());\n pp = addFront(words[left],pp);\n }\n return pp;\n }\n string shortestSuperstring(vector<string>& words) {\n int n = words.size();\n // cout<<n<<"\\n";\n if(n==1) return words[0];\n vector<vector<int>> adj[n];\n\n for(int i=0;i<words.size();i++)\n {\n for(int j=0;j<words.size();j++)\n {\n if(i==j) continue;\n string common = addFront(words[j],words[i]);\n int cost = common.size() - words[i].size();\n adj[i].push_back({j,cost});\n }\n }\n vector<vector<int>> dp(n,vector<int> (2<<n , -1));\n vector<vector<int>> path(n,vector<int> (2<<n, -1));\n int ans = 1e9;\n string pathAns;\n for(int i=0;i<words.size();i++){\n \n // fill(dp);\n // fill(path);\n int start = words[i].size();\n int val = solve(i,0,adj,dp,n,words,path)+start;\n if(val<ans)\n {\n ans = val;\n set<int> vis;\n for(int k=0;k<n;k++) vis.insert(k);\n pathAns = getPath(i,path,vis,words);\n // reverse(order.begin(),order.end());\n \n ans = val;\n }\n }\n return pathAns;\n\n }\n};\n```
| 1
| 0
|
['C++']
| 2
|
find-the-shortest-superstring
|
C++ | DP + BFS | Cleaner than official
|
c-dp-bfs-cleaner-than-official-by-lowkey-xb60
|
Intuition\n Describe your first thoughts on how to solve this problem. \nVery hard problem for mortals and probably will not be on interview but worth doing to
|
lowkeyandgrace
|
NORMAL
|
2023-02-11T19:10:58.767932+00:00
|
2023-02-11T19:11:27.133278+00:00
| 412
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nVery hard problem for mortals and probably will not be on interview but worth doing to improve skills and expand DP understanding.\n\nNot immediately obviously that it\'s DP problem. We want build word paths with help of memoize (dp) of best score based on mask and last word in current path. Runtime reduction here is that multiple paths can end up at the same mask / last visited.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nDon\'t be put off by bitmask, it\'s just a clean as possible way of tracking which words have been visited. This tests if you know basic bit manipulations well - which by itself is an easy problem. This problem is hard since it puts so many concepts together.\n\nThe official solution (at time of writing) uses a loop to go through the dp search space but it\'s more intuitive to do BFS. Once you have a path, you know that other paths are just adding each of the possible words left.\n\nKeep a parent array to let us back trace back.\n\nOnce DP step is done, take highest score that ends with mask of all words used (11111...111). Then use the parent vector to backtrace.\n\n# Runtime\n\n# Code\n```\nclass Solution {\npublic:\n string shortestSuperstring(vector<string>& words) {\n const size_t N = words.size();\n vector<vector<int>> overlap = vector<vector<int>>(N, vector<int>(N, 0));\n // pre-calculate the distance (number of shared characters) between each word pair in each direction \n for (int i = 0; i < N-1; i++)\n {\n for (int j = i+1; j < N; j++)\n {\n overlap[i][j] = Overlap(words[i], words[j]);\n overlap[j][i] = Overlap(words[j], words[i]);\n }\n }\n\n const size_t R = pow(2, N);\n DP dp = DP(R, vector<int>(N, 0));\n DP parent = DP(R, vector<int>(N,0));\n vector<bool> visited = vector<bool>(R,0);\n \n list<int> q{};\n for (int i = 0; i < N; i++)\n {\n const int mask = 1 << i;\n q.emplace_back(1 << i);\n }\n\n while (!q.empty())\n {\n int mask = q.front(); q.pop_front();\n for (int i = 0; i < N; i++)\n {\n if ((mask & (1 << i)) == 0) continue;\n \n int prev = mask ^ (1<<i);\n if (prev == 0) continue;\n for (int j = 0; j < N; j++)\n {\n if ((prev & (1<<j)) == 0) continue;\n \n int score = dp[prev][j] + overlap[j][i];\n if (score >= dp[mask][i])\n {\n dp[mask][i] = score;\n parent[mask][i] = j;\n }\n }\n }\n\n for (int i = 0; i < N; i++)\n {\n int next = mask | (1 << i);\n if (!visited[next])\n {\n visited[next] = true;\n q.emplace_back(next);\n }\n }\n }\n\n int curr = 0;\n int max_score = *max_element(dp[R-1].begin(), dp[R-1].end()); \n for (int i = 0; i < N; i++)\n {\n if (dp[R-1][i] == max_score) curr = i;\n }\n\n list<int> path{curr};\n int curr_mask = R-1;\n for(int i = 1; i < N; i++)\n {\n int prev = curr;\n curr = parent[curr_mask][curr];\n curr_mask = curr_mask & (~(1 << prev));\n path.emplace_front(curr);\n }\n\n auto prev = path.begin();\n string res = words[*prev];\n for (auto it = ++path.begin(); it != path.end(); it++)\n {\n res += words[*it].substr(overlap[*prev][*it]);\n prev = it;\n }\n\n return res;\n }\nprivate:\n using DP = vector<vector<int>>;\n\n inline int Overlap(string front, string end)\n {\n int max_overlap = min(front.size(),end.size());\n while (max_overlap > 0)\n {\n int j = 0;\n bool possible = true;\n for (int i = front.size()-max_overlap; i < front.size() && possible; i++)\n {\n if (front[i] != end[j]) possible = false;\n j++;\n }\n if (possible) return max_overlap;\n max_overlap--;\n }\n return 0;\n }\n};\n```
| 1
| 0
|
['C++']
| 0
|
find-the-shortest-superstring
|
[python] dp + bitmask
|
python-dp-bitmask-by-vl4deee11-4p3r
|
\nclass Solution:\n def shortestSuperstring(self, words: List[str]) -> str:\n rbm=[0]\n for i in range(len(words)):rbm[0]|=(1<<i)\n def
|
vl4deee11
|
NORMAL
|
2022-11-11T05:02:38.520937+00:00
|
2022-11-11T05:03:43.652362+00:00
| 111
| false
|
```\nclass Solution:\n def shortestSuperstring(self, words: List[str]) -> str:\n rbm=[0]\n for i in range(len(words)):rbm[0]|=(1<<i)\n def isc(prev,curr):\n i=0\n i2=0\n mi2=0\n while i<len(prev):\n i1=i\n while i1<len(prev) and i2<len(curr) and prev[i1]==curr[i2]:\n i1+=1\n i2+=1\n if i1==len(prev):return True\n i+=1\n return False\n \n def geta(prev,curr):\n i=max(0,len(prev)-len(curr)-1)\n i2=0\n mi2=0\n while i<len(prev):\n i1=i\n i2=0\n while i1<len(prev) and i2<len(curr) and prev[i1]==curr[i2]:\n i1+=1\n i2+=1\n if i1==len(prev):mi2=max(mi2,i2)\n i+=1\n return curr[mi2:]\n\n gr=defaultdict(list)\n gr[-1]=[i for i in range(len(words))]\n for i in range(len(words)):\n for j in range(len(words)):\n f=isc(words[i],words[j])\n if not f:continue\n gr[i].append(j)\n \n @cache\n def dp(bm,pi):\n if bm==rbm[0]:\n return "",True\n a=""\n x=False\n for ni in gr[pi]:\n k=1<<ni\n if k&bm!=0:continue\n if pi==-1:\n add=words[ni]\n else:\n add=geta(words[pi],words[ni])\n r,f=dp(bm|k,ni)\n if not f:continue\n if len(r)+len(add)<len(a) or not x:\n a=add+r\n x=True\n if not x:\n for ni in range(len(words)):\n k=1<<ni\n if k&bm!=0:continue\n if pi==-1:\n add=words[ni]\n else:\n add=geta(words[pi],words[ni])\n r,f=dp(bm|k,ni)\n if not f:continue\n if len(r)+len(add)<len(a) or not x:\n a=add+r\n x=True\n return a,x\n \n r,_=dp(0,-1)\n return r\n```
| 1
| 0
|
[]
| 0
|
find-the-shortest-superstring
|
C++|Clean DP solution
|
cclean-dp-solution-by-endless_mercury-5iwe
|
Breaking stereotype of using dp for storing only integers or boolean.\nSimple Solution using bitmask dp and trying all combinations\n\nclass Solution {\npublic:
|
endless_mercury
|
NORMAL
|
2022-10-29T11:19:33.269350+00:00
|
2022-10-29T11:19:33.269393+00:00
| 301
| false
|
Breaking stereotype of using dp for storing only integers or boolean.\nSimple Solution using bitmask dp and trying all combinations\n```\nclass Solution {\npublic:\n string solve(int last,int mask,int n,int need,map<int,map<int,int>>&mp,vector<string>&words,vector<vector<string>>&dp){\n if(mask==need){\n return "";\n }\n if(dp[last+1][mask]!="")\n return dp[last+1][mask];\n string curr="";\n for(int i=0;i<n;i++){\n if((mask>>i)&1)\n continue;\n string temp=words[i].substr(mp[last][i]);\n int temp_mask=(mask|(1<<i));\n temp+=solve(i,temp_mask,n,need,mp,words,dp);\n if(curr==""||temp.length()<curr.length()){\n curr=temp;\n }\n }\n return dp[last+1][mask]=curr;\n }\n string shortestSuperstring(vector<string>& words) {\n map<int,map<int,int>> mp;\n int n=words.size();\n for(int i=0;i<n;i++){\n mp[-1][i]=0;\n for(int j=0;j<n;j++){\n int m=words[i].length();\n int m2=words[j].length();\n mp[i][j]=0;\n for(int l=1;l<min(m,m2);l++){\n string temp=words[i].substr(m-l);\n string temp2=words[j].substr(0,l);\n if(temp==temp2){\n mp[i][j]=l;\n }\n }\n }\n }\n int mask=0;\n int need=(1<<n)-1;\n int last=-1;\n vector<vector<string>> dp(n+1,vector<string>(need,""));\n return solve(last,mask,n,need,mp,words,dp);\n\n }\n};\n```\nUpvote if helped :)
| 1
| 0
|
['Dynamic Programming', 'C']
| 2
|
find-the-shortest-superstring
|
klickh baith soluution
|
klickh-baith-soluution-by-utkarsh190-k8oa
|
"When you meet your God tell him to leave me alone" - Guts\n\nclass Solution {\nprivate:\n int calcOverlap(string a, string b){\n if(a == "" || b == "
|
utkarsh190
|
NORMAL
|
2022-05-17T17:48:30.710453+00:00
|
2022-05-17T17:48:30.710501+00:00
| 139
| false
|
"When you meet your God tell him to leave me alone" - Guts\n```\nclass Solution {\nprivate:\n int calcOverlap(string a, string b){\n if(a == "" || b == "") return 0;\n int n = a.length();\n for(int len = min(a.length()-1, b.length()-1); len >= 0; len--){\n bool found = true;\n for(int i = 0; i < len; i++){\n if(a[n-len+i] != b[i]){\n found = false; break;\n }\n }\n if(found) return len;\n }\n return 0;\n }\n string dp(int idx, int state, vector<string>&ar, vector<vector<string>>&memo, vector<vector<int>>&overlap){\n int n = ar.size();\n if(state == (1<<n) - 1) return ar[idx];\n if(memo[idx][state] != "-1") return memo[idx][state];\n \n string res = "-1";\n for(int i = 0; i < n; i++){\n if((state & (1<<i)) == 0){\n string cur, next = dp(i, state | (1<<i), ar, memo, overlap);\n if(idx < n){\n int len = overlap[idx][i];\n cur = ar[idx].substr(0, ar[idx].size()-len) + next;\n } else cur = next;\n \n if(res == "-1" || cur.length() < res.length()){\n res = cur;\n }\n }\n }\n\n memo[idx][state] = res;\n return res;\n }\npublic:\n string shortestSuperstring(vector<string>& ar) {\n int n = ar.size();\n vector<vector<string>> memo(15, vector<string> (1<<ar.size(), "-1"));\n vector<vector<int>> overlap(n, vector<int>(n, 50));\n for(int i = 0; i < n; i++){\n for(int j = 0; j < n; j++){\n if(i == j) continue;\n overlap[i][j] = calcOverlap(ar[i], ar[j]);\n }\n }\n return dp(14, 0, ar, memo, overlap);\n }\n};\n```
| 1
| 0
|
[]
| 0
|
find-the-shortest-superstring
|
Python | TSP | Simple Code with Bit Mask
|
python-tsp-simple-code-with-bit-mask-by-bk6q2
|
bitmask: contains information of nodes that are visited currently\ndfs(bitmask, i): shortest superstring after i with visited nodes bitmask\n```\nclass Solution
|
aryonbe
|
NORMAL
|
2022-04-13T06:17:00.010830+00:00
|
2022-04-22T10:46:55.086478+00:00
| 408
| false
|
bitmask: contains information of nodes that are visited currently\ndfs(bitmask, i): shortest superstring after i with visited nodes bitmask\n```\nclass Solution:\n def shortestSuperstring(self, A):\n @lru_cache(None)\n def suffix(i,j):\n for k in range(min(len(A[i]),len(A[j])),0,-1):\n if A[j].startswith(A[i][-k:]):\n return A[j][k:]\n return A[j]\n n = len(A)\n @lru_cache(None)\n def dfs(bitmask, i):\n if bitmask + 1 == 1 << n: return ""\n return min([suffix(i, j)+dfs(bitmask | 1<<j, j) for j in range(n) if not(bitmask & 1<<j)], key = len)\n return min([A[i]+dfs(1<<i,i) for i in range(n)], key = len)
| 1
| 0
|
['Bit Manipulation', 'Python']
| 0
|
find-the-shortest-superstring
|
Java Bitmask DP
|
java-bitmask-dp-by-zerocool1989-kfd8
|
This is a varaint of the travelling salesman problem.\n\n\nclass Solution {\n \n public String shortestSuperstring(String[] words) {\n String[][] t
|
zerocool1989
|
NORMAL
|
2021-10-10T17:00:30.223275+00:00
|
2021-10-10T17:00:30.223314+00:00
| 175
| false
|
This is a varaint of the travelling salesman problem.\n\n```\nclass Solution {\n \n public String shortestSuperstring(String[] words) {\n String[][] toAdd = new String[words.length][words.length];\n String[][] dp = new String[words.length + 1][(1 << (words.length + 1))];\n\n for (int i = 0; i < words.length; i++) {\n for (int j = 0; j < words.length; j++) {\n if (i == j) continue;\n for (int k = 0; k < words[i].length(); k++) {\n String str = words[i].substring(k);\n if (words[j].startsWith(str)) {\n toAdd[i][j] = words[j].substring(str.length());\n break;\n }\n }\n if (toAdd[i][j] == null) {\n toAdd[i][j] = words[j];\n }\n }\n }\n String ans = "";\n int minLen = Integer.MAX_VALUE;\n for (int i = 0; i < words.length; i++) {\n String str = words[i] + solve(words, toAdd, i, (1 << i), dp);\n if (str.length() < minLen) {\n minLen = str.length();\n ans = str;\n }\n }\n return ans;\n }\n\n private String solve(String[] arr, String[][] toAdd, int last, int mask, String[][] dp) {\n if (mask == (1 << arr.length)-1) {\n return "";\n }\n if (dp[last][mask] != null) {\n return dp[last][mask];\n }\n int minLen = Integer.MAX_VALUE;\n String ret = "";\n for (int i = 0; i < arr.length; i++) {\n if ((mask & (1 << i)) == 0) {\n String curr = toAdd[last][i] + solve(arr, toAdd, i, mask | (1 << i), dp);\n if (curr.length() < minLen) {\n minLen = curr.length();\n ret = curr;\n }\n }\n }\n return dp[last][mask] = ret;\n }\n}\n```
| 1
| 0
|
[]
| 0
|
find-the-shortest-superstring
|
Easy Recursive Solution in Java Using DP Bitmask
|
easy-recursive-solution-in-java-using-dp-k7mn
|
I have used recursive memoized approach as the iterative appraoch would be hard to understand. Similar to TSP Problem.\nThe first call is to a dummy node.\n\n``
|
rite2riddhi
|
NORMAL
|
2021-08-10T04:38:12.372393+00:00
|
2021-08-10T04:38:51.210766+00:00
| 355
| false
|
I have used recursive memoized approach as the iterative appraoch would be hard to understand. Similar to TSP Problem.\nThe first call is to a dummy node.\n\n```class Solution {\n private String dp[][];\n private int n;\n private int [][] graph;\n \n private int overlap(String word1 , String word2)\n {\n int word1Len = word1.length();\n int word2Len = word2.length();\n for(int i = 0 ; i < word1Len ; i ++)\n {\n if(word2.startsWith(word1.substring(i)))\n return (word2Len - word1Len + i);\n }\n return word2Len;\n }\n \n private void computeGraph(String[] words)\n {\n for(int i = 0 ; i < n ; i ++)\n for(int j = 0 ; j < n ; j ++)\n graph[i][j] = overlap(words[i] , words[j]);\n }\n \n private String getMinString(int mask , int u , String[] words)\n {\n if(mask == ((1 << n) - 1))\n return "";\n \n if(dp[mask][u] != null)\n return dp[mask][u];\n \n int minCost = Integer.MAX_VALUE;\n String minString = "";\n for(int nextIndex = 0 ; nextIndex < n ; nextIndex ++)\n {\n if( (mask & (1 << nextIndex)) == 0)\n {\n int cost = (mask == 0) ? words[nextIndex].length() : graph[u][nextIndex];\n String cur = (mask == 0) ? words[nextIndex] : words[nextIndex].substring(words[nextIndex].length() - graph[u][nextIndex]);\n \n String next = getMinString(mask | (1 << nextIndex) , nextIndex , words);\n cost += next.length();\n if(cost < minCost)\n {\n minString = cur + next;\n minCost = cost;\n }\n }\n }\n \n return (dp[mask][u] = minString);\n \n }\n \n public String shortestSuperstring(String[] words) {\n n = words.length;\n dp = new String[(1 << n)][n];\n \n graph = new int[n][n];\n \n computeGraph(words);\n \n return getMinString(0 , 0 , words);\n }\n}
| 1
| 0
|
[]
| 1
|
find-the-shortest-superstring
|
Java using dp bitmask beats 97%
|
java-using-dp-bitmask-beats-97-by-julian-vg8x
|
\nclass Solution {\n public String shortestSuperstring(String[] words) { \n int n = words.length;\n int[][] cost = buildGraph(words); // runti
|
julianzheng
|
NORMAL
|
2021-07-11T06:12:41.041040+00:00
|
2021-07-11T06:12:41.041086+00:00
| 248
| false
|
```\nclass Solution {\n public String shortestSuperstring(String[] words) { \n int n = words.length;\n int[][] cost = buildGraph(words); // runtime O(N^2 * L^2)\n \n // dp[i][j]: the minimal cost to get to state i with words[j] as the last word\n int[][] dp = new int[1 << n][n];\n int[][] precursor = new int[1 << n][n];\n \n // Runtime: O(N^2 * 2^N )\n for (int state = 1; state < (1 << n); state++) {\n for (int curr = 0; curr < n; curr++) {\n if ((state & (1 << curr)) == 0) continue; // check if it is a valid state ending with words[curr]\n int prevState = state ^ (1 << curr); // find its precursor by removing that bit\n if (prevState == 0) { // if the precursor is empty string\n dp[state][curr] = words[curr].length(); // the cost would be the string it selft\n precursor[state][curr] = -1;\n continue;\n }\n int tempMin = Integer.MAX_VALUE;\n int tempParent = -1;\n for (int prev = 0; prev < n; prev++) {\n if ((prevState & (1 << prev)) == 0) continue;\n if (dp[prevState][prev] + cost[prev][curr] < tempMin) {\n tempMin = dp[prevState][prev] + cost[prev][curr];\n tempParent = prev;\n }\n }\n dp[state][curr] = tempMin;\n precursor[state][curr] = tempParent;\n }\n }\n \n int globalMin = Integer.MAX_VALUE;\n int last = -1; // the last word to add in the optimal solution\n for (int i = 0; i < n; i++) {\n if (globalMin > dp[(1 << n) - 1][i]) {\n globalMin = dp[(1 << n) - 1][i];\n last = i;\n }\n }\n \n // reconstruct the answer to return using the dp table\n StringBuilder res = new StringBuilder();\n int state = (1 << n) - 1; // read the dp table backwards starting with the state where all bits are 1\n while ((state ^ (1 << last)) > 0) {\n int prev = precursor[state][last];\n res.insert(0, words[last].substring(words[last].length() - cost[prev][last]));\n state = state ^ (1 << last);\n last = prev;\n }\n res.insert(0, words[last]);\n return res.toString();\n }\n \n private int[][] buildGraph(String[] words) {\n int n = words.length;\n int[][] g = new int[n][n];\n for (int i = 0; i < n; i++) {\n for (int j = i + 1; j < n; j++) {\n g[i][j] = getCost(words[i], words[j]);\n g[j][i] = getCost(words[j], words[i]);\n }\n }\n return g;\n }\n \n private int getCost(String s1, String s2) {\n int i = 0;\n while (i < s1.length()) {\n if (s1.charAt(i) == s2.charAt(0)) {\n int k = i;\n int p = 0;\n while (k < s1.length()) {\n if (s1.charAt(k) == s2.charAt(p)) {\n k++;\n p++;\n } else {\n break;\n }\n }\n if (k == s1.length()) return s2.length() - p; \n }\n i++;\n }\n return s2.length();\n }\n}\n```
| 1
| 0
|
[]
| 0
|
find-the-shortest-superstring
|
javascript use graph + bitmask dp
|
javascript-use-graph-bitmask-dp-by-henry-iw2b
|
reference:\nhttps://leetcode.com/problems/find-the-shortest-superstring/discuss/195487/python-bfs-solution-with-detailed-explanation(with-extra-Chinese-explanat
|
henrychen222
|
NORMAL
|
2021-05-26T21:03:27.476808+00:00
|
2021-05-26T23:21:20.590960+00:00
| 257
| false
|
reference:\nhttps://leetcode.com/problems/find-the-shortest-superstring/discuss/195487/python-bfs-solution-with-detailed-explanation(with-extra-Chinese-explanation)\nTLE fixed by @fdglchen\nhttps://leetcode.com/problems/find-the-shortest-superstring/discuss/195487/python-bfs-solution-with-detailed-explanation(with-extra-Chinese-explanation)/950172\n\nMain idea: Question can be transformed in this way, In a graph, start from a point, traverse all points, to make the path longest. use bfs\n\nRuntime: 5772ms a little slow.\n```\nconst getDistance2 = (s1, s2) => {\n let n = s1.length;\n for (let i = 1; i < n; i++) {\n if (s2.startsWith(s1.slice(i))) return n - i + 1; // +1 to be able to handle edge 0\n }\n return 1;\n};\n\nconst getResFromPath2 = (w, G, path) => {\n let res = w[path[0]];\n let n = path.length;\n for (let i = 1; i < n; i++) {\n let [prev, cur] = [path[i - 1], path[i]];\n let idx = G[prev][cur] - 1; // -1 to handle edge 0\n res += w[cur].slice(idx);\n }\n return res;\n};\n\nconst shortestSuperstring = (w) => {\n let n = w.length;\n let G = initialize2DArrayNew(n, n);\n for (let i = 0; i < n; i++) {\n for (let j = i + 1; j < n; j++) {\n G[i][j] = getDistance2(w[i], w[j]);\n G[j][i] = getDistance2(w[j], w[i]);\n }\n }\n let dp = initialize2DArrayNew(1 << n, n);\n let q = [];\n for (let i = 0; i < n; i++) q.push([i, 1 << i, [i], 0]);\n let maxDis = -1;\n let p = [];\n let final_mask = (1 << n) - 1;\n while (q.length) { // bfs\n let [node, mask, path, dis] = q.shift();\n if (dis < dp[mask][node]) continue;\n if (mask == final_mask && dis > maxDis) {\n [p, maxDis] = [path, dis];\n continue;\n }\n for (let i = 0; i < n; i++) {\n if (1 << i & mask) continue;\n let next_mask = mask | 1 << i;\n let potential_overlap = dp[mask][node] + G[node][i];\n if (potential_overlap > dp[next_mask][i]) { // >= will TLE, have duplicated calculation. figured out by @fdglchen in original post comments\n dp[next_mask][i] = potential_overlap;\n q.push([i, next_mask, path.concat([i]), potential_overlap]);\n }\n }\n }\n return getResFromPath2(w, G, p);\n};\n\nconst initialize2DArrayNew = (n, m) => {\n let data = [];\n for (let i = 0; i < n; i++) {\n let tmp = Array(m).fill(0);\n data.push(tmp);\n }\n return data;\n};\n```\nSolution 2: Travelling salesman https://en.wikipedia.org/wiki/Travelling_salesman_problem\nreference: https://leetcode.com/problems/find-the-shortest-superstring/discuss/194932/Travelling-Salesman-Problem\nRuntime: 152ms 90.07%\n```\nconst getDistance3 = (s1, s2) => {\n let n = s1.length;\n let m = s2.length;\n for (let i = 1; i < n; i++) {\n if (s2.startsWith(s1.slice(i))) return m - n + i;\n }\n return m;\n};\n\nconst getResFromPath3 = (w, G, p, last) => {\n let n = w.length;\n let res = \'\';\n let cur = (1 << n) - 1;\n let st = [];\n while (cur > 0) {\n st.push(last);\n let tmp = cur;\n cur -= 1 << last;\n last = p[tmp][last];\n }\n let i = st.pop();\n res += w[i];\n while (st.length) {\n let j = st.pop();\n res += w[j].slice(w[j].length - G[i][j]);\n i = j;\n }\n return res;\n};\n\nconst MAX = Number.MAX_SAFE_INTEGER;\nconst shortestSuperstring = (w) => {\n let n = w.length;\n let G = initialize2DArrayNew(n, n);\n for (let i = 0; i < n; i++) {\n for (let j = 0; j < n; j++) {\n G[i][j] = getDistance3(w[i], w[j]);\n G[j][i] = getDistance3(w[j], w[i]);\n }\n }\n let dp = initialize2DArrayNew(1 << n, n);\n let p = initialize2DArrayNew(1 << n, n);\n let [last, min, final_mask] = [-1, MAX, (1 << n) - 1];\n for (let i = 1; i < 1 << n; i++) {\n dp[i].fill(MAX);\n for (let j = 0; j < n; j++) {\n if ((i & 1 << j) > 0) {\n let prev = i - (1 << j);\n if (prev == 0) {\n dp[i][j] = w[j].length;\n } else {\n for (let k = 0; k < n; k++) {\n let potential_overlap = dp[prev][k] + G[k][j];\n if (dp[prev][k] < MAX && potential_overlap < dp[i][j]) {\n dp[i][j] = potential_overlap;\n p[i][j] = k;\n }\n }\n }\n }\n if (i == final_mask && dp[i][j] < min) {\n min = dp[i][j];\n last = j;\n }\n }\n }\n return getResFromPath3(w, G, p, last);\n};\n\nconst initialize2DArrayNew = (n, m) => {\n let data = [];\n for (let i = 0; i < n; i++) {\n let tmp = Array(m).fill(0);\n data.push(tmp);\n }\n return data;\n};\n```
| 1
| 0
|
['Graph', 'Bitmask', 'JavaScript']
| 0
|
find-the-shortest-superstring
|
(C++) 943. Find the Shortest Superstring
|
c-943-find-the-shortest-superstring-by-q-272u
|
top-down\n\nclass Solution {\npublic:\n string shortestSuperstring(vector<string>& words) {\n int n = size(words); \n vector<vector<int>> ovlp(
|
qeetcode
|
NORMAL
|
2021-05-26T15:31:01.887441+00:00
|
2021-05-26T19:51:03.776997+00:00
| 895
| false
|
**top-down**\n```\nclass Solution {\npublic:\n string shortestSuperstring(vector<string>& words) {\n int n = size(words); \n vector<vector<int>> ovlp(n, vector<int>(n, 0)); \n \n for (int i = 0; i < n; ++i) \n for (int j = 0; j < n; ++j) \n for (int k = 0; k < min(size(words[i]), size(words[j])); ++k) \n if (words[i].substr(size(words[i])-k) == words[j].substr(0, k))\n ovlp[i][j] = k; // extra length upon appending j to i \n \n map<pair<int, int>, pair<int, int>> memo; \n \n function<pair<int, int>(int, int)> fn = [&](int prev, int mask) {\n pair key = make_pair(prev, mask); \n if (memo.find(key) == memo.end()) {\n if (mask == 0) return make_pair(0, 0); \n int vv = INT_MAX, kk = -1; \n for (int k = 0; k < n; ++k) {\n if (mask & 1 << k) {\n auto [v, tmp] = fn(k, mask ^ 1 << k); \n int offset = prev == -1 ? size(words[k]) : size(words[k]) - ovlp[prev][k]; \n if (v + offset < vv) {\n vv = v + offset; \n kk = k; \n }\n }\n }\n memo[key] = make_pair(vv, kk); \n } \n return memo[key]; \n };\n \n string ans; \n int prev = -1, mask = (1 << n) - 1; \n while (mask) {\n auto [tmp, k] = fn(prev, mask); \n if (ans.size()) ans += words[k].substr(ovlp[prev][k]); \n else ans += words[k]; \n prev = k; \n mask ^= 1 << k; \n }\n return ans; \n }\n};\n```\n\nshorter but slower\n```\nclass Solution {\npublic:\n string shortestSuperstring(vector<string>& words) {\n int n = size(words); \n vector<vector<int>> ovlp(n, vector<int>(n, 0)); \n \n for (int i = 0; i < n; ++i) \n for (int j = 0; j < n; ++j) \n for (int k = 0; k < min(size(words[i]), size(words[j])); ++k) \n if (words[i].substr(size(words[i])-k) == words[j].substr(0, k))\n ovlp[i][j] = k;\n \n map<pair<int, int>, string> memo; \n \n function<string(int, int)> fn = [&](int prev, int mask) {\n pair key = make_pair(prev, mask); \n if (memo.find(key) == memo.end()) {\n if (mask == 0) return string(); \n string ss = string(250, \'*\'); \n for (int k = 0; k < n; ++k) {\n if (mask & 1<<k) {\n auto s = fn(k, mask ^ 1<<k); \n int offset = prev == -1 ? 0 : ovlp[prev][k]; \n if (size(words[k]) - offset + size(s) < size(ss)) {\n ss = words[k].substr(offset) + s; \n }\n }\n }\n memo[key] = ss; \n } \n return memo[key]; \n };\n \n return fn(-1, (1<<n) - 1);\n }\n};\n```\n\n**bottom-up**\n```\nclass Solution {\npublic:\n string shortestSuperstring(vector<string>& words) {\n int n = size(words); \n \n vector<vector<int>> ovlp (n, vector<int>(n)); \n for (int i = 0; i < n; ++i) \n for (int j = 0; j < n; ++j)\n for (int k = 0; k < min(size(words[i]), size(words[j])); ++k)\n if (words[i].substr(size(words[i]) - k) == words[j].substr(0, k)) {\n ovlp[i][j] = k; \n }\n \n vector<vector<int>> dp(1<<n, vector<int>(n)); // min length of mask ending at bit \n vector<vector<int>> parent(1<<n, vector<int>(n, -1)); \n for (int mask = 0; mask < (1 << n); ++mask) {\n for (int bit = 0; bit < n; ++bit) {\n if (mask & 1<<bit) {\n int pmask = mask ^ (1<<bit); \n if (pmask) {\n for (int i = 0; i < n; ++i) {\n if (pmask & 1<<i) {\n int val = dp[pmask][i] + size(words[bit]) - ovlp[i][bit]; \n if (dp[mask][bit] == 0 || val < dp[mask][bit]) {\n dp[mask][bit] = val; \n parent[mask][bit] = i; \n }\n }\n }\n }\n else dp[mask][bit] = size(words[bit]); \n }\n }\n }\n \n auto it = min_element(begin(dp.back()), end(dp.back())); \n int mask = (1<<n) - 1, p = it - begin(dp.back()); \n string ans; \n while (mask) {\n int pp = parent[mask][p]; \n if (pp == -1) ans = words[p] + ans; \n else ans = words[p].substr(ovlp[pp][p]) + ans; \n mask ^= 1 << p; \n p = pp; \n }\n return ans; \n }\n}; \n```
| 1
| 1
|
['C']
| 1
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.