question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
minimum-difference-between-largest-and-smallest-value-in-three-moves | Python Solution | Explained | O(n) time, O(1) space complexity | python-solution-explained-on-time-o1-spa-kc7s | Python Solution | Explained | O(n) time, O(1) space complexity\n\nThe current problem can be easily solved after observing the following:\n\n1. Only the largest | aragorn_ | NORMAL | 2020-07-31T01:47:51.523275+00:00 | 2020-07-31T01:58:16.061769+00:00 | 950 | false | **Python Solution | Explained | O(n) time, O(1) space complexity**\n\nThe current problem can be easily solved after observing the following:\n\n1. Only the largest and smallest values found in the array affect the solution, since they cause the greatest differences. For example, if we imagine the sorted array [a, b, c, d, e, f, g, h, i, j, k], the optimal answer will be found after removing elements from [a,d] and/or [h,k]. Only the top-4 elements at each side are important. \n\n2. While sorting makes sense (under the previous context), we can find the top-4 highest and lowest elements of the array using an algorithm with O(n) time complexity (sorting is O(n log n) ). Different O(n) algorithms can be chosen. The code below uses heaps of size=4 to find the top-4 values at each side. This still has a time complexity of O(n), because O( n * log(4) ) = O(n).\n\n3. To avoid unnecesary calculations, we notice that it\'s always optimal to delete "x" elements from one side, and "3-x" elements from the other extreme. As a result, we can find the optimal answer with only 4 queries for each side ( x= [0,1,2,3] removals).\n\n4. Since our algorithm only stored small arrays up to size=4, we can conclude that our solution has O(1) space complexity.\n\n```\nimport heapq\nclass Solution:\n def minDifference(self, A):\n # 1) Trivial cases\n if len(A)<=4:\n return 0\n #\n # 2) Find: routine to find the top-4 highest or lowest elements (both cases are covered)\n def find(high):\n k = 1 if high else -1\n heap = [ k*x for x in A[:4] ]\n heapq.heapify(heap)\n for x in A[4:]:\n heapq.heappushpop(heap,k*x)\n return sorted([ k*x for x in heap ])\n #\n # 3) Fetch the top-4 elements at each extreme\n big = find(high=True)\n small = find(high=False)\n #\n # 4) Find the optimal answer\n return min([ (big[-4+i] - small[i]) for i in range(4) ])\n```\n\n**PS. Shorter Version**\nI recently learned about the existence of the functions "nlargest" and "nsmallest" in the "heapq" library, which simplify the code a lot. The time and space complexity are still O(n) and O(1) respectively. Cheers,\n\n```\n\nimport heapq\nclass Solution:\n def minDifference(self, A):\n # 1) Trivial case\n if len(A)<=4:\n return 0\n #\n # 2) Fetch the top-4 elements at each extreme\n big = heapq.nlargest(4,A)[::-1]\n small = heapq.nsmallest(4,A)\n #\n # 4) Find the optimal answer\n return min([ (big[-4+i] - small[i]) for i in range(4) ])\n```\n**Appendix: Sorting Method (Not Recommended)**\n\nWhile this algorithm isn\'t recommended due to its higher time complexity O( n log n), LeetCode might rate it as equally fast since most test cases involve small arrays, where the log(n) difference is negligible. \n\n```\nclass Solution:\n def minDifference(self, A):\n if len(A)<=4:\n return 0\n #\n A.sort()\n return min([ (A[-4+i] - A[i]) for i in range(4) ])\n``` | 6 | 0 | ['Python', 'Python3'] | 2 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | Python Complete Explanation (Prefix+suffix =3 elements) | python-complete-explanation-prefixsuffix-50fi | 1)Sort the array so we have a window with indicess of [0,n-1] represent [min,max].\n2)Now,changing either the left or right results in the change in the answer | akhil_ak | NORMAL | 2020-07-11T17:32:06.662761+00:00 | 2020-07-12T02:41:50.851293+00:00 | 553 | false | 1)Sort the array so we have a window with indicess of [0,n-1] represent [min,max].\n2)Now,changing either the left or right results in the change in the answer .so,changing just means removing a number and adding a new number.We are asked change a total of 3 elements here.\n3) number of elements that can be removed from [left,right] are [0,3],[1,2],[2,1],[3,0]\n4)when 0 elements removed from left, min remains the same,so answer = nums[-4] - nums[0]\n5)Similarly,we do for all the rest of prefix+suffix possibilities and obtain the minimum of all.\n\nConfused? why did i call changing an element as removal?\n```\neg: input = [0,1,1,4,6,6,6]\nAssume [left,right] = [2,1],Here why the answer has nothing to do with first 2 elements and last 1 element? Because,we make all of them as equal.\nExplanation:\n\t[0,1] [1,4,6,6] [6] is of form `prefix-window-suffix` so we convert all elements in prefix to window[0] and all elements in suffix to window[-1] hence maintaining the window validity to true.\n```\n`Time:O(nlogn) Space:O(1)`\n\n\tclass Solution:\n\t\tdef minDifference(self, nums: List[int]) -> int:\n\t\t\tn = len(nums)\n\t\t\tif n<=4:\n\t\t\t\treturn 0\n\t\t\tnums.sort()\n\t\t\tans = float(\'inf\')\n\t\t\ti,j = 3,n-1\n\t\t\twhile i>=0 and j>=0:\n\t\t\t\tans = min(ans,nums[j]-nums[i])\n\t\t\t\ti-=1\n\t\t\t\tj-=1\n\n\t\t\treturn ans\nThis same method works well for any general k as well. In my opinion this is also a typical sliding window.please leave an upvote to help this post reach those trying to understand this question. :) | 6 | 2 | ['Python', 'Python3'] | 2 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | C++ | O(nlogn) | c-onlogn-by-di_b-562o | ```\nint minDifference(vector& nums) {\n int n = nums.size();\n if(n < 5)\n return 0;\n sort(nums.begin(), nums.end());\n | di_b | NORMAL | 2020-07-11T16:04:28.131538+00:00 | 2020-07-11T16:04:28.131569+00:00 | 923 | false | ```\nint minDifference(vector<int>& nums) {\n int n = nums.size();\n if(n < 5)\n return 0;\n sort(nums.begin(), nums.end());\n int res = min({nums[n-4]-nums[0], nums[n-1]-nums[3], nums[n-3]-nums[1], nums[n-2]-nums[2]});\n return res;\n } | 6 | 1 | ['C'] | 0 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | ✅Simple and Clear Python3 Code✅ | simple-and-clear-python3-code-by-moazmar-pr12 | \n### Explanation\n\nIntuition\nIf the length of nums is 4 or less, we can make all elements equal by removing up to three elements, resulting in a difference o | moazmar | NORMAL | 2024-07-03T20:16:08.558077+00:00 | 2024-07-03T20:16:08.558099+00:00 | 4 | false | \n### Explanation\n\n**Intuition**\nIf the length of `nums` is 4 or less, we can make all elements equal by removing up to three elements, resulting in a difference of 0.\n\n**Approach**\n1. **Edge Case Handling**: If the length of `nums` is less than or equal to 4, return 0 immediately since we can remove enough elements to make the array equal.\n2. **Sort the Array**: Sorting the array helps in easily finding the minimum and maximum values after potential removals.\n3. **Calculate Possible Differences**: After sorting, consider the following four scenarios to remove elements such that the remaining array has the smallest difference between the maximum and minimum values:\n - Remove the three smallest elements.\n - Remove the two smallest elements and the largest element.\n - Remove the smallest element and the two largest elements.\n - Remove the three largest elements.\n4. **Return the Minimum Difference**: The minimum of the four calculated differences is the answer.\n\n### Complexity\n\n- **Time Complexity**: $$O(n \\log n)$$, where `n` is the length of `nums`, due to the sorting operation.\n- **Space Complexity**: $$O(1)$$, since no additional space proportional to the input size is used beyond the input and a few extra variables.\n\n# Code\n```\nclass Solution:\n def minDifference(self, nums: List[int]) -> int:\n n=len(nums)\n if n<5:\n return 0\n nums.sort()\n return min([nums[-1]-nums[3],nums[-2]-nums[2], nums[-3]-nums[1],nums[-4]-nums[0]])\n``` | 5 | 0 | ['Python3'] | 0 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | solved with just basics(noobie technique) | solved-with-just-basicsnoobie-technique-dn2uc | Intuition\n Describe your first thoughts on how to solve this problem. \nThe key observation is that by removing three elements from the array, we can only remo | utkarsh_the_co | NORMAL | 2024-07-03T17:32:35.536638+00:00 | 2024-07-03T17:32:35.536668+00:00 | 79 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe key observation is that by removing three elements from the array, we can only remove elements from either the start (smallest elements) or the end (largest elements) of the sorted array. This is because removing elements from anywhere else would not help in minimizing the difference between the remaining maximum and minimum values. Thus, the solution involves sorting the array and considering the best possible scenarios where we remove three elements from either end.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nHandle Small Arrays: If the array size is less than or equal to 4, then we can remove all elements to make the array empty or with a single element, hence the minimum difference is 0.\n\nSort the Array: Sorting the array helps us easily access the smallest and largest elements.\n\nConsider Possible Removals:\n\nRemove the three largest elements.\nRemove the two largest and one smallest element.\nRemove the one largest and two smallest elements.\nRemove the three smallest elements.\n\n# Complexity\n- Time complexity: O(NLogN)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int minDifference(vector<int>& nums) {\n int n = nums.size();\n if(n<=4)\n {\n return 0;\n }\n sort(nums.begin(),nums.end());\n vector<int> ans;\n \n \n ans.push_back(abs(nums[n-4]-nums[0]));\n ans.push_back(abs(nums[3]-nums[n-1]));\n ans.push_back(abs(nums[2]-nums[n-2]));\n ans.push_back(abs(nums[1]-nums[n-3]));\n sort(ans.begin(),ans.end());\n return ans[0];\n }\n};\n``` | 5 | 0 | ['Array', 'Sorting', 'C++'] | 1 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | Easy Way | easy-way-by-layan_am-3yrb | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | layan_am | NORMAL | 2024-07-03T14:46:13.966940+00:00 | 2024-07-03T14:46:13.966959+00:00 | 459 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int minDifference(int[] arr) {\n int n = arr.length;\n if (n <= 4) {\n return 0;\n }\n Arrays.sort(arr);\n int res = Integer.MAX_VALUE;\n for (int i = 0; i < 4; i++) {\n res = Math.min(res, arr[n - 1 - 3 + i] - arr[i]);\n }\n return res;\n }\n}\n``` | 5 | 0 | ['Java'] | 1 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | 💠 Ruby one-liner solution | ruby-one-liner-solution-by-lowie-oty8 | Intuition\n\nIf the length of the array is $4$ or less, we could easily see that the answer is $0$, because we have enough operations to turn all elements of th | lowie_ | NORMAL | 2024-07-03T04:18:27.521337+00:00 | 2024-07-03T04:18:27.521372+00:00 | 64 | false | # Intuition\n\nIf the length of the array is $4$ or less, we could easily see that the answer is $0$, because we have enough operations to turn all elements of the array to the same number.\n\nOtherwise, we can see that to achieve the best answer, we would have to remove some largest, or some smallest numbers, or both, from the array.\n\n# Approach\n\nLet\'s set $nums\' = sort(nums)$, the answer will be one of four:\n\n- $nums\'[n - 4] - num\'[0]$.\n- $nums\'[n - 3] - num\'[1]$.\n- $nums\'[n - 2] - num\'[2]$.\n- $nums\'[n - 1] - num\'[3]$.\n\nTherefore, we will try some way to create the enumerator with these 4 elements and use `min` function on it.\n\nWe will also use `sort!` to modify `nums`, instead of `sort` which would just return the sorted array without any modification. Note that this is not a good practice at all, but it would help solving the one-liner challenge.\n\n# Complexity\n- Time complexity: $O(n * log(n))$\n\n- Space complexity: $O(1)$\n\n# Code\n```\n# @param {Integer[]} nums\n# @return {Integer}\ndef min_difference(nums)\n nums.sort!.length <= 4 ? 0 : 4.times.map { |i| nums[i - 4] - nums[i] }.min\nend\n``` | 5 | 0 | ['Ruby'] | 1 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | simple approach | JAVA | simple-approach-java-by-sukritisinha0717-0opf | \n\n# Approach\n Describe your approach to solving the problem. \n1. Begin the minDifference method which takes an array of integers as input.\n2. Calculate the | sukritisinha0717 | NORMAL | 2024-07-03T03:21:01.959761+00:00 | 2024-07-03T03:21:01.959792+00:00 | 11 | false | \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Begin the minDifference method which takes an array of integers as input.\n2. Calculate the length of the input array and store it in numsSize.\n3. If the numsSize is less than or equal to 4, return 0 as there are not enough numbers to form a difference.\n4. Sort the input array in ascending order using Arrays.sort(nums).\n5. Initialize a variable minDiff to store the minimum difference as Integer.MAX_VALUE.\n6. Loop through the array from 0 to 3 (inclusive) using the variable left.\n7. Calculate the corresponding right index as numsSize - 4 + left.\n8. Update minDiff by taking the minimum of its current value and the difference between nums[right] and nums[left].\n9. Return the value stored in minDiff.\n\n# Complexity\n- Time complexity:O(n\u22C5logn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n) or O(logn)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n\n public int minDifference(int[] nums) {\n int numsSize = nums.length;\n if (numsSize <= 4) return 0;\n\n Arrays.sort(nums);\n\n int minDiff = Integer.MAX_VALUE;\n\n for (int left = 0, right = numsSize - 4; left < 4; left++, right++) {\n minDiff = Math.min(minDiff, nums[right] - nums[left]);\n }\n\n return minDiff;\n }\n}\n``` | 5 | 0 | ['Java'] | 1 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | Easy C++ solution using deque | easy-c-solution-using-deque-by-manan14-8e9u | \nclass Solution {\npublic:\n int ans=INT_MAX;\n void solve(deque<int> &dq,int cnt)\n {\n if(cnt==3)\n {\n ans=min(ans,dq.back | Manan14 | NORMAL | 2022-07-04T10:32:27.620889+00:00 | 2022-07-04T10:32:27.620931+00:00 | 337 | false | ```\nclass Solution {\npublic:\n int ans=INT_MAX;\n void solve(deque<int> &dq,int cnt)\n {\n if(cnt==3)\n {\n ans=min(ans,dq.back()-dq.front());\n return;\n }\n int temp=dq.front();\n dq.pop_front();\n solve(dq,cnt+1);\n dq.push_front(temp);\n temp=dq.back();\n dq.pop_back();\n solve(dq,cnt+1);\n dq.push_back(temp);\n }\n int minDifference(vector<int>& nums) {\n deque<int> dq;\n if(nums.size()<=4) return 0;\n sort(nums.begin(),nums.end());\n for(auto &x:nums) dq.push_back(x);\n solve(dq,0);\n return ans;\n }\n};\n``` | 5 | 0 | ['Queue'] | 2 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | Javascript Easy to understand | javascript-easy-to-understand-by-louisve-zmcv | This solutions is so easy, it doesn\'t need explaining.\n\n\n/**\n * @param {number[]} nums\n * @return {number}\n */\nvar minDifference = function(nums) {\n | louisvelz | NORMAL | 2021-04-14T13:37:04.633476+00:00 | 2021-04-14T13:37:04.633508+00:00 | 679 | false | This solutions is so easy, it doesn\'t need explaining.\n\n```\n/**\n * @param {number[]} nums\n * @return {number}\n */\nvar minDifference = function(nums) {\n if (nums.length <= 4) return 0\n nums.sort((a,b) => a-b)\n \n let i = 0;\n let j = nums.length - 4\n let min = Infinity\n \n while(i <= 3){\n min = Math.min(nums[j] - nums[i], min)\n i++\n j++\n }\n \n \n return min\n \n};\n\n``` | 5 | 0 | ['Sorting', 'JavaScript'] | 2 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | Short Easy Java | short-easy-java-by-branmazz-pla2 | Any array that has 4 numbers, you can change any 3 of the numbers to the remaining so it will always be 0.\nOtherwise, sort the array.\n\nNow the distance betwe | branmazz | NORMAL | 2020-12-24T22:36:56.413196+00:00 | 2020-12-24T22:36:56.413236+00:00 | 483 | false | Any array that has 4 numbers, you can change any 3 of the numbers to the remaining so it will always be 0.\nOtherwise, sort the array.\n\nNow the distance between the min and max is the distance between the first element and the last element.\nCheck all the combos for min distance and return.\n\nCombos are:\nchange the 3 smallest\nchange the 2 smallest and the 1 largest\nchange the 1 smallest and the 2 largest\nchange the 3 largest\n\n\n``` \n public int minDifference(int[] nums) {\n if(nums.length <= 4) return 0;\n int minDistance = Integer.MAX_VALUE;\n \n Arrays.sort(nums);\n for(int i = 0; i<=3; i++){\n minDistance = Math.min(minDistance,nums[nums.length-1-i] - nums[3-i]);\n }\n \n return minDistance;\n }\n | 5 | 0 | [] | 2 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | [JAVA] Generalized solution for K moves | java-generalized-solution-for-k-moves-by-iv6d | \tpublic int minDifference(int[] nums) {\n \n int k = 3;\n int n = nums.length;\n \n if(n < k + 2)\n return 0;\n | pikapikaa | NORMAL | 2020-08-09T17:26:11.318528+00:00 | 2020-08-09T17:26:23.995097+00:00 | 366 | false | \tpublic int minDifference(int[] nums) {\n \n int k = 3;\n int n = nums.length;\n \n if(n < k + 2)\n return 0;\n \n Arrays.sort(nums);\n \n int min = Integer.MAX_VALUE;\n \n for(int i = 0; i <= k; i++){\n min = Math.min(nums[n-1-i] - nums[k-i], min);\n }\n \n return min;\n } | 5 | 1 | ['Sorting', 'Java'] | 1 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | Python | Greedy | python-greedy-by-khosiyat-lrdc | see the Successfully Accepted Submission\n\n# Code\n\nclass Solution:\n def minDifference(self, nums: List[int]) -> int:\n if len(nums) <= 4:\n | Khosiyat | NORMAL | 2024-07-03T08:28:02.229333+00:00 | 2024-07-03T08:28:02.229368+00:00 | 197 | false | [see the Successfully Accepted Submission](https://leetcode.com/problems/minimum-difference-between-largest-and-smallest-value-in-three-moves/submissions/1308006366/?envType=daily-question&envId=2024-07-03)\n\n# Code\n```\nclass Solution:\n def minDifference(self, nums: List[int]) -> int:\n if len(nums) <= 4:\n return 0\n \n nums.sort()\n n = len(nums)\n \n return min(nums[n-1] - nums[3], # Remove the three smallest elements\n nums[n-2] - nums[2], # Remove the two smallest and the largest\n nums[n-3] - nums[1], # Remove the smallest and the two largest\n nums[n-4] - nums[0]) # Remove the three largest elements\n \n```\n\n# Step-by-Step Approach to Minimize Difference in Array\n\n## Understand the Objective\nWe want to minimize the difference between the largest and smallest values in the array. If we can change up to three elements, we should aim to either reduce the largest values, increase the smallest values, or a combination of both.\n\n## Consider Edge Cases\n- If the array has fewer than or exactly four elements, we can directly change all elements to be the same (since we can make up to three changes), resulting in a difference of 0.\n- If the array has more than four elements, we need a strategy to handle the more complex scenarios.\n\n## Sorting the Array\nSorting the array will help us easily access the largest and smallest elements that might need to be changed.\n\n## Evaluate Possible Moves\n- Change the three largest elements.\n- Change the two largest elements and one smallest element.\n- Change the one largest element and two smallest elements.\n- Change the three smallest elements.\n\nEach of these strategies will result in different maximum and minimum values, and we need to choose the one with the smallest difference.\n\n## Calculate the Minimum Difference\nAfter sorting the array, evaluate the possible minimum differences resulting from the above strategies and return the smallest one.\n\n## Explanation\n- **Edge Case Handling**: If there are fewer than or exactly four elements, we return 0 because we can always make all elements equal with at most three changes.\n- **Sorting**: We sort the array to easily access the smallest and largest elements.\n- **Evaluating Moves**: We compute the difference for the four possible strategies and return the minimum of these differences.\n\n\n | 4 | 0 | ['Python3'] | 0 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | Easy Java Code | easy-java-code-by-kundan25-p28h | Intuition\n- The task is to minimize the difference between the maximum and minimum values in an array after removing up to three elements. This can be effectiv | kundan25 | NORMAL | 2024-07-03T02:53:15.906562+00:00 | 2024-07-03T02:53:15.906596+00:00 | 506 | false | # Intuition\n- The task is to minimize the difference between the maximum and minimum values in an array after removing up to three elements. This can be effectively approached by considering the smallest and largest elements in a sorted array.\n\n# Approach\n1. If the length of the array is less than or equal to 4, the result is 0 because we can remove all elements or no elements, leading to a difference of 0.\n1. Sort the array.\n1. Check the difference between the highest and lowest elements after removing up to three elements from either end:\n - Remove 3 smallest elements.\n - Remove 2 smallest and 1 largest element.\n - Remove 1 smallest and 2 largest elements.\n - Remove 3 largest elements. \n4. Return the minimum difference obtained from these scenarios.\n\n# Complexity\n- Time complexity:- \uD835\uDC42( \uD835\uDC5B log\uD835\uDC5B)\n\n- Space complexity:- O(1) as only a fixed amount of extra space is used.\n\n# Code\n```\nclass Solution {\n public int minDifference(int[] nums) {\n int n = nums.length;\n if (n <= 4) return 0;\n Arrays.sort(nums);\n int res = Integer.MAX_VALUE;\n for (int i = 0; i <= 3; i++) {\n res = Math.min(res, nums[n - 4 + i] - nums[i]);\n }\n return res;\n }\n}\n```\n# **Conclusion**\n- By sorting the array and considering the removal of different combinations of three elements, we can effectively minimize the difference between the largest and smallest values in the modified array. This approach ensures that we evaluate all possible scenarios efficiently, leading to an optimal solution with a time complexity of O(nlogn). | 4 | 0 | ['Java'] | 1 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | Simple Code C++ | simple-code-c-by-agam_swarup-g0yj | Approach and Intuition\nProblem Understanding:\nThe problem asks for the minimum difference between the largest and smallest numbers in the array after making a | agam_swarup | NORMAL | 2024-07-03T02:40:35.314889+00:00 | 2024-07-03T02:40:35.314920+00:00 | 782 | false | # Approach and Intuition\nProblem Understanding:\nThe problem asks for the minimum difference between the largest and smallest numbers in the array after making at most three changes to the array. The changes are essentially removing up to three elements from the array to minimize the difference between the remaining elements.\n\nIntuition:\nIf we sort the array, the smallest possible difference between the maximum and minimum values in the array will be among the following four scenarios:\n\nRemove the three largest elements.\nRemove the two largest elements and the smallest element.\nRemove the largest element and the two smallest elements.\nRemove the three smallest elements.\nIn each case, the resulting array will be shorter by three elements, so we can find the difference between the smallest and largest numbers in the remaining array. Sorting the array helps us easily access these candidates for removal.\n\nDetailed Steps:\nCheck if the array size is less than or equal to 4. If it is, we can remove all elements, resulting in a minimum difference of 0.\nSort the array.\nCalculate the difference in the following scenarios:\nRemove the three largest elements: nums[n-4] - nums[0]\nRemove the two largest and the smallest element: nums[n-3] - nums[1]\nRemove the largest and the two smallest elements: nums[n-2] - nums[2]\nRemove the three smallest elements: nums[n-1] - nums[3]\nReturn the minimum of these differences.\n\n# Complexity\n- Time complexity:\nSorting the array takes O(nlogn)\nFinding the minimum difference among four candidates takes O(1)\n\nThus, the overall time complexity is O(nlogn).\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution {\npublic:\n int minDifference(vector<int>& nums) {\n if(nums.size()<=4)return 0;\n int n = nums.size();\n sort(nums.begin(),nums.end());\n return min((nums[n-4]-nums[0]),min((nums[n-3]-nums[1]),min((nums[n-2]-nums[2]),(nums[n-1]-nums[3]))\n ));\n\n }\n};\n``` | 4 | 0 | ['Array', 'Greedy', 'Sorting', 'C++'] | 4 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | JAVA EASIEST SOLUTION | java-easiest-solution-by-anurag015-ll37 | A = [1,5,6,13,14,15,16,17]\nn = 8\n\nCase 1: kill 3 biggest elements\n\nAll three biggest elements can be replaced with 14\n[1,5,6,13,14,15,16,17] -> [1,5,6,13, | anurag015 | NORMAL | 2022-06-02T05:33:52.674517+00:00 | 2022-06-02T05:38:25.047441+00:00 | 329 | false | A = [1,5,6,13,14,15,16,17]\nn = 8\n\nCase 1: kill 3 biggest elements\n\nAll three biggest elements can be replaced with 14\n[1,5,6,13,14,15,16,17] -> [1,5,6,13,14,14,14,14] == can be written as A[n-4] - A[0] == (14-1 = 13)\n\nCase 2: kill 2 biggest elements + 1 smallest elements\n\n[1,5,6,13,14,15,16,17] -> [5,5,6,13,14,15,15,15] == can be written as A[n-3] - A[1] == (15-5 = 10)\n\nCase 3: kill 1 biggest elements + 2 smallest elements\n\n[1,5,6,13,14,15,16,17] -> [6,6,6,13,14,15,16,16] == can be written as A[n-2] - A[2] == (16-6 = 10)\n\nCase 4: kill 3 smallest elements\n\n[1,5,6,13,14,15,16,17] -> [13,13,13,13,14,15,16,17] == can be written as A[n-1] - A[3] == (17-13 = 4)\n\nAnswer is minimum of all these cases!\n\n\nclass Solution {\n\n public int minDifference(int[] nums) {\n Arrays.sort(nums);\n \n int n=nums.length;\n if(n<=4)\n return 0;\n \n int res=Integer.MAX_VALUE;\n for(int i=0;i<=3;i++)\n {\n res=Math.min(res,nums[n-4+i]-nums[i]);\n }\n return res; \n }\n} | 4 | 0 | ['Sorting', 'Java'] | 1 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | C++, sort + sliding window, time: O(nlogn), space: O(n + logn) | c-sort-sliding-window-time-onlogn-space-a82bt | \nclass Solution {\npublic:\n \n // sorting + sliding window\n int minDifference(vector<int>& nums) {\n \n if (nums.size() < 5) {\n | hsuedw | NORMAL | 2021-10-03T00:44:42.806465+00:00 | 2022-11-19T10:22:37.225274+00:00 | 332 | false | ```\nclass Solution {\npublic:\n \n // sorting + sliding window\n int minDifference(vector<int>& nums) {\n \n if (nums.size() < 5) {\n // If the number of elements is less than or equal to four, \n // we can always adjust the values and let the minimum difference\n // to be zero.\n return 0;\n }\n \n // nums.size() >= 5;\n \n // Sort nums in ascending order.\n sort(begin(nums), end(nums));\n \n // Use the idea of sliding window to find the minimum defference after three moves.\n // Because nums is sorted, we can treat nums as circular array and choose three consecutive elements to find the answer.\n // After we choose three consecutive elements as our window, assume the three consecutive elements are reset to the\n // maximum value outside the window.\n int lastIdx = nums.size() - 1;\n \n // Now, the first three elements are our window.\n // The maximum value outside the window is the last element.\n // Change the values of the first three elements to the value of nums[lastIdx].\n int minDiff = nums[lastIdx] - nums[3]; \n \n // Treat nums as a circular array and choose nums[0], nums[1] and nums[lastIdx] to be our window.\n // The maximum value outside the window is nums[lastIdx - 1].\n // Change the values of nums[0], nums[1] and nums[lastIdx] to the value of nums[lastIdx - 1].\n minDiff = min(minDiff, nums[lastIdx - 1] - nums[2]);\n \n // Based upon the idea described above, choose nums[0], nums[lastIdx] and nums[lastIdx - 1] to be our window.\n // Change the values of nums[0], nums[lastIdx] and nums[lastIdx - 1] to the value of num[lastIdx - 2].\n minDiff = min(minDiff, nums[lastIdx - 2] - nums[1]);\n \n // Based upon the idea described above, choose the last three elements to be our window.\n // Change the values of the last three elements to the value of nums[last - 3].\n minDiff = min(minDiff, nums[lastIdx - 3] - nums[0]);\n \n // Since nums has been sorted, we don\'t have to iterate through the whole array.\n // After the silding window covers the first three and last three elements,\n // we can find the minimum difference.\n \n return minDiff;\n }\n};\n``` | 4 | 0 | ['C++'] | 2 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | [Python] straightforward solution with 2 heaps | python-straightforward-solution-with-2-h-ud6p | \nfrom heapq import *\nclass Solution:\n def minDifference(self, nums: List[int]) -> int:\n if len(nums) <= 4:\n return 0\n \n | jyung616 | NORMAL | 2021-08-24T21:24:22.592756+00:00 | 2021-08-25T02:08:56.907497+00:00 | 585 | false | ```\nfrom heapq import *\nclass Solution:\n def minDifference(self, nums: List[int]) -> int:\n if len(nums) <= 4:\n return 0\n \n maxHeap, minHeap = [], []\n \n for n in nums:\n heappush(maxHeap, -n)\n heappush(minHeap, n)\n if len(maxHeap) > 4:\n heappop(maxHeap)\n heappop(minHeap)\n \n # e.g. [1,5,0,10,14]\n\t\t#print(maxHeap) #[-10, -5, 0, -1]\n #print(minHeap) #[1, 5, 14, 10]\n \n minNums = sorted([-1*n for n in maxHeap]) # [0, 1, 5, 10]\n maxNums = sorted(minHeap, reverse = True) # [10, 14, 5, 1]\n \n res = float("inf") \n for i in range(4):\n res = min(res, maxNums[3-i]-minNums[i])\n return res \n\t\t\n``` | 4 | 0 | ['Heap (Priority Queue)', 'Python', 'Python3'] | 2 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | Simple Python3 with Detailed Explanation | simple-python3-with-detailed-explanation-kz1p | First, we eliminate the simple case of arrays with less than 5 elements. If an array has less than 5 elements, we can change all the elements to match. For exam | gillcmc2342 | NORMAL | 2021-08-18T20:07:27.176465+00:00 | 2021-08-18T20:07:27.176522+00:00 | 277 | false | First, we eliminate the simple case of arrays with less than 5 elements. If an array has less than 5 elements, we can change all the elements to match. For example [1,2,3,4] could be changed to [1,1,1,1]. Thus any array with less than 5 elements will always return 0. \n\nNext, we sort the array. With a sorted array, there are 4 distinct solution possibliltes. \n\n1. The three highest numbers need to be changed changed. An example of this would be [2,3,4,35,46,78,88]. Assuming we remove the 3 highest, the solution of our minimum will be the 4th highest minus the lowest. In the code below, this is expressed as `nums[l-4] - nums[0]`\n2. The second use case is elminating two high numbers and one low number. An example would be [1,33,34,35,65,67]. In this case, we change the two highest and the lowest, meaning we subtract the 3rd largest number from the second smallest number: `nums[l-3] - nums[1`\n3. Th third case is removing the highest number and the two smallest numbers. Ex. [1,2,33,34,35,71]. Expressed as `nums[l-2]-nums[2]`\n4. Finally, the fourth case involves elminating the three smallest numbers. Ex. [1,2,3,96,97,98,99]. Expressed as `nums[l-1]-nums[3]`\n\nNow all that remains is to select the smallest number of these four choices, and return that value. \n\n```\ndef minDifference(self, nums: List[int]) -> int:\n\n l = len(nums)\n if l < 5:\n return 0\n nums.sort()\n \n return min(nums[l-4]-nums[0], nums[l-3]-nums[1], nums[l-2]-nums[2], nums[l-1]-nums[3])\n``` | 4 | 0 | [] | 0 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | 4 lines C++ code, runtime beats: 93.86% | 4-lines-c-code-runtime-beats-9386-by-pus-0fzc | \nclass Solution {\npublic:\n int minDifference(vector<int>& nums) {\n int n = nums.size();\n if(n<=4) return 0;\n \n sort(nums.b | push_pop_top | NORMAL | 2021-08-17T19:27:33.701746+00:00 | 2021-08-17T19:27:33.701791+00:00 | 251 | false | ```\nclass Solution {\npublic:\n int minDifference(vector<int>& nums) {\n int n = nums.size();\n if(n<=4) return 0;\n \n sort(nums.begin(), nums.end());\n return min({nums[n-4] - nums[0],\n nums[n-3] - nums[1],\n nums[n-2] - nums[2],\n nums[n-1] - nums[3]\n });\n }\n};\n```\n**Please upvote if you like** | 4 | 0 | ['Sorting'] | 1 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | Straight forward Java Solution: O(nlogn) time O(1) space | straight-forward-java-solution-onlogn-ti-7lzu | \nclass Solution {\n public int minDifference(int[] nums) {\n int length = nums.length;\n if (length <= 4) {\n return 0;\n }\n Arrays.sort(num | supunwijerathne | NORMAL | 2021-08-02T18:47:37.985616+00:00 | 2021-08-02T18:47:58.517175+00:00 | 598 | false | ```\nclass Solution {\n public int minDifference(int[] nums) {\n int length = nums.length;\n if (length <= 4) {\n return 0;\n }\n Arrays.sort(nums);\n int min = Integer.MAX_VALUE;\n min = Math.min(min, nums[length - 1] - nums[3]);\n min = Math.min(min, nums[length - 2] - nums[2]);\n min = Math.min(min, nums[length - 3] - nums[1]);\n min = Math.min(min, nums[length - 4] - nums[0]);\n return min;\n }\n}\n``` | 4 | 0 | ['Java'] | 1 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | A/C Python 3 solution, easy to understand | ac-python-3-solution-easy-to-understand-lhs1b | \nclass Solution:\n def minDifference(self, nums: List[int]) -> int:\n nums.sort()\n n = len(nums)\n if (n <= 4 ):\n return 0 | willysde | NORMAL | 2021-06-27T21:52:14.072587+00:00 | 2021-06-27T21:52:14.072630+00:00 | 256 | false | ```\nclass Solution:\n def minDifference(self, nums: List[int]) -> int:\n nums.sort()\n n = len(nums)\n if (n <= 4 ):\n return 0\n \n res = nums[-1] - nums[0]\n # kill 3 biggest elements\n res = min(res, nums[-4] - nums[0])\n # kill 2 biggest elements + 1 smallest elements\n res = min(res, nums[-3] - nums[1])\n # kill 1 biggest elements + 2 smallest elements\n res = min(res, nums[-2] - nums[2])\n # kill 3 smallest elements\n res = min(res, nums[-1] - nums[3])\n \n return res\n \n``` | 4 | 1 | [] | 1 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | Python Simplest 4 line solution | python-simplest-4-line-solution-by-gsgup-hj22 | \nclass Solution:\n def minDifference(self, nums: List[int]) -> int:\n if len(nums)<=4:\n return 0\n nums.sort()\n return min | gsgupta11 | NORMAL | 2020-11-20T18:38:23.100533+00:00 | 2020-11-20T18:38:23.100571+00:00 | 380 | false | ```\nclass Solution:\n def minDifference(self, nums: List[int]) -> int:\n if len(nums)<=4:\n return 0\n nums.sort()\n return min(nums[-3]-nums[1],nums[-4]-nums[0],nums[-1]-nums[3],nums[-2]-nums[2])\n``` | 4 | 0 | [] | 1 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | C# Solution - 2 Lines | c-solution-2-lines-by-leonhard_euler-7ujh | \npublic class Solution \n{\n public int MinDifference(int[] A) \n {\n Array.Sort(A);\n return A.Length <= 4 ? 0 : new int[] { A[^1] - A[3], | Leonhard_Euler | NORMAL | 2020-07-11T18:19:15.081217+00:00 | 2020-07-11T18:25:04.996448+00:00 | 118 | false | ```\npublic class Solution \n{\n public int MinDifference(int[] A) \n {\n Array.Sort(A);\n return A.Length <= 4 ? 0 : new int[] { A[^1] - A[3], A[^2] - A[2], A[^3] - A[1], A[^4] - A[0] }.Min();\n }\n}\n``` | 4 | 0 | [] | 2 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | Ugly O(n) or Simple and Sweet O(n *log n) [Java] | ugly-on-or-simple-and-sweet-on-log-n-jav-7pny | Either \na) the array is short (4 or less elements) and you can affort in 3 move to change values, such the array has only 1 value\nb) for a longer array , if y | florin5 | NORMAL | 2020-07-11T16:01:26.636118+00:00 | 2020-07-11T16:20:16.043148+00:00 | 814 | false | Either \na) the array is short (4 or less elements) and you can affort in 3 move to change values, such the array has only 1 value\nb) for a longer array , if you have it sorted :** [m-1][m-2] [m-3] [m-4]**[ middle of the array] **[M-4][M-3] [M-2][M-1]** and you will replace some of the lower side of the array m-1 :m -4 or upper side of the array M-4-M-1. \nFor example if you replace k smallest elements and 3-k bigger elements the spread (Max-min) of the array will be [M-1-(3-k)] -[m-1-k]\n\n```\nclass Solution {\n public int minDifference(int[] nums) {\n if (nums.length <=4) {return 0;}\n Arrays.sort(nums);\n int r = nums[nums.length-1] - nums[0];\n for(int i=0;i<4;i++) {\n r = Math.min(r, nums[nums.length-(4-i)] - nums[i]);\n }\n return r;\n }\n}\n```\n\nO(n*log(n)) Complexity is steming from sorting, but since only the 3 lowest and highes elements of the arrays need to be sorted , that can be done in O(n):\n1) select 4 smalles and highes elemenst with with `[quick select](https://en.wikipedia.org/wiki/Quickselect)`.\n2) sort 4 smallest/highest elements - wich is a constant time operation | 4 | 0 | [] | 2 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | 99% Running time | SLIDING WINDOW | Easy to understand | 99-running-time-sliding-window-easy-to-u-mdv2 | Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem asks to minimize the difference between the maximum and minimum values of a | LinhNguyen310 | NORMAL | 2024-07-04T14:20:35.598347+00:00 | 2024-07-04T14:20:35.598395+00:00 | 2 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem asks to minimize the difference between the maximum and minimum values of an array after making at most three moves. Each move can change any one element to any other value. If we can make at most three moves, the optimal strategy involves focusing on the smallest and largest elements, as these contribute the most to the difference.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSort the Array: Sorting helps in easily accessing the smallest and largest elements.\nHandle Small Arrays: If the array has four or fewer elements, the difference can always be reduced to zero since we can change each element in three moves or less.\nEvaluate Possible Changes: For arrays with more than four elements, consider the four smallest and four largest elements. By examining different combinations of three moves on these elements, we can determine the minimum possible difference.\nWe can consider removing combinations of three elements from the start or end, or a mix of both.\nCalculate the Differences: Calculate the differences between appropriate elements after removing three elements from consideration.\n# Complexity\n- Time complexity:O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution(object):\n def minDifference(self, nums):\n """\n :type nums: List[int]\n :rtype: int\n """\n #iwthin 3 moves\n # every move can change 1 val to any val\n n = len(nums)\n if n <= 4:\n return 0\n nums.sort()\n count = 0\n minGap = float("inf")\n mergedList = []\n if n == 5:\n for i in range(n - 3, n):\n mergedList.append((i, nums[i]))\n for i in range(2):\n mergedList.append((i, nums[i]))\n else:\n for i in range(n - 3, n):\n mergedList.append((i, nums[i]))\n for i in range(3):\n mergedList.append((i, nums[i]))\n \n i, j = 0, 2\n res = []\n while j < len(mergedList):\n firstPosition, secondPosition = mergedList[i][0], mergedList[j][0]\n res *= 0\n if firstPosition == n - 3 and secondPosition == n - 1:\n res = nums[: n - 3]\n elif firstPosition == 0 and secondPosition == 2:\n res = nums[3:]\n else:\n minPosition = min(firstPosition, secondPosition)\n maxPosition = max(firstPosition, secondPosition)\n res = nums[minPosition + 1:maxPosition]\n gap = abs(res[-1] - res[0])\n minGap = min(gap, minGap)\n i += 1\n j += 1\n return minGap\n```\n\n\n | 3 | 0 | ['Python'] | 0 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | TC: O(n) | without STL | Simple Intuition | Recursion | tc-on-without-stl-simple-intuition-recur-xz9z | Intuition\nYou don\'t need to sort entire array.\nJust 4 smallest and 4 biggest elements are required.\n\nThen Apply recursion or iteration to get minDifference | AnishDhomase | NORMAL | 2024-07-03T17:16:35.677582+00:00 | 2024-07-03T17:16:35.677604+00:00 | 10 | false | # Intuition\nYou don\'t need to sort entire array.\nJust 4 smallest and 4 biggest elements are required.\n\nThen Apply recursion or iteration to get minDifference.\n change last 3 elements\n change last 2 elements & first 1 element\n change last 1 element & first 2 element\n change first 3 elements\nchanging: change to new max elem or new min elem\n\nnextSmallestElem() function will give you next Smallest Elem\nnextLargestElem() function will give you next Largest Elem\n\n# Code\n```\nclass Solution {\n int nextLargestElem(vector<int> &nums, vector<int> &smallCopy, unordered_set<int> &st){\n int n = nums.size(), ind = -1;\n int largest = INT_MAX, smallest = INT_MIN; \n if(smallCopy.size() > 4)\n largest = smallCopy.back();\n for(int i=0; i<n; i++){\n if(smallest <= nums[i] && nums[i] <= largest){\n if(st.find(i) == st.end()){\n smallest = nums[i];\n ind = i;\n }\n }\n }\n st.insert(ind);\n return nums[ind];\n }\n int nextSmallestElem(vector<int> &nums, vector<int> &smallCopy, unordered_set<int> &st){\n int n = nums.size(), ind = -1;\n int smallest = INT_MIN, largest = INT_MAX; \n if(smallCopy.size())\n smallest = smallCopy.back();\n for(int i=0; i<n; i++){\n if(smallest <= nums[i] && nums[i] <= largest){\n if(st.find(i) == st.end()){\n largest = nums[i];\n ind = i;\n }\n }\n }\n st.insert(ind);\n return nums[ind];\n }\n void findMinDiff(int start, int end, int moves, long long &minDiff, vector<int> &smallCopy){\n if(moves == 3){ \n minDiff = min<long long>((long long)smallCopy[end] - (long long)smallCopy[start], minDiff);\n return;\n }\n findMinDiff(start+1, end, moves+1, minDiff, smallCopy);\n findMinDiff(start, end-1, moves+1, minDiff, smallCopy);\n }\npublic:\n int minDifference(vector<int>& nums) {\n int n = nums.size();\n long long minDiff = 1e15;\n vector<int> smallCopy;\n unordered_set<int> st;\n if(n <= 4) return 0;\n if(n < 8){\n for(auto num: nums) smallCopy.push_back(num);\n sort(smallCopy.begin(), smallCopy.end());\n }\n else{\n for(int i=0; i<4; i++)\n smallCopy.push_back(nextSmallestElem(nums, smallCopy, st));\n for(int i=0; i<4; i++)\n smallCopy.push_back(nextLargestElem(nums, smallCopy, st));\n reverse(smallCopy.begin()+4, smallCopy.end());\n }\n findMinDiff(0, smallCopy.size()-1, 0, minDiff, smallCopy);\n return minDiff;\n }\n};\n``` | 3 | 0 | ['C++'] | 0 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | General solution for k moves using recursion and dp | general-solution-for-k-moves-using-recur-39kr | Intuition\nWe are Supposed to return difference(minimum) between smallest and largest number. It immediately strikes sorting! After sorting we will be able to g | Aditya_Garg17 | NORMAL | 2024-07-03T11:52:38.895010+00:00 | 2024-07-03T11:52:38.895043+00:00 | 4 | false | # Intuition\nWe are Supposed to return difference(minimum) between smallest and largest number. It immediately strikes sorting! After sorting we will be able to get minimum and maximum number without traversing. To lower the difference we have to either increase the minimum number or decrease the maximum element. And at a time, we can only do either of them. So by using recursion we are taking cases like if we removed start element, or if we removed end element then returning minimum of them. Pure Recursion will give pretty bad solution with time complexity O(2^n) hence we use dp to optimize it to O(n^2), although we can do this question in O(nlogn), I though this solution is pretty easy to figure out, without playing with indexes. \n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nPretty much self explainatory!\nK is the number of moves.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nTime complexity will be O(n^2*k)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n*k)\n\n# Code\n```\nclass Solution {\npublic:\n int helper(vector<int>& nums, int moves,int start,int end,vector<vector<int>>& dp){\n if(moves==0){\n return nums[end]-nums[start];\n }\n if (dp[start][moves]!=-1) {\n return dp[start][moves];\n }\n int remStart=helper(nums,moves-1,start+1,end,dp);\n int remEnd=helper(nums,moves-1,start,end-1,dp);\n return dp[start][moves]=min(remStart,remEnd);\n }\n int minDifference(vector<int>& nums) {\n int n=nums.size();\n if(n<=4){\n return 0;\n }\n //k is number of moves\n int k=3;\n sort(nums.begin(),nums.end());\n vector<vector<int>> dp(n, vector<int>(k + 1, -1));\n return helper(nums,3,0,nums.size()-1,dp);\n \n \n }\n\n};\n``` | 3 | 0 | ['C++'] | 0 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | Greedy Case Work | Java | C++ | greedy-case-work-java-c-by-lazy_potato-j03u | Intuition, approach, and complexity discussed in video solution in detail\nhttps://youtu.be/xEPTygm6rdI\n\n# Code\nJava\n\nclass Solution {\n public int minD | Lazy_Potato_ | NORMAL | 2024-07-03T07:21:33.083727+00:00 | 2024-07-03T07:21:33.083759+00:00 | 258 | false | # Intuition, approach, and complexity discussed in video solution in detail\nhttps://youtu.be/xEPTygm6rdI\n\n# Code\nJava\n```\nclass Solution {\n public int minDifference(int[] nums) {\n int size = nums.length;\n if (size <= 4) {\n return 0;\n }\n PriorityQueue<Integer> minHeap = new PriorityQueue<>();\n PriorityQueue<Integer> maxHeap = new PriorityQueue<>((a, b)->(b - a));\n for (var num : nums) {\n maxHeap.offer(num);\n if (maxHeap.size() > 4) {\n maxHeap.poll();\n }\n minHeap.offer(num);\n if (minHeap.size() > 4) {\n minHeap.poll();\n }\n }\n List<Integer> minFour = new ArrayList<>(maxHeap);\n List<Integer> maxFour = new ArrayList<>(minHeap);\n Collections.sort(minFour);\n Collections.sort(maxFour);\n int minDif = Integer.MAX_VALUE;\n for (int indx = 0; indx < 4; indx++) {\n int currDiff = maxFour.get(indx) - minFour.get(indx);\n minDif = Math.min(minDif, currDiff);\n }\n return minDif;\n }\n}\n```\nC++\n```\nclass Solution {\npublic:\n int minDifference(vector<int>& nums) {\n int size = nums.size();\n if (size <= 4) {\n return 0;\n }\n \n priority_queue<int, vector<int>, greater<int>> minHeap;\n priority_queue<int> maxHeap;\n \n for (int num : nums) {\n maxHeap.push(num);\n if (maxHeap.size() > 4) {\n maxHeap.pop();\n }\n minHeap.push(num);\n if (minHeap.size() > 4) {\n minHeap.pop();\n }\n }\n \n vector<int> minFour, maxFour;\n while (!maxHeap.empty()) {\n minFour.push_back(maxHeap.top());\n maxHeap.pop();\n }\n while (!minHeap.empty()) {\n maxFour.push_back(minHeap.top());\n minHeap.pop();\n }\n \n sort(minFour.begin(), minFour.end());\n sort(maxFour.begin(), maxFour.end());\n \n int minDif = INT_MAX;\n for (int indx = 0; indx < 4; ++indx) {\n int currDiff = maxFour[indx] - minFour[indx];\n minDif = min(minDif, currDiff);\n }\n \n return minDif;\n }\n};\n\n``` | 3 | 0 | ['Array', 'Greedy', 'C++', 'Java'] | 2 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | Simple and Beginner-Friendly Solution w/ Sorting and Greedy Method 😊😊 | simple-and-beginner-friendly-solution-w-jsnb5 | Intuition\nThe problem asks us to find the minimum difference between three numbers from a given list. The key is to realize that we can achieve the smallest di | briancode99 | NORMAL | 2024-07-03T06:23:24.459424+00:00 | 2024-07-29T06:24:46.393569+00:00 | 20 | false | # Intuition\nThe problem asks us to find the minimum difference between three numbers from a given list. The key is to realize that we can achieve the smallest difference by focusing on the extremes of the sorted list. If we pick three numbers from the extremes (smallest and largest), we are likely to find the smallest difference.\n\n# Approach\n1. Sort the input list: This will allow us to easily access the smallest and largest numbers.\n2. Iterate through possible combinations: We need to consider all possible combinations of three numbers that can be selected from the sorted list.\n3. Calculate the difference: For each combination, calculate the difference.\n4. Update the minimum difference: Keep track of the minimum difference found so far and update it if a smaller difference is encountered.\n5. Return the minimum difference: After iterating through all possible combinations, return the minimum difference.\n\n# Complexity\n- Time complexity: O(n log n)\n\n- Space complexity: O(1)\n\n# Code\n```\n/**\n * @param {number[]} nums\n * @return {number}\n */\nvar minDifference = function (nums) {\n if (nums.length <= 3) {\n return 0;\n }\n\n let min = Infinity;\n nums = nums.sort((a, b) => a - b);\n\n let left = 0;\n let right = nums.length - 1;\n\n // left left left\n min = Math.min(min, Math.abs(nums[left + 3] - nums[right]));\n\n // left left right\n min = Math.min(min, Math.abs(nums[left + 2] - nums[right - 1]));\n\n // left right right\n min = Math.min(min, Math.abs(nums[left + 1] - nums[right - 2]));\n\n // right right right\n min = Math.min(min, Math.abs(nums[left] - nums[right - 3]));\n\n return min;\n};\n``` | 3 | 0 | ['Array', 'Greedy', 'Sorting', 'JavaScript'] | 0 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | 🥷🏻✔️ Time: O(nlogn), Space: O(1): Go, Javascript, PHP, Typescript 🔥🥷🏻 | time-onlogn-space-o1-go-javascript-php-t-exbf | javascript []\nfunction minDifference(nums) {\n if (nums.length <= 4) return 0;\n\n nums.sort((a,b)=>a-b);\n\n let result = Number.MAX_VALUE;\n let | samandareshmamatov | NORMAL | 2024-07-03T05:37:02.501781+00:00 | 2024-07-03T05:37:02.501816+00:00 | 90 | false | ```javascript []\nfunction minDifference(nums) {\n if (nums.length <= 4) return 0;\n\n nums.sort((a,b)=>a-b);\n\n let result = Number.MAX_VALUE;\n let n = nums.length;\n let i = 0;\n\n while (i <= 3) {\n result = Math.min(result, nums[n - 4 + i] - nums[i]);\n i++;\n }\n\n return result;\n};\n```\n```PHP []\nclass Solution {\n\n /**\n * @param Integer[] $nums\n * @return Integer\n */\n function minDifference($nums) {\n if (count($nums) <= 4) {\n return 0;\n }\n\n sort($nums);\n\n $result = INF;\n $n = count($nums);\n $i = 0;\n\n while ($i <= 3) {\n $result = min($result, $nums[$n - 4 + $i] - $nums[$i]);\n $i++;\n }\n\n return $result;\n }\n}\n```\n```Typescript []\nfunction minDifference(nums: number[]): number {\n if (nums.length <= 4) return 0;\n\n nums.sort((a,b)=>a-b);\n\n let result: number = Number.MAX_VALUE;\n let n: number = nums.length;\n let i: number = 0;\n\n while (i <= 3) {\n result = Math.min(result, nums[n - 4 + i] - nums[i]);\n i++;\n }\n\n return result;\n};\n```\n```Go []\nfunc minDifference(nums []int) int {\n n := len(nums)\n if n <= 4 {\n return 0\n }\n\n sort.Ints(nums)\n\n result := math.Inf(1)\n i := 0\n\n for i <= 3 {\n result = math.Min(result, float64(nums[n-4+i]-nums[i]))\n i++\n }\n\n return int(result)\n}\n``` | 3 | 0 | ['Go'] | 1 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | Simple solution along with Follow up for 'K' | Java | C++ | Python | simple-solution-along-with-follow-up-for-3uhy | Intuition\nFirst lets understand for k = 3\nYou can remove in this manner \n1. Remove first three and last zero elements (3,0) --> nums[n-1] - nums[3]\n2. Remov | androiprogrammers | NORMAL | 2024-07-03T05:11:29.060993+00:00 | 2024-07-03T05:11:29.061026+00:00 | 205 | false | # Intuition\nFirst lets understand for k = 3\nYou can remove in this manner \n1. Remove first three and last zero elements (3,0) --> nums[n-1] - nums[3]\n2. Remove first two and last one (2,1) --> nums[n-2] - nums[2]\n3. Remove first one and last two (1,2) --> nums[n-3] - nums[1]\n4. Remove first zero and last three elements (0,3) --> nums[n-4] - nums[0]\n\nSo we take the minimum of these. \n\nSo for k we can solve like this\n1. remove (k,0)\n2. remove (k-1,1)\n3. remove (k-2,2)\n4. so on..... \n\n\n# Approach\n\nWe will use sliding window technique to solve for k\nIf you want to know the reference for this idea checkout this problem [https://leetcode.com/problems/maximum-points-you-can-obtain-from-cards/description/]()\n\nNow for the first k we will solve and then slide as shown\n\n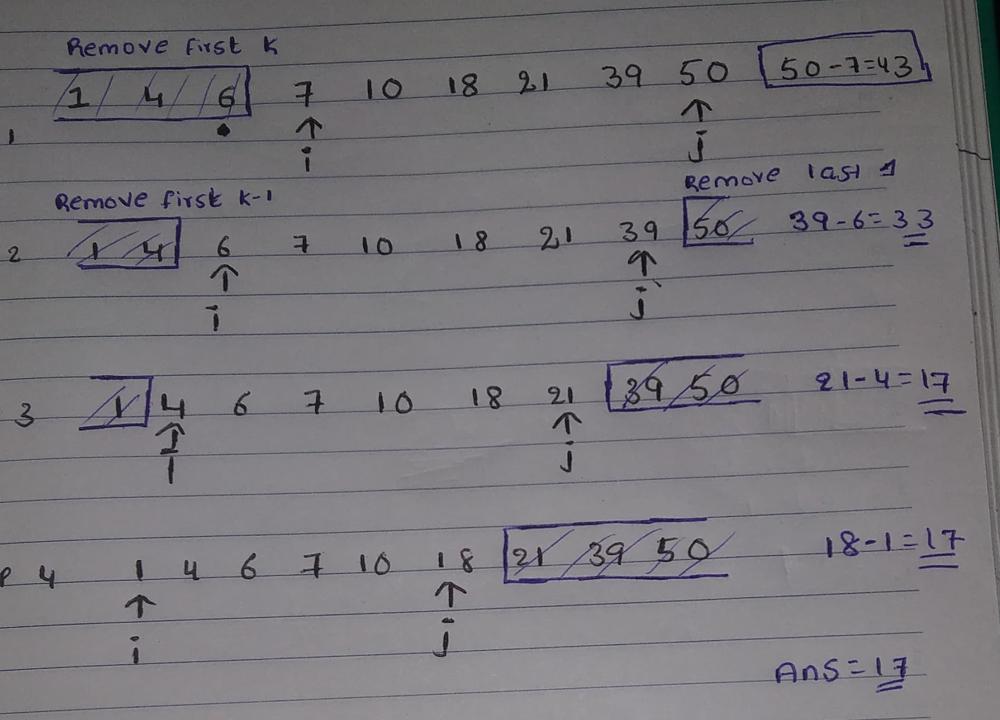\n\n\n# Complexity\n- Time complexity:\n$$O(nlogn)$$\n\n- Space complexity:\n$$O(1)$$\n\n# Code\n```java []\nclass Solution {\n public int minDifference(int[] nums) {\n return solve(nums,3); \n }\n public int solve(int[] nums,int k){\n int n = nums.length;\n Arrays.sort(nums);\n if(n<=k){\n return 0;\n }\n int i = k, j = n-1;\n int ans = Integer.MAX_VALUE;\n while(i>=0){\n ans = Math.min(nums[j]-nums[i],ans);\n i--;\n j--;\n }\n return ans;\n }\n}\n\n```\n```python []\nclass Solution:\n def minDifference(self, nums):\n return self.solve(nums, 3)\n\n def solve(self, nums, k):\n nums.sort()\n n = len(nums)\n if n <= k:\n return 0\n i = k\n j = n - 1\n ans = float(\'inf\')\n while i >= 0:\n ans = min(nums[j] - nums[i], ans)\n i -= 1\n j -= 1\n return ans\n```\n```C++ []\n#include <vector>\n#include <algorithm>\n#include <climits>\n\nclass Solution {\npublic:\n int minDifference(std::vector<int>& nums) {\n return solve(nums, 3);\n }\n\n int solve(std::vector<int>& nums, int k) {\n std::sort(nums.begin(), nums.end());\n int n = nums.size();\n if (n <= k) {\n return 0;\n }\n int i = k, j = n - 1;\n int ans = INT_MAX;\n while (i >= 0) {\n ans = std::min(nums[j] - nums[i], ans);\n i--;\n j--;\n }\n return ans;\n }\n};\n```\n\n | 3 | 0 | ['Array', 'Two Pointers', 'Greedy', 'Sliding Window', 'Sorting', 'Python', 'C++', 'Java', 'Python3'] | 1 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | Solution for Leetcode#1509 | solution-for-leetcode1509-by-samir023041-kmhp | \n\n# Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \nStep-01: At first | samir023041 | NORMAL | 2024-07-03T05:08:09.098433+00:00 | 2024-07-03T05:08:09.098465+00:00 | 85 | false | \n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nStep-01: At first, need to sort the arrray\nStep-02: Follow the below four options how 3 moves are done\nStep-03: Find the minimum difference among all options\n\n\n\n\n# Complexity\n- Time complexity: O(nLog(n))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n\nCoding Option-01: (Using **JAVA**)\n```\nclass Solution {\n public int minDifference(int[] nums) {\n int n=nums.length;\n if(n<=3){\n return 0;\n } \n Arrays.sort(nums);\n \n int result=Integer.MAX_VALUE;\n\n result=Math.min(result, nums[n-4] - nums[0]);\n result=Math.min(result, nums[n-3] - nums[1]);\n result=Math.min(result, nums[n-2] - nums[2]);\n result=Math.min(result, nums[n-1] - nums[3]);\n \n return result; \n }\n\n}\n```\n\nCoding Option-02: (Using **JAVA**)\n```\nclass Solution {\n public int minDifference(int[] nums) {\n int n=nums.length;\n if(n<=3){\n return 0;\n } \n Arrays.sort(nums); \n \n int result=Integer.MAX_VALUE;\n\n for(int i=0; i<4; i++){\n result = Math.min( result, nums[n-(4-i)]-nums[i] );\n }\n\n return result;\n }\n\n}\n``` | 3 | 0 | ['Java'] | 0 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | Beats 96% | Best Solution | Explained💯 | beats-96-best-solution-explained-by-sury-3htz | Intuition\n\nThoughts:\n1. Two pointer : Failed when realised you can\'t make more than 3 moves\n2. Recursion : As there were 4 possibilites strinking, but migh | suryanshnevercodes | NORMAL | 2024-07-03T03:48:52.655662+00:00 | 2024-07-03T05:33:33.819341+00:00 | 346 | false | # Intuition\n\nThoughts:\n1. Two pointer : Failed when realised you can\'t make more than 3 moves\n2. Recursion : As there were 4 possibilites strinking, but might give TLE\n3. Sorting and Greedy : THIS WORKS!\n\n# Approach\n\nSo I realised that if we can sort the array we just have to deal with the maximum and minimum elements in order to minimise the difference, so let\'s find out with an example:\n\nSuppose, I have `[1,5,0,10,14]`\n\nThe current minimum and maximum is 0 and 14, but we can do 3 operations on any of the 3 to minimise the difference, so let\'s observe that after sorting it becomes `[0,1,5,10,14]`. Now maximum difference with no operations is 14-0 = 14. \n\n$$Operation 1 :$$ So let\'s change either the 0 to 14 or 14 to 0, now it becomes `[0,1,5,10,0]`.\n\n$$Operation 2 :$$ Now maximum difference is 10-0 = 10, so lets change the 10 to 0 or 0 to 10, now it becomes `[0,1,5,0,0]`.\n\n$$Operation 3 :$$ Now difference is 5-0 = 5, so lets change 5 to 0 as well, now finally it becomes `[0,1,0,0,0]`.\n\nFinally we have exhausted all the operations and our answer is 1. Did you notice something?\n\nWe applied operations on the last 3 elements of the array in order to minimise it, thus applying on last 3 is a possibility. Similarly we can also apply on first three to make them equal of the 3 greater elements in order to minimise difference in the middle. Another one can be change the first two elements and change the last element and finally change the last two elements and first element only.\n\nThis works because the array is sorted and the elements that can create the maximum difference are residing at the extremes only.\n\nSo, to conclude:\n\n1. Sort the array\n2. $$Possibility 1$$ : `Change the last 3 elements`. So we can return n[n-4] - n[0];\n3. $$Possibility 2$$ : `Change the first 3 elements`. So we can return n[n-1] - n[3];\n4. $$Possibility 3$$ : `Change the last 2 and first 1 elements`. So we can return n[n-3] - n[1];\n5. $$Possibility 4$$ : `Change the last 1 and first 2 elements`. So we can return n[n-2] - n[2];\n\nThis all works for array length > 5. What is the array is of smaller length? It will always yeild answer as 0. How? TRY TO THINK. :)\n\n\n# Complexity\n- Time complexity: `O(n.log(n))`\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: `O(1)`\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n\n```java []\nclass Solution {\n public int minDifference(int[] nums) {\n if(nums.length < 5) return 0;\n Arrays.sort(nums);\n int p1 = nums[nums.length - 1] - nums[3];\n int p2 = nums[nums.length - 2] - nums[2];\n int p3 = nums[nums.length - 3] - nums[1];\n int p4 = nums[nums.length - 4] - nums[0];\n return Math.min(p1, Math.min(p2, Math.min(p3, p4)));\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int minDifference(std::vector<int>& nums) {\n if (nums.size() < 5) return 0;\n std::sort(nums.begin(), nums.end());\n int p1 = nums[nums.size() - 1] - nums[3];\n int p2 = nums[nums.size() - 2] - nums[2];\n int p3 = nums[nums.size() - 3] - nums[1];\n int p4 = nums[nums.size() - 4] - nums[0];\n return std::min({p1, p2, p3, p4});\n }\n};\n\n```\n```python []\nclass Solution:\n def minDifference(self, nums):\n if len(nums) < 5:\n return 0\n nums.sort()\n p1 = nums[-1] - nums[3]\n p2 = nums[-2] - nums[2]\n p3 = nums[-3] - nums[1]\n p4 = nums[-4] - nums[0]\n return min(p1, p2, p3, p4)\n```\n```Javascript []\nclass Solution {\n minDifference(nums) {\n if (nums.length < 5) return 0;\n nums.sort((a, b) => a - b);\n let p1 = nums[nums.length - 1] - nums[3];\n let p2 = nums[nums.length - 2] - nums[2];\n let p3 = nums[nums.length - 3] - nums[1];\n let p4 = nums[nums.length - 4] - nums[0];\n return Math.min(p1, p2, p3, p4);\n }\n}\n```\n# UPVOTE PLEASE \uD83E\uDD79\uD83D\uDE4F | 3 | 0 | ['Array', 'Greedy', 'Sorting', 'Python', 'C++', 'Java', 'Python3', 'JavaScript'] | 1 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | {C++} Sliding Window, 7 LOC, clean & concise. | c-sliding-window-7-loc-clean-concise-by-1to8e | 3 Moves 3rd of July \u2B50\n\n## Intuition\n \nSince It is a greedy problem we can easily solve it through sorting \u2705.\n\n## Approach\n Describe your approa | Ashmit_Mehta | NORMAL | 2024-07-03T02:58:59.486238+00:00 | 2024-07-12T03:18:09.695775+00:00 | 145 | false | > ***3 Moves 3rd of July \u2B50***\n\n## Intuition\n \nSince It is a **greedy problem** we can easily solve it through **sorting** \u2705.\n\n## Approach\n<!-- Describe your approach to solving the problem. -->\n- Firstly handle the edge cases where `n<=4` as the `ans` will always be `0` for them. \n\n- Sort the vector `nums`.\n\n- Make a window of size 3.\n\n- The window will start from the right end of the vector and move towards the right too.\n\n- Check the difference b/w the Min & Max element outside the window.\n\n- After checking the difference outside all the windows return the minimum difference.\n\n\n\n<br>\n\n```cpp\nclass Solution {\npublic:\n int minDifference(vector<int>& nums) {\n int n = nums.size();\n if(n<5) return 0;\n\n sort(nums.begin(),nums.end());\n\n int j=n-4, i = 0;\n int ans = INT_MAX;\n\n while(j<n) ans = min(ans,nums[j++]-nums[i++]);\n\nreturn ans;\n\n }\n};\n```\n\n\n#### Complexity\n- Time complexity: $$O(nlogn)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n\n\n> #### *~ Please upvote if you found it helpful\u2764\uFE0F*\n\n<br>\n\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n\n\n\n\n\n | 3 | 0 | ['Array', 'Greedy', 'Sliding Window', 'Sorting', 'C++'] | 0 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | simple and easy Python solution with explanation 😍❤️🔥 | simple-and-easy-python-solution-with-exp-op8h | if it\'s help, please up \u2B06 vote! \u2764\uFE0F\n\n\n# Code\n\nclass Solution(object):\n def minDifference(self, nums):\n if len(nums) <= 3:\n | shishirRsiam | NORMAL | 2024-07-03T01:32:31.374674+00:00 | 2024-07-03T01:32:31.374705+00:00 | 590 | false | # if it\'s help, please up \u2B06 vote! \u2764\uFE0F\n\n\n# Code\n```\nclass Solution(object):\n def minDifference(self, nums):\n if len(nums) <= 3:\n return 0\n \n nums.sort()\n ans = float(\'inf\')\n \n # frist three remove\n ans = min(ans, nums[-1] - nums[3])\n\n # last three remove\n ans = min(ans, nums[-4] - nums[0])\n\n # first 2 remove, last 1 remove\n ans = min(ans, nums[-2] - nums[2])\n\n # first 1 remove, last 2 remove\n ans = min(ans, nums[-3] - nums[1])\n return ans\n``` | 3 | 0 | ['Array', 'Greedy', 'Sorting', 'Python', 'Python3'] | 6 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | [Python3] ✅✅✅ Easy Solution Beats 98.82% 🔥🔥 -> O(1) Space ✅✅✅ | python3-easy-solution-beats-9882-o1-spac-8lpp | \n\n\n# Complexity\n- Time complexity: O(n.logn)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(1)\n Add your space complexity here, e.g. | OsamaAlhasanat | NORMAL | 2024-07-03T01:13:32.048826+00:00 | 2024-07-03T08:25:36.013581+00:00 | 234 | false | # \n\n\n# Complexity\n- Time complexity: O(n.logn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minDifference(self, nums: List[int]) -> int:\n n = len(nums)\n if n < 5: return 0\n nums.sort()\n f = lambda a, b: abs(a - b)\n return min(f(nums[0], nums[-4]), f(nums[1], nums[-3]), f(nums[2], nums[-2]), f(nums[3], nums[-1]))\n``` | 3 | 0 | ['Array', 'Greedy', 'Sorting', 'Python', 'Python3'] | 2 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | Minimum Difference After Changing Four Elements | minimum-difference-after-changing-four-e-kpz2 | Intuition\n- The goal of this function is to minimize the difference between the largest and smallest elements in the array after changing at most four elements | logusivam | NORMAL | 2024-05-09T08:20:33.703852+00:00 | 2024-05-09T08:20:33.703883+00:00 | 155 | false | # Intuition\n- The goal of this function is to minimize the difference between the largest and smallest elements in the array after changing at most four elements. To do this, the function sorts the array and considers four different cases of which elements to change to minimize the difference.\n\n# Approach\n1. Check if the length of the array is 4 or less. If so, return 0 because we can make all elements equal.\n2. Sort the array in non-decreasing order to easily identify the smallest and largest elements.\n3. Consider four possible cases by calculating the differences between:\n - The largest element and the third-largest element\n - The second-largest element and the second-smallest element\n - The third-smallest element and the second-smallest element\n - The smallest element and the fourth-smallest element\n4. Return the minimum difference among these four cases.\n\n# Complexity\n- **Time complexity:** O(n log n) due to the sorting operation, where n is the length of the input array.\n- **Space complexity:** O(1). The function uses a constant amount of extra space for storing temporary variables.\n\n# Code\n```\nvar minDifference = function(nums) {\n const n = nums.length;\n if (n <= 4) return 0; // If there are 4 or fewer elements, we can make them all equal\n \n nums.sort((a, b) => a - b); // Sort the array in non-decreasing order\n \n // Consider the four possible cases:\n // 1. Change the largest three elements\n // 2. Change the smallest element and the largest two elements\n // 3. Change the two smallest elements and the largest element\n // 4. Change the three smallest elements\n return Math.min(\n nums[n - 1] - nums[3],\n nums[n - 2] - nums[2],\n nums[n - 3] - nums[1],\n nums[n - 4] - nums[0]\n );\n};\n\n``` | 3 | 0 | ['JavaScript'] | 2 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | Sorting ||| Greedy | sorting-greedy-by-seal541-ijlc | Cover all the cases:\n\n- If\n - The number of elements are $\u2264 4$ then we can simply make largest 3 equal to smallest\n- Else\n - Return the minimum | seal541 | NORMAL | 2024-01-26T13:02:07.185549+00:00 | 2024-01-26T13:02:07.185569+00:00 | 606 | false | # Cover all the cases:\n\n- If\n - The number of elements are $\u2264 4$ then we can simply make largest 3 equal to smallest\n- Else\n - Return the minimum of converting smallest 3 to 4th smallest\n - smallest $2$ elements to $3^{rd}$ smallest, and largest to $2^{nd}$ largest\n - smallest $1$ to $2^{nd}$ smallest and the 2 largest to $3^{rd}$ largest\n - $3$ largest elements to the $4^{th}$ largest.\n - and do the difference for each case, with the largest of new with the smallest of the new.\n# Code\n```\nclass Solution {\npublic:\n int minDifference(vector<int>& nums) {\n sort(nums.rbegin(), nums.rend());\n if(nums.size()<=4){\n return 0;\n }\n cout<<nums[3]-nums[0]<<endl;\n\n return min(nums[3]-nums[nums.size()-1], min(nums[0]-nums[nums.size()-4], min(nums[1]-nums[nums.size()-3],nums[2]-nums[nums.size()-2])));\n }\n};\n``` | 3 | 0 | ['Array', 'Greedy', 'Sorting', 'C++'] | 1 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | Only 4 cases possible||Beats 91% | only-4-cases-possiblebeats-91-by-vikalp_-ftgb | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | vikalp_07 | NORMAL | 2023-08-13T14:23:06.645639+00:00 | 2023-08-13T14:23:06.645660+00:00 | 531 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int minDifference(vector<int>& nums) {\n int n = nums.size();\n if(n<=4)\n {\n return 0;\n }\n\n sort(nums.begin(),nums.end());\n int ans1 = abs(nums[0]-nums[n-4]);\n int ans2 = abs(nums[3]-nums[n-1]);\n int ans3 = abs(nums[1]-nums[n-3]);\n int ans4 = abs(nums[2]-nums[n-2]);\n\n return min(min(ans1,ans2),min(ans3,ans4));\n }\n};\n``` | 3 | 0 | ['C++'] | 3 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | 5 Lines Code || DP || Easy C++ || Beats 100% ✅✅ | 5-lines-code-dp-easy-c-beats-100-by-deep-rg5e | Approach\n Describe your approach to solving the problem. \nWe have to remove three numbers from 3 minimum + 3 maximum but which three elements will we choose.. | Deepak_5910 | NORMAL | 2023-08-06T10:41:40.993981+00:00 | 2023-08-06T16:19:33.605189+00:00 | 493 | false | # Approach\n<!-- Describe your approach to solving the problem. -->\nWe have to **remove three number**s from **3 minimum + 3 maximum** but which three elements will we **choose**.........\uD83E\uDD14\uD83E\uDD14\uD83E\uDD14\uD83E\uDD14\nHere I used **dp concept** to select three elements so as to **reduce the difference**.\n\n**Note:- Same Problem with Same Approach**\nLink:-https://leetcode.com/problems/minimum-score-by-changing-two-elements/solutions/3872837/5-lines-code-dp-easy-c-beats-100/\n\n# Complexity\n- Time complexity:O(N * Log(N))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int solve(vector<int> arr,int i,int j,int k)\n {\n if(k==3) return arr[j]-arr[i];\n return min(solve(arr,i+1,j,k+1),solve(arr,i,j-1,k+1));\n }\n int minDifference(vector<int>& arr) {\n if(arr.size()<=4) return 0;\n sort(arr.begin(),arr.end());\n return solve(arr,0,arr.size()-1,0);\n }\n};\n```\n\n | 3 | 0 | ['Array', 'Dynamic Programming', 'C++'] | 4 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | c++ | easy | short | c-easy-short-by-venomhighs7-ppik | \n# Code\n\nclass Solution {\npublic:\n int minDifference(vector<int>& nums) {\n\tint n = nums.size();\n if(n < 5)\n\t\treturn 0;\n\tpartial_sort(nums.begin | venomhighs7 | NORMAL | 2022-10-11T04:01:24.377648+00:00 | 2022-10-11T04:01:24.377698+00:00 | 882 | false | \n# Code\n```\nclass Solution {\npublic:\n int minDifference(vector<int>& nums) {\n\tint n = nums.size();\n if(n < 5)\n\t\treturn 0;\n\tpartial_sort(nums.begin(), nums.begin() + 4, nums.end());\n partial_sort(nums.rbegin(), nums.rbegin() + 4, nums.rend(), greater<int>());\n\t\n\tint min_diff = INT_MAX;\n\tfor(int i = 0, j = n - 4; i < 4; ++i, ++j)\n\t\tmin_diff = min(min_diff, nums[j] - nums[i]);\n \n\treturn min_diff;\n}\n};\n``` | 3 | 0 | ['C++'] | 0 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | C++ || EASY TO UNDERSTAND || Simple Solution || Commented | c-easy-to-understand-simple-solution-com-ikzo | \nclass Solution {\npublic:\n int minDifference(vector<int>& nums) {\n int n=nums.size();\n if(n<=4)\n return 0;\n sort(nums.begi | aarindey | NORMAL | 2022-04-17T21:17:43.876532+00:00 | 2022-04-17T21:17:43.876577+00:00 | 114 | false | ```\nclass Solution {\npublic:\n int minDifference(vector<int>& nums) {\n int n=nums.size();\n if(n<=4)\n return 0;\n sort(nums.begin(),nums.end());\n //changing first second and third smallest to next smallest\n int res=nums[n-1]-nums[3];\n //changing last three greatest numbers\n res=min(res,nums[n-4]-nums[0]);\n //changing 2 smallest+1 greatest\n res=min(res,nums[n-2]-nums[2]);\n //changing 2 greatest+ 1 smallest;\n res=min(res,nums[n-3]-nums[1]);\n return res;\n }\n};\n```\n**Please upvote to motivate me in my quest of documenting all leetcode solutions(to help the community). HAPPY CODING:)\nAny suggestions and improvements are always welcome** | 3 | 0 | [] | 0 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | ✔️[C++] || optimized Simple Code || Explained || TC: O( n ) , SC: O( 1 ) | c-optimized-simple-code-explained-tc-o-n-y11i | Please Upvote if it helps\u2B06\uFE0F\nWhy we will go for priority queue not for sorting ?\n--> Because this method only takes O( n ) time complexity and O( 1 ) | anant_0059 | NORMAL | 2022-03-26T11:51:20.213571+00:00 | 2022-03-26T17:23:25.108755+00:00 | 213 | false | #### *Please Upvote if it helps\u2B06\uFE0F*\n**Why we will go for priority queue not for sorting ?**\n*--> Because this method only takes O( n ) time complexity and O( 1 ) space complexity. But in sorting takes O( n log(n) ) time complexity. \nThe time comlexity for using priority queue is O( n ) because we restricted the size of priority queue to 4. So, total time complexity is O( n log(4) ) i.e. we can write it O( n ).*\n\n**We require only 4 largest element and 4 smallest element only for the required answer.**\nThe explanation of this is here: https://leetcode.com/problems/minimum-difference-between-largest-and-smallest-value-in-three-moves/discuss/730567/JavaC%2B%2BPython-Straight-Forward\n\n```\n\tint minDifference(vector<int>& nums) {\n int n=nums.size();\n if(n<5) return 0;\n priority_queue<int> pq_min;\n priority_queue <int, vector<int>, greater<int>> pq_max;\n for(int i=0;i<n;++i){\n if(pq_max.size()<4) pq_max.push(nums[i]), pq_min.push(nums[i]);\n else{\n if(pq_max.top()<nums[i]) pq_max.pop(), pq_max.push(nums[i]);\n if(pq_min.top()>nums[i]) pq_min.pop(), pq_min.push(nums[i]);\n }\n }\n \n vector<int> min_four(4);\n for(int i=0;i<4;++i) min_four[3-i]=pq_min.top(), pq_min.pop();\n \n int ans=INT_MAX;\n for(int i=0;i<4;++i){\n ans=min(ans, pq_max.top()-min_four[i]);\n pq_max.pop();\n }\n return ans;\n }\n``` | 3 | 0 | ['C'] | 0 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | Explanation of intuition | explanation-of-intuition-by-abhinav_sing-2oa9 | \n\n\nclass Solution {\npublic:\n int minDifference(vector<int>& nums) {\n int n = nums.size();\n // If size is 4 then we can make 3 elements e | abhinav_singh22 | NORMAL | 2022-03-15T08:16:59.098519+00:00 | 2022-03-15T08:16:59.098552+00:00 | 144 | false | \n\n```\nclass Solution {\npublic:\n int minDifference(vector<int>& nums) {\n int n = nums.size();\n // If size is 4 then we can make 3 elements equal to the\n // 4th element and the difference will be 0.\n // If size is less than 4 then we can make elements equal to\n // each other and the difference will be 0\n if (n <= 4) return 0;\n \n sort(nums.begin(), nums.end());\n \n return min({\n nums[n-3] - nums[1],\n nums[n-4] - nums[0],\n nums[n-1] - nums[3],\n nums[n-2] - nums[2]\n });\n }\n};\n```\n\nTime Complexity: O(nlogn) | 3 | 0 | ['Greedy'] | 1 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | Python solution in O(n) and O(1) extra memory | python-solution-in-on-and-o1-extra-memor-n0rz | \ndef minDifference(self, nums: List[int]) -> int:\n """\n Runtime O(n) and O(1) extra memory. One pass the collect 4 smallest and largest elements. \n | ozymandiaz147 | NORMAL | 2022-02-06T17:14:12.313270+00:00 | 2022-02-06T17:14:12.313308+00:00 | 239 | false | ```\ndef minDifference(self, nums: List[int]) -> int:\n """\n Runtime O(n) and O(1) extra memory. One pass the collect 4 smallest and largest elements. \n Then 4 comparisons of endpoints.\n """\n n = len(nums)\n if n <= 4:\n return 0\n min4 = nums[:4]\n max4 = nums[:4]\n for num in nums[4:]:\n idx, num_other = max([(i, val) for i, val in enumerate(min4)], key=lambda x: x[1])\n if num_other > num:\n min4[idx] = num\n idx, num_other = min([(i, val) for i, val in enumerate(max4)], key=lambda x: x[1])\n if num_other < num:\n max4[idx] = num\n nums8 = sorted(min4) + sorted(max4)\n minDiff = sys.maxsize\n for i in range(4):\n minDiff = min(minDiff, abs(nums8[i] - nums8[8 - 3 - 1 + i]))\n return minDiff\n\t``` | 3 | 0 | [] | 1 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | Java | O(n) with explanation using priorityQueues WITHOUT SORTING THE WHOLE ARRAY | java-on-with-explanation-using-priorityq-qgsc | We only need the 4 (3 possible changes plus 1) highest and 4 lowest numbers, as in case we take the 3 lowest numbers and convert them into the 4th (let\'s call | eldavimost | NORMAL | 2021-09-29T20:32:42.239314+00:00 | 2021-09-29T20:32:42.239365+00:00 | 439 | false | We only need the 4 (3 possible changes plus 1) highest and 4 lowest numbers, as in case we take the 3 lowest numbers and convert them into the 4th (let\'s call it the minNumberInRangeIndex), the difference would be the max number(nums[maxNumberInRangeIndex]) minus the nums[minNumberInRangeIndex].\nWe use a sliding window technique to see if any of the other possible options might give us a lowest difference: we substract 1 from maxNumberInRange and minNumberInRange, check the difference between their values and save it as the min if it\'s less.\n\nAs we don\'t need all numbers, we don\'t need to sort the whole array. We can just go over it and collect the 4 lowest and 4 highest numbers with 2 priorityqueues. As each priority queue would be at most 4 of size, this gives us a runtime of O(n log 4) = O(n).\n\nThis solution runs in 31 ms though, instead of 14 ms that runs just sorting all the elems. This is because the tests are done with a very small n. If n was larger as the problem states (1 <= nums.length <= 10^5) this probably would be way faster than sorting. \n\nLet me know if I\'m wrong, it\'s my first post!\n\n```\nclass Solution {\n public int minDifference(int[] nums) {\n final int numberOfChanges = 3;\n if (nums.length <= numberOfChanges + 1) {\n return 0;\n }\n int[] numsSimplified = getSimplifiedArray(nums, numberOfChanges);\n return minDifferenceSlidingWindow(numsSimplified, numberOfChanges);\n }\n \n private int[] getSimplifiedArray(int[] nums, int numberOfChanges) {\n Queue<Integer> higher = new PriorityQueue<>(); // Want to have the lowest number of the high numbers first\n Queue<Integer> lower = new PriorityQueue<>(Collections.reverseOrder()); // Want to have the higher of the lowest\n for (int i = 0; i < nums.length; i++) {\n higher.add(nums[i]);\n if (higher.size() > numberOfChanges + 1) {\n int value = higher.remove();\n lower.add(value);\n if (lower.size() > numberOfChanges + 1) {\n lower.remove();\n }\n }\n }\n int[] nums2 = new int[higher.size() + lower.size()];\n while (lower.size() > 0) {\n int value = lower.remove().intValue();\n nums2[lower.size()] = value;\n }\n while (higher.size() > 0) {\n int value = higher.remove().intValue();\n nums2[nums2.length - higher.size() - 1] = value;\n }\n return nums2;\n }\n \n private int minDifferenceSlidingWindow(int[] nums, int numberOfChanges) {\n int maxIndex = nums.length - 1;\n int minIndex = numberOfChanges;\n int min = Integer.MAX_VALUE;\n for (; minIndex >= 0; minIndex--, maxIndex--) {\n int diff = nums[maxIndex] - nums[minIndex];\n min = Math.min(min, diff);\n }\n return min;\n }\n}\n``` | 3 | 1 | ['Heap (Priority Queue)', 'Java'] | 2 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | Simplest C++ Solution | Explanation | Clean Code | | simplest-c-solution-explanation-clean-co-brvx | We had to replace three element in the array to make the amplitude (difference between max and min) minimum.\nWe can choose these elements from anywhere but to | yash2711 | NORMAL | 2021-09-23T04:36:03.634672+00:00 | 2021-09-23T04:36:03.634710+00:00 | 422 | false | We had to replace three element in the array to make the amplitude (difference between max and min) minimum.\nWe can choose these elements from anywhere but to minimize the amplitude, we have to choose them from either ends of the array.\nSo we have following possiblities:\n1. 0 start + 3 end\n2. 1 start + 2 end\n3. 2 start + 1 end\n4. 3 start + 0 end\n\nIf number of element is <= 4, we can always choose 3 from starting or ending and make the amplitude zero. So this becomes our edge case.\n\nWe simple use a for loop.\n\n```\nclass Solution {\npublic:\n int minDifference(vector<int>& arr) {\n if(arr.size() <= 4) return 0;\n int res = INT_MAX;\n sort(arr.begin(), arr.end());\n for(int i = 0; i <= 3; i++)\n {\n res = min(res,(arr[arr.size()-4+i] - arr[i]));\n }\n return res;\n }\n};\n```\nDo upvote if it helped you! | 3 | 1 | ['C', 'Sorting'] | 0 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | Sort array and quickly check 3 cases | Time Complexity O(nlogn) | sort-array-and-quickly-check-3-cases-tim-ribs | just sort the array.\n\nnow we have 4 possible combinations of cases:\n1. we can change first 3 elemenet with 4th element of array.\n2. we can change Last 3 el | codeankit | NORMAL | 2021-08-28T19:08:02.983900+00:00 | 2021-08-28T19:08:02.983929+00:00 | 307 | false | just **sort** the array.\n\n**now we have 4 possible combinations of cases**:\n1. we can change first 3 elemenet with 4th element of array.\n2. we can change Last 3 elemenet with 4th last element.\n3. we can change First 2 element with with 3rd element and last element with 2nd last element.\n4. we can change Last 2 element with 3rd last element and 1st element with 2nd element.\n\nJust find out all 4 possible combinations and return miniumn our of it.\n\n\n```\nclass Solution {\npublic:\n int minDifference(vector<int>& nums) {\n int len=nums.size();\n \n if(len < 5)\n return 0;\n \n sort(nums.begin(), nums.end());\n \n int min1= min( nums[len-1]-nums[3], nums[len-4]-nums[0] );\n \n int min2= min(nums[len-2]-nums[2], nums[len-3]-nums[1]);\n \n return min( min1, min2);\n }\n};\n``` | 3 | 1 | ['C', 'Sorting'] | 0 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | Javascript Simple With explanation | javascript-simple-with-explanation-by-ba-zewb | \nvar minDifference = function(nums) {\n let len = nums.length;\n if (len < 5) return 0;\n\n nums.sort((a,b) => a-b)\n \n return Math.min(\n | back_to_basics | NORMAL | 2021-07-30T16:29:56.412681+00:00 | 2021-07-30T16:30:20.334801+00:00 | 269 | false | ```\nvar minDifference = function(nums) {\n let len = nums.length;\n if (len < 5) return 0;\n\n nums.sort((a,b) => a-b)\n \n return Math.min(\n \n ( nums[len-1] - nums[3] ), // 3 elements removed from start 0 from end\n ( nums[len-4] - nums[0] ), // 3 elements removed from end 0 from start\n ( nums[len-2] - nums[2] ), // 2 elements removed from start 1 from end\n ( nums[len-3] - nums[1] ), // 2 elements removed from end 1 from start\n \n\n)\n \n \n \n \n};\n``` | 3 | 0 | ['JavaScript'] | 0 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | C++ Solution || Using Sorting || Clear Code | c-solution-using-sorting-clear-code-by-k-mug7 | Using Bubble and Selection Sort\n\nclass Solution {\npublic:\n int minDifference(vector<int>& nums) {\n int n = nums.size();\n if(n <= 3) retur | kannu_priya | NORMAL | 2021-07-07T18:48:48.173597+00:00 | 2021-07-07T18:51:30.048183+00:00 | 395 | false | **Using Bubble and Selection Sort**\n```\nclass Solution {\npublic:\n int minDifference(vector<int>& nums) {\n int n = nums.size();\n if(n <= 3) return 0;\n \n //using bubble sort (4 greatest elements will go at its right position)\n for(int i = 0; i < 4; i++)\n for(int j = 0; j < n-1-i; j++)\n if(nums[j] > nums[j+1]) swap(nums[j], nums[j+1]);\n \n //using selection sort (4 smallest elements will go at its right position)\n int mini, index;\n for(int i = 0; i < 4; i++){\n mini = nums[i], index = i;\n for(int j = i+1; j < n; j++){\n if(mini > nums[j]){\n mini = nums[j];\n index = j;\n }\n }\n swap(nums[i], nums[index]);\n }\n \n int first = nums[n-1] - nums[3]; //remove first 3 elements\n int second = nums[n-4] - nums[0]; //remove last 3 elements\n int third = nums[n-2] - nums[2]; //remove first 2 and 1 last elements\n int forth = nums[n-3] - nums[1]; //remove first 1 and 2 last elements\n \n return min(min(first, second), min(third, forth));\n }\n};\n```\n\n**Using STL sort function**\n```\nclass Solution {\npublic:\n int minDifference(vector<int>& nums) {\n int n = nums.size();\n if(n <= 3) return 0;\n sort(nums.begin(), nums.end());\n \n int first = nums[n-1] - nums[3]; //remove first 3 elements\n int second = nums[n-4] - nums[0]; //remove last 3 elements\n int third = nums[n-2] - nums[2]; //remove first 2 and 1 last elements\n int forth = nums[n-3] - nums[1]; //remove first 1 and 2 last elements\n \n return min(min(first, second), min(third, forth));\n }\n};\n``` | 3 | 0 | ['C', 'Sorting', 'C++'] | 1 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | Java based solution using Sliding Window O(nLogn) | java-based-solution-using-sliding-window-p6db | Intuition\nHere you have to find the minumum difference between the largest and the smallest number by making/considering any other three numbers in the array e | azmishra | NORMAL | 2021-07-04T18:14:05.035404+00:00 | 2021-07-04T18:14:05.035446+00:00 | 341 | false | **Intuition**\nHere you have to find the minumum difference between the largest and the smallest number by making/considering any other three numbers in the array equal to whatever number from the same array. Confused? I was too . \n\nIt\'s actually simple, all you have to do is to see this problem in a different way. It\'s asking us to return the minimum difference between smallest and largest number of the array considering there are only N - 3 element at each run (N - length of array). \nThe reason we substracted by 3 is because in the problem it says we can replace any number using three move. Using this we will just increment our pointers (walker and looper) and get the difference between the first element and the last element in that range and get the minimum from it to get the result.\n``` n-3-1 ``` will be the last element in the first interation.\n\nOne more thing for array with length between 0 - 4 the answer will always be 0, reason being we can just replace the maximum number with the other three and then difference will be 0.\n\n```\nclass Solution {\n public int minDifference(int[] nums) {\n int n = nums.length;\n if(n < 5) return 0;\n Arrays.sort(nums);//O(nLogn) this uses TimSort\n int walker = 0, looper = n - 3 - 1;\n int res = Integer.MAX_VALUE;\n while(walker < n && looper < n) {\n res = Math.min(res, (nums[looper++] - nums[walker++]));\n }\n return res;\n }\n}\n```\n\nReference \n1. [LeetCode Discuss](https://leetcode.com/problems/minimum-difference-between-largest-and-smallest-value-in-three-moves/discuss/731233/Similar-to-1423.-Maximum-Points-You-Can-Obtain-from-Cards) | 3 | 0 | ['Sliding Window', 'Sorting', 'Java'] | 0 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | just Follow pattern Runtime: 72 ms, faster than 95.87% | just-follow-pattern-runtime-72-ms-faster-bgk1 | \nstatic auto speedup = [](){\n std::ios::sync_with_stdio(false);\n std::cin.tie(nullptr);\n std::cout.tie(nullptr);\n return nullptr;\n}();\n\nclas | cs_balotiya | NORMAL | 2021-06-11T10:36:08.695461+00:00 | 2021-06-11T10:36:08.695506+00:00 | 98 | false | ```\nstatic auto speedup = [](){\n std::ios::sync_with_stdio(false);\n std::cin.tie(nullptr);\n std::cout.tie(nullptr);\n return nullptr;\n}();\n\nclass Solution {\npublic:\n int minDifference(vector<int>& nums) {\n \n\t\t int n = nums.size();\n\t\t\t\t\n\t\t if(n <= 3)\n return 0;\n\t\t\t\n sort(nums.begin(), nums.end());\n \n int p1 = abs(nums[0] - nums[n-4]); // 0 3\n int p2 = abs(nums[1] - nums[n-3]); // 1 2\n int p3 = abs(nums[2] - nums[n-2]); // 2 2\n int p4 = abs(nums[3] - nums[n-1]); // 3 0\n \n return min(min(p1, p2),min(p3,p4));\n }\n};\n``` | 3 | 1 | [] | 1 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | O(N) find 4 smallest and 4 largest, 82% speed | on-find-4-smallest-and-4-largest-82-spee-ikm9 | Runtime: 332 ms, faster than 81.63% of Python3 online submissions for Minimum Difference Between Largest and Smallest Value in Three Moves.\nMemory Usage: 24.1 | evgenysh | NORMAL | 2021-04-28T12:59:00.029835+00:00 | 2021-04-28T12:59:00.029864+00:00 | 670 | false | Runtime: 332 ms, faster than 81.63% of Python3 online submissions for Minimum Difference Between Largest and Smallest Value in Three Moves.\nMemory Usage: 24.1 MB, less than 75.23% of Python3 online submissions for Minimum Difference Between Largest and Smallest Value in Three Moves.\n```\nclass Solution:\n def minDifference(self, nums) -> int:\n if len(nums) > 4:\n s1 = s2 = s3 = s4 = float("inf")\n l1 = l2 = l3 = l4 = float("-inf")\n for n in nums:\n if n < s1:\n s4 = s3\n s3 = s2\n s2 = s1\n s1 = n\n elif n < s2:\n s4 = s3\n s3 = s2\n s2 = n\n elif n < s3:\n s4 = s3\n s3 = n\n elif n < s4:\n s4 = n\n if n > l1:\n l4 = l3\n l3 = l2\n l2 = l1\n l1 = n\n elif n > l2:\n l4 = l3\n l3 = l2\n l2 = n\n elif n > l3:\n l4 = l3\n l3 = n\n elif n > l4:\n l4 = n\n return min(l4 - s1, l3 - s2, l2 - s3, l1 - s4)\n return 0\n```\n | 3 | 1 | ['Python', 'Python3'] | 1 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | C++ sort and recursion with explanation | c-sort-and-recursion-with-explanation-by-9rqo | \nclass Solution {\npublic:\n int minDifference(vector<int>& nums) {\n // Sort the array first. Then for each move we have 2 options:\n // 1) M | chase1991 | NORMAL | 2021-02-26T03:30:38.528927+00:00 | 2021-02-26T03:30:38.528983+00:00 | 181 | false | ```\nclass Solution {\npublic:\n int minDifference(vector<int>& nums) {\n // Sort the array first. Then for each move we have 2 options:\n // 1) Move the smallest number to the next larger number, OR\n // 2) Move the largest number to the next smaller number.\n // We need to compare the difference of 1) and 2), and choose the minimum value.\n sort(nums.begin(), nums.end());\n return minDifference(nums, 3, 0, nums.size() - 1);\n }\n \nprivate:\n int minDifference(const vector<int>& nums, int moves, int left, int right)\n {\n if (left > right)\n {\n return 0; // all elements are equal\n }\n \n if (moves == 0)\n {\n return nums[right] - nums[left]; // no more moves\n }\n \n int n1 = minDifference(nums, moves - 1, left + 1, right); // move smallest to the next larger\n int n2 = minDifference(nums, moves - 1, left, right - 1); // move largest to the next smaller\n return n1 < n2 ? n1 : n2;\n }\n};\n``` | 3 | 0 | [] | 0 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | Simple C++ Solution | simple-c-solution-by-indrajohn-quk7 | \nclass Solution {\npublic:\n int minDifference(vector<int>& nums) {\n sort(nums.begin(), nums.end());\n int count = 0;\n if (nums.size( | indrajohn | NORMAL | 2021-02-15T11:12:15.851263+00:00 | 2021-02-15T11:12:15.851297+00:00 | 279 | false | ```\nclass Solution {\npublic:\n int minDifference(vector<int>& nums) {\n sort(nums.begin(), nums.end());\n int count = 0;\n if (nums.size() <= 4) return 0;\n \n int n = nums.size();\n int a = nums[n - 1] - nums[3], b = nums[n - 2] - nums[2], \n c = nums[n - 3] - nums[1], d = nums[n - 4]- nums[0];\n return min(min(a, b), min(c, d));\n }\n};\n``` | 3 | 0 | [] | 0 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | C# - Simple Solution Easy to Understand | c-simple-solution-easy-to-understand-by-nqr72 | \npublic class Solution {\n public int MinDifference(int[] nums) {\n \n if(nums.Length<=4)\n return 0;\n Array.Sort(nums);\n | karanverma39 | NORMAL | 2021-02-15T07:08:42.178296+00:00 | 2021-02-15T07:08:42.178340+00:00 | 169 | false | ```\npublic class Solution {\n public int MinDifference(int[] nums) {\n \n if(nums.Length<=4)\n return 0;\n Array.Sort(nums);\n \n int result = int.MaxValue;\n \n for(int i = 0; i < 4; i++){\n result = Math.Min(result,(nums[nums.Length-1-3+i]-nums[i]));\n }\n return result;\n }\n}\n``` | 3 | 0 | ['Sorting'] | 0 |
minimum-difference-between-largest-and-smallest-value-in-three-moves | My Java Solution | my-java-solution-by-vrohith-ko4y | \nclass Solution {\n public int minDifference(int[] nums) {\n if (nums.length < 5)\n return 0;\n Arrays.sort(nums);\n int res | vrohith | NORMAL | 2020-09-05T06:36:34.755621+00:00 | 2020-09-05T06:36:34.755657+00:00 | 518 | false | ```\nclass Solution {\n public int minDifference(int[] nums) {\n if (nums.length < 5)\n return 0;\n Arrays.sort(nums);\n int result = Integer.MAX_VALUE;\n for (int i=0; i<4; i++) {\n result = Math.min(result, nums[nums.length-4+i] - nums[i]);\n }\n return result;\n }\n}\n``` | 3 | 0 | ['Array', 'Sorting', 'Java'] | 2 |
split-message-based-on-limit | [Python] Find the number of substrings | python-find-the-number-of-substrings-by-kp24z | Explanation\nThe key question is to find out the number of split parts k.\n\ncur is the total string length of all indices,\nlike the string length for "123" is | lee215 | NORMAL | 2022-11-12T17:07:32.123238+00:00 | 2022-11-13T04:01:05.578380+00:00 | 6,441 | false | # **Explanation**\nThe key question is to find out the number of split parts `k`.\n\n`cur` is the total string length of all indices,\nlike the string length for "123" is 3.\n`</>` takes 3 characters.\nThe number `k` takes `len(str(k))` characters.\n\nIf `cur + len(s) + (3 + len(str(k))) * k > limit * k`,\nmeans not enough characters to split `s`.\n\nIf `3 + len(str(k)) * 2 >= limit`,\n`k` means `<k/k>` already takes `limit` characters,\nit is impossible to split message as required.\n\nWe increment `k` from 0 until we find `k` that can split message `s` as required.\n<br>\n\n# **Complexity**\nTime `O(n)`\nSpace `O(n)`\n<br>\n\n**Python**\n```py\n def splitMessage(self, s: str, limit: int) -> List[str]:\n cur = k = i = 0\n while 3 + len(str(k)) * 2 < limit and cur + len(s) + (3 + len(str(k))) * k > limit * k:\n k += 1\n cur += len(str(k))\n res = []\n if 3 + len(str(k)) * 2 < limit:\n for j in range(1, k + 1):\n l = limit - (len(str(j)) + 3 + len(str(k)))\n res.append(\'%s<%s/%s>\' % (s[i:i + l], j, k))\n i += l\n return res\n```\n | 71 | 1 | ['Python'] | 14 |
split-message-based-on-limit | ✅ [Python] binary search is redundant, just brute force it (explained) | python-binary-search-is-redundant-just-b-jbq4 | \u2705 IF YOU LIKE THIS SOLUTION, PLEASE UPVOTE.\n*\nThis solution employs a brute force approach to find the minimal number of parts needed to split the string | stanislav-iablokov | NORMAL | 2022-11-12T18:12:19.821564+00:00 | 2022-11-12T18:34:18.502193+00:00 | 3,023 | false | **\u2705 IF YOU LIKE THIS SOLUTION, PLEASE UPVOTE.**\n****\nThis solution employs a brute force approach to find the minimal number of parts needed to split the string into parts of limited length with appended suffixes. Time complexity is linear: **O(N)**. Space complexity is linear: **O(N)**.\n\n**Comment.** Given the boundaries for this problem, i.e. `len(message) <= 10000`, and considering the fact that the minimal size of each part is `len("_<1/1>") = 6`, we colcude that the maximal number of iterations in case of using a brute-force approach is `10000 / 6 = 1667`. That\'s very cheap for a linear scan, so let\'s brute force the number of parts `p` then use it to format a list of parts.\n\n**Python.**\n```\nclass Solution:\n def splitMessage(self, msg: str, lim: int) -> List[str]:\n \n def sz(n) : return len(str(n)) # a helper function to get a number of digits\n \n p = a = 1 # a number of parts and a total length of a-indices\n \n while p * (sz(p) + 3) + a + len(msg) > p * lim: # [1] check that current number of parts is not enough...\n if 3 + sz(p) * 2 >= lim : return [] # [2] ...or break if the separation is not possible\n p += 1 # [3] try an increased number of parts\n a += sz(p) # [4] also, increase the total length of a-indices\n \n parts = [] # [5] at this point, we either obtained the minimal number \n # of parts \'p\' or have returned an empty list \n for i in range(1,p+1):\n j = lim - (sz(p)+sz(i)+3) # [6] for each part, find how many symbols to bite off \n part, msg = msg[0:j], msg[j:] # [7] bite off a piece of string...\n parts.append(f"{part}<{i}/{p}>") # [8] ...and format a suffix-tagged part\n \n return parts\n``` | 43 | 0 | [] | 8 |
split-message-based-on-limit | ✔✔✔ Brute Force ⁉ || Simple Approach || C++ || Explained | brute-force-simple-approach-c-explained-1jb02 | As the problem required to find minimum number of parts, Let us traverse from 1 to see if we can divide our message with current number of parts.\n\nLet us do s | brehampie | NORMAL | 2022-11-12T16:01:40.297319+00:00 | 2022-11-13T12:31:24.286042+00:00 | 2,235 | false | As the problem required to find minimum number of parts, Let us traverse from 1 to see if we can divide our message with current number of parts.\n\nLet us do some calculation now.\n\n<b>What will be the length of the string after we attach the extra info "<a/b>" with each part?</b>\n\nLet the number of parts = <b>N</b>\nThen with each part we will attach "</>". Hence we need extra <b>3*N</b> character.\nWe will also attach the value b= N with each part.Then we need extra <b>Nx(number of digits in N)</b>.\nFinally we will attach the value of <b>a </b> with each part, which requires the <b>sum of number of digits from 1 to N</b>.\nHence the actual size of string will be = <b>N + 3*N + Nx(number of digits in N) + <span>Σ</span>(number of digits from 1 to N)<b>\n\nNow we just need to check if we can divide the size in N parts where each part will contain <b>limit</b> characters except the last one.\n\nSample Code:\n```\nclass Solution {\npublic:\n vector<string> splitMessage(string message, int limit) {\n vector<int>dig(10001),cum_sum(10001);// contains number of digits in N and cumulative sum of number of digits.\n // find number of digits in X.\n auto number_of_digits=[](int x){\n int ret = 0;\n while(x){\n ret++;\n x/=10;\n }\n return ret;\n };\n for(int i=1;i<=10000;i++){\n dig[i] = number_of_digits(i); \n cum_sum[i] = cum_sum[i-1]+dig[i];\n }\n \n int actual_size = message.size();\n vector<string>ret;\n for(int N=1;N<=actual_size;N++){\n int newSize = actual_size+3*N+dig[N]*N+cum_sum[N];\n \n //check if possible to achieve the result.\n if((newSize+limit-1)/limit==N){\n string s;\n int cur = 1;\n //for each part we need to add <a/b> with it\n int extra = dig[N]+3;//as a part changes we do it in runtime\n for(char&c:message){\n s+=c;\n if(s.size()+dig[cur]+extra==limit){\n s+="<"+to_string(cur)+"/"+to_string(N)+">";\n ret.push_back(s);\n s.clear();\n cur++;\n }\n }\n //if last part contains less than limit characters.\n if(s.size()){\n s+="<"+to_string(cur)+"/"+to_string(N)+">";\n ret.push_back(s);\n s.clear();\n }\n return ret;\n }\n }\n return ret;\n }\n};\n```\n\n | 32 | 8 | ['C'] | 8 |
split-message-based-on-limit | Binary search does not work - counterexample added | binary-search-does-not-work-counterexamp-i1eo | Counter example\n\n"abbababbbaaa aabaa a"\n8\n\n\nThe above test can be split into 7 tokens, can\'t be split into 10 tokens and it can be split again into 11 to | przemysaw2 | NORMAL | 2022-11-16T02:59:18.485281+00:00 | 2022-11-28T17:27:15.557413+00:00 | 1,400 | false | # Counter example\n```\n"abbababbbaaa aabaa a"\n8\n```\n\nThe above test can be split into 7 tokens, can\'t be split into 10 tokens and it can be split again into 11 tokens. This problem does not have the BS property.\n\nSome of the incorrect BS solutions passed these tests, because of the order in which they check the values.\n\nIf they hit 11 first, they detect, it is possible, so they go to the left and they find the 7 solution later.\n\nIf they hit 10 first, they detect it is impossible and they go right, finding the 11 solution. It is possible to design the test cases to kill all BS solutions though. | 21 | 0 | ['C++'] | 8 |
split-message-based-on-limit | ✅ Most Descriptive Solution So Far | most-descriptive-solution-so-far-by-hrid-n3qu | \u2705 It surprises me how posts with absolutely no explanation receive so many upvotes!!\n\n# Code\nJava []\nclass Solution {\n // returns the number of cha | hridoy100 | NORMAL | 2024-08-09T01:19:37.957279+00:00 | 2024-08-09T01:21:22.369186+00:00 | 1,571 | false | ### \u2705 It surprises me how posts with absolutely no explanation receive so many upvotes!!\n\n# Code\n``` Java []\nclass Solution {\n // returns the number of characters in an integer\n int charLen(int value) {\n int len = 0;\n while(value!=0) {\n len++;\n value /=10;\n }\n return len;\n }\n // segments = k\n int checkValidity(String message, int limit, int segments) {\n int charLenSoFar = 0;\n int msgLen = message.length();\n for(int i=1; i<=segments; i++) {\n // if total character length we have collected so far\n // increases the message length, then we have taken too many segments\n // We need to look on the left, return -1\n if(charLenSoFar >= msgLen) {\n return -1;\n }\n int formatLen = 3 + charLen(i) + charLen(segments); // "<" + i + "/" + segments + ">"\n int remLen = limit - formatLen;\n // if the remaining length of a chunk is less than or eq 0,\n // then we won\'t be able to add any character to it\n if(remLen <= 0) {\n return -1;\n }\n // we can take remLen (remaining length) characters from the message string\n charLenSoFar += remLen;\n }\n\n // if characters we were able to collect so far is less than the message length,\n // we need to increase our segments, so, look on the right side, return 1\n if(charLenSoFar < msgLen) {\n return 1;\n }\n\n // we were able to confine all the characters of message\n // using this segments. So, this is a happy case and possible answer.\n return 0;\n }\n\n public String[] splitMessage(String message, int limit) {\n int left = 1;\n int right = message.length();\n int segments = Integer.MAX_VALUE;\n\n while(left <= right) {\n int mid = left + (right-left)/2;\n\n int segmentValidity = checkValidity(message, limit, mid);\n if(segmentValidity == 0) {\n segments = Math.min(segments, mid);\n right = mid - 1;\n left = 1;\n }\n // we need to look on the left side\n else if(segmentValidity == -1) {\n right = mid - 1;\n }\n // we need to look on the right side\n else {\n left = mid + 1;\n }\n }\n // if we never found any happy case, there\'s no answer\n if(segments == Integer.MAX_VALUE) {\n return new String[0];\n }\n else {\n // construct the string with minimum segments we were able to determine\n return getFormattedStrings(message, limit, segments);\n }\n }\n\n // segments = k\n String[] getFormattedStrings(String message, int limit, int segments) {\n String[] res = new String[segments];\n int msgLen = message.length();\n int charLenSoFar = 0;\n\n for(int i=1; i<=segments; i++) {\n String format = "<" + i + "/" + segments + ">";\n int remaining = limit - format.length();\n\n int startIdx = charLenSoFar;\n int endIdx = charLenSoFar + remaining;\n // we don\'t want it to go out of bound..\n endIdx = Math.min(msgLen, endIdx);\n\n res[i-1] = message.substring(startIdx, endIdx) + format;\n\n // update charLenSoFar (characters so far seen) value \n // as we were able to acquire remaining size of characters\n charLenSoFar += remaining;\n }\n\n return res;\n }\n}\n``` | 14 | 0 | ['String', 'Binary Search', 'Java'] | 0 |
split-message-based-on-limit | 💥💥 O(n) on runtime and memory [EXPLAINED] | on-on-runtime-and-memory-explained-by-r9-jb20 | IntuitionSplit a long message into smaller parts, each with a specific length, and append a suffix showing its index and total number of parts. The suffix must | r9n | NORMAL | 2024-12-26T05:39:53.235782+00:00 | 2024-12-26T05:39:53.235782+00:00 | 303 | false | # Intuition
Split a long message into smaller parts, each with a specific length, and append a suffix showing its index and total number of parts. The suffix must fit within the given length limit, and we need to minimize the number of parts while ensuring all parts, when combined, reconstruct the original message.
# Approach
Start by determining the number of parts needed based on the length limit and the space taken by the suffix; once the number of parts is found, slice the message into parts and append the suffix for each part.
# Complexity
- Time complexity:
O(n), where n is the length of the message. We traverse the message and the parts only once.
- Space complexity:
O(n), as we store the result in a list of strings that hold each part of the message.
# Code
```rust []
impl Solution {
pub fn split_message(message: String, limit: i32) -> Vec<String> {
let limit = limit as usize;
// Helper function to calculate suffix length
let get_suff_len = |a: usize, b: usize| format!("<{}/{}>", a, b).len();
// Variables to determine the number of parts
let mut num_parts = 0;
let mut prefix_length_so_far = 0;
// Find the number of parts required
while 3 + (num_parts.to_string().len() * 2) < limit &&
(num_parts * limit)
- prefix_length_so_far
- (num_parts * (3 + num_parts.to_string().len()))
< message.len()
{
num_parts += 1;
prefix_length_so_far += num_parts.to_string().len();
}
// Check if we have enough capacity for the message
if (num_parts * limit)
- prefix_length_so_far
- (num_parts * (3 + num_parts.to_string().len()))
< message.len()
{
return vec![];
}
// Construct the resulting parts
let mut result = Vec::new();
let mut l = 0;
for i in 1..=num_parts {
let data_length = limit - get_suff_len(i, num_parts);
let end = (l + data_length).min(message.len());
let token = format!("{}<{}/{}>", &message[l..end], i, num_parts);
l += data_length;
result.push(token);
}
result
}
}
``` | 11 | 0 | ['String', 'Binary Search', 'Rust'] | 0 |
split-message-based-on-limit | Java divide stage solution | java-divide-stage-solution-by-wts2accura-8rba | \nclass Solution {\n public String[] splitMessage(String message, int limit) {\n int[] stgTable = {\n (limit - 5) * 9,\n | david_chiang_job | NORMAL | 2022-11-12T16:13:06.018526+00:00 | 2022-11-12T16:13:06.018564+00:00 | 1,409 | false | ```\nclass Solution {\n public String[] splitMessage(String message, int limit) {\n int[] stgTable = {\n (limit - 5) * 9,\n (limit - 6) * 9 + (limit - 7) * 90,\n (limit - 7) * 9 + (limit - 8) * 90 + (limit - 9) * 900,\n (limit - 8) * 9 + (limit - 9) * 90 + (limit - 10) * 900 + (limit - 11) * 9000,\n };\n int l = message.length(), stg = 0;\n while (stg < stgTable.length) {\n if (stgTable[stg] >= l) break;\n stg++;\n }\n if (stg == stgTable.length) return new String[0];\n ArrayList<String> list = new ArrayList<>();\n int idx = 1, strIdx = 0;\n for (int i = 0; i <= stg; i++) {\n int size = limit - 5 - stg - i;\n for (int j = 0; j < 9 * Math.pow(10, i) && strIdx < message.length(); j++) {\n list.add(message.substring(strIdx, Math.min(message.length(), strIdx + size)) + "<" + idx);\n strIdx += size;\n idx++;\n }\n }\n String[] res = list.toArray(new String[]{});\n for (int i = 0; i < res.length; i++)\n res[i] = res[i] + "/" + (idx - 1) + ">";\n return res;\n }\n}\n``` | 10 | 0 | ['Java'] | 2 |
split-message-based-on-limit | [Python] Simple dumb O(N) solution, no binary search needed | python-simple-dumb-on-solution-no-binary-ejv5 | Intuition\nThe idea is to figure out how many characters the parts count take up. Once we know that, generating all the parts is trivial.\n\n# Approach\nSimply | vu-dinh-hung | NORMAL | 2022-11-12T17:01:28.669676+00:00 | 2023-01-01T04:16:16.905877+00:00 | 1,633 | false | # Intuition\nThe idea is to figure out how many characters the parts count take up. Once we know that, generating all the parts is trivial.\n\n# Approach\nSimply check if 9, 99, 999, or 9999 parts are enough to split the whole message, since 9, 99, 999, or 9999 are the maximum possible parts count for 1, 2, 3, or 4 characters.\n\nLet\'s say a message splits into 14 parts. For that string, the `splitable` function below will return `True` for 99, but `False` for 9 -> we need to reserve 2 characters for the parts count.\n\n# Complexity\n- Time complexity: O(n)\n- Space complexity: O(n)\n\n# Code\n```\nclass Solution:\n def splitMessage(self, message: str, limit: int) -> List[str]:\n def splitable_within(parts_limit):\n # check the message length achievable with <parts_limit> parts\n length = sum(limit - len(str(i)) - len(str(parts_limit)) - 3 for i in range(1, parts_limit + 1))\n return length >= len(message)\n \n parts_limit = 9\n if not splitable_within(parts_limit):\n parts_limit = 99\n if not splitable_within(parts_limit):\n parts_limit = 999\n if not splitable_within(parts_limit):\n parts_limit = 9999\n if not splitable_within(parts_limit):\n return []\n \n # generate the actual message parts\n parts = []\n m_index = 0 # message index\n for part_index in range(1, parts_limit + 1):\n if m_index >= len(message): break\n length = limit - len(str(part_index)) - len(str(parts_limit)) - 3\n parts.append(message[m_index:m_index + length])\n m_index += length\n \n return [f\'{part}<{i + 1}/{len(parts)}>\' for i, part in enumerate(parts)]\n\n``` | 9 | 0 | ['Python3'] | 1 |
split-message-based-on-limit | Java Easy to Understand Code | java-easy-to-understand-code-by-sajedjal-2oxu | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | sajedjalil | NORMAL | 2024-02-05T03:18:06.543536+00:00 | 2024-02-05T03:18:06.543570+00:00 | 928 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n log n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public String[] splitMessage(String message, int limit) {\n \n int low = 1, high = message.length();\n int result = Integer.MAX_VALUE;\n\n while( low<=high ) {\n int mid = low + (high-low)/2;\n\n int value = checkValidity(message, limit, mid); \n // System.out.println(mid+" "+value);\n if(value == 0) {\n result = Math.min(result, mid);\n high = mid - 1;\n low = 1;\n }\n else if( value == -1 ) high = mid - 1;\n else low = mid + 1;\n }\n // System.out.println(result);\n\n if( result == Integer.MAX_VALUE) return new String[0];\n else return getFormattedStrings(message, limit, result);\n }\n\n private int checkValidity(String message, int limit, int k) {\n\n int idx = 0;\n for(int i=1; i<=k; i++) {\n\n if( idx >= message.length() ) return -1;\n String format = "<"+i+"/"+k+">";\n int left = limit - format.length();\n\n if( left <= 0 ) return -1;\n\n idx += left;\n\n\n }\n\n if( idx < message.length()) return 1;\n\n return 0;\n }\n\n private String[] getFormattedStrings(String message, int limit, int k) {\n String [] result = new String[k];\n\n int idx = 0;\n for(int i=1; i<=k; i++) {\n String format = "<"+i+"/"+k+">";\n int diff = limit-format.length();\n \n if( idx+diff > message.length() ) result[i-1] = message.substring(idx)+format;\n else result[i-1] = message.substring(idx, idx+diff)+format;\n\n idx += diff;\n }\n return result; \n }\n}\n``` | 7 | 0 | ['Java'] | 2 |
split-message-based-on-limit | Java || concise and clear solution | java-concise-and-clear-solution-by-chris-2lkc | \nclass Solution {\n public String[] splitMessage(String message, int limit) {\n int size = message.length();\n int lenOfIndice = 1, total = 1; | Chris___Yang | NORMAL | 2022-11-17T21:37:18.269940+00:00 | 2022-11-17T21:37:18.269968+00:00 | 1,054 | false | ```\nclass Solution {\n public String[] splitMessage(String message, int limit) {\n int size = message.length();\n int lenOfIndice = 1, total = 1;\n while (size + (3 + len(total)) * total + lenOfIndice > limit * total) {\n if (3 + len(total) * 2 >= limit) return new String[0];\n total += 1;\n lenOfIndice += len(total);\n }\n \n return formStrings(message, limit, total);\n }\n private String[] formStrings(String message, int limit, int total) {\n int index = 0;\n String[] result = new String[total];\n for (int i = 1; i <= total; ++i) {\n String suffix = String.format("<%d/%d>", i, total);\n // do not exceed the length of the "message" using Math.min()\n String prefix = message.substring(index, Math.min(index + limit - suffix.length(), message.length()));\n result[i - 1] = prefix + suffix;\n index += limit - suffix.length();\n }\n return result;\n }\n private int len(int number) {\n return String.valueOf(number).length();\n }\n\n}\n``` | 7 | 0 | ['Java'] | 1 |
split-message-based-on-limit | C++ Solution with explanation | c-solution-with-explanation-by-rac101ran-3dai | \n// First I thought of binary search , but realised soon , I can iterate over all the b\'s.\n// Let\'s say answer is of size x , We know x-1 words will have le | rac101ran | NORMAL | 2022-11-14T19:01:35.124502+00:00 | 2022-11-30T07:03:57.660849+00:00 | 684 | false | ```\n// First I thought of binary search , but realised soon , I can iterate over all the b\'s.\n// Let\'s say answer is of size x , We know x-1 words will have length limit & last word should be <=limit\n// Validate the last word , picking b greedily :)\nclass Solution {\npublic:\n vector<string> splitMessage(string message, int limit) {\n int b = 0 , cnt = 0 , sm = 0;\n vector<string> ans;\n for(int i=1; i<=10000; i++) {\n sm+=Size(i); // sum of length of (\'1\') + (\'2\')... (\'i\') , we are calculating sum of length of all a\'s.\n int cnt = ((3 + Size(i)) * i) + message.size() + sm; // sum of (3 is "</>" + i\'s size ) * i times , message , sm \n int len = (i-1) * limit; // till second last\n if(cnt - len <= limit) { // if last is bigger than limit , its invalid!\n b = i;\n break;\n }\n }\n string s = "";\n cnt = 1;\n for(int i=0; i<message.size(); i++) {\n if(limit - (3 + Size(cnt) + Size(b) + (int)s.size())>0) {\n s+=message[i];\n }else {\n string word = s + "<" + to_string(cnt) + "/" + to_string(b) + ">";\n ans.push_back(word);\n s = message[i];\n cnt++;\n }\n }\n string word = s + "<" + to_string(cnt) + "/" + to_string(b) + ">";\n ans.push_back(word);\n if(cnt>b || word.size()>limit) return {}; // cnt is last value of a , which should never be > than b , also last word size should be <= limit!\n return ans;\n }\n int Size(int n) {\n return to_string(n).size();\n }\n};\n``` | 7 | 0 | ['Math', 'C'] | 3 |
split-message-based-on-limit | Python, Go | Simple solution with explanation | O(N) | python-go-simple-solution-with-explanati-zjjt | Intuition\n Describe your first thoughts on how to solve this problem. \nLet\'s consider a scenario where we merge the split string back without excluding the s | globaldjs | NORMAL | 2024-02-04T04:18:16.698154+00:00 | 2024-02-04T04:18:16.698183+00:00 | 1,242 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nLet\'s consider a scenario where we merge the split string back without excluding the suffixes. Knowing the **original size** of the string and the **number** of its parts, we can calculate the overall size of this combined string.\n\nExample: `"short mess<1/2>age<2/2>"`\n\u2022 Original length: 13\n\u2022 Number of parts: 2\n\u2022 Length of each suffix: 5\n\u2022 Total length: 13 + 2 * 5 = 23\n\nNote that `limit * parts >= total_length`. Knowing the original size of the string, limit and total size of the suffixes, it is possible to find out the number of parts\n\u2022 Limit: 15\n\u2022 `15 * parts >= 13 + parts * 5; parts >= 13 / (15 - 5); parts >= 1.3`\n\u2022 Fractions cannot represent parts, so `parts = ceil(1.3) = 2`\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nLet\'s apply it to all possible ranges of the parts (1-10000)\n**\u2022 1 <= parts < 10**\ntotal_length = msg_length + parts * 5\nlimit * parts >= msg_length + parts * 5\nparts >= msg_length / (limit - 5)\n\n**\u2022 10 <= parts < 100**\ntotal_length = msg_length + 9 * 6 + (parts - 9) * 7\n*Explanation*: 9 parts with "<K/NN>" suffixes AND (total_parts - 9) parts with "<KK/NN>" suffixes.\nlimit * parts >= msg_length - 9 + parts * 7\nparts >= (msg_length - 9) / (limit - 7)\n\n**\u2022 100 <= parts < 1000**\ntotal_length = msg_length + 9 * 7 + 90 * 8 + (parts - 99) * 9\nlimit * parts >= msg_length - 108 + parts * 9\nparts >= (msg_length - 108) / (limit - 9)\n\n**\u2022 1000 <= parts < 10000**\ntotal_length = msg_length + 9 * 8 + 90 * 9 + 900 * 10 + (parts - 999) * 11\nlimit * parts >= msg_length - 1107 + parts * 11\nparts >= (msg_length - 1107) / (limit - 11)\n\n**\u2022 parts = 10000**\ntotal_length = msg_length + 9 * 9 + 90 * 10 + 900 * 11 + 9000 * 12 + 13\nlimit * parts >= msg_length + 118894\nparts >= (msg_length + 118894) / limit\n\nDetermining the exact number of parts to split the string require approximation, as the initial result could potentially fall into the next interval.\n\n# Code\n```python3 []\nimport math\n\n\nclass Solution:\n def getNumberOfParts(self, message: str, limit: int) -> int:\n if limit < 6:\n return 0\n length = len(message)\n parts = math.ceil(length / (limit - 5))\n if 10 <= parts < 100:\n parts = math.ceil((length - 9) / (limit - 7)) if limit > 7 else 0\n if 100 <= parts < 1000:\n parts = math.ceil((length - 108) / (limit - 9)) if limit > 9 else 0\n if 1000 <= parts < 10000:\n parts = math.ceil((length - 1107) / (limit - 11)) if limit > 11 else 0\n if parts > 10000:\n parts = math.ceil((length + 118894) / limit)\n if parts > 10000:\n parts = 0\n return parts\n\n def splitMessage(self, message: str, limit: int) -> List[str]:\n res = []\n start, end = 0, 0\n parts = self.getNumberOfParts(message, limit)\n for i in range(parts):\n suffix = f"<{i+1}/{parts}>"\n end = start + limit - len(suffix)\n res.append(f"{message[start:end]}{suffix}")\n start = end\n return res\n```\n```Go []\nimport (\n\t"fmt"\n\t"math"\n)\n\nfunc numberOfParts(message string, limit int) int {\n\tif limit < 6 {\n\t\treturn 0\n\t}\n\tlength := len(message)\n\tparts := int(math.Ceil(float64(length) / float64(limit-5)))\n\tif parts >= 10 && parts < 100 {\n\t\tif limit < 8 {\n\t\t\treturn 0\n\t\t}\n\t\tparts = int(math.Ceil(float64(length-9) / float64(limit-7)))\n\t}\n\tif parts >= 100 && parts < 1000 {\n\t\tif limit < 10 {\n\t\t\treturn 0\n\t\t}\n\t\tparts = int(math.Ceil(float64(length-108) / float64(limit-9)))\n\t}\n\tif parts >= 1000 && parts < 10000 {\n\t\tif limit < 12 {\n\t\t\treturn 0\n\t\t}\n\t\tparts = int(math.Ceil(float64(length-1107) / float64(limit-11)))\n\t}\n if parts > 10000 {\n parts = int(math.Ceil(float64(length + 118894) / float64(limit)))\n if parts > 10000 {\n parts = 0\n }\n }\n\treturn parts\n}\n\nfunc splitMessage(message string, limit int) []string {\n\tvar start int\n\tvar res []string\n\tparts := numberOfParts(message, limit)\n\tfor i := 0; i < parts; i++ {\n\t\tsuffix := fmt.Sprintf("<%d/%d>", i+1, parts)\n\t\tend := min(start+limit-len(suffix), len(message))\n\t\tres = append(res, message[start:end]+suffix)\n\t\tstart = end\n\t}\n\treturn res\n}\n```\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n | 6 | 0 | ['Go', 'Python3'] | 2 |
split-message-based-on-limit | Binary Search | binary-search-by-votrubac-bls0 | This is an old problem known as SMS split (SMS messages are limited to 160 characters).\n\nWe can use a binary search to find out the number of messages. We jus | votrubac | NORMAL | 2022-11-13T23:07:28.969901+00:00 | 2022-11-16T06:30:12.204191+00:00 | 1,357 | false | This is an old problem known as SMS split (SMS messages are limited to 160 characters).\n\nWe can use a binary search to find out the number of messages. We just need to make this search efficient (e.g. no string creation).\n\n> Note that first we need to find the smallest number of digits in `b`, e.g. 1 (up to 9 parts), 2 (up to 99), 3 (up to 999), and so on.\n\nKnowing the number of messages, we then can build out splits.\n\n**C++**\n```cpp\nbool binarySearch(int sz, int limit, int m) {\n int len_a = 1, up = 9, len_b = to_string(m).size();\n for (int a = 1; a <= m && sz > 0; ++a) {\n sz -= limit - 3 - len_a - len_b;\n if (a == up) {\n ++len_a;\n up = up * 10 + 9;\n }\n }\n return sz <= 0;\n}\nvector<string> splitMessage(string mess, int limit) {\n int l = 1, r = 9, sz = mess.size();\n vector<string> res;\n while (l <= sz && !binarySearch(sz, limit, r)) {\n l *= 10;\n r = min(r * 10 + 9, sz + 1);\n }\n if (l <= sz) {\n while (l < r)\n if (int m = (l + r) / 2; binarySearch(sz, limit, m))\n r = m;\n else\n l = m + 1;\n for (int i = 0, a = 1; a <= l; ++a) {\n string suff = "<" + to_string(a) + "/" + to_string(l) + ">";\n res.push_back(mess.substr(i, limit - suff.size()) + suff);\n i += limit - suff.size();\n }\n }\n return res;\n}\n``` | 6 | 0 | ['C'] | 2 |
split-message-based-on-limit | C++ | Try to find the optimal b, since it is affecting suffix length | c-try-to-find-the-optimal-b-since-it-is-by80r | we know that the <a/b> suffix is dependent on b and a goes till b, so if we can somehow try to find the optimal b, we should be able to get the answer.\n\nHow | ajay_5097 | NORMAL | 2022-11-13T06:33:58.802082+00:00 | 2022-11-13T06:35:03.741186+00:00 | 320 | false | we know that the `<a/b>` suffix is dependent on `b` and `a` goes till `b`, so if we can somehow try to find the optimal `b`, we should be able to get the answer.\n\nHow to find optimal `b` - \n\nWe know that exact `b` does not matter, the only thing that matters is the length of `b`. Since the length of the input string is `10^4`, we know `b` would never have more than `4` digits in suffix.\n\nFirst we try to find out what would be length of `b` in the optimal answer. and we try to build the string. since `a` goes till `b` If we were able to find an optimal `b` then last `a` is your `b` since we are iterating from smallest length to largest length of `b`.\n\n```cpp\nclass Solution {\npublic:\n int getLength(int n) {\n return to_string(n).size();\n }\n \n int getPossibleB(const string &message, int &limit) {\n int n = message.size();\n for (int b = 1; b <= 4; ++b) {\n bool isPossible = true;\n int a = 1;\n for (int j = 0; j < n; ) {\n if (getLength(a) > b) {\n isPossible = false;\n break;\n }\n int suffix = 1 + getLength(a) + 1 + b + 1; //<a/b>\n int rem = limit - suffix;\n j += rem;\n ++a;\n }\n if (isPossible) return a - 1;\n }\n return -1;\n }\n \n vector<string> getSplitString(const string &message, int &limit, int &b) {\n int n = message.size();\n int a = 1;\n vector<string> res;\n string bstring = to_string(b);\n for (int j = 0; j < n; ) {\n string suffix = \'<\' + to_string(a) + \'/\' + bstring + \'>\';\n int rem = limit - suffix.size();\n ++a;\n res.push_back(message.substr(j, rem) + suffix);\n j += rem;\n }\n return res;\n }\n \n vector<string> splitMessage(string message, int limit) {\n int b = getPossibleB(message, limit);\n if (b == -1) return {};\n return getSplitString(message, limit, b);\n }\n};\n``` | 5 | 0 | [] | 1 |
split-message-based-on-limit | Simple Approach || C++ || Check For every Number of Spilit | simple-approach-c-check-for-every-number-ngjz | \nclass Solution {\npublic:\n string getSuffix(int a,int b){\n string suffix = "<" + to_string(a) + "/" + to_string(b) + ">";\n return suffix; | PRINCE_____RAJ | NORMAL | 2022-11-12T17:42:40.488492+00:00 | 2022-11-13T10:36:48.043066+00:00 | 483 | false | ```\nclass Solution {\npublic:\n string getSuffix(int a,int b){\n string suffix = "<" + to_string(a) + "/" + to_string(b) + ">";\n return suffix; \n }\n vector<string> splitMessage(string s, int limit) {\n if(limit < 6)\n return {};\n int sum = 0;\n int i;\n for(i = 1;true;i++){\n string a = to_string(i);\n\t\t\tsum += 3 + a.size(); //space required to adjust "<a/>" after ith spilit\n\t\t\t/*\n\t\t\t\tlimit*i = total space we get after ith spilit\n\t\t\t\tsum = space required to adjust "<a/>" after ith spilit\n\t\t\t\ta.size()*i = space required to adjust "b" after the ith spilit\n\t\t\t\tthen (limit*i - sum - a.size()*i ) represent the space used for adjusting the string\n\t\t\t\tand when it is greater than size of string we got the total numner of spilit required\n\t\t\t*/\n if(limit*i - sum - a.size()*i >= s.size()) \n break;\n\t\t\t\t\n\t\t\t// if the total space is used for adjusting the suffix part only then we can\'t spilit and return\n if(limit <= 3 + a.size() + a.size())\n return {};\n }\n int k = 0;\n vector<string> res(i,"");\n for(int j = 1;j <= i;j++){\n string suffix = getSuffix(j,i);\n for(int l = 0;l < limit - suffix.size() && l +k < s.size();l++)\n res[j-1] += s[l+k];\n \n \n res[j-1] += suffix;\n k += limit - suffix.size();\n }\n return res;\n }\n};\n```\n\n | 5 | 1 | [] | 2 |
split-message-based-on-limit | Python tricky solution | python-tricky-solution-by-faceplant-v9a6 | python\nr = -1\nn = len(message)\ns = (limit - 5) * 9\nif s >= n:\n\tr = 9 - (s - n) // (limit - 5)\nelse:\n\ts = (limit - 6) * 9 + (limit - 7) * 90\n\tif s >= | FACEPLANT | NORMAL | 2022-11-12T16:11:04.181944+00:00 | 2022-11-12T16:20:29.649480+00:00 | 1,083 | false | ```python\nr = -1\nn = len(message)\ns = (limit - 5) * 9\nif s >= n:\n\tr = 9 - (s - n) // (limit - 5)\nelse:\n\ts = (limit - 6) * 9 + (limit - 7) * 90\n\tif s >= n:\n\t\tr = 99 - (s - n) // (limit - 7)\n\telse:\n\t\ts = (limit - 7) * 9 + (limit - 8) * 90 + (limit - 9) * 900\n\t\tif s >= n:\n\t\t\tr = 999 - (s - n) // (limit - 9)\n\t\telse:\n\t\t\ts = (limit - 8) * 9 + (limit - 9) * 90 + (limit - 10) * 900 + (limit - 11) * 9000\n\t\t\tif s >= n:\n\t\t\t\tr = 9999 - (s - n) // (limit - 11)\n\t\t\telse:\n\t\t\t\ts = (limit - 9) * 9 + (limit - 10) * 90 + (limit - 11) * 900 + (limit - 12) * 9000 + (limit - 13) * 90000\n\t\t\t\tif s >= n:\n\t\t\t\t\tr = 99999 - (s - n) // (limit - 13)\nif r == -1:\n\treturn []\nj = 0\nres = []\nfor i in range(1, r + 1):\n\tt = "<" + str(i) + "/" + str(r) + ">"\n\td = limit - len(t)\n\tres.append(message[j : j + d] + t)\n\tj += d\nreturn res\n```\n | 5 | 1 | [] | 1 |
split-message-based-on-limit | Binary search for optimal split | binary-search-for-optimal-split-by-theab-ltfj | \nclass Solution:\n def getsuffixes(self, n):\n return [f"<{i}/{n}>" for i in range(1, n + 1)]\n \n def splitMessage(self, message: str, limit: | theabbie | NORMAL | 2022-11-12T16:00:40.868219+00:00 | 2022-11-12T16:00:40.868251+00:00 | 1,164 | false | ```\nclass Solution:\n def getsuffixes(self, n):\n return [f"<{i}/{n}>" for i in range(1, n + 1)]\n \n def splitMessage(self, message: str, limit: int) -> List[str]:\n n = len(message)\n if n + 5 <= limit:\n return [f"{message}<1/1>"]\n beg = 1\n end = n\n finalres = []\n while beg <= end:\n l = (beg + end) // 2\n suff = self.getsuffixes(l)\n res = []\n i = 0\n for j in range(l):\n k = limit - len(suff[j])\n res.append(f"{message[i : i + k]}{suff[j]}")\n i += k\n if i < n:\n beg = l + 1\n elif len(res[-2]) != limit:\n end = l - 1\n else:\n finalres = res\n break\n return finalres\n``` | 5 | 2 | ['Python'] | 4 |
split-message-based-on-limit | Binary Search || Simple Approach || C++ || Explaination || Clear Code | binary-search-simple-approach-c-explaina-nsfo | In this problem, we are sure that if we give 1 token to every element we get the one possible distribution but it is not the ans, but if we take it as one possi | Sriyansh2001 | NORMAL | 2022-11-12T19:52:47.203943+00:00 | 2022-11-12T19:56:13.803563+00:00 | 979 | false | In this problem, we are sure that if we give 1 token to every element we get the one possible distribution but it is not the ans, but if we take it as one possible chance of answer so our distribution will be from 1 to n (length of the string). \nNow first we check for the middle one. If the answer is possible we can return it. but If answer is not possible from that partition and the size of string is greater than the token size than it is sure that the ans present in the lower half then we skip it upper and check for the lower half and vice versa.\nFor elimination the halfs we use binary search O(log n) and to check the possibility of ans we traverse to whole string O(n).\nSo the time Complexity of program is O(n log n).\n\n\n\n```\nclass Solution {\npublic:\n vector<string> splitMessage(string message, int limit) {\n return solution(message,limit,message.size());\n }\nprivate:\n vector<string> solution(string m,int limit,int n) {\n int i=1,j=n;\n while(i<=j) {\n int mid = (i+j)/2;\n pair<vector<string>,int> ans = get_str(m,limit,mid);\n if(ans.second == 0) return ans.first;\n else if(ans.second==-1) i = mid+1;\n else j = mid-1;\n }\n return {};\n }\n \n pair<vector<string>,int> get_str(string m,int limit,int total) {\n string temp = to_string(total);\n string pre = "";\n int num = 1;\n string check = to_string(num);\n vector<string> ans;\n for(int i=0 ; i<m.length() ; ++i) {\n if(check.length()+temp.length()+3 >= limit) return {{},-1};\n if(pre.size()+check.length()+temp.length()+3 == limit) {\n string insert = pre;\n insert.push_back(\'<\');\n insert.append(check);\n insert.push_back(\'/\');\n insert.append(temp);\n insert.push_back(\'>\');\n ans.push_back(insert);\n pre = "";\n i-=1;\n num+=1;\n check = to_string(num);\n }\n else {\n pre.push_back(m[i]);\n }\n }\n string insert = pre;\n insert.push_back(\'<\');\n insert.append(check);\n insert.push_back(\'/\');\n insert.append(temp);\n insert.push_back(\'>\');\n ans.push_back(insert);\n if(num == total) return {ans,0};\n else if(num > total) return {{},-1};\n return {{},1};\n }\n};\n``` | 4 | 0 | ['Binary Search', 'C++'] | 2 |
split-message-based-on-limit | Straightforward solution | straightforward-solution-by-xiangthepooh-csyj | Code\npy\nclass Solution:\n def splitMessage(self, message: str, limit: int) -> List[str]:\n def mysum(parts):\n if parts < 10: return part | Xiangthepoohead | NORMAL | 2024-08-17T03:10:04.366474+00:00 | 2024-08-17T03:10:04.366514+00:00 | 523 | false | # Code\n```py\nclass Solution:\n def splitMessage(self, message: str, limit: int) -> List[str]:\n def mysum(parts):\n if parts < 10: return parts\n if parts < 100: return 2*(parts-9) + mysum(9)\n if parts < 1000: return 3*(parts-99) + mysum(99)\n if parts < 10000: return 4*(parts-999)+mysum(999)\n return 5 + mysum(9999)\n for parts in range(1, len(message)+1):\n #O(n) - bad\n # totalLen = len(message) + sum(len(\'<{}/{}>\'.format(i,parts)) for i in range(1,parts+1))\n #O(1) - good\n totalLen = len(message) + 3*parts + mysum(parts) + parts * len(str(parts))\n if ceil(totalLen / limit) == parts:\n #Run simulation\n ret = []\n ind = 0\n for i in range(1, parts+1):\n counter = \'<{}/{}>\'.format(i,parts)\n j = ind + limit - len(counter)\n ret.append(message[ind:j]+counter)\n ind = j\n return ret\n return []\n``` | 3 | 0 | ['Python3'] | 0 |
split-message-based-on-limit | Detailed explanation with code | Both O(n) and Binary Search solution | C++ | detailed-explanation-with-code-both-on-a-xfsm | Intuition\n Describe your first thoughts on how to solve this problem. \nIt\'s pretty obvious from the question that the key thing we need to find out is minimu | ayan_27 | NORMAL | 2024-05-02T07:28:00.442291+00:00 | 2024-05-02T07:30:28.859782+00:00 | 272 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIt\'s pretty obvious from the question that the key thing we need to find out is **minimum number of total splits**. If we know in how many parts we can split the message so that every part except the last one satisfying the limit condition, we can easily build the answer.\nThe bruteforce will be trying every possible total number of part (starting from 1..) and check which one is satisfying the condition. But that will be too much.\n\nBut but but... do we really need to know the exact number of total splits? let\'s take one example\n\nString = "this is really a very awesome message", limit=9\n\nle\'s try splitting the string in **7** parts:\n`"this<1/7>", " is <2/7>", "real<3/7>", "ly a<4/7>", " ver<5/7>", "y aw<6/7>", "esom<7/7>", "e me<8/7>", "ssag<9/7>", "e<10/7>"` -> not possible (need 10 parts)\n\nlet\'s try with **9** parts:\n`"this<1/9>", " is <2/9>", "real<3/9>", "ly a<4/9>", " ver<5/9>", "y aw<6/9>", "esom<7/9>", "e me<8/9>", "ssag<9/9>", "e<10/9>"` -> not possible (need 10 parts)\n\n\nlet\'s try with **10** parts:\n`"thi<1/10>","s i<2/10>","s r<3/10>","eal<4/10>","ly <5/10>","a v<6/10>","ery<7/10>"," aw<8/10>","eso<9/10>","me<10/10>"," m<11/10>","es<12/10>","sa<13/10>", "ge<14/10>"` -> not possible (need 14 parts)\n<br>wait..what? why 10 part is not working? -> becuse number of characters required by the total part number has increased :)\n\nlet\'s try with **14** parts:\n`"thi<1/14>","s i<2/14>","s r<3/14>","eal<4/14>","ly <5/14>","a v<6/14>","ery<7/14>"," aw<8/14>","eso<9/14>","me<10/14>"," m<11/14>","es<12/14>","sa<13/14>","ge<14/14>"` -> possible\n\nlet\'s try with **15** parts:\n`"thi<1/15>","s i<2/15>","s r<3/15>","eal<4/15>","ly <5/15>","a v<6/15>","ery<7/15>"," aw<8/15>","eso<9/15>","me<10/15>"," m<11/15>","es<12/15>","sa<13/15>","ge<14/15>"` -> not possible (need 14 parts)\n\nKey Observations:\n1. While trying with 7 or 9 or you can try with any single digit part number, we will always see that the actual number of parts require is 10\n2. Similarly, while trying with any 2 digit part number, we will always see require total part is 14.\n\nThought:\n1. The number of parts depends on the number of digits of `total parts`, as that will determine how many character of the message we can put into a single part. And ultimately that will decide how many actual total parts we will require.\n2. Therefor, if we try to split the message into a total number of parts with `d` digits and after splitting we get the number of digits in actual `total number of parts`(let\'s say b) d digits only, then we know b is the exact total number of parts we require (becaseue it satisfying the condition of d digits). \n\nModified Problem Statement:\n1. Find total number of digits require for b\n\n\n# Approach I\n<!-- Describe your approach to solving the problem. -->\nFrom the constraint we can observer that `message.length<=10^4`, therefor we can safely deduce from that b will be always lesser than `10^4`, i.e., number of digits in b will be atmost `5` (10000 -> 5 digits).\n\nWith this small range (1 to 5), we can easily check for each number of digits which one is satisfying the condition. (we require the minimum number of digits)\n\n# Code\n```\nclass Solution {\npublic:\n int isValidTotalPart(string& message, int limit, int numberOfDigit) {\n int a = 0, i=0;\n limit = limit - 3 - numberOfDigit; // substract size of \'</>\' and b\n if(limit<=0) return 0;\n while(i<message.size()) {\n a++; // -> part number\n int l = limit - to_string(a).size(); // -> substract size of a\n if(l<=0) return 0; //-> if there is no space of message, then it\'s not possible\n i+=l; //-> use remaining space for message\n }\n return a; //-> return how many actual total parts required\n }\n\n vector<string> splitMessage(string message, int limit) {\n int b = 0;\n for(int numberOfDigit=1; numberOfDigit<=5; numberOfDigit++) {\n int totalPart = isValidTotalPart(message,limit, numberOfDigit);\n if(totalPart>0 && to_string(totalPart).size()==numberOfDigit) { // check if number of digits in actual totalPart is equal to what we tried\n b=totalPart;\n break;\n }\n }\n\n if(b==0) return {};\n\n // build the answer\n vector<string> ans(b); // we know b number of parts will be required\n limit = limit - 3 - to_string(b).size();\n int i=0;\n for(int a=1; a<=b; a++) {\n int l = limit - to_string(a).size();\n ans[a-1] = message.substr(i, l) + "<" + to_string(a) + "/" + to_string(b) + ">";\n i+=l;\n }\n\n return ans;\n }\n};\n```\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n) -> `isValidTotalPart()` will be called 5 times and each pass will take O(n) where n is size of message\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n) - for storing the `ans` vector\n\n---\n\n# Approach II (Binary Search)\n<!-- Describe your approach to solving the problem. -->\nIf the range for number of digits is quite large, then the above approach will take O(n*k), where k is range of digits. We can optimise it further in that scenario by performing binary search on the range of k.\n\n# Code\n```\nclass Solution {\npublic:\n int isValidTotalPart(string& message, int limit, int numberOfDigit) {\n int a = 0, i=0;\n limit = limit - 3 - numberOfDigit; // substract size of \'</>\' and b\n if(limit<=0) return 0;\n while(i<message.size()) {\n a++; // -> part number\n int l = limit - to_string(a).size(); // -> substract size of a\n if(l<=0) return 0; //-> if there is no space of message, then it\'s not possible\n i+=l; //-> use remaining space for message\n }\n return a; //-> return how many actual total parts required\n }\n\n vector<string> splitMessage(string message, int limit) {\n int l = 1, r = 5;\n int b = 0;\n\n while(l<=r) {\n int mid = l+(r-l)/2;\n int totalPart = isValidTotalPart(message, limit, mid);\n\n if(totalPart==0 || to_string(totalPart).size()<mid) r=mid-1; //if number of digits require is less than what we have tried for, shift the search space to left\n else if(to_string(totalPart).size()==mid) {\n b = totalPart;\n r=mid-1; // shift to left to search for lesser number of digit\n } // if more number of digits require is more, shift search space to right\n else l=mid+1;\n }\n //cout<<"Total part "<<b<<endl;\n\n if(b==0) return {};\n\n\n // build the answer\n vector<string> ans(b); // we know b number of parts will be \n limit = limit - 3 - to_string(b).size();\n int i=0;\n for(int a=1; a<=b; a++) {\n int l = limit - to_string(a).size();\n ans[a-1] = message.substr(i, l) + "<" + to_string(a) + "/" + to_string(b) + ">";\n i+=l;\n }\n\n return ans;\n }\n};\n```\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(nlogk) -> `isValidTotalPart()` will be called log(k) times and each pass will take O(n) where k is the range of number of digits and n is the message size\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n) - for storing the `ans` vector\n | 3 | 0 | ['Binary Search', 'C++'] | 1 |
split-message-based-on-limit | JAVA soln with explanation | java-soln-with-explanation-by-vibh04-ehf3 | The basic idea for this problem is to determine the appropriate number of parts to divide our input string to, such that each part length is within limit define | Vibh04 | NORMAL | 2022-11-12T18:35:57.228921+00:00 | 2022-11-12T18:35:57.228959+00:00 | 285 | false | The basic idea for this problem is to determine the appropriate number of parts to divide our input string to, such that each part length is within limit defined. One way to determine it is to loop on possible part values and then divide the modified string (containing original string plus all instances of <a/part>) by the part value. This will give us the maximum length of each string part.\n\nAs specified in the question we want the max length of a string part to be lesser or equal to `limit` along with the minimum part value. Thus we loop part in an ascending manner and as soon we get max length of part to be <= `limit`, we break the loop.\n\nFinally after calculating the minimum possible parts, we construct our string array as per requirement.\n```\nclass Solution {\n public String[] splitMessage(String message, int limit) {\n int len = message.length(), part;\n StringBuilder partSb = new StringBuilder();\n for(part=1;part<=len;part++){\n int numChars = 0;\n numChars = part*3; //Accounting for all </> characters in modified string\n numChars += ((Integer.toString(part)).length())*part; //Accounting for repeated b in modified string\n partSb.append(Integer.toString(part)); \n numChars += partSb.length(); //Accounting for a from 1 to b in modified string\n float remainChars = (float)len+numChars;\n\t\t\t//Finally checking below if the average string length per part is lesser or equal to limit,\n\t\t\t//if yes we get our part value else we continue;\n if(remainChars/(float)part <= ((float)limit))\n break;\n }\n if(part>len) return new String[]{}; //No suitable part found, return empty string\n String[] res = new String[part];\n int idx = 0;\n\t\t//Construct res array as required based on the number of parts determined\n for(int i=1;i<=part;i++){\n StringBuilder suffix = new StringBuilder();\n suffix.append("<").append(Integer.toString(i)).append("/").append(Integer.toString(part)).append(">");\n StringBuilder prefix = new StringBuilder();\n if(idx + limit-suffix.length()<=len)\n prefix.append(message.substring(idx, idx + limit-suffix.length()));\n else\n prefix.append(message.substring(idx, len));\n idx += prefix.length();\n prefix.append(suffix);\n res[i-1] = prefix.toString();\n }\n return res;\n }\n}\n//TC : O(n^2) Since we are iterating on all parts and also calculating substring (O(n) operation) in each part,\n//WC complexity would O(n^2) as parts can be almost equal to length of the `message`.\n//SC : O(n) StringBuilder to store part value for each iteration ~ O(n).\n``` | 3 | 0 | ['Java'] | 0 |
split-message-based-on-limit | Java check all possible suffix lengths | java-check-all-possible-suffix-lengths-b-lz53 | \nclass Solution {\n public String[] splitMessage(String message, int limit) {\n // since message length can be at most 10^4, we cant\n // poss | zadeluca | NORMAL | 2022-11-12T16:06:00.307232+00:00 | 2022-11-12T16:06:00.307273+00:00 | 429 | false | ```\nclass Solution {\n public String[] splitMessage(String message, int limit) {\n // since message length can be at most 10^4, we cant\n // possibly have more than 10^5-1 parts, or 5 digits in length\n for (int numDigits = 1; numDigits <= 5; numDigits++) {\n int maxParts = (int)Math.pow(10, numDigits) - 1;\n \n // determine if we can reach the end of message with the\n // maximum number of parts, if so we have our answer\n int idx = 0;\n for (int part = 1; part <= maxParts; part++) {\n int suffixLen = String.valueOf(part).length() + numDigits + 3;\n idx += limit - suffixLen;\n \n if (idx >= message.length()) {\n // System.out.println(part);\n return createOutput(message, limit, part);\n }\n }\n }\n \n return new String[0];\n }\n \n private String[] createOutput(String message, int limit, int numParts) {\n String[] output = new String[numParts];\n int idx = 0;\n \n for (int i = 1; i <= numParts; i++) {\n String suffix = "<" + i + "/" + numParts + ">";\n int contentLen = limit - suffix.length();\n \n // be sure to handle last part being shorter than limit\n int end = Math.min(idx + contentLen, message.length());\n \n output[i - 1] = message.substring(idx, end) + suffix;\n idx += contentLen;\n }\n \n return output;\n }\n}\n``` | 3 | 0 | [] | 1 |
split-message-based-on-limit | Java - Binary search fails. Simple brute force works like charm. | java-binary-search-fails-simple-brute-fo-x5kx | My inital thought was to find the y in . Basically how many parts. I tried binary search and almost 91/94 test cases passed then. I will my binary search code b | vijaygtav | NORMAL | 2024-03-10T01:31:42.650782+00:00 | 2024-03-10T01:31:42.650805+00:00 | 193 | false | My inital thought was to find the y in <x/y>. Basically how many parts. I tried binary search and almost 91/94 test cases passed then. I will my binary search code below, very stright forward binary search. Later with the failed example, i realized that if we find some number is failing, doesn\'t mean all the number below it are failing which is the basis of binary search, in this question its happeing such a way, a particular number might fail but a number below it will pass, due to len of the numbers in x/y, as the y is a larger, combined with x, the total occupancy will be something like <783/1023>. this itself occupy 11 chars, if say limit is 10, it doesnt work, so our binary search might try something even larger for this problem, but thats the not case, a smaller one like 756/986 might work. Thats with binary search. I just keep all the code and delted the binary search part.\n\nRegarding how to solve it, check if a parituclar y in my code (base vairable) is allowing us to complete the divion, i start from 1 and search linearly, firrst number which works is the best division possible.\n\nExplaining paritiuclar segment of the code to understanbd, once you understand the segment, it is easy to read the code.\n\nint delimit_start = 4 + (int) Math.ceil(Math.log10(base+1));\n\ngiven base, i want to find the delimit starting size, with single number base, it will be <1/9> which is off size 5, without base it is 4, <1/>, so it should 4 + size (len) of the base, Math.log10(base) gives that, but for 10 itself, it will give 1, i add 1 to make it 11, to get 2.\n\nlen -= (Math.min(base, (9 * Math.pow(10, count))) * (limit - delimit_start));\n\nwe need to know for 0 - 9, 10 - 99, 100 - 999, how many len we are dividing successfully, which is Math.pow(10, count) gives us it is 9, or 90, 900 etc for the group. then limit - delimit_start tells how much remaining for the string, multiplying those two will give how much string len we consued in this part of the calcalation. why math.min in Math.min(base, (9 * Math.pow(10, count)), if remaining string segment is less than 9 or 90, or 900 then we only can take base * (limit - delimit_start).\n\nreturn len <= 0;\n\nif len is covered, we are good.\n\nconstruct method is heavily inspried and kind of repeation of the possible method, just that, we skip 9, 90, 900 in the possible method, here we need to go and construct each string segment. so two loops. outside while is same as possible method, the inside for loop is to construct each string segment.\n\nI know, i didnt explain very well, i fought it hard about which part i should stress in my explation, so gave what i thought might be the burning issue in your head, if you want specific clarificaiton, please let me know in the comments, i will try my best. Thanks.\n# Code\n```\nclass Solution {\n public String[] splitMessage(String message, int limit) {\n for(int i=1; i<=message.length(); i++)\n if(possible(message.length(), i, limit))\n return construct(message, i, limit);\n\n return new String[0];\n }\n\n public String[] construct(String message, int base, int limit) {\n String[] ret = new String[base];\n\n int delimit_start = 4 + (int) Math.ceil(Math.log10(base+1));\n\n int ret_index = 0, i = 0, count = 0;\n\n while(i < message.length()) {\n for(int p = 1; p <= 9 * Math.pow(10, count) && i < message.length(); p++) {\n \n int offset = Math.min(message.length(), i + (limit - delimit_start));\n\n ret[ret_index++] = message.substring(i, offset) + "<" + ret_index + "/" + base + ">";\n i += (limit - delimit_start);\n }\n count++;\n delimit_start++;\n }\n\n return ret;\n }\n\n public boolean possible(int len, int base, int limit) {\n int delimit_start = 4 + (int) Math.ceil(Math.log10(base+1));\n int count = 0;\n while(len > 0 && base > 0) {\n len -= (Math.min(base, (9 * Math.pow(10, count))) * (limit - delimit_start));\n delimit_start++;\n base -= (9 * Math.pow(10, count));\n count++;\n }\n\n return len <= 0;\n }\n}\n``` | 2 | 0 | ['Java'] | 0 |
split-message-based-on-limit | [Python] Easy Pattern Detection with thought process when being asked during interviews | python-easy-pattern-detection-with-thoug-cuhg | Pattern Detection\nThe difficulty of this problem come from 2 parts. For the sake of eay understanding, let\'s use i as the index of each part and X as the tota | jandk | NORMAL | 2023-12-10T19:49:09.628608+00:00 | 2023-12-10T19:49:53.161862+00:00 | 115 | false | ### Pattern Detection\nThe difficulty of this problem come from 2 parts. For the sake of eay understanding, let\'s use `i` as the index of each part and `X` as the total number of parts.\n1. The total number of parts `X` is determined by the number of characters each part can hold which is various as index `i` increases. If `i` is less than `10`, the length of charactor the part can hold is `limit - 5`, if `i` is greater than `10` and less than `100`, the length is `limit - 6`.\n2. What maximum length of index `i` can have is determined by the `X`. \n\nSo, it seems both are dependent to each other. \nThen what we are going to do is to break the circular dependency by simplying the problem.\n\nLet\'s assume the `X` is less than `10`. \n### X <= 9\nthen the length of charactor each part holds is `limit - 5`\n```\nlen(message) <= 9 * (limit - 5) == 9 * limit - 9 * 5\n```\n\n### X <= 99\nwe know it must contain the first 9 parts, so we can simply subtract the first 9 parts and caculate how many parts we can have so that `X` is less than `100`.\nNote, since the `X` is with 2 digits, so it is `limit - 6` for the first 9 parts instead of `limit - 5`.\n```\nlen(message) - 9 * (limit - 6) <= 90 * (limit - 7) == 99 * limit - 90 * 7 - 9 * 6\n```\n\n### X <= 999\nSimilarly, we know the first 99 parts must be included, so we subtract them and caculuate the `X`\n```\nlen(message) - 9 * (limit - 7) - 90 * (limit - 8) <= 900 * (limit - 9) == 900 * limit - 900 * 9 - 90 * 8 - 9 * 7\n```\n\nDo you see the pattern? leaving the part for `X <= 9999` for you to figure out.\nTherefore, we can simply check which range the length of `message` falls in and know the length of `X`, which helps to split the `message`.\n\n\n```python\ndef splitMessage(self, message: str, limit: int) -> List[str]:\n\n\tif limit < 6:\n\t\treturn []\n \n\tdef process(length_x):\n\t\tindex = 1\n i = 0\n pieces = []\n while i < n:\n\t\t\tlength = 3 + length_x + len(str(index)) \n\t\t pieces.append((message[i: i + (limit - length)], str(index)))\n i += limit - length\n index += 1\n\t\treturn [\'\'.join([piece[0], \'<\', piece[1], \'/\', str(index - 1), \'>\']) for piece in pieces] \n \n\tn = len(message)\n\tif n <= 9 * limit - 9 * 5:\n\t\treturn process(1)\n\tif n <= 99 * limit - 90 * 7 - 9 * 6: \n\t return process(2)\n\tif n <= 999 * limit - 900 * 9 - 90 * 8 - 9 * 7:\n\t\treturn process(3)\n\tif n <= 9999 * limit - 9000 * 11 - 900 * 10 - 90 * 9 - 9 * 8:\n\t\treturn process(4)\n\treturn []\n```\n\n*Time Complexity* = **O(N)**\n*Space Complexity* = **O(N)**\n | 2 | 0 | [] | 0 |
split-message-based-on-limit | Java || 99.02% fast || Simple & Easy to Understand | java-9902-fast-simple-easy-to-understand-tszj | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \nAssume 1 <= num(page) < | x1x2x3xzzz | NORMAL | 2023-08-21T20:20:10.122256+00:00 | 2023-08-21T20:20:10.122275+00:00 | 282 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nAssume $$1 <= num(page) <= 9$$, confirm whether there is enough space for current message to be stored.\n\nIf so, compute the exact $$num(page)$$.\nIf not, assume $$10 <= num(page) <= 99$$ and check again until find the exact $$num(page)$$.\n\n\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n private int getPages(int l, int limit) {\n int curLen = limit - 5; // length of "<1/3>" is 5\n int curCapacity = 9;\n int extraSpace = 0;\n while (l > curLen * curCapacity + extraSpace) {\n curLen -= 2;\n extraSpace += curCapacity; // "***<5/23>" has extra space than "**<12/23>"\n curCapacity = Integer.parseInt(curCapacity + "9");\n if (curLen <= 0) return 0;\n }\n int ans = (l - extraSpace) / curLen;\n if ((l - extraSpace) % curLen != 0) ++ans;\n return ans;\n }\n\n public String[] splitMessage(String message, int limit) {\n int l = message.length();\n int pages = getPages(l, limit);\n String[] ans = new String[pages];\n int curPos = 0;\n for (int i=0; i<pages; ++i) {\n String tag = "<" + (i+1) + "/" + pages + ">";\n int infoLen = limit - tag.length();\n ans[i] = message.substring(curPos, Math.min(l, curPos + infoLen)) + tag;\n curPos += infoLen;\n }\n return ans;\n }\n}\n``` | 2 | 0 | ['Java'] | 2 |
split-message-based-on-limit | Binary Search solution with digit-count check(It passes "abbababbbaaa aabaa a" test case ) | binary-search-solution-with-digit-count-u4spx | Approach\nBinary Search is not very necessary for this problem. just increase b one by one and check whether there are remain message. It takes O(n) so still ac | qian48 | NORMAL | 2022-11-24T01:38:52.402710+00:00 | 2022-11-24T01:56:22.768572+00:00 | 297 | false | # Approach\nBinary Search is not very necessary for this problem. just increase `b` one by one and check whether there are remain message. It takes O(n) so still acceptable.\n\nFor binary search solution, one important thing to notice is that `b` is not monotone for different digit-count.\n\nExample:\nmessage = "abbababbbaaa aabaa a", limit = 8\nA simple BS solution will determine `b` as 11. But cutting into 7 parts also works.\n\nTo resolve this issue, we should **determine BS search range beforehand**. `b` is monotone inside range 1-9,10-99,100-999... \nFirst check whether cut it into 9 part would suffice. If not then there must be at least 10 parts. Then we check if cutting into 99 parts suffice. If not then there must be at least 100 parts. Keep the process until digit-count is found.\n\nAfter `b`\'s digit count is determined, we ensure the BS search range is monotone and can proceed with following process.\n\n\n\n# Code\n```python\nclass Solution:\n def splitMessage(self, message: str, limit: int) -> List[str]:\n if limit <= 5: return []\n \n # Important: Determine number of digit of b. BS monotone holds for same digit-count \n # This will fix the testcase like: message = "abbababbbaaa aabaa a", limit = 8\n nd = -1\n for dc in range(1, 7):\n remain = len(message)\n for d in range(1, dc+1): \n if limit - 3 - d - dc < 0: break\n remain -= (limit - 3 - d - dc)*9*10**(d-1)\n if remain <= 0:\n nd = dc\n break\n if nd == -1: return []\n \n # binary search of b\n start, end = 10**(nd - 1), 10 ** nd\n while start != end:\n mid = (start + end) // 2\n dc = len(str(mid))\n remain = len(message) \n for d in range(1, dc):\n remain -= (limit - 3 - d - dc)*9*10**(d-1)\n for i in range(10**(dc-1), mid + 1):\n remain -= limit - 3 - 2*dc \n if remain < 0: break\n # print(start, end, mid, remain)\n if remain > 0: start = mid + 1\n else: end = mid\n\n # construct answer\n ans = []\n dc = len(str(start))\n cur = 0\n for d in range(1, dc + 1):\n for i in range(10**(d-1), 10**d):\n nxt = min(cur + limit - 3 - d - dc, len(message))\n ans.append(message[cur:nxt] + \'<\' + str(i) + \'/\' + str(start) + \'>\')\n cur = nxt\n if nxt >= len(message): break\n \n if cur < len(message): return []\n return ans\n \n``` | 2 | 0 | ['Python3'] | 0 |
split-message-based-on-limit | C++ O(n) simple solution | c-on-simple-solution-by-shashankzobb-yoke | Let the total number of part is total_num.\nLet\'s see. Every part is in the form of "_". The "<", ">", "/" are constant. The value of index does not depend on | ShashankZobb | NORMAL | 2022-11-15T19:11:37.970703+00:00 | 2022-11-15T19:13:31.165746+00:00 | 280 | false | Let the total number of part is total_num.\nLet\'s see. Every part is in the form of "_<index/total_num>". The "<", ">", "/" are constant. The value of index does not depend on our choice so we can treat it as constant. So the only remaining variables are **no of digit** in total_num and no of characters. Since there is a limit, the no of character depend on the **no of digit** in total_num. \nSince the size of message can be atmost 10<sup>4</sup>. No of digit will be atmost 4.\n```\nint digit(int num){\n\tif(num == 0)return 1;\n\tint ans = 0;\n\twhile(num > 0){\n\t\tans++;\n\t\tnum /= 10;\n\t}\n\treturn ans;\n}\nvector<string> splitMessage(string message, int limit) {\n\tif(limit <= 4)return {};\n\tint ans = 1e9;\n\tfor(int dig = 1;dig <= 5;dig++){\n\t\tint index = 1, max_no_of_char = limit-(digit(index)+dig+3), no_of_char = 0, flag = 1;\n\t\tfor(char &i:message){\n\t\t\tno_of_char++;\n\t\t\tif(no_of_char > max_no_of_char){\n\t\t\t\tindex++;\n\t\t\t\tmax_no_of_char = limit-(digit(index)+dig+3);\n\t\t\t\tno_of_char = 1;\n\t\t\t\tif(max_no_of_char <= 0){ // No space left to put a character\n\t\t\t\t\tflag = 0;\n\t\t\t\t\tbreak;\n\t\t\t\t}\n\t\t\t}\n\t\t}\n\t\tif(digit(index) > dig){ // The no of digit of last index is more than the allowed value.\n\t\t\tflag = 0;\n\t\t}\n\t\tif(flag == 1){\n\t\t\tans = index;\n\t\t\tbreak;\n\t\t}\n\t}\n\tif(ans == 1e9)return {};\n\tvector<string>v;\n\tstring str;\n\tint index = 1;\n\tint max_no_of_char = limit-(digit(ans)+digit(index)+3), no_of_char = 0;\n\tfor(char &i:message){\n\t\tstr += i;\n\t\tno_of_char++;\n\t\tif(no_of_char == max_no_of_char){\n\t\t\tstr += \'<\';\n\t\t\tstr += to_string(index);\n\t\t\tstr += \'/\';\n\t\t\tstr += to_string(ans);\n\t\t\tstr += \'>\';\n\t\t\tv.push_back(str);\n\t\t\tstr = "";\n\t\t\tindex++;\n\t\t\tno_of_char = 0;\n\t\t\tmax_no_of_char = limit-(digit(ans)+digit(index)+3);\n\t\t}\n\t}\n\tif(no_of_char > 0){\n\t\tstr += \'<\';\n\t\tstr += to_string(index);\n\t\tstr += \'/\';\n\t\tstr += to_string(ans);\n\t\tstr += \'>\';\n\t\tv.push_back(str);\n\t}\n\treturn v;\n}\n``` | 2 | 0 | ['C'] | 0 |
split-message-based-on-limit | C++| Simple Linear Search + Maths | O(N) | c-simple-linear-search-maths-on-by-kumar-89hy | \nclass Solution {\npublic:\n int find(int n){\n int re = 0;\n while(n){re++;n/=10;}\n return re;\n }\n void dopart(vector<string> | kumarabhi98 | NORMAL | 2022-11-15T13:11:37.605594+00:00 | 2022-11-15T13:11:37.605632+00:00 | 115 | false | ```\nclass Solution {\npublic:\n int find(int n){\n int re = 0;\n while(n){re++;n/=10;}\n return re;\n }\n void dopart(vector<string>& re,string s,int limit,int n){\n int j = 0;\n string k = to_string(n);\n for(int i = 1; i<=n;++i){\n int size = limit-(3+find(n)+find(i));\n string temp;\n while(size-- && j<s.size()){ temp+= string(1,s[j]); j++;}\n temp+="<"+to_string(i)+"/"+k+">";\n re.push_back(temp);\n }\n }\n vector<string> splitMessage(string s, int limit) {\n vector<string> re;\n int n = s.size(),sum = 0; \n for(int i = 1; i<=n;++i){\n sum+=find(i); // sum = lenght(1)+length(2)+...+length(i) \n int size = 3*i + i*find(i) + sum; // total size of string after adding all suffix\n int last = 3 + 2*find(i); // length of last suffix\n if(last>limit) break;\n int k = s.size()+size - limit*(i-1); // size of the last part of resulting string\n if(k>=0 && k<=limit){ // check atmost limit condition for last last\n dopart(re,s,limit,i); // do partition of string \n break;\n }\n }\n return re;\n }\n};\n``` | 2 | 0 | ['Math', 'C'] | 0 |
split-message-based-on-limit | [C++] Direct search for minimum target part number | c-direct-search-for-minimum-target-part-dxkc2 | Think of the string "xxxx<a/b>" where b is a fixed upper bound with a < b.\nGiven a limit, one must reserve 3 characters for < / >.\nThe spaces allowed for putt | hy0913 | NORMAL | 2022-11-12T17:40:02.138332+00:00 | 2022-11-13T04:16:44.542659+00:00 | 307 | false | Think of the string `"xxxx<a/b>"` where b is a fixed upper bound with `a < b`.\nGiven a limit, one must reserve 3 characters for `<` `/` `>`.\nThe spaces allowed for putting characters would be `limit - 3 - len(b) - len(a)`.\n\n\n\n\nDue to the observation, we try to fix baseDigit and search for the minium part number through `getMinumPartNum()`.\nThis function bascially fulfills the following logic:\n\nWe use variable `baseDigit` for the digit count of upper bound b.\nAssume the baseDigit is 3, we try to consume the characters from message.\nPart Index: [1-9], 9 parts with len(a) =1, each consumes `limit - 3 - baseDigit - 1` characters.\nPart Index: [10 - 99], 90 parts with len(a) = 2 , each consumes `limit - 3 - baseDigit - 2` characters.\nIf there is no enough characters before reaching index 100, we can return false to early stop.\nFor the remaing part count with index >= 100, it would be `ceil(remainCharCnt / (limit - 3 - 2 * baseDigit))`\nSince there is at most 999 parts with baseDigit = 3, we still need to check if the final part number does not exceed this contraint.\n\nGiven that we\'ve found the minimum part number, to form the final part vector would be trivial.\n\n```\nclass Solution {\npublic:\n vector<string> splitMessage(string message, int limit) {\n int n = message.size();\n int baseDigit = 1;\n int minPartNum = INT_MAX;\n while (limit - 3 - 2 * baseDigit > 0) {\n if (getMinumPartNum(n, baseDigit, limit, minPartNum))\n break;\n baseDigit++;\n }\n if (minPartNum == INT_MAX) return {};\n \n vector<string> ans;\n formPart(message, limit, minPartNum, ans);\n return ans;\n }\n \n bool getMinumPartNum(int n, int baseDigit, int limit, int &minPartNum) {\n double remainCharCnt = n;\n int cnt = 0;\n for (int d = 1; d <= baseDigit; d++) {\n if (d != baseDigit) {\n remainCharCnt -= 9 * pow(10, d - 1) * (limit - 3 - baseDigit - d);\n if (remainCharCnt < 0) return false;\n } else\n cnt = ceil(remainCharCnt/ (limit - 3 - 2 * baseDigit));\n }\n\n int finalPartNum = pow(10, baseDigit - 1) - 1 + cnt;\n if (finalPartNum >= pow(10, baseDigit)) return false;\n minPartNum = finalPartNum; \n return true;\n }\n \n void formPart(string message, int limit, int partNum, vector<string> &ans) {\n int idx = 0;\n int n = message.size();\n for (int i = 1; i <= partNum; i++) {\n string postfix = "<" + to_string(i) + "/" + to_string(partNum) + ">";\n int remain = limit - postfix.size();\n string token = message.substr(idx, min(remain, n - idx)) + postfix;\n idx += remain;\n ans.push_back(token);\n } \n }\n};\n``` | 2 | 0 | ['C'] | 0 |
split-message-based-on-limit | Java solution using simple Math | java-solution-using-simple-math-by-kriti-vut1 | \nclass Solution {\n public String[] splitMessage(String message, int limit) {\n try{\n for(int parts=1;parts<=100000;parts++)\n | kritikmodi | NORMAL | 2022-11-12T16:26:02.451715+00:00 | 2022-11-12T16:26:02.451754+00:00 | 1,104 | false | ```\nclass Solution {\n public String[] splitMessage(String message, int limit) {\n try{\n for(int parts=1;parts<=100000;parts++)\n {\n int extralen=(3+Integer.toString(parts).length())*parts;\n int extra=0;\n if(parts>=10000)\n extra=9+90*2+900*3+9000*4+1*5;\n else if(parts>=1000)\n extra=9+90*2+900*3+(parts-1000+1)*4;\n else if(parts>=100)\n extra=9+90*2+(parts-100+1)*3;\n else if(parts>=10)\n extra=9+(parts-10+1)*2;\n else\n extra=parts;\n extralen+=extra;\n int totallen=extralen+message.length();\n if((limit*(parts-1)<totallen)&&(totallen-limit*(parts-1)<=limit))\n {\n String ans[]=new String[parts];\n int i=0;\n for(int currpart=0;currpart<ans.length;currpart++)\n {\n String num=Integer.toString(currpart+1);\n String deno=Integer.toString(parts);\n String suffix="<"+num+"/"+deno+">";\n int len=limit-suffix.length();\n if(currpart==ans.length-1)\n ans[currpart]=message.substring(i,message.length())+suffix;\n else\n ans[currpart]=message.substring(i,i+len)+suffix;\n i+=len;\n }\n return ans;\n }\n }\n }catch(Exception e)\n {\n return new String[0];\n }\n return new String[0];\n }\n}\n``` | 2 | 0 | ['Math', 'String', 'Java'] | 0 |
split-message-based-on-limit | [Python] Easy to understand O(N) solution with clear explanations | on-python-solution-with-clear-explanatio-wtpm | IntuitionThis is a hard problem at first glance.
You need to know total number of parts (which we call N) the message will be broken into to start breaking down | ashkankzme | NORMAL | 2025-04-10T16:48:44.554284+00:00 | 2025-04-10T19:18:02.305385+00:00 | 12 | false | # Intuition
This is a hard problem at first glance.
You need to know total number of parts (which we call N) the message will be broken into to start breaking down the message, but you won't have that number until you have actually split the message. So what can be done?
# Approach
The key idea here is that you'll only need to know how many digits N is. From the problem description, N can only have between 1 to 4 digits.
In the longest case, if limit is a small number and message is super long (less than 10^4 characters), you'll get fewer than 10,000 parts, which makes N into 4 digits. In the short case, limit will be long and message will be smaller than the limit, meaning you'll get a single digit N.
Since we only need to know how many digits N must have to start, we can test for all possible cases and pick the smallest N that matches our initial guess for count of digits of N.
# Complexity
- Time complexity:
$$O(n)$$ because you will have at most 4x loops over the message length.
- Space complexity:
Also $$O(n)$$ because you will be storing the results in a new list. If output is excluded from space constraints, space complexity reduces to O(1).
# Code
```python3 []
class Solution:
def splitMessage(self, message: str, limit: int) -> List[str]:
# i think key is that the optimal solution is brute force
# but even if you brute force, you will still be O(N)
# bc the part lengths is unknown but it can atmost be 4 digits in worse case
# so you'll loop 4 times at most
# We will call total number of parts N
# N is unknown in the beginning and we will try to find it by trying different lengths of N (how many digits in N)
# at the beginning, we will reserve placeholder characters for N
# at the end when N is known, we will try to replace the placeholder,
# but if the len of characters doesn't match, then we will try increasing len of N by 1 and doing the same thing
message_len = len(message)
for len_n in range(1, 5): # N will have between 1-4 digits
parts = []
i = 0
n_placeholder = '?' * len_n
while i < message_len:
item_idx = str(len(parts) + 1)
suffix = '<'+item_idx+'/'+n_placeholder+'>'
# what happens if suffix > limit?
if len(suffix) >= limit:
return []
# for now let's assume suffix < limit
msg_part = message[i: min(i+ limit-len(suffix), len(message))]
parts.append(msg_part + suffix)
i += limit-len(suffix)
if len(str(len(parts))) == len_n:
# it means we have found the answer!
N = str(len(parts))
for i, part in enumerate(parts):
parts[i] = part.replace(n_placeholder, N)
return parts
return []
``` | 1 | 0 | ['Python3'] | 0 |
split-message-based-on-limit | Java | Binary Search | java-binary-search-by-wa11ace-zzc8 | Intuition\nOnce the number of parts is decided, the problem can be solved easily.\nTo determine the number of parts, first decide the length this number has, an | wa11ace | NORMAL | 2024-03-12T19:28:14.220438+00:00 | 2024-03-12T19:28:14.220473+00:00 | 93 | false | # Intuition\nOnce the number of parts is decided, the problem can be solved easily.\nTo determine the number of parts, first decide the length this number has, and run binary search over all numbers of this length to find the minimum number.\n\n# Complexity\n- Time complexity:\n$$O(n)$$, given $$1 <= \\text{message.length} <= 10^{4}$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\nclass Solution {\n public String[] splitMessage(String message, int limit) {\n \n int n = message.length();\n int l = 1, r = 9;\n\n while( !isValid(n, limit, r) ) r = r*10 + 9;\n l = (int)Math.pow( 10, (int)Math.log10(r) );\n\n while( l<r ){\n int mid = (l+r)/2;\n if( isValid(n, limit, mid) ) r=mid;\n else l = mid+1;\n }\n if(l>n) return new String[0];\n\n String[] res = new String[l];\n int i=1;\n int curr = 0;\n int nsfx = (int)Math.log10(l)+1 + 3;\n while(i<=l) {\n int totsfx = nsfx + (int)Math.log10(i)+1;\n int nmsg = limit - totsfx;\n String s = message.substring( curr, Math.min(curr+nmsg, n) );\n res[i-1] = s+"<"+String.valueOf(i)+"/"+String.valueOf(l)+">";\n curr += nmsg;\n i++;\n }\n return res;\n\n }\n\n private boolean isValid( int len, int limit, int num ) {\n int totsuffix = ((int)Math.log10(num)+1 + 3) * num;\n int curr = num;\n for(int nd=4; nd>=1; nd--) {\n int ln = (int)Math.pow(10, nd-1);\n if( curr>=ln ) {\n totsuffix += nd*(curr-ln+1);\n curr = ln-1;\n }\n }\n\n int nmsg = limit*num - totsuffix;\n return nmsg >= len;\n }\n\n}\n``` | 1 | 0 | ['Java'] | 0 |
split-message-based-on-limit | Why not just simply counting from 1 to 4? | why-not-just-simply-counting-from-1-to-4-xzsi | Intuition\nThe only thing unknown is how many parts will be there. However, we don\'t need to know that ahead of time. The only reason we cannot determine the h | shawn996 | NORMAL | 2024-03-09T02:19:36.035454+00:00 | 2024-03-09T02:20:21.921839+00:00 | 298 | false | # Intuition\nThe only thing unknown is how many parts will be there. However, we don\'t need to know that ahead of time. The only reason we cannot determine the how many non-suffix space a part could take is unknown of the LENGTH of total parts, but we can use placeholder for this unknown. Since the message length is less than 10^4, there are only 4 placeholders possible. "-", "--", "---", "----", for example, "<1/--->"\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n4 * O(n) = O(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def splitMessage(self, message: str, limit: int) -> List[str]:\n n = len(message)\n\n def createValid(digits):\n res = []\n i, idx = 0, 1\n placeholder = digits * "-"\n \n while i < n:\n if len(res) >= 10 ** digits: return []\n suffix = "<" + str(idx) + "/" + placeholder + ">"\n remaining = limit - len(suffix)\n if remaining < 0:\n return []\n res.append(message[i:min(n, i+remaining)] + suffix)\n i += remaining\n idx += 1\n \n count = str(len(res))\n if len(count) == digits:\n for j in range(len(res)):\n res[j] = res[j].replace(placeholder, count)\n return res\n\n return []\n \n for i in range(1, 5):\n res = createValid(i)\n if res: return res\n \n return []\n\n``` | 1 | 0 | ['Python3'] | 1 |
split-message-based-on-limit | O(n) solution with O(1) space with "simple" math and problem constraints analysis | on-solution-with-o1-space-with-simple-ma-16v9 | Intuition\nThe intuition is that no matter how many parts you have, they will always follow a pattern of digits. Any number between 100 and 999, for example, wi | vtfr | NORMAL | 2023-12-13T20:08:31.934519+00:00 | 2023-12-13T20:17:15.605980+00:00 | 175 | false | # Intuition\nThe intuition is that no matter how many parts you have, they will always follow a pattern of digits. Any number between 100 and 999, for example, will always have 3 digits. So instead of combining everything and seeing if it magically works (I\'m looking at you brute-forcers), we can calculate how many parts we actually need by trying all possible max part **digits** combinations, which are constrained by the problem.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(1)$$, as the output does not count as space\n\n# Code\n```\nfrom typing import Optional, List, Tuple\nimport math\n\nclass Solution:\n\n # O(n)\n def splitMessage(self, message: str, limit: int) -> List[str]:\n # Consider the smallest possible suffix: <1/1>\n # It\'s already 5 digits. Can\'t work with that...\n if limit <= 5:\n return []\n \n # O(1)\n def find_max_part() -> Optional[int]:\n # Consider that at most we\'ll have 5 digits for the\n # total part, as the problem is constrained to:\n #\n # 1 <= limit <= 10**4\n # 1 <= message.length <= 10**4\n #\n # In the worst case scenario, for the biggest message\n # possible and the smallest (viable) limit, we can\n # partition it in less than or equal to:\n #\n # 10 ** 4 = 10_000 parts (which has 5 digits) [1]\n #\n # [1] This was revealed to me in a dream.\n for total_digits in range(1, 5 + 1):\n remaining = len(message)\n parts = 0\n\n # Start reducing the message. First we start by the\n # 1 digit numbers, then 2 digit numbers, until we reach\n # the current total_digits maximum.\n for part_digits in range(1, total_digits + 1):\n # The maximum part can be calculated as such.\n #\n # This wields the following values:\n # [1, 9 ] => 10 - 1 = 9 items\n # [10, 99 ] => 100 - 10 = 90 items\n # [100, 999] => 1000 - 100 = 900 items\n max_part = 10 ** part_digits - 10 ** (part_digits - 1)\n\n suffix_len = 3 + part_digits + total_digits\n message_len = limit - suffix_len\n\n # No possible combination satisfies this. And \n # no possible >future< combination will neither, as\n # we\'re always increasing the number of digits.\n if message_len <= 0:\n return None\n\n # Calculate how many items we can fit here.\n # Be careful with the maximum this chunk can hold\n items_for_part = min(math.ceil(remaining / message_len), max_part)\n remaining -= items_for_part * message_len\n parts += items_for_part\n\n if remaining <= 0:\n return parts\n \n return None\n\n max_part = find_max_part()\n if not max_part:\n return []\n\n max_parts_str = str(max_part)\n \n i = 0\n partitions = []\n \n # Simply build the partitions.\n # O(n)\n for part in range(1, max_part + 1):\n part_str = str(part)\n message_chunk_len = limit - (3 + len(part_str) + len(max_parts_str))\n message_chunk = message[i:i+message_chunk_len]\n i += message_chunk_len\n\n partitions.append(f"{message_chunk}<{part_str}/{max_parts_str}>")\n \n return partitions\n\n``` | 1 | 0 | ['Python3'] | 0 |
split-message-based-on-limit | Modified binary search | modified-binary-search-by-demon_code-led1 | as it says make minimum splits as much as u can...\nso first try 1 to 9 , 10 to 99 , 100 to 999 , then 1000 to 9999 that\'s it\nso why doing this insted o | demon_code | NORMAL | 2023-08-17T04:52:40.654902+00:00 | 2024-10-22T11:26:22.013488+00:00 | 734 | false | as it says make minimum splits as much as u can...\nso first try 1 to 9 , 10 to 99 , 100 to 999 , then 1000 to 9999 that\'s it\nso why doing this insted of making low=1 and high=10000 and apply once the problem here is the binary search solution works for numbers which have same digit count \neg: \n"abbababbbaaa aabaa a"\n8\n\nhere if we just follow simple binary search with low=1 & high=10000 we end up on 11 but their is a solution at 7 splits which is better \nusual binary search fails to ensure the solution on range which have lesser digits than current mid\nso we need to search in ranges so why not jsut start from 1 to 9 best possible splits and if it fails then move forward \n**see the solve function implimentation**\nit will give us the correct value of spilts needed and then it\'s just easy problem just iterate and finished\n\n\n```\n\n class Solution {\npublic:\n \n string s="";\n int limit=0;\n bool safe(int m)\n {\n int n=s.size();\n int c=to_string(m).size();\n int t=1;\n for(int i=1; i<=m; i++)\n {\n int tem=to_string(t).size();\n t++;\n n-=(limit-3-c-tem);\n }\n \n if(n<=0) return true;\n return false;\n }\n int solve(int l, int h)\n {\n int n=s.size();\n \n int ans=-1;\n while(l<=h)\n {\n int m=l+((h-l)/2);\n \n if(safe(m))\n {\n // cout<<m<<endl;\n ans=m;\n h=m-1;\n }\n else l=m+1;\n }\n \n if(ans==-1) // if answer not found\n {\n if(h>=n) return -1;\n return solve(h+1, h*10+9);\n }\n else\n return ans;\n }\n \n vector<string> splitMessage(string s1, int t) \n {\n limit=t;\n \n if(t<=5) return {};\n s=s1;\n int p=solve(1,9);\n \n if(p==-1) return {};\n // cout<<safe(7)<<endl; \n string left="/"+to_string(p)+">";\n int c=left.size(); //constant\n \n \n string second="";\n int k=0;\n \n int rem=0;\n \n int n=s.size();\n \n vector<string> ans; \n \n for(int i=1; i<=p; i++)\n {\n \n second="<"+ to_string(i)+left;\n rem=(limit-(int)second.size());\n if(rem==0) return {};//if no remaining space for char so return{} \n \n string tem="";\n for(int j=0; j<rem; j++)// add remaining character\n {\n tem+=s[k];\n k++;\n if(k==n) break;\n }\n \n tem+=second;\n ans.push_back(tem);\n \n if(k==n) break;\n }\n return ans;\n \n }\n};\n\n``` | 1 | 0 | ['Greedy', 'Binary Search Tree', 'C'] | 1 |
split-message-based-on-limit | Kotlin Solution with Math | kotlin-solution-with-math-by-lararicardo-c84c | Approach\nWe can solve this problem doing pure math calculations.\n\n1. We first try to split it with at most 9 copies. We know the suffix will be of the form " | lararicardo386 | NORMAL | 2023-07-30T05:48:27.291016+00:00 | 2023-07-30T05:48:27.291034+00:00 | 20 | false | # Approach\nWe can solve this problem doing pure math calculations.\n\n1. We first try to split it with at most 9 copies. We know the suffix will be of the form "<1/9>", which will always have 5 chars. This means that we have only (limit -5) chars that we can extract from the original string. Therefore we would need (Message Length / (Limit-5)) Copies. If number of copies is greater than 9 then we know we need to check now with at most 99\n2. Now we try to split it with at most 9 copies. We know we will have 9 copies of the following form "<1/99>" whose length is (Limit -6) and then we will have 90 copies of the form "<10/99>" whose length is (Limit-7). To get how many copies we will need we can do quick math.\n\nFor other cases we have similar logic\n\n# Code\n\nCode can be simplify but tried to keep it self explained.\n```\nimport kotlin.math.ceil\nimport kotlin.math.min\nclass Solution {\n\n fun splitAtMost9(length: Int, limit: Int):Int{\n if(limit <= 5) return -1\n val numberOfCopies = ceil(length/(limit - 5).toFloat()).toInt()\n return if(numberOfCopies <= 9)numberOfCopies else -1\n }\n\n fun splitWithAtMost99(length: Int, limit: Int):Int{\n if(limit <= 7) return -1\n val restOfStringLength = length - (limit-6)*9\n val numberOfCopies = ceil(restOfStringLength/(limit-7).toFloat()).toInt() + 9\n return if(numberOfCopies <= 99) numberOfCopies else -1\n }\n\n fun splitWithAtMost999(length: Int, limit: Int):Int{\n if(limit <= 9) return -1\n var restOfStringLength = length - (limit-7)*9\n restOfStringLength = restOfStringLength - (limit-8)*90\n\n val numberOfCopies = ceil(restOfStringLength/(limit-9).toFloat()).toInt() + 99\n return if(numberOfCopies <= 999) numberOfCopies else -1\n }\n\n fun splitWithAtMost9999(length: Int, limit: Int):Int{\n if(limit <= 9) return -1\n var restOfStringLength = length - (limit-8)*9\n restOfStringLength = restOfStringLength - (limit-9)*90\n restOfStringLength = restOfStringLength - (limit-10)*900\n\n val numberOfCopies = ceil(restOfStringLength/(limit-11).toFloat()).toInt() + 999\n return if(numberOfCopies <= 9999) numberOfCopies else -1\n }\n\n fun splitMessage(message: String, limit: Int): Array<String> {\n var copies = splitAtMost9(message.length,limit)\n if(copies == -1){\n copies = splitWithAtMost99(message.length,limit)\n }\n if(copies == -1){\n copies = splitWithAtMost999(message.length,limit)\n }\n if(copies == -1){\n copies = splitWithAtMost9999(message.length,limit)\n }\n if(copies <= 0 ){\n return emptyArray<String>()\n }\n val ans = Array<String>(copies){""}\n var appended = 0\n for(i in 1..copies){\n val toAppendLength = limit - "<$i/$copies>".length\n ans[i-1] = message.substring(appended,min(appended+toAppendLength,message.length)) + "<$i/$copies>"\n appended = appended+toAppendLength\n }\n\n return ans\n \n }\n}\n``` | 1 | 0 | ['Kotlin'] | 0 |
split-message-based-on-limit | Golang solution with explanation | golang-solution-with-explanation-by-msfs-aalf | Intuition\nThe length of the suffix (<x/y>) determines everything else. Since the constraints say that that the length of the message is <= 10^4, that means tha | msfspinolo | NORMAL | 2023-02-14T16:52:26.254269+00:00 | 2023-02-14T16:52:26.254318+00:00 | 60 | false | # Intuition\nThe length of the suffix (`<x/y>`) determines everything else. Since the constraints say that that the length of the message is <= 10^4, that means that the mesage can be split into at most 10^4 parts, which means that the length of `y` in our suffix is at most 4.\n\n# Approach\nTry to split the message assuming `y` is length 1 (i.e., less than 10 parts), and increment the length of `y` when that assumption is violated. The first viable solution will be the least number of splits since we used the shortest possible suffix.\n\n# Complexity\n- Time complexity: O(N). We iterate the message at most 4 times.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N). We store the splits in a string slice and have a few other variables of constant size.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport "fmt"\nimport "math"\n\nfunc splitMessage(message string, limit int) []string {\n // This will be the final result. If we don\'t find a workable\n // solution this will return empty by default.\n var result []string\n\n // Start by assuming the denominator (total number of splits) is\n // one digit long, and work up from there.\n for denomDigits := 1; denomDigits <= 4; denomDigits++ {\n // Track how many splits/parts we have so far\n numParts := 0\n // Make a copy of the message that we can slice up for\n // each attempt with a given denominator length\n m := message\n // This will contain the message pieces without suffix. We\n // can\'t know the correct suffix until we\'re done splitting.\n var splits []string\n\n // We\'re going to slice off the message bit by bit, so we\n // know we\'re done when it\'s empty.\n for len(m) > 0 {\n numParts++\n // The number of digits in the current message number\n // is the base-10 logarithm of the message number,\n // truncated to an int, plus 1.\n // Example:\n // - mesage #4\n // math.Log10(4.0) == 0.6020599913279624\n // truncate to int => 0\n // add 1 => 1\n numDigits := int(math.Log10(float64(numParts))) + 1\n\n // If this is true, we aren\'t reserving enough digits\n // for the total number of splits. Try again with\n // more digits.\n if numDigits > denomDigits {\n splits = nil\n break\n }\n\n // The number of characters we grab is based on the limit.\n // We have to make room for:\n // - The number of digits in the message number\n // - The number of digits in the total number of splits\n // - The 3 standard suffix characters "</>"\n toGrab := limit - numDigits - denomDigits - 3\n\n // We don\'t have room to grab anything, so this won\'t\n // work. Try again with more digits.\n if toGrab <= 0 {\n splits = nil\n break\n }\n\n // Edge case, we are grabbing the last bit of the string\n // and there\'s not enough left to hit the limit.\n if toGrab > len(m) {\n toGrab = len(m)\n }\n\n // Add our split to the list and slice off the message.\n splits = append(splits, m[0:toGrab])\n m = m[toGrab:]\n }\n\n // We found a viable solution.\n if splits != nil {\n // d is the total number of splits\n d := len(splits)\n for i, s := range splits {\n // i + 1 because we number 1 to d instead of 0 to\n // d -1\n result = append(result, fmt.Sprintf("%s<%d/%d>", s, i + 1, d))\n }\n break\n }\n }\n return result\n}\n``` | 1 | 0 | ['Go'] | 1 |
split-message-based-on-limit | 2 steps solution - easy understanding | 2-steps-solution-easy-understanding-by-g-sgdt | Intuition\n 2 steps to split message\n\n# Approach\n Step 1: calculate an array whose item is the chars amount that can be spliited at a specific suffix l | Gang-Li | NORMAL | 2022-12-26T00:09:41.755157+00:00 | 2022-12-26T00:09:41.755189+00:00 | 202 | false | # Intuition\n 2 steps to split message\n\n# Approach\n Step 1: calculate an array whose item is the chars amount that can be spliited at a specific suffix length.\n Step 2: calcuate the total number of splitted message. Based on the array from step 1, copy meessage into final answer array.\n \n\n# Complexity\n- Time complexity:\n O(N)\n\n- Space complexity:\n O(N)\n\n# Code\n```\n/**\n * @param {string} message\n * @param {number} limit\n * @return {string[]}\n */\nvar splitMessage = function (message, limit) {\n if (limit <= 5) return [];\n\n const MESSAGE_LEN = message.length;\n const NINE = 9;\n\n /* \n // the suffix is in format <index/total>, both index and total are number type\n\n When given digits value, calcuate an array.\n Item of the array is the total chars can be spliited from message, at this level the suffix is same length.\n But the next item of the array, the suffix length will be ONE more than previous. \n\n digits: digit length of the [total number] of splitted message\n value 1: means range of [1, 9] messages allowed to be splitted.\n value 2: means range of [1, 99] messages allowed to be splitted.\n value 3: means range of [1, 999] messages allowed to be splitted.\n ...etc\n */\n function calcuate(digits) {\n let sum = 0;\n let charsAmountArr = [];\n\n // the suffix is in format <index/total>, both index and total are number type\n for (let idxLen = 1; idxLen <= digits; idxLen++) {\n let countCanSplit = NINE * Math.pow(10, idxLen - 1);\n let charsCanSplit = countCanSplit * (limit - 3 - digits - idxLen);\n charsAmountArr.push(charsCanSplit);\n sum += charsCanSplit;\n }\n\n if (sum < MESSAGE_LEN) return [];\n else return charsAmountArr;\n }\n\n let charsAmountArr = [];\n for (let i = 1; i <= limit - 5; i++) {\n charsAmountArr = calcuate(i);\n if (charsAmountArr.length > 0) break;\n }\n if (charsAmountArr.length < 1) return [];\n\n // the suffix is in format <index/total>, both index and total are number\n // Now, we need calcuate the total value\n let remaining = MESSAGE_LEN;\n let arrLen = charsAmountArr.length;\n for (let i = 0; i < arrLen - 1; i++) remaining -= charsAmountArr[i];\n let base = Math.pow(10, arrLen - 1) - 1;\n let chars = limit - 3 - 2 * arrLen;\n let total = base + Math.ceil(remaining / chars);\n\n let ans = [];\n let copyStartIndex = 0;\n let splitIndex = 1;\n for (let i = 0; i < arrLen; i++) {\n let charsAmount = charsAmountArr[i];\n let chars = limit - 3 - arrLen - (i + 1);\n for (let j = 0; j < charsAmount / chars; j++) {\n let copyEndIdx = Math.min(copyStartIndex + chars, MESSAGE_LEN);\n ans.push(\n `${message.substring(\n copyStartIndex,\n copyEndIdx\n )}<${splitIndex}/${total}>`\n );\n if (copyEndIdx === MESSAGE_LEN) return ans;\n\n splitIndex++;\n copyStartIndex = copyEndIdx;\n }\n }\n\n return ans;\n};\n``` | 1 | 0 | ['JavaScript'] | 0 |
split-message-based-on-limit | [Python3] linear search | python3-linear-search-by-ye15-4l0f | Please pull this commit for solutions of biweekly 91. \n\n\nclass Solution:\n def splitMessage(self, message: str, limit: int) -> List[str]:\n prefix | ye15 | NORMAL | 2022-11-19T19:37:29.416866+00:00 | 2022-11-19T19:37:29.416894+00:00 | 182 | false | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/e8b87d04cc192c5227286692921910fe93fee05d) for solutions of biweekly 91. \n\n```\nclass Solution:\n def splitMessage(self, message: str, limit: int) -> List[str]:\n prefix = b = 0 \n while 3 + len(str(b))*2 < limit and len(message) + prefix + (3+len(str(b)))*b > limit * b: \n b += 1\n prefix += len(str(b))\n ans = []\n if 3 + len(str(b))*2 < limit: \n i = 0 \n for a in range(1, b+1): \n step = limit - (len(str(a)) + len(str(b)) + 3)\n ans.append(f"{message[i:i+step]}<{a}/{b}>")\n i += step \n return ans \n``` | 1 | 0 | ['Python3'] | 1 |
split-message-based-on-limit | Golang 87 ms 7.3 MB | golang-87-ms-73-mb-by-maxhero90-c8nw | \nfunc max(a, b int) int {\n\tif a >= b {\n\t\treturn a\n\t}\n\treturn b\n}\n\nfunc splitMessage(message string, limit int) []string {\n\tfor totalDigitCount := | maxhero90 | NORMAL | 2022-11-14T23:00:29.462194+00:00 | 2022-11-14T23:00:29.462229+00:00 | 239 | false | ```\nfunc max(a, b int) int {\n\tif a >= b {\n\t\treturn a\n\t}\n\treturn b\n}\n\nfunc splitMessage(message string, limit int) []string {\n\tfor totalDigitCount := 1; totalDigitCount < 5; totalDigitCount++ {\n\t\tprevMaxPayload, maxPayload := 0, 0\n\t\tmultiplier := 1\n\t\tfor curDigitCount := 1; curDigitCount <= totalDigitCount; curDigitCount, multiplier = curDigitCount+1, multiplier*10 {\n\t\t\tprevMaxPayload = maxPayload\n\t\t\tmaxPayload += max(0, (limit-3-totalDigitCount-curDigitCount)*9*multiplier)\n\t\t}\n\t\tif maxPayload < len(message) {\n\t\t\tcontinue\n\t\t}\n\t\tlastPartsLen := limit - 3 - totalDigitCount*2\n\t\ttotalPartsCount := multiplier/10 - 1 + (len(message)-prevMaxPayload+lastPartsLen-1)/lastPartsLen\n\t\ttotalPartsCountSuffix := "/" + strconv.Itoa(totalPartsCount) + ">"\n\t\tresult := make([]string, totalPartsCount)\n\t\tcIdx := 0\n\t\tfor i := 1; i < totalPartsCount; i++ {\n\t\t\tsuffix := "<" + strconv.Itoa(i) + totalPartsCountSuffix\n\t\t\tcIdx2 := limit - len(suffix) + cIdx\n\t\t\tresult[i-1] = message[cIdx:cIdx2] + suffix\n\t\t\tcIdx = cIdx2\n\t\t}\n\t\tresult[len(result)-1] = message[cIdx:] + "<" + strconv.Itoa(totalPartsCount) + totalPartsCountSuffix\n\t\treturn result\n\t}\n\treturn nil\n}\n``` | 1 | 0 | ['Go'] | 0 |
split-message-based-on-limit | [Golang] Brute Force 🤝💪✅✅✅ || Runtime = 142 ms || Memory = 7.4 MB | golang-brute-force-runtime-142-ms-memory-it8j | \nfunc splitMessage(message string, limit int) []string {\n\tp := 1\n\ta := 1\n\n\tfor p*(size(p)+3)+a+len(message) > p*limit {\n\t\tif 3+size(p)*2 >= limit {\n | a-n-k-r | NORMAL | 2022-11-14T09:29:44.788071+00:00 | 2022-11-14T09:31:02.935511+00:00 | 47 | false | ```\nfunc splitMessage(message string, limit int) []string {\n\tp := 1\n\ta := 1\n\n\tfor p*(size(p)+3)+a+len(message) > p*limit {\n\t\tif 3+size(p)*2 >= limit {\n\t\t\treturn []string{}\n\t\t}\n\t\tp += 1\n\t\ta += size(p)\n\t}\n\n\tparts := make([]string, 0)\n\n\tfor i := 1; i < p+1; i++ {\n\t\tj := Min(limit - (size(p) + size(i) + 3), len(message))\n\t\tpart := message[0:j]\n\t\tmessage = message[j:]\n\t\tparts = append(parts, fmt.Sprintf("%s<%d/%d>", part, i, p))\n\t}\n\n\treturn parts\n}\n\nfunc Min(x, y int) int {\n\tif x < y {\n\t\treturn x\n\t}\n\treturn y\n}\n\nfunc size(n int) int {\n\treturn len(strconv.Itoa(n))\n}\n\n``` | 1 | 0 | ['Go'] | 0 |
split-message-based-on-limit | [C++] Brute force with O(N) time complexity | c-brute-force-with-on-time-complexity-by-ystx | \nclass Solution {\npublic:\n int digits(int n) {\n int cnt = 0;\n while (n) {\n n /= 10;\n cnt++;\n }\n re | kaminyou | NORMAL | 2022-11-13T07:56:45.289834+00:00 | 2022-11-18T18:10:54.348436+00:00 | 310 | false | ```\nclass Solution {\npublic:\n int digits(int n) {\n int cnt = 0;\n while (n) {\n n /= 10;\n cnt++;\n }\n return cnt;\n }\n vector<string> splitMessage(string message, int limit) {\n int n = message.size();\n for (int length = 1; length * 2 + 3 < limit; ++length) {\n int cnt = (pow(10, length) - 1);\n int available = cnt * limit;\n available -= 3 * cnt;\n available -= length * cnt;\n for (int i = 1; i <= length; ++i) {\n available -= i * (pow(10, i) - pow(10, i - 1));\n }\n if (available >= n) return generate(message, limit, length);\n }\n \n return {};\n }\n vector<string> generate(string& message, int limit, int length) {\n int n = message.size();\n vector<string> res;\n int index = 0;\n int cnt = 1;\n while (index < n) {\n int remain = limit - 3;\n remain -= digits(cnt);\n remain -= length;\n int extract = min(remain, n - index);\n string temp = message.substr(index, extract) + "<" + to_string(cnt) + "/";\n res.push_back(temp);\n index += extract;\n cnt++;\n }\n string blockCnt = to_string(cnt - 1);\n for (auto& word : res) {\n word += blockCnt + ">";\n }\n return res;\n }\n};\n\n``` | 1 | 0 | ['C', 'Binary Tree'] | 2 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.