question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
longest-uploaded-prefix | ✅✅Faster || Easy To Understand || C++ Code | faster-easy-to-understand-c-code-by-__kr-w9ub | Array\n\n\nclass LUPrefix {\npublic:\n \n vector<int> arr;\n \n // longest will keep track of untill (longest - 1) we have got the longest uploaded | __KR_SHANU_IITG | NORMAL | 2022-10-01T17:41:19.515131+00:00 | 2022-10-01T17:41:19.515175+00:00 | 72 | false | * ***Array***\n\n```\nclass LUPrefix {\npublic:\n \n vector<int> arr;\n \n // longest will keep track of untill (longest - 1) we have got the longest uploaded prefix\n \n int longestt = 1;\n \n LUPrefix(int n) {\n \n arr.assign(n + 1, 0);\n }\n \n void upload(int video) {\n \n arr[video]++;\n }\n \n int longest() {\n \n while(longestt < arr.size())\n {\n if(arr[longestt])\n {\n longestt++;\n }\n else\n {\n break;\n }\n }\n \n return longestt - 1;\n }\n};\n``` | 1 | 0 | ['Array', 'C', 'C++'] | 0 |
longest-uploaded-prefix | Java Solution | Small Code | java-solution-small-code-by-_thepassenge-znlk | \nclass LUPrefix {\n \n Set<Integer> set;\n int maxVideoPrefix = 0;\n \n public LUPrefix(int n) {\n set = new HashSet<>();\n }\n \n | _thepassenger | NORMAL | 2022-10-01T17:38:01.503506+00:00 | 2022-10-01T17:38:29.638836+00:00 | 51 | false | ```\nclass LUPrefix {\n \n Set<Integer> set;\n int maxVideoPrefix = 0;\n \n public LUPrefix(int n) {\n set = new HashSet<>();\n }\n \n public void upload(int video) {\n set.add(video);\n while(set.contains(maxVideoPrefix+1)) {\n maxVideoPrefix++;\n }\n }\n \n public int longest() {\n return maxVideoPrefix;\n }\n}\n\n``` | 1 | 0 | ['Java'] | 0 |
longest-uploaded-prefix | C++ || Set || Simple Explanation | c-set-simple-explanation-by-anis23-wi02 | Approach:\n\n keep storing the values in the set\n keep track of the max_length\n whenever we encounter the longest() function\n\t start from the last stored ma | anis23 | NORMAL | 2022-10-01T17:29:55.121117+00:00 | 2022-10-01T17:29:55.121155+00:00 | 48 | false | **Approach:**\n\n* keep storing the values in the set\n* keep track of the max_length\n* whenever we encounter the longest() function\n\t* start from the last stored max value\n\t* now keep increasing it to the number that has not been added yet\n* example:\n\t* let currently m = 3\n\t* set = {1,2,3,5,6,7,9}\n\t* because the longest has all number from 1 to i that\'s why m is 3\n\t* now we add 4\n\t* now we got the longest() function\n\t\t* so start from 3\n\t\t* check if we have 4 in the set, we do have 4 so inc m\n\t\t* after doing this ... we will reach at 7 the new max value\n\t\t* so return 7\n\n**Code:**\n\n```\nclass LUPrefix\n{\npublic:\n set<int> st;\n int m = 0; // max value so far\n LUPrefix(int n)\n {\n }\n\n void upload(int video)\n {\n st.insert(video);\n }\n\n int longest()\n {\n while (st.find(m + 1) != st.end())\n m++;\n return m;\n }\n};\n``` | 1 | 0 | ['C', 'Ordered Set'] | 0 |
longest-uploaded-prefix | 🤯 [Python] Made Easy | Pointer based approach | Explained | python-made-easy-pointer-based-approach-7wn8f | We maintain a pointer to return the longest prefix size. At start the pointer stays at 0, Since we know there cant be a 0 video, so the pointer stays at 0 until | ramsudharsan | NORMAL | 2022-10-01T16:49:55.320988+00:00 | 2022-10-01T16:49:55.321027+00:00 | 85 | false | We maintain a pointer to return the longest prefix size. At start the pointer stays at 0, Since we know there cant be a 0 video, so the pointer stays at 0 until the 1st video is uploaded. As soon as the 1st video gets uploaded, we increase the pointer till the end of the array or till it finds another 0.\n\n**Upvote if you understood the logic :)**\n\n```\nclass LUPrefix:\n\n def __init__(self, n: int):\n self.arr = [0] * n\n self.point = 0\n\n def upload(self, video: int) -> None:\n self.arr[video - 1] = video\n \n while self.point < len(self.arr) and self.arr[self.point] > 0:\n self.point += 1\n \n\n def longest(self) -> int:\n return self.point\n``` | 1 | 0 | ['Python'] | 0 |
longest-uploaded-prefix | simple and clean solution using vector<bool> | simple-and-clean-solution-using-vectorbo-sxaa | \nclass LUPrefix {\npublic:\n vector<bool> v;\n int a=1;\n int b;\n LUPrefix(int n) {\n v.resize(n+1,false);\n b=n;\n }\n \n | aniketpawar | NORMAL | 2022-10-01T16:49:52.479031+00:00 | 2022-10-01T16:49:52.479066+00:00 | 24 | false | ```\nclass LUPrefix {\npublic:\n vector<bool> v;\n int a=1;\n int b;\n LUPrefix(int n) {\n v.resize(n+1,false);\n b=n;\n }\n \n void upload(int video) {\n v[video]=true;\n }\n \n int longest() {\n while(a<=b)\n {\n if(v[a]==false)break;\n a++;\n }\n return a-1;\n \n }\n};\n\n``` | 1 | 0 | [] | 0 |
longest-uploaded-prefix | python solution faster 90% | python-solution-faster-90-by-dugu0607-llzc | class LUPrefix:\n\n def init(self, n: int):\n self.arr = [False] * n\n self.minTrue = -1\n \n\n def upload(self, video: int) -> None: | Dugu0607 | NORMAL | 2022-10-01T16:49:46.099505+00:00 | 2022-10-01T16:49:46.099531+00:00 | 45 | false | class LUPrefix:\n\n def __init__(self, n: int):\n self.arr = [False] * n\n self.minTrue = -1\n \n\n def upload(self, video: int) -> None:\n video -= 1\n self.arr[video] = True\n if self.minTrue == video - 1:\n while video + 1 < len(self.arr) and self.arr[video + 1]:\n video += 1\n self.minTrue = video\n \n \n def longest(self) -> int:\n \n return self.minTrue + 1 | 1 | 0 | ['Python'] | 0 |
longest-uploaded-prefix | Union Find | with concise comment | union-find-with-concise-comment-by-lucie-0pcs | \nclass LUPrefix {\npublic:\n const int OFFLINE = -1;\n const int MAIN_SERVER = 1;\n vector<int> root;\n vector<int> rank;\n LUPrefix(int n) {\n | lucienlo | NORMAL | 2022-10-01T16:37:02.371479+00:00 | 2022-10-01T16:42:22.178785+00:00 | 58 | false | ```\nclass LUPrefix {\npublic:\n const int OFFLINE = -1;\n const int MAIN_SERVER = 1;\n vector<int> root;\n vector<int> rank;\n LUPrefix(int n) {\n root = vector<int>(n+1, OFFLINE);\n rank = vector<int>(n+1, 1);\n }\n\n int find (const int i) {\n if (i == -1 || root[i] == i)\n return i;\n return root[i] = find(root[i]);\n }\n \n void merge(const int i, const int j) {\n int u = find(i), v = find(j);\n \n if (v > u) //adopt the fareset server as our server root\n swap(u, v);\n \n root[v] = root[u];\n rank[u] += rank[v];\n }\n\n void upload(const int video) {\n root[video] = video; //active the server of current video\n \n if (video+1 < root.size() && find(root[video+1]) != OFFLINE) // nearby left server has been actived\n merge(video, video+1);\n\n if (video-1 >= 0 && find(root[video-1]) != OFFLINE) // nearby right server has been actived\n merge(video, video-1);\n\n }\n \n int longest() {\n return find(root[MAIN_SERVER]) == OFFLINE ? 0 : find(root[MAIN_SERVER]); //return which the farest server that ROOT server can reach\n }\n};\n``` | 1 | 0 | ['Union Find', 'C'] | 1 |
longest-uploaded-prefix | C++ | Vector | Easy & Short Solution | c-vector-easy-short-solution-by-shubhamr-suzw | \nclass LUPrefix {\n vector<int> mp;\n int i = 1;\n int len;\npublic:\n LUPrefix(int n) {\n mp.resize(n+1);\n len = n;\n }\n \n | shubhamrwt2001 | NORMAL | 2022-10-01T16:35:37.559486+00:00 | 2022-10-01T16:35:37.559518+00:00 | 29 | false | ```\nclass LUPrefix {\n vector<int> mp;\n int i = 1;\n int len;\npublic:\n LUPrefix(int n) {\n mp.resize(n+1);\n len = n;\n }\n \n void upload(int video) {\n mp[video] = 1;\n while( i <= len && mp[i] ){\n i++;\n }\n }\n \n int longest() {\n return i-1;\n }\n};\n``` | 1 | 0 | ['C'] | 0 |
longest-uploaded-prefix | Java | Easy Understanding | java-easy-understanding-by-singhmohit971-4mg1 | Hi Family,\n\nI did this question using Array\n\n\nclass LUPrefix {\n \n // declare the array\n int ar[];\n int max_cnt = 1;\n\n public LUPrefix( | singhmohit9718 | NORMAL | 2022-10-01T16:29:09.465604+00:00 | 2022-10-01T16:29:09.465640+00:00 | 44 | false | Hi Family,\n\nI did this question using Array\n\n```\nclass LUPrefix {\n \n // declare the array\n int ar[];\n int max_cnt = 1;\n\n public LUPrefix(int n) {\n //initialize the array\n ar = new int[n+2];\n }\n \n public void upload(int video) {\n ar[video] = 1;\n // check everytime from the max index \n while (ar[max_cnt] == 1) {\n max_cnt++;\n }\n }\n \n public int longest() {\n \n return max_cnt-1;\n }\n}\n```\n\n**If you liked the code Please Please Please Upvote it**\n\n\n**Thanks!!!**\n\n | 1 | 0 | ['Array', 'Java'] | 0 |
longest-uploaded-prefix | Simple Java solution | simple-java-solution-by-damingqisheng-kort | \nclass LUPrefix {\n boolean[] videos;\n int pointer = 0;\n public LUPrefix(int n) {\n videos = new boolean[n+1];\n }\n \n public void | damingqisheng | NORMAL | 2022-10-01T16:28:17.204611+00:00 | 2022-10-01T16:28:17.204651+00:00 | 30 | false | ```\nclass LUPrefix {\n boolean[] videos;\n int pointer = 0;\n public LUPrefix(int n) {\n videos = new boolean[n+1];\n }\n \n public void upload(int video) {\n videos[video] = true;\n }\n \n public int longest() {\n while(pointer < videos.length-1 && videos[pointer+1]) {\n pointer++;\n }\n return pointer;\n }\n}\n``` | 1 | 0 | ['Array', 'Java'] | 0 |
longest-uploaded-prefix | Python UnionFind | python-unionfind-by-yeung9613-2oza | Expand size of neighbors if they are at least 1. longest() just returns the size of parent of 0.\n\nTime:\n- upload: amortized O(1)\n- longest: amortized O(1)\n | yeung9613 | NORMAL | 2022-10-01T16:27:17.406751+00:00 | 2022-10-01T19:18:25.755779+00:00 | 110 | false | Expand size of neighbors if they are at least 1. longest() just returns the size of parent of 0.\n\nTime:\n- upload: amortized O(1)\n- longest: amortized O(1)\n\nSpace: O(n)\n\n```python\nclass UF:\n def __init__(self, n):\n self.parents = [i for i in range(n)]\n self.size = [0] * n\n \n def find(self, x):\n px = self.parents[x]\n if x != px:\n self.parents[x] = self.find(px)\n \n return self.parents[x]\n \n def union(self, x, y):\n px, py = self.find(x), self.find(y)\n if px != py:\n self.parents[px] = py\n self.size[py] += self.size[px]\n\t\t\t\n def getsize(self, x):\n return self.size[self.find(x)]\n\t\t\nclass LUPrefix:\n\n def __init__(self, n: int):\n self.uf = UF(n)\n self.n = n\n \n def upload(self, video: int) -> None:\n i = video - 1\n self.uf.size[i] += 1\n if i > 0 and self.uf.getsize(i-1) > 0:\n self.uf.union(i, i-1)\n if i+1 < self.n and self.uf.getsize(i+1) > 0:\n self.uf.union(i, i+1)\n \n def longest(self) -> int:\n return self.uf.getsize(0)\n``` | 1 | 0 | ['Union Find', 'Python'] | 0 |
longest-uploaded-prefix | Easy to understand using array. | easy-to-understand-using-array-by-kamal0-sus4 | \nclass LUPrefix:\n\n def __init__(self, n: int):\n self.i = 0\n self.l = [0]*(n+1)\n self.n = n\n\n def upload(self, video: int) -> | kamal0308 | NORMAL | 2022-10-01T16:19:42.042572+00:00 | 2022-10-01T16:25:41.568663+00:00 | 28 | false | ```\nclass LUPrefix:\n\n def __init__(self, n: int):\n self.i = 0\n self.l = [0]*(n+1)\n self.n = n\n\n def upload(self, video: int) -> None:\n if video==1:\n self.i = 1\n self.l[video]=1\n while(self.i<self.n):\n if self.l[self.i+1]==1:\n self.i+=1\n else:\n break\n def longest(self) -> int:\n return self.i\n``` | 1 | 1 | ['Python', 'Python3'] | 0 |
longest-uploaded-prefix | c++, Very easy, O(n) | c-very-easy-on-by-chaser_aim-mjui | \'\'\'\nThe key point here is to increase the value uploaded prefix whenever we are getting continuous number.\n \n vector v;\n int ans = 0;\n LUPre | chaser_aim | NORMAL | 2022-10-01T16:18:19.009209+00:00 | 2022-10-30T09:30:26.786390+00:00 | 39 | false | \'\'\'\nThe key point here is to increase the value uploaded prefix whenever we are getting continuous number.\n \n vector<bool> v;\n int ans = 0;\n LUPrefix(int n) {\n\t\n\t\t// defining a vector of size 1 greater n;\n v.resize(n + 1);\n for(int i = 0;i <n; i++){\n\t\t\n\t\t// false means the number is not uploaded\n v[i] = false; \n }\n }\n \n void upload(int video) {\n\t\n\t// true means the number is uploaded\n v[video - 1] = true;\n\t\t\n\t// counting the number of continuous numbers from 1\n while(v[ans] == true){\n ans++;\n } \n }\n \n int longest() {\n return ans;\n }\n\'\'\' | 1 | 0 | ['C'] | 0 |
longest-uploaded-prefix | Java | Set and Union Find | Easy explanation ✅ | java-set-and-union-find-easy-explanation-eswh | Terminology\nLet\'s call a contiguous section of videos a component.\nEx: [1,2,4,5,6,8,9]\nComponents: [1,2], [4,5,6], [8,9]\n\n#### Logic:\n Keep a set for see | Saumay_Khandelwal | NORMAL | 2022-10-01T16:15:43.624997+00:00 | 2022-10-01T16:28:53.232456+00:00 | 117 | false | #### Terminology\nLet\'s call a contiguous section of videos a component.\nEx: [1,2,4,5,6,8,9]\nComponents: [1,2], [4,5,6], [8,9]\n\n#### Logic:\n* Keep a set for seen elements.\n* Maintain a union find set with n+1 elements\n\t* Larger root will become the root while doing union operation. Thus, root of an element would be the largest element of that component.\n* upload():\n\t* add the element to set\n\t* if neighbors are already uploaded, union with them as well\n* longest():\n\t* return the root of 0(the largest element of the component having 0).\n\n```\nclass LUPrefix {\n \n private Set<Integer> seen;\n private DisjointSet ds;\n \n public LUPrefix(int n) {\n seen = new HashSet<>();\n seen.add(0);\n \n ds = new DisjointSet(n+1);\n }\n \n public void upload(int video) {\n seen.add(video);\n \n if(seen.contains(video-1))\n ds.union(video-1, video);\n if(seen.contains(video+1))\n ds.union(video, video+1);\n }\n \n public int longest() {\n return ds.find(0);\n }\n}\n\nclass DisjointSet {\n int[] root;\n\n public DisjointSet(int n) {\n root = new int[n+1];\n\n for(int i=0 ; i<n+1 ; i++) {\n root[i] = i;\n }\n }\n\n public void union(int x, int y) {\n int rootX = find(x);\n int rootY = find(y);\n\n if(rootX != rootY) {\n if(rootX > rootY)\n root[rootY] = rootX;\n else\n root[rootX] = rootY;\n }\n }\n\n public int find(int x) {\n if(root[x]==x)\n return root[x];\n\n root[x] = find(root[x]);\n return root[x];\n }\n}\n``` | 1 | 0 | ['Union Find', 'Ordered Set', 'Java'] | 0 |
longest-uploaded-prefix | Java Priority Queue Solution | java-priority-queue-solution-by-abascus-z3tf | \nclass LUPrefix {\n \n PriorityQueue<Integer> pq;\n int previousValue;\n\n public LUPrefix(int n) {\n pq = new PriorityQueue<>();\n p | abascus | NORMAL | 2022-10-01T16:10:57.910988+00:00 | 2022-10-01T16:10:57.911029+00:00 | 34 | false | ```\nclass LUPrefix {\n \n PriorityQueue<Integer> pq;\n int previousValue;\n\n public LUPrefix(int n) {\n pq = new PriorityQueue<>();\n previousValue = 0;\n }\n \n public void upload(int video) {\n pq.offer(video);\n \n while(!pq.isEmpty() && pq.peek().equals(previousValue + 1)) {\n pq.poll();\n previousValue += 1;\n }\n }\n \n public int longest() {\n return previousValue;\n }\n}\n\n/**\n * Your LUPrefix object will be instantiated and called as such:\n * LUPrefix obj = new LUPrefix(n);\n * obj.upload(video);\n * int param_2 = obj.longest();\n */\n ```\n \n Time complexity :- 0(nlogn) | 1 | 0 | [] | 0 |
longest-uploaded-prefix | Easiest Solution Ever C++ | easiest-solution-ever-c-by-rishabhsingha-ogws | \nclass LUPrefix {\n vector<int> ds;\n int count = 1;\n int len;\npublic:\n LUPrefix(int n) {\n len = n;\n ds = vector<int>(n+1);\n | Rishabhsinghal12 | NORMAL | 2022-10-01T16:09:18.028515+00:00 | 2022-10-01T16:12:52.895399+00:00 | 42 | false | ```\nclass LUPrefix {\n vector<int> ds;\n int count = 1;\n int len;\npublic:\n LUPrefix(int n) {\n len = n;\n ds = vector<int>(n+1);\n }\n \n void upload(int video) \n {\n if(video == count)\n {\n ds[video]++;\n count++;\n video++;\n while(video <= len and ds[video] != 0){count++;video++;}\n }\n else\n {\n ds[video]++;\n \n }\n }\n \n int longest() \n {\n if(count == 1)return 0;\n return count-1;\n \n }\n};\n\n/**\n * Your LUPrefix object will be instantiated and called as such:\n * LUPrefix* obj = new LUPrefix(n);\n * obj->upload(video);\n * int param_2 = obj->longest();\n */\n``` | 1 | 0 | ['C', 'C++'] | 0 |
longest-uploaded-prefix | C++ || Easy || Similar to Find Mes number in Array problem | c-easy-similar-to-find-mes-number-in-arr-3k80 | \tclass LUPrefix {\n\tpublic:\n\t\tset st;\n\t\tunordered_map mp;\n\t\tLUPrefix(int n) \n\t\t{\n\t\t\tst.insert(1);\n\t\t}\n\n\t\tvoid upload(int video) \n\t\t{ | _Falcon | NORMAL | 2022-10-01T16:08:38.193381+00:00 | 2022-10-01T16:13:49.101010+00:00 | 28 | false | \tclass LUPrefix {\n\tpublic:\n\t\tset<long long> st;\n\t\tunordered_map<int, int> mp;\n\t\tLUPrefix(int n) \n\t\t{\n\t\t\tst.insert(1);\n\t\t}\n\n\t\tvoid upload(int video) \n\t\t{\n\t\t\tif (!mp[video + 1])\n\t\t\t{\n\t\t\t\tst.insert(video + 1);\n\t\t\t}\n\t\t\tst.erase(video);\n\t\t\tmp[video]++;\n\t\t}\n\n\t\tint longest() \n\t\t{\n\t\t\treturn *st.begin() - 1; \n\t\t}\n\t};\n\n\t/**\n\t * Your LUPrefix object will be instantiated and called as such:\n\t * LUPrefix* obj = new LUPrefix(n);\n\t * obj->upload(video);\n\t * int param_2 = obj->longest();\n\t */ | 1 | 0 | [] | 0 |
longest-uploaded-prefix | Easy solution | C++ | easy-solution-c-by-__abcd-w9g7 | solution 1:\n\nclass LUPrefix {\npublic:\n int len = 1, a[100001] = {0};\n LUPrefix(int n) {}\n void upload(int video) {\n a[video] = 1;\n | __Abcd__ | NORMAL | 2022-10-01T16:04:43.081259+00:00 | 2022-10-01T17:52:40.954194+00:00 | 26 | false | **solution 1:**\n```\nclass LUPrefix {\npublic:\n int len = 1, a[100001] = {0};\n LUPrefix(int n) {}\n void upload(int video) {\n a[video] = 1;\n while(a[len])++len;\n }\n \n int longest() {\n return len-1;\n }\n};\n\n/**\n * Your LUPrefix object will be instantiated and called as such:\n * LUPrefix* obj = new LUPrefix(n);\n * obj->upload(video);\n * int param_2 = obj->longest();\n */\n```\n**solution 2:**\n```\nclass LUPrefix {\npublic:\n set<int> s;\n LUPrefix(int n) {\n for (int i=1; i<=n+1; i++) s.insert(i);\n }\n \n void upload(int video) {\n s.erase(video);\n }\n int longest() {\n return *s.begin()-1;\n }\n};\n\n/**\n * Your LUPrefix object will be instantiated and called as such:\n * LUPrefix* obj = new LUPrefix(n);\n * obj->upload(video);\n * int param_2 = obj->longest();\n */\n``` | 1 | 0 | [] | 0 |
longest-uploaded-prefix | Easy Java Solution | easy-java-solution-by-sumitk7970-ywxc | ```\nclass LUPrefix {\n boolean[] uploaded;\n int lPrefix = 0;\n\n public LUPrefix(int n) {\n uploaded = new boolean[n+1];\n }\n \n pub | Sumitk7970 | NORMAL | 2022-10-01T16:01:14.910856+00:00 | 2022-10-01T16:09:41.242343+00:00 | 102 | false | ```\nclass LUPrefix {\n boolean[] uploaded;\n int lPrefix = 0;\n\n public LUPrefix(int n) {\n uploaded = new boolean[n+1];\n }\n \n public void upload(int video) {\n uploaded[video] = true;\n for(int i=lPrefix+1; i<uploaded.length; i++) {\n if(uploaded[i]) {\n lPrefix++;\n } else {\n break;\n }\n }\n }\n \n public int longest() {\n return lPrefix;\n }\n}\n | 1 | 0 | ['Java'] | 0 |
longest-uploaded-prefix | Very Very Easy| O(N) | very-very-easy-on-by-charitramehlawat-jeoa | \nclass LUPrefix {\npublic:\n vector<int>v;\n int count = 0;// will act as the index and the count of prefix\n LUPrefix(int n) {\n v.resize(n+5, | charitramehlawat | NORMAL | 2022-10-01T16:01:14.485735+00:00 | 2022-10-01T16:04:31.824639+00:00 | 143 | false | ```\nclass LUPrefix {\npublic:\n vector<int>v;\n int count = 0;// will act as the index and the count of prefix\n LUPrefix(int n) {\n v.resize(n+5,0);\n }\n \n void upload(int video) {\n // Set video-1->index as 1\n v[video-1] = 1;\n // take count as the index and increment it until we get 0 on the index\n while(v[count]!=0)count++; \n }\n \n int longest() {\n // As we are using 0 based indexing so the where the count is zero all the prev elements are 1 \n return count;\n }\n};\n\n/**\n * Your LUPrefix object will be instantiated and called as such:\n * LUPrefix* obj = new LUPrefix(n);\n * obj->upload(video);\n * int param_2 = obj->longest();\n */\n``` | 1 | 0 | ['C', 'C++'] | 0 |
longest-uploaded-prefix | Union Find - C++ | union-find-c-by-shivanshudobhal-u1sv | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | shivanshudobhal | NORMAL | 2025-04-10T16:21:52.074438+00:00 | 2025-04-10T16:21:52.074438+00:00 | 1 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class DSU{
public:
vector<int> par,size;
DSU(int n){
par.resize(n);
size.resize(n,1);
for(int i=0;i<n;i++){
par[i]=i;
}
}
int findUPar(int node){
if(par[node]==node) return node;
return par[node] = findUPar(par[node]);
}
void unionBySize(int u, int v){
int up_u = findUPar(u);
int up_v = findUPar(v);
if(up_u==up_v) return;
else if(size[up_u]<size[up_v]){
par[up_u] = up_v;
size[up_v]+=size[up_u];
} else {
par[up_v] = up_u;
size[up_u]+=size[up_v];
}
}
};
class LUPrefix {
public:
vector<int> vis;
int x = 0;
DSU ds;
LUPrefix(int n): ds(n+1) {
vis.resize(n+1,0);
}
void upload(int video) {
vis[video] = 1;
// for(int i=1;i<vis.size()-1;i++){
// if(vis[i]==0 || vis[i+1]==0)
// break;
// ds.unionBySize(i,i+1);
// }
if(vis.size()-1 > 1){
if(video==1){
if(vis[video+1]==1)
ds.unionBySize(video,video+1);
} else if(video == vis.size()-1){
if(vis[video-1]==1)
ds.unionBySize(video,video-1);
} else {
if(vis[video+1]==1)
ds.unionBySize(video,video+1);
if(vis[video-1]==1)
ds.unionBySize(video,video-1);
}
}
}
int longest() {
if(vis.size()-1==1)
return vis[1] == 1;
return vis[1]==0?0:ds.size[ds.findUPar(1)];
}
};
/**
* Your LUPrefix object will be instantiated and called as such:
* LUPrefix* obj = new LUPrefix(n);
* obj->upload(video);
* int param_2 = obj->longest();
*/
``` | 0 | 0 | ['Union Find', 'C++'] | 0 |
longest-uploaded-prefix | easy solution | easy-solution-by-owenwu4-q86o | Intuitionobserve that starts at 1ApproachComplexity
Time complexity:
Space complexity:
Code | owenwu4 | NORMAL | 2025-04-04T21:16:52.925687+00:00 | 2025-04-04T21:16:52.925687+00:00 | 1 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
observe that starts at 1
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class LUPrefix:
def __init__(self, n: int):
self.n = n
self.myset = set()
self.start = 1
def upload(self, video: int) -> None:
self.myset.add(video)
#print(self.myset)
while self.start in self.myset:
self.start += 1
def longest(self) -> int:
#print(self.start)
return self.start - 1
# Your LUPrefix object will be instantiated and called as such:
# obj = LUPrefix(n)
# obj.upload(video)
# param_2 = obj.longest()
``` | 0 | 0 | ['Python3'] | 0 |
longest-uploaded-prefix | O(N) Approach | very easy in java | on-approach-very-easy-in-java-by-harikri-ove0 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | harikrishnakharikrishnak42 | NORMAL | 2025-03-09T16:36:54.759505+00:00 | 2025-03-09T16:36:54.759505+00:00 | 4 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class LUPrefix {
int[] fre ;
int max ;
int ind ;
public LUPrefix(int n) {
fre = new int[n + 1] ;
max = 0 ;
ind = 1 ;
}
public void upload(int video) {
fre[video] = 1 ;
}
public int longest() {
while (ind <= fre.length - 1 && fre[ind] == 1) {
ind++;
}
return ind - 1;
}
}
/**
* Your LUPrefix object will be instantiated and called as such:
* LUPrefix obj = new LUPrefix(n);
* obj.upload(video);
* int param_2 = obj.longest();
*/
``` | 0 | 0 | ['Java'] | 0 |
longest-uploaded-prefix | C++ solution with array | c-solution-with-array-by-oleksam-zwn8 | Please, upvote if you like it. Thanks :-)Complexity
Time complexity:
O(1)
Space complexity:
O(n)
Code | oleksam | NORMAL | 2025-03-07T20:49:04.474515+00:00 | 2025-03-07T20:49:04.474515+00:00 | 4 | false | Please, upvote if you like it. Thanks :-)
# Complexity
- Time complexity:
O(1)
- Space complexity:
O(n)
# Code
```cpp []
class LUPrefix {
public:
LUPrefix(int n) {
videos.resize(n + 1);
}
void upload(int video) {
videos[video] = 1;
while (maxUploaded + 1 < videos.size() && videos[maxUploaded + 1] == 1)
maxUploaded++;
}
int longest() {
return maxUploaded;
}
private:
int maxUploaded = 0;
vector<int> videos;
};
``` | 0 | 0 | ['Array', 'Design', 'C++'] | 0 |
longest-uploaded-prefix | Python3 O(N) Solution with count sorting (99.05% Runtime) | python3-on-solution-with-count-sorting-9-drvg | IntuitionApproach
Define an array for count sorting and iteratively update corresnponding index.
Return the current index of the array and update it if needed. | missingdlls | NORMAL | 2025-02-21T06:55:50.507773+00:00 | 2025-02-21T06:55:50.507773+00:00 | 8 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
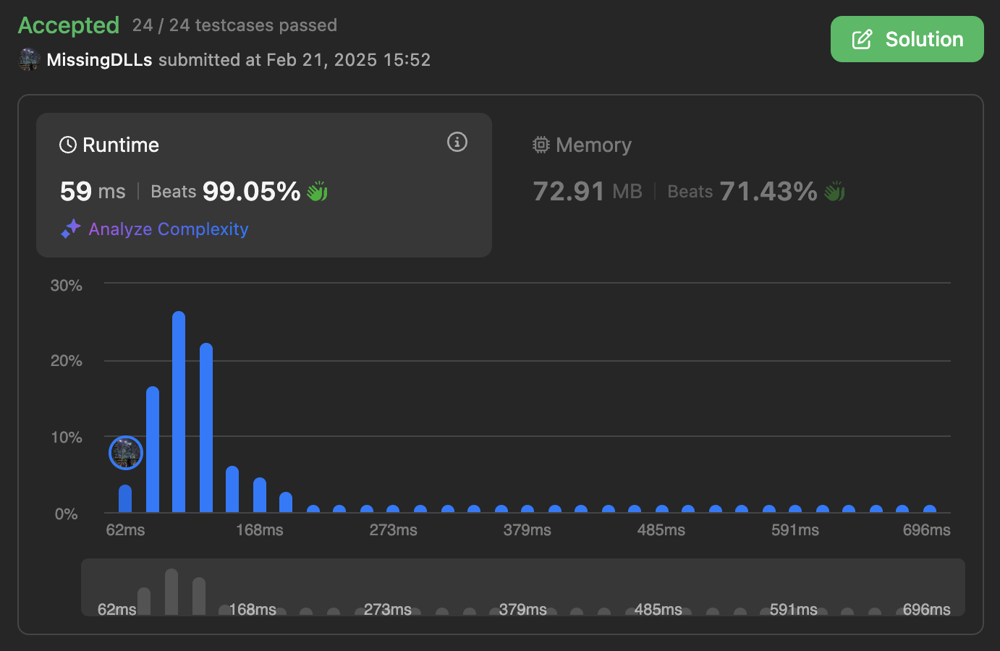
# Approach
<!-- Describe your approach to solving the problem. -->
- Define an array for count sorting and iteratively update corresnponding index.
- Return the current index of the array and update it if needed.
# Complexity
- Time complexity: O(N)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(N)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
If this solution is similar to yours or helpful, upvote me if you don't mind
```python3 []
class LUPrefix:
def __init__(self, n: int):
self.n=n
self.m=n+1
self.a=[False]*(self.m)
self.i=1
def upload(self, video: int) -> None:
self.a[video]=True
def longest(self) -> int:
while self.i<=self.n and self.a[self.i]:
self.i+=1
return self.n if self.i==self.m else self.i-1
# Your LUPrefix object will be instantiated and called as such:
# obj = LUPrefix(n)
# obj.upload(video)
# param_2 = obj.longest()
``` | 0 | 0 | ['Array', 'Math', 'Design', 'Queue', 'Counting', 'Monotonic Queue', 'Counting Sort', 'Python', 'Python3'] | 0 |
longest-uploaded-prefix | Python3 solution using list O(1) time, O(n) memory | python3-solution-using-list-o1-time-on-m-f9wu | IntuitionApproachComplexity
Time complexity:
O(1) for each of operations, O(n) if we include array initialization in constructor.
Space complexity:
O(n)
Cod | saitama1v1 | NORMAL | 2025-02-01T19:25:39.740407+00:00 | 2025-02-01T19:25:39.740407+00:00 | 12 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
O(1) for each of operations, O(n) if we include array initialization in constructor.
- Space complexity:
O(n)
# Code
```python3 []
class LUPrefix:
def __init__(self, n: int):
self.array = [0]*n
self.n = n
def upload(self, video: int) -> None:
idx = video - 1
max_len_left = 0
if idx > 0:
max_len_left = self.array[idx - 1]
max_len_right = 0
if idx < self.n - 1:
max_len_right = self.array[idx + 1]
new_size = max_len_left + max_len_right + 1
self.array[idx] = new_size
if idx - max_len_left >= 0:
self.array[idx - max_len_left] = new_size
if idx + max_len_right < self.n:
self.array[idx + max_len_right] = new_size
def longest(self) -> int:
return self.array[0]
# Your LUPrefix object will be instantiated and called as such:
# obj = LUPrefix(n)
# obj.upload(video)
# param_2 = obj.longest()
``` | 0 | 0 | ['Python3'] | 0 |
longest-uploaded-prefix | Easy way to solve beat 100% | easy-way-to-solve-beat-100-by-anayet_has-8n5o | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | Anayet_Hasan_Niloy | NORMAL | 2025-02-01T00:31:22.693676+00:00 | 2025-02-01T00:31:22.693676+00:00 | 4 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class LUPrefix {
public:
LUPrefix(int n) {
}
void upload(int video) {
uploadedVideos.insert(video);
while (uploadedVideos.count(longestSequence + 1)) {
++longestSequence;
}
}
int longest() {
return longestSequence;
}
private:
int longestSequence = 0;
unordered_set<int> uploadedVideos;
};
/**
* Your LUPrefix object will be instantiated and called as such:
* LUPrefix* obj = new LUPrefix(n);
* obj->upload(video);
* int param_2 = obj->longest();
*/
``` | 0 | 0 | ['C++'] | 0 |
longest-uploaded-prefix | 2424. Longest Uploaded Prefix | 2424-longest-uploaded-prefix-by-g8xd0qpq-xw6i | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | G8xd0QPqTy | NORMAL | 2025-01-18T14:46:36.229383+00:00 | 2025-01-18T14:46:36.229383+00:00 | 10 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class LUPrefix:
def __init__(self, n: int):
self.uploaded = [False] * (n + 1)
self.max_prefix = 0
def upload(self, video: int):
self.uploaded[video] = True
while self.max_prefix + 1 <= len(self.uploaded) - 1 and self.uploaded[self.max_prefix + 1]:
self.max_prefix += 1
def longest(self) -> int:
return self.max_prefix
``` | 0 | 0 | ['Python3'] | 0 |
longest-uploaded-prefix | Using DSU || Simple Beginner Friendly Solution with Dry Run | using-dsu-simple-beginner-friendly-solut-vpam | Intuitionprerequisite : DSU. If you don't know what this is then I'll recommend u to study that first. You can follow this to study dsu: DSU by StriverNow that | 5umit_kun | NORMAL | 2025-01-12T20:29:17.629749+00:00 | 2025-01-12T20:29:17.629749+00:00 | 9 | false | # Intuition
**prerequisite** : DSU. If you don't know what this is then I'll recommend u to study that first. You can follow this to study dsu: [DSU by Striver](https://takeuforward.org/data-structure/disjoint-set-union-by-rank-union-by-size-path-compression-g-46/)
Now that you know what dsu is lets understand why dsu can be used here to efficiently track the longest prefix length.
**The intuition behind using a DSU in this problem is to efficiently track and manage consecutive uploaded videos as a single connected component.**
The longest prefix of uploaded videos starting from 1 can be determined by checking the size of the connected component that starts from video 1.
Here each time we add a video, we can (i):Connect to its next video (if uploaded) and (ii): Connect to its previous video (if uploaded).
Note that here we wont be doing union by size or union by rank, instead we will connect the larger video number to the smaller video number (here video number does not means size) and add the size of ultimate parent of larger video number to ultimate parent of smaller video number so that for each chunk , the size[start] stores the size of the component.
By merging these groups, DSU ensures that all consecutive uploaded videos are treated as one connected component.
# Approach
Inorder to check whether the next and previous videos have been uploaded we will maintain an array. This will also help us to check whether '1' has been uploaded previously at any particular moment.
# Upload function:
- Connect the video with the next video(if the next video is visited) by taking a union between them.
- Connect the video with the prev video(if the prev one is visited or already added) by taking a union between them.
- Now mark the current video as visited or available.
- Then check if the video '1' is already available if it is the size[1] is the length of the component starting from '1', update the variable which stores the maximum length prefix.
> Dry run: Suppose we already have videos 1 and 3 and now we want to upload 2
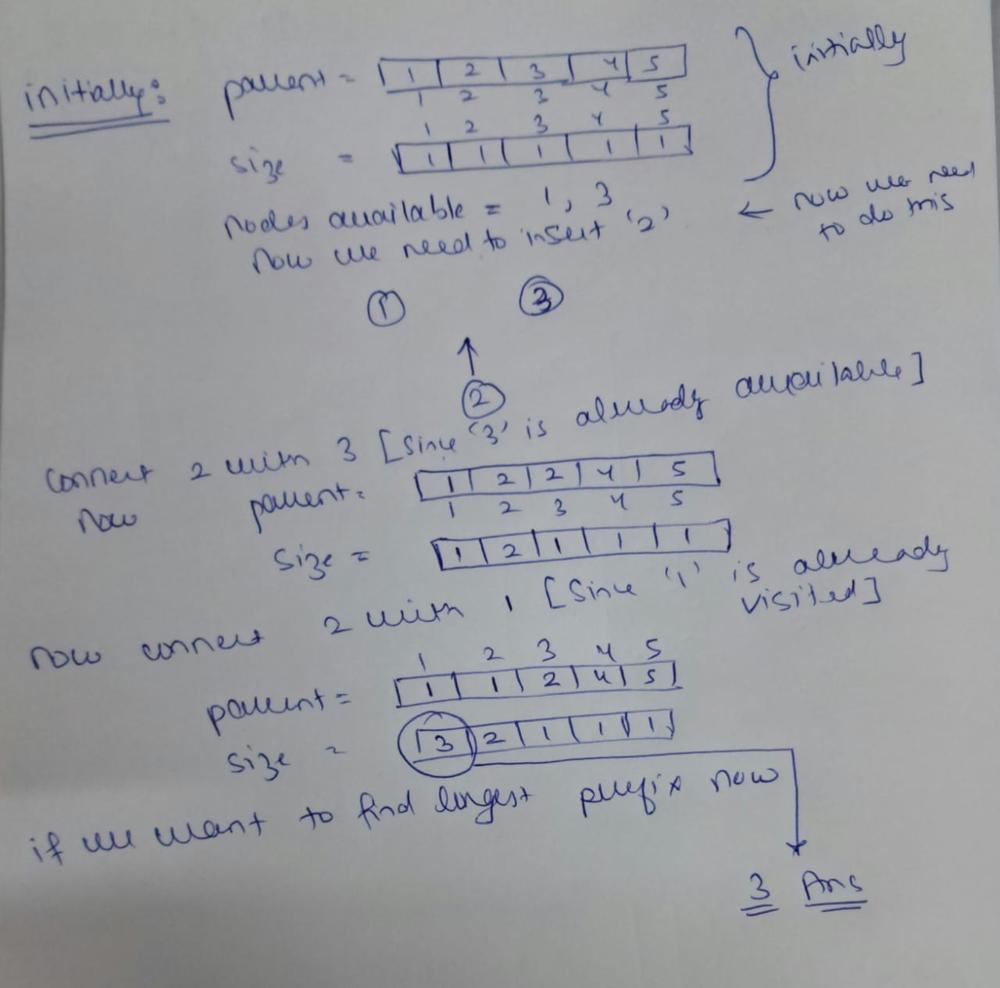
# longest function:
just return the variable that we have used to maintain the maximum prefix length.
# Code
```cpp []
class DisjointSet{
public:
vector<int>parent;
vector<int>size;
DisjointSet(int n){
parent.resize(n);
size.resize(n);
for(int i=0;i<n;i++){
parent[i]=i;
size[i]=1;
}
}
int findUPar(int node){
if(parent[node]==node){
return node;
}
return parent[node]=findUPar(parent[node]);
}
void un(int u,int v){
//u mein smaller bhejo
int uu=findUPar(u);
int uv=findUPar(v);
if(uu==uv){
return;
}
parent[uv]=uu;
size[uu]+=size[uv];
}
};
class LUPrefix {
public:
DisjointSet* ds=NULL;
vector<int>v;
int maxi=0;
int n;
LUPrefix(int n) {
ds=new DisjointSet(n+1);
v.resize(n+1,0);
this->n=n;
}
void upload(int video) {
if(video<n){
if(v[video+1]==1){
ds->un(video,video+1);
}
}
if(video>1){
if(v[video-1]==1){
ds->un(video-1,video);
}
}
v[video]=1;
if(v[1]==1){
maxi=max(maxi,ds->size[1]);
}
}
int longest() {
return maxi;
}
};
/**
* Your LUPrefix object will be instantiated and called as such:
* LUPrefix* obj = new LUPrefix(n);
* obj->upload(video);
* int param_2 = obj->longest();
*/
``` | 0 | 0 | ['Union Find', 'C++'] | 0 |
longest-uploaded-prefix | Beats 99% - simple boolean array O(1) Amortized | beats-99-simple-boolean-array-o1-amortiz-8lja | IntuitionCreate a boolean array of size n.
Keep track of where the longest prefix should be (initially 0);
Decrement each video for easier indexing.
If we uploa | aginton3 | NORMAL | 2025-01-08T21:25:41.032006+00:00 | 2025-01-08T21:25:41.032006+00:00 | 5 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Create a boolean array of size `n`.
Keep track of where the longest prefix should be (initially 0);
Decrement each video for easier indexing.
If we upload a video to longest position, then we know we have a block of at least length longest, i.e., from [0, longest]. Then, we can scan adjacent cells to the right that are true, incrementing total and giving us the total size of longest.
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
Amortized Complexity of upload(int video)
Worst Case:
In a single upload, the while loop may iterate over 𝑂(𝑛) indices (e.g., when all elements in mem are true after the upload).
Best Case:
The while loop does not execute (e.g., if the uploaded video index is not equal to longest).
Key Observation: The longest variable is only incremented and updated once per index during the lifetime of the program. This means the total work across all calls to upload is proportional to 𝑂(𝑛)
Thus, the amortized time complexity of each call to upload is O(1).
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class LUPrefix {
boolean[] mem;
int longest = 0;
public LUPrefix(int n) {
mem = new boolean[n];
}
public void upload(int video) {
video--;
mem[video]=true;
if (video == longest){
longest++;
while (longest < mem.length && mem[longest]){
longest++;
}
}
}
public int longest() {
return longest;
}
}
/**
* Your LUPrefix object will be instantiated and called as such:
* LUPrefix obj = new LUPrefix(n);
* obj.upload(video);
* int param_2 = obj.longest();
*/
``` | 0 | 0 | ['Java'] | 0 |
longest-uploaded-prefix | Lazy Calc Longest, constant upload, using array | lazy-calc-longest-constant-upload-using-5x56z | Intuitionwhen the longest is requested, start from the previously calculated longest and step forward and capture any additional uploads to prefix.ApproachMost | sajackson | NORMAL | 2025-01-03T21:40:40.462717+00:00 | 2025-01-03T21:40:40.462717+00:00 | 2 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
when the longest is requested, start from the previously calculated longest and step forward and capture any additional uploads to prefix.
# Approach
Most other solutions do the longest calculation at the end of upload(), this keeps the calculation time averaged, but is also unnecessary work in the case where longest() is not called after upload(). So I did the calculation at the beginning of longest(), essentially a lazier approach.
# Complexity
- Time complexity:
upload: O(1)
longest: O(1) amortized, no more than O(n)
- Space complexity:
O(n)
# Code
```typescript []
class LUPrefix {
data: boolean[];
long_pre: number;
constructor(n: number) {
this.data = new Array(n);
this.long_pre = 0;
}
upload(video: number): void {
this.data[video-1] = true;
}
longest(): number {
while (this.data[this.long_pre]) this.long_pre++;
return this.long_pre;
}
}
/**
* Your LUPrefix object will be instantiated and called as such:
* var obj = new LUPrefix(n)
* obj.upload(video)
* var param_2 = obj.longest()
*/
``` | 0 | 0 | ['TypeScript'] | 0 |
longest-uploaded-prefix | Python (Simple BIT) | python-simple-bit-by-rnotappl-oybu | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | rnotappl | NORMAL | 2025-01-01T07:50:45.546448+00:00 | 2025-01-01T07:50:45.546448+00:00 | 10 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class BIT:
def __init__(self,n):
self.ans = [0]*(n+1)
def update(self,i,val):
while i < len(self.ans):
self.ans[i] += val
i += i&-i
def query(self,i):
total = 0
while i:
total += self.ans[i]
i -= i&-i
return total
class LUPrefix:
def __init__(self, n):
self.res = BIT(n)
self.n = n
def upload(self, video):
self.res.update(video,1)
def longest(self):
low, high = 1, self.n
while low <= high:
mid = (low+high)//2
if self.res.query(mid) == mid:
low = mid + 1
else:
high = mid - 1
return high
``` | 0 | 0 | ['Python3'] | 0 |
longest-uploaded-prefix | bitset fun | bitset-fun-by-aneeshsaripalli-cqll | Intuition\nWe need one-bit per index.\n\nWe\'ll have some left-padded block of bits. An upload may extend this block, or add a bit somewhere else in our storage | aneeshsaripalli | NORMAL | 2024-11-30T22:11:54.424271+00:00 | 2024-11-30T22:11:54.424302+00:00 | 2 | false | # Intuition\nWe need one-bit per index.\n\nWe\'ll have some left-padded block of bits. An upload may extend this block, or add a bit somewhere else in our storage.\n\nWe can just move our count pointer left to right when longest() is called This looks at every element which is O(N), so O(1) amortized cost.\n\nWe can use the natural word size of 64-bit processors to check if all bits within a 64-bit value are set without checking all 64-bits in a scalar fashion (note that all 1s in a register is equal to -1 unsigned).\n\n# Approach\nUse STL\'s bitset to store a bit per index, up to the max count of 1e5. We set the 0 bit for convenience. We later have to subtract this out.\n\nWe keep track of the last known contiguous bit index so that we don\'t restart from the start of the list. `known_ = N` implies `[0... N]` are set.\n\nOn every call to `longest()` we see how far we can push `known_` (this is non-decreasing between calls to `longest()`). The `get()` function relies on `bitset` being typically implemented as a value type comparable to `std::array<std::uint64_t, CEIL(SIZE/64)>`. This is technically undefined behavior but tbh I don\'t care, it works in practice. `index>>6` is the same as `index/64`, and gives us the offset of the 64-bit address that stores out `n = index/64`th 64-bit word.\n\nWe handle 64-bits at a time until the next 64-bit word isn\'t all set. At this point we call `countr_one` to count the number of right padded 1s in the register. The lowest indexed bits are in the lowest bits of the register (i.e. if `b_[64*i + 1] == 1`, then `get(64*i) & 1 == 1`) so we can use countr_one to count the remanining low-contiguous 1s. \n\nWe only care for `[1...N]` (excluding our 0 at the front) so we subtract out 1 when we return a value in `longest()`.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass LUPrefix {\npublic:\n bitset<100001> b_{};\n\n size_t known_{};\n\n\n LUPrefix(int n): b_{} {\n b_[0] = true;\n }\n\n std::uint64_t const get(\n size_t index\n ) {\n return *(std::bit_cast<uint64_t const*>(&b_) + (index >> 6));\n }\n\n void upload(int video) {\n b_.set(video);\n }\n \n int longest() {\n while(get(known_) == -1UL){\n known_ += 64;\n }\n return known_ + countr_one(get(known_)) - 1;\n }\n};\n\n/**\n * Your LUPrefix object will be instantiated and called as such:\n * LUPrefix* obj = new LUPrefix(n);\n * obj->upload(video);\n * int param_2 = obj->longest();\n */\n``` | 0 | 0 | ['C++'] | 0 |
longest-uploaded-prefix | faster than 95%, CPP, O(n) worst case | faster-than-95-cpp-on-worst-case-by-lyjw-nqms | 1.\tvector<bool> done:\n \u2022\tThis vector is used to keep track of which videos have been uploaded. The index of the vector corresponds to the video I | LYjwjScNHF | NORMAL | 2024-11-24T18:51:49.642535+00:00 | 2024-11-24T18:51:49.642610+00:00 | 2 | false | 1.\t`vector<bool> done`:\n \u2022\tThis vector is used to keep track of which videos have been uploaded. The index of the vector corresponds to the video ID, and the value at that index indicates whether the video has been uploaded (`true`) or not (`false`).\n\t2.\t`int longestTillNow`:\n\t\u2022\tThis variable keeps track of the longest continuous sequence of uploaded videos starting from video 1. For example, if videos 1, 2, and 3 are uploaded, `longestTillNow` would be 3.\n\t3.\t`int total`:\n\t\u2022\tThis variable stores the total number of videos plus one (to account for indexing from 1). It is initialized to `n + 1`, where `n` is the total number of videos.\n\n Constructor: `LUPrefix(int n)`\n \u2022\tThe constructor initializes the `done` vector with a size of `n + 1`, setting all values to `false` (0). It also initializes `longestTillNow` to 0 and sets `total` to `n + 1`.\n Method: `upload(int video)`\n \u2022\tThis method is called when a video is uploaded:\n \u2022\tIt marks the corresponding index in the `done` vector as `true`, indicating that the video has been uploaded.\n \u2022\tIf the uploaded video ID matches `longestTillNow + 1`, it increments `longestTillNow`. This means if the next expected video (in sequential order) has been uploaded, it extends the longest sequence.\n Method: `longest()`\n \u2022\tThis method returns the length of the longest continuous sequence of uploaded videos:\n \u2022\tIt uses a while loop to check if the next video in sequence (`longestTillNow + 1`) has been uploaded. If it has, it increments `longestTillNow`.\n \u2022\tThe loop continues until it finds a gap (i.e., a video that hasn\u2019t been uploaded).\n \u2022\tFinally, it returns the current value of `longestTillNow`.\n\n# Code\n```cpp []\nclass LUPrefix {\npublic:\n vector<bool> done;\n int longestTillNow;\n int total;\n LUPrefix(int n) {\n done = vector<bool>(n+1, 0);\n longestTillNow = 0;\n total = n+1;\n }\n \n void upload(int video) {\n done[video]=true; \n if(video==longestTillNow+1){\n longestTillNow++;\n }\n }\n \n int longest() {\n while(longestTillNow+1<=total && done[longestTillNow+1]) longestTillNow++;\n return longestTillNow;\n }\n};\n\n/**\n * Your LUPrefix object will be instantiated and called as such:\n * LUPrefix* obj = new LUPrefix(n);\n * obj->upload(video);\n * int param_2 = obj->longest();\n */\n``` | 0 | 0 | ['C++'] | 0 |
longest-uploaded-prefix | SImple solution without binary search | simple-solution-without-binary-search-by-mhqz | \njava []\nclass LUPrefix {\n int max;\n int[]l;\n TreeSet<Integer>ts;\n // boolean \n public LUPrefix(int n) {\n max=0;\n l | risabhuchiha | NORMAL | 2024-11-23T23:11:46.514392+00:00 | 2024-11-23T23:11:46.514432+00:00 | 0 | false | \n```java []\nclass LUPrefix {\n int max;\n int[]l;\n TreeSet<Integer>ts;\n // boolean \n public LUPrefix(int n) {\n max=0;\n l=new int[n+2];\n ts=new TreeSet<>((a,b)->b-a);\n }\n \n public void upload(int v) {\n int ll=l[v-1];\n int rl=l[v+1];\n int nl=ll+rl+1;\n l[v]=nl;\n l[v-ll]=nl;\n l[v+rl]=nl;\n\n }\n \n public int longest() {\n return l[1];\n }\n}\n\n/**\n * Your LUPrefix object will be instantiated and called as such:\n * LUPrefix obj = new LUPrefix(n);\n * obj.upload(video);\n * int param_2 = obj.longest();\n */\n``` | 0 | 0 | ['Java'] | 0 |
number-of-orders-in-the-backlog | [Java/C++/Python] Priority Queue | javacpython-priority-queue-by-lee215-kn4u | Complexity\nTime O(nlogn)\nSpace O(n)\n\n\nJava\njava\n public int getNumberOfBacklogOrders(int[][] orders) {\n PriorityQueue<int[]> buy = new Priorit | lee215 | NORMAL | 2021-03-21T06:55:16.501446+00:00 | 2021-03-21T06:55:16.501475+00:00 | 9,673 | false | # **Complexity**\nTime `O(nlogn)`\nSpace `O(n)`\n<br>\n\n**Java**\n```java\n public int getNumberOfBacklogOrders(int[][] orders) {\n PriorityQueue<int[]> buy = new PriorityQueue<>((a, b) -> (b[0] - a[0]));\n PriorityQueue<int[]> sell = new PriorityQueue<>((a, b) -> (a[0] - b[0]));\n for (int[] o : orders) {\n if (o[2] == 0)\n buy.offer(o);\n else\n sell.offer(o);\n while (!buy.isEmpty() && !sell.isEmpty() && sell.peek()[0] <= buy.peek()[0]) {\n int k = Math.min(buy.peek()[1], sell.peek()[1]);\n buy.peek()[1] -= k;\n sell.peek()[1] -= k;\n if (buy.peek()[1] == 0) buy.poll();\n if (sell.peek()[1] == 0) sell.poll();\n }\n\n }\n int res = 0, mod = 1000000007;\n for (int[] o : sell)\n res = (res + o[1]) % mod;\n for (int[] o : buy)\n res = (res + o[1]) % mod;\n return res;\n }\n```\n\n**C++**\n```cpp\n int getNumberOfBacklogOrders(vector<vector<int>>& orders) {\n priority_queue<vector<int>>buy;\n priority_queue<vector<int>, vector<vector<int>>, greater<vector<int>>>sell;\n for (auto& o : orders) {\n if (o[2] == 0)\n buy.push(o);\n else\n sell.push(o);\n while (buy.size() && sell.size() && sell.top()[0] <= buy.top()[0]) {\n int k = min(buy.top()[1], sell.top()[1]);\n vector<int> tmp = buy.top(); buy.pop();\n tmp[1] -= k;\n if (tmp[1]) buy.push(tmp);\n\n tmp = sell.top(); sell.pop();\n tmp[1] -= k;\n if (tmp[1]) sell.push(tmp);\n }\n\n }\n int res = 0, mod = 1e9 + 7;\n while (sell.size())\n res = (res + sell.top()[1]) % mod, sell.pop();\n while (buy.size())\n res = (res + buy.top()[1]) % mod, buy.pop();\n return res;\n }\n```\n\n**Python**\n```py\n def getNumberOfBacklogOrders(self, orders):\n sell, buy = [], []\n for p, a, t in orders:\n if t == 0:\n heapq.heappush(buy, [-p, a])\n else:\n heapq.heappush(sell, [p, a])\n while sell and buy and sell[0][0] <= -buy[0][0]:\n k = min(buy[0][1], sell[0][1])\n buy[0][1] -= k\n sell[0][1] -= k\n if buy[0][1] == 0: heapq.heappop(buy)\n if sell[0][1] == 0: heapq.heappop(sell)\n return sum(a for p, a in buy + sell) % (10**9 + 7)\n```\n | 131 | 5 | [] | 28 |
number-of-orders-in-the-backlog | Java/Python Heap Solution | javapython-heap-solution-by-admin007-ewv8 | If you got WA, you might need to see the following requirements:\nIf the order is a buy order, you look at the sell order with the smallest price in the backlog | admin007 | NORMAL | 2021-03-21T04:01:16.350877+00:00 | 2021-03-21T04:14:46.937593+00:00 | 3,559 | false | If you got WA, you might need to see the following requirements:\n**If the order is a buy order, you look at the sell order with the smallest price in the backlog.**\n**if the order is a sell order, you look at the buy order with the largest price in the backlog**\n\n**Please upvote for this if you find it is helpful!**\n\n**Java:**\n\n```\n public int getNumberOfBacklogOrders(int[][] orders) { \n PriorityQueue<int[]> buy = new PriorityQueue<>((a, b) -> (b[0] - a[0]));\n PriorityQueue<int[]> sell = new PriorityQueue<>((a, b) -> (a[0] - b[0]));\n for (int[] o : orders) {\n if (o[2] == 0) { // processing buy orders:\n while (!sell.isEmpty() && o[0] >= sell.peek()[0] && o[1] >= sell.peek()[1]) {\n o[1] -= sell.peek()[1];\n sell.poll();\n }\n if (!sell.isEmpty() && o[0] >= sell.peek()[0] && o[1] > 0) {\n sell.peek()[1] -= o[1];\n o[1] = 0;\n }\n if (o[1] > 0) {\n buy.offer(o);\n }\n } else { // processing sell orders:\n while (!buy.isEmpty() && o[0] <= buy.peek()[0] && o[1] >= buy.peek()[1]) {\n o[1] -= buy.peek()[1];\n buy.poll();\n }\n if (!buy.isEmpty() && o[0] <= buy.peek()[0] && o[1] > 0) {\n buy.peek()[1] -= o[1];\n o[1] = 0;\n }\n if (o[1] > 0) {\n sell.offer(o);\n }\n } \n }\n long res = 0;\n for (int[] o : sell) {\n res += o[1];\n }\n for (int[] o : buy) {\n res += o[1];\n }\n return (int)(res % 1000000007);\n }\n```\n\n**Python:**\n\n```\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n buy = []\n sell = []\n for price, amount, orderType in orders :\n if orderType == 0 :\n # buy\n while amount > 0 and len(sell) > 0 :\n pt = sell[0]\n if pt[0] > price :\n break\n deal = min(amount, pt[1])\n amount -= deal\n pt[1] -= deal\n if pt[1] == 0 :\n heapq.heappop(sell)\n if amount > 0 :\n heapq.heappush(buy, [-price, amount])\n else :\n # sell\n while amount > 0 and len(buy) > 0 :\n pt = buy[0]\n if -pt[0] < price :\n break\n deal = min(amount, pt[1])\n amount -= deal\n pt[1] -= deal\n if pt[1] == 0 :\n heapq.heappop(buy)\n if amount > 0 :\n heapq.heappush(sell, [price, amount])\n res = sum([t[1] for t in buy]) + sum([t[1] for t in sell])\n return res % (10**9+7)\n```\n | 29 | 0 | [] | 3 |
number-of-orders-in-the-backlog | C++ 2 Heaps | c-2-heaps-by-votrubac-yp4e | A practical problem on how to process level 2 quotes. It took me a while to implement during the contest.\n\nWe can use min (for sell) and max (for buy) heaps. | votrubac | NORMAL | 2021-03-22T17:05:30.871238+00:00 | 2021-03-26T19:40:08.959661+00:00 | 1,736 | false | A practical problem on how to process [level 2 quotes](https://stockstotrade.com/understanding-level-2-quotes-infographic/). It took me a while to implement during the contest.\n\nWe can use min (for sell) and max (for buy) heaps. Note that we do not process an order right away, but just put it into one of the heaps. Then, we just fulfill orders while we can, pulling them from the heads of our heaps.\n\nThe intuition here is that, if there are existing orders in the heaps, those are orders that we could not process before.\n\n**C++**\nNote that we are pushing negative prices to `sell` to turn in from max heap to min heap.\n\n```cpp\nint getNumberOfBacklogOrders(vector<vector<int>>& orders) {\n priority_queue<array<int, 2>> buy, sell;\n long res = 0;\n for (auto &o : orders) {\n res += o[1];\n if (o[2])\n sell.push({-o[0], o[1]});\n else\n buy.push({o[0], o[1]});\n while (!sell.empty() && !buy.empty() && -sell.top()[0] <= buy.top()[0]) {\n auto [sell_p, sell_a] = sell.top(); sell.pop();\n auto [buy_p, buy_a] = buy.top(); buy.pop();\n auto execute = min(sell_a, buy_a);\n res -= 2 * execute;\n if (sell_a > execute)\n sell.push({sell_p, sell_a - execute});\n if (buy_a > execute)\n buy.push({buy_p, buy_a - execute}); \n }\n }\n return res % 1000000007;\n}\n``` | 18 | 0 | [] | 4 |
number-of-orders-in-the-backlog | C++ solution | priority queues | easy to implement| Beats 100% | c-solution-priority-queues-easy-to-imple-mxbk | we initialise two priority queues, one of buy and other sell, after that we iterate through the orders, \nfor every order , we have two choices:\n-> ordertype i | srinivasteja18 | NORMAL | 2021-03-21T04:07:39.010106+00:00 | 2021-03-22T05:39:10.509606+00:00 | 1,356 | false | we initialise two priority queues, one of buy and other sell, after that we iterate through the orders, \nfor every order , we have two choices:\n-> ordertype is `0-buy`, here we check three cases,\n* \t\tif sell.size() ==0, we just push our current order into buy\n* \t\tif sell.top()[0] > p , that means smallest price of sell is greater that current price of buy, so we push into buy\n* \t\tif number of order n>0\nSame with the case of ordertype 1, \n\nFinally, we count the number of orders left in both `buy` and `sell`\n\n**Please Upvote** if you find it helpful.\n\n```\n int getNumberOfBacklogOrders(vector<vector<int>>& orders) {\n priority_queue<vector<int>>buy;\n priority_queue<vector<int>,vector<vector<int>>,greater<vector<int>>>sell;\n for(vector<int>temp : orders){\n int p=temp[0], n = temp[1], t = temp[2];\n if(t==0){\n while(sell.size() && sell.top()[0] <= p && n){\n vector<int>cur = sell.top();\n if(cur[1] > n){\n cur[1] -= n;\n sell.pop();\n sell.push(cur);\n n=0;\n }else{\n n -= cur[1];\n sell.pop();\n }\n }\n if(n) buy.push({p,n,t});\n }\n else{\n while(buy.size() && buy.top()[0]>=p && n){\n vector<int>cur = buy.top();\n if(cur[1] > n){\n cur[1] -= n;\n buy.pop();\n buy.push(cur);\n n=0;\n }else{\n n -= cur[1];\n buy.pop();\n }\n }\n if(n) sell.push({p,n,t});\n }\n } \n long long int res=0;\n while(buy.size()>0){\n res += buy.top()[1];\n buy.pop();\n }\n while(sell.size()>0){\n res += sell.top()[1];\n sell.pop();\n }\n return res%1000000007;\n }\n``` | 14 | 2 | [] | 2 |
number-of-orders-in-the-backlog | Python 3 || 9 lines, w/ explanation | python-3-9-lines-w-explanation-by-spauld-sll0 | Here\'s the plan:\n1. Establish maxheap buy for buy orders and minheap sell for sell orders.\n2. Iterate through orders. Push each element onto the appropriate | Spaulding_ | NORMAL | 2023-01-03T21:07:24.565235+00:00 | 2024-06-10T20:26:20.242880+00:00 | 1,980 | false | Here\'s the plan:\n1. Establish maxheap `buy` for buy orders and minheap `sell` for sell orders.\n2. Iterate through `orders`. Push each element onto the appropriate heap.\n3. During each iteration, peak at the heads of each list and determine whether they allow a transaction. If so, pop both heads, and if one has a positive amount after the transaction, push it back on its heap, and check the new heads (lather, rinse, repeat... `while`)\n4. After the iteration,`return`the sum of`amt`in the heaps.\n\n```\nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n\n buy,sell = [], [] # <-- 1\n\n for price,amt,order in orders: # <-- 2\n if order: heappush(sell, ( price, amt)) #\n else : heappush(buy , (-price, amt)) #\n \n while buy and sell and -buy[0][0] >= sell[0][0]: # <-- 3\n #\n (buyPrice,buyAmt), (sellPrice,sellAmt) = heappop(buy), heappop(sell) #\n #\n if buyAmt > sellAmt: heappush(buy , (buyPrice , buyAmt -sellAmt)) #\n elif buyAmt < sellAmt: heappush(sell, (sellPrice, sellAmt- buyAmt)) #\n\n return sum(amt for _,amt in buy+sell)% (1000000007) # <-- 4\n```\n[https://leetcode.com/problems/number-of-orders-in-the-backlog/submissions/870707453/](http://)\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(*N*). | 13 | 0 | ['Python3'] | 1 |
number-of-orders-in-the-backlog | Heap/PQ solution with logic [Python] | heappq-solution-with-logic-python-by-_ny-99ou | Logic is:\n Since we need to do a lot of find min/max operations: use 2 heaps:\n\t max-heap b for buy, min-heap s for sell\n\t So, max buy offer is on top of he | _nyctophiliac_ | NORMAL | 2021-03-21T04:05:37.900132+00:00 | 2021-03-21T05:55:24.565258+00:00 | 1,346 | false | Logic is:\n* Since we need to do a lot of **find min/max** operations: use 2 heaps:\n\t* max-heap `b` for buy, min-heap `s` for sell\n\t* So, max buy offer is on top of heap `b`\n\t* Min sell offer is on top of heap `s`\n* Each element of heap is an array: `[price, amount]`\n* *For* each buy/sell order:\n\t* Check for the **good** condition\n\t\t* Good condition is when:\n\t\t\t* Both `b` and `s` are non-empty\n\t\t\t* Top elements satisfy: `s[0][0] <= -b[0][0]` - means `sell price <= buy price`\n\t\t\t* If **good** condition is true: a *sale* will definitely happen\n\t* *While* condition stays **good**, keep performing *sales*\n\t\t* A *sale* means:\n\t\t\t* Pick the top element of both heaps\n\t\t\t* Call their amounts `a1` and `a2`\n\t\t\t* Reduce `a1` and `a2` until one of them becomes `0`\n\t\t\t* If either `a1` or `a2` becomes `0`, pop the heap to which it belongs\n\t\t* Check if the new top of the heap satisfies **good** condition\n* Count the sum of amounts in each heap\n\n```\nclass Solution:\n def getNumberOfBacklogOrders(self, orders):\n b, s = [], []\n heapq.heapify(b)\n heapq.heapify(s)\n \n for p,a,o in orders:\n if o == 0:\n heapq.heappush(b, [-p, a])\n \n elif o == 1:\n heapq.heappush(s, [p, a])\n \n # Check "good" condition\n while s and b and s[0][0] <= -b[0][0]:\n a1, a2 = b[0][1], s[0][1]\n \n if a1 > a2:\n b[0][1] -= a2\n heapq.heappop(s)\n elif a1 < a2:\n s[0][1] -= a1\n heapq.heappop(b)\n else:\n heapq.heappop(b)\n heapq.heappop(s)\n \n count = sum([a for p,a in b]) + sum([a for p,a in s])\n return count % (10**9 + 7)\n ``` \n | 10 | 0 | ['Heap (Priority Queue)', 'Python', 'Python3'] | 2 |
number-of-orders-in-the-backlog | [Python3] priority queue | python3-priority-queue-by-ye15-sqcf | \n\nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n ans = 0\n buy, sell = [], [] # max-heap & min-heap | ye15 | NORMAL | 2021-03-21T04:03:58.847538+00:00 | 2021-03-22T00:02:37.904534+00:00 | 1,278 | false | \n```\nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n ans = 0\n buy, sell = [], [] # max-heap & min-heap \n \n for p, q, t in orders: \n ans += q\n if t: # sell order\n while q and buy and -buy[0][0] >= p: # match \n pb, qb = heappop(buy)\n ans -= 2*min(q, qb)\n if q < qb: \n heappush(buy, (pb, qb-q))\n q = 0 \n else: q -= qb \n if q: heappush(sell, (p, q))\n else: # buy order \n while q and sell and sell[0][0] <= p: # match \n ps, qs = heappop(sell)\n ans -= 2*min(q, qs)\n if q < qs: \n heappush(sell, (ps, qs-q))\n q = 0 \n else: q -= qs \n if q: heappush(buy, (-p, q))\n \n return ans % 1_000_000_007\n```\n\nA conciser implementation by @lee215\n```\nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n buy, sell = [], [] # max-heap & min-heap \n for p, q, t in orders: \n if t: heappush(sell, [p, q])\n else: heappush(buy, [-p, q])\n \n while buy and sell and -buy[0][0] >= sell[0][0]: \n qty = min(buy[0][1], sell[0][1])\n buy[0][1] -= qty\n sell[0][1] -= qty\n if not buy[0][1]: heappop(buy)\n if not sell[0][1]: heappop(sell)\n return (sum(q for _, q in sell) + sum(q for _, q in buy)) % 1_000_000_007\n``` | 8 | 1 | ['Python3'] | 3 |
number-of-orders-in-the-backlog | Java Simple and easy solution, using Priority Queue, T O(n Log(n)), S O(n) clean code with comments | java-simple-and-easy-solution-using-prio-3tjd | PLEASE UPVOTE IF YOU LIKE THIS SOLUTION\n\n\n\n\nclass Solution {\n \n PriorityQueue<Order> buyBackLog;\n PriorityQueue<Order> sellBackLog;\n \n | satyaDcoder | NORMAL | 2021-03-30T13:20:47.454235+00:00 | 2021-03-30T13:20:47.454265+00:00 | 822 | false | **PLEASE UPVOTE IF YOU LIKE THIS SOLUTION**\n\n\n\n```\nclass Solution {\n \n PriorityQueue<Order> buyBackLog;\n PriorityQueue<Order> sellBackLog;\n \n static int MOD = 1_000_000_007;\n \n \n public int getNumberOfBacklogOrders(int[][] orders) {\n \n //max heap, heapify on price\n buyBackLog = new PriorityQueue<Order>((a, b) -> (b.price - a.price));\n //min heap, heapify on price\n sellBackLog = new PriorityQueue<Order>((a, b) -> (a.price - b.price));\n \n \n //handle all order\n for(int[] order : orders){\n int price = order[0];\n int quantity = order[1];\n int orderType = order[2];\n \n if(orderType == 0){\n //buy order \n handleBuyOrder(new Order(price, quantity));\n \n }else if(orderType == 1){ \n //sell order\n handleSellOrder(new Order(price, quantity));\n }\n }\n \n long counts = 0L;\n \n //count buy backlog\n while(!buyBackLog.isEmpty()){\n counts += buyBackLog.remove().quantity; \n counts %= MOD;\n }\n \n //count sell backlog\n while(!sellBackLog.isEmpty()){\n counts += sellBackLog.remove().quantity; \n counts %= MOD;\n }\n \n \n return (int) (counts % MOD);\n }\n \n \n \n \n private void handleBuyOrder(Order buyOrder){\n //just add buyorder, if there is no sell back log\n if(sellBackLog.isEmpty()){\n buyBackLog.add(buyOrder);\n return;\n }\n \n \n while(!sellBackLog.isEmpty() && buyOrder.price >= sellBackLog.peek().price && buyOrder.quantity > 0){\n //selloder with minumum price\n Order sellOrder = sellBackLog.remove();\n \n if(buyOrder.quantity >= sellOrder.quantity){\n buyOrder.quantity -= sellOrder.quantity;\n sellOrder.quantity = 0;\n } else {\n //decrement sell order, add remaining sellorder\n sellOrder.quantity -= buyOrder.quantity;\n sellBackLog.add(sellOrder);\n \n buyOrder.quantity = 0;\n }\n }\n \n //add reaming buyorder\n if(buyOrder.quantity > 0){\n buyBackLog.add(buyOrder);\n }\n }\n \n \n private void handleSellOrder(Order sellOrder){\n //just add sell order, if there is no buy backlog\n if(buyBackLog.isEmpty()){\n sellBackLog.add(sellOrder);\n return;\n }\n \n \n while(!buyBackLog.isEmpty() && buyBackLog.peek().price >= sellOrder.price && sellOrder.quantity > 0){\n //buy order with maximum price\n Order buyOrder = buyBackLog.remove();\n \n if(sellOrder.quantity >= buyOrder.quantity){\n sellOrder.quantity -= buyOrder.quantity;\n buyOrder.quantity = 0;\n \n }else{\n //decrement buy order quantity, add remaining buyorder\n buyOrder.quantity -= sellOrder.quantity;\n buyBackLog.add(buyOrder);\n \n sellOrder.quantity = 0;\n }\n }\n \n //add remaining sell order\n if(sellOrder.quantity > 0){\n sellBackLog.add(sellOrder);\n }\n }\n}\n\nclass Order{\n int price;\n int quantity;\n \n public Order(int price, int quantity){\n this.price = price;\n this.quantity = quantity;\n }\n}\n``` | 5 | 1 | ['Heap (Priority Queue)', 'Java'] | 1 |
number-of-orders-in-the-backlog | [Python] Concise Heap Implementation | python-concise-heap-implementation-by-za-klzt | Introduction\n\nWe need to find the total amount of orders that remain un-executed in the backlog of orders after a series of buy and sell orders have passed. A | zayne-siew | NORMAL | 2022-04-23T16:08:51.670524+00:00 | 2022-04-28T04:32:05.255954+00:00 | 806 | false | ### Introduction\n\nWe need to find the total amount of orders that remain un-executed in the backlog of orders after a series of buy and sell orders have passed. A buy order is executed if there exists a sell order in the backlog that has a selling price lower than or equal to the buying price, and a sell order is executed if there exists a buy order in the backlog that has a buying price greater than or equal to the selling price. Each time a buy/sell order comes, we need to compare its price with the sell/buy order with the smallest/greatest price, respectively.\n\nSince we need to obtain the smallest/greatest prices per order, a heap (priority queue) data structure is ideal for this task. For the buy order log, we require a max heap to obtain the greatest buying price; for the sell order log, we require a min heap to obtain the smallest buying price. Note that Python\'s `heapq` library implements a min heap, hence, to maintain a max heap, we need to **negate the buying prices**.\n\nTherefore, each time a buy/sell order with a given buying/selling price and the amount of orders is processed, we retrieve the sell/buy order with the smallest/largest price and execute the orders if the criteria (as mentioned above) is met. We continue to retrieve the sell/buy orders until;\n\n1. The criteria for executing the orders is no longer met.\n2. There are no more orders in the backlog to execute.\n3. There are no more orders in the current order to execute.\n\nAfter which, any remaining un-executed orders gets appended to its corresponding backlog.\n\n---\n\n### Base Implementation\n\nThis implementation features heavily on readability, and is meant to provide readers with a good understanding of how the code should work. If anything here is unclear or could be written better, please let me know in the comments.\n\n```python\nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n # note that: buy_log - max heap; sell_log - min heap\n buy_log, sell_log = [], []\n for price, amount, order_type in orders:\n target_log = buy_log if order_type else sell_log\n while amount and target_log:\n # check that the appropriate buy/sell order fits the criteria\n # if order type is sell, ensure buy order price >= current price\n # else if order type is buy, ensure sell order price <= current price\n if (order_type and abs(target_log[0][0]) < price) or \\\n (not order_type and target_log[0][0] > price):\n break\n current_price, current_amount = heappop(target_log)\n # cancel buy and sell orders\n min_amount = min(amount, current_amount)\n amount -= min_amount\n current_amount -= min_amount\n # check if there are remaining target orders\n if current_amount:\n heappush(target_log, (current_price, current_amount))\n # check if there are remaining current orders\n if amount:\n heappush(sell_log if order_type else buy_log,\n # negate price if order type is buy\n # so as to maintain a max heap for buy orders\n (price if order_type else -price, amount))\n return (sum(log_amount for _, log_amount in buy_log) + \\\n sum(log_amount for _, log_amount in sell_log))%int(1e9+7)\n```\n\n---\n\n### Concise Implementation\n\nInstead of having two separate heaps to manage the buy and sell logs, we can combine them into one tuple and use the order type to access the proper logs. If implemented correctly, taking the different comparison operators / min/max heap into account, we can save a lot of lines because none of the code is repeated.\n\nThe following code has been revised for readability, as suggested by [@daBozz](https://leetcode.com/daBozz/).\n\n```python\nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n backlog = ([], []) # (buy (max-heap), sell (min-heap))\n for price, amount, order_type in orders:\n # check that the appropriate buy/sell order fits the criteria in the while loop\n # note that le, ge come from the Python operator library\n # equivalent to: le - lambda a, b: a <= b\n # ge - lambda a, b: a >= b\n while amount > 0 and \\\n (target_log := backlog[1-order_type]) and \\\n (le, ge)[order_type](abs(target_log[0][0]), price):\n curr_price, curr_amount = heappop(target_log)\n if (amount := amount-curr_amount) < 0: # there are remaining target orders\n heappush(target_log, (curr_price, -amount))\n if amount > 0: # there are remaining current orders\n heappush(backlog[order_type], (price if order_type else -price, amount))\n # note that itemgetter comes from the Python operator library\n # equivalent to: lambda t: t[1]\n return sum(sum(map(itemgetter(1), log)) for log in backlog)%int(1e9+7)\n```\n\n**TC: O(nlogk)**, where `n` is the number of orders and `k` is the maximum length of either the buy or sell backlogs.\n**SC: O(n)**, taking both backlogs into account.\n\n---\n\nPlease upvote if this has helped you! Appreciate any comments as well :) | 4 | 0 | ['Heap (Priority Queue)', 'Python', 'Python3'] | 1 |
number-of-orders-in-the-backlog | Java TreeMap | java-treemap-by-mayank12559-uydh | \npublic int getNumberOfBacklogOrders(int[][] orders) {\n TreeMap<Integer, Long> buy = new TreeMap();\n TreeMap<Integer, Long> sell = new TreeMap( | mayank12559 | NORMAL | 2021-03-21T04:00:39.673759+00:00 | 2021-03-21T04:00:39.673791+00:00 | 461 | false | ```\npublic int getNumberOfBacklogOrders(int[][] orders) {\n TreeMap<Integer, Long> buy = new TreeMap();\n TreeMap<Integer, Long> sell = new TreeMap();\n for(int []order: orders){\n long orderCount = order[1];\n if(order[2] == 0){\n while(true){\n Map.Entry<Integer, Long> me = sell.firstEntry();\n if(orderCount == 0 || me == null || me.getKey() > order[0]){\n break;\n }\n if(me.getValue() <= orderCount){\n sell.remove(me.getKey());\n }else{\n sell.put(me.getKey(), me.getValue() - orderCount);\n }\n orderCount = Math.max(0, orderCount - me.getValue());\n }\n if(orderCount != 0)\n buy.put(order[0], buy.getOrDefault(order[0], 0L) + orderCount);\n }else{\n while(true){\n Map.Entry<Integer, Long> me = buy.lastEntry();\n if(orderCount == 0 || me == null || me.getKey() < order[0]){\n break;\n }\n if(me.getValue() <= orderCount){\n buy.remove(me.getKey());\n }else{\n buy.put(me.getKey(), me.getValue() - orderCount);\n }\n orderCount = Math.max(0, orderCount - me.getValue());\n }\n if(orderCount != 0)\n sell.put(order[0], sell.getOrDefault(order[0], 0L) + orderCount);\n }\n }\n long ans = 0;\n for(Long i: buy.values()){\n ans += i;\n }\n for(Long i: sell.values()){\n ans += i;\n }\n return (int)(ans % 1000000007);\n }\n``` | 4 | 1 | [] | 3 |
number-of-orders-in-the-backlog | Java || 2 Priority Queues || 1ms Beats 90% | java-2-priority-queues-1ms-beats-90-by-d-7dgj | \nclass Order implements Comparable<Order> {\n int price, amount, orderType;\n Order(int price, int amount, int orderType) {\n this.price = price;\ | devansh2805 | NORMAL | 2022-04-14T08:16:11.302601+00:00 | 2022-04-14T08:16:11.302629+00:00 | 706 | false | ```\nclass Order implements Comparable<Order> {\n int price, amount, orderType;\n Order(int price, int amount, int orderType) {\n this.price = price;\n this.amount = amount;\n this.orderType = orderType;\n }\n \n @Override\n public int compareTo(Order order) {\n return this.price - order.price;\n }\n}\n\nclass Solution {\n static final int BUY = 0, SELL = 1, mod = 1000000007;\n public int getNumberOfBacklogOrders(int[][] orders) {\n PriorityQueue<Order> sellBacklog = new PriorityQueue<>();\n PriorityQueue<Order> buyBacklog = new PriorityQueue<>(Collections.reverseOrder());\n for(int[] order: orders) {\n int price = order[0], amount = order[1], orderType = order[2];\n Order orderInstance = new Order(price, amount, orderType);\n if(orderType == SELL) {\n Order topBuy = buyBacklog.peek();\n while(topBuy != null && \n topBuy.price >= orderInstance.price && \n orderInstance.amount > 0) {\n int buysRemaining = Math.max(0, topBuy.amount - orderInstance.amount);\n int orderRemainig = Math.max(0, orderInstance.amount - topBuy.amount);\n topBuy.amount = buysRemaining;\n if(buysRemaining == 0) {\n buyBacklog.poll();\n }\n orderInstance.amount = orderRemainig; \n topBuy = buyBacklog.peek();\n }\n if(orderInstance.amount > 0) {\n sellBacklog.add(orderInstance);\n }\n } else {\n Order topSell = sellBacklog.peek();\n while(topSell != null && \n topSell.price <= orderInstance.price && \n orderInstance.amount > 0) {\n int sellsRemaining = Math.max(0, topSell.amount - orderInstance.amount);\n int orderRemaining = Math.max(0, orderInstance.amount - topSell.amount);\n topSell.amount = sellsRemaining;\n if(sellsRemaining == 0) {\n sellBacklog.poll();\n }\n orderInstance.amount = orderRemaining;\n topSell = sellBacklog.peek();\n }\n if(orderInstance.amount > 0) {\n buyBacklog.add(orderInstance);\n }\n }\n }\n int total = 0;\n while(!sellBacklog.isEmpty()) {\n Order sell = sellBacklog.poll();\n total = (total + sell.amount) % mod;\n }\n while (!buyBacklog.isEmpty()) {\n Order buy = buyBacklog.poll();\n total = (total + buy.amount) % mod;\n }\n return total;\n }\n}\n``` | 3 | 0 | ['Heap (Priority Queue)', 'Java'] | 0 |
number-of-orders-in-the-backlog | [C++] 2 Heaps | c-2-heaps-by-aparna_g-m61n | \nclass Solution {\npublic:\n int getNumberOfBacklogOrders(vector<vector<int>>& orders) {\n int n = orders.size();\n //0 - buy , 1 - sell; \n | aparna_g | NORMAL | 2021-07-18T18:49:08.605822+00:00 | 2021-07-18T18:49:25.443370+00:00 | 387 | false | ```\nclass Solution {\npublic:\n int getNumberOfBacklogOrders(vector<vector<int>>& orders) {\n int n = orders.size();\n //0 - buy , 1 - sell; \n priority_queue<vector<int>> buyBacklog;\n priority_queue<vector<int> , vector<vector<int>> , greater<vector<int>>> sellBacklog;\n \n for(auto order : orders) {\n if(order[2] == 0) \n buyBacklog.push(order);\n else \n sellBacklog.push(order);\n \n while(!buyBacklog.empty() && !sellBacklog.empty() && sellBacklog.top()[0] <= buyBacklog.top()[0]) {\n auto btop = buyBacklog.top();\n buyBacklog.pop();\n auto stop = sellBacklog.top();\n sellBacklog.pop();\n int diff = btop[1] - stop[1];\n if(diff > 0) {\n btop[1] = diff;\n buyBacklog.push(btop);\n }\n else if(diff<0) {\n stop[1] = abs(diff);\n sellBacklog.push(stop);\n }\n }\n }\n \n int ans = 0 , mod = 1e9+7;\n while(!buyBacklog.empty()){\n ans = (ans +buyBacklog.top()[1])%mod;\n buyBacklog.pop();\n }\n while(!sellBacklog.empty()){\n ans = (ans+ sellBacklog.top()[1])%mod;\n sellBacklog.pop();\n }\n return ans;\n }\n};\n``` | 3 | 0 | ['C', 'Heap (Priority Queue)', 'C++'] | 0 |
number-of-orders-in-the-backlog | Python // 2 Heaps // Readable code with dataclass | python-2-heaps-readable-code-with-datacl-gtwu | The readability of your code is as important as the correctness of your solution.\n\nWhenever possible, I like to convert input arrays into custom objects with | GroovySpoon | NORMAL | 2021-05-22T19:57:45.295861+00:00 | 2021-05-22T19:57:45.295918+00:00 | 607 | false | The readability of your code is as important as the correctness of your solution.\n\nWhenever possible, I like to convert input arrays into custom objects with readable field names.\n\n```Python\nfrom enum import IntEnum\nfrom dataclasses import dataclass, field\n\nclass oType(IntEnum):\n BUY = 0\n SELL = 1\n\n# Sort based on price. (Other fields not used in compare).\n@dataclass(order = True)\nclass Order:\n price: int\n amount: int = field(compare = False)\n orderType: oType = field(compare = False)\n\n\nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n orders = [Order(*o) for o in orders]\n \n buyHeap: Order = []\n sellHeap: Order = []\n \n for incomingOrder in orders:\n if incomingOrder.orderType == oType.BUY:\n while sellHeap and sellHeap[0].price <= incomingOrder.price:\n sellOrder = heapq.heappop(sellHeap)\n if sellOrder.amount < incomingOrder.amount:\n incomingOrder.amount -= sellOrder.amount\n elif sellOrder.amount == incomingOrder.amount:\n incomingOrder.amount = 0\n break\n elif sellOrder.amount > incomingOrder.amount:\n sellOrder.amount = sellOrder.amount - incomingOrder.amount\n incomingOrder.amount = 0\n heapq.heappush(sellHeap, sellOrder)\n break\n if incomingOrder.amount > 0:\n # negate for max heap\n incomingOrder.price = -incomingOrder.price\n heapq.heappush(buyHeap, incomingOrder)\n elif incomingOrder.orderType == oType.SELL:\n while buyHeap and -buyHeap[0].price >= incomingOrder.price:\n buyOrder = heapq.heappop(buyHeap)\n if buyOrder.amount < incomingOrder.amount:\n incomingOrder.amount -= buyOrder.amount\n elif buyOrder.amount == incomingOrder.amount:\n incomingOrder.amount = 0\n break\n elif buyOrder.amount > incomingOrder.amount:\n buyOrder.amount = buyOrder.amount - incomingOrder.amount\n incomingOrder.amount = 0\n heapq.heappush(buyHeap, buyOrder)\n break\n if incomingOrder.amount > 0:\n heapq.heappush(sellHeap, incomingOrder)\n \n buySum = sum([order.amount for order in buyHeap])\n sellSum = sum([order.amount for order in sellHeap])\n return (buySum + sellSum) % (10**9 + 7)\n```\n \n \n \n | 3 | 0 | [] | 1 |
number-of-orders-in-the-backlog | C++ | priority Queue | solution | c-priority-queue-solution-by-quantico_ku-debk | \nclass Solution {\npublic:\n int mod = 1e9+7;\n int getNumberOfBacklogOrders(vector<vector<int>>& orders) {\n priority_queue<pair<int, int>>buy;\n | quantico_kush | NORMAL | 2021-03-21T11:51:40.273407+00:00 | 2021-03-21T11:59:31.080414+00:00 | 228 | false | ```\nclass Solution {\npublic:\n int mod = 1e9+7;\n int getNumberOfBacklogOrders(vector<vector<int>>& orders) {\n priority_queue<pair<int, int>>buy;\n priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> sell;\n for(auto x : orders)\n {\n int cnt = x[1];\n if(x[2]==1)\n { \n while(!buy.empty() && cnt)\n { // if orderType is sell, then we look for\n int f = buy.top().first; //all largest value in buy, and decrease the amount \n if(f>=x[0])\n {\n int s = buy.top().second;\n buy.pop();\n int mn = min(s, cnt); \n s -= mn;\n cnt -=mn; \n if(s) buy.push({f, s});\n }else break; \n }\n if(cnt) sell.push({x[0], cnt}); // if still amount is left we push into sell heap\n }\n else\n {\n while(!sell.empty() && cnt)\n { // if orderType is buy, then we look for\n int f = sell.top().first; //all smallest value in sell, and decrease the amount \n if(f<=x[0])\n {\n int s = sell.top().second; \n sell.pop(); \n int mn = min(s, cnt); \n s -= mn;\n cnt -=mn; \n if(s) sell.push({f, s});\n }else break;\n }\n if(cnt) buy.push({x[0], cnt}); // if still amount is left we push into buy heap\n }\n }\n // calculating remaining orders\n int ans = 0;\n while(!sell.empty())\n {\n ans = (ans + sell.top().second)%mod;\n sell.pop();\n }\n while(!buy.empty())\n {\n ans = (ans + buy.top().second)%mod;\n buy.pop();\n }\n return ans%mod;\n }\n};\n``` | 3 | 0 | ['Heap (Priority Queue)'] | 0 |
number-of-orders-in-the-backlog | Python - Priority Queue Solution - O(nlogn) | python-priority-queue-solution-onlogn-by-myr3 | Maintain two priority queues. One for the buy orders and the other for the sell orders\n\nfrom queue import PriorityQueue\nclass Solution:\n def getNumberOfB | incomingoogle | NORMAL | 2021-03-21T07:36:11.165924+00:00 | 2021-03-21T07:52:22.219947+00:00 | 161 | false | Maintain two priority queues. One for the buy orders and the other for the sell orders\n```\nfrom queue import PriorityQueue\nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n buy_q = PriorityQueue()\n sell_q = PriorityQueue()\n\n for odr in orders:\n if odr[2] == 1: #sell\n while buy_q.qsize()>0 and odr[1] > 0: #while there is backlog and odr[1]!=0\n price, quant = buy_q.get() \n if -price < odr[0]: #if the highest order price in buy_q is less than current order price\n buy_q.put((price,quant))\n break\n \n deal = min(quant, odr[1]) #max buy backlog that can be removed from buy\n odr[1] -= deal #subract from the current sell quantity\n \n if deal != quant: buy_q.put((price, quant - deal)) #push the remaining buy backlog the the buy_q\n \n if odr[1]>0:\n sell_q.put((odr[0], odr[1])) #push the remaning sell items to the sell_q\n \n else: #buy\n while sell_q.qsize()>0 and odr[1] > 0: #while there is backlog and odr[1]!=0\n price, quant = sell_q.get() \n if price > odr[0]: #if the lowest order price in sell_q is less than current order price\n sell_q.put((price,quant))\n break\n \n deal = min(quant, odr[1]) #max sell backlog that can be removed from sell\n odr[1] -= deal #subract from the current buy quantity\n \n if deal != quant: sell_q.put((price, quant - deal)) #push the remaining sell backlog the the sell_q\n \n if odr[1]>0:\n buy_q.put((-odr[0], odr[1])) #push the remaning buy items to the buy_q\n \n total_back = 0 #total backlog\n while sell_q.qsize()>0:\n total_back += sell_q.get()[1]\n\n while buy_q.qsize() > 0:\n total_back += buy_q.get()[1]\n \n return total_back%(10**9 + 7)\n```\n | 3 | 1 | [] | 0 |
number-of-orders-in-the-backlog | C++ | Map Solution | Question Explained | c-map-solution-question-explained-by-bla-odvp | The description of the question is quite difficult to understand. I\'ll put it in an easier way:\n\n1. when you buy (stock), you buy from the lowest sell orders | blackhole99 | NORMAL | 2021-03-21T05:08:20.515917+00:00 | 2021-03-24T16:28:47.668500+00:00 | 141 | false | The description of the question is quite difficult to understand. I\'ll put it in an easier way:\n\n1. when you buy (stock), you buy from the lowest sell orders up to your limit price, until everything available is exhausted;\n2. when you sell (stock), you sell to the highest buy orders to until your own limit price, until everything higher (or equal) than your limit price is exhausted.\n\n```\nclass Solution {\npublic:\n int getNumberOfBacklogOrders(vector<vector<int>>& orders) { \n map<int, long> buys, sells;\n for (auto& order : orders) {\n if (order[2] == 0) { // buy order\n int amount = order[1];\n while (amount > 0 && !sells.empty() && sells.begin()->first <= order[0]) {\n auto it = sells.begin();\n int have = it->second;\n it->second -= amount;\n amount -= have;\n if (it->second <= 0) {\n sells.erase(it);\n }\n }\n \n if (amount > 0) {\n if (buys.find(order[0]) == buys.end()) {\n buys[order[0]] = amount;\n } else {\n buys[order[0]] += amount;\n }\n } \n } else { // sell order\n int amount = order[1];\n while (amount > 0 && !buys.empty() && buys.rbegin()->first >= order[0]) {\n auto it = prev(buys.end());\n int have = it->second;\n it->second -= amount;\n amount -= have;\n if (it->second <= 0) {\n buys.erase(it);\n }\n }\n \n if (amount > 0) {\n if (sells.find(order[0]) == sells.end()) {\n sells[order[0]] = amount;\n } else {\n sells[order[0]] += amount;\n }\n }\n }\n }\n \n int res = 0, MOD = 1000000007;\n for (auto it = buys.begin(); it != buys.end(); it++) {\n res += it->second;\n res %= MOD;\n }\n \n for (auto it = sells.begin(); it != sells.end(); it++) {\n res += it->second;\n res %= MOD;\n }\n \n return res;\n }\n};\n``` | 3 | 2 | ['Tree', 'C'] | 0 |
number-of-orders-in-the-backlog | [Python] Heapq | python-heapq-by-qubenhao-arf0 | Buy list order by negative price so that it can be from greater to smaller.\n\npython\n def getNumberOfBacklogOrders(self, orders):\n """\n :ty | qubenhao | NORMAL | 2021-03-21T04:07:00.788957+00:00 | 2021-03-21T04:08:02.797754+00:00 | 381 | false | Buy list order by negative price so that it can be from greater to smaller.\n\n```python\n def getNumberOfBacklogOrders(self, orders):\n """\n :type orders: List[List[int]]\n :rtype: int\n """\n import heapq\n sells = []\n buys = []\n for p,a,t in orders:\n if t == 0:\n while sells:\n p_, a_ = heapq.heappop(sells)\n if p_ <= p:\n if a >= a_:\n a -= a_\n else:\n heapq.heappush(sells, (p_, a_-a))\n a = 0\n break\n else:\n heapq.heappush(sells, (p_, a_))\n break\n if a:\n heapq.heappush(buys, (-p, a))\n else:\n while buys:\n p_, a_ = heapq.heappop(buys)\n p_ = -p_\n if p_ >= p:\n if a >= a_:\n a -= a_\n else:\n heapq.heappush(buys, (-p_, a_-a))\n a = 0\n break\n else:\n heapq.heappush(buys, (-p_, a_))\n break\n if a:\n heapq.heappush(sells, (p, a))\n return (sum(x[1] for x in sells) + sum(x[1] for x in buys)) % (10**9+7)\n``` | 3 | 0 | ['Python'] | 0 |
number-of-orders-in-the-backlog | c++ | easy | fast | c-easy-fast-by-venomhighs7-hy0t | \n\n# Code\n\nclass Solution {\npublic:\n int getNumberOfBacklogOrders(vector<vector<int>>& orders) {\n priority_queue<vector<int>>buy;\n pr | venomhighs7 | NORMAL | 2022-11-21T05:34:20.116523+00:00 | 2022-11-21T05:34:20.116563+00:00 | 805 | false | \n\n# Code\n```\nclass Solution {\npublic:\n int getNumberOfBacklogOrders(vector<vector<int>>& orders) {\n priority_queue<vector<int>>buy;\n priority_queue<vector<int>, vector<vector<int>>, greater<vector<int>>>sell;\n for (auto& o : orders) {\n if (o[2] == 0)\n buy.push(o);\n else\n sell.push(o);\n while (buy.size() && sell.size() && sell.top()[0] <= buy.top()[0]) {\n int k = min(buy.top()[1], sell.top()[1]);\n vector<int> tmp = buy.top(); buy.pop();\n tmp[1] -= k;\n if (tmp[1]) buy.push(tmp);\n\n tmp = sell.top(); sell.pop();\n tmp[1] -= k;\n if (tmp[1]) sell.push(tmp);\n }\n\n }\n int res = 0, mod = 1e9 + 7;\n while (sell.size())\n res = (res + sell.top()[1]) % mod, sell.pop();\n while (buy.size())\n res = (res + buy.top()[1]) % mod, buy.pop();\n return res;\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
number-of-orders-in-the-backlog | C++ two priority queue (EASY😈) | c-two-priority-queue-easy-by-rajwardhan2-0uql | \nclass Solution {\npublic:\n int mod=1e9+7;\n int getNumberOfBacklogOrders(vector<vector<int>>& nums) {\n priority_queue<pair<int,long long int>>b | Rajwardhan22 | NORMAL | 2022-08-02T09:58:46.791058+00:00 | 2022-08-02T09:58:46.791097+00:00 | 367 | false | ```\nclass Solution {\npublic:\n int mod=1e9+7;\n int getNumberOfBacklogOrders(vector<vector<int>>& nums) {\n priority_queue<pair<int,long long int>>buy;\n priority_queue<pair<int,long long int>,vector<pair<int,long long int>>,greater<pair<int,long long int>>>sell;\n int maxi1=0,maxi2=0;\n \n \n for(int i=0;i<nums.size();i++){\n if(nums[i][2]==0){//buy\n bool b=false;\n \n while(!sell.empty() and sell.top().first<=nums[i][0] and nums[i][1]>0){\n pair<int,long long int>p=sell.top();\n sell.pop();\n if(p.second>nums[i][1]){\n b=true;\n sell.push({p.first,p.second-nums[i][1]});\n break;\n }\n nums[i][1]=abs(p.second - nums[i][1]);\n }\n if(b){continue;}\n \n if(nums[i][1]>0 ){\n maxi1=nums[i][1];\n buy.push({nums[i][0],nums[i][1]});\n }\n }\n else{//sell\n bool b=false;\n \n while(!buy.empty() and buy.top().first>=nums[i][0] and nums[i][1]>0){\n pair<int,long long int>p=buy.top();\n buy.pop();\n if(p.second>nums[i][1]){\n b=true;\n buy.push({p.first,p.second-nums[i][1]});\n break;\n }\n nums[i][1]=abs(p.second - nums[i][1]);\n }\n if(b){continue;}\n \n if(nums[i][1]>0 ){\n maxi2=nums[i][1];\n sell.push({nums[i][0],nums[i][1]});\n }\n \n }\n }\n \n int cnt=0;\n while(!sell.empty()){\n cnt=(cnt+((sell.top().second % mod)))%mod;\n sell.pop();\n }\n while(!buy.empty()){\n cnt=(cnt+((buy.top().second % mod)))%mod;\n buy.pop();\n }\n return cnt;\n \n }\n};\n``` | 2 | 0 | ['C', 'Heap (Priority Queue)', 'C++'] | 0 |
number-of-orders-in-the-backlog | Modular | Good for interviews | Simulating stock market matching engine with Min and Max Heaps | modular-good-for-interviews-simulating-s-7dvr | \nfrom heapq import heappush, heappop\n\nclass MatchingEngine(object):\n \n def __init__(self):\n self.buy_orders = [] # Max heap\n self.se | jbond_007 | NORMAL | 2021-12-06T04:37:05.350410+00:00 | 2021-12-06T04:37:05.350451+00:00 | 1,818 | false | ```\nfrom heapq import heappush, heappop\n\nclass MatchingEngine(object):\n \n def __init__(self):\n self.buy_orders = [] # Max heap\n self.sell_orders = [] # Min heap \n \n def buy(self, buy_price, quantity):\n while len(self.sell_orders) > 0 and buy_price >= self.sell_orders[0][0] and quantity > 0:\n sell_price, sell_quantity = heappop(self.sell_orders)\n if sell_quantity > quantity:\n heappush(self.sell_orders, (sell_price, sell_quantity - quantity))\n quantity = 0\n else:\n quantity -= sell_quantity\n if quantity != 0:\n heappush(self.buy_orders, (-buy_price, quantity))\n \n def sell(self, sell_price, quantity):\n while len(self.buy_orders) > 0 and sell_price <= -self.buy_orders[0][0] and quantity > 0:\n buy_price, buy_quantity = heappop(self.buy_orders)\n if buy_quantity > quantity:\n heappush(self.buy_orders, (buy_price, buy_quantity - quantity))\n quantity = 0\n else:\n quantity -= buy_quantity\n if quantity != 0:\n heappush(self.sell_orders, (sell_price, quantity))\n \n def get_pending_orders(self):\n pending = lambda arr : sum(map(lambda item: item[1], arr))\n return (pending(self.buy_orders) + pending(self.sell_orders)) % (10**9 + 7)\n \n\nclass Solution(object):\n def getNumberOfBacklogOrders(self, orders):\n """\n :type orders: List[List[int]]\n :rtype: int\n """\n \n engine = MatchingEngine()\n \n for price, quantity, oType in orders:\n if oType == 0:\n engine.buy(price, quantity)\n else:\n engine.sell(price, quantity)\n \n return engine.get_pending_orders()\n``` | 2 | 0 | ['Heap (Priority Queue)'] | 0 |
number-of-orders-in-the-backlog | (C++) 1801. Number of Orders in the Backlog | c-1801-number-of-orders-in-the-backlog-b-wer5 | \n\nclass Solution {\npublic:\n int getNumberOfBacklogOrders(vector<vector<int>>& orders) {\n priority_queue<pair<int, int>> buy; // max-heap \n | qeetcode | NORMAL | 2021-06-08T20:09:34.205672+00:00 | 2021-06-08T20:09:34.205703+00:00 | 285 | false | \n```\nclass Solution {\npublic:\n int getNumberOfBacklogOrders(vector<vector<int>>& orders) {\n priority_queue<pair<int, int>> buy; // max-heap \n priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> sell; // min-heap \n \n for (auto& order : orders) {\n auto price = order[0], qty = order[1], type = order[2]; \n if (type == 0) buy.emplace(price, qty); \n else sell.emplace(price, qty); \n \n while (size(buy) && size(sell) && buy.top().first >= sell.top().first) {\n auto [bp, bq] = buy.top(); buy.pop(); \n auto [sp, sq] = sell.top(); sell.pop(); \n if (bq > sq) {\n bq -= sq; \n buy.emplace(bp, bq); \n } else if (bq < sq) {\n sq -= bq; \n sell.emplace(sp, sq); \n }\n }\n }\n \n int ans = 0; \n while (size(buy)) { ans = (ans + buy.top().second) % 1\'000\'000\'007; buy.pop(); }\n while (size(sell)) { ans = (ans + sell.top().second) % 1\'000\'000\'007; sell.pop(); }\n return ans; \n }\n};\n``` | 2 | 0 | ['C'] | 0 |
number-of-orders-in-the-backlog | Python [max/min heap] | python-maxmin-heap-by-gsan-tdci | Buy orders are ranked from largest to smallest in price.\nSell orders are ranked from smallest to largest in price.\nWe add the orders in the order they arrive, | gsan | NORMAL | 2021-03-21T06:04:46.967197+00:00 | 2021-03-21T06:04:46.967229+00:00 | 135 | false | Buy orders are ranked from largest to smallest in price.\nSell orders are ranked from smallest to largest in price.\nWe add the orders in the order they arrive,\nwhen there is a match in prices we do the transaction.\n\n```python\nclass Solution:\n def getNumberOfBacklogOrders(self, orders):\n maxhp = []\n minhp = []\n for x,y,z in orders:\n if z==0: #buy\n heapq.heappush(maxhp, (-x, y))\n else: #sell\n heapq.heappush(minhp, (x, y))\n \n #if there is match, do the transaction\n while maxhp and minhp and -maxhp[0][0] >= minhp[0][0]:\n xbuy, ybuy = heapq.heappop(maxhp)\n xsell, ysell = heapq.heappop(minhp)\n if ybuy > ysell:\n heapq.heappush(maxhp, (xbuy, ybuy-ysell))\n elif ybuy < ysell:\n heapq.heappush(minhp, (xsell, ysell-ybuy))\n \n ans = sum(y for _,y in maxhp) + sum(y for _,y in minhp)\n ans = ans % (10**9 + 7)\n return ans\n``` | 2 | 0 | [] | 0 |
number-of-orders-in-the-backlog | [C++] Solution with Two Priority_queues | c-solution-with-two-priority_queues-by-d-1hah | Idea:\nThis problem is like a trading system. With a bunch of sell orders, when a buying order comes in, the system would match the buying order with the sellin | davidchai | NORMAL | 2021-03-21T04:55:10.460337+00:00 | 2021-03-21T04:55:10.460362+00:00 | 1,491 | false | Idea:\nThis problem is like a trading system. With a bunch of sell orders, when a buying order comes in, the system would match the buying order with the selling orders whose prices is less than or equal to the buying prices. Same thing goes with the buy orders. In order to find which one is the best match, or there is no match at all, we can use the priority_queue(heap) to simulate the process.\n\nCode:\n```\nclass Solution {\npublic:\n int getNumberOfBacklogOrders(vector<vector<int>>& orders) {\n priority_queue<pair<int,int>, vector<pair<int,int>>, BuyComp> buy;\n priority_queue<pair<int,int>, vector<pair<int,int>>, SellComp> sell;\n long res = 0;\n \n for (vector<int>& order : orders) {\n int sum = order[1];\n // buy order\n if (order.back() == 0) {\n while (!sell.empty() && sell.top().first <= order[0] && order[1]) {\n int amount = min(order[1], sell.top().second);\n if (sell.top().second == amount) {\n sell.pop();\n } else {\n pair<int,int> cur = sell.top();\n sell.pop();\n cur.second -= amount;\n sell.push(cur);\n }\n order[1] -= amount;\n }\n if (order[1] > 0) {\n buy.push(make_pair(order[0], order[1]));\n }\n\t\t\t// sell order\n } else {\n while (!buy.empty() && buy.top().first >= order[0] && order[1]) {\n int amount = min(order[1], buy.top().second);\n if (buy.top().second == amount) {\n buy.pop();\n } else {\n pair<int,int> cur = buy.top();\n buy.pop();\n cur.second -= amount;\n buy.push(cur);\n }\n order[1] -= amount;\n }\n if (order[1] > 0) {\n sell.push(make_pair(order[0], order[1]));\n }\n }\n res += order[1]*2 - sum;\n }\n return res%mod;\n }\nprivate:\n const int mod = 1e9+7;\n \n // price, amount\n struct BuyComp {\n bool operator() (pair<int,int>& a, pair<int,int>& b) {\n return a.first < b.first;\n }\n };\n \n struct SellComp {\n bool operator() (pair<int,int>& a, pair<int,int>& b) {\n return a.first > b.first;\n }\n };\n};\n``` | 2 | 0 | ['C', 'Heap (Priority Queue)'] | 4 |
number-of-orders-in-the-backlog | Ruby - Keep sorted queues for buy and sell orders. | ruby-keep-sorted-queues-for-buy-and-sell-sdil | Keep buy queue sorted by price descending.\nKeep sell queue sorted by price ascending.\nBuy by the best price (minimum price - first in the sell queue) while ca | shhavel | NORMAL | 2021-03-21T04:54:38.171541+00:00 | 2021-03-21T06:50:11.392853+00:00 | 104 | false | Keep buy queue sorted by price descending.\nKeep sell queue sorted by price ascending.\nBuy by the best price (minimum price - first in the sell queue) while can.\nSell by the best price (maximum price - first in the buy queue) while can.\n\n```ruby\ndef get_number_of_backlog_orders(orders)\n bq = []; sq = [] # buy queue and sell queue\n for price, amount, order_type in orders\n if order_type == 0 # buy\n amount -= sq.shift[1] while amount > 0 && sq.any? && sq[0][0] <= price && sq[0][1] <= amount\n if sq.any? && sq[0][0] <= price\n sq[0][1] -= amount\n else\n bq.insert(bq.bsearch_index { |p,| p <= price } || bq.size, [price, amount]) if amount > 0\n end\n else # sell\n amount -= bq.shift[1] while amount > 0 && bq.any? && bq[0][0] >= price && bq[0][1] <= amount\n if bq.any? && bq[0][0] >= price\n bq[0][1] -= amount\n else\n sq.insert(sq.bsearch_index { |p,| p >= price } || sq.size, [price, amount]) if amount > 0\n end\n end\n end\n (bq.sum(&:last) + sq.sum(&:last)) % 1000000007\nend\n``` | 2 | 0 | ['Binary Tree', 'Ruby'] | 1 |
number-of-orders-in-the-backlog | C++ beats 100% | c-beats-100-by-subbuffer-kp7t | Used two maps for each of the buys and sells; and using the iterator pointers, I would decrement the necessary map values.\n\nclass Solution {\npublic:\n int | SubBuffer | NORMAL | 2021-03-21T04:04:23.971530+00:00 | 2021-03-21T04:10:26.443268+00:00 | 323 | false | Used two maps for each of the buys and sells; and using the iterator pointers, I would decrement the necessary map values.\n```\nclass Solution {\npublic:\n int getNumberOfBacklogOrders(vector<vector<int>>& orders) {\n map<int,long> mpBuy;\n map<int,long> mpSell;\n int count = 0;\n for (int i = 0;i<orders.size();i++){\n if (orders[i][2]==0 && mpBuy.find(orders[i][0])!=mpBuy.end()){\n mpBuy[orders[i][0]] += orders[i][1];\n continue;\n }\n if (orders[i][2]==1 && mpSell.find(orders[i][0])!=mpSell.end()){\n mpSell[orders[i][0]] += orders[i][1];\n continue;\n }\n if (orders[i][2]==0){\n if (mpSell.size()==0){\n mpBuy[orders[i][0]] += orders[i][1];\n continue;\n }\n auto it = mpSell.begin();\n count = orders[i][1];\n while(count>0){\n if ((*it).first<=orders[i][0] && (*it).second>count){\n (*it).second -= count;\n count = 0;\n break;\n }\n if ((*it).first<=orders[i][0] && (*it).second<=count){\n count -= (*it).second;\n auto it2 = it;\n it++;\n mpSell.erase((*it2).first);\n }\n if (mpSell.size()==0){\n break;\n }\n if ((*it).first>orders[i][0]){\n break;\n }\n }\n if (count!=0){\n mpBuy[orders[i][0]] += count;\n }\n continue;\n }\n if (orders[i][2]==1){\n if (mpBuy.size()==0){\n mpSell[orders[i][0]] += orders[i][1];\n continue;\n }\n auto it = mpBuy.end();\n it--;\n count = orders[i][1];\n while(count>0){\n if ((*it).first>=orders[i][0] && (*it).second>count){\n (*it).second -= count;\n count = 0;\n break;\n }\n if ((*it).first>=orders[i][0] && (*it).second<=count){\n count -= (*it).second;\n auto it2 = it;\n it--;\n mpBuy.erase((*it2).first);\n }\n if (mpBuy.size()==0){\n break;\n }\n if ((*it).first<orders[i][0]){\n break;\n }\n }\n if (count!=0){\n mpSell[orders[i][0]] += count;\n }\n continue;\n }\n }\n long sum = 0;\n for (auto it = mpBuy.begin();it!=mpBuy.end();++it){\n sum += (*it).second;\n }\n for (auto it = mpSell.begin();it!=mpSell.end();++it){\n sum += (*it).second;\n }\n sum %= (int)1e9+7;\n return sum;\n }\n};\n``` | 2 | 0 | [] | 1 |
number-of-orders-in-the-backlog | [Python3] Clean and Clear - Two heaps | python3-clean-and-clear-two-heaps-by-_br-1y6q | \nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n buy, sell, MOD = [], [], 10**9 + 7\n \n def pr | _brian | NORMAL | 2021-03-21T04:03:05.238388+00:00 | 2021-03-21T04:03:05.238421+00:00 | 272 | false | ```\nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n buy, sell, MOD = [], [], 10**9 + 7\n \n def process_buy(buy_price, buy_amount):\n while buy_amount > 0:\n if not sell:\n break\n sell_price, sell_amount = heapq.heappop(sell)\n if sell_price > buy_price:\n heapq.heappush(sell, (sell_price, sell_amount))\n break\n \n if sell_amount - buy_amount > 0:\n heapq.heappush(sell, (sell_price, sell_amount - buy_amount))\n buy_amount -= sell_amount\n if buy_amount > 0:\n heapq.heappush(buy, (-buy_price, buy_amount))\n \n def process_sell(sell_price, sell_amount):\n while sell_amount > 0:\n if not buy:\n break\n buy_price, buy_amount = heapq.heappop(buy)\n buy_price *= -1 # min heap only in Python\n if sell_price > buy_price:\n heapq.heappush(buy, (-buy_price, buy_amount))\n break\n \n if buy_amount - sell_amount > 0:\n heapq.heappush(buy, (-buy_price, buy_amount - sell_amount))\n sell_amount -= buy_amount\n if sell_amount > 0:\n heapq.heappush(sell, (sell_price, sell_amount))\n \n for price, amount, order_type in orders:\n if order_type == 0:\n process_buy(price, amount)\n else:\n process_sell(price, amount)\n\n return (sum([x[1] for x in buy]) + sum([x[1] for x in sell])) % MOD\n``` | 2 | 0 | [] | 1 |
number-of-orders-in-the-backlog | [Java] Easy 2 Heap solution | java-easy-2-heap-solution-by-ytchouar-tge8 | java\nclass Solution {\n public int getNumberOfBacklogOrders(final int[][] orders) {\n final Queue<int[]> buy = new PriorityQueue<>((a, b) -> b[0] - a | YTchouar | NORMAL | 2024-06-14T04:01:44.541378+00:00 | 2024-06-14T04:01:44.541460+00:00 | 326 | false | ```java\nclass Solution {\n public int getNumberOfBacklogOrders(final int[][] orders) {\n final Queue<int[]> buy = new PriorityQueue<>((a, b) -> b[0] - a[0]);\n final Queue<int[]> sell = new PriorityQueue<>((a, b) -> a[0] - b[0]);\n\n for(final int[] order : orders) {\n if(order[2] == 0)\n buy.offer(new int[] { order[0], order[1] });\n else\n sell.offer(new int[] { order[0], order[1] });\n\n while(!buy.isEmpty() && !sell.isEmpty() && sell.peek()[0] <= buy.peek()[0]) {\n final int[] sellOrder = sell.peek(), buyOrder = buy.peek();\n\n final int processed = Math.min(sellOrder[1], buyOrder[1]);\n\n sellOrder[1] -= processed;\n buyOrder[1] -= processed;\n\n if(sellOrder[1] == 0)\n sell.poll();\n\n if(buyOrder[1] == 0)\n buy.poll();\n }\n }\n\n int backlog = 0;\n\n while(!buy.isEmpty())\n backlog = (backlog + buy.poll()[1]) % 1000000007;\n\n while(!sell.isEmpty())\n backlog = (backlog + sell.poll()[1]) % 1000000007;\n\n return backlog;\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
number-of-orders-in-the-backlog | JS || Solution by Bharadwaj | js-solution-by-bharadwaj-by-manu-bharadw-hd8j | Code\n\nvar getNumberOfBacklogOrders = function (orders) {\n var bq = new MaxPriorityQueue({ priority: (bid) => bid[0] });\n var sq = new MinPriorityQueue | Manu-Bharadwaj-BN | NORMAL | 2024-03-01T06:33:40.846400+00:00 | 2024-03-01T06:33:40.846427+00:00 | 69 | false | # Code\n```\nvar getNumberOfBacklogOrders = function (orders) {\n var bq = new MaxPriorityQueue({ priority: (bid) => bid[0] });\n var sq = new MinPriorityQueue({ priority: (bid) => bid[0] });\n var backlog = [bq, sq];\n orders.forEach(order => {\n let [price, amount, type] = order;\n if (type === 0) {\n while (!sq.isEmpty() && amount > 0) {\n var cur = sq.front().element;\n if (cur[0] <= price) {\n if (amount <= cur[1]) {\n cur[1] -= amount;\n amount = 0;\n break;\n }\n else {\n amount -= cur[1];\n sq.dequeue();\n }\n } else {\n break;\n }\n }\n\n if (amount > 0) {\n bq.enqueue([price, amount]);\n }\n }\n else {\n while (!bq.isEmpty() && amount > 0) {\n var cur = bq.front().element;\n if (cur[0] >= price) {\n if (amount <= cur[1]) {\n cur[1] -= amount;\n amount = 0;\n break;\n }\n else {\n amount -= cur[1];\n bq.dequeue();\n }\n } else {\n break;\n }\n }\n if (amount > 0) {\n sq.enqueue([price, amount]);\n }\n }\n });\n\n var res = 0;\n var mod = 1000000007;\n while (!bq.isEmpty()) {\n var cur = bq.front().element;\n res = (res + cur[1]) % mod;\n bq.dequeue();\n }\n while (!sq.isEmpty()) {\n var cur = sq.front().element;\n res = (res + cur[1]) % mod;\n sq.dequeue();\n }\n return res;\n};\n``` | 1 | 0 | ['JavaScript'] | 1 |
number-of-orders-in-the-backlog | [C] Heap | c-heap-by-leetcodebug-tvzo | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | leetcodebug | NORMAL | 2023-11-30T04:47:04.338256+00:00 | 2023-11-30T04:47:04.338288+00:00 | 9 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(nlogn)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/*\n * 1801. Number of Orders in the Backlog\n *\n * You are given a 2D integer array orders, where each orders[i] = \n * [pricei, amounti, orderTypei] denotes that amounti orders have \n * been placed of type orderTypei at the price pricei. \n * The orderTypei is:\n *\n * 0 if it is a batch of buy orders, or\n * 1 if it is a batch of sell orders.\n * Note that orders[i] represents a batch of amounti independent orders \n * with the same price and order type. All orders represented by orders[i] \n * will be placed before all orders represented by orders[i+1] for all \n * valid i.\n *\n * There is a backlog that consists of orders that have not been executed. \n * The backlog is initially empty. When an order is placed, the following happens:\n * \n * If the order is a buy order, you look at the sell order with the smallest \n * price in the backlog. If that sell order\'s price is smaller than or equal \n * to the current buy order\'s price, they will match and be executed, and that \n * sell order will be removed from the backlog. Else, the buy order is added \n * to the backlog.\n * Vice versa, if the order is a sell order, you look at the buy order with \n * the largest price in the backlog. If that buy order\'s price is larger than \n * or equal to the current sell order\'s price, they will match and be executed, \n * and that buy order will be removed from the backlog. Else, the sell order \n * is added to the backlog.\n * Return the total amount of orders in the backlog after placing all the orders \n * from the input. Since this number can be large, return it modulo 10^9 + 7.\n *\n * 1 <= orders.length <= 10^5\n * orders[i].length == 3\n * 1 <= pricei, amounti <= 10^9\n * orderTypei is either 0 or 1.\n */\n\ntypedef struct item {\n int price;\n unsigned int amount;\n} item_t;\n\n#define HEAP_SIZE 100000\n\nitem_t max_heap[HEAP_SIZE];\nint max_idx;\n\nitem_t min_heap[HEAP_SIZE];\nint min_idx;\n\nvoid max_init()\n{\n max_idx = -1;\n}\n\nint max_push(item_t *item)\n{\n if (max_idx + 1 == HEAP_SIZE) {\n return -1;\n }\n\n max_idx++;\n max_heap[max_idx] = *item;\n\n for (int i = max_idx; i > 0; ) {\n int parent = (i - 1) / 2;\n\n if (max_heap[i].price > max_heap[parent].price) {\n item_t tmp = max_heap[i];\n max_heap[i] = max_heap[parent];\n max_heap[parent] = tmp;\n }\n\n i = parent;\n }\n\n return 0;\n}\n\nint max_pop(item_t *item)\n{\n if (max_idx == -1) {\n return -1;\n }\n\n *item = max_heap[0];\n max_heap[0] = max_heap[max_idx];\n max_idx--;\n\n for (int i = 1; i <= max_idx; ) {\n\n int parent = (i - 1) / 2;\n\n if (i + 1 <= max_idx && max_heap[i + 1].price > max_heap[i].price) {\n i = i + 1;\n }\n\n if (max_heap[i].price > max_heap[parent].price) {\n item_t tmp = max_heap[i];\n max_heap[i] = max_heap[parent];\n max_heap[parent] = tmp;\n }\n\n i = i * 2 + 1;\n\n }\n\n return 0;\n}\n\nvoid min_init()\n{\n min_idx = -1;\n}\n\nint min_push(item_t *item)\n{\n if (min_idx + 1 == HEAP_SIZE) {\n return -1;\n }\n\n min_idx++;\n min_heap[min_idx] = *item;\n\n for (int i = min_idx; i > 0; ) {\n int parent = (i - 1) / 2;\n\n if (min_heap[i].price < min_heap[parent].price) {\n item_t tmp = min_heap[i];\n min_heap[i] = min_heap[parent];\n min_heap[parent] = tmp;\n }\n\n i = parent;\n }\n\n return 0;\n}\n\nint min_pop(item_t *item)\n{\n if (min_idx == -1) {\n return -1;\n }\n\n *item = min_heap[0];\n min_heap[0] = min_heap[min_idx];\n min_idx--;\n\n for (int i = 1; i <= min_idx; ) {\n\n int parent = (i - 1) / 2;\n\n if (i + 1 <= min_idx && min_heap[i + 1].price < min_heap[i].price) {\n i = i + 1;\n }\n\n if (min_heap[i].price < min_heap[parent].price) {\n item_t tmp = min_heap[i];\n min_heap[i] = min_heap[parent];\n min_heap[parent] = tmp;\n }\n\n i = i * 2 + 1;\n\n }\n\n return 0;\n}\n\nint getNumberOfBacklogOrders(int** orders, int ordersSize, int* ordersColSize){\n\n /*\n * Input:\n * **orders\n * ordersSize\n * *ordersColSize\n */\n\n item_t item;\n int ans = 0;\n\n max_init();\n min_init();\n\n for (int i = 0; i < ordersSize; i++) {\n /* Buy */\n if (orders[i][2] == 0) {\n /* Search sell backlog and find out the lowest price */\n for (; orders[i][1] && min_pop(&item) == 0; ) {\n\n if (item.price <= orders[i][0]) {\n if (item.amount <= orders[i][1]) {\n orders[i][1] -= item.amount;\n }\n else {\n item.amount -= orders[i][1];\n orders[i][1] = 0;\n min_push(&item);\n }\n }\n else {\n min_push(&item);\n break;\n }\n }\n\n /* Put the remain order to max heap */\n if (orders[i][1] != 0) {\n item.price = orders[i][0];\n item.amount = orders[i][1];\n max_push(&item);\n }\n }\n /* Sell */\n else if (orders[i][2] == 1) {\n /* Search sell backlog and find out the lowest price */\n for (; orders[i][1] && max_pop(&item) == 0; ) {\n\n if (item.price >= orders[i][0]) {\n if (item.amount <= orders[i][1]) {\n orders[i][1] -= item.amount;\n }\n else {\n item.amount -= orders[i][1];\n orders[i][1] = 0;\n max_push(&item);\n }\n }\n else {\n max_push(&item);\n break;\n }\n }\n\n /* Put the remain order to min heap */\n if (orders[i][1] != 0) {\n item.price = orders[i][0];\n item.amount = orders[i][1];\n min_push(&item);\n }\n }\n }\n\n while (max_pop(&item) == 0) {\n ans += item.amount;\n ans %= 1000000007;\n }\n\n while (min_pop(&item) == 0) {\n ans += item.amount;\n ans %= 1000000007;\n }\n\n /*\n * Output:\n * Return the total amount of orders in the backlog after placing all the orders \n * from the input. Since this number can be large, return it modulo 10^9 + 7.\n */\n\n return ans;\n} \n``` | 1 | 0 | ['Array', 'C', 'Heap (Priority Queue)'] | 0 |
number-of-orders-in-the-backlog | Heap | cpp | heap-cpp-by-tan_b-v39p | \nclass Solution\n{\n public:\n struct cmp\n {\n bool operator()(pair<int, int> a, pair<int, int> b)\n {\n | Tan_B | NORMAL | 2023-01-02T14:46:58.676072+00:00 | 2023-01-02T14:46:58.676103+00:00 | 173 | false | ```\nclass Solution\n{\n public:\n struct cmp\n {\n bool operator()(pair<int, int> a, pair<int, int> b)\n {\n return a.first > b.first;\n }\n };\n void fun(priority_queue<pair<int, int>, vector< pair<int, int>>, cmp> &sell, priority_queue< pair<int, int>> &buy)\n {\n while (buy.size() and sell.size() and buy.top().first >= sell.top().first)\n {\n auto x = buy.top();\n auto y = sell.top();\n buy.pop();\n sell.pop();\n if (x.second < y.second)\n {\n y.second -= x.second;\n x.second = 0;\n sell.push(y);\n }\n else if (y.second < x.second)\n {\n x.second -= y.second;\n y.second = 0;\n buy.push(x);\n }\n else\n {\n x.second = 0;\n y.second = 0;\n }\n }\n }\n int getNumberOfBacklogOrders(vector<vector < int>> &orders)\n {\n int mod = 1e9 + 7;\n priority_queue<pair<int, int>, vector< pair<int, int>>, cmp> sell;\n priority_queue<pair<int, int>> buy;\n long ans = 0;\n for (int x = 0; x < orders.size(); x++)\n {\n if (orders[x][2] == 1) sell.push({ orders[x][0],orders[x][1] });\n else buy.push({ orders[x][0],orders[x][1] });\n\n fun(sell, buy);\n }\n fun(sell, buy);\n while (buy.size())\n {\n ans = (ans + buy.top().second) % mod;\n buy.pop();\n }\n while (sell.size())\n {\n ans = (ans + sell.top().second) % mod;\n sell.pop();\n }\n return ans;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
number-of-orders-in-the-backlog | Java Sol: Number of Orders in the Backlog | java-sol-number-of-orders-in-the-backlog-ahm7 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\nminHeap for sell.\nmaxHeap for buy.\n Describe your approach to solving t | gyanendras1898 | NORMAL | 2023-01-01T08:50:11.036889+00:00 | 2023-01-01T08:50:11.036919+00:00 | 304 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nminHeap for sell.\nmaxHeap for buy.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n- O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n- O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n final static int MOD = (int) (1e9 + 7);\n class Order{\n int price;\n int amount;\n Order(int price, int amount){\n this.price = price;\n this.amount = amount;\n }\n }\n public int getNumberOfBacklogOrders(int[][] orders) {\n PriorityQueue<Order> sell = new PriorityQueue<>((Order o1,Order o2)->{\n return o1.price - o2.price;\n });\n PriorityQueue<Order> buy = new PriorityQueue<>((Order o1,Order o2)->{\n return o2.price - o1.price;\n });\n\n boolean flag;\n for(int[] ord : orders){\n int amount = ord[1];\n int price = ord[0];\n if(ord[2] == 0){ //buy\n while(amount>0 && !sell.isEmpty() && sell.peek().price<=price){\n Order front = sell.poll();\n if(front.amount>=amount){\n front.amount = front.amount - amount;\n amount = 0;\n if(front.amount>0) sell.add(front);\n } \n else\n amount = amount - front.amount; \n }\n if(amount > 0) buy.add(new Order(price, amount));\n }else{ //sell\n while(amount>0 && !buy.isEmpty() && buy.peek().price>=price){\n Order front = buy.poll();\n if(front.amount>=amount){\n front.amount = front.amount - amount;\n amount = 0;\n if(front.amount>0) buy.add(front);\n } \n else\n amount = amount - front.amount; \n }\n if(amount > 0) sell.add(new Order(price, amount));\n }\n }\n long ans = 0;\n while(!sell.isEmpty())\n ans= (ans + sell.poll().amount) % MOD;\n \n while(!buy.isEmpty())\n ans= (ans + buy.poll().amount) % MOD;\n\n return (int) ans%MOD;\n \n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
number-of-orders-in-the-backlog | [GO] Use two heaps | go-use-two-heaps-by-zhouhaibing089-7jr5 | Intuition\n\nThis is a typical use case to find maximum and minimum elements with heap. The buy orders are the ones which we would like to find its highest pric | zhouhaibing089 | NORMAL | 2022-12-04T08:47:31.633517+00:00 | 2022-12-04T08:47:31.633559+00:00 | 68 | false | # Intuition\n\nThis is a typical use case to find maximum and minimum elements with heap. The buy orders are the ones which we would like to find its highest price at any point of time, and thus is a maximum heap, and similarly, the sell orders are the ones which we would like to find its lowest price at any point of time, and thus is a minimum heap.\n\n# Approach\n\n1. For any new buy order, we look at: a) whethere there is any sell orders, if no, push into buy orders heap. b) is the sell order within the price range, if no, push into buy orders heap. c) if it is within the range, then simply update the amount in the corresponding sell order, and pop it up if it is 100% fullfilled. d) if this buy order is not 100% fullfilled, continue to the next loop\n2. For any new sell order, we look at: a) whethere there is any buy orders, if no, push into sell orders heap. b) is the buy order within the price range, if no, push into sell orders heap. c) if it is within the range, then simply update the amount in the corresponding buy order, and pop it up if it is 100% fullfilled. d) if this sell order is not 100% fullfilled, continue to the next loop.\n\n# Complexity\n- Time complexity: $$O(n log n)$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n```\nfunc getNumberOfBacklogOrders(orders [][]int) int {\n var sells = &sellAsc{}\n\tvar buys = &buyDesc{}\n\n\tfor i, o := range orders {\n\t\tif o[2] == 0 {\n\t\t\t// this is a buy order, find the smallest sell order\n\t\t\tfor {\n\n\t\t\t\tif len(*sells) == 0 {\n\t\t\t\t\theap.Push(buys, order{price: o[0], amount: o[1], term: i})\n\t\t\t\t\tbreak\n\t\t\t\t}\n\t\t\t\tpeek := (*sells)[0]\n\t\t\t\tif peek.price > o[0] {\n\t\t\t\t\theap.Push(buys, order{price: o[0], amount: o[1], term: i})\n\t\t\t\t\tbreak\n\t\t\t\t}\n\t\t\t\t// can be fullfilled\n\t\t\t\tif peek.amount > o[1] {\n\t\t\t\t\t(*sells)[0].amount = peek.amount - o[1]\n\t\t\t\t\to[1] = 0\n\t\t\t\t} else {\n\t\t\t\t\theap.Pop(sells)\n\t\t\t\t\to[1] = o[1] - peek.amount\n\t\t\t\t}\n\t\t\t\tif o[1] == 0 {\n\t\t\t\t\tbreak\n\t\t\t\t}\n\t\t\t}\n\t\t} else {\n\t\t\t// this is a sell order, find the largest buy order\n\t\t\tfor {\n\t\t\t\tif len(*buys) == 0 {\n\t\t\t\t\theap.Push(sells, order{price: o[0], amount: o[1], term: i})\n\t\t\t\t\tbreak\n\t\t\t\t}\n\t\t\t\tpeek := (*buys)[0]\n\t\t\t\tif peek.price < o[0] {\n\t\t\t\t\theap.Push(sells, order{price: o[0], amount: o[1], term: i})\n\t\t\t\t\tbreak\n\t\t\t\t}\n\t\t\t\t// can be fullfilled\n\t\t\t\tif peek.amount > o[1] {\n\t\t\t\t\t(*buys)[0].amount = peek.amount - o[1]\n\t\t\t\t\to[1] = 0\n\t\t\t\t} else {\n\t\t\t\t\theap.Pop(buys)\n\t\t\t\t\to[1] = o[1] - peek.amount\n\t\t\t\t}\n\t\t\t\tif o[1] == 0 {\n\t\t\t\t\tbreak\n\t\t\t\t}\n\t\t\t}\n\t\t}\n\t}\n\n\tvar left int\n\tfor _, o := range *buys {\n\t\tleft = left + o.amount\n\t\tif left >= 1000000007 {\n\t\t\tleft = left % 1000000007\n\t\t}\n\t}\n\tfor _, o := range *sells {\n\t\tleft = left + o.amount\n\t\tif left >= 1000000007 {\n\t\t\tleft = left % 1000000007\n\t\t}\n\t}\n\treturn left\n}\n\ntype order struct {\n\tamount int\n\tprice int\n\tterm int\n}\n\ntype sellAsc []order\n\nfunc (s sellAsc) Len() int {\n\treturn len(s)\n}\n\nfunc (s sellAsc) Less(i, j int) bool {\n\tif s[i].price < s[j].price {\n\t\treturn true\n\t}\n\tif s[i].price > s[j].price {\n\t\treturn false\n\t}\n\treturn s[i].term < s[j].term\n}\n\nfunc (s sellAsc) Swap(i, j int) {\n\ts[i], s[j] = s[j], s[i]\n}\n\nfunc (s *sellAsc) Push(x interface{}) {\n\t*s = append(*s, x.(order))\n}\n\nfunc (s *sellAsc) Pop() interface{} {\n\told := *s\n\tn := len(old)\n\to := old[n-1]\n\t*s = old[:n-1]\n\treturn o\n}\n\ntype buyDesc []order\n\nfunc (b buyDesc) Len() int {\n\treturn len(b)\n}\n\nfunc (b buyDesc) Less(i, j int) bool {\n\tif b[i].price > b[j].price {\n\t\treturn true\n\t}\n\tif b[i].price < b[j].price {\n\t\treturn false\n\t}\n\treturn b[i].term < b[j].term\n}\n\nfunc (b buyDesc) Swap(i, j int) {\n\tb[i], b[j] = b[j], b[i]\n}\n\nfunc (b *buyDesc) Push(x interface{}) {\n\t*b = append(*b, x.(order))\n}\n\nfunc (b *buyDesc) Pop() interface{} {\n\told := *b\n\tn := len(old)\n\to := old[n-1]\n\t*b = old[:n-1]\n\treturn o\n}\n``` | 1 | 0 | ['Go'] | 1 |
number-of-orders-in-the-backlog | Multiset Solution | Clean Code | Easy to Understand | multiset-solution-clean-code-easy-to-und-nhbm | Idea?\n Track the pairs {price,amount} for sell orders and buy orders seperately in a multiset.\n Whenever we have a buy order, keep popping out the selling ord | sunny_38 | NORMAL | 2022-04-03T08:00:20.059111+00:00 | 2022-04-03T08:01:11.051063+00:00 | 138 | false | **Idea?**\n* Track the pairs **{price,amount**} for sell orders and buy orders seperately in a **multiset**.\n* Whenever we have a *buy orde*r, **keep popping out the selling orders** present in the backlog that are less than or equal to current price and number of orders left is still positive.\n* Also, Whenever we have a *sell orde*r, **keep popping out the buying orders** present in the backlog that are greater than or equal to current price and number of orders is still positive.\n* Finally, add all the number of amounts that are present in the selling as well as buying backlog.\n\n```\nclass Solution {\npublic:\n\t// Time Complexity:- O(NlogN)\n\t// Space Complexity:- O(N)\n #define ll long long\n #define MOD 1000000007\n int getNumberOfBacklogOrders(vector<vector<int>>& orders) {\n ll ans = 0;\n multiset<pair<int,int>> sell;\n multiset<pair<int,int>,greater<pair<int,int>>> buy;\n for(auto& order:orders){\n int price = order[0],amount = order[1],orderType = order[2];\n if(orderType==0){\n while(!sell.empty() and amount>0 and sell.begin()->first<=price){\n int available_price = sell.begin()->first;\n int available_amount = sell.begin()->second;\n sell.erase(sell.begin());\n \n int take = min(amount,available_amount);\n \n amount -= take;\n available_amount -= take;\n \n if(available_amount){\n sell.insert({available_price,available_amount});\n }\n }\n \n if(amount){\n buy.insert({price,amount});\n }\n }\n else{\n while(!buy.empty() and amount>0 and buy.begin()->first>=price){\n int available_price = buy.begin()->first;\n int available_amount = buy.begin()->second;\n buy.erase(buy.begin());\n \n int take = min(amount,available_amount);\n \n amount -= take;\n available_amount -= take;\n \n if(available_amount){\n buy.insert({available_price,available_amount});\n }\n }\n \n if(amount){\n sell.insert({price,amount});\n }\n }\n }\n for(auto& x:buy){\n ans += x.second;\n ans %= MOD;\n }\n for(auto& x:sell){\n ans += x.second;\n ans %= MOD;\n }\n return (int)ans;\n }\n};\n```\n**DOn\'t Forget to Upvote!** | 1 | 0 | ['C'] | 0 |
number-of-orders-in-the-backlog | Python solution using minheap and maxheap | python-solution-using-minheap-and-maxhea-l7fp | \nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n \'\'\'\n 2D array orders \n orders[i] = [price | ikna | NORMAL | 2021-11-06T04:11:07.974336+00:00 | 2021-11-06T04:11:07.974380+00:00 | 168 | false | ```\nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n \'\'\'\n 2D array orders \n orders[i] = [price, amount, orderType]\n 0 = buy\n 1 = sell\n \n backlog = []\n \n if order == buy:\n if any get the sell_order with smallest price. \n - sell removed from the backlog\n else:\n - buy is added to the backlog\n if sell:\n if any get the buy_order with largest price,\n - buy order is removed from the backlog\n else:\n - sell is added to the backlog\n \n \'\'\'\n minheap = []\n maxheap = []\n \n BUY, SELL = 0, 1\n \n for price, order, typ in orders:\n consume = 0\n if typ is BUY:\n while minheap and order and minheap[0][0] <= price:\n sellPrice, sellOrder = heappop(minheap)\n consume = min(order, sellOrder)\n sellOrder -= consume\n order -= consume\n if sellOrder:\n heappush(minheap, (sellPrice, sellOrder))\n \n if order: #if any buy orders are remaining\n heappush(maxheap, (-price, order))\n \n else: #order is SELL\n while maxheap and order and -maxheap[0][0] >= price:\n buyPrice, buyOrder = heappop(maxheap)\n consume = min(order, buyOrder)\n buyOrder -= consume\n order -= consume\n if buyOrder:\n heappush(maxheap, (buyPrice, buyOrder))\n \n if order: #if any sell orders are remaining\n heappush(minheap, (price, order))\n \n totorder = 0\n for _,order in minheap:\n totorder += order\n \n for _,order in maxheap:\n totorder += order\n \n return totorder % (10**9 + 7)\n \n``` | 1 | 0 | ['Heap (Priority Queue)', 'Python'] | 0 |
number-of-orders-in-the-backlog | C++ priority Queue based solution || beginner friendly code | c-priority-queue-based-solution-beginner-zh5n | \nclass Solution {\npublic:\n int getNumberOfBacklogOrders(vector<vector<int>>& orders) {\n \n priority_queue<pair<int,int>,vector<pair<int,int | 007shaswatkumar | NORMAL | 2021-08-11T18:33:51.989179+00:00 | 2021-08-11T18:33:51.989219+00:00 | 271 | false | ```\nclass Solution {\npublic:\n int getNumberOfBacklogOrders(vector<vector<int>>& orders) {\n \n priority_queue<pair<int,int>,vector<pair<int,int>> > buy; //max queue for buy\n priority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int>> >sell;//min queue for sell\n \n for(auto x:orders){\n \n if(x[2]==0){\n buy.push({x[0],x[1]});\n int flag=0;\n while(sell.size()>0 && sell.top().first<=x[0] && x[1]>0){\n flag=1;\n buy.pop();\n auto t = sell.top();\n sell.pop();\n if(t.second<x[1]){\n \n buy.push({x[0],x[1]-t.second});\n x[1] = x[1] - t.second;//decrease the size of remaining items as well\n \n }\n else{\n sell.push({t.first,t.second-x[1]});\n x[1] = 0;//all the items got finished\n }\n }\n \n \n \n \n \n }\n \n if(x[2]==1){\n \n int flag=0;\n sell.push({x[0],x[1]});\n while(buy.size()>0 && buy.top().first>=x[0] && x[1]>0){\n flag=1;\n auto t = buy.top();\n sell.pop();\n buy.pop();\n if(t.second<x[1]){\n \n sell.push({x[0],x[1]-t.second});\n x[1]= x[1] -t.second;//decrement the remaining item\n }\n else{\n buy.push({t.first,t.second-x[1]});\n x[1] = 0;//all the item got finished\n }\n }\n \n \n \n \n \n }\n \n }\n\t\t//now count the number of items remaining in the queues;\n int count =0;\n while(buy.size()){\n \n count = (count + buy.top().second)%1000000007;\n buy.pop();\n }\n \n while(sell.size()){\n \n count = (count + sell.top().second)%1000000007;\n sell.pop();\n }\n \n return count;\n \n }\n};\n```\n\n**Hit like if you liked:: ,, Happy Coding :)** | 1 | 0 | ['C', 'Heap (Priority Queue)', 'C++'] | 0 |
number-of-orders-in-the-backlog | c++(196ms 99%) two maps | c196ms-99-two-maps-by-zx007pi-ngk8 | Runtime: 196 ms, faster than 98.82% of C++ online submissions for Number of Orders in the Backlog.\nMemory Usage: 64.5 MB, less than 39.53% of C++ online submis | zx007pi | NORMAL | 2021-07-19T16:34:16.041777+00:00 | 2021-07-19T16:40:15.189254+00:00 | 149 | false | Runtime: 196 ms, faster than 98.82% of C++ online submissions for Number of Orders in the Backlog.\nMemory Usage: 64.5 MB, less than 39.53% of C++ online submissions for Number of Orders in the Backlog.\n```\nclass Solution {\npublic:\n int getNumberOfBacklogOrders(vector<vector<int>>& orders) {\n map<int, long> buy, sell;\n \n for(auto &it: orders) \n if(it[2]){ //buy\n auto b = buy.rbegin();\n while(b != buy.rend() && it[0] <= b->first){ //if we can buy\n it[1] -= b->second;\n if(it[1] < 0) {b->second = -it[1]; break;}\n \n int tmp = b->first; \n b++; \n buy.erase(tmp);\n if(it[1] == 0) break;\n }\n if(it[1] > 0) sell[it[0]] += it[1];\n }\n else { //sell\n auto s = sell.begin();\n while(s != sell.end() && it[0] >= s->first){ //if we can sell\n it[1] -= s->second;\n if(it[1] < 0) {s->second = -it[1]; break;}\n \n int tmp = s->first;\n s++;\n sell.erase(tmp);\n if(it[1] == 0) break;\n }\n if(it[1] > 0) buy[it[0]] += it[1];\n } \n \n \n long answer = 0;\n for(auto &it: buy ) answer += it.second;\n for(auto &it: sell) answer += it.second;\n \n return answer % 1000000007;\n }\n};\n``` | 1 | 0 | ['C', 'C++'] | 0 |
number-of-orders-in-the-backlog | Python easy to understand with comments (heaps) | python-easy-to-understand-with-comments-rgi25 | A simple implmentation using Heaps (creds to ye15 for a guideline)\n\n\ndef getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n buy_heap, sell_ | riyasat | NORMAL | 2021-03-24T19:41:43.450284+00:00 | 2021-03-24T19:41:43.450326+00:00 | 180 | false | A simple implmentation using Heaps (creds to ye15 for a guideline)\n\n```\ndef getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n buy_heap, sell_heap = [], [] #max heap for buy order, min heap for sell orders\n \n for p, a, t in orders:\n #sell order\n if t:\n #while the quantity of the sell order is not satisfied and there is a match\n while a and buy_heap and -buy_heap[0][0] >= p:\n #quantity of the best buy order avialable\n buy_amount = buy_heap[0][1]\n #if there is enough buy_amount, we can execute this sell order and exit the loop\n if buy_amount > a:\n #assign new amount after sell order\n buy_heap[0][1] -= a\n a = 0\n #there is not enough of the best buy order to execute the sell order\n else:\n #remove the current buy order (alredy used) and work with the next best buy order\n heapq.heappop(buy_heap)\n #update the remaining sell order\n a -= buy_amount\n #if the sell order is not fulfilled, add it to the sell backlog (sell heap)\n if a > 0:\n heapq.heappush(sell_heap, [p, a])\n #buy order \n else:\n #same idea for buy order\n while a and sell_heap and sell_heap[0][0] <= p:\n sell_amount = sell_heap[0][1]\n if(sell_amount > a):\n sell_heap[0][1] -= a\n a = 0\n else:\n heapq.heappop(sell_heap)\n a-=sell_amount\n if(a > 0):\n heapq.heappush(buy_heap, [-p, a])\n \n #return the remaining orders in the backlog\n return sum(a for _, a in buy_heap+sell_heap) % (10**9 + 7)\n``` | 1 | 1 | ['Heap (Priority Queue)', 'Python'] | 0 |
number-of-orders-in-the-backlog | Java | Priority Queue | java-priority-queue-by-bhattfrequent-b4p5 | \nclass Solution {\n public int getNumberOfBacklogOrders(int[][] orders) {\n PriorityQueue<BO> pqBo = new PriorityQueue(new BOComp());\n Priori | bhattfrequent | NORMAL | 2021-03-23T03:14:35.236267+00:00 | 2021-03-23T03:14:35.236304+00:00 | 134 | false | ```\nclass Solution {\n public int getNumberOfBacklogOrders(int[][] orders) {\n PriorityQueue<BO> pqBo = new PriorityQueue(new BOComp());\n PriorityQueue<SO> pqSo = new PriorityQueue(new SOComp());\n // IF BUY CHECK SMALLEST SELL, SELL SHOULD BE LESS\n // IF SELL CHECK LARGEST BUY, BUY SHOULD BE MORE\n for(int[] item : orders){\n boolean isBo = false;\n BO buyBlog = null;\n SO sellBlog = null;\n if(item[2] == 0){\n buyBlog = new BO(item[0], item[1]);\n if(pqSo.peek() == null){\n pqBo.add(buyBlog);\n }else{\n sellBlog = pqSo.poll();\n }\n isBo = true;\n }else{\n sellBlog = new SO(item[0], item[1]);\n if(pqBo.peek() == null){\n pqSo.add(sellBlog);\n }else{\n buyBlog = pqBo.poll();\n }\n }\n if(buyBlog == null || sellBlog == null) continue;\n if(isBo == true){\n if(sellBlog.getPrice() <= buyBlog.getPrice()){\n if(sellBlog.getQty() >= buyBlog.getQty()){\n sellBlog.setQty(sellBlog.getQty() - buyBlog.getQty());\n if(sellBlog.getQty() > 0){\n pqSo.add(sellBlog);\n }\n }else{\n buyBlog.setQty(buyBlog.getQty() - sellBlog.getQty());\n while(buyBlog.getQty() > 0 && pqSo.peek() != null && pqSo.peek().getPrice() <= buyBlog.getPrice()){\n if(buyBlog.getQty() > pqSo.peek().getQty()){\n buyBlog.setQty(buyBlog.getQty() - pqSo.poll().getQty());\n }else{\n pqSo.peek().setQty(pqSo.peek().getQty() - buyBlog.getQty() );\n buyBlog.setQty(0);\n }\n \n }\n if(buyBlog.getQty() > 0){\n pqBo.add(buyBlog);\n }\n }\n }else{\n pqSo.add(sellBlog);\n pqBo.add(buyBlog);\n }\n }else{\n \n if(sellBlog.getPrice() <= buyBlog.getPrice()){\n if(sellBlog.getQty() >= buyBlog.getQty()){\n sellBlog.setQty(sellBlog.getQty() - buyBlog.getQty());\n \n while(sellBlog.getQty() > 0 && pqBo.peek() != null && pqBo.peek().getPrice() >= sellBlog.getPrice()){\n \n if(sellBlog.getQty() > pqBo.peek().getQty()){\n sellBlog.setQty(sellBlog.getQty() - pqBo.poll().getQty());\n }else{\n pqBo.peek().setQty(pqBo.peek().getQty() - sellBlog.getQty() );\n sellBlog.setQty(0);\n }\n \n }\n \n if(sellBlog.getQty() > 0){\n pqSo.add(sellBlog);\n }\n }else{\n buyBlog.setQty(buyBlog.getQty() - sellBlog.getQty());\n if(buyBlog.getQty() > 0){\n pqBo.add(buyBlog);\n }\n }\n }else{\n pqBo.add(buyBlog);\n pqSo.add(sellBlog);\n }\n }\n }\n BO buyBlog = null;\n SO sellBlog = null;\n int blogQty = 0;\n int max = (int )(Math.pow(10,9) + 7);\n while(!pqBo.isEmpty()){\n buyBlog = pqBo.poll();\n blogQty = (blogQty + buyBlog.getQty()) % max;\n }\n while(!pqSo.isEmpty()){\n sellBlog = pqSo.poll();\n blogQty = (blogQty + sellBlog.getQty()) % max;\n }\n return blogQty;\n }\n \n}\n\nclass BO {\n private int price;\n private int qty;\n public BO(int price, int qty){\n this.price = price;\n this.qty = qty;\n }\n public int getPrice(){\n return this.price;\n }\n public int getQty(){\n return this.qty;\n }\n public void setQty(int qty){\n this.qty = qty;\n }\n @Override\n public String toString(){\n return "Price is " + this.getPrice() + " Qty is " + this.getQty();\n }\n}\n\nclass SO {\n private int price;\n private int qty;\n public SO(int price, int qty){\n this.price = price;\n this.qty = qty;\n }\n public int getPrice(){\n return this.price;\n }\n public int getQty(){\n return this.qty;\n }\n public void setQty(int qty){\n this.qty = qty;\n }\n @Override\n public String toString(){\n return "Price is " + this.getPrice() + " Qty is " + this.getQty();\n }\n}\n\nclass BOComp implements Comparator<BO>{\n public int compare(BO itemA,BO itemB){\n return itemA.getPrice() < itemB.getPrice()? 1: -1;\n }\n}\n\nclass SOComp implements Comparator<SO>{\n public int compare(SO itemA,SO itemB){\n return itemA.getPrice() > itemB.getPrice()? 1: -1;\n }\n}\n``` | 1 | 0 | [] | 1 |
number-of-orders-in-the-backlog | C# SortedSet - O(N*LogN) time | c-sortedset-onlogn-time-by-xenfruit-b4f3 | SortedSet works as a priority queue here. SortedSet.Min, SortedSet.Max, SortedSet.Add and SortedSet.Remove methods take LogN time each which leads to O(NLogN) t | xenfruit | NORMAL | 2021-03-22T04:18:24.421930+00:00 | 2021-03-29T15:13:11.142541+00:00 | 107 | false | SortedSet works as a priority queue here. SortedSet.Min, SortedSet.Max, SortedSet.Add and SortedSet.Remove methods take LogN time each which leads to O(NLogN) time complexity overall.\nWe need method AddOrder because SortedSet doesn\'t allow to store duplicates.\n```\npublic class Solution\n{\n public int GetNumberOfBacklogOrders(int[][] orders)\n {\n var buyQueue = new SortedSet<Tuple<int, int>>();\n var sellQueue = new SortedSet<Tuple<int, int>>();\n for (int i = 0; i < orders.Length; i++)\n {\n var price = orders[i][0];\n var amount = orders[i][1];\n if (orders[i][2] == 0)\n {\n while (amount > 0 && sellQueue.Count > 0)\n {\n var min = sellQueue.Min;\n var minPrice = min.Item1;\n if (minPrice > price)\n break;\n amount = DecreaseAmount(amount, sellQueue, min);\n }\n if (amount > 0)\n AddOrder(price, amount, buyQueue);\n }\n else\n {\n while (amount > 0 && buyQueue.Count > 0)\n {\n var max = buyQueue.Max;\n var maxPrice = max.Item1;\n if (maxPrice < price)\n break;\n amount = DecreaseAmount(amount, buyQueue, max);\n }\n if (amount > 0)\n AddOrder(price, amount, sellQueue);\n }\n }\n var result = 0;\n foreach (var item in buyQueue)\n result = (result + item.Item2) % (int)(1e9 + 7);\n foreach (var item in sellQueue)\n result = (result + item.Item2) % (int)(1e9 + 7);\n return result;\n }\n \n private int DecreaseAmount(int amount, SortedSet<Tuple<int, int>> queue, Tuple<int, int> order)\n {\n queue.Remove(order);\n var orderPrice = order.Item1;\n var orderAmount = order.Item2;\n if (orderAmount > amount)\n {\n AddOrder(orderPrice, orderAmount - amount, queue);\n return 0;\n }\n return amount - orderAmount;\n }\n \n private void AddOrder(int price, int amount, SortedSet<Tuple<int, int>> queue)\n {\n var order = Tuple.Create(price, amount);\n while (queue.Contains(order))\n {\n queue.Remove(order);\n order = Tuple.Create(price, order.Item2 * 2);\n }\n queue.Add(order);\n }\n}\n``` | 1 | 0 | [] | 0 |
number-of-orders-in-the-backlog | Java Solution with Priority Queue | java-solution-with-priority-queue-by-raj-i25q | \nclass Solution {\n static int mod = 1000000007;\n \n public int getNumberOfBacklogOrders(int[][] orders) {\n Queue<int[]> buyBacklog = new Pri | rajanpupa | NORMAL | 2021-03-21T22:18:15.802549+00:00 | 2021-03-21T22:18:15.802592+00:00 | 86 | false | ```\nclass Solution {\n static int mod = 1000000007;\n \n public int getNumberOfBacklogOrders(int[][] orders) {\n Queue<int[]> buyBacklog = new PriorityQueue<>((a,b) -> b[0]-a[0]);\n Queue<int[]> sellBacklog = new PriorityQueue<>((a,b) -> a[0]-b[0]);\n \n \n \n for(int[] order: orders) {\n if(order[2] == 0) { // buy\n while (!sellBacklog.isEmpty() && sellBacklog.peek()[0] <= order[0]) {\n int [] minSell = sellBacklog.peek();\n \n if(minSell[1] > order[1]) {\n // more to sell than buy\n minSell[1] -= order[1];\n order[1] = 0;\n break;\n } else if(minSell[1] == order[1]) {\n // buy quantity and sell quantity are same\n sellBacklog.remove();\n order[1] = 0;\n break;\n } else{\n // buy more quantity than this batch has to sell\n order[1] -= minSell[1];\n sellBacklog.remove();\n }\n } // while\n if(order[1] > 0) {\n buyBacklog.add(order);\n }\n } else { // sell\n while(!buyBacklog.isEmpty() && buyBacklog.peek()[0] >= order[0]) {\n int[] maxBuy = buyBacklog.peek();\n \n if(maxBuy[1] > order[1]) {\n // more buy than sell\n maxBuy[1] -= order[1];\n order[1] = 0;\n break;\n } else if (maxBuy[1] == order[1]) {\n // equal buy and sell\n order[1] = 0;\n buyBacklog.remove();\n break;\n } else {\n // less to buy than sell\n order[1] -= maxBuy[1];\n buyBacklog.remove();\n }\n } // while\n if(order[1] > 0) {\n sellBacklog.add(order);\n }\n }\n } // for\n long batch = 0;\n \n for(int[] buy: buyBacklog) batch = (batch+buy[1])%mod;\n for(int[] sell: sellBacklog) batch = (batch+sell[1])%mod;\n \n return (int) batch;\n }\n}\n``` | 1 | 0 | [] | 0 |
number-of-orders-in-the-backlog | Java | Runtime and Memory 100% | java-runtime-and-memory-100-by-ryanrehma-7tj6 | \nclass Solution {\n int MOD = 1000000007;\n public void insert(int elem, ArrayList<Integer> backlog, int[][] orders) {\n int left = 0, right = bac | ryanrehman99 | NORMAL | 2021-03-21T09:15:47.785073+00:00 | 2021-03-21T09:15:47.785106+00:00 | 77 | false | ```\nclass Solution {\n int MOD = 1000000007;\n public void insert(int elem, ArrayList<Integer> backlog, int[][] orders) {\n int left = 0, right = backlog.size();\n while (left < right) {\n int mid = left + (right - left) / 2;\n if (orders[elem][0] > orders[backlog.get(mid)][0])\n left = mid+1;\n else\n right = mid;\n }\n backlog.add(left, elem);\n }\n \n public void buy(int i, ArrayList<Integer> buy_backlog, ArrayList<Integer> sell_backlog, int[][] orders) {\n while (orders[i][1] > 0 && sell_backlog.size() > 0) {\n int min_sell = sell_backlog.get(0);\n if (orders[min_sell][0] > orders[i][0]) break;\n \n int delete = Math.min(orders[min_sell][1], orders[i][1]);\n orders[min_sell][1] -= delete;\n orders[i][1] -= delete;\n if (orders[min_sell][1] == 0) sell_backlog.remove(0);\n }\n \n if (orders[i][1] != 0) insert(i, buy_backlog, orders);\n }\n \n public void sell(int i, ArrayList<Integer> buy_backlog, ArrayList<Integer> sell_backlog, int[][] orders) {\n while (orders[i][1] > 0 && buy_backlog.size() > 0) {\n int n = buy_backlog.size() - 1;\n int max_buy = buy_backlog.get(n);\n if (orders[max_buy][0] < orders[i][0]) break;\n \n int delete = Math.min(orders[max_buy][1], orders[i][1]);\n orders[max_buy][1] -= delete;\n orders[i][1] -= delete;\n if (orders[max_buy][1] == 0) buy_backlog.remove(n);\n }\n if (orders[i][1] != 0) insert(i, sell_backlog, orders);\n }\n\n public int getNumberOfBacklogOrders(int[][] orders) {\n ArrayList<Integer> buy_backlog = new ArrayList<>();\n ArrayList<Integer> sell_backlog = new ArrayList<>();\n\n for (int i=0; i<orders.length; i++) {\n if (orders[i][2] == 0)\n buy(i, buy_backlog, sell_backlog, orders);\n else\n sell(i, buy_backlog, sell_backlog, orders);\n }\n \n int ct = 0;\n for (int i : buy_backlog) ct = (ct + orders[i][1]) % MOD;\n for (int i : sell_backlog) ct = (ct + orders[i][1]) % MOD;\n \n return ct;\n }\n}\n``` | 1 | 0 | [] | 0 |
number-of-orders-in-the-backlog | Java PriorityQueue. Simple and Straightforward | java-priorityqueue-simple-and-straightfo-twy3 | Idea is very simple. Maintain a min heap for sell backlogs and maxHeap for buy backlogs.\nWhen order is sell order we will tye to fullfill it from buy backlog w | Jenjoy | NORMAL | 2021-03-21T07:28:26.405356+00:00 | 2021-03-21T07:36:25.816639+00:00 | 91 | false | Idea is very simple. Maintain a min heap for sell backlogs and maxHeap for buy backlogs.\nWhen order is sell order we will tye to fullfill it from buy backlog with making sure conditions are met and vice versa.\n\nAt the end go through both the backlogs and compute total backlogs orders\n\nMore commets and explaination inline\n```\n public int getNumberOfBacklogOrders(int[][] orders) { \n\t\tQueue<int[]> sellBacklog = new PriorityQueue<int[]>((a, b) -> a[0] - b[0]);\n\t\tQueue<int[]> buyBacklog = new PriorityQueue<int[]>((a, b) -> b[0] - a[0]);\n\n\t\tfor (int[] order : orders) {\n\t\t\tint price = order[0], amt = order[1], type = order[2];\n\t\t\tif (type == 0) { // buy order\n\t\t\t\twhile (!sellBacklog.isEmpty() && sellBacklog.peek()[0] <= price && amt > 0) {\n\t\t\t\t\tif (sellBacklog.peek()[1] > amt) {\n\t\t\t\t\t\t// we have more than required for current buy order so update this sell order and this order is fully completed\n\t\t\t\t\t\tsellBacklog.peek()[1] -= amt;\n\t\t\t\t\t\tamt = 0;\n\t\t\t\t\t} else {\n\t\t\t\t\t\t// this whole sell order will be used to fullfil this buy order\n\t\t\t\t\t\tamt -= sellBacklog.remove()[1];\n\t\t\t\t\t}\n\t\t\t\t}\n\n\t\t\t\t// we still have few more order to fullfil so add it to buy backlog\n\t\t\t\tif (amt > 0) {\n\t\t\t\t\tbuyBacklog.add(new int[] { price, amt });\n\t\t\t\t}\n\t\t\t} else { // sell order\n\t\t\t\twhile (!buyBacklog.isEmpty() && buyBacklog.peek()[0] >= price && amt > 0) {\n\t\t\t\t\tif (buyBacklog.peek()[1] > amt) {\n\t\t\t\t\t\t// we have more than required for current sell order so update this buy order and this sell order is fully completed\n\t\t\t\t\t\tbuyBacklog.peek()[1] -= amt;\n\t\t\t\t\t\tamt = 0;\n\t\t\t\t\t} else {\n\t\t\t\t\t\t// this whole buy order will be used to fullfil current sell order\n\t\t\t\t\t\tamt -= buyBacklog.remove()[1];\n\t\t\t\t\t}\n\t\t\t\t}\n\n\t\t\t\t// we still have few more order to fullfil so add it to sell backlog\n\t\t\t\tif (amt > 0) {\n\t\t\t\t\tsellBacklog.add(new int[] { price, amt });\n\t\t\t\t}\n\n\t\t\t}\n\t\t}\n\n // compute total backlog\n\t\tlong result = 0;\n\t\tfor (int[] order : sellBacklog) result += order[1];\t\t\n\t\tfor (int[] order : buyBacklog) result += order[1];\n\t\t\n\t\treturn (int)(result % 1000000007);\n }\n``` | 1 | 0 | [] | 0 |
number-of-orders-in-the-backlog | The Example to Practice DRY | the-example-to-practice-dry-by-haoel-2edi | \n\nclass Order {\npublic:\n int price;\n int amount;\n};\n\nenum COMP { GREATER, LESS };\n\ntemplate <COMP op>\nclass OrderComp {\npublic:\n bool oper | haoel | NORMAL | 2021-03-21T07:12:41.995627+00:00 | 2021-03-21T07:12:41.995660+00:00 | 106 | false | \n```\nclass Order {\npublic:\n int price;\n int amount;\n};\n\nenum COMP { GREATER, LESS };\n\ntemplate <COMP op>\nclass OrderComp {\npublic:\n bool operator() (const Order& lhs, const Order& rhs) {\n if (op == GREATER) {\n return lhs.price > rhs.price;\n }\n return lhs.price < rhs.price;\n }\n};\n\n\nclass Solution {\nprivate:\n template<typename T1, typename T2>\n void processOrder(T1& q1, T2& q2, COMP op, int price, int amount, string n1="q1", string n2="q2") {\n if (q2.size() == 0) {\n q1.push(Order{price, amount});\n return;\n }\n \n while(!q2.empty() && amount > 0 ){\n Order order = q2.top(); \n if (op == GREATER && order.price > price ) break;\n if (op == LESS && order.price < price) break;\n\n q2.pop();\n //cout << "=> deQueue("<< n2 << "): " << order.price << ", "<< order.amount << endl;\n\n int amt = min(order.amount, amount);\n order.amount -= amt;\n amount -= amt;\n if (order.amount > 0) {\n //cout << "<= enQueue("<< n2 <<"): " << order.price << ", "<< order.amount << endl;\n q2.push(order);\n }\n }\n if (amount > 0) {\n //cout << "<= enQueue("<< n1 <<"): " << price << ", "<< amount << endl;\n q1.push(Order{price, amount});\n }\n }\n \n template<typename T>\n void countQ(T& q, int& amount){\n while(!q.empty()) {\n amount = (amount + q.top().amount) % 1000000007;\n q.pop();\n }\n }\npublic:\n int getNumberOfBacklogOrders(vector<vector<int>>& orders) {\n \n priority_queue<Order, vector<Order>, OrderComp<GREATER>> sell;\n priority_queue<Order, vector<Order>, OrderComp<LESS>> buy;\n \n for (auto& order : orders) {\n int& price = order[0];\n int& amount = order[1];\n \n if (order[2] == 0) { //buy order\n processOrder(buy, sell, GREATER, price, amount, "buy", "sell");\n }else { // sell order\n processOrder(sell, buy, LESS, price, amount, "sell", "buy");\n }\n }\n \n int amount = 0;\n countQ(sell, amount);\n countQ(buy, amount);\n return amount ;\n }\n};\n``` | 1 | 0 | [] | 0 |
number-of-orders-in-the-backlog | [JavaScript] 2 Heap Solution w/ explanation | javascript-2-heap-solution-w-explanation-ua1r | javascript\nvar getNumberOfBacklogOrders = function(orders) {\n const buyHeap = new Heap((child, parent) => child.price > parent.price)\n const sellHeap = | stevenkinouye | NORMAL | 2021-03-21T07:05:41.505823+00:00 | 2021-03-21T07:07:05.858663+00:00 | 227 | false | ```javascript\nvar getNumberOfBacklogOrders = function(orders) {\n const buyHeap = new Heap((child, parent) => child.price > parent.price)\n const sellHeap = new Heap((child, parent) => child.price < parent.price)\n \n for (let [price, amount, orderType] of orders) {\n \n // sell\n if (orderType) {\n \n // while there are amount to be decremented from the sell,\n // orders to in the buy backlog, and the price of the largest\n // price is greater than the sell price decrement the\n // amount of the order with the largest price by the amount\n while (amount > 0 && buyHeap.peak() && buyHeap.peak().price >= price) {\n if (buyHeap.peak().amount > amount) {\n buyHeap.peak().amount -= amount\n amount = 0\n } else {\n amount -= buyHeap.pop().amount\n }\n }\n \n // if there is any amount left, add it to the sale backlog\n if (amount) {\n sellHeap.push({ price, amount })\n }\n\n // buy\n } else {\n \n // while there are amount to be decremented from the buy,\n // orders to in the sell backlog, and the price of the smallest\n // price is less than the buy price decrement the\n // amount of the order with the smallest price by the amount\n while (amount > 0 && sellHeap.peak() && sellHeap.peak().price <= price) {\n if (sellHeap.peak().amount > amount) {\n sellHeap.peak().amount -= amount\n amount = 0\n } else {\n amount -= sellHeap.pop().amount;\n }\n }\n \n // if there is any amount left, add it to the buy backlog\n if (amount) {\n buyHeap.push({ price, amount })\n }\n }\n }\n \n // total all of the amounts in both backlogs and return the result\n let accumultiveAmount = 0;\n for (const { amount } of buyHeap.store) {\n accumultiveAmount += amount;\n }\n for (const { amount } of sellHeap.store) {\n accumultiveAmount += amount;\n }\n return accumultiveAmount % 1000000007\n};\n\nclass Heap {\n constructor(fn) {\n this.store = [];\n this.fn = fn;\n }\n \n peak() {\n return this.store[0];\n }\n \n size() {\n return this.store.length;\n }\n \n pop() {\n if (this.store.length < 2) {\n return this.store.pop();\n }\n const result = this.store[0];\n this.store[0] = this.store.pop();\n this.heapifyDown(0);\n return result;\n }\n \n push(val) {\n this.store.push(val);\n this.heapifyUp(this.store.length - 1);\n }\n \n heapifyUp(child) {\n while (child) {\n const parent = Math.floor((child - 1) / 2);\n if (this.shouldSwap(child, parent)) {\n [this.store[child], this.store[parent]] = [this.store[parent], this.store[child]]\n child = parent;\n } else {\n return child;\n }\n }\n }\n \n heapifyDown(parent) {\n while (true) {\n let [child, child2] = [1,2].map((x) => parent * 2 + x).filter((x) => x < this.size());\n if (this.shouldSwap(child2, child)) {\n child = child2\n }\n if (this.shouldSwap(child, parent)) {\n [this.store[child], this.store[parent]] = [this.store[parent], this.store[child]]\n parent = child;\n } else {\n return parent;\n }\n }\n }\n \n shouldSwap(child, parent) {\n return child && this.fn(this.store[child], this.store[parent]);\n }\n}\n``` | 1 | 0 | ['Heap (Priority Queue)', 'JavaScript'] | 1 |
number-of-orders-in-the-backlog | Python 3, Heap and Dictionary | python-3-heap-and-dictionary-by-silvia42-d7wb | We use two heaps:\nlogBuy is storing MINUS prices, because we will need the highest price first.\nlogSell is storing prices, because we will need the lowest pri | silvia42 | NORMAL | 2021-03-21T05:15:18.291466+00:00 | 2021-03-21T13:25:09.069889+00:00 | 112 | false | We use two heaps:\n```logBuy``` is storing MINUS prices, because we will need the highest price first.\n```logSell``` is storing prices, because we will need the lowest price first.\n\nWe use two dictonaries:\n```dictBuy[k]``` is number of prices ```-k``` in ```Buy Backlog```\n```dictSell[k]``` is number of prices ```k``` in ```Sell Backlog```\n\nFirst we are iterating over ```orders``` and updating heaps and dictionaries.\nFinally we are counting, how many items is in Backlogs and return that value.\n\n```\nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n logBuy=[]\n dictBuy={}\n logSell=[]\n dictSell={}\n # price,amount,type\n for p,a,t in orders:\n if t: # type=1 = SELL\n dictSell[p]=dictSell.get(p,0) + a\n heapq.heappush(logSell,p) \n else: # type=0 = BUY\n dictBuy[-p]=dictBuy.get(-p,0) + a\n heapq.heappush(logBuy,-p)\n ok=1\n while ok and logBuy and logSell:\n ok=0\n buy=heapq.heappop(logBuy)\n sell=heapq.heappop(logSell)\n b=dictBuy[buy]\n s=dictSell[sell]\n if b and s and -buy>=sell:\n ok=1\n amount=min(b,s)\n dictBuy[buy]-=amount\n dictSell[sell]-=amount\n if dictBuy[buy]:\n heapq.heappush(logBuy,buy)\n if dictSell[sell]:\n heapq.heappush(logSell,sell) \n return (sum(v for k,v in dictBuy.items()) + sum(v for k,v in dictSell.items())) % (10**9+7)\n``` | 1 | 0 | ['Heap (Priority Queue)', 'Python'] | 0 |
number-of-orders-in-the-backlog | [Python3] Simple Solution with Priority Queue (100 % Time & Space Efficiency) | python3-simple-solution-with-priority-qu-2wml | \nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n buy, sell = [], []\n \n for order in orders:\n | leonardthong | NORMAL | 2021-03-21T04:25:18.242163+00:00 | 2021-03-21T04:26:07.477654+00:00 | 71 | false | ```\nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n buy, sell = [], []\n \n for order in orders:\n if order[2] == 0:\n while len(sell) > 0:\n if 0 >= len(sell) or 0 == order[1]: break\n\n se = heapq.heappop(sell)\n if order[0] >= se[0]:\n t = min(order[1], se[1])\n order[1] -= t\n se[1] -= t\n \n if se[1] != 0:\n heapq.heappush(sell, se)\n break\n else:\n heapq.heappush(sell, se)\n break\n \n if order[1] != 0:\n order[0] = -order[0]\n heapq.heappush(buy, order)\n \n else:\n while len(buy) > 0:\n if 0 >= len(buy) or 0 == order[1]: break\n \n bu = heapq.heappop(buy)\n if order[0] <= (bu[0] * -1):\n t = min(order[1], bu[1])\n order[1] -= t\n bu[1] -= t\n \n if bu[1] != 0:\n heapq.heappush(buy, bu)\n break\n else:\n heapq.heappush(buy, bu)\n break\n \n if order[1] != 0:\n heapq.heappush(sell, order)\n\n\n x = 0 \n for b in buy:\n x += b[1]\n x %= (1000000000 + 7)\n \n for s in sell:\n x += s[1]\n x %= (1000000000 + 7)\n \n return x\n``` | 1 | 0 | [] | 0 |
number-of-orders-in-the-backlog | [Kotlin]Good problem. Let's implement the core datastruct of a matching engine. | kotlingood-problem-lets-implement-the-co-tu9n | It\'s really a good problem. It\'s the core datastruct of a matching engine. I really know it cause my job is about it.\n\nUsually we use the the LMAX Architect | azzssss | NORMAL | 2021-03-21T04:13:14.528484+00:00 | 2021-03-21T04:20:17.618719+00:00 | 431 | false | It\'s really a good problem. It\'s the core datastruct of a matching engine. I really know it cause my job is about it.\n\nUsually we use the the LMAX Architecture to implement a mathing engine. If you are interested in it, you can read this article [The LMAX Architecture](https://martinfowler.com/articles/lmax.html).\n\nBut unfortunately, I got a Time Limit Exceeded. I want to sovle this problem as usual as what we do when we implement it in a real situation. But it did not work in the contest. sad.\n\nA depthLine means a set of orders with the same price.\n\n```\nclass `Number of Orders in the Backlog` {\n\n val buy = TreeMap<Int, DepthLine> { a, b ->\n b - a\n }\n\n val sell = TreeMap<Int, DepthLine> { a, b ->\n a - b\n }\n\n val BUY = 0\n\n val SELL = 1\n\n val mod = 1000000007\n\n fun getNumberOfBacklogOrders(orders: Array<IntArray>): Int {\n for (order in orders) {\n for (i in 0 until order[1]) {\n match(Order(order[0], order[2]))\n }\n }\n var res = 0\n buy.forEach {\n res += it.value.size()\n res = res % mod\n }\n sell.forEach {\n res += it.value.size()\n res = res % mod\n }\n return res\n }\n\n fun match(order: Order) {\n if (order.type == SELL) {\n match(order, buy, sell)\n } else {\n match(order, sell, buy)\n }\n }\n\n private fun match(order: Order, book: TreeMap<Int, DepthLine>, oppositeBook: TreeMap<Int, DepthLine>) {\n var matched = false\n for ((price, depthLine) in book) {\n if (order.type == SELL) {\n if (price > order.price && depthLine.size() > 0) {\n depthLine.poll()\n matched = true\n break\n }\n } else {\n if (price < order.price && depthLine.size() > 0) {\n depthLine.poll()\n matched = true\n break\n }\n }\n }\n if (!matched) {\n val depthLine = oppositeBook[order.price]\n if (depthLine == null) {\n val depthLine = DepthLine(order.price)\n oppositeBook[order.price] = depthLine\n depthLine.offer(Order(order.price, SELL))\n } else {\n depthLine.offer(Order(order.price, SELL))\n }\n }\n }\n\n class DepthLine(val price: Int) {\n val orderList = LinkedList<Order>()\n\n fun size(): Int {\n return orderList.size\n }\n\n fun offer(order: Order) {\n orderList.offer(order)\n }\n\n fun poll() {\n orderList.poll()\n }\n }\n\n class Order(val price: Int, val type: Int)\n}\n``` | 1 | 1 | [] | 0 |
number-of-orders-in-the-backlog | C++ priority queue | c-priority-queue-by-navysealsniper-34lz | \n\n int getNumberOfBacklogOrders(vector>& orders) {\n std::priority_queue, vector\>> buy;\n auto cmp = {return a[0] > b[0];};\n std::p | navysealsniper | NORMAL | 2021-03-21T04:08:12.044211+00:00 | 2021-03-21T04:08:12.044253+00:00 | 68 | false | \n\n int getNumberOfBacklogOrders(vector<vector<int>>& orders) {\n std::priority_queue<vector<int>, vector<vector<int>>> buy;\n auto cmp = [](vector<int>& a, vector<int>& b) {return a[0] > b[0];};\n std::priority_queue<vector<int>, vector<vector<int>>, decltype(cmp)> sell(cmp);\n int mod = 1e9 + 7;\n for(auto& o : orders) {\n if (o[2] == 0) { // buy option, looking for smallest in sell queue, the price has to be <= \n \n int price = o[0];\n int amount = o[1];\n \n while(!sell.empty() && amount > 0) {\n auto cur = sell.top();\n \n if (cur[0] <= o[0]) {\n int cnt = cur[1];\n \n if (cnt >= amount) {\n cnt -= amount;\n amount = 0;\n sell.pop();\n if (cnt > 0) {\n sell.push({cur[0], cnt, 1});\n }\n } else {\n amount -= cnt;\n sell.pop();\n }\n } else {\n break;\n }\n }\n \n if (amount > 0) {\n buy.push({price, amount, 0});\n amount = 0;\n }\n \n } else { // sell, looking for larest buy, >= \n int price = o[0];\n int amount = o[1];\n \n while(!buy.empty() && amount > 0) {\n auto cur = buy.top();\n \n if (cur[0] >= price) {\n int cnt = cur[1];\n \n if (cnt >= amount) {\n cnt -= amount;\n amount = 0;\n buy.pop();\n if (cnt > 0) {\n buy.push({cur[0], cnt, 0});\n }\n } else {\n amount -= cnt;\n buy.pop();\n }\n \n } else {\n break;\n }\n }\n \n if (amount > 0) {\n sell.push({price, amount, 1});\n amount = 0;\n }\n \n }\n }\n \n long long res = 0;\n \n while(!buy.empty()) {\n auto cur = buy.top();\n buy.pop();\n \n res += cur[1];\n }\n \n while(!sell.empty()) {\n auto cur = sell.top();\n sell.pop();\n \n res += cur[1];\n }\n \n return res % mod;\n } | 1 | 0 | [] | 0 |
number-of-orders-in-the-backlog | [TypeScript] Skew Heap | typescript-skew-heap-by-shinkashi-t0i3 | I like Skew Heap. It\'s much simpler than usual healps and easy to customise.\n\ntypescript\nconst MOD = 10 ** 9 + 7;\n\nclass Node {\n constructor(\n | shinkashi | NORMAL | 2021-03-21T04:04:36.714479+00:00 | 2021-03-21T04:04:36.714511+00:00 | 93 | false | I like Skew Heap. It\'s much simpler than usual healps and easy to customise.\n\n```typescript\nconst MOD = 10 ** 9 + 7;\n\nclass Node {\n constructor(\n public price: number,\n public amount: number,\n public left: Node | null = null,\n public right: Node | null = null\n ) { };\n}\n\n// Skew Heap\nfunction meld(a: Node | null, b: Node | null, maxheap: boolean): Node | null {\n if (!a) return b;\n if (!b) return a;\n const cmp: boolean = maxheap ? a.price < b.price : a.price > b.price\n if (cmp) [b, a] = [a, b];\t\t\n a.right = meld(a.right, b, maxheap);\n [a.left, a.right] = [a.right, a.left];\n return a;\n}\n\nfunction getNumberOfBacklogOrders(orders: number[][]): number {\n let buyBacklog: Node | null = null;\n let sellBacklog: Node | null = null;\n\n for (let [price, amount, orderType] of orders) {\n if (orderType == 0) {\n // buy order\n while (amount > 0) {\n if (!sellBacklog || sellBacklog.price > price) {\n buyBacklog = meld(buyBacklog, new Node(price, amount), true);\n break;\n }\n else {\n const am = Math.min(amount, sellBacklog.amount);\n amount -= am;\n const cur = new Node(sellBacklog.price, sellBacklog.amount - am);\n sellBacklog = meld(sellBacklog.left, sellBacklog.right, false)\n if (cur.amount > 0) {\n sellBacklog = meld(sellBacklog, cur, false);\n }\n }\n }\n } else if (orderType == 1) {\n // sell order\n while (amount > 0) {\n if (!buyBacklog || buyBacklog.price < price) {\n sellBacklog = meld(sellBacklog, new Node(price, amount), false);\n break;\n }\n else {\n const am = Math.min(amount, buyBacklog.amount);\n amount -= am;\n const cur = new Node(buyBacklog.price, buyBacklog.amount - am);\n buyBacklog = meld(buyBacklog.left, buyBacklog.right, true)\n if (cur.amount > 0) {\n buyBacklog = meld(buyBacklog, cur, true);\n }\n }\n }\n }\n }\n\n // console.log({ buyBacklog, sellBacklog })\n\n const countHeap = (n: Node | null): number => {\n if (!n) return 0;\n let amount = n.amount;\n amount += countHeap(n.left) + countHeap(n.right);\n amount %= MOD;\n return amount;\n }\n\n return (countHeap(buyBacklog) + countHeap(sellBacklog)) % MOD;\n}\n\n``` | 1 | 0 | [] | 0 |
number-of-orders-in-the-backlog | [C++] Priority Queue Solution | c-priority-queue-solution-by-vector_long-awly | The problem description is really confusing.\n\nIntuition:\n\nDo what the description states.\n\nUsing a priority queue to store buy and sell respectively, sell | vector_long_long | NORMAL | 2021-03-21T04:01:48.986509+00:00 | 2021-03-21T04:02:28.708492+00:00 | 363 | false | The problem description is really confusing.\n\n**Intuition**:\n\nDo what the description states.\n\nUsing a priority queue to store buy and sell respectively, sell sorted from smallest to largest, buy sorted from largest to smallest.\n\nA very important insight is that do not store individual orders, instead, store the **number of orders** in that particular amount in total.\n\nThen every time grab the top element and compare.\n\n```\nclass Solution {\npublic:\n int getNumberOfBacklogOrders(vector<vector<int>>& orders) {\n // value, amount (buy smallest in sell, sell largest in buy), sell sorted from smallest to largest, buy sorted from largest to smallest\n long ans = 0;\n priority_queue<pair<int,long>, vector<pair<int,long>>, greater<pair<int,long>>> sell;\n priority_queue<pair<int,long>> buy;\n for(vector<int> order:orders){\n if(order[2]){\n if(buy.empty() || buy.top().first < order[0]){\n sell.push(make_pair(order[0],order[1]));\n continue;\n }\n while(!buy.empty() && order[1] > 0 && buy.top().first >= order[0]){\n if(buy.top().second >= order[1]){\n pair<int,long> cur = buy.top();\n cur.second -= order[1];\n buy.pop();\n buy.push(cur);\n order[1] = 0;\n break;\n }\n order[1] -= buy.top().second;\n buy.pop();\n }\n if(order[1] > 0) sell.push(make_pair(order[0],order[1]));\n } else{\n if(sell.empty() || sell.top().first > order[0]){\n buy.push(make_pair(order[0],order[1]));\n continue;\n }\n while(!sell.empty() && order[1] > 0 && sell.top().first <= order[0]){\n if(sell.top().second >= order[1]){\n pair<int,long> cur = sell.top();\n cur.second -= order[1];\n sell.pop();\n sell.push(cur); \n order[1] = 0;\n break;\n }\n order[1] -= sell.top().second;\n sell.pop();\n }\n if(order[1] > 0) buy.push(make_pair(order[0],order[1]));\n }\n }\n while(!sell.empty()){\n ans += sell.top().second; sell.pop();\n }\n ans %= 1000000007;\n while(!buy.empty()){\n ans += buy.top().second; buy.pop();\n }\n return ans % 1000000007;\n }\n};\n``` | 1 | 0 | ['C', 'Heap (Priority Queue)', 'C++'] | 1 |
number-of-orders-in-the-backlog | Min and max Heap | min-and-max-heap-by-wei130-2rfy | \tclass Solution(object):\n\t\tdef getNumberOfBacklogOrders(self, orders):\n\t\t\t"""\n\t\t\t:type orders: List[List[int]]\n\t\t\t:rtype: int\n\t\t\t"""\n\t\t\t | wei130 | NORMAL | 2021-03-21T04:01:31.150154+00:00 | 2021-03-21T04:01:31.150187+00:00 | 205 | false | \tclass Solution(object):\n\t\tdef getNumberOfBacklogOrders(self, orders):\n\t\t\t"""\n\t\t\t:type orders: List[List[int]]\n\t\t\t:rtype: int\n\t\t\t"""\n\t\t\tbuy = []\n\t\t\tsell = []\n\t\t\tfor i in range(len(orders)):\n\t\t\t\torder = orders[i]\n\t\t\t\tif order[2] == 0:\n\t\t\t\t\twhile sell and sell[0][0] <= order[0] and order[1] > 0:\n\t\t\t\t\t\tnode = heapq.heappop(sell)\n\t\t\t\t\t\tif node[1] >= order[1]:\n\t\t\t\t\t\t\tnode[1] -= order[1]\n\t\t\t\t\t\t\torder[1] = 0\n\t\t\t\t\t\t\theapq.heappush(sell, ([node[0], node[1]]))\n\t\t\t\t\t\telse:\n\t\t\t\t\t\t\torder[1] -= node[1]\n\t\t\t\t\tif order[1] > 0:\n\t\t\t\t\t\theapq.heappush(buy, ([-order[0], order[1]]))\n\t\t\t\telse:\n\t\t\t\t\twhile buy and abs(buy[0][0]) >= order[0] and order[1] > 0:\n\t\t\t\t\t\tnode = heapq.heappop(buy)\n\t\t\t\t\t\tif node[1] >= order[1]:\n\t\t\t\t\t\t\tnode[1] -= order[1]\n\t\t\t\t\t\t\torder[1] = 0\n\t\t\t\t\t\t\theapq.heappush(buy, ([node[0], node[1]]))\n\t\t\t\t\t\telse:\n\t\t\t\t\t\t\torder[1] -= node[1]\n\t\t\t\t\tif order[1] > 0:\n\t\t\t\t\t\theapq.heappush(sell, ([order[0], order[1]]))\n\t\t\tres = 0\n\t\t\tfor a, b in buy:\n\t\t\t\tres += b\n\t\t\tfor a, b in sell:\n\t\t\t\tres += b\n\t\t\treturn res % (10**9 + 7) | 1 | 0 | [] | 0 |
number-of-orders-in-the-backlog | Easy to understand 2 order queue solution for javascript | easy-to-understand-2-order-queue-solutio-t7pz | NotesSeems like all the JavasScript solution out there is using outdated syntax. We need to use an external library unlike python. This is an answer that'll act | alexanderyst | NORMAL | 2025-04-12T01:29:35.854850+00:00 | 2025-04-12T01:29:35.854850+00:00 | 1 | false | # Notes
Seems like all the JavasScript solution out there is using outdated syntax. We need to use an external library unlike python. This is an answer that'll actually pass.
# Approach
Maintain a max queue for buy orders (since we always want the highest price) and min queue for sell orders (since we always want the lowest price). As orders comes in
If it's a sell order
1. We compare the sell order to the buy order with the highest price
2. If the highest priced buy order has a higher price than the sell order, we execute however buy orders are available.
3. We continue the process until there are no more buy orders that meet the requirement (buyer price >= sell price).
4. Out of while loop, if there are still remaining sell orders, we add it to the queue.
If it's a buy order
- Same logic for buy order but instead of finding the highest price in seller queue, we are finding the lowest price in seller queue and see if the seller order is less than or equal to the buy order.
At the end we add up all the amounts in both queues and return
# Complexity
- Time complexity:
O(nlogn)
- Space complexity:
O(n)
# Code
```javascript []
/**
* @param {number[][]} orders
* @return {number}
*/
var getNumberOfBacklogOrders = function(orders) {
const buyQueue = new MaxPriorityQueue((order) => order[0]);
const sellQueue = new MinPriorityQueue((order) => order[0]);
for (let order of orders) {
let [price, amount, type] = order;
if(type) {
//sell
while(!buyQueue.isEmpty() && (buyQueue.front()[0] >= price) && (amount > 0)) {
let [buyPrice, buyAmount, buyType] = buyQueue.front();
const minAmount = Math.min(buyAmount, amount);
amount = amount - minAmount;
buyQueue.front()[1] = buyAmount - minAmount;
if(buyAmount === 0) {
buyQueue.dequeue();
}
}
if(amount) {
sellQueue.enqueue([price, amount, type]);
}
} else {
//buy
while(!sellQueue.isEmpty() && (sellQueue.front()[0] <= price) && (amount > 0)) {
let [sellPrice, sellAmount, sellType] = sellQueue.front();
const minAmount = Math.min(sellAmount, amount);
amount = amount - minAmount;
sellQueue.front()[1] = sellAmount - minAmount;
if(sellAmount === 0) {
sellQueue.dequeue();
}
}
if(amount) {
buyQueue.enqueue([price, amount, type]);
}
}
}
let ans = 0;
const mod = 1e9 + 7;
for(let buyOrder of buyQueue) {
ans = (ans + buyOrder[1])%mod
}
for(let sellOrder of sellQueue) {
ans = (ans + sellOrder[1])%mod;
}
return ans;
};
``` | 0 | 0 | ['JavaScript'] | 0 |
number-of-orders-in-the-backlog | priority queue | priority-queue-by-rajeshkumar1130-euq7 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | rajeshkumar1130 | NORMAL | 2025-04-03T05:55:16.289090+00:00 | 2025-04-03T05:55:16.289090+00:00 | 2 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```csharp []
public class Solution {
public int GetNumberOfBacklogOrders(int[][] orders) {
PriorityQueue<int[], int> buy = new();
PriorityQueue<int[], int> sell = new();
foreach(var order in orders)
{
if(order[2] == 0)
{
while(sell.Count>0 && sell.Peek()[0]<=order[0] && order[1]>0)
{
if(order[1]>=sell.Peek()[1])
{
order[1] -= sell.Peek()[1];
sell.Dequeue();
}
else
{
sell.Peek()[1] -= order[1];
order[1] = 0;
}
}
if(order[1]>0)
{
buy.Enqueue(order, -1*order[0]);
}
}
else
{
while(buy.Count>0 && buy.Peek()[0]>=order[0] && order[1]>0)
{
if(order[1]>=buy.Peek()[1])
{
order[1] -= buy.Peek()[1];
buy.Dequeue();
}
else
{
buy.Peek()[1] -= order[1];
order[1] = 0;
}
}
if(order[1]>0)
{
sell.Enqueue(order, order[0]);
}
}
}
int ans = 0;
while(sell.Count>0)
{
ans= (ans+sell.Peek()[1])%(1000000000+7);
sell.Dequeue();
}
while(buy.Count>0)
{
ans = (ans+buy.Peek()[1])%(1000000000+7);
buy.Dequeue();
}
return ans;
}
}
``` | 0 | 0 | ['C#'] | 0 |
number-of-orders-in-the-backlog | two priority_queue | two-priority_queue-by-johnchen-umqk | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | johnchen | NORMAL | 2025-03-28T14:51:17.487658+00:00 | 2025-03-28T14:51:17.487658+00:00 | 5 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
constexpr static int mod = 1e9 + 7;
public:
int getNumberOfBacklogOrders(vector<vector<int>>& orders) {
priority_queue<pair<int, int>, vector<pair<int, int>>, less<>> buy;
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> sell;
for (const vector<int>& order: orders)
{
switch (order.back())
{
case 0:
buy.emplace(order[0], order[1]);
break;
case 1:
sell.emplace(order[0], order[1]);
break;
default:
break;
}
while (!buy.empty() && !sell.empty() && buy.top().first >= sell.top().first)
{
if (const int amount = min(buy.top().second, sell.top().second);
buy.top().second > sell.top().second)
{
const int buyPrice = buy.top().first;
const int buyAmount = buy.top().second - amount;
sell.pop();
buy.pop();
buy.emplace(buyPrice, buyAmount);
}
else if (buy.top().second < sell.top().second)
{
const int sellPrice = sell.top().first;
const int sellAmount = sell.top().second - amount;
buy.pop();
sell.pop();
sell.emplace(sellPrice, sellAmount);
}
else
{
sell.pop();
buy.pop();
}
}
}
int res = 0;
while (!buy.empty())
{
res = (res + buy.top().second) % mod;
buy.pop();
}
while (!sell.empty())
{
res = (res + sell.top().second) % mod;
sell.pop();
}
return res;
}
};
``` | 0 | 0 | ['C++'] | 0 |
number-of-orders-in-the-backlog | Wouldn't the time complexity be O(N^2 logN) using priority queues? | wouldnt-the-time-complexity-be-on2-logn-qws3q | IntuitionUsing two priority queues like most of the solutions posted here.ApproachComplexity
Time complexity:
Inside the for loop, there is a while loop that mi | xzw0005 | NORMAL | 2025-03-03T00:45:45.355174+00:00 | 2025-03-03T00:45:45.355174+00:00 | 7 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Using two priority queues like most of the solutions posted here.
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
Inside the for loop, there is a while loop that might iterate all existing elements in the priority queue (which would exist $O(n)$ of them). In that case, wouldn't the time complexity be $O(N^2 logN)$?
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
To simulate the process of iterating over the orders:
```python3 []
class Solution:
def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:
buyMaxHeap, sellMinHeap = [], []
for p, k, t in orders:
if t == 0: ## buy order
while sellMinHeap and sellMinHeap[0][0] <= p and k > 0:
sell = heapq.heappop(sellMinHeap)
if sell[1] <= k:
k -= sell[1]
else:
heapq.heappush(sellMinHeap, (sell[0], sell[1]-k))
k = 0
break
if k > 0:
heapq.heappush(buyMaxHeap, (-p, k))
else: ## sell order
while buyMaxHeap and -buyMaxHeap[0][0] >= p and k > 0:
buy = heapq.heappop(buyMaxHeap)
if buy[1] <= k:
k -= buy[1]
else:
heapq.heappush(buyMaxHeap, (buy[0], buy[1]-k))
k = 0
break
if k > 0:
heapq.heappush(sellMinHeap, (p, k))
MOD = 10**9+7
return sum([k for p, k in buyMaxHeap + sellMinHeap]) % MOD
```
For conciseness and readability:
```
class Solution:
def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:
buyMaxHeap, sellMinHeap = [], []
for p, k, t in orders:
if t == 0: ## buy order
heapq.heappush(buyMaxHeap, (-p, k))
else:
heapq.heappush(sellMinHeap, (p, k))
while buyMaxHeap and sellMinHeap and -buyMaxHeap[0][0] >= sellMinHeap[0][0]:
buy, sell = heapq.heappop(buyMaxHeap), heapq.heappop(sellMinHeap)
if buy[1] > sell[1]:
heapq.heappush(buyMaxHeap, (buy[0], buy[1] - sell[1]))
elif buy[1] < sell[1]:
heapq.heappush(sellMinHeap, (sell[0], sell[1] - buy[1]))
MOD = 10**9+7
return sum([k for p, k in buyMaxHeap + sellMinHeap]) % MOD
``` | 0 | 0 | ['Python3'] | 0 |
number-of-orders-in-the-backlog | C++ easy solution using 2 priority queues | c-easy-solution-using-2-priority-queues-ta42x | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | hunny123 | NORMAL | 2025-02-12T20:03:27.668910+00:00 | 2025-02-12T20:03:27.668910+00:00 | 4 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int getNumberOfBacklogOrders(vector<vector<int>>& orders) {
priority_queue<pair<int,int>>p;
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
for(int i=0;i<orders.size();i++)
{
if(orders[i][2]==0)
{
p.push({orders[i][0],orders[i][1]});
}
else{
pq.push({orders[i][0],orders[i][1]});
}
while(!p.empty()&&!pq.empty()&&(p.top().first>=pq.top().first))
{
int p1=p.top().first;
int q1=p.top().second;
int p2=pq.top().first;
int q2=pq.top().second;
p.pop();
pq.pop();
if(q1>q2)
{
q1=q1-q2;
p.push({p1,q1});
}
else if(q2>q1)
{
q2=q2-q1;
pq.push({p2,q2});
}
} }
int ans=0;
while(!p.empty())
{
ans=(ans+p.top().second)%1000000007;
p.pop();
}
while(!pq.empty())
{
ans=(ans+pq.top().second)%1000000007;
pq.pop();
}
return ans;
}
};
``` | 0 | 0 | ['C++'] | 0 |
number-of-orders-in-the-backlog | количество заказов в бэклоге | kolichestvo-zakazov-v-bekloge-by-elliot0-nj8o | ИнтуицияПодходСложность
Временная сложность:
Сложность пространства:
Код | Elliot0-1 | NORMAL | 2025-02-08T15:17:02.238739+00:00 | 2025-02-08T15:17:02.238739+00:00 | 4 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```javascript []
let getNumberOfBacklogOrders = function (orders) {
let buy = []
let sell = []
let stop=true
function sortBuyandSell(arr, elem) {
let start = 0;
let end = arr.length;
while (start < end) {
const mid = Math.floor((start + end) / 2);
if (arr[mid][0] < elem[0]) {
start = mid + 1;
} else {
end = mid;
}
}
arr.splice(start, 0, elem);
return start;
}
function differenceAmount(num,indexBuy,indexSell){
if(num>0){
buy[indexBuy][1] =num
sell.splice(indexSell,1)
}
else if(num<0){
sell[indexSell][1]=Math.abs(num)
buy.splice(indexBuy,1)
}
else{
buy.splice(indexBuy,1)
sell.splice(indexSell,1)
stop = false
}
}
function addBackLog(elem){
if(elem[2]===0){
if(sell.length > 0 && elem[0] >= sell[0][0]){
let indexBuy=sortBuyandSell(buy,elem)
while(stop && buy.length>indexBuy && sell.length > 0 && (buy[indexBuy][0] >= sell[0][0])){
let num=buy[indexBuy][1]-sell[0][1]
differenceAmount(num,indexBuy,0)
}
stop=true
}
else {
sortBuyandSell(buy,elem)
}
}
else if(elem[2]===1){
if(buy.length > 0 && elem[0] <= buy[buy.length-1][0]){
let indexSell=sortBuyandSell(sell,elem)
while(stop && buy.length>0 && sell.length > indexSell && sell[indexSell][0] <= buy[buy.length-1][0]){
let num=buy[buy.length-1][1]-sell[indexSell][1]
differenceAmount(num,buy.length-1,indexSell )
}
stop=true
}
else {
sortBuyandSell(sell,elem)
}
}
}
for(let i=0;i<orders.length;i++){
addBackLog(orders[i])
}
let buyAmount=buy.map(el=>el[1]).reduce((a,b)=>a+b,0)
let sellAmount=sell.map(el=>el[1]).reduce((a,b)=>a+b,0)
return (buyAmount+sellAmount) % (1000000000 + 7 )
};
``` | 0 | 0 | ['JavaScript'] | 0 |
number-of-orders-in-the-backlog | C# 100% best runtime 90% best memory using only two priority queues | c-100-best-runtime-90-best-memory-using-ypxla | ProofIntuition + ApproachWe need to keep track of low sell price because problem says we need to match buys with the smallest sell price.We need to keep track o | gabida | NORMAL | 2025-02-04T21:32:50.664188+00:00 | 2025-02-04T21:32:50.664188+00:00 | 7 | false | # Proof
# Intuition + Approach
We need to keep track of low sell price because problem says we need to match buys with the smallest sell price.
We need to keep track of high buy price to match it with sell prices.
Data strucutre that keep ordering in c# with payloads is PriorityQueue<T, V>.
There are 3 states for each new order:
1. We can't match it ? => we push it to its queue, if it buy we push it to buyQueue, if it is sell we push it sell queue,
2. We totaly match it:
- Using one order.
- Using multiple orders.
3. We partialy match it.
# Complexity
- Time complexity:
Inserting in priority queue is O(logn) and we iterate over all orders which is O(n) the total is O(nlong)
- Space complexity:
We can store up to n order which is O(n).
# Code
```csharp []
public class Solution {
public int GetNumberOfBacklogOrders(int[][] orders)
{
var priotirySell = new PriorityQueue<int[], int>();
var priorityBuy = new PriorityQueue<int[], int>(Comparer<int>.Create((x, y) => y.CompareTo(x)));
long allAmount = 0;
foreach(int[] order in orders)
{
bool isBuy = order[2] == 0;
int price = order[0];
int amount = order[1];
var takeFrom = isBuy ? priotirySell : priorityBuy;
var pushTo = isBuy ? priorityBuy : priotirySell;
bool orderSatified = false;
do{
if(takeFrom.Count == 0)
{
// we can't satisfy the order
orderSatified = true;
allAmount += amount;
pushTo.Enqueue(order, order[0]);
}
else
{
var temp = takeFrom.Peek();
if((isBuy && temp[0] <= price) || (!isBuy && price <= temp[0]))
{
if(amount <= temp[1])
{
orderSatified = true;
allAmount -= amount;
if(amount - temp[1] == 0)
{
takeFrom.Dequeue();
}else{
temp[1] = temp[1] - amount;
}
}else{
amount -= temp[1];
allAmount -= temp[1];
order[1] -= temp[1];
takeFrom.Dequeue();
}
}else
{
pushTo.Enqueue(order, order[0]);
allAmount += amount;
orderSatified = true;
}
}
}while(!orderSatified);
}
return (int)(allAmount % 1_000_000_007);
}
}
``` | 0 | 0 | ['C#'] | 0 |
number-of-orders-in-the-backlog | Easy to understand Java solution - Using 2 Priority queues | easy-to-understand-java-solution-using-2-8jhi | IntuitionThe goal is to simulate the orders executions with 2 backlogs. When there is a buy order, we need to find the sell order with the smallest price. The q | pushkardg | NORMAL | 2025-01-13T00:26:27.981606+00:00 | 2025-01-13T00:26:27.981606+00:00 | 9 | false | # Intuition
The goal is to simulate the orders executions with 2 backlogs. When there is a buy order, we need to find the sell order with the smallest price. The quickest way to find this would be by storeing the sell orders in a Priority queue, which is sorted by the price.
Similarly, when there is a sell order, we need to find the buy order with the smallest price, which can be done using a PriorityQueue.
So we use 2 Priority queues in the code and simulate buy/sell orders by iterating through the entire list.
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
class Order{
int price;
int amount;
public Order(int price, int amount){
this.price = price;
this.amount = amount;
}
}
public int getNumberOfBacklogOrders(int[][] orders) {
PriorityQueue<Order> buyBacklog = new PriorityQueue<>( (a,b) -> Integer.compare(b.price, a.price) );
PriorityQueue<Order> sellBacklog = new PriorityQueue<>( (a,b) -> Integer.compare(a.price, b.price) );
for( int i = 0; i< orders.length ; i++){
int price = orders[i][0];
int amount = orders[i][1];
int orderType = orders[i][2];
if( orderType == 0){
//BUy order
while(!sellBacklog.isEmpty() && sellBacklog.peek().price <= price ){
Order sellOrder = sellBacklog.poll();
int remainingQty = sellOrder.amount;
if( remainingQty < amount ){
amount-=remainingQty;
}else{
Order updatedSellOrder = new Order(sellOrder.price, remainingQty - amount);
amount = 0;
sellBacklog.offer( updatedSellOrder);
break;
}
}
if( amount > 0){
buyBacklog.offer( new Order( price, amount));
}
}else{
//Sell order
while( !buyBacklog.isEmpty() && buyBacklog.peek().price >= price){
Order buyOrder = buyBacklog.poll();
int remainingQty = buyOrder.amount;
if( remainingQty < amount ){
amount-=remainingQty;
}else{
Order updatedBuyOrder = new Order( buyOrder.price , remainingQty - amount);
amount =0;
buyBacklog.offer(updatedBuyOrder );
break;
}
}
if( amount > 0){
sellBacklog.offer( new Order(price, amount));
}
}
}
long totalOrdersRemaining = 0;
while( !buyBacklog.isEmpty() ){
totalOrdersRemaining+= buyBacklog.poll().amount;
}
while( !sellBacklog.isEmpty() ){
totalOrdersRemaining+= sellBacklog.poll().amount;
}
return (int)(totalOrdersRemaining % (Math.pow(10, 9) + 7));
}
}
``` | 0 | 0 | ['Java'] | 0 |
number-of-orders-in-the-backlog | Heap | Simulation | heap-simulation-by-anonymous_k-cdm1 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | anonymous_k | NORMAL | 2025-01-08T20:49:03.627829+00:00 | 2025-01-08T20:49:03.627829+00:00 | 9 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:
'''
smallest
largest
This can be simulated with heap, because we only care about samllest and largest.
'''
M = int(1e9) + 7
sellBacklog, buyBacklog = [], []
for price, amount, orderType in orders:
if orderType:
# sell
while buyBacklog and -buyBacklog[0][0] >= price and amount:
buyPrice, buyAmount = heapq.heappop(buyBacklog)
minimum = min(buyAmount, amount)
buyAmount -= minimum
amount -= minimum
if buyAmount: heapq.heappush(buyBacklog, (buyPrice, buyAmount))
if amount: heapq.heappush(sellBacklog, (price, amount))
else:
# buy
while sellBacklog and sellBacklog[0][0] <= price and amount:
sellPrice, sellAmount = heapq.heappop(sellBacklog)
minimum = min(sellAmount, amount)
sellAmount -= minimum
amount -= minimum
if sellAmount: heapq.heappush(sellBacklog, (sellPrice, sellAmount))
if amount: heapq.heappush(buyBacklog, (-price, amount))
return (sum(amount for _, amount in sellBacklog) + sum(amount for _, amount in buyBacklog)) % M
``` | 0 | 0 | ['Python3'] | 0 |
number-of-orders-in-the-backlog | build an order-book and match-orders | build-an-order-book-and-match-orders-by-zrbz3 | IntuitionFirst thought: I need a sorted data structure to provide me min and max on pricesApproachCould use binary-search-tree or priority-queue; opted for PQ, | asafbu | NORMAL | 2024-12-28T11:01:02.435233+00:00 | 2024-12-28T11:01:02.435233+00:00 | 15 | false | # Intuition
First thought: I need a sorted data structure to provide me min and max on prices
# Approach
Could use binary-search-tree or priority-queue; opted for PQ, because I really do not need to sort each node, just need the min for asks and max for bids.
# Complexity
- Time complexity:
O(nlogn)
- Space complexity:
O(n)
# Code
```java []
class Solution {
final int BUY = 0, ASK = 1;
final PriorityQueue<int[]> asks = new PriorityQueue<>((a, b) -> a[0] - b[0]);
final PriorityQueue<int[]> bids = new PriorityQueue<>((a, b) -> b[0] - a[0]);
public int getNumberOfBacklogOrders(int[][] orders) {
for (int[] newOrder : orders) {
if (newOrder[2] == BUY) bids.offer(newOrder);
else asks.offer(newOrder);
matchOrders();
}
return (int) (remainingQuantity() % 1000_000_007);
}
void matchOrders() {
while (bids.size() > 0 && asks.size() > 0 && bids.peek()[0] >= asks.peek()[0]) {
int quantityTraded = Integer.min(bids.peek()[1], asks.peek()[1]);
bids.peek()[1] -= quantityTraded;
asks.peek()[1] -= quantityTraded;
if (bids.peek()[1] == 0) bids.poll();
if (asks.peek()[1] == 0) asks.poll();
}
}
long remainingQuantity() {
long totalQuantity = 0;
while (bids.size() > 0 || asks.size() > 0) {
totalQuantity += bids.size() > 0 ? bids.poll()[1] : 0;
totalQuantity += asks.size() > 0 ? asks.poll()[1] : 0;
}
return totalQuantity;
}
}
``` | 0 | 0 | ['Array', 'Sorting', 'Heap (Priority Queue)', 'Java'] | 0 |
number-of-orders-in-the-backlog | OOP Design Solution | oop-design-solution-by-deydev-77af | null | deydev | NORMAL | 2024-12-27T09:13:13.130731+00:00 | 2024-12-31T02:23:50.061103+00:00 | 12 | false |
```python []
BUY_ORDERS = 0
SELL_ORDERS = 1
MOD = int(1e9 + 7)
class OrderBook:
def __init__(self, order_type) -> None:
self.order_type = order_type
self.price_orders_map: dict[int, int] = {}
self.price_heap: list[int] = []
self.backlog = 0
def push(self, price, orders) -> None:
if price not in self.price_orders_map:
heappush(self.price_heap, self._heapPriceMap(price))
self.price_orders_map[price] = orders
else:
self.price_orders_map[price] += orders
self.backlog += orders
def pop(self, orders):
best_price = self.peekPrice()
remaining_orders = self.price_orders_map[best_price] - orders
if remaining_orders == 0:
heappop(self.price_heap)
del self.price_orders_map[best_price]
else:
self.price_orders_map[best_price] = remaining_orders
self.backlog -= orders
def peekPrice(self) -> int:
return self._heapPriceMap(self.price_heap[0])
def orders(self, price) -> int:
return self.price_orders_map[price]
def empty(self) -> int:
return len(self.price_heap) == 0
def _heapPriceMap(self, price) -> int:
return -price if self.order_type == BUY_ORDERS else price
class Solution:
def __init__(self):
self.buy_book = OrderBook(BUY_ORDERS)
self.sell_book = OrderBook(SELL_ORDERS)
def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:
for price, quantity, transaction in orders:
if transaction == BUY_ORDERS:
self.settleTrades(price, quantity, BUY_ORDERS)
else:
self.settleTrades(price, quantity, SELL_ORDERS)
res = self.buy_book.backlog + self.sell_book.backlog
return res % MOD
def settleTrades(self, price, orders, order_type):
append_book = self.buy_book if order_type == BUY_ORDERS else self.sell_book
opposing_book = self.sell_book if order_type == BUY_ORDERS else self.buy_book
while orders > 0 and not opposing_book.empty():
# Check if the trade can happen
best_opposing_price = opposing_book.peekPrice()
if order_type == BUY_ORDERS and price < best_opposing_price:
break
if order_type == SELL_ORDERS and price > best_opposing_price:
break
# Perform trade by matching orders
opposing_orders = opposing_book.orders(best_opposing_price)
matched_orders = min(orders, opposing_orders)
orders -= matched_orders
opposing_book.pop(matched_orders)
# If there's any unmatched orders, add it to backlog
if orders > 0:
append_book.push(price, orders)
```
``` cpp []
const int BUY_ORDERS = 0;
const int SELL_ORDERS = 1;
const int MOD = 1e9 + 7;
class DynamicComparator {
public:
DynamicComparator(int orderType) : orderType(orderType) {}
bool operator() (int lhs, int rhs) const {
if (orderType == BUY_ORDERS) {
return lhs < rhs; // Max-heap for BUY_ORDER
} else {
return lhs > rhs; // Min-heap for SELL_ORDER
}
}
private:
int orderType;
};
class OrderBook {
public:
long backlog;
OrderBook(int orderType)
: backlog(0),
priceHeap(DynamicComparator(orderType)) {};
void push(int price, int orders) {
if (!priceOrdersMap.contains(price)) {
priceOrdersMap[price] = orders;
priceHeap.push(price);
} else {
priceOrdersMap[price] += orders;
}
backlog += orders;
}
void pop(int orders) {
int topPrice = priceHeap.top();
int remainingOrders = priceOrdersMap[topPrice] - orders;
if (remainingOrders == 0) {
priceHeap.pop();
priceOrdersMap.erase(topPrice);
} else {
priceOrdersMap[topPrice] = remainingOrders;
}
backlog -= orders;
}
tuple<int, int> peek() {
int topPrice = priceHeap.top();
int topPriceOrders = priceOrdersMap[topPrice];
return make_tuple(topPrice, topPriceOrders);
}
size_t size() {
return priceHeap.size();
}
private:
unordered_map<int, int> priceOrdersMap;
priority_queue<int, vector<int>, DynamicComparator> priceHeap;
};
class Solution {
private:
OrderBook buyBook;
OrderBook sellBook;
public:
Solution() : buyBook(BUY_ORDERS), sellBook(SELL_ORDERS) {};
int getNumberOfBacklogOrders(vector<vector<int>>& orders) {
for (auto& order : orders) {
settleTrades(order[0], order[1], order[2]);
}
return (buyBook.backlog + sellBook.backlog) % MOD;
}
void settleTrades(int price, int orders, int orderType) {
OrderBook& appendBook = orderType == BUY_ORDERS ? buyBook : sellBook;
OrderBook& matchBook = orderType == BUY_ORDERS ? sellBook : buyBook;
while (matchBook.size() and orders) {
auto [bestOpposingPrice, bestOpposingPriceOrders] = matchBook.peek();
if (orderType == BUY_ORDERS && price < bestOpposingPrice) break;
if (orderType == SELL_ORDERS && price > bestOpposingPrice) break;
int matchedOrders = min(orders, bestOpposingPriceOrders);
orders -= matchedOrders;
matchBook.pop(matchedOrders);
}
if (orders > 0) {
appendBook.push(price, orders);
}
}
};
``` | 0 | 0 | ['Design', 'Heap (Priority Queue)', 'Simulation', 'C++', 'Python3'] | 0 |
number-of-orders-in-the-backlog | TypeScript Clean Min & Max Heaps Solution | typescript-clean-min-max-heaps-solution-n77yy | IntuitionKeep two heaps, max heap for buy, min heap for sell backlogs.ApproachJust simulate the process as explained in the question.Complexity
Time complexity | shtanriverdi | NORMAL | 2024-12-24T08:21:39.091156+00:00 | 2024-12-24T08:21:39.091156+00:00 | 10 | false | # Intuition
Keep two heaps, max heap for buy, min heap for sell backlogs.
# Approach
Just simulate the process as explained in the question.
# Complexity
- Time complexity:
O(N log N)
- Space complexity:
O(N)
# Code
```typescript []
function getNumberOfBacklogOrders(orders: number[][]): number {
const buyMaxHeapBacklog = new MaxPriorityQueue({ priority: (tuple) => tuple[0] });
const sellMinHeapBacklog = new MinPriorityQueue({ priority: (tuple) => tuple[0] });
for (let [price, amount, type] of orders) {
// Buy look for '<='
if (type === 0) {
while (!sellMinHeapBacklog.isEmpty() && amount > 0 && sellMinHeapBacklog.front().priority <= price) {
const { priority, element } = sellMinHeapBacklog.dequeue();
const [sellOrderPrice, sellOrderAmount] = element;
const amountToSubstract = Math.min(sellOrderAmount, amount)
const updatedSellOrderAmount = sellOrderAmount - amountToSubstract;
amount -= amountToSubstract;
if (updatedSellOrderAmount > 0) {
sellMinHeapBacklog.enqueue([sellOrderPrice, updatedSellOrderAmount]);
}
}
if (amount > 0) {
buyMaxHeapBacklog.enqueue([price, amount]);
}
}
// Sell look for '>='
else {
while (!buyMaxHeapBacklog.isEmpty() && amount > 0 && buyMaxHeapBacklog.front().priority >= price) {
const { priority, element } = buyMaxHeapBacklog.dequeue();
const [buyOrderPrice, buyOrderAmount] = element;
const amountToSubstract = Math.min(buyOrderAmount, amount)
const updatedBuyOrderAmount = buyOrderAmount - amountToSubstract;
amount -= amountToSubstract;
if (updatedBuyOrderAmount > 0) {
buyMaxHeapBacklog.enqueue([buyOrderPrice, updatedBuyOrderAmount]);
}
}
if (amount > 0) {
sellMinHeapBacklog.enqueue([price, amount]);
}
}
}
let amountSum = 0;
amountSum += sellMinHeapBacklog.toArray().reduce((sum, cur) => sum + cur.element[1], 0);
amountSum += buyMaxHeapBacklog.toArray().reduce((sum, cur) => sum + cur.element[1], 0);
const MOD = 1000000007;
return amountSum % MOD;
};
``` | 0 | 0 | ['Array', 'Heap (Priority Queue)', 'Simulation', 'TypeScript'] | 0 |
number-of-orders-in-the-backlog | C++ solutions Two Heaps | c-solutions-two-heaps-by-oleksam-tl48 | \n// Please, upvote if you like it. Thanks :-)\n// TC - O(nlog(n))\n// SC - O(n)\ntypedef pair<int, int> pii;\nint getNumberOfBacklogOrders(vector<vector<int>>& | oleksam | NORMAL | 2024-12-06T14:57:02.554166+00:00 | 2024-12-06T14:57:02.554208+00:00 | 3 | false | ```\n// Please, upvote if you like it. Thanks :-)\n// TC - O(nlog(n))\n// SC - O(n)\ntypedef pair<int, int> pii;\nint getNumberOfBacklogOrders(vector<vector<int>>& orders) {\n\tpriority_queue<pii> buy;\n\tpriority_queue<pii, vector<pii>, greater<pii>> sell;\n\tfor (const auto& order : orders) {\n\t\tint price = order[0], amount = order[1], type = order[2];\n\t\tif (type == 0) { // buy\n\t\t\twhile (amount > 0 && !sell.empty() && sell.top().first <= price) {\n\t\t\t\tauto [sell_price, sell_amount] = sell.top();\n\t\t\t\tsell.pop();\n\t\t\t\tif (sell_amount > amount) {\n\t\t\t\t\tsell.push( { sell_price, sell_amount - amount } );\n\t\t\t\t\tamount = 0;\n\t\t\t\t}\n\t\t\t\telse\n\t\t\t\t\tamount -= sell_amount;\n\t\t\t}\n\t\t\tif (amount > 0)\n\t\t\t\tbuy.push( { price, amount } );\n\t\t}\n\t\telse {\n\t\t\twhile (amount > 0 && !buy.empty() &&\n\t\t\t\t\tbuy.top().first >= price) {\n\t\t\t\tauto [buy_price, buy_amount] = buy.top();\n\t\t\t\tbuy.pop();\n\t\t\t\tif (buy_amount > amount) {\n\t\t\t\t\tbuy.push( { buy_price, buy_amount - amount } );\n\t\t\t\t\tamount = 0;\n\t\t\t\t}\n\t\t\t\telse\n\t\t\t\t\tamount -= buy_amount;\n\t\t\t}\n\t\t\tif (amount > 0)\n\t\t\t\tsell.push( { price, amount } );\n\t\t}\n\t}\n\tint res = 0, mod = 1e9+7;\n\twhile (!buy.empty()) {\n\t\tres = (res + buy.top().second) % mod;\n\t\tbuy.pop();\n\t}\n\twhile (!sell.empty()) {\n\t\tres = (res + sell.top().second) % mod;\n\t\tsell.pop();\n\t}\n\treturn res;\n}\n``` | 0 | 0 | ['Greedy', 'C', 'Heap (Priority Queue)', 'C++'] | 0 |
number-of-orders-in-the-backlog | Python3. Heap | python3-heap-by-srptv-vt4w | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | srptv | NORMAL | 2024-11-11T16:47:34.704970+00:00 | 2024-11-11T16:47:34.705010+00:00 | 5 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def getNumberOfBacklogOrders(self, orders: List[List[int]]) -> int:\n\n buy = []\n sell = []\n\n for order in orders:\n price, amount, tp = order\n\n if tp == 0:\n while sell and sell[0][0] <= price:\n tmp = heapq.heappop(sell)\n if amount < tmp[1]:\n heapq.heappush(sell, (tmp[0], tmp[1] - amount))\n amount = 0\n break\n else:\n amount = amount - tmp[1]\n \n if amount != 0:\n heapq.heappush(buy, (-price, amount))\n\n if tp == 1:\n while buy and -buy[0][0] >= price:\n tmp = heapq.heappop(buy)\n if amount < tmp[1]:\n heapq.heappush(buy, (tmp[0], tmp[1] - amount))\n amount = 0\n break\n else:\n amount = amount - tmp[1]\n \n if amount != 0:\n heapq.heappush(sell, (price, amount))\n\n cnt = 0\n\n while sell:\n tmp = heapq.heappop(sell)\n cnt += tmp[1]\n\n while buy:\n tmp = heapq.heappop(buy)\n cnt += tmp[1]\n\n return cnt % (10 ** 9 + 7)\n``` | 0 | 0 | ['Python3'] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.