question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
find-the-array-concatenation-value | Beat 95.65% 55ms Python3 two pointer | beat-9565-55ms-python3-two-pointer-by-am-i87w | \n\n# Code\n\nclass Solution:\n def findTheArrayConcVal(self, nums: List[int]) -> int:\n i, j, count = 0, len(nums)-1, 0\n while i <= j:\n | amitpandit03 | NORMAL | 2023-03-06T16:53:25.480533+00:00 | 2023-03-06T16:53:32.287885+00:00 | 37 | false | \n\n# Code\n```\nclass Solution:\n def findTheArrayConcVal(self, nums: List[int]) -> int:\n i, j, count = 0, len(nums)-1, 0\n while i <= j:\n if i != j: count += int(str(nums[i]) + str(nums[j]))\n else: count += nums[j]\n i += 1\n j -= 1\n return count\n``` | 1 | 0 | ['Array', 'Two Pointers', 'Simulation', 'Python3'] | 0 |
find-the-array-concatenation-value | Simple Java Solution 0ms | beats 100% | two pointer approach and No conversion to String needed | simple-java-solution-0ms-beats-100-two-p-mb79 | Intuition\nUse the two pointer approach to iterate through the array from both ends and conactenate the correspinding numbers till start<end.\n\nNote: please ma | ayushprakash1912 | NORMAL | 2023-02-19T06:06:31.363565+00:00 | 2023-02-19T06:06:31.363619+00:00 | 10 | false | # Intuition\nUse the two pointer approach to iterate through the array from both ends and conactenate the correspinding numbers till start<end.\n\n**Note: please make sure to use \'long\' variable while adding otherwise theoutput will overflow.**\n\n# Approach\n1. Place two pointers and both left and right end of the array and itarate through moving them towards each other.\n2. If start<end, concatenate the numbers and add them to the output variable. You may not need to convert the number to String to concatenate. Simple arithematic operation will also do it in O(1) due to input contraints. Please refer the code for this.\n3. If start==end, simply add the number to the result and return it.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution {\n public long findTheArrayConcVal(int[] nums) {\n \n long result=0;\n int start=0, end=nums.length-1;\n\n while(start<end) {\n result = result + concat((long)nums[start], (long)nums[end]);\n start++;\n end--;\n }\n\n if(start==end) {\n result = result+nums[start];\n }\n\n return result;\n }\n\n public long concat(long a, long b) {\n \n if (b < 10) {\n return a * 10 + b;\n } else if (b < 100) {\n return a * 100 + b;\n } else if (b < 1000) {\n return a * 1000 + b;\n } else if (b < 10000) {\n return a * 10000 + b;\n }\n\n return a * 100000 + b;\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
find-the-array-concatenation-value | Use StringBuilder to solve | use-stringbuilder-to-solve-by-niok-as2r | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Niok | NORMAL | 2023-02-18T06:03:16.319923+00:00 | 2023-02-18T06:03:16.319953+00:00 | 648 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public long findTheArrayConcVal(int[] nums) {\n long res = 0L;\n StringBuilder sb = new StringBuilder();\n int i = 0;\n int j = nums.length - 1;\n while(j >= i){\n if(j == i){\n sb.append(nums[i]);\n }else{\n sb.append(nums[i]).append(nums[j]);\n }\n int temp = Integer.parseInt(sb.toString());\n sb.setLength(0);\n res += temp;\n j--;\n i++;\n }\n return res;\n }\n}\n``` | 1 | 0 | ['Java'] | 1 |
find-the-array-concatenation-value | Simple Python Solution | simple-python-solution-by-saiavunoori418-2ssy | \n\nSolution:\n\nclass Solution:\n def findTheArrayConcVal(self, nums: List[int]) -> int:\n conc = 0\n if len(nums) == 1:\n return n | saiavunoori4187 | NORMAL | 2023-02-18T05:22:29.309346+00:00 | 2023-02-18T05:22:29.309396+00:00 | 78 | false | \n\nSolution:\n\n```class Solution:\n def findTheArrayConcVal(self, nums: List[int]) -> int:\n conc = 0\n if len(nums) == 1:\n return nums[0]\n while len(nums)>1:\n temp = int(str(nums[0])+str(nums[-1]))\n conc+=temp\n nums = nums[1:len(nums)-1]\n if len(nums)==1:\n conc+=nums[0]\n return conc``` | 1 | 0 | [] | 0 |
find-the-array-concatenation-value | One-for solution | one-for-solution-by-ods967-7k4b | Code\n\n/**\n * @param {number[]} nums\n * @return {number}\n */\nvar findTheArrayConcVal = function(nums) {\n let res = 0;\n for (let i = 0; i < nums.len | ods967 | NORMAL | 2023-02-17T04:49:50.249762+00:00 | 2023-02-17T04:49:50.249903+00:00 | 95 | false | # Code\n```\n/**\n * @param {number[]} nums\n * @return {number}\n */\nvar findTheArrayConcVal = function(nums) {\n let res = 0;\n for (let i = 0; i < nums.length / 2; i++) {\n const rightIndex = nums.length - 1 - i;\n res += i === rightIndex ? nums[i] : Number(\'\' + nums[i] + nums[rightIndex]);\n }\n return res;\n};\n``` | 1 | 0 | ['JavaScript'] | 0 |
find-the-array-concatenation-value | JavaScript | Two pointer | O(n) | javascript-two-pointer-on-by-akey_9-07pz | Approach\n Describe your approach to solving the problem. \nTwo pointer\n\n# Complexity\n- Time complexity: O(n)\n Add your time complexity here, e.g. O(n) \n\n | akey_9 | NORMAL | 2023-02-13T13:37:17.554923+00:00 | 2023-02-13T13:37:17.554968+00:00 | 94 | false | # Approach\n<!-- Describe your approach to solving the problem. -->\nTwo pointer\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code - I\n```\n/**\n * @param {number[]} nums\n * @return {number}\n */\nvar findTheArrayConcVal = function(nums) {\n let i = 0, j = nums.length-1, sum = 0;\n while(i<j) {\n sum += Number(nums[i]+\'\'+nums[j]);\n i++;\n j--;\n }\n if(i===j) sum += nums[i];\n return sum;\n};\n```\n# Code - II\n```\n/**\n * @param {number[]} nums\n * @return {number}\n */\nvar findTheArrayConcVal = function(nums) {\n let i = 0, j = nums.length-1, sum = 0;\n while(i<=j) {\n sum += Number(i===j ? nums[i] : `${nums[i]}`+`${nums[j]}`);\n i++; j--;\n }\n return sum;\n};\n``` | 1 | 0 | ['Two Pointers', 'JavaScript'] | 0 |
find-the-array-concatenation-value | Simple JavaScript | simple-javascript-by-dsinkey-1yt2 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | dsinkey | NORMAL | 2023-02-12T14:48:03.805149+00:00 | 2023-02-12T14:48:03.805184+00:00 | 280 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * @param {number[]} nums\n * @return {number}\n */\nvar findTheArrayConcVal = function(nums) {\n let sum = 0;\n\n while(nums.length) {\n const first = nums.shift();\n const last = nums.pop();\n const concat = first?.toString() + last?.toString();\n sum += parseInt(concat);\n }\n\n return sum;\n};\n``` | 1 | 0 | ['JavaScript'] | 0 |
find-the-array-concatenation-value | Beats 100 % || 2 lines || 39ms | beats-100-2-lines-39ms-by-codequeror-65dr | Upvote it\n\nclass Solution:\n def findTheArrayConcVal(self, nums: List[int]) -> int:\n ans = sum(int(str(nums[i]) + str(nums[len(nums) - 1 - i])) for | Codequeror | NORMAL | 2023-02-12T13:07:09.460195+00:00 | 2023-02-12T13:07:09.460226+00:00 | 8 | false | # Upvote it\n```\nclass Solution:\n def findTheArrayConcVal(self, nums: List[int]) -> int:\n ans = sum(int(str(nums[i]) + str(nums[len(nums) - 1 - i])) for i in range(len(nums) // 2))\n return ans if len(nums) % 2 == 0 else ans + nums[len(nums) // 2]\n``` | 1 | 0 | ['Python3'] | 0 |
find-the-array-concatenation-value | Simple solution using String || Beginner Friendly || JAVA | simple-solution-using-string-beginner-fr-6h0j | \n\n# Code\n\nclass Solution {\n public long findTheArrayConcVal(int[] nums) {\n long out=0;\n\n for(int i=0;i<nums.length/2;i++)\n | PAPPURAJ | NORMAL | 2023-02-12T12:48:43.571756+00:00 | 2023-02-12T12:48:43.571787+00:00 | 115 | false | \n\n# Code\n```\nclass Solution {\n public long findTheArrayConcVal(int[] nums) {\n long out=0;\n\n for(int i=0;i<nums.length/2;i++)\n out+=Long.parseLong(String.valueOf(nums[i])+String.valueOf(nums[nums.length-1-i]));\n if(nums.length%2==1)\n out+=nums[nums.length/2];\n return out; \n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
find-the-array-concatenation-value | Beats 100% Speed easy Python solution | beats-100-speed-easy-python-solution-by-7wiqn | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Pavellver | NORMAL | 2023-02-12T11:13:41.918978+00:00 | 2023-02-12T11:13:41.919040+00:00 | 68 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findTheArrayConcVal(self, nums: List[int]) -> int:\n summary = 0\n a = nums.copy()\n for i in nums[:len(a) // 2]:\n summary += int(str(i) + str(nums[-1]))\n nums.pop(-1)\n return summary if len(a)%2 == 0 else summary + nums[-1] \n \n``` | 1 | 0 | ['Python3'] | 0 |
find-the-array-concatenation-value | Simple Easy Python Solution | simple-easy-python-solution-by-debasish3-77ke | Runtime: 62 ms, faster than 66.67% of Python3 online submissions for Find the Array Concatenation Value.\n\nMemory Usage: 14.1 MB, less than 61.11% of Python3 o | Debasish365 | NORMAL | 2023-02-12T09:29:04.984632+00:00 | 2023-02-12T09:29:04.984673+00:00 | 19 | false | Runtime: 62 ms, faster than 66.67% of Python3 online submissions for Find the Array Concatenation Value.\n\nMemory Usage: 14.1 MB, less than 61.11% of Python3 online submissions for Find the Array Concatenation Value.\n\n\n```class Solution:\n def findTheArrayConcVal(self, nums: List[int]) -> int:\n l = len(nums)//2\n ans = 0\n rem = ""\n if len(nums)%2 !=0:\n ans += nums[l]\n for i in range(l):\n if len(nums) == 1:\n ans = ans + nums[-1]\n break\n ans += int(str(nums[0]) + str(nums[-1]))\n nums.pop(0)\n nums.pop(-1)\n return ans | 1 | 0 | [] | 0 |
find-the-array-concatenation-value | 4 Solutions || Brute >> Better >> Optimal || c++ || Faster than 100% || 0ms | 4-solutions-brute-better-optimal-c-faste-p1uy | Intuition\n\nwe need to concatinate the first and last digits \nfor example [7,52,2,4]\nans = 522 + 14 = 596 ;\nso 52 and 2 make 522 by (52 * 100) + 2\nsimilar | ketansarna | NORMAL | 2023-02-12T08:03:15.571875+00:00 | 2023-02-12T08:03:15.571911+00:00 | 159 | false | # Intuition\n\nwe need to concatinate the first and last digits \nfor example [7,52,2,4]\nans = 522 + 14 = 596 ;\nso 52 and 2 make 522 by (52 * 100) + 2\nsimilarly \nfor 7 and 4 \n(7 * 10) + 4 = 74\n\nin colclusion we just need to find the power of 10 which we need to multiply the first digit \n\n\n\n# Approach 1 \n// credit goes to ganesh_2023 for this solution\nwe can use a while loop and keep dividing last element to find out the power needed\n\n# Code\n\nclass Solution {\npublic:\n long long findTheArrayConcVal(vector<int>& nums) {\n long long int ans=0,x,b;\n int i = 0, j = nums.size()-1;\n while(i<j){\n x = nums[j], b = 0;\n while(x){\n b++;\n x /= 10;\n }\n ans = ans + nums[i]*1LL*pow(10,b)+nums[j];\n i++;\n j--;\n }\n if(i==j){\n ans += nums[i];\n }return ans;\n }\n};\n\n# Approach 2\nusing log and pow \n\n# Code\nclass Solution {\npublic:\n long long findTheArrayConcVal(vector<int>& nums) {\n int i=0;\n int j=nums.size()-1;\n long long ans=0;\n while(i<j)\n {\n ans = ans + (nums[i] * pow(10, (int)log10(nums[j]) + 1 )) + nums[j];\n i++;\n j--;\n }\n if(i==j) ans += nums[i];\n return ans;\n }\n};\n\n# Approach 3\nusing stol and to_string() and simply adding\n\n# Code\n\nclass Solution {\npublic:\n long long findTheArrayConcVal(vector<int>& nums) {\n\n int i = 0;\n int j = nums.size()-1;\n long long ans = 0;\n\n while(i<j)\n {\n string temp = to_string(nums[i]) + to_string(nums[j]);\n ans += stol(temp);\n i++;\n j--;\n }\n if(i==j)\n ans += nums[i];\n return ans;\n \n }\n};\n\n# approach 4\nthis is the fastest and is feasiable only beacause of the constraints given\n\nwe simply use if else to find the power \n\n# Code\n\nclass Solution {\npublic:\n long long findTheArrayConcVal(vector<int>& nums) {\n \n int i=0;\n int j=nums.size()-1;\n long long concat =0;\n while(i<=j)\n {\n if(i==j)\n {\n concat += nums[i];\n break;\n }\n if(nums[j]<10)\n {\n concat += nums[i]*10 + nums[j];\n i++;\n j--;\n continue;\n }\n if(nums[j]<100)\n {\n concat += nums[i]*100 + nums[j];\n i++;\n j--;\n continue;\n }\n if(nums[j]<1000)\n {\n concat += nums[i]*1000 + nums[j];\n i++;\n j--;\n continue;\n }\n if(nums[j]<10000)\n {\n concat += nums[i]*10000 + nums[j];\n i++;\n j--;\n continue;\n }\n if(nums[j]<100000)\n {\n concat += nums[i]*100000 + nums[j];\n i++;\n j--;\n continue;\n }\n }\n return concat;\n \n }\n};\n | 1 | 0 | ['C++'] | 0 |
find-the-array-concatenation-value | 100% Fast Easy Simple C++ Solution ✔✔ | 100-fast-easy-simple-c-solution-by-akank-7y6b | Complexity\n- Time complexity: O(n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(1)\n Add your space complexity here, e.g. O(n) \n\n# Co | akanksha984 | NORMAL | 2023-02-12T07:26:55.633954+00:00 | 2023-02-12T07:26:55.633987+00:00 | 40 | false | ## Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n long long findTheArrayConcVal(vector<int>& nums) {\n long long ans=0;\n int i=0; int j= nums.size()-1;\n while (i<=j){\n if (i==j){\n ans+= nums[i];\n break;\n }\n int fir= nums[i]; int sec= nums[j];\n int dem= nums[j];\n int test= 0;\n while (dem>0){test++; dem/=10;}\n while (test--)fir*=10;\n fir+=sec;\n ans+= fir;\n i++; j--;\n }\n return ans;\n }\n};\n``` | 1 | 0 | ['Array', 'Math', 'Two Pointers', 'String', 'C++'] | 0 |
find-the-array-concatenation-value | Easy Solution || C++ | easy-solution-c-by-kd_5304-237k | Code\n\n#define ll long long\nclass Solution {\npublic:\n ll concat(int a,int b){\n int c=b,d=1;\n while(c!=0){\n d*=10;\n | kd_5304 | NORMAL | 2023-02-12T05:39:00.531438+00:00 | 2023-02-12T05:39:00.531493+00:00 | 105 | false | # Code\n```\n#define ll long long\nclass Solution {\npublic:\n ll concat(int a,int b){\n int c=b,d=1;\n while(c!=0){\n d*=10;\n c/=10;\n }\n return (ll)(a*d+b);\n }\n ll findTheArrayConcVal(vector<int>& nums) {\n ll ans=0; int l=nums.size();\n if(l==1) return (ll)nums[0];\n for(int i=0,j=l-1;i<j;i++,j--)\n ans+=concat(nums[i],nums[j]);\n if(l%2!=0)\n ans+=nums[l/2];//since the middle element gets left in the for loop\n return ans; \n }\n};\n```\n# Upvote if this helped!~\n\n | 1 | 0 | ['Array', 'Math', 'C++'] | 0 |
find-the-array-concatenation-value | very easy java solution | very-easy-java-solution-by-logesh_7-0ads | \nclass Solution {\n public long findTheArrayConcVal(int[] nums) {\n ArrayList<Integer>a=new ArrayList();\n for(int x:nums){\n a.add | logesh_7_ | NORMAL | 2023-02-12T05:24:50.388283+00:00 | 2023-02-12T05:24:50.388323+00:00 | 24 | false | ```\nclass Solution {\n public long findTheArrayConcVal(int[] nums) {\n ArrayList<Integer>a=new ArrayList();\n for(int x:nums){\n a.add(x);\n \n }\n long sum=0;\n String b="";\n while(a.size()>0){\n if(a.size()>1){\n b+=a.get(0)+""+a.get(a.size()-1)+"";\n sum+=Long.parseLong(b);\n b="";\n a.remove(0);\n a.remove(a.size()-1);\n //System.out.println(sum);\n }\n else{\n b+=a.get(0)+"";\n a.remove(0);\n sum+=Long.parseLong(b);\n }\n }return sum;\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
find-the-array-concatenation-value | c++ | c-by-prabhdeep0007-e107 | ~~~\nclass Solution {\npublic:\n long long findTheArrayConcVal(vector& nums) {\n long long n=nums.size(),ans=0;\n for(int i=0;i<n/2;i++)\n | prabhdeep0007 | NORMAL | 2023-02-12T05:24:33.372168+00:00 | 2023-02-12T05:24:33.372206+00:00 | 16 | false | ~~~\nclass Solution {\npublic:\n long long findTheArrayConcVal(vector<int>& nums) {\n long long n=nums.size(),ans=0;\n for(int i=0;i<n/2;i++)\n {\n string s1=to_string(nums[i]);\n string s2=to_string(nums[n-i-1]);\n s1=s1+s2;\n cout<<s1<<endl;\n ans+=stoi(s1);\n }\n if(n%2!=0) \n {\n ans+=nums[n/2];\n }\n return ans;\n }\n}; | 1 | 0 | ['C'] | 0 |
find-the-array-concatenation-value | Easiest C++ solution using single for loop | easiest-c-solution-using-single-for-loop-f3b7 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | vishu_0123 | NORMAL | 2023-02-12T04:58:57.495794+00:00 | 2023-02-12T04:58:57.495847+00:00 | 38 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n long long findTheArrayConcVal(vector<int>& nums) {\n long long n=nums.size(),sum=0;\n for(int i=0;i<n/2;i++){\n int a=log10(nums[n-1-i]);\n int b=(nums[i]*(pow(10,a+1)))+nums[n-1-i];\n sum=sum+b;\n }\n if(n%2==1) return sum+nums[n/2];\n else return sum;\n \n }\n};\nDo UPVOTE if you like\n``` | 1 | 0 | ['C++'] | 0 |
find-the-array-concatenation-value | Simple C++| | string to int | | int to string conversion | simple-c-string-to-int-int-to-string-con-cxyf | \n# Approach\nuse two pointer technique to solve the problem\n Describe your approach to solving the problem. \n\n# Complexity\n- Time complexity: O(n*n)\n Add | yashpal_97 | NORMAL | 2023-02-12T04:46:01.047037+00:00 | 2023-02-12T04:46:01.047081+00:00 | 55 | false | \n# Approach\nuse two pointer technique to solve the problem\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n*n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:o(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n long long findTheArrayConcVal(vector<int>& nums) {\n string s="";\n long long ans=0;\n int n=nums.size();\n int st=0,e=n-1;\n if(n==1){\n return nums[0];\n }\n while(st<e){\n s+=to_string(nums[st]);\n s+=to_string(nums[e]);\n int yk=stoi(s);\n ans+=yk;\n s="";\n st++;e--;\n }\n st=0;e=n-1;\n if(n&1){\n int mid=(st+e)/2;\n return ans+nums[mid];\n }\n else{\n return ans;\n }\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
find-the-array-concatenation-value | [Python3] simulation | python3-simulation-by-ye15-6rbp | \n\nclass Solution:\n def findTheArrayConcVal(self, nums: List[int]) -> int:\n n = len(nums)\n ans = 0 \n for i in range((n+1)//2): \n | ye15 | NORMAL | 2023-02-12T04:38:14.718112+00:00 | 2023-02-12T04:38:14.718140+00:00 | 214 | false | \n```\nclass Solution:\n def findTheArrayConcVal(self, nums: List[int]) -> int:\n n = len(nums)\n ans = 0 \n for i in range((n+1)//2): \n if i == n-1-i: ans += nums[i]\n else: ans += int(str(nums[i]) + str(nums[n-1-i]))\n return ans \n``` | 1 | 0 | ['Python3'] | 0 |
find-the-array-concatenation-value | easy short efficient clean code | easy-short-efficient-clean-code-by-maver-dxuy | \nclass Solution {\npublic:\ntypedef long long ll;\nlong long findTheArrayConcVal(vector<int>&v) {\n ll n=v.size(), ans=0, l=0, r=n-1;\n while(l<r){\n | maverick09 | NORMAL | 2023-02-12T04:24:37.366006+00:00 | 2023-02-12T04:28:43.573428+00:00 | 52 | false | ```\nclass Solution {\npublic:\ntypedef long long ll;\nlong long findTheArrayConcVal(vector<int>&v) {\n ll n=v.size(), ans=0, l=0, r=n-1;\n while(l<r){\n ans+=stoll(to_string(v[l++])+to_string(v[r--]));\n }\n if(l==r){\n ans+=v[l];\n }\n return ans;\n}\n};\n``` | 1 | 0 | ['C'] | 0 |
find-the-array-concatenation-value | Python Short and Simple | python-short-and-simple-by-aqxa2k-rfqg | Solution \n\nI use a left and right pointer and increment my answer at each step of the time, by concatenating the two numbers in their string form and converti | aqxa2k | NORMAL | 2023-02-12T04:03:17.292999+00:00 | 2023-02-12T04:03:17.293046+00:00 | 84 | false | # Solution \n\nI use a left and right pointer and increment my answer at each step of the time, by concatenating the two numbers in their string form and converting back to int. If the middle element is left (or if $N$ is odd), simply add it to the answer. \n\nAlternatively, you can just simulate what is stated in the problem. For languages like C++ where vector.erase(0) works in $O(N)$, you could use a deque or similar data structure, although it is not necessary, as $O(N^2)$ passes under the small constraints. \n\n# Complexity\n- Time complexity: $O(N)$\n- Space complexity: $O(1)$ (extra space)\n\n### \n\n```py\nclass Solution:\n def findTheArrayConcVal(self, nums: List[int]) -> int:\n l = 0\n r = len( nums)-1 \n ans = 0 \n \n while (l < r): \n x = str( nums[l]) \n y = str( nums[r]) \n x += y \n ans += int(x)\n l += 1\n r -= 1 \n \n if l == r: \n ans += nums[l] \n \n return ans\n``` | 1 | 0 | ['Python3'] | 0 |
find-the-array-concatenation-value | ✅ C++ || Easy | c-easy-by-lc_tushar-4rpx | \nclass Solution {\npublic:\n long long findTheArrayConcVal(vector<int>& nums) \n {\n long long ans = 0;\n int i = 0,j = nums.size()-1;\n | lc_Tushar | NORMAL | 2023-02-12T04:02:45.488321+00:00 | 2023-02-12T04:02:45.488371+00:00 | 65 | false | ```\nclass Solution {\npublic:\n long long findTheArrayConcVal(vector<int>& nums) \n {\n long long ans = 0;\n int i = 0,j = nums.size()-1;\n string temp = "";\n while(i<j)\n {\n temp = "";\n temp+=to_string(nums[i])+to_string(nums[j]);\n ans+=stoi(temp);\n i++;j--;\n }\n if(nums.size()%2)\n {\n ans+=nums[i];\n }\n return ans;\n }\n};\n``` | 1 | 0 | ['C', 'C++'] | 0 |
find-the-array-concatenation-value | C++ || simple to_string() use | c-simple-to_string-use-by-up1512001-rncn | \nclass Solution {\npublic:\n long long findTheArrayConcVal(vector<int>& nums) {\n long long ans=0;\n for(int i=0,j=nums.size()-1;i<nums.size() | up1512001 | NORMAL | 2023-02-12T04:02:13.112514+00:00 | 2023-02-12T04:02:13.112562+00:00 | 84 | false | ```\nclass Solution {\npublic:\n long long findTheArrayConcVal(vector<int>& nums) {\n long long ans=0;\n for(int i=0,j=nums.size()-1;i<nums.size()/2;i++,j--){\n string s = to_string(nums[i])+to_string(nums[j]);\n ans += stoll(s);\n }\n if(nums.size()%2==1) ans += nums[nums.size()/2];\n return ans;\n }\n};\n``` | 1 | 0 | ['C', 'C++'] | 0 |
find-the-array-concatenation-value | C++ | c-by-s1ddharth-h97g | \nclass Solution {\npublic:\n long long findTheArrayConcVal(vector<int>& nums) {\n deque<int> dq;\n for(auto &it: nums) {\n dq.push_ | s1ddharth | NORMAL | 2023-02-12T04:01:57.615161+00:00 | 2023-02-12T04:01:57.615206+00:00 | 49 | false | ```\nclass Solution {\npublic:\n long long findTheArrayConcVal(vector<int>& nums) {\n deque<int> dq;\n for(auto &it: nums) {\n dq.push_back(it);\n }\n long long con = 0;\n while(dq.size() > 0) {\n if(dq.size() > 1) {\n auto first = to_string(dq.front());\n auto last = to_string(dq.back());\n dq.pop_front();\n dq.pop_back();\n string temp = first + last;\n con += stoi(temp);\n }\n else {\n auto first = to_string(dq.front());\n dq.pop_front();\n string temp = first;\n con += stoi(temp);\n }\n }\n return con;\n }\n};\n``` | 1 | 0 | ['C'] | 0 |
find-the-array-concatenation-value | Two Pointer Simple C++ | two-pointer-simple-c-by-stupidly_logical-fgg9 | \n# Code\n\nclass Solution {\npublic:\n long long findTheArrayConcVal(vector<int>& nums) {\n int n = nums.size(), l, r;\n l = 0; r = n-1;\n | stupidly_logical | NORMAL | 2023-02-12T04:00:59.905079+00:00 | 2023-02-13T10:54:25.609528+00:00 | 102 | false | \n# Code\n```\nclass Solution {\npublic:\n long long findTheArrayConcVal(vector<int>& nums) {\n int n = nums.size(), l, r;\n l = 0; r = n-1;\n long long int ans = 0;\n while (l <= r) {\n if (l == r) {\n ans += nums[l];\n break;\n }\n string a = to_string(nums[l++]);\n string b = to_string(nums[r--]);\n a = a+b;\n ans += stoi(a);\n }\n return ans;\n }\n};\n``` | 1 | 0 | ['Two Pointers', 'C++'] | 0 |
find-the-array-concatenation-value | Two Pointer ✅ | Array 🦾 | Easy 😉 | Python3 | 🥳 | two-pointer-array-easy-python3-by-sourab-5t3p | IntuitionThe problem requires performing pairwise concatenation from both ends of the array until it's empty. A two-pointer approach came to mind: one pointer s | Sourabhishere | NORMAL | 2025-04-08T18:30:12.882924+00:00 | 2025-04-08T18:30:12.882924+00:00 | 1 | false | # Intuition
The problem requires performing pairwise concatenation from both ends of the array until it's empty. A two-pointer approach came to mind: one pointer starts at the beginning (i), and one at the end (j). We concatenate the values at these pointers as strings, convert the result back to an integer, and add to the total. If i == j, we only add the middle element once.
# Approach
We initialize two pointers i and j at the start and end of the array, respectively. A variable sums holds the final concatenation value. We use a while loop to iterate as long as i <= j:
- If i == j, there’s only one element left, so we add it directly to sums.
- Otherwise, we concatenate nums[i] and nums[j] as strings, convert the result to an integer, and add it to sums.
- Increment i and decrement j to continue processing the inner elements.
We return sums once the loop ends.
# Complexity
- Time complexity: **O(n)**
We visit each element at most once, performing constant-time operations per iteration.
- Space complexity: **O(1)**
We only use a few variables for tracking indices and the total sum. The temporary string concatenation and conversion are done in constant space per iteration.
# Code
```python3 []
class Solution:
def findTheArrayConcVal(self, nums: List[int]) -> int:
i , j = 0, len(nums)-1
sums = 0
while i <= j:
if i == j:
sums += int(str(nums[i]))
else:
sums += int(str(nums[i]) + str(nums[j]))
i += 1
j -= 1
return sums
```
---
# If you find it useful

- Thank You ☺️
- Hope your day Goes well 😉
| 0 | 0 | ['Array', 'Two Pointers', 'Python3'] | 0 |
find-the-array-concatenation-value | TypeScript solution, beats 100% | typescript-solution-beats-100-by-alkons-vwaq | IntuitionWe can solve this problem with O(n/2)ApproachWe need to iterate through a half of the array.
Starting from 0 and picking values: left = nums[0], right | alkons | NORMAL | 2025-04-02T08:57:56.719377+00:00 | 2025-04-02T08:57:56.719377+00:00 | 2 | false | # Intuition
We can solve this problem with O(n/2)
# Approach
We need to iterate through a half of the array.
Starting from 0 and picking values: left = nums[0], right = nums[nums.length - 1 - 0].
Then iterate until we calculate all the elements.
# Complexity
# Time complexity:
O(n)
(O(n/2) to be precise)
# Code
```typescript []
function findTheArrayConcVal(nums: number[]): number {
let result = 0;
for (let i = 0; i < Math.ceil(nums.length / 2); i++) {
const left = nums[i];
const rightIndex = nums.length - 1 - i;
if (rightIndex === i) {
result += left;
continue;
}
const concatenated = Number.parseInt(left.toString() + nums[rightIndex].toString());
result += concatenated;
}
return result;
}
``` | 0 | 0 | ['TypeScript'] | 0 |
find-the-array-concatenation-value | ✅💯🔥Simple Code📌🚀| 🎓🧠using two pointers | O(n) Time Complexity💀💯 | simple-code-using-two-pointers-on-time-c-sddg | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | kotla_jithendra | NORMAL | 2025-03-31T11:12:45.689058+00:00 | 2025-03-31T11:12:45.689058+00:00 | 2 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def findTheArrayConcVal(self, nums: List[int]) -> int:
l=0
r=len(nums)-1
concat=0
while l<r:
sum=int(str(nums[l])+str(nums[r]))
concat+=sum
l+=1
r-=1
if l==r:
concat+=nums[l]
return concat
``` | 0 | 0 | ['Array', 'Two Pointers', 'Python', 'Python3'] | 0 |
find-the-array-concatenation-value | Java Solution Optimized Simple Approach Beat 85% ✅💯 | java-solution-optimized-simple-approach-s593n | Intuition1. Initialization:
ans: A variable of type long is used to store the result, which is the sum of concatenated values.
si: A pointer to the start of the | UnratedCoder | NORMAL | 2025-03-29T06:29:54.713364+00:00 | 2025-03-29T06:29:54.713364+00:00 | 2 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
**1. Initialization:**
- ans: A variable of type long is used to store the result, which is the sum of concatenated values.
- si: A pointer to the start of the array (initialized to 0).
- ei: A pointer to the end of the array (initialized to nums.length - 1).
**2. While Loop:**
- The while loop runs as long as si <= ei:
- Concatenation & Summation:
- If si is not equal to ei, the elements at si and ei are concatenated as strings. The string concatenation is achieved by converting each element to a string using Integer.toString(nums[si]) and Integer.toString(nums[ei]), and then adding them together. The resulting string is then parsed back to an integer, which is added to the result (ans).
- If si equals ei, it means we are at the middle element (in case of an odd-length array). In this case, we simply add the value of nums[ei] to ans (as no concatenation happens here).
- After each operation, si is incremented (move toward the right) and ei is decremented (move toward the left).
**3. Return the Result:**
- After the loop completes, the accumulated value of ans is returned, which represents the sum of concatenated values from the array.
# Approach
<!-- Describe your approach to solving the problem. -->
**1. Initialization:**
- ans: A variable of type long is used to store the result, which is the sum of concatenated values.
- si: A pointer to the start of the array (initialized to 0).
- ei: A pointer to the end of the array (initialized to nums.length - 1).
**2. While Loop:**
- The while loop runs as long as si <= ei:
- Concatenation & Summation:
- If si is not equal to ei, the elements at si and ei are concatenated as strings. The string concatenation is achieved by converting each element to a string using Integer.toString(nums[si]) and Integer.toString(nums[ei]), and then adding them together. The resulting string is then parsed back to an integer, which is added to the result (ans).
- If si equals ei, it means we are at the middle element (in case of an odd-length array). In this case, we simply add the value of nums[ei] to ans (as no concatenation happens here).
- After each operation, si is incremented (move toward the right) and ei is decremented (move toward the left).
**3. Return the Result:**
- After the loop completes, the accumulated value of ans is returned, which represents the sum of concatenated values from the array.
# Complexity
- Time complexity: O(n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public long findTheArrayConcVal(int[] nums) {
long ans = 0;
int si = 0;
int ei = nums.length - 1;
while (si <= ei) {
if (si != ei) {
int temp = Integer.parseInt(Integer.toString(nums[si]) + Integer.toString(nums[ei]));
ans += temp;
} else {
ans += nums[ei];
}
si++;
ei--;
}
return ans;
}
}
``` | 0 | 0 | ['Array', 'Two Pointers', 'Simulation', 'Java'] | 0 |
find-the-array-concatenation-value | Optimized simple solution - beats 95.78%🔥 | optimized-simple-solution-beats-9578-by-25ydm | Complexity
Time complexity: O(N)
Space complexity: O(1)
Code | cyrusjetson | NORMAL | 2025-03-28T11:24:54.906692+00:00 | 2025-03-28T11:24:54.906692+00:00 | 2 | false | # Complexity
- Time complexity: O(N)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public long findTheArrayConcVal(int[] nums) {
long ans = 0;
int l = 0;
int r = nums.length - 1;
while (l < r) {
int n1 = nums[l];
int n2 = nums[r];
int t = n2;
int p = 10;
while (t != 0) {
t /= 10;
p *= 10;
}
if (p != 10) {
ans += n1 * p / 10 + n2;
}
l++;
r--;
}
if (l == r) {
ans += nums[l];
}
return ans;
}
}
``` | 0 | 0 | ['Java'] | 0 |
find-the-array-concatenation-value | Simple and 100% beats solution | simple-and-100-beats-solution-by-vignesh-vnn3 | Intuition ApproachWe have two pointers in which one moves from left and other from right, while doing this we concatenate the numbera concatenate b is given bya | vignesharavindh_ | NORMAL | 2025-03-28T06:44:30.352693+00:00 | 2025-03-28T06:44:30.352693+00:00 | 2 | false | # Intuition Approach
<!-- Describe your first thoughts on how to solve this problem. -->
We have two pointers in which one moves from left and other from right, while doing this we concatenate the number
a concatenate b is given by
a * number of places to move for b + b
number of places to move for b is given by the 10 power the number of digits in b, so that adding b to a doesnt affect a.
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(n)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(1)
# Code
```cpp []
class Solution {
public:
long long num_digits(int value)
{
int num = 1;
while(value)
{
value = value / 10;
num *= 10;
}
return num;
}
long long findTheArrayConcVal(vector<int>& nums) {
int n = nums.size();
int left = 0;
int right = n - 1;
long long sum = 0;
while(left <= right)
{
if(left == right)
{
sum += nums[left];
}
else
{
sum += nums[left] * num_digits(nums[right]) + nums[right];
}
left ++;
right --;
}
return sum;
}
};
``` | 0 | 0 | ['Math', 'Two Pointers', 'C++'] | 0 |
find-the-array-concatenation-value | find-the-array-concatenation-value | find-the-array-concatenation-value-by-ad-ntbh | IntuitionApproachComplexity
Time complexity:
O(n)
Space complexity:
O(1)
Code | Aditya1234563 | NORMAL | 2025-03-24T14:14:15.692785+00:00 | 2025-03-24T14:14:15.692785+00:00 | 3 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
O(n)
- Space complexity:
O(1)
# Code
```java []
class Solution {
public long findTheArrayConcVal(int[] nums) {
int n=nums.length;
int i=0;
int j=n-1;
long ans=0;
if (n%2!=0) {
int k=n/2;
ans+=(nums[k]);
}
while(i<j){
String s=String.valueOf(nums[i])+String.valueOf(nums[j]);
ans+=(Long.parseLong(s));
i++;
j--;
}
return ans;
}
}
``` | 0 | 0 | ['Java'] | 0 |
find-the-array-concatenation-value | Easy Solution | easy-solution-by-adhi_m_s-gbd5 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | Adhi_M_S | NORMAL | 2025-03-24T07:01:36.952613+00:00 | 2025-03-24T07:01:36.952613+00:00 | 2 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def findTheArrayConcVal(self, nums: List[int]) -> int:
left,right=0,len(nums)-1
tem=[]
while left<=right:
if left!=right:
tem.append(int(str(nums[left])+str(nums[right])))
elif left==right:
tem.append(nums[left])
left+=1
right-=1
return sum(tem)
``` | 0 | 0 | ['Python3'] | 0 |
find-the-array-concatenation-value | TP | tp-by-sangram1989-8eaj | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | Sangram1989 | NORMAL | 2025-03-23T13:38:06.154458+00:00 | 2025-03-23T13:38:06.154458+00:00 | 2 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public long findTheArrayConcVal(int[] nums) {
int i=0;
int j=nums.length-1;
long finalsum=0;
while(i<=j){
String sum="";
if(i==j){
finalsum=finalsum+nums[j];
return finalsum;
}
sum=sum+String.valueOf(nums[i])+String.valueOf(nums[j]);
finalsum=finalsum+Long.parseLong(sum);
i++;
j--;
}
return finalsum;
}
}
``` | 0 | 0 | ['Java'] | 0 |
find-the-array-concatenation-value | Sum of Concatenated Pairs in an Array | sum-of-concatenated-pairs-in-an-array-by-c0fd | IntuitionApproachInitialize two pointers:i at the start (0)j at the end (len(nums) - 1)Maintain a variable concat to store the sum of concatenated numbers.Use a | jadhav_omkar_12 | NORMAL | 2025-03-22T19:16:52.078420+00:00 | 2025-03-22T19:16:52.078420+00:00 | 1 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->The problem requires forming numbers by concatenating the first and last elements of the array and summing them. If the array has an odd length, the middle element is added separately. The two-pointer approach is a natural way to solve this, as it allows efficient pairing of elements.
# Approach
Initialize two pointers:
i at the start (0)
j at the end (len(nums) - 1)
Maintain a variable concat to store the sum of concatenated numbers.
Use a while loop to process pairs (nums[i] and nums[j]):
Convert both numbers to strings and concatenate them.
Convert the concatenated string back to an integer and add it to concat.
Move the left pointer i forward and the right pointer j backward.
If there is a single unpaired middle element (for odd-length arrays), add it separately.
Return concat.
# Complexity
- Time complexity:
O(n)
- Space complexity:
O(1)
# Code
```python3 []
class Solution:
def findTheArrayConcVal(self, nums: List[int]) -> int:
if(len(nums)==1):
return nums[0]
i=0
j=len(nums)-1
concat=0
while(i<j):
concat+=int(str(nums[i])+str(nums[j]))
i+=1
j-=1
if i == j:
concat += nums[i]
return concat
``` | 0 | 0 | ['Python3'] | 0 |
maximum-number-of-consecutive-values-you-can-make | [Java/C++/Python] Accumulate the Coins | javacpython-accumulate-the-coins-by-lee2-f918 | Intuition\n"Return the maximum number ... you can make with your coins starting from and including 0"\nthis equals to\n"Return the minimum number that you can | lee215 | NORMAL | 2021-03-20T16:01:38.530454+00:00 | 2021-03-21T05:27:06.571414+00:00 | 8,876 | false | # **Intuition**\n"Return the maximum number ... you can make with your coins starting from and **including 0**"\nthis equals to\n"Return the minimum number that you can not make .."\n<br>\n\n# **Explanation**\nBecause samll values can only discompose to samller numbers,\nwe sort the input array and check from the small coins.\n\n`res` means the next value we want to make,\nand we can already make `0,1,2,3...res-1`.\n\nWe iterate the array,\nIf `a > res`, all remaining numbers are bigger than `res`,\nwe can not make `res` in all means,\nso we break the loop and return `res`\n\nIf `a <= res`,\nwe could make from `0` to `res - 1`,\nnow with `a` so we can make from `a` to `res + a - 1`,\nand `a <= res`, so our next goal becomes `res + a` now.\nso in this case, we simply `res += a`\n<br>\n\n# **Complexity**\nTime `O(sort)`\nSpace `O(sort)`\n<br>\n\n**Java**\n```java\n public int getMaximumConsecutive(int[] A) {\n Arrays.sort(A);\n int res = 1;\n for (int a: A) {\n if (a > res) break;\n res += a;\n }\n return res;\n }\n```\n\n**C++**\n```cpp\n int getMaximumConsecutive(vector<int>& A) {\n sort(A.begin(), A.end());\n int res = 1;\n for (int a: A) {\n if (a > res) break;\n res += a;\n }\n return res;\n }\n```\n\n**Python**\n```py\n def getMaximumConsecutive(self, A):\n res = 1\n for a in sorted(A):\n if a > res: break\n res += a\n return res\n```\n | 257 | 4 | [] | 41 |
maximum-number-of-consecutive-values-you-can-make | C++/Java/Python with picture | cjavapython-with-picture-by-votrubac-bpa4 | The intuition for this one is cool. Got a few TLE before figuring it out.\n\nThis is the realization: if we reached number i, that means that we can make all va | votrubac | NORMAL | 2021-03-20T16:01:29.290903+00:00 | 2021-03-26T18:12:35.789115+00:00 | 5,402 | false | The intuition for this one is cool. Got a few TLE before figuring it out.\n\nThis is the realization: if we reached number `i`, that means that we can make all values `0...i`. So, if we add a coin with value `j`, we can also make values `i+1...i+j`.\n\nThe only case when we can have a gap is the coin value is greater than `i + 1 `. So we sort the coins to make sure we process smaller coins first.\n\nFor example, let\'s assume that we can make all values `0...7`. Adding a nickel allows us to make values `8..12` (`7+1...7+5`).\n\n\n\n**C++**\n```cpp\nint getMaximumConsecutive(vector<int>& c) {\n sort(begin(c), end(c));\n int max_val = 1;\n for (auto i = 0; i < c.size() && c[i] <= max_val; ++i)\n max_val += c[i];\n return max_val;\n} \n```\n**Java**\n```java\npublic int getMaximumConsecutive(int[] c) {\n Arrays.sort(c);\n int max_val = 1;\n for (int i = 0; i < c.length && c[i] <= max_val; ++i)\n max_val += c[i];\n return max_val; \n}\n```\n**Python 3**\n```python\nclass Solution:\n def getMaximumConsecutive(self, coins: List[int]) -> int:\n max_val = 1\n for c in sorted(coins):\n if c > max_val:\n break\n max_val += c\n return max_val\n``` | 142 | 4 | [] | 12 |
maximum-number-of-consecutive-values-you-can-make | ✅Short & Easy w/ Explanation | Greedy Approach | short-easy-w-explanation-greedy-approach-5l80 | We can understand this algorithm through an example. \nIf we have coins [1], we can form the sequence 0, 1. For extending sequence we need coin <= 2.\nIf we hav | archit91 | NORMAL | 2021-03-20T16:04:18.376983+00:00 | 2021-03-20T16:33:51.313480+00:00 | 2,256 | false | We can understand this algorithm through an example. \nIf we have coins `[1]`, we can form the sequence `0, 1`. For extending sequence we need coin <= 2.\nIf we have coing `[1, 2]`, we can form `0, 1, 2, 3`. For extending sequence we need coin <= 4.\nIf we have coing `[1, 2, 3]`, we can form `0, 1, 2, 3, 4, 5, 6`. For extending sequence we need coin <= 7.\nIn each of the above case, ***if the next coin we get is greater than the maximum sequence currently formed, we cannot extend the sequence in any case whatsoever***.\n\nSuppose we get another 1 coin and have `[1,1,2,3]`, we can form `0, 1, 2, 3, 4, 5, 6, 7`. \nWe can see we extended the previous sequence by 1 and now we would need coin of 8 or less value.\n\nNow, if we get a coin 9, then there\'s no way we can extend the sequence. The sequence previously formed was upto 7 and we needed to get a coin of value less than or equal to 8 to extend the sequence.\n\n------------\n\n**We can generalize pattern** - we can extend the current consecutive sequence, if the coin we are going to choose is less than or equal to the `current sum + 1`.\n\n```\nint getMaximumConsecutive(vector<int>& coins) {\n\tsort(begin(coins), end(coins));\n\tint curSum = 0;\n\tfor(auto& coin : coins)\n\t\tif(coin <= curSum + 1) curSum += coin;\n\t\telse break;\n\n\treturn curSum + 1;\n}\n```\n\n**Time Complexity :** **`O(NlogN)`**\n**Space Complexity :** **`O(1)`**, ignoring the implicit space required by the sort algorithm\n\n------------\n------------ | 55 | 1 | ['C'] | 2 |
maximum-number-of-consecutive-values-you-can-make | C++/Python/Javascript Solution, O(NLogN) Time and O(logn) space | cpythonjavascript-solution-onlogn-time-a-8ojk | The space complexity is O(logn), There are logN stack frame when running quick sort.\nThanks @lee215 to point it out.\n\n#### Idea\n- sort the Array\n- We start | chejianchao | NORMAL | 2021-03-20T16:00:24.153796+00:00 | 2021-03-20T16:28:22.675602+00:00 | 1,048 | false | The space complexity is O(logn), There are logN stack frame when running quick sort.\nThanks @lee215 to point it out.\n\n#### Idea\n- sort the Array\n- We start from 0 as current, means we can cover all the number from 0 ~ current, and if current + 1 >= next_number, that means we can cover all the number from 0 ~ current + next_number, so current += next_number.\n\n#### Complexity\n- Time: O(NLogN)\n- Space: O(1)\n#### C++\n```\nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) {\n sort(coins.begin(), coins.end());\n int cur = 0;\n for(int i = 0; i < coins.size(); ++i) {\n if(cur + 1 >= coins[i]) {\n cur += coins[i];\n }\n }\n return cur + 1;\n }\n};\n```\n\n#### Python\n```\nclass Solution(object):\n def getMaximumConsecutive(self, coins):\n """\n :type coins: List[int]\n :rtype: int\n """\n coins.sort();\n cur = 0;\n for i in range(0, len(coins)):\n if cur + 1 >= coins[i]:\n cur += coins[i]\n \n return cur + 1\n```\n\n#### Javascript\n```\nvar getMaximumConsecutive = function(coins) {\n coins.sort((a, b) => a - b);\n let cur = 0;\n for(let i = 0; i < coins.length; ++i) {\n if(cur + 1 >= coins[i]) {\n cur += coins[i];\n }\n }\n return cur + 1;\n};\n``` | 15 | 4 | [] | 3 |
maximum-number-of-consecutive-values-you-can-make | [Python 3] with explanation. | python-3-with-explanation-by-bakerston-kgxs | Suppose we have a coin of value c[i], we can use this coin to extend current consecutive values, only if we have already built consecutive values no less than c | Bakerston | NORMAL | 2021-03-20T16:04:46.364234+00:00 | 2021-03-20T17:07:15.829204+00:00 | 687 | false | Suppose we have a coin of value ```c[i]```, we can use this coin to extend current consecutive values, only if we have already built consecutive values no less than ```c[i] - 1```. \n\nSo just sort coins by value, for each ```coin[i]```, check if ```c[i]``` satisfies ```c[i] <= cur_max + 1```. If so, increase the maximum value from ```cur_max``` to ```cur_max + coin[i]```, otherwise, return ```c[i] + 1``` (No need to try any following coins because coin with larger value can not cover ```cur_max + 1``` neither). \n\n* For example:```\nvalues = [0,1,2,3,4,5,6],\nnew_c = 7```\nTherefore we can build ```[7, 8, ... , 13]``` with ```new value = 7```, now the consecutive value list is ```[0, 1, ... , 13]```\n\nHowever, if the new value is 2 more larger than the maximum number, we can not find a way to fill the ```value = max_values + 1```\n\n* For example:```\nvalues = [0,1,2,3,4,5,6],\nnew_c = 8```\nIn this case, ```max_value = 6```, we cant fit the value 7 with current coins, meaning the maximum value we can reach is max_value, ```ans = max_value + 1``` (including 0)\n\n```\ndef getMaximumConsecutive(self, coins: List[int]) -> int:\n coins.sort()\n cur = 0\n for idx in range(len(coins)):\n if coins[idx] - 1 > cur:\n break\n cur += coins[idx]\n return cur + 1\n``` | 9 | 0 | [] | 1 |
maximum-number-of-consecutive-values-you-can-make | Java Simple Explanation (beats 99) | java-simple-explanation-beats-99-by-vani-yu7e | \nclass Solution {\n public int getMaximumConsecutive(int[] c) {\n Arrays.sort(c);\n int n = c.length;\n int sum = 1;\n for(int i | vanir | NORMAL | 2021-04-03T11:43:05.104555+00:00 | 2021-04-03T12:30:30.038008+00:00 | 519 | false | ```\nclass Solution {\n public int getMaximumConsecutive(int[] c) {\n Arrays.sort(c);\n int n = c.length;\n int sum = 1;\n for(int i=0;i<n;i++){\n if(c[i]<=sum) sum=sum+c[i];\n else break;\n }\n return sum;\n \n \n }\n}\n```\n\nYou want to get the value of the biggest sum you can make using consecutive integers and these integers should be from the array.\n\nLet us say,\ncurrently,\nthe consecutive sum I want is stored in \'sum\'.\n(initialised as sum=1)\nNow\nif my current coin is equal to sum,\nthen I am done! (Because I was looking for that sum value and a coin serves it)\n\nif my current coing is smaller than sum,\nthen that means I can pick the largest sum (which is sum itself) and add my coin value to it, to extend my reach of the sum.\n\nIf your current sum is say 6 and then coin you got is y, then you can extend your range! Why? Because 1,2,3...,y,...6 are already there. You add your y to all these numbers and the max reach is 6+y, that is your new sum. You are able to form all the sums between 6 to 6+y now.\nIf you cannot, extend the range, then that is the maximum you could have gone...\n\n\n\n\n | 7 | 0 | [] | 0 |
maximum-number-of-consecutive-values-you-can-make | [C++] O(nlgn) Time, Constant Space DP Solution Explained | c-onlgn-time-constant-space-dp-solution-5v96x | I started to tackle this problem in a kind of crude DP fashion (you know, preparing all the cells up to the sum of all the provided coins), when it occurred to | ajna | NORMAL | 2021-03-20T20:57:06.537903+00:00 | 2021-03-20T20:57:06.537940+00:00 | 1,159 | false | I started to tackle this problem in a kind of crude DP fashion (you know, preparing all the cells up to the sum of all the provided coins), when it occurred to me that there was a simpler way, less memory demanding way and that is the one I am going to explore and explaing now :)\n\nTo proceed, we will first of all initialise `res`, our usual accumulator variable, to be `1`, since we can always do at least a combination (`0`, no matter what coins are we given).\n\nThe magic starts now: we will sort `coins` so that they are in increasing order, then we will loop through them and for each `coin` we will check if its value is `<` res, which means we could actually get to use it to gain `res + coin` more combinations, since our loop invariant is that we could reach `res` without any gaps. As soon as we find a coin bigger than `res`, it implies that we would have gap, so we quit.\n\nAt the end of the loop, we can just return `res` and be done with it.\n\nLet\'s try with a couple of simple examples, starting with (already sorted) `coins == {1, 1, 4}`.\n\nWe will have initially:\n\n```cpp\nres = 1; // we can reach a value of 0 with the coins\ncoin = 1\n```\n\nSince `coin <= res`, we know that we can reach `res` as a value, so we increase `res` by `1` and we move on:\n\n```cpp\nres = 2; // we can reach a value of 1 with the coins, so we have 2 combinations available\ncoin = 1\n```\n\nAgain, we want to know if we can reach `2` with our coins so far and it turns out we can, since `coins < res`:\n\n```cpp\nres = 3; // we can reach a value of 2 with the coins, so we have 3 possible combinations\ncoin = 4\n```\n\nAnd here we stop, since `coin > res` (`4 > 3`), which means we cannot reach `4` with any of the smaller coins (and of course if we had bigger coins, they would not help either).\n\nIf we had `coins = {1, 1, 1, 4}`, you can easily verify how the last step would lead us to have\n\n```cpp\nres = 4; // we can reach a value of 3 with the coins, so we have 4 valid combinations\ncoin = 4\n```\n\nAnd then we might be able to return `res == 4 + 4 == 8` different combinations; if we had `5` or higher as a last coin, it is easy to visualise how we might have not gone back to a `5` or more cells ago in an ideal DP computation of all the possible combinations with it, not without gaps.\n\nThe code:\n\n```cpp\nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) {\n // support variables\n int res = 1;\n // preparing coins\n sort(begin(coins), end(coins));\n for (int coin: coins) {\n // checking if we could have reached coin without gaps\n if (res >= coin) res += coin;\n else break;\n }\n return res;\n }\n};\n``` | 7 | 0 | ['Dynamic Programming', 'C', 'Combinatorics', 'C++'] | 3 |
maximum-number-of-consecutive-values-you-can-make | Python O(NlogN) time solution. Explained | python-onlogn-time-solution-explained-by-rd9v | The idea behind it is simple:\nsort the coins, and every time we take the smallest available (greedy and dp like)\ncur_max tracks the max consecutive we can mak | dyxuki | NORMAL | 2021-08-29T11:08:56.094043+00:00 | 2021-08-30T07:36:21.056461+00:00 | 487 | false | The idea behind it is simple:\nsort the coins, and every time we take the smallest available (greedy and dp like)\ncur_max tracks the max consecutive we can make.\n* if we have a "1", then we know for sure we can make the next number (so: cur_max +=1) (Actually this case is already covered in the next if condition "coin <= cur_max+1", but I hope by separating this case out there, things are clearer)\n* if we have a coin "k+1" but cur_max is "k", that means we can make any number from 0 to k, so by just adding k to them, we can also make any number from k to k+(k+1). The same applies if we have any coin "j" where j < k. (we can make numbers from 0 to k+j)\n* if we have a coin that\'s bigger than the cur_max+1, we know we cannot make cur_max + 1. As the coins are sorted, we don\'t need to look further.\n\nwe return cur_max + 1 because we don\'t return the max number we can make, but the amount of numbers. From 0 to cur_max, there are exactly (cur_max + 1) numbers.\n\n```\nclass Solution:\n def getMaximumConsecutive(self, coins: List[int]) -> int:\n cur_max = 0\n coins.sort()\n \n for coin in coins:\n if coin == 1:\n cur_max += 1\n elif coin <= cur_max+1:\n cur_max += coin\n else: #coin > cur_max + 1\n break\n \n return cur_max+1\n```\n\nTime complexity is O(NlogN) because of the sorting\nSpace complexity is O(N) (timsort in python) | 5 | 1 | ['Python'] | 0 |
maximum-number-of-consecutive-values-you-can-make | Clean Python 3, Greedy O(sort) | clean-python-3-greedy-osort-by-lenchen11-b54c | Sort first, and use largest to save the current possible consecutive largest value\nif current coin is larger than largest, it should be largest + 1.\nOtherwise | lenchen1112 | NORMAL | 2021-03-20T16:01:07.685074+00:00 | 2021-03-20T16:01:29.903027+00:00 | 379 | false | Sort first, and use `largest` to save the current possible consecutive largest value\nif current coin is larger than `largest`, it should be largest + 1.\nOtherwise there will be a gap.\n\nTime: `O(sort)`\nSpace: `O(sort)`\n```\nclass Solution:\n def getMaximumConsecutive(self, coins: List[int]) -> int:\n largest = 0\n for coin in sorted(coins):\n if coin > largest + 1: break\n largest += coin\n return largest + 1\n``` | 5 | 2 | [] | 0 |
maximum-number-of-consecutive-values-you-can-make | C++ | Short Iterative Greedy solution | Explained | Fast solution with less memory usage | c-short-iterative-greedy-solution-explai-2fto | Intuition\n Describe your first thoughts on how to solve this problem. \nNote: For complete code, please scroll to the end. Detailed explanation continues below | DebasritoLahiri | NORMAL | 2022-12-21T23:54:36.374975+00:00 | 2022-12-22T00:02:28.099264+00:00 | 289 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n***Note:*** *For complete code, please scroll to the end. Detailed explanation continues below.*\n\nSuppose we have already achieved a value of x. Now our next coin can be either equal to x+1 or less/greater than x+1. If our next coin is equal to x+1 then we can surely form x+1 amount using that coin alone. However, if our next coin is not equal to x+1 then either we can form x+1 using our next coin and some previous coin(s) or we can\'t form it.\n\nNow in case our next coin is greater than x+1, then we can\'t form our next value as that will require subtracting some amount from next coin which is not possible as we can only use a specific coin or sum of some coins and we also already know no combination of our previous coins can give next value.\n\nIn case our next coin is less than x+1, then we have to make sure that the difference in amount can be made up from our remaining coins. It it can be then we can proceed else we can\'t.\n\nAlso when proceeding, if we have a value x and we can form x+1 using either next coin alone or in combination with some other coins, then we can also form till x+(the value of next coin) as:\n\nWe have been checking in a contiguous manner for the maximum sum possible. So for a coin value of v, we can combine it with previous coins to make sums of (v+1),(v+2),(v+3)........(v+x) where x is the previous value we have achieved till now without considering the coin with value v.\n\nAlso note that we will be starting with 0 as max value as that is the least value we can achieve anytime as it will not require any coins and then we will keep increasing on this.\n\n# Detailed Explanation/Approach\n<!-- Describe your approach to solving the problem. -->\nFirst we sort the input as we will be starting from 0 and incrementing our maximum value in every iteration in an increasing manner. Our maximum value will be maintained in the variable val. Also for our iteration we take the total size of our input in size variable.\n```\nsort(coins.begin(),coins.end());\nint val=0;\nint size=coins.size();\n```\nNow we will loop over our coins input and keep increasing the value of val. Only if we either reach the end of our input or if we can\'t increase the value of val to the next value we need to achieve(which is previous value + 1), then we will break from the loop.\n```\nfor(int i=0;i<size;i++){\n if(.......)\n .....\n else\n break;\n }\n```\nHere, we determine we can achieve next value if any of the below condition satisfies:\n1. The next coin value is equal to the next value we want to achieve:`coins[i]==val+1`\n2. The next coin value is less than our next required value:`coins[i]<val+1` and the difference between the next required value and our next coin value can be made up using previous coins (i.e is less than or equal to our current max value): `(val+1)-coins[i]<=val`\nIf none of the above conditions satisfy then we can\'t achieve our next value and we break from the loop.\n```\nfor(int i=0;i<size;i++){\n if(coins[i]==val+1 || (coins[i]<val+1 && (val+1)-coins[i]<=val))\n ....\n else\n break;\n }\n```\nIf we can achieve our next value, then we increase our max value variable val by the value of the next coin(i.e our max value becomes the sum of our next coin value and current max value), as we can also achieve in this case the values upto the sum of our coin value and current max value.\n```\nfor(int i=0;i<size;i++){\n if(coins[i]==val+1 || (coins[i]<val+1 && (val+1)-coins[i]<=val))\n val+=coins[i];\n else\n break;\n }\n```\nFinally we have our max achievable value in the val variable. However, the problem is asking for the maximum number of **consecutive integers** we can form. This means that we have to count all the integers from 0 till our max value which is simply equal to our max value+1. So we return val+1.\n```\nreturn val+1;\n```\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nIn our program we are using only 1 for loop for iterating over all the input elements only once which should make our TC O(n). However, for sorting we are using an inbuilt function, which basically does a quicksort (we can also implemenet this ourselves instead of using library function). This makes the total TC O(n^2) in worst case and O(nlogn) in average and best cases.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nWe are not using any other extra space except our variables that hold the max value and the input size. But these take constant space. So our total SC is O(1).\n\n# Complete Code\n```\nint getMaximumConsecutive(vector<int>& coins) {\n sort(coins.begin(),coins.end());\n int val=0;\n int size=coins.size();\n for(int i=0;i<size;i++){\n if(coins[i]==val+1 || (coins[i]<val+1 && (val+1)-coins[i]<=val))\n val+=coins[i];\n else\n break;\n }\n return val+1;\n}\n```\n\n\n\n\nIf this helped you, please leave an upvote. Thanks. \uD83D\uDE0A\uD83C\uDF08\n | 4 | 0 | ['C++'] | 0 |
maximum-number-of-consecutive-values-you-can-make | Greedy Solution || Java || Time O(NlogN) and Space:O(1) | greedy-solution-java-time-onlogn-and-spa-lay7 | \n\n public int getMaximumConsecutive(int[] coins) {\n Arrays.sort(coins);\n int result=1;\n \n int idx=0;\n while(idx<coins. | himanshuchhikara | NORMAL | 2021-03-20T16:39:16.956244+00:00 | 2021-03-20T16:39:16.956268+00:00 | 366 | false | \n```\n public int getMaximumConsecutive(int[] coins) {\n Arrays.sort(coins);\n int result=1;\n \n int idx=0;\n while(idx<coins.length && result>=coins[idx]){\n result+=coins[idx];\n idx++;\n }\n return result;\n }\n\t``` | 3 | 1 | ['Greedy', 'Sorting', 'Java'] | 0 |
maximum-number-of-consecutive-values-you-can-make | Easy C++ Solution | easy-c-solution-by-nehagupta_09-am97 | \n\n# Code\n\nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) {\n sort(coins.begin(),coins.end());\n int count=1;\n | NehaGupta_09 | NORMAL | 2024-06-21T07:57:17.685744+00:00 | 2024-06-21T07:57:17.685772+00:00 | 50 | false | \n\n# Code\n```\nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) {\n sort(coins.begin(),coins.end());\n int count=1;\n for(int i=0;i<coins.size();i++)\n {\n if(coins[i]<=count){\n count+=coins[i];\n }\n else\n {\n return count;\n }\n }\n return count;\n }\n};\n``` | 2 | 0 | ['Array', 'Greedy', 'Sorting', 'C++'] | 0 |
maximum-number-of-consecutive-values-you-can-make | c++ | easy | fast | c-easy-fast-by-venomhighs7-9h74 | \n\n# Code\n\nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& A) {\n sort(A.begin(), A.end());\n int res = 1;\n f | venomhighs7 | NORMAL | 2022-11-21T05:35:04.657504+00:00 | 2022-11-21T05:35:04.657549+00:00 | 486 | false | \n\n# Code\n```\nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& A) {\n sort(A.begin(), A.end());\n int res = 1;\n for (int a: A) {\n if (a > res) break;\n res += a;\n }\n return res;\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
maximum-number-of-consecutive-values-you-can-make | TIME O(nlogn) || SPACE O(1) || C++ || SIMPLE | time-onlogn-space-o1-c-simple-by-abhay_1-4d33 | \nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) {\n sort(coins.begin(),coins.end());\n int ans = 0;\n int su | abhay_12345 | NORMAL | 2022-10-01T10:47:54.997976+00:00 | 2022-10-01T10:47:54.998008+00:00 | 646 | false | ```\nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) {\n sort(coins.begin(),coins.end());\n int ans = 0;\n int sum = 0;\n for(auto &i: coins){\n if(sum+1<i){\n return sum+1;\n }\n sum += i;\n }\n return sum+1;\n }\n};\n``` | 2 | 0 | ['Greedy', 'C', 'Sorting', 'C++'] | 0 |
maximum-number-of-consecutive-values-you-can-make | c++ solution using Hashing | c-solution-using-hashing-by-bhardwajsahi-5jg0 | \nint getMaximumConsecutive(vector<int>& a) {\n \n map<int, int> mp;\n \n int n = a.size();\n \n for(int i=0;i<n;i++){ | bhardwajsahil | NORMAL | 2021-08-01T05:34:51.110645+00:00 | 2021-08-01T05:34:51.110689+00:00 | 309 | false | ```\nint getMaximumConsecutive(vector<int>& a) {\n \n map<int, int> mp;\n \n int n = a.size();\n \n for(int i=0;i<n;i++){\n if(!mp[a[i]]){\n mp[a[i]] = 0;\n }\n mp[a[i]]++;\n }\n \n int ans = 0;\n \n for(auto i : mp){\n int x = i.first * i.second;\n if(ans+1 >= (i.first)){\n ans += x;\n }\n else\n break;\n }\n return ans+1;\n }\n``` | 2 | 0 | [] | 2 |
maximum-number-of-consecutive-values-you-can-make | [Python] step-by-step explanation | python-step-by-step-explanation-by-kuanc-udy6 | python\nclass Solution:\n def getMaximumConsecutive(self, coins: List[int]) -> int:\n # 1) if we can use first k coins to make values 0...v,\n | kuanc | NORMAL | 2021-07-28T00:29:28.653119+00:00 | 2021-07-28T00:29:28.653166+00:00 | 210 | false | ```python\nclass Solution:\n def getMaximumConsecutive(self, coins: List[int]) -> int:\n # 1) if we can use first k coins to make values 0...v,\n # it means the combination of first k coins can cover values 0...v\n # 2) what\'s the condition for k + 1 coin s.t. we can make v + 1\n # if it\'s 1 ==> (v) + 1 = v + 1\n # if it\'s 2 ==> (v - 1) + 2 = v + 1\n # if it\'s v ==> (1) + v = v + 1\n # if it\'s v + 1 ==> (0) + v + 1 = v + 1\n # if it\'s v + 2 ==> No solution\n # 3) actually:\n # if it\'s 1 ==> (0...v) + 1 = 0...(v + 1)\n # if it\'s v + 1 ==> (0...v) + v + 1 = 0...(v + v + 1)\n # 4) now we can conclude that\n # if i-th coin <= v + 1 ==> we can make v + 1 + i-th coin\n \n coins.sort()\n v = 0 # we can make 0...v\n for i in range(len(coins)):\n if coins[i] <= v + 1:\n v += coins[i]\n else:\n break\n return v + 1 # [0...v]: v + 1 values\n \n # T: O(sort) + O(n)\n # S: O(sort)\n``` | 2 | 0 | [] | 0 |
maximum-number-of-consecutive-values-you-can-make | Python3 Simple Solution | python3-simple-solution-by-victor72-7z1q | Time Complexity: 94% (approximately)\nSpace Complexity: 84% (approximately)\n\n\nclass Solution:\n def getMaximumConsecutive(self, coins: List[int]) -> int:\ | victor72 | NORMAL | 2021-04-11T17:54:27.190507+00:00 | 2021-04-11T17:54:27.190544+00:00 | 330 | false | **Time Complexity:** 94% (approximately)\n**Space Complexity:** 84% (approximately)\n\n```\nclass Solution:\n def getMaximumConsecutive(self, coins: List[int]) -> int:\n coins.sort()\n \n res = 1\n \n for coin in coins:\n if (res >= coin):\n res += coin\n \n return res\n```\n | 2 | 1 | ['Python', 'Python3'] | 0 |
maximum-number-of-consecutive-values-you-can-make | [Python] Thinking from presum | python-thinking-from-presum-by-qubenhao-k4ck | Given a list of numbers, the maximum we could reach is the sum of the array. What if we keep trying from left to right (after sorting)? For every coins[i], it c | qubenhao | NORMAL | 2021-03-21T01:36:43.101939+00:00 | 2021-03-21T02:18:49.532187+00:00 | 523 | false | Given a list of numbers, the maximum we could reach is the sum of the array. What if we keep trying from left to right (after sorting)? For every coins[i], it can construct every number from `coins[i]` to `coins[i] + persum[i-1]`.\n\n```\n def getMaximumConsecutive(self, coins):\n """\n :type coins: List[int]\n :rtype: int\n """\n coins.sort()\n persum = [0] * len(coins)\n ans = 1\n for i,c in enumerate(coins):\n persum[i] += persum[i-1] + c\n\n if persum[0] != 1:\n return ans\n ans += 1\n for i in range(1,len(persum)):\n if persum[i] == ans:\n ans += 1\n elif coins[i] <= ans:\n ans = persum[i] + 1\n else:\n return ans\n return ans\n```\n\nFrom the code above, we can see that ans is actually exactly persum, so we don\'t need a list of persum anymore.\n\n```\n def getMaximumConsecutive(self, coins):\n """\n :type coins: List[int]\n :rtype: int\n """\n ans = 1\n for coin in sorted(coins):\n if coin <= ans:\n ans += coin\n else:\n return ans\n return ans\n``` | 2 | 0 | ['Python'] | 0 |
maximum-number-of-consecutive-values-you-can-make | python3 Sorting O(nlogn) solution | python3-sorting-onlogn-solution-by-swap2-0wp0 | ```\nclass Solution:\n def getMaximumConsecutive(self, coins: List[int]) -> int:\n coins.sort()\n ans = 0\n for i in range(len(coins)):\ | swap2001 | NORMAL | 2021-03-20T16:10:55.811362+00:00 | 2021-03-20T16:10:55.811387+00:00 | 263 | false | ```\nclass Solution:\n def getMaximumConsecutive(self, coins: List[int]) -> int:\n coins.sort()\n ans = 0\n for i in range(len(coins)):\n if coins[i]<=ans+1:\n ans += coins[i]\n else:\n break\n return ans+1 | 2 | 1 | ['Sorting', 'Python3'] | 1 |
maximum-number-of-consecutive-values-you-can-make | [Java] greedy | java-greedy-by-66brother-tepj | \nclass Solution {\n public int getMaximumConsecutive(int[] A) {\n Arrays.sort(A);\n int res=1;\n for(int i=0;i<A.length;i++){\n | 66brother | NORMAL | 2021-03-20T16:02:38.827740+00:00 | 2021-03-20T16:02:38.827768+00:00 | 82 | false | ```\nclass Solution {\n public int getMaximumConsecutive(int[] A) {\n Arrays.sort(A);\n int res=1;\n for(int i=0;i<A.length;i++){\n if(A[i]>res)break;\n res+=A[i];\n }\n \n return res;\n \n }\n}\n``` | 2 | 0 | [] | 0 |
maximum-number-of-consecutive-values-you-can-make | [Python3] greedy | python3-greedy-by-ye15-milc | \n\nclass Solution:\n def getMaximumConsecutive(self, coins: List[int]) -> int:\n ans = 1\n for x in sorted(coins): \n if ans < x: b | ye15 | NORMAL | 2021-03-20T16:01:47.052813+00:00 | 2021-03-21T00:42:00.460881+00:00 | 243 | false | \n```\nclass Solution:\n def getMaximumConsecutive(self, coins: List[int]) -> int:\n ans = 1\n for x in sorted(coins): \n if ans < x: break \n ans += x\n return ans\n``` | 2 | 1 | ['Python3'] | 0 |
maximum-number-of-consecutive-values-you-can-make | GREEDY | INTUITION | C++ SOLUTION | greedy-intuition-c-solution-by-haribhakt-iv3g | Intuition\nWe can have a prefixSum which will indicate sum of all elements from start till current index. If curr_index >= prefixSum + 1, which means it is unat | HariBhakt | NORMAL | 2024-06-18T02:27:35.679833+00:00 | 2024-06-18T02:27:35.679852+00:00 | 229 | false | # Intuition\nWe can have a prefixSum which will indicate sum of all elements from start till current index. If curr_index >= prefixSum + 1, which means it is unattainable.\n\n# Approach\nHave a prefixSum which checks if coins[curr_idx] >= prefixSum + 1.If yes, break the loop and return ans;\n\n# Complexity\n- Time complexity: $$O(nlogn)$$ \n\n- Space complexity: $$O(1)$$ \n\n# Code\n```\nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) {\n sort(coins.begin(), coins.end());\n int preSum = 0;\n \n for(int coin: coins){\n if(coin <= preSum + 1){\n preSum += coin;\n }\n else break;\n }\n\n return preSum + 1;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
maximum-number-of-consecutive-values-you-can-make | [Python3] O(NlogN) Greedy solution + explanation | python3-onlogn-greedy-solution-explanati-1prg | Intuition\nThe problem requires determining the maximum number of consecutive integer values that can be made using the given coins, starting from 0. The key ob | pipilongstocking | NORMAL | 2024-06-16T05:46:50.162088+00:00 | 2024-06-16T05:46:50.162115+00:00 | 121 | false | # Intuition\nThe problem requires determining the maximum number of consecutive integer values that can be made using the given coins, starting from 0. The key observation here is that if we can create all values up to a certain integer `x`, and the next coin has a value less than or equal to `x`, then we can extend the range of consecutive values we can create.\n\n# Approach\n1. **Sort the Coins**: Start by sorting the coins in ascending order. This allows us to iteratively build the range of consecutive sums in a structured manner.\n \n2. **Initialize**: Initialize `next_coin` to 1. This variable represents the smallest value that we cannot currently form with the given subset of coins.\n\n3. **Iterate Through Coins**: Iterate through each coin:\n - If the value of the coin is less than or equal to `next_coin`, it means we can use this coin to extend our range of consecutive sums.\n - Update `next_coin` by adding the value of the current coin. This extends the range of consecutive sums we can form.\n\n4. **Break Condition**: If a coin\'s value is greater than `next_coin`, break the loop as we can no longer form consecutive sums with the remaining coins.\n\n5. **Return Result**: The value of `next_coin` after the loop completes will be the maximum number of consecutive integers that can be formed.\n\n# Complexity\n- Time complexity: $$O(n \\log n)$$\n - Sorting the coins takes $$O(n \\log n)$$ time.\n - Iterating through the coins takes $$O(n)$$ time.\n \n- Space complexity: $$O(1)$$\n - Only a few variables are used, regardless of the input size.\n\n# Code\n```python\nclass Solution:\n def getMaximumConsecutive(self, coins: List[int]) -> int:\n coins.sort()\n next_coin = 1\n for coin in coins:\n if next_coin - coin < 0: \n break\n next_coin += coin\n return next_coin\n | 1 | 0 | ['Greedy', 'Sorting', 'Python3'] | 0 |
maximum-number-of-consecutive-values-you-can-make | Easy Java Solution || Beats 100% | easy-java-solution-beats-100-by-ravikuma-n2ti | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | ravikumar50 | NORMAL | 2024-04-26T16:58:11.846773+00:00 | 2024-04-26T16:58:11.846809+00:00 | 341 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int getMaximumConsecutive(int[] A) {\n Arrays.sort(A);\n int res = 1;\n for (int a: A) {\n if (a > res) break;\n res += a;\n }\n return res;\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
maximum-number-of-consecutive-values-you-can-make | solution | solution-by-shree_govind_jee-z5ql | Intuition\nThis is the realization: if we reached number i, that means that we can make all values 0...i. So, if we add a coin with value j, we can also make va | Shree_Govind_Jee | NORMAL | 2024-01-22T02:44:02.946301+00:00 | 2024-01-22T02:44:02.946325+00:00 | 238 | false | # Intuition\nThis is the realization: if we reached number i, that means that we can make all values 0...i. So, if we add a coin with value j, we can also make values i+1...i+j.\n\nThe only case when we can have a gap is the coin value is greater than i + 1 . So we sort the coins to make sure we process smaller coins first.\n\nFor example, let\'s assume that we can make all values 0...7. Adding a nickel allows us to make values 8..12 (7+1...7+5).\n\n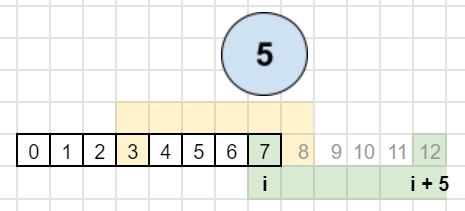\n\n# Complexity\n- Time complexity:$$O(n+sorting)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int getMaximumConsecutive(int[] coins) {\n Arrays.sort(coins);\n\n int maxV = 1;\n for (int coin : coins) {\n if (coin <= maxV)\n maxV += coin;\n }\n return maxV;\n }\n}\n``` | 1 | 0 | ['Array', 'Greedy', 'Java'] | 0 |
maximum-number-of-consecutive-values-you-can-make | [Python3] memory usage: less than 100% | python3-memory-usage-less-than-100-by-le-02ri | ```\nclass Solution:\n def getMaximumConsecutive(self, coins: List[int]) -> int:\n cur = ans = sum(coins);\n coins.sort();\n while cur > | leehjworking | NORMAL | 2022-08-23T01:54:25.734673+00:00 | 2022-08-23T01:57:36.617977+00:00 | 221 | false | ```\nclass Solution:\n def getMaximumConsecutive(self, coins: List[int]) -> int:\n cur = ans = sum(coins);\n coins.sort();\n while cur > 1 and coins: \n half = cur//2;\n cur += -coins.pop(); \n #we cannot make half with the remaining coins\n if cur < half:\n ans = cur;\n \n return ans + 1;\n""" \nmax = 4 [1,3]\nmax = 1 < 2 -> max = 1\n\nmax = 7 [1,1,1,4]\nmax = 3 >=3 [1,1,1]\nmax = 2 >=1 [1,1]\nmax = 1 >=0 [1]\n\n\nmax = 19 [1,1,3,4,10]\nmax = 9 >=9 [1,1,3,4]\nmax = 5 >=4 [1,1,3]\nmax = 2 >=2 [1,1]\nmax = 1 >=1 [1]\n\n\nmax = 18 [1,3,4,10]\nmax = 8 < 9 [1,3,4]\nmax = 4 >=4 [1,3]\nmax = 1 < 2 [1]\n\n""" | 1 | 0 | [] | 0 |
maximum-number-of-consecutive-values-you-can-make | Easy and clean C++ code | easy-and-clean-c-code-by-19je0894-canm | ```\nclass Solution {\npublic:\n int getMaximumConsecutive(vector& coins) {\n sort(coins.begin() , coins.end());\n \n // initially we ha | 19JE0894 | NORMAL | 2022-08-07T11:38:29.062886+00:00 | 2022-08-07T11:38:29.062918+00:00 | 213 | false | ```\nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) {\n sort(coins.begin() , coins.end());\n \n // initially we have zero as max and min values\n int mn = 0 , mx = 0;\n \n for(auto x : coins){\n int temp_mn = mn + x;\n int temp_mx = mx + x;\n \n // here if temp_mn > mx + 1 then there wont be the continuity so check for this here\n if(temp_mn <= mx + 1){\n mx = max(mx , temp_mx);\n }else\n break;\n }\n \n \n return mx - mn + 1;\n }\n}; | 1 | 0 | [] | 0 |
maximum-number-of-consecutive-values-you-can-make | C++ Simple Explanation | Clean Code | O(NlogN) time, O(1) space | c-simple-explanation-clean-code-onlogn-t-p1rq | just try to dry run this after reading this explanation!\non this example\n\n[1,2,4,9,10,11]\n\nAfter sorting the array what we basically try to do is traverse | kartikeya_0607 | NORMAL | 2022-06-21T21:39:57.154706+00:00 | 2022-06-22T08:45:17.077468+00:00 | 235 | false | just try to dry run this after reading this explanation!\non this example\n```\n[1,2,4,9,10,11]\n```\nAfter sorting the array what we basically try to do is traverse the array and in each iteration we check whether its possible to move ahead. If yes we do otherwise we simply break.\n\n1. the ``sum`` variable basically depicts the max value that it is possible to reach so far. So intially it\'s intialised with zero.\n2. After that we start traversing the array\n3. At every step we check that wether we have created all the numbers ``>= current_number-1``, because all the numbers from the ( ``current_number`` to ``current_number+sum`` ) can be created with the help of this ``current_number``. Thus after ensuring that all those numbers can be created (just checking ``sum >= curr - 1`` ), we can simply update our ``sum`` variable and move to the next iteration. If it\'s not valid to move forward we simply break.\n4. We simply return ``sum+1`` (the +1 just to account ``0`` that has to be counted extra)\n\nTime Complexity: `O(NlogN)`, just sorting and then a single traversal.\nSpace Complexity: `O(1)`, as we are using no extra arrays, just some variables.\n\n**Please Upvote if you liked the solution and it helped you!!\u2764\uFE0F\uD83D\uDE03\uD83D\uDC4D**\n\n**C++**\n```\nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) {\n int n = coins.size();\n int sum = 0;\n sort(coins.begin(), coins.end());\n for(int i = 0; i < n; i++) {\n int curr = coins[i];\n if(sum >= (curr-1)) {\n sum += curr;\n }else {\n break;\n }\n }\n return sum+1;\n }\n};\n```\n**Javascript**\n```\nfunction compare(a, b) {\n if(a > b) return 1;\n if(a < b) return -1;\n return 0;\n}\nvar getMaximumConsecutive = function(coins) {\n const n = coins.length\n let sum = 0\n coins.sort(compare)\n coins.forEach((coin) => {\n if(sum >= coin-1) {\n sum += coin\n }else {\n return sum + 1;\n }\n })\n return sum + 1;\n};\n```\n | 1 | 0 | ['Greedy', 'Sorting'] | 0 |
maximum-number-of-consecutive-values-you-can-make | [cpp] simple 6 liner code | cpp-simple-6-liner-code-by-tushargupta98-jr3f | \nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) {\n sort(coins.begin(), coins.end());\n int min = 0;\n for(i | tushargupta9800 | NORMAL | 2022-05-07T17:13:03.347542+00:00 | 2022-05-07T17:13:03.347588+00:00 | 66 | false | ```\nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) {\n sort(coins.begin(), coins.end());\n int min = 0;\n for(int i: coins){\n if(i <= min+1) min = i+min;\n else break;\n }\n \n return min+1;\n }\n};\n``` | 1 | 0 | [] | 0 |
maximum-number-of-consecutive-values-you-can-make | Short C++, O(NLogN) Time and O(1) Space | short-c-onlogn-time-and-o1-space-by-adar-6xw4 | \tclass Solution {\n\tpublic:\n int getMaximumConsecutive(vector& coins) {\n int n=coins.size();\n sort(coins.begin(),coins.end());\n in | adarsh_190701 | NORMAL | 2022-02-03T07:04:25.128433+00:00 | 2022-02-03T07:04:25.128470+00:00 | 228 | false | \tclass Solution {\n\tpublic:\n int getMaximumConsecutive(vector<int>& coins) {\n int n=coins.size();\n sort(coins.begin(),coins.end());\n int ans=1;\n for(int i=0;i<n;i++){\n if(coins[i]<=ans) ans+=coins[i];\n }\n return ans;\n }\n\t}; | 1 | 0 | ['C', 'C++'] | 0 |
maximum-number-of-consecutive-values-you-can-make | very easy maths logic C++ | very-easy-maths-logic-c-by-adarshxd-ofpw | \nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) {\n sort(coins.begin(), coins.end());\n if (!coins.size()) return 1 | AdarshxD | NORMAL | 2021-12-05T19:35:48.532116+00:00 | 2022-01-26T11:32:00.023286+00:00 | 185 | false | ```\nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) {\n sort(coins.begin(), coins.end());\n if (!coins.size()) return 1;\n if(coins.size()==1 and coins[0]==1) return 2;\n \n //then we have 2 or more than 2\n int max=0;\n if(coins[0]==1){\n max=1;\n int i=1;\n while(i<coins.size()){\n //main logic\n if (coins[i]<=max+1) max+=coins[i];\n else break;\n i++;\n }\n return max+1;\n }\n return 1;\n }\n};\n``` | 1 | 0 | ['Sorting'] | 1 |
maximum-number-of-consecutive-values-you-can-make | C++ | Sort | Similar to Patching Array | c-sort-similar-to-patching-array-by-shru-zyd9 | ```\nclass Solution {\npublic:\n int getMaximumConsecutive(vector& coins) {\n int mis = 1, i =0;\n sort(coins.begin(),coins.end());\n wh | shruti985 | NORMAL | 2021-09-12T08:59:02.764472+00:00 | 2021-09-12T08:59:02.764501+00:00 | 121 | false | ```\nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) {\n int mis = 1, i =0;\n sort(coins.begin(),coins.end());\n while(i<coins.size() && mis>=coins[i])\n mis += coins[i++];\n return mis;\n }\n}; | 1 | 0 | [] | 0 |
maximum-number-of-consecutive-values-you-can-make | Java Solution | java-solution-by-jxie418-nlkd | \nclass Solution {\n public int getMaximumConsecutive(int[] coins) {\n Arrays.sort(coins);\n int x = 0;\n\t\tfor (int v: coins) {\n\t\t\tif (v | jxie418 | NORMAL | 2021-08-07T17:59:40.056340+00:00 | 2021-08-07T17:59:40.056383+00:00 | 105 | false | ```\nclass Solution {\n public int getMaximumConsecutive(int[] coins) {\n Arrays.sort(coins);\n int x = 0;\n\t\tfor (int v: coins) {\n\t\t\tif (v <=x+) \n\t\t\t x +=v;\n\t\t\telse\n\t\t\t break;\n\t\t}\n\t\treturn x+1;\n }\n}\n``` | 1 | 2 | [] | 1 |
maximum-number-of-consecutive-values-you-can-make | Proof that sorting + greedy works | proof-that-sorting-greedy-works-by-decom-dgez | The coding part is straightforward from the hints. However, it is the proof that sorting + greedy works the interviewer would be asking.\n1. If coins[:i] has su | decomplexifier | NORMAL | 2021-07-26T05:02:25.191042+00:00 | 2021-07-26T05:05:32.948552+00:00 | 148 | false | The coding part is straightforward from the hints. However, it is the proof that sorting + greedy works the interviewer would be asking.\n1. If `coins[:i]` has subset sums `0, 1, ..., x`, then for `coins[:i+1]` we can have these new sums by adding `v=coins[i]`: `v, v+1, ..., v+x`. If `v <= x+1`, then there is no gap between these two sequences, and thus we can have subset sums up to `v+x`. Note that this part does not require `coins` be to sorted.\n2. If `coins[:i]` has subset sums `0, 1, ..., x`, and `coins[i] > x+1`, then the max subset sum for `coins[:i+1]` remains `x`. Proof by contradiction: suppose otherwise `coins[:i+1]` can have a subset of sum `x+1` (or greater), then this newly larger sum must be contributed by `coins[i]`, namely there exists a subset `S in range(i)` such that `sum([coins[j] for j in S]) + coins[i] = x + 1`. Since the values are all positive, we must the sum of subset `S` must be nonnegative, and thus `coins[i] <= x + 1`, a contradiction. Note that this part also does not require `coins` to be sorted.\n3. Note that (1) & (2) only prove that `v+x` is *achievable* for `coins[:i+1]`; we yet to prove that it can not be larger than that. Again proof by contradiction: suppose `v=coins[i] <= x + 1`, and there exists a subset `S in range(i+1)` such that `sum([coins[j] for j in S]) = v+x+1`. Note that `i` is not necessarily in `S`.\n 3(a). If `i` is in `S`, then the sum of subset `S-{i}` is `x+1`, which contradicts that `coins[:i]` can only have consecutive subset sums up to `x`.\n\t3(b). If `i` is not in `S`, remove an arbitrary element `k` in `S` (doable because `S` is clearly not empty), denoted as `S2`. This time we need `coins[:i+1]` to be **sorted**: since `coins[i]>=coins[j]` for any j in `S`, we must have `sum([coins[j] for j in S2]) = (v-coins[k]) + x + 1 >= x + 1`, which contradicts that `coins[:i]` can only has consecutive sums up to `x`. \n\n```\nclass Solution:\n def getMaximumConsecutive(self, coins: List[int]) -> int:\n coins.sort()\n x = 0\n for v in coins:\n if v <= x + 1:\n x += v\n return x + 1\n``` | 1 | 0 | [] | 0 |
maximum-number-of-consecutive-values-you-can-make | o(nlog(n)) | cpp | easy to solve | onlogn-cpp-easy-to-solve-by-mayankpatel8-6myw | class Solution {\npublic:\n int getMaximumConsecutive(vector& coins) {\n \n sort(coins.begin(),coins.end());\n long long i,j,k=0,l,m;\n | mayankpatel8011 | NORMAL | 2021-05-27T13:17:37.967108+00:00 | 2021-07-08T02:36:43.638815+00:00 | 177 | false | class Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) {\n \n sort(coins.begin(),coins.end());\n long long i,j,k=0,l,m;\n i=j=0;\n while(j<coins.size())\n {\n if(k>=coins[j])\n {\n k+=coins[j];\n j++;\n }\n else if(k+1==coins[j])\n {\n k+=coins[j];\n j++;\n \n }\n else\n return k+1;\n }\n return k+1;\n \n }\n}; | 1 | 0 | [] | 1 |
maximum-number-of-consecutive-values-you-can-make | Easy Java O(nlogn) Solution | easy-java-onlogn-solution-by-jalwal-rn5a | \nclass Solution {\n public int getMaximumConsecutive(int[] nums) {\n int len = nums.length;\n Arrays.sort(nums);\n int ans = 1;\n | jalwal | NORMAL | 2021-05-16T14:48:38.150443+00:00 | 2021-05-16T14:48:38.150474+00:00 | 288 | false | ```\nclass Solution {\n public int getMaximumConsecutive(int[] nums) {\n int len = nums.length;\n Arrays.sort(nums);\n int ans = 1;\n for(int i = 0 ; i < len ; i++) {\n if(nums[i] > ans) break;\n ans += nums[i];\n }\n return ans;\n }\n}\n``` | 1 | 0 | ['Greedy', 'Sorting', 'Java'] | 0 |
maximum-number-of-consecutive-values-you-can-make | Simple c++ solution with detailed explaintion | simple-c-solution-with-detailed-explaint-tnbl | \n/*\n\tIf we are able to form any number in the range [s,e].\n\tIf we take a number A and include it with every number of the range [s,e]. We will be able to f | akhil_trivedi | NORMAL | 2021-04-19T05:33:30.550927+00:00 | 2021-04-19T05:33:30.550969+00:00 | 164 | false | ```\n/*\n\tIf we are able to form any number in the range [s,e].\n\tIf we take a number A and include it with every number of the range [s,e]. We will be able to form ant number in the range[s+A,e+A].\n\tNow lets consider the two ranges:\n\t\t[s,e] - formed without taking A\n\t\t[s+A,e+A] - formed by taking A with every number in the range [s,e]\n\tSo, the range of numbers we can form with or without taking A is [s,e] U [s+A,e+A]\n\tIf s+A <= e+1, then [s,e] U [s+A,e+A] will form a continous sequence [s,e+A]\n\tNow suppose s+A > e+1, this means we cannot form e+1\n\t\tNow lets take another number B >= A.\n\t\tThe smallest number we can form considering the range [s,e] with B is s+B\n\t\tBut B >= a => s+B >= s+A > e+1 => s+B > e+1. Thie means we cannot form e+1 by considering B or rather any number greater than A.\n\t\tThis implies e+1 will be the smallest number which cannot be formed considering the elements of the array.\n\tIf we keep forming continous sequence still at the end we will get e+1 as the required answer.\t\t\n*/\nint getMaximumConsecutive(vector<int>& coins){\n\t// To implement the above algorithm we need to sort the array so that each number is greater than or equal to the previous number\n\tsort(coins.begin(),coins.end());\n\t// 0 can always be formed by taking no elements\n\tif(coins[0] != 1)\n\t\treturn 1;\n\t// Setting the initial range as [0,1] and then implementing the above algorithm\n\tint s = 0, e = 1, n = coins.size();\n\tfor(int i=1;i<n;i++){\n\t\tint l = s + coins[i], r = e + coins[i];\n\t\tif(l <= e + 1){\n\t\t\te = r;\n\t\t}\n\t\telse{\n\t\t\treturn e + 1;\n\t\t}\n\t}\n\treturn e + 1; \n}\n``` | 1 | 0 | [] | 0 |
maximum-number-of-consecutive-values-you-can-make | Incorrect test? | incorrect-test-by-icholy-tw1p | I\'m getting the following test failure:\n\n\nInput: [1,3,4]\nOutput: 3\nExpected: 2\n\n\nI might be misunderstanding the problem, but it seems like the longest | icholy | NORMAL | 2021-04-04T17:16:24.530111+00:00 | 2021-04-04T17:16:24.530160+00:00 | 118 | false | I\'m getting the following test failure:\n\n```\nInput: [1,3,4]\nOutput: 3\nExpected: 2\n```\n\nI might be misunderstanding the problem, but it seems like the longest consecutive values are 3,4,5:\n\n```\n- 3: take [3]\n- 4: take [4]\n- 5: take [4, 1]\n``` | 1 | 1 | [] | 2 |
maximum-number-of-consecutive-values-you-can-make | Short Easy C++ Code | short-easy-c-code-by-aryan29-6qrw | \nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) {\n sort(coins.begin(),coins.end());\n int n=coins.size();\n | aryan29 | NORMAL | 2021-03-25T06:27:27.185128+00:00 | 2021-03-25T06:27:27.185170+00:00 | 146 | false | ```\nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) {\n sort(coins.begin(),coins.end());\n int n=coins.size();\n int till=1; //1 + point where we can reach now\n for(int i=0;i<n;i++)\n {\n if(coins[i]>till) // we could only make sum to (till-1) yet and so integer we require should have max value=till it can have less value than that too\n break;\n till+=coins[i]; \n\t\t\t// as we have already reached all point to till-1 we can reach all points to till-1+coins[i] now\n }\n return till;\n \n }\n};\n``` | 1 | 0 | [] | 0 |
maximum-number-of-consecutive-values-you-can-make | C++ (there was a leetcode problem really similar to this?) | c-there-was-a-leetcode-problem-really-si-bu84 | Cannot remember the # of that problem. But the underlying algorithm is almost the same.\n\n\nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int | wzypangpang | NORMAL | 2021-03-22T01:56:07.817539+00:00 | 2021-03-22T01:56:07.817569+00:00 | 162 | false | Cannot remember the # of that problem. But the underlying algorithm is almost the same.\n\n```\nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) {\n sort(coins.begin(), coins.end());\n int sum = 0;\n for(int i=0; i<coins.size(); i++) {\n if(coins[i] > sum + 1) return sum + 1;\n sum += coins[i];\n }\n \n return sum + 1;\n }\n};\n``` | 1 | 0 | [] | 1 |
maximum-number-of-consecutive-values-you-can-make | Java solution 100% faster without using Arrays.sort() | java-solution-100-faster-without-using-a-h84y | \nclass Solution {\n public int getMaximumConsecutive(int[] coins) {\n if(coins.length==0 && coins==null)\n return 0;\n TreeMap<Integer,In | kanojiyakaran | NORMAL | 2021-03-21T17:58:10.323455+00:00 | 2021-03-21T17:58:10.323492+00:00 | 191 | false | ```\nclass Solution {\n public int getMaximumConsecutive(int[] coins) {\n if(coins.length==0 && coins==null)\n return 0;\n TreeMap<Integer,Integer> map=new TreeMap<Integer,Integer>();\n for(int i:coins)\n map.put(i,map.getOrDefault(i,0)+1);\n int range=0;\n for(int i:map.keySet()){\n if(range==0 && i==1)\n range=i*map.get(i);\n else if(range!=0 && range+1>=i)\n range+=i*map.get(i);\n else \n break;\n }\n return range+1;\n }\n}\n``` | 1 | 0 | ['Tree', 'Java'] | 0 |
maximum-number-of-consecutive-values-you-can-make | javascript greedy 176ms | javascript-greedy-176ms-by-henrychen222-1sh9 | \nconst getMaximumConsecutive = (c) => {\n c.sort((x, y) => x - y);\n let res = 0;\n for (const e of c) {\n if (e <= res + 1) res += e;\n }\n | henrychen222 | NORMAL | 2021-03-20T17:40:10.159335+00:00 | 2021-03-20T17:40:10.159365+00:00 | 154 | false | ```\nconst getMaximumConsecutive = (c) => {\n c.sort((x, y) => x - y);\n let res = 0;\n for (const e of c) {\n if (e <= res + 1) res += e;\n }\n return res + 1;\n};\n``` | 1 | 0 | ['Greedy', 'JavaScript'] | 0 |
maximum-number-of-consecutive-values-you-can-make | sort and use prefix sum c++ | sort-and-use-prefix-sum-c-by-sguox002-j5ay | stop when there is a gap.\n\n int getMaximumConsecutive(vector<int>& coins) {\n sort(begin(coins),end(coins));\n int n=coins.size();\n i | sguox002 | NORMAL | 2021-03-20T16:13:36.572846+00:00 | 2021-03-21T02:15:27.402712+00:00 | 137 | false | stop when there is a gap.\n```\n int getMaximumConsecutive(vector<int>& coins) {\n sort(begin(coins),end(coins));\n int n=coins.size();\n int mx=0,pre=0;\n for(int i: coins){\n if(i>pre+1) return pre+1;\n pre+=i;\n }\n return pre+1;\n }\n``` | 1 | 0 | [] | 0 |
maximum-number-of-consecutive-values-you-can-make | Javascript Solution With Explanation | javascript-solution-with-explanation-by-90k1y | \n// we iterate from the smallest number while maintaining an integer sum. sum means that we can produce all number from 0 to sum.\n// when we can make numbers | thebigbadwolf | NORMAL | 2021-03-20T16:02:47.550815+00:00 | 2021-03-20T16:02:47.550857+00:00 | 148 | false | ```\n// we iterate from the smallest number while maintaining an integer sum. sum means that we can produce all number from 0 to sum.\n// when we can make numbers from 0 to sum, and we encounter a new number, lets say arr[2].\n// it is obvious that we can create all numbers from sum to sum + arr[2].\n// if there is a gap if(arr[i] > sum+1) it means no combinations could create that number and we stop.\nvar getMaximumConsecutive = function(coins) {\n coins.sort((a,b) => a-b);\n let sum = 1;\n for(let i = 0; i < coins.length; i++) {\n if(coins[i] <= sum) {\n sum += coins[i];\n } else {\n break;\n }\n }\n return sum;\n};\n``` | 1 | 0 | ['JavaScript'] | 1 |
maximum-number-of-consecutive-values-you-can-make | [Java / Python / C++] Clean and Correct solution | java-python-c-clean-and-correct-solution-v25h | Java:\n\nclass Solution {\n int getMaximumConsecutive(int[] coins) {\n Arrays.sort(coins);\n int val=0;\n for(int i : coins){\n | lokeshsk1 | NORMAL | 2021-03-20T16:01:30.149843+00:00 | 2021-03-20T16:05:03.279840+00:00 | 222 | false | **Java:**\n```\nclass Solution {\n int getMaximumConsecutive(int[] coins) {\n Arrays.sort(coins);\n int val=0;\n for(int i : coins){\n if(i <= val+1)\n val += i;\n else\n break;\n }\n return val+1;\n }\n}\n```\n\n**Python:**\n```\nclass Solution:\n def getMaximumConsecutive(self, coins: List[int]) -> int:\n val = 0\n for i in sorted(coins):\n if i <= val+1:\n val+=i\n else:\n break\n return val+1\n```\n\n**C++:**\n```\nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) {\n sort(coins.begin(),coins.end());\n int val=0;\n for(int i : coins){\n if(i <= val+1)\n val += i;\n else\n break;\n }\n return val+1;\n }\n};\n``` | 1 | 0 | [] | 0 |
maximum-number-of-consecutive-values-you-can-make | Java Simple and Short | java-simple-and-short-by-mayank12559-esmg | \n public int getMaximumConsecutive(int[] coins) {\n Arrays.sort(coins);\n int max = 1;\n for(Integer i: coins){\n if(i > max | mayank12559 | NORMAL | 2021-03-20T16:00:35.799574+00:00 | 2021-03-20T16:00:35.799605+00:00 | 167 | false | ```\n public int getMaximumConsecutive(int[] coins) {\n Arrays.sort(coins);\n int max = 1;\n for(Integer i: coins){\n if(i > max)\n return max;\n max += i;\n }\n return max;\n }\n``` | 1 | 1 | [] | 0 |
maximum-number-of-consecutive-values-you-can-make | easy java solution | easy-java-solution-by-phani40-ao5z | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | phani40 | NORMAL | 2025-03-23T06:08:16.249716+00:00 | 2025-03-23T06:08:16.249716+00:00 | 2 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
import java.util.Arrays;
class Solution {
public int getMaximumConsecutive(int[] coins) {
Arrays.sort(coins); // Sort coins to work sequentially
int count = 0; // Start with 0 consecutive values
for (int i = 0; i < coins.length; i++) {
if (coins[i] > count + 1) {
break; // Stop if a gap is found
}
count += coins[i]; // Add the current coin to the consecutive range
}
return count + 1; // Add 1 to include "0" in the count
}
}
``` | 0 | 0 | ['Java'] | 0 |
maximum-number-of-consecutive-values-you-can-make | 1798. Maximum Number of Consecutive Values You Can Make | 1798-maximum-number-of-consecutive-value-k9zs | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | G8xd0QPqTy | NORMAL | 2025-01-15T03:42:26.018543+00:00 | 2025-01-15T03:42:26.018543+00:00 | 10 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def getMaximumConsecutive(self, coins: list[int]) -> int:
coins.sort()
ans = 0
for coin in coins:
if coin > ans + 1:
break
ans += coin
return ans + 1
``` | 0 | 0 | ['Python3'] | 0 |
maximum-number-of-consecutive-values-you-can-make | [Python3] O(n) | Simple Solution | python3-on-simple-solution-by-huangweiji-qxu5 | IntuitionGiven that I can express values ranging from 0 to x with n coins, when a new coin of value y is introduced, I can express values from 0 to x + y using | huangweijing | NORMAL | 2025-01-09T02:30:01.244789+00:00 | 2025-01-09T02:30:01.244789+00:00 | 5 | false | # Intuition
Given that I can express values ranging from 0 to x with n coins, when a new coin of value y is introduced, I can express values from 0 to x + y using these n + 1 coins.
# Complexity
- Time complexity:
$$O(n)$$
- Space complexity:
$$O(1)$$
# Code
```python3 []
from typing import List
class Solution:
def getMaximumConsecutive(self, coins: List[int]) -> int:
coins.sort()
max_expressable = 0
for coin in coins:
if coin > max_expressable + 1:
break
max_expressable += coin
return max_expressable + 1
``` | 0 | 0 | ['Python3'] | 0 |
maximum-number-of-consecutive-values-you-can-make | Greedy Prefix | greedy-prefix-by-theabbie-xbry | \nclass Solution:\n def getMaximumConsecutive(self, coins: List[int]) -> int:\n coins.sort()\n if coins[0] > 1:\n return 1\n | theabbie | NORMAL | 2024-10-15T15:58:16.260137+00:00 | 2024-10-15T15:58:16.260195+00:00 | 2 | false | ```\nclass Solution:\n def getMaximumConsecutive(self, coins: List[int]) -> int:\n coins.sort()\n if coins[0] > 1:\n return 1\n p = 0\n for i in range(len(coins)):\n p += coins[i]\n if i == len(coins) - 1 or p + 1 < coins[i + 1]:\n return p + 1\n``` | 0 | 0 | ['Python'] | 0 |
maximum-number-of-consecutive-values-you-can-make | Python Medium | python-medium-by-lucasschnee-9jd1 | python3 []\nclass Solution:\n def getMaximumConsecutive(self, coins: List[int]) -> int:\n coins.sort()\n \n\n best = 1\n\n\n for | lucasschnee | NORMAL | 2024-08-28T01:18:16.978500+00:00 | 2024-08-28T01:18:16.978520+00:00 | 1 | false | ```python3 []\nclass Solution:\n def getMaximumConsecutive(self, coins: List[int]) -> int:\n coins.sort()\n \n\n best = 1\n\n\n for x in coins:\n if x <= best:\n best += x\n else:\n return best\n\n return best\n``` | 0 | 0 | ['Python3'] | 0 |
maximum-number-of-consecutive-values-you-can-make | simple solution - Beats 100% Runtime | simple-solution-beats-100-runtime-by-las-b3e4 | Intuition\nThe problem requires finding the maximum number of consecutive integers starting from 1 that can be formed using the given set of coins. The first th | lashaka | NORMAL | 2024-08-15T04:55:48.776045+00:00 | 2024-08-15T04:55:48.776071+00:00 | 1 | false | # Intuition\nThe problem requires finding the maximum number of consecutive integers starting from 1 that can be formed using the given set of coins. The first thought is to sort the coins and then iteratively check whether each coin can extend the range of consecutive numbers that can be formed. If a coin is greater than the current possible range + 1, then it\'s impossible to form the next number, and the solution should stop.\n\n# Approach\n1. Sort the Coins: Start by sorting the coins in ascending order to make it easier to consider the smallest possible combinations first.\n2. Initialize a Counter: Start with a counter at 1, representing the smallest possible sum you can form (with no coins used).\n3. Iterate through the Coins: For each coin, check if it can be used to extend the current range of possible sums. If the coin\'s value is greater than the current counter, you can\'t form the next consecutive number, so break out of the loop.\n4. Update the Counter: If the coin can be used, add its value to the counter and continue.\n5. Return the Counter: The counter will now hold the maximum number of consecutive integers that can be formed starting from 1.\n\n# Complexity\n- Time complexity:\nSorting the array takes \uD835\uDC42(\uD835\uDC5Blog\uD835\uDC5B)\nIterating through the sorted coins takes \uD835\uDC42(\uD835\uDC5B)\nTherefore, the overall time complexity is \uD835\uDC42(\uD835\uDC5Blog\uD835\uDC5B)\n- Space complexity:\nThe space complexity is \uD835\uDC42(1)\nO(1), assuming the sorting is done in-place and only a few extra variables are used.\n# Code\n```\npublic class Solution {\n public int GetMaximumConsecutive(int[] coins) {\n Array.Sort(coins);\n int counter = 1;\n for(int i = 0;i<coins.Length;i++) {\n if(coins[i] > counter) break;\n counter+=coins[i];\n }\n return counter;\n }\n}\n``` | 0 | 0 | ['C#'] | 0 |
maximum-number-of-consecutive-values-you-can-make | Easy CPP Solution | easy-cpp-solution-by-clary_shadowhunters-zvrn | \n# Code\n\nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) \n {\n sort(coins.begin(),coins.end());\n int cur=0;\n | Clary_ShadowHunters | NORMAL | 2024-08-14T18:50:25.627155+00:00 | 2024-08-14T18:50:25.627172+00:00 | 4 | false | \n# Code\n```\nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) \n {\n sort(coins.begin(),coins.end());\n int cur=0;\n for (auto it: coins)\n {\n if (it<=cur) cur+=it;\n else if (it==cur+1) cur+=it;\n else return cur+1;\n }\n return cur+1;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
maximum-number-of-consecutive-values-you-can-make | O(nlogn) Soln | onlogn-soln-by-ozzyozbourne-sba0 | Complexity\n- Time complexity:O(nlogn)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity:O(1)\n Add your space complexity here, e.g. O(n) \n\n# | ozzyozbourne | NORMAL | 2024-07-23T12:58:55.028387+00:00 | 2024-07-23T12:58:55.028418+00:00 | 20 | false | # Complexity\n- Time complexity:$$O(nlogn)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` java []\nfinal class Solution {\n public int getMaximumConsecutive(final int[] coins) {\n Arrays.sort(coins);\n int s = 0;\n for(final var c: coins){\n if (s < c - 1) break;\n s += c;\n }return s + 1;\n }\n}\n```\n``` python []\nclass Solution:\n def getMaximumConsecutive(self, coins: List[int]) -> int:\n coins.sort()\n s = 0;\n for c in coins:\n if s < c - 1:\n break\n s += c\n return s + 1\n```\n``` rust []\nimpl Solution {\n pub fn get_maximum_consecutive(mut coins: Vec<i32>) -> i32 {\n coins.sort_unstable();\n let mut s = 0;\n for c in coins{\n if s < c - 1 {\n break;\n }\n s += c;\n }\n s + 1\n }\n}\n```\n``` Erlang []\n-spec get_maximum_consecutive(Coins :: [integer()]) -> integer().\nget_maximum_consecutive(Coins) ->\n SortedCoins = lists:sort(Coins), \n helper(SortedCoins, 0).\n\n-spec helper(Coins :: [integer()], Acc :: integer()) -> integer().\nhelper([], Acc) -> Acc + 1;\nhelper([H | T], Acc) when Acc < H - 1 -> Acc + 1;\nhelper([H | T], Acc) -> helper(T, Acc + H).\n```\n``` Elixir []\ndefmodule Solution do\n @spec get_maximum_consecutive(coins :: [integer]) :: integer\n def get_maximum_consecutive(coins) do\n coins = Enum.sort(coins)\n helper(coins, 0) \n end\n\n @spec helper(coins :: [integer], acc :: integer) :: integer\n defp helper([], acc), do: acc + 1\n defp helper([h | t], acc) when acc < h - 1, do: acc + 1\n defp helper([h | t], acc), do: helper(t, acc + h)\nend\n``` | 0 | 0 | ['Prefix Sum', 'Python', 'Java', 'Rust', 'Elixir', 'Erlang'] | 0 |
maximum-number-of-consecutive-values-you-can-make | beats 100 in performance | beats-100-in-performance-by-ayoublaar-z4iu | Intuition\n Describe your first thoughts on how to solve this problem. \nSuppose we have a list starting from 0 to n :\n[ 0, 1, 2, ...., n ]\nIf you add a numbe | AyoubLaar | NORMAL | 2024-07-19T12:47:01.686269+00:00 | 2024-07-19T12:47:01.686301+00:00 | 1 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSuppose we have a list starting from 0 to n :\n[ 0, 1, 2, ...., n ]\nIf you add a number m to all elements in the list, you\'ll have a new list like this :\n[ m, m+1, m+2, ...., n+m]\nJoin the two lists and you\'ll have :\n[ 0, 1, 2, ...., n, m, m+1, m+2, ...., m+n]\n\nFor the list to be valid as prescripred in the description we need : 1 <= m <= n+1\nAt the lowest range we will have without duplicates: \n[ 0, 1, 2, ...., n, n+1]\nAt the highest range we will have without duplicates:\n[ 0, 1, 2, ...., n, n+1, n+2, ...., n+m]\n# Approach\n<!-- Describe your approach to solving the problem. -->\nyou keep iterating over the array, adding the values which are less or equal to the next val, and then making them negative so you don\'t add them again in the next iteration, if in the real case you don\'t want to modify the coins array, you would have to either create a copy or revert the negative values. \n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n) but not really since you keep iterating over the array until there is no more change in the next val, performs better than if you sort the array. \n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n\n# Code\n```\nint getMaximumConsecutive(int* coins, int coinsSize) {\n int next = 1, current =0;\n while(next != current){\n current = next;\n for(int i = 0 ; i < coinsSize ; i++){\n if( coins[i] > 0 && coins[i] <= next ){\n next += coins[i];\n coins[i] *= -1;\n }\n }\n }\n return next;\n}\n``` | 0 | 0 | ['C'] | 0 |
maximum-number-of-consecutive-values-you-can-make | TIME O(nlogn) || SPACE O(1) || C++ || SIMPLE | time-onlogn-space-o1-c-simple-by-priyans-wzjy | Intuition\nThe problem requires us to find the maximum number of consecutive integers (starting from 1) that can be formed using given coins. Intuitively, if we | priyanshu_2012 | NORMAL | 2024-06-22T17:02:06.425081+00:00 | 2024-06-22T17:02:06.425108+00:00 | 2 | false | # Intuition\nThe problem requires us to find the maximum number of consecutive integers (starting from 1) that can be formed using given coins. Intuitively, if we sort the coins and iterate through them, we can keep a running sum of the coin values. As long as the next coin can be added to this sum to form a consecutive sequence, we continue; otherwise, we break out of the loop. The key insight is that if the next coin is larger than sum + 1, we cannot form the next consecutive number.\n\n\n\n# Approach\nSort the coins in ascending order.\nInitialize a variable sum to keep track of the running total of the coin values.\nIterate through the sorted coins:\nIf the current coin can be used to extend the sequence of consecutive integers (i.e., sum + 1 >= coin), add the coin\'s value to sum.\nIf the current coin cannot be used to extend the sequence, break out of the loop.\nReturn sum + 1 as the maximum number of consecutive integers that can be formed.\n# Complexity\n- Time complexity:\n O(nlogn)\n- Space complexity:\n\uD835\uDC42(1)\n\n\n# Code\n```\nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) {\n \n int sum = 0;\n sort(coins.begin(),coins.end());\n for(int i=0;i<coins.size();i++){\n if(sum + 1 >= coins[i]){\n sum += coins[i];\n }else{\n break;\n }\n }\n return sum+1;\n }\n};\n``` | 0 | 0 | ['Array', 'Greedy', 'Sorting', 'C++'] | 0 |
maximum-number-of-consecutive-values-you-can-make | beat 100% | beat-100-by-ankushgurjar839-v2wg | \n# Complexity\n- Time complexity:\nO(n)+O(nlogn)\n\n- Space complexity:\nO(1)\n\n# Code\n\nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int> | ankushgurjar839 | NORMAL | 2024-06-20T12:56:04.153990+00:00 | 2024-06-20T12:56:04.154029+00:00 | 1 | false | \n# Complexity\n- Time complexity:\nO(n)+O(nlogn)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) {\n\n sort(coins.begin(),coins.end());\n int i=0;\n int n=coins.size();\n int range=0;\n\n while(i<n){\n if(coins[i]<=range+1){\n range+=coins[i];\n i++;\n }\n else break;\n }\n return range+1; \n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
maximum-number-of-consecutive-values-you-can-make | !!!! | Easy && Best | C++ Solution | using sorting | | easy-best-c-solution-using-sorting-by-su-f7cc | Intuition\n- sort the numbers\n- try to generate consecutive number greedily\n\n# Approach\nGreedy Approach\n\n# Complexity\n- Time complexity:\nO(nlogn)\n\n- S | sumitcoder01 | NORMAL | 2024-06-18T07:35:40.728949+00:00 | 2024-06-18T07:35:40.728974+00:00 | 7 | false | # Intuition\n- sort the numbers\n- try to generate consecutive number greedily\n\n# Approach\nGreedy Approach\n\n# Complexity\n- Time complexity:\n$$O(nlogn)$$\n\n- Space complexity:\n$$O(1)$$\n\n# Code\n```\nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) {\n int ans = 1;\n sort(coins.begin(),coins.end());\n for(int coin:coins){\n if(coin > ans) break;\n ans += coin;\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
maximum-number-of-consecutive-values-you-can-make | Greedy :: Sorting :: Beats 91.67% | greedy-sorting-beats-9167-by-akhil_pathi-l3s0 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | akhil_pathivada_ | NORMAL | 2024-06-17T08:15:10.246198+00:00 | 2024-06-17T08:15:10.246227+00:00 | 8 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int getMaximumConsecutive(int[] coins) {\n Arrays.sort(coins);\n int result = 1;\n for (int coin : coins) {\n if (result < coin) {\n break;\n }\n result += coin;\n }\n return result;\n }\n}\n``` | 0 | 0 | ['Greedy', 'Sorting', 'Java'] | 0 |
maximum-number-of-consecutive-values-you-can-make | Nlog(N) || Easy to understand | nlogn-easy-to-understand-by-arpit2804-6b5i | \n\n# Code\n\nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) {\n sort(coins.begin(),coins.end());\n int l = 0,r=0;\n | arpit2804 | NORMAL | 2024-06-17T06:26:14.324557+00:00 | 2024-06-17T06:26:14.324592+00:00 | 2 | false | \n\n# Code\n```\nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) {\n sort(coins.begin(),coins.end());\n int l = 0,r=0;\n int maxi = 0;\n for(int i=0;i<coins.size();i++){\n int newl = l+coins[i];\n int newr = r+coins[i];\n\n if(newl<=r+1){\n r=newr;\n }\n else{\n maxi = max(maxi,r-l+1);\n l = newl;\n r = newr;\n }\n }\n maxi = max(maxi,r-l+1);\n return maxi;\n }\n};\n``` | 0 | 0 | ['Greedy', 'Sorting', 'C++'] | 0 |
maximum-number-of-consecutive-values-you-can-make | Basic greedy solution with some intuition | basic-greedy-solution-with-some-intuitio-9zvc | Intuition\n Describe your first thoughts on how to solve this problem. \nwhat is the amount you can reach with no coins? i.e 0 and with 1 coin of value 1? i.e 1 | Pawaneet56 | NORMAL | 2024-06-16T21:15:15.874275+00:00 | 2024-06-16T21:15:15.874313+00:00 | 8 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nwhat is the amount you can reach with no coins? i.e 0 and with 1 coin of value 1? i.e 1 , but what if i have another coin of value 3 then you will not be able to reach 2 , but if you had a coin of value 2 you can reach 2 , 3->(1+2) so the point is now if you have 3 , then you can reach all the values from 3..6 , because you can add 3 to all the previous reachable values. So if you sort the coins and then traverse each coin, if you get a value which is greater than the current reach + 1 then you cannot get the consecutive values and that\'s where you have to break.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe code can be written in a short format as well , but i have tried to keep it basic , we will have a variable reach which tells the amount we can reach till now , and we will sort the array in ascending order, now if the current value of coin < reach + 1 , then we can increase the reach by the value of coin as we can reach all the values in between as well but in the else case we cannot have any more consecutive values, so we need to break the loop and we have got our output.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(nlogn)$$\nfor sorting the array\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\nsince we are just using one variable reach.\n# Code\n```\nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) {\n int reach=0;\n int sz=coins.size();\n int i=0;\n sort(coins.begin(),coins.end());\n while(i<sz){\n if(coins[i]<=reach+1){\n reach+=coins[i++];\n }\n else{\n break;\n }\n }\n return reach+1;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
maximum-number-of-consecutive-values-you-can-make | scala unfold oneliner | scala-unfold-oneliner-by-vititov-h89z | same as "330. Patching Array" ( https://leetcode.com/problems/patching-array )\n\nobject Solution {\n def getMaximumConsecutive(coins: Array[Int]): Int =\n | vititov | NORMAL | 2024-06-16T12:46:57.299066+00:00 | 2024-06-16T12:46:57.299093+00:00 | 3 | false | same as "330. Patching Array" ( https://leetcode.com/problems/patching-array )\n```\nobject Solution {\n def getMaximumConsecutive(coins: Array[Int]): Int =\n (1 +: LazyList.unfold((1,coins.toList.sorted)){case (num, l) =>\n //Option.unless(l.headOption.forall(num < _)){(num+l.head,(num+l.head, l.tail))}\n Option.when(l.headOption.exists(num >= _)){(num+l.head,(num+l.head, l.tail))}\n }).last\n}\n``` | 0 | 0 | ['Greedy', 'Recursion', 'Line Sweep', 'Sorting', 'Scala'] | 0 |
maximum-number-of-consecutive-values-you-can-make | Easy C++ Greedy Solution With Explanation | easy-c-greedy-solution-with-explanation-vn8rj | Approach\nTo solve the problem, we can use a greedy algorithm. The key insight is to sort the coins and then iteratively check if the current coin can extend th | whatspumpkin | NORMAL | 2024-06-16T10:07:22.560733+00:00 | 2024-06-16T10:07:22.560763+00:00 | 19 | false | # Approach\nTo solve the problem, we can use a greedy algorithm. The key insight is to sort the coins and then iteratively check if the current coin can extend the range of consecutive values we can form.\n\n1. **Sort the Coins**:\n - First, we sort the array of coins. This allows us to consider the smallest coins first, which helps in forming the smallest possible values consecutively.\n\n2. **Iterate and Extend**:\n - We initialize a variable `currNum` to 1, which represents the smallest value that we cannot form yet.\n - We iterate through the sorted coins. For each coin, if the coin\'s value is less than or equal to `currNum`, it means we can use this coin to extend the range of consecutive values we can form. We then add the coin\'s value to `currNum`.\n - If the coin\'s value is greater than `currNum`, it means there is a gap, and we cannot form `currNum` using the current set of coins. Hence, we return `currNum` as the result.\n\n3. **Return the Result**:\n - If we can iterate through all the coins without finding a gap, we return `currNum` as the maximum number of consecutive values we can form.\n\n# Complexity\n- Time complexity: $$O(n \\log n)$$ due to the sorting step.\n- Space complexity: $$O(1)$$ as we are using a constant amount of extra space.\n\n# Code\n```cpp\nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) {\n sort(coins.begin(), coins.end());\n int currNum = 1;\n\n for(int i = 0; i < coins.size(); i++){\n if(coins[i] <= currNum){\n currNum += coins[i];\n }\n else{\n return currNum;\n }\n }\n return currNum;\n }\n};\n```\n\n# Example Walkthrough\nLet\'s walk through the example to see how the code works:\n- Input: coins = [1, 1, 1, 4]\n- Output: 8\n\n**Step-by-Step Execution:**\n1. Sort the coins: [1, 1, 1, 4]\n2. Initialize `currNum` to 1.\n3. Iterate through the sorted coins:\n - For coins[0] = 1: Since 1 <= 1, update `currNum` to 2.\n - For coins[1] = 1: Since 1 <= 2, update `currNum` to 3.\n - For coins[2] = 1: Since 1 <= 3, update `currNum` to 4.\n - For coins[3] = 4: Since 4 <= 4, update `currNum` to 8.\n4. All coins are processed, and the maximum number of consecutive values we can form is 8.\n\nThus, the total number of consecutive integer values that can be made starting from 0 is 8. | 0 | 0 | ['Greedy', 'C++'] | 0 |
maximum-number-of-consecutive-values-you-can-make | Simple C Solution | simple-c-solution-by-p_more-lhz0 | Code\n\nint cmp(const void * a , const void *b)\n{\n return *(int*)a - *(int*)b;\n}\nint getMaximumConsecutive(int* coins, int coinsSize) {\n int prev = 0 | P_More | NORMAL | 2024-06-16T09:28:25.516046+00:00 | 2024-06-16T09:28:25.516096+00:00 | 2 | false | # Code\n```\nint cmp(const void * a , const void *b)\n{\n return *(int*)a - *(int*)b;\n}\nint getMaximumConsecutive(int* coins, int coinsSize) {\n int prev = 0 ;\n qsort(coins,coinsSize,sizeof(int),cmp);\n for(int i = 0 ; i < coinsSize ; i++)\n {\n if(prev + 1 < coins[i])\n return prev + 1;\n prev = prev + coins[i];\n }\n return prev + 1 ;\n}\n``` | 0 | 0 | ['C'] | 0 |
maximum-number-of-consecutive-values-you-can-make | 1798. Maximum Number of Consecutive Values You Can Make.cpp | 1798-maximum-number-of-consecutive-value-gcu0 | Code\n\nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) {\n sort(coins.begin(),coins.end());\n int ans=0;\n in | 202021ganesh | NORMAL | 2024-06-16T08:16:13.779298+00:00 | 2024-06-16T08:16:13.779339+00:00 | 1 | false | **Code**\n```\nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) {\n sort(coins.begin(),coins.end());\n int ans=0;\n int curr=1;\n int n=coins.size();\n for( int i=0;i<n;i++){\n if(curr==coins[i]){ \n curr*=2;\n ans=curr-1;\n }\n else if(curr>coins[i]){\n curr+=coins[i];\n ans=curr-1;\n }\n else {\n break;\n }\n }\n return ans+1; \n }\n};\n``` | 0 | 0 | ['C'] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.