question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
minimum-swaps-to-make-sequences-increasing | C++ Solution| Dp | O(n) | Well commented code and well explained | c-solution-dp-on-well-commented-code-and-l3ko | Here we are taking dp[n][2] where for any index i there are 2 case-\n-->dp[i][0] - when we don\'t want to swap the ith state\n-->dp[i][1]- when we want to swap | yash_kothari | NORMAL | 2021-03-19T12:16:02.226969+00:00 | 2021-03-19T12:16:02.227000+00:00 | 362 | false | Here we are taking dp[n][2] where for any index i there are 2 case-\n-->dp[i][0] - when we don\'t want to swap the ith state\n-->dp[i][1]- when we want to swap the ith state \nThen for any index i we have two situations as follows-\n--> A[i-1]<A[i] && B[i-1]<B[i] then\n\t\t------> if we don\'t swap the ith state dp[i][0]=dp[i-1][0]\n\t\t------>if we swap the ith state then we need to swap the i-1th state also dp[i][1]=dp[i-1][1]+1 //+1 is cost of swapping\n-->A[i-1]<B[i] && B[i-1]<A[i] then\n------->if we don\'t swap ith index we need to swap the i-1th state dp[i][0]=dp[i-1][1]\n------->if we swap the ith index then we don\'t need to swap the i-1th state dp[i][1]=dp[i-1][0]+1 //+1 is cost of swaping\n```\nclass Solution {\npublic:\n int minSwap(vector<int>& A, vector<int>& B) {\n int n=A.size();\n vector<vector<int>> dp(n,vector<int>(2,INT_MAX));\n //base case\n dp[0][0]=0;//if we don\'t swap no cost\n dp[0][1]=1;// if we swap then cost is 1\n for(int i=1;i<n;i++)\n {\n if(A[i-1]<A[i] && B[i-1]<B[i])//this is the when the array is increasing\n {\n dp[i][0]=min(dp[i][0],dp[i-1][0]);//if ith is unchanged it would have value of dp[i-1][0] since the i-1th state will also remain unchanged\n dp[i][1]=min(dp[i][1],dp[i-1][1]+1);//if ith state is change that means that i-1th state must also be changed because the are following the rule of increasing\n }\n if(A[i-1]<B[i] && B[i-1]<A[i])//this is the case when array is not increasing\n {\n dp[i][0]=min(dp[i][0],dp[i-1][1]);//if we donot swap the ith state it means the we are swapping 0..(i-1) th state and ith state remains unchanged\n dp[i][1]=min(dp[i][1],dp[i-1][0]+1);//if we are swaping the ith state then it means that we are not swaping the 0....(i-1)th state\n }\n }\n int ans=min(dp[n-1][0],dp[n-1][1]);\n return ans;\n }\n}; | 2 | 0 | [] | 3 |
minimum-swaps-to-make-sequences-increasing | Python DP solution O(n) time O(1) space | python-dp-solution-on-time-o1-space-by-h-ud74 | \nclass Solution:\n def minSwap(self, A: List[int], B: List[int]) -> int:\n \n # DP\n # \n # state: f(i, s) := min swaps to make | hooraywhoami | NORMAL | 2021-02-21T23:37:35.876466+00:00 | 2021-02-21T23:42:45.452110+00:00 | 220 | false | ```\nclass Solution:\n def minSwap(self, A: List[int], B: List[int]) -> int:\n \n # DP\n # \n # state: f(i, s) := min swaps to make A[:i+1] B[:i+1] strckly increasing, s indicating if last bit is swapped or not\n # funct: \n # f(i, 0) = min(f(i-1, 0), f(i-1, 1)) (check if strictly increasing with the last 2 steps)\n # f(i, 1) = min(f(i-1, 0), f(i-1, 1)) + 1 (check if strictly increasing with the last 2 steps)\n # start: f(0, 0) = 0, f(0, 1) = 1\n # final: min(f(n, 0), f(n, 1))\n #\n # Can trivially modify code and optimize to constant space since each dp cell only depends on last cell\n # Kept it this way to make it a bit more readable.\n \n dp = [[None] * 2 for _ in range(len(A))]\n dp[0][0], dp[0][1] = 0, 1\n for i in range(1, len(A)):\n dp[i][0] = min([dp[i-1][0] if A[i] > A[i-1] and B[i] > B[i-1] else float(\'inf\'),\n dp[i-1][1] if A[i] > B[i-1] and B[i] > A[i-1] else float(\'inf\')])\n dp[i][1] = min([dp[i-1][0] if B[i] > A[i-1] and A[i] > B[i-1] else float(\'inf\'),\n dp[i-1][1] if B[i] > B[i-1] and A[i] > A[i-1] else float(\'inf\')]) + 1\n return min(dp[-1][0], dp[-1][1])\n```\n\nUpdate: The O(1) space version\n```\n dp = [0, 1]\n for i in range(1, len(A)):\n dp = [min([dp[0] if A[i] > A[i-1] and B[i] > B[i-1] else float(\'inf\'),\n dp[1] if A[i] > B[i-1] and B[i] > A[i-1] else float(\'inf\')]),\n min([dp[0] if B[i] > A[i-1] and A[i] > B[i-1] else float(\'inf\'),\n dp[1] if B[i] > B[i-1] and A[i] > A[i-1] else float(\'inf\')]) + 1]\n return min(dp)\n``` | 2 | 0 | [] | 0 |
minimum-swaps-to-make-sequences-increasing | Clean Python Solution (With Other Similar Problems) | clean-python-solution-with-other-similar-xu3n | python\nclass Solution(object):\n def minSwap(self, A, B):\n keep = [float(\'inf\') for _ in xrange(len(A))]\n swap = [float(\'inf\') for _ in | christopherwu0529 | NORMAL | 2021-02-14T07:04:47.213467+00:00 | 2021-02-14T07:04:47.213515+00:00 | 179 | false | ```python\nclass Solution(object):\n def minSwap(self, A, B):\n keep = [float(\'inf\') for _ in xrange(len(A))]\n swap = [float(\'inf\') for _ in xrange(len(A))]\n \n keep[0] = 0\n swap[0] = 1\n \n for i in xrange(1, len(A)):\n \n if A[i]>A[i-1] and B[i]>B[i-1]:\n keep[i] = keep[i-1]\n swap[i] = swap[i-1]+1\n \n if A[i]>B[i-1] and B[i]>A[i-1]:\n keep[i] = min(keep[i], swap[i-1])\n swap[i] = min(swap[i], keep[i-1]+1)\n \n return min(keep[-1], swap[-1])\n"""\nSimilar Problems: 198, 213, 309, 740, 790, 801\nFor more other topics similar problems, check out my GitHub.\nIt took me a lots of time to make the solution. Becuase I want to help others like me.\nPlease give me a star if you like it. Means a lot to me.\nhttps://github.com/wuduhren/leetcode-python\n"""\n``` | 2 | 0 | [] | 1 |
minimum-swaps-to-make-sequences-increasing | Python DP solution with explanation | python-dp-solution-with-explanation-by-a-hzpo | \nclass Solution(object):\n def minSwap(self, A, B):\n if len(A) != len(B) or len(A) == 0:\n return -1 \n \n # | amadiaos | NORMAL | 2020-12-03T16:03:00.346849+00:00 | 2020-12-03T16:03:00.346896+00:00 | 186 | false | ```\nclass Solution(object):\n def minSwap(self, A, B):\n if len(A) != len(B) or len(A) == 0:\n return -1 \n \n #it shows the starting status at 0 position\n #pkeep stores the previous no swap minimum value, so at 0 position, the value is 0 if no swap\n #pswap stores the previous swap minimum value, so at 0 postion, the value is 1 if swap\n pkeep, pswap = 0, 1 \n \n \n for i in range(1, len(A)):\n keep = swap = float(\'inf\') #they are the current statuses\' values, by default we put maximum as initialization\n \n #both A and B are in ascend order for i and i-1 elements\n #we can choose to swap both or not at all\n #pay attention here, we can\'t just swap i or i-1, because the if condition doesn\'t guarantee A[i] > B[i]\n if A[i] > A[i-1] and B[i] > B[i-1]: \n keep = pkeep \n swap = pswap+1 \n \n #the if condition checks A and B are in ascending trend for crossing case\n #we can choose to swap i or swap i-1, but you can\'t swap twice\n if A[i] > B[i-1] and B[i] > A[i-1]:\n keep = min(keep, pswap)\n swap = min(pkeep+1, swap)\n #finally we make sure the status is propagated to the next \n pswap = swap\n pkeep = keep\n \n return min(keep, swap)\n``` | 2 | 0 | [] | 0 |
minimum-swaps-to-make-sequences-increasing | logically swap or not swap recursively O(n) a solution explanation you can understand | logically-swap-or-not-swap-recursively-o-fq6r | At each index, we compare the results after swapping and not swapping A and B.\n\nwe need to know from the previous step, if A and B are swapped, if so previous | coolgk | NORMAL | 2020-11-11T23:48:32.341397+00:00 | 2020-11-11T23:53:58.925772+00:00 | 207 | false | **At each index, we compare the results after swapping and not swapping A and B.**\n\n**we need to know from the previous step, if A and B are swapped, if so `previous a` becomes `previous b`, and `previous b` becomes `previous a`**\n\n**when `current a > previous b` AND `current b > previous a`, swap action is possible, caldulate the result of swap.**\n\n**when `current a <= previous a` OR `current b <= previous b`, must swap, return the result of swap above**\n\n**when swap is not a must, return min(swap, notSwap)**\n\n```javascript\nfunction rc (a, b, index = 0, previousOneSwapped = false) {\n if (index >= a.length) return 0;\n\n\t// if from the previous step, a and b are swapped, previous a becomes previous b and previous b becomes previous a\n const [previousA, previousB] = previousOneSwapped ? [b[index - 1], a[index - 1]] : [a[index - 1], b[index - 1]];\n \n const canSwap = index === 0 || a[index] > previousB && b[index] > previousA;\n const mustSwap = index > 0 && (a[index] <= previousA || b[index] <= previousB);\n\n let swapCurrent = Infinity;\n if (canSwap) swapCurrent = 1 + rc(a, b, index + 1, true, memo);\n if (mustSwap) return swapCurrent;\n\n const doNotSwapCurrent = rc(a, b, index + 1, false, memo);\n \n return Math.min(swapCurrent, doNotSwapCurrent);\n}\n```\n\n**ADD MEMOISATION**\n\n```javascript\nfunction rc (a, b, index = 0, swapped = false, memo = {}) {\n if (index >= a.length) return 0;\n\n const memoKey = `${index},${swapped}`\n if (memo[memoKey] !== undefined) return memo[memoKey]\n\n const [previousA, previousB] = swapped ? [b[index - 1], a[index - 1]] : [a[index - 1], b[index - 1]];\n\n let swapCurrent = Infinity;\n if (index === 0 || a[index] > previousB && b[index] > previousA) swapCurrent = 1 + rc(a, b, index + 1, true, memo);\n if (index > 0 && (a[index] <= previousA || b[index] <= previousB)) return memo[memoKey] = swapCurrent;\n \n return memo[memoKey] = Math.min(swapCurrent, rc(a, b, index + 1, false, memo));\n}\n```\n\n**Iterative DP**\n\n**The trcky bit of the iterative solution is the meaning of `a[i] > b[i - 1] && b[i] > a[i - 1]` and `a[i] > a[i - 1] && b[i] > b[i - 1]`** \n\nRead the code first, then come back here.\n\n**`a[i] > b[i - 1] && b[i] > a[i - 1]` means `current a > previous b && current b > previous a` when `noSwap[i - 1]` is used in calculation i.e. no swap from the previous step**\n\n**However, the same `a[i] > b[i - 1] && b[i] > a[i - 1]` means `current a > previous A && current b > previous B` when `swap[i - 1]` is used in calculation i.e. a and b have been swapped from the previous step**\n\n**Same logic for `a[i] > a[i - 1] && b[i] > b[i - 1]`**\n\n**it means `current a > previous a && current b > previous b` if `notSwap[i - 1]` used in calculation**\n**it means `current a > previous b && current b > previous a` if `swap[i - 1]` used in calculation**\n\n```javascript\nfunction dp (a, b) {\n const swap = Array(a.length).fill(0);\n const notSwap = Array(a.length).fill(0);\n swap[0] = 1;\n \n for (let i = 1; i < a.length; i++) {\n swap[i] = Infinity;\n notSwap[i] = Infinity;\n \n if (a[i] > b[i - 1] && b[i] > a[i - 1]) {\n swap[i] = Math.min(swap[i], 1 + notSwap[i - 1]);\n notSwap[i] = Math.min(notSwap[i], swap[i - 1]);\n }\n \n if (a[i] > a[i - 1] && b[i] > b[i - 1]) {\n swap[i] = Math.min(swap[i], 1 + swap[i - 1]);\n notSwap[i] = Math.min(notSwap[i], notSwap[i - 1]);\n }\n }\n \n return Math.min(swap[a.length - 1], notSwap[a.length - 1]);\n}\n``` | 2 | 0 | [] | 0 |
minimum-swaps-to-make-sequences-increasing | Java explanation using DP | java-explanation-using-dp-by-alex_molina-ytux | The idea is that you have an array int[][] dp = new int[A.length][2], where dp[i][0] means we have the min number of swaps up to index i assuming we didnt swap | alex_molina | NORMAL | 2020-10-01T22:14:21.846581+00:00 | 2020-10-01T22:17:01.749332+00:00 | 187 | false | The idea is that you have an array int[][] dp = new int[A.length][2], where dp[i][0] means we have the min number of swaps up to index i assuming we didnt swap the ith column entries, and dp[i][1] means we have the min number of swaps up to index i assuming we swapped the ith column entries.\n\nTo get the next column entries there are four cases:\n\n1.) we swapped column i and swapped column i+1\n2.) we didnt swap column i and didnt swap column i+1\n3.) we swapped column i but not swap i+1\n4.) we didnt swap column i but did swap column i+1\n\nThe first two cases can be encapsulated by the conditional:\n\n```\nif(A[i-1] < A[i] && B[i-1] < B[i]){\n\t\t// this means A[i-1] and A[i] can either be in array A, or array B.\n\t\t// likewise for B[i-1] and B[i]\n}\n```\n\nThus in the above conditional we check the cases for dp[i][0] and dp[i][1], corresponding to case 2 and 1 respectively. For cases 3 and 4, we use the conditional:\n\n```\nif(A[i-1] < B[i] && B[i-1] < A[i]){\n\t\t// this means A[i-1] and B[i] can either be in array A, or array B.\n\t\t// likewise for B[i-1] and A[i]\n}\n```\n\nWhere we check for case dp[i][0] and dp[i][1]. We take the mins for each one.\n\nThe final code is as follows:\n\n```\nclass Solution {\n public int minSwap(int[] A, int[] B) {\n \n int[][] dp = new int[A.length][2];\n dp[0][0] = 0; \n dp[0][1] = 1; \n\n for(int i=1; i<A.length; i++){\n \n dp[i][0] = Integer.MAX_VALUE;\n dp[i][1] = Integer.MAX_VALUE;\n \n if(A[i-1] < A[i] && B[i-1] < B[i]){\n dp[i][0] = Math.min(dp[i][0],dp[i-1][0]); //dont swap i and dont swap i-1\n dp[i][1] = Math.min(dp[i][1],dp[i-1][1]+1); //swap i and i-1\n }\n \n if(A[i-1] < B[i] && B[i-1] < A[i]){\n dp[i][1] = Math.min(dp[i][1],dp[i-1][0]+1); //dont swap i-1 and swap i\n dp[i][0] = Math.min(dp[i][0],dp[i-1][1]); // dont swap i and swap i-1\n }\n \n }\n\n return Math.min(dp[dp.length-1][0],dp[dp.length-1][1]); \n }\n}\n```\n\nA final exercise to the reader is converting the above DP approach to constant space (this is how you get the answer provided as an explanation). | 2 | 0 | [] | 0 |
minimum-swaps-to-make-sequences-increasing | [C] Non-DP easy-to-understand O(n) solution O(1) space | c-non-dp-easy-to-understand-on-solution-ytma2 | The DP solution is difficult to figure out. Below is my solution.\n\nFor the input arrays A, B of length n, denoted by problem (A, B, n), define an index e to b | hang_er | NORMAL | 2020-04-25T20:53:06.235136+00:00 | 2020-04-26T00:06:16.377891+00:00 | 232 | false | The DP solution is difficult to figure out. Below is my solution.\n\nFor the input arrays A, B of length n, denoted by problem (A, B, n), define an index e to be "good" if e=0 OR min{A[e], B[e]} > max{A[e-1], B[e-1]}. Whether or not to swap a "good" index e is not affected by the subarrays [0 ... e-1].\n\nFor the example A = [0, 4, 4, 5, 9] and B = [0, 1, 6, 8, 10], there are 3 "good" indices, 0, 1, and 4. The observation below is key to solving the problem:\n\nSuppose there are *k* good indices for the given problem (A, B, n), denoted by e0 = 0, e1, ... e_{k-1}, 1 <= k <= n, then the subarrays A[e_i ... e_{i+1}-1], B[e_i ... e_{i+1}-1] are completely determined once A[e_i] and B[e_i] are fixed. It can be proved by induction.\n\nSo, for each pair of subarrays e_i, ..., e_{i+1}-1, there are two possible ways to make them increasing, namely, swap and not swap A[e_i], B[e_i]. Denoted them by P1 and P2. In practice, we only need to solve one of them because of the following relation:\n\nNumber of swaps of P1 + Number of swaps of P2 = subarray length.\n\nWe solve the problem by adding the solution to each subproblem confined to e_i, ... e_{i+1}-1. Running time is Theta(n).\n```\n#define MIN(a, b) (a <= b? a : b)\n#define MAX(a, b) (a >= b? a : b)\n\nint minSwap(int* A, int ASize, int* B, int BSize){\n int ans = 0;\n int e = 0; // the max. good index before the current iteration i\n int curSwaps = 0; // record no. of swaps in the current subproblem\n for (int i = 1; i < ASize; i++) {\n if (MIN(A[i], B[i]) > MAX(A[i-1], B[i-1])) { // if i is a good index\n ans += MIN(curSwaps, i-e-curSwaps); // select min. swaps of the two configurations\n e = i;\n curSwaps = 0;\n continue;\n }\n if (A[i-1] >= A[i] || B[i-1] >= B[i]) { // if need to swap i\n int temp = A[i];\n A[i] = B[i];\n B[i] = temp;\n curSwaps++;\n }\n } // end for\n ans += MIN(curSwaps, ASize-e-curSwaps);\n return ans;\n}\n``` | 2 | 0 | ['C'] | 0 |
minimum-swaps-to-make-sequences-increasing | Java dp solution | java-dp-solution-by-cuny-66brother-dc9n | \nclass Solution {\n int MAX=2000;\n public int minSwap(int[] A, int[] B) {\n MAX=A.length+10;\n if(A.length==1)return 0;\n int dp[][ | CUNY-66brother | NORMAL | 2020-03-02T22:04:34.195345+00:00 | 2020-03-02T22:04:34.195395+00:00 | 210 | false | ```\nclass Solution {\n int MAX=2000;\n public int minSwap(int[] A, int[] B) {\n MAX=A.length+10;\n if(A.length==1)return 0;\n int dp[][]=new int[2][A.length]; //[Nonswap,swap]\n dp[0][0]=0;dp[1][0]=1;\n for(int i=1;i<A.length;i++){\n //Non swap\n int nonA=A[i];\n int nonB=B[i];\n int val=MAX;\n if(nonA>A[i-1]&&nonB>B[i-1]){//not swap pre\n val=Math.min(val,dp[0][i-1]);\n }\n if(nonA>B[i-1]&&nonB>A[i-1]){//swap pre\n val=Math.min(val,dp[1][i-1]); \n }\n dp[0][i]=val;\n //Swap\n int swapA=B[i];\n int swapB=A[i];\n val=MAX;\n if(swapA>A[i-1]&&swapB>B[i-1]){\n val=Math.min(val,1+dp[0][i-1]);\n }\n if(swapA>B[i-1]&&swapB>A[i-1]){\n val=Math.min(val,1+dp[1][i-1]);\n }\n dp[1][i]=val;\n }\n return Math.min(dp[0][dp[0].length-1],dp[1][dp[0].length-1]);\n }\n \n}\n``` | 2 | 1 | [] | 0 |
minimum-swaps-to-make-sequences-increasing | C++ beat 99.3% with clear explanations | c-beat-993-with-clear-explanations-by-sk-t6m8 | \nclass Solution {\npublic:\n int minSwap(vector<int> &A, vector<int> &B) {\n int vec_len = A.size();\n /*dp[i][0]: the cost if do not exchange | sktzwhj | NORMAL | 2018-10-18T00:32:22.910511+00:00 | 2018-10-18T00:32:22.910561+00:00 | 398 | false | ```\nclass Solution {\npublic:\n int minSwap(vector<int> &A, vector<int> &B) {\n int vec_len = A.size();\n /*dp[i][0]: the cost if do not exchange at position i. dp[i][1]: the cost of changing at position i*/\n vector <vector<int>> dp = vector <vector< int >> (vec_len, vector<int>(2, INT32_MAX));\n dp[0][0] = 0;\n dp[0][1] = 1;\n for (int i = 1; i < vec_len; ++i) {\n if (A[i] > A[i - 1] && B[i] > B[i - 1]) {\n /*condition already satisfied, no change. if last position has changed,\n the current one needs to change to keep ascending order*/\n dp[i][0] = dp[i - 1][0];\n dp[i][1] = dp[i - 1][1] + 1;\n }\n if (A[i] > B[i - 1] && B[i] > A[i - 1]) {\n /*if change is not harmful, you can either change the last position or not */\n dp[i][0] = min(dp[i][0], dp[i - 1][1]);\n dp[i][1] = min(dp[i][1], dp[i - 1][0] + 1);\n }\n }\n\n return min(dp[vec_len - 1][0], dp[vec_len - 1][1]);\n }\n};\n``` | 2 | 1 | [] | 0 |
minimum-swaps-to-make-sequences-increasing | Simple DP in Java with time:O(N) space:O(1) | simple-dp-in-java-with-timeon-spaceo1-by-qo42 | \nIf you use the recursive function, the recursion would be something like:\n\nO swapped X not swapped\n\n[0] O X\n[1] | luckman | NORMAL | 2018-04-30T01:04:30.983599+00:00 | 2018-04-30T01:04:30.983599+00:00 | 613 | false | ```\nIf you use the recursive function, the recursion would be something like:\n\nO swapped X not swapped\n\n[0] O X\n[1] O X O X\n[2] O X O X O X O X \n :\n \n \nOptimal Subtructure would be:\n \n [i] O + 1\n min(/ \\)\n [i+1] O X\n\n [i] X + 0\n min(/ \\)\n [i+1] O X\n \nAll possible conditions are shown below: \n\n[i] --> (Not Swapped) A B \n[i+1] --> (Swapped) B A (Not Swapped) A B\n\n[i] --> (Swapped) B A \n[i+1] --> (Swapped) B A (Not Swapped) A B\n\n```\nThe following is the code.\n```\npublic int minSwap(int[] A, int[] B) {\n int l = A.length;\n int[] pre = new int[]{0, 1};\n for(int i = l - 2; i >= 0; i--) {\n int[] cur = new int[]{0, 1};\n /* dp[0] --> not swap current */\n int min = Integer.MAX_VALUE;\n if(A[i] < A[i + 1] && B[i] < B[i + 1]) min = Math.min(min, pre[0]);\n if(A[i] < B[i + 1] && B[i] < A[i + 1]) min = Math.min(min, pre[1]); \n cur[0] += min;\n\n /* dp[1] --> swap current */\n min = Integer.MAX_VALUE;\n if(B[i] < A[i + 1] && A[i] < B[i + 1]) min = Math.min(min, pre[0]);\n if(B[i] < B[i + 1] && A[i] < A[i + 1]) min = Math.min(min, pre[1]);\n cur[1] += min;\n\n /* update pre */\n pre = cur;\n }\n return Math.min(pre[0], pre[1]);\n}\n``` | 2 | 0 | [] | 0 |
minimum-swaps-to-make-sequences-increasing | very easy to understand python solution | very-easy-to-understand-python-solution-6ixd3 | \nclass Solution(object):\n def minSwap(self, A, B):\n """\n :type A: List[int]\n :type B: List[int]\n :rtype: int\n """\n | medi_ | NORMAL | 2018-03-19T15:19:14.697973+00:00 | 2018-03-19T15:19:14.697973+00:00 | 477 | false | ```\nclass Solution(object):\n def minSwap(self, A, B):\n """\n :type A: List[int]\n :type B: List[int]\n :rtype: int\n """\n \n keep=[float(\'inf\') for i in range(len(A))]\n swap=[float(\'inf\') for i in range(len(A))]\n \n # first element you can either keep it or swap it\n keep[0]=0\n swap[0]=1\n \n for i in range(1,len(A)):\n if A[i]>A[i-1] and B[i]>B[i-1]:\n keep[i]=min(keep[i-1],keep[i])\n if A[i]>B[i-1] and B[i]>A[i-1]:\n keep[i]=min(keep[i],swap[i-1])\n if A[i]>B[i-1] and B[i]>A[i-1]: \n swap[i] =min(keep[i-1]+1,swap[i])\n if A[i]>A[i-1] and B[i]>B[i-1]:\n swap[i] =min(swap[i-1]+1,swap[i])\n return min(swap[-1],keep[-1])\n``` | 2 | 1 | [] | 0 |
minimum-swaps-to-make-sequences-increasing | Best C++ Solution || Space optimize approach | best-c-solution-space-optimize-approach-jnmxk | Complexity
Time complexity:O(n)
Space complexity:O(1)
Code | kansalhimanshu123 | NORMAL | 2025-04-04T18:32:49.926456+00:00 | 2025-04-04T18:32:49.926456+00:00 | 21 | false |
# Complexity
- Time complexity:O(n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int Solve(vector<int>&nums1,vector<int>&nums2){
int n=nums1.size();
vector<int>next(2,0);
vector<int>curr(2,0);
for(int i=n-1; i>0; i--){
for(int j=0; j<2; j++){
int ans=INT_MAX;
int prev1=nums1[i-1];
int prev2=nums2[i-1];
if(j) swap(prev1,prev2);
if(nums1[i]>prev1 && nums2[i]>prev2){
ans=next[0];
}
if(nums1[i]>prev2 && nums2[i]>prev1){
ans=min(ans,(1+next[1]));
}
curr[j]=ans;
}
next=curr;
}
return min(curr[0],curr[1]);
}
int minSwap(vector<int>& nums1, vector<int>& nums2) {
nums1.insert(nums1.begin(),-1);
nums2.insert(nums2.begin(),-1);
return Solve(nums1,nums2);
}
};
``` | 1 | 0 | ['Array', 'Dynamic Programming', 'C++'] | 0 |
minimum-swaps-to-make-sequences-increasing | Easy Solution using dp + memo+ tabulation | easy-solution-using-dp-memo-tabulation-b-5xrx | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | HYDRO2070 | NORMAL | 2025-01-01T18:19:40.337893+00:00 | 2025-01-01T18:19:40.337893+00:00 | 22 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int minSwap(vector<int>& nums1, vector<int>& nums2) {
int n = nums1.size();
vector<vector<int>> dp(n, vector<int>(2, INT_MAX));
dp[0][0] = 0;
dp[0][1] = 1;
for (int i = 1; i < n; ++i) {
if (nums1[i] > nums1[i - 1] && nums2[i] > nums2[i - 1]) {
dp[i][0] = dp[i - 1][0];
dp[i][1] = dp[i - 1][1] + 1;
}
if (nums1[i] > nums2[i - 1] && nums2[i] > nums1[i - 1]) {
dp[i][0] = min(dp[i][0], dp[i - 1][1]);
dp[i][1] = min(dp[i][1], dp[i - 1][0] + 1);
}
}
return min(dp[n - 1][0], dp[n - 1][1]);
}
};
``` | 1 | 0 | ['Array', 'Dynamic Programming', 'C', 'C++'] | 1 |
minimum-swaps-to-make-sequences-increasing | Easiest optimized || C++ | easiest-optimized-c-by-radhakrishnaaaa-8wz8 | Complexity
Time complexity: O(n)
Space complexity: O(n)
Code | RadhaKrishnaaaa | NORMAL | 2025-01-01T02:33:05.957731+00:00 | 2025-01-01T02:33:05.957731+00:00 | 53 | false | # Complexity
- Time complexity: O(n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(n)
<!-- Add your space coacasmplexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
vector<vector<int>>dp;
int solve (int i, bool prev_swapped, vector<int>& nums1, vector<int>& nums2){
if(i == nums1.size()) return 0;
if(dp[i][prev_swapped] != -1) return dp[i][prev_swapped];
int prev1 = -1;
int prev2 = -1;
if(i > 0){
if(prev_swapped){
prev1 = nums2[i-1];
prev2 = nums1[i-1];
}
else{
prev1 = nums1[i-1];
prev2 = nums2[i-1];
}
}
int res = INT_MAX;
if(nums1[i] > prev1 && nums2[i] > prev2){ // may or may not swap
res = min(res, solve(i+1, false, nums1, nums2));
}
if(nums1[i] > prev2 && nums2[i] > prev1){ // this condition is must, when we have to swap;
res = min(res, 1+solve(i+1, true, nums1, nums2));
}
return dp[i][prev_swapped] = res;
}
int minSwap(vector<int>& nums1, vector<int>& nums2) {
int n = nums1.size();
dp.resize(n+1, vector<int>(2, -1));
return solve(0, false, nums1, nums2);
}
};
``` | 1 | 0 | ['Dynamic Programming', 'C++'] | 0 |
minimum-swaps-to-make-sequences-increasing | Python O(n) time, O(1) space | python-on-time-o1-space-by-babos-ranj | \npython3 []\nclass Solution:\n def minSwap(self, nums1: List[int], nums2: List[int]) -> int:\n dp = [0, 1]\n\n for i in range(1, len(nums1)):\ | babos | NORMAL | 2024-11-19T06:45:56.559040+00:00 | 2024-11-19T06:45:56.559067+00:00 | 77 | false | \n```python3 []\nclass Solution:\n def minSwap(self, nums1: List[int], nums2: List[int]) -> int:\n dp = [0, 1]\n\n for i in range(1, len(nums1)):\n noSwap, yesSwap = 0, 0\n\n # check valid configurations\n if (nums1[i-1] >= nums1[i]) or (nums2[i-1] >= nums2[i]): \n noSwap = dp[1] # prev must be swapped if not swapping cur\n yesSwap = dp[0] + 1 # prev cannot be swapped if swapping cur\n elif (nums1[i-1] >= nums2[i]) or (nums2[i-1] >= nums1[i]):\n noSwap = dp[0] # prev cannot be swapped if not swapping cur\n yesSwap = dp[1] + 1 # prev must be swapped if swapping cur\n else:\n noSwap = min(dp[0], dp[1])\n yesSwap = min(dp[0], dp[1]) + 1\n\n dp = [noSwap, yesSwap]\n return min(dp)\n``` | 1 | 0 | ['Python3'] | 0 |
minimum-swaps-to-make-sequences-increasing | All approach ...Recursion To.......DP............/\/\/\/\.................... | all-approach-recursion-todp-by-ghanshyam-p6vb | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Ghanshyam_bunkar016 | NORMAL | 2024-08-23T05:24:47.664015+00:00 | 2024-08-23T05:24:47.664047+00:00 | 2 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int solve(vector<int>& nums1, vector<int>& nums2,int index,bool swapped){\n if(index==nums1.size()){\n return 0;\n }\n\n int prev1=nums1[index-1];\n int prev2=nums2[index-1];\n int ans=INT_MAX;\n\n if(swapped){\n swap(prev1,prev2);\n }\n\n if(nums1[index]>prev1&&nums2[index]>prev2){\n ans=solve(nums1,nums2,index+1,0);\n }\n\n if(nums1[index]>prev2&&nums2[index]>prev1){\n ans=min(ans,1+solve(nums1,nums2,index+1,1));\n }\n\n return ans;\n }\n\n int solveMem(vector<int>& nums1, vector<int>& nums2,int index,bool swapped,vector<vector<int>>&dp){\n if(index==nums1.size()){\n return 0;\n }\n\n if(dp[index][swapped]!=-1){\n return dp[index][swapped];\n }\n int prev1=nums1[index-1];\n int prev2=nums2[index-1];\n int ans=INT_MAX;\n\n if(swapped){\n swap(prev1,prev2);\n }\n\n if(nums1[index]>prev1&&nums2[index]>prev2){\n ans=solveMem(nums1,nums2,index+1,0,dp);\n }\n\n if(nums1[index]>prev2&&nums2[index]>prev1){\n ans=min(ans,1+solveMem(nums1,nums2,index+1,1,dp));\n }\n\n return dp[index][swapped]=ans;\n }\n\n int solveTab(vector<int>& nums1, vector<int>& nums2){\n int n=nums1.size();\n vector<vector<int>>dp(n+1,vector<int>(2,0));\n\n for(int index=n-1;index>=1;index--){\n for(int swapped=1;swapped>=0;swapped--){\n int prev1=nums1[index-1];\n int prev2=nums2[index-1];\n int ans=INT_MAX;\n\n if(swapped){\n swap(prev1,prev2);\n }\n\n if(nums1[index]>prev1&&nums2[index]>prev2){\n ans=dp[index+1][0];\n }\n\n if(nums1[index]>prev2&&nums2[index]>prev1){\n ans=min(ans,1+dp[index+1][1]);\n }\n\n dp[index][swapped]=ans;\n }\n }\n return dp[1][0];\n }\n\n int solveSOP(vector<int>& nums1, vector<int>& nums2){\n int n=nums1.size();\n \n int swap=0;\n int noswap=0;\n int currswap=0;\n int currnoswap=0;\n\n for(int index=n-1;index>=1;index--){\n for(int swapped=1;swapped>=0;swapped--){\n int prev1=nums1[index-1];\n int prev2=nums2[index-1];\n int ans=INT_MAX;\n\n if(swapped){\n int temp=prev1;\n prev1=prev2;\n prev2=temp;\n // swap(prev1,prev2);\n }\n\n if(nums1[index]>prev1&&nums2[index]>prev2){\n ans=noswap;\n }\n\n if(nums1[index]>prev2&&nums2[index]>prev1){\n ans=min(ans,1+swap);\n }\n\n if(swapped)\n currswap=ans;\n\n else\n currnoswap=ans;\n }\n swap=currswap;\n noswap=currnoswap;\n }\n return min(swap,noswap);\n }\n\n int minSwap(vector<int>& nums1, vector<int>& nums2) {\n nums1.insert(nums1.begin(),-1);\n nums2.insert(nums2.begin(),-1);\n bool swapped=0;\n int n=nums1.size();\n\n // return solve(nums1,nums2,1,swapped);\n\n // vector<vector<int>>dp(n,vector<int>(2,-1));\n // return solveMem(nums1,nums2,1,swapped,dp);\n\n // return solveTab(nums1,nums2);\n\n return solveSOP(nums1,nums2);\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
minimum-swaps-to-make-sequences-increasing | space optimized || using dynamic programming || beats (runtime -> 94.41%) (memory-> 90.65%)🔥 | space-optimized-using-dynamic-programmin-pwg2 | Time complexity:\nO(N)\n\n- Space complexity:\nO(1)\n\n# Code\n\nclass Solution {\npublic:\n\nusing recursion\n\n\n int rec(vector<int>& nums1, vector<int>& | arnavmehta290 | NORMAL | 2023-09-17T10:21:06.344515+00:00 | 2023-09-17T10:21:06.344538+00:00 | 8 | false | - Time complexity:\nO(N)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution {\npublic:\n```\nusing recursion\n```\n\n int rec(vector<int>& nums1, vector<int>& nums2, int swaps, int i){\n if(i>=nums1.size()){\n return 0;\n }\n int prev1 = nums1[i-1];\n int prev2 = nums2[i-1];\n\n if(swaps){\n swap(prev1, prev2);\n }\n\n // no swap\n int ans=INT_MAX;\n\n if(nums1[i]> prev1 && nums2[i]>prev2){\n ans = rec(nums1, nums2, 0, i+1);\n }\n\n // swap\n\n if(nums1[i] > prev2 && nums2[i] > prev1){\n ans = min(ans, 1+rec(nums1, nums2, 1, i+1));\n }\n\n return ans;\n\n }\n```\nrecursion and memoization\n```\n int recMem(vector<int>& nums1, vector<int>& nums2, int i , int swaps, vector<vector<int>>& dp){\n if(i==nums1.size()){\n return 0;\n }\n if(dp[i][swaps] != -1) return dp[i][swaps];\n\n int prev1 = nums1[i-1];\n int prev2 = nums2[i-1];\n\n if(swaps) swap(prev1, prev2);\n\n int ans = INT_MAX;\n\n // no swap\n if(nums1[i]> prev1 && nums2[i]>prev2){\n ans = recMem(nums1, nums2, i+1, 0, dp);\n }\n\n // swap\n\n if(nums1[i] > prev2 && nums2[i] > prev1){\n ans = min(ans, 1+recMem(nums1, nums2, i+1, 1, dp));\n }\n\n return dp[i][swaps]=ans;\n\n }\n```\n using tabulation\n```\n int table(vector<int>& nums1, vector<int>& nums2){\n\n int n = nums1.size();\n\n vector<vector<int>> dp(n+1, vector<int>(2, 0));\n\n for(int i = n-1;i>=1;i--){\n for(int j = 1;j>=0;j--){\n\n int ans = INT_MAX;\n int prev1 = nums1[i-1];\n int prev2 = nums2[i-1];\n\n if(j) swap(prev1, prev2);\n\n // no swap\n if(nums1[i]> prev1 && nums2[i]>prev2){\n ans = dp[i+1][0];\n }\n\n // swap\n\n if(nums1[i] > prev2 && nums2[i] > prev1){\n ans = min(ans, 1+dp[i+1][1]);\n }\n\n dp[i][j]=ans;\n\n }\n }\n\n return dp[1][0];\n }\n```\nspace optimaization\n\n```\n int spaceOPT(vector<int>& nums1, vector<int>& nums2){\n\n int n = nums1.size();\n\n int swap =0;\n int noswap =0;\n int currswap=0;\n int currnoswap=0;\n\n for(int i = n-1;i>=1;i--){\n\n // for curr swap------------------\n int ans = INT_MAX;\n int prev1 = nums1[i-1];\n int prev2 = nums2[i-1];\n\n int temp = prev1;\n prev1 = prev2;\n prev2 = temp;\n\n // no swap\n if(nums1[i]> prev1 && nums2[i]>prev2){\n ans = min(ans, noswap);\n }\n\n // swap\n\n if(nums1[i] > prev2 && nums2[i] > prev1){\n ans = min(ans, 1+swap);\n }\n currswap=ans;\n\n // --------------------------------------\n // for curr no swap\n ans = INT_MAX;\n prev1 = nums1[i-1];\n prev2 = nums2[i-1];\n\n // no swap\n if(nums1[i]> prev1 && nums2[i]>prev2){\n ans = min(ans, noswap);\n }\n\n // swap\n\n if(nums1[i] > prev2 && nums2[i] > prev1){\n ans = min(ans, 1+swap);\n }\n\n currnoswap=ans;\n\n // --------------------------------\n\n swap = currswap;\n noswap = currnoswap;\n\n\n }\n\n return min(currswap, currnoswap);\n }\n\n```\nmain function\n```\n int minSwap(vector<int>& nums1, vector<int>& nums2) {\n\n nums1.insert(nums1.begin(), -1);\n nums2.insert(nums2.begin(), -1);\n int n = nums1.size();\n // return rec(nums1, nums2, 0, 1);\n\n // vector<vector<int>> dp(n, vector<int>(2, -1));\n // return recMem(nums1, nums2, 1, 0, dp);\n\n return spaceOPT(nums1, nums2);\n\n }\n};\n``` | 1 | 0 | ['Array', 'Dynamic Programming', 'Recursion', 'Memoization', 'Queue', 'C++'] | 0 |
minimum-swaps-to-make-sequences-increasing | Java with explanation. DFS + Memoization. SC: O(N), TC: O(N) | java-with-explanation-dfs-memoization-sc-eh6p | \n# Code\n\nclass Solution {\n Integer[][] memo;\n int SWAPPED = 0;\n int NOT_SWAPPED = 1;\n\n int NOT_VALID = (int) Math.pow(10, 6);\n public in | vera_uva | NORMAL | 2023-08-29T15:06:46.614822+00:00 | 2023-08-29T15:06:46.614854+00:00 | 216 | false | \n# Code\n```\nclass Solution {\n Integer[][] memo;\n int SWAPPED = 0;\n int NOT_SWAPPED = 1;\n\n int NOT_VALID = (int) Math.pow(10, 6);\n public int minSwap(int[] nums1, int[] nums2) {\n this.memo = new Integer[nums1.length][2];\n return dfs(nums1, nums2, 0, NOT_SWAPPED);\n }\n\n private int dfs(int[] nums1, int[] nums2, int index, int swapped) {\n if (index == nums1.length) return 0;\n\n if (memo[index][swapped] != null) return memo[index][swapped];\n\n // we have 2 option: 1) swap our arr[index] or not\n int option1 = NOT_VALID;\n // before proceed any option check: is it valid? \n // Is arr[i] > arr[i-1]?\n if (isValidOption(nums1, nums2, index)) {\n // we didn\'t swapped our arr[i], amount of operations the same\n option1 = dfs(nums1, nums2, index + 1, NOT_SWAPPED);\n }\n\n // swap, dfs and swap again\n swap(nums1, nums2, index);\n int option2 = NOT_VALID;\n if (isValidOption(nums1, nums2, index) && nums1[index] != nums2[index]) {\n // we swapped our arr[i], amount of operations increased by 1\n option2 = dfs(nums1, nums2, index + 1, SWAPPED) + 1;\n }\n swap(nums1, nums2, index);\n\n // take the minimum amount of operations\n int result = Math.min(option1, option2);\n \n // we have 2 ways to save data:\n // if our PREVIOUS index was swapped hold 0, opposite 1\n memo[index][swapped] = result;\n return result;\n }\n\n private boolean isValidOption(int[] nums1, int[] nums2, int index) {\n if (index == 0) return true;\n return nums1[index] > nums1[index - 1] && nums2[index] > nums2[index - 1];\n }\n\n\n private void swap(int[] arr1, int[] arr2, int i) {\n int temp = arr1[i];\n arr1[i] = arr2[i];\n arr2[i] = temp;\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
minimum-swaps-to-make-sequences-increasing | Rust | Bottom-up DP, One-Pass, no extra space | rust-bottom-up-dp-one-pass-no-extra-spac-yf6x | Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n\npub fn solve(\n vec_0: Vec<u32>,\n vec_1: Vec<u32>,\n) -> usize {\n let | soyflourbread | NORMAL | 2023-08-05T02:17:40.393864+00:00 | 2023-08-05T02:17:40.393890+00:00 | 8 | false | # Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(1)$$\n\n# Code\n```\npub fn solve(\n vec_0: Vec<u32>,\n vec_1: Vec<u32>,\n) -> usize {\n let mut dp = [usize::MIN, 1];\n\n for i in 1..vec_0.len() {\n let (e0, e1) = (vec_0[i], vec_1[i]);\n let (p0, p1) = (vec_0[i - 1], vec_1[i - 1]);\n\n let mut dp_next = [usize::MAX; 2];\n \n if p0 < e0 && p1 < e1 {\n dp_next[0] = dp_next[0].min(dp[0]);\n dp_next[1] = dp_next[1].min(dp[1] + 1);\n } // try not swapping\n \n if p1 < e0 && p0 < e1 {\n dp_next[0] = dp_next[0].min(dp[1]);\n dp_next[1] = dp_next[1].min(dp[0] + 1);\n } // try swapping\n\n dp = dp_next;\n }\n\n *dp.into_iter().min().unwrap()\n}\n\nimpl Solution {\n fn preproc(vec: Vec<i32>) -> Vec<u32> {\n vec.into_iter()\n .map(|e| e as u32)\n .collect::<Vec<_>>()\n }\n\n pub fn min_swap(vec_0: Vec<i32>, vec_1: Vec<i32>) -> i32 {\n let vec_0 = Self::preproc(vec_0);\n let vec_1 = Self::preproc(vec_1);\n\n solve(vec_0, vec_1) as i32\n }\n}\n``` | 1 | 0 | ['Dynamic Programming', 'Rust'] | 0 |
minimum-swaps-to-make-sequences-increasing | C++ || DP || MEMOIZATION DP | c-dp-memoization-dp-by-hey_himanshu-mh0f | REC + MEMO\n\nclass Solution {\npublic:\n int solve(vector<int>& nums1, vector<int>& nums2 , int index , int swapped , vector<vector<int>> &dp){\n\n | Hey_Himanshu | NORMAL | 2023-06-14T07:24:38.593830+00:00 | 2023-06-14T07:24:38.593851+00:00 | 455 | false | REC + MEMO\n```\nclass Solution {\npublic:\n int solve(vector<int>& nums1, vector<int>& nums2 , int index , int swapped , vector<vector<int>> &dp){\n\n // base case \n if(index == nums1.size()){\n return 0 ;\n }\n\n int ans = INT_MAX ;\n int prev1 = nums1[index-1] ;\n int prev2 = nums2[index-1 ];\\\n\n if(dp[index][swapped] != -1){\n return dp[index][swapped] ;\n }\n\n if(swapped){\n swap(prev1 , prev2) ;\n\n }\n\n // NO SWAPP\n if(nums1[index] > prev1 && nums2[index] >prev2){\n ans = solve(nums1 , nums2 , index+1 , 0 , dp);\n }\n\n // SWAPPED\n if(nums1[index] > prev2 && nums2[index] > prev1){\n ans = min(ans , 1+solve(nums1 , nums2 , index+1 , 1,dp)) ;\n }\n return dp[index][swapped] = ans ;\n }\n\n int minSwap(vector<int>& nums1, vector<int>& nums2) {\n\n // st1 : add -1 at the begninng of both the arrays \n nums1.insert(nums1.begin() , -1);\n nums2.insert(nums2.begin() , -1);\n int n = nums1.size() ;\n bool swapped = 0 ;\n\n vector<vector<int>> dp(n , vector<int> (2,-1)) ;\n return solve(nums1, nums2 , 1 , swapped , dp); \n }\n};\n``` | 1 | 0 | ['Dynamic Programming', 'C', 'C++'] | 0 |
minimum-swaps-to-make-sequences-increasing | Solution | solution-by-deleted_user-9ezd | C++ []\nconst int ZERO = []() {\n ios_base::sync_with_stdio(false);\n cin.tie(nullptr);\n return 0;\n}();\nclass Solution {\npublic:\n int minSwap(v | deleted_user | NORMAL | 2023-05-01T00:08:37.700242+00:00 | 2023-05-01T01:05:02.880695+00:00 | 1,974 | false | ```C++ []\nconst int ZERO = []() {\n ios_base::sync_with_stdio(false);\n cin.tie(nullptr);\n return 0;\n}();\nclass Solution {\npublic:\n int minSwap(vector<int>& a, vector<int>& b) {\n int n = static_cast<int>(a.size());\n vector<int> swaps(n, n);\n vector<int> noswaps(n, n);\n swaps[0] = 1;\n noswaps[0] = 0;\n for (int i = 1; i < n; ++i) {\n if (a[i] > a[i-1] && b[i] > b[i-1]) {\n swaps[i] = swaps[i-1] + 1;\n noswaps[i] = noswaps[i-1];\n }\n if (a[i] > b[i-1] && b[i] > a[i-1]) {\n swaps[i] = min(swaps[i], noswaps[i-1] + 1);\n noswaps[i] = min(noswaps[i], swaps[i-1]);\n }\n }\n return min(swaps.back(), noswaps.back());\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def minSwap(self, A: List[int], B: List[int]) -> int:\n ans = sm = lg = mx = 0\n for x, y in zip(A, B): \n if mx < min(x, y):\n ans += min(sm, lg)\n sm = lg = 0 \n mx = max(x, y)\n if x < y: sm += 1 # count "x < y"\n elif x > y: lg += 1 # count "x > y"\n return ans + min(sm, lg)\n```\n\n```Java []\nclass Solution {\n public int minSwap(int[] A, int[] B) {\n int swapRecord = 1, fixRecord = 0;\n for (int i = 1; i < A.length; i++) {\n if (A[i - 1] >= B[i] || B[i - 1] >= A[i]) {\n swapRecord++;\n } else if (A[i - 1] >= A[i] || B[i - 1] >= B[i]) {\n int temp = swapRecord;\n swapRecord = fixRecord + 1;\n fixRecord = temp;\n } else {\n int min = Math.min(swapRecord, fixRecord);\n swapRecord = min + 1;\n fixRecord = min;\n }\n }\n return Math.min(swapRecord, fixRecord);\n }\n}\n```\n | 1 | 0 | ['C++', 'Java', 'Python3'] | 0 |
minimum-swaps-to-make-sequences-increasing | C++ simple solution 96.04% faster 中文註解 | c-simple-solution-9604-faster-zhong-wen-abuk6 | \n\n// 801. Minimum Swaps To Make Sequences Increasing\nclass Solution {\npublic:\n int minSwap(std::vector<int>& nums1, std::vector<int>& nums2) {\n | paulchen2713 | NORMAL | 2022-10-10T05:05:47.834685+00:00 | 2022-10-10T05:05:47.834712+00:00 | 62 | false | \n```\n// 801. Minimum Swaps To Make Sequences Increasing\nclass Solution {\npublic:\n int minSwap(std::vector<int>& nums1, std::vector<int>& nums2) {\n // \u7576\u524D\u4F4D\u7F6E i \u662F\u5426\u8981\u4EA4\u63DB, \u53EA\u53D6\u6C7A\u65BC\u7576\u524D\u4F4D\u548C\u524D\u4E00\u4F4D\u662F\u5426\u662F\u56B4\u683C\u905E\u589E, \u800C\u524D\u4E00\u4F4D\u4E5F\u6709\u4EA4\u63DB\u6216\u4E0D\u4EA4\u63DB\n // \u5169\u7A2E\u72C0\u614B, \u4E5F\u5C31\u662F\u8AAA\u524D\u4E00\u4F4D\u7684\u4E0D\u540C\u72C0\u614B\u4E5F\u6703\u5F71\u97FF\u5230\u7576\u524D\u4F4D\u662F\u5426\u4EA4\u63DB \u8DDF 714. Best Time to Buy \n // and Sell Stock with Transaction Fee \u9019\u984C\u5F88\u50CF, \u9700\u8981\u7DAD\u8B77\u5169\u7A2E\u72C0\u614B\u4E0D\u505C\u5207\u63DB\n const int n = nums1.size();\n\n // do_swap[i] \u8868\u793A\u7BC4\u570D [0, i] \u7684\u56B4\u683C\u905E\u589E\u5B50\u9663\u5217 \u4E14\u7576\u524D\u4F4D\u7F6E i \u9700\u8981\u4EA4\u63DB \u7684\u6700\u5C0F\u4EA4\u63DB\u6B21\u6578\n // no_swap[i] \u8868\u793A\u7BC4\u570D [0, i] \u7684\u56B4\u683C\u905E\u589E\u5B50\u9663\u5217 \u4E14\u7576\u524D\u4F4D\u7F6E i \u4E0D\u9700\u8981\u4EA4\u63DB \u7684\u6700\u5C0F\u4EA4\u63DB\u6B21\u6578\n std::vector<int> do_swap(n, n), no_swap(n, n);\n\n // \u7531\u65BC\u9700\u8981\u8DDF\u524D\u4E00\u4F4D\u6BD4\u8F03, \u6703\u5F9E\u7B2C\u4E8C\u500B\u6578\u5B57\u958B\u59CB\u904D\u6B77, \u6240\u4EE5\u9700\u8981\u5148\u521D\u59CB\u5316 do_swap \u548C no_swap \u7684\n // \u7B2C\u4E00\u4F4D, do_swap[0] \u8A2D\u70BA 1 \u8868\u793A i \u4F4D\u7F6E\u9700\u8981\u4EA4\u63DB, no_swap[0] \u8A2D\u70BA 0 \u8868\u793A i \u4F4D\u7F6E\u4E0D\u9700\u8981\u4EA4\u63DB\n do_swap[0] = 1; no_swap[0] = 0;\n\n // \u72C0\u614B\u8F49\u79FB\u65B9\u7A0B\u5206\u6790, \u7531\u65BC\u9019\u984C\u6709\u9650\u5236\u8AAA "\u4E00\u5B9A\u80FD" \u901A\u904E\u4EA4\u63DB\u751F\u6210\u5169\u500B\u540C\u6642\u56B4\u683C\u905E\u589E\u7684\u9663\u5217, \u5247\u5169\u500B\u9663\u5217\n // \u7684\u7576\u524D\u4F4D\u7F6E\u548C\u524D\u4E00\u4F4D\u7F6E\u9593\u7684\u95DC\u4FC2\u5C31\u6703\u53EA\u6709\u5169\u7A2E, \u4E00\u7A2E\u662F\u4E0D\u7528\u4EA4\u63DB, \u7576\u524D\u4F4D\u7F6E\u7684\u6578\u5B57\u5DF2\u7D93\u5206\u5225\u5927\u65BC\u524D\u4E00\u500B\n // \u4F4D\u7F6E, \u53E6\u4E00\u7A2E\u662F\u9700\u8981\u4EA4\u63DB, \u800C\u4EA4\u63DB\u5F8C\u7576\u524D\u4F4D\u7F6E\u7684\u6578\u5B57\u624D\u80FD\u5206\u5225\u5927\u65BC\u524D\u4E00\u500B\u6578\u5B57\n\n for (int i = 1; i < n; i++) {\n // \u5982\u679C\u7576\u524D\u4F4D\u7F6E\u5DF2\u7D93\u5206\u5225\u5927\u65BC\u524D\u4E00\u4F4D\u7F6E\u7684\u6578, \u90A3\u7167\u7406\u8AAA\u662F\u4E0D\u9700\u8981\u518D\u9032\u884C\u4EA4\u63DB, \u4F46 do_swap[i] \u7684\u8A2D\u8A08\u9650\u5B9A\n // \u6211\u5011\u5FC5\u9808\u8981\u4EA4\u63DB\u7576\u524D\u4F4D\u7F6E i, \u65E2\u7136\u7576\u524D\u4F4D\u7F6E\u8981\u4EA4\u63DB, \u5247\u524D\u4E00\u500B\u4F4D\u7F6E i - 1 \u4E5F\u5F97\u4EA4\u63DB, \u540C\u6642\u4EA4\u63DB\u624D\u80FD\u7E7C\u7E8C\n // \u4FDD\u8B49\u540C\u6642\u905E\u589E, \u9019\u6A23 do_swap[i] \u5C31\u53EF\u4EE5\u8CE6\u503C\u70BA do_swap[i - 1] + 1, \u800C no_swap[i] \u5C31\u76F4\u63A5\u8CE6\u503C\n // \u70BA no_swap[i - 1] \u5373\u53EF, \u56E0\u70BA\u4E0D\u9700\u8981\u4EA4\u63DB\u4E86, \u9019\u662F\u7B2C\u4E00\u7A2E\u60C5\u6CC1\n if (nums1[i] > nums1[i - 1] && nums2[i] > nums2[i - 1]) {\n do_swap[i] = do_swap[i - 1] + 1;\n no_swap[i] = no_swap[i - 1];\n }\n // \u7B2C\u4E8C\u7A2E\u60C5\u6CC1\u662F\u9700\u8981\u4EA4\u63DB\u7576\u524D\u4F4D\u7F6E, \u624D\u80FD\u4FDD\u8B49\u905E\u589E, \u800C do_swap[i] \u6B63\u597D\u4E5F\u662F\u8981\u4EA4\u63DB\u7576\u524D\u4F4D\u7F6E, \u800C\u524D\u4E00\u4F4D\u7F6E\n // \u4E0D\u80FD\u4EA4\u63DB, \u9019\u6A23\u53EF\u7528 no_swap[i - 1] + 1 \u4F86\u66F4\u65B0 do_swap[i], \u800C no_swap[i] \u662F\u4E0D\u80FD\u4EA4\u63DB\u7576\u524D\u4F4D\u7F6E, \n // \u5247\u53EF\u4EE5\u901A\u904E\u4EA4\u63DB\u524D\u4E00\u500B\u4F4D\u7F6E\u4F86\u540C\u6A23\u5BE6\u73FE\u905E\u589E, \u5373\u53EF\u7528 do_swap[i - 1] \u66F4\u65B0 no_swap[i]\n if (nums1[i] > nums2[i - 1] && nums2[i] > nums1[i - 1]) {\n do_swap[i] = std::min(do_swap[i], no_swap[i - 1] + 1);\n no_swap[i] = std::min(no_swap[i], do_swap[i - 1]);\n }\n }\n // \u6700\u5F8C\u7576\u5FAA\u74B0\u7D50\u675F, \u5728 do_swap[n - 1] \u548C no_swap[n - 1] \u4E4B\u4E2D\u56DE\u50B3\u8F03\u5C0F\u503C\u5373\u53EF\n return std::min(do_swap[n - 1], no_swap[n - 1]);\n }\n};\n```\n```\n117 / 117 test cases passed. Status: Accepted\nRuntime: 204 ms, faster than 96.04% of C++ online submissions for Minimum Swaps To Make Sequences Increasing.\nMemory Usage: 94.2 MB, less than 76.86% of C++ online submissions for Minimum Swaps To Make Sequences Increasing.\n```\n | 1 | 0 | ['C'] | 0 |
minimum-swaps-to-make-sequences-increasing | Recursive -> TopDown -> BottomUP -> Space Optimized | recursive-topdown-bottomup-space-optimiz-z1i2 | \nclass Solution {\nprivate:\n int recursive(vector<int>& nums1, vector<int>& nums2, int idx, int swapped){\n cout << idx << " " << swapped << endl;\n | krishnajsw | NORMAL | 2022-09-28T14:19:05.988158+00:00 | 2022-09-28T14:19:05.988224+00:00 | 64 | false | ```\nclass Solution {\nprivate:\n int recursive(vector<int>& nums1, vector<int>& nums2, int idx, int swapped){\n cout << idx << " " << swapped << endl;\n if(idx == nums1.size()) return 0;\n int ans = INT_MAX;\n if(idx == 0 || nums1[idx] > nums1[idx - 1] && nums2[idx] > nums2[idx - 1]){\n ans = recursive(nums1, nums2, idx + 1, 0);\n }\n if(idx == 0 || nums1[idx] > nums2[idx - 1] && nums2[idx] > nums1[idx - 1]){\n swap(nums1[idx], nums2[idx]);\n ans = min(ans, 1 + recursive(nums1, nums2, idx + 1, 1));\n swap(nums1[idx], nums2[idx]);\n }\n return ans;\n }\n int topDown(vector<int>& nums1, vector<int>& nums2, int idx, int swapped, vector<vector<int>> &dp){\n if(idx == nums1.size()) return 0;\n if(dp[idx][swapped] != -1) return dp[idx][swapped];\n int ans = INT_MAX;\n if(idx == 0 || nums1[idx] > nums1[idx - 1] && nums2[idx] > nums2[idx - 1]){\n ans = topDown(nums1, nums2, idx + 1, 0, dp);\n }\n if(idx == 0 || nums1[idx] > nums2[idx - 1] && nums2[idx] > nums1[idx - 1]){\n swap(nums1[idx], nums2[idx]);\n ans = min(ans, 1 + topDown(nums1, nums2, idx + 1, 1, dp));\n swap(nums1[idx], nums2[idx]);\n }\n return dp[idx][swapped] = ans;\n }\n int bottomUp(vector<int>& nums1, vector<int>& nums2){\n vector<vector<int>> dp(nums1.size() + 1, vector<int>(2, 0));\n for(int idx = nums1.size() - 1 ; idx >= 0 ; idx--){\n for(int swapped = 1; swapped >= 0; swapped--){\n int ans = INT_MAX;\n if(swapped){\n swap(nums1[idx], nums2[idx]);\n }\n if(idx == 0 || nums1[idx] > nums1[idx - 1] && nums2[idx] > nums2[idx - 1]){\n ans = dp[idx + 1][0];\n }\n if(idx == 0 || nums1[idx] > nums2[idx - 1] && nums2[idx] > nums1[idx - 1]){\n ans = min(ans, 1 + dp[idx + 1][1]);\n }\n if(swapped){\n swap(nums1[idx], nums2[idx]);\n\n }\n dp[idx][swapped] = ans; \n }\n }\n return dp[0][0];\n }\n\n int spaceOptimized(vector<int>& nums1, vector<int>& nums2){\n vector<int> dp(2, 0);\n for(int idx = nums1.size() - 1 ; idx >= 0 ; idx--){\n vector<int> temp(2);\n for(int swapped = 1; swapped >= 0; swapped--){\n int ans = INT_MAX;\n if(swapped){\n swap(nums1[idx], nums2[idx]);\n }\n if(idx == 0 || nums1[idx] > nums1[idx - 1] && nums2[idx] > nums2[idx - 1]){\n ans = dp[0];\n }\n if(idx == 0 || nums1[idx] > nums2[idx - 1] && nums2[idx] > nums1[idx - 1]){\n ans = min(ans, 1 + dp[1]);\n }\n if(swapped){\n swap(nums1[idx], nums2[idx]);\n\n }\n temp[swapped] = ans; \n }\n dp = temp;\n }\n return dp[0];\n }\n\npublic:\n int minSwap(vector<int>& nums1, vector<int>& nums2) {\n\n int swapped = 0;\n // return recursive(nums1, nums2, 1, swapped);\n \n //topDown\n // vector<vector<int>> dp(nums1.size(), vector<int>(2, -1));\n // return topDown(nums1, nums2, 0, swapped, dp);\n \n //Bottom Up\n // return bottomUp(nums1, nums2);\n return spaceOptimized(nums1, nums2);\n\n }\n};\n``` | 1 | 0 | ['Dynamic Programming', 'Recursion'] | 0 |
minimum-swaps-to-make-sequences-increasing | C++ DP Solution [Tabulation] | c-dp-solution-tabulation-by-iamanjali-iw0k | \nclass Solution {\npublic:\n int minSwap(vector<int>& nums1, vector<int>& nums2) {\n \n int n = nums1.size();\n \n vector<vector | iamanjali | NORMAL | 2022-09-28T09:58:15.035938+00:00 | 2022-09-28T09:58:15.035980+00:00 | 51 | false | ```\nclass Solution {\npublic:\n int minSwap(vector<int>& nums1, vector<int>& nums2) {\n \n int n = nums1.size();\n \n vector<vector<int>> dp(n, vector<int>(2,-1));\n \n dp[0][0] = 0;\n dp[0][1] = 1;\n \n \n \n for(int i=1;i<n;i++) {\n \n bool a = (nums1[i-1] < nums1[i] && nums2[i-1] < nums2[i]); \n bool b = (nums1[i-1] < nums2[i] && nums2[i-1] < nums1[i]);\n \n if(a && b) {\n dp[i][0] = min(dp[i-1][0] , dp[i-1][1]) ;\n dp[i][1] = min(dp[i-1][0], dp[i-1][1]) + 1;\n }\n else if(a) {\n dp[i][0] = dp[i-1][0];\n dp[i][1] = dp[i-1][1] + 1;\n \n }\n else {\n dp[i][0] = dp[i-1][1];\n dp[i][1] = dp[i-1][0] + 1;\n \n }\n }\n \n return min(dp[n-1][0], dp[n-1][1]);\n \n }\n};\n``` | 1 | 0 | ['Dynamic Programming', 'C'] | 0 |
minimum-swaps-to-make-sequences-increasing | Java ||Recursion and Memoization Solution || clears understanding | java-recursion-and-memoization-solution-8hy3v | ```\nclass Solution {\n \n int [][] dp;\n public int minSwap(int[] nums1, int[] nums2) {\n List list1 = new ArrayList<>();\n \n for( | kurmiamreet44 | NORMAL | 2022-09-17T08:09:55.954800+00:00 | 2022-09-17T08:09:55.954837+00:00 | 102 | false | ```\nclass Solution {\n \n int [][] dp;\n public int minSwap(int[] nums1, int[] nums2) {\n List<Integer> list1 = new ArrayList<>();\n \n for(int x : nums1)\n {\n list1.add(x);\n }\n list1.add(0,-1);\n \n List<Integer> list2 = new ArrayList<>();\n for(int x : nums2)\n {\n list2.add(x);\n }\n list2.add(0,-1);\n \n dp = new int[list1.size()][2];\n for(int []arr: dp)\n {\n Arrays.fill(arr,-1);\n }\n \n return solve(list1,list2, 1,0);\n \n }\n \n public int solve(List<Integer> list1, List<Integer> list2,int index , int swapped )\n {\n if(index==list1.size())\n {\n return 0; \n }\n \n if(dp[index][swapped]!=-1)\n {\n return dp[index][swapped];\n }\n \n int prev1 = list1.get(index-1);\n int prev2 = list2.get(index-1);\n \n \n if(swapped==1)\n {\n int temp=prev1;\n prev1=prev2;\n prev2=temp;\n }\n \n // first option : dont swap the values \n int ans = Integer.MAX_VALUE;\n if(prev1 < list1.get(index) && prev2< list2.get(index))\n {\n ans= solve(list1, list2, index+1,0);\n }\n \n // second option :swap the values\n if(prev1 < list2.get(index) && prev2< list1.get(index))\n {\n ans =Math.min(ans,1 + solve(list1,list2, index+1, 1));\n }\n \n return dp[index][swapped]= ans;\n }\n} | 1 | 0 | ['Java'] | 0 |
minimum-swaps-to-make-sequences-increasing | c++ | RECURSION + MEMOIZATION | (DP Approach) | c-recursion-memoization-dp-approach-by-l-0tgc | Brute Force Recursion Approach\n\nint bruteForce()(vector<int>& v1, vector<int>& v2, int i){\n\tint n = v1.size();\n\tif(i>1 && (v1[i-2]>= v1[i-1] || v2[i-2]>=v | lokesh_0 | NORMAL | 2022-08-16T10:10:37.015925+00:00 | 2022-08-16T10:10:37.015950+00:00 | 119 | false | **Brute Force Recursion Approach**\n```\nint bruteForce()(vector<int>& v1, vector<int>& v2, int i){\n\tint n = v1.size();\n\tif(i>1 && (v1[i-2]>= v1[i-1] || v2[i-2]>=v2[i-1])) return 1e6;\n\tif(i==n) return 0;\n\n\t// Swap for current index so 1 + getMinSwap(...);\n\tint min_swaps = INT_MAX;\n\t// swapping for current index \n\tswap(v1[i], v2[i]);\n\tmin_swaps = 1 + getMinSwaps(v1, v2, i+1, 1);\n\n\n\t// reverting the array to form it was in \n\t// before doing the above swapping call\n\tswap(v1[i], v2[i]);\n\n\t// dont swap current for current index\n\treturn min_swaps = min(min_swaps, getMinSwaps(v1, v2, i+1, 0));\n}\n```\n \n \n** RECURSION + MEMOIZATION ** \n \n```\nint dp[100005][2];\n\nint getMinSwaps(vector<int>& v1, vector<int>& v2, int i, int p = 0){\n\tint n = v1.size();\n\tif(i>1 && (v1[i-2]>= v1[i-1] || v2[i-2]>=v2[i-1])) return 1e6;\n\tif(i==n) return 0;\n\tif(dp[i][p] != -1) return dp[i][p];\n\n\n\t// The two states that are changing are \n\t// 1) index (i.e. i)\n\t// 2) swapping for current index (i.e. p)\n\t// so if swapped than p = 1 \n\t// else p = 0\n\tswap(v1[i], v2[i]);\n\t// swapped so p = 1\n\tdp[i][p] = 1 + getMinSwaps(v1, v2, i+1, 1);\n\tswap(v1[i], v2[i]);\n\n\t// no swapped so p = 0\n\treturn dp[i][p] = min(dp[i][p], getMinSwaps(v1, v2, i+1, 0));\n}\n```\n\n | 1 | 0 | ['Dynamic Programming', 'Recursion', 'Memoization', 'C'] | 1 |
minimum-swaps-to-make-sequences-increasing | c++ easy memonization DP | c-easy-memonization-dp-by-code_in_red-9qrq | \nclass Solution {\npublic:\n int dp[100005][5];\n int help(vector<int>&a,vector<int>&b,int i,int s){\n if(i==a.size())return 0;\n if(dp[i][ | code_in_red | NORMAL | 2022-05-30T07:46:52.507635+00:00 | 2022-05-30T07:46:52.507666+00:00 | 129 | false | ```\nclass Solution {\npublic:\n int dp[100005][5];\n int help(vector<int>&a,vector<int>&b,int i,int s){\n if(i==a.size())return 0;\n if(dp[i][s]!=-1)return dp[i][s];\n int r=INT_MAX;\n if(s){ //previous element was swapped\n if(i-1>=0&&a[i]>b[i-1]&&b[i]>a[i-1]) r=min(r,help(a,b,i+1,0));\n if(i-1>=0&&b[i]>b[i-1]&&a[i]>a[i-1]) r=min(r,1+help(a,b,i+1,1)); //we are swapping ith element\n if(i==0) r=min({r,help(a,b,i+1,0),1+help(a,b,i+1,1)}); \n }else{\n if(i-1>=0&&a[i]>a[i-1]&&b[i]>b[i-1]) r=min(r,help(a,b,i+1,0));\n if(i-1>=0&&a[i]>b[i-1]&&b[i]>a[i-1]) r=min(r,1+help(a,b,i+1,1));\n if(i==0) r=min({r,help(a,b,i+1,0),1+help(a,b,i+1,1)});\n }\n return dp[i][s]=r;\n \n }\n int minSwap(vector<int>& nums1, vector<int>& nums2) {\n memset(dp,-1,sizeof(dp));\n return help(nums1,nums2,0,0);\n }\n};\n``` | 1 | 0 | ['Dynamic Programming', 'Memoization', 'C'] | 0 |
minimum-swaps-to-make-sequences-increasing | ✅ Memoization | With Explanation | Simple | C++ | memoization-with-explanation-simple-c-by-hg7g | \nclass Solution {\npublic:\n vector <vector <int>> dp;\n // dp[i][0] -> swaps needed to make array from index i to n stricly increasing considering index | vinoltauro | NORMAL | 2022-04-01T06:39:09.008889+00:00 | 2022-04-01T06:39:09.008927+00:00 | 201 | false | ```\nclass Solution {\npublic:\n vector <vector <int>> dp;\n // dp[i][0] -> swaps needed to make array from index i to n stricly increasing considering index i is not swapped\n // dp[i][1] -> swaps needed to make array from index i to n stricly increasing considering index i is swapped\n \n int helper(vector<int> &nums1, vector<int>& nums2, int i, int p1, int p2){\n \n\t\t// Base Case -> if we reach the end of the array return 0\n if(i >= nums1.size())\n return 0;\n \n // if answer to the current index for both the states is found, return saved answer\n if((dp[i][0] != INT_MAX and dp[i][1] != INT_MAX))\n return min (dp[i][0], dp[i][1]);\n \n int option1 = INT_MAX;\n // if x1 in nums1 and x2 in nums2 is greater than their previous, there is no need to swap\n if(p1 < nums1[i] and p2 < nums2[i])\n option1 = helper(nums1, nums2, i + 1, nums1[i], nums2[i]);\n \n // save answer of not swapping\n dp[i][0] = option1;\n \n // swap the current numbers\n swap(nums1[i], nums2[i]);\n \n int option2 = INT_MAX;\n // now if the current numbers are greater than previous, we add 1 operation and return the rest of operations from index i + 1\n if(p1 < nums1[i] and p2 < nums2[i]){\n option2 = 1 + helper(nums1, nums2, i +1 , nums1[i], nums2[i]);\n //save answer of swapping\n dp[i][1] = option2;\n }\n \n \n // unswap the current number for the recursion tree to continue\n swap(nums1[i], nums2[i]);\n\t\t\n // also consider a case where \n // 1. current numbers are greater than their previous \n // 2. if we swap the numbers, the current now is also greater than their previous\n // eg A = [1,7] B = [5,9]\n // at i = 1 we can afford to swap the current index and also afford to not swap it\n // therefore the answer will be the minimum of swapping and not swapping\n \n\n return min (option1, option2);\n \n \n }\n \n \n int minSwap(vector<int>& nums1, vector<int>& nums2) {\n \n dp.resize(nums1.size(), vector <int> (2, INT_MAX));\n return helper(nums1, nums2, 0, -1, -1);\n }\n};\n``` | 1 | 0 | [] | 0 |
minimum-swaps-to-make-sequences-increasing | JAVA: EASY DP | java-easy-dp-by-nicolas2lee-aubs | The idea is very simple, enumerate all cases.\ndp[i][0] do not swap current pair \ndp[i][1] swap current pair\n\n* a1\nif (a1<b2 && b1<a2){\n dp[i][0] = Math | nicolas2lee | NORMAL | 2022-03-06T19:40:29.927509+00:00 | 2022-03-06T19:43:38.601196+00:00 | 413 | false | The idea is very simple, enumerate all cases.\ndp[i][0] do not swap current pair \ndp[i][1] swap current pair\n\n* a1<a2 && b1<b2\n\n```\nif (a1<b2 && b1<a2){\n dp[i][0] = Math.min(Math.min(dp[i-1][0], dp[i-1][1]), dp[i][0]);\n dp[i][1] = Math.min(Math.min(dp[i-1][0]+1,dp[i-1][1]+1), dp[i][1]);\n}else{\n dp[i][0] = Math.min(dp[i-1][0], dp[i][0]);\n dp[i][1] = Math.min(dp[i-1][1]+1, dp[i][1]);\n}\n```\n\n* a1<a2 && b1>b2\n\n```\nif (a1<b2 && b1<a2)\n\tdp[i][0] = min(dp[i-1][1], dp[i][0])\n\tdp[i][1] = min(dp[i-1][0]+1, dp[i][1])\n```\n\n* a1>a2 && b1<b2\n```\nif (a1<b2 && b1<a2)\n\tdp[i][0] = min(dp[i-1][1], dp[i][0])\n\tdp[i][1] = min(dp[i-1][0]+1, dp[i][1])\n```\n\n* a1>a2 && b1>b2\n```\nif (a1<b2 && b1<a2)\n\tdp[i][0] = min(dp[i-1][1], dp[i][0])\n\tdp[i][1] = min(dp[i-1][0]+1, dp[i][1])\n```\nSo we can simplify \n```\nclass Solution {\n public int minSwap(int[] nums1, int[] nums2) {\n int[][] dp = new int[nums1.length][2];\n //dp[0][0] = 0; if we do not swap, then nb of swap is 0\n dp[0][1] = 1; // if we swap the first, then nb of swap is 1 \n for (int i=1; i<nums1.length; i++){\n int a1 = nums1[i-1];\n int a2 = nums1[i];\n int b1 = nums2[i-1];\n int b2 = nums2[i];\n dp[i][0] = Integer.MAX_VALUE;\n dp[i][1] = Integer.MAX_VALUE;\n if (a1<a2 && b1 <b2){\n if (a1<b2 && b1<a2){\n dp[i][0] = Math.min(Math.min(dp[i-1][0], dp[i-1][1]), dp[i][0]);\n dp[i][1] = Math.min(Math.min(dp[i-1][0]+1,dp[i-1][1]+1), dp[i][1]);\n }else{\n dp[i][0] = Math.min(dp[i-1][0], dp[i][0]);\n dp[i][1] = Math.min(dp[i-1][1]+1, dp[i][1]);\n }\n }else{\n dp[i][0] = Math.min(dp[i-1][1], dp[i][0]);\n dp[i][1] = Math.min(dp[i-1][0]+1, dp[i][1]);\n }\n // System.out.print(dp[i][0]+","+dp[i][1]+" ");\n }\n //System.out.println();\n return Math.min(dp[nums1.length-1][0], dp[nums1.length-1][1]);\n }\n}\n``` | 1 | 0 | ['Dynamic Programming', 'Java'] | 1 |
minimum-swaps-to-make-sequences-increasing | A graspable recursive solution | a-graspable-recursive-solution-by-su7ss-7uah | \nclass Solution {\n public int minSwap(int[] nums1, int[] nums2) {\n Map<String, Integer> memo = new HashMap<>();\n return Math.min(dfs(nums1, | su7ss | NORMAL | 2022-01-24T05:37:15.936577+00:00 | 2022-01-24T05:37:15.936619+00:00 | 177 | false | ```\nclass Solution {\n public int minSwap(int[] nums1, int[] nums2) {\n Map<String, Integer> memo = new HashMap<>();\n return Math.min(dfs(nums1, nums2, 1, false, memo), \n dfs(nums1, nums2, 1, true, memo) + 1);\n }\n \n private int dfs(int[] nums1, int[] nums2, int index, boolean prevSwap, Map<String, Integer> memo){\n if(index == nums1.length){\n return 0;\n }\n \n int a = nums1[index - 1];\n int b = nums2[index - 1];\n \n if(prevSwap){\n a = nums2[index - 1];\n b = nums1[index - 1];\n }\n \n String key = index + ":" + prevSwap;\n if(memo.containsKey(key)){\n return memo.get(key);\n }\n \n int res = Integer.MAX_VALUE;\n \n if(nums1[index] > a && nums2[index] > b){\n res = Math.min(res, dfs(nums1, nums2, index + 1, false, memo));\n }\n \n if(nums1[index] > b && nums2[index] > a){\n res = Math.min(res, dfs(nums1, nums2, index + 1, true, memo) + 1);\n }\n \n memo.put(key, res);\n return res;\n }\n}\n``` | 1 | 1 | ['Recursion', 'Memoization'] | 1 |
minimum-swaps-to-make-sequences-increasing | C++ DP O(N) Time and O(1) space solution | c-dp-on-time-and-o1-space-solution-by-ha-a1s8 | \nclass Solution {\npublic:\n int minSwap(vector<int> &one, vector<int> &two)\n {\n int n = one.size();\n int swap = 1;\n int noSwap = 0;\n\n for | haidermalik | NORMAL | 2022-01-04T08:03:42.478587+00:00 | 2022-01-04T08:03:42.478621+00:00 | 358 | false | ```\nclass Solution {\npublic:\n int minSwap(vector<int> &one, vector<int> &two)\n {\n int n = one.size();\n int swap = 1;\n int noSwap = 0;\n\n for (int i = 1; i < n; i++)\n {\n int oldSwap = swap;\n int oldNoSwap = noSwap;\n\n if (one[i] > one[i - 1] and one[i] > two[i - 1] and two[i] > two[i - 1] and two[i] > one[i - 1])\n {\n swap = 1 + min(oldSwap, oldNoSwap);\n noSwap = min(oldSwap, oldNoSwap);\n }\n else if (one[i] <= one[i - 1] or two[i] <= two[i - 1])\n {\n swap = 1 + oldNoSwap;\n noSwap = oldSwap;\n }\n else if (one[i] > one[i - 1] and two[i] > two[i - 1] and (one[i] <= two[i - 1] or two[i] <= one[i - 1]))\n {\n swap = 1 + oldSwap;\n noSwap = oldNoSwap;\n }\n }\n return min(swap, noSwap);\n }\n};\n``` | 1 | 0 | ['Dynamic Programming', 'C'] | 1 |
minimum-swaps-to-make-sequences-increasing | [Java] DP Iterative solution | java-dp-iterative-solution-by-ailyasov-z6lp | DP Iterative solution\nFor each element in both arrays we should maintain the invariant:\nnums[i - 1] < nums[i]\n\nStates:\ndp[i][0] minimum number of swaps to | ailyasov | NORMAL | 2022-01-03T20:00:38.500777+00:00 | 2022-01-28T21:07:41.273920+00:00 | 243 | false | **DP Iterative solution**\nFor each element in both arrays we should maintain the invariant:\n`nums[i - 1] < nums[i]`\n\nStates:\n`dp[i][0]` minimum number of swaps to have [0:i] sorted and no swap made at i index\n`dp[i][1] ` minimum number of swaps to have [0:i] sorted and swap i index of both arrays\n\nFor each element we make sure that nums[i - 1] < nums[i]\nThere are 4 cases:\n1. i - 1 elements not swapped, i elements not swapped. Because no swaps happened array values at index i - 1 and i remain the same. And we update not swapped state.\n```\nif(nums1[i - 1] < nums1[i] && nums2[i - 1] < nums2[i]) {\n\tdp[i][0] = dp[i - 1][0]; \n}\n```\nCompare this case with the remaining 3 keeping into account changes in values at i - 1 and i indices.\n\n2. i - 1 elements swapped, i element not swapped. Because i - 1 element swapped, array values at i - 1 changed: nums1[i - 1] = nums2[i - 1], and nums2[i - 1] = nums1[i - 1] so we do similar check, but with that difference. And we update not swapped state and read previous swapped state.\n```\nif(nums2[i - 1] < nums1[i] && nums1[i - 1] < nums2[i]) {\n\tdp[i][0] = Math.min(dp[i][0], dp[i - 1][1]);\n}\n```\n3. i - 1 elements not swapped, i elements swapped. Because i index is swapped, array values at index i changed so that nums1[i] = nums2[i] and nums2[i] = nums1[i]. So we should take that into account when comparing. And we update swapped state with the previous not swapped value.\n```\nif(nums1[i - 1] < nums2[i] && nums2[i - 1] < nums1[i]) {\n\tdp[i][1] = dp[i - 1][0] + 1; \n}\n```\n4. i - 1 elements swapped, i elements swapped. Because array values at both i - 1 and i indices changed that means both i - 1 and i indices of nums1 array now have values from nums2 array. Similarly both i - 1 and i indices of nums2 array now have values from nums1 array. And we update swapped state with the previous swapped state.\n```\nif(nums2[i - 1] < nums2[i] && nums1[i - 1] < nums1[i]) {\n\tdp[i][1] = Math.min(dp[i][1], dp[i - 1][1] + 1);\n}\n```\n\n**Code:**\n```\nclass Solution {\n final static int INF = (int) 1e9 + 7;\n public int minSwap(int[] nums1, int[] nums2) {\n int n = nums1.length;\n int[][] dp = new int[n][2];\n dp[0][0] = 0;\n dp[0][1] = 1; \n for(int i = 1; i < n; i++) {\n dp[i][0] = dp[i][1] = INF;\n //last time no swap and this time no swap\n if(nums1[i - 1] < nums1[i] && nums2[i - 1] < nums2[i]) {\n dp[i][0] = dp[i - 1][0]; \n }\n //last time swap this time no swap\n if(nums2[i - 1] < nums1[i] && nums1[i - 1] < nums2[i]) {\n dp[i][0] = Math.min(dp[i][0], dp[i - 1][1]);\n }\n //last time no swap this time swap\n if(nums1[i - 1] < nums2[i] && nums2[i - 1] < nums1[i]) {\n dp[i][1] = dp[i - 1][0] + 1; \n }\n //last time swap this time swap\n if(nums2[i - 1] < nums2[i] && nums1[i - 1] < nums1[i]) {\n dp[i][1] = Math.min(dp[i][1], dp[i - 1][1] + 1);\n } \n }\n \n return Math.min(dp[n - 1][0], dp[n - 1][1]);\n }\n}\n``` | 1 | 0 | ['Dynamic Programming', 'Iterator', 'Java'] | 0 |
minimum-swaps-to-make-sequences-increasing | [C++] Dynamic programming with O(n) Time and O(n) Space | c-dynamic-programming-with-on-time-and-o-n69n | We easily see that the position of any element of the two provided arrays is fixed, either we choose to swap it or keep it as original. Thus, at any position th | trieutrng | NORMAL | 2021-11-24T09:07:38.478054+00:00 | 2021-11-24T10:45:35.123763+00:00 | 406 | false | We easily see that the position of any element of the two provided arrays is fixed, either we choose to swap it or keep it as original. Thus, at any position there are 2 states we can maintain, I call them **keep** and **swap** (keep if we choose to keep the elements as original, and swap is the opposite case).\n\nAt any position we can choose to keep it as original if the value of the element of **nums1** greater than the previous one in the same array, the same for the element of **nums2**. In the other hand, we can choose to swap the elements of the 2 arrays if and only if the value of the element of **nums1** is greater than the element of **nums2** which has position less than position of the mentioned element of **nums1** array.\n\nAs the statement of this problem, we need to make the 2 provided arrays **strictly increasing**. And they guaranteed that the test case we received is always possible to find the minimum result. Therefore, there are at least one state we can choose at any position (**keep** or **swap** the elements). \n\nWe can use the dynamic programming technique to solve this problem. The base state is at position 0 and the result is the minimum value of 2 state of the last.\n\nHere is the code:\n\n```\nint minSwap(vector<int>& nums1, vector<int>& nums2) {\n\tint n=nums1.size();\n\tvector<int> swap(n, INT_MAX), keep(n, INT_MAX);\n\n\tkeep[0]=0;\n\tswap[0]=1;\n\n\tfor(int i=1; i<n; i++) {\n\t\tif(nums1[i]>nums1[i-1] && nums2[i]>nums2[i-1]) {\n\t\t\tkeep[i]=keep[i-1];\n\t\t\tswap[i]=swap[i-1]+1;\n\t\t} \n\t\tif(nums1[i]>nums2[i-1] && nums2[i]>nums1[i-1]) {\n\t\t\tkeep[i]=min(swap[i-1],keep[i]);\n\t\t\tswap[i]=min(keep[i-1]+1,swap[i]);\n\t\t}\n\t}\n\n\treturn min(keep[n-1],swap[n-1]);\n}\n```\n\n\tTime complexity: O(n)\n\tSpace complexity: O(n) | 1 | 0 | ['Dynamic Programming', 'C'] | 0 |
minimum-swaps-to-make-sequences-increasing | Python DP solution O(n) Time and O(1) Space | python-dp-solution-on-time-and-o1-space-ffyxz | \nclass Solution:\n def minSwap(self, nums1: List[int], nums2: List[int]) -> int:\n dp_none_swapped = 0\n dp_swapped = 1\n n = len(nums1 | chang_liu | NORMAL | 2021-10-14T19:16:59.701693+00:00 | 2021-10-14T19:16:59.701741+00:00 | 226 | false | ```\nclass Solution:\n def minSwap(self, nums1: List[int], nums2: List[int]) -> int:\n dp_none_swapped = 0\n dp_swapped = 1\n n = len(nums1)\n for i in range(1, n):\n #First, if at i, we don\'t swap\n #Then, if at i, we swap \n new_none_swapped = n + n\n new_swapped = n + n\n if nums1[i] > nums1[i-1] and nums2[i] > nums2[i-1]:\n new_none_swapped = min(new_none_swapped, dp_none_swapped)\n new_swapped = min(dp_swapped + 1, new_swapped)\n if nums1[i] > nums2[i-1] and nums2[i] > nums1[i-1]:\n new_none_swapped = min(dp_swapped, new_none_swapped)\n new_swapped = min(dp_none_swapped + 1, new_swapped)\n \n dp_none_swapped = new_none_swapped\n dp_swapped = new_swapped\n \n return min(dp_none_swapped, dp_swapped)\n``` | 1 | 0 | [] | 0 |
binary-tree-coloring-game | [Java/C++/Python] Simple recursion and Follow-Up | javacpython-simple-recursion-and-follow-edk24 | Intuition\nThe first player colors a node,\nthere are at most 3 nodes connected to this node.\nIts left, its right and its parent.\nTake this 3 nodes as the roo | lee215 | NORMAL | 2019-08-04T04:02:55.997216+00:00 | 2019-10-22T17:23:33.627274+00:00 | 22,669 | false | # **Intuition**\nThe first player colors a node,\nthere are at most 3 nodes connected to this node.\nIts left, its right and its parent.\nTake this 3 nodes as the root of 3 subtrees.\n\nThe second player just color any one root,\nand the whole subtree will be his.\nAnd this is also all he can take,\nsince he cannot cross the node of the first player.\n<br>\n\n# **Explanation**\n`count` will recursively count the number of nodes,\nin the left and in the right.\n`n - left - right` will be the number of nodes in the "subtree" of parent.\nNow we just need to compare `max(left, right, parent)` and `n / 2`\n<br>\n\n# **Complexity**\nTime `O(N)`\nSpace `O(height)` for recursion\n<br>\n\n**Java:**\n```java\n int left, right, val;\n public boolean btreeGameWinningMove(TreeNode root, int n, int x) {\n val = x;\n count(root);\n return Math.max(Math.max(left, right), n - left - right - 1) > n / 2;\n }\n\n private int count(TreeNode node) {\n if (node == null) return 0;\n int l = count(node.left), r = count(node.right);\n if (node.val == val) {\n left = l;\n right = r;\n }\n return l + r + 1;\n }\n```\n\n**C++:**\n```cpp\n int left, right, val;\n bool btreeGameWinningMove(TreeNode* root, int n, int x) {\n val = x, n = count(root);\n return max(max(left, right), n - left - right - 1) > n / 2;\n }\n\n int count(TreeNode* node) {\n if (!node) return 0;\n int l = count(node->left), r = count(node->right);\n if (node->val == val)\n left = l, right = r;\n return l + r + 1;\n }\n```\n\n**Python:**\n```python\n def btreeGameWinningMove(self, root, n, x):\n c = [0, 0]\n def count(node):\n if not node: return 0\n l, r = count(node.left), count(node.right)\n if node.val == x:\n c[0], c[1] = l, r\n return l + r + 1\n return count(root) / 2 < max(max(c), n - sum(c) - 1)\n```\n\n# **Fun Moment of Follow-up**:\nAlex and Lee are going to play this turned based game.\nAlex draw the whole tree. `root` and `n` will be given.\nNote the `n` will be odd, so no tie in the end.\n\nNow Lee says that, this time he wants to color the node first.\n1. Return `true` if Lee can ensure his win, otherwise return `false`\n\n2. Could you find the set all the nodes,\nthat Lee can ensure he wins the game?\nReturn the size of this set.\n\n3. What is the complexity of your solution?\n\n\n# Solution to the follow up 1\n\nYes, similar to the solution [877. Stone Game](https://leetcode.com/problems/stone-game/discuss/154610/DP-or-Just-return-true)\nJust return true.\nBut this time, Lee\'s turn to ride shotgun today! Bravo.\n\n**Java/C++**\n```java\n return true;\n```\n**Python:**\n```python\n return True\n```\n\n# Solution to the follow up 2\nThere will one and only one node in the tree,\nthat can Lee\'s win.\n\n**Java/C++**\n```java\n return 1\n```\n**Python:**\n```python\n return 1\n```\n\n# Solution to the follow up 3\nIt can be solve in `O(N)`.\n | 317 | 4 | [] | 35 |
binary-tree-coloring-game | Easy to understand for everyone | easy-to-understand-for-everyone-by-mudin-nq27 | Count left and right children\'s nodes of the player 1\'s initial node with value x. Lets call countLeft and countRight.\n1. if countLeft or countRight are big | mudin | NORMAL | 2019-08-04T05:31:27.921010+00:00 | 2019-08-04T05:31:27.921065+00:00 | 8,700 | false | Count left and right children\'s nodes of the player 1\'s initial node with value `x`. Lets call `countLeft` and `countRight`.\n1. if `countLeft` or `countRight` are bigger than `n/2`, player 2 chooses this child of the node and will win.\n2. If `countLeft + countRight + 1` is smaller than `n/2`, player 2 chooses the parent of the node and will win;\n3. otherwise, player 2 has not chance to win.\n\n```\nvar btreeGameWinningMove = function(root, n, x) {\n \n let leftCount = 0;\n let rightCount = 0;\n \n function countNodes(t) {\n if(!t) return 0;\n let l = countNodes(t.left);\n let r = countNodes(t.right);\n if (t.val == x) {\n leftCount = l;\n rightCount = r;\n }\n return l + r + 1;\n }\n \n countNodes(root); // calculate node count\n \n // if player2 chooses player1\'s parent node and payer1 node\'s count is smaller than n/2, playr2 will win\n if(leftCount+rightCount+1<n/2) return true;\n \n // if player2 chooses player1\'s left or right node and its count is bigger than n/2, playr2 will win\n if(leftCount>n/2 || rightCount>n/2) return true;\n \n return false;\n};\n``` | 123 | 1 | [] | 12 |
binary-tree-coloring-game | Simple Clean Java Solution | simple-clean-java-solution-by-ayyild1z-1wlo | Short explanation:\n\nWhen you find the selected node, there are three different paths you can block: left right parent In order to guarantee your win, one of t | ayyild1z | NORMAL | 2019-08-26T18:49:04.297051+00:00 | 2019-08-26T18:57:24.285030+00:00 | 3,054 | false | **Short explanation:**\n\nWhen you find the selected node, there are three different paths you can block: `left` `right` `parent` In order to guarantee your win, one of those paths should include more nodes than the sum of other two paths. \n\n.\n\n```java\npublic boolean btreeGameWinningMove(TreeNode root, int n, int x) {\n\tif(root == null) return false;\n\n\tif(root.val == x){\n\t\tint left = count(root.left);\n\t\tint right = count(root.right);\n\t\tint parent = n - (left+right+1);\n\n\t\treturn parent > (left + right) || left > (parent + right) || right > (left + parent);\n\t}\n\n\treturn btreeGameWinningMove(root.left, n, x) || btreeGameWinningMove(root.right, n, x);\n}\n\nprivate int count(TreeNode node){\n\tif(node == null) return 0;\n\treturn count(node.left) + count(node.right) + 1;\n}\n``` | 83 | 0 | ['Java'] | 5 |
binary-tree-coloring-game | c++,0ms, modular, beats 100% (both time and memory) with algo and image | c0ms-modular-beats-100-both-time-and-mem-q64g | The second player will pick y as either left child, right child or parent (depending on which one has max nodes in their vicinity) of the node picked by first p | goelrishabh5 | NORMAL | 2019-08-04T04:51:06.711368+00:00 | 2019-08-04T05:23:19.484788+00:00 | 3,710 | false | The second player will pick y as either left child, right child or parent (depending on which one has max nodes in their vicinity) of the node picked by first player.\nIf the no of nodes available for second player is greater than first, he wins \nNote : Equal case will never arise since n is odd\n\nFor example : \n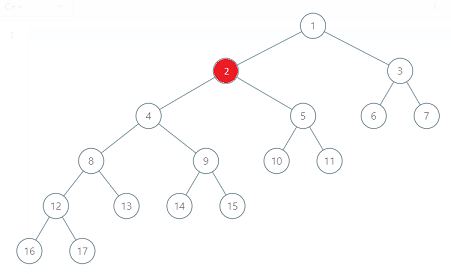 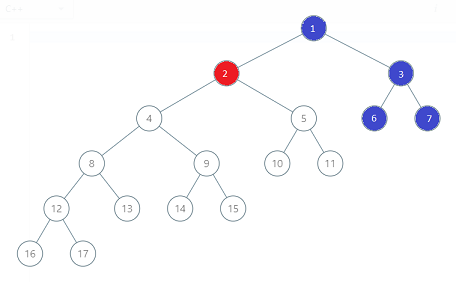 **parent(b:4)** 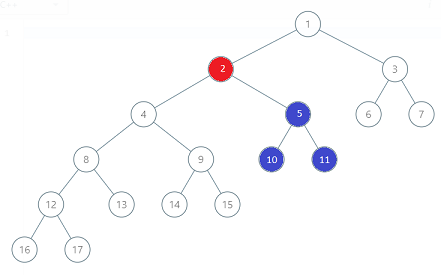 **right child (b:3)** 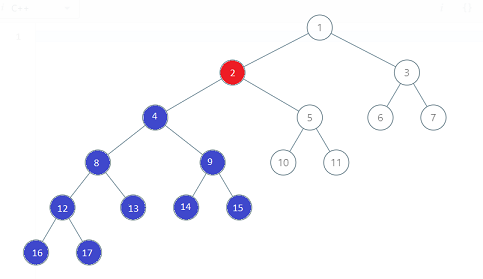 **left child (b:9)** \n\nHere, blue wins since it will pick left child. Thus, 9 will be left for blue and for red , 8 will be left\n\n```\nTreeNode* findNode(TreeNode* root,int x)\n {\n TreeNode* temp = NULL;\n if(root)\n {\n if(root->val==x)\n temp = root;\n else\n {\n temp = findNode(root->left,x);\n if(!temp)\n temp = findNode(root->right,x);\n }\n }\n return temp;\n }\n \n void countChildren(TreeNode* root, int &no)\n {\n if(root)\n {\n no++;\n countChildren(root->left,no);\n countChildren(root->right,no); \n }\n }\n \n bool btreeGameWinningMove(TreeNode* root, int n, int x) {\n \n int left=0,right=0,parent=0,blue=0;\n TreeNode* temp = findNode(root,x); // find node\n countChildren(temp->left,left); // count no of nodes in left subtree\n countChildren(temp->right,right); // count no of nodes in right subtree\n blue=max(left,right);\n if(temp->val!=root->val)\n parent = n-(left+right+1); // count no of nodes apart from given node\'s subtree\n blue=max(blue,parent);\n \n return (blue)>(n-blue);\n }\n``` | 67 | 2 | ['C', 'Binary Tree'] | 4 |
binary-tree-coloring-game | C++ count nodes in x subtree | c-count-nodes-in-x-subtree-by-votrubac-ngy7 | Intuition\nAfter the first player choose x node, the best options for the second player are:\n- Choose the parent of x. Second player will color all nodes outsi | votrubac | NORMAL | 2019-08-04T04:56:28.317478+00:00 | 2019-08-04T05:14:45.739827+00:00 | 2,128 | false | # Intuition\nAfter the first player choose ```x``` node, the best options for the second player are:\n- Choose the parent of ```x```. Second player will color all nodes outside ```x``` subtree.\n- Choose the left child of ```x```. Second player will color all nodes in the left child.\n- ... or the right child.\n# Solution\nCount the number of nodes in the left and right subtree of ```x```, and compare to ```n``` to determine if the second player can color more nodes.\n```\nint x_l = 0, x_r = 0;\nint count(TreeNode* root, int x) {\n if (root == nullptr) return 0;\n auto l = count(root->left, x), r = count(root->right, x);\n if (root->val == x) x_l = l, x_r = r;\n return 1 + l + r;\n}\nbool btreeGameWinningMove(TreeNode* r, int n, int x) {\n count(r, x);\n return x_r + x_l < n / 2 || x_l > n / 2 || x_r > n / 2;\n}\n```\n# Complexity Analysis\nRuntime: O(n)\nMemory: O(h), where h is the height of the tree (for the recursion).\n\t | 36 | 1 | [] | 1 |
binary-tree-coloring-game | Confusing problem statement | confusing-problem-statement-by-nice_dev-kdlp | Can anyone make me understand what does the problem statement mean? I looked at this example \n\n\nInput: root = [1,2,3,4,5,6,7,8,9,10,11], n = 11, x = 3\nOutpu | nice_dev | NORMAL | 2019-08-04T09:02:35.094664+00:00 | 2019-08-04T09:02:35.094696+00:00 | 2,362 | false | Can anyone make me understand what does the problem statement mean? I looked at this example \n\n```\nInput: root = [1,2,3,4,5,6,7,8,9,10,11], n = 11, x = 3\nOutput: true\nExplanation: The second player can choose the node with value 2.\n```\n\nWhy node with value `2`? Why not any other node? | 33 | 1 | [] | 6 |
binary-tree-coloring-game | Python 3 | DFS | One pass & Three pass | Explanation | python-3-dfs-one-pass-three-pass-explana-hhi7 | Intuition\n- When first player chose a node x, then there are 3 branches left there for second player to choose (left subtree of x, right subtree of x, parent e | idontknoooo | NORMAL | 2020-08-17T20:34:26.323020+00:00 | 2020-08-17T20:34:26.323065+00:00 | 1,184 | false | ### Intuition\n- When first player chose a node `x`, then there are 3 branches left there for second player to choose (left subtree of `x`, right subtree of `x`, parent end of `x`. \n- For the second player, to ensure a win, we need to make sure that there is one branch that dominate the sum of the other 2 branches. As showed at below.\n\t- left + right < parent\n\t- parent + right < left\n\t- parent + left < right\n### Three-pass solution\n```\nclass Solution:\n def btreeGameWinningMove(self, root: TreeNode, n: int, x: int) -> bool:\n first = None\n def count(node):\n nonlocal first\n total = 0\n if node: \n if node.val == x: first = node\n total += count(node.left) + count(node.right) + 1\n return total\n \n s = count(root) # Get total number of nodes, and x node (first player\'s choice)\n l = count(first.left) # Number of nodes on left branch \n r = count(first.right) # Number of nodes on right branch \n p = s-l-r-1 # Number of nodes on parent branch (anything else other than node, left subtree of node or right subtree of node)\n return l+r < p or l+p < r or r+p < l\n```\n\n### One-pass solution\n- Once you understand the idea of three-pass solution, it\'s pretty easy to modify the code to a one-pass solution\n```\nclass Solution:\n def btreeGameWinningMove(self, root: TreeNode, n: int, x: int) -> bool:\n l = r = 0\n def count(node):\n nonlocal l, r\n total = 0\n if node: \n l_count, r_count = count(node.left), count(node.right)\n if node.val == x: \n l, r = l_count, r_count\n total += l_count + r_count + 1\n return total\n s = count(root) \n p = s-l-r-1 \n return l+r < p or l+p < r or r+p < l\n``` | 18 | 0 | ['Depth-First Search', 'Python', 'Python3'] | 2 |
binary-tree-coloring-game | C++ Easy To Understand Code with Explanation | c-easy-to-understand-code-with-explanati-p3at | Given that total nodes are n.\n###### For any node x, \n###### a.find the count of nodes in the left subtree \n###### b.and the count of nodes in the right subt | pratyush63 | NORMAL | 2020-05-07T11:33:03.956399+00:00 | 2020-05-07T11:34:01.301722+00:00 | 699 | false | ###### Given that total nodes are n.*\n###### For any node x, \n###### a.find the count of nodes in the left subtree \n###### b.and the count of nodes in the right subtree\n###### c.Count of nodes above node x(remaining tree) will be n-(a)-(b)-1\n###### If player 2 picks the right child, the right subtree is blocked for player 1\n###### If he picks the left child, the left subtree is blocked.Similary on picking the parent node, the remaining nodes are blocked\n###### Condition for player 2 to win:\n###### a>b+c or b>a+c or c>a+b*\n\n class Solution {\n public:\n\n int count(TreeNode* root)\n {\n if(root==NULL) return 0;\n \n return 1+count(root->left)+count(root->right);\n }\n \n TreeNode* find(TreeNode*root,int x)\n {\n if(root==NULL)\n return NULL;\n if(root->val==x)\n return root;\n \n TreeNode* l=find(root->left,x);\n TreeNode* r=find(root->right,x);\n if(l==NULL) return r;\n return l;\n }\n bool btreeGameWinningMove(TreeNode* root, int n, int x) {\n TreeNode* xpos=find(root,x);\n int a=count(xpos->left);\n int b=count(xpos->right);\n int c=n-a-b-1;\n if(a>b+c) return true;\n if(b>a+c) return true;\n if(c>a+b) return true;\n return false;\n }\n }; | 13 | 0 | [] | 2 |
binary-tree-coloring-game | Iterative BFS, python with my explanation | iterative-bfs-python-with-my-explanation-t5rj | There are three "zones" in the tree:\n1. Left subtree under Red\n2. Right subtree under Red\n3. The remainder of the tree "above" Red\n\nBlue can pick the left | bookra | NORMAL | 2020-01-04T04:49:14.940282+00:00 | 2020-01-04T04:49:14.940332+00:00 | 1,246 | false | There are three "zones" in the tree:\n1. Left subtree under Red\n2. Right subtree under Red\n3. The remainder of the tree "above" Red\n\nBlue can pick the left child, right child, or parent of Red to control zones 1, 2, or 3, respectivley.\n\nTherefore we count the number of nodes in two of the zones. The third zone is simply n - sum(the other two zones) -1\n\nIf one of the zones is larger than the other two combined (plus 1 for the Red node), then we (Blue) can control it and win the game. Otherwise we lose :(\n\nSo I utilized a BFS to iterativley count Zone 3 first , leaving aside Red and its subtree(s) for the next BFS. Comments below:\n\n```python\nfrom collections import deque\ndef btreeGameWinningMove(self, root: TreeNode, n: int, x: int) -> bool:\n\toutside_red, red_ltree, red_rtree = 0, 0, 0\n\tred_node = None\n\tq = deque([root])\n\twhile len(q):\n\t\tcurr_node = q.pop()\n\t\tif curr_node.val ==x:\n\t\t\t# we won\'t append any children this go-around\n\t\t\tred_node = curr_node\n\t\telse:\n\t\t\toutside_red += 1\n\t\t\tq.extendleft([x for x in [curr_node.left, curr_node.right] if x])\n\t#now check left subtree. If it\'s empty that makes our job easier because red_rtree = n-outside_red-1\n\tif red_node.left:\n\t\tq.append(red_node.left)\n\t\twhile len(q):\n\t\t\tcurr_node = q.pop()\n\t\t\tred_ltree +=1\n\t\t\tq.extend([x for x in [curr_node.left, curr_node.right] if x])\n\telse:\n\t\tred_ltree = 0\n\tred_rtree = n - outside_red - red_ltree - 1\n\t[low, med, high] = sorted([outside_red, red_ltree, red_rtree])\n\treturn high > med+low+1\n\t\t``` | 11 | 0 | ['Breadth-First Search', 'Python3'] | 1 |
binary-tree-coloring-game | ✅ [C++] Easy Intuitive solution with Explanation | c-easy-intuitive-solution-with-explanati-jaqu | This question is easy once you figure out what to do. We need to check if we can win or not. Its simple. Just reduce the win chances of your opponent. \nHow do | biT_Legion | NORMAL | 2022-05-19T11:27:25.255112+00:00 | 2022-05-19T11:27:25.255155+00:00 | 1,135 | false | This question is easy once you figure out what to do. We need to check if we can win or not. **Its simple**. Just reduce the win chances of your opponent. \n***How do we do that?***\nWe will try to block the movement of the oppenent(Lets call him red) by choosing one of his neighbour. That way, he will have no choice and he will be forced to move in the only remaining two directions. Here, three directions are \n* toward his parent, \n* towards his left child, \n* towards his right child\n\nNow, to ensure our win, we will block the one having more number of nodes connected to it. To check the number of nodes, we maintain a child array. This child array will store the number of children of a node. So, if we color the parent of red node, we will have `child[root]-child[rednode]` nodes to color while red node will have `child[rednode]` nodes. \n**Why `child[root]-child[rednode]`?**\nWell, every parent of a node is also its neighbour. So we can also move upwards, towards parent of each node. Thus, we have to count all those nodes as well. Therefore, we check directly for child[root], and since some of the nodes are already occupied by red node, thus we need to subtract those froom child[root]. Similiarly, we do for the left node and right node and check if we can win or not. \n\n```\nclass Solution {\npublic:\n TreeNode* X;\n bool btreeGameWinningMove(TreeNode* root, int n, int x) {\n vector <int> child(n+1,0);\n \n dfs(root,0,x,child);\n \n if(child[root->val]>2*child[x]) return true;\n if(X->left and 2*child[X->left->val]>child[root->val]) return true;\n if(X->right and 2*child[X->right->val]>child[root->val]) return true;\n return false;\n }\nprotected:\n int dfs(TreeNode* root, int parent, int x, vector<int>&child){\n if(!root) return 0;\n \n // Since we would need to access left and right child too. We can also have two int variables for the same\n if(root->val == x) X=root;\n \n int left = dfs(root->left,root->val,x,child);\n int right = dfs(root->right,root->val,x,child);\n \n return child[root->val] = 1+left+right;\n }\n};\n``` | 10 | 1 | ['Depth-First Search', 'C', 'C++'] | 0 |
binary-tree-coloring-game | Python 3 || 12 lines, w/ explanation and example || T/S: 98% / 93% | python-3-12-lines-w-explanation-and-exam-g3q7 | The problem reduces to whether any of the three subgraphs with edges to node x have at least (n+1)//2 nodes.\n\nHere\'s the plan:\n- Traverse the tree with dfs | Spaulding_ | NORMAL | 2022-12-30T22:47:02.108506+00:00 | 2024-06-01T15:54:43.429995+00:00 | 761 | false | The problem reduces to whether any of the three subgraphs with edges to node `x` have at least `(n+1)//2` nodes.\n\nHere\'s the plan:\n- Traverse the tree with `dfs` recursively.\n- For each `node`, rewrite `node.val` with the count of nodes in its subtree.\n- Evaluate whether `node` is x, and if so, determine whether one of its neighbors is greater than `(n+1)//2`.\n- Return `True` if so, of if either child returns `True`. If not, return `False`\n```\nclass Solution:\n def btreeGameWinningMove(self, root: TreeNode, n: int, x: int) -> bool:\n\n most = (n+1)//2\n\n def dfs(node):\n if not node: return False\n\n if dfs(node.left) or dfs(node.right): return True\n is_x = node.val == x\n \n l = node.left .val if node.left else 0\n r = node.right.val if node.right else 0\n\n if is_x and (l >= most or r >= most): return True\n\n node.val = 1 + l + r\n\n if is_x: return node.val < most\n\n return False\n\n return dfs(root)\n```\n[https://leetcode.com/problems/binary-tree-coloring-game/submissions/1274328962/](https://leetcode.com/problems/binary-tree-coloring-game/submissions/1274328962/)\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(*N*), in which *N* ~ the number of nodes. | 8 | 0 | ['Python3'] | 0 |
binary-tree-coloring-game | Simple recursive solution in C++ with explanation [0ms] | simple-recursive-solution-in-c-with-expl-kk94 | Because the game is played on a tree there are no cycles in the graph, and marking a node divides-off a part of the graph, making it forever inaccessible to the | ahcox | NORMAL | 2019-11-07T17:50:25.835479+00:00 | 2019-11-07T17:53:23.827868+00:00 | 548 | false | Because the game is played on a tree there are no cycles in the graph, and marking a node divides-off a part of the graph, making it forever inaccessible to the other player. Therefore, a first move which cuts off more of the tree than remains accessible to the other player is an automatic winning one. The best such move must be adjacent to the selection of the first player because any other move will always increase the number of nodes it cuts off if it is adjusted towards the node chosen by player one by one edge in the graph.\n\nOur choice is therefore between the zero to three neighbouring nodes of the node chosen by player 1. We can evaluate which of these is best by counting the nodes connected through them. The left and right subtrees can be counted by a simple recursive depth first search. The part of the tree connected through the parent of this node can be counted implcitly since we were given the total node count in parameter _n_. We simply subtract the left and right subtree counts from _n_ and one more for the node chosen by player 1 to give the number of nodes reachable through the parent. \n\n### Algorithm \n\n* Search the tree for the node of the player\'s first move.\n* Walk the tree down the the left and right branches from that, counting nodes in each.\n* There will be up to 3 groups of nodes:\n * left: counted\n\t* right: counted:\n\t* parent: n - (left + right + 1);\n\nIf one of these counts is larger than the other two combined, there exists a move separating that subtree from player 1 which means player one can never win no matter what other moves follow.\n\n### C++ Code\n\n```c++\n constexpr const TreeNode* find(const TreeNode* node, const int val){\n if(node->val == val) return node;\n\t\t\n const TreeNode* found = nullptr; \n if(node->left) found = find(node->left, val);\n if(!found && node->right) found = find(node->right, val);\n return found;\n }\n \n constexpr const unsigned count(const TreeNode* node){\n unsigned counter = 1;\n if(node->left) counter += count(node->left);\n if(node->right) counter += count(node->right);\n return counter;\n }\n \n class Solution {\n public:\n constexpr\n bool btreeGameWinningMove(TreeNode* root, int n, int x) const\n {\n const TreeNode*const p1_move = find(root, x);\n const unsigned left_count = p1_move->left != nullptr ? count(p1_move->left) : 0;\n const unsigned right_count = p1_move->right != nullptr ? count(p1_move->right) : 0;\n const unsigned parent_count = n - (left_count + right_count + 1);\n if(left_count > 1 + parent_count + right_count ||\n right_count > 1 + parent_count + left_count ||\n parent_count > 1 + left_count + right_count)\n {\n return true;\n }\n return false;\n }\n };\n``` | 7 | 0 | ['Depth-First Search', 'Recursion', 'C', 'Binary Tree'] | 0 |
binary-tree-coloring-game | SIMPLE JAVA APPROACH WITH EXPLANATION | simple-java-approach-with-explanation-by-49fp | \t// time complexity O(N) , space complexity O(height)\n\t/ approach :\n\t\t\t--> as we are given the starting red color node(x), the only place to start color | the_moonLight | NORMAL | 2021-01-26T08:48:35.537604+00:00 | 2021-01-26T08:48:35.537643+00:00 | 304 | false | \t// time complexity O(N) , space complexity O(height)\n\t/* approach :\n\t\t\t--> as we are given the starting red color node(x), the only place to start coloring blue that ensures blue to win is to color any adjacent node of x to blue.\n\t\t\t--> if we color left child of x to blue then we can stop the red color player to color any node of subtree starting from the left child of x.\n\t\t\t--> similar goes for right child for x.\n\t\t\t--> if we initially color parent node of x to blue , then we can stop the red color player to color upper nodes of x and their remaining children.\n\t\t\t--> in either case blue player will be coloring only 1 part(left subtree/right subtree/ parent tree) and rest 2 parts are colored by red.\n\t\t\t--> find # nodes in any 1 part > # of nodes in remaining 2 parts , if yes then blue can win else cann\'t.\n\t*/\n\tclass Solution {\n\t\tpublic boolean btreeGameWinningMove(TreeNode root, int n, int x) {\n\t\t\tTreeNode redColor = findRedColor(root,x);\n\t\t\tint leftSubtree = count(redColor.left,null);\n\t\t\tint rightSubtree = count(redColor.right,null);\n\t\t\tint parentTree = count(root,redColor);\n\t\t\tif(leftSubtree> rightSubtree + parentTree)return true;\n\t\t\tif(rightSubtree> leftSubtree + parentTree)return true;\n\t\t\tif(parentTree> rightSubtree + leftSubtree)return true;\n\t\t\treturn false;\n\t\t}\n\n\t\tprivate TreeNode findRedColor(TreeNode root,int x){\n\t\t\tif(root==null)return null;\n\t\t\tif(root.val==x)return root;\n\t\t\tTreeNode l = findRedColor(root.left,x);\n\t\t\tif(l!=null)return l;\n\t\t\treturn findRedColor(root.right,x);\n\t\t}\n\t\tprivate int count(TreeNode root, TreeNode redColor){\n\t\t\tif(root==null || root==redColor)return 0;\n\t\t\treturn 1 + count(root.left,redColor) + count(root.right,redColor);\n\t\t}\n\t} | 5 | 0 | [] | 0 |
binary-tree-coloring-game | Java solution beats 100% time: Break the problem down into two easier problems | java-solution-beats-100-time-break-the-p-5ew4 | \nclass Solution {\n int count;\n public boolean btreeGameWinningMove(TreeNode root, int n, int x) {\n if (root == null)\n return false; | jasonhey93 | NORMAL | 2020-01-27T20:59:57.943745+00:00 | 2020-01-27T21:00:21.137142+00:00 | 399 | false | ```\nclass Solution {\n int count;\n public boolean btreeGameWinningMove(TreeNode root, int n, int x) {\n if (root == null)\n return false;\n \n // find the node with value x\n TreeNode target = search(root, x);\n \n // separate the tree into three parts around the target: left subtrees, right subtrees, and others\n int left = subtreeCount(target.left);\n int right = subtreeCount(target.right);\n int remain = n - left - right - 1;\n \n // return true if the count of any two part is greater than the count of the third part\n return (remain > left + right + 1) || (left > remain + right + 1) || (right > left + remain + 1);\n }\n \n private TreeNode search(TreeNode root, int x) {\n if (root == null)\n return null;\n \n if (root.val == x)\n return root;\n \n TreeNode left = search(root.left, x);\n TreeNode right = search(root.right, x);\n if (left == null && right == null)\n return null;\n else if (left != null)\n return left;\n return right;\n }\n \n private int subtreeCount(TreeNode root) {\n if (root == null)\n return 0;\n \n int leftNodes = subtreeCount(root.left);\n int rightNodes = subtreeCount(root.right);\n return leftNodes + rightNodes + 1;\n }\n}\n``` | 5 | 0 | ['Recursion', 'Java'] | 0 |
binary-tree-coloring-game | c++ 0ms easy solution !!!! | c-0ms-easy-solution-by-shivanshu0287-h574 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | shivanshu0287 | NORMAL | 2023-09-13T08:18:32.578821+00:00 | 2023-09-13T08:18:32.578843+00:00 | 265 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\n int length(TreeNode* root){\n if(root==0)return 0;\n return 1+length(root->left)+length(root->right);\n }\n TreeNode* search(TreeNode* root,int x){\n if(root==0)return 0;\n if(root->val==x){\n return root;\n }\n auto left=search(root->left,x);\n auto right=search(root->right,x);\n if(left)return left;\n if(right)return right;\n return 0;\n }\npublic:\n bool btreeGameWinningMove(TreeNode* root, int n, int x) {\n if(root->val==x){\n if(length(root->left)==length(root->right))\n return false;\n else\n return true;\n }\n auto temp=search(root,x);\n int y=length(temp);\n int x1=n-y;\n if(x1>y)return true;\n int l1=length(temp->left);\n int l2=length(temp->right);\n if(x1+1+l1<l2)return true;\n if(x1+1+l2<l1)return true;\n return false;\n }\n};\n``` | 4 | 0 | ['C++'] | 1 |
binary-tree-coloring-game | [C++] Simplest - Recursive - 2 solutions. | c-simplest-recursive-2-solutions-by-user-kexn | \n\n\nThis is a game theory question so instead of just making moves, \'blue\' need to damage \'red\'. \nThe idea is that every node can have at max 3 neighbou | user2085X | NORMAL | 2022-04-14T11:08:48.323428+00:00 | 2022-04-14T11:08:48.323464+00:00 | 303 | false | 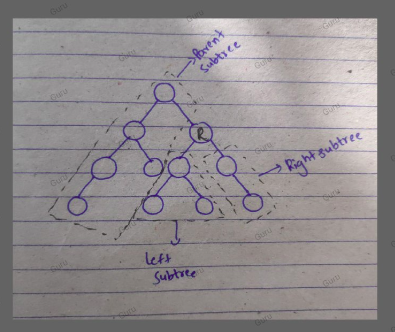\n\n\nThis is a game theory question so instead of just making moves, \'blue\' need to damage \'red\'. \nThe idea is that every node can have at max 3 neighbour nodes(1> parent, 2> left child, 3> right child), \'red\' node will also have at max 3 neighbours. All these 3 neighbours will further have 3 subtrees, for \'blue\' to win we need to mark one of these neighbours as blue so that one probable path for \'red\' to paint red will be blocked. \n\n1> find red node\n2> count no. of nodes for red node\'s left and right child.\n3> cout no. of nodes to the other side of red node\'s parent node = total no. of nodes(n) - count of nodes in red node\'s left subtree - count of node\'s in red nodes\' right subtree - 1(for red node) \n4> if max of these three count is greater than the sum of other two -> \'blue\' wins.\nHere\'s the simple solution : \n```\nclass Solution {\npublic:\n int arr[3];\n bool btreeGameWinningMove(TreeNode* root, int n, int x) {\n findRedNode(root, x);\n arr[2] = n - arr[0] - arr[1] - 1;\n sort(arr, arr+3);\n \n if(arr[2] > arr[0] + arr[1]) return true;\n return false;\n }\nprivate: \n void findRedNode(TreeNode* root, int x) {\n if(root == NULL) return;\n \n if(root -> val == x) {\n arr[0] = countNodes(root -> left);\n arr[1] = countNodes(root -> right);\n return;\n }\n \n findRedNode(root -> left, x);\n findRedNode(root -> right, x);\n }\n \n int countNodes(TreeNode* node) {\n if(node == NULL) return 0;\n return (1+ countNodes(node -> left) + countNodes(node -> right));\n }\n};\n\n```\n\ntime complexity of this code is just greater than O(n), in order to decrease it we can both find red node plus count nodes to it\'s left and right subtree in one pass as a result time complexity will be under O(n).\n\n\nhere\'s my code: \n```\nclass Solution {\npublic:\n int arr[3];\n bool btreeGameWinningMove(TreeNode* root, int n, int x) {\n findAndCount(root, x);\n arr[2] = n - arr[0] - arr[1] - 1;\n sort(arr, arr+3);\n \n if(arr[2] > arr[0] + arr[1]) return true;\n return false;\n }\nprivate: \n int findAndCount(TreeNode* root, int x) {\n if(root == NULL) return 0;\n int l = findAndCount(root -> left, x);\n int r = findAndCount(root -> right, x);\n \n if(root -> val == x) {\n arr[0] = l;\n arr[1] = r;\n }\n \n return l+r+1;\n }\n \n};\n\n``` | 4 | 0 | ['Backtracking', 'Depth-First Search', 'Recursion', 'Binary Tree'] | 0 |
binary-tree-coloring-game | JAVA | Explained | beginner friendly | java-explained-beginner-friendly-by-code-idvc | \n\t// When you find the selected node, there are three different paths you can block: left ,right or parent \n\t// if i color left(a) node blue, then red perso | codewizard27 | NORMAL | 2022-01-18T15:50:39.079836+00:00 | 2022-01-18T15:50:39.079877+00:00 | 398 | false | \n\t// When you find the selected node, there are three different paths you can block: left ,right or parent \n\t// if i color left(a) node blue, then red person can color all right and parent nodes red\n\t// if i color right (b) node blue, then red person can color all left and parent nodes red\n\t// if i color parent(c) node blue, then red person can color all right and left nodes red\n\t// so i can only win if i choose a node which contains elements greater than the count of elements in otther 2 nodes i.e a>b+c i color a node blue, or b>a+c i color b node blue , or c>a+b i color c node blue\n\t// if none of these 3 conditions hold true then red person wins bcoz he has more nodes to color\n\tclass Solution {\n\t\tpublic boolean btreeGameWinningMove(TreeNode root, int n, int x) {\n\t\t\tif(root==null) return false;\n\t\t\tif(root.val==x){\n\t\t\t\tint a=countofnodes(root.left);\n\t\t\t\tint b=countofnodes(root.right);\n\t\t\t\tint c=n-a-b-1; // 1 for root\n\t\t\t\tif(a>b+c || b>c+a || c>a+b) return true;\n\t\t\t\treturn false;\n\t\t\t}\n\t\t\tboolean left=btreeGameWinningMove(root.left,n,x);\n\t\t\tif(left) return true;\n\t\t\tboolean right=btreeGameWinningMove(root.right,n,x);\n\t\t\tif(right) return true;\n\n\t\t\treturn false;\n\t\t}\n\t\tpublic int countofnodes(TreeNode root){\n\t\t\tif(root==null) return 0;\n\t\t\treturn countofnodes(root.left)+countofnodes(root.right)+1;\n\t\t}\n\t}\n | 4 | 0 | ['Java'] | 1 |
binary-tree-coloring-game | C++ || Easy Solution | c-easy-solution-by-shubham_0221-pbuk | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | shubham_0221 | NORMAL | 2023-02-20T11:41:44.260591+00:00 | 2023-02-20T11:41:44.260641+00:00 | 455 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n int l=0,r=0;\n int fun(TreeNode*root,int x){\n if(root==NULL)return 0;\n int left=fun(root->left,x);\n int right=fun(root->right,x);\n if(root->val==x){\n l=left;\n r=right;\n }\n return left+right+1;\n }\n bool btreeGameWinningMove(TreeNode* root, int n, int x) {\n fun(root,x);\n int p=n-(l+r+1);\n int node=max(p,max(l,r));\n if(node>n/2)\n return true;\n return false;\n }\n};\n``` | 3 | 0 | ['C++'] | 0 |
binary-tree-coloring-game | 0ms | BFS | Diagram | Tree as Graph | Explained | 0ms-bfs-diagram-tree-as-graph-explained-8un2t | This is a standard simulation problem. You don\'t need to think of all the cases of expansion just deal with the stopping case, i.e. when both red and blue are | aryanjofficial57 | NORMAL | 2022-10-07T08:35:10.121223+00:00 | 2022-10-07T08:35:10.121257+00:00 | 251 | false | This is a standard simulation problem. You don\'t need to think of all the cases of *expansion* just deal with the **stopping case**, i.e. when both **red** and **blue** are fully expanded leaving no **uncolored** node.\n\n*The key is to imagine this **tree as graph** with parent and childrens as adjacent neighbors *\n\nThe idea is simple we need to pick a **blue** such that **red** can not expand too much : ***count(blue) > count ( red)*** , this is my **winning** condition\n\nYou can observe that if we pick a **blue** immediately next to **red** then *expansion of red is blocked* in that direction so we drastically reduce the number of reds, \n\n# **BUT**\n\n***we have three candidates for blue ( red->left , red->right & red->parent) then which one to pick?***\n\nSolution- Pick a **blue** among these three such that **sum of count** from the rest two nodes +**1** should be still **lesser** than count from the node you\'re painting **blue** \nHere look at this diagram:\n\n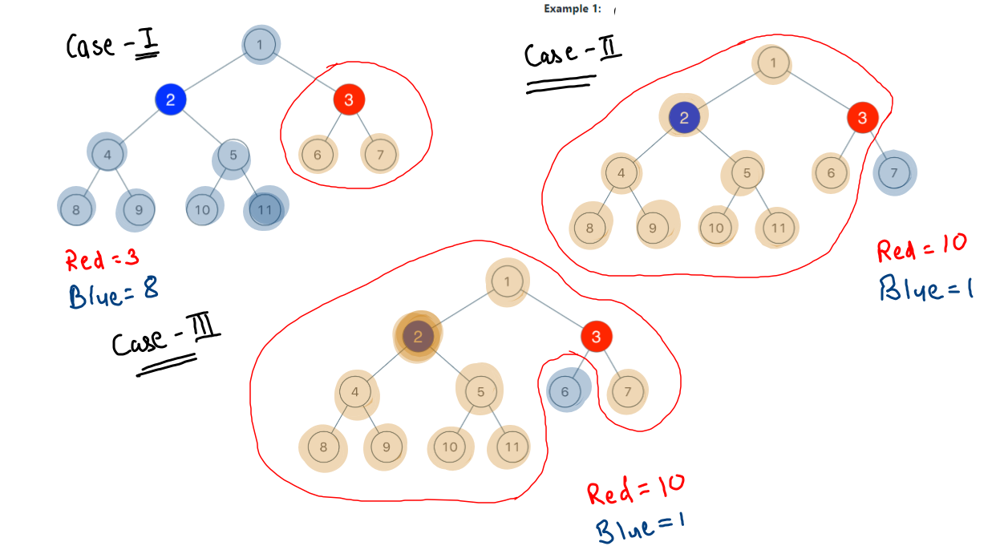\n\nThis results in **three** cases for winning:\n\n **Case1:** Pick **parent** of x as blue: *Count( left subtree) + Count( right subtree ) + 1(for x) < Count( Parent)*\n \n **Case2:** Pick **left** of x as blue: *Count( parent subtree) + Count( right subtree ) + 1< Count( Left)*\n \n **Case3:** Pick **right** of x as blue: *Count( left subtree) + Count( parent subtree ) + 1< Count( Right)*\n \n\nIf any of case becomes **true** we can return **true **\n\nelse return **false** \n\n# Code:\n\n```\nclass Solution {\npublic:\n TreeNode* rootx;\n unordered_map<int, TreeNode*> mp;\n \n \n int bfs(TreeNode* root){\n \n queue<TreeNode*> q; q.push(root);\n int count=0;\n if(!root) return 0;\n \n while(!q.empty()){\n auto curr=q.front();q.pop();\n int t=curr->val;\n curr->val=0;\n count++;\n \n if(curr->left && curr->left->val!=0 ) q.push(curr->left);\n if(curr->right && curr->right->val!=0 ) q.push(curr->right);\n if(mp[t] && mp[t]->val!=0 ) q.push(mp[t]);\n }\n \n return count;\n }\n \n void preorder(TreeNode* root,int x){\n \n if(!root) return;\n \n if(root->val==x) rootx=root;\n if(root->left) mp[root->left->val]=root;\n if(root->right) mp[root->right->val]=root;\n preorder(root->left,x);\n preorder(root->right,x);\n }\n \n bool btreeGameWinningMove(TreeNode* root, int n, int x) {\n \n preorder(root,x);\n mp[root->val]=NULL;\n \n rootx->val=0;\n int a=bfs(mp[x]);\n int b=bfs(rootx->left);\n int c=bfs(rootx->right);\n \n if(a+b+1<c) return true;\n \n if(b+c+1<a) return true;\n \n if(c+a+1<b) return true;\n \n return false;\n }\n};\n\n\n```\n\n**If you like the explanation then feel free to upvote. Cheers!!** | 3 | 0 | ['Tree', 'Breadth-First Search', 'Graph'] | 1 |
binary-tree-coloring-game | C++ Easy To Understand Solution | Recursion | Node Count | c-easy-to-understand-solution-recursion-hz6mv | \n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0) | abhinandan__22 | NORMAL | 2022-03-02T19:43:48.481941+00:00 | 2022-03-02T19:43:48.481988+00:00 | 260 | false | ```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n \n TreeNode* find_node(TreeNode* a,int x)\n {\n if(a)\n {\n if(a->val==x)\n return a;\n TreeNode* h = find_node(a->left,x);\n if(h)\n return h;\n h = find_node(a->right,x);\n return h;\n }\n return a;\n }\n \n int count_node(TreeNode* a)\n {\n if(a)\n {\n int h = count_node(a->left);\n int k = count_node(a->right);\n return h+k+1;\n }\n return 0;\n \n }\n \n bool btreeGameWinningMove(TreeNode* a, int n, int x) {\n \n TreeNode *x_node = find_node(a,x);\n \n int Left_node = count_node(x_node->left);\n int Right_node = count_node(x_node->right);\n int Upper_node = n-Left_node-Right_node-1;\n \n int y = max(Upper_node,max(Left_node,Right_node));\n \n x = n-y;\n \n if(y>x)\n return 1;\n return 0;\n \n \n }\n};\n``` | 3 | 0 | ['C'] | 0 |
binary-tree-coloring-game | C++ Recursion Solution | c-recursion-solution-by-ahsan83-bvkj | Runtime: 4 ms, faster than 82.92% of C++ online submissions for Binary Tree Coloring Game.\nMemory Usage: 11.6 MB, less than 5.05% of C++ online submissions for | ahsan83 | NORMAL | 2020-10-31T01:57:57.458205+00:00 | 2020-10-31T02:00:12.907321+00:00 | 207 | false | Runtime: 4 ms, faster than 82.92% of C++ online submissions for Binary Tree Coloring Game.\nMemory Usage: 11.6 MB, less than 5.05% of C++ online submissions for Binary Tree Coloring Game.\n\nPlayer 1 chooses Node x first which has 3 neighbor nodes (parent, left, right). \nPlayer 2 will choose one of those 3 neighbor nodes at first which has maximum childs in its subtree and all\nthe nodes of that subtree will be the count of Player 2. \nIf max node count of Player 2 is greater than n/2 then he WIN, otherwise he LOSE. \n\n```\nclass Solution {\npublic:\n \n // find neighbor nodes of node x\n void findNodes(TreeNode *root, int x, vector<TreeNode*>&neighbors)\n {\n if(!root) return;\n \n // found target node x\n if(root->val==x)\n {\n neighbors.push_back(root->left);\n neighbors.push_back(root->right);\n \n return;\n }\n \n findNodes(root->left,x,neighbors);\n findNodes(root->right,x,neighbors); \n }\n \n // count nodes of the subtree\n int countNodes(TreeNode *root)\n {\n if(!root) return 0;\n \n return countNodes(root->left) + countNodes(root->right) + 1;\n }\n \n bool btreeGameWinningMove(TreeNode* root, int n, int x) {\n \n // store neighbor node of node x\n vector<TreeNode*>neighbors;\n \n // find neighbor nodes\n findNodes(root,x,neighbors);\n \n // count left child neighbor subtree nodes\n int leftSubtreeCount = countNodes(neighbors[0]);\n \n // count right child neighbor subtree nodes \n int rightSubtreeCount = countNodes(neighbors[1]);\n \n // count parent neighbor subtree nodes\n int parentSubtreeCount = n - 1 - leftSubtreeCount - rightSubtreeCount;\n \n // return true if max node count of player 2 is greater than n/2 which player 2 can choose to WIN\n // otherwise return false means player 2 lose\n return max({leftSubtreeCount,rightSubtreeCount,parentSubtreeCount}) > n/2;\n }\n};\n``` | 3 | 0 | ['Depth-First Search', 'Recursion', 'C'] | 0 |
binary-tree-coloring-game | [C++] beats 100% in time and memory [Detailed Explanantion] | c-beats-100-in-time-and-memory-detailed-z7mt7 | \n/*\n https://leetcode.com/problems/binary-tree-coloring-game/\n \n Idea is to find the total nodes in the left, right and before node x. Then the sec | cryptx_ | NORMAL | 2020-01-13T17:01:37.433000+00:00 | 2020-01-13T17:01:37.433046+00:00 | 285 | false | ```\n/*\n https://leetcode.com/problems/binary-tree-coloring-game/\n \n Idea is to find the total nodes in the left, right and before node x. Then the second player can just\n choose to color the branch with majority nodes(> N/2). If such a node is there then he can win, otherwise not possible.\n \n TC: O(n)\n \n*/\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode(int x) : val(x), left(NULL), right(NULL) {}\n * };\n */\nclass Solution {\npublic:\n \n int postTraversal(TreeNode* root, int& x, bool& can_win, int n) {\n if(!root)\n return 0;\n \n int left = postTraversal(root->left, x, can_win, n);\n int right = postTraversal(root->right, x, can_win, n);\n \n // if the current node is the one chosen by first player\n if(root->val == x) {\n // In order for the second player to win, he needs to select a neighouring branch\n // which has more nodes than the combined nodes of other two neighbouring branches\n // +1 for including the current node\n int num_nodes_before = n - (1 + left + right);\n can_win = (num_nodes_before > left + right) || \n (left > num_nodes_before + right) ||\n (right > num_nodes_before + left);\n }\n \n // total no. of nodes int the subtree with the current node as root \n return left + right + 1;\n }\n \n bool btreeGameWinningMove(TreeNode* root, int n, int x) {\n // whether second player can win or not\n bool can_win = false;\n postTraversal(root, x, can_win, n);\n return can_win;\n }\n};\n``` | 3 | 0 | [] | 0 |
binary-tree-coloring-game | Java. 100% faster. Easy to understand | java-100-faster-easy-to-understand-by-mc-sho7 | \nclass Solution {\n \n private int countOpenNodes(TreeNode n, int selected) {\n if(n == null || n.val == selected) { return 0; }\n \n | mc1234 | NORMAL | 2019-09-11T19:10:07.111999+00:00 | 2019-09-11T19:10:07.112049+00:00 | 609 | false | ```\nclass Solution {\n \n private int countOpenNodes(TreeNode n, int selected) {\n if(n == null || n.val == selected) { return 0; }\n \n return 1 + countOpenNodes(n.left, selected) + countOpenNodes(n.right, selected);\n }\n \n private TreeNode findNode(TreeNode n, int val) {\n if(n == null || n.val == val) { return n; }\n \n TreeNode found = findNode(n.left, val);\n if(found != null) { return found; }\n \n return findNode(n.right, val); \n }\n \n public boolean btreeGameWinningMove(TreeNode root, int n, int x) {\n \n TreeNode selected = findNode(root, x);\n \n int leftCnt = countOpenNodes(selected.left, x);\n int rightCnt = countOpenNodes(selected.right, x);\n int parentCnt = n - (1 + leftCnt + rightCnt);\n \n if(parentCnt > 1 + leftCnt + rightCnt) { return true; }\n if(rightCnt > 1 + parentCnt + leftCnt) { return true; }\n if(leftCnt > 1 + parentCnt + rightCnt) { return true; }\n \n return false;\n }\n}\n``` | 3 | 0 | [] | 2 |
binary-tree-coloring-game | Java O(N) | 100% Faster Solution | java-on-100-faster-solution-by-tbekpro-d0lr | Complexity\n- Time complexity: O(N)\n\n# Code\n\nclass Solution {\n public boolean btreeGameWinningMove(TreeNode root, int n, int x) {\n TreeNode[] re | tbekpro | NORMAL | 2023-12-15T14:03:12.195467+00:00 | 2023-12-16T23:15:03.548545+00:00 | 492 | false | # Complexity\n- Time complexity: O(N)\n\n# Code\n```\nclass Solution {\n public boolean btreeGameWinningMove(TreeNode root, int n, int x) {\n TreeNode[] red = new TreeNode[1];\n findNode(root, x, red);\n int[] countLeft = new int[1], countRight = new int[1];\n countNodes(red[0].left, countLeft);\n countNodes(red[0].right, countRight);\n\n int l = countLeft[0], r = countRight[0];\n\n return l > n - l || r > n - r || l + r + 1 < n - l - r - 1; \n }\n\n private void countNodes(TreeNode node, int[] count) {\n if (node == null) return;\n \n count[0]++;\n countNodes(node.left, count);\n countNodes(node.right, count);\n }\n\n private void findNode(TreeNode node, int x, TreeNode[] res) {\n if (node == null) return;\n \n if (node.val == x) {\n res[0] = node;\n return;\n }\n \n findNode(node.left, x, res);\n findNode(node.right, x, res);\n }\n}\n``` | 2 | 0 | ['Java'] | 0 |
binary-tree-coloring-game | Java 0ms - DFS | java-0ms-dfs-by-_sikarwar-zg79 | \n Describe your first thoughts on how to solve this problem. \n\n Descre your approach to solving the problem. \n\n# Complexity\n- Time complexity: O(n)\n Add | _sikarwar_ | NORMAL | 2022-12-27T13:15:28.444240+00:00 | 2022-12-27T13:15:28.444270+00:00 | 836 | false | \n<!-- Describe your first thoughts on how to solve this problem. -->\n\n<!-- Descre your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n * TreeNode(int val) { this.val = val; }\n * TreeNode(int val, TreeNode left, TreeNode right) {\n * this.val = val;\n * this.left = left;\n * this.right = right;\n * }\n * }\n */\nclass Solution {\n private int countNodes(TreeNode root){\n if(root == null){\n return 0;\n }\n return 1 + countNodes(root.left) + countNodes(root.right);\n }\n private TreeNode findX(TreeNode root, int x){\n if(root == null || root.val == x){\n return root;\n }\n TreeNode left = findX(root.left, x);\n if(left != null){\n return left;\n }\n return findX(root.right, x);\n }\n public boolean btreeGameWinningMove(TreeNode root, int n, int x) {\n TreeNode nodeX = findX(root, x);\n int leftCount = countNodes(nodeX.left);\n int rightCount = countNodes(nodeX.right);\n return (leftCount + rightCount < n / 2) || (leftCount > n - leftCount) || (rightCount > n - rightCount);\n }\n}\n``` | 2 | 0 | ['Tree', 'Depth-First Search', 'Binary Tree', 'Java'] | 0 |
binary-tree-coloring-game | Python, DFS | python-dfs-by-swepln-q35h | Intuition\nWe have 3 different ways to choose the element that will beat opponent.\n1. Choose left sub-tree of opponent node\n2. Choose right sub-tree of oppone | swepln | NORMAL | 2022-11-20T01:17:19.036397+00:00 | 2022-11-20T01:17:19.036430+00:00 | 396 | false | # Intuition\nWe have 3 different ways to choose the element that will beat opponent.\n1. Choose left sub-tree of opponent node\n2. Choose right sub-tree of opponent node\n3. Choose parent of opponent node\n\nThen we should calculate amount of nodes in left and right sub-trees. If one of them grater than sum of others - we can win.\n\nAnother edge case when opponent choose root. In this case we can win only if amount of left and right sub-trees are different.\n\n# Complexity\n- Time complexity:\nO(N)\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def btreeGameWinningMove(self, root, n: int, x: int) -> bool:\n\n def calculateNodes(node):\n if not node:\n return 0\n \n result = 1\n \n if node.left:\n result += calculateNodes(node.left)\n if node.right:\n result += calculateNodes(node.right)\n\n return result\n\n if root.val == x:\n return calculateNodes(root.left) != calculateNodes(root.right)\n\n def dfs(node):\n if node.val == x:\n a = calculateNodes(node.left)\n b = calculateNodes(node.right)\n c = n - (a + b + 1)\n\n return a > b + c or b > a + c or c > a + b\n\n if node.left:\n result = dfs(node.left)\n if result != None:\n return result\n if node.right:\n result = dfs(node.right)\n if result != None:\n return result\n\n return None\n\n return dfs(root)\n``` | 2 | 0 | ['Python3'] | 0 |
binary-tree-coloring-game | Simple java solution with basic intuition | simple-java-solution-with-basic-intuitio-7po6 | If you carefully notice then you will observe that whichever player(player 1 or player 2) color more than half nodes will win the game, this is basic intuition | 404_coder | NORMAL | 2021-06-07T09:57:01.179882+00:00 | 2021-06-07T09:57:01.179911+00:00 | 132 | false | If you carefully notice then you will observe that whichever player(player 1 or player 2) color more than half nodes will win the game, this is basic intuition of this problem. Now given the node choosen by player 1, player 2 can choose a node either from left or from right child or it can choose parent of given node. \nSo what we will do is we will find number of nodes in left and right of node selected by player 1 and then number of nodes player2 can color if he not choose node from left and right of node choosen by player1(above nodes) = n - left nodes - right nodes -1 and if max(left nodes,right nodes,above nodes) > n/2 then player 2 will win else he will lose.\n\n\nclass Solution {\n public boolean btreeGameWinningMove(TreeNode root, int n, int x) {\n \n TreeNode x_node=find(root,x); // find node chossen by player 1\n int left_nodes=nodes(x_node.left); // number of nodes in left side\n int right_nodes=nodes(x_node.right); // number of nodes in right side\n int above_nodes=(n-left_nodes-right_nodes-1); // number of nodes above the choosen node\n \n \n int max_nodes=Math.max(above_nodes,Math.max(left_nodes,right_nodes));\n if(max_nodes>n/2)\n {\n return true;\n }\n return false;\n }\n \n public int nodes(TreeNode root)\n {\n if(root==null)\n {\n return 0;\n }\n return 1+nodes(root.left)+nodes(root.right);\n }\n public TreeNode find(TreeNode root,int x)\n {\n if(root==null)\n {\n return null;\n }\n if(root.val==x)\n {\n return root;\n }\n TreeNode left_node=find(root.left,x);\n if(left_node!=null && left_node.val==x)\n {\n return left_node;\n }\n TreeNode right_node=find(root.right,x);\n if(right_node!=null && right_node.val==x)\n {\n return right_node;\n }\n return null;\n }\n}\n\nThanks for reading :-) | 2 | 0 | [] | 0 |
binary-tree-coloring-game | Simple python O(n) solution that beats 100% | simple-python-on-solution-that-beats-100-i075 | We need to count tree sizes of children of x node. \nThen the tree size of the rest of the tree could be calculated directly from these findings.\nx_parent = n | avakatushka | NORMAL | 2020-12-05T10:47:42.254229+00:00 | 2020-12-05T10:47:42.254263+00:00 | 126 | false | We need to count **tree sizes** of children of x node. \nThen the tree **size of the rest of the tree** could be calculated directly from these findings.\nx_parent = n - x_left - x_right - 1\nIf any of the tree sizes gets the majority, it\'s possible for us to win:\ncapacity > n - capacity \n```\ndef btreeGameWinningMove(self, root, n, x):\n tree = {\'x_left\' : 0, \'x_right\' : 0, \'x_parent\' : 0}\n def dfs(node):\n if not node:\n return 0\n left = dfs(node.left)\n right = dfs(node.right)\n if node.val == x:\n tree[\'x_left\'] = left\n tree[\'x_right\'] = right\n return left + 1 + right\n dfs(root)\n \n tree[\'x_parent\'] = n - tree[\'x_left\'] - 1 - tree[\'x_right\']\n \n for capacity in tree.values():\n if capacity > n - capacity:\n return True\n return False\n```\nThis solution is O(n) time and O(n) space for recursion stack | 2 | 0 | [] | 0 |
binary-tree-coloring-game | Explained | C++ | explained-c-by-harshjoeyit-wsxx | Approach\n1. It is always best case for use if either choose y \n\na) left child of x\n\tthis case works when number of nodes in left subtree of x are > n/2\n\n | harshjoeyit | NORMAL | 2020-08-21T14:04:24.565810+00:00 | 2020-08-21T14:05:03.834579+00:00 | 188 | false | > Approach\n1. It is always best case for use if either choose y \n\na) left child of x\n\tthis case works when number of nodes in left subtree of x are > n/2\n\nb) right chilf of x\n\tthis case works when number of nodes in right subtree of x are > n/2\n\nc) parent of x\n\tthis case works when number in nodes in tree of x < (n+1)/2\n\t\n2. If we satisfy any of the three condition then we return true\n3. We might not even satisty any of the three condition, then we return false;\n\t\n> Algorithm\n\n```\n\tint go(TreeNode *root) {\n if(!root) {\n return 0;\n }\n return 1 + go(root->left) + go(root->right);\n }\n \n int l, r;\n \n void findNode(TreeNode *root, int x) {\n if(!root) {\n return;\n }\n if(root->val == x) {\n l = go(root->left);\n r = go(root->right);\n return;\n }\n findNode(root->left, x);\n findNode(root->right, x);\n }\n \n bool btreeGameWinningMove(TreeNode* root, int n, int x) {\n if(n == 1) {\n return false;\n }\n \n l = r = 0;\n\t\t\n\t\t// find the root and count the left and right children\n findNode(root, x);\n \n\t\t// case 1 and 2 \n if(l > n/2 || r > n/2) {\n return true;\n }\n \n\t\t// case 3\n return (l + r + 1) < (n+1)/2;\n }\n``` | 2 | 0 | [] | 0 |
binary-tree-coloring-game | Java Recursion | java-recursion-by-kylinzhuo-i8fo | \n\n\nLet\'s assume the first player took Node 3 in the above tree. \n\nThere are 3 areas to consider: \n- {Node 3\'s left sub tree} (area 1)\n- {Node 3\'s rig | kylinzhuo | NORMAL | 2020-04-04T04:55:13.036821+00:00 | 2020-04-13T07:12:00.138082+00:00 | 208 | false | 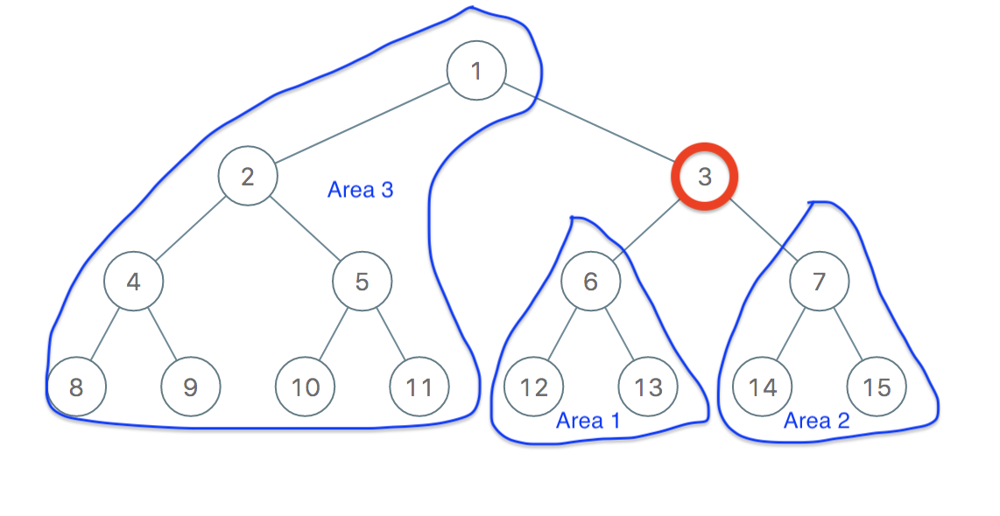\n\n\nLet\'s assume the first player took Node 3 in the above tree. \n\nThere are 3 areas to consider: \n- {Node 3\'s left sub tree} (area 1)\n- {Node 3\'s right sub tree} (area 2)\n- {whole tree - subtree with Node 3 as the root} (area 3)\n\nIf player 2 takes Node 3\'s parent node, it means Area 3 cannot be chosen by player 1 anymore, that is to say, It has been RESERVED for player 2 to finish choosing. In this way, Area 1 and 2 are all belonging to Player 1 because of the rule.\n\nIf player 2 takes Node 3\' child node, either Node 6 or Node 7, then Area 3 belongs to Player 1. In addition, if Player 2 chooses Area 1, Area 2 goes to **Player 1** (*p.s. thanks @leetcodenob for pointing the typo out, it was wrong as Player 2*); else if Player 2 chooses Area 2, Area 1 will belong to Player 1. \n\n\n\n\n```java\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode(int x) { val = x; }\n * }\n */\nclass Solution {\n \n int left; // Area 1\n int right; // Area 2\n \n public boolean btreeGameWinningMove(TreeNode root, int n, int x) {\n count(root, x);\n int p = n - (this.left + this.right + 1); // Area 3\n return Math.max(p, Math.max(this.left, this.right)) > n/2;\n }\n \n int count(TreeNode node, int x) {\n if (node == null) {\n return 0;\n }\n int left = count(node.left, x);\n int right = count(node.right, x);\n\t\t\n if (node.val == x) { // assign the value to Area 1 and Area 2\n this.left = left;\n this.right = right;\n }\n return 1 + left + right;\n }\n}\n``` | 2 | 0 | [] | 2 |
binary-tree-coloring-game | Beats 100% 100% - With Explanation - Java | beats-100-100-with-explanation-java-by-b-qo7j | \nidea is simple,\nsecond player has 3 options to block player one,\n1. Block moving to its left child\n2. Block moving to its right child\n3. Block moving to i | bkatwal | NORMAL | 2020-02-03T11:59:20.339917+00:00 | 2020-02-03T12:00:13.425923+00:00 | 187 | false | \nidea is simple,\nsecond player has 3 options to block player one,\n1. Block moving to its left child\n2. Block moving to its right child\n3. Block moving to its parent\n\nAs player one started first the win is only possible if you have more than n/2 nodes in either one of them, beacuse player one can chose again after you pick.\n\nAlgo\n1. For a node x, get count of left and right -> post order will do\n2. Num of nodes in parent side = n - (leftCount + rightCount) - 1\n3. If max(leftCount, rightCount, parentCount) > n/2 -> win possible, return tru\n\nSo, we need a node that has more than n/2 nodes to win \n\n```\nclass Solution {\n int leftCount, rightCount;\n\n public boolean btreeGameWinningMove(TreeNode root, int n, int x) {\n count(root, x);\n return Math.max(Math.max(leftCount, rightCount), n - leftCount - rightCount - 1) > n / 2;\n }\n\n private int count(TreeNode node, int x) {\n if (node == null)\n return 0;\n int l = count(node.left, x);\n int r = count(node.right, x);\n if (node.val == x) {\n leftCount = l;\n rightCount = r;\n }\n return l + r + 1;\n }\n\n}\n``` | 2 | 0 | [] | 0 |
binary-tree-coloring-game | Java Solution with explanation | java-solution-with-explanation-by-pulkit-h2s8 | My approach is a bit lengthy.\nI broke down the problem into 2 subcases.\n\nCASE 1\nWe calcaulate the number of nodes in the subtree rooted at X, and if the num | pulkitjainn | NORMAL | 2019-09-12T06:37:08.133765+00:00 | 2019-09-12T06:39:31.088842+00:00 | 415 | false | My approach is a bit lengthy.\nI broke down the problem into 2 subcases.\n\n**CASE 1**\nWe calcaulate the number of nodes in the subtree rooted at `X`, and if the number of nodes in in this subtree is greater then the count of rest of the nodes in the tree we return false.\n\n**CASE 2**\nIn this approach, we calcaculate the number of nodes in the left and right sub tree of the tree rooted at `X`, now comes the tricky part, we would choose the `maximumOf(leftSubtreeCount, rightSubtreeCount)` as `Y`. Now since `Y` is one of the child of `X`, so the nodes above `X` would be coloured by `X`. In short,\n```\nCount of X = mininmumOf(leftSubtreeCount, rightSubtreeCount) + rest of the nodes in tree\nCounf of Y = maximumOf(leftSubtreeCount, rightSubtreeCount)\n\nif(Count of X < Count of Y){\n\treturn true;\n}\n```\nIn the end with return the `OR` of the cases.\n\n**CODE**\n```\nclass Solution { \n public boolean btreeGameWinningMove(TreeNode root, int n, int x) {\n \n // Case 1\n TreeNode nodex = findX(root, x);\n int countofx = countNodes(nodex);\n int countofy = n - countofx;\n boolean case1 = countofy>countofx;\n \n //Case 2\n boolean case2 = helper(root,x,n,0);\n\n return case1 || case2; \n }\n \n \n public static boolean helper(TreeNode root, int x, int n, int count){\n if(root==null){\n return false;\n } \n if(root.val == x){\n int leftsubtree = countNodes(root.left);\n int rightsubtree = countNodes(root.right);\n \n int temp = Math.min(rightsubtree,leftsubtree) + n-(rightsubtree+leftsubtree+1);\n return temp < Math.max(leftsubtree,rightsubtree);\n } \n boolean l = helper(root.left, x, n, count+1);\n boolean r = helper(root.right, x, n, count+1);\n return l||r;\n }\n \n //Method to find the node with value X\n public static TreeNode findX(TreeNode root, int x){\n if(root==null){\n return null;\n } \n if(root.val == x){\n return root;\n }\n TreeNode lft = findX(root.left,x);\n if(lft!=null){\n return lft;\n }\n return findX(root.right,x);\n }\n \n \n //Method to count number of nodes\n public static int countNodes(TreeNode root){\n if(root==null){\n return 0;\n }\n return 1+ countNodes(root.left)+countNodes(root.right);\n } \n}\n``` | 2 | 1 | [] | 0 |
binary-tree-coloring-game | python | python-by-cybernanana-8v2k | \nclass Solution(object):\n def btreeGameWinningMove(self, root, n, x):\n """\n :type root: TreeNode\n :type n: int\n :type x: in | cybernanana | NORMAL | 2019-08-14T02:10:07.675193+00:00 | 2019-08-14T02:10:07.675227+00:00 | 277 | false | ```\nclass Solution(object):\n def btreeGameWinningMove(self, root, n, x):\n """\n :type root: TreeNode\n :type n: int\n :type x: int\n :rtype: bool\n """\n self.left = None\n self.right = None\n self.helper(root, x)\n parent = n - 1 - self.left - self.right\n return max(parent, max(self.left, self.right)) > n / 2\n \n def helper(self, root, x):\n if not root:\n return 0\n l = self.helper(root.left, x)\n r = self.helper(root.right, x)\n if root.val == x:\n self.left = l\n self.right = r\n return 1 + r + l\n``` | 2 | 0 | ['Python3'] | 0 |
binary-tree-coloring-game | [C++] Simple strategy (and some DFS as an afterthought) | c-simple-strategy-and-some-dfs-as-an-aft-6fqt | The optimal strategy is to make y either the parent of x, or a child. Any other choice is suboptimal, as x could always first grow their territory towards you, | mhelvens | NORMAL | 2019-08-04T10:23:24.360101+00:00 | 2019-08-04T10:23:24.360131+00:00 | 154 | false | The optimal strategy is to make `y` either the parent of `x`, or a child. Any other choice is suboptimal, as `x` could always first grow their territory _towards_ you, stealing points that you would otherwise have blocked off.\n\n* If `y` is a child, it gets the number of nodes in that sub-tree, and `x` gets all other nodes.\n* If `y` is the parent, `x` gets the number of nodes in its own sub-tree, and `y` gets all other nodes.\n\nThe code below just tests whether `x` comes out ahead in any of those three scenarios. There are two utility-methods employing DFS to find and count nodes.\n\n```C++\nclass Solution {\npublic:\n bool btreeGameWinningMove(TreeNode* root, int n, int x) {\n auto xNode = getNode(root, x);\n int xLeftCount = countNodes(xNode->left);\n int xRightCount = countNodes(xNode->right);\n\tint xCount = 1 + xLeftCount + xRightCount;\n return xLeftCount > n/2 ||\n xRightCount > n/2 ||\n\t\t xNode != root && xCount <= n/2;\n }\n \nprivate:\n TreeNode* getNode(TreeNode* root, int val) {\n if (!root) return nullptr;\n if (root->val == val) return root;\n auto left = getNode(root->left, val);\n if (left) return left;\n return getNode(root->right, val);\n }\n \n int countNodes(TreeNode* root) {\n if (root) return 1 + countNodes(root->left) + countNodes(root->right);\n else return 0;\n }\n};\n``` | 2 | 1 | ['Depth-First Search', 'C'] | 0 |
binary-tree-coloring-game | Simple Cpp solution passes all test cases | simple-cpp-solution-passes-all-test-case-2clr | When the first player choses a node there are three options available for the second player.\nHe can either choose the parent or left child or right child. By d | player007 | NORMAL | 2019-08-04T04:30:30.552459+00:00 | 2019-08-04T14:38:26.140583+00:00 | 118 | false | When the first player choses a node there are three options available for the second player.\nHe can either choose the parent or left child or right child. By doing so he is blocking the chosen path for the first player as in a tree there is only one path between two nodes.\nSo what we can do is to chose the node out of three say lv(left child), rv (right child), or par(parent) and calculate the no. of nodes in that subtree. In doing so we only need lv and rv as par can be calculated using par =n - lv - rv - 1.\nNow we will choose the max among the three value if our max comes out to be greater than n/2\nthen it is possible for us to win the game.\n\nint count(TreeNode* root) {\n if(!root)\n return 0;\n return count(root->left) + count(root->right) + 1;\n }\n \n TreeNode* find(TreeNode* root, int x) {\n if(!root)\n return NULL;\n if(root->val == x)\n return root;\n TreeNode* lv = find(root->left, x);\n TreeNode* rv = find(root->right, x);\n return lv ? lv : rv;\n }\n \n bool btreeGameWinningMove(TreeNode* root, int n, int x) {\n if(n == 1)\n return false;\n TreeNode* temp = find(root, x);\n int lv = count(temp->left);\n int rv = count(temp->right);\n int par = n - lv - rv - 1;\n int mx = max(lv, max(rv, par));\n cout << lv << " " << rv << " " << par << " mx";\n if(mx > n-mx)\n return true;\n return false;\n } | 2 | 0 | [] | 0 |
binary-tree-coloring-game | Simple Python, Easy to understand | simple-python-easy-to-understand-by-davy-jtm8 | The node selected by the first person divides the tree by three parts: left, right, parent. We can only choose one region.\n\nclass Solution:\n def btreeGame | davyjing | NORMAL | 2019-08-04T04:06:53.470328+00:00 | 2019-08-04T04:07:07.714527+00:00 | 210 | false | The node selected by the first person divides the tree by three parts: left, right, parent. We can only choose one region.\n```\nclass Solution:\n def btreeGameWinningMove(self, root: TreeNode, n: int, x: int) -> bool:\n self.loc = None\n def dfs(node):\n if not node:\n return\n if node.val == x:\n self.loc = node\n return\n else:\n dfs(node.left)\n dfs(node.right)\n dfs(root)\n self.l = 0\n self.r = 0\n def cnt_l(node):\n if node:\n self.l += 1\n cnt_l(node.left)\n cnt_l(node.right)\n def cnt_r(node):\n if node:\n self.r += 1\n cnt_r(node.left)\n cnt_r(node.right)\n cnt_l(self.loc.left)\n cnt_r(self.loc.right)\n t = n - 1 -self.l - self.r\n return max(t,max(self.l,self.r)) > n/2\n``` | 2 | 2 | [] | 0 |
binary-tree-coloring-game | Python based on left, right and above | python-based-on-left-right-and-above-by-cxjrm | The first step is to calculate the size of the subtree rooted at each node.\nOnce we have this info, it boils down to we as Player 2 choosing the node, that is | Cubicon | NORMAL | 2019-08-04T04:02:46.019858+00:00 | 2019-08-04T04:09:49.199920+00:00 | 234 | false | The first step is to calculate the size of the subtree rooted at each node.\nOnce we have this info, it boils down to we as Player 2 choosing the node, that is either parent of X, or left child of X or right child of X.\n\nLets definte "Above" = number of nodes that are not in my subtree.\n\nIf we choose the parent of X =. we can color everythin Above, while X can color his left and right subtree.\nIf we choose X\'s left subtree, then X can choose his right subtree + Above\nIf we choose X\'s right subtree, then X can shoose his left subtree + Above.\n\nFinally we see if we can win, by choosing the best of the above 3 options.\n\n```\ndef btreeGameWinningMove(self, root: TreeNode, n: int, x: int) -> bool:\n def traverse(node):\n if not node: return 0\n res = 1 + traverse(node.left) + traverse(node.right)\n d[node.val] = res\n return res\n \n def find(node, above):\n if not node: return False\n leftval = node.left.val if node.left else 0\n rightval = node.right.val if node.right else 0\n if node.val == x:\n return above > d[node.val] or d[rightval] > above + d[leftval] or d[leftval] > above + d[rightval]\n return find(node.left, 1 + above + d[rightval]) or find(node.right, 1 + above + d[leftval])\n \n d = defaultdict(int)\n traverse(root)\n return find(root, 0)\n``` | 2 | 2 | [] | 1 |
binary-tree-coloring-game | Java Solution | java-solution-by-zqin9-wkaf | \n\t// value of left node of x.\n int left = 0;\n // value of right node of x.\n int right = 0;\n public boolean btreeGameWinningMove(TreeNode root, | zqin9 | NORMAL | 2019-08-04T04:02:39.766601+00:00 | 2019-08-04T04:05:14.307477+00:00 | 234 | false | ```\n\t// value of left node of x.\n int left = 0;\n // value of right node of x.\n int right = 0;\n public boolean btreeGameWinningMove(TreeNode root, int n, int x) {\n if (root.left == null && root.right == null) {\n return false;\n }\n int[] numOfChildren = new int[n];\n traverse(root, numOfChildren, x);\n if ((n - (numOfChildren[x - 1])) > (numOfChildren[x - 1])) {\n\t\t\t// We can choose the nodes that do not belong to subtree of x.\n return true;\n } else {\n\t\t\t// We can choose one of the subtrees of x.\n if (left != 0 && numOfChildren[left - 1] > n - numOfChildren[left - 1]) {\n return true;\n }\n if (right != 0 && numOfChildren[right - 1] > n - numOfChildren[right - 1]) {\n return true;\n }\n }\n return false;\n }\n\n // Find the number of nodes for each subtree.\n private int traverse(TreeNode root, int[] numOfChildren, int x) {\n if (root == null) {\n return 0;\n }\n if (root.val == x) {\n if (root.left != null) {\n left = root.left.val;\n }\n if (root.right != null) {\n right = root.right.val;\n }\n }\n int left = traverse(root.left, numOfChildren, x);\n int right = traverse(root.right, numOfChildren, x);\n numOfChildren[root.val - 1] = left + right + 1;\n return left + right + 1;\n }\n``` | 2 | 1 | [] | 0 |
binary-tree-coloring-game | C++ O(N) recursive | c-on-recursive-by-murkyautomata-y1sl | Optimal strategy is choosing a node adjacent to your opponents to claim the region beyond it.\n\nclass Solution {\npublic:\n int nLeft, nRight, nAbove, y;\n | murkyautomata | NORMAL | 2019-08-04T04:02:37.756648+00:00 | 2019-08-04T04:02:37.756687+00:00 | 248 | false | Optimal strategy is choosing a node adjacent to your opponents to claim the region beyond it.\n```\nclass Solution {\npublic:\n int nLeft, nRight, nAbove, y;\n bool btreeGameWinningMove(TreeNode* root, int n, int x) {\n nLeft=0, nRight=0, nAbove=0, y=x;\n count(root);\n return (\n nLeft > nRight + nAbove\n || nRight > nLeft + nAbove\n || nAbove > nLeft + nRight \n );\n }\n \n void count(TreeNode* node){\n if(!node) return;\n \n if(node->val==y){\n countBelow(node->left, nLeft );\n countBelow(node->right, nRight);\n return;\n }\n ++nAbove;\n count(node->left);\n count(node->right);\n }\n \n void countBelow(TreeNode* node, int &t){\n if(!node) return;\n \n ++t;\n countBelow(node->left, t);\n countBelow(node->right, t);\n }\n};\n``` | 2 | 1 | [] | 0 |
binary-tree-coloring-game | simple JAVA O(n) solution with explanation | simple-java-on-solution-with-explanation-nc7d | Given a red node the best chance we can win is to blue-color its parent or either of its children.\nWhy?\nBecause by doing so we block the first player in one o | may6 | NORMAL | 2019-08-04T04:01:18.623591+00:00 | 2019-08-04T04:35:56.350279+00:00 | 361 | false | Given a red node the best chance we can win is to blue-color its parent or either of its children.\nWhy?\nBecause by doing so we block the first player in one of the three directions. We hence take all the rest of the nodes as our own. \nAny other options can\'t beat these three. A simple proof of condradiction can prove this arguement.\n\nSo we simply calculate the score in the three scenerios and check if any of them can win.\n```\nclass Solution {\n public boolean btreeGameWinningMove(TreeNode root, int n, int x) {\n TreeNode red = find(root, x);\n int leftNum = count(red.left);\n int rightNum = count(red.right);\n int parentNum = n - leftNum - rightNum - 1;\n if(leftNum > n - leftNum || rightNum > n - rightNum || parentNum > n - parentNum) {\n return true;\n } else {\n return false;\n }\n }\n private TreeNode find(TreeNode root, int x) {\n if(root == null) {\n return null;\n }\n if(root.val == x) {\n return root;\n } else {\n TreeNode left = find(root.left, x);\n TreeNode right = find(root.right, x);\n if(left != null) {\n return left;\n }\n if(right != null) {\n return right;\n }\n return null;\n }\n }\n private int count(TreeNode red) {\n if(red == null) {\n return 0;\n }\n return 1 + count(red.left) + count(red.right);\n }\n}\n``` | 2 | 1 | [] | 1 |
binary-tree-coloring-game | Python - Recursive Solution ✅ | python-recursive-solution-by-itsarvindhe-wiad | The idea is to keep track of the parent nodes of each node first. That will be required when we have to traverse towards the top of a node.\n\nThen, we will che | itsarvindhere | NORMAL | 2024-06-05T05:24:59.383142+00:00 | 2024-06-05T05:26:40.257844+00:00 | 111 | false | The idea is to keep track of the parent nodes of each node first. That will be required when we have to traverse towards the top of a node.\n\nThen, we will check how many nodes each subtree has which has root as the node which is the neighbor of the node that "x" selects initially.\n\n\n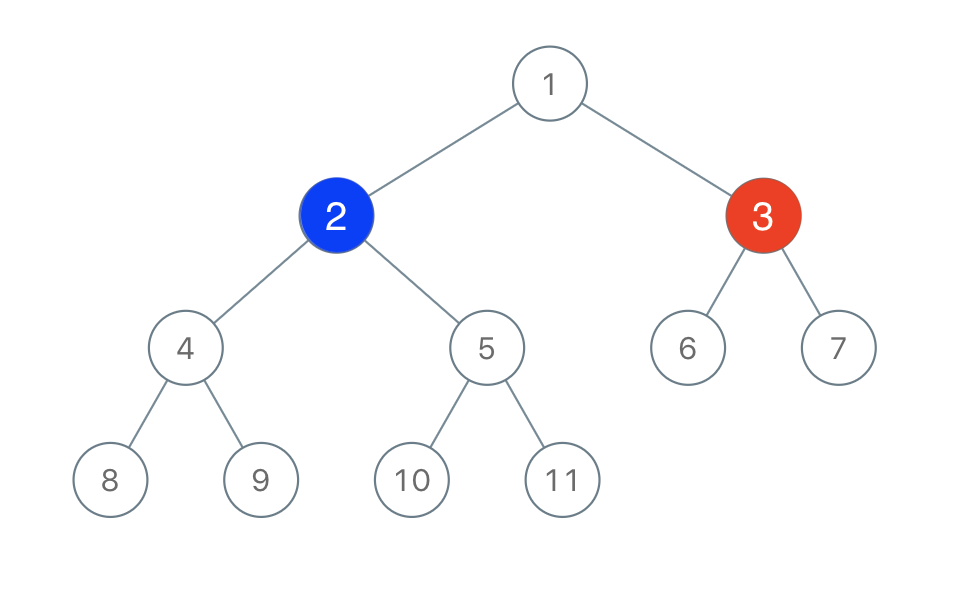\n\n\nFor example, if in the above example, "x" selects the node "3" initially, then "y" has three choices. It can either select node "1" or it can select node "6" or it can select node "7".\n\nThe reason why we want "y" to select neighbors of node "3" is because that will ensure that "y" will get that entire subtree to itself and hence all the nodes. So, if we know the count of nodes in each of these three subtrees rooted at "1", "6" and "7", we can know if "y" has a chance to win or not.\n\nFor example, for the tree with root as "1", the number of nodes are 8 (1,2,4,5,8,9,10,11)\nFor the tree with root as "6", the number of nodes are 1 (6)\nFor the tree with root as "7", the number of nodes are 1 (7)\n\nAnd we see that one subtree has more nodes than other two. It means, if "y" selects the root of this first subtree, then it ensures that "y" will win. Because then, "y" will get all the "8" nodes to itself, whereas "x" will get only 2 more nodes.\n\nAnd that\'s the whole idea.\n\n```\nclass Solution:\n \n \n # To get the data about parent nodes\n def getParentNodes(self, root, parent, node1, x, parentNodes):\n \n # Base Case\n if not root: return\n \n # Update the parent node\n if parent: parentNodes[root] = parent\n \n if root.val == x: node1[0] = root\n \n # Traverse left\n self.getParentNodes(root.left, root, node1, x, parentNodes)\n \n # Traverse right\n self.getParentNodes(root.right, root, node1, x, parentNodes)\n \n # Helper function to count nodes in a tree rooted at "root"\n def count(self, root, node1, parentNodes, visited):\n \n # Base Case\n if not root or root == node1 or root in visited: return 0\n \n # Add to the visited set\n visited.add(root)\n \n # Traverse top\n topCount = 0\n if root in parentNodes: \n topCount = self.count(parentNodes[root], node1, parentNodes, visited)\n \n # Traverse left\n leftCount = self.count(root.left, node1, parentNodes, visited)\n \n # Traverse right\n rightCount = self.count(root.right, node1, parentNodes, visited)\n \n # Return the total count\n return topCount + leftCount + 1 + rightCount\n \n def btreeGameWinningMove(self, root: Optional[TreeNode], n: int, x: int) -> bool:\n \n # To keep track of the parent nodes\n parentNodes = {}\n \n # Also get the node that first player selected\n node1 = [None]\n \n # Traverse the tree and get information about parent nodes\n self.getParentNodes(root, None, node1, x, parentNodes)\n \n # Count of nodes in the subtree with root = parent of node1 (if it is not root itself)\n countTop = 0\n if node1[0] in parentNodes: countTop = self.count(parentNodes[node1[0]], node1[0], parentNodes, set())\n \n # Count of nodes in the subtree with root = left child of node1 (if it exists)\n countLeft = self.count(node1[0].left, node1[0], parentNodes, set())\n \n # Count of nodes in the subtree with root = right child of node1( (if it exists)\n countRight = self.count(node1[0].right, node1[0], parentNodes, set())\n \n # The second player can only win if among all the three subtrees around the node that "x" has chosen,\n # One subtree has more nodes than the other two\n return countTop > countLeft + countRight or countLeft > countTop + countRight or countRight > countTop + countLeft\n``` | 1 | 0 | ['Tree', 'Depth-First Search', 'Recursion', 'Binary Tree', 'Python3'] | 0 |
binary-tree-coloring-game | Simple Explanation with example in Java | simple-explanation-with-example-in-java-jvj0x | Intuition\n Describe your first thoughts on how to solve this problem. \nIn the case where the game goes until all nodes are selected, you need n/2+1 nodes to w | pdube | NORMAL | 2024-04-14T23:38:19.087395+00:00 | 2024-04-14T23:38:19.087412+00:00 | 68 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIn the case where the game goes until all nodes are selected, you need `n/2+1` nodes to win.\n\nBased on the opponent\'s choice, you can select 3 options: the parent, the left branch or the right branch. If there is one of those choices that contains at least the number of nodes to win, it is possible for you to win. If not, it isn\'t possible.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFirst, walk the Tree to find the opponent\'s choice. Then count the nodes of each child branch. Compare the number of nodes with the number of nodes to win (`n/2+1`) to determine if it\'s possible for you to win.\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n * TreeNode(int val) { this.val = val; }\n * TreeNode(int val, TreeNode left, TreeNode right) {\n * this.val = val;\n * this.left = left;\n * this.right = right;\n * }\n * }\n */\nclass Solution {\n\n public boolean btreeGameWinningMove(TreeNode root, int n, int x) {\n //find opponent max potential plays\n TreeNode opponentNode = find(root, x);\n int left = count(opponentNode.left);\n int right = count(opponentNode.right);\n\n // need at least n/2 + 1 nodes to win\n int countToWin = n/2+1;\n //if a child branch has enough nodes to win, select child branch and win\n if(left >= countToWin || right >= countToWin) return true;\n //if opponent\'s child branches do not have to win, select parent and win\n if(left + right + 1 < countToWin) return true;\n return false;\n }\n\n public int count(TreeNode node){\n if(node == null) {\n return 0;\n }\n int l = count(node.left);\n int r = count(node.right);\n return 1 + l + r;\n }\n\n public TreeNode find(TreeNode node, int target) {\n if(node == null) return null;\n \n if(node.val == target) {\n return node;\n }\n\n TreeNode l = find(node.left, target);\n if(l != null) {\n return l;\n }\n TreeNode r = find(node.right, target);\n if(r != null) {\n return r;\n }\n return null;\n }\n\n}\n``` | 1 | 0 | ['Java'] | 0 |
binary-tree-coloring-game | Block Corona | C++ | Easy to understand | block-corona-c-easy-to-understand-by-son-tz5j | Intuition\n Describe your first thoughts on how to solve this problem. \nBlock Corona\n\n# Approach\n Describe your approach to solving the problem. \nUnderstan | sonitish | NORMAL | 2023-12-19T17:50:49.159462+00:00 | 2023-12-19T17:52:56.337726+00:00 | 203 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nBlock Corona\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUnderstand it like red is corona and it can spread in 3 direction(upper, leftBottom, rightBottom) and you can block it\'s any one direction and you have to minimize the spread so minimum people die which side you will block?\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n int countNode(TreeNode *root, TreeNode *obstacle){\n if(root == NULL || root == obstacle) return 0;\n int l = countNode(root->left, obstacle);\n int r = countNode(root->right, obstacle);\n return l + r + 1;\n }\n TreeNode *findXNode(TreeNode *root, int x){\n if(root == NULL) return NULL;\n if(root->val == x) return root;\n TreeNode *l = findXNode(root->left,x);\n TreeNode *r = findXNode(root->right,x);\n if(l != NULL) return l;\n if(r != NULL) return r;\n return NULL;\n }\n bool btreeGameWinningMove(TreeNode* root, int n, int x) {\n TreeNode *xNode = findXNode(root, x);\n int p1 = countNode(xNode->left, NULL);\n int p2 = countNode(xNode->right, NULL);\n int p3 = countNode(root,xNode);\n if(p1 > p2 && p1 > p3){ // i am assuming i will block p1 dir\n return p1 > p2 + p3;\n }\n if(p2 > p1 && p2 > p3){ i am assuming i will block p2 dir\n return p2 > p1 + p3;\n }\n if(p3 > p1 && p3 > p2){ i am assuming i will block p3 dir\n return p3 > p1 + p2;\n }\n return false;\n }\n};\n``` | 1 | 0 | ['C++'] | 2 |
binary-tree-coloring-game | Boring ||Easy||beats 100% ,0ms || left, right, parent | boring-easybeats-100-0ms-left-right-pare-7wxk | Intuition\n Describe your first thoughts on how to solve this problem. \njust 3 ways\npick leftsubtree\npick rightsubtree\npick parent node\n# Approach\n Descri | vikas_dor | NORMAL | 2023-11-29T09:07:38.525633+00:00 | 2023-11-29T09:07:38.525662+00:00 | 216 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\njust 3 ways\npick leftsubtree\npick rightsubtree\npick parent node\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(H)\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n\n int getsubtree(TreeNode* root, int &key, int &left, int &right, int &cur ){\n if(root == NULL) return 0;\n\n int lefty = getsubtree(root->left, key, left, right, cur);\n int righty = getsubtree(root->right, key, left, right, cur);\n if(root->val == key){\n left = lefty;\n right = righty;\n cur = lefty + righty+1;\n } \n\n\n return lefty + righty+1;\n }\n\n //3 options pick any of two child or its parent\n bool btreeGameWinningMove(TreeNode* root, int n, int x) {\n int leftchild_subtree = -1;\n int rightchild_subtree = -1;\n int cursubtree = -1;\n\n getsubtree(root, x, leftchild_subtree, rightchild_subtree, cursubtree);\n\n if(leftchild_subtree > n-leftchild_subtree){\n return true;\n }\n if(rightchild_subtree > n-rightchild_subtree){\n return true;\n }\n if(n - cursubtree > cursubtree){\n return true;\n }\n\n return false;\n\n }\n};\n``` | 1 | 0 | ['Binary Tree', 'C++'] | 0 |
binary-tree-coloring-game | simple python dfs beats 98% solution | simple-python-dfs-beats-98-solution-by-p-7is8 | We first build a undirectd acyclic graph \nAs player 1 choose a node first, the only chance for player 2 to win is to choose a children of node with value x , w | Pseudo_intelligent | NORMAL | 2023-01-16T00:52:02.562754+00:00 | 2023-01-16T00:52:02.562784+00:00 | 119 | false | ***We first build a undirectd acyclic graph \n*As player 1 choose a node first, the only chance for player 2 to win is to choose a children of node with value x , which are \'chances\' . We always choose node next to player 1\'s node, major reason is only \none edge between 2 nodes, this act like a \'separator\'.\n We know that n is always odd, as if n is even, player 2 always can win, as player 2 can choose a neighbour node which partites the graph into equal number of nodes (at minimum), and player 1 will always run out of node first \n We hope the number of nodes in the sub tree, \'chances\', at least greater than (n-1)/2 in order to win player 1.\n Choosing the closest neighbour node to player 1 node in a tree always guarantee to maximize your chance of winning***\n\n```\n\nclass Solution:\n def build_graph(self,rt,parent):\n if rt:\n if parent:\n self.graph[rt.val].add(parent.val)\n if rt.left:\n self.graph[rt.val].add(rt.left.val)\n if rt.right:\n self.graph[rt.val].add(rt.right.val)\n self.build_graph(rt.left,rt)\n self.build_graph(rt.right,rt)\n return \n \n def dfs_node(self,node,visited):\n if node:\n visited.add(node)\n nc = 1\n for neighbour in self.graph[node]:\n if neighbour not in visited:\n nc += self.dfs_node(neighbour,visited)\n return nc\n else:\n return 0\n \n def btreeGameWinningMove(self, root: Optional[TreeNode], n: int, x: int) -> bool:\n self.graph = defaultdict(lambda:set())\n self.build_graph(root,None)\n for chances in self.graph[x]:\n node_counts = self.dfs_node(chances,set([x]))\n if node_counts > (n-1)/2:\n return True\n return False | 1 | 0 | [] | 0 |
binary-tree-coloring-game | C++ : 0 ms, faster than 100.00% of C++ online submissions for Binary Tree Coloring Game. | c-0-ms-faster-than-10000-of-c-online-sub-h7cm | \nclass Solution {\npublic:\n TreeNode *chosen = NULL;\n \n bool btreeGameWinningMove(TreeNode* root, int n, int x) {\n preorder(root , x);\n | sonud | NORMAL | 2022-08-16T05:09:21.329092+00:00 | 2022-08-16T05:09:21.329139+00:00 | 327 | false | ```\nclass Solution {\npublic:\n TreeNode *chosen = NULL;\n \n bool btreeGameWinningMove(TreeNode* root, int n, int x) {\n preorder(root , x);\n \n int leftnodes = countNodes(chosen -> left);\n int rightnodes = countNodes(chosen -> right);\n int upNodes = n - (leftnodes + rightnodes) - 1;\n\n if((leftnodes + rightnodes) < upNodes || (leftnodes + upNodes) < rightnodes || (rightnodes + upNodes) < leftnodes){\n return true;\n }\n \n return false;\n \n }\n \n int countNodes(TreeNode *root){\n if(root == NULL) return 0;\n \n return 1 + countNodes(root -> left) + countNodes(root -> right);\n }\n \n void preorder(TreeNode *root , int x){\n if(root == NULL){\n return;\n }\n \n if(root -> val == x){\n chosen = root;\n return;\n }\n preorder(root -> left , x);\n preorder(root -> right , x);\n }\n};\n``` | 1 | 0 | ['Depth-First Search', 'C'] | 0 |
binary-tree-coloring-game | C++ solution 100% better Using Recursion | c-solution-100-better-using-recursion-by-05rk | class Solution {\npublic:\n\n int total_descent(TreeNode root)\n {\n \n if(root==NULL)\n {\n return 0;\n }\n els | dippatel11 | NORMAL | 2022-07-15T09:13:15.323846+00:00 | 2022-07-15T09:13:15.323889+00:00 | 129 | false | class Solution {\npublic:\n\n int total_descent(TreeNode* root)\n {\n \n if(root==NULL)\n {\n return 0;\n }\n else if(root->left==NULL&&root->right==NULL)\n {\n return 1;\n }\n else\n {\n int ans=0;\n ans+=total_descent(root->left);\n ans+=total_descent(root->right);\n return ans+1;\n }\n \n \n \n }\n \n bool findx(TreeNode* root,int n,int x)\n {\n if(root==NULL)\n {\n return false;\n }\n if(root->val==x)\n {\n \n \n int l=total_descent(root->left);\n int r=total_descent(root->right);\n int u=n-l-r-1;\n \n if((l<(u+r+1))&&(r<(u+l+1)&&(u<l+r+1)))\n {\n return false;\n }\n else\n {\n return true;\n }\n \n } \n else\n {\n \n bool l=findx(root->left,n,x);\n bool r=findx(root->right,n,x);\n return l||r; \n }\n }\n \n bool btreeGameWinningMove(TreeNode* root, int n, int x) \n {\n \n if(root->val==x)\n {\n int l=total_descent(root->left);\n int r=total_descent(root->right);\n \n if(l==r)\n {\n return false;\n }\n else{\n return true;\n }\n }\n \n return findx(root,n,x);\n \n }\n \n}; | 1 | 0 | [] | 1 |
binary-tree-coloring-game | A java starightforward and stepwise solution(comments included) || 0ms | a-java-starightforward-and-stepwise-solu-xybe | class Solution {\n public boolean btreeGameWinningMove(TreeNode root, int n, int x) {\n TreeNode red=getNode(root,x); //getting the x node\n | knuckleHEADd | NORMAL | 2022-07-10T08:49:00.926370+00:00 | 2022-07-10T17:26:37.826639+00:00 | 206 | false | ```class Solution {\n public boolean btreeGameWinningMove(TreeNode root, int n, int x) {\n TreeNode red=getNode(root,x); //getting the x node\n int countPar=getCount(root,red); //count if I set blue as parent of red\n int countLeft=getCount(red.left,red); //count if I set blue as leftChild of red\n int countRight=getCount(red.right,red); //count if I set blue as rightChild of red\n return countPar>n/2||countLeft>n/2||countRight>n/2; \n\t\t/*n/2 is the max either color node can have, and since n is odd, one will definitely be greater than the other. For example->5(2,3)*/\n }\n \n public TreeNode getNode(TreeNode root,int x){\n if(root==null)return null;\n TreeNode left=getNode(root.left,x);\n TreeNode right=getNode(root.right,x);\n if(left!=null&&left.val==x)return left;\n if(right!=null&&right.val==x)return right;\n if(root.val==x)return root;\n return null;\n }\n \n public int getCount(TreeNode node,TreeNode block){\n if(node==null||node==block)return 0; //if node encounters the red node or null-> return\n int left=getCount(node.left,block);\n int right=getCount(node.right,block);\n return left+right+1;\n }\n}\n```\n\nPS: Don\'t get confused with the statement that the nodes "take turns" | 1 | 0 | ['Binary Tree', 'Java'] | 0 |
binary-tree-coloring-game | PYTHON SOL | LINEAR TIME | EXPLAINED WITH PICTURE | EASY | TRAVERSING | | python-sol-linear-time-explained-with-pi-xyhm | TIME AND SPACE COMPLEXITY\nRuntime: 36 ms, faster than 89.14% of Python3 online submissions for Binary Tree Coloring Game.\nMemory Usage: 14 MB, less than 52.72 | reaper_27 | NORMAL | 2022-07-03T12:18:14.577734+00:00 | 2022-07-03T12:18:14.577767+00:00 | 212 | false | # TIME AND SPACE COMPLEXITY\nRuntime: 36 ms, faster than 89.14% of Python3 online submissions for Binary Tree Coloring Game.\nMemory Usage: 14 MB, less than 52.72% of Python3 online submissions for Binary Tree Coloring Game.\n\n\n# EXPLANATION\n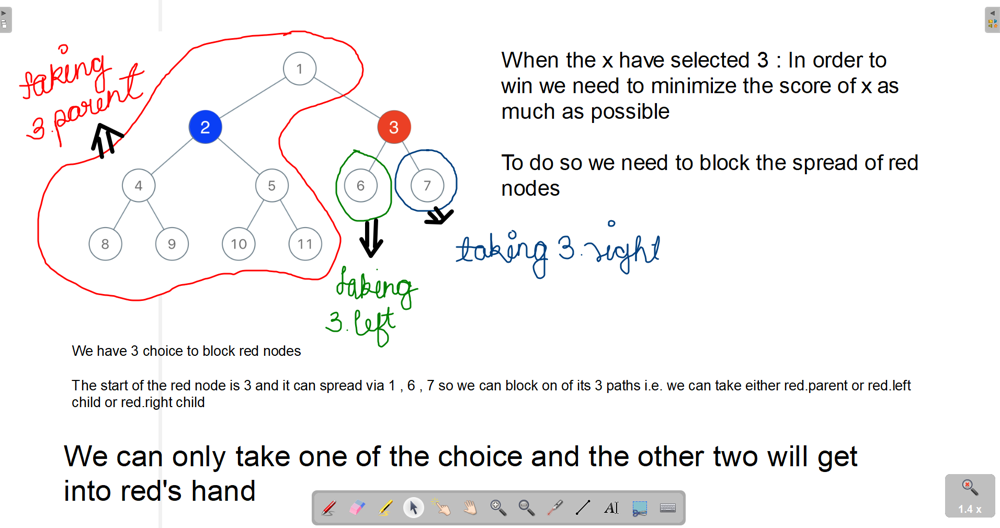\n\n# CODE\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def findParent(self,node,par = None):\n if node:\n self.parent[node.val] = par\n self.findParent(node.left,node)\n self.findParent(node.right,node)\n \n def traverse(self,node,done):\n if node:\n if node in done: return 0\n done[node] = True\n a = self.traverse(self.parent[node.val],done)\n b = self.traverse(node.left,done)\n c = self.traverse(node.right,done)\n return a + b + c + 1\n return 0\n \n def btreeGameWinningMove(self, root: Optional[TreeNode], n: int, x: int) -> bool:\n self.parent = {}\n self.findParent(root)\n parent = self.parent[x]\n node = root if root.val == x else parent.left if parent and parent.left and parent.left.val == x else parent.right\n up = self.traverse(parent,{node:True})\n left = self.traverse(node.left,{node:True})\n right = self.traverse(node.right,{node:True})\n return (up > left + right) or (left > up + right) or (right > up + left)\n```\n | 1 | 0 | ['Depth-First Search', 'Python', 'Python3'] | 0 |
binary-tree-coloring-game | easy to understand C++ and 100% runtime | easy-to-understand-c-and-100-runtime-by-6kmsj | ```TreeNode tg=NULL;\n int rec(TreeNode root){\n if(root==NULL)return 0;\n return rec(root->left)+rec(root->right)+1;\n }\n \n void fi | ishanudr | NORMAL | 2022-06-13T07:48:39.690555+00:00 | 2022-06-13T07:48:39.690585+00:00 | 115 | false | ```TreeNode* tg=NULL;\n int rec(TreeNode* root){\n if(root==NULL)return 0;\n return rec(root->left)+rec(root->right)+1;\n }\n \n void fi(TreeNode* root,int x){\n if(root==NULL)return;\n if(root->val==x){\n tg=root;\n return;\n }\n fi(root->right,x);\n fi(root->left,x);\n }\n \n bool btreeGameWinningMove(TreeNode* root, int n, int x) {\n tg=NULL;\n fi(root,x);\n if(tg==NULL)return false;\n int b=rec(tg->right);\n int c=rec(tg->left);\n int a=n-b-c-1;\n if(a>b+c || b>a+c || c>a+b)return true;\n return false;\n } | 1 | 1 | ['Recursion', 'C'] | 0 |
binary-tree-coloring-game | Java Binary Tree | java-binary-tree-by-manishen-gj85 | \n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n | Manishen | NORMAL | 2022-06-09T15:12:38.820410+00:00 | 2022-06-09T15:12:38.820452+00:00 | 213 | false | ```\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n * TreeNode(int val) { this.val = val; }\n * TreeNode(int val, TreeNode left, TreeNode right) {\n * this.val = val;\n * this.left = left;\n * this.right = right;\n * }\n * }\n */\nclass Solution {\n static int xkaleft;\n static int xkaright;\n \n public static int size(TreeNode node,int x){\n if(node == null){\n return 0;\n }\n \n int ls = size(node.left,x);\n int rs = size(node.right,x);\n \n int ts = ls + rs + 1;\n \n if(node.val == x){\n xkaleft = ls;\n xkaright = rs;\n }\n return ts;\n \n }\n public boolean btreeGameWinningMove(TreeNode root, int n, int x) {\n \n size(root,x);\n \n int otherside = n - (xkaleft + xkaright + 1);\n int maxofthree = Math.max(otherside,Math.max(xkaleft,xkaright));\n \n int rest = n - maxofthree;\n \n if(maxofthree > rest){\n return true;\n }\n \n return false;\n \n }\n}\n``` | 1 | 0 | ['Binary Tree', 'Java'] | 0 |
binary-tree-coloring-game | JAVA AC solution || 0ms | java-ac-solution-0ms-by-priyansh007-pzfx | intuition that i got is if the player x already took his chance we have to greedily choose max of (left subtree of x,right subtree of x,other subtree)\nas we ch | Priyansh007 | NORMAL | 2022-05-26T15:49:32.888478+00:00 | 2022-05-26T15:49:32.888515+00:00 | 64 | false | intuition that i got is if the player x already took his chance we have to greedily choose max of (left subtree of x,right subtree of x,other subtree)\nas we choose this then if the other size is still greater than our choosed size we cant win\nelse we can win\n```\nclass Solution {\n int xRightSubtreeSum=0;\n int xLeftSubtreeSum=0;\n public int size(TreeNode root,int x){\n if(root==null)return 0;\n \n int leftSize=size(root.left,x);\n int rightSize=size(root.right,x);\n \n if(root.val==x){\n xRightSubtreeSum=rightSize;\n xLeftSubtreeSum=leftSize;\n }\n return leftSize+rightSize+1;\n }\n public boolean btreeGameWinningMove(TreeNode root, int n, int x) {\n size(root,x);\n \n int otherSubtreeSize=n-(xLeftSubtreeSum+xRightSubtreeSum+1);\n \n //we try to take max possible subtree\n int yMax=Math.max(otherSubtreeSize,Math.max(xLeftSubtreeSum,xRightSubtreeSum));\n \n int rest=n-yMax;\n \n if(rest>yMax){//after taking max... the rest is still greater then we cant win\n return false;\n }\n return true;\n }\n}\n``` | 1 | 0 | ['Recursion', 'Game Theory', 'Java'] | 0 |
binary-tree-coloring-game | Simple Java Solution using DFS | Easy to Understand | simple-java-solution-using-dfs-easy-to-u-gdy3 | Please upvote, if you find it useful :)\n\n\nclass Solution {\n \n public int xleft;\n public int xright;\n \n public int size(TreeNode node, int | kxbro | NORMAL | 2022-05-18T17:30:53.197060+00:00 | 2022-05-18T17:30:53.197105+00:00 | 201 | false | Please upvote, if you find it useful :)\n\n```\nclass Solution {\n \n public int xleft;\n public int xright;\n \n public int size(TreeNode node, int x) {\n if(node == null) {\n return 0;\n }\n \n int ls = size(node.left, x);\n int rs = size(node.right, x);\n \n if(node.val == x){\n xleft = ls;\n xright = rs;\n }\n \n return ls + rs + 1;\n }\n \n public boolean btreeGameWinningMove(TreeNode root, int n, int x) {\n size(root, x);\n int otherSize = n - xleft - xright - 1;\n int max = Math.max(otherSize, Math.max(xleft, xright));\n \n int rest = n - max;\n if(max > rest) {\n return true;\n }\n \n return false;\n }\n}\n``` | 1 | 0 | ['Depth-First Search', 'Java'] | 1 |
binary-tree-coloring-game | Python easy solution (DFS) | python-easy-solution-dfs-by-ganyue246-40v4 | \n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.lef | ganyue246 | NORMAL | 2022-03-31T01:58:47.294749+00:00 | 2022-03-31T01:58:47.294800+00:00 | 145 | false | ```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def btreeGameWinningMove(self, root: Optional[TreeNode], n: int, x: int) -> bool:\n \n # Do DFS on 3 direction of opponent\n # if one side is greater than the other 2 direction, you win!\n \n opponent = None\n \n def DFS(root):\n if not root:\n return 0\n \n nonlocal x\n if root.val == x:\n nonlocal opponent\n opponent = root\n return 0\n \n return 1 + DFS(root.left) + DFS(root.right)\n \n above = DFS(root)\n left = DFS(opponent.left)\n right = DFS(opponent.right)\n \n if (above > left + right) or (left > above + right) or (right > above + left):\n return True\n \n return False\n \n \n \n``` | 1 | 0 | ['Python', 'Python3'] | 0 |
binary-tree-coloring-game | C++ | DFS | Commented | c-dfs-commented-by-singhabhinavv-vjgs | \n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0) | singhabhinavv | NORMAL | 2022-03-23T06:07:53.934643+00:00 | 2022-03-23T06:07:53.934686+00:00 | 88 | false | ```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n int total = 0;\n TreeNode* found;\n void find(TreeNode* root, int x) {\n if(!root) return ;\n ++total;\n if(root->val == x) {\n found = root;\n }\n find(root->left, x);\n find(root->right, x);\n }\n int cnt = 0;\n void dfs(TreeNode* root) {\n if(!root) return;\n cnt++;\n dfs(root->left);\n dfs(root->right);\n }\n bool btreeGameWinningMove(TreeNode* root, int n, int x) {\n // We have three options to sucessfullly restrict the red color\n // 1. We color the parent of the node x blue so that red expands \n // only to its children.\n // 2. We color the left child of the node x blue so that red\n // expands only to its right children and it\'s ancestor.\n // 3. We color the right child of the node x blue so that red \n // expands only to it\'s left and it\'s ancestor\n // Among these three options if in any case we get more blues than reds\n // Our answer will be true;\n \n // 1.\n find(root, x);\n TreeNode* nr = found;\n dfs(nr);\n int red = cnt;\n int blue = total - cnt;\n cnt = 0;\n if(blue > red) return true;\n // 2.\n dfs(nr->left);\n blue = cnt;\n red = total - cnt;\n cnt = 0;\n if(blue > red) return true;\n // 3.\n dfs(nr->right);\n blue = cnt;\n red = total - blue;\n if(blue > red) return true;\n return false;\n }\n};\n``` | 1 | 0 | ['Binary Tree'] | 0 |
binary-tree-coloring-game | python | python-by-hzhaoc-n2gf | if x is root, it cuts tree into two parts: left child, right child. Only when the two parts are same num of nodes, player 2 will never win\n- if x is not root, | hzhaoc | NORMAL | 2022-01-06T04:07:56.595277+00:00 | 2022-01-06T04:07:56.595322+00:00 | 46 | false | - if x is root, it cuts tree into two parts: left child, right child. Only when the two parts are same num of nodes, player 2 will never win\n- if x is not root, it cuts tree into three parts: left child, right child, parent. Only when the largest part of three are more than half of total nodes, player 2 will win.\n\n```python\n def btreeGameWinningMove(self, root: Optional[TreeNode], n: int, x: int) -> bool:\n def search(node):\n\t\t\'\'\'count num of nodes at or below this node\'\'\'\n if not node:\n return 0\n \n l = search(node.left)\n r = search(node.right)\n \n if node.val == x:\n self.l, self.r = l, r\n \n return 1 + l + r\n \n if x == root.val:\n c1 = search(root.left)\n return c1 != n // 2\n \n self.l, self.r = 0, 0\n search(root)\n return max([self.l, self.r, n - 1 - self.l - self.r]) > n //2\n \n``` | 1 | 0 | [] | 0 |
binary-tree-coloring-game | py3: binary tree coloring game | py3-binary-tree-coloring-game-by-snalli-ra40 | \n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.lef | snalli | NORMAL | 2021-12-12T21:58:07.346704+00:00 | 2021-12-12T22:00:12.278660+00:00 | 64 | false | ```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def btreeGameWinningMove(self, root: Optional[TreeNode], n: int, x: int) -> bool:\n \n node = None\n queue = [root]\n # find the node x\n while queue:\n node = queue.pop(0)\n if node.val == x:\n break\n if node.left: queue.append(node.left)\n if node.right: queue.append(node.right)\n \n def dfs(t):\n if not t:\n return 0\n \n return 1 + dfs(t.left) + dfs(t.right)\n """\n There are atmost 3 nodes connected to x: parent, left, right\n As a blue player, you must block off the path that would give you\n the maximum number of nodes to color.\n """\n l,r = dfs(node.left), dfs(node.right)\n # num parents of x\n p = n-1-l-r\n \n return l > p+r+1 or r > p+l+1 or p > l+r+1\n``` | 1 | 0 | [] | 0 |
binary-tree-coloring-game | C++ | Faster than 100% | Winning Strategy | c-faster-than-100-winning-strategy-by-ap-ihau | Essentially, the (possible) winning strategy is to choose a neighbor node to color \'BLUE\'. This will block the \'RED\' player from moving into the part of the | apartida | NORMAL | 2021-11-03T17:53:31.203662+00:00 | 2021-11-03T17:53:31.203692+00:00 | 128 | false | Essentially, the (possible) winning strategy is to choose a neighbor node to color \'BLUE\'. This will block the \'RED\' player from moving into the part of the tree that has the most nodes. To this, the optimal \'BLUE\' (neighbor) node is the one that contains the most nodes. \n\n```\n /* Pointer to \'RED\' node. */\n TreeNode* RED = nullptr;\n \n /* Perform depth-first search of the tree. */\n int dfs(TreeNode* node, int x) {\n /* Reached a leaf node. */\n if (node == nullptr) return 0;\n \n /* Reached the \'RED\' node. */\n if (node->val == x) {\n RED = node; /* Save the pointer. */\n return 0;\n }\n \n return 1 + dfs(node->left, x) + dfs(node->right, x);\n }\n \n bool btreeGameWinningMove(TreeNode* root, int n, int x) {\n \n /* Boundary case. */\n if (n <= 1) return false;\n \n /* Number of blue nodes based on move. */\n int numBlueNodes = 0;\n \n /* Initialize the \'RED\' node. */\n RED = root;\n \n /* Choose the parent node (if available). */\n if (root->val != x) numBlueNodes = dfs(root, x);\n if (numBlueNodes > (n/2)) return true;\n \n /* Choose the right child node (if available). */\n numBlueNodes = dfs(RED->right, x);\n if (numBlueNodes > (n/2)) return true;\n \n /* Choose the left child node (if available). */\n numBlueNodes = dfs(RED->left, x);\n if (numBlueNodes > (n/2)) return true;\n \n /* No winning moves. */\n return false;\n \n } | 1 | 0 | ['Depth-First Search', 'C'] | 0 |
binary-tree-coloring-game | C++ beat 100%, explained | c-beat-100-explained-by-wzypangpang-m88c | The trick here is in order to optimally choose y, there are only 3 options\n1) parent node of x\n2) left child of x\n3) right child of x\n\nNote that once we ch | wzypangpang | NORMAL | 2021-09-18T19:20:16.091236+00:00 | 2021-09-18T19:20:16.091277+00:00 | 141 | false | The trick here is in order to optimally choose y, there are only 3 options\n1) parent node of x\n2) left child of x\n3) right child of x\n\nNote that once we choose y, the tree is "split" into 2 subtrees (you can think of cutting the edge connecting x and y).\nthe following actions of 2 players are constrained within their correspoding subtree. Therefore, the comparing the sizes of subtrees determines whether the second player can win.\n\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n int count(TreeNode* root) {\n if(!root) return 0;\n return 1 + count(root->left) + count(root->right);\n } \n \n TreeNode* find(TreeNode* root, int x) {\n if(!root) return nullptr;\n if(root->val == x) return root;\n \n auto n = find(root->left, x);\n if(n) return n;\n n = find(root->right, x);\n return n;\n }\n \n bool btreeGameWinningMove(TreeNode* root, int n, int x) {\n TreeNode* node = find(root, x);\n \n int left = count(node->left);\n int right = count(node->right);\n int threshold = n / 2;\n \n if(left > threshold || right > threshold || (n - 1 - left - right) > threshold) {\n return true;\n }\n return false;\n }\n};\n``` | 1 | 0 | [] | 0 |
binary-tree-coloring-game | C++ || DFS || Neat and Simple Code | c-dfs-neat-and-simple-code-by-dharineesh-qm5v | \nclass Solution {\npublic:\n bool btreeGameWinningMove(TreeNode* root, int n, int x) {\n TreeNode* xNode = findNode(root, x);\n int leftCount | Dharineesh | NORMAL | 2021-07-31T09:01:30.829595+00:00 | 2021-07-31T09:01:30.829635+00:00 | 187 | false | ```\nclass Solution {\npublic:\n bool btreeGameWinningMove(TreeNode* root, int n, int x) {\n TreeNode* xNode = findNode(root, x);\n int leftCount = countNodes(xNode->left);\n int rightCount = countNodes(xNode->right);\n int parentCount = n - leftCount - rightCount - 1;\n \n int max = (leftCount > rightCount && leftCount > parentCount) ? leftCount : (rightCount > parentCount) ? rightCount : parentCount;\n if( max > n/2)\n return true;\n return false;\n }\n \n int countNodes(TreeNode* root){\n if(!root)\n return 0;\n return countNodes(root->left) + countNodes(root->right) + 1;\n \n }\n \n TreeNode* findNode(TreeNode* root, int x){\n if(!root)\n return NULL;\n if(root->val == x)\n return root;\n TreeNode* left = findNode(root->left, x);\n TreeNode* right = findNode(root->right, x);\n return (left) ? left : right;\n }\n};\n``` | 1 | 0 | ['Depth-First Search', 'Recursion', 'C'] | 0 |
binary-tree-coloring-game | C++ 100% faster | c-100-faster-by-mohammeddeifallah-50qu | Just counting the nodes in the subtree rooted at x.\n\n/**\n * Definition for a binary tree node.\n * * struct TreeNode {\n * int val;\n * TreeNode *le | mohammeddeifallah | NORMAL | 2021-07-29T21:47:59.466628+00:00 | 2021-07-29T21:48:25.925583+00:00 | 133 | false | Just counting the nodes in the subtree rooted at `x`.\n```\n/**\n * Definition for a binary tree node.\n * * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\nprivate:\n int countNodes(TreeNode* node){\n if(!node){\n return 0;\n }\n return 1 + countNodes(node -> left) + countNodes(node -> right);\n }\npublic:\n bool btreeGameWinningMove(TreeNode* root, int n, int x) {\n queue<TreeNode*> q;\n q.push(root);\n TreeNode* target;\n while(!q.empty()){\n TreeNode* node = q.front();\n q.pop();\n if(node -> val == x){\n target = node;\n while(q.size()){\n q.pop();\n }\n break;\n }\n if(node -> left) q.push(node -> left);\n if(node -> right) q.push(node -> right);\n }\n \n int left = countNodes(target -> left);\n int right = countNodes(target -> right);\n if(left + right + 1 <= n / 2){\n return true;\n }\n \n if(left > n / 2 || right > n / 2){\n return true;\n }\n return false;\n \n }\n};\n``` | 1 | 0 | ['Breadth-First Search', 'Recursion', 'Queue', 'C'] | 0 |
binary-tree-coloring-game | Easy Simple Java solution with Approach || 100% fast | easy-simple-java-solution-with-approach-bwy5x | Approach \nEveryone loves winning Therefore in this game we also want to win so for that we will block the first player\'s right subtree or left subtree or pare | amitverma1050 | NORMAL | 2021-07-04T18:31:08.770483+00:00 | 2021-07-04T18:32:51.789210+00:00 | 139 | false | **Approach** \nEveryone loves winning Therefore in this game we also want to win so for that we will block the first player\'s right subtree or left subtree or parent subtree on the basis of most nodes in subtree .\ncount1 -> we find the count of left subtree\ncount2 -> we find the count of right subtree\nn-count1-count2-1 -> count of parent subtree\n\nif any one of them have greater than half of total number of nodes we will win. \n\n```\npublic boolean btreeGameWinningMove(TreeNode root, int n, int x) {\n TreeNode node = find(root,x); // find the given node of first player\n if(node.left == null && node.right == null) return true;\n int count1 = countOfSubtree(node.left); // count of left subtree\n int count2 = countOfSubtree(node.right); // count of right subtree\n return (count1 > n/2 || count2 > n/2 || n-count1-count2-1 >n/2);\n }\n \n public TreeNode find(TreeNode root,int x){\n if(root == null) return null;\n if(root.val == x) return root;\n TreeNode left = find(root.left,x);\n if(left != null) return left;\n TreeNode right = find(root.right,x);\n if(right != null) return right;\n return null;\n }\n \n public int countOfSubtree(TreeNode root){\n if(root == null) return 0;\n int count =0;\n count += countOfSubtree(root.left);\n count += countOfSubtree(root.right);\n return count + 1;\n }\n``` | 1 | 0 | [] | 0 |
binary-tree-coloring-game | C++| Java | 100% Faster | 0 ms | Easy Solution | c-java-100-faster-0-ms-easy-solution-by-j506q | C++\n### \n\nExplanation:\n\nThe node with value x divides the tree in three parts, parent region, left child region and right child region. If number of nodes | kush_yadav | NORMAL | 2021-06-09T19:12:16.398036+00:00 | 2021-11-06T07:11:57.850623+00:00 | 190 | false | ### **C++**\n### \n\n**Explanation:**\n\nThe node with value x divides the tree in three parts, parent region, left child region and right child region. If number of nodes in any of those regions is more that n/2 then y can win.\n\n```\nclass Solution {\n //This node will store the node with value X\n TreeNode* X = NULL;\n //This function will assign the node with value x to X.\n void findX(TreeNode* root, int x){\n if(!root||X) return;\n if(root->val==x) X=root;\n findX(root->left,x);\n findX(root->right,x);\n }\n \n\t//This function will return the child count\n int child_count(TreeNode* root){\n if(!root) return 0;\n return child_count(root->left)+child_count(root->right)+1;\n }\n \npublic:\n bool btreeGameWinningMove(TreeNode* root, int n, int x) {\n findX(root,x);\n int lc = child_count(X->left);\n int rc = child_count(X->right);\n\t\t//Get max from all three regions and return true if its greater than n/2\n return max(max(lc,rc),n-lc-rc-1)>n/2;\n }\n};\n\n```\n\n\n\n### **Java**\n### \n```\nclass Solution {\n public boolean btreeGameWinningMove(TreeNode root, int n, int x) {\n find(root,x);\n int lc = count(p1.left);\n int rc = count(p1.right);\n return Math.max(Math.max(lc,rc),n-lc-rc-1)>n/2;\n }\n \n TreeNode p1 = null;\n \n public void find(TreeNode root,int x){\n if(root == null || p1!=null) return;\n if(root.val == x) p1 = root;\n find(root.left, x);\n find(root.right,x);\n }\n \n public int count(TreeNode root){\n if(root == null) return 0;\n return count(root.left)+count(root.right)+1;\n }\n}\n\n``` | 1 | 0 | ['C', 'Java'] | 0 |
binary-tree-coloring-game | VERY EASY 0 MS SOLUTION | very-easy-0-ms-solution-by-xxsidxx-wdnt | \n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n | xxsidxx | NORMAL | 2021-05-11T13:50:49.368243+00:00 | 2021-05-11T13:50:49.368291+00:00 | 72 | false | ```\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n * TreeNode(int val) { this.val = val; }\n * TreeNode(int val, TreeNode left, TreeNode right) {\n * this.val = val;\n * this.left = left;\n * this.right = right;\n * }\n * }\n */\nclass Solution {\n int left=0;\n int right=0;\n public boolean btreeGameWinningMove(TreeNode root, int n, int x) {\n int total= dfs(root,x);\n \n int parent= total-left-right-1;\n \n\n if(parent>left+right){\n return true;\n }else if(left>parent+right){\n return true;\n }else if(right>parent+left){\n return true;\n }\n \n return false;\n \n }\n public int dfs(TreeNode root,int x){\n \n if(root==null)return 0;\n \n int l= dfs(root.left,x);\n int r= dfs(root.right,x);\n \n \n if(root.val==x){\n left=l;\n right=r;\n }\n \n \n return l+r+1;\n \n \n }\n\n \n}\n\n\n``` | 1 | 0 | [] | 0 |
binary-tree-coloring-game | Java: Easy solution | java-easy-solution-by-abhi192-q77v | ```\n// three positions are candidates of y\n// case 1: left child of x has greater number of elements\n//case 2: right child of x has greater number of element | abhi192 | NORMAL | 2021-04-26T10:36:23.657213+00:00 | 2021-04-26T10:36:23.657259+00:00 | 140 | false | ```\n// three positions are candidates of y\n// case 1: left child of x has greater number of elements\n//case 2: right child of x has greater number of elements\n// case 3: parent has greater number of elements \n\nclass Solution {\n int xlc,xrc; \n public boolean btreeGameWinningMove(TreeNode root, int n, int x) {\n getChildCount(root,x);\n int xsub = 1 + xlc + xrc; \n \n if(xlc>n-xlc || xrc>n-xrc || xsub<n-xsub)\n return true;\n return false;\n }\n \n // gives me count of left subtree and right subtree below x\n public int getChildCount(TreeNode node, int x){\n if(node==null)\n return 0;\n int ans =1;\n int lc= getChildCount(node.left,x);\n int rc= getChildCount(node.right,x);\n if(node.val==x){\n xlc=lc;\n xrc=rc;\n }\n ans+=lc+rc;\n return ans;\n }\n} | 1 | 0 | ['Java'] | 0 |
binary-tree-coloring-game | Python dfs iteration + recursion w/comments | python-dfs-iteration-recursion-wcomments-utsa | py\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.l | leovam | NORMAL | 2021-02-28T01:50:57.112302+00:00 | 2021-02-28T01:50:57.112328+00:00 | 153 | false | ```py\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\n\'\'\'\nw: tree traversal + greedy\nh: the node x partiton the tree into three parts:\n 1: its left subtree\n 2: its right right subtree\n 3: its parent and the other subtree of its parent\n in order to win the game, we should have as many as blue node, so we do it greedily:\n color x\'s parent or x\'left child or x\'s right child to block x\n \n so if there is a partition which contains more node than the other two, we will win\n\'\'\'\nclass Solution:\n def btreeGameWinningMove(self, root: TreeNode, n: int, x: int) -> bool:\n # 1. find x\n stack = []\n node = root\n x_node = None\n while stack or node:\n while node:\n if node.val == x:\n x_node = node\n stack.append(node)\n node = node.left\n \n node = stack.pop()\n if node.val == x:\n x_node = node\n node = node.right\n \n \n # 2. count the three partition\n def dfs(node, cnt):\n if not node:\n return 0\n cnt[0] += 1\n dfs(node.left, cnt)\n dfs(node.right, cnt)\n \n p1 = [0]\n p2 = [0]\n dfs(x_node.left, p1)\n dfs(x_node.right, p2)\n \n remain = n - p1[0] - p2[0] - 1\n \n if remain > p1[0] + p2[0] + 1 or p1[0] > remain + p2[0] + 1 or p2[0] > remain + p1[0] + 1:\n return True\n else:\n return False\n``` | 1 | 0 | ['Depth-First Search', 'Python'] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.