question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
maximum-number-of-consecutive-values-you-can-make | Thought Process behind the Solution|| C++ || Easy & Clean Code. | thought-process-behind-the-solution-c-ea-6vqc | Approach\nWhy res Starts at 1\nInitial Smallest Missing Number:\n The smallest positive integer is 1. Starting res at 1 means we are initially considering 1 | nikk_05 | NORMAL | 2024-06-16T08:11:40.546512+00:00 | 2024-06-16T08:11:40.546542+00:00 | 10 | false | # Approach\n***Why res Starts at 1***\nInitial Smallest Missing Number:\n The smallest positive integer is 1. Starting res at 1 means we are initially considering 1 as the smallest integer that we can\'t form with the given coins.\n If we can form 1, we will increment res to 2, meaning we are now considering 2 as the next smallest integer we can\'t form, and so on.\n \n\n***Let\'s break down the logic:***\n\n- Sort the Coins:\n\nThe coins are sorted in ascending order to ensure that we consider smaller denominations first. This helps us to build the smallest consecutive numbers step by step.\n\n- Iterate Through the Coins:\n\nFor each coin in the sorted list, we check if it can be used to form the current smallest missing number res.\n\n- Check If Coin Can Form res:\n\nIf the coin value a is greater than res, it means we cannot form the number res with the current set of coins, so we break out of the loop.\nIf the coin value a is less than or equal to res, it means we can form the number res and all numbers up to res + a - 1 with the current set of coins. Therefore, we update res to res + a.\n****\n**Example Walkthrough**\n\nConsider coins = [1, 2, 2, 5]:\nInitialization:\nres = 1\n\n**First Iteration (coin = 1):**\ncoin (1) <= res (1)\nUpdate res = res + coin = 1 + 1 = 2\nNow we can form numbers {1}.\n\n**Second Iteration (coin = 2):**\ncoin (2) <= res (2)\nUpdate res = res + coin = 2 + 2 = 4\nNow we can form numbers {1, 2, 3}.\n\n**Third Iteration (coin = 2):**\ncoin (2) <= res (4)\nUpdate res = res + coin = 4 + 2 = 6\nNow we can form numbers {1, 2, 3, 4, 5}.\n\n**Fourth Iteration (coin = 5):**\ncoin (5) > res (6)\nBreak the loop, as we can\'t form res (6) with the current set of coins.\n\nThe maximum number of consecutive integers that can be formed is 5.\n\n# Complexity\n- Time complexity:\nO(nlogn)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) {\n sort(coins.begin(), coins.end());\n int missing = 1;\n for (int coin : coins) {\n if (coin > missing)\n break;\n missing += coin;\n }\n return missing;\n }\n};\n``` | 0 | 0 | ['Array', 'Greedy', 'Sorting', 'C++'] | 0 |
maximum-number-of-consecutive-values-you-can-make | [C++] Sort then Greedy | c-sort-then-greedy-by-amanmehara-3b5l | Complexity\n- Time complexity: O(nlogn)\n- Space complexity: O(1)\n\n# Code\n\nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) {\n | amanmehara | NORMAL | 2024-06-16T08:11:07.724991+00:00 | 2024-06-16T08:11:07.725015+00:00 | 2 | false | # Complexity\n- Time complexity: $$O(nlogn)$$\n- Space complexity: $$O(1)$$\n\n# Code\n```\nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) {\n sort(coins.begin(), coins.end());\n int curr = 0;\n for (const auto& coin : coins) {\n if (coin > curr + 1) {\n break;\n }\n curr += coin;\n }\n return curr + 1;\n }\n};\n``` | 0 | 0 | ['Array', 'Greedy', 'Sorting', 'C++'] | 0 |
maximum-number-of-consecutive-values-you-can-make | ✅99.55% Better than Other C++ Users|| Easy ||Concept Explained...! | 9955-better-than-other-c-users-easy-conc-4fj4 | Intuition\nWhen you first see this problem, you might think about how you can create a range of consecutive numbers starting from 1 using the given coins. The k | kaditya67 | NORMAL | 2024-06-16T07:29:24.438811+00:00 | 2024-06-16T07:29:24.438841+00:00 | 6 | false | ### Intuition\nWhen you first see this problem, you might think about how you can create a range of consecutive numbers starting from 1 using the given coins. The key insight here is to use a greedy approach to always use the smallest available coin to extend the range of consecutive numbers you can make. By sorting the coins and iterating through them, you can ensure that you are always using the optimal coin to extend your range.\n\n### Approach\n1. **Sort the Array:** Start by sorting the coins array. This allows you to consider the smallest coin first, ensuring that you build up the range of consecutive values in the most efficient way possible.\n2. **Initialize maxReach:** This variable keeps track of the maximum number of consecutive values you can make starting from 1.\n3. **Iterate through the coins:** For each coin, check if it can extend the range of consecutive values. If the current coin is greater than `maxReach + 1`, you can\'t make `maxReach + 1` and thus, you return `maxReach + 1`. If the current coin can extend the range, add it to `maxReach`.\n4. **Return the Result:** After processing all the coins, return `maxReach + 1`, as this represents the maximum number of consecutive values you can make.\n\n### Complexity\n- **Time complexity:** \\(O(n \\log n)\\) due to sorting the array of coins.\n- **Space complexity:** \\(O(1)\\) since we are using a constant amount of extra space for the `maxReach` variable and loop indices.\n\n### Code\nHere\'s the implementation in C++:\n\n```cpp\nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) {\n ios_base::sync_with_stdio(0);\n sort(coins.begin(), coins.end());\n int maxReach = 0;\n int n = coins.size();\n for (int i = 0; i < n; i++) {\n if (coins[i] > maxReach + 1) {\n return maxReach + 1;\n } else {\n maxReach += coins[i];\n }\n }\n return maxReach + 1;\n }\n};\n```\n\n### Explanation\n- **Sorting the Coins:** Sorting ensures that you always consider the smallest coin first.\n- **Updating maxReach:** For each coin, if it is less than or equal to `maxReach + 1`, you can add it to `maxReach` and extend the range. Otherwise, if it\'s larger, you cannot make the next consecutive number, so you return `maxReach + 1`.\n- **Result:** The final result is `maxReach + 1`, indicating the maximum number of consecutive values you can make starting from 1.\n\nThis solution is efficient and leverages the greedy algorithm to ensure that you are always making the optimal choice at each step. | 0 | 0 | ['C++'] | 0 |
maximum-number-of-consecutive-values-you-can-make | Simple Greedy | simple-greedy-by-abhimanyu_185724-jdn7 | Intuition\nIf we can form all integers from 0 to x using the current elements of the array, and we have a new value v, then we can form all integers from 0 to x | Abhimanyu_185724 | NORMAL | 2024-06-16T07:19:11.668145+00:00 | 2024-06-16T07:24:34.603395+00:00 | 3 | false | # Intuition\nIf we can form all integers from 0 to x using the current elements of the array, and we have a new value v, then we can form all integers from 0 to x+v if and only if v\u2264x+1.\nExplanation with an Example\n\nGiven an array [1,1,4], we start with the initial set S={0}:\n\n Step 1: Adding the first element a[0]=1\n Current set S={0}\n By adding 1, we can form {0,1}\n Now, x=1\n\n Step 2: Adding the second element a[1]=1\n Current set S={0,1}\n By adding 1 to each element of S, we get {0+1,1+1}={1,2}\n Combining with the current set S, we get {0,1,2}\n Now, x=2\n\n Step 3: Adding the third element a[2]=4\n Current set S={0,1,2}\n By adding 4 to each element of S, we get {0+4,1+4,2+4}={4,5,6}\n Combining with the current set S, we get {0,1,2,4,5,6}\n Notice that we cannot form the integer 3 because there is no way to create 3 by adding 4 to any element in {0,1,2}\n\nThe critical condition is a[i]\u2264x+1. If a[i] is greater than x+1, there will be gaps in the sequence of integers we can form. In our example, a[2]=4 and x+1=3, 4\u22643 does not hold, resulting in the gap at 3.\n\n# Similar Problems\n[Minimum Number of Coins to be Added](https://leetcode.com/problems/minimum-number-of-coins-to-be-added/)\n[Patching Array](https://leetcode.com/problems/patching-array/description/)\n# Approach\n- Sort the array. and make a x=0.\n- check if x+1>=coins[i]\n- if yes then update x -> x+coins[i]\n- else return x+1\n# Complexity\n- Time complexity: O(NlogN)\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) {\n sort(coins.begin(), coins.end());\n int x=0;\n for(auto coin:coins){\n if(coin<=x+1)\n x+=coin;\n else break;\n }\n return x+1;\n }\n};\n``` | 0 | 0 | ['Greedy', 'C++'] | 0 |
maximum-number-of-consecutive-values-you-can-make | Summing | summing-by-azizkaz-zcod | Intuition\n Describe your first thoughts on how to solve this problem. \nAt first we need to sort the $coins$ array.\nIf we can construct all sums in the range | azizkaz | NORMAL | 2024-06-16T06:57:25.494061+00:00 | 2024-06-16T06:58:00.989191+00:00 | 1 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAt first we need to sort the $coins$ array.\nIf we can construct all sums in the range $[1, k]$ inclusive, and we have the next number from $coins[i]$, then using this number we can construct all sums in the range $[1, k + coins[i]]$\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSumming\n\n# Complexity\n- Time complexity: $O(n \\cdot logn)$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(n)$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nwhere $n$ is the length of the $coins$ array\n\n# Code\n```\nimpl Solution {\n pub fn get_maximum_consecutive(mut coins: Vec<i32>) -> i32 {\n coins.sort_unstable();\n \n let mut s = 0;\n\n for c in coins {\n if s < c - 1 {\n break;\n }\n s += c;\n }\n\n s + 1\n }\n}\n``` | 0 | 0 | ['Prefix Sum', 'Rust'] | 0 |
maximum-number-of-consecutive-values-you-can-make | C++||Greedy & Sorting | cgreedy-sorting-by-prathmeshr-hlj7 | Intuition\nSorting the array which will make easy to check consecutive numbers.\n\nwe will start with tmp = 0 and will check that coins[i] is less or eqaul to t | PrathmeshR | NORMAL | 2024-06-16T06:31:48.362560+00:00 | 2024-06-16T06:31:48.362583+00:00 | 2 | false | # Intuition\nSorting the array which will make easy to check consecutive numbers.\n\nwe will start with tmp = 0 and will check that coins[i] is less or eqaul to tmp + 1.\n\ntmp represent upto which number we are able to make series of consecutive numbers.\n\nif coins[i] is greater than tmp + 1 means some number is missing in tmp.\n\nso,that it will become consecutive number of coins[i]. so break the loop and while returning ans just add 1 to ans for 0.\n\n# Complexity\n- Time complexity:\nO(nlogn)\n\n- Space complexity:\nO(1)\n\n\n\n\n# Code\n```\nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) {\n sort(coins.begin(),coins.end());\n int ans = 0;\n int tmp = 0;\n int i = 0;\n while(i < coins.size()){\n if(coins[i]-1 <= tmp){\n tmp+=coins[i];\n }else{\n break;\n }\n i++;\n }\n return tmp + 1;\n }\n};\n``` | 0 | 0 | ['Greedy', 'Sorting', 'C++'] | 0 |
maximum-number-of-consecutive-values-you-can-make | easy cpp soln | easy-cpp-soln-by-pratima-bakshi-60xb | Complexity\n- Time complexity:\n O(NLogN)\n\n- Space complexity:\n O(1)\n\n# Code\n\nclass Solution {\npublic:\n \n int getMaximumConsecutive(vector | Pratima-Bakshi | NORMAL | 2024-06-16T05:59:19.305882+00:00 | 2024-06-16T05:59:19.305907+00:00 | 1 | false | # Complexity\n- Time complexity:\n O(NLogN)\n\n- Space complexity:\n O(1)\n\n# Code\n```\nclass Solution {\npublic:\n \n int getMaximumConsecutive(vector<int>& coins) \n {\n long long sum = 0;\n int i =0;\n sort(coins.begin(),coins.end());\n while(sum<=1e10)\n {\n if(i<coins.size() && coins[i]<=sum+1)\n {\n sum+=coins[i];\n i++;\n }\n else\n {\n return sum+1;\n }\n }\n return sum+1;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
maximum-number-of-consecutive-values-you-can-make | Easy to understand C++ solution, beats 96% in time and 79% in space. | easy-to-understand-c-solution-beats-96-i-rfmc | \nPlease upvote if u find this useful <3\n\n# Intuition\n- If we can make first x values and we have a value y, we can make all the values that <= x+y and >=y\n | notisora | NORMAL | 2024-06-16T05:08:01.522662+00:00 | 2024-06-16T05:08:01.522684+00:00 | 5 | false | 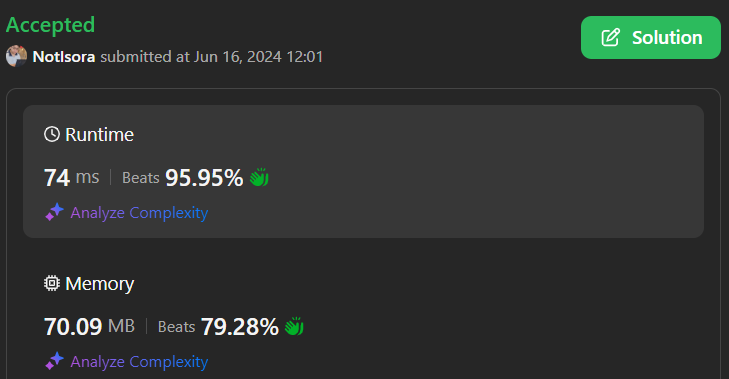\n**Please upvote if u find this useful <3**\n\n# Intuition\n- If we can make first x values and we have a value y, we can make all the values that <= x+y and >=y\n- => X would start at 0 and if x <=coins[i], x would be x+coins[i]\n\n# Complexity\n- Time complexity:\n**O(n*log2(n))**\n\n- Space complexity:\n**O(1)**\n\n# Code\n```\nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) {\n sort(coins.begin(),coins.end());\n int n=coins.size(),consecutive=1;\n for(int i=0;i<n;i++){\n if (coins[i]<=consecutive){\n consecutive+=coins[i];\n } \n }\n return consecutive;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
maximum-number-of-consecutive-values-you-can-make | Fastest and Easiest solution in python🔥 | fastest-and-easiest-solution-in-python-b-umld | \n\n\n\n# Approach\nAnswer lies in the hint:\nIf you can make the first x values and you have a value v, then you can make all the values \u2264 v + x\n\nThe co | avoynath2005 | NORMAL | 2024-06-16T01:57:18.088538+00:00 | 2024-06-16T01:57:18.088565+00:00 | 35 | false | \n\n\n\n# Approach\nAnswer lies in the hint:\nIf you can make the first x values and you have a value v, then you can make all the values \u2264 v + x\n\nThe code is self explainatory\n\n# Code\n```\nclass Solution:\n def getMaximumConsecutive(self, coins: List[int]) -> int:\n coins.sort()\n r=1\n\n for c in coins:\n if c>r:\n break\n else:\n r+=c\n return r\n \n``` | 0 | 0 | ['Python3'] | 0 |
maximum-number-of-consecutive-values-you-can-make | Set - TLE | set-tle-by-wangcai20-01if | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | wangcai20 | NORMAL | 2024-05-18T16:15:22.764051+00:00 | 2024-05-18T16:15:22.764082+00:00 | 14 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int getMaximumConsecutive(int[] coins) {\n // math\n Arrays.sort(coins);\n int res = 1;\n for (int val : coins)\n if (val > res)\n break;\n else\n res += val;\n return res;\n }\n\n public int getMaximumConsecutive_TLE(int[] coins) {\n // set, O(N^2)\n Set<Integer> set = new HashSet<>(List.of(0));\n for (int newVal : coins)\n for (int val : set.toArray(new Integer[] {}))\n set.add(val + newVal);\n // System.out.println(set);\n int res = 0;\n for (int i = 0; i < set.size(); i++, res++)\n if (!set.contains(i))\n break;\n return res;\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
maximum-number-of-consecutive-values-you-can-make | simple maths || easy to understand || o(N) time && o(1) space || | simple-maths-easy-to-understand-on-time-14yxm | Code\n\nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) {\n \n //if i dont take anything that will sum to 0\n | akshat0610 | NORMAL | 2024-05-14T09:39:53.686019+00:00 | 2024-05-14T09:39:53.686048+00:00 | 11 | false | # Code\n```\nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) {\n \n //if i dont take anything that will sum to 0\n int maxVal = 0;\n sort(coins.begin(),coins.end());\n for(int i = 0 ; i < coins.size() ; i++){\n //we cannot add the coins\n if(coins[i] == (maxVal+1)){\n maxVal = ((2*maxVal)+1);\n }else if(coins[i] > (maxVal+1)){\n return maxVal+1;\n }else if(coins[i] < (maxVal+1)){\n maxVal = maxVal + coins[i];\n }\n }\n return maxVal+1;\n }\n};\n``` | 0 | 0 | ['Array', 'Greedy', 'Sorting', 'C++'] | 0 |
maximum-number-of-consecutive-values-you-can-make | Easy JS with O(nlogn) time complexity | easy-js-with-onlogn-time-complexity-by-m-3j3z | Complexity\n- Time complexity: O(nlogn)\n- Space complexity: O(n)\n\n# Idea\nJust check: if any coins[i] > sum(coins, i - 1) + 1 THEN cannot find elements with | Maduro29 | NORMAL | 2024-04-20T07:37:01.518378+00:00 | 2024-04-20T07:37:01.518408+00:00 | 4 | false | # Complexity\n- Time complexity: O(nlogn)\n- Space complexity: O(n)\n\n# Idea\nJust check: if any coins[i] > sum(coins, i - 1) + 1 THEN cannot find elements with sum coins[i] - 1\n\n# Code\n```\n/**\n * @param {number[]} coins\n * @return {number}\n */\nvar getMaximumConsecutive = function(coins) {\n coins.sort((a, b) => a - b)\n let sum = 0\n for (let i = 0; i < coins.length; i++) {\n if (coins[i] > sum + 1) {\n break\n }\n sum += coins[i]\n }\n return sum + 1\n};\n``` | 0 | 0 | ['JavaScript'] | 0 |
maximum-number-of-consecutive-values-you-can-make | Straightforward Python | straightforward-python-by-jabezng2-dwje | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Jabezng2 | NORMAL | 2024-04-12T14:12:52.498476+00:00 | 2024-04-12T14:12:52.498508+00:00 | 30 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getMaximumConsecutive(self, coins: List[int]) -> int:\n # [1, 1, 3, 4, 10]\n # 0: []\n # 1: [1]\n # 2: [1, 1]\n # We have 3 and we can make up to 2 so we can make till 5\n # 5: [1, 1, 3]\n # We have 4 and we can make up to 5 so we can make till 9\n # 9: [1, 1, 3, 4]\n # We have 10 and we can make up to 9 so we can make till 19\n # 19 + 1 = 20 (becos zero index)\n # for the case of [1, 3]\n # we can make up till 1 but we cant make 2 so since 3 > 2 then we break\n coins.sort()\n res = 1\n for coin in coins:\n if coin > res:\n break\n res += coin\n return res\n \n\n \n``` | 0 | 0 | ['Python3'] | 0 |
maximum-number-of-consecutive-values-you-can-make | Shortest, Easiest, Clean & Clear | To the Point & Beginners Friendly Approach (❤️ ω ❤️) | shortest-easiest-clean-clear-to-the-poin-gc90 | Code\n\nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) {\n int x=1;\n sort(coins.begin(),coins.end());\n for( | Nitansh_Koshta | NORMAL | 2024-04-10T13:06:52.370480+00:00 | 2024-04-10T13:06:52.370516+00:00 | 3 | false | # Code\n```\nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) {\n int x=1;\n sort(coins.begin(),coins.end());\n for(auto i:coins){\n if(i<=x)x+=i;\n else break;\n }\n return x;\n\n// if you like my approach then please UpVOTE o((>\u03C9< ))o\n }\n};\n```\n\n\n | 0 | 0 | ['C++'] | 0 |
maximum-number-of-consecutive-values-you-can-make | Python (Simple Greedy) | python-simple-greedy-by-rnotappl-19tc | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | rnotappl | NORMAL | 2024-03-17T16:27:50.299381+00:00 | 2024-03-17T16:27:50.299414+00:00 | 26 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getMaximumConsecutive(self, coins):\n n, running_sum = len(coins), 0\n\n coins.sort()\n\n for i in coins:\n if i > running_sum+1:\n return running_sum+1\n running_sum += i \n\n return running_sum+1\n``` | 0 | 0 | ['Python3'] | 0 |
maximum-number-of-consecutive-values-you-can-make | JS || Solution by Bharadwaj | js-solution-by-bharadwaj-by-manu-bharadw-eqxw | Code\n\nvar getMaximumConsecutive = function (coins) {\n coins.sort((a, b) => a - b);\n let count = 0;\n for (let coin of coins) {\n if (coin <= | Manu-Bharadwaj-BN | NORMAL | 2024-03-02T04:58:14.268094+00:00 | 2024-03-02T04:58:14.268160+00:00 | 32 | false | # Code\n```\nvar getMaximumConsecutive = function (coins) {\n coins.sort((a, b) => a - b);\n let count = 0;\n for (let coin of coins) {\n if (coin <= count + 1) {\n count += coin;\n }\n }\n return count + 1;\n};\n``` | 0 | 0 | ['JavaScript'] | 1 |
maximum-number-of-consecutive-values-you-can-make | 1798. Maximum Number of Consecutive Values You Can Make | 1798-maximum-number-of-consecutive-value-scp9 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\nPure math\n\n\ncoin value is <= sum+1\n\n\n\n# Complexity\n- Time complex | pgmreddy | NORMAL | 2024-02-26T14:56:30.296918+00:00 | 2024-02-26T14:56:30.296953+00:00 | 5 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nPure math\n\n`\ncoin value is <= sum+1\n`\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n\n---\n\n```\nvar getMaximumConsecutive = function (cs) {\n cs.sort((a, b) => a - b)\n let s = 0\n for (let c of cs) {\n if (c <= s + 1) {\n s += c\n }\n }\n return s + 1\n};\n```\n\n---\n | 0 | 0 | ['JavaScript'] | 0 |
maximum-number-of-consecutive-values-you-can-make | submission beats 100% of other submissions' runtime. | submission-beats-100-of-other-submission-6471 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | PriyanshuNiranjan | NORMAL | 2024-02-16T14:07:43.151357+00:00 | 2024-02-16T14:07:43.151386+00:00 | 31 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int getMaximumConsecutive(int[] coins) {\n Arrays.sort(coins);\n int maxv = 1;\n for (int c : coins) {\n if (c > maxv)\n break;\n\n maxv += c;\n }\n return maxv;\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
maximum-number-of-consecutive-values-you-can-make | consecutive | consecutive-by-aman_17000s-6wg2 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | aman_17000s | NORMAL | 2024-02-06T07:45:22.317299+00:00 | 2024-02-06T07:45:22.317320+00:00 | 3 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) {\n sort(coins.begin(),coins.end());\n int ans=0;\n int curr=1;\n int n=coins.size();\n for( int i=0;i<n;i++){\n if(curr==coins[i]){\n \n curr*=2;\n ans=curr-1;\n }\n else if(curr>coins[i]){\n curr+=coins[i];\n ans=curr-1;\n }\n else {\n break;\n }\n }\n return ans+1;\n \n }\n};\n``` | 0 | 0 | ['Greedy', 'Sorting', 'C++'] | 0 |
maximum-number-of-consecutive-values-you-can-make | greedy | greedy-by-ns7653900-n79u | \n\n# Code\n\nclass Solution:\n def getMaximumConsecutive(self, coins: List[int]) -> int:\n coins.sort()\n ans=0\n tot=0\n for i | ns7653900 | NORMAL | 2024-01-24T05:16:29.714569+00:00 | 2024-01-24T05:16:29.714602+00:00 | 23 | false | \n\n# Code\n```\nclass Solution:\n def getMaximumConsecutive(self, coins: List[int]) -> int:\n coins.sort()\n ans=0\n tot=0\n for i in range(len(coins)):\n if tot-coins[i]>=-1:\n tot+=coins[i]\n ans=tot\n else:\n break\n return ans+1\n\n\n \n``` | 0 | 0 | ['Python3'] | 0 |
maximum-number-of-consecutive-values-you-can-make | same as patching array||c++||ditto same as patching array | same-as-patching-arraycditto-same-as-pat-tcll | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | kartik_pandey07 | NORMAL | 2024-01-19T16:39:40.481528+00:00 | 2024-01-19T16:39:40.481567+00:00 | 5 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) {\n sort(coins.begin(),coins.end());\n int sum=0;\n int i=0;\n while(i<coins.size())\n {\n if(coins[i]<=sum+1)\n {\n sum+=coins[i];\n i++;//i++ yaha pe krnge ham..same logic as in patching array and minimum coin needed to make such that sum lies in rage from [1,target]\n }\n else\n {\n break;//loop se break kr ja is time kyuki consecutiveness yaha pe break ho jiga..mean vo number missing hai mean consecutiveness break hua na...to jaha consecutive break ho rha hai hame waha pe ruk jana hai bhai\n }\n }\n return sum+1;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
maximum-number-of-consecutive-values-you-can-make | 🔥🔥🔥easy to understand [JAVA] | easy-to-understand-java-by-chakribontha9-3ta0 | maximum number we can make == minimum number we can\'t make from array\nhow we can find minimum number ???\nAns:-SORT ARRAY\nwhy sort?? \nAns:-[[2] 1 5]]\nminel | chakribontha9 | NORMAL | 2024-01-04T10:35:29.744623+00:00 | 2024-01-04T10:35:29.744653+00:00 | 20 | false | **maximum number we can make == minimum number we can\'t make from array**\nhow we can find minimum number ???\nAns:-SORT ARRAY\nwhy sort?? \nAns:-[[2] 1 5]]\nminele=1\nminele is 1 first ele is greater than minele --itsfailed\nexample [ 1 3 ]\n [1 **[2]** 3] \n\n```\nclass Solution {\n public int getMaximumConsecutive(int[] coins) {\n Arrays.sort(coins);\n int res=1;\n \n for(int ele:coins){\n if(ele>res){\n break;\n }\n res+=ele;\n }\n return res;\n }\n}\n// 1 1 3 4 10\n``` | 0 | 0 | ['Greedy', 'Java'] | 0 |
maximum-number-of-consecutive-values-you-can-make | merge sort | merge-sort-by-a36466136-t873 | Intuition\n Describe your first thoughts on how to solve this problem. \nmerge sort\n# Approach\n Describe your approach to solving the problem. \n\n# Complexit | a36466136 | NORMAL | 2023-12-14T02:24:33.545701+00:00 | 2023-12-14T02:24:33.545754+00:00 | 21 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nmerge sort\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(nlogn)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n# Code\n```\nclass Solution:\n def getMaximumConsecutive(self, coins: List[int]) -> int:\n coins.sort()\n prev = 0\n for c in coins:\n if c > prev + 1:\n return prev + 1\n prev += c\n return prev + 1\n \n``` | 0 | 0 | ['Python3'] | 0 |
maximum-number-of-consecutive-values-you-can-make | Simple C++ Solution | simple-c-solution-by-ikharabhishek-4lus | Intuition\n# There is 1 observation here. so if we find the consecutive sequence till "x" then if we have new interger let say "val" then we can obtained a cons | ikharabhishek | NORMAL | 2023-12-05T07:16:25.862230+00:00 | 2023-12-05T07:16:25.862259+00:00 | 8 | false | # Intuition\n# **There is 1 observation here. so if we find the consecutive sequence till "x" then if we have new interger let say "val" then we can obtained a consecutive sequence from 0 ... val+x . But only case when it is not possible is when x+1 < val.**\n\n# Approach\n1. Sort the coins array.\n2. Initialize the ans with 1, as 0 can be obtainable so we have to find from 1.\n3. We will traverse over each and every element of an coins array till coins[i]<=ans and add the coins[i] in our ans as per the intuition.\n4. Finally return the ans.\n\n# Complexity\n- Time complexity:\nO(nlogn+n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution {\npublic:\n \n int getMaximumConsecutive(vector<int>& c) {\n int n = c.size();\n sort(c.begin(),c.end());\n int ans=1;\n for(int i=0;i<n && c[i]<=ans;i++){\n ans += c[i];\n }\n return ans;\n } \n};\n``` | 0 | 0 | ['C++'] | 0 |
maximum-number-of-consecutive-values-you-can-make | Python greedy with sorting with explanation (330 and 2952 variant) | python-greedy-with-sorting-with-explanat-h6mm | Intuition\n Describe your first thoughts on how to solve this problem. \n1. Initialize res = 1 since we count from 0;\n2. Sort coins;\n3. For each coin in coins | nanzhuangdalao | NORMAL | 2023-12-03T22:00:58.698420+00:00 | 2023-12-03T22:06:02.800181+00:00 | 20 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n1. Initialize res = 1 since we count from 0;\n2. Sort coins;\n3. For each coin in coins:\n - if coin > res, then the consecutive values cannot expand to the right;\n - if coin == res, then the consecutive values can be just perfectly expanded, res = coin + res;\n - if coin < res, then the consecutive values can be expanded, but not as "efficient" as above, res = coin + res.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nGreedy with sorting.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n * log(n))\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n) due to sorting in Python\n# Code\n```\nclass Solution:\n def getMaximumConsecutive(self, coins: List[int]) -> int:\n res = 1\n coins.sort()\n for coin in coins:\n if coin > res:\n break\n else:\n res += coin\n \n return res\n``` | 0 | 0 | ['Python3'] | 0 |
maximum-number-of-consecutive-values-you-can-make | [Rust] Sort + Greedy value coverage extension | rust-sort-greedy-value-coverage-extensio-pdq9 | Intuition\nThe intuition behind solving this problem is based on the realization that if we can create every sum up to a certain value with the given coins, the | phi9t | NORMAL | 2023-12-03T19:48:20.977176+00:00 | 2023-12-03T19:48:20.977204+00:00 | 2 | false | # Intuition\nThe intuition behind solving this problem is based on the realization that if we can create every sum up to a certain value with the given coins, then any additional coin can only increase or maintain this range. The key lies in identifying the smallest value that we cannot attain. Since the coins don\'t necessarily come in a sequence (like 1, 2, 3, etc.), there might be gaps. Our goal is to find the first gap in the consecutive sums that we can create.\n\n# Approach\n1. **Sort the Coins:** Start by sorting the coins in ascending order. This step is crucial as it allows us to methodically build up sums from the smallest coin upwards, ensuring we don\'t miss any possible sums.\n\n2. **Iterative Summation:**\n - Initialize a variable `cover` to 0, which represents the highest sum we can create consecutively from the given coins.\n - Iterate through the sorted coins. For each coin, check if the next coin is larger than `cover + 1`. If it is, this means we cannot create the sum `cover + 1` with the given coins, and hence we\'ve found our gap.\n - If the coin is equal to or less than `cover + 1`, add it to `cover`. This increases the range of sums we can create.\n\n3. **Result:**\n - Once the first gap is found (or if all coins are used), the result is `cover + 1`, which is the smallest sum we cannot create.\n\n# Complexity\n- Time Complexity: **O(n log n)**\n - The most time-consuming operation in this algorithm is the sorting of the coins, which takes O(n log n) time, where `n` is the number of coins. The subsequent linear scan of the sorted array is O(n), which is overshadowed by the sorting step.\n\n- Space Complexity: **O(1)**\n - The space complexity is constant. We only use a few variables (`cover` and iteration variables) and do not allocate any additional data structures that scale with the input size. The sorting is done in place, so no extra space is needed for that operation.\n\n# Code\n```\n// Define a struct named Solution. This is a common pattern in competitive programming where\n// functions are defined as static methods on a struct.\nimpl Solution {\n // Define a public static method on the Solution struct.\n // It takes a vector of integers as input and returns an integer.\n pub fn get_maximum_consecutive(coins: Vec<i32>) -> i32 {\n // Create a mutable copy of the coins vector. \'mut\' keyword is used for mutability.\n let mut vals = coins;\n // Sort the vector in-place. Rust\'s sort method is similar to C++\'s sort() and Python\'s sort().\n vals.sort();\n \n // Initialize a variable \'cover\' to 0. It will keep track of the highest consecutive integer\n // we can make with the given set of coins.\n let mut cover = 0;\n \n // Iterate over the sorted coin values.\n for val in vals {\n // Check if the next coin is larger than the smallest unattainable value (cover + 1).\n // If it is, we can\'t cover that value with the current set of coins, so break the loop.\n if cover + 1 < val {\n break;\n }\n // Add the current coin\'s value to the cover. This extends the range of consecutive\n // values we can create.\n cover += val;\n }\n \n // Return the smallest unattainable value, which is one more than the current cover.\n cover + 1\n }\n}\n\n``` | 0 | 0 | ['Rust'] | 0 |
maximum-number-of-consecutive-values-you-can-make | Easy JavaScript Solution | easy-javascript-solution-by-surajkales11-kp4u | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | surajkales111 | NORMAL | 2023-12-03T05:21:26.610960+00:00 | 2023-12-03T05:21:26.610988+00:00 | 5 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * @param {number[]} coins\n * @return {number}\n */\nvar getMaximumConsecutive = function (coins) {\ncoins.sort((a,b) => a- b);\nlet reach = 0;\nlet i = 0;\nwhile (i < coins.length) {\nif (i < coins.length && coins[i] <= reach + 1) {\nreach += coins[i];\ni++;\n} else {\nbreak;\n}\n}\nreturn reach + 1;\n};\n``` | 0 | 0 | ['JavaScript'] | 0 |
maximum-number-of-consecutive-values-you-can-make | Easy to understand JavaScript solution (Greedy) | easy-to-understand-javascript-solution-g-ak46 | Complexity\n- Time complexity:\nO(nlogn)\n\n- Space complexity:\nO(1)\n\n# Code\n\nvar getMaximumConsecutive = function(coins) {\n let result = 1;\n\n coi | tzuyi0817 | NORMAL | 2023-11-09T02:55:16.152681+00:00 | 2023-11-09T02:55:16.152717+00:00 | 5 | false | # Complexity\n- Time complexity:\n$$O(nlogn)$$\n\n- Space complexity:\n$$O(1)$$\n\n# Code\n```\nvar getMaximumConsecutive = function(coins) {\n let result = 1;\n\n coins.sort((a, b) => a - b);\n\n for (const coin of coins) {\n if (coin > result) return result;\n result += coin;\n }\n return result;\n};\n``` | 0 | 0 | ['JavaScript'] | 0 |
maximum-number-of-consecutive-values-you-can-make | C# Solution Using Concatenation | c-solution-using-concatenation-by-jack00-5pur | Intuition\n\n\n# Approach\nassume we have found [0..biggest], in order for the consecutive, the next coin value have to be <=biggest+1, if that satisfies, we ca | jack0001 | NORMAL | 2023-10-07T17:32:36.351034+00:00 | 2023-10-07T17:32:36.351072+00:00 | 6 | false | # Intuition\n\n\n# Approach\nassume we have found [0..biggest], in order for the consecutive, the next coin value have to be <=biggest+1, if that satisfies, we can concatenate the smallest we found and the biggest would be this coin value plus "biggest" we found before.\n\n# Complexity\n- Time complexity:\nO(nlogn)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\npublic class Solution {\n public int GetMaximumConsecutive(int[] coins) {\n int lastSml = 0, lastBig = 0;\n int largest = 1;\n\n Array.Sort(coins);\n\n for(int i=0; i<coins.Length; ++i){\n int val = coins[i];\n int sml, big;\n if(val > lastBig+1){\n sml = val;\n break;\n }\n else{\n sml = lastSml;\n }\n\n lastSml = sml;\n lastBig = val + lastBig;\n largest = Math.Max(largest, lastBig-lastSml+1);\n }\n\n return largest;\n }\n}\n``` | 0 | 0 | ['C#'] | 0 |
maximum-number-of-consecutive-values-you-can-make | Easiest C++ Solution... | easiest-c-solution-by-parthbansal2047-6u7b | \n\n# Complexity\n- Time complexity: O(n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(1)\n Add your space complexity here, e.g. O(n) \ | parthbansal2047 | NORMAL | 2023-09-17T20:44:58.784884+00:00 | 2023-09-17T20:44:58.784911+00:00 | 13 | false | \n\n# Complexity\n- Time complexity: *O(n)*\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: *O(1)*\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) {\n int ans=0;\n sort(coins.begin(), coins.end());\n for(int i=0; i<coins.size(); i++){\n if(ans+1>=coins[i]){\n ans+=coins[i];\n }\n }\n return ans+1;\n }\n};\n``` | 0 | 0 | ['Array', 'Greedy', 'C++'] | 0 |
maximum-number-of-consecutive-values-you-can-make | C++/Python, greedy solution with explanation | cpython-greedy-solution-with-explanation-brrw | sort coins first.\n[0, m] are coin we can construct.\n\nand current coin is c,\nso if we use current coin c, we can construct m + c at most.\n\nand if current c | shun6096tw | NORMAL | 2023-08-30T08:50:36.639222+00:00 | 2023-08-30T08:50:36.639240+00:00 | 27 | false | sort coins first.\n[0, m] are coin we can construct.\n\nand current coin is c,\nso if we use current coin c, we can construct m + c at most.\n\nand if current coin c > m + 1,\nthere is no way to construct m + 1 because other coins after conic c >= c.\n\ntc is O(nlogn), sc is O(1).\n### python\n```python\nclass Solution:\n def getMaximumConsecutive(self, coins: List[int]) -> int:\n coins.sort()\n mx = 0\n for c in coins:\n if c > mx + 1: break\n mx += c\n return mx + 1\n```\n### c++\n```cpp\nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) {\n sort(coins.begin(), coins.end());\n int mx = 0;\n for (int& c: coins) {\n if (c > mx + 1) break;\n mx += c;\n }\n return mx + 1;\n }\n};\n``` | 0 | 0 | ['Greedy', 'C', 'Sorting', 'Python'] | 0 |
maximum-number-of-consecutive-values-you-can-make | Fast solution O(N*logN) time and O(1) space | fast-solution-onlogn-time-and-o1-space-b-2pdy | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | devvikram34 | NORMAL | 2023-08-20T16:27:43.336513+00:00 | 2023-08-20T16:28:28.228057+00:00 | 16 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(N*log N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public:\n int getMaximumConsecutive ( vector<int>& a ) {\n int ans = 1 , k = 0;\n sort ( a.begin ( ) , a.end ( ) );\n for ( auto&& i : a ) {\n if ( i - k <= 1 ) {\n k += i;\n if ( i != k + 1 ) ans += i;\n else ++ans;\n }\n }\n return ans;\n }\n };\n``` | 0 | 0 | ['C++'] | 0 |
maximum-number-of-consecutive-values-you-can-make | Maximum Number of Consecutive Values You Can Make solve with python | maximum-number-of-consecutive-values-you-l4qc | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | suryasoto45 | NORMAL | 2023-06-10T15:51:18.541197+00:00 | 2023-06-10T15:51:18.541232+00:00 | 74 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getMaximumConsecutive(self, coins: List[int]) -> int:\n ans = 1 # next value we want to make\n\n for coin in sorted(coins):\n if coin > ans:\n return ans\n ans += coin\n\n return ans\n\n``` | 0 | 0 | ['Python3'] | 0 |
maximum-number-of-consecutive-values-you-can-make | C++ | O(nlogn) + O(n) | c-onlogn-on-by-seekerm-0xen | Intuition\nFirst sort the elements. Why ??\nFor e.g. coins = [1,1,1,4]. Here the numbers less than 4 can only be generated by elements in the coins array with v | SeekerM | NORMAL | 2023-05-12T10:51:08.281129+00:00 | 2023-05-12T10:51:08.281177+00:00 | 51 | false | # Intuition\nFirst sort the elements. Why ??\nFor e.g. coins = [1,1,1,4]. Here the numbers less than 4 can only be generated by elements in the coins array with value less than 4. There to generate the numbers starting from 1 to ... we need coins to be sorted order.\n\nExplanation for: \n if(x <= rv+1)rv += x;\n else return rv+1;\n\nIf on reaching a number x in the sorted coins array, we still not have x-1, then we cannot generate x-1 because the smallest number that can be generated using x, is x. \n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Code\n```\nclass Solution {\npublic:\n int getMaximumConsecutive(vector<int>& coins) {\n \n sort(coins.begin(), coins.end());\n \n int rv = 0;\n for(int x: coins){\n if(x <= rv+1)rv += x;\n else return rv+1;\n }\n return rv+1;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
maximum-number-of-consecutive-values-you-can-make | Rust solution! | rust-solution-by-zhoutianyi0805-hl7i | Newbie in rust, any suggestion welcome\n# Code\n\n\nimpl Solution {\n pub fn get_maximum_consecutive(coins: Vec<i32>) -> i32 {\n let mut c = coins.clone | zhoutianyi0805 | NORMAL | 2023-05-05T22:38:59.927987+00:00 | 2023-05-05T22:38:59.928019+00:00 | 24 | false | Newbie in rust, any suggestion welcome\n# Code\n```\n\nimpl Solution {\n pub fn get_maximum_consecutive(coins: Vec<i32>) -> i32 {\n let mut c = coins.clone();\n c.sort();\n let mut res = 0;\n let mut ans = c.iter()\n .try_fold(0, |accum, &val| {\n if accum < val - 1 {\n res = accum;\n None\n } else {\n Some(accum + val)\n }\n }).unwrap_or(res);\n ans+1\n }\n}\n\n``` | 0 | 0 | ['Rust'] | 0 |
minimum-swaps-to-make-sequences-increasing | Java O(n) DP Solution | java-on-dp-solution-by-wangzi6147-7dws | swapRecord means for the ith element in A and B, the minimum swaps if we swap A[i] and B[i]\nfixRecord means for the ith element in A and B, the minimum swaps i | wangzi6147 | NORMAL | 2018-03-19T04:20:01.859505+00:00 | 2018-10-21T05:49:21.762728+00:00 | 35,253 | false | ```swapRecord``` means for the ith element in A and B, the minimum swaps if we swap ```A[i]``` and ```B[i]```\n```fixRecord``` means for the ith element in A and B, the minimum swaps if we DONOT swap ```A[i]``` and ```B[i]```\n```\nclass Solution {\n public int minSwap(int[] A, int[] B) {\n int swapRecord = 1, fixRecord = 0;\n for (int i = 1; i < A.length; i++) {\n if (A[i - 1] >= B[i] || B[i - 1] >= A[i]) {\n\t\t// In this case, the ith manipulation should be same as the i-1th manipulation\n // fixRecord = fixRecord;\n swapRecord++;\n } else if (A[i - 1] >= A[i] || B[i - 1] >= B[i]) {\n\t\t// In this case, the ith manipulation should be the opposite of the i-1th manipulation\n int temp = swapRecord;\n swapRecord = fixRecord + 1;\n fixRecord = temp;\n } else {\n // Either swap or fix is OK. Let\'s keep the minimum one\n int min = Math.min(swapRecord, fixRecord);\n swapRecord = min + 1;\n fixRecord = min;\n }\n }\n return Math.min(swapRecord, fixRecord);\n }\n}\n```\n\nLet me firstly explain the O(n) space DP solution which uses swapRecord[n] and fixRecord[n]. It would be more explicit.\n\nOne thing should be kept in mind is, the array A and B would always be valid after you do the swap manipulation or not for each element. Take an example:\n\n```\nindex 0 1 2 3 4\nA 1 3 5 4 9\nB 1 2 3 7 10 \nswapRecord 1 1 2 1 2\nfixRecord 0 0 0 2 1\n```\n\n```swapRecord[i]``` means for the ith element in A and B, the minimum swaps if we swap A[i] and B[i]\n```fixRecord[i]``` means for the ith element in A and B, the minimum swaps if we DONOT swap A[i] and B[i]\n\nObviously, ```swapRecord[0] = 1``` and ```fixRecord[0] = 0```.\n\nFor ```i = 1```, either swap or fix is OK. So we take the minimum previous result, ```min = min(swapRecord[0], fixRecord[0]) = 0```. ```swapRecord[1] = min + 1 = 1```, ```fixRecord[1] = min = 0```\nFor ```i = 2```, notice that A[1] >= B[2], which means the manipulation of ```A[2] and B[2]``` should be same as ```A[1] and B[1]```, if A[1] and B[1] swap, A[2] and B[2] should swap, vice versa. Make sense, right? So ```swapRecord[2] = swapRecord[1] + 1``` and ```fixRecord[2] = fixRecord[1]```\nFor ```i = 3```, notice that A[2] >= A[3], which mean the manipulation of ```A[3] and B[3]``` and ```A[2] and B[2]``` should be opposite. In this case, ```swapRecord[3] = fixRecord[2] + 1``` and ```fixRecord[3] = swapRecord[2]```\nFor the last elements, it\'s similiar as the elements when i = 1. Either swap or fix is OK. You can try to figure this out. :D\n\nFinally, we get the minimum of last swapRecord and fixRecord. It should be the result.\n\nNotice that every ith swapRecord and fixRecord is only relevant with the previous one. So the algorithm should be optimized to an O(1) space version. Just like the code I write above. | 408 | 7 | [] | 42 |
minimum-swaps-to-make-sequences-increasing | [Java/C++/Python] DP O(N) Solution | javacpython-dp-on-solution-by-lee215-xrdk | Explanation\nswap[n] means the minimum swaps to make the A[i] and B[i] sequences increasing for 0 <= i <= n,\nin condition that we swap A[n] and B[n]\nnot_swap[ | lee215 | NORMAL | 2018-03-19T08:27:53.829176+00:00 | 2020-11-29T10:23:48.824046+00:00 | 32,570 | false | # **Explanation**\n```swap[n]``` means the minimum swaps to make the ```A[i]``` and ```B[i]``` sequences increasing for ```0 <= i <= n```,\nin condition that we swap ```A[n]``` and ```B[n]```\n```not_swap[n]``` is the same with ```A[n]``` and ```B[n]``` not swapped.\n\n@Acker help explain:\n1. `A[i - 1] < A[i] && B[i - 1] < B[i]`.\nIn this case, if we want to keep A and B increasing before the index i, can only have two choices.\n-> 1.1 don\'t swap at (i-1) and don\'t swap at i, we can get `not_swap[i] = not_swap[i-1]`\n-> 1.2 swap at (i-1) and swap at i, we can get `swap[i] = swap[i-1]+1`\nif swap at (i-1) and do not swap at i, we can not guarantee A and B increasing.\n\n2. `A[i-1] < B[i] && B[i-1] < A[i]`\nIn this case, if we want to keep A and B increasing before the index i, can only have two choices.\n-> 2.1 swap at (i-1) and do not swap at i, we can get `notswap[i] = Math.min(swap[i-1], notswap[i] )`\n-> 2.2 do not swap at (i-1) and swap at i, we can get `swap[i]=Math.min(notswap[i-1]+1, swap[i])`\n<br>\n\n# Complexty\nTime `O(N)`\nSpace `O(N)`\n<br>\n\n**C++**\n```cpp\n int minSwap(vector<int>& A, vector<int>& B) {\n int N = A.size();\n int not_swap[1000] = {0};\n int swap[1000] = {1};\n for (int i = 1; i < N; ++i) {\n not_swap[i] = swap[i] = N;\n if (A[i - 1] < A[i] && B[i - 1] < B[i]) {\n swap[i] = swap[i - 1] + 1;\n not_swap[i] = not_swap[i - 1];\n }\n if (A[i - 1] < B[i] && B[i - 1] < A[i]) {\n swap[i] = min(swap[i], not_swap[i - 1] + 1);\n not_swap[i] = min(not_swap[i], swap[i - 1]);\n }\n }\n return min(swap[N - 1], not_swap[N - 1]);\n }\n```\n**Java**\n```java\n public int minSwap(int[] A, int[] B) {\n int N = A.length;\n int[] swap = new int[1000];\n int[] not_swap = new int[1000];\n swap[0] = 1;\n for (int i = 1; i < N; ++i) {\n not_swap[i] = swap[i] = N;\n if (A[i - 1] < A[i] && B[i - 1] < B[i]) {\n swap[i] = swap[i - 1] + 1;\n not_swap[i] = not_swap[i - 1];\n }\n if (A[i - 1] < B[i] && B[i - 1] < A[i]) {\n swap[i] = Math.min(swap[i], not_swap[i - 1] + 1);\n not_swap[i] = Math.min(not_swap[i], swap[i - 1]);\n }\n }\n return Math.min(swap[N - 1], not_swap[N - 1]);\n }\n```\n**Python**\n```py\n def minSwap(self, A, B):\n N = len(A)\n not_swap, swap = [N] * N, [N] * N\n not_swap[0], swap[0] = 0, 1\n for i in range(1, N):\n if A[i - 1] < A[i] and B[i - 1] < B[i]:\n swap[i] = swap[i - 1] + 1\n not_swap[i] = not_swap[i - 1]\n if A[i - 1] < B[i] and B[i - 1] < A[i]:\n swap[i] = min(swap[i], not_swap[i - 1] + 1)\n not_swap[i] = min(not_swap[i], swap[i - 1])\n return min(swap[-1], not_swap[-1])\n```\n<br>\n\n# Solution 2\nTime O(N)\nSpace only `O(1)`\n**Java**\n```java\n public int minSwap(int[] A, int[] B) {\n int N = A.length;\n int swap = 1, not_swap = 0;\n for (int i = 1; i < N; ++i) {\n int not_swap2 = N, swap2 = N;\n if (A[i - 1] < A[i] && B[i - 1] < B[i]) {\n swap2 = swap + 1;\n not_swap2 = not_swap;\n }\n if (A[i - 1] < B[i] && B[i - 1] < A[i]) {\n swap2 = Math.min(swap2, not_swap + 1);\n not_swap2 = Math.min(not_swap2, swap);\n }\n swap = swap2;\n not_swap = not_swap2;\n }\n return Math.min(swap, not_swap);\n }\n```\n**C++**\n```cpp\n int minSwap(vector<int>& A, vector<int>& B) {\n int N = A.size(), swap = 1, not_swap = 0;\n for (int i = 1; i < N; ++i) {\n int not_swap2 = N, swap2 = N;\n if (A[i - 1] < A[i] && B[i - 1] < B[i]) {\n swap2 = swap + 1;\n not_swap2 = not_swap;\n }\n if (A[i - 1] < B[i] && B[i - 1] < A[i]) {\n swap2 = min(swap2, not_swap + 1);\n not_swap2 = min(not_swap2, swap);\n }\n swap = swap2;\n not_swap = not_swap2;\n }\n return min(swap, not_swap);\n }\n```\n**Python**\n```py\n def minSwap(self, A, B):\n N = len(A)\n not_swap, swap = 0, 1\n for i in range(1, N):\n not_swap2 = swap2 = N\n if A[i - 1] < A[i] and B[i - 1] < B[i]:\n swap2 = swap + 1\n not_swap2 = not_swap\n if A[i - 1] < B[i] and B[i - 1] < A[i]:\n swap2 = min(swap2, not_swap + 1)\n not_swap2 = min(not_swap2, swap)\n swap, not_swap = swap2, not_swap2\n return min(swap, not_swap)\n``` | 317 | 3 | [] | 36 |
minimum-swaps-to-make-sequences-increasing | Bottom-up DP with Optimization (Java / Python) | bottom-up-dp-with-optimization-java-pyth-82kn | state\t\nwhether we swap the element at index i to make A[0..i] and B[0..i] both increasing can uniquely identify a\xA0state, i.e. a node in the state graph.\n | gracemeng | NORMAL | 2018-08-21T01:59:58.096686+00:00 | 2018-10-17T19:14:32.933059+00:00 | 8,992 | false | **state**\t\nwhether we swap the element at index i to make A[0..i] and B[0..i] both increasing can uniquely identify a\xA0state, i.e. a node in the state graph.\n**state function**\t\n`state(i, 0)`\xA0is the minimum swaps to make A[0..i] and B[0..i] both increasing if we donot swap A[i] with B[i]\n`state(i, 1)`\xA0is the minimum swaps to make A[0..i] and B[0..i] both increasing if we do swap A[i] with B[i]\n**goal state**\t\n`min{state(n - 1, 0), state(n - 1, 1)}` where n = A.length\n**state transition**\t\nWe define `areBothSelfIncreasing: A[i - 1] < A[i] && B[i - 1] < B[i], areInterchangeIncreasing: A[i - 1] < B[i] && B[i - 1] < A[i]`.\nSince *\'the given input always makes it possible\'*, at least one of the two conditions above should be satisfied.\n```\nif i == 0, \n\t state(0, 0) = 0; \n\t state(0, 1) = 1;\n\t\t\t\nGenerally speaking,\n\tif areBothSelfIncreasing && areInterchangeIncreasing\n\t // Doesn\'t matter whether the previous is swapped or not.\n\t state(i, 0) = Math.min(state(i - 1, 0), state(i - 1, 1));\n\t state(i, 1) = Math.min(state(i - 1, 0), state(i - 1, 1)) + 1;\n\telse if areBothSelfIncreasing\n\t // Following the previous action.\n\t state(i, 0) = state(i - 1, 0);\n\t state(i, 1) = state(i - 1, 1) + 1;\n\telse if areInterchangeIncreasing\n\t // Opposite to the previous action.\n\t state(i, 0) = state(i - 1, 1);\n\t state(i, 1) = state(i - 1, 0) + 1;\n```\n**Java 0.0**\n```\n public int minSwap(int[] A, int[] B) {\n int n = A.length;\n \n /* \n\t\t state[i][0] is min swaps too make A[0..i] and B[0..i] increasing if we do not swap A[i] and B[i]; \n\t\t state[i][1] is min swaps too make A[0..i] and B[0..i] increasing if we swap A[i] and B[i].\n */\n int[][] state = new int[n][2];\n state[0][1] = 1;\n \n for (int i = 1; i < n; i++) {\n boolean areBothSelfIncreasing = A[i - 1] < A[i] && B[i - 1] < B[i];\n boolean areInterchangeIncreasing = A[i - 1] < B[i] && B[i - 1] < A[i];\n \n if (areBothSelfIncreasing && areInterchangeIncreasing) {\n state[i][0] = Math.min(state[i - 1][0], state[i - 1][1]);\n state[i][1] = Math.min(state[i - 1][0], state[i - 1][1]) + 1;\n } else if (areBothSelfIncreasing) {\n state[i][0] = state[i - 1][0];\n state[i][1] = state[i - 1][1] + 1;\n } else { // if (areInterchangeIncreasing)\n state[i][0] = state[i - 1][1];\n state[i][1] = state[i - 1][0] + 1;\n }\n }\n \n return Math.min(state[n - 1][0], state[n - 1][1]);\n }\n```\n**Optimization**\nSince current state depends on its previous state only, we may use variables to save states rather than the state array.\n**Java 0.1**\n```\n public int minSwap(int[] A, int[] B) {\n int n = A.length, prevNotSwap = 0, prevSwap = 1;\n \n for (int i = 1; i < n; i++) {\n boolean areBothSelfIncreasing = A[i - 1] < A[i] && B[i - 1] < B[i];\n boolean areInterchangeIncreasing = A[i - 1] < B[i] && B[i - 1] < A[i];\n \n if (areBothSelfIncreasing && areInterchangeIncreasing) {\n int newPrevNotSwap = Math.min(prevNotSwap, prevSwap);\n prevSwap = Math.min(prevNotSwap, prevSwap) + 1;\n prevNotSwap = newPrevNotSwap;\n } else if (areBothSelfIncreasing) {\n prevSwap++;\n } else { // if (areInterchangeIncreasing)\n int newPrevNotSwap = prevSwap;\n prevSwap = prevNotSwap + 1;\n prevNotSwap = newPrevNotSwap;\n }\n }\n \n return Math.min(prevSwap, prevNotSwap);\n }\n```\n**Python**\n```\n def minSwap(self, A, B):\n n = len(A)\n prevNotSwap = 0\n prevSwap = 1\n for i in range(1, n):\n areBothSelfIncreasing = A[i - 1] < A[i] and B[i - 1] < B[i] \n areInterchangeIncreasing = A[i - 1] < B[i] and B[i - 1] < A[i]\n if areBothSelfIncreasing and areInterchangeIncreasing:\n newPrevNotSwap = min(prevNotSwap, prevSwap)\n prevSwap = min(prevNotSwap, prevSwap) + 1\n prevNotSwap = newPrevNotSwap\n elif areBothSelfIncreasing:\n prevSwap += 1 \n else: # if areInterchangeIncreasing:\n newPrevNotSwap = prevSwap\n prevSwap = prevNotSwap + 1\n prevNotSwap = newPrevNotSwap\n return min(prevNotSwap, prevSwap)\n```\n**(\u4EBA \u2022\u0348\u1D17\u2022\u0348)** Thanks for voting! | 275 | 0 | [] | 21 |
minimum-swaps-to-make-sequences-increasing | Recursive with memoization (beats 100.00 %): | recursive-with-memoization-beats-10000-b-eob0 | \nclass Solution { \n\n int[][] dp;\n \n public int minSwap(int[] A, int[] B) {\n dp = new int[A.length][2];\n for (int[] row: dp)\n | yogi_bear | NORMAL | 2019-03-26T06:16:30.430676+00:00 | 2020-04-12T20:26:10.015676+00:00 | 7,320 | false | ```\nclass Solution { \n\n int[][] dp;\n \n public int minSwap(int[] A, int[] B) {\n dp = new int[A.length][2];\n for (int[] row: dp)\n Arrays.fill(row, -1);\n return minSwapHelper(A, B, 0, -1, -1, 0);\n }\n \n private int minSwapHelper(int[] A, int[] B, int i, int prevA, int prevB, int swapped) {\n if(i == A.length) return 0;\n \tif(dp[i][swapped] != -1) return dp[i][swapped];\n int minSwaps = Integer.MAX_VALUE;\n if(A[i] > prevA && B[i] > prevB) {\n minSwaps = minSwapHelper(A, B, i + 1, A[i], B[i], 0);\n }\n swap(A, B, i);\n if(A[i] > prevA && B[i] > prevB) {\n minSwaps = Math.min(minSwaps, minSwapHelper(A, B, i + 1, A[i], B[i], 1) + 1);\n }\n swap(A, B, i);\n dp[i][swapped] = minSwaps;\n return minSwaps;\n }\n \n private void swap(int[] A, int[] B, int i) {\n int t = A[i];\n A[i] = B[i];\n B[i] = t;\n }\n}\n```\n\n##### Minor improvements (no swap call)\n\n```\nclass Solution {\n \n Integer[][] dp;\n final int MAX = 10_000;\n \n public int minSwap(int[] A, int[] B) {\n dp = new Integer[A.length][2]; \n return minSwapHelper(A, B, 0, -1, -1, 0);\n }\n \n private int minSwapHelper(int[] A, int[] B, int i, int prevA, int prevB, int swapped) {\n \n if(i == A.length) return 0;\n \tif(dp[i][swapped] != null) return dp[i][swapped];\n \n int minSwaps = MAX;\n \n if(A[i] > prevA && B[i] > prevB) { // with-no-swap\n minSwaps = minSwapHelper(A, B, i + 1, A[i], B[i], 0);\n }\n \n if(B[i] > prevA && A[i] > prevB) { // with-swap\n minSwaps = Math.min(minSwaps, minSwapHelper(A, B, i + 1, B[i], A[i], 1) + 1);\n }\n\n dp[i][swapped] = minSwaps;\n return minSwaps;\n }\n \n}\n``` | 106 | 0 | [] | 17 |
minimum-swaps-to-make-sequences-increasing | Python 14-line O(1) space O(n) time DP solution | python-14-line-o1-space-on-time-dp-solut-mo7d | This problem can be solved using dynamic programming, at each position, we can choose to swap or not. Since we want two sorted arrays, at each position, whether | luckypants | NORMAL | 2018-03-19T03:45:50.604272+00:00 | 2018-10-21T05:21:55.360369+00:00 | 7,910 | false | This problem can be solved using dynamic programming, at each position, we can choose to swap or not. Since we want two sorted arrays, at each position, whether to swap or not depends on the choice at previous position, so we can form a recursive formula.\n\n```\nN = len(A)\ndp = [[maxint]*2 for _ in range(N)]\n```\n\nLet initialize a N*2 array dp, \n\n* dp[i][0] means the least swaps used to make A[:i+1] and B[:i+1] sorted having no swap at i-th position.\n* dp[i][1] means the least swaps used to make A[:i+1] and B[:i+1] sorted having swap at i-th position.\n\n**Picture explanation:**\n\n\n\nHere is the recursive formula:\n\nThere are two cases that can make the two arrays sorted:\n\n```\nA . B\nC . D\n```\n\nHere our cases are `A<B and C<D` and `A<D and C<B`.\n\nBecause the possible combination to be sorted are only `A B` in array1 `C D` in array2 or `A D` in array1 `C B` in array2, so only the 2 cases, and they can holds at the same time: for example `A=1, B=2, C=1, D=2`. If both don\'t hold, swapping can\'t make them in order.\n\nFor $i in [1, N]$:\n\nIf A[i]>A[i-1] and B[i]>B[i-1] (they are in order without swap):\ndp[i][0]=min(dp[i][0], dp[i-1][0]) (no swap at i-1 and no swap at i)\ndp[i][1]=min(dp[i][1], dp[i-1][1]+1) (swap at i-1 so swap at i to make in order)\n\nIf A[i]>B[i-1] and B[i]>A[i-1] (they are in order with a swap):\ndp[i][0]=min(dp[i][0], dp[i-1][1]) (swap at i-1, no need to swap at i)\ndp[i][1]=min(dp[i][1], dp[i-1][0]+1) (no swap at i-1, so swap at i)\n\nThe two cases don\'t conflict with each other, so we choose minimum of them when both holds.\n\nWhat we want to return is min(dp[N-1][0], dp[N-1][1]).\n\nAt every recursion, we only need the last result, so we can use less space, from O(N) to O(1), time complexity O(N).\n\n20-Line Python Solution\uFF1A\n\n```\ndef minSwap(self, A, B):\n """\n :type A: List[int]\n :type B: List[int]\n :rtype: int\n """\n n = len(A)\n pre = [0, 1]\n for i in range(1, n):\n cur = [sys.maxsize, sys.maxsize]\n if A[i]>A[i-1] and B[i]>B[i-1]:\n cur[0] = min(cur[0], pre[0])\n cur[1] = min(cur[1], pre[1]+1)\n if A[i]>B[i-1] and B[i]>A[i-1]:\n cur[0] = min(cur[0], pre[1])\n cur[1] = min(cur[1], pre[0]+1)\n pre = cur\n return min(pre)\n``` | 70 | 1 | [] | 17 |
minimum-swaps-to-make-sequences-increasing | C++ solution with explanation | c-solution-with-explanation-by-snorlaxny-sbvq | Here let me rephrase the solution by @lee215.\n\nhttps://leetcode.com/problems/minimum-swaps-to-make-sequences-increasing/discuss/119879/Easy-Understood-DP-Solu | snorlaxnyc | NORMAL | 2018-03-24T03:17:45.497684+00:00 | 2018-09-19T07:19:21.100653+00:00 | 5,663 | false | Here let me rephrase the solution by @lee215.\n\nhttps://leetcode.com/problems/minimum-swaps-to-make-sequences-increasing/discuss/119879/Easy-Understood-DP-Solution-C++JavaPython\n\nThis problem can be solved using dynamic programming, at each position, we can choose to swap or not. Since we want two sorted arrays, at each position, whether to swap or not depends on the choice at previous position, so we can form a recursive formula.\n\nWhen ```A[0, i-1]``` and ```B[0, i - 1]``` are sorted, since "It is guaranteed that the given input always makes it possible.". There are two cases on index ```i```:\n\n1. They are both still sorted when add number at index i, ```A[i] > A[i - 1] && B[i] > B[i - 1]```\n2. They are not sorted when add number at index i, in this case, only ```A[i] > B[i - 1] && B[i] > A[i - 1]``` can guarantee that "the given input always makes it possible".\n\nHere we use :\n\n* ```swap[i]``` to represent the minimum swaps to make the ```A[0, i]``` and ```B[0, i]``` sequences increasing for ```0 <= i <= n``` in condition that we swap ```A[i]``` and ```B[i]```. \n* ```no_swap[i]``` to represent the minimum swaps to make the ```A[0, i]``` and ```B[0, i]``` sequences increasing for ```0 <= i <= n``` in condition that we don\'t swap ```A[i]``` and ```B[i]```.\n\n```cpp\nclass Solution {\npublic:\n int minSwap(vector<int>& A, vector<int>& B) {\n const size_t n = A.size();\n vector<int> swap(n, n), no_swap(n, n);\n swap[0] = 1;\n no_swap[0] = 0;\n for (size_t i = 1; i < n; ++i) {\n if (A[i] > A[i - 1] && B[i] > B[i - 1]) {\n // If we swap position i, we need to swap position i - 1.\n swap[i] = swap[i - 1] + 1;\n \n // If we don\'t swap position i , we should not swap position i - 1.\n no_swap[i] = no_swap[i - 1];\n }\n \n if (A[i] > B[i - 1] && B[i] > A[i - 1]) {\n // If we swap position i, we should not swap position i - 1.\n swap[i] = std::min(swap[i], no_swap[i - 1] + 1);\n \n // If we don\'t swap position i, we should swap position i - 1.\n no_swap[i] = std::min(no_swap[i], swap[i - 1]);\n }\n }\n \n return std::min(swap.back(), no_swap.back());\n }\n};\n```\n | 54 | 3 | [] | 5 |
minimum-swaps-to-make-sequences-increasing | FULLY EXPLAINED SOLUTION FOR BEGINNER . ( Recursion+Memoization) | fully-explained-solution-for-beginner-re-bqwb | The basic idea behind this problem is same what we uses in 0 1 knapsack.\nSo what is the idea in 0 1 knapsack. The idea is that we provide some condition during | rahul_81 | NORMAL | 2022-03-14T18:17:21.203731+00:00 | 2023-03-13T06:08:09.881085+00:00 | 2,952 | false | The basic idea behind this problem is same what we uses in 0 1 knapsack.\nSo what is the idea in **0 1 knapsack**. The idea is that we provide some condition during function call, and if condition is satisfied then we have two options (i,e) either include the current element or do not include the current element.But if condition is not satisfied then we have only one option (i,e) we do not include the current element.\n\nWe will use that same idea here.\nSo what are the different conditions here.\n\nCondition 1 - Ok lets suppose we have two arrays as follows :-\n\tnums1[] = [3,2]\n\tnums2[] = [1,4]\n\tand we are at index 1.we can see that for nums1 we have nums1[ind-1]>= nums1[ind], So for this condition we have only one option i,e we have to swap the elements so that array can be made strictly increasing. So we will swap elements and recursively call next functions.\n\t\n\tAfter swapping element at index 1 array will now becomes nums1[] = {3,4} and nums2[] = {1,2} (i,e strictly increasing)\n\t\nCondition 2- lets take another example:-\nnums1[] = {1,2}\nnums2[] = {3,4}\nindex = 1;\n\nif we do swapping of the current element then our array will be nums1[] = {1,4} and nums2[] = {3,2}. We can see that the elements in nums2 is not in increasing order.\n\nTherefore if (nums1[ind-1] >= nums2[ind] || nums2[ind-1] >= nums1[ind] ) we cannot swap the current element.\n\nCondition 3 -\nNow lets take another example \nnums1[] = {1,5}\nnums2[] = {3,4}\nindex = 1;\n\nHere we have two options either we swap the current element or we do not swap. So here we will take the minimum answer of both the option and return the answer.\n\nAny suggestions are welcome.\nThanks\n**Do upvote if you like the explaination !!!**\n\nclass Solution {\n\n public int minSwap(int[] nums1, int[] nums2) {\n\t\n int dp[] = new int[nums1.length];\n Arrays.fill(dp,-1);\n \n int ans = solve(nums1,nums2,0,dp);\n \n return ans;\n }\n \n public int solve(int nums1[],int nums2[],int ind,int[] dp){\n \n if(ind == nums1.length) return 0;\n \n\t\t// Condition 1\n\t\t\n if(ind>0 && (nums1[ind-1]>=nums1[ind] || nums2[ind-1]>=nums2[ind])) {\n \n\t\t\t\t//\tnums1[] = [3,2]\n\t\t\t\t//\tnums2[] = [1,4]\n\t\t\t\t\n int t = nums1[ind];\n nums1[ind] = nums2[ind];\n nums2[ind] = t;\n \n int val = 1+solve(nums1,nums2,ind+1,dp);\n \n\t\t\t// Since after swapping array becomes \n\t\t\t// nums1[] = [3,4]\n\t\t\t// nums2[] = [1,2]\n\t\t\t// therefore we have to swap it back so that we can have our original array.\n\t\t\t\n t = nums1[ind];\n nums1[ind] = nums2[ind];\n nums2[ind] = t;\n \n return val;\n \n } \n\t\t// Condition 2\n\t\t\n\t\telse if(ind>0 && (nums1[ind-1]>=nums2[ind] || nums2[ind-1]>=nums1[ind])) {\n\t\t\t\treturn solve(nums1,nums2,ind+1,dp);\n }\n\t\t// Condition 3\n\t\t\n else {\n if(dp[ind] != -1) return dp[ind];\n \n int tempAns1 = solve(nums1,nums2,ind+1,dp);\n \n int t = nums1[ind];\n nums1[ind] = nums2[ind];\n nums2[ind] = t;\n \n int tempAns2 = 1+solve(nums1,nums2,ind+1,dp);\n \n t = nums1[ind];\n nums1[ind] = nums2[ind];\n nums2[ind] = t;\n \n return dp[ind] = Math.min(tempAns1,tempAns2);\n }\n \n }\n}\n\nA pictorial representation of why we are updating dp[] array only in condition 3.\n**nums1[] = [4,4,5];\nnums2[] = [1,6,8];**\n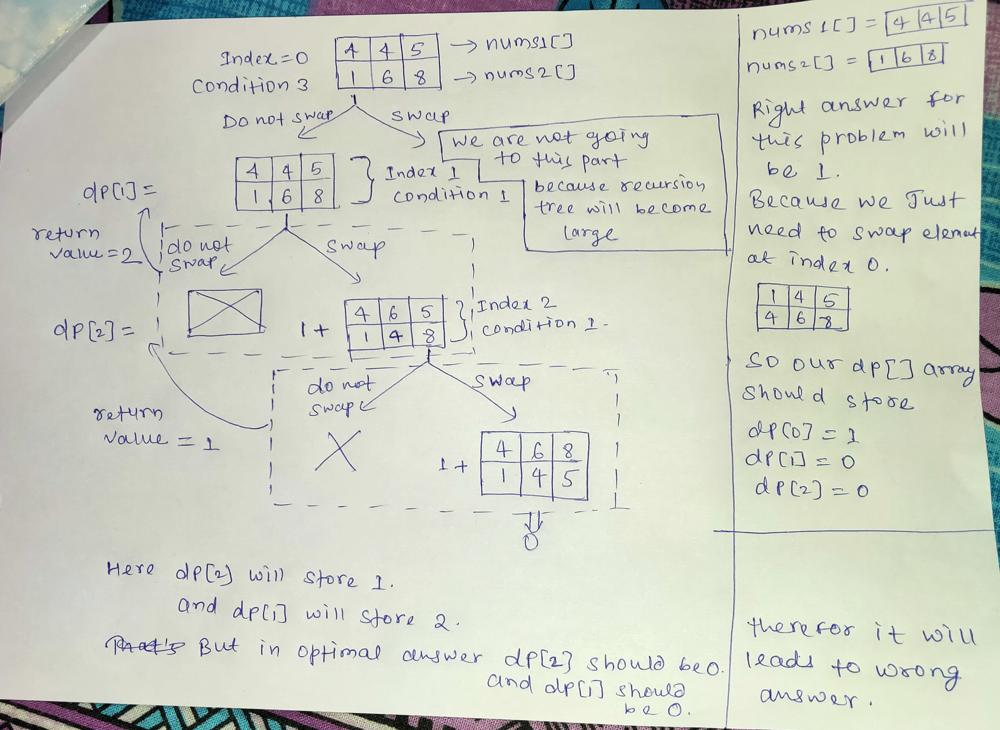\n\n | 45 | 0 | ['Java'] | 4 |
minimum-swaps-to-make-sequences-increasing | Super Intuitive solution(recursive + memoization) | super-intuitive-solutionrecursive-memoiz-7qw0 | \nclass Solution {\n public int minSwap(int[] A, int[] B) {\n Integer[][] dp = new Integer[A.length][2];//0 no swap, 1:swap\n\n return dfs( | job | NORMAL | 2018-11-11T17:57:15.734051+00:00 | 2018-11-11T17:57:15.734091+00:00 | 3,265 | false | ```\nclass Solution {\n public int minSwap(int[] A, int[] B) {\n Integer[][] dp = new Integer[A.length][2];//0 no swap, 1:swap\n\n return dfs(A,B,0,dp,0);\n }\n public int dfs(int[] A,int[] B, int i,Integer[][] dp,int swap){\n\n if(i==A.length){\n return 0;\n }\n if(dp[i][swap]!=null)\n return dp[i][swap];\n int min1=Integer.MAX_VALUE;\n if(i==0 || A[i] > A[i-1] && B[i] > B[i-1]){\n min1=dfs(A,B,i+1,dp,0);\n }\n int min2=Integer.MAX_VALUE;\n if(i==0 || A[i] > B[i-1] && B[i] >A[i-1]){\n swap(A,B,i);\n min2=dfs(A,B,i+1,dp,1)+1;\n swap(A,B,i);\n }\n dp[i][swap]=Math.min(min1,min2);\n return dp[i][swap];\n }\n public void swap(int[] A,int[] B, int idx){\n int temp=A[idx];\n A[idx]=B[idx];\n B[idx]=temp;\n }\n}\n``` | 40 | 2 | [] | 3 |
minimum-swaps-to-make-sequences-increasing | Java DP 2ms solution with comments | java-dp-2ms-solution-with-comments-by-ar-64kq | \npublic int minSwap(int[] A, int[] B) {\n int n = A.length;\n int not_swap[] = new int[n]; \n //not_swap[i] -> min swaps to make {A[0]~A[i | arjun_sharma | NORMAL | 2019-04-07T21:41:19.287307+00:00 | 2019-04-07T21:41:19.287374+00:00 | 2,385 | false | ```\npublic int minSwap(int[] A, int[] B) {\n int n = A.length;\n int not_swap[] = new int[n]; \n //not_swap[i] -> min swaps to make {A[0]~A[i]} and {B[0]~B[i]} without swapping A[i] and B[i]\n int swap[] = new int[n];\n //swap[i] -> min swaps to make {A[0]~A[i]} and {B[0]~B[i]} with swapping A[i] and B[i]\n Arrays.fill(not_swap, Integer.MAX_VALUE);\n Arrays.fill(swap, Integer.MAX_VALUE);\n not_swap[0] = 0;\n swap[0] = 1;\n \n for(int i = 1; i < n; i++) {\n if(A[i - 1] < A[i] && B[i - 1] < B[i]) {\n swap[i] = swap[i - 1] + 1; //swap both A[i - 1], B[i - 1] & A[i], B[i]\n not_swap[i] = not_swap[i - 1]; //don\'t swap both A[i - 1], B[i - 1] & A[i], B[i]\n }\n if(A[i] > B[i - 1] && B[i] > A[i - 1]) {\n swap[i] = Math.min(swap[i], not_swap[i - 1] + 1); //if we swap A[i],B[i], we don\'t need to swap A[i - 1],B[i - 1] \n //not_swap[i - 1] + 1 because we didn\'t swap A[i - 1] & B[i - 1] and +1 for current swap \n not_swap[i] = Math.min(not_swap[i], swap[i - 1]); //if we swap A[i - 1],B[i - 1], we don\'t need to swap A[i],B[i]\n }\n }\n \n return Math.min(swap[n - 1], not_swap[n - 1]);\n }\n``` | 32 | 1 | [] | 7 |
minimum-swaps-to-make-sequences-increasing | From Recursion to DP (4 Solutions) [Java] | from-recursion-to-dp-4-solutions-java-by-jywc | Approach\nThere are two states possible,\n1. Don\'t swap elements at the current index\n2. Swap elements at the current index\n\nWe just have to find out which | redocsuomynona | NORMAL | 2021-06-16T19:41:37.592879+00:00 | 2021-06-16T19:41:37.592915+00:00 | 2,495 | false | **Approach**\nThere are two states possible,\n1. Don\'t swap elements at the current index\n2. Swap elements at the current index\n\nWe just have to find out which one gives the minimum number of swaps for the rest of the array. That is, we will compute answer for both the states. The answer for the current state is dependent on the relation between the element at the current index and the previous index.\n\nIf they are already in increasing order, then the state for the current index is applied to the previous index (that is, no swap remains no swap, swap remains swap). Else, the state for the current index is reversed for the previous index. But, what if swap and no swap both achieve the increasing order? In this case, we take the minimum of both states from the previous index.\n\n**Implementations**\nN = size of nums1/nums2 array\n\n**1. Recursion**\nTime complexiy: O(2^N)\nSpace complexity: O(N)\n\n```java\nclass Solution {\n public int minSwap(int[] nums1, int[] nums2) {\n return Math.min(recurse(nums1, nums2, nums1.length - 1, 0),\n recurse(nums1, nums2, nums1.length - 1, 1));\n }\n \n private int recurse(int[] nums1, int[] nums2, int i, int swap) {\n // base case\n if (i == 0)\n return swap;\n \n // default is set as max\n int res = Integer.MAX_VALUE;\n \n // if array is increasing without swapping\n if (nums1[i] > nums1[i - 1] && nums2[i] > nums2[i - 1])\n res = recurse(nums1, nums2, i - 1, swap);\n \n // if array is increasing with swapping\n if (nums1[i] > nums2[i - 1] && nums2[i] > nums1[i - 1])\n res = Math.min(res, \n recurse(nums1, nums2, i - 1, 1 - swap));\n \n return swap == 0 ? res : res + 1;\n }\n}\n```\n\n**2. Memoization**\nTime complexiy: O(N)\nSpace complexity: O(N)\n\n```java\nclass Solution {\n public int minSwap(int[] nums1, int[] nums2) {\n int n = nums1.length;\n \n // initialize dp table\n int[][] memo = new int[2][n];\n Arrays.fill(memo[0], -1);\n Arrays.fill(memo[1], -1);\n memo[0][0] = 0;\n memo[1][0] = 1;\n \n return Math.min(recurse(nums1, nums2, n - 1, 0, memo),\n recurse(nums1, nums2, n - 1, 1, memo));\n }\n \n private int recurse(int[] nums1, int[] nums2, int i, int swap, int[][] memo) {\n //check dp table\n if (memo[swap][i] != -1)\n return memo[swap][i];\n \n // initial value is set as max\n int res = Integer.MAX_VALUE;\n \n // if array is increasing without swapping\n if (nums1[i] > nums1[i - 1] && nums2[i] > nums2[i - 1])\n res = recurse(nums1, nums2, i - 1, swap, memo);\n \n // if array is increasing with swapping\n if (nums1[i] > nums2[i - 1] && nums2[i] > nums1[i - 1])\n res = Math.min(res, \n recurse(nums1, nums2, i - 1, 1 - swap, memo));\n \n memo[swap][i] = swap == 0 ? res : res + 1;\n return memo[swap][i];\n }\n}\n```\n\n**3. Tabulation**\nTime complexiy: O(N)\nSpace complexity: O(N)\n\n```java\nclass Solution {\n public int minSwap(int[] nums1, int[] nums2) {\n int n = nums1.length;\n \n // initialize dp table\n int[][] table = new int[2][n];\n table[0][0] = 0;\n table[1][0] = 1;\n \n for (int i = 1; i < n; i++) {\n // initial value\n table[0][i] = Integer.MAX_VALUE;\n table[1][i] = Integer.MAX_VALUE;\n \n // if array is increasing without swapping\n if (nums1[i] > nums1[i - 1] && nums2[i] > nums2[i - 1]) {\n table[0][i] = table[0][i - 1];\n table[1][i] = 1 + table[1][i - 1];\n }\n \n // if array is increasing with swapping\n if (nums1[i] > nums2[i - 1] && nums2[i] > nums1[i - 1]) {\n table[0][i] = Math.min(table[0][i], table[1][i - 1]);\n table[1][i] = Math.min(table[1][i], 1 + table[0][i - 1]);\n }\n }\n \n return Math.min(table[0][n - 1], table[1][n - 1]);\n }\n}\n```\n\n**4. Tabulation with Constant Space**\nTime complexiy: O(N)\nSpace complexity: O(1)\n\n```java\nclass Solution {\n public int minSwap(int[] nums1, int[] nums2) {\n int n = nums1.length;\n \n // initialize current res\n int curNoSwap = 0, curSwap = 1;\n \n for (int i = 1; i < n; i++) {\n // update previous values\n int prevNoSwap = curNoSwap, prevSwap = curSwap;\n \n // reset cur values\n curNoSwap = Integer.MAX_VALUE;\n curSwap = Integer.MAX_VALUE;\n \n // if array is increasing without swapping\n if (nums1[i] > nums1[i - 1] && nums2[i] > nums2[i - 1]) {\n curNoSwap = prevNoSwap;\n curSwap = 1 + prevSwap;\n }\n \n // if array is increasing with swapping\n if (nums1[i] > nums2[i - 1] && nums2[i] > nums1[i - 1]) {\n curNoSwap = Math.min(curNoSwap, prevSwap);\n curSwap = Math.min(curSwap, 1 + prevNoSwap);\n }\n }\n \n return Math.min(curNoSwap, curSwap);\n }\n}\n``` | 31 | 0 | ['Dynamic Programming', 'Recursion', 'Java'] | 1 |
minimum-swaps-to-make-sequences-increasing | Java neat and easy to understand DP O(n) solution! | java-neat-and-easy-to-understand-dp-on-s-9np2 | We create a dp[n][2] array. dp[i][0] means the minimun swaps when we do not swap in position i, while dp[i][1] means otherwise.\n\nBasically, there are three ca | kylewzk | NORMAL | 2018-03-20T07:11:09.824075+00:00 | 2018-09-27T02:07:46.355571+00:00 | 3,079 | false | We create a dp[n][2] array. dp[i][0] means the minimun swaps when we do not swap in position i, while dp[i][1] means otherwise.\n\nBasically, there are three cases:\na) We either swap or not in position i for condition: A[i]>A[i-1] && A[i]>B[i-1] && B[i] > A[i-1] && B[i] > B[i-1].\nb) If i-1 swaps, i swaps. If i-1 does not swap, i does not swap. A[i]>A[i-1] && B[i]>B[i-1]\nc) If i-1 swaps, i does not swaps. If i-1 does not swap, i swaps.\n\n```\n\n public int minSwap(int[] A, int[] B) {\n int[][] dp = new int[A.length][2];\n \n dp[0][0] = 0;\n dp[0][1] = 1;\n \n for(int i=1; i<A.length; i++) {\n if(A[i]>A[i-1] && A[i]>B[i-1] && B[i] > A[i-1] && B[i] > B[i-1]) {\n dp[i][0] = Math.min(dp[i-1][0], dp[i-1][1]);\n dp[i][1] = Math.min(dp[i-1][0], dp[i-1][1])+1;\n } else if (A[i]>A[i-1] && B[i]>B[i-1]) {\n dp[i][0] = dp[i-1][0];\n dp[i][1] = dp[i-1][1]+1;\n } else {\n dp[i][0] = dp[i-1][1];\n dp[i][1] = dp[i-1][0]+1;\n }\n }\n\t\t\t\t\n return Math.min(dp[A.length-1][0], dp[A.length-1][1]);\n }\n\t\t\n\t\t\n\t\t\n```\n\nBelow is optimized O(1) space solution:\n\n```\n\n public int minSwap(int[] A, int[] B) {\n int pre_swap = 1, pre_not_swap = 0;\n \n for(int i=1; i<A.length; i++) {\n int cur_swap, cur_not_swap;\n if(A[i]>A[i-1] && A[i]>B[i-1] && B[i] > A[i-1] && B[i] > B[i-1]) {\n cur_not_swap = Math.min(pre_swap, pre_not_swap);\n cur_swap = Math.min(pre_swap, pre_not_swap)+1;\n } else if (A[i]>A[i-1] && B[i]>B[i-1]) {\n cur_not_swap = pre_not_swap;\n cur_swap = pre_swap+1;\n } else {\n cur_not_swap = pre_swap;\n cur_swap = pre_not_swap+1;\n }\n \n pre_swap = cur_swap;\n pre_not_swap = cur_not_swap;\n }\n \n return Math.min(pre_swap, pre_not_swap);\n }\n``` | 31 | 0 | [] | 6 |
minimum-swaps-to-make-sequences-increasing | [Python] DP solution with explanations | python-dp-solution-with-explanations-by-k33wf | Explanations: For each i, we can either swap or keep the two respective value. Since the best options can come from either swap or keep as well, we need to have | codingasiangirll | NORMAL | 2020-05-19T16:05:22.748574+00:00 | 2020-05-19T18:14:38.356542+00:00 | 951 | false | **Explanations**: For each `i`, we can either swap or keep the two respective value. Since the best options can come from either swap or keep as well, we need to have 2 array to record two actions at each `i`. Here, `dp[0][:]` will record keep and `dp[1][:]` will record swap. \nFor `dp[0][i]`, number of swaps needed, if at `i`, we do nothing. (Therefore, `dp[0][0] = 0`)\nFor `dp[1][i]`, number of swaps needed, if at `i`, we swap `A[i]` and `B[i]`. (Therefore, `dp[1][0] = 1`)\n\nThere are two cases that will result in keep and swap:\n1. `A[i] > A[i - 1] and B[i] > B[i - 1]`: A, B are both increasing. \n If at `i`, we choose to keep, `i-1` will also have to keep to make it valid.\n\t If at `i`, we choose to swap, `i-1` will also have to swap to make it valid and since we swap at `i`, we need to add one.\n2. `A[i] > B[i - 1] and B[i] > A[i - 1]`: A is bigger than B\' prior and B is bigger than A\'s prior.\n If at `i`, we choose to keep, `i-1` will have to swap to make it valid. We also have to compare and restore the smallest number of swaps for `dp[0][i]` incase Case 1 is also valid statement.\n\t If at `i`, we choose to swap, `i-1` will have to keep.\n\n**Complexity**: Time O(N), N is length of A. Space O(N)\n```\nclass Solution:\n def minSwap(self, A: List[int], B: List[int]) -> int:\n n = len(A)\n dp = [[float(\'inf\')] * n for _ in range(2)]\n dp[0][0], dp[1][0] = 0, 1 # keep # swap \n for i in range(1, n):\n if A[i] > A[i - 1] and B[i] > B[i - 1]:\n # keep i\n dp[0][i] = dp[0][i - 1]\n # swap i\n dp[1][i] = dp[1][i - 1] + 1\n if A[i] > B[i - 1] and B[i] > A[i - 1]:\n # keep i\n dp[0][i] = min(dp[0][i], dp[1][i - 1])\n # swap i\n dp[1][i] = min(dp[1][i], dp[0][i - 1] + 1)\n return min(dp[0][n - 1], dp[1][n - 1])\n``` | 19 | 0 | ['Dynamic Programming'] | 1 |
minimum-swaps-to-make-sequences-increasing | [C++/Java/Python] Simple DP O(n) Time O(1) Space with Explanation | cjavapython-simple-dp-on-time-o1-space-w-q3ex | Explanation\n\nThis problem relies on the fact that it is possible for both nums1 and nums2 to be strictly increasing in the end. Since we can only perform swap | zayne-siew | NORMAL | 2021-11-07T11:53:11.114942+00:00 | 2021-11-07T11:54:35.252004+00:00 | 1,631 | false | ### Explanation\n\nThis problem relies on the fact that it is possible for both `nums1` and `nums2` to be strictly increasing in the end. Since we can only perform swaps between elements with the same index, i.e. we can only swap `nums1[i]` with `nums2[i]` for `0 <= i < n` (where `n` is the length of the arrays), we can therefore deduce that **it is possible for both subarrays of `nums1` and `nums2` from index `0` to `i` (`0 <= i < n`) to be strictly increasing**.\n\nTherefore, at any given index `i` (`1 <= i < n`), we can assert that both subarrays of `nums1` and `nums2` from index `0` to `i-1` are strictly increasing. When the next element at index `i` is introduced, we need to decide what to do at the index: swap `nums1[i]` and `nums2[i]`, or leave it as it is. To help us make that decision, we have the following two cases:\n\n1. **The subarrays of `nums1` and `nums2` from index `0` to `i` is already strictly increasing.**\n\n```text\nnums1: [ 1, 2, 3, ... ]\n ^\n i\n\t\t\t v\nnums2: [ 2, 3, 4, ... ]\n```\n\nThis means that we don\'t actually need to do anything. Hence, if we chose to leave the `i-1`<sup>th</sup> index unswapped previously, we can similarly leave the `i`<sup>th</sup> index unswapped. However, if we chose to swap `nums1[i-1]` and `nums2[i-1]` previously, we now need to perform one more swap to "cancel out" the effects of the previous swap and maintain the order of the arrays. We can write this as the following two equations:\n\n```text\nCASE 1 (already strictly increasing):\n\tkeep[i] = keep[i-1] --> subarrays from index 0 to i-1 left unswapped, so leave nums1[i] and nums2[i] unswapped\n\tswap[i] = swap[i-1] + 1 --> if nums1[i-1] and nums2[i-1] were previously swapped, swap nums1[i] and nums2[i] also\n```\n\n2. **The subarrays of `nums1` and `nums2` from index `0` to `i` is strictly increasing AFTER swapping `nums1[i]` and `nums2[i]`.**\n\n```text\nnums1: [ 0, 3, 2, ... ]\n ^\n i\n\t\t\t v\nnums2: [ 0, 1, 4, ... ]\n```\n\nSimple enough, we just perform the swap, right? Not really, since our comparison depends on what we did previously. If we had swapped `nums1[i-1]` and `nums2[i-1]` prior to the comparison, then there would be a discrepancy in comparison since the code doesn\'t actually modify the array and thus cannot \'see\' the swap performed previously:\n\n```text\n WHAT THE CODE SEES WHAT THE ARRAYS LOOKS LIKE CURRENTLY*\nnums1: [ 0, 3, 2, ... ] nums1: [ 0, 1, 2, ... ]\n ^ ^\n i VS i\n\t\t\t v \t\t\t v\nnums2: [ 0, 1, 4, ... ] nums2: [ 0, 3, 4, ... ]\n\n*after swapping nums1[i-1] and nums2[i-1]\n```\n\nHence, counterintuitively, if we had previously swapped `nums1[i-1]` and `nums2[i-1]`, we can choose to leave `nums1[i]` and `nums2[i]` unswapped and thus no additional swaps are needed. Likewise, if we had left `nums1[i-1]` and `nums2[i-1]` unswapped, we can choose to swap `nums1[i]` and `nums2[i]` and thus 1 additional swap is needed. We can write this as the following two equations:\n\n```text\nCASE 2 (requires swapping first):\n\tkeep[i] = swap[i-1] --> nums1[i-1] and nums2[i-1] was already swapped, so leave nums1[i] and nums2[i] unswapped\n\tswap[i] = keep[i-1] + 1 --> if nums1[i-1] and nums2[i-1] were previously unswapped, then swap nums1[i] and nums2[i]\n```\n\nNote that these 2 cases are not mutually exclusive. However, as mentioned previously, each index `i` will fulfil at least one of these two cases, since it is guaranteed that the subarrays up to index `i` can be strictly increasing. Thus, we can compute the number of swaps required for each case, and take the minimum number afterward.\n\n---\n\n### Implementation\n\n- Use variables `keep` and `swap` to keep track of the previous minimum swaps given the action taken (swapping or leaving unswapped).\n- Check cases via comparing `nums1[i-1]`, `nums1[i]`, `nums2[i-1]` and `nums2[i]` appropriately, in a sliding-window fashion.\n- Iterate through each index to ensure the subarrays up to the index are strictly increasing, and perform the necessary actions if needed.\n\n<iframe src="https://leetcode.com/playground/ckNCn9Lq/shared" frameBorder="0" width="900" height="450"></iframe>\n\n---\n\nPlease upvote if this has helped you! Appreciate any comments as well :) | 15 | 0 | ['Dynamic Programming', 'Python', 'C++', 'Java'] | 2 |
minimum-swaps-to-make-sequences-increasing | Clear Python o(n) Time, o(n) Space solution with comments | clear-python-on-time-on-space-solution-w-2xtx | bottom up dp python solution with comments\n\nTime: o(n)\nSpace: o(n)\n\n\n\nclass Solution:\n def minSwap(self, A: List[int], B: List[int]) -> int:\n | ay6xp123 | NORMAL | 2020-02-02T17:38:54.607061+00:00 | 2020-02-02T17:38:54.607111+00:00 | 936 | false | bottom up dp python solution with comments\n\nTime: o(n)\nSpace: o(n)\n\n\n```\nclass Solution:\n def minSwap(self, A: List[int], B: List[int]) -> int:\n \n n = len(A)\n \n # In this problem, we have two states that we need to keep track at element i; \n # what happens if we swap or do not swap at i?\n \n # min number of swaps to get ascending order if we SWAP at i \n swap = [0] * n\n \n # min number of swaps to get ascending order if we do NOT SWAP at i\n noswap = [0] * n\n \n # base case: swapping 0th element\n swap[0] = 1\n\n for i in range(1, n):\n strictly_increasing = A[i] > A[i-1] and B[i] > B[i-1]\n strictly_xincreasing = A[i] > B[i-1] and B[i] > A[i-1]\n \n # we can swap here, but we also do not have too\n if strictly_increasing and strictly_xincreasing: \n \n # if we decide to swap at i, we can consider the state of either swapping or not swapping i-1, since doing either\n # will not break out strictly increasing for either array rule\n swap[i] = min(noswap[i-1], swap[i-1]) + 1\n \n # we chose not to swap at i, so we can consider states if we swap at i - 1 or not swap, since again we will not break the strictly increasing rule\n noswap[i] = min(noswap[i-1], swap[i-1])\n \n \n # we can not swap at i, since we know that A[i] is not greater than B[i-1], or that B[i] is not greater than A[i-1]\n elif strictly_increasing:\n \n \n \n # if we swap at i, then to keep increasing condition, we must also swap at i-1, we are essentially just swapping both i and i-1 and get the same thing \n swap[i] = swap[i-1] + 1\n \n # if we do not swap at i, then we must also chose to not swap at i-1 to keep the problem conditions true\n noswap[i] = noswap[i-1]\n \n \n # we must swap, since A[i] is not greater than A[i-1], or B[i] is not greater than B[i-1]\n # but we know that A[i] > B[i-1] and that B[i] > A[i-1]\n elif strictly_xincreasing:\n\n # if we swap at i, then we must have not swapped at i-1\n swap[i] = noswap[i-1] + 1\n \n # if we do not swap at i, then we must have swapped at i-1 for the problem conditions to be true\n noswap[i] = swap[i-1]\n \n \n \n # take min of both state paths to see who holds the better result\n return min(noswap[n-1], swap[n-1])\n\n\n``` | 15 | 1 | ['Dynamic Programming', 'Python3'] | 3 |
minimum-swaps-to-make-sequences-increasing | C++, Time O(n), Space O(1), 4ms, beats 100% | c-time-on-space-o1-4ms-beats-100-by-pjin-nmtq | If A[i] > B[i], we say, we have a upward node, elsewise we have a downward note.\n\nIf a node max(A[i],B[i]) < min(A[i+1],B[i+1]), we name it a free node.\nBeca | pjincz | NORMAL | 2018-11-17T01:04:03.217804+00:00 | 2018-11-17T01:04:03.217862+00:00 | 1,139 | false | If A[i] > B[i], we say, we have a upward node, elsewise we have a downward note.\n\nIf a node max(A[i],B[i]) < min(A[i+1],B[i+1]), we name it a free node.\nBecause it can changed freely.\nOtherwise, a non-free node should have same direction with next node.\n\nSo, we find a chain, left of first node is a free node, end with a free node. All other node in chain should be non-free nodes.\nWe known: all nodes in chain should have same direction.\nFixup a chain need min(upward nodes, downward nodes) steps.\n\nSo we got the solution: just scan all chains!\n\n```C++\nstatic const int _ = []() {\n ios::sync_with_stdio(false);\n cin.tie(nullptr);\n return 0;\n}();\n\nclass Solution {\npublic:\n int minSwap(vector<int>& A, vector<int>& B) {\n int swaps = 0;\n int up = 0, down = 0;\n for (int i = 0; i < A.size(); ++i) {\n if (A[i] > B[i])\n up += 1;\n else\n down += 1;\n\n if (i == A.size() - 1 || std::max(A[i], B[i]) < std::min(A[i + 1], B[i + 1])) {\n // free node\n swaps += std::min(up, down);\n up = down = 0;\n }\n }\n return swaps;\n }\n};\n``` | 15 | 0 | [] | 2 |
minimum-swaps-to-make-sequences-increasing | DP Simple O(n) time O(1) Space with detailed explanation | dp-simple-on-time-o1-space-with-detailed-tw3d | Think of the problem as finding the best path from n-1th index to nth index\nSuppose Array \n A=[0,7,8,10,10,11,12,13,19,18] and\n\t B=[4,4,5, 7,11,1 | prajwalroxman | NORMAL | 2019-06-29T08:10:08.637306+00:00 | 2019-06-29T08:40:49.042877+00:00 | 1,218 | false | Think of the problem as finding the best path from n-1th index to nth index\nSuppose Array \n A=[0,7,8,10,10,11,12,13,19,18] and\n\t B=[4,4,5, 7,11,14,15,16,17,20]\n\t\t\t\t\t\t\t\t\t\t\t ^\nInitially,\t\t\t\t\t\t\t\t\t\t\t \nswap =[0,0,0,0,0,0,0,0,0,1]\nunswap=[0,0,0,0,0,0,0,0,0,0]\n\t\t\t\t\t\t\t\t\t\t ^\t\t\t\t\t\t\t\t\t\t \nImplies If we are at last index we can swap the values(cost=1) and reach destination OR we can directly reach without swap(cost=0)\n\nWe can encounter 3 cases while traversing the array from right to left:\n```1 case:``` Both A[i] and B[i] are in strictly increasing order\n```A[i]<A[i+1] && A[i]<B[i+1] &&B[i]<A[i+1]&& B[i]<B[i+1]```\nHere the current action will be independent of next values \ni.e.``` swap[i]=1+ min(swap[i+1],unswap[i+1])```\n``` unswap[i]=0+ min(swap[i+1],unswap[i+1])```\n\n```2 case:```Either A or B violates its own sequence.\n```A[i]>=A[i+1] || B[i]>=B[i+1]```\nHere we have to make sure that current and next are alternate.\nImplies either swap current and unswap next OR swap next and unswap current\ni.e.``` swap[i]=1+ unswap[i+1]```\n``` unswap[i]=0+ swap[i+1]```\n\n```3 case:```Either A or B violates the other\'s sequence.\n```A[i]>=B[i+1] || B[i]>=A[i+1]```\nHere we have to make sure that current and next are in same order.\nImplies either swap current and swap next OR unswap current and unswap next\ni.e.``` swap[i]=1+ swap[i+1]```\n``` unswap[i]=0+ unswap[i+1]```\n\nThe code in JavaScript is as follows\n```\n/**\n * @param {number[]} A\n * @param {number[]} B\n * @return {number}\n */\nvar minSwap = function(A, B) {\n let swap = new Array(A.length).fill(0);\n let unswap = new Array(A.length).fill(0);\n swap[A.length-1]=1;\n unswap[A.length-1]=0;\n for(let i=A.length-2;i>=0;i--){\n /*Case 1 a<c,d &b <c,d*/\n if(A[i]<A[i+1]&&A[i]<B[i+1]&&B[i]<A[i+1]&&B[i]<B[i+1]){\n swap[i]=1+Math.min(swap[i+1],unswap[i+1]);\n unswap[i]=0+Math.min(swap[i+1],unswap[i+1]);\n continue;\n }\n /*Case 2 a>=c || b>=d*/\n if(A[i]>=A[i+1]||B[i]>=B[i+1]){\n swap[i]=1+unswap[i+1];\n unswap[i]=0+swap[i+1];\n continue;\n }\n /*Case 3 a>=d ||b >=c*/ \n if(A[i]>=B[i+1]||B[i]>=A[i+1]){\n swap[i]=1+swap[i+1];\n unswap[i]=0+unswap[i+1];\n continue;\n }\n \n }\n return Math.min(swap[0],unswap[0]);\n};\n```\n\nWe only need 2 variables so we can optimize space and make it O(1) Space\n```\n/**\n * @param {number[]} A\n * @param {number[]} B\n * @return {number}\n */\nvar minSwap = function(A, B) {\n let swap=1;\n let unswap=0;\n for(let i=A.length-2;i>=0;i--){\n let temp=swap;\n /*Case 1 a<c,d &b <c,d*/\n if(A[i]<A[i+1]&&A[i]<B[i+1]&&B[i]<A[i+1]&&B[i]<B[i+1]){ \n swap=1+Math.min(swap,unswap);\n unswap=0+Math.min(temp,unswap);\n continue;\n }\n /*Case 2 a>=c || b>=d*/\n if(A[i]>=A[i+1]||B[i]>=B[i+1]){\n swap=1+unswap;\n unswap=0+temp;\n continue;\n }\n /*Case 3 a>=d ||b >=c*/ \n if(A[i]>=B[i+1]||B[i]>=A[i+1]){\n swap=1+swap;\n unswap=0+unswap;\n continue;\n }\n \n }\n return Math.min(swap,unswap);\n};\n``` | 14 | 0 | [] | 2 |
minimum-swaps-to-make-sequences-increasing | ✅✅Faster || Easy To Understand || C++ Code | faster-easy-to-understand-c-code-by-__kr-wrql | Approach 1 :- Using Recursion && Memoization\n\n Time Complexity :- O(N)\n\n Space Complexity :- O(N)\n\n\nclass Solution {\npublic:\n \n int dp[100005][2 | __KR_SHANU_IITG | NORMAL | 2022-07-04T07:40:21.185771+00:00 | 2022-07-04T07:40:21.185843+00:00 | 1,085 | false | * ***Approach 1 :- Using Recursion && Memoization***\n\n* ***Time Complexity :- O(N)***\n\n* ***Space Complexity :- O(N)***\n\n```\nclass Solution {\npublic:\n \n int dp[100005][2];\n \n int dfs(vector<int>& nums1, vector<int>& nums2, int i, int n, int prev1, int prev2, bool swap)\n {\n if(i == n)\n return 0;\n \n // if already calculated\n \n if(dp[i][swap] != -1)\n return dp[i][swap];\n \n int ans = INT_MAX;\n \n // no swaps have been made\n \n if(nums1[i] > prev1 && nums2[i] > prev2)\n {\n ans = min(ans, dfs(nums1, nums2, i + 1, n, nums1[i], nums2[i], false));\n }\n \n // swaps have been made\n \n if(nums1[i] > prev2 && nums2[i] > prev1)\n {\n ans = min(ans, 1 + dfs(nums1, nums2, i + 1, n, nums2[i], nums1[i], true));\n }\n \n // store in dp\n \n return dp[i][swap] = ans;\n }\n \n int minSwap(vector<int>& nums1, vector<int>& nums2) {\n \n int n = nums1.size();\n \n memset(dp, -1, sizeof(dp));\n \n return dfs(nums1, nums2, 0, n, -1, -1, false);\n }\n};\n``` | 12 | 0 | ['Dynamic Programming', 'Recursion', 'Memoization', 'C'] | 1 |
minimum-swaps-to-make-sequences-increasing | C++: Solution with explanation | c-solution-with-explanation-by-bingabid-y8ah | To make both array strictly increasing till \'i\' index, there is two possibility\n\n1. we do not swap the \'i\' elements.\n2. we swap the \'i\' elements.\n\nMi | bingabid | NORMAL | 2020-06-10T11:11:28.283212+00:00 | 2020-06-10T11:13:01.296999+00:00 | 884 | false | To make both array strictly increasing till \'i\' index, there is two possibility\n```\n1. we do not swap the \'i\' elements.\n2. we swap the \'i\' elements.\n\nMinimum of the above two possibility is the minimum number of swap needed \nto make both the array strictly increasing till \'i\' index.\n```\n\nlet \'n\' is the size of array and take two auxilary array\n```\nnot_swap[i]: it stores the minimum swap needed to make the array strictly increasing till \'i\' index without making swap at \'i\' index.\nswap[i] : it stores the minimum swap needed to make the array strictly increasing till \'i\' index with making swap at \'i\' index.\n```\n\nAssume we have computed till \'i-1\' element i.e\n``` \nnot_swap[i-1] : minimum swapping needed without swapping \'i-1\' element\nswap[i-1] : minimum swapping needed with swapping \'i-1\' element\t\n```\nNow observe two condition carefully, \n1. if \'i-1\' & \'i\' elements from both array are in strictly increasing order i.e \n```\n\tif(A[i-1]<A[i] and B[i-1]<B[i]) then \n\tnot_swap[i] = not_swap[i-1], coz by definition we do not want to swap at \'i\' index.\n\tswap[i] = swap[i-1]+1, since we swapped at \'i-1\' index and (\'i-1\' & \'i\') already strictly increasing,\n\t we have to reverse our previous swapping of \'i-1\' index by swapping at again at \'i\' index.\n```\n2. if cross \'i-1\' & \'i\' elements from both arrays are in strictly increasing order i.e (A[i-1]<B[i] && B[i-1]<B[i]) we can make it strictly incresing by swapping either at \'i-1\' index or \'i\' index.\n``` \n if consider \'i-1\' index swaping then we do not have to swap at \'i\' index (not_swap[i] case)\n if consider swapping \'i\' index then we do not have to swap at \'i-1\' index (swap[i] case). So,\n \n\tif(A[i-1]<B[i] && B[i-1]<B[i]) then\n\tnot_swap[i] = min ( not_swap[i] ----> existing value from previous steps (1st step),\n\t\t\t\t\t\tY[i-1] ----> since by definition we are not allowed to make swap here for \'not_swap\' case, take value from \'i-1\' \'swap\' case)\n\tswap[i] = min( swap[i] ----> existing value from previous steps (1st step),\n\t\t\t\t not_swap[i-1] + 1 ----> since by definition we must swap at \'i\' index for \'swap\' case, take value from \'i-1\' \'not_swap\' case & add 1\n\t\t\t\t)\n```\n\t\n\nIf the explanation is good enough for you, then implementation is a cake walk . Still my implementation is as follows:\n\n```\nclass Solution {\npublic:\n int minSwap(vector<int>& A, vector<int>& B) {\n int n = A.size();\n vector<int> x(n,0); /*without swap at \'i\' index*/\n vector<int> y(n,1); /*with swap at \'i\' index*/\n for(int i=1;i<n;i++){\n\t\t\t/*assign any large value like infinity, INT_MAX or \n\t\t\tanything which is more than maximum possible answer i.e n*/\n x[i] = y[i] = n; \n if(A[i-1]<A[i] && B[i-1]<B[i]){\n x[i] = x[i-1];\n y[i] = y[i-1]+1;\n }\n if(A[i-1]<B[i] && B[i-1]<A[i]){\n x[i] = min(x[i],y[i-1]);\n y[i] = min(y[i],x[i-1]+1);\n }\n }\n return min(x[n-1],y[n-1]);\n }\n};\n``` | 11 | 0 | [] | 1 |
minimum-swaps-to-make-sequences-increasing | 💥 Runtime beats 100.00%, Memory beats 66.67% [EXPLAINED] | runtime-beats-10000-memory-beats-6667-ex-apig | Intuition\nImagine you\'re trying to make two sequences of numbers strictly increasing. You have two arrays, nums1 and nums2, and you can swap elements at the s | r9n | NORMAL | 2024-09-06T16:55:59.090570+00:00 | 2024-09-06T16:55:59.090595+00:00 | 220 | false | # Intuition\nImagine you\'re trying to make two sequences of numbers strictly increasing. You have two arrays, nums1 and nums2, and you can swap elements at the same index between these arrays. Your goal is to find the minimum number of swaps required to make both arrays strictly increasing.\n\nThink of it like organizing two rows of numbers so that each number is smaller than the one that comes after it. If you need to swap some numbers between the rows to achieve this, you want to minimize the number of swaps.\n\n# Approach\nStart Small:\n\nBegin with the first element. If it\'s not swapped, the number of swaps required is zero (dp0[0] = 0). If it\'s swapped, you\'ll need one swap (dp1[0] = 1).\n\nMove Step-by-Step:\n\nFor each subsequent element, decide whether to swap or not based on whether the current and previous numbers in both arrays are strictly increasing. You\'ll keep track of two things:\n\ndp0[i]: Minimum swaps needed up to index i without swapping the current index.\ndp1[i]: Minimum swaps needed up to index i with swapping the current index.\n\nUpdate Your Decisions:\n\nAt each step, update the minimum swaps required based on whether you swap or not:\n\nIf you don\'t swap, check if the previous element conditions are satisfied without swapping.\nIf you swap, check if the previous element conditions are satisfied with swapping.\n\nChoose the Best Option:\n\nAfter processing all elements, you\u2019ll have two possible values for the last index: either you didn\u2019t swap or you did. The result will be the minimum of these two values.\n\n# Complexity\n- Time complexity:\nO(n): The approach involves a single pass through the arrays (from the start to the end), making it linear in terms of time. For each element, we do constant-time work (checking and updating values).\n\n- Space complexity:\nO(n): We use arrays dp0 and dp1 to keep track of the minimum swaps up to each index. Since these arrays are of size n (the length of the input arrays), the space used is linear with respect to the number of elements.\n\n# Code\n```typescript []\nfunction minSwap(nums1: number[], nums2: number[]): number {\n const n = nums1.length;\n let dp0 = new Array(n).fill(Infinity); // Minimum swaps without swap at index i\n let dp1 = new Array(n).fill(Infinity); // Minimum swaps with swap at index i\n\n // Initialize for the first index\n dp0[0] = 0;\n dp1[0] = 1;\n\n for (let i = 1; i < n; i++) {\n const noSwap = nums1[i - 1] < nums1[i] && nums2[i - 1] < nums2[i];\n const swap = nums1[i - 1] < nums2[i] && nums2[i - 1] < nums1[i];\n\n if (noSwap) {\n dp0[i] = Math.min(dp0[i], dp0[i - 1]);\n dp1[i] = Math.min(dp1[i], dp1[i - 1] + 1);\n }\n \n if (swap) {\n dp0[i] = Math.min(dp0[i], dp1[i - 1]);\n dp1[i] = Math.min(dp1[i], dp0[i - 1] + 1);\n }\n }\n\n return Math.min(dp0[n - 1], dp1[n - 1]);\n}\n\n``` | 9 | 0 | ['TypeScript'] | 1 |
minimum-swaps-to-make-sequences-increasing | C++ Easy and simple solution Recrusive->TopDown->BottomUp | c-easy-and-simple-solution-recrusive-top-bcpn | Guy\'s if you find this solution helpful \uD83D\uDE0A, PLEASE do UPVOTE. By doing that it motivate\'s me to create more better post like this \u270D\uFE0F\n\nTh | ayushluthra62 | NORMAL | 2022-10-12T13:48:31.251289+00:00 | 2022-10-12T13:48:31.251335+00:00 | 1,064 | false | **Guy\'s if you find this solution helpful \uD83D\uDE0A, PLEASE do UPVOTE. By doing that it motivate\'s me to create more better post like this \u270D\uFE0F**\n\n**There are Different method to solve This question**. \n* **Recursive (TLE)**\n* **Recursive** + **Dp** (Accepted) \n* **Bottom Up (DP)** (Accepted) \n\n**Approach** 1: **Recursive (TLE)**\n```\nclass Solution {\npublic:\n int solve(vector<int>& nums1, vector<int>& nums2,int index, bool swapped){\n if(index==nums1.size()) return 0;\n int ans=INT_MAX;\n int prev1=nums1[index-1];\n int prev2=nums2[index-1];\n \n if(swapped){\n swap(prev1,prev2);\n }\n \n if(nums1[index]>prev1 && nums2[index]>prev2)\n ans=min(ans,solve(nums1,nums2, index+1, 0));\n if(nums1[index]> prev2 && nums2[index]>prev1)\n ans=min(ans,1+solve(nums1,nums2,index+1,1));\n \n return ans;\n }\n int minSwap(vector<int>& nums1, vector<int>& nums2) {\n\n //it means that previous index were swapped or not \n nums1.insert(nums1.begin(),-1);\n nums2.insert(nums2.begin(),-1);\n bool swapped=0;\n return solve(nums1, nums2,1,swapped);\n \n } \n};\n```\n\n**Approach** 2 : **Recursive**+**Dp**\n\n```\nclass Solution {\npublic:\n int solve(vector<int>& nums1, vector<int>& nums2,int index, bool swapped,vector<vector<int>>&dp){\n if(index==nums1.size()) return 0;\n if(dp[index][swapped]!=-1) return dp[index][swapped];\n int ans=INT_MAX;\n int prev1=nums1[index-1];\n int prev2=nums2[index-1];\n \n if(swapped){\n swap(prev1,prev2);\n }\n \n if(nums1[index]>prev1 && nums2[index]>prev2)\n ans=min(ans,solve(nums1,nums2, index+1, 0,dp));\n if(nums1[index]> prev2 && nums2[index]>prev1)\n ans=min(ans,1+solve(nums1,nums2,index+1,1,dp));\n \n return dp[index][swapped]=ans;\n }\n int minSwap(vector<int>& nums1, vector<int>& nums2) {\n\n //it means that previous index were swapped or not \n nums1.insert(nums1.begin(),-1);\n nums2.insert(nums2.begin(),-1);\n bool swapped=0;\n vector<vector<int>>dp(nums1.size()+1,vector<int>(2,-1));\n return solve(nums1, nums2,1,swapped,dp);\n \n } \n};\n```\nApproach 3: **Bottom up**\n```\nclass Solution {\npublic:\n int minSwap(vector<int>& nums1, vector<int>& nums2) {\n\n //it means that previous index were swapped or not \n \n nums1.insert(nums1.begin(),-1);\n nums2.insert(nums2.begin(),-1);\n bool swapped=0;\n vector<vector<int>>dp(nums1.size()+1,vector<int>(2,0));\n \n for(int index=nums1.size()-1;index>=1;index--){\n for(int swapped=1;swapped>=0;swapped--){\n int ans=INT_MAX;\n int prev1=nums1[index-1];\n int prev2=nums2[index-1];\n\n if(swapped){\n swap(prev1,prev2);\n }\n\n if(nums1[index]>prev1 && nums2[index]>prev2)\n ans=min(ans,dp[index+1][0]);\n if(nums1[index]> prev2 && nums2[index]>prev1)\n ans=min(ans,1+dp[index+1][1]);\n\n dp[index][swapped]=ans;\n }\n }\n return dp[1][1];\n \n } \n};\n\n```\n****Guy\'s if you find this solution helpful \uD83D\uDE0A, PLEASE do UPVOTE. By doing that it motivate\'s me to create more better post like this \u270D\uFE0F**** | 9 | 1 | ['Recursion', 'C', 'C++'] | 2 |
minimum-swaps-to-make-sequences-increasing | [Python3] two counters | python3-two-counters-by-ye15-s24v | Algo \nThis solution is different from the mainstream solutions. Given that we know a solution exists, if we put larger of A[i] and B[i] to A and smaller of A[i | ye15 | NORMAL | 2020-11-11T22:30:06.699064+00:00 | 2020-11-11T22:30:06.699107+00:00 | 710 | false | Algo \nThis solution is different from the mainstream solutions. Given that we know a solution exists, if we put larger of `A[i]` and `B[i]` to `A` and smaller of `A[i]` and `B[i]` to `B`. The resulting sequence satisfies the requirement of increasing `A` and increasing `B`. In the spirit of this idea, we can count the occurrence of `A[i] < B[i]` in `sm` and count the occurrence of `A[i] > B[i]` in `lg`. The minimum of `sm` and `lg` gives enough swap to get two increasing sequences. The issue is that it is more than enough as there can be cases where `max(A[i-1], B[i-1]) < min(A[i], B[i])`. In such a case, we treat the array as two subarrays ending at `i-1` and starting at `i`. The sum of all such pieces gives the correct answer. \n\nImplementation (72ms, 99.18%)\n```\nclass Solution:\n def minSwap(self, A: List[int], B: List[int]) -> int:\n ans = sm = lg = mx = 0\n for x, y in zip(A, B): \n if mx < min(x, y): # prev max < current min\n ans += min(sm, lg) # update answer & reset \n sm = lg = 0 \n mx = max(x, y)\n if x < y: sm += 1 # count "x < y"\n elif x > y: lg += 1 # count "x > y"\n return ans + min(sm, lg)\n``` | 9 | 0 | ['Python3'] | 1 |
minimum-swaps-to-make-sequences-increasing | 4 Approaches || Recursion || Memoization || Tabulation || Space Optimization ( O(1) ) || Beats 100% | 4-approaches-recursion-memoization-tabul-cxvh | Approach 1: Recursive Approach\n Describe your approach to solving the problem. \n- The function solve uses recursion to explore all possibilities at each index | prayashbhuria931 | NORMAL | 2024-08-29T19:59:51.024040+00:00 | 2024-08-29T19:59:51.024072+00:00 | 419 | false | # Approach 1: Recursive Approach\n<!-- Describe your approach to solving the problem. -->\n- The function solve uses recursion to explore all possibilities at each index in the sequences.\n- Parameters:\n - nums1 and nums2: The input sequences.\n - index: The current index being processed.\n - swapped: A boolean flag indicating whether the previous elements (at index-1) were swapped.\n- Logic:\n - Base Case: If index equals the size of the arrays, return 0 because no more swaps are needed.\n - Previous Values: prev1 and prev2 store the previous elements of nums1 and nums2 respectively. If swapped is true, the values of prev1 and prev2 are swapped to reflect the fact that the previous elements were swapped.\n - No Swap: If the current elements (nums1[index] and nums2[index]) are greater than their respective previous elements, recursively solve the problem without swapping (swapped = 0).\n - Swap: If swapping the current elements maintains the strictly increasing property, recursively solve the problem with a swap (swapped = 1) and increment the swap count.\n- Return: The minimum of the results from the two options.\n\n# Complexity\n- Time complexity: O(2^n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\nprivate:\n int solve(vector<int>& nums1, vector<int>& nums2,int index,int swapped)\n {\n //base case\n if(index==nums1.size()) return 0;\n\n int ans=INT_MAX;\n\n int prev1=nums1[index-1];\n int prev2=nums2[index-1];\n\n //catch\n if(swapped) swap(prev1,prev2);\n\n //noswap\n if(nums1[index]>prev1 && nums2[index]>prev2) ans=solve(nums1,nums2,index+1,0);\n \n //swap\n if(nums1[index]>prev2 && nums2[index]>prev1)\n {\n ans=min(ans,1+solve(nums1,nums2,index+1,1));\n }\n\n return ans;\n }\n\npublic:\n int minSwap(vector<int>& nums1, vector<int>& nums2) {\n nums1.insert(nums1.begin(),-1);\n nums2.insert(nums2.begin(),-1);\n //it means that the previous indexes were swapped or not \n bool swapped=0;\n return solve(nums1,nums2,1,swapped);\n\n }\n};\n```\n\n# Approach 2: Memoization\n<!-- Describe your approach to solving the problem. -->\n- This approach adds a memoization table dp to store results of subproblems to avoid recomputation.\n- Parameters:\n - Similar to solve, but with an additional dp table to store results for each (index, swapped) pair.\n- Logic:\n - If a result for (index, swapped) is already computed, return it from dp.\n - Otherwise, compute it similarly to solve and store the result in dp.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\nprivate:\n int solveMem(vector<int>& nums1, vector<int>& nums2,int index,int swapped,vector<vector<int>> &dp)\n {\n //base case\n if(index==nums1.size()) return 0;\n\n if(dp[index][swapped]!=-1) return dp[index][swapped];\n\n int ans=INT_MAX;\n\n int prev1=nums1[index-1];\n int prev2=nums2[index-1];\n\n //catch\n if(swapped) swap(prev1,prev2);\n\n //noswap\n if(nums1[index]>prev1 && nums2[index]>prev2) ans=solveMem(nums1,nums2,index+1,0,dp);\n \n //swap\n if(nums1[index]>prev2 && nums2[index]>prev1)\n {\n ans=min(ans,1+solveMem(nums1,nums2,index+1,1,dp));\n }\n\n return dp[index][swapped]=ans;\n }\n\n\npublic:\n int minSwap(vector<int>& nums1, vector<int>& nums2) {\n\n nums1.insert(nums1.begin(),-1);\n nums2.insert(nums2.begin(),-1);\n //it means that the previous indexes were swapped or not \n bool swapped=0;\n\n int n=nums1.size();\n\n vector<vector<int>> dp(n,vector<int> (2,-1));\n return solveMem(nums1,nums2,1,swapped,dp);\n }\n};\n```\n\n\n# Approach 3: Tabulation\n<!-- Describe your approach to solving the problem. -->\n- This method builds the solution iteratively from the last index to the first.\n- Parameters:\n - A dp table is created with dimensions [n+1][2] where n is the size of the arrays, and the second dimension represents the swapped state (0 or 1).\n- Logic:\n - Iterate backward through the arrays, considering both swap and no swap scenarios.\n - Fill the dp table based on the conditions described above.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\nprivate:\n int solveTab(vector<int> &nums1,vector<int> &nums2)\n {\n int n=nums1.size();\n vector<vector<int>> dp(n+1,vector<int> (2,0));\n\n for(int index=n-1;index>=1;index--)\n {\n for(int swapped=1;swapped>=0;swapped--)\n {\n \n int ans=INT_MAX;\n\n int prev1=nums1[index-1];\n int prev2=nums2[index-1];\n\n //catch\n if(swapped) swap(prev1,prev2);\n\n //noswap\n if(nums1[index]>prev1 && nums2[index]>prev2) ans=dp[index+1][0];\n \n //swap\n if(nums1[index]>prev2 && nums2[index]>prev1)\n {\n ans=min(ans,1+dp[index+1][1]);\n }\n\n dp[index][swapped]=ans; \n }\n }\n return dp[1][0];\n }\npublic:\n int minSwap(vector<int>& nums1, vector<int>& nums2) {\n nums1.insert(nums1.begin(),-1);\n nums2.insert(nums2.begin(),-1);\n\n return solveTab(nums1,nums2);\n }\n};\n```\n\n\n# Approach 4: Space Optimization\n<!-- Describe your approach to solving the problem. -->\n- This approach further optimizes space by using only two variables to keep track of the current and previous results (swapp and noswap).\n- Parameters:\n - Instead of a full dp table, use only two sets of variables (currswap, currnoswap) to store results for the current index.\n- Logic:\n - Process each index similarly but only keep track of the necessary values for the next iteration.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\nprivate:\n int solveSO(vector<int> &nums1,vector<int> &nums2)\n {\n int n=nums1.size();\n\n int swapp=0;\n int noswap=0;\n int currswap=0;\n int currnoswap=0;\n\n\n for(int index=n-1;index>=1;index--)\n {\n for(int swapped=1;swapped>=0;swapped--)\n {\n \n int ans=INT_MAX;\n\n int prev1=nums1[index-1];\n int prev2=nums2[index-1];\n\n //catch\n if(swapped) swap(prev1,prev2);\n\n //noswap\n if(nums1[index]>prev1 && nums2[index]>prev2) ans=noswap;\n \n //swap\n if(nums1[index]>prev2 && nums2[index]>prev1)\n {\n ans=min(ans,1+swapp);\n }\n\n if(swapped) currswap=ans;\n else currnoswap=ans; \n }\n swapp=currswap;\n noswap=currnoswap;\n }\n return min(swapp,noswap);\n }\npublic:\n int minSwap(vector<int>& nums1, vector<int>& nums2) {\n nums1.insert(nums1.begin(),-1);\n nums2.insert(nums2.begin(),-1);\n\n return solveSO(nums1,nums2);\n\n }\n};\n```\n\n | 8 | 0 | ['Array', 'Dynamic Programming', 'Recursion', 'Memoization', 'C++'] | 1 |
minimum-swaps-to-make-sequences-increasing | 99.51 % Faster Runtime ✅✅ || Recursive + Memoization || Easy to Understand | 9951-faster-runtime-recursive-memoizatio-pz9b | Recursively go to every index and check possibility for swapping\n Describe your first thoughts on how to solve this problem. \n\n# Approach : \n> 1.) If we are | unknown_ajay | NORMAL | 2023-07-07T05:10:41.470478+00:00 | 2023-07-07T05:11:40.701639+00:00 | 1,370 | false | # Recursively go to every index and check possibility for swapping\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach : \n> 1.) If we are at index Zero we can either swap it or not because zero does not have any previous index \n2.) Calculate previous index\'s value for both the vectors and store them in some variables ( prevP and prevQ in my code )\n3.) If it is possible to either swap or not then try out both the possibilities \n4.) If it is mandatory to swap then swap it\n5.) else no need to swap\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nint dp[100010][2]; \n// [100010] -> to keep track of current index \n// [2] -> to check last index swapped or not \n\nint rec(vector<int> &p,vector<int> &q,int idx,bool prev)\n{\n if(idx==p.size()) return 0;\n int ans = 1e6; // some big number \n \n if(dp[idx][prev] != -1) return dp[idx][prev]; // memoization\n \n int prevP , prevQ; // previous element for both p and q vectors\n if(idx!=0)\n {\n if(prev) // it means previous index was swapped \n {\n prevP = q[idx-1];\n prevQ = p[idx-1];\n }else \n {\n prevP = p[idx-1];\n prevQ = q[idx-1];\n }\n }\n\n if(idx!=0) // returning big number for cases where nothing can be done \n {\n if( (prevP >= p[idx] || prevQ >= q[idx] ) && (prevQ >= p[idx] || prevP >= q[idx]) ) return 1e6;\n }\n\n\n if(idx==0)\n {\n ans = min(ans,rec(p,q,idx+1,false)); // No Swap\n ans = min(ans,1+rec(p,q,idx+1,true)); // Swap\n }else\n {\n if( (prevP < p[idx] && prevQ < q[idx]) && (prevQ < p[idx] && prevP < q[idx]) ) \n {\n // IF we swap or not this idx does not have any problem So\n ans = min(ans,rec(p,q,idx+1,false)); // No Swap\n ans = min(ans,1+rec(p,q,idx+1,true)); // Swap\n }else if( prevP >= p[idx] || prevQ >= q[idx] )\n {\n // Swap is must \n ans = min(ans,1+rec(p,q,idx+1,true)); // Swap \n } else \n {\n // No need to swap \n ans = min(ans,rec(p,q,idx+1,false));\n }\n }\n\n return dp[idx][prev] = ans;\n}\n\n\n\n\nclass Solution {\npublic:\n int minSwap(vector<int>& p, vector<int>& q) \n {\n ios_base::sync_with_stdio(false); cin.tie(NULL);\n memset(dp,-1,sizeof(dp));\n return rec(p,q,0,false); \n }\n};\n``` | 8 | 0 | ['Dynamic Programming', 'Recursion', 'Memoization', 'C++'] | 0 |
minimum-swaps-to-make-sequences-increasing | Python recursion with cache | python-recursion-with-cache-by-cubicon-m7ns | \n def _minSwap(self, A, B, i, cache, swapped):\n if (swapped, i) in cache:\n return cache[(swapped, i)]\n if i == len(A):\n | Cubicon | NORMAL | 2018-03-19T05:01:07.621798+00:00 | 2018-09-05T02:33:32.197113+00:00 | 1,413 | false | ```\n def _minSwap(self, A, B, i, cache, swapped):\n if (swapped, i) in cache:\n return cache[(swapped, i)]\n if i == len(A):\n return 0\n l_min = math.inf if i > 0 and (A[i] <= A[i - 1] or B[i] <= B[i - 1]) else self._minSwap(A, B, i + 1, cache, 0)\n A[i], B[i] = B[i], A[i]\n r_min = math.inf if i > 0 and (A[i] <= A[i - 1] or B[i] <= B[i - 1]) else self._minSwap(A, B, i + 1, cache, 1)\n A[i], B[i] = B[i], A[i]\n cache[(swapped, i)] = min(l_min, r_min + 1)\n return cache[(swapped, i)]\n\n def minSwap(self, A, B):\n if len(A) == 1: return 0\n return self._minSwap(A, B, 0, {}, 0)\n``` | 8 | 1 | [] | 0 |
minimum-swaps-to-make-sequences-increasing | recursion -> memoization | recursion-memoization-by-abhishekaaru-aatj | Recursion (TLE)\n\nclass Solution {\npublic:\n int solve(vector<int> num1,vector<int> num2,int i,int prev1,int prev2){\n int n = num1.size();\n | abhishekaaru | NORMAL | 2022-06-04T01:24:01.508813+00:00 | 2022-06-04T01:24:01.508848+00:00 | 595 | false | **Recursion (TLE)**\n```\nclass Solution {\npublic:\n int solve(vector<int> num1,vector<int> num2,int i,int prev1,int prev2){\n int n = num1.size();\n if(i == n){\n return 0;\n }\n \n int noSwap=1e9;\n if(num1[i]>prev1 && num2[i]>prev2){\n noSwap = solve(num1,num2,i+1,num1[i],num2[i]);\n }\n \n int swap=1e9;\n if(num1[i]>prev2 && num2[i]>prev1){\n swap = 1 + solve(num1,num2,i+1,num2[i],num1[i]);\n }\n \n return min(swap,noSwap);\n }\n int minSwap(vector<int>& nums1, vector<int>& nums2) {\n int n=nums1.size();\n int m=nums2.size();\n \n return solve(nums1,nums2,0,-1,-1);\n }\n};\n```\n**Memoization**\n```\nclass Solution {\npublic:\n vector<vector<int>> dp;\n \n int solve(vector<int> &num1,vector<int> &num2,int i,int prev1,int prev2,bool swaped){\n int n = num1.size();\n if(i == n){\n return 0;\n }\n \n if(dp[i][swaped] != -1){\n return dp[i][swaped];\n }\n \n int noSwap=1e9;\n if(num1[i]>prev1 && num2[i]>prev2){\n noSwap = solve(num1,num2,i+1,num1[i],num2[i],false);\n }\n \n int swap=1e9;\n if(num1[i]>prev2 && num2[i]>prev1){\n swap = 1 + solve(num1,num2,i+1,num2[i],num1[i],true);\n }\n \n return dp[i][swaped] = min(swap,noSwap);\n }\n \n \n int minSwap(vector<int>& nums1, vector<int>& nums2) {\n int n=nums1.size();\n dp.resize(n+1,vector<int> (2,-1));\n \n return solve(nums1,nums2,0,-1,-1,0);\n }\n};\n``` | 7 | 0 | ['Dynamic Programming', 'Recursion', 'Memoization', 'C'] | 3 |
minimum-swaps-to-make-sequences-increasing | C++ Solution with Very Detailed Explanation | c-solution-with-very-detailed-explanatio-n36d | For each ith index, we have two options - either swap or do not swap them. We have to calculate the moves for both of them until the last index.\n1. We have ini | rootkonda | NORMAL | 2020-05-23T08:14:27.113666+00:00 | 2020-05-23T08:15:20.950988+00:00 | 396 | false | For each ith index, we have two options - either swap or do not swap them. We have to calculate the moves for both of them until the last index.\n1. We have initialized two arrays with MAX value, which is N as we are going to calculate minimum.\n2. For index 0, if we swap then swap[0] = 1 and if we do not swap then noswap[0] =0\n3. For index 1 and all other indices, we check two conditions and determine the values of noswap[i] and swap[i]:\n4. In a normal scenario(First If Condition, either swap them both or don\'t), where the given two numbers in both the arrays are sorted i.e. A[i-1]<A[i] and B[i-1]<B[i]. Our goal is to keep them sorted. However we calculate the noswap[1] and swap[1] like this:\n\ta. If we have swapped A[0] and B[0] and we are also swapping A[1] and B[1] then swap[1] will be count of previous swaps plus 1. i.e. swap[i] = swap[i-1]+1;\n\tb. Similarly, if we did not swap A[0] and B[0] and we are also not swapping A[1] and B[1] so moves remain same as previous noswap[i] = noswap[i-1];\n\tc. The key point here is either swap A[0] and A[1] elements with B[0] and B[1] or do not swap them both. We cannot choose either or here because when you think about it, two elements are sorted in A and two elements are sorted in B but we don\'t know if swapping one of them alone will hold this property true. That\'s why we have to swap them both or don\'t.\n5. Second if condition, swap either one of them i.e 0th or 1st when the condition satisfies.\n\t a. For example, if we swap A[0] and B[0] then we have to check if B[0] < A[1] and similarly A[0]<B[1] because thats how its gonna be after swapping and they have to be strictly increasing.\n\t b. If we swap A[1] with B[1] then we cannot swap A[0] with B[0](we have already considered that scenario in the first If condition). Now we try this scenario of swapping only one of them either A[0] or A[1]. So if we swap A[1] and B[1], then swap[1] = min(swap[1],noswap[0]+1), noswap[0]+1 is because ony A[1] is swapped so +1 with noswap[0] as A[0] is not swapped.\n\t c. Similarly, if we do not swap A[1] and B[1] then noswap[1] = min(noswap[1],swap[0]) we are doing +1 because current element is not swapped. \n6. Finally, the minimum of swap[n-1] and noswap[n-1] is the answer.\nHope it is clear !\n\n```\nclass Solution {\npublic:\n int minSwap(vector<int>& A, vector<int>& B) \n {\n int n = A.size();\n vector<int> swap(n,n);\n vector<int> noswap(n,n);\n swap[0] = 1;\n noswap[0] = 0;\n for(int i=1;i<n;i++)\n {\n if(A[i-1]<A[i] and B[i-1]<B[i])\n {\n swap[i] = swap[i-1]+1;\n noswap[i] = noswap[i-1];\n }\n if(A[i-1]<B[i] and B[i-1]<A[i])\n {\n swap[i] = min(noswap[i-1]+1,swap[i]);\n noswap[i] = min(swap[i-1],noswap[i]);\n }\n }\n return min(swap[n-1],noswap[n-1]);\n }\n};\n\n\n``` | 7 | 0 | [] | 1 |
minimum-swaps-to-make-sequences-increasing | Python | DP | Memoization | Simplest Solution With Explanation | python-dp-memoization-simplest-solution-4ex8j | Logic\n1. Instead of checking everytime the entire array to be strictly increasing, we could check at each index whether the element is greater than its previou | akash3anup | NORMAL | 2022-05-09T06:16:04.857833+00:00 | 2022-05-09T06:16:27.933077+00:00 | 616 | false | ### Logic\n1. Instead of checking everytime the entire array to be strictly increasing, we could check at each index whether the element is greater than its previous index or not. If it is then the array is strictly increasing till this index.\n2. So if the index reaches the end of array it means the array is strictly increasing.\n3. Now for each index, \n\t- We will check whether the element at the current index for both the arrays can be swapped or not. If it can be swapped then we have one swap and then we can recur for further indexes.\n\t- We also need to check whether can we go for further recurrence without swapping\n4. The minimum of above two scenarios would be the answer.\n\n```\nclass Solution: \n def dp(self, nums1, nums2, prev1, prev2, i, swapped, lookup):\n if i == len(nums1):\n return 0\n \n key = (i, swapped)\n if key not in lookup:\n minSwaps = sys.maxsize\n # Swap\n if nums2[i] > prev1 and nums1[i] > prev2:\n minSwaps = 1 + self.dp(nums1, nums2, nums2[i], nums1[i], i+1, 1, lookup)\n # Dont swap\n if nums2[i] > prev2 and nums1[i] > prev1:\n minSwaps = min(minSwaps, self.dp(nums1, nums2, nums1[i], nums2[i], i+1, 0, lookup))\n lookup[key] = minSwaps\n return lookup[key]\n \n def minSwap(self, nums1: List[int], nums2: List[int]) -> int:\n return self.dp(nums1, nums2, -1, -1, 0, 0, {})\n \n```\n\n***If you liked the above solution then please upvote!*** | 6 | 0 | ['Dynamic Programming', 'Memoization', 'Python'] | 2 |
minimum-swaps-to-make-sequences-increasing | C++ || Easy & Simple Code || DP | c-easy-simple-code-dp-by-agrasthnaman-ws3m | \nclass Solution {\npublic:\n int minSwap(vector<int>& A, vector<int>& B) {\n int swaps = 0,up = 0, down = 0;\n for (int i = 0; i < A.size(); + | agrasthnaman | NORMAL | 2022-03-18T21:41:58.292242+00:00 | 2022-03-18T21:41:58.292271+00:00 | 519 | false | ```\nclass Solution {\npublic:\n int minSwap(vector<int>& A, vector<int>& B) {\n int swaps = 0,up = 0, down = 0;\n for (int i = 0; i < A.size(); ++i) {\n if (A[i] > B[i]){up += 1;}\n else{down += 1;}\n\n if (i == A.size() - 1 || max(A[i], B[i]) < min(A[i + 1], B[i + 1])) {\n swaps += min(up, down);\n up = down = 0;\n }\n }\n return swaps;\n }\n};\n```\nDo upvote if it helped :) | 6 | 0 | ['Dynamic Programming', 'C'] | 1 |
minimum-swaps-to-make-sequences-increasing | C++ Recursive (TLE) --> Memoization | c-recursive-tle-memoization-by-thechildw-pgn9 | If you have any doubts : Please Contact : https://www.linkedin.com/in/shubham-dangwal-307347197/\nC++ Recursive CODE=>TLE \n\nclass Solution {\npublic:\n \n | thechildwholovesyou | NORMAL | 2022-01-24T06:31:53.246741+00:00 | 2022-01-24T18:26:11.841068+00:00 | 851 | false | If you have any doubts : Please Contact : https://www.linkedin.com/in/shubham-dangwal-307347197/\nC++ Recursive CODE=>TLE \n```\nclass Solution {\npublic:\n \n int helper(vector<int>& a, vector<int>& b, int i,int prevA, int prevB, bool swap)\n {\n if(i==a.size()) return 0;\n int res=INT_MAX;\n \n // no swaps\n if(a[i]>prevA and b[i]>prevB)\n res=helper(a,b,i+1,a[i],b[i],0);\n // swaps\n if(b[i]>prevA and a[i]>prevB)\n res=min(res,helper(a,b,i+1,b[i],a[i],1)+1);\n return res;\n }\n int minSwap(vector<int>& nums1, vector<int>& nums2) {\n return helper(nums1, nums2,0,-1,-1,0);\n }\n};\n```\n\nC++ Memoized CODE \n\n```\nclass Solution {\npublic:\n \n \n int helper(vector<int>& a, vector<int>& b, int i,int prevA, int prevB, bool swap,vector<vector<int>>&dp)\n {\n if(i==a.size()) return 0;\n if(dp[i][swap]!=-1) return dp[i][swap];\n int res=INT_MAX;\n \n // no swaps\n if(a[i]>prevA and b[i]>prevB)\n res=helper(a,b,i+1,a[i],b[i],0,dp);\n // swaps\n if(b[i]>prevA and a[i]>prevB)\n res=min(res,helper(a,b,i+1,b[i],a[i],1,dp)+1);\n return dp[i][swap]=res;\n }\n\n int minSwap(vector<int>& nums1, vector<int>& nums2) {\n vector<vector<int>>dp(nums1.size()+1, vector<int>(2,-1));\n return helper(nums1, nums2,0,-1,-1,0,dp);\n }\n};\n``` | 6 | 1 | ['Recursion', 'Memoization'] | 1 |
minimum-swaps-to-make-sequences-increasing | C++, O(n), With detailed explanation | c-on-with-detailed-explanation-by-user78-5zr5 | \n\n\tint minSwap(vector& nums1, vector& nums2) {\n /\n At any index i, min number of swaps to maintain 0 to i in order = \n min(minimu | user7862p | NORMAL | 2021-06-06T02:54:33.952607+00:00 | 2021-06-06T02:54:33.952643+00:00 | 414 | false | \n\n\tint minSwap(vector<int>& nums1, vector<int>& nums2) {\n /*\n At any index i, min number of swaps to maintain 0 to i in order = \n min(minimum number of swaps required to maintain 0 to i in order by swapping ith numbers, \n minimum number of swaps required to maintain 0 to i in order by not swapping ith numbers)\n \n if we maintain these 2 variables for every index i, then we can easily find the answer for n.\n \n Following cases arises:\n 1. Numbers are already in order. Swapping again disturbs the order:\n Since, swapping only ith distubs the order, if we need to swap ith, we must also swap i-1th\n \n 2. Numbers are already in order. Swapping again does not matter.\n Since swapping ith again does not matter, if we swap ith, previous numbers can be swapped or \n not swapped. Find the min of 2 cases.\n If we do not swap ith, since i-1th can be swapped or not swapped, find the min of 2 cases.\n \n 3. Numbers are not in order. We must swap to order.\n Since we need to swap ith to make order, i-1th cannot be swapped. \n \n In the code below, \n prevSwap - min number of swaps by swapping i-1th to keep 0 to i-1 in order\n prevNoSwap - min number of swaps by not swapping i-1th to keep 0 to i-1 in order\n */\n int prevSwap = 1, prevNoSwap = 0;\n for (int i = 1; i<nums1.size(); i++) {\n int curSwap = 0, curNoSwap = 0;\n \n // case: already in the proper order\n if (nums1[i-1] < nums1[i] && nums2[i-1] < nums2[i]) {\n \n // case 2: if we swap ith, it do not disturb the order, so find the min of both case\n if (nums1[i] > nums2[i-1] && nums2[i] > nums1[i-1]) {\n // if we swap ith, i-1th can be swapped or not swapped. In both cases order is maintained; \n // so find min of the two cases\n curSwap = min(prevNoSwap, prevSwap) + 1;\n // if we do not swap the ith, i-1th can be swapped or not swapped\n curNoSwap = min(prevSwap, prevNoSwap);\n } else {\n // case 1: if we swap ith, it disturbs the order, so do not swap ith\n \n // if we have to swap ith, then we must swap i-1th also to retain the order\n curSwap = prevSwap + 1;\n // if we do not swap ith, then nothing to do for i-1th as well; count remains same as prev\n curNoSwap = prevNoSwap;\n }\n } else {\n // case 3: order is not proper, we must swap the ith element\n \n // if we swap ith, we must not swap i-1th.\n curSwap = prevNoSwap + 1;\n // if we do not swap ith, i-1th must be swapped to maintain order\n curNoSwap = prevSwap;\n }\n\n prevSwap = curSwap;\n prevNoSwap = curNoSwap;\n }\n \n return min(prevSwap, prevNoSwap);\n } | 6 | 0 | [] | 0 |
minimum-swaps-to-make-sequences-increasing | c++ 98% dp. easy to explain and impl in 10mins. cheers! | c-98-dp-easy-to-explain-and-impl-in-10mi-ulyy | \n#include <vector>\n#include <limits>\n\nusing namespace std;\n\nconst int INF = 1e5;\n\nclass Solution {\npublic:\n int minSwap(vector<int>& A, vector<int> | solaaoi | NORMAL | 2018-10-12T06:01:57.075979+00:00 | 2018-10-17T20:56:11.273140+00:00 | 828 | false | ```\n#include <vector>\n#include <limits>\n\nusing namespace std;\n\nconst int INF = 1e5;\n\nclass Solution {\npublic:\n int minSwap(vector<int>& A, vector<int>& B) {\n if (A.empty()) {\n return 0;\n }\n \n int n = A.size();\n \n vector<vector<int>> dp(n, vector<int>(2, INF));\n dp[0][0] = 0;\n dp[0][1] = 1;\n for (int i = 1; i < n; ++i) {\n if (A[i] > A[i - 1] && B[i] > B[i - 1]) {\n dp[i][0] = min(dp[i][0], dp[i - 1][0]);\n dp[i][1] = min(dp[i][1], dp[i - 1][1] + 1);\n }\n if (A[i] > B[i - 1] && B[i] > A[i - 1]) {\n dp[i][0] = min(dp[i][0], dp[i - 1][1]);\n dp[i][1] = min(dp[i][1], dp[i - 1][0] + 1);\n }\n }\n \n return min(dp[n - 1][0], dp[n - 1][1]);\n }\n};\n\n\n``` | 6 | 2 | [] | 1 |
minimum-swaps-to-make-sequences-increasing | Most Efficient Way🔥| Time And Space Optimized| 4 Different Ways| Complexity Analysis | most-efficient-way-time-and-space-optimi-e7l2 | Complexity\n\n\n\n\n# Pure Recursion\n\nclass Solution {\npublic:\n int solve(vector<int>& nums1, vector<int>& nums2, int index, int isSwapped) {\n // | vaib8557 | NORMAL | 2024-06-26T15:29:23.626325+00:00 | 2024-06-26T15:29:23.626343+00:00 | 402 | false | # Complexity\n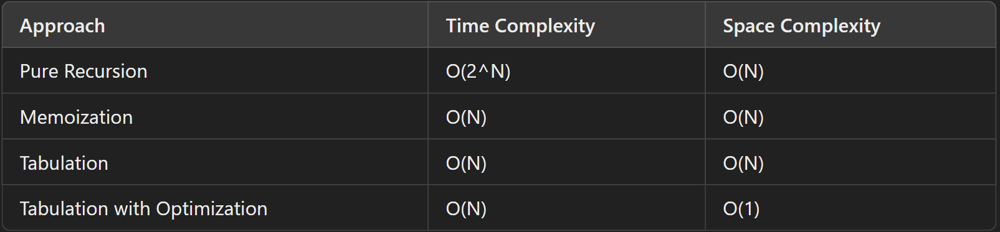\n\n\n\n# Pure Recursion\n```\nclass Solution {\npublic:\n int solve(vector<int>& nums1, vector<int>& nums2, int index, int isSwapped) {\n // Base case: if index is out of bounds, no more swaps needed\n if (index >= nums1.size()) return 0;\n\n // Initialize the minimum number of swaps needed as a large number\n int minSwaps = INT_MAX;\n\n // Get the previous elements of nums1 and nums2\n int prev1 = nums1[index - 1];\n int prev2 = nums2[index - 1];\n\n // If the previous elements are needed to swap, swap them for comparison\n if (isSwapped) swap(prev1, prev2);\n\n // Case 1: No swap at current index\n if (nums1[index] > prev1 && nums2[index] > prev2) {\n minSwaps = solve(nums1, nums2, index + 1, 0);\n }\n\n // Case 2: Swap at current index\n if (nums1[index] > prev2 && nums2[index] > prev1) {\n minSwaps = min(minSwaps, 1 + solve(nums1, nums2, index + 1, 1));\n }\n\n return minSwaps;\n }\n\n int minSwap(vector<int>& nums1, vector<int>& nums2) {\n // Insert dummy elements at the beginning to simplify indexing\n nums1.insert(nums1.begin(), -1);\n nums2.insert(nums2.begin(), -1);\n\n // Start solving from the first actual element, with no swaps initially\n return solve(nums1, nums2, 1, 0);\n }\n};\n```\n\n# Memoization\n```\nclass Solution {\npublic:\n int solve(vector<int>& nums1, vector<int>& nums2, int index, int isSwapped, vector<vector<int>>& memo) {\n // Base case: if index is out of bounds, no more swaps needed\n if (index >= nums1.size()) return 0;\n\n // If the result is already computed, return it\n if (memo[index][isSwapped] != -1) return memo[index][isSwapped];\n\n // Initialize the minimum number of swaps needed as a large number\n int minSwaps = INT_MAX;\n\n // Get the previous elements of nums1 and nums2\n int prev1 = nums1[index - 1];\n int prev2 = nums2[index - 1];\n\n // If the previous elements are needed to swap, swap them for comparison\n if (isSwapped) swap(prev1, prev2);\n\n // Case 1: No swap at current index\n if (nums1[index] > prev1 && nums2[index] > prev2) {\n minSwaps = solve(nums1, nums2, index + 1, 0, memo);\n }\n\n // Case 2: Swap at current index\n if (nums1[index] > prev2 && nums2[index] > prev1) {\n minSwaps = min(minSwaps, 1 + solve(nums1, nums2, index + 1, 1, memo));\n }\n\n // Store the result in the memoization table and return it\n return memo[index][isSwapped] = minSwaps;\n }\n\n int minSwap(vector<int>& nums1, vector<int>& nums2) {\n // Insert dummy elements at the beginning to simplify indexing\n nums1.insert(nums1.begin(), -1);\n nums2.insert(nums2.begin(), -1);\n\n // Initialize memoization table with -1\n vector<vector<int>> memo(nums1.size(), vector<int>(2, -1));\n\n // Start solving from the first actual element, with no swaps initially\n return solve(nums1, nums2, 1, 0, memo);\n }\n};\n```\n\n# Tabulation \n```\nclass Solution {\npublic:\n int minSwap(vector<int>& nums1, vector<int>& nums2) {\n // Insert dummy elements at the beginning to simplify indexing\n nums1.insert(nums1.begin(), -1);\n nums2.insert(nums2.begin(), -1);\n\n // Initialize DP table with default values\n vector<vector<int>> dp(nums1.size() + 1, vector<int>(2, 0));\n\n // Iterate from the end to the beginning\n for (int i = nums1.size() - 1; i >= 1; --i) {\n for (int isSwapped = 1; isSwapped >= 0; --isSwapped) {\n // Initialize the minimum number of swaps needed as a large number\n int minSwaps = INT_MAX;\n\n // Get the previous elements of nums1 and nums2\n int prev1 = nums1[i - 1];\n int prev2 = nums2[i - 1];\n\n // If the previous elements are needed to swap then swap them for comparison\n if (isSwapped) swap(prev1, prev2);\n\n // Case 1: No swap at current index\n if (nums1[i] > prev1 && nums2[i] > prev2) {\n minSwaps = dp[i + 1][0];\n }\n\n // Case 2: Swap at current index\n if (nums1[i] > prev2 && nums2[i] > prev1) {\n minSwaps = min(minSwaps, 1 + dp[i + 1][1]);\n }\n\n // Store the result in the DP table\n dp[i][isSwapped] = minSwaps;\n }\n }\n\n // Return the minimum number of swaps needed to make both arrays strictly increasing\n return dp[1][0];\n }\n};\n```\n\n# Tabulation With Space Optimization\n```\nclass Solution {\npublic:\n int minSwap(vector<int>& nums1, vector<int>& nums2) {\n // Insert dummy elements at the beginning to simplify indexing\n nums1.insert(nums1.begin(), -1);\n nums2.insert(nums2.begin(), -1);\n\n // Initialize variables to store the results of the previous iteration\n int noSwapPrev = 0, swapPrev = 0;\n int noSwapCurr = 0, swapCurr = 0;\n\n // Iterate from the end to the beginning\n for (int i = nums1.size() - 1; i >= 1; --i) {\n for (int isSwapped = 1; isSwapped >= 0; --isSwapped) {\n // Initialize the minimum number of swaps needed as a large number\n int minSwaps = INT_MAX;\n\n // Get the previous elements of nums1 and nums2\n int prev1 = nums1[i - 1];\n int prev2 = nums2[i - 1];\n\n // If the previous elements are needed to swap then swap them for comparison\n if (isSwapped) swap(prev1, prev2);\n\n // Case 1: No swap at current index\n if (nums1[i] > prev1 && nums2[i] > prev2) {\n minSwaps = noSwapPrev;\n }\n\n // Case 2: Swap at current index\n if (nums1[i] > prev2 && nums2[i] > prev1) {\n minSwaps = min(minSwaps, 1 + swapPrev);\n }\n\n // Store the result for the current iteration\n if (isSwapped == 0) {\n noSwapCurr = minSwaps;\n } else {\n swapCurr = minSwaps;\n }\n }\n\n // Update the results for the next iteration\n noSwapPrev = noSwapCurr;\n swapPrev = swapCurr;\n }\n\n // Return the minimum number of swaps needed to make both arrays strictly increasing\n return noSwapCurr;\n }\n};\n``` | 5 | 0 | ['Dynamic Programming', 'Backtracking', 'Recursion', 'Memoization', 'C++'] | 0 |
minimum-swaps-to-make-sequences-increasing | ✅ [Python3] DP Solution O(n) Time | python3-dp-solution-on-time-by-samirpaul-6ykm | \nclass Solution:\n def minSwap(self, nums1: List[int], nums2: List[int]) -> int:\n dp = [[-1]*2 for i in range(len(nums1))]\n \n def so | SamirPaulb | NORMAL | 2022-10-08T06:23:52.368651+00:00 | 2022-10-08T07:27:38.273851+00:00 | 1,051 | false | ```\nclass Solution:\n def minSwap(self, nums1: List[int], nums2: List[int]) -> int:\n dp = [[-1]*2 for i in range(len(nums1))]\n \n def solve(prev1, prev2, i, swaped):\n if i >= len(nums1): return 0\n if dp[i][swaped] != -1: return dp[i][swaped]\n \n ans = 2**31\n \n # No Swap\n if nums1[i] > prev1 and nums2[i] > prev2:\n ans = solve(nums1[i], nums2[i], i+1, 0) \n \n # Swap\n if nums1[i] > prev2 and nums2[i] > prev1:\n ans = min(ans, 1 + solve(nums2[i], nums1[i], i+1, 1)) \n \n dp[i][swaped] = ans\n return ans\n \n return solve(-1, -1, 0, 0) \n``` | 5 | 0 | ['Dynamic Programming', 'Recursion', 'Memoization', 'Python', 'Python3'] | 1 |
minimum-swaps-to-make-sequences-increasing | Python easy peasy // clear and simple 7 lines solution | python-easy-peasy-clear-and-simple-7-lin-6adw | \nclass Solution:\n def minSwap(self, A, B):\n non_swapped, swapped = [0] * len(A), [1] + [0] * (len(A) - 1)\n for i in range(1, len(A)):\n | cenkay | NORMAL | 2018-05-04T14:09:12.652981+00:00 | 2018-05-04T14:09:12.652981+00:00 | 988 | false | ```\nclass Solution:\n def minSwap(self, A, B):\n non_swapped, swapped = [0] * len(A), [1] + [0] * (len(A) - 1)\n for i in range(1, len(A)):\n swps, no_swps = set(), set()\n if A[i - 1] < A[i] and B[i - 1] < B[i]: swps.add(swapped[i - 1] + 1 ); no_swps.add(non_swapped[i - 1])\n if B[i - 1] < A[i] and A[i - 1] < B[i]: swps.add(non_swapped[i - 1] + 1); no_swps.add(swapped[i - 1])\n swapped[i], non_swapped[i] = min(swps), min(no_swps)\n return min(swapped[-1], non_swapped[-1])\n``` | 5 | 1 | [] | 0 |
minimum-swaps-to-make-sequences-increasing | 0(N) Solution | 0n-solution-by-2005115-8dai | \n# PLS UPVOTE IF YOU LIKE MY SOLUTION\n# Approach\nModify the solve function to take nums1, nums2, and the current index index as parameters. Also, pass a bool | 2005115 | NORMAL | 2023-07-18T12:10:44.451526+00:00 | 2023-07-18T12:10:44.451554+00:00 | 436 | false | \n# PLS UPVOTE IF YOU LIKE MY SOLUTION\n# Approach\nModify the solve function to take nums1, nums2, and the current index index as parameters. Also, pass a boolean variable swapped to keep track of whether the elements are swapped at the current index.\n\nAdd a base case to the solve function. When the current index reaches the end of the arrays (i.e., index == nums1.size()), return 0 as there are no more elements to consider.\n\nAdd a memoization check in the solve function to avoid redundant calculations. If the result for the current index and swapped state is already calculated, return it from the memoization table dp.\n\nInitialize the variable ans to store the minimum number of swaps required. Set it to INT_MAX initially.\n\nCalculate the previous elements prev1 and prev2 based on the swapped flag and the elements at the previous index.\n\nCheck if swapping is not required (nums1[index] > prev1 and nums2[index] > prev2). In this case, make a recursive call to solve with the next index and the swapped flag set to 0. Update ans with the returned value.\n\nCheck if swapping is required (nums1[index] > prev2 and nums2[index] > prev1). In this case, make a recursive call to solve with the next index and the swapped flag set to 1. Add 1 to the returned value and update ans with the minimum value between ans and the sum.\n\nStore the result in the memoization table dp[index][swapped] and return ans.\n\nIn the minSwap function, insert a dummy element (-1) at the beginning of both nums1 and nums2. This is done to match the indices with the solve function.\n\nCreate a memoization table dp with dimensions [n][2], where n is the size of the modified arrays nums1 and nums2. Initialize all values with -1.\n\nSet the swapped flag to 0 initially.\n\nCall the solve function with nums1, nums2, starting index 1, swapped flag, and the memoization table dp.\n\nReturn the result.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:0(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:0(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\nint solve(vector<int>& nums1, vector<int>& nums2,int index,bool swapped,vector<vector<int>>&dp)\n{\n if(index==nums1.size())\n return 0;\n if(dp[index][swapped]!=-1)\n {\n return dp[index][swapped];\n }\n int ans=INT_MAX;\n int prev1=nums1[index-1];\n int prev2=nums2[index-1];\n if(swapped)\n swap(prev1,prev2);\n\n if(nums1[index]>prev1 && nums2[index]>prev2 )\n {\n ans =solve(nums1,nums2,index+1,0,dp);\n }\n if(nums1[index]>prev2 && nums2[index]>prev1)\n {\n ans =min(ans,1+solve(nums1,nums2,index+1,1,dp));\n }\n return dp[index][swapped]=ans;\n\n}\n int minSwap(vector<int>& nums1, vector<int>& nums2) {\n nums1.insert(nums1.begin(),-1);\n nums2.insert(nums2.begin(),-1);\n int n = nums1.size();\n vector<vector<int>>dp(n,vector<int>(2,-1));\n bool swapped=0;\n\n return solve(nums1,nums2,1,swapped,dp); \n }\n};\n```\n# PLS HELP ME IN THIS .THIS IS 0(1) SOLUTION BUT IM NOT ABLE TO FIX THE ERROR \n# Code\n```\nclass Solution {\npublic:\nbool solve(vector<int>nums , int n , int t)\n{\n vector<int>curr(t+1,0);\n vector<int>next(t+1,0);\n curr[0]=1;\n next[0]=1;\n\n for (int index=n-1;index>=0;index--)\n {\n for(int target=0;target<=t;target++)\n {\n bool include =false;\n if(target-nums[index]>=0)\n {\n include= next[target-nums[index]];\n }\n bool exclude = next[target];\n curr[target]=include or exclude;\n }\n next =curr;\n }\n return next[t];\n\n}\n bool canPartition(vector<int>& nums) {\n int n = nums.size();\n int target=0;\n for(int i =0;i<n;i++)\n {\n target+=nums[i];\n }\n if(target%2==1)return 0;\n return solve(nums,n,target/2);\n }\n};\n``` | 4 | 0 | ['Array', 'Dynamic Programming', 'C++'] | 0 |
minimum-swaps-to-make-sequences-increasing | Java | 1D DP | easy-understanding | java-1d-dp-easy-understanding-by-6862win-ifbg | There are only 2 cases for each pair of numbers; otherwise, the input is invalid.\n (a) nums1[i] > nums1[i - 1] && nums2[i] > nums2[i - 1]\n\t(b) nums1[i] > | 6862wins | NORMAL | 2021-11-25T22:23:26.883767+00:00 | 2021-11-25T22:23:26.883794+00:00 | 610 | false | 1. There are only 2 cases for each pair of numbers; otherwise, the input is invalid.\n (a) nums1[i] > nums1[i - 1] && nums2[i] > nums2[i - 1]\n\t(b) nums1[i] > nums2[i - 1] && nums2[i] > nums1[i - 1]\n2. For each pair of numbers in the arrays, there are 2 states: swap or no swap\n3. State transition for Case (a)\n \t\t\tnoSwap[i] = noSwap[i - 1];\n \t\t\tswap[i] = swap[i - 1] + 1;\n4. State transition for Case (b)\n \t\t\tnoSwap[i] = swap[i - 1];\n \t\t\tswap[i] = noSwap[i - 1] + 1;\n```\n public int minSwap(int[] nums1, int[] nums2) {\n \tint n = nums1.length;\n \tint[] swap = new int[n], noSwap = new int[n];\n swap[0] = nums1[0] == nums2[0] ? 0 : 1;\n \tfor (int i = 1; i < n; i++) {\n \t\tnoSwap[i] = swap[i] = n; // the value is initialized because Math.min( ) is used in the following codes\n \t\tif (nums1[i] > nums1[i - 1] && nums2[i] > nums2[i - 1]) {\n \t\t\tnoSwap[i] = noSwap[i - 1];\n \t\t\tswap[i] = swap[i - 1] + 1;\n \t\t} \n \t\tif (nums1[i] > nums2[i - 1] && nums2[i] > nums1[i - 1]) {\n \t\t\tnoSwap[i] = Math.min(noSwap[i], swap[i - 1]);\n \t\t\tswap[i] = Math.min(swap[i], noSwap[i - 1] + 1);\n \t\t}\n \t}\n \treturn Math.min(swap[n - 1], noSwap[n - 1]);\n }\n\n | 4 | 0 | ['Dynamic Programming', 'Java'] | 0 |
minimum-swaps-to-make-sequences-increasing | Detailed Explanation of The Solution | detailed-explanation-of-the-solution-by-topgx | You have looked at the solution and you are wondering about the logic behind the if conditions, aren\'t you? Well, you are at the right place. I am writing this | 19mihir98 | NORMAL | 2021-03-12T22:53:58.817374+00:00 | 2021-04-24T07:19:26.510818+00:00 | 313 | false | You have looked at the solution and you are wondering about the logic behind the if conditions, aren\'t you? Well, you are at the right place. I am writing this post as there are many posts explaining the code but no one seem to clearly explain the logic and the thought process behind it. \n\n```\nint minSwap(vector<int>& A, vector<int>& B) {\n\tint N = A.size();\n\tint not_swap[1000] = {0};\n\tint swap[1000] = {1};\n\tfor (int i = 1; i < N; ++i) {\n\t\tnot_swap[i] = swap[i] = N;\n\t\tif (A[i - 1] < A[i] && B[i - 1] < B[i]) {\n\t\t\tswap[i] = swap[i - 1] + 1;\n\t\t\tnot_swap[i] = not_swap[i - 1];\n\t\t}\n\t\tif (A[i - 1] < B[i] && B[i - 1] < A[i]) {\n\t\t\tswap[i] = min(swap[i], not_swap[i - 1] + 1);\n\t\t\tnot_swap[i] = min(not_swap[i], swap[i - 1]);\n\t\t}\n\t}\n\treturn min(swap[N - 1], not_swap[N - 1]);\n}\n```\n\nCode Author: @Lee215\n\nHave a look at the problem statement once again:\n\n*Given A and B, return the minimum number of swaps to make both sequences strictly increasing. **It is guaranteed that the given input always makes it possible.***\n\nThe statement in bold is essential in understanding the logic behind the if conditions in the code. Let me explain why:\n\n```\nif (A[i - 1] < A[i] && B[i - 1] < B[i]) {\n\t\t\tswap[i] = swap[i - 1] + 1;\n\t\t\tnot_swap[i] = not_swap[i - 1];\n\t\t}\n```\n\nThe first if condition is relatively easy and straightforward to understand. It simply means that if there is a situation where A[i - 1] < A[i] && B[i - 1] < B[i] you either swap both A[i] and A[i-1] with B[i] and B[i-1] respectively or do not swap at all. \n\nNow, lets look at the second condition and this one is a bit tricky: \n```\nif (A[i - 1] < B[i] && B[i - 1] < A[i]) {\n\t\t\tswap[i] = min(swap[i], not_swap[i - 1] + 1);\n\t\t\tnot_swap[i] = min(not_swap[i], swap[i - 1]);\n\t\t}\n```\n\nThe reason behind why we have formed this condition ( A[i - 1] < B[i] && B[i - 1] < A[i] ) is because of the fact that the inputs provided are such that it is possible to make the array increasing by swapping A[i] with B[i]. This condition is essential to understand because it eliminates the case which makes it impossible to have swaping of elements resulting in the formation increasing array.\n\n ```\n A = [a1, a2] \n B = [b1, b2]\n```\n\nSay, if a1>b2 and b1>a2 and a1>a2 and b1>b2:\n\nAn example of such case would be:\n\n```\nA = [10, 5]\nB = [6, 3]\n```\n\nThis is an invalid test case to this problem as it is strictly decreasing and follows a1>b2 and b1>a2 which blocks the possibility of making the sequece increasing by swapping any one of those. \n\nTherefore, the only cases where it is possible to make the sequence increasing is when for any i, either it is already strictly increasing ( *A[i - 1] < A[i] && B[i - 1] < B[i]* ) where we can swap both or do not swap both or if it is possible to get the order correct by a single swap ( *A[i - 1] < B[i] && B[i - 1] < A[i]* ) \n\nI hope this helps. If you still need help, feel free to comment. \n\n\n\n\n | 4 | 0 | [] | 1 |
minimum-swaps-to-make-sequences-increasing | Recursive wit memo in C++ | recursive-wit-memo-in-c-by-anmolgera-hpvp | \nclass Solution {\npublic:\n \n int knap(vector<int>&A, vector<int>&B, int prevA, int prevB, int swap, int idx, vector<vector<int>> &dp) {\n \n | anmolgera | NORMAL | 2021-01-16T20:26:05.351535+00:00 | 2021-01-16T20:26:05.351569+00:00 | 330 | false | ```\nclass Solution {\npublic:\n \n int knap(vector<int>&A, vector<int>&B, int prevA, int prevB, int swap, int idx, vector<vector<int>> &dp) {\n \n if(idx==A.size()){\n return 0;\n }\n \n if(dp[idx][swap]!=-1){\n return dp[idx][swap];\n }\n int minswaps = INT_MAX;\n \n if(A[idx]>prevA && B[idx]>prevB){\n minswaps = knap(A,B,A[idx],B[idx],0,idx+1,dp);\n }\n \n if(B[idx]>prevA && A[idx]>prevB){\n minswaps = min(minswaps, knap(A,B,B[idx],A[idx],1,idx+1,dp)+1);\n }\n \n return dp[idx][swap] = minswaps;\n }\n \n \n \n \n \n \n int minSwap(vector<int>& A, vector<int>& B) {\n //int dp[A.size()+1][2];\n vector<vector<int>>dp(A.size()+1, vector<int>(2,-1));\n //emset(dp,-1,sizeof(dp));\n return knap(A,B,-1,-1,0,0,dp);\n }\n};\n``` | 4 | 0 | [] | 2 |
minimum-swaps-to-make-sequences-increasing | C++ program without DP int time complexity of O(n) and space complexity O(1) | c-program-without-dp-int-time-complexity-m03c | \nclass Solution {\npublic:\n int minSwap(vector<int>& A, vector<int>& B) {\n int c=0,k=1,temp;\n for(int i=1;i<A.size();i++){\n if | arpit0891 | NORMAL | 2020-11-09T18:40:03.060256+00:00 | 2020-11-09T18:40:03.060310+00:00 | 591 | false | ```\nclass Solution {\npublic:\n int minSwap(vector<int>& A, vector<int>& B) {\n int c=0,k=1,temp;\n for(int i=1;i<A.size();i++){\n if (min(A[i],B[i])>max(A[i-1],B[i-1]))\n { c=min(c,k);\n k=min(c,k)+1; \n }\n else if (A[i] > A[i-1] and B[i] > B[i-1])\n k=k+1;\n else{\n temp=c;\n c=k;\n k=temp+1;\n }\n }\n return min(c,k);\n }\n};\n``` | 4 | 1 | ['C'] | 0 |
minimum-swaps-to-make-sequences-increasing | Python easy peasy bottom up DP | python-easy-peasy-bottom-up-dp-by-prabhj-xvle | Here dp[i] means, minimum no. of swaps to make A[:i+1] and B[:i+1] increasing.\ndp[i][0] means, when ith index is not swapped.\ndp[i][1] means, when ith index i | prabhjyot28 | NORMAL | 2020-03-30T16:30:09.603921+00:00 | 2020-03-30T16:30:09.603958+00:00 | 510 | false | Here dp[i] means, minimum no. of swaps to make A[:i+1] and B[:i+1] increasing.\ndp[i][0] means, when ith index is not swapped.\ndp[i][1] means, when ith index is swapped.\n\n```\ndef usingDP(self, A, B):\n dp = [[float(\'inf\'), float(\'inf\')] for i in range(len(A))] #[NotSwapped, Swapped]\n \n dp[0][0] = 0\n dp[0][1] = 1\n \n for i in range(1, len(dp)):\n if A[i]>A[i-1] and B[i]>B[i-1]:\n dp[i][0] = min(dp[i][0], dp[i-1][0])\n \n if A[i]>B[i-1] and B[i]>A[i-1]:\n dp[i][0] = min(dp[i][0], dp[i-1][1])\n \n if B[i]>A[i-1] and A[i]>B[i-1]:\n dp[i][1] = min(dp[i][1], dp[i-1][0]+1)\n \n if B[i]>B[i-1] and A[i]>A[i-1]:\n dp[i][1] = min(dp[i][1], dp[i-1][1]+1)\n \n return min(dp[-1])\n```\n\n | 4 | 1 | ['Dynamic Programming', 'Python3'] | 0 |
minimum-swaps-to-make-sequences-increasing | Hope It helps dp O(n) | hope-it-helps-dp-on-by-savecancel-txs0 | inspired from @SolaAoi \n\nclass Solution {\npublic:\n int minSwap(vector<int>& A, vector<int>& B) \n {\n int n=A.size();\n \n int d | savecancel | NORMAL | 2019-12-18T17:50:17.453376+00:00 | 2019-12-27T09:05:10.431588+00:00 | 263 | false | inspired from @SolaAoi \n```\nclass Solution {\npublic:\n int minSwap(vector<int>& A, vector<int>& B) \n {\n int n=A.size();\n \n int dp[n][2];\n \n \n for(int i=0;i<n;i++)\n {\n dp[i][0]=INT_MAX;\n dp[i][1]=INT_MAX;\n }\n \n \n dp[0][0]=0;\n dp[0][1]=1;\n \n \n for (int i = 1; i < n; ++i) \n {\n if (A[i] > A[i - 1] && B[i] > B[i - 1]) \n {\n \n// we donot swap the A[i],B[i] the answer is same as prev one\n dp[i][0] = dp[i - 1][0];\n// if we swap the to make it in order we have to use the prev swapped result\n \n// 3 6 --------> 3 9 to make it order we have to swap previous pair 8 9 \n// 8 9 8 6 3 6 \n \n dp[i][1] = dp[i - 1][1] + 1;\n }\n if (A[i] > B[i - 1] && B[i] > A[i - 1])\n {\n \n// 3 15 \n// 9 12\n// we have two choices \n// 1)not the current pair\n// 2)swap\n \n// 1) in choice we have another option that is we can swap prev pair but then order is maintaines\n \n// 3 15 ----> 9 15 we can see the order is maintained\n// 9 12 3 12\n dp[i][0] = min(dp[i][0], dp[i - 1][1]);\n \n// if we swap the current pair the also then order is maintained there is no need to swap the prev pair \n \n// 3 15 -----> 3 12\n// 9 12 9 15\n dp[i][1] = min(dp[i][1], dp[i - 1][0] + 1);\n }\n }\n \n return min(dp[n-1][0],dp[n-1][1]);\n }\n \n \n};\n``` | 4 | 0 | [] | 1 |
minimum-swaps-to-make-sequences-increasing | Approach + Memoization solution | approach-memoization-solution-by-pranayh-w8fi | \n## (1) why dp? why not simple linar search - greedy?\nnums1 = [0, 4, 4, 5, 9]\nnums2 = [0, 1, 6, 8, 10]\n\nsometimes we can do only 1 coll, either of them\nbu | pranayharishchandra | NORMAL | 2024-08-07T09:20:46.056883+00:00 | 2024-08-07T09:51:12.916935+00:00 | 199 | false | \n## (1) why dp? why not simple linar search - greedy?\nnums1 = [0, 4, 4, 5, 9]\nnums2 = [0, 1, 6, 8, 10]\n\nsometimes we can do only 1 coll, either of them\nbut if the: idx = 1\nprev1 = 0 prev2 = 0\ncurr1 = 4 curr2 = 1\n\nin this case both the calls, swap or not swap will be done\nand greedy will not work \nas we meed to find out most optimal \nand for that we need to try all ways using recursion/dynammic programming\n\n---\n\n## (2) why adding -1?\n- 0 <= nums1[i], nums2[i] <= 2 * 105 (non negative elements)\n- you need to compare the "index = 0" element (1st element of the array) with someting\nso we can swap them \n\n---\n\n## (3)\n// Case 2: if you swap the current index - i.e. swap(nums1[index], nums2[index])\n// then the current condition will become \nif (nums2[index] > prev1 && nums1[index] > prev2) {\n\n\n---\n\n## (4) Tabulation: we will make the loop of isSwap from 0 to 1, even when it was not done in memoization\nthen this the reason \nWHY MEMOIZATION DON\'T FILL THE COMPLETE DP TABLE \nAND TABULATION DO ALL TYPE OF CALLS SO IT FILLS UP THE DP TABLE\nand this is why in some problems when we need table we use Tabulation and memo can\'t be used \n(as it don\'t fills up the dp table)\n\n"""\nfor (int i = nums1.size() - 1; i >= 1; --i) {\n for (int isSwapped = 1; isSwapped >= 0; --isSwapped) {\n"""\n\n---\n\n# Approach + Code\n```\n// https://leetcode.com/problems/minimum-swaps-to-make-sequences-increasing/solutions/5373146/most-efficient-way-time-and-space-optimized-4-different-ways-complexity-analysis/\n/*\n(1) why dp? why not simple linar search - greedy?\nnums1 = [0, 4, 4, 5, 9]\nnums2 = [0, 1, 6, 8, 10]\n\nsometimes we can do only 1 coll, either of them\nbut if the: idx = 1\nprev1 = 0 prev2 = 0\ncurr1 = 4 curr2 = 1\n\nin this case both the calls, swap or not swap will be done\nand greedy will not work \nas we meed to find out most optimal \nand for that we need to try all ways using recursion/dynammic programming\n\n(2) why adding -1?\n- 0 <= nums1[i], nums2[i] <= 2 * 105 (non negative elements)\n- you need to compare the "index = 0" element (1st element of the array) with someting\nso we can swap them \n\n(3)\n// Case 2: if you swap the current index - i.e. swap(nums1[index], nums2[index])\n// then the current condition will become \nif (nums2[index] > prev1 && nums1[index] > prev2) {\n\n(4) Tabulation: we will make the loop of isSwap from 0 to 1, even when it was not done in memoization\nthen this the reason \nWHY MEMOIZATION DON\'T FILL THE COMPLETE DP TABLE \nAND TABULATION DO ALL TYPE OF CALLS SO IT FILLS UP THE DP TABLE\nand this is why in some problems when we need table we use Tabulation and memo can\'t be used \n(as it don\'t fills up the dp table)\n\n"""\nfor (int i = nums1.size() - 1; i >= 1; --i) {\n for (int isSwapped = 1; isSwapped >= 0; --isSwapped) {\n"""\n */\n\n\nclass Solution {\npublic:\n int solve(vector<int>& nums1, vector<int>& nums2, int index, int isSwapped, vector<vector<int>>& memo) {\n // Base case: if index is out of bounds, no more swaps needed\n if (index >= nums1.size()) return 0;\n\n // If the result is already computed, return it\n if (memo[index][isSwapped] != -1) return memo[index][isSwapped];\n\n // Initialize the minimum number of swaps needed as a large number\n int minSwaps = INT_MAX;\n\n // Get the previous elements of nums1 and nums2\n int prev1 = nums1[index - 1];\n int prev2 = nums2[index - 1];\n\n // If the previous elements are needed to swap, swap them for comparison\n if (isSwapped) swap(prev1, prev2);\n\n // Case 1: No swap at current index\n if (nums1[index] > prev1 && nums2[index] > prev2) {\n minSwaps = solve(nums1, nums2, index + 1, 0, memo);\n }\n\n // Case 2: if you swap the current index - i.e. swap(nums1[index], nums2[index])\n // then the current condition will become \n if (nums2[index] > prev1 && nums1[index] > prev2) {\n minSwaps = min(minSwaps, 1 + solve(nums1, nums2, index + 1, 1, memo));\n }\n\n // Store the result in the memoization table and return it\n return memo[index][isSwapped] = minSwaps;\n }\n\n int minSwap(vector<int>& nums1, vector<int>& nums2) {\n // Insert dummy elements at the beginning to simplify indexing\n nums1.insert(nums1.begin(), -1);\n nums2.insert(nums2.begin(), -1);\n\n // Initialize memoization table with -1\n vector<vector<int>> memo(nums1.size(), vector<int>(2, -1));\n\n // Start solving from the first actual element, with no swaps initially\n return solve(nums1, nums2, 1, 0, memo);\n }\n};\n```\n\n--- \nthis is solution taught by Love Babbar | 3 | 0 | ['C++'] | 0 |
minimum-swaps-to-make-sequences-increasing | Easy Recursive approach, Memoisation, Tabulation, and space Optimised | easy-recursive-approach-memoisation-tabu-5i4p | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | ironblade | NORMAL | 2023-02-11T05:38:40.265083+00:00 | 2023-02-11T05:38:40.265123+00:00 | 931 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n\n int solve(int index, vector<int> &nums1, vector<int> &nums2, bool flag){\n int n = nums1.size();\n // base case\n if(index == n) return 0;\n\n int ans = INT_MAX;\n int prev1 = nums1[index-1];\n int prev2 = nums2[index-1];\n\n if(flag) // we flag is true then we swap prev1 and prev2\n swap(prev1,prev2);\n \n //noswap\n if(prev1< nums1[index] && prev2< nums2[index]){\n ans = solve(index+1,nums1,nums2,0);\n }\n\n //swap\n if(prev1< nums2[index] && prev2< nums1[index]){\n ans = min(ans, 1+ solve(index+1,nums1,nums2,1));\n }\n return ans;\n }\n\n int solveMem(int index, vector<int> &nums1, vector<int> &nums2, bool flag, vector<vector<int>> &dp){\n int n = nums1.size();\n // base case\n if(index == n) return 0;\n\n if(dp[index][flag]!= -1) return dp[index][flag];\n\n int ans = INT_MAX;\n int prev1 = nums1[index-1];\n int prev2 = nums2[index-1];\n\n if(flag) // we flag is true then we swap prev1 and prev2\n swap(prev1,prev2);\n \n //noswap\n if(prev1< nums1[index] && prev2< nums2[index]){\n ans = solveMem(index+1,nums1,nums2,0,dp);\n }\n\n //swap\n if(prev1< nums2[index] && prev2< nums1[index]){\n ans = min(ans, 1+ solveMem(index+1,nums1,nums2,1,dp));\n }\n return dp[index][flag] = ans; \n }\n\n int solveTab(vector<int> &nums1,vector<int> &nums2){\n int n = nums1.size();\n vector<vector<int>> dp(n+1,vector<int>(2,0));\n\n for(int index=n-1;index>=1;index--){\n for(int flag =1;flag>=0;flag--){\n int ans = INT_MAX;\n int prev1 = nums1[index-1];\n int prev2 = nums2[index-1];\n\n if(flag) // we flag is true then we swap prev1 and prev2\n swap(prev1,prev2);\n \n //noswap\n if(prev1< nums1[index] && prev2< nums2[index]){\n ans = dp[index+1][0];\n }\n\n //swap\n if(prev1< nums2[index] && prev2< nums1[index]){\n ans = min(ans, 1+ dp[index+1][1]);\n }\n dp[index][flag]= ans;\n }\n }\n return dp[1][0];\n }\n\n int solveSO(vector<int> &nums1, vector<int> &nums2){\n int n = nums1.size();\n vector<int> curr(2,0);\n vector<int> next(2,0);\n\n for(int index=n-1;index>=1;index--){\n for(int flag =1;flag>=0;flag--){\n int ans = INT_MAX;\n int prev1 = nums1[index-1];\n int prev2 = nums2[index-1];\n\n if(flag) // we flag is true then we swap prev1 and prev2\n swap(prev1,prev2);\n \n //noswap\n if(prev1< nums1[index] && prev2< nums2[index]){\n ans = next[0];\n }\n\n //swap\n if(prev1< nums2[index] && prev2< nums1[index]){\n ans = min(ans, 1+ next[1]);\n }\n curr[flag]= ans;\n }\n next = curr;\n }\n return next[0];\n }\n\n int minSwap(vector<int>& nums1, vector<int>& nums2) {\n int n = nums1.size();\n nums1.insert(nums1.begin(),-1);\n nums2.insert(nums2.begin(),-1);\n\n bool flag = 0;\n // return solve(1,nums1,nums2,flag);\n\n // vector<vector<int>> dp(n+1, vector<int>(2,-1));\n // return solveMem(1,nums1,nums2,flag,dp);\n\n\n // return solveTab(nums1,nums2);\n\n return solveSO(nums1,nums2);\n }\n};\n``` | 3 | 0 | ['C++'] | 1 |
minimum-swaps-to-make-sequences-increasing | ✅✅C++ || Recursive (MEMORIZED SOLUTION) || TOP DOWN | c-recursive-memorized-solution-top-down-zlgva | \nclass Solution {\npublic: \n int dp[100001][2];\n // in this i am checking for the last to front so i am \n // finding the decreaing sequence from th | MAXXER_17 | NORMAL | 2022-08-05T05:57:00.613538+00:00 | 2022-08-05T05:57:00.613596+00:00 | 865 | false | ```\nclass Solution {\npublic: \n int dp[100001][2];\n // in this i am checking for the last to front so i am \n // finding the decreaing sequence from the last to front\n int findans(vector<int>&a,vector<int>&b,int i,int val)\n {\n if(i==0)\n return 0;\n if(dp[i][val]!=-1)\n return dp[i][val];\n int ans=INT_MAX-1;\n // 1 denote precious values were swapped \n // 0 denoted previous values were not swapped\n \n if(val==1)\n {\n // not swapping the current values\n if(a[i]>b[i-1] && b[i]>a[i-1])\n {\n ans=min(ans,findans(a,b,i-1,0));\n }\n // swapping the current values\n if(a[i]>a[i-1] && b[i]>b[i-1])\n {\n ans=min(ans,1+findans(a,b,i-1,1));\n }\n }\n else\n {\n // not swapping the current values\n if(a[i]>a[i-1] && b[i]>b[i-1])\n {\n ans=min(ans,findans(a,b,i-1,0));\n }\n // swapping the current values\n if(a[i]>b[i-1] && b[i]>a[i-1])\n {\n ans=min(ans,1+findans(a,b,i-1,1));\n }\n }\n // return the min ans\n return dp[i][val]=ans;\n }\n int minSwap(vector<int>& a, vector<int>& b) {\n memset(dp,-1,sizeof(dp));\n int n=a.size();\n // return the min of if last values were swapped or not\n return min(findans(a,b,n-1,0),1+findans(a,b,n-1,1));\n }\n};\n```\n\nConsider UPVOTE If you like it | 3 | 0 | ['Dynamic Programming', 'Recursion', 'Memoization', 'C', 'C++'] | 0 |
minimum-swaps-to-make-sequences-increasing | [C++] code like poetry | Top-down | c-code-like-poetry-top-down-by-onesucces-x4hh | \nclass Solution {\n public:\n \n vector<vector<int>> memo;\n \n int f(vector<int> &A, vector<int> &B, int i, bool shouldSwap) {\n int n = A | onesuccess | NORMAL | 2020-11-06T23:12:23.075314+00:00 | 2020-11-06T23:12:23.075340+00:00 | 449 | false | ```\nclass Solution {\n public:\n \n vector<vector<int>> memo;\n \n int f(vector<int> &A, vector<int> &B, int i, bool shouldSwap) {\n int n = A.size();\n if (i == n) return 0;\n if (memo[shouldSwap][i] != -1) return memo[shouldSwap][i];\n int a = A[i - 1], b = B[i - 1];\n if (shouldSwap) swap(a, b);\n int o1 = INT_MAX, o2 = INT_MAX;\n if (B[i] > b && A[i] > a) o1 = f(A, B, i + 1, false);\n if (A[i] > b && B[i] > a) o2 = 1 + f(A, B, i + 1, true);\n return memo[shouldSwap][i] = min(o1, o2);\n }\n \n int minSwap(vector<int> &A, vector<int> &B) {\n memo.resize(2, vector<int> (A.size(), -1));\n return min(f(A, B, 1, false), 1 + f(A, B, 1, true));\n }\n};\n``` | 3 | 2 | ['C'] | 0 |
minimum-swaps-to-make-sequences-increasing | [Python] Top Down and Bottom Up DP Solutions | python-top-down-and-bottom-up-dp-solutio-3tld | Top Down Expanded for Readability: 112 ms\npython\ndef minSwap(self, A: List[int], B: List[int]) -> int:\n\n\tif len(A) == 1: return 0\n\n\[email protected]_cache | rowe1227 | NORMAL | 2020-11-02T08:20:16.650896+00:00 | 2020-11-02T08:20:16.650938+00:00 | 209 | false | **Top Down Expanded for Readability: 112 ms**\n```python\ndef minSwap(self, A: List[int], B: List[int]) -> int:\n\n\tif len(A) == 1: return 0\n\n\[email protected]_cache(None)\n\tdef helper(i, prev_swap):\n\n\t\tif i == len(A):\n\t\t\treturn 0\n\n\t\t# if the previous values (A[i-1] and B[i-1]) were swapped then a = B[i-1] and b = A[i-1]\n\t\ta,b = (B[i-1], A[i-1]) if prev_swap else (A[i-1], B[i-1])\n\n\t\toptions = []\n\n\t\t# don\'t swap A[i] and B[i]\n\t\tif A[i] > a and B[i] > b:\n\t\t\toptions.append(helper(i+1, False))\n\n\t\t# swap A[i] and B[i]\n\t\tif A[i] > b and B[i] > a:\n\t\t\toptions.append(1 + helper(i+1, True))\n\n\t\t# Choose the option that requires less total swaps\n\t\treturn min(options)\n\n\treturn min(helper(1, False), 1 + helper(1, True))\n```\n\n<br>\n\n**Top Down DP written more concicely: 108ms**\n```python\ndef minSwap(self, A: List[int], B: List[int]) -> int:\n\n\[email protected]_cache(None)\n\tdef helper(i, prev_swap):\n\t\tif i == len(A): return 0\n\t\ta,b = (B[i-1], A[i-1]) if prev_swap else (A[i-1], B[i-1])\n\t\treturn min(helper(i+1, False) if A[i] > a and B[i] > b else float(\'inf\'), 1 + helper(i+1, True) if A[i] > b and B[i] > a else float(\'inf\'))\n\treturn min(helper(1, False), 1 + helper(1, True)) if len(A) > 1 else 0\n```\n\n<br>\n\n**Bottom Up DP: 108 ms**\n```python\ndef minSwap(self, A: List[int], B: List[int]) -> int:\n\n\tn = len(A)\n\tdp = [[0 for _ in range(2)] for _ in range(n+1)]\n\tfor i in range(n-1, -1, -1):\n\t\tfor prev_swap in range(2):\n\t\t\ta,b = (B[i-1], A[i-1]) if prev_swap else (A[i-1], B[i-1])\n\t\t\tdp[i][prev_swap] = min(dp[i+1][0] if A[i] > a and B[i] > b else float(\'inf\'), 1 + dp[i+1][1] if A[i] > b and B[i] > a else float(\'inf\'))\n\n\treturn min(dp[1][0], 1 + dp[1][1]) if len(A) > 1 else 0\n``` | 3 | 0 | [] | 0 |
minimum-swaps-to-make-sequences-increasing | [Python] O(N) Time O(1) Space DP solution with explainations | python-on-time-o1-space-dp-solution-with-067i | For each pair of elements of A and B, (A[i], B[i]), there are only two status \'not swap\' or \'swap\'. Set two variables, n_swap, swap, to store the min number | licpotis | NORMAL | 2020-10-27T12:18:55.211167+00:00 | 2020-10-27T12:27:16.677135+00:00 | 640 | false | For each pair of elements of A and B, (A[i], B[i]), there are only two status \'not swap\' or \'swap\'. Set two variables, n_swap, swap, to store the min number of swaps to make subarray A[:i+1] and B[:i+1] strict increasing. \n\nFor i-th pair of (A[i], B[i]), there are only three possible cases since it is guaranteed that at least an possible A and B exits after some swaps:\n\t1. (A[i], B[i]) and (A[i - 1], B[i - 1]) need to be the same status, i.e. if (i-1)th pair swap, i-th pair need to swap; if (i-1)th pair doesn\'t swap, i-th pair must not swap to satisfiy the strict increasing condition.\n\t2. (A[i], B[i]) and (A[i - 1], B[i - 1]) need to be the opposite status. i.e. if (i-1)th pair swap, then ith pair must not swap, vice versa.\n\t3. (A[i], B[i]) could be either same or opposite status of (A[i - 1], B[i - 1]), the strict increasing condition will be satisfied.\n\nHere is my code with comments:\n```\nclass Solution:\n def minSwap(self, A: List[int], B: List[int]) -> int:\n # to store min number of swaps of two status: not swap and swap\n n_swap, swap = 0, 1\n for i in range(1, len(A)):\n # Case III: ith pair of (a, b) could be any status\n if max(A[i - 1], B[i - 1]) < min(A[i], B[i]):\n n_swap = min(n_swap, swap)\n swap = n_swap + 1\n # Case I: same status of ith and (i-1)th pair of (a, b)\n elif A[i - 1] < A[i] and B[i - 1] < B[i]:\n swap += 1\n # Case I: diff status of ith and (i-1)th pair of (a, b)\n else:\n n_swap, swap = swap, n_swap + 1\n return min(n_swap, swap)\n```\n\n | 3 | 0 | ['Dynamic Programming', 'Python', 'Python3'] | 0 |
minimum-swaps-to-make-sequences-increasing | C++ | O( N ) | Detailed Explanation and comments | c-o-n-detailed-explanation-and-comments-p78li | Credits to : lee215\nI will be explaining the approach here.\n swap[i] = total no. of swaps required to keep array from 0 to i in increasing order when we swap | Might_Guy | NORMAL | 2020-04-25T15:07:42.154336+00:00 | 2020-04-25T15:10:26.084652+00:00 | 303 | false | Credits to : [lee215](https://leetcode.com/lee215)\nI will be explaining the approach here.\n* swap[i] = total no. of swaps required to keep array from 0 to i in increasing order when we swap the ith positions\n* notswap[i] = total no. of swaps required to keep array from 0 to i in increasing order when we do not swap the ith positions\n\nIf condition ( A [ i ] > A [ i - 1] & & B [ i ]> B [ i - 1 ] ) is satisfied then \n* if we swap ith and we have to swap i-1 th also.\n* if we do not swap ith and we can not swap i-1 th also.\n\nIf condition ( A [ i ] > B [ i - 1 ] && B [ i ]> A [ i - 1 ] ) is satisfied then \n* if we swap ith then we can not swap i-1 th.\n* if we do not swap ith then we have to swap i-1 th.\n\nThe two conditions can be met simuntaneously for a given i.\n( It is not a if and else ) that is why in second if we have min to keep the minimum obtained for swap[i] and notswap[i] on following these two conditions.\n\n\n```\nclass Solution {\npublic:\n int minSwap(vector<int>& A, vector<int>& B) {\n int n = A.size();\n vector<int>notswap(n);\n vector<int>swap(n,1);\n for(int i=1;i<n;i++){\n swap[i]=n;\n notswap[i]=n;\n if(A[i]>A[i-1] && B[i]>B[i-1]){\n\t\t\t\t//swapped i so cant swap at i-1 hence notswap[i-1] and add one for swap at i\n swap[i] = swap[i-1]+1;\n\t\t\t\t//not swapped at i so can do at i-1 also hence notswap[i]=notswap[i-1];\n notswap[i]=notswap[i-1];\n }\n\t\t\t // we take min just to get min out of thsese two if conditions\n if(A[i]>B[i-1] && B[i]>A[i-1]){\n\t\t\t\t// swap at i so cant swap at i-1 hence notswap[i-1] and add one for swap at i\n swap[i] = min(notswap[i-1]+1,swap[i]);\n\t\t\t\t//notswap[i] so we have to swap at i-1 hence swap[i-1] add zero for no swap at i\n notswap[i]= min(swap[i-1],notswap[i]);\n }\n }\n return min({swap[n-1],notswap[n-1]});\n }\n};\n``` | 3 | 0 | [] | 1 |
minimum-swaps-to-make-sequences-increasing | DP and not greedy explaination | dp-and-not-greedy-explaination-by-sthakk-o0gm | Thoughts\n\n- Greedy is not the solution, why?\n\t- First thought came of greedy, i.e. iterate over all the indices (A and B same), then wherever condition brea | sthakkar411 | NORMAL | 2020-03-21T15:12:39.591944+00:00 | 2020-03-21T15:12:39.591980+00:00 | 157 | false | ***Thoughts***\n\n- ***Greedy is not the solution, why?***\n\t- First thought came of greedy, i.e. iterate over all the indices (A and B same), then wherever condition breaks, swap it, do moves++ and move further\n\t- But in the above approach, whenever condition fails, we are swapping current index elements, we could also have swapped previous index elements, which could have given us the best answer.\n\t- Consider the example :\n\t\t\t- 1, 7, 8, 9\n\t\t\t- 6, 2, 3, 4\n\t- In the above example, if we do greedy, then we would end up swapping 2, 3, 4, thus 3 moves, but answer is 1 move\n\t- But now, thought comes, what if we calculate moves using greedy, and return min(moves, n - moves)\n\t- But there is problem with this approach, consider the array is divided into 3 sections, Left, middle and right section.\n\t- Left section has problem, we calculate moves in left as leftMoves, similarly for right as rightMoves, and say middle section is perfect, strictly increasing.\n\t- Now we cannot do min (leftMoves+rightMoves, n - (leftMoves+rightMoves))\n\t- Because second part in minimum says, swap middle part also, which is not required, we should have just done min in leftPart + min in rightPart\n\t- Thus, this question cannot be solved using greedy\n\n\n- ***Recursion (or Dynamic Programming)***\n\t- Now we know that whenever condition breaks, we could have either swapped previous one or current one.\n\t- But if we swapped previous one, it could have broken the previous part of array\n\t- So for each index, we will calculate 2 answers, min swaps required till now, if current one is not swapped and min swaps requried till now, if current one is swapped.\n\t- This way, current both answers can be used to caclulate next both answers\n\t- But in this approach, calculate answers, if possible, i.e. it could be possible to swap only, not leave the arrays as it is (without swapping), as may not lead to strictly increasing arrays\n\t- Moreover, we will not use DP of space N, since current both answers just depend upon previous 2 answers, thus 4 variables will solve the problem\n\t- Otherwise, we could have required 2D array for DP = new int[N][2]\n\t- Time : O(N), Space : O(1)\n\n***Solution***\n\n```\nclass Solution {\n public int minSwap(int[] A, int[] B) {\n if (A == null || A.length == 0) return 0;\n int len = A.length;\n int prevNonSwap = 0, prevSwap = 1, currSwap = len, currNonSwap = len;\n for (int idx = 1; idx < len; idx++) {\n if ((A[idx] > A[idx-1]) && (B[idx] > B[idx-1])) {\n currNonSwap = prevNonSwap;\n currSwap = prevSwap+1;\n }\n if ((A[idx] > B[idx-1]) && (B[idx] > A[idx-1])) {\n currNonSwap = Math.min(currNonSwap, prevSwap);\n currSwap = Math.min(currSwap, prevNonSwap+1);\n }\n prevSwap = currSwap;\n prevNonSwap = currNonSwap;\n currSwap = len;\n currNonSwap = len;\n }\n return Math.min(prevSwap, prevNonSwap);\n }\n}\n``` | 3 | 0 | [] | 0 |
minimum-swaps-to-make-sequences-increasing | C++ 8ms 97% DP solution, O(n) time O(1) space w/ explanation | c-8ms-97-dp-solution-on-time-o1-space-w-svzsz | Took me a while to figure out the specific DP logic and mentally prove its correctness. The basic idea is this:\n\nAssume you arrive at index i of both arrays. | guccigang | NORMAL | 2020-01-03T05:27:25.740424+00:00 | 2020-01-03T06:12:14.915908+00:00 | 225 | false | Took me a while to figure out the specific DP logic and mentally prove its correctness. The basic idea is this:\n\nAssume you arrive at index `i` of both arrays. There are two things you can do. You can either keep `A[i]` and `B[i`] the way they are (do not flip them), or swap `A[i]` and `B[i]` (flip them). Of course there are restrictions. You can only keep (or flip) `A[i]`, `B[i]` if the result is *valid*. This means after either keeping or flipping the result should be: `A[i] > A[i-1] && B[i] > B[i-1]`. \n\nOther than the restriction of strictly increasing array, we also need to ensure we have the *minimum* number of swaps. So we have to choose the best option based on our previously calculated result. \n\nThe next step is to write out the DP logic based on what we can do:\n\nFirst we define two boolean quantities:\n\n`t1 = A[i] > A[i-1] && B[i] > B[i-1]`\n`t2 = A[i] > B[i-1] && B[i] > A[i-1]`\n\nCondition `t1` is true if the array is valid without flipping. Condition `t2` is true if the array is valid with flipping. It is important to notice that these two conditions are **not mutually exclusive**. \n\nTo start off, we need two arrays, one remembering **minimum flips if we choose not to flip**, and the other **minimum flips if we choose to flip**. We will label them as `no_flip` and `flip`. `no_flip[i]` is defined as the number of moves required to make the arrays valid from `0 ... i`, and we do not flip at index `i`. `flip[i]` is defined as the number of moves required to make the arrays valid from `0 ... i`, but we *must* flip at index `i`. \n\n* **Assume at index `i` we do not want to flip.** What would be the required number of flips to make the arrays valid from `0 ... i` ?\nIf `t1` is true, then we don\'t have to do anything. Thus, the number of flips would be the same as those required from `no_flip[i-1]`.\nIf `t2` is true, then we *could* flip the previous pair `(A[i-1], B[i-1]`, whilethe arrays are still valid, so the number of flips required for that would be `flip[i-1]`. \nIf `t1` and `t2` are true, we have two options. Naturally, we pick the minimum, which would be `min(no_flip[i-1], flip[ i-1])`. If we only have one option, then we must choose that option. \nIf both options are invalid (guaranteed to not happen in this case), then we should put an arbitrary (large) number to indicate "impossible". \n\n* **Assume at index `i` we want to flip.** What would be the required number of flips to make the arrays valid from `0 ... i` ?\nIf `t1` is true, then we have an interesting scenario. We *must* flip at `i`, so then to be consistent with `t1` we need to also flip at `i-1`. Thus, the number of flips would be the same as those required from `flip[i-1]`.\nIf `t2` is true, since we are already flipping at `i` we do not flip at `i-1`, so the number of flips required for that would be `no_flip[i-1]`. \nIf `t1` and `t2` are true, we have two options. Naturally, we pick the minimum, which would be `min(flip[i-1], no_flip[i-1])`. If we only have one option, then we must choose that option. \nBecause we are flipping at index `i`, we need to **add 1** to our minimum flip count.\nIf both options are invalid (guaranteed to not happen in this case), then we should put an arbitrary (large) number to indicate "impossible". \n\nUsing this DP logic, our update rule is as follows:\n\n`no_flip[i-1] = t1 && t2 ? min(no_flip[i-1], flip[i-1]) : t1 ? no_flip[i-1] ; t2 ? flip[i-1] : 9001`\n`flip[i-1] = t1 && t2 ? 1 + min(flip[i-1], no_flip[i-1]) : t1 ? flip[i-1] ; t2 ? no_flip[i-1] : 9001`\n\nI used over 9000 as "impossible" here.\n\nTo begin, we have a single element which is always strictly sorted. Thus, `no_flip[0] = 0` and `flip[0] = 1`. `flip[0]` is 1 because the previous (empty array) is valid with 0 flips and we must flip at current index, which leads to `flip[0] = 0 + 1 = 1`.\n\nOnce we get values for `flip` and `no_flip` at the last index, we can simply take the minimum again to get the answer. This forms the DP solution for this problem, with run-time `O(n)` and space `O(n)`. \n\nTo convert the `O(n)` space DP solution to `O(1)` space, I combined the two required vectors (`no_flip` and `flip`) so that I keep the state of the previous iteration. In my code the vector `n` is defined as `n = {no_flip[i-1]. flip[i-1]}` and `other = {no_flip[i], flip[i]}`. \n\n**O(n) space**\n```\nclass Solution {\npublic:\n int minSwap(vector<int>& A, vector<int>& B) {\n int size = A.size(), count = 0;\n vector<int> n(size, 0), f(size, 0); // n = no_flip, f = flip\n f[0] = 1;\n for(int i = 1; i < size; ++i) {\n const bool t1 = A[i] > A[i-1] && B[i] > B[i-1], t2 = A[i] > B[i-1] && B[i] > A[i-1];\n n[i] = t1 && t2 ? min(n[i-1], f[i-1]) : t1 ? n[i-1] : t2 ? f[i-1] : 9001;\n f[i] = t1 && t2 ? 1 + min(n[i-1], f[i-1]) : t2 ? 1 + n[i-1] : t1 ? 1 + f[i-1] : 9001;\n } \n return min(n.back(), f.back());\n }\n};\n\nauto gucciGang = []() {std::ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);return 0;}();\n```\n\n\n**O(1) space** \n\n```\nclass Solution {\npublic:\n int minSwap(vector<int>& A, vector<int>& B) {\n int size = A.size(), count = 0;\n vector<int> n(2, 0), other(2, 0); // index 0 = no_flip, index 1 = flip\n n[1] = 1;\n for(int i = 1; i < size; ++i) {\n const bool t1 = A[i] > A[i-1] && B[i] > B[i-1], t2 = A[i] > B[i-1] && B[i] > A[i-1];\n other[0] = t1 && t2 ? min(n[0], n[1]) : t1 ? n[0] : t2 ? n[1] : 9001;\n other[1] = t1 && t2 ? 1 + min(n[0], n[1]) : t2 ? 1 + n[0] : t1 ? 1 + n[1] : 9001;\n swap(n, other);\n } \n return min(n[0], n[1]);\n }\n};\n\nauto gucciGang = []() {std::ios::sync_with_stdio(false);cin.tie(nullptr);cout.tie(nullptr);return 0;}();\n``` | 3 | 0 | [] | 0 |
minimum-swaps-to-make-sequences-increasing | Python dp With Clear Explanation | python-dp-with-clear-explanation-by-sash-sjuz | Minimum swaps To make Sequences Increasing\n\n### Given 2 arrays, find minimum same indexed swaps that need to occur to make both arrays strictly increasing\n\n | sashank007 | NORMAL | 2019-10-01T23:10:12.367784+00:00 | 2019-10-02T07:12:08.510804+00:00 | 351 | false | ## Minimum swaps To make Sequences Increasing\n\n### Given 2 arrays, find minimum same indexed swaps that need to occur to make both arrays strictly increasing\n\n1. Firstly, at each stage , we need to store the value of count if we swap A[i] and B[i] and if we don\'t swap A[i] and B[i].\n2. If they are increasing without a swap, then we don\'t need to do anything when we don\'t swap. We take the previous value stored for not swapping and store in current index. For swap, that means the swap which occurred previously was a faulty one , so we need to rectify that so swap[i-1] +1\n3. If they are increasing with a swap, that means B[i-1] < A[i] and A[i-1] < B[i]. This means if we want to swap A[i] and B[i], we can either keep[i-1] + 1 or swap[i-1] +1 (we can swap both or keep one and swap one . Both will work). We take the minimum of these two values. For noswap array, we take the minimum of swap[i-1] and noswap[i].\n4. In the end, the minimum of both final values (noswap and swap) are taken as the final result.\n\n```\nclass Solution:\n def minSwap(self, A: List[int], B: List[int]) -> int:\n n = len(A)\n noswap = [ float(\'inf\')] * n\n swap = [float(\'inf\')] * n\n noswap[0] = 0\n swap[0]=1\n for i in range(1 , n):\n incr_without_swap = A[i] >A[i-1] and B[i] >B[i-1]\n incr_with_swap = A[i]>B[i-1] and B[i] > A[i-1]\n if incr_without_swap:\n #you can keep both values or swap both values\n noswap[i]=noswap[i-1]\n swap[i]= swap[i-1]+1\n if incr_with_swap:\n swap[i] = min(noswap[i-1] +1,swap[i])\n noswap[i]= min(swap[i-1],noswap[i])\n return min(noswap[-1],swap[-1])\n``` | 3 | 0 | [] | 0 |
minimum-swaps-to-make-sequences-increasing | Beats 99.29% Python | beats-9929-python-by-gracemeng-msut | \n def minSwap(self, A, B):\n n = len(A)\n prevNotSwap = 0\n prevSwap = 1\n for i in range(1, n):\n areBothSelfIncreas | gracemeng | NORMAL | 2018-12-20T01:29:43.367625+00:00 | 2018-12-20T01:29:43.367687+00:00 | 449 | false | ```\n def minSwap(self, A, B):\n n = len(A)\n prevNotSwap = 0\n prevSwap = 1\n for i in range(1, n):\n areBothSelfIncreasing = A[i - 1] < A[i] and B[i - 1] < B[i] \n areInterchangeIncreasing = A[i - 1] < B[i] and B[i - 1] < A[i]\n if areBothSelfIncreasing and areInterchangeIncreasing:\n newPrevNotSwap = min(prevNotSwap, prevSwap)\n prevSwap = min(prevNotSwap, prevSwap) + 1\n prevNotSwap = newPrevNotSwap\n elif areBothSelfIncreasing:\n prevSwap += 1 \n else: # if areInterchangeIncreasing:\n newPrevNotSwap = prevSwap\n prevSwap = prevNotSwap + 1\n prevNotSwap = newPrevNotSwap\n return min(prevNotSwap, prevSwap)\n```\n**(\u4EBA \u2022\u0348\u1D17\u2022\u0348)** Thanks for voting! | 3 | 0 | [] | 0 |
minimum-swaps-to-make-sequences-increasing | C++ O(n) time, O(1) space | c-on-time-o1-space-by-babos-is8e | cpp []\nclass Solution {\npublic:\n int minSwap(vector<int>& nums1, vector<int>& nums2) {\n int swap = 1;\n int noSwap = 0;\n \n | babos | NORMAL | 2024-11-19T06:48:32.619547+00:00 | 2024-11-19T06:48:32.619580+00:00 | 55 | false | ```cpp []\nclass Solution {\npublic:\n int minSwap(vector<int>& nums1, vector<int>& nums2) {\n int swap = 1;\n int noSwap = 0;\n \n for (int i = 1; i < nums1.size(); i++) {\n int curSwap = 0;\n int curNoSwap = 0;\n\n if (nums1[i] <= nums1[i-1] || nums2[i] <= nums2[i-1]) {\n // musn\'t have swapped if swapping; else must have swapped\n curSwap = noSwap + 1;\n curNoSwap = swap;\n } else if (nums1[i] <= nums2[i-1] || nums2[i] <= nums1[i-1]) {\n // must have swapped if swapping; else musn\'t have\n curSwap = swap + 1;\n curNoSwap = noSwap;\n } else {\n curSwap = min(swap, noSwap) + 1;\n curNoSwap = min(swap, noSwap);\n }\n\n swap = curSwap;\n noSwap = curNoSwap;\n }\n\n return min(swap, noSwap);\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
minimum-swaps-to-make-sequences-increasing | 🔥🎯Clean O(n) DP approach🎯🔥 | clean-on-dp-approach-by-msrathore1612-m4rb | Intuition\nFor every index i we can either swap it if the strictly increasing rule is being broken or keep it as it is.\n\u2234 We have two Choices.\n\n# Approa | msrathore1612 | NORMAL | 2024-07-25T16:38:20.512692+00:00 | 2024-07-25T16:38:20.512725+00:00 | 491 | false | # Intuition\nFor every index i we can either swap it if the strictly increasing rule is being broken or keep it as it is.\n\u2234 We have two $$Choices$$.\n\n# Approach\nIf at any index $$i$$ we have the swaps needed for sub array [ $$i+1$$ to $$n$$ ]\nthen we can calculate result for $$i$$ $$th$$ index.\n\n### Case1 : \n**Invalide case**\nCurrent element of nums1 / nums2 is greater or equal to next element.\n\n - We **have** to swap **either** $$i$$ $$th$$ elements **or** $$i+1$$ $$th$$ elements. \n\n **Note :** if you swap both $$i$$ $$th$$ elements and $$i+1$$ $$th$$ elements you will atain the same Invalid case again.\n\n - So we will add the ( result / cost / number of operations needed ) of $$swapping$$ $$i$$ $$th$$ elements with $$notSwapping$$ of $$i+1$$ $$th$$ index and vice versa.\n\n### Case2 : \n**Valide case**\nCurrent element of nums1 and nums2 is smaller then to next element.\nHere there are two senarios :\n\n - If after swapping $$i$$ $$th$$ elements **Invalid case** is attained then we will have to swap $$i+1$$ $$th$$ elements too, else we can go with or without swapping $$i+1$$ $$th$$ elements it doesn\'t matter. \n\n\n# Complexity\n- Time complexity: **O(n)**\n\n- Space complexity: **O(n)**\n\n# Code\n```\nclass Solution {\npublic:\n\n int solveTab(vector<int> &nums1, vector<int> &nums2){\n int n = nums1.size();\n vector<int>swap(n, 0); //considering swapping senario\n vector<int>noSwap(n, 0); //considering not swapping \n int ans=0;\n if(nums1.back()<=nums1[n-2] || nums2.back()<=nums2[n-2] ) ans=1; \n swap[n-1]=1; // base case\n\n for(int i=n-2; i>=0; i--){\n if(nums1[i]>=nums1[i+1] || nums2[i]>=nums2[i+1]){\n //invalid case either swap i or swap i+1\n swap[i]=1+noSwap[i+1];\n noSwap[i]=swap[i+1];\n ans=max(ans, min(swap[i], noSwap[i]));\n }else{\n //No swap needed\n if(nums2[i]>=nums1[i+1] || nums1[i]>=nums2[i+1]){\n //If swapped it will become Invalid so you would have to swap again\n swap[i]=1+swap[i+1];\n noSwap[i]=noSwap[i+1];\n }else{\n swap[i]=1+min(swap[i+1], noSwap[i+1]);\n noSwap[i]=min(swap[i+1], noSwap[i+1]);\n }\n ans=max(ans, min(swap[i], noSwap[i]));\n }\n }\n return ans;\n }\n\n int minSwap(vector<int>& nums1, vector<int>& nums2) {\n return solveTab(nums1, nums2);\n }\n};\n``` | 2 | 0 | ['Dynamic Programming', 'C++'] | 0 |
minimum-swaps-to-make-sequences-increasing | EASY UNDERSTANDING DP (FOUR APPROACHES) | easy-understanding-dp-four-approaches-by-d1c3 | RECURSION \n\n \nint solve(vector<int>& nums1, vector<int>& nums2, int index, bool swapped)\n {\n if(index >= nums1.size())\n {\n re | 20122 | NORMAL | 2024-02-24T18:58:50.535310+00:00 | 2024-02-24T18:58:50.535335+00:00 | 197 | false | **RECURSION **\n\n ```\nint solve(vector<int>& nums1, vector<int>& nums2, int index, bool swapped)\n {\n if(index >= nums1.size())\n {\n return 0;\n }\n \n int ans = INT_MAX;\n \n int prev1 = nums1[index-1];\n int prev2 = nums2[index-1];\n \n \n //if only one element to swap or swap count ==1 \n if(swapped)\n {\n swap(prev1, prev2);\n }\n \n //Non-Swappped \n if(nums1[index] > prev1 && nums2[index] > prev2)\n {\n ans = solve(nums1, nums2, index+1, 0);\n }\n \n //swapped\n if(nums1[index] > prev2 && nums2[index] > prev1)\n {\n ans = min(ans, 1 + solve(nums1, nums2, index+1, 1)); \n }\n \n return ans;\n }\n \n```\n\n**MEMOIZATION **\n\n```\nint solveMem(vector<int>& nums1, vector<int>& nums2, int index, bool swapped, vector<vector<int>>& dp)\n {\n if(index >= nums1.size())\n {\n return 0;\n }\n \n if(dp[index][swapped] != -1)\n {\n return dp[index][swapped];\n }\n \n int ans = INT_MAX;\n \n int prev1 = nums1[index-1];\n int prev2 = nums2[index-1];\n \n \n //if only one element to swap or swap count ==1 \n if(swapped)\n {\n swap(prev1, prev2);\n }\n \n //Non-Swappped \n if(nums1[index] > prev1 && nums2[index] > prev2)\n {\n ans = solveMem(nums1, nums2, index+1, 0, dp);\n }\n \n //swapped\n if(nums1[index] > prev2 && nums2[index] > prev1)\n {\n ans = min(ans, 1 + solveMem(nums1, nums2, index+1, 1,dp)); \n }\n \n \n return dp[index][swapped] = ans;\n }\n \n```\n\n**Tabulation**\n\n```\nint solveTab(vector<int>& nums1, vector<int>& nums2)\n {\n int n = nums1.size();\n vector<vector<int>> dp(n+1, vector<int> (2,0));\n \n for(int index = n-1; index >=1; index --)\n {\n for(int swapped = 1; swapped >=0; swapped--)\n {\n int ans = INT_MAX;\n \n int prev1 = nums1[index-1];\n int prev2 = nums2[index-1];\n \n \n //if only one element to swap or swap count ==1 \n if(swapped)\n {\n swap(prev1, prev2);\n }\n \n //Non-Swappped \n if(nums1[index] > prev1 && nums2[index] > prev2)\n {\n ans = dp[index+1][0];\n }\n \n //swapped\n if(nums1[index] > prev2 && nums2[index] > prev1)\n {\n ans = min(ans, 1 + dp[index+1][1]); \n }\n \n dp[index][swapped] = ans;\n \n }\n }\n return dp[1][0];\n }\n```\n\n**SPACE OPTIMIZATION**\n\n```\n int spaceOpti(vector<int>& nums1, vector<int>& nums2)\n {\n int swap = 0;\n int noswap = 0;\n int currSwap = 0;\n int currNoSwap =0;\n int n = nums1.size();\n \n for(int index = n-1; index >=1; index --)\n {\n for(int swapped = 1; swapped >=0; swapped--)\n {\n int ans = INT_MAX;\n \n int prev1 = nums1[index-1];\n int prev2 = nums2[index-1];\n \n \n //if only one element to swap or swap count ==1 \n if(swapped)\n {\n int temp = prev2;\n prev2 = prev1;\n prev1 = temp;\n }\n \n //Non-Swappped \n if(nums1[index] > prev1 && nums2[index] > prev2)\n {\n ans = noswap;\n }\n \n //swapped\n if(nums1[index] > prev2 && nums2[index] > prev1)\n {\n ans = min(ans, 1 + swap); \n }\n \n if(swapped)\n {\n currSwap = ans; \n }\n else{\n currNoSwap = ans;\n }\n \n }\n swap = currSwap;\n noswap = currNoSwap;\n }\n return min(swap,noswap);\n }``\n```\n\n# UPVOTE IF YOU FIND IT UNDERSTANDABLE****** | 2 | 0 | ['Recursion', 'Memoization', 'C'] | 1 |
minimum-swaps-to-make-sequences-increasing | Detailed Explanation : O(n) Solution using 2 cases for Multisequences DP | Javascript | C++ | detailed-explanation-on-solution-using-2-ys3d | Intuition\nDynamic Programming Approach:\nThe idea is to keep track of two states at each index i: swap[i] and not_swap[i].\n\nswap[i] represents the minimum nu | rbssmtkr | NORMAL | 2023-08-11T04:28:35.796430+00:00 | 2023-08-11T04:29:01.805283+00:00 | 75 | false | # Intuition\n**Dynamic Programming Approach:**\nThe idea is to keep track of two states at each index i: swap[i] and not_swap[i].\n\n`swap[i]` represents the minimum number of swaps required to make `A[0...i]` and `B[0...i]` strictly increasing, considering that you swap elements at index i.\n\n`not_swap[i]` represents the minimum number of swaps required to make `A[0...i]` and `B[0...i]` strictly increasing, considering that you do not swap elements at index i.\n\n\n**Transition Rules:**\n\nIf `A[i-1] < A[i] and B[i-1] < B[i]`, you can keep the same arrangement or swap elements. So, `swap[i] = swap[i-1] + 1 and not_swap[i] = not_swap[i-1]`.\n\nIf `A[i-1] < B[i] and B[i-1] < A[i]`, you can swap at index i or not swap. So, `swap[i] = min(swap[i]`, `not_swap[i-1] + 1)` and n`ot_swap[i] = min(not_swap[i], swap[i-1])`\n\n# Approach\n\nCase 1 : `A[i] > A[i-1] and B[i] > B[i-1]`\n\n`swap[i] = swap[i-1] + 1 `\nif you swapped at i - 1 then swap at i \n\n`not_swap[i] = not_swap[i-1];`\nif you didn\'t swap at i - 1 dont swap here as well\n\n\nCase 2 : `A[i] > B[i-1] and B[i] > A[i-1]`\n\nBoth may not be sorted or one is not sorted in this case\n\nif swapped at [i - 1] index dont swap again otherwise swap here as only one of the 2 swaps are required\n`swap[i] = min( swap[i] , not_swap[i-1] + 1 )`\n\n`not_swap[i] = min( not_swap[i] , swap[i-1] )`\n\nthere can be both possibilities together or singly so its taking a minimum of the possibilities in the process of calculation\n\n# Complexity\n- Time complexity: $$O(N)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(N)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n\n```javascript []\nvar minSwap = function(A, B) {\n\n const N = A.length;\n const swap = new Array(N).fill(1);\n const not_swap = new Array(N).fill(0);\n\n for (let i = 1; i < N; i++) {\n not_swap[i] = swap[i] = N;\n\n if (A[i - 1] < A[i] && B[i - 1] < B[i]) {\n swap[i] = swap[i - 1] + 1;\n not_swap[i] = not_swap[i - 1];\n }\n\n if (A[i - 1] < B[i] && B[i - 1] < A[i]) {\n swap[i] = Math.min(swap[i], not_swap[i - 1] + 1); \n// swapped at [i] th index\n not_swap[i] = Math.min(not_swap[i], swap[i - 1]); \n// swapped at [i - 1] th index\n }\n }\n return Math.min(swap[N - 1], not_swap[N - 1]);\n\n \n};\n```\n```cpp []\nclass Solution {\npublic:\n int minSwap(vector<int>& A, vector<int>& B) {\n\n int N = A.size();\n vector<int> swap(N,1) , not_swap(N,0);\n for( int i = 1 ; i < N ; i++)\n {\n not_swap[i] = swap[i] = N;\n\n if( A[i-1] < A[i] && B[i-1] < B[i] )\n {\n swap[i] = swap[i-1] + 1;\n not_swap[i] = not_swap[i-1];\n }\n\n if( A[i-1] < B[i] && B[i-1] < A[i] )\n {\n swap[i] = min( swap[i] , not_swap[i-1] + 1 ); // swapped at [i] th index\n not_swap[i] = min( not_swap[i] , swap[i-1] ); // swapped at [i - 1] th index\n }\n }\n return min( swap[N-1] , not_swap[N-1] );\n }\n};\n``` | 2 | 0 | ['Array', 'Dynamic Programming', 'C++', 'JavaScript'] | 0 |
minimum-swaps-to-make-sequences-increasing | [Python 3] O(n) Time, O(1) Space, Detailed Explanation | python-3-on-time-o1-space-detailed-expla-a1j8 | Intuition\n Describe your first thoughts on how to solve this problem. \nThere are 3 different cases to consider when looking at the border between two pairs of | KellerWheat | NORMAL | 2023-07-29T23:41:27.528382+00:00 | 2023-07-29T23:43:38.441912+00:00 | 172 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThere are 3 different cases to consider when looking at the border between two pairs of numbers (a pair being numbers in nums1 and nums2 with the same index):\n1. The numbers are increasing, and if either pair was flipped they would still be increasing (ex. nums1 = [1, 3] and nums2 = [2, 4])\n2. The numbers are increasing, but if either pair flipped they would not be increasing (ex. nums1 = [1, 2] and nums2 = [3, 4])\n3. The numbers are not increasing (since there is a guaranteed solution this means that if either pair is flipped they will be increasing, ex. nums1 = [6, 5] and nums2 = [4, 7])\n\nTwo observations that lead to this approach:\n1. In the first case above, these borders can be used to divide the problem into independent subproblems, as the chosen flips of each will not affect the other\n2. Within each subsection, Every boundary between numbers now falls into the second or third case above. As a result, there are only two sets of flips that are valid, and they are mirrors of each other.\n\nIf the second observation is confusing, try drawing out some examples to build intuition. Think of every flippable pair as being "aligned" a certain direction and all pairs needing to be "aligned" the same way for both arrays to be increasing\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThese two observations give us a relatively straightforward solution:\n1. Divide the problem into sections on borders where the arrays are increasing no matter whether the numbers are flipped or not\n2. In each subsection, take a greedy approach and flip any pair of numbers when necessary, counting the number of flips needed to make the subsection strictly increasing.\n3. After making all necessary flips in a subsection, add the count to the total. Note that the exact opposite set of flips would also results in an increasing subsection, so the real count is min(count, length of subsection - count)\n\nThe code below keeps track of each subsection as it goes, allowing the algorithm to be completed in one pass and without any extra memory.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def minSwap(self, nums1: List[int], nums2: List[int]) -> int:\n sectionSwaps = 0\n sectionLength = 1\n minSwaps = 0\n for x in range(0, len(nums1) - 1):\n # If the end of the subsection has been reached,\n # add the minimum number of steps to the total\n if max(nums1[x], nums2[x]) < min(nums1[x + 1], nums2[x + 1]):\n minSwaps += min(sectionSwaps, sectionLength - sectionSwaps)\n sectionLength = 1\n sectionSwaps = 0\n continue\n sectionLength += 1\n # Flip the next pair if it does not align with the current one\n if nums1[x] >= nums1[x + 1] or nums2[x] >= nums2[x + 1]:\n sectionSwaps += 1\n temp = nums1[x + 1]\n nums1[x + 1] = nums2[x + 1]\n nums2[x + 1] = temp\n # The last subsection is not handled in the for loop\n minSwaps += min(sectionSwaps, sectionLength - sectionSwaps)\n return minSwaps\n``` | 2 | 0 | ['Python3'] | 0 |
minimum-swaps-to-make-sequences-increasing | solution using recursion and memoization | solution-using-recursion-and-memoization-d74c | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | uwais67 | NORMAL | 2023-03-02T18:38:37.256941+00:00 | 2023-03-02T18:38:37.257002+00:00 | 257 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\nint solve(int i,int p,vector<int> &nums1,vector<int> &nums2,vector<vector<int>> &dp){\n int n=nums1.size();\n if(i==n) return 0;\n if(dp[i][p]!=-1) return dp[i][p];\n int p1,p2;\n if(i>0&&p==0) {\n p1=nums1[i-1];\n p2=nums2[i-1];\n }\n else if(i>0&&p==1){\n p1=nums2[i-1];\n p2=nums1[i-1];\n }\n if(i!=0){\n if((nums1[i]<=p1||nums2[i]<=p2)&&(nums1[i]<=p2||nums2[i]<=p1)) return INT_MAX-1;\n }\n int sp=INT_MAX;\n int np=INT_MAX;\n if(i==0){\n sp=1+solve(i+1,1,nums1,nums2,dp);\n np=solve(i+1,0,nums1,nums2,dp);\n }\n else{\n if((nums1[i]>p1&&nums2[i]>p2)&&(nums1[i]>p2&&nums2[i]>p1)) {\n sp=1+solve(i+1,1,nums1,nums2,dp);\n np=solve(i+1,0,nums1,nums2,dp);\n }\n else if(nums1[i]<=p1||nums2[i]<=p2)\n sp=1+solve(i+1,1,nums1,nums2,dp);\n else\n np=solve(i+1,0,nums1,nums2,dp);\n }\n return dp[i][p]= min(sp,np);\n}\n int minSwap(vector<int>& nums1, vector<int>& nums2) {\n int n=nums1.size();\n vector<vector<int>> dp(n+1,vector<int>(2,-1));\n return solve(0,0,nums1,nums2,dp);\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
minimum-swaps-to-make-sequences-increasing | C++ dp solution with simple explanation | c-dp-solution-with-simple-explanation-by-7kpg | Intuition\n Describe your first thoughts on how to solve this problem. \nTo find min number of swaps at a particular position, following information at previous | pranabpandey | NORMAL | 2022-10-03T19:33:00.844314+00:00 | 2022-10-03T19:33:00.844347+00:00 | 1,524 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo find min number of swaps at a particular position, following information at previous position is required \n-min swaps if swap at previous position\n-min swaps if no swap at previous position\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFor each position, find minimum number of swaps if current position is swapped, also if current position is not swapped.\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$ (can be easily optimized, since only information about previous position is required)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int minSwap(vector<int>& v1, vector<int>& v2) {\n int n=v1.size();\n int dp[n][2];\n for(int i=0;i<n;i++){dp[i][0]=INT_MAX; dp[i][1]=INT_MAX;}\n dp[0][0]=0;\n dp[0][1]=1;\n int prev1,prev2;\n for(int i=1;i<n;i++){\n //prev position swapped\n prev1=v2[i-1];\n prev2=v1[i-1];\n if(dp[i-1][1]!=INT_MAX){\n //swap at current position\n if(v2[i]>prev1 && v1[i]>prev2){\n dp[i][1]=1+dp[i-1][1];\n }\n //no swap at current position\n if(v1[i]>prev1 && v2[i]>prev2){\n dp[i][0]=dp[i-1][1];\n }\n }\n\n //prev position no swap\n prev1=v1[i-1];\n prev2=v2[i-1];\n if(dp[i-1][0]!=INT_MAX){\n //swap at current position\n if(v2[i]>prev1 && v1[i]>prev2){\n dp[i][1]=min(dp[i][1],1+dp[i-1][0]);\n }\n //no swap at current position\n if(v1[i]>prev1 && v2[i]>prev2){\n dp[i][0]=min(dp[i][0],dp[i-1][0]);\n }\n }\n }\n return min(dp[n-1][0],dp[n-1][1]);\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
minimum-swaps-to-make-sequences-increasing | [C++] Memoization -> Space Optimization, O(1) Space, clean code | c-memoization-space-optimization-o1-spac-tgks | 1. Memoization\n\n\nclass Solution {\nprivate:\n int solve(vector<int> &nums1, vector<int> &nums2, int index, int swapped, vector<vector<int> > &dp){\n | hardikjain40153 | NORMAL | 2022-07-22T11:25:35.753387+00:00 | 2022-07-22T11:25:35.753427+00:00 | 427 | false | ***1. Memoization***\n\n```\nclass Solution {\nprivate:\n int solve(vector<int> &nums1, vector<int> &nums2, int index, int swapped, vector<vector<int> > &dp){\n if(index >= nums1.size()) return 0;\n \n if(dp[index][swapped]!=-1) return dp[index][swapped];\n \n int prev1 = nums1[index-1];\n int prev2 = nums2[index-1];\n int ans = INT_MAX;\n //if elements at last index were swapped then we need to swap our prev1 and prev2, logically.\n if(swapped) swap(prev1, prev2);\n \n //check if swap needed for elements at \'index\'.\n if(nums1[index] > prev1 && nums2[index] > prev2){\n //no need of swap\n ans = min(ans, solve(nums1, nums2, index+1, 0, dp)) ;\n }\n if(nums1[index]>prev2 && nums2[index]>prev1){\n //swap, count +1;\n ans = min(ans, 1+solve(nums1, nums2, index+1, 1, dp));\n }\n \n return dp[index][swapped] = ans;\n }\npublic:\n int minSwap(vector<int>& nums1, vector<int>& nums2) {\n //we put some -1 at the start of each array to make comparison easy.\n nums1.insert(nums1.begin(), -1);\n nums2.insert(nums2.begin(), -1);\n \n //this variable will show if the last index was swapped or not(if swapped 1, else 0);\n int swapped = 0, index = 1;\n vector<vector<int> > dp(nums1.size(), vector<int>(2, -1));\n return solve(nums1, nums2, index, swapped, dp);\n }\n};\n```\n\n***2. Tabulation***\n\n```\nclass Solution {\npublic:\n int minSwap(vector<int>& nums1, vector<int>& nums2) {\n //we put some -1 at the start of each array to make comparison easy.\n int n = nums1.size();\n nums1.insert(nums1.begin(), -1);\n nums2.insert(nums2.begin(), -1);\n\n vector<vector<int> > dp(n+2, vector<int>(2, 0));\n \n for(int index = n; index >= 1; index--){\n for(int swapped = 0; swapped < 2; swapped++){\n int prev1 = nums1[index-1];\n int prev2 = nums2[index-1];\n int ans = INT_MAX;\n //if elements at last index were swapped then we need to swap our prev1 and prev2, logically.\n if(swapped) swap(prev1, prev2);\n\n //check if swap needed for elements at \'index\'.\n if(nums1[index] > prev1 && nums2[index] > prev2){\n //no need of swap\n ans = min(ans, dp[index+1][0]) ;\n }\n if(nums1[index]>prev2 && nums2[index]>prev1){\n //swap, count +1;\n ans = min(ans, 1 + dp[index+1][1]);\n }\n\n dp[index][swapped] = ans;\n }\n }\n return dp[1][0];\n }\n};\n```\n\n***3. Space Optimization, Constant space***\n\n```\nclass Solution {\npublic:\n int minSwap(vector<int>& nums1, vector<int>& nums2) {\n int n = nums1.size(), prev1, prev2, ans;\n \n //we put some -1 at the start of each array to make comparison easy.\n nums1.insert(nums1.begin(), -1);\n nums2.insert(nums2.begin(), -1);\n \n vector<int> next(2, 0), cur(2, 0);\n \n for(int index = n; index >= 1; index--){\n for(int swapped = 0; swapped < 2; swapped++){\n prev1 = nums1[index-1];\n prev2 = nums2[index-1];\n ans = INT_MAX;\n //if elements at last index were swapped then we need to swap our prev1 and prev2, logically.\n if(swapped) swap(prev1, prev2);\n\n //check if swap needed for elements at \'index\'.\n if(nums1[index] > prev1 && nums2[index] > prev2){\n //no need of swap\n ans = min(ans, next[0]) ;\n }\n if(nums1[index]>prev2 && nums2[index]>prev1){\n //swap, count +1;\n ans = min(ans, 1 + next[1]);\n }\n cur[swapped] = ans;\n }\n next = cur;\n }\n return next[0];\n }\n};\n```\n\n*Comment below for any queries.\nUpvote if it helps.* | 2 | 0 | ['Dynamic Programming', 'Recursion', 'Memoization', 'C', 'C++'] | 0 |
minimum-swaps-to-make-sequences-increasing | DP O(n) Solution | Recursion & Memoization | Explained with comments | dp-on-solution-recursion-memoization-exp-oagh | \nclass Solution {\npublic:\n \n int solve(vector<int>& nums1, vector<int>& nums2, vector<vector<int>>& dp, int index, int max1, int max2, bool swap){\n | _vedang_ | NORMAL | 2022-07-09T04:52:30.343009+00:00 | 2022-07-09T04:52:30.343051+00:00 | 397 | false | ```\nclass Solution {\npublic:\n \n int solve(vector<int>& nums1, vector<int>& nums2, vector<vector<int>>& dp, int index, int max1, int max2, bool swap){\n if(index == nums1.size()) return 0;\n if(dp[index][swap] != -1) return dp[index][swap];\n \n if(nums1[index] <= max1 || nums2[index] <= max2) //if current array not strictly increasing, then swapping is the only option\n return dp[index][swap] = 1 + solve(nums1, nums2, dp, index + 1, nums2[index], nums1[index], true);\n \n //if current array is strictly increasing, try swapping and not swapping and choose minimum\n //swap only if the array formed after swapping is then strictly increasing, else assign a very large number to avoid it in minimum\'s calculation\n int Swap = (nums1[index] > max2 && nums2[index] > max1) ? 1 + solve(nums1, nums2, dp, index + 1, nums2[index], nums1[index], true) : 1000000;\n int notSwap = solve(nums1, nums2, dp, index + 1, nums1[index], nums2[index], false);\n \n //return best of swapping and non-swapping options\n return dp[index][swap] = min(Swap, notSwap);\n }\n \n int minSwap(vector<int>& nums1, vector<int>& nums2) {\n vector<vector<int>> dp(nums1.size() + 1, vector<int>(2, -1));\n return min(solve(nums1, nums2, dp, 1, nums1[0], nums2[0], false), 1 + solve(nums1, nums2, dp, 1, nums2[0], nums1[0], true));\n }\n};\n\n``` | 2 | 0 | ['Dynamic Programming', 'C', 'C++'] | 0 |
minimum-swaps-to-make-sequences-increasing | Recursion || C++ | recursion-c-by-leetcode_hard-t889 | \n// We have two choices either swap ith or don\'t swap ith since we want increasing order so if ith is in increasing order then we can choose not to swap and i | LeetCode_Hard | NORMAL | 2022-04-10T15:27:53.697454+00:00 | 2022-04-10T15:27:53.697491+00:00 | 256 | false | ```\n// We have two choices either swap ith or don\'t swap ith since we want increasing order so if ith is in increasing order then we can choose not to swap and if swapping them also result in increasing then we can choose to swap.\n\nclass Solution {\npublic:\n vector<vector<int>>dp;\n int minSwap(vector<int>& nums1, vector<int>& nums2) {\n \n // appending -1 in nums1 and nums2 for convinience instead of appending we can call min(first swapped, first unswapped)\n nums1.insert(nums1.begin(),-1); \n nums2.insert(nums2.begin(),-1);\n \n dp.resize(nums1.size(),vector<int>(2,-1));\n return solve(1,0,nums1,nums2);\n }\n \n int solve(int i,bool swapped,vector<int>&nums1,vector<int>&nums2){\n \n if(i==nums1.size()) return 0;\n if(dp[i][swapped]!=-1) return dp[i][swapped];\n \n int ans=INT_MAX;\n int pre1=nums1[i-1],pre2=nums2[i-1];\n if(swapped){ // if previous one is swapped\n swap(pre1,pre2);\n }\n \n if(nums1[i]>pre1 && nums2[i]>pre2){ // choice 1 we don\'t swap if it is in increasing\n ans=solve(i+1,0,nums1,nums2);\n }\n \n if(nums1[i]>pre2 && nums2[i]>pre1){ // choice 2 we swap if swapping result in increasing order\n ans=min(ans,solve(i+1,1,nums1,nums2)+1);\n }\n \n return dp[i][swapped]=ans;\n \n }\n};\n```\n\n// https://leetcode.com/problems/minimum-swaps-to-make-sequences-increasing/discuss/262241/Recursive-with-memoization-(beats-100.00-): | 2 | 0 | ['Recursion', 'C'] | 0 |
minimum-swaps-to-make-sequences-increasing | Simple Python Top-Down DFS + @cache (12 lines) | simple-python-top-down-dfs-cache-12-line-76ta | dfs(i, a, b) returns the minimum swaps to ensure that a < nums1[i] and b < nums2[i]. If nums1[i] and nums2[i] are already greater than the things that come befo | jaredlwong | NORMAL | 2022-02-18T04:11:10.406530+00:00 | 2022-02-18T04:11:27.773090+00:00 | 265 | false | `dfs(i, a, b)` returns the minimum swaps to ensure that `a < nums1[i]` and `b < nums2[i]`. If `nums1[i]` and `nums2[i]` are already greater than the things that come before we don\'t need to swap, otherwise we have to swap.\n\nIt\'s still O(n)\n\n```\nfrom functools import cache\nclass Solution:\n def minSwap(self, nums1: List[int], nums2: List[int]) -> int:\n @cache\n def dfs(i, a, b):\n if i == len(nums1): return 0\n min_swaps = float(\'inf\')\n if a < nums1[i] and b < nums2[i]:\n min_swaps = min(min_swaps, dfs(i+1, nums1[i], nums2[i]))\n if a < nums2[i] and b < nums1[i]:\n min_swaps = min(min_swaps, 1+dfs(i+1, nums2[i], nums1[i]))\n return min_swaps\n return dfs(0, float(\'-inf\'), float(\'-inf\'))\n``` | 2 | 0 | ['Depth-First Search', 'Python', 'Python3'] | 0 |
minimum-swaps-to-make-sequences-increasing | [Python] Top down DP - Clean & Concise | python-top-down-dp-clean-concise-by-hiep-0g6l | Solution 1: Top down DP\n\nclass Solution:\n def minSwap(self, nums1: List[int], nums2: List[int]) -> int:\n @lru_cache(None)\n def dp(i, isSwa | hiepit | NORMAL | 2021-07-27T12:15:26.033734+00:00 | 2021-07-27T13:03:54.049746+00:00 | 411 | false | **Solution 1: Top down DP**\n```\nclass Solution:\n def minSwap(self, nums1: List[int], nums2: List[int]) -> int:\n @lru_cache(None)\n def dp(i, isSwap):\n if i == len(nums1):\n return 0\n \n cand = []\n if i == 0:\n last1 = last2 = -math.inf\n elif isSwap:\n last1, last2 = nums2[i-1], nums1[i-1]\n else:\n last1, last2 = nums1[i-1], nums2[i-1]\n \n if nums1[i] > last1 and nums2[i] > last2:\n cand.append(dp(i+1, False)) # Case 1: Dont swap\n if nums2[i] > last1 and nums1[i] > last2:\n cand.append(dp(i+1, True) + 1) # Case 2: Swap\n \n return min(cand) if cand else math.inf\n \n return dp(0, False)\n```\nComplexity:\n- Time: `O(4 * N)`, where `N <= 10^5` is length of `nums1` or `nums2`.\n- Space: `O(2 * N)` | 2 | 4 | [] | 1 |
minimum-swaps-to-make-sequences-increasing | C++ & Rust: One Pass Scan Counting Greedy O(N) | c-rust-one-pass-scan-counting-greedy-on-jcumv | The reasining is pretty much the same essentially as most other post. \n1) Let n be the lenth of the arrays and count be the number of swaps of a way to make bo | xiaoping3418 | NORMAL | 2021-06-28T08:42:08.129161+00:00 | 2022-07-16T13:19:47.442604+00:00 | 443 | false | The reasining is pretty much the same essentially as most other post. \n1) Let n be the lenth of the arrays and count be the number of swaps of a way to make both arrays strictly incresing. Alternately, we can make n - count swaps to arcgive the same goal. Therefore, the answer is min(count, n - count).\n2) As matter of fact, above conclusion is not valid if both elements at a position are greater than either elements in front of the position. One nice thing needs to be noticed is that any swap after the position has no impact. Therefore, the partial result we get up current could added to the final solution and the remaining problem could be resolved as if cuttent position is the start position. \n3) Added Rust solution on 07/16/2022 \n~~~\n// Rust Solution\nuse std::mem;\n\nimpl Solution {\n pub fn min_swap(nums1: Vec<i32>, nums2: Vec<i32>) -> i32 {\n let n = nums1.len();\n \n let (mut nums1, mut nums2) = (nums1, nums2);\n let (mut count, mut groupSize, mut ret) = (0, 1, 0);\n \n for i in 1..n {\n if nums1[i - 1].max(nums2[i - 1]) < nums1[i].min(nums2[i]) {\n ret += count.min(groupSize - count);\n count = 0;\n groupSize = 1;\n } else {\n groupSize += 1;\n if nums1[i - 1] <= nums1[i] && nums2[i - 1] <= nums2[i] { continue; }\n \n mem::swap(&mut nums1[i], &mut nums2[i]);\n count += 1;\n\t\t\t\t\n if i == n - 1 { ret += count.min(groupSize - count); } \n }\n }\n \n ret\n }\n}\n\n// C++ Solution\nclass Solution {\npublic:\n int minSwap(vector<int>& nums1, vector<int>& nums2) {\n int n = nums1.size(), count = 0, groupSize = 1, ret = 0;\n for (int i = 1; i < n; ++i) {\n int &a = nums1[i - 1], &b = nums2[i - 1], &c = nums1[i], &d = nums2[i]; \n if (max(a, b) < min(c, d)) {\n ret += min(groupSize - count, count);\n count = 0;\n groupSize = 1;\n } else {\n ++groupSize;\n if (a >= c || b >= d) {\n swap(c, d);\n ++count;\n }\n\t\t\t\tif (i == n - 1) ret += min(count, groupSize - count); \n };\n }\n return ret;\n }\n};\n~~~ | 2 | 0 | ['C', 'Rust'] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.