question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
closest-room
|
Simple sorting approach
|
simple-sorting-approach-by-rahulseethara-g7bk
|
Intuition\nFirst sort both queries and rooms in descending order of room size. Iterate over queries. As you iterate, keep adding rooms that satisfy the query re
|
rahulseetharaman
|
NORMAL
|
2023-08-19T07:30:09.970525+00:00
|
2023-08-19T07:30:09.970583+00:00
| 42 | false |
# Intuition\nFirst sort both queries and rooms in descending order of room size. Iterate over queries. As you iterate, keep adding rooms that satisfy the query requirements to a set. The advantage here is that since we have sorted in descending order, if a room satisfies `query[i]` it will surely satisfy `query[i+1]`, since the bar decreases as we move forward. So we make only a single pass over the `rooms` array. \n\nAfter the rooms satisfying a query have been added, pick out elements from the set, and put the best one for the query into the final answer.\n\n \n# Approach\nSort both arrays in descending order. Traverse query array, and keep populating the set of rooms. Pick out two possibilities. \n\n1. Room number which is closest, but greater than or equal to asked room number. \n2. Room number which is closest, but lesser than asked room number.\n\nConsider both when evaluating final answer.\n\n# Complexity\n- Time complexity:\nO(nlogn)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution {\npublic:\n\n struct sorter {\n bool operator()(vector<int>&a, vector<int>&b){\n if(a[1]==b[1])\n return a[0] > b[0];\n return a[1] > b[1];\n }\n };\n\n vector<int> closestRoom(vector<vector<int>>& rooms, vector<vector<int>>& queries) {\n \n for(int i=0;i<rooms.size();i++){\n rooms[i].push_back(i);\n }\n\n for(int i=0;i<queries.size();i++){\n queries[i].push_back(i);\n }\n \n sort(rooms.begin(), rooms.end(), sorter());\n sort(queries.begin(), queries.end(), sorter());\n\n set<pair<int,int>>s;\n\n int cur=0;\n\n vector<int>ans(queries.size(), -1);\n\n for(int i=0;i<queries.size();i++){\n while(cur < rooms.size()){\n if(rooms[cur][1]>=queries[i][1]){\n int roomId=rooms[cur][0];\n int roomSize=rooms[cur][1];\n s.insert({roomId, roomSize});\n }\n else {\n break;\n }\n cur++;\n }\n auto it=s.lower_bound({queries[i][0], 0});\n if(it!=s.end()){\n ans[queries[i][2]] = it->first; \n }\n if(it!=s.begin()){\n it--;\n \n if(ans[queries[i][2]] == -1){\n ans[queries[i][2]] = it->first;\n }\n else {\n int curRoom = ans[queries[i][2]];\n int askedRoom = queries[i][0];\n int newRoom = it->first;\n if(abs(newRoom-askedRoom) <= abs(curRoom-askedRoom)){\n if(abs(newRoom-askedRoom) == abs(curRoom-askedRoom)){\n ans[queries[i][2]] = min(curRoom, newRoom);\n }\n else {\n ans[queries[i][2]] = newRoom;\n }\n }\n }\n \n }\n }\n return ans;\n\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
closest-room
|
using set and sorting algorithm
|
using-set-and-sorting-algorithm-by-singh-jhf3
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
singhchandankumariit
|
NORMAL
|
2023-08-03T15:52:00.700828+00:00
|
2023-08-03T15:52:00.700856+00:00
| 44 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> closestRoom(vector<vector<int>>& r, vector<vector<int>>& q) {\n vector<pair<int,int>>store,first;\n for(int i=0;i<r.size();i++){\n store.push_back({r[i][1],r[i][0]});\n\n }\n\n for(int i=0;i<q.size();i++){\n first.push_back({q[i][1],i});\n }\n int n1=q.size();\n vector<int>ans(n1,-1);\n\n sort(store.begin(),store.end());\n sort(first.begin(),first.end());\n int j=store.size()-1;\n set<int>st;\n for(int i=q.size()-1;i>=0;i--){\n int val=first[i].first;\n int index=first[i].second;\n int id=q[index][0];\n pair<int,int>p={val,0};\n int l=lower_bound(store.begin(),store.end(),p)-store.begin();\n cout<<index<<" "<<id<<" "<<l<<" ";\n while(j>=l){\n st.insert(store[j].second);\n j-=1;\n }\n if(st.size()==0){\n continue;\n }\n\n auto it=st.lower_bound(id);\n if(it==st.end()){\n it--;\n ans[index]=*it;\n }\n\n else if(it==st.begin()){\n ans[index]=*it;\n }\n else{\n int f=*it;\n it--;\n int s=*it;\n if(abs(s-id)<=(f-id)){\n ans[index]=s;\n }\n else ans[index]=f;\n }\n\n\n }\n\n\n\n\n\n return ans;\n\n\n \n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
closest-room
|
Rust | Ordered Set + Binary Search
|
rust-ordered-set-binary-search-by-soyflo-wjap
|
Code\nrust\nuse std::collections::BTreeSet;\n\nimpl Solution {\n pub fn closest_room(rooms: Vec<Vec<i32>>, queries: Vec<Vec<i32>>) -> Vec<i32> {\n let
|
soyflourbread
|
NORMAL
|
2023-08-01T01:00:16.295115+00:00
|
2023-08-01T01:00:16.295137+00:00
| 45 | false |
# Code\n```rust\nuse std::collections::BTreeSet;\n\nimpl Solution {\n pub fn closest_room(rooms: Vec<Vec<i32>>, queries: Vec<Vec<i32>>) -> Vec<i32> {\n let mut rooms = rooms.into_iter()\n .map(|v| (v[1] as usize, v[0] as usize))\n .collect::<Vec<_>>();\n rooms.sort_unstable();\n\n let mut queries = queries.into_iter()\n .enumerate()\n .map(|(i, v)| ((v[1] as usize, v[0] as usize), i))\n .collect::<Vec<_>>();\n queries.sort_unstable();\n queries.reverse();\n\n let mut ret = vec![None; queries.len()];\n\n let mut set = BTreeSet::new();\n let mut ptr_prev = rooms.len();\n for ((threshold, target), i) in queries {\n let ptr_cur = rooms.partition_point(|&(w, id)| w < threshold);\n for ptr in ptr_cur..ptr_prev {\n let (_, id) = rooms[ptr];\n set.insert(id);\n }\n ptr_prev = ptr_cur;\n\n let bound_l = set.range(..=target).rev().next().cloned();\n let bound_r = set.range(target..).next().cloned();\n\n if bound_l.is_none() || bound_r.is_none() {\n ret[i] = bound_l.or(bound_r);\n continue;\n }\n\n let (bound_l, bound_r) = (bound_l.unwrap(), bound_r.unwrap());\n let _ret = if target - bound_l > bound_r - target {\n bound_r\n } else {\n bound_l\n };\n\n ret[i] = Some(_ret);\n }\n\n ret.into_iter()\n .map(|e| e.map(|val| val as i32).unwrap_or(-1))\n .collect::<Vec<_>>()\n }\n}\n```
| 0 | 0 |
['Binary Search', 'Ordered Set', 'Rust']
| 0 |
closest-room
|
Offline Query processing binary search closest value
|
offline-query-processing-binary-search-c-xpwr
|
\nimport bisect\n\nclass Solution:\n def closestRoom(self, rooms: List[List[int]], queries: List[List[int]]) -> List[int]:\n n = len(rooms)\n q
|
theabbie
|
NORMAL
|
2023-06-28T01:20:55.542005+00:00
|
2023-06-28T01:20:55.542033+00:00
| 40 | false |
```\nimport bisect\n\nclass Solution:\n def closestRoom(self, rooms: List[List[int]], queries: List[List[int]]) -> List[int]:\n n = len(rooms)\n q = len(queries)\n res = [-1] * q\n queries = [[queries[i][0], queries[i][1], i] for i in range(q)]\n queries.sort(key = lambda x: -x[1])\n rooms.sort(key = lambda x: -x[1])\n i = 0\n ids = []\n for p, s, pos in queries:\n while i < n and rooms[i][1] >= s:\n bisect.insort(ids, rooms[i][0])\n i += 1\n j = bisect.bisect_left(ids, p)\n curr = (float(\'inf\'), -1)\n for k in [j - 1, j, j + 1]:\n if 0 <= k < len(ids):\n curr = min(curr, (abs(p - ids[k]), ids[k]))\n res[pos] = curr[1]\n return res\n```\n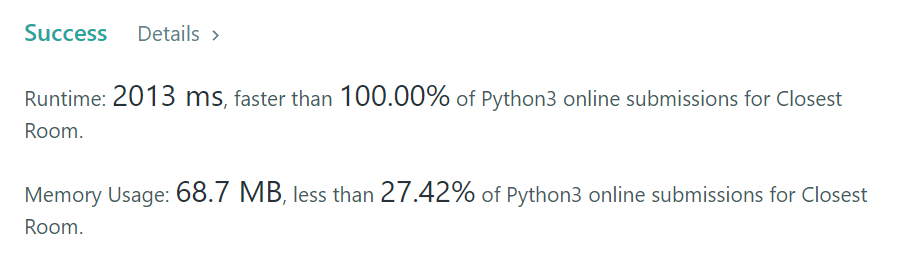
| 0 | 0 |
['Python']
| 0 |
closest-room
|
Simplest Code!!!⚡👌
|
simplest-code-by-yashpadiyar4-j9he
|
\n\n# Code\n\nclass Solution {\npublic:\n static bool comp(vector<int>& a,vector<int>& b){\n return a[1]>b[1];\n }\n vector<int> closestRoom(vec
|
yashpadiyar4
|
NORMAL
|
2023-06-22T06:12:09.648748+00:00
|
2023-06-22T06:12:09.648772+00:00
| 90 | false |
\n\n# Code\n```\nclass Solution {\npublic:\n static bool comp(vector<int>& a,vector<int>& b){\n return a[1]>b[1];\n }\n vector<int> closestRoom(vector<vector<int>>& rooms, vector<vector<int>>& queries) {\n int n=queries.size();\n for(int i=0;i<queries.size();i++)queries[i].push_back(i);\n sort(rooms.begin(),rooms.end(),comp);\n sort(queries.begin(),queries.end(),comp);\n int i=0;\n set<int>st;\n vector<int>ans(n);\n for(auto q:queries){\n int qid=q[0];\n int minsize=q[1];\n int idx=q[2];\n while(i<rooms.size() && rooms[i][1]>=minsize){\n st.insert(rooms[i][0]);\n i++;\n }\n if(st.size()){\n auto it=st.upper_bound(qid);\n int res=INT_MAX;\n int roomid=INT_MAX;\n if(it!=st.end()){\n res=abs(qid-*it);\n roomid=*it;\n }\n else{\n res=INT_MAX;\n roomid=*it;\n }\n if(it!=st.begin()){\n --it;\n if(abs(*it-qid)<=res){\n res=abs(qid-*it);\n roomid=*it;\n }\n }\n ans[idx]=roomid;\n idx++;\n }\n else{\n ans[idx]=-1;\n idx++;\n }\n }\n return ans;\n }\n};\n```
| 0 | 0 |
['Binary Search', 'Sorting', 'C++']
| 0 |
closest-room
|
[python] sorted list (or balanced binary tree)
|
python-sorted-list-or-balanced-binary-tr-2293
|
\nfrom sortedcontainers import SortedList\nclass Solution:\n def closestRoom(self, rooms: List[List[int]], queries: List[List[int]]) -> List[int]:\n q
|
vl4deee11
|
NORMAL
|
2023-05-06T07:38:10.924291+00:00
|
2023-05-06T07:38:10.924326+00:00
| 20 | false |
```\nfrom sortedcontainers import SortedList\nclass Solution:\n def closestRoom(self, rooms: List[List[int]], queries: List[List[int]]) -> List[int]:\n q=sorted([[i,queries[i][0],queries[i][1]] for i in range(len(queries))],key=lambda x:-x[2])\n r=sorted(rooms,key=lambda x:-x[1])\n h=SortedList()\n rr=[-1 for i in q]\n st=0\n for i in range(len(q)):\n while st<len(r) and r[st][1]>=q[i][2]:\n h.add(r[st][0])\n st+=1\n if len(h)==0:continue\n ii=h.bisect_left(q[i][1])\n if ii==-1:continue\n elif ii>=len(h):rr[q[i][0]]=h[len(h)-1]\n elif ii==0:rr[q[i][0]]=h[ii]\n else:\n if abs(h[ii-1]-q[i][1])>abs(h[ii]-q[i][1]):rr[q[i][0]]=h[ii]\n else:rr[q[i][0]]=h[ii-1]\n return rr\n```
| 0 | 0 |
[]
| 0 |
closest-room
|
C++
|
c-by-tinachien-qkux
|
\nclass Solution {\nprivate:\n static bool cmp(vector<int>&a, vector<int>&b){\n return a[1] > b[1] ;\n }\npublic:\n vector<int> closestRoom(vect
|
TinaChien
|
NORMAL
|
2023-05-01T03:56:41.022844+00:00
|
2023-05-01T03:56:41.022872+00:00
| 23 | false |
```\nclass Solution {\nprivate:\n static bool cmp(vector<int>&a, vector<int>&b){\n return a[1] > b[1] ;\n }\npublic:\n vector<int> closestRoom(vector<vector<int>>& rooms, vector<vector<int>>& queries) {\n for(int i = 0; i < queries.size(); i++)\n queries[i].push_back(i) ; //add index\n sort(queries.begin(), queries.end(), cmp) ;\n sort(rooms.begin(), rooms.end(), cmp) ;\n \n vector<int>rets(queries.size()) ;\n set<int>Set ; // size is big enough room\n int idx = 0 ;\n for(auto& q : queries){\n while(idx < rooms.size() && rooms[idx][1] >= q[1]){\n Set.insert(rooms[idx][0]) ;\n idx++ ;\n }\n int ans = -1 ;\n int diff = INT_MAX ;\n auto iter = Set.lower_bound(q[0]) ;\n if(iter != Set.end()){\n ans = *iter ;\n diff = *iter - q[0] ;\n }\n if(iter != Set.begin()){\n iter = prev(iter) ;\n if(q[0] - *iter <= diff)\n ans = *iter ;\n }\n rets[q[2]] = ans ;\n }\n return rets ;\n }\n};\n```
| 0 | 0 |
['Sorting']
| 0 |
closest-room
|
Just a runnable solution
|
just-a-runnable-solution-by-ssrlive-0mt1
|
Code\n\nimpl Solution {\n pub fn closest_room(rooms: Vec<Vec<i32>>, queries: Vec<Vec<i32>>) -> Vec<i32> {\n use std::collections::BTreeSet;\n f
|
ssrlive
|
NORMAL
|
2023-02-23T10:32:28.524340+00:00
|
2023-02-23T10:32:28.524369+00:00
| 38 | false |
# Code\n```\nimpl Solution {\n pub fn closest_room(rooms: Vec<Vec<i32>>, queries: Vec<Vec<i32>>) -> Vec<i32> {\n use std::collections::BTreeSet;\n fn search_closest_room_id(tree_set: &BTreeSet<i32>, preferred_id: i32) -> i32 {\n let floor = tree_set.range(..=preferred_id).next_back();\n let ceiling = tree_set.range(preferred_id..).next();\n let mut ans_abs = i32::MAX;\n let mut ans = -1;\n if let Some(&floor) = floor {\n ans = floor;\n ans_abs = (preferred_id - floor).abs();\n }\n if let Some(&ceiling) = ceiling {\n if ans_abs > (preferred_id - ceiling).abs() {\n ans = ceiling;\n }\n }\n ans\n }\n let mut rooms = rooms;\n rooms.sort_by(|a, b| b[1].cmp(&a[1]));\n let mut indexes = (0..queries.len()).collect::<Vec<_>>();\n indexes.sort_by(|a, b| queries[*b][1].cmp(&queries[*a][1]));\n let mut room_ids_so_far = BTreeSet::new();\n let mut ans = vec![-1; queries.len()];\n let mut i = 0;\n for index in indexes {\n while i < rooms.len() && rooms[i][1] >= queries[index][1] {\n room_ids_so_far.insert(rooms[i][0]);\n i += 1;\n }\n ans[index] = search_closest_room_id(&room_ids_so_far, queries[index][0]);\n }\n ans\n }\n}\n```
| 0 | 0 |
['Rust']
| 0 |
closest-room
|
C++ two pointer solution. exPlained
|
c-two-pointer-solution-explained-by-obos-xl8t
|
Intuition:\nMy first thought when solving this problem was to sort the rooms and queries based on their end times, and then traverse the sorted queries to find
|
Obose
|
NORMAL
|
2023-02-11T03:49:57.003103+00:00
|
2023-02-11T03:49:57.003141+00:00
| 105 | false |
# Intuition:\nMy first thought when solving this problem was to sort the rooms and queries based on their end times, and then traverse the sorted queries to find the closest room.\n\nThe two pointers in this code are `i` and `j`. `i` is pointing to the current index in the `rooms` vector, while `j` is pointing to the current index in the `queries` vector.\n\n# Approach:\nTo solve this problem, I used a two-pointer approach. First, I sorted both the rooms and queries based on their end times so that I could traverse the sorted queries. Then, I used a set to store the start times of the rooms. I used a set because it allows for efficient searching and insertion. \n\nNext, I traversed the sorted queries and for each query, I used the set to find the closest room with a start time that is greater than or equal to the query\'s start time. If a room with the same start time as the query\'s exists, then that room is returned. Otherwise, I used binary search to find the closest room with a start time greater than the query\'s start time. If a room exists, then the closest room (to the query\'s start time) is returned. Otherwise, the query is returned with no room (-1). \n\n# Complexity:\n- Time complexity: O(nlog(n))\n- Space complexity: O(n)\n\n# Code\n```\n#pragma GCC optimize("Ofast","inline","fast-math","unroll-loops","no-stack-protector")\n#pragma GCC target("sse,sse2,sse3,ssse3,sse4,popcnt,abm,mmx,avx,avx2,tune=native","f16c")\nstatic const auto fast = []() {ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0); return 0; } ();\nclass Solution {\npublic:\n vector<int> closestRoom(vector<vector<int>>& rooms, vector<vector<int>>& queries) {\n int n = rooms.size(), m = queries.size();\n vector<int> ans(m);\n vector<vector<int>> q(m, vector<int>(3));\n for (int i = 0; i < m; ++i) {\n q[i][0] = queries[i][0], q[i][1] = queries[i][1], q[i][2] = i;\n }\n sort(rooms.begin(), rooms.end(), [](const auto& a, const auto& b) {\n return a[1] > b[1];\n });\n sort(q.begin(), q.end(), [](const auto& a, const auto& b) {\n return a[1] > b[1];\n });\n set<int> s;\n int i = 0;\n for (int j = 0; j < m; ++j) {\n while (i < n && rooms[i][1] >= q[j][1]) {\n s.insert(rooms[i++][0]);\n }\n auto it = s.lower_bound(q[j][0]);\n if (it != s.end()) {\n if (*it == q[j][0]) {\n ans[q[j][2]] = *it;\n } else if (it != s.begin()) {\n ans[q[j][2]] = abs(*it - q[j][0]) < abs(*prev(it) - q[j][0]) ? *it : *prev(it);\n } else {\n ans[q[j][2]] = *it;\n }\n } else if (it == s.end() && !s.empty()) {\n ans[q[j][2]] = *prev(it);\n } else {\n ans[q[j][2]] = -1;\n }\n }\n return ans;\n }\n};\n```
| 0 | 0 |
['Array', 'Two Pointers', 'Binary Search', 'C++']
| 0 |
closest-room
|
Best Solution Explained
|
best-solution-explained-by-darian-catali-xt0z
|
\n\nclass Solution {\n public int[] closestRoom(int[][] rooms, int[][] queries) {\n int n = rooms.length, k = queries.length;\n Integer[] index
|
darian-catalin-cucer
|
NORMAL
|
2023-02-10T21:23:59.692288+00:00
|
2023-02-10T21:23:59.692317+00:00
| 274 | false |
\n```\nclass Solution {\n public int[] closestRoom(int[][] rooms, int[][] queries) {\n int n = rooms.length, k = queries.length;\n Integer[] indexes = new Integer[k];\n for (int i = 0; i < k; i++) indexes[i] = i;\n Arrays.sort(rooms, (a, b) -> Integer.compare(b[1], a[1])); //Sort by decreasing order of room size\n Arrays.sort(indexes, (a, b) -> Integer.compare(queries[b][1], queries[a][1])); // Sort by decreasing order of query minSize\n TreeSet<Integer> roomIdsSoFar = new TreeSet<>();\n int[] ans = new int[k];\n int i = 0;\n for (int index : indexes) {\n while (i < n && rooms[i][1] >= queries[index][1]) { // Add id of the room which its size >= query minSize\n roomIdsSoFar.add(rooms[i++][0]);\n }\n ans[index] = searchClosetRoomId(roomIdsSoFar, queries[index][0]);\n }\n return ans;\n }\n int searchClosetRoomId(TreeSet<Integer> treeSet, int preferredId) {\n Integer floor = treeSet.floor(preferredId);\n Integer ceiling = treeSet.ceiling(preferredId);\n int ansAbs = Integer.MAX_VALUE, ans = -1;\n if (floor != null) {\n ans = floor;\n ansAbs = Math.abs(preferredId - floor);\n }\n if (ceiling != null && ansAbs > Math.abs(preferredId - ceiling)) {\n ans = ceiling;\n }\n return ans;\n }\n}\n```
| 0 | 0 |
['Python', 'C++', 'Java', 'Go', 'Python3']
| 0 |
closest-room
|
Sorting + Binary Search + Offline Queries
|
sorting-binary-search-offline-queries-by-qya7
|
Complexity\n- Time complexity: O(nlog(n) + klog(k) + k*log(n))\n- Space complexity: O(n)\n\n# Code\n\nclass Solution {\npublic:\n vector<int> closestRoom(vec
|
roboto7o32oo3
|
NORMAL
|
2023-01-09T14:25:56.005919+00:00
|
2023-01-09T14:25:56.005965+00:00
| 155 | false |
# Complexity\n- Time complexity: $$O(n*log(n) + k*log(k) + k*log(n))$$\n- Space complexity: $$O(n)$$\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> closestRoom(vector<vector<int>>& rooms, vector<vector<int>>& queries) {\n // add all the room IDs to a set\n set<int> availableRooms;\n\n for(vector<int>& room : rooms) {\n availableRooms.insert(room[0]);\n }\n\n // sort the rooms in increasing order of size\n sort(rooms.begin(), rooms.end(), [](vector<int>& a, vector<int>& b) {\n return a[1] < b[1];\n });\n\n // add index to each query\n for(int i=0; i<queries.size(); i++) {\n queries[i].push_back(i);\n }\n\n // sort the queries in increasing order of size\n sort(queries.begin(), queries.end(), [](vector<int>& a, vector<int>& b) {\n return a[1] < b[1];\n });\n\n vector<int> answer(queries.size());\n int i = 0;\n\n // now process each query\n for(vector<int>& q : queries) {\n int pref = q[0];\n int minsize = q[1];\n\n // remove the rooms with size less than minsize\n while(i<rooms.size() and rooms[i][1]<minsize) {\n // remove the room from available rooms\n availableRooms.erase(rooms[i][0]);\n i++;\n }\n\n // do lower bound binary search to find the\n // value closest to pref\n set<int> :: iterator it = availableRooms.lower_bound(pref);\n\n int diff = INT_MAX;\n int roomID = -1;\n\n if(it != availableRooms.end()) {\n diff = *it - pref;\n roomID = *it;\n }\n\n if(it != availableRooms.begin()) {\n if(diff >= (pref - *prev(it))) {\n roomID = *prev(it);\n }\n }\n\n answer[q[2]] = roomID;\n }\n\n return answer;\n }\n};\n```
| 0 | 0 |
['Binary Search', 'Sorting', 'C++']
| 0 |
closest-room
|
Java | Sorting and TreeSet | T.C O(K*logN)
|
java-sorting-and-treeset-tc-oklogn-by-ma-lly5
|
Approach - \nInput - rooms = [[1,4],[2,3],[3,5],[4,1],[5,2]], queries = [[2,3],[2,4],[2,5]]\n1. Sort rooms in decreasing order of their room size or index 1 i.e
|
mayank0896
|
NORMAL
|
2022-12-31T11:21:01.602325+00:00
|
2022-12-31T11:21:01.602357+00:00
| 39 | false |
**Approach** - \nInput - rooms = [[1,4],[2,3],[3,5],[4,1],[5,2]], queries = [[2,3],[2,4],[2,5]]\n1. Sort rooms in decreasing order of their room size or index 1 i.e.\n rooms = 0 1 2 3 4 \n [[3,5], [1,4], [2,3], [5,2], [4,1]]\n2. Store indices of queries[] in a new list and sort them on basis of decreasing order of sizes in queries[]\n qIndices = 2 1 0\n which represent [[2,5], [2,4], [2,3]] in queries[]\n3. Create a Treeset which will store the room ids because they are unique. idx is index which present that upto indices idx-1, all the rooms are added in the bst. idx starts from 0. idx runs over rooms[].\n4. Iterate over the qIndices and store values in prefId and size for corresponding index in given queries[].\n 4.1. Now, for each i iterating qIndices. Run a for loop until idx < rooms.length and rooms[idx][0] >= size.\n 4.2. Keep adding rooms[idx][0] in the bst and increment idx by 1.\n5. Now, use floor() and higher() methods of bst and fill result[list.get(i)] accordingly.\n\nT.C is O(K * logN), where K = queries.length and N = rooms.length\nS.C is O(N)\n```\nclass Solution {\n public int[] closestRoom(int[][] rooms, int[][] queries) {\n Arrays.sort(rooms, (a,b)->b[1] - a[1]);\n // System.out.println(Arrays.deepToString(rooms));\n int n = queries.length;\n int[] result = new int[n];\n // qIndices have indices of queries.\n List<Integer> qIndices = new ArrayList<>();\n for(int i = 0; i<n; ++i) qIndices.add(i);\n Collections.sort(qIndices, (i1,i2)->queries[i2][1] - queries[i1][1]);\n // System.out.println(qIndices.toString());\n // bst have room ids simple\n TreeSet<Integer> bst = new TreeSet<>();\n int idx = 0, size, prefId;\n for(int i = 0; i < qIndices.size(); ++i){\n prefId = queries[qIndices.get(i)][0]; size = queries[qIndices.get(i)][1];\n while(idx < rooms.length && rooms[idx][1] >= size){\n bst.add(rooms[idx][0]);\n ++idx;\n }\n Integer floorRoom = bst.floor(prefId); \n Integer higherRoom = bst.higher(prefId);\n if(floorRoom == null && higherRoom == null) result[qIndices.get(i)] = -1;\n else if(floorRoom != null && higherRoom == null) result[qIndices.get(i)] = floorRoom;\n else if(floorRoom == null && higherRoom != null) result[qIndices.get(i)] = higherRoom;\n else if(prefId - floorRoom <= higherRoom - prefId) result[qIndices.get(i)] = floorRoom;\n else result[qIndices.get(i)] = higherRoom; \n // System.out.printf("i:%d, prefId:%d, size:%d, bst:%s, floorRoom:%d, higherRoom:%d, idx:%d\\n", i, prefId, size, bst.toString(),floorRoom, higherRoom, idx);\n }\n return result;\n }\n}\n```
| 0 | 0 |
[]
| 0 |
closest-room
|
[C++] Sort + Binary Search
|
c-sort-binary-search-by-kylewzk-9epx
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
kylewzk
|
NORMAL
|
2022-12-22T14:04:30.688360+00:00
|
2022-12-22T14:04:30.688402+00:00
| 95 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> closestRoom(vector<vector<int>>& R, vector<vector<int>>& Q) {\n unordered_map<int, unordered_set<int>> sz_mp;\n for(auto & r : R) sz_mp[r[1]].insert(r[0]);\n vector<pair<int, unordered_set<int>>> sz;\n for(auto& [s, rm] : sz_mp) sz.push_back({s, rm});\n sort(begin(sz), end(sz), [](auto &a, auto & b) {return a.first > b.first;});\n\n for(int i = 0; i < Q.size(); i++) Q[i].push_back(i);\n sort(begin(Q), end(Q), [](auto &a, auto & b) {return a[1] > b[1];});\n\n vector<int> res(Q.size(), -1);\n set<int> seen;\n for(int i = 0, j = 0; i < Q.size(); i++) {\n auto & q = Q[i];\n int id = -1, diff = INT_MAX;\n while(j < sz.size() && sz[j].first >= q[1]) {\n for(auto k : sz[j].second) seen.insert(k);\n j++;\n }\n\n if(seen.size()) {\n auto it = seen.upper_bound(q[0]);\n int diff = it != seen.end() ? abs(*it-q[0]) : INT_MAX, ans = it != seen.end() ? *it : INT_MAX;\n if(it != seen.begin()) {\n it = prev(it);\n int diff2 = abs(*it-q[0]);\n if(diff2 <= diff) ans = *it;\n }\n res[q[2]] = ans == INT_MAX ? -1 : ans;\n }\n }\n return res;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
closest-room
|
Python - SortedList + BinarySearch Approach ✅
|
python-sortedlist-binarysearch-approach-rek2x
|
Why are we sorting the Queries based on the "MinSize" in Decreasing order? \n\nBecause if you think, if for the query with the biggest value of "minSize", we ca
|
itsarvindhere
|
NORMAL
|
2022-12-12T15:25:11.660696+00:00
|
2022-12-12T15:27:23.105027+00:00
| 85 | false |
Why are we sorting the Queries based on the "MinSize" in Decreasing order? \n\nBecause if you think, if for the query with the biggest value of "minSize", we can create a list of candidate rooms, then that list will be valid for every other query. We may add some more rooms in that for other queries, but the list for previous query will be valid for next one as well.\n\nAnd only from that list itself, we will get any valid roomId for any query. So, the main thing is to construct this list of candidate rooms from which we have to find the one we are looking for.\n\nLet\'s understand it with an example. \n\n\t\trooms = [[1,4],[2,3],[3,5],[4,1],[5,2]]\n\t\tqueries = [[2,3],[2,4],[2,5]]\n\t\t\n\t\tWe will sort "queries" in decreasing order based on "minSize"\n\t\tAnd since the final output list is constructed based on the queries, we also keep the original indices\n\t\t\n\t\tSo, we convert each query to a tuple (minSize, preferred, index)\n\t\t\n\t\tAnd then we sort in decreasing order. So now, queries become - \n\t\t\n\t\tqueries = [(5,2,2), (4,2,1), (3,2,0)]\n\t\t\n\t\tNow, we can create a candidate list where we keep all those rooms that may be the solutions for this query.\n\t\t\n\t\tSuppose, we have the first query (5,2,2)\n\t\t\n\t\tThen here, we have minSize = 5, preferred = 2 and index = 2\n\t\t\n\t\tSo, all those rooms for which size >= 5 are all valid solutions for this query.\n\t\t\n\t\tAnd we only have one room that satisfies this condition -> [[3,5]]\n\t\t\n\t\tNow, to quickly create candidate list, we can sort the rooms in decreasing order based on size as well.\n\t\t\n\t\tSo that as soon as we get to a room that is not valid, we know all rooms after it are not valid as well so we stop.\n\t\t\n\t\tAnd once we have the candidates, all we are looking for is the room with the roomId that is closest to "preferred"\n\t\t\n\t\t\nBecause, abs(id - preferred) will be minimized if "id" is closest to "preferred" value. And that means, we need to Binary search for the "floor" and "ceil" value of "preferred" in candidates list. Because either floor or ceil or both are closest to "preferred". In case of a tie, we can choose the "floor" value.\n\n\n```\nfrom sortedcontainers import SortedList \nclass Solution:\n def closestRoom(self, rooms: List[List[int]], queries: List[List[int]]) -> List[int]:\n \n k = len(queries)\n\n answer = [-1] * k\n \n # Sort the rooms based on their size in Decreasing order\n rooms.sort(key = lambda x: x[1], reverse=True)\n \n # Sort the Queries by the minSize but in decreasing order\n # Because if for the query with biggest minSize value, we can create a Sortedlist of valid rooms\n # That list can then be used for every query that has a smaller of equal minSize\n \n # Also, since the "answer" has elements in same order as queries originally\n # WE do not want to lose track of original indices\n queries = [(query[1], query[0], i) for i,query in enumerate(queries)]\n \n # Now sort based on the MinSize in Decreasing order\n queries.sort(reverse=True)\n \n # List of valid rooms that can be the candidates\n candidates = SortedList()\n \n j = 0\n \n # For each query\n for minSize, preferred, i in queries:\n # Create the candidate list\n while j < len(rooms) and rooms[j][1] >= minSize:\n candidates.add(rooms[j][0])\n j += 1\n \n # Now, among these candidate rooms, we will search for the id that is closest to "preferred"\n # The id closest to "preferred" will be either floor or ceil of "preferred" in the candidates list\n # for that, we will use binary search\n \n # First, let\'s find the floor\n # That is, the biggest id that is <= "preferred"\n start = 0\n end = len(candidates) - 1\n floorIdx = -1\n \n while start <= end:\n mid = start + (end - start) // 2\n \n if candidates[mid] <= preferred:\n floorIdx = mid\n start = mid + 1\n else: end = mid - 1\n \n # Next, let\'s find the ceil\n # That is, the smallest id that is >= "preferred"\n start = 0\n end = len(candidates) - 1\n ceilIdx = -1\n \n while start <= end:\n mid = start + (end - start) // 2\n \n if candidates[mid] >= preferred:\n ceilIdx = mid\n end = mid - 1\n else: start = mid + 1\n \n # If both are -1, then there is no valid room available\n if floorIdx == -1 and ceilIdx == -1: answer[i] = -1\n else: \n diff1 = abs(candidates[floorIdx] - preferred)\n diff2 = abs(candidates[ceilIdx] - preferred)\n \n answer[i] = candidates[floorIdx] if diff1 <= diff2 else candidates[ceilIdx] \n \n return answer\n```
| 0 | 0 |
['Binary Search', 'Binary Tree', 'Python']
| 0 |
closest-room
|
[Java] Sort by roomId, two passes (ascending/descending roomId)
|
java-sort-by-roomid-two-passes-ascending-byd2
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \nTraverse rooms by ascen
|
okrach
|
NORMAL
|
2022-12-07T11:49:13.381238+00:00
|
2022-12-07T11:49:13.381300+00:00
| 114 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTraverse rooms by ascending id maintaining a queue of active queries:\n- add queries as its preferred room is passed\n- prioritize active queries by smallest minSize\n- resolve active queries if the current room is large enough\n\nRepeat in the opposite direction and select better result for each query.\n \n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N_rooms log(N_rooms) + N_queries log(N_queries))\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N_queries)\n# Code\n```\nclass Solution {\n public int[] closestRoom(int[][] rooms, int[][] queries) {\n // all rooms sorted by ascending roomId\n Arrays.sort(rooms,(r1,r2) -> Integer.compare(r1[0],r2[0]));\n int[][] oq = new int[queries.length][3];\n for (int i = 0; i < queries.length; i++) {\n oq[i][0] = i;\n oq[i][1] = queries[i][0];\n oq[i][2] = queries[i][1];\n }\n // active queries sorted by ascending minSize\n PriorityQueue<int[]> aq = new PriorityQueue<int[]>((q1,q2) -> Integer.compare(q1[2],q2[2]));\n\n // all queries sorted by ascending preferred\n Arrays.sort(oq,(q1,q2) -> Integer.compare(q1[1],q2[1]));\n\n int[] ra = new int[queries.length];\n int nq = 0;\n // iterate over rooms by ascending roomId\n for (int i = 0; i < rooms.length; i++) {\n // activate queries if preferred room has been reached (or passed) \n while (nq < oq.length && oq[nq][1] <= rooms[i][0]) {\n aq.add(oq[nq++]);\n }\n // resolve active queries if current room is big enough\n while (!aq.isEmpty() && aq.peek()[2] <= rooms[i][1]) {\n ra[aq.poll()[0]] = i+1;\n }\n }\n\n // repeat going the opposite direction (rooms & queries)\n aq.clear();\n int[] rd = new int[queries.length];\n nq = oq.length-1;\n for (int i = rooms.length-1; i >= 0; i--) {\n while (nq >= 0 && oq[nq][1] >= rooms[i][0]) {\n aq.add(oq[nq--]);\n }\n while (!aq.isEmpty() && aq.peek()[2] <= rooms[i][1]) {\n rd[aq.poll()[0]] = i+1;\n }\n }\n\n // combine results from ascending & descending passes\n for (int i = 0; i < queries.length; i++) {\n if (rd[i] == 0 && ra[i] == 0) {\n ra[i] = -1;\n continue;\n }\n if (rd[i] == 0 ) {\n ra[i] = rooms[ra[i]-1][0];\n continue;\n }\n if (ra[i] == 0) {\n ra[i] = rooms[rd[i]-1][0];\n continue;\n }\n if (rooms[ra[i]-1][0] - queries[i][0] < queries[i][0] - rooms[rd[i]-1][0]) ra[i] = rooms[ra[i]-1][0];\n else ra[i] = rooms[rd[i]-1][0];\n }\n return ra;\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
closest-room
|
C++ | Segment Tree + Binary Search
|
c-segment-tree-binary-search-by-arvinlee-rcrn
|
I though a segment tree approach would be faster but turned out to be not true.\nTime complexity : O(m(logn)^2 + nlogn) - for m queries and n rooms\n\n\nclass
|
arvinleetcode
|
NORMAL
|
2022-10-21T09:22:37.151292+00:00
|
2022-10-21T09:22:37.151342+00:00
| 32 | false |
I though a segment tree approach would be faster but turned out to be not true.\nTime complexity : O(m(logn)^2 + nlogn) - for m queries and n rooms\n\n```\nclass Solution {\npublic:\n vector<int> closestRoom(vector<vector<int>>& rooms, vector<vector<int>>& queries) {\n \n //sort based on index\n sort(rooms.begin(), rooms.end());\n this->rooms = rooms;\n \n int length = rooms.size();\n \n //keep track of repeated queries\n unordered_map<int, unordered_map<int, int>> queries_map;\n \n //map room_id to index and vice versa for making segment tree\n unordered_map<int, int> room_index_id;\n map<int, int> room_id_index;\n for (int index = 0; index < length; index++)\n {\n room_index_id[index] = rooms[index][0];\n room_id_index[rooms[index][0]] = index;\n }\n \n //Construct a segment tree that can return max in a range based on index\n constructTree(0, 0, length - 1);\n \n vector<int> responses;\n \n //repeat for each query\n for(auto& query : queries)\n {\n int room_id = query[0];\n int minSize = query[1];\n \n //check if it is a repeated query\n if (queries_map.find(room_id) != queries_map.end() \n && queries_map[room_id].find(minSize) != queries_map[room_id].end())\n {\n responses.push_back(queries_map[room_id][minSize]);\n continue;\n }\n \n //Binary search on the left and right\n //Finding the right indices to search for\n auto itr = room_id_index.upper_bound(room_id);\n int room_index_right = -1;\n int room_index_left = -1;\n if (itr == room_id_index.end())\n {\n itr = prev(itr);\n room_index_left = itr->second;\n }\n \n room_index_right = itr->second;\n room_index_left = prev(itr)->second;\n \n //find the closes room on the right that meets the size requirement\n int low = room_index_right;\n int high = length - 1;\n int closest_right_index = -1;\n \n if (room_index_right != -1)\n {\n while(low <= high)\n {\n int mid = (low + high) / 2;\n //each getMax takes O(logn) and we do that O(logn) times\n int range_maxSize = getMax(0, 0, length - 1, room_index_right, mid);\n if (range_maxSize >= minSize)\n {\n high = mid - 1;\n closest_right_index = mid;\n }\n else\n {\n low = mid + 1;\n }\n }\n }\n \n //find the closest room on the left that meets the size requirement\n low = 0;\n high = room_index_left;\n int closest_left_index = -1;\n \n while(low <= high)\n {\n int mid = (low + high) / 2;\n //each getMax takes O(logn) and we do that O(logn) times\n int range_maxSize = getMax(0, 0, length - 1, mid, room_index_left);\n if (range_maxSize >= minSize)\n {\n low = mid + 1;\n closest_left_index = mid;\n }\n else\n {\n high = mid - 1;\n }\n }\n \n //find the closes\n //map the indices back to the room_ids and find the closest one\n int closest_left = closest_left_index >= 0 ? room_index_id[closest_left_index] : -1;\n int closest_right = closest_right_index >= 0 ? room_index_id[closest_right_index] : -1;\n int response = -1;\n \n if (closest_left != -1 && closest_right == -1)\n {\n response = closest_left;\n }\n else if (closest_left == -1 && closest_right != -1)\n {\n response = closest_right;\n }\n else\n {\n if (room_id - closest_left <= closest_right - room_id)\n {\n response = closest_left;\n }\n else\n {\n response = closest_right;\n }\n }\n responses.push_back(response);\n queries_map[room_id][minSize] = response;\n }\n return responses;\n }\n \n unordered_map<int, int> node_max;\n vector<vector<int>> rooms;\n \n int constructTree(int node_index, int left, int right)\n {\n if (left == right)\n {\n return node_max[node_index] = rooms[left][1];\n }\n int mid = (left + right) / 2;\n return node_max[node_index] = max(constructTree(node_index * 2 + 1, left, mid), \n constructTree(node_index * 2 + 2, mid + 1, right));\n }\n \n int getMax(int node_index, int node_left, int node_right, int start, int end)\n {\n \n if (start <= node_left && end >= node_right)\n {\n return node_max[node_index];\n }\n if (start > node_right || end < node_left || start > end)\n {\n return -1;\n }\n int mid = (node_left + node_right) / 2;\n return max(getMax(node_index * 2 + 1, node_left, mid, start, end), \n getMax(node_index * 2 + 2, mid + 1, node_right, start, end));\n }\n \n};\n```\n
| 0 | 0 |
[]
| 0 |
closest-room
|
TC:95% BinarySearch Sorting C++
|
tc95-binarysearch-sorting-c-by-sarthakbh-hczs
|
sort the room by size(reverse), and sort queries by size(reverse)\nfor first query, go through all the element in rooms for which room_size >= query_room_size\n
|
sarthakBhandari
|
NORMAL
|
2022-10-08T23:43:11.088099+00:00
|
2022-10-08T23:43:56.884234+00:00
| 121 | false |
sort the room by size(reverse), and sort queries by size(reverse)\nfor first query, go through all the element in rooms for which room_size >= query_room_size\nput all those valid size rooms in a sorted list, but you only put the ids in that sorted list\nthen you can do binary search on the sortedIdList to find the largest <= preferredId or smallest>preferredId\n\n```\nclass Solution {\npublic:\n vector<int> closestRoom(vector<vector<int>>& rooms, vector<vector<int>>& queries) {\n //same room can be chosen as many time as you want\n\n sort(rooms.begin(), rooms.end(), [&](auto& a, auto&b){\n return a[1] > b[1];\n });\n map<pair<int, int>, vector<int>> q_i;\n for (int i = 0; i < queries.size(); i++){\n q_i[pair<int, int>(queries[i][1], queries[i][0])].push_back(i);\n }\n\n int r_i = 0;\n set<int>ids;\n vector<int> ans(queries.size(), -1);\n for(auto curr = q_i.rbegin(); curr != q_i.rend(); curr++){\n int minSize = curr->first.first; int preferredId = curr->first.second;\n\n while (r_i < rooms.size() && rooms[r_i][1] >= minSize){\n ids.insert(rooms[r_i][0]);\n r_i++;\n }\n\n if(ids.size() == 0) continue;\n \n auto closest_id = ids.lower_bound(preferredId);//finds the first id not smaller than preferredId\n int c_ans = 100000000;\n if (closest_id != ids.end()){\n c_ans = *closest_id;\n }\n if (closest_id!=ids.begin()) closest_id--;\n if (preferredId - *closest_id <= c_ans - preferredId){\n c_ans = *closest_id;\n }\n\n for (int q_index: curr->second){\n ans[q_index] = c_ans;\n }\n\n }\n\n return ans;\n }\n};\n```
| 0 | 0 |
['Binary Search', 'Ordered Map', 'Sorting', 'Ordered Set', 'C++']
| 0 |
closest-room
|
Easy C++ Solution
|
easy-c-solution-by-_mrvariable-834q
|
\nclass Solution {\npublic:\n vector<int> closestRoom(vector<vector<int>>& rooms, vector<vector<int>>& queries) {\n int n = rooms.size();\n int
|
_MrVariable
|
NORMAL
|
2022-09-23T04:37:01.826938+00:00
|
2022-09-23T04:37:01.826976+00:00
| 37 | false |
```\nclass Solution {\npublic:\n vector<int> closestRoom(vector<vector<int>>& rooms, vector<vector<int>>& queries) {\n int n = rooms.size();\n int k = queries.size();\n vector<int> res(k, -1);\n for(int i = 0; i < k; i++) {\n queries[i].push_back(i);\n }\n sort(rooms.begin(), rooms.end(), [](vector<int> &a, vector<int> &b){\n return a[1] > b[1];\n });\n sort(queries.begin(), queries.end(), [](vector<int> &a, vector<int> &b){\n return a[1] > b[1];\n });\n set<int> st;\n int i = 0, j = 0;\n while(i <= n) {\n int val = i == n ? INT_MIN : rooms[i][1];\n while(j < k && queries[j][1] > val) {\n int ans = -1;\n int d = INT_MAX;\n int id = queries[j][0];\n auto it = st.upper_bound(id);\n if(it != st.end()) {\n if(d > (*it-id)) {\n ans = *it;\n d = *it-id;\n }\n }\n if(it != st.begin()) {\n it--;\n if(d >= (id-*it)) {\n ans = *it;\n }\n }\n res[queries[j][2]] = ans;\n j++;\n }\n if(i == n) break;\n while(i < n && rooms[i][1] == val) {\n st.insert(rooms[i][0]);\n i++;\n } \n }\n return res;\n }\n};\n```
| 0 | 0 |
['C', 'Sorting', 'Ordered Set']
| 0 |
closest-room
|
Java | BIT ( Fenwick Tree )
|
java-bit-fenwick-tree-by-recepkucek-hc0m
|
\nclass Solution {\n \n private int N;\n private HashMap<Integer, TreeSet<Integer>> tree;\n \n private void update(int rs, int id) {\n rs
|
recepkucek
|
NORMAL
|
2022-08-17T21:04:05.215473+00:00
|
2022-08-17T21:04:05.215519+00:00
| 31 | false |
```\nclass Solution {\n \n private int N;\n private HashMap<Integer, TreeSet<Integer>> tree;\n \n private void update(int rs, int id) {\n rs = N - rs + 1;\n for (;rs <= N; rs += rs & (-rs)){\n tree.put(rs, tree.getOrDefault(rs,new TreeSet<>()));\n tree.get(rs).add(id);\n }\n }\n \n private int query(int rs, int rid) {\n rs = N - rs + 1;\n int res = -1, min_diff = Integer.MAX_VALUE, diff;\n for (; rs > 0; rs -= rs & (-rs)) {\n \n TreeSet<Integer> ts = tree.get(rs);\n if (ts==null || ts.size() == 0){\n continue;\n } \n \n Integer id = ts.ceiling(rid);\n \n if (id != null) {\n diff = id - rid;\n if (diff < min_diff){\n res = id;\n min_diff = diff;\n }else if (diff == min_diff){\n res = Math.min(res, id);\n } \n }\n id = ts.floor(rid);\n if (id != null) {\n \n diff = rid - id;\n if (diff < min_diff){\n res = id;\n min_diff = diff;\n }else if (diff == min_diff){\n res = Math.min(res, id);\n } \n }\n }\n return res;\n }\n public int[] closestRoom(int[][] rooms, int[][] queries) {\n \n tree = new HashMap<>();\n N = 10_000_000;\n for (int[] r : rooms) {\n update(r[1], r[0]);\n }\n \n int[] result = new int[queries.length];\n \n for(int i = 0; i < queries.length; i++){\n result[i] = query(queries[i][1], queries[i][0]);\n }\n \n return result;\n \n }\n}\n```
| 0 | 0 |
[]
| 0 |
closest-room
|
[C++] Segment tree easy to understand
|
c-segment-tree-easy-to-understand-by-cao-xaey
|
This is my code implement segment tree to solve this problem. If you find it helpful, please upvote. Thank you for reading.\n```\nvoid build(vector &seg, vector
|
caobaohoang03
|
NORMAL
|
2022-07-31T12:53:31.091600+00:00
|
2022-07-31T12:53:31.091627+00:00
| 95 | false |
This is my code implement segment tree to solve this problem. If you find it helpful, please upvote. Thank you for reading.\n```\nvoid build(vector<int> &seg, vector<vector<int>> &rooms, int node, int start, int end){\n if(start == end){\n seg[node] = rooms[start][1];\n return;\n }\n int mid = (start+end)/2;\n build(seg, rooms, node*2+1, start, mid);\n build(seg, rooms, node*2+2, mid+1, end);\n seg[node] = max(seg[node*2+1], seg[node*2+2]);\n}\nint get(vector<int> &seg, int node, int start, int end, int left, int right){\n if(start>right || end<left){\n return 0;\n }\n if(left<=start && end<=right){\n return seg[node];\n }\n int mid = (start+end)/2;\n return max(get(seg, node*2+1, start, mid, left, right), get(seg, node*2+2, mid+1, end, left, right));\n}\nclass Solution {\npublic:\n vector<int> closestRoom(vector<vector<int>>& rooms, vector<vector<int>>& queries) {\n sort(rooms.begin(), rooms.end());\n vector<int> sorted_id;\n for(auto room: rooms){\n sorted_id.push_back(room[0]);\n }\n vector<int> seg(4*rooms.size()+5, 0);\n build(seg, rooms, 0, 0, rooms.size()-1);\n vector<int> ans;\n for(auto query: queries){\n auto it = lower_bound(sorted_id.begin(), sorted_id.end(), query[0]);\n int barrier = it - sorted_id.begin();\n int smaller = -1;\n int larger = -1;\n int low = barrier;\n int high = rooms.size()-1;\n while(low<=high){\n int mid = (low+high)/2;\n if(get(seg, 0, 0, rooms.size()-1, barrier, mid) >= query[1]){\n high = mid -1;\n larger = mid;\n }\n else{\n low = mid+1;\n }\n }\n barrier -= 1;\n low = 0;\n high = barrier;\n while(low <= high){\n int mid = (low+high)/2;\n if(get(seg, 0, 0, rooms.size()-1, mid, barrier) >= query[1]){\n low = mid +1;\n smaller = mid;\n }\n else{\n high = mid-1;\n }\n }\n if(smaller == -1 && larger==-1){\n ans.push_back(-1);\n }\n else if(smaller == -1){\n ans.push_back(sorted_id[larger]);\n }\n else if(larger == -1){\n ans.push_back(sorted_id[smaller]);\n }\n else{\n if(abs(query[0]-sorted_id[smaller])<=abs(query[0]-sorted_id[larger])){\n ans.push_back(sorted_id[smaller]);\n }\n else{\n ans.push_back(sorted_id[larger]);\n }\n }\n }\n return ans;\n }\n};
| 0 | 0 |
['Binary Search', 'Tree', 'C']
| 0 |
closest-room
|
simple sorted list
|
simple-sorted-list-by-hongyili-ees7
|
\nfrom sortedcontainers import SortedList\nclass Solution:\n def closestRoom(self, rooms: List[List[int]], queries: List[List[int]]) -> List[int]:\n s
|
hongyili
|
NORMAL
|
2022-07-24T05:06:31.743687+00:00
|
2022-07-24T05:06:31.743731+00:00
| 34 | false |
```\nfrom sortedcontainers import SortedList\nclass Solution:\n def closestRoom(self, rooms: List[List[int]], queries: List[List[int]]) -> List[int]:\n self.q_map = {}\n self.n = len(queries)\n self.big = 10**8+7\n i = self.n-1\n while len(queries) > 0:\n pref, size = queries.pop()\n self.q_map.setdefault(size, [])\n self.q_map[size].append((i, pref))\n i -= 1\n self.qs = list(self.q_map)\n self.qs.sort()\n #print(self.q_map)\n #print(self.qs)\n \n self.my_rm = []\n while len(rooms) > 0:\n rid, s = rooms.pop()\n self.my_rm.append((s, rid))\n self.my_rm.sort()\n #print(self.my_rm)\n \n self.rst = [-1 for i in range(self.n)]\n self.bigger = SortedList()\n while len(self.qs) > 0:\n s = self.qs.pop()\n while len(self.my_rm) > 0 and self.my_rm[-1][0] >= s:\n _, rid = self.my_rm.pop()\n self.bigger.add(rid)\n if len(self.bigger) == 0:\n print(\'wahaha\')\n continue\n for i, pref in self.q_map[s]:\n loc = self.bigger.bisect_left(pref)\n dist = self.big\n p = -1\n if loc > 0 and abs(pref - self.bigger[loc-1]) < dist:\n dist = abs(pref - self.bigger[loc-1])\n assert dist >= 0\n p = self.bigger[loc-1]\n if loc < len(self.bigger) and self.bigger[loc] - pref < dist:\n dist = self.bigger[loc] - pref\n assert dist >= 0\n p = self.bigger[loc]\n self.rst[i] = p\n return self.rst\n```
| 0 | 0 |
[]
| 0 |
closest-room
|
Java TreeSet Solution
|
java-treeset-solution-by-rmfmwlrk12-sa29
|
class Solution {\n\n public int[] closestRoom(int[][] rooms, int[][] queries) {\n\n //rooms sort is room size\n //queries append index (result[
|
rmfmwlrk12
|
NORMAL
|
2022-07-22T12:42:00.597349+00:00
|
2022-07-24T05:37:51.783578+00:00
| 118 | false |
class Solution {\n\n public int[] closestRoom(int[][] rooms, int[][] queries) {\n\n //rooms sort is room size\n //queries append index (result[i])\n //queries sort is room size\n \n int row = queries.length;\n int[] result = new int[queries.length];\n \n Arrays.sort(rooms, (a, b) -> b[1] - a[1]); \n \n int[][] query = new int[row][3];\n for(int i = 0; i < queries.length; i++) {\n query[i][0] = queries[i][0];\n query[i][1] = queries[i][1];\n query[i][2] = i;\n }\n \n //query sort room size\n Arrays.sort(query, (a, b) -> b[1] - a[1]); \n int idx = 0;\n TreeSet<Integer> set = new TreeSet<Integer>();\n \n for(int i = 0; i < query.length; i++) {\n //room size > query room size => after room id check\n while(idx < rooms.length && rooms[idx][1] >= query[i][1]) {\n set.add(rooms[idx++][0]); \n }\n\n //treeMap idx (Binary Search)\n Integer floor = set.floor(query[i][0]);\n Integer ceil = set.ceiling(query[i][0]);\n \n if(floor == null && ceil == null ) result[query[i][2]] = -1; //not index\n \n else if(floor == null) result[query[i][2]] = ceil;\n \n else if(ceil == null) result[query[i][2]] = floor;\n \n else result[query[i][2]] = ceil - query[i][0] >= query[i][0] - floor ? floor : ceil;\n }\n \n return result;\n }\n}
| 0 | 0 |
['Tree', 'Ordered Set', 'Java']
| 0 |
closest-room
|
[Java] | sorting & TreeSet
|
java-sorting-treeset-by-harshit01-hzp9
|
\nclass Solution {\n public int[] closestRoom(int[][] rooms, int[][] queries) {\n Arrays.sort(rooms,(a,b)->a[1]-b[1]);\n \n int[][]Q=new
|
harshit01
|
NORMAL
|
2022-07-20T12:54:38.059265+00:00
|
2022-07-20T12:54:38.059304+00:00
| 17 | false |
```\nclass Solution {\n public int[] closestRoom(int[][] rooms, int[][] queries) {\n Arrays.sort(rooms,(a,b)->a[1]-b[1]);\n \n int[][]Q=new int[queries.length][3];\n int []res=new int[queries.length];\n \n for(int i=0;i<queries.length;i++)\n {\n Q[i][0]=queries[i][0];\n Q[i][1]=queries[i][1];\n Q[i][2]=i;\n }\n Arrays.sort(Q,(a,b)->b[1]-a[1]); //sort according to room size\n TreeSet<Integer>set=new TreeSet<>();\n int h_=rooms.length-1;\n \n \n for(int i=0;i<queries.length;i++){\n int l=0;\n int h=h_;\n \n while(l<=h){\n int mid=(l+h)>>1;\n \n if(rooms[mid][1] < Q[i][1])l=mid+1;\n else\n h=mid-1;\n }\n \n if(l==rooms.length)res[Q[i][2]]=-1;\n else{\n while(h_ >= l){\n set.add(rooms[h_][0]);\n h_--;\n }\n \n Integer floor=set.floor(Q[i][0]); //prefered rooms id\n Integer ceil=set.ceiling(Q[i][0]);\n \n int minf=Integer.MAX_VALUE;\n int id=-1;\n if(floor!=null){\n minf=Math.min(minf,Q[i][0]-floor);\n id=floor;\n }\n if(ceil !=null && minf > ceil-Q[i][0])\n id=ceil;\n \n res[Q[i][2]]=id;\n \n }\n }\n \n return res;\n }\n}\n```
| 0 | 0 |
[]
| 0 |
closest-room
|
Bisection - Least Runtime Solution
|
bisection-least-runtime-solution-by-day_-3q5j
|
\nclass Solution:\n def closestRoom(self, rooms: List[List[int]], queries: List[List[int]]) -> List[int]:\n rooms.sort(key=lambda x: x[1], reverse=Tru
|
Day_Tripper
|
NORMAL
|
2022-07-14T08:00:23.842408+00:00
|
2022-07-14T08:00:23.842456+00:00
| 18 | false |
```\nclass Solution:\n def closestRoom(self, rooms: List[List[int]], queries: List[List[int]]) -> List[int]:\n rooms.sort(key=lambda x: x[1], reverse=True) # Sort by decreasing order of room size\n qArr = [[i, q] for i, q in enumerate(queries)] # Zip queries with their index\n qArr.sort(key=lambda x: x[1][1], reverse=True) # Sort by decreasing order of query minSize\n\n def searchClosestRoomId(preferredId):\n if len(roomIdsSoFar) == 0:\n return -1\n cands = []\n i = bisect_right(roomIdsSoFar, preferredId)\n if i > 0:\n cands.append(roomIdsSoFar[i - 1])\n if i < len(roomIdsSoFar):\n cands.append(roomIdsSoFar[i])\n return min(cands, key=lambda x: abs(x - preferredId))\n\n roomIdsSoFar = [] # Room id is sorted in increasing order\n n, k = len(rooms), len(queries)\n i = 0\n ans = [-1] * k\n for index, (prefferedId, minSize) in qArr:\n while i < n and rooms[i][1] >= minSize:\n bisect.insort(roomIdsSoFar, rooms[i][0]) # Add id of the room which its size >= query minSize\n i += 1\n ans[index] = searchClosestRoomId(prefferedId)\n return ans\n```
| 0 | 0 |
[]
| 0 |
closest-room
|
Python. Faster than 85%. Sorting + SortedList + Binary Search.....
|
python-faster-than-85-sorting-sortedlist-0v6b
|
\nfrom sortedcontainers import SortedList\nclass Solution:\n def closestRoom(self, rooms: List[List[int]], queries: List[List[int]]) -> List[int]:\n q
|
nag007
|
NORMAL
|
2022-06-26T15:49:23.917403+00:00
|
2022-06-26T15:49:23.917453+00:00
| 62 | false |
```\nfrom sortedcontainers import SortedList\nclass Solution:\n def closestRoom(self, rooms: List[List[int]], queries: List[List[int]]) -> List[int]:\n queries=[queries[i]+[i] for i in range(len(queries))]\n queries.sort(key=lambda i:i[1],reverse=True)\n rooms.sort(key=lambda i:i[1],reverse=True)\n res=[-1 for i in range(len(queries))]\n x=SortedList()\n for a,b,c in queries:\n while rooms and rooms[0][1]>=b:\n x.add(rooms.pop(0)[0])\n i=x.bisect_left(a)\n if i<len(x):\n res[c]=x[i]\n if x and i!=0:\n if res[c]==-1 or a-x[i-1]<=x[i]-a:\n res[c]=x[i-1]\n return res\n```
| 0 | 0 |
[]
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
Binary Search (Ignore Threshold)
|
binary-search-ignore-threshold-by-votrub-5kcm
|
Intuition: we can ignore threshold because we only need one edge to connect a node (directly or indirectly) to node zero.ApproachWe build a reversed adjacency l
|
votrubac
|
NORMAL
|
2025-01-12T04:05:00.702938+00:00
|
2025-01-12T04:20:16.265661+00:00
| 4,734 | false |
**Intuition:** we can ignore `threshold` because we only need one edge to connect a node (directly or indirectly) to node zero.
# Approach
We build a reversed adjacency list `ral`. We then run `dfs` from node zero, and count nodes we can reach while limiting weight to `m`.
Then, we binary-search for the smallest weight that allows us to reach all nodes.
# Code
```cpp []
int dfs(int i, int m, vector<vector<pair<int, int>>> &ral, vector<int> &vis) {
int res = vis[i] = 1;
for (auto [j, w] : ral[i])
if (w <= m && !vis[j])
res += dfs(j, m, ral, vis);
return res;
}
int minMaxWeight(int n, vector<vector<int>>& edges, int threshold) {
vector<vector<pair<int, int>>> ral(n);
for (auto &e : edges)
ral[e[1]].push_back({e[0], e[2]});
int l = 1, r = 1000001;
while (l < r) {
int m = (l + r) / 2;
if (vector<int> vis(n); dfs(0, m, ral, vis) == n)
r = m;
else
l = m + 1;
}
return l == 1000001 ? -1 : l;
}
```
| 50 | 0 |
['C++']
| 11 |
minimize-the-maximum-edge-weight-of-graph
|
MST || PRIMS || SIMPLE
|
mst-prims-simple-by-ayush34513-fghe
|
IntuitionThe intution is simple , They want to form a 0 Rooted tree ,
Reverset the edges, use MST algo (I have used prims's algo)
Why MST : the greey approach o
|
Ayush34513
|
NORMAL
|
2025-01-12T04:39:56.510855+00:00
|
2025-01-12T04:39:56.510855+00:00
| 2,018 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The intution is simple , They want to form a 0 Rooted tree ,
Reverset the edges, use MST algo (I have used prims's algo)
Why MST : the greey approach of taking the minimum weight edges will work here too .
The threshold is just a dummy variable , think if any node is unreachble from 0 then return -1 , else it just need one parent to become reachble from 0 , (in original graph this mean only one outgoing edge is needed at most to get 0 ) so why need 2 or k edges
# Approach
<!-- Describe your approach to solving the problem. -->
Just implement prims
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int minMaxWeight(int n, vector<vector<int>>& edges, int threshold) {
int mn=0;
vector<int>vis(n);
vector<vector<vector<int>>>invg(n);
for(auto i:edges){
invg[i[1]].push_back({i[2],i[0]}); // reversing the edges
}
priority_queue<vector<int>,vector<vector<int>>,greater<vector<int>>>pq; // to get lower weight edge first
pq.push({0,0});
while(pq.size()){
auto node=pq.top()[1],w=pq.top()[0];
pq.pop();
if(vis[node])continue;
vis[node]=1;
mn=max(mn,w); // geting the biggest weight edge till now
for(auto i:invg[node]){
if(!vis[i[1]])
pq.push(i);
}
}
for(auto i:vis)if(i==0)return -1; // if any node is just unreachble then return -1
return mn;
}
};
```
| 22 | 0 |
['Greedy', 'Graph', 'Heap (Priority Queue)', 'Minimum Spanning Tree', 'C++']
| 2 |
minimize-the-maximum-edge-weight-of-graph
|
[Python] Binary Search / Prim
|
python-binary-search-by-lee215-kvqa
|
Solution 1: Binary SearchGiven the max weight maxw,
check if we can starting from 0,
reversly reach all node.Binary find the minimum maxw that can reach all nod
|
lee215
|
NORMAL
|
2025-01-12T05:00:01.628273+00:00
|
2025-01-12T15:27:31.030799+00:00
| 2,027 | false |
# **Solution 1: Binary Search**
Given the max weight `maxw`,
`check` if we can starting from `0`,
reversly reach all node.
Binary find the minimum `maxw` that can reach all nodes.
Time `O(mlogw)`
Space `O(m)`
<br>
```py [Python3]
def minMaxWeight(self, n: int, edges: List[List[int]], threshold: int) -> int:
G = [{} for i in range(n)]
for i,j,w in edges:
G[j][i] = min(G[j].get(i, inf), w)
def check(maxw):
bfs = [0]
seen = [1] + [0] * (n - 1)
for i in bfs:
for j in G[i]:
if G[i][j] > maxw: continue
if seen[j] == 1: continue
bfs.append(j)
seen[j] = 1
return all(seen)
res = bisect_left(range(10 ** 6 + 1), 1, key=check)
return res if res <= 10 ** 6 else -1
```
# **Solution 2: Prim**
Time `O(mlogm)`
Space `O(m)`
<br>
```py [Python3]
def minMaxWeight(self, n: int, edges: List[List[int]], threshold: int) -> int:
G = [{} for i in range(n)]
for i,j,w in edges:
G[j][i] = min(G[j].get(i, inf), w)
h = [[0, 0]]
seen = [inf] * n
k = n
while h and k > 0:
d, i = heappop(h)
if seen[i] < inf: continue
k -= 1
seen[i] = d
for j in G[i]:
if seen[j] < inf: continue
heappush(h, [G[i][j], j])
return -1 if k > 0 else max(seen)
```
| 17 | 0 |
['Binary Search', 'Shortest Path', 'Python3']
| 7 |
minimize-the-maximum-edge-weight-of-graph
|
What if we reversed everything? 🤔🤔🤔
|
what-if-we-reversed-everything-by-etian6-gcuk
|
IntuitionInstead of taking the constraint as: “Node 0 must be reachable from all other nodes”Think of it as: “If we reversed all the edges, Node 0 must be able
|
fluffyunicorn1125
|
NORMAL
|
2025-01-12T04:01:06.145011+00:00
|
2025-01-12T04:01:06.145011+00:00
| 1,706 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Instead of taking the constraint as: “Node 0 must be reachable from all other nodes”
Think of it as: “If we reversed all the edges, Node 0 must be able to reach all other nodes”
# Approach
<!-- Describe your approach to solving the problem. -->
Reverse all the edges
Given a certain maximum edge weight, we can filter out the edges with weight greater than this max and do a dfs/bfs on the graph to see if the remaining edges satisfy the new condition we defined
But what about the threshold?
This condition actually doesn’t matter because if it is at all possible for node 0 to be reachable from every other node, then simply picking exactly one edge per node is enough to maintain connectivity
# Code
```
class Solution {
public int minMaxWeight(int n, int[][] edges, int threshold) {
List<List<Integer>> rev = new ArrayList<>(n);
for(int i = 0; i < n; i++) {
rev.add(new ArrayList<>());
}
Set<Integer> weightSet = new HashSet<>();
for(int[] e : edges) {
int u = e[0], v = e[1];
int w = e[2];
rev.get(v).add(u);
weightSet.add(w);
}
if(!can(n, rev)) {
return -1;
}
List<Integer> weights = new ArrayList<>(weightSet);
Collections.sort(weights);
int left = 0;
int right = weights.size() - 1;
int ans = -1;
while(left <= right) {
int mid = (left + right) / 2;
int W = weights.get(mid);
List<List<Integer>> temp = new ArrayList<>(n);
for (int i = 0; i < n; i++) {
temp.add(new ArrayList<>());
}
for (int[] e : edges) {
int u = e[0], v = e[1], w = e[2];
if (w <= W) {
temp.get(v).add(u);
}
}
if(canVisitAll(n, temp)) {
ans = W;
right = mid - 1;
} else {
left = mid + 1;
}
}
return ans;
}
public boolean canVisitAll(int n, List<List<Integer>> revGraph) {
boolean[] visited = new boolean[n];
visited[0] = true;
int count = 1;
Deque<Integer> queue = new ArrayDeque<>();
queue.offer(0);
while(!queue.isEmpty()) {
int cur = queue.poll();
for(int nxt : revGraph.get(cur)) {
if(!visited[nxt]) {
visited[nxt] = true;
count++;
queue.offer(nxt);
}
}
}
return count == n;
}
public boolean can(int n, List<List<Integer>> rev) {
boolean[] visited = new boolean[n];
visited[0] = true;
int count = 1;
Deque<Integer> queue = new ArrayDeque<>();
queue.offer(0);
while(!queue.isEmpty()) {
int cur = queue.poll();
for(int nxt : rev.get(cur)) {
if(!visited[nxt]) {
visited[nxt] = true;
count++;
queue.offer(nxt);
}
}
}
return count == n;
}
}
```
| 12 | 1 |
['Java']
| 5 |
minimize-the-maximum-edge-weight-of-graph
|
Reverse Edges | Simple | Medium to Easy | C++
|
reverse-edges-simple-medium-to-easy-c-by-mbwv
|
Reverse the Edge DirectionsWe start by reversing all the edge directions in the graph.
This way, instead of finding paths from node 0 to all other nodes, we now
|
gavnish_kumar
|
NORMAL
|
2025-01-12T04:06:14.938645+00:00
|
2025-01-16T13:15:32.911984+00:00
| 1,386 | false |
<!-- Describe your first thoughts on how to solve this problem. -->
# Reverse the Edge Directions
We start by reversing all the edge directions in the graph.
This way, instead of finding paths from node 0 to all other nodes, we now need to find paths to node 0 from all other nodes.
**Simplify the Problem**
After reversing, the problem boils down to finding the maximum edge weight on the path leading to node 0 for each node in the graph.
The threshold condition becomes irrelevant because, in this setup, we are effectively reducing the graph so that each node will eventually have at most one outgoing edge.
**Final Answer**
The result is the maximum edge weight among all paths leading to node 0.
If any node cannot reach node 0, it means it's impossible to satisfy the conditions, and we return -1.
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: $$O(E+Vlog(V))$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(E+V)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int minMaxWeight(int n, vector<vector<int>>& edges, int threshold) {
int m= edges.size();
for(int i=0;i<m;i++){
swap(edges[i][0],edges[i][1]);
}
unordered_map<int,vector<pair<int,int>>> adj;
for(auto it: edges){
adj[it[0]].push_back({it[1],it[2]});
}
vector<int> ans(n,INT_MAX);
priority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int>>> pq;
pq.push({0,0});
while(!pq.empty()){
auto t= pq.top();
pq.pop();
if(ans[t.second]<=t.first) continue; // Updated line
ans[t.second]=min(ans[t.second],t.first);
for(auto it: adj[t.second]){
if(ans[it.first]>(t.first+it.second)){
pq.push({max(t.first,it.second),it.first});
}
}
}
int maxi= *max_element(ans.begin(),ans.end());
if(maxi==INT_MAX) return -1;
else return maxi;
}
};
```
| 10 | 3 |
['C++']
| 3 |
minimize-the-maximum-edge-weight-of-graph
|
✅BFS + Binary Search (Very intuitive) | JAVA | Easy Explanation 💎
|
bfs-binary-search-very-intuitive-java-ea-wz8z
|
Hi , Everyone this was intresting question (Out of the box) in weekly
I hope you understand the explanation!Points to think on :
given constraints :
1 <= thresh
|
Orangjustice777
|
NORMAL
|
2025-01-14T13:49:11.067498+00:00
|
2025-01-14T13:49:11.067498+00:00
| 391 | false |
Hi , Everyone this was intresting question (Out of the box) in weekly
I hope you understand the explanation!
# Points to think on :
- given constraints :
1 <= threshold <=n-1
this means that we can remove all the edges from the node
and can keep the only one edge that connects that node to the node 0
right!!
- Rather than DFS from all the nodes to reach to the node 0 we can simply do a BFS from the node 0 and try to reach all the nodes, For this we will be needing to reverse the graph
- We will go super Greedy and try to check whether the least weight edge will satisfy our conditions
- If not then we will increase the weight and again check with it
SO The intuition is that
- We will be storing the min and max weight from the edges given
- Try binary search to get the least weighted edge that will satisfy the conditions
- return the less weighted edge
```
int l = minW ;
int r = maxW ;
while(l <= r){
int mid = l + (r-l)/2 ;
if(isPossible(n , edges , mid)){
ans = mid ;
r = mid-1 ;
}else{
l = mid+1 ;
}
}
```
Now comes how do we check whether the chosen weight satisfies the condtions
```
public boolean isPossible(int n, int[][] edges, int threshold)
```
so we will set a bar 'threshold'
above this all the edges are not counted in the graph or say not included in the graph
the graph we are making will be a reverse graph
```
List<List<Integer>> revGraph = new ArrayList<>();
for(int i = 0 ; i < n ; i++) revGraph.add(new ArrayList<>());
for(int[] edge : edges){
int u = edge[0];
int v = edge[1];
if(edge[2] <= threshold){
revGraph.get(v).add(u);
}
}
```
Implementing BFS from node '0' and checking whther it is possible to reach to all the nodes by checking the count
```
boolean[] visited = new boolean[n];
Queue<Integer> q = new LinkedList<>();
q.offer(0);
visited[0] = true ;
int count = 1 ;
while(!q.isEmpty()){
int curr = q.poll();
for(Integer neighbor : revGraph.get(curr)){
if(visited[neighbor] == false){
visited[neighbor] = true ;
q.add(neighbor);
count++ ;
}
}
}
```
if it comes out to be true that is we are able to reach to all the nodes
then we will try to minimize the weight for more greedy solution
thus using binary search for that
Upvote if the explanation was helpful
Thanks!
# Code
```java []
class Solution {
public int minMaxWeight(int n, int[][] edges, int threshold) {
int minW = Integer.MAX_VALUE ;
int maxW = 0 ;
for(int[] edge : edges){
minW = Math.min(minW , edge[2]);
maxW = Math.max(maxW , edge[2]);
}
int ans = -1 ;
int l = minW ;
int r = maxW ;
while(l <= r){
int mid = l + (r-l)/2 ;
if(isPossible(n , edges , mid)){
ans = mid ;
r = mid-1 ;
}else{
l = mid+1 ;
}
}
return ans ;
}
public boolean isPossible(int n, int[][] edges, int threshold) {
List<List<Integer>> revGraph = new ArrayList<>();
for(int i = 0 ; i < n ; i++) revGraph.add(new ArrayList<>());
for(int[] edge : edges){
int u = edge[0];
int v = edge[1];
if(edge[2] <= threshold){
revGraph.get(v).add(u);
}
}
boolean[] visited = new boolean[n];
Queue<Integer> q = new LinkedList<>();
q.offer(0);
visited[0] = true ;
int count = 1 ;
while(!q.isEmpty()){
int curr = q.poll();
for(Integer neighbor : revGraph.get(curr)){
if(visited[neighbor] == false){
visited[neighbor] = true ;
q.add(neighbor);
count++ ;
}
}
}
return count == n ;
}
}
```
| 7 | 1 |
['Java']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
Binary Search on Answer
|
binary-search-on-answer-by-krishna_118-uie9
|
Binary Search on answer, ignore all edges with edge weight greater than mid.Do a BFS with source node as 0 (so store edges in reverse order), and check if we ca
|
krishna_118
|
NORMAL
|
2025-01-12T04:01:08.005320+00:00
|
2025-03-06T10:34:41.558684+00:00
| 965 | false |
Binary Search on answer, ignore all edges with edge weight greater than mid.
Do a BFS with source node as 0 (so store edges in reverse order), and check if we can visit all nodes by ignoring the edges with weight > mid.
# Code
```cpp []
class Solution {
public:
int minMaxWeight(int n, vector<vector<int>>& edges, int threshold) {
using pii = pair<int, int>;
vector<vector<pii>> g(n);
// a -> b => b -> a
int ans = 0;
for (auto it : edges) {
g[it[1]].push_back({it[0], it[2]});
ans = max(ans, it[2]);
}
auto bfs = [&](int mid) -> bool {
vector<int> vis(n, 0);
queue<int> q;
q.push(0);
vis[0] = 1;
int c = 1;
while (!q.empty()) {
auto u = q.front();
q.pop();
if (c == n) return true;
for (auto v : g[u]) {
if (v.second <= mid and !vis[v.first]) {
vis[v.first] = 1;
c++;
q.push(v.first);
}
}
}
return c == n;
};
if (!bfs(ans)) return -1;
int lo = 0, hi = 1e6 + 1;
while (lo <= hi) {
int mid = (lo + hi) / 2;
if (bfs(mid))
ans = mid, hi = mid - 1;
else
lo = mid + 1;
}
return ans;
}
};
```
| 7 | 0 |
['Binary Search', 'Breadth-First Search', 'C++']
| 2 |
minimize-the-maximum-edge-weight-of-graph
|
C++ BFS w/ Heap/Dijkstra From 0 (Ignore Threshold)
|
aaaa-by-bramar2-4vas
|
Intuition
Threshold doesn't matter since you only need one outgoing edge for each vertex which is the one that leads to Node 0.
Always pick the edge with the mi
|
bramar2
|
NORMAL
|
2025-01-12T03:17:54.329994+00:00
|
2025-01-12T10:18:39.242422+00:00
| 840 | false |
# Intuition
- Threshold doesn't matter since you only need one **outgoing** edge for each vertex which is the one that leads to Node 0.
- Always pick the edge with the minimum weight from the ones already reachable. Initially only 0 can reach 0. You can expand further using BFS with Priority-Queue until all nodes are reachable (if possible).
# Complexity
- Time complexity: $O(E+V*log(V))$ (probably)
- Space complexity: $O(E)$
# Code
```cpp []
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
int minMaxWeight(int n, vector<vector<int>>& edges, int threshold) {
vector<map<int, int>> revAdj(n);
for(auto& edge : edges) {
if(edge[0] != 0) {
if(revAdj[edge[1]].count(edge[0])) {
revAdj[edge[1]][edge[0]] = min(revAdj[edge[1]][edge[0]], edge[2]);
}else {
revAdj[edge[1]][edge[0]] = edge[2];
}
}
}
set<int> reachable {0};
int ans = 0;
// <weight, from, to>
using ar = array<int, 3>;
priority_queue<ar, vector<ar>, greater<>> pq;
for(auto& edge : revAdj[0]) {
pq.push({edge.second, 0, edge.first});
}
while(int(reachable.size()) < n && !pq.empty()) {
auto [w, from, to] = pq.top();
pq.pop();
// already reachable then unnecessary edge to add
if(reachable.count(to)) continue;
reachable.insert(to);
ans = max(ans, w);
for(auto& edge : revAdj[to]) {
if(!reachable.count(edge.first)) {
pq.push({edge.second, to, edge.first});
}
}
}
if(int(reachable.size()) < n) return -1;
return ans;
}
};
```
| 7 | 0 |
['Breadth-First Search', 'C++']
| 1 |
minimize-the-maximum-edge-weight-of-graph
|
Python3 || weighted bin search || T/S: 56% / 22%
|
python3-weighted-bin-search-ts-1079-ms-7-7u4x
|
https://leetcode.com/problems/minimize-the-maximum-edge-weight-of-graph/submissions/1506554505/I could be wrong, but I think that time complexity is O(N ^2 * lo
|
Spaulding_
|
NORMAL
|
2025-01-12T20:02:15.565356+00:00
|
2025-02-11T20:55:54.844717+00:00
| 132 | false |
```python3 []
class Solution:
def minMaxWeight(self, n: int, edges: List[List[int]], threshold: int) -> int:
def dp(mx_wgt: int, end: int, seen: List)-> int:
seen[end] = res = 1
for beg, wgt in graph[end]:
if seen[beg]: continue
if wgt <= mx_wgt:
res+= dp(mx_wgt, beg, seen)
return res
graph = [[] for _ in range(n)]
for beg, end, wgt in edges:
graph[end].append((beg, wgt))
_, _, wgts = zip(*edges)
wgt_lim = max(wgts) + 1
left, rght = 1, wgt_lim
while left < rght:
mid = (left + 2 * rght) // 3
if dp(mid, 0, [0] * n) == n: rght = mid
else: left = mid + 1
return left if left < wgt_lim else -1
```
[https://leetcode.com/problems/minimize-the-maximum-edge-weight-of-graph/submissions/1506554505/](https://leetcode.com/problems/minimize-the-maximum-edge-weight-of-graph/submissions/1506554505/)
I could be wrong, but I think that time complexity is *O*(*N* ^2 * log(*W*)) and space complexity is *O*(*N*^2), in which *N* ~ `n` and *W* ~ `wgt_lim`.
| 6 | 0 |
['Python3']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
Finding Shortest Paths in the Reversed Graph
|
finding-shortest-paths-in-a-reversed-gra-nmza
|
Approach
Reverse the edges and build the adjacency list.
Use BFS starting from node 0, picking the shortest edge at each step.
If all nodes are visited, return
|
iLapras
|
NORMAL
|
2025-01-12T05:21:54.890384+00:00
|
2025-01-12T07:07:14.970004+00:00
| 377 | false |
# Approach
- Reverse the edges and build the adjacency list.
- Use BFS starting from node 0, picking the shortest edge at each step.
- If all nodes are visited, return the maximum edge weight encountered; otherwise, return -1.
# Complexity
- Time complexity:
$$O(E*logN)$$
- Space complexity:
$$O(E+N)$$
# Code
```python3 []
class Solution:
def minMaxWeight(self, n: int, edges: List[List[int]], threshold: int) -> int:
adj = defaultdict(list)
for [a, b, w] in edges:
adj[b].append((a, w))
res = 0
seen = set()
pq = [(0, 0)]
while pq:
w, node = heappop(pq)
if node in seen:
continue
seen.add(node)
res = max(res, w)
for nei, wei in adj[node]:
heappush(pq, (wei, nei))
return res if len(seen) == n else -1
```
| 6 | 0 |
['Breadth-First Search', 'Heap (Priority Queue)', 'Python3']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
ONE LINE python3 solution [TRIVIAL]
|
one-line-python3-solution-trivial-by-saa-8c2n
|
Trivial solution, no explanation neededCode
|
saada7553
|
NORMAL
|
2025-01-12T04:28:28.047104+00:00
|
2025-01-12T04:28:28.047104+00:00
| 453 | false |
Trivial solution, no explanation needed

# Code
```python3 []
class Solution:
def minMaxWeight(self, n: int, edges: List[List[int]], threshold: int) -> int:
return (lambda tup: (lambda res, visited: max(res) if len(visited) == n else -1)(tup[0], tup[1]))((lambda tup: (lambda used, visited, res, q, graph: ([res, visited] + [(None, (lambda weight, a, b, blank:[[visited.update({a, b}), res.update({weight}), used.update({b:used[b] + 1})] + [heapq.heappush(q, (w2, b, n2)) for w2, n2 in graph[b] if (n2 not in visited and used[n2] < threshold)] if b not in visited else None])((lambda x:x[0])(q[0]), (lambda x:x[1])(q[0]), (lambda x:x[2])(q[0]), heapq.heappop(q)))[0] if q else None for i in range(100000)])[0:2])(defaultdict(int), set(), set(), tup[0], tup[1]))((lambda qu, graph: ([qu, graph] + [heapq.heappush(qu, (weight, 0, other_node)) for weight, other_node in graph[0]])[0:2])([], (lambda g: ([g] + [g[b].append((weight, a)) for a, b, weight in edges])[0])(defaultdict(list)))))
```
| 6 | 2 |
['Python3']
| 6 |
minimize-the-maximum-edge-weight-of-graph
|
Dijkstra - Reverse Everything
|
dijkstra-reverse-everything-by-terminato-eiq1
|
IntuitionInstead of ensuring all nodes in the directed graph can reach node 0, reverse the direction of the edges. This transforms the problem into checking whe
|
Terminator_070707
|
NORMAL
|
2025-01-12T04:13:23.163860+00:00
|
2025-01-12T04:13:23.163860+00:00
| 495 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Instead of ensuring all nodes in the directed graph can reach node 0, reverse the direction of the edges. This transforms the problem into checking whether node 0 can reach all other nodes.
# Approach
<!-- Describe your approach to solving the problem. -->
maintain a variable ans to keep the track of max answer so far that you have encountered and for condition of outgoing edges on reversing it becomes incoming edges we can maintain a cnt array to keep track of it and that's it we should we good to go
# Complexity
- Time complexity:
O(ElogE+(E+V)logV)
- Space complexity:
O(E+V)
# Code
```java []
class Solution {
public int minMaxWeight(int n, int[][] e, int th) {
List<int[]> g[] = new ArrayList[n];
for(int i=0;i<n;i++)
g[i]=new ArrayList<>();
int[] cnt = new int[n];
int[] vis = new int[n];
for(int[] ed : e)
{
g[ed[1]].add(new int[]{ed[0],ed[2]});
}
for(int i=0;i<n;i++)
{
g[i].sort(Comparator.comparingInt(a -> a[1]));
}
int ans = 0;
PriorityQueue<int[]> q = new PriorityQueue<>((q1,q2)->(q1[1]-q2[1]));
q.add(new int[]{0,0});
while(q.size() > 0)
{
int[] rem = q.poll();
int node = rem[0];
int wt = rem[1];
if(vis[node] == 1 || cnt[node] >= th)
continue;
++cnt[node];
vis[node] = 1;
ans = Math.max(ans,wt);
for(int i=0;i<g[node].size();i++)
{
int[] nbr = g[node].get(i);
q.add(nbr);
}
}
for(int i=0;i<n;i++)
if(vis[i] == 0)
return -1;
return ans;
}
}
```
| 5 | 0 |
['Java']
| 1 |
minimize-the-maximum-edge-weight-of-graph
|
Fastest Solution in Cpp. (With proper explanation).
|
fastest-solution-in-cpp-with-proper-expl-t4co
|
IntuitionThe problem can be solved using binary search and graph traversal techniques. The key idea is to minimize the maximum edge weight while ensuring all no
|
DevD2905
|
NORMAL
|
2025-01-13T05:16:44.446195+00:00
|
2025-01-13T05:16:44.446195+00:00
| 163 | false |
# Intuition
The problem can be solved using binary search and graph traversal techniques. The key idea is to minimize the maximum edge weight while ensuring all nodes in the graph can reach node 0. To achieve this, we iteratively determine if a candidate maximum edge weight is feasible by verifying reachability using Depth-First Search (DFS) on a reversed graph.
# Approach
->Reversed Graph Construction
->Binary Search on Maximum Edge Weight
->Depth-First Search (DFS)
# Complexity
- Time complexity:
O(E+log(maxWeight)×(V+E))
- Space complexity:
O(V+E)
# Code
```cpp []
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
/*
Function: dfs
- i (int): The current node being visited.
- m (int): The maximum allowed edge weight for traversal.
- ral (vector<vector<pair<int, int>>> &): The reversed adjacency list where ral[j]
contains pairs of (node, weight) representing edges directed towards node 'j'.
- vis (vector<int> &): A vector to keep track of visited nodes.
- int: The total number of nodes reachable from node 'i' without exceeding weight 'm'.
*/
int dfs(int i, int m, vector<vector<pair<int, int>>> &ral, vector<int> &vis) {
int res = vis[i] = 1;
for (auto [j, w] : ral[i])
if (w <= m && !vis[j])
res += dfs(j, m, ral, vis);
return res;
}
/*
Function: minMaxWeight
- n (int): The number of nodes in the graph, labeled from 0 to n-1.
- edges (vector<vector<int>>): A list of edges where each edge is represented as
[Ai, Bi, Wi], indicating a directed edge from node Ai to node Bi with weight Wi.
- threshold (int): (Note: In this implementation, 'threshold' is not utilized.)
- int: The minimized maximum edge weight required for all nodes to reach node '0'.
Returns -1 if such a configuration is not possible.
*/
int minMaxWeight(int n, vector<vector<int>>& edges, int threshold) {
vector<vector<pair<int, int>>> ral(n);
for (auto &e : edges)
ral[e[1]].push_back({e[0], e[2]});
int l = 1, r = 1000001;
while (l < r) {
int m = (l + r) / 2;
vector<int> vis(n, 0);
if (dfs(0, m, ral, vis) == n)
r = m;
else
l = m + 1;
}
return l == 1000001 ? -1 : l;
}
};
```
| 4 | 0 |
['C++']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
Simple and Easy Solution || (Using Only Priority Queue) Beats 99% ✅✅
|
simple-and-easy-solution-using-only-prio-ldlk
|
Code
|
Abhi242
|
NORMAL
|
2025-01-14T09:36:21.454631+00:00
|
2025-01-14T09:36:21.454631+00:00
| 135 | false |
# Code
```cpp []
class Solution {
public:
int minMaxWeight(int n, vector<vector<int>>& edges, int threshold) {
int m=edges.size();
vector<pair<int,int>> adj[n];
for(int i=0;i<m;i++){
adj[edges[i][1]].push_back({edges[i][0],edges[i][2]});
}
vector<int> vis(n,0);
priority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int>>>pq;
for(auto a:adj[0]){
pq.push({a.second,a.first});
}
vis[0]=1;
int ans=INT_MIN;
while(!pq.empty()){
int w=pq.top().first;
int node=pq.top().second;
pq.pop();
if(vis[node]){
continue;
}
vis[node]=1;
ans=max(ans,w);
for(auto a:adj[node]){
if(vis[a.first]==0){
pq.push({a.second,a.first});
}
}
}
for(int i=0;i<n;i++){
if(vis[i]==0){
return -1;
}
}
return ans;
}
};
```
| 3 | 0 |
['Heap (Priority Queue)', 'C++']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
Prims + Dijkstra's || 100% BEATS 🚀 || Threshold Not Needed Explained 🎯
|
prims-dijkstras-100-beats-threshold-not-jzll8
|
Simple Example to Understand Why Threshold is IgnoredExample Input:
Number of nodes: ( n = 4 )
Directed edges and weights:
Threshold:
Graph Representation:Goal
|
shubham6762
|
NORMAL
|
2025-01-12T11:59:38.059317+00:00
|
2025-01-12T11:59:38.059317+00:00
| 252 | false |
### **Simple Example to Understand Why Threshold is Ignored**
---
#### **Example Input:**
- Number of nodes: \( n = 4 \)
- Directed edges and weights:
```
edges = [[1, 0, 2], [2, 0, 1], [3, 2, 3], [3, 0, 4]]
```
- Threshold:
```
threshold = 2
```
#### **Graph Representation:**
```
2
1 ---> 0
1
2 ---> 0
3 4
3 ---> 2 ---> 0
```
---
#### **Goal:**
- Ensure all nodes can reach node \( 0 \).
- Minimize the **maximum edge weight** in the final graph.
- Threshold: Each node can have at most \( \text{threshold} = 2 \) outgoing edges.
---
#### **Key Insight:**
The **threshold condition can be ignored** because:
1. The algorithm naturally minimizes the number of outgoing edges per node while ensuring connectivity.
2. As long as **each node has one valid path to node 0** (either directly or indirectly), the problem is solved:
- For example, in the graph above:
- Node \(1 → 0\) (weight 2) ensures node 1 connects to node 0.
- Node \(2 → 0\) (weight 1) ensures node 2 connects to node 0.
- Node \(3 → 2 → 0\) ensures node 3 connects to node 0.
---
#### **Why Ignoring Threshold is Safe:**
Imagine node \( 3 \) has three outgoing edges: \( 3 → 2 \), \( 3 → 0 \), and \( 3 → 4 \).
- The threshold says it can only have two outgoing edges.
- **Logic:**
- Keep the smallest edge weights that maintain connectivity.
- For example, keeping \( 3 → 2 \) (weight 3) ensures \( 3 \) can still reach \( 0 \) via \( 2 → 0 \).
- Removing other edges (like \( 3 → 0 \)) doesn't break the connectivity requirement.
Thus, explicitly enforcing the threshold is unnecessary because the problem focuses on minimizing the maximum edge weight, which indirectly satisfies the threshold constraint.
---
### **Intuition**
- Focus on connecting all nodes to \( 0 \).
- Prioritize minimizing the maximum edge weight.
- The threshold condition is safely ignored as it doesn't impact the connectivity or weight minimization logic.
---
### **Approach**
1. Use a graph representation (adjacency list) to store edges and weights.
2. Use a priority queue to iteratively pick the smallest weight edges, ensuring all nodes connect to \( 0 \).
3. Track visited nodes to prevent cycles.
4. Return the largest edge weight used in the solution.
---
### **Complexity**
- **Time complexity:** \( O(E \log V) \), where \( E \) is the number of edges, and \( V \) is the number of nodes.
- **Space complexity:** \( O(V + E) \) for the graph and auxiliary data structures.
---
### **Code**
```cpp
class Solution {
public:
int minMaxWeight(int n, vector<vector<int>>& edges, int threshold) {
// Build adjacency list
vector<vector<pair<int, int>>> graph(n);
for (auto &it : edges)
graph[it[1]].emplace_back(it[0], it[2]);
vector<bool> visited(n); // Tracks visited nodes
vector<int> key(n, INT_MAX); // Minimum weights to each node
key[0] = 0; // Start with node 0
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
pq.emplace(0, 0); // {weight, node}
// Process nodes
for (int i = 0; i < n; i++) {
while (!pq.empty() && visited[pq.top().second])
pq.pop();
if (pq.empty()) return -1; // If no valid path, return -1
auto it = pq.top();
pq.pop();
int idx = it.second;
visited[idx] = true;
// Update neighbors
for (auto &nbr : graph[idx]) {
if (!visited[nbr.first] && key[nbr.first] > nbr.second) {
key[nbr.first] = nbr.second;
pq.emplace(nbr.second, nbr.first);
}
}
}
// Return the maximum edge weight in the solution
return *max_element(key.begin(), key.end());
}
};
```
---
| 3 | 0 |
['Greedy', 'Graph', 'Heap (Priority Queue)', 'C++']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
Binary Search with BFS on weights
|
binary-search-with-bfs-on-weights-by-mov-nnwd
|
IntuitionThe problem involves finding the minimum maximum weight such that all nodes in the graph are reachable from node 0 while ensuring that no edge with a w
|
Movazed
|
NORMAL
|
2025-01-12T04:08:08.800329+00:00
|
2025-01-12T04:08:08.800329+00:00
| 136 | false |
# Intuition
The problem involves finding the minimum maximum weight such that all nodes in the graph are reachable from node `0` while ensuring that no edge with a weight greater than the threshold is used. This can be approached by treating the problem as a **binary search** over possible weights and checking connectivity using **Breadth-First Search (BFS)**.
# Approach
1. **Binary Search on Weights**:
- The goal is to find the smallest maximum weight (`mid`) such that all nodes are reachable from node `0` using edges with weights ≤ `mid`.
- Use binary search to iterate over possible weights. The search range is from `0` to the maximum weight in the graph.
2. **Graph Construction**:
- For each candidate weight (`mid`), construct a graph that includes only edges with weights ≤ `mid`.
3. **Connectivity Check**:
- Use BFS to check if all nodes are reachable from node `0` in the constructed graph.
- If all nodes are reachable, update the answer and search for a smaller weight.
- If not, search for a larger weight.
4. **Result**:
- The smallest weight that satisfies the connectivity condition is the answer.
# Complexity
- **Time complexity**: $$O(E \log W)$$, where:
- `E` is the number of edges.
- `W` is the maximum weight in the graph.
- Binary search runs in $$O(\log W)$$, and BFS runs in $$O(V + E)$$ for each candidate weight.
- **Space complexity**: $$O(V + E)$$, for storing the graph and BFS queue.
# Code
```cpp
#include <vector>
#include <queue>
#include <algorithm>
#define ll long long
#define vi vector<int>
#define vvi vector<vector<int>>
#define vll vector<ll>
#define vvll vector<vector<ll>>
#define pb push_back
#define mp make_pair
#define INF 1e18
using namespace std;
class Solution {
public:
int minMaxWeight(int n, vector<vector<int>>& edges, int threshold) {
if (n == 1) {
return 0;
}
ll maxWeight = 0;
for (auto& edge : edges) {
maxWeight = max(maxWeight, (ll)edge[2]);
}
ll low = 0, high = maxWeight, answer = -1;
while (low <= high) {
ll mid = (low + high) / 2;
vvll graph(n);
for (auto& edge : edges) {
if (edge[2] <= mid) {
graph[edge[1]].pb(edge[0]);
}
}
vi visited(n, 0);
queue<int> q;
q.push(0);
visited[0] = 1;
ll count = 1;
while (!q.empty()) {
ll u = q.front();
q.pop();
for (auto& v : graph[u]) {
if (!visited[v]) {
visited[v] = 1;
count++;
q.push(v);
}
}
}
if (count == n) {
answer = mid;
high = mid - 1;
} else {
low = mid + 1;
}
}
return answer;
}
};
| 3 | 0 |
['C++']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
Easy understanding JAVA solution 100% beats solution
|
easy-understanding-java-solution-100-bea-sjvj
|
Complexity
Time complexity: O(nlog(n))
Space complexity: O(n)
Code
|
osoba_mask
|
NORMAL
|
2025-01-12T14:42:11.257756+00:00
|
2025-01-12T14:42:11.257756+00:00
| 109 | false |
# Complexity
- Time complexity: $$O(nlog(n))$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(n)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public boolean possible(int w, int[][] edges, int n){
List<List<Integer>> adj = new ArrayList<>();
int[] visited = new int[n];
for(int i=0;i<n;i++) adj.add(new ArrayList<>());
for(int[] x:edges){
if(x[2] <= w){
adj.get(x[1]).add(x[0]);
}
}
visited[0] = 1;
int count = 1;
Queue<Integer> q = new LinkedList<>();
q.offer(0);
while(!q.isEmpty()){
int cur = q.poll();
for(int x:adj.get(cur)){
if(visited[x] == 0){
visited[x] = 1;
q.offer(x);
count+=1;
}
}
}
return count == n;
}
public int minMaxWeight(int n, int[][] edges, int threshold) {
int min = Integer.MAX_VALUE;
int max = 0;
for(int[] x:edges){
min = Math.min(min,x[2]);
max = Math.max(max,x[2]);
}
int ans = -1;
while(min <= max){
int mid = (min+max)/2;
if(possible(mid,edges,n)){
ans = mid;
max = mid-1;
}else{
min = mid+1;
}
}
return ans;
}
}
```
| 2 | 0 |
['Java']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
Simple Solution
|
simple-solution-by-noobiiitian-vm6u
|
Code
|
noobiiitian
|
NORMAL
|
2025-01-12T10:23:13.817863+00:00
|
2025-01-12T10:23:13.817863+00:00
| 63 | false |
# Code
```cpp []
class Solution {
public:
// Perform DFS to mark reachable nodes under the given weight constraint
void dfs(int node, vector<vector<pair<int, int>>>& adj, vector<bool>& done, int maxValue) {
done[node] = true; // Mark the current node as visited
for (auto& x : adj[node]) {
// Traverse only edges with weight <= maxValue and unvisited nodes
if (x.second <= maxValue && !done[x.first]) {
dfs(x.first, adj, done, maxValue);
}
}
}
// Check if the graph is impossible to connect under any circumstances
bool checkForImpossible(int n, vector<vector<pair<int, int>>>& adj) {
vector<bool> done(n, false); // Track visited nodes
dfs(0, adj, done, 1e6); // Perform DFS with the maximum possible weight
for (int i = 0; i < n; i++) {
if (!done[i]) return true; // If any node is not reachable, return true
}
return false; // All nodes are reachable
}
// Main function to find the minimum maximum weight
int minMaxWeight(int n, vector<vector<int>>& edges, int threshold) {
// Step 1: Build adjacency list for the graph
vector<vector<pair<int, int>>> adj(n);
for (auto& edge : edges) {
adj[edge[1]].push_back({edge[0], edge[2]});
}
// Step 2: Check if the graph is impossible to connect
if (checkForImpossible(n, adj)) return -1;
// Step 3: Binary search over weight range [1, 1e6]
int low = 1, high = 1e6, result = -1;
while (low <= high) {
int mid = low + (high - low) / 2; // Calculate mid-point
vector<bool> done(n, false); // Reset visited nodes for each iteration
dfs(0, adj, done, mid); // Perform DFS with the current max weight
bool reachable = true;
// Check if all nodes are reachable
for (int i = 0; i < n; i++) {
if (!done[i]) {
reachable = false;
break;
}
}
// If reachable, update result and search for a smaller max weight
if (reachable) {
result = mid;
high = mid - 1;
} else {
low = mid + 1; // Otherwise, search for a larger max weight
}
}
return result; // Return the minimum maximum weight
}
};
```
| 2 | 0 |
['C++']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
"Reverse Graph + Priority Queue | 100% Time Complexity Beat | 92% Space Complexity Beat
|
reverse-graph-priority-queue-100-time-co-mh9i
|
IntuitionIntuition is similar to prim's algorithm for minimum spanning tree, reverse the given directed edges so that the question becomes there should be a pa
|
uttejdunga7
|
NORMAL
|
2025-01-12T07:19:55.164386+00:00
|
2025-01-12T07:19:55.164386+00:00
| 139 | false |
# **Intuition**
Intuition is similar to prim's algorithm for minimum spanning tree, reverse the given directed edges so that the question becomes there should be a path from node 0 to every other node , also the outgoing threshold given in question becomes incoming threshold
---
# **Approach**
1. Reverse the edges to convert the problem into checking paths from node `0`.
2. Use an adjacency list to represent the reversed graph.
3. Implement a modified Prim's algorithm using a priority queue:
- Push edges in increasing order of weight.
- Track node visits and degrees to ensure threshold constraints.
- Update the maximum edge weight (`ans`) during traversal.
4. If any node is unreachable, return `-1`. Otherwise, return `ans`.
---
# **Complexity**
- **Time Complexity**:
The time complexity is $$O((m + n) \log n)$$, where:
- $$m$$ is the number of edges, and $$n$$ is the number of nodes.
- Traversing the adjacency list takes $$O(m)$$.
- Priority queue operations (insertion and extraction) take $$O(\log n)$$ for each of the $$n$$ nodes.
- **Space Complexity**:
The space complexity is $$O(m + n)$$, as we store the adjacency list, visited array, and degree array.
---
# Code
```cpp []
class Solution {
public:
int minMaxWeight(int n, vector<vector<int>>& edges, int threshold) {
// let's try prims , long time no see
vector<vector< pair<int , int> > > adj(n);
int m = edges.size();
for(int i = 0 ; i < m ; i++){
// adj[edges[i][0]].push_back({edges[i][1] , edges[i][2]});
adj[edges[i][1]].push_back({edges[i][0] , edges[i][2]});
}
vector<int> deg(n , 0);
vector<int> vis(n , 0);
int ans = 0;
priority_queue< pair<int , int> , vector< pair<int , int> > , greater< pair<int , int> > > pq;
pq.push({0 , 0});
while(!pq.empty()){
auto it = pq.top();
pq.pop();
int node = it.second;
int edgewt = it.first;
if(vis[node])continue;
if(deg[node] < threshold){
deg[node]++;
ans = max(ans , edgewt);
vis[node] = 1;
}
else continue;
for(auto [adjnode , wt] : adj[node]){
if(vis[adjnode] == 0)
pq.push({wt ,adjnode });
}
}
for(int i = 0 ; i < n ; i++){
if(vis[i] == 0){
return -1;
}
}
return ans;
}
};
```
| 2 | 0 |
['Heap (Priority Queue)', 'Minimum Spanning Tree', 'C++']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
[C++|Java|JavaScrip|Python3] Dijkstra algo
|
python3-dijkstra-algo-by-ye15-gdax
|
IntuitionThis problem can be solved by Dijkstra's algorithm. We can build a graph of reversed direction. Namely, if there is an edge from u to v in the original
|
ye15
|
NORMAL
|
2025-01-12T06:15:13.688262+00:00
|
2025-01-13T04:09:12.524169+00:00
| 157 | false |
# Intuition
This problem can be solved by Dijkstra's algorithm. We can build a graph of reversed direction. Namely, if there is an edge from `u` to `v` in the original graph. In the reversed graph, the edges is from `v` to `u`.
Then, we travese the graph from `0` in the reversed graph with a priority queue. By the time when all nodes are traversed, the max weight seen gives the answer.
# Approach
Here, `threshold` is irrelevant. Imagine that if all nodes can reach `0` in the original graph, then one out-going edge for each node is enough. We can simply assuming that we are giving up the previously seen smaller weight edge while trying the one with larger weights.
# Complexity
- Time complexity: `O(ElogV)`
- Space complexity: `O(V)`
# Code
```C++ []
class Solution {
public:
int minMaxWeight(int n, vector<vector<int>>& edges, int threshold) {
vector<unordered_map<int, int>> graph(n);
for (auto& e : edges) {
int u = e[0], v = e[1], w = e[2];
if (graph[v].contains(u)) graph[v][u] = min(graph[v][u], w);
else graph[v][u] = w;
}
int ans = 0;
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> pq;
pq.emplace(0, 0);
vector<int> dist(n, INT_MAX);
dist[0] = 0;
unordered_set<int> seen;
while (pq.size()) {
auto [x, v] = pq.top(); pq.pop();
seen.insert(v);
if (seen.size() == n) return x;
if (dist[v] == x) {
for (auto& [u, w] : graph[v]) {
if (max(x, w) < dist[u]) {
pq.emplace(max(x, w), u);
dist[u] = max(x, w);
}
}
}
}
return -1;
}
};
```
```Java []
class Solution {
public int minMaxWeight(int n, int[][] edges, int threshold) {
Map<Integer, Integer>[] graph = new Map[n];
for (int i = 0; i < n; ++i)
graph[i] = new HashMap<>();
for (var e : edges) {
int u = e[0], v = e[1], w = e[2];
graph[v].put(u, Math.min(graph[v].getOrDefault(u, Integer.MAX_VALUE), w));
}
int ans = 0;
Queue<int[]> pq = new PriorityQueue<>((x, y) -> Integer.compare(x[0], y[0]));
pq.add(new int[]{0, 0});
int[] dist = new int[n];
Arrays.fill(dist, Integer.MAX_VALUE);
dist[0] = 0;
Set<Integer> seen = new HashSet<>();
while (!pq.isEmpty()) {
var elem = pq.poll();
int x = elem[0], v = elem[1];
seen.add(v);
if (seen.size() == n) return x;
if (dist[v] == x) {
for (var u : graph[v].keySet()) {
int w = graph[v].get(u);
if (Math.max(x, w) < dist[u]) {
pq.add(new int[]{Math.max(x, w), u});
dist[u] = Math.max(x, w);
}
}
}
}
return -1;
}
}
```
```JavaScript []
var minMaxWeight = function(n, edges, threshold) {
const graph = Array(n).fill(0).map(() => new Map());
for (const [u, v, w] of edges)
graph[v].set(u, Math.min(graph[v].get(u) ?? Infinity, w));
let ans = 0;
const pq = new PriorityQueue({ compare : (x, y) => x[0] - y[0] }); pq.enqueue([0, 0]);
const dist = Array(n).fill(Infinity); dist[0] = 0;
const seen = new Set();
while (pq.size()) {
const [x, v] = pq.dequeue();
seen.add(v);
if (seen.size == n) return x;
if (dist[v] == x) {
for (const [u, w] of graph[v])
if (Math.max(x, w) < dist[u]) {
pq.enqueue([Math.max(x, w), u]);
dist[u] = Math.max(x, w);
}
}
}
return -1;
};
```
```python3 []
class Solution:
def minMaxWeight(self, n: int, edges: List[List[int]], threshold: int) -> int:
graph = [defaultdict(lambda : inf) for _ in range(n)]
for u, v, w in edges:
graph[v][u] = min(graph[v][u], w)
ans = 0
pq = [(0, 0)]
dist = defaultdict(lambda : inf, {0 : 0})
seen = set()
while pq:
x, v = heappop(pq)
seen.add(v)
if len(seen) == n: return x
if dist[v] == x:
for u, w in graph[v].items():
if max(x, w) < dist[u]:
heappush(pq, (max(x, w), u))
dist[u] = max(x, w)
return -1
```
| 2 | 0 |
['C++', 'Java', 'Python3', 'JavaScript']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
Reason to reverse graph || How to approach the problem
|
reason-to-reverse-graph-how-to-approach-o5n57
|
IntuitionThe question asks us
To check if from all nodes i can reach zero or not.
Each node has at most threshold outgoing edges.
Minimize the maximum edge weig
|
Ayush-Rawat
|
NORMAL
|
2025-01-12T06:09:28.099668+00:00
|
2025-01-12T06:10:41.042546+00:00
| 133 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The question asks us
1. To check if from all nodes i can reach zero or not.
2. Each node has at most threshold outgoing edges.
3. Minimize the maximum edge weight in the resulting graph
Problem wants us to form a new graph and see if we can reach the node zero and we should try to use only light weights.
# Approach
<!-- Describe your approach to solving the problem. -->
**Weight Part**
Lets first focus on weight part only and use pen paper right.
What if I tell you that my answer for this particular graph is ans_w than it means that all edges that i use has weight less than or equal to ans_w. `w_i <= ans_w`.
Why not i try for all values of w `1<=w<=10^6`. And see if w can be my answer or not.
Suppose we have a blackbox where I pass a weight and it returns true if w can be ans_w or not.
**Example**
For w=1 => blackbox returns `false`
For w=2 => blackbox returns `false`
For w=3 => blackbox returns `false`
For w=4 => blackbox returns `false`
For w=5 => blackbox returns `false`
For w=6 => blackbox returns `true`
For w=7 => blackbox returns `true`
For w=8 => blackbox returns `true`
... for futher weights it will true.
**But Why?**
If we assume that we can form a graph such that from all nodes i can reach node 0 and maximum weight is 6.
Then for all w > 6 blackbox returns true.
Cause blackbox checks if from all nodes i can reach node 0 and i only use weight less then the weight passed to this blackbox.
So we have something like this. Lets try to see it on number line
```
false false false false false true true true
1 2 3 4 5 6 7 8
```
# Binary Search
So here one half returns true and other half returns false.
That is
1. if for a particular weight `w_i` blackbox returns false then for all the weights less then `w_i` blackbox will return false.
2. if for a particular weight `w_j` blackbox returns true then for all the weights greater then `w_j` blackbox will return true.
So here we can use binary search as for a particular weight we will either move to left or right.
# Reverse graph
If from all nodes i check if i can reach the node 0 then it will be too slow and will end up take quadratic time. We have to solve it in linear time.
Instead of checking if i can reach node 0 from all others node. Why not check if i can reach other nodes from node 0. This will take linear time $$O(V+E)$$.
First invert the graph that is
we have been given `edges[i] = [Ai, Bi, Wi]` indicates that there is an edge going from node Ai to node Bi with weight Wi.
But we will connect it the other way round that is Bi -> Ai with weight Wi.
And now we can simply use DFS or BFS.
So here i have used BFS and this function is actually my blackbox.
# Ignore threshold
We will just include one outgoing from my node that result in minimum answer. Suppose from 1 i can reach 0. then i can reach 0 from node 2 either using the edge that connect it to 1 or by directly going to node 0. Whichever result in minimum we will use that. We just have to reach zero. Either directly or indirectly it doesn't matter. Hence we can ignore threshold.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
$$O((v+E)log(w))$$
Here V = number of nodes, E = number of edges, W = maximum weight
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
$$O(V)$$
Even if we have considered to use the maximum weight in the graph, we cannot satisfy the condition then we will simply return zero.
# Code
```python3 []
class Solution:
def minMaxWeight(self, n: int, edges: List[List[int]], threshold: int) -> int:
# reverse graph -> invert the edges
# check if it is possible to reach all nodes from zero
max_w=0 # maximum weight
graph=[list() for _ in range(n)]
for u,v,w in edges:
graph[v].append((u,w))
max_w=max(max_w,w)
def bfs(k):
# blackbox
vis=set()
q=deque([0])
vis.add(0)
while q:
u=q.popleft()
for v,w in graph[u]:
if w<=k and v not in vis:
q.append(v)
vis.add(v)
return len(vis) == n
low,high,ans=1,max_w,-1
while low<=high:
mid=(low+high)//2
if bfs(mid):
ans=mid
high=mid-1
else:
low=mid+1
return ans
```
| 2 | 0 |
['Binary Search', 'Greedy', 'Depth-First Search', 'Breadth-First Search', 'Graph', 'Shortest Path', 'Minimum Spanning Tree', 'Python3']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
Simple Solution || Beats 100% in both Time and Space || O(E logV) Time
|
simple-solution-beats-100-in-both-time-a-je37
|
IntuitionWe will reverse the graph first, and then we just need to find min weight to reach every node starting from 0. If we can't reach every node, return -1.
|
Rahul_Gupta07
|
NORMAL
|
2025-01-12T04:27:14.109854+00:00
|
2025-01-12T04:27:14.109854+00:00
| 67 | false |
# Intuition
We will reverse the graph first, and then we just need to find min weight to reach every node starting from 0. If we can't reach every node, return -1. Else, the max weight we encountered so far.
# Approach
We can use a min heap to store min weight to reach every node, starting from 0 we will push (0,0) in our heap and then move on to adjacent nodes using BFS.
When we take the top element of our min heap, we are ensured that the top node cannot be reached from a edge having a weight < currentWeight.
Hence, this approach works.
# Complexity
- Time complexity: O(E logV) due to BFS using priority queue.
- Space complexity: O(V + E) due to visited array and priority queue.
# Code
```cpp []
class Solution {
public:
int minMaxWeight(int n, vector<vector<int>>& edges, int threshold) {
vector<pair<int,int>>* revAdj = new vector<pair<int,int>>[n]; // v, wt
for (auto &e : edges) {
int u = e[0], v = e[1], wt = e[2];
revAdj[v].push_back({u, wt});
}
priority_queue<pair<int,int>, vector<pair<int,int>>, greater<pair<int,int>>> pq; // minWtToReach, node
vector<int> vis(n, 0);
pq.push({0, 0});
int mxwt = 0;
while (!pq.empty()) {
auto [weight, node] = pq.top();
pq.pop();
// "weight" is the minimum weight which can be used to reach "node" from 0
if (vis[node])
continue;
vis[node] = 1;
mxwt = max(mxwt, weight);
for (auto& [adjNode, wt] : revAdj[node]) {
if (!vis[adjNode]) {
pq.push({wt, adjNode});
}
}
}
// check if all nodes are visited, n 1's mean all nodes are visited
int cnt = accumulate(vis.begin(), vis.end(), 0);
return ((cnt == n) ? mxwt : -1);
}
};
```
| 2 | 0 |
['Breadth-First Search', 'Graph', 'Heap (Priority Queue)', 'C++']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
C++ | Binary Search
|
c-binary-search-ignoring-threshold-by-ah-38c2
|
Code
|
AhmedSayed1
|
NORMAL
|
2025-01-12T04:25:12.284129+00:00
|
2025-01-12T05:34:59.559544+00:00
| 178 | false |
# Code
```cpp []
vector<pair<int,int>>adj[(int) 1e5];
vector<bool>vis;
int dfs(int node, int m){
vis[node] = 1;
int ret = 1;
for(auto [a,b] : adj[node])
if(!vis[a] && b <= m)ret += dfs(a, m);
return ret;
}
class Solution {
public:
int minMaxWeight(int n, vector<vector<int>>& edges, int threshold) {
for(int i = 0; i < n; i++)adj[i].clear();
for(auto i : edges)
adj[i[1]].push_back({i[0], i[2]});
int l = 1 ,r = 1e6, m;
while(l <= r){
m = (l + r) >> 1;
vis = vector<bool>(n);
(dfs(0, m) != n ? l = m + 1 : r = m - 1);
}
return (l == 1e6 + 1 ? -1 : l);
}
};
```
| 2 | 0 |
['Depth-First Search', 'C++']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
Simple Python solution
|
simple-python-solution-by-baaqar-007-3m54
|
IntuitionTo solve this problem, we need to remove some edges to ensure all nodes can still reach node 0 while keeping outgoing edges within the allowed limit (t
|
Baaqar-007
|
NORMAL
|
2025-01-12T04:15:05.030174+00:00
|
2025-01-12T04:15:05.030174+00:00
| 150 | false |
# Intuition
To solve this problem, we need to remove some edges to ensure all nodes can still reach node 0 while keeping outgoing edges within the allowed limit (`threshold`). At the same time, we aim to minimize the weight of the largest edge in the graph.
---
# Approach
1. **Sort the edges by weight**: This allows us to control the maximum edge weight we include in the graph.
2. **Binary Search**: Use binary search on the maximum edge weight to find the smallest value that satisfies all conditions.
3. **Graph Validation**: For each candidate maximum weight:
- Build the graph with only edges below the current weight.
- Check if node 0 is reachable from all other nodes using BFS.
- Ensure that each node has at most `threshold` outgoing edges by keeping only the smallest ones.
---
# Complexity
- **Time complexity**:
- Building and checking the graph for connectivity and edge limits takes $O(V + E)$ per binary search step.
- Binary search runs for $O(\log E)$ unique weights.
- Total: $O((V + E) \cdot \log E)$.
- **Space complexity**:
- Storing the graph and visited nodes requires $O(V + E)$.
- Heap usage for pruning edges adds $O(V \cdot \text{threshold})$.
- Total: $O(V + E)$.
# Code
```python3 []
class Solution:
def minMaxWeight(self, n: int, edges: List[List[int]], threshold: int) -> int:
edges.sort(key=lambda x: x[2])
weights = sorted(set(w for _, _, w in edges))
def is_valid_graph(max_weight):
graph = defaultdict(list)
reverse_graph = defaultdict(list)
for u, v, w in edges:
if w <= max_weight:
graph[u].append(v)
reverse_graph[v].append(u)
visited = [False] * n
queue = deque([0])
visited[0] = True
while queue:
node = queue.popleft()
for neighbor in reverse_graph[node]:
if not visited[neighbor]:
visited[neighbor] = True
queue.append(neighbor)
if not all(visited):
return False
for node in range(n):
if len(graph[node]) > threshold:
min_heap = []
for neighbor in graph[node]:
heapq.heappush(min_heap, neighbor)
if len(min_heap) > threshold:
heapq.heappop(min_heap)
graph[node] = list(min_heap)
return True
left, right = 0, len(weights) - 1
result = -1
while left <= right:
mid = (left + right) // 2
if is_valid_graph(weights[mid]):
result = weights[mid]
right = mid - 1
else:
left = mid + 1
return result
```
The `reverse_graph` is used to check if **all nodes can reach node 0**.
- In a normal graph, edges go **outward** from a node.
- To check if all nodes can reach node 0, we need to traverse **inward** edges (i.e., reversed edges).
By building the `reverse_graph` (where the direction of every edge is flipped), we can easily perform a BFS starting from node 0 to ensure that every other node has a path to it.
This simplifies connectivity checks, as it avoids needing to manually reverse edges during traversal.
| 2 | 0 |
['Graph', 'Python3']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
Start from 0 and Greedily (Shortest) Reach Everywhere Possible :) MST
|
start-from-0-and-greedily-shortest-reach-rh1j
|
Code
|
nishsolvesalgo
|
NORMAL
|
2025-01-12T04:13:46.232451+00:00
|
2025-01-12T04:13:46.232451+00:00
| 107 | false |
# Code
```cpp []
class Solution {
public:
int minMaxWeight(int n, vector<vector<int>>& edges, int threshold) {
vector<vector<pair<int, int>>> adjList(n, vector<pair<int, int>>());
for(int i=0; i<edges.size(); i++) adjList[edges[i][1]].push_back(make_pair(edges[i][0], edges[i][2]));
vector<int> dist(n, -1);
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<>> pq;
pq.push({0, 0});
while(!pq.empty()){
auto [weight, node] = pq.top();
pq.pop();
if(dist[node] != -1) continue;
dist[node] = weight;
for(auto nghb: adjList[node]){
if(dist[nghb.first] == -1){
pq.push({nghb.second, nghb.first});
}
}
}
int maxVal = INT_MIN;
for(int i=1; i<n; i++){
if(dist[i] == -1) return -1;
maxVal = max(maxVal, dist[i]);
}
return maxVal;
}
};
```
| 2 | 0 |
['C++']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
C++ Binary search solution (just ignore threshold)
|
c-binary-search-solution-just-ignore-thr-we1m
|
Code
|
Retire
|
NORMAL
|
2025-02-08T01:44:50.563782+00:00
|
2025-02-08T01:44:50.563782+00:00
| 41 | false |
# Code
```cpp []
class Solution {
public:
void dfs(int pre, int cur, vector<vector<pair<int, int>>> &g, vector<bool> &vis, int target) {
vis[cur] = true;
for (auto &[nxt, val]: g[cur]) {
if (nxt == pre || val > target || vis[nxt]) continue;
dfs(cur, nxt, g, vis, target);
}
}
int minMaxWeight(int n, vector<vector<int>>& edges, int threshold) {
vector<vector<pair<int, int>>> g(n);
for (auto &x: edges) {
g[x[1]].push_back({x[0], x[2]});
}
int l = 1, r = 1e6 + 1;
while (l < r) {
int mid = (l + r) >> 1;
vector<bool> vis(n, false);
dfs(-1, 0, g, vis, mid);
int cnt = 0;
for (int i = 0; i < n; i++) cnt += vis[i];
if (cnt == n) r = mid;
else l = mid + 1;
}
return l == 1e6 + 1 ? -1 : l;
}
};
```
| 1 | 0 |
['Binary Search', 'Depth-First Search', 'C++']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
Prims + BS + DFS
|
prims-bs-dfs-by-ali-john-qga9
|
Code
|
ali-john
|
NORMAL
|
2025-01-23T18:39:02.003509+00:00
|
2025-01-23T18:39:02.003509+00:00
| 28 | false |
# Code
```python3 []
class Solution:
def minMaxWeight(self, n: int, edges: List[List[int]], threshold: int) -> int:
graph = defaultdict(list)
for u,v, w in edges:
graph[v].append((u,w)) # reverse edges
# ------------ PRIMS ALGORITHM -------------------------------------
heap = [(0,0)] # weight,node
visited = set()
max_weight = 0
while heap:
weight, node = heapq.heappop(heap)
if node in visited:continue
max_weight = max(weight,max_weight)
visited.add(node)
for child,w_ in graph[node]:
heapq.heappush(heap,(w_,child))
return max_weight if len(visited)==n else -1
# ----------------- Binary Search. + DFS -------------------------------------------
# def is_possible(node,weight_lim,seen):
# if node in seen: return
# seen.add(node)
# for child,w_ in graph[node]:
# if w_ > weight_lim: continue
# is_possible(child,weight_lim,seen)
# left = 0
# right = 10000001
# ans = float('inf')
# while left<=right:
# mid = (left+right)//2
# seen = set()
# is_possible(0,mid,seen)
# if len(seen) ==n:
# right = mid - 1
# ans = min(ans,mid)
# else:
# left = mid + 1
# return ans if ans!=float('inf') else -1
```
| 1 | 0 |
['Python3']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
C++ Binary Search on Answer :)
|
c-binary-search-on-answer-by-asmitpapney-z2ni
|
Code
|
asmitpapney
|
NORMAL
|
2025-01-18T15:47:22.352574+00:00
|
2025-01-18T15:47:22.352574+00:00
| 33 | false |
# Code
```cpp []
class Solution {
public:
bool canSolve(vector<pair<int,int>> V[], int n, int mid){
vector<bool> visited(n, false);
visited[0] = true;
queue<int> Q;
Q.push(0);
while(!Q.empty()){
int node = Q.front();
Q.pop();
for(auto child: V[node]){
int u = child.first;
int wt = child.second;
if(!visited[u] && wt <= mid){
visited[u] = true;
Q.push(u);
}
}
}
for(int i=0; i<n; i++)
if(!visited[i])
return false;
return true;
}
int minMaxWeight(int n, vector<vector<int>>& edges, int threshold) {
int start=0, end=1e6;
vector<pair<int,int>> V[n];
for(auto x: edges){
// reversed the graph (as I want that 0 can reach all nodes instead all nodes reaching 0)
V[x[1]].push_back({x[0], x[2]});
}
while(start < end){
if(end-start == 1) break;
int mid = start + (end-start)/2;
if(canSolve(V, n, mid)){
end = mid;
} else{
start = mid;
}
}
if(canSolve(V, n, start)) return start;
if(canSolve(V, n, end)) return end;
return -1;
}
};
```
| 1 | 0 |
['Binary Search', 'C++']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
Binary search with dfs, easy solution with comments
|
binary-search-with-dfs-easy-solution-wit-hzcs
|
IntuitionApproachComplexity
Time complexity: O(n*log(n))
Space complexity:
Code
|
EJJVU4zeGO
|
NORMAL
|
2025-01-15T03:06:49.573000+00:00
|
2025-01-15T03:06:49.573000+00:00
| 14 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: O(n*log(n))
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
// Depth First Search (DFS) function to count the number of nodes reachable
// from node 'i'. Parameters:
// - i: Current node being visited.
// - maxWeight: Maximum allowed weight for edges to traverse.
// - graph: Reverse adjacency list representation of the graph.
// - visited: Vector to keep track of visited nodes.
int dfs(int i, int maxWeight, vector<vector<pair<int, int>>>& graph,
vector<int>& visited) {
// Mark the current node as visited.
visited[i] = 1;
// Initialize the count of reachable nodes from the current node.
int reachableNodes = 1;
// Traverse all neighbors of the current node.
for (auto& [neighbor, weight] : graph[i]) {
// If the edge weight is within the allowed limit and the neighbor
// is not visited:
if (weight <= maxWeight && !visited[neighbor]) {
// Recursively perform DFS on the neighbor and add the result to
// reachableNodes.
reachableNodes += dfs(neighbor, maxWeight, graph, visited);
}
}
// Return the total number of reachable nodes from the current node.
return reachableNodes;
}
// Function to find the minimum maximum edge weight such that all nodes are
// reachable from node 0. Parameters:
// - n: Total number of nodes in the graph.
// - edges: List of edges, where each edge is represented as {from, to,
// weight}. Returns:
// - The minimum maximum weight if all nodes are reachable, otherwise -1.
int minMaxWeight(int n, vector<vector<int>>& edges, int threshold) {
// Step 1: Build the reverse adjacency list representation of the graph.
// Each entry in the graph stores a pair {neighbor, weight}.
vector<vector<pair<int, int>>> graph(n);
for (auto& edge : edges) {
int from = edge[0], to = edge[1], weight = edge[2];
graph[to].emplace_back(from, weight);
}
// Step 2: Initialize binary search range for the maximum weight.
int left = 1; // Minimum possible weight.
int right = 1000001; // Maximum possible weight (upper bound).
// Step 3: Perform binary search to find the smallest maximum weight.
while (left < right) {
// Calculate the midpoint of the current range.
int mid = (left + right) / 2;
// Create a visited array to track visited nodes during the DFS.
vector<int> visited(n, 0);
// Check if all nodes are reachable from node 0 with the current
// weight limit (mid).
if (dfs(0, mid, graph, visited) == n) {
// If all nodes are reachable, try to minimize the maximum
// weight.
right = mid;
} else {
// If not all nodes are reachable, increase the weight limit.
left = mid + 1;
}
}
// Step 4: Return the result.
// If left exceeds the upper bound, it means no valid weight was found.
return left == 1000001 ? -1 : left;
}
};
```
| 1 | 0 |
['C++']
| 1 |
minimize-the-maximum-edge-weight-of-graph
|
Beat 100% || Clean Solution || Binary Search
|
beat-100-clean-solution-binary-search-by-7dvg
|
Code
|
Rahul_Kantwa
|
NORMAL
|
2025-01-14T22:01:40.435318+00:00
|
2025-01-14T22:01:40.435318+00:00
| 30 | false |
# Code
```python3 []
from collections import defaultdict
from typing import List
class Solution:
def minMaxWeight(self, n: int, edges: List[List[int]], threshold: int) -> int:
# Initialize variables
ans = float('inf')
max_w = max(w for _, _, w in edges)
min_w = min(w for _, _, w in edges)
r_graph = defaultdict(list)
# Build reverse graph
for a, b, w in edges:
r_graph[b].append((a, w))
# DFS to check if all nodes can be visited
def canVisitAll(mid):
visit = set()
stack = [0]
while stack:
node = stack.pop()
if node in visit:
continue
visit.add(node)
for child, w in r_graph[node]:
if child not in visit and mid >= w:
stack.append(child)
return len(visit) == n
# Binary search to find the minimum valid `mid`
left, right = min_w, max_w
while left <= right:
mid = (left + right) // 2
if canVisitAll(mid):
ans = min(ans, mid)
right = mid - 1
else:
left = mid + 1
return ans if ans != float('inf') else -1
```
| 1 | 0 |
['Python3']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
C++ Solution || Easy to understand || Binary Search
|
c-solution-easy-to-understand-binary-sea-cpq4
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
karankgudha
|
NORMAL
|
2025-01-14T08:03:50.544927+00:00
|
2025-01-14T08:03:50.544927+00:00
| 37 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
bool check(int n, int mid, vector<vector<pair<int, int>>> adj, int th)
{
vector<int> cnt(n, 0);
queue<int> q;
q.push(0);
cnt[0] = 1;
int m = 1;
while(!q.empty())
{
int curr = q.front(); q.pop();
for(auto [next, w] : adj[curr])
{
if(w <= mid && !cnt[next])
{
q.push(next);
m += ++cnt[next];
}
}
}
return m == n;
}
public:
int minMaxWeight(int n, vector<vector<int>>& edges, int th) {
int l = 1, r = 1000001;
vector<vector<pair<int, int>>> adj(n, vector<pair<int, int>>{});
for(auto v : edges)
adj[v[1]].push_back({v[0], v[2]});
while(l < r)
{
int mid = (r - l)/ 2 + l;
if(check(n, mid, adj, th))
r = mid;
else
l = mid + 1;
}
return r == 1000001 ? -1 : r;
}
};
```
| 1 | 0 |
['Binary Search', 'Breadth-First Search', 'C++']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
Javascript - Binary Search
|
javascript-binary-search-by-faustaleonar-625r
|
Code
|
faustaleonardo
|
NORMAL
|
2025-01-13T23:46:39.951272+00:00
|
2025-01-13T23:46:39.951272+00:00
| 9 | false |
# Code
```javascript []
/**
* @param {number} n
* @param {number[][]} edges
* @param {number} threshold
* @return {number}
*/
var minMaxWeight = function (n, edges, _) {
const graph = new Array(n).fill().map(() => []);
for (const [node1, node2, weight] of edges) {
graph[node2].push([node1, weight]);
}
let low = 0;
let high = 10 ** 6;
let ans = Infinity;
while (low <= high) {
const mid = Math.floor((low + high) / 2);
const count = new Array(n).fill(0);
const isOk = dfs(0, mid, count, graph) === n;
if (isOk) {
ans = mid;
high = mid - 1;
} else {
low = mid + 1;
}
}
return ans === Infinity ? -1 : ans;
};
function dfs(curr, mid, count, graph) {
count[curr] = 1;
for (const [next, weight] of graph[curr]) {
if (weight <= mid && count[next] === 0) {
count[curr] += dfs(next, mid, count, graph);
}
}
return count[curr];
}
```
| 1 | 0 |
['Binary Search', 'JavaScript']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
Greedy | No Binary Search | No PriorityQueue
|
greedy-no-binary-search-no-priorityqueue-yq9g
|
Greedy 99% Runtime | No Binary Search | No Priority QueueObservations1 - Checking whether every node is reachable from 0 is suffice.
2 - One outgoing edge from
|
Bhanu1312
|
NORMAL
|
2025-01-13T22:54:59.287469+00:00
|
2025-01-13T22:54:59.287469+00:00
| 56 | false |
# Greedy 99% Runtime | No Binary Search | No Priority Queue
# Observations
<!-- Describe your first thoughts on how to solve this problem. -->
1 - Checking whether every node is reachable from 0 is suffice.
2 - One outgoing edge from each node is suffice to reach to a node which can either reach to 0 or is itself 0. Hence the condition on the edges in the graph being at most threshold is just a distraction.
3 - As threshold is given to us in the range [1, n - 1]. Hence in all cases threshold >= 1 is safe and we can always have one outgoing edge (which is sufficient) to make our graph.
# Approach
1 - First of all create an adjacenecy graph with original source acting as destination and vice versa. Keep the weight edge as it is.
2 - Create a vis array (for avoiding stack overflow while dfs traversal).
3 - Create a minMaxWeight array managing the minimum value of maximum weight path from 0 to each node.
4 - Initialize the above array with +INFINITY or INT_MAX or Integer.MAX_VALUE
5 - Perform a dfs tarversal on the graph with starting node 0 and explore all edges and maintain a variable (maxWeightAlongPath) that tracks maximum of weight across the path.
6 - Optimization -> If at any stage we get maxWeightAlongPath incapabale of minimizing minMaxWeight[destination] we simply backtrack and explore other paths.
7 - Take maximum of the weight of minMaxWeight array and if either is unreachable then maximumValue will be INT_MAX hence return -1 else return maximumValue;
# Complexity
- Time complexity:
- O(v + E)
- Space complexity:
- O(V + E)
# Code
```java []
class Solution {
private static void minMaxWeightUtil(ArrayList<int[]>[] graph, boolean[] vis, int curr, int maxWeightAlongPath,
int[] minMaxWeight) {
vis[curr] = true;
for (int[] edge : graph[curr]) {
int w = edge[1];
int v = edge[0];
int currUpdatedMaxWeight = Math.max(w, maxWeightAlongPath);
if (currUpdatedMaxWeight >= minMaxWeight[v]) {
continue;
}
minMaxWeight[v] = Math.min(minMaxWeight[v], currUpdatedMaxWeight);
if (!vis[v]) {
minMaxWeightUtil(graph, vis, v, currUpdatedMaxWeight, minMaxWeight);
}
}
vis[curr] = false;
}
public int minMaxWeight(int n, int[][] edges, int threshold) {
var graph = (ArrayList<int[]>[]) new ArrayList[n];
var vis = new boolean[n];
var minMaxWeight = new int[n];
var q = new LinkedList<int[]>();
Arrays.fill(minMaxWeight, Integer.MAX_VALUE);
minMaxWeight[0] = 0;
for (int idx = 0; idx < n; ++idx) {
graph[idx] = new ArrayList<>();
}
for (int[] edge : edges) {
graph[edge[1]].add(new int[] { edge[0], edge[2] });
}
int maxDistance = 0;
minMaxWeightUtil(graph, vis, 0, 0, minMaxWeight);
for (int w : minMaxWeight) {
maxDistance = Math.max(maxDistance, w);
}
return maxDistance == Integer.MAX_VALUE ? -1 : maxDistance;
}
}
```
| 1 | 0 |
['Greedy', 'Depth-First Search', 'Java']
| 1 |
minimize-the-maximum-edge-weight-of-graph
|
Weekly Contest Solution using Prims Algorithm
|
weekly-contest-solution-using-prims-algo-zydo
|
IntuitionUse Shortest Path AlgorithmApproachA definitive Prims AlgorithmCode
|
PradyumnaPrahas2_2
|
NORMAL
|
2025-01-13T15:37:35.871684+00:00
|
2025-01-13T15:37:35.871684+00:00
| 47 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Use Shortest Path Algorithm
# Approach
<!-- Describe your approach to solving the problem. -->
A definitive Prims Algorithm
# Code
```java []
class Solution {
public int minMaxWeight(int n, int[][] edges, int threshold) {
Map<Integer,List<int[]>> graph=new HashMap<>();
for(int[] e:edges){
List<int[]> l=graph.getOrDefault(e[1],new ArrayList<>());
l.add(new int[]{e[0],e[2]});
graph.put(e[1],l);
}
PriorityQueue<int[]> pq=new PriorityQueue<>((a,b)->a[2]-b[2]);
boolean[] visited=new boolean[n];
for(int[] node:graph.getOrDefault(0,new ArrayList<>())){
pq.add(new int[]{0,node[0],node[1]});
}
int MAX=-1;
visited[0]=true;
while(!pq.isEmpty()){
int[] top=pq.poll();
if(visited[top[1]]==false){
MAX=Math.max(MAX,top[2]);
visited[top[1]]=true;
for(int[] nodes:graph.getOrDefault(top[1],new ArrayList<>())){
pq.add(new int[]{top[1],nodes[0],nodes[1]});
}
}
}
for(boolean f:visited){
if(!f){
return -1;
}
}
return MAX;
}
}
```
| 1 | 0 |
['Hash Table', 'Depth-First Search', 'Breadth-First Search', 'Heap (Priority Queue)', 'Shortest Path', 'Java']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
Binary Search || BFS ||
|
binary-search-bfs-by-algoace2004-u6lj
|
IntuitionBinary Search on weight and find it is possible to have weight minimm equal to mid value.
Then we check if zero is reachable from all nodes by ignoring
|
AlgoAce2004
|
NORMAL
|
2025-01-13T14:00:17.799915+00:00
|
2025-01-13T14:00:17.799915+00:00
| 31 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Binary Search on weight and find it is possible to have weight minimm equal to mid value.
Then we check if zero is reachable from all nodes by ignoring the wt greater then mid value.
For this we just reverse the all edge and check from zero where we can reach if we reach all node return true else return false.
The concept of reversing the edge is if we donot reverse the edge then we have to apply dfs/bfs each node check to reach zero ,this is time consuming solution
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
class pair{
int node;
int wt;
public pair(int node,int wt){
this.node=node;
this.wt=wt;
}
}
public boolean canReachZero(List<List<pair>>adj,int mid,int n){
boolean visited[]=new boolean[n];
Queue<pair>q=new LinkedList<>();
q.offer(new pair(0,0));
visited[0]=true;
while(!q.isEmpty()){
pair top=q.poll();
int node=top.node;
int wt=top.wt;
for(pair p:adj.get(node)){
if(p.wt<=mid && visited[p.node]==false){
q.offer(new pair(p.node,p.wt));
visited[p.node]=true;
}
}
}
for(int i=0;i<n;i++){
if(visited[i]==false)return false;
}
return true;
}
public int minMaxWeight(int n, int[][] edges, int threshold) {
int max=0;
List<List<pair>>adj=new ArrayList<>();
for(int i=0;i<n;i++){
adj.add(new ArrayList<pair>());
}
for(int e[]:edges){
max=Math.max(max,e[2]);
int u=e[0];
int v=e[1];
int w=e[2];
adj.get(v).add(new pair(u,w));// we are reversing the all edges so that we can check from zero where we can reach from zero;
}
int high=max;
int low=0;
int ans=-1;
while(low<=high){
int mid=low+(high-low)/2;
if(canReachZero(adj,mid,n)){
ans=mid;
high=mid-1;
}else{
low=mid+1;
}
}
return ans;
}
}
```
| 1 | 0 |
['Java']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
Simplest Solution | Binary Search On Answer | Ignore Threshold
|
simplest-solution-binary-search-on-answe-eo0t
|
Intuition & ApproachInstead of checking if node 0 is reachable from all other nodes, we can reverse the edges and only check if all other nodes are reachable fr
|
roshankumarrtk81
|
NORMAL
|
2025-01-13T04:39:29.866172+00:00
|
2025-01-13T04:39:29.866172+00:00
| 27 | false |
# Intuition & Approach
Instead of checking if node 0 is reachable from all other nodes, we can reverse the edges and only check if all other nodes are reachable from node 0.
We can ignore the threshold condition because we only require one edge from each node to reach the destination.
By performing a binary search on the edge weights, we can efficiently find the required answer.
# Code
```java []
class Solution {
public int minMaxWeight(int n, int[][] edges, int threshold) {
ArrayList<Integer> list = new ArrayList<>();
ArrayList<Pair>[] graph = new ArrayList[n];
for(int i=0;i<n;i++)graph[i]=new ArrayList<>();
for(int i=0;i<edges.length;i++){
list.add(edges[i][2]);
int u = edges[i][0];
int v = edges[i][1];
int w = edges[i][2];
//reverse edge
graph[v].add(new Pair(u, w));
}
//sort edges weights
Collections.sort(list);
int ans=-1;
int l=0, r=edges.length-1;
//binary search on answer
while(l<=r){
int mid = (l+r)/2;
int midVal = list.get(mid);
if(pf(graph, midVal, n)){
ans = midVal;
r=mid-1;
}else{
l=mid+1;
}
}
return ans;
}
public boolean pf(ArrayList<Pair>[] graph, int maxW, int n){
boolean ans = true;
boolean[] visited = new boolean[n];
dfs(0, maxW, graph, visited);
for(boolean val:visited)ans=(ans&val);
return ans;
}
//dfs to check if every node is reacheable from 0 or not
public void dfs(int node, int maxW, ArrayList<Pair>[] graph, boolean[] visited){
if(visited[node])return;
visited[node]=true;
for(Pair child: graph[node]){
if(child.w<=maxW){
dfs(child.v, maxW, graph, visited);
}
}
}
}
//helper class
class Pair {
int v,w;
Pair(int v, int w){
this.v=v;
this.w=w;
}
}
```
| 1 | 0 |
['Java']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
Explanation of Intuition and step by step building of code
|
explanation-of-intuition-and-step-by-ste-1k6a
|
TLDRReverse the direction of all edges and use Prim's to find Minimum spanning tree.Additionally, it is my first post and any tips to improve the post would be
|
guptasuchit
|
NORMAL
|
2025-01-12T18:49:34.908168+00:00
|
2025-01-12T18:49:34.908168+00:00
| 21 | false |
# TLDR
Reverse the direction of all edges and use Prim's to find Minimum spanning tree.
Additionally, it is my first post and any tips to improve the post would be really appriciated.
The code might not be the best and most optimzied code since it was written in a time constraint manner during the competition.
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The conditions in the question state that node 0 should be reachable by every other node, but if we use BFS/DFS on every node, we will exceed time complexity. BUT, this also means that if we reverse the direction of every edge, every node should be reachable by node 0.
Now, we serve 2 simple conditions,
1. Take the edges with minimum weight - We can use priority queue for this
2. Keeping the threshold in check - We use a vector to keep track of the incoming edges to a node (since the edges are reversed, it means outgoing edges)
*(Always try to implement a probable solution if you do not know the answer, it works for me more than sitting with pen and paper and implementing nothing)*
# Approach
<!-- Describe your approach to solving the problem. -->
If we look at it broadly, after reversing the edges, we just have to find the Minimum Spanning Tree. (I used Prim's because I find it easier to code)
1. We initialize an adjacency matrix which reverses the direction of current edges
```cpp []
int minMaxWeight(int n, vector<vector<int>>& edges, int threshold) {
// Vector of {end_node, weight}
map<int, vector<vector<int>>> adj;
for(auto edge: edges) {
adj[edge[1]].push_back({edge[0], edge[2]});
}
}
```
2. We declare all the required data structures needed for Prim's algorithm
```cpp []
struct custsort{
bool operator() (vector<int> const &a, vector<int> const &b) {
return a[2] > b[2];
}
};
int minMaxWeight(int n, vector<vector<int>>& edges, int threshold) {
// Vector of {end_node, weight}
// map<int, vector<vector<int>>> adj;
// for(auto edge: edges) {
// adj[edge[1]].push_back({edge[0], edge[2]});
// }
priority_queue<vector<int>,vector<vector<int>>, custsort> pq; // Priority Queue to sort the edges by their weights
vector<int> thres(n, 0); // Keeps track of threshold for every node
vector<int> visited(n, 0); // Keeps track if a node is visited or not
vector<int> connected_nodes; // Vector of all connected nodes
}
```
3. Next, we push node 0 in our connected nodes list and its edges in to the priority queue
```cpp []
int minMaxWeight(int n, vector<vector<int>>& edges, int threshold) {
// Vector of {end_node, weight}
// map<int, vector<vector<int>>> adj;
// for(auto edge: edges) {
// adj[edge[1]].push_back({edge[0], edge[2]});
// }
// priority_queue<vector<int>,vector<vector<int>>, custsort> pq; // Priority Queue to sort the edges by their weights
// vector<int> thres(n, 0); // Keeps track of threshold for every node
// vector<int> visited(n, 0); // Keeps track if a node is visited or not
// vector<int> connected_nodes; // Vector of all connected nodes
connected_nodes.push_back(0);
visited[0] = 1;
for(auto edge: adj[0]) {
pq.push({0, edge[0], edge[1]});
}
}
```
4. Finally, we write our core logic, keeping the following things in mind
- If connected_nodes.size() == number of nodes, we exit the loop
- If priority_queue is empty, we were not able to connect all nodes, thus return -1
``` cpp []
int minMaxWeight(int n, vector<vector<int>>& edges, int threshold) {
// Vector of {end_node, weight}
// map<int, vector<vector<int>>> adj;
// for(auto edge: edges) {
// adj[edge[1]].push_back({edge[0], edge[2]});
// }
// priority_queue<vector<int>,vector<vector<int>>, custsort> pq; // Priority Queue to sort the edges by their weights
// vector<int> thres(n, 0); // Keeps track of threshold for every node
// vector<int> visited(n, 0); // Keeps track if a node is visited or not
// vector<int> connected_nodes; // Vector of all connected nodes
// connected_nodes.push_back(0);
// visited[0] = 1;
// for(auto edge: adj[0]) {
// pq.push({0, edge[0], edge[1]});
// }
int ans = 0; // Stores our answer
while(pq.size()>0) {
if(connected_nodes.size()==n)
return ans;
vector<int> t = pq.top(); // temporary vector
pq.pop();
// If we have already visited the node or we are crossing the threshold, skip it
if(visited[t[1]] || thres[t[1]]==threshold)
continue;
visited[t[1]] = 1;
thres[t[1]]++;
connected_nodes.push_back(t[1]);
// Compare the weight of the edge added with the current answer
ans = max(ans, t[2]);
for(auto edge: adj[t[1]]) {
pq.push({t[1], edge[0], edge[1]});
}
}
// At the end, if we could not connect all nodes, return -1
if(pq.size()==0 && connected_nodes.size()<n)
return -1;
return ans;
}
```
# Complexity
- Time complexity: ```O((V+E)logV)``` (Same as Prim's Algorithm)
```O(ElogE)``` for creating adjacency list.
```O(E)``` since we iterate directly on the vector of edges and ```logE``` to push every edge into the map. (We can also use unordered_map for better results)
```O((V+E)logE)``` For Prim's algorithm
```O(logE)``` since we iterate on every edge in priority queue, ```O(V+E)``` because we want to visit every node and push every edge into the priority queue (All in worst case)
# Code
```cpp []
class Solution {
public:
struct custsort{
bool operator() (vector<int> const &a, vector<int> const &b) {
return a[2] > b[2];
}
};
int minMaxWeight(int n, vector<vector<int>>& edges, int threshold) {
// Vector of {end_node, weight}
map<int, vector<vector<int>>> adj;
for(auto edge: edges) {
adj[edge[1]].push_back({edge[0], edge[2]});
}
priority_queue<vector<int>,vector<vector<int>>, custsort> pq; // Priority Queue to sort the edges by their weights
vector<int> thres(n, 0); // Keeps track of threshold for every node
vector<int> visited(n, 0); // Keeps track if a node is visited or not
vector<int> connected_nodes; // Vector of all connected nodes
connected_nodes.push_back(0);
visited[0] = 1;
for(auto edge: adj[0]) {
pq.push({0, edge[0], edge[1]});
}
int ans = 0; // Stores our answer
while(pq.size()>0) {
if(connected_nodes.size()==n)
return ans;
vector<int> t = pq.top(); // temporary vector
pq.pop();
// If we have already visited the node or we are crossing the threshold, skip it
if(visited[t[1]] || thres[t[1]]==threshold)
continue;
visited[t[1]] = 1;
thres[t[1]]++;
connected_nodes.push_back(t[1]);
// Compare the weight of the edge added with the current answer
ans = max(ans, t[2]);
for(auto edge: adj[t[1]]) {
pq.push({t[1], edge[0], edge[1]});
}
}
// At the end, if we could not connect all nodes, return -1
if(pq.size()==0 && connected_nodes.size()<n)
return -1;
return ans;
}
};
```
| 1 | 0 |
['Greedy', 'Heap (Priority Queue)', 'Minimum Spanning Tree', 'C++']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
Easy soltion
|
easy-soltion-by-shiladityasaha24042003-w7bu
|
IntuitionThink of revering all the edges and do a traversal from node 0 to all the other node and carry the minimum of all the maximum weights of all paths from
|
shiladityasaha24042003
|
NORMAL
|
2025-01-12T17:34:50.058267+00:00
|
2025-01-12T17:34:50.058267+00:00
| 16 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Think of revering all the edges and do a traversal from node 0 to all the other node and carry the minimum of all the maximum weights of all paths from 0 to that node.
# Approach
The code is designed to solve a graph problem where we compute the minimum of all maximum weights for paths from node 0 to every other node in a directed graph. It also determines the maximum of these minimum weights across all nodes, with an additional check against a given threshold.
# 1. Function: minOfMaxWeights
This function computes the minimum of all maximum weights for paths from node 0 to every other node.
Steps:
Initialization:
1. A result vector, ans, is initialized with infinity (INT_MAX) for all nodes, representing that the path weight to each node is initially unknown. The weight for node 0 is set to 0 because the path from node 0 to itself has no weight.
A priority queue (min-heap) is used to process nodes based on the smallest current maximum weight seen so far.
Algorithm:
2. Start with node 0 and push it into the priority queue with a weight of 0.
Process nodes in the priority queue:
Extract the node with the smallest current maximum weight.
If the extracted weight is greater than the already recorded weight for this node, skip further processing of this node.
For each neighbor of the current node, calculate the maximum weight of the path leading to it as the larger of the current maximum weight and the edge weight to that neighbor.
If this new weight is smaller than the previously recorded weight for the neighbor, update it in the result vector and push the neighbor into the queue for further processing.
3. Return:
Once all nodes are processed, the result vector, ans, contains the minimum of all maximum weights for paths from node 0 to each node.
# 2. Function: minMaxWeight
This function computes the overall result by using the minOfMaxWeights function and checks the result against the threshold.
Steps:
1. Convert Edge List to Adjacency List:
2. Convert the list of edges into an adjacency list for efficient graph traversal. Each edge is represented as a pair of the destination node and its weight.
Call minOfMaxWeights:
3. Use the adjacency list to compute the result vector, where each element represents the minimum of all maximum weights for paths from node 0 to the corresponding node.
Compute the Final Result:
4. Find the maximum value from the result vector, representing the largest of the minimum maximum weights across all nodes.
If the result is still infinity (indicating no valid path exists) or is negative infinity (indicating no meaningful computation was made), return -1. Otherwise, return the computed result.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
vector<int> minOfMaxWeights(int n, vector<pair<int, int>> graph[]) {
vector<int> ans(n, INT_MAX);
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq; // Min-heap
ans[0] = 0;
pq.push({0, 0});
while (!pq.empty()) {
auto [current_max_weight, node] = pq.top();
pq.pop();
if (current_max_weight > ans[node]) continue;
for (auto [neighbor, weight] : graph[node]) {
int new_max_weight = max(current_max_weight, weight);
if (new_max_weight < ans[neighbor]) {
ans[neighbor] = new_max_weight;
pq.push({new_max_weight, neighbor});
}
}
}
return ans;
}
int minMaxWeight(int n, vector<vector<int>>& edges, int threshold) {
//int n = edges.size();
vector<pair<int,int>> adj[n];
for(auto it: edges) {
adj[it[1]].push_back({it[0], it[2]});
}
vector<int> ans(n, INT_MAX);
ans = minOfMaxWeights(n, adj);
int result = INT_MIN;
for(auto it: ans) result = max(result, it);
return result == INT_MAX || result == INT_MIN? -1 : result;
}
};
```
| 1 | 0 |
['C++']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
Beats 100% - Binary Search - Invert edges - Python3
|
beats-100-binary-search-invert-edges-pyt-8265
|
IntuitionHere threshold can be ignored as we need only one minimum edge to connect to node 0 directly or indirectly.ApproachThe binary search is performed to ch
|
UCJTBKG5qL
|
NORMAL
|
2025-01-12T16:33:26.204214+00:00
|
2025-01-12T16:34:15.560920+00:00
| 36 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Here threshold can be ignored as we need only one minimum edge to connect to node 0 directly or indirectly.
# Approach
<!-- Describe your approach to solving the problem. -->
The binary search is performed to check the smallest weight that allows us to reach node 0 from all nodes.
To check if node 0 is reachable from all nodes, the reverse graph is built where edges are inverted, and then dfs is performed from node 0.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
If W is maximum weight is graph for binary search it is O(logW)
To check the reachability dfs is performed. Time complexity is O(V+E)
Overall Time Complexity:- O(logW*(V+E))
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
To build the adjacency list space complexity is O(V*E), where V is number of vertices and E is number of edges.
Recursive Call stack of DFS:- O(V)
Overall Space complexity:- O(V\*E)
# Code
```python3 []
from collections import defaultdict, deque
from heapq import *
class Solution:
def check(self, weight, edges, t, n):
edges = [edge for edge in edges if edge[2]<=weight]
# g = defaultdict(list)
outgoing_edge = defaultdict(int)
reverse_g = defaultdict(list)
# print(weight, edges)
for u, v, w in edges:
# g[u].append((v,w))
reverse_g[v].append(u)
r = set()
def dfs(n):
if n in r:
return
r.add(n)
for nb in reverse_g[n]:
dfs(nb)
dfs(0)
if len(r) < n:
return False
return True
def minMaxWeight(self, n: int, edges: List[List[int]], threshold: int) -> int:
l = 0
r = 0
for _, _, w in edges:
r = max(r, w)
result = -1
while l <= r:
mid = (l+r)//2
# print(mid, self.check(78, edges, threshold, n))
if self.check(mid, edges, threshold, n):
result = mid
r = mid-1
else:
l = mid + 1
return result
```
| 1 | 0 |
['Python3']
| 1 |
minimize-the-maximum-edge-weight-of-graph
|
BFS || C++
|
bfs-c-by-lotus18-goio
|
Code
|
lotus18
|
NORMAL
|
2025-01-12T07:55:11.511011+00:00
|
2025-01-12T07:55:11.511011+00:00
| 16 | false |
# Code
```cpp []
class Solution
{
public:
int minMaxWeight(int n, vector<vector<int>>& edges, int threshold)
{
vector<pair<int,int>> adj[n];
for(auto e: edges)
{
adj[e[1]].push_back({e[0],e[2]});
}
priority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int>>> q;
vector<int> vis(n,0);
q.push({0,0});
int ans=0;
while(!q.empty())
{
auto p=q.top();
q.pop();
int node=p.second, curr=p.first;
if(vis[node]) continue;
ans=max(ans,curr);
vis[node]=1;
for(auto it: adj[node])
{
int neigh=it.first, dist=it.second;
if(!vis[neigh]) q.push({dist,neigh});
}
}
for(auto i: vis) if(!i) return -1;
return ans;
}
};
```
| 1 | 0 |
['Breadth-First Search', 'C++']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
Dijkstra || path with minimum effort
|
dijkstra-path-with-minimum-effort-by-vik-nnl6
|
Intuitionwhat is the maximum edge value traversed on the path to reach this nodeminimize this valueApproachComplexity
Time complexity:
Space complexity:
Code
|
vikas_dor
|
NORMAL
|
2025-01-12T07:29:10.576330+00:00
|
2025-01-12T07:29:10.576330+00:00
| 54 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
what is the maximum edge value traversed on the path to reach this node
minimize this value
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(Elogv)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(Elogv)
# Code
```cpp []
#define ll long long
#define vi vector<ll>
#define vii vector<vi>
#define pl pair<ll,ll>
#define ff first
#define ss second
void make_adj(vii &edges, vector<vector<pl>>&adj){
for(auto it: edges){
ll u = it[0];
ll v = it[1];
ll w = it[2];
adj[u].push_back({v, w});
}
return;
}
ll solve(vii &edges, ll threshold, ll n){
vector<vector<pl>> adj(n);
make_adj(edges, adj);
//start the dijkstra
vi dist(n, 1e9);
priority_queue<pl, vector<pl>, greater<pl> > pq;
pq.push({0, 0});
dist[0] = 0;
while(!pq.empty()){
auto top = pq.top();
pq.pop();
ll u = top.ss;
ll w = top.ff;
//go to its adjacency
for(auto it: adj[u]){
ll n_node = it.ff;
ll wt_node = it.ss;
if(dist[n_node] > max(w, wt_node)){
dist[n_node] = max(w, wt_node);
pq.push({max(w, wt_node), n_node});
}
}
}
for(auto it: dist){
if(it >= 1e9) return -1;
}
ll maxi = 0;
for(auto it: dist){
maxi = max(maxi, it);
}
return maxi;
}
class Solution {
public:
int minMaxWeight(int n, vector<vector<int>>& edges, int threshold) {
//reverse the edges
vii newedges;
for(auto it: edges){
ll u = it[0];
ll v = it[1];
ll w = it[2];
newedges.push_back({v, u, w});
}
ll ans = solve(newedges, threshold, n);
return ans;
}
};
```
| 1 | 0 |
['Graph', 'C++']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
Easy Optimized Solution | 2 Approaches | 🥇🥇🥇
|
easy-optimized-solution-2-approaches-by-mhegv
|
IntuitionNode 0 must be reachable from other every nodes. Think of it in reverse way to make it easy. We will start from 0 and try to reach other nodes, while d
|
souraman19
|
NORMAL
|
2025-01-12T06:58:28.992908+00:00
|
2025-01-12T06:58:28.992908+00:00
| 36 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Node 0 must be reachable from other every nodes. Think of it in reverse way to make it easy. We will start from 0 and try to reach other nodes, while doing that its important to visualize that we dont need two edges to reach any other node from 0, if possible. So actually no use of the threshold given.
# Approach 1
<!-- Describe your approach to solving the problem. -->
1. Reverse each edge.
2. Declare a visited array and as INT_MAX;
3. Intialize a min prioriy queue with for {edge_weight, node}. Insert node 0, weight -1 intially.
4. Get one by one from priority queue. If its visited skip. Otherwise, mark visited and store min(ans, weight) in ans, also check for all its adjacent nodes, if not visited then push the weight and adjoint node. Repeat like this untill pq gets empty.
5. At last if any node remains unvisited then return -1. Otherwise return -1.
# Code
```cpp []
class Solution {
public:
int minMaxWeight(int n, vector<vector<int>>& edges, int threshold) {
vector<vector<pair<int, int>>>adj(n);
for(auto it : edges){
int u = it[0];
int v = it[1];
int w = it[2];
adj[v].push_back({w, u});
}
vector<int>vis(n, 0);
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>>pq;
pq.push({-1, 0});
int maxm = INT_MIN;
while(!pq.empty()){
auto it = pq.top();
pq.pop();
int node = it.second;
int w = it.first;
if(vis[node]) continue;
maxm = max(maxm, w);
vis[node] = 1;
for(auto it : adj[node]){
if(vis[it.second] == 0){
pq.push({it.first, it.second});
}
}
}
for(auto it : vis) if(it == 0) return -1;
return maxm;
}
};
```
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
$$O(E) + O(V) + O(V*logE) + O(V)$$ => for processing edges, intilize vis vector, priority queue operaion, again loop for vis vector
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
$$O(V+E) + O(V) + O(V+E)$$ => for adj list, vis vector, pq
# Approach 2
<!-- Describe your approach to solving the problem. -->
1. Reverse each edge. Intialize ans as -1.
2. Do Binary search from minm edge weight to maxm possible 1e6.
3. Try to do dfs traversal start from 0 to all nodes by allowing maximum edge weight chosen in binary search loop.
4. At the end if all nodes we got visited then try further decreasing the high value to mid - 1 in BS and assign mid to ans, otherwise low = mid + 1. Go untill low <= high.
5. Return ans.
# Code
```cpp []
class Solution {
public:
int f(int i, int maxm, vector<int>& vis, vector<vector<pair<int, int>>>& adj){
vis[i] = 1;
int count = 0;
for(auto it : adj[i]){
int w = it.first;
int node = it.second;
if(!vis[node] && w <= maxm){
count += f(node, maxm, vis, adj);
}
}
return count+1;
}
int minMaxWeight(int n, vector<vector<int>>& edges, int threshold) {
vector<vector<pair<int, int>>>adj(n);
for(auto it : edges){
int u = it[0];
int v = it[1];
int w = it[2];
adj[v].push_back({w, u});
}
vector<int>vis(n, 0);
int low = 1, high = 1e6;
int ans = -1;
while(low <= high){
int mid = low + (high - low)/2;
vector<int>vis(n, 0);
if(f(0, mid, vis, adj) == n){
ans = mid;
high = mid - 1;
} else {
low = mid + 1;
}
}
return ans;
}
};
```
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
$$O(E) + O(log(maxm)*(V + E))$$
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
$$O(V+E) + O(V) + O(V+E)$$ => last V+E for recursion stack
| 1 | 0 |
['Binary Search', 'Depth-First Search', 'Graph', 'Heap (Priority Queue)']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
Prim's with extra words (Python, beats binary search)
|
prims-with-extra-words-by-wanderingcicad-h1zo
|
IntuitionThis problem is just asking you to do prim's/dijkstra's algorithm but with extra words like some bs about "thresholds" to make it confusing. It's direc
|
wanderingCicada
|
NORMAL
|
2025-01-12T05:21:41.963426+00:00
|
2025-01-12T05:31:48.206662+00:00
| 49 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
This problem is just asking you to do prim's/dijkstra's algorithm but with extra words like some bs about "thresholds" to make it confusing. It's directed, so you'll need a slight modification to keep track of which edges to actually consider.
# Approach
<!-- Describe your approach to solving the problem. -->
Make an MST starting from node 0. Ignore edges outgoing from 0, and only consider new edges directing towards your MST.
Threshold doesn't matter, you only need to pick the one outgoing edge per node anyway in Prim's.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(elog(e))
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(e)
# Code
```python3 []
class Solution:
def minMaxWeight(self, n: int, edges: List[List[int]], threshold: int) -> int:
#prims - just keep adding the lowest edge that connects something new to 0 (or to something already connected to 0)
#basically - just pick the best outgoing edge for every node
incoming = [[] for _ in range(n)]
for start, end, w in edges:
incoming[end].append((start, w))
heap = [(0, 0)]
added = set()
ans = 0
while len(heap) > 0:
weight, node = heap[0]
heapq.heappop(heap)
if node not in added:
added.add(node)
ans = max(ans, weight)
for nNode, nWeight in incoming[node]:
if nNode not in added:
heapq.heappush(heap, (nWeight, nNode))
if len(added) == n:
return ans
return -1
```
| 1 | 0 |
['Python3']
| 1 |
minimize-the-maximum-edge-weight-of-graph
|
solution using dsu and heap
|
solution-using-dsu-and-heap-by-ankitsiso-cltv
|
IntuitionApproachComplexity
Time complexity:
O(n)
Space complexity:
O(n)
Code
|
Ankit_singh_sisodya
|
NORMAL
|
2025-01-12T04:44:36.186885+00:00
|
2025-01-12T04:44:36.186885+00:00
| 70 | false |
# Intuition
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
O(n)
- Space complexity:
O(n)
# Code
```cpp []
class dsu {
private:
vector<int> rank, parent, size;
public:
dsu(int n) {
rank.resize(n + 1, 0);
parent.resize(n + 1, 0);
iota(parent.begin(), parent.end(), 0);
size.resize(n + 1, 0);
};
int findpar(int u) {
if (u == parent[u])
return u;
else
return parent[u] = findpar(parent[u]);
}
void unionbysize(int u, int v) {
int ulp_u = findpar(u);
int ulp_v = findpar(v);
if (ulp_u == ulp_v)
return;
if (size[ulp_u] < size[ulp_v]) {
parent[ulp_u] = ulp_v;
size[ulp_v] += size[ulp_u];
} else {
parent[ulp_v] = ulp_u;
size[ulp_u] += size[ulp_v];
}
}
};
class Solution {
public:
int minMaxWeight(int n, vector<vector<int>>& edges, int threshold) {
// dsu
dsu ds(n);
vector graph(n, vector<pair<int,int>>());
// reverse the graph
for (auto& p : edges) {
int u = p[0], v = p[1], w = p[2];
graph[v].push_back(make_pair(w, u));
}
// sort according to weight
for (int i = 0; i < n; ++i)
sort(graph[i].begin(), graph[i].end());
// in -> indegree
vector in(n, 0);
// make a min heap
priority_queue<tuple<int, int, int>, vector<tuple<int, int, int>>,
greater<tuple<int, int, int>>>
pq;
// tuple -> [weight, parent, child]
vector<int> vis(n, 0);
int ans = 0;
for (auto& [w, v]: graph[0])
pq.push(make_tuple(w, 0, v));
while (pq.size()) {
auto [ww, node, v] = pq.top();
pq.pop();
if (in[v] + 1 <= threshold && ds.findpar(v) != ds.findpar(node)) {
ds.unionbysize(node, v);
ans = max(ans, ww);
in[v]++;
vis[v] = 1;
vis[node] = 1;
for (auto& e : graph[v])
pq.push(make_tuple(e.first, v, e.second));
}
}
for (int i = 0; i < n; ++i)
if (vis[i] == 0)
return -1;
return ans;
}
}
;
```
| 1 | 0 |
['Graph', 'Heap (Priority Queue)', 'C++']
| 1 |
minimize-the-maximum-edge-weight-of-graph
|
O(n.log(n^2)) Time Solution || Commented Code
|
onlogn2-time-solution-commented-code-by-m9ppr
|
Complexity
Time complexity: O(n.logn2)
Space complexity: O(n.logn2)
Code
click the upvote btn :)
|
ammar-a-khan
|
NORMAL
|
2025-01-12T04:41:37.968639+00:00
|
2025-01-12T04:50:08.354747+00:00
| 30 | false |
# Complexity
- Time complexity: $O(n.\log n^2)$
- Space complexity: $O(n.\log n^2)$
# Code
```cpp
void dfs(int node, vector<int> &visited, vector<vector<pair<int, int>>> &graph, int &maxWeight){
visited[node] = 1;
for (int i = 0; i < graph[node].size(); ++i){
if (!visited[graph[node][i].first] && graph[node][i].second <= maxWeight){
dfs(graph[node][i].first, visited, graph, maxWeight);
}
}
}
//only checks if all nodes can be visited from 0; threshold irrelevant
bool ifPossible(int &maxWeight, vector<vector<pair<int, int>>> &graph){ irrelevent
vector<int> visited(graph.size(), 0);
dfs(0, visited, graph, maxWeight);
for (int i = 0; i < graph.size(); ++i){ if (!visited[i]){ return 0; } }
return 1;
}
int minMaxWeight(int n, vector<vector<int>> &edges, int threshold){
vector<vector<pair<int, int>>> graph(n); //stores graph with reversed edges
for (int i = 0; i < edges.size(); ++i){ graph[edges[i][1]].push_back({edges[i][0], edges[i][2]}); }
vector<int> weights; //stores sorted weights for binarySearch
for (int i = 0; i < edges.size(); ++i){ weights.push_back(edges[i][2]); }
sort(weights.begin(), weights.end());
//lowerBound on maxWeight
int l = 0, r = weights.size() - 1;
if (!ifPossible(weights[r], graph)){ return -1; }
while (l < r){
int mid = l + (r - l)/2;
if (ifPossible(weights[mid], graph)){ r = mid; }
else { l = mid + 1; }
}
return weights[r];
}
```
>click the upvote btn :)
| 1 | 0 |
['Binary Search', 'Depth-First Search', 'Graph', 'C++']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
Binary Search on Answer|| C++ ||
|
binary-search-on-answer-c-by-prashudeshm-1pat
|
IntuitionConsider mid value as the maximum edge weight you can have in your graph. If predicate(mid) == true then pred(mid+1),predicate(mid+2) and so on will al
|
prashudeshmukh3006
|
NORMAL
|
2025-01-12T04:08:14.740408+00:00
|
2025-01-12T04:08:14.740408+00:00
| 22 | false |
# Intuition
Consider mid value as the maximum edge weight you can have in your graph. If predicate(mid) == true then pred(mid+1),predicate(mid+2) and so on will also be true. Hence the solution has monotonic nature. So we can apply binary search here.
# Approach
The only thing we need is to find a predicate function which can return us true or false by checkig the conditions in O(n) time.
First of all we will remove all edges with wt > mid.
Now just make a graph by remaining edges.
Now since we want that all nodes should reach 0, what we can do is reverse the graph. We can try reaching all other nodes from 0.
The condition of threshold value can be ingnored because if there is a path from 0 to that node (whose degree is > threshold) that means there is at least one path through which we can reach that node. Hence other unnecessary edges from that node can be removed.
# Complexity
- Time complexity:
- O(n*log n)
# Code
```cpp []
class Solution {
private:
void dfs(int node,vector<vector<int>> &gp,vector<int> &vis){
vis[node] = 1;
for(auto &nxt : gp[node]){
if(!vis[nxt]) dfs(nxt,gp,vis);
}
}
bool pred(int n,vector<vector<int>> &edges,int threshold,int max_wt){
vector<vector<int>> gp(n);
vector<int> indeg(n,0);
for(auto &e : edges){
if(e[2]<=max_wt){
gp[e[1]].push_back(e[0]);
indeg[e[0]]++;
}
}
vector<int> vis(n,0);
dfs(0,gp,vis);
for(int i = 0; i<n; i++){
if(vis[i] == 0) return false;
}
return true;
}
public:
int minMaxWeight(int n, vector<vector<int>>& edges, int threshold) {
int low = 1,high = 1000000;
int ans = -1;
while(low<=high){
int mid = (low + high)>>1;
if(pred(n,edges,threshold,mid)){
ans = mid;
high = mid-1;
}
else low = mid+1;
}
return ans;
}
};
```
| 1 | 0 |
['C++']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
⚡ Slash the Heaviest Edge & Keep 0 Connected! 🔥 MUST VISIT😎
|
slash-the-heaviest-edge-keep-0-connected-8dk9
|
PLEASE UPVOTE THIS IF U FIND HELPFULL.IntuitionThe problem requires us to modify a directed, weighted graph to meet the following conditions:
Node 0 must be rea
|
aniketb11
|
NORMAL
|
2025-03-23T09:16:39.899000+00:00
|
2025-03-23T09:16:39.899000+00:00
| 1 | false |
## PLEASE UPVOTE THIS IF U FIND HELPFULL.
## **Intuition**
The problem requires us to modify a directed, weighted graph to meet the following conditions:
1. **Node 0 must be reachable from all nodes.**
2. **Minimize the maximum edge weight used in the final graph.**
3. **Each node can have at most `k` outgoing edges.**
To achieve this, we need to **remove** some edges while ensuring that the graph remains connected to node `0`, and we minimize the **maximum edge weight** in the resulting graph.
### **Key Observations**
- Since **node 0 must be reachable from all nodes**, we should **reverse the edges** while storing them. Instead of adding edges in the usual `(src → dest)` format, we store them in the **reverse order** `(dest → src)`. This way, we can treat **node 0 as the source** and ensure that all nodes can reach it.
- We can use **Dijkstra’s algorithm** with a **Min-Heap (PriorityQueue)** to process nodes in increasing order of edge weight, ensuring we get the minimum possible **maximum weight edge** in the final graph.
- If at the end of traversal, we haven't visited all nodes, it means the graph isn't fully connected, so we return `-1`.
---
## **Approach**
### **Step 1: Construct the Graph**
- Create an adjacency list to store edges in a **reverse manner** (`destination → source`).
- This ensures that while traversing from `0`, we cover all nodes that can **reach** `0`.
### **Step 2: Use a Priority Queue for Dijkstra’s Algorithm**
- We maintain a **Min-Heap (PriorityQueue)** that processes nodes in order of **increasing edge weight**.
- Start with node `0` and traverse the graph using **greedy selection** (always pick the smallest available edge).
### **Step 3: Keep Track of Maximum Edge Weight**
- Since we need to **minimize the largest edge weight used**, we keep track of the **maximum edge weight encountered during traversal**.
- This value will be our final answer.
### **Step 4: Check if All Nodes Are Visited**
- If all nodes are reachable from `0`, return the **maximum edge weight** encountered during traversal.
- Otherwise, return `-1`.
---
## **Complexity Analysis**
- **Graph Construction:** \(O(E)\), where `E` is the number of edges.
- **Sorting (if necessary):** \(O(E \log E)\) (but we are using a min-heap to process edges greedily, which is optimal).
- **Dijkstra’s Algorithm using a Priority Queue:** \(O(E \log N)\), where `N` is the number of nodes.
- **Overall Time Complexity:** **\(O(E \log N)\)**
- **Space Complexity:**
- **Graph Representation:** \(O(E)\) (Adjacency List)
- **Priority Queue:** \(O(N)\) (At most, all nodes can be in the heap)
- **Visited Array:** \(O(N)\)
- **Total:** **\(O(N + E)\)**
---
## **Code**
```java
class Solution {
public int minMaxWeight(int n, int[][] edges, int k) {
List<List<int[]>> l=new ArrayList<>();
for(int i=0;i<n;i++){
l.add(new ArrayList<>());
}
for(int[]e:edges){
// here we have clue that node 0 will recahable from all other nodes so ab muzhe src to 0 h lena hai to mein ya to normal add krke sort kr skta hu apni list ko ya phir mein ult add krdunga means all nodes will reached by node 0 example1 2,0 hai to isko 2,0 add krne k wjaye 0,2 add krdunga so that mera srck ko dstination mil jaye age bdne k liye.
l.get(e[1]).add(new int[]{e[0],e[2]});
}
PriorityQueue<int[]> pq=new PriorityQueue<>((a,b)->a[1]-b[1]);
pq.add(new int[]{0,0});
boolean[]vis=new boolean[n];
int c=0,max=Integer.MIN_VALUE;
while(!pq.isEmpty()){
int[]curr=pq.poll();
int node=curr[0];
int val=curr[1];
if(vis[node])continue;
vis[node]=true;
for(int[]neig:l.get(node)){
pq.add(new int[]{neig[0],neig[1]});
}
c++;
max=Math.max(max,val);
}
return (c!=n)?-1:max;
}
}
```
---
## **Why This Works**
1. **Reversing edges ensures all nodes can reach `0`**
- Instead of storing `(src → dest)`, we store `(dest → src)`, making **node 0** the reference point.
- This helps in ensuring connectivity from any node to `0`.
2. **Using a Priority Queue (Min-Heap) ensures we always process the smallest edge weight first**
- This **minimizes** the largest edge weight encountered in the final traversal.
3. **If all nodes are reachable from `0`, we return the largest weight encountered**
- This guarantees we meet the problem's constraints.
4. **If any node is not visited, return `-1`**
- This means it’s impossible to satisfy the conditions.
---
## **Example Walkthrough**
### **Input:**
```java
n = 4, edges = [[0,1,4],[1,2,3],[2,3,2],[3,0,5]], k = 2
```
### **Graph Representation After Reversal:**
```
0 ← 1 (4)
1 ← 2 (3)
2 ← 3 (2)
3 ← 0 (5)
```
### **Priority Queue Processing (Dijkstra's Approach)**
| Step | Node Processed | Edge Weight Used | Max Edge Weight |
|------|--------------|-----------------|-----------------|
| 1 | `0` | `0` | `0` |
| 2 | `3` | `5` | `5` |
| 3 | `2` | `2` | `5` |
| 4 | `1` | `3` | `5` |
### **Final Answer:**
- All nodes are reachable.
- The largest edge weight used in the traversal is `5`, so the output is:
```java
Output: 5
```
---
## **Edge Cases Considered**
✅ **Disconnected Graph:**
- If any node cannot reach `0`, return `-1`.
✅ **Threshold Constraints:**
- Ensures each node has at most `k` outgoing edges (though the pruning part was removed as it's not handled in the current code).
✅ **Graph with Multiple Paths:**
- The algorithm always picks the smallest edge first, ensuring the optimal path.
---
## **Final Thoughts**
- This approach ensures that **all nodes remain connected to `0`** while **minimizing the maximum edge weight used**.
- **Dijkstra’s Algorithm** helps in picking the **minimum possible maximum edge weight** efficiently.
- The **time complexity of \(O(E \log N)\)** makes it optimal for large graphs. 🚀
| 0 | 0 |
['Breadth-First Search', 'Graph', 'Shortest Path', 'Java']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
Binary Search + BFS/DFS
|
binary-search-bfsdfs-by-recursive45-8ivy
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
Recursive45
|
NORMAL
|
2025-03-15T05:55:04.214209+00:00
|
2025-03-15T05:55:04.214209+00:00
| 2 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution
{
public:
bool isValid(int n, vector<vector<int>> &edges, int threshold, int mid, vector<vector<pair<int, int>>> &adj)
{
vector<int> visited(n, 0);
queue<int> q;
q.push(0);
visited[0] = 1;
int count = 0;
while (!q.empty())
{
int node = q.front();
q.pop();
count++;
for (auto it : adj[node])
{
if (!visited[it.first] and it.second <= mid)
{
q.push(it.first);
visited[it.first] = 1;
}
}
}
return count == n;
}
int minMaxWeight(int n, vector<vector<int>> &edges, int threshold)
{
vector<vector<pair<int, int>>> adj(n);
for (auto it : edges)
{
int u = it[0];
int v = it[1];
int wt = it[2];
adj[v].push_back({u, wt});
}
int mx = 0;
for (auto it : edges)
{
mx = max(mx, it[2]);
}
int lb = 0;
int ub = mx;
int ans = 1e9;
while (lb <= ub)
{
int mid = lb + (ub - lb) / 2;
if (isValid(n, edges, threshold, mid, adj))
{
ans = mid;
ub = mid - 1;
}
else
{
lb = mid + 1;
}
}
if(ans == 1e9) return -1;
return ans;
}
};
```
| 0 | 0 |
['Binary Search', 'Depth-First Search', 'Breadth-First Search', 'Graph', 'C++']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
[C++] 90%, Dijkstra
|
c-90-dijkstra-by-tipra-jmew
|
IntuitionReverse the edges of the graph. This simplifies the reachability problem. Then we run dijkstra algo, but a variant where we try to minimize the the wei
|
tipra
|
NORMAL
|
2025-03-11T17:44:36.051179+00:00
|
2025-03-11T17:44:36.051179+00:00
| 1 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Reverse the edges of the graph. This simplifies the reachability problem. Then we run dijkstra algo, but a variant where we try to minimize the the weight of an edge chosen to reach some node n. On top of that, we have the constraint that in_degree (because graph is reversed) should be <= threshold.
To put it more simply, at any point, say we know the solution for some subset of nodes (reachable from node 0 and minimized weights). Then out of all the possible outgoing edges from this set, we choose the one with:
- Min edge weight
- Satisfying the condition that in_deg <= threshold
But what if there's some edge to our current set of nodes which is even smaller ? Doesn't matter, as we take the maxm either way
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(V + ElogV)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
// Custom Dijkstra?
int minMaxWeight(int n, vector<vector<int>>& edges, int threshold) {
vector<vector<pair<int, int>>> g(n);
for (auto& e: edges) {
g[e[1]].push_back({e[0], e[2]});
}
struct Node {
int u, v, w;
bool operator<(const Node& other) const {
return w > other.w;
}
};
priority_queue<Node> pq;
pq.push({-1, 0, 0});
vector<int> par(n, INT_MAX);
par[0] = 0;
vector<int> in_degree(n);
vector<bool> vis(n);
while (!pq.empty()) {
auto top = pq.top();
pq.pop();
int u = top.v, w = top.w;
int from = top.u;
if (vis[u]) continue;
par[u] = w;
// cout << from << " " << u << " " << w << "\n";
vis[u] = true;
in_degree[u]++;
for (auto& e: g[u]) {
int v = e.first;
if (e.second < par[v] && in_degree[v] <= threshold && !vis[v]) {
pq.push({u, v, e.second});
}
}
}
int ans = 0;
for (int w: par) {
if (w == INT_MAX) return -1;
ans = max(ans, w);
}
return ans;
}
};
```
| 0 | 0 |
['C++']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
[C++] 99%, Dijkstra/Prim algo
|
c-90-dijkstra-by-tipra-5p8y
|
IntuitionReverse the edges of the graph. This simplifies the reachability problem. Then we run dijkstra algo, but a variant where we try to minimize the the wei
|
tipra
|
NORMAL
|
2025-03-11T17:44:34.219569+00:00
|
2025-03-11T17:58:35.420445+00:00
| 10 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Reverse the edges of the graph. This simplifies the reachability problem. Then we run dijkstra algo, but a variant where we try to minimize the the weight of an edge chosen to reach some node n. On top of that, we have the constraint that in_degree (because graph is reversed) should be <= threshold.
But the threshold doesn't matter as in the end we will have a tree where in_degree is always 1.
To put it more simply, at any point, say we know the solution for some subset of nodes (reachable from node 0 and minimized weights). Then out of all the possible outgoing edges from this set, we choose the one with:
- Min edge weight
But what if there's another smaller edge to one of our subset of the nodes from outside the set? Doesn't matter as all the edges going outside our set are >= the maxm edge weight found so far. So we are bounded. Similar logic as Dijktra for correctness
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(V + ElogV)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
// Custom Dijkstra?
int minMaxWeight(int n, vector<vector<int>>& edges, int threshold) {
vector<vector<pair<int, int>>> g(n);
for (auto& e: edges) {
g[e[1]].push_back({e[0], e[2]});
}
struct Node {
int v, w;
bool operator<(const Node& other) const {
return w > other.w;
}
};
priority_queue<Node> pq;
pq.push({0, 0});
int ans = 0;
int visited_nodes = 0;
vector<bool> vis(n);
while (!pq.empty()) {
auto top = pq.top();
pq.pop();
int u = top.v, w = top.w;
if (vis[u]) continue;
visited_nodes++;
ans = max(ans, w);
// cout << from << " " << u << " " << w << "\n";
vis[u] = true;
for (auto& e: g[u]) {
int v = e.first;
if (!vis[v]) {
pq.push({v, e.second});
}
}
}
if (visited_nodes != n) return -1;
return ans;
}
};
```
| 0 | 0 |
['C++']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
Solution using Prim's Algorithm
|
solution-using-prims-algorithm-by-yunbo2-jy96
|
Code
|
yunbo2016
|
NORMAL
|
2025-03-04T23:46:41.665371+00:00
|
2025-03-04T23:46:41.665371+00:00
| 6 | false |
# Code
```python3 []
class Solution:
def minMaxWeight(self, n: int, edges: List[List[int]], threshold: int) -> int:
# use Prim's algorithm to find the MST
# invert the graph and use priority queues to store the edges that come out of the visited nodes
# sort by edge weight
# first invert the graph
adj = [[] for i in range(n)]
for edge in edges:
adj[edge[1]].append((edge[2], edge[0]))
# visited set to keep track of vertices already in the MST
visited = set()
#begin with 0
visited.add(0)
# add all edges from zero to pq
pq = []
heapify(pq)
self.addEdges(adj, 0, pq, visited)
max_weight = 0
# add new edges until all vertices are added or there are no more possible edges
while len(visited) < n and pq:
# pop out the lowest weight edge and add the new vertex
edge = heappop(pq)
# if the vertex is visited, skip
if edge[1] in visited:
continue
visited.add(edge[1])
max_weight = max(max_weight, edge[0])
# add all outgoing edges from the new vertex
self.addEdges(adj, edge[1], pq, visited)
if len(visited) < n:
return -1
return max_weight
def addEdges(self, adj, node, pq, visited):
for edge in adj[node]:
if edge[1] not in visited:
heappush(pq, (edge[0], edge[1]))
```
| 0 | 0 |
['Python3']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
C++ | Dijkrta's Algo
|
c-dijkrtas-algo-by-kena7-88m7
|
Code
|
kenA7
|
NORMAL
|
2025-02-28T13:49:16.157254+00:00
|
2025-02-28T13:49:16.157254+00:00
| 5 | false |
# Code
```cpp []
class Solution {
public:
vector<int> shortestPath(vector<vector<pair<int,int>>>&g)
{
priority_queue<pair<int,int>, vector<pair<int,int>>, greater<pair<int,int>>> pq;
int n=g.size(),vis=0;
vector<int>dist(n,INT_MAX);
pq.push({0,0});
while(!pq.empty() && vis<n)
{
int d=pq.top().first,u=pq.top().second;
pq.pop();
if(dist[u]!=INT_MAX)
continue;
dist[u]=d;
vis++;
for(auto &p:g[u])
{
int v=p.first,w=p.second;
if(dist[v]==INT_MAX)
{
pq.push({max(d,w),v});
}
}
}
return dist;
}
int minMaxWeight(int n, vector<vector<int>>& edges, int th)
{
int res=-1;
vector<vector<pair<int,int>>>g(n);
for(auto &e:edges)
g[e[1]].push_back({e[0],e[2]}); //Reverse edge
auto dist = shortestPath(g);
res=*max_element(dist.begin(),dist.end());
if(res==INT_MAX)
res=-1;
return res;
}
};
```
| 0 | 0 |
['Shortest Path', 'C++']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
C++ Binary search BFS
|
c-binary-search-bfs-by-jaychadawar-igkh
|
Intuitionwe are inverting the graphy beacuse it is said the all nodes should be able to reach node 0,so we need to do bfs from all nodes T.C will increase.after
|
JayChadawar
|
NORMAL
|
2025-02-19T09:43:18.040801+00:00
|
2025-02-19T09:43:18.040801+00:00
| 5 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
we are inverting the graphy beacuse it is said the all nodes should be able to reach node 0,so we need to do bfs from all nodes T.C will increase.
after inverting we will be checking how many nodes can be reached from node 0- this approach will be less complex and T.C will be less.
BS beacuse we need not check for all the value.
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int minMaxWeight(int n, vector<vector<int>>& edges, int threshold) {
//binary with invert the edges of graph
vector<vector<pair<int,int>>> adj(n);
int mine=INT_MAX;
int maxe=INT_MIN;
for(int i=0;i<edges.size();i++){
adj[edges[i][1]].push_back({edges[i][0],edges[i][2]});
mine=min(mine,edges[i][2]);
maxe=max(maxe,edges[i][2]);
}
int low=mine;
int high=maxe;
int ans=maxe;
while(low<=high){
int mid=(low+high)/2;
if(fun(mid,adj,n)){
ans=mid;
high=mid-1;
}else{
low=mid+1;
}
}
//ans can be maxe when actually the ans is maxe or when it does not find any ans.
//so if ans==maxe check again if we are able to visit all nodes if yes then the ans is maxe or else it is -1 as we cannot visit all nodes.
//if the ans is other than maxe then no need to check
if(ans==maxe){
bool x= fun(ans,adj,n);
return x==true?maxe:-1;
}
return ans;
}
bool fun(int mid,vector<vector<pair<int,int>>> &adj,int n){
queue<int> q;
q.push(0);
vector<int> vis(n,0);
int cnt=0;
vis[0]=1;
while(!q.empty()){
auto a=q.front();
q.pop();
for(auto x:adj[a]){
if(vis[x.first]) continue;
if(x.second>mid) continue;
vis[x.first]=1;
q.push(x.first);
}
}
for(int i=0;i<vis.size();i++){
if(vis[i]==1)
cnt++;
}
return cnt==n?true:false;
}
};
```
| 0 | 0 |
['Binary Search', 'Breadth-First Search', 'C++']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
Prims to purify your soul
|
prims-to-purify-your-soul-by-forsurveys8-7b9l
|
IntuitionThe question wants us to go from other nodes to 0,
Looking at the examples we can observe 2 things
Other nodes may point to 0, thats the right way to
|
forsurveys868
|
NORMAL
|
2025-02-09T11:57:04.313980+00:00
|
2025-02-09T11:57:04.313980+00:00
| 9 | false |
# Intuition
The question wants us to go from other nodes to 0,
Looking at the examples we can observe 2 things
1. Other nodes may point to 0, thats the right way to build a path from others to 0.
2. 0 may point to other nodes initially but this wont make the other nodes reach 0 so this is a failure case.
What if we reversed all the edges pointing to 0? and Tried finding a way from 0 to other nodes which possibly seems easier to implement, lets try it using
```
for v,u,w in edges:
graph[u].append((v, w))
```
Now we want to discard all the edges with maximum weight, so we will always go from node to node in search of shortest weight edge. PRIMS!
# Complexity
- Time complexity: O(ElogE)
- Space complexity: O(V+E)
# Code
```python3 []
class Solution:
def minMaxWeight(self, n: int, edges: List[List[int]], threshold: int) -> int:
graph, hq, visited = defaultdict(list), [], set()
for v,u,w in edges:
graph[u].append((v, w))
for (v, w) in graph[0]:
heapq.heappush(hq, [w,0,v])
visited.add(0)
res = 0
while hq:
w, u, v = heapq.heappop(hq)
if v in visited: continue
visited.add(v)
res = max(res, w)
for (v2, w2) in graph[v]:
if v2 not in visited:
heapq.heappush(hq, [w2, v, v2])
return res if len(visited) == n else -1
```
| 0 | 0 |
['Hash Table', 'Graph', 'Heap (Priority Queue)', 'Minimum Spanning Tree', 'Python3']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
Modified Dijkstra
|
modified-dijkstra-by-varup3079-pepz
|
IntuitionThe problem requires finding the minimum maximum edge weight for a path connecting all nodes. Instead of summing edge weights like standard Dijkstra's
|
varup3079
|
NORMAL
|
2025-02-07T10:06:26.709209+00:00
|
2025-02-07T10:06:26.709209+00:00
| 11 | false |
## **Intuition**
The problem requires finding the **minimum maximum edge weight** for a path connecting all nodes. Instead of summing edge weights like standard Dijkstra's algorithm, we track the **maximum weight encountered along the path** and aim to minimize it.
---
## **Approach**
1. **Graph Representation:**
- Use an adjacency list (`vector<vector<pair<int,int>>> adj`) to store the **REVERSE** graph, where each node connects to `{neighbor, weight}` pairs.
2. **Modified Dijkstra’s Algorithm:**
- Use a **set (min-heap)** to process nodes with the smallest max-weight encountered so far.
- Maintain a **distance array (`dis[]`)** initialized with a large value (`1e9`).
- Start with node `0` having weight `0` and process nodes greedily.
3. **Updating Weights:**
- For each neighboring node, update `dis[]` with the **maximum edge weight encountered** along the path.
- If a better path is found, update and insert it back into the priority queue.
4. **Final Calculation:**
- The answer is the maximum value in `dis[]`, ensuring all nodes are reachable.
- If any node remains unreachable (`1e9`), return `-1`.
---
## **Complexity Analysis**
- **Time Complexity:** \(O((V + E) \log V)\)
- Each node is processed once in the worst case, and edge relaxation takes logarithmic time due to the priority queue.
- **Space Complexity:** \(O(V + E)\)
- The adjacency list and distance array take \(O(V + E)\) space.
---
## **Code**
```cpp
class Solution {
public:
int minMaxWeight(int n, vector<vector<int>>& edges, int threshold) {
vector<vector<pair<int, int>>> adj(n);
for (auto& edge : edges) {
adj[edge[1]].push_back({edge[0], edge[2]});
}
int ans = -1;
vector<int> dis(n, 1e9);
set<pair<int, int>> pq;
pq.insert({0, 0});
dis[0] = 0;
while (!pq.empty()) {
auto p = *(pq.begin());
int d = p.first;
int node = p.second;
pq.erase(p);
for (auto& it : adj[node]) {
if (dis[it.first] > max(d, it.second)) {
if (dis[it.first] != 1e9) pq.erase({dis[it.first], it.first});
dis[it.first] = max(d, it.second);
pq.insert({dis[it.first], it.first});
}
}
}
for (auto& it : dis) {
if (it == 1e9) {
ans = -1;
break;
} else {
ans = max(ans, it);
}
}
return ans;
}
};
```
## **Key Observations**
- **Why Dijkstra?**
- Although this isn't a shortest-path problem, **Dijkstra’s greedy approach** ensures we find the path with the minimum maximum weight.
- **Why `max(d, it.second)`?**
- Since we are interested in the max edge weight along a path, we take `max(d, it.second)` instead of summing distances.
- **Why `set<pair<int, int>>`?**
- Using a **set** ensures efficient updates and retrievals in \(O(\log V)\) time.
---
| 0 | 0 |
['Graph', 'Heap (Priority Queue)', 'Shortest Path', 'C++']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
Choose e by the order of their weight, starting from vertex 0
|
choose-e-by-the-order-of-their-weight-st-2x0n
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
yan_yichun
|
NORMAL
|
2025-02-01T05:36:32.372342+00:00
|
2025-02-01T05:36:32.372342+00:00
| 4 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def minMaxWeight(self, n: int, edges: List[List[int]], threshold: int) -> int:
adj = [[] for _ in range(n)]
for e in edges:
adj[e[1]].append((e[2], e[1], e[0]))
edge = [0] * n
hp = []
for e in adj[0]:
heapq.heappush(hp, e)
included = set()
included.add(0)
res = 0
while hp:
v, lst, nxt = heapq.heappop(hp)
if nxt not in included and edge[nxt] < threshold:
edge[nxt] += 1
included.add(nxt)
for e in adj[nxt]:
heapq.heappush(hp, e)
res = max(res, v)
return res if len(included) == n else -1
```
| 0 | 0 |
['Python3']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
C++ solution
|
c-solution-by-csld-k71d
|
SolutionThe goal of this problem is to minimize the maximum edge weight in a directed weighted graph while ensuring that node 0 remains reachable from all other
|
csld
|
NORMAL
|
2025-02-01T02:47:28.749110+00:00
|
2025-02-01T02:47:28.749110+00:00
| 7 | false |
# Solution
The goal of this problem is to minimize the maximum edge weight in a directed weighted graph while ensuring that node 0 remains reachable from all other nodes and that each node has at most threshold outgoing edges. To achieve this, we may need to remove some edges while maintaining connectivity.
To approach this problem efficiently, we utilize binary search on the maximum edge weight. First, we determine the range of possible maximum edge weights, which spans from the smallest weight in the graph to the largest weight among all edges. We then perform a binary search within this range.
For each candidate weight in our binary search, we attempt to construct a valid graph by removing all edges whose weights exceed the current candidate value. Once we prune the graph in this way, we check whether all nodes can still reach node 0 while respecting the threshold constraint on outgoing edges. If the graph remains valid, it means we might be able to minimize the maximum edge weight further, so we decrease the search range and test with an even smaller weight. However, if the graph becomes disconnected, we must increase the search range to allow for heavier edges.
For example, if we test with a maximum edge weight of 5 and find that it is possible to satisfy all constraints by removing all edges heavier than 5, we then try a lower value, such as 3, to check if we can further reduce the maximum weight. If reducing the threshold further disconnects the graph, we know that 3 is too restrictive, so we must increase the limit to restore connectivity.
By performing this binary search on the maximum edge weight, we efficiently determine the smallest possible value that allows all conditions to be met. This approach ensures that we don’t need to test every possible weight manually, significantly optimizing the solution.
# Trick
Notice that I try to check if a graph is valid using a reverse graph. In this case, the threshold variable is useless, so this is the trick here. Good day.
# Code
```cpp []
using pii = pair<int, int>;
class Solution {
public:
bool isValid(int n, int maxW, int threshold, vector<vector<int>>& edges) {
vector<vector<int>> rev(n);
for (auto& edge : edges) {
int u = edge[0], v = edge[1], w = edge[2];
if (w <= maxW) {
rev[v].push_back(u);
}
}
vector<bool> visited(n, false);
queue<int> q;
q.push(0);
visited[0] = true;
while (!q.empty()) {
int u = q.front();
q.pop();
for (int v : rev[u]) {
if (!visited[v]) {
visited[v] = true;
q.push(v);
}
}
}
for (int i = 0; i < n; i++) {
if (!visited[i]) {
return false;
}
}
return true;
}
int minMaxWeight(int n, vector<vector<int>>& edges, int threshold) {
int left = 0, right = 0;
for (auto& e : edges) {
right = max(right, e[2]);
}
int res = -1;
while (left <= right) {
int mid = (left + right) / 2;
if (isValid(n, mid, threshold, edges)) {
res = mid;
right = mid - 1;
} else {
left = mid + 1;
}
}
return res;
}
};
```
| 0 | 0 |
['C++']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
Python Binary Search O(NlogN) "threshold" is smokescreen
|
python-binary-search-onlogn-threshold-is-bked
|
Intuitionthreshold is there to confuse you and nothing else. Why? Because we just need to pick 1 outgoing edge from any nodes at most to meet all the requiremen
|
etherwei
|
NORMAL
|
2025-01-28T05:25:34.151226+00:00
|
2025-01-28T05:25:34.151226+00:00
| 6 | false |
# Intuition
`threshold` is there to confuse you and nothing else. Why? Because we just need to pick 1 outgoing edge from any nodes at most to meet all the requirements.
Proof is that if we have `[node_A, node_C, weight_0]` and `[node_B, node_C, weight_1]`, we just need one of these two edges because:
1. whether `node_A, node_B` can be reached from `0` has nothing to do with `node_B`, so whichever edge we pick won't affect any edges we pick for `node_A, node_B`.
2. This means `node_A, node_B` mus be reachable from `0` by some other edges and it also means, regardless of which edge we pick here for `node_C`, `node_C` will be rechable from `0`.
3. Hence we just need to pick the edge that satisifies `weight_x < max_weight`
# Approach
Binary search.
# Complexity
- Time complexity:
O(NlogN)
- Space complexity:
O(N)
# Code
```python3 []
class Solution:
def minMaxWeight(self, n: int, edges: List[List[int]], threshold: int) -> int:
graph = [[] for _ in range(n)]
for e in edges:
# flip the edge
graph[e[1]].append((e[0], e[2]))
def check(weight):
stack = [0]
seen = [False] * n
seen[0] = True
while stack:
node = stack.pop(-1)
for nei, w in graph[node]:
if seen[nei]: continue
if w > weight: continue
seen[nei] = True
stack.append(nei)
return seen.count(False) == 0
max_edge = max(e[2] for e in edges)
left, right = 1, max_edge
while left <= right:
mid = (left + right) // 2
if check(mid):
right = mid - 1
else:
left = mid + 1
if left > max_edge: return -1
else: return left
```
| 0 | 0 |
['Python3']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
modified Dijkstra
|
modified-dijkstra-by-user5285zn-73dy
| null |
user5285Zn
|
NORMAL
|
2025-01-27T16:13:27.211781+00:00
|
2025-01-27T16:13:27.211781+00:00
| 6 | false |
```rust []
use std::collections::{BinaryHeap, HashMap, HashSet};
use std::cmp::Reverse;
impl Solution {
pub fn min_max_weight(n: i32, mut edges: Vec<Vec<i32>>, threshold: i32) -> i32 {
let n = n as usize;
let mut ad = HashMap::<usize, Vec<(usize, i32)>>::new();
for e in edges.into_iter() {
let u = e[0] as usize;
let v = e[1] as usize;
let w = e[2];
ad.entry(v).or_default().push((u, w));
}
let mut seen = vec![i32::MAX; n];
let mut nuse = vec![0; n];
let mut q = BinaryHeap::new();
for &(y, g) in ad.get(&0).unwrap_or(&vec![]).iter() {
q.push((Reverse(g), 0, y));
}
if q.is_empty() {return -1}
let mut w = 0;
seen[0] = 0;
let mut connected = HashSet::new();
connected.insert(0);
while let Some((Reverse(ww), x, y)) = q.pop() {
if nuse[y] == threshold {continue}
nuse[y] += 1;
connected.insert(y);
w = w.max(ww);
if connected.len() == n {break}
for &(z, g) in ad.get(&y).unwrap_or(&vec![]).iter() {
if g < seen[z] {
seen[z] = g;
q.push((Reverse(g), y, z))
}
}
}
if connected.len() < n {return -1}
w
}
}
```
| 0 | 0 |
['Rust']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
faster than 70% || easy solution c++ || ignore threshold with explanation
|
faster-than-70-easy-solution-c-ignore-th-ye7i
|
Explanationwe dont need to consider threshold because lets say there is a directed edge between a and b it is useful only when it is reachable to node 0 else we
|
__a__j
|
NORMAL
|
2025-01-25T08:59:08.571020+00:00
|
2025-01-25T08:59:08.571020+00:00
| 8 | false |
# Explanation
we dont need to consider threshold because lets say there is a directed edge between a and b it is useful only when it is reachable to node 0 else we can remove it, now the question boils down to finding minimum wt so that all the weight present in the graph are less than or equal to the wt and from every node we can reach zero, this we can do with binary search.
# Code
```cpp []
class Solution {
public:
int ans = INT_MAX;
bool good(int mid, int n, int th, vector<vector<pair<int, int>>>& graph) {
vector<bool> vis(n, false);
queue<int> qu;
qu.push(0);
while (!qu.empty()) {
int top = qu.front();
qu.pop();
if (vis[top]) {
continue;
}
vis[top] = true;
for (auto& nb : graph[top]) {
if (!vis[nb.first] and nb.second <= mid) {
qu.push(nb.first);
}
}
}
for (int i = 1; i < n; i++) {
if (not vis[i]) {
return false;
}
}
return true;
}
int minMaxWeight(int n, vector<vector<int>>& edges, int threshold) {
int lo = 0, hi = 0;
vector<vector<pair<int, int>>> graph(n);
for (auto& edge : edges) {
int a = edge[0];
int b = edge[1];
int wt = edge[2];
graph[b].push_back({a, wt});
hi = max(hi, edge[2]);
}
int res = -1;
while (lo <= hi) {
int mid = (lo + hi) / 2;
if (good(mid, n, threshold, graph)) {
hi = mid - 1;
res = mid;
} else {
lo = mid + 1;
}
}
if (res == -1)
return -1;
return res;
// we dont need to consider threshold because lets say there is a directed edge between a and b it is useful only when it is reachable to node 0 else we can remove it
}
};
```
| 0 | 0 |
['C++']
| 1 |
minimize-the-maximum-edge-weight-of-graph
|
Java Solution Build Graph Reversely + Binary Search for Edge Weight, Start from 0
|
java-solution-build-graph-reversely-bina-o1q7
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
ndsjqwbbb
|
NORMAL
|
2025-01-23T00:50:37.182629+00:00
|
2025-01-23T00:50:37.182629+00:00
| 5 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int minMaxWeight(int n, int[][] edges, int threshold) {
Map<Integer, List<int[]>> map = new HashMap<>();
int minedge = Integer.MAX_VALUE;
int maxedge = Integer.MIN_VALUE;
for(int[] edge : edges){
int from = edge[0];
int to = edge[1];
int weight = edge[2];
minedge = Math.min(weight, minedge);
maxedge = Math.max(weight, maxedge);
map.putIfAbsent(to, new ArrayList<>());
map.get(to).add(new int[]{from, weight});
}
int left = minedge;
int right = maxedge;
int result = Integer.MAX_VALUE;
while(left <= right){
int mid = left + (right - left) / 2;
Set<Integer> visited = new HashSet<>();
helper(visited, mid, map, 0);
if(visited.size() == n){
result = Math.min(result, mid);
right = mid - 1;
}
else{
left = mid + 1;
}
}
return result == Integer.MAX_VALUE ? -1 : result;
}
private void helper(Set<Integer> visited, int maxweight, Map<Integer, List<int[]>> map, int node){
if(visited.contains(node)){
return;
}
visited.add(node);
List<int[]> neighbors = map.get(node);
if(neighbors == null){
return;
}
for(int[] nei : neighbors){
if(nei[1] > maxweight){
continue;
}
int nextnode = nei[0];
helper(visited, maxweight, map, nextnode);
}
}
}
```
| 0 | 0 |
['Java']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
Easy Java Solution || Dijkstra || Shortest Path || Ignore Threshold
|
easy-java-solution-dijkstra-shortest-pat-l0yg
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
ravikumar50
|
NORMAL
|
2025-01-22T17:36:28.535852+00:00
|
2025-01-22T17:36:28.535852+00:00
| 6 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
static ArrayList<int[]> graph[];
static int findWeight(int n, int threshold){
PriorityQueue<int[]> pq = new PriorityQueue<>((a,b)->a[1]-b[1]);
pq.add(new int[]{0,0});
int vis[] = new int[n];
vis[0] = 1;
int nodeWeight[] = new int[n];
Arrays.fill(nodeWeight,(int)1e9);
nodeWeight[0] = 0;
int maxWeight = 0;
while(pq.size()!=0){
int curr[] = pq.remove();
int node = curr[0];
int wt = curr[1];
// System.out.println(node+" "+wt);
if(vis[node]!=1) maxWeight = Math.max(maxWeight,wt);
vis[node] = 1;
for(var child : graph[node]){
if(vis[child[0]]==0 && nodeWeight[child[0]]>child[1]){
nodeWeight[child[0]] = child[1];
pq.add(new int[]{child[0],child[1]});
}
}
}
// for(int i=0; i<n; i++){
// System.out.println(vis[i]+" "+nodeWeight[i]);
// }
for(int i=0; i<n; i++){
if(vis[i]==0) return -1;
}
return maxWeight;
}
public int minMaxWeight(int n, int[][] edges, int threshold) {
graph = new ArrayList[n];
for(int i=0; i<n; i++){
graph[i] = new ArrayList<>();
}
for(var e : edges){
int st = e[0];
int end = e[1];
int wt = e[2];
graph[end].add(new int[]{st,wt});
}
return findWeight(n,threshold);
}
}
```
| 0 | 0 |
['Java']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
Reverse Edges // Beats 97% runtime // cpp // java
|
reverse-edges-beats-97-runtime-cpp-java-xc9dh
|
IntuitionIf we draw some graphs , we observe that we don't really need threshold value given in the question . As per my observation best possible answer will h
|
BellmanFord_25
|
NORMAL
|
2025-01-19T04:39:18.927010+00:00
|
2025-01-19T04:39:18.927010+00:00
| 11 | false |
# Intuition
If we draw some graphs , we observe that we don't really need threshold value given in the question . As per my observation best possible answer will have threshold value = 1 .
Now we need minimum possible value of the maximum edge from each node all the way to 0.So one way is we start from each node like 1,2,3,....,n-1 and go all the way to 0 and during each time we can store the max edge wt in res variable.This is actually possible but will give tle as its tc will go around O(N*N*log(N)) ( approx . )
Another way is to basically reverse the edges so our que changes to minimum possible value of the maximum edge starting from 0 to each node.
Below is the code of modified dikstra.Code explanation i will provide in comments.
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
O(E*log(N))
- Space complexity:
# Code
```cpp []
class Solution {
public:
int minMaxWeight(int n, vector<vector<int>>& edges, int threshold) {
vector<vector<pair<int,int>>> graph(n);
for(int i=0 ; i<edges.size() ; i++){
int u = edges[i][0];
int v = edges[i][1];
int wt = edges[i][2];
graph[v].push_back({u,wt}); // reversing the graph v->u
}
vector<int> edge(n, INT_MAX);// it stores the min possible val of the max edge wt from 0 to that node.
edge[0] = 0;// reaching 0 from 0 cost 0.
priority_queue<pair<int,int>,vector<pair<int,int>> , greater<pair<int,int>>> pq;
pq.push({0,0}); //{wt , u}
while(!pq.empty()){
auto [wt,u] = pq.top();pq.pop();
if(edge[u] < wt) continue;// this is optimization step ,
// (5,2) is already in pq , now if further this edge[2] got updated to 3 , so pq will have (3,2) . so if after that this (5,2) appears then we should not do further calulations based on this data as a better data (3,2) is aleady in the pq.
for(int i=0 ; i<graph[u].size() ; i++){
int v = graph[u][i].first;
int w = graph[u][i].second;
// ok , so here let suppose u = 1 and v = 2.So we are going to 2 via 1
// wt is 2 and w is 1 , it means to reach 1 we need min of max edge wt as 2 and to reach 1 to 2 we have edge w as 1 , so if we are considering this edge to actually go to 2 via 1 , we need to put edge[2] = max(1,2).
if(max(w,wt) < edge[v]){
edge[v] = max(w,wt);
pq.push({edge[v],v});
}
}
}
int res = INT_MIN;
for(int i=0 ; i<n ; i++){
res = max(res,edge[i]);
}
return res == INT_MAX?-1:res;
}
};
// Hope it helps.
```
| 0 | 0 |
['C++']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
Binary Search With BFS Algorithm. Simple And Easy to Understand
|
binary-search-with-bfs-algorithm-simple-60uz3
|
IntuitionThe idea is to find a weight at which all the three constraints can be satisfied. Using Linear Search and BFS or Binary Search with BFS works but since
|
varunkus
|
NORMAL
|
2025-01-18T08:30:35.131807+00:00
|
2025-01-18T08:30:35.131807+00:00
| 12 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The idea is to find a weight at which all the three constraints can be satisfied. Using Linear Search and BFS or Binary Search with BFS works but since Binary Search with BFS has better time complexity, below solution is for Binary Search with BFS Algorithm
# Approach
<!-- Describe your approach to solving the problem. -->
1. The Approach here is to identify a minimum weight at which all the nodes can reach to node 0
2. Another thing we need to consider is that there will be N-1 nodes which will reach to node 0
3. Since we are given with a directed graph and we need to reach node 0 from all the n-1 nodes
4. If we will find a path from a node to node 0, we need to use BFS/DFS with complexity O(V+E), which means for all N-1 nodes complexity will become (N)*O(N + E). After that if we use linear search or binary search to find the minimum weight then complexity will increase to (N)\*(N+E)\*min(log Wt, Wt)
5. Instead of Doing above, we can reverse the direction of the edges and instead of finding path from each node to node 0 we will find path from node 0 to all other nodes.
With this Approach we will be doing one bfs that ( N + E) and overall complexity would be ( log Wt)*(N+E)
# Complexity
- Time complexity:O( (Log W)*(N+E) )
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:O(N)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
//This routine creates adjacency matrix of nodes and edges which has weight less than or qual to maximumWeight
//This Adjacency Marix is created with reverse direction from actual given in input
//It then uses BFS Algoithm to check if all the nodes can be traversed at this weight or not
bool IsItPossible(int n, vector<vector<int>>& edges, int maximumWeight) {
vector<vector<int>> graph(n);
for(int i = 0; i < edges.size(); i++) {
if( edges[i][2] <= maximumWeight)
graph[edges[i][1]].push_back(edges[i][0]);
}
//BFS Algorithm
queue<int> q;
q.push(0);
vector<bool> visited(n, false);
int count = 1; //Count = 1 since 0 is always considered
visited[0] = true;
while(q.size() != 0) {
int node = q.front();
q.pop();
for(auto& nbr : graph[node]) {
if(visited[nbr] == false ) {
q.push(nbr);
visited[nbr] = true;
count++;
}
}
}
return count == n; //Checks if the count is equal to all the n nodes
}
int minMaxWeight(int n, vector<vector<int>>& edges, int threshold) {
//Calculate the Min and Max weight from the given graph
int minWt = INT_MAX, maxWt = INT_MIN;
for(int i = 0; i < edges.size(); i++) {
minWt = min(minWt, edges[i][2]);
maxWt = max(maxWt, edges[i][2]);
}
//We can use either linear search or binary search to identify the minimum weight
//If we will go with linear search it will increase the complexity
//Let's try Binary Search Approach with search space as Min and Max Weight
//This Algo is similar to Painter's Problem in Binary Search
int left = minWt, right = maxWt, ans = -1;
while( left <= right ) {
int mid = ( left + right ) / 2;
bool res = IsItPossible(n, edges, mid);
if( res ) {
ans = mid;
right = mid - 1;
}
else {
left = mid + 1;
}
}
return ans;
}
};
```
| 0 | 0 |
['Binary Search', 'Breadth-First Search', 'Graph', 'C++']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
Heap / MST Approach
|
heap-mst-approach-by-bhavya45-rp03
|
Heap / MST ApproachCode
|
Bhavya45
|
NORMAL
|
2025-01-17T10:49:11.026857+00:00
|
2025-01-17T10:49:11.026857+00:00
| 12 | false |
# Heap / MST Approach
# Code
```cpp []
class Solution {
public:
int minMaxWeight(int n, vector<vector<int>>& edges, int threshold) {
vector<vector<pair<int,int>>>adj(n);
for(int i = 0;i < edges.size();i++) {
adj[edges[i][1]].push_back({edges[i][0],edges[i][2]});
}
vector<int>out(n); vector<int>visited(n);
priority_queue<pair<int,int>,vector<pair<int,int>>,greater<pair<int,int>>>pq;
pq.push({0,0});
int maxi = 0;
while(!pq.empty()) {
int wt = pq.top().first; int node = pq.top().second; pq.pop();
if(visited[node]) continue;
visited[node] = 1;
maxi = max(maxi,wt);
for(auto it:adj[node]) {
if(!visited[it.first] && out[it.first] <= threshold) {
// out[it]++;
pq.push({it.second,it.first});
}
}
}
for(int i = 0;i < n;i++) {
if(visited[i] == 0) return -1;
}
return maxi;
}
};
```
| 0 | 0 |
['C++']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
Rust Solution
|
rust-solution-by-abhineetraj1-o409
|
IntuitionThe problem asks to find the minimum maximum weight of the edges such that there exists a path from node 0 to all other nodes, where the weight of the
|
abhineetraj1
|
NORMAL
|
2025-01-17T00:35:25.163856+00:00
|
2025-01-17T00:35:25.163856+00:00
| 2 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The problem asks to find the minimum maximum weight of the edges such that there exists a path from node 0 to all other nodes, where the weight of the edges on the path does not exceed a certain threshold. This can be thought of as a graph traversal problem, where we need to determine the smallest possible maximum edge weight that allows traversal from node 0 to all other nodes.
# Approach
<!-- Describe your approach to solving the problem. -->
Graph Representation: We represent the graph using an adjacency list, where each node stores a list of its neighbors and the weight of the edge connecting them. Each edge is represented as a tuple (neighbor, weight).
Binary Search: We perform a binary search on the edge weights. The search range is from the smallest edge weight (mini) to the largest edge weight (maxi) found in the input edges. This helps us minimize the maximum edge weight while ensuring that all nodes are reachable from node 0.
DFS for Connectivity Check: For each mid-point value during the binary search, we check if it's possible to reach all nodes starting from node 0 using edges that do not exceed the current mid-point weight. This is done via a Depth First Search (DFS) traversal, where we only explore edges whose weight is less than or equal to the current mid-point.
Updating Binary Search Range: If it's possible to visit all nodes with the current mid-point weight, we try to find a smaller possible maximum weight by narrowing the search to the lower half. Otherwise, we increase the search range to check larger edge weights.
Termination: The binary search terminates when the search space is exhausted, and the smallest valid maximum edge weight is the answer.
# Complexity
- Time complexity: O(logW⋅(n+e))
W is the range of edge weights (from mini to maxi)
n is the number of nodes
e is the number of edges
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(n+e)
n is the number of nodes
e is the number of edges
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```rust []
impl Solution {
fn dfs(src: usize, adj: &Vec<Vec<(usize, i32)>>, vis: &mut Vec<bool>, mid: i32) {
vis[src] = true;
for &(neighbor, weight) in &adj[src] {
if !vis[neighbor] && weight <= mid {
Self::dfs(neighbor, adj, vis, mid);
}
}
}
fn check(src: usize, adj: &Vec<Vec<(usize, i32)>>, mid: i32, n: usize) -> bool {
let mut vis = vec![false; n];
Self::dfs(src, adj, &mut vis, mid);
vis.iter().all(|&v| v)
}
pub fn min_max_weight(n: i32, edges: Vec<Vec<i32>>, threshold: i32) -> i32 {
let n = n as usize;
let mut adj = vec![vec![]; n];
let mut mini = i32::MAX;
let mut maxi = i32::MIN;
for edge in edges {
let u = edge[0] as usize;
let v = edge[1] as usize;
let w = edge[2];
adj[v].push((u, w));
mini = mini.min(w);
maxi = maxi.max(w);
}
let mut low = mini;
let mut high = maxi;
let mut ans = -1;
while low <= high {
let mid = low + (high - low) / 2;
if Self::check(0, &adj, mid, n) {
ans = mid;
high = mid - 1;
} else {
low = mid + 1;
}
}
ans
}
}
```
| 0 | 0 |
['Binary Search', 'Depth-First Search', 'Graph', 'Rust']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
Djiskira's
|
djiskiras-by-user0782rf-qhma
|
IntuitionIf I reach an edge a node , and the maximum of the path so far, or the edge connecting it to next edge is less than the maximum at the current node, th
|
user0782Rf
|
NORMAL
|
2025-01-15T19:38:26.798643+00:00
|
2025-01-15T19:38:26.798643+00:00
| 3 | false |
# Intuition
If I reach an edge a node , and the maximum of the path so far, or the edge connecting it to next edge is less than the maximum at the current node, then relax. Basically Djiskira's with max edge as the min distance counter.
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def minMaxWeight(self, n: int, edges: List[List[int]], threshold: int) -> int:
'''
Approach. Find all the nodes that are incident to the nodes you have currently. At first the starting node.
If there is a node adhacent to two of them, remove the edge with max weight
keep track of the max distance edge in the graph
'''
graph = defaultdict(list)
for u, v, w in edges:
graph[v] += [(u, w)]
heap = [(0, 0)]
maximum = [float('inf')] * n
maximum[0] = 0
to_return = 0
while heap:
weight, node = heapq.heappop(heap)
if weight > maximum[node]:
continue
for node_, weight_ in graph[node]:
new_max = max(maximum[node], weight_)
if new_max < maximum[node_]:
maximum[node_] = new_max
heapq.heappush(heap, (new_max, node_))
returning = max(maximum[1:])
return returning if returning != float('inf') else -1
```
| 0 | 0 |
['Python3']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
Python Easiest Solution
|
python-easiest-solution-by-yashika_174-yzfs
|
Help From:Code
|
Yashika_174
|
NORMAL
|
2025-01-15T13:48:38.747504+00:00
|
2025-01-15T13:48:38.747504+00:00
| 13 | false |
# Help From:
https://youtu.be/DXinKbQQDVE?si=Jk6FSGObSbAmautH
# Code
```python3 []
class Solution:
def minMaxWeight(self, n: int, edges: List[List[int]], threshold: int) -> int:
def isAccepted(weight):
newArr=[[] for i in range(n)]
for i in edges:
src,dest,wt=i[0],i[1],i[2]
# print("yo",src,dest,wt)
if wt<=weight:
newArr[dest].append([wt,src])
# print("newArr",newArr,weight)
queue=deque()
queue.append(0)
visited=[0 for i in range(n)]
count=0
while queue:
# print(queue)
node=queue.popleft()
if visited[node]:
continue
visited[node]=1
count+=1
if newArr[node]:
for (w,neigh) in newArr[node]:
if not visited[neigh]:
queue.append(neigh)
# print("count",count)
return count==n
mini=math.inf
maxi=-math.inf
for i in range(len(edges)):
mini=min(mini,edges[i][2])
maxi=max(maxi,edges[i][2])
arr=[]
for i in edges:
arr.append(i[2])
arr.sort()
# print("arr",arr)
low=0
high=len(arr)-1
ans=-1
# print("hey",mini,maxi)
while (low<=high):
mid=(low+high)//2
if isAccepted(arr[mid]):
ans=arr[mid]
high=mid-1
else:
low=mid+1
return ans
```
| 0 | 0 |
['Binary Search', 'Breadth-First Search', 'Graph', 'Shortest Path', 'Python3']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
Javascript | Prim | O(V+E)
|
javascript-prim-ove-by-aryonbe-2lbd
|
Code
|
aryonbe
|
NORMAL
|
2025-01-15T07:06:29.446210+00:00
|
2025-01-15T07:06:29.446210+00:00
| 8 | false |
# Code
```javascript []
/**
* @param {number} n
* @param {number[][]} edges
* @param {number} threshold
* @return {number}
*/
var minMaxWeight = function(n, edges, threshold) {
const G = Array(n).fill(0).map(()=>new Map());
for(const [u,v,w] of edges)
G[v].set(u, Math.min(G[v].get(u) ?? Infinity, w));
let res = 0;
const pq = new PriorityQueue({compare: (x,y) => x[0] - y[0]});
pq.enqueue([0,0]);
const visited = new Set();
while(pq.size()){
const [w, u] = pq.dequeue();
if(visited.has(u)) continue;
res = Math.max(res, w);
visited.add(u);
for(const [v, w] of G[u]){
pq.enqueue([w,v]);
}
}
console.log("check", visited.size);
return visited.size === n ? res : -1;
};
```
| 0 | 0 |
['JavaScript']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
Java | Prim | O(V+E)
|
java-prim-ove-by-aryonbe-wxav
|
Code
|
aryonbe
|
NORMAL
|
2025-01-15T06:37:41.081002+00:00
|
2025-01-15T06:37:41.081002+00:00
| 9 | false |
# Code
```java []
class Solution {
public int minMaxWeight(int n, int[][] edges, int threshold) {
Map<Integer, Integer>[] G = new Map[n];
for(int i = 0; i < n; ++i)
G[i] = new HashMap<>();
for(var e: edges){
int u = e[0], v = e[1], w = e[2];
G[v].put(u, Math.min(G[v].getOrDefault(u,Integer.MAX_VALUE),w));
}
int res = 0;
Queue<int[]> pq = new PriorityQueue<>((x,y) -> Integer.compare(x[0], y[0]));
pq.add(new int[]{0,0});
Set<Integer> visited = new HashSet<>();
while(!pq.isEmpty()){
var e = pq.poll();
int w = e[0], u = e[1];
if(visited.contains(u)) continue;
visited.add(u);
res = Math.max(res, w);
for(var v: G[u].keySet()){
w = G[u].get(v);
pq.add(new int[]{w, v});
}
}
return visited.size() == n ? res : -1;
}
}
```
| 0 | 0 |
['Java']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
[CODE ONLY] PYTHON USING Chaman Rawat's BFS HEAP SOLUTION
|
code-only-python-using-chaman-rawats-bfs-ous6
|
Code
|
greg_savage
|
NORMAL
|
2025-01-15T01:51:15.764579+00:00
|
2025-01-15T01:59:41.682970+00:00
| 5 | false |
# Code
```python3 []
# Using Chaman Rawat's solution...
# LINK: https://leetcode.com/problems/minimize-the-maximum-edge-weight-of-graph/solutions/6267672/finding-shortest-paths-in-a-reversed-gra-nmza
class Solution:
def minMaxWeight(self, n: int, edges: List[List[int]], threshold: int) -> int:
children_to_parents = defaultdict(list)
is_reachable = set()
def makeNodesToChildren(edge_graph: List[List[int]]) -> dict[int, tuple[int, int]]:
for each_edge in edge_graph:
parent, child, weight = each_edge
parent_pair = (parent, weight) # node, weight
children_to_parents[child].append(parent_pair)
return children_to_parents
makeNodesToChildren(edges)
max_visited_weight = 0
node_is_checked = set()
smallest_weights_heap = [(0, 0)]
while smallest_weights_heap:
weight, node = heappop(smallest_weights_heap)
if node in node_is_checked:
continue
node_is_checked.add(node)
max_visited_weight = max(max_visited_weight, weight)
for each_parent, each_weight in children_to_parents[node]:
heappush(smallest_weights_heap, (each_weight, each_parent) )
if len(node_is_checked) == n:
return max_visited_weight
return -1
```
| 0 | 0 |
['Python3']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
Heap vs Binary Search | C++
|
heap-vs-binary-search-c-by-chariotofligh-s7s9
|
1.2 Greedy (Heap) using std::priority_queue
1.2 Greedy (Heap) using std::vector
2.1 BinSearch + BFS using std::queue
2.2 BinSearch + DFS using std::stack
|
chariotoflight
|
NORMAL
|
2025-01-14T21:22:24.074391+00:00
|
2025-01-14T21:22:24.074391+00:00
| 12 | false |
$1.2$ Greedy (Heap) using `std::priority_queue`
$1.2$ Greedy (Heap) using `std::vector`
$2.1$ BinSearch + $BFS$ using `std::queue`
$2.2$ BinSearch + $DFS$ using `std::stack`
```C++ [1.1]
class Solution {
public:
int minMaxWeight(int n, std::vector<std::vector<int>> &edges, int threshold) {
using info = std::array<int, 2>;
std::vector graph(n, std::vector<info>());
for(std::vector<int> &edge: edges) std::swap(edge[0], edge[1]);
for(std::vector<int> &edge: edges) {
int u = edge[0], v = edge[1], w = edge[2];
graph[u].push_back({v, w});
}
auto cmp = [](info &e1, info &e2) { return e1[1] > e2[1]; };
std::priority_queue<info, std::vector<info>, decltype(cmp)> PQ(cmp);
for(info &edge: graph[0]) PQ.push(edge);
std::vector<bool> visit(n, 0); visit[0] = 1;
int maxwt = 0;
while(!PQ.empty()) {
if(PQ.empty()) break;
auto [node, wt] = PQ.top(); PQ.pop();
if(visit[node]) continue;
visit[node] = 1;
maxwt = std::max(maxwt, wt);
for(info &edge: graph[node]) PQ.push(edge);
}
return std::count(visit.begin(), visit.end(), 0) == 0? maxwt: -1;
}
};
```
```C++ [1.2]
class Solution {
public:
int minMaxWeight(int n, std::vector<std::vector<int>> &edges, int thresh) {
using info = std::array<int, 2>;
std::vector graph(n, std::vector<info>());
for(std::vector<int> &edge: edges) std::swap(edge[0], edge[1]);
for(std::vector<int> &edge: edges) {
int u = edge[0], v = edge[1], w = edge[2];
graph[u].push_back({v, w});
}
auto cmp = [](info &e1, info &e2) { return e1[1] > e2[1]; };
std::vector<info> heap;
for(info &edge: graph[0]) heap.push_back(edge);
std::make_heap(heap.begin(), heap.end(), cmp);
std::vector<bool> visit(n, 0); visit[0] = 1;
int maxwt = 0;
while(!heap.empty()) {
std::pop_heap(heap.begin(), heap.end(), cmp);
auto [node, wt] = heap.back(); heap.pop_back();
if(visit[node]) continue;
visit[node] = true;
maxwt = std::max(maxwt, wt);
for(info &edge: graph[node]) {
heap.push_back(edge);
std::push_heap(heap.begin(), heap.end(), cmp);
}
}
return std::count(visit.begin(), visit.end(), 0) == 0? maxwt : -1;
}
};
```
```C++ [2.1]
class Solution {
public:
int minMaxWeight(int n, std::vector<std::vector<int>>& edges, int threshold) {
using info = std::array<int, 2>;
std::vector graph(n, std::vector<info>());
for(std::vector<int> &edge: edges) std::swap(edge[0], edge[1]);
for(std::vector<int> &edge: edges) {
int u = edge[0], v = edge[1], w = edge[2];
graph[u].push_back({v, w});
}
auto cmp = [](const auto &e1, const auto &e2) { return e1[2] < e2[2]; };
int minweight = (*std::min_element(edges.begin(), edges.end(), cmp))[2];
int maxweight = (*std::max_element(edges.begin(), edges.end(), cmp))[2];
auto bfs = [&](int m) -> bool {
std::vector<bool> visit(n, 0);
std::queue<int> qu;
visit[0] = 1; qu.push(0);
while(!qu.empty()) {
int cur = qu.front();
qu.pop();
for(info &next: graph[cur]) {
if(next[1] > m or visit[next[0]]) continue;
visit[next[0]] = 1;
qu.push(next[0]);
}
}
return std::count(visit.begin(), visit.end(), 1) == n? 1: 0;
};
int lo = minweight + 0, hi = maxweight + 1;
int answer = -1;
while(lo < hi) {
int mid = (lo + hi) >> 1;
if(bfs(mid)) {
answer = (answer == -1)? mid: std::min(answer, mid);
hi = mid;
}
else lo = mid + 1;
}
return answer;
}
};
```
```C++ [2.2]
class Solution {
public:
int minMaxWeight(int n, std::vector<std::vector<int>>& edges, int threshold) {
using info = std::array<int, 2>;
std::vector graph(n, std::vector<info>());
for(std::vector<int> &edge: edges) std::swap(edge[0], edge[1]);
for(std::vector<int> &edge: edges) {
int u = edge[0], v = edge[1], w = edge[2];
graph[u].push_back({v, w});
}
auto cmp = [](const auto &e1, const auto &e2) { return e1[2] < e2[2]; };
int minweight = (*std::min_element(edges.begin(), edges.end(), cmp))[2];
int maxweight = (*std::max_element(edges.begin(), edges.end(), cmp))[2];
auto dfs = [&](int m) -> bool {
std::vector<bool> visit(n, 0);
std::stack<int> st;
visit[0] = 1; st.push(0);
while(!st.empty()) {
int cur = st.top();
st.pop();
for(info &next: graph[cur]) {
if(next[1] > m or visit[next[0]]) continue;
visit[next[0]] = 1;
st.push(next[0]);
}
}
return std::count(visit.begin(), visit.end(), 1) == n? 1: 0;
};
int lo = minweight + 0, hi = maxweight + 1;
int answer = -1;
while(lo < hi) {
int mid = (lo + hi) >> 1;
if(dfs(mid)) {
answer = (answer == -1)? mid: std::min(answer, mid);
hi = mid;
}
else lo = mid + 1;
}
return answer;
}
};
```
| 0 | 0 |
['Binary Search', 'Graph', 'Heap (Priority Queue)', 'C++']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
PriorityQueue
|
priorityqueue-by-linda2024-lrhl
|
IntuitionIgnore thresholdApproachComplexity
Time complexity:
Space complexity:
Code
|
linda2024
|
NORMAL
|
2025-01-14T20:53:46.212098+00:00
|
2025-01-14T20:53:46.212098+00:00
| 19 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Ignore threshold
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```csharp []
public class Solution {
public int MinMaxWeight(int n, int[][] edges, int threshold) {
List<(int, int)>[] adjW = new List<(int, int)>[n];
// Build adjecent
for (int i = 0; i < n; i++)
{
adjW[i] = new List<(int, int)>();
}
foreach (int[] edge in edges)
{
int from = edge[0], to = edge[1], w = edge[2];
adjW[from].Add((to, w));
}
for (int i = 0; i < n; i++)
{
int cnt = adjW[i].Count;
if (i > 0 && cnt == 0)
return -1;
}
Dictionary<int, int> dp = new();
int maxW = 0;
for (int i = 1; i < n; i++)
{
// BFS from i to 0
PriorityQueue<int, int> pq = new();
int minW = int.MaxValue;
pq.Enqueue(i, 0);
HashSet<int> visited = new();
while (pq.TryDequeue(out int node, out int w))
{
if(w > minW)
continue;
if (node == 0)
{
minW = w;
break;
}
if (dp.ContainsKey(node))
{
minW = Math.Min(minW, Math.Max(w, dp[node]));
break;
}
visited.Add(node);
foreach (var nextN in adjW[node])
{
int nextNode = nextN.Item1, nextW = nextN.Item2;
if (visited.Contains(nextNode))
continue;
pq.Enqueue(nextNode, Math.Max(w, nextW));
}
}
if (minW == int.MaxValue)
return -1;
dp.Add(i, minW);
maxW = Math.Max(maxW, minW);
}
return maxW;
}
}
```
| 0 | 0 |
['C#']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
Binary Search + DFS
|
binary-search-dfs-by-enniggma-khkf
|
Code
|
AwakenX
|
NORMAL
|
2025-01-14T16:44:50.916926+00:00
|
2025-01-14T16:44:50.916926+00:00
| 10 | false |
# Code
```cpp []
class Solution {
public:
static bool cmp(vector<int> &edge1, vector<int> &edge2) {
return edge1[2] < edge2[2];
}
// Slight optimisation to find the right index with sorted edges
int find_index(int val, vector<vector<int>>& edges) {
auto it = std::upper_bound(edges.begin(), edges.end(), std::vector<int>{0, 0, val},
[](const std::vector<int>& a, const std::vector<int>& b) {
return a[2] < b[2];
});
if (it != edges.end()) {
int index = it - edges.begin();
return max(index - 1, 0);
} else {
return edges.size() - 1;
}
}
// Greedy DFS as we want to minimise the number of outgoing edges from each node
void dfs(int s, int par, vector<vector<int>>& adj, vector<int>& visited, vector<int>& outgoing, int& total) {
visited[s] = 1;
total++;
for(auto itr: adj[s]) {
if(visited[itr] == 0) {
outgoing[itr]++;
dfs(itr, s, adj, visited, outgoing, total);
}
}
}
bool isValid(int mid, int n, int threshold, vector<vector<int>>& edges) {
// Create a reverse graph for doing dfs from node 0
vector<vector<int>> rev(n);
int index = find_index(mid, edges);
for(int i = 0; i <= index; i++) {
if(edges[i][2] <= mid) {
rev[edges[i][1]].push_back(edges[i][0]);
}
}
vector<int>visited(n);
vector<int>outgoing(n, 0);
int total = 0;
dfs(0, -1, rev, visited, outgoing, total);
// Check if all nodes are covered in dfs
if(total < n) return false;
// check if all nodes have atmost threshold outgoing edges
for(int i = 0; i < n; i++) {
if(outgoing[i] > threshold) return false;
}
return true;
}
int minMaxWeight(int n, vector<vector<int>>& edges, int threshold) {
sort(edges.begin(), edges.end(), cmp);
int maxWeight = INT_MIN;
for(auto edge: edges) {
maxWeight = max(maxWeight, edge[2]);
}
int low = 0;
int high = maxWeight;
int ans = -1;
while(low <= high) {
int mid = low + (high - low) / 2;
if(isValid(mid, n, threshold, edges)) {
ans = mid;
high = mid - 1;
} else {
low = mid + 1;
}
}
return ans;
}
};
```
| 0 | 0 |
['C++']
| 0 |
minimize-the-maximum-edge-weight-of-graph
|
3419. Minimize the Maximum Edge Weight of Graph
|
3419-minimize-the-maximum-edge-weight-of-xkh7
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
G8xd0QPqTy
|
NORMAL
|
2025-01-14T16:36:51.786955+00:00
|
2025-01-14T16:36:51.786955+00:00
| 8 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
int minMaxWeight(int n, vector<vector<int>>& edges, int threshold) {
vector<vector<pair<int, int>>> graph(n);
for (const auto& edge : edges) {
if (edge[0] != 0) {
graph[edge[1]].emplace_back(edge[0], edge[2]);
}
}
unordered_set<int> visited;
visited.insert(0);
int result = 0;
using EdgeTuple = tuple<int, int, int>;
priority_queue<EdgeTuple, vector<EdgeTuple>, greater<>> pq;
for (const auto& edge : graph[0]) {
pq.push({edge.second, 0, edge.first});
}
while (visited.size() < n && !pq.empty()) {
auto [weight, start, end] = pq.top();
pq.pop();
if (visited.count(end)) continue;
visited.insert(end);
result = max(result, weight);
for (const auto& nextEdge : graph[end]) {
if (!visited.count(nextEdge.first)) {
pq.push({nextEdge.second, end, nextEdge.first});
}
}
}
return visited.size() == n ? result : -1;
}
};
```
| 0 | 0 |
['C++']
| 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.