question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
smallest-subtree-with-all-the-deepest-nodes
|
Simple Java dfs recursion function with explanation
|
simple-java-dfs-recursion-function-with-034s1
|
First Root to Leaf: return the deep level of every node\nThen Leaf to Root: only when the its left node and right node both have the deepthest level, update the
|
binglelove
|
NORMAL
|
2018-07-08T05:10:19.208163+00:00
|
2018-10-22T02:35:27.951058+00:00
| 5,823 | false |
First `Root` to `Leaf`: return the deep level of every node\nThen `Leaf` to `Root`: only when the its left node and right node both have the deepthest level, update the result node\n```Java\nclass Solution {\n \n int deepestLevel = 0;\n TreeNode res = null;\n \n public TreeNode subtreeWithAllDeepest(TreeNode root) {\n dfs(root, 0);\n return res;\n }\n \n private int dfs(TreeNode root, int level) {\n if (root == null) return level;\n \n int leftLevel = dfs(root.left, level + 1);\n int rightLevel = dfs(root.right, level + 1);\n \n int curLevel = Math.max(leftLevel, rightLevel);\n deepestLevel = Math.max(deepestLevel, curLevel);\n if (leftLevel == deepestLevel && rightLevel == deepestLevel)\n res = root;\n return curLevel;\n }\n}\n\n```
| 166 | 1 |
[]
| 21 |
smallest-subtree-with-all-the-deepest-nodes
|
C++ - Simple O(n) Solution with BFS+LCA with thought process explained
|
c-simple-on-solution-with-bfslca-with-th-12nb
|
The thought process goes like this - Find all deepest nodes by traversing the tree using BFS. The required node is nothing but the LCA of all the deepest nodes.
|
pavan5
|
NORMAL
|
2018-07-08T03:00:35.273997+00:00
|
2018-10-19T04:46:00.290470+00:00
| 5,225 | false |
The thought process goes like this - Find all deepest nodes by traversing the tree using BFS. The required node is nothing but the LCA of all the deepest nodes. Finding LCA of all nodes at the same level is equivalent to finding LCA of the `leftMost` and `rightMost` node. Keep track of `leftMost` and `rightMost` nodes while doing BFS and finally return their LCA.\n\n```\nclass Solution {\npublic:\n TreeNode* lca( TreeNode* root, TreeNode* p, TreeNode* q ) {\n if ( !root || root == p || root == q ) return root;\n TreeNode *left = lca( root->left, p, q );\n TreeNode *right = lca (root->right, p, q );\n\n return !left? right: !right? left: root;\n }\n \n TreeNode* subtreeWithAllDeepest(TreeNode* root) {\n if ( !root || !root->left && !root->right ) return root;\n TreeNode *leftMost = NULL;\n TreeNode *rightMost = NULL;\n \n queue<TreeNode*> q;\n q.push(root);\n while( !q.empty() ) {\n int levelSize = q.size();\n for(int level = 0; level < levelSize; level++ ) {\n TreeNode* node = q.front(); q.pop();\n if ( level == 0 ) leftMost = node;\n if ( level == levelSize - 1 ) rightMost = node;\n \n if (node->left) q.push(node->left);\n if (node->right) q.push(node->right);\n \n }\n }\n return lca( root, leftMost, rightMost );\n }\n};\n```
| 113 | 2 |
[]
| 8 |
smallest-subtree-with-all-the-deepest-nodes
|
Simple recursive Java Solution
|
simple-recursive-java-solution-by-the-tr-o6hn
|
\n\tpublic int depth(TreeNode root){\n\t\tif(root == null ) return 0;\n\t\treturn Math.max(depth(root.left),depth(root.right))+1;\n\t}\n\tpublic TreeNode subtre
|
the-traveller
|
NORMAL
|
2018-07-08T03:06:11.094854+00:00
|
2018-09-28T03:32:31.024158+00:00
| 7,490 | false |
```\n\tpublic int depth(TreeNode root){\n\t\tif(root == null ) return 0;\n\t\treturn Math.max(depth(root.left),depth(root.right))+1;\n\t}\n\tpublic TreeNode subtreeWithAllDeepest(TreeNode root) {\n\t\t\tif( root == null ) return null;\n\t\t\tint left = depth(root.left);\n\t\t\tint right = depth(root.right);\n\t\t\tif( left == right ) return root;\n\t\t\tif( left > right ) return subtreeWithAllDeepest(root.left);\n\t\t\treturn subtreeWithAllDeepest(root.right);\n\t}\n```\n\t\t\n\nThe time complexity of above code is O(N^2) since a binary tree can degenerate to a linked list, the worst complexity to calculate depth is O(N) and so the overall time complexity is O(N^2). Here is the memoized version:\n\nTime complexity: O(N)\n\n ```\n public int depth(TreeNode root,HashMap<TreeNode,Integer> map){\n if(root == null ) return 0;\n if( map.containsKey(root) ) return map.get(root); \n int max = Math.max(depth(root.left,map),depth(root.right,map))+1;\n map.put(root,max); \n return max;\n }\n public TreeNode dfs(TreeNode root, HashMap<TreeNode,Integer> map){\n int left = depth(root.left,map);\n int right = depth(root.right,map);\n if( left == right ) return root;\n if( left > right ) return dfs(root.left,map);\n return dfs(root.right,map);\n }\n public TreeNode subtreeWithAllDeepest(TreeNode root) {\n if( root == null ) return null;\n HashMap<TreeNode,Integer> map = new HashMap<>();\n depth(root,map);\n return dfs(root,map);\n }\n```\n\t\t
| 72 | 3 |
[]
| 15 |
smallest-subtree-with-all-the-deepest-nodes
|
Python Solution | O(n)
|
python-solution-on-by-tolujimoh-03h9
|
\n # Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, x):\n# self.val = x\n# self.left = None\n# self.rig
|
tolujimoh
|
NORMAL
|
2019-06-18T02:22:31.112344+00:00
|
2020-08-23T19:32:15.511359+00:00
| 2,945 | false |
```\n # Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, x):\n# self.val = x\n# self.left = None\n# self.right = None\n\nclass Solution:\n def subtreeWithAllDeepest(self, root: TreeNode) -> TreeNode:\n \n def deepestDepth(node, depth):\n \n if not node:\n return node, depth\n \n\t\t\t\n left, leftDepth = deepestDepth(node.left, depth + 1)\n right, rightDepth = deepestDepth(node.right, depth + 1) \n\n\t\t\t# If the deepest node on the left subtree is deeper than the deepest node \n\t\t\t# on the right subtree return the left subtree and the left deepest depth \n if leftDepth > rightDepth:\n return left, leftDepth\n \n\t\t\t# If the deepest node on the right subtree is deeper than the deepest node \n\t\t\t# on the left subtree return the right subtree and the right deepest depth \n if rightDepth > leftDepth:\n return right, rightDepth\n \n\t\t\t\n\t\t\t# If the above two conditions isn\'t met, then leftDepth == rightDepth\n\t\t\t#\n\t\t\t# leftDepth equal rightDepth means that the deepest node\n\t\t\t# in the left subtree has the same depth as the deepest node \n\t\t\t# in the right subtree, as such, we should return the current node \n\t\t\t# as it is the root of the current subtree that contains the deepest \n\t\t\t# nodes on the left and right subtree.\n\t\t\t#\n\t\t\t# return statment can also be `return node, rightDepth`\n return node, leftDepth\n \n return deepestDepth(root, 0)[0]\n```
| 65 | 1 |
['Depth-First Search', 'Python']
| 6 |
smallest-subtree-with-all-the-deepest-nodes
|
Short and concise C++ solution using DFS, 3~5 lines
|
short-and-concise-c-solution-using-dfs-3-rp4v
|
cpp []\nint depth(TreeNode *root) {\n return !root ? 0 : max(depth(root->left), depth(root->right)) + 1;\n}\n\nTreeNode* subtreeWithAllDeepest(TreeNode* root
|
mzchen
|
NORMAL
|
2018-07-08T04:29:36.405570+00:00
|
2024-01-24T02:52:37.735920+00:00
| 4,405 | false |
```cpp []\nint depth(TreeNode *root) {\n return !root ? 0 : max(depth(root->left), depth(root->right)) + 1;\n}\n\nTreeNode* subtreeWithAllDeepest(TreeNode* root) {\n int d = depth(root->left) - depth(root->right);\n return !d ? root : subtreeWithAllDeepest(d > 0 ? root->left : root->right);\n}\n```\n\nUpdate:\nSince some of you suggested that the original solution visits each node multiple times, I added below another version that addresses the issue at the cost of two additional lines.\n```cpp []\npair<int, TreeNode*> dfs(TreeNode *root) {\n if (!root) return {0, nullptr};\n auto [d1, r1] = dfs(root->left);\n auto [d2, r2] = dfs(root->right);\n return {max(d1, d2) + 1, d1 == d2 ? root : d1 > d2 ? r1 : r2};\n}\n\nTreeNode* subtreeWithAllDeepest(TreeNode* root) {\n return dfs(root).second;\n}\n```
| 34 | 2 |
['Depth-First Search', 'C++']
| 9 |
smallest-subtree-with-all-the-deepest-nodes
|
Video solution | Intuition explained in detail | C++
|
video-solution-intuition-explained-in-de-s72z
|
Video\nHey everyone, i have created a video solution for this problem, I have solved this problem by using maximum depth of binary tree , i have taken advantage
|
_code_concepts_
|
NORMAL
|
2024-08-02T10:49:01.569686+00:00
|
2024-08-02T10:49:01.569706+00:00
| 404 | false |
# Video\nHey everyone, i have created a video solution for this problem, I have solved this problem by using **maximum depth of binary tree** , i have taken advantage of background procees of recursion and explained the same in video, how to use recursion to solve this problem, this video is part of my Trees playlist.\nVideo link: https://youtu.be/oqH6mnNxOB4\nPlaylist link: https://www.youtube.com/playlist?list=PLICVjZ3X1Aca0TjUTcsD7mobU001CE7GL\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n TreeNode* res = nullptr;\n int deepestLevel = 0;\n\n int dfs(TreeNode* root, int height) {\n if (!root) return height;\n int leftHeight = dfs(root->left, height + 1);\n int rightHeight = dfs(root->right, height + 1);\n int currLevel= max(leftHeight, rightHeight);\n if(currLevel>=deepestLevel){\n deepestLevel=currLevel;\n if(leftHeight==deepestLevel && rightHeight==deepestLevel){\n res=root;\n }\n \n }\n \n return max(leftHeight, rightHeight);\n }\n\n TreeNode* subtreeWithAllDeepest(TreeNode* root) {\n dfs(root, 0);\n return res;\n }\n};\n\n\n```
| 17 | 0 |
['C++']
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
C++ The Simplest Solution, Easy to Understand, Recursive, faster than 85%
|
c-the-simplest-solution-easy-to-understa-6xs7
|
\nclass Solution {\npublic:\n int getDepth(TreeNode* root) {\n if (!root)\n return 0;\n return max(getDepth(root->right), getDepth(r
|
yehudisk
|
NORMAL
|
2020-12-12T17:05:43.371865+00:00
|
2020-12-12T17:05:43.371907+00:00
| 735 | false |
```\nclass Solution {\npublic:\n int getDepth(TreeNode* root) {\n if (!root)\n return 0;\n return max(getDepth(root->right), getDepth(root->left)) + 1;\n }\n \n TreeNode* subtreeWithAllDeepest(TreeNode* root) {\n if (!root)\n return NULL;\n \n int right_depth = getDepth(root->right);\n int left_depth = getDepth(root->left);\n \n if (right_depth == left_depth)\n return root;\n \n if (right_depth > left_depth) \n return subtreeWithAllDeepest(root->right);\n \n else \n return subtreeWithAllDeepest(root->left);\n }\n};\n```\n**Like it? please upvote...**
| 17 | 1 |
['C']
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
C++ : using recursion : 85% faster
|
c-using-recursion-85-faster-by-u11292-bbnv
|
```\nclass Solution {\npublic:\n TreeNode subtreeWithAllDeepest(TreeNode root) {\n if (root == NULL) return NULL;\n int left = getDepth(root-
|
u11292
|
NORMAL
|
2020-12-12T10:36:45.115599+00:00
|
2020-12-12T10:36:45.115632+00:00
| 1,131 | false |
```\nclass Solution {\npublic:\n TreeNode* subtreeWithAllDeepest(TreeNode* root) {\n if (root == NULL) return NULL;\n int left = getDepth(root->left);\n int right = getDepth(root->right);\n if (left == right) return root;\n else if (left > right) return subtreeWithAllDeepest(root->left);\n else return subtreeWithAllDeepest(root->right);\n }\n \nprivate :\n int getDepth(TreeNode* node)\n {\n if (node == NULL) return 0;\n return 1 + std::max(getDepth(node->left),getDepth(node->right));\n }\n};
| 17 | 0 |
[]
| 2 |
smallest-subtree-with-all-the-deepest-nodes
|
Same as LCA O(2N)
|
same-as-lca-o2n-by-cxk_123-da0r
|
1.get deepest nodes\n2.use LCA \nTime O(N) space O(N)\nyou can reduce space by using just one set\n\n public TreeNode subtreeWithAllDeepest(TreeNode root) {\
|
cxk_123
|
NORMAL
|
2018-07-08T03:05:31.238243+00:00
|
2018-07-08T03:05:31.238243+00:00
| 1,271 | false |
1.get deepest nodes\n2.use LCA \nTime O(N) space O(N)\nyou can reduce space by using just one set\n\n public TreeNode subtreeWithAllDeepest(TreeNode root) {\n Map<Integer, Set<TreeNode>> map = new HashMap<>();\n Queue<TreeNode> queue = new LinkedList<>();\n int level = 0;\n queue.offer(root);\n \n while(!queue.isEmpty()) {\n int size = queue.size();\n Set<TreeNode> list = new HashSet<>();\n \n for(int i = 0; i < size; i++) {\n TreeNode current = queue.poll();\n list.add(current);\n \n if(current.left != null) {\n queue.offer(current.left);\n }\n \n if(current.right != null) {\n queue.offer(current.right);\n }\n }\n map.put(level, list);\n level++;\n }\n Set<TreeNode> nodes = map.get(level - 1);\n return LCA(root, nodes); \n }\n \n private TreeNode LCA(TreeNode root, Set<TreeNode> set) {\n if(root == null ||set.contains(root)) {\n return root;\n }\n \n TreeNode left = LCA(root.left, set);\n TreeNode right = LCA(root.right, set);\n \n if(left != null && right != null) {\n return root;\n }\n \n return left == null ? right : left;\n }\n
| 13 | 2 |
[]
| 4 |
smallest-subtree-with-all-the-deepest-nodes
|
Java - O(1) space excluding recursion stack - O(N) time
|
java-o1-space-excluding-recursion-stack-ow3tr
|
The idea it to propogate a depth val until we reach a null and then return back the maximum depth that was found in the subtree. If both the left and right subt
|
shreyansh94
|
NORMAL
|
2018-07-08T03:04:14.324552+00:00
|
2018-10-18T22:58:31.977043+00:00
| 1,811 | false |
The idea it to propogate a depth `val` until we reach a `null` and then return back the maximum depth that was found in the subtree. If both the left and right subtree return the same depth, which is also equal to the maximum depth of tree, update the result. \n\n```\nclass Solution {\n\n int maxDepth = -1; \n TreeNode[] result = new TreeNode[1]; \n\t\t\n public TreeNode subtreeWithAllDeepest (TreeNode root) {\n if(root == null)\n return root; \n result[0] = null; \n getNode(root , 0); \n return result[0]; \n }\n public int getNode (TreeNode root, int depth){\n if(root == null)\n return depth; \n int l = getNode(root.left, depth+1); \n int r = getNode(root.right, depth+1); \n\t\t\t\t\n\t\t\t\t// both left and right depth are same and if it is greater than or equal to the maxDepth so far, UPDATE result. \n\t\t\t\t// `=` in l >= maxDepth, implies that the all the nodes with maximum depth are considered. \n if(l == r && l >= maxDepth ){\n maxDepth = l; \n result[0] = root; \n }\n\t\t\t\t\n\t\t\t\t// return the maximum depth that was found in this subtree. \n return Math.max(l,r);\n }\n}\n```
| 13 | 1 |
[]
| 8 |
smallest-subtree-with-all-the-deepest-nodes
|
[Pyton] O(n) time/O(h) space, explained
|
pyton-on-timeoh-space-explained-by-dbabi-fmua
|
Let us use dfs(level, node) function, where:\n\n1. level is distance between root of our tree and current node we are in.\n2. result of this function is the dis
|
dbabichev
|
NORMAL
|
2020-12-12T10:28:43.753474+00:00
|
2020-12-12T10:48:28.456367+00:00
| 895 | false |
Let us use `dfs(level, node)` function, where:\n\n1. `level` is distance between root of our tree and current `node` we are in.\n2. result of this function is the distance between `node` and its farthest children: that is the largest numbers of steps we need to make to reach leaf.\n\nSo, how exactly this function will work:\n1. If `not node`, then we are in the leaf and result is `0`.\n2. in other case, we run recursively `dfs` for `node.left` and `node.right`.\n3. What we keep in our `cand`: in first value sum of distances to root and to farthest leaf, second value is distance to root and final value is current node. Note, that `cand[0]` represent length of the longest path going from root to leaf, through our `node`.\n4. `if cand[0] > self.ans[0]:` it means that we found node with longer path going from root to leaf, and it means that we need to update `self.ans`.\n5. Also, if `cand[0] = self.ans[0]` and also `lft = rgh`, it means that we are now on the longest path from root to leaf and we have a **fork**: we can go either left or right and in both cases will have longest paths. Note, that we start from root of our tree, so it this way we will get **fork** which is the closest to our root, and this is exactly what we want in the end.\n6. Finally, we return `cand[0] - cand[1]`: distance from node to farthest children.\n\n**Complexity**: time complexity is `O(n)`: to visit all nodes in tree. Space complexity is `O(h)`, where `h` is height of tree.\n\n```\nclass Solution:\n def subtreeWithAllDeepest(self, root):\n self.ans = (0, 0, None)\n def dfs(lvl, node):\n if not node: return 0\n lft = dfs(lvl + 1, node.left)\n rgh = dfs(lvl + 1, node.right)\n cand = (max(lft, rgh) + 1 + lvl, lvl, node)\n\n if cand[0] > self.ans[0] or cand[0] == self.ans[0] and lft == rgh:\n self.ans = cand\n \n return cand[0] - cand[1]\n \n dfs(0, root)\n return self.ans[2]\n```\n\nIf you have any questions, feel free to ask. If you like solution and explanations, please **Upvote!**
| 12 | 0 |
[]
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
[Python] BFS and Euler Path - with picture
|
python-bfs-and-euler-path-with-picture-b-utt3
|
The Euler path is a useful tool to have for solving any LCA problem here is how it works:\n1. Find the deepest nodes using BFS\n2. Traverse the graph visiting r
|
rowe1227
|
NORMAL
|
2020-12-12T08:53:03.287968+00:00
|
2020-12-13T18:05:21.222141+00:00
| 951 | false |
The Euler path is a useful tool to have for solving any LCA problem here is how it works:\n1. Find the deepest nodes using BFS\n2. Traverse the graph visiting **root, left, root, right, root** to make a Euler Path\n3. Return the node (LCA) that is at the lowest depth between **p** and **q** in the Euler Path\n\n<img src="https://assets.leetcode.com/users/images/062b2e0e-65a1-4203-a51d-18fff04f8b2c_1604555931.5770352.png" width="50%">\n\n**In this problem, p and q would be the two of the deepest nodes in the tree 7 and 4\nand the lowest depth node between them is node 2 ~ which is the LCA of 7 and 4**\n\n<br>\n\n```python\ndef subtreeWithAllDeepest(self, root: TreeNode) -> TreeNode:\n\t\n\tdef get_deepest_nodes(root):\n\t\tq = [root]\n\t\twhile q:\n\t\t\tnext_level = []\n\t\t\tfor node in q:\n\t\t\t\tif node.left:\n\t\t\t\t\tnext_level.append(node.left)\n\t\t\t\tif node.right:\n\t\t\t\t\tnext_level.append(node.right)\n\n\t\t\tif next_level:\n\t\t\t\tq = next_level\n\t\t\telse:\n\t\t\t\tbreak\n\t\treturn q\n\n\tdef euler_path(node, d):\n\t\tnonlocal depth, path\n\n\t\tpath.append(node)\n\t\tdepth.append(d)\n\n\t\tif node.left:\n\t\t\teuler_path(node.left, d+1)\n\t\t\tpath.append(node)\n\t\t\tdepth.append(d)\n\n\t\tif node.right:\n\t\t\teuler_path(node.right, d+1)\n\t\t\tpath.append(node)\n\t\t\tdepth.append(d)\n\n\tif not root.left and not root.right: return root\n\t\n\t# Make an Euler path\n\tpath = []\n\tdepth = []\n\teuler_path(root, 0)\n\t\n\t# Find the deepest nodes\n\tdeepest_nodes = get_deepest_nodes(root)\n\t\n\t# Find the LCA of the deepest nodes\n\ti = min(path.index(node) for node in deepest_nodes)\n\tj = max(path.index(node) for node in deepest_nodes)\n\treturn path[min(range(i, j+1), key = lambda k: depth[k])]\n```
| 12 | 0 |
[]
| 2 |
smallest-subtree-with-all-the-deepest-nodes
|
C++✅✅ || Easiest solution using BFS || Beats 90%
|
c-easiest-solution-using-bfs-beats-90-by-vyx9
|
Intuition\n Describe your first thoughts on how to solve this problem. \nMy approach was to perform BFS and store only the first and last node at the deepest le
|
ayush220802
|
NORMAL
|
2022-12-24T17:46:52.279800+00:00
|
2022-12-24T18:29:51.520158+00:00
| 903 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nMy approach was to perform BFS and store only the first and last node at the deepest level.\n\nFind the LCA of first and last node.\n\nThus it is ensured that all the other nodes between the first and last node will be part of the LCA found.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe first use BFS, i.e., Level Order Traversal on the tree and find out the first and last nodes of the deepest level. Then we return their lca using the standard recursive procedure. Although, it is a two pass solution, it\'s really easy to understand how it works\n# Complexity\n- Time complexity:O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n TreeNode* subtreeWithAllDeepest(TreeNode *root) {\n queue<TreeNode*> q;\n q.push(root);\n TreeNode *first, *last;\n while(!q.empty()) {\n first = q.front(); last = q.back();\n int sz = q.size();\n while(sz--) {\n auto node = q.front(); q.pop();\n if(node -> left) q.push(node -> left);\n if(node -> right) q.push(node -> right);\n }\n }\n return lca(root, first, last);\n }\n \n TreeNode* lca(TreeNode *root, TreeNode *p, TreeNode *q) {\n if(!root || root == p || root == q) return root;\n auto left = lca(root -> left, p, q);\n auto right = lca(root -> right, p, q);\n return left ? right ? root : left : right;\n }\n};\n```
| 11 | 0 |
['Tree', 'Breadth-First Search', 'C++']
| 1 |
smallest-subtree-with-all-the-deepest-nodes
|
[C++] 4 Solutions Compared and Explained, 100% Time, 100% Space
|
c-4-solutions-compared-and-explained-100-ts3h
|
Fantastic problem you can tackle from multiple directions - as I did with pleasure :)\n\nMy first approach was to run a plain DFS call to build a vector represe
|
ajna
|
NORMAL
|
2020-12-13T09:02:34.813911+00:00
|
2020-12-13T09:29:39.911910+00:00
| 1,035 | false |
Fantastic problem you can tackle from multiple directions - as I did with pleasure :)\n\nMy first approach was to run a plain DFS call to build a vector represeting the path up to the node itself and then check if it was one of the deepest one, in order to then take the first and the last of them to find their common ancestor.\n\nTo do so, I declared a couple of variables, at class level:\n* `paths` is a vector of `TreeNode` vectors and it will store all our deeper ones;\n* `tmp` is the vector used in our DFS calls to store the way to the currently parsed node.\n\nIn our main function, we will then first of all populate `paths`, with a call to our `dfs` helper function.\n\nThis function takes 2 parameters, the currently parsed node `root` and:\n* updates `tmp` pushing `root` in;\n* checks if now `tmp` is either the first elements that would be pushed in paths or longer (ie: deeper) than the last inserted one, in which case it overwrites `paths` to just contain it;\n* alternatively checks if `tmp` is as long/deep as the last element in `paths`, in which case `tmp` gets appended to it;\n* calls itself recursively on the children branches, if any;\n* backtracks `tmp` popping `root` out.\n\nYou might save yourself some unnecessary checks removing `paths.empty()` from the first conditional, if you just push `{{root}}` into `paths` before calling `dfs` the first time, but I think it is not that much of a difference and I found more elegant to keep it in - just consider discussing this option if you are interviewing and want to show a keen eye for performances.\n\nOnce done, we loop as long as the last node in the first and the last path in `paths` are different (which also implies no looping at all in case we only had a single deepest path stored there, which is perfect), popping the last element out of both of them.\n\nFor example, with the provided sample input (`{3,5,1,6,2,0,8,null,null,7,4}`), we will end up having as deepest paths in `paths`:\n\n```cpp\n{3, 5, 2, 7}\n{3, 5, 2, 4}\n```\n\nTheir last element does not match, so we pop it out from both and get:`paths`:\n\n```cpp\n{3, 5, 2}\n{3, 5, 2}\n```\n\nNow their last element is the same, so that is our solution!\n\nOnce done, we can return the last element of the first (or of the last, it does not matter) path in `paths` :)\n\nThe code, who had decent time and somehow average memory consumption:\n\n```cpp\nclass Solution {\npublic:\n // support variables\n vector<vector<TreeNode*>> paths;\n vector<TreeNode*> tmp;\n // DFSing the deepest paths\n void dfs(TreeNode* root) {\n // updating tmp\n tmp.push_back(root);\n // if tmp is the new deepest, we overwrite paths\n if (paths.empty() || tmp.size() > paths.back().size()) paths = {tmp};\n // if tmp is as deep as the last element in paths, we add it\n else if (tmp.size() == paths.back().size()) paths.push_back(tmp);\n // recursive calls to the children, if any\n if (root->left) dfs(root->left);\n if (root->right) dfs(root->right);\n // backtracking on tmp\n tmp.pop_back();\n }\n TreeNode* subtreeWithAllDeepest(TreeNode* root) {\n // extracting the longest paths\n dfs(root);\n // reducing the 2 extreme paths to the common node\n while (paths.front().back() != paths.back().back()) paths.front().pop_back(), paths.back().pop_back();\n return paths.front().back();\n }\n};\n```\n\nThen I cam up with another alternative: to go recursively and take the depth of the left and right branch respectively, then compare them:\n* if they are equal, by definition we know that `root` is the one node that connects all the deepest ones;\n* otherwise, we call the function recursively on the deeper branch of the 2.\n\nThe code, that performs surprisingly very fast, despite recomputing over and over again the depth of several nodes (I try to optimise that part, but check below the code to know how it went):\n\n```cpp\nclass Solution {\npublic:\n int getDepth(TreeNode *root) {\n return root ? 1 + max(getDepth(root->left), getDepth(root->right)) : 0;\n }\n\n TreeNode* subtreeWithAllDeepest(TreeNode* root) {\n int l = getDepth(root->left), r = getDepth(root->right);\n return l == r ? root : subtreeWithAllDeepest(l > r ? root->left : root->right);\n }\n};\n```\n\nI wanted to try a memoised version of it, but it does run significantly slower, to my surprise - not sure if searching through the map or the compiler being unable to properly work it with tail recursions is the culprit here.\n\nThe code of this disappointed experiment (which is of course burning some more memory for no gain):\n\n```cpp\nclass Solution {\npublic:\n unordered_map<TreeNode*, int> depths;\n int getMemoisedDepth(TreeNode *root) {\n return root ? depths.find(root) != end(depths) ? depths[root] : depths[root] = 1 + max(getMemoisedDepth(root->left), getMemoisedDepth(root->right)) : 0;\n }\n\n TreeNode* subtreeWithAllDeepest(TreeNode* root) {\n int l = getMemoisedDepth(root->left), r = getMemoisedDepth(root->right);\n return l == r ? root : subtreeWithAllDeepest(l > r ? root->left : root->right);\n }\n};\n```\n\nLast but not least, I took the idea of using Euler path from [here](https://leetcode.com/problems/smallest-subtree-with-all-the-deepest-nodes/discuss/969164/Python-BFS-and-Euler-Path-with-picture) and tweaked it a bit to fit my idea (and optimise it as much as I could, of course).\n\nCheck the link above for a full, illustrated description of it, but the idea is to go with an in-order traversal (left-root-right) storing each element and the matching depth into 2 containers, that I declared respectively as `nodes` and `depths`, iterating though them with my usual pointer `pos`, that by the end of the process will also be the value of the number of nodes parsed (and thus the length of the array to actually be considered).\n\nFor example, running the first provided sample input (`{3,5,1,6,2,0,8,null,null,7,4}`) we will get:\n\n```cpp\n6 5 7 2 4 3 0 1 8 //nodes\n2 1 3 2 3 0 2 1 2 //depths\n```\n\nAs described in [rowe1227](https://leetcode.com/rowe1227)\'s solution, we now need to go and find the deeper nodes, then return the shallowest node between them.\n\nAnd I wanted to give myself an extra challenge: can we do it not just only in linear time, but in a single pass?\n\nTurns out there is a way!\n\nWe will need a few support variables:\n* `res` and `shallowestNode` are 2 `TreeNode` pointers;\n* `maxDepth` and `minDepth` are 2 others to store, as their name implies, the maximum depth found so far and the minimum depth found after each deepest node - I declared them conveniently at loop level, since we won\'t need them outside the loop - also note that we want to initialise the former as `-1`, in order to correctly register even the provided `root` as the deeper one, in the edge case of getting a single-noded tree as an input.\n\nThen we iterate through all the indexes `i` in the `0 - (pos - 1)` range and:\n* check if the current depth is the new maximum, in which case we:\n\t* we set both `maxDepth` and `minDepth` to the value of the current depth;\n\t* we set `res` to the value of the matching node;\n* check if instead the current depth is equal to the current maximim `maxDepth`, in which case we just set the node matching the shallowest depth found after the maximum as the new `res`;\n* check if instead the current depth is lesser than `minDepth`, in which case we:\n\t* update `minDepth` to its value;\n\t* update `shallowestNode` to the matching value in `nodes`.\n\nIt is not the most intuitive pattern ever, but you can check how it works: if you will find only a single node with the maximumm depth, than that is your answer; if you are going to find more than one, then the shallowest one you found in the middle is what you need to return.\n\nIt really works!\n\nAnd thus, once we are done, we can just return `res` :)\n\nThe code, which is rather fast and with average memory usage:\n\n```cpp\nclass Solution {\npublic:\n // support variable - note: no need to initialise the arrays\n int depths[500], pos = 0;\n TreeNode *nodes[500];\n void dfs(TreeNode* root, int depth = 0) {\n // in-order traversal\n if (root->left) dfs(root->left, depth + 1);\n nodes[pos] = root, depths[pos++] = depth;\n if (root->right) dfs(root->right, depth + 1);\n }\n TreeNode* subtreeWithAllDeepest(TreeNode* root) {\n // support variables\n TreeNode *res, *shallowestNode;\n // populating the Euler path\n dfs(root);\n // finding the lowest depth and the highest node inside the first and last deeper node\n for (int i = 0, maxDepth = -1, minDepth; i < pos; i++) {\n // a deeper node is found\n if (depths[i] > maxDepth) {\n maxDepth = minDepth = depths[i];\n res = nodes[i];\n }\n // another node as deep as maxDepth is found\n else if (depths[i] == maxDepth) {\n res = shallowestNode;\n }\n // updating the shallowest node found so far\n else if (depths[i] < minDepth) {\n minDepth = depths[i];\n shallowestNode = nodes[i];\n }\n }\n return res;\n }\n};\n```
| 11 | 1 |
['Depth-First Search', 'Graph', 'C', 'C++']
| 1 |
smallest-subtree-with-all-the-deepest-nodes
|
Python solution
|
python-solution-by-zitaowang-6lea
|
First use BFS to find the deepest nodes, then find the lowest common ancestor (LCA) of these nodes. \n\nTime complexity: O(n), space complexity: O(n).\n\nclass
|
zitaowang
|
NORMAL
|
2018-12-22T11:37:36.914003+00:00
|
2018-12-22T11:37:36.914045+00:00
| 445 | false |
First use BFS to find the deepest nodes, then find the lowest common ancestor (LCA) of these nodes. \n\nTime complexity: O(n), space complexity: O(n).\n```\nclass Solution:\n def subtreeWithAllDeepest(self, root):\n """\n :type root: TreeNode\n :rtype: TreeNode\n """\n if not root:\n return\n\t\t\t\n\t\t# BFS to find the deepest nodes\n q = collections.deque([(root,0)])\n maxdepth = -float(\'inf\')\n res = []\n dic = {} # keep track of the parent\n while q:\n u, depth = q.popleft()\n if depth > maxdepth:\n maxdepth = depth\n res = [u]\n elif depth == maxdepth:\n res.append(u)\n if u.left:\n q.append((u.left, depth+1))\n dic[u.left] = u\n if u.right:\n q.append((u.right, depth+1))\n dic[u.right] = u\n\t\t\t\t\n\t\t# find the LCA of nodes in res\n if len(res) == 1:\n return res[0]\n else:\n while True:\n parent = []\n for u in res:\n if not parent:\n parent.append(dic[u])\n else:\n if dic[u] != parent[0]:\n parent.append(dic[u])\n if len(parent) == 1:\n return parent[0]\n else:\n res = parent\n```
| 10 | 0 |
[]
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
DFS C++ - <10 LOC
|
dfs-c-10-loc-by-miguelmartin75-idfi
|
\npair<int, TreeNode*> f(TreeNode* root) {\n if(root == nullptr) return {0, root};\n \n auto l = f(root->left);\n auto r = f(root->right);\n
|
miguelmartin75
|
NORMAL
|
2018-07-09T03:28:47.989468+00:00
|
2018-07-09T03:28:47.989468+00:00
| 716 | false |
```\npair<int, TreeNode*> f(TreeNode* root) {\n if(root == nullptr) return {0, root};\n \n auto l = f(root->left);\n auto r = f(root->right);\n \n if(l.first == r.first) return {1 + l.first, root};\n else if(l.first > r.first) return {1 + l.first, l.second};\n else return {1 + r.first, r.second};\n}\n \nTreeNode* subtreeWithAllDeepest(TreeNode* root) {\n return f(root).second;\n}\n```
| 10 | 1 |
[]
| 2 |
smallest-subtree-with-all-the-deepest-nodes
|
[Python3] dfs O(N)
|
python3-dfs-on-by-ye15-b71r
|
Algo \nTraverse the tree. At each node, compare the height of left subtree to the height of right subtree. \n1) if left == right, return node;\n2) if left > rig
|
ye15
|
NORMAL
|
2020-11-18T20:07:43.752531+00:00
|
2020-12-13T05:40:51.919076+00:00
| 898 | false |
Algo \nTraverse the tree. At each node, compare the height of left subtree to the height of right subtree. \n1) if left == right, return node;\n2) if left > right, move to left subtree;\n3) if left < right, move to right subtree. \n\nImplementation\n```\nclass Solution:\n def subtreeWithAllDeepest(self, root: TreeNode) -> TreeNode:\n \n @lru_cache(None)\n def fn(node):\n """Return height of tree rooted at node."""\n if not node: return 0\n return 1 + max(fn(node.left), fn(node.right))\n \n node = root\n while node: \n left, right = fn(node.left), fn(node.right)\n if left == right: return node\n elif left > right: node = node.left\n else: node = node.right \n```\n\nAnalysis\nTime complexity `O(N)`\nSpace complexity `O(N)`\n\nEdited on 12/13/2020\n```\nclass Solution:\n def subtreeWithAllDeepest(self, root: TreeNode) -> TreeNode:\n fn = lru_cache(None)(lambda x: 1 + max(fn(x.left), fn(x.right)) if x else 0)\n \n node = root\n while node: \n if fn(node.left) == fn(node.right): return node \n elif fn(node.left) < fn(node.right): node = node.right\n else: node = node.left\n return node \n```
| 9 | 0 |
['Python3']
| 1 |
smallest-subtree-with-all-the-deepest-nodes
|
[Java] Super easy | 100% & 99%
|
java-super-easy-100-99-by-akberovr-u5r7
|
\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n
|
akberovr
|
NORMAL
|
2020-09-02T09:32:13.581195+00:00
|
2020-09-02T09:39:29.524047+00:00
| 881 | false |
```\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n * TreeNode(int val) { this.val = val; }\n * TreeNode(int val, TreeNode left, TreeNode right) {\n * this.val = val;\n * this.left = left;\n * this.right = right;\n * }\n * }\n */\nclass Solution {\n public TreeNode subtreeWithAllDeepest(TreeNode root) {\n if(root == null)\n return null;\n \n if(checkHeight(root.left) == checkHeight(root.right))\n return root;\n else if(checkHeight(root.left) > checkHeight(root.right))\n return subtreeWithAllDeepest(root.left);\n else\n return subtreeWithAllDeepest(root.right); \n }\n \n private int checkHeight(TreeNode root){\n if(root == null) return 0;\n int res = Math.max(checkHeight(root.left), checkHeight(root.right))+1;\n return res;\n }\n}\n```
| 9 | 0 |
['Java']
| 3 |
smallest-subtree-with-all-the-deepest-nodes
|
JavaScript Solution - DFS Approach (Last Updated 10/01/20)
|
javascript-solution-dfs-approach-last-up-3oon
|
\nvar subtreeWithAllDeepest = function(root) {\n let height = 0;\n let maxNode = null;\n \n dfs(root, 0);\n \n return maxNode;\n \n func
|
Deadication
|
NORMAL
|
2020-05-23T04:01:57.465324+00:00
|
2020-10-02T14:35:11.742275+00:00
| 579 | false |
```\nvar subtreeWithAllDeepest = function(root) {\n let height = 0;\n let maxNode = null;\n \n dfs(root, 0);\n \n return maxNode;\n \n function dfs(node, currDepth) {\n if (node == null) return currDepth - 1;\n \n height = Math.max(height, currDepth);\n \n const leftDepth = dfs(node.left, currDepth + 1);\n const rightDepth = dfs(node.right, currDepth + 1);\n \n if (leftDepth == height && rightDepth == height) {\n maxNode = node;\n }\n \n return Math.max(leftDepth, rightDepth);\n }\n};\n```
| 9 | 0 |
['Depth-First Search', 'JavaScript']
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
Simple Python BFS + LCA Solution; faster than 98.7% at the time of writing
|
simple-python-bfs-lca-solution-faster-th-0e6a
|
Understanding of the Problem:\n\n Find the nodes at the deepest level in the tree. It can be just one node with the maximum depth. There can be many nodes with
|
anubhav_j
|
NORMAL
|
2019-06-15T20:49:07.031980+00:00
|
2019-06-15T20:49:07.032038+00:00
| 695 | false |
**Understanding of the Problem:**\n\n* Find the nodes at the deepest level in the tree. It can be just one node with the maximum depth. There can be many nodes with the same maximum depth, i.e. the same level in BFS.\n\n* The problem asks for the common parent node of these deepest nodes.\n\t* In case when there is just one deepest node, it is the result.\n\t* In case there are many nodes at the deepest level, the result is the Least Common Ancestor(LCA) of the leftmost and the rightmost nodes.\n\n**Solving**\n\n* Use BFS to find the left-most and right-most deepest nodes. In the queue, the tuple (node,depth) is pushed to keep track of every level. All the next levels of node are marked with depth+1\n\n* Keep track of maximum depth. ``` depth > max_depth``` takes care of storing the leftmost deepest node. ``` depth >= max_depth ``` takes care of storing the rightmost deepest node. The *equals* helps to keep on updating the last one at the same level.\n\n* Once you have the two nodes, simply return their LCA.\n\n```\ndef subtreeWithAllDeepest(self, root):\n """\n :type root: TreeNode\n :rtype: TreeNode\n """\n \n # Find left-most deepest(lmd) node\n # Find right-most deepest(rmd) node\n # Find LCA of those two\n \n lmd = rmd = root\n from collections import deque\n q = deque()\n q.append((root,0)) # (TreeNode, depth)\n max_depth = 0\n while q:\n \n node, depth = q.popleft()\n if depth>max_depth:\n max_depth = depth\n lmd = node\n if depth>=max_depth:\n max_depth = depth\n rmd = node\n if node.left:\n q.append((node.left, depth+1))\n if node.right:\n q.append((node.right, depth+1))\n \n if lmd is rmd:\n return lmd\n return self.lca(root, lmd, rmd)\n \n def lca(self, root, lmd, rmd):\n \n if not root:\n return None\n if root.val==lmd.val or root.val==rmd.val:\n return root\n \n lh = self.lca(root.left, lmd, rmd)\n rh = self.lca(root.right, lmd, rmd)\n \n if lh and rh:\n return root\n if lh and not rh:\n return lh\n if rh and not lh:\n return rh\n return None\n```\n\n*Above code can definitely have some optimizations.* I just shared my idea+implementation.\n
| 8 | 0 |
[]
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
Python. || one traverse, 9 lines || T/S: 91% / 93%
|
python-one-traverse-9-lines-ts-91-93-by-5osz4
|
Here\'s the plan:\n\n- We use the function dfs to traverse each node\'s subtree and return the maximum level in the subtree.\n- We determine whether dfs(node.le
|
Spaulding_
|
NORMAL
|
2022-07-05T18:03:34.476842+00:00
|
2024-05-30T22:16:31.232278+00:00
| 237 | false |
###### Here\'s the plan:\n\n- We use the function `dfs` to traverse each node\'s subtree and return the maximum level in the subtree.\n- We determine whether `dfs(node.left) == dfs(node.right)`; if so, then node is a candidate for the answer. \n- We store the most recent candidate node in `d` by `key = maxLevel`\nfor the subtree. \n- We return the actual maximum level as `d[dfs(root)]`.\n\n```\nclass Solution:\n def subtreeWithAllDeepest(self, root: TreeNode) -> TreeNode:\n \n def dfs(node = root, level = 0):\n if not node:\n return level-1\n \n l, r = dfs(node.left, level+1), dfs(node.right, level+1)\n \n if l == r:\n d[l] = node\n \n return max(l,r)\n \n d = {}\n return d[dfs()]\n```\n\n[https://leetcode.com/problems/smallest-subtree-with-all-the-deepest-nodes/submissions/1272760997/](https://leetcode.com/problems/smallest-subtree-with-all-the-deepest-nodes/submissions/1272760997/)\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(*N*), in which *N* ~ the number of nodes.\n\n\n\n
| 7 | 0 |
['Python']
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
Java BFS
|
java-bfs-by-emichaux-179b
|
Use BFS to traverse the tree and get the last level. Then iterate through the last level\'s parents until you get the shared parent node.\n\n\nclass Solution {\
|
emichaux
|
NORMAL
|
2019-08-03T15:44:00.610210+00:00
|
2019-08-04T16:34:53.198788+00:00
| 689 | false |
Use BFS to traverse the tree and get the last level. Then iterate through the last level\'s parents until you get the shared parent node.\n\n```\nclass Solution {\n public TreeNode subtreeWithAllDeepest(TreeNode root) {\n Queue<TreeNode> q = new LinkedList<TreeNode>();\n\t\tif (root == null)\n\t\t\treturn root;\n \n q.add(root);\n HashMap<TreeNode, TreeNode> mapOfNodes = new HashMap<>();\n \n while (!q.isEmpty()) {\n Queue<TreeNode> tempQ = new LinkedList<TreeNode>();\n for(TreeNode t: q) { \n if(t.left != null) {\n tempQ.add(t.left);\n mapOfNodes.put(t.left, t);\n }\n\n if(t.right != null) {\n tempQ.add(t.right);\n mapOfNodes.put(t.right, t);\n }\n }\n if(tempQ.size() == 0) {\n break;\n }\n else {\n q = tempQ;\n }\n }\n \n return getSharedParent(q, mapOfNodes);\n }\n \n private TreeNode getSharedParent(Queue<TreeNode> q, HashMap<TreeNode, TreeNode> mapOfNodes) {\n while(!q.isEmpty()) {\n if(q.size() == 1) return q.poll();\n \n Queue<TreeNode> tempQ = new LinkedList<TreeNode>();\n for(TreeNode t: q) {\n if(!tempQ.contains(mapOfNodes.get(t))) {\n tempQ.add(mapOfNodes.get(t));\n }\n }\n q = tempQ;\n }\n return null;\n }\n}\n```
| 7 | 0 |
['Breadth-First Search', 'Java']
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
LCA of multiple nodes
|
lca-of-multiple-nodes-by-xp336-f84x
|
The solution is very straight forward. like of problem we solved before LCA of two nodes in a binary tree.Now instead of two nodes we have multiple nodes.\n\ncl
|
xp336
|
NORMAL
|
2018-10-31T06:15:19.572127+00:00
|
2018-10-31T06:15:19.572171+00:00
| 1,311 | false |
The solution is very straight forward. like of problem we solved before LCA of two nodes in a binary tree.Now instead of two nodes we have multiple nodes.\n```\nclass Solution {\n public TreeNode subtreeWithAllDeepest(TreeNode root) {\n Set<TreeNode> deepestNodes = getDeepestNodes(root);\n return helper(root, deepestNodes);\n }\n \n private TreeNode helper(TreeNode root, Set<TreeNode> deepestNodes){\n if(root == null) return null;\n if(deepestNodes.contains(root)) return root;\n TreeNode left = helper(root.left, deepestNodes);\n TreeNode right = helper(root.right, deepestNodes);\n if(left == null){\n return right;\n }\n if(right == null){\n return left;\n }\n return root;\n }\n \n private Set<TreeNode> getDeepestNodes(TreeNode root){\n Queue<TreeNode> queue = new LinkedList<>();\n queue.offer(root);\n Set<TreeNode> set = new HashSet<>();\n while(!queue.isEmpty()){\n int size = queue.size();\n set = new HashSet<>();\n for(int i = 0; i < size; i++){\n TreeNode poped = queue.poll();\n set.add(poped);\n if(poped.left != null){\n queue.offer(poped.left);\n }\n if(poped.right != null){\n queue.offer(poped.right);\n }\n }\n \n }\n return set;\n }\n}\n```
| 7 | 0 |
[]
| 1 |
smallest-subtree-with-all-the-deepest-nodes
|
C++ | Used pair instead of defining new Class| 100% faster 0ms | dfs
|
c-used-pair-instead-of-defining-new-clas-4w98
|
\nclass Solution {\npublic:\n \n pair<TreeNode* , int> helper(TreeNode* root)\n {\n if(root == NULL) return {NULL,0}; \n pair l = h
|
pratham7711
|
NORMAL
|
2022-01-10T05:47:22.449684+00:00
|
2022-01-10T05:47:22.449731+00:00
| 179 | false |
```\nclass Solution {\npublic:\n \n pair<TreeNode* , int> helper(TreeNode* root)\n {\n if(root == NULL) return {NULL,0}; \n pair l = helper(root->left) , r = helper(root->right);\n if(l.second > r.second) return {l.first , l.second + 1};\n if(l.second < r.second) return {r.first , r.second + 1};\n return {root,l.second + 1};\n }\n TreeNode* subtreeWithAllDeepest(TreeNode* root) {\n return helper(root).first;\n }\n};\n```
| 6 | 0 |
['Depth-First Search', 'C']
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
Hints That Will Guide You To The Solution Yourself
|
hints-that-will-guide-you-to-the-solutio-ycww
|
😇 Actually Good Hints
Hint 1.
Think about how DFS or finding depth could solve this question?
Hint 2.
Find the maxDepth of the binary tree. T
|
LeadingTheAbyss
|
NORMAL
|
2025-04-04T01:22:31.172636+00:00
|
2025-04-04T01:22:31.172636+00:00
| 182 | false |
# 😇 Actually Good Hints
<details>
<summary><span style="font-size:20px;"><strong>Hint 1.</strong></span></summary>
<span style="font-size:18px;">Think about how <strong>DFS</strong> or <strong>finding depth</strong> could solve this question?</span>
</details>
<br>
<details>
<summary><span style="font-size:20px;"><strong>Hint 2.</strong></span></summary>
<span style="font-size:18px;">Find the <strong>maxDepth</strong> of the binary tree. Try solving
<a href="https://leetcode.com/problems/maximum-depth-of-binary-tree/" target="_blank">104. Maximum Depth of Binary Tree</a> first if needed.</span>
</details>
<br>
<details>
<summary><span style="font-size:20px;"><strong>Hint 3.</strong></span></summary>
<span style="font-size:18px;">Try to use recursion until you reach <code>maxDepth - 1</code> and return that node.</span>
</details>
<br>
<details>
<summary><span style="font-size:20px;"><strong>Hint 4.</strong></span></summary>
<span style="font-size:18px;">
Maintain a <code>currentLength</code> counter during recursion and keep using <strong>DFS</strong> until you reach <code>maxDepth - 1</code>. When you reach that level, you can return the current node:
<br>
<code>if (maxi - 1 == currentLength) return root;</code>
<br>
</span>
</details>
<br>
<details>
<summary><span style="font-size:20px;"><strong>Hint 5.</strong></span></summary>
<span style="font-size:18px;">
After recursing on both sides, combine their results as follows:
<br>
<code>if (left && right) return root;<br>return left ? left : right;</code>
<br>
This means if both <strong>left</strong> and <strong>right</strong> return <strong>non-null</strong> values, the <strong>current node</strong> is the <strong>lowest common ancestor</strong>. Otherwise, return the non-null child.
</span>
</details>
<br>
</details><br>
<details><summary><span style="font-size:20px;"><strong>Disclaimer [This is the solution]</strong></span></summary> <span style="font-size:18px;"></span>
```cpp []
class Solution {
public:
TreeNode* subtreeWithAllDeepest(TreeNode* root) {
int maxi = maxDepth(root); // maxi is the max depth
return dfs(root, maxi, 0);
}
TreeNode* dfs(TreeNode* root, int maxi, int len) {
if (!root) return nullptr;
if (maxi - 1 == len) return root;
TreeNode* left = dfs(root->left, maxi, len + 1);
TreeNode* right = dfs(root->right, maxi, len + 1);
if (left && right) return root;
return left ? left : right;
}
int maxDepth(TreeNode* root) {
if (!root) return 0;
return 1 + max(maxDepth(root->left), maxDepth(root->right));
}
};
```
```Python []
class Solution(object):
def subtreeWithAllDeepest(self, root) {
def maxDepth(node):
if not node:
return 0
return 1 + max(maxDepth(node.left), maxDepth(node.right))
def dfs(node, maxi, length):
if not node:
return None
if maxi - 1 == length:
return node
left = dfs(node.left, maxi, length + 1)
right = dfs(node.right, maxi, length + 1)
if left and right:
return node
return left if left else right
maxi = maxDepth(root) # maxi is the max depth
return dfs(root, maxi, 0)
```
```Java []
class Solution {
TreeNode* subtreeWithAllDeepest(TreeNode* root) {
int maxi = maxDepth(root); // maxi is the max depth
return dfs(root, maxi, 0);
}
private TreeNode dfs(TreeNode root, int maxi, int len) {
if (root == null) return null;
if (maxi - 1 == len) return root;
TreeNode left = dfs(root.left, maxi, len + 1);
TreeNode right = dfs(root.right, maxi, len + 1);
if (left != null && right != null) return root;
return left != null ? left : right;
}
private int maxDepth(TreeNode root) {
if (root == null) return 0;
return 1 + Math.max(maxDepth(root.left), maxDepth(root.right));
}
}
</details> <br>
<img src="https://assets.leetcode.com/users/images/cc496d84-0690-4377-b8a3-f621f326df8f_1742786890.68028.png" width="400">
| 5 | 0 |
['Tree', 'Breadth-First Search', 'Binary Tree', 'Python', 'C++', 'Java']
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
C++/DFS
|
cdfs-by-blue_tiger-yo55
|
\n\n// The simple logic behind this problem is that u need to check the height of the left and right subtree for every node. \n// case-1: If both left and right
|
Blue_tiger
|
NORMAL
|
2022-05-19T07:42:54.561473+00:00
|
2022-05-30T09:00:39.080162+00:00
| 102 | false |
\n\n// The simple logic behind this problem is that u need to check the height of the left and right subtree for every node. \n// case-1: If both left and right height are same ans will be root.\n// case-2: Else If left height is greater than ans will be root->left.\n// case-3: Ese ans will be root->right.\n\n// 1st solution: TC=O(N)\nclass Solution {\npublic:\n \n TreeNode *ans=NULL;\n int height(TreeNode *root)\n {\n if (root == NULL)\n return -1;\n else\n {\n int lHeight = height(root->left);\n int rHeight = height(root->right);\n return 1+max(lHeight,rHeight);\n }\n }\n \n void dfs(TreeNode *root)\n {\n int lh=height(root->left);\n int rh=height(root->right);\n if(lh==rh)\n {\n ans=root;\n return ;\n }\n else if(lh>rh)\n {\n ans=root->left;\n dfs(root->left);\n }\n else\n {\n ans=root->right;\n dfs(root->right);\n }\n }\n TreeNode* subtreeWithAllDeepest(TreeNode* root) {\n if(!root) return NULL;\n if(!root->left && !root->right) return root;\n dfs(root);\n \n return ans;\n }\n};\n\n// 2nd Solution O(N2)-(worse case)\nclass Solution {\npublic:\n \n\n pair<TreeNode*,int> dfs(TreeNode *root)\n {\n if(!root) return {NULL,0};\n if(!root->left && !root->right) return {root,1};\n pair<TreeNode*,int>left=dfs(root->left);\n pair<TreeNode*,int>right=dfs(root->right);\n if(left.second==right.second)\n {\n return {root,left.second+1};\n }\n else if(left.second>right.second)\n return {left.first,left.second+1};\n else\n return {right.first,right.second+1};\n }\n TreeNode* subtreeWithAllDeepest(TreeNode* root) {\n if(!root) return NULL;\n if(!root->left && !root->right) return root;\n pair<TreeNode*,int>ans=dfs(root);\n \n return ans.first;\n }\n};
| 5 | 0 |
[]
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
C++ | Most Unique Approach | O(n) ONLY 100% Faster | With Explanations
|
c-most-unique-approach-on-only-100-faste-mqhy
|
We will use a pair in the solution.\nThe first part of the pair will contain the node and the second part will contain the deepest level.\nAt base condition we
|
ama29n
|
NORMAL
|
2022-01-07T11:41:34.862755+00:00
|
2022-01-07T11:44:28.439147+00:00
| 217 | false |
We will use a pair in the solution.\nThe first part of the pair will contain the node and the second part will contain the deepest level.\nAt base condition we will return a pair as ```{NULL, -1}```. \n\nAt every position in the tree we will check the deepest level i.e., ```pair.second``` of left and right subtree.\n\nNow there are 2 cases possible here:\n1. deepest level of right and left subtree is same i.e., ```l.second == r.second``` - This means that the current node is the subtree having the deepest nodes. Thus, we will return a pair having ```p.first = root (current node)```. Now, how to ensure that it is the deepest subtree? simple answer is to set its level as ```l.second + 1``` or ```r.second + 1``` and return it. How it is working takes us to the second condition.\n\n2. Now let us assume we get left and right subtrees with different levels. In this case, we will return the pair of subtree with deeper level but will increment its level by 1. \n\nNow, from 1st condition we got a subtree having the deepest nodes and we are always incrementing it\'s level by 1. **So, no matter what if we even get another subtree whose level is lesser than the one which is deepest it will not be returned. And if we get another subtree whose level is deeper it will be retuned due to 2nd condition and if they both have same deepest level, we will return that subtree instead**.\n\nNow, this algorithm also ensures that only a **complete subtree is being returned due to the 1st condition**.\n\n\n```\n\t// pair.first = node\n // pair.second = deepest level\n \n pair<TreeNode*, int> deepest(TreeNode* root) {\n if(!root) return {NULL, -1};\n\t\t\n pair<TreeNode*, int> l = deepest(root->left), r = deepest(root->right), p;\n \n if(l.second == r.second) { \n p.second = l.second + 1;\n p.first = root;\n return p;\n }\n \n if(l.second > r.second) {l.second += 1; return l;}\n else {r.second += 1; return r;}\n }\n \n TreeNode* subtreeWithAllDeepest(TreeNode* root) {\n pair<TreeNode*, int> p = deepest(root);\n return p.first;\n }\n```
| 5 | 0 |
['Tree', 'Depth-First Search', 'Breadth-First Search', 'Binary Tree']
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
EASY JAVA SOLUTION
|
easy-java-solution-by-21arka2002-o6by
|
Code\n\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode(
|
21Arka2002
|
NORMAL
|
2023-03-08T08:02:41.670953+00:00
|
2023-03-08T08:02:41.671004+00:00
| 428 | false |
# Code\n```\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n * TreeNode(int val) { this.val = val; }\n * TreeNode(int val, TreeNode left, TreeNode right) {\n * this.val = val;\n * this.left = left;\n * this.right = right;\n * }\n * }\n */\nclass Solution {\n public TreeNode subtreeWithAllDeepest(TreeNode root) {\n if(root==null)return null;\n int lh=height(root.left);\n int rh=height(root.right);\n if(lh==rh)return root;\n else if(lh>rh)return subtreeWithAllDeepest(root.left);\n else return subtreeWithAllDeepest(root.right);\n }\n public int height(TreeNode root)\n {\n if(root==null)return 0;\n return (int)Math.max(height(root.left),height(root.right))+1;\n }\n}\n```
| 4 | 0 |
['Binary Tree', 'Java']
| 1 |
smallest-subtree-with-all-the-deepest-nodes
|
EASY DFS C++ SOLUTION
|
easy-dfs-c-solution-by-sahib5730-o9gx
|
\nclass Solution {\npublic:\n TreeNode* ans;\n int help(TreeNode* root){\n if(!root)return 0;\n int l = help(root->left);\n int r = h
|
sahib5730
|
NORMAL
|
2022-07-19T05:11:57.215787+00:00
|
2022-07-19T05:11:57.215829+00:00
| 550 | false |
```\nclass Solution {\npublic:\n TreeNode* ans;\n int help(TreeNode* root){\n if(!root)return 0;\n int l = help(root->left);\n int r = help(root->right);\n return max(l,r)+1;\n }\n bool help2(TreeNode*root,int ht){\n if(ht==0)\n return true;\n if(!root)return false;\n bool l = help2(root->left,ht-1);\n bool r = help2(root->right,ht-1);\n if(l and r){\n // cout<<root->val<<" ";\n ans = root;\n }\n return l or r;\n }\n TreeNode* subtreeWithAllDeepest(TreeNode* root) {\n int ht=0;\n ht = help(root);\n help2(root,ht);\n return ans;\n }\n};\n```
| 4 | 0 |
['Depth-First Search', 'Recursion', 'C++']
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
BFS one pass beats 100% with clear explanation
|
bfs-one-pass-beats-100-with-clear-explan-q2lc
|
All node have highest depth should all located on the last row of the input tree.\n2. If there is only one node on last row. We just need to return that node.\n
|
skrmao
|
NORMAL
|
2019-03-08T22:29:17.334932+00:00
|
2019-03-08T22:29:17.334981+00:00
| 387 | false |
1. All node have highest depth should all located on the last row of the input tree.\n2. If there is only one node on last row. We just need to return that node.\n3. If there are multiple nodes on the last row the we have to find the lowest common ancestor of the most left node and most right node.\n4. We can achieve this by doing one level-order-traversal to find the last row of the input tree and meanwhile use a hashmap to store the parent-child relationship of all node.\n\n```\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * public int val;\n * public TreeNode left;\n * public TreeNode right;\n * public TreeNode(int x) { val = x; }\n * }\n */\n public class Solution {\n\n public TreeNode SubtreeWithAllDeepest(TreeNode root)\n {\n if (root == null) return root;\n\t Dictionary<TreeNode, TreeNode> dict = new Dictionary<TreeNode, TreeNode>();\n var q = new Queue<TreeNode>();\n var lastrow = new List<TreeNode>(); \n\t \n\t //Find the last row of input tree same as level order traversal\n q.Enqueue(root);\n\n while(q.Count != 0)\n {\n lastrow = new List<TreeNode>();\n var level = q.Count;\n for(int i = 0; i< level;i++)\n {\n var temp = q.Dequeue();\n if(temp.left != null) {\n q.Enqueue(temp.left);\n dict.Add(temp.left, temp);\n }\n if(temp.right != null) {\n q.Enqueue(temp.right);\n dict.Add(temp.right, temp);\n }\n lastrow.Add(temp);\n }\n\n } \n \n if(lastrow.Count == 1) return lastrow.First();\n\t// find the lowest common ancestor of most left and most right node on last row\n var left = lastrow.First();\n var right = lastrow.Last();\n\n while(dict[left] != dict[right])\n {\n left = dict[left];\n right = dict[right];\n }\n\n return dict[left];\n }\n}\n```
| 4 | 0 |
['Breadth-First Search']
| 1 |
smallest-subtree-with-all-the-deepest-nodes
|
0 ms JS/C++. DFS. Beats 100.00%
|
0-ms-jsc-dfs-beats-10000-by-nodeforce-zk2c
|
ApproachDFS. Check the depth of the left and right child, if they are equal to the maximum depth, then the node is the lca(Lowest Common Ancestor) of Deepest Le
|
nodeforce
|
NORMAL
|
2025-04-04T11:46:24.179332+00:00
|
2025-04-04T12:16:31.938849+00:00
| 95 | false |
# Approach
DFS. Check the depth of the left and right child, if they are equal to the maximum depth, then the node is the `lca`(Lowest Common Ancestor) of Deepest Leaves. The solution is the same as [1123. Lowest Common Ancestor of Deepest Leaves](https://leetcode.com/problems/lowest-common-ancestor-of-deepest-leaves/solutions/6614672/0-ms-jsc-dfs-beats-10000-by-nodeforce-x7wp).
# Complexity
- Time complexity: $$O(n)$$.
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(n)$$, because of recursion.
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
static TreeNode* subtreeWithAllDeepest(TreeNode* r) {
int maxDepth = -1;
TreeNode* lca = nullptr;
const function<int(TreeNode*, int)> dfs = [&maxDepth, &lca, &dfs](TreeNode* n, int d) {
const int dleft = n->left ? dfs(n->left, d + 1) : d;
const int dright = n->right ? dfs(n->right, d + 1) : d;
if (d > maxDepth) maxDepth = d;
if (dleft == maxDepth && dright == maxDepth) lca = n;
return max(dleft, dright);
};
dfs(r, 0);
return lca;
}
};
```
```javascript []
const subtreeWithAllDeepest = (r) => {
let maxDepth = -1;
let lca = null;
const dfs = (n, d) => {
const dleft = n.left ? dfs(n.left, d + 1) : d;
const dright = n.right ? dfs(n.right, d + 1) : d;
if (d > maxDepth) maxDepth = d;
if (dleft === maxDepth && dright === maxDepth) lca = n;
return Math.max(dleft, dright);
};
dfs(r, 0);
return lca;
};
```
| 3 | 0 |
['Tree', 'Depth-First Search', 'Recursion', 'C', 'Binary Tree', 'C++', 'TypeScript', 'JavaScript']
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
Solution
|
solution-by-deleted_user-tk9q
|
C++ []\nclass Solution {\npublic:\n int height(TreeNode* root) {\n if (!root) return 0;\n return max(height(root->left) + 1, height(root->right
|
deleted_user
|
NORMAL
|
2023-05-08T06:21:18.255618+00:00
|
2023-05-08T07:20:33.738660+00:00
| 838 | false |
```C++ []\nclass Solution {\npublic:\n int height(TreeNode* root) {\n if (!root) return 0;\n return max(height(root->left) + 1, height(root->right) + 1); \n }\n TreeNode* subtreeWithAllDeepest(TreeNode* root) {\n if (!root) return NULL;\n\n int left = height(root->left); \n int right = height(root->right);\n\n if (left == right) return root;\n if (left > right) return subtreeWithAllDeepest(root->left);\n return subtreeWithAllDeepest(root->right);\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def subtreeWithAllDeepest(self, root: TreeNode) -> TreeNode:\n found = False\n ans = TreeNode(-1)\n \n def dfs(node,p,q):\n nonlocal found, ans\n if not node: return []\n \n left = dfs(node.left,left_node,right_node)\n right = dfs(node.right,left_node,right_node)\n \n total = [*left,*right]\n total.append(node.val)\n \n if p.val in total and q.val in total and not found: \n ans = (node)\n found = True\n \n return total\n\n def find_depth(root):\n q = deque()\n q.append(root)\n\n while q:\n l,r = None,None\n no_nodes = len(q)\n for i in range(len(q)):\n a = q.popleft()\n if i == 0: l = a\n if i == no_nodes-1: r = a\n\n if a.left: q.append(a.left)\n if a.right: q.append(a.right)\n \n return l,r\n \n left_node,right_node = find_depth(root)\n dfs(root,left_node,right_node)\n \n return ans\n```\n\n```Java []\nclass Solution {\n int maxDepth = Integer.MIN_VALUE;\n TreeNode result = null;\n public TreeNode subtreeWithAllDeepest(TreeNode root) {\n postOrder(root, 0);\n return result;\n }\n public int postOrder(TreeNode node, int deep) {\n if (node == null) {\n return deep;\n }\n int left = postOrder(node.left, deep + 1);\n int right = postOrder(node.right, deep + 1);\n int curDepth = Math.max(left, right);\n maxDepth = Math.max(maxDepth, curDepth);\n if (left == maxDepth && right == maxDepth) {\n result = node;\n }\n return curDepth;\n }\n}\n```\n
| 3 | 0 |
['C++', 'Java', 'Python3']
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
Solution in C++
|
solution-in-c-by-ashish_madhup-z6w5
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
ashish_madhup
|
NORMAL
|
2023-03-01T16:25:01.757788+00:00
|
2023-03-01T16:25:01.757832+00:00
| 531 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution \n{\npublic:\n TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {\n if (!root) return NULL;\n if (root==p || root==q) return root;\n TreeNode *l = lowestCommonAncestor(root->left,p,q);\n TreeNode *r = lowestCommonAncestor(root->right,p,q);\n if (l&&r) return root;\n if (l) return l;\n return r;\n } \n vector<vector<TreeNode*>> bfs(TreeNode* root)\n {\n vector<vector<TreeNode*>> ret;\n queue<TreeNode*> q;\n q.push(root);\n while(!q.empty()) {\n int currlen = q.size();\n vector<TreeNode*> row;\n for (int i=0; i<currlen; i++) {\n auto curr = q.front(); q.pop();\n row.push_back(curr);\n if (curr->left) q.push(curr->left);\n if (curr->right) q.push(curr->right);\n }\n ret.push_back(row);\n }\n return ret;\n }\n TreeNode* subtreeWithAllDeepest(TreeNode* root)\n {\n vector<vector<TreeNode*>> level = bfs(root);\n vector<TreeNode*> tmp = level.back();\n if (tmp.size()==1) return tmp[0];\n return lowestCommonAncestor(root, tmp[0], tmp.back());\n }\n};\n```
| 3 | 0 |
['C++']
| 1 |
smallest-subtree-with-all-the-deepest-nodes
|
C++ easy fast and short code
|
c-easy-fast-and-short-code-by-divyansh-x-rwnt
|
\nclass Solution {\npublic:\n \n unordered_set <TreeNode*> m;\n int n;\n TreeNode *ans = NULL;\n \n int solve(TreeNode *root)\n {\n
|
divyansh-xz
|
NORMAL
|
2022-10-05T05:25:10.925677+00:00
|
2022-10-05T05:25:10.925716+00:00
| 474 | false |
```\nclass Solution {\npublic:\n \n unordered_set <TreeNode*> m;\n int n;\n TreeNode *ans = NULL;\n \n int solve(TreeNode *root)\n {\n if(!root or ans) return 0;\n \n int left = solve(root->left);\n int right = solve(root->right);\n \n int x = left+right;\n \n if(m.find(root)!=m.end())\n x++;\n \n if(x==n and !ans)\n ans = root;\n \n return x;\n }\n \n TreeNode* subtreeWithAllDeepest(TreeNode* root) {\n queue<TreeNode*> q, temp;\n q.push(root);\n \n while(q.size())\n {\n temp = q;\n int n = q.size();\n for(int i = 0;i<n;i++)\n {\n TreeNode *r = q.front();\n q.pop();\n \n if(r->left)\n q.push(r->left);\n \n if(r->right)\n q.push(r->right);\n }\n }\n \n while(temp.size())\n {\n m.insert(temp.front());\n temp.pop();\n }\n n = m.size();\n \n solve(root);\n return ans;\n }\n \n};\n```\n**UPVOTE!**
| 3 | 0 |
['C']
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
100% faster C++ depth comparison, optimized with hashmap
|
100-faster-c-depth-comparison-optimized-jvztf
|
\nunordered_map<int,int> mp;\n \n int depth(TreeNode* root){\n if(!root) return 0;\n if(mp.find(root->val)!=mp.end()) return mp[root->val];\
|
reetisharma
|
NORMAL
|
2021-09-29T15:09:58.369003+00:00
|
2021-09-29T15:09:58.369052+00:00
| 124 | false |
```\nunordered_map<int,int> mp;\n \n int depth(TreeNode* root){\n if(!root) return 0;\n if(mp.find(root->val)!=mp.end()) return mp[root->val];\n return mp[root->val] = 1 + max(depth(root->left), depth(root->right));\n }\n TreeNode* subtreeWithAllDeepest(TreeNode* root) {\n if(!root) return root;\n \n int l,r;\n \n if(root->left && mp.find(root->left->val)!=mp.end()) l = mp[root->left->val];\n else l = depth(root->left);\n \n if(root->right && mp.find(root->right->val)!=mp.end()) r = mp[root->right->val];\n else r = depth(root->right);\n \n if(l==r)return root;\n else if(l>r) return subtreeWithAllDeepest(root->left);\n else return subtreeWithAllDeepest(root->right);\n }\n```
| 3 | 0 |
[]
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
Simple 0ms DFS PostOrder Solution.
|
simple-0ms-dfs-postorder-solution-by-bud-z4or
|
The question simple wants to ask the lca of the deepest nodes, so what we are doing is, first we call and get the the deepest height of both the sides, and if t
|
budhirajamadhav
|
NORMAL
|
2021-07-07T02:10:18.477637+00:00
|
2021-07-07T02:10:18.477670+00:00
| 71 | false |
The question simple wants to ask the lca of the deepest nodes, so what we are doing is, first we call and get the the deepest height of both the sides, and if they come the same and it is greater than the previous deepest height then this node is the lca and both deepest lie on either of its sides.\n\n```\n TreeNode answer = null;\n int curDepth = 0;\n \n public int lcaOfDeepest(TreeNode node, int level){\n \n if(node == null) return level;\n \n int leftDepth = lcaOfDeepest(node.left, level + 1);\n int rightDepth = lcaOfDeepest(node.right, level + 1);\n \n if(leftDepth == rightDepth && leftDepth >= curDepth){\n \n curDepth = leftDepth;\n answer = node;\n return leftDepth;\n \n }\n \n return Math.max(leftDepth, rightDepth);\n \n }\n \n public TreeNode subtreeWithAllDeepest(TreeNode root) {\n \n lcaOfDeepest(root, 1);\n return answer;\n \n }\n\n```
| 3 | 1 |
[]
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
Python, BFS + LCA
|
python-bfs-lca-by-iamcookie-erpd
|
Find the deepest nodes using BFS. If there is nothing left in queues, that means all the nodes in current level are the deepest nodes. After we got all the deep
|
iamcookie
|
NORMAL
|
2021-03-02T22:01:17.762908+00:00
|
2021-03-02T22:02:21.269168+00:00
| 322 | false |
Find the deepest nodes using BFS. If there is nothing left in queues, that means all the nodes in current level are the deepest nodes. After we got all the deepest nodes, then we want find the lowest common ancestor (LCA) of all the node using recursion.\n```\nclass Solution:\n def subtreeWithAllDeepest(self, root: TreeNode) -> TreeNode:\n leafs = self.bfs(root)\n return self.LCA(root, leafs)\n \n def bfs(self, node):\n q = [node]\n while q:\n level = []\n for i in range(len(q)):\n node = q.pop(0)\n if node.left:\n q.append(node.left)\n if node.right:\n q.append(node.right)\n level.append(node)\n if not q:\n return level #return a list\n \n \n def LCA(self, node, nodes): #nodes going to be list of deepest nodes\n if not node:\n return None\n \n if node in nodes:\n return node\n \n left = self.LCA(node.left, nodes)\n right = self.LCA(node.right, nodes)\n \n if left and right:\n return node\n \n else:\n return left or right\n```
| 3 | 0 |
['Breadth-First Search', 'Python']
| 1 |
smallest-subtree-with-all-the-deepest-nodes
|
[Simple] [C++] solution
|
simple-c-solution-by-hackhim18-n9w5
|
Runtime: 4 ms, faster than 85.18% of C++ online submissions for Smallest Subtree with all the Deepest Nodes.\nMemory Usage: 14.5 MB, less than 100.00% of C++ on
|
hackhim18
|
NORMAL
|
2021-01-13T22:48:49.985423+00:00
|
2021-01-13T22:48:49.985471+00:00
| 134 | false |
*Runtime: 4 ms, faster than 85.18% of C++ online submissions for Smallest Subtree with all the Deepest Nodes.\nMemory Usage: 14.5 MB, less than 100.00% of C++ online submissions for Smallest Subtree with all the Deepest Nodes.*\n\n```\nclass Solution {\npublic:\n TreeNode* subtreeWithAllDeepest(TreeNode* root) {\n if(root == NULL){\n return NULL;\n }\n int leftDepth = getDepth(root->left); \n int rightDepth = getDepth(root->right);\n if(leftDepth == rightDepth){\n return root;\n }\n else{\n if(leftDepth > rightDepth){\n return subtreeWithAllDeepest(root->left);\n }else {\n return subtreeWithAllDeepest(root->right); \n }\n }\n }\n //to calculate the height\n int getDepth(TreeNode* node){\n if(node == NULL){\n return 0;\n }\n return 1 + max(getDepth(node->left), getDepth(node->right));\n }\n \n};\n```
| 3 | 0 |
['Recursion', 'C']
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
Python O(n) by DFS [w/ Comment]
|
python-on-by-dfs-w-comment-by-brianchian-e27f
|
Python O(n) by DFS \n\n---\n\nImplementation:\n\n\nclass Solution:\n def subtreeWithAllDeepest(self, root: TreeNode) -> TreeNode:\n \n # ------
|
brianchiang_tw
|
NORMAL
|
2020-12-12T10:01:16.055780+00:00
|
2020-12-12T10:41:05.259373+00:00
| 430 | false |
Python O(n) by DFS \n\n---\n\n**Implementation**:\n\n```\nclass Solution:\n def subtreeWithAllDeepest(self, root: TreeNode) -> TreeNode:\n \n # --------------------------------------------\n def helper(node: TreeNode) -> (int, TreeNode):\n \n # first return item is depth\n # second return item is root of smallest subtree with deepest nooes\n \n if not node:\n\t\t\t\n # base case\n # empty node or empty tree\n return 0, None\n \n l_depth, l_node = helper(node.left)\n r_depth, r_node = helper(node.right)\n \n if l_depth > r_depth:\n\t\t\t\n # left subtree is deeper\n return l_depth+1, l_node\n \n elif r_depth > l_depth:\n\t\t\t\n # right subtree is deeper\n return r_depth+1, r_node\n \n else:\n\t\t\t\n # both subtrees are the same\n # current node is the root of smallest subtree with deepest nodes\n return l_depth+1, node\n \n # --------------------------------------------\n \n # second return item is the answer\n return helper(root)[1]\n```\n\n---\n\nRelated leetcode challenge:\n\n[Leetcode #104 Maximum Depth of Binary Tree](https://leetcode.com/problems/maximum-depth-of-binary-tree/)
| 3 | 0 |
['Depth-First Search', 'Recursion', 'Python', 'Python3']
| 1 |
smallest-subtree-with-all-the-deepest-nodes
|
[Java] Two pass | Clean solution | 100% / 98%
|
java-two-pass-clean-solution-100-98-by-a-kkud
|
1) Get the height of the deepest node\n2) Start returning the deepest node\n3) For those who are not the deepest nodes return null from them\n4) if left and rig
|
aksharkashyap
|
NORMAL
|
2020-07-21T15:08:32.959338+00:00
|
2020-07-21T15:22:28.212625+00:00
| 234 | false |
1) Get the height of the deepest node\n2) Start returning the deepest node\n3) For those who are not the deepest nodes return null from them\n4) if left and right subtree of a certain node returned the deepest nodes then return(propagate) the node itself\n5) if left subtree returned deepest node but right subtree returned null, propagate the deepest node(left) further\n6) if right subtree returned deepest node but left subtree returned null, propagate the deepest node(right) further\n```\nclass Solution {\n \n int getHeight(TreeNode root){\n if(root == null) return 0;\n int left = getHeight(root.left)+1;\n int right = getHeight(root.right)+1;\n return Math.max(left,right);\n }\n \n TreeNode getNode(TreeNode root,int h, int H){\n if(root == null) return null;\n if(h == H) return root;\n TreeNode left = getNode(root.left,h+1,H);\n TreeNode right = getNode(root.right,h+1,H);\n if(left != null && right != null) return root; \n return left != null ? left : right; \n }\n \n public TreeNode subtreeWithAllDeepest(TreeNode root) {\n return getNode(root,1,getHeight(root));\n }\n}\n```
| 3 | 0 |
['Java']
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
Java - Easy solution by comparing Depth - with comments
|
java-easy-solution-by-comparing-depth-wi-ehz6
|
\nclass Solution {\n public TreeNode subtreeWithAllDeepest(TreeNode root) {\n if (root == null) {\n return null;\n }\n int le
|
meltawab
|
NORMAL
|
2020-06-12T18:45:55.284979+00:00
|
2020-06-12T18:45:55.285014+00:00
| 179 | false |
```\nclass Solution {\n public TreeNode subtreeWithAllDeepest(TreeNode root) {\n if (root == null) {\n return null;\n }\n int leftDepth = getDepth(root.left); // get depth of left\n int rightDepth = getDepth(root.right); // get depth of right\n if (leftDepth == rightDepth) {\n return root; // You got it!\n } else {\n // Go with the deepest side \n if(leftDepth > rightDepth){\n return subtreeWithAllDeepest(root.left);\n } else {\n return subtreeWithAllDeepest(root.right);\n }\n }\n }\n \n // Method to get depth of tree at any node.\n public int getDepth (TreeNode node) {\n if (node == null) {\n return 0;\n }\n return 1 + Math.max(getDepth(node.left), getDepth(node.right)); \n }\n}\n```
| 3 | 0 |
['Depth-First Search', 'Java']
| 1 |
smallest-subtree-with-all-the-deepest-nodes
|
recursive python solution
|
recursive-python-solution-by-shuuchen-690q
|
```\nclass Solution:\n def subtreeWithAllDeepest(self, root: TreeNode) -> TreeNode:\n def helper(node):\n if not node:\n ret
|
shuuchen
|
NORMAL
|
2019-08-15T14:05:44.082057+00:00
|
2019-08-15T14:05:44.082103+00:00
| 284 | false |
```\nclass Solution:\n def subtreeWithAllDeepest(self, root: TreeNode) -> TreeNode:\n def helper(node):\n if not node:\n return 0, None\n ld, ln = helper(node.left)\n rd, rn = helper(node.right)\n \n return max(ld, rd) + 1, node if ld == rd else ln if ld > rd else rn\n \n return helper(root)[1]
| 3 | 0 |
[]
| 1 |
smallest-subtree-with-all-the-deepest-nodes
|
C# Solution
|
c-solution-by-leonhard_euler-a5eb
|
\npublic class Solution \n{\n public TreeNode SubtreeWithAllDeepest(TreeNode root) \n {\n if(root == null) return root;\n int l = GetDepth(r
|
Leonhard_Euler
|
NORMAL
|
2019-08-06T05:17:00.289974+00:00
|
2019-08-06T05:17:00.290035+00:00
| 104 | false |
```\npublic class Solution \n{\n public TreeNode SubtreeWithAllDeepest(TreeNode root) \n {\n if(root == null) return root;\n int l = GetDepth(root.left), r = GetDepth(root.right);\n if(l == r) return root;\n if(l > r) return SubtreeWithAllDeepest(root.left);\n return SubtreeWithAllDeepest(root.right);\n }\n \n private int GetDepth(TreeNode root)\n {\n return root == null ? 0 : 1 + Math.Max(GetDepth(root.left), GetDepth(root.right));\n }\n}\n```
| 3 | 0 |
[]
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
⚡CLEAN CODE⚡| ✅✅BEATS 100%🍨| 🗝️ EASY EXPLANATION🧊 | Using Depth-First-Search
|
clean-code-beats-100-easy-explanation-us-1mee
|
IntuitionGiven the root of a binary tree, the depth of each node is the shortest distance to the root.Return the smallest subtree such that it contains all the
|
Happy-Singh-Chauhan
|
NORMAL
|
2025-04-04T09:32:03.894437+00:00
|
2025-04-04T09:32:03.894437+00:00
| 102 | false |
# Intuition
Given the root of a binary tree, the depth of each node is the shortest distance to the root.
Return the smallest subtree such that it contains all the deepest nodes in the original tree.
A node is called the deepest if it has the largest depth possible among any node in the entire tree.
The subtree of a node is a tree consisting of that node, plus the set of all descendants of that node.
This question is same as 1123:[https://leetcode.com/problems/lowest-common-ancestor-of-deepest-leaves/description/]()
# Approach
1. Initialize a treenode res for storing end result and maxDepth initially -1 as global variable.
2. Using function dfs recursively :
* Base Condition : If the root node is pointing null, return maximum of maxDepth and current depth.
* Check for left and right of root node recursively.
* If left is equal to right and maxDepth, we are in the maxDepth so just update res as that root node.
* Else return maximum of left and right node.
# Complexity
- Time complexity:
O(n)
- Space complexity:
O(n)
# Code
```java []
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
TreeNode res;
int maxDepth=-1;
public int dfs(TreeNode root,int depth){
if(root == null){
maxDepth=Math.max(maxDepth,depth);
return depth;
}
int left=dfs(root.left,depth+1);
int right=dfs(root.right,depth+1);
if(left == right && left == maxDepth)res=root;
return Math.max(left,right);
}
public TreeNode subtreeWithAllDeepest(TreeNode root) {
dfs(root,0);
return res;
}
}
```
```c++ []
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
TreeNode* res = nullptr;
int maxDepth = -1;
int dfs(TreeNode* root, int depth) {
if (root == nullptr) {
maxDepth = std::max(maxDepth, depth);
return depth;
}
int left = dfs(root->left, depth + 1);
int right = dfs(root->right, depth + 1);
if (left == right && left == maxDepth) {
res = root;
}
return std::max(left, right);
}
public:
TreeNode* subtreeWithAllDeepest(TreeNode* root) {
dfs(root, 0);
return res;
}
};
```
```python []
# Definition for a binary tree node.
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution:
def __init__(self):
self.res = None
self.maxDepth = -1
def dfs(self, root, depth):
if not root:
self.maxDepth = max(self.maxDepth, depth)
return depth
left = self.dfs(root.left, depth + 1)
right = self.dfs(root.right, depth + 1)
if left == right and left == self.maxDepth:
self.res = root
return max(left, right)
def subtreeWithAllDeepest(self, root: TreeNode) -> TreeNode:
self.dfs(root, 0)
return self.res
```

| 2 | 0 |
['Tree', 'Depth-First Search', 'Binary Tree', 'C++', 'Java', 'Python3']
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
Python Intuitive Solution🔥Single Pass DFS LCA Approach [Beats 100% ⚡]
|
python-intuitive-solutionsingle-pass-dfs-e6hn
|
IntuitionFind a node whose left and right subtree depths are equal (since we are looking for the lowest common ancestor of the deepest nodes in those subtrees.)
|
user8043Na
|
NORMAL
|
2025-01-12T15:50:04.155366+00:00
|
2025-01-12T15:50:04.155366+00:00
| 251 | false |
# Intuition
Find a node whose left and right subtree depths are equal (since we are looking for the lowest common ancestor of the deepest nodes in those subtrees.). Among such nodes, choose the one that is:
- Has the greatest subtree depths (implying it covers all deepest nodes).
- If multiple nodes exist, choose the one at the shallowest depth in the tree.
```
3 [l=3, r=2]
/ \
5 [l=2, r=3] 1 [l=1, r=2]
/ \ \
6 [l=2, r=2] 2 [l=3, r=3] 8 [l=2, r=2]
/ \
7 [l=3, r=3] 4 [l=3, r=3]
```
The required node is the one which follows all these conditions:
$$ l(node) == r(node) , \\l(node) = max(l), \\ depth(node) = min(depth)$$
From above example, Node 2 follows the criterion.
# Complexity
## Time complexity:
It only requires a single pass depth first search making it a $O(n)$ solution.
## Space complexity: $O(1)$
# Code
```python3 []
# Definition for a binary tree node.
class TreeNode(object):
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution(object):
def __init__(self):
# Stores the node that covers all the deepest nodes in the tree
self.target_node = None
# Minimum depth at which the target node is found (used for tie-breaking)
self.min_depth = 1000
# Maximum depth at which the deepest nodes are found
self.max_depth = -1
def dfs(self, node, depth):
"""
Perform depth-first search to calculate the depth of left and right subtrees.
Intuition:
- Find a node whose left and right subtree depths are equal (implying it covers all deepest nodes).
- Among such nodes, choose the one that is:
1. At the greatest depth for the deepest nodes.
2. If multiple nodes exist, choose the one at the shallowest depth in the tree.
"""
if node is None:
# Return the depth just above the null node
return depth - 1
# Recursively calculate the maximum depth of the left and right subtrees
depth_l = self.dfs(node.left, depth + 1)
depth_r = self.dfs(node.right, depth + 1)
# Check if this node is a potential target node
if depth_l == depth_r:
# Condition 1: If the subtree depth is greater than the previously known max depth
if depth_l > self.max_depth or \
(depth_l == self.max_depth and depth < self.min_depth):
# Condition 2: If the subtree depth matches the max depth, but this node is at a shallower depth
self.target_node = node
self.min_depth = depth
self.max_depth = depth_l
# Return the maximum depth found in the left or right subtree
return max(depth_l, depth_r)
def subtreeWithAllDeepest(self, root):
self.dfs(root, 0)
return self.target_node
```
| 2 | 0 |
['Python3']
| 1 |
smallest-subtree-with-all-the-deepest-nodes
|
Easiest java solution explained | Beats 100%
|
easiest-java-solution-explained-beats-10-byzq
|
# IntuitionThe task is to find the subtree with all the deepest nodes in a binary tree. The deepest nodes are the ones that lie at the maximum depth of the tree
|
atharva9412
|
NORMAL
|
2024-12-16T12:40:11.094316+00:00
|
2024-12-26T07:32:47.881311+00:00
| 158 | false |
### **# Intuition**
The task is to find the **subtree with all the deepest nodes** in a binary tree. The deepest nodes are the ones that lie at the maximum depth of the tree.
- To solve this, we need to identify the **depth** of the left and right subtrees.
- We then recursively explore the subtree with the deeper depth until we reach the common ancestor of all the deepest nodes.
---
### **# Approach**
1. **Recursive Subtree Traversal:**
- Start from the root of the tree and calculate the heights of the left and right subtrees.
- If the heights are equal, it means the root of the current subtree is the common ancestor of all the deepest nodes, and we can return it.
- If one side is deeper (greater height), move to that side and repeat the process recursively.
2. **Height Calculation:**
- Use a helper function `getHeight()` to calculate the height of a node. The height is defined as the number of edges from the node to the deepest leaf.
- For each node, the height is the maximum of the left and right subtree heights, plus one for the current node.
3. **Termination Condition:**
- If we reach a leaf node (or a null node), we stop and return the corresponding height (0 for null, 1 for a leaf node).
---
### **# Complexity**
- **Time Complexity:**
- For each node, we calculate the height of its subtrees. Since the height calculation involves a traversal of each node, the overall complexity is O(n), where n is the number of nodes in the tree.
- **Space Complexity:**
- The space complexity is O(h), where h is the height of the tree, because we use recursion (which adds to the stack space).
---
### **# Code Explanation**
```java
class Solution {
// Function to find the subtree containing all the deepest nodes
public TreeNode subtreeWithAllDeepest(TreeNode root) {
if (root == null) {
return null; // Base case: If root is null, return null
}
// Calculate the heights of the left and right subtrees
int leftHeight = getHeight(root.left);
int rightHeight = getHeight(root.right);
// If left and right heights are equal, return the current root
if (leftHeight == rightHeight) {
return root;
}
// Otherwise, recurse into the deeper subtree
if (leftHeight > rightHeight) {
return subtreeWithAllDeepest(root.left); // Explore left subtree
} else {
return subtreeWithAllDeepest(root.right); // Explore right subtree
}
}
// Helper function to calculate the height of a node
public int getHeight(TreeNode node) {
if (node == null) {
return 0; // Base case: height of null node is 0
}
// Recursively calculate the height of the left and right subtrees
return Math.max(getHeight(node.left), getHeight(node.right)) + 1;
}
}
```
---
### **How the Code Works:**
1. **`subtreeWithAllDeepest()`**:
- It first checks the heights of the left and right subtrees using `getHeight()`.
- If both heights are the same, it means the current node is the common ancestor of all the deepest nodes, so it is returned.
- If one subtree is deeper than the other, the function recursively calls itself on the deeper side.
2. **`getHeight()`**:
- It computes the height of a subtree by returning the maximum depth between the left and right subtrees, incremented by one for the current node.
---
### **Example Run:**
Consider the following binary tree:
```
1
/ \
2 3
/ \ \
4 5 6
/ / \
7 8 9
```
- The deepest nodes are `7`, `8`, and `9`, all at level 4.
- The common ancestor of all these nodes is node `3` because it is the root of the subtree that contains all of them.
#### Explanation:
1. The height of the left subtree of node `1` is 3 (`[2, 4]`), and the right subtree is 3 (`[3, 6, 8, 9]`).
2. The left and right heights of node `1` are equal, so the subtree rooted at node `1` contains all the deepest nodes.
3. The result is the subtree rooted at node `1`.
---
### **Key Points:**
- The tree is traversed recursively to find the subtree that includes all the deepest nodes.
- The recursive depth comparisons guide the solution to the correct ancestor node.
#### Thank You !!
| 2 | 0 |
['Tree', 'Depth-First Search', 'Binary Tree', 'Java']
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
Beats 100% || Easy understandable c++
|
beats-100-easy-understandable-c-by-srimu-pudu
|
\n\n# Approach\n\nDo a preorder traversal of the whole tree and then find all the Tree Nodes with highest depth, and then by using lowest common ancestor of any
|
srimukheshsuru
|
NORMAL
|
2024-07-05T18:33:15.718804+00:00
|
2024-07-05T18:33:15.718832+00:00
| 115 | false |
\n\n# Approach\n\nDo a preorder traversal of the whole tree and then find all the Tree Nodes with highest depth, and then by using lowest common ancestor of any two nodes find the lowest common ancestor of all the nodes with highest depth \n\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\n\nclass Solution {\npublic:\n TreeNode* lca(TreeNode* root, TreeNode* p, TreeNode* q) {\n if(root== NULL) return root;\n if(root==p || root == q) return root;\n TreeNode* l1 = lca(root->left,p,q);\n TreeNode* l2 = lca(root->right,p,q);\n if(l1==NULL) return l2;\n if(l2==NULL) return l1; \n if( (l1 ==p && l2 ==q) ||(l1 ==q && l2 ==p) ) return root;\n return NULL;\n }\n void preord(TreeNode* root,vector<pair<TreeNode*,int>>&v,int d){\n if(root == NULL) return;\n v.push_back({root,d});\n preord(root->left,v,d+1);\n preord(root->right,v,d+1);\n }\n TreeNode* subtreeWithAllDeepest(TreeNode* root) {\n vector<pair<TreeNode*,int>>v;\n preord(root,v,0);\n vector<TreeNode*>deeps;\n int maxdeep = 0;\n for(int i=0;i<v.size();i++){\n maxdeep = max(maxdeep,v[i].second);\n }\n for(int i=0;i<v.size();i++){\n if(v[i].second == maxdeep){\n deeps.push_back(v[i].first);\n }\n }\n if(deeps.size() == 1) return deeps[0];\n TreeNode* ans ;\n ans = lca(root,deeps[0],deeps[1]);\n for(int i=2;i<deeps.size();i++){\n ans = lca(root,ans,deeps[i]);\n }\n return ans;\n }\n};\n```
| 2 | 0 |
['Tree', 'Depth-First Search', 'C++']
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
c++ (clean code) ✅✅ || using DFS || beats 100% time
|
c-clean-code-using-dfs-beats-100-time-by-s5mb
|
Approach\n\n\n\n\n- Go down while calculating the depth.\n \n int l = subtree(root->left, c+1);\n int r = subtree(root->right, c+1);\n\n- If de
|
vikas107sharma
|
NORMAL
|
2024-04-19T21:29:36.305665+00:00
|
2024-04-19T21:29:36.305684+00:00
| 95 | false |
# Approach\n\n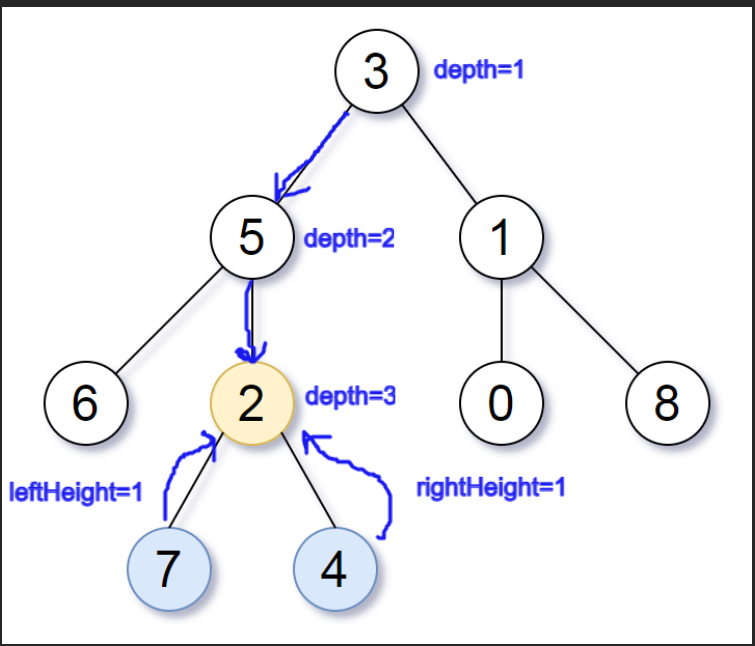\n\n\n- Go down while calculating the depth.\n ```\n int l = subtree(root->left, c+1);\n int r = subtree(root->right, c+1);\n ```\n- If depth+leftHeight == depth+rightHeight, here we get a valid node which could be our finalans\n ```\n if(c+l == c+r) {\n if(maxh<=c+l) {\n ans = root;\n maxh=c+l;\n }\n }\n ```\n- Update maxh when new height obtained is greater than maxh\n\n\n# Complexity\n\n```\nTime complexity: O(N)\n```\n```\nSpace complexity: O(N)\n```\n\n# Code\n```\nclass Solution {\npublic:\n\n TreeNode* ans;\n int maxh;\n int subtree(TreeNode* root, int c) {\n if(!root) return 0;\n int l = subtree(root->left, c+1);\n int r = subtree(root->right, c+1);\n if(c+l == c+r) {\n if(maxh<=c+l) {\n ans = root;\n maxh=c+l;\n }\n }\n return 1+max(l,r);\n }\n\n TreeNode* subtreeWithAllDeepest(TreeNode* root) {\n maxh=0;\n subtree(root,1);\n return ans;\n }\n};\n```\n\n```\nif(helpful) Upvote++ ;\n\uD83D\uDC4D\uD83D\uDC4D\uD83D\uDC4D\uD83D\uDC4D\n```
| 2 | 0 |
['Tree', 'Depth-First Search', 'Binary Tree', 'C++']
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
Breadth-first search and LCA
|
breadth-first-search-and-lca-by-rishabba-p8ns
|
Intuition\n Describe your first thoughts on how to solve this problem. \nLowest Common Ancestor\n\n# Approach\n Describe your approach to solving the problem. \
|
RishabBaid
|
NORMAL
|
2024-01-13T16:15:27.726365+00:00
|
2024-01-13T16:15:27.726397+00:00
| 123 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nLowest Common Ancestor\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFind out the last level of the tree and store the left and right nodes of that level, then we can simply find the lowest common ancestor of those 2 nodes and return that as the answer.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {\n if(!root || root == p || root == q)\n return root;\n TreeNode* left = lowestCommonAncestor(root->left, p, q);\n TreeNode* right = lowestCommonAncestor(root->right, p, q);\n if(!left)\n return right;\n if(!right)\n return left;\n return root;\n }\n TreeNode* subtreeWithAllDeepest(TreeNode* root) {\n vector<vector<TreeNode*>> vec;\n queue<TreeNode*> q;\n q.push(root);\n while(!q.empty()) {\n int n = q.size();\n vector<TreeNode*> temp;\n while(n--) {\n TreeNode* node = q.front();\n q.pop();\n temp.push_back(node);\n if(node->left)\n q.push(node->left);\n if(node->right)\n q.push(node->right);\n }\n vec.push_back(temp);\n }\n vector<TreeNode*> lastlvl = vec[vec.size()-1];\n TreeNode* left = lastlvl[0];\n TreeNode* right = lastlvl[lastlvl.size()-1];\n return lowestCommonAncestor(root, left, right);\n }\n};\n```
| 2 | 0 |
['Breadth-First Search', 'C++']
| 3 |
smallest-subtree-with-all-the-deepest-nodes
|
BFS O(N) Solution | Python
|
bfs-on-solution-python-by-rtassaramiller-2sph
|
Approach\n- Create a parent hash table (key: node | value: parent node)\n- Create a levels hash table to store the nodes at each height\n- Perform BFS normally
|
rtassaramiller
|
NORMAL
|
2023-09-10T16:24:50.465593+00:00
|
2023-09-10T16:25:09.098787+00:00
| 266 | false |
# Approach\n- Create a `parent` hash table (key: node | value: parent node)\n- Create a `levels` hash table to store the nodes at each height\n- Perform BFS normally while storing the parents and nodes at each level\n- We can find the LCA by traversing upwards the leftmost and rightmost nodes of the last level. If both variables point to the same node, it means we found the LCA.\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\n\nclass Solution:\n def subtreeWithAllDeepest(self, root: TreeNode) -> TreeNode:\n \n from collections import deque, defaultdict\n\n parents = {root: None}\n levels = defaultdict(list)\n max_depth = 0\n\n queue = deque([(root, 0)])\n\n while queue:\n node, depth = queue.popleft()\n levels[depth].append(node)\n max_depth = max(max_depth, depth)\n \n if node.left:\n parents[node.left] = node\n queue.append((node.left, depth + 1))\n\n if node.right:\n parents[node.right] = node\n queue.append((node.right, depth + 1))\n\n leftmost = levels[max_depth][0]\n rightmost = levels[max_depth][-1]\n\n while leftmost != rightmost:\n leftmost = parents[leftmost]\n rightmost = parents[rightmost]\n return leftmost\n\n```
| 2 | 0 |
['Breadth-First Search', 'Binary Tree', 'Python', 'Python3']
| 1 |
smallest-subtree-with-all-the-deepest-nodes
|
BEATS 80% -- RECURSIVE SOLUTION -- INTUTIVE -- EASY
|
beats-80-recursive-solution-intutive-eas-w3ce
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n see comments for exp
|
Skaezr73
|
NORMAL
|
2023-09-02T06:59:25.183939+00:00
|
2023-09-02T06:59:25.183961+00:00
| 61 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n <B> see comments for explanation!</B>\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n int height(TreeNode* root) { // find height of tree\n if (root == nullptr) return 0;\n else return 1 + max(height(root->left), height(root->right));\n }\n\n TreeNode* dfs(TreeNode* root, int h, int curh) {\n if (root == nullptr) { // if reached to end node having height less than max height!\n return nullptr;\n } else {\n curh++; // increase current height by 1\n TreeNode* lef = dfs(root->left, h, curh); //check whether left subtree has that max depth node or not\n \n TreeNode* rig = dfs(root->right, h,curh); // check whether right subtree has max depth node or not\n\n if (curh == h) {\n return root; // if present node is max depth return it!\n } else if (lef != nullptr && rig != nullptr) {\n return root; // if both left nad right subtree have that "max depth node" return their ancestor!\n } else if (lef != nullptr) {\n return lef;// if left subtree has "max depth node" return the pointer which was generated recursively\n } else if (rig != nullptr) {\n return rig; // apropos to above step!\n } else {\n return nullptr; // if right and left subtree dont have "max depth node" return null!\n }\n }\n }\n\n TreeNode* subtreeWithAllDeepest(TreeNode* root) {\n int h = height(root);\n int curh = 0;\n TreeNode* ans = dfs(root, h, curh);\n return ans;\n }\n};\n\n```
| 2 | 0 |
['C++']
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
Simple DFS solution || O(N)time || BFS+LCA
|
simple-dfs-solution-ontime-bfslca-by-shr-mhou
|
\n\n# Code\n\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNod
|
Shristha
|
NORMAL
|
2023-02-04T07:35:37.243811+00:00
|
2023-02-04T07:35:37.243852+00:00
| 253 | false |
\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\n\n //idea is find all nodes in last level & then find the least common ancestor for extreme left node & extreme right node.\nclass Solution {\npublic:\n TreeNode* lca( TreeNode* root, TreeNode* p, TreeNode* q ) {\n if ( !root || root == p || root == q ) return root;\n TreeNode *left = lca( root->left, p, q );\n TreeNode *right = lca (root->right, p, q );\n\n return !left? right: !right? left: root;\n }\n \n TreeNode* subtreeWithAllDeepest(TreeNode* root) {\n if ( !root || !root->left && !root->right ) return root;\n TreeNode *leftMost = NULL;\n TreeNode *rightMost = NULL;\n \n queue<TreeNode*> q;\n q.push(root);\n while( !q.empty() ) {\n int levelSize = q.size();\n for(int level = 0; level < levelSize; level++ ) {\n TreeNode* node = q.front(); q.pop();\n if ( level == 0 ) leftMost = node;\n if ( level == levelSize - 1 ) rightMost = node;\n \n if (node->left) q.push(node->left);\n if (node->right) q.push(node->right);\n \n }\n }\n return lca( root, leftMost, rightMost );\n }\n};\n\n```
| 2 | 0 |
['Breadth-First Search', 'C++']
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
Simple DFS solution || O(N)time || BFS+LCS
|
simple-dfs-solution-ontime-bfslcs-by-shr-2krj
|
\n\n# Code\n\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNod
|
Shristha
|
NORMAL
|
2023-02-04T07:33:45.804605+00:00
|
2023-02-04T07:33:45.804651+00:00
| 236 | false |
\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\n\n //idea is find all nodes in last level & then find the least common ancestor for extreme left node & extreme right node.\nclass Solution {\npublic:\n TreeNode* lca( TreeNode* root, TreeNode* p, TreeNode* q ) {\n if ( !root || root == p || root == q ) return root;\n TreeNode *left = lca( root->left, p, q );\n TreeNode *right = lca (root->right, p, q );\n\n return !left? right: !right? left: root;\n }\n \n TreeNode* subtreeWithAllDeepest(TreeNode* root) {\n if ( !root || !root->left && !root->right ) return root;\n TreeNode *leftMost = NULL;\n TreeNode *rightMost = NULL;\n \n queue<TreeNode*> q;\n q.push(root);\n while( !q.empty() ) {\n int levelSize = q.size();\n for(int level = 0; level < levelSize; level++ ) {\n TreeNode* node = q.front(); q.pop();\n if ( level == 0 ) leftMost = node;\n if ( level == levelSize - 1 ) rightMost = node;\n \n if (node->left) q.push(node->left);\n if (node->right) q.push(node->right);\n \n }\n }\n return lca( root, leftMost, rightMost );\n }\n};\n\n```
| 2 | 0 |
['Breadth-First Search', 'C++']
| 1 |
smallest-subtree-with-all-the-deepest-nodes
|
C++ easy fast and short code
|
c-easy-fast-and-short-code-by-akshat0610-59pw
|
\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0)
|
akshat0610
|
NORMAL
|
2022-10-27T06:40:10.449093+00:00
|
2022-10-27T06:40:10.449120+00:00
| 339 | false |
```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n TreeNode* subtreeWithAllDeepest(TreeNode* root) \n{\n return fun(root); \n}\nTreeNode* fun(TreeNode* root)\n{\n\t\n int left_h = geth(root->left);\n int right_h = geth(root->right);\n \n //if on the curr root -->\n \n //if we have left_h more than the right_h --> deepest leaves are present in the left then we would go in the left to generate the ans\n if(left_h > right_h)\n {\n \treturn fun(root->left);\n\t}\n\t//if we have right_h more than the right_h -->deepest leaves are present in the right then we would go in the right to generat the ans\n\telse if(right_h > left_h)\n\t{\n\t\treturn fun(root->right);\n\t}\n\telse if(right_h == left_h)\n\t{\n\t\treturn root;\n\t}\n return NULL;\n}\nint geth(TreeNode* root)\n{\n\tif(root==NULL)\n\t{\n\t\treturn 0;\n\t}\n\treturn 1 + max(geth(root->left),geth(root->right));\n}\n};\n```
| 2 | 0 |
['Depth-First Search', 'Recursion', 'C', 'C++']
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
Cpp Solution Using LCA
|
cpp-solution-using-lca-by-sanket_jadhav-2qkm
|
```\nclass Solution {\npublic:\n TreeNode lca(TreeNode root,TreeNode p,TreeNode q){\n if(!root)return NULL;\n if(root==p || root==q)return root
|
Sanket_Jadhav
|
NORMAL
|
2022-08-27T13:44:25.832783+00:00
|
2022-08-27T13:44:25.832813+00:00
| 233 | false |
```\nclass Solution {\npublic:\n TreeNode* lca(TreeNode* root,TreeNode* p,TreeNode* q){\n if(!root)return NULL;\n if(root==p || root==q)return root;\n \n TreeNode *left=lca(root->left,p,q);\n TreeNode *right=lca(root->right,p,q);\n \n if(!left)return right;\n if(!right)return left;\n \n return root;\n \n } \n \n TreeNode* subtreeWithAllDeepest(TreeNode* root) {\n if(!root)return root;\n \n vector<TreeNode*>v;\n \n queue<TreeNode*>q;\n q.push(root);\n \n while(!q.empty()){\n int n=q.size();\n vector<TreeNode*>a;\n \n for(int i=0;i<n;i++){\n auto ptr=q.front();\n q.pop();\n a.push_back(ptr);\n \n if(ptr->left)q.push(ptr->left);\n if(ptr->right)q.push(ptr->right);\n }\n v=a;\n }\n \n if(v.size()==1)return v[0];\n TreeNode* ptr=root;\n return lca(ptr,v[0],v[v.size()-1]);\n \n }\n};
| 2 | 0 |
['C++']
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
c++ solution || easy to understand
|
c-solution-easy-to-understand-by-tejraj-mjc78
|
class Solution {\npublic:\n TreeNode subtreeWithAllDeepest(TreeNode root) {\n unordered_map mp;\n mp[root]=NULL;\n queue q;\n q.p
|
Tejraj-Singh
|
NORMAL
|
2022-08-18T11:59:06.386022+00:00
|
2022-08-18T11:59:06.386052+00:00
| 116 | false |
class Solution {\npublic:\n TreeNode* subtreeWithAllDeepest(TreeNode* root) {\n unordered_map<TreeNode*,TreeNode*> mp;\n mp[root]=NULL;\n queue<TreeNode*> q;\n q.push(root);\n while(!q.empty()){\n int n=q.size();\n for(int i=0;i<n;i++){\n TreeNode* r=q.front(); q.pop();\n if(r->left){\n q.push(r->left);\n mp[r->left]=r;\n } \n if(r->right){\n q.push(r->right);\n mp[r->right]=r;\n } \n }\n }\n queue<TreeNode*> q1;\n q1.push(root);\n vector<TreeNode*> v1;\n while(!q1.empty()){\n v1.clear();\n int n=q1.size();\n for(int i=0;i<n;i++){\n TreeNode* r=q1.front(); q1.pop();\n v1.push_back(r);\n if(r->left) q1.push(r->left);\n if(r->right) q1.push(r->right);\n }\n }\n int n=v1.size()-1;\n TreeNode* t=NULL;\n unordered_map<TreeNode*,int> mp1;\n while(t==NULL){\n for(int i=0;i<v1.size();i++){\n if(mp1[v1[i]]==n && v1[i]!=NULL) t=v1[i];\n mp1[v1[i]]++;\n v1[i]=mp[v1[i]];\n }\n }\n return t;\n }\n};
| 2 | 0 |
[]
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
Python two pass beats 99%
|
python-two-pass-beats-99-by-ashkan-leo-qydy
|
The idea is to compute the depth and the parent of each vertex in the tree. Then, find the deepest nodes in the tree and climb up starting from them until we re
|
ashkan-leo
|
NORMAL
|
2022-04-30T22:25:59.159149+00:00
|
2022-04-30T22:26:15.346390+00:00
| 312 | false |
The idea is to compute the depth and the parent of each vertex in the tree. Then, find the deepest nodes in the tree and climb up starting from them until we reach a common ancestor. I use dfs to compute the depths and parents, and then perform the climbing using them.\n\n```python\nclass Solution:\n def subtreeWithAllDeepest(self, root: TreeNode) -> TreeNode:\n parent, depth = {root: None}, {root: 0}\n def dfs(node):\n if node.right:\n parent[node.right] = node\n depth[node.right] = depth[node] + 1\n dfs(node.right)\n if node.left:\n parent[node.left] = node\n depth[node.left] = depth[node] + 1\n dfs(node.left)\n dfs(root)\n \n max_depth = max(depth.values())\n deepest_nodes = set(node for node in parent.keys() if depth[node] == max_depth)\n while len(deepest_nodes) > 1:\n deepest_nodes = set(parent[node] for node in deepest_nodes)\n \n return deepest_nodes.pop()\n```
| 2 | 0 |
['Depth-First Search', 'Python', 'Python3']
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
[Python][Interview] LCA of M nodes in an N-ary Tree
|
pythoninterview-lca-of-m-nodes-in-an-n-a-9p4i
|
Posting this as I got this question in an interview\nFind the LCA of m nodes in an n-ary tree, which can be reworded to find the smallest subtree of all m nodes
|
deafcon
|
NORMAL
|
2022-03-25T22:10:53.061163+00:00
|
2022-03-25T22:10:53.061198+00:00
| 228 | false |
Posting this as I got this question in an interview\nFind the LCA of m nodes in an n-ary tree, which can be reworded to find the smallest subtree of all m nodes.\n\nKeep a count of the m nodes found in each subtree. Once count == len(m) this is the LCA and return the ans\n\nExample:\nm = `2,1,3` -> LCA is 5\nm = `7,3` -> 1\nm = `1,3` -> 1\nm = `1,3,6` -> 5\n\n``` \n\t5\n / | \\\n2 1 6\n / \\\n 7 3\ndef soln(root, m):\n return recurse(root, m)[1]\n\ndef recurse(node, m):\n if not node:\n return (0, None) #return the count of m nodes seen and ans\n \n count = 0\n ans = None\n for child in node.children:\n seen, prev = self.recurse(child, m)\n if seen == -1:\n # this means we have already foundthe ans\n return (-1, prev)\n ans = prev\n count+=seen\n \n if node in m:\n count+=1\n prev = node # use this node now as LCA\n \n if count == len(m):\n return (-1, root)\n return (count, prev)\n```
| 2 | 0 |
['Depth-First Search', 'Python']
| 1 |
smallest-subtree-with-all-the-deepest-nodes
|
Java| 0MS 100% FASTER | WITH COMMENTS
|
java-0ms-100-faster-with-comments-by-aad-nrl7
|
\nclass Solution {\n TreeNode root1;\n public TreeNode subtreeWithAllDeepest(TreeNode root) {\n int d=depth(root);\n helper(root,d,0);\n
|
aadishjain__
|
NORMAL
|
2022-01-07T12:44:58.401391+00:00
|
2022-01-07T12:44:58.401432+00:00
| 126 | false |
```\nclass Solution {\n TreeNode root1;\n public TreeNode subtreeWithAllDeepest(TreeNode root) {\n int d=depth(root);\n helper(root,d,0);\n return root1;\n }\n public int helper(TreeNode root,int level,int last)\n {\n if(root==null)\n {\n return last;\n }\n \n int l=helper(root.left,level,last+1);\n int r=helper(root.right,level,last+1);\n \n if(l==level && r==level) //it will take us to last mode or deepest node\n {\n root1=root; \n }\n return Math.max(l,r);\n \n }\n public int depth(TreeNode root) // it is used to find max depth or last level of nodes\n {\n if(root==null)\n {\n return 0;\n }\n int l=depth(root.left);\n int r=depth(root.right);\n int th=Math.max(l,r)+1;\n return th;\n }\n}\n \n \n \n\n```
| 2 | 0 |
['Depth-First Search', 'Java']
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
Simple recursion with python (easy to understand) with explanation
|
simple-recursion-with-python-easy-to-und-f9u0
|
In short if both child has same depth, you return parent otherwise you return child with the max depth.\n```\n# Definition for a binary tree node.\n# class Tree
|
kaichamp101
|
NORMAL
|
2021-12-23T20:20:50.308778+00:00
|
2021-12-23T20:20:50.308821+00:00
| 199 | false |
In short if both child has same depth, you return parent otherwise you return child with the max depth.\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def findDepth(self, node):\n if not node:\n return 0\n return 1 + max(self.findDepth(node.left), self.findDepth(node.right))\n \n def subtreeWithAllDeepest(self, root: TreeNode) -> TreeNode:\n if self.findDepth(root.left) == self.findDepth(root.right):\n return root\n elif self.findDepth(root.left) > self.findDepth(root.right):\n return self.subtreeWithAllDeepest(root.left)\n else:\n return self.subtreeWithAllDeepest(root.right)
| 2 | 0 |
['Recursion', 'Python']
| 1 |
smallest-subtree-with-all-the-deepest-nodes
|
Java 100% Fast
|
java-100-fast-by-pagalpanda-4h28
|
\n public TreeNode subtreeWithAllDeepest(TreeNode root) {\n if(root == null) return root;\n \n int leftH = height(root.left);\n int
|
pagalpanda
|
NORMAL
|
2021-08-19T02:49:56.777719+00:00
|
2021-08-19T02:49:56.777748+00:00
| 102 | false |
```\n public TreeNode subtreeWithAllDeepest(TreeNode root) {\n if(root == null) return root;\n \n int leftH = height(root.left);\n int rightH = height(root.right);\n if(leftH == rightH) {\n return root;\n } else if(leftH > rightH) {\n return subtreeWithAllDeepest(root.left);\n }\n return subtreeWithAllDeepest(root.right);\n }\n \n int height(TreeNode root) {\n if(root == null) return 0;\n int left = height(root.left);\n int right = height(root.right);\n return 1 + Math.max(left, right);\n }\n```
| 2 | 0 |
['Java']
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
Java + HashMap recursive Solution
|
java-hashmap-recursive-solution-by-mysur-i1y9
|
```\nMap map = new HashMap<>();\n public TreeNode subtreeWithAllDeepest(TreeNode root) {\n //check the case if the both left subtree height == right s
|
mysururaja
|
NORMAL
|
2021-07-05T07:54:00.301302+00:00
|
2021-07-05T07:56:20.400913+00:00
| 45 | false |
```\nMap<TreeNode,Integer> map = new HashMap<>();\n public TreeNode subtreeWithAllDeepest(TreeNode root) {\n //check the case if the both left subtree height == right subtree height, if true return root else traverse left & right recursively to check for height\n \n if(root==null || (height(root.left)==height(root.right))) return root;\n return subtreeWithAllDeepest(height(root.left)>height(root.right) ? root.left : root.right);\n }\n \n public int height(TreeNode root){\n if(root==null) return 0;\n \n //maintain the hashmap with nodes & its coresponding height\n if(map.containsKey(root)) return map.get(root);\n \n map.put(root,1+Math.max(height(root.left),height(root.right)));\n \n return map.get(root);\n }
| 2 | 0 |
[]
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
[C++] Simple Solution
|
c-simple-solution-by-siddhantsmedar21-ceja
|
\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0)
|
siddhantsmedar21
|
NORMAL
|
2021-02-15T06:56:28.527060+00:00
|
2021-02-15T06:56:28.527102+00:00
| 48 | false |
```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\n int depthOfTree(TreeNode* root){\n if(!root) return 0;\n if(root->left == NULL && root->right == NULL) return 1;\n else return(max(depthOfTree(root->left), depthOfTree(root->right)))+1;\n }\n void findNode(TreeNode* root, TreeNode*& result){\n if(!root) return;\n \n int left = depthOfTree(root->left);\n int right = depthOfTree(root->right);\n \n if(left > right){\n findNode(root->left, result);\n }\n else if(right > left){\n findNode(root->right, result);\n }\n else{\n result = root;\n return;\n }\n }\npublic:\n TreeNode* subtreeWithAllDeepest(TreeNode* root) {\n TreeNode* result = NULL;\n findNode(root, result);\n return result;\n }\n};\n```
| 2 | 1 |
[]
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
Java || Postorder || 0ms || beats 100% || O(n)
|
java-postorder-0ms-beats-100-on-by-legen-e1zl
|
\n \n public class Pair {\n\t\tTreeNode root;\n\t\tint depth;\n\n\t\tpublic Pair(TreeNode node, int depth) {\n\t\t\tthis.root = node;\n\t\t\tthis.depth =
|
LegendaryCoder
|
NORMAL
|
2021-02-07T15:09:53.022629+00:00
|
2021-02-07T15:09:53.022677+00:00
| 66 | false |
\n \n public class Pair {\n\t\tTreeNode root;\n\t\tint depth;\n\n\t\tpublic Pair(TreeNode node, int depth) {\n\t\t\tthis.root = node;\n\t\t\tthis.depth = depth;\n\t\t}\n\t}\n \n // O(n)\n\tpublic TreeNode subtreeWithAllDeepest(TreeNode root) {\n\t\treturn subtreeWithAllDeepestHelper(root, 0).root;\n\t}\n\n\t// O(n)\n\tpublic Pair subtreeWithAllDeepestHelper(TreeNode root, int depth) {\n\n\t\tif (root == null)\n\t\t\treturn null;\n\n\t\tif (root.left == null && root.right == null)\n\t\t\treturn new Pair(root, depth);\n\n\t\tPair left = subtreeWithAllDeepestHelper(root.left, depth + 1);\n\t\tPair right = subtreeWithAllDeepestHelper(root.right, depth + 1);\n\n\t\tif (left == null)\n\t\t\treturn right;\n\n\t\tif (right == null)\n\t\t\treturn left;\n\n\t\treturn (left.depth == right.depth) ? new Pair(root, left.depth) : (left.depth > right.depth) ? left : right;\n\t}\n
| 2 | 0 |
[]
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
[JAVA] Clean Code, 100% Faster Solution, O(N) Time Complexity
|
java-clean-code-100-faster-solution-on-t-fwzu
|
\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n
|
anii_agrawal
|
NORMAL
|
2020-12-13T16:08:46.584848+00:00
|
2020-12-13T16:08:46.584882+00:00
| 82 | false |
```\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n * TreeNode(int val) { this.val = val; }\n * TreeNode(int val, TreeNode left, TreeNode right) {\n * this.val = val;\n * this.left = left;\n * this.right = right;\n * }\n * }\n */\n\nclass Solution {\n \n private int maxDepth (TreeNode root) {\n \n if (root == null) {\n return 0;\n }\n \n return 1 + Math.max (maxDepth (root.left), maxDepth (root.right));\n }\n \n public TreeNode subtreeWithAllDeepest(TreeNode root) {\n \n if (root == null) {\n return root;\n }\n \n int leftDepth = maxDepth (root.left);\n int rightDepth = maxDepth (root.right);\n \n if (leftDepth == rightDepth) {\n return root;\n }\n \n return leftDepth > rightDepth ? subtreeWithAllDeepest (root.left) : subtreeWithAllDeepest (root.right);\n }\n}\n```\n\nPlease help to **UPVOTE** if this post is useful for you.\nIf you have any questions, feel free to comment below.\n**HAPPY CODING :)\nLOVE CODING :)**
| 2 | 0 |
[]
| 1 |
smallest-subtree-with-all-the-deepest-nodes
|
[C++] DFS
|
c-dfs-by-codedayday-knxt
|
\nclass Solution {\npublic: \n int depth(TreeNode *root) {\n return !root ? 0 : 1 + max(depth(root->left), depth(root->right));\n }\n\n TreeNo
|
codedayday
|
NORMAL
|
2020-12-12T22:42:23.582118+00:00
|
2020-12-12T22:47:36.681267+00:00
| 112 | false |
```\nclass Solution {\npublic: \n int depth(TreeNode *root) {\n return !root ? 0 : 1 + max(depth(root->left), depth(root->right));\n }\n\n TreeNode* subtreeWithAllDeepest(TreeNode* root) {\n int d = depth(root->left) - depth(root->right);\n return d==0 ? root : subtreeWithAllDeepest(d > 0 ? root->left : root->right);\n }\n};\n```\nreference:\nhttps://leetcode.com/problems/smallest-subtree-with-all-the-deepest-nodes/discuss/146842/Short-and-concise-C%2B%2B-solution-using-DFS-3~5-lines
| 2 | 0 |
[]
| 2 |
smallest-subtree-with-all-the-deepest-nodes
|
Simple java by just using two global variables 0ms runtime
|
simple-java-by-just-using-two-global-var-2ls9
|
Using a global variable to store max height at each instance and the result root at that instance.\nTraversing the left subtree first and then the right subtree
|
holaleetcode
|
NORMAL
|
2020-10-26T11:45:29.112311+00:00
|
2020-10-26T11:48:07.208159+00:00
| 105 | false |
Using a global variable to store max height at each instance and the result root at that instance.\nTraversing the left subtree first and then the right subtree and calculating the height of left and right subtree and if they are equal to maximum height till that moment then then the current node becomes the smallest subtree with the deepest nodes so store it in variable res and repeat this for all the nodes.\n\n```\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n * TreeNode(int val) { this.val = val; }\n * TreeNode(int val, TreeNode left, TreeNode right) {\n * this.val = val;\n * this.left = left;\n * this.right = right;\n * }\n * }\n */\nclass Solution {\n int maxHeight;\n TreeNode res;\n public TreeNode subtreeWithAllDeepest(TreeNode root) {\n res = root;\n traverse(root, 0);\n return res;\n }\n int traverse(TreeNode root, int height){\n if(root == null){\n if(height > maxHeight) maxHeight = height;\n return height;\n }\n int left = traverse(root.left, height+1);\n int right = traverse(root.right, height+1);\n if(left == maxHeight && right == maxHeight){\n res = root;\n }\n return Math.max(left, right);\n }\n}\n\n```
| 2 | 0 |
['Recursion', 'Java']
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
[C++] O(n) Easier to understand with explanation. 93%
|
c-on-easier-to-understand-with-explanati-vjys
|
\nclass Solution {\n int maxDepth = 0;\n \n TreeNode* helper(TreeNode* root, int& depth) {\n if (root == NULL) {\n return NULL;\n
|
theoddredbit
|
NORMAL
|
2020-08-15T03:51:51.335090+00:00
|
2020-08-15T03:52:40.431298+00:00
| 200 | false |
```\nclass Solution {\n int maxDepth = 0;\n \n TreeNode* helper(TreeNode* root, int& depth) {\n if (root == NULL) {\n return NULL;\n }\n \n depth++; // for this node.\n // identify if this is a leaf node.\n if (root->left == NULL && root->right == NULL) {\n return root;\n }\n \n int leftDepth = depth; \n // if either exist, we want to ask the children.\n TreeNode* left = helper(root->left, leftDepth);\n \n int rightDepth = depth;\n TreeNode* right = helper(root->right, rightDepth);\n \n // if both sides are equal then this node is the contendor for LCA.\n if (rightDepth == leftDepth) {\n depth = leftDepth;\n return root;\n }\n \n if (rightDepth > leftDepth) {\n depth = rightDepth;\n return right;\n } else {\n depth = leftDepth;\n return left;\n }\n \n // now when it returns to the parent, the parent has the choice again to check against\n // its left and right. And again if the length from both the sides is equal, the\n // LCA contender will change, until it reaches the root.\n }\npublic:\n TreeNode* subtreeWithAllDeepest(TreeNode* root) {\n // so for a node to know the deepest node, the depth of its left and right subtrees should be same.\n // if the right is deeper than the left, then its not the deepest.\n // so every node passes the max depth it has seen to the parent. \n int depth = 0;\n return helper(root, depth);\n }\n};\n```
| 2 | 0 |
['C']
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
java beats 100%
|
java-beats-100-by-zinking-6f2k
|
\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n
|
zinking
|
NORMAL
|
2020-07-16T15:07:11.243012+00:00
|
2020-07-16T15:07:11.243060+00:00
| 92 | false |
```\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n * TreeNode(int val) { this.val = val; }\n * TreeNode(int val, TreeNode left, TreeNode right) {\n * this.val = val;\n * this.left = left;\n * this.right = right;\n * }\n * }\n */\nclass Solution {\n TreeNode result;\n int hmax = 0;\n public TreeNode subtreeWithAllDeepest(TreeNode root) {\n if (root == null) {\n return root;\n } else {\n this.result = root;\n pstVisit(root, 0);\n return result;\n }\n \n }\n \n private int pstVisit(TreeNode nd, int lvl) {\n if (nd == null) {\n return lvl - 1;\n }\n \n if (nd.left == null && nd.right == null) {\n if (lvl >= hmax) {\n result = nd;\n hmax = lvl;\n }\n return lvl;\n } else {\n int hl = pstVisit(nd.left, lvl + 1);\n int hr = pstVisit(nd.right, lvl + 1);\n \n if (hl == hr && hl >= hmax) {\n result = nd;\n hmax = hl;\n }\n return Math.max(hl, hr);\n }\n }\n}\n```
| 2 | 0 |
[]
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
C++ Recursive Easy APproach
|
c-recursive-easy-approach-by-peeyushbh19-37i0
|
\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0)
|
peeyushbh1998
|
NORMAL
|
2020-05-13T10:33:21.772560+00:00
|
2020-05-13T10:33:21.772612+00:00
| 215 | false |
```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n int hei(TreeNode* rt){\n if(rt==NULL) return 10000;\n return 1+max(hei(rt->left),hei(rt->right));\n }\n TreeNode* subtreeWithAllDeepest(TreeNode* root) {\n if(root==NULL) return NULL;\n if(root->left==NULL && root->right==NULL){\n return root;\n }\n if(hei(root->left)==hei(root->right)){\n return root;\n }\n else if(hei(root->left)>hei(root->right)){\n return subtreeWithAllDeepest(root->left);\n }\n else{\n return subtreeWithAllDeepest(root->right); \n }\n }\n};\n```
| 2 | 0 |
['Recursion', 'C', 'C++']
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
Java recursion
|
java-recursion-by-vikrant_pc-ypxo
|
\nint maxDepth = 0;\nTreeNode result = null;\npublic TreeNode subtreeWithAllDeepest(TreeNode root) {\n\tdepth(root, 0);\n\treturn result;\n}\npublic int depth(T
|
vikrant_pc
|
NORMAL
|
2020-03-09T06:43:38.070755+00:00
|
2020-03-10T01:44:34.895388+00:00
| 127 | false |
```\nint maxDepth = 0;\nTreeNode result = null;\npublic TreeNode subtreeWithAllDeepest(TreeNode root) {\n\tdepth(root, 0);\n\treturn result;\n}\npublic int depth(TreeNode root, int depth) {\n\tif(root == null) return depth-1;\n\tif(maxDepth<depth) maxDepth = depth;\n\tint left = depth(root.left, depth +1);\n\tint right = depth(root.right, depth +1);\n\tif(left == maxDepth && right == maxDepth) result = root;\n\treturn Math.max(left,right);\n}\n```
| 2 | 0 |
[]
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
[C++] Short, Concise and Easy to understand. Beats 100% time. With comments
|
c-short-concise-and-easy-to-understand-b-8hfw
|
\nclass Solution {\npublic:\n int height(TreeNode* r) {\n return (r) ? 1 + max(height(r->left), height(r->right)) : 0;\n }\n TreeNode* subtreeWi
|
dummydummydummyda
|
NORMAL
|
2019-07-26T13:08:41.268861+00:00
|
2019-07-26T13:10:39.981995+00:00
| 181 | false |
```\nclass Solution {\npublic:\n int height(TreeNode* r) {\n return (r) ? 1 + max(height(r->left), height(r->right)) : 0;\n }\n TreeNode* subtreeWithAllDeepest(TreeNode* root) {\n if(!root) return NULL;\n int lh = height(root->left);\n int rh = height(root->right);\n \n if(lh == rh) return root; // if height of left and right subtrees are same, this is the answer\n if(lh > rh) return subtreeWithAllDeepest(root->left); // go with the one with more height as LCA lies there\n return subtreeWithAllDeepest(root->right);\n }\n};\n```
| 2 | 0 |
[]
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
Go 100% 0ms/3MB solution
|
go-100-0ms3mb-solution-by-scoot_lin-50mt
|
\n/**\n * Definition for a binary tree node.\n * type TreeNode struct {\n * Val int\n * Left *TreeNode\n * Right *TreeNode\n * }\n */\n// var maxDep
|
scoot_lin
|
NORMAL
|
2019-06-19T02:58:38.592097+00:00
|
2019-06-19T02:58:38.592129+00:00
| 96 | false |
```\n/**\n * Definition for a binary tree node.\n * type TreeNode struct {\n * Val int\n * Left *TreeNode\n * Right *TreeNode\n * }\n */\n// var maxDepth int = 0\n// var level int = 0\n// var recmap map[int]TreeNode\nfunc subtreeWithAllDeepest(root *TreeNode) *TreeNode {\n _,maxDepth := search(root)\n return maxDepth\n}\n\nfunc search(root *TreeNode)(int,*TreeNode){\n if root == nil{\n return 0,nil\n }\n ldep,lnode := search(root.Left)\n rdep,rnode := search(root.Right)\n max := Max(ldep, rdep) + 1\n if ldep == rdep{\n return max,root\n }\n if ldep > rdep{\n return max,lnode\n }else{\n return max,rnode\n }\n}\n\nfunc Max(x, y int) int {\n if x > y {\n return x\n }\n return y\n}\n```\n
| 2 | 0 |
[]
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
Swift tuple
|
swift-tuple-by-qzjian-tyd0
|
\nclass Solution {\n func subtreeWithAllDeepest(_ root: TreeNode?) -> TreeNode? {\n return deep(root).1\n }\n\n func deep(_ root: TreeNode?) ->
|
qzjian
|
NORMAL
|
2019-01-18T13:44:16.065782+00:00
|
2019-01-18T13:44:16.065841+00:00
| 151 | false |
```\nclass Solution {\n func subtreeWithAllDeepest(_ root: TreeNode?) -> TreeNode? {\n return deep(root).1\n }\n\n func deep(_ root: TreeNode?) -> (Int, TreeNode?) {\n if root == nil { return (0, root)}\n let l = deep(root?.left) ,r = deep(root?.right)\n let d1 = l.0 , d2 = r.0\n return (max(d1, d2)+1, d1==d2 ? root : d1>d2 ? l.1 : r.1)\n }\n}\n```
| 2 | 0 |
[]
| 1 |
smallest-subtree-with-all-the-deepest-nodes
|
Super-simple Java, beats 100% despite poor algorithm :-)
|
super-simple-java-beats-100-despite-poor-n3we
|
Very easy, but worst case, this is O(n^2), which is bad. However, it beats 100%! We need bigger/uglier test cases. ``` public TreeNode subtreeWithAllDeepe
|
jpv
|
NORMAL
|
2018-11-09T18:33:37.002272+00:00
|
2018-11-09T18:33:37.002315+00:00
| 168 | false |
Very easy, but worst case, this is O(n^2), which is bad. However, it beats 100%! We need bigger/uglier test cases.
```
public TreeNode subtreeWithAllDeepest(TreeNode root) {
if( root==null ) return root;
int L=height(root.left);
int R=height(root.right);
if( L==R ) return root;
if( L<R ) return subtreeWithAllDeepest( root.right );
else return subtreeWithAllDeepest( root.left );
}
private static int height( TreeNode node )
{
if( node==null ) return 0;
return 1+Math.max( height(node.left), height(node.right) );
}
```
| 2 | 0 |
[]
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
Need more examples and detailed explanation.
|
need-more-examples-and-detailed-explanat-mz1d
|
It\'s not clear from start which node you need to return. Also it\'s not clear what to do if node is deepest and it hasn\'t any child. For example:\n\n1 -> 2 ->
|
ivadimko
|
NORMAL
|
2018-10-24T17:15:31.641520+00:00
|
2018-10-24T17:15:31.641563+00:00
| 158 | false |
It\'s not clear from start which node you need to return. Also it\'s not clear what to do if node is deepest and it hasn\'t any child. For example:\n```\n1 -> 2 -> 3\n```\nWhat do we need to return? 3 as deepest one or 2 as root which has deepest node.\n\nI\'ve solved this problem and the hardest thing was to understand the description. Everything else is just simple `DFS`
| 2 | 1 |
[]
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
BFS solution
|
bfs-solution-by-h379wang-1f0k
|
\n\nclass Solution:\n def subtreeWithAllDeepest(self, root):\n if not root: return\n parent = {} # child: its parent\n queue = set([root
|
h379wang
|
NORMAL
|
2018-08-23T02:57:20.368238+00:00
|
2018-08-23T02:58:56.565434+00:00
| 264 | false |
```\n\nclass Solution:\n def subtreeWithAllDeepest(self, root):\n if not root: return\n parent = {} # child: its parent\n queue = set([root])\n while queue:\n new_queue = set()\n for n in queue:\n if n.left:\n new_queue.add(n.left)\n parent[n.left] = n\n if n.right:\n new_queue.add(n.right)\n parent[n.right] = n\n if not new_queue:\n break\n else:\n queue = new_queue\n # queue == all the deepest nodes\n # find its closest shared parent\n while queue:\n if len(queue) == 1:\n return queue.pop()\n new_queue = set()\n for n in queue:\n new_queue.add(parent[n])\n queue = new_queue\n```
| 2 | 0 |
[]
| 1 |
smallest-subtree-with-all-the-deepest-nodes
|
concise kotlin recursion
|
concise-kotlin-recursion-by-edroid-kaeh
|
\nfun subtreeWithAllDeepest(root: TreeNode?): TreeNode? {\n if (root == null) return root\n\n val a = findMax(root.left)\n val b = findMax(root.right)\n if
|
edroid
|
NORMAL
|
2018-07-10T20:09:01.091201+00:00
|
2018-07-10T20:09:01.091201+00:00
| 81 | false |
```\nfun subtreeWithAllDeepest(root: TreeNode?): TreeNode? {\n if (root == null) return root\n\n val a = findMax(root.left)\n val b = findMax(root.right)\n if (a == b) return root\n\n return subtreeWithAllDeepest(if (a > b) root.left else root.right)\n}\n\nfun findMax(root: TreeNode?) : Int {\n return if (root == null) return 0 else 1 + Math.max(findMax(root.left), findMax(root.right))\n}\n```
| 2 | 0 |
[]
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
BFS + LCA
|
bfs-lca-by-gracemeng-dgfc
|
What is depth of a node?\n> \n> The distance from the root to a node\n \n>How do we tell if a node is deepest?\n>\n>By BFS level order traversal. Nodes in the l
|
gracemeng
|
NORMAL
|
2018-07-08T08:34:00.620620+00:00
|
2019-08-09T01:58:03.993628+00:00
| 250 | false |
> What is depth of a node?\n> \n> The distance from the root to a node\n \n>How do we tell if a node is deepest?\n>\n>By BFS level order traversal. Nodes in the last level should be deepest (if root is at level 0).\n\n> The problem is actually asking the LCA among deepest nodes\n> \n> For deepest nodes `[ leftmost , ..., rightmost ]` (nodes are in order), `lca(leftmost , ..., rightmost) = lca(leftmost, rightmost)`\n>\n> So during BFS level order traversal, we only have to keep track of the leftmost and rightmost node.\n****\n```\n public TreeNode subtreeWithAllDeepest(TreeNode root) {\n if (root == null) {\n return null;\n }\n // Get list of deepest nodes\n List<TreeNode> deepestNodes = getDeepestNodes(root);\n \n TreeNode lca = deepestNodes.get(0);\n for (int i = 1; i < deepestNodes.size(); i++) {\n lca = getLowestCommonAncestor(root, lca, deepestNodes.get(i));\n }\n \n return lca;\n }\n \n private List<TreeNode> getDeepestNodes(TreeNode root) {\n List<TreeNode> levelNodes = new ArrayList<>();\n \n Queue<TreeNode> queue = new LinkedList<>();\n queue.offer(root);\n \n while (!queue.isEmpty()) {\n int size = queue.size();\n levelNodes = new ArrayList<>();\n for (int i = 0; i < size; i++) {\n TreeNode node = queue.poll();\n levelNodes.add(node);\n \n if (node.left != null) {\n queue.offer(node.left);\n } \n if (node.right != null) {\n queue.offer(node.right);\n }\n }\n }\n \n return levelNodes;\n }\n \n private TreeNode getLowestCommonAncestor(TreeNode root, TreeNode left, TreeNode right) {\n if (root == null) {\n return null;\n }\n if (root == left || root == right) {\n return root;\n }\n TreeNode leftAns = getLowestCommonAncestor(root.left, left, right);\n TreeNode rightAns = getLowestCommonAncestor(root.right, left, right);\n if (leftAns != null && rightAns != null) {\n return root;\n } else if (leftAns == null) {\n return rightAns;\n } else { // if (rightAns == null) {\n return leftAns;\n } \n }\n```
| 2 | 0 |
[]
| 2 |
smallest-subtree-with-all-the-deepest-nodes
|
Find the Deepest Roots, the Jedi's Quest
|
find-the-deepest-roots-the-jedis-quest-b-4zx1
|
IntuitionHmm... The deepest nodes we must find, and their common ancestor identify. Like seeking the source of the dark side, to the roots we must travel.Approa
|
x7Fg9_K2pLm4nQwR8sT3vYz5bDcE6h
|
NORMAL
|
2025-04-07T16:02:29.313084+00:00
|
2025-04-07T16:02:29.313084+00:00
| 11 | false |
# Intuition
Hmm... The deepest nodes we must find, and their common ancestor identify. Like seeking the source of the dark side, to the roots we must travel.
# Approach
1. findv: Performs DFS to find a path to a target value (p or q), storing the path in ans and setting res=true if found.
2. FindValue: Locates a node with a specific value in the tree.
3. lowestCommonAncestor: Uses findv to get paths for p and q, then compares paths to find their last common node (LCA).
4. solve: Recursively finds all leaf nodes and their depths, storing them in ans.
5. subtreeWithAllDeepest:
- Collects all deepest leaves using solve.
- Finds their LCA by iteratively computing pairwise LCAs.
# Complexity
- Time complexity: $$O(n^2)$$
- Space complexity: $$O(n)$$
# Code
```cpp []
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
void findv (TreeNode* root, int value, vector<int>&ans, bool &res){
if (root==NULL||res){return;}
ans.push_back(root->val);
if (root->val==value){res=true;return;}
findv(root->left,value,ans,res);
findv(root->right,value,ans,res);
if (!res){ans.pop_back();}
}
TreeNode* FindValue (TreeNode* root, int Value){
if (root==NULL){return NULL;}
if (root->val==Value){return root;}
TreeNode* left=FindValue(root->left,Value);
if (left){return left;}
return FindValue(root->right,Value);
}
TreeNode* lowestCommonAncestor(TreeNode* root, int p, int q) {
vector<int>ans1,ans2;
bool res=false;
findv(root,p,ans1,res);
res=false;
findv(root,q,ans2,res);
int x=ans1[0],size=min(ans1.size(),ans2.size());
for (int i=1;i<size;i++){if (ans1[i]==ans2[i]){x=ans1[i];}}
return FindValue(root,x);
}
void solve(TreeNode* root, int d, vector<vector<int>>&ans){
if (root==NULL){return;}
if (root->left==NULL && root->right==NULL){
ans.push_back({d,root->val});
}
solve(root->left,d+1,ans);
solve(root->right,d+1,ans);
}
TreeNode* subtreeWithAllDeepest(TreeNode* root) {
if (root->left==NULL && root->right==NULL){return root;}
vector<vector<int>>ans;
vector<int>a;
solve(root,0,ans);
sort(ans.begin(),ans.end());
int d=ans[ans.size()-1][0],s=0;
for (int i=ans.size()-1;i>=0;i--){
if (ans[i][0]==d){a.push_back(ans[i][1]);}
}
if (a.size()==1){return lowestCommonAncestor(root,a[0],a[0]);}
TreeNode* op=lowestCommonAncestor(root,a[0],a[1]);
while (a.size()>1){
op=lowestCommonAncestor(root,a[a.size()-1],a[a.size()-2]);
a.pop_back();
a.pop_back();
a.push_back(op->val);
}
return op;
}
};
```
| 1 | 0 |
['C++']
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
Same Code as a LCA Question Just find deepest two Nodes and get their LCA & done || Runs 0ms
|
same-code-as-a-lca-question-just-find-de-ot3y
|
Approach
It is a same as a LCA question but here we will have to find the nodes who are deepest in levels So, their LCA will be the root who is at shortest dist
|
Harsh-X
|
NORMAL
|
2025-04-07T01:51:59.733342+00:00
|
2025-04-07T01:51:59.733342+00:00
| 12 | false |
# Approach
<!-- Describe your approach to solving the problem. -->
- It is a same as a LCA question but here we will have to find the nodes who are deepest in levels So, their LCA will be the root who is at shortest distance from them.
- So, we can simply find the two nodes which are in deepest levels.
- Then we can find those node's LCA & thats it done
# Complexity
- Time complexity: **O(N)**
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: **O(H)**
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
int maxDepth = 0;
TreeNode* deepestLeave1 = NULL;
TreeNode* deepestLeave2 = NULL;
public:
void GetDeepestLeaves(TreeNode* &root, int depth){
if(!root){
return;
}
if(!root->left && !root->right){
// If we found the node depth greater than maxDepth then pick that node
if(depth > maxDepth){
maxDepth = depth;
deepestLeave1 = deepestLeave2 = root;
}
// if we found that depth again we can simply update our deepestLeaves2 since deepestLeaves1 is already picked another node.
else if(depth == maxDepth){
deepestLeave2 = root;
}
return;
}
GetDeepestLeaves(root->left, depth+1);
GetDeepestLeaves(root->right, depth+1);
}
// This is a normal/common LCA code to find LCA of two nodes
TreeNode* Solve(TreeNode* &root){
if(!root || root == deepestLeave1 || root == deepestLeave2){
return root;
}
TreeNode* left = Solve(root->left);
TreeNode* right = Solve(root->right);
if(left && right){
return root;
}
else if(left){
return left;
}
return right;
}
TreeNode* subtreeWithAllDeepest(TreeNode* root) {
GetDeepestLeaves(root, 0);
return Solve(root);
}
};
```

| 1 | 0 |
['Tree', 'Depth-First Search', 'Binary Tree', 'C++']
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
Python3. Algorithm: Depth-First Search
|
python3-algorithm-depth-first-search-by-x1156
| null |
RuslanTsykaliak
|
NORMAL
|
2025-04-05T11:18:36.763519+00:00
|
2025-04-05T11:18:36.763519+00:00
| 11 | false |
```python3 []
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def subtreeWithAllDeepest(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
def dfs(node):
if not node:
return 0, None
left_depth, left_node = dfs(node.left)
right_depth, right_node = dfs(node.right)
if left_depth > right_depth:
return left_depth + 1, left_node
elif left_depth < right_depth:
return right_depth + 1, right_node
else:
return left_depth + 1, node
return dfs(root)[1]
```
| 1 | 0 |
['Depth-First Search', 'Binary Tree', 'Python3']
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
100% beats Solution | Java | DFS
|
100-beats-solution-java-dfs-by-swykoon-bnrn
|
IntuitionWe need to return the least common ancestor of the deepest leaves. The deepest leaves are the leaf nodes which are situated at (height of tree - 1)th l
|
SwyKoon
|
NORMAL
|
2025-04-04T18:44:43.641164+00:00
|
2025-04-04T18:44:43.641164+00:00
| 19 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
We need to return the least common ancestor of the deepest leaves. The deepest leaves are the leaf nodes which are situated at (height of tree - 1)th level. Since we need to find the deepest leaves ancestor we can use DFS as it will traverse each branch of tree as deeply as possible.
The least common ancestor would be one in which both left and right subtree would be able to reach the same level as seen in example 1. It is also clear from example 3, that if a node is single child of its parent, or in other words the depth which each child of a parent can reach are different, then the node would be the least common ancestor.
# Approach
<!-- Describe your approach to solving the problem. -->
We run a DFS over the tree, maintaining the depth we reach when we visit a node. We use post order traversal since it allows us to reach the maximum depth possible in a branch, thus allowing us to find the least common ancestor, when we backtrack upwards in the tree.
Once we reach the end of a branch we check if we have reached the maximum depth we can. If yes, then we update the maximum depth and store the node reached as a possible answer. If we have not gone deeper then the previous maximum depth we reached, that means we can not go any deeper and should now focus on finding least common ancestor. So we check if the maximum depth we can reach from the left and right children are the same. If yes, we have found our least common ancestor and we store it.
When recursion gets over, we can safely return the least common ancestor we found.
# Complexity
- Time complexity: O(N)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
We visit each node in tree once.
- Space complexity: O(N)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
The space the recursion stack takes
# Code
```java []
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
TreeNode answer = null;
int max_depth = 0;
public TreeNode lcaDeepestLeaves(TreeNode root) {
DFS(root, 0);
return answer;
}
private int DFS(TreeNode root, int depth)
{
if(root == null)
return depth - 1;
// We try to go as deep in the tree as possible
int leftDepth = DFS(root.left, depth + 1);
int rightDepth = DFS(root.right, depth + 1);
// If current depth is the maximum we have reached, then this possibly could be the node we are looking for (if it is single child)
if(depth > max_depth)
{
max_depth = depth;
answer = root;
}
// Other wise we will return the common ancestor which would be node, for which both left depth and right depth would be equal
else if(leftDepth == rightDepth && leftDepth == max_depth)
answer = root;
// We return the maximum of the depths reached
return Math.max(leftDepth, rightDepth);
}
}
```
| 1 | 0 |
['Tree', 'Depth-First Search', 'Breadth-First Search', 'Binary Tree', 'Java']
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
DFS
|
dfs-by-khaled-alomari-1ytz
|
Complexity
Time complexity:
O(n)
Space complexity:
O(n)
Code
|
khaled-alomari
|
NORMAL
|
2025-04-04T18:14:32.197485+00:00
|
2025-04-04T18:14:32.197485+00:00
| 16 | false |
# Complexity
- Time complexity:
$$O(n)$$
- Space complexity:
$$O(n)$$
# Code
```typescript []
function subtreeWithAllDeepest(root: TreeNode | null): TreeNode | null {
const dfs = (node: typeof root, depth: number): number => {
if (!node) return depth;
const left = dfs(node.left, ++depth);
const right = dfs(node.right, depth);
if (left === right && left > resDepth) {
resDepth = left - 1, resHead = node;
}
return Math.max(left, right);
};
let resHead = root, resDepth = 0;
dfs(root, 0);
return resHead;
}
```
```javascript []
function subtreeWithAllDeepest(root) {
const dfs = (node, depth) => {
if (!node) return depth;
const left = dfs(node.left, ++depth);
const right = dfs(node.right, depth);
if (left === right && left > resDepth) {
resDepth = left - 1, resHead = node;
}
return Math.max(left, right);
};
let resHead = root, resDepth = 0;
dfs(root, 0);
return resHead;
}
```
| 1 | 0 |
['Tree', 'Depth-First Search', 'Recursion', 'Simulation', 'Binary Tree', 'TypeScript', 'JavaScript']
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
🔥BEAT 100% with the easiest solution (with explanation) 💯💯
|
beat-100-with-the-easiest-solution-with-1wa1d
|
Smallest Subtree with all the Deepest NodesIntuitionThe task is to return the smallest subtree that contains all the deepest nodes of the binary tree.The intuit
|
bob_dylan
|
NORMAL
|
2025-04-04T16:07:11.838417+00:00
|
2025-04-04T16:09:50.278751+00:00
| 30 | false |
# Smallest Subtree with all the Deepest Nodes
## Intuition
The task is to return the smallest subtree that contains all the **deepest** nodes of the binary tree.
The intuition is to:
- Traverse the entire tree to find the maximum depth.
- Use **post-order DFS** to compute the depth of each node’s left and right subtree.
- If both left and right subtree depths are equal and match the **maximum depth**, then this node is the **Lowest Common Ancestor (LCA)** of all deepest nodes.
## Approach
1. Use a recursive DFS function to:
- Compute and propagate the depth of each subtree.
- Track the **maximum depth** encountered globally.
- Update the `lca` variable if the current node’s left and right depths are the same and equal to the maximum depth.
2. Finally, return the node stored in the `lca` variable, which will be the root of the smallest subtree containing all deepest nodes.
## Complexity
- **Time Complexity:** $$O(n)$$ — We visit each node once to compute depths and identify the LCA.
- **Space Complexity:** $$O(h)$$ — Where *h* is the height of the tree due to recursion stack (worst case O(n) for skewed trees).
### If you found this helpful, PLEASE UPVOTE 🥹🥹
## Code
### C++
```cpp []
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* lca = NULL;
int dfs(TreeNode* root, int depth, int &maxDepth) {
maxDepth = max(maxDepth, depth);
if (root == NULL) return depth;
int leftDepth = dfs(root->left, depth + 1, maxDepth);
int rightDepth = dfs(root->right, depth + 1, maxDepth);
int bigDepth = max(leftDepth, rightDepth);
if (leftDepth == rightDepth && bigDepth == maxDepth) {
lca = root;
}
return bigDepth;
}
TreeNode* subtreeWithAllDeepest(TreeNode* root) {
lca = root;
int maxDepth = 0;
dfs(root, 0, maxDepth);
return lca;
}
};
```
```python []
class Solution:
def __init__(self):
self.lca = None
def dfs(self, root, depth, maxDepth):
maxDepth[0] = max(maxDepth[0], depth)
if not root:
return depth
left = self.dfs(root.left, depth + 1, maxDepth)
right = self.dfs(root.right, depth + 1, maxDepth)
if left == right and max(left, right) == maxDepth[0]:
self.lca = root
return max(left, right)
def subtreeWithAllDeepest(self, root):
maxDepth = [0]
self.dfs(root, 0, maxDepth)
return self.lca
```
```java []
class Solution {
TreeNode lca = null;
public TreeNode subtreeWithAllDeepest(TreeNode root) {
int[] maxDepth = new int[1];
dfs(root, 0, maxDepth);
return lca;
}
private int dfs(TreeNode node, int depth, int[] maxDepth) {
maxDepth[0] = Math.max(maxDepth[0], depth);
if (node == null) return depth;
int left = dfs(node.left, depth + 1, maxDepth);
int right = dfs(node.right, depth + 1, maxDepth);
if (left == right && Math.max(left, right) == maxDepth[0]) {
lca = node;
}
return Math.max(left, right);
}
}
```
```javascript []
var subtreeWithAllDeepest = function(root) {
let lca = null;
let maxDepth = 0;
const dfs = (node, depth) => {
maxDepth = Math.max(maxDepth, depth);
if (!node) return depth;
const left = dfs(node.left, depth + 1);
const right = dfs(node.right, depth + 1);
if (left === right && Math.max(left, right) === maxDepth) {
lca = node;
}
return Math.max(left, right);
};
dfs(root, 0);
return lca;
};
```
# Summary
- We use a DFS traversal to compute the depth of all nodes.
- By comparing the depths of the left and right subtrees, we detect the node where the deepest leaves meet.
- This solution efficiently returns the smallest subtree that contains all the deepest nodes.
| 1 | 0 |
['Tree', 'Depth-First Search', 'Binary Tree', 'Python', 'C++', 'Java', 'JavaScript']
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
DFS || Python
|
dfs-python-by-sadhashivaaeshala-p79f
|
Code
|
SadhaShivaAeshala
|
NORMAL
|
2025-04-04T13:39:07.400502+00:00
|
2025-04-04T13:39:07.400502+00:00
| 22 | false |
# Code
```python3 []
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def subtreeWithAllDeepest(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
def dfs(node, depth):
if not node:
return (None, depth + 1)
leftNode, leftDepth = dfs(node.left, depth + 1)
rightNode, rightDepth = dfs(node.right, depth + 1)
if leftDepth > rightDepth:
return (leftNode, leftDepth)
elif rightDepth > leftDepth:
return (rightNode, rightDepth)
return (node, leftDepth)
node, _ = dfs(root, 0)
return node
```
| 1 | 0 |
['Python3']
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
"🌳🔍 Mastering the Depths: Efficient LCA Search to Rule Them All! | Beats 100% 💯🚀
|
mastering-the-depths-efficient-lca-searc-q8mz
|
IntuitionThe goal of the problem is to find the lowest common ancestor (LCA) of the deepest leaves in a binary tree. The LCA of two nodes in a binary tree is th
|
udit_s05
|
NORMAL
|
2025-04-04T13:16:16.607943+00:00
|
2025-04-04T13:16:16.607943+00:00
| 22 | false |
# Intuition
The goal of the problem is to find the lowest common ancestor (LCA) of the deepest leaves in a binary tree. The LCA of two nodes in a binary tree is the lowest node that is an ancestor of both nodes. To solve the problem, we first need to determine the deepest leaves and then find the LCA of those nodes. This can be done by performing a level-order traversal (breadth-first search) of the tree, identifying the deepest level, and then using the LCA algorithm to find the common ancestor of all nodes at that level.
# Approach
Perform a level-order traversal (BFS) to collect all the nodes at the deepest level of the tree. This is done by iterating through each level of the tree until the queue is empty.
The last set of nodes added to the queue corresponds to the deepest leaves.
Use the lowestCommonAncestor function to find the LCA of all the deepest leaves. Start with the first node in the deepest level and iteratively find the LCA with the subsequent nodes.
Return the LCA of all the deepest leaves.
# Complexity
- Time complexity:
The time complexity is O(N), where N is the total number of nodes in the tree. The level-order traversal visits every node once, and the lowestCommonAncestor function is invoked at most once per pair of nodes.
- Space complexity:
The space complexity is O(N) for the queue used in level-order traversal, where N is the number of nodes in the tree. Additionally, the space required to store the deepest leaves is O(L), where L is the number of nodes at the deepest level.
# Code
```cpp []
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(root == NULL || root == p || root == q) return root;
TreeNode *left = lowestCommonAncestor(root->left, p, q);
TreeNode *right = lowestCommonAncestor(root->right, p, q);
if(left == NULL) return right;
else if(right == NULL) return left;
return root;
}
TreeNode* subtreeWithAllDeepest(TreeNode* root) {
vector<TreeNode*> child;
queue<TreeNode*> q;
q.push(root);
while(!q.empty()){
int n = q.size();
child.clear();
while(n--){
TreeNode *node = q.front();
q.pop();
child.push_back(node);
if(node->left) {q.push(node->left);}
if(node->right) {q.push(node->right);}
}
}
TreeNode *p = child[0];
for(int i=1; i<child.size(); i++){
p = lowestCommonAncestor(root, p, child[i]);
}
return p;
}
};
```
| 1 | 0 |
['C++']
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
DFS
|
dfs-by-akshaypatidar33-9ndo
|
Code
|
akshaypatidar33
|
NORMAL
|
2025-04-04T12:51:52.594360+00:00
|
2025-04-04T12:51:52.594360+00:00
| 15 | false |
# Code
```cpp []
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
pair<TreeNode*, int> solve(TreeNode* root, int depth){
if(root==NULL) return {root, depth+1};
pair<TreeNode*, int> l = solve(root->left, depth+1);
pair<TreeNode*, int> r = solve(root->right, depth+1);
if(l.second<r.second) return r;
else if(l.second>r.second) return l;
return {root, l.second};
}
TreeNode* subtreeWithAllDeepest(TreeNode* root) {
return solve(root, 0).first;
}
};
```
| 1 | 0 |
['Tree', 'Depth-First Search', 'Binary Tree', 'C++']
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
simple py solution - beats 100%, same solution as problem 1123
|
simple-py-solution-beats-100-same-soluti-5rtk
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
noam971
|
NORMAL
|
2025-04-04T12:45:19.541175+00:00
|
2025-04-04T12:45:19.541175+00:00
| 10 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def subtreeWithAllDeepest(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
def lca(root):
if not root:
return (0, None)
d_l, l_lca = lca(root.left) # d_l = depth_left
d_r, r_lca = lca(root.right) # d_r = depth_right
if d_l == d_r:
return d_r + 1, root
return (d_r + 1, r_lca) if d_l < d_r else (d_l + 1, l_lca)
return lca(root)[1]
```
| 1 | 0 |
['Python3']
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
World's most easy Solution You Will Ever Find.. Beats 100%..
|
worlds-most-easy-solution-you-will-ever-xwjds
|
IntuitionWe want to find the Lowest Common Ancestor (LCA) of the deepest leaf nodes in a binary tree.First, we find the maximum depth of the tree (i.e., the dee
|
Tanishcoder123
|
NORMAL
|
2025-04-04T06:55:22.307936+00:00
|
2025-04-04T06:55:22.307936+00:00
| 74 | false |
# Intuition
We want to find the Lowest Common Ancestor (LCA) of the deepest leaf nodes in a binary tree.
First, we find the maximum depth of the tree (i.e., the deepest level).
Then, we do a DFS traversal, and at each node:
If both left and right children contain deepest leaves, then this node is the LCA.
If only one side has deepest leaves, we return that side up the recursion.
The moment both sides return non-null, that node becomes the LCA.
# Approach
Find the maximum depth using a simple recursive function maxDepth.
Do a second DFS (dfs function):
Track the current depth (len).
When you reach depth == maxDepth - 1, return the node (it's one level before deepest).
For each node, recursively check left and right children.
If both return non-null, current node is the LCA of deepest leaves.
# Complexity
- Time complexity:
O(n)
- Space complexity:
O(h)
# Code
```cpp []
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
TreeNode* subtreeWithAllDeepest(TreeNode* root)
{
int maxD = maxDepth(root);
return dfs(root,maxD,0);
}
TreeNode* dfs(TreeNode* root,int maxD,int len)
{
if(root == NULL) return NULL;
if(maxD-1 == len) return root;
TreeNode* left = dfs(root->left,maxD,len+1);
TreeNode* right = dfs(root->right,maxD,len+1);
if(left && right) return root;
return left?left:right;
}
int maxDepth(TreeNode* root)
{
if(root == NULL) return 0;
return 1 + max(maxDepth(root->left),maxDepth(root->right));
}
};
```
| 1 | 0 |
['C++']
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
✅ Easy to Understand & Beginner Friendly | 100% Faster | Detailed Video Explanation🔥
|
easy-to-understand-beginner-friendly-100-vluy
|
IntuitionThe problem requires finding the Lowest Common Ancestor (LCA) of the deepest leaves in a binary tree.
Since the deepest leaves are the farthest nodes f
|
sahilpcs
|
NORMAL
|
2025-04-04T03:49:54.670954+00:00
|
2025-04-04T03:49:54.670954+00:00
| 95 | false |
# Intuition
The problem requires finding the Lowest Common Ancestor (LCA) of the deepest leaves in a binary tree.
Since the deepest leaves are the farthest nodes from the root, their LCA must be the node where the left and right subtrees have the same height.
# Approach
1. **Compute Height:** Define a helper function `height(TreeNode root)` that calculates the height of a subtree.
2. **Compare Heights:** Recursively compare the heights of the left and right subtrees:
- If the heights are equal, the current node is the LCA.
- If the left subtree is taller, the LCA must be in the left subtree.
- If the right subtree is taller, the LCA must be in the right subtree.
3. **Recursive Traversal:** Recursively move down towards the deeper subtree until the LCA is found.
# Complexity
- **Time complexity:**
- Each call to `lcaDeepestLeaves()` makes two recursive `height()` calls.
- The height function runs in $$O(n)$$ and is called multiple times, leading to an overall complexity of **$$O(n^2)$$** in the worst case.
- This could be optimized using a bottom-up approach with a single traversal.
- **Space complexity:**
- In the worst case (skewed tree), the recursion depth can reach **$$O(n)$$** due to the recursive stack.
- In a balanced tree, the depth is **$$O(\log n)$$**.
# Code
```java []
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode subtreeWithAllDeepest(TreeNode root) {
return lcaDeepestLeaves(root);
}
/**
* Finds the Lowest Common Ancestor (LCA) of the deepest leaves in a binary tree.
* @param root The root node of the binary tree.
* @return The LCA of the deepest leaves.
*/
public TreeNode lcaDeepestLeaves(TreeNode root) {
if (root == null) return null; // Base case: if tree is empty, return null
int lh = height(root.left); // Compute the height of the left subtree
int rh = height(root.right); // Compute the height of the right subtree
// If both subtrees have the same height, the current node is the LCA
if (lh == rh) return root;
// If left subtree is deeper, move towards left subtree
if (lh > rh)
return lcaDeepestLeaves(root.left);
// Otherwise, move towards right subtree
return lcaDeepestLeaves(root.right);
}
/**
* Calculates the height of a given binary tree.
* @param root The root node of the tree.
* @return The height of the tree.
*/
private int height(TreeNode root) {
if (root == null) return 0; // Base case: null node has height 0
return 1 + Math.max(height(root.left), height(root.right)); // Compute height recursively
}
}
```
https://youtu.be/Q9uK_iuJMBw
| 1 | 0 |
['Tree', 'Depth-First Search', 'Binary Tree', 'Java']
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
Smallest SubTree With Deepest Nodes in cpp
|
smallest-subtree-with-deepest-nodes-in-c-bt2r
|
IntuitionThe goal is to determine the lowest common ancestor (LCA) of the deepest leaves in a binary tree. Here's the thought process:
Calculate the depth of t
|
Champians_Knight
|
NORMAL
|
2025-04-04T02:06:25.888491+00:00
|
2025-04-04T02:06:25.888491+00:00
| 72 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The goal is to determine the lowest common ancestor (LCA) of the deepest leaves in a binary tree. Here's the thought process:
1. Calculate the depth of the left subtree (denoted as x).
2. Similarly, calculate the depth of the right subtree (denoted as y).
Compare the depths:
If x > y, recursively move to root->left.
If y > x, recursively move to root->right.
If x == y, update ans to the current root node (since it serves as the LCA of the deepest leaves).
4. Finally, return ans.
# Approach
<!-- Describe your approach to solving the problem. -->
This problem can be approached using a post-order traversal to calculate the depth of subtrees and recursively search for the LCA:
1. Define a helper function to calculate the depth of the tree.
2. Implement the main function to compare depths of left and right subtrees and recursively navigate toward the deepest leaves.
3. Update the LCA if the depths are equal.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
$$O(n)$$, where
𝑛
is the number of nodes in the tree. We traverse each node once to calculate depths.
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
$$O(h)$$, where
ℎ
is the height of the tree. This accounts for the recursive stack.
# Code
```cpp []
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
TreeNode* ans;
int depth(TreeNode* root)
{
if (!root) return -1;
int DOL = depth(root -> left);
int DOR = depth(root -> right);
return max(DOL , DOR) + 1;
}
public:
TreeNode* subtreeWithAllDeepest(TreeNode* root) {
int DOL = depth(root -> left);
int DOR = depth(root -> right);
if (DOL > DOR) subtreeWithAllDeepest(root -> left);
else if (DOR > DOL) subtreeWithAllDeepest(root -> right);
else ans = root;
return ans;
}
};
```
| 1 | 0 |
['C++']
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
Two Lines!
|
two-lines-by-charnavoki-h68i
| null |
charnavoki
|
NORMAL
|
2025-04-04T00:55:51.986809+00:00
|
2025-04-04T00:55:51.986809+00:00
| 25 | false |
```javascript []
const subtreeWithAllDeepest = f = (n, x = d(n.right), y = d(n.left)) =>
x === y ? n : f(x > y ? n.right : n.left);
const d = (n) => n ? 1 + Math.max(d(n.left), d(n.right)) : 0;
```
| 1 | 0 |
['JavaScript']
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
Smallest Subtree with all the Deepest Nodes | Beats 100%
|
smallest-subtree-with-all-the-deepest-no-wi55
|
IntuitionThe problem requires finding the smallest subtree that contains all the deepest nodes in a binary tree.
The deepest nodes are the ones with the maximum
|
s_sinha
|
NORMAL
|
2025-04-04T00:45:25.979905+00:00
|
2025-04-04T00:45:25.979905+00:00
| 29 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The problem requires finding the smallest subtree that contains all the deepest nodes in a binary tree.
- The deepest nodes are the ones with the maximum depth in the tree.
- The smallest subtree means the lowest common ancestor (LCA) of all these deepest nodes.
Our first thought is to traverse the tree and find the deepest nodes' LCA using Depth-First Search (DFS).
# Approach
<!-- Describe your approach to solving the problem. -->
1. Use a DFS helper function that returns a pair containing:
- The node representing the LCA of the deepest nodes.
- The depth of that node.
2. Base Case:
- If the node is null, return (null, 0), meaning no LCA and depth 0.
3. Recursive Case:
- Recursively call DFS on the left and right subtrees.
- Compare the depths of the left and right subtrees:
- If left depth > right depth, return the left subtree as it contains the LCA.
- If right depth > left depth, return the right subtree as it contains the LCA.
- If both depths are equal, return the current node as it is the LCA of the deepest nodes.
4. Final Result:
- The DFS function is called on the root, and the LCA is returned
# Complexity
- Time complexity: O(N)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(N)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode subtreeWithAllDeepest(TreeNode root) {
return dfs(root).getKey();
}
public Pair<TreeNode,Integer> dfs(TreeNode root){
if(root == null)
return new Pair<>(null,0);
Pair<TreeNode,Integer> left = dfs(root.left);
Pair<TreeNode,Integer> right = dfs(root.right);
if(left.getValue() > right.getValue())
return new Pair<>(left.getKey(),left.getValue()+1);
if(right.getValue() > left.getValue())
return new Pair<>(right.getKey(),right.getValue()+1);
return new Pair(root,left.getValue()+1);
}
}
```
| 1 | 0 |
['Java']
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
Beats 100% | DFS | Python3
|
beats-100-dfs-python3-by-alpha2404-x18x
|
Please UpvoteCode
|
Alpha2404
|
NORMAL
|
2025-03-21T10:27:20.678616+00:00
|
2025-03-21T10:27:20.678616+00:00
| 70 | false |
# Please Upvote
# Code
```python3 []
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def subtreeWithAllDeepest(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
self.candidate = None
self.max_depth = -1
self.dfs(root,0)
return self.candidate
def dfs(self,node, depth):
if not node:
return -1
if not node.left and not node.right:
if depth>self.max_depth:
self.candidate = node
self.max_depth = depth
return depth
l_depth = self.dfs(node.left,depth+1)
r_depth = self.dfs(node.right,depth+1)
if l_depth==r_depth==self.max_depth:
self.candidate = node
return max(l_depth, r_depth)
```
| 1 | 0 |
['Depth-First Search', 'Binary Tree', 'Python3']
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
Straightforward one pass, O(H) space
|
straightforward-one-pass-oh-space-by-_tl-78ri
|
IntuitionAs long as, left depth == right depth, it should be the "local" answer.
post order helps find the global answer.Code
|
_TLE
|
NORMAL
|
2025-03-06T06:56:54.004028+00:00
|
2025-03-06T06:56:54.004028+00:00
| 9 | false |
# Intuition
As long as, left depth == right depth, it should be the "local" answer.
post order helps find the global answer.
# Code
```python3 []
class Solution:
def subtreeWithAllDeepest(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
def dfs(node, depth=0):
if not node: return (node, depth)
ansL, depthL = dfs(node.left, depth+1)
ansR, depthR = dfs(node.right, depth+1)
if depthL == depthR: return (node, depthL)
if depthL > depthR: return (ansL, depthL)
return (ansR, depthR)
return dfs(root)[0]
```
| 1 | 0 |
['Python3']
| 0 |
smallest-subtree-with-all-the-deepest-nodes
|
bfs(find deepest nodes)->postorder(to gets smallest sub-tree)
|
bfsfind-deepest-nodes-postorderto-gets-s-gngs
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
2manas1
|
NORMAL
|
2024-08-14T16:48:04.589320+00:00
|
2024-08-14T16:48:04.589350+00:00
| 206 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n * TreeNode(int val) { this.val = val; }\n * TreeNode(int val, TreeNode left, TreeNode right) {\n * this.val = val;\n * this.left = left;\n * this.right = right;\n * }\n * }\n */\nclass Solution {\n public TreeNode subtreeWithAllDeepest(TreeNode root) {\n\n //we first apply bfs to find the last layer nodes and store in a list.\n // apply postorder left->right->node, so that we can find the smallest tree with all the deepest nodes\n// we first have to find the deepest level\n\n List<Integer>s1 =new ArrayList<>();\n Queue<TreeNode>queue = new LinkedList<>();\n queue.offer(root);\n\n while(!queue.isEmpty()){\n List<Integer>s3 = new ArrayList<>();\n int ll = queue.size();\n for(int i=0;i<ll;i++){\n TreeNode tar = queue.poll();\n s3.add(tar.val);\n if(tar.left!=null){\n queue.offer(tar.left);\n }\n if(tar.right!=null){\n queue.offer(tar.right);\n }\n }\n if(queue.isEmpty()){\n for(int r=0;r<s3.size();r++){\n s1.add(s3.get(r));\n }\n }\n }\n\n // now we have obtained our all the nodes in the list s1\n //applying postorder to check the smallest tree\n Queue<TreeNode>rt = new LinkedList<>();\n postorder(root,rt,s1);\n\n return rt.poll();\n }\n\n public void postorder(TreeNode root, Queue<TreeNode>s5,List<Integer>s3){\n if(root==null){\n return;\n }\n\n postorder(root.left,s5,s3);\n postorder(root.right,s5,s3);\n if(s5.isEmpty() && check(root,s3)){\n s5.offer(root);\n }\n }\n\n public boolean check(TreeNode root,List<Integer>s1){\n\n List<Integer>ch = new ArrayList<>();\n preorder(root,ch);\n int cc =0; \n for(int i=0;i<s1.size();i++){\n int elm = s1.get(i);\n if(ch.contains(elm)){\n cc++;\n }\n }\n\n return cc==s1.size();\n\n}\n\npublic void preorder(TreeNode root,List<Integer>ch){\nif(root==null){\n return;\n}\nch.add(root.val);\npreorder(root.left,ch);\npreorder(root.right,ch);\n}\n}\n```
| 1 | 0 |
['Java']
| 1 |
smallest-subtree-with-all-the-deepest-nodes
|
🌳56. ⭐ Recursive [ DFS ] || Post Order Traversal || Short & Sweet Code !! || C++ Code Reference !!
|
56-recursive-dfs-post-order-traversal-sh-c4bo
|
Intuition\n- Post Order Traversal !!\n# Code\ncpp [There You Go !!]\n\n pair<TreeNode*,int>f(TreeNode* a)\n {\n if(!a) return {nullptr,0};\n\n
|
Amanzm00
|
NORMAL
|
2024-07-10T09:51:51.162250+00:00
|
2024-07-10T09:51:51.162284+00:00
| 169 | false |
# Intuition\n- Post Order Traversal !!\n# Code\n```cpp [There You Go !!]\n\n pair<TreeNode*,int>f(TreeNode* a)\n {\n if(!a) return {nullptr,0};\n\n pair<TreeNode*,int> l=f(a->left);\n pair<TreeNode*,int> r=f(a->right);\n\n if(r.second>l.second) return {r.first,r.second+1};\n else if(l.second>r.second) return {l.first,l.second+1};\n else return {a,l.second+1};\n }\n\npublic:\n TreeNode* subtreeWithAllDeepest(TreeNode* a) {\n return f(a).first;\n }\n\n\n```\n\n---\n# *Guy\'s Upvote Pleasee !!* \n\n\n# ***(\u02E3\u203F\u02E3 \u035C)***
| 1 | 0 |
['Hash Table', 'Tree', 'Depth-First Search', 'Breadth-First Search', 'Recursion', 'Binary Tree', 'C++']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Explained - Simple DFS and count node with in K depth
|
explained-simple-dfs-and-count-node-with-gya8
|
Intuition\n- To know how many nodes are there wher the edges are less than k, we can simply run dfs from the start node with depth count equal to k.\n- Also we
|
kreakEmp
|
NORMAL
|
2024-12-01T06:51:25.054285+00:00
|
2024-12-02T00:56:03.349062+00:00
| 1,647 | false |
# Intuition\n- To know how many nodes are there wher the edges are less than k, we can simply run dfs from the start node with depth count equal to k.\n- Also we can observe that we will always connect to the same node of the second tree where the linked nodes count at a distance of k-1 is largest. k-1 => because we need to 1 connection from tree1 to tree2 so remaining we have k-1 edges.\n\n# Approach\n- Build 2 graphs -> g1 and g2 from the given edges list\n- Now find the maximum node count that is possible by doing dfs from each node of g2 with a max depth of k-1 levels.\n- Interate over the nodes of the g1 and then do dfs from it as well. Finally add the max count that we computed before and the current node count to the ans list\n\n\n# Complexity\n- Time complexity: O(N.N + M.M)\n\n- Space complexity: O(N + M)\n\n# Code\n```cpp []\n\nvector<vector<int>> buildGraph(vector<vector<int>>& edges){\n vector<vector<int>> g(edges.size() +1 );\n for(auto e: edges){\n g[e[0]].push_back(e[1]); g[e[1]].push_back(e[0]);\n }\n return g;\n}\n\nint dfs(vector<vector<int>>& g, int root, int par, int k, int count = 1){\n if(k < 0) return 0;\n for(auto node: g[root]) count += (node != par)?dfs(g, node, root, k-1): 0;\n return count; \n}\n\nvector<int> maxTargetNodes(vector<vector<int>>& edges1, vector<vector<int>>& edges2, int k) {\n auto g1 = buildGraph(edges1), g2 = buildGraph(edges2);\n int count = 0, n = edges1.size()+1, m = edges2.size()+1;\n vector<int> ans;\n for(int i = 0; i < m; ++i) count = max(count, dfs(g2, i, -1, k-1));\n for(int i = 0; i < n; ++i) ans.push_back(count + dfs(g1, i, -1, k));\n return ans;\n}\n```\n\n\n\n---\n\n\n<b>Here is an article of my interview experience - A Journey to FAANG Company, I recomand you to go through this to know which all resources I have used & how I cracked interview at Amazon:\nhttps://leetcode.com/discuss/interview-experience/3171859/Journey-to-a-FAANG-Company-Amazon-or-SDE2-(L5)-or-Bangalore-or-Oct-2022-Accepted\n\n\n---\n
| 16 | 2 |
['C++']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
DFS From Each Node
|
dfs-from-each-node-by-votrubac-68o3
|
For the first tree, we run DFS from each node for up to k edges.\n\nFor the second tree, we run DFS from each node for up to k - 1 edges. We track the maximum o
|
votrubac
|
NORMAL
|
2024-12-01T04:31:57.127053+00:00
|
2024-12-01T05:44:40.994735+00:00
| 1,135 | false |
For the first tree, we run DFS from each node for up to `k` edges.\n\nFor the second tree, we run DFS from each node for up to `k - 1` edges. We track the maximum of targets in `max2`.\n\nWe need to add `max2` to the final result for each node in the first tree.\n\n**C++**\n```cpp\nint dfs(int i, int p, vector<vector<int>> &al, int k) {\n if (k <= 0)\n return k == 0;\n int res = 1;\n for (int j : al[i])\n if (j != p)\n res += dfs(j, i, al, k - 1);\n return res;\n}\nvector<vector<int>> adjacencyList(vector<vector<int>>& edges) {\n vector<vector<int>> al(edges.size() + 1);\n for (auto &e: edges) {\n al[e[0]].push_back(e[1]);\n al[e[1]].push_back(e[0]); \n } \n return al;\n}\nvector<int> maxTargetNodes(vector<vector<int>>& e1, vector<vector<int>>& e2, int k) {\n int m = e1.size() + 1, n = e2.size() + 1, max2 = 0;\n auto al1 = adjacencyList(e1), al2 = adjacencyList(e2);\n vector<int> res(m);\n for (int i = 0; i < n; ++i)\n max2 = max(max2, dfs(i, -1, al2, k - 1));\n for (int i = 0; i < m; ++i)\n res[i] = max2 + dfs(i, -1, al1, k); \n return res;\n}\n```
| 13 | 2 |
[]
| 4 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.