question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
[Python3] brute-force
|
python3-brute-force-by-ye15-vgfv
|
Intuition\nEssentially, this is a brute-force approach. For the two trees, we calculate the target nodes. For tree 1, we run DFS on each node to count its targe
|
ye15
|
NORMAL
|
2024-12-01T04:39:51.996685+00:00
|
2024-12-01T04:57:57.573950+00:00
| 420 | false |
**Intuition**\nEssentially, this is a brute-force approach. For the two trees, we calculate the target nodes. For tree 1, we run DFS on each node to count its target nodes of `k`. For tree 2, we do similar but count target nodes of `k-1`. This is to account for the cost of the added edge. For tree 2, we want the largest count of target nodes and apply it to all nodes of tree 1. \n\n**Analysis**\nTime complexity `O(N^2 + M^2)`\nSpace complexity `O(N + M)`\n\n**Implementation**\n```\nclass Solution:\n def maxTargetNodes(self, edges1: List[List[int]], edges2: List[List[int]], k: int) -> List[int]:\n \n def fn(edges, k): \n n = len(edges)+1\n tree = [[] for _ in range(n)]\n for u, v in edges: \n tree[u].append(v)\n tree[v].append(u)\n ans = [0]*n\n for x in range(n): \n stack = [(x, -1, 0)]\n while stack: \n u, p, d = stack.pop()\n if d <= k: ans[x] += 1\n for v in tree[u]: \n if v != p: \n stack.append((v, u, d+1))\n return ans \n \n most = max(fn(edges2, k-1))\n return [x+most for x in fn(edges1, k)]\n```
| 11 | 0 |
['Python3']
| 1 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Python3 || dfs || T/S: 98% / 94%
|
python3-dfs-ts-98-94-by-spaulding-lk8o
|
python3 []\nclass Solution:\n def maxTargetNodes(self, edges1: List[List[int]], \n edges2: List[List[int]], k: int) -> List[int]:\n\n
|
Spaulding_
|
NORMAL
|
2024-12-03T03:34:23.361419+00:00
|
2024-12-04T22:08:40.948396+00:00
| 134 | false |
```python3 []\nclass Solution:\n def maxTargetNodes(self, edges1: List[List[int]], \n edges2: List[List[int]], k: int) -> List[int]:\n\n def dfs(node: int, level: int, par: int, count = 1) -> int:\n\n if level < k:\n for chd in graph[node]:\n if chd == par: continue\n count += dfs(chd, level + 1, node)\n return count\n\n\n n, m, mx = len(edges1) + 1, len(edges2) + 1, 0\n if k == 0: return [1] * n\n\n graph = [[] for _ in range(m)]\n\n for u, v in edges2:\n graph[u].append(v)\n graph[v].append(u)\n\n for node in range(m):\n mx = max(mx, dfs(node, 1, -1))\n\n graph = [[] for _ in range(n)]\n for u, v in edges1:\n graph[u].append(v)\n graph[v].append(u)\n\n return [dfs(node, 0, -1) + mx for node in range(n)]\n```\n\n[https://leetcode.com/problems/maximize-the-number-of-target-nodes-after-connecting-trees-i/submissions/1468842261/](https://leetcode.com/problems/maximize-the-number-of-target-nodes-after-connecting-trees-i/submissions/1468842261/)\n\nI could be wrong, but I think that time complexity is *O*(*NK* + *MK*) and space complexity is *O*(*N* + *M* + *K*), in which *N*, *M*, *K* ~ `n`, `m`, `k`.
| 9 | 0 |
['Python3']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Centroid Decomposition - O(n log n + m log m) solution
|
centroid-decomposition-on-log-n-m-log-m-vbuht
|
Intuition\n- For a tree with size n, the key task is to find for each node the number of nodes with distance \leq k.\n- Centroid decomposition is an efficient
|
sykobeli
|
NORMAL
|
2024-12-02T07:28:56.351871+00:00
|
2024-12-02T07:28:56.351891+00:00
| 202 | false |
# Intuition\n- For a tree with size $$n$$, the key task is to find for each node the number of nodes with distance $$\\leq k$$.\n- Centroid decomposition is an efficient algorithm dealing with distances between any two nodes in a tree. A centroid is a node such that when being the root, no subtree has size $$\\geq n/2$$. After finding a centroid for a tree, we recursively repeat it for the subtrees, resulting in at most $$O(\\log n)$$ centroids.\n- Note that any simple path between two nodes in a tree must pass through a common centroid ancestor, going from one subtree to another subtree. The distance between the two nodes is simply the sum of the distances from the centroid to the two nodes. \n\n# Approach\nWe iterate through each centroid. For each centroid, we first find the distances from the centroid to the nodes in each subtree, and count the frequencies. For each node in a subtree, we only need to consider the paths from that node to the centroid, then going into any other subtrees. The number of such paths with length $$\\leq k$$ can be obtained using prefix sums. Note that all these computations take $$O(n)$$ time for each centroid.\n\n# Complexity\n- Time complexity:\n$$O(n\\log n+m\\log m)$$\n\n- Space complexity:\n$$O(n+m)$$\n\nThe below code takes around 200 ms.\n\n# Code\n```python3 []\nfrom collections import defaultdict\n\nclass Solution:\n def maxTargetNodes(self, edges1: List[List[int]], edges2: List[List[int]], k: int) -> List[int]:\n def subtreeSizes(node, parent):\n nonlocal sizes\n for child in adj[node]:\n if child == parent or child in visited:\n continue\n sizes[node] += subtreeSizes(child, node)\n return sizes[node]\n\n def findCentroid(node, parent, root):\n for child in adj[node]:\n if child == parent or child in visited:\n continue\n if sizes[child] > sizes[root] // 2:\n return findCentroid(child, node, root)\n return node\n\n def findDistances(node, parent, depth, count):\n if depth > k:\n return\n if len(count) == depth - 1:\n count.append(1)\n else:\n count[depth - 1] += 1\n for child in adj[node]:\n if child == parent or child in visited:\n continue\n findDistances(child, node, depth + 1, count)\n\n def countTarget(node, parent, depth, total, curr):\n if depth > k:\n return\n nonlocal result\n result[node] += total[min(k - depth, len(total) - 1)] - curr[min(k - depth, len(curr) - 1)]\n for child in adj[node]:\n if child == parent or child in visited:\n continue\n countTarget(child, node, depth + 1, total, curr)\n\n def centroidDecomposition(node):\n nonlocal visited, result, sizes\n sizes = [1] * n\n subtreeSizes(node, -1)\n centroid = findCentroid(node, -1, node)\n visited.add(centroid)\n prefixes = {}\n maxlen = 1\n for child in adj[centroid]:\n if child in visited:\n continue\n count = []\n findDistances(child, centroid, 1, count)\n prefixes[child] = [0]\n for i in range(len(count)):\n prefixes[child].append(prefixes[child][-1] + count[i])\n maxlen = max(maxlen, len(prefixes[child]))\n total = [1] * maxlen\n for child in prefixes:\n for i in range(maxlen):\n total[i] += prefixes[child][min(i, len(prefixes[child]) - 1)]\n result[centroid] += total[min(k, len(total) - 1)]\n for child in adj[centroid]:\n if child in visited:\n continue\n countTarget(child, centroid, 1, total, prefixes[child])\n for child in adj[centroid]:\n if child in visited:\n continue\n centroidDecomposition(child)\n\n k -= 1\n if k < 0:\n maxcount = 0\n else:\n adj = defaultdict(list)\n for edge in edges2:\n adj[edge[0]].append(edge[1])\n adj[edge[1]].append(edge[0])\n n = len(edges2) + 1\n sizes = []\n visited = set()\n result = [0] * n\n centroidDecomposition(0)\n maxcount = max(result)\n k += 1\n adj = defaultdict(list)\n for edge in edges1:\n adj[edge[0]].append(edge[1])\n adj[edge[1]].append(edge[0])\n n = len(edges1) + 1\n sizes = []\n visited = set()\n result = [maxcount] * n\n centroidDecomposition(0)\n return result\n```
| 5 | 0 |
['Python3']
| 2 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Step-By-Step BFS Implementation 🔥 | Simple Beginner Friendly Explanation With Inturition
|
step-by-step-bfs-implementation-simple-b-rdjy
|
IntuitionTo maximize the number of nodes "target" to each node in the first tree:
Compute how many nodes are reachable within k steps in the first tree.
Compute
|
atharvaparab9160
|
NORMAL
|
2024-12-01T06:55:08.374693+00:00
|
2024-12-25T07:51:33.493444+00:00
| 429 | false |
# Intuition
#### To maximize the number of nodes "target" to each node in the first tree:
1. Compute how many nodes are reachable within k steps in the first tree.
2. Compute how many nodes are reachable within k−1 steps in the second tree (since connecting adds one edge).
3. For each node in the first tree, the best result is its reachable count plus the maximum reachable count from the second tree.
# Approach
1. **Precompute Reachable Nodes**:
Use BFS to calculate how many nodes each node can reach within k steps for the first tree.
Use BFS to calculate how many nodes each node can reach within k−1 steps for the second tree.
1. **Find Maximum Boost**:
Find the maximum reachable nodes in the second tree.
1. **Combine Results**:
- For each node i in the first tree:
answer[i]=reachableCount1[i]+max(reachableCount2)
Return the result array answer.
# Key Concepts in the Code
1. **Breadth-First Search (BFS)**:
BFS is used to traverse the tree level by level and compute distances.
2. **Adjacency List Representation**:
Efficient representation of the tree structure for traversal.
3. **Combining Results**:
Since queries are independent, we can compute results for tree 1 and tree 2 separately and combine them.
# Complexity
- **Time complexity:**
- The calculateReachableNodes_BFS function is called separately for each tree. Within it:
- For each node in the tree (say n for the first tree, m for the second tree):
-BFS is performed starting from that node.
-BFS visits each node and edge once for each traversal.
**The total cost for BFS across all nodes in a tree is:**
O(num_nodes×(num_nodes+num_edges))=O(n×n) for tree 1 and O(m×m) for tree 2.
||**Overall Time Complexity is : O(n^2+m^2)**||
- **Space complexity:**
***Adjacency Lists*** : O(n+m) space.
***Visited Arrays*** : Each BFS requires a visited array of size O(n) or O(m).
***Queue for BFS*** : The queue in BFS has a maximum size proportional to the number of nodes, O(n) or O(m).
***Result Arrays*** : Storing reachable counts for each tree: O(n+m).
||**Total space complexity is:O(n+m)**||
# Code
```python3 []
from collections import deque
from typing import List
class Solution:
def maxTargetNodes(self, edges1: List[List[int]], edges2: List[List[int]], k: int) -> List[int]:
# Base case: if k is 0, all nodes can only reach themselves.
if k == 0:
return [1] * (len(edges1) + 1)
# Initialize adjacency lists for both trees
adjacencyList1 = [[] for _ in range(len(edges1) + 1)]
adjacencyList2 = [[] for _ in range(len(edges2) + 1)]
# Build adjacency list for the first tree
for u, v in edges1:
adjacencyList1[u].append(v)
adjacencyList1[v].append(u)
# Build adjacency list for the second tree
for u, v in edges2:
adjacencyList2[u].append(v)
adjacencyList2[v].append(u)
# Function to calculate reachable nodes within a given distance for a tree
def calculateReachableNodes_BFS(adjacencyList, maxDistance):
reachCounts = [0] * len(adjacencyList)
for startNode in range(len(adjacencyList)):
# Perform BFS to calculate reachable nodes
queue = deque([startNode])
visited = [False] * len(adjacencyList)
visited[startNode] = True
level = 0
# level signifies distance of node from the startNode
# if (distance increses more than k) or (queue becomes empty) then the bfs stops
# and return the total number of neighbours reachable from the startNode
while len(queue)!=0 and level < maxDistance:
level += 1
# this FOR loop ensures that only the elements at that specific level from startNode are seen
lenQ = len(queue)
for _ in range(lenQ):
currentNode = queue.popleft()
for neighbor in adjacencyList[currentNode]:
if not visited[neighbor]:
visited[neighbor] = True
queue.append(neighbor)
# Store the count of reachable nodes from the current start node
reachCounts[startNode] = sum(visited)
return reachCounts
# Calculate reachable nodes for the first tree within distance k
reachableCount1 = calculateReachableNodes_BFS(adjacencyList1, k)
# Calculate reachable nodes for the second tree within distance k-1
# we arw using k-1 bcs when we connect tree 1 and tree 2 there will be a edge created there
reachableCount2 = calculateReachableNodes_BFS(adjacencyList2, k - 1)
# Find the maximum reachable nodes in the second tree
maxReachableInTree2 = max(reachableCount2)
# Add the maximum from the second tree to each node's reachable count in the first tree
for i in range(len(reachableCount1)):
reachableCount1[i] += maxReachableInTree2
return reachableCount1
```
```C++ []
#include <vector>
#include <queue>
#include <algorithm>
using namespace std;
class Solution {
public:
vector<int> maxTargetNodes(vector<vector<int>>& edges1, vector<vector<int>>& edges2, int k) {
// Base case: if k is 0, all nodes can only reach themselves.
if (k == 0) {
return vector<int>(edges1.size() + 1, 1);
}
// Initialize adjacency lists for both trees
int n1 = edges1.size() + 1, n2 = edges2.size() + 1;
vector<vector<int>> adjacencyList1(n1), adjacencyList2(n2);
// Build adjacency list for the first tree
for (auto& edge : edges1) {
adjacencyList1[edge[0]].push_back(edge[1]);
adjacencyList1[edge[1]].push_back(edge[0]);
}
// Build adjacency list for the second tree
for (auto& edge : edges2) {
adjacencyList2[edge[0]].push_back(edge[1]);
adjacencyList2[edge[1]].push_back(edge[0]);
}
// Function to calculate reachable nodes within a given distance for a tree
auto calculateReachableNodes_BFS = [](vector<vector<int>>& adjacencyList, int maxDistance) {
int n = adjacencyList.size();
vector<int> reachCounts(n, 0);
for (int startNode = 0; startNode < n; ++startNode) {
vector<bool> visited(n, false);
queue<int> q;
q.push(startNode);
visited[startNode] = true;
int level = 0;
while (!q.empty() && level < maxDistance) {
int lenQ = q.size();
++level;
for (int i = 0; i < lenQ; ++i) {
int currentNode = q.front();
q.pop();
for (int neighbor : adjacencyList[currentNode]) {
if (!visited[neighbor]) {
visited[neighbor] = true;
q.push(neighbor);
}
}
}
}
reachCounts[startNode] = count(visited.begin(), visited.end(), true);
}
return reachCounts;
};
// Calculate reachable nodes for the first tree within distance k
vector<int> reachableCount1 = calculateReachableNodes_BFS(adjacencyList1, k);
// Calculate reachable nodes for the second tree within distance k-1
vector<int> reachableCount2 = calculateReachableNodes_BFS(adjacencyList2, k - 1);
// Find the maximum reachable nodes in the second tree
int maxReachableInTree2 = *max_element(reachableCount2.begin(), reachableCount2.end());
// Add the maximum from the second tree to each node's reachable count in the first tree
for (int i = 0; i < reachableCount1.size(); ++i) {
reachableCount1[i] += maxReachableInTree2;
}
return reachableCount1;
}
};
```
```Java []
import java.util.*;
class Solution {
public int[] maxTargetNodes(int[][] edges1, int[][] edges2, int k) {
if (k == 0) {
int[] result = new int[edges1.length + 1];
Arrays.fill(result, 1);
return result;
}
// Create adjacency lists
List<List<Integer>> adj1 = new ArrayList<>(edges1.length + 1);
List<List<Integer>> adj2 = new ArrayList<>(edges2.length + 1);
// Initialize adjacency lists
for (int i = 0; i <= edges1.length; i++) {
adj1.add(new ArrayList<>());
}
for (int i = 0; i <= edges2.length; i++) {
adj2.add(new ArrayList<>());
}
// Populate adjacency list for first graph
for (int[] edge : edges1) {
int u = edge[0], v = edge[1];
adj1.get(u).add(v);
adj1.get(v).add(u);
}
// Populate adjacency list for second graph
for (int[] edge : edges2) {
int u = edge[0], v = edge[1];
adj2.get(u).add(v);
adj2.get(v).add(u);
}
// Calculate target nodes for first graph
int[] ans1 = new int[edges1.length + 1];
for (int i = 0; i < adj1.size(); i++) {
ans1[i] = bfs(adj1, i, k);
}
// Calculate target nodes for second graph
int[] ans2 = new int[edges2.length + 1];
for (int i = 0; i < adj2.size(); i++) {
ans2[i] = bfs(adj2, i, k - 1);
}
// Find maximum value in ans2
int maxi = Arrays.stream(ans2).max().orElse(0);
// Combine results
for (int i = 0; i < ans1.length; i++) {
ans1[i] += maxi;
}
return ans1;
}
private int bfs(List<List<Integer>> adj, int start, int maxDepth) {
Queue<Integer> q = new LinkedList<>();
boolean[] visited = new boolean[adj.size()];
q.offer(start);
visited[start] = true;
int depth = 1;
while (!q.isEmpty() && depth <= maxDepth) {
int size = q.size();
for (int i = 0; i < size; i++) {
int current = q.poll();
for (int neighbor : adj.get(current)) {
if (!visited[neighbor]) {
visited[neighbor] = true;
q.offer(neighbor);
}
}
}
depth++;
}
// Count visited nodes
int visitedCount = 0;
for (boolean v : visited) {
if (v) visitedCount++;
}
return visitedCount;
}
}
```
| 4 | 0 |
['Tree', 'Breadth-First Search', 'Graph', 'Shortest Path', 'Python', 'C++', 'Java', 'Python3']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
bfs java solution
|
bfs-java-solution-by-adityachauhan_27-635h
|
Intuition\n1. Generate both trees using edges arrays\n2. use bfs to count no of nodes within distance k-1 in tree 2 starting at each node and take the max value
|
adityachauhan_27
|
NORMAL
|
2024-12-01T04:36:25.972576+00:00
|
2024-12-01T04:36:25.972606+00:00
| 312 | false |
# Intuition\n1. Generate both trees using edges arrays\n2. use bfs to count no of nodes within distance k-1 in tree 2 starting at each node and take the max value.\n3. use bfs to count no of nodes within distance k in tree1 for each node and add max value from step 2\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public void bfs(ArrayList<ArrayList<Integer>> tree,int node,int[] arr,int k){\n int res=0;\n Queue<Integer> q=new LinkedList<>();\n HashSet<Integer> visited=new HashSet<>();\n q.add(node);\n int count=0;\n while(!q.isEmpty() && count<=k){\n int size=q.size();\n for(int i=0;i<size;i++){\n int temp=q.poll();\n visited.add(temp);\n for(int x:tree.get(temp)){\n if(!visited.contains(x)){\n q.offer(x);\n }\n }\n }\n count++;\n }\n arr[node]=visited.size();\n }\n \n public int[] maxTargetNodes(int[][] edges1, int[][] edges2, int k) {\n int n=edges1.length+1;\n int m=edges2.length+1;\n\n ArrayList<ArrayList<Integer>> tree1=new ArrayList<>();\n ArrayList<ArrayList<Integer>> tree2=new ArrayList<>();\n\n for(int i=0;i<n;i++)tree1.add(new ArrayList<>());\n for(int i=0;i<m;i++)tree2.add(new ArrayList<>());\n\n for(int[] e:edges1){\n tree1.get(e[0]).add(e[1]);\n tree1.get(e[1]).add(e[0]);\n }\n\n for(int[] e:edges2){\n tree2.get(e[0]).add(e[1]);\n tree2.get(e[1]).add(e[0]);\n }\n\n int[] tar1=new int[n];\n int[] tar2=new int[m];\n\n for(int i=0;i<m;i++){\n bfs(tree2,i,tar2,k-1);\n }\n \n int max=0;\n for(int i:tar2){\n max=Math.max(i,max);\n }\n\n for(int i=0;i<n;i++){\n bfs(tree1,i,tar1,k);\n }\n \n for(int i=0;i<n;i++){\n tar1[i]+=max;\n }\n \n return tar1;\n }\n}\n```
| 4 | 0 |
['Breadth-First Search', 'Java']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Javascript 🎉🎉🎉
|
javascript-by-csathnere-fctb
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
csathnere
|
NORMAL
|
2024-12-01T04:39:38.073976+00:00
|
2024-12-01T04:39:38.074004+00:00
| 168 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```javascript []\n/**\n * @param {number[][]} edges1\n * @param {number[][]} edges2\n * @param {number} k\n * @return {number[]}\n */\nvar maxTargetNodes = function(edges1, edges2, k) {\n const n = edges1.length + 1;\n const m = edges2.length + 1;\n\n const adj1 = Array.from({ length: n }, () => []);\n const adj2 = Array.from({ length: m }, () => []);\n\n for (const [u, v] of edges1) {\n adj1[u].push(v);\n adj1[v].push(u);\n }\n for (const [u, v] of edges2) {\n adj2[u].push(v);\n adj2[v].push(u);\n } \n const good1 = new Array(n).fill(0);\n const good2 = new Array(m).fill(0);\n\n const dfs = (node, parent, distance, root, k, good, adj) => {\n if (distance >= k) return;\n good[root]++;\n for (const neighbor of adj[node]) {\n if (neighbor !== parent) {\n dfs(neighbor, node, distance + 1, root, k, good, adj);\n }\n }\n };\n for (let i = 0; i < n; i++) {\n dfs(i, -1, 0, i, k + 1, good1, adj1);\n }\n\n for (let i = 0; i < m; i++) {\n dfs(i, -1, 0, i, k, good2, adj2);\n }\n\n const mx = Math.max(...good2);\n\n return good1.map(value => value + mx);\n\n};\n```
| 2 | 0 |
['JavaScript']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
🔥Simple DFS⚡ || ✅Clean & Best Code💯
|
simple-dfs-clean-best-code-by-adish_21-kzu8
|
\n\n# Complexity\n\n- Time complexity:\nO(m * m + n * n)\n\n- Space complexity:\nO(m + v)\n\n\n# Code\n## Please Upvote if it helps\uD83E\uDD17\ncpp []\nclass S
|
aDish_21
|
NORMAL
|
2024-12-04T18:33:39.694448+00:00
|
2024-12-04T18:33:39.694488+00:00
| 63 | false |
\n\n# Complexity\n```\n- Time complexity:\nO(m * m + n * n)\n\n- Space complexity:\nO(m + v)\n```\n\n# Code\n## Please Upvote if it helps\uD83E\uDD17\n```cpp []\nclass Solution {\npublic:\n int cnt = 0;\n void dfs(int node, vector<vector<int>>& adj, int k, int val, vector<bool>& vis){\n vis[node] = true;\n if(val > k)\n return ;\n cnt++;\n for(auto it : adj[node]){\n if(!vis[it])\n dfs(it, adj, k, val + 1, vis);\n }\n }\n\n vector<int> maxTargetNodes(vector<vector<int>>& edges1, vector<vector<int>>& edges2, int k) {\n int n = edges1.size() + 1, m = edges2.size() + 1;\n vector<int> ans(n);\n vector<vector<int>> adj1(n), adj2(m);\n for(auto it : edges1){\n int x = it[0], y = it[1];\n adj1[x].push_back(y);\n adj1[y].push_back(x);\n }\n for(auto it : edges2){\n int x = it[0], y = it[1];\n adj2[x].push_back(y);\n adj2[y].push_back(x);\n }\n int maxi = 0;\n for(int i = 0 ; i < m ; i++){\n cnt = 0;\n vector<bool> vis(m);\n dfs(i, adj2, k - 1, 0, vis);\n maxi = max(maxi, cnt);\n }\n for(int i = 0 ; i < n ; i++){\n cnt = 0;\n vector<bool> vis(n);\n dfs(i, adj1, k, 0, vis);\n ans[i] = cnt + maxi;\n }\n return ans;\n }\n};\n```
| 1 | 0 |
['Tree', 'Depth-First Search', 'C++']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
✅✅✅Easy To Understand C++ Code||BFS
|
easy-to-understand-c-codebfs-by-shubham_-w4bq
|
Intuition\n Describe your first thoughts on how to solve this problem. \nbrute force :finding answer for every node independently as constraints are too low.\n#
|
codeblunderer
|
NORMAL
|
2024-12-03T20:35:39.112098+00:00
|
2024-12-03T20:35:39.112124+00:00
| 99 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nbrute force :finding answer for every node independently as constraints are too low.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUsing bfs finding how many nodes can be reached from every other node for tree1 .\nNow, we need to draw one edge from tree1 to tree2 we will greedily find which node of tree2 can traverse to maximum number of nodes to a max distance of k-1 as 1 distance will be used in connecting 2 trees\nnow adding this ans in every node of tree1 \n# Code\n```cpp []\nclass Solution {\npublic:\n int bfs(vector<int>adj[],int k,int node,int n){\n queue<int>q;\n vector<bool>vis(n,false);\n int cnt=k>=0?1:0;\n // if k is less than 0 we can\'t travel from any of the node \n q.push(node);\n vis[node]=1;\n while(!q.empty() && k>0){\n int size=q.size();\n while(size--){\n int x=q.front();q.pop();\n for(auto it:adj[x]){\n if(!vis[it]){\n vis[it]=1;\n q.push(it);\n cnt++;\n }\n }\n }\n k--;\n }\n return cnt;\n }\n vector<int> maxTargetNodes(vector<vector<int>>& edges1, vector<vector<int>>& edges2, int k) {\n int n=edges1.size(),m=edges2.size(),maxi=0;\n vector<int>adj1[n+1],adj2[m+1];\n // creating adjacency for graph1\n for(auto it:edges1){\n adj1[it[0]].push_back(it[1]);\n adj1[it[1]].push_back(it[0]);\n }\n // creating adjacency for graph2\n for(auto it:edges2){\n adj2[it[0]].push_back(it[1]);\n adj2[it[1]].push_back(it[0]);\n }\n //finding the node with greatest travel capacity in graph2\n for(int i=0;i<=m;i++){\n maxi=max(maxi,bfs(adj2,k-1,i,m+1));\n }\n //findind total number of nodes at\n // a distance of k and adding nodes of graph2 \n vector<int>ans(n+1);\n for(int i=0;i<=n;i++){\n ans[i]=bfs(adj1,k,i,n+1)+maxi;\n }\n return ans;\n }\n};\n```
| 1 | 0 |
['Tree', 'Breadth-First Search', 'C++']
| 2 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
100% Beats BFS Optimal Solution in JAVA,C++ & Python
|
100-beats-bfs-optimal-solution-in-javac-ksx74
|
Counting Nodes at Distance k in a Graph \uD83C\uDF10\n\nIn graph theory, a graph is a set of nodes connected by edges, and often we need to perform certain task
|
dipesh1203
|
NORMAL
|
2024-12-02T09:56:35.256244+00:00
|
2024-12-02T09:57:20.006441+00:00
| 135 | false |
## Counting Nodes at Distance `k` in a Graph \uD83C\uDF10\n\nIn graph theory, a **graph** is a set of nodes connected by edges, and often we need to perform certain tasks based on the distance between nodes. For instance, one task might be to count the number of nodes within a certain distance from a given node. Let\'s explore a solution to count the number of nodes within distance `k` in an undirected graph using BFS (Breadth-First Search).\n\n### Problem Overview \uD83E\uDD14\nGiven two graphs represented by edge lists (`edges1` and `edges2`), we need to:\n1. Count how many nodes are at a distance of `k` from each node in the graph.\n2. Find the node with the maximum count of reachable nodes at distance `k` and combine the results from both graphs.\n\nThis problem requires BFS traversal to explore nodes within a specified distance from the starting node.\n\n### Steps to Solve \uD83D\uDCC8\n1. **Create the Graph**: The graph is represented as an adjacency list. We will build the graph from the given edges.\n2. **BFS Traversal**: For each node, we use BFS to explore the nodes within the given distance `k`. During the traversal, we keep track of the distances of nodes from the start node.\n3. **Counting Nodes**: We count how many nodes are at a distance less than or equal to `k`.\n4. **Combine Results**: We combine the results of the two graphs and return the final node counts.\n\n### Solution \uD83D\uDCBB\n\n```java []\nimport java.util.*;\n\nclass Solution {\n class edge {\n int src, dest;\n public edge(int src, int dest) {\n this.src = src;\n this.dest = dest;\n }\n }\n\n public void createGraph(ArrayList<edge>[] graph, int[][] edges) {\n for (int i = 0; i < graph.length; i++) {\n graph[i] = new ArrayList<>();\n }\n for (int[] e : edges) {\n int src = e[0];\n int dest = e[1];\n graph[src].add(new edge(src, dest));\n graph[dest].add(new edge(dest, src)); // Since it\'s undirected\n }\n }\n\n public int countNodesWithinDistanceK(ArrayList<edge>[] graph, int startNode, int k) {\n Queue<Integer> queue = new LinkedList<>();\n boolean[] visited = new boolean[graph.length];\n int[] distance = new int[graph.length];\n\n queue.add(startNode);\n visited[startNode] = true;\n\n int count = 0; // To count nodes within distance <= k\n\n while (!queue.isEmpty()) {\n int current = queue.poll();\n if (distance[current] <= k) {\n count++;\n }\n\n for (edge e : graph[current]) {\n if (!visited[e.dest]) {\n queue.add(e.dest);\n visited[e.dest] = true;\n distance[e.dest] = distance[current] + 1;\n }\n }\n }\n\n return count;\n }\n\n public void count(ArrayList<edge>[] graph, int k, int[] res) {\n for (int i = 0; i < graph.length; i++) {\n res[i] = countNodesWithinDistanceK(graph, i, k);\n }\n }\n\n public int[] maxTargetNodes(int[][] edges1, int[][] edges2, int k) {\n Set<Integer> node1 = new HashSet<>();\n Set<Integer> node2 = new HashSet<>();\n \n // Fill the sets with nodes from both graphs\n for (int[] edge : edges1) {\n node1.add(edge[0]);\n node1.add(edge[1]);\n }\n for (int[] edge : edges2) {\n node2.add(edge[0]);\n node2.add(edge[1]);\n }\n\n ArrayList<edge>[] graph1 = new ArrayList[node1.size()];\n ArrayList<edge>[] graph2 = new ArrayList[node2.size()];\n\n createGraph(graph1, edges1);\n createGraph(graph2, edges2);\n\n int[] count1 = new int[graph1.length];\n int[] count2 = new int[graph2.length];\n \n count(graph1, k, count1);\n count(graph2, k - 1, count2); // For second graph, we reduce the distance by 1\n\n int max = Integer.MIN_VALUE;\n for (int i = 0; i < count2.length; i++) {\n max = Math.max(max, count2[i]); // Find the maximum count from the second graph\n }\n\n int[] res = new int[graph1.length];\n for (int i = 0; i < count1.length; i++) {\n res[i] = count1[i] + max; // Combine results from both graphs\n }\n\n return res;\n }\n}\n```\n```cpp []\n#include <iostream>\n#include <vector>\n#include <queue>\n#include <unordered_set>\n#include <algorithm>\n\nusing namespace std;\n\nclass Solution {\npublic:\n struct Edge {\n int src, dest;\n Edge(int src, int dest) : src(src), dest(dest) {}\n };\n\n void createGraph(vector<Edge> graph[], vector<vector<int>>& edges) {\n for (auto& e : edges) {\n int src = e[0], dest = e[1];\n graph[src].push_back(Edge(src, dest));\n graph[dest].push_back(Edge(dest, src));\n }\n }\n\n int countNodesWithinDistanceK(vector<Edge> graph[], int startNode, int k, int n) {\n vector<bool> visited(n, false);\n vector<int> distance(n, -1);\n queue<int> q;\n q.push(startNode);\n visited[startNode] = true;\n distance[startNode] = 0;\n\n int count = 0;\n while (!q.empty()) {\n int current = q.front();\n q.pop();\n\n if (distance[current] <= k) {\n count++;\n }\n\n for (auto& e : graph[current]) {\n if (!visited[e.dest]) {\n visited[e.dest] = true;\n distance[e.dest] = distance[current] + 1;\n q.push(e.dest);\n }\n }\n }\n return count;\n }\n\n vector<int> maxTargetNodes(vector<vector<int>>& edges1, vector<vector<int>>& edges2, int k) {\n unordered_set<int> node1, node2;\n for (auto& e : edges1) {\n node1.insert(e[0]);\n node1.insert(e[1]);\n }\n for (auto& e : edges2) {\n node2.insert(e[0]);\n node2.insert(e[1]);\n }\n\n int n1 = node1.size(), n2 = node2.size();\n vector<Edge> graph1[n1], graph2[n2];\n\n createGraph(graph1, edges1);\n createGraph(graph2, edges2);\n\n vector<int> count1(n1), count2(n2);\n for (int i = 0; i < n1; i++) {\n count1[i] = countNodesWithinDistanceK(graph1, i, k, n1);\n }\n for (int i = 0; i < n2; i++) {\n count2[i] = countNodesWithinDistanceK(graph2, i, k - 1, n2);\n }\n\n int max = *max_element(count2.begin(), count2.end());\n vector<int> res(n1);\n for (int i = 0; i < n1; i++) {\n res[i] = count1[i] + max;\n }\n return res;\n }\n};\n```\n```python []\nfrom collections import deque\n\nclass Solution:\n class Edge:\n def __init__(self, src, dest):\n self.src = src\n self.dest = dest\n\n def createGraph(self, graph, edges):\n for e in edges:\n src, dest = e\n graph[src].append(self.Edge(src, dest))\n graph[dest].append(self.Edge(dest, src)) # Since it\'s undirected\n\n def countNodesWithinDistanceK(self, graph, startNode, k):\n visited = [False] * len(graph)\n distance = [-1] * len(graph)\n queue = deque([startNode])\n visited[startNode] = True\n distance[startNode] = 0\n\n count = 0\n while queue:\n current = queue.popleft()\n\n if distance[current] <= k:\n count += 1\n\n for e in graph[current]:\n if not visited[e.dest]:\n visited[e.dest] = True\n distance[e.dest\n\n] = distance[current] + 1\n queue.append(e.dest)\n return count\n\n def maxTargetNodes(self, edges1, edges2, k):\n node1, node2 = set(), set()\n for e in edges1:\n node1.update(e)\n for e in edges2:\n node2.update(e)\n\n graph1 = [[] for _ in range(len(node1))]\n graph2 = [[] for _ in range(len(node2))]\n\n self.createGraph(graph1, edges1)\n self.createGraph(graph2, edges2)\n\n count1 = [self.countNodesWithinDistanceK(graph1, i, k) for i in range(len(graph1))]\n count2 = [self.countNodesWithinDistanceK(graph2, i, k - 1) for i in range(len(graph2))]\n\n maxCount = max(count2)\n res = [count1[i] + maxCount for i in range(len(count1))]\n return res\n```\n\n\n### Explanation of Code \uD83D\uDCDC\n\n1. **Graph Representation**: We create a graph using an adjacency list. Each node has a list of edges connected to it.\n2. **`countNodesWithinDistanceK()` Method**:\n - We start a BFS traversal from a given `startNode`.\n - As we traverse, we calculate the distance from the start node for each other node.\n - If a node\u2019s distance is less than or equal to `k`, we increment the count.\n3. **`count()` Method**:\n - This method counts the nodes within distance `k` for each node in the graph.\n4. **`maxTargetNodes()` Method**:\n - We combine results from two different graphs (`edges1` and `edges2`) by first counting the nodes within distance `k` for each node in both graphs, and then adding the maximum result from the second graph to the first graph.\n\n### Conclusion \uD83C\uDFC1\n\nThis blog demonstrated a solution to count the number of nodes within distance `k` in a graph. The approach uses BFS to traverse the graph and counts nodes within the given distance range. We discussed the solution in **Java**, **C++**, and **Python**, with the added benefit of clear explanations and emojis for a fun, engaging read! \uD83D\uDE80
| 1 | 0 |
['Breadth-First Search', 'Graph', 'Python', 'C++', 'Java', 'Python3']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
O((N + M) * K) Tree DP using a Single DFS on Each Tree | Detailed Explanation & Comments
|
on-m-k-tree-dp-using-a-single-dfs-on-eac-ankf
|
Intuition\n- We can arbitrarily root each tree at a vertex (0 in accompanying code), then perform DFS on this root.\n- Tree structure: By rooting the tree and p
|
chanlvh
|
NORMAL
|
2024-12-01T23:34:31.629306+00:00
|
2024-12-02T00:07:14.597374+00:00
| 70 | false |
# Intuition\n- We can **arbitrarily root each tree** at a vertex (`0` in accompanying code), then **perform DFS on this root**.\n- **Tree structure**: By rooting the tree and performing DFS traversal on the root, each node in the tree will have a single parent (except the root), and optionally some children.\n- Observe that paths of length `d` from a vertex `v` can go in 1 of 2 directions: either i) **forward** down to `v`\'s descendants, or ii) **backward** up to `v`\'s parent.\n- We can accurately **calculate the number of forward paths during DFS**. **Every** forward path of length `d` from `v` contributes **one** corresponding forward path of length `d + 1` to `v`\u2019s parent. Recurrence relation, for any distance `d`:\n$$\\text{fwd\\_paths}[v][d] = \\sum_{\\text{child } u \\text{ of } v} \\text{fwd\\_paths}[u][d - 1]$$.\n- Determination of the number of **backward paths** requires that we process each node **in topological order**, such that all paths, in any directions, of any distance from a parent node must have been calculated before we can process its children.\n- For a vertex `v` with parent `p`, a **backward** path of length `d` can take 1 of 2 directions:\n - i) The path starts from `v`, passes through `p` then goes **forward** (relative to `p`) through another child of `p` and ending in some descendants of `p` .\n - ii) The path also starts from `v` and passes through `p` but continues to move **backward** (relative to `p`) through `p`\'s parent.\n- The **first type of backward paths** from `v` with length `d` ends up going **forward** from `p` .\n - So the length of the segment from `p` of such paths will be `d - 1` to account for the edge `(v, p)`. There are $\\text{fwd\\_paths}[p][d-1]$ such paths.\n - However, note that these also include paths that go through `v` which we do not want (i.e. we only want paths that, after starting from `v` and passing `p`, will cross some other children of `p`). There are $\\text{fwd\\_paths}[v][d-2]$ paths that start from `p` and passes through `v` with length `d - 1`, so we can subtract these from our calculation.\n - Thus, the recurrence relation for these paths is:\n$$\\text{bckwd\\_paths\\_type\\_i}[v][d]=\\text{fwd\\_paths}[p][d-1] - \\text{fwd\\_paths}[v][d-2]$$.\n- The **second type of backward paths** from `v` with length `d` goes backward from `p`. Again, the length of the segment from `p` of such paths is `d - 1`. So the recurrence relation for these paths is:\n$$\\text{bckwd\\_paths\\_type\\_ii}[v][d] = \\text{bckwd\\_paths}[p][d-1]$$.\n- The **total number of backward paths** from `v` with a particular length `d` is just the sum of the aforementioned two sub-types. So, in summary:\n$$\\text{bckwd\\_paths}[v][d] = \\text{fwd\\_paths}[p][d-1]-\\text{fwd\\_paths}[v][d-2] + \\text{bckwd\\_paths}[p][d-1]$$.\n- Thus, for any node `v` in either tree, before joining them, the total number of paths of length **at most** `k` is just the **sum of both forward and backward paths** from `v` with lengths **at most** `k`: (note that we don\u2019t count backward paths of length `0` to avoid double-counting paths of length `0`):\n$$\\text{count}[v]_k=\\sum_{d_1=0}^{k}\\text{fwd\\_paths}[v][d_1] + \\sum_{d_2=1}^{k}\\text{bckwd\\_paths}[v][d_2]$$.\n- Back to our original problem, to **maximize** the number of nodes with distance `<= k` to any node `v` from the first tree, we want to connect `v` of the first tree with a node `u` in the second tree such that `u` has the **maximum** number of nodes with distance `<= k - 1` from `u` (subtract `1` to account for the node `(u, v)`).\nSo, if we define `maxConnection` as the max number of nodes with distance `<= k - 1` from any node in the second tree: $\\text{maxConnection} = \\text{max}_{u \\in V_2}(\\text{count2}[u]_{k-1})$, then for any vertex `v` in the first tree, the answer after joining the two trees would be:\n$$\\text{count1}[v]_{k, {\\text{ after\\_join}}} = \\text{count1}[v]_{k, {\\text{ before\\_join}}} + \\text{maxConnection } (\\forall v \\in V_1)$$.\n\n# Approach\n- **Edge case** of `k = 0`: return an array of all `1`\'s.\n- Build the **adjacency lists** for both trees and store in `tree1` and `tree2`.\n- **Perform DFS** on each tree to calculate **forward paths**:\n - Use a pre-order queue (or post-order stack) to keep track of topological order.\n - Store the parent `p` of this node `v` in a `parent` array such that `parent[v] = p`.\n - Store the number of **forward** paths with length `d` from vertex `v` in `dp[v][d]` :\n - Base case (at start of DFS): `dp[v][0] = 1` because there is exactly 1 node of distance 0 from `v` (itself).\n - (At end of DFS) For each distance `d = 1` through `d = k`, merge the current node\u2019s contribution to its parent\u2019s number of forward paths: `dp[p][d] += dp[v][d - 1]`.\n- Traverse each node in each tree in topological order to calculate **backward** **paths** and **total** number of paths using **DP**.\n - Store the number of backward paths with length `d` from vertex `v` in `backtrack[v][d]`, and the total number of paths (both forward and backward) with length **at most** `k` (or `k - 1` for the second tree) from vertex `v` in `count[v]`.\n - If `v` is not the root, then `backtrack[v][1] = 1` (there is 1 backward path of length 1, which is the path back to `v`\'s parent `p`).\n - If `v` is not the root, then for any distance `1 < d <= k` (or `<= k - 1` for the second tree) , the number of backward paths from node `v` with parent `p` is `backtrack[v][d] = dp[p][d - 1] - dp[v][d - 2] + backtrack[p][d - 1]`.\n - **Sum all forward and backward paths** and store in `count[v]`.\n- Iterate through all the values in `count2` (the `count` array associated with the second tree) to find the `maxConnectivity`.\n- Iterate through all the values in `count1` (the `count` array associated with the first tree) and add `maxConnectivity` to each, which yields the desired result.\n- Return `count1` .\n# Complexity\n- Time complexity: $$\\text{O}((N + M) \\cdot K)$$\n- Space complexity: $$\\text{O}((N + M) \\cdot K)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n \n public int[] maxTargetNodes(int[][] edges1, int[][] edges2, int k) {\n final int N = edges1.length + 1;\n final int M = edges2.length + 1;\n\n if (k == 0) {\n int[] res = new int[N];\n Arrays.fill(res, 1);\n return res;\n }\n\n // build adjacency lists\n List<Integer>[] tree1 = buildAdj(edges1, N);\n List<Integer>[] tree2 = buildAdj(edges2, M);\n\n // dp1[v][d] stores number of descendants of v in tree1 at distance d from v (forward paths)\n // dp2[v][d] stores number of descendants of v in tree2 at distance d from v (forward paths)\n int[][] dp1 = new int[N][k + 1]; // distance ranging 0 to k\n int[][] dp2 = new int[M][k]; // distance ranging 0 to (k - 1)\n int[] parent1 = new int[N];\n int[] parent2 = new int[M];\n Queue<Integer> q1 = new LinkedList<>();\n Queue<Integer> q2 = new LinkedList<>();\n\n dfs(0, -1, tree1, parent1, dp1, q1, k); // root tree1 arbitrarily at node 0\n dfs(0, -1, tree2, parent2, dp2, q2, k - 1); // root tree2 arbitrarily at node 0\n // only interested in paths of length up to k - 1 in tree2 to account for 1 edge\n // connecting the 2 trees\n\n // backtrack1[v][d] stores number of paths in tree1 of length d that start from v and\n // passes through the parent of v (backward paths)\n int[][] backtrack1 = new int[N][k + 1]; // distance ranging 0 to k\n int[][] backtrack2 = new int[M][k]; // distance ranging 0 to (k - 1)\n int[] count1 = new int[N]; // store all paths of lengths <= k in tree1 that start from v in any direction\n int[] count2 = new int[M]; // store all paths of lengths <= k - 1 in tree2 that start from v in any direction\n\n // populate the backtrack and count arrays\n calcBacktrack(q1, parent1, dp1, backtrack1, count1, k);\n calcBacktrack(q2, parent2, dp2, backtrack2, count2, k - 1);\n\n int maxConnectivity = 1;\n for (int count : count2)\n maxConnectivity = Math.max(maxConnectivity, count);\n \n // overwrite answer onto count1\n for (int v = 0; v < N; v++)\n count1[v] += maxConnectivity;\n \n return count1;\n }\n\n private List<Integer>[] buildAdj(int[][] edges, int vertexCount) {\n List<Integer>[] tree = new List[vertexCount];\n int u, v;\n for (int[] edge : edges) {\n u = edge[0];\n v = edge[1];\n if (tree[u] == null) tree[u] = new LinkedList<Integer>();\n if (tree[v] == null) tree[v] = new LinkedList<Integer>();\n tree[u].add(v);\n tree[v].add(u);\n }\n return tree;\n }\n\n private void dfs(int v, int p, List<Integer>[] adj, int[] parent, int[][] dp, Queue<Integer> q, int k) {\n dp[v][0] = 1; // distance of 0\n q.offer(v); // pre-order queue\n parent[v] = p; // mark p as the parent of v\n\n if (adj[v] != null)\n for (int u : adj[v]) {\n if (u == p) continue;\n dfs(u, v, adj, parent, dp, q, k);\n }\n\n // at this point all children nodes have been processed\n if (p == -1) // if this is the root node\n return;\n \n // merge current node\'s contributions to its parent\n for (int d = 1; d <= k; d++)\n dp[p][d] += dp[v][d - 1]; \n }\n\n private void calcBacktrack(Queue<Integer> q, int[] parent, int[][] dp, int[][] backtrack, int[] count, int k) {\n int v, p;\n\n // populating the backtrack matrix requires processing nodes in topological order\n // so that data for a parent is fully computed by the time start processing child\n // can use either a preorder queue like here, or postorder stack\n while (!q.isEmpty()) {\n v = q.poll();\n p = parent[v];\n \n // distance 0 from v\n count[v] = dp[v][0];\n\n // distance 1 from v\n if (k >= 1) {\n if (p != -1) // cannot backtrack if v is the root node\n backtrack[v][1] = 1;\n // from v to descendants, and from v back through parent of v\n count[v] += dp[v][1] + backtrack[v][1];\n }\n\n // distances 1 < d <= k from v\n for (int d = 2; d <= k; d++) {\n if (p != -1) // cannot backtrack if v is the root node\n \n // paths of distance d from v, that goes from v back to the parent of v (p)\n // then either go through another child of p, or back to grandparent\n \n // paths from p will have length d - 1 to account for edge (p-v)\n \n // when using dp[p][d - 1] this number also includes forward paths that\n // go through v which we don\'t want, so we have to subtract these sub-paths\n backtrack[v][d] = dp[p][d - 1] - dp[v][d - 2] + backtrack[p][d - 1];\n\n // from v to descendants, and from v back through parent of v\n count[v] += dp[v][d] + backtrack[v][d];\n }\n }\n }\n}\n```
| 1 | 0 |
['Dynamic Programming', 'Depth-First Search', 'Java']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Java Solution Using DFS
|
java-solution-using-dfs-by-ramanshuraj00-dmk0
|
Approach\nStep 1: Represent the Trees\nUse adjacency lists to represent the graphs tree1 and tree2 for efficient traversal.\n\nStep 2: Compute Reachable Nodes f
|
ramanshuraj001
|
NORMAL
|
2024-12-01T19:11:07.577481+00:00
|
2024-12-01T19:11:07.577518+00:00
| 72 | false |
# Approach\nStep 1: Represent the Trees\nUse adjacency lists to represent the graphs tree1 and tree2 for efficient traversal.\n\nStep 2: Compute Reachable Nodes for tree1\nFor each node in tree1, perform a DFS (or BFS) up to a depth of k. During the DFS:\nTrack visited nodes to avoid cycles.\nCount the number of nodes reachable within k moves.\n\nStep 3: Compute the Maximum Reachable Nodes for tree2\nFor all nodes in tree2, perform a DFS (or BFS) up to a depth of k-1. During the DFS:\nTrack visited nodes to avoid cycles.\nFind the maximum number of reachable nodes for any starting node in tree2.\n\nStep 4: Combine Results\nFor each node in tree1, add the precomputed reachable nodes (from Step 2) to the maximum reachable nodes in tree2 (from Step 3).\n\nStep 5: Return the Results\nReturn an array where each entry corresponds to the sum of reachable nodes in tree1 and the maximum reachable nodes in tree2.\n\n# Complexity\n- Time complexity:\nO((n + m)*k);\n\n- Space complexity:\nO(n + m + k);\n\n# Code\n```java []\nimport java.util.*;\n\nclass Solution {\n public int[] maxTargetNodes(int[][] edges1, int[][] edges2, int k) {\n int n = edges1.length + 1;\n int m = edges2.length + 1;\n int[] answer = new int[n];\n ArrayList<Integer>[] tree1 = new ArrayList[n];\n ArrayList<Integer>[] tree2 = new ArrayList[m];\n\n for (int i = 0; i < n; i++) tree1[i] = new ArrayList<>();\n for (int i = 0; i < m; i++) tree2[i] = new ArrayList<>();\n\n for (int[] edge : edges1) {\n tree1[edge[0]].add(edge[1]);\n tree1[edge[1]].add(edge[0]);\n }\n\n for (int[] edge : edges2) {\n tree2[edge[0]].add(edge[1]);\n tree2[edge[1]].add(edge[0]);\n }\n\n int[] temp = new int[n];\n for (int i = 0; i < n; i++) {\n boolean[] visited = new boolean[n];\n visited[i] = true;\n temp[i] = dfs(tree1, i, k, visited);\n }\n\n int max = 0;\n for (int i = 0; i < m; i++) {\n boolean[] visited = new boolean[m];\n visited[i] = true;\n max = Math.max(max, dfs(tree2, i, k - 1, visited));\n }\n\n for (int i = 0; i < n; i++) {\n answer[i] = temp[i] + max;\n }\n\n return answer;\n }\n\n public int dfs(ArrayList<Integer>[] graph, int src, int k, boolean[] visited) {\n if (k < 0) return 0;\n int cnt = 1;\n for (int nbr : graph[src]) {\n if (!visited[nbr]) {\n visited[nbr] = true;\n cnt += dfs(graph, nbr, k - 1, visited);\n }\n }\n return cnt;\n }\n}\n\n```
| 1 | 0 |
['Depth-First Search', 'Java']
| 1 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Heavily Commented code Using DFS
|
heavily-commented-code-using-dfs-by-sapi-hp4c
|
\n# Code\ncpp []\nclass Solution {\nprivate:\n // Depth-First Search (DFS) function to explore the tree\n void dfs(int temp, int mom, int dist, int root,
|
LeadingTheAbyss
|
NORMAL
|
2024-12-01T04:41:54.839293+00:00
|
2024-12-01T04:41:54.839315+00:00
| 60 | false |
\n# Code\n```cpp []\nclass Solution {\nprivate:\n // Depth-First Search (DFS) function to explore the tree\n void dfs(int temp, int mom, int dist, int root, int maxi, vector<int>& res, vector<vector<int>>& nums) {\n // If the current distance exceeds or equals the maximum allowed distance, stop\n if (dist >= maxi) return;\n\n // Increment the result for the current root node (this tracks the number of nodes\n // reachable within the distance limit for a given root)\n res[root]++;\n\n // Explore all adjacent nodes (neighbors) of the current node\n for (int adj : nums[temp]) {\n // Make sure we don\'t revisit the parent node (avoid cycles)\n if (adj != mom) {\n // Perform DFS on the adjacent node with the current node as the parent\n dfs(adj, temp, dist + 1, root, maxi, res, nums);\n }\n }\n }\n\npublic:\n vector<int> maxTargetNodes(vector<vector<int>>& edg1, vector<vector<int>>& edg2, int k) {\n // Calculate the number of nodes in each graph\n int n1 = edg1.size() + 1; // Number of nodes in the first graph\n int n2 = edg2.size() + 1; // Number of nodes in the second graph\n\n // Initialize adjacency lists for both graphs\n vector<vector<int>> nums2(n1), nums1(n2);\n\n // Populate the adjacency list for the first graph (edges from edg1)\n for (auto& edge : edg1) {\n int u = edge[0], v = edge[1];\n nums2[u].push_back(v); // Add v as a neighbor of u\n nums2[v].push_back(u); // Add u as a neighbor of v (undirected graph)\n }\n\n // Populate the adjacency list for the second graph (edges from edg2)\n for (auto& edge : edg2) {\n int u = edge[0], v = edge[1];\n nums1[u].push_back(v); // Add v as a neighbor of u\n nums1[v].push_back(u); // Add u as a neighbor of v (undirected graph)\n }\n\n // Initialize result vectors for both graphs, set all values to 0\n vector<int> r1(n1, 0), r2(n2, 0);\n\n // Perform DFS for each node in the first graph, with a maximum distance of k+1\n for (int i = 0; i < n1; i++) {\n dfs(i, -1, 0, i, k + 1, r1, nums2); // DFS starting from node i in nums2\n }\n\n // Perform DFS for each node in the second graph, with a maximum distance of k\n for (int i = 0; i < n2; i++) {\n dfs(i, -1, 0, i, k, r2, nums1); // DFS starting from node i in nums1\n }\n\n // Find the maximum value in the r2 array (the maximum number of nodes reachable from any node in graph 2)\n int maxi = *max_element(r2.begin(), r2.end());\n\n // Initialize the result vector for the final answer (to store the result for each node in graph 1)\n vector<int> res(n1);\n\n // For each node in graph 1, calculate the total result as the sum of reachable nodes from that node in graph 1\n // and the maximum reachable nodes from any node in graph 2\n for (int i = 0; i < n1; i++) {\n res[i] = r1[i] + maxi;\n }\n\n // Return the result vector\n return res;\n }\n};\n\n```
| 1 | 0 |
['C++']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
C++ BFS Tree 1 and 2
|
c-bfs-tree-1-and-2-by-bramar2-80x0
|
Intuition\n- To connect to tree 2, there will always be one vertex that is best for everything. You can find it by using BFS on every Tree 2 vertex. $O(m^2)$\n-
|
bramar2
|
NORMAL
|
2024-12-01T04:19:33.146771+00:00
|
2024-12-01T04:22:00.719627+00:00
| 55 | false |
# Intuition\n- To connect to tree 2, there will always be one vertex that is best for everything. You can find it by using BFS on every Tree 2 vertex. $O(m^2)$\n- Then, you need to get the **reachable count of vertices** for each vertex in Tree 1. You can find it by also using BFS on every Tree 1 vertex. $O(n^2)$\n\n# Complexity\n- Time complexity: $O(n^2+m^2)$\n\n- Space complexity: $O(n+m)$\n\n# Code\n```cpp []\n#include <bits/stdc++.h>\nusing namespace std;\n\nclass Solution {\npublic:\n vector<int> maxTargetNodes(vector<vector<int>>& edges1, vector<vector<int>>& edges2, int k) {\n \tint n = edges1.size() + 1, m = edges2.size() + 1;\n\n \tif(k == 0) return vector<int>(n, 1);\t\n\n\n \tvector<vector<int>> adj1(n), adj2(m);\n\n\t\tfor(auto& e : edges1) {\n \t\tadj1[e[0]].push_back(e[1]);\n \t\tadj1[e[1]].push_back(e[0]);\n \t}\n\n \tfor(auto& e : edges2) {\n \t\tadj2[e[0]].push_back(e[1]);\n \t\tadj2[e[1]].push_back(e[0]);\n \t}\n\n \tvector dist1(n, vector<int>(n, 0)), dist2(m, vector<int>(m, 0));\n \tauto bfs = [&](auto& dist, auto& adj, int start) -> void {\n vector<bool> visited(max(n, m) + 1, false);\n \t\tdeque<int> q;\n \t\tvisited[start] = true;\n \t\tq.push_back(start);\n \t\tint currDist = 0;\n \t\twhile(!q.empty()) {\n \t\t\tint sz = q.size();\n \t\t\tdist[currDist] += sz;\n \t\t\twhile(sz--) {\n \t\t\t\tint v = q.front();\n \t\t\t\tq.pop_front();\n \t\t\t\tfor(int o : adj[v]) {\n if(!visited[o]) {\n visited[o] = true;\n q.push_back(o);\n }\n }\n \t\t\t}\n \t\t\t++currDist;\n \t\t}\n \t};\n\n \tfor(int i = 0; i < n; i++) {\n \t\tbfs(dist1[i], adj1, i);\n // prefix sum so dist[i][d] = num of verts in <= d distance\n \t\tfor(int j = 1; j < n; j++) dist1[i][j] += dist1[i][j - 1];\n \t}\n\n \tint best = 1;\n \tfor(int i = 0; i < m; i++) {\n \t\tbfs(dist2[i], adj2, i);\n // prefix sum so dist[i][d] = num of verts in <= d distance\n \t\tfor(int j = 1; j < m; j++) dist2[i][j] += dist2[i][j - 1];\n // check best vert for (k - 1) [-1 because you need to travel from tree1 to tree2 first]\n \t\tbest = max(best, dist2[i][min(k - 1, m - 1)]);\n \t}\n\n\n \tvector<int> res(n);\n \tfor(int i = 0; i < n; i++) {\n \t\tres[i] = dist1[i][min(k, n - 1)] + best;\n \t}\n \treturn res;\n }\n};\n```
| 1 | 0 |
['C++']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
only using BFS
|
only-using-bfs-by-sudip_basak-ehf1
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
sudip_basak
|
NORMAL
|
2025-04-05T06:02:08.274103+00:00
|
2025-04-05T06:02:08.274103+00:00
| 1 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int[] maxTargetNodes(int[][] edges1, int[][] edges2, int k) {
int n = edges1.length+1;
int m = edges2.length+1;
List<List<Integer>> tree1 =buildGraph(edges1,n);
List<List<Integer>> tree2 =buildGraph(edges2,m);
List<Set<Integer>> allcombi = new ArrayList<>();
for(int i=0;i<m;i++){
Set<Integer> ans = bfs(tree2,i,k-1);
allcombi.add(ans);
}
int ans[] = new int[n];
for(int i=0;i<n;i++){
Set<Integer> reach = bfs(tree1,i,k);
int maxi = Integer.MIN_VALUE;
for(int j=0;j<m;j++){
maxi = Math.max(reach.size() + allcombi.get(j).size(),maxi );
}
ans[i]=maxi;
}
return ans;
}
public Set<Integer> bfs(List<List<Integer>> list, int start, int k){
HashSet<Integer> set = new HashSet<>();
if (k < 0) return set;
Queue<int[]> q = new LinkedList<>();
q.offer(new int[]{start,0});
set.add(start);
while(!q.isEmpty()){
int size = q.size();
for(int i=0;i<size;i++){
int val[] = q.poll();
int node = val[0];
int level = val[1];
if(level == k) continue;
for(int neigbor : list.get(node)){
if(!set.contains(neigbor)){
q.offer(new int[]{neigbor,level+1});
set.add(neigbor);
}
}
}
}
return set;
}
private List<List<Integer>> buildGraph(int[][] edges, int size) {
List<List<Integer>> graph = new ArrayList<>();
for (int i = 0; i < size; i++) graph.add(new ArrayList<>());
for (int[] edge : edges) {
int u = edge[0], v = edge[1];
graph.get(u).add(v);
graph.get(v).add(u);
}
return graph;
}
}
```
| 0 | 0 |
['Java']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Python3 solution | BFS | Brute force
|
python3-solution-bfs-brute-force-by-flor-xh6e
|
IntuitionBrute force.ApproachIterate over all the nodes from tree2 and for each one get the number of nodes which are at a distance <= k and get the maximum sco
|
FlorinnC1
|
NORMAL
|
2025-03-07T20:13:26.781832+00:00
|
2025-03-07T20:13:26.781832+00:00
| 2 | false |
# Intuition
Brute force.
# Approach
Iterate over all the nodes from tree2 and for each one get the number of nodes which are at a distance <= k and get the maximum score. Iterate over tree1 and for each node get the number of nodes which are at a distance <= k+1 and add to the maximum score from tree2.
# Complexity
- Time complexity:
$$O(n*n+m*m)$$
- Space complexity:
$$O(n+m)$$
# Code
```python3 []
class Solution:
def maxTargetNodes(self, edges1: List[List[int]], edges2: List[List[int]], k: int) -> List[int]:
tree1, tree2 = defaultdict(lambda: []), defaultdict(lambda: [])
ans = []
for i in range(len(edges1)):
tree1[edges1[i][0]].append(edges1[i][1])
tree1[edges1[i][1]].append(edges1[i][0])
for i in range(len(edges2)):
tree2[edges2[i][0]].append(edges2[i][1])
tree2[edges2[i][1]].append(edges2[i][0])
max_score_tree2 = 0
for i, element in enumerate(tree2):
max_score_tree2 = max(max_score_tree2, self.bfs(element, tree2, k))
for i in range(len(tree1)):
current_score_tree1 = self.bfs(i, tree1, k+1) + max_score_tree2
ans.append(current_score_tree1)
return ans
def bfs(self, start_node, graph, k):
count_nodes = 0
queue = [start_node]
visited = set()
level = {start_node: 1}
visited.add(start_node)
while queue:
current_node = queue.pop(0)
if level[current_node] <= k:
count_nodes += 1
for neigh_node in graph[current_node]:
if neigh_node not in visited:
level[neigh_node] = level[current_node] + 1
visited.add(neigh_node)
queue.append(neigh_node)
else:
break
return count_nodes
```
| 0 | 0 |
['Breadth-First Search', 'Python3']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Py3 Solution Leveraging Standard BFS/DFS count nodes (k-1) away in tree 2 and (k) away in tree 1
|
py3-solution-leveraging-standard-bfsdfs-zansh
|
URL := https://leetcode.com/problems/maximize-the-number-of-target-nodes-after-connecting-trees-i/description/
3372. Maximize the Number of Target Nodes After C
|
2018hsridhar
|
NORMAL
|
2025-03-04T02:39:09.431893+00:00
|
2025-03-04T02:39:09.431893+00:00
| 1 | false |
URL := https://leetcode.com/problems/maximize-the-number-of-target-nodes-after-connecting-trees-i/description/
3372. Maximize the Number of Target Nodes After Connecting Trees I
# Intuition and Approach
For each node in tree 2, how many nodes are visitable in distance k-1?
For each node in tree 1, count nodes visitable in distance k
Add the node with maximal nodes visited - according to distance (k-1) - in tree 2 - to tree 1
can be any node : think greedily here ( disconnected components ) single edge always needed
# Code
```python3 []
class Solution:
def maxTargetNodes(self, edges1: List[List[int]], edges2: List[List[int]], k: int) -> List[int]:
adjListOne = self.makeAdjList(edges1)
adjListTwo = self.makeAdjList(edges2)
maxNodesVisitedGraphTwo = 0
visited = set()
for nodeTwo, adjNodes in adjListTwo.items():
numVisitedFromTwo = self.countNodesAtDistance(adjListTwo,visited, nodeTwo, k-1)
visited.clear()
maxNodesVisitedGraphTwo = max(maxNodesVisitedGraphTwo, numVisitedFromTwo)
# oh assuming we fill out for each node in one ( ok careful here )
nodesInOne = []
for nodeOne, adjNodes in adjListOne.items():
nodesInOne.append(nodeOne)
nodesInOne.sort()
answers = [0 for idx in range(len(nodesInOne))]
for index, nodeOne in enumerate(nodesInOne):
numVisitedFromOne = self.countNodesAtDistance(adjListOne, visited, nodeOne, k)
visited.clear()
maxVisitedAtNode = numVisitedFromOne + maxNodesVisitedGraphTwo
answers[index] = maxVisitedAtNode
return answers
# BFS/DFS - 1K nodes at max - shouldn't be to inefficient ( I hope ) ?
def countNodesAtDistance(self, adjList:dict, visited:set(), root:int, dist:int) -> int:
criteriaCount = 0
if(root not in visited and dist >= 0):
visited.add(root)
criteriaCount = 1
children = adjList[root]
for child in children:
childDist = dist - 1
childCount = self.countNodesAtDistance(adjList,visited,child,childDist)
criteriaCount += childCount
return criteriaCount
# we lack nodal counts here, sadly
# of just use items anyways
def makeAdjList(self, edges:List[List[int]]) -> dict:
adjList = dict()
for [src,dst] in edges:
if(src not in adjList):
adjList[src] = set()
if(dst not in adjList):
adjList[dst] = set()
adjList[src].add(dst)
adjList[dst].add(src)
return adjList
```
| 0 | 0 |
['Depth-First Search', 'Breadth-First Search', 'Python3']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Kotlin | BFS
|
kotlin-bfs-by-jschnall-o9k8
|
IntuitionPassed first try. :) See comment at top for my thought process.Complexity
Time complexity:
O(n2+m2+e+f) To create the maps it was necessary to iterate
|
jschnall
|
NORMAL
|
2025-02-28T21:08:45.716039+00:00
|
2025-02-28T21:12:23.684365+00:00
| 1 | false |
# Intuition
Passed first try. :) See comment at top for my thought process.
# Complexity
- Time complexity:
$$O(n^2 + m^2 + e + f)$$ To create the maps it was necessary to iterate through each of the adjacency lists, so this would be equal to the number of edges in each graph (let's call them e and f), then do bfs with a maximum depth of k, but potentially all nodes are within k hops away, so this would be n^2 for each of the maps.
- Space complexity:
$$O(n + m + max(e, f))$$ Created graphs from the adjacency lists, store a level in the graph during bfs
# Code
```kotlin []
class Solution {
fun maxTargetNodes(edges1: Array<IntArray>, edges2: Array<IntArray>, k: Int): IntArray {
// You always want to connect at the node in the first tree that you're trying to maximize for,
// so the newly added nodes are as close as possible
// for the second tree, calculate the number of nodes within k-1 distance from each node, and connect to the max
// Can do this with BFS of depth k-1 from each node. There may be a more efficient method
val graph1 = mutableMapOf<Int, MutableSet<Int>>()
val graph2 = mutableMapOf<Int, MutableSet<Int>>()
for (edge in edges1) {
graph1.getOrPut(edge[0]) { mutableSetOf<Int>() }.add(edge[1])
graph1.getOrPut(edge[1]) { mutableSetOf<Int>() }.add(edge[0])
}
for (edge in edges2) {
graph2.getOrPut(edge[0]) { mutableSetOf<Int>() }.add(edge[1])
graph2.getOrPut(edge[1]) { mutableSetOf<Int>() }.add(edge[0])
}
var max = 0
for (node in graph2.keys) {
max = maxOf(max, bfs(graph2, node, k - 1))
}
return IntArray(graph1.size) { i -> max + bfs(graph1, i, k) }
}
fun bfs(graph: Map<Int, Set<Int>>, start: Int, depth: Int): Int {
if (depth < 0) return 0
var queue = ArrayDeque<Int>()
val visited = mutableSetOf<Int>()
var count = 0
var distance = 0
queue.add(start)
visited.add(start)
while (queue.isNotEmpty() && distance <= depth) {
val level = ArrayDeque<Int>()
while (queue.isNotEmpty()) {
val node = queue.removeFirst()
count++
for (neighbor in graph.getOrDefault(node, mutableSetOf<Int>())) {
if (neighbor !in visited) {
level.add(neighbor)
visited.add(neighbor)
}
}
}
queue = level
distance++
}
return count
}
}
```
| 0 | 0 |
['Kotlin']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
BFS, Dictionary
|
bfs-dictionary-by-gdjk97-o8ws
|
Complexity
Time complexity:O(nlogn)
Space complexity:O(n)
Code
|
gdjk97
|
NORMAL
|
2025-02-20T03:25:02.069217+00:00
|
2025-02-20T03:25:02.069217+00:00
| 4 | false |
# Complexity
- Time complexity:
O(nlogn)
- Space complexity:
O(n)
# Code
```python3 []
from collections import deque
from operator import itemgetter
class Solution:
def maxTargetNodes(self, edges1: List[List[int]], edges2: List[List[int]], k: int) -> List[int]:
# build an adjacency list
def buildGraph(edges):
graph = defaultdict(list)
for u, v in edges:
graph[u].append(v)
graph[v].append(u)
return graph
def getReachCount(edges, reach):
edges = buildGraph(edges)
reachCount = {}
for i in edges.keys():
# BFS approach essentially
q = deque()
if reach < 1:
reachCount[i] = 1 if reach >= 0 else 0
continue
q.append((i, 0, None))
count = 0
while q:
node, dist, prev = q.popleft()
if dist + 1 > reach:
continue
for edge in edges[node]:
# so that we don't loop around
if edge == prev:
continue
q.append((edge, dist + 1, node))
count += 1
# the +1 is to account for the
reachCount[i] = count + 1
return reachCount
rc1 = getReachCount(edges1, k)
# distance = 1 to attach it to the other node, kence k-1
rc2 = getReachCount(edges2, k-1)
# get the best match
max_reach2 = max(rc2.values())
# sorte based on the graph nodes as a dictionary
# does not maintain order
rc1 = sorted(rc1.items(), key=itemgetter(0))
ans = [i[1] + max_reach2 for i in rc1]
return ans
```
| 0 | 0 |
['Python3']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Simple Java Solution
|
simple-java-solution-by-sakshikishore-4csf
|
Code
|
sakshikishore
|
NORMAL
|
2025-02-18T04:09:33.435152+00:00
|
2025-02-18T04:09:33.435152+00:00
| 4 | false |
# Code
```java []
public class Node
{
int ele,count;
public Node(int e, int cnt)
{
ele=e;
count=cnt;
}
}
class Solution {
public int[] maxTargetNodes(int[][] edges1, int[][] edges2, int k) {
HashMap<Integer,ArrayList<Integer>> h1=new HashMap<Integer,ArrayList<Integer>>();
for(int i=0;i<edges1.length;i++)
{
if(!h1.containsKey(edges1[i][0]))
{
ArrayList<Integer> l=new ArrayList<Integer>();
l.add(edges1[i][1]);
h1.put(edges1[i][0],l);
}
else
{
ArrayList<Integer> l=h1.get(edges1[i][0]);
l.add(edges1[i][1]);
h1.put(edges1[i][0],l);
}
if(!h1.containsKey(edges1[i][1]))
{
ArrayList<Integer> l=new ArrayList<Integer>();
l.add(edges1[i][0]);
h1.put(edges1[i][1],l);
}
else
{
ArrayList<Integer> l=h1.get(edges1[i][1]);
l.add(edges1[i][0]);
h1.put(edges1[i][1],l);
}
}
int arr[]=new int[edges1.length+1];
for(int i=0;i<=edges1.length;i++)
{
Queue<Node> q=new LinkedList<Node>();
q.add(new Node(i,0));
HashSet<Integer> hset=new HashSet<Integer>();
hset.add(i);
while(q.size()>0)
{
Node node=q.poll();
if(node.count<=k)
{
arr[i]++;
}
ArrayList<Integer> l=h1.get(node.ele);
for(int j=0;j<l.size();j++)
{
if(!hset.contains(l.get(j)))
{
q.add(new Node(l.get(j),node.count+1));
hset.add(l.get(j));
}
}
}
}
HashMap<Integer,ArrayList<Integer>> h2=new HashMap<Integer,ArrayList<Integer>>();
for(int i=0;i<edges2.length;i++)
{
if(!h2.containsKey(edges2[i][0]))
{
ArrayList<Integer> l=new ArrayList<Integer>();
l.add(edges2[i][1]);
h2.put(edges2[i][0],l);
}
else
{
ArrayList<Integer> l=h2.get(edges2[i][0]);
l.add(edges2[i][1]);
h2.put(edges2[i][0],l);
}
if(!h2.containsKey(edges2[i][1]))
{
ArrayList<Integer> l=new ArrayList<Integer>();
l.add(edges2[i][0]);
h2.put(edges2[i][1],l);
}
else
{
ArrayList<Integer> l=h2.get(edges2[i][1]);
l.add(edges2[i][0]);
h2.put(edges2[i][1],l);
}
}
int max=0;
for(int i=0;i<=edges2.length;i++)
{
Queue<Node> q=new LinkedList<Node>();
q.add(new Node(i,0));
HashSet<Integer> hset=new HashSet<Integer>();
hset.add(i);
int m=0;
while(q.size()>0)
{
Node node=q.poll();
if(node.count<k)
{
m++;
}
ArrayList<Integer> l=h2.get(node.ele);
for(int j=0;j<l.size();j++)
{
if(!hset.contains(l.get(j)))
{
q.add(new Node(l.get(j),node.count+1));
hset.add(l.get(j));
}
}
}
if(m>max)
{
max=m;
}
}
for(int i=0;i<arr.length;i++)
{
arr[i]+=max;
}
return arr;
}
}
```
| 0 | 0 |
['Java']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Java Solution BFS
|
java-solution-bfs-by-ndsjqwbbb-2uaf
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
ndsjqwbbb
|
NORMAL
|
2025-01-28T20:46:10.919276+00:00
|
2025-01-28T20:46:10.919276+00:00
| 4 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int[] maxTargetNodes(int[][] edges1, int[][] edges2, int k) {
Map<Integer, List<Integer>> graph1 = new HashMap<>();
Map<Integer, List<Integer>> graph2 = new HashMap<>();
buildgraph(edges1, graph1);
buildgraph(edges2, graph2);
int maxedge1 = 0;
for(int[] edge : edges1){
maxedge1 = Math.max(maxedge1, edge[0]);
maxedge1 = Math.max(maxedge1, edge[1]);
}
maxedge1++;
int maxedge2 = 0;
for(int[] edge : edges2){
maxedge2 = Math.max(maxedge2, edge[0]);
maxedge2 = Math.max(maxedge2, edge[1]);
}
maxedge2++;
int[][] tree1reachable = computereachable(graph1, maxedge1, k);
int[][] tree2reachable = computereachable(graph2, maxedge2, k - 1);
int[] tree2maxreachable = computetree2maxreachable(tree2reachable, maxedge2, k);
int[] result = new int[maxedge1];
for(int i = 0; i < maxedge1; i++){
int counttree1 = (k < tree1reachable[i].length) ? tree1reachable[i][k] : tree1reachable[i][tree1reachable[i].length - 1];
int counttree2 = k >= 1 ? tree2maxreachable[k - 1] : 0;
result[i] = counttree1 + counttree2;
}
return result;
}
private void buildgraph(int[][] edges, Map<Integer, List<Integer>> graph){
for(int[] edge : edges){
int from = edge[0];
int to = edge[1];
graph.putIfAbsent(from, new ArrayList<>());
graph.get(from).add(to);
graph.putIfAbsent(to, new ArrayList<>());
graph.get(to).add(from);
}
}
private int[][] computereachable(Map<Integer, List<Integer>> graph, int numnodes, int maxdepth){
int[][] reachable = new int[numnodes][maxdepth + 1];
for(int i = 0; i < numnodes; i++){
reachable[i] = bfscount(graph, i, maxdepth);
}
return reachable;
}
private int[] bfscount(Map<Integer, List<Integer>> graph, int start, int maxdepth){
if(maxdepth < 0){
return new int[0];
}
int[] count = new int[maxdepth + 1];
Queue<Integer> queue = new ArrayDeque<>();
queue.offer(start);
Set<Integer> visited = new HashSet<>();
visited.add(start);
count[0] = 1;
int depth = 1;
while(!queue.isEmpty() && depth <= maxdepth){
int size = queue.size();
for(int i = 0; i < size; i++){
int current = queue.poll();
List<Integer> list = graph.get(current);
if(list == null){
continue;
}
for(int next : list){
if(visited.contains(next)){
continue;
}
visited.add(next);
count[depth] += 1;
queue.offer(next);
}
}
depth++;
}
for(int i = 1; i <= maxdepth; i++){
count[i] += count[i - 1];
}
return count;
}
private int[] computetree2maxreachable(int[][] tree2reachable, int m, int k){
int[] maxreachable = new int[k];
for(int i = 0; i < m; i++){
for(int j = 0; j < k; j++){
if(j < tree2reachable[i].length){
maxreachable[j] = Math.max(maxreachable[j], tree2reachable[i][j]);
}
}
}
return maxreachable;
}
}
```
| 0 | 0 |
['Java']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
3372. Maximize the Number of Target Nodes After Connecting Trees I
|
3372-maximize-the-number-of-target-nodes-dp60
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
G8xd0QPqTy
|
NORMAL
|
2025-01-24T14:04:16.834213+00:00
|
2025-01-24T14:04:16.834213+00:00
| 1 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```dart []
class Solution {
List<int> maxTargetNodes(List<List<int>> edges1, List<List<int>> edges2, int k) {
int n = edges1.length + 1;
int m = edges2.length + 1;
int maxCount = 0;
if (k == 0) return List.filled(n, 1);
List<List<int>> graph = List.generate(m, (_) => []);
for (var edge in edges2) {
graph[edge[0]].add(edge[1]);
graph[edge[1]].add(edge[0]);
}
int dfs(int node, int level, int parent, [int count = 1]) {
if (level < k) {
for (var child in graph[node]) {
if (child == parent) continue;
count += dfs(child, level + 1, node);
}
}
return count;
}
for (int node = 0; node < m; node++) {
maxCount = max(maxCount, dfs(node, 1, -1));
}
graph = List.generate(n, (_) => []);
for (var edge in edges1) {
graph[edge[0]].add(edge[1]);
graph[edge[1]].add(edge[0]);
}
List<int> result = [];
for (int node = 0; node < n; node++) {
result.add(dfs(node, 0, -1) + maxCount);
}
return result;
}
}
```
| 0 | 0 |
['Dart']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Maximum Target Nodes in Two Trees with BFS and Precomputation.
|
maximum-target-nodes-in-two-trees-with-b-qsx9
|
IntuitionApproachComplexity
Time complexity:
O(n^2 + m^2).
Space complexity:
O(n + m).
Code
|
RishiINSANE
|
NORMAL
|
2025-01-20T13:17:28.745638+00:00
|
2025-01-20T13:17:28.745638+00:00
| 4 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
O(n^2 + m^2).
- Space complexity:
O(n + m).
# Code
```cpp []
class Solution {
public:
vector<int> maxTargetNodes(vector<vector<int>>& edges1,
vector<vector<int>>& edges2, int k) {
int n = edges1.size() + 1, m = edges2.size() + 1;
vector<int> ans(n, 0);
vector<vector<int>> adj1(n), adj2(m);
for (auto it : edges1) {
int u = it[0];
int v = it[1];
adj1[u].push_back(v);
adj1[v].push_back(u);
}
for (auto it : edges2) {
int u = it[0];
int v = it[1];
adj2[u].push_back(v);
adj2[v].push_back(u);
}
vector<int> V1 = precomputeValues(n, k, adj1);
vector<int> V2 = precomputeValues(m, k - 1, adj2);
int mV2 = *max_element(V2.begin(),V2.end());
for (int i = 0; i < n; i++) {
ans[i] = V1[i] + mV2;
}
return ans;
}
vector<int> precomputeValues(int n, int k, vector<vector<int>>& adj) {
vector<int> value(n);
for (int i = 0; i < n; i++) {
vector<int> vis(n);
value[i] += bfs(i, k, vis, adj);
}
return value;
}
int bfs(int node, int k, vector<int>& vis, vector<vector<int>>& adj) {
if (k < 0)
return 0;
queue<pair<int, int>> q;
int cnt = 0;
//{lvl,node}
q.push({0, node});
vis[node] = 1;
while (!q.empty()) {
auto it = q.front();
q.pop();
int lvl = it.first;
int cnode = it.second;
if (lvl > k)
continue;
cnt++;
for (auto it : adj[cnode]) {
if (!vis[it]) {
q.push({lvl + 1, it});
vis[it] = 1;
}
}
}
return cnt;
}
};
```
| 0 | 0 |
['C++']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
c++ solution using dfs
|
c-solution-using-dfs-by-dilipsuthar60-zyay
|
\nclass Solution {\npublic:\n // step 1. create graph give edges \n vector<vector<int>>createGraph(vector<vector<int>>&edges){\n int n=edges.size()
|
dilipsuthar17
|
NORMAL
|
2024-12-26T16:47:41.082387+00:00
|
2024-12-26T16:47:41.082427+00:00
| 5 | false |
```\nclass Solution {\npublic:\n // step 1. create graph give edges \n vector<vector<int>>createGraph(vector<vector<int>>&edges){\n int n=edges.size();\n vector<vector<int>>graph(n+1);\n for(auto &edge:edges){\n graph[edge[0]].push_back(edge[1]);\n graph[edge[1]].push_back(edge[0]);\n }\n return graph;\n }\n int countNodes(vector<vector<int>>&edges,int node,int k,int p=-1){\n if(k<0){\n return 0;\n }\n int count=1;\n for(auto &child:edges[node]){\n if(p!=child){\n count+=countNodes(edges, child, k-1, node);\n }\n }\n return count;\n }\n vector<int> maxTargetNodes(vector<vector<int>>& edges1, vector<vector<int>>& edges2, int k) {\n int n=edges1.size();\n int m=edges2.size();\n auto graph1=createGraph(edges1);\n auto graph2=createGraph(edges2);\n int maxNodeCount=0;\n for(int i=0;i<=m;i++){\n maxNodeCount=max(maxNodeCount,countNodes(graph2,i,k-1));\n }\n vector<int>ans;\n for(int i=0;i<=n;i++){\n int value=maxNodeCount+countNodes(graph1,i,k);\n ans.push_back(value);\n }\n return ans;\n }\n};\n```
| 0 | 0 |
['Depth-First Search', 'C', 'C++']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
DFS || Easy To Understand || C++
|
dfs-easy-to-understand-c-by-lotus18-ohw8
|
Code
|
lotus18
|
NORMAL
|
2024-12-25T07:08:54.036367+00:00
|
2024-12-25T07:08:54.036367+00:00
| 6 | false |
# Code
```cpp []
class Solution
{
public:
int countNodes(int node, int distance, int d, vector<int> &vis, vector<int> adj[])
{
if(d>distance) return 0;
vis[node]=1;
int cnt=1;
for(auto it: adj[node])
{
if(!vis[it]) cnt+=countNodes(it,distance, d+1,vis,adj);
}
return cnt;
}
vector<int> maxTargetNodes(vector<vector<int>>& edges1, vector<vector<int>>& edges2, int k)
{
int n=edges1.size(), m=edges2.size();
vector<int> adj1[n+1], adj2[m+1];
for(auto it: edges1)
{
adj1[it[0]].push_back(it[1]);
adj1[it[1]].push_back(it[0]);
}
for(auto it: edges2)
{
adj2[it[0]].push_back(it[1]);
adj2[it[1]].push_back(it[0]);
}
vector<int> ans(n+1);
for(int x=0; x<=n; x++)
{
vector<int> vis(n+1,0);
ans[x]=countNodes(x,k,0,vis,adj1);
}
int mx=0;
for(int x=0; x<=m; x++)
{
vector<int> vis(m+1,0);
mx=max(mx,countNodes(x,k-1,0,vis,adj2));
}
for(int x=0; x<=n; x++) ans[x]+=mx;
return ans;
}
};
```
| 0 | 0 |
['Depth-First Search', 'C++']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Good Question Bad Description
|
good-question-bad-description-by-hilaksh-6cpi
|
IntuitionThe question asks you to connect two trees by adding a single edge between a node from the first tree and a node from the second tree. After the connec
|
HiLakshya
|
NORMAL
|
2024-12-24T18:51:16.258165+00:00
|
2024-12-24T18:51:16.258165+00:00
| 2 | false |
# Intuition
The question asks you to connect two trees by adding a single edge between a node from the first tree and a node from the second tree. After the connection, you need to determine the maximum number of nodes that can be reached from a specific node in the first tree within a distance of k edges. The goal is to maximize this count for each node in the first tree.
# About the k-1 logic in the code
When you connect a node u in the first tree to a node v in the second tree, the edge between u and v consumes one distance unit. Hence for the second tree only nodes within k−1 distance from 𝑣 v can be considered.
# Code
```cpp []
class Solution {
int numberofnodes(unordered_map<int, vector<int>>& graph, int node, int k) {
if(k == 0) return 1;
queue<pair<int, int>> q;
q.push({node, 0});
vector<bool> visited(graph.size(), false);
int count = 1;
while (!q.empty()) {
auto node = q.front();
q.pop();
int curr = node.first;
int dist = node.second;
visited[curr] = true;
for (auto& neighbor : graph[curr]) {
if (!visited[neighbor]) {
if(dist + 1 <= k) {
count++;
q.push({neighbor, dist + 1});
}
}
}
}
return count;
}
public:
vector<int> maxTargetNodes(vector<vector<int>>& edges1, vector<vector<int>>& edges2, int k) {
unordered_map<int, vector<int>> graph1, graph2;
for (auto& edge : edges1) {
graph1[edge[0]].push_back(edge[1]);
graph1[edge[1]].push_back(edge[0]);
}
for (auto& edge : edges2) {
graph2[edge[0]].push_back(edge[1]);
graph2[edge[1]].push_back(edge[0]);
}
vector<int> ans1;
for (int i = 0; i < graph1.size(); i++) {
ans1.push_back(numberofnodes(graph1, i, k));
// cout << ans1[i] << " ";
}
if(k == 0) {
return ans1; // GG testcase 724
}
int ans2 = 1;
for (int i = 0; i < graph2.size(); i++) {
ans2 = max(ans2, numberofnodes(graph2, i, k-1));
}
// cout << ans2 << endl;
for(int i = 0; i < ans1.size(); i++) {
ans1[i] =ans1[i]+ ans2;
}
return ans1;
}
};
```
| 0 | 0 |
['C++']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Graph + DFS
|
graph-dfs-by-linda2024-fk6f
|
Intuition
Build Graphs based on edges array;
Calculate the max nodes number with deps <= k-1;
Loop nodes in first graph, and get nodes with deps <= k and plus t
|
linda2024
|
NORMAL
|
2024-12-20T19:28:14.965386+00:00
|
2024-12-20T19:28:14.965386+00:00
| 7 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
1. Build Graphs based on edges array;
2. Calculate the max nodes number with deps <= k-1;
3. Loop nodes in first graph, and get nodes with deps <= k and plus the max nodes calculated in step 2;
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```csharp []
public class Solution {
private Dictionary<int, HashSet<int>> BuildGraph(int[][] edges)
{
Dictionary<int, HashSet<int>> g = new();
foreach(int[] e in edges)
{
int u = e[0], v = e[1];
if(!g.ContainsKey(u))
g.Add(u, new HashSet<int>());
if(!g.ContainsKey(v))
g.Add(v, new HashSet<int>());
g[u].Add(v);
g[v].Add(u);
}
return g;
}
private int DFS(Dictionary<int, HashSet<int>> graph, int cur, int par, int steps, int count = 1)
{
// Console.WriteLine($"In DFS, cur is {cur}, parent is {par}, steps are {steps}");
if(steps < 0 || cur == par)
return 0;
foreach(int next in graph[cur])
{
count += ((next == par)? 0 : DFS(graph, next, cur, steps-1));
// Console.WriteLine($"in loop: next is {next}, count is {count}");
}
return count;
}
public int[] MaxTargetNodes(int[][] edges1, int[][] edges2, int k) {
var g1 = BuildGraph(edges1);
var g2 = BuildGraph(edges2);
int n1Cnt = edges1.Length + 1, n2Cnt = edges2.Length+1;
// Get max Count for edge path < k in graph2:
int maxCnt2 = 0;
for(int i = 0; i < n2Cnt; i++)
{
maxCnt2 = Math.Max(maxCnt2, DFS(g2, i, -1, k-1));
}
int[] res = new int[n1Cnt];
// Console.WriteLine($"max Count in graph 2 is {maxCnt2}");
for(int i = 0; i < n1Cnt; i++)
{
res[i] = maxCnt2 + DFS(g1, i, -1, k);
}
return res;
}
}
```
| 0 | 0 |
['C#']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Easy Cpp
|
easy-cpp-by-gps_357-9epz
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
gps_357
|
NORMAL
|
2024-12-14T09:27:53.205166+00:00
|
2024-12-14T09:27:53.205166+00:00
| 3 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\nmap<int,vector<int>> t1,t2;\n\nint dfs(int node,int par,int d ,int k , map<int,vector<int>>& t){\nif(d == k) return 0;\nint a = 0;\n for(auto i : t[node]){\n if(i!=par){\n a += dfs(i,node,d+1,k,t)+1;\n }\n }\n\n return a ;\n}\n\n\nvector<int> maxTargetNodes(vector<vector<int>>& e1, vector<vector<int>>& e2, int k) {\n vector<int> ans;\n for(auto i : e1){\n t1[i[0]].push_back(i[1]);\n t1[i[1]].push_back(i[0]);\n }\n\n for(auto i : e2){\n t2[i[0]].push_back(i[1]);\n t2[i[1]].push_back(i[0]);\n }\n ans.resize(e1.size()+1);\n // memset(ans,0,sizeof(ans));\n int a = 0;\n\n if(k!= 0){\n for(int i = 0;i<e2.size()+1;i++){\n int x = dfs(i,-1,0,k-1,t2)+1 ; \n\n cout<<i<<" a val"<<x<<endl; \n a = max(a,x) ;\n }\n cout<<a<<endl;\n }\n \n\n\n\n for(int i =0 ;i<ans.size();i++){\n \n int x = dfs(i,-1,0,k,t1)+1;\n // cout<<x<<endl;\n ans[i] = x+a ;\n\n }\n \n\n return ans;\n \n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Maximizing Reachable Nodes Across Two Graphs Using DFS
|
maximizing-reachable-nodes-across-two-gr-rqr9
|
IntuitionThe problem involves finding the maximum number of target nodes reachable in two graphs given a certain depth. We use Depth First Search (DFS) to explo
|
YuviG_1188
|
NORMAL
|
2024-12-13T17:25:56.174607+00:00
|
2024-12-13T17:25:56.174607+00:00
| 4 | false |
# Intuition\nThe problem involves finding the maximum number of target nodes reachable in two graphs given a certain depth. We use Depth First Search (DFS) to explore the graphs and determine the count of reachable nodes. Combining the results from both graphs allows us to compute the desired maximum target nodes.\n\n# Approach\n1. Represent the two graphs as adjacency lists.\n2. Use a DFS function to explore nodes up to a depth `k` and count the reachable nodes.\n3. For each node in the second graph, compute the maximum number of nodes reachable.\n4. For each node in the first graph, compute the total reachable nodes by adding the DFS result for that node and the maximum result from the second graph.\n5. Return the results as a vector.\n\n# Complexity\n- **Time complexity:**\n - Building adjacency lists: $$O(E_1 + E_2)$$, where $$E_1$$ and $$E_2$$ are the number of edges in the two graphs.\n - Performing DFS for each node: $$O((V_1 + V_2) \\times k)$$, where $$V_1$$ and $$V_2$$ are the number of nodes in the two graphs, and $$k$$ is the depth limit.\n - Overall: $$O(E_1 + E_2 + (V_1 + V_2) \\times k)$$.\n- **Space complexity:**\n - Storing adjacency lists: $$O(E_1 + E_2)$$.\n - Recursion stack for DFS: $$O(k)$$.\n - Visited arrays: $$O(V_1 + V_2)$$.\n - Overall: $$O(E_1 + E_2 + V_1 + V_2)$$.\n\n# Code\n```cpp\nclass Solution {\npublic:\n int dfs(vector<vector<int>>& adj, int source, int level, vector<int>& visited, int k) {\n if (k == 0) return 1; // Base case: depth 0 reached\n if (k < 0) return 0; // Invalid depth\n if (k == level) return 1; // Reached the required depth\n if (visited[source]) return 0; // Already visited\n\n visited[source] = true; // Mark as visited\n int sum = 0;\n for (auto next : adj[source]) {\n if (visited[next]) continue; // Skip already visited nodes\n sum += dfs(adj, next, level + 1, visited, k); // Recursive DFS\n }\n visited[source] = false; // Backtrack\n return sum + 1; // Include the current node\n }\n\n vector<int> maxTargetNodes(vector<vector<int>>& edges1, vector<vector<int>>& edges2, int k) {\n int n = edges1.size() + 1; // Number of nodes in the first graph\n int m = edges2.size() + 1; // Number of nodes in the second graph\n\n // Build adjacency lists\n vector<vector<int>> adj1(n);\n vector<vector<int>> adj2(m);\n for (auto edge : edges1) {\n int u = edge[0], v = edge[1];\n adj1[u].push_back(v);\n adj1[v].push_back(u);\n }\n for (auto edge : edges2) {\n int u = edge[0], v = edge[1];\n adj2[u].push_back(v);\n adj2[v].push_back(u);\n }\n\n // Find the maximum reachable nodes in the second graph\n int max2 = INT_MIN;\n for (int i = 0; i < m; i++) {\n vector<int> visited(m, false);\n max2 = max(max2, dfs(adj2, i, 0, visited, k - 1));\n }\n\n // Compute the results for the first graph\n vector<int> answer(n);\n for (int i = 0; i < n; i++) {\n vector<int> visited(n, false);\n int res = dfs(adj1, i, 0, visited, k);\n answer[i] = res + max2;\n }\n\n return answer;\n }\n};\n
| 0 | 0 |
['C++']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Java | DFS | With Detailed Explanation | Well Commented
|
java-dfs-with-detailed-explanation-well-6taeb
|
Problem Description\n There exist two undirected trees with n and m nodes, with distinct labels in ranges [0, n - 1] and [0, m - 1], respectively.\n\n## You are
|
Paramveer01
|
NORMAL
|
2024-12-08T12:32:10.259384+00:00
|
2024-12-08T12:32:10.259420+00:00
| 6 | false |
# Problem Description\n There exist two undirected trees with `n` and `m` nodes, with distinct labels in ranges `[0, n - 1]` and `[0, m - 1]`, respectively.\n\n## You are also provided:\n\n1. edges1 (a 2D integer array of size n - 1) which represents edges in the first tree, where `edges1[i] = [a_i, b_i]` indicates an edge between nodes a_i and b_i.\n2. edges2 (a 2D integer array of size m - 1) which represents edges in the second tree, where `edges2[i] = [u_i, v_i]` indicates an edge between nodes u_i and v_i.\n3. An integer k.\n\n## Target Node \nA node `u` is target to node `v` if the number of edges on the path from `u` to `v` is less than or equal to `k`. Note that a node is always target to itself.\n\n## Task\nReturn an array of size n, where the i-th value is the maximum possible number of nodes target to node i of the first tree if you connect one node from the first tree to another node in the second tree.\n\n# Intuition\nWe have to calculate maximum number of target nodes for all nodes of 1st tree, if we have to connect one node from the 1st tree to 2nd tree.\n\nLet we take the given example :- k = 2\n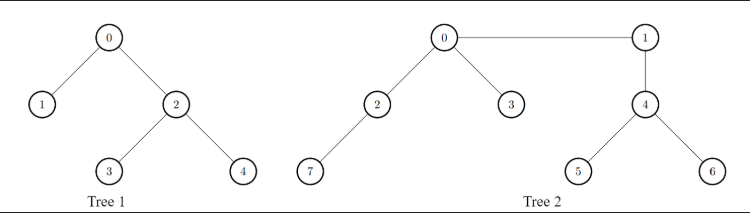\n\n1. Calculate the maximum number of target node for ech node of tree1 without connecting . That will be : \n answer = {5,3,5,4,4}.\n\n - From node 0 we can visit (0,1,2,3,4)\n - From node 1 we can visit (0,1,2) and so on\n2. Now we have to attach one node from tree1 to tree2. For this we can follow this .\n \n `ans[i] = tar nodes in T1 from i node + node with max tar nodes in T2 for k=k-1`\n\n3. For k = k-1 in Tree2 \n\n - From node 0 = 4 i.e {0,1,2,3}\n - From node 1 = 3 i.e {0,1,4}\n - From node 2 = 4 i.e {0,2,7}\n - From node 3 = 2 i.e {0,3}\n - From node 4 = 4 i.e {1,4,5,6}\n - So on.\n4. So in Tree 2 max is 4 . Now when we add it in answer we got resultant array.\n` answer = {9,7,9,8,8} `\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nLooking From the constrains we can perform dfs for every node i.e.\n> 2 <= n, m <= 1000\n\n1. Build Graph from the given edges array\n2. Use DFS traversal to find max value of taget nodes that can be visited for each node in tree2 with k = k-1.\n3. Use again DFS to find maximum number of target node we can visit from a node in tree1 for each node and store in a result array.\n4. Adding max value in answer of each node of tree1 and return it.\n\n\n# Complexity\n- Time complexity: $$O(nk+mk)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n Graphs : $$O(n+m)$$\n\n# Code\n```java []\nclass Solution {\n public int[] maxTargetNodes(int[][] edges1, int[][] edges2, int k) {\n int n = edges1.length;\n int m = edges2.length;\n\n // Pre calculation Array for both graphs\n int[] arr1 = new int[n+1];\n int[] arr2 = new int[m+1];\n\n // Making graph from edges\n HashMap<Integer,ArrayList<Integer>> g1 = new HashMap<>();\n HashMap<Integer,ArrayList<Integer>> g2 = new HashMap<>();\n \n if(k==0){\n Arrays.fill(arr1,1);\n return arr1;\n }\n\n for(int[] i: edges1){\n if(!g1.containsKey(i[0])) g1.put(i[0],new ArrayList<>());\n if(!g1.containsKey(i[1])) g1.put(i[1],new ArrayList<>());\n g1.get(i[0]).add(i[1]);\n g1.get(i[1]).add(i[0]);\n }\n\n for(int[] i: edges2){\n if(!g2.containsKey(i[0])) g2.put(i[0],new ArrayList<>());\n if(!g2.containsKey(i[1])) g2.put(i[1],new ArrayList<>());\n g2.get(i[0]).add(i[1]);\n g2.get(i[1]).add(i[0]);\n }\n int max = 0;\n\n for(int i=0;i<=m;i++){\n max = Math.max(max,dfs(g2,k-1,i,new boolean[m+1]));\n }\n max++;\n for(int i=0;i<=n;i++){\n arr1[i] = dfs(g1,k,i,new boolean[n+1])+1+max;\n }\n\n return arr1;\n\n\n }\n\n public int dfs(HashMap<Integer,ArrayList<Integer>> g1, int k, int u,boolean[] vis){\n if(k==0) return 0;\n int min = 0;\n vis[u] = true;\n for(int i:g1.get(u)){\n if(!vis[i]){\n min += dfs(g1,k-1,i,vis)+1;\n }\n }\n return min;\n }\n \n}\n```
| 0 | 0 |
['Tree', 'Depth-First Search', 'Breadth-First Search', 'Graph', 'Recursion', 'Java']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Graph Traversal for each node
|
graph-traversal-for-each-node-by-techtin-39iu
|
\n\n# Complexity\n- Time complexity:O(n^2+m^2)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity:O(n+m)\n Add your space complexity here, e.g. O
|
TechTinkerer
|
NORMAL
|
2024-12-07T07:04:55.409854+00:00
|
2024-12-07T07:04:55.409879+00:00
| 21 | false |
\n\n# Complexity\n- Time complexity:O(n^2+m^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n+m)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n void dfs(int node,int par,unordered_map<int,vector<int>> &adj,int k,int level,int &ans){\n\n if(level<=k)\n ans++;\n\n for(auto i:adj[node]){\n if(i!=par)\n dfs(i,node,adj,k,level+1,ans);\n }\n }\n vector<int> maxTargetNodes(vector<vector<int>>& edges1, vector<vector<int>>& edges2, int k) {\n unordered_map<int,vector<int>> adj1,adj2;\n\n for(auto e:edges1){\n adj1[e[0]].push_back(e[1]);\n adj1[e[1]].push_back(e[0]);\n }\n\n for(auto e:edges2){\n adj2[e[0]].push_back(e[1]);\n adj2[e[1]].push_back(e[0]);\n }\n\n int m=edges1.size()+1;\n int n=edges2.size()+1;\n\n\n vector<int> v(m,0);\n\n for(int i=0;i<m;i++){\n int ans=0;\n dfs(i,-1,adj1,k,0,ans);\n v[i]=ans;\n }\n int maxi=0;\n for(int i=0;i<n;i++){\n int ans=0;\n dfs(i,-1,adj2,k-1,0,ans);\n maxi=max(ans,maxi);\n }\n\n \n\n for(int i=0;i<m;i++){\n v[i]+=maxi;\n }\n\n return v;\n\n\n }\n};\n```
| 0 | 0 |
['Tree', 'Depth-First Search', 'Breadth-First Search', 'C++']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
DFS with Detailed Explanation | Java |
|
dfs-with-detailed-explanation-java-by-ga-5w7l
|
Intuition\nThe problem is as follows: We are given two graphs or trees (referred to as graphs) with sizes n and m, respectively, and an integer k. We need to re
|
GauravAvghade
|
NORMAL
|
2024-12-06T13:41:06.597391+00:00
|
2024-12-06T13:41:06.597414+00:00
| 3 | false |
# Intuition\nThe problem is as follows: We are given two graphs or trees (referred to as graphs) with sizes `n` and `m`, respectively, and an integer `k`. We need to return an array of length `n`, where the `i-th` index in the array represents:\n\n*( The number of nodes that can be reached from the `i-th` node in `graph1` within a distance `k` ) plus `+`\n( The maximum number of nodes that can be reached in `graph2` from a single node in `graph2` within a distance `k\u22121`).*\n\n**Explanation of** "*the maximum number of nodes that can be reached in `graph2` from a node in `graph2` with distance `k\u22121`*":\n- This means we need to find a single node in `graph2` that can reach the maximum number of nodes in `graph2` within a distance `k\u22121`.\n \n- The `k\u22121` distance accounts for the fact that connecting a node in `graph2` to a node in `graph1` incurs a cost of 1 distance.\n\nWe must perform this calculation for every node in `graph1` and return the result as an array.\n\n**Observations**:\n- For any node in `graph1`, we need to account for the fact that it can always reach itself at a distance of `0`, which is less than or equal to `k`. Hence, if `k = 0`, we can simply return an array of all ones since no other nodes can be reached.\n\n- Why do we consider a single node in `graph2`? Because we can connect any node from `graph1` to `graph2`. To maximize the result, we simply need to find a single node in `graph2` that can reach the maximum number of nodes in `graph2` within a distance `k\u22121`. This ensures the optimal connection between the graphs.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Create two unidirectional graphs, `graph1` and `graph2`, based on the input edge arrays `edges1` and `edges2`.\n\n- Use either Depth First Search (**DFS**) or Breadth First Search (**BFS**) to find the node in `graph2` that can reach the maximum number of nodes within a distance `k\u22121`. Store this value as `max`.\n\n- For each node `i` in `graph1`, calculate the number of nodes it can reach within a distance `k` using **BFS** or **DFS**. Add this value to `max` and store the result in the answer array.\n\nThe final answer array will represent, for each node in `graph1`, the sum of:\n\n- The number of nodes reachable from the node in `graph1` within distance `k`, and\n\n- The maximum number of nodes reachable in `graph2` from a single node within distance `k\u22121`.\n\n# Complexity\n**Time complexity**:` O(V2 * (V2 + E2)) + O(V1 * (V1 + E1))`\n- O(V2 * (V2 + E2)) Computing the maximum reachable nodes in `graph2`.\n\n- O(V1 * (V1 + E1)) Computing the result for each node in `graph1`.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n**Space complexity**: `O(V1 + E1 + V2 + E2 + K)`\n- O(V1 + E1) Storing `graph1`.\n\n- O(V2 + E2) Storing `graph2`.\n\n- O(K) Stack space for recursion.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int[] maxTargetNodes(int[][] edges1, int[][] edges2, int k) {\n int[] res = new int[edges1.length + 1];\n if(k == 0) {\n Arrays.fill(res, 1);\n return res;\n }\n List<List<Integer>> graph1 = new ArrayList<>();\n for(int i = 0; i < edges1.length + 1; ++i)\n graph1.add(new ArrayList<>());\n\n List<List<Integer>> graph2 = new ArrayList<>();\n for(int i = 0; i < edges2.length + 1; ++i)\n graph2.add(new ArrayList<>());\n \n for(int[] edge : edges1) {\n graph1.get(edge[0]).add(edge[1]);\n graph1.get(edge[1]).add(edge[0]);\n }\n\n for(int[] edge : edges2) {\n graph2.get(edge[0]).add(edge[1]);\n graph2.get(edge[1]).add(edge[0]);\n }\n\n boolean[] visited = new boolean[edges2.length + 1] ;\n int max = 0;\n for(int i = 0; i < edges2.length + 1; ++i) \n max = Math.max(max, dfs(graph2, i, k - 1, visited));\n\n visited = new boolean[edges1.length + 1] ;\n for(int i = 0; i < edges1.length + 1; ++i) \n res[i] = max + dfs(graph1, i, k, visited);\n\n return res;\n }\n private int dfs(List<List<Integer>> list, int node, int k, boolean[] visited) {\n if(k < 0) return 0;\n int ans = 1;\n visited[node] = true;\n for(int cur: list.get(node)) \n if(!visited[cur]) ans += dfs(list, cur, k - 1, visited);\n visited[node] = false;\n return ans;\n }\n}\n```\n\n
| 0 | 0 |
['Java']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
JAVA | BFS | Clean Implementation
|
java-bfs-clean-implementation-by-keshavj-kqmb
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
keshavjoshi_ca
|
NORMAL
|
2024-12-06T01:50:45.706814+00:00
|
2024-12-06T01:50:45.706845+00:00
| 2 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n HashMap<Integer, List<Integer>> graph1 = new HashMap<>();\n HashMap<Integer, List<Integer>> graph2 = new HashMap<>();\n \n HashMap<Integer, Integer> map = new HashMap<>();\n int maxNode = -1;\n\n public int bfs(int index, int k, HashMap<Integer, List<Integer>> graph){\n Queue<Integer> q = new LinkedList<>();\n HashSet<Integer> seen = new HashSet<>();\n q.add(index);\n seen.add(index);\n\n int level = 0, count=1;\n while(!q.isEmpty()){\n int size = q.size();\n for(int i=0; i<size; i++){\n int node = q.poll();\n for(Integer neighbour: graph.get(node)){\n if(!seen.contains(neighbour) && level < k){\n q.add(neighbour);\n seen.add(neighbour);\n count++;\n }\n }\n }\n level++;\n }\n\n return count;\n }\n\n public int[] maxTargetNodes(int[][] edges1, int[][] edges2, int k) {\n int n = edges1.length, m=edges2.length;\n\n for(int[] row: edges1){\n graph1.computeIfAbsent(row[0], x->new ArrayList<Integer>()).add(row[1]);\n graph1.computeIfAbsent(row[1], x->new ArrayList<Integer>()).add(row[0]);\n }\n for(int[] row: edges2){\n graph2.computeIfAbsent(row[0], x->new ArrayList<Integer>()).add(row[1]);\n graph2.computeIfAbsent(row[1], x->new ArrayList<Integer>()).add(row[0]);\n }\n\n for(int i=0; i<=n; i++){\n // count total nodes at K distance from ith node\n int totalNodes = bfs(i, k, graph1);\n map.put(i, totalNodes);\n }\n for(int i=0; i<=m; i++){\n // count total nodes at K-1 distance from ith node\n int totalNodes = bfs(i, k-1, graph2);\n maxNode = Math.max(maxNode, totalNodes);\n }\n\n int[] result = new int[n+1];\n for(int i=0; i<=n; i++){\n result[i] += map.get(i);\n if(k > 0){\n result[i] += maxNode;\n }\n }\n return result;\n }\n}\n```
| 0 | 0 |
['Breadth-First Search', 'Java']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Easy BFS || Clean Code || JAVA
|
easy-bfs-clean-code-java-by-owaispatel95-3m2e
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
owaispatel95
|
NORMAL
|
2024-12-05T19:05:55.799459+00:00
|
2024-12-05T19:05:55.799511+00:00
| 5 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public static class Tree {\n public int size;\n public List<List<Integer>> adjList;\n\n public Tree(final int size) {\n this.size = size;\n }\n\n public static class Node {\n public int ele, count;\n\n public Node(final int ele, final int count) {\n this.ele = ele;\n this.count = count;\n }\n }\n\n public void construct(final int[][] edges) {\n this.adjList = new ArrayList<>();\n\n for (int i = 0; i < size; i++) adjList.add(new ArrayList<>());\n\n for (final int[] edge : edges) {\n adjList.get(edge[0]).add(edge[1]);\n adjList.get(edge[1]).add(edge[0]);\n }\n }\n\n public int kDistBfs(final int node, final int k) {\n final boolean[] visited = new boolean[size];\n final Queue<Node> queue = new ArrayDeque<>();\n\n visited[node] = true;\n queue.add(new Node(node, 0));\n\n int count = 0;\n\n while(!queue.isEmpty()) {\n final Node cur = queue.remove();\n\n count++;\n\n for (final int child : adjList.get(cur.ele)) {\n if (!visited[child] && cur.count + 1 <= k) {\n visited[child] = true;\n\n queue.add(new Node(child, cur.count + 1));\n }\n }\n }\n\n return count;\n }\n\n public int[] kNearestCount(final int k) {\n final int[] kNearest = new int[size];\n\n for (int i = 0; i < size; i++) {\n kNearest[i] = kDistBfs(i, k);\n }\n\n return kNearest;\n }\n }\n\n public int[] maxTargetNodes(int[][] edges1, int[][] edges2, int k) {\n final int n = edges1.length + 1;\n final int m = edges2.length + 1;\n\n final Tree t1 = new Tree(n);\n final Tree t2 = new Tree(m);\n\n t1.construct(edges1);\n t2.construct(edges2);\n\n final int[] t1KNearest = t1.kNearestCount(k);\n final int[] t2KNearest = t2.kNearestCount(k - 1);\n\n if (k == 0) return t1KNearest;\n\n int max = 0;\n\n for (int i = 0; i < m; i++) {\n max = Integer.max(max, t2KNearest[i]);\n }\n\n for (int i = 0; i < n; i++) {\n t1KNearest[i] += max;\n }\n\n return t1KNearest;\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
BFS javascript
|
bfs-javascript-by-craftyfox-fa14
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
craftyfox
|
NORMAL
|
2024-12-05T08:37:07.172343+00:00
|
2024-12-05T08:37:07.172382+00:00
| 6 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```javascript []\n/**\n * @param {number[][]} edges1\n * @param {number[][]} edges2\n * @param {number} k\n * @return {number[]}\n */\n var bfs=function(adj,n,k,start){\n let queue=[];\n queue.push(start);\n let visited = Array.from({ length: n }, () => false);\n visited[start]=true;\n\n let cnt=0,d=0;\n while(queue.length && d<=k){\n let sz=queue.length;\n while(sz-->0)\n {\n let node = queue.shift();\n cnt++;\n for (let n of adj[node]) {\n if (!visited[n]) {\n visited[n] = true;\n queue.push(n);\n }\n }\n }\n d++;\n \n }\n return cnt;\n\n }\nvar maxTargetNodes = function(edges1, edges2, k) {\n const n = edges1.length + 1;\n const m = edges2.length + 1;\n\n const adj1 = Array.from({ length: n }, () => []);\n const adj2 = Array.from({ length: m }, () => []);\n\n for (const [u, v] of edges1) {\n adj1[u].push(v);\n adj1[v].push(u);\n }\n for (const [u, v] of edges2) {\n adj2[u].push(v);\n adj2[v].push(u);\n } \n\n \n\n\n\n const good1 = new Array(n).fill(0);\n const good2 = new Array(m).fill(0);\n for(let i=0;i<n;i++)\n good1[i]=bfs(adj1,n,k,i)\n\n let ans = 0;\n\n for(let i=0;i<m;i++)\n ans=Math.max(ans,bfs(adj2,m,k-1,i));\n for(let i=0;i<n;i++)\n good1[i]+=ans;\n return good1;\n\n\n\n};\n```
| 0 | 0 |
['Breadth-First Search', 'JavaScript']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Python3 Double DFS O(km+kn) (Beats 99.3%)
|
python3-double-dfs-okmkn-beats-993-by-ch-klrd
|
\nclass Solution:\n def maxTargetNodes(self, edges1: List[List[int]], edges2: List[List[int]], k: int) -> List[int]:\n if k == 0:\n return
|
cheetaslo
|
NORMAL
|
2024-12-05T08:26:56.502824+00:00
|
2024-12-05T08:26:56.502864+00:00
| 18 | false |
```\nclass Solution:\n def maxTargetNodes(self, edges1: List[List[int]], edges2: List[List[int]], k: int) -> List[int]:\n if k == 0:\n return [1] * (len(edges1)+1)\n \n def wrapper(edges, k):\n n = len(edges) + 1\n g = [[] for _ in range(n)]\n \n for u, v in edges:\n g[u].append(v)\n g[v].append(u)\n \n cnt = [[0]*(k+1) for _ in range(n)] # cnt[i][j] is number of nodes has distance j to node i\n \n def dfs1(to, fa):\n nonlocal cnt\n cnt[to][0] += 1\n for nei in g[to]:\n if nei == fa:\n continue\n dfs1(nei, to)\n for d in range(1, k+1):\n cnt[to][d] += cnt[nei][d-1]\n return\n \n dfs1(0, -1)\n \n # propagate\n def dfs2(to, fa):\n nonlocal cnt\n for nei in g[to]:\n if nei == fa:\n continue\n for d in range(k, 0, -1):\n if d == 1:\n cnt[nei][d] += cnt[to][d-1]\n else:\n cnt[nei][d] += cnt[to][d-1] - cnt[nei][d-2]\n dfs2(nei, to)\n \n dfs2(0, -1)\n return cnt\n \n cnt1 = wrapper(edges1, k)\n cnt2 = wrapper(edges2, k-1)\n tree2_max = max(sum(l) for l in cnt2)\n return [sum(l) + tree2_max for l in cnt1]\n \n \n\n```
| 0 | 0 |
['Depth-First Search', 'Python3']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
3372. Maximize the Number of Target Nodes After Connecting Trees I | DFS Solution ✨✅
|
3372-maximize-the-number-of-target-nodes-xqmf
|
\uD83C\uDF33 Connecting Two Trees with a Limit - Intuition and Approach Explained\n\n## Intuition\n\nThe problem revolves around two trees with n and m nodes an
|
ayushkumar08032003
|
NORMAL
|
2024-12-04T13:58:31.459661+00:00
|
2024-12-04T13:58:31.459696+00:00
| 3 | false |
# \uD83C\uDF33 **Connecting Two Trees with a Limit - Intuition and Approach Explained**\n\n## **Intuition**\n\nThe problem revolves around **two trees** with `n` and `m` nodes and asks us to compute how many nodes from both trees can be reached from a node in the first tree with a **distance limit of k edges**. \n\n- A node in the second tree is only reachable if we consider connecting one node from the first tree to it. \n- We need to efficiently compute the **maximum number of reachable nodes** from each node in the first tree, considering this **virtual connection**.\n\nThe approach leverages **Depth-First Search (DFS)** to calculate reachable nodes and ensures that the operations are performed efficiently on the given graphs.\n\n---\n\n## **Approach**\n\n### **Step-by-Step Solution**\n\n1. **Graph Representation:**\n - Use adjacency lists (`graph1` and `graph2`) to represent the two trees, making traversal straightforward.\n\n2. **DFS Traversal:**\n - Implement a recursive DFS function that counts how many nodes can be reached from a given node within `k` edges.\n - If the path length exceeds `k`, terminate the DFS for that path.\n\n3. **Pre-computation for Tree 2:**\n - Compute the **maximum reachable nodes** from any node in the second tree (`tree2`) with `k-1` edges. \n - This helps as every query node in the first tree will benefit from connecting to this optimized configuration of the second tree.\n\n4. **Query Each Node in Tree 1:**\n - For each node in the first tree, perform a DFS to calculate how many nodes can be reached within `k` edges.\n - Add the precomputed maximum from the second tree to this count.\n\n5. **Result Compilation:**\n - Store the computed values for each node in the first tree in an array and return the result.\n\n---\n\n## **Complex Coding Topics Simplified**\n\n### **1. DFS in Trees**\n - DFS is ideal for traversing nodes connected in a graph/tree structure.\n - It uses a **recursive backtracking approach**, marking nodes as visited to avoid revisits.\n\n### **2. Pre-computation**\n - By calculating the best possible result for the second tree independently, we save repeated calculations during queries for the first tree.\n\n---\n\n## **Code Explanation**\n\n```cpp\n#define vi vector<int>\n#define vvi vector<vi>\n\nclass Solution {\npublic:\n // Helper DFS function to count reachable nodes within the distance `k`.\n int dfs(int node, int cnt, vvi &graph, vector<bool> &vis, int k) {\n // If the current path exceeds the distance limit, terminate.\n if (cnt > k) return 0;\n\n vis[node] = true; // Mark the current node as visited.\n int count = 1; // Count the current node.\n\n // Traverse all connected nodes.\n for (int neighbor : graph[node]) {\n if (!vis[neighbor]) {\n count += dfs(neighbor, cnt + 1, graph, vis, k);\n }\n }\n\n return count; // Return the total count of reachable nodes.\n }\n\n // Helper function to compute the best possible result for the second tree.\n int help(int m, vvi &graph2, int k) {\n int maxNodes = 0;\n\n // Iterate over all nodes in the second tree.\n for (int i = 0; i < m; ++i) {\n vector<bool> vis(m, false); // Reset visited nodes for each DFS call.\n int reachable = dfs(i, 0, graph2, vis, k - 1); // Max reach within k-1.\n maxNodes = max(maxNodes, reachable); // Update the maximum.\n }\n\n return maxNodes; // Return the best possible result for the second tree.\n }\n\n // Main function to calculate the result for all nodes in the first tree.\n vector<int> maxTargetNodes(vector<vector<int>>& edges1, \n vector<vector<int>>& edges2, int k) {\n int n = edges1.size() + 1, m = edges2.size() + 1;\n\n // Build adjacency lists for both trees.\n vvi graph1(n), graph2(m);\n for (vector<int> &edge : edges1) {\n graph1[edge[0]].push_back(edge[1]);\n graph1[edge[1]].push_back(edge[0]);\n }\n\n for (vector<int> &edge : edges2) {\n graph2[edge[0]].push_back(edge[1]);\n graph2[edge[1]].push_back(edge[0]);\n }\n\n // Precompute the best result for the second tree.\n int tree2Result = help(m, graph2, k);\n\n vector<int> result; // To store results for all nodes in the first tree.\n\n // Query each node in the first tree.\n for (int i = 0; i < n; ++i) {\n vector<bool> vis(n, false); // Reset visited nodes for each DFS call.\n int reachable = dfs(i, 0, graph1, vis, k); // Max reach in the first tree.\n reachable += tree2Result; // Add the precomputed result from the second tree.\n result.push_back(reachable);\n }\n\n return result; // Return the result array.\n }\n};\n```\n\n---\n\n## **Complexity Analysis**\n\n1. **Time Complexity:**\n - **Graph Construction:** \\( O(n + m) \\), where \\( n \\) and \\( m \\) are the number of nodes in the two trees.\n - **DFS Traversals:**\n - For Tree 1: \\( O(n * k) \\), as each DFS explores up to \\( k \\) edges.\n - For Tree 2: \\( O(m * k) \\).\n - **Overall:** \\( O(n * k + m * k) \\).\n\n2. **Space Complexity:**\n - **Graph Storage:** \\( O(n + m) \\) for adjacency lists.\n - **Visited Array:** \\( O(max(n, m)) \\).\n - **Overall:** \\( O(n + m) \\).\n\n---\n\n# **PLEASE UPVOTE IF YOU LIKED IT \u2705**
| 0 | 0 |
['C++']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Easy to UnderStand || Begginer Friendly
|
easy-to-understand-begginer-friendly-by-cwnxo
|
Intuition\n\nThe problem involves two graphs represented by edge lists e1 and e2. The goal is to maximize the number of nodes reachable in the first graph, give
|
tinku_tries
|
NORMAL
|
2024-12-04T13:04:23.543448+00:00
|
2024-12-04T13:04:23.543497+00:00
| 4 | false |
# Intuition\n\nThe problem involves two graphs represented by edge lists `e1` and `e2`. The goal is to maximize the number of nodes reachable in the first graph, given a constraint on the number of steps (`k`) that can be taken in the second graph.\n\nTo achieve this:\n1. Use `e2` to determine the maximum number of nodes reachable within `k-1` steps.\n2. Combine this with the result of iterating over `e1` for all possible starting points.\n\n---\n\n# Approach\n\n1. **Graph Construction**:\n - Build adjacency lists for both graphs from `e1` and `e2`.\n\n2. **DFS Traversal**:\n - Write a recursive function `IterateOnGraph` that performs a depth-first search (DFS) to calculate the number of nodes reachable from a given node within a specified number of steps (`k`).\n\n3. **Precompute Maximum Nodes in `G2`**:\n - Iterate over all nodes in `G2` and calculate the maximum number of nodes reachable within `k-1` steps.\n\n4. **Calculate Results for `G1`**:\n - For each node in `G1`, calculate the total number of reachable nodes by combining its DFS result with the precomputed maximum from `G2`.\n\n5. **Return Results**:\n - Store the results for each node in `G1` in a vector and return it.\n\n---\n\n# Complexity\n\n- **Time Complexity**:\n - **Graph Construction**: `O(n + m)`, where `n` is the number of nodes and `m` is the number of edges.\n - **DFS Traversals**: `O(n k)` for `G1` and `O(m k)` for `G2`.\n - Overall: `O((n + m) k)`.\n\n- **Space Complexity**:\n - Adjacency lists require `O(n + m)`.\n - Recursive stack in DFS has a maximum depth of `k`.\n - Overall: `O(n + m + k)`.\n\n---\n# Beats\n\n\n---\n\n# Code\n\n```cpp\nclass Solution {\npublic:\n // DFS function to calculate reachable nodes within \'k\' steps\n int IterateOnGraph(int node, int parent, vector<vector<int>>& graph, int k) {\n if (k <= 0) return (k == 0); // Base case: If no steps are left\n int count = 1; // Count the current node\n for (auto& neighbor : graph[node]) {\n if (neighbor != parent) { // Avoid revisiting the parent node\n count += IterateOnGraph(neighbor, node, graph, k - 1);\n }\n }\n return count;\n }\n\n vector<int> maxTargetNodes(vector<vector<int>>& e1, vector<vector<int>>& e2, int k) {\n int n1 = e1.size() + 1, n2 = e2.size() + 1;\n vector<vector<int>> G1(n1), G2(n2);\n\n // Construct adjacency lists for both graphs\n for (auto& edge : e1) {\n G1[edge[0]].push_back(edge[1]);\n G1[edge[1]].push_back(edge[0]);\n }\n for (auto& edge : e2) {\n G2[edge[0]].push_back(edge[1]);\n G2[edge[1]].push_back(edge[0]);\n }\n\n // Precompute the maximum reachable nodes in G2 within k-1 steps\n int maxG2 = 0;\n for (int i = 0; i < n2; i++) {\n maxG2 = max(maxG2, IterateOnGraph(i, -1, G2, k - 1));\n }\n\n // Calculate results for G1\n vector<int> result;\n for (int i = 0; i < n1; i++) {\n result.push_back(IterateOnGraph(i, -1, G1, k) + maxG2);\n }\n\n return result;\n }\n};\n```\n\n---\n\n# Explanation of the Code\n\n1. **Graph Construction**:\n - Convert `e1` and `e2` edge lists into adjacency lists `G1` and `G2`.\n\n2. **DFS Traversal**:\n - `IterateOnGraph` is a recursive function that counts all nodes reachable from a given starting point within `k` steps.\n\n3. **Maximizing Nodes in `G2`**:\n - Iterate over all nodes in `G2` and calculate the maximum nodes reachable within `k-1` steps.\n\n4. **Combining Results**:\n - For each node in `G1`, calculate the total nodes reachable by summing its DFS result and the precomputed maximum for `G2`.\n\n5. **Result**:\n - Store the total for each node in `G1` and return as the output.\n\n---\n\n# Edge Cases\n\n1. **Disconnected Graph**:\n - If some nodes are not connected in `G1` or `G2`, ensure the result accounts for isolated nodes.\n\n2. **Small `k`**:\n - For \\(k = 1\\), only the current node can be considered in `G1`.\n\n3. **No Edges**:\n - If `e1` or `e2` is empty, the graphs will only have isolated nodes.
| 0 | 0 |
['Tree', 'Depth-First Search', 'C++']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Simple UnderStanding
|
simple-understanding-by-alvin121202-t8dl
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\nDFS AND FIND MAX\n\n# Complexity\n- Time complexity:\n Add your time comp
|
Alvin121202
|
NORMAL
|
2024-12-04T08:40:47.557001+00:00
|
2024-12-04T08:40:47.557027+00:00
| 5 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nDFS AND FIND MAX\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int[] maxTargetNodes(int[][] edges1, int[][] edges2, int k) {\n \n int []arr1 = helper(edges1,k);\n System.out.println();\n int []arr2 = helper(edges2,k-1);\n int max = 0;\n for(int i=0;i<arr2.length;i++) max = Math.max(arr2[i],max);\n for(int i=0;i<arr1.length;i++) arr1[i] += max;\n return arr1;\n \n\n }\n\n public int[] helper(int[][] edges1,int k){\n HashMap<Integer,ArrayList<Integer>> map = new HashMap<>();\n\n for(int []ch:edges1){\n int start = ch[0];\n int end = ch[1];\n\n map.computeIfAbsent(start,key -> new ArrayList<>()); \n map.computeIfAbsent(end,key -> new ArrayList<>()); \n\n map.get(start).add(end);\n map.get(end).add(start);\n }\n int []arr1 = new int[edges1.length+1];\n \n \n for(int i=0;i<=edges1.length;i++){\n HashSet<Integer> v = new HashSet<>();\n dfs(map,i,v,0,k);\n arr1[i] = v.size();\n System.out.print(arr1[i] + " ");\n }\n\n return arr1;\n }\n public void dfs(HashMap<Integer,ArrayList<Integer>> map,int index,HashSet<Integer> visited,int count,int k){\n if(k < 0) return;\n visited.add(index); \n if(count == k) return;\n for(int node : map.get(index)){\n if(!visited.contains(node)){\n dfs(map,node,visited,count+1,k);\n }\n }\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
DFS recursive python. As simple as possible, hopefully it helps others : )
|
dfs-recursive-python-as-simple-as-possib-7gar
|
Intuition\n- Find the number of targets for each node in graph1 (for k)\n- Find the number of targets for each node in graph2 (for k-1 since we use one edge to
|
mattachea
|
NORMAL
|
2024-12-04T03:03:02.815369+00:00
|
2024-12-04T03:03:02.815433+00:00
| 10 | false |
# Intuition\n- Find the number of targets for each node in graph1 (for k)\n- Find the number of targets for each node in graph2 (for k-1 since we use one edge to connect graph1 to graph2)\n- We only care about the max number from graph2 since we will always connect graph1 to that node.\n\n\n(using extra space helped with debugging)\n\n\n# Code\n```python3 []\nclass Solution:\n def maxTargetNodes(self, edges1: List[List[int]], edges2: List[List[int]], k: int) -> List[int]:\n\n # Recursively get the number of targets from \'node\' \n def getNumTargets(node, parent, adj, k) -> int:\n if k <= 0:\n return 1\n\n count = 1\n for nei in adj[node]:\n if nei != parent:\n count += getNumTargets(nei, node, adj, k-1)\n return count\n\n # Create graph \n def getGraph(edges):\n adj = collections.defaultdict(list)\n for u, v in edges:\n adj[u].append(v)\n adj[v].append(u)\n return adj\n\n\n # Handle edge case\n if k == 0: return [1] * (len(edges1)+1)\n\n # Process Graph 1\n adj1 = getGraph(edges1)\n targets1 = {node: getNumTargets(node, -1, adj1, k) for node in adj1}\n \n # Process graph2, use k-1 since the connection from graph1 to graph2 takes one edge\n adj2 = getGraph(edges2)\n targets2 = {node: getNumTargets(node, -1, adj2, k - 1) for node in adj2}\n\n maxNumTargets2 = max(targets2.values())\n return [targets1[i] + maxNumTargets2 for i in range(len(edges1)+1)]\n \n```
| 0 | 0 |
['Python3']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Solution
|
solution-by-aadib123-xuol
|
Intuition\nThe very first thought that comes in the mind is that since we have to find number of all nodes upto level k from node u so it can be level order tra
|
aadib123
|
NORMAL
|
2024-12-03T17:23:28.318545+00:00
|
2024-12-03T17:23:28.318587+00:00
| 1 | false |
# Intuition\nThe very first thought that comes in the mind is that since we have to find number of all nodes upto level k from node u so it can be level order traversing.\n\n# Approach\nAs we can understand this problem can further be break into two subproblems the first one is for every node in first tree we have to find number of all nodes upto level k. The other subproblem is we have to find a node in second tree such that it has maximum number of nodes upto level k-1(It is till level k-1 because 1 connection is always require to connect the both trees).It can be seem very easily that both subproblem are independent as for any node i from first tree we can always select the node j from second tree for maximum nodes(j is the solution for our second subproblem).We can find solutions to both subproblem by applying BFS. For second subproblem we can apply BFS for every node and keep track of maximum nodes so far.The constraints given in the problem allows us to do so.Finally we can add the answers of both these subproblems to finally get the answer.\n\n# Complexity\n- Time complexity:\nWe are applying BFS for every node so in worstscenario time complexity is O(n^2+m^2).\n\n- Space complexity:\nSince the maximum number of vertices in the queue is bounded by the number of vertices in the graph, the space complexity of the queue is O(max(n,m)).\n\n# Code\n```cpp []\nclass Solution {\npublic:\n\nint help(vector<vector<int>> &v,int k,int i)\n{\n\n\n\tvector<bool> vis(v.size(),false);\n\n\tint sum=0;\n\tint level=0;\n\n\t\tif(k<level)\n\t\treturn sum;\n\n\t\t\n\t\tqueue<int> q;\n\t\tq.push(i);\n\t\tvis[i]=true;\n\t\tsum++;\n\t\t\n\n\t\twhile(!q.empty())\n\t\t{\n\t\tif(k==level)\n\t\t\treturn sum;\n\n\n\t\tint x=q.size();\n\t\twhile(x--)\n\t\t{\n\t\tint f=q.front();\n\t\tq.pop();\n\t\tfor(auto j:v[f])\n\t\t{\n\t\tif(!vis[j])\n\t\t{\n\t\n\t\tq.push(j);\n\t\tvis[j]=true;\n\t\tsum++;\n\t\n\t\t}\n\t\n\t\n\t\t}\n\t\t}\n\t\tlevel++;\n\n\n\n \n\t\t}\n\t\treturn sum;\n}\n vector<int> maxTargetNodes(vector<vector<int>>& edges1, vector<vector<int>>& edges2, int k) {\nvector<vector<int>> t1(edges1.size()+1,vector<int>()),t2(edges2.size()+1,vector<int>());\n\nfor(auto i:edges1)\n{\n t1[i[0]].push_back(i[1]);\n t1[i[1]].push_back(i[0]);\n\n}\nfor(auto i:edges2)\n{\n t2[i[0]].push_back(i[1]);\n t2[i[1]].push_back(i[0]);\n\n}\nvector<int> ans(edges1.size()+1);\nint maxi=0;\n\nint loc;\nfor(int i=0;i<t2.size();i++)\n{\n loc=help(t2,k-1,i);\n maxi=max(maxi,loc);\n \n\n}\ncout<<maxi;\nfor(int i=0;i<t1.size();i++)\n{\nans[i]=help(t1,k,i);\nans[i]+=maxi;\n\n}\n\nreturn ans;\n \n }\n};\n```
| 0 | 0 |
['Tree', 'Breadth-First Search', 'C++']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
BFS
|
bfs-by-eskandar1-5rs6
|
\n# Complexity\n- Time complexity:\n Add your time complexity here, e.g. O(n) \nO(n(E1+V1)) + O(m(E2+V2))\n- E1 = n \n- E2 = m\n* O(n^2 + v1) + O(m^2 + v2) ==
|
Eskandar1
|
NORMAL
|
2024-12-03T13:26:31.340373+00:00
|
2024-12-03T13:26:31.340410+00:00
| 7 | false |
\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n*(E1+V1)) + O(m*(E2+V2))\n- E1 = n \n- E2 = m\n* O(n^2 + v1) + O(m^2 + v2) == O(n^2 + m^2) == O(n^2)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(v)\n---\n# Code\n```cpp []\nclass Solution {\npublic:\nvector<int>adj1[1000];\nvector<int>adj2[1000];\nint ans[1000], vis[1000];\nint mx=0;\nvoid BFS(int u, int k, bool f){\n queue<pair<int, int>>q;\n q.push({u, 0});\n while(q.size()){\n auto it=q.front();\n int x=it.first, y=it.second;\n q.pop();\n vis[x]=1;\n \n if(f==1 && y<=k) {\n ans[u]++;\n for(auto v: adj1[x]){\n if(vis[v]==1) continue;\n q.push({v, y+1});\n }\n }\n else if(f == 0 && y <= k-1) {\n mx= mx+1;\n for(auto v: adj2[x]){\n if(vis[v]==1) continue;\n q.push({v, y+1});\n }\n }\n }\n}\n\n vector<int> maxTargetNodes(vector<vector<int>>& edges1, vector<vector<int>>& edges2, int k) {\n int n = edges1.size(), m = edges2.size();\n for(auto it: edges1){\n adj1[it[0]].push_back(it[1]);\n adj1[it[1]].push_back(it[0]);\n }\n for(auto it: edges2){\n adj2[it[0]].push_back(it[1]);\n adj2[it[1]].push_back(it[0]);\n }\n //////////////////////////////////\n \n for(int i=0; i<=n; i++){\n for(int i=0; i<=n; i++) vis[i]=0;\n BFS(i, k, 1);\n }\n\n int mxCount=0;\n for(int i=0; i<=m; i++){\n for(int i=0; i<=m; i++) vis[i]=0;\n BFS(i, k, 0);\n mxCount = max(mxCount, mx);\n mx=0;\n }\n vector<int>res(n+1);\n for(int i=0; i<=n; i++) res[i] = ans[i]+mxCount;\n return res;\n }\n};\n```
| 0 | 0 |
['Tree', 'Depth-First Search', 'Breadth-First Search', 'C++']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
BFS Solution || Detailed Explanation || C++ || Easy to understand
|
bfs-solution-detailed-explanation-c-easy-mk0f
|
Intuition\n Describe your first thoughts on how to solve this problem. \nTo determine the maximum number of nodes that can be reached within a distance k in two
|
Abhishekjha6908
|
NORMAL
|
2024-12-03T10:56:46.732398+00:00
|
2024-12-03T10:56:46.732424+00:00
| 10 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo determine the maximum number of nodes that can be reached within a distance `k` in two graphs, we can use Breadth-First Search (BFS). BFS is ideal for exploring nodes layer by layer, making it easy to track nodes within a limited distance. By leveraging BFS, we can count reachable nodes in one graph and use this result to enhance counts from the other graph.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Adjacency List Construction:\n - Convert edges1 and edges2 into adjacency lists (adj1 and adj2) to represent the graphs.\n - Add edges as bidirectional to simulate undirected graphs.\n\n2. BFS Implementation:\n - For a given start node, BFS explores nodes level by level, maintaining a count of reachable nodes and using a distance limit (k).\n - Use a visited array to prevent revisiting nodes.\n\n3. Compute Maximum BFS Count for Graph 2:\n - Iterate over all nodes in adj2 and compute the maximum count of reachable nodes within k-1 distance.\n\n4. Combine Results for Graph 1:\n - For each node in adj1, perform BFS up to distance k and add the maximum count from adj2.\n\n5. Return Results:\n - The result array contains combined counts for each node in adj1.\n# Complexity\n- Time complexity:$$O(V1\u22C5(E1/V1+k)+V2\u22C5(E2/V2+k))$$\n - BFS runs for each node in both graphs, iterating over edges.\n - Let V1 and E1 be the vertices and edges in edges1, and V2 and E2 in edges2. \n - $$O(V1\u22C5(E1/V1+k)+V2\u22C5(E2/V2+k))$$, approximately linear in nodes and edges. \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n - BFS uses a queue (O(V)), a visited array (O(V)), and adjacency lists (O(E)), where V and E depend on the graph size.\n - O(V1+E1+V2+E2) in total. \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\n int BfsCount(vector<vector<int>>& adj,int k,int start,int size){\n queue<int> q;\n q.push(start);\n vector<bool> visited(size,false);\n visited[start] = true;\n int count = 0;\n int dist = 0;\n\n while(!q.empty() && dist<=k){\n int qs = q.size();\n for(int i=0;i<qs;i++){\n int Node = q.front();\n q.pop();\n count++;\n for(auto it: adj[Node]){\n if(!visited[it]){\n visited[it] = true;\n q.push(it);\n }\n }\n }\n \n dist++;\n }\n return count;\n }\n\npublic:\n vector<int> maxTargetNodes(vector<vector<int>>& edges1, vector<vector<int>>& edges2, int k) {\n int n = edges1.size()+1;\n int m = edges2.size()+1;\n vector<vector<int>> adj1(n), adj2(m);\n for(const auto& it: edges1){\n adj1[it[0]].push_back(it[1]);\n adj1[it[1]].push_back(it[0]);\n }\n\n for(const auto& it: edges2){\n adj2[it[0]].push_back(it[1]);\n adj2[it[1]].push_back(it[0]);\n }\n\n int max_BfsCount_v = 0;\n\n for(int i=0;i<m;i++){\n int cnt = BfsCount(adj2,k-1,i,m);\n if(cnt> max_BfsCount_v) max_BfsCount_v = cnt;\n }\n\n vector<int> ans(n);\n for(int i=0;i<n;i++){\n ans[i] = BfsCount(adj1,k,i,n)+max_BfsCount_v;\n }\n\n return ans;\n }\n};\n```
| 0 | 0 |
['Tree', 'Breadth-First Search', 'C++']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Easy Method Using BFS
|
easy-method-using-bfs-by-mdjabir786c-hcuz
|
Bold# Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n-
|
mdjabir786
|
NORMAL
|
2024-12-03T04:58:29.077105+00:00
|
2024-12-03T04:58:29.077135+00:00
| 2 | false |
**Bold**# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(N+M)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(N+M)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\nvector<int> bfs(vector<int>adj[],int n,int k) \n{\n vector<int>ans(n,0); \n for(int i=0;i<n;i++) \n {\n int c=0; \n vector<int>boo(n,0); \n queue<pair<int,int>>q; \n q.push({i,0}); \n boo[i]=1; \n while(!q.empty()) \n {\n int node=q.front().first; \n int d=q.front().second;\n q.pop(); \n if(d>k) continue; \n c++; \n for(int j:adj[node]) \n {\n if(boo[j]==0) \n {\n boo[j]=1; \n q.push({j,d+1}); \n }\n \n }\n }\n ans[i]=c; \n }\n return ans; \n}\n vector<int> maxTargetNodes(vector<vector<int>>& edges1, vector<vector<int>>& edges2, int k) {\n // converting Edges to Adj Matrix; \n int n=edges1.size()+1; \n vector<int>adj1[1001]; \n /* \n 0->1,2 \n 1->0 \n 2->0,3,4 \n 3->2 */ \n for(auto i:edges1) \n {\n adj1[i[0]].push_back(i[1]); \n adj1[i[1]].push_back(i[0]); \n }\n int m=edges2.size()+1; \n vector<int>adj2[1001]; \n for(auto i:edges2) \n {\n adj2[i[0]].push_back(i[1]); \n adj2[i[1]].push_back(i[0]); \n }\n /* ,\n 0->1,2,3 \n 1->0,4 \n 2->0,7\n 3->0 \n 4->1,5,6\n 5->4\n 6->4\n 7->2 */ \n\n vector<int>ans1=bfs(adj1,n,k); \n vector<int>ans2=bfs(adj2,m,k-1); \n vector<int>ans; \n for(int i=0;i<n;i++) \n {\n int jabir=0; \n for(int j=0;j<m;j++) \n {\n jabir=max(jabir,ans1[i]+ans2[j]); \n }\n ans.push_back(jabir); \n }\n return ans; \n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
BFS by Java (Explained)
|
bfs-by-java-explained-by-judyzwy2021-esxh
|
Intuition\n Describe your first thoughts on how to solve this problem. \nThe number of target nodes is calculated by adding the number of target nodes on the or
|
JudyZWY2021
|
NORMAL
|
2024-12-03T00:25:57.404745+00:00
|
2024-12-03T00:25:57.404773+00:00
| 5 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe number of target nodes is calculated by adding the number of target nodes on the original tree and the number of target nodes after connecting another tree. As the 2 trees are independent, we could calculate these 2 numbers seperately.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Use adjacent lists to describe the graphs\n2. Find the number of target nodes for each node on 2 trees\n - Tree1: the number of edges on the path $u$ to $v$ is no larger than k (We need number for each node, the result should be store in an array)\n - Tree2: the number of edges on the path $u$ to $v$ is no larger than k-1 (We only need the maximum value, the result is only an integer)\n3. Add the number from Tree2 to each number in Tree1\n\n# Complexity\n- Time complexity: $$O(N_1 + N_2+K)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(N_1 + N_2)$$ where $N_1$ is the length of $edges1$ and $N_2$ is the length of $edges2$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int[] maxTargetNodes(int[][] edges1, int[][] edges2, int k) {\n int n1 = edges1.length+1; \n int[] result = new int[n1];\n \n // if k equals to 0, we could not connect 2 trees together and every node has the only one target node, which is itself.\n if (k == 0) {\n Arrays.fill(result, 1);\n return result;\n }\n\n // find the adjacent list of each node in 2 trees\n List<List<Integer>> adj1 = adjcentList(edges1);\n List<List<Integer>> adj2 = adjcentList(edges2);\n \n // for the first tree, find the number of target nodes for each node\n for(int i=0; i<n1; i++) {\n result[i] = bfs(adj1, k, i);\n }\n\n int n2 = edges2.length+1;\n int maxValue = 0;\n // we only need the node that has the maximum number of targer nodes for the second tree\n for(int i=0; i<n2; i++) {\n // as we need 1 edge to connect 2 trees, \n maxValue = Math.max(bfs(adj2, k-1, i), maxValue);\n }\n\n // add the maximum number of target nodes from the second tree to each node on the first tree\n for(int i=0; i<n1; i++) {\n result[i] += maxValue;\n }\n \n return result;\n }\n\n private List<List<Integer>> adjcentList(int[][] edges1) {\n List<List<Integer>> adj = new ArrayList<>();\n int n = edges1.length+1;\n for(int i=0; i<n; i++) {\n adj.add(new ArrayList<>());\n }\n // add edges to both nodes\n for(int[] edges: edges1) {\n adj.get(edges[0]).add(edges[1]);\n adj.get(edges[1]).add(edges[0]);\n }\n return adj;\n }\n\n // return the number of target nodes\n private int bfs(List<List<Integer>> adj, int k, int i) {\n Queue<Integer> queue = new LinkedList<>();\n boolean[] visited = new boolean[adj.size()];\n queue.offer(i);\n int temp = k;\n int result = 1;\n // The number of nodes is smaller than k\n while (temp-- > 0) {\n int size = queue.size();\n for(int j=0; j<size; j++) {\n int curr = queue.poll();\n // mark the visited nodes\n visited[curr] = true;\n for(int num: adj.get(curr)) {\n // if the child nodes are unvistied, we add it to the queue\n if (!visited[num]) {\n queue.offer(num);\n }\n }\n }\n result += queue.size();\n }\n return result;\n }\n}\n```
| 0 | 0 |
['Breadth-First Search', 'Queue', 'Java']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Python efficeient O((n+m)*k) solution Real Solution , Fast , Python3 , dfs solution
|
python-efficeient-onmk-solution-real-sol-i57o
|
Intuition\nThe problem involves two graphs represented by edges1 and edges2. We need to determine the maximum number of nodes reachable within k steps from each
|
adi_bhai_god
|
NORMAL
|
2024-12-02T22:57:52.934387+00:00
|
2024-12-02T22:57:52.934441+00:00
| 11 | false |
# Intuition\nThe problem involves two graphs represented by `edges1` and `edges2`. We need to determine the maximum number of nodes reachable within `k` steps from each node in both graphs and return a list of these values.\n\nTo achieve this, a depth-first search (DFS) is used to explore nodes up to a depth of `k` for each starting node.\n\n# Approach\n1. **Data Structures**:\n - Use two `defaultdict` objects (`dp1` and `dp2`) to represent adjacency lists for `edges1` and `edges2`.\n\n2. **DFS Functions**:\n - `dfs_spl`: Computes the number of nodes reachable within `k` steps from a given node in the second graph (`dp2`).\n - `dfs_spl2`: Computes the number of nodes reachable within `k` steps from a given node in the first graph (`dp1`).\n\n3. **Main Logic**:\n - For each node in `edges2`, calculate the reachable nodes within `k` steps and store them in the `ans` list.\n - For each node in `edges1`, calculate the reachable nodes within `k` steps and store them in the `ans2` list.\n - Find the maximum value from `ans` and update `ans2` with this value when `k > 0`.\n\n4. **Return**:\n - Return the final list `ans2`.\n\n# Complexity\n- **Time Complexity**: \n $$O((n + m) \\times k)$$ \n - Constructing the adjacency lists takes \\(O(n + m)\\), where \\(n\\) is the number of nodes and \\(m\\) is the number of edges. \n - Each DFS explores nodes up to a depth of `k`, and we perform DFS for each node in both graphs. Hence, the total time complexity is \\(O((n + m) \\times k)\\).\n\n- **Space Complexity**: \n $$O(n + m)$$ \n Space is used for adjacency lists (`dp1` and `dp2`), recursion stack (which can go up to depth `k`), and the result lists (`ans` and `ans2`). Hence, the space complexity is linear with respect to the number of nodes and edges.\n\n# Code\n```python\nfrom typing import List\nfrom collections import defaultdict\n\nclass Solution:\n def maxTargetNodes(self, edges1: List[List[int]], edges2: List[List[int]], k: int) -> List[int]:\n dp1 = defaultdict(list)\n dp2 = defaultdict(list)\n\n # Build adjacency lists for both graphs\n for i, j in edges1:\n dp1[i].append(j)\n dp1[j].append(i)\n\n for i, j in edges2:\n dp2[i].append(j)\n dp2[j].append(i)\n\n ans = [1] * (len(edges2) + 1)\n\n # DFS for the second graph\n def dfs_spl(i, par, k):\n if k <= 0:\n return 0\n ct = 0\n for j in dp2[i]:\n if j != par:\n ct += (1 + dfs_spl(j, i, k - 1))\n return ct\n\n # DFS for the first graph\n def dfs_spl2(i, par, k):\n if k <= 0:\n return 0\n ct = 0\n for j in dp1[i]:\n if j != par:\n ct += (1 + dfs_spl2(j, i, k - 1))\n return ct\n\n # Calculate reachable nodes for graph 2\n for i in range(len(edges2) + 1):\n ans[i] += dfs_spl(i, -1, k - 1)\n\n ans2 = [1] * (len(edges1) + 1)\n\n # Calculate reachable nodes for graph 1\n for i in range(len(edges1) + 1):\n ans2[i] += dfs_spl2(i, -1, k)\n\n # Find max reachable nodes in graph 2 and add to graph 1\'s result\n q = max(ans)\n for i in range(len(ans2)):\n if k > 0:\n ans2[i] += q\n\n return ans2\n
| 0 | 0 |
['Depth-First Search', 'Python3']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
BFS solution
|
bfs-solution-by-jaifer07-lxzv
|
Intuition\n Describe your first thoughts on how to solve this problem. \nGot this problem in the contest\nThis is a Graph problem\n\n# Approach\n Describe your
|
jaifer07
|
NORMAL
|
2024-12-02T17:46:53.465103+00:00
|
2024-12-02T17:46:53.465127+00:00
| 1 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nGot this problem in the contest\nThis is a Graph problem\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nCan be broken down to below steps:\n1. Generate adjacency lists, adj1 and adj2\n2. Find max of **no of nodes at distance <= k from every nodes in adj2** \n3. Find **no of nodes at distance <= k for each node in adj1** in an array **say, ans[ ]**\n4. Final answer for each node of **adj2 = ans[i] + (result from step 2)**\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int[] maxTargetNodes(int[][] edges1, int[][] edges2, int k) {\n \n List<List<Integer>> adj1 = generateGraph(edges1);\n List<List<Integer>> adj2 = generateGraph(edges2);\n \n int n2 = edges2.length + 1;\n int n1 = edges1.length + 1;\n \n // no of nodes at dist <= k\n int[] ans = new int[n1];\n\n // find max of no:of nodes at distance <= k among every nodes in second graph\n // (since g1 can be connected to any nodes of g2)\n int max2 = -1;\n for (int j = 0; j < n2; j++) {\n max2 = Math.max(max2, getNoOfNodes(adj2, j, k-1));\n }\n\n // find no of nodes at distance <= k from each node of first graph\n // add max2 to each values\n for (int i = 0; i < n1; i++) {\n ans[i] = getNoOfNodes(adj1, i, k) + max2;\n }\n\n return ans;\n }\n\n /**\n * Get no of nodes at distance <= k from given root\n * uses BFS. We can also use dfs with less lines\n */\n private int getNoOfNodes(List<List<Integer>> adj, int root, int k) {\n Queue<Integer> queue = new LinkedList<>();\n queue.add(root);\n boolean[] visited = new boolean[adj.size()];\n visited[root] = true;\n\n int count = 0;\n int dist = 0;\n while (!queue.isEmpty()) {\n int size = queue.size();\n if (dist <= k) {\n count += size;\n } else {\n break;\n }\n for (int i = 0; i < size; i++) {\n int curr = queue.remove();\n List<Integer> adjNodes = adj.get(curr);\n for (int adjNode: adjNodes) {\n if (visited[adjNode]) continue;\n visited[adjNode] = true;\n queue.add(adjNode);\n }\n }\n dist++;\n }\n return count;\n }\n\n private List<List<Integer>> generateGraph(int[][] edges) {\n int n = edges.length + 1;\n List<List<Integer>> adj = new ArrayList<>();\n \n for (int i = 0; i < n; i++) adj.add(new ArrayList<>());\n \n for (int[] edge: edges) {\n adj.get(edge[0]).add(edge[1]);\n adj.get(edge[1]).add(edge[0]);\n }\n\n return adj;\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
100% time and space complexity. Java Easy Solution with Explanation
|
100-time-and-space-complexity-java-easy-h0puf
|
Intuition\n * For tree 2 - we need to calculate the max nodes at a distance of k-1 for any node\n * For tree 1 - we need to get no of nodes at k distance from g
|
GokulBansal
|
NORMAL
|
2024-12-02T17:20:27.403395+00:00
|
2024-12-02T17:20:27.403415+00:00
| 6 | false |
# Intuition\n * For tree 2 - we need to calculate the max nodes at a distance of k-1 for any node\n * For tree 1 - we need to get no of nodes at k distance from given node\n\n# Approach\n * For tree 2 - we need to calculate the max nodes at a distance of k-1 for any node\n * For tree 1 - we need to get no of nodes at k distance from given node\n\n# Complexity\n- Time complexity:\nO(n*n) - no of nodes * get max nodes\n\n- Space complexity:\nO(n2 + m2) - adjacency list of n nodes with n edges\n\n# Code\n```java []\nclass Solution {\n\n public static int getMaxNodes (ArrayList<List<Integer>> adjList, int k, int currNode, int n, boolean[] visited) {\n if(k == 0) {\n return 1;\n }\n if(k < 1) {\n return 0;\n }\n visited[currNode] = true;\n int output = 1;\n List<Integer> adjNodes = adjList.get(currNode);\n\n for(int node : adjNodes) {\n if(visited[node] != true) {\n output += getMaxNodes(adjList, k-1, node, n, visited);\n }\n }\n return output;\n }\n\n public static int getMaxNodes (ArrayList<List<Integer>> adjList, int k, int currNode, int n) {\n if(k == 0) {\n return 1;\n }\n if(k < 1) {\n return 0;\n }\n boolean[] visited = new boolean[n];\n visited[currNode] = true;\n int output = 1;\n List<Integer> adjNodes = adjList.get(currNode);\n\n for(int node : adjNodes) {\n output += getMaxNodes(adjList, k-1, node, n, visited);\n }\n return output;\n }\n\n public int[] maxTargetNodes(int[][] edges1, int[][] edges2, int k) {\n int n = edges1.length + 1;\n int m = edges2.length + 1;\n\n ArrayList<List<Integer>> adjList1 = new ArrayList<List<Integer>>();\n ArrayList<List<Integer>> adjList2 = new ArrayList<List<Integer>>();\n\n for(int i = 0; i < n; i++) {\n List<Integer> temp = new ArrayList<Integer>();\n adjList1.add(temp);\n }\n\n for(int i = 0; i < m; i++) {\n List<Integer> temp = new ArrayList<Integer>();\n adjList2.add(temp);\n }\n\n for(int i = 0; i < n-1; i++) {\n int u = edges1[i][0];\n int v = edges1[i][1];\n List<Integer> temp1 = adjList1.get(u);\n temp1.add(v);\n List<Integer> temp2 = adjList1.get(v);\n temp2.add(u);\n\n adjList1.set(u, temp1);\n adjList1.set(v, temp2);\n }\n\n for(int i = 0; i < m-1; i++) {\n int u = edges2[i][0];\n int v = edges2[i][1];\n\n List<Integer> temp1 = adjList2.get(u);\n temp1.add(v);\n List<Integer> temp2 = adjList2.get(v);\n temp2.add(u);\n\n adjList2.set(u, temp1);\n adjList2.set(v, temp2);\n }\n\n int maxNodes = 0;\n for(int i = 0; i < m; i++) {\n int value = getMaxNodes(adjList2, k-1, i, m);\n maxNodes = Math.max(maxNodes, value);\n }\n\n int[] output = new int[n];\n\n for(int i = 0; i < n; i++) {\n int value = getMaxNodes(adjList1, k, i, n) + maxNodes;\n output[i] = value;\n }\n\n return output;\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
c++
|
c-by-sougataroy893-c9xj
|
\tclass Solution {\n\tpublic:\n\n\t\tvoid mk(vector> &e,vector> &g){\n\t\t\tfor(auto i: e){\n\t\t\t\tg[i[0]].push_back(i[1]);\n\t\t\t\tg[i[1]].push_back(i[0]);\
|
sougataroy893
|
NORMAL
|
2024-12-02T08:51:35.962104+00:00
|
2024-12-02T08:51:35.962132+00:00
| 0 | false |
\tclass Solution {\n\tpublic:\n\n\t\tvoid mk(vector<vector<int>> &e,vector<vector<int>> &g){\n\t\t\tfor(auto i: e){\n\t\t\t\tg[i[0]].push_back(i[1]);\n\t\t\t\tg[i[1]].push_back(i[0]);\n\t\t\t}\n\t\t}\n\t\tunordered_map<int,int> s;\n\t\tint f(int u,vector<int> &a,vector<vector<int>> &g,int k,int p){\n\t\t\tif(k<=0){\n\t\t\t\treturn 0;\n\t\t\t}\n\t\t\ts[u]++;\n\t\t\tint c=0;\n\t\t\tfor(auto i: g[u]){\n\t\t\t\tif(s.find(i)==s.end()){\n\t\t\t\t\tc+=1;\n\t\t\t\t}\n\t\t\t}\n\t\t\tfor(auto i: g[u]){\n\t\t\t\tif(i!=p){\n\t\t\t\t\tc+=f(i,a,g,k-1,u);\n\t\t\t\t}\n\t\t\t}\n\t\t\treturn c;\n\t\t}\n\t\tvector<int> maxTargetNodes(vector<vector<int>>& e1, vector<vector<int>>& e2, int k) {\n\t\t\tint n=e1.size(),m=e2.size();\n\t\t\tvector<int> a(n+1,0),b(m+1,0);\n\t\t\tvector<vector<int>> g1(n+1),g2(m+1);\n\t\t\tmk(e1,g1);\n\t\t\tmk(e2,g2);\n\t\t\tfor(int i=0;i<n+1;i++){\n\t\t\t\ts.clear();\n\t\t\t\ta[i]=(f(i,a,g1,k,-1))+1;\n\t\t\t}\n\t\t\tint c=0;\n\t\t\tfor(int i=0;i<m+1;i++){\n\t\t\t\tif(k-1<0) break;\n\t\t\t\ts.clear();\n\t\t\t\tb[i]=(f(i,b,g2,k-1,-1))+1;\n\t\t\t\tc=max(c,b[i]);\n\t\t\t}\n\t\t\tvector<int> ans;\n\t\t\tfor(auto i: a){\n\t\t\t\tans.push_back(i+c);\n\t\t\t}\n\t\t\treturn ans;\n\t\t}\n\t};
| 0 | 0 |
[]
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Java O(n*n + m*m)
|
java-onn-mm-by-xuyiouqd-4sjo
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \nfor each tree, try to m
|
xuyiouqd
|
NORMAL
|
2024-12-02T06:23:19.629031+00:00
|
2024-12-02T06:23:19.629060+00:00
| 1 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nfor each tree, try to memorize the level list which memorize the num of nodes on each level, at the same time, we calculate the preSum of the node\'s numbers.\n\nfor each node in tree1, we use tree1\'s preSum of Min(k,lastLevel) + tree2\'s max preSum of Min(k-1,lastLevel)\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n*n+m*m)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n+m)$$\n# Code\n```java []\nclass Solution {\n public int[] maxTargetNodes(int[][] edges1, int[][] edges2, int k) {\n int n = edges1.length+1, m = edges2.length+1;\n Map<Integer,List<Integer>> map1 = new HashMap<>();\n for(int[] e1 : edges1){\n map1.putIfAbsent(e1[0],new ArrayList<>());\n map1.get(e1[0]).add(e1[1]);\n map1.putIfAbsent(e1[1],new ArrayList<>());\n map1.get(e1[1]).add(e1[0]);\n }\n Map<Integer,List<Integer>> levelMap1 = new HashMap<>();\n for(int i=0;i<n;i++){\n levelMap1.putIfAbsent(i,new ArrayList<>());\n List<Integer> levelList = levelMap1.get(i);\n dfs(i,-1,0,map1,levelList);\n for(int j=1;j<levelList.size();j++){\n levelList.set(j,levelList.get(j-1)+levelList.get(j));\n }\n }\n Map<Integer,List<Integer>> map2 = new HashMap<>();\n for(int[] e2 : edges2){\n map2.putIfAbsent(e2[0],new ArrayList<>());\n map2.get(e2[0]).add(e2[1]);\n map2.putIfAbsent(e2[1],new ArrayList<>());\n map2.get(e2[1]).add(e2[0]);\n }\n Map<Integer,List<Integer>> levelMap2 = new HashMap<>();\n for(int i=0;i<m;i++){\n levelMap2.putIfAbsent(i,new ArrayList<>());\n List<Integer> levelList = levelMap2.get(i);\n dfs(i,-1,0,map2,levelList);\n for(int j=1;j<levelList.size();j++){\n levelList.set(j,levelList.get(j-1)+levelList.get(j));\n }\n }\n int[] ans = new int[n];\n for(int i=0;i<n;i++){\n List<Integer> levelList1 = levelMap1.get(i);\n ans[i] += levelList1.get(Math.min(k,levelList1.size()-1));\n if(k==0) continue;\n int maxK = 0;\n for(int j=0;j<m;j++){\n List<Integer> levelList2 = levelMap2.get(j);\n maxK = Math.max(maxK,levelList2.get(Math.min(k-1,levelList2.size()-1)));\n }\n ans[i] += maxK;\n \n }\n return ans;\n }\n void dfs(int cur , int p, int level, Map<Integer,List<Integer>> map, List<Integer> levelList){\n if(level >=levelList.size()){\n levelList.add(1);\n }else{\n levelList.set(level,levelList.get(level)+1);\n }\n for(int next : map.get(cur)){\n if(next == p) continue;\n dfs(next,cur,level+1,map,levelList);\n }\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
BFS traversal for every node to maintain count with K dist
|
bfs-traversal-for-every-node-to-maintain-miyh
|
\nint bfs(int node,int k,vector<vector<int>>&adj,int n){ \n vector<int> vis(n,0);\n queue<int> q;\n q.push(node);\n vis[node]=1;\n
|
Sahil1107
|
NORMAL
|
2024-12-02T05:32:20.822463+00:00
|
2024-12-02T05:32:20.822487+00:00
| 8 | false |
```\nint bfs(int node,int k,vector<vector<int>>&adj,int n){ \n vector<int> vis(n,0);\n queue<int> q;\n q.push(node);\n vis[node]=1;\n int cnt=0;\n int tot=0;\n while(!q.empty()){\n int l=q.size();\n if(cnt<=k){\n tot+=l;\n }\n if(cnt>k){\n return tot;\n }\n for(int i=0;i<l;i++){\n int node=q.front();\n q.pop();\n for(auto it:adj[node]){\n if(vis[it]==0){\n vis[it]=1;\n q.push(it);\n }\n }\n }\n cnt++;\n }\n return tot;\n\n }\n vector<int> maxTargetNodes(vector<vector<int>>& edges1, vector<vector<int>>& edges2, int k) {\n int n=edges1.size();\n int m=edges2.size();\n vector<int> bfs1(n+1,0);\n vector<int> ans(n+1);\n int maxi=INT_MIN;\n vector<vector<int>> adj1(n+1);\n for(int i=0;i<n;i++){\n int u=edges1[i][0];\n int v=edges1[i][1];\n adj1[u].push_back(v);\n adj1[v].push_back(u);\n }\n vector<vector<int>> adj2(m+1);\n for(int i=0;i<m;i++){\n int u=edges2[i][0];\n int v=edges2[i][1];\n adj2[u].push_back(v);\n adj2[v].push_back(u);\n }\n for(int i=0;i<n+1;i++){\n bfs1[i]=bfs(i,k,adj1,n+1);\n }\n\n\n for(int i=0;i<m+1;i++){\n maxi=max(maxi,bfs(i,k-1,adj2,m+1));\n \n }\n for(int i=0;i<n+1;i++){\n ans[i]=bfs1[i]+maxi;\n }\n \n return ans;\n }\n\t```
| 0 | 0 |
['Breadth-First Search', 'Graph', 'C']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Two-Way DP | O(n+m) time, O(n+m) space | C++
|
two-way-dp-onm-time-onm-space-c-by-haris-wt81
|
Intuition\nTo maximize the number of target nodes, we need to compute the number of nodes reachable from each node in the trees for a given distance k. This req
|
HariShankarKarthik
|
NORMAL
|
2024-12-02T05:10:19.525669+00:00
|
2024-12-02T05:10:19.525693+00:00
| 4 | false |
# Intuition\nTo maximize the number of target nodes, we need to compute the number of nodes reachable from each node in the trees for a given distance $$k$$. This requires efficiently combining information from both trees to calculate the contribution of each node.\n\n# Approach\n1. **Tree Representation**: Represent both trees as adjacency lists.\n2. **Target Node Calculation for $$Tree_1$$**: Perform two DFS traversals (forward and backward) to calculate the number of target nodes reachable from each node up to distance $$k$$.\n3. **Target Node Calculation for $$Tree_2$$**: Repeat the calculation for $$Tree_2$$ but for $$k\u22121$$ since we need to connect it to $$Tree_1$$.\n4. **Aggregate Results**: Use the computed results from $$Tree_2$$ to calculate the maximum additional nodes that can be reached when connecting the trees. Combine this with $$Tree_1$$\u2019s reachability to compute the final result.\n\n# Complexity\n- Time complexity: $$O(n_1 + n_2)$$\n- Space complexity: $$O(n_1 + n_2)$$\n\nwhere $$n_1$$ and $$n_2$$ are the number of nodes in $$Tree_1$$ and $$Tree_2$$, respectively. Each node and edge is visited once.\n\n# Code\n```cpp []\nclass Solution {\n // Helper function to compute target nodes reachable from the subtree of each node\n void forwardDFS(const vector<vector<int>> &graph, vector<vector<int>> &targets, const int &k, const int &curr, const int &prev) {\n targets[curr][0] = 1; // Base case: current node can reach itself\n for(const auto &next: graph[curr]) {\n if(next == prev) {\n continue; // Avoid revisiting the parent node\n }\n forwardDFS(graph, targets, k, next, curr); // Recursive DFS for children\n for(int i = 1; i <= k; i++) {\n targets[curr][i] += targets[next][i - 1]; // Add reachable nodes from the child\n }\n }\n }\n \n // Helper function to compute additional target nodes considering nodes outside the subtree\n void backwardDFS(const vector<vector<int>> &graph, vector<vector<int>> &targets, const int &k, const int &curr, const int &prev) {\n for(const auto &next: graph[curr]) {\n if(next == prev) {\n continue; // Avoid revisiting the parent node\n }\n for(int i = k; i > 1; i--) {\n targets[next][i] += targets[curr][i - 1] - targets[next][i - 2]; // Adjust for parent contribution\n }\n targets[next][1] += targets[curr][0]; // Add parent node itself\n backwardDFS(graph, targets, k, next, curr); // Recursive DFS for children\n }\n }\n \n // Calculates the number of target nodes reachable from each node for a given k\n vector<vector<int>> getTargetNodes(const vector<vector<int>> &graph, const int &k) {\n const int n = graph.size();\n vector<vector<int>> targets(n, vector<int>(k + 1, 0)); // DP table for reachable nodes\n forwardDFS(graph, targets, k, 0, -1); // First DFS to populate targets in subtrees\n backwardDFS(graph, targets, k, 0, -1); // Second DFS to adjust for targets outside subtree\n return targets;\n }\n\npublic:\n // Main function to compute the maximum target nodes reachable after connecting two trees\n vector<int> maxTargetNodes(vector<vector<int>>& edges1, vector<vector<int>>& edges2, int k) {\n const int n1 = 1 + edges1.size(); // Number of nodes in first tree\n const int n2 = 1 + edges2.size(); // Number of nodes in second tree\n vector<int> result(n1, 1); // Default result: each node reaches itself\n \n if(k == 0) {\n return result; // If k=0, no additional nodes can be reached\n }\n\n vector<vector<int>> graph1(n1), graph2(n2); // Graph representations for both trees\n for(const auto &edge: edges1) {\n graph1[edge[0]].push_back(edge[1]);\n graph1[edge[1]].push_back(edge[0]); // Build adjacency list for tree 1\n }\n \n if(k == 1) {\n for(int i = 0; i < n1; i++) {\n result[i] = 2 + graph1[i].size(); // Immediate neighbors and self\n }\n return result;\n }\n\n for(const auto &edge: edges2) {\n graph2[edge[0]].push_back(edge[1]);\n graph2[edge[1]].push_back(edge[0]); // Build adjacency list for tree 2\n }\n\n vector<vector<int>> targets1 = getTargetNodes(graph1, k); // Targets for tree 1\n vector<vector<int>> targets2 = getTargetNodes(graph2, k - 1); // Targets for tree 2\n\n int maxExtra = 0; // Max additional targets from tree 2\n for(const auto &target: targets2) {\n maxExtra = max(maxExtra, accumulate(target.begin(), target.end(), 0)); // Aggregate tree 2 contributions\n }\n\n for(int i = 0; i < n1; i++) {\n result[i] = maxExtra + accumulate(targets1[i].begin(), targets1[i].end(), 0); // Total reachable nodes\n }\n return result;\n }\n};\n\n```
| 0 | 0 |
['C++']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
C++ SIMPLE SOLUTION
|
c-simple-solution-by-sai_sohan-cj1m
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
sai_sohan
|
NORMAL
|
2024-12-02T05:06:15.420792+00:00
|
2024-12-02T05:06:15.420834+00:00
| 1 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n vector<int> maxTargetNodes(vector<vector<int>>& edges1, vector<vector<int>>& edges2, int k) {\n unordered_map<int, vector<int>> mp1, mp2;\n vector<int> ans;\n\n // Build adjacency lists\n for (auto& edge : edges1) {\n mp1[edge[0]].push_back(edge[1]);\n mp1[edge[1]].push_back(edge[0]);\n }\n for (auto& edge : edges2) {\n mp2[edge[0]].push_back(edge[1]);\n mp2[edge[1]].push_back(edge[0]);\n }\n\n // Handle edge case when k == 0\n if (k == 0) {\n for (auto& [node, _] : mp1) {\n ans.push_back(1); // Each node can reach only itself\n }\n return ans;\n }\n\n vector<int> v1(mp1.size());\n vector<int> v2(mp2.size());\n int u = INT_MIN;\n\n // BFS for graph 1 (mp1)\n for (auto& [start, _] : mp1) {\n int h = k, c = 1;\n unordered_set<int> visited;\n queue<int> q;\n\n visited.insert(start);\n q.push(start);\n\n while (!q.empty() && h > 0) {\n int size = q.size();\n while (size--) {\n int current = q.front();\n q.pop();\n\n for (int neighbor : mp1[current]) {\n if (visited.find(neighbor) == visited.end()) {\n visited.insert(neighbor);\n q.push(neighbor);\n c++;\n }\n }\n }\n h--;\n }\n v1[start] = c;\n }\n\n // BFS for graph 2 (mp2)\n for (auto& [start, _] : mp2) {\n int h = k - 1, c = 1;\n unordered_set<int> visited;\n queue<int> q;\n\n visited.insert(start);\n q.push(start);\n\n while (!q.empty() && h > 0) {\n int size = q.size();\n while (size--) {\n int current = q.front();\n q.pop();\n\n for (int neighbor : mp2[current]) {\n if (visited.find(neighbor) == visited.end()) {\n visited.insert(neighbor);\n q.push(neighbor);\n c++;\n }\n }\n }\n h--;\n }\n u = max(u, c);\n }\n\n // Combine results\n for (auto& count : v1) {\n ans.push_back(count + u);\n }\n\n return ans;\n }\n};\n\n```
| 0 | 0 |
['C++']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
3372. Maximize the Number of Target Nodes After Connecting Trees I
|
3372-maximize-the-number-of-target-nodes-nwnl
|
Intuition\n Describe your first thoughts on how to solve this problem. \nGiven two trees, T1 and T2, and an integer k, we want to find the maximum number of nod
|
crypto6knight9
|
NORMAL
|
2024-12-02T02:50:46.894333+00:00
|
2024-12-02T02:50:46.894357+00:00
| 4 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nGiven two trees, T1 and T2, and an integer k, we want to find the maximum number of nodes in T1 that are at most k edges away from each node i in T1 after connecting i to a node in T2.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFor each tree, calculate the distance from each node to all other nodes. This can be done using a simple Breadth-First Search (BFS) traversal.\nStore the distances in a 2D matrix for each tree.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int[] maxTargetNodes(int[][] edges1, int[][] edges2, int k) {\n int n = edges1.length + 1, m = edges2.length + 1;\n List<Integer>[] adj = new List[m];\n for (int i = 0; i < m; i++) {\n adj[i] = new ArrayList<>();\n }\n for (int[] e : edges2) {\n adj[e[0]].add(e[1]);\n adj[e[1]].add(e[0]);\n }\n int max = 0;\n for (int i = 0; i < m; i++) {\n max = Math.max(max, bfs(adj, m, i, k - 1));\n }\n adj = new List[n];\n for (int i = 0; i < n; i++) {\n adj[i] = new ArrayList<>();\n }\n for (int[] e : edges1) {\n adj[e[0]].add(e[1]);\n adj[e[1]].add(e[0]);\n }\n int[] res = new int[n];\n for (int i = 0; i < n; i++) {\n res[i] = bfs(adj, n, i, k) + max;\n }\n return res;\n }\n\n static int bfs(List<Integer>[] adj, int n, int start, int k) {\n if (k < 0) {\n return 0;\n }\n boolean[] seen = new boolean[n];\n Queue<Integer> q = new LinkedList<>();\n q.add(start);\n seen[start] = true;\n int res = 0, step = 0;\n while (!q.isEmpty() && step <= k) {\n int sz = q.size();\n res += sz;\n for (int i = 0; i < sz; i++) {\n int node = q.poll();\n for (int neighbor : adj[node]) {\n if (!seen[neighbor]) {\n seen[neighbor] = true;\n q.add(neighbor);\n }\n }\n }\n step++;\n }\n return res;\n }\n \n}\n```
| 0 | 0 |
['Java']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
BFS level order traversal
|
bfs-level-order-traversal-by-punitpunde-mjbb
|
Intuition\nUse BFS to compute the number of nodes reachable within \n\uD835\uDC58\nk levels in both trees. Combine these results to find the maximum possible no
|
PunitPunde
|
NORMAL
|
2024-12-02T01:41:25.276946+00:00
|
2024-12-02T01:41:25.277000+00:00
| 5 | false |
# Intuition\nUse BFS to compute the number of nodes reachable within \n\uD835\uDC58\nk levels in both trees. Combine these results to find the maximum possible nodes reachable for each node in Tree 1.\n\n# Approach\n1. Build adjacency lists for both trees.\nUse BFS to calculate the maximum reachable nodes in Tree 2 for all possible roots.\n2. For each node in Tree 1, compute the sum of its reachable nodes (using BFS) and the precomputed maximum from Tree 2.\n\n# Complexity\n- Time complexity: $$O(n* n + m * m)$$ \n\n- Space complexity: $$O(n + m)$$\n\n# Code\n```java []\nimport java.util.*;\n\nclass Solution {\n public int[] maxTargetNodes(int[][] edges1, int[][] edges2, int k) {\n int n = edges1.length + 1;\n int m = edges2.length + 1;\n List<List<Integer>> tree1 = buildAdjList(n, edges1);\n List<List<Integer>> tree2 = buildAdjList(m, edges2);\n int max = 0;\n for (int i = 0; i < m; i++) {\n max = Math.max(bfs(tree2, i, k - 1), max);\n }\n int ans[] = new int[n];\n for (int i = 0; i < n; i++) {\n ans[i] = bfs(tree1, i, k) + max;\n }\n return ans;\n }\n private int bfs(List<List<Integer>> tree, int start, int k) {\n if (k == -1) {\n return 0;\n }\n\n Queue<Integer> q = new LinkedList<>();\n int[] vis = new int[tree.size()];\n vis[start] = 1;\n q.add(start);\n int c = 1;\n\n while (k > 0 && !q.isEmpty()) {\n int size = q.size(); // Number of nodes at the current level\n for (int i = 0; i < size; i++) {\n int curr = q.poll();\n for (int a : tree.get(curr)) {\n if (vis[a] == 0) {\n vis[a] = 1;\n q.add(a);\n c++;\n }\n }\n }\n k--; // Decrement k after finishing the current level\n }\n\n return c;\n }\n private List<List<Integer>> buildAdjList(int nodes, int[][] edges) {\n List<List<Integer>> adj = new ArrayList<>();\n for (int i = 0; i < nodes; i++) {\n adj.add(new ArrayList<>());\n }\n for (int[] edge : edges) {\n adj.get(edge[0]).add(edge[1]);\n adj.get(edge[1]).add(edge[0]);\n }\n return adj;\n }\n}\n\n```
| 0 | 0 |
['Java']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Simple DFS
|
simple-dfs-by-opsac123-749r
|
O(n + m)\n\n# Code\npython3 []\nclass Solution:\n def maxTargetNodes(self, edges1: List[List[int]], edges2: List[List[int]], k: int) -> List[int]:\n \
|
Oretrestw375
|
NORMAL
|
2024-12-02T00:14:44.586385+00:00
|
2024-12-02T00:14:44.586428+00:00
| 12 | false |
O(n + m)\n\n# Code\n```python3 []\nclass Solution:\n def maxTargetNodes(self, edges1: List[List[int]], edges2: List[List[int]], k: int) -> List[int]:\n \n graph2 = defaultdict(list)\n for start, end in edges2:\n graph2[start].append(end)\n graph2[end].append(start)\n\n def dfs(node, steps):\n if steps == k or node in self.seen:\n return\n \n self.cnt += 1\n self.seen.add(node)\n for child in self.graph[node]:\n dfs(child, steps + 1)\n \n lookup2 = defaultdict(int)\n self.graph = deepcopy(graph2)\n\n # we look uptill depth k - 1 for graph2\n for i in range(0, len(edges2) + 1):\n self.cnt = 0\n self.seen = set()\n dfs(i, 0)\n lookup2[i] = self.cnt\n\n graph1 = defaultdict(list)\n for start, end in edges1:\n graph1[start].append(end)\n graph1[end].append(start)\n\n lookup1 = defaultdict(int)\n self.graph = deepcopy(graph1)\n\n # we look uptill depth k for graph1\n for i in range(0, len(edges1) + 1):\n self.cnt = 0\n self.seen = set()\n dfs(i, -1)\n lookup1[i] = self.cnt\n\n max_key_2 = max(lookup2.values())\n \n ans = []\n for i in range(0, len(edges1) + 1):\n ans.append(lookup1[i] + max_key_2)\n \n return ans\n```
| 0 | 0 |
['Python3']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Java - BFS
|
java-bfs-by-biolearning-bhwp
|
\n\n# Code\njava []\nclass Solution {\n public int[] maxTargetNodes(int[][] edges1, int[][] edges2, int k) {\n Map<Integer, List<Integer>> graph1 = bu
|
biolearning
|
NORMAL
|
2024-12-01T23:48:40.103900+00:00
|
2024-12-01T23:48:40.103931+00:00
| 3 | false |
\n\n# Code\n```java []\nclass Solution {\n public int[] maxTargetNodes(int[][] edges1, int[][] edges2, int k) {\n Map<Integer, List<Integer>> graph1 = buildGraph(edges1);\n int n = edges1.length + 1;\n int[] cnt1 = new int[n];\n for (int from = 0; from < n; from++) {\n cnt1[from] = getNodesWithinK(graph1, from, k);\n }\n\n Map<Integer, List<Integer>> graph2 = buildGraph(edges2);\n int m = edges2.length + 1;\n int[] cnt2 = new int[m];\n int max = -1;\n for (int from = 0; from < m; from++) {\n cnt2[from] = getNodesWithinK(graph2, from, k-1);\n max = Math.max(max, cnt2[from]);\n };\n\n // System.out.println("cnt1: " + Arrays.toString(cnt1));\n // System.out.println("cnt2: " + Arrays.toString(cnt2));\n\n int[] res = new int[n];\n for (int i = 0; i < n; i++) {\n res[i] = cnt1[i] + max;\n }\n return res;\n }\n\n int getNodesWithinK (Map<Integer, List<Integer>> graph, int from, int k) {\n Queue<int[]> queue = new LinkedList<>();\n queue.offer(new int[]{from, -1});\n\n int cnt = 0;\n int layer = 0;\n while (!queue.isEmpty() && layer <= k) {\n int size = queue.size();\n for (int i = 0; i < size; i++) {\n int[] arr = queue.poll();\n int curr = arr[0], parent = arr[1];\n for (int next : graph.get(curr)) {\n if (next == parent) continue;\n queue.offer(new int[]{next, curr});\n }\n cnt++;\n }\n layer++;\n }\n return cnt;\n }\n\n Map<Integer, List<Integer>> buildGraph(int[][] edges) {\n int n = edges.length + 1;\n Map<Integer, List<Integer>> graph = new HashMap<>();\n\n for (int[] edge : edges) {\n int a = edge[0], b = edge[1];\n graph.computeIfAbsent(a, k -> new ArrayList<>()).add(b);\n graph.computeIfAbsent(b, k -> new ArrayList<>()).add(a);\n }\n\n return graph;\n } \n}\n```
| 0 | 0 |
['Java']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
USING BFS in both trees
|
using-bfs-in-both-trees-by-shubh_gupta21-0g8m
|
Intuition\n Describe your first thoughts on how to solve this problem. \nUSING BFS in both tree to count node at distance k in tree1 and maximum number of node
|
shubh_gupta21
|
NORMAL
|
2024-12-01T20:48:08.091151+00:00
|
2024-12-01T20:48:08.091195+00:00
| 13 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUSING BFS in both tree to count node at distance k in tree1 and maximum number of node at distance k-1 in tree 2 .\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(V.(V+E))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(V+E)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n // int s;\n int solve(unordered_map<int, vector<int>>& adj, int start, int k, int s) {\n queue<int> q;\n vector<int> vis(s + 1, 0);\n int cnt = 0;\n q.push(start);\n int dist = 0;\n vis[start] = 1;\n\n while (!q.empty() and dist <= k) {\n int n = q.size();\n\n for (int i = 0; i < n; i++) {\n\n auto it = q.front();\n q.pop();\n\n int node = it;\n\n cnt++;\n\n for (auto adjNode : adj[node]) {\n if (!vis[adjNode]) {\n q.push(adjNode);\n vis[adjNode] = 1;\n }\n }\n }\n dist++;\n }\n return cnt;\n }\n vector<int> maxTargetNodes(vector<vector<int>>& edges1,\n vector<vector<int>>& edges2, int k) {\n unordered_map<int, vector<int>> adj1;\n unordered_map<int, vector<int>> adj2;\n\n int n1 = edges1.size();\n int n2 = edges2.size();\n\n vector<int> temp1;\n vector<int> ans;\n int maxi = INT_MIN;\n\n for (int i = 0; i < n1; i++) {\n int u = edges1[i][0];\n int v = edges1[i][1];\n\n adj1[u].push_back(v);\n adj1[v].push_back(u);\n }\n\n for (int i = 0; i < n2; i++) {\n int u = edges2[i][0];\n int v = edges2[i][1];\n\n adj2[u].push_back(v);\n adj2[v].push_back(u);\n }\n\n for (int i = 0; i < adj1.size(); i++) {\n int cnt = solve(adj1, i, k, adj1.size());\n temp1.push_back(cnt);\n }\n\n for (int i = 0; i < adj2.size(); i++) {\n\n int cnt = solve(adj2, i, k - 1, adj2.size());\n maxi = max(maxi, cnt);\n }\n\n for (int i = 0; i < adj1.size(); i++) {\n ans.push_back(temp1[i] + maxi);\n }\n return ans;\n }\n};\n```
| 0 | 0 |
['Tree', 'Breadth-First Search', 'Graph', 'C++']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Java Map & DFS Solution
|
java-map-dfs-solution-by-solved-9eua
|
\nclass Solution {\n public int[] maxTargetNodes(int[][] edges1, int[][] edges2, int k) {\n Map<Integer, List<Integer>> tree1 = new HashMap<>();\n
|
solved
|
NORMAL
|
2024-12-01T20:46:10.304527+00:00
|
2024-12-01T20:46:10.304560+00:00
| 1 | false |
```\nclass Solution {\n public int[] maxTargetNodes(int[][] edges1, int[][] edges2, int k) {\n Map<Integer, List<Integer>> tree1 = new HashMap<>();\n Map<Integer, List<Integer>> tree2 = new HashMap<>();\n constructGraph(edges1, tree1);\n constructGraph(edges2, tree2);\n int tree1Size = calculateTreeSize(edges1);\n int tree2Size = calculateTreeSize(edges2);\n int[] result = new int[tree1Size];\n for (int i = 0; i < tree1Size; i++) {\n Set<Integer> set = new HashSet<>();\n set.add(i);\n int size = findKClosest(tree1, i, k, set);\n result[i] = size;\n }\n int maxValue = 0;\n for (int i = 0; i < tree2Size; i++) {\n Set<Integer> set = new HashSet<>();\n set.add(i);\n int size = findKClosest(tree2, i, k - 1, set);\n maxValue = Math.max(maxValue, size);\n }\n for (int i = 0; i < tree1Size; i++) {\n result[i] = result[i] + maxValue;\n }\n return result;\n }\n public void constructGraph(int[][] edges, Map<Integer, List<Integer>> tree) {\n for (int i = 0; i < edges.length; i++) {\n int[] edge = edges[i];\n int start = edge[0];\n int end = edge[1];\n if (tree.containsKey(start)) {\n List<Integer> list = tree.get(start);\n list.add(end);\n tree.put(start, list);\n } else {\n List<Integer> list = new ArrayList<>();\n list.add(end);\n tree.put(start, list);\n } \n if (tree.containsKey(end)) {\n List<Integer> list = tree.get(end);\n list.add(start);\n tree.put(end, list);\n } else {\n List<Integer> list = new ArrayList<>();\n list.add(start);\n tree.put(end, list);\n } \n }\n }\n public int calculateTreeSize(int[][] edges) {\n int size = 0;\n for (int i = 0; i < edges.length; i++) {\n int[] edge = edges[i];\n size = Math.max(size, edge[0]);\n size = Math.max(size, edge[1]);\n }\n return size + 1;\n }\n public int findKClosest(Map<Integer, List<Integer>> map, int node, int k, Set<Integer> visited) {\n if (!map.containsKey(node) || k < 0) {\n return 0;\n }\n int sum = 1;\n List<Integer> neighbors = map.get(node);\n for (int i = 0; i < neighbors.size(); i++) {\n int neighbor = neighbors.get(i);\n if (!visited.contains(neighbor)) {\n visited.add(neighbor);\n sum = sum + findKClosest(map, neighbor, k - 1, visited);\n }\n }\n return sum;\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
beats 100%
|
beats-100-by-bimal_23-12-ntyj
|
Intuition\nfind the indegree of both tree for every node:\nfind the max indegree of second tree: \nthen add the indegree of every node of first tree with max:\n
|
Bimal_23-12
|
NORMAL
|
2024-12-01T19:14:04.052614+00:00
|
2024-12-01T19:14:04.052643+00:00
| 4 | false |
# Intuition\nfind the indegree of both tree for every node:\nfind the max indegree of second tree: \nthen add the indegree of every node of first tree with max:\n\n\n\n# Complexity\n- Time complexity:\nk(n+m)\n\n\n\n# Code\n```java []\nclass Solution {\n class Pair{\n int node;int edgecount;\n Pair(int node,int edgecount)\n {\n this.node=node;\n this.edgecount=edgecount;\n }\n }\n public int[] maxTargetNodes(int[][] edges1, int[][] edges2, int k) \n {\n int n=edges1.length;int m=edges2.length;\n int firsttree[]=new int[n+1];int secondtree[]=new int[m+1];\n List<List<Integer>> adj1=new ArrayList<>();\n List<List<Integer>> adj2=new ArrayList<>();\n for(int i=0;i<n+1;i++)\n {\n adj1.add(new ArrayList<>());\n }\n for(int i=0;i<m+1;i++)\n {\n adj2.add(new ArrayList<>());\n }\n for(int i=0;i<n;i++)\n {\n adj1.get(edges1[i][0]).add(edges1[i][1]);\n adj1.get(edges1[i][1]).add(edges1[i][0]);\n }\n for(int i=0;i<m;i++)\n {\n adj2.get(edges2[i][0]).add(edges2[i][1]);\n adj2.get(edges2[i][1]).add(edges2[i][0]);\n }\n for(int i=0;i<n+1;i++)\n {\n Queue<Pair> queue=new LinkedList<>();\n boolean visited[]=new boolean[n+1];\n queue.add(new Pair(i,0));\n firsttree[i]=bfs(queue,visited,k,adj1);\n }\n for(int i=0;i<m+1 && k>0;i++)\n {\n Queue<Pair> queue=new LinkedList<>();\n boolean visited[]=new boolean[m+1];\n queue.add(new Pair(i,0));\n secondtree[i]=bfs(queue,visited,k-1,adj2); \n }\n int max=0;\n for(int i:secondtree)\n {\n max=Math.max(max,i);\n }\n int [] ans=new int[n+1];\n for(int i=0;i<=n;i++)\n {\n ans[i]=firsttree[i]+max;\n }\n return ans;\n }\n int bfs(Queue<Pair> q,boolean visited [],int k,List<List<Integer>> adj)\n {\n int count=0;\n while(!q.isEmpty())\n {\n Pair p=q.poll();\n \n int nd=p.node;\n int ed=p.edgecount;\n if(visited[nd]) continue;\n visited[nd]=true;\n count+=1;\n for(int neighbour:adj.get(nd))\n {\n if(!visited[neighbour] && ed<k)\n {\n q.add(new Pair(neighbour,ed+1));\n }\n }\n }\n return count;\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Easy Implementation || BFS
|
easy-implementation-bfs-by-dodrairob-cdyn
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
dodrairob
|
NORMAL
|
2024-12-01T19:09:23.321931+00:00
|
2024-12-01T19:31:53.727408+00:00
| 5 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n vector<int> maxTargetNodes(vector<vector<int>>& edges1,\n vector<vector<int>>& edges2, int k) {\n ios::sync_with_stdio(false);\n cin.tie(0);\n cout.tie(0);\n vector<vector<int>> adj(4000, vector<int>());\n int n = edges1.size(), m = edges2.size();\n for (auto a : edges1) {\n adj[a[0]].push_back(a[1]);\n adj[a[1]].push_back(a[0]);\n }\n for (auto a : edges2) {\n adj[2000 + a[0]].push_back(2000 + a[1]);\n adj[2000 + a[1]].push_back(2000 + a[0]);\n }\n vector<int> temp(4000, 0);\n for (int i = 0; i <= n; i++) {\n queue<int> q;\n q.push(i);\n int l = 0;\n vector<int> v(4000, 0);\n v[i] = 1;\n bool ch = false;\n while (!q.empty()) {\n int s = q.size();\n for (int j = 0; j < s; j++) {\n int a = q.front();\n q.pop();\n if (l <= k)\n temp[i]++;\n else {\n ch = true;\n break;\n }\n for (auto c : adj[a]) {\n if (v[c] == 0) {\n q.push(c);\n v[c] = 1;\n }\n }\n }\n if (ch)\n break;\n l++;\n }\n }\n for (int i = 2000; i <= (2000 + m); i++) {\n queue<int> q;\n q.push(i);\n int l = 0;\n vector<int> v(4000, 0);\n v[i] = 1;\n bool ch = false;\n while (!q.empty()) {\n int s = q.size();\n for (int j = 0; j < s; j++) {\n int a = q.front();\n q.pop();\n if (l <= k - 1)\n temp[i]++;\n else {\n ch = true;\n break;\n }\n for (auto c : adj[a]) {\n if (v[c] == 0) {\n q.push(c);\n v[c] = 1;\n }\n }\n }\n if (ch)\n break;\n l++;\n }\n }\n vector<int> ans;\n int q = 0;\n for (int j = 2000; j <= (2000 + m); j++) {\n q = max(q, temp[j]);\n }\n for (int i = 0; i <= n; i++) {\n int l = 0;\n int p = temp[i];\n l = p + q;\n ans.push_back(l);\n }\n return ans;\n }\n};\n```
| 0 | 0 |
['Breadth-First Search', 'Graph', 'C++']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
BFS with Levels || C++ || First thought
|
bfs-with-levels-c-first-thought-by-james-6run
|
Complexity\n- Time complexity: O(N^2 + M^2)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(N + M)\n Add your space complexity here, e.g. O
|
james_thorn
|
NORMAL
|
2024-12-01T18:22:12.269247+00:00
|
2024-12-01T18:22:12.269296+00:00
| 7 | false |
# Complexity\n- Time complexity: O(N^2 + M^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N + M)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int BFS(int i, vector<vector<int>> &adj, int k, vector<int> vis)\n {\n queue<int> q;\n q.push(i);\n vis[i] = 1;\n int sum = 0;\n\n while(!q.empty() && k>0)\n {\n int sz = q.size();\n while(sz--)\n {\n int node = q.front();\n q.pop();\n\n for(auto it : adj[node])\n {\n if(!vis[it])\n {\n sum++;\n vis[it] = 1;\n q.push(it);\n }\n\n }\n }\n k--;\n }\n\n return sum;\n }\n\n vector<int> maxTargetNodes(vector<vector<int>>& edges1, vector<vector<int>>& edges2, int k) {\n int n = edges1.size() + 1;\n int m = edges2.size() + 1;\n vector<int> vis1(n,0) , vis2(m,0);\n vector<vector<int>> adj1(n) , adj2(m);\n\n for(int i=0; i<n-1; i++)\n {\n adj1[edges1[i][0]].push_back(edges1[i][1]);\n adj1[edges1[i][1]].push_back(edges1[i][0]);\n }\n\n for(int i=0; i<m-1; i++)\n {\n adj2[edges2[i][0]].push_back(edges2[i][1]);\n adj2[edges2[i][1]].push_back(edges2[i][0]);\n }\n\n\n int add = 0;\n for(int i=0; i<m; i++)\n {\n int x = BFS(i,adj2,k-1,vis2); // for graph2 finding the max possible\n add = max(add,x); // value with one less edge thats why k-1\n }\n\n vector<int> answer(n,add+1); // every node is a target of itself\n\n for(int i=0; i<n; i++)\n {\n int sum = BFS(i,adj1,k,vis1);\n answer[i] += sum;\n if(k>=1) answer[i]++; // adding 1 for connection to graph2\n }\n\n return answer;\n\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
DFS From every Node
|
dfs-from-every-node-by-yaswanth58-7az1
|
Intuition\n Describe your first thoughts on how to solve this problem. \nFind Max Possible DFS in Tree2 with k-1 which will be inturn added to DFS of each node
|
yaswanth58
|
NORMAL
|
2024-12-01T18:14:59.906984+00:00
|
2024-12-01T18:14:59.907034+00:00
| 4 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFind Max Possible DFS in Tree2 with k-1 which will be inturn added to DFS of each node in Tree1.\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int dfs(int i, int p, vector<vector<int>> &al, int k) {\n if (k <= 0)\n return k == 0;\n int res = 1;\n for (int j : al[i])\n if (j != p)\n res += dfs(j, i, al, k - 1);\n return res;\n}\n\nvector<vector<int>> adjacencyList(vector<vector<int>>& edges) {\nvector<vector<int>> al(edges.size() + 1);\nfor (auto &e: edges) {\n al[e[0]].push_back(e[1]);\n al[e[1]].push_back(e[0]); \n} \nreturn al;\n}\n\n vector<int> maxTargetNodes(vector<vector<int>>& e1, vector<vector<int>>& e2, int k) {\n int m = e1.size() + 1, n = e2.size() + 1, max2 = 0;\n auto al1 = adjacencyList(e1), al2 = adjacencyList(e2);\n vector<int> res(m); \n for(int i=0;i<n;i++)\n {\n max2=max(max2,dfs(i,-1,al2,k-1));\n } \n\n for(int i=0;i<m;i++)\n {\n res[i]=dfs(i,-1,al1,k)+max2;\n }\n return res;\n\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Java Solution using BFS (Finding Max Neighbors at a fixed distance)
|
java-solution-using-bfs-finding-max-neig-gjs3
|
Intuition\nWe can observe that adding an edge from one tree to another should be done in a way which maximises the total target nods.(i.e nodes which are reacha
|
lohith17
|
NORMAL
|
2024-12-01T17:53:56.639668+00:00
|
2024-12-01T17:53:56.639711+00:00
| 4 | false |
# Intuition\nWe can observe that adding an edge from one tree to another should be done in a way which maximises the total target nods.(i.e nodes which are reachable from the current node within the distance k), this can only happen when we attach an edge from the current node to the node which has max neighbors at depth (k-1) in the second tree. Once we identify this max node, we can find the max neighbors in the first tree for each node and add the max neighbors from the second tree.\n\n\n# Code\n```java []\nclass Solution {\n Map<Integer, List<Integer>> hm2;\n Map<Integer, List<Integer>> hm1;\n \n public int tree1bfs(int node, int count){\n int neighborCount = 0;\n Deque<Integer> queue = new LinkedList<>();\n queue.offer(node);\n Set<Integer> visited = new HashSet<>();\n while(!queue.isEmpty() && count >= 0){\n int size = queue.size();\n neighborCount += size;\n for(int i = 0; i < size; i++){\n int n = queue.pollFirst();\n if(!visited.contains(n)){\n visited.add(n);\n if(hm1.containsKey(n)){\n List<Integer> neighbor = hm1.get(n);\n for(int j = 0; j < neighbor.size(); j++){\n if(!visited.contains(neighbor.get(j))){\n queue.offer(neighbor.get(j));\n }\n }\n }\n }\n }\n count -= 1;\n }\n\n return neighborCount;\n }\n \n public int bfs(int node, int count){\n int neighborCount = 0;\n Deque<Integer> queue = new LinkedList<>();\n queue.offer(node);\n Set<Integer> visited = new HashSet<>();\n while(!queue.isEmpty() && count >= 0){\n int size = queue.size();\n neighborCount += size;\n for(int i = 0; i < size; i++){\n int n = queue.pollFirst();\n if(!visited.contains(n)){\n visited.add(n);\n if(hm2.containsKey(n)){\n List<Integer> neighbor = hm2.get(n);\n for(int j = 0; j < neighbor.size(); j++){\n if(!visited.contains(neighbor.get(j))){\n queue.offer(neighbor.get(j));\n }\n }\n }\n }\n }\n count -= 1;\n }\n\n return neighborCount;\n }\n public int[] maxTargetNodes(int[][] edges1, int[][] edges2, int k) {\n // get the count of max nodes reachable with k-1 edges in tree 2\n hm2 = new HashMap<>();\n for(int i = 0; i < edges2.length; i++){\n int from = edges2[i][0];\n int to = edges2[i][1];\n if(hm2.containsKey(from)){\n List<Integer> li = hm2.get(from);\n li.add(to);\n hm2.put(from, li);\n }\n else{\n List<Integer> li = new ArrayList<>();\n li.add(to);\n hm2.put(from, li);\n }\n if(hm2.containsKey(to)){\n List<Integer> li = hm2.get(to);\n li.add(from);\n hm2.put(to, li);\n }\n else{\n List<Integer> li = new ArrayList<>();\n li.add(from);\n hm2.put(to, li);\n }\n }\n\n int max = Integer.MIN_VALUE;\n for(int i = 0; i <= edges2.length; i++){\n int neighborCount = bfs(i, k-1);\n if(neighborCount > max){\n max = neighborCount;\n }\n }\n\n\n //get the count of elements which are reachable within k depth in tree 1\n\n hm1 = new HashMap<>();\n for(int i = 0; i < edges1.length; i++){\n int from = edges1[i][0];\n int to = edges1[i][1];\n if(hm1.containsKey(from)){\n List<Integer> li = hm1.get(from);\n li.add(to);\n hm1.put(from, li);\n }\n else{\n List<Integer> li = new ArrayList<>();\n li.add(to);\n hm1.put(from, li);\n }\n if(hm1.containsKey(to)){\n List<Integer> li = hm1.get(to);\n li.add(from);\n hm1.put(to, li);\n }\n else{\n List<Integer> li = new ArrayList<>();\n li.add(from);\n hm1.put(to, li);\n }\n }\n\n int[] ans = new int[edges1.length+1];\n for(int i = 0; i <= edges1.length; i++){\n ans[i] = tree1bfs(i, k) + max;\n }\n return ans;\n }\n}\n```
| 0 | 0 |
['Breadth-First Search', 'Java']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Easy BFS Solution || C++
|
easy-bfs-solution-c-by-nayandubey08-d03n
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n/\n1.Make Adjacency Lis
|
nayandubey08
|
NORMAL
|
2024-12-01T17:44:36.139676+00:00
|
2024-12-01T17:44:36.139723+00:00
| 7 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n/*\n1.Make Adjacency List for both the given graph(make it directed)\n2.Apply BFS for each node in each graph and find how many nodes have been connected with each source node\n 2.1-> for graph1 consider for K range\n 2.2-> for graph2 consider for K-1 range (because 1 edge will be added while connecting node from graph1 to node from graph2)\n3.Prepare result for each node and take only maxCount of node in graph2\n*/\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n/*\n1.Make Adjacency List for both the given graph(make it directed)\n2.Apply BFS for each node in each graph and find how many nodes have been connected with each source node\n 2.1-> for graph1 consider for K range\n 2.2-> for graph2 consider for K-1 range (because 1 edge will be added while connecting node from graph1 to node from graph2)\n3.Prepare result for each node and take only maxCount of node in graph2\n*/\n vector<int> maxTargetNodes(vector<vector<int>>& edges1, vector<vector<int>>& edges2, int k) {\n int m=edges1.size();\n int n=edges2.size();\n vector<vector<int>> adj1(m+1);\n vector<vector<int>> adj2(n+1);\n //make adjacency list for 1 tree with m nodes\n for(auto arr:edges1)\n {\n adj1[arr[0]].push_back(arr[1]);\n adj1[arr[1]].push_back(arr[0]);\n }\n //make adjacency list for 2 tree with n nodes\n for(auto arr:edges2)\n {\n adj2[arr[0]].push_back(arr[1]);\n adj2[arr[1]].push_back(arr[0]);\n }\n // take map to count ,how many nodes have connected with src node in a K range for 1 tree\n // take map to count ,how many nodes have connected with src node in a K-1 range for 2 tree\n unordered_map<int,int> m1,m2;\n int largest=0;\n for(int node=0;node<=m;node++)\n {\n queue<pair<int,int>> q;\n vector<int> visited(m+1,-1);\n q.push({node,0});\n visited[node]=1;\n m1[node]++;\n while(q.size()!=0)\n {\n int n=q.front().first;\n int h=q.front().second;\n q.pop();\n if(h+1>k) break;\n for(auto itr:adj1[n])\n {\n if(visited[itr]==-1)\n {\n m1[node]++;\n visited[itr]=1;\n q.push({itr,h+1});\n }\n }\n }\n }\n for(int node=0;node<=n;node++)\n {\n queue<pair<int,int>> q;\n vector<int> visited(n+1,-1);\n q.push({node,0});\n visited[node]=1;\n if(k>0) m2[node]++;\n while(q.size()!=0)\n {\n int n=q.front().first;\n int h=q.front().second;\n q.pop();\n if(h+1>k-1) break;\n for(auto itr:adj2[n])\n {\n if(visited[itr]==-1)\n {\n m2[node]++;\n visited[itr]=1;\n q.push({itr,h+1});\n }\n }\n }\n //we are taking maxCount in 2 tree ,bcz it will max our result\n largest=max(m2[node],largest);\n }\n //iterating for each node in tree1\n vector<int> result(m+1);\n for(int i=0;i<=m;i++)\n {\n result[i]=m1[i]+largest;\n }\n return result;\n }\n};\n```
| 0 | 0 |
['Graph', 'C++']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Bread first search | Brute force
|
bread-first-search-brute-force-by-chirag-yi0q
|
Code\njava []\n\nclass Solution {\n public int[] maxTargetNodes(int[][] edges1, int[][] edges2, int k) {\n int n = edges1.length + 1;\n int m =
|
chiragnayak10
|
NORMAL
|
2024-12-01T16:30:18.554663+00:00
|
2024-12-01T16:30:18.554701+00:00
| 1 | false |
# Code\n```java []\n\nclass Solution {\n public int[] maxTargetNodes(int[][] edges1, int[][] edges2, int k) {\n int n = edges1.length + 1;\n int m = edges2.length + 1;\n\n List<List<Integer>> tree1 = new ArrayList<>();\n List<List<Integer>> tree2 = new ArrayList<>();\n\n for (int i = 0; i < n; i++) tree1.add(new ArrayList<>());\n for (int i = 0; i < m; i++) tree2.add(new ArrayList<>());\n\n for (int[] edge : edges1) {\n tree1.get(edge[0]).add(edge[1]);\n tree1.get(edge[1]).add(edge[0]);\n }\n\n\n for (int[] edge : edges2) {\n tree2.get(edge[0]).add(edge[1]);\n tree2.get(edge[1]).add(edge[0]);\n }\n\n int f2 = 0;\n for (int i = 0; i < m; i++) {\n f2 = Math.max(f2, bfs(tree2, k - 1, i));\n }\n\n int[] answer = new int[n];\n for (int i = 0; i < n; i++) {\n answer[i] = f2 + bfs(tree1, k, i);\n }\n\n return answer;\n }\n\n public int bfs(List<List<Integer>> graph, int k, int src) {\n Queue<Integer> q = new LinkedList<>();\n boolean[] visited = new boolean[graph.size()];\n q.add(src);\n visited[src] = true;\n int cnt = 0;\n\n while (k >= 0) {\n int sz = q.size();\n cnt += sz;\n\n for (int i = 0; i < sz; i++) {\n int curr = q.poll();\n for (int neighbor : graph.get(curr)) {\n if (!visited[neighbor]) {\n q.add(neighbor);\n visited[neighbor] = true;\n }\n }\n }\n k--;\n }\n\n return cnt;\n }\n}\n\n```
| 0 | 0 |
['Tree', 'Breadth-First Search', 'Queue', 'Java']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
bfs on all nodes: a working solution
|
bfs-on-all-nodes-a-working-solution-by-l-0hz1
|
Intuition\n- the targets reachable from u with at most k edges,is obviously bfs doable, with O(N^2)\n\n \n\n# Code\ncpp []\nclass Solution {\npublic:\n vecto
|
lambdacode-dev
|
NORMAL
|
2024-12-01T16:08:18.046282+00:00
|
2024-12-01T16:08:18.046309+00:00
| 0 | false |
# Intuition\n- the targets reachable from `u` with at most `k` edges,is obviously `bfs` doable, with `O(N^2)`\n\n \n\n# Code\n```cpp []\nclass Solution {\npublic:\n vector<int> maxTargetNodes(vector<vector<int>>& edges1, vector<vector<int>>& edges2, const int k) {\n int n = edges1.size() + 1; vector<unordered_set<int>> adj1(n);\n int m = edges2.size() + 1; vector<unordered_set<int>> adj2(m);\n auto mkadj = [](vector<vector<int>>& edges,vector<unordered_set<int>>& adj) {\n for(auto const& e : edges) {\n int u = e[0], v = e[1];\n adj[u].insert(v);\n adj[v].insert(u);\n }\n };\n mkadj(edges1, adj1);\n mkadj(edges2, adj2);\n \n auto bfs = [](vector<unordered_set<int>>const& adj, int u, int k) {\n if(k < 0) return 0;\n int reaches = 0;\n queue<int> q;\n q.push(u);\n unordered_set<int> visited;\n while(!q.empty() && k-- >= 0) {\n for(int sz = q.size(); sz; --sz) {\n int a = q.front();\n q.pop();\n ++reaches;\n visited.insert(a);\n for(auto b : adj[a]) {\n if(!visited.contains(b)) \n q.push(b);\n }\n }\n }\n return reaches;\n };\n vector<int> t1(n); for(int u = 0; u < n; ++u) t1[u] = bfs(adj1, u, k);\n vector<int> t2(m); for(int u = 0; u < m; ++u) t2[u] = bfs(adj2, u, k-1);\n int maxt2 = *max_element(t2.begin(), t2.end());\n for(auto & a : t1) a += maxt2;\n return t1;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Simple DFS Based Solution With proper comments
|
simple-dfs-based-solution-with-proper-co-jviz
|
Intuition\nDFS to find sum of nodes upto\n 1. k-1th level in tree 2\n 2. kth level in tree 1\n\n \nSum above 2\n\n# Complexity\n- Time complexity: O(n) \n Add y
|
SJ4u
|
NORMAL
|
2024-12-01T15:31:20.799446+00:00
|
2024-12-01T15:31:20.799484+00:00
| 0 | false |
# Intuition\nDFS to find sum of nodes upto\n 1. k-1th level in tree 2\n 2. kth level in tree 1\n\n \nSum above 2\n\n# Complexity\n- Time complexity: $$O(n)$$ \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$ \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n\n //simple dfs to get sum of nodes uptil level k\n int compute_at_k(int node,int level,int k,unordered_map<int,vector<int>>&graph,unordered_map<int,int>&visited){\n\n if(level>k)\n return 0;\n if(level==k)\n return 1;\n \n int ans = 1;\n visited[node] = 1;\n for(auto x:graph[node]){\n if(!visited[x]){\n visited[x] = 1;\n ans+=compute_at_k(x,level+1,k,graph,visited);\n }\n }\n return ans;\n }\n vector<int> maxTargetNodes(vector<vector<int>>& edges1, vector<vector<int>>& edges2, int k) {\n int n = edges1.size(),m=edges2.size(),max_pot=1;\n unordered_map<int,vector<int>>graph1,graph2;\n unordered_map<int,int>visited;\n vector<int>ans;\n\n //constructing graphs here\n for(auto x:edges2){\n graph2[x[0]].push_back(x[1]);\n graph2[x[1]].push_back(x[0]);\n }\n for(auto x:edges1){\n graph1[x[0]].push_back(x[1]);\n graph1[x[1]].push_back(x[0]);\n }\n\n\n //finding max_potential i.e. max nodes at k-1 level in graph2\n if(k!=0){\n for(int i=0;i<=m;i++){\n visited.clear();\n max_pot = max(max_pot,compute_at_k(i,0,k-1,graph2,visited));\n }\n } else{\n max_pot = 0;\n }\n\n cout<<"Max_Potential :"<<max_pot<<endl; \n\n for(int i=0;i<=n;i++){\n visited.clear();\n int nodes_at_k = compute_at_k(i,0,k,graph1,visited);\n ans.push_back(max_pot+nodes_at_k);\n }\n\n return ans; \n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
BFS solution - Python3
|
bfs-solution-python3-by-g_asritha-2jfa
|
Intuition\nWe have to the target nodes at \'k\' distance which gives us the idea to use BFS.\n\n# Approach\nWe are asked to maximize the output in the quesion.
|
g_asritha
|
NORMAL
|
2024-12-01T14:38:16.928345+00:00
|
2024-12-01T14:38:16.928393+00:00
| 8 | false |
# Intuition\nWe have to the target nodes at \'k\' distance which gives us the idea to use BFS.\n\n# Approach\nWe are asked to maximize the output in the quesion. If we see carefully, the only changing parameter in the output array is the node from tree1. Which means we can get the maximum degree of a node from tree2 connect that node to every node from tree1 to get the maximum output.\nNote - Since we are connecting a node from tree1 to tree2 the distance reduces to \'k-1\' for tree2.\nSo, we can get the node which has the maximum target nodes in tree2 at distance "K-1" and add this value to every node from tree1 in the resultant array.\n\n# Complexity\n- Time complexity:\nFor tree2 - O(M*(V2 + E2))\nFor tree1 - O(N*(V1 + E1))\nTotal = M^2 + N^2 (in the worst case if k is very high)\n\n(Please correct me if I am wrong!)\n\n- Space complexity:\nTotal = O(N + M) (using a hashmap to store trees)\n\n# Code\n```python3 []\nclass Solution:\n def maxTargetNodes(self, edges1: List[List[int]], edges2: List[List[int]], k: int) -> List[int]:\n tree2 = defaultdict(list)\n for u,v in edges2:\n tree2[u].append(v)\n tree2[v].append(u)\n\n # bfs to find the no of nodes at dist \'d\' from the curr node in tree\n def bfs(node, d, tree):\n q = deque([node])\n visited = set()\n res = 0\n while q and d>=0: # every node is target to itself\n res += len(q)\n for _ in range(len(q)):\n curr = q.popleft()\n visited.add(curr)\n for ele in tree[curr]:\n if ele not in visited:\n q.append(ele)\n d -= 1\n return res\n\n # getting the maximum degree from tree2 so that node from tree1 can connect and maximixe it\'s target nodes.\n max_d2 = float(\'-inf\')\n for node in tree2:\n d2 = bfs(node, k-1, tree2)\n max_d2 = max(max_d2, d2)\n \n tree1 = defaultdict(list)\n for u,v in edges1:\n tree1[u].append(v)\n tree1[v].append(u)\n \n # getting the degree from tree1 first and then adding the max value we have from tree2 to maximize the overall output.\n res = [0]*len(tree1)\n for node in tree1:\n d1 = bfs(node, k, tree1)\n res[node] = (d1 + max_d2)\n return res\n```
| 0 | 0 |
['Python3']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
JAVA Solution
|
java-solution-by-ayushsarda-yu6v
|
Intuition\nFirst of all the question wants us to calculate how many nodes satisfy target condition, which essentially means number of nodes which can be reached
|
ayushsarda
|
NORMAL
|
2024-12-01T13:59:18.333018+00:00
|
2024-12-01T13:59:18.333050+00:00
| 6 | false |
# Intuition\nFirst of all the question wants us to calculate how many nodes satisfy target condition, which essentially means number of nodes which can be reached with atmost k edges. We need to calculate maximum of this if you are allowed to take any node from tree1 and connect it to tree2.\n\n# Approach\nThe solution is pretty simple. You just need to calculate target nodes for each node from tree1 with k as the maximum edge count.\nIf you connect one node randomly with a node from tree2, you are creating one edge to make that connection. You need to calculate target nodes for each node in tree2 with (k - 1) as the maximum edge count. This is done to ensure the edge made from tree1, when accounted for, will result in target nodes from tree2 with k as edge count.\nA simple BFS on the entire tree is done for both of them with k and (k - 1) respectively, as the deciding parameter to satisfy target count. Once that is done, you just need to find the maximum value of target nodes amongst all the nodes from tree2. Add the maximum value to the target nodes of tree1 for each node and that is your answer.\n\n# Code\n```java []\nclass Solution {\n\n // add null after each layer of nodes is complete to be able to count number layers we are deep\n private void computeTargetNodes(Map<Integer, List<Integer>> graph, Map<Integer, Integer> target, int i, int n, int k) {\n Queue<Integer> q = new LinkedList<>();\n int[] visited = new int[n];\n q.add(i);\n q.add(null);\n visited[i] = 1;\n int layers = 0;\n int targetNodesCount = 0;\n while (!q.isEmpty()) {\n if (layers > k) break;\n Integer el = q.poll();\n if (el == null && !q.isEmpty()) {\n q.add(null);\n layers++;\n } else if (el != null) {\n targetNodesCount++;\n for (int node: graph.getOrDefault(el, new ArrayList<>())) {\n if (visited[node] == 0) {\n q.add(node);\n visited[node] = 1;\n }\n }\n }\n }\n target.put(i, targetNodesCount);\n return;\n }\n\n public int[] maxTargetNodes(int[][] edges1, int[][] edges2, int k) {\n int n = edges1.length + 1;\n int m = edges2.length + 1;\n\n // create graphs\n Map<Integer, List<Integer>> g1 = new HashMap<>();\n for (int[] e: edges1) {\n List<Integer> arr = g1.getOrDefault(e[0], new ArrayList<>());\n arr.add(e[1]);\n g1.put(e[0], arr);\n\n arr = g1.getOrDefault(e[1], new ArrayList<>());\n arr.add(e[0]);\n g1.put(e[1], arr);\n }\n\n Map<Integer, List<Integer>> g2 = new HashMap<>();\n for (int[] e: edges2) {\n List<Integer> arr = g2.getOrDefault(e[0], new ArrayList<>());\n arr.add(e[1]);\n g2.put(e[0], arr);\n\n arr = g2.getOrDefault(e[1], new ArrayList<>());\n arr.add(e[0]);\n g2.put(e[1], arr);\n }\n\n // calculate target nodes for each node\n Map<Integer, Integer> target1 = new HashMap<>();\n for (int i = 0; i < n; i++) {\n computeTargetNodes(g1, target1, i, n, k);\n }\n\n Map<Integer, Integer> target2 = new HashMap<>();\n for (int i = 0; i < m; i++) {\n computeTargetNodes(g2, target2, i, m, k - 1);\n }\n\n // compute max count of target nodes amongst all nodes from tree2\n int mx = Integer.MIN_VALUE;\n for (Map.Entry<Integer, Integer> el: target2.entrySet()) {\n mx = Math.max(mx, el.getValue());\n }\n\n // add that to each node of tree1 to get the answer\n int[] ans = new int[n];\n for (Map.Entry<Integer, Integer> el: target1.entrySet()) {\n ans[el.getKey()] = el.getValue() + mx;\n }\n\n return ans;\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
C++ | BruteForce | BFS |
|
c-bruteforce-bfs-by-n1kh1l-zlzg
|
Intuition\nwe need at most k distance count of nodes for tree1 and maximum distance cout for any node in tree2 we will just add the count from tree1 to max of t
|
n1kh1l
|
NORMAL
|
2024-12-01T13:53:27.888393+00:00
|
2024-12-01T13:53:27.888413+00:00
| 9 | false |
# Intuition\nwe need at most k distance count of nodes for tree1 and maximum distance cout for any node in tree2 we will just add the count from tree1 to max of tree2\n\n# Approach\nuse bfs to count k distance nodes\n\n# Complexity\n- Time complexity:\nO(N * N + M * M)\n\n- Space complexity:\nO(N + M);\n\n# Code\n```cpp []\nclass Solution {\npublic:\n\n int bfs (int root, vector<vector<int>>& adj, int k) {\n\n queue<int> q;\n q.push(root);\n vector<bool> vis(1001, false);\n int level = 0, res = 1;\n while (!q.empty() && level < k) {\n level++;\n int sz = q.size();\n for (int i = 0; i < sz; i++) {\n int node = q.front();\n q.pop();\n vis[node] = true;\n for (auto nbr : adj[node]) {\n if (vis[nbr] == false)\n res++, q.push(nbr);\n }\n }\n }\n return res;\n }\n vector<int> maxTargetNodes(vector<vector<int>>& edges1, vector<vector<int>>& edges2, int k) {\n \n ios::sync_with_stdio(false);\n cin.tie(0); cout.tie(0);\n vector<vector<int>> adj1(edges1.size() + 1), adj2(edges2.size() + 1);\n for (int i = 0; i < edges1.size(); i++) {\n adj1[edges1[i][0]].push_back(edges1[i][1]);\n adj1[edges1[i][1]].push_back(edges1[i][0]);\n }\n for (int i = 0; i < edges2.size(); i++) {\n adj2[edges2[i][0]].push_back(edges2[i][1]);\n adj2[edges2[i][1]].push_back(edges2[i][0]);\n }\n int mx = 0;\n for (int i = 0; i < adj2.size(); i++) {\n mx = max(mx, bfs(i, adj2, k - 1));\n }\n vector<int> res(edges1.size() + 1, 0);\n for (int i = 0; i < adj1.size(); i++) {\n if (k == 0)\n res[i] = 1;\n else\n res[i] = (mx + bfs(i, adj1, k));\n }\n return res;\n\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
C++ 🧠 Solution Explanation ✅
|
c-solution-explanation-by-gismet-wxnn
|
Intuition\nEvery node of the first tree must be linked to a node with the maximum number of target nodes for k = k - 1 in the second tree. \n\nFor instance, in
|
Gismet
|
NORMAL
|
2024-12-01T13:09:48.284314+00:00
|
2024-12-01T13:09:48.284354+00:00
| 5 | false |
# Intuition\nEvery node of the first tree must be linked to a node with the maximum number of target nodes for k = k - 1 in the second tree. \n\nFor instance, in the first example, such a node in the second tree is either node `0` or node `4` with maximum number of 4 target nodes. \n\nWe find the number of nodes target to node `i` in the first tree and add the maximum value (for exmaple 1, it is 4). \n\nWe use `DFS` to find the number of nodes target to a node `i` in a tree.\n\n\n\n# Complexity\n- Time complexity:\n`O(n^2)` where n is the number of nodes in the first tree. \n\n- Space complexity:\n`O(1)` \n\n# Code\n```cpp []\n#define vv vector\n\n\nint dfs(vv<vv<int>> &tree, int v, int p, int k)\n{\n if (k == 0)\n return 1;\n\n int ans = 1;\n for (int u : tree[v])\n {\n if (u != p)\n {\n ans += dfs(tree, u, v, k - 1);\n }\n }\n\n return ans;\n}\n\nclass Solution {\npublic:\n vector<int> maxTargetNodes(vector<vector<int>>& edges1, vector<vector<int>>& edges2, int k) {\n int n = edges1.size() + 1;\n int m = edges2.size() + 1;\n vv<vv<int>> tree1(n), tree2(m);\n for (auto &edge : edges1)\n {\n tree1[edge[0]].push_back(edge[1]);\n tree1[edge[1]].push_back(edge[0]);\n }\n\n for (auto &edge : edges2)\n {\n tree2[edge[0]].push_back(edge[1]);\n tree2[edge[1]].push_back(edge[0]);\n }\n\n int mx = 0;\n for (int i = 0; i < m && k != 0; i++)\n {\n mx = max(mx, dfs(tree2, i, -1, k - 1));\n }\n\n vv<int> ans(n);\n for (int i = 0; i < n; i++)\n {\n ans[i] = dfs(tree1, i, -1, k) + mx;\n }\n\n return ans;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
C++ || Solution Explanation✅
|
c-solution-explanation-by-gismet-stzu
|
Intuition\nEvery node of the first tree must be linked to a node with the maximum number of target nodes for k = k - 1 in the second tree. \n\nFor instance, in
|
Gismet
|
NORMAL
|
2024-12-01T13:08:32.347247+00:00
|
2024-12-01T13:08:32.347284+00:00
| 0 | false |
# Intuition\nEvery node of the first tree must be linked to a node with the maximum number of target nodes for k = k - 1 in the second tree. \n\nFor instance, in the first example, such a node in the second tree is either node `0` or node `4` with maximum number of 4 target nodes. \n\nWe find the number of nodes target to node `i` in the first tree and add the maximum value (for exmaple 1, it is 4). \n\nWe use `DFS` to find the number of nodes target to a node `i` in a tree.\n\n\n\n# Complexity\n- Time complexity:\n`O(n^2)` where n is the number of nodes in the first tree. \n\n- Space complexity:\n`O(1)` \n\n# Code\n```cpp []\n#define vv vector\n\n\nint dfs(vv<vv<int>> &tree, int v, int p, int k)\n{\n if (k == 0)\n return 1;\n\n int ans = 1;\n for (int u : tree[v])\n {\n if (u != p)\n {\n ans += dfs(tree, u, v, k - 1);\n }\n }\n\n return ans;\n}\n\nclass Solution {\npublic:\n vector<int> maxTargetNodes(vector<vector<int>>& edges1, vector<vector<int>>& edges2, int k) {\n int n = edges1.size() + 1;\n int m = edges2.size() + 1;\n vv<vv<int>> tree1(n), tree2(m);\n for (auto &edge : edges1)\n {\n tree1[edge[0]].push_back(edge[1]);\n tree1[edge[1]].push_back(edge[0]);\n }\n\n for (auto &edge : edges2)\n {\n tree2[edge[0]].push_back(edge[1]);\n tree2[edge[1]].push_back(edge[0]);\n }\n\n int mx = 0;\n for (int i = 0; i < m && k != 0; i++)\n {\n mx = max(mx, dfs(tree2, i, -1, k - 1));\n }\n\n vv<int> ans(n);\n for (int i = 0; i < n; i++)\n {\n ans[i] = dfs(tree1, i, -1, k) + mx;\n }\n\n return ans;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Using bfs
|
using-bfs-by-risabhuchiha-isj3
|
\njava []\nclass Solution {\n public int[] maxTargetNodes(int[][] e1, int[][] e2, int k) {\n int[]ans=new int[e1.length+1]; \n if(k==0){\n
|
risabhuchiha
|
NORMAL
|
2024-12-01T13:02:27.943637+00:00
|
2024-12-01T13:02:27.943663+00:00
| 5 | false |
\n```java []\nclass Solution {\n public int[] maxTargetNodes(int[][] e1, int[][] e2, int k) {\n int[]ans=new int[e1.length+1]; \n if(k==0){\n Arrays.fill(ans,1);\n return ans;\n }\n ArrayList<ArrayList<Integer>>adj1=new ArrayList<>();\n for(int i=0;i<ans.length;i++){\n adj1.add(new ArrayList<>());\n }\n for(int[]it:e1){\n adj1.get(it[0]).add(it[1]);\n adj1.get(it[1]).add(it[0]);\n }\n ArrayList<ArrayList<Integer>>adj2=new ArrayList<>();\n for(int i=0;i<e2.length+1;i++){\n adj2.add(new ArrayList<>());\n }\n for(int[]it:e2){\n adj2.get(it[0]).add(it[1]);\n adj2.get(it[1]).add(it[0]);\n }\n int max=0;\n int node=-1;\n for(int i=0;i<adj2.size();i++){\n int pp=bfs(i,adj2,k-1);\n if(pp>max){\n max=pp;\n node=i;\n }\n }\n for(int i=0;i<ans.length;i++){\n ans[i]=2+bfs(i,adj1,k)+max;\n \n }\n return ans;\n }\n public int bfs(int r,ArrayList<ArrayList<Integer>>adj,int k){\n Queue<int[]>x=new ArrayDeque<>();\n x.offer(new int[]{r,0});\n int[]vis=new int[adj.size()];\n vis[r]=0;\n int ans=0;\n while(x.size()>0){\n int[] p=x.poll();\n vis[p[0]]=1;\n for(int it:adj.get(p[0])){\n if(vis[it]==0){\n if(p[1]+1<=k){\n ans++;\n x.offer(new int[]{it,p[1]+1});\n vis[it]=1;\n } \n \n \n }\n }\n }\n \n return ans;\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Not so hard bfs
|
not-so-hard-bfs-by-jovamilenkovic-651u
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
jovamilenkovic
|
NORMAL
|
2024-12-01T13:02:21.271593+00:00
|
2024-12-01T13:02:21.271628+00:00
| 7 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```csharp []\npublic class Solution {\n public int[] MaxTargetNodes(int[][] e1, int[][] e2, int k) {\n Dictionary <int, List<int>> d1= new Dictionary <int, List<int>>();\n Dictionary <int, List<int>> d2= new Dictionary <int, List<int>>();\n for(int i=0; i< e1.Length; i++){\n if(d1.ContainsKey(e1[i][0]))d1[e1[i][0]].Add(e1[i][1]);\n else d1.Add(e1[i][0], new List<int>(){e1[i][1]});\n if(d1.ContainsKey(e1[i][1]))d1[e1[i][1]].Add(e1[i][0]);\n else d1.Add(e1[i][1], new List<int>(){e1[i][0]});\n }\n for(int i=0; i< e2.Length; i++){\n if(d2.ContainsKey(e2[i][0]))d2[e2[i][0]].Add(e2[i][1]);\n else d2.Add(e2[i][0], new List<int>(){e2[i][1]});\n if(d2.ContainsKey(e2[i][1]))d2[e2[i][1]].Add(e2[i][0]);\n else d2.Add(e2[i][1], new List<int>(){e2[i][0]});\n }\n int[] a1= new int [e1.Length+1];\n foreach(int a in d1.Keys){\n bool[] seen= new bool[ e1.Length+1];\n seen[a]=true;\n Queue<int> q= new Queue<int>();\n q.Enqueue(a);\n int s=0;\n while( q.Count>0 && s<k){\n int l=q.Count;\n for (int i=0; i<l; i++){\n int x=q.Dequeue();\n for(int j=0; j< d1[x].Count; j++){\n if(!seen[d1[x][j]]){\n seen[d1[x][j]]=true;\n a1[a]++;\n q.Enqueue(d1[x][j]);\n }\n }\n }\n s++;\n }\n }\n int[] a2= new int [e2.Length+1];\n foreach(int a in d2.Keys){\n bool[] seen= new bool[ e2.Length+1];\n seen[a]=true;\n Queue<int> q= new Queue<int>();\n q.Enqueue(a);\n int s=0;\n while( q.Count>0 && s<k-1){\n int l=q.Count;\n for (int i=0; i<l; i++){\n int x=q.Dequeue();\n for(int j=0; j< d2[x].Count; j++){\n if(!seen[d2[x][j]]){\n seen[d2[x][j]]=true;\n a2[a]++;\n q.Enqueue(d2[x][j]);\n }\n }\n }\n s++;\n }\n }\n int max=0;\n for (int i=0; i< a2.Length; i++){\n max=Math.Max(max,a2[i] );\n }\n int []ans = new int[e1.Length+1];\n if(k>0) for(int i=0; i< a1.Length; i++){\n ans[i]=max+2+a1[i];\n }\n else Array.Fill(ans,1);\n return ans;\n\n }\n}\n```
| 0 | 0 |
['C#']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Simple python3 solution | DFS + Counting
|
simple-python3-solution-dfs-counting-by-3cdwm
|
Complexity\n- Time complexity: O(n^2 + m^2)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(n + m)\n Add your space complexity here, e.g. O
|
tigprog
|
NORMAL
|
2024-12-01T12:53:41.943355+00:00
|
2024-12-01T12:55:15.562938+00:00
| 18 | false |
# Complexity\n- Time complexity: $$O(n^2 + m^2)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n + m)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def maxTargetNodes(self, edges1: List[List[int]], edges2: List[List[int]], k: int) -> List[int]:\n def get_vs(edges):\n vs = defaultdict(list)\n for u, v in edges:\n vs[u].append(v)\n vs[v].append(u)\n return vs, len(vs)\n \n vs_1, n = get_vs(edges1)\n if k == 0:\n return [1] * n\n vs_2, m = get_vs(edges2)\n\n def dfs(node, vs, distance):\n stack = [(node, distance)]\n in_progress = {node}\n while stack:\n u, dist = stack.pop()\n if dist == 0:\n continue\n for v in vs[u]:\n if v not in in_progress:\n in_progress.add(v)\n stack.append((v, dist - 1))\n return len(in_progress)\n\n second_max = max(\n dfs(node, vs_2, k - 1)\n for node in range(m)\n )\n\n return [\n dfs(node, vs_1, k) + second_max\n for node in range(n)\n ]\n```
| 0 | 0 |
['Depth-First Search', 'Graph', 'Counting', 'Python3']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Simple Breath First Search
|
simple-breath-first-search-by-b_charan-c450
|
Intuition\nSIMPLE BFS \n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time complexity:\nO(N+M+K)\n\n- Space complexity:\nO(N+
|
B_charan
|
NORMAL
|
2024-12-01T12:45:26.165496+00:00
|
2024-12-01T12:45:26.165575+00:00
| 4 | false |
# Intuition\nSIMPLE BFS \n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(N+M+K)\n\n- Space complexity:\nO(N+M)\n\n# Code\n```cpp []\nclass Solution {\npublic:\n //To find the no of target nodes for the given node in the graph\n int find_target(vector<vector<int>> &adj1,int n,int k,int start)\n {\n queue<int> q;\n q.push(start);\n int s,node,ans=0;\n vector<bool> visted(n+1,false);\n for(int i=0;i<=k;i++)\n {\n s=q.size();\n ans+=s;\n if(s==0)\n break;\n for(int j=0;j<s;j++)\n {\n node=q.front();\n visted[node]=true;\n q.pop();\n for(auto l:adj1[node])\n {\n if(visted[l]!=true)\n q.push(l);\n }\n }\n }\n return ans;\n }\n vector<int> maxTargetNodes(vector<vector<int>>& edges1,\n vector<vector<int>>& edges2, int k) {\n int n=edges1.size();\n int m=edges2.size();\n vector<int> tree1(n+1);\n vector<int> tree2(m+1);\n vector<vector<int>> adj1(n+1);\n vector<vector<int>> adj2(m+1);\n for(auto i:edges1)\n {\n adj1[i[0]].push_back(i[1]);\n adj1[i[1]].push_back(i[0]);\n }\n for(auto i:edges2)\n {\n adj2[i[0]].push_back(i[1]);\n adj2[i[1]].push_back(i[0]);\n }\n for(int i=0;i<=n;i++)\n {\n tree1[i]=find_target(adj1,n,k,i);\n }\n for(int i=0;i<=m;i++)\n {\n tree2[i]=find_target(adj2,m,k-1,i);\n }\n vector<int> ans(n+1,0);\n for(int i=0;i<=n;i++)\n {\n for(int j=0;j<=m;j++)\n {\n ans[i]=max(ans[i],tree1[i]+tree2[j]);\n }\n }\n return ans;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Simple DFS - C++ - O(k(m+n)) -> O(m+n)
|
simple-dfs-c-okmn-omn-by-lyjwjscnhf-0u0m
|
Code\ncpp []\nclass Solution {\npublic:\n void bfs2(int s, vector<int>& ans, vector<vector<int>>& adj, int k){\n vector<int> vis(adj.size(), 0);\n
|
LYjwjScNHF
|
NORMAL
|
2024-12-01T12:45:00.377058+00:00
|
2024-12-01T12:45:00.377093+00:00
| 38 | false |
# Code\n```cpp []\nclass Solution {\npublic:\n void bfs2(int s, vector<int>& ans, vector<vector<int>>& adj, int k){\n vector<int> vis(adj.size(), 0);\n queue<pair<int, int>> q;\n q.push({s, 0});\n vis[s]=1;\n while(!q.empty()){\n pair<int, int> top = q.front();\n q.pop();\n int node = top.first;\n int dist = top.second;\n if(dist<=k){\n ans[s]++;\n }else{\n continue;\n }\n for(int ngb: adj[node]){\n if(ngb==s || vis[ngb]!=0) continue;\n q.push({ngb, dist+1});\n vis[ngb]=1;\n }\n vis[node]=2;\n }\n }\n vector<int> maxTargetNodes(vector<vector<int>>& edges1, vector<vector<int>>& edges2, int k) {\n int n = edges1.size()+1;\n int m = edges2.size()+1;\n vector<vector<int>> adj1(n, vector<int>()), adj2(m, vector<int>());\n for(auto edge: edges1){\n int u = edge[0];\n int v = edge[1];\n adj1[u].push_back(v);\n adj1[v].push_back(u);\n }\n for(auto edge: edges2){\n int u = edge[0];\n int v = edge[1];\n adj2[u].push_back(v);\n adj2[v].push_back(u);\n }\n vector<int> t2kminus1(m, 0);\n int maxT2 = 0;\n for(int i=0; i<m; i++){\n bfs2(i, t2kminus1, adj2, k-1);\n maxT2 = max(maxT2, t2kminus1[i]);\n }\n cout<<maxT2<<endl;\n vector<int> ans(n, maxT2);\n for(int i=0; i<n; i++){\n bfs2(i, ans, adj1, k);\n }\n return ans;\n }\n};\n```
| 0 | 0 |
['C++']
| 1 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
✅✅✅[Editor's Choice]✅✅✅ Simplest solution beating the rest - Please upvote for more such easy solves
|
editors-choice-simplest-solution-beating-dba3
|
\n\n\n# Code\njava []\nclass Solution {\n public int[] maxTargetNodes(int[][] edges1, int[][] edges2, int k) {\n \n List<List<Integer>> tree1 =
|
sachinab
|
NORMAL
|
2024-12-01T12:32:50.309920+00:00
|
2024-12-01T12:32:50.309956+00:00
| 4 | false |
\n\n\n# Code\n```java []\nclass Solution {\n public int[] maxTargetNodes(int[][] edges1, int[][] edges2, int k) {\n \n List<List<Integer>> tree1 = buildTree(edges1);\n List<List<Integer>> tree2 = buildTree(edges2);\n int t2Tars = getMaxTargets(tree2,k-1);\n System.out.println(t2Tars);\n\n int res[] = new int[edges1.length+1];\n for(int i=0; i<res.length; i++){\n res[i]=getSurrTars(tree1,i,k)+t2Tars;\n }\n return res;\n }\n\n private List<List<Integer>> buildTree(int[][] edges){\n List<List<Integer>> tree = new ArrayList<>();\n for(int i=0; i<=edges.length; i++){\n tree.add(new ArrayList<>());\n }\n\n for(int[] edge : edges){\n tree.get(edge[0]).add(edge[1]);\n tree.get(edge[1]).add(edge[0]);\n }\n return tree;\n } \n\n private int getSurrTars(List<List<Integer>> tree, int i, int depth){\n\n Queue<Integer> q = new LinkedList<>();\n q.offer(i);\n int res = 0;\n Set<Integer> visited = new HashSet<>();\n while(!q.isEmpty() && depth>=0){\n int n = q.size();\n for(int j=0; j<n; j++){\n int p = q.poll();\n res++;\n visited.add(p);\n for(int nbr : tree.get(p)){\n if(!visited.contains(nbr)){\n q.offer(nbr);\n }\n }\n }\n depth--;\n }\n return res;\n }\n\n private int getMaxTargets(List<List<Integer>> tree, int depth){\n int max = 0;\n for(int i=0; i<tree.size(); i++){\n max = Math.max(max, getSurrTars(tree,i,depth));\n }\n return max;\n }\n\n\n}\n```
| 0 | 0 |
['Java']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
✅✅✅[Editor's Choice]✅✅✅ Simplest solution beating all - Please upvote for more such easy solutions.
|
editors-choice-simplest-solution-beating-l5if
|
\n\n\n# Code\njava []\nclass Solution {\n public int[] maxTargetNodes(int[][] edges1, int[][] edges2, int k) {\n \n List<List<Integer>> tree1 =
|
sachinab
|
NORMAL
|
2024-12-01T12:31:40.067974+00:00
|
2024-12-01T12:31:40.068009+00:00
| 1 | false |
\n\n\n# Code\n```java []\nclass Solution {\n public int[] maxTargetNodes(int[][] edges1, int[][] edges2, int k) {\n \n List<List<Integer>> tree1 = buildTree(edges1);\n List<List<Integer>> tree2 = buildTree(edges2);\n int t2Tars = getMaxTargets(tree2,k-1);\n System.out.println(t2Tars);\n\n int res[] = new int[edges1.length+1];\n for(int i=0; i<res.length; i++){\n res[i]=getSurrTars(tree1,i,k)+t2Tars;\n }\n return res;\n }\n\n private List<List<Integer>> buildTree(int[][] edges){\n List<List<Integer>> tree = new ArrayList<>();\n for(int i=0; i<=edges.length; i++){\n tree.add(new ArrayList<>());\n }\n\n for(int[] edge : edges){\n tree.get(edge[0]).add(edge[1]);\n tree.get(edge[1]).add(edge[0]);\n }\n return tree;\n } \n\n private int getSurrTars(List<List<Integer>> tree, int i, int depth){\n\n Queue<Integer> q = new LinkedList<>();\n q.offer(i);\n int res = 0;\n Set<Integer> visited = new HashSet<>();\n while(!q.isEmpty() && depth>=0){\n int n = q.size();\n for(int j=0; j<n; j++){\n int p = q.poll();\n res++;\n visited.add(p);\n for(int nbr : tree.get(p)){\n if(!visited.contains(nbr)){\n q.offer(nbr);\n }\n }\n }\n depth--;\n }\n return res;\n }\n\n private int getMaxTargets(List<List<Integer>> tree, int depth){\n int max = 0;\n for(int i=0; i<tree.size(); i++){\n max = Math.max(max, getSurrTars(tree,i,depth));\n }\n return max;\n }\n\n\n}\n```
| 0 | 0 |
['Java']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Readable and Maintainable code | Java | Easy to understand | Beginner friendly
|
readable-and-maintainable-code-java-easy-ahio
|
Intuition\n\n//initial intuition\nBased on the questino, It\'s just how many nodes can we reach from a given node. So, a simple BFS would give us the result of
|
omnitrix_joy
|
NORMAL
|
2024-12-01T12:23:20.122505+00:00
|
2024-12-01T12:23:20.122541+00:00
| 7 | false |
# Intuition\n\n//initial intuition\nBased on the questino, It\'s just how many nodes can we reach from a given node. So, a simple BFS would give us the result of how many nodes we can travel in an undirected graph given a node "i".\n\n//greedy\nSince we can connect a node "i" from graph1 to any node in grahp2, its is always best to connect to the best possible node in graph2 right ? So, yes, greedily we can just take the best possible node in graph2. Because once we know this, we can always connect any node in graph1 to always the best possible node in graph2.\n\n# Approach\nBFS + greedy + graph creation\n\n# Complexity\nIf N is number of nodes in graph1 and M is number of nodes in graph2, then \n- Time complexity:\nn^2 + m^2 + m + n\n\n- Space complexity:\nFor graph -> n + m (since undirected graph, we need to store u,v and v,u)\nFor BFS Queue -> h (height of graph)\ntotally -> n + m + h\n\n# Code\n```java []\nclass Solution {\n public int[] maxTargetNodes(int[][] edges1, int[][] edges2, int k) {\n Map<Integer,List<Integer>> graph1 = new HashMap<>();\n Map<Integer,List<Integer>> graph2 = new HashMap<>();\n\n createGraph(graph1, edges1);\n createGraph(graph2, edges2);\n\n //check best node in graph2\n int maxInGraph2 = getMaxTargetFromGraph2(graph2, k-1);\n\n int n = graph1.size();\n int[] result = new int[n];\n for(int i=0;i<n;i++){\n int nodesVisited = bfs(i, graph1, k) + maxInGraph2;\n result[i]=nodesVisited;\n }\n \n return result;\n\n }\n\n private int getMaxTargetFromGraph2(Map<Integer,List<Integer>> graph, int k){\n if(k==-1){\n return 0;\n }\n int n = graph.size();\n int max = 1;\n for(int i=0;i<n;i++){\n int nodes = bfs(i, graph, k);\n max = Math.max(max, nodes);\n }\n return max;\n }\n\n private int bfs(int node, Map<Integer,List<Integer>> graph, int k){\n int nodesVisited = 1;\n Queue<int[]> q = new LinkedList<>();\n q.add(new int[]{node,-1});\n while(!q.isEmpty() && k>0){\n int n = q.size();\n k--;\n for(int i=0;i<n;i++){\n int[] curr = q.poll();\n for(int neighbor : graph.get(curr[0])){\n if(curr[1]==neighbor) continue;\n q.add(new int[]{neighbor,curr[0]});\n nodesVisited++;\n }\n }\n }\n return nodesVisited;\n }\n\n private void createGraph(Map<Integer,List<Integer>> graph, int[][] edges){\n for(int[] edge: edges){\n graph.putIfAbsent(edge[0], new ArrayList<>());\n graph.putIfAbsent(edge[1], new ArrayList<>());\n graph.get(edge[0]).add(edge[1]);\n graph.get(edge[1]).add(edge[0]);\n }\n }\n}\n```
| 0 | 0 |
['Greedy', 'Breadth-First Search', 'Graph', 'Java']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
DP O(k * max(n, m))
|
dp-ok-maxn-m-by-hidden_i-q6qj
|
Intuition & approach\n- While thinking solution, main trouble was whether we can avoid recomputing somehow.\n- Say we want to compute for k = 2, and we have nod
|
hidden_i
|
NORMAL
|
2024-12-01T12:04:51.627285+00:00
|
2024-12-01T12:05:22.041399+00:00
| 21 | false |
# Intuition & approach\n- While thinking solution, main trouble was whether we can avoid recomputing somehow.\n- Say we want to compute for $$k = 2$$, and we have node with index $$0$$ which is connected to node $$1$$ of the same tree i.e. we want $$DP[2][0][Answer]$$.\n- $$DP[k=2][0][Answer]$$ should be $$DP[k = 1][1][Answer]$$ but here we have also double counted edge between $$0-1$$ because $$DP[k = 1][1][Answer]$$ which be equal to count of neighbors of node $$1$$.\n- Hence, we can deduct that value which helped form $$DP[k = 1][1][Answer]$$ corresponding to node $$0$$.\n\n# Complexity\nNote: Size of looping over adjaceny matrix for a tree should be equalivalent to going over each edge where number of edges is equal to $$O(n)$$.\n- Time complexity: $$O(k * max(n, m))$$\n- Space complexity: $$O(max(n, m))$$\n\n# Code\n```cpp []\nclass Solution {\n vector<vector<unordered_map<int, int>>> solve(int n, int k, vector<vector<int>>& adjMat) {\n vector<vector<unordered_map<int, int>>> dp(3, vector<unordered_map<int, int>>(n));\n for (int i = 0; i < n; i += 1) {\n for (int j = 0; j < adjMat[i].size(); j += 1)\n dp[0][i][adjMat[i][j]] = 0;\n dp[0][i][-1] = 1;\n }\n for (int i = 0; i < n; i += 1) {\n for (int j = 0; j < adjMat[i].size(); j += 1)\n dp[1][i][adjMat[i][j]] = 1;\n dp[1][i][-1] = adjMat[i].size() + 1;\n }\n for (int x = 2; x <= k; x += 1)\n for (int i = 0; i < n; i += 1) {\n dp[x % 3][i][-1] = 1;\n for (int j = 0; j < adjMat[i].size(); j += 1) {\n dp[x % 3][i][adjMat[i][j]] = \n dp[(x - 1) % 3][adjMat[i][j]][-1] - \n dp[(x - 1) % 3][adjMat[i][j]][i];\n dp[x % 3][i][-1] += dp[x % 3][i][adjMat[i][j]];\n }\n }\n return dp;\n }\n\npublic:\n vector<int> maxTargetNodes(\n vector<vector<int>>& edges1,\n vector<vector<int>>& edges2, \n int k) {\n\n int n = edges1.size() + 1;\n if (k == 0) {\n vector<int> answer(n, 1);\n return answer;\n }\n \n vector<vector<int>> adjMat1(n);\n for (auto& edge : edges1) {\n int a = edge[0], b = edge[1];\n adjMat1[a].push_back(b);\n adjMat1[b].push_back(a);\n }\n auto dp1 = solve(n, k, adjMat1);\n\n if (k == 1) {\n vector<int> answer(n);\n for (int i = 0; i < n; i += 1)\n answer[i] = dp1[k % 3][i][-1] + 1;\n return answer;\n }\n\n int m = edges2.size() + 1;\n vector<vector<int>> adjMat2(m);\n for (auto& edge : edges2) {\n int a = edge[0], b = edge[1];\n adjMat2[a].push_back(b);\n adjMat2[b].push_back(a);\n }\n auto dp2 = solve(m, k, adjMat2);\n \n int maxSum = 0;\n for (int i = 0; i < m; i += 1)\n maxSum = max(maxSum, dp2[(k - 1) % 3][i][-1]);\n\n vector<int> answer(n);\n for (int i = 0; i < n; i += 1)\n answer[i] = dp1[k % 3][i][-1] + maxSum;\n return answer;\n }\n};\n```
| 0 | 0 |
['Dynamic Programming', 'C++']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
My Solutions
|
my-solutions-by-hope_ma-x4th
|
1. Use the BFS\n\n/**\n * Time Complexity: O(n1 * n1 + n2 * n2)\n * Space Complexity: O(n1 + n2)\n * where `n1` is the length of the vector `edges1`\n * `
|
hope_ma
|
NORMAL
|
2024-12-01T10:17:06.583702+00:00
|
2024-12-01T10:45:16.952963+00:00
| 1 | false |
**1. Use the BFS**\n```\n/**\n * Time Complexity: O(n1 * n1 + n2 * n2)\n * Space Complexity: O(n1 + n2)\n * where `n1` is the length of the vector `edges1`\n * `n2` is the length of the vector `edges2`\n */\nclass Solution {\n public:\n vector<int> maxTargetNodes(const vector<vector<int>> &edges1,\n const vector<vector<int>> &edges2,\n const int k) {\n vector<int> ret = get_all_nodes(edges1, k);\n vector<int> nodes = get_all_nodes(edges2, k - 1);\n const int max_node = *max_element(nodes.begin(), nodes.end());\n for (int &item : ret) {\n item += max_node;\n }\n return ret;\n }\n \n private:\n /**\n * @return: a vector<int> `ret`,\n * whose length is the number of the nodes of the tree,\n * represented by the vector `edges`,\n * each element `ret[i]` of which is the number of the nodes\n * whose distance to the node `i` is less than or equal to `distance`\n */\n vector<int> get_all_nodes(const vector<vector<int>> &edges, const int distance) {\n const int n = static_cast<int>(edges.size()) + 1;\n vector<int> tree[n];\n for (const vector<int> &edge : edges) {\n tree[edge.front()].emplace_back(edge.back());\n tree[edge.back()].emplace_back(edge.front());\n }\n \n vector<int> ret(n);\n for (int node = 0; node < n; ++node) {\n ret[node] = get_one_nodes(tree, node, distance);\n }\n return ret;\n }\n \n /**\n * @return: the number of the nodes whose distance to the node `node` is less than\n * or equal to `distance`\n */\n int get_one_nodes(const vector<int> *tree, const int root, const int distance) {\n /**\n * <0>: the node\n * <1>: the parent node\n */\n using q_node_t = array<int, 2>;\n constexpr int invalid_parent = -1;\n int ret = 0;\n queue<q_node_t> q({q_node_t{root, invalid_parent}});\n for (int d = 0; d < distance + 1 && !q.empty(); ++d) {\n ret += static_cast<int>(q.size());\n for (size_t qs = q.size(); qs > 0; --qs) {\n const auto [node, parent] = q.front();\n q.pop();\n for (const int child : tree[node]) {\n if (child == parent) {\n continue;\n }\n q.emplace(q_node_t{child, node});\n }\n }\n }\n return ret;\n }\n};\n```\n**2. Use the DFS**\n```\n/**\n * Time Complexity: O(n1 * n1 + n2 * n2)\n * Space Complexity: O(n1 + n2)\n * where `n1` is the length of the vector `edges1`\n * `n2` is the length of the vector `edges2`\n */\nclass Solution {\n public:\n vector<int> maxTargetNodes(const vector<vector<int>> &edges1,\n const vector<vector<int>> &edges2,\n const int k) {\n vector<int> ret = get_all_nodes(edges1, k);\n vector<int> nodes = get_all_nodes(edges2, k - 1);\n const int max_node = *max_element(nodes.begin(), nodes.end());\n for (int &item : ret) {\n item += max_node;\n }\n return ret;\n }\n \n private:\n /**\n * @return: a vector<int> `ret`,\n * whose length is the number of the nodes of the tree,\n * represented by the vector `edges`,\n * each element `ret[i]` of which is the number of the nodes\n * whose distance to the node `i` is less than or equal to `distance`\n */\n vector<int> get_all_nodes(const vector<vector<int>> &edges, const int distance) {\n const int n = static_cast<int>(edges.size()) + 1;\n vector<int> tree[n];\n for (const vector<int> &edge : edges) {\n tree[edge.front()].emplace_back(edge.back());\n tree[edge.back()].emplace_back(edge.front());\n }\n \n vector<int> ret(n);\n for (int node = 0; node < n; ++node) {\n ret[node] = get_one_nodes(tree, node, distance);\n }\n return ret;\n }\n \n /**\n * @return: the number of the nodes whose distance to the node `node` is less than\n * or equal to `distance`\n */\n int get_one_nodes(const vector<int> *tree, const int root, const int distance) {\n constexpr int invalid_parent = -1;\n return dfs(tree, root, invalid_parent, 0, distance);\n }\n \n int dfs(const vector<int> *tree,\n const int node,\n const int parent,\n const int current_distance,\n const int distance) {\n if (current_distance > distance) {\n return 0;\n }\n \n int ret = 1;\n for (const int child : tree[node]) {\n if (child == parent) {\n continue;\n }\n ret += dfs(tree, child, node, current_distance + 1, distance);\n }\n return ret;\n }\n};\n```
| 0 | 0 |
[]
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
C++ Well Commented and Explained Code
|
c-well-commented-and-explained-code-by-s-o3ir
|
Problem Description\n\nYou are given two undirected trees with n and m nodes. The nodes have distinct labels in the ranges [0, n - 1] and [0, m - 1], respective
|
sumitgarg380
|
NORMAL
|
2024-12-01T09:59:38.112373+00:00
|
2024-12-01T09:59:38.112413+00:00
| 68 | false |
# Problem Description\n\nYou are given two undirected trees with `n` and `m` nodes. The nodes have distinct labels in the ranges `[0, n - 1]` and `[0, m - 1]`, respectively.\n\nYou are also provided:\n- `edges1` (a 2D integer array of size `n - 1`) which represents edges in the first tree, where `edges1[i] = [a_i, b_i]` indicates an edge between nodes `a_i` and `b_i`.\n- `edges2` (a 2D integer array of size `m - 1`) which represents edges in the second tree, where `edges2[i] = [u_i, v_i]` indicates an edge between nodes `u_i` and `v_i`.\n- An integer `k`.\n\n### Target Node\nA node `u` is **target** to node `v` if the number of edges on the path from `u` to `v` is less than or equal to `k`. Note that a node is always target to itself.\n\n### Task\nReturn an array of size `n`, where the `i-th` value is the maximum possible number of nodes **target** to node `i` of the first tree if you connect one node from the first tree to another node in the second tree.\n\n### Constraints\n- Queries are **independent**, meaning after processing each query, the added edge is removed.\n\n---\n\n## Intuition\n\n1. **DFS for Target Count**:\n - Use a DFS to calculate the number of nodes in a tree that are within a distance of `k` edges from a given node.\n - This gives us the count of target nodes for both trees independently.\n\n2. **Merge Trees Virtually**:\n - For each node in the second tree, compute the maximum number of nodes target to it.\n - Simulate adding an edge between every node of the first tree and each node of the second tree.\n - For each query, combine the results of the two trees and return the maximum.\n\n3. **Optimization**:\n - Precompute the DFS results for all nodes in both trees to avoid redundant calculations.\n\n---\n\n## Approach\n\n1. **Build the Adjacency List**:\n - Represent the two trees using adjacency lists for easier traversal.\n\n2. **DFS Traversal**:\n - Implement a helper function `dfs` to compute the number of target nodes for a given node and a specific `k`.\n\n3. **Iterate Over Nodes**:\n - For each node in the second tree, calculate the maximum target nodes.\n - For each node in the first tree, calculate the total target nodes by combining results from both trees.\n\n4. **Store Results**:\n - Store the results in an array and return it.\n\n---\n\n## Complexity\n\n- **Time Complexity**: \n - Building adjacency lists: \\( O(n + m) \\) \n - DFS for all nodes in both trees: \\( O(nk + mk) \\) \n - Combining results: \\( O(nm) \\) \n **Total**: \\( O(nk + mk + nm) \\)\n\n- **Space Complexity**: \n - Adjacency lists: \\( O(n + m) \\) \n - DFS recursion stack: \\( O(k) \\)\n\n---\n\n## Code\n\n```cpp\nclass Solution {\npublic:\n // Perform DFS to count target nodes\n int dfs(int i, int p, vector<vector<int>> &adj, int k) {\n if (k <= 0) return k == 0;\n int res = 1; // Include current node\n for (int j : adj[i]) {\n if (j != p) {\n res += dfs(j, i, adj, k - 1);\n }\n }\n return res;\n }\n\n vector<int> maxTargetNodes(vector<vector<int>>& edges1, vector<vector<int>>& edges2, int k) {\n int m = edges1.size() + 1; // Nodes in first tree\n int n = edges2.size() + 1; // Nodes in second tree\n\n // Build adjacency list for the first tree\n vector<vector<int>> adj1(m);\n for (auto &edge : edges1) {\n adj1[edge[0]].push_back(edge[1]);\n adj1[edge[1]].push_back(edge[0]);\n }\n\n // Build adjacency list for the second tree\n vector<vector<int>> adj2(n);\n for (auto &edge : edges2) {\n adj2[edge[0]].push_back(edge[1]);\n adj2[edge[1]].push_back(edge[0]);\n }\n\n // Precompute the maximum target nodes for each node in the second tree\n int maxSecondTreeTargets = 0;\n for (int i = 0; i < n; ++i) {\n maxSecondTreeTargets = max(maxSecondTreeTargets, dfs(i, -1, adj2, k - 1));\n }\n\n // Compute results for each node in the first tree\n vector<int> result(m);\n for (int i = 0; i < m; ++i) {\n result[i] = maxSecondTreeTargets + dfs(i, -1, adj1, k);\n }\n\n return result;\n }\n};\n
| 0 | 0 |
['Tree', 'Depth-First Search', 'C++']
| 1 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
BFS - find nodes with k distance
|
bfs-find-nodes-with-k-distance-by-naveen-jb0c
|
Intuition\n From each node in tree1, we can visit all nodes with k distance. To connect with tree2, we have to connect an edge with takes a distance of 1. Hence
|
NaveenprasanthSA
|
NORMAL
|
2024-12-01T09:52:10.972870+00:00
|
2024-12-01T09:53:33.284344+00:00
| 8 | false |
# Intuition\n* From each node in tree1, we can visit all nodes with k distance. To connect with tree2, we have to connect an edge with takes a distance of 1. Hence we can visit all nodes in tree2 within k-1 distance. \n* Where should we connect the edge? We can connect each node of tree1 with the node of tree2 from where we can visit max number of nodes within k-1 distance.\n\n# Approach\n* For each node u in the first tree, find the number of nodes at a distance of at most k from node u.\n\n* For each node v in the second tree, find the number of nodes at a distance of at most k - 1 from node v.\n\n# Complexity\n- Time complexity:\nTree1: To find nodes with k dist for each node = O(M^2) \nTree2: To find nodes with k dist for each node = O(N^2) \nO(M^2 + N^2)\n\n- Space complexity:\nO(M^2 + N^2)\n\n\n\n# Code\n```python3 []\nclass Solution:\n def maxTargetNodes(self, edges1: List[List[int]], edges2: List[List[int]], k: int) -> List[int]:\n \n\n def find(edges, k):\n\n graph = defaultdict(list)\n\n for i,j in edges:\n graph[i].append(j)\n graph[j].append(i)\n \n n = len(graph)\n\n nodes_within_k_dist = [0] * n\n if k<0: return nodes_within_k_dist\n\n for src in range(n): \n q = [[src,0]] \n visited = set()\n visited.add(src)\n count = 1\n\n while q:\n node,steps = q.pop(0)\n for nei in graph[node]:\n if nei not in visited and steps < k:\n count += 1\n q.append([nei,steps+1])\n visited.add(nei)\n \n nodes_within_k_dist[src] = count\n\n return nodes_within_k_dist\n \n count1 = find(edges1,k)\n count2 = find(edges2,k-1)\n max_count2 = max(count2)\n\n res = []\n for count in count1:\n res.append(count + max_count2) \n \n return res\n\n\n\n \n \n\n\n\n\n\n\n\n```
| 0 | 0 |
['Python3']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
C++ Easy approach
|
c-easy-approach-by-kumarbytes-bz14
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
kumarbytes
|
NORMAL
|
2024-12-01T09:47:03.558244+00:00
|
2024-12-01T09:47:03.558280+00:00
| 0 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\n vector<vector<int>>populateGraph(vector<vector<int>>& edges){\n int n = edges.size();\n vector<vector<int>>graph(n+1);\n for(auto& edge:edges){\n graph[edge[1]].push_back(edge[0]);\n graph[edge[0]].push_back(edge[1]);\n }\n return graph;\n }\n int numOfNodeAtDistHelper(vector<vector<int>>&graph,int node,int dist){\n int n = graph.size();\n queue<pair<int,int>>q;\n vector<int>visited(n,0);\n q.push({node,0});\n int cnt = 0;\n while(q.size()){\n auto curr = q.front();\n q.pop();\n if(visited[curr.first]) continue;\n visited[curr.first]++;\n cnt++;\n if(curr.second == dist)continue;\n for(auto nbr:graph[curr.first]){\n if(visited[nbr])continue;\n q.push({nbr,curr.second+1});\n }\n }\n return cnt;\n }\n unordered_map<int,int>numOfNodeAtDist(vector<vector<int>>&graph,int dist){\n int n= graph.size();\n unordered_map<int,int>nodeCountMap;\n // will do bfs for each node and return\n for(int i=0;i<n;i++){\n int cnt = numOfNodeAtDistHelper(graph,i,dist);\n cout<<cnt<<",";\n nodeCountMap[i]= cnt;\n }\n return nodeCountMap;\n }\n\npublic:\n vector<int> maxTargetNodes(vector<vector<int>>& edges1, vector<vector<int>>& edges2, int k) {\n int n = edges1.size();\n int m = edges2.size();\n vector<int>ans(n+1,1);\n if(k==0)return ans; // only that node is target to itself\n vector<vector<int>>graph1 = populateGraph(edges1);\n vector<vector<int>>graph2 = populateGraph(edges2);\n unordered_map<int,int>numOfNodeAtDist1 = numOfNodeAtDist(graph1,k);\n unordered_map<int,int>numOfNodeAtDist2 = numOfNodeAtDist(graph2,k-1);\n int maxi = 0;\n for(auto val :numOfNodeAtDist2){\n maxi = max(maxi,val.second);\n }\n for(int i=0; i<=n; i++){\n ans[i]= numOfNodeAtDist1[i]+maxi;\n }\n return ans;\n \n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
C++ | BFS Simple approach
|
c-bfs-simple-approach-by-pradygup-bb6t
|
Intuition\nThis one i couldn\'t solve in contest but the approach i was thinking around was quite right.\nWe can calculate cnt of nodes who are at lesser then o
|
pradygup
|
NORMAL
|
2024-12-01T09:22:00.318171+00:00
|
2024-12-01T09:22:00.318206+00:00
| 14 | false |
# Intuition\nThis one i couldn\'t solve in contest but the approach i was thinking around was quite right.\nWe can calculate cnt of nodes who are at lesser then or equal to k distance from me and then make a count array for both the graphs seperately.After that we simply add them at each index because when we join a node with an edge to other graph just 1 edge is added extra which is 1 dist. So if we calculate nodes lesser then k-1 for graph 2 it would become lesser then equal to k. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(n*(n+E)+m*(m+E))\n\n- Space complexity:\nO(n+m)\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int shortestPath(int src,vector<vector<int>>adj,int N,int k){\n if(k<0)return 0;\n //bfs traversal to determine all least distances\n queue<pair<int,int>>q;\n q.push({0,src});\n int cnt=1;\n \n vector<int>vis(N,0);\n vis[src]=1;\n while(!q.empty()){\n auto it=q.front();\n int node=it.second;\n int dist=it.first;\n q.pop();\n // if(dist<=k)\n for(auto it:adj[node]){\n if(dist+1<=k && !vis[it]){\n vis[it]=1;\n cnt++;\n q.push({dist+1,it});\n }\n }\n }\n return cnt;\n }\n vector<int> maxTargetNodes(vector<vector<int>>& edges1, vector<vector<int>>& edges2, int k) {\n int maxNode1 = 0, maxNode2 = 0;\n for (auto& edge : edges1) {\n maxNode1 = max(maxNode1, max(edge[0], edge[1]));\n }\n for (auto& edge : edges2) {\n maxNode2 = max(maxNode2, max(edge[0], edge[1]));\n }\n int n=edges1.size();\n int m=edges2.size();\n // Create adjacency lists for both graphs.\n // vector<vector<int>> adj1(maxNode1 + 1);\n // vector<vector<int>> adj2(maxNode2 + 1);\n vector<vector<int>> adj1(n + 1);\n vector<vector<int>> adj2(m + 1);\n\n // Build adjacency list for graph 1.\n for (auto& edge : edges1) {\n adj1[edge[0]].push_back(edge[1]);\n adj1[edge[1]].push_back(edge[0]);\n }\n\n // Build adjacency list for graph 2.\n for (auto& edge : edges2) {\n adj2[edge[0]].push_back(edge[1]);\n adj2[edge[1]].push_back(edge[0]);\n }\n // int n=maxNode1,m=maxNode2;\n vector<int>answer(n+1,0);\n vector<int>cnt(n+1,0);\n for(int i=0;i<=n;i++){\n cnt[i]=shortestPath(i,adj1,n+1,k);\n }\n\n vector<int>cnt2(m+1,0);\n for(int i=0;i<=m;i++){\n cnt2[i]=shortestPath(i,adj2,m+1,k-1);\n }\n int goldenNodeCnt=0;\n for(int i=0;i<=m;i++){\n goldenNodeCnt=max(goldenNodeCnt,cnt2[i]);\n }\n\n for(int i=0;i<=n;i++){\n answer[i]=goldenNodeCnt+cnt[i];\n }\n return answer;\n }\n};\n```
| 0 | 0 |
['Breadth-First Search', 'Shortest Path', 'C++']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Easy Java Solution
|
easy-java-solution-by-vansh_goel-8b4t
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
vg_85
|
NORMAL
|
2024-12-01T09:16:19.246782+00:00
|
2024-12-01T09:16:19.246810+00:00
| 9 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int dfs(List<List<Integer>> adj,int i,int par,int k){\n if(k<0) return 0;\n int c=1;\n for(int j:adj.get(i)){\n if(j!=par) c+=dfs(adj,j,i,k-1);\n }\n return c;\n }\n public int[] find(int edges[][],int k){\n int n=edges.length+1;\n List<List<Integer>> adj=new ArrayList<>();\n for(int i=0;i<n;i++) adj.add(new ArrayList<>());\n for(int i[]:edges){\n adj.get(i[0]).add(i[1]);\n adj.get(i[1]).add(i[0]);\n }\n int ans[]=new int[n];\n for(int i=0;i<n;i++){\n int c=dfs(adj,i,-1,k);\n ans[i]=c;\n }\n return ans;\n }\n public int[] maxTargetNodes(int[][] edges1, int[][] edges2, int k) {\n int c1[]=find(edges1,k);\n int c2[]=find(edges2,k-1);\n int max=Arrays.stream(c2).max().getAsInt();\n for(int i=0;i<c1.length;i++) c1[i]+=max;\n return c1;\n }\n}\n```
| 0 | 0 |
['Depth-First Search', 'Java']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
DarkNerd | ✅
|
darknerd-by-darknerd-vbhi
|
Intuition:\n\nThe task is to compute the maximum number of nodes reachable from each node in the first graph within distance k while considering the maximum con
|
darknerd
|
NORMAL
|
2024-12-01T09:10:50.127880+00:00
|
2024-12-01T09:10:50.127922+00:00
| 1 | false |
### Intuition:\n\nThe task is to compute the maximum number of nodes reachable from each node in the first graph within distance `k` while considering the maximum contribution from nodes in the second graph within distance `k-1`. \nThis involves exploring the neighborhood of each node using BFS and combining results efficiently.\n\n---\n\n### Approach:\n\n1. **Parse Graphs from Edge Lists:**\n - Construct adjacency lists for both graphs (`mp1` for `edges1` and `mp2` for `edges2`) using an unordered map.\n - Track the maximum node indices in both graphs to determine the total number of nodes (`n` for the first graph and `m` for the second graph).\n\n2. **Breadth-First Search (BFS) Implementation:**\n - Implement a BFS helper function that calculates the number of reachable nodes within a distance `k` from a starting node.\n - Use a queue for level-wise traversal and a visited array to prevent revisiting nodes.\n\n3. **Calculate Reachable Nodes:**\n - For each node in the first graph, calculate the number of reachable nodes within distance `k` using BFS and store results in `vec1`.\n - Similarly, for each node in the second graph, calculate reachable nodes within distance `k-1` using BFS and store results in `vec2`.\n\n4. **Combine Results:**\n - Find the maximum reachable nodes in `vec2`.\n - For each node in the first graph, calculate the sum of reachable nodes from `vec1` and the maximum value from `vec2`, storing the result in the answer array `ans`.\n\n5. **Return the Result:**\n - Return the `ans` array, which contains the maximum number of reachable nodes for each node in the first graph combined with the maximum from the second graph.\n\n---\n\n\n\n### Time Complexity:\n\n1. **Graph Construction:**\n - Parsing the edges for both graphs takes $$O(E_1 + E_2)$$, where $$E_1$$ and $$E_2$$ are the number of edges in `edges1` and `edges2`.\n\n2. **BFS for Reachable Nodes:**\n - For each node in both graphs, the BFS traversal takes $$O(V + E)$$ per graph, where $$V$$ is the number of nodes and $$E$$ is the number of edges. Across all nodes:\n - First graph: $$O(n \\times (n + E_1))$$\n - Second graph: $$O(m \\times (m + E_2))$$\n\n3. **Result Combination:**\n - Finding the maximum in `vec2` and combining results for `ans` takes $$O(n + m)$$.\n\nOverall time complexity: \n$$O(n^2 + m^2 + E_1 + E_2)$$\n\n---\n\n### Space Complexity:\n\n1. **Adjacency Lists:**\n - Storage for adjacency lists `mp1` and `mp2`: $$O(E_1 + E_2)$$.\n\n2. **Visited Arrays:**\n - BFS uses a visited array of size $$O(n)$$ for the first graph and $$O(m)$$ for the second graph.\n\n3. **Result Arrays:**\n - Arrays `vec1`, `vec2`, and `ans` store $$O(n + m)$$ values.\n\nOverall space complexity: \n$$O(n + m + E_1 + E_2)$$\n\n# Code\n```cpp []\nclass Solution {\n int bfs(unordered_map<int, vector<int>>& mp, int node, int k, int n) {\n if(k<0){\n return 0;\n }\n vector<int> visited(n, 0);\n queue<int> qu;\n int ct = 1, level = 0;\n qu.push(node);\n visited[node] = 1;\n while (!qu.empty() && level < k) {\n int size = qu.size();\n while (size-- > 0) {\n int top = qu.front();\n qu.pop();\n for (int i : mp[top]) {\n if (visited[i]) {\n continue;\n }\n qu.push(i);\n visited[i] = 1;\n ct++;\n }\n }\n level++;\n }\n return ct;\n }\n\npublic:\n vector<int> maxTargetNodes(vector<vector<int>>& edges1, vector<vector<int>>& edges2, int k) {\n unordered_map<int, vector<int>> mp1, mp2;\n int n = 0, m = 0;\n\n for (auto& edge : edges1) {\n mp1[edge[0]].push_back(edge[1]);\n mp1[edge[1]].push_back(edge[0]);\n n = max({n, edge[0], edge[1]});\n }\n for (auto& edge : edges2) {\n mp2[edge[0]].push_back(edge[1]);\n mp2[edge[1]].push_back(edge[0]);\n m = max({m, edge[0], edge[1]});\n }\n\n n++, m++;\n vector<int> vec1(n, 0), vec2(m, 0);\n\n for (int i = 0; i < n; i++) {\n vec1[i] = bfs(mp1, i, k, n);\n }\n for (int i = 0; i < m; i++) {\n vec2[i] = bfs(mp2, i, k-1, m);\n }\n\n vector<int> ans(n, 0);\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < m; j++) {\n ans[i] = max(ans[i], vec1[i] + vec2[j]);\n }\n }\n return ans;\n }\n};\n\n```
| 0 | 0 |
['C++']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Swift DFS
|
swift-dfs-by-liampronan-i8qc
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n- see code comments. \n
|
liampronan
|
NORMAL
|
2024-12-01T08:44:55.984120+00:00
|
2024-12-01T08:44:55.984147+00:00
| 3 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- see code comments. \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```swift []\nclass Solution {\n func maxTargetNodes(_ edges1: [[Int]], _ edges2: [[Int]], _ k: Int) -> [Int] {\n var (adjList1, adjList2) = buildAdjLists(edges1, edges2)\n\n // build up res by summing all target nodes for each i \n var res = Array(repeating: 0, count: adjList1.count) \n for i in 0...edges1.count {\n var visited = Set<Int>()\n visited.insert(i)\n res[i] = dfs(adjList1, node: i, k: k, visited: &visited)\n }\n \n var counter2 = [Int: Int]()\n // for the 2nd tree, we\'re really only concerned with the max value \n // also, we set k to k-1 since we will "use" an edge to connect tree2 to tree1 \n var maxVal = Int.min\n for i in 0...edges2.count {\n var visited = Set<Int>()\n visited.insert(i)\n counter2[i] = dfs(adjList2, node: i, k: k - 1, visited: &visited)\n maxVal = max(maxVal, counter2[i]!)\n }\n \n return res.map { $0 + maxVal }\n }\n\n\n\n func dfs(_ adjList: [Int: [Int]], node: Int, k: Int, visited: inout Set<Int>) -> Int {\n if k < 0 { return 0 }\n if k == 0 { return 1 }\n\n var sum = 0\n for neighbor in adjList[node, default: []] {\n guard !visited.contains(neighbor) else { continue }\n visited.insert(neighbor)\n sum += dfs(adjList, node: neighbor, k: k - 1, visited: &visited) \n }\n\n return sum + 1\n }\n\n func buildAdjLists(_ edges1: [[Int]], _ edges2: [[Int]]) -> ([Int: [Int]], [Int: [Int]]) {\n var adjList1 = (0...edges1.count).reduce(into: [Int: [Int]]()) { acc, v in \n acc[v] = []\n }\n var adjList2 = (0...edges2.count).reduce(into: [Int: [Int]]()) { acc, v in \n acc[v] = []\n }\n\n for edge in edges1 {\n adjList1[edge[0]]!.append(edge[1])\n adjList1[edge[1]]!.append(edge[0])\n }\n for edge in edges2 {\n adjList2[edge[0]]!.append(edge[1])\n adjList2[edge[1]]!.append(edge[0])\n }\n return (adjList1, adjList2)\n }\n}\n```
| 0 | 0 |
['Swift']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
DFS || Beats 100% || Trees
|
dfs-beats-100-trees-by-dheeraj_001-vopw
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
dheeraj_001
|
NORMAL
|
2024-12-01T08:16:33.638400+00:00
|
2024-12-01T08:16:33.638434+00:00
| 8 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n\nint bfs(int i , vector<vector<int>>&adj, int k,int par=-1)\n{\n\n if(k<0)\n return 0;\n if(k==0)\n return 1;\n int res=1;\n for(auto P :adj[i])\n {\n if(P==par)\n continue;\n // if it come s to parent //loop exit\n res+=bfs(P,adj,k-1,i);\n }\n return res;\n}\n vector<int> maxTargetNodes(vector<vector<int>>& edges1, vector<vector<int>>& edges2, int k) {\n\n int n=edges1.size()+1;\n int m=edges2.size()+1;\n\n vector<vector<int>> adj1(n), adj2(m);\n\n\n for(int i=0;i<n-1;i++)\n {\n int u=edges1[i][0];\n int v=edges1[i][1];\n adj1[u].push_back(v);\n adj1[v].push_back(u);\n }\n for(int i=0;i<m-1;i++)\n {\n int u=edges2[i][0];\n int v=edges2[i][1];\n adj2[v].push_back(u);\n adj2[u].push_back(v);\n }\n\n // we need to add node which has maximum neig in 2nd tree\n\n int maxi=0;\n for(int i=0;i<m;i++)\n {\n // one connection is mae we havve k-1 edges left;\n maxi=max(maxi,bfs(i,adj2,k-1));\n // after traversing all node we got best maxi from trr2 , to ad to each node in tree 1\n }\n vector<int>ans;\n\n for(int i=0;i<n;i++)\n {\n int res=0;\n // we have k edges left , we havent used any\n res+=bfs(i,adj1,k);\n res+=maxi;\n ans.push_back(res);\n }\n return ans;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Python || Simple Solution || BFS || 100% beats
|
python-simple-solution-bfs-100-beats-by-l1oxf
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
vilaparthibhaskar
|
NORMAL
|
2024-12-01T08:14:59.896145+00:00
|
2024-12-01T08:18:04.097008+00:00
| 14 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def maxTargetNodes(self, edges1: List[List[int]], edges2: List[List[int]], k: int) -> List[int]:\n n, m = len(edges1) + 1, len(edges2) + 1\n if k == 0:\n return [1] * (n)\n t1 = defaultdict(list)\n t2 = defaultdict(list)\n for i in edges1:\n [st, ed] = i\n t1[st].append(ed)\n t1[ed].append(st)\n for i in edges2:\n [st, ed] = i\n t2[st].append(ed)\n t2[ed].append(st)\n\n\n def helper2(node, k):\n self.s.add(node)\n if k == 0:\n return 1\n sm = 1\n for i in t2[node]:\n if i not in self.s:\n sm += helper2(i, k - 1)\n return sm\n\n \n def helper1(node, k):\n self.s.add(node)\n if k == 0:\n return 1\n sm = 1\n for i in t1[node]:\n if i not in self.s:\n sm += helper1(i, k - 1)\n return sm\n\n mx = -math.inf\n for i in range(m):\n self.s = set()\n mx = max(mx, helper2(i, k - 1))\n\n ans = [0] * n\n for i in range(n):\n self.s = set()\n val = helper1(i, k)\n ans[i] = val + mx\n return ans\n```
| 0 | 0 |
['Breadth-First Search', 'Python3']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Java solution using bfs beats 100%
|
java-solution-using-bfs-beats-100-by-tan-v7v9
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n BFS to Count Nodes Wit
|
TanmayYadav
|
NORMAL
|
2024-12-01T08:14:59.827235+00:00
|
2024-12-01T08:14:59.827274+00:00
| 7 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n BFS to Count Nodes Within Distance\nUsing a helper function f, we:\n\nStart a BFS traversal from a given node i.\nCount all nodes within a distance k for Tree 1 and k-1 for Tree 2.\n Iterate and Compute Results\nFor each node in Tree 1:\nCompute the maximum number of nodes within k-1 distance in Tree 2 (by iterating over all nodes in Tree 2).\nAdd this value to the number of nodes within k distance in Tree 1.\nFinally, store the sum in the results array. \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int[] maxTargetNodes(int[][] edges1, int[][] edges2, int k) {\n int[]ans=new int[edges1.length+1];\n if(k==0) {\n Arrays.fill(ans,1);\n return ans;\n }\n List<List<Integer>> list1=createGraph(edges1);\n List<List<Integer>> list2=createGraph(edges2);\n int max=0;\n for(int i=0;i<=edges2.length;i++) {\n max=Math.max(max,f(i,list2,k-1));\n }\n for(int i=0;i<=edges1.length;i++) {\n ans[i] = max + f(i,list1,k);\n }\n return ans;\n }\n private List<List<Integer>> createGraph(int[][]arr) {\n int m =arr.length;\n List<List<Integer>> graph=new ArrayList<>();\n for(int i=0;i<=m;i++) graph.add(new ArrayList<>());\n for(int[]i:arr) {\n graph.get(i[0]).add(i[1]);\n graph.get(i[1]).add(i[0]);\n }\n return graph;\n }\n private int f(int i,List<List<Integer>>graph,int k) {\n Queue<int[]>q=new LinkedList<>();\n q.add(new int[]{i,0});\n boolean[]vis=new boolean[graph.size()];\n vis[i]=true;\n int cnt=0;\n while(!q.isEmpty()) {\n int[]curr=q.poll();\n cnt++;\n if(curr[1]==k) continue;\n for(int j:graph.get(curr[0])) {\n if(!vis[j]) {\n vis[j]=true;\n q.add(new int[]{j,curr[1]+1});\n }\n }\n }\n return cnt;\n }\n}\n```
| 0 | 0 |
['Breadth-First Search', 'Java']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Python (Simple DFS)
|
python-simple-dfs-by-rnotappl-x4mu
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
rnotappl
|
NORMAL
|
2024-12-01T07:26:04.476612+00:00
|
2024-12-01T07:26:04.476638+00:00
| 13 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def maxTargetNodes(self, edges1, edges2, k):\n n, m, graph1, graph2 = len(edges1)+1, len(edges2)+1, defaultdict(list), defaultdict(list)\n\n for i,j in edges1:\n graph1[i].append(j)\n graph1[j].append(i)\n\n for i,j in edges2:\n graph2[i].append(j)\n graph2[j].append(i)\n\n def function(node,graph,d):\n stack, ans, visited = [(node,0)], {node}, {node}\n\n while stack:\n nd,dist = stack.pop()\n\n if dist <= d:\n ans.add(nd)\n\n for neighbor in graph[nd]:\n if neighbor not in visited:\n stack.append((neighbor,dist+1))\n visited.add(neighbor)\n\n return len(ans)\n\n res1 = [function(i,graph1,k) for i in range(n)]\n res2 = max([function(i,graph2,k-1) for i in range(m)])\n\n return [i+res2 for i in res1] if k > 0 else [1]*n\n```
| 0 | 0 |
['Python3']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Java Solution
|
java-solution-by-saicharansarikonda51-rfmi
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
saicharansarikonda51
|
NORMAL
|
2024-12-01T07:18:40.624044+00:00
|
2024-12-01T07:18:40.624088+00:00
| 5 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n int[] distance2;\n int[] distance1;\n public int[] maxTargetNodes(int[][] edges1, int[][] edges2, int k) {\n\n List<List<Integer>> adj1 = new ArrayList<>();\n List<List<Integer>> adj2 = new ArrayList<>();\n\n for(int i=0;i<edges1.length+1;i++)\n {\n adj1.add(new ArrayList<>());\n }\n\n for(int[] edge:edges1)\n {\n adj1.get(edge[0]).add(edge[1]);\n adj1.get(edge[1]).add(edge[0]);\n }\n\n for(int i=0;i<edges2.length+1;i++)\n {\n adj2.add(new ArrayList<>());\n }\n\n for(int[] edge:edges2)\n {\n adj2.get(edge[0]).add(edge[1]);\n adj2.get(edge[1]).add(edge[0]);\n }\n\n int[] ans = new int[edges1.length+1];\n\n distance1 = new int[adj1.size()];\n for(int i=0;i<distance1.length;i++)\n {\n distance1[i] = bfs(i,k,adj1);\n }\n\n distance2 = new int[adj2.size()];\n for(int i=0;i<distance2.length;i++)\n {\n distance2[i] = bfs(i,k-1,adj2);\n }\n\n int val = Integer.MIN_VALUE;\n for(int j=0;j<distance2.length;j++)\n {\n val = Math.max(val,distance2[j]);\n }\n\n for(int i=0;i<ans.length;i++)\n {\n ans[i]=distance1[i];\n ans[i]+=val;\n }\n\n return ans;\n \n }\n\n \n\n public int bfs(int i,int k, List<List<Integer>> adj)\n {\n int ans = 0;\n Queue<int[]> queue = new LinkedList<>();\n queue.add(new int[]{i,0});\n int count = 0;\n HashSet<Integer> visited = new HashSet<>();\n visited.add(i);\n\n while(queue.size()>0)\n {\n int[] curr = queue.poll();\n if(curr[1]>k)\n {\n continue;\n }\n count+=1;\n\n for(Integer j:adj.get(curr[0]))\n {\n if(!visited.contains(j))\n {\n queue.add(new int[]{j,curr[1]+1});\n visited.add(j);\n }\n }\n \n }\n\n return count;\n }\n}\n```
| 0 | 0 |
['Breadth-First Search', 'Java']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Java Solution
|
java-solution-by-saicharansarikonda51-znx1
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
saicharansarikonda51
|
NORMAL
|
2024-12-01T07:16:48.883124+00:00
|
2024-12-01T07:16:48.883162+00:00
| 0 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n int[] distance2;\n int[] distance1;\n public int[] maxTargetNodes(int[][] edges1, int[][] edges2, int k) {\n\n List<List<Integer>> adj1 = new ArrayList<>();\n List<List<Integer>> adj2 = new ArrayList<>();\n\n for(int i=0;i<edges1.length+1;i++)\n {\n adj1.add(new ArrayList<>());\n }\n\n for(int[] edge:edges1)\n {\n adj1.get(edge[0]).add(edge[1]);\n adj1.get(edge[1]).add(edge[0]);\n }\n\n for(int i=0;i<edges2.length+1;i++)\n {\n adj2.add(new ArrayList<>());\n }\n\n for(int[] edge:edges2)\n {\n adj2.get(edge[0]).add(edge[1]);\n adj2.get(edge[1]).add(edge[0]);\n }\n\n int[] ans = new int[edges1.length+1];\n\n distance1 = new int[adj1.size()];\n for(int i=0;i<distance1.length;i++)\n {\n distance1[i] = bfs(i,k,adj1);\n }\n\n distance2 = new int[adj2.size()];\n for(int i=0;i<distance2.length;i++)\n {\n distance2[i] = bfs(i,k-1,adj2);\n }\n\n int val = Integer.MIN_VALUE;\n for(int j=0;j<distance2.length;j++)\n {\n val = Math.max(val,distance2[j]);\n }\n\n for(int i=0;i<ans.length;i++)\n {\n ans[i]=distance1[i];\n // System.out.println("1. i "+i+" ans[i] "+ans[i]);\n //System.out.println("val is "+val);\n ans[i]+=val;\n //System.out.println("2. i "+i+" ans[i] "+ans[i]);\n }\n\n return ans;\n \n }\n\n \n\n public int bfs(int i,int k, List<List<Integer>> adj)\n {\n int ans = 0;\n Queue<int[]> queue = new LinkedList<>();\n queue.add(new int[]{i,0});\n int count = 0;\n HashSet<Integer> visited = new HashSet<>();\n visited.add(i);\n\n while(queue.size()>0)\n {\n int[] curr = queue.poll();\n if(curr[1]>k)\n {\n continue;\n }\n count+=1;\n\n for(Integer j:adj.get(curr[0]))\n {\n if(!visited.contains(j))\n {\n queue.add(new int[]{j,curr[1]+1});\n visited.add(j);\n }\n }\n \n }\n\n return count;\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Simple BFS solution
|
simple-bfs-solution-by-avik56-3k7h
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
avik56
|
NORMAL
|
2024-12-01T07:05:01.580353+00:00
|
2024-12-01T07:05:01.580433+00:00
| 12 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n\n int bfs(vector<vector<int>>& adj,int index,int k,int n)\n {\n vector<int> visited(n+1,0);\n queue<int> q;\n q.push(index);\n int ans = 1;\n visited[index] = 1;\n while(!q.empty())\n {\n int count = q.size();\n if(!count || !k)\n break;\n k--;\n while(count--)\n {\n int curr = q.front();\n q.pop();\n for(auto node:adj[curr])\n {\n if(!visited[node])\n {\n ans++;\n q.push(node);\n visited[node]=1;\n }\n } \n }\n }\n return ans;\n }\n\n\n vector<int> maxTargetNodes(vector<vector<int>>& edges1, vector<vector<int>>& edges2, int k) {\n \n int n = edges1.size();\n int m = edges2.size();\n vector<int> ans(n+1,1);\n\n if(k==0)\n return ans;\n\n vector<vector<int>> adj1(n+1);\n vector<vector<int>> adj2(m+1);\n\n for(auto edge:edges1)\n {\n adj1[edge[0]].push_back(edge[1]);\n adj1[edge[1]].push_back(edge[0]);\n }\n\n for(auto edge:edges2)\n {\n adj2[edge[0]].push_back(edge[1]);\n adj2[edge[1]].push_back(edge[0]);\n }\n\n int target = 0;\n for(int i=0;i<=m;i++)\n target = max(target,bfs(adj2,i,k-1,m));\n \n for(int i=0;i<=n;i++)\n {\n ans[i] = (target + bfs(adj1,i,k,n));\n }\n \n return ans;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Video Explanation Solution easy to understand | Programming with Pirai | Half Moon Coder.
|
video-explanation-solution-easy-to-under-pcxh
|
\n# Code\npython3 []\nclass Solution:\n def maxTargetNodes(self, edges1: List[List[int]], edges2: List[List[int]], k: int) -> List[int]:\n v=set()\n
|
Piraisudan_02
|
NORMAL
|
2024-12-01T06:06:50.406365+00:00
|
2024-12-01T06:06:50.406394+00:00
| 20 | false |
\n# Code\n```python3 []\nclass Solution:\n def maxTargetNodes(self, edges1: List[List[int]], edges2: List[List[int]], k: int) -> List[int]:\n v=set()\n adj1={}\n adj2={}\n n=m=0\n for a,b in edges1:\n if a not in adj1: adj1[a]=[]\n if b not in adj1: adj1[b]=[]\n adj1[a].append(b)\n adj1[b].append(a)\n n=max(n,a,b)\n for x,y in edges2:\n if x not in adj2: adj2[x]=[]\n if y not in adj2: adj2[y]=[]\n adj2[x].append(y)\n adj2[y].append(x)\n m=max(m,x,y)\n \n def tree2(root,k,adj):\n if k==-1 or root in v: return 0\n res=1\n v.add(root)\n for i in adj[root]:\n res+=tree2(i,k-1,adj)\n v.remove(root)\n return res\n \n ans=0\n for i in range(m+1):\n ans=max(tree2(i,k-1,adj2),ans)\n \n res=[]\n for i in range(n+1):\n val=tree2(i,k,adj1)\n # print(val)\n res.append(val+ans)\n return res\n```
| 0 | 0 |
['Depth-First Search', 'Breadth-First Search', 'Graph', 'Python3']
| 0 |
maximize-the-number-of-target-nodes-after-connecting-trees-i
|
Clean BFS | JAVA
|
clean-bfs-java-by-kesarwaniankit4812-s8th
|
Code\njava []\nclass Solution {\n public int[] maxTargetNodes(int[][] edges1, int[][] edges2, int k) {\n int m = edges1.length, n = edges2.length;\n\n
|
kesarwaniankit4812
|
NORMAL
|
2024-12-01T06:04:43.874231+00:00
|
2024-12-01T06:04:43.874267+00:00
| 11 | false |
# Code\n```java []\nclass Solution {\n public int[] maxTargetNodes(int[][] edges1, int[][] edges2, int k) {\n int m = edges1.length, n = edges2.length;\n\n if (k == 0) {\n int [] res = new int[m + 1];\n Arrays.fill(res, 1);\n\n return res;\n }\n\n List<List<Integer>> adj1 = new ArrayList<>();\n for (int i=0; i<=m; i++) {\n adj1.add(new ArrayList<>());\n }\n\n for (int [] edge : edges1) {\n adj1.get(edge[0]).add(edge[1]);\n adj1.get(edge[1]).add(edge[0]);\n }\n\n List<List<Integer>> adj2 = new ArrayList<>();\n for (int i=0; i<=n; i++) {\n adj2.add(new ArrayList<>());\n }\n\n for (int [] edge : edges2) {\n adj2.get(edge[0]).add(edge[1]);\n adj2.get(edge[1]).add(edge[0]);\n }\n\n int max = 1;\n for (int i=0; i<=n; i++) {\n max = Math.max(max, helper(adj2, i, k - 1));\n }\n\n int [] res = new int[m + 1];\n for (int i=0; i<=m; i++) {\n res[i] = max + helper(adj1, i, k);\n }\n\n return res;\n }\n\n private int helper(List<List<Integer>> adj, int u, int dist) {\n int count = 0;\n\n Queue<Integer> queue = new LinkedList<>();\n Set<Integer> visited = new HashSet<>();\n queue.offer(u);\n visited.add(u);\n\n int lvl = 0;\n while (!queue.isEmpty()) {\n if (lvl > dist) {\n break;\n }\n\n int size = queue.size();\n for (int i=0; i<size; i++) {\n int curr = queue.poll();\n count++;\n\n for (int child : adj.get(curr)) {\n if (!visited.contains(child)) {\n queue.offer(child);\n visited.add(child);\n }\n }\n }\n lvl++;\n }\n\n return count;\n }\n}\n```
| 0 | 0 |
['Depth-First Search', 'Breadth-First Search', 'Java']
| 0 |
subsequence-with-the-minimum-score
|
Right and Left O(n)
|
right-and-left-on-by-votrubac-iu8t
|
Based on the problem description, we need to find the longest prefix + suffix of t that is a subsequence of s.\n\nWe first match t starting from the right.\n\nF
|
votrubac
|
NORMAL
|
2023-02-12T04:02:39.538894+00:00
|
2023-02-12T08:45:40.949452+00:00
| 8,935 | false |
Based on the problem description, we need to find the longest prefix + suffix of `t` that is a subsequence of `s`.\n\nWe first match `t` starting from the right.\n\nFor each matched character in `t`, we remember the corresponding point in `s` in the `dp` array. This is our suffix.\n\nThen we go left-to-right building our prefix. For each prefix, we determine the longest suffix using `dp`.\n\n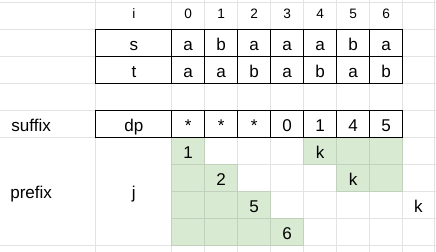\n\n**C++**\n```cpp\nint minimumScore(string s, string t) {\n int ss = s.size(), st = t.size(), k = st - 1;\n vector<int> dp(st, -1);\n for (int i = ss - 1; i >= 0 && k >= 0; --i)\n if (s[i] == t[k])\n dp[k--] = i;\n int res = k + 1;\n for (int i = 0, j = 0; i < ss && j < st && res > 0; ++i)\n if (s[i] == t[j]) {\n for (; k < t.size() && dp[k] <= i; ++k);\n res = min(res, k - (++j));\n }\n return res;\n}\n```\n**Java**\n```java\npublic int minimumScore(String s, String t) {\n int ss = s.length(), st = t.length(), k = st - 1;\n int[] dp = new int[st];\n Arrays.fill(dp, -1);\n for (int i = ss - 1; i >= 0 && k >= 0; --i)\n if (s.charAt(i) == t.charAt(k))\n dp[k--] = i;\n int res = k + 1;\n for (int i = 0, j = 0; i < ss && j < st && res > 0; ++i)\n if (s.charAt(i) == t.charAt(j)) {\n for (; k < st && dp[k] <= i; ++k);\n res = Math.min(res, k - (++j));\n }\n return res;\n}\n```
| 100 | 4 |
['C', 'Java']
| 15 |
subsequence-with-the-minimum-score
|
🔥Python3🔥 Greedy with comments
|
python3-greedy-with-comments-by-meidache-5ars
|
Observation: Everything in between left and right can be removed.\n\npython\nclass Solution:\n def minimumScore(self, s: str, t: str) -> int:\n # Take
|
MeidaChen
|
NORMAL
|
2023-02-12T05:02:25.994251+00:00
|
2024-01-04T19:27:30.390823+00:00
| 1,411 | false |
**Observation**: Everything in between ```left``` and ```right``` can be removed.\n\n```python\nclass Solution:\n def minimumScore(self, s: str, t: str) -> int:\n # Take care of the case where t is already a substring of s, return 0 in this case.\n j = 0\n for i in range(len(s)):\n if s[i]==t[j]: j+=1\n if j==len(t): return 0\n \n # Moving forward, store the first letter\'s index in t that needs to be removed if s ends at i.\n firstRemovedIndexFromLeft = [0]*len(s)\n left = 0\n for i in range(len(s)):\n if s[i]==t[left]:\n left += 1\n firstRemovedIndexFromLeft[i] = left\n\n # Worest case, we remove the first and last letter in t.\n res = len(t)\n \n # Moving backward, at each position i in s, there are two cases:\n # (1) the firstRemovedIndexFromLeft[i] <= first removed index from right,\n # This is a valid case in the sense that we can \n # basically, remove everything in between these two indices, including these two indices.\n # i.e.,\n # s = \'aabbbaa\'\n # t = \'aazzzaa\'\n # firstRemovedIndexFromLeft = [1, 2, 2, 2, 2, 2, 2]\n # firstRemovedIndexFromRight = [4, 4, 4, 4 ,4, 5, 6] (We don\'t actually put the right in arr like this, but just for easy understanding here)\n # when i=3, firstRemovedIndexFromLeft[i] = 2 and right = 4, \n # so we try to update res, if the score (right-left+1) is smaller.\n #\n # (2) left > right, this is an invalid case to consider both indices.\n # In this case, we basically just remove everything from 0 to index right, \n # score is (right - 0 + 1), where 0 is the left index. Update res if score is smaller.\n right = len(t) -1 \n for i in reversed(range(len(s))):\n if right>=firstRemovedIndexFromLeft[i]:\n res = min(right-firstRemovedIndexFromLeft[i]+1,res)\n if s[i] == t[right]:\n right -= 1\n res = min(res, right+1)\n \n return res\n```\nIs this called greedy approach or dp? Or it has an other name? Plesse leave a comment if you know the answer, thanks.\n\n**Upvote** if you like this post.\n\n**Connect with me on [LinkedIn](https://www.linkedin.com/in/meida-chen-938a265b/)** if you\'d like to discuss other related topics\n\n\uD83C\uDF1F If you are interested in **Machine Learning** || **Deep Learning** || **Computer Vision** || **Computer Graphics** related projects and topics, check out my **[YouTube Channel](https://www.youtube.com/@meidachen8489)**! Subscribe for regular updates and be part of our growing community.
| 21 | 0 |
[]
| 1 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.