question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
matrix-cells-in-distance-order
|
C++ O(RC) time, O(1) additional space
|
c-orc-time-o1-additional-space-by-asbest-5h4b
|
Idea: start from (r0, c0) and add elements around it to the answer vector layer by layer, each layer having a diamond shape as in the below picture.\n\n\n\n\n\n
|
asbest
|
NORMAL
|
2020-07-06T12:50:58.685595+00:00
|
2020-07-06T12:55:07.878462+00:00
| 154 | false |
Idea: start from (r0, c0) and add elements around it to the answer vector layer by layer, each layer having a diamond shape as in the below picture.\n\n\n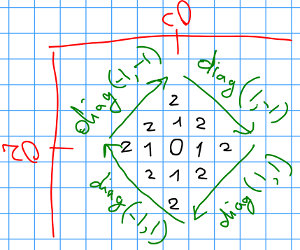\n\n\n```\n vector<vector<int>> allCellsDistOrder(int R, int C, int r0, int c0) {\n vector<vector<int>> ans;\n int l = 1, x = r0, y = c0;\n \n auto diag = [&ans, R, C, &l, &x, &y] (int dir_row, int dir_col) {\n for (int j = 1; j <= l; j++) {\n x += dir_row, y += dir_col;\n if (0 <= x && x < R && 0 <= y && y < C)\n ans.push_back({x, y});\n }\n };\n \n ans.push_back({x, y});\n while (l < R + C) {\n x = r0 - l; y = c0;\n diag(1,-1); diag(1,1); diag(-1,1); diag(-1,-1);\n l++;\n }\n \n return ans;\n }\n```
| 2 | 0 |
[]
| 0 |
matrix-cells-in-distance-order
|
C++ solution using Hashtable without lambda function
|
c-solution-using-hashtable-without-lambd-6bza
|
\tclass Solution {\n\tpublic:\n\t\tvector> allCellsDistOrder(int R, int C, int r0, int c0) {\n\t\t\tvector> res;\n\t\t\tfor(int i=0;i<R;i++)\n\t\t\t\tfor(int j=
|
jasperjoe
|
NORMAL
|
2020-01-07T16:22:45.865346+00:00
|
2020-01-07T16:22:45.865384+00:00
| 262 | false |
\tclass Solution {\n\tpublic:\n\t\tvector<vector<int>> allCellsDistOrder(int R, int C, int r0, int c0) {\n\t\t\tvector<vector<int>> res;\n\t\t\tfor(int i=0;i<R;i++)\n\t\t\t\tfor(int j=0;j<C;j++){\n\t\t\t\t\tres.push_back({i,j});\n\t\t\t\t}\n\t\t\tset<int> cnt;\n\t\t\tunordered_map<int,vector<vector<int>>> m;\n\t\t\tfor(auto x:res){\n\t\t\t\tint dis=abs(x[0]-r0)+abs(x[1]-c0);\n\t\t\t\tcnt.insert(dis);\n\t\t\t\tm[dis].push_back(x);\n\t\t\t}\n\t\t\tvector<int> cur{cnt.begin(),cnt.end()};//convert set into vector\n\t\t\tsort(cur.begin(),cur.end());\n\t\t\tvector<vector<int>> ans;\n\t\t\tfor(int i=0;i<cur.size();i++){\n\t\t\t\tfor(auto x:m[cur[i]]){\n\t\t\t\t\tans.push_back(x);\n\t\t\t\t}\n\t\t\t}\n\n\t\t\treturn ans;\n\t\t}\n\t};
| 2 | 1 |
['Hash Table', 'C', 'C++']
| 1 |
matrix-cells-in-distance-order
|
JAVA - BFS Solution (Easy to Understand)
|
java-bfs-solution-easy-to-understand-by-f2245
|
\npublic int[][] allCellsDistOrder(int R, int C, int r0, int c0) {\n\tint[][] sol = new int[R*C][2];\n\tQueue<int[]> q = new LinkedList<>();\n\tboolean[][] visi
|
anubhavjindal
|
NORMAL
|
2019-12-16T07:53:10.103368+00:00
|
2019-12-16T07:53:10.103420+00:00
| 152 | false |
```\npublic int[][] allCellsDistOrder(int R, int C, int r0, int c0) {\n\tint[][] sol = new int[R*C][2];\n\tQueue<int[]> q = new LinkedList<>();\n\tboolean[][] visited = new boolean[R][C];\n\tq.offer(new int[] {r0,c0});\n\tint i = 0;\n\twhile(!q.isEmpty()) {\n\t\tint[] curr = q.poll();\n\t\tint r = curr[0], c = curr[1];\n\t\tif(r<0 || c<0 || r>=R || c>=C)\n\t\t\tcontinue;\n\t\tif(visited[r][c])\n\t\t\tcontinue;\n\t\tvisited[r][c] = true;\n\t\tsol[i++] = curr;\n\t\tq.offer(new int[]{r,c+1});\n\t\tq.offer(new int[]{r,c-1});\n\t\tq.offer(new int[]{r+1,c});\n\t\tq.offer(new int[]{r-1,c});\n\t}\n\treturn sol;\n}\n```
| 2 | 0 |
[]
| 0 |
matrix-cells-in-distance-order
|
javascript solution 140 ms, faster than 100.00%
|
javascript-solution-140-ms-faster-than-1-25ap
|
\nvar allCellsDistOrder = function(R, C, r0, c0) {\n var arr = new Array();\n for(let i = 0; i < R; i++){\n for(let j = 0; j < C; j++){\n
|
tommy_giser
|
NORMAL
|
2019-07-01T08:26:33.841739+00:00
|
2019-07-01T08:26:33.841776+00:00
| 105 | false |
```\nvar allCellsDistOrder = function(R, C, r0, c0) {\n var arr = new Array();\n for(let i = 0; i < R; i++){\n for(let j = 0; j < C; j++){\n arr.push([i, j]);\n }\n }\n\n arr.sort((v1, v2) => {\n return Math.abs(v1[0] - r0) + Math.abs(v1[1] - c0) - (Math.abs(v2[0] - r0) + Math.abs(v2[1] - c0));\n });\n\n return arr;\n};\n```
| 2 | 0 |
[]
| 0 |
matrix-cells-in-distance-order
|
python O(n) bfs & O(nlogn) sort
|
python-on-bfs-onlogn-sort-by-jason003-uegb
|
python\nclass Solution:\n def allCellsDistOrder(self, R: int, C: int, r0: int, c0: int) -> List[List[int]]:\n # O(nlogn), sort\n # return sorte
|
jason003
|
NORMAL
|
2019-04-28T05:20:20.273287+00:00
|
2019-04-28T05:20:20.273318+00:00
| 231 | false |
```python\nclass Solution:\n def allCellsDistOrder(self, R: int, C: int, r0: int, c0: int) -> List[List[int]]:\n # O(nlogn), sort\n # return sorted([(a, b) for a in range(R) for b in range(C)], key = lambda x: abs(x[0] - r0) + abs(x[1] - c0))\n \n # O(n), BFS\n dq = collections.deque([(r0, c0)])\n res = [(r0, c0)]\n seen = {(r0, c0)}\n while dq:\n sz = len(dq)\n for _ in range(sz):\n x, y = dq.popleft()\n for dx, dy in ((1, 0), (-1, 0), (0, 1), (0, -1)):\n xx, yy = x + dx, y + dy\n if 0 <= xx < R and 0 <= yy < C and (xx, yy) not in seen:\n seen.add((xx, yy))\n res.append((xx, yy))\n dq.append((xx, yy))\n return res\n```
| 2 | 0 |
[]
| 0 |
matrix-cells-in-distance-order
|
Simple Java solution with Comparator
|
simple-java-solution-with-comparator-by-6x98n
|
\tclass Solution {\n\t\tpublic int[][] allCellsDistOrder(int R, int C, int r0, int c0) {\n\t\t\tint[][] res = new int[R*C][1];\n\t\t\tint x =0;\n\t\t\tfor(int i
|
tanvir3
|
NORMAL
|
2019-04-23T08:28:42.575176+00:00
|
2019-04-23T08:28:42.575245+00:00
| 176 | false |
\tclass Solution {\n\t\tpublic int[][] allCellsDistOrder(int R, int C, int r0, int c0) {\n\t\t\tint[][] res = new int[R*C][1];\n\t\t\tint x =0;\n\t\t\tfor(int i=0;i<R;i++){\n\t\t\t\tfor(int j=0;j<C;j++){\n\t\t\t\t\tres[x++]= new int[]{i,j};\n\t\t\t\t}\n\t\t\t}\n\n\t\t\tArrays.sort(res,new Comparator<int[]>(){\n\t\t\t\tpublic int compare(int[] a,int[] b){\n\t\t\t\t\treturn (Math.abs(r0-a[0]) + Math.abs(c0-a[1]))-(Math.abs(r0-b[0]) + Math.abs(c0-b[1]));\n\t\t\t\t}\n\t\t\t});\n\n\t\t\treturn res;\n\t\t}\n\t}
| 2 | 0 |
[]
| 1 |
matrix-cells-in-distance-order
|
C# One line solution
|
c-one-line-solution-by-qw123-jhyl
|
\npublic class Solution {\n public int[][] AllCellsDistOrder(int R, int C, int r0, int c0) => Enumerable.Range(0,R*C).Select(i=>new int[]{i/C,i%C}).OrderBy(x
|
qw123
|
NORMAL
|
2019-04-22T00:58:56.905211+00:00
|
2019-04-22T00:58:56.905280+00:00
| 154 | false |
```\npublic class Solution {\n public int[][] AllCellsDistOrder(int R, int C, int r0, int c0) => Enumerable.Range(0,R*C).Select(i=>new int[]{i/C,i%C}).OrderBy(x=> Math.Abs(x[0]-r0)+Math.Abs(x[1]-c0)).ToArray();\n}\n```
| 2 | 0 |
[]
| 0 |
matrix-cells-in-distance-order
|
Explained Short Javascript O(n) Beats 100%
|
explained-short-javascript-on-beats-100-0gsrz
|
\n```\nvar allCellsDistOrder = function(R, C, r0, c0) {\n\t// Create a 2D array which holds the maximum number of possible distances.\n let ordered = [...Arr
|
jcode-dev
|
NORMAL
|
2019-04-21T23:38:12.562479+00:00
|
2019-04-21T23:38:12.562521+00:00
| 150 | false |
\n```\nvar allCellsDistOrder = function(R, C, r0, c0) {\n\t// Create a 2D array which holds the maximum number of possible distances.\n let ordered = [...Array(R*C)].map(e => [])\n\t\n\t// Traverse the whole grid\n for(let j = 0; j < R; j++) {\n for(let i = 0; i < C; i++) {\n\t\t\t// Get Manhattan distance\n let d = Math.abs(j-r0) + Math.abs(i-c0)\n\t\t\t// Add to the 2D array in an ordered manner\n ordered[d].push([j,i])\n }\n }\n // Use ES6 spread operator to flatten\n return [].concat([].concat(...ordered))\n};
| 2 | 0 |
[]
| 0 |
matrix-cells-in-distance-order
|
Very Simple C# Solution
|
very-simple-c-solution-by-christris-t2qm
|
csharp\n\npublic class Solution\n{ \n class Point : IComparable<Point>\n {\n public readonly int x;\n public readonly int y;\n
|
christris
|
NORMAL
|
2019-04-21T06:16:15.669938+00:00
|
2019-04-21T06:16:15.669995+00:00
| 253 | false |
``` csharp\n\npublic class Solution\n{ \n class Point : IComparable<Point>\n {\n public readonly int x;\n public readonly int y;\n public static Point origin;\n \n public Point(int x, int y)\n {\n this.x = x;\n this.y = y; \n }\n \n public int CompareTo(Point other)\n {\n return (Math.Abs(x - origin.x) + Math.Abs(y - origin.y)) \n - (Math.Abs(other.x - origin.x) + Math.Abs(other.y - origin.y));\n }\n }\n \n public int[][] AllCellsDistOrder(int R, int C, int r0, int c0) { \n List<Point> points = new List<Point>();\n Point.origin = new Point(r0, c0);\n\t\t \n for(int r = 0; r < R; r++)\n {\n for(int c = 0; c < C; c++)\n {\n points.Add(new Point(r, c)); \n } \n } \n \n return points.OrderBy(p => p).Select(p => new int[] { p.x, p.y}).ToArray(); \n }\n}\n```
| 2 | 1 |
[]
| 0 |
matrix-cells-in-distance-order
|
Priority Queue Solution in java
|
priority-queue-solution-in-java-by-ravit-7zmq
|
\nclass Solution {\n public int[][] allCellsDistOrder(int R, int C, int r0, int c0) {\n \n PriorityQueue<int[]> pq = new PriorityQueue<>((a,b)-
|
ravitejathoram
|
NORMAL
|
2019-04-21T04:45:50.457961+00:00
|
2019-04-21T04:45:50.457991+00:00
| 128 | false |
```\nclass Solution {\n public int[][] allCellsDistOrder(int R, int C, int r0, int c0) {\n \n PriorityQueue<int[]> pq = new PriorityQueue<>((a,b)->a[2]-b[2]);\n \n for(int r=0;r < R;r++){\n for(int c=0;c < C;c++){\n int dist = Math.abs(r-r0) + Math.abs(c-c0);\n pq.offer(new int[]{r,c,dist});\n }\n }\n int[][] res = new int[R*C][2];\n int k = 0;\n while(!pq.isEmpty()){\n int[] val = pq.poll();\n res[k][0] = val[0];\n res[k][1] = val[1];\n k++;\n }\n return res;\n }\n}\n```\n\n
| 2 | 0 |
['Heap (Priority Queue)']
| 0 |
matrix-cells-in-distance-order
|
Python Straightforward 5-Line O(N) Code
|
python-straightforward-5-line-on-code-by-1k1o
|
Go through the cells and classify them according to their distances towards (r0, c0). Finally, output them sequentially.\n\nclass Solution:\n def allCellsDis
|
infinute
|
NORMAL
|
2019-04-21T04:05:57.399894+00:00
|
2019-04-21T04:05:57.399928+00:00
| 353 | false |
Go through the cells and classify them according to their distances towards `(r0, c0)`. Finally, output them sequentially.\n```\nclass Solution:\n def allCellsDistOrder(self, R: int, C: int, r0: int, c0: int) -> List[List[int]]:\n res = [[] for _ in range(R + C)]\n for row in range(R):\n for col in range(C):\n res[abs(row - r0) + abs(col - c0)].append([row, col])\n return sum(res, [])\n```\n\nOf course, you can do it in one line with the builtin `sort`.\n```\nclass Solution:\n def allCellsDistOrder(self, R: int, C: int, r0: int, c0: int) -> List[List[int]]:\n return sorted([[row, col] for row in range(R) for col in range(C)], key=lambda x: abs(x[0] - r0) + abs(x[1] - c0))\n```
| 2 | 1 |
['Python']
| 2 |
matrix-cells-in-distance-order
|
Java straighforward
|
java-straighforward-by-never-give-up-ruly
|
class Solution {\n \n public int[][] allCellsDistOrder(int R, int C, int r0, int c0) {\n List<int[]> result = new ArrayList<int[]>();\n \n
|
never-give-up
|
NORMAL
|
2019-04-21T04:01:56.169296+00:00
|
2019-04-21T04:01:56.169341+00:00
| 263 | false |
```class Solution {\n \n public int[][] allCellsDistOrder(int R, int C, int r0, int c0) {\n List<int[]> result = new ArrayList<int[]>();\n \n for (int i = 0; i < R; i++) {\n for (int j = 0; j < C; j++) {\n int[] tmp = new int[2];\n \n tmp[0] = i;\n tmp[1] = j;\n \n result.add(tmp);\n }\n }\n \n Collections.sort(result, new Comparator<int[]>() {\n public int compare(int[] a, int[] b) {\n int l1 = Math.abs(a[0] - r0) + Math.abs(a[1] - c0);\n int l2 = Math.abs(b[0] - r0) + Math.abs(b[1] - c0);\n \n return l1 - l2;\n }\n });\n \n int[][] arr = result.toArray(new int[result.size()][2]);\n \n return arr;\n }\n}```
| 2 | 1 |
[]
| 0 |
matrix-cells-in-distance-order
|
SIMPLE AND EASY PYTHON CODE
|
simple-and-easy-python-code-by-harsh_519-w3t2
|
Here's a concise Python solution that meets the requirements:Explanation:
Generate the Coordinates:A list comprehension creates a list of all cells in the matr
|
harsh_5191
|
NORMAL
|
2025-02-19T06:07:06.840645+00:00
|
2025-02-19T06:07:06.840645+00:00
| 72 | false |
Here's a concise Python solution that meets the requirements:
```python
def allCellsDistOrder(rows: int, cols: int, rCenter: int, cCenter: int):
# Create a list of all cell coordinates in the matrix
cells = [[r, c] for r in range(rows) for c in range(cols)]
# Sort the cells by their Manhattan distance from (rCenter, cCenter)
cells.sort(key=lambda cell: abs(cell[0] - rCenter) + abs(cell[1] - cCenter))
return cells
```
### Explanation:
1. **Generate the Coordinates:**
A list comprehension creates a list of all cells in the matrix.
2. **Sort by Manhattan Distance:**
The `sort` method uses a lambda function to compute the Manhattan distance for each cell:
\[
\text{distance} = |r - rCenter| + |c - cCenter|
\]
The cells are sorted in increasing order of this distance.
3. **Return the Result:**
Finally, the sorted list is returned.
This approach is straightforward and efficient for the problem constraints.

| 1 | 0 |
['Python']
| 0 |
matrix-cells-in-distance-order
|
[Chaining] - Very Short Code
|
chaining-very-short-code-by-charnavoki-6ix8
| null |
charnavoki
|
NORMAL
|
2025-01-25T17:51:49.050258+00:00
|
2025-01-25T17:51:49.050258+00:00
| 82 | false |
```javascript []
const allCellsDistOrder = (r, c, x, y, m = Math.abs) =>
Array(r).fill(0)
.map((_, i) => Array(c).fill().map((_, j) => [i, j] )).flat()
.sort(([i, j], [a, b]) => m(j-y) + m(i-x) - m(b-y) - m(a-x));
```
| 1 | 0 |
['JavaScript']
| 0 |
matrix-cells-in-distance-order
|
Brute Force 👀 🎊 | | C++
|
brute-force-c-by-varuntyagig-ax44
|
Complexity
Time complexity:
O(Rows∗Cols∗Log(Rows∗Cols))
Space complexity:
O(Rows∗Cols)
Code
|
varuntyagig
|
NORMAL
|
2025-01-23T06:56:53.739516+00:00
|
2025-01-23T06:56:53.739516+00:00
| 157 | false |
# Complexity
- Time complexity:
$$O(Rows∗Cols∗Log(Rows∗Cols))$$
- Space complexity:
$$O(Rows*Cols)$$
# Code
```cpp []
class Solution {
public:
vector<vector<int>> allCellsDistOrder(int rows, int cols, int rCenter,
int cCenter) {
vector<int> storeDistance;
vector<vector<int>> storeCordinates, answer;
for (int i = 0; i < rows; i++) {
for (int j = 0; j < cols; j++) {
int r1 = i;
int c1 = j;
storeDistance.push_back(abs(r1 - rCenter) + abs(c1 - cCenter));
storeCordinates.push_back({i, j});
}
}
sort(storeDistance.begin(), storeDistance.end());
for (int i = 0; i < storeDistance.size(); i++) {
for (int j = 0; j < storeCordinates.size(); j++) {
int r1 = storeCordinates[j][0];
int c1 = storeCordinates[j][1];
int dis = abs(r1 - rCenter) + abs(c1 - cCenter);
if (dis == storeDistance[i]) {
answer.push_back({r1, c1});
storeCordinates[j][0] = -1000;
storeCordinates[j][1] = -1000;
break;
}
}
}
return answer;
}
};
```
| 1 | 0 |
['Array', 'Sorting', 'Matrix', 'C++']
| 0 |
matrix-cells-in-distance-order
|
Python3 Solution | Beats 96.01% | Explain Step by Step
|
python3-solution-beats-9601-explain-step-fywi
|
Intuition
Use a dictionary distance_dict to record distance.
Sort distance_dict according to keys -> sorted_dict.
Use sorted_dict to return the final answe
|
ChrisLee0688
|
NORMAL
|
2025-01-05T01:19:34.644357+00:00
|
2025-01-05T01:19:34.644357+00:00
| 167 | false |
# Intuition
1. Use a dictionary `distance_dict` to record distance.
2. Sort `distance_dict` according to keys -> `sorted_dict`.
3. Use `sorted_dict` to return the final answer `ans`.
# Approach
# **1. Fill `distance_dict` while iterating matrix.**
- Initialize an empty dictionary `distance_dict`.
```python3 []
distance_dict = {}
```
- Iterate through the matrix and calculate the distance.
```python3 []
for r in range(rows):
for c in range(cols):
distance = abs(r - rCenter) + abs(c - cCenter)
```
- Update `distance_dict`:
```python3 []
if distance in distance_dict:
distance_dict[distance].append([r, c])
else:
distance_dict[distance] = [[r, c]]
```
# **2. Sort the distance_dict**
- Sort the dict by key (by distance) in non-decreasing order.
# **3. Return the final answer**
```python3 []
ans = []
for value in sorted_dict.values():
ans.extend(value)
return ans
```
# Complexity
- Time complexity: $$O(n^2)$$, iterate through every grid of the matrix.
- Space complexity: $$O(n)$$, the cost of the dictionary.
# Code
```python3 []
import math
class Solution:
def allCellsDistOrder(self, rows: int, cols: int, rCenter: int, cCenter: int) -> List[List[int]]:
# Fill distance_dict while iterating matrix
# Key represents the distance
# Value represents the list including all cells that have the same distance
distance_dict = {}
for r in range(rows):
for c in range(cols):
distance = abs(r - rCenter) + abs(c - cCenter)
if distance in distance_dict:
distance_dict[distance].append([r, c])
else:
distance_dict[distance] = [[r, c]]
# Sort the distance_dict
sorted_keys = sorted(distance_dict.keys())
sorted_dict = {x: distance_dict[x] for x in sorted_keys}
# Use sorted_dict to return the final answer
ans = []
for value in sorted_dict.values():
ans.extend(value)
return ans
```
| 1 | 0 |
['Sorting', 'Matrix', 'Python3']
| 0 |
matrix-cells-in-distance-order
|
Single line solution python
|
single-line-solution-python-by-jralphw-zudn
|
Return list first created by generator statement then sorted using lambda function as key\n\n# Code\npython3 []\nclass Solution:\n def allCellsDistOrder(self
|
jralphw
|
NORMAL
|
2024-09-27T00:47:32.424151+00:00
|
2024-09-27T00:47:32.424210+00:00
| 73 | false |
Return list first created by generator statement then sorted using lambda function as key\n\n# Code\n```python3 []\nclass Solution:\n def allCellsDistOrder(self, rows: int, cols: int, rCenter: int, cCenter: int) -> List[List[int]]:\n return sorted([[i, j] for i in range(rows) for j in range(cols) ], key = lambda s: abs(s[0]-rCenter)+abs(s[1]-cCenter))\n```
| 1 | 0 |
['Python3']
| 1 |
matrix-cells-in-distance-order
|
🔥✅Python Easy Solution✅ Beat 87.63% | ✅ With Explanation🔥
|
python-easy-solution-beat-8763-with-expl-8o9a
|
PLEASE UPVOTE\n\n\n# Intuition\n\nWhen faced with the task of sorting matrix cells by their distance from a specific cell, the immediate thought is to leverage
|
abdulrehmanadeem14
|
NORMAL
|
2024-03-24T10:32:58.358436+00:00
|
2024-03-24T10:32:58.358467+00:00
| 418 | false |
# **PLEASE UPVOTE**\n\n\n# Intuition\n\nWhen faced with the task of sorting matrix cells by their distance from a specific cell, the immediate thought is to leverage the Manhattan distance formula due to its simplicity and relevance in grid-based problems. This problem\'s essence lies not just in calculating distances but also in efficiently organizing the cells according to these distances. Recognizing that the Manhattan distance provides a straightforward way to compare the proximity between any two points on a grid, we can use it to fulfill the sorting requirement.\n\nimage.png\n\n\n# Approach\n\n1. **Generate Coordinates**: Create a list of all cell coordinates in the matrix. This is straightforward in a grid where each cell can be represented by a pair of row and column indices.\n \n2. **Sort by Distance**: Use the Manhattan distance formula to sort these coordinates. The formula, |r1 - r2| + |c1 - c2|, is applied between the center cell `(rCenter, cCenter)` and each cell in the grid. Sorting based on this distance ensures that cells closer to the center are placed before those farther away.\n\n3. **Return Sorted List**: After sorting, the list of cells now respects the order of increasing distance from the center cell. This sorted list is exactly what is needed as output.\n\n# Complexity\n\n- **Time Complexity**: $$O(n \\log n)$$\n\n - Generating all cell coordinates takes $$O(n)$$ time, where \\(n\\) is the total number of cells in the matrix (`rows * cols`).\n - Sorting these cells by their distance from the center cell takes $$O(n \\log n)$$ time, as sorting algorithms typically have this complexity.\n\n- **Space Complexity**: $$O(n)$$\n\n - The space complexity is determined by the storage of all cell coordinates in a list, requiring $$O(n)$$ space, where \\(n\\) is the total number of cells.\n\n# Code\n\n```python\nfrom typing import List\n\nclass Solution:\n def allCellsDistOrder(self, rows: int, cols: int, rCenter: int, cCenter: int) -> List[List[int]]:\n # Generate all cells\n all_cells = [[r, c] for r in range(rows) for c in range(cols)]\n \n # Sort cells by Manhattan distance from (rCenter, cCenter)\n all_cells.sort(key=lambda x: abs(x[0] - rCenter) + abs(x[1] - cCenter))\n \n # Return sorted cells\n return all_cells\n```\n
| 1 | 0 |
['Array', 'Math', 'Matrix', 'Python', 'C++', 'Java', 'Python3']
| 1 |
matrix-cells-in-distance-order
|
Matrix Cells in Distance Order || JAVASCRIPT || Solution by Bharadwaj
|
matrix-cells-in-distance-order-javascrip-685p
|
Approach\nHashing\n\n# Complexity\n- Time complexity:\nTime: O(r*c)\n\n- Space complexity:\nO(r+c)\n\n# Code\n\nvar allCellsDistOrder = function(r, c, r0, c0) {
|
Manu-Bharadwaj-BN
|
NORMAL
|
2023-11-25T13:19:21.357095+00:00
|
2023-11-25T13:19:21.357127+00:00
| 34 | false |
# Approach\nHashing\n\n# Complexity\n- Time complexity:\nTime: O(r*c)\n\n- Space complexity:\nO(r+c)\n\n# Code\n```\nvar allCellsDistOrder = function(r, c, r0, c0) {\n let buckets = [];\n let ret = [];\n for(let i = 0; i < r; ++i){\n for(let j = 0; j < c; ++j){\n let dis = Math.abs(i - r0) + Math.abs(j - c0);\n if(buckets[dis] === undefined) buckets[dis] = [];\n buckets[dis].push([i, j]);\n }\n }\n for(let bucket of buckets){\n ret.push(...bucket);\n }\n return ret;\n};\n```
| 1 | 0 |
['JavaScript']
| 0 |
matrix-cells-in-distance-order
|
Swift Solution
|
swift-solution-by-danilovdev-6ppa
|
Intuition\nCalculate distance for every cell and sort by this distance.\n\n# Approach\nCalculate distance from center cell for every other cell in matrix, and p
|
danilovdev
|
NORMAL
|
2023-10-07T15:22:31.302868+00:00
|
2023-10-07T15:22:31.302896+00:00
| 10 | false |
# Intuition\nCalculate distance for every cell and sort by this distance.\n\n# Approach\nCalculate distance from center cell for every other cell in matrix, and put to array along with each cell coordinates. Then sort array by distance and get only cells coordinates from this array.\n\n# Complexity\n- Time complexity:\nO(rows X cols) Because we iterate all elements in matrix\n\n- Space complexity:\nO(rows X cols) Because we store all elements\n\n# Code\n```\nclass Solution {\n func allCellsDistOrder(_ rows: Int, _ cols: Int, _ rCenter: Int, _ cCenter: Int) -> [[Int]] {\n var cells: [(cell: [Int], dist: Int)] = [] \n for i in 0..<rows {\n for j in 0..<cols {\n let dist = abs(i - rCenter) + abs(j - cCenter)\n cells.append(([i, j], dist))\n }\n }\n return cells.sorted(by: { $0.dist < $1.dist }).map { $0.cell }\n }\n}\n```
| 1 | 0 |
['Swift']
| 1 |
matrix-cells-in-distance-order
|
C# Priority Queue Solution
|
c-priority-queue-solution-by-siriusq-rn2l
|
Code\n\npublic class Solution {\n public int[][] AllCellsDistOrder(int rows, int cols, int rCenter, int cCenter) {\n PriorityQueue<int[], int> pq = ne
|
Siriusq
|
NORMAL
|
2023-08-25T07:24:06.690373+00:00
|
2023-08-25T07:24:06.690399+00:00
| 12 | false |
# Code\n```\npublic class Solution {\n public int[][] AllCellsDistOrder(int rows, int cols, int rCenter, int cCenter) {\n PriorityQueue<int[], int> pq = new PriorityQueue<int[], int>();\n for (int i = 0; i < rows; i++)\n {\n for (int j = 0; j < cols; j++)\n {\n pq.Enqueue(new int[] { i, j }, Math.Abs(i - rCenter) + Math.Abs(j - cCenter));\n }\n }\n int[][] res = new int[rows * cols][];\n int count = 0;\n while (pq.Count > 0)\n {\n res[count] = pq.Dequeue();\n count++;\n }\n \n return res;\n }\n}\n```
| 1 | 0 |
['C#']
| 0 |
matrix-cells-in-distance-order
|
1 line, linq
|
1-line-linq-by-3s_akb-jh3s
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
3S_AKB
|
NORMAL
|
2023-06-30T21:42:11.734290+00:00
|
2023-06-30T21:42:11.734311+00:00
| 18 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\npublic class Solution {\n public int[][] AllCellsDistOrder(int Y, int X, int YY, int XX) {\n return Enumerable.Range(0, X*Y).\n Select(x => (x / X, x % X, Math.Abs(YY - x / X) + Math.Abs(XX - x % X))).\n OrderBy(x=>x.Item3).Select(x=> new int[] {x.Item1, x.Item2}).ToArray();\n }\n}\n```
| 1 | 0 |
['C#']
| 1 |
matrix-cells-in-distance-order
|
Python3 || One-liner based on list comprehesion &sorted() || beats 95.3% runtime & 85.6% mem usage
|
python3-one-liner-based-on-list-comprehe-hvf0
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Molot84
|
NORMAL
|
2023-04-05T10:56:33.055668+00:00
|
2023-04-05T10:56:33.055702+00:00
| 75 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def allCellsDistOrder(self, rows: int, cols: int, rCenter: int, cCenter: int) -> List[List[int]]:\n return sorted([[r, c] for r in range(rows) for c in range(cols)], key=lambda x: abs(x[0] - rCenter) + abs(x[1] - cCenter))\n```
| 1 | 0 |
['Python3']
| 0 |
matrix-cells-in-distance-order
|
Python3 - Nasty 1 liner
|
python3-nasty-1-liner-by-spankem-o4op
|
\n# Complexity\n- Time complexity:\nO(nlogn) \n\n- Space complexity:\no(n)\n\n# Code\n\nclass Solution:\n def allCellsDistOrder(self, rows: int, cols: int, r
|
spankem
|
NORMAL
|
2023-03-15T11:13:00.162535+00:00
|
2023-03-15T11:14:16.771349+00:00
| 52 | false |
\n# Complexity\n- Time complexity:\nO(nlogn) \n\n- Space complexity:\no(n)\n\n# Code\n```\nclass Solution:\n def allCellsDistOrder(self, rows: int, cols: int, rCenter: int, cCenter: int) -> List[List[int]]:\n\n return sorted(\n [[r, c] for r in range(0, rows, 1) for c in range(0, cols, 1)],\n key=lambda coord: abs(coord[0] - rCenter) + abs(coord[1] - cCenter),\n )\n\n```
| 1 | 0 |
['Python3']
| 0 |
matrix-cells-in-distance-order
|
Beats 98%
|
beats-98-by-codequeror-4t00
|
Upvote it :)\n\nclass Solution:\n def allCellsDistOrder(self, rows: int, cols: int, rCenter: int, cCenter: int) -> List[List[int]]:\n d, res = default
|
Codequeror
|
NORMAL
|
2023-01-26T09:00:00.443916+00:00
|
2023-01-26T09:00:00.443972+00:00
| 79 | false |
# Upvote it :)\n```\nclass Solution:\n def allCellsDistOrder(self, rows: int, cols: int, rCenter: int, cCenter: int) -> List[List[int]]:\n d, res = defaultdict(list), []\n for i in range(rows):\n x = abs(i - rCenter)\n for j in range(cols):\n dist = x + abs(j - cCenter)\n d[dist].append([i, j])\n for i in sorted(d): res += d[i]\n return res\n\n```
| 1 | 0 |
['Python', 'Python3']
| 0 |
matrix-cells-in-distance-order
|
python3 Solution
|
python3-solution-by-motaharozzaman1996-ji37
|
\n\nclass Solution:\n def allCellsDistOrder(self, rows: int, cols: int, rCenter: int, cCenter: int) -> List[List[int]]:\n res=[]\n for r in ran
|
Motaharozzaman1996
|
NORMAL
|
2023-01-07T11:34:25.816304+00:00
|
2023-01-07T11:34:25.816357+00:00
| 612 | false |
\n```\nclass Solution:\n def allCellsDistOrder(self, rows: int, cols: int, rCenter: int, cCenter: int) -> List[List[int]]:\n res=[]\n for r in range(rows):\n for c in range(cols):\n res.append([r,c])\n \n res.sort(key=lambda x:abs(x[0]-rCenter)+ abs(x[1]-cCenter))\n return res\n```
| 1 | 0 |
['Python3']
| 0 |
matrix-cells-in-distance-order
|
C++ || CLEAN COMPARATOR SOLUTION || EASY TO UNDERSTAND
|
c-clean-comparator-solution-easy-to-unde-7fug
|
\nclass Solution {\npublic:\n vector<vector<int>> allCellsDistOrder(int rows, int cols, int rCenter, int cCenter) {\n vector<vector<int>> ans;\n
|
aaronbargotta
|
NORMAL
|
2022-09-23T23:24:55.468856+00:00
|
2022-09-23T23:24:55.468894+00:00
| 984 | false |
```\nclass Solution {\npublic:\n vector<vector<int>> allCellsDistOrder(int rows, int cols, int rCenter, int cCenter) {\n vector<vector<int>> ans;\n for (int r = 0; r < rows; r++) {\n for (int c = 0; c < cols; c++) {\n ans.push_back({r, c});\n }\n }\n\n sort(ans.begin(), ans.end(), DistFromCenterSorter(rCenter, cCenter));\n return ans;\n }\n\nprivate:\n struct DistFromCenterSorter {\n int rCenter;\n int cCenter;\n DistFromCenterSorter(int rCenter, int cCenter) {\n this->rCenter = rCenter;\n this->cCenter = cCenter;\n }\n\n bool operator()(const vector<int>& cell1, const vector<int>& cell2) {\n return distFromCenter(cell1) < distFromCenter(cell2);\n }\n\n int distFromCenter(const vector<int>& cell) {\n return abs(cell[0] - this->rCenter) + abs(cell[1] - this->cCenter);\n }\n };\n};\n```\n\nIf you found this useful, an upvote would be appreciated! :)
| 1 | 0 |
[]
| 0 |
matrix-cells-in-distance-order
|
I am not a big fan of one-liner, but this is hard to refrain...
|
i-am-not-a-big-fan-of-one-liner-but-this-oin7
|
\nclass Solution:\n def allCellsDistOrder(self, rows: int, cols: int, rCenter: int, cCenter: int) -> List[List[int]]:\n return sorted([[x,y] for x in
|
huikinglam02
|
NORMAL
|
2022-08-19T04:32:10.209555+00:00
|
2022-08-19T04:32:10.209580+00:00
| 118 | false |
```\nclass Solution:\n def allCellsDistOrder(self, rows: int, cols: int, rCenter: int, cCenter: int) -> List[List[int]]:\n return sorted([[x,y] for x in range(rows) for y in range(cols)], key = lambda x: abs(x[0] - rCenter) + abs(x[1] - cCenter))\n```
| 1 | 0 |
[]
| 0 |
matrix-cells-in-distance-order
|
Using helper function & sort
|
using-helper-function-sort-by-andrewnerd-lzje
|
\nclass Solution:\n def allCellsDistOrder(self, rows: int, cols: int, rCenter: int, cCenter: int) -> List[List[int]]:\n # create a r, c matrix given t
|
andrewnerdimo
|
NORMAL
|
2022-08-07T21:57:56.802066+00:00
|
2022-08-07T21:57:56.802092+00:00
| 371 | false |
```\nclass Solution:\n def allCellsDistOrder(self, rows: int, cols: int, rCenter: int, cCenter: int) -> List[List[int]]:\n # create a r, c matrix given the rows & cols\n # each element represents a list [r, c] where r is the row & c the col\n # find find the distances of all cells from the center (append to res)\n # sort the result by distance function\n # Time O(M + N) Space O(M + N)\n \n \n def distance(p1, p2):\n return abs(p1[0] - p2[0]) + abs(p1[1] - p2[1])\n \n matrix = [[i, j] for i in range(rows) for j in range(cols)]\n center = [rCenter, cCenter]\n matrix.sort(key=lambda c: distance(c, center))\n \n return matrix\n```
| 1 | 0 |
['Python', 'Python3']
| 0 |
matrix-cells-in-distance-order
|
Matrix Cells in Distance Order | Java | Easy | Queue | BFS | Sorting | 2 methods
|
matrix-cells-in-distance-order-java-easy-3rd4
|
\n//--------------------Method 1----------------------\n\nclass Solution {\n public int[][] allCellsDistOrder(int rows, int cols, int rCenter, int cCenter) {
|
Paridhicodes
|
NORMAL
|
2022-07-13T14:50:37.163239+00:00
|
2022-07-13T14:59:33.465135+00:00
| 390 | false |
```\n//--------------------Method 1----------------------\n\nclass Solution {\n public int[][] allCellsDistOrder(int rows, int cols, int rCenter, int cCenter) {\n \n int [][]res=new int[rows*cols][2];\n \n int idx=0;\n \n for(int i=0;i<rows;i++){\n for(int j=0;j<cols;j++){\n res[idx][0]=i;\n res[idx][1]=j;\n idx++;\n }\n }\n \n Arrays.sort(res,(a,b)->{\n int d1=Math.abs(a[0]-rCenter)+Math.abs(a[1]-cCenter);\n int d2=Math.abs(b[0]-rCenter)+Math.abs(b[1]-cCenter);\n \n return d1-d2;\n });\n \n return res;\n }\n}\n\n//--------------------Method 2--------------------\n\n// class Solution {\n// public int[][] allCellsDistOrder(int rows, int cols, int rCenter, int cCenter) {\n \n// boolean [][]vis=new boolean[rows][cols];\n// int [][]ans=new int[rows*cols][2];\n \n// Queue<Pair> q=new LinkedList<>();\n// q.add(new Pair(rCenter,cCenter));\n// int idx=0;\n// vis[rCenter][cCenter]=true;\n// int [][]dir={{0,1},{1,0},{-1,0},{0,-1}};\n \n// while(!q.isEmpty()){\n// Pair curr=q.remove();\n// ans[idx][0]=curr.r;\n// ans[idx][1]=curr.c;\n// idx++;\n \n// for(int []d:dir){\n// int nr=curr.r+d[0];\n// int nc=curr.c+d[1];\n \n// if(nr>=0 && nr<rows && nc>=0 && nc<cols && !vis[nr][nc]){\n// vis[nr][nc]=true;\n// q.add(new Pair(nr,nc));\n// }\n// }\n// }\n \n// return ans;\n// }\n// }\n\n// class Pair{\n// int r;\n// int c;\n \n// public Pair(int r, int c){\n// this.r=r;\n// this.c=c;\n// }\n// }\n```
| 1 | 0 |
['Breadth-First Search', 'Queue', 'Java']
| 0 |
matrix-cells-in-distance-order
|
Java | Easy | Sorting Solution
|
java-easy-sorting-solution-by-pranav_bob-6yd7
|
```class Solution {\n public int[][] allCellsDistOrder(int rows, int cols, int rCenter, int cCenter) {\n int [][] ans = new int [rows*cols][2];\n
|
pranav_bobade
|
NORMAL
|
2022-06-09T09:36:40.790778+00:00
|
2022-06-09T09:36:40.790815+00:00
| 109 | false |
```class Solution {\n public int[][] allCellsDistOrder(int rows, int cols, int rCenter, int cCenter) {\n int [][] ans = new int [rows*cols][2];\n // creating an 2d array to store coordinates / total pairs(i,j) \n for(int i = 0; i < rows; i++)\n {\n for(int j = 0; j < cols; j++)\n {\n int bno = i * cols + j; //ans. array index\n ans[bno][0] = i;\n ans[bno][1] = j;\n }\n }\n \n Arrays.sort(ans,(a,b) ->{\n int d1 = Math.abs(a[0] - rCenter) + Math.abs(a[1] - cCenter);\n int d2 = Math.abs(b[0] - rCenter) + Math.abs(b[1] - cCenter);\n\n return d1 - d2;\n });\n // (a,b) is each 1d array on ans array\'s index\n return ans;\n }\n}
| 1 | 0 |
[]
| 1 |
matrix-cells-in-distance-order
|
super clear 🐍 illustrated explanation
|
super-clear-illustrated-explanation-by-w-txbg
|
<-- please vote\n\n\n\n\nBFS solution\n\n def allCellsDistOrder(self, rows: int, cols: int, rCenter: int, cCenter: int) -> List[List[int]]:\n """ O(NM
|
wilmerkrisp
|
NORMAL
|
2022-05-06T12:17:19.988366+00:00
|
2022-05-06T12:18:23.986381+00:00
| 27 | false |
<-- please vote\n\n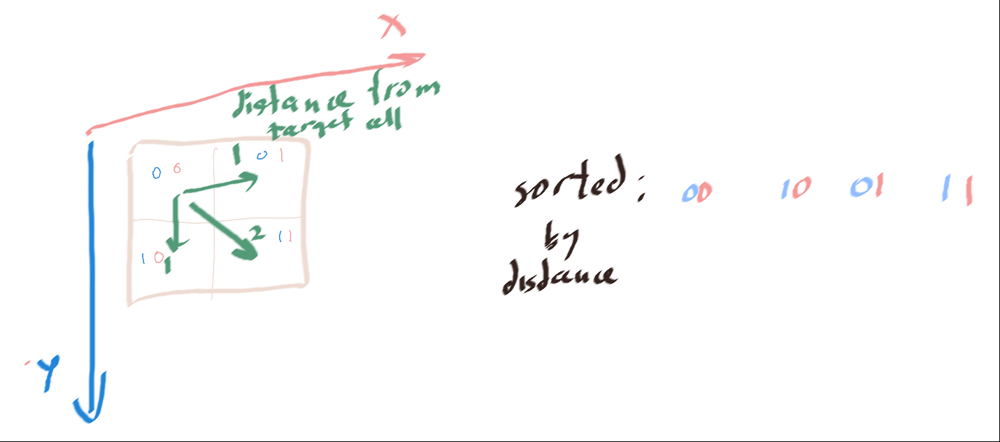\n\n\nBFS solution\n\n def allCellsDistOrder(self, rows: int, cols: int, rCenter: int, cCenter: int) -> List[List[int]]:\n """ O(NM)TS """\n grid = {(y, x): 1 for y in range(rows) for x in range(cols) if (y, x) != (rCenter, cCenter)}\n\n def fn(level):\n if level:\n yield from level\n yield from fn([pt for y, x in level for pt in ((y + 1, x), (y - 1, x), (y, x - 1), (y, x + 1)) if grid.pop(pt, False)])\n\n return fn([(rCenter, cCenter)])\n\n def allCellsDistOrder(self, rows: int, cols: int, rCenter: int, cCenter: int) -> List[List[int]]:\n """ O(NM)TS """\n grid = {(y, x): 1 for y in range(rows) for x in range(cols) if (y, x) != (rCenter, cCenter)}\n level = [(rCenter, cCenter)]\n while level:\n yield from level\n level = [(y, x) for y_, x_ in level for y, x in ((y_ + 1, x_), (y_ - 1, x_), (y_, x_ - 1), (y_, x_ + 1)) if grid.pop((y, x), False)]\n\nsort solution\n\n def allCellsDistOrder(self, rows: int, cols: int, rCenter: int, cCenter: int) -> List[List[int]]:\n """ O(NM log NM)T O(NM)S """\n arr = list(itertools.product(range(rows), range(cols)))\n fn = lambda t: abs(t[0] - rCenter) + abs(t[1] - cCenter)\n arr.sort(key=fn)\n return arr
| 1 | 0 |
[]
| 0 |
matrix-cells-in-distance-order
|
4 solutions & best: O(m*n) time and O(1) extra space
|
4-solutions-best-omn-time-and-o1-extra-s-tk2q
|
\nclass Solution {\npublic:\n vector<vector<int>> allCellsDistOrder(int rows, int cols, int rCenter, int cCenter) {\n // return bruteForceSolution(row
|
anwesha-lc
|
NORMAL
|
2022-04-29T06:44:13.771324+00:00
|
2022-04-29T06:44:13.771349+00:00
| 45 | false |
```\nclass Solution {\npublic:\n vector<vector<int>> allCellsDistOrder(int rows, int cols, int rCenter, int cCenter) {\n // return bruteForceSolution(rows, cols, rCenter, cCenter);\n // return usingOrderedMap(rows, cols, rCenter, cCenter);\n // return sortResultDirectly(rows, cols, rCenter, cCenter);\n return distanceOrderConcentricCircles(rows, cols, rCenter, cCenter);\n }\nprivate:\n //O(m*n log(m*n)) time, O(m*n) extra space\n vector<vector<int>> bruteForceSolution(int rows, int cols, int rCenter, int cCenter) {\n vector<vector<int>> result(rows*cols, vector<int>(2)); // array of coordinates\n vector<vector<int>> arr(rows*cols, vector<int>(3)); // array of (dist, i, j)\n \n //O(rows*cols)\n for(int i = 0; i < rows; ++i) {\n for(int j = 0; j < cols; ++j) {\n int d = abs(i - rCenter) + abs(j - cCenter);\n int k = i*cols + j;\n arr[k][0] = d;\n arr[k][1] = i;\n arr[k][2] = j;\n }\n }\n \n //O(rows*cols + log(rows*cols))\n sort(arr.begin(), arr.end()); //sort by distance\n \n //O(rows*cols)\n for(int k = 0; k < arr.size(); ++k) {\n result[k][0] = arr[k][1]; //row index\n result[k][1] = arr[k][2]; //column index;\n }\n return result;\n }\n //O(m*n log(m*n)) time, O(m*n) extra space\n vector<vector<int>> usingOrderedMap(int rows, int cols, int rCenter, int cCenter) {\n multimap<int, vector<int>> a;\n for(int i = 0; i < rows; ++i) {\n for(int j = 0; j < cols; ++j) {\n int d = abs(i - rCenter) + abs(j - cCenter);\n a.insert({d, {i,j}}); // O(log (rows*cols)) bBST -> sorted linkedlist\n }\n }\n \n vector<vector<int>> res; // [i,j]\n for(auto item : a) {\n res.push_back(item.second);\n }\n return res;\n }\n //O(m*n log(m*n)) time, O(1) extra space\n vector<vector<int>> sortResultDirectly(int rows, int cols, int rCenter, int cCenter) {\n vector<vector<int>> result(rows*cols, vector<int>(2)); //array of coordinates(i,j)\n \n //O(rows*cols)\n for(int i = 0; i < rows; ++i) {\n for(int j = 0; j < cols; ++j) {\n int k = i*cols + j;\n result[k][0] = i;\n result[k][1] = j;\n }\n }\n \n //O(rows*cols + lof(rows*cols))\n sort(result.begin(), result.end(), //lambda function\n //cell1 and cell2 are parameters and rCenter and cCenter we have to mention even tho they are global variables since lambda funcion is anonymous only complier can see them\n [rCenter, cCenter] (vector<int>& cell1, vector<int>& cell2) {\n int d1 = abs(cell1[0] - rCenter) + abs(cell1[1] - cCenter);\n int d2 = abs(cell2[0] - rCenter) + abs(cell2[1] - cCenter);\n return d1 < d2;\n } \n );\n return result;\n }\n // O(m*n) time O(1) extra space\n vector<vector<int>> distanceOrderConcentricCircles(int rows, int cols, int rCenter, int cCenter) {\n vector<int> cell {rCenter, cCenter};\n vector<vector<int>> res;\n res.push_back(cell);\n \n int count = 1;\n int d = 0;\n while(count < rows * cols) {\n ++d;\n int roffset = 0, coffset = d;\n while(coffset > 0) {\n cell[0] = rCenter + roffset;\n cell[1] = cCenter + coffset;\n if(cell[0] >= 0 && cell[0] < rows && cell[1] >=0 && cell[1] < cols) {\n res.push_back(cell);\n ++count;\n }\n --roffset;\n --coffset;\n }\n while(coffset > -d) {\n cell[0] = rCenter + roffset;\n cell[1] = cCenter + coffset;\n if(cell[0] >= 0 && cell[0] < rows && cell[1] >=0 && cell[1] < cols) {\n res.push_back(cell);\n ++count;\n }\n ++roffset;\n --coffset;\n }\n while(coffset < 0) {\n cell[0] = rCenter + roffset;\n cell[1] = cCenter + coffset;\n if(cell[0] >= 0 && cell[0] < rows && cell[1] >=0 && cell[1] < cols) {\n res.push_back(cell);\n ++count;\n }\n ++roffset;\n ++coffset;\n }\n while(coffset < d) {\n cell[0] = rCenter + roffset;\n cell[1] = cCenter + coffset;\n if(cell[0] >= 0 && cell[0] < rows && cell[1] >=0 && cell[1] < cols) {\n res.push_back(cell);\n ++count;\n }\n --roffset;\n ++coffset;\n }\n }\n return res;\n }\n\n};\n```
| 1 | 0 |
[]
| 0 |
matrix-cells-in-distance-order
|
easy python code
|
easy-python-code-by-dakash682-tozp
|
\nclass Solution:\n def allCellsDistOrder(self, rows: int, cols: int, rCenter: int, cCenter: int) -> List[List[int]]:\n matrix = []\n output =
|
dakash682
|
NORMAL
|
2022-04-19T02:47:02.560602+00:00
|
2022-04-19T02:47:02.560631+00:00
| 111 | false |
```\nclass Solution:\n def allCellsDistOrder(self, rows: int, cols: int, rCenter: int, cCenter: int) -> List[List[int]]:\n matrix = []\n output = []\n d = {}\n for i in range(rows):\n for j in range(cols):\n matrix.append([i,j])\n for i in matrix:\n dist = abs(rCenter - i[0]) + abs(cCenter - i[1])\n if dist in d:\n d[dist].append(i)\n else:\n d[dist] = []\n d[dist].append(i)\n for i in range(len(d)):\n for j in d[i]:\n output.append(j)\n return output\n```\nif this helped, plz consider **upvote**
| 1 | 0 |
['Python', 'Python3']
| 0 |
matrix-cells-in-distance-order
|
[C++] Hash table
|
c-hash-table-by-amithm7-gu5y
|
cpp\nvector<vector<int>> allCellsDistOrder(int rows, int cols, int rCenter, int cCenter) {\n\tvector<vector<vector<int>>> dis(199); // cells grouped by index as
|
amithm7
|
NORMAL
|
2022-04-05T11:05:14.899150+00:00
|
2022-04-05T11:11:34.027727+00:00
| 94 | false |
```cpp\nvector<vector<int>> allCellsDistOrder(int rows, int cols, int rCenter, int cCenter) {\n\tvector<vector<vector<int>>> dis(199); // cells grouped by index as distance\n\tvector<vector<int>> ans;\n\tint d;\n\n\t// map distances\n\tfor(int i = 0; i < rows; ++i)\n\t\tfor(int j = 0; j < cols; ++j)\n\t\t\td = abs(i - rCenter) + abs(j - cCenter),\n\t\t\tdis[d].push_back({i, j});\n\n\t// retrieve cells by distance\n\tfor(auto &v: dis)\n\t\tfor(auto &p: v)\n\t\t\tans.push_back({p[0], p[1]});\n\n\treturn ans;\n}\n```
| 1 | 0 |
['C']
| 1 |
matrix-cells-in-distance-order
|
Python solution 70% faster, 76% memory
|
python-solution-70-faster-76-memory-by-g-ozem
|
python\nclass Solution:\n def allCellsDistOrder(self, rows: int, cols: int, rCenter: int, cCenter: int) -> List[List[int]]:\n p = [rCenter, cCenter]\n
|
gilbendavid11
|
NORMAL
|
2022-03-31T07:52:14.460995+00:00
|
2022-03-31T07:52:14.461036+00:00
| 51 | false |
```python\nclass Solution:\n def allCellsDistOrder(self, rows: int, cols: int, rCenter: int, cCenter: int) -> List[List[int]]:\n p = [rCenter, cCenter]\n dists = [[] for i in range(rows+cols)]\n \n def calc_dist(p1, p2):\n return sum(abs(i - j) for i, j in zip(p1,p2))\n for r in range(rows):\n for c in range(cols):\n dists[calc_dist(p, (r, c))].append([r, c])\n sorted_dists = [point for points in dists for point in points]\n return sorted_dists\n```
| 1 | 0 |
[]
| 0 |
matrix-cells-in-distance-order
|
Java | 5 liner | Simple
|
java-5-liner-simple-by-prashant404-jjhl
|
T/S: O(rows x cols)/O(rows x cols)\n\npublic int[][] allCellsDistOrder(int rows, int cols, int rCenter, int cCenter) {\n\tvar triplets = new ArrayList<List<Inte
|
prashant404
|
NORMAL
|
2022-03-07T05:13:37.432794+00:00
|
2022-03-07T05:13:37.432839+00:00
| 218 | false |
**T/S:** O(rows x cols)/O(rows x cols)\n```\npublic int[][] allCellsDistOrder(int rows, int cols, int rCenter, int cCenter) {\n\tvar triplets = new ArrayList<List<Integer>>(rows * cols);\n\tvar ordered = new int[distances.size()][2];\n\n\t// create triplets of (row, column, distance)\n\tfor (var i = 0; i < rows; i++)\n\t\tfor (var j = 0; j < cols; j++)\n\t\t\ttriplets.add(List.of(i, j, Math.abs(rCenter - i) + Math.abs(cCenter - j)));\n\n\t// sort triplets by distance\n\ttriplets.sort(Comparator.comparingInt(cell -> cell.get(2)));\n\n\treturn triplets.stream()\n\t\t\t\t .map(triplets -> new int[]{triplet.get(0), triplet.get(1)})\n\t\t\t\t .toArray(int[][]::new);\n}\n```\n***Please upvote if this helps***
| 1 | 1 |
['Java']
| 0 |
matrix-cells-in-distance-order
|
Simple C++ solution | Custom comparator sorting
|
simple-c-solution-custom-comparator-sort-lel4
|
\nclass Solution {\npublic:\n \n vector<vector<int>> allCellsDistOrder(int rows, int cols, int rCenter, int cCenter) \n {\n int x=rCenter,y=cCen
|
newmutant
|
NORMAL
|
2022-02-19T13:38:45.318597+00:00
|
2022-02-19T13:38:45.318623+00:00
| 63 | false |
```\nclass Solution {\npublic:\n \n vector<vector<int>> allCellsDistOrder(int rows, int cols, int rCenter, int cCenter) \n {\n int x=rCenter,y=cCenter;\n vector<vector<int>>ans;\n for(int i=0;i<rows;i++)\n {\n for(int j=0;j<cols;j++)\n {\n ans.push_back({i-x,j-y}); // pushing the coordinate by subtracting x and y\n }\n }\n sort(ans.begin(),ans.end(),[](vector<int>&a, vector<int>&b)\n {\n return (abs(a[0])+abs(a[1]))<(abs(b[0])+abs(b[1]));\n });\n int n=ans.size();\n for(int i=0;i<n;i++)\n {\n ans[i][0]+=x; // now adding x and y in the coordinates\n ans[i][1]+=y;\n }\n return ans;\n }\n};\n```\n1. Take all coordinates and substract with rCenter and cCenter and push the coordinates into array.\n2. Sort with custom comparator by taking abs values of individual item\n3. Now iterate the all coordinates and add rCenter and cCenter
| 1 | 0 |
[]
| 0 |
matrix-cells-in-distance-order
|
C++ easy to understand, using multi map
|
c-easy-to-understand-using-multi-map-by-bqmd9
|
\nclass Solution {\npublic:\n int distance(int r, int c, int kr, int kc){\n return (fabs(r - kr) + fabs(c - kc));\n }\n vector<vector<int>> allC
|
RiteshKhan
|
NORMAL
|
2022-02-15T16:54:34.424995+00:00
|
2022-03-27T17:20:07.726810+00:00
| 44 | false |
```\nclass Solution {\npublic:\n int distance(int r, int c, int kr, int kc){\n return (fabs(r - kr) + fabs(c - kc));\n }\n vector<vector<int>> allCellsDistOrder(int rows, int cols, int rCenter, int cCenter) {\n multimap<int,vector<int>> s;\n vector<vector<int>> vec;\n for (int i = 0; i < rows; ++i)\n {\n for (int j = 0; j < cols; ++j)\n\t\t\t{\n vector<int> v(2);\n int d;\n v[0] = i;\n v[1] = j;\n d = distance(i, j, rCenter, cCenter);\n s.insert({d, v});\n }\n }\n for (auto itr = s.begin(); itr != s.end(); ++itr)\n\t\t{\n vec.push_back(itr->second);\n }\n return vec;\n }\n};\n```\n**If you like it please upvote**
| 1 | 0 |
['C', 'Matrix']
| 0 |
matrix-cells-in-distance-order
|
Simple C++ solution without sort, storing distance of each cell
|
simple-c-solution-without-sort-storing-d-e7wq
|
We use the dist vector to store all the cells corresponding to their distance from Center.\n\ndist[0] = {All cells at distance 0 from center}\ndist[1] = {All ce
|
shardul08
|
NORMAL
|
2022-02-15T06:26:23.188307+00:00
|
2022-02-15T06:28:41.069794+00:00
| 51 | false |
We use the `dist` vector to store all the cells corresponding to their distance from Center.\n```\ndist[0] = {All cells at distance 0 from center}\ndist[1] = {All cells at distance 1 from center}\ndist[2] = {All cells at distance 2 from center}\n```\nand so on\n\n```\nvector<vector<int>> allCellsDistOrder(int rows, int cols, int rCenter, int cCenter) {\n \n int max_dist = rows + cols + 1;\n vector<vector<vector<int>>> dist(max_dist,vector<vector<int>>());\n \n for(int i=0; i<rows; i++) {\n for(int j=0; j<cols; j++) {\n int d = abs(rCenter-i) + abs(cCenter-j);\n dist[d].push_back({i,j});\n }\n }\n \n vector<vector<int>> res;\n \n for(int i=0; i<max_dist; i++) {\n for(auto v : dist[i])\n res.push_back(v);\n }\n \n return res;\n }\n```
| 1 | 0 |
[]
| 0 |
matrix-cells-in-distance-order
|
[C++]Easy to Understand || Simple C++ Code || Better than 90% Memory Utilization
|
ceasy-to-understand-simple-c-code-better-fpt6
|
Upvote if you like it!!!\n\nvector<vector<int>> allCellsDistOrder(int rows, int cols, int rCenter, int cCenter){\n vector<vector<int>> result(rows*cols,vecto
|
shubham_bhardwaj007
|
NORMAL
|
2022-02-08T04:50:10.286485+00:00
|
2022-02-08T04:50:10.286542+00:00
| 107 | false |
Upvote if you like it!!!\n```\nvector<vector<int>> allCellsDistOrder(int rows, int cols, int rCenter, int cCenter){\n vector<vector<int>> result(rows*cols,vector<int>(3));\n int counter=0;\n for(int row=0;row<rows;row++)\n {\n for(int column=0;column<cols;column++)\n {\n result.at(counter++)={row,column,(abs(row-rCenter)+abs(column-cCenter))};\n }\n }\n sort(result.begin(),result.end(),[](vector<int>& c1,vector<int>& c2)\n {\n return c1[2]<c2[2];\n });\n for(vector<int>&element: result)\n {\n element.pop_back();\n }\n return result;\n}\n```
| 1 | 0 |
['C']
| 0 |
matrix-cells-in-distance-order
|
C++ solution vector<vector<int>>
|
c-solution-vectorvectorint-by-vipul_tejy-0rkv
|
\nclass Solution {\npublic:\n vector<vector<int>> allCellsDistOrder(int rows, int cols, int rCenter, int cCenter) {\n vector<vector<int>> res(rows*col
|
vipul_tejyan
|
NORMAL
|
2022-02-01T20:30:07.766826+00:00
|
2022-02-01T20:30:07.766868+00:00
| 97 | false |
```\nclass Solution {\npublic:\n vector<vector<int>> allCellsDistOrder(int rows, int cols, int rCenter, int cCenter) {\n vector<vector<int>> res(rows*cols);\n \n for(int i=0;i<rows;i++){\n for(int j=0;j<cols;j++){\n int boxNo=((i*cols)+j);\n res[boxNo].push_back(i);\n res[boxNo].push_back(j);\n }\n }\n sort(res.begin(),res.end(),[rCenter,cCenter](vector<int> a,vector<int> b){\n int d1=abs(a[0]-rCenter)+abs(a[1]-cCenter);\n int d2=abs(b[0]-rCenter)+abs(b[1]-cCenter);\n \n return d1<d2;\n });\n return res;\n }\n};\n```
| 1 | 0 |
[]
| 0 |
matrix-cells-in-distance-order
|
JAVA Counting Sort Clean code soln
|
java-counting-sort-clean-code-soln-by-an-r2xa
|
\'\'\'\npublic int[][] allCellsDistOrder(int R, int C, int r0, int c0) {\n int [][]ans=new int[R*C][2];\n int count[]=new int[R+C-1];\n \
|
anshulpro27
|
NORMAL
|
2022-02-01T13:09:46.469782+00:00
|
2022-02-01T13:09:46.469834+00:00
| 72 | false |
\'\'\'\npublic int[][] allCellsDistOrder(int R, int C, int r0, int c0) {\n int [][]ans=new int[R*C][2];\n int count[]=new int[R+C-1];\n \n for(int i=0;i<R;i++)\n {\n for(int j=0;j<C;j++)\n {\n int dis=Math.abs(r0-i) +Math.abs(c0-j);\n count[dis]++;\n }\n }\n \n for(int i=1;i<count.length;i++) count[i]+=count[i-1];\n \n for(int i=0;i<R;i++)\n {\n for(int j=0;j<C;j++)\n {\n int dis=Math.abs(r0-i) +Math.abs(c0-j);\n \n if(dis==0)ans[0]=new int[]{i,j};\n else{\n ans[count[dis-1]]=new int[]{i,j};\n count[dis-1]++;\n } \n }\n }\n return ans;\n }\n\'\'\'
| 1 | 0 |
[]
| 0 |
matrix-cells-in-distance-order
|
JAVA EASY SOLUTION [ SORTING ]
|
java-easy-solution-sorting-by-aniket7419-wo5k
|
\nclass Node{\n int i,j,distance;\n Node(int i,int j,int distance){\n this.i=i;\n this.j=j;\n this.distance=distance;\n }\n}\n\n\n
|
aniket7419
|
NORMAL
|
2021-12-26T11:32:44.035398+00:00
|
2021-12-26T11:32:44.035435+00:00
| 126 | false |
```\nclass Node{\n int i,j,distance;\n Node(int i,int j,int distance){\n this.i=i;\n this.j=j;\n this.distance=distance;\n }\n}\n\n\nclass Solution {\n ArrayList<Node> list=new ArrayList<>();\n public int[][] allCellsDistOrder(int rows, int cols, int rCenter, int cCenter) {\n \n for(int i=0;i<rows;i++) for(int j=0;j<cols;j++) list.add(new Node(i,j,Math.abs(rCenter-i)+Math.abs(cCenter-j)));\n Collections.sort(list,(a,b)->a.distance-b.distance);\n int result[][]=new int[list.size()][2];\n for(int i=0;i<list.size();i++)\n {\n result[i][0]=list.get(i).i;\n result[i][1]=list.get(i).j;\n }\n return result; \n }\n}\n```
| 1 | 0 |
[]
| 0 |
matrix-cells-in-distance-order
|
Python 3 90% Faster Solution : One Liner
|
python-3-90-faster-solution-one-liner-by-80ut
|
\nclass Solution:\n def allCellsDistOrder(self, rows: int, cols: int, rCenter: int, cCenter: int) -> List[List[int]]:\n return sorted([[i,j] for i in
|
deleted_user
|
NORMAL
|
2021-12-01T13:27:31.361612+00:00
|
2021-12-01T13:27:31.361654+00:00
| 135 | false |
```\nclass Solution:\n def allCellsDistOrder(self, rows: int, cols: int, rCenter: int, cCenter: int) -> List[List[int]]:\n return sorted([[i,j] for i in range(rows) for j in range(cols)] , key = lambda x: abs(x[0]-rCenter)+abs(x[1]-cCenter))\n```
| 1 | 0 |
['Python3']
| 0 |
reconstruct-a-2-row-binary-matrix
|
C++/Java 5 lines
|
cjava-5-lines-by-votrubac-ed45
|
Intuition\nIf the column sum is 2 or 0, the choice is obvius.\n\nIf it\'s 1, we set the upper bit if upper is larger than lower, and lower bit otherwise.\n\nC++
|
votrubac
|
NORMAL
|
2019-11-10T20:33:59.984344+00:00
|
2019-11-11T02:10:48.054626+00:00
| 5,024 | false |
#### Intuition\nIf the column sum is `2` or `0`, the choice is obvius.\n\nIf it\'s `1`, we set the upper bit if `upper` is larger than `lower`, and lower bit otherwise.\n\n**C++**\n> See Java version below for less compacted version :)\n```\nvector<vector<int>> reconstructMatrix(int u, int l, vector<int>& cs) {\n vector<vector<int>> res(2, vector<int>(cs.size()));\n for (auto i = 0; i < cs.size(); u -= res[0][i], l -= res[1][i++]) {\n res[0][i] = cs[i] == 2 || (cs[i] == 1 && l < u);\n res[1][i] = cs[i] == 2 || (cs[i] == 1 && !res[0][i]);\n }\n return u == 0 && l == 0 ? res : vector<vector<int>>();\n}\n```\n**Java**\n```\npublic List<List<Integer>> reconstructMatrix(int u, int l, int[] cs) {\n boolean[][] res = new boolean[2][cs.length];\n for (int i = 0; i < cs.length; ++i) {\n res[0][i] = cs[i] == 2 || (cs[i] == 1 && l < u);\n res[1][i] = cs[i] == 2 || (cs[i] == 1 && !res[0][i]);\n u -= res[0][i] ? 1 : 0;\n l -= res[1][i] ? 1 : 0;\n }\n return l == 0 && u == 0 ? new ArrayList(Arrays.asList(res[0], res[1])) : new ArrayList(); \n}\n```
| 55 | 3 |
[]
| 7 |
reconstruct-a-2-row-binary-matrix
|
[Python3] Easy Greedy Solution
|
python3-easy-greedy-solution-by-localhos-u55j
|
\nclass Solution:\n def reconstructMatrix(self, upper: int, lower: int, colsum: List[int]) -> List[List[int]]:\n n = len(colsum)\n upper_list =
|
localhostghost
|
NORMAL
|
2019-11-14T04:50:36.338608+00:00
|
2019-11-14T04:55:00.229739+00:00
| 2,024 | false |
```\nclass Solution:\n def reconstructMatrix(self, upper: int, lower: int, colsum: List[int]) -> List[List[int]]:\n n = len(colsum)\n upper_list = [0 for _ in range(n)]\n lower_list = [0 for _ in range(n)]\n \n for i, v in enumerate(colsum):\n if v == 1:\n if upper > lower:\n upper_list[i] = 1\n upper -= 1\n else: \n lower_list[i] = 1\n lower -= 1\n elif v == 2: \n upper_list[i] = lower_list[i] = 1\n upper, lower = upper - 1, lower - 1\n \n return [upper_list, lower_list] if upper == lower == 0 else []\n```
| 20 | 0 |
[]
| 4 |
reconstruct-a-2-row-binary-matrix
|
Detailed Explanation using Greedy Approach
|
detailed-explanation-using-greedy-approa-g8st
|
Intuition\n* First, intialize both the rows as 0. Now, fill the indices where the vertical column sum is 2 (as they don\'t have a choice). So, now we only need
|
just__a__visitor
|
NORMAL
|
2019-11-10T04:12:19.408423+00:00
|
2019-11-10T05:21:24.356284+00:00
| 2,829 | false |
# Intuition\n* First, intialize both the rows as `0`. Now, fill the indices where the vertical column sum is `2` (as they don\'t have a choice). So, now we only need to make choices for the columns with sum `1`. Find out the current sum of the first row. Compare it with the required amount. If the difference becomes negative, it means that there is no solution. Else, greedily fill the required `1s` in the top row and the remaining `1s` in the bottom row. Finally, check if the sum of the bottom row equals `lower`\n\n```cpp\nclass Solution\n{\npublic:\n vector<vector<int>> reconstructMatrix(int upper, int lower, vector<int>& colsum);\n};\n\nvector<vector<int>> Solution :: reconstructMatrix(int upper, int lower, vector<int>& colsum)\n{\n int n = colsum.size();\n vector<vector<int>> mat(2, vector<int> (n, 0));\n \n for(int i = 0; i < n; i++)\n if(colsum[i] == 2)\n mat[0][i] = 1, mat[1][i] = 1;\n \n auto& first_row = mat[0];\n int current_upper_sum = accumulate(first_row.begin(), first_row.end(), 0);\n \n int diff = upper - current_upper_sum;\n \n if(diff < 0)\n return vector<vector<int>>();\n \n for(int i = 0; i < n; i++)\n {\n if(colsum[i] == 1)\n {\n if(diff > 0)\n mat[0][i] = 1, diff--;\n else \n mat[1][i] = 1;\n }\n }\n \n auto& second_row = mat[1];\n int current_lower_sum = accumulate(second_row.begin(), second_row.end(), 0);\n \n if(current_lower_sum != lower)\n return vector<vector<int>> ();\n \n return mat;\n \n}\n```
| 20 | 3 |
[]
| 1 |
reconstruct-a-2-row-binary-matrix
|
O(n) time Java Solution Easy to understand with Comments and Explaination
|
on-time-java-solution-easy-to-understand-8zy5
|
We count the number of columns for which we need 1 in both rows(colsum[i] == 2), similarly we count the number of columns for which we need column-sum as 1 and
|
manrajsingh007
|
NORMAL
|
2019-11-10T04:02:53.996059+00:00
|
2019-11-11T08:10:34.968338+00:00
| 1,751 | false |
We count the number of columns for which we need 1 in both rows(colsum[i] == 2), similarly we count the number of columns for which we need column-sum as 1 and column-sum as 0.\n\n\nFor the columns where we need the column-sum as 2, we definitely know that we need 1 in both the rows, similarly if the column-sum is 0 we know we need to place 0s in both the rows.\n\n\nFor the case where we need column-sum as 1, we need to see if we can have a 1 in row1 or do we have to have a 1 in row2. \nFor those cases I have done a precomputation and followed a somewhat greedy approach.\nThe number of columns where we need a 1 in row1 and 0 in row2 is say count1 (as mentioned in code). \nWe start assigning values to the two rows now by iterating over each value in the colsum array. If we encounter a colsum[i] == 2 or colsum[i] == 0, we assign 1s to both the rows and 0s to both the rows respectively.\n**For the cases where colsum[i] == 1, we check value of count1 variable which will tell us if we can assign a 1 to row1 or not. If value of count1 > 0, we can assign 1 to row1 and 0 to row2 and we simultaneously decrement count1. Else if count1 == 0, we assign a 0 to row1 and 1 to row2.**\n\n```\nclass Solution {\n public List<List<Integer>> reconstructMatrix(int upper, int lower, int[] colsum) {\n \n int n = colsum.length;\n int sum0 = 0; // no. of columns with colsum 0\n int sum1 = 0; // no. of columns with colsum 1\n int sum2 = 0; // no. of columns with colsum 2\n \n for(int i = 0; i < n; i++){\n if(colsum[i] == 0) sum0 ++;\n else if(colsum[i] == 1) sum1 ++;\n else sum2 ++;\n }\n \n int count1 = upper - sum2; // no. of columns with 1 in 1st row and 0 in 2nd row\n int count2 = lower - sum2; // no. of columns with 0 in 1st row and 1 in 2nd row\n \n // check if arrangement is possible or not\n if(count1 < 0 || count2 < 0 || count1 + count2 != sum1) return new ArrayList<>();\n \n List<List<Integer>> ans = new ArrayList<>();\n for(int i = 0; i < 2; i++) ans.add(new ArrayList<>());\n \n for(int i = 0; i < n; i++){\n if(colsum[i] == 2){\n ans.get(0).add(1);\n ans.get(1).add(1);\n }\n else if(colsum[i] == 0){\n ans.get(0).add(0);\n ans.get(1).add(0);\n }\n else{\n if(count1 > 0){\n count1 --;\n ans.get(0).add(1);\n ans.get(1).add(0);\n }\n else{\n ans.get(0).add(0);\n ans.get(1).add(1);\n }\n }\n }\n \n return ans;\n }\n}
| 18 | 6 |
['Greedy']
| 2 |
reconstruct-a-2-row-binary-matrix
|
C++ Simple Explanation
|
c-simple-explanation-by-physics_alpaca-6t9j
|
This problem can be solved using a greedy approach. We can iterate through each column and determine how we assign values to the upper cell and lower cell based
|
physics_alpaca
|
NORMAL
|
2021-05-04T02:54:54.009681+00:00
|
2021-05-04T02:57:03.836295+00:00
| 627 | false |
This problem can be solved using a greedy approach. We can iterate through each column and determine how we assign values to the upper cell and lower cell based on `colsum[i]`.\n\nWe can break down the greedy decision into 3 cases:\n\n1. `colsum[i]==0`\nWe don\'t do anything in this case, clearly both upper and lower cells are 0.\n\n2. `colsum[i]==2`\nWe set both upper and lower cells to 1 and decrement both upper and lower.\n\n3. `colsum[i]==1`\nEither the upper or lower cell is a 1. We make the choice based on whichever is larger - upper or lower. The intuition behind assigning the 1 to the larger quantity is to balance them out in anticipation for Case 2. Think about it this way: we only benefit by assigning in this manner. Suppose after we make this choice we only encounter Case 1 and 3, then it wouldn\'t matter the way we assigned the 1. However, if we instead encounter many instances of Case 2, we could end up having an invalid solution if upper and lower aren\'t balanced, as we\'d be decrementing both of them at the same time.\n\nHere\'s a sample input. Try going through it by not balancing upper and lower vs. balancing upper and lower. You can imagine not balancing as always assigning to upper until upper = 0, then assigning to lower. \n```\n5\n5\n[2,1,2,0,1,0,1,2,0,1]\n```\n\nAfter iterating through each column, we have to validate that both upper and lower are exactly 0. It\'s most convenient to perform this check outside the loop as if we\'d put this check inside the loop, we could only check the case where either upper or lower is less than 0.\n\nC++ code:\n```\nclass Solution {\npublic:\n vector<vector<int>> reconstructMatrix(int upper, int lower, vector<int>& colsum) {\n vector<vector<int>> ans(2, vector<int>(colsum.size()));\n for (int i=0; i<colsum.size(); ++i) {\n if (colsum[i]==2) {\n ans[0][i]=1;\n ans[1][i]=1;\n --upper;\n --lower;\n }\n else if (colsum[i]==1) {\n if (upper>lower) {\n ans[0][i]=1;\n --upper;\n }\n else {\n ans[1][i]=1;\n --lower;\n }\n }\n }\n if (upper!=0 || lower!=0) return {};\n return ans;\n }\n};\n```\n\nTime complexity: O(n)\nSpace complexity: O(n)
| 9 | 0 |
['Greedy', 'C']
| 1 |
reconstruct-a-2-row-binary-matrix
|
Java Simple greedy with pitfalls
|
java-simple-greedy-with-pitfalls-by-hobi-6qk5
|
greedy is simple, \n1, if colsum is 0, or 2, aka colsum % 2 == 0, assign colsum / 2 to upper and lower row each;\n2, Otherwise, colsum is 1, based on diff = upp
|
hobiter
|
NORMAL
|
2020-06-29T02:48:42.390772+00:00
|
2020-06-29T02:48:42.390820+00:00
| 701 | false |
greedy is simple, \n1, if colsum is 0, or 2, aka colsum % 2 == 0, assign colsum / 2 to upper and lower row each;\n2, Otherwise, colsum is 1, based on diff = upper - lower, to assign 1 and 0, remember to update diff\n3, check if diff != 0 || upper + lower != sum, invalid, return empty list;\n\n```\n public List<List<Integer>> reconstructMatrix(int upper, int lower, int[] colsum) {\n List<List<Integer>> res = new ArrayList<>();\n List<Integer> up = new ArrayList<>(), lo = new ArrayList<>();\n int diff = upper - lower, sum = 0;\n for (int i : colsum) {\n sum += i;\n if (i % 2 == 0) { // colsum 0, or 2\n up.add(i / 2);\n lo.add(i / 2);\n } else { //colsum is 1\n if (diff >= 0) {\n up.add(1);\n lo.add(0);\n diff--;\n } else {\n up.add(0);\n lo.add(1);\n diff++;\n }\n }\n }\n if (diff != 0 || upper + lower != sum) return res;\n res.add(up);\n res.add(lo);\n return res;\n }\n```
| 7 | 1 |
[]
| 1 |
reconstruct-a-2-row-binary-matrix
|
✅✅Java || 🚀🚀100% beats ||🔥 Simple || Explanation
|
java-100-beats-simple-explanation-by-rob-emo6
|
Intuition\nIf a column sum is 2, both the upper and lower rows must contain a 1 in that column. If a column sum is 0, both rows will have a 0 in that column. Th
|
robin_kumar_rk
|
NORMAL
|
2024-03-03T13:39:46.800371+00:00
|
2024-07-20T11:14:26.539126+00:00
| 226 | false |
# Intuition\nIf a column sum is 2, both the upper and lower rows must contain a 1 in that column. If a column sum is 0, both rows will have a 0 in that column. Therefore, our primary focus should be on managing columns where the column sum is 1.\n\n# Approach\n1. **Initialization :** Start by initializing two arrays to represent the upper and lower rows of the matrix, both filled with zeros.\n\n2. **Handling Columns with Sum = 2 :** \n For columns where the column sum is 2, set both the upper and lower rows to 1 in those columns. Decrease the upper and lower counts accordingly since we\'ve used up one 1 from each row.\n\n3. **Handling Columns with Sum = 1:** \n\n - For columns where the column sum is 1, first try to place a 1 in the upper row if the remaining upper count is greater than 0. If successful, place 1 in the upper row and 0 in the lower row, then decrease the upper count.\n\n - If the upper count is 0, try to place a 1 in the lower row if the remaining lower count is greater than 0. If successful, place 1 in the lower row and 0 in the upper row, then decrease the lower count.\n\n - If neither the upper nor the lower rows can accommodate the 1, it means constructing the matrix is not possible, and we should return an empty list.\n\n4. **Validation :** After processing all columns, check if both the upper and lower counts are 0. If not, return an empty list as it indicates that the matrix construction failed.\n \n5. **Final answer :** Convert the upper and lower row arrays into lists and add them to the result list. Return the result list as the final reconstructed matrix.\n\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution {\n public List<List<Integer>> reconstructMatrix(int upper, int lower, int[] colsum) {\n int n = colsum.length;\n List<List<Integer>> result = new ArrayList<>();\n Integer upperRow[] = new Integer[n];\n Integer lowerRow[] = new Integer[n];\n \n // Initialize both rows with zeros\n Arrays.fill(upperRow, 0);\n Arrays.fill(lowerRow, 0);\n \n // First pass: handle columns where colsum[i] is 2\n for (int i = 0; i < n; i++) {\n if (colsum[i] == 2) {\n // Both rows must have a 1 in the i-th column\n upperRow[i] = 1;\n lowerRow[i] = 1;\n upper--;\n lower--;\n }\n }\n \n // Second pass: handle columns where colsum[i] is 1\n for (int i = 0; i < n; i++) {\n if (colsum[i] == 1) {\n if (upper > 0) {\n // Place 1 in the upper row if possible\n upperRow[i] = 1;\n upper--;\n } else if (lower > 0) {\n // Otherwise, place 1 in the lower row\n lowerRow[i] = 1;\n lower--;\n } else {\n // If neither row can accommodate the 1, return an empty list\n return result;\n }\n }\n }\n \n // Check if all the required 1\'s are placed correctly\n if (upper != 0 || lower != 0) {\n return result;\n }\n \n // Convert arrays to lists and add to the result\n result.add(Arrays.asList(upperRow));\n result.add(Arrays.asList(lowerRow));\n return result;\n }\n}\n\n```
| 6 | 0 |
['Java']
| 3 |
reconstruct-a-2-row-binary-matrix
|
[C++], 100ms, faster than 100%
|
c-100ms-faster-than-100-by-ishaan20-tonr
|
\nclass Solution {\npublic:\n vector<vector<int>> reconstructMatrix(int upper, int lower, vector<int>& colsum) {\n ios_base::sync_with_stdio(false);\n
|
ishaan20
|
NORMAL
|
2020-07-26T06:22:00.660586+00:00
|
2020-07-26T06:22:00.660623+00:00
| 404 | false |
```\nclass Solution {\npublic:\n vector<vector<int>> reconstructMatrix(int upper, int lower, vector<int>& colsum) {\n ios_base::sync_with_stdio(false);\n cin.tie(NULL);\n int n = colsum.size();\n vector<vector<int> > res(2, vector<int>(n, 0));\n int sumUp = 0, sumLo = 0;\n for(int i = 0; i < n; i++)\n if(colsum[i] == 2)\n res[0][i] = 1, res[1][i] = 1, sumUp++, sumLo++;\n for(int i = 0; i < n; i++)\n {\n if(colsum[i] == 1)\n {\n if(sumUp < upper)\n res[0][i] = 1, sumUp++;\n else\n res[1][i] = 1, sumLo++;\n }\n }\n if(sumUp != upper || sumLo != lower)\n return {};\n return res;\n }\n};\n```
| 4 | 0 |
[]
| 0 |
reconstruct-a-2-row-binary-matrix
|
C++ straightforward two-pass solution
|
c-straightforward-two-pass-solution-by-j-b5io
|
The idea is simple, first fill all 2s. Then fill ones, and try to fill upper first. \n\n\nclass Solution {\npublic:\n vector<vector<int>> reconstructMatrix(i
|
jiangleetcode
|
NORMAL
|
2020-04-28T03:57:32.562737+00:00
|
2020-04-28T03:57:32.562783+00:00
| 289 | false |
The idea is simple, first fill all 2s. Then fill ones, and try to fill upper first. \n\n```\nclass Solution {\npublic:\n vector<vector<int>> reconstructMatrix(int upper, int lower, vector<int>& colsum) {\n vector<vector<int>> ret, empty;\n \n int n = colsum.size();\n ret.resize(2);\n ret[0].resize(n);\n ret[1].resize(n);\n for( int i=0; i<n; i++ )\n {\n if ( colsum[i] == 2 )\n {\n ret[0][i] = 1;\n ret[1][i] = 1;\n upper--;\n lower--;\n }\n if ( upper < 0 || lower < 0 )\n return empty;\n }\n \n for( int i=0; i<n; i++ )\n {\n if ( colsum[i] == 1 )\n {\n if ( upper > 0 )\n {\n ret[0][i] = 1;\n upper--;\n }\n else\n {\n ret[1][i] = 1;\n lower --;\n }\n }\n if ( upper < 0 || lower < 0 )\n return empty;\n }\n \n if ( upper!=0 || lower!=0 )\n return empty;\n else\n return ret;\n }\n};\n```\n
| 4 | 0 |
[]
| 0 |
reconstruct-a-2-row-binary-matrix
|
🔥C++ greedy Solution O(N)
|
c-greedy-solution-on-by-igi17-vw0q
|
\tIntuition- I am checking greedily that First I am checking for colsum value 2\n\t if at any given point of time I do not have enough lower and upper to make
|
igi17
|
NORMAL
|
2022-02-18T18:00:31.344551+00:00
|
2022-02-18T18:00:31.344586+00:00
| 324 | false |
**\tIntuition- I am checking greedily that First I am checking for colsum value 2\n\t if at any given point of time I do not have enough lower and upper to make sum 2\n\t i will return false , otherwise will check for 0 and 1 in next loop.**\n\t \n\t\tclass Solution {\n\t\tpublic:\n\t\t\tvector<vector<int>> reconstructMatrix(int upper, int lower, vector<int>& colsum) {\n\t\t\t\t\t vector<vector<int>> ans(2,vector<int>(colsum.size(),0));\n\t\t\t\t\t bool flag=true;\n\t\t\t\t\tfor(int i=0;i<colsum.size();i++){\n\t\t\t\t\t\tif(colsum[i]==2){\n\t\t\t\t\t\t\tif(lower<=0 || upper<=0){\n\t\t\t\t\t\t\t\tflag=false;\n\t\t\t\t\t\t\t\tbreak;\n\t\t\t\t\t\t\t}\n\t\t\t\t\t\t\tans[0][i]=ans[1][i]=1;\n\t\t\t\t\t\t\tupper--;\n\t\t\t\t\t\t\tlower--;\n\t\t\t\t\t\t}\n\t\t\t\t\t}\n\t\t\t\tif(!flag) return {};\n\t\t\t\t\t for(int i=0;i<colsum.size();i++){\n\t\t\t\t\t\t if(colsum[i]==2) continue;\n\t\t\t\t\t\t else if(colsum[i]==0) ans[0][i]=ans[1][i]=0;\n\t\t\t\t\t\t else{\n\t\t\t\t\t\t\t if(lower>0){\n\t\t\t\t\t\t\t\t ans[1][i]=1;\n\t\t\t\t\t\t\t\t ans[0][i]=0;\n\t\t\t\t\t\t\t\t lower--;\n\t\t\t\t\t\t\t }\n\t\t\t\t\t\t\t else if(upper>0){\n\t\t\t\t\t\t\t\t ans[0][i]=1;\n\t\t\t\t\t\t\t\t ans[1][i]=0;\n\t\t\t\t\t\t\t\t upper--;\n\t\t\t\t\t\t\t }\n\t\t\t\t\t\t\t else {\n\t\t\t\t\t\t\t\t flag=false;\n\t\t\t\t\t\t\t\t break;\n\t\t\t\t\t\t\t }\n\t\t\t\t\t\t }\n\t\t\t\t\t }\n\t\t\t\tif(!flag || lower>0 || upper>0) return {};\n\t\t\t\treturn ans;\n\t\t\t} \n\t\t};
| 3 | 0 |
['Greedy', 'C']
| 0 |
reconstruct-a-2-row-binary-matrix
|
Python 3 | Greedy | Explanations
|
python-3-greedy-explanations-by-idontkno-iy5u
|
Explanation\n- Ultimately, we have to fill out 2 row and use exactly upper+lower values, so simply take the greedy apporach\n\t- if upper + lower != sum(colsum)
|
idontknoooo
|
NORMAL
|
2020-09-14T01:39:28.832081+00:00
|
2020-09-14T01:39:28.832124+00:00
| 635 | false |
### Explanation\n- Ultimately, we have to fill out 2 row and use exactly `upper+lower` values, so simply take the greedy apporach\n\t- if `upper + lower != sum(colsum)`, `return []`\n\t- when `colsum[i] == 2` and `upper` and `lower` are available, place both row and decrement variables\n\t- when `colsum[i] == 1` take whoever is larger and place `1` on cooresponding row\n\t- when `colsum[i] == 0` ignore and `continue`\n\t- else `return []`\n- `u`: first row\n- `d`: second row\n### Implementation\n```\nclass Solution:\n def reconstructMatrix(self, upper: int, lower: int, colsum: List[int]) -> List[List[int]]:\n s, n = sum(colsum), len(colsum)\n if upper + lower != s: return []\n u, d = [0] * n, [0] * n\n for i in range(n):\n if colsum[i] == 2 and upper > 0 and lower > 0:\n u[i] = d[i] = 1\n upper, lower = upper-1, lower-1\n elif colsum[i] == 1: \n if upper > 0 and upper >= lower:\n u[i], upper = 1, upper-1\n elif lower > 0 and lower > upper:\n d[i], lower = 1, lower-1\n else: return [] \n elif not colsum[i]: continue\n else: return []\n return [u, d] \n```
| 3 | 0 |
['Greedy', 'Python', 'Python3']
| 0 |
reconstruct-a-2-row-binary-matrix
|
Java Greedy Solution
|
java-greedy-solution-by-ayyild1z-eh5b
|
Java\npublic List<List<Integer>> reconstructMatrix(int upper, int lower, int[] colsum) {\n\tList<List<Integer>> res = new ArrayList<List<Integer>>(){{\n\t\tadd(
|
ayyild1z
|
NORMAL
|
2019-12-01T01:29:22.496363+00:00
|
2019-12-01T01:29:22.496411+00:00
| 321 | false |
```Java\npublic List<List<Integer>> reconstructMatrix(int upper, int lower, int[] colsum) {\n\tList<List<Integer>> res = new ArrayList<List<Integer>>(){{\n\t\tadd(new ArrayList<Integer>());\n\t\tadd(new ArrayList<Integer>());\n\t}};\n\n\tfor(int i=0; i < colsum.length; i++){\n\t\tif(colsum[i] == 2){\n\t\t\tres.get(0).add(1);\n\t\t\tres.get(1).add(1);\n\t\t\tupper--;\n\t\t\tlower--;\n\t\t}else if(colsum[i] == 1){\n\t\t\tif(upper > lower){\n\t\t\t\tres.get(0).add(1);\n\t\t\t\tres.get(1).add(0);\n\t\t\t\tupper--;\n\t\t\t}else{\n\t\t\t\tres.get(0).add(0);\n\t\t\t\tres.get(1).add(1);\n\t\t\t\tlower--;\n\t\t\t}\n\t\t}else{\n\t\t\tres.get(0).add(0);\n\t\t\tres.get(1).add(0);\n\t\t}\n\t}\n\n\tif(lower != 0 || upper != 0){\n\t\treturn Collections.emptyList();\n\t}\n\n\treturn res; \n}\n```
| 3 | 0 |
['Java']
| 1 |
reconstruct-a-2-row-binary-matrix
|
Java, counting, greedy, beats 100%, explained
|
java-counting-greedy-beats-100-explained-cujf
|
We can solve this doing traversal and distribute numbers as per sum at each step. If in the end upper and lower limits are not 0s it means than solution is not
|
gthor10
|
NORMAL
|
2019-11-11T01:23:31.431731+00:00
|
2019-11-11T01:23:31.431768+00:00
| 377 | false |
We can solve this doing traversal and distribute numbers as per sum at each step. If in the end upper and lower limits are not 0s it means than solution is not possible.\nFor the distribution use greedy approach - because we can return any correct solution just start fill with 1-s from the upper row.\nDetailed logic:\ncount how many 2s we have. we need to reserve it and not use to early\nthe rest of upper and lower we can distribute as we like, starting from upper row (actual order doesn\'t really matter)\nwe have only 3 cases - colsum[i] is 0 - it means both numbers are 0, it\'s 1 - it means only one is 1, and 2 - this is only when both upper and lower are 1\nwhile distributing we decrement upper and lower. At each step and in the end we need to check if lower and upper are ok.\n\nO(len(colsum)) time - iterate over colsum 2 times, one to count 2s, second to form the result. O(1) space - no extra space used except for resulting lists.\n\n```\n public List<List<Integer>> reconstructMatrix(int upper, int lower, int[] colsum) {\n List<List<Integer>> res = new ArrayList();\n //check number of 2-s in colsum\n int t = 0;\n for (int n : colsum) {\n if (n == 2 ) ++t;\n }\n List<Integer> up = new ArrayList(), down = new ArrayList();\n //decrement number of 2s from upper and lower so it contribution reserved\n upper-=t;\n lower-=t;\n //check every number in colsum in greedy manner starting from the upper\n for (int n : colsum) {\n //start from 0, it covers case when n == 0\n int x = 0, y = 0;\n //if sum for the col is 2 the only way to get it is to make up and low both 1\n if (n == 2) {\n x = y = 1;\n } else if (n == 1) {\n //if it\'s 1 it means only one from up/lower is 1. Start from upper always\n if (upper > 0) {\n --upper;\n x = 1;\n y = 0;\n } else {\n --lower;\n x = 0;\n y = 1;\n }\n }\n //check if we out of limits \n if (upper < 0 || lower < 0)\n return res;\n //add number to upper and lower rows\n up.add(x); down.add(y);\n }\n //check if we have used exact number for each row sum\n if (lower == 0 && upper == 0) {\n res.add(up); res.add(down);\n }\n return res;\n }\n```
| 3 | 0 |
['Greedy', 'Counting', 'Java']
| 1 |
reconstruct-a-2-row-binary-matrix
|
🔥Beats 93.72%🔥✅Easiest (C++/Java/Python) Solution With Detailed Explanation✅
|
beats-9372easiest-cjavapython-solution-w-iz2s
|
Intuition\nThe intuition for reconstructing a 2D matrix involves first checking if the total upper and lower row sums match the required column sums, then alloc
|
suyogshete04
|
NORMAL
|
2024-02-14T03:23:35.563474+00:00
|
2024-02-14T03:23:35.563508+00:00
| 595 | false |
# Intuition\nThe intuition for reconstructing a 2D matrix involves first checking if the total upper and lower row sums match the required column sums, then allocating 1s to each row based on column sum values, prioritizing columns with a sum of 2, followed by distributing the remaining 1s between the two rows while respecting the upper and lower limits.\n\n\n\n\n# Approach\n\n1. **Initialization**: The code initializes variables to keep track of the number of columns that should have a sum of 1 and 2, based on the `colsum` array. It also calculates the initial sums for the upper and lower rows after accommodating columns with a sum of 2.\n\n2. **Feasibility Check**: Before attempting to construct the matrix, the code checks if the desired configuration is possible by comparing the total sum of `upper` and `lower` with the total sum required by `colsum`. If the total sum doesn\'t match, or if the adjusted sums for upper or lower rows (after accounting for columns with a sum of 2) are negative, the function immediately returns an empty matrix, indicating that reconstruction is not possible.\n\n3. **Matrix Construction**: The algorithm then proceeds to construct the matrix row by row, column by column. For columns with a `colsum` of 2, it places a 1 in both the upper and lower rows. For columns with a `colsum` of 1, it prefers to place a 1 in the upper row until the upper sum is fully allocated, after which any remaining columns with a `colsum` of 1 are allocated to the lower row. This step continues until all columns are processed.\n\n4. **Result**: If the algorithm can successfully allocate the sums according to the `colsum` while respecting the `upper` and `lower` constraints, it returns the constructed matrix. Otherwise, it has already returned an empty matrix in the feasibility check step.\n\n\n# Complexity\n1. **Time Complexity**: The overall time complexity is \\(O(n)\\), where \\(n\\) is the length of the `colsum` array. This is because the algorithm iterates through the `colsum` array exactly once to construct the matrix, and the initial counting of 1s and 2s in `colsum` also requires a single pass through the array.\n\n2. **Space Complexity**: The space complexity is \\(O(n)\\) due to the storage requirements of the resulting 2D matrix, which has 2 rows and `n` columns. The rest of the variables used for counting and tracking the sum allocations are of constant space, not dependent on the input size.\n\n# Code\n```C++ []\nclass Solution {\npublic:\n vector<vector<int>> reconstructMatrix(int upper, int lower,\n vector<int>& colsum) {\n int n = colsum.size();\n\n int count1 = 0;\n int count2 = 0;\n\n for (int i = 0; i < n; i++) {\n if (colsum[i] == 1)\n count1++;\n\n if (colsum[i] == 2)\n count2 += 2;\n }\n\n if (((upper + lower) - (count1 + count2)) != 0)\n return {};\n\n int upp = upper-(count2/2);\n int low = lower-(count2/2);\n\n if (upp < 0 || low < 0)\n return {};\n\n vector<vector<int>> res(2, vector<int>(n, 0));\n\n for (int i = 0; i < n; i++) {\n if (colsum[i] == 2) {\n res[0][i] = 1;\n res[1][i] = 1;\n }\n else if (colsum[i] == 1 && upp) {\n res[0][i] = 1;\n upp--;\n }\n else if (colsum[i] == 1 && low)\n {\n res[1][i] = 1;\n low--;\n }\n }\n\n return res;\n }\n};\n```\n```Java []\nimport java.util.ArrayList;\nimport java.util.Arrays;\nimport java.util.List;\n\npublic class Solution {\n public List<List<Integer>> reconstructMatrix(int upper, int lower, int[] colsum) {\n int n = colsum.length;\n int count1 = 0;\n int count2 = 0;\n\n for (int i = 0; i < n; i++) {\n if (colsum[i] == 1) count1++;\n if (colsum[i] == 2) count2 += 2;\n }\n\n if ((upper + lower) - (count1 + count2) != 0) return new ArrayList<>();\n\n int upp = upper - count2 / 2;\n int low = lower - count2 / 2;\n\n if (upp < 0 || low < 0) return new ArrayList<>();\n\n List<List<Integer>> res = new ArrayList<>();\n res.add(new ArrayList<>());\n res.add(new ArrayList<>());\n\n for (int i = 0; i < n; i++) {\n if (colsum[i] == 2) {\n res.get(0).add(1);\n res.get(1).add(1);\n } else if (colsum[i] == 1) {\n if (upp > 0) {\n res.get(0).add(1);\n res.get(1).add(0);\n upp--;\n } else {\n res.get(0).add(0);\n res.get(1).add(1);\n low--;\n }\n } else {\n res.get(0).add(0);\n res.get(1).add(0);\n }\n }\n\n return res;\n }\n}\n\n```\n```Python []\nfrom typing import List\n\nclass Solution:\n def reconstructMatrix(self, upper: int, lower: int, colsum: List[int]) -> List[List[int]]:\n n = len(colsum)\n \n # Check if the total sum matches the desired row sums\n if upper + lower != sum(colsum):\n return []\n \n # Initialize the result matrix\n res = [[0 for _ in range(n)] for _ in range(2)]\n \n for i in range(n):\n # If colsum[i] is 2, both rows must have a 1 in the i-th column\n if colsum[i] == 2:\n if upper > 0 and lower > 0:\n res[0][i], res[1][i] = 1, 1\n upper -= 1\n lower -= 1\n else:\n return [] # Not enough sums to distribute\n # If colsum[i] is 1, distribute it to either row according to the remaining sums\n elif colsum[i] == 1:\n if upper > lower:\n res[0][i] = 1\n upper -= 1\n elif lower >= upper:\n res[1][i] = 1\n lower -= 1\n else:\n return [] # Not a valid scenario\n \n # Check if we correctly distributed all sums\n if upper == 0 and lower == 0:\n return res\n else:\n return [] # Sums were not correctly distributed\n\n```
| 2 | 0 |
['Greedy', 'Matrix', 'C++', 'Java', 'Python3']
| 1 |
reconstruct-a-2-row-binary-matrix
|
C++ | BEATS 95 % | explained with comments
|
c-beats-95-explained-with-comments-by-kr-tvlu
|
\n# Code\n\nclass Solution {\npublic:\n vector<vector<int>> reconstructMatrix(int u, int l, vector<int>& c) {\n\n vector<vector<int>> ans;\n// sum all
|
kr_vishnu
|
NORMAL
|
2023-01-17T07:20:29.331967+00:00
|
2023-01-17T07:20:29.332003+00:00
| 356 | false |
\n# Code\n```\nclass Solution {\npublic:\n vector<vector<int>> reconstructMatrix(int u, int l, vector<int>& c) {\n\n vector<vector<int>> ans;\n// sum all elements in colsum vector and count no of 2\'s present in colsum;\n// if sum is not equal to lower + upper or if no of 2\'s is greater than lower than return empty vector.\n int cs=0; int cnt2=0;\n for(int i=0; i<c.size(); i++){\n cs+=c[i]; \n if(c[i]==2) cnt2++;\n } \n if(cs != u+l || l<cnt2) return ans;\n//create two vector for upper and lower row. Initialize them with zero;\n int n=c.size();\n vector<int> v1(n,0);\n vector<int> v2(n,0);\n//if column sum for any matrix cell is 2, we will assign them 1. Since for column sum =2, we need 1 in both upper and lower row for that column\n for(int i=0; i<n; i++){\n if(c[i]==2){\n v1[i]=1;\n u--; c[i]--;\n }\n } \n//For upper row, if upper sum>0 and colsum> 0, assign it with 1; Repeat same for lower vector too\n for(int i=0; i<n; i++){\n if(u && c[i] && !v1[i]){\n v1[i]=1;\n u--; c[i]--;\n }\n }\n for(int i=0; i<n; i++){\n if(l && c[i]){\n v2[i]=1;\n l--; c[i]--;\n }\n }\n ans.push_back(v1);\n ans.push_back(v2);\n return ans;\n }\n};\n```
| 2 | 0 |
['C++']
| 0 |
reconstruct-a-2-row-binary-matrix
|
C++ | Easy and Clean code | Simple logic
|
c-easy-and-clean-code-simple-logic-by-va-4a0p
|
Intuition\nIf number of 2\'s in colsum is represented by cnt, that means upper and lower must be equal to or greater than cnt.\n\n# Approach\n Describe your app
|
VAIBHAV_SHORAN
|
NORMAL
|
2023-01-01T10:36:15.744325+00:00
|
2023-01-01T10:37:34.526105+00:00
| 665 | false |
# Intuition\nIf number of 2\'s in colsum is represented by cnt, that means upper and lower must be equal to or greater than cnt.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution {\npublic:\n vector<vector<int>> reconstructMatrix(int upper, int lower, vector<int>& colsum) {\n vector<vector<int>> ans;\n int cnt = 0;\n\n int temp = 0;\n for(int i=0; i<colsum.size(); i++){\n temp += colsum[i];\n if(colsum[i] == 2) cnt++;\n }\n\n if(temp != upper + lower) return ans;\n if(lower < cnt || upper < cnt) return ans;\n\n int n = colsum.size();\n vector<int> a(n, 0);\n vector<int> b(n, 0);\n\n for(int i=0; i<colsum.size(); i++){\n if(colsum[i] == 1){\n if(upper >= lower){\n a[i] = 1;\n upper--;\n }\n else{\n b[i] = 1;\n lower--;\n }\n }\n if(colsum[i] == 2){\n a[i] = 1;\n b[i] = 1;\n upper--;\n lower--;\n }\n }\n\n ans.push_back(a);\n ans.push_back(b);\n return ans;\n }\n};\n```
| 2 | 0 |
['C++']
| 0 |
reconstruct-a-2-row-binary-matrix
|
C++ || EASY TO UNDERSTAND || O(n) complexity || Greedy
|
c-easy-to-understand-on-complexity-greed-8pml
|
\nclass Solution {\npublic:\n vector<vector<int>> reconstructMatrix(int upper, int lower, vector<int>& colsum) {\n int m=colsum.size();\n vecto
|
aarindey
|
NORMAL
|
2022-02-24T05:02:42.553663+00:00
|
2022-02-24T05:02:42.553702+00:00
| 191 | false |
```\nclass Solution {\npublic:\n vector<vector<int>> reconstructMatrix(int upper, int lower, vector<int>& colsum) {\n int m=colsum.size();\n vector<vector<int> > ans(2,vector<int>(m));\n int total=accumulate(colsum.begin(),colsum.end(),0);\n if(total!=upper+lower)\n {\n return {};\n }\n \n for(int j=0;j<m;j++)\n {\n if(colsum[j]==2)\n {\n ans[0][j]=1;\n ans[1][j]=1;\n upper--;\n lower--;\n }\n else if(colsum[j]==1)\n {\n if(upper>lower)\n {\n ans[0][j]=1;\n upper--;\n }\n else\n {\n ans[1][j]=1;\n lower--;\n }\n } \n }\n if(upper!=0||lower!=0)\n return {};\n return ans;\n }\n};\n```
| 2 | 0 |
[]
| 0 |
reconstruct-a-2-row-binary-matrix
|
[C++] One Pass Solution , O(N) Time & O(1) Space
|
c-one-pass-solution-on-time-o1-space-by-q4sse
|
\nclass Solution\n{\npublic:\n vector<vector<int>> reconstructMatrix(int upper, int lower, vector<int> &colsum)\n {\n int n = 2, m = colsum.size();
|
jayesh2604
|
NORMAL
|
2021-11-14T11:27:42.224890+00:00
|
2021-11-14T11:27:42.224953+00:00
| 140 | false |
```\nclass Solution\n{\npublic:\n vector<vector<int>> reconstructMatrix(int upper, int lower, vector<int> &colsum)\n {\n int n = 2, m = colsum.size();\n vector<vector<int>> A(n, vector<int>(m, 0));\n for (int i = 0; i < m; i++)\n {\n if (colsum[i] == 2)\n {\n A[0][i] = 1;\n A[1][i] = 1;\n upper--;\n lower--;\n }\n else if (colsum[i] == 0)\n {\n A[0][i] = 0;\n A[1][i] = 0;\n }\n else\n {\n if (upper >= lower)\n {\n A[0][i] = 1;\n A[1][i] = 0;\n upper--;\n }\n else\n {\n A[0][i] = 0;\n A[1][i] = 1;\n lower--;\n }\n }\n }\n if (lower != 0 || upper != 0)\n {\n A.clear();\n }\n return A;\n }\n};\n```
| 2 | 0 |
[]
| 0 |
reconstruct-a-2-row-binary-matrix
|
JAVA EASY SOLUTION O(N) SINGLE PASS
|
java-easy-solution-on-single-pass-by-ani-olim
|
\nclass Solution {\n \n public List<List<Integer>> reconstructMatrix(int upper, int lower, int[] colsum) {\n List<List<Integer>> list=new ArrayLis
|
aniket7419
|
NORMAL
|
2021-10-30T09:50:53.251995+00:00
|
2021-10-30T09:50:53.252025+00:00
| 121 | false |
```\nclass Solution {\n \n public List<List<Integer>> reconstructMatrix(int upper, int lower, int[] colsum) {\n List<List<Integer>> list=new ArrayList<>();\n ArrayList<Integer> up=new ArrayList<>();\n ArrayList<Integer> down=new ArrayList<>();\n \n \n \n for(int i=0;i<colsum.length;i++){\n if(colsum[i]==2){\n up.add(1);\n down.add(1);\n upper--;\n lower--;\n }\n else if(colsum[i]==0){\n up.add(0);\n down.add(0);\n \n }\n else{\n if(upper>=lower){\n up.add(1);\n down.add(0);\n upper--;\n \n }\n else{\n down.add(1);\n up.add(0);\n lower--;\n }\n }\n }\n if(upper==0&&lower==0){\n list.add(up);\n list.add(down);\n }\n \n return list;\n }\n \n \n \n}\n```
| 2 | 0 |
[]
| 0 |
reconstruct-a-2-row-binary-matrix
|
C++ | Very Simple Solution | With Explanation
|
c-very-simple-solution-with-explanation-gg5cb
|
When colsum[i] is 2, then it is obviously 1 in both rows for ith column.\nWhen colsum[i] is 1, then first set the row based on which sum is bigger i.e. Give pre
|
rootkonda
|
NORMAL
|
2020-06-06T19:26:08.050897+00:00
|
2020-06-06T19:26:08.050950+00:00
| 119 | false |
When colsum[i] is 2, then it is obviously 1 in both rows for ith column.\nWhen colsum[i] is 1, then first set the row based on which sum is bigger i.e. Give preference to the row sum which is greater and then the row with lower sum. \n\n```\nclass Solution {\npublic:\n vector<vector<int>> reconstructMatrix(int upper, int lower, vector<int>& colsum) \n {\n int n = colsum.size();\n vector<vector<int>> ans(2,vector<int>(n,0)); \n for(int i=0;i<n;i++)\n {\n if(lower<0 or upper<0)\n return {};\n if(colsum[i]==2)\n {\n ans[0][i] = 1;\n ans[1][i] = 1;\n upper--;\n lower--;\n }\n else if(colsum[i]==1)\n {\n if(upper>lower)\n {\n ans[0][i]=1;\n upper--;\n } \n else\n {\n ans[1][i]=1;\n lower--;\n }\n }\n }\n if(lower!=0 or upper!=0)\n return {};\n return ans;\n }\n};\n```
| 2 | 0 |
[]
| 0 |
reconstruct-a-2-row-binary-matrix
|
Simple Proof of the Greedy Approach
|
simple-proof-of-the-greedy-approach-by-n-50y6
|
if column[i] if 0 or 2, we know the value of the 2-row binary matrix for sure, for those remaining column[j] == 1 elements, suppose we have a solution uuullluul
|
nate17
|
NORMAL
|
2019-11-11T04:17:45.599826+00:00
|
2019-11-12T04:40:55.192215+00:00
| 128 | false |
if column[i] if 0 or 2, we know the value of the 2-row binary matrix for sure, for those remaining column[j] == 1 elements, suppose we have a solution `uuullluull...` where `u` denoting the upper j th column element is 1 and `l` denoting the lower j th column element is 1. Since column[j] == 1 is symmetric for `u` and `l` positions, we therefore could arrange `u` and `l` in any order, and there are a total of `count of u` combination out of `count of sum of u and l` solutions. Here is the code to find one of those solutions:\n```python\nclass Solution:\n def reconstructMatrix(self, upper: int, lower: int, colsum: List[int]) -> List[List[int]]:\n n = len(colsum)\n res = [[0]*n for _ in range(2)]\n for i in range(n):\n if colsum[i] == 2:\n res[0][i] = 1\n res[1][i] = 1\n upper -= 1\n lower -= 1\n elif colsum[i] == 1:\n if upper > lower:\n res[0][i] = 1\n upper -= 1\n else:\n res[1][i] = 1\n lower -= 1\n if lower != 0 or upper != 0:\n return []\n return res \n```
| 2 | 1 |
[]
| 0 |
reconstruct-a-2-row-binary-matrix
|
Python 3 (nine lines) (beats 100%)
|
python-3-nine-lines-beats-100-by-junaidm-hffx
|
```\nclass Solution:\n def reconstructMatrix(self, U: int, L: int, C: List[int]) -> List[List[int]]:\n M, u = [[0]*len(C) for _ in range(2)], C.count(
|
junaidmansuri
|
NORMAL
|
2019-11-10T05:00:09.358529+00:00
|
2019-11-10T05:01:08.563603+00:00
| 324 | false |
```\nclass Solution:\n def reconstructMatrix(self, U: int, L: int, C: List[int]) -> List[List[int]]:\n M, u = [[0]*len(C) for _ in range(2)], C.count(2)\n if U + L != sum(C) or u > min(L,U): return []\n for j,s in enumerate(C):\n if s == 2: M[0][j] = M[1][j] = 1\n for j,s in enumerate(C):\n if s == 1:\n if u < U: M[0][j], u = 1, u + 1\n else: M[1][j] = 1\n return M\n \n\t\t\t\n- Junaid Mansuri
| 2 | 1 |
['Python', 'Python3']
| 0 |
reconstruct-a-2-row-binary-matrix
|
C++ solution easy to understand
|
c-solution-easy-to-understand-by-yanjing-f7q3
|
\nclass Solution {\npublic:\n vector<vector<int>> reconstructMatrix(int upper, int lower, vector<int>& colsum) {\n if(colsum.size() == 0) return {};\n
|
yanjing328681
|
NORMAL
|
2019-11-10T04:04:56.475787+00:00
|
2019-11-10T04:04:56.475823+00:00
| 149 | false |
```\nclass Solution {\npublic:\n vector<vector<int>> reconstructMatrix(int upper, int lower, vector<int>& colsum) {\n if(colsum.size() == 0) return {};\n int n = colsum.size();\n vector<vector<int>> res(2, vector<int>(n, 0));\n int up = 0, low = 0;\n for(int j = 0; j < n; ++j)\n {\n if(colsum[j] == 2)\n {\n res[0][j] = 1;\n res[1][j] = 1;\n up++;\n low++;\n }\n else if(colsum[j] == 0)\n {\n res[0][j] = 0;\n res[1][j] = 0;\n }\n }\n if(up == upper && low == lower) return res;\n if(up > upper || low > lower) return {};\n for(int j = 0; j < n; ++j)\n {\n if(colsum[j] != 1) continue;\n if(upper - up >= lower - low)\n {\n res[0][j] = 1;\n res[1][j] = 0;\n up++;\n }\n else \n {\n res[0][j] = 0;\n res[1][j] = 1;\n low++;\n }\n }\n if(up != upper || low != lower) return {};\n return res;\n }\n};\n```
| 2 | 2 |
[]
| 0 |
reconstruct-a-2-row-binary-matrix
|
[Java] Greedy O(n) Solution
|
java-greedy-on-solution-by-sun_wukong-mxjp
|
\nclass Solution {\n public List<List<Integer>> reconstructMatrix(int upper, int lower, int[] colsum) {\n int sum = 0, count2 = 0;\n for (int c
|
sun_wukong
|
NORMAL
|
2019-11-10T04:03:13.336796+00:00
|
2019-11-10T04:05:01.844732+00:00
| 301 | false |
```\nclass Solution {\n public List<List<Integer>> reconstructMatrix(int upper, int lower, int[] colsum) {\n int sum = 0, count2 = 0;\n for (int cs : colsum) {\n sum += cs;\n count2 += cs/2;\n }\n \n if (upper + lower != sum || upper < count2 || lower < count2) return new ArrayList();\n \n List<List<Integer>> matrix = new ArrayList();\n matrix.add(new ArrayList());\n matrix.add(new ArrayList());\n \n for (int i = 0; i < colsum.length; i++) {\n if (colsum[i] == 2) {\n matrix.get(0).add(1);\n matrix.get(1).add(1);\n } else if (colsum[i] == 1) {\n matrix.get(0).add(upper > lower ? 1 : 0);\n matrix.get(1).add(upper > lower ? 0 : 1);\n } else {\n matrix.get(0).add(0);\n matrix.get(1).add(0);\n }\n upper -= matrix.get(0).get(i);\n lower -= matrix.get(1).get(i);\n }\n return matrix;\n }\n}\n```
| 2 | 2 |
['Greedy']
| 3 |
reconstruct-a-2-row-binary-matrix
|
c++ easy solution
|
c-easy-solution-by-geetanjali-18-0vah
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
geetanjali-18
|
NORMAL
|
2024-07-20T07:54:12.183359+00:00
|
2024-07-20T07:54:12.183431+00:00
| 33 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<vector<int>> reconstructMatrix(int upper, int lower, vector<int>& colsum) {\n int n = colsum.size();\n vector<vector<int>>ans(2, vector<int>(n));\n vector<vector<int>>temp;\n if(upper+lower != accumulate(colsum.begin(), colsum.end(), 0)) return temp;\n for(int i=0;i<n;i++){\n if(colsum[i]==2){\n ans[0][i] = 1;\n ans[1][i] = 1;\n upper--;\n lower--;\n }\n else if(colsum[i]==1){\n if(upper>lower){\n ans[0][i] = 1;\n upper--;\n }\n else{\n ans[1][i] = 1;\n lower--;\n }\n }\n }\n if(lower!=0 || upper!=0) return temp;\n return ans;\n }\n};\n```
| 1 | 0 |
['C++']
| 0 |
reconstruct-a-2-row-binary-matrix
|
JavaScript | Simple Greedy Solution | O(N)
|
javascript-simple-greedy-solution-on-by-867zc
|
Approach\nThe solution implements a greedy approach to reconstruct two rows, row1 and row2, based on a given column sum array (colsum), upper and lower constrai
|
christinashoe22
|
NORMAL
|
2024-01-23T21:55:09.380614+00:00
|
2024-01-23T21:55:09.380636+00:00
| 59 | false |
# Approach\nThe solution implements a greedy approach to reconstruct two rows, row1 and row2, based on a given column sum array (colsum), upper and lower constraints. The algorithm iterates through each column, making decisions on how to distribute ones in both rows to match the column sums efficiently. It uses conditions to handle cases where colsum is 0, skips unnecessary iterations, and adjusts the distribution based on the values of upper and lower. The code ensures the total sum of the reconstructed rows aligns with the given upper and lower constraints, returning a valid reconstruction or an empty array if not possible.\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(n)\n\n# Code\n```\n/**\n * @param {number} upper\n * @param {number} lower\n * @param {number[]} colsum\n * @return {number[][]}\n */\nvar reconstructMatrix = function(upper, lower, colsum) {\n const length = colsum.length; \n const row1 = new Array(length).fill(0);\n const row2 = new Array(length).fill(0);\n let totalSum = colsum.reduce((acc, currValue)=> acc + currValue, 0);\n\n if(totalSum!==upper+lower) return [];\n \n for(let i = 0 ; i<colsum.length; i++){\n if(upper <0 || lower<0) return [];\n if(colsum[i]===0) continue;\n if(colsum[i]===2) {\n row1[i] = 1;\n upper--;\n row2[i] = 1;\n lower--;\n } \n else if(upper>lower) {\n upper--;\n row1[i]++;\n }\n else {\n lower--;\n row2[i]++;\n }\n }\n return [row1, row2];\n};\n```
| 1 | 0 |
['Greedy', 'JavaScript']
| 0 |
reconstruct-a-2-row-binary-matrix
|
Simple Python Greedy O(n) Solution
|
simple-python-greedy-on-solution-by-jsod-ylov
|
Code\n\nclass Solution:\n def reconstructMatrix(self, upper: int, lower: int, colsum: List[int]) -> List[List[int]]:\n \n n = len(colsum)\n
|
jsod
|
NORMAL
|
2023-11-20T16:48:14.967624+00:00
|
2023-11-20T16:48:14.967650+00:00
| 38 | false |
# Code\n```\nclass Solution:\n def reconstructMatrix(self, upper: int, lower: int, colsum: List[int]) -> List[List[int]]:\n \n n = len(colsum)\n matrix = [[0] * n for _ in range(2)]\n if upper + lower != sum(colsum): return []\n\n for i in range(n):\n if colsum[i] == 2:\n matrix[0][i] = 1\n matrix[1][i] = 1\n upper -= 1\n lower -= 1\n elif colsum[i] == 1:\n if lower <= upper:\n matrix[0][i] = 1\n upper -= 1\n else:\n matrix[1][i] = 1\n lower -= 1\n \n if upper > 0 or lower > 0:\n return []\n \n return matrix\n```
| 1 | 0 |
['Python3']
| 0 |
reconstruct-a-2-row-binary-matrix
|
Simple and clear python3 solutions | 524 ms - faster than 94.4% solutions
|
simple-and-clear-python3-solutions-524-m-ujw9
|
Complexity\n- Time complexity: O(n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(n) (only for answer)\n Add your space complexity here,
|
tigprog
|
NORMAL
|
2023-10-03T09:58:26.565023+00:00
|
2023-10-03T09:58:26.565042+00:00
| 44 | false |
# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$ (only for answer)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` python3 []\nclass Solution:\n def reconstructMatrix(self, upper: int, lower: int, colsum: List[int]) -> List[List[int]]:\n n = len(colsum)\n if upper > n or lower > n:\n return []\n\n deuces = sum(1 for elem in colsum if elem == 2)\n if upper < deuces or lower < deuces:\n return []\n\n if upper + lower != sum(colsum):\n return []\n \n result = [[0] * n for _ in range(2)]\n upper -= deuces\n lower -= deuces\n\n for i, s in enumerate(colsum):\n if s == 2:\n result[0][i] = 1\n result[1][i] = 1\n elif s == 1:\n if upper:\n result[0][i] = 1\n upper -= 1\n else:\n result[1][i] = 1\n lower -= 1\n\n return result\n```
| 1 | 0 |
['Math', 'Greedy', 'Python3']
| 0 |
reconstruct-a-2-row-binary-matrix
|
c++| easy approach | understandable
|
c-easy-approach-understandable-by-venomh-atzx
|
```\nvector> reconstructMatrix(int upper, int lower, vector& colsum) {\n \n vector> ans(2,vector(colsum.size(),0));\n for(int i=0;ilower)\n
|
venomhighs7
|
NORMAL
|
2022-09-20T03:50:39.311026+00:00
|
2022-09-20T03:50:39.311141+00:00
| 370 | false |
```\nvector<vector<int>> reconstructMatrix(int upper, int lower, vector<int>& colsum) {\n \n vector<vector<int>> ans(2,vector<int>(colsum.size(),0));\n for(int i=0;i<colsum.size();i++)\n {\n if(colsum[i]==1)\n {\n if(upper>lower)\n {\n ans[0][i]=1;\n upper--; // 1 less sum of 0th row as we make the cell as 1\n }\n \n else\n {\n ans[1][i]=1;\n lower--; // 1 less sum of 1st row as we make the cell as 1\n }\n \n }\n \n if(colsum[i]==2)\n {\n ans[0][i]=1;\n ans[1][i]=1;\n \n upper--; // 1 less sum of 0th row as we make the cell as 1\n lower--; // 1 less sum of 1st row as we make the cell as 1\n }\n \n if(upper<0 or lower<0) //sum exceeds of any row then not possible to form \n return {};\n }\n \n //0th row sum and 1st row sum should be completely made by forming the matrix\n if(upper!=0 or lower!=0) \n return {};\n \n return ans;\n \n }
| 1 | 0 |
[]
| 0 |
reconstruct-a-2-row-binary-matrix
|
✅C++ || Logic Explained in detail || EASY
|
c-logic-explained-in-detail-easy-by-abhi-wkny
|
\n\nLogic->You cannot do anything about colsum[i] = 2 case or colsum[i] = 0 case. Then you put colsum[i] = 1 case to the upper row until upper has reached. Then
|
abhinav_0107
|
NORMAL
|
2022-08-08T10:15:51.149412+00:00
|
2022-08-08T10:15:51.149457+00:00
| 322 | false |
\n\n***Logic->You cannot do anything about colsum[i] = 2 case or colsum[i] = 0 case. Then you put colsum[i] = 1 case to the upper row until upper has reached. Then put the rest into lower row.***\n\n**T->O(n) && S->O(n * 2)**\n\n\t\tclass Solution {\n\t\tpublic:\n\t\t\tvector<vector<int>> reconstructMatrix(int upper, int lower, vector<int>& colsum) {\n\t\t\t\tint n=colsum.size();\n\t\t\t\tvector<vector<int>>mat(2,vector<int>(n,0));\n\t\t\t\tif(lower+upper!=accumulate(colsum.begin(),colsum.end(),0))return {};\n\t\t\t\tfor(int j=0;j<n;j++){\n\t\t\t\t\tif(colsum[j]==2){\n\t\t\t\t\t\tmat[1][j]=mat[0][j]=1;\n\t\t\t\t\t\tcolsum[j]=0;\n\t\t\t\t\t\tupper--;\n\t\t\t\t\t\tlower--;\n\t\t\t\t\t} \n\t\t\t\t}\n\t\t// Upper\n\t\t\t\tfor(int j=0;j<n;j++){\n\t\t\t\t\tif(upper && colsum[j]){\n\t\t\t\t\t\tmat[0][j]=1;\n\t\t\t\t\t\tupper--;\n\t\t\t\t\t\tcolsum[j]--;\n\t\t\t\t\t} \n\t\t\t\t}\n\t\t// Lower\n\t\t\t\tfor(int j=0;j<n;j++){\n\t\t\t\t\tif(lower && colsum[j]){\n\t\t\t\t\t\tmat[1][j]=1;\n\t\t\t\t\t\tlower--;\n\t\t\t\t\t\tcolsum[j]--;\n\t\t\t\t\t} \n\t\t\t\t}\n\t\t\t\tif(lower || upper)return {};\n\t\t\t\treturn mat;\n\t\t\t}\n\t\t};
| 1 | 0 |
['C', 'C++']
| 0 |
reconstruct-a-2-row-binary-matrix
|
c++ || greedy approach
|
c-greedy-approach-by-ayushanand245-56zp
|
\nclass Solution {\npublic:\n vector<vector<int>> reconstructMatrix(int upper, int lower, vector<int>& col) {\n int m = col.size();\n vector<ve
|
ayushanand245
|
NORMAL
|
2022-03-28T07:51:35.923376+00:00
|
2022-03-28T07:52:01.246625+00:00
| 72 | false |
```\nclass Solution {\npublic:\n vector<vector<int>> reconstructMatrix(int upper, int lower, vector<int>& col) {\n int m = col.size();\n vector<vector<int>> temp(2,vector<int>(m));\n vector<int> row = {upper,lower};\n int rowSum = accumulate(row.begin(), row.end(), 0);\n int colSum = accumulate(col.begin(), col.end(), 0);\n if(rowSum != colSum) return vector<vector<int>>();\n \n for(int j=0;j<m;j++){\n if(col[j] == 2){\n temp[0][j]=1; row[0]--;\n temp[1][j]=1; row[1]--;\n }\n else if(col[j]==1){\n if(row[0] > row[1]){\n temp[0][j]=1; row[0]--;\n }\n else{\n temp[1][j]=1; row[1]--;\n }\n }\n }\n if(row[0]!=0 || row[1]!=0) return {};\n return temp;\n }\n};\n```
| 1 | 0 |
[]
| 0 |
reconstruct-a-2-row-binary-matrix
|
greedy approach
|
greedy-approach-by-kumarambuj-9cbz
|
\nclass Solution:\n def reconstructMatrix(self, upper: int, lower: int, colsum: List[int]) -> List[List[int]]:\n if (upper+lower)!=sum(colsum):\n
|
kumarambuj
|
NORMAL
|
2022-01-07T15:40:06.093395+00:00
|
2022-01-07T15:40:06.093432+00:00
| 97 | false |
```\nclass Solution:\n def reconstructMatrix(self, upper: int, lower: int, colsum: List[int]) -> List[List[int]]:\n if (upper+lower)!=sum(colsum):\n return []\n \n res=[[0 for i in range(len(colsum))] for j in range(2)]\n \n for i in range(len(colsum)):\n if colsum[i]==2:\n if upper>0 and lower>0:\n lower-=1\n upper-=1\n res[0][i]=1\n res[1][i]=1\n else:\n return []\n for i in range(len(colsum)):\n \n if colsum[i]==1:\n \n if upper>0:\n res[0][i]=1\n upper-=1\n elif lower>0:\n res[1][i]=1\n lower-=1\n else:\n return []\n return res\n```
| 1 | 0 |
['Greedy', 'Python']
| 0 |
reconstruct-a-2-row-binary-matrix
|
Easy C++ Greedy solution || commented
|
easy-c-greedy-solution-commented-by-sait-3myo
|
\nclass Solution {\npublic:\n vector<vector<int>> reconstructMatrix(int upper, int lower, vector<int>& colsum) {\n \n //first fill the cols who
|
saiteja_balla0413
|
NORMAL
|
2021-11-04T12:52:50.667158+00:00
|
2021-11-04T12:53:56.448788+00:00
| 97 | false |
```\nclass Solution {\npublic:\n vector<vector<int>> reconstructMatrix(int upper, int lower, vector<int>& colsum) {\n \n //first fill the cols whose colsum[i]==2 \n \n vector<vector<int>> empty;\n int len=colsum.size();\n vector<vector<int>> res(2,vector<int>(len,0));\n \n //the count of cols whose colsum[i]==1\n int ones=0;\n for(int i=0;i<len;i++)\n {\n if(colsum[i]==1)\n ones++;\n else if(colsum[i]==2)\n {\n if(upper==0 || lower==0)\n return empty;\n res[0][i]=res[1][i]=1;\n upper--;\n lower--;\n }\n }\n\t\t// we cant fill the cols whose colsum is 1\n if(ones!=(lower+upper))\n return empty;\n \n for(int i=0;i<len;i++)\n {\n if(colsum[i]==1)\n {\n if(upper)\n { \n\t\t\t\t //fill the first row\n res[0][i]=1;\n upper--;\n }\n else{\n\t\t\t\t//fill the second row\n res[1][i]=1;\n lower--;\n }\n }\n }\n return res;\n }\n};\n```
| 1 | 0 |
['Greedy', 'C']
| 0 |
reconstruct-a-2-row-binary-matrix
|
Easy and Simple Solution In JS
|
easy-and-simple-solution-in-js-by-prabha-kw2c
|
```\n/*\n * @param {number} upper\n * @param {number} lower\n * @param {number[]} colsum\n * @return {number[][]}\n /\nvar reconstructMatrix = function(upper, l
|
Prabhatsingh
|
NORMAL
|
2021-10-15T18:51:39.736868+00:00
|
2021-10-15T18:51:39.736903+00:00
| 117 | false |
```\n/**\n * @param {number} upper\n * @param {number} lower\n * @param {number[]} colsum\n * @return {number[][]}\n */\nvar reconstructMatrix = function(upper, lower, colsum){\n let dp = new Array(2)\n for(let i = 0; i< dp.length; i++){\n dp[i] = new Array(colsum.length)\n }\n let first = upper\n let second = lower\n let upsum = 0\n let losum= 0\n \n for(let i = 0; i< colsum.length; i++){\n if(colsum[i] === 2){\n dp[0][i] = 1\n dp[1][i] = 1\n upsum++\n losum++\n }\n else if(colsum[i] === 1){\n if(lower < upper){\n dp[0][i] =1\n dp[1][i] = 0\n upper--\n upsum++\n }\n else{\n dp[0][i] = 0\n dp[1][i] = 1\n lower--\n losum++\n }\n }\n else if(colsum[i] === 0){\n dp[0][i] = 0\n dp[1][i] = 0\n }\n else{\n return []\n }\n }\n if(losum !== second || upsum !== first) return []\n return dp\n}
| 1 | 0 |
['JavaScript']
| 0 |
reconstruct-a-2-row-binary-matrix
|
C++ || O(n) || Greedy || Easy To Understand ✔
|
c-on-greedy-easy-to-understand-by-ajay_m-887u
|
here colsum[i] = 0 or 1 or 2\nfor colsum[i] == 0 => both upper and lower row has value 0\nfor colsum[i] == 2 => both upper and lower row has value 1\nfor colsum
|
AJAY_MAKVANA
|
NORMAL
|
2021-09-24T07:39:05.340131+00:00
|
2021-09-24T07:39:05.340162+00:00
| 172 | false |
here `colsum[i] = 0 or 1 or 2`\nfor `colsum[i] == 0 => both upper and lower row has value 0`\nfor `colsum[i] == 2 => both upper and lower row has value 1`\nfor `colsum[i] == 1 => if upper > lower then upper row value = 1 else lower row value = 1`\n\n```\nclass Solution {\npublic:\n\tvector<vector<int>> reconstructMatrix(int upper, int lower, vector<int>& colsum) {\n\t\tint n = colsum.size();\n\t\tvector<vector<int>> ans(2, vector<int>(n, 0));\n\t\tfor (int i = 0; i < n; i++)\n\t\t{\n\t\t\tif (colsum[i] == 2)\n\t\t\t{\n\t\t\t\tans[0][i] = 1;\n\t\t\t\tans[1][i] = 1;\n\t\t\t\tupper--;\n\t\t\t\tlower--;\n\t\t\t}\n\t\t\telse if (colsum[i] == 1)\n\t\t\t{\n\t\t\t\tif (upper > lower)\n\t\t\t\t{\n\t\t\t\t\tans[0][i] = 1;\n\t\t\t\t\tupper--;\n\t\t\t\t}\n\t\t\t\telse\n\t\t\t\t{\n\t\t\t\t\tans[1][i] = 1;\n\t\t\t\t\tlower--;\n\t\t\t\t}\n\t\t\t}\n\t\t}\n\t\tif (lower == 0 && upper == 0)\n\t\t{\n\t\t\treturn ans;\n\t\t}\n\t\treturn {};\n\t}\n};\n```\n\n**If find Helpful *Upvote It* \uD83D\uDC4D**
| 1 | 0 |
['Greedy', 'C', 'C++']
| 1 |
reconstruct-a-2-row-binary-matrix
|
C++ Solution
|
c-solution-by-ahsan83-7fi7
|
Runtime: 88 ms, faster than 23.00% of C++ online submissions for Reconstruct a 2-Row Binary Matrix.\nMemory Usage: 62.6 MB, less than 13.67% of C++ online submi
|
ahsan83
|
NORMAL
|
2021-08-06T15:10:57.400561+00:00
|
2021-08-06T15:10:57.400607+00:00
| 125 | false |
Runtime: 88 ms, faster than 23.00% of C++ online submissions for Reconstruct a 2-Row Binary Matrix.\nMemory Usage: 62.6 MB, less than 13.67% of C++ online submissions for Reconstruct a 2-Row Binary Matrix.\n\n\nGiven array is Binary and so the max col value can be 2. So, we first put both in upper and lower row in ith\ncolumn if column value is 2. Then we iteratively put 1 in those columns of upper or lower row if upper sum\nand ith column is greater than 0 or lower sum and ith column is greater than 0. Then we again check the\nupper sum and lower sum and specific column sum for the valdity of the result. Any invalid case makes\nresult impossible.\n\n```\nclass Solution {\npublic:\n vector<vector<int>> reconstructMatrix(int upper, int lower, vector<int>& col) {\n \n\n int n = col.size();\n vector<vector<int>>res(2,vector<int>(n,0));\n vector<int>colsum(col.begin(),col.end());\n \n int rowsum [2] = {upper,lower};\n \n // make res[0][j] && res[1][j] 1 if col[j]==2\n for(int j=0;j<n;j++)\n {\n if(colsum[j]==2)\n {\n res[0][j] = 1;\n res[1][j] = 1;\n colsum[j] = 0;\n rowsum[0] -= 1;\n rowsum[1] -= 1;\n }\n }\n \n // make res[i][j] 1 if both rowsum[i]>0 && colsum[j]>0\n for(int i=0;i<2;i++)\n {\n for(int j=0;j<n;j++)\n {\n if(res[i][j]!=1)\n {\n res[i][j] = (rowsum[i]>0 && colsum[j]>0) ? 1 : 0;\n rowsum[i] -= res[i][j];\n colsum[j] -= res[i][j];\n }\n } \n }\n \n // check validity of the result vector with given costraints\n int t_upper = 0;\n int t_lower = 0;\n for(int i=0;i<n;i++)\n {\n t_upper+=res[0][i];\n t_lower+=res[1][i];\n \n if(col[i]!=(res[0][i]+res[1][i]))return {}; // invalid\n }\n \n if(t_upper != upper || t_lower!=lower)return {}; // invalid\n \n \n return res;\n }\n};\n```
| 1 | 0 |
['Array', 'C']
| 0 |
reconstruct-a-2-row-binary-matrix
|
C++ | Greedy
|
c-greedy-by-kena7-5qp7
|
\nclass Solution {\npublic:\n vector<vector<int>> reconstructMatrix(int upper, int lower, vector<int>& colsum) \n {\n int n=colsum.size();\n
|
kenA7
|
NORMAL
|
2021-05-25T09:33:36.087374+00:00
|
2021-05-25T09:33:36.087416+00:00
| 84 | false |
```\nclass Solution {\npublic:\n vector<vector<int>> reconstructMatrix(int upper, int lower, vector<int>& colsum) \n {\n int n=colsum.size();\n vector<vector<int>>res(2,vector<int>(n,0));\n for(int i=0;i<n;i++)\n {\n if(colsum[i]==2)\n {\n upper--;\n lower--;\n res[0][i]=1;\n res[1][i]=1;\n }\n }\n if(upper<0 || lower<0)\n return {};\n for(int i=0;i<n;i++)\n {\n if(colsum[i]==1)\n {\n if(upper)\n {\n upper--;\n res[0][i]=1;\n }\n else\n {\n lower--;\n res[1][i]=1;\n }\n }\n }\n if(upper!=0 || lower!=0)\n return {};\n return res;\n }\n};\n```
| 1 | 0 |
[]
| 0 |
reconstruct-a-2-row-binary-matrix
|
Python - first remove 2, then remove ones arbitrarily
|
python-first-remove-2-then-remove-ones-a-zfmi
|
First remove sum==2s since we do not have a choice there.\nThen we can arbitrarily choose either upper or lower when sum==1.\nMake sure do some check such as up
|
mahsaelyasi
|
NORMAL
|
2021-03-19T01:18:24.728777+00:00
|
2021-03-19T01:18:58.182664+00:00
| 113 | false |
First remove sum==2s since we do not have a choice there.\nThen we can arbitrarily choose either upper or lower when sum==1.\nMake sure do some check such as upper + lower == sum(colsum)\n```\ndef reconstructMatrix(self, upper: int, lower: int, colsum: List[int]) -> List[List[int]]:\n if sum(colsum) != upper + lower: return []\n m, n = len(colsum), 2\n ans = [[0] * m for _ in range(n)]\n for i in range(m):\n if colsum[i] == 2:\n if upper > 0 and lower > 0:\n upper -= 1\n lower -= 1\n ans[0][i] = 1\n ans[1][i] = 1\n else:\n return []\n \n for i in range(m):\n if colsum[i] == 1 and upper > 0:\n ans[0][i] = 1\n upper -= 1\n\n for i in range(m):\n if colsum[i] == 1 and ans[0][i] == 0 and lower > 0:\n ans[1][i] = 1\n lower -= 1\n \n return ans\n```
| 1 | 0 |
[]
| 0 |
reconstruct-a-2-row-binary-matrix
|
Very easy and commented solution in c++(no complex code)
|
very-easy-and-commented-solution-in-cno-nnr48
|
\tclass Solution {\n\tpublic:\n\t\tvector> reconstructMatrix(int upper, int lower, vector& colsum) {\n\t\t\tint n=colsum.size();\n\t\t\tint i=0;\n\t\t\tvector>r
|
shubhamsinhanitt
|
NORMAL
|
2021-03-17T07:43:43.350591+00:00
|
2021-03-17T07:43:43.350620+00:00
| 96 | false |
\tclass Solution {\n\tpublic:\n\t\tvector<vector<int>> reconstructMatrix(int upper, int lower, vector<int>& colsum) {\n\t\t\tint n=colsum.size();\n\t\t\tint i=0;\n\t\t\tvector<vector<int>>res(2,vector<int>(n,0));\n\t\t\tvector<vector<int>>res1;\n\t\t\twhile(i<n)\n\t\t\t{\n\t\t\t\tif(colsum[i]==2&&upper>0&&lower>0)// if both lower and upper are above 0 then we can only have 2 as column sum\n\t\t\t\t{\n\t\t\t\t\tres[0][i]=1;\n\t\t\t\t\tres[1][i]=1;\n\t\t\t\t\tupper--;\n\t\t\t\t\tlower--;\n\t\t\t\t}\n\t\t\t\telse if(colsum[i]==2)// else return empty vector\n\t\t\t\t{\n\t\t\t\t\treturn res1;\n\t\t\t\t}\n\t\t\t\telse if(colsum[i]==1)\n\t\t\t\t{\n\t\t\t\t\tif(upper>lower&&upper>0)// check if upper > lower and also upper should be greater than 0\n\t\t\t\t\t{\n\t\t\t\t\t\tres[0][i]=1;\n\t\t\t\t\t\tupper--;\n\t\t\t\t\t}\n\t\t\t\t\telse if(lower>=upper&&lower>0)// check if lower>upper and also lower is greater than 0\n\t\t\t\t\t{\n\t\t\t\t\t\tres[1][i]=1;\n\t\t\t\t\t\tlower--;\n\t\t\t\t\t}\n\t\t\t\t\telse\n\t\t\t\t\t{\n\t\t\t\t\t\treturn res1;// return empty vector\n\t\t\t\t\t}\n\t\t\t\t}\n\t\t\t\ti++;\n\t\t\t}\n\n\t\t\tif(upper==0&&lower==0)// at last if we have assigned number of 1 in both rows equals to upper and lower so we are checking if both of them are 0\n\t\t\t{\n\t\t\t\treturn res;\n\t\t\t}\n\t\t\treturn res1; // else return empty vector\n\n\n\n\t\t}\n\t};
| 1 | 0 |
[]
| 0 |
reconstruct-a-2-row-binary-matrix
|
Python solution beats 97% with comments
|
python-solution-beats-97-with-comments-b-bf7m
|
class Solution:\n\n def reconstructMatrix(self, upper: int, lower: int, colsum: List[int]) -> List[List[int]]:\n if sum(colsum) != upper+lower:\n
|
flyingspa
|
NORMAL
|
2021-03-06T10:49:43.334822+00:00
|
2021-03-06T10:49:43.334855+00:00
| 215 | false |
class Solution:\n\n def reconstructMatrix(self, upper: int, lower: int, colsum: List[int]) -> List[List[int]]:\n if sum(colsum) != upper+lower:\n return []\n ans = [[0]*len(colsum) for _ in range(2)]\n for i in range(len(colsum)): #if colsum is equal to 2, we have no choice but put 1 in both rows\n if colsum[i] == 2:\n ans[0][i] = 1\n ans[1][i] = 1\n upper-=1\n lower-=1\n \n for i in range(len(colsum)):\n if colsum[i] == 1: \n if upper>0: #try to put into the upper row first \n ans[0][i] = 1\n upper-=1\n elif lower > 0: # and then the lower row\n ans[1][i] = 1\n lower -= 1\n if upper <0 or lower <0: # if any negative value found, return \n return []\n return ans
| 1 | 0 |
['Python']
| 0 |
reconstruct-a-2-row-binary-matrix
|
c++ greedy faster than 100%
|
c-greedy-faster-than-100-by-panbowang001-jy7q
|
c++\n// \u5982\u679C\u7B49\u4E8E 2,\u4E24\u884C\u90FD\u4E3A 1\n// \u5982\u679C\u7B49\u4E8E1\uFF0C\u53D6\u503C\u5269\u4F59\u5927\u7684\u4E00\u884C\u6539\u4E3A1\n
|
panbowang001
|
NORMAL
|
2021-02-26T10:36:00.751118+00:00
|
2021-02-26T10:36:00.751153+00:00
| 70 | false |
```c++\n// \u5982\u679C\u7B49\u4E8E 2,\u4E24\u884C\u90FD\u4E3A 1\n// \u5982\u679C\u7B49\u4E8E1\uFF0C\u53D6\u503C\u5269\u4F59\u5927\u7684\u4E00\u884C\u6539\u4E3A1\nclass Solution {\npublic:\n vector<vector<int>> reconstructMatrix(int upper, int lower, vector<int>& colsum) {\n\t\tint n = colsum.size();\n vector<vector<int>> ret(2, vector<int>(n, 0));\n\t\tfor (int i = 0; i < n; ++i) {\n\t\t\tif (colsum[i] == 2) {\n\t\t\t\tret[0][i] = 1;\n\t\t\t\tret[1][i] = 1;\n\t\t\t\t--upper;\n\t\t\t\t--lower;\n\t\t\t} else if (colsum[i] == 1) {\n\t\t\t\tif (lower > upper) {\n\t\t\t\t\tret[1][i] = 1;\n\t\t\t\t\t--lower;\n\t\t\t\t} else {\n\t\t\t\t\tret[0][i] = 1;\n\t\t\t\t\t--upper;\n\t\t\t\t}\n\t\t\t}\n\t\t}\n\t\tif (upper != 0 || lower != 0) {\n\t\t\treturn vector<vector<int>>();\n\t\t}\n\t\t\n\t\treturn ret;\n }\n};\n```
| 1 | 0 |
[]
| 0 |
reconstruct-a-2-row-binary-matrix
|
Easy to understand java solution
|
easy-to-understand-java-solution-by-nir1-ex3c
|
\nclass Solution {\n public List<List<Integer>> reconstructMatrix(int upper, int lower, int[] colsum) {\n int l = colsum.length;\n \n Li
|
nir16r
|
NORMAL
|
2020-12-29T09:59:41.860695+00:00
|
2020-12-29T09:59:41.860735+00:00
| 174 | false |
```\nclass Solution {\n public List<List<Integer>> reconstructMatrix(int upper, int lower, int[] colsum) {\n int l = colsum.length;\n \n List<List<Integer>> out = new ArrayList<>();\n List<Integer> upperList = new ArrayList<>();\n List<Integer> lowerList = new ArrayList<>();\n \n for(int i=0;i<l;i++){\n if(colsum[i] == 2){\n upperList.add(1);\n lowerList.add(1);\n upper-=1;\n lower-=1;\n }else if(colsum[i] == 0){\n upperList.add(0);\n lowerList.add(0);\n }else if(colsum[i] == 1){\n if(upper > lower){\n upperList.add(1);\n lowerList.add(0);\n upper-=1;\n }else{\n upperList.add(0);\n lowerList.add(1);\n lower-=1;\n }\n }\n }\n \n if(upper != 0 || lower != 0){\n return out;\n }\n out.add(upperList);\n out.add(lowerList);\n return out;\n \n }\n}\n```
| 1 | 0 |
['Java']
| 1 |
reconstruct-a-2-row-binary-matrix
|
JAVA 100% : This row save my life - return new ArrayList(Arrays.asList(a1, a2));
|
java-100-this-row-save-my-life-return-ne-qk4w
|
\nclass Solution {\n public List<List<Integer>> reconstructMatrix(int upper, int lower, int[] colsum) {\n int n = colsum.length;\n int[] a1 = n
|
tea_93
|
NORMAL
|
2020-10-14T03:29:48.772863+00:00
|
2020-10-14T03:31:36.798358+00:00
| 289 | false |
```\nclass Solution {\n public List<List<Integer>> reconstructMatrix(int upper, int lower, int[] colsum) {\n int n = colsum.length;\n int[] a1 = new int[n];\n int[] a2 = new int[n];\n \n for (int i = 0; i < n; i++) {\n if (colsum[i] == 2) {\n a1[i] = 1;\n a2[i] = 1;\n upper--;\n lower--;\n }\n else if (colsum[i] == 1) {\n if (upper >= lower) {\n a1[i] = 1;\n upper--;\n } else {\n a2[i] = 1;\n lower--;\n }\n }\n }\n \n if (upper != 0 || lower != 0)\n return new ArrayList();\n \n return new ArrayList(Arrays.asList(a1, a2));\n }\n}\n```
| 1 | 0 |
[]
| 1 |
reconstruct-a-2-row-binary-matrix
|
Different method in python 3
|
different-method-in-python-3-by-mintukri-ewwp
|
\nclass Solution:\n def reconstructMatrix(self, upper: int, lower: int, colsum: List[int]) -> List[List[int]]: \n \n sum=0\n for i i
|
mintukrish
|
NORMAL
|
2020-10-13T18:22:39.509230+00:00
|
2020-10-13T18:22:39.509272+00:00
| 199 | false |
```\nclass Solution:\n def reconstructMatrix(self, upper: int, lower: int, colsum: List[int]) -> List[List[int]]: \n \n sum=0\n for i in range(len(colsum)):\n sum+=colsum[i]\n if upper+lower!=sum:\n return []\n num_two = colsum.count(2)\n \n if num_two > lower or num_two > upper:\n return []\n \n matrix=[[0 for i in range(len(colsum)) ]for j in range(2) ]\n \n \n def insert(j,position,i,matrix,colsum):\n if colsum[j]>0 and position>0:\n matrix[i][j]=1\n position-=1\n colsum[j]-=1\n return j,position,matrix,colsum\n \n for j in range(len(colsum)):\n if(upper<lower):\n j,lower,matrix,colsum=insert(j,lower,1,matrix,colsum)\n j,upper,matrix,colsum=insert(j,upper,0,matrix,colsum)\n else:\n j,upper,matrix,colsum=insert(j,upper,0,matrix,colsum)\n j,lower,matrix,colsum=insert(j,lower,1,matrix,colsum)\n\n return(matrix)\n```
| 1 | 0 |
['Python', 'Python3']
| 0 |
reconstruct-a-2-row-binary-matrix
|
Python: find indexes of 2 and 1 (596 - 604 ms / ~ 100%)
|
python-find-indexes-of-2-and-1-596-604-m-zkzo
|
The idea is pretty straight forward. Find out all indexes of 2 in colsum and then distribute 1 to the rest of columns.\npython\ndef reconstructMatrix(self, uppe
|
rnoro
|
NORMAL
|
2020-09-26T22:17:24.612417+00:00
|
2020-09-26T22:17:24.612462+00:00
| 121 | false |
The idea is pretty straight forward. Find out all indexes of `2` in `colsum` and then distribute `1` to the rest of columns.\n```python\ndef reconstructMatrix(self, upper, lower, colsum):\n # check sum\n if upper+lower != sum(colsum): \n return []\n \n n = len(colsum)\n ret = [[0]*n for _ in range(2)]\n \n ind = collections.defaultdict(list)\n for i, x in enumerate(colsum):\n ind[x].append(i)\n \n # simple inference\n if lower < len(ind[2]) or upper < len(ind[2]):\n return []\n \n # distribute numbers\n u = upper\n for i in ind[2]:\n ret[0][i] = ret[1][i] = 1\n u -= 1\n \n for i in ind[1]:\n if u:\n ret[0][i] = 1\n u -= 1\n else:\n ret[1][i] = 1\n \n return ret\n```
| 1 | 0 |
['Python']
| 0 |
reconstruct-a-2-row-binary-matrix
|
simple cpp solution
|
simple-cpp-solution-by-_mrbing-gnkh
|
Runtime: 152 ms, faster than 82.34% of C++ online submissions for Reconstruct a 2-Row Binary Matrix.\nMemory Usage: 60.5 MB, less than 100.00% of C++ online sub
|
_mrbing
|
NORMAL
|
2020-05-26T08:01:36.528445+00:00
|
2020-05-26T08:01:36.528479+00:00
| 60 | false |
Runtime: 152 ms, faster than 82.34% of C++ online submissions for Reconstruct a 2-Row Binary Matrix.\nMemory Usage: 60.5 MB, less than 100.00% of C++ online submissions for Reconstruct a 2-Row Binary Matrix.\n```\n class Solution {\npublic:\n vector<vector<int>> reconstructMatrix(int upper, int lower, vector<int>& colsum) {\n int i= 0, j, m = colsum.size();\n int k = 0;\n vector<vector<int>> output(2, (vector<int> (m, 0)));\n while(k < m){\n if(upper + lower < colsum[k]){\n vector<vector<int>> empty;\n return empty;\n }\n if(colsum[k] == 2){\n output[0][i] = 1;\n output[1][i] = 1;\n upper--;\n lower--;\n }else if(colsum[k] == 1){\n if(upper >= lower){\n output[0][i] = 1;\n upper--;\n }else{\n output[1][i] = 1;\n lower--;\n }\n }\n k++;\n i++;\n }\n if(upper != 0 || lower != 0){\n vector<vector<int>> empty;\n return empty;\n }\n\n return output;\n }\n};
| 1 | 1 |
['C++']
| 0 |
reconstruct-a-2-row-binary-matrix
|
Python / C++: One Pass Greedy with Detailed Explanation
|
python-c-one-pass-greedy-with-detailed-e-b71m
|
We use the greedy approach to solve this problem. We campare the sum of upper row and lower row in each iteration, and use the bigger one to reconstruct the mat
|
nissekl
|
NORMAL
|
2020-05-05T19:45:23.271851+00:00
|
2020-05-05T19:50:27.097036+00:00
| 142 | false |
We use the greedy approach to solve this problem. We campare the sum of upper row and lower row in each iteration, and use the bigger one to reconstruct the matrix. After the for loop, we check whether the upper and lower row are 0. If it is, it means that the matrix is successful reconstructed. \n\nFor example 1:\n\nupper = 5, \nlower = 5,\ncolsum = [2,1,2,0,1,0,1,2,0,1]\n\nbeacuse firsr element is 2, both have to add 1\nupperM=[1,\nlowerM =[1,\nupper->4\nlower->4\n\n2nd element is 1 and upper=>lower, we choose upper to add 1 \nupperM=[1,1\nlowerM=[1,0\nupper->3\nlower->4\n\n3nd element is 2,both have to add 1\nupperM=[1,1,1\nlowerM=[1,0.1\nupper->2\nlower->3\n\n4th element is 0, do nothing\nupperM=[1,1,1,0\nlowerM=[1,0.1,0\n\n5th element is 1 and upper<lower, we choose lower to add 1 \nupperM=[1,1,1,0,0\nlowerM=[1,0.1,0,1\nupper->2\nlower->2\n.\n..\n...and so on\n\n\nAfter all reconstruction is completed,we check whether both upper and lower are 0 (perfectly used) or remained positive (hadn\'t been used) or negative (over used).\nIf it both are 0 return the result, if it is not return empty list.\n\nBecause it is one pass, the time complexity is O(n).\nI create an array which length is n to store all the result, so the space is O(n).\n\n\nC++\n```\nclass Solution {\npublic:\n vector<vector<int>> reconstructMatrix(int upper, int lower, vector<int>& colsum) {\n vector<vector<int>> res(2,vector<int>(colsum.size(),0));\n for(int i=0;i<colsum.size();i++){\n \n if(colsum[i]==2){ \n upper--;\n lower--;\n res[0][i]=1;\n res[1][i]=1;\n }\n else if(colsum[i]==1){\n \n if(upper<=lower){\n lower--;\n res[1][i]=1;\n }\n \n else{ \n upper--;\n res[0][i]=1;\n }\n\n }\n \n }\n \n return (upper==0 && lower==0) ? res:vector<vector<int>> {};\n }\n};\n```\n\nPython\n```\nclass Solution:\n def reconstructMatrix(self, upper: int, lower: int, colsum: List[int]) -> List[List[int]]:\n res = [[0]*len(colsum) for _ in range(2)]\n for i in range(len(colsum)):\n if colsum[i]==2:\n upper-=1\n lower-=1\n res[0][i]=1\n res[1][i]=1\n elif colsum[i]==1:\n if upper<=lower:\n lower-=1\n res[1][i]=1\n else:\n upper-=1\n res[0][i]=1\n return res if upper==lower==0 else []\n```
| 1 | 0 |
[]
| 0 |
reconstruct-a-2-row-binary-matrix
|
C++ code
|
c-code-by-vivekkshukla-cn5h
|
\nclass Solution {\npublic:\n vector<vector<int>> reconstructMatrix(int upper, int lower, vector<int>& colsum) {\n int sum=0, twos=0;\n for(int
|
vivekkshukla
|
NORMAL
|
2019-12-30T10:14:06.090820+00:00
|
2019-12-30T10:14:06.090870+00:00
| 154 | false |
```\nclass Solution {\npublic:\n vector<vector<int>> reconstructMatrix(int upper, int lower, vector<int>& colsum) {\n int sum=0, twos=0;\n for(int i = 0; i < colsum.size(); ++i){\n sum += colsum[i];\n if(colsum[i] == 2) ++twos;\n }\n if(upper + lower != sum || upper < twos || lower < twos) \n return {};\n \n vector<int> upper_row(colsum.size(), 0);\n for(int i = 0; i < colsum.size() && upper > 0; ++i){\n if(colsum[i] == 2 || colsum[i] == 1){\n upper_row[i] = 1;\n colsum[i]-= upper_row[i];\n upper--;\n }\n }\n \n return {upper_row, colsum};\n }\n};\n```
| 1 | 0 |
[]
| 1 |
reconstruct-a-2-row-binary-matrix
|
Java concise solution
|
java-concise-solution-by-iknownothingabo-ay5s
|
\nclass Solution {\n public List<List<Integer>> reconstructMatrix(int upper, int lower, int[] colsum) {\n List<List<Integer>> matrix = new ArrayList()
|
iknownothingaboutcoding
|
NORMAL
|
2019-12-23T07:14:00.139990+00:00
|
2019-12-23T07:14:00.140042+00:00
| 222 | false |
```\nclass Solution {\n public List<List<Integer>> reconstructMatrix(int upper, int lower, int[] colsum) {\n List<List<Integer>> matrix = new ArrayList();\n List<Integer> top = new ArrayList();\n List<Integer> bottom = new ArrayList();\n for (int num : colsum) {\n if (num == 0) {\n top.add(0);\n bottom.add(0);\n } else if (num == 2) {\n top.add(1);\n bottom.add(1);\n upper--;\n lower--;\n } else if (upper == 0 && lower == 0) {\n return matrix;\n } else if (upper > lower) {\n top.add(1);\n bottom.add(0);\n upper--;\n } else {\n top.add(0);\n bottom.add(1);\n lower--;\n }\n }\n if (upper != 0 || lower != 0)\n return new ArrayList<>();\n matrix.add(top);\n matrix.add(bottom);\n return matrix;\n }\n}\n```
| 1 | 0 |
[]
| 1 |
reconstruct-a-2-row-binary-matrix
|
Python Greedy very easy with comments
|
python-greedy-very-easy-with-comments-by-fyri
|
\nclass Solution:\n def reconstructMatrix(self, upper: int, lower: int, colsum: List[int]) -> List[List[int]]:\n result, sums = [[0 for i in range(len
|
raunit
|
NORMAL
|
2019-12-01T06:09:44.892829+00:00
|
2019-12-01T06:10:12.422298+00:00
| 187 | false |
```\nclass Solution:\n def reconstructMatrix(self, upper: int, lower: int, colsum: List[int]) -> List[List[int]]:\n result, sums = [[0 for i in range(len(colsum))] for j in range(2)], [upper, lower]\n\t\t# no solution possible\n if sum(sums) != sum(colsum):\n return []\n for i, val in enumerate(colsum):\n if not sums[0] and not sums[1]:\n break\n\t\t\t# if it is a 0 or a 2 then we add 0 or 1 to both the cells\n if val == 2 or val == 0:\n result[0][i], result[1][i] = val // 2, val // 2\n for i in range(2):\n sums[i] -= val // 2\n else:\n\t\t\t # Add 1 to the row where more 1s are to be assigned\n index = 0 if sums[0] > sums[1] else 1\n result[index][i] = 1\n sums[index] -= 1\n\t\t# The solution found is invalid meaning no solution is possible\n if sum(result[0]) != upper or sum(result[1]) != lower:\n return []\n return result\n```
| 1 | 0 |
[]
| 0 |
reconstruct-a-2-row-binary-matrix
|
python3 greedy with explanation
|
python3-greedy-with-explanation-by-xz273-mzgv
|
1.If the sum of columns isn\'t equal to upper + lower: return []\n2.Since column sum 0 means the 2 rows are 0 and sum 2 mean the 2 rows are 2, we can add these
|
xz2737
|
NORMAL
|
2019-11-15T00:20:05.515629+00:00
|
2019-11-15T00:20:05.515670+00:00
| 96 | false |
1.If the sum of columns isn\'t equal to upper + lower: return []\n2.Since column sum 0 means the 2 rows are 0 and sum 2 mean the 2 rows are 2, we can add these numbers first.\n0 -->...0 and 2 --> 2\nrow2....0..................2\n3. We just need to decide which row to place 1 when column sum is 1, here we can use greedy and the problem is solved.\n\n\n```\n\t\tif sum(colsum) != upper+lower:\n return []\n nums = []\n for t in range(2):\n tem = []\n for i in range(len(colsum)):\n tem.append(\'#\')\n nums.append(tem)\n for i in range(len(colsum)):\n if colsum[i] == 2:\n nums[0][i] = 1\n nums[1][i] = 1\n upper -= 1\n lower -= 1\n elif colsum[i] == 0:\n nums[0][i] = 0\n nums[1][i] = 0\n \n for i in range(len(colsum)):\n if colsum[i] == 1:\n if upper > 0:\n nums[0][i] = 1\n nums[1][i] = 0\n upper -= 1\n else:\n nums[1][i] = 1\n nums[0][i] = 0\n lower -= 1\n if lower < 0 or upper < 0:\n return []\n return nums\n```
| 1 | 0 |
[]
| 0 |
reconstruct-a-2-row-binary-matrix
|
python greedy solution
|
python-greedy-solution-by-shuuchen-2cbh
|
It is straightforward when S[i] is 0 or 2,\n When S[i] is 1, minus max(U, L) by one and set 1 to the corresponding position in res,\n Don\' t forget to check U
|
shuuchen
|
NORMAL
|
2019-11-14T03:06:05.858434+00:00
|
2019-11-14T03:10:41.215810+00:00
| 119 | false |
* It is straightforward when S[i] is 0 or 2,\n* When S[i] is 1, minus max(U, L) by one and set 1 to the corresponding position in res,\n* Don\' t forget to check U and L are both 0 in the end.\n\n```\nclass Solution:\n def reconstructMatrix(self, U: int, L: int, S: List[int]) -> List[List[int]]:\n \n res = [[0] * len(S) for _ in range(2)]\n \n for i in range(len(S)):\n if S[i] == 2:\n if U > 0 and L > 0:\n res[0][i] = res[1][i] = 1\n U -= 1\n L -= 1\n else:\n return []\n elif S[i] == 1:\n if U > L:\n res[0][i] = 1\n U -= 1\n elif L > 0:\n res[1][i] = 1\n L -= 1\n else:\n return []\n \n return res if U == L == 0 else []
| 1 | 0 |
[]
| 0 |
reconstruct-a-2-row-binary-matrix
|
Java dumb solution
|
java-dumb-solution-by-swilor-7j0e
|
\n\n\nclass Solution {\n public List<List<Integer>> reconstructMatrix(int upper, int lower, int[] colsum) {\n List<List<Integer>> matrix = new ArrayLi
|
swilor
|
NORMAL
|
2019-11-14T02:06:17.825676+00:00
|
2019-11-14T02:06:17.825730+00:00
| 156 | false |
\n\n```\nclass Solution {\n public List<List<Integer>> reconstructMatrix(int upper, int lower, int[] colsum) {\n List<List<Integer>> matrix = new ArrayList<>();\n matrix.add(new ArrayList<>(colsum.length));\n matrix.add(new ArrayList<>(colsum.length));\n \n for(int j = 0; j < colsum.length; j++){\n if(colsum[j] == 0){\n matrix.get(0).add(0);\n matrix.get(1).add(0);\n }else if(colsum[j] == 2){\n matrix.get(0).add(1);\n matrix.get(1).add(1);\n upper--;\n lower--;\n }else if(colsum[j] == 1){\n if(upper > lower){\n matrix.get(0).add(1);\n matrix.get(1).add(0);\n upper--;\n }else{\n matrix.get(0).add(0);\n matrix.get(1).add(1);\n lower--;\n }\n }\n }\n \n if(upper == 0 && lower == 0) return matrix;\n else return new ArrayList<>();\n }\n}\n```
| 1 | 0 |
[]
| 0 |
reconstruct-a-2-row-binary-matrix
|
C++ solution with detailed explanation
|
c-solution-with-detailed-explanation-by-52pvb
|
Explanation:\n1. traverse every single number in colsum and assign initial values to the cells\n2. Before applying swaps on upper cell and its corresponding low
|
waeaqar
|
NORMAL
|
2019-11-10T19:57:44.387936+00:00
|
2019-11-10T19:57:44.388030+00:00
| 61 | false |
Explanation:\n1. traverse every single number in colsum and assign initial values to the cells\n2. Before applying swaps on upper cell and its corresponding lower cell, we check if the answer can be achieved.\n3. Apply swaps\n4. done\n\n```\nvector<vector<int>> reconstructMatrix(int upper, int lower, vector<int>& colsum) {\n int n = colsum.size();\n int count_two;\n vector<vector<int>> mat(2, vector<int>(n, 0));\n \n\t\t//traverse colsum\n for (int i = 0; i < colsum.size(); i++){\n\t\t\t////if 2, then both upper and lower cell is 1 for sure\n if (colsum[i] == 2){\n mat[0][i] = 1;\n mat[1][i] = 1;\n count_two++;\n } \n\t\t\t//we give upper cell value of 1 if colsum[i] is 1\n\t\t\t//lower cell value is 0\n\t\t\telse if (colsum[i] == 1){\n mat[0][i] = 1;\n mat[1][i] = 0;\n }\n }\n \n //now we calculate the value of the upper and lower cell\n int count_upper = 0;\n int count_lower = 0;\n \n for (int i = 0; i < colsum.size(); i++){\n count_upper += mat[0][i];\n count_lower += mat[1][i];\n }\n \n\t\t//since all the 1s are assigned to the upper cells, \n\t\t//if count_upper is still smaller than upper, \n\t\t//there is no possible moves we can apply to make count_upper larger\n\t\t//hence output empty array\n if (count_upper < upper){\n return {};\n }\n\t\t\n bool flag = true;\n int diff = abs(count_upper - upper);\n \n //now we need to compare four values below:\n\t\t//count_upper, upper, count_lower, lower\n\t\t//there must be an even number of even and odd numbers for the four values above\n int odd_count = 0;\n int even_count = 0;\n \n if (count_upper % 2 == 1){\n odd_count++;\n } else {\n even_count++;\n }\n if (count_lower % 2 == 1){\n odd_count++;\n } else {\n even_count++;\n }\n if (upper % 2 == 1){\n odd_count++;\n } else {\n even_count++;\n }\n if (lower % 2 == 1){\n odd_count++;\n } else {\n even_count++;\n }\n //if does not pass the check.. return empty string\n if( odd_count % 2 == 1 || even_count % 2== 1 || count_upper + count_lower != upper + lower){\n return {};\n }\n \n if (diff == 0){\n return mat;\n }\n \n if (diff > 0){\n flag = true;\n } else {\n flag = false;\n }\n \n \n for (int i = 0; i < colsum.size() && diff > 0; i++){\n if (mat[0][i] == 1 && mat[1][i] == 0 && flag == true){\n swap(mat[0][i], mat[1][i]);\n diff--;\n }\n \n if (mat[0][i] == 0 && mat[1][i] == 1 && flag == false){\n swap(mat[0][i], mat[1][i]);\n diff--;\n }\n }\n \n return mat;\n }
| 1 | 1 |
[]
| 0 |
reconstruct-a-2-row-binary-matrix
|
Single pass C++ solution
|
single-pass-c-solution-by-rajeshk92-gmq3
|
\nclass Solution {\npublic:\n vector<vector<int>> reconstructMatrix(int upper, int lower, vector<int>& colsum) {\n int n = colsum.size();\n \n
|
rajeshk92
|
NORMAL
|
2019-11-10T17:40:43.519633+00:00
|
2019-11-11T14:01:32.258576+00:00
| 109 | false |
```\nclass Solution {\npublic:\n vector<vector<int>> reconstructMatrix(int upper, int lower, vector<int>& colsum) {\n int n = colsum.size();\n \n // create 2 vectors - one filled with zeros and another empty\n vector<vector<int>> result (2, vector<int> (n,0) );\n vector<vector<int>> empty;\n \n\t\t// if upper or lower cannot be greater than colsum.size(), n\n if(upper > n || lower > n) {\n return empty;\n } \n \n\t\t// check the colsum array while also constructing the new matrix\n for(int i = 0; i < n; i++) {\n if(colsum[i] == 2) {\n\t\t\t // both are 1 if colsum is 2\n result[0][i] = 1;\n result[1][i] = 1;\n upper--;\n lower--;\n }\n else if(colsum[i] == 1) {\n if(upper>lower) {\n\t\t\t\t // make upper row 1 only if upper is greater than lower\n\t\t\t\t\t// this ensures that if a 2 comes later we still have sufficient upper counts left to insert 1 in upper row \n result[0][i] = 1;\n upper--;\n }\n else {\n result[1][i] = 1;\n lower--;\n }\n }\n }\n \n // upper and lower will be larger or smaller than 0 if we are not able to form matrix\n if(upper != 0 || lower != 0) {\n return empty;\n }\n \n return result;\n }\n};\n```
| 1 | 1 |
['C']
| 1 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.