question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
check-if-digits-are-equal-in-string-after-operations-ii
|
Easy Java Solution || Using The Lucas Theorem || Beats 100% of Java Users .
|
easy-java-solution-using-the-lucas-theor-1n7v
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
zzzz9
|
NORMAL
|
2025-02-23T14:23:40.954320+00:00
|
2025-02-23T14:23:40.954320+00:00
| 90 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public boolean hasSameDigits(String s) {
int n = s.length();
if (n == 2) {
return s.charAt(0) == s.charAt(1);
}
long a = 0;
long b = 0;
for (int i = 0; i < n - 1; i++) {
int coeff = comb10( i , n-2 ) ;
a = (a + coeff * (s.charAt(i) - '0')) % 10;
b = (b + coeff * (s.charAt(i + 1) - '0')) % 10;
}
return a == b;
}
public int comb10(int k ,int n ){
if( k == 0 || k == n ){
return 1 ;
}
int a = comb2( k , n ) ;
int b = comb5( k , n ) ;
for( int i=0 ; i<10 ; ++i ){
if( i%2 == a && i%5 == b ){
return i ;
}
}
return -1 ;
}
public int comb2(int k , int n ){
while( k >0 || k>0 ){
if( (k&1) > (n&1) ){
return 0 ;
}
n >>= 1 ;
k >>= 1 ;
}
return 1 ;
}
public int comb5( int k , int n ){
int rs = 1 ;
while( k>0 || n>0 ){
int a = k%5 ;
int b = n%5 ;
if( a > b ){
return 0 ;
}
rs = rs * helper( a , b ) % 5 ;
n /= 5 ;
k /= 5 ;
}
return rs ;
}
public int helper( int k , int n ){
int[] fact = new int[]{ 1 , 1 , 2 , 6 , 24 } ;
int up = fact[n] ;
int denominent = fact[k]*fact[n-k] ;
int rs = up/denominent ;
return rs%5 ;
}
}
```
| 1 | 0 |
['Combinatorics', 'Number Theory', 'Java']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
No Lucas
|
no-lucas-by-mintujupally-34a9
|
IntuitionLet the given number bed0d1d2...dn−1. On iteratively adding the digits as stated in the problem, the final two digits would be:
n−2C0 d0+n−2C1 d
|
mintujupally
|
NORMAL
|
2025-02-23T10:45:52.459735+00:00
|
2025-02-23T11:03:23.165400+00:00
| 128 | false |
# Intuition
Let the given number be $$d_0 d_1 d_2 ... d_{n-1}$$. On iteratively adding the digits as stated in the problem, the final two digits would be:
1. $$^{n-2}C_{0}\ d_0 + ^{n-2}C_{1}\ d_1 + ^{n-2}C_{2}\ d_2 + ... ^{n-2}C_{n-2}\ d_{n-2} $$
2. $$^{n-2}C_{0}\ d_1 + ^{n-2}C_{1}\ d_2 + ^{n-2}C_{2}\ d_3 + ... ^{n-2}C_{n-2}\ d_{n-1} $$
# Challenge
<!-- Describe your approach to solving the problem. -->
The main and only challenge in the calculation is modulo 10 being asked in the problem. As 10 is not a prime number modulo inverse does not always exist, causing it difficult to compute the required divisions over modulo.
# Approach
To tackle this problem, as 10 can be prime factorized as $$2 \times 5$$, we compute the binomial coefficient at every step by keeping track of the value using three different values as $$\ x,\ y\ $$and$$\ z$$, where:
1. $$x\ $$ is the power of 2
2. $$y\ $$ is the power of 5
3. $$z\ $$ is the remaining factor
i.e. assume we are computing $$^{n-2}C_{i}\ $$, then: $$^{n-2}C_{i}\ = 2^{x}\ 5^{y}\ z$$
We will also be employing the relation (here $$\ m\ $$ would be $$\ n-2\ $$):
$$^{m}C_{i+1}=^{m}C_{i}\ \frac{m-r}{r+1}$$
## NOTE:
In the modInverse calculation, `3` is passed as the second parameter to `powerMod` because $$\phi(10) = 4\ $$. This is from Euler's theorem for modular inverse, which states:
> For any number $${m}$$ where $$gcd(a, m)=1$$:
$$a^{\phi(m)}\equiv1\ (mod\ m)$$
$$a^{-1}\equiv\ a^{\phi(m)-1}\ (mod\ m)$$
1. $$\phi(m)$$ is Euler's totient function whose value is number of coprimes to $$m$$ which are $$\ \leq m$$.
2. For a number $$m=p_1 ^{x_1}\ p_2 ^{x_2}\ p_3 ^{x_3}\ ...p_k ^{x_k}\ $$:
$$\phi(m) = m\ (1-\frac{1}{p_1})(1-\frac{1}{p_2})(1-\frac{1}{p_3})\ ...\ (1-\frac{1}{p_k})$$
3. Hence $$\ \phi(10) = 10 \times (1-\frac{1}{2})\times(1-\frac{1}{5})=4$$
```
int modInverse(int a) {
return powerMod(a, 3);
}
```
# Complexity
- Time complexity: $$O(n)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(1)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int powerMod(int a, int b) {
int mod = 10;
int res = 1;
a = a % mod;
while (b > 0) {
if (b & 1)
res = (1LL * res * a) % mod;
a = (1LL * a * a) % mod;
b >>= 1;
}
return res;
}
int modInverse(int a) {
return powerMod(a, 3);
}
int calc(int x, int y, int z)
{
int ans=powerMod(2, x);
ans=(ans*powerMod(5, y))%10;
ans=(ans*z)%10;
return ans;
}
bool hasSameDigits(string s) {
int n=s.size();
int m=n-1;
int x=0, y=0, z=1;
int a=0;
for(int i=0; i<m; i++)
{
int c=s[i]-'0';
int f=calc(x, y, z);
a=(a+(c*f)%10)%10;
int num=m-1-i;
int den=i+1;
while(num>0 && num%2==0) ++x, num/=2;
while(den>0 && den%2==0) --x, den/=2;
while(num>0 && num%5==0) ++y, num/=5;
while(den>0 && den%5==0) --y, den/=5;
num%=10;
z=(((z*num)%10)*modInverse(den))%10;
}
x=0, y=0, z=1;
int b=0;
for(int i=0; i<m; i++)
{
int c=s[i+1]-'0';
int f=calc(x, y, z);
b=(b+(c*f)%10)%10;
int num=m-1-i;
int den=i+1;
while(num>0 && num%2==0) ++x, num/=2;
while(den>0 && den%2==0) --x, den/=2;
while(num>0 && num%5==0) ++y, num/=5;
while(den>0 && den%5==0) --y, den/=5;
num%=10;
z=(((z*num)%10)*modInverse(den))%10;
}
return a==b;
}
};
```
| 1 | 0 |
['C++']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
Java most detailed and beginner friendly solution with proper explanation for each step.
|
java-most-detailed-and-beginner-friendly-yyec
|
IntuitionThe intution for this problem comes from observing the patterns, let's see few examples:
Eg: 2 digits (a b)The final 2 digits are a%10 & b%10
Eg: 3 dig
|
1_mohit_1
|
NORMAL
|
2025-02-23T08:33:31.950687+00:00
|
2025-02-23T08:33:31.950687+00:00
| 72 | false |
# Intuition
The intution for this problem comes from observing the patterns, let's see few examples:
**Eg: 2 digits (a b)**
The final 2 digits are a%10 & b%10
**Eg: 3 digits (a b c)**
Final ans: (a+b)%10 & (b+c)%10
**Eg: 4 digits (a b c d)**
Final ans: (a+2b+c)%10 & (b+2c+d)%10
**Eg: 5 digits (a b c d e)**
Final ans: (a+3b+3c+d)%10 & (b+3c+3d+e)%10
**Eg: 6 digits (a b c d e f)**
Final ans: (a+4b+6c+4d+e)%10 & (b+4c+6d+4e+f)%10
If we see the ans can be computed quickly if we can find out the coefficient at every step and if we closely look these coefficients are binomial coefficients mod 10 which is (n-2)Ck mod 10.
**Eg: 6 digits**
n = 6, n-2 = 4
0th coefficient => k=0 => 4C0 mod 10 -> 1
1st coefficient => k=1 => 4C1 mod 10 -> 4
2nd coefficient => k=2 => 4C2 mod 10 -> 6
and so on...
To efficiently calculate these coefficients we make use of Lucas algorithm and Chinese Reminder Theorem.
# Approach
**Lucas algorithm:**

Since we see that for lucas algorithm p must be a prime so we break 10 into 2 primes 2 and 5 and find the binomial coefficient for 2 and 5.
**Let's take an example of 2:
n=6, k=3, p=2**
n=6, in base 2 -> 110 -> 1 * 2^2 + 1 * 2^1 + 0 * 2^0 = 6
k=3, in base 2 -> 011 -> 0 * 2^2 + 1 * 2^1 + 1 * 2^0 = 3
Now we need to take digits at every position in both n & k and do (niCki) mod p.
Now using Lucas algorithm, 6C3 mod 2 is ((1C0 mod 2) * (1C1 mod 2) * (0C1 mod 2)) mod 2.
**Important point to note is if for any digit k>n, then the entire product becomes 0, since there is no way to choose more k from less n. i.e.
if k > n then answer is 0**
**Hence we see if the n&k is equal to k that means all the digits in k should have only 1s where n also has 1s if not at that point k>n and hence product is zero.**
**So for 2 -> n&k==k then answer is 1 or it's 0.**
**For 5 for the same example:
n=6, k=3, p=2**
n=6 in base 5 -> 11 -> 1 * 5^1 + 1 * 5^0 = 6
k=3 in base 5 -> 03 -> 0 * 5^1 + 3 * 5^0 = 3
Now using Lucas algorithm, 6C3 mod 5 is ((1C0 mod 5) * (1C3 mod 5)) mod 5
Pascal's triangle helps us quickly find the values for nck mod p
Pascal's triangle for mod 5
**In pascal's triangle p[i][j]=p[i-1][j-1]+p[i-1][j]**
1 -> 0th row
1 1 -> 1st row
1 2 1 -> 2nd row
1 3 3 1 -> 3rd row
1 4 1 4 1 -> 4th row (the reason why 3rd column here is 1 is (3+3)%5=1)
So, eg: 4C2 will be 1, 4C1 will be 4, 3C1 will be 3 and so on...
Hence 6C3 mod 5 = ((1C0 mod 5) * (1C3 mod 5)) mod 5
= (p[1][0] * p[1][3]) % 5
= (1 * 0) % 5
= 0
**Chinese reminder theorem(CRT): The reason we need to use CRT is because the Lucas algorithm works for only prime modulo(10 is not a prime), so now to get nCk mod 10 from nCk mod 2 and nCk mod 5, we use CRT.**

# Complexity
- Time complexity:
O(n*logn) -> where log here is with base 5.
- Space complexity:
We don't use any extra space hence it's O(1)
# Code
```java []
class Solution {
public boolean hasSameDigits(String s) {
int n=s.length()-2,x=0,y=0;
for(int k=0;k<=n;k++){
int bcoeff=binMod10(n,k);
x=(x+((s.charAt(k)-'0')*bcoeff))%10;
y=(y+((s.charAt(k+1)-'0')*bcoeff))%10;
}
return x==y;
}
// Use chinese reminder theorem to combine binMod2 and binMod5
public int binMod10(int n,int k){
int bm2=binMod2(n,k);
int bm5=binMod5(n,k);
for(int x=0;x<=9;x++){
if(x%2==bm2 && x%5==bm5) return x;
}
return 0;
}
// Find binMod2 using Lucas algorithm, simplified since it's 2
// See the explaination why this will work
public int binMod2(int n,int k){
return (n&k)==k ? 1 : 0;
}
// Find binMod5 using Lucas algorithm
public int binMod5(int n,int k){
int pascalTriangleMod5[][] = {
{1},
{1,1},
{1,2,1},
{1,3,3,1},
{1,4,1,4,1}
};
int ans=1;
while(n>0 || k>0){
int ndigit=n%5,kdigit=k%5;
if(kdigit>ndigit) return 0;
ans=(ans*pascalTriangleMod5[ndigit][kdigit])%5;
n/=5;k/=5;
}
return ans;
}
}
```
| 1 | 1 |
['Math', 'Java']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
☕ Java solution
|
java-solution-by-barakamon-ghu3
| null |
Barakamon
|
NORMAL
|
2025-02-23T07:04:15.206060+00:00
|
2025-02-23T07:04:15.206060+00:00
| 70 | false |

```java []
class Solution {
public boolean hasSameDigits(String s) {
int size = s.length();
int X = size - 2;
int x = 0, y = 0;
for (int j = 0; j <= X; j++) {
int coeff = binomialMod10(X, j);
x = (x + coeff * (s.charAt(j) - '0')) % 10;
y = (y + coeff * (s.charAt(j + 1) - '0')) % 10;
}
return x == y;
}
private int binomialMod10(int n, int k) {
int i = binomialMod2(n, k);
int j = binomialMod5(n, k);
for (int x = 0; x < 10; x++) {
if (x % 2 == i && x % 5 == j) {
return x;
}
}
return 0;
}
private int binomialMod2(int n, int k) {
return ((n & k) == k) ? 1 : 0;
}
private int binomialMod5(int n, int k) {
int[][] tuples = {
{1},
{1, 1},
{1, 2, 1},
{1, 3, 3, 1},
{1, 4, 1, 4, 1}
};
int result = 1;
while (n > 0 || k > 0) {
int nthd = n % 5;
int kthd = k % 5;
if (kthd > nthd) return 0;
result = (result * tuples[nthd][kthd]) % 5;
n /= 5;
k /= 5;
}
return result;
}
}
```
| 1 | 0 |
['Java']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
Easy to understand
|
easy-to-understand-by-ujjwalbharti13-24l5
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
UjjwalBharti13
|
NORMAL
|
2025-02-23T06:41:54.617996+00:00
|
2025-02-23T06:41:54.617996+00:00
| 114 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
vector<int> get_base5_digits(int n) {
vector<int> res;
if (n == 0) {
res.push_back(0);
return res;
}
while (n > 0) {
res.push_back(n % 5);
n /= 5;
}
return res;
}
bool hasSameDigits(string s) {
int n = s.size();
if (n == 2) {
return s[0] == s[1];
}
int m = n - 2;
int mod5_table[5][5] = {
{1, 0, 0, 0, 0}, // n=0
{1, 1, 0, 0, 0}, // n=1
{1, 2, 1, 0, 0}, // n=2
{1, 3, 3, 1, 0}, // n=3
{1, 4, 1, 4, 1} // n=4
};
int mod10_table[2][5] = {
{0, 6, 2, 8, 4}, // a=0
{5, 1, 7, 3, 9} // a=1
};
vector<int> m_digits = get_base5_digits(m);
vector<int> coefficients(m + 1);
for (int j = 0; j <= m; ++j) {
int mod2 = ((j & m) == j) ? 1 : 0;
vector<int> j_digits = get_base5_digits(j);
if (j_digits.size() > m_digits.size()) {
coefficients[j] = mod10_table[mod2][0];
continue;
}
int mod5 = 1;
for (int d = 0; d < m_digits.size(); ++d) {
int jd = (d < j_digits.size()) ? j_digits[d] : 0;
if (jd > m_digits[d]) {
mod5 = 0;
break;
}
mod5 = (mod5 * mod5_table[m_digits[d]][jd]) % 5;
}
int b = mod5 % 5;
coefficients[j] = mod10_table[mod2][b];
}
int sum1 = 0, sum2 = 0;
for (int i = 0; i <= m; ++i) {
sum1 = (sum1 + (s[i] - '0') * coefficients[i]) % 10;
}
for (int i = 0; i <= m; ++i) {
sum2 = (sum2 + (s[i + 1] - '0') * coefficients[i]) % 10;
}
return sum1 == sum2;
}
};
```
| 1 | 0 |
['C++']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
🔥🔥Luca's Theorem 🔥| Combinatorics | Easy, when you do dry run or hard forever 🔥🔥|
|
lucas-theorem-combinatorics-easy-when-yo-laqe
|
IntuitionApproachN = [N1, N2, ... N-kth term] in p base
M = [M1, M2, ... M-kth term] in p base
p is a prime and may or may not multiple of N or MThen, according
|
Sourav19
|
NORMAL
|
2025-02-23T05:30:53.381831+00:00
|
2025-03-22T22:10:00.126769+00:00
| 140 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
N = [N1, N2, ... N-kth term] in p base
M = [M1, M2, ... M-kth term] in p base
p is a prime and may or may not multiple of N or M
Then, according to Lucas Theorem -->
c(N, M) = N! / (M! * (N-M)!)
c(N, M) % p = c(N1, M1) * c(N2, M2) * ... * c(N(kth term), M(kth term)) % p
Afterthat, by breaking down binomial coefficients modulo10 using mod 2 and mod5 separately and then reconstructing them via the Chinese Remainder Theorem(CRT), the approach avoids redundant calculations, making it highly efficient.
# Complexity
- Time complexity:O(N*LogN)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
// If gcd(b, mod) != 1 (No Modular Inverse Exists)
// Here, mod is very low, so Simple moduler division is not possible here.
// That's why we need to use some other theorem i.e, Luca's Theorem
class Solution {
public:
int nCr(int n, int r) {
int ans = 1 ;
for(int i=1 ; i<=r ; i++)
{
ans *= n-i+1 ;
ans /= i ; // Here No problem will occur, because [r < mod]. And mod is very small, as well as we are not doing any moduler operations
}
return ans ;
}
int nCr_mod_Lucas_Theorem(int n, int r, int mod)
{
if(r > n) return 0 ;
int res = 1 ;
while(n>0 && r>0)
{
res *= nCr(n%mod, r%mod) ;
res %= mod ;
n /= mod ;
r /= mod ;
}
return res ;
}
bool hasSameDigits(string s) {
int n = s.length() ;
int num1 = 0, num2 = 0 ;
for(int i=0 ; i<n-1 ; i++)
{
int res2 = nCr_mod_Lucas_Theorem(n-2, i, 2) ; // Instead -> return ((n&r) == r) ;
int res5 = nCr_mod_Lucas_Theorem(n-2, i, 5) ;
int res10 = -1 ;
for(int decimalVal=0 ; decimalVal<=9 ; decimalVal++)
{
if(decimalVal%2 == res2 && decimalVal%5 == res5)
{
res10 = decimalVal ;
}
}
num1 = (num1 + res10 * (s[i]-'0')) % 10 ;
num2 = (num2 + res10 * (s[i+1]-'0')) % 10 ;
}
return num1 == num2 ;
}
};
```

| 1 | 0 |
['Math', 'Combinatorics', 'Number Theory', 'C++']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
Fast modulo of Pascal triangle || Python O(n) || WUCG
|
fast-modulo-of-pascal-triangle-wucg-by-t-t2pi
|
IntuitionLetnbe the number of digit ins.The first element was the digit given by the following∑k=0n−1(nk)int(s[k])And the second element was the digit given b
|
Trance-0
|
NORMAL
|
2025-02-23T04:24:55.277806+00:00
|
2025-02-23T04:29:46.332760+00:00
| 182 | false |
# Intuition
Let $n$ be the number of digit in `s`.
The first element was the digit given by the following $$
\sum_{k=0}^{n-1} \begin{pmatrix}n\\k\end{pmatrix}int(s[k])
$$
And the second element was the digit given by the following $$
\sum_{k=1}^n \begin{pmatrix}n\\k\end{pmatrix}int(s[k])
$$
<!-- Describe your first thoughts on how to solve this problem. -->
Remember that in modular arithmetic $(a\cdot b)\mod 10=(a\mod 10)\cdot (c\mod 10)$
# Approach
<!-- Describe your approach to solving the problem. -->
The key is to build modular of $$\begin{pmatrix}n\\k\end{pmatrix}\mod 10$$ quickly, here, we use the solution from
[fast modulo](https://stackoverflow.com/questions/76357846/numbers-of-combinations-modulo-m-efficiently)
to help us compute the desired result in $$O(n)$$
# Complexity
- Time complexity: $$O(n)$$ for the modulo
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(n)$$ for storing array and results
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def hasSameDigits(self, s: str) -> bool:
n=len(s)
# generic approach for checking, no modular.
# p = []
# for k in range(n-2):
# p.append(p[k] * (n-2-k) // (k+1))
# fast modulo: https://stackoverflow.com/questions/76357846/numbers-of-combinations-modulo-m-efficiently
def fast(n, m):
res=[1]
c = 1
G = 1
for k in range(n):
mul = n - k
while (g := gcd(mul, m)) > 1:
mul //= g
G *= g
div = k + 1
while (g := gcd(div, m)) > 1:
div //= g
G //= g
# build modular inverse use pow(div, -1, m)
c = c * mul * pow(div, -1, m) % m
res.append(c * G % m)
return res
p = fast(n-2, 10)
# print(p)
a,b=0,0
for i,e in enumerate(s[:n-1]):
# print(min(i+1,n-i-1),i+1,n-i-1)
a=(a+int(e)*p[i])%10
for i,e in enumerate(s[1:]):
b=(b+int(e)*p[i])%10
# print(a,b)
return a==b
```
Please upvote if you find the solution helpful so that more people can get inspirations from it, Thanks! :)
| 1 | 0 |
['Math', 'Python3']
| 1 |
check-if-digits-are-equal-in-string-after-operations-ii
|
Easy Java Solution
|
easy-java-solution-by-anupamkumar25-75ee
|
IntuitionWe reinterpret the repeated adjacent-sum operation as a convolution with the vector [1, 1]. Repeating this operation (n–2) times is equivalent to convo
|
anupamKumar25
|
NORMAL
|
2025-04-10T05:15:28.172698+00:00
|
2025-04-10T05:15:28.172698+00:00
| 3 | false |
# Intuition
We reinterpret the repeated adjacent-sum operation as a convolution with the vector [1, 1]. Repeating this operation (n–2) times is equivalent to convolving the original digit sequence with the binomial coefficients from the expansion of (1+x)^(n–2) modulo 10. Thus, the two final digits can be expressed as linear combinations of the original digits with these binomial coefficients. The "rare CP concept" here is to compute the required binomial coefficients modulo 10 using Lucas’s theorem (applied separately modulo 2 and 5) and then combine them via the Chinese Remainder Theorem.
# Approach
1. Represent the final two digits as:
- f0 = sum_{j=0}^{n–2} (binom(n–2, j) * digit_j) mod 10
- f1 = sum_{j=0}^{n–2} (binom(n–2, j) * digit_{j+1}) mod 10
2. Instead of computing huge binomials directly, use Lucas’s theorem to compute binom(n–2, j) modulo 2 and modulo 5. Then combine these two residues using the Chinese Remainder Theorem to get the coefficient modulo 10.
3. Sum up the contributions for f0 and f1 and check if they are equal modulo 10.
# Complexity
- Time complexity: O(n * (log(n) base p)) where p ∈ {2,5}; effectively O(n)
- Space complexity: O(1)
# Code
```java []
class Solution {
int[][] binom2;
int[][] binom5;
public Solution() {
binom2 = new int[2][2];
binom2[0][0] = 1;
binom2[1][0] = 1;
binom2[1][1] = 1;
binom5 = new int[5][5];
for (int i = 0; i < 5; i++) {
for (int j = 0; j <= i; j++) {
if (j == 0 || j == i)
binom5[i][j] = 1;
else
binom5[i][j] = (binom5[i - 1][j - 1] + binom5[i - 1][j]) % 5;
}
}
}
int lucas(int n, int k, int p) {
int res = 1;
while (n > 0 || k > 0) {
int ni = n % p;
int ki = k % p;
if (ki > ni) return 0;
if (p == 2)
res = (res * binom2[ni][ki]) % 2;
else if (p == 5)
res = (res * binom5[ni][ki]) % 5;
n /= p;
k /= p;
}
return res;
}
int binomMod10(int n, int k) {
int mod2 = lucas(n, k, 2);
int mod5 = lucas(n, k, 5);
for (int x = mod5; x < 10; x += 5) {
if (x % 2 == mod2) return x;
}
return 0;
}
public boolean hasSameDigits(String s) {
int n = s.length();
int m = n - 2;
int f0 = 0, f1 = 0;
for (int j = 0; j <= m; j++) {
int c = binomMod10(m, j);
int d = s.charAt(j) - '0';
f0 = (f0 + c * d) % 10;
}
for (int j = 0; j <= m; j++) {
int c = binomMod10(m, j);
int d = s.charAt(j + 1) - '0';
f1 = (f1 + c * d) % 10;
}
return f0 == f1;
}
}
```
| 0 | 0 |
['Java']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
Chinese Theorem + Lucas' Theorem
|
chinese-theorem-lucas-theorem-by-joshler-mfwp
|
ApproachLucas' Theorem: Allows one to calculate C(n, k) mod p for primes p by breaking the numbers down into digits in base p.Chinese Theorem: Combines the resu
|
JoshlerBoy
|
NORMAL
|
2025-04-05T11:37:16.090957+00:00
|
2025-04-05T11:37:16.090957+00:00
| 1 | false |
# Approach
<!-- Describe your approach to solving the problem. -->
Lucas' Theorem: Allows one to calculate C(n, k) mod p for primes p by breaking the numbers down into digits in base p.
Chinese Theorem: Combines the results mod 2 and 5 to obtain the coefficient mod 10.
# Complexity
- Time complexity:NLogN
# Code
```csharp []
public class Solution {
public bool HasSameDigits(string s) {
int n = s.Length;
if (n == 2) return s[0] == s[1];
int k = n - 2;
// Предварительно вычисленные биномиальные коэффициенты для p=2 и p=5
int[,] comb2 = new int[2, 2] { { 1, 0 }, { 1, 1 } };
int[,] comb5 = new int[5, 5] {
{ 1, 0, 0, 0, 0 },
{ 1, 1, 0, 0, 0 },
{ 1, 2, 1, 0, 0 },
{ 1, 3, 3, 1, 0 },
{ 1, 4, 1, 4, 1 }
};
int sumFirst = 0, sumSecond = 0;
for (int i = 0; i <= k; i++) {
int mod2 = Lucas(k, i, 2, comb2);
int mod5 = Lucas(k, i, 5, comb5);
int mod10 = (5 * mod2 + 6 * mod5) % 10;
sumFirst = (sumFirst + (s[i] - '0') * mod10) % 10;
sumSecond = (sumSecond + (s[i + 1] - '0') * mod10) % 10;
}
return sumFirst == sumSecond;
}
private int Lucas(int n, int k, int p, int[,] comb) {
int result = 1;
while (n > 0 || k > 0) {
int a = n % p;
int b = k % p;
if (b > a) return 0;
result = (result * comb[a, b]) % p;
n /= p;
k /= p;
}
return result;
}
}
```
| 0 | 0 |
['C#']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
modular arithmetic || functional js
|
modular-arithmetic-functional-js-by-hawk-y2rj
|
IntuitionThe problem asks us to determine if two substrings, formed from the given string s, have the same sum when combined with a certain combinatorial functi
|
hawk2a
|
NORMAL
|
2025-04-04T23:31:55.050917+00:00
|
2025-04-04T23:32:41.731017+00:00
| 6 | false |
# Intuition
The problem asks us to determine if two substrings, formed from the given string `s`, have the same sum when combined with a certain combinatorial function. The idea here involves understanding how to efficiently calculate these sums using modular arithmetic and binomial coefficients modulo 5 and 10.
---
# Approach
1. **Binomial Coefficient Modulo Calculations:**
- Two helper functions are defined: `binomMod5` and `binomMod10`, which calculate binomial coefficients modulo 5 and 10, respectively.
- `binomMod5` uses a precomputed table for binomial coefficients modulo 5, reducing computational complexity.
- `binomMod10` utilizes both `binomMod5` and some additional conditions to compute the result modulo 10.
2. **Iterating Over Substrings:**
- We loop over all positions in the string `s` and compute a weighted sum of the digits using the binomial coefficient results.
- We accumulate values `x` and `y` from the two substrings based on their weighted sums.
3. **Comparison:**
- If the two sums, `x` and `y`, are equal, return `true`. Otherwise, return `false`.
---
# Complexity
- **Time complexity:**
$$O(n)$$ — Iterating through the string and performing constant-time binomial calculations for each digit.
- **Space complexity:**
$$O(1)$$ — Only a few integer variables and precomputed tables are used.
---
# Code
```javascript
const hasSameDigits = s => {
const binomMod5 = (n, r) => {
const table = [
[1, 0, 0, 0, 0],
[1, 1, 0, 0, 0],
[1, 2, 1, 0, 0],
[1, 3, 3, 1, 0],
[1, 4, 1, 4, 1]
];
let res = 1;
while (n || r) {
const n_digit = n % 5;
const r_digit = r % 5;
if (r_digit > n_digit) return 0;
res = (res * table[n_digit][r_digit]) % 5;
n = Math.floor(n / 5);
r = Math.floor(r / 5);
}
return res;
};
const binomMod10 = (k, j) => {
const r2 = ((j & ~k) === 0) ? 1 : 0;
const r5 = binomMod5(k, j);
return (5 * r2 + 6 * r5) % 10;
};
const n = s.length;
const k = n - 2;
let x = 0;
let y = 0;
for (let j = 0; j <= k; j++) {
const c = binomMod10(k, j);
x = (x + c * (s[j] - '0')) % 10;
y = (y + c * (s[j + 1] - '0')) % 10;
}
return x === y;
};
```
| 0 | 0 |
['JavaScript']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
extremely easy, 100% optimized golang 24ms, 8.38mb (beats 95%)
|
extremely-easy-100-optimized-golang-24ms-gcmj
|
Approachsimple CRT + lucas theorumCode
|
pratyushking
|
NORMAL
|
2025-03-22T11:45:22.670527+00:00
|
2025-03-22T11:46:23.360120+00:00
| 11 | false |
# Approach
simple CRT + lucas theorum
# Code
```golang []
func hasSameDigits(s string) bool {
n := len(s);
m := n - 2;
mDigits := make([]int, 10);
mSize := 0;
temp := m;
if temp == 0 {
mDigits[mSize] = 0;
mSize++;
} else {
for temp > 0 {
mDigits[mSize] = temp % 5;
mSize++;
temp /= 5;
}
}
small := [5][5]int{
{1, 0, 0, 0, 0},
{1, 1, 0, 0, 0},
{1, 2, 1, 0, 0},
{1, 3, 3, 1, 0},
{1, 4, 1, 4, 1},
};
diff := 0;
for j := 0; j <= m; j++ {
res5 := 1;
x := j;
for i := 0; i < mSize; i++ {
d := x % 5;
x /= 5;
a := mDigits[i];
if d > a {
res5 = 0;
break;
}
res5 = (res5 * small[a][d]) % 5;
}
c2 := 0;
if (m & j) == j {
c2 = 1;
}
coeff := res5;
if (res5&1) != c2 {
coeff += 5;
}
delta := int(s[j] - '0') - int(s[j+1] - '0');
diff = (diff + coeff * delta) % 10;
if diff < 0 {
diff += 10;
}
}
return diff == 0;
}
```
| 0 | 0 |
['Go']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
Java Beats 94% (pascal triangle + CRT)
|
java-beats-94-pascal-triangle-crt-by-fye-on0l
|
IntuitionCompute last row of Pascals triangle and add accordingly.ApproachCompute last row mod 5 and mod 2 (since we can divide in Z5,Z2 this case so we can d
|
fyeon
|
NORMAL
|
2025-03-19T11:36:31.829894+00:00
|
2025-03-19T11:36:31.829894+00:00
| 7 | false |
# Intuition
Compute last row of Pascals triangle and add accordingly.
# Approach
Compute last row mod 5 and mod 2 (since we can divide in $Z_5,Z_2$ this case so we can do it $O(nlog(n))$ and use CRT do find the results $\mod 10$
# Complexity
- Time complexity:
$O(nlog(n))$
- Space complexity:
$O(n)$
# Code
```java []
import java.math.BigInteger;
class Solution {
public boolean hasSameDigits(String s) {
int n = s.length();
int[] mod5 = new int[n - 1]; // mod[i] = i choose (n - 1) mod 5
int[] fac2 = new int[n -1]; // counts 2 factors (we only need to check divisibility)
int[] fac5 = new int[n - 1]; // counts 5 factor
int[] inverse5 = {0, 1, 3, 2, 4};
fac2[0] = 0;
fac2[n - 2] = 0;
mod5[0] = 1;
mod5[n - 2] = 1;
fac5[0] = 0;
fac5[n -2] = 0;
for(int i = 1; i <= n - 3; i++){
// Track factors mod 2
Pair a_2 = factors(i, 2); // divisor
Pair a_5 = factors(i,5); // divisor
Pair b_2 = factors(n -i - 1, 2);
Pair b_5 = factors(n - i - 1, 5);
fac2[i] = fac2[i - 1] + b_2.count - a_2.count;
fac5[i] = fac5[i - 1] + b_5.count - a_5.count;
mod5[i] = mod5[i - 1]*b_5.modulo*inverse5[a_5.modulo] %5;
}
int[] arr = new int[n - 1];
for(int i = 0; i < n - 1; i++){
int m5 = fac5[i] != 0 ? 0 : mod5[i];
int m2 = fac2[i] != 0 ? 0 : 1;
arr[i] = m5 % 2 == m2 ? m5 : m5 + 5;
}
int a = 0;
int b = 0;
for(int i = 0; i < n -1; i++){
a += (arr[i]*((int) s.charAt(i)))%10;
b += (arr[i]*((int) s.charAt(i+1)))%10;
}
return (a%10) == (b%10);
}
public Pair factors(int n, int div){
Pair res = new Pair(0,0);
while(n % div == 0){
n /= div;
res.count++;
}
res.modulo = n % div;
return res;
}
}
class Pair {
int count;
int modulo;
Pair(int cnt, int mod){
count = cnt;
modulo = mod;
}
}
```
| 0 | 0 |
['Java']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
Mathematical Proof Solution || Beats 100%
|
mathematical-proof-solution-beats-100-by-kdbg
|
Mathematical Proof for "Check If Digits Are Equal in String After Operations II"Problem StatementGiven a string s consisting of digits, perform the following op
|
brandonyee-cs
|
NORMAL
|
2025-03-18T13:11:06.269603+00:00
|
2025-03-18T13:11:06.269603+00:00
| 13 | false |
# Mathematical Proof for "Check If Digits Are Equal in String After Operations II"
## Problem Statement
Given a string $s$ consisting of digits, perform the following operation repeatedly until the string has exactly two digits:
* For each pair of consecutive digits in $s$, calculate a new digit as the sum of the two digits modulo 10.
* Replace $s$ with the sequence of newly calculated digits, maintaining the order.
Return `true` if the final two digits in $s$ are the same; otherwise, return `false`.
## Key Insight
The solution uses a combinatorial approach based on the fact that after successive operations, each position in the resulting string can be expressed as a linear combination of the original digits, with coefficients being binomial coefficients.
## Mathematical Derivation
Let $s^{(k)}[j]$ represent the $j$-th digit after $k$ operations. By induction, we can prove:
$$s^{(k)}[j] = \left(\sum_{i=0}^{k} \binom{k}{i} \cdot s[j+i]\right) \bmod 10$$
After $n-2$ operations (where $n$ is the string length), we have:
$$s^{(n-2)}[0] = \left(\sum_{i=0}^{n-2} \binom{n-2}{i} \cdot s[i]\right) \bmod 10$$
$$s^{(n-2)}[1] = \left(\sum_{i=0}^{n-2} \binom{n-2}{i} \cdot s[i+1]\right) \bmod 10$$
For these digits to be equal, their difference must be 0 (mod 10):
$$\left(\sum_{i=0}^{n-2} \binom{n-2}{i} \cdot (s[i] - s[i+1])\right) \bmod 10 = 0$$
## Implementation Analysis
### Number Representation
The solution uses tuples $(y, a, b)$ where a number is represented as $y \cdot 2^a \cdot 5^b$ with $\gcd(y,10)=1$. This factorization efficiently handles modular arithmetic with powers of 10.
### Binomial Coefficient Calculation
The `compute_comb` function calculates binomial coefficients using the recurrence relation:
$$\binom{N}{k} = \binom{N-1}{k-1} \cdot \frac{N-k+1}{k}$$
### Modular Arithmetic Optimizations
The solution only needs coefficient values modulo 10, handled efficiently by the `toInt` function which leverages these properties:
* If both $a \geq 1$ and $b \geq 1$, then $2^a \cdot 5^b \equiv 0 \pmod{10}$
* If $b \geq 1$, then $y \cdot 5^b \equiv 5 \pmod{10}$ when $y$ is coprime to 10
* Powers of 2 modulo 10 follow the cycle $[6, 2, 4, 8]$
### Final Calculation
The `hasSameDigits` function computes:
$$\sum_{i=0}^{n-2} \left(\text{toInt}(C[i]) \cdot (s[i] - s[i+1])\right) \bmod 10$$
where $C[i]$ represents $\binom{n-2}{i}$ in our factorized representation.
## Time Complexity Analysis
The solution achieves $O(n)$ time complexity versus $O(n^2)$ for a simulation-based approach, as it directly computes the final result without simulating each intermediate step.
## Correctness
The algorithm correctly determines if the final two digits will be equal by computing their mathematical relationship to the original digits, rather than performing the operations explicitly.
## Implementation Details
The code leverages several optimizations:
1. The `factor()` function decomposes integers into the $(y, a, b)$ representation
2. The `inverse()` function efficiently computes modular multiplicative inverses
3. The `toInt()` function handles special cases for efficient modular evaluation
4. The combinatorial identity allows us to compute the result in linear time
By using these mathematical properties, the solution avoids the expensive operation of actually simulating the digit transformations, resulting in a much more efficient algorithm.
``` C+++
using int3 = array<int, 3>; // (y, a, b) where x = y * 2^a * 5^b and gcd(y,10) = 1
int3 C[100000];
int inv10[10]={0, 1, 0, 7, 0, 0, 0, 3, 0, 9};// inv10[x]*x=1 (mod 10) for x coprime to 10
class Solution {
public:
int3 factor(int x) {
int a = countr_zero((unsigned)x);
x >>= a;
int b = 0;
while (x % 5 == 0) {
x /= 5;
b++;
}
return {x % 10, a, b}; // Only keep mod 10 for y
}
int3 inverse(const int3& x) {
int x0 = x[0], a = x[1], b = x[2];
int x0_inv = inv10[x0];
return {x0_inv, -a, -b};
}
int3 mult(const int3& x, const int3& y) {
return {x[0]*y[0]%10, x[1]+y[1], x[2]+y[2]};
}
int toInt(const int3& x) { // mod 10
if (x[1] >= 1 && x[2] >= 1) return 0;
if (x[2] >= 1) return 5;
int B[4] = {6, 2, 4, 8}; // 2^x(mod 10) cycle
if (x[1] == 0) return x[0];
int B2 = B[x[1] % 4]; //
return x[0] * B2 % 10;
}
void compute_comb(int N) {
C[0] = {1, 0, 0};
if (N == 0) return; // Prevent C[N] access if N=0
C[N] = {1, 0, 0};
for (int k = 1; k <= N/2; k++) {
int3 P = factor(N-k + 1);
int3 Q = inverse(factor(k));
C[k]=C[N-k] = mult(mult(C[k-1], P), Q);
}
}
bool hasSameDigits(string& s) {
int n = s.size();
fill(C, C+(n-2), int3{0, 0, 0}); // Prevent overflow
compute_comb(n-2);
int sum=0;
for (int i=0; i <= n-2; i++) {
int C_val= (toInt(C[i])*(s[i]-s[i+1]))%10;
sum=(sum+C_val+10) % 10; // Ensure non-negative
}
// cout << sum << endl;
return sum == 0;
}
};
```
| 0 | 0 |
['Math', 'Combinatorics', 'Number Theory', 'C++']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
binomial coefficient reduction for final digit equivalence
|
binomial-coefficient-reduction-for-final-n80m
|
Intuitionthe idea is that after repeatedly summing adjacent digits mod 10, the final two digits can be expressed as a weighted sum of the original digits. the w
|
Ban_Brian
|
NORMAL
|
2025-03-14T22:11:34.010327+00:00
|
2025-03-14T22:11:34.010327+00:00
| 7 | false |
# Intuition
the idea is that after repeatedly summing adjacent digits mod 10, the final two digits can be expressed as a weighted sum of the original digits. the weights come from the binomial coefficients in the n-2 row of pascal's triangle, taken mod 10.
# Approach
- convert the input string to a list of digits.
- note that the final digits are given by:
- f0 = sum(binom(n-2, i) * digit[i]) mod 10
- f1 = sum(binom(n-2, i) * digit[i+1]) mod 10
- compute the binomial coefficients mod 10 using lucas' theorem by calculating them mod 2 and mod 5, then combining the results.
-- compare the two final digits and return true if they are the same; otherwise, return false.
# Complexity
- Time complexity:
o(n)
- Space complexity:
o(n)
# Code
```python3 []
class Solution:
def hasSameDigits(self, s: str) -> bool:
n = len(s)
if n == 2:
return s[0] == s[1]
digits = list(map(int, s))
N = n - 2
mod = 10
F0, F1 = 0, 0
for i in range(n - 1):
c2 = self.binom_mod2(N, i)
c5 = self.binom_mod5(N, i, 5)
r = (5 * c2 + 6 * c5) % mod
F0 = (F0 + r * digits[i]) % mod
F1 = (F1 + r * digits[i+1]) % mod
return F0 == F1
def binom_mod2(self, n: int, k: int) -> int:
if k > n:
return 0
return 1 if (n & k) == k else 0
def binom_mod5(self, n: int, k: int, p: int) -> int:
if k > n:
return 0
res = 1
while n or k:
n_i = n % p
k_i = k % p
if k_i > n_i:
return 0
res = (res * self.small_binom(n_i, k_i, p)) % p
n //= p
k //= p
return res
def small_binom(self, n: int, k: int, p: int) -> int:
if k > n:
return 0
fact = [1] * p
for i in range(1, p):
fact[i] = (fact[i-1] * i) % p
inv_fact = [1] * p
inv_fact[p-1] = pow(fact[p-1], p-2, p)
for i in range(p-2, -1, -1):
inv_fact[i] = (inv_fact[i+1] * (i+1)) % p
return (fact[n] * inv_fact[k] * inv_fact[n-k]) % p
```
| 0 | 0 |
['Python3']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
Finally learnt Lucas's Theorem and CRT (solution with resource links for references)
|
finally-learnt-lucass-theorem-and-crt-so-ec9t
|
IntuitionThe question is related to Pascial triangle:say the digits are: a + b + c + d + e + f
We are comparing the modulus 10 of pairwise-reduction-sum (the op
|
ericlauchiho
|
NORMAL
|
2025-03-13T06:53:37.522218+00:00
|
2025-03-13T06:56:22.097457+00:00
| 17 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The question is related to Pascial triangle:
say the digits are: a + b + c + d + e + f
We are comparing the modulus 10 of pairwise-reduction-sum (the operation in the question) of (a + b + c + d + e) and (b + c + d + e + f).
And we can observe that the pairwise-reduction-sum is actually the sum of each digit multiplying nCr (Binomial coefficient/Pascal's triangle/combination/whatever it is called):
```
a + b + c + d + e
(a + b) + (b + c) + (c + d) + (d + e)
(a + 2b + c) + (b + 2c + d) + (c + 2d + e)
(a + 3b + 3c + d) + (b + 3c + 3d + e)
a + 4b + 6c + 4d + e
1 4 6 4 1 <-- this is the 4-th row of Pascal's triangle (n = 4 for nCr).
```
# Approach
I have tried the following ways to calculate the nCr, and then mod 10 it, but all got TLE:
- calculate it directly n! / (k!(n-k)!)
- construct the triangle from top to n-th row
- construct the row from left to right using nCr = nC(r-1) * (n-r+1)/r
probably because n can go very large making the factorial or even simple multiplication very slow.
To make it pass all tests, as the hint stated, we can use Lucas's theorem to efficiently calculate `nCr mod 5` and `nCr mod 2`, and then use Chinese Remainder Theorem (CRT) to get `nCr mod 10`.
# Code
```python3 []
from math import comb
def egcd(a, b):
if a == 0:
return (b, 0, 1)
else:
g, y, x = egcd(b % a, a)
return (g, x - (b // a) * y, y)
def modinv(a, m):
'''
https://stackoverflow.com/questions/4798654/modular-multiplicative-inverse-function-in-python
'''
g, x, y = egcd(a, m)
return x % m
def numberToBase(n, b):
if n == 0:
return [0]
digits = []
while n:
digits.append(int(n % b))
n //= b
return digits
def CRT(a, m):
'''
https://cp-algorithms.com/algebra/chinese-remainder-theorem.html#implementation
'''
M = 1
for m_i in m:
M *= m_i
ans = 0
for i in range(len(a)):
a_i = a[i]
m_i = M / m[i]
n_i = modinv(m_i, m[i])
ans = (ans + a_i * m_i % M * n_i) % M
return ans
def lucasTheorem(n, r, p):
'''
https://brilliant.org/wiki/lucas-theorem/
'''
nDigits = numberToBase(n, p)
rDigits = numberToBase(r, p)
ans = 1
for i in range(len(nDigits)):
ni = nDigits[i]
if i < len(rDigits):
ri = rDigits[i]
else:
ri = 0
ans *= comb(ni, ri)
return ans
class Solution:
def hasSameDigits(self, s: str) -> bool:
# Convert the string to a list of integers once
digits = [int(ch) for ch in s]
n = len(digits) - 2 # Based on your original logic
# Initialize accumulators with the first two digits
acc1 = digits[0]
acc2 = digits[1]
comb = 1 # This will hold C(n, 0), then C(n, 1), etc. in turn
# We already accounted for r = 0 in acc1, acc2, so start from r = 1
for r in range(1, n + 1):
# calculate mod 10 of the binomial coefficient
nCr_mod_5 = lucasTheorem(n, r, 5)
nCr_mod_2 = lucasTheorem(n, r, 2)
nCr_mod_10 = CRT([nCr_mod_5, nCr_mod_2], [5, 2])
# Update the last-digit sums
acc1 = (acc1 + digits[r] * nCr_mod_10) % 10
acc2 = (acc2 + digits[r + 1] * nCr_mod_10) % 10
return acc1 == acc2
```
| 0 | 0 |
['Python3']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
Solution in C# using a class for computations modulo 10
|
solution-in-c-using-a-class-for-computat-cpqz
|
IntuitionI noticed the relation to Pascals triangles. I hoped using BigIntegers would suffice, but alas.ApproachThis solution uses the same approach as others I
|
igloo81
|
NORMAL
|
2025-03-12T11:38:19.930775+00:00
|
2025-03-12T11:38:19.930775+00:00
| 17 | false |
# Intuition
I noticed the relation to Pascals triangles. I hoped using BigIntegers would suffice, but alas.
# Approach
This solution uses the same approach as others I've examined. However it is the only one in C#.
We have to compute pascal's triangle modulo 10. This is tricky because you can't just divide modulo 10 (because 10 is not a prime, ask ChatGPT for more information). We get around this by introducing the class NumberModulo10. This class supports multiplication and division modulo 0. It qas quite finicky to write, it needed tests.
The idea behind NumberModulo10 is to keep track how many factors 2 and 5 the numbers has and store the remainder modulo 10. Creation and multiplication is easy to implement. However, division & conversion to an int is harder.
For division we have to compute the inverse of the remainder. This isdone via a short switch statement.
For conversion to an integer the two's cause some complexities. Fortunately the sequence is kinda simple, [2, 4, 8, 16, 32, 64, 128]. So the sequence mod 10 becomes [2, 4, 8, 6, 2, ...], which we put in another switch statement.
# Complexity
- Time complexity: $$O(n log(n))$$
- Space complexity: $$O(n)$$
# Code
```csharp []
public class Solution {
public bool HasSameDigits(string s) {
InitializeFactorials();
//TestModulo10Computations();
var counts = ComputePermutationsModulo10_2(s.Length-1).ToArray();
var digits = s.Select(character => character - '0').ToArray();
var left = 0;
for (var i = 0; i < digits.Length - 1; i++)
left += digits[i] * counts[i];
left = left % 10;
var right = 0;
for (var i = 0; i < digits.Length - 1; i++)
right += digits[i +1] * counts[i];
right = right % 10;
return left == right;
}
internal static NumberModulo10[] Factorials = null;
public IEnumerable<int> ComputePermutationsModulo10(int n)
{
BigInteger result = 1;
yield return (int)result;
for (var i = 1; i < n; i++)
{
result = result * (n-i);
result /= i;
yield return (int)(result % 10);
}
}
internal void InitializeFactorials()
{
if (Factorials != null)
return;
var max = 100005;
Factorials = new NumberModulo10[max + 1];
Factorials[0] = new NumberModulo10(0, 0, 1);
for (var i = 1; i <= max; i++)
Factorials[i] = NumberModulo10.Mult(Factorials[i-1], NumberModulo10.Create(i));
}
internal IEnumerable<int> ComputePermutationsModulo10_2(int n)
{
for (var i = 0; i < n; i++)
yield return NumberModulo10.Divide(Factorials[n-1], NumberModulo10.Mult(Factorials[i], Factorials[n-1-i])).ToNumber();
}
internal void TestModulo10Computations()
{
//TestCreation();
//TestMult();
TestKnownCaseInDetail();
TestCombinations();
}
internal void TestCreation()
{
for (var t = 1; t < 20; t++)
Console.WriteLine($"{t} {NumberModulo10.Create(t).ToNumber()}");
}
internal void TestMult()
{
for (var t = 1; t < 10; t++)
Console.WriteLine($"{(t*t)%10} {NumberModulo10.Mult(NumberModulo10.Create(t), NumberModulo10.Create(t)).ToNumber()}");
}
internal void TestKnownCaseInDetail()
{
Console.WriteLine($"{Factorials[9]}, {NumberModulo10.Mult(Factorials[2], Factorials[7])}, {NumberModulo10.Divide(Factorials[9], NumberModulo10.Mult(Factorials[2], Factorials[7]))}");
}
internal void TestCombinations()
{
Console.WriteLine(string.Join(" ", ComputePermutationsModulo10(9).Select(_ => _.ToString())));
Console.WriteLine(string.Join(" ", ComputePermutationsModulo10_2(9).Select(_ => _.ToString())));
}
public record NumberModulo10(int Twos, int Fives, int Remainder)
{
public static NumberModulo10 Create(int number)
{
var twos = 0;
var fives = 0;
var remainder = number;
while (remainder % 2 == 0)
{
twos += 1;
remainder = remainder / 2;
}
while (remainder % 5 == 0)
{
fives += 1;
remainder = remainder / 5;
}
return new NumberModulo10(twos, fives, remainder);
}
public static NumberModulo10 Mult(NumberModulo10 left, NumberModulo10 right) =>
new NumberModulo10(left.Twos + right.Twos, left.Fives + right.Fives, (left.Remainder * right.Remainder) % 10);
public static NumberModulo10 Divide(NumberModulo10 left, NumberModulo10 right) =>
new NumberModulo10(left.Twos - right.Twos, left.Fives - right.Fives, (left.Remainder * Inverse(right.Remainder)) % 10);
public int ToNumber()
{
if (Twos > 0 && Fives > 0)
return 0;
else if (Twos > 0)
{
return (Twos % 4) switch
{
0 => (6 * Remainder) % 10,
1 => (2 * Remainder) % 10,
2 => (4 * Remainder) % 10,
3 => (8 * Remainder) % 10,
};
}
else if (Fives > 0)
return (5 * Remainder) % 10;
else
return Remainder;
}
internal static int Inverse(int value)
{
return value switch
{
1 => 1,
3 => 7,
7 => 3,
9 => 9,
_ => throw new Exception($"{value} has no inverse modulo 10")
};
}
}
}
```
| 0 | 0 |
['C#']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
Using lucas theorem(lucas theorem code generated from gpt)
|
using-lucas-theoremlucas-theorem-code-ge-hxcw
| null |
risabhuchiha
|
NORMAL
|
2025-03-03T19:28:41.944682+00:00
|
2025-03-03T19:28:41.944682+00:00
| 15 | false |
```java []
class Solution {
public boolean hasSameDigits(String s) {
int n=s.length();
int m=n-2;
int a=0;
int b=0;
for(int i=0;i<s.length()-1;i++){
int bc=f(m,i);
System.out.println(bc);
a=(a+bc*(s.charAt(i)-'0'));
b=(b+bc*(s.charAt(i+1)-'0'));
}
return a%10==b%10;
}
public int f(int m,int j){
int a=l(m,j,5);
int b=l(m,j,2);
for(int i=0;i<=9;i++){
if((i%2==b)&&(i%5==a)){
return i;
}
}
return 0;
}
public int power(int x, int y, int p) {
int res = 1;
x = x % p;
while (y > 0) {
if ((y & 1) == 1)
res = (res * x) % p;
y = y >> 1;
x = (x * x) % p;
}
return res;
}
// Function to compute modular inverse of n under modulo p
// Using Fermat's Little Theorem: n^(p-2) % p is the inverse of n modulo p when p is prime
public int modInverse(int n, int p) {
return power(n, p - 2, p);
}
// Function to compute nCr % p using factorials and modular inverses
public int nCrModP(int n, int r, int p) {
if (r > n)
return 0;
if (r == 0)
return 1;
int[] fact = new int[(int)n + 1];
fact[0] = 1;
for (int i = 1; i <= n; i++) {
fact[i] = (fact[i - 1] * i) % p;
}
int result = fact[(int)n];
result = (result * modInverse(fact[(int)r], p)) % p;
result = (result * modInverse(fact[(int)(n - r)], p)) % p;
return result;
}
// Lucas' Theorem implementation to compute C(n, r) % p
public int l(int n, int r, int p) {
if (r == 0)
return 1;
return (l(n / p, r / p, p) * nCrModP(n % p, r % p, p)) % p;
}
//39024
// 3 +9 9+0 0+2 2+4
// 3+9+9+0 9+0+0+2 0+2+2+4
//3+9+9+0+9+0+0+2 9+0+0+2+0+2+2+4
}
```
| 0 | 0 |
['Java']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
Using lucas theorem(lucas theorem code generated from gpt)
|
using-lucas-theoremlucas-theorem-code-ge-fdgr
| null |
risabhuchiha
|
NORMAL
|
2025-03-03T19:28:38.306836+00:00
|
2025-03-03T19:28:38.306836+00:00
| 6 | false |
```java []
class Solution {
public boolean hasSameDigits(String s) {
int n=s.length();
int m=n-2;
int a=0;
int b=0;
for(int i=0;i<s.length()-1;i++){
int bc=f(m,i);
System.out.println(bc);
a=(a+bc*(s.charAt(i)-'0'));
b=(b+bc*(s.charAt(i+1)-'0'));
}
return a%10==b%10;
}
public int f(int m,int j){
int a=l(m,j,5);
int b=l(m,j,2);
for(int i=0;i<=9;i++){
if((i%2==b)&&(i%5==a)){
return i;
}
}
return 0;
}
public int power(int x, int y, int p) {
int res = 1;
x = x % p;
while (y > 0) {
if ((y & 1) == 1)
res = (res * x) % p;
y = y >> 1;
x = (x * x) % p;
}
return res;
}
// Function to compute modular inverse of n under modulo p
// Using Fermat's Little Theorem: n^(p-2) % p is the inverse of n modulo p when p is prime
public int modInverse(int n, int p) {
return power(n, p - 2, p);
}
// Function to compute nCr % p using factorials and modular inverses
public int nCrModP(int n, int r, int p) {
if (r > n)
return 0;
if (r == 0)
return 1;
int[] fact = new int[(int)n + 1];
fact[0] = 1;
for (int i = 1; i <= n; i++) {
fact[i] = (fact[i - 1] * i) % p;
}
int result = fact[(int)n];
result = (result * modInverse(fact[(int)r], p)) % p;
result = (result * modInverse(fact[(int)(n - r)], p)) % p;
return result;
}
// Lucas' Theorem implementation to compute C(n, r) % p
public int l(int n, int r, int p) {
if (r == 0)
return 1;
return (l(n / p, r / p, p) * nCrModP(n % p, r % p, p)) % p;
}
//39024
// 3 +9 9+0 0+2 2+4
// 3+9+9+0 9+0+0+2 0+2+2+4
//3+9+9+0+9+0+0+2 9+0+0+2+0+2+2+4
}
```
| 0 | 0 |
['Java']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
Solution You are Looking For
|
solution-you-are-looking-for-by-abmishra-zayw
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
abmishra1234
|
NORMAL
|
2025-03-03T05:09:24.930611+00:00
|
2025-03-03T05:09:24.930611+00:00
| 16 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
from typing import List
# Precomputed small binomials mod 5 for n < 5:
_small = {
0: [1],
1: [1, 1],
2: [1, 2, 1],
3: [1, 3, 3, 1],
4: [1, 4, 1, 4, 1]
}
def nCr_mod2(n: int, r: int) -> int:
"""Compute C(n, r) mod 2 using Lucas theorem for mod 2."""
if r > n:
return 0
# In mod 2, C(n, r) = 1 if and only if r's binary representation is a subset of n's.
while n or r:
if (r & 1) > (n & 1):
return 0
n //= 2
r //= 2
return 1
def nCr_mod5(n: int, r: int) -> int:
"""Compute C(n, r) mod 5 using Lucas theorem."""
if r > n:
return 0
if n < 5:
return _small[n][r]
n0, r0 = n % 5, r % 5
# If r0 > n0, then the small binom is 0.
if r0 > n0:
return 0
return (_small[n0][r0] * nCr_mod5(n // 5, r // 5)) % 5
def nCr_mod10(n: int, r: int) -> int:
"""Combine results mod 2 and mod 5 using CRT to get binom(n, r) mod 10."""
a = nCr_mod2(n, r) # mod 2 result
b = nCr_mod5(n, r) # mod 5 result
# We need x mod 10 such that:
# x ≡ a (mod 2) and x ≡ b (mod 5)
# The possibilities for x given b are b and b+5.
for candidate in (b, b + 5):
if candidate % 2 == a:
return candidate % 10
return 0 # fallback; though one candidate must work.
class Solution:
def hasSameDigits(self, s: str) -> bool:
n = len(s)
# Convert string to list of integers.
digits = [int(ch) for ch in s]
# Number of operations = n - 2, so we need row r = n - 2 of Pascal's triangle.
r = n - 2
F0, F1 = 0, 0
# Iterate j from 0 to r (inclusive).
for j in range(r + 1):
coef = nCr_mod10(r, j)
F0 = (F0 + coef * digits[j]) % 10
F1 = (F1 + coef * digits[j + 1]) % 10
return F0 == F1
# Example usage:
# if __name__ == "__main__":
# sol = Solution()
# # Provided test cases:
# print("s = '3902' ->", sol.hasSameDigits("3902")) # Expected True
# print("s = '34789' ->", sol.hasSameDigits("34789")) # Expected False
# # The problematic test case:
# print("s = '8506969' ->", sol.hasSameDigits("8506969")) # Expected True
```
| 0 | 0 |
['Python3']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
Explanation with Lucas Theorem and Chinese remainder theorem - O(n log n)
|
explanation-with-lucas-theorem-and-chine-8e6x
|
IntuitionYou need to have an understanding of pascals triangle, lucas theorem and chinese remainder thm.Now, if you do the steps of forming the two digits strin
|
SaketCodeScribe
|
NORMAL
|
2025-03-02T12:17:54.204253+00:00
|
2025-03-02T12:17:54.204253+00:00
| 14 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
You need to have an understanding of pascals triangle, lucas theorem and chinese remainder thm.
Now, if you do the steps of forming the two digits string, you'll see pascal triangle
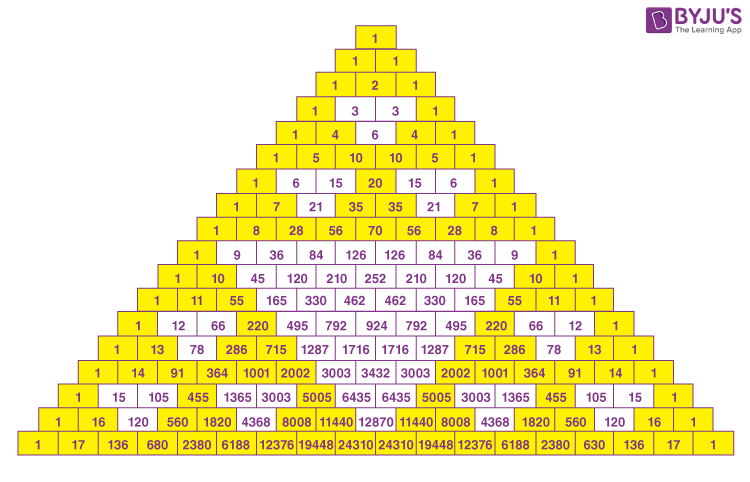
now, as per lucas thm, you can calculate nck mod p (binomial coefficient of n the row and kth column in pascal triagnle).
If you select p as 2 and 5.
Then with Chinese Thm you can calculate mod 10 using the formula which I used.
```
X = (a1*M1*InvM1 + a2*M2*InvM2) mod M
m1 = 2, m2 = 5, M = m1*m2
a1 = nck mod 2, a2 = nck mod 5
M1 = M/m1, M2 = M/m2
M1 * InvM1 ≅ 1 (mod m1)
M2 * InvM2 ≅ 1 (mod m2)
```
# Complexity
- Time complexity: $$O(n logn)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(1)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
double[] fact = {1, 1, 2, 6, 24};
public boolean hasSameDigits(String s) {
return CheckLastTwoDigitsAreEqual(s, s.length());
}
public boolean CheckLastTwoDigitsAreEqual(String s, int n){
int i, val1 = 0, val2 = 0;
for(i=0; i<n-1; i++){
int coeff = findMod10(n-2, i);
val1 = (val1%10+((s.charAt(i)-'0')%10*coeff)%10)%10;
val2 = (val2%10+((s.charAt(i+1)-'0')%10*coeff)%10)%10;
}
return val1 == val2;
}
public int findMod10(int n, int k){
// to find Mod 10, apply chinese remainder theorem with p1 = 2 and p2 = 5
int a1 = lucasTheorem(n, k, 2);
int a2 = lucasTheorem(n, k, 5);
int M1 = 5, M2 = 2;
// calculate multiplicative inverse of M1 and M2
int invM1 = findInv(M1, 2), invM2 = findInv(M2, 5);
return (a1*M1*invM1+a2*M2*invM2)%10;
}
public int findInv(int a, int b){
// Since M1 = 2 and M2 = 5 always, we can directly return the
// multiplicative inverse
return b == 2 ? 1 : 3;
}
public int lucasTheorem(int d, int k, int num){
// lucasTheorem
int a, b;
double prod = 1;
while(d != 0 || k != 0){
if (d == 0){
b = k%num;
if (b != 0){
return 0;
}
}
else if (k != 0){
a = d%num;
b = k%num;
if (b > a){
return 0;
}
prod *= fact[a]/(fact[b]*fact[a-b]);
}
d /= num;
k /=num;
}
return (int)prod;
}
}
```
| 0 | 0 |
['Java']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
explaination of why Luca's thm.
|
explaination-of-why-lucas-thm-by-joshuad-c18t
|
Intuitionso i think the problem is clear, we recognised a pattern (nth row of pascal's triangle) and we need to get that row and multiply its elements with the
|
joshuadlima
|
NORMAL
|
2025-03-01T13:59:35.151833+00:00
|
2025-03-01T13:59:35.151833+00:00
| 17 | false |
# Intuition
so i think the problem is clear, we recognised a pattern (nth row of pascal's triangle) and we need to get that row and multiply its elements with the corresponding digits in the string and get the sum.
This pattern can also be recognised by simply dry running. (check the comment at the bottom of my code)
The issue we face is to calculate nCr for such huge numbers and modulo it with 10.
1. 10 isnt prime -> fix: break 10 into 2 x 5 and merge the results of individual nCr of each.
How?
if ncr mod 2 is 0 -> the value is even
thus is ncr mod 5 is 0, 1, 2, 3, 4 => the ncr mod 10 will be 0, 6, 2, 8, 4 respectively
similarly for the case where ncr mod 2 is 1
2. our traditional methods of calculating ncr could be DP (not viable because n * n is too big) and using inverse modulo (which we compute using fermat's little theorem)
-> we cant using inverse modulo (ncr = factorial(n) * inverse_factorial(n - r) * inverse_factorial(r)) because fermat's little theorem makes an assumption that p (the prime number that needs to be modded) and the value (here factorial) are both co-prime.. if not, then the inverse modulo doesnt exist. for this reason we cant precompute inverse factorial mod 2 and mod 5.
Thus we are left with Luca's theorem which also leverages the fact that p is very small.
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
#define ll long long
class Solution {
public:
int fact[10];
int nCrSmall(ll n, ll r, ll p) {
if (n < r)
return 0;
else
return (fact[n] / (fact[n - r] * fact[r])) % p;
}
int nCrModpLuca(int n, int r, int p)
{
if (r==0)
return 1;
int ni = n % p, ri = r % p;
return (nCrModpLuca(n / p, r / p, p) * nCrSmall(ni, ri, p)) % p;
}
ll nCrMod10(int n, int r) {
ll mod2 = nCrModpLuca(n, r, 2);
ll mod5 = nCrModpLuca(n, r, 5);
if(mod5 == 0)
return mod2 ? 5 : 0;
else if(mod5 == 1)
return mod2 ? 1 : 6;
else if(mod5 == 2)
return mod2 ? 7 : 2;
else if(mod5 == 3)
return mod2 ? 3 : 8;
else
return mod2 ? 9 : 4;
}
bool hasSameDigits(string s) {
fact[0] = 1;
for(int i = 1; i < 10; i++)
fact[i] = fact[i - 1] * i;
ll d1 = 0, d2 = 0;
for(int i = 0; i < s.size() - 1; i++){
int ncr10 = nCrMod10(s.size() - 2, i);
d1 = (d1 + (s[i] - '0') * ncr10) % 10;
d2 = (d2 + (s[i + 1] - '0') * ncr10) % 10;
}
// cout << d1 << " " << d2 << "\n";
return d1 == d2;
}
};
/*
3 4 7 8 9
3+4 4+7 7+8 8+9
3+4+4+7 4+7+7+8 7+8+8+9
3+4+4+7+4+7+7+8 4+7+7+8+7+8+8+9
(pascal triangle)
0761
737
00
*/
```
| 0 | 0 |
['C++']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
33ms Runtime in C. Modular Arithmetic. GCD and Factor Removal
|
37ms-runtime-in-c-modular-arithmetic-gcd-q7ag
|
ApproachModular Arithmetic:We use two modulus values (2 and 5)GCD and Factor Removal:We use the greatest common divisor (GCD) to simplify numbers where necessar
|
dotis101
|
NORMAL
|
2025-02-27T20:30:57.208032+00:00
|
2025-03-01T17:35:12.066078+00:00
| 30 | false |
# Approach
<!-- Describe your approach to solving the problem. -->
**Modular Arithmetic:**
We use two modulus values (2 and 5)
**GCD and Factor Removal:**
We use the greatest common divisor (GCD) to simplify numbers where necessary, and we remove factors of 2 and 5 from the numbers to reduce them modulo the target value.
**Key Insight:**
We break the problem into two independent tests: one for modulus 2 and another for modulus 5.
# Complexity
- Time complexity: **O(n)**
- Space complexity: **O(1)**
# Code
```c []
// Computes the greatest common divisor of a and b.
static inline int32_t gcd(int32_t a, int32_t b) {
while (b) {
a ^= b ^= a ^= b; // XOR trick to swap a and b
b %= a;
}
return a;
}
/* Removes factors of mod from a.
Returns in *r the value a reduced modulo */
static inline void cal(int32_t a, int32_t mod, int32_t *r, int32_t *cnt) {
int32_t count = 0;
while (a > 0 && a % mod == 0) {
count++;
a /= mod;
}
*r = a % mod;
*cnt = count;
}
// Computes the modular inverse of a modulo mod.
static inline int32_t modinv(int32_t a, int32_t mod) {
for (int32_t i = 1; i < mod; i++) {
if ((a * i) % mod == 1)
return i;
}
return 0;
}
/* Performs the test for a given modulus(2 or 5)
based on the difference between weighted sums. */
static bool test(int32_t mod, const char *s) {
int32_t n = strlen(s);
int32_t res = 0, r = 1, c = 0;
for (int32_t i = 0; i < n - 1; i++) {
if (c == 0) {
res = (res + r * ((s[i] - '0') - (s[i + 1] - '0'))) % mod;
if (res < 0) res += mod;
}
int32_t rr, cc;
cal(n - 2 - i, mod, &rr, &cc);
r = (r * rr) % mod;
c += cc;
cal(i + 1, mod, &rr, &cc);
r = (r * modinv(rr, mod)) % mod;
c -= cc;
}
return (res % mod) == 0;
}
/* Checks if the final two digits are the same.
Returns true if they are the same, false otherwise. */
static bool hasSameDigits(const char *s) {
return test(2, s) && test(5, s);
}
```
| 0 | 0 |
['C']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
Check If Digits Are Equal in String After Operations II
|
check-if-digits-are-equal-in-string-afte-6306
|
Complexity
Time complexity: O(N)
Space complexity: O(1)
Code
|
Ansh1707
|
NORMAL
|
2025-02-27T16:02:57.426631+00:00
|
2025-02-27T16:02:57.426631+00:00
| 21 | false |
# Complexity
- Time complexity: O(N)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python []
class Solution(object):
def hasSameDigits(self, s):
"""
:type s: str
:rtype: bool
"""
def is_valid(mod):
def decompose(x, mod):
cnt = 0
while x > 1 and x % mod == 0:
x //= mod
cnt += 1
return x, cnt
res = cnt = 0
curr = 1
n = len(s) - 1
for i in xrange(n):
if cnt == 0:
res = (res + curr * (ord(s[i]) - ord(s[i + 1]))) % mod
x, c = decompose(n - i - 1, mod)
curr = (curr * x) % mod
cnt += c
x, c = decompose(i + 1, mod)
curr = (curr * pow(x, mod - 2, mod)) % mod
cnt -= c
return res == 0
return is_valid(2) and is_valid(5)
```
| 0 | 0 |
['Math', 'String', 'Combinatorics', 'Number Theory', 'Python']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
Optimisation O(n) pour l'Égalité des Chiffres Finaux
|
optimisation-on-pour-legalite-des-chiffr-3oes
|
IntuitionAu lieu de simuler naïvement chaque opération, qui conduirait à une complexité en O(n²) pour des chaînes de longueur pouvant atteindre 10⁵, on remarque
|
cxIo7G1ot6
|
NORMAL
|
2025-02-27T13:03:38.480920+00:00
|
2025-02-27T13:03:38.480920+00:00
| 13 | false |
# Intuition
Au lieu de simuler naïvement chaque opération, qui conduirait à une complexité en O(n²) pour des chaînes de longueur pouvant atteindre 10⁵, on remarque que l'opération est linéaire (modulo 10). Ainsi, les deux chiffres finaux peuvent être exprimés comme des sommes pondérées des chiffres initiaux, où les coefficients sont les binomiaux de la ligne correspondante de Pascal.
# Approach
L'idée est de reformuler le problème en calculant directement les deux chiffres finaux. après avoir effectué (L–2) opérations (pour une chaîne de longueur L), on peut montrer que :
Le premier chiffre final est une somme pondérée des premiers L–1 chiffres de la chaîne avec des coefficients binomiaux.
Le second chiffre final est une somme pondérée des derniers L–1 chiffres, décalée d'une position.
La difficulté réside dans le calcul des coefficients binomiaux modulo 10. Puisque 10 n'est pas premier, il n'est pas possible d'utiliser directement une inversion modulaire pour la division. Pour contourner ce problème, on décompose chaque coefficient en :
Une partie résiduelle « copremière » avec 10.
Les puissances de 2 et 5 qui forment le 10.
Ainsi, pour chaque coefficient, si on possède à la fois un facteur 2 et un facteur 5, le coefficient est nul modulo 10. Sinon, on calcule la contribution modulo 10 en combinant la partie copremière et le facteur 2 ou 5 restant. Ce calcul est effectué en une boucle linéaire, garantissant une optimisation suffisante pour traiter des cas de grande taille.
# Complexity
- Time complexity:
Chaque coefficient est calculé en une seule itération sur la chaîne (avec n = L – 2), et les opérations à l’intérieur de la boucle se font en temps constant.
- Space complexity:
L’algorithme utilise un nombre constant de variables supplémentaires (en dehors de la chaîne d’entrée).
# Code
```java []
class Solution {
public boolean hasSameDigits(String s) {
int L = s.length();
int n = L - 2;
int A = 0, B = 0;
int res = 1;
int cnt2 = 0;
int cnt5 = 0;
for (int j = 0; j <= n; j++) {
int cVal;
if (cnt2 > 0 && cnt5 > 0) {
cVal = 0;
} else if (cnt2 > 0) {
cVal = (int) ( (long) res * pow2(cnt2) % 10 );
} else if (cnt5 > 0) {
cVal = (int) ( (long) res * 5 % 10 );
} else {
cVal = res % 10;
}
int digitA = s.charAt(j) - '0';
int digitB = s.charAt(j+1) - '0';
A = (A + cVal * digitA) % 10;
B = (B + cVal * digitB) % 10;
if (j < n) {
int numerator = n - j;
int denominator = j + 1;
int num2 = 0, num5 = 0;
int tmp = numerator;
while (tmp % 2 == 0) { num2++; tmp /= 2; }
while (tmp % 5 == 0) { num5++; tmp /= 5; }
int numCoprime = tmp % 10;
int den2 = 0, den5 = 0;
tmp = denominator;
while (tmp % 2 == 0) { den2++; tmp /= 2; }
while (tmp % 5 == 0) { den5++; tmp /= 5; }
int denCoprime = tmp % 10;
res = (res * numCoprime) % 10;
cnt2 += num2;
cnt5 += num5;
int inv = modInv(denCoprime);
res = (res * inv) % 10;
cnt2 -= den2;
cnt5 -= den5;
}
}
return A == B;
}
private int pow2(int exp) {
if(exp == 0) return 1;
switch(exp % 4) {
case 1: return 2;
case 2: return 4;
case 3: return 8;
default: return 6;
}
}
private int modInv(int x) {
switch(x) {
case 1: return 1;
case 3: return 7;
case 7: return 3;
case 9: return 9;
default: return 1;
}
}
public static void main(String[] args) {
Solution sol = new Solution();
System.out.println("s = \"3902\" -> " + sol.hasSameDigits("3902"));
System.out.println("s = \"34789\" -> " + sol.hasSameDigits("34789"));
String s = "8511091174243970293830342753059959793455377893239051540927082033187240124651229102505421365397729731740624985976268193161909092667482162609105851918329325410229303096145203285966520320429119384446770055324289454442954597630606378451482361366896910776550615973749924980365499549511704675725195663107728081029608575109725399732672058587256993726863276501858883662007362560815246884096259020234496053459165914113397087333641562001970404358712101566463126129305760602714410261720198595772192756949994361450529207454149673035573098830421831309194263544594007550188801321953486900418288916392541385847578758551708294616501456816524717438312058500300288868953422115931462276486885913112671552112754119767267621269560618674030131754128856353720751335308105588014754553778617501267029280240423832512177715508236759500474945035840428596745739268598933476010552810416514316060195958059404368153600344223160971369308987776658691971723970769376180896862840723518439341935614206767582388604235193637092402433663668727253863972978514229601582421448166527144131253387154395775592358019590680702190704499241496925111130194219795706800345173303260442653604447578003347631943913218385257512925060165807340873922438201432922853019264090389581305644965200572122806139177551973435419645514198562152315885392561597057958489927226094303976667008461440816384107700958082762054062862978877164156340331810298614797596471444329253938876072843770795718420670993562025309405464921097647102127112753047141132213852170185177941108947208851591877874428506536720569272960446163857345970157074777262657467919343799385582135456166613132027220067090289431721832069601432323573404866372353541042870928620955868755334424571763936184484330974970756512179803681363021075184601757687640941008917712631764272527828638442519961130805821109137312058154056088794778667809778520891462897389040931374831253566950261285451732547782440546368493373827016874592373107472040883380959501216070238219495029145308865413087337192076688648645267137352032821663013782324960261680805708481713272384569339945696255637747022170099488797844015341942650394639976630537358294896083644891306864428090342753841957230297332886715097445715870047132909598527580066721731847355525276473254280573636687108825582815472218447930101385552289625287402143639205489747896990810626817492093426862879930237761595807688491386266037305034155993242960325800766341555409447456085209442690249493319595974410499461472889992743304042638661402936492751134153618438719122659779278593454345562856939161533956406664062082948502192616188359181424778685153097822238878650684606450186365367824787969956896239686299711473952543244454407437972621019129858045855802669740924346562271755789922776852966015983373223984515681628996744657357266074345956404557430495922634049229408654918041656688799879520877100522487922957705935017704071417671856380551133496181712641524172716734775879858208226434051731656057563966349762268670773167064345059714223679637100751184692572787651829263323319095148243753853280906286968525848051465210590600256007080343223858268670720042068419494674887376834277991448904219871084565845566765609281789755289059876005460861951378749415901441459192337407041165444863382494204852095924440945180423738602946245407515741984712673149515067375321667553297489332356750942403610336886254800514132765055130423896419669598451107787594693528731655017976186383968755105230110421192185775629168145593057911559376473844619261209489258070880197188964305822209497843893720207883604806732462355187403570140697897014178540619928507223798723141945207998863064388718759430755734127925254545618782725641065676253642825199669088788157091153054087652424968346143752354760700188475028543129035231781427786570123258459465262727961004609483163242709460058271249800801401170601368826025839065359868446587778315774995596977318361459374351686542010357910338611548104543410042691137071879894419360441632041055110202794163";
System.out.println("Cas long -> " + sol.hasSameDigits(s));
}
}
```
| 0 | 0 |
['Java']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
Rust | Binomial coefficients using modular inverse
|
rust-binomial-coefficients-using-modular-1jx7
|
ApproachI don't understand Lucas's theorem, but I was able to figure out a solution using modular inverses.Iteratively calculate all the coefficients in a row o
|
primbin
|
NORMAL
|
2025-02-26T22:35:40.630071+00:00
|
2025-02-26T22:35:40.630071+00:00
| 20 | false |
# Approach
I don't understand Lucas's theorem, but I was able to figure out a solution using modular inverses.
Iteratively calculate all the coefficients in a row of pascal's triangle modulo m, while keeping track of how many multiples of m need to be divided out of each coefficient. If there's at least 1 multiple of m in the coefficient, then it's 0 mod m.
# Code
```rust []
// Compute modular inverse using extended euclid's algorithm
// Multiply this instead of dividing when computing the binomial coefficients
// I got this off of wikipedia
pub fn modular_inverse(x: i32, m: i32) -> Option<i32> {
let (mut t, mut newt) = (0,1);
let (mut r, mut newr) = (m,x);
while newr != 0 {
let q = r / newr;
(t, newt) = (newt, t - q * newt);
(r, newr) = (newr, r - q * newr);
}
if r > 1 {
return None;
}
if t < 0 {
t = t + m;
}
return Some(t);
}
// Decompose n into a * m^b
pub fn decomp(mut n: i32, m: i32) -> (i32,i32) {
let mut r = 0;
if n == 0 || m == 0 {
return (0,0);
}
while (n % m == 0) {
n /= m;
r += 1;
}
return (n,r);
}
// Get the nth row of pascal's triangle mod m
pub fn pascal_row(n: i32,m: i32) -> impl Iterator<Item=i32> {
return (0..(n+1)).scan(
// Keep track of the number of multiples of m are in the prime factorization,
// As well as the remainder mod m, after dividing out the multiples
(0,1),
move |&mut (ref mut multiples,ref mut rem),i| {
if i > 0 {
// Break down the numerator and denominator into x_p * m^x
let (num,num_p) = decomp(n+1-i,m);
let (denom,denom_p) = decomp(i,m);
*multiples = &*multiples + num_p - denom_p;
// Call unwrap here because we should be dividing out any factors of m beforehand
let top = num%m;
let bottom = modular_inverse(denom%m,m).unwrap();
// Multiplicative formula for n choose k, from wikipedia
*rem = (&*rem * top * bottom) % m;
}
assert!(*multiples >= 0, "The prime factorization can't have a negative exponent");
// If the number of multiples in this coefficient > 0, then the coefficient is 0 mod m
if *multiples > 0 {
return Some(0);
}
return Some(*rem);
}
);
}
pub fn atoi_byte(c: u8) -> i32 {
return c as i32 - 48;
}
// Return the digit that we'd get from the string s after applying the whole process, mod m (where m is prime)
pub fn get_final_digit(s: &str,m:i32) -> i32 {
let row = pascal_row(s.len() as i32-1,m);
return s
.as_bytes()
.iter()
.zip(row)
.map(|(&digit,coeff)| atoi_byte(digit)*coeff)
.fold(0,|a,x|(a+x)%m);
}
impl Solution {
pub fn has_same_digits(s: String) -> bool {
// Use chinese remainder theorem -- if it works for both mod 2 and mod 5, then it should work for mod 10
let mod_2 = get_final_digit(&s[..s.len()-1],2) == get_final_digit(&s[1..], 2);
let mod_5 = get_final_digit(&s[..s.len()-1],5) == get_final_digit(&s[1..], 5);
return mod_2 && mod_5;
}
}
```
| 0 | 0 |
['Rust']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
Simple and Intuitive Python Solution – No Need for Lucas’ Theorem
|
simple-and-intuitive-python-solution-no-e5gtc
|
ApproachIf the input string is "abcde", the the calculation chain:a, b, c, d, e
(a + b), (b + c), (c + d), (d + e)
(a + 2b + c), (b + 2c + d), (c + 2d + e)
(a +
|
user1871i
|
NORMAL
|
2025-02-26T18:34:06.136211+00:00
|
2025-02-26T18:34:06.136211+00:00
| 25 | false |
# Approach
<!-- Describe your approach to solving the problem. -->
If the input string is "abcde", the the calculation chain:
a, b, c, d, e
(a + b), (b + c), (c + d), (d + e)
(a + 2b + c), (b + 2c + d), (c + 2d + e)
(a + 3b + 3c + d), (b + 3c + 3d + e)
Each step has binomial coefficients. If input length is n (eg. 5 for 'abcde'), then we'll need the binomial coefficients for (1 + x)^(n-2) (eg. (1 + x)^3 which is 1, 3, 3, 1).
# Complexity
- Time complexity:$$O(n)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:$$O(n)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def hasSameDigits(self, s: str) -> bool:
s = [int(c) for c in s]
def generateBinomials(n):
"""
generate binomial coefficients
if n = 3, res = [1, 3, 3, 1]
if n = 4, res = [1, 4, 6, 4, 1]
"""
res = [1] * (n + 1)
# calculate only half of the binomial coefficients
for i in range(1, n // 2 + 1):
res[i] = res[i - 1] * (n - i + 1) // i
# use only last digit
res = [r % 10 for r in res]
# copy other half
for i in range(n, n // 2, -1):
res[i] = res[n - i]
return res
# get the binomial coefficients
binomials = generateBinomials(len(s) - 2)
# get the last two results
x = sum(i * j % 10 for i, j in zip(binomials, s[:-1]))
y = sum(i * j % 10 for i, j in zip(binomials, s[1:]))
return x % 10 == y % 10
```
| 0 | 0 |
['Python3']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
Has Same Digits Javascript Solution
|
has-same-digits-javascript-solution-by-a-q963
|
Intuition
This problem requires checking whether alternating sums of binomial coefficients modulo 10 are equal.
The key observation is that binomial coefficient
|
ak1919
|
NORMAL
|
2025-02-26T00:46:22.811087+00:00
|
2025-02-26T00:46:22.811087+00:00
| 62 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
* This problem requires checking whether alternating sums of binomial coefficients modulo 10 are equal.
* The key observation is that binomial coefficients have properties that can be used for efficient computation.
# Approach
<!-- Describe your approach to solving the problem. -->
* 1. Compute alternating sums using binomial coefficients modulo 10.
* 2. Use modular arithmetic properties of binomial coefficients with respect to 2 and 5.
* 3. Compare the computed sums.
# Complexity
- Time complexity: O(n), where n is the length of the string (each binomial coefficient calculation is efficient).
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1), since only a few variables are used.
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```javascript []
var hasSameDigits = function (s) {
// Step 1: Initialize Variables
let size = s.length;
let X = size - 2;
let x = 0, y = 0;
// Step 2: Compute Alternating Sum Using Binomial Coefficients
for (let j = 0; j <= X; j++) {
let coeff = binomialMod10(X, j);
x = (x + coeff * (s.charCodeAt(j) - '0'.charCodeAt(0))) % 10;
y = (y + coeff * (s.charCodeAt(j + 1) - '0'.charCodeAt(0))) % 10;
}
// Step 3: Compare Alternating Sums
return x === y;
};
// Step 4: Compute Binomial Coefficient Modulo 10
var binomialMod10 = function (n, k) {
let i = binomialMod2(n, k);
let j = binomialMod5(n, k);
for (let x = 0; x < 10; x++) {
if (x % 2 === i && x % 5 === j) {
return x;
}
}
return 0;
};
// Step 5: Compute Binomial Coefficient Modulo 2
var binomialMod2 = function (n, k) {
return ((n & k) === k) ? 1 : 0;
};
// Step 6: Compute Binomial Coefficient Modulo 5 Using Lookup Table
var binomialMod5 = function (n, k) {
const tuples = [
[1],
[1, 1],
[1, 2, 1],
[1, 3, 3, 1],
[1, 4, 1, 4, 1]
];
let result = 1;
while (n > 0 || k > 0) {
let nthd = n % 5;
let kthd = k % 5;
if (kthd > nthd) return 0;
result = (result * tuples[nthd][kthd]) % 5;
n = Math.floor(n / 5);
k = Math.floor(k / 5);
}
return result;
};
```
| 0 | 0 |
['JavaScript']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
Lucas' theorem || Explained
|
lucas-theorem-explained-by-saifyssk04-je8b
|
IntuitionThe problem requires us to repeatedly transform a string of digits until only two digits remain, then check if they are equal. Instead of simulating th
|
saifyssk04
|
NORMAL
|
2025-02-25T06:18:48.999062+00:00
|
2025-02-25T06:18:48.999062+00:00
| 40 | false |
### Intuition
The problem requires us to repeatedly transform a string of digits until only two digits remain, then check if they are equal. Instead of simulating the entire transformation process, we can leverage combinatorial mathematics and number theory (Lucas' theorem) to determine the final two digits directly.
### Approach
1. **Understanding the Transformation:**
- Each transformation step replaces the string with a new sequence where each digit is calculated as `(s[i] + s[i+1]) % 10`.
- The number of digits reduces in each iteration until only two remain.
2. **Optimization Using Combinatorial Coefficients:**
- Instead of simulating every step, we can compute the final two digits using **binomial coefficients modulo 10**.
- The approach is based on properties of **Lucas' theorem** for modulus 5 and properties of binomial coefficients modulo 2.
3. **Precomputing Small Binomial Coefficients Modulo 5:**
- We precompute binomial coefficients modulo 5 up to size 5.
- This allows us to efficiently compute any binomial coefficient modulo 5 using **Lucas' theorem**.
4. **Using Lucas' Theorem for Modulo 5 Computation:**
- We define a function `lucas_mod5(n, k)`, which calculates binomial coefficients using the theorem.
- This theorem breaks down `C(n, k) mod 5` into smaller calculations based on digits in base 5.
5. **Calculating the Coefficients for Each Digit:**
- The binomial coefficient modulo 2 is determined using `(m & j) == j`.
- The modulo 5 result is adjusted so that it remains congruent modulo 2.
- The final coefficient is used to determine the weighted sum of digits.
6. **Computing the Final Two Digits:**
- Using the derived coefficients, we compute two final sums and return `true` if they are equal.
### Complexity Analysis
- **Time Complexity:**
- Computing binomial coefficients up to size 5 is **O(1)**.
- The transformation calculations require **O(n)** operations.
- Overall, the approach runs in **O(n)** time.
- **Space Complexity:**
- Only a few integer variables and a small coefficient table are used.
- The space complexity is **O(1)**.
### Code
```cpp
class Solution {
public:
bool hasSameDigits(string s) {
int n = s.size();
int m = n - 2;
// Precompute small binomials mod 5 for Lucas' theorem.
int comb[5][5] = {0};
for (int i = 0; i < 5; i++){
for (int j = 0; j <= i; j++){
if (j == 0 || j == i)
comb[i][j] = 1;
else
comb[i][j] = (comb[i-1][j-1] + comb[i-1][j]) % 5;
}
}
// Lucas' theorem for p = 5.
auto lucas_mod5 = [&](int n, int k) -> int {
int res = 1;
while (n > 0 || k > 0) {
int n_i = n % 5;
int k_i = k % 5;
if (k_i > n_i) return 0;
res = (res * comb[n_i][k_i]) % 5;
n /= 5;
k /= 5;
}
return res;
};
// For m = n-2, binom(m, j) mod 2 is 1 if (m & j) == j, else 0.
auto getCoeff = [&](int j) -> int {
int a = ((m & j) == j) ? 1 : 0;
int b = lucas_mod5(m, j); // b is in {0,1,2,3,4}
int coeff;
if ((b % 2) == a)
coeff = b;
else
coeff = (b + 5) % 10; // b+5 is in {5,6,7,8,9}
return coeff;
};
// Compute the two sums:
int sum0 = 0, sum1 = 0;
for (int j = 0; j <= m; j++) {
int coeff = getCoeff(j);
int digit0 = s[j] - '0';
int digit1 = s[j+1] - '0';
sum0 = (sum0 + coeff * digit0) % 10;
sum1 = (sum1 + coeff * digit1) % 10;
}
return sum0 == sum1;
}
};
| 0 | 0 |
['Math', 'Number Theory', 'C++']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
[Python] lucas theorem + CRT beats 100%
|
python-lucas-theorem-crt-beats-100-by-kn-rj70
|
The hardest part of this problem is the calculation of nCk % 10. The naive approach will take O(k) times. However we can speed it up to O(logN) time by using lu
|
knatti
|
NORMAL
|
2025-02-24T15:51:50.966255+00:00
|
2025-02-24T16:01:44.668110+00:00
| 37 | false |
The hardest part of this problem is the calculation of nCk % 10. The naive approach will take O(k) times. However we can speed it up to O(logN) time by using lucas theorem. For mod 2 we can use the fact that nCk % m is odd when n&k ==k.
```python3 []
class Solution:
def lucas(self,n, k):
res = 1
while n or k:
(n, n_i), (k, k_i) = divmod(n,5),divmod(k,5)
res = (res * (comb(n_i, k_i)%5)) % 5
return res
def crt(self,n, k):
r2 = n & k == k
r5 = self.lucas(n, k)
for c in range(10):
if c%2 == r2 and c%5 == r5:
return c
def hasSameDigits(self, s: str) -> bool:
mods = [self.crt(len(s)-2,i) for i in range(len(s)-1)]
return sum(int(c)*mods[i] for i,c in enumerate(s[:-1]))%10 == sum(int(c)*mods[i] for i,c in enumerate(s[1:]))%10
```
| 0 | 0 |
['Python3']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
Extending the common idea of computing binomial coefficient mod prime
|
extending-the-common-idea-of-computing-b-eazp
|
IntuitionWe see a lot of problems in contests requiring us to compute binomial coefficients mod a large prime (for example109+7). This is possible because we kn
|
jianstanleya
|
NORMAL
|
2025-02-24T10:16:12.010480+00:00
|
2025-02-24T10:16:12.010480+00:00
| 26 | false |
# Intuition
We see a lot of problems in contests requiring us to compute binomial coefficients mod a large prime (for example $10^9+7$). This is possible because we know factorials with relatively small factors will always be coprime with this large prime. In this problem, we must find a workaround for mod 10 because the factorials are probably not coprime with it.
# Approach
We can derive the coefficient mod 10 if we find it mod 2 and mod 5. However, the factorials may contain factors of 2 and 5. Therefore, we should find the factorials rid of factors of 2 and 5 to allow safe computation of multiplicative inverse, while keeping track of whether the coefficient is a multiple of 2 or 5.
# Complexity
- Time complexity: $O(N)$
- Space complexity: $O(N)$
# Code
```cpp []
static constexpr int lookup[2][5] = {
{0, 6, 2, 8, 4},
{5, 1, 7, 3, 9}
}, minv2[2] = {-1, 1}, minv5[5] = {-1, 1, 3, 2, 4};
class Solution {
public:
bool hasSameDigits(string s) {
int n = s.size(), a = 0, b = 0;
vector<int> facno2(n), facno5(n), freq2(n, 0), freq5(n, 0);
facno2[0] = facno5[0] = 1;
for(int i = 1; i < n; ++i) {
int p = i, q = i;
while(p % 2 == 0) {
p /= 2;
++freq2[i];
}
while(q % 5 == 0) {
q /= 5;
++freq5[i];
}
facno2[i] = (facno2[i - 1] * p) % 2;
facno5[i] = (facno5[i - 1] * q) % 5;
freq2[i] += freq2[i - 1];
freq5[i] += freq5[i - 1];
}
auto binom2 = [&](int n, int k) {
if(freq2[n] - freq2[n - k] - freq2[k] > 0) return 0;
return (facno2[n] * minv2[facno2[n - k]] * minv2[facno2[k]]) % 2;
};
auto binom5 = [&](int n, int k) {
if(freq5[n] - freq5[n - k] - freq5[k] > 0) return 0;
return (facno5[n] * minv5[facno5[n - k]] * minv5[facno5[k]]) % 5;
};
auto binom10 = [&](int n, int k) {
return lookup[binom2(n, k)][binom5(n, k)];
};
for(int i = 0; i <= (n - 2) / 2; ++i) {
a += binom10(n - 2, i) * (s[i] - '0');
b += binom10(n - 2, i) * (s[i + 1] - '0');
}
for(int i = n - 2; i > (n - 2) / 2; --i) {
a += binom10(n - 2, n - 2 - i) * (s[i] - '0');
b += binom10(n - 2, n - 2 - i) * (s[i + 1] - '0');
}
return a % 10 == b % 10;
}
};
```
| 0 | 0 |
['C++']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
C++, memory beats 100% users, no multiplicative inverse needed, straightforward, simple coding.
|
c-memory-beats-100-users-no-multiplicati-qxe0
|
Although a lot of people are way smarter than I do, I might as well just post my own implementation here, for the sake of joining the party of thousands of leet
|
slothalan
|
NORMAL
|
2025-02-24T04:20:53.884961+00:00
|
2025-02-24T09:59:10.448568+00:00
| 46 | false |
Although a lot of people are way smarter than I do, I might as well just post my own implementation here, for the sake of joining the party of thousands of leetcoders online (-_-). This code's memory usage beats 100% users though.
### Intuition
Quick recap: we can change the base of numbers using simple division.
e.g. 462 (base 10)
= 92 * 5 + 2
= 18 * 5 + 2
= 3 * 5 + 3
= 0 * 5 + 3
= 3322 (base 5)
let string s = "abcdef", each character is a digit.
[a,b,c,d,e,f]
[g,h,i,j,k]
[l,m,n,o]
[p,q,r]
[**A**,**B**]
g=a+b, h=b+c (1 a 2 b 1 c)
l=g+h = (a+b+b+c)+(b+c+c+d) (1 a 3 b 3 c 1 d)
Ha ha, yet another way to represent the mighty Pascal triangle values (-_-)
0C0=1
1C0=1, 1C1=1
2C0=1, 2C1=2, 2C2=1
3C0=1, 3C1=3, 3C2=3, 3C3=1
**A** = a * nC0 +...+ e * nCr
n = string s.length()-2
r = n
s.length() can be 100000. It is not possible to compute, let's say 100000C50000 without causing overflow.
But, with the so-called mighty "Lucas's theorm", nCr mod p, where p is a prime, is equal to:
$${{n}\choose{r}}={{a_{p^{l}}}\choose{b_{p^{l}}}}\times{{c_{p^{l-1}}}\choose{d_{p^{l-1}}}}\times\dots\times{{e_{p^{0}}}\choose{f_{p^{0}}}}$$
Where l is the maximum power such that the coefficient of either n or r with base as p is not zero, and a,b,c,d,e,f are all coefficients.
If the coefficients of either n or r or both with base as p for some power l is 0, then $${{a_{p^{l}}}\choose{b_{p^{l}}}}$$ is 0.
For example:
11C6 (mod 5)
11 (base 10) = 21 (base 5)
6 (base 10) = 11 (base 5)
So, 11C6 = 2C1 * 1C1 = 2 (mod 5)
Using such property, we can identify the last digit of a very large nCr (mod p).
Next, consider this table:
|digit|mod 2|mod 5|
|---|---|---|
|0|0|0|
|1|1|1|
|2|0|2|
|3|1|3|
|4|0|4|
|5|1|0|
|6|0|1|
|7|1|2|
|8|0|3|
|9|1|4|
If we want to identify the last digit of the number, we perform a mod 10, and 10 = 2 * 5, and 2 and 5 are primes.
So, by Lucas's theorem, we can determine the nCr (mod 2) and nCr (mod 5) values, and determine the last digit using the table above.
We cannot directly apply mod 10 to a multiplied value mod by any other values to get the last digit (of course).
Now we can compute **A** as follows:
**A** = (a * (last digit of nC0) +...+ e * (last digit of nCr)) mod 10.
Calculate **B** as well and check whether **A** == **B**.
### Approach
Just directly implement the idea in code.
### Complexity
- Time complexity: $$O(N)$$
- Space complexity: $$O(1)$$
Somehow, there are many different implementations and ideas out there. Here's mine:
### Code
```cpp []
typedef long long int lld;
class Solution {
public:
int M[10][2]={
{0,0},{1,1},{2,0},{3,1},{4,0},
{0,1},{1,0},{2,1},{3,0},{4,1}
};
int C[10][10];
int getOptMod(int n, int r, int p) {
int res=1;
while (n&&r) {
res*=C[n%p][r%p]; res%=p;
n/=p;r/=p;
}
return res;
}
int getD(int& f2, int& f5) {
for (int i=0; i<10; i++) {
if (M[i][0]==f5&&M[i][1]==f2) {return i;}
}
return -1;
}
int getVal(string& s, int st, int en) {
int n=en-st;
int res=0;
for (int i=st; i<=en; i++) {
int d=(int)(s[i]-'0');
int f2=getOptMod(n,i-st,2);
int f5=getOptMod(n,i-st,5);
int mag=getD(f2,f5);
d*=mag;
res+=d;
res%=10;
}
return res;
}
bool hasSameDigits(string s) {
int slen=s.length();
memset(C,0,sizeof(C));
C[0][0]=1;
for (int i=1; i<10; i++) {
C[i][0]=C[i][i]=1;
for (int j=1; j<i; j++) {
C[i][j]=C[i-1][j]+C[i-1][j-1];
}
}
return getVal(s,0,slen-2)==getVal(s,1,slen-1);
}
};
```
Without the Internet, I do not believe that LeetCode would have existed and been used by millions of people.
And solving math and logic puzzles is always a discouraging process for me. Numbers and well-proven formulas are concrete, stubborn, and will never change, and thus a lot of artists always claimed that their creativity supersedes rigid logic. But, when talking about proofing the correctness of formulas, finding new mathematical facts, using math operators to find new truths, or assigning a different meaning to existing facts, all these involves a great deal of creativity and, sometimes, quite counter-intuitive.
I am always saddened by the fact that I have an ordinary brain and being stuck at performing rudimentary work, and I cannot even excel at my job, which is disappointing. If I ever have gifted genetics to accompany with my strong will and justifiable moral values, I could have done so much more in real life and to experience a multitude of intellectual and spiritual activities beyond my current imagination. I think I always deserve it, and I am stuck now.
I do not believe that having more vacations, socializing more with others, etc., will ever make a slight positive change to my own conditions. All these activities will only make use of basic cognitive and physical abilities that everyone knows. I am not trying to be special. I just want a different life experience that money can never buy.
| 0 | 0 |
['C++']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
Check If Digits Are Equal in String After Operations II || Beat 100% Time and Space
|
check-if-digits-are-equal-in-string-afte-grqg
|
Beat 100% Time and Space Complexity Solution for "Check If Digits Are Equal in String After Operations II"This solution efficiently solves the problem using mat
|
hoanghung3011
|
NORMAL
|
2025-02-24T03:02:52.172213+00:00
|
2025-02-24T03:02:52.172213+00:00
| 40 | false |
# Beat 100% Time and Space Complexity Solution for "Check If Digits Are Equal in String After Operations II"
This solution efficiently solves the problem using mathematical insights from combinatorics, modular arithmetic, and Lucas's theorem. The approach avoids repeated string manipulations and leverages precomputed mappings to achieve optimal performance.
---
## Intuition
The problem involves repeatedly summing consecutive digits modulo 10 until only two digits remain. Instead of simulating this process iteratively (which would be computationally expensive for large strings), we recognize that the final result depends on weighted sums of the original digits, where the weights are determined by binomial coefficients modulo 10. Using properties of modular arithmetic and Lucas's theorem, we can compute these weights efficiently.
---
## Approach
1. **Key Insight**:
- The final two digits after all operations depend on weighted sums of the original digits.
- These weights are given by binomial coefficients $ C(L, j) \mod 10 $, where $ L = n - 2 $ (length of the string minus 2).
2. **Efficient Computation**:
- Use Lucas's theorem to compute $ C(n, k) \mod 5 $ efficiently.
- Combine results modulo 2 and modulo 5 to determine $ C(n, k) \mod 10 $ using a precomputed mapping.
3. **Implementation Steps**:
- Precompute mappings for $ C(n, k) \mod 10 $ based on its behavior modulo 2 and modulo 5.
- Compute the weighted sums $ f_0 $ and $ f_1 $ for the first $ L+1 $ and last $ L+1 $ digits, respectively.
- Compare $ f_0 $ and $ f_1 $. If they are equal, return `true`; otherwise, return `false`.
4. **Optimization**:
- Avoid redundant calculations by leveraging bitwise operations for modulo 2 checks.
- Use precomputed small binomial coefficients modulo 5 for efficient computation.
---
## Complexity
- **Time Complexity**: $ O(n) $
- Each digit is processed once, and binomial coefficients are computed in constant time using precomputed tables.
- **Space Complexity**: $ O(1) $
- The solution uses a fixed amount of space for precomputed mappings and temporary variables.
---
## Code
```java
class Solution {
// Precomputed mapping for nCr mod 10:
private static final int[][] MOD10_MAPPING = {
{0, 6, 2, 8, 4}, // when nCr mod2 = 0
{5, 1, 7, 3, 9} // when nCr mod2 = 1
};
public boolean hasSameDigits(String s) {
int n = s.length();
int L = n - 2; // Length of the final operation sequence
int f0 = 0, f1 = 0;
// Compute weighted sums for indices 0..L and 1..(L+1)
for (int j = 0; j <= L; j++) {
int coeff = binomMod10(L, j); // Binomial coefficient mod 10
f0 = (f0 + coeff * (s.charAt(j) - '0')) % 10;
f1 = (f1 + coeff * (s.charAt(j + 1) - '0')) % 10;
}
return f0 == f1;
}
// Compute nCr mod 10 by combining mod2 and mod5 parts
private int binomMod10(int n, int k) {
int mod2 = binomMod2(n, k); // Either 0 or 1
int mod5 = binomMod5(n, k); // Value in {0,1,2,3,4}
return MOD10_MAPPING[mod2][mod5];
}
// nCr mod 2: nCr mod 2 == 1 if and only if every 1-bit in k is contained in n
private int binomMod2(int n, int k) {
return ((n & k) == k) ? 1 : 0;
}
// nCr mod 5 computed via Lucas's theorem
private int binomMod5(int n, int k) {
// Precomputed small binomial coefficients mod 5 for numbers 0..4
int[][] t = {
{1},
{1, 1},
{1, 2, 1},
{1, 3, 3, 1},
{1, 4, 1, 4, 1}
};
int res = 1;
while (n > 0 || k > 0) {
int nDigit = n % 5;
int kDigit = k % 5;
if (kDigit > nDigit) return 0;
res = (res * t[nDigit][kDigit]) % 5;
n /= 5;
k /= 5;
}
return res;
}
}
| 0 | 0 |
['Math', 'Combinatorics', 'Java']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
🔥 Efficient Solution Using Pascal's Triangle, Lucas' Theorem & CRT
|
efficient-solution-using-pascals-triangl-myzt
|
IntuitionAfter Getting Tle haam saab 😭😭Here's the observation:The final two digits are determined by a pattern of additions that follows Pascal's Triangle.Eac
|
BaO0Xk2Xmf
|
NORMAL
|
2025-02-23T18:34:16.623015+00:00
|
2025-02-23T18:34:16.623015+00:00
| 24 | false |
# Intuition
**After Getting Tle haam saab 😭😭**
Here's the observation:
The final two digits are determined by a pattern of additions that follows Pascal's Triangle.
Each digit's contribution to the result can be represented by binomial coefficients.
Instead of running the entire transformation, we can directly compute the two final digits using properties of modular arithmetic and binomial coefficients.
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach


<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: **O(nlogn)**
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: **O(1)**
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int nCrModP(int n, int r, int p) {
if (r == 0) return 1;
int ni = n % p, ri = r % p;
return (nCrModP(n / p, r / p, p) * nCrSmall(ni, ri, p)) % p;
}
int nCrSmall(int n, int r, int p) {
if (r > n) return 0;
if (r == 0 || r == n) return 1;
int res = 1;
for (int i = 0; i < r; i++) {
res = res * (n - i) % p;
res = res * modInverse(i + 1, p) % p;
}
return res;
}
int modInverse(int a, int p) {
int res = 1;
int power = p - 2;
while (power) {
if (power % 2) res = (res * a) % p;
a = (a * a) % p;
power /= 2;
}
return res;
}
int crt(int a, int b) {
for (int i = 0; i < 10; i++) {
if (i % 2 == a && i % 5 == b) {
return i;
}
}
return 0;
}
bool hasSameDigits(string s) {
int n = s.length();
if (n == 2) return s[0] == s[1];
int d1 = 0, d2 = 0;
for (int i = 0; i < n - 1; i++) {
int coef = crt(nCrModP(n - 2, i, 2), nCrModP(n - 2, i, 5));
d1 = (d1 + (s[i] - '0') * coef) % 10;
}
for (int i = 1; i < n; i++) {
int coef = crt(nCrModP(n - 2, i - 1, 2), nCrModP(n - 2, i - 1, 5));
d2 = (d2 + (s[i] - '0') * coef) % 10;
}
return d1 == d2;
}
};
```
| 0 | 0 |
['Math', 'Combinatorics', 'C++']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
NOT Luca's theorem ahh solution✅Both 100%
|
not-lucas-theorem-ahh-solutionboth-100-b-42h4
|
Complexity :
Time complexity:O(n)
Space complexity:O(n)
Code :
|
zabakha
|
NORMAL
|
2025-02-23T17:39:34.394398+00:00
|
2025-02-23T17:39:34.394398+00:00
| 46 | false |
----
# Complexity :
- Time complexity: $O(n)$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $O(n)$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
---
# Code :
```cpp []
class Solution {
int invMod10[10];
int pow2mod10(long long p) {
switch (p % 4) {
case 0: return 6;
case 1: return 2;
case 2: return 4;
default: return 8;
}
}
void factor(int n, int &c2, int &c5, int &r) {
c2 = 0; c5 = 0;
while (n and n % 2 == 0) { n /= 2; c2++; }
while (n and n % 5 == 0) { n /= 5; c5++; }
r = n % 10;
}
int getFinalValue(long long c2, long long c5, int v) {
if (c2 > 0 && c5 > 0) return 0;
int ans = v;
if (c2 > 0) ans = (ans * pow2mod10(c2)) % 10;
if (c5 > 0) ans = (ans * 5) % 10;
return ans;
}
vector<int> getPascalsTriangleRowMod10(int x) {
for(int i=0;i<10;i++) invMod10[i] = -1;
invMod10[1] = 1; invMod10[3] = 7; invMod10[7] = 3; invMod10[9] = 9;
vector<int> res(x+1);
res[0] = 1;
long long c2 = 0, c5 = 0;
int val = 1;
for(int k=1; k<=x; k++){
int a2,a5,rem; factor(x - k + 1, a2, a5, rem);
c2 += a2; c5 += a5; val = (val * rem) % 10;
int b2,b5,brem; factor(k, b2, b5, brem);
c2 -= b2; c5 -= b5; val = (val * invMod10[brem]) % 10;
res[k] = getFinalValue(c2, c5, val);
}
return res;
}
public:
bool hasSameDigits(string s) {
vector<int> p = getPascalsTriangleRowMod10(s.length() - 2);
int res = 0;
for(int i = 0; i < p.size(); i++) {
res = (res + (s[i] - s[i+1]) * p[i] % 10) % 10;
}
return res % 10 == 0;
}
};
```
| 0 | 0 |
['C++']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
Combinatorics
|
combinatorics-by-maxorgus-mrx0
|
Code
|
MaxOrgus
|
NORMAL
|
2025-02-23T15:36:27.063983+00:00
|
2025-02-23T15:36:27.063983+00:00
| 30 | false |
# Code
```python3 []
@cache
def comb2(a,b):
res = 1
while a > 0 or b > 0:
a1 = a % 2
b1 = b % 2
if a1>=b1:
res *= comb(a1,b1)
else: return 0
a = a // 2
b = b // 2
res = res % 2
return res
@cache
def comb5(a,b):
res = 1
while a > 0 or b > 0:
a1 = a % 5
b1 = b % 5
if a1>=b1:
res *= comb(a1,b1)
else: return 0
a = a // 5
b = b // 5
res = res % 5
return res
class Solution:
def hasSameDigits(self, s: str) -> bool:
N = len(s)
a2,b2,a5,b5 = 0,0,0,0
for i in range(N-1):
p = int(s[i])
q = int(s[i+1])
a2 = (a2 + p*comb2(N-2,i)) % 2
b2 = (b2 + q*comb2(N-2,i)) % 2
a5 = (a5 + p*comb5(N-2,i)) % 5
b5 = (b5 + q*comb5(N-2,i)) % 5
return a2==b2 and a5==b5
```
| 0 | 0 |
['Combinatorics', 'Python3']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
My Solution
|
my-solution-by-hope_ma-tduu
| null |
hope_ma
|
NORMAL
|
2025-02-23T13:38:02.777989+00:00
|
2025-02-23T13:38:02.777989+00:00
| 24 | false |
```
/**
* Time Complexity: O(n * log(n))
* Space Complexity: O(1)
* where `n` is the length of the string `s`
*/
class Solution {
private:
static constexpr int mod = 10;
static constexpr int prime_factor2 = 2;
static constexpr int prime_factor5 = 5;
public:
bool hasSameDigits(const string &s) {
constexpr int max_mod = 5;
constexpr char zero = '0';
const int n = static_cast<int>(s.size());
vector<vector<int>> comb(max_mod, vector<int>(max_mod, 0));
for (int i = 0; i < max_mod; ++i) {
for (int j = 0; j < i + 1; ++j) {
if (j == 0) {
comb[i][j] = 1;
} else {
comb[i][j] = comb[i - 1][j] + comb[i - 1][j - 1];
}
}
}
int a1 = 0;
int a2 = 0;
for (int i = 0; i < n - 1; ++i) {
const int c = crt(n - 2, i, comb);
a1 = (a1 + c * (s[i] - zero)) % mod;
a2 = (a2 + c * (s[i + 1] - zero)) % mod;
}
return a1 == a2;
}
private:
int lucas(const int n, const int m, const int p, const vector<vector<int>> &comb) {
if (m == 0) {
return 1;
}
return (lucas(n / p, m / p, p, comb) * comb[n % p][m % p]) % p;
}
int crt(const int n, const int m, const vector<vector<int>> &comb) {
return (prime_factor2 * lucas(n, m, prime_factor5, comb) +
prime_factor5 * lucas(n, m, prime_factor2, comb)) % mod;
}
};
```
| 0 | 0 |
['C++']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
🚀 Lucas' Theorem + CRT | O(n log n) | With Resources 🎯
|
lucas-theorem-crt-on-log-n-with-resource-01vo
|
ResourcesLucas' Theorem
Chinese Remainder TheoremIntuitionInstead of simulating the operations until the string length reduces to 2, we can track how often each
|
piyushk1264
|
NORMAL
|
2025-02-23T11:59:57.882902+00:00
|
2025-02-23T11:59:57.882902+00:00
| 38 | false |
# Resources
[Lucas' Theorem](https://en.wikipedia.org/wiki/Lucas%27s_theorem)
[Chinese Remainder Theorem](https://en.wikipedia.org/wiki/Chinese_remainder_theorem#Systematic_search)
# Intuition
Instead of simulating the operations until the string length reduces to 2, we can track how often each digit contributes to the final two digits. This contribution follows binomial coefficients.
Thus, the problem reduces to efficiently computing binomial coefficients modulo 10.
Using number theory, we compute $$\binom{n}{k} \mod 10$$ by first calculating $$\binom{n}{k} \mod 2$$ and $$\binom{n}{k} \mod 5$$ separately (since $$2 \times 5 = 10$$) and then combining the results using the Chinese Remainder Theorem.
# Approach
1. Compute $$\binom{n}{k} \bmod 10$$
- Here, $$n = \text{s.length} - 2$$.
2. Use Lucas’ Theorem to compute $$\binom{n}{k} \bmod p$$
- This is equivalent to computing $$\binom{n_i}{k_i} \bmod p$$ for each digit in the base $$p$$ representation of $$n$$ and $$k$$.
3. Combine results using the Chinese Remainder Theorem (CRT)
- Given:
- $$x \equiv \text{res}_2 \pmod{2}$$
- $$x \equiv \text{res}_5 \pmod{5}$$
- We solve for $$x$$ modulo 10.
4. Compute the final two digits
- Iterate over adjacent pairs in $$s$$ and use the computed coefficients to track their contribution.
- Compare the resulting first and second digits.
# Complexity
- Time complexity:
Efficiently computed using Lucas’ theorem and CRT, reducing operations to $$O(n \log n)$$
- Space complexity:
$$O(1)$$ as only a few integers are stored
# Code
```cpp []
class Solution {
int binom10(int n, int k) {
int res2 = lucas(n, k, 2);
int res5 = lucas(n, k, 5);
return chineseRemainder(res2, res5, 2, 5);
}
// Naive binomial coefficient
// https://en.wikipedia.org/wiki/Binomial_coefficient#Multiplicative_formula
int binom(int n, int k) {
double product = 1;
for (int i=1; i<=k; i++) {
product *= 1.0 * (n + 1 - i) / i;
}
return (int)product;
}
// https://en.wikipedia.org/wiki/Lucas%27s_theorem
int lucas(int n, int k, int p) {
int product = 1;
while (n > 0 || k > 0) {
int ni = n%p;
int ki = k%p;
if (ki > ni) return 0;
int b = binom(ni, ki);
product = (product * b) % p;
n /= p;
k /= p;
}
return product;
}
// https://en.wikipedia.org/wiki/Chinese_remainder_theorem#Systematic_search
int chineseRemainder(int a1, int a2, int n1, int n2) {
int N = n1*n2;
for (int x=0; x<N; x++) {
if (x % n1 == a1 && x % n2 == a2) {
return x;
}
}
throw "No solution";
}
public:
bool hasSameDigits(string s) {
int n = s.length();
int l = n-2;
int a = 0, b = 0;
for (int i=0; i<n-1; i++) {
int w = binom10(l, i);
int d1 = s[i] - '0';
int d2 = s[i+1] - '0';
a = (a + w * d1) % 10;
b = (b + w * d2) % 10;
}
return a == b;
}
};
```
| 0 | 0 |
['C++']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
[Java] Super fast pre-calculation solution
|
java-super-fast-pre-calculation-solution-wrzd
|
IntuitionNoticed that for somens, the value of(kn)mod10is very sparse, meaning for thosens, there are very limited number ofks that makes(kn)mod10=0.Then we
|
wddd
|
NORMAL
|
2025-02-23T10:46:37.013628+00:00
|
2025-02-23T10:46:37.013628+00:00
| 61 | false |
# Intuition
Noticed that for some $$n$$s, the value of $${n \choose k} \mod 10$$ is very sparse, meaning for those $$n$$s, there are very limited number of $$k$$s that makes $${n \choose k} \mod 10 \ne 0$$.
Then we can try to find those $$n$$s and reduce the input size using them. In the end we can just bruteforcely calculate the final result.
The key is to find those $$n$$s, and pick up about $${\log_2 n}$$ of them.
It is not so easy to have a definite way to find them (requires knowledge of the Lucas theorem), but inituitively, those $$n$$ should likely end with many $$0$$s.
# Complexity
- Time complexity:
About $$O(nlogn)$$
- Space complexity:
$$O(n)$$
# Code
```java []
/*
Runtime 65 ms
Beats 100.00% of users with Java
Memory 46.5 MB
Beats 100.00% of users with Java
*/
class Solution {
static TreeMap<Integer, int[][]> BC_MOD_PRE = new TreeMap<>();
static {
int size = 5;
BC_MOD_PRE.put(size, new int[][] {{0,1},{1,5},{4,5},{5,1}});
size = 20;
BC_MOD_PRE.put(size, new int[][] {{0,1},{4,5},{5,4},{10,6},{15,4},{16,5},{20,1}});
size = 50;
BC_MOD_PRE.put(size, new int[][] {{0,1},{2,5},{16,5},{18,5},{25,2},{32,5},{34,5},{48,5},{50,1}});
size = 130;
BC_MOD_PRE.put(size, new int[][] {{0,1},{2,5},{5,6},{125,6},{128,5},{130,1}});
size = 260;
BC_MOD_PRE.put(size, new int[][] {{0,1},{4,5},{5,2},{10,6},{125,2},{130,4},{135,2},{250,6},{255,2},{256,5},{260,1}});
size = 640;
BC_MOD_PRE.put(size, new int[][] {{0,1},{5,8},{10,8},{15,6},{128,5},{512,5},{625,6},{630,8},{635,8},{640,1}});
size = 1280;
BC_MOD_PRE.put(size, new int[][] {{0,1},{5,6},{25,6},{30,6},{256,5},{625,2},{630,2},{650,2},{655,2},{1024,5},{1250,6},{1255,6},{1275,6},{1280,1}});
size = 3200;
BC_MOD_PRE.put(size, new int[][] {{0,1},{25,8},{50,8},{75,6},{128,5},{1024,5},{1152,5},{2048,5},{2176,5},{3072,5},{3125,6},{3150,8},{3175,8},{3200,1}});
size = 6400;
BC_MOD_PRE.put(size, new int[][] {{0,1},{25,6},{125,6},{150,6},{256,5},{2048,5},{2304,5},{3125,2},{3150,2},{3250,2},{3275,2},{4096,5},{4352,5},{6144,5},{6250,6},{6275,6},{6375,6},{6400,1}});
size = 16400;
BC_MOD_PRE.put(size, new int[][] {{0,1},{16,5},{25,6},{125,6},{150,6},{625,6},{650,6},{750,6},{775,6},{15625,6},{15650,6},{15750,6},{15775,6},{16250,6},{16275,6},{16375,6},{16384,5},{16400,1}});
size = 53250;
BC_MOD_PRE.put(size, new int[][] {{0,1},{2,5},{125,6},{3125,2},{3250,2},{4096,5},{4098,5},{6250,6},{6375,6},{15625,8},{15750,8},{16384,5},{16386,5},{18750,6},{18875,6},{20480,5},{20482,5},{21875,8},{22000,8},{31250,8},{31375,8},{32768,5},{32770,5},{34375,6},{34500,6},{36864,5},{36866,5},{37500,8},{37625,8},{46875,6},{47000,6},{49152,5},{49154,5},{50000,2},{50125,2},{53125,6},{53248,5},{53250,1}});
size = 82000;
BC_MOD_PRE.put(size, new int[][] {{0,1},{16,5},{64,5},{80,5},{125,6},{625,6},{750,6},{3125,6},{3250,6},{3750,6},{3875,6},{16384,5},{16400,5},{16448,5},{16464,5},{65536,5},{65552,5},{65600,5},{65616,5},{78125,6},{78250,6},{78750,6},{78875,6},{81250,6},{81375,6},{81875,6},{81920,5},{81936,5},{81984,5},{82000,1}});
}
public boolean hasSameDigits(String s) {
List<Integer> digits = new ArrayList<>();
for (char c : s.toCharArray()) {
digits.add(c - '0');
}
int n = digits.size() - 2;
Integer last = BC_MOD_PRE.floorKey(n);
while (last != null) {
List<Integer> next = new ArrayList<>();
for (int i = 0; i + last < digits.size(); i++) {
int result = 0;
for (int[] map : BC_MOD_PRE.get(last)) {
result += map[1] * digits.get(i + map[0]);
}
next.add(result % 10);
}
digits = next;
n = digits.size() - 2;
last = BC_MOD_PRE.floorKey(n);
}
if (digits.size() == 2) {
return digits.get(0) == digits.get(1);
}
return hasSameDigits(digits);
}
private boolean hasSameDigits(List<Integer> digits) {
int n = digits.size() - 2;
long b = 1;
int[] bc = new int[n + 1];
bc[0] = 1;
for (int i = 1; i <= n / 2; i++) {
b = b * (n - i + 1) / i;
bc[i] = (int) (b % 10);
}
int r1 = 0;
for (int i = 0; i < digits.size() - 1; i++) {
r1 += digits.get(i) * bc[Math.min(i, n - i)];
r1 %= 10;
}
int r2 = 0;
for (int i = 1; i < digits.size(); i++) {
r2 += digits.get(i) * bc[Math.min(i - 1, n - i + 1)];
r2 %= 10;
}
return r1 == r2;
}
}
```
| 0 | 0 |
['Math', 'Java']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
Binomial coefficient | Simple solution with 100% beaten
|
binomial-coefficient-simple-solution-wit-4qxf
|
Has Same Digits CheckIntuitionThe goal is to check if a given string of digits can be reduced to two identical digits using a transformation rule based on binom
|
Takaaki_Morofushi
|
NORMAL
|
2025-02-23T08:46:05.873650+00:00
|
2025-02-23T08:46:05.873650+00:00
| 41 | false |
# Has Same Digits Check
## Intuition
The goal is to check if a given string of digits can be reduced to two identical digits using a transformation rule based on binomial coefficients modulo 10.
## Approach
1. Compute binomial coefficients modulo 10 efficiently using properties of mod 2 and mod 5.
2. Use the Chinese Remainder Theorem to combine results.
3. Sum the transformed digits and check if the last two remaining digits are the same.
## Complexity
- **Time Complexity:** $$O(n \log n)$$ due to efficient binomial coefficient calculations.
- **Space Complexity:** $$O(1)$$ since we use only a few integer variables.
## Code
```cpp
#include <vector>
#include <string>
using namespace std;
class Solution {
public:
bool hasSameDigits(string s) {
int n = s.size();
if (n < 2) return false; // Edge case
int N = n - 2, f0 = 0, f1 = 0;
for (int j = 0; j <= N; j++) {
int c = binomMod10(N, j);
f0 = (f0 + c * (s[j] - '0')) % 10;
f1 = (f1 + c * (s[j + 1] - '0')) % 10;
}
return f0 == f1;
}
private:
int binomMod10(int n, int k) {
int r2 = (n & k) == k; // C(n, k) mod 2
int r5 = binomMod5(n, k); // C(n, k) mod 5
return chineseRemainder(r2, 2, r5, 5);
}
int binomMod5(int n, int k) {
static const int t[5][5] = {
{1}, {1, 1}, {1, 2, 1}, {1, 3, 3, 1}, {1, 4, 1, 4, 1}
};
int res = 1;
while (n || k) {
int nd = n % 5, kd = k % 5;
if (kd > nd) return 0;
res = (res * t[nd][kd]) % 5;
n /= 5, k /= 5;
}
return res;
}
int chineseRemainder(int r1, int m1, int r2, int m2) {
for (int x = 0; x < m1 * m2; x++) {
if (x % m1 == r1 && x % m2 == r2) return x;
}
return 0;
}
};
```
| 0 | 0 |
['C++']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
Why is using the mod feature wrong?
|
why-is-using-the-mod-feature-wrong-by-yl-fh03
|
Can some one help me to find out why using the mod feature is wrong?We know the mod feature that (x%10 + y%10)%10 == (x+y)%10.Suppose the string is: abcdefAfter
|
ylf951
|
NORMAL
|
2025-02-23T08:37:10.871572+00:00
|
2025-02-23T08:37:10.871572+00:00
| 50 | false |
Can some one help me to find out why using the mod feature is wrong?
We know the mod feature that (x%10 + y%10)%10 == (x+y)%10.
Suppose the string is: abcdef
After the 1st loop, we'll get: ```(a+b) %10, (b+c) %10, (c+d)%10, (d+e)%10, (e+f)%10```.
Since ```(x%10 + y%10)%10 == (x+y)%10```, we should have ```((a+b) %10, (b+c) %10)%10 -> (a+2b+c)%10```.
After the 2nd loop, we'll get: ```(a+2b+c)%10, (b+2c+d)%10, (c+2d+e)%10, (d+2e+f)%10```.
After the 3rd loop, we'll get: ```(a+3b+3c+d)%10, (b+3c+3d+e)%10, (c+3d+3e+f)%10```.
After the 4th loop, we'll get: ```(a+4b+4c+4d+e)%10, (b+4c+4d+4e+f)%10```.
Based on this, for case "321881" which a=3, b=2, c=1, d=8, e=8, f=1,
The final 2 digits should be ```(a+4b+4c+4d+e)%10``` and ```(b+4c+4d+4e+f)%10``` which is ```(3+4*(2+1+8)+8)%10, (2+4*(1+8+8)+1)%10 -> 5,1```.
But the actual result is the following:
321881
1st loop: 5, 3, 9, 6, 9
2nd loop: 8, 2, 5, 5
3rd loop: 0, 7, 0
4th loop: 7, 7
These two results -- (5,1) and (7,7) -- are not the same, why? I cannot find out where is wrong...
| 0 | 0 |
['C++']
| 2 |
check-if-digits-are-equal-in-string-after-operations-ii
|
Binomial Approach + Code + Video Explanation
|
binomial-approach-code-video-explanation-9cl5
|
Video ExplanationCode
|
akgupta0777
|
NORMAL
|
2025-02-23T08:28:31.616446+00:00
|
2025-02-23T08:28:31.616446+00:00
| 43 | false |
# Video Explanation
https://www.youtube.com/watch?v=g5Ygoa9uRQc
# Code
```cpp []
static int boost = [](){std::ios::sync_with_stdio(0);cin.tie(nullptr);cout.tie(nullptr);return 0;}();
class Solution {
public:
int getBinCoeffMod10(int n, int k) {
int coeffMod2 = getBinCoeffMod2(n, k);
int coeffMod5 = getBinCoeffMod5(n, k);
for (int i = 0; i < 10; i++) {
if (i % 2 == coeffMod2 && i % 5 == coeffMod5)
return i;
}
return 0;
}
int getBinCoeffMod2(int n, int k) {
while (k > 0) {
if ((k & 1) > (n & 1))
return 0;
n >>= 1;
k >>= 1;
}
return 1;
}
int getBinCoeffMod5(int n, int k) {
int res = 1;
while (n > 0 || k > 0) {
int nd = n % 5;
int kd = k % 5;
if (kd > nd)
return 0;
res = (res * getBinCoeff(nd, kd)) % 5;
n /= 5;
k /= 5;
}
return res;
}
int getBinCoeff(int n, int k) {
if (k > n)
return 0;
int fact[5] = {1, 1, 2, 1, 4};
int numerator = fact[n];
int denominator = (fact[k] * fact[n - k]) % 5;
int deninv = 0;
for (int i = 0; i < 5; i++) {
if ((denominator * i) % 5 == 1) {
deninv = i;
break;
}
}
return (numerator * deninv) % 5;
}
bool hasSameDigits(string s) {
int n = s.size();
int iterations = n - 2;
int first = 0, second = 0;
for (int i = 0; i <= iterations; ++i) {
int coefficient = getBinCoeffMod10(iterations, i);
int digit1 = s[i] - '0';
int digit2 = s[i + 1] - '0';
first = (first + coefficient * digit1) % 10;
second = (second + coefficient * digit2) % 10;
}
return first == second;
}
};
```
| 0 | 0 |
['Math', 'Bit Manipulation', 'Combinatorics', 'C++']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
Just the explanation
|
just-the-explanation-by-shivambangia-d0xh
|
Let’s break down what the explanation means:1. The Problem Setup:You’re given a string of digits. You need to reduce this string repeatedly by taking every pair
|
shivambangia
|
NORMAL
|
2025-02-23T08:05:28.992121+00:00
|
2025-02-23T08:05:28.992121+00:00
| 25 | false |
Let’s break down what the explanation means:
1. The Problem Setup:
You’re given a string of digits. You need to reduce this string repeatedly by taking every pair of adjacent digits, adding them together, and then taking the result modulo 10 (i.e. keeping only the last digit of the sum). You do this repeatedly until only two digits remain. Finally, you check if these two remaining digits are the same.
2. The Key Observation – Connection to Binomial Expansion:
Although it might look like you’re just doing a series of additions, there’s a hidden structure. If you write out how each digit from the original string affects the final two digits, you’ll notice that the process is similar to a binomial expansion. In a binomial expansion (like (a + b)^n), each term has a coefficient (a binomial coefficient) that tells you how many ways that term can be formed.
Here, each digit’s contribution to the final result can be thought of as being multiplied by a certain binomial coefficient—this tells you “how many times” (or with what weight) that digit shows up in the final two digits.
3. Working Modulo 10:
Since every operation is done modulo 10, you only care about these coefficients modulo 10. However, 10 is a composite number (10 = 2 × 5), so directly computing binomial coefficients modulo 10 is tricky.
4. Efficient Computation with Lucas’ Theorem:
To handle this, you break the problem into two parts:
• Compute the binomial coefficients modulo 2.
• Compute the binomial coefficients modulo 5.
Lucas’ Theorem is a mathematical tool that makes it easier to compute binomial coefficients modulo a prime (or a prime power). After you get the coefficients modulo 2 and modulo 5, you combine them using the Chinese Remainder Theorem (which is a way to solve congruences) to obtain the coefficients modulo 10.
5. Using the Coefficients to Compute the Final Result:
Once you have the relevant binomial coefficients modulo 10, you can use them to determine the contribution of each digit in the original string toward the final two digits. You do this using modular arithmetic, accumulating the contributions into two sums (let’s call them s1 and s2 for the two final digits).
6. Checking the Answer:
Finally, after computing these sums (again, modulo 10), you compare the two digits. If they’re the same, you return true; otherwise, false.
7. Complexity Considerations:
The explanation also mentions time and space complexity. Although it doesn’t give exact numbers in the snippet, it hints that by using properties of binomial coefficients and Lucas’ Theorem, the solution can be made efficient despite the underlying combinatorial nature of the problem.
| 0 | 0 |
['C++']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
LeetCode (X) LeetMath (O) C++ solution with Lucas' Theorem for Pascal's triangle
|
leetcode-x-leetmath-o-c-solution-with-lu-a1bl
|
IntuitionSince the length of s can be up to 100,000, the only feasible approach is to use Lucas' Theorem to compute the (n−2)th row of Pascal's triangle.A brute
|
william6715
|
NORMAL
|
2025-02-23T06:10:06.133443+00:00
|
2025-02-23T10:21:23.904456+00:00
| 70 | false |
# Intuition
Since the length of s can be up to 100,000, the only feasible approach is to use Lucas' Theorem to compute the (n−2)th row of Pascal's triangle.
A brute-force approach will inevitably result in an overflow in any programming language.
The math theory background is needed.
Lucas' Theorem: https://en.wikipedia.org/wiki/Pascal%27s_triangle
# Approach
We can easy know that the final two word can be calculate with $$\Sigma s[i]*\binom{n-2}{i}$$ and $$\Sigma s[i+1]*\binom{n-2}{i}$$.
However, the n can be 100000, and the $$\binom{n}{n/2}$$ can be 30000 digits. No any type can handle it.
Therefore, we need to use Lucas' Theorem to module the number first.
$${\displaystyle {\binom {m}{n}}\equiv \prod _{i=0}^{k}{\binom {m_{i}}{n_{i}}}{\pmod {p}}}$$
p can only be prime number, so we use 2 and 5.
# Complexity
- Time complexity:
O(n)
- Space complexity:
O(n)
# Code
```cpp []
class Solution {
public:
bool hasSameDigits(string s) {
int n = s.size();
vector<int> matrix(n-1);
for(int i=0; i<n-1; ++i){
// Use Lucas's theorem, Calculate C(n-2,i)
matrix[i] = Lucas(n-2, i);
}
int first = 0;
int second = 0;
for(int i=0; i<n-1; ++i){ // i: 0 ~ n-2 and i+1: 1 ~ n-1
first += (s[i]-'0') * matrix[i];
second += (s[i+1]-'0') * matrix[i];
}
first %= 10;
second %= 10;
return first == second;
}
int Lucas(int n, int k){
int val2 = Lucas2(n, k);
int val5 = Lucas5(n, k);
return val5 % 2 == val2? val5 : val5 + 5;
}
int Lucas2(int n, int k){
while(k > 0){ // when k < 0, C(X,0) is always 1
int nn = n%2;
int kk = k%2;
if(kk > nn) return 0;
n/=2;
k/=2;
}
return 1; // both C(1,0) or C(0,0) is 1
}
int Lucas5(int n, int k){
int res = 1;
while(k > 0){ // when k < 0, C(X,0) is always 1
int nn = n%5;
int kk = k%5;
if(kk > nn) return 0;
res *= combination(nn, kk);
n/=5;
k/=5;
}
return res % 5;
}
// Calculate C(n,k)
int combination(int n, int k){
int res = 1;
for(int i=0; i<k; ++i){
res *= n-i;
res /= i+1;
}
return res;
}
};
```
| 0 | 0 |
['C++']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
Hack! Just for fun
|
hack-just-for-fun-by-dzeko-l278
|
Just a hackCode
|
dzeko
|
NORMAL
|
2025-02-23T04:58:01.375790+00:00
|
2025-02-23T04:58:01.375790+00:00
| 131 | false |
Just a hack
# Code
```python3 []
class Solution:
def hasSameDigits(self, s: str) -> bool:
n = len(s) - 2
first, second = 0, 0
c = [1]
coeff = 1
for k in range(n + 1):
mod_coeff = coeff % 10
first = (first + mod_coeff * (ord(s[k]) - ord('0'))) % 10
second = (second + mod_coeff * (ord(s[k + 1]) - ord('0'))) % 10
if k < n//2 :
if coeff % 10000000 == 0:
coeff = 0
else:
coeff = coeff * (n - k) // (k + 1) if k < n else 1
c.append(coeff)
else:
coeff = c[n - 1 - k]
c.append(coeff)
# print(c[:15])
# print(c[-15:])
return first == second
```
| 0 | 0 |
['Python3']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
O(N) Solution | Easy explanation
|
on-solution-easy-explanation-by-sarthak_-i589
|
IntuitionThe sum of all digits (modulo 10) should be zero for the number to have digits satisfying the condition.This ensures that the number retains its origin
|
Sarthak_0909k
|
NORMAL
|
2025-02-23T04:10:41.668040+00:00
|
2025-02-23T04:10:41.668040+00:00
| 282 | false |
# Intuition
The sum of all digits (modulo 10) should be zero for the number to have digits satisfying the condition.This ensures that the number retains its original properties when considering mod constraints.
# Complexity
- Time complexity:O(N)
- Space complexity: (1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
bool hasSameDigits(string number) {
string original = number;
int length = number.size();
int lastIndex = length - 2;
int sumFirstPattern = 0, sumSecondPattern = 0;
for (int i = 0; i <= lastIndex; ++i) {
int patternMod2 = computeCombinationMod(lastIndex, i, 2);
int patternMod5 = computeCombinationMod(lastIndex, i, 5);
int multiplier = getMultiplier(patternMod2, patternMod5);
sumFirstPattern = (sumFirstPattern + multiplier * (number[i] - '0')) % 10;
sumSecondPattern = (sumSecondPattern + multiplier * (number[i + 1] - '0')) % 10;
}
return sumFirstPattern == sumSecondPattern;
}
private:
int computeFactorialMod(int num, int r, int mod) {
if (r > num) return 0;
if (mod == 2) {
return ((r & ~num) == 0) ? 1 : 0;
} else {
int factorial[5], modularInverse[5];
factorial[0] = 1;
for (int i = 1; i < 5; ++i) {
factorial[i] = (factorial[i - 1] * i) % 5;
}
for (int i = 0; i < 5; ++i) {
modularInverse[i] = computeModularInverse(factorial[i], 3, 5);
}
return ((factorial[num] * modularInverse[r]) % 5 * modularInverse[num - r]) % 5;
}
}
int computeCombinationMod(int num, int r, int mod) {
int result = 1;
while (num || r) {
int numMod = num % mod, rMod = r % mod;
if (rMod > numMod) return 0;
result = (result * computeFactorialMod(numMod, rMod, mod)) % mod;
num /= mod;
r /= mod;
}
return result;
}
int getMultiplier(int mod2, int mod5) {
for (int i = 0; i < 10; ++i) {
if (i % 2 == mod2 && i % 5 == mod5) return i;
}
return 0;
}
int computeModularInverse(int base, int exponent, int mod) {
int result = 1;
while (exponent) {
if (exponent & 1) result = (result * base) % mod;
base = (base * base) % mod;
exponent /= 2;
}
return result;
}
bool isPalindrome(string str) {
int left = 0, right = str.size() - 1;
while (left < right) {
if (str[left++] != str[right--]) return false;
}
return true;
}
vector<int> sieve(int maxLimit) {
vector<int> isPrime(maxLimit + 1, 1);
isPrime[0] = isPrime[1] = 0;
for (int i = 2; i <= maxLimit; ++i) {
if (isPrime[i]) {
for (int j = i * i; j <= maxLimit; j += i)
isPrime[j] = 0;
}
}
vector<int> primes;
for (int i = 2; i <= maxLimit; ++i) {
if (isPrime[i]) primes.push_back(i);
}
return primes;
}
int factorialMod(int num) {
int result = 1;
for (int i = 2; i <= num; ++i)
result = (1LL * result * i) % 1000000007;
return result;
}
int modularExponentiation(long long base, long long exponent, long long mod) {
long long result = 1;
while (exponent) {
if (exponent & 1) result = (result * base) % mod;
base = (base * base) % mod;
exponent >>= 1;
}
return result;
}
long long modularInverse(long long num, long long mod) {
return modularExponentiation(num, mod - 2, mod);
}
};
```
| 0 | 1 |
['C++']
| 2 |
kth-smallest-product-of-two-sorted-arrays
|
[Python] binary search solution, explained
|
python-binary-search-solution-explained-x2rtt
|
The idea of this problem is to use binary search: let check(x) be the answer to the question: how many products are less or equal than x. Then we use binary sea
|
dbabichev
|
NORMAL
|
2021-10-16T16:00:41.165294+00:00
|
2021-10-16T18:15:43.598947+00:00
| 10,697 | false |
The idea of this problem is to use binary search: let `check(x)` be the answer to the question: how many products are less or equal than `x`. Then we use binary search and find the first moment where we have exactly `k` such numbers.\n\n1. If `n1` is positive, then values in `nums2 * n1` go in increasing order, so we use bisect to find number of values which are `<= x//n1`.\n2. If `n1` is negative, then values in `nums2 * n1` going in decreasing order, so we need to take the right part.\n3. If `n1` equal to `0`, than all values in `nums2 * n1` are equal to `0`. So, we update `total` only if `x >= 0`.\n\n#### Complexity\nTime complexity is `O(n*log m* log N)`, where `n = len(nums1)`, `m = len(nums2)` and `N = 10**10 + 10` is the maximum value of product. Space complexity is `O(1)`\n\n\n#### Code\n```python\nfrom bisect import bisect, bisect_left\n\nclass Solution:\n def kthSmallestProduct(self, nums1, nums2, k):\n def check(x):\n total = 0\n for n1 in nums1:\n if n1 > 0: total += bisect(nums2, x//n1)\n if n1 < 0: total += len(nums2) - bisect_left(nums2, ceil(x/n1))\n if n1 == 0 and x >= 0: total += len(nums2)\n\n return total\n\n beg, end = -10**10 - 1, 10**10 + 1\n\n while beg + 1 < end:\n mid = (beg + end)//2\n if check(mid) >= k:\n end = mid\n else:\n beg = mid\n\n return beg + 1\n```\n\nIf you have any questoins, feel free to ask. If you like the solution and explanation, please **upvote!**
| 107 | 6 |
['Binary Search']
| 17 |
kth-smallest-product-of-two-sorted-arrays
|
[Python] Binary Search, O((m+n)log10^10)
|
python-binary-search-omnlog1010-by-lee21-osy9
|
Intuition\nBinary search the result, and count the number of smaller product.\n\nWe can firstly consider the simple situation with no negatives.\nThe base of th
|
lee215
|
NORMAL
|
2021-10-16T16:19:21.387996+00:00
|
2021-10-16T16:19:21.388024+00:00
| 10,240 | false |
# **Intuition**\nBinary search the result, and count the number of smaller product.\n\nWe can firstly consider the simple situation with no negatives.\nThe base of this question is the two sum problem.\n\nIn two sum problem,\nwe can count the number of pair with sum <= x.\n\nIn this two product problem,\nwe need to count the number of pair with product <= x.\n<br>\n\n# **Complexity**\nTime `O((m+n)log10^10)`\nSpace `O(n+m)`\n<br>\n\n**Python**\n```py\n def kthSmallestProduct(self, A, B, k):\n n, m = len(A), len(B)\n A1,A2 = [-a for a in A if a < 0][::-1], [a for a in A if a >= 0]\n B1,B2 = [-a for a in B if a < 0][::-1], [a for a in B if a >= 0]\n\n neg = len(A1) * len(B2) + len(A2) * len(B1)\n if k > neg:\n k -= neg\n s = 1\n else:\n k = neg - k + 1\n B1, B2 = B2,B1\n s = -1\n\n def count(A, B, x):\n res = 0\n j = len(B) - 1\n for i in xrange(len(A)):\n while j >= 0 and A[i] * B[j] > x:\n j -= 1\n res += j + 1\n return res\n\n left, right = 0, 10**10\n while left < right:\n mid = (left + right) / 2\n if count(A1, B1, mid) + count(A2, B2, mid) >= k:\n right = mid\n else:\n left = mid + 1\n return left * s\n```\n
| 82 | 6 |
[]
| 17 |
kth-smallest-product-of-two-sorted-arrays
|
Binary Search and Two Pointers
|
binary-search-and-two-pointers-by-votrub-qh6s
|
There are a few problems like this. Generating products directly is expensive.\n\nHowever, finding how many products are less than a given number m can be done
|
votrubac
|
NORMAL
|
2021-10-18T08:58:12.238522+00:00
|
2021-10-18T17:50:45.033399+00:00
| 7,829 | false |
There are a few problems like this. Generating products directly is expensive.\n\nHowever, finding how many products are *less* than a given number `m` can be done in a linear time by using the two pointers approach. Initially, `p1` points to the first element in the first array, and `p2` - the last element in the second array. For each element `p1`, we move `p2` to the left if the product is higher than `m`. The number of products therefore is defined by the position of `p2` in each step.\n\nFor example, we have `19` products less than `15` for these arrays `[1, 2, 3, 4, 5] [1, 2, 3, 4, 5]`:\n\n| p1 | p2 | products |\n| - | - | - | \n|[1]|[5]|[1, 2, 3, 4, 5]\n|[2]|[5]|[2,4,6,8,10]|\n|[3]|[4]|[3, 6, 9, 12]|\n|[4]|[3]|[4, 8, 12]|\n|[5]|[2]|[5, 10]|\n\nSo, we binary-search for a value `m`, count products less than `m`, and return the smallest value where the number of products is exactly `k`.\n\nThe trick here is that we have both positive and negative numbers. I broke my head trying to figure out the pointers algebra. So, instead I just created new arrays for positives, negatives, and the reverse versions of those. The `count` function uses two pointers to count values. We use the same function for all four cases, though we will need to pass array in the correct order, depending on:\n- All numbers are non-negative (positive and zero).\n\t- Original order for both arrays\n- All numbers are negative.\n\t- Reverse order for both arrays\n- One array is negative, and the other is positive.\n\t- Reverse order for the positive one, original for negative.\n\n**C++**\n```cpp\nlong long count(vector<int>& n1, vector<int>& n2, long long m) {\n long long cnt = 0;\n for (int p1 = 0, p2 = n2.size() - 1; p1 < n1.size(); ++p1) {\n while (p2 >= 0 && (long long)n1[p1] * n2[p2] > m)\n --p2;\n cnt += p2 + 1;\n }\n return cnt;\n}\nlong long kthSmallestProduct(vector<int>& n1, vector<int>& n2, long long k) {\n auto lp = lower_bound(begin(n1), end(n1), 0), rp = lower_bound(begin(n2), end(n2), 0);\n vector<int> neg1(begin(n1), lp), neg2(begin(n2), rp);\n vector<int> pos1(lp, end(n1)), pos2(rp, end(n2));\n vector<int> pos1_r(rbegin(pos1), rend(pos1)), pos2_r(rbegin(pos2), rend(pos2));\n vector<int> neg1_r(rbegin(neg1), rend(neg1)), neg2_r(rbegin(neg2), rend(neg2)); \n long long l = -10000000000, r = 10000000000;\n while (l < r) {\n long long m = (l + r - 1) / 2, cnt = 0;\n if (m >= 0)\n cnt = count(neg1_r, neg2_r, m) + count(pos1, pos2, m) \n + neg1.size() * pos2.size() + neg2.size() * pos1.size();\n else\n cnt = count(pos2_r, neg1, m) + count(pos1_r, neg2, m);\n if (cnt < k) \n l = m + 1;\n else\n r = m;\n }\n return l;\n}\n```
| 53 | 1 |
[]
| 8 |
kth-smallest-product-of-two-sorted-arrays
|
Java Double Binary Search O(log10^10 x MlogN)
|
java-double-binary-search-olog1010-x-mlo-p074
|
Thinking Process\n I can put the index pair for the two arrays in a priority queue and compute the answer gradually. However, the K can be up to 10^9. This will
|
hdchen
|
NORMAL
|
2021-10-16T16:36:10.972799+00:00
|
2021-10-16T17:22:57.833429+00:00
| 6,474 | false |
**Thinking Process**\n* I can put the index pair for the two arrays in a priority queue and compute the answer gradually. However, the K can be up to 10^9. This will lead to TLE.\n* The element can be negative. Maybe I need to know the number of negative elements and handle 4 different combinations: (negative array 1, negative array 2), (negative array 1, positive array 2), (positive array 1, negative array 2), (positive array 1, positive array 2). At least, I can know the number of products of each combination and locate k-th product among them.\n* Even though I know which combination the k-th product belongs to, it doesn\'t guarantee I can use the priority queue approach. I need another hint.\n* Continue with above, I think I need some way to eliminate some number of products step by step to reach the goal.\n* Since the array is sorted, if I turn my attention on nums1[i] x nums2[j], I can know there are j + 1 products which are less than or equal to nums1[i] x nums2[j] that are generated by nums1[i]. Then I realize that I should try the binary search.\n\n**Algorithm**\n* Binary search the answer\n* For each nums1[i], count the number of products that are less than or equal to the current guess\n\n**Quick Implementation during the contest** \n```\nclass Solution {\n static long INF = (long) 1e10;\n public long kthSmallestProduct(int[] nums1, int[] nums2, long k) {\n int m = nums1.length, n = nums2.length;\n long lo = -INF - 1, hi = INF + 1;\n while (lo < hi) { \n long mid = lo + ((hi - lo) >> 1), cnt = 0;\n for (int i : nums1) {\n if (0 <= i) {\n int l = 0, r = n - 1, p = 0;\n while (l <= r) {\n int c = l + ((r - l) >> 1);\n long mul = i * (long) nums2[c];\n if (mul <= mid) {\n p = c + 1;\n l = c + 1;\n } else r = c - 1;\n }\n cnt += p;\n } else {\n int l = 0, r = n - 1, p = 0;\n while (l <= r) {\n int c = l + ((r - l) >> 1);\n long mul = i * (long) nums2[c];\n if (mul <= mid) {\n p = n - c;\n r = c - 1;\n } else l = c + 1;\n }\n cnt += p;\n }\n }\n if (cnt >= k) {\n hi = mid;\n } else lo = mid + 1L;\n }\n return lo;\n }\n}\n```
| 46 | 2 |
['Binary Tree', 'Java']
| 3 |
kth-smallest-product-of-two-sorted-arrays
|
C++ | Answer on Binary Search
|
c-answer-on-binary-search-by-chandanagra-q798
|
The idea of this problem is to use binary search on answer -\nLet check(x) be the answer to the question: how many products are less or equal than x. \nThen we
|
chandanagrawal23
|
NORMAL
|
2021-10-16T16:33:14.940831+00:00
|
2021-10-16T16:47:50.378916+00:00
| 5,967 | false |
The idea of this problem is to use binary search on answer -\nLet check(x) be the answer to the question: how many products are less or equal than x. \nThen we use binary search and find the first moment where we have exactly k such numbers .\n```\nclass Solution {\npublic:\n bool check(long long midval,vector<int>& nums1, vector<int>& nums2, long long k){\n long long cnt=0;\n for(int i=0;i<nums1.size();i++)\n {\n long long val=nums1[i];\n \n\t\t\t//If val == 0, product of val and each element in nums2 will be 0. And if midval>=0, then because all\n\t\t\t//products are 0, all products will be smaller or equal to midval. So we can add all products in the answer\n\t\t\tif(val==0 and midval>=0)\n cnt+=nums2.size();\n \n else if(val>0)\n cnt+=findmaxIndex(nums2,val,midval);\n \n else if(val<0)\n cnt+=findminIndex(nums2,val,midval);\n }\n return cnt>=k;\n }\n \n int findmaxIndex(vector<int>&nums2 , long long val , long long midval)\n {\n int l = 0 , r = nums2.size()-1 , res= -1;\n while(l<=r)\n {\n long long mid = (l+r)/2;\n if(val*nums2[mid]<=midval)\n {\n res=mid;\n l=mid+1;\n }\n else r=mid-1;\n }\n return res+1;\n }\n \n int findminIndex(vector<int>&nums2 , long long val , long long midval)\n {\n int l = 0 , r = nums2.size()-1 , res= r+1;\n while(l<=r)\n {\n long long mid = (l+r)/2;\n if(val*nums2[mid]<=midval)\n {\n res=mid;\n r=mid-1;\n }\n else l=mid+1;\n }\n return nums2.size()-res;\n }\n \n long long kthSmallestProduct(vector<int>& nums1, vector<int>& nums2, long long k) {\n long long l=-1e10,r=1e10,res=-1;\n while(l<=r){\n long long mid = (l+r)/2;\n // cout<<mid<<endl;\n if(check(mid,nums1,nums2,k)) {\n res=mid;\n r=mid-1;\n }\n else l=mid+1;\n }\n return res;\n }\n};\n```\n\nAlso If you can try , try this - "https://codingcompetitions.withgoogle.com/kickstart/round/0000000000201b77/0000000000201c95#problem"
| 45 | 2 |
['C', 'Binary Tree']
| 5 |
kth-smallest-product-of-two-sorted-arrays
|
Binary search with detailed explanation
|
binary-search-with-detailed-explanation-v5xqg
|
Note: credit goes to lee215 for the inverse/reverse trick\n\n### Step 1. k\'th smallest product for lists with only positive numbers\n\nImagine that there are o
|
sebnyberg
|
NORMAL
|
2021-10-16T22:17:58.943896+00:00
|
2022-10-27T14:20:02.461397+00:00
| 3,168 | false |
***Note: credit goes to lee215 for the inverse/reverse trick***\n\n### Step 1. k\'th smallest product for lists with only positive numbers\n\nImagine that there are only positive numbers, and we want to find the k\'th smallest number.\n\nConsider the two lists `a=[1,2,3]` and `b=[1,5,8]`. Their products form a matrix:\n\n| - | 1 | 2 | 3 |\n| --- | --- | --- | --- |\n| __1__ | 1 | 2 | 3 |\n| __5__ | 5 | 10 | 15 |\n| __8__ | 8 | 18 | 24 |\n\nAssuming that we guess a number `x`, then it\'s possible to quickly determine how many numbers are smaller than `x`. Just iterate row by row, moving a right pointer left until the condition is satisfied and count the number of elements before the pointer:\n\n```go\nfunc count(a, b []int, val int) int {\n\tvar count int\n\tj := len(b) - 1\n\tfor i := range a {\n\t\tfor j >= 0 && a[i]*b[j] > val {\n\t\t\tj--\n\t\t}\n\t\tcount += j + 1\n\t}\n\treturn count\n}\n```\n\nWith this approach, it\'s easy to find the k\'th positive number using binary search:\n\n```go\nvar lo, hi int = 0, 1e10\nfor lo < hi {\n\tmid := (lo + hi) / 2\n\tres := count(a, b, mid)\n\tif res >= int(k) {\n\t\thi = mid\n\t} else {\n\t\tlo = mid + 1\n\t}\n}\nreturn lo\n```\n\n### Step 2. Mixed numbers\n\nSo far so good. The problem is with the negative numbers. When the lists contain negative numbers, then their products form a kind of criss-cross pattern. Positive numbers are the result of combining numbers diagonally across in the matrix, and negative numbers are the result of combining numbers vertically:\n\n```\n \\ | - | + |\n - | + | - |\n + | - | + |\n```\n\nIn order to search numbers, input lists are split into two halves:\n\n```bash\na = [ -5, -2, -1, 0, 1, 2 ]\n |----[a1]---|---[a2]--]\n\nb = [ -8, -5, -2, 3, 5 ]\n |----[b1]---|-[b2]-|\n```\n\nThe first thing to note is that the number of positive / negative numbers can be counted by multiplying the lengths of each section:\n\n```go\nnegCount := len(a1)*len(b2) + len(b1)*len(a2)\n```\n\nKnowing how many numbers exist, if a request is made for `k <= negCount`, then that product must be in one of the negative quadrants, and vice versa for `k > negCount`. This tells us which sections to combine when searching for an answer.\n\nHowever, simply multiplying elements in order from different segments yield different signs and orderings:\n\n| first | second | sign | order |\n| --- | --- | --- | --- |\n| a1 | b1 | + | desc |\n| a1 | b2 | - | no order |\n| a2 | b1 | - | no order |\n| a2 | b2 | + | asc |\n\nThe first trick here is to reverse negative portions, which results in ordered outputs:\n\n| first | second | sign | order |\n| --- | --- | --- | --- |\n| rev(a1) | rev(b1) | + | asc |\n| rev(a1) | b2 | - | desc |\n| a2 | rev(b1) | - | desc |\n| a2 | b2 | + | asc |\n\nAt this point it would be possible to write two different binary search functions, one for searching from the right, and one from the left. But there is one final trick to make the code cleaner. \n\nBy inverting negative values (making them positive), it\'s possible to search in the same way for negative and positive numbers. However, the k\'th result will no longer be the k\'th smallest, but rather the k\'th largest number:\n\n| first | second | sign | order |\n| --- | --- | --- | --- |\n| inv(rev(a1)) | inv(rev(b1)) | + | asc |\n| inv(rev(a1)) | b2 | + | desc |\n| a2 | inv(rev(b1)) | + | desc |\n| a2 | b2 | + | asc |\n\n### Final solution:\n\n```go\nfunc kthSmallestProduct(nums1 []int, nums2 []int, k int64) int64 {\n\taSplit := sort.SearchInts(nums1, 0)\n\tbSplit := sort.SearchInts(nums2, 0)\n\ta1, a2 := rev(inv(nums1[:aSplit])), nums1[aSplit:]\n\tb1, b2 := rev(inv(nums2[:bSplit])), nums2[bSplit:]\n\n\tnegCount := len(a1)*len(b2) + len(b1)*len(a2)\n\n\tsign := 1\n\tif int(k) > negCount {\n\t\tk -= int64(negCount) // => kth smallest number from non-negative part\n\t} else {\n\t\tk = int64(negCount) - k + 1 // => kth largest number after transform\n\t\tb1, b2 = b2, b1 // swap to fix combination\n\t\tsign = -1\n\t}\n\n\tvar lo, hi int = 0, 1e10\n\tfor lo < hi {\n\t\tmid := (lo + hi) / 2\n\t\tif rcount(a1, b1, mid) + count(a2, b2, mid) >= int(k) {\n\t\t\thi = mid\n\t\t} else {\n\t\t\tlo = mid + 1\n\t\t}\n\t}\n\treturn int64(sign * lo)\n}\n\nfunc count(a, b []int, val int) int {\n\tvar count int\n\tj := len(b) - 1\n\tfor i := range a {\n\t\tfor j >= 0 && a[i]*b[j] > val {\n\t\t\tj--\n\t\t}\n\t\tcount += j + 1\n\t}\n\treturn count\n}\n\nfunc inv(a []int) []int {\n\tfor i := range a {\n\t\ta[i] = -a[i]\n\t}\n\treturn a\n}\n\nfunc rev(a []int) []int {\n\tfor l, r := 0, len(a)-1; l < r; l, r = l+1, r-1 {\n\t\ta[l], a[r] = a[r], a[l]\n\t}\n\treturn a\n}\n\n```
| 33 | 2 |
['Go']
| 2 |
kth-smallest-product-of-two-sorted-arrays
|
(C++) 2040. Kth Smallest Product of Two Sorted Arrays
|
c-2040-kth-smallest-product-of-two-sorte-mjfv
|
\n\nclass Solution {\npublic:\n long long kthSmallestProduct(vector<int>& nums1, vector<int>& nums2, long long k) {\n \n auto fn = [&](double v
|
qeetcode
|
NORMAL
|
2021-10-16T18:18:46.403076+00:00
|
2021-10-16T18:18:46.403114+00:00
| 2,305 | false |
\n```\nclass Solution {\npublic:\n long long kthSmallestProduct(vector<int>& nums1, vector<int>& nums2, long long k) {\n \n auto fn = [&](double val) {\n long long ans = 0; \n for (auto& x : nums1) {\n if (x < 0) ans += nums2.end() - lower_bound(nums2.begin(), nums2.end(), ceil(val/x)); \n else if (x == 0) {\n if (0 <= val) ans += nums2.size(); \n } else ans += upper_bound(nums2.begin(), nums2.end(), floor(val/x)) - nums2.begin(); \n }\n return ans; \n }; \n \n long long lo = -pow(10ll, 10), hi = pow(10ll, 10)+1;\n while (lo < hi) {\n long long mid = lo + (hi - lo)/2; \n if (fn(mid) < k) lo = mid + 1; \n else hi = mid; \n }\n return lo; \n }\n};\n```
| 18 | 0 |
['C']
| 6 |
kth-smallest-product-of-two-sorted-arrays
|
[Java] Binary Search on the Answer
|
java-binary-search-on-the-answer-by-nirv-4kez
|
Binary search on the answer and use a helper function to count the number of products that are less than mid.\nSimilar problem from AtCoder - https://atcoder.jp
|
nirvana_rsc
|
NORMAL
|
2021-10-16T18:54:50.788136+00:00
|
2021-10-16T19:22:30.181716+00:00
| 2,500 | false |
Binary search on the answer and use a helper function to count the number of products that are less than mid.\nSimilar problem from AtCoder - https://atcoder.jp/contests/abc155/tasks/abc155_d\n\n```\n public long kthSmallestProduct(int[] nums1, int[] nums2, long k) {\n long lo = (long) -1e10;\n long hi = (long) 1e10;\n while (lo < hi) {\n final long mid = lo + hi + 1 >> 1;\n if (f(nums1, nums2, mid) < k) {\n lo = mid;\n } else {\n hi = mid - 1;\n }\n }\n return lo;\n }\n\n private static long f(int[] nums1, int[] nums2, long mid) {\n long count = 0;\n for (int num : nums1) {\n int lo = 0;\n int hi = nums2.length;\n if (num < 0) {\n while (lo < hi) {\n final int m = lo + hi >>> 1;\n if ((long) nums2[m] * num >= mid) {\n lo = m + 1;\n } else {\n hi = m;\n }\n }\n count += nums2.length - lo;\n } else {\n while (lo < hi) {\n final int m = lo + hi >>> 1;\n if ((long) nums2[m] * num < mid) {\n lo = m + 1;\n } else {\n hi = m;\n }\n }\n count += lo;\n }\n }\n return count;\n }\n```
| 14 | 0 |
[]
| 5 |
kth-smallest-product-of-two-sorted-arrays
|
O(M+N) using old algorithm on virtual matrix
|
omn-using-old-algorithm-on-virtual-matri-tm3d
|
O(M+N) solution, where M and N are the lengths of the two arrays. Using an O(n) solution for finding the kth-smallest element in a sorted n×n matrix. Applied to
|
stefan4trivia
|
NORMAL
|
2021-10-17T06:28:27.810960+00:00
|
2021-10-17T07:00:30.899397+00:00
| 618 | false |
O(M+N) solution, where M and N are the lengths of the two arrays. Using an [O(n) solution for finding the kth-smallest element in a sorted n×n matrix](https://leetcode.com/problems/kth-smallest-element-in-a-sorted-matrix/discuss/85170/O(n)-from-paper.-Yes-O(rows).). Applied to a virtual matrix I build. "Virtual" meaning I compute its elements on-the-fly, only the elements the algorithm needs to look at. Because building the whole matrix explicitly would take O(MN).\n\nFor example for the arrays `[-2,-1,0,1,2]` and `[-3,-1,2,4,5]` with `k=3`, I first figure out that there are ten negative products, so the kth-smallest product is negative. And thus I build the following virtual matrix of all negative products and find the 7-th smallest element (7 because k=3 and the four -\u221E elements):\n```\n[-\u221E, -\u221E, -10, -8, -4]\n[-\u221E, -\u221E, -5, -4, -2]\n[-6, -2, \u221E, \u221E, \u221E]\n[-3, -1, \u221E, \u221E, \u221E]\n[ \u221E, \u221E, \u221E, \u221E, \u221E]\n```\nThe lower-left "quadrant" is the positive values from the first array multiplied with the negative values from the second array. The upper-right quadrant is negatives from first multiplied with positives from second.\n\nThe same arrays `[-2,-1,0,1,2]` and `[-3,-1,2,4,5]` but with `k=20` turns into finding the 9th-smallest element in the virtual matrix of *positive* products:\n```\n[-\u221E, -\u221E, 2, 4, 5]\n[-\u221E, -\u221E, 4, 8, 10]\n[ 1, 3, \u221E, \u221E, \u221E]\n[ 2, 6, \u221E, \u221E, \u221E]\n[ \u221E, \u221E, \u221E, \u221E, \u221E]\n```\nLower-left are (negatives of first)×(negatives of second).\nUpper-right are (positives of first)×(positives of second).\n\nThe solution code, the bottom half is the `kthSmallest` function from the old problem:\n\n```\nclass Solution:\n def kthSmallestProduct(self, A, B, k):\n \n # Analyze negatives, positives, zeros\n negA = [a for a in A if a < 0]\n posA = [a for a in A if a > 0]\n negB = [b for b in B if b < 0]\n posB = [b for b in B if b > 0]\n nA, pA, nB, pB = map(len, (negA, posA, negB, posB))\n negatives = nA * pB + pA * nB\n positives = nA * nB + pA * pB\n zeros = len(A) * len(B) - negatives - positives\n \n # Configure the matrix and adjust k.\n\t\t# A1 and A2 become the factors for the rows (top and bottom part)\n\t\t# B1 and B2 become the factors for the columns (left and right part)\n if k <= negatives:\n A1, A2 = negA, posA[::-1]\n B1, B2 = negB, posB[::-1]\n else:\n k -= negatives\n if k <= zeros:\n return 0\n k -= zeros\n A1, A2 = posA, negA[::-1]\n B1, B2 = negB[::-1], posB\n \n # Build the virtual matrix\n a1, a2, b1, b2 = map(len, (A1, A2, B1, B2))\n k += a1 * b1\n m = len(A1 + A2)\n n = len(B1 + B2)\n class Row:\n def __init__(self, i):\n if i < a1:\n get = lambda j: -inf if j < b1 else A1[i] * B2[j-b1] if j < n else inf\n elif i < m:\n get = lambda j: A2[i-a1] * B1[j] if j < b1 else inf\n else:\n get = lambda j: inf\n self.get = get\n def __getitem__(self, j):\n return self.get(j)\n matrix = list(map(Row, range(max(m, n))))\n \n # Debugging/visualization: print the matrix\n if 0:\n print(k)\n for i in range(len(matrix)):\n print([matrix[i][j] for j in range(len(matrix))])\n \n # Let the matrix solution do the hard work\n return self.kthSmallest(matrix, k)\n\n def kthSmallest(self, matrix, k):\n\n # The median-of-medians selection function.\n def pick(a, k):\n if k == 1:\n return min(a)\n groups = (a[i:i+5] for i in range(0, len(a), 5))\n medians = [sorted(group)[len(group) // 2] for group in groups]\n pivot = pick(medians, len(medians) // 2 + 1)\n smaller = [x for x in a if x < pivot]\n if k <= len(smaller):\n return pick(smaller, k)\n k -= len(smaller) + a.count(pivot)\n return pivot if k < 1 else pick([x for x in a if x > pivot], k)\n\n # Find the k1-th and k2th smallest entries in the submatrix.\n def biselect(index, k1, k2):\n\n # Provide the submatrix.\n n = len(index)\n def A(i, j):\n return matrix[index[i]][index[j]]\n \n # Base case.\n if n <= 2:\n nums = sorted(A(i, j) for i in range(n) for j in range(n))\n return nums[k1-1], nums[k2-1]\n\n # Solve the subproblem.\n index_ = index[::2] + index[n-1+n%2:]\n k1_ = (k1 + 2*n) // 4 + 1 if n % 2 else n + 1 + (k1 + 3) // 4\n k2_ = (k2 + 3) // 4\n a, b = biselect(index_, k1_, k2_)\n\n # Prepare ra_less, rb_more and L with saddleback search variants.\n ra_less = rb_more = 0\n L = []\n jb = n # jb is the first where A(i, jb) is larger than b.\n ja = n # ja is the first where A(i, ja) is larger than or equal to a.\n for i in range(n):\n while jb and A(i, jb - 1) > b:\n jb -= 1\n while ja and A(i, ja - 1) >= a:\n ja -= 1\n ra_less += ja\n rb_more += n - jb\n L.extend(A(i, j) for j in range(jb, ja))\n \n # Compute and return x and y.\n x = a if ra_less <= k1 - 1 else \\\n b if k1 + rb_more - n*n <= 0 else \\\n pick(L, k1 + rb_more - n*n)\n y = a if ra_less <= k2 - 1 else \\\n b if k2 + rb_more - n*n <= 0 else \\\n pick(L, k2 + rb_more - n*n)\n return x, y\n\n # Set up and run the search.\n n = len(matrix)\n start = max(k - n*n + n-1, 0)\n k -= n*n - (n - start)**2\n return biselect(list(range(start, min(n, start+k))), k, k)[0]\n```
| 13 | 2 |
[]
| 1 |
kth-smallest-product-of-two-sorted-arrays
|
[Python3] binary search
|
python3-binary-search-by-ye15-gj0s
|
\n\nclass Solution:\n def kthSmallestProduct(self, nums1: List[int], nums2: List[int], k: int) -> int:\n \n def fn(val):\n """Return
|
ye15
|
NORMAL
|
2021-10-16T16:01:41.031445+00:00
|
2021-10-16T19:10:10.123109+00:00
| 2,399 | false |
\n```\nclass Solution:\n def kthSmallestProduct(self, nums1: List[int], nums2: List[int], k: int) -> int:\n \n def fn(val):\n """Return count of products <= val."""\n ans = 0\n for x in nums1: \n if x < 0: ans += len(nums2) - bisect_left(nums2, ceil(val/x))\n elif x == 0: \n if 0 <= val: ans += len(nums2)\n else: ans += bisect_right(nums2, floor(val/x))\n return ans \n \n lo, hi = -10**10, 10**10 + 1\n while lo < hi: \n mid = lo + hi >> 1\n if fn(mid) < k: lo = mid + 1\n else: hi = mid\n return lo \n```\n\n```\nclass Solution:\n def kthSmallestProduct(self, nums1: List[int], nums2: List[int], k: int) -> int:\n neg = [x for x in nums1 if x < 0]\n pos = [x for x in nums1 if x >= 0]\n \n def fn(val):\n """Return count of products <= val."""\n ans = 0\n lo, hi = 0, len(nums2)-1\n for x in neg[::-1] + pos if val >= 0 else neg + pos[::-1]: \n if x < 0: \n while lo < len(nums2) and x*nums2[lo] > val: lo += 1\n ans += len(nums2) - lo\n elif x == 0: \n if 0 <= val: ans += len(nums2)\n else: \n while 0 <= hi and x*nums2[hi] > val: hi -= 1\n ans += hi+1\n return ans \n \n lo, hi = -10**10, 10**10 + 1\n while lo < hi: \n mid = lo + hi >> 1\n if fn(mid) < k: lo = mid + 1\n else: hi = mid\n return lo \n```
| 12 | 2 |
['Python3']
| 1 |
kth-smallest-product-of-two-sorted-arrays
|
Java Solution | Binary Search
|
java-solution-binary-search-by-hcrocks00-xcaq
|
So we want to find out k-th smallest product from the two sorted arrays. Let\'s first find out the range of our answer. So the minimum value it can go is if we
|
hcrocks007
|
NORMAL
|
2021-12-13T08:42:29.702082+00:00
|
2021-12-13T08:42:29.702110+00:00
| 2,984 | false |
So we want to find out k-th smallest product from the two sorted arrays. Let\'s first find out the range of our answer. So the minimum value it can go is if we have elements -10^5 in both the arrays so the minimum value is -10^10 and similarly for maximum value it is 10^10. Now we can do a binary search in our range and for every current product we can check whether we have atleast k products that are less than current product. If we do have atleast k products that are less than current product then we move our window left, otherwise to the right.\n\nOk so now we know what we have to do, lets now see how would we do what we wanna do?\n\nSo we iterate over nums1 and count the number of products that are less than current product.\nHere three cases arise:\n1. currentElement = 0: 0 * any number in nums2 will be 0. So if current product>=0 then we know that the whole array(nums2) would be included in our count.\n2. currentElement>0: then we find maximum index in nums2 such that currentElement * nums2[maxIndex] is less than equal to current product. Then we can add maxIndex+1 elements into our count as they are less that equal to current product.\n3. currentElement<0: then we do exact reverse of what we did in the previous case. We find minimum element that satisfies currentElement * nums2[minIndex]<= current product.\n\nCode :\n```\nclass Solution {\n public long kthSmallestProduct(int[] nums1, int[] nums2, long k) {\n long l = (long)-1e11;\n long r = (long)1e11;\n long res = 0;\n while ( l<=r ) {\n long mid = (l+r)/2;\n // checking whether we have k at least k elements whose product is less than the current product\n // if yes then we know we have to move left\n if ( check(mid, nums1, nums2, k) ) {\n r = mid - 1;\n res = mid;\n } else {\n l = mid + 1;\n }\n }\n return res;\n }\n public boolean check ( long mid, int[] nums1, int[] nums2, long k ) {\n long cnt = 0;\n for ( int i=0; i<nums1.length; i++ ) {\n long val = (long) nums1[i];\n // if current element is 0 and we out current product is >= 0 then we can add the whole second array because 0*anything will be 0\n if ( val==0 && mid>=0 ) {\n cnt += nums2.length;\n } else if ( val<0 ) {\n // If we encounter negative value we find the minimum index in the second array such that this element * minIndexElement <= current product\n cnt += findMinIndex(val, mid, nums2);\n } else if ( val>0 ) {\n // if we encounter positive element we find max index in the second array such that this element * maxIndexElement <= current product\n cnt += findMaxIndex(val, mid, nums2);\n }\n }\n // if we have atleast k elements whose product is less than current product\n return cnt>=k;\n }\n public long findMaxIndex( long val, long mid, int[] nums2 ) {\n int l = 0;\n int r = nums2.length - 1;\n // when no element in second array when multiplied by the current element of the first array yields result less that current product we will return res+1 hence -1 + 1 hence 0 coz there are no elements which when multiplied by current element of the first array yield result less than current product.\n long res = -1;\n while ( l<=r ) {\n int m = (l+r)/2;\n if ( val*nums2[m]<=mid ) {\n // if our current product is >= val*current element then we move the window to right side in order to find max index with which when multiplied the element of the first array is still less than current product.\n res = (long)m;\n l = m + 1; \n } else {\n r = m - 1;\n }\n }\n // so we have found res+1 elements who satisfy our condition. +1 coz res would give index\n return res+1;\n }\n public long findMinIndex( long val, long mid, int[] nums2 ) {\n int l = 0;\n int r = nums2.length - 1;\n // when all elements of second array multiplied by current element of first array yield result > current product then we return 0 coz there are no elements which would yield us result.\n long res = r + 1;\n while ( l<=r ) {\n int m = (l+r)/2;\n if ( val*nums2[m]<=mid ) {\n r = m - 1;\n res = (long)m;\n } else {\n l = m + 1;\n }\n }\n return nums2.length - res;\n }\n}\n```
| 11 | 0 |
['Binary Tree', 'Java']
| 3 |
kth-smallest-product-of-two-sorted-arrays
|
C++ || Detailed Explanation || Binary Search || Counting ||
|
c-detailed-explanation-binary-search-cou-j7qt
|
Intuition\n###### The key intuition to solve this problem is to use binary search on the answer space rather than generating all possible products. Instead of a
|
khalidalam980
|
NORMAL
|
2024-10-05T18:22:41.273435+00:00
|
2024-10-05T18:22:41.273468+00:00
| 607 | false |
# Intuition\n###### The key intuition to solve this problem is to use **`binary search`** on the answer space rather than generating all possible products. Instead of asking "what is the **`kth`** smallest product?", we transform the question to "how many products are less than or equal to a given value **`x`**?". If we can efficiently answer this question, we can binary search for the **`kth`** smallest product. The tricky part is counting these products quickly. Since we\'re dealing with multiplication, we need to consider **three** **cases**: when the first number is **positive**, **negative**, or **zero**, as this affects how we count valid pairs. For positive numbers, we\'re looking for products less than **`x`**, so we need the second number to be less than **`x`** divided by our first number. For negative numbers, the inequality flips, so we need the second number to be greater than **`x`** divided by our first number. Since our second array is sorted, we can use binary search (**`upper_bound`** for **positive**, **`lower_bound`** for **negative**) to quickly count how many numbers satisfy these conditions. Zero is a special case that\'s easy to handle separately. By leveraging this counting method within our binary search on the answer space, we can efficiently find the **`kth`** smallest product without actually generating all possible products, giving us a solution that\'s much faster than a brute force approach.\n\n# Approach\n###### The solution uses binary search on the answer space **`[-10^10, 10^10]`** to find the **`kth`** smallest product \n- For each potential answer **`x`**, we count how many products are **`\u2264 x`** \n- For efficient counting, we iterate through each number **`a`** in **`nums1`** and handle three cases: **positive**, **negative**, and **zero** \n - For **positive** **`a`**, we find how many **`b`** in **`nums2`** satisfy **`b \u2264 x/a`** using **`upper_bound`** \n - For **negative** **`a`**, we find how many **`b`** in **`nums2`** satisfy **`b \u2265 x/a`** using **`lower_bound`** (since the inequality flips) \n - For **zero**, we count all numbers in **`nums2`** if **`x \u2265 0`** \n - The counting function can terminate early if we find **`k`** or more valid products \n- If we find **`\u2265 k`** products **`\u2264 x`**, we store **`x`** as a potential answer and try a smaller value in our binary search \n- If we find **`< k`** products, we need to try a larger value \n- Binary search continues until we find the smallest **`x`** that has at least **`k`** products less than or equal to it \n- The solution avoids generating all possible products, instead using binary search twice: once for the answer and once for counting, making it efficient for large inputs.\n\n# Code Walkthrough\n- The binary search implementation:\n ```\n ll low = -1e10;\n ll high = 1e10;\n ll ans = 0;\n while(low <= high) {\n ll mid = low + (high-low)/2;\n if(isPossible(mid, nums1, nums2, k)) {\n ans = mid;\n high = mid-1;\n } else {\n low = mid+1;\n }\n }\n ```\n - ###### This is trying to find the smallest value \'x\' such that there are at least k pairs whose product is less than or equal to x.\n- The crucial part is the isPossible function:\n ```\n bool isPossible(ll x, vector<int>& nums1, vector<int>& nums2, ll k)\n ```\n - ###### This function checks if there are at least **`k`** pairs whose product is less than or equal to **`x`**.\n - \n###### Let\'s understand the **three cases**:\n###### **a)** When **`nums1[i] < 0`** (negative number):\n```\nif(nums1[i] < 0) {\n ll rem = ceil((double)x/nums1[i]);\n int ind = lower_bound(nums2.begin(), nums2.end(), rem) - nums2.begin();\n count += (n2-ind);\n}\n```\n###### When multiplying a negative number, the inequality reverses. So, for **`nums1[i] * nums2[j] <= x`**:\n- We need **`nums2[j] >= x/nums1[i]`**\n- We use ceil because we want the smallest number that satisfies this\n- lower_bound finds the first element **`>= rem`**\n- All elements from this index to the end will satisfy our condition\n\n###### **b)** When **`nums1[i] > 0`** (positive number):\n```\nelse if(nums1[i] > 0) {\n ll rem = floor((double)x/nums1[i]);\n int ind = upper_bound(nums2.begin(), nums2.end(), rem) - nums2.begin();\n count += ind;\n}\n```\n###### For positive numbers:\n- We need **`nums2[j] <= x/nums1[i]`**\n- We use floor because we want the largest number that satisfies this\n- **`upper_bound`** finds the first **`element > rem`**\n- All elements before this index will satisfy our condition\n\n###### **c)** When **`nums1[i] == 0`**:\n```\nelse {\n if(x >= 0) {\n count += n2;\n }\n}\n```\n###### When multiplying by **`zero`**:\n- If **`x >= 0`**, all products (which will be 0) are **`<= x`**\n- If **`x < 0`**, no products satisfy the condition\n\n###### The function returns **`true`** if the total count of satisfying pairs is **`>= k`**.\n\n# Special Focus(Dry Run):\n\n###### Let\'s dive deeper into these two cases with examples.\n\n###### **A)** When **`nums1[i] < 0`** (Negative Number Case)\n###### Let\'s take an example:\n```\nnums1[i] = -2\nnums2 = [1, 3, 5, 7]\nx = 10\n```\n###### We want to find how many products **`(-2 * nums2[j])`** are less than or equal to **`10`**.\n\n- ###### First, we calculate **`rem = ceil(x/nums1[i])`**\n ```\n rem = ceil(10/-2) = ceil(-5) = -5\n ```\n- ###### Now, the inequality we\'re solving:\n ```\n -2 * nums2[j] \u2264 10\n nums2[j] \u2265 -5 (dividing both sides by -2, inequality sign flips)\n ```\n- ###### We use **`lower_bound`** to find the first element in **`nums2`** that is **`\u2265 -5`**. In our example, all elements are **`\u2265 -5`**, so **`index = 0`**\n- ###### **`Count`** is incremented by **`(n2 - index) = 4 - 0 = 4`**\n\n###### This means all four products ($$-2\\times1$$ = -2, $$-2\\times3$$ = -6, $$-2\\times5$$ = -10, $$-2\\times 7$$ = -14) are **`\u2264 10`**.\n\n###### **B)** When nums1[i] > 0 (Positive Number Case)\n###### Let\'s take another example:\n```\nnums1[i] = 2\nnums2 = [1, 3, 5, 7]\nx = 10\n```\n###### We want to find how many products **`(2 * nums2[j])`** are less than or equal to **`10`**.\n\n- First, we calculate rem = floor(x/nums1[i])\n ```\n rem = floor(10/2) = floor(5) = 5\n ```\n- The inequality we\'re solving:\n ```\n 2 * nums2[j] \u2264 10\n nums2[j] \u2264 5 (dividing both sides by 2, inequality sign remains the same)\n ```\n- We use upper_bound to find the first element in nums2 that is > 5. In our example, this is the index 3 (element 7)\n- Count is incremented by this index: 3\n\n###### This means three products ($$2*1 = 2,~~2*3 = 6,~~2*5 = 10$$) are **`\u2264 10`**.\n\n###### **Why the difference in approach?**\n\n- **Ceiling vs Floor**\n\n - For negative numbers, we use ceiling because when we divide by a negative number, we want to round up to get the smallest number that satisfies our inequality\nFor positive numbers, we use floor because we want the largest number that satisfies our inequality\n\n\n- **Lower_bound vs Upper_bound**\n\n - For negative numbers, we use lower_bound because we\'re looking for numbers greater than or equal to our calculated rem\nFor positive numbers, we use upper_bound because we\'re looking for the point where numbers become greater than our calculated rem\n\n\n- **Counting**\n\n - For negative numbers, we count from the found index to the end\n - For positive numbers, we count from the beginning to the found index\n\n\n\n###### **Here\'s a visualization:**\n```\nNegative case (-2):\nnums2: 1 3 5 7\nx/n1: -5 -5 -5 -5\n \u2191 \u2191 \u2191 \u2191\n All count because all \u2265 -5\n\nPositive case (2):\nnums2: 1 3 5 7\nx/n1: 5 5 5 5\n \u2191 \u2191 \u2191 \n These count \u2934 This doesn\'t\n because \u2264 5\n```\n\n# Complexity\n- **Time complexity:**\n - Binary search takes $$O(log(10^{10}))$$ iterations\n - For each iteration, isPossible function takes O(n1 * log(n2))\n - Total: $$O(n1 * log(n2) * log(10^{10}))$$\n\n- **Space complexity:** $$O(1)$$\n\n# Code\n```cpp []\nclass Solution {\npublic:\n using ll = long long;\n bool isPossible(ll x, vector<int>& nums1, vector<int>& nums2, ll k){\n int n1 = nums1.size();\n int n2 = nums2.size();\n ll count=0;\n for(int i=0;i<n1;i++){\n if(nums1[i]<0){\n ll rem = ceil((double)x/nums1[i]);\n int ind = lower_bound(nums2.begin(), nums2.end(), rem)-nums2.begin();\n count += (n2-ind);\n }else if(nums1[i]>0){\n ll rem = floor((double)x/nums1[i]);\n int ind = upper_bound(nums2.begin(), nums2.end(), rem)-nums2.begin();\n count += ind;\n }else{\n if(x>=0){\n count += n2;\n }\n }\n if(count>=k) return true;\n }\n return count>=k;\n }\n ll kthSmallestProduct(vector<int>& nums1, vector<int>& nums2, ll k) {\n int n1 = nums1.size();\n int n2 = nums2.size();\n ll low = -1e10;\n ll high = 1e10;\n ll ans=0;\n while(low<=high){\n ll mid = low+(high-low)/2;\n if(isPossible(mid, nums1, nums2, k)){\n ans = mid;\n high = mid-1;\n }else{\n low = mid+1;\n }\n }\n return ans;\n }\n};\n```\n## If you found this helpful, an upvote would be greatly appreciated!\n## Comment any doubt or suggestions.
| 9 | 0 |
['Array', 'Binary Search', 'Counting', 'C++']
| 1 |
kth-smallest-product-of-two-sorted-arrays
|
C++ | Both Approaches | 2 Pointer & Binary search | Easy to understand |
|
c-both-approaches-2-pointer-binary-searc-e1h4
|
Approach 1 : 2 pointers\n\nclass Solution {\npublic:\n long long kthSmallestProduct(vector<int>& nums1, vector<int>& nums2, long long k) {\n \n
|
aavishkarmishra
|
NORMAL
|
2022-07-02T19:34:24.584661+00:00
|
2022-07-02T19:36:59.040844+00:00
| 1,408 | false |
**Approach 1 : 2 pointers**\n```\nclass Solution {\npublic:\n long long kthSmallestProduct(vector<int>& nums1, vector<int>& nums2, long long k) {\n \n auto fn = [&](double val) {\n long long ans = 0; \n for (auto& x : nums1) {\n if (x < 0) ans += nums2.end() - lower_bound(nums2.begin(), nums2.end(), ceil(val/x)); \n else if (x == 0) {\n if (0 <= val) ans += nums2.size(); \n } else ans += upper_bound(nums2.begin(), nums2.end(), floor(val/x)) - nums2.begin(); \n }\n return ans; \n }; \n \n long long lo = -pow(10ll, 10), hi = pow(10ll, 10)+1;\n while (lo < hi) {\n long long mid = lo + (hi - lo)/2; \n if (fn(mid) < k) lo = mid + 1; \n else hi = mid; \n }\n return lo; \n }\n};\n\n```\n**Approach 2 : Binary Search**\nThe idea of this problem is to use binary search on answer -\nLet check(x) be the answer to the question: how many products are less or equal than x.\nThen we use binary search and find the first moment where we have exactly k such numbers .\n```\nclass Solution {\npublic:\n bool check(long long midval,vector<int>& nums1, vector<int>& nums2, long long k){\n long long cnt=0;\n for(int i=0;i<nums1.size();i++)\n {\n long long val=nums1[i];\n \n\t\t\t//If val == 0, product of val and each element in nums2 will be 0. And if midval>=0, then because all\n\t\t\t//products are 0, all products will be smaller or equal to midval. So we can add all products in the answer\n\t\t\tif(val==0 and midval>=0)\n cnt+=nums2.size();\n \n else if(val>0)\n cnt+=findmaxIndex(nums2,val,midval);\n \n else if(val<0)\n cnt+=findminIndex(nums2,val,midval);\n }\n return cnt>=k;\n }\n \n int findmaxIndex(vector<int>&nums2 , long long val , long long midval)\n {\n int l = 0 , r = nums2.size()-1 , res= -1;\n while(l<=r)\n {\n long long mid = (l+r)/2;\n if(val*nums2[mid]<=midval)\n {\n res=mid;\n l=mid+1;\n }\n else r=mid-1;\n }\n return res+1;\n }\n \n int findminIndex(vector<int>&nums2 , long long val , long long midval)\n {\n int l = 0 , r = nums2.size()-1 , res= r+1;\n while(l<=r)\n {\n long long mid = (l+r)/2;\n if(val*nums2[mid]<=midval)\n {\n res=mid;\n r=mid-1;\n }\n else l=mid+1;\n }\n return nums2.size()-res;\n }\n \n long long kthSmallestProduct(vector<int>& nums1, vector<int>& nums2, long long k) {\n long long l=-1e10,r=1e10,res=-1;\n while(l<=r){\n long long mid = (l+r)/2;\n // cout<<mid<<endl;\n if(check(mid,nums1,nums2,k)) {\n res=mid;\n r=mid-1;\n }\n else l=mid+1;\n }\n return res;\n }\n};\n```
| 4 | 0 |
['Two Pointers', 'Binary Search', 'C', 'Binary Tree', 'C++']
| 1 |
kth-smallest-product-of-two-sorted-arrays
|
c++ | binary search | easy to understand
|
c-binary-search-easy-to-understand-by-ve-637d
|
\n# Code\n\nclass Solution {\npublic:\n bool check(long long midval,vector<int>& nums1, vector<int>& nums2, long long k){\n long long cnt=0;\n
|
venomhighs7
|
NORMAL
|
2022-09-30T12:42:34.455707+00:00
|
2022-09-30T12:42:34.455737+00:00
| 1,311 | false |
\n# Code\n```\nclass Solution {\npublic:\n bool check(long long midval,vector<int>& nums1, vector<int>& nums2, long long k){\n long long cnt=0;\n for(int i=0;i<nums1.size();i++)\n {\n long long val=nums1[i];\n\t\t\tif(val==0 and midval>=0)\n cnt+=nums2.size();\n \n else if(val>0)\n cnt+=findmaxIndex(nums2,val,midval);\n \n else if(val<0)\n cnt+=findminIndex(nums2,val,midval);\n }\n return cnt>=k;\n }\n \n int findmaxIndex(vector<int>&nums2 , long long val , long long midval)\n {\n int l = 0 , r = nums2.size()-1 , res= -1;\n while(l<=r)\n {\n long long mid = (l+r)/2;\n if(val*nums2[mid]<=midval)\n {\n res=mid;\n l=mid+1;\n }\n else r=mid-1;\n }\n return res+1;\n }\n \n int findminIndex(vector<int>&nums2 , long long val , long long midval)\n {\n int l = 0 , r = nums2.size()-1 , res= r+1;\n while(l<=r)\n {\n long long mid = (l+r)/2;\n if(val*nums2[mid]<=midval)\n {\n res=mid;\n r=mid-1;\n }\n else l=mid+1;\n }\n return nums2.size()-res;\n }\n \n long long kthSmallestProduct(vector<int>& nums1, vector<int>& nums2, long long k) {\n long long l=-1e10,r=1e10,res=-1;\n while(l<=r){\n long long mid = (l+r)/2;\n if(check(mid,nums1,nums2,k)) {\n res=mid;\n r=mid-1;\n }\n else l=mid+1;\n }\n return res;\n }\n};\n```
| 3 | 0 |
['C++']
| 0 |
kth-smallest-product-of-two-sorted-arrays
|
✅ C++ Simple Binary Search Solution with comments | Easy to understand
|
c-simple-binary-search-solution-with-com-dbjt
|
We can\'t apply priority queue over here just because of the constraints, that would give us TLE.\nBut we can apply Binary Search over here.\n\nApproach\nWe can
|
gaurav31200
|
NORMAL
|
2022-08-03T05:02:38.870143+00:00
|
2022-08-03T05:04:04.873937+00:00
| 692 | false |
We can\'t apply priority queue over here just because of the constraints, that would give us TLE.\nBut we can apply *Binary Search* over here.\n\n**Approach**\nWe can apply the Binary search over the range [-1e10,1e10] (minimum product of the pairs,maximum product of the pairs).We can count the number of pair products and decrease our search space accordingly\n\nNow the question arises, how can we count the number of pair products without getting tle?\nThe answer is, we can apply Binary search here as well.\n\n**Keep this in mind -** There can be negative elements also and when we consider the negative element the logic got reversed.\n\n**C++ Code**\n```\nclass Solution {\npublic:\n long long countSmallerProducts(vector<int>& nums1, vector<int>& nums2, long long product){\n long long count=0;\n for(int num:nums1){\n if(num>=0){\n int l=0,h=nums2.size()-1,temp=-1;\n while(l<=h){\n int mid=l+(h-l)/2;\n if((long long)num*nums2[mid] <= product){\n temp=mid;\n l=mid+1;\n }else h=mid-1;\n }\n count+=temp+1;\n }else{\n int l=0,h=nums2.size()-1,temp=nums2.size();\n while(l<=h){\n int mid=l+(h-l)/2;\n if((long long)num*nums2[mid] <= product){\n temp=mid;\n h=mid-1;\n }else l=mid+1;\n }\n count+=(nums2.size()-temp);\n }\n }\n return count;\n }\n long long kthSmallestProduct(vector<int>& nums1, vector<int>& nums2, long long k) {\n long long s=-1e10,e=1e10,ans=0;\n \n \n while(s<=e){\n long long mid = (s+e)/2;\n if(countSmallerProducts(nums1,nums2,mid)>=k){\n ans=mid;\n e=mid-1;\n }else s=mid+1;\n }\n \n return ans;\n }\n};\n```
| 3 | 0 |
['C', 'Binary Tree']
| 0 |
kth-smallest-product-of-two-sorted-arrays
|
Python 3 AC Solution with detailed math derivation
|
python-3-ac-solution-with-detailed-math-5mdik
|
\nclass Solution:\n def kthSmallestProduct(self, nums1: List[int], nums2: List[int], k: int) -> int:\n """\n Binary Search\n find first
|
cara22
|
NORMAL
|
2022-06-17T22:22:41.461575+00:00
|
2022-06-17T22:27:19.313828+00:00
| 710 | false |
```\nclass Solution:\n def kthSmallestProduct(self, nums1: List[int], nums2: List[int], k: int) -> int:\n """\n Binary Search\n find first number that makes countSmallerOrEqual(number) >= k\n return number\n """\n boundary = [nums1[0]*nums2[0], nums1[0] * nums2[-1], nums1[-1] * nums2[0], nums1[-1] * nums2[-1]]\n low, high = min(boundary), max(boundary)\n while low + 1 < high:\n mid = low + (high - low) // 2\n if self.countSmallerOrEqual(mid, nums1, nums2) >= k:\n high = mid\n else:\n low = mid + 1\n if self.countSmallerOrEqual(low, nums1, nums2) >= k:\n return low\n else:\n return high\n \n def countSmallerOrEqual(self, m, nums1, nums2):\n """\n Two pointers solution\n use monotonic property of both nums1 and nums2\n return the number of products nums1[i] * nums2[j] <= m\n l1, l2 = len(nums1), len(nums2)\n \n 1) if m >= 0, \n ***Given nums1[i] < 0***\n find j such that nums2[j] >= m/nums1[i]\n i increases - > nums1[i] increases -> m/nums1[i] decreases -> index j decreases\n j monotonically moves left\n return j:l2 -> l2 - j + 1\n *** Given nums1[i] = 0\n return l2\n ***Given nums1[i] > 0***\n find j such that nums2[j] <= m/nums1[i]\n i increases - > nums1[i] increases -> m/nums1[i] decreases -> index j decreases\n j monotonically moves left\n return 0:j -> j + 1\n\n 2) if m < 0, \n ***Given nums1[i] < 0***\n find j such that nums2[j] >= m/nums1[i]\n i increases - > nums1[i] increases -> m/nums1[i] increases -> index j increases\n j monotonically moves right\n return j:l2 -> l2 - j + 1\n *** Given nums1[i] = 0\n return 0\n ***Given nums1[i] > 0***\n find j such that nums2[j] <= m/nums1[i]\n i increases - > nums1[i] increases -> m/nums1[i] increases -> index j increases\n j monotonically moves right\n return 0:j -> j + 1\n \n """\n l1, l2 = len(nums1), len(nums2)\n ans = 0\n if m >= 0:\n j1, j2 = l2-1, l2-1\n for i in range(l1):\n if nums1[i] < 0:\n while j1 >=0 and nums2[j1] >= m/nums1[i]:\n j1 -= 1\n ans += l2 - j1 - 1\n elif nums1[i] > 0:\n while j2 >=0 and nums2[j2] > m/nums1[i]:\n j2 -= 1\n ans += j2 + 1\n else:\n ans += l2\n else:\n j1, j2 = 0, 0\n for i in range(l1):\n if nums1[i] < 0:\n while j1 < l2 and nums2[j1] < m/nums1[i]:\n j1 += 1\n ans += l2 - j1\n elif nums1[i] > 0:\n while j2 < l2 and nums2[j2] <= m/nums1[i]:\n j2 += 1\n ans += j2\n return ans\n```\n \n
| 3 | 0 |
['Two Pointers', 'Binary Tree', 'Python3']
| 0 |
kth-smallest-product-of-two-sorted-arrays
|
Java | Binary Search Solution
|
java-binary-search-solution-by-aswinb-aeo8
|
2040. Kth Smallest Product of Two Sorted Arrays\n\nPlease \uD83D\uDD3C upvote this post if you find the answer useful & do comment about your thoughts \uD83D\uD
|
aswinb
|
NORMAL
|
2022-05-17T11:21:28.306760+00:00
|
2022-05-19T07:09:33.240528+00:00
| 1,049 | false |
# [2040. Kth Smallest Product of Two Sorted Arrays](https://leetcode.com/problems/kth-smallest-product-of-two-sorted-arrays/)\n\n**Please** \uD83D\uDD3C **upvote this post if you find the answer useful & do comment about your thoughts** \uD83D\uDCAC\n\n## Java | Binary Search Solution\n\n### Java Code\n\n```\nclass Solution {\n public long kthSmallestProduct(int[] nums1, int[] nums2, long k) {\n return kthSmallest(nums1, nums2, k);\n }\n\n\tpublic static long kthSmallest(int[] nums1, int[] nums2, long k) {\n\n\t\tlong lo = -1000_000_0000l;\n\t\tlong hi = 1000_000_0000l;\n\t\tlong ans = 0;\n\n\t\t// Binary Search\n\t\twhile (lo <= hi) {\n\t\t\tlong mid = (lo + hi) / 2;\n\t\t\tif (countNumberOfElements(nums1, nums2, mid) >= k) {\n\t\t\t\tans = mid;\n\t\t\t\thi = mid - 1;\n\t\t\t} else {\n\t\t\t\tlo = mid + 1;\n\t\t\t}\n\t\t}\n\t\treturn ans;\n\n\t}\n\n\tpublic static long countNumberOfElements(int[] arr1, int[] arr2, long Dot_pot) {\n\t\tlong ans = 0;\n\t\tfor (int e1 : arr1) {\n\t\t\tint count = 0;\n\t\t\tif (e1 >= 0) {\n\t\t\t\tint lo = 0;\n\t\t\t\tint hi = arr2.length - 1;\n\t\t\t\twhile (lo <= hi) {\n\t\t\t\t\tint mid = (lo + hi) / 2;\n\t\t\t\t\tif ((long) e1 * arr2[mid] <= Dot_pot) {\n\t\t\t\t\t\tcount = mid + 1;\n\t\t\t\t\t\tlo = mid + 1;\n\t\t\t\t\t} else {\n\t\t\t\t\t\thi = mid - 1;\n\t\t\t\t\t}\n\t\t\t\t}\n\t\t\t\tans = ans + count;\n\n\t\t\t}\n\n\t\t\telse {\n\n\t\t\t\tint lo = 0;\n\t\t\t\tint hi = arr2.length - 1;\n\t\t\t\twhile (lo <= hi) {\n\t\t\t\t\tint mid = (lo + hi) / 2;\n\t\t\t\t\tif ((long) e1 * arr2[mid] <= Dot_pot) {\n\t\t\t\t\t\tcount = arr2.length - mid;\n\t\t\t\t\t\thi = mid - 1;\n\n\t\t\t\t\t} else {\n\t\t\t\t\t\tlo = mid + 1;\n\t\t\t\t\t}\n\t\t\t\t}\n\t\t\t\tans = ans + count;\n\n\t\t\t}\n\n\t\t}\n\t\treturn ans;\n\t}\n\n}\n```
| 3 | 0 |
['Binary Tree', 'Java']
| 1 |
kth-smallest-product-of-two-sorted-arrays
|
Java Binary Search Solution with Explanation
|
java-binary-search-solution-with-explana-dsgs
|
\nclass Solution {\n public long kthSmallestProduct(int[] nums1, int[] nums2, long k) {\n // 1. define search space\n long left = (long)-1e11;\
|
yeoubi
|
NORMAL
|
2022-05-04T02:39:39.485132+00:00
|
2022-05-04T02:39:39.485162+00:00
| 990 | false |
```\nclass Solution {\n public long kthSmallestProduct(int[] nums1, int[] nums2, long k) {\n // 1. define search space\n long left = (long)-1e11;\n long right = (long)1e11;\n while(left < right){\n long mid = left + (right - left) / 2;\n if(countSmaller(nums1, nums2, mid) >= k){\n right = mid;\n } else {\n left = mid + 1;\n }\n }\n // At the end, left is the product that has k smaller products before it, so the kth smallest product is left - 1\n return left - 1;\n }\n \n private long countSmaller(int[] nums1, int[] nums2, long product){\n long count = 0;\n for(int i = 0; i < nums1.length; i++){\n // count all nums2[j] such that nums1[i] * nums2[j] < product\n if(nums1[i] >= 0){\n int left = 0;\n int right = nums2.length;\n while(left < right){\n int mid = left + (right - left) / 2;\n // if nums1[i] > 0, find the first occurrence of nums2[j] where nums1[i] * nums2[j] >= product\n if((long) nums1[i] * nums2[mid] < product){\n left = mid + 1;\n } else {\n right = mid;\n } \n }\n count += left;\n } else {\n int left = 0;\n int right = nums2.length;\n while(left < right){\n int mid = left + (right - left) / 2;\n // since nums1[i] is negative, nums2 is sorted\n // nums[j] * nums[i] will be in descending order from [0...nums2.length-1]\n // take [-4,-2,0,3] as an example, product with a negative number will become smaller if the number gets bigger\n // want to find the last nums2[j] such that nums1[i] * nums2[j] is not smaller than product\n if((long) nums1[i] * nums2[mid] >= product){\n left = mid + 1;\n } else {\n right = mid;\n }\n }\n count += nums2.length - left;\n }\n }\n return count;\n }\n}\n```
| 3 | 0 |
['Binary Tree', 'Java']
| 1 |
kth-smallest-product-of-two-sorted-arrays
|
[C] Binary search, explanation with examples
|
c-binary-search-explanation-with-example-zfnc
|
The idea is to use binary search on the answer.\nWe are searching for the least x, such that there are at least k products less than or equal to x.\n\nFor each
|
johndevou
|
NORMAL
|
2021-10-17T22:16:17.657383+00:00
|
2021-10-17T22:16:17.657459+00:00
| 423 | false |
The idea is to use binary search on the answer.\nWe are searching for the least x, such that there are at least k products less than or equal to x.\n\nFor each element in the array *a[n]* we perform a special binary search on the array *b[m]*, hence a total running time of *O(n.log(m).log(Range))*.\nSince the order of *a* and *b* is irrelevant, this bound can further be improved to *O(min(n,m).log(max(n,m)).log(Range))*.\n\n*How exactly do we perform the search?*\n\nLet *the upper-bound of y* be the number of elements in *b* that are less than or equal to y.\n\nLet x\u22650. Let w>0 be an element of *a* and we want to know how many products of w with an element of *b* are less than or equal to x.\nThe numbers of these products is exactly *the upper-bound of (x div w)*, for instance:\n\nx=31, w=10, b=[-5, -4, -3, -3, -2, -1, 2, 3, 3, 4, 6, 12, 13].\nThe number of products, less than or equal to 31 is 9.\nThis corresponds to the range [-5, -4, -3, -3, -2, -1, 2, 3, 3], which directly corresponds to *the upper-bound of 3*.\n\nIn case w<0 we are interested in *m - the upper-bound of (x div w)-1*.\nFor instance x=31, w=-10 in the above example.\nThe valid range of products is [-3, -3, -2, -1, 2, 3, 3, 4, 6, 12, 13].\nThe number of elemets here is exactly *m - the upper-bound of -4*, since the later corresponds to the remaining range [-5, -4].\n\nIn case x<0, we have some special cases, depending on whether w divides x or not.\n\nFor w>0 and w divides x we are again searching for *the upper-bound of (x div w)*.\nFor instance x=-30, w=10 in the above example.\nThe valid range is [-5, -4, -3, -3], which corresponds to the products [-50, -40, -30, -30], all less than or equal to -30.\n\nHowever if w does not divide x we are searching for *the upper-bound of (x div w)-1*.\nFor instance x=-31, w=10. \nThe valid range is now [-5, -4], which corresponds to the producuts [-50, -40].\nNote that -3 is no longer in the valid range, since -30 > -31.\n\nFor w<0 and w divides x we are again searching for *m - the upper-bound of (x div w)-1*.\nFor instance x=-30, w=-10. \nThe valid range is now [3, 3, 4, 6, 12, 13], which corresponds to the products [-30, -30, -40, -60, -120, -130], all less than or equal to -30.\n\nHowever if w does not divide x we are searching for *m - the upper-bound of (x div w)*.\nFor instance x=-31, w=-10.\nThe valid range is now [4, 6, 12, 13], which corresponds to the products [-40, -60, -120, -130].\nNote that 3 is now longer in the valid range, since -30 > -31.\n\nThe last remaining case is w=0, which is trivial, since all resulting products are equal to 0.\nIn case x\u22650, we have m products less than or equal to x and in case x<0 we have no such products.\n\nThe following C solution is a straight-forward illustration of the above idea.\n```\nint ub(int* a, int l, int r, long long x){\n int m;\n while (l <= r){\n m = (l+r)/2;\n if (a[m] <= x) l = m+1;\n else r = m-1;\n }\n \n return l;\n}\n\nlong long kthSmallestProduct(int* a, int n, int* b, int m, long long k){\n long long r = (long long)(1e10), l = -r, x, c;\n \n int i;\n \n while (l <= r){\n x = (l+r)/2;\n \n c = 0;\n for (i = 0; i < n; i++){\n if (a[i] > 0) c += ub(b, 0, m-1, x/a[i] - (x<0 && x%a[i]));\n else if (a[i] < 0) c += m - ub(b, 0, m-1, x/a[i] - !(x<0 && x%a[i]));\n else if (x >= 0) c += m;\n \n if (c > k-1) break;\n }\n \n if (c <= k-1) l = x+1;\n else r = x-1;\n }\n \n return l;\n}\n```
| 3 | 0 |
[]
| 0 |
kth-smallest-product-of-two-sorted-arrays
|
[C++] Binary Search, O((m + n)log(Max - Min)), Explained
|
c-binary-search-om-nlogmax-min-explained-gck2
|
Divide nums1 and nums2 into two parts by sign, with left half <= 0, right half > 0, denoted as l1, r1, l2, r2, so 4 combinations of subarrays of nums1 and nums2
|
cwcu
|
NORMAL
|
2021-10-16T19:08:36.862216+00:00
|
2021-10-16T22:31:08.088958+00:00
| 1,031 | false |
1. Divide nums1 and nums2 into two parts by sign, with left half <= 0, right half > 0, denoted as l1, r1, l2, r2, so 4 combinations of subarrays of nums1 and nums2 in total, i.e. (l1, l2), (l1, r2), (r1, l2), (r1, r2)\n2. Binary search the answer, which is guaranteed to be in the range of [Min, Max], where Min and Max are the minimum and maximum product. So initialize the search range as [left = Min, right = Max], for each mid = (left + right) >> 1, count how many products <= mid in the 4 combinations / matrices above. And reverse the subarrays to make the matrices sorted when necessary. \n3. If the number of products <= mid is exactly k, return the Max product <= mid.\n\nNote: \n1. For subarrays a[0, 1, ..., n - 1] and b[0, 1 ..., m - 1], their products can be represented as a matrix c[x][y] = a[x] * b[y] (We don\'t really represent it because that would be O(nm) complexity). And for the matrix to be sorted: we actually mean every row and column are sorted ascendingly.\n2. To find how many elements in a sorted matrix <= mid, please refer https://leetcode.com/problems/kth-smallest-element-in-a-sorted-matrix/\n\n\n\n```\n#define ll long long\n\nclass Solution {\npublic:\n // refer: https://leetcode.com/problems/kth-smallest-element-in-a-sorted-matrix/\n inline ll countInMatrix(vector<ll>& a, vector<ll>& b, ll mid, ll& Max) {\n ll n = a.size(), m = b.size();\n // matrix c[x][y] := a[x] * b[y]\n ll x = n - 1, y = 0;\n ll cnt = 0;\n \n while (x >= 0 && y < m) {\n if (a[x] * b[y] <= mid) {\n Max = max(Max, a[x] * b[y]);\n cnt += x + 1;\n y++;\n }\n else {\n x--;\n }\n }\n \n return cnt;\n }\n \n long long kthSmallestProduct(vector<int>& nums1, vector<int>& nums2, long long k) {\n // divide into four combinations by positive / negative, represented in 4 sorted matrices\n // binary search by value\n // suppose mid = (left + right) >> 1; count how many elements <= mid in those 4 matrices\n \n ll n1 = nums1.size(), n2 = nums2.size();\n ll p1, p2;\n for (ll i = 0; i <= n1; ++i) {\n if (i == n1 || nums1[i] > 0) {\n p1 = i;\n break;\n }\n }\n for (ll i = 0; i <= n2; ++i) {\n if (i == n2 || nums2[i] > 0) {\n p2 = i;\n break;\n }\n }\n \n vector<ll> l1(nums1.begin(), nums1.begin() + p1);\n vector<ll> r1(nums1.begin() + p1, nums1.end());\n vector<ll> l2(nums2.begin(), nums2.begin() + p2);\n vector<ll> r2(nums2.begin() + p2, nums2.end());\n \n vector<ll> l1r(l1); // l1 reverse\n vector<ll> r1r(r1);\n vector<ll> l2r(l2);\n vector<ll> r2r(r2);\n reverse(l1r.begin(), l1r.end());\n reverse(r1r.begin(), r1r.end());\n reverse(l2r.begin(), l2r.end());\n reverse(r2r.begin(), r2r.end());\n \n ll left = LLONG_MAX, right = LLONG_MIN;\n vector<ll> t1 = {0, p1 - 1, p1, n1 - 1};\n vector<ll> t2 = {0, p2 - 1, p2, n2 - 1};\n for (ll i = 0; i < 4; ++i) {\n if (t1[i] < 0 || t1[i] >= n1) continue;\n for (ll j = 0; j < 4; ++j) {\n if (t2[j] < 0 || t2[j] >= n2) continue;\n left = min(left, (ll)nums1[t1[i]] * nums2[t2[j]]);\n right = max(right, (ll)nums1[t1[i]] * nums2[t2[j]]);\n }\n }\n \n while (left <= right) {\n ll mid = (left + right) >> 1;\n \n ll cur = 0;\n ll Max = LLONG_MIN;\n cur += countInMatrix(l1, r2r, mid, Max);\n cur += countInMatrix(l1r, l2r, mid, Max);\n cur += countInMatrix(r1r, l2, mid, Max);\n cur += countInMatrix(r1, r2, mid, Max);\n \n if (cur == k) return Max;\n else if (cur > k) right = mid - 1;\n else left = mid + 1;\n }\n \n return left;\n }\n};\n```
| 3 | 0 |
['C', 'Binary Tree']
| 0 |
kth-smallest-product-of-two-sorted-arrays
|
short and concise C++ code
|
short-and-concise-c-code-by-cychiu77-nns2
|
IntuitionBinary SearchApproachIterate througth nums1 and denote current elemnt as num.
In each iteration, count the number of elements in nums2 such that their
|
gwku77
|
NORMAL
|
2025-01-17T12:10:24.998506+00:00
|
2025-01-17T12:35:34.511778+00:00
| 201 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Binary Search
# Approach
<!-- Describe your approach to solving the problem. -->
Iterate througth `nums1` and denote current elemnt as `num`.
In each iteration, count the number of elements in `nums2` such that their product <= `mid`.
Divide into three cases. Dry running test cases makes it easier to understand.
1. `num > 0`
2. `num == 0`
3. `num < 0`
Compute `mid` with `floor` to get rid of infinite loop since `l` and `r` may be negative numbers.
# Complexity
- Time complexity: $$O(N1 ∗ Log(N2) ∗ Log(2 * 10^{10}))$$
- Space complexity: $$O(1)$$
# Code
```cpp []
class Solution {
public:
long long kthSmallestProduct(vector<int>& nums1, vector<int>& nums2, long long k) {
int n1 = nums1.size(), n2 = nums2.size();
if (n1 > n2) {
swap(n1, n2);
nums1.swap(nums2);
}
long long l = -1e10, r = 1e10;
while (l < r) {
long long mid = floor((l + r) / 2.);
long long cnt = 0;
for (auto &num : nums1) {
if (num == 0) {
if (mid >= 0) cnt += n2;
}
else if (num > 0) {
double target = (double)mid / num;
int j = upper_bound(begin(nums2), end(nums2), target) - begin(nums2);
cnt += j;
}
else {
double target = (double)mid / num;
int j = lower_bound(begin(nums2), end(nums2), target) - begin(nums2);
cnt += (n2 - j);
}
}
if (cnt >= k) {
r = mid;
}
else {
l = mid + 1;
}
}
return l;
}
};
```
| 2 | 0 |
['C++']
| 0 |
kth-smallest-product-of-two-sorted-arrays
|
Binary Search - Simple C++ Solution with explanation
|
binary-search-simple-c-solution-with-exp-btjk
|
Intuition\n\nWe will start with the binary search finding how many numbers are less than the current value. And will go to the left or right side based on the n
|
Sajal0701
|
NORMAL
|
2024-11-18T16:57:40.602657+00:00
|
2024-11-18T16:57:40.602694+00:00
| 158 | false |
# Intuition\n\nWe will start with the binary search finding how many numbers are less than the current value. And will go to the left or right side based on the no. of elements smaller than our current value.\n\nChecking for numbers smaller than a value. Now we will iterate over the first array. \n\nNow if the current element is negative, then we will find the largest number in nums2 which is lesser than or equal to the number x/nums1[i]( removing the part added by first array). Now since the current element was negative we will take all the elements on the right side because we need all the elements that are greater.\n\nNow if the element of nums1 is postive than we will simply find the smallest number that is greater than the x/nums1[i]. Now after counting for each index if at any point the count is greater than or equal to k , we will return true else false;\n\nNow if the function returns true it means that this could be the possible answer and we will shift the binary search to the left as we want kth smallest element and currently we are getting more than k smaller elements on the left.\n\n\n\n# Approach\n\nStart with the binary search and call the isPossible function for the every possible value of mid , and move the binary search window based on its output.\n\nwe will keep a count and iterate over the first array.\n\nNow if the current element is negative we will find all the numbers such than nums[i]*nums2[j] should be greater than x. Thus we will find the lower bound of x/nums1[i] and increase the count by n2-ind where ind is the index of largest value of nums2 which is lesser than x/nums1[i].\n\nElse if the current element is positive we will find all the numbers such that nums[i]*nums2[j] is lesser than x. thus we will find upper bound of x/nums1[i] and increase the count by ind.\n\nif at any point count >= k , it means this is possible value and we return true which means shift the window to the left as there are more smaller elements on the left side.\n\n# Complexity\n- Time complexity:\n$$O(nlogn)$$\n\n- Space complexity:\n$$O(1)$$\n\n# Code\n```cpp []\nclass Solution {\npublic:\n bool isPossible(vector<int>& nums1, vector<int>& nums2, long long k,\n long long x) {\n \n int n1 = nums1.size();\n int n2 = nums2.size();\n long long count = 0;\n\n for(int i = 0; i<n1; i++){\n if(nums1[i] < 0){\n long long rem = ceil((double)x/nums1[i]);\n int ind = lower_bound(nums2.begin(), nums2.end() , rem) -nums2.begin();\n count += (n2-ind);\n }\n else if( nums1[i] > 0) {\n long long rem = floor((double)x/nums1[i]);\n int ind = upper_bound(nums2.begin(), nums2.end(), rem) - nums2.begin();\n count += ind;\n }\n else {\n if(x>=0) count += n2;\n }\n if(count >= k) return true;\n }\n return count >=k;\n\n }\n\n long long kthSmallestProduct(vector<int>& nums1, vector<int>& nums2,\n long long k) {\n long long s = -1e10;\n long long n = nums1.size();\n long long m = nums2.size();\n long long e = 1e10;\n\n long long ans = 0;\n\n while (s <= e) {\n long long mid = s + (e - s) / 2;\n\n if (isPossible(nums1, nums2, k, mid)) {\n ans = mid;\n e = mid - 1;\n } else\n s = mid + 1;\n }\n\n return ans;\n }\n};\n```
| 2 | 0 |
['Binary Search', 'C++']
| 0 |
kth-smallest-product-of-two-sorted-arrays
|
Easy Solution :)
|
easy-solution-by-user20222-fi25
|
Code\n\nclass Solution {\npublic:\n long long f(vector<int>&v1,vector<int>&v2,long long k,long long t){\n long long ct=0;\n for(long long i=0;i
|
user20222
|
NORMAL
|
2024-06-03T11:52:19.123422+00:00
|
2024-06-03T11:52:19.123467+00:00
| 446 | false |
# Code\n```\nclass Solution {\npublic:\n long long f(vector<int>&v1,vector<int>&v2,long long k,long long t){\n long long ct=0;\n for(long long i=0;i<v1.size();i++){\n if(v1[i]==0){\n if(t>=0)ct+=v2.size();\n }\n else if(v1[i]>0){\n long long val = floor((double)t/v1[i]);\n auto it = upper_bound(v2.begin(),v2.end(),val);\n if(it==v2.end()||(*it)>val)it--;\n ct+=(it-v2.begin()+1);\n }else{\n long long val = ceil((double)t/v1[i]);\n auto it = lower_bound(v2.begin(),v2.end(),val); \n ct+=(v2.end()-it);\n }\n if(ct>k)return ct;\n }\n return ct;\n }\n long long kthSmallestProduct(vector<int>& nums1, vector<int>& nums2, long long k) {\n long long low = min({nums1[0]*1LL*nums2.back(),nums1.back()*1LL*nums2[0],nums1[0]*1LL*nums2[0]}),high = max({nums1[0]*1LL*nums2[0],nums1.back()*1LL*nums2.back(),nums1[0]*1LL*nums2.back(),nums2[0]*1LL*nums1.back()}),ans = 0; \n while(low<=high){\n long long mid = low+(high-low)/2;\n long long x = f(nums1,nums2,k,mid); \n if(x<k){\n low = mid+1;\n }else{\n ans = mid;\n high =mid-1;\n }\n } \n return ans;\n }\n};\n```
| 2 | 0 |
['C++']
| 0 |
kth-smallest-product-of-two-sorted-arrays
|
Java Solution Binary Search Approach Used
|
java-solution-binary-search-approach-use-o72b
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \nBinary Search Approach
|
NamanSaini18
|
NORMAL
|
2023-07-12T10:59:49.763712+00:00
|
2023-07-12T10:59:49.763734+00:00
| 925 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. --> \nBinary Search Approach Used\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n \n public long kthSmallestProduct(int[] nums1, int[] nums2, long k)\n {\n long si = -1000_000_0000l;\n long ei = 1000_000_0000l;\n long ans = 0;\n while(si <= ei)\n {\n long mid = si + (ei - si) / 2;\n long count = 0;\n if(countofProduct(nums1,nums2,mid) >= k)\n {\n ans = mid;\n ei = mid - 1;\n }\n else\n {\n si = mid + 1;\n }\n\n\n }\n\n return ans;\n\n\n }\n\n private static long countofProduct(int[] nums1, int[] nums2, long prod)\n {\n long res = 0;\n for(int e1 : nums1)\n {\n if(e1 >= 0)\n {\n int count = 0;\n int low = 0;\n int high = nums2.length - 1;\n while (low <= high)\n {\n int mid = low + (high - low) / 2;\n if((long) e1 * nums2[mid] <= prod)\n {\n count = mid + 1;\n low = mid + 1;\n }\n else {\n high = mid - 1;\n }\n }\n res += count;\n\n }\n else {\n int count = 0;\n int low = 0;\n int high = nums2.length - 1;\n while (low <= high)\n {\n int mid = low + (high - low) / 2;\n if((long) e1 * nums2[mid] <= prod)\n {\n count = nums2.length - mid;\n high = mid - 1;\n }\n else {\n low = mid + 1;\n }\n }\n res += count;\n }\n\n }\n return res;\n\n\n }\n}\n```
| 2 | 0 |
['Java']
| 0 |
kth-smallest-product-of-two-sorted-arrays
|
Binary Search wtih explnation JAVA
|
binary-search-wtih-explnation-java-by-ve-ysun
|
Intuition\n Describe your first thoughts on how to solve this problem. \nThe given arrays are already sorted. We need find the kth smallest product.\n\n##### Br
|
venkatpselvam1
|
NORMAL
|
2023-02-18T16:47:47.400797+00:00
|
2023-02-18T16:47:47.400839+00:00
| 254 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe given arrays are already sorted. We need find the $$k$$th smallest product.\n\n##### Brute Force approach:\nWe can create a PriorityQueue with k Length and we can iterate each element in nums1 with each element in nums2. The product we can put in the Priority Queue. But this appraoch will take $$O( (n*m) log n)$$.\n\n##### Binary Search:\nAs the arrays are already sorted, we can use BST to find the no of products which are less than or equal to current value. This current value can vary between Long.MIN_VALUE to Long.MAX_VALUE.\n\ne.g:\n[1,2,3,4,5]\n[1,2,3,4,5]\nAll the products are \n```\n[ (1,2,3,4,5), (2,4,6,8,10), (3,6,9,12,15), (4,8,12,16,20), (5,10,15,20,25)]\n```\n\nFor the given no 8, the no of products <= 8 are :\n```\n[ (1,2,3,4,5), (2,4,6,8), (3,6), (4,8), (5)]\nAns = 5 + 4 + 2 + 2+ 1 = 14\n```\n\nSo if we have a method which gives no of products which are less than equal to given value than we can use BST as follows to solve the problem.\n\n```\nl = long.MIN_VALUE\nh = long.MAX_VALUE\nwhile(l < h)\n{\n m = l +(h-l)/2;\n val = getProductsLessThanOrEqualToM(m);\n if(val >= k) h = m\n else l = m\n}\nreturn h\n```\n\n##### How to get no of products less than given value\n\nFor simplicity lets consider both of our array only contains postive value.\n\n```\nIndex: 0,1,2,3,4\nNums1: 1,2,3,4,5\nNums2: 1,2,3,4,5\n\nWe want to get all the products less than 8\n[0, 4] -> 1 * 5 = 5 so it indicates all the index (0 to 3 also will have the product less than 8) => 5\n\n[1, 4] -> 2 * 5 = 10 which is greater than 8\n[1, 3] -> 2 * 4 = 8 which is equal to 8. So all index b/w [0,3] also will have the product less than 8 => 4\n\n//we don\'t need to consider [2,4] as [1,4] already not in the list\n[2,3] -> 3 * 4 = 12 which is greater than 8\n[2,2] -> 3 * 3 = 9 which is greater than 9\n[2,1] -> 3 * 2 = 6 so all the index b/w [0,1] have the product less than 8 => 2\n\n[3,1] -> 4 * 2 => 8 so all the index b/w [0,1] have the product less than 8 =>2\n\n[4,1] -> 5 * 2 => 10 which is greater than 8\n[4,0] -> 5 * 1 => 5 so the only 0 the index of nums2 will contibute => 1\n\nTotal ans: 5 + 4 + 2 + 2 + 1 = 14\n\n```\n\n##### How to handle postivie and negative nos?\nWhen nums1 is positive and nums2 is positive.\n\n```\n*\n1,2,3,4,5\n1,2,3,4,5\n *\nThe start index:\nfor nums1: 0\nfor nums2: 4\n```\n\nWhen nums1 is positive and nums2 is negative.\n```\n *\n1,2,3,4,5\n-5,-4,-3,-2,-1\n *\nThe start index:\nfor nums1: 4\nfor nums2: 4\n```\n\nWhen nums1 is negative and nums2 is negative.\n```\n *\n-5,-4,-3,-2,-1\n-5,-4,-3,-2,-1\n*\nThe start index:\nfor nums1: 4\nfor nums2: 0\n```\n\nWhen nums1 is negative and nums2 is positive.\n```\n*\n-5,-4,-3,-2,-1\n1,2,3,4,5\n*\nThe start index:\nfor nums1: 0\nfor nums2: 0\n```\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\nn - no of elements in the array 1\nm - no of elements in the array 2\n- Time complexity: $$O( (n+m) log n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int findMaxNegativeIndex(int[] nums)\n {\n var low = 0;//negtive no\n var high = nums.length -1;//not a negative no\n if(nums[low] > 0) return -1;//don\'t not have any negative value\n if(nums[high] < 0) return high;//all numbers are negative\n while(low < high)\n {\n var m = (low + high + 1)/2;\n if(nums[m] < 0)\n {\n low = m;\n }else{\n if(high == m) break;\n high = m;\n }\n }\n return low;\n }\n public long kthSmallestProduct(int[] nums1, int[] nums2, long k) {\n long low = Long.MIN_VALUE/2;//have less than k no product than this\n long high = Long.MAX_VALUE/2;//have atleast k no product less than this\n var negInd1 = findMaxNegativeIndex(nums1);\n var negInd2 = findMaxNegativeIndex(nums2);\n while(low < high)\n {\n long m = low + (high-low)/2;\n var val = getNoOfProductLessThan(m, nums1, nums2, negInd1, negInd2);\n if(k <= val){\n high = m;\n }else{\n if(low == m) break;\n low = m;\n }\n }\n\n return high;\n }\n public long getNoOfProductLessThan(long m, int[] nums1, int[] nums2, int f, int s)\n {\n var l1 = nums1.length;\n var l2 = nums2.length;\n \n long ans = 0;\n\n //when nums1 pos and nums2 is pos\n var j = l2-1;\n for(int i = f+1; i < l1; i++)\n {\n //special case when nums1[i] == 0\n if(nums1[i] == 0)\n {\n if(m >= 0) ans+= l2;\n continue;\n }\n while(j > s && ( (long)nums1[i] * (long)nums2[j] > m) )\n {\n j--;\n }\n if(j > s) ans+= j-s;\n }\n\n //when nums1 pos and nums2 is neg\n j = s;\n for(int i = l1-1; i > f; i--)\n {\n if(nums1[i] == 0) break;\n while(j >= 0 && ( (long)nums1[i] * (long)nums2[j] > m) )\n {\n j--;\n }\n if(j >= 0) ans += (j+1);\n }\n\n //when nums1 neg and nums2 is neg\n j = 0;\n for(int i = f; i >= 0; i--)\n {\n while(j <= s && ( (long)nums1[i] * (long)nums2[j] > m) )\n {\n j++;\n }\n if(j <= s) ans+= (s-j+1);\n }\n\n //when nums1 neg and nums2 is pos\n j = s+1;\n for(int i = 0; i <= f; i++)\n {\n while(j < l2 && ( (long)nums1[i] * (long)nums2[j] > m) )\n {\n j++;\n }\n if(j < l2) ans += (l2 - j);\n }\n return ans;\n }\n}\n```
| 2 | 0 |
['Java']
| 0 |
kth-smallest-product-of-two-sorted-arrays
|
c++ solution using binary search
|
c-solution-using-binary-search-by-dilips-a7ou
|
\nclass Solution {\npublic:\n int n,m;\n using ll =long long;\n ll find(vector<int>&nums1,vector<int>&nums2,ll product)\n {\n ll count=0;\n
|
dilipsuthar17
|
NORMAL
|
2022-01-26T14:11:57.643035+00:00
|
2022-01-26T14:39:50.309225+00:00
| 1,039 | false |
```\nclass Solution {\npublic:\n int n,m;\n using ll =long long;\n ll find(vector<int>&nums1,vector<int>&nums2,ll product)\n {\n ll count=0;\n for(int i=0;i<n;i++)\n {\n long long val=nums1[i];\n if(val>=0)\n {\n ll l=0;\n ll r=m-1;\n ll ans=-1;\n while(l<=r)\n {\n ll mid=(l+r)/2;\n if((val*nums2[mid])<=product)\n {\n ans=mid;\n l=mid+1;\n }\n else\n {\n r=mid-1;\n }\n }\n count+=ans+1;\n }\n else\n {\n ll l=0;\n ll r=m-1;\n ll ans=m;\n while(l<=r)\n {\n ll mid=(l+r)/2;\n if((val*nums2[mid])<=product)\n {\n ans=mid;\n r=mid-1;\n }\n else\n {\n l=mid+1;\n }\n }\n count+=m-ans;\n }\n }\n return count;\n }\n long long kthSmallestProduct(vector<int>& nums1, vector<int>& nums2, long long k) \n {\n n=nums1.size();\n m=nums2.size();\n ll f1=nums1[0];\n ll f2=nums1[n-1];\n ll f3=nums2[0];\n ll f4=nums2[m-1];\n ll l=min({f1*f2,f1*f3,f1*f4,f2*f3,f2*f4,f3*f4});\n ll r=max({f1*f2,f1*f3,f1*f4,f2*f3,f2*f4,f3*f4});\n ll ans=-1;\n while(l<=r)\n {\n ll mid=(l+r)/2;\n if(find(nums1,nums2,mid)>=k)\n {\n ans=mid;\n r=mid-1;\n }\n else\n {\n l=mid+1;\n }\n }\n return ans;\n }\n};\n```
| 2 | 0 |
['C', 'Binary Tree', 'C++']
| 0 |
kth-smallest-product-of-two-sorted-arrays
|
[Python] Variation of finding Kth value in 2D Ascending Array
|
python-variation-of-finding-kth-value-in-80m9
|
1) We split each sorted arrays into positive and negative parts pos1,neg1, pos2, neg2. \n2) We can compute how many multiplied numbers are positive, negative or
|
irt
|
NORMAL
|
2021-10-20T18:44:31.065347+00:00
|
2021-10-21T04:33:57.024267+00:00
| 549 | false |
1) We split each sorted arrays into positive and negative parts pos1,neg1, pos2, neg2. \n2) We can compute how many multiplied numbers are positive, negative or zeros. Return 0 if k falls between.\n3) If k<=number of negatives, we need to check multiplied numbers from (pos1, neg2) and (pos2, neg1). Else we need to check multiplied numbers from (pos1,pos2) and (neg1, neg2). \n4) If k<= number of negatives, just make negative parts positive and reverse the arrays neg1 and neg2. It does not matter, we can make the result negative. But in this case, kth smallest number would be actually the (number_of_negatives-k+1)th smallest number when we reverse the negaive parts with their absoulte values. \n5) Now the problem is same as finding kth smallest number in a two dimensional array where numbers in each row/column is increasing since the 2D matrix can be thought of as `Val[row][col]= pair1[row]*pair2[col]`. We can compute the rank of an arbitrary value in each pairs in `O(m+n)` time. We just need to compute rank from the two pairs `O(logV)` time. \n```\nimport bisect\nclass Solution:\n def kthSmallestProduct(self, nums1: List[int], nums2: List[int], k: int) -> int:\n n1,n2 = len(nums1), len(nums2)\n l1, r1 = bisect.bisect_left(nums1, 0),bisect.bisect_right(nums1, 0)\n l2, r2 = bisect.bisect_left(nums2, 0),bisect.bisect_right(nums2, 0)\n num_of_negatives = l1*(n2-r2)+ l2*(n1-r1)\n num_of_positives = l1*l2+ (n1-r1)*(n2-r2)\n num_of_zeros = (r1-l1)*n2 + (r2-l2)*n1- (r1-l1)*(r2-l2)\n nums1_n, nums1_p = nums1[:l1], nums1[r1:]\n nums2_n, nums2_p = nums2[:l2], nums2[r2:]\n nums1_n, nums2_n = [-d for d in nums1_n], [-d for d in nums2_n]\n nums1_n.reverse(), nums2_n.reverse()\n if k<= num_of_negatives:\n return -self.compute(nums1_n, nums2_p, nums2_n, nums1_p, num_of_negatives-k+1)\n elif k<=num_of_negatives+num_of_zeros:\n return 0\n else:\n return self.compute(nums1_n, nums2_n, nums1_p, nums2_p, k-num_of_negatives-num_of_zeros)\n \n def compute(self, pair_1r,pair_1c, pair_2r, pair_2c, k):\n start,end = float(\'inf\'), float(\'-inf\')\n if pair_1r and pair_1c:\n start = min(pair_1r[0]*pair_1c[0], start)\n end = max(pair_1r[-1]*pair_1c[-1], end)\n if pair_2r and pair_2c:\n start = min(pair_2r[0]*pair_2c[0], start)\n end = max(pair_2r[-1]*pair_2c[-1], end)\n while start<end:\n mid = (start+end)//2\n k1, low1, high1 = self.get_rank(pair_1r,pair_1c, mid)\n k2, low2, high2 = self.get_rank(pair_2r,pair_2c, mid)\n if k1+k2==k:\n return max(low1,low2)\n elif k1+k2<k:\n start = min(high1, high2)\n else:\n end = max(low1, low2)\n return start\n def get_rank(self,pair_r, pair_c,mid):\n m, n = len(pair_r), len(pair_c)\n if m==0 or n==0:\n return 0, float(\'-inf\'), float(\'inf\')\n row, col = m-1, 0\n low, high = float(\'-inf\'), float(\'inf\')\n ans = 0\n while row>=0:\n while col<n and pair_r[row]*pair_c[col]<=mid:\n low = max(low, pair_r[row]*pair_c[col])\n col +=1\n if col<n: \n high = min(high, pair_r[row]*pair_c[col])\n ans += col\n row -= 1\n return ans, low, high\n```
| 2 | 0 |
['Binary Tree']
| 0 |
kth-smallest-product-of-two-sorted-arrays
|
C++/Rust solution
|
crust-solution-by-6cdh-wfzw
|
We execute 4 simple algorithm on 4 sorted sub matrix to process negative rather than 1 complex algorithm.\n\nTime: O(n * log(10^10))\nSpace: O(1)\n\nRust\n\nThe
|
6cdh
|
NORMAL
|
2021-10-18T11:32:30.215649+00:00
|
2021-10-18T11:32:30.215690+00:00
| 333 | false |
We execute 4 simple algorithm on 4 sorted sub matrix to process negative rather than 1 complex algorithm.\n\nTime: O(n * log(10^10))\nSpace: O(1)\n\nRust\n\nThe space complexity of this rust code is not O(1) since I\'m still a newbee on rust and\ndon\'t know how to implement it.\n\n```rust\nimpl Solution {\n pub fn kth_smallest_product(nums1: Vec<i32>, nums2: Vec<i32>, k: i64) -> i64 {\n let (neg1, pos1): (Vec<i32>, Vec<i32>) = nums1.iter().partition(|&&x| x < 0);\n let (neg2, pos2): (Vec<i32>, Vec<i32>) = nums2.iter().partition(|&&x| x < 0);\n let rneg1: Vec<i32> = neg1.iter().cloned().rev().collect();\n let rneg2: Vec<i32> = neg2.iter().cloned().rev().collect();\n let rpos1: Vec<i32> = pos1.iter().cloned().rev().collect();\n let rpos2: Vec<i32> = pos2.iter().cloned().rev().collect();\n let countle = |mid: i64| {\n Solution::countle_in_sorted_matrix(&neg1, &rpos2, mid)\n + Solution::countle_in_sorted_matrix(&rneg1, &rneg2, mid)\n + Solution::countle_in_sorted_matrix(&rpos1, &neg2, mid)\n + Solution::countle_in_sorted_matrix(&pos1, &pos2, mid)\n };\n\n let limit = 10_i64.pow(10);\n let mut r = (-limit, limit);\n while r.0 != r.1 {\n let mid = r.0 + (r.1 - r.0) / 2;\n if countle(mid) < k {\n r.0 = mid + 1;\n } else {\n r.1 = mid;\n }\n }\n r.0\n }\n\n fn countle_in_sorted_matrix(nums1: &[i32], nums2: &[i32], k: i64) -> i64 {\n let mut j = nums2.len();\n let mut cnt: i64 = 0;\n for &v in nums1 {\n while j != 0 && (nums2[j - 1] as i64) * (v as i64) > k {\n j -= 1;\n }\n cnt += j as i64;\n }\n\n cnt\n }\n}\n```\n\nC++\n\nO(1) space\n\n```cpp\nclass Solution {\n public:\n long long kthSmallestProduct(vector<int>& nums1,\n vector<int>& nums2,\n long long k) {\n int64_t l = -1e10;\n int64_t r = 1e10;\n while (l != r) {\n const auto mid = l + (r - l) / 2;\n if (countle(nums1, nums2, mid) < k) {\n l = mid + 1;\n } else {\n r = mid;\n }\n }\n return l;\n }\n\n int64_t countle(const vector<int>& nums1,\n const vector<int>& nums2,\n int64_t k) {\n const auto pos1 = partition_point(nums1.begin(),\n nums1.end(),\n [](const auto& x) { return x < 0; });\n const auto pos2 = partition_point(nums2.begin(),\n nums2.end(),\n [](const auto& x) { return x < 0; });\n const auto first1 = nums1.begin();\n const auto last1 = nums1.end();\n const auto first2 = nums2.begin();\n const auto last2 = nums2.end();\n return countle_in_sorted_matrix(pos1, last1, pos2, last2, k) +\n countle_in_sorted_matrix(first1,\n pos1,\n make_reverse_iterator(last2),\n make_reverse_iterator(pos2),\n k) +\n countle_in_sorted_matrix(make_reverse_iterator(pos1),\n make_reverse_iterator(first1),\n make_reverse_iterator(pos2),\n make_reverse_iterator(first2),\n k) +\n countle_in_sorted_matrix(make_reverse_iterator(last1),\n make_reverse_iterator(pos1),\n first2,\n pos2,\n k);\n }\n\n template <class It1, class It2>\n int64_t countle_in_sorted_matrix(\n It1 first1, It1 last1, It2 first2, It2 last2, int64_t k) {\n int64_t cnt = 0;\n auto j = last2;\n for (auto it = first1; it != last1; ++it) {\n while (j != first2 && j[-1] * int64_t(*it) > k) {\n --j;\n }\n cnt += distance(first2, j);\n }\n return cnt;\n }\n};\n```
| 2 | 0 |
['C', 'Rust']
| 0 |
kth-smallest-product-of-two-sorted-arrays
|
My notes
|
my-notes-by-lilydenris-2t5t
|
My notes on this Q. You are welcome if it helped you otherwise let me know how I can improve.\n\nI know this is binary search but the implementation details kil
|
lilydenris
|
NORMAL
|
2021-10-16T22:40:26.101680+00:00
|
2021-10-16T22:45:49.119994+00:00
| 337 | false |
My notes on this Q. You are welcome if it helped you otherwise let me know how I can improve.\n\nI know this is binary search but the implementation details killed me.\n\nThe first puzzle is what should the check function return. I see most solution is to return true if number of x*y <= answer is >= k. \n\nwhy both has =? Can we return true if number of x*y < answer is > k and still make it work? I still don\'t know the answer.\n\nLet me explain why return true **if number of x*y <= answer is >= k** works with my binary search template:\n\n```\nint start = 0, end = max_val;\nwhile (start + 1 < end) {\n\tint mid = (start + end)/2;\n\t\n\tif (number of x*y <= mid is >= k) // we can tell the ans is in [start, mid]\n\t\tend = mid;\n else\n\t start = mid;\n}\n\nif (number of x*y <= start is >= k) // if start is satsified then end will also return true, so return start.\n\treturn start;\nelse\n\treturn end;\n```\nThis is when I feel my binary search template is not very good to solve this kind of questions, because I am not confident what check() should return.\n\nOk, the next step is to work on the check function. My C++ nlogn solution will TLE everytime, the complexity is 5*10^4 * log(5*10^4) * log(10^10) = 5 *10000 * 16 * 34 = 27,200,000. I will still mention as I keep getting WA during the contest.\n```\nans = 30, x = 4 then we are looking for y <=7\nans = 30, x = -4 then we are looking for y >= -7\nans = -30, x = 4 then we are looking for y <= -8 \nans = -30, x = -4 then we are looking for y >= 8\n```\n \nThe last two cases screwed me over. Below is the binary search check() function that will TLE.\n```\nclass Solution {\npublic:\n // <= target\n bool check(long long target, vector<int> & nums1, vector<int> & nums2, long long k) {\n long long cnt = 0;\n for (int i = 0; i < nums1.size(); i++) {\n if (nums1[i] == 0) {\n if (target >= 0) {\n cnt += nums2.size();\n }\n } else {\n if (nums1[i] < 0) {\n // we need to patch the value by 1 \n long long x = target / nums1[i];\n if (target % nums1[i] != 0) {\n if (target < 0)\n x++;\n }\n auto it = lower_bound(nums2.begin(), nums2.end(), x);\n cnt += nums2.size() - (it - nums2.begin());\n } else {\n // we need to patch the value by 1 \n long long x = target / nums1[i];\n if (target % nums1[i] != 0) {\n if (target < 0)\n x--;\n }\n auto it = upper_bound(nums2.begin(), nums2.end(), x);\n\n cnt += it - nums2.begin();\n }\n }\n }\n\n return cnt >= k;\n }\n \n long long kthSmallestProduct(vector<int>& nums1, vector<int>& nums2, long long k) {\n long long start = -1e10, end = 1e10;\n while (start + 1 < end) {\n long long mid = start + end >> 1;\n if (check(mid, nums1, nums2, k)) {\n end = mid;\n } else {\n start = mid;\n }\n }\n \n if (check(start, nums1, nums2, k))\n return start;\n \n return end;\n }\n}; \n```\n\nSo we need to do better and we can use two pointers to make it O(m+n). It is much easier if all numbers are positive. Otherwise we need to break it down into 4 scenarios to make sure monotonicity\uFF08\u5355\u8C03\u6027\uFF09of x*y.\n\nThe idea is to separate the two array into two negatives and two positive(include 0) and count all 4 combinations.\n\n```\ntypedef long long LL;\n\nclass Solution {\npublic:\n vector<LL> neg1, neg2, pos1, pos2;\n \n // <= target\n bool check(long long target, long long k) {\n long long cnt = 0;\n \n if (target >= 0) {\n cnt += neg1.size() * pos2.size();\n cnt += neg2.size() * pos1.size();\n // neg1 and neg2\n LL i = 0, j = neg2.size()-1;\n for (; i < neg1.size(); i++) {\n while (j >= 0 && neg1[i] * neg2[j] <= target) {\n j--;\n }\n \n cnt += (LL)neg2.size() - j - 1;\n }\n \n // pos1 and pos2\n i = 0, j = pos2.size()-1;\n for (; i < pos1.size(); i++) {\n while (j >= 0 && pos1[i] * pos2[j] > target) {\n j--;\n }\n \n cnt += j + 1;\n }\n \n } else {\n // neg1 and pos2 \n LL i = 0, j = 0;\n for (; i < neg1.size(); i++) {\n while (j < pos2.size() && neg1[i] * pos2[j] > target) {\n j++;\n }\n \n cnt += (LL)pos2.size() - j;\n }\n \n // pos1 and neg2\n i = 0, j = 0;\n for (; i < neg2.size(); i++) {\n while (j < pos1.size() && neg2[i] * pos1[j] > target) {\n j++;\n }\n \n cnt += (LL)pos1.size() - j;\n }\n \n }\n \n return cnt >= k;\n }\n \n \n long long kthSmallestProduct(vector<int>& nums1, vector<int>& nums2, long long k) {\n long long start = -1e10, end = 1e10;\n \n for (int num : nums1) {\n if (num < 0)\n neg1.push_back(num);\n else\n pos1.push_back(num);\n }\n \n for (int num : nums2) {\n if (num < 0)\n neg2.push_back(num);\n else\n pos2.push_back(num);\n }\n \n \n while (start + 1 < end) {\n long long mid = start + end >> 1;\n if (check(mid, k)) {\n end = mid;\n } else {\n start = mid;\n }\n }\n \n if (check(start, k))\n return start;\n \n return end;\n }\n}; \n```\n
| 2 | 0 |
[]
| 0 |
kth-smallest-product-of-two-sorted-arrays
|
[Kotlin]Double binary search
|
kotlindouble-binary-search-by-joy32812-cezg
|
binary search answer\n2. For each answer p, find out the number (product >= p). (iterate first array and binary search the second array)\n\n\n/**\n * Double bin
|
joy32812
|
NORMAL
|
2021-10-16T16:05:49.745062+00:00
|
2021-10-16T16:05:49.745101+00:00
| 415 | false |
1. binary search answer\n2. For each answer p, find out the number (product >= p). (iterate first array and binary search the second array)\n\n```\n/**\n * Double binary search\n */\nfun kthSmallestProduct(nums1: IntArray, nums2: IntArray, k: Long): Long {\n\n val orderNums2 = nums2.toList()\n val reversedNums2 = nums2.reversed()\n fun doGetLessEqual(a: Long, p: Long, nums: List<Int>): Long {\n if (a * nums.first() > p) return 0\n\n var l = 0\n var r = nums.size\n while (l < r) {\n val m = (l + r) / 2\n if (a * nums[m] > p) r = m\n else l = m + 1\n }\n return 1L * l\n }\n\n fun getLessEqual(a: Long, p: Long): Long {\n if (a > 0) return doGetLessEqual(a, p, orderNums2)\n if (a < 0) return doGetLessEqual(a, p, reversedNums2)\n\n return if (p >= 0) 1L * nums2.size else 0\n }\n\n\n // min and max will be in this list.\n val limits = listOf(\n 1L * nums1[0] * nums2[0],\n 1L * nums1[0] * nums2.last(),\n 1L * nums1.last() * nums2[0],\n 1L * nums1.last() * nums2.last()\n )\n var l = limits.min()!!\n var r = limits.max()!!\n while (l < r) {\n val m = l + (r - l) / 2\n\n var lessEqualCnt = nums1.map { getLessEqual(1L * it, m) }.sum()\n if (lessEqualCnt >= k) r = m\n else l = m + 1\n }\n\n return l\n}\n\n```
| 2 | 0 |
[]
| 0 |
kth-smallest-product-of-two-sorted-arrays
|
[Python] NumPy
|
python-numpy-by-atf-bjdy
|
It\'s kind of rare to see a use case for np.searchsorted but it makes the code fairly concise.\n\npython\nimport numpy as np\n\nclass Solution:\n def kthSmal
|
atf
|
NORMAL
|
2021-10-16T16:02:57.146440+00:00
|
2021-10-16T16:02:57.146473+00:00
| 663 | false |
It\'s kind of rare to see a use case for np.searchsorted but it makes the code fairly concise.\n\n```python\nimport numpy as np\n\nclass Solution:\n def kthSmallestProduct(self, nums1: List[int], nums2: List[int], k: int) -> int:\n A = np.sort(nums1)\n B = np.sort(nums2)\n Aneg, Azero, Apos = A[A < 0], A[A == 0], A[A > 0]\n\n def f(x):\n # Count number of a * b <= x, casing on the sign of a\n countZero = len(Azero) * len(B) if x >= 0 else 0\n countPos = np.searchsorted(B, x // Apos, side="right").sum()\n countNeg = len(Aneg) * len(B) - np.searchsorted(B, (-x - 1) // (-Aneg), side="right").sum()\n return countNeg + countZero + countPos\n\n lo = -(10 ** 10)\n hi = 10 ** 10\n while lo < hi:\n mid = (lo + hi) // 2\n if f(mid) >= k:\n hi = mid\n else:\n lo = mid + 1\n return hi\n```\n\nProblem https://atcoder.jp/contests/abc155/tasks/abc155_d is similar.
| 2 | 0 |
[]
| 0 |
kth-smallest-product-of-two-sorted-arrays
|
Solution using Binary Seach without any libraries (no bisect) | Interview friendly
|
solution-using-binary-seach-without-any-i9f6j
|
IntuitionThe goal is to find the k-th smallest product of pairs formed by elements from two sorted arrays. Since the products can be both positive and negative,
|
alshadows
|
NORMAL
|
2025-03-10T14:41:23.997444+00:00
|
2025-03-10T14:41:23.997444+00:00
| 100 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The goal is to find the **k-th smallest product** of pairs formed by elements from two sorted arrays. Since the products can be both positive and negative, we need to efficiently count the number of products less than or equal to a given value using binary search.
# Approach
<!-- Describe your approach to solving the problem. -->
1. **Binary Search on Product Values:**
- Identify the search space based on the minimum and maximum possible products.
- Use binary search to efficiently find the k-th smallest product.
2. **Counting Function:**
- For each number in `nums1`, determine how many pairs from `nums2` produce a product less than or equal to the target value (`mid`).
# Complexity
- Time complexity:
$$O((m + n) \log X)$$ where `m` and `n` are the array lengths and `X` is the search space range (max product - min product).
- Space complexity:
$$O(1)$$ (excluding recursion stack for binary search).
# Code
```python
from typing import List
class Solution:
def kthSmallestProduct(self, nums1: List[int], nums2: List[int], k: int) -> int:
# Ensure nums1 is the smaller array to reduce iterations
if len(nums1) > len(nums2):
nums1, nums2 = nums2, nums1
# Establish binary search boundaries based on product extremes
products = [nums1[0] * nums2[-1], nums1[0] * nums2[0], nums1[-1] * nums2[0], nums1[-1] * nums2[-1]]
l, r = min(products), max(products)
# Binary search for the k-th smallest product
while l < r:
mid = (l + r) // 2
if self.countLessEqual(nums1, nums2, mid) >= k: # Check if mid is a valid k-th product
r = mid
else:
l = mid + 1
return l
# Helper function to count products <= mid
def countLessEqual(self, nums1, nums2, mid):
count = 0
for i in nums1:
if i < 0: # Handling negative numbers in nums1
if nums2[0] * i <= mid: # All pairs in nums2 are valid
count += len(nums2)
elif nums2[-1] * i > mid: # All pairs exceed mid
continue
else: # Binary search for boundary in nums2
l, r = 0, len(nums2) - 1
while l < r:
m = (l + r) // 2
if nums2[m] * i <= mid:
r = m
else:
l = m + 1
count += len(nums2) - l
elif i > 0: # Handling positive numbers in nums1
if nums2[-1] * i <= mid: # All pairs are valid
count += len(nums2)
elif nums2[0] * i > mid: # All pairs exceed mid
continue
else: # Binary search for boundary in nums2
l, r = 0, len(nums2) - 1
while l < r:
m = (l + r + 1) // 2
if nums2[m] * i <= mid:
l = m
else:
r = m - 1
count += l + 1
else: # Special case where element in nums1 is zero
count += len(nums2) if mid >= 0 else 0
return count
| 1 | 0 |
['Binary Search', 'Python3']
| 0 |
kth-smallest-product-of-two-sorted-arrays
|
C++ || short code
|
c-short-code-by-colecantcode-xj9k
|
\nclass Solution {\n typedef long long ll;\n #define all(a) begin(a), end(a)\npublic:\n ll kthSmallestProduct(vector<int>& nums1, vector<int>& nums2, l
|
colecantcode
|
NORMAL
|
2023-05-20T01:32:44.232535+00:00
|
2023-05-20T01:32:44.232587+00:00
| 133 | false |
```\nclass Solution {\n typedef long long ll;\n #define all(a) begin(a), end(a)\npublic:\n ll kthSmallestProduct(vector<int>& nums1, vector<int>& nums2, ll k) {\n ll l = -1e10, r = 1e10;\n ll ans;\n while (l <= r) {\n ll m = (l+r) / 2;\n \n ll cnt = 0;\n for (int x : nums1) {\n if (x == 0) cnt += (m >= 0) * size(nums2);\n else if (x > 0) cnt += upper_bound(all(nums2), m / x - (m < 0 && m % x)) - begin(nums2);\n else cnt += end(nums2) - lower_bound(all(nums2), m / x + (m < 0 && m % x));\n }\n if (cnt < k) l = m+1;\n else ans = m, r = m-1;\n }\n return ans;\n }\n};\n```
| 1 | 0 |
['Binary Search', 'C']
| 1 |
kth-smallest-product-of-two-sorted-arrays
|
one of the best intitution for 2 binary search used and reduse time complexity in <=1 sec
|
one-of-the-best-intitution-for-2-binary-n1h2r
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
SharmaAyush121
|
NORMAL
|
2023-05-11T08:59:00.877411+00:00
|
2023-05-11T08:59:00.877459+00:00
| 276 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n#define ll long long\nclass Solution {\npublic:\n\n\tll countKaroProducts(vector<int>& a, vector<int>& b, long long mid) {\n\t\tll totalNumbersLessThanMid = 0;\n\t\tfor (auto el : a) {\n\t\t\tint cnt = 0;\n\n\t\t\tif (el >= 0) { //positive number check number >=0\n\t\t\t\tll s = 0, e = b.size() - 1; //0 to n-1\n\t\t\t\twhile (s <= e) {\n\t\t\t\t\tll m = (s + e) / 2;\n\t\t\t\t\tif ((ll)((ll)el * (ll)b[m]) <= mid) {\n\t\t\t\t\t\tcnt = m + 1; //if number is less then mid then we can say all less no are negetive\n\t\t\t\t\t\ts = m + 1;\n\t\t\t\t\t}\n\t\t\t\t\telse {\n\t\t\t\t\t\te = m - 1;\n\t\t\t\t\t}\n\t\t\t\t}\n\n\t\t\t\ttotalNumbersLessThanMid += cnt;\n\t\t\t}\n\t\t\telse { //negetive number search\n\t\t\t\tll s = 0, e = b.size() - 1;\n\t\t\t\twhile (s <= e) {\n\t\t\t\t\tll m = (s + e) / 2;\n\t\t\t\t\tif ((ll)((ll)el * (ll)b[m]) <= mid) {\n\t\t\t\t\t\tcnt = b.size() - m;\n\t\t\t\t\t\te = m - 1; //check any elemet left from mid-1 if then include\n\t\t\t\t\t}\n\t\t\t\t\telse {\n\t\t\t\t\t\ts = m + 1;\n\t\t\t\t\t}\n\t\t\t\t}\n\n\t\t\t\ttotalNumbersLessThanMid += cnt;\n\t\t\t}\n\t\t}\n\n\t\treturn totalNumbersLessThanMid;\n\t}\n\n\tlong long kthSmallestProduct(vector<int>& nums1, vector<int>& nums2, long long k) {\n\t\tll s = -1e10;\n\t\tll e = 1e10;\n\t\tll ans;\n\t\twhile (s <= e) { // log(2*10^10)\n\t\t\tll mid = ((ll)(s + e)) / 2;\n\t\t\tif (countKaroProducts(nums1, nums2, mid) >= k) {\n\t\t\t\tans = mid; \n\t\t\t\te = mid - 1;\n\t\t\t}\n\t\t\telse {\n\t\t\t\ts = mid + 1; \n\t\t\t}\n\t\t}\n\t\treturn ans;\n\t}\n};\n```
| 1 | 0 |
['Binary Search', 'Binary Search Tree', 'Binary Tree', 'C++']
| 0 |
kth-smallest-product-of-two-sorted-arrays
|
[C++] || Code for Beginners || Binary Search || Reference for future me :)
|
c-code-for-beginners-binary-search-refer-crs1
|
Binary search for the Kth value, in the isPossible function check how hany products can be formed from nums1, nums2 whose product is less than your assumed valu
|
Decode_Apocalypse
|
NORMAL
|
2022-10-25T13:17:40.107169+00:00
|
2022-10-25T13:20:21.784890+00:00
| 1,013 | false |
Binary search for the Kth value, in the isPossible function check how hany products can be formed from nums1, nums2 whose product is less than your assumed value. It should be greater than k, otherwise its quite obvious you would not get kth value if your number of elements are less than K\n\nTo find the products from both array, loop on array1 and binary search on array2 to find the count of products which can be less than your guessed value.\n\nIf your element in array1 is positive, obviously, you need to multiply it with smallest negatives to minimise the product and hopefully make it smaller than your guessed value\nand\nIf your element in array1 is negative, you need to multiply it with all the largest positives in array2 such that the product becomes less than guessed value\n\n```\nclass Solution {\npublic:\n int maximiseSmall(vector<int> &nums2 ,long long val ,long long midval){\n int l=0;\n int r=nums2.size()-1;\n int res= -1;\n while(l<=r){\n long long mid=(l+r)/2;\n if(val*nums2[mid]<=midval){ /* maximise the left side of nums2 as val is positive\n\t\t\t\t\t\t\t\t\t\t\tand hence we need to have as many negative/small\n\t\t\t\t\t\t\t\t\t\t\tnumbers which are mostly found on left side */\n res=mid;\n l=mid+1;\n }\n else{\n r=mid-1;\n }\n }\n return res+1;\n }\n \n int maximiseLarge(vector<int> &nums2 ,long long val ,long long midval){\n int l=0;\n int r=nums2.size()-1;\n int res=nums.size()+1;\n while(l<=r){\n long long mid=(l+r)/2;\n if(val*nums2[mid]<=midval){ /* maximise the right side of nums2 as val is negative\n\t\t\t\t\t\t\t\t\t\t and hence we need to have as many positive/large\n\t\t\t\t\t\t\t\t\t\t\tnumbers which are mostly found on right side,\n\t\t\t\t\t\t\t\t\t\t\tas negative*positive=negative. So finally we subtract\n\t\t\t\t\t\t\t\t\t\t\tres from nums2.size() to get how many numbers were on \n\t\t\t\t\t\t\t\t\t\t\tthe right side */\n res=mid;\n r=mid-1;\n }\n else{\n l=mid+1;\n }\n }\n return nums2.size()-res;\n }\n \n bool isPossible(vector<int> &nums1, vector<int> nums2, long long midval, long long k){\n long long cnt=0;\n for(int i=0;i<nums1.size();i++){\n long long val=nums1[i]; \n\t\t\t/* If val == 0, product of val and each element in nums2 will be 0. And if midval>=0, \n\t\t\tthen because all products are 0, all products will be smaller or equal to midval. \n\t\t\tSo we can add all products in the answer */\n\t\t\tif(val==0 && midval>=0){\n cnt+=nums2.size();\n }\n else if(val>0){\n cnt+=maximiseSmall(nums2,val,midval);\n }\n else if(val<0){\n cnt+=maximiseLarge(nums2,val,midval);\n }\n }\n return cnt>=k;\n }\n \n long long kthSmallestProduct(vector<int>& nums1, vector<int>& nums2, long long k) {\n long long low=-1e10;\n long long high=1e10;\n long long res=0;\n while(low<=high){\n long long mid=(high+low)/2;\n if(isPossible(nums1,nums2,mid,k)==true){\n res=mid;\n high=mid-1;\n }\n else{\n low=mid+1;\n }\n }\n return res;\n }\n};\n```
| 1 | 0 |
['C', 'Binary Tree']
| 0 |
kth-smallest-product-of-two-sorted-arrays
|
Python - Binary Search - Clean Code
|
python-binary-search-clean-code-by-jivig-625e
|
\nclass Solution:\n def kthSmallestProduct(self, nums1: List[int], nums2: List[int], k: int) -> int:\n n = len(nums1)\n m = len(nums2)\n
|
jiviG
|
NORMAL
|
2022-06-28T21:06:26.677791+00:00
|
2022-06-28T21:06:26.677820+00:00
| 249 | false |
```\nclass Solution:\n def kthSmallestProduct(self, nums1: List[int], nums2: List[int], k: int) -> int:\n n = len(nums1)\n m = len(nums2)\n \n nPos = [num for num in nums1 if num >= 0]\n nNeg = [-num for num in nums1 if num < 0][::-1]\n mPos = [num for num in nums2 if num >= 0]\n mNeg = [-num for num in nums2 if num < 0][::-1]\n \n numOfNegatives = len(nPos) * len(mNeg) + len(mPos) * len(nNeg)\n sign = 1\n if k > numOfNegatives:\n k -= numOfNegatives\n else:\n k = numOfNegatives - k + 1\n temp = mPos\n mPos = mNeg\n mNeg = temp\n sign = -1\n \n \n def count(n, m, target):\n result = 0\n right = len(m) - 1\n \n for left in range(len(n)):\n while right >= 0 and n[left] * m[right] > target:\n right -= 1\n result += right + 1\n return result\n \n \n left = 0\n right = 10**10\n \n while left < right:\n mid = left + (right - left) // 2\n \n countPos = count(nPos, mPos, mid) + count(nNeg, mNeg, mid)\n \n if countPos >= k:\n right = mid\n else:\n left = mid + 1\n \n return left * sign\n```
| 1 | 0 |
[]
| 1 |
kth-smallest-product-of-two-sorted-arrays
|
Java solution | Binary Search | TC = O(nlogm)
|
java-solution-binary-search-tc-onlogm-by-ct2a
|
\n// Tc = O(nlogm) => dependent on count function\n\nclass Solution {\n public long kthSmallestProduct(int[] nums1, int[] nums2, long k) {\n long lo
|
ankitbaghel
|
NORMAL
|
2022-06-22T09:21:46.625566+00:00
|
2022-06-22T09:21:46.625599+00:00
| 563 | false |
```\n// Tc = O(nlogm) => dependent on count function\n\nclass Solution {\n public long kthSmallestProduct(int[] nums1, int[] nums2, long k) {\n long low = (long)-1e10, high = (long)1e10;\n \n while(low <= high){\n long dotProduct = (low+high)/2;\n if(countNoOfElements(nums1, nums2, dotProduct) < k) \n low = dotProduct+1;\n else\n high = dotProduct-1;\n }\n return high;\n }\n \n private long countNoOfElements(int[] nums1, int[] nums2, long dotProduct){ // this function will return the no. of elements(after product) which are less than dotProduct\n long count = 0;\n for(int element : nums1){\n if(element >= 0){ // if positve\n int low = 0, high = nums2.length; // binary search on nums2\n while(low < high){\n int mid = (low+high)/2;\n if((long)element * nums2[mid] < dotProduct)\n low = mid+1;\n else\n high = mid;\n }\n count += low; // no. of elemets after product with element smaller than dotproduct\n }\n else{ //if negative => binary search in some reverse order\n int low = 0, high = nums2.length;\n while(low < high){\n int mid = (low+high)/2;\n if((long) element * nums2[mid] >= dotProduct)\n low = mid+1;\n else\n high = mid;\n }\n \n count += nums2.length - low; // in negative element case smaller element will be on right side\n }\n \n }\n return count;\n }\n}\n```
| 1 | 1 |
['Binary Tree', 'Java']
| 0 |
kth-smallest-product-of-two-sorted-arrays
|
[JavaScript] 2 Solutions - Binary Search
|
javascript-2-solutions-binary-search-by-rs8tv
|
Time O((n + m) * log(10 ^ 10))\n\nvar kthSmallestProduct = function(nums1, nums2, k) {\n let rProduct = 10 ** 10, lProduct = -rProduct;\n const negativeN
|
tmohan
|
NORMAL
|
2022-05-01T09:00:46.700165+00:00
|
2022-07-03T10:24:30.799279+00:00
| 139 | false |
**Time O((n + m) * log(10 ^ 10))**\n```\nvar kthSmallestProduct = function(nums1, nums2, k) {\n let rProduct = 10 ** 10, lProduct = -rProduct;\n const negativeNums1 = nums1.filter((num) => num < 0);\n const positiveNums1 = nums1.filter((num) => num >= 0);\n const negativeNums2 = nums2.filter((num) => num < 0);\n const positiveNums2 = nums2.filter((num) => num >= 0);\n const negativeNums1Reverse = [...negativeNums1].reverse();\n const positiveNums1Reverse = [...positiveNums1].reverse();\n const negativeNums2Reverse = [...negativeNums2].reverse();\n const positiveNums2Reverse = [...positiveNums2].reverse();\n\n const findRank = (list1, list2, product) => {\n let rank = 0;\n\n for (let i = list1.length - 1, j = 0; i >= 0; i--) {\n\t\t\tfor (; j < list2.length && list2[j] * list1[i] <= product; j++);\n rank += j;\n }\n \n return rank;\n };\n\n while (lProduct < rProduct) {\n const midProduct = Math.floor((lProduct + rProduct) / 2);\n\n if (midProduct >= 0) {\n var rank = negativeNums1.length * positiveNums2.length +\n negativeNums2.length * positiveNums1.length +\n findRank(negativeNums1Reverse, negativeNums2Reverse, midProduct) +\n findRank(positiveNums1, positiveNums2, midProduct)\n } else {\n var rank = findRank(positiveNums1Reverse, negativeNums2, midProduct) +\n findRank(positiveNums2Reverse, negativeNums1, midProduct);\n }\n\n rank < k ? (lProduct = midProduct + 1) : (rProduct = midProduct);\n }\n \n return lProduct;\n};\n```\n\n**Time O(n * log(m) * log(10 ^ 10))**\n```\nvar kthSmallestProduct = function(nums1, nums2, k) {\n let rProduct = 10 ** 10, lProduct = -rProduct;\n\n while (lProduct < rProduct) {\n const midProduct = Math.floor((lProduct + rProduct) / 2);\n let rank = 0;\n \n for (const num1 of nums1) {\n if (num1 < 0) {\n let l = 0, r = nums2.length;\n while (l < r) {\n const mid = (l + r) >> 1;\n nums2[mid] * num1 <= midProduct ? (r = mid) : (l = mid + 1);\n }\n\n rank += nums2.length - l;\n } else if (num1 > 0) {\n let l = -1, r = nums2.length - 1;\n while (l < r) {\n const mid = (l + r + 1) >> 1;\n nums2[mid] * num1 <= midProduct ? (l = mid) : (r = mid - 1);\n }\n\n rank += l + 1;\n } else {\n rank += midProduct >= 0 ? nums2.length : 0;\n }\n }\n \n rank < k ? lProduct = midProduct + 1 : rProduct = midProduct;\n }\n\n return lProduct;\n};\n```
| 1 | 0 |
[]
| 0 |
kth-smallest-product-of-two-sorted-arrays
|
C# Solution
|
c-solution-by-drstrangedotnet-w0ow
|
Solution is C# version of this \n\npublic class Solution \n{\n static long INF = (long) 1e10;\n \n public long KthSmallestProduct(int[] nums1, int[] nu
|
drStrangeDotNet
|
NORMAL
|
2022-04-12T05:01:18.338952+00:00
|
2022-04-12T05:01:18.339000+00:00
| 135 | false |
Solution is C# version of [this ](https://leetcode.com/problems/kth-smallest-product-of-two-sorted-arrays/discuss/1524349/Java-Double-Binary-Search-O(log1010-x-MlogN))\n```\npublic class Solution \n{\n static long INF = (long) 1e10;\n \n public long KthSmallestProduct(int[] nums1, int[] nums2, long k) \n {\n int m = nums1.Length, n = nums2.Length;\n\t\tlong lo = -INF - 1, hi = INF + 1;\n \n\t\twhile (lo < hi)\n\t\t{\n\t\t\tlong mid = lo + ((hi - lo) >> 1), cnt = 0;\n\t\t\t\n foreach (int i in nums1)\n\t\t\t{\n\t\t\t\tif (0 <= i)\n\t\t\t\t{\n\t\t\t\t\tint l = 0, r = n - 1, p = 0;\n\t\t\t\t\twhile (l <= r)\n\t\t\t\t\t{\n\t\t\t\t\t\tint c = l + ((r - l) >> 1);\n\t\t\t\t\t\tlong mul = i * (long)nums2[c];\n\t\t\t\t\t\tif (mul <= mid)\n\t\t\t\t\t\t{\n\t\t\t\t\t\t\tp = c + 1;\n\t\t\t\t\t\t\tl = c + 1;\n\t\t\t\t\t\t}\n\t\t\t\t\t\telse\n\t\t\t\t\t\t{\n\t\t\t\t\t\t\tr = c - 1;\n\t\t\t\t\t\t}\n\t\t\t\t\t}\n\t\t\t\t\tcnt += p;\n\t\t\t\t}\n\t\t\t\telse\n\t\t\t\t{\n\t\t\t\t\tint l = 0, r = n - 1, p = 0;\n\t\t\t\t\twhile (l <= r)\n\t\t\t\t\t{\n\t\t\t\t\t\tint c = l + ((r - l) >> 1);\n\t\t\t\t\t\tlong mul = i * (long)nums2[c];\n\t\t\t\t\t\tif (mul <= mid)\n\t\t\t\t\t\t{\n\t\t\t\t\t\t\tp = n - c;\n\t\t\t\t\t\t\tr = c - 1;\n\t\t\t\t\t\t}\n\t\t\t\t\t\telse\n\t\t\t\t\t\t{\n\t\t\t\t\t\t\tl = c + 1;\n\t\t\t\t\t\t}\n\t\t\t\t\t}\n\t\t\t\t\tcnt += p;\n\t\t\t\t}\n\t\t\t}\n\t\t\tif (cnt >= k)\n\t\t\t{\n\t\t\t\thi = mid;\n\t\t\t}\n\t\t\telse\n\t\t\t{\n\t\t\t\tlo = mid + 1L;\n\t\t\t}\n\t\t}\n\t\treturn lo;\n \n }\n}\n```
| 1 | 0 |
[]
| 0 |
kth-smallest-product-of-two-sorted-arrays
|
Binary search
|
binary-search-by-ankush093-v06t
|
\n\nclass Solution {\n //function for counting valid elements whose product with elements of second vector(nums2) is less than or equal to val when the eleme
|
Ankush093
|
NORMAL
|
2022-02-07T17:27:43.402879+00:00
|
2022-02-07T17:27:43.402909+00:00
| 643 | false |
\n```\nclass Solution {\n //function for counting valid elements whose product with elements of second vector(nums2) is less than or equal to val when the element of first vector(nums1) is negative\n int getvalue1(long long x,vector<int>& nums2,int m,long long val){\n int l = 0 ,r = m - 1;\n int ans = m;\n while( l <= r){\n int mid = l + (r-l)/2;\n if(x *1LL* nums2[mid] <= val){\n ans = mid;\n r = mid -1;\n }\n else\n l = mid + 1;\n }\n return m - ans;\n }\n //function for counting valid elements whose product with elements of second vector(nums2) is less than or equal to val when the element of first vector(nums1) is positive\n int getvalue2(long long x,vector<int>& nums2,int m,long long val){\n int l = 0 ,r = m - 1;\n int ans = 0;\n while( l <= r){\n int mid = l + (r-l)/2;\n if(x *1LL* nums2[mid] <= val){\n ans = mid +1;\n l = mid +1;\n }\n else\n r = mid - 1;\n }\n return ans;\n }\n \n bool valid(vector<int>& nums1, vector<int>& nums2,int n ,int m,long long mid,long long k){\n long long ans = 0;\n //counting the valid pairing of each element of first vector(nums1) with the elements of second vector(nums2)\n for(int i = 0 ; i < n ; i++){\n if(nums1[i] < 0)\n ans += getvalue1(nums1[i],nums2,m,mid);\n else\n ans +=getvalue2(nums1[i],nums2,m,mid);\n }\n return ans >= k;\n }\npublic:\n long long kthSmallestProduct(vector<int>& nums1, vector<int>& nums2, long long k) {\n \n int n = nums1.size() , m = nums2.size() ;\n long long ans = 0;\n long long mini = min(nums1[0],nums2[0]),maxi = max(nums1[n - 1],nums2[m - 1]);\n long long l = min(mini*maxi,mini),r=max(mini*mini,maxi*maxi);\n while(l <= r){\n \n long long mid = l + (r - l)/2;\n \n if(valid(nums1,nums2,n,m,mid,k)){\n ans = mid ;\n r = mid - 1;\n }\n else\n l = mid + 1;\n }\n return ans;\n }\n};\n```
| 1 | 0 |
['Binary Tree', 'C++']
| 0 |
kth-smallest-product-of-two-sorted-arrays
|
[C++] Binary Search O(NlogNlogA), (1728 ms, 24.71% / 89.7 MB, 74.15% )
|
c-binary-search-onlognloga-1728-ms-2471-k7re2
|
My main idea is to rewrite the problem description as follows,\n"Find the minimum integer which is larger than at least k products made with nums1 and nums2.".\
|
HirofumiTsuda
|
NORMAL
|
2021-12-28T05:05:52.885364+00:00
|
2021-12-28T05:05:52.885414+00:00
| 356 | false |
My main idea is to rewrite the problem description as follows,\n"Find the minimum integer which is larger than at least k products made with nums1 and nums2.".\nThis problem can be solved by a binary search technique.\n\nThe complexity is O(NlogNlogA), where N denotes max(nums1.size(), nums2.size()) and A denotes the size of the range. Here,\nthe range is set [-1e10, 1e10] so A is 2e10.\n\n\n```c++\ntypedef long long int ll;\n\nclass Solution {\npublic:\n long long kthSmallestProduct(vector<int>& nums1, vector<int>& nums2, long long k) {\n ll left = -(ll)(1e10) - 1;\n ll right = (ll)(1e10) + 1;;\n while(right - left > 1){\n ll c = (left + right)/2;\n ll num = 0;\n for(int n : nums1){\n if(n == 0){\n if(c >= 0){\n num += nums2.size();\n }\n }else if(n > 0){\n ll f = floor(c/(double)n);\n auto iter = upper_bound(nums2.begin(), nums2.end(), f);\n num += iter - nums2.begin();\n }else{\n ll f = ceil(c / (double)n);\n auto iter = lower_bound(nums2.begin(), nums2.end(), f);\n num += nums2.size() - (iter - nums2.begin()); \n }\n }\n if(num >= k){\n right = c;\n }else{\n left = c;\n }\n }\n return right;\n }\n}\n```
| 1 | 1 |
['Binary Tree']
| 0 |
kth-smallest-product-of-two-sorted-arrays
|
[Python3] Brute Force in TLE passing 82/112 test cases
|
python3-brute-force-in-tle-passing-82112-b6ny
|
This is just a brute force way to solve the problem. Obviously, this gets into time limit exceed, but I just want to share this solution for beginners like me f
|
yugo9081
|
NORMAL
|
2021-11-25T22:24:40.005013+00:00
|
2021-11-25T22:24:40.005066+00:00
| 674 | false |
This is just a brute force way to solve the problem. Obviously, this gets into time limit exceed, but I just want to share this solution for beginners like me for technical interview. \n\nPassed 82/112 test cases.\n\nCorrect me if I need to edit this solution! :)\n\n```\nclass Solution:\n def kthSmallestProduct(self, nums1: List[int], nums2: List[int], k: int) -> int:\n result = []\n for i in range(len(nums1)):\n for j in range(len(nums2)):\n temp = nums1[i]*nums2[j]\n result.append(temp)\n result.sort()\n return result[k-1]\n```
| 1 | 1 |
['Python', 'Python3']
| 2 |
kth-smallest-product-of-two-sorted-arrays
|
[Java] Binary Search Approach
|
java-binary-search-approach-by-vinsinin-614h
|
Thanks to @hdchen took reference from the solution and made a concise version of it.\n\nApproach\n Do Binary Search from negative limit -1e10 to positive limit
|
vinsinin
|
NORMAL
|
2021-11-22T04:17:07.987044+00:00
|
2021-11-22T04:32:22.984962+00:00
| 935 | false |
Thanks to [@hdchen](https://leetcode.com/problems/kth-smallest-product-of-two-sorted-arrays/discuss/1524349/Java-Double-Binary-Search-O(log1010-x-MlogN)) took reference from the solution and made a concise version of it.\n\n**Approach**\n* Do Binary Search from negative limit `-1e10` to positive limit `1e10` for the value `val` from the first array\n* Do Binary search for the length of the second array from `0` to `nums2.length - 1`\n* Multiply the value each time with the mid value from the second array and see if its less that or greater and count `cnt` accordingly\n* Eventually the `k` smallest element will be found and the `lo` value will be returned\n\n```\nclass Solution {\n public long kthSmallestProduct(int[] nums1, int[] nums2, long k) {\n long lo = (long) -1e10; \n long hi = (long) 1e10;\n \n while (lo < hi) {\n long mid = lo + ((hi - lo) >> 1);\n long cnt = 0;\n \n for (int val : nums1) \n cnt += (val >= 0) ? binary_search(mid, val, nums2, true) : binary_search(mid, val, nums2, false);\n \n if (cnt >= k) hi = mid;\n else lo = mid + 1;\n }\n return lo;\n }\n \n public long binary_search(long mid, int i, int[] nums2, boolean positive){\n int l = 0;\n int r = nums2.length - 1;\n int res = 0;\n \n while (l <= r) {\n int c = l + ((r - l) >> 1);\n long mul = i * (long) nums2[c];\n if (mul <= mid) {\n if (positive){\n l = c + 1;\n res = c + 1; \n }\n else{\n r = c - 1;\n res = nums2.length - c;\n } \n }\n else{\n if (positive) r = c - 1; \n else l = c + 1;\n }\n }\n return res;\n }\n}\n```
| 1 | 0 |
['Binary Tree', 'Java']
| 1 |
kth-smallest-product-of-two-sorted-arrays
|
[C++] Binary Search, clean and short, O((M+N)lgV)
|
c-binary-search-clean-and-short-omnlgv-b-ucbt
|
c++\nclass Solution {\npublic:\n long long kthSmallestProduct(vector<int>& a, vector<int>& b, long long k) {\n int n = a.size(), m = b.size();\n
|
slo
|
NORMAL
|
2021-11-14T12:44:34.662383+00:00
|
2021-11-14T12:45:43.663925+00:00
| 550 | false |
```c++\nclass Solution {\npublic:\n long long kthSmallestProduct(vector<int>& a, vector<int>& b, long long k) {\n int n = a.size(), m = b.size();\n int x = lower_bound(begin(a), end(a), 0) - begin(a);\n int y = lower_bound(begin(b), end(b), 0) - begin(b);\n auto lt = [&](int i, int j) { return 1LL * a[x - 1 - i] * b[y - 1 - j]; };\n auto rt = [&](int i, int j) { return 1LL * a[i] * b[m - 1 - j]; };\n auto lb = [&](int i, int j) { return 1LL * a[n - 1 - i] * b[j]; };\n auto rb = [&](int i, int j) { return 1LL * a[x + i] * b[y + j]; };\n auto count = [](auto& f, int n, int m, long long v) {\n long long c = 0;\n for(int i = n - 1, j = 0; j < m && i >= 0; ++j) {\n while (i >= 0 && 1LL * f(i, j) > v) --i;\n c += i + 1;\n }\n return c;\n };\n long long L = -1e10 - 1, R = 1e10;\n while (L + 1 < R) {\n auto M = (L + R) >> 1;\n auto cnt = count(lt, x, y, M) +\n count(rt, x, m - y, M) +\n count(lb, n - x, y, M) +\n count(rb, n - x, m - y, M);\n if (cnt < k) L = M;\n else R = M;\n }\n return R;\n }\n};\n```
| 1 | 0 |
[]
| 0 |
kth-smallest-product-of-two-sorted-arrays
|
[Java] Binary Search
|
java-binary-search-by-a_love_r-cgp8
|
~~~java\n\nclass Solution {\n public long kthSmallestProduct(int[] nums1, int[] nums2, long k) {\n if (nums1 == null || nums2 == null) {\n
|
a_love_r
|
NORMAL
|
2021-10-31T17:50:26.931257+00:00
|
2021-10-31T17:50:26.931287+00:00
| 485 | false |
~~~java\n\nclass Solution {\n public long kthSmallestProduct(int[] nums1, int[] nums2, long k) {\n if (nums1 == null || nums2 == null) {\n return -1;\n }\n \n long left = (long) -1e10;\n long right = (long) 1e10;\n while (left + 1 < right) {\n long mid = left + (right - left) / 2;\n long count = countSmallerOrEqual(nums1, nums2, mid);\n if (count < k) {\n left = mid + 1;\n } else {\n right = mid;\n }\n }\n\n return countSmallerOrEqual(nums1, nums2, left) >= k ? left : right;\n }\n \n private long countSmallerOrEqual(int[] nums1, int[] nums2, long target) {\n long count = 0;\n \n for (int n1 : nums1) {\n int left = 0, right = nums2.length - 1;\n \n while (left + 1 < right) {\n int mid = left + (right - left) / 2;\n long prod = (long)n1 * nums2[mid];\n \n if (n1 >= 0) {\n if (prod <= target) {\n left = mid;\n } else {\n right = mid - 1;\n }\n } else {\n if (prod <= target) {\n right = mid;\n } else {\n left = mid + 1;\n }\n }\n } \n \n long currCount = 0;\n if (n1 >= 0) {\n if ((long) n1 * nums2[right] <= target) {\n currCount = right + 1;\n } else if ((long) n1 * nums2[left] <= target) {\n currCount = left + 1;\n } else {\n currCount = 0;\n }\n } else {\n if ((long) n1 * nums2[left] <= target) {\n currCount = nums2.length - left;\n } else if ((long) n1 * nums2[right] <= target) {\n currCount = nums2.length - right;\n } else {\n currCount = 0;\n }\n }\n count += currCount;\n }\n \n return count;\n }\n}\n\n~~~
| 1 | 0 |
[]
| 0 |
kth-smallest-product-of-two-sorted-arrays
|
best soln
|
best-soln-by-gaurav_205-teve
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
gaurav_205
|
NORMAL
|
2025-03-21T14:53:02.203460+00:00
|
2025-03-21T14:53:02.203460+00:00
| 6 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int check(long long mid,vector<int>& nums1, vector<int>& nums2, long long k)
{
long long count=0;
for (int i = 0; i<nums1.size(); i++) {
if (nums1[i] > 0) {
count += upper_bound(nums2.begin(), nums2.end(),floor((double) mid / nums1[i]) ) - nums2.begin();
} else if (nums1[i] < 0) {
long long rem = ceil((double)mid/nums1[i]);
int ind = lower_bound(nums2.begin(), nums2.end(), rem) - nums2.begin();
count += (nums2.size()-ind);
} else {
if (mid >= 0) count += nums2.size();
}
}
return count>=k;
}
long long kthSmallestProduct(vector<int>& nums1, vector<int>& nums2, long long k) {
int n=nums1.size(),m=nums2.size();
long long lo=-1e18;
long long hi=1e18;
long long ans=-1;
while(lo<=hi)
{
long long mid=lo+(hi-lo)/2;
if(check(mid,nums1,nums2,k))
{
ans=mid;
hi=mid-1;
}else{
lo=mid+1;
}
}
return ans;
}
};
```
| 0 | 0 |
['Array', 'Binary Search', 'C++']
| 0 |
kth-smallest-product-of-two-sorted-arrays
|
Simple Java code with Binary search with comments.
|
simple-java-code-with-binary-search-with-9zjq
|
IntuitionSimple Java coding using Binary SearchCode
|
raghuvansh
|
NORMAL
|
2025-03-15T07:56:20.516026+00:00
|
2025-03-15T07:59:23.246294+00:00
| 24 | false |
# Intuition
Simple Java coding using Binary Search
# Code
```java []
class Solution {
private long INF = (long) 1e10;
public long kthSmallestProduct(int[] nums1, int[] nums2, long k) {
long min = -INF - 1;
long max = INF + 1;
while (min <= max) {
long mid = max + (min - max) / 2;
long s = countOfProductLessThanEqNum(mid, nums1, nums2);
if (s >= k) {
max = mid - 1;
} else {
min = mid + 1;
}
}
return min;
}
private long countOfProductLessThanEqNum(long num, int nums1[], int nums2[]) {
long countOfProductLessThanEqNum = 0;
int m = nums2.length;
for (long num1 : nums1) {
if (num1 < 0) {
// Since num1 is -ve, its product with all nums2 will be in descresing order.
// Pivote is the index where product of num1 and num2 is small or eq to num.
int left = 0;
int right = m - 1;
int pivot = 0;
while (left <= right) {
int mid = (left + right) / 2;
long product = num1 * nums2[mid];
if (product <= num) {
/**
* eg num1 = -2, num = -5
* nums2 = {-3,2,3}
* for this the pivot is at 3 so number of products less than -5 is 1 only -6
* from (6,-4,-6)
*/
pivot = m - mid;
right = mid - 1;
} else
left = mid + 1;
}
countOfProductLessThanEqNum += pivot;
}
else {
int left = 0;
int right = m - 1;
int pivot = 0;
while (left <= right) {
int mid = (left + right) / 2;
long product = num1 * nums2[mid];
if (product <= num) {
pivot = mid + 1;
left = mid + 1;
} else
right = mid - 1;
}
countOfProductLessThanEqNum += pivot;
}
}
return countOfProductLessThanEqNum;
}
}
```
| 0 | 0 |
['Java']
| 0 |
kth-smallest-product-of-two-sorted-arrays
|
Optimal Approach ✅
|
optimal-approach-by-santoshpal_47-jdui
|
K-th Smallest Product of Two Sorted ArraysProblem StatementGiven two sorted arrays, nums1 and nums2, containing integers (both positive and negative), we need t
|
Santoshpal_47
|
NORMAL
|
2025-03-06T17:44:40.855009+00:00
|
2025-03-06T17:44:40.855009+00:00
| 10 | false |
## **K-th Smallest Product of Two Sorted Arrays**
### **Problem Statement**
Given two sorted arrays, `nums1` and `nums2`, containing integers (both positive and negative), we need to find the **k-th smallest product** formed by multiplying one element from `nums1` and one from `nums2`.
---
### **Approach: Binary Search on Answer**
Since the arrays are sorted, the products formed by pairing their elements are also partially ordered. We leverage **binary search on the product range** to efficiently determine the k-th smallest product.
#### **Steps:**
1. **Define the Search Space:**
- The smallest possible product is \( -10^{10} \) (minimum negative product).
- The largest possible product is \( 10^{10} \) (maximum positive product).
- Set `s = -1e10` and `e = 1e10`.
2. **Binary Search on `x`:**
- Check if `x` can be the k-th smallest product using `isPossible()`.
- If at least `k` products are **≤ `x`**, update `ans = x` and shrink the search space (`e = mid - 1`).
- Otherwise, move right (`s = mid + 1`).
3. **Counting Products ≤ `x` (`isPossible` function):**
- For each `nums1[i]`, find how many products with `nums2[j]` are ≤ `x`.
- Use **binary search (`lower_bound` / `upper_bound`)** to efficiently count:
- **If `nums1[i] < 0`**, find the first `nums2[j]` such that `nums1[i] * nums2[j]` is ≥ `x`.
- **If `nums1[i] > 0`**, find the last `nums2[j]` such that `nums1[i] * nums2[j]` is ≤ `x`.
- **If `nums1[i] == 0`**, count all elements in `nums2` when `x ≥ 0`.
---
### **Code Implementation**
```cpp
class Solution {
public:
bool isPossible(vector<int>& nums1, vector<int>& nums2, long long k, long long x) {
int n1 = nums1.size();
int n2 = nums2.size();
long long count = 0;
for (int i = 0; i < n1; i++) {
if (nums1[i] < 0) {
long long rem = ceil((double)x / nums1[i]);
int ind = lower_bound(nums2.begin(), nums2.end(), rem) - nums2.begin();
count += (n2 - ind);
} else if (nums1[i] > 0) {
long long rem = floor((double)x / nums1[i]);
int ind = upper_bound(nums2.begin(), nums2.end(), rem) - nums2.begin();
count += ind;
} else {
if (x >= 0) count += n2;
}
if (count >= k) return true;
}
return count >= k;
}
long long kthSmallestProduct(vector<int>& nums1, vector<int>& nums2, long long k) {
long long s = -1e10, e = 1e10, ans = 0;
while (s <= e) {
long long mid = s + (e - s) / 2;
if (isPossible(nums1, nums2, k, mid)) {
ans = mid;
e = mid - 1;
} else {
s = mid + 1;
}
}
return ans;
}
};
```
---
### **Complexity Analysis**
#### **Time Complexity:**
$$O(n \log m \log (10^{10}))$$
- **Binary search on product range:** \( O(\log (10^{10})) \)
- **Counting valid products (`isPossible` function)**:
- Iterates through `nums1` → \( O(n) \)
- Each `lower_bound` / `upper_bound` operation → \( O(\log m) \)
- **Total:** \( O(n \log m \log (10^{10})) \)
#### **Space Complexity:**
$$
O(1)
$$
- Only a few integer variables are used; no extra space required.
---
### **Why This Works Efficiently**
- **Avoids Sorting Large Lists:** Unlike naive approaches that generate all possible products, this uses **binary search on the result**.
- **Binary Search + Two-Pointer Counting:** Efficiently counts elements ≤ `x` using **binary search**, reducing unnecessary computations.
This method ensures that we find the **exact k-th smallest product efficiently**, even when `nums1` and `nums2` are large. 🚀
| 0 | 0 |
['Array', 'Binary Search', 'C++']
| 0 |
kth-smallest-product-of-two-sorted-arrays
|
Optimized Binary Search in with Explanation
|
optimized-binary-search-in-with-explanat-n9ra
|
IntuitionApproachComplexity
Time complexity: O((m + n) * log (hi - lo))
Space complexity: O(m + n)
Code
|
stalebii
|
NORMAL
|
2025-03-01T17:12:19.360991+00:00
|
2025-03-01T17:15:51.079965+00:00
| 53 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: O((m + n) * log (hi - lo))
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(m + n)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def kthSmallestProduct(self, nums1: List[int], nums2: List[int], k: int) -> int:
def get_count(target):
nonlocal neg1, pos1, neg2, pos2
# there are four combinations to count for : (neg1, neg2), (neg1, pos2), (pos1, neg2), (pos1, pos2)
res = 0
# case1; (neg1, neg2)
i = len(neg1) - 1 # i starts from tail of neg1 (maximum value)
j = 0 # j starts from the head of neg2 (minimum value)
while i >= 0 and j < len(neg2):
# found a valid pair; anything comes after j in neg2 can be paired with neg1[i]
if neg1[i] * neg2[j] <= target:
# count all the values after j
res += (len(neg2) - j)
# i is fully covered; decrease it then
i -= 1
else:
j += 1
# case2; (neg1, pos2)
i = 0 # i starts from head of neg1 (minimum value)
j = 0 # j starts from the head of pos2 (minimum value)
while i < len(neg1) and j < len(pos2):
# found a valid pair; anything comes after j in pos2 can be paired with neg1[i]
if neg1[i] * pos2[j] <= target:
res += (len(pos2) - j)
# i is fully covered; increase it then
i += 1
else:
j += 1
# case 3; (pos1, neg2)
i = len(pos1) - 1 # i starts from tail of pos1 (maximum value)
j = len(neg2) - 1 # j starts from tail of neg2 (maximum value)
while i >= 0 and j >= 0:
# found a valid pair; anything comes before j in pos2 can be paired with neg1[i]
if pos1[i] * neg2[j] <= target:
res += (j + 1)
# i is fully covered; decrease it then
i -= 1
else:
j -= 1
# case4; (pos1, pos2)
i = 0 # i starts from head of pos1 (minimum value)
j = len(pos2) - 1 # j starts from tail of pos2 (maximum value)
while i < len(pos1) and j >= 0:
# found a valid pair; anything comes before j in pos2 can be paired with pos1[i]
if pos1[i] * pos2[j] <= target:
res += (j + 1)
# i is fully covered; increase it then
i += 1
else:
j -= 1
return res
# 1. split nums1 into neg1 & pos1 arrays
neg1 = [num for num in nums1 if num < 0]
pos1 = nums1[len(neg1):]
# 2. split nums2 into neg2 & pos2 arrays
neg2 = [num for num in nums2 if num < 0]
pos2 = nums2[len(neg2):]
# 3. calculate lower & upper bounds for the product of values
lo = min(nums1[0] * nums2[0], nums1[-1] * nums2[0],
nums1[0] * nums2[-1], nums1[-1] * nums2[-1])
hi = max(nums1[0] * nums2[0], nums1[-1] * nums2[0],
nums1[0] * nums2[-1], nums1[-1] * nums2[-1])
# 4. run binary search till reaching the right pair
while lo <= hi:
mid = (lo + hi) // 2
# count the number of valid indices for product value of mid
count = get_count(mid)
# infeasible; search the right side
if count < k:
lo = mid + 1
# feasible; search the left side
else:
hi = mid - 1
return lo
```
| 0 | 0 |
['Array', 'Binary Search', 'Python', 'Python3']
| 0 |
kth-smallest-product-of-two-sorted-arrays
|
Template Binary Search + Correct Bounds
|
template-binary-search-correct-bounds-by-qn0g
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
lex217
|
NORMAL
|
2025-01-29T04:55:57.299499+00:00
|
2025-01-29T04:55:57.299499+00:00
| 9 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python []
class Solution(object):
def kthSmallestProduct(self, nums1, nums2, k):
"""
:type nums1: List[int]
:type nums2: List[int]
:type k: int
:rtype: int
"""
def count_pairs(x):
"""Count number of pairs (nums1[i], nums2[j]) where nums1[i] * nums2[j] <= x."""
count = 0
for num in nums1:
if num > 0:
# Count nums2[j] <= x / num using binary search
count += bisect_right(nums2, x // num)
if num < 0:
# Count nums2[j] >= x / num using binary search
count += len(nums2) - bisect_left(nums2, ceil(x/float(num)))# this is python fuckery
if num == 0 and x >=0:
# If num is zero, all products are zero (valid if x >= 0)
count += len(nums2)
return count
# Define search space for the product
A = [nums1[0], nums1[-1]]
B = [nums2[0], nums2[-1]]
cartesian_product = [i*j for i, j in list(itertools.product(A, B))]
left, right = min(cartesian_product), max(cartesian_product)
while left < right:
mid = (left + right) // 2
if count_pairs(mid) < k:
left = mid + 1
else:
right = mid
return left
```
| 0 | 0 |
['Python']
| 0 |
kth-smallest-product-of-two-sorted-arrays
|
2040. Kth Smallest Product of Two Sorted Arrays
|
2040-kth-smallest-product-of-two-sorted-3cywq
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
G8xd0QPqTy
|
NORMAL
|
2025-01-17T14:28:12.323773+00:00
|
2025-01-17T14:28:12.323773+00:00
| 71 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
from bisect import bisect_left, bisect_right
from math import ceil
class Solution:
def kthSmallestProduct(self, nums1, nums2, k):
def valid_pairs(x):
count = 0
for num in nums1:
if num > 0:
count += bisect_right(nums2, x // num)
elif num < 0:
count += len(nums2) - bisect_left(nums2, ceil(x / num))
elif num == 0 and x >= 0:
count += len(nums2)
return count
low, high = -10**10 - 1, 10**10 + 1
while low + 1 < high:
mid = (low + high) // 2
if valid_pairs(mid) >= k:
high = mid
else:
low = mid
return low + 1
```
| 0 | 0 |
['Python3']
| 0 |
kth-smallest-product-of-two-sorted-arrays
|
C# Binary Search On Answer Solution
|
c-binary-search-on-answer-solution-by-ge-jr3g
|
IntuitionApproachWe search between a very wide range of possible products (from
−10^10 to 10^10).
For each midpoint (mid), we count how many products are less t
|
GetRid
|
NORMAL
|
2025-01-03T18:48:10.284073+00:00
|
2025-01-03T18:48:10.284073+00:00
| 12 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->My intuition was to convert the problem from sorting products explicitly to leveraging binary search to simulate the sorting process indirectly.
___
# Approach
<!-- Describe your approach to solving the problem. --> Binary Search (KthSmallestProduct):
We search between a very wide range of possible products (from
−10^10 to 10^10).
For each midpoint (mid), we count how many products are less than or equal to mid using CountLessOrEqual.
Counting Products (CountLessOrEqual):
For each element in nums1, we count the number of elements in nums2 that can form a product less than or equal to mid.
Split into CountPositive (when num1 >= 0) and CountNegative (when num1 < 0).
Efficient Counting (CountPositive and CountNegative):
Use binary search to quickly count the number of valid products in nums2 for a given value of nums1[i].
___
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->O(m * log*(n)).
___
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->O(1).
___
# Code
```csharp []
public class Solution {
public long KthSmallestProduct(int[] nums1, int[] nums2, long k) {
long left = -10000000000L; // Smallest possible product
long right = 10000000000L; // Largest possible product
while (left < right) {
long mid = left + (right - left) / 2;
if (CountLessOrEqual(nums1, nums2, mid) >= k) {
right = mid; // Narrow down to smaller range
} else {
left = mid + 1; // Narrow down to larger range
}
}
return left;
}
private long CountLessOrEqual(int[] nums1, int[] nums2, long target) {
long count = 0;
foreach (int num1 in nums1) {
if (num1 >= 0) {
count += CountPositive(nums2, num1, target);
} else {
count += CountNegative(nums2, num1, target);
}
}
return count;
}
private long CountPositive(int[] nums, int num, long target) {
int low = 0, high = nums.Length - 1;
while (low <= high) {
int mid = low + (high - low) / 2;
if ((long)num * nums[mid] <= target) {
low = mid + 1;
} else {
high = mid - 1;
}
}
return low;
}
private long CountNegative(int[] nums, int num, long target) {
int low = 0, high = nums.Length - 1;
while (low <= high) {
int mid = low + (high - low) / 2;
if ((long)num * nums[mid] <= target) {
high = mid - 1;
} else {
low = mid + 1;
}
}
return nums.Length - low;
}
}
```
| 0 | 0 |
['Array', 'Binary Search', 'C#']
| 0 |
kth-smallest-product-of-two-sorted-arrays
|
EASY TO UNDERSTAND | CLEAN CODE | 2X BINARY SEARCH
|
easy-to-understand-clean-code-2x-binary-mulwz
|
Binary Search on Answer.For each index i in nums1 , find the point in nums2 till which the product is less than the value in the binary search on answer.For fin
|
braindroid
|
NORMAL
|
2024-12-18T20:33:07.897274+00:00
|
2024-12-18T20:33:07.897274+00:00
| 21 | false |
Binary Search on Answer. \n\nFor each index i in nums1 , find the point in nums2 till which the product is less than the value in the binary search on answer.\n\nFor finding the point we can just observe that if nums1[i] <= 0 then it is better to perform the binary search for the point on the array sorted in descending order & if nums[i] > 0 then we can just perform binary search for the point in ascending order. As they form monotonic product pairs.\n\n\n# Code\n```cpp []\nclass Solution {\npublic:\n vector<int>a;\n vector<int>b;\n vector<int>nums;\n long long k;\n\n bool ok(long long x) {\n int m = (int)nums.size();\n int n = (int)a.size();\n long long cnt = 0;\n for(int i = 0 ; i < m ; i++) {\n int l = -1;\n int r = n;\n while(r > l + 1) {\n int m = (l+r) >> 1;\n int val;\n if(nums[i] <= 0) {\n val = b[m];\n } else {\n val = a[m];\n }\n if(nums[i] *1LL* val <= x) {\n l = m;\n } else {\n r = m;\n }\n }\n cnt += (l+1);\n }\n return cnt >= k;\n }\n\n long long kthSmallestProduct(vector<int>& nums1, vector<int>& nums2, long long _k) {\n k = _k;\n nums = nums1;\n a = nums2;\n b = nums2;\n sort(a.begin(),a.end());\n sort(b.rbegin(),b.rend());\n long long l = -1e11;\n long long r = 1e11;\n while(r > l + 1) {\n long long m = (l+r) >> 1;\n if(ok(m)) {\n r = m;\n } else {\n l = m;\n }\n }\n return r;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
kth-smallest-product-of-two-sorted-arrays
|
8 lines scala double binary search and virtual Array.reverse
|
8-lines-scala-double-binary-search-and-v-m80h
|
scala []\nobject Solution {\n def kthSmallestProduct(nums1: Array[Int], nums2: Array[Int], k: Long): Long =\n def bs(check: Long => Boolean, lo: Long, hi: L
|
vititov
|
NORMAL
|
2024-11-17T20:32:37.528266+00:00
|
2024-11-17T20:35:44.874106+00:00
| 3 | false |
```scala []\nobject Solution {\n def kthSmallestProduct(nums1: Array[Int], nums2: Array[Int], k: Long): Long =\n def bs(check: Long => Boolean, lo: Long, hi: Long):Long =\n lazy val mid = lo + (hi - lo) / 2\n if(hi-lo<=1) hi else if(check(mid)) bs(check,lo,mid) else bs(check,mid,hi)\n def count(mid:Long): Long = nums1.iterator.map(_.toLong).map(n1 =>\n if(n1>=0) bs(i=>n1*nums2(i.toInt)>mid ,-1, nums2.length)\n else nums2.length-bs(i => n1*nums2(i.toInt)<=mid,-1, nums2.length)\n ).sum\n bs(count(_)>=k, -10_000_000_001L, 10_000_000_000L)\n}\n```
| 0 | 0 |
['Array', 'Binary Search', 'Scala']
| 0 |
kth-smallest-product-of-two-sorted-arrays
|
Java | Binary Search | Beats 100% Solutions
|
java-binary-search-beats-100-solutions-b-5pw7
|
Code\njava []\nclass Solution {\n public long kthSmallestProduct(int[] nums1, int[] nums2, long k) {\n int segregated1[][] = segregate(nums1);\n
|
tushar_goyal
|
NORMAL
|
2024-11-02T16:09:00.894621+00:00
|
2024-11-02T16:09:00.894653+00:00
| 54 | false |
# Code\n```java []\nclass Solution {\n public long kthSmallestProduct(int[] nums1, int[] nums2, long k) {\n int segregated1[][] = segregate(nums1);\n int neg1[] = segregated1[0];\n int pos1[] = segregated1[1];\n int segregated2[][] = segregate(nums2);\n int neg2[] = segregated2[0];\n int pos2[] = segregated2[1];\n \n long negProd = (long) neg1.length * pos2.length + (long) pos1.length * neg2.length;\n\n int arr1[], arr2[], arr3[], arr4[];\n if(k <= negProd) {\n reverse(pos1);\n reverse(pos2);\n arr1 = neg1;\n arr2 = pos2;\n arr3 = neg2;\n arr4 = pos1;\n } else {\n k -= negProd;\n reverse(neg1);\n reverse(neg2);\n inverse(neg1);\n inverse(neg2);\n arr1 = neg1;\n arr2 = neg2;\n arr3 = pos1;\n arr4 = pos2;\n }\n long start = (long) -1e10, end = (long) 1e10;\n while(start <= end) {\n long mid = start + (end - start) / 2;\n long count = countSmallerEqual(arr1, arr2, mid) + countSmallerEqual(arr3, arr4, mid);\n if(count < k) {\n start = mid + 1;\n } else {\n end = mid - 1;\n }\n }\n return start;\n }\n\n private long countSmallerEqual(int A[], int B[], long num) {\n int i = 0, j = B.length - 1;\n long count = 0;\n while(i < A.length && j >= 0) {\n if(num < (long) A[i] * B[j]) {\n j--;\n } else {\n count += j + 1;\n i++;\n }\n }\n return count;\n }\n\n private void inverse(int nums[]) {\n for(int i = 0; i < nums.length; i++) {\n nums[i] = -nums[i];\n }\n }\n\n private void reverse(int nums[]) {\n int i = 0, j = nums.length - 1;\n while(i < j) {\n int temp = nums[i];\n nums[i] = nums[j];\n nums[j] = temp;\n i++;\n j--;\n }\n }\n\n private int[][] segregate(int nums[]) {\n ArrayList<Integer> negatives = new ArrayList<>(); \n ArrayList<Integer> positives = new ArrayList<>(); \n for(int i = 0; i < nums.length; i++) {\n if(nums[i] < 0) {\n negatives.add(nums[i]);\n } else {\n positives.add(nums[i]);\n }\n }\n int[] negativeArray = negatives.stream().mapToInt(i -> i).toArray();\n int[] positiveArray = positives.stream().mapToInt(i -> i).toArray();\n return new int[][]{negativeArray, positiveArray};\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.