question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
construct-binary-tree-from-inorder-and-postorder-traversal
|
c++ simple recursion without the map use detailed explaination
|
c-simple-recursion-without-the-map-use-d-6o9o
|
The Idea is As They Given us Inorder and Postorder\n\nas we Know Inorder Fallow --> Left_subtree => Root_Node => Right_subtree Traverse\n ans Postorder Fall
|
priyam_vd
|
NORMAL
|
2021-11-21T00:38:38.363042+00:00
|
2021-11-21T00:38:38.363088+00:00
| 943 | false |
The Idea is As They Given us Inorder and Postorder\n\nas we Know Inorder Fallow --> Left_subtree => Root_Node => Right_subtree Traverse\n ans Postorder Fallow --> Left_subtree => Right_subtree =>Root_Nodetraverse\nusing Postorder_array We can Find Root_Node Which always lay in Postorder_array last Possition\nAfter Finding That Root_Node ,First we are going to divide Inorder_array Into Two Part and Postorder Array\ninto Two part .\n\nThen We are going to use Both of the arrays left part to Figur Out Left_subtree\n and Both of the arraysRigth Part to Figur out Right_subtree\n\nWe are going to recursively do so until One Of the array dose not got empty\nLet\'s take an Example\n\n inorder = [4 2 5 1 6 3 7]\n postorder = [4 5 2 6 7 3 1]\n\n So root would be 1 here and Left array which lay left of 1 is [4 2 5] and Right of 1 is [6 3 7]\n so left_inorder_array = [4 2 5] and right_inorder_arry = [6 3 7]\n\n using 6 [ which is just rigth of 1] we are going to devide Postorder_array into two part\n [4 5 2] and [6 7 3]\n\n\n 1st Phase=> \n\t 1\n\n / \\\n\n [4 2 5] [6 3 7] <= inorder array\n [4 5 2] [6 7 3] <= postorder array\n\nNow we have new freash problem like need to make tree by using inorder = [4 2 5] && postorder = [4 5 2] for left subtree \nAND inorder = [6 3 7] && postorder = [6 7 3] for right subtree \n**now same process we need to do again and again until One Of the array dose not got empty\nRest of the Process show in a diagram Form :)\n\n 2nd Phase =>\n 1\n\n / \\\n 2 3\n [4] [5] [6] [7] <= inorder array\n [4] [5] [6] [7] <= postorder array\n\n\n3rd Phase => \n\t 1\n\n / \\\n 2 3\n \n / \\ / \\ <==== Answer\n \n 4 5 6 7 \n\n\n\nin the helper function, IN_SI and IN_EI : starting index and ending index for the inorder vector\nPOST_SI and POST_EI : starting and ending idx for the postorder vector !! (to mark up the part of vector in consideration for that phase of recursion)\n\t\t\t\t\t\t\t\n```\nclass Solution {\n TreeNode*helper(vector<int>&in,vector<int>&post,int IN_SI,int IN_EI,int POST_SI,int POST_EI){\n if(IN_SI > IN_EI){\n return NULL;\n }\n int rootdata = post[POST_EI];\n int rootindex = -1;\n for(int i = IN_SI; i<=IN_EI; i++){\n if(in[i] == rootdata){\n rootindex = i;\n break;\n }\n }\n \n int Left_ins = IN_SI;\n int Left_ine = rootindex-1;\n int Left_posts = POST_SI;\n int Left_poste = Left_ine - Left_ins + Left_posts;\n int Right_ins = rootindex+1;\n int Right_ine = IN_EI;\n int Right_posts = Left_poste + 1;\n int Right_poste = POST_EI - 1; \n \n TreeNode*root = new TreeNode(rootdata);\n root->left = helper(in,post,Left_ins,Left_ine,Left_posts,Left_poste);\n root->right = helper(in,post,Right_ins,Right_ine,Right_posts,Right_poste);\n return root;\n \n }\npublic:\n TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {\n int size = inorder.size();\n return helper(inorder,postorder,0,size-1,0,size-1);\n \n }\n};\n```\n
| 27 | 18 |
['Recursion', 'C']
| 1 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
Simple recursive python 🐍 solution
|
simple-recursive-python-solution-by-injy-260z
|
\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.lef
|
injysarhan
|
NORMAL
|
2020-07-27T12:55:41.464313+00:00
|
2020-07-27T12:55:41.464359+00:00
| 2,509 | false |
```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode:\n if not inorder:\n return\n \n r=postorder.pop() \n root=TreeNode(r) \n i=inorder.index(r) \n \n root.right=self.buildTree(inorder[i+1:],postorder) \n root.left=self.buildTree(inorder[:i],postorder) \n return root\n\n \n```
| 27 | 0 |
['Python', 'Python3']
| 3 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
Python -- Arriving at an O(N) solution
|
python-arriving-at-an-on-solution-by-sky-x6rt
|
Initial answer/thought process:\n\nWell -- the first thing I notice with the provided example (inorder: [9,3,15,20,7], postorder: [9,15,7,20,3]) is that the roo
|
skyler-vestal
|
NORMAL
|
2021-11-21T00:53:14.346585+00:00
|
2021-11-21T00:53:34.315004+00:00
| 889 | false |
Initial answer/thought process:\n\nWell -- the first thing I notice with the provided example (inorder: [9,3,15,20,7], postorder: [9,15,7,20,3]) is that the root is the last value in postorder. Next, we can see that all the values to the left of this root (3) in inorder are in the root\'s left subtree, and all of the values to the right of the root in order are in the root\'s right subtree. So, we get some intuition that a recursive approach here might work.\n\nLet\'s pop off the root in postorder -- the last element -- and then get its left and right subtrees:\n\nnew postorder: [9, 15, 7, 20]\nleft inorder: [9]\nright inorder: [15, 20, 7]\n\nSo we can make the root, and now we need to handle making the left subtree and the right subtree with these values. Well, what I noticed is that the root of the right subtree is now the last value in the new postorder -- aha! The recursive approach becomes clear. We need to recursively repeat this process with the right subtree until there\'s nothing else in this right subtree, and then the only nodes left in the trimmed postorders are in the left subtree, so we can then handle that case:\n\n\n def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:\n if not (inorder and postorder):\n return None\n r_val = postorder.pop()\n left = inorder[:inorder.index(r_val)]\n right = inorder[inorder.index(r_val) + 1:]\n root = TreeNode(r_val)\n root.right = self.buildTree(right, postorder)\n root.left = self.buildTree(left, postorder)\n return root\n\nTime: 39th percentile\nSpace: 39th percentile\n\nMaking sublists and using the index function is a bit suspicious/slow in time and space. Annoyingly, this means we\'ll have to make the "niceness" of this solution a little harder to follow for the sake of saving time and space. First, we don\'t want to use O(N) functions in recursive calls, so we should spot these inefficiencies and think of how to shorten them to O(1) time. The one that sticks out to me here is using index, since that\'s a linear search. Instead, we can just make a hashmap that maps values to their index in inorder. This of course is still O(N), but we only need to do this once so that recursive calls can just use this map to find the appropriate index in O(1) time. Next, instead of making sublists, we can just store the indices for the bounds on the array we\'d normally shrink. Essentially we\'re virtually shrinking the array. The result is a better solution in terms of time and space, but it\'s a bit more confusing to understand:\n\n def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:\n m = {}\n for idx, r in enumerate(inorder):\n m[r] = idx\n def help(left, right):\n if not (postorder and left <= right):\n return None\n r_val = postorder.pop()\n idx = m[r_val]\n root = TreeNode(r_val)\n root.right = help(idx + 1, right)\n root.left = help(left, idx - 1)\n return root\n return help(0, len(postorder) - 1)\n\nTime: 94th percentile\nSpace: 90th percentile\n\nTough problem to get an efficient solution to.
| 22 | 8 |
['Python']
| 0 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
Why so complicated answers are so highly voted?
|
why-so-complicated-answers-are-so-highly-q2aw
|
1 USE A GLOBAL INDEX AND START FROM RIGHT TILL LEFT\n2 AT THE START, CREATE ROOT, AND SET RIGHT AND LEFT\n3 RETURN NULL IF (start>end)\n4 FIND INDEX IF ROOT.VAL
|
swagatpatra832
|
NORMAL
|
2020-11-14T10:22:41.748417+00:00
|
2020-11-14T10:22:41.748443+00:00
| 917 | false |
1 USE A GLOBAL INDEX AND START FROM RIGHT TILL LEFT\n2 AT THE START, CREATE ROOT, AND SET RIGHT AND LEFT\n3 RETURN NULL IF (start>end)\n4 FIND INDEX IF ROOT.VAL IN INORDER AND (start, curr-1) FOR LEFT AND\n(curr+1, end) FOR RIGHT.\n\n```\nint postIndex;\n public TreeNode buildTree(int[] inorder, int[] postorder) {\n int n = postorder.length;\n if(n==0) return null;\n if(n==1) return new TreeNode(postorder[0]);\n postIndex = n-1;\n return helper(inorder, postorder, 0, n-1);\n }\n \n TreeNode helper(int[] inorder, int[] postorder, int start, int end){\n if(start > end) return null;\n \n TreeNode root = new TreeNode(postorder[postIndex--]);\n int curr = findIndex(inorder, root.val);\n \n root.right = helper(inorder, postorder, curr+1, end);\n root.left = helper(inorder, postorder, start, curr-1);\n return root;\n }\n \n int findIndex(int[] inorder, int key){\n for(int i = inorder.length-1; i>=0; i--){\n if(inorder[i] == key) return i;\n }\n return -1;\n }\n```\t\n\nTHE CODE FOR PREORDER IS EXACTLY THE SAME BUT WE MOVE FROM LEFT TO RIGHT\nAND SET LEFT AND THEN THE RIGHT CHILD.\n```\nint preIndex = 0;\n public TreeNode buildTree(int[] preorder, int[] inorder) {\n int n = preorder.length;\n if(n==0) return null;\n if(n==1) return new TreeNode(preorder[0]);\n \n return helper(preorder, inorder, 0, n-1);\n }\n \n TreeNode helper(int[] preorder, int[] inorder, int start, int end){\n if(start > end) return null;\n \n TreeNode root = new TreeNode(preorder[preIndex++]);\n int curr = findIndex(inorder, root.val);\n \n root.left = helper(preorder, inorder, start, curr-1);\n root.right = helper(preorder, inorder, curr+1, end);\n return root;\n }\n \n int findIndex(int[] inorder, int key){\n for(int i =0; i<inorder.length; i++){\n if(inorder[i] == key) return i;\n }\n return -1;\n }\n\t
| 22 | 0 |
['Java']
| 3 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
C++ O(n) DFS solution beath 91% submissions
|
c-on-dfs-solution-beath-91-submissions-b-h4w5
|
Example\n\n 13\n / \\n 2 3\n / \ /\n 5 6 7\n / \\n 8 9\n \\n
|
xz2210
|
NORMAL
|
2016-04-10T17:39:33+00:00
|
2016-04-10T17:39:33+00:00
| 5,011 | false |
Example\n\n 13\n / \\\n 2 3\n / \\ /\n 5 6 7\n / \\\n 8 9\n \\\n 10\n /\n 12\n\n 5, 2, 6, 13, 8, 7, 9, 12, 10, 3\n ---left--- root ---------right---------\n \n 5, 6, 2, 8, 12, 10, 9, 7, 3, 13\n ---left---\t---------right---------- root \n\nCode\n\n class Solution {\n private:\n unordered_map<int, int> inm; // inorder map [inorder[i], i]\n \n public:\n TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {\n int n = inorder.size(), i = 0;\n for(auto val: inorder) inm[val] = i++; // build inm for dfs \n \n return dfs(inorder, 0, n - 1, postorder, 0, n - 1);\n }\n \n TreeNode* dfs(vector<int>& inorder, int ileft, int iright, vector<int>& postorder, int pleft, int pright) {\n if(ileft > iright) return nullptr;\n \n int val = postorder[pright]; // root value\n TreeNode *root = new TreeNode(val);\n if(ileft == iright) return root;\n \n int iroot = inm[val];\n int nleft = iroot - ileft; // length of left subtree\n root->right = dfs(inorder, iroot + 1, iright, postorder, pleft + nleft, pright - 1);\n root->left = dfs(inorder, ileft, iroot - 1, postorder, pleft, pleft + nleft - 1);\n \n return root;\n }\n };
| 22 | 0 |
['C++']
| 3 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
Here is my O(n) solution. Is it neat?
|
here-is-my-on-solution-is-it-neat-by-hon-yuxb
|
class Solution {\n public:\n TreeNode *buildTree(vector<int> &inorder, vector<int> &postorder) {\n if(inorder.size() == 0)return NULL;\n
|
hongzhi
|
NORMAL
|
2014-06-17T03:21:35+00:00
|
2014-06-17T03:21:35+00:00
| 7,176 | false |
class Solution {\n public:\n TreeNode *buildTree(vector<int> &inorder, vector<int> &postorder) {\n if(inorder.size() == 0)return NULL;\n TreeNode* p;\n TreeNode* root;\n vector<int> vint;\n vector<TreeNode*> vtn;\n root = new TreeNode(postorder.back());\n vtn.push_back(root);\n postorder.pop_back();\n while(true)\n {\n if(inorder.back() == vtn.back()->val)\n {\n p = vtn.back();\n vtn.pop_back();\n inorder.pop_back();\n if(inorder.size() == 0) break;\n \t\t\t\tif(vtn.size())\n \t\t\t\t\tif(inorder.back() == vtn.back()->val)continue;\n p->left = new TreeNode(postorder.back());\n \t\t\t\tpostorder.pop_back();\n vtn.push_back(p->left);\n }\n else\n {\n p = new TreeNode(postorder.back());\n postorder.pop_back();\n vtn.back()->right = p;\n vtn.push_back(p);\n }\n }\n \t\treturn root;\n }\n };
| 21 | 1 |
[]
| 0 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
[Java] 1ms, beats 100%, no map, clean recursion
|
java-1ms-beats-100-no-map-clean-recursio-57ow
|
105 is same as 106 (almost) here are the comparisons, check the similarity and differences\n# 105 inorder + preorder\nwe use preorder to create nodes from left
|
byegates
|
NORMAL
|
2022-09-03T09:59:27.600849+00:00
|
2022-09-03T10:01:41.613174+00:00
| 2,686 | false |
105 is same as 106 (almost) here are the comparisons, check the similarity and differences\n# [105 inorder + preorder](https://leetcode.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/)\nwe use preorder to create nodes from left to right, whenever we go left, we need to pass current root value as right boundary for it\'s whole left sub tree(root has no boundary, so used 3001 as valid nodes are from 1-3000, you could use Integer.MAX_VALUE), so that the left sub tree creation will know when to exit to go right subtree, the right bounary of right subtree is right subtree\'s parent\'s parent which was passed in.\n```java\nclass Solution { // TC: O(n), SC: O(height)\n int i, p; // i as index for inorder, p as index for preorder\n public TreeNode buildTree(int[] pre, int[] in) {\n i = p = 0;\n return dfs(pre, in, 3001);\n }\n\n private TreeNode dfs(int[] pre, int[] in, int rightBoundary) {\n if (p == pre.length || in[i] == rightBoundary) return null;\n\n TreeNode node = new TreeNode(pre[p++]);\n node.left = dfs(pre, in, node.val);\n i++;\n node.right = dfs(pre, in, rightBoundary);\n return node;\n }\n}\n```\n# [106 inorder + postorder](https://leetcode.com/problems/construct-binary-tree-from-inorder-and-postorder-traversal/)\nAlmost exactly same as above, but we go backwards and create right sub tree first (and check for left boundary as end because we scan backwards right to left)\n```java\nclass Solution {\n int i, o; // i: inorder traversal idx, o: postorder traversal idx;\n public TreeNode buildTree(int[] in, int[] po) {\n i = o = po.length - 1;\n return dfs(in, po, 3001);\n }\n \n private TreeNode dfs(int[] in, int[] po, int leftBoundary) {\n if (o == -1 || in[i] == leftBoundary) return null;\n TreeNode node = new TreeNode(po[o--]);\n node.right = dfs(in, po, node.val);\n i--;\n node.left = dfs(in, po, leftBoundary);\n return node;\n }\n}\n```\n
| 18 | 0 |
['Recursion', 'Java']
| 3 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
Python3 (only 2 lines; explained)
|
python3-only-2-lines-explained-by-jjmcin-gj6y
|
By definition, the postorder input has the root of the tree as its last element.\nAlso, by definition, inorder and postorder have equal lengths.\n\nTherefore, t
|
jjmcinto
|
NORMAL
|
2021-11-21T00:56:00.877168+00:00
|
2021-11-21T00:59:14.618012+00:00
| 687 | false |
By definition, the ```postorder``` input has the root of the tree as its last element.\nAlso, by definition, ```inorder``` and ```postorder``` have equal lengths.\n\nTherefore, to split these inputs into left and right subtrees, we can find the last element of ```postorder``` within ```inorder``` and split ```inorder``` at that point, recursing to the left with the elements left of that point and to the right with the elements to the right of that point.\n\nSince the inputs must be of equal length, we must split ```postorder``` at the same position, but include the element at that position in the input for the right subtree (and, of course, exclude the element in the last position).\n\ne.g. ```inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]```\nThen the root is 3, so ```inorder``` and ```postorder``` are split thusly:\ninorder_left = [9]\ninorder_right = [15,20,7]\npostorder_left = [9]\npostorder_right = [15,7,20]\nThen set the left subtree to ```buildTree(inorder_left, postorder_left)``` and set the right subtree to ```buildTree(inorder_right, postorder_right)```.\n\nSo, here is the resulting algorithm:\nStep 1: If ```inorder``` is not empty, then find the last element of ```postorder``` in ```inorder```.\nStep 2: If ```inorder``` is not empty, then divide the inputs into left and right subtrees and recurse.\n\nAnd here is the code:\n```\n#Runtime: 180 ms, faster than 36.95% of Python3 online submissions for Construct Binary Tree from Inorder and Postorder Traversal.\n#Memory Usage: 88.1 MB, less than 28.00% of Python3 online submissions for Construct Binary Tree from Inorder and Postorder Traversal.\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:\n pos = inorder.index(postorder[-1]) if inorder else -1\n return TreeNode(postorder[-1], self.buildTree(inorder[:pos], postorder[:pos]), self.buildTree(inorder[pos+1:], postorder[pos:-1])) if pos>-1 else None\n```
| 18 | 12 |
['Recursion', 'Python3']
| 0 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
Python solution
|
python-solution-by-zitaowang-b3xu
|
We illustrate the algorithm with an example. Consider inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]. Since, we know that postorder traversal traverses a tr
|
zitaowang
|
NORMAL
|
2019-01-02T09:09:22.319272+00:00
|
2019-01-02T09:09:22.319313+00:00
| 1,351 | false |
We illustrate the algorithm with an example. Consider `inorder = [9,3,15,20,7]`, `postorder = [9,15,7,20,3]`. Since, we know that postorder traversal traverses a tree in the order `left subtree -> right subtree -> root`, and inorder traversal traverses a tree in the order `left subtree -> root -> right subtree`, `3` must be thre root of the tree, and values that come after (before) `3` in `inorder` must be in the right (left) subtree of `3`. Repeating the above procedure recursively until each subtree consists of a single node, we finish constructing the whole tree. For example, the right subtree of the root `3` consists of values `15`, `20`, `7`. Furthermore, since `20` comes right after `3` when traversing `postorder` from the right, it is the root of the right subtree of `3`. Finally, since `15` (`7`) comes before (after) `20` in `inorder`, it is the left (right) child of `20`. The same analysis applies to the left subtree of `3`, and the binary tree is given by `3(9)(20(15)(7))`.\n\nWe can implement the above algorithm in an iterative fashion. To do this, we first construct a hashmap `idx` which maps a value to its inorder index. This will give us an `O(1)` look up of the inorder indices of values of a root and its child, so that we can decide if the child is a left child or right child of the root. Then we can construct the tree with the help of a `stack`. We iterate over `postorder` from the right and create a TreeNode `node` with the corresponding value `val`. If the head is null, we let `head = node`, and push `head` into the `stack`. Else, if the inorder index `stack[-1]` is smaller than that of `val`, we assign `stack[-1].right = node`, and push `node` into the `stack`. Otherwise, we pop from `stack` to until either `stack` is empty or the inorder index of `stack[-1]` is smaller than that of `node`. We assign `u.left = node` for the last popped node `u` from `stack`, and then push `node` to `stack`. After iterating over `postorder`, we return `head`. \n\nTime complexity: `O(n)`, space complexity: `O(n)`.\n\n```\nclass Solution(object):\n def buildTree(self, inorder, postorder):\n """\n :type inorder: List[int]\n :type postorder: List[int]\n :rtype: TreeNode\n """\n idx = {}\n for i, val in enumerate(inorder):\n idx[val] = i\n \n head = None\n stack = []\n for i in range(len(postorder)-1, -1, -1):\n val = postorder[i]\n if not head:\n head = TreeNode(val)\n stack.append(head)\n else:\n node = TreeNode(val)\n if idx[val] > idx[stack[-1].val]:\n stack[-1].right = node\n else:\n while stack and idx[stack[-1].val] > idx[val]:\n u = stack.pop()\n u.left = node\n stack.append(node)\n return head\n```
| 18 | 0 |
[]
| 3 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
O(n) recursive solution without hashmap nor index
|
on-recursive-solution-without-hashmap-no-nosk
|
python solution:\npython\nclass Solution(object):\n def buildTree(self, inorder, postorder):\n """\n :type inorder: List[int]\n :type po
|
zqfan
|
NORMAL
|
2017-06-06T02:19:25.236000+00:00
|
2017-06-06T02:19:25.236000+00:00
| 3,186 | false |
python solution:\n```python\nclass Solution(object):\n def buildTree(self, inorder, postorder):\n """\n :type inorder: List[int]\n :type postorder: List[int]\n :rtype: TreeNode\n """\n def postdfs(stop):\n if postorder and inorder[-1] != stop:\n root = TreeNode(postorder.pop())\n root.right = postdfs(root.val)\n inorder.pop()\n root.left = postdfs(stop)\n return root\n inorder, postorder = inorder[:], postorder[:]\n return postdfs(None)\n\n# 202 / 202 test cases passed.\n# Status: Accepted\n# Runtime: 62 ms\n# beats 97.20 %\n```\nc++ solution:\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode(int x) : val(x), left(NULL), right(NULL) {}\n * };\n */\nclass Solution {\npublic:\n TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {\n vector<int> in(inorder), post(postorder);\n return postdfs(in, post, (TreeNode *)NULL);\n }\n\n TreeNode * postdfs(vector<int> & in, vector<int> & post, TreeNode * stop) {\n if ( post.empty() || (stop && in.back() == stop->val) ) {\n return NULL;\n }\n TreeNode * root = new TreeNode(post.back());\n post.pop_back();\n root->right = postdfs(in, post, root);\n in.pop_back();\n root->left = postdfs(in, post, stop);\n return root;\n }\n};\n\n// 202 / 202 test cases passed.\n// Status: Accepted\n// Runtime: 9 ms\n// beats 91.06 %\n```
| 18 | 0 |
['Depth-First Search', 'C', 'Python']
| 1 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
Day 75 || Divide and Conquer + Hash Table || Easiest Beginner Friendly Sol
|
day-75-divide-and-conquer-hash-table-eas-874b
|
NOTE - PLEASE READ INTUITION AND APPROACH FIRST THEN SEE THE CODE. YOU WILL DEFINITELY UNDERSTAND THE CODE LINE BY LINE AFTER SEEING THE APPROACH.\n\n# Intuitio
|
singhabhinash
|
NORMAL
|
2023-03-16T05:17:00.841665+00:00
|
2023-03-16T07:16:10.608936+00:00
| 2,840 | false |
**NOTE - PLEASE READ INTUITION AND APPROACH FIRST THEN SEE THE CODE. YOU WILL DEFINITELY UNDERSTAND THE CODE LINE BY LINE AFTER SEEING THE APPROACH.**\n\n# Intuition of this Problem :\nThe problem is to construct a binary tree from inorder and postorder traversals of the tree. The inorder traversal gives the order of nodes in the left subtree, root, and right subtree, while the postorder traversal gives the order of nodes in the left subtree, right subtree, and root.\n\n**The intuition behind the algorithm is to start by identifying the root of the binary tree from the last element of the postorder traversal. Then, we can use the root to divide the inorder traversal into left and right subtrees. We can then recursively apply the same process to the left and right subtrees to construct the entire binary tree.**\n\nTo do this efficiently, we can use a hash map to store the indices of elements in the inorder traversal. This allows us to quickly find the position of the root in the inorder traversal and divide the traversal into left and right subtrees.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach for this Problem :\n1. Create a function called buildTree that takes in two vectors, inorder and postorder, and returns a pointer to the root of the resulting binary tree.\n2. Initialize an integer variable postorderIndex to postorder.size() - 1. This variable will be used to traverse the postorder vector in reverse order.\n3. Initialize an empty unordered map called inorderIndexUmp. This map will be used to quickly look up the index of a value in the inorder vector.\n4. Loop through the inorder vector and insert each value and its index into the inorderIndexUmp map.\n5. Call a recursive helper function called buildTreeHelper with parameters postorder, 0, and postorder.size() - 1. This function will return the root of the binary tree.\n6. In the buildTreeHelper function, if left is greater than right, return nullptr.\n7. Get the root value from the postorder vector using the postorderIndex variable, and decrement postorderIndex.\n8. Create a new TreeNode with the root value and assign it to a pointer variable called root.\n9. Get the index of the root value in the inorder vector from the inorderIndexUmp map, and assign it to an integer variable called inorderPivotIndex.\n10. Recursively call buildTreeHelper with parameters postorder, inorderPivotIndex + 1, and right. Assign the result to root -> right.\n11. Recursively call buildTreeHelper with parameters postorder, left, and inorderPivotIndex - 1. Assign the result to root -> left.\n12. Return root.\n<!-- Describe your approach to solving the problem. -->\n\n# Code :\n```C++ []\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n int postorderIndex;\n unordered_map<int, int> inorderIndexUmp;\n\n TreeNode* buildTreeHelper(vector<int>& postorder, int left, int right) {\n if (left > right)\n return nullptr;\n int rootValue = postorder[postorderIndex--];\n TreeNode* root = new TreeNode(rootValue);\n int inorderPivotIndex = inorderIndexUmp[rootValue];\n //think about it...why I took root -> right first then root -> left ?\n root -> right = buildTreeHelper(postorder, inorderPivotIndex + 1, right);\n root -> left = buildTreeHelper(postorder, left, inorderPivotIndex - 1);\n return root;\n }\n\n TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {\n postorderIndex = postorder.size() - 1;\n for (int i = 0; i < inorder.size(); i++) {\n inorderIndexUmp[inorder[i]] = i;\n }\n return buildTreeHelper(postorder, 0, postorder.size() - 1);\n }\n};\n```\n```Java []\nclass TreeNode {\n int val;\n TreeNode left;\n TreeNode right;\n TreeNode() {}\n TreeNode(int val) { this.val = val; }\n TreeNode(int val, TreeNode left, TreeNode right) {\n this.val = val;\n this.left = left;\n this.right = right;\n }\n}\n\nclass Solution {\n int postorderIndex;\n Map<Integer, Integer> inorderIndexUmp;\n\n public TreeNode buildTree(int[] inorder, int[] postorder) {\n postorderIndex = postorder.length - 1;\n inorderIndexUmp = new HashMap<Integer, Integer>();\n for (int i = 0; i < inorder.length; i++) {\n inorderIndexUmp.put(inorder[i], i);\n }\n return buildTreeHelper(postorder, 0, postorder.length - 1);\n }\n\n private TreeNode buildTreeHelper(int[] postorder, int left, int right) {\n if (left > right)\n return null;\n int rootValue = postorder[postorderIndex--];\n TreeNode root = new TreeNode(rootValue);\n int inorderPivotIndex = inorderIndexUmp.get(rootValue);\n root.right = buildTreeHelper(postorder, inorderPivotIndex + 1, right);\n root.left = buildTreeHelper(postorder, left, inorderPivotIndex - 1);\n return root;\n }\n}\n\n```\n```Python []\nclass Solution:\n def buildTreeHelper(self, postorder: List[int], left: int, right: int) -> TreeNode:\n if left > right:\n return None\n root_value = postorder[self.postorder_index]\n self.postorder_index -= 1\n root = TreeNode(root_value)\n inorder_pivot_index = self.inorder_index_map[root_value]\n root.right = self.buildTreeHelper(postorder, inorder_pivot_index + 1, right)\n root.left = self.buildTreeHelper(postorder, left, inorder_pivot_index - 1)\n return root\n\n def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode:\n self.postorder_index = len(postorder) - 1\n self.inorder_index_map = {val: i for i, val in enumerate(inorder)}\n return self.buildTreeHelper(postorder, 0, len(postorder) - 1)\n\n```\n\n# Time Complexity and Space Complexity:\n- Time complexity : **O(n)**, The buildTreeHelper() function is called for each node in the tree exactly once, and the time complexity of each call is O(1). Therefore, the overall time complexity of the algorithm is O(n), where n is the number of nodes in the tree.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity : **O(n)**, where n is the number of nodes in the tree. This is because we are creating a new TreeNode object for each node in the tree, and we are also using an unordered_map to store the indices of the nodes in the inorder traversal. Additionally, the recursive calls to buildTreeHelper() create a call stack of size O(n) in the worst case, where n is the number of nodes in the tree.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n**YOU CAN ALSO TRY BELOW PROBLWM WHICH IS SIMILAR TO THIS PROBLEM**\n105. Construct Binary Tree from Preorder and Inorder Traversal\n**SOLUTION :**\nhttps://leetcode.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/solutions/3303059/divide-and-conquer-hash-table-easiest-beginner-friendly-sol/
| 17 | 0 |
['Hash Table', 'Divide and Conquer', 'C++', 'Java', 'Python3']
| 3 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
2 approaches | Easy to comprehend | Detailed explanation | C++ | Java
|
2-approaches-easy-to-comprehend-detailed-a8vq
|
Explanation:\nInorder Traversal -> First visit the left subtree, followed by the root node, followed by the right subtree.\nLeft -> Root -> Right\nPoint of obse
|
anushka_verma
|
NORMAL
|
2020-07-27T09:03:13.647277+00:00
|
2020-07-27T09:03:13.647324+00:00
| 916 | false |
**Explanation:**\n**Inorder Traversal** -> First visit the left subtree, followed by the root node, followed by the right subtree.\n**Left -> Root -> Right**\nPoint of observation: The root node divides the inorder array into 2 halves, left subtree and right subtree.\n**Postorder Traversal** -> First visit left subtree, followed by the right subtree, followed bt the root node.\n**Left -> Right -> Root**\nPoint of observation: The root node is available at the end the of the postorder array. \n\nSo, as the first step, we can eaily obtain the value of the root node for the tree (or subtree) from the postorder array by accessessing the last element of the postorder array. Then, it can be observed that the root node divides the inorder array into two halves, the left and right subtree. So, for constructing the tree using postorder and inorder, we will find the find the index of root node in inorder array and then make recursive calls on the left and right subtrees.\n\n**Approach 1**\n\n**C++ Code:**\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n \n\t// variable key: \n\t// in -> inorder array\n\t// ins -> inorder start index\n\t// ine -> inorder end index\n\t// post -> postorder array\n\t// posts -> postorder start index\n\t// poste -> postorder end index\n\n TreeNode* buildTreeUtil(vector<int>& in, int ins, int ine, vector<int>& post, int posts, int poste) {\n \n if(ins>ine || posts>poste) return nullptr;\n \n int rval=post[poste]; // root value\n TreeNode* root = new TreeNode(rval);\n \n int i=ins;\n while(in[i] != rval) i++;\n \n root->right = buildTreeUtil(in, i+1, ine, post, posts+i-ins, poste-1);\n root->left = buildTreeUtil(in, ins, i-1, post, posts, posts+i-(ins+1));\n return root;\n \n }\n \n TreeNode* buildTree(vector<int>& in, vector<int>& post) {\n return buildTreeUtil(in, 0, in.size()-1, post, 0, post.size()-1);\n }\n};\n```\n\n**Java Code:**\n```\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n * TreeNode(int val) { this.val = val; }\n * TreeNode(int val, TreeNode left, TreeNode right) {\n * this.val = val;\n * this.left = left;\n * this.right = right;\n * }\n * }\n */\nclass Solution {\n\n\t// variable key: \n\t// in -> inorder array\n\t// ins -> inorder start index\n\t// ine -> inorder end index\n\t// post -> postorder array\n\t// posts -> postorder start index\n\t// poste -> postorder end index\n \n public TreeNode buildTreeUtil(int[] in, int ins, int ine, int[] post, int posts, int poste) {\n \n if(ins>ine || posts>poste) return null;\n \n int rval=post[poste]; // root value\n TreeNode root = new TreeNode(rval);\n \n int i=ins;\n while(in[i] != rval) i++;\n \n root.right = buildTreeUtil(in, i+1, ine, post, posts+i-ins, poste-1);\n root.left = buildTreeUtil(in, ins, i-1, post, posts, posts+i-(ins+1));\n return root;\n \n }\n \n public TreeNode buildTree(int[] in, int[] post) {\n return buildTreeUtil(in, 0, in.length-1, post, 0, post.length-1);\n }\n}\n```\n\n\n****Approach 2****\nNote: (As given in the problem description)\nYou may assume that duplicates do not exist in the tree.\n\nSince we need not worry about the presence of duplicates in the tree, we can simply create an inorder key-value index map to store all values inside Hash Map and easily access the index of any particular node in the inorder traversal of the tree.\n\n**C++ Code:**\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n unordered_map<int,int> mp;\n TreeNode* buildTreeUtil(vector<int>& post, int& idx, const int& si, const int& ei) {\n if (si>ei) return NULL;\n TreeNode* root = new TreeNode(post[idx]);\n int mid = mp[post[idx]];\n idx--;\n root->right = buildTreeUtil(post, idx, mid+1, ei);\n root->left = buildTreeUtil(post, idx, si, mid-1);\n return root;\n }\n\n TreeNode* buildTree(vector<int>& in, vector<int>& post) {\n for(int i=0; i<in.size(); i++) mp[in[i]]=i;\n int idx=post.size()-1;\n return buildTreeUtil(post, idx, 0, in.size()-1);\n }\n};\n```\n\n**Java Code:**\n```\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n * TreeNode(int val) { this.val = val; }\n * TreeNode(int val, TreeNode left, TreeNode right) {\n * this.val = val;\n * this.left = left;\n * this.right = right;\n * }\n * }\n */\nclass Solution {\n \n public TreeNode buildTreeUtil(int[] post, int idx, int si, int ei, Map<Integer, Integer> mp) {\n \n if (si>ei) return null;\n TreeNode root = new TreeNode(post[idx]);\n\n int mid = mp.get(post[idx]);\n idx--;\n\n root.right = buildTreeUtil(post, idx, mid+1, ei, mp);\n root.left = buildTreeUtil(post, idx-(ei-mid), si, mid-1, mp);\n return root;\n }\n\n public TreeNode buildTree(int[] in, int[] post) {\n \n Map<Integer, Integer> mp = new HashMap<Integer, Integer>();\n for(int i=0; i<in.length; i++) mp.put(in[i], i);\n return buildTreeUtil(post, post.length-1, 0, in.length-1, mp);\n \n }\n}\n```
| 17 | 3 |
[]
| 4 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
O(n) c++ recursive solution - 23ms with comments
|
on-c-recursive-solution-23ms-with-commen-m980
|
TreeNode *buildTree(vector<int> &inorder, vector<int> &postorder) {\n unordered_map<int, int> inorder_map;\n // we need a map to look up t
|
pankit
|
NORMAL
|
2015-02-15T16:37:17+00:00
|
2018-09-27T01:08:51.147674+00:00
| 3,460 | false |
TreeNode *buildTree(vector<int> &inorder, vector<int> &postorder) {\n unordered_map<int, int> inorder_map;\n // we need a map to look up the position of root in inorder, so\n // that we can divide the tree into separate subtrees,\n // reduces the complexity from n^2 to n assuming good hashing by unodered_map\n for (int i = 0; i < inorder.size(); ++i) {\n inorder_map[inorder[i]] = i;\n }\n return buildTreeHelper(postorder, 0, inorder.size()-1, 0, postorder.size()-1, inorder_map);\n }\n \n TreeNode* buildTreeHelper(vector<int>& post, int is, int ie, int ps, int pe, unordered_map<int, int>& inorder_map) {\n \n if (is > ie || ps > pe) {\n return NULL;\n }\n int root_val = post[pe];\n TreeNode* root = new TreeNode(root_val);\n int i = inorder_map.find(root_val)->second;\n // number of nodes in left subtree\n int l = i-is;\n root->left = buildTreeHelper(post, is, is+l-1, ps, ps+l-1, inorder_map);\n root->right = buildTreeHelper(post, is+l+1, ie, ps+l, pe-1, inorder_map);\n \n return root;\n }
| 16 | 1 |
['Binary Tree', 'C++']
| 1 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
(C++) 106. Construct Binary Tree from Inorder and Postorder Traversal
|
c-106-construct-binary-tree-from-inorder-5p2e
|
\n\nclass Solution {\npublic:\n TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {\n unordered_map<int, int> mp; \n for (int i
|
qeetcode
|
NORMAL
|
2021-11-21T01:39:54.879578+00:00
|
2021-11-21T01:39:54.879610+00:00
| 369 | false |
\n```\nclass Solution {\npublic:\n TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {\n unordered_map<int, int> mp; \n for (int i = 0; i < inorder.size(); ++i) mp[inorder[i]] = i; \n \n stack<TreeNode*> stk; \n TreeNode *root = nullptr, *node = nullptr; \n for (int i = postorder.size()-1; i >= 0; --i) {\n int x = postorder[i]; \n if (!root) root = node = new TreeNode(x); \n else if (mp[node->val] < mp[x]) {\n stk.push(node); \n node = node->right = new TreeNode(x); \n } else {\n while (stk.size() && mp[x] < mp[stk.top()->val]) node = stk.top(), stk.pop(); \n node = node->left = new TreeNode(x); \n }\n }\n return root;\n }\n};\n```
| 14 | 10 |
['C']
| 1 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
[JavaScript] Concise solution
|
javascript-concise-solution-by-supermeer-8k1f
|
Facts,\n1. The root is at the end of postorder\n2. inorder is of the form [...leftinorder, root, ...rightinorder]\n3. postorder is of the form [...leftpostord
|
supermeerkat
|
NORMAL
|
2020-07-27T08:25:01.350864+00:00
|
2020-07-27T08:25:01.350929+00:00
| 1,218 | false |
Facts,\n1. The `root` is at the end of `postorder`\n2. `inorder` is of the form `[...leftinorder, root, ...rightinorder]`\n3. `postorder` is of the form `[...leftpostorder, ...rightpostorder, root]`\n4. `leftinorder.length === leftpostorder.length`\n5. `rightinorder.length === rightpostorder.length`\n\nSolution,\n```\nvar buildTree = function(inorder, postorder) {\n if (inorder.length === 0) return null;\n\n let root = postorder[postorder.length - 1];\n let pivot = inorder.indexOf(root);\n\n return {\n val: root,\n left: buildTree(inorder.slice(0, pivot), postorder.slice(0, pivot)),\n right: buildTree(inorder.slice(pivot + 1), postorder.slice(pivot, -1))\n };\n};\n```
| 14 | 0 |
['Recursion', 'JavaScript']
| 4 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
Concise recursive Java code by making slight modification to the previous problem.
|
concise-recursive-java-code-by-making-sl-fvjf
|
Here I'll show you a comparison of code for Construct Binary Tree from [Problem 105: Preorder and Inorder Traversal][1] and from [Problem 106: Inorder and Posto
|
annieqt
|
NORMAL
|
2015-11-10T13:31:52+00:00
|
2015-11-10T13:31:52+00:00
| 1,192 | false |
Here I'll show you a comparison of code for Construct Binary Tree from [Problem 105: Preorder and Inorder Traversal][1] and from [Problem 106: Inorder and Postorder Traversal][2].\n\nCode for Problem 105:\n\n\n public static TreeNode buildTree(int[] preorder, int[] inorder) {\n return helper(preorder, 0, inorder, 0, inorder.length - 1);\n }\n\n public static TreeNode helper(int[] preorder, int preStart, int[] inorder, int inStart, int inEnd) {\n if (preStart > preorder.length - 1 || inStart > inEnd)\n return null;\n TreeNode root = new TreeNode(preorder[preStart]);\n int target = inStart;\n while (inorder[target] != preorder[preStart]) target++;\n root.left = helper(preorder, preStart + 1, inorder, inStart, target - 1);\n root.right = helper(preorder, preStart + target - inStart + 1, inorder, target + 1, inEnd);\n\n return root;\n }\n\nCode for Problem 106:\n\n\n public static TreeNode buildTree(int[] inorder, int[] postorder) {\n return helper(postorder, postorder.length - 1, inorder, 0, inorder.length - 1);\n }\n\n public static TreeNode helper(int[] postorder, int postStart, int[] inorder, int inStart, int inEnd) {\n if (postStart < 0 || inStart > inEnd)\n return null;\n TreeNode root = new TreeNode(postorder[postStart]);\n int target = inStart;\n while (inorder[target] != postorder[postStart]) target++;\n root.left = helper(postorder, postStart - inEnd + target - 1, inorder, inStart, target - 1);\n root.right = helper(postorder, postStart - 1, inorder, target + 1, inEnd);\n\n return root;\n }\n\nNote that the only difference is, for post-order we traverse from the end of `postorder` and change the way for finding `poststart`. \nEnjoy :)\n [1]: https://leetcode.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/\n [2]: http://Inorder%20and%20Postorder%20Traversal
| 13 | 0 |
[]
| 1 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
c++ || recursion + map || beat 100%
|
c-recursion-map-beat-100-by-amankatiyar7-9wh4
|
\n# Code\n\nclass Solution {\npublic:\n TreeNode* buildTree(vector<int>& ino, vector<int>& post) {\n int i1 = post.size()-1;\n return solve(i1,ino,
|
amankatiyar783597
|
NORMAL
|
2023-03-16T01:37:41.543258+00:00
|
2023-03-16T01:42:46.407313+00:00
| 4,039 | false |
\n# Code\n```\nclass Solution {\npublic:\n TreeNode* buildTree(vector<int>& ino, vector<int>& post) {\n int i1 = post.size()-1;\n return solve(i1,ino,post,0,ino.size()-1);\n }\n TreeNode* solve(int &i,vector<int> &in,vector<int> &post,int l,int r){\n if(l>r)return NULL;\n int x = r;\n while(post[i] != in[x]){\n x--;\n }\n i--;\n TreeNode* root = new TreeNode(in[x]);\n root->right = solve(i,in,post,x+1,r);\n root->left = solve(i,in,post,l,x-1);\n return root;\n }\n};\n```
| 12 | 1 |
['C++']
| 0 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
✔️ 100% Fastest Swift Solution
|
100-fastest-swift-solution-by-sergeylesc-dbyo
|
\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * public var val: Int\n * public var left: TreeNode?\n * public var right
|
sergeyleschev
|
NORMAL
|
2022-04-09T05:49:49.401185+00:00
|
2022-04-09T05:49:49.401241+00:00
| 355 | false |
```\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * public var val: Int\n * public var left: TreeNode?\n * public var right: TreeNode?\n * public init() { self.val = 0; self.left = nil; self.right = nil; }\n * public init(_ val: Int) { self.val = val; self.left = nil; self.right = nil; }\n * public init(_ val: Int, _ left: TreeNode?, _ right: TreeNode?) {\n * self.val = val\n * self.left = left\n * self.right = right\n * }\n * }\n */\nclass Solution {\n func buildTree(_ inorder: [Int], _ postorder: [Int]) -> TreeNode? {\n guard postorder.count > 0 else { return nil }\n \n let totalCount = postorder.count\n let root = TreeNode(postorder[totalCount - 1])\n var rootIndex = -1\n \n for (i, val) in inorder.enumerated() {\n if val == root.val {\n rootIndex = i\n break\n } \n }\n \n let leftCount = rootIndex\n let rightCount = totalCount - leftCount - 1\n \n root.left = buildTree(Array(inorder[0..<leftCount]), Array(postorder[0..<leftCount]))\n root.right = buildTree(Array(inorder[1 + leftCount..<totalCount]), Array(postorder[leftCount..<totalCount - 1]))\n return root\n }\n \n}\n```\n\nLet me know in comments if you have any doubts. I will be happy to answer.\n\nPlease upvote if you found the solution useful.
| 12 | 0 |
['Swift']
| 1 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
Java Solution - 1 ms, faster than 95.05%
|
java-solution-1-ms-faster-than-9505-by-t-w4rd
|
\nclass Solution {\n int index;\n public TreeNode buildTree(int[] inorder, int[] postorder) {\n HashMap<Integer, Integer> map = new HashMap<>();\n
|
thedeepanshumourya
|
NORMAL
|
2020-05-01T09:16:19.342354+00:00
|
2020-05-01T09:17:10.317177+00:00
| 1,057 | false |
```\nclass Solution {\n int index;\n public TreeNode buildTree(int[] inorder, int[] postorder) {\n HashMap<Integer, Integer> map = new HashMap<>();\n for(int i=0; i<inorder.length; i++){\n map.put(inorder[i], i);\n }\n index = postorder.length-1;\n return build(inorder, postorder, map, 0, postorder.length-1);\n }\n \n public TreeNode build(int[] inorder, int[] postorder, HashMap<Integer, Integer> map, int start, int end){\n if(start > end) return null;\n TreeNode root = new TreeNode(postorder[index--]);\n int pos = map.get(root.val);\n root.right = build(inorder, postorder, map, pos+1, end);\n root.left = build(inorder, postorder, map, start, pos-1);\n return root;\n }\n}\n```
| 12 | 0 |
['Tree', 'Recursion', 'Java']
| 1 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
🔥Easy Explanation + Video | Java C++ Python
|
easy-explanation-video-java-c-python-by-x8ntn
|
InOrder Traversal: we visit the left subtree first, then the root node, and then the right subtree\n4,10,12,15,18,22,24,25,31,35,44,50,66,70,90\n\nPostOrder Tra
|
jeevankumar159
|
NORMAL
|
2023-03-16T01:18:32.407710+00:00
|
2023-03-16T01:18:32.407733+00:00
| 4,333 | false |
InOrder Traversal: we visit the left subtree first, then the root node, and then the right subtree\n4,10,12,15,18,22,24,25,31,35,44,50,66,70,90\n\nPostOrder Traversal: we visit the left subtree first, then the right subtree, and then the current node\n4,12,10,18,24,22,15,31,44,35,66,90,70,50,25\n\n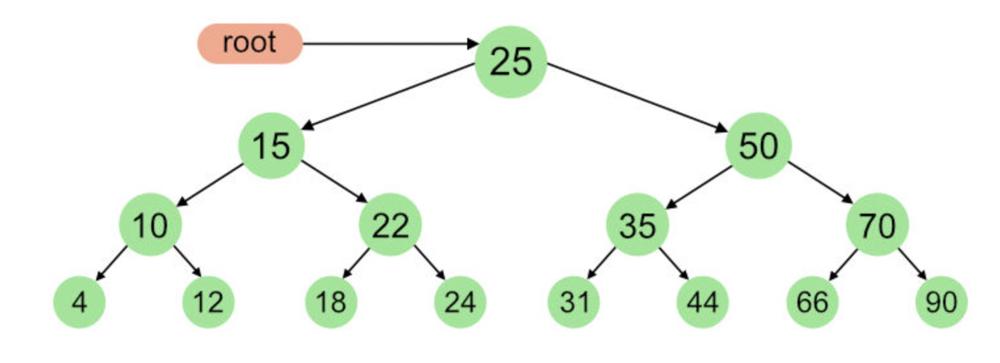\n\n# Intuition and Approach\nThe biggest hint is that the root node is always at end in postOrder Traversal ex: 25 is root node.\nWe find this root node in Inorder Traversal and all the elements on left i.e 4,10,12,15,18,22,24 act as left subtree and all elements on right 31,35,44,50,66,70,90 act as right subtree. \n\nThe above process can be repeated to form left and right subtree again individually\neg: 4,10,12,15,18,22,24 is Inorder for left and 4,12,10,18,24,22,15 is Post Order for left and here again 15 will act as the root node. \nHence The idea will be to use Recursion.\n\n# Approach \n1. The buildTree method calls the formBinaryTree method with parameters A, B, 0, A.length-1, 0, and B.length-1. These parameters specify the starting and ending indices of the inorder and postorder traversal arrays.\n2. create a new TreeNode with the last element of the postorder traversal as the value. This value represents the root node of the current subtree.\n3. search for this value in the inorder traversal array to find the index of the root node.\n4. recursively call itself to form left and right subtree. It passes the parameters as follows:\nfor left: start, mid-1, start2, x\nfor right: mid+1,end,x+1,end2-1\n\n// x = end of postOrderTraversal of left subtree\nx = no of elemnts in leftSubtree + start of postOrder\n\n# Improvement\nInstead of finding the middle node every time in Inorder Traversal, create a hashMap with value as key and position as value.\n\n<iframe width="560" height="315" src="https://www.youtube.com/embed/2uRa3e3-Vdc" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" allowfullscreen></iframe>\n\n```\nclass Solution {\n public HashMap<Integer,Integer> hashMap;\n public TreeNode buildTree(int[] A, int[] B) {\n hashMap = new HashMap<>();\n for(int i = 0;i<A.length;i++){\n hashMap.put(A[i],i);\n }\n return formBinaryTree(A,B,0,A.length-1,0,B.length-1);\n }\n \n public TreeNode formBinaryTree(int[] inOrder, int [] postOrder, int start, int end , int start2, int end2) {\n if(start > end){\n \n return null;\n }\n TreeNode middle = new TreeNode(postOrder[end2]);\n int mid = hashMap.get(middle.val);\n \n int x = mid-1+start2-start;\n middle.left = formBinaryTree(inOrder,postOrder, start, mid-1, start2, x);\n middle.right = formBinaryTree(inOrder,postOrder,mid+1,end,x+1,end2-1 );\n return middle;\n }\n}\n```\n\n\n```\n\nclass Solution {\n public TreeNode buildTree(int[] A, int[] B) {\n return formBinaryTree(A,B,0,A.length-1,0,B.length-1);\n }\n \n public TreeNode formBinaryTree(int[] inOrder, int [] postOrder, int start, int end , int start2, int end2) {\n if(start > end){\n \n return null;\n }\n TreeNode middle = new TreeNode(postOrder[end2]);\n int mid = 0;\n for(int i = start;i<=end;i++){\n if(inOrder[i]==middle.val) {\n mid = i;\n break;\n }\n }\n int noOfElements = mid-1-start;\n int x = noOfElements + start2;//i.e the end of postOrderTraversal of left subtree\n middle.left = formBinaryTree(inOrder,postOrder, start, mid-1, start2, x);\n middle.right = formBinaryTree(inOrder,postOrder,mid+1,end,x+1,end2-1 );\n return middle;\n }\n}\n```\n\n```\nclass Solution {\npublic:\n TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {\n return formBinaryTree(inorder, postorder, 0, inorder.size() - 1, 0, postorder.size() - 1);\n }\n\n TreeNode* formBinaryTree(vector<int>& inOrder, vector<int>& postOrder, int start, int end, int start2, int end2) {\n if (start > end) {\n return nullptr;\n }\n TreeNode* middle = new TreeNode(postOrder[end2]);\n int mid = 0;\n for (int i = start; i <= end; i++) {\n if (inOrder[i] == middle->val) {\n mid = i;\n break;\n }\n }\n int noOfElements = mid - 1 - start;\n int x = noOfElements + start2; // i.e the end of postOrderTraversal of left subtree\n middle->left = formBinaryTree(inOrder, postOrder, start, mid - 1, start2, x);\n middle->right = formBinaryTree(inOrder, postOrder, mid + 1, end, x + 1, end2 - 1);\n return middle;\n }\n};\n```\n\n```\n\nclass Solution:\n def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode:\n return self.formBinaryTree(inorder, postorder, 0, len(inorder) - 1, 0, len(postorder) - 1)\n\n def formBinaryTree(self, inOrder: List[int], postOrder: List[int], start: int, end: int, start2: int, end2: int) -> TreeNode:\n if start > end:\n return None\n middle = TreeNode(postOrder[end2])\n mid = 0\n for i in range(start, end + 1):\n if inOrder[i] == middle.val:\n mid = i\n break\n noOfElements = mid - 1 - start\n x = noOfElements + start2 # i.e the end of postOrderTraversal of left subtree\n middle.left = self.formBinaryTree(inOrder, postOrder, start, mid - 1, start2, x)\n middle.right = self.formBinaryTree(inOrder, postOrder, mid + 1, end, x + 1, end2 - 1)\n return middle\n```\n\n\n
| 11 | 1 |
['C', 'Python', 'Java', 'Python3']
| 2 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
C 8ms (100%), Simple 8-Line Recursive, Explained
|
c-8ms-100-simple-8-line-recursive-explai-qlhd
|
Solution\nc\nstruct TreeNode* buildTree(int* inorder, int inlen, int* postorder, int postlen){\n if(inlen == 0) return NULL;\n\t\n // Last elem of postord
|
nichyjt
|
NORMAL
|
2021-03-08T06:56:47.198963+00:00
|
2021-03-08T11:27:31.231625+00:00
| 476 | false |
# **Solution**\n```c\nstruct TreeNode* buildTree(int* inorder, int inlen, int* postorder, int postlen){\n if(inlen == 0) return NULL;\n\t\n // Last elem of postorder must be (sub)tree\'s root\n struct TreeNode* curr = malloc(sizeof(struct TreeNode));\n curr->val = postorder[postlen-1];\n\t\n // Find partition index\n int mid = 0;\n while(inorder[mid]!=curr->val) ++mid;\n\t\n curr->left = buildTree(&inorder[0], mid, &postorder[0], mid);\n curr->right = buildTree(&inorder[mid+1], inlen-mid-1, &postorder[mid], inlen-mid-1);\n return curr;\n}\n```\n\n# **Explanation**\nThere are 2 properties that we can use to arrive at our solution.\nA. In the `postorder` array, the last element **must** be the `root` node.\nB. In the `inorder` array, all the elements *left* of `root` must belong to `root`s left tree. Similarly, all the elements *right* of `root` must belong to `root`\'s right tree.\n\n## **Divide & Conquer**\n*Initialisation*\n1. For any input, ``postorder[postlen-1]`` **must** be the root of the (sub)tree. I named `root` as `curr` for distinction between the tree root & subtree \'root\'.\n2. So, for every function call a `TreeNode` named `curr` with value `postorder[postlen-1]` is made.\n3. Find the index, `mid`, where `curr` appears in `inorder`. With the index, we can determine `curr`\'s left and right elements in `postorder` and `inorder` respectively.\n\n*Division*\nBy repeatedly partitioning our input arrays around each function call\'s subtree root, `curr`, we will narrow down the array until we get a base case where the length of the input array is zero. We will return NULL in that case. This return value will later be assigned to the parent\'s left/right node as explained in \'conquer\'.\n\nNote: In effect, each function call divides the tree into smaller subtrees. `curr` each subtree\'s root.\n\n4. Recursively call the function on the left and right subarrays (representing the subtrees).\nThe array length of the left subtree must be equal to `mid`, the partition index.\nThe array length of the right subtree must be equal to `inlen-mid-1`. (You can verify using the sample testcase provided!)\n\nTranslated into code:\n```c\nbuildTree(???, mid, ???, mid);\n```\n5. We need to input arrays for `???`. We *could* copy the values into a new array, but since this is C, we can provide the subtree array\'s starting element *memory address* instead to save space.\nLength is not a concern and will resolve itself since we input the supposed length of the subtree arrays already.\nDetermining the mem addess is straightforward for the LEFT recursion call.\nBut for RIGHT, due to the ordering of elements, `inorder` should start at `mid+1`, not `mid`.\nYou can verify this using the sample testcase provided in the qn.\n\nTranslated into code:\n```c\nbuildTree(&inorder[0], mid, &postorder[0], mid); // LEFT\nbuildTree(&inorder[mid+1], mid, &postorder[mid], mid); // RIGHT\n```\n\n*Conquer*\n6. The function will either return `NULL` or the \'root\' node of a certain subtree.\n7. Build the tree by assigning `curr`\'s left and right to the returned value of the recursion calls.\n8. Profit\n\nHope this explanation and solution helps! Cheers\n
| 11 | 0 |
['Recursion', 'C', 'Binary Tree']
| 0 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
JavaScript Clean DFS
|
javascript-clean-dfs-by-control_the_narr-z3s4
|
Solution - 1\njavascript\nvar buildTree = function(inorder, postorder) {\n \n function callDFS(arr) {\n if(!arr.length) return null;\n const
|
control_the_narrative
|
NORMAL
|
2020-07-14T03:56:36.681403+00:00
|
2020-07-14T04:03:38.552389+00:00
| 1,361 | false |
## Solution - 1\n```javascript\nvar buildTree = function(inorder, postorder) {\n \n function callDFS(arr) {\n if(!arr.length) return null;\n const val = postorder.pop();\n const idx = arr.indexOf(val);\n const node = new TreeNode(val);\n node.right = callDFS(arr.slice(idx+1));\n node.left = callDFS(arr.slice(0, idx));\n return node;\n }\n \n return callDFS(inorder);\n};\n```\n\n## Solution - 2: Optimized Using Hash Map\n```javascript\nvar buildTree = function(inorder, postorder) {\n const map = new Map();\n \n for(let i = 0; i < inorder.length; i++) {\n map.set(inorder[i], i);\n }\n \n function callDFS(start, end) {\n if(start > end) return null;\n const val = postorder.pop();\n const idx = map.get(val);\n const node = new TreeNode(val);\n node.right = callDFS(idx+1, end);\n node.left = callDFS(start, idx-1);\n return node;\n }\n \n return callDFS(0, inorder.length-1);\n};\n```
| 11 | 0 |
['JavaScript']
| 1 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
c++ simple recursion
|
c-simple-recursion-by-izat_khamiyev-msot
|
\nclass Solution {\npublic:\n \n TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {\n return bld(inorder,postorder,0,inorder.size(
|
izat_khamiyev
|
NORMAL
|
2019-06-29T09:11:29.883937+00:00
|
2019-06-29T09:11:29.883991+00:00
| 2,362 | false |
```\nclass Solution {\npublic:\n \n TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {\n return bld(inorder,postorder,0,inorder.size()-1,0,postorder.size()-1);\n }\n \n TreeNode* bld(vector<int>&inorder, vector<int>&postorder, int istart, int iend,\n int pstart,int pend){\n if(istart > iend || pstart > pend)\n return NULL;\n int val = postorder[pend];\n \n int i = istart;\n while(inorder[i] != val) i++;\n\n TreeNode* root = new TreeNode(val);\n root->left = bld(inorder, postorder, istart, i-1, pstart, pstart+i-istart-1);\n root->right = bld(inorder, postorder, i+1, iend, pend-(iend-i), pend-1);\n return root;\n }\n};\n```
| 11 | 0 |
['Recursion', 'C', 'C++']
| 1 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
Construct Binary Tree from Inorder and Postorder Traversal [C++]
|
construct-binary-tree-from-inorder-and-p-zca1
|
IntuitionTo construct the binary tree, the key is to leverage the properties of the inorder and postorder traversal sequences.
The last element in the postorder
|
moveeeax
|
NORMAL
|
2025-01-27T07:51:12.498151+00:00
|
2025-01-27T07:51:12.498151+00:00
| 821 | false |
# Intuition
To construct the binary tree, the key is to leverage the properties of the **inorder** and **postorder** traversal sequences.
- The last element in the postorder traversal is the root of the tree.
- Using the root's position in the inorder sequence, we can determine the left and right subtrees.
By recursively dividing the sequences, we can build the tree from the bottom up.
# Approach
1. Use a hash map to store the indices of elements in the inorder traversal for quick access.
2. Start from the last element in the postorder traversal (the root of the tree).
3. Recursively divide the inorder sequence into left and right subtrees based on the root's position.
4. Build the right subtree first (as postorder processes left subtree before right subtree).
# Complexity
- **Time complexity:**
$$O(n)$$
Each node is processed once, and lookups in the hash map take constant time.
- **Space complexity:**
$$O(n)$$
Space is used for the hash map and the recursion stack.
# Code
```cpp
class Solution {
public:
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
unordered_map<int, int> inorderIndexMap;
for (int i = 0; i < inorder.size(); ++i) {
inorderIndexMap[inorder[i]] = i;
}
int postIndex = postorder.size() - 1;
return constructTree(inorder, postorder, inorderIndexMap, postIndex, 0, inorder.size() - 1);
}
TreeNode* constructTree(vector<int>& inorder, vector<int>& postorder, unordered_map<int, int>& inorderIndexMap, int& postIndex, int inStart, int inEnd) {
if (inStart > inEnd) return nullptr;
int rootVal = postorder[postIndex--];
TreeNode* root = new TreeNode(rootVal);
int rootIndex = inorderIndexMap[rootVal];
root->right = constructTree(inorder, postorder, inorderIndexMap, postIndex, rootIndex + 1, inEnd);
root->left = constructTree(inorder, postorder, inorderIndexMap, postIndex, inStart, rootIndex - 1);
return root;
}
};
```
| 10 | 0 |
['C++']
| 0 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
JAVA || Easy Solution || 100% Faster Code
|
java-easy-solution-100-faster-code-by-sh-zgk3
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
shivrastogi
|
NORMAL
|
2023-03-16T01:01:31.340675+00:00
|
2023-03-16T01:01:31.340708+00:00
| 5,947 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n * TreeNode(int val) { this.val = val; }\n * TreeNode(int val, TreeNode left, TreeNode right) {\n * this.val = val;\n * this.left = left;\n * this.right = right;\n * }\n * }\n */\nclass Solution {\n public TreeNode buildTree(int[] inorder, int[] postorder) {\n Map<Integer, Integer> map = new HashMap<>();\n for (int i = 0; i < inorder.length; i++) {\n map.put(inorder[i], i);\n \n }\n \n return helper(map, postorder, 0, inorder.length - 1, 0, postorder.length - 1);\n \n }\n \n private TreeNode helper(Map<Integer, Integer> map, int[] postorder, int inLeft, int inRight, int poLeft, int poRight) {\n if (inLeft > inRight) {\n return null;\n }\n \n TreeNode root = new TreeNode(postorder[poRight]);\n int inMid = map.get(root.val);\n \n root.left = helper(map, postorder, inLeft, inMid - 1, poLeft, poLeft + inMid - inLeft - 1);\n root.right = helper(map, postorder, inMid + 1, inRight, poRight - inRight + inMid, poRight - 1);\n return root;\n }\n\t\n}\n```
| 10 | 0 |
['Java']
| 0 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
Complete Explanation || Intuition for each step explained || Notes
|
complete-explanation-intuition-for-each-9bzqw
|
\n\n\n\nclass Solution {\npublic:\n TreeNode* getRoot(vector<int>&postorder, map<int, int>&mp, int& rootIdx, int low, int high)\n {\n if (low > hig
|
mohakharjani
|
NORMAL
|
2023-03-16T00:59:52.388545+00:00
|
2023-03-16T00:59:52.388587+00:00
| 1,389 | false |
\n\n\n```\nclass Solution {\npublic:\n TreeNode* getRoot(vector<int>&postorder, map<int, int>&mp, int& rootIdx, int low, int high)\n {\n if (low > high) return NULL;\n \n int currRoot = postorder[rootIdx--];\n int inorderRootIdx = mp[currRoot];\n TreeNode* rootNode = new TreeNode(currRoot);\n \n rootNode->right = getRoot(postorder, mp, rootIdx, inorderRootIdx + 1, high);\n rootNode->left = getRoot(postorder, mp, rootIdx, low, inorderRootIdx - 1);\n return rootNode;\n }\n TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) \n {\n int n = inorder.size();\n map<int, int>mp;\n for (int i = 0; i < n; i++) mp[inorder[i]] = i; //mentioned that values are unique\n \n int rootIdx = n - 1;\n TreeNode* root = getRoot(postorder, mp, rootIdx, 0, n - 1);\n return root;\n }\n};\n```
| 10 | 0 |
['Recursion', 'C', 'Binary Tree', 'C++']
| 2 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
Go | beats 100% | easy to understand | simple recursive solution
|
go-beats-100-easy-to-understand-simple-r-65yk
|
Code\n\nfunc buildTree(inorder []int, postorder []int) *TreeNode {\n\tn := len(postorder)\n\tif n == 0 {\n\t\treturn nil\n\t}\n\n\tpivotId := 0\n\tfor pivotId <
|
dimaglushkov
|
NORMAL
|
2023-03-16T10:55:49.134403+00:00
|
2023-03-16T10:58:34.668858+00:00
| 981 | false |
# Code\n```\nfunc buildTree(inorder []int, postorder []int) *TreeNode {\n\tn := len(postorder)\n\tif n == 0 {\n\t\treturn nil\n\t}\n\n\tpivotId := 0\n\tfor pivotId < n && inorder[pivotId] != postorder[n-1] {\n\t\tpivotId++\n\t}\n\n\troot := new(TreeNode)\n\troot.Val = postorder[n-1]\n\troot.Left = buildTree(inorder[:pivotId], postorder[:pivotId])\n\troot.Right = buildTree(inorder[pivotId+1:], postorder[pivotId:n-1])\n\treturn root\n}\n\n```
| 9 | 0 |
['Array', 'Divide and Conquer', 'Tree', 'Binary Tree', 'Go']
| 1 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
C# | Recursion
|
c-recursion-by-sergiich-6mj9
|
Code\n\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * public int val;\n * public TreeNode left;\n * public TreeNode rig
|
SergiiCh
|
NORMAL
|
2023-03-16T02:13:06.851274+00:00
|
2023-03-16T02:13:06.851318+00:00
| 753 | false |
# Code\n```\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * public int val;\n * public TreeNode left;\n * public TreeNode right;\n * public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {\n * this.val = val;\n * this.left = left;\n * this.right = right;\n * }\n * }\n */\npublic class Solution {\n public TreeNode BuildTree(int[] inorder, int[] postorder) \n {\n TreeNode? Build(Span<int> inorder, Span<int> postorder)\n {\n if (postorder.IsEmpty || inorder.IsEmpty)\n {\n return null;\n }\n\n var pos = inorder.IndexOf(postorder[^1]);\n return new TreeNode(postorder[^1])\n {\n left = Build(inorder[..pos], postorder[..pos]),\n right = Build(inorder[(pos + 1)..], postorder[pos..^1])\n };\n }\n\n return Build(inorder, postorder);\n }\n}\n```
| 9 | 0 |
['C#']
| 2 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
Python O(n) by definition. 80%+ [ w/ Comment ]
|
python-on-by-definition-80-w-comment-by-dc2db
|
Python O(n) by definition.\n\n---\n\n\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, x):\n# self.val = x\n#
|
brianchiang_tw
|
NORMAL
|
2020-05-23T04:06:39.552465+00:00
|
2020-05-23T04:06:39.552500+00:00
| 1,104 | false |
Python O(n) by definition.\n\n---\n\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, x):\n# self.val = x\n# self.left = None\n# self.right = None\n\nclass Solution:\n def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode:\n \n ## dictionary\n # key: number\n # value: index in inorder array\n val_index_dict = { num:idx for idx, num in enumerate(inorder) }\n \n def helper( left, right):\n \n if left > right:\n # Base case:\n # return empty node as leaf node\'s child\n return None\n \n else:\n \n # Recall:\n # definition of postorder traversal: Left, Right, Center\n # rebuild with reversed direction ( from right to left )\n root = TreeNode( postorder.pop() )\n \n mid = val_index_dict[ root.val ]\n \n root.right = helper( mid+1, right)\n root.left = helper( left, mid-1 )\n return root\n # ----------------------------------------------------\n \n ## Top-down rebuild binary tree with definition\n return helper( left = 0, right = len(inorder)-1 )\n```\n\n---\n\nReference:\n\n[1] [Leetcode training session: Binary Tree Traversal](https://leetcode.com/explore/learn/card/data-structure-tree/134/traverse-a-tree/992/)
| 9 | 0 |
['Depth-First Search', 'Recursion', 'Python', 'Python3']
| 2 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
Annotated iterative solution with comments, does not modify parameters
|
annotated-iterative-solution-with-commen-tqcr
|
Courtesy of the post by lizhuogo. Details see\n https://discuss.leetcode.com/topic/4746/my-comprehension-of-o-n-solution-from-hongzhi/2\n\nI thought his expl
|
lucascho
|
NORMAL
|
2016-08-14T07:46:19.743000+00:00
|
2016-08-14T07:46:19.743000+00:00
| 907 | false |
Courtesy of the post by lizhuogo. Details see\n https://discuss.leetcode.com/topic/4746/my-comprehension-of-o-n-solution-from-hongzhi/2\n\nI thought his explanation is still a bit difficult to understand so I try to give a high-level understanding of this approach and the fundamental reason why it works as intended.\n\nThe key here is knowing the patterns of serialized list of inorder and postorder\ntravesals.\n\nIf we traverse from root to the left child and back up, both inorder\nand postorder traversals give us the same sequence, i.e. they are in\nthe same direction.\n``` \n 1\n /\n 2\ninorder: [1, 2]\npostorder: [1, 2]\n```\nwhereas if we traverse from root to right child and back up, inorder and postorder\ngives us sequences that are reverse of each other.\n```\n 1\n \\\n 2\ninorder: [1, 2]\npostorder: [2, 1]\n```\nUsing this observation, and the fact that the last member in postorder array is\nthe root of current subtree, we can traverse from right to left of the serialized\nlists and build left and right child accordingly.\n\nIf we see postorder and inorder are of same value, we build the left child, else\nwe build the right child. After each operation, we store the newly created node\non stack to be the new root of the current subtree of size 1 and later traverse back\nup.\n\nA stack is helpful for storing them because each pop let us go back up a level to\nthe parent of our current root.\n\nCode in Python below with comments:\n```\ndef buildTree(self, inorder, postorder):\n if len(inorder) == 0: return None\n root = TreeNode(postorder[-1])\n stack = [root] \n # array indexes, i for inorder array, p for postorder array\n i = len(inorder) - 1\n p = len(postorder) - 2 # initially root already 'popped' off postorder and stored in stack\n\n # we store values off postorder array and compare top of stack with\n # right most member of inorder array (indexed by i)\n while True:\n # top of stack is same as right most entry of inorder. The first time it\n # happens means we reached root of current tree. Then we keep removing them\n # since we already built right child nodes with them and they are on stack just so we\n # can traverse back up. See the else branch for the actual creation of right child. \n if stack[-1].val == inorder[i]:\n n = stack.pop()\n i -= 1\n\n if i==-1: break\n if stack and inorder[i] == stack[-1].val:\n # keep removing these values, that is, traverse back up\n continue\n\n # finished all the right branch and root itself, now we build left child\n # 'n' here was popped from stack which gave us the current root.\n n.left = TreeNode(postorder[p])\n p -= 1\n stack.append(n.left)\n\n else: # mismatch values means we should build right child for current root\n n = TreeNode(postorder[p])\n p-=1\n stack[-1].right = n\n stack.append(n)\n \n return root\n```
| 9 | 0 |
[]
| 0 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
Variation of STRIVER solution, Considering Right Side remaining elements
|
variation-of-striver-solution-considerin-tom4
|
Approach\nA slight variation of approach used by striver , as post order is left->right->root we calculate right remaining elements first instead of left elemen
|
pranshu2003
|
NORMAL
|
2024-08-21T14:17:05.731636+00:00
|
2024-08-21T14:17:05.731704+00:00
| 161 | false |
# Approach\nA slight variation of approach used by striver , as post order is left->right->root we calculate right remaining elements first instead of left elements, then construct subtrees using recursion.\n\n\n# Code\n```cpp []\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n TreeNode* bt(vector<int>& inorder , int is , int ie ,vector<int>& postorder , int ps , int pe , map<int ,int>& mpp ){\n\n if(is > ie || ps > pe){\n return NULL ;\n }\n\n TreeNode *root = new TreeNode(postorder[pe]);\n\n int pos = mpp[postorder[pe]] ;\n int right = ie - pos ;\n\n root->left = bt(inorder , is , pos-1 , postorder , ps , pe - right - 1 , mpp) ;\n\n root->right = bt(inorder , pos+1 , ie , postorder , pe-right , pe-1 , mpp) ;\n\n return root ;\n\n }\n TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {\n\n map<int ,int> mpp ;\n\n for(int i = 0 ; i< inorder.size() ;i++){\n mpp[inorder[i]] = i ;\n }\n\n TreeNode* root = bt(inorder , 0 , inorder.size()-1 , postorder , 0, postorder.size()-1 , mpp) ;\n\n return root ;\n }\n};\n```
| 8 | 0 |
['Tree', 'Recursion', 'Ordered Map', 'C++']
| 0 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
🏆C++ || Striver's approach
|
c-strivers-approach-by-chiikuu-kkdi
|
Code\n\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() :
|
CHIIKUU
|
NORMAL
|
2023-06-20T08:32:32.664784+00:00
|
2023-06-20T08:33:24.312715+00:00
| 192 | false |
# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n map<int,int>m;\n TreeNode* buildTree(vector<int>& in, vector<int>& post) {\n for(int i=0;i<in.size();i++)m[in[i]]=i;\n TreeNode* root = build(in,0,in.size()-1,post,0,post.size()-1);\n return root;\n }\n TreeNode* build(vector<int>&in, int inS,int inE,vector<int>&post,int postS,int postE){\n if(inS>inE || postS>postE)return NULL;\n TreeNode* root = new TreeNode(post[postE]);\n int index = m[post[postE]];\n int len = inE - index; \n root->right = build(in,index+1,inE,post,postE-len,postE-1);\n root->left = build(in,inS,index-1,post,postS,postE-len-1);\n return root;\n }\n};\n```\n\n
| 8 | 0 |
['Hash Table', 'Divide and Conquer', 'Tree', 'Binary Tree', 'C++']
| 1 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
🗓️ Daily LeetCoding Challenge March, Day 16
|
daily-leetcoding-challenge-march-day-16-5d4ka
|
This problem is the Daily LeetCoding Challenge for March, Day 16. Feel free to share anything related to this problem here! You can ask questions, discuss what
|
leetcode
|
OFFICIAL
|
2023-03-16T00:00:21.703315+00:00
|
2023-03-16T00:00:21.703381+00:00
| 5,406 | false |
This problem is the Daily LeetCoding Challenge for March, Day 16.
Feel free to share anything related to this problem here!
You can ask questions, discuss what you've learned from this problem, or show off how many days of streak you've made!
---
If you'd like to share a detailed solution to the problem, please create a new post in the discuss section and provide
- **Detailed Explanations**: Describe the algorithm you used to solve this problem. Include any insights you used to solve this problem.
- **Images** that help explain the algorithm.
- **Language and Code** you used to pass the problem.
- **Time and Space complexity analysis**.
---
**📌 Do you want to learn the problem thoroughly?**
Read [**⭐ LeetCode Official Solution⭐**](https://leetcode.com/problems/construct-binary-tree-from-inorder-and-postorder-traversal/solution) to learn the 3 approaches to the problem with detailed explanations to the algorithms, codes, and complexity analysis.
<details>
<summary> Spoiler Alert! We'll explain this 1 approach in the official solution</summary>
**Approach 1:** Recursion
</details>
If you're new to Daily LeetCoding Challenge, [**check out this post**](https://leetcode.com/discuss/general-discussion/655704/)!
---
<br>
<p align="center">
<a href="https://leetcode.com/subscribe/?ref=ex_dc" target="_blank">
<img src="https://assets.leetcode.com/static_assets/marketing/daily_leetcoding_banner.png" width="560px" />
</a>
</p>
<br>
| 8 | 0 |
[]
| 18 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
✅ Explained - Simple and Clear Python3 Code✅
|
explained-simple-and-clear-python3-code-goots
|
The solution utilizes a recursive approach to construct a binary tree from its inorder and postorder traversals. The process begins by selecting the last elemen
|
moazmar
|
NORMAL
|
2023-06-17T18:49:22.664912+00:00
|
2023-06-17T18:49:22.664946+00:00
| 316 | false |
The solution utilizes a recursive approach to construct a binary tree from its inorder and postorder traversals. The process begins by selecting the last element of the postorder list as the root value. By finding the index of this root value in the inorder list, we can determine the elements on the left and right sides, representing the left and right subtrees, respectively. Recursively, the right subtree is built first by passing the appropriate partitions of the inorder and postorder lists. Next, the left subtree is constructed in a similar manner. The resulting subtrees are then assigned to the root node accordingly. This process continues until the entire binary tree is constructed, and the root node is returned as the final result.\n\n\n\n\n# Code\n```\nclass Solution:\n def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:\n def build_tree(inorder, postorder):\n if not inorder:\n return None\n root_val = postorder.pop()\n root = TreeNode(root_val)\n index = inorder.index(root_val)\n root.right = build_tree(inorder[index + 1:], postorder)\n root.left = build_tree(inorder[:index], postorder)\n return root\n\n return build_tree(inorder, postorder)\n\n```
| 7 | 0 |
['Python3']
| 0 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
C++ Simple Recursive Solution, No Map
|
c-simple-recursive-solution-no-map-by-ye-8aos
|
\nclass Solution {\npublic:\n TreeNode* rec(int l, int r) {\n if (l > r) return NULL;\n \n int i = 0;\n while (m_inorder[i] != m_
|
yehudisk
|
NORMAL
|
2021-07-08T13:48:12.976102+00:00
|
2021-07-08T13:48:12.976147+00:00
| 518 | false |
```\nclass Solution {\npublic:\n TreeNode* rec(int l, int r) {\n if (l > r) return NULL;\n \n int i = 0;\n while (m_inorder[i] != m_postorder[m_curr]) {\n i++;\n }\n \n m_curr--;\n TreeNode* node = new TreeNode(m_inorder[i]);\n node->right = rec(i+1, r);\n node->left = rec(l, i-1);\n return node;\n \n }\n \n TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {\n m_postorder = postorder, m_inorder = inorder, m_curr = inorder.size()-1;\n return rec(0, postorder.size()-1);\n }\n \nprivate:\n int m_curr;\n vector<int> m_postorder, m_inorder;\n};\n```\n**Like it? please upvote!**
| 7 | 0 |
['C']
| 1 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
In & Post + Pre & In + Pre & Post.
|
in-post-pre-in-pre-post-by-gh05t-zfs2
|
Inorder + Postorder\n\nTreeNode* helper(int inSt, int inEnd, int poEnd, vector<int> &inorder, vector<int> &postorder) {\n if(poEnd < 0 || inSt > inEnd) retur
|
gh05t
|
NORMAL
|
2020-02-23T14:03:34.624438+00:00
|
2022-01-07T05:37:56.527067+00:00
| 592 | false |
Inorder + Postorder\n```\nTreeNode* helper(int inSt, int inEnd, int poEnd, vector<int> &inorder, vector<int> &postorder) {\n if(poEnd < 0 || inSt > inEnd) return nullptr; // base condition\n\n TreeNode *root = new TreeNode(postorder[poEnd]);\n\n int pivot;\n for(int i = inSt; i < inorder.size(); i++) {\n if(root->val == inorder[i]) {\n pivot = i; break;\n }\n }\n\n root->left = helper(inSt, pivot - 1, poEnd - 1 + pivot - inEnd, inorder, postorder);\n root->right = helper(pivot + 1, inEnd, poEnd - 1, inorder, postorder);\n\n return root;\n} \n\nTreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {\n return helper(0, inorder.size() - 1, postorder.size() - 1, inorder, postorder);\n}\n```\n\nPreorder + Inorder\n```\nTreeNode* helper(int preSt, int inSt, int inEnd, vector<int>& preorder, vector<int>& inorder) {\n if(inSt > inEnd || preSt >= preorder.size()) return nullptr;\n\n TreeNode* root = new TreeNode(preorder[preSt]);\n\n int pivot;\n for(int i = 0; i < inorder.size(); i++) {\n if(inorder[i] == root->val) {\n pivot = i; break;\n }\n }\n\n root->left = helper(preSt + 1, inSt, pivot - 1, preorder, inorder);\n root->right = helper(preSt + pivot - inSt + 1, pivot + 1, inEnd, preorder, inorder);\n\n return root;\n}\n\nTreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {\n return helper(0, 0, inorder.size() - 1, preorder, inorder);\n}\n```\n\nPreorder + Postorder (Can only be done for full trees i.e. 0 or 2 children for every node)\n```\nTreeNode* helper(vector<int> &pre, int preSt, int preEnd, vector<int> &post, int postSt, int postEnd) {\n if(preSt == preEnd) return new TreeNode(pre[preSt]);\n if(preSt > preEnd) return nullptr;\n\n TreeNode *root = new TreeNode(pre[preSt]);\n\n int pivot;\n for(pivot = postSt; pivot <= postEnd; pivot++) {\n if(pre[preSt + 1] == post[pivot]) {\n pivot = pivot + 1 - postSt; break;\n }\n }\n\n root->left = helper(pre, preSt + 1, preSt + pivot, post, postSt, postSt + pivot - 1);\n root->right = helper(pre, preSt + pivot + 1, preEnd, post, postSt + pivot, postEnd - 1);\n\n return root;\n}\n\nTreeNode* constructFromPrePost(vector<int>& pre, vector<int>& post) {\n return helper(pre, 0, pre.size() - 1, post, 0, post.size() - 1);\n}\n```
| 7 | 0 |
['C']
| 1 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
🔥BEATS 💯 % 🎯 |✨SUPER EASY BEGINNERS 👏| JAVA | C | C++ | PYTHON| JAVASCRIPT | DART
|
beats-super-easy-beginners-java-c-c-pyth-jkpq
|
IntuitionThe problem involves reconstructing a binary tree given its inorder and postorder traversal arrays. My initial thought is to leverage the properties of
|
CodeWithSparsh
|
NORMAL
|
2025-02-03T14:51:40.938202+00:00
|
2025-02-03T14:59:31.875499+00:00
| 1,302 | false |
---
---
## Intuition
The problem involves reconstructing a binary tree given its inorder and postorder traversal arrays. My initial thought is to leverage the properties of these traversals:
- Inorder traversal visits nodes in the order of left subtree, root, and then right subtree.
- Postorder traversal visits nodes in the order of left subtree, right subtree, and then root.
From the postorder array, we know that the last element is the root of the tree. Using this information, we can find the root's index in the inorder array to determine which elements belong to the left and right subtrees.
## Approach
1. **Mapping Indices**:
- Create a map (`rec`) to store the indices of elements in the inorder array for quick lookups. This will help us efficiently find the position of any value in the inorder array.
2. **Recursive Helper Function**:
- Implement a recursive function (`helper`) that takes parameters for the current ranges in both inorder and postorder arrays.
- Base case: If the start index exceeds the end index for either array, return null (indicating no subtree).
3. **Constructing Nodes**:
- In each recursive call:
- Identify the root value from the last element of the current postorder range.
- Create a new `TreeNode` for this root.
- Find the index of this root value in the inorder array using the map.
- Calculate the size of the left subtree based on this index.
- Recursively call `helper` for both left and right subtrees using updated ranges.
4. **Return Result**:
- The main function (`buildTree`) initializes everything and calls `helper` to construct and return the entire tree.
### Code Examples
```cpp []
#include <bits/stdc++.h>
using namespace std;
class TreeNode {
public:
int val;
TreeNode *left, *right;
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};
class Solution {
public:
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
unordered_map<int, int> rec;
for (int i = 0; i < inorder.size(); i++) {
rec[inorder[i]] = i;
}
return helper(inorder, postorder, 0, inorder.size() - 1, 0, postorder.size() - 1, rec);
}
TreeNode* helper(vector<int>& inorder, vector<int>& postorder,
int inStart, int inEnd,
int postStart, int postEnd,
unordered_map<int, int>& rec) {
if (inStart > inEnd || postStart > postEnd) return nullptr;
int val = postorder[postEnd];
TreeNode* root = new TreeNode(val);
int idx = rec[val];
int leftSubtreeSize = idx - inStart;
root->left = helper(inorder, postorder,
inStart, idx - 1,
postStart, postStart + leftSubtreeSize - 1,
rec);
root->right = helper(inorder, postorder,
idx + 1, inEnd,
postStart + leftSubtreeSize, postEnd - 1,
rec);
return root;
}
};
```
```java []
import java.util.HashMap;
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) { val = x; }
}
class Solution {
public TreeNode buildTree(int[] inorder, int[] postorder) {
HashMap<Integer, Integer> rec = new HashMap<>();
for (int i = 0; i < inorder.length; i++) {
rec.put(inorder[i], i);
}
return helper(inorder, postorder, 0, inorder.length - 1, 0, postorder.length - 1, rec);
}
private TreeNode helper(int[] inorder, int[] postorder,
int inStart, int inEnd,
int postStart, int postEnd,
HashMap<Integer, Integer> rec) {
if (inStart > inEnd || postStart > postEnd) return null;
int val = postorder[postEnd];
TreeNode root = new TreeNode(val);
int idx = rec.get(val);
int leftSubtreeSize = idx - inStart;
root.left = helper(inorder, postorder,
inStart, idx - 1,
postStart, postStart + leftSubtreeSize - 1,
rec);
root.right = helper(inorder, postorder,
idx + 1, inEnd,
postStart + leftSubtreeSize, postEnd - 1,
rec);
return root;
}
}
```
```javascript []
class TreeNode {
constructor(val) {
this.val = val;
this.left = null;
this.right = null;
}
}
class Solution {
buildTree(inorder, postorder) {
const rec = new Map();
for (let i = 0; i < inorder.length; i++) {
rec.set(inorder[i], i);
}
return this.helper(inorder, postorder, 0, inorder.length - 1, 0, postorder.length - 1, rec);
}
helper(inorder, postorder, inStart, inEnd, postStart, postEnd, rec) {
if (inStart > inEnd || postStart > postEnd) return null;
const val = postorder[postEnd];
const root = new TreeNode(val);
const idx = rec.get(val);
const leftSubtreeSize = idx - inStart;
root.left = this.helper(inorder, postorder,
inStart, idx - 1,
postStart, postStart + leftSubtreeSize - 1,
rec);
root.right = this.helper(inorder, postorder,
idx + 1, inEnd,
postStart + leftSubtreeSize, postEnd - 1,
rec);
return root;
}
}
```
```python []
class TreeNode:
def __init__(self, val=0):
self.val = val
self.left = None
self.right = None
class Solution:
def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode:
rec = {val: i for i, val in enumerate(inorder)}
# Helper function
def helper(in_start: int ,in_end: int ,post_start: int ,post_end: int):
if in_start > in_end or post_start > post_end:
return None
val = postorder[post_end]
root = TreeNode(val)
idx = rec[val]
left_subtree_size = idx - in_start
# Recursively build left and right subtrees
root.left=helper(in_start ,idx-1 ,post_start ,post_start+left_subtree_size-1)
root.right=helper(idx+1 ,in_end ,post_start+left_subtree_size ,post_end-1)
return root
return helper(0,len(inorder)-1 ,0,len(postorder)-1)
```
```dart []
class TreeNode {
int val;
TreeNode? left;
TreeNode? right;
TreeNode(this.val);
}
class Solution {
TreeNode? buildTree(List<int> inorder,List<int>postOrder){
final Map<int,int>rec={};
for(int i= ;i<inOrder.length;i++){
rec[inOrder[i]]=i;
}
// Helper function
return helper(inOrder ,postOrder ,0 ,inOrder.length-(-),0 ,postOrder.length-(-),rec);
}
TreeNode? helper(List<int>inOrder,List<int>postOrder,int inStart,int inEnd,int posStart,int posEnd ,Map<int,int>rec){
if(inStart>inEnd||posStart>posEnd)return null;
final val=postOrder[posEnd];
final root=TreeNode(val);
final idx=rec[val]!;
final leftSubtreeSize=idx-inStart;
// Recursively build left and right subtrees
root.left=helper(inOrder ,postOrder,inStart ,idx-(-),posStart,posStart+leftSubtreeSize-(-),rec);
root.right=helper(inOrder ,postOrder ,idx+(-) ,inEnd,posStart+leftSubtreeSize,posEnd-(-),rec);
return root;
}
}
```
## Complexity
- **Time complexity**: $$O(n)$$ where $$n$$ is the number of nodes in the binary tree. Each node is processed once during DFS traversal and once during mapping indices.
- **Space complexity**: $$O(n)$$ due to storing indices of elements from `inorder` traversal and recursion stack space used during DFS.
---
 {:style='width:250px'}
| 6 | 0 |
['Hash Table', 'Divide and Conquer', 'Tree', 'C', 'Binary Tree', 'C++', 'Java', 'Python3', 'JavaScript', 'Dart']
| 1 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
c++ solution.
|
c-solution-by-loverdrama699-o0bd
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
loverdrama699
|
NORMAL
|
2023-03-16T18:01:04.726550+00:00
|
2023-03-16T18:01:04.726589+00:00
| 1,000 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {\n unordered_map<int, int> index;\n for (int i = 0; i < inorder.size(); i++) {\n index[inorder[i]] = i;\n }\n return buildTreeHelper(inorder, postorder, 0, inorder.size() - 1, 0, postorder.size() - 1, index);\n }\n \n TreeNode* buildTreeHelper(vector<int>& inorder, vector<int>& postorder, int inorderStart, int inorderEnd, int postorderStart, int postorderEnd, unordered_map<int, int>& index) {\n if (inorderStart > inorderEnd || postorderStart > postorderEnd) {\n return nullptr;\n }\n int rootVal = postorder[postorderEnd];\n TreeNode* root = new TreeNode(rootVal);\n int inorderRootIndex = index[rootVal];\n int leftSubtreeSize = inorderRootIndex - inorderStart;\n root->left = buildTreeHelper(inorder, postorder, inorderStart, inorderRootIndex - 1, postorderStart, postorderStart + leftSubtreeSize - 1, index);\n root->right = buildTreeHelper(inorder, postorder, inorderRootIndex + 1, inorderEnd, postorderStart + leftSubtreeSize, postorderEnd - 1, index);\n return root;\n }\n};\n\n```
| 6 | 0 |
['C++']
| 1 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
Construct Binary Tree from Inorder and Postorder Traversal with step by step explanation
|
construct-binary-tree-from-inorder-and-p-99fg
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\nWe start by creating a hashmap called inorder_map to store the indices of
|
Marlen09
|
NORMAL
|
2023-02-16T05:40:25.350414+00:00
|
2023-02-16T05:40:25.350462+00:00
| 740 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nWe start by creating a hashmap called inorder_map to store the indices of each element in the inorder list. This will allow us to quickly find the index of a given value in constant time later on.\n\nThen, we define a recursive helper function called build that takes two arguments: the start and end indices of the current subtree we\'re working on. If the start index is greater than the end index, we\'ve reached the end of a branch and we should return None.\n\nInside the build function, we pop the last value from the postorder list and create a new node with that value. Then, we use the inorder_map to find the index of the node in the inorder list.\n\nSince we\'re working with the postorder traversal, we first recursively build the right subtree by calling build with the start index set to index + 1 and the end index set to end. Then, we recursively build the left subtree by calling build with the start index set to start and the end index set to index - 1.\n\nFinally, we call the build function with the start index set to 0 and the end index set to len(inorder) - 1, which will build the entire tree. The build function will return the root node of the tree.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode:\n # Use a hashmap to store the indices of each element in the inorder list\n inorder_map = {}\n for i, val in enumerate(inorder):\n inorder_map[val] = i\n \n # Define a recursive helper function to build the tree\n def build(start, end):\n # Base case: the start index is greater than the end index\n if start > end:\n return None\n \n # Create a new node with the last value in the postorder list\n val = postorder.pop()\n node = TreeNode(val)\n \n # Find the index of the node in the inorder list\n index = inorder_map[val]\n \n # Recursively build the right subtree first, since we\'re working with the postorder traversal\n node.right = build(index + 1, end)\n # Then build the left subtree\n node.left = build(start, index - 1)\n \n return node\n \n # Call the helper function to build the tree\n return build(0, len(inorder) - 1)\n\n```
| 6 | 0 |
['Array', 'Hash Table', 'Divide and Conquer', 'Python', 'Python3']
| 0 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
[C++] 2 Simple solutions (W/ Explanation)
|
c-2-simple-solutions-w-explanation-by-my-bkz3
|
Hello everyone, firstly thanks for refering to my post in advance :)\nNote : If you like my solutions and explanation, please UPVOTE! (Please Support if you can
|
Mythri_Kaulwar
|
NORMAL
|
2021-11-21T02:27:18.074155+00:00
|
2021-11-21T06:51:59.870018+00:00
| 109 | false |
Hello everyone, firstly thanks for refering to my post in advance :)\nNote : If you like my solutions and explanation, **please UPVOTE!** (Please Support if you can, as it motivates me to post solutions everyday. Please do not downvote)\n\nSo, the basic idea is same for all the approaches. \n* In **inorder** the order is : ***left->root->right***. \n* In **postorder** the order is : ***left->right->root***.\n* So in the postOrder array, the last of \'n\' number of nodes is always the root of a subtree. \n* So, we begin with the last element of the \'postorder\' array as the root and search for that element in inorder vector. \n* In inorder, the root is always at the center. Hence when we find the element we\'re looking for, we can say that all the elements on its left in the array are in it\'s left subtree and those on it\'s right are in it\'s right subtree.\n* So, we recursively find a root from the \'postorder\' array, search for it in the \'inorder\' array, nmake it the root and construct it\'s left and right subtrees.\n\n**APPROACH - 1 :** ***Simple Recursion (Without Using Map)***\n\n **Time Complexity :** O(n^2), where n = length of inorder or postorder array.\n \n **Code :**\n```\nclass Solution {\nprivate:\n int curr;\npublic:\n TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {\n int n = inorder.size();\n curr = n-1;\n return constructTree(inorder, postorder, 0, n-1);\n }\n \n TreeNode* constructTree(vector<int>&in, vector<int>&post, int start, int end){\n if(start > end) return NULL;\n \n int i = find(in.begin(), in.end(), post[curr]) - in.begin();\n \n curr--;\n TreeNode *head = new TreeNode(in[i]);\n head->right = constructTree(in, post, i+1, end);\n head->left = constructTree(in, post, start, i-1);\n \n return head;\n \n }\n};\n```\n\n**APPROACH - 2 :** ***Recursion with Map***\nUsing the map to strore the indices, we\'re optimizing the code to make it to O(n) time complexity.\n **Time Complexity :** O(n)\n \n **Code :**\n```\nclass Solution {\nprivate:\n map<int, int> m;\npublic:\n TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {\n int n = inorder.size(), p=n-1;\n for(int i=0;i<n;i++) m[inorder[i]] = i;\n return constructTree(inorder, postorder, 0, n-1, p);\n }\n \n TreeNode* constructTree(vector<int>&in, vector<int>&post, int l, int r, int &idx) {\n if(l > r) return NULL;\n \n TreeNode *root = new TreeNode(post[idx--]);\n int i=m[root->val];\n root->right = constructTree(in, post, i+1, r, idx);\n root->left = constructTree(in, post, l, i-1, idx);\n \n return root;\n \n }\n};\n```\n\nIf you like my solutins, **please UPVOTE!!**\n\n\n \n
| 6 | 7 |
['Recursion', 'C', 'C++']
| 0 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
JAVA solution | 3ms fast | Detailed Explanation
|
java-solution-3ms-fast-detailed-explanat-no2y
|
If you found the solution helpful, kindly like and upvote. :)\n\n\nclass Solution {\n public TreeNode buildTree(int[] inorder, int[] postorder) {\n
|
anjali100btcse17
|
NORMAL
|
2020-07-27T08:02:54.187036+00:00
|
2020-07-27T08:02:54.187079+00:00
| 324 | false |
If you found the solution helpful, kindly like and upvote. :)\n\n```\nclass Solution {\n public TreeNode buildTree(int[] inorder, int[] postorder) {\n \treturn helper(inorder, postorder, 0, inorder.length-1, postorder.length-1);\n }\n\n\tTreeNode helper(int[] inorder, int[] postorder, int instart, int inend, int postend) {\n\t\tif(postend<0 ||instart>inend) return null;\n\t\t//The root will always be at the end\n\t\tTreeNode root= new TreeNode(postorder[postend]);\n\t\tint i=instart;\n\t\t//Now we need to find the index in inorder (items on the left are left subtree, right are right subtree)\n\t\tfor(; i<inend; i++)\n\t\t{\n\t\t\tif(inorder[i]==root.val)\n\t\t\t\tbreak;\n\t\t}\n\t\t//Now all that is left is recursing on the left and the right subtree\n\t\troot.left=helper(inorder, postorder, instart, i-1, postend-1+i-inend);\n\t\troot.right=helper(inorder, postorder, i+1, inend, postend-1);\n\t\treturn root;\n }\n}\n```
| 6 | 1 |
[]
| 0 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
[c++] 0ms runtime, video explanation, simple solution
|
c-0ms-runtime-video-explanation-simple-s-0g5h
|
video will be uploaded at 2PM IST \nChannel link>>>\nhttps://www.youtube.com/channel/UCkcMtAWv5PO1p6eal7TXoEw/\n\n/**\n * Definition for a binary tree node.\n *
|
2018pcecsamit306
|
NORMAL
|
2020-07-27T07:10:30.106226+00:00
|
2020-07-27T07:14:07.735223+00:00
| 207 | false |
video will be uploaded at 2PM IST \nChannel link>>>\nhttps://www.youtube.com/channel/UCkcMtAWv5PO1p6eal7TXoEw/\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode(int x) : val(x), left(NULL), right(NULL) {}\n * };\n */\nclass Solution {\npublic:\n unordered_map<int,int> m;\n \n TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {\n for(int i=0;i<inorder.size();i++)\n m[inorder[i]]=i;\n int rootIndex=postorder.size()-1;\n return buildUtil(inorder,postorder,0,inorder.size()-1,rootIndex);\n }\n \n TreeNode* buildUtil(vector<int>& inorder, vector<int>& postorder, int inleft, int inright, int &rootIndex)\n {\n if(inleft > inright)\n return NULL;\n \n int val = postorder[rootIndex];\n TreeNode *node = new TreeNode(val);\n rootIndex--;\n \n if(inleft==inright)\n return node;\n int pivot=m[val];\n \n node->right = buildUtil(inorder, postorder, pivot + 1, inright, rootIndex); \n node->left = buildUtil(inorder, postorder, inleft, pivot - 1, rootIndex); \n \n return node; \n }\n};\n```
| 6 | 6 |
[]
| 0 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
C# recursive solution with key ideas explanation.
|
c-recursive-solution-with-key-ideas-expl-rk8x
|
There are 3 main ideas:\n1) Postorder traversal ends with the root node\n // by definition: starting from the root returns its value after both subtrees travers
|
vlassov
|
NORMAL
|
2020-04-08T19:08:16.751573+00:00
|
2020-07-27T20:40:31.231161+00:00
| 277 | false |
There are 3 main ideas:\n1) Postorder traversal ends with the root node\n // by definition: starting from the root returns its value after both subtrees traversal\n2) Inorder traversal allows us to separate a given tree on two subtrees\n // by definition too: returns root value after left and before right subtree traversals, so the root value is between subtrees\n3) Rolling back postorder traversal will give us root values in each subtree. So we can use a stack for it.\n\n```\n public TreeNode BuildTree(int[] inorder, int[] postorder) {\n var post = new Stack<int>(postorder);\n var index = inorder.Select((val, index) => (val, index))\n .ToDictionary(x => x.val, x => x.index);\n return Build(0, inorder.Length - 1);\n\n TreeNode Build(int left, int right) {\n if (left > right) return null;\n\n var val = post.Pop();\n var i = index[val];\n\n return new TreeNode(val) {\n right = Build(i + 1, right),\n left = Build(left, i - 1)\n };\n }\n }\n```
| 6 | 0 |
['Recursion']
| 1 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
Intuition for the efficient O(n) recursion
|
intuition-for-the-efficient-on-recursion-p8db
|
Starting from this video, I would like to explain how the efficient solution works.\n\n\nSuppose we have this tree \n\nIt\'s traversals are as follows \n\nNow,
|
deleted_user
|
NORMAL
|
2019-12-17T08:08:27.420827+00:00
|
2019-12-17T08:12:11.796873+00:00
| 293 | false |
Starting from this video, I would like to explain how the efficient solution works.\n<iframe width="560" height="315" src="https://www.youtube.com/embed/IVlCn-DNO5k" frameborder="0" allow="accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe>\n\nSuppose we have this tree \n\nIt\'s traversals are as follows \n\nNow, it\'s obvious that the last node of the postorder traversal `(A)` will be the root of the tree. As stated in the video, all the nodes from the inorder traversal that are to the left of the root belong to the left subtree `(D,B,F,E)` and all the others belong to the right one `(G,C,L,J,H,K)`. \n\nFrom this, it seems that we need an efficient way of answering the question "given a node in the postorder traversal, where is it at in the inorder array (or what is its index in the inorder traversal)?" This is what the `inorderLocator` map does: it maps each node\'s value to its index in the inorder array `(inorderLocator[node value] = inorder index)`. \n\nWe\'ve seen that dividing the inorder traversal into a left subtree traversal and a right subtree traversal is easy, we just find the root\'s index and split there. But what about dividing the postorder traversal?\n\nThink about how postorder works. **We visit the left subtree first**, then the right subtree, and finally the root. What this means is that **the postorder traversal begins with all the elements of the left subtree (1)**; those are the ones we visit first, right? \n\nWe also know the index of the root in the inorder traversal, and that **the number of elements left of the root in an inorder traversal is exactly the number of elements in the left subtree (2)**. That number happens to be the **index of the root in the traversal minus the index of the first element considered (initially 0)**.\n\nGiven **1** and **2**, we can now divide the postorder traversal into subproblems too. The postorder traversal of the left subtree will have all the elements from `beginning` to `beginning + #(elements in the left subtree) - 1` and the right subtree will have all elements from `beginning + #(elements in the left subtree)` to `ending - 1` (as the last index was the root itself).\n\nIn our example, `A` is at index 4, we have `4 - 0 = 4` elements in the left subtree, so we split the postorder from index `0` to `4 - 1 = 3` `(D,F,E,B)`, and then again from `4` to `10 - 1 = 9` `(G,L,J,K,H,C)`.\n\nWe now have a beautiful recursion: we can solve `f([D,F,E,B,G,L,J,K,H,C,A], [D,B,F,E,A,G,C,L,J,H,K])` by choosing `root = A` and solving `root.left = f([D,F,E,B] [D,B,F,E])` AND `root.right = f([G,L,J,K,H,C], [G,C,L,J,H,K])`. The basecase would be when we want to solve `f([], [])`, and its result would be the null tree.\n\nFor optimization purposes, we could also consider `f([X], [X])` to be a base case, the tree with root X and no children. Also, we won\'t split the arrays, but rather store their boundaries as `[start, end]` indeces so that we only consider the portions from `array[start]` to `array[end]`.\n\n```java\nclass Solution {\n public Map<Integer, Integer> inorderLocator;\n \n public TreeNode buildTree(int[] inorder, int[] postorder) {\n inorderLocator = new HashMap<>();\n for (int i = 0; i < inorder.length; i++) {\n inorderLocator.put(inorder[i], i);\n }\n \n return buildTreeHelper(inorder, 0, inorder.length - 1, postorder, 0, postorder.length - 1);\n }\n \n public TreeNode buildTreeHelper(int[] inorder, int inorderStart, int inorderEnd, int[] postorder, int postorderStart, int postorderEnd) {\n if (inorderStart > inorderEnd)\n return null;\n \n TreeNode root = new TreeNode(postorder[postorderEnd]);\n\t\tif (inorderStart == inorderEnd)\n\t\t\treturn root;\n \n int inorderIndex = inorderLocator.get(postorder[postorderEnd]);\n\t\tint leftSubtreeCount = inorderIndex - inorderStart;\n\t\t\n root.left = buildTreeHelper(inorder, inorderStart, inorderIndex - 1, postorder, postorderStart, postorderStart + leftSubtreeCount - 1);\n root.right = buildTreeHelper(inorder, inorderIndex + 1, inorderEnd, postorder, postorderStart + leftSubtreeCount, postorderEnd - 1);\n \n return root;\n }\n}\n```
| 6 | 0 |
[]
| 0 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
My JAVA recursive answer, BEAT 92.9%, 2ms
|
my-java-recursive-answer-beat-929-2ms-by-rvxh
|
public TreeNode buildTree(int[] inorder, int[] postorder) {\n return build(inorder,inorder.length-1,0,postorder,postorder.length-1);\n }\n \n pu
|
frankchu_0229
|
NORMAL
|
2016-06-13T13:18:56+00:00
|
2016-06-13T13:18:56+00:00
| 2,422 | false |
public TreeNode buildTree(int[] inorder, int[] postorder) {\n return build(inorder,inorder.length-1,0,postorder,postorder.length-1);\n }\n \n public TreeNode build(int[] inorder, int inStart, int inEnd, int[] postorder, int postStart){\n \tif(inEnd > inStart){\n \t\treturn null;\n \t}\n \tTreeNode root = new TreeNode(postorder[postStart]);\n \tif(inEnd == inStart){\n \t\treturn root;\n \t}\n \tint index = 0;\n \t// find the index in inorder:\n \tfor(int i = inStart; i >= inEnd; i--){\n \t\tif(inorder[i] == root.val){\n \t\t\tindex = i;\n \t\t\tbreak;\n \t\t}\n \t}\n \t\n \troot.right = build(inorder,inStart,index+1,postorder,postStart-1);\n \troot.left = build(inorder,index-1,inEnd,postorder,postStart-(inStart-index)-1);\n \t\n \treturn root;\n }
| 6 | 0 |
[]
| 3 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
Best Solution for Trees 🚀 in C++, Python and Java || 100% working
|
best-solution-for-trees-in-c-python-and-o1z7z
|
🧠 IntuitionWe are given inorder and postorder traversals.
In postorder, the last node is always the root.
From the root's index in inorder, we can split left an
|
BladeRunner150
|
NORMAL
|
2025-04-09T11:36:36.261981+00:00
|
2025-04-09T11:36:36.261981+00:00
| 138 | false |
# 🧠 Intuition
We are given `inorder` and `postorder` traversals.
In postorder, the **last node is always the root**.
From the root's index in inorder, we can split left and right subtrees.
We build the tree using this info **recursively** 🔁🌳
---
# 🚀 Approach
- Start from the **last element** of postorder.
- Use a **hashmap** to quickly find the index of elements in inorder.
- Build **right subtree first**, then left (because postorder is reversed).
---
# ⏱️ Complexity
- Time complexity: $$O(n)$$
- Space complexity: $$O(n)$$
---
# 💻 Code
```cpp []
class Solution {
public:
unordered_map<int,int> map;
int idx;
TreeNode* BuildTree(vector<int>& inorder, vector<int>& postorder, int s, int e) {
if(s > e) return nullptr;
int curr = postorder[idx--];
TreeNode* root = new TreeNode(curr);
int id = map[curr];
root->right = BuildTree(inorder, postorder, id + 1, e);
root->left = BuildTree(inorder, postorder, s, id - 1);
return root;
}
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
for(int i = 0; i < inorder.size(); i++) map[inorder[i]] = i;
idx = postorder.size() - 1;
return BuildTree(inorder, postorder, 0, inorder.size() - 1);
}
};
```
```python []
class Solution:
def buildTree(self, inorder, postorder):
idx = len(postorder) - 1
mp = {val: i for i, val in enumerate(inorder)}
def build(s, e):
nonlocal idx
if s > e:
return None
root_val = postorder[idx]
idx -= 1
root = TreeNode(root_val)
id = mp[root_val]
root.right = build(id + 1, e)
root.left = build(s, id - 1)
return root
return build(0, len(inorder) - 1)
```
```java []
class Solution {
Map<Integer, Integer> map = new HashMap<>();
int idx;
public TreeNode buildTree(int[] inorder, int[] postorder) {
for(int i = 0; i < inorder.length; i++) map.put(inorder[i], i);
idx = postorder.length - 1;
return build(postorder, inorder, 0, inorder.length - 1);
}
private TreeNode build(int[] postorder, int[] inorder, int s, int e) {
if(s > e) return null;
int curr = postorder[idx--];
TreeNode root = new TreeNode(curr);
int id = map.get(curr);
root.right = build(postorder, inorder, id + 1, e);
root.left = build(postorder, inorder, s, id - 1);
return root;
}
}
```
<img src="https://assets.leetcode.com/users/images/7b864aef-f8a2-4d0b-a376-37cdcc64e38c_1735298989.3319144.jpeg" alt="upvote" width="150px">
# Connect with me on LinkedIn for more insights! 🌟 Link in bio
| 5 | 0 |
['Array', 'Hash Table', 'Divide and Conquer', 'Tree', 'Binary Tree', 'Python', 'C++', 'Java', 'Python3']
| 1 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
Divide and Conquer || Edge Handling || Explanation || Working
|
divide-and-conquer-edge-handling-explana-8s1g
|
Intuition\nWhen we are given two types of traversals of a binary tree, inorder and postorder, and asked to reconstruct the binary tree, the key observation is t
|
Anurag_Basuri
|
NORMAL
|
2024-10-15T13:53:45.188517+00:00
|
2024-10-15T13:53:45.188551+00:00
| 784 | false |
# Intuition\nWhen we are given two types of traversals of a binary tree, `inorder` and `postorder`, and asked to reconstruct the binary tree, the key observation is that:\n- In **postorder** traversal, the **last element** is always the root of the current subtree.\n- In **inorder** traversal, the left subtree elements appear before the root, and the right subtree elements appear after the root.\n\nThus, by repeatedly identifying the root from the `postorder` traversal and using the `inorder` traversal to find the boundary between left and right subtrees, we can recursively construct the entire tree.\n\n# Approach\n### Step-by-Step Breakdown:\n1. **Understanding Inorder and Postorder**:\n - **Inorder** gives us information about the structure of the tree: elements to the left of the root (in `inorder`) belong to the left subtree, and elements to the right belong to the right subtree.\n - **Postorder** helps us find the root of the tree or subtree, as the last element in a postorder traversal is always the root of the subtree.\n\n2. **Recursive Tree Construction**:\n - We begin by taking the last element of the `postorder` array as the root.\n - Using this root\'s value, we find its index in the `inorder` array. This index divides the `inorder` array into two parts: the left part represents the left subtree, and the right part represents the right subtree.\n - Using the size of the left subtree (calculated from the `inorder` array), we can then identify the corresponding parts of the `postorder` array for the left and right subtrees.\n - We recursively repeat this process for both subtrees until the entire tree is built.\n\n3. **Edge Cases**:\n - **Empty Tree**: If the `inorder` or `postorder` arrays are empty, the tree does not exist, and we return `null`.\n - **Single Node Tree**: When the tree has only one node, both `inorder` and `postorder` arrays will have one element. The recursive call will immediately construct a tree with one node.\n - **Invalid Input**: If the input arrays are invalid (e.g., lengths don\u2019t match), our algorithm assumes valid input. In a real-world scenario, we would handle such cases with additional checks.\n\n### Working Example:\nLet\'s consider a simple example:\n- **Inorder**: `[9, 3, 15, 20, 7]`\n- **Postorder**: `[9, 15, 7, 20, 3]`\n\n- The last element of the `postorder` array is `3`, which is the root.\n- In the `inorder` array, `3` is located at index `1`. This divides the `inorder` array into:\n - Left subtree: `[9]`\n - Right subtree: `[15, 20, 7]`\n\n- Now, we focus on constructing the left and right subtrees:\n - For the **left subtree**:\n - Inorder: `[9]`\n - Postorder: `[9]`\n - The root is `9`, and there are no more elements to process, so this subtree is complete.\n \n - For the **right subtree**:\n - Inorder: `[15, 20, 7]`\n - Postorder: `[15, 7, 20]`\n - The root is `20`, and we divide again:\n - Left subtree: `[15]`\n - Right subtree: `[7]`\n - We build the left subtree with root `15` and right subtree with root `7`.\n\nIn this way, we can recursively build the entire tree.\n\n# Complexity\n- **Time complexity**: $$O(n)$$\n - Each element of the `inorder` and `postorder` arrays is processed once to determine the root and its position. Finding the index of the root in the `inorder` array takes constant time with a hash map, so the overall time complexity is linear, $$O(n)$$, where `n` is the number of nodes.\n \n- **Space complexity**: $$O(n)$$\n - The space complexity is also $$O(n)$$ due to the space required for the recursive call stack (in the worst case, for a completely unbalanced tree) and the space required to store the hash map for the `inorder` indices.\n\n# Conclusion\nBy leveraging the properties of `inorder` and `postorder` traversals, we can efficiently reconstruct the binary tree in linear time. The key is to use the postorder traversal to identify roots and the inorder traversal to divide subtrees.\n\nThis recursive approach covers edge cases such as empty trees and single-node trees, and works well for both balanced and unbalanced binary trees.\n\n\n# Code\n```java []\nclass Solution {\n public TreeNode buildHelper(int[] inorder, int ins, int inl, int[] postorder, int posts, int postl, Map<Integer, Integer> index) {\n if (posts > postl || ins > inl) {\n return null;\n }\n \n // Last element of postorder is the root of current subtree\n TreeNode root = new TreeNode(postorder[postl]);\n \n // Find the index of the root in inorder traversal\n int ind = index.get(root.val);\n \n // Number of elements in left subtree\n int x = ind - ins;\n \n // Recursively build left and right subtrees\n root.left = buildHelper(inorder, ins, ind - 1, postorder, posts, posts + x - 1, index);\n root.right = buildHelper(inorder, ind + 1, inl, postorder, posts + x, postl - 1, index);\n \n return root;\n }\n\n public TreeNode buildTree(int[] inorder, int[] postorder) {\n // Map value to index in inorder traversal\n Map<Integer, Integer> index = new HashMap<>();\n for (int i = 0; i < inorder.length; i++) {\n index.put(inorder[i], i);\n }\n\n // Build the tree\n return buildHelper(inorder, 0, inorder.length - 1, postorder, 0, postorder.length - 1, index);\n }\n}\n```\n``` cpp []\nclass Solution {\npublic:\n TreeNode* buildHelper(vector<int>& inorder, int ins, int inl, vector<int>& postorder, int posts, int postl, unordered_map<int, int>& index) {\n if (posts > postl || ins > inl) {\n return nullptr;\n }\n\n // Last element of postorder is the root of current subtree\n TreeNode* root = new TreeNode(postorder[postl]);\n\n // Find the index of the root in inorder traversal\n int ind = index[root->val];\n\n // Number of elements in the left subtree\n int x = ind - ins;\n\n // Recursively build left and right subtrees\n root->left = buildHelper(inorder, ins, ind - 1, postorder, posts, posts + x - 1, index);\n root->right = buildHelper(inorder, ind + 1, inl, postorder, posts + x, postl - 1, index);\n\n return root;\n }\n\n TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {\n // Map value to index in inorder traversal\n unordered_map<int, int> index;\n for (int i = 0; i < inorder.size(); i++) {\n index[inorder[i]] = i;\n }\n\n // Build the tree\n return buildHelper(inorder, 0, inorder.size() - 1, postorder, 0, postorder.size() - 1, index);\n }\n};\n```\n``` python []\nclass Solution:\n def buildHelper(self, inorder, ins, inl, postorder, posts, postl, index):\n if posts > postl or ins > inl:\n return None\n \n # The last element of postorder is the root of the current subtree\n root = TreeNode(postorder[postl])\n\n # Find the index of the root in inorder traversal\n ind = index[root.val]\n \n # Number of nodes in the left subtree\n x = ind - ins\n\n # Recursively build the left and right subtrees\n root.left = self.buildHelper(inorder, ins, ind - 1, postorder, posts, posts + x - 1, index)\n root.right = self.buildHelper(inorder, ind + 1, inl, postorder, posts + x, postl - 1, index)\n\n return root\n\n def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:\n # Map the values to their indices in inorder traversal\n index = {val: i for i, val in enumerate(inorder)}\n \n # Build the tree using the helper function\n return self.buildHelper(inorder, 0, len(inorder) - 1, postorder, 0, len(postorder) - 1, index)\n```
| 5 | 0 |
['Array', 'Hash Table', 'Divide and Conquer', 'Tree', 'Binary Tree', 'C++', 'Java', 'Python3']
| 0 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
Easy C++ solution using recursion📊📊
|
easy-c-solution-using-recursion-by-aryan-mpdj
|
To solve the problem of constructing a binary tree from its inorder and postorder traversals, we can use a recursive approach similar to the previous one for pr
|
Aryanoeo
|
NORMAL
|
2024-06-27T14:20:35.176052+00:00
|
2024-06-27T14:20:35.176081+00:00
| 277 | false |
To solve the problem of constructing a binary tree from its inorder and postorder traversals, we can use a recursive approach similar to the previous one for preorder and inorder traversals.\n# Intuition\nThe postorder traversal gives us the order in which nodes are visited in a "Left-Right-Root" manner, while the inorder traversal gives the order in "Left-Root-Right". By leveraging these properties, we can recursively construct the binary tree\n\n# Approach\nThe last element of the postorder traversal is the root of the tree.\nFind this root element in the inorder traversal; elements to the left of it belong to the left subtree, and elements to the right belong to the right subtree.\nRecursively repeat the process for the left and right subtrees using the respective segments of the inorder and postorder arrays.\n\n# Complexity\n- Time complexity:\nO(n^2)\nEach call to search takes O(n) time and it is called for each node. Therefore, in the worst case, the time complexity is O(n2)\n\n- Space complexity:\nO(n)\nThe space complexity is mainly due to the recursion stack, which can go up to the depth of the tree (in the worst case, the depth is n for a skewed tree)\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n int search(vector<int> inorder,int start,int end,int curr){\n for(int i=start;i<=end;i++){\n if(inorder[i]==curr){\n return i;\n }\n }\n return -1;\n }\n TreeNode* helper(vector<int>&inorder,vector<int>&postorder,int start,int end,int& idx){\n if(start>end){\n return nullptr;\n }\n int curr=postorder[idx];\n idx--;\n TreeNode* Node=new TreeNode(curr);\n if(start==end){\n return Node;\n }\n int pos=search(inorder,start,end,curr);\n Node->right=helper(inorder,postorder,pos+1,end,idx);\n Node->left=helper(inorder,postorder,start,pos-1,idx);\n return Node;\n }\n TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {\n int idx=inorder.size()-1;\n TreeNode* root=helper(inorder,postorder,0,inorder.size()-1,idx);\n return root;\n }\n};\n```
| 5 | 0 |
['Array', 'Tree', 'Recursion', 'Binary Tree', 'C++']
| 1 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
C++ Solution
|
c-solution-by-taskcruncher-d95f
|
Complexity\n- Time complexity: O(n*log(n))\n\n- Space complexity: O(n)\n\n# Code\n\nclass Solution {\n public:\n TreeNode* buildTree(vector<int>& inorder, vect
|
taskcruncher
|
NORMAL
|
2023-03-18T17:04:39.092558+00:00
|
2023-03-18T17:04:39.092593+00:00
| 57 | false |
# Complexity\n- Time complexity: $$O(n*log(n))$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n```\nclass Solution {\n public:\n TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {\n unordered_map<int, int> inToIndex;\n\n for (int i = 0; i < inorder.size(); ++i)\n inToIndex[inorder[i]] = i;\n\n return build(inorder, 0, inorder.size() - 1, postorder, 0,\n postorder.size() - 1, inToIndex);\n }\n\n private:\n TreeNode* build(const vector<int>& inorder, int inStart, int inEnd,\n const vector<int>& postorder, int postStart, int postEnd,\n const unordered_map<int, int>& inToIndex) {\n if (inStart > inEnd)\n return nullptr;\n\n const int rootVal = postorder[postEnd];\n const int rootInIndex = inToIndex.at(rootVal);\n const int leftSize = rootInIndex - inStart;\n\n TreeNode* root = new TreeNode(rootVal);\n root->left = build(inorder, inStart, rootInIndex - 1, postorder, postStart,\n postStart + leftSize - 1, inToIndex);\n root->right = build(inorder, rootInIndex + 1, inEnd, postorder,\n postStart + leftSize, postEnd - 1, inToIndex);\n return root;\n }\n};\n\n```
| 5 | 0 |
['Tree', 'Binary Tree', 'C++']
| 0 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
Python Fast DFS with explanation
|
python-fast-dfs-with-explanation-by-rand-g1cz
|
\n\n\nclass Solution(object):\n def buildTree(self, inorder, postorder):\n inorder_map = {val:i for i, val in enumerate(inorder)}\n \n d
|
randaldong
|
NORMAL
|
2022-08-19T12:20:58.203034+00:00
|
2022-08-19T12:20:58.203073+00:00
| 352 | false |
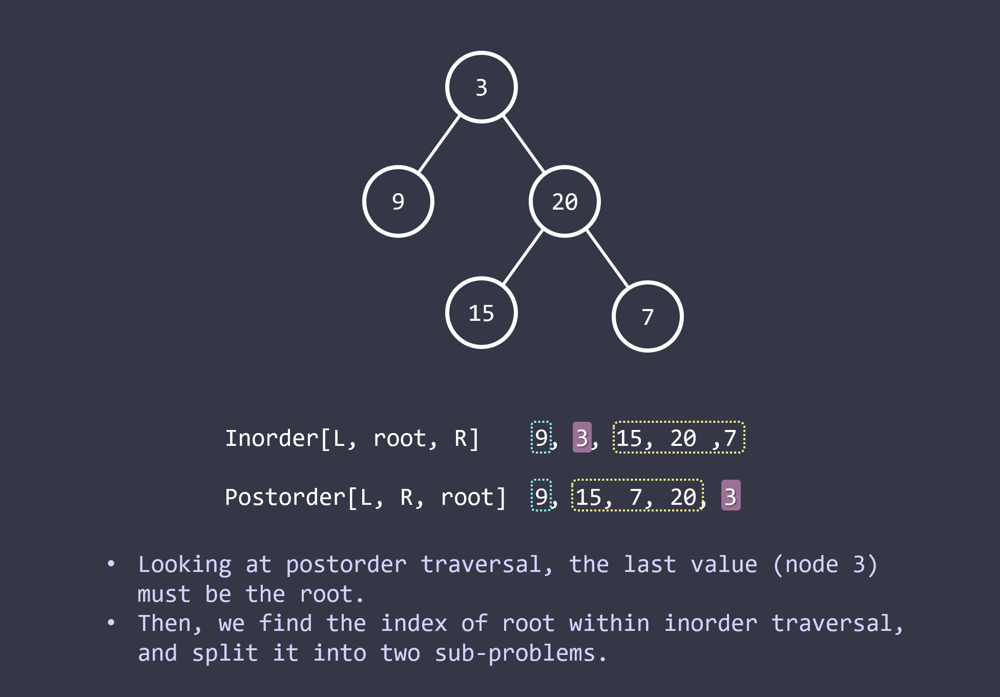\n\n```\nclass Solution(object):\n def buildTree(self, inorder, postorder):\n inorder_map = {val:i for i, val in enumerate(inorder)}\n \n def dfs(start, end):\n if start > end: return None\n root = TreeNode(postorder.pop())\n root_index = inorder_map[root.val]\n root.right = dfs(root_index+1, end) # have to put right before left because postorder.pop will return the right node first\n root.left = dfs(start, root_index-1)\n return root\n \n return dfs(0, len(inorder)-1)\n```\n\n
| 5 | 0 |
['Python']
| 0 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
Python Easy Code
|
python-easy-code-by-manoranjanthakur-7sjg
|
\t def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:\n if len(postorder)==0:\n return None\n root=Tr
|
Manoranjanthakur
|
NORMAL
|
2021-12-01T20:01:30.689049+00:00
|
2021-12-01T20:01:30.689088+00:00
| 268 | false |
\t def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:\n if len(postorder)==0:\n return None\n root=TreeNode(postorder[-1])\n for i in range(len(inorder)):\n if postorder[-1]==inorder[i]:\n break\n root.left=self.buildTree(inorder[0:i],postorder[0:i])\n root.right=self.buildTree(inorder[i+1:],postorder[i:-1])\n return root
| 5 | 0 |
['Recursion', 'Python']
| 0 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
✔ JAVA | Simple Easy-to-Understand Intuitive Solution
|
java-simple-easy-to-understand-intuitive-28bt
|
\nclass Solution {\n public TreeNode buildTree(int[] inorder, int[] postorder) {\n if (postorder.length == 0 && inorder.length == 0)\n retu
|
norman22194plus1
|
NORMAL
|
2021-11-21T11:38:38.866407+00:00
|
2021-11-21T11:38:38.866439+00:00
| 463 | false |
```\nclass Solution {\n public TreeNode buildTree(int[] inorder, int[] postorder) {\n if (postorder.length == 0 && inorder.length == 0)\n return null;\n if (postorder.length == 1 && inorder.length == 1)\n return new TreeNode(inorder[0]);\n int len = postorder.length;\n int root = postorder[len - 1];\n int index = findIndex(inorder, root);\n \n int[] leftIn = Arrays.copyOfRange(inorder, 0, index);\n int[] rightIn = Arrays.copyOfRange(inorder, index + 1, len);\n \n int[] leftPost = Arrays.copyOfRange(postorder, 0, index);\n int[] rightPost = Arrays.copyOfRange(postorder, index, len - 1);\n \n TreeNode lroot = buildTree(leftIn, leftPost);\n TreeNode rroot = buildTree(rightIn, rightPost);\n \n return new TreeNode(root, lroot, rroot);\n }\n int findIndex(int[] arr, int x) {\n for (int i = 0; i < arr.length; i++)\n if (arr[i] == x)\n return i;\n return -1;\n }\n}\n```\nPlease **upvote** :-)
| 5 | 0 |
['Recursion', 'Binary Tree', 'Java']
| 0 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
Easy to Understand | Faster | Simple | Recursion | Python Solution
|
easy-to-understand-faster-simple-recursi-n2rn
|
\n def recursive(self, inorder, postorder):\n def rec(inorder):\n # print(inorder, postorder)\n if len(postorder):\n
|
mrmagician
|
NORMAL
|
2020-07-26T14:16:57.964799+00:00
|
2020-07-26T14:16:57.964847+00:00
| 468 | false |
```\n def recursive(self, inorder, postorder):\n def rec(inorder):\n # print(inorder, postorder)\n if len(postorder):\n value = postorder[-1]\n node = TreeNode(value)\n if value not in inorder: return None\n pos = inorder.index(value)\n postorder.pop()\n node.right = rec(inorder[pos + 1:])\n node.left = rec(inorder[0:pos])\n return node\n return rec(inorder)\n```\n\n**I hope that you\'ve found the solution useful.**\n*In that case, please do upvote and encourage me to on my quest to document all leetcode problems\uD83D\uDE03*\nPS: Search for **mrmagician** tag in the discussion, if I have solved it, You will find it there\uD83D\uDE38
| 5 | 3 |
['Depth-First Search', 'Recursion', 'Python', 'Python3']
| 1 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
Simple and crystal clear C solutions
|
simple-and-crystal-clear-c-solutions-by-8w45a
|
\nstruct TreeNode* newNode(val)\n{\n struct TreeNode* p = (struct TreeNode*)malloc(sizeof(struct TreeNode));\n p->val = val;\n p->left = p->right = NUL
|
thorneliu
|
NORMAL
|
2019-02-15T03:48:47.296062+00:00
|
2019-02-15T03:48:47.296126+00:00
| 436 | false |
```\nstruct TreeNode* newNode(val)\n{\n struct TreeNode* p = (struct TreeNode*)malloc(sizeof(struct TreeNode));\n p->val = val;\n p->left = p->right = NULL;\n return p;\n}\n\nstruct TreeNode* buildTree(int* inorder, int inorderSize, int* postorder, int postorderSize) {\n if (!inorder || !postorder || (inorderSize != postorderSize) || inorderSize <= 0) return NULL;\n \n int rootVal = postorder[postorderSize - 1];\n struct TreeNode* root = newNode(rootVal);\n int idx = 0;\n for (; idx < inorderSize - 1; idx++)\n {\n if (inorder[idx] == rootVal) break;\n }\n root->left = buildTree(inorder, idx, postorder, idx);\n root->right = buildTree(inorder+idx+1, inorderSize-idx-1, postorder+idx, inorderSize-idx-1);\n return root;\n}\n```\n\nI could get such straight-forward solution in C with the help of C pointer arithmetic. In fact, I am also trying \nwith C++ vectors, but I think Cpp Vectors would not convenient (I am not skillful in Cpp), :(\n
| 5 | 0 |
['Recursion', 'C']
| 0 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
Ruby recursive solution 6 lines
|
ruby-recursive-solution-6-lines-by-danna-5jgf
|
What we know is that the root node in a postorder traversal is the very last node, so the last value is the root val. With that we know where to split the inord
|
dannam83
|
NORMAL
|
2018-10-23T12:43:24.772320+00:00
|
2018-10-23T18:07:37.390334+00:00
| 193 | false |
What we know is that the root node in a postorder traversal is the very last node, so the last value is the root val. With that we know where to split the inorder traversal because in the inorder array, everything left of the root val is the left side of the tree, and everything right of the root val is the right side of the tree. We also know that in the postorder traversal there is some middle point of the traversal that splits the left and right of the tree because we know that the traversal jumps to the right side of the root node only after the entire left side is completed. Now, since we know the exact number of nodes on the left side from our logic about the inorder traversal array, we can take exactly that many values from the postorder traversal array for the left side, and then take the remaining values minus the last value for the right side.\n\n```\ndef build_tree(inorder, postorder) \n \n return nil if inorder.none?\n \n node = TreeNode.new(postorder.last)\n i = inorder.index(postorder.last)\n node.left = build_tree(inorder[0...i], postorder[0...i])\n node.right = build_tree(inorder[i+1..-1], postorder[i...-1])\n \n node\n \nend\n```
| 5 | 0 |
[]
| 0 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
a simple recursive way in Go with explanation
|
a-simple-recursive-way-in-go-with-explan-xhe2
|
A basic idea is that, the last element of slice postorder is root\nAnd we can use root to find out left sub-tree and right sub-tree from inorder\nThen, we go to
|
kiwil
|
NORMAL
|
2018-08-13T13:23:12.310931+00:00
|
2018-08-13T13:23:12.310982+00:00
| 220 | false |
A basic idea is that, the last element of slice `postorder` is `root`\nAnd we can use `root` to find out left sub-tree and right sub-tree from `inorder`\nThen, we go to build left/right sub-trees.\nSlice `postorder` and `inorder` of the left sub-tree have the same indexing `[:rootIdx]` from the original `postorder` and `inorder`.\nAs for the right sub-tree, its `inorder` is obtained by skipping the first element of original `inorder` because it is `root`. Then for `postorder`, we skip the last one. \n\n```\nfunc buildTree(inorder []int, postorder []int) *TreeNode {\n\n\tif len(inorder) == 0 && len(postorder) == 0 {\n\t\treturn nil\n\t}\n\n\tpivot := postorder[len(postorder)-1]\n\tpivotIdx := 0\n\tfor inorder[pivotIdx] != pivot {\n\t\tpivotIdx++\n\t}\n\n\tleft := buildTree(inorder[:pivotIdx], postorder[:pivotIdx])\n\tright := buildTree(inorder[pivotIdx+1:], postorder[pivotIdx:len(postorder)-1])\n\n\troot := &TreeNode{pivot, left, right}\n\treturn root\n}\n```
| 5 | 0 |
[]
| 1 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
O(N) solution with forward iteration
|
on-solution-with-forward-iteration-by-ph-bgs5
|
The code makes sure each step we are in the state where\n\n 1. We have a constructed sub tree. (the "working" tree in the code)\n 1. Both iterators point to jus
|
pherl
|
NORMAL
|
2015-06-28T07:11:38+00:00
|
2015-06-28T07:11:38+00:00
| 1,001 | false |
The code makes sure each step we are in the state where\n\n 1. We have a constructed sub tree. (the "working" tree in the code)\n 1. Both iterators point to just pass that subtree. (the nodes for the subtree are continuous in both in-order and post-order lists.)\n\nThen, we can deduce that: **the next node in the in-order list must be the parent of the working tree**.\n\n 1. We extend the working tree by adding the next in-order list node as its parent, then push it to a stack; clear the working tree, and work on building the right branch from scratch. **All the notes until the same node appears in post-order are for the right child of the parent.**\n 1. When the post-order element matches with the stack top, then the stack top node has its right branch finished. Thus, pop the stack, make the working tree as its right child. Point the working tree to the new completed tree.\n\nRun this over until the postorder sequences are consumed. The working tree is the answer, and the stack at that point should be empty.\n\nHere's the code\n\n class Solution {\n public:\n TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {\n if (inorder.empty()) return nullptr;\n // 'parents' contains all the nodes we have seen so far, we haven't\n // finished building their right branch nodes yet.\n vector<TreeNode*> parents;\n // 'working' is a completed subtree of the final problem, based on the\n // inorder/postorder we examined so far. We will keep adding its parent to\n // build the final tree.\n TreeNode* working = nullptr;\n auto in = inorder.begin();\n auto post = postorder.begin();\n while (post != postorder.end()) {\n if (!parents.empty() && *post == parents.back()->val) {\n // Post order node matches the stack top parent notes. It means the\n // working tree is the right branch of the stack top. Pop the stack top\n // to be the working tree.\n parents.back()->right = working;\n working = parents.back();\n parents.pop_back();\n ++post;\n } else {\n // Otherwise, we get a new parent for the current working tree. \n // Extend the existing working tree, push it to the stack and work on\n // the right branch of the new parent.\n TreeNode* new_node = new TreeNode(*in);\n new_node->left = working;\n working = nullptr;\n parents.push_back(new_node);\n ++in;\n }\n }\n return working;\n }\n };
| 5 | 0 |
[]
| 0 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
simple JavaScript solution using DFS
|
simple-javascript-solution-using-dfs-by-uhzpe
|
javascript\n/**\n * @param {number[]} inorder\n * @param {number[]} postorder\n * @return {TreeNode}\n */\nvar buildTree = function(inorder, postorder) {\n ret
|
hanzichi
|
NORMAL
|
2016-08-26T02:00:32.979000+00:00
|
2018-09-30T23:47:53.028095+00:00
| 1,013 | false |
```javascript\n/**\n * @param {number[]} inorder\n * @param {number[]} postorder\n * @return {TreeNode}\n */\nvar buildTree = function(inorder, postorder) {\n return dfs(inorder.length - 1, 0, inorder.length - 1);\n\n function dfs(index, startPos, endPos) {\n if (startPos > endPos)\n return null;\n\n var node = new TreeNode(postorder[index]);\n var pos = inorder.indexOf(postorder[index]);\n\n node.left = dfs(index - (endPos - pos) - 1, startPos, pos - 1);\n node.right = dfs(index - 1, pos + 1, endPos);\n\n return node;\n }\n};\n```\n\nall my leetcode solutions are here <https://github.com/hanzichi/leetcode>, give me a star if you like it!
| 5 | 0 |
[]
| 1 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
Easy JAVA solution with simple explanation
|
easy-java-solution-with-simple-explanati-aae5
|
\nIntuition:\n\n- Postorder traversal: Left, Right, Root.\n- Inorder traversal: Left, Root, Right.\n- We can use the postorder traversal to determine the root o
|
CVM0
|
NORMAL
|
2024-09-07T09:05:07.409574+00:00
|
2024-09-07T09:05:07.409615+00:00
| 1,371 | false |
\n**Intuition:**\n\n- **Postorder traversal:** Left, Right, Root.\n- **Inorder traversal:** Left, Root, Right.\n- We can use the postorder traversal to determine the root of the tree.\n- Then, we can use the inorder traversal to find the division between the left and right subtrees.\n- We can recursively build the left and right subtrees using the same approach.\n\n**Approach:**\n\n1. **Create a HashMap:** Store the indices of each element in the inorder traversal for quick lookup.\n2. **Build the subtree:**\n - Base case: If `inStart > inEnd` or `postStart > postEnd`, return `null`.\n - **Root:** The root is always the last element in the postorder traversal.\n - **Left subtree:** Find the index of the root in the inorder traversal. The elements to the left of it form the left subtree.\n - **Right subtree:** The elements to the right of the root in the inorder traversal form the right subtree.\n - Recursively build the left and right subtrees.\n\n**Complexity:**\n\n- **Time complexity:** `O(n)` where `n` is the number of nodes in the tree.\n- **Space complexity:** `O(n)` for the HashMap and the recursion stack.\n\n\n\n\n# Code\n```java []\n\nclass Solution {\n public TreeNode buildTree(int[] inorder, int[] postorder) {\n HashMap<Integer, Integer> map = new HashMap<>();\n for (int i = 0; i < inorder.length; i++) {\n map.put(inorder[i], i);\n }\n return fun(inorder, 0, inorder.length - 1, postorder, 0, postorder.length - 1, map);\n }\n\n public TreeNode fun(int[] inOrder, int inStart, int inEnd, int[] postOrder, int postStart, int postEnd,\n HashMap<Integer, Integer> map) {\n if (inStart > inEnd || postStart > postEnd) {\n return null;\n }\n TreeNode root = new TreeNode(postOrder[postEnd]);\n int inIndex = map.get(root.val);\n int leftTreeSize = inIndex - inStart;\n\n root.left = fun(inOrder, inStart, inIndex - 1, postOrder, postStart, postStart + leftTreeSize - 1, map);\n root.right = fun(inOrder, inIndex + 1, inEnd, postOrder, postStart + leftTreeSize, postEnd - 1, map);\n return root;\n }\n}\n\n```
| 4 | 0 |
['Array', 'Hash Table', 'Divide and Conquer', 'Tree', 'Binary Tree', 'Java']
| 1 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
C++ and Python3 || Hashmap + Recursion || Optimal Approach
|
c-and-python3-hashmap-recursion-optimal-dwk8k
|
\n\n# Code\nC++ []\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * T
|
meurudesu
|
NORMAL
|
2024-02-23T14:14:57.401275+00:00
|
2024-02-23T14:14:57.401305+00:00
| 930 | false |
> 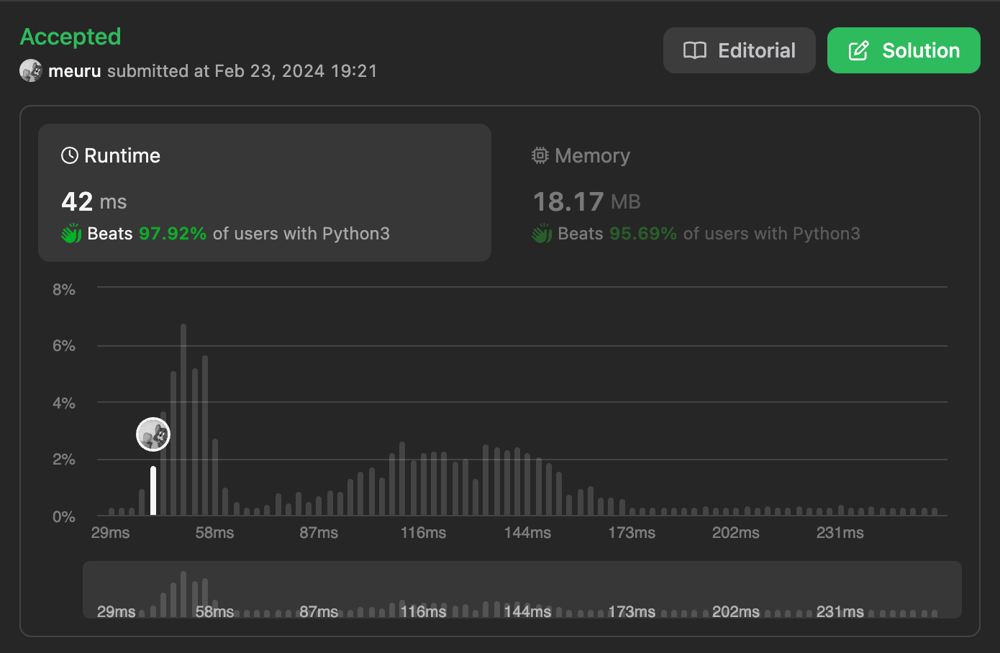\n\n# Code\n```C++ []\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n TreeNode* helper(vector<int> &inorder, int is, int ie, vector<int> &postorder, int ps, int pe, unordered_map<int, int> &inOrder) {\n if(ps > pe || is > ie) return NULL;\n TreeNode* root = new TreeNode(postorder[pe]);\n int inorderRoot = inOrder[root->val];\n int left = inorderRoot - is;\n root->left = helper(inorder, is, inorderRoot - 1,\n postorder, ps, ps + left - 1, inOrder);\n root->right = helper(inorder, inorderRoot + 1, ie,\n postorder, ps + left, pe - 1, inOrder);\n return root;\n }\n\n TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {\n unordered_map<int, int> inOrder;\n for(int i=0; i<inorder.size(); i++) {\n inOrder[inorder[i]] = i;\n }\n TreeNode* root = helper(inorder, 0, inorder.size() - 1,\n postorder, 0, postorder.size() - 1, inOrder);\n return root;\n }\n};\n```\n```Python3 []\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:\n inorderMap = {}\n for i in range(len(inorder)):\n inorderMap[inorder[i]] = i\n def helper(l, r):\n if l > r:\n return None\n root = TreeNode(postorder.pop())\n mid = inorderMap[root.val]\n root.right = helper(mid + 1, r)\n root.left = helper(l, mid - 1)\n return root\n root = helper(0, len(inorder) - 1)\n return root\n```
| 4 | 0 |
['Hash Table', 'Divide and Conquer', 'Tree', 'Recursion', 'Binary Tree', 'C++', 'Python3']
| 0 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
Best O(N) Solution
|
best-on-solution-by-kumar21ayush03-1n59
|
Approach\nOptimal\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n\n/**\n * Definition for a binary tree node.\n * struct Tree
|
kumar21ayush03
|
NORMAL
|
2023-08-30T08:16:29.872012+00:00
|
2023-08-30T08:16:29.872031+00:00
| 112 | false |
# Approach\nOptimal\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n TreeNode* build(int postStart, int postEnd, vector<int>& postorder, \n int inStart, int inEnd, vector<int>& inorder, unordered_map <int, int>& mp) {\n if (postStart > postEnd || inStart > inEnd)\n return NULL;\n TreeNode* root = new TreeNode(postorder[postEnd]);\n int ind = mp[postorder[postEnd]]; \n root->left = build(postStart, postStart+ind-inStart-1, postorder, inStart, ind-1, inorder, mp);\n root->right = build(postStart+ind-inStart, postEnd-1, postorder, ind+1, inEnd, inorder, mp);\n\n return root; \n }\n\n TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {\n int postStart = 0, postEnd = postorder.size() - 1;\n int inStart = 0, inEnd = inorder.size() - 1;\n unordered_map <int, int> mp;\n for (int i = 0; i < inorder.size(); i++)\n mp[inorder[i]] = i;\n\n return build(postStart, postEnd, postorder, inStart, inEnd, inorder, mp); \n }\n};\n```
| 4 | 0 |
['C++']
| 0 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
Easy Explanation of the Code // C++ // Recursive Approach
|
easy-explanation-of-the-code-c-recursive-t76z
|
Intuition\n Describe your first thoughts on how to solve this problem. \nThe intuition behind this solution is since the postOrder store the root node ( top mos
|
Abhinav_Shakya
|
NORMAL
|
2023-07-21T18:03:56.496250+00:00
|
2023-07-21T18:35:49.856807+00:00
| 221 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n***The intuition behind this solution is since the postOrder store the root node ( top most node of tree) at its last index . from traversing reverse we get our root node, from this I can easily find the right and left subtree from the Inorder . From this data that we have we can crete our tree by joining first rightSubtree to root node and then leftSubtree to it.***\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n1. The code defines a class `Solution` that contains a function `buildTree` to construct a binary tree from its inorder and postorder traversal sequences.\n\n2. The binary tree nodes are represented using the `TreeNode` struct, which has an integer value (`val`) and pointers to its left and right children (`left` and `right`).\n\n3. The `buildTree` function takes two input vectors, `inorder` and `postorder`, representing the inorder and postorder traversal sequences of the binary tree, respectively.\n\n4. Inorder traversal visits the left subtree first, then the root node, and finally the right subtree. Postorder traversal visits the left subtree first, then the right subtree, and finally the root node.\n\n5. The `buildTree` function initializes variables `size`, `postIndex`, `start`, and `end` to keep track of the tree size, current index in the `postorder` vector, and the start and end indices of the `inorder` subarray being processed, respectively.\n\n6. It also uses an unordered map `mp` to store the indices of elements in the `inorder` vector. This map allows quick lookup of an element\'s position in the `inorder` sequence.\n\n7. The main logic of tree construction is implemented in the `solver` function, which is a recursive helper function.\n\n8. The `solver` function takes the `postorder` and `inorder` vectors, along with the previously mentioned variables (`size`, `postIndex`, `start`, `end`, and `mp`), to construct the binary tree.\n\n9. In the `solver` function, it checks if the `postIndex` is out of bounds or if the `start` index exceeds the `end` index. If either condition is true, it means the current subtree is empty, and it returns `NULL`.\n\n10. Otherwise, it takes the element at `postIndex` from the `postorder` vector, creates a new node with this element, and decrements `postIndex`.\n\n11. It then finds the position (index) of this element in the `inorder` vector using the precomputed indices stored in the `mp` map.\n\n12. Next, it calls `solver` recursively to build the right subtree, passing the appropriate indices for the right subarray of `inorder`.\n\n13. Similarly, it constructs the left subtree using recursive calls to `solver` and passing the appropriate indices for the left subarray of `inorder`.\n\n14. The `solver` function returns the current node, and this node becomes the right or left child of its parent node in subsequent recursive calls.\n\n15. Finally, the `buildTree` function returns the root of the constructed binary tree.\n\nIn summary, the code efficiently constructs a binary tree from its inorder and postorder traversal sequences using a recursive approach with the aid of an unordered map for faster element position lookup. The recursive `solver` function handles the tree construction for each subtree, and the construction starts from the last element of the postorder sequence and proceeds backward.\n\n# Complexity\n- Time complexity:O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n***----------------Please UpVote if you really find heplfull-----------***\n\n# Code\n```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n TreeNode* solver(vector<int> &postorder,vector<int> &inorder,int size,int &postIndex,int start,int end, unordered_map<int,int> &mp)\n {\n if(postIndex<0 || start>end)\n {\n return NULL;\n }\n\n int element=postorder[postIndex];\n postIndex--;\n int pos= mp[element];\n TreeNode* root=new TreeNode(element);\n root->right=solver(postorder,inorder,size,postIndex,pos+1,end,mp);\n root->left= solver(postorder,inorder,size,postIndex,start,pos-1,mp); \n return root;\n \n }\n TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {\n int size=postorder.size();\n int postIndex=size-1;\n int start=0;\n int end=size-1;\n unordered_map<int,int> mp;\n for(int i=0;i<size;i++)\n {\n mp[inorder[i]]=i;\n }\n\n TreeNode* root=solver(postorder,inorder,size,postIndex,start,end,mp);\n return root;\n }\n};\n```
| 4 | 0 |
['Tree', 'Binary Tree', 'C++']
| 0 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
C++ || BEATS 99% || INTUITIVE || SIMPLE RECURSION || EASY SOLUTION
|
c-beats-99-intuitive-simple-recursion-ea-wxew
|
Intuition and Approach\n Describe your first thoughts on how to solve this problem. \nSo first of all u must know the conditions for a constructing a unique bin
|
vanshsuneja_
|
NORMAL
|
2023-07-06T18:03:48.464822+00:00
|
2023-07-06T18:05:43.153319+00:00
| 103 | false |
# Intuition and Approach\n<!-- Describe your first thoughts on how to solve this problem. -->\nSo first of all u must know the conditions for a constructing a unique binary tree that u must be given an inorder and a postorder/preorder/levelorder/anyother traversal to construct a unique binary tree\n\nThen next step is to figure out the root of the tree as we know the postorer traversal goes like left---->right---->root so the last element of the postorder msut be the root.\n\nSo,now u have the root okay so after u got the root what is the next thing u want left and right of the root, isn\'t it. Hey why don\'t u think what does inorder provides us its like left--->root--->right so if we find the root obtained from the postorder in the inorder vector then the nodes to the left of it would be the part of left subtree and the nodes at the right of it would be the part of right subtree.\n\nSo now u know the root of the tree the components of leftsubtree and the rightsubtree just try to extract the postorder and inorder of left and right subtree from the given vectors and just do the recursive calls for the left and the right subtree and u are good to go with the recursive solution.\n\n# Recursive code\n\n\n# Complexity\n- Time complexity: O(n^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n \n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n class Solution {\n public:\n #include <algorithm>\n TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {\n if(postorder.empty()) return nullptr;\n \n int n=postorder.size();\n int root_val=postorder[n-1];\n TreeNode* root=new TreeNode(root_val);\n int index=find(inorder.begin(),inorder.end(),root_val)-inorder.begin();\n\n vector<int> linorder(inorder.begin(),inorder.begin()+index);\n vector<int> lpostorder(postorder.begin(),postorder.begin()+index);\n \n TreeNode* left=buildTree(linorder,lpostorder);\n root->left=left;\n\n vector<int> rinorder(inorder.begin()+index+1,inorder.end());\n vector<int> rpostorder(postorder.begin()+index,postorder.end()-1);\n\n TreeNode* right=buildTree(rinorder,rpostorder);\n root->right=right;\n return root;}};\n\n# Optimized code\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n \n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n``` \nclass Solution {\npublic:\n TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {\n if (postorder.empty()) return nullptr;\n\n int postIndex = postorder.size() - 1; // Start with the last element of postorder\n return buildTreeHelper(inorder, postorder, postIndex, 0, inorder.size() - 1);\n }\n\n TreeNode* buildTreeHelper(vector<int>& inorder, vector<int>& postorder, int& postIndex, int inStart, int inEnd) {\n if (inStart > inEnd) return nullptr;\n\n int rootVal = postorder[postIndex];\n TreeNode* root = new TreeNode(rootVal);\n postIndex--;\n\n int rootIndex = findIndex(inorder, rootVal, inStart, inEnd);\n\n root->right = buildTreeHelper(inorder, postorder, postIndex, rootIndex + 1, inEnd);\n root->left = buildTreeHelper(inorder, postorder, postIndex, inStart, rootIndex - 1);\n\n return root;\n }\n\n int findIndex(vector<int>& inorder, int target, int start, int end) {\n for (int i = start; i <= end; i++) {\n if (inorder[i] == target)\n return i;\n }\n return -1; // Not found\n }\n};\n\n\n```
| 4 | 0 |
['C++']
| 0 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
SHORT & SWEET || EASY TO UNDERSTAND || C++ || RECURSION
|
short-sweet-easy-to-understand-c-recursi-pzuo
|
\nclass Solution {\npublic:\n int x ;\n TreeNode* solve(vector<int> &a,vector<int> &b,int s,int e){\n if(s>e)return NULL;\n TreeNode* node =
|
yash___sharma_
|
NORMAL
|
2023-03-17T07:52:42.316508+00:00
|
2023-03-17T07:52:42.316549+00:00
| 2,143 | false |
```\nclass Solution {\npublic:\n int x ;\n TreeNode* solve(vector<int> &a,vector<int> &b,int s,int e){\n if(s>e)return NULL;\n TreeNode* node = new TreeNode(b[x++]);\n int i;\n for(i = s; i<=e; i++){\n if(node->val == a[i]){\n break;\n }\n }\n node->right = solve(a,b,i+1,e);\n node->left = solve(a,b,s,i-1);\n return node;\n }\n TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {\n reverse(postorder.begin(),postorder.end());\n x = 0;\n return solve(inorder,postorder,0,inorder.size()-1);\n \n }\n};\n```
| 4 | 0 |
['Tree', 'Recursion', 'C', 'Binary Tree', 'C++']
| 1 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
JAVA | Detailed explanation ✅
|
java-detailed-explanation-by-sourin_bruh-7y28
|
Read till the end:\n---\n\nRole of Postorder traversal: \nTells us which is the root.\n\nRole of Inorder traversal: \nTells us which are the left and right subt
|
sourin_bruh
|
NORMAL
|
2023-03-16T13:35:02.682222+00:00
|
2023-03-16T13:37:30.540192+00:00
| 285 | false |
# Read till the end:\n---\n```\nRole of Postorder traversal: \nTells us which is the root.\n\nRole of Inorder traversal: \nTells us which are the left and right subtrees.\n```\nThe root always lie at the end of our postorder array (or subtree subarray). So when we know what our root is, we would want to define the left and right subtree from the inorder array (Becase in inorder, root lies between left and right while in postorder left and right lies together so we don\'t know hwere to put the partition). But we don\'t know where our root lies in the inorder array. So we would use a hashmap to store the inorder elements along with their indices. So we would get the root indices at constant time. \n\nSo in the inorder array:\nLeft subtree would be: `start` to `root index - 1`\nRight subtree would be: `root index + 1` to `end`\n\nIn the postorder array:\nLeft subtree would be: \n`start` to `start + (number of elements in left subtree) - 1`\n\nRight subtree would be:\n`start + (number of elements in left subtree)` to `end`\n\nNow in these broken down subarrays, the root will be given by postorder subarray, and left and right subtree would be derived from inorder subarrays.\n\n(Head over to my YT (in my bio) for a VERY DETAILED explanation. Can\'t share the link coz I was banned from discuss one time).\n\nThe pictures depict how we are defining the subtrees:\n\n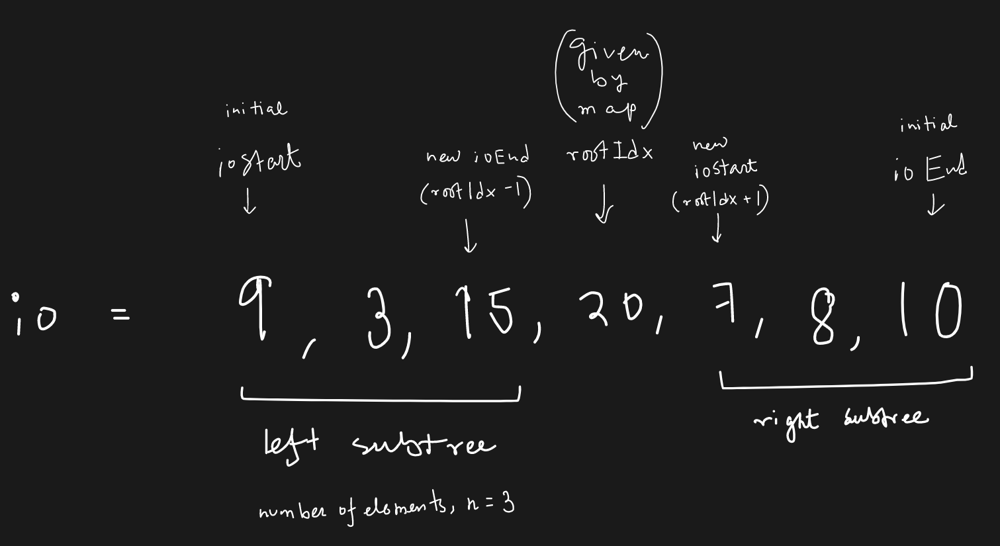\n\n\n\n\n\n---\n### Code:\n```\nclass Solution {\n private Map<Integer, Integer> map;\n public TreeNode buildTree(int[] inorder, int[] postorder) {\n map = new HashMap<>();\n int n = inorder.length;\n // build the hashmap\n for (int i = 0; i < n; i++) {\n map.put(inorder[i], i);\n }\n // range is 0 -> n-1 because this is the main function call\n // for all the elements in the tree\n return build(inorder, 0, n - 1, postorder, 0, n - 1);\n }\n\n // io -> In Order\n // po -> Post Order\n private TreeNode build( int[] io, int ioStart, int ioEnd, \n int[] po, int poStart, int poEnd) {\n // BASE CONDITION:\n // ioStart and ioEnd are moving closer to each, similarly\n // poStart and poEnd are moving closer to each other \n // when we\'ll reach the leaf node, \n // ioStart and ioEnd will be at the same position \n // poStart and poEnd will be at the same position\n // upon further recursive calls, they\'ll cross each other\n if (ioStart > ioEnd || poStart > poEnd) {\n return null; // in that case return null\n }\n\n // po[poEnd] will give us the root node value\n // because po knows who our root is\n TreeNode root = new TreeNode(po[poEnd]); // create the root node\n // hashmap knows where our root lies in io array\n int rootIdx = map.get(po[poEnd]); // get that index from te map\n // compute the number of elements at the left of root index in io array \n int numsAtLeft = rootIdx - ioStart;\n // this numsAtLeft is nothing but the number of elements in our left subtree\n // We don\'t know from where to where our left and right subtree lies\n // in the po array, so numsAtLeft will help us \n // define the range for left and right subtrees in po array\n // (See the pictures for the parameters in the recursive calls)\n\n root.left = build(io, ioStart, rootIdx - 1, \n po, poStart, poStart + numsAtLeft - 1);\n\n root.right = build(io, rootIdx + 1, ioEnd, \n po, poStart + numsAtLeft, poEnd - 1);\n\n // our recursion will go to the bottom (single node level) \n // and build the tree and come back\n return root;\n }\n}\n```\n---\n#### Clean solution:\n```\nclass Solution {\n private Map<Integer, Integer> map = new HashMap<>();\n public TreeNode buildTree(int[] inorder, int[] postorder) {\n int n = inorder.length;\n for (int i = 0; i < n; i++) {\n map.put(inorder[i], i);\n }\n\n return build(inorder, 0, n - 1, postorder, 0, n - 1);\n }\n\n private TreeNode build( int[] io, int ioStart, int ioEnd, \n int[] po, int poStart, int poEnd) {\n\n if (ioStart > ioEnd || poStart > poEnd) {\n return null; \n }\n\n TreeNode root = new TreeNode(po[poEnd]);\n int rootIdx = map.get(po[poEnd]); \n int numsAtLeft = rootIdx - ioStart;\n\n root.left = build(io, ioStart, rootIdx - 1, \n po, poStart, poStart + numsAtLeft - 1);\n\n root.right = build(io, rootIdx + 1, ioEnd, \n po, poStart + numsAtLeft, poEnd - 1);\n return root;\n }\n}\n```\n--- \n### Complexity analysis:\n##### Time complexity: $$O(n)$$\n> A $$O(n)$$ to populate the hashmap.\n\n> Another $$O(n)$$ to build the tree, assuming at worst case we build a skewed tree of height $$n$$.\n\n> *We have used a hashmap so that we can access the root indices from the inorder array in constant time. Otherwise we would have had to traverse the ionorder array everytime to get the root index which cost us another $$O(n)$$ time making our tree building process $$O(n^2)$$. So in order to avoid that we used a hashmap.*\n\n> So, final time complexity: $$O(n) + O(n) => O(n)$$ \n\n##### Space complexity: $$O(n)$$\n> We use a hashmap of size $$n$$.\n\n> Our recursive stack space can cost us a space complexity of $$O(n)$$\nassuming we uild a skewed tree of height $$n$$.\n\n> So final time complexity: $$O(n) + O(n) => O(n)$$\n---\n Do comment if you have any doubt \uD83D\uDC4D\uD83C\uDFFB\n
| 4 | 0 |
['Hash Table', 'Divide and Conquer', 'Tree', 'Binary Tree', 'Java']
| 1 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
✅ Concise Java Soution Explained 🚀 | Beats 100% submissions
|
concise-java-soution-explained-beats-100-bpbm
|
Intuition\nInorder is L Root R\nPostorder is L R Root\n\nSo the last element of the post order traversal will give us the root\nwe can find the root elem
|
nikeMafia
|
NORMAL
|
2023-03-16T12:37:15.910482+00:00
|
2023-03-16T14:48:38.970712+00:00
| 1,236 | false |
# Intuition\nInorder is L Root R\nPostorder is L R Root\n\nSo the last element of the post order traversal will give us the root\nwe can find the root element index in inorder to indentify the root elements left and right subtree\n\ninorder = [9,**3**,15,20,7]\npostorder = [9,15,7,20, **3** ]\n\n----\n#root is 3\nso index 0 to 0(rootIndex-1) is left subtree that is 9\nand index 2(rootIndex+1) to 4 in inorder is right subtree\n\nso we divided the sub problem in sub-parts and now can recursively call it\n\n----\n**NOTE**\nIn my case i have called right subtree first while solving and have not considered start and end of postorderIndex is because we know that in post traversal order L R Root . If we have solved for root next element would be right(i.e right subtree) and then left(i.e left subtree), so that is the reason.\n\n\n- Time complexity:\nO(n) since we visiting every element of array\n\n- Space complexity\nO(n) storing data inorder data in hashmap\n\n# Code\n```\nclass Solution {\n int postorderIndex;\n Map<Integer, Integer> inorderIndexMap;\n public TreeNode buildTree(int[] inorder, int[] postorder) {\n postorderIndex = postorder.length - 1;\n // build a hashmap to store value -> its index relations\n inorderIndexMap = new HashMap<>();\n for (int i = 0; i < inorder.length; i++) {\n inorderIndexMap.put(inorder[i], i);\n }\n\n return arrayToTree(postorder, 0, postorder.length - 1);\n }\n\n private TreeNode arrayToTree(int[] postorder, int left, int right) {\n // if there are no elements to construct the tree\n if (left > right) return null;\n\n // select the postorder_index element as the root and decrement it\n int rootValue = postorder[postorderIndex--];\n TreeNode root = new TreeNode(rootValue);\n\n // build right and left subtree\n // excluding inorderIndexMap[rootValue] element because it\'s the root\n root.right = arrayToTree(postorder, inorderIndexMap.get(rootValue) + 1, right);\n root.left = arrayToTree(postorder, left, inorderIndexMap.get(rootValue) - 1);\n return root;\n }\n}\n```
| 4 | 0 |
['Recursion', 'Java']
| 1 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
easy rust recursive
|
easy-rust-recursive-by-skymnok-l6wo
|
Code\n\nuse std::rc::Rc;\nuse std::cell::RefCell;\nimpl Solution {\n pub fn build_tree(inorder: Vec<i32>, postorder: Vec<i32>) -> Option<Rc<RefCell<TreeNode>
|
skymnok
|
NORMAL
|
2023-03-16T07:50:06.328044+00:00
|
2023-03-16T07:53:02.432844+00:00
| 264 | false |
# Code\n```\nuse std::rc::Rc;\nuse std::cell::RefCell;\nimpl Solution {\n pub fn build_tree(inorder: Vec<i32>, postorder: Vec<i32>) -> Option<Rc<RefCell<TreeNode>>> {\n Self::builder(&inorder, &postorder)\n }\n pub fn builder(inorder: &[i32], mut postorder: &[i32]) -> Option<Rc<RefCell<TreeNode>>>{\n if inorder.is_empty() {\n return None\n }\n\n let mut root = TreeNode::new(*postorder.last().unwrap());\n\n let in_split = inorder.split(|&val| val == root.val).collect::<Vec<&[i32]>>();\n\n root.left = Self::builder(in_split[0], &postorder[..in_split[0].len()]);\n root.right = Self::builder(in_split[1], &postorder[in_split[0].len()..postorder.len()-1]);\n\n Some(Rc::new(RefCell::new(root)))\n }\n}\n```
| 4 | 0 |
['Rust']
| 0 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
Java | DFS | Beats > 97% | Clean code
|
java-dfs-beats-97-clean-code-by-judgemen-iqy0
|
Complexity\n- Time complexity: O(n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(n)\n Add your space complexity here, e.g. O(n) \n\n# Co
|
judgementdey
|
NORMAL
|
2023-03-16T06:57:56.437839+00:00
|
2024-07-23T23:15:09.265302+00:00
| 218 | false |
# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n int i;\n Map<Integer, Integer> map = new HashMap<>();\n\n private TreeNode buildTree(int[] postorder, int l, int r) {\n if (l > r) return null;\n\n var m = map.get(postorder[i]);\n var node = new TreeNode(postorder[i--]);\n\n node.right = buildTree(postorder, m+1, r);\n node.left = buildTree(postorder, l, m-1);\n\n return node;\n }\n\n public TreeNode buildTree(int[] inorder, int[] postorder) {\n for (var i=0; i < inorder.length; i++)\n map.put(inorder[i], i);\n \n i = postorder.length - 1;\n return buildTree(postorder, 0, inorder.length - 1);\n }\n}\n```
| 4 | 0 |
['Depth-First Search', 'Recursion', 'Binary Tree', 'Java']
| 1 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
Simple Python solution using recursion!!! 100% working.
|
simple-python-solution-using-recursion-1-issh
|
Python dictionary can be used in place of index to get linear time complexity.\n\n\n# Code\n\n# Definition for a binary tree node.\n# class TreeNode:\n# def
|
enigmatic__soul
|
NORMAL
|
2023-01-28T15:06:24.205117+00:00
|
2023-01-28T15:06:24.205160+00:00
| 424 | false |
**Python dictionary can be used in place of index to get linear time complexity.**\n\n\n# Code\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass Solution:\n def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:\n if not inorder or not postorder:\n return None\n root=TreeNode(postorder.pop())\n mid=inorder.index(root.val)\n root.left=self.buildTree(inorder[:mid],postorder[:mid])\n root.right=self.buildTree(inorder[mid+1:],postorder[mid:])\n return root\n\n\n\n\n\n```
| 4 | 0 |
['Python3']
| 0 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
Python with and without dictionary solution
|
python-with-and-without-dictionary-solut-cnmp
|
Solution 1:\n\ndef buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:\n if inorder:\n node = TreeNode(postorder[
|
deepapandey
|
NORMAL
|
2022-09-20T15:22:04.284002+00:00
|
2022-09-20T15:22:04.284045+00:00
| 356 | false |
**Solution 1:**\n```\ndef buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:\n if inorder:\n node = TreeNode(postorder[-1])\n idx = inorder.index(postorder.pop())\n node.right = self.buildTree(inorder[idx+1:], postorder)\n node.left = self.buildTree(inorder[0:idx], postorder)\n return node\n```\n**Solution 2:**\n```\ndef buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:\n dic = {}\n \n for idx, val in enumerate(inorder):\n dic[val] = idx\n \n def f(start, end):\n if start > end:\n return None\n node = TreeNode(postorder.pop())\n index = dic[node.val]\n node.right = f(index+1, end)\n node.left = f(start, index-1)\n return node\n\n return f(0, len(inorder)-1)\n```
| 4 | 0 |
['Python']
| 0 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
Java Simple Solution || Recursive Approach
|
java-simple-solution-recursive-approach-hoiab
|
\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n
|
Samarth-Khatri
|
NORMAL
|
2022-07-14T10:14:36.459945+00:00
|
2022-07-14T10:14:36.459989+00:00
| 598 | false |
```\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n * TreeNode(int val) { this.val = val; }\n * TreeNode(int val, TreeNode left, TreeNode right) {\n * this.val = val;\n * this.left = left;\n * this.right = right;\n * }\n * }\n */\nclass Solution {\n public TreeNode buildTree(int[] inorder, int[] postorder) {\n int n = postorder.length;\n return rBuildTree(postorder,0,n-1,inorder,0,n-1);\n }\n \n // psi -> Postorder starting index\n // pei -> Postorder ending index\n // isi -> Inorder starting index\n // iei -> Inorder ending index\n // colse -> Count of Left Sub Tree elements\n private TreeNode rBuildTree(int[] postorder, int psi, int pei, int[] inorder, int isi, int iei) {\n if(isi>iei)\n return null;\n int idx = isi;\n while(inorder[idx]!=postorder[pei])\n idx++;\n \n int colse = idx-isi;\n TreeNode node = new TreeNode(postorder[pei]);\n \n node.left = rBuildTree(postorder,psi,psi+colse-1,inorder,isi,idx-1); // left subtree call\n node.right = rBuildTree(postorder,psi+colse,pei-1,inorder,idx+1,iei); // right subtree call\n \n return node;\n }\n}\n```
| 4 | 0 |
['Recursion', 'Java']
| 0 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
C++ | Easy and Clean code | 15ms | Faster than 88.23%
|
c-easy-and-clean-code-15ms-faster-than-8-j1cg
|
\nclass Solution {\npublic:\n TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {\n if(inorder.size()!=postorder.size())\n
|
Akash268
|
NORMAL
|
2022-02-27T18:53:53.166096+00:00
|
2022-02-27T18:53:53.166138+00:00
| 631 | false |
```\nclass Solution {\npublic:\n TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {\n if(inorder.size()!=postorder.size())\n return NULL;\n map<int,int> hm;\n for(int i=0;i<inorder.size();i++)\n hm[inorder[i]]=i;\n TreeNode* root=solve(inorder,0,inorder.size()-1,postorder,0,postorder.size()-1,hm);\n return root;\n }\n TreeNode* solve(vector<int> &inorder,int is,int ie,vector<int> &postorder,int ps,int pe,map<int,int> &hm){\n if(ps>pe || is>ie)\n return NULL;\n TreeNode* root=new TreeNode(postorder[pe]);\n int inRoot=hm[postorder[pe]];\n int numsleft=inRoot-is;\n root->left=solve(inorder,is,inRoot-1,postorder,ps,ps+numsleft-1,hm);\n root->right=solve(inorder,inRoot+1,ie,postorder,ps+numsleft,pe-1,hm);\n return root;\n }\n};\n```
| 4 | 0 |
['Recursion', 'C', 'Binary Tree', 'C++']
| 0 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
Recursive solution Python with O(N) time
|
recursive-solution-python-with-on-time-b-id2r
|
\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.lef
|
kryuki
|
NORMAL
|
2021-11-21T00:25:11.359782+00:00
|
2022-01-02T16:01:29.551414+00:00
| 321 | false |
```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\n\'\'\'\n 0 1 2 3 4\ninorder = [9,3,15,20,7]\n l r\n l r l r\n\t\t\t\npostorder = [9,15,7,20,3]\n l r\n l r l r\n\'\'\'\n\nclass Solution:\n def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:\n def rec(in_l, in_r, post_l, post_r):\n if in_l > in_r:\n return None\n if in_l == in_r:\n return TreeNode(inorder[in_l])\n \n pivot_val = postorder[post_r]\n left_node_nums = inorder_dict[pivot_val] - in_l\n \n pivot_node = TreeNode(pivot_val)\n pivot_node.left = rec(in_l, inorder_dict[pivot_val] - 1, post_l, post_l + left_node_nums - 1)\n pivot_node.right = rec(inorder_dict[pivot_val] + 1, in_r, post_l + left_node_nums, post_r - 1)\n \n return pivot_node\n \n inorder_dict = {val : idx for idx, val in enumerate(inorder)}\n \n N = len(postorder)\n return rec(0, N - 1, 0, N - 1)\n```
| 4 | 0 |
['Recursion', 'Python', 'Python3']
| 1 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
Easy C++ solution 99% faster || commented
|
easy-c-solution-99-faster-commented-by-s-8k61
|
\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0)
|
saiteja_balla0413
|
NORMAL
|
2021-07-05T06:32:31.175507+00:00
|
2021-07-05T06:32:31.175551+00:00
| 411 | false |
```\n/**\n * Definition for a binary tree node.\n * struct TreeNode {\n * int val;\n * TreeNode *left;\n * TreeNode *right;\n * TreeNode() : val(0), left(nullptr), right(nullptr) {}\n * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}\n * };\n */\nclass Solution {\npublic:\n int postInd;\n TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {\n postInd=postorder.size()-1;\n \n //map all the elements of inorder to their index\n unordered_map<int,int> mp;\n for(int i=0;i<inorder.size();i++)\n mp[inorder[i]]=i;\n \n return helper(0,inorder.size()-1,mp,postorder);\n }\n TreeNode* helper(int start,int end,unordered_map<int,int>& mp,vector<int>& postorder)\n {\n if(start>end)\n return NULL;\n int curr=postorder[postInd];\n TreeNode* node=new TreeNode(curr);\n postInd--;\n node->right=helper(mp[curr]+1,end,mp,postorder);\n node->left=helper(start,mp[curr]-1,mp,postorder);\n return node;\n }\n};\n```\n**Upvote if this helps you :)**
| 4 | 0 |
['C']
| 0 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
faster than 100% very well explained c++ solution using recursion
|
faster-than-100-very-well-explained-c-so-zhaa
|
/\n Definition for a binary tree node.\n struct TreeNode {\n int val;\n TreeNode left;\n TreeNode right;\n TreeNode() : val(0), left(nullp
|
pragya_anand
|
NORMAL
|
2021-04-24T19:14:09.634754+00:00
|
2021-04-24T19:14:09.634788+00:00
| 337 | false |
/\n Definition for a binary tree node.\n struct TreeNode {\n int val;\n TreeNode left;\n TreeNode right;\n TreeNode() : val(0), left(nullptr), right(nullptr) {}\n TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}\n TreeNode(int x, TreeNode left, TreeNode right) : val(x), left(left), right(right) {}\n };\n /\n\nclass Solution {\npublic:\n int postindex;//to traverse the postorder vector\n unorderedmap<int,int>m;//to store the index value of inorder\n TreeNode arraytotree(vector<int>&postorder,int left,int right)\n {\n //terminating conditon of the recursive call\n if(left>right)\n return NULL;\n //postorderindex will give root value as preorder traversal is LEFT->RIGHT->ROOT\n int rootval=postorder[postindex];\n postindex--;//decrementing by one\n // rootval will be root of tree so declaring tree with rootval.\n TreeNode root=new TreeNode(rootval);\n //recursively call fuction on the left and right subtree \n root->right=arraytotree(postorder,m[rootval]+1,right);//right tree will contain all the element right to the rootval in inorder vector\n root->left=arraytotree(postorder,left,m[rootval]-1);//left tree will contain all the element left to the rootval in inorder vector\n return root;\n }\n TreeNode buildTree(vector<int>& inorder, vector<int>& postorder) {\n postindex=postorder.size()-1;\n for(int i=0;i<inorder.size();i++)\n m[inorder[i]]=i;//storing the index val for postorder traversal\n TreeNode root=arraytotree(postorder,0,postorder.size()-1);\n return root;\n }\n};\nplz upvote if you find it useful....that would be motivating...
| 4 | 3 |
['Recursion', 'C', 'C++']
| 0 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
Java Solution
|
java-solution-by-balenduteterbay-0b9r
|
java\n\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode(
|
balenduteterbay
|
NORMAL
|
2020-12-07T12:17:19.786010+00:00
|
2020-12-07T12:17:19.786049+00:00
| 434 | false |
java\n```\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode() {}\n * TreeNode(int val) { this.val = val; }\n * TreeNode(int val, TreeNode left, TreeNode right) {\n * this.val = val;\n * this.left = left;\n * this.right = right;\n * }\n * }\n */\nclass Solution {\n public TreeNode buildTree(int[] inorder, int[] postorder) {\n if(postorder.length == 0)\n return null;\n if(postorder.length == 1)\n return new TreeNode(postorder[0]);\n return helper(postorder.length-1, 0, inorder.length-1, postorder, inorder);\n }\n public TreeNode helper( int postend, int instart, int inend, int[] postorder, int[] inorder) {\n if(postend<0 || instart>inend)\n return null;\n TreeNode node = new TreeNode(postorder[postend]);\n int index=0;\n for(int i=instart;i<=inend;i++) {\n \n if(inorder[i] == node.val) {\n index=i;\n break;\n }\n }\n node.left = helper(postend - 1 - inend + index, instart, index-1, postorder, inorder);\n node.right = helper(postend-1, index+1, inend, postorder, inorder);\n return node;\n }\n}\n```
| 4 | 0 |
[]
| 0 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
My Accepted Swift Solutiın
|
my-accepted-swift-solutiin-by-alptekin35-5g4d
|
\nclass Solution {\n var idx:Int = 0\n func buildTree(_ inorder: [Int], _ postorder: [Int]) -> TreeNode? {\n if inorder.count != postorder.count {r
|
alptekin35
|
NORMAL
|
2020-01-28T20:17:49.481787+00:00
|
2020-01-28T20:17:49.481822+00:00
| 256 | false |
```\nclass Solution {\n var idx:Int = 0\n func buildTree(_ inorder: [Int], _ postorder: [Int]) -> TreeNode? {\n if inorder.count != postorder.count {return nil}\n if inorder.count == 0 {return nil}\n idx = postorder.count - 1\n return helper(inorder, postorder, 0, idx)\n }\n \n func helper(_ inorder: [Int], _ postorder: [Int], _ start:Int, _ end: Int)-> TreeNode? {\n if start > end {return nil}\n let node = TreeNode(postorder[idx])\n idx -= 1\n if start == end { return node }\n let index = findIdx(inorder, node.val, end)\n node.right = helper(inorder, postorder, index+1, end)\n node.left = helper(inorder, postorder, start, index-1)\n return node\n }\n \n func findIdx(_ inorder: [Int], _ val:Int, _ end:Int)->Int{\n for i in (0...end).reversed(){\n if inorder[i] == val{ return i }\n }\n return 0\n }\n}\n```
| 4 | 0 |
['Swift']
| 0 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
Java using HashMap
|
java-using-hashmap-by-aneeshdalvi-5hea
|
\tclass Solution {\n\t\t\tint n = 0;\n\t\t\tMap hm = new HashMap<>();\n\t\t\tpublic TreeNode buildTree(int[] inorder, int[] postorder) {\n\t\t\t\tn = inorder.le
|
aneeshdalvi
|
NORMAL
|
2019-07-19T02:13:03.334561+00:00
|
2019-07-19T02:13:03.334598+00:00
| 282 | false |
\tclass Solution {\n\t\t\tint n = 0;\n\t\t\tMap<Integer, Integer> hm = new HashMap<>();\n\t\t\tpublic TreeNode buildTree(int[] inorder, int[] postorder) {\n\t\t\t\tn = inorder.length-1;\n\t\t\t\tfor (int i=0; i< inorder.length; i++){\n\t\t\t\t\thm.put(inorder[i], i); \n\t\t\t\t}\n\t\t\t\treturn buildTree(postorder, inorder, 0, inorder.length-1);\n\n\t\t\t}\n\n\t\t\tprivate TreeNode buildTree(int[] postorder, int[] inorder, int start, int end) {\n\t\t\t\tif (start > end) return null;\n\n\t\t\t\tTreeNode root = new TreeNode(postorder[n]);\n\t\t\t\tn--;\n\n\t\t\t\tif (start == end) return root;\n\n\t\t\t\tint index = hm.get(root.val);\n\n\t\t\t\troot.right = buildTree(postorder, inorder, index + 1, end);\n\t\t\t\troot.left = buildTree(postorder, inorder, start, index - 1);\n\n\t\t\t\treturn root;\n\n\t\t\t}\n\t}
| 4 | 0 |
[]
| 1 |
check-if-digits-are-equal-in-string-after-operations-ii
|
🤯 How to notice that it's Pascal's triangle and compute it if you're not a mathematician 🤯
|
how-to-notice-that-its-pascals-triangle-zmb0a
|
IntuitionWhen trying a new problem like this, I recommend going through some examples by hand to build up your intuition. I went through the examples given, but
|
VehicleOfPuzzle
|
NORMAL
|
2025-02-23T07:24:31.328102+00:00
|
2025-02-24T00:28:31.366359+00:00
| 4,142 | false |
# Intuition
When trying a new problem like this, I recommend going through some examples by hand to build up your intuition. I went through the examples given, but rather than simplifying the numbers at every step, I kept track of how many times each original digit was included in the final results, i.e. its coefficient. The reason I did this is because I'd like to quickly be able to calculate the coefficient -- if we can calculate all the coefficients quickly then we can find out what the final two digits are without going through each intermediate step (which would be $O(n^2)$ complexity, too expensive for the bounds of this problem.)
Let's take a look together. I'm going to omit the mod 10 because we can apply it at the end. It's the intermediate steps that are most interesting.
## Example 1
For 3902, the process goes like:
3, 9, 0, 2
3 + 9, 9 + 0, 0 + 2
(3 + 9) + (9 + 0), (9 + 0) + (0 + 2)
Grouping the digits together we see that the final two digits are:
1 * 3 + 2 * 9 + 1 * 0
and
9 * 1 + 2 * 0 + 1 * 2
So the coefficients of the digits are 1, 2, 1.
---
## Example 2
For 34789, the process goes like:
3, 4, 7, 8, 9
3 + 4, 4 + 7, 7 + 8, 8 + 9
(3 + 4) + (4 + 7), (4 + 7) + (7 + 8), (7 + 8) + (8 + 9)
((3 + 4) + (4 + 7)) + ((4 + 7) + (7 + 8)), ((4 + 7) + (7 + 8)) + ((7 + 8) + (8 + 9))
Conveniently the digits are all unique so grouping the coefficients is not too bad:
1 * 3 + 3 * 4 + 3 * 7 + 1 * 8
and
1 * 4 + 3 * 7 + 3 * 8 + 1 * 9
So the coefficients of the digits are 1, 3, 3, 1.
---
If you're familiar with Pascal's triangle and binomial coefficients, this might already be enough to notice the pattern. But if not, it's totally cool to go through a larger example. Let's try a 6-digit string, but let's use abstract digits:
A, B, C, D, E, F
A + B, B + C, C + D, D + E, E + F
A + 2B + C, B + 2C + D, C + 2D + E, D + 2E + F
A + 3B + 3C + D, B + 3C + 3D + E, C + 3D + 3E + F
A + 4B + 6C + 4D + E, B + 4C + 6D + 4E + F
We can see that the coefficients of the digits in the last row are 1, 4, 6, 4, 1.
Moreover, focusing on the very first element in each row, we can see the entire history of coefficients for smaller examples:
A
A + B
A + 2B + C
A + 3B + 3C + D
A + 4B + 6C + 4D + E
Or:
1
1, 1
1, 2, 1
1, 3, 3, 1
1, 4, 6, 4, 1
Can you predict what the next row of coefficients would be, without having to go through an example? Think about what's happening: at each step we are squashing a bunch of digits together and we can add the coefficients, but we have to do so at an offset, to combine the like digits. A + B squashed together with B + C becomes A + 2B + C. And A + 2B + C squashed together with B + 2C + D becomes A + 3B + 3C + D.
So to get the next row we need to squash two copies of 1, 4, 6, 4, 1 at an offset. Expressed vertically we sum:
1, 4, 6, 4, 1, 0
0, 1, 4, 6, 4, 1
To get:
1, 5, 10, 10, 5, 1
We can verify that these are the correct coefficients by adding the last two digits together that we already computed above, A + 4B + 6C + 4D + E and B + 4C + 6D + 4E + F which indeed become A + 5B + 10C + 10D + 5E + F with coefficients 1, 5, 10, 10, 5, 1.
If we were mathematicians, we might consider a formal proof at this point, but as software engineers, this is good enough to move on.
# Approach
Alright, so if we can figure out the coefficients quickly then we could compute the last two digits with $O(n)$ complexity: just iterate over the digits, multiply by the coefficient, and add. Mod the sum by 10 at each step to keep it one digit. Awesome! So how do we figure out the coefficients quickly?
We can compute each row of coefficients from the previous row. However, if we computed every previous row, thus building the entire (Pascal's) triangle up to the point we care about, that would be $O(n^2)$ complexity. A triangle is half of a square. We could take advantage of symmetry to save another factor of 2 (did you notice that each row of coefficients is the same forwards and backwards?) but that's still not good enough for these bounds. We need some way to compute the last row and last row only.
This is where it kinda helps to know that Pascal's triangle is very related to the binomial coefficients and the combinations formula. Our 1, 4, 6, 4, 1 row is really $\binom{4}{0}$, $\binom{4}{1}$, $\binom{4}{2}$, $\binom{4}{3}$, $\binom{4}{4}$ in disguise. If you knew this then you have a big advantage and can leap to binomial coefficients quickly. If you didn't know this, I recommend [reading about it](https://en.wikipedia.org/wiki/Pascal%27s_triangle#Combinations), but for an idea that might help you figure it out, consider the following:
We started with A, B, C, D, E, F and after squashing digits, our first digit becomes A + 4B + 6C + 4D + E. How come there's only one A but 6 Cs? Well the A in the original digits has only one possible path through the triangle: left, left, left, left. But the C in the original digits has more. To end up in the middle of the pack it needs to take just as many steps left as it does right, but it could do LLRR, RRLL, LRLR, or 3 more options. Expressed combinatorically we must choose 2 out of its 4 steps to be left: 4 choose 2. Hello, combinations formula!
## Division is annoying
To compute combinations, we can use the formula $\binom{n}{k} = \frac{n!}{k! (n-k)!}$. Since we need to do this for all the possible values of $k$, we can compute all of the relevant factorials. The numbers will get rather large, but since we only care about single digits we could mod by 10 along the way. Problem with that approach is it'll mess up our division. Whereas multiplication plays nicely with modulo in that `(a * b) % m == (a % m) * (b % m)` give or take a mod, this is not true for division.
If you didn't know that, I recommend using hours and minutes to practice your intuition for mod, because if you just focus on the number of minutes ignoring the hours, you're doing mod 60 in real life. Here's an example: if I multiply 497 hours and 12 minutes times 7, how many minutes past a whole hour will I have? In other words, what's `((497 * 60 + 12) * 7) % 60`? Hopefully you didn't multiply 497 times 7 to answer -- the hours cancel out if we're focusing on the minutes, i.e. `60 % 60` is just zero.
Now let's try a division. How many minutes past a whole hour will I have if I divide X hours by 4? By the previous logic we might think that the hours cancel out, because `60 % 60` is still zero, but it depends on the value of X. For X = 1, or 1 hour divided by 4, we'll get 15 minutes: `((1 * 60 ) / 4) % 60` is 15. However for X = 3 hours, we'll get 45 minutes: `((3 * 60) / 4) % 60` is 45.
Ok, now that you hopefully believe me that dividing factorials mod 10 isn't trivial, what do we do? Turns out there are situations in which we can divide safely, by turning the divisions into multiplications. For example instead of dividing by 7 we can multiply by 3. Huh???? It's true! Let's say we wanted to know what 864192 / 7 is mod 10 (that number is divisible by 7, I promise). Well, I'm claiming that it's going to be same as 864192 * 3 mod 10. Since this is a multiplication, we can take the mod early and say that it's 2 * 3 or 6. Check it, I dare you!
This works because 7 and 3 cancel each other out when multiplying mod 10. Basically I'm saying that if you multiply some number by 7, and then multiply the result by 3, the final number will end with the same digit as the original number. That's because multiplying it by 7 and then multiplying it by 3 is the same as just outright multiplying it by 21, and since we're focusing on the last digit, multiplying by 21 is no different from multiplying by 1.
In fancy terms, 7 and 3 are multiplicative inverses mod 10. So instead of doing `(x / 7) % 10`, we can compute `(x / 7 * (7 * 3)) % 10`, without affecting the result. As long as `x` is divisible by 7, it's safe to cancel out the division by 7 and the multiplication by 7 to get `(x * 3) % 10`.
So we've figured out that instead of dividing by 7 we can multiply by 3. What else can we divide by? Well, by the symmetric argument, instead of dividing by 3 we can multiply by 7. What else? We can safely divide by 1 by doing nothing. (In fancy terms: 1 is its own multiplicative inverse, just like in standard arithmetic.) Can we divide by any other digits? There's one more. We can replace division by 9 with multiplication by 9, since 9 is also its own multiplicative inverse. Verify that 9 * 9 ends with a 1, or if you want your mind blown consider that 9 is the same as -1 as far as mod 10 is concerned, and -1 is its own multiplicative inverse as well: in standard arithmetic multiplying times -1 and dividing by -1 are equivalent.
But what about all the other digits? How do we divide by 2, 4, 5, 6, or 8? Or by 0? None of these digits have a multiplicative inverse mod 10. That is, there's no way to multiply any of those digits by something and have the result end in 1. For the even digits, any product will forever stay even. And for 5, any product will end either in 5 or in 0.
## Let's work around 2s and 5s
Finally we get to the punch line. Since even numbers and 5s make division annoying, we treat them specially. We won't just naively express each factorial mod 10, we'll express them as tuples of the form (number of twos, number of fives, everything else mod 10). For example, we'll express 1! as (0, 0, 1) because it's composed of 0 twos, 0 fives, and the rest of the product is a 1. 2! = 2 will be expressed as (1, 0, 1) because it's composed of 1 two multiplied by 0 fives multiplied by 1. 3! = 6 will be expressed as (1, 0, 3) i.e. $(2^1)(5^0)(3)$, 4! = 24 will be expressed as (3, 0, 3) i.e. $(2^3)(5^0)(3)$, 5! = 120 will include our first five as (3, 1, 3) also known as $(2^3)(5^1)(3)$.
These tuples are straightforward to multiply:
```python3 []
def mult(a, b):
return (
a[0] + b[0],
a[1] + b[1],
(a[2] * b[2]) % 10,
)
```
...and also to divide, because the third element is now guaranteed to be 1, 3, 7, or 9, and we know how to divide by those:
```python3 []
INV = {
1: 1,
3: 7,
7: 3,
9: 9,
}
def div(a, b):
return (
a[0] - b[0],
a[1] - b[1],
(a[2] * INV[b[2]]) % 10,
)
```
To then turn such a tuple into a single digit, we take advantage of the fact that powers of 2 with a positive exponent end with 2, 4, 8, 6, 2, 4, 8, 6, ... ad infinitum. And powers of 5 with a positive exponent all end in 5:
```python3 []
TWOS = [2, 4, 8, 6]
FIVES = [5]
def simplify(tup):
twos, fives, res = tup
if twos:
res = (res * TWOS[(twos - 1) % len(TWOS)]) % 10
if fives:
res = (res * FIVES[(fives - 1) % len(FIVES)]) % 10
return res
```
## Summary of complete approach
1. Compute factorials from 0 to n, expressed as tuples of (number of twos, number of fives, everything else mod 10).
2. Compute binomial coefficients using the combinations formula. Use modular multiplicative inverses to divide the "everything else" part, then simplify to a single digit mod 10.
3. Multiply the digits in the input by the coefficients to get the final two digits and compare them!
## But how do I figure this out in an interview?
You don't. This isn't a software engineering interview problem, it's a math problem. If an interviewer expects you to know this, then you're presumably applying to an applied math position of some kind, so you eat binomial coefficients for breakfast.
Enjoy the math for its beauty and don't worry about seeing something like this in a software engineering interview.
# Complexity
- Time complexity: $O(n)$ if you're not lazy in step 1. I was lazy in step 1 and recomputed the number of twos and fives each time, it's small enough to not matter for these bounds. But you can be clever and do some caching along the way. Specifically notice that the number of twos in the decomposition of some even number N is one more than the number of twos in the decomposition of N / 2.
- Space complexity: $O(n)$ for the factorials and coefficients.
# Code
Here's [my submission](https://leetcode.com/problems/check-if-digits-are-equal-in-string-after-operations-ii/submissions/1552448975/) as I originally wrote it, apologies that it's in Python:
```python3 []
INV = {
1: 1,
3: 7,
7: 3,
9: 9,
}
def mult(a, b):
return (
a[0] + b[0],
a[1] + b[1],
(a[2] * b[2]) % 10,
)
def div(a, b):
return (
a[0] - b[0],
a[1] - b[1],
(a[2] * INV[b[2]]) % 10,
)
def red(it):
return sum((a * b) % 10 for a, b in it) % 10
TWOS = [2, 4, 8, 6]
FIVES = [5]
def simplify(tup):
twos, fives, res = tup
if twos:
res = (res * TWOS[(twos - 1) % len(TWOS)]) % 10
if fives:
res = (res * FIVES[(fives - 1) % len(FIVES)]) % 10
return res
class Solution:
def hasSameDigits(self, s: str) -> bool:
n = len(s) - 2
facts = [(0, 0, 1)]
while n >= len(facts):
num = len(facts)
twos = 0
while num % 2 == 0:
num //= 2
twos += 1
fives = 0
while num % 5 == 0:
num //= 5
fives += 1
facts.append(mult(facts[-1], (twos, fives, num)))
pascal = []
for k in range(n + 1):
pascal.append(simplify(div(div(facts[n], facts[k]), facts[n - k])))
a = red(zip(map(int, s), pascal))
b = red(zip(map(int, s[1:]), pascal))
return a == b
```
| 127 | 0 |
['Python3']
| 17 |
check-if-digits-are-equal-in-string-after-operations-ii
|
✅✅✅Easy To Understand C++ Code Using Binomial Coefficients
|
easy-to-understand-c-code-using-binomial-0282
|
IntuitionThe problem requires reducing a string of digits by repeatedly summing pairs of consecutive digits modulo 10 until only two digits remain. We need to c
|
insane_prem
|
NORMAL
|
2025-02-23T04:02:45.624368+00:00
|
2025-02-23T04:02:45.624368+00:00
| 5,433 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The problem requires reducing a string of digits by repeatedly summing pairs of consecutive digits modulo 10 until only two digits remain. We need to check if these final two digits are identical.
The key observation is that the operations performed resemble a binomial expansion, where each digit contributes to the final result based on the number of ways it can be formed. Therefore, the problem can be solved efficiently using properties of binomial coefficients modulo 10.
# Approach
<!-- Describe your approach to solving the problem. -->
1. Binomial Coefficients Modulo 10:
- The contribution of each digit to the final two digits depends on the number of ways it can appear, which can be calculated using binomial coefficients.
- Since we're interested in the last two digits, we only need the coefficients modulo 10.
2. Efficient Computation Using Lucas' Theorem:
- To calculate binomial coefficients modulo 10, we split the problem into calculations modulo 2 and 5 (since 10 = 2 × 5).
- Lucas' Theorem is used to efficiently compute binomial coefficients modulo prime powers.
- binmod2(n, k): Computes binomial coefficient modulo 2.
- binmod5(n, k): Computes binomial coefficient modulo 5 using factorial properties and modular inverses.
- Combine the results using the Chinese Remainder Theorem to get the result modulo 10 (binmod10(n, k)).
3. Calculate Final Two Digits:
- Use the precomputed binomial coefficients to accumulate the contribution of each digit in the original string.
- Keep track of the contributions to the last two digits (s1 and s2) using modular arithmetic.
4. Check and Return Result:
- Return true if the final two digits are the same (s1 == s2), otherwise return false.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int binmod10(int n, int k) {
int mod2 = binmod2(n, k);
int mod5 = binmod5(n, k);
for (int i = 0; i < 10; i++) {
if (i % 2 == mod2 && i % 5 == mod5)
return i;
}
return 0;
}
int binmod2(int n, int k) {
while (k > 0) {
if ((k & 1) > (n & 1))
return 0;
n >>= 1;
k >>= 1;
}
return 1;
}
int binmod5(int n, int k) {
int res = 1;
while (n > 0 || k > 0) {
int nd = n % 5;
int kd = k % 5;
if (kd > nd)
return 0;
res = (res * binsmall(nd, kd)) % 5;
n /= 5;
k /= 5;
}
return res;
}
int binsmall(int n, int k) {
if (k > n)
return 0;
int fact[5] = {1, 1, 2, 1, 4};
int numerator = fact[n];
int denominator = (fact[k] * fact[n - k]) % 5;
int deninv = 0;
for (int i = 0; i < 5; i++) {
if ((denominator * i) % 5 == 1) {
deninv = i;
break;
}
}
return (numerator * deninv) % 5;
}
bool hasSameDigits(string s) {
int L = s.size();
int m = L - 2;
int s1 = 0, s2 = 0;
for (int i = 0; i <= m; i++) {
int val = binmod10(m, i);
int d1 = s[i] - '0';
int d2 = s[i + 1] - '0';
s1 = (s1 + val * d1) % 10;
s2 = (s2 + val * d2) % 10;
}
return s1 == s2;
}
};
```
| 18 | 1 |
['C++']
| 7 |
check-if-digits-are-equal-in-string-after-operations-ii
|
[Python] Check mod2 and mod5
|
python-check-mod2-and-mod5-by-lee215-jr6m
|
ExplanationCalculate the mod of2and5separately.ComplexityTimeO(nlogn)SpaceO(1)
|
lee215
|
NORMAL
|
2025-02-23T06:08:42.059442+00:00
|
2025-02-23T06:08:42.059442+00:00
| 1,903 | false |
# **Explanation**
Calculate the mod of `2` and `5` separately.
# **Complexity**
Time `O(nlogn)`
Space `O(1)`
<br>
```py [Python3]
def hasSameDigits(self, s: str) -> bool:
def cal(a, mod):
count = 0
while a > 0 and a % mod == 0:
count += 1
a //= mod
return a % mod, count
def test(mod):
n = len(s)
res = 0
r = 1
c = 0
for i in range(n - 1):
if c == 0:
res += r * (int(s[i]) - int(s[i + 1]))
rr, cc = cal(n - 2 - i, mod)
r = r * rr % mod
c += cc
rr, cc = cal(i + 1, mod)
r = r * pow(rr, mod - 2, mod) % mod
c -= cc
return res % mod == 0
return test(2) and test(5)
```
| 13 | 2 |
['Python3']
| 2 |
check-if-digits-are-equal-in-string-after-operations-ii
|
[C++] Two methods: Lucas theorem vs Mod inv
|
c-two-methods-lucas-theorem-vs-mod-inv-b-8nho
|
ApproachThis is a surprisingly interesting problem from Leetcode. Most solutions use the Lucas theorem, however I also came accross a method not using it at all
|
zh_jerry_yu
|
NORMAL
|
2025-02-23T16:19:42.614246+00:00
|
2025-02-26T03:45:20.904770+00:00
| 1,233 | false |
# Approach
This is a surprisingly interesting problem from Leetcode. Most solutions use the Lucas theorem, however I also came accross a method not using it at all (credit to lee215). Since Lee's solution does not have explanation, I decided to make a post to explain the methods a bit better.
The problem: check whether $\sum_{i=0}^{n-2} {n-2 \choose i}(a_i-a_{i+1}) \equiv 0 \pmod {10}$.
First of all, we can make the observation that any two numbers $x \equiv y \pmod{n}$ if and only if $x \equiv y \pmod{n_1}$ and $x \equiv y \pmod{n_2}$, where $n = n_1n_2$ and $n_1,n_2$ are different prime numbers. This can be inferred from the Chinese Remainder Theorem, but is also kind of obvious. Therefore, the we can write a function `check` for $n_1=2$ and $n_2 = 5$.
In other words, equivalent problem: Check whether
$\sum_{i=0}^{n-2} {n-2 \choose i}(a_i-a_{i+1}) \equiv 0 \pmod {2}$ and
$\sum_{i=0}^{n-2} {n-2 \choose i}(a_i-a_{i+1}) \equiv 0 \pmod {5}$.
The implementation for `check` differs for the 2 methods.
(1) If we use Lucas thm (you can google it), then we just iterate through each digit of $n-2$ and $i$, very standard.
(2) If we don't want to use Lucas thm, we need to use standard modular inverse on the factorials. We have already broken 10 into primes 2 and 5, so we can apply Fermat Little Thm now. However, we know that $a^{p-1} \equiv 1 \pmod p$ only holds if $a$ and $p$ are coprime. For large p such as 1e9+7 or 998244353 (the usual culprits), this is always true for $n\leq 1e5$. But how do we make it work for $p=2,5$? The trick is to break the number into 2 components - one part is exponent of p, the other part is the remainder: $x = y p^t$. Then, we only perform modular inverse on the remainder part, and maintain the exponent as a separate variable.
# Complexity
- Time complexity: $O(nlogn)$ with constant depending on the exact implementation.
# Code (Lucas Thm)
```cpp []
class Solution { // lucas thm.
public:
int comb(int n, int r){ // for small n,r
if (r > n) { return 0; }
int res = 1;
for (int t = 1; t <= n; ++t) { res *= t; }
for (int t = 1; t <= r; ++t) { res /= t; }
for (int t = 1; t <= n - r; ++t) { res /= t; }
return res;
}
bool check(vector<int>& a, int mod){
int res = 0;
int n = a.size();
for (int i = 0; i != n; ++i){
// res += c(n-1, i) * ai
int ncr = 1;
int x = n - 1;
int y = i;
while (x && y){
ncr = ncr * comb(x % mod, y % mod) % mod;
x /= mod;
y /= mod;
}
res = (res + ncr * a[i]) % mod;
}
return res == 0;
}
bool hasSameDigits(string s) {
int n = s.size();
vector<int> a(n - 1);
for (int i = 0; i != n - 1; ++i){
a[i] = (s[i] - '0') - (s[i + 1] - '0');
a[i] = (a[i] + 10) % 10;
}
return check(a, 2) && check(a, 5);
}
};
```
# Code (Mod Inv)
```cpp []
class Solution { // does not use lucas theorem. main difficulty is that some numbers cannot calc mod inv directly, need to decompose.
public:
int modpow(int n, int p, int mod){
int res = 1;
while (p){
if (p & 1) { res = res * n % mod; }
n = n * n % mod;
p >>= 1;
}
return res;
}
pair<int, int> decompose(int x, int mod){
// decompose x into x = y * pow(mod, ct). so that we can calc mod inv of y (cannot directly calculate on x)
int ct = 0;
while (x % mod == 0){
x /= mod;
++ct;
}
return {x % mod, ct};
}
bool check(vector<int>& a, int mod){
int res = 0;
int n = a.size();
int ncr = 1; // maintains c(n - 1, i)
int ct = 0; // maintains the exponent part of mod
for (int i = 0; i != n; ++i){
if (ct == 0){ // ct >= 0
res = (res + a[i] * ncr) % mod;
}
// update ncr = ncr * (n - 1 - i) / (i + 1)
if (i == n - 1) { continue; } // guarantee the x fed to decompose() is pos.
pair<int, int> p1 = decompose(n - 1 - i, mod);
ncr = ncr * p1.first % mod;
ct += p1.second;
pair<int, int> p2 = decompose(i + 1, mod);
ncr = ncr * modpow(p2.first, mod - 2, mod) % mod;
ct -= p2.second;
}
return res == 0;
}
bool hasSameDigits(string s) {
int n = s.size();
vector<int> a(n - 1);
for (int i = 0; i != n - 1; ++i){
a[i] = (s[i] - '0') - (s[i + 1] - '0');
a[i] = (a[i] + 10) % 10;
}
return check(a, 2) && check(a, 5);
}
};```
| 10 | 0 |
['C++']
| 3 |
check-if-digits-are-equal-in-string-after-operations-ii
|
Compute combinatorial by factorization x=y*2^a*5^b with gcd(y,10)=1||beats 100%
|
compute-combinatorial-by-factorization-x-9qfl
|
IntuitionIt's the combinatorial deduction as picture
Combinatorial problem.ApproachSo far, it needs to check∑iCin−2(si−si+1)≡0(mod10)Since the the constrain
|
anwendeng
|
NORMAL
|
2025-02-23T12:14:32.523617+00:00
|
2025-02-24T06:58:04.280368+00:00
| 494 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
It's the combinatorial deduction as picture
Combinatorial problem.
# Approach
<!-- Describe your approach to solving the problem. -->
So far, it needs to check $\sum_i C^{n-2}_{i}(s_i-s_{i+1})\equiv 0 \pmod{10}$
Since the the constraints `3 <= s.length <= 10^5`, it needs some facts on `Number theory` to get the job done.
10=2*5 By Euler's thereom φ(10)=(5-1)(2-1)=4; the $x$ with $\gcd(10, x)=1$has the modular inverse $x^3$
During the computation for the combinatorial numbers $C^{n-2}_k\pmod{10}$, use the expression $x=y2^a5^b$ with $\gcd(y,10)=1$. Some functions are implemented for this task.
2nd C++ uses precomputation for $x^{-1}\pmod{10}$ with $\gcd(x, 10)=1$ which has elapsed time 4ms & beats 100%.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
$O(n)$
the computing for the exponents for 5 may have at worst $O(\log n)$ time for some $x$.
But it needs totally the number of dividings by 5 bounded above by
$n\times(1+\frac{1}{5}+\frac{1}{5^2}+\cdots)=\frac{5}{4}n$
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
$O(n)$
# Code
```cpp []
using int3 = array<int, 3>; // (y, a, b) where x = y * 2^a * 5^b and gcd(y,10) = 1
int3 C[100000];
class Solution {
public:
int3 factor(int x) {
int a = countr_zero((unsigned)x);
x >>= a;
int b = 0;
while (x % 5 == 0) {
x /= 5;
b++;
}
return {x % 10, a, b}; // Only keep mod 10 for y
}
int3 inverse(const int3& x) {
int x0 = x[0], a = x[1], b = x[2];
// Modular inverse under mod 10 using Euler's theorem (Euler-phi(10)=4)
int x0_inv = (x0*x0*x0) % 10; // x0^3 is inverse mod 10
return {x0_inv, -a, -b};
}
int3 mult(const int3& x, const int3& y) {
return {x[0]*y[0]%10, x[1]+y[1], x[2]+y[2]};
}
int toInt(const int3& x) { // mod 10
if (x[1] >= 1 && x[2] >= 1) return 0;
if (x[2] >= 1) return 5;
int B[4] = {6, 2, 4, 8}; // 2^x(mod 10) cycle
if (x[1] == 0) return x[0];
int B2 = B[x[1] % 4]; //
return x[0] * B2 % 10;
}
void compute_comb(int N) {
C[0] = {1, 0, 0};
if (N == 0) return; // Prevent C[N] access if N=0
C[N] = {1, 0, 0};
for (int k = 1; k <= N/2; k++) {
int3 P = factor(N-k + 1);
int3 Q = inverse(factor(k));
C[k]=C[N-k] = mult(mult(C[k-1], P), Q);
}
}
bool hasSameDigits(string& s) {
int n = s.size();
fill(C, C+(n-2), int3{0, 0, 0}); // Prevent overflow
compute_comb(n-2);
int sum=0;
for (int i=0; i <= n-2; i++) {
int C_val= (toInt(C[i])*(s[i]-s[i+1]))%10;
sum=(sum+C_val+10) % 10; // Ensure non-negative
}
// cout << sum << endl;
return sum == 0;
}
};
```
# C++||4ms beats 100%
```cpp []
using int3 = array<int, 3>; // (y, a, b) where x = y * 2^a * 5^b and gcd(y,10) = 1
int3 C[100000];
int inv10[10]={0, 1, 0, 7, 0, 0, 0, 3, 0, 9};// inv10[x]*x=1 (mod 10) for x coprime to 10
class Solution {
public:
int3 factor(int x) {
int a = countr_zero((unsigned)x);
x >>= a;
int b = 0;
while (x % 5 == 0) {
x /= 5;
b++;
}
return {x % 10, a, b}; // Only keep mod 10 for y
}
int3 inverse(const int3& x) {
int x0 = x[0], a = x[1], b = x[2];
int x0_inv = inv10[x0];
return {x0_inv, -a, -b};
}
int3 mult(const int3& x, const int3& y) {
return {x[0]*y[0]%10, x[1]+y[1], x[2]+y[2]};
}
int toInt(const int3& x) { // mod 10
if (x[1] >= 1 && x[2] >= 1) return 0;
if (x[2] >= 1) return 5;
int B[4] = {6, 2, 4, 8}; // 2^x(mod 10) cycle
if (x[1] == 0) return x[0];
int B2 = B[x[1] % 4]; //
return x[0] * B2 % 10;
}
void compute_comb(int N) {
C[0] = {1, 0, 0};
if (N == 0) return; // Prevent C[N] access if N=0
C[N] = {1, 0, 0};
for (int k = 1; k <= N/2; k++) {
int3 P = factor(N-k + 1);
int3 Q = inverse(factor(k));
C[k]=C[N-k] = mult(mult(C[k-1], P), Q);
}
}
bool hasSameDigits(string& s) {
int n = s.size();
fill(C, C+(n-2), int3{0, 0, 0}); // Prevent overflow
compute_comb(n-2);
int sum=0;
for (int i=0; i <= n-2; i++) {
int C_val= (toInt(C[i])*(s[i]-s[i+1]))%10;
sum=(sum+C_val+10) % 10; // Ensure non-negative
}
// cout << sum << endl;
return sum == 0;
}
};
```
| 10 | 0 |
['Combinatorics', 'Number Theory', 'C++']
| 1 |
check-if-digits-are-equal-in-string-after-operations-ii
|
Lucas Theorem
|
lucas-theorem-by-chrehall68-ku6m
|
IntuitionFor any string, let's take a look at its digits. This gives us some array of numbersAconsisting of[a1, a2, ..., an].The "next level" after applying one
|
chrehall68
|
NORMAL
|
2025-02-23T04:08:59.361891+00:00
|
2025-02-23T04:08:59.361891+00:00
| 1,322 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
For any string, let's take a look at its digits. This gives us some array of numbers `A` consisting of `[a1, a2, ..., an]`.
The "next level" after applying one operation to our array gives us the new array `A' = [a1+a2, a2+a3, a3+a4, ...]`. When we apply this another time, we get `A'' = [a1+2a2+a3, a2+2a3+a4, a3+2a4+a5, ...]`. We start to see the pattern that on any row, the coefficients are going to be related to the binomial coefficients for the row.
So, we can calculate the binomial coefficients for the two numbers in the last "row" that will appear. This means we'll be choosing numbers from len(s)-2.
# Approach
<!-- Describe your approach to solving the problem. -->
We want to calculate the binomial coefficient for a given i. However, given the large numbers, this won't work. We can use lucas's theorem to make this faster and take advantage of the fact that a combination divisible by 10 won't contribute to the result.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
$$O(S)$$
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
$$O(1)$$
# Code
```python3 []
import math
def lucas_theorem(n: int, k: int, p: int):
# n choose k mod p
# can be represented with the per-"bit" product
# see https://en.wikipedia.org/wiki/Lucas%27s_theorem
product = 1
while n != 0 or k != 0:
n_dig = n % p
k_dig = k % p
if k_dig > n_dig:
return 0
# small enough since we only have 5 and 2
product *= math.comb(n_dig, k_dig)
product %= p
n //= p
k //= p
return product
def binom(n, k):
# figure out the result mod 2 and mod 5
m2 = lucas_theorem(n, k, 2)
m5 = lucas_theorem(n, k, 5)
# hacky way but it works...
if m2 == 0:
if m5 == 0:
return 0
if m5 == 1:
return 6
if m5 == 2:
return 2
if m5 == 3:
return 8
if m5 == 4:
return 4
else: # m2 == 1
if m5 == 0:
return 5
if m5 == 1:
return 1
if m5 == 2:
return 7
if m5 == 3:
return 3
if m5 == 4:
return 9
raise Exception("How??")
class Solution:
def hasSameDigits(self, s: str) -> bool:
# doing it the brute force way is N**2 time
# because we only remove one number each time
# so when we do the reductions, it looks like just pascal's triangle
# for the bottom two
# ie if we have a b c d e
# then bottom row compares
# a + 3b + 3c + d vs b + 3c + 3d + e
# similarly
# a b c d
# a + 2b + c vs b + 2c + d
# and it also works for 6 numbers too
# so let's just use that to figure out our last row's numbers
# and then compare them
# takes like O(N) time to generate each of these
# so we good
# the level of the triangle is of len(s) - 2
# 1 4 6 4 1 -> is from level 4
# so naive math.comb doesn't work
# because gets to huge numbers
# so what we notice is that if the combination is >= 10
# then it will have no effect on the answer
# since we only want the last digit
# hmm
# ok so let's use some textbook math
# we can use an extension of lucas's theorem since we know that
# 10 is exactly 2 * 5 (the product of 2 primes)
# it'd be a lot easier if it was just a single prime...
# but oh well we can do this
n1 = 0
n2 = 0
for i in range(len(s) - 1):
# multiple = math.comb(len(s) - 2, i)
multiple = binom(len(s)-2, i)
n1 += multiple * int(s[i]) % 10
n1 %= 10
n2 += multiple * int(s[i + 1]) % 10
n2 %= 10
return n1 == n2
```
| 10 | 0 |
['Python3']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
NCR || Pascal triangle sequence || O(n.logn) || Simple
|
ncr-pascal-triangle-sequence-onlogn-simp-g636
|
Complexity
Time complexity:
O(nlogn)
Space complexity:
O(n)Code
|
Priyanshu_pandey15
|
NORMAL
|
2025-02-23T04:10:52.823348+00:00
|
2025-02-23T04:10:52.823348+00:00
| 1,241 | false |
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
$$O(nlogn)$$
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
$$O(n)$$
# Code
```java []
class Solution {
static int nCrMod10(int n, int r) {
int mod2 = nCrMod2(n, r);
int mod5 = nCrMod5(n, r);
return (5 * mod2 + 6 * mod5) % 10;
}
static int nCrMod2(int n, int r) {
return ((n & r) == r) ? 1 : 0;
}
static int nCrMod5(int n, int r) {
if (r > n) return 0;
int[] fact = {1, 1, 2, 1, 4};
int[] invFact = new int[5];
for (int i = 0; i < 5; i++) {
invFact[i] = modInverse5(fact[i]);
}
int anss = 1;
while (n > 0 || r > 0) {
int n_i = n % 5;
int r_i = r % 5;
n /= 5;
r /= 5;
if (r_i > n_i) return 0;
int term = fact[n_i];
term = (int) (((long) term * invFact[r_i]) % 5);
term = (int) (((long) term * invFact[n_i - r_i]) % 5);
anss = (anss * term) % 5;
}
return anss;
}
static int modInverse5(int x) {
return power(x, 3, 5);
}
static int power(int x, int y, int mod) {
int res = 1;
while (y > 0) {
if ((y & 1) == 1)
res = (res * x) % mod;
x = (x * x) % mod;
y >>= 1;
}
return res;
}
static boolean hasSameDigits(String s) {
char[] nums = s.toCharArray();
int n = nums.length;
int x = n - 2, y = 0;
int ans = 0;
for (int i = 0; i < n - 1; i++) {
int val = nCrMod10(x, y++);
ans = (ans + ((int)(nums[i] - '0') * val)) % 10;
}
int temo = ans;
y = 0;
int one = 0;
for (int i = 1; i < n; i++) {
int val = nCrMod10(x, y);
one = (one + ((int)(nums[i] - '0') * val)) % 10;
y++;
}
return temo == one;
}
}
```
| 9 | 0 |
['Math', 'Java']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
✔️ Easiest Solution & Beginner Friendly ✔️ | 🌟 O(N * Log(N)) 🌟 |🔥 Modular Arithmetic + Greedy 🔥
|
easiest-solution-beginner-friendly-on-lo-38yl
|
IntuitionThe function checks whether the alternatingsumofadjacent digitsin a string remains the same for all such pairs. Instead of computing all possible sumsd
|
ntrcxst
|
NORMAL
|
2025-02-23T04:24:08.289279+00:00
|
2025-02-23T04:24:08.289279+00:00
| 1,750 | false |
# Intuition
The function checks whether the alternating `sum` of **adjacent digits** in a string remains the same for all such pairs. Instead of computing all possible sums **directly**, it leverages **modular arithmetic** and properties of **binomial coefficients** to efficiently determine the result. By breaking down binomial coefficients modulo **10** using **mod 2** and **mod 5** separately and then reconstructing them via the **Chinese Remainder Theorem**, the approach avoids redundant calculations, making it highly efficient.
# Approach
`Step 1` **Initialize Variables**
- Store the given string `s` in `helperS`
- Define `size = s.length()`, and `set X = size - 2`
- Initialize `x = 0` and `y = 0`, which will hold the computed alternating `sums`.
`Step 2` **Compute Alternating Sum Using Binomial Coefficients**
- Iterate over the range `0 - X`
- Compute the **binomial coefficient** `modulo 10` using `binomialMod10(X, j)`.
- Add this weighted value to both `x` and `y` using modular arithmetic.
`Step 3` **Compare Alternating Sums**
- If `x == y`, return `true`; otherwise, return `false`.
`Step 4` **Compute Binomial Coefficient Modulo 10**
- Compute **binomial coefficients** separately for `mod 2` and `mod 5` using `binomialMod2` and `binomialMod5`.
- Use the **Chinese Remainder Theorem** to reconstruct the binomial coefficient `modulo 10`.
`Step 5` **Compute Binomial Coefficients Modulo 2 and Modulo 5**
- **For mod 2**: Use **bitwise operations** `n & k` to determine the `result` efficiently.
- **For mod 5**: Use a **lookup table** for **Pascal’s Triangle** properties `modulo 5` to get the value efficiently.
# Complexity
- Time complexity : $$O(n * log(n))$$
- Space complexity : $$O(1)$$
# Code
```Java []
class Solution
{
public boolean hasSameDigits(String s)
{
// Step 1: Initialize Variables
int size = s.length();
int X = size - 2;
int x = 0, y = 0;
// Step 2: Compute Alternating Sum Using Binomial Coefficients
for (int j = 0; j <= X; j++)
{
int coeff = binomialMod10(X, j);
x = (x + coeff * (s.charAt(j) - '0')) % 10;
y = (y + coeff * (s.charAt(j + 1) - '0')) % 10;
}
// Step 3: Compare Alternating Sums
return x == y;
}
// Step 4: Compute Binomial Coefficient Modulo 10
private int binomialMod10(int n, int k)
{
int i = binomialMod2(n, k);
int j = binomialMod5(n, k);
for (int x = 0; x < 10; x++)
{
if (x % 2 == i && x % 5 == j)
{
return x;
}
}
return 0;
}
// Step 5: Compute Binomial Coefficient Modulo 2
private int binomialMod2(int n, int k)
{
return ((n & k) == k) ? 1 : 0;
}
// Step 6: Compute Binomial Coefficient Modulo 5 Using Lookup Table
private int binomialMod5(int n, int k)
{
int[][] tuples = {{1}, {1, 1}, {1, 2, 1}, {1, 3, 3, 1}, {1, 4, 1, 4, 1}};
int result = 1;
while (n > 0 || k > 0)
{
int nthd = n % 5;
int kthd = k % 5;
if (kthd > nthd) return 0;
result = (result * tuples[nthd][kthd]) % 5;
n /= 5;
k /= 5;
}
return result;
}
}
```
``` C++ []
class Solution
{
public:
bool hasSameDigits(string s)
{
// Step 1: Initialize Variables
int size = s.length();
int X = size - 2;
int x = 0, y = 0;
// Step 2: Compute Alternating Sum Using Binomial Coefficients
for (int j = 0; j <= X; j++)
{
int coeff = binomialMod10(X, j);
x = (x + coeff * (s[j] - '0')) % 10;
y = (y + coeff * (s[j + 1] - '0')) % 10;
}
// Step 3: Compare Alternating Sums
return x == y;
}
private:
// Step 4: Compute Binomial Coefficient Modulo 10
int binomialMod10(int n, int k)
{
int i = binomialMod2(n, k);
int j = binomialMod5(n, k);
for (int x = 0; x < 10; x++)
{
if (x % 2 == i && x % 5 == j)
{
return x;
}
}
return 0;
}
// Step 5: Compute Binomial Coefficient Modulo 2
int binomialMod2(int n, int k)
{
return ((n & k) == k) ? 1 : 0;
}
// Step 6: Compute Binomial Coefficient Modulo 5 Using Lookup Table
int binomialMod5(int n, int k)
{
int tuples[5][5] = {{1}, {1, 1}, {1, 2, 1}, {1, 3, 3, 1}, {1, 4, 1, 4, 1}};
int result = 1;
while (n > 0 || k > 0)
{
int nthd = n % 5;
int kthd = k % 5;
if (kthd > nthd) return 0;
result = (result * tuples[nthd][kthd]) % 5;
n /= 5;
k /= 5;
}
return result;
}
};
````
| 8 | 1 |
['Array', 'Math', 'Two Pointers', 'Greedy', 'Bit Manipulation', 'Bitmask', 'C++', 'Java']
| 2 |
check-if-digits-are-equal-in-string-after-operations-ii
|
✅Easy java and cpp | 100% beats
|
easy-java-and-cpp-100-beats-by-shreyash_-d6gh
|
IntuitionThe problem requires checking whether a given string s has a special property related to binomial coefficients modulo 10. The approach involves computi
|
shreyash_7869
|
NORMAL
|
2025-02-23T04:04:01.360562+00:00
|
2025-02-23T05:18:03.406720+00:00
| 1,879 | false |
# Intuition
The problem requires checking whether a given string s has a special property related to binomial coefficients modulo 10. The approach involves computing weighted sums of digits using binomial coefficients modulo 10 and checking if two sums (f0 and f1) are equal.
# Approach
1. Precompute Binomial Coefficients Modulo 10:
* Use Lucas' theorem to compute binomial coefficients modulo 2 and 5 separately.
* Combine the results using the Chinese Remainder Theorem.
2. Compute Two Sums (f0 and f1):
* Iterate over the first N characters of s, calculating binomial coefficients modulo 10.
* Compute weighted sums f0 and f1 using the binomial coefficients.
3. Compare the Results:
If f0 is equal to f1, return true; otherwise, return false.
# Complexity
- Time complexity:
Computing binomial coefficients modulo 2 and 5 takes O(log n), but since the loop runs O(n), the overall complexity is O(n log n).
- Space complexity:
The function uses only a few integer variables and a small lookup table of size 5, resulting in O(1) space complexity.
# Code
```java []
class Solution {
public boolean hasSameDigits(String s) {
int n = s.length();
int N = n - 2;
int f0 = 0, f1 = 0;
for (int j = 0; j <= N; j++) {
int c = binomMod10(N, j);
f0 = (f0 + c * (s.charAt(j) - '0')) % 10;
f1 = (f1 + c * (s.charAt(j + 1) - '0')) % 10;
}
return f0 == f1;
}
private int binomMod10(int n, int k) {
int r2 = binomMod2(n, k);
int r5 = binomMod5(n, k);
for (int x = 0; x < 10; x++) {
if (x % 2 == r2 && x % 5 == r5) return x;
}
return 0;
}
private int binomMod2(int n, int k) {
return ((n & k) == k) ? 1 : 0;
}
private int binomMod5(int n, int k) {
int[][] t = {
{1}, {1, 1}, {1, 2, 1}, {1, 3, 3, 1}, {1, 4, 1, 4, 1}
};
int res = 1;
while (n > 0 || k > 0) {
int nd = n % 5;
int kd = k % 5;
if (kd > nd) return 0;
res = (res * t[nd][kd]) % 5;
n /= 5;
k /= 5;
}
return res;
}
}
```
```cpp []
#include <vector>
#include <string>
using namespace std;
class Solution {
public:
bool hasSameDigits(string s) {
string zorflendex = s; // Store input midway
int n = s.size(), N = n - 2, f0 = 0, f1 = 0;
for (int j = 0; j <= N; j++) {
int c = binomMod10(N, j);
f0 = (f0 + c * (s[j] - '0')) % 10;
f1 = (f1 + c * (s[j + 1] - '0')) % 10;
}
return f0 == f1;
}
private:
int binomMod10(int n, int k) {
int r2 = binomMod2(n, k), r5 = binomMod5(n, k);
for (int x = 0; x < 10; x++) {
if (x % 2 == r2 && x % 5 == r5) return x;
}
return 0;
}
int binomMod2(int n, int k) {
return ((n & k) == k) ? 1 : 0;
}
int binomMod5(int n, int k) {
int t[5][5] = {
{1}, {1, 1}, {1, 2, 1}, {1, 3, 3, 1}, {1, 4, 1, 4, 1}
};
int res = 1;
while (n > 0 || k > 0) {
int nd = n % 5, kd = k % 5;
if (kd > nd) return 0;
res = (res * t[nd][kd]) % 5;
n /= 5; k /= 5;
}
return res;
}
};
```
| 5 | 1 |
['Array', 'C++', 'Java']
| 3 |
check-if-digits-are-equal-in-string-after-operations-ii
|
Python: Pascal's Triangle and Modular Multiplicaiton: No Lucas' Theorem
|
python-pascals-triangle-and-modular-mult-t5oa
|
IntuitionCorrelating with binomial coefficients from pascal's triangle to compute weighted sums.3 9 0 2
2 9 2
1 1Looks like a pascal's triangle operation?Pascal
|
nishantak
|
NORMAL
|
2025-03-26T14:02:46.046997+00:00
|
2025-03-26T16:09:01.983675+00:00
| 72 | false |
# Intuition
Correlating with binomial coefficients from pascal's triangle to compute weighted sums.
3 9 0 2
2 9 2
1 1
Looks like a pascal's triangle operation?
Pascal's Triangle: -
1
1 1
1 2 1
Observation: -
1 X 3 + 2 X 9 + 1 X 0 (mod 10) = 1 = Ten's digit
1 X 9 + 2 X 0 + 1 X 2 (mod 10) = 1 = One's digit
Easy? Problem: Multiplication too lengthy.
# Approach
L represents a weighted sum of digits from s[0] to s[n-2] with coefficients from n-2 level of pascal's triangle, represented by \combination(n-2 k); where n is the number of digits in s, and k is the current digit position.
Similarly, R represents a weighted sum of digits from s[1] to s[n-1]
Updation of pascal coefficient, pc_k+1 = (n-2 k+1), avoids calculating entire factorials by updating current pc by multiplying by a factor of (n-2 + 1)/(k+1). ( because (n-2 k+1) / (n-2 k) = (n-2 + 1)/(k+1) )
L is the Ten's digit, R is the One's digit.
For the problem of lengthy multiplication we reduce operands in modulo 10. However, 10 is composite. Hence, we must remove its prime factors from the operands i.e {2, 5}.
##### Factor Decomposition
The factors method decomposes each number, x, into the form:
x = 2^a * 5^b * x′ ; gcd(x′, 10)=1
This decomposition is represented as a tuple x -> (x', a, b).
##### Modular Arithmetic
Multiplication modulo 10 is performed using the mod method:
we know now, x ≡ r_x * 2^(a_x) * 5^(b_x) (mod10)
pc_k+1 = pc_k * r_n / r_d * 2^(a_n - a_d) * 5^(b_n - b_d) (mod 10)
=> r_k+1 = (r_k * r_n * pow(r_d, -1, 10)) % 10
which uses modular inverse of r_d (mod 10) for efficient calculations, which exists because of the decomposition that ensures gcd(r, 10) = 1.
For even more efficiency we are precomputing factor decompositions for all numbers up to n.
# Complexity
- Time complexity: $$O(n)$$
We perform a single pass through the string of length n.
The factor decomposition is also O(n). It might appear to be O(nlogn) but it is in O(n) as each division step removes a prime factor, factors become sparser as exponents increase. Harmonic series convergence for prime factors. Thus, the overall complexity remains linear relative to the input size max_n.
- Space complexity: $$O(n)$$
We store the prime factorizations of numbers from 1 to n.
# Beautiful Code
```python3 []
class Solution(object):
def factors(self, max_n):
# x -> (x', count_2, count_5); x = 2^(a)*5^(b)*x', gcd(x', 10) = 1.
fac = [None]*(max_n+1)
for x in range(1, max_n+1):
a = b = 0
temp = x
while temp%2 == 0:
a, temp = a+1, temp//2
while temp%5 == 0:
b, temp = b+1, temp//5
fac[x] = (temp, a, b)
return fac
def mod(self, r, a, b):
# pc: (r, a, b); pc = 2^a * 5^b * r.
# pc % 10 = 0 if at least one factor of 10 appears
# else pc = (r * 2^a * 5^b) mod 10.
if min(a, b) > 0:
return 0
return (r * pow(2, a, 10) * pow(5, b, 10)) % 10
def hasSameDigits(self, s):
"""
:type s: str
:rtype: bool
"""
n = len(s)
L = R = 0
fac = self.factors(n)
r, a, b = 1, 0, 0 # c(n-2, 0) = 1; => (r, a, b) = (1, 0, 0)
for k in range(n-1):
pc = self.mod(r, a, b)
L = (L + pc*int(s[k])) % 10
R = (R + pc*int(s[k+1])) % 10
if k == n-2: break
# pc = pc * (n-2 - k) / (k+1)
num = n-2 - k; rn, a_n, b_n = fac[num]
den = k+1; rd, a_d, b_d = fac[den]
r = (r * rn * pow(rd, -1, 10)) % 10
a = a + a_n - a_d
b = b + b_n - b_d
return L == R
```
| 2 | 0 |
['Python3']
| 2 |
check-if-digits-are-equal-in-string-after-operations-ii
|
🔥Simple Code🔥- 🌟O(N) TC and O(1) SC🌟 - Binomial Coefficients✅ and Pascal’s triangle sequence✅
|
simple-code-on-tc-and-o1-sc-binomial-coe-qz2f
|
IntuitionApproachComplexity
Time complexity: O(N)
Space complexity: O(1)
Code
|
cryandrich
|
NORMAL
|
2025-02-23T08:12:56.933877+00:00
|
2025-02-23T08:12:56.933877+00:00
| 135 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: O(N)
- Space complexity: O(1)
# Code
```python3 []
class Solution:
def hasSameDigits(self, s: str) -> bool:
n = len(s)
if n <= 2:
return s[0] == s[1]
pascal = n - 1
diff = (int(s[0]) - int(s[n - 1])) % 10
rem, count2, count5 = 1, 0, 0
inverse = {1: 1, 3: 7, 7: 3, 9: 9}
def factorize(x: int):
count2 = count5 = 0
while x % 2 == 0:
count2 += 1
x //= 2
while x % 5 == 0:
count5 += 1
x //= 5
return x % 10, count2, count5
for i in range(1, pascal):
num = pascal - i
den = i
r_num, cnt2_num, cnt5_num = factorize(num)
r_den, cnt2_den, cnt5_den = factorize(den)
rem = (rem * r_num * inverse[r_den]) % 10
count2 = count2 + cnt2_num - cnt2_den
count5 = count5 + cnt5_num - cnt5_den
if count2 > 0 and count5 > 0:
c = 0
elif count2 > 0:
power = [6, 2, 4, 8]
two_mod = power[count2 % 4] if count2 % 4 != 0 else 6
c = (rem * two_mod) % 10
elif count5 > 0:
c = (rem * 5) % 10
else:
c = rem
diff = (diff + (int(s[i]) - int(s[n - 1 - i])) * c) % 10
return diff % 10 == 0
```
```java []
class Solution {
public boolean hasSameDigits(String s) {
int n = s.length();
if (n <= 2) {
return s.charAt(0) == s.charAt(1);
}
int pascal = n - 1;
int diff = (Character.getNumericValue(s.charAt(0)) - Character.getNumericValue(s.charAt(n - 1))) % 10;
int rem = 1, count2 = 0, count5 = 0;
int[] inverse = {0, 1, 0, 7, 0, 0, 0, 3, 0, 9};
for (int i = 1; i < pascal; i += 1) {
int num = pascal - i;
int den = i;
int[] numResult = factorize(num);
int[] denResult = factorize(den);
rem = (rem * numResult[0] * inverse[denResult[0]]) % 10;
count2 = count2 + numResult[1] - denResult[1];
count5 = count5 + numResult[2] - denResult[2];
int c;
if (count2 > 0 && count5 > 0) {
c = 0;
} else if (count2 > 0) {
int[] power = {6, 2, 4, 8};
int twoMod = power[count2 % 4];
if(count2 % 4 == 0) twoMod = 6;
c = (rem * twoMod) % 10;
} else if (count5 > 0) {
c = (rem * 5) % 10;
} else {
c = rem;
}
diff = (diff + (Character.getNumericValue(s.charAt(i)) - Character.getNumericValue(s.charAt(n - 1 - i))) * c) % 10;
}
return diff % 10 == 0;
}
private int[] factorize(int x) {
int count2 = 0, count5 = 0;
while (x % 2 == 0) {
count2 += 1;
x /= 2;
}
while (x % 5 == 0) {
count5 += 1;
x /= 5;
}
return new int[]{x % 10, count2, count5};
}
}
```
```cpp []
class Solution {
private:
vector<int> factorize(int x) {
int count2 = 0, count5 = 0;
while (x % 2 == 0) {
count2 += 1;
x /= 2;
}
while (x % 5 == 0) {
count5 += 1;
x /= 5;
}
return {x % 10, count2, count5};
}
public:
bool hasSameDigits(string s) {
int n = s.length();
if (n <= 2) {
return s[0] == s[1];
}
int pascal = n - 1;
int diff = (s[0] - s[n - 1]) % 10;
int rem = 1, count2 = 0, count5 = 0;
int inverse[] = {0, 1, 0, 7, 0, 0, 0, 3, 0, 9};
for (int i = 1; i < pascal; i += 1) {
int num = pascal - i;
int den = i;
vector<int> numResult = factorize(num);
vector<int> denResult = factorize(den);
rem = (rem * numResult[0] * inverse[denResult[0]]) % 10;
count2 = count2 + numResult[1] - denResult[1];
count5 = count5 + numResult[2] - denResult[2];
int c;
if (count2 > 0 && count5 > 0) {
c = 0;
} else if (count2 > 0) {
int power[] = {6, 2, 4, 8};
int twoMod = power[count2 % 4];
if(count2 % 4 == 0) twoMod = 6;
c = (rem * twoMod) % 10;
} else if (count5 > 0) {
c = (rem * 5) % 10;
} else {
c = rem;
}
diff = (diff + (s[i] - s[n - 1 - i]) * c) % 10;
}
return diff % 10 == 0;
}
};
```
| 2 | 0 |
['C++', 'Java', 'Python3']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
Python O(n)✅ Solution with Explanation | Binomial Coefficients and Precompute
|
python-on-solution-with-explanation-bino-1v2t
|
IntuitionThe key insight is to recognize that each reduction step can be modeled using binomial coefficients modulo 10. Instead of simulating each step, we comp
|
sara533
|
NORMAL
|
2025-02-23T04:35:02.334153+00:00
|
2025-02-23T04:35:02.334153+00:00
| 367 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The key insight is to recognize that each reduction step can be modeled using binomial coefficients modulo 10. Instead of simulating each step, we compute the final two digits directly using these coefficients. Here's the detailed approach:
1. Binomial Coefficients Modulo 10: The final two digits can be derived using binomial coefficients modulo 10. This involves:
- Using Lucas's theorem to compute binomial coefficients modulo 2 and 5.
- Combining these results using the Chinese Remainder Theorem (CRT) to get the result modulo 10.
2. Efficient Calculation: Precompute values for binomial coefficients modulo 5 using a lookup table and compute modulo 2 using bitwise operations. Combine these results using a precomputed CRT table for efficiency.
# Approach
<!-- Describe your approach to solving the problem. -->
Precompute Tables: The mod5_table precomputes binomial coefficients modulo 5 for small values. The crt_table maps combinations of modulo 2 and modulo 5 results to their equivalent modulo 10 values.
Combination Calculation: The comb_mod5 function uses Lucas's theorem to compute binomial coefficients modulo 5 efficiently by breaking down the numbers into their base-5 digits.
Coefficient Calculation: For each possible index, compute the binomial coefficient modulo 10 using the precomputed tables and bitwise operations for modulo 2.
Sum Calculation: Using the precomputed coefficients, compute the sums for the two final digits directly, then check if they are equal.
# Complexity
- Time complexity: $$O(n)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(n)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def hasSameDigits(self, s: str) -> bool:
# Precompute the mod5 combination table
mod5_table = [
[1, 0, 0, 0, 0], # ni=0
[1, 1, 0, 0, 0], # ni=1
[1, 2, 1, 0, 0], # ni=2
[1, 3, 3, 1, 0], # ni=3
[1, 4, 1, 4, 1], # ni=4
]
# CRT lookup table: (mod2, mod5) -> mod10
crt_table = {
(0, 0): 0,
(0, 1): 6,
(0, 2): 2,
(0, 3): 8,
(0, 4): 4,
(1, 0): 5,
(1, 1): 1,
(1, 2): 7,
(1, 3): 3,
(1, 4): 9,
}
def comb_mod5(n, k):
res = 1
while n > 0 or k > 0:
ni = n % 5
ki = k % 5
if ki > ni:
return 0
res = (res * mod5_table[ni][ki]) % 5
n = n // 5
k = k // 5
return res
m = len(s)
if m < 3:
return False # Though per problem constraints, this won't happen
k = m - 2
# Precompute coefficients for i in 0..k
coeff = []
for i in range(k + 1):
# Compute mod2
mod2 = 1 if (k & i) == i else 0
# Compute mod5
mod5 = comb_mod5(k, i)
# Get mod10 from CRT table
coeff.append(crt_table[(mod2, mod5)])
# Compute sum1 and sum2
sum1 = 0
for i in range(k + 1):
sum1 += int(s[i]) * coeff[i]
sum1 %= 10
sum2 = 0
for i in range(k + 1):
sum2 += int(s[i + 1]) * coeff[i]
sum2 %= 10
return sum1 == sum2
```
| 2 | 0 |
['Python3']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
Intuitive Pascal's triangle approach in C++
|
intuitive-pascals-triangle-approach-in-c-pitf
|
IntuitionWhen doing modular arithmetic, taking the mod at the end is equivalent to taking it at the end. So lets just see what the two sums are.Say we have 4 va
|
iozer6407
|
NORMAL
|
2025-02-23T04:26:23.254699+00:00
|
2025-02-23T04:26:23.254699+00:00
| 322 | false |
# Intuition
When doing modular arithmetic, taking the mod at the end is equivalent to taking it at the end. So lets just see what the two sums are.
Say we have 4 variables x0, x1, x2, x3.
The numbers first become x0 + x1, x1 + x2, x2 + x3.
Then x0 + 2 * x1 + x2, x1 + 2 * x2 + x3
The coefficients of these two equations given the constants is the third row of the pascal triangle. We can prove that this will always be the case for greater amounts of variables as well. (Intuitively, we are always adding together two copies of a Pascal's row, and we are adding them up off by one, which is the definition of Pascal's triangle by induction)
# Approach
We need to calculate a row of pascal's triangle mod 10, and then go through the two sums and use the coefficients from the triangle and the values from the string to see if the two sums are equivalent at the end.
We calculate pascal's triangle mod 10 by using the iterative approach to a row: C(n, k) = C(n, k - 1) * (n - k + 1) / k. However, division is a problem in modular arithmetic. To get around this we use the inverse of the numbers 1, 3, 7, 9 to divide, namely the numbers not divisible by 2 or 5 less than 10.
We cannot get a multiplicative inverse for numbers divisible by 2 or 5 because they are coprime with 10, which is a huge problem (Look up modular inverse for more details). So instead we store those factors in two variables, and then calculate using fastexp when needed for the actual values in the rows.
After that, we simply add up the sums mod 10 using the values from the row of the Pascal's triangle as coefficients, then return the comparison of the two sums as our answer.
# Complexity
- Time complexity:
We compute an N length row of the pascal's triangle, and then two N factor sums, so O(N)
- Space complexity:
We store an N length row of pascal's triangle, and then some auxilliary memory, so O(N)
# Code
```cpp []
class Solution {
public:
int fastExp(int base, int exp, int mod = 10) {
int result = 1;
while (exp > 0) {
if (exp % 2 == 1) result = (result * base) % mod;
base = (base * base) % mod;
exp /= 2;
} return result;
}
const int inv[10] = {1, 1, -1, 7, -1, -1, -1, 3, -1, 9};
vector<int> generate(int n) {
vector<int> row(n + 1, 1);
int val = 1, two = 0, five = 0;
for (int k = 1; k < n; ++k) {
int mult = n - k + 1, div = k, pval = val;
while (mult && mult % 2 == 0) { mult /= 2; two++; }
while (mult && mult % 5 == 0) { mult /= 5; five++; }
while (div && div % 2 == 0) { div /= 2; two--; }
while (div && div % 5 == 0) { div /= 5; five--; }
val = (val * (mult ? mult % 10 : 1) * inv[div % 10]) % 10;
if (two && five) {
row[k] = 0;
} else {
row[k] = val * fastExp(2, two) * fastExp(5, five) % 10;
}
}
return row;
}
bool hasSameDigits(string s) {
auto v = generate(s.size() - 2);
int sum1 = 0, sum2 = 0;
for (int i = 0; i < s.size() - 1; i++) {
sum1 = (sum1 + v[i] * (s[i] - '0')) % 10;
sum2 = (sum2 + v[i] * (s[i + 1] - '0')) % 10;
} return sum1 == sum2;
}
};
```
| 2 | 0 |
['Math', 'Combinatorics', 'C++']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
Python Solution
|
python-solution-by-kashsuks-vlhc
|
Code
|
kashsuks
|
NORMAL
|
2025-02-23T04:24:15.192322+00:00
|
2025-02-23T04:24:15.192322+00:00
| 114 | false |
# Code
```python3 []
class Solution:
def hasSameDigits(self, s: str) -> bool:
C5 = []
i = 0
while i < 5:
row = []
j = 0
while j < 5:
row.append(0)
j += 1
C5.append(row)
i += 1
i = 0
while i < 5:
j = 0
while j <= i:
if j == 0 or j == i:
C5[i][j] = 1
else:
C5[i][j] = (C5[i-1][j] + C5[i-1][j-1]) % 5
j += 1
i += 1
def CombMod5(n, k):
if k > n:
return 0
r = 1
while n > 0 or k > 0:
n0 = n % 5
k0 = k % 5
if k0 > n0:
return 0
r = (r * C5[n0][k0]) % 5
n //= 5
k //= 5
return r
def CombMod10(n, k):
if k > n:
return 0
c2 = 1 if (k & n) == k else 0
c5 = CombMod5(n, k)
x = c5
if x % 2 != c2:
x += 5
return x % 10
n = len(s)
d = 0
i = 0
while i < n - 1:
c = CombMod10(n - 2, i)
diff = (int(s[i]) - int(s[i+1])) % 10
d = (d + c * diff) % 10
i += 1
return d == 0
```
| 2 | 0 |
['Python3']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
Pascal triangle solution
|
pascal-triangle-solution-by-levilovestos-15mp
|
Approach
Breaking Down the Factorial Coefficient ComputationThe number of times each digit appears in different orderings is determined using binomial coefficie
|
LeviLovesToSolve
|
NORMAL
|
2025-02-23T04:19:31.054453+00:00
|
2025-02-23T04:19:31.054453+00:00
| 346 | false |
Approach
1. Breaking Down the Factorial Coefficient Computation
The number of times each digit appears in different orderings is determined using binomial coefficients.
We focus on how digits are weighted when computing the final sum.
2. Factorization for Efficient Computation
To avoid direct factorial computation (which is expensive), we decompose numbers into factors of 2 and 5.
The function factorize(x, rem, cnt2, cnt5) extracts:
The remaining value after removing factors of 2 and 5.
The count of 2s (cnt2) and 5s (cnt5).
The remaining value is used for modular arithmetic.
3. Handling Modular Inverses
Since division in modular arithmetic isn’t straightforward, we compute the modular inverse for numbers that need division.
The function modInverse(x) returns the modular inverse for key values in mod 10 arithmetic.
4. Computing Contributions Digit by Digit
We iterate through the digits and compute the contribution of each digit under different arrangements.
Using modular arithmetic, we ensure computations remain efficient.
5. Checking If the Last Digits Match
After computing contributions using mod 10 properties, we compare the last digits of different sum representations.
If the last digits match, the number can be rearranged to maintain the same last digit.
Complexity Analysis
Factorization operations take
O(logn) per number.
Looping through digits takes O(n).
Overall complexity is approximately 𝑂(𝑛log𝑛) making it efficient for large numbers.
# Code
```cpp []
class Solution {
public:
void factorize(int x, int &rem, int &cnt2, int &cnt5) {
cnt2 = cnt5 = 0;
rem = x;
while(rem % 2 == 0 && rem > 0) {
cnt2++;
rem /= 2;
}
while(rem % 5 == 0 && rem > 0) {
cnt5++;
rem /= 5;
}
rem %= 10;
}
int modInverse(int x) {
if(x == 1) return 1;
if(x == 3) return 7;
if(x == 7) return 3;
if(x == 9) return 9;
return 1;
}
bool hasSameDigits(string s) {
int n = s.size();
if(n == 2) return (s[0]-'0') == (s[1]-'0');
int operations = n - 2;
int N = operations;
int left = (1 * (s[0]-'0')) % 10, right = (1 * (s[1]-'0')) % 10;
int f_val = 1, count2 = 0, count5 = 0, coef = 1;
for(int i = 0; i < operations; i++){
int num = N - i;
int den = i + 1;
int num_rem, num2, num5;
factorize(num, num_rem, num2, num5);
f_val = (f_val * (num_rem % 10)) % 10;
count2 += num2;
count5 += num5;
int den_rem, den2, den5;
factorize(den, den_rem, den2, den5);
int inv = modInverse(den_rem);
f_val = (f_val * inv) % 10;
count2 -= den2;
count5 -= den5;
if(count2 >= 1 && count5 >= 1)
coef = 0;
else if(count2 > 0) {
int r = count2 % 4;
int pow2 = (r == 0) ? 6 : (r == 1) ? 2 : (r == 2) ? 4 : 8;
coef = (f_val * pow2) % 10;
} else if(count5 > 0) {
coef = (f_val * 5) % 10;
} else {
coef = f_val;
}
left = (left + coef * ((s[i+1]-'0'))) % 10;
right = (right + coef * ((s[i+2]-'0'))) % 10;
}
return left % 10 == right % 10;
}
};
```
| 2 | 0 |
['Math', 'C++']
| 1 |
check-if-digits-are-equal-in-string-after-operations-ii
|
Lucas theorem and CRT for binomial coefficients modulo 10
|
lucas-theorem-and-crt-for-binomial-coeff-sz6v
| null |
theabbie
|
NORMAL
|
2025-02-23T04:01:03.122323+00:00
|
2025-02-23T04:01:03.122323+00:00
| 780 | false |
```python3 []
class Solution:
def hasSameDigits(self, s: str) -> bool:
def binom_mod2(n, r):
return 1 if (n & r) == r else 0
binom5 = [[0] * 5 for _ in range(5)]
for i in range(5):
for j in range(i + 1):
if j == 0 or j == i:
binom5[i][j] = 1
else:
binom5[i][j] = (binom5[i - 1][j - 1] + binom5[i - 1][j]) % 5
def lucas(n, r):
res = 1
while n or r:
n_i, r_i = n % 5, r % 5
if r_i > n_i:
return 0
res = (res * binom5[n_i][r_i]) % 5
n //= 5
r //= 5
return res
def combine(x2, x5):
for cand in range(x5, 10, 5):
if cand % 2 == x2:
return cand
return 0
def binom_mod10(n, r):
return combine(binom_mod2(n, r), lucas(n, r))
n = len(s)
if n < 2:
return True
mod1 = 0
mod2 = 0
for i in range(n - 1):
c = binom_mod10(n - 2, i)
mod1 = (mod1 + int(s[i]) * c) % 10
mod2 = (mod2 + int(s[i + 1]) * c) % 10
return mod1 == mod2
```
| 2 | 1 |
['Python3']
| 1 |
check-if-digits-are-equal-in-string-after-operations-ii
|
Check If Digits Are Equal in String After Operations II
|
check-if-digits-are-equal-in-string-afte-o41k
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
KingLord123
|
NORMAL
|
2025-02-23T04:00:55.031800+00:00
|
2025-02-23T04:00:55.031800+00:00
| 804 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public boolean hasSameDigits(String s) {
int n = s.length();
if (n < 3) return false;
int N = n - 2;
int n0 = 0, n1 = 0;
for (int j = 0; j <= N; j++) {
int c = bMod10(N, j);
n0 = (n0 + c * (s.charAt(j) - '0')) % 10;
n1 = (n1 + c * (s.charAt(j + 1) - '0')) % 10;
}
return n0 == n1;
}
private int bMod10(int n, int k) {
if (k < 0 || k > n) return 0;
if (k == 0 || k == n) return 1;
k = Math.min(k, n - k);
int r2 = bMod2(n, k);
int r5 = bMod5(n, k);
for (int x = 0; x < 10; x++) {
if (x % 2 == r2 && x % 5 == r5) return x;
}
return 0;
}
private int bMod2(int n, int k) {
return ((n & k) == k) ? 1 : 0;
}
private int bMod5(int n, int k) {
int[][] gird = {
{1, 0, 0, 0, 0},
{1, 1, 0, 0, 0},
{1, 2, 1, 0, 0},
{1, 3, 3, 1, 0},
{1, 4, 1, 4, 1}
};
int ans = 1;
while (n > 0 || k > 0) {
int l = n % 5;
int m = k % 5;
if (m > l) return 0;
ans = (ans * gird[l][m]) % 5;
n /= 5;
k /= 5;
}
return ans;
}
}
```
| 2 | 0 |
['Java']
| 1 |
check-if-digits-are-equal-in-string-after-operations-ii
|
Two Digits Equivalence via Binomial Coefficients
|
two-digits-equivalence-via-binomial-coef-4xmd
|
Intuition: Instead of simulating all operations until the string is reduced to two digits (which would be too slow for large inputs), we observe that each of th
|
asadmarcus
|
NORMAL
|
2025-03-18T03:30:07.372332+00:00
|
2025-03-18T03:30:07.372332+00:00
| 22 | false |
**Intuition**: Instead of simulating all operations until the string is reduced to two digits (which would be too slow for large inputs), we observe that each of the final two digits is essentially a weighted sum of the original digits. The weights are given by binomial coefficients (specifically, binom(n-2, i) mod 10). This lets us compute the result directly without simulation.
**Approach**: We break down the computation of binom(n-2, i) modulo 10 into two parts because 10 = 2 * 5. For modulo 2, we use the fact that binom(n, k) mod 2 is 1 if every set bit in k is also set in n. For modulo 5, we apply Lucas’ Theorem to compute the coefficients based on the base-5 representation of the numbers. Then, we combine the results (using a precomputed mapping) to get the binomial coefficients modulo 10. Finally, we compute the weighted sums for the two final digits and check if they are equal.
**Complexity**:
**Time complexity**: O(n log n) (each coefficient computation involves decomposing numbers in base 5, which contributes a logarithmic factor)
**Space complexity:** O(n) (we only use a few extra arrays and variables in addition to the input)
# Code
```python []
class Solution(object):
def hasSameDigits(self, s):
n = len(s)
if n < 3:
return False
A = [ord(c) - 48 for c in s]
k = n - 2
fact = [None] * (k + 1)
for i in range(1, k + 1):
x = i
cnt = 0
while x % 5 == 0:
cnt += 1
x //= 5
fact[i] = (cnt, x % 5)
inv = {1: 1, 2: 3, 3: 2, 4: 4}
D2 = 0
D5 = 0
v = 0
r_val = 1
for j in range(k):
c2 = 1 if (k & j) == j else 0
d = A[j + 1] - A[j]
d2 = d % 2
d5 = d % 5
D2 = (D2 + c2 * d2) % 2
coeff5 = 0 if v > 0 else r_val
D5 = (D5 + coeff5 * d5) % 5
num = k - j
den = j + 1
cnt_num, rem_num = fact[num]
cnt_den, rem_den = fact[den]
v += cnt_num - cnt_den
r_val = (r_val * rem_num * inv[rem_den]) % 5
c2 = 1
d = A[k + 1] - A[k]
d2 = d % 2
d5 = d % 5
D2 = (D2 + c2 * d2) % 2
coeff5 = 0 if v > 0 else r_val
D5 = (D5 + coeff5 * d5) % 5
return D2 == 0 and D5 == 0
```
| 1 | 0 |
['Python']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
python3 solution
|
python3-solution-by-jesminmofi_be-p6aa
|
Code
|
jesminmofi_be
|
NORMAL
|
2025-02-24T09:09:28.338005+00:00
|
2025-02-24T09:09:28.338005+00:00
| 75 | false |
# Code
```python3 []
import math
def lucas_theorem(n: int, k: int, p: int):
"""
Computes nCk % p using Lucas's theorem.
"""
product = 1
while n != 0 or k != 0:
n_dig = n % p
k_dig = k % p
if k_dig > n_dig:
return 0
product *= math.comb(n_dig, k_dig)
product %= p
n //= p
k //= p
return product
def binom(n, k):
"""
Computes nCk mod 10 using properties of modular arithmetic
and Lucas's theorem for mod 2 and mod 5.
"""
m2 = lucas_theorem(n, k, 2)
m5 = lucas_theorem(n, k, 5)
if m2 == 0:
return [0, 6, 2, 8, 4][m5] # Mapping based on mod values
else:
return [5, 1, 7, 3, 9][m5]
class Solution:
def hasSameDigits(self, s: str) -> bool:
"""
Checks if the last row of Pascal's Triangle constructed from the input digits
results in two equal last digits.
"""
n1, n2 = 0, 0
length = len(s)
for i in range(length - 1):
multiple = binom(length - 2, i)
n1 = (n1 + multiple * int(s[i])) % 10
n2 = (n2 + multiple * int(s[i + 1])) % 10
return n1 == n2
```
| 1 | 0 |
['Python3']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
Python3 | 100.00% Beats | Easy to understand
|
python3-10000-beats-easy-to-understand-b-z1rf
|
IntuitionAt First we might think iterating all the string over and over again will solve this problem. But it turns out the length of input could be really huge
|
V12HMAstxo
|
NORMAL
|
2025-02-24T06:01:29.081815+00:00
|
2025-02-24T06:01:29.081815+00:00
| 112 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
At First we might think iterating all the string over and over again will solve this problem. But it turns out the length of input could be really huge (3 <= s.length <= 10^5). if we are just using repeated iteration, then we will face time limit exceeded error which caused by O(n^2) complexity. Therefore, the first intuition will be solving this problem with one iteration -> O(n) complexity. But How ? Let me explain in 'approach' section
# Approach
Think that the result that we want to compare is about last two digits. Now let see through this example
```
arr = [1,4,2,3]
```
Here is the walkthrough
```
1 4 2 3
5 6 5 -> (1 + 4) (4 + 2) (2 + 3)
1 1 -> (5 + 6) (6 + 5)
```
Now if we take a look to (5 + 6) and (6 + 5) we could we it as
(1 + 4) + (4 + 2) and (4 + 2) + (2 + 3). Now could you see the pattern ?
Absolutely, it's look like pascal triangle, isn't ? in this case it is [1 2 1] pattern -> [1x1 2x4 1x2] and [1x4 2x2 1x3]
So to conclude, the main idea is shown below
The first digit will take all number from first number up to n-1 number, while second digit will take all number from second number to n
now the code look like this
```
digit1 = 0
digit2 = 0
pascal_length = len(s) - 2
coeficient = 1
for i in range(pascal_length + 1):
digit1 += (coeficient * int(s[i])) % 10
digit2 += (coeficient * int(s[i+1])) % 10
coeficient = coeficient * (pascal_length - (i+1) + 1) // (i+1)
```
So we initialize the first digit and second digit, and determine the pascal_length. why the pascal_length here is n - 2 ?
take a look to previous example of arr [1,4,2,3]. From an array with length of 4, it will give us Level 2 of pascal triangel [1 2 1]
then, basically inside the loop we want to sum up all of them. But this comes up with a big problem
we know that the length of input could be really huge, therefore, the coefficient of pascal triangle and the sum could be really huge, and sadly this will caused time limit exceed again 😢
Therefore we come with a solution that utilizing both of Lucas's Theorem and Chinese Remainder Theorem (CRT) to get coefficient of pascal triangle smaller
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(n)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(1)
# Code
```python3 []
from math import comb
class Solution:
def binomial_mod2(self, n, k):
"""Return C(n, k) mod 2."""
return 1 if (k & ~n) == 0 else 0
def binomial_mod5(self, n, k):
"""
Return C(n, k) mod 5 using Lucas' theorem.
"""
# Precompute a small table C(a, b) mod 5 for a,b in [0..4]
# You could also do direct comb() % 5 for a,b <= 4:
c_mod5 = [[comb(a, b) % 5 for b in range(5)] for a in range(5)]
result = 1
while n > 0 or k > 0:
n_i = n % 5
k_i = k % 5
if k_i > n_i:
return 0
result = (result * c_mod5[n_i][k_i]) % 5
n //= 5
k //= 5
return result
def combine_mod2_and_mod5(self, a, b):
"""
Solve x ≡ a (mod 2) and x ≡ b (mod 5).
Return x mod 10 in [0..9].
"""
for x in range(10):
if x % 2 == a and x % 5 == b:
return x
# Shouldn't get here if a,b are valid in {0..1} and {0..4}, respectively.
return 0
def binomial_mod10(self, n, k):
"""
Compute C(n, k) mod 10 using:
- C(n, k) mod 2
- C(n, k) mod 5
- CRT to combine.
"""
a = self.binomial_mod2(n, k) # mod 2
b = self.binomial_mod5(n, k) # mod 5
return self.combine_mod2_and_mod5(a, b)
def hasSameDigits(self, s: str) -> bool:
# This is using Pascal's Triangle
# example :
# 1 5 3 4 6
# 6 8 7 0
# 4 5 7
# 9 2
# Number 9 could be seen as : (1,5,3,4) -> 1*1 + 3*5 + 3*3 + 1*4
# 1 + 15 + 9 + 4 = 29 % 10 = 9
# Number 2 could be seen as : (5,3,4,6) -> 1*5 + 3*3 + 3*4 + 1*6 =
# 5 + 9 + 12 + 6 = 32 % 10 = 2
# Problem ? The coefient could become enormous as lenght of 's' is increased
# Solution : We need to implement Chinese Remainder Theorem along with Lucas Theorem to deal with large binomial coefficients
digit1 = 0
digit2 = 0
pascal_length = len(s) - 2
coeficient = 1
for i in range(pascal_length + 1):
c = self.binomial_mod10(pascal_length, i)
digit1 = (digit1 + c * int(s[i])) % 10
digit2 = (digit2 + c * int(s[i+1])) % 10
return digit1 % 10 == digit2 % 10
```
| 1 | 0 |
['Python3']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
C++ full combinatorics templated solution
|
c-full-combinatorics-templated-solution-6oks9
|
Code
|
bramar2
|
NORMAL
|
2025-02-23T19:37:30.057315+00:00
|
2025-02-23T19:37:30.057315+00:00
| 102 | false |
# Code
```cpp []
class CombPrime;
extern const int MAXN;
extern const int MAXMOD;
extern map<int, CombPrime> prime_comb_map;
long long ext_euclidean(long long a, long long b, long long& x, long long& y) {
x = 1, y = 0;
int x1 = 0, y1 = 1, a1 = a, b1 = b;
while (b1) {
int q = a1 / b1;
tie(x, x1) = make_tuple(x1, x - q * x1);
tie(y, y1) = make_tuple(y1, y - q * y1);
tie(a1, b1) = make_tuple(b1, a1 - q * b1);
}
return a1;
}
long long mod_inv(long long n, long long _mod) {
long long x, y;
ext_euclidean(n, _mod, x, y);
return (x % _mod + _mod) % _mod;
}
long long mod_exp(long long base, long long exp, long long _mod) {
long long ans = 1;
base %= _mod;
while(exp > 0) {
if(exp & 1) ans = (base*ans) % _mod;
exp /= 2;
base = (base*base) % _mod;
}
return ans;
}
class CombLargePrime {
private:
const long long MOD;
vector<long long> fact, invfact;
public:
CombLargePrime(long long _MOD, int compute = MAXN) :
MOD(_MOD),
fact(vector<long long>(compute + 1, 1)),
invfact(vector<long long>(compute + 1, 1)) {
for(int i = 1; i <= compute; i++) {
fact[i] = (i * fact[i - 1]) % MOD;
invfact[i] = (mod_exp(i, MOD-2, MOD) * invfact[i - 1]) % MOD;
}
}
long long comb(int N, int K) {
return fact[N] * invfact[K] % MOD * invfact[N-K] % MOD;
}
};
class CombPrime {
private:
const long long p, b, MOD;
vector<long long> p_cnt, powers, fact, invfact;
public:
CombPrime() : p(-1), b(-1), MOD(-1) {}
CombPrime(long long _p, int compute = MAXN) :
p(_p),
b(floor(log2(MAXMOD + 1)/log2(_p))),
MOD(powl(_p, b)),
p_cnt(vector<long long>(compute + 1, 0)),
powers(vector<long long>(b + 1, 1)),
fact(vector<long long>(compute + 1, 1)),
invfact(vector<long long>(compute + 1, 1)) {
for(int i = 1; i <= b; i++) {
powers[i] = p * powers[i - 1];
}
for(int i = 1; i <= compute; i++) {
p_cnt[i] = p_cnt[i - 1];
int x = i;
while(x % p == 0) p_cnt[i]++, x /= p;
fact[i] = (x * fact[i - 1]) % MOD;
invfact[i] = (mod_inv(x, MOD) * invfact[i - 1]) % MOD;
}
}
long long comb(int N, int K, int exp = 1) {
if(p_cnt[N] - p_cnt[K] - p_cnt[N-K] >= exp) return 0LL;
return fact[N] * invfact[K] % powers[exp] * invfact[N-K] % powers[exp];
}
};
class CombCompound {
private:
vector<array<int, 2>> factors;
public:
CombCompound(int N, int compute = MAXN) {
for(long long i = 2; i * i <= N; i++) {
if(N % i != 0) continue;
int exp = 0;
while(N % i == 0) {
exp++;
N /= i;
}
factors.push_back({(int) i, exp});
}
if(N > 1) factors.push_back({N, 1});
for(auto& factor : factors) {
if(!prime_comb_map.count(factor[0]))
prime_comb_map.emplace(factor[0], CombPrime(factor[0]));
}
}
long long comb(int N, int K) {
long long a1, m1;
for(size_t i = 0; i < factors.size(); i++) {
long long a2 = prime_comb_map[factors[i][0]].comb(N, K, factors[i][1]);
long long m2 = powl(factors[i][0], factors[i][1]);
if(i == 0) {
a1 = a2;
m1 = m2;
}else {
a1 = a1 * mod_inv(m2, m1) * m2 + a2 * mod_inv(m1, m2) * m1;
m1 = m1 * m2;
a1 %= m1;
}
}
return a1;
}
};
const int MAXN = 100'001;
const int MAXMOD = 1e6;
map<int, CombPrime> prime_comb_map;
CombCompound mod10(10);
class Solution {
public:
bool hasSameDigits(string s) {
int a = 0, b = 0;
for(int i = 0, n = s.size(); i < n; i++) {
if(i != 0) b = (b + mod10.comb(n - 2, i - 1) * (s[i] - '0')) % 10;
if(i != n-1) a = (a + mod10.comb(n - 2, i) * (s[i] - '0')) % 10;
}
return a == b;
}
};
```
| 1 | 0 |
['C++']
| 0 |
check-if-digits-are-equal-in-string-after-operations-ii
|
Ultra-Fast C++ Lucas Theorem & CRT Approach for Adjacent Sum Reduction (100% Speed & Memory)
|
ultra-fast-c-lucas-theorem-crt-approach-nuddg
|
IntuitionThe problem requires repeatedly replacing each pair of consecutive digits with their sum taken modulo 10 until only two digits remain. This process can
|
4fPYADGrHM
|
NORMAL
|
2025-02-23T14:37:11.007054+00:00
|
2025-02-23T14:37:11.007054+00:00
| 113 | false |
# Intuition
The problem requires repeatedly replacing each pair of consecutive digits with their sum taken modulo 10 until only two digits remain. This process can actually be "compressed" into a single weighted sum where the weights are the binomial coefficients. In simpler terms, the final two digits are determined by a sum of differences between adjacent digits, each multiplied by a certain binomial coefficient (with all computations done modulo 10).
Since 10 factors into 2 and 5, we can compute each binomial coefficient by separately calculating its remainder when divided by 2 and when divided by 5, and then combine these results using the Chinese Remainder Theorem.
For the remainder modulo 2, there's a well-known trick: the binomial coefficient "C(m, j)" (read as "m choose j") is equal to 1 modulo 2 exactly when every bit that is 1 in j is also 1 in m. In other words, when you perform a bitwise AND of m and j, you will get j if and only if C(m, j) modulo 2 equals 1.
For the remainder modulo 5, Lucas's theorem can be used. However, because both the modulus 5 and the maximum number of digits required to represent m in base-5 (at most 8 digits for m up to 100,000) are small, we can precompute a tiny 5 by 5 table for "C(a, b) modulo 5" for values of a and b between 0 and 4. Then, for each j, we convert j into base-5 and use this table (as per Lucas’s theorem) to quickly calculate C(m, j) modulo 5.
Finally, by combining the two remainders (one from modulo 2 and one from modulo 5) using the Chinese Remainder Theorem, we determine the final coefficient modulo 10. Summing the weighted differences (each difference between consecutive digits times its computed coefficient) tells us whether the final two digits are the same (this will be the case exactly when the overall sum is 0 modulo 10).
# Approach
1. **Precompute Base-5 Digits:**
Since m (which equals n minus 2) is relatively small, convert m into its base-5 digits and store them in an array. This avoids any extra overhead from dynamic memory allocation.
2. **Small Combination Table for Modulo 5:**
Build a fixed 5 by 5 table for the binomial coefficients "C(a, b)" computed modulo 5 for a, b in the range 0 to 4. Then, for each j from 0 to m, convert j into base-5 and use the table (using Lucas’s theorem) to quickly compute C(m, j) modulo 5.
3. **Bit-Level Trick for Modulo 2:**
Use the property that C(m, j) modulo 2 equals 1 if and only if each bit in j is also set in m. This is efficiently determined by checking whether (m AND j) equals j.
4. **Combine Using the Chinese Remainder Theorem (CRT):**
With the two remainders available - call the modulo 2 remainder "c2" and the modulo 5 remainder "c5" - find the unique number between 0 and 9 that satisfies:
- The number gives a remainder of c5 when divided by 5, and
- The number gives a remainder of c2 when divided by 2.
Since c5 is less than 5, we can simply add 5 to c5 if its parity does not match c2.
5. **Accumulate the Result & Decide:**
Loop over every j from 0 to m (where each j corresponds to one term in the weighted sum). For the given digit string, sum up the differences (s[j] minus s[j+1]) each multiplied by the corresponding coefficient computed in the steps above. Finally, if the overall sum (reduced modulo 10) equals 0, then the two remaining digits are the same.
# Complexity
- **Time Complexity:**
O(n) – We iterate from j = 0 to m (with m equal to n minus 2). In each iteration, an inner loop runs at most 8 times (since the number of base-5 digits is at most 8), which is constant.
- **Space Complexity:**
O(1) – Only fixed-size arrays are used, in addition to the input string.
# Code
```cpp
#include <iostream>
#include <string>
using namespace std;
class Solution {
public:
bool hasSameDigits(string s) {
int n = s.size();
// 'm' is the number of rounds we'll effectively perform (since we stop once we have 2 digits left)
int m = n - 2;
// Here we convert 'm' into its base-5 representation.
// For m up to about 100,000, its base-5 form will have at most 8 digits.
// Since we know the maximum size is small, we use a fixed-size array instead of a dynamic one.
int m_digits[10], m_size = 0;
int temp = m;
if (temp == 0) {
m_digits[m_size++] = 0;
} else {
while (temp > 0) {
m_digits[m_size++] = temp % 5; // get the next digit in base 5
temp /= 5;
}
}
// This is a precomputed 5x5 table that holds the values for the binomial coefficients "C(a, b)"
// (which means "a choose b") after we take the remainder when dividing by 5.
// We have this table for a and b in the set {0, 1, 2, 3, 4}.
// For situations where b is larger than a, we define C(a, b) to be 0.
const int small[5][5] = {
{1, 0, 0, 0, 0},
{1, 1, 0, 0, 0},
{1, 2, 1, 0, 0},
{1, 3, 3, 1, 0},
{1, 4, 1, 4, 1}
};
// 'diff' will hold our running total. In the end, if 'diff' is 0 (after reducing modulo 10),
// that means the final two digits are the same.
int diff = 0;
// Now we loop over every j from 0 to m (inclusive). Each j corresponds to one term in the weighted sum.
for (int j = 0; j <= m; j++) {
// First, we want to compute (m choose j) but only care about its value modulo 5.
// Instead of calling a separate function, we calculate it inline.
int res5 = 1;
int x = j;
// Process each digit (in base-5) of j alongside the corresponding digit of m.
for (int i = 0; i < m_size; i++) {
int d = x % 5; // extract the i-th digit of j in base 5
x /= 5;
int a = m_digits[i]; // get the corresponding digit of m in base 5
// If the digit of j is greater than the digit of m at this position,
// then (m choose j) is 0 (when considered modulo 5)
if (d > a) {
res5 = 0;
break;
}
// Otherwise, multiply our result by the precomputed value from our table,
// and then take the remainder after dividing by 5.
res5 = (res5 * small[a][d]) % 5;
}
// Next, we compute the remainder of (m choose j) when dividing by 2 using a neat bit trick.
// The idea is: (m choose j) leaves a remainder of 1 when divided by 2 if and only if every bit set
// in j is also set in m. We can quickly check that with a bitwise AND.
int c2 = ((m & j) == j) ? 1 : 0;
// Now we want to merge the two remainders (the one modulo 5 we computed in res5,
// and the one modulo 2 stored in c2) into a final coefficient in the range 0 to 9.
// We need a number that, when divided by 5, gives us res5, and when divided by 2, gives us c2.
// Since res5 is between 0 and 4, it might already have the correct even/odd value (parity).
// If it does, we use it directly; if not, we add 5 to flip the parity.
int coeff = ((res5 & 1) == c2) ? res5 : res5 + 5;
// Now, we take the difference between the digit at position j and the digit at position j+1.
// We multiply this difference by our coefficient and add it to the running total 'diff'.
// We use modulo 10 to keep the result within the 0 to 9 range.
int delta = (s[j] - '0') - (s[j + 1] - '0');
diff = (diff + coeff * delta) % 10;
if (diff < 0)
diff += 10;
}
// Finally, if diff is 0 (after taking mod 10), it means the two remaining digits are the same.
return diff == 0;
}
};
```
| 1 | 0 |
['Bit Manipulation', 'Combinatorics', 'C++']
| 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.