question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
next-greater-element-ii
|
C++ most easiest solution and easy to understand
|
c-most-easiest-solution-and-easy-to-unde-1b1u
|
```\nclass Solution {\npublic:\n vector nextGreaterElements(vector& nums) {\n int n=nums.size();\n vectorans(n,0);\n stacks;\n fo
|
trojancode
|
NORMAL
|
2021-03-03T20:57:31.661824+00:00
|
2021-03-03T21:14:40.335091+00:00
| 1,511 | false |
```\nclass Solution {\npublic:\n vector<int> nextGreaterElements(vector<int>& nums) {\n int n=nums.size();\n vector<int>ans(n,0);\n stack<int>s;\n for(int i=n-1;i>=0;i--) {\n s.push(nums[i]);\n }\n \n for(int i=n-1;i>=0;i--) {\n while(!s.empty() && nums[i]>=s.top()) s.pop();\n if(s.empty()) ans[i]=-1;\n else ans[i]=s.top();\n s.push(nums[i]);\n }\n return ans;\n }\n};\n
| 13 | 0 |
['Stack', 'C']
| 2 |
next-greater-element-ii
|
503: Solution with step by step explanation
|
503-solution-with-step-by-step-explanati-ke1i
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n1. Initialize a stack to keep track of indices of elements we haven\'t fo
|
Marlen09
|
NORMAL
|
2023-03-12T04:26:14.908046+00:00
|
2023-03-12T04:26:14.908076+00:00
| 2,975 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Initialize a stack to keep track of indices of elements we haven\'t found a next greater element for.\n\n2. Initialize the result list to contain all -1s (assuming we won\'t find any next greater element).\n\n3. Loop through the array twice (to handle circularity) and process each element:\na. For each element i in the array:\ni. Pop elements off the stack if they are less than the current element and update their result to the current element.\nii. Add the current index i to the stack.\n\n4. Return the result list.\n\nThis algorithm works because it processes each element in the array twice, allowing it to handle circularity. During the first pass, it looks for next greater elements to the right of each element. During the second pass, it looks for next greater elements to the left of each element that haven\'t been found yet. By using a stack to keep track of indices of elements we haven\'t found a next greater element for, we can easily update their results when we find a greater element.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def nextGreaterElements(self, nums: List[int]) -> List[int]:\n # Initialize a stack to keep track of indices of elements we haven\'t found a next greater element for\n stack = []\n \n # Initialize the result list to contain all -1s (assuming we won\'t find any next greater element)\n result = [-1] * len(nums)\n \n # Loop through the array twice (to handle circularity) and process each element\n for _ in range(2):\n for i in range(len(nums)):\n # Pop elements off the stack if they are less than the current element and update their result\n while stack and nums[stack[-1]] < nums[i]:\n result[stack.pop()] = nums[i]\n \n # Add the current index to the stack\n stack.append(i)\n \n # Return the result list\n return result\n\n```
| 12 | 0 |
['Array', 'Stack', 'Monotonic Stack', 'Python', 'Python3']
| 0 |
next-greater-element-ii
|
Python Stack 98.78% faster | Simplest solution with explanation | Beg to Adv | Monotonic Stack
|
python-stack-9878-faster-simplest-soluti-04cl
|
Basic Idea:\n\n1. Well loop once, in that way we get the Next Greater Number of a normal array.\n2. Well Loop second time, then we will get the Next Greater Num
|
rlakshay14
|
NORMAL
|
2022-09-02T18:52:04.340132+00:00
|
2022-09-02T18:54:05.345187+00:00
| 2,751 | false |
**Basic Idea:**\n\n1. We`ll loop once, in that way we get the Next Greater Number of a normal array.\n2. We`ll Loop second time, then we will get the Next Greater Number of a circular array.\n\n**Optimised solution :**\n```\nclass Solution:\n def nextGreaterElements(self, nums: List[int]) -> List[int]:\n stack, res = [], [-1] * len(nums) # taking an empty stack for storing index, a list with the lenght same as of nums so that we wont add unnecessary elements.\n # [-1] * len(nums) = this will produce a list with len of nums and all elems will be -1.\n for i in list(range(len(nums))) * 2: # see explanation below.\n while stack and (nums[stack[-1]] < nums[i]): # stack is not empty and nums previous elem is less then current, i.e 1<2. \n res[stack.pop()] = nums[i] # then we`ll pop the index in stack and in the res on the same index will add the current num. \n stack.append(i) # if stack is empty then we`ll add the index of num in it for comparision to the next element in the provided list. \n return res # returing the next greater number for every element in nums.\n```\n\n >**for i in list(range(len(nums))) * 2:**\n > As we know the given array is circular integer array, so we have to run the for loop twice so that we could compare last elments of the list to the first elements. \n > In python 3, just `for i in range(len(nums)) * 2` will thrown exception `TypeError: unsupported operand type(s) for *: \'range\' and \'int\'`, however if we put range inside it`ll work fine. Using list() is a little hack to make it work. \n\n**Expantion of the above solution :**\n```python\nstack, r = [], [-1] * len(nums)\n for i in range(len(nums)):\n while stack and (nums[stack[-1]] < nums[i]):\n r[stack.pop()] = nums[i]\n stack.append(i)\n for i in range(len(nums)):\n while stack and (nums[stack[-1]] < nums[i]):\n r[stack.pop()] = nums[i]\n if stack == []:\n break\n return r\n```\n\n***Found helpful, Do upvote !!***
| 12 | 0 |
['Stack', 'Monotonic Stack', 'Python', 'Python3']
| 2 |
next-greater-element-ii
|
Brute Intuitive solution✔️✔️✅ Beats 98% Monotonic Pattern
|
brute-intuitive-solution-beats-98-monoto-9lng
|
503. Next Greater Element II\njava []\npublic class Solution {\n public int[] nextGreaterElements(int[] A) {\n int n = A.length;\n int[] res =
|
Dixon_N
|
NORMAL
|
2024-05-24T12:54:15.597623+00:00
|
2024-05-24T21:46:32.365519+00:00
| 1,072 | false |
## 503. Next Greater Element II\n```java []\npublic class Solution {\n public int[] nextGreaterElements(int[] A) {\n int n = A.length;\n int[] res = new int[n]; \n Arrays.fill(res, -1); // Initialize result array with -1 \n Stack<Integer> stack = new Stack<>(); // Stack to store indices\n\n // Iterate through the array twice to handle circular nature\n for (int i = 0; i < n * 2; i++) { \n // Use modulo to wrap around the array\n while (!stack.isEmpty() && A[stack.peek()] < A[i % n]) { \n \n res[stack.pop()] = A[i % n];\n }\n stack.push(i % n); // Push current index (mod n) onto the stack\n }\n return res; // Return the result array\n }\n}\n\n```\n\nLearn Next Greater element, then next smaller element(**right**), previous smaller element (NSE **left**) its follow up questions notable 84. Largest Rectangle in Histogram and 85. Maximal Rectangle\n\n\n\n```java []\n//Next Greater Element\nimport java.util.Arrays;\nimport java.util.Stack;\n\npublic class NextGreaterElement {\n\n public static int[] nextGreaterElement(int[] nums) {\n int n = nums.length;\n int[] result = new int[n];\n Arrays.fill(result, -1);\n Stack<Integer> stack = new Stack<>();\n\n for (int i = 0; i < n; i++) {\n while (!stack.isEmpty() && nums[stack.peek()] < nums[i]) {\n result[stack.pop()] = nums[i];\n }\n stack.push(i);\n }\n\n return result;\n }\n\n public static void main(String[] args) {\n int[] nums = {4, 5, 2, 25};\n int[] result = nextGreaterElement(nums);\n System.out.println(Arrays.toString(result)); // Output: [5, 25, 25, -1]\n }\n}\n\n```\n```java []\nimport java.util.Arrays;\nimport java.util.Stack;\n\npublic class PreviousGreaterElement {\n\n public static int[] previousGreaterElement(int[] nums) {\n int n = nums.length;\n int[] result = new int[n];\n Arrays.fill(result, -1);\n Stack<Integer> stack = new Stack<>();\n\n for (int i = 0; i < n; i++) {\n while (!stack.isEmpty() && nums[stack.peek()] <= nums[i]) {\n stack.pop();\n }\n if (!stack.isEmpty()) {\n result[i] = nums[stack.peek()];\n }\n stack.push(i);\n }\n\n return result;\n }\n}\n\n```\n```java []\n//Next Smaller Element\nimport java.util.Arrays;\nimport java.util.Stack;\n\npublic class NextSmallerElement {\n\n public static int[] nextSmallerElement(int[] nums) {\n int n = nums.length;\n int[] result = new int[n];\n Arrays.fill(result, -1);\n Stack<Integer> stack = new Stack<>();\n\n for (int i = 0; i < n; i++) {\n while (!stack.isEmpty() && nums[stack.peek()] > nums[i]) {\n result[stack.pop()] = nums[i];\n }\n stack.push(i);\n }\n\n return result;\n }\n}\n\n```\n```java []\n//Previous Smaller Element\nimport java.util.Arrays;\nimport java.util.Stack;\n\npublic class PreviousSmallerElement {\n\n public static int[] previousSmallerElement(int[] nums) {\n int n = nums.length;\n int[] result = new int[n];\n Arrays.fill(result, -1);\n Stack<Integer> stack = new Stack<>();\n\n for (int i = 0; i < n; i++) {\n while (!stack.isEmpty() && nums[stack.peek()] >= nums[i]) {\n stack.pop();\n }\n if (!stack.isEmpty()) {\n result[i] = nums[stack.peek()];\n }\n stack.push(i);\n }\n\n return result;\n }\n}\n\n```\n\n## Next Greater Element I\n\n# Code\n```\npublic class Solution {\n public int[] nextGreaterElement(int[] nums1, int[] nums2) {\n Map<Integer, Integer> map = new HashMap<>(); // map from x to next greater element of x\n Stack<Integer> stack = new Stack<>();\n \n // Iterate through nums2 and fill the map with next greater elements\n for (int num : nums2) {\n while (!stack.isEmpty() && stack.peek() < num) {\n map.put(stack.pop(), num);\n }\n stack.push(num);\n } \n \n // Update nums1 with the next greater elements found in the map, or -1 if not found\n for (int i = 0; i < nums1.length; i++) {\n nums1[i] = map.getOrDefault(nums1[i], -1);\n }\n \n return nums1;\n }\n}\n\n```\n\n## 84. Largest Rectangle in Histogram\n### Next Smaller Element to right\n\n```java []\n//Next Smaller Element to the right pattern \n\n/*for (int i = 0; i < n; i++) {\n while (!stack.isEmpty() && arr[stack.peek()] > arr[i]) {\n ans[stack.pop()] = arr[i]; //Next Smaller Element to the right pattern \n }\n stack.push(i);\n}\n\n*/\nimport java.util.Stack;\n\npublic class Solution {\n\n\n public int largestRectangleArea(int[] heights) {\n int maxArea = 0;\n Stack<Pair> stack = new Stack<>();\n\n for (int i = 0; i < heights.length; i++) {\n int start = i;\n // Pop elements from stack while the current height is less than the height at stack\'s top\n while (!stack.isEmpty() && stack.peek().height > heights[i]) {\n Pair pair = stack.pop();\n int index = pair.index;\n int height = pair.height;\n maxArea = Math.max(maxArea, height * (i - index));\n start = index; // Update start to the index of the popped element\n }\n stack.push(new Pair(start, heights[i])); // Push current index and height as a pair\n }\n\n // Process remaining elements in the stack\n for (Pair pair : stack) {\n int index = pair.index;\n int height = pair.height;\n maxArea = Math.max(maxArea, height * (heights.length - index));\n }\n\n return maxArea;\n }\n class Pair {\n int index;\n int height;\n\n Pair(int index, int height) {\n this.index = index;\n this.height = height;\n }\n }\n}\n```\n## 85. Maximal Rectangle\n\n```java []\nimport java.util.Stack;\n\npublic class Solution {\n public int maximalRectangle(char[][] matrix) {\n int n = matrix.length;\n if (n == 0) return 0;\n int m = matrix[0].length;\n if (m == 0) return 0;\n\n int[][] mat = new int[n][m];\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < m; j++) {\n mat[i][j] = matrix[i][j] == \'1\' ? 1 : 0;\n }\n }\n\n return maximalAreaOfSubMatrixOfAll1(mat, n, m);\n }\n\n public int maximalAreaOfSubMatrixOfAll1(int[][] mat, int n, int m) {\n int maxArea = 0;\n int[] height = new int[m];\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < m; j++) {\n if (mat[i][j] == 1) {\n height[j]++;\n } else {\n height[j] = 0;\n }\n }\n int area = largestRectangleArea(height);\n maxArea = Math.max(maxArea, area);\n }\n return maxArea;\n }\n\n public int largestRectangleArea(int[] heights) {\n int maxArea = 0;\n Stack<Pair> stack = new Stack<>();\n\n for (int i = 0; i < heights.length; i++) {\n int start = i;\n // Pop elements from stack while the current height is less than the height at stack\'s top\n while (!stack.isEmpty() && stack.peek().height > heights[i]) {\n Pair pair = stack.pop();\n int index = pair.index;\n int height = pair.height;\n maxArea = Math.max(maxArea, height * (i - index));\n start = index; // Update start to the index of the popped element\n }\n stack.push(new Pair(start, heights[i])); // Push current index and height as a pair\n }\n\n // Process remaining elements in the stack\n for (Pair pair : stack) {\n int index = pair.index;\n int height = pair.height;\n maxArea = Math.max(maxArea, height * (heights.length - index));\n }\n\n return maxArea;\n }\n class Pair {\n int index;\n int height;\n\n Pair(int index, int height) {\n this.index = index;\n this.height = height;\n }\n }\n}\n```\n11. Container With Most Water\n42. Trapping Rain Water(similair)\n2517. Maximum Tastiness of Candy Basket (similair)\n2560. House Robber IV (similair)\n198. House Robber (DP)\n213. House Robber II(DP)\n337. House Robber III (DP)\n[907. Sum of Subarray Minimums](https://leetcode.com/problems/sum-of-subarray-minimums/solutions/5165808/monotonic-patter-continuation/)\n\nIntroduction To stack and NEG pattern - **4 variations** covered in\n\n[232. Implement Queue using Stacks](https://leetcode.com/problems/implement-queue-using-stacks/solutions/5203561/implement-queue-using-stacks/)\n[225. Implement Stack using Queues](https://leetcode.com/problems/implement-stack-using-queues/solutions/5203563/implement-stacks-using-queue/)\n[155. Min Stack](https://leetcode.com/problems/min-stack/solutions/4185675/java-simple-solution-using-two-stack-and-one-stack/)\n[496. Next Greater Element I](https://leetcode.com/problems/next-greater-element-i/solutions/5164552/must-read-intuitive-pattern-for-deep-understanding-of-nge-and-nsm/) **very very important**\n[503. Next Greater Element II](https://leetcode.com/problems/next-greater-element-ii/solutions/5201809/brute-intuitive-solution-beats-98-monotonic-pattern/)\n[907. Sum of Subarray Minimums](https://leetcode.com/problems/sum-of-subarray-minimums/solutions/5165808/monotonic-patter-continuation/) **pattern**\n[11. Container With Most Water](https://leetcode.com/problems/container-with-most-water/solutions/5165076/must-read-maximum-water-pattern/)\n[42. Trapping Rain Water](https://leetcode.com/problems/trapping-rain-water/solutions/5165626/building-intuitive-solution-one-step-at-a-time/)\n[1856. Maximum Subarray Min-Product](https://leetcode.com/problems/maximum-subarray-min-product/solutions/5167159/must-read-monotonic-stack-pattern-variations/)\n[735. Asteroid Collision](https://leetcode.com/problems/asteroid-collision/solutions/5166334/brute-solution/)\n[402. Remove K Digits](https://leetcode.com/problems/remove-k-digits/solutions/5166502/beast-intuitive-approach-step-by-step-nsg-to-right/)\n[2104. Sum of Subarray Ranges](https://leetcode.com/problems/sum-of-subarray-ranges/solutions/5166891/beastt-solution/)\n[84. Largest Rectangle in Histogram](https://leetcode.com/problems/largest-rectangle-in-histogram/solutions/5172029/monotonic-stack-pattern-deep-understanding/)\n[85. Maximal Rectangle](https://leetcode.com/problems/maximal-rectangle/solutions/5201947/brute-intuitive-solution-beats-98-monotonic-stack-pattern-deep-understanding/)\n[739. Daily Temperatures](https://leetcode.com/problems/daily-temperatures/solutions/5167031/must-read-monotonic-stack-pattern-variations/) **Fundamental**\n[853. Car Fleet](https://leetcode.com/problems/car-fleet/solutions/5167204/must-read-monotonic-stack-pattern-variations/)\n[150. Evaluate Reverse Polish Notation](https://leetcode.com/problems/evaluate-reverse-polish-notation/solutions/5172161/stack-intuitive-solution/)\n[895. Maximum Frequency Stack](https://leetcode.com/problems/maximum-frequency-stack/solutions/5172171/stack-implementation-problem/) **VVI** Implementation problem\n[173. Binary Search Tree Iterator](https://leetcode.com/problems/binary-search-tree-iterator/solutions/5172179/brute-solution/)\n[682. Baseball Game](https://leetcode.com/problems/baseball-game/solutions/5172183/straight-forward-approach/)\n[1209. Remove All Adjacent Duplicates in String II](https://leetcode.com/problems/remove-all-adjacent-duplicates-in-string-ii/solutions/5172210/stack-solution-pattern/) **Must Go through**\n[456. 132 Pattern](https://leetcode.com/problems/132-pattern/solutions/5202876/monotonic-stack/)\n[22. Generate Parentheses](https://leetcode.com/problems/generate-parentheses/solutions/5202882/monotonic-stack/)\n[460. LFU Cache]()\n[146. LRU Cache]()\n[901. Online Stock Span](https://leetcode.com/problems/online-stock-span/solutions/5172217/stack-nge-and-nse-deep-understanding/) **Must Read**\n[239. Sliding Window Maximum](https://leetcode.com/problems/sliding-window-maximum/solutions/5175931/nge-pattern/) **All three solution**\n[856. Score of Parentheses](https://leetcode.com/problems/score-of-parentheses/solutions/5203496/scoreofparentheses/)\n[844. Backspace String Compare](https://leetcode.com/problems/backspace-string-compare/solutions/5203544/brute-and-optimized-backspacecompare-beats-100/)\n[71. Simplify Path](https://leetcode.com/problems/simplify-path/solutions/5203538/simplifypath/)\n\n<br/>\n\n\n\n
| 9 | 0 |
['Java']
| 1 |
next-greater-element-ii
|
JAVA CODE | 6ms | Two iterations | NGETR
|
java-code-6ms-two-iterations-ngetr-by-ab-tx5q
|
\nclass Solution {\n public int[] nextGreaterElements(int[] arr) {\n int ngetr[] = new int[arr.length];\n Stack<Integer> st = new Stack<>();\n
|
abhishekgusain2705
|
NORMAL
|
2021-04-02T09:04:30.917312+00:00
|
2021-04-02T09:06:23.914564+00:00
| 1,553 | false |
```\nclass Solution {\n public int[] nextGreaterElements(int[] arr) {\n int ngetr[] = new int[arr.length];\n Stack<Integer> st = new Stack<>();\n st.push(0);\n //1st iteration\n for(int i = 1 ; i < arr.length ; i++){\n while(st.size() > 0 && arr[st.peek()] < arr[i])\n { //this is the logic for NGETR\n ngetr[st.peek()] = arr[i];\n st.pop();\n }\n st.push(i);\n }\n //second iteration as array is cyclic\n for(int i = 0 ; i < arr.length ; i++){\n while(arr[st.peek()] < arr[i])\n {\n ngetr[st.peek()] = arr[i];\n st.pop();\n }\n }\n while(st.size() > 0){\n ngetr[st.peek()] = -1;\n st.pop();\n }\n return ngetr;\n }\n\t//NGETR => Next Greater Element to Right\n}\n```\n***Plz Upvote If you like the solution***
| 9 | 0 |
['Stack', 'Java']
| 3 |
next-greater-element-ii
|
Using Stack in java
|
using-stack-in-java-by-tryambak_trivedi-14wt
|
\n# Code\n\nclass Solution {\n public int[] nextGreaterElements(int[] nums) {\n Stack<Integer> st = new Stack<Integer>();\n int v[]= new int[nums.leng
|
Tryambak_Trivedi
|
NORMAL
|
2024-03-09T06:32:25.509327+00:00
|
2024-03-09T06:32:25.509362+00:00
| 380 | false |
\n# Code\n```\nclass Solution {\n public int[] nextGreaterElements(int[] nums) {\n Stack<Integer> st = new Stack<Integer>();\n int v[]= new int[nums.length];\n for(int i=nums.length-1;i>=0;i--)\n st.push(nums[i]);\n\n for(int i= nums.length-1 ;i>=0;i--)\n {\n while(!st.isEmpty() && st.peek()<=nums[i])\n {\n st.pop();\n }\n if(st.isEmpty())\n v[i]=-1;\n else\n v[i]=st.peek();\n \n st.push(nums[i]);\n }\n return(v);\n }\n}\n```
| 8 | 0 |
['Java']
| 1 |
next-greater-element-ii
|
🔥[Python 3] Monotonic stack 2 traversal approaches
|
python-3-monotonic-stack-2-traversal-app-ssy6
|
Iteration from start to end:\npython3\nclass Solution:\n def nextGreaterElements(self, nums: List[int]) -> List[int]:\n stack, L = [], len(nums)\n
|
yourick
|
NORMAL
|
2023-07-21T17:09:47.702356+00:00
|
2023-07-21T17:09:47.702382+00:00
| 1,087 | false |
## Iteration from start to end:\n```python3\nclass Solution:\n def nextGreaterElements(self, nums: List[int]) -> List[int]:\n stack, L = [], len(nums)\n res = [-1] * L\n\n for i in range(L*2):\n idx = i % L\n while stack and nums[stack[-1]] < nums[idx]:\n res[stack.pop()] = nums[idx]\n stack.append(idx)\n return res\n```\n## Iteration from end to start:\n```\nclass Solution:\n def nextGreaterElements(self, nums: List[int]) -> List[int]:\n stack, L = [], len(nums)\n res = [-1] * L\n\n for i in reversed(range(L * 2 - 1)):\n idx = i % L\n while stack and stack[-1] <= nums[idx]:\n stack.pop()\n res[idx] = stack[-1] if stack else -1\n stack.append(nums[idx])\n \n return res\n```\n\n
| 8 | 0 |
['Monotonic Stack', 'Python', 'Python3']
| 0 |
next-greater-element-ii
|
JAVA SOLUTION✅✅ || STEP BY STEP EXPLAINED🤗
|
java-solution-step-by-step-explained-by-3otgo
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
abhiyadav05
|
NORMAL
|
2023-04-29T17:37:19.104479+00:00
|
2023-04-29T17:37:19.104518+00:00
| 1,166 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->O(N)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->O(N)\n\n\n\n# Code\n```\nclass Solution {\n public int[] nextGreaterElements(int[] nums) {\n \n int n = nums.length;\n Stack<Integer> st = new Stack<>(); // create a stack to store indices of elements\n\n // first loop to find the next greater element for each element in nums (except the last one)\n for(int i = n-2; i >= 0; i--){\n\n // while the stack is not empty and the top element is smaller than or equal to the current element in nums\n while(st.size() > 0 && st.peek() <= nums[i]){\n st.pop(); // remove the top element from stack\n }\n st.push(nums[i]); // push the current element in nums into stack\n }\n\n int ans[] = new int[nums.length];\n\n // second loop to find the next greater element for the remaining elements (including the last one)\n for(int i = n-1; i >= 0; i--){\n\n // while the stack is not empty and the top element is smaller than or equal to the current element in nums\n while(st.size() > 0 && nums[i] >= st.peek()){\n st.pop(); // remove the top element from stack\n }\n \n if(st.size() == 0){\n ans[i] = -1; // if stack is empty, set the answer to -1 (no next greater element found)\n }else{\n ans[i] = st.peek(); // otherwise, set the answer to the top element of the stack\n }\n\n st.push(nums[i]); // push the current element in nums into stack\n }\n return ans; // return the answer array\n }\n}\n\n```
| 8 | 0 |
['Array', 'Stack', 'Java']
| 0 |
next-greater-element-ii
|
✅Accepted | | ✅Easy solution || ✅Short & Simple || ✅Best Method
|
accepted-easy-solution-short-simple-best-6yhh
|
\n# Code\n\nclass Solution {\npublic:\n vector<int> nextGreaterElements(vector<int>& nums) {\n int n=nums.size();\n vector<int> ans(n, -1);\n
|
sanjaydwk8
|
NORMAL
|
2023-01-25T12:07:36.589367+00:00
|
2023-01-25T12:07:36.589411+00:00
| 2,087 | false |
\n# Code\n```\nclass Solution {\npublic:\n vector<int> nextGreaterElements(vector<int>& nums) {\n int n=nums.size();\n vector<int> ans(n, -1);\n stack<int> st;\n for(int i=0;i<2*n;i++)\n {\n while(!st.empty() && nums[i%n]>nums[st.top()%n])\n {\n ans[st.top()%n]=nums[i%n];\n st.pop();\n }\n st.push(i%n);\n }\n return ans;\n }\n};\n```\nPlease **UPVOTE** if it helps \u2764\uFE0F\uD83D\uDE0A\nThank You and Happy To Help You!!
| 8 | 0 |
['C++']
| 1 |
next-greater-element-ii
|
C++ Solution with O(n) Time complexity
|
c-solution-with-on-time-complexity-by-pr-fasd
|
\n# Code\n\nclass Solution {\npublic:\n vector<int> nextGreaterElements(vector<int>& nums) {\n vector<int> temp;\n vector<int> temp2(2*nums.siz
|
prins_kraj
|
NORMAL
|
2022-11-11T19:30:10.553398+00:00
|
2022-11-11T19:30:10.553428+00:00
| 1,237 | false |
\n# Code\n```\nclass Solution {\npublic:\n vector<int> nextGreaterElements(vector<int>& nums) {\n vector<int> temp;\n vector<int> temp2(2*nums.size());\n for(int i=0; i<nums.size(); i++){\n temp.push_back(nums[i]);\n }\n for(int i=0; i<nums.size(); i++){\n temp.push_back(nums[i]);\n }\n stack<int> st;\n for(int i=temp.size()-1; i>=0; i--){\n int k=temp[i];\n while(!st.empty() && st.top()<=k){\n st.pop();\n }\n int nge;\n if(st.empty()){\n nge=-1;\n }\n else{\n nge=st.top();\n }\n temp2[i]=nge;\n st.push(k);\n }\n vector<int> ans;\n for(int i=0; i<nums.size(); i++){\n ans.push_back(temp2[i]);\n }\n return ans;\n }\n};\n```
| 8 | 0 |
['Stack', 'C++']
| 1 |
next-greater-element-ii
|
Javascript easy stack solution
|
javascript-easy-stack-solution-by-gauran-fe6i
|
```\nvar nextGreaterElements = function(nums) {\n let n = nums.length;\n let stack =[];\n let result = new Array(n).fill(-1)\n for(let i=0; i<2*n;i+
|
gaurang9
|
NORMAL
|
2021-03-06T08:03:55.012866+00:00
|
2021-03-06T08:03:55.012911+00:00
| 1,500 | false |
```\nvar nextGreaterElements = function(nums) {\n let n = nums.length;\n let stack =[];\n let result = new Array(n).fill(-1)\n for(let i=0; i<2*n;i++){\n while(stack.length && nums[i%n]>nums[stack[stack.length-1]]){\n result[stack.pop()]= nums[i%n]\n }\n stack.push(i%n)\n }\n return result;\n};
| 8 | 0 |
['Stack', 'JavaScript']
| 1 |
next-greater-element-ii
|
Simple Java Solution
|
simple-java-solution-by-allabakash-s4ns
|
\nclass Solution {\n \n public int[] nextGreaterElements(int[] nums) {\n \n Stack<Integer> stack = new Stack<>();\n \n int[] resu
|
allabakash
|
NORMAL
|
2020-07-15T04:51:46.625549+00:00
|
2020-07-15T04:51:46.625585+00:00
| 1,905 | false |
```\nclass Solution {\n \n public int[] nextGreaterElements(int[] nums) {\n \n Stack<Integer> stack = new Stack<>();\n \n int[] result = new int[nums.length];\n \n process(nums, result, stack, true);\n \n process(nums, result, stack, false); \n \n while (!stack.isEmpty()) {\n \n result[stack.pop()] = -1;\n }\n \n return result;\n }\n \n private void process(int[] nums, int[] result, Stack<Integer> stack, boolean push) {\n \n for (int i = 0; i < nums.length; i++) {\n \n while (!stack.isEmpty() && nums[stack.peek()] < nums[i]) {\n \n result[stack.pop()] = nums[i];\n }\n \n if (push)\n stack.push(i);\n }\n }\n}\n```
| 8 | 0 |
['Java']
| 1 |
next-greater-element-ii
|
Simply Simple Python Solution - two pass - O(n) - Stack
|
simply-simple-python-solution-two-pass-o-wd52
|
\tdef nextGreaterElements(self, nums: List[int]) -> List[int]:\n ln = len(nums)\n if ln == 0:\n return []\n stack = []\n
|
limitless_
|
NORMAL
|
2019-09-21T20:46:50.954328+00:00
|
2019-09-21T20:46:50.954378+00:00
| 1,825 | false |
\tdef nextGreaterElements(self, nums: List[int]) -> List[int]:\n ln = len(nums)\n if ln == 0:\n return []\n stack = []\n res = [-1] * ln\n # Run it twice. After first iteration\n # the stack has the increasing order of elements from starting\n # so in second iteration you will get the next greater from stack\n # which was on the left side of that node\n for _ in range(2):\n for i in range(ln - 1, -1, -1):\n while len(stack) > 0 and stack[-1] <= nums[i]:\n stack.pop()\n if len(stack) > 0:\n res[i] = stack[-1]\n \n stack.append(nums[i])\n \n return res
| 8 | 1 |
['Python', 'Python3']
| 1 |
next-greater-element-ii
|
🚀 Elegant Python3 Solution | Monotonic Stack | Beats 99.41% 🔥
|
elegant-python3-solution-monotonic-stack-5mb9
|
IntuitionTo solve the problem, we need to find the next greater element for each number in the circular array. A monotonic stack is ideal for this task, as it a
|
justsmartboy
|
NORMAL
|
2025-01-05T17:37:53.644942+00:00
|
2025-01-05T17:38:10.745285+00:00
| 1,085 | false |
[](https://leetcode.com/problems/next-greater-element-ii/submissions/1498746841/)
# Intuition
To solve the problem, we need to find the next greater element for each number in the circular array. A **monotonic stack** is ideal for this task, as it allows us to efficiently track the next greater elements while iterating. By traversing the array twice (to simulate its circular nature), we can ensure all elements are covered.
---
# Approach
1. **Simulate Circular Array**:
- To handle the circular nature of the array, iterate over it twice using `i % len(nums)` to access elements.
2. **Use a Monotonic Stack**:
- Maintain a stack to store elements in decreasing order. This helps efficiently find the next greater element.
- As we traverse, pop elements from the stack that are smaller than or equal to the current element because they can’t be the next greater element.
3. **Result Array**:
- Initialize a result array `res` with `-1` to represent elements with no next greater value.
- Update `res[i]` with the top of the stack when the next greater element is found.
4. **Push to Stack**:
- Add the current element to the stack for future comparisons.
---
# Complexity
- **Time complexity**:
$$O(n)$$
Each element is pushed and popped from the stack at most once, where \(n\) is the length of the array.
- **Space complexity**:
$$O(n)$$
The stack may store up to \(n\) elements in the worst case.
---
# Code
```python
class Solution:
def nextGreaterElements(self, nums: List[int]) -> List[int]:
n = len(nums)
res = [-1] * n # Initialize the result array with -1
stack = [] # Monotonic stack to track next greater elements
# Iterate through the array twice to simulate circularity
for i in range(2 * n - 1, -1, -1):
num = nums[i % n] # Current element (handle circular index)
# Remove elements from the stack that are <= the current element
while stack and stack[-1] <= num:
stack.pop()
# If the stack is not empty, the top of the stack is the next greater element
if stack:
res[i % n] = stack[-1]
# Push the current element onto the stack
stack.append(num)
return res
```

| 7 | 0 |
['Array', 'Stack', 'Monotonic Stack', 'Python', 'Python3']
| 0 |
next-greater-element-ii
|
simple and easy understanding c++ code
|
simple-and-easy-understanding-c-code-by-3ya2q
|
\ncpp []\nclass Solution {\npublic:\n vector<int> nextGreaterElements(vector<int>& nums) {\n int n=nums.size();\n vector<int>arr(n,-1);\n
|
sampathkumar718
|
NORMAL
|
2024-09-01T14:33:31.455024+00:00
|
2024-09-01T14:33:31.455056+00:00
| 922 | false |
\n```cpp []\nclass Solution {\npublic:\n vector<int> nextGreaterElements(vector<int>& nums) {\n int n=nums.size();\n vector<int>arr(n,-1);\n for(int i=0;i<n;i++){\n for(int j=1;j<n;j++){\n int a=(i+j)%n;\n if(nums[a]>nums[i]){\n arr[i]=nums[a];\n break;\n }\n }\n }\n \n return arr;\n }\n};\n```
| 7 | 0 |
['C++']
| 1 |
next-greater-element-ii
|
Very Short and Simple Approach. 🔥
|
very-short-and-simple-approach-by-harshr-tbcr
|
\nPLEASE UPVOTE IF U LIKE \uD83D\uDC4D\n\n# Complexity\n- Time complexity:O(n^2)\n\n- Space complexity:O(1) \njavascript []\n/**\n * @param {number[]} nums\n *
|
HarshRaj130102
|
NORMAL
|
2024-06-14T13:21:58.712106+00:00
|
2024-06-14T13:23:59.177880+00:00
| 1,914 | false |
```\nPLEASE UPVOTE IF U LIKE \uD83D\uDC4D\n```\n# Complexity\n- Time complexity:$$O(n^2)$$\n\n- Space complexity:$$O(1)$$ \n```javascript []\n/**\n * @param {number[]} nums\n * @return {number[]}\n */\nvar nextGreaterElements = function(nums) {\n let ans = new Array(nums.length).fill(-1);\n for (let i = 0; i < nums.length; i++) {\n let j = (i + 1) % nums.length;\n while (i !== j) {\n if (nums[j] > nums[i]) {\n ans[i] = nums[j];\n break;\n } else {\n j = (j + 1) % nums.length;\n }\n }\n }\n return ans;\n};\n\n```\n```python []\nclass Solution:\n def nextGreaterElements(self, nums):\n ans = [-1] * len(nums)\n for i in range(len(nums)):\n j = (i + 1) % len(nums)\n while i != j:\n if nums[j] > nums[i]:\n ans[i] = nums[j]\n break\n else:\n j = (j + 1) % len(nums)\n return ans\n\n```\n```c++ []\n#include <vector>\nusing namespace std;\n\nclass Solution {\npublic:\n vector<int> nextGreaterElements(vector<int>& nums) {\n vector<int> ans(nums.size(), -1);\n for (int i = 0; i < nums.size(); ++i) {\n int j = (i + 1) % nums.size();\n while (i != j) {\n if (nums[j] > nums[i]) {\n ans[i] = nums[j];\n break;\n } else {\n j = (j + 1) % nums.size();\n }\n }\n }\n return ans;\n }\n};\n\n```\n```java []\nclass Solution {\n public int[] nextGreaterElements(int[] nums) {\n int ans[] = new int[nums.length];\n for(int i = 0 ; i<nums.length ; i++){\n ans[i] = -1;\n int j = (i+1)%nums.length;\n while(i != j){\n if(nums[j] > nums[i]){\n ans[i] = nums[j];\n break;\n }\n else{\n j = (j+1)%nums.length;\n }\n }\n }\n return ans;\n }\n}\n```
| 7 | 0 |
['Python', 'C++', 'Java', 'JavaScript']
| 1 |
next-greater-element-ii
|
Using increasing stack , 95.21% efficient.
|
using-increasing-stack-9521-efficient-by-92fw
|
Intuition\n Describe your first thoughts on how to solve this problem. \nTo use stack as it works on lifo method and make it an increasing stack by appending an
|
Shrishti007
|
NORMAL
|
2024-01-19T08:34:47.634825+00:00
|
2024-01-19T08:34:47.634847+00:00
| 1,160 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo use stack as it works on lifo method and make it an increasing stack by appending and popping so that the next greater element is the top of the stack.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUse a stack and a result array, make sure that the stack is in increasing order and traverse the array given as it is circular can traverse in inverse manner, then check if the stack exist and if the top element is less than the visting element in the given array then pop out that element as we are trying to maintain the stack in increasing manner, to get result check if we are in nums and then if the stack exist add the top to the result else add the element to the stack.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N) as the while loop is not travers only the traversing the whole nums, only the element present in the stack.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N)\n\n# Code\n```\nclass Solution:\n def nextGreaterElements(self, nums: List[int]) -> List[int]:\n # Initializing the ans and stack \n n = len(nums)\n result = [-1] * n\n st = []\n # Traversing through the array by 2n-1 as we are using an imaginary \n # array of size n and as the array is circular we can traverse in reversibly also\n # It will not affect the ans\n for i in range(2*n-1,-1,-1):\n # Using while loop to remove the element which are less than the element \n # we are traversing at in the stack\n # using index as that because this is a circular array\n while st and st[-1] <= nums[i%n]:\n st.pop()\n # When we are before the end of the nums if stack exist then add the \n # top value of the stack to the result array as this will be the nge\n if (i <n):\n if st:\n result[i] = st[-1]\n # else append the value in the stack as the stack is in increaing order\n # no element is smaller than the visiting element in the stack\n st.append(nums[i%n])\n return result\n\n \n```
| 7 | 0 |
['Python3']
| 0 |
next-greater-element-ii
|
Explanation of the high rated solution
|
explanation-of-the-high-rated-solution-b-281g
|
Try to explain Ya Chen Chang\'s solution. It\'s concise and elegant but I could get the main idea at the first glance. I hope this could help to make it clear t
|
hcaulfield
|
NORMAL
|
2020-07-22T21:45:47.043340+00:00
|
2020-07-22T21:45:47.043383+00:00
| 674 | false |
Try to explain [Ya Chen Chang](https://leetcode.com/problems/next-greater-element-ii/discuss/145374/Python-beats-100http://)\'s solution. It\'s concise and elegant but I could get the main idea at the first glance. I hope this could help to make it clear that how it works.\n\nThe code:\n```\nclass Solution(object):\n def nextGreaterElements(self, nums):\n n = len(nums)\n ret = [-1] * n\n stack = nums[::-1]\n for i in range(n - 1, -1, -1):\n while stack and stack[-1] <= nums[i]:\n stack.pop()\n if stack:\n ret[i] = stack[-1]\n stack.append(nums[i])\n return ret\n```\n\nFirst ignore that it\'s a circular array. Then the code is almost the same except that stack should be initisalized as an emplty stack:\n```\nclass Solution(object):\n def nextGreaterElements(self, nums):\n n = len(nums)\n ret = [-1] * n\n stack1 = []\n # stack = nums[::-1]\n for i in range(n - 1, -1, -1):\n while stack1 and stack1[-1] <= nums[i]:\n stack1.pop()\n if stack1:\n ret[i] = stack1[-1]\n stack1.append(nums[i])\n return ret\n```\nThen consider the circular condition. When stack1 is empty, we still could try to find the next greater element from the begining of the array. The code is like this:\n```\nclass Solution(object):\n def nextGreaterElements(self, nums): \n n = len(nums)\n ret = [-1] * n\n stack1 = []\n stack2 = nums[::-1]\n for i in range(n - 1, -1, -1):\n while stack1 and stack1[-1] <= nums[i]:\n stack1.pop()\n if stack1:\n ret[i] = stack1[-1]\n else:\n while stack2 and stack2[-1] <= nums[i]:\n stack2.pop()\n if stack2:\n ret[i] = stack2[-1] \n stack1.append(nums[i])\n return ret\n```\nBut there\'s no need to distinguish stack1 and stack2, so the original code follows.
| 7 | 1 |
[]
| 1 |
next-greater-element-ii
|
Java use a stack
|
java-use-a-stack-by-hobiter-mpmb
|
More concise version:\n\n public int[] nextGreaterElements(int[] nums) {\n Stack<Integer> st = new Stack<>();\n int[] res = new int[nums.length
|
hobiter
|
NORMAL
|
2020-01-06T03:40:25.734003+00:00
|
2020-05-26T06:37:53.348013+00:00
| 806 | false |
More concise version:\n```\n public int[] nextGreaterElements(int[] nums) {\n Stack<Integer> st = new Stack<>();\n int[] res = new int[nums.length];\n for (int cnt = 0; cnt < 2; cnt++) {\n for (int i = 0; i < nums.length; i++) {\n while (!st.isEmpty() && nums[i] > nums[st.peek()]) res[st.pop()] = nums[i];\n if (cnt == 0) st.push(i);\n }\n }\n while (!st.isEmpty()) res[st.pop()] = -1;\n return res;\n }\n```
| 7 | 0 |
[]
| 2 |
next-greater-element-ii
|
Most general code using stack without trick and 4-th variant I met on my OA
|
most-general-code-using-stack-without-tr-gkxi
|
Algorithm:\nMono Stack as you know\n\n---\nFinal code:\n\njava\nclass Solution {\n public int[] nextGreaterElements(int[] nums) {\n // corner case\n
|
416486188
|
NORMAL
|
2019-04-24T06:07:27.396234+00:00
|
2019-04-24T06:07:27.396261+00:00
| 1,122 | false |
**Algorithm**:\n**Mono Stack** as you know\n\n---\nFinal code:\n\n```java\nclass Solution {\n public int[] nextGreaterElements(int[] nums) {\n // corner case\n if(nums == null) return null;\n \n int n = nums.length;\n int[] res = new int[n];\n \n Deque<Integer> stack = new ArrayDeque<>(); // to store idx\n for(int i = 0; i < 2 * n; i++){ \n int num = nums[i % n];\n while(!stack.isEmpty() && num > nums[stack.peekFirst()]){\n int idx = stack.pollFirst();\n res[idx] = num;\n }\n \n if(i < n) stack.offerFirst(i);\n }\n \n // set the max\'s greater element to be -1\n while(!stack.isEmpty()){\n int idx = stack.pollFirst();\n res[idx] = -1;\n }\n\n return res;\n }\n}\n```\n\n---\nTime complexity: `O(n)`\nSpace complexity: `O(n)` \n- If the array is sorted in descending order like `[5, 4, 3, 2, 1]` or \n- All the elements in the array are the same like `[5, 5, 5, 5, 5]`\n\n---\n**What\'s the trick of other OP?**\n\n```java\n public int[] nextGreaterElements(int[] nums) {\n int n = nums.length, next[] = new int[n];\n Arrays.fill(next, -1); // difference!!!\n Stack<Integer> stack = new Stack<>(); // index stack\n for (int i = 0; i < n * 2; i++) {\n int num = nums[i % n]; \n while (!stack.isEmpty() && nums[stack.peek()] < num)\n next[stack.pop()] = num;\n if (i < n) stack.push(i);\n } \n\t\t\n\t\t// no polling all nodes in stack and set max\'s greater element to be -1\n\t\t// because of the difference!!!\n\t\t\n return next;\n }\n```\n**One trick hidden** if you notice: `Arrays.fill(res, -1);`, have you wondered why we initalize the `res` to `-1` here ?\n**Guess**: according to the definition? \nNope, `-1` means there is no greater number exists, i.e. currrent number is the max number, but initially we just don\'t know if there is a greater number, doesn\'t mean that there is no one.\n**Reason** is that it can help us **save extra operations** to set the greater element of the max number to be `-1`! As we know, at last there **are** only indices of the max number in the stack. For example: `[1, 5, 3, 5, 4]`, at last the stack will be: `[2, 3]` which is the indices of number `5`. If we initialize them to be `-1`, nothing we need to take care of. \n**Question**: can we do without it?\nYes, we just need to pop all the elements in stack, and set corresponding greater value in `res[]` to be `-1`. It leads to the code below:\n**Compare**: which is better?\nHonestly, I like my own. Since I now have a clear picture of what the whole process is like especially at the end.\n\n---\n**How to deal with circular array? 3 variations to deal with circular array**:\n1. we can scan the array twice using 2 for loop, but will cause redundancy code\n2. we can expand the original array, but can be simplified by method 3\n3. we can simulate expanding the original array like the author\'s code\n\n---\nNote: we push elements to stack in the 1st round, but only pop elements in the 2nd round!!!\n\n---\n**Variant**\n**Closest greater element**\nlike the name, find the the greater element which is most cloest to it, if have 2 elements having same distance to an element, choose the greater element with the smallest index. For example: `[4, 2 ,1, 3]`, return `[-1, 4, 2, 4]`.
| 7 | 0 |
['Stack', 'Java']
| 0 |
next-greater-element-ii
|
Circular Next Greater Element Solution using Stack
|
circular-next-greater-element-solution-u-c773
|
Complete this problem before attempting [Next Greater Element]\n# Intuition\nThe problem asks us to find the next greater element for each element in the circul
|
vanshwari
|
NORMAL
|
2024-02-17T09:40:12.567991+00:00
|
2024-06-28T12:03:13.059959+00:00
| 354 | false |
Complete this problem before attempting [[Next Greater Element](https://leetcode.com/problems/next-greater-element-i/)]\n# Intuition\nThe problem asks us to find the next greater element for each element in the circular array `a`. To solve this, we can use a stack to keep track of elements in `a`. We\'ll iterate through `a` twice, effectively treating it as a circular array. For each element in `a`, we\'ll find the next greater element using the same approach as in the Next Greater Element I problem.\n\n# Approach\n1. Initialize a stack to keep track of elements in `a` and a vector `ans` to store the next greater element for each element in `a`. Initialize all elements of `ans` to -1.\n2. Iterate through `a` twice.\n - For each element in `a`, pop elements from the stack until we find an element greater than the current element.\n - If there\'s an element in the stack, store it as the next greater element for the current element; otherwise, store `-1`.\n - Push the current element into the stack.\n3. Return `ans`.\n\n# Complexity\n- Time complexity: \\( O(n) \\), where \\( n \\) is the size of `a`. We iterate through `a` twice, effectively making it \\( 2n \\), but in terms of complexity analysis, we consider it \\( O(n) \\).\n- Space complexity: \\( O(n) \\), where \\( n \\) is the size of `a`. We use a stack and a vector to store elements and their next greater elements.\n\n# Code\n```cpp\nclass Solution {\npublic:\n vector<int> nextGreaterElements(vector<int>& a) {\n int n = a.size();\n vector<int> ans(n, -1);\n stack<int> st;\n \n // Iterate through a twice\n for (int k = 0; k < 2; ++k) {\n for (int i = n - 1; i >= 0; --i) {\n while (!st.empty() && st.top() <= a[i]) {\n st.pop();\n }\n if (!st.empty()) {\n ans[i] = st.top();\n }\n st.push(a[i]);\n }\n }\n return ans;\n }\n};\n```
| 6 | 0 |
['Stack', 'C++']
| 0 |
next-greater-element-ii
|
Best O(N) Solution
|
best-on-solution-by-kumar21ayush03-dq0y
|
Approach 1\nBrute-Force\n\n# Complexity\n- Time complexity:\nO(n^2)\n\n- Space complexity:\nO(1) \n\n# Code\n\nclass Solution {\npublic:\n vector<int> nextGr
|
kumar21ayush03
|
NORMAL
|
2023-02-08T13:27:33.158437+00:00
|
2023-02-08T13:27:33.158469+00:00
| 1,302 | false |
# Approach 1\nBrute-Force\n\n# Complexity\n- Time complexity:\n$$O(n^2)$$\n\n- Space complexity:\n$$O(1)$$ \n\n# Code\n```\nclass Solution {\npublic:\n vector<int> nextGreaterElements(vector<int>& nums) {\n int n = nums.size();\n vector <int> ans;\n for (int i = 0; i < n; i++) {\n int NGE = -1;\n for (int j = 1; j < n; j++) {\n int k = (i + j) % n;\n if (nums[k] > nums[i]) {\n NGE = nums[k];\n break;\n }\n }\n ans.push_back(NGE);\n }\n return ans;\n }\n};\n```\n\n# Approach 2\nUsing Stack\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(n)$$ \n\n# Code\n```\nclass Solution {\npublic:\n vector<int> nextGreaterElements(vector<int>& nums) {\n int n = nums.size();\n vector <int> ans;\n stack <int> s;\n for (int i = 2 * n - 1; i >= 0; i--) {\n while (s.empty() == false && s.top() <= nums[i % n])\n s.pop();\n if (i < n) {\n int NGE = s.empty() ? -1 : s.top();\n ans.push_back(NGE);\n } \n s.push(nums[i % n]);\n }\n reverse(ans.begin(), ans.end());\n return ans;\n }\n};\n```
| 6 | 0 |
['C++']
| 0 |
next-greater-element-ii
|
Easy Stack Solution
|
easy-stack-solution-by-2005115-rrdm
|
\n# Approach\nApproach:\n\nThis problem can be solved easily and efficiently by using the stack data structure as it is based on the Last in First out (LIFO) pr
|
2005115
|
NORMAL
|
2023-07-29T08:50:29.107998+00:00
|
2023-07-29T08:50:29.108027+00:00
| 627 | false |
\n# Approach\nApproach:\n\nThis problem can be solved easily and efficiently by using the stack data structure as it is based on the Last in First out (LIFO) principle.\n\nTo make it a bit easier let\u2019s first try to solve without considering the array as circular. To find the next greater element we start traversing the given array from the right. As for the rightmost element, there is no other element at its right. Hence, we assign -1 at its index in the resultant array. Since this can be the next greater element (NGE) for some other element, we push it in the stack S. We keep checking for other elements. Let\u2019s say we are checking for an element at index i. We keep popping from the stack until the element at the top of the stack is smaller than A[i]. The main intuition behind popping them is that these elements can never be the NGE for any element present at the left of A[i] because A[i] is greater than these elements. Now, if the top element of S is greater than A[i] then this is NGE of A[i] and we will assign it to res[i], where res is the resultant array. If the stack becomes empty then it implies that no element at the right of A[i] is greater than it and we assign -1. At last, we push A[i] in S.\n\nDry run: Let\u2019s apply this algorithm for A[] = {5,7,1,2,6,0}:\n\n\n\nSo, the resultant array is {7,-1,2,6,-1,-1}. Remember that we have considered the array to be non-circular. For a circular array, the resultant array should be {7,-1,2,6,7,5}. \n\nNow we need to make this algorithm work for a circular array. The only difference between a circular and non-circular array is that while searching for the next greater element in a non-circular array we don\u2019t consider the elements left to the concerned element. This can be easily done by inserting the elements of the array A at the end of A, thus making its size double. But we actually don\u2019t require any extra space. We can just traverse the array twice. We actually run a loop 2*N times, where N is the size of the given array.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:0(2N+2N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:0(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> nextGreaterElements(vector<int>& nums) {\n stack<int>st;\n int n = nums.size();\n vector<int>ans(n,-1);\n for (int i = 2 * n - 1; i >= 0; i--)\n {\n while(!st.empty() && st.top() <= nums[i % n])\n {\n st.pop();\n }\n if(i<n)\n {\n if(!st.empty())\n {\n ans[i]=st.top();\n }\n \n }\n st.push(nums[i%n]);\n }\n return ans;\n }\n};\n```
| 5 | 0 |
['Stack', 'C++']
| 0 |
next-greater-element-ii
|
✅ C++ | 2 Stacks and 1 stack Approach | 98% Faster | Linear Time
|
c-2-stacks-and-1-stack-approach-98-faste-b5hr
|
503. Next Greater Element II\n\n1. Using Two Stacks :\nTime Complexity : O(n)\nSpace Complexity : O(2*n)\n\n\nvector<int> nextGreaterElements(vector<int>& nums)
|
CodeMars
|
NORMAL
|
2022-10-06T08:17:06.026555+00:00
|
2022-10-06T08:17:06.026592+00:00
| 825 | false |
[**503. Next Greater Element II**](https://leetcode.com/problems/next-greater-element-ii/)\n\n**1. Using Two Stacks :**\n**`Time Complexity : O(n)`**\n**`Space Complexity : O(2*n)`**\n\n```\nvector<int> nextGreaterElements(vector<int>& nums) {\n stack<int>st1, st2;\n for(int i=nums.size()-1; i>=0; i--)st1.push(nums[i]);\n vector<int>ans(nums.size(), -1);\n for(int i=nums.size()-1; i>=0; i--){\n bool flag=false;\n while(!st2.empty()){\n if(st2.top()>nums[i]){\n ans[i]=st2.top();\n flag=true;\n break;\n }\n st2.pop();\n }\n while(!flag and !st1.empty()){\n if(st1.top()>nums[i]){\n ans[i]=st1.top();\n flag=true;\n break;\n }\n st1.pop();\n }\n st2.push(nums[i]);\n }\n return ans;\n }\n```\n**2. Using One Stack :**\n**`Time Complexity : O(n)`**\n**`Space Complexity : O(n)`**\n\n```\nvector<int> nextGreaterElements(vector<int>& nums) {\n stack<int>st;\n int n=nums.size();\n vector<int>ans(n, -1);\n for(int i=0; i<2*n-1; i++){\n while(!st.empty() and nums[st.top()]<nums[i%n]){\n ans[st.top()]=nums[i%n];\n st.pop();\n }\n st.push(i%n);\n }\n return ans;\n }\n```\n***Happy Coding :)***\n```\nif(liked(\u2764\uFE0F)==true) Upvote(\u2B06\uFE0F);\nelse Comment(\uD83D\uDCDD);\nreturn Thank You\uD83D\uDE01;\n```\n\n
| 5 | 0 |
['Stack', 'C']
| 1 |
next-greater-element-ii
|
🔥100%✅Fastest solution | Detailed explanation | Easy understand
|
100fastest-solution-detailed-explanation-ax4p
|
Read the below approach to understand the logic\n\nPlease upvote it you like it!!!!!\n\nApproach\n\nThe approach is simple, As mentioned in problem considred gi
|
pranjal9424
|
NORMAL
|
2022-09-10T21:01:49.743468+00:00
|
2022-09-10T21:01:49.743504+00:00
| 684 | false |
**Read the below approach to understand the logic**\n\n***Please upvote it you like it!!!!!***\n\n**Approach**\n\nThe approach is simple, As mentioned in problem considred given array as a cyclic, So firstly take a stack and push all the elments of given array from last to first. Take an another loop iterate from last to first index and inside this loop perform below operation.\n* Take another loop and pop stack elements till stack top element is less than or equal to current index element and stack is not empty.\n* after previous iterations if stack became empty then set -1 as current index element. Else set the stack top value.\n\n**~Time complexity: O(N)**\n\n**~Space complexity: O(N)**\n\n**Code:-**\n\n```\nclass Solution {\npublic:\n vector<int> nextGreaterElements(vector<int>& nums) {\n int n=nums.size();\n stack<int> st;\n st.push(INT_MIN);\n for(int i=n-1;i>=0;i--){\n st.push(nums[i]);\n }\n for(int i=n-1;i>=0;i--){\n int curr=nums[i];\n while(st.top()!=INT_MIN and st.top()<=curr){\n st.pop();\n }\n nums[i]=st.top()==INT_MIN?-1:st.top();\n st.push(curr);\n }\n return nums;\n }\n};\n```
| 5 | 0 |
['Stack', 'C', 'C++']
| 0 |
next-greater-element-ii
|
Next Greater Element II || C++ || Easy Solution
|
next-greater-element-ii-c-easy-solution-f8myj
|
class Solution\n{\npublic:\n vector nextGreaterElements(vector &nums)\n {\n int n = nums.size();\n stack st;\n vector v(n);\n
|
Code_Ranjit
|
NORMAL
|
2022-05-03T07:02:43.406272+00:00
|
2022-05-03T07:02:43.406305+00:00
| 1,159 | false |
class Solution\n{\npublic:\n vector<int> nextGreaterElements(vector<int> &nums)\n {\n int n = nums.size();\n stack<int> st;\n vector<int> v(n);\n for (int i = 2 * n - 1; i >= 0; i--)\n {\n\n while (!st.empty() && st.top() <= nums[i % n])\n {\n st.pop();\n }\n if (st.empty())\n v[i % n] = -1;\n else\n v[i % n] = st.top();\n st.push(nums[i % n]);\n }\n\n return v;\n }\n};
| 5 | 0 |
['Stack', 'C', 'Monotonic Stack', 'C++']
| 0 |
next-greater-element-ii
|
C++ | Short and easy to understand code | O(N) time and space
|
c-short-and-easy-to-understand-code-on-t-lqvk
|
Please upvote if you like this approach \ solution \uD83D\uDE0A\n\n\tclass Solution {\n\t\tpublic:\n\t\t\tvector nextGreaterElements(vector& nums) {\n\t\t\t\tin
|
codeninja_24
|
NORMAL
|
2022-03-09T06:51:06.257486+00:00
|
2022-03-09T06:51:06.257533+00:00
| 523 | false |
**Please upvote if you like this approach \\ solution \uD83D\uDE0A**\n\n\tclass Solution {\n\t\tpublic:\n\t\t\tvector<int> nextGreaterElements(vector<int>& nums) {\n\t\t\t\tint n = nums.size(); \n\t\t\t\tvector<int> v(n, -1);\n\t\t\t\tstack<int> st; \n\n\t\t\tfor(int i = 2*n-1; i>=0; i--) {\n\t\t\t\twhile(!st.empty() && st.top() <= nums[i%n]) {\n\t\t\t\t\tst.pop(); \n\t\t\t\t}\n\t\t\t\tv[i%n] = st.empty() ? -1 : st.top();\n\t\t\t\tst.push(nums[i%n]);\n\t\t\t}\n\t\t\treturn v; \n\t\t}\n\t};\n
| 5 | 0 |
['Stack', 'C', 'C++']
| 1 |
next-greater-element-ii
|
Using Stack, Simple & Concise, [C++]
|
using-stack-simple-concise-c-by-akashsah-476c
|
Implementation\n\nUsing Stack\nTime Complexity = O(2N), Space Complexity = O(N)\n\nclass Solution {\npublic:\n vector<int> nextGreaterElements(vector<int>& n
|
akashsahuji
|
NORMAL
|
2021-12-11T16:22:49.493597+00:00
|
2021-12-11T16:22:49.493623+00:00
| 351 | false |
Implementation\n\n**Using Stack\nTime Complexity = O(2N), Space Complexity = O(N)**\n```\nclass Solution {\npublic:\n vector<int> nextGreaterElements(vector<int>& nums) {\n int n = nums.size();\n stack<int> s; \n vector<int> res(n, -1);\n for(int itr = 2*n-1; itr >= 0; itr--){\n while(!s.empty() && s.top() <= nums[itr%n]) s.pop();\n if(!s.empty()) res[itr%n] = s.top();\n s.push(nums[itr%n]);\n }\n return res;\n }\n};\n```\nIf you find any issue in understanding the solution then comment below, will try to help you.\nIf you found my solution useful.\nSo **please do upvote and encourage me** to document all leetcode problems\uD83D\uDE03\nHappy Coding **:)**
| 5 | 1 |
['Stack', 'C']
| 0 |
next-greater-element-ii
|
C++ Different Solution
|
c-different-solution-by-ama29n-k0rl
|
\nclass Solution {\npublic:\n vector<int> nextGreaterElements(vector<int> &nums)\n{\n stack<int> s;\n int idx = 0;\n int max = nums[0];\n for (in
|
ama29n
|
NORMAL
|
2021-09-13T09:53:37.036780+00:00
|
2021-09-13T09:53:37.036813+00:00
| 292 | false |
```\nclass Solution {\npublic:\n vector<int> nextGreaterElements(vector<int> &nums)\n{\n stack<int> s;\n int idx = 0;\n int max = nums[0];\n for (int i = 0; i < nums.size(); i++) // Finding the maximum element in the array\n if (nums[i] > max)\n {\n max = nums[i];\n idx = i;\n }\n\n vector<int> greater(nums.size());\n greater[idx] = -1;\n s.push(nums[idx]);\n\n// Finding the next greater element from the starting till the maximum element with normal apprach\n for (int i = idx - 1; i >= 0; i--) \n {\n while (s.size() > 0 && nums[i] >= s.top()) s.pop();\n greater[i] = s.size() == 0 ? -1 : s.top();\n s.push(nums[i]);\n }\n\n// Now we already have the previous elements from the maximum element in the stack \n// and we will find the next greater element for remaining elements using same stack with normal approach\n for (int i = nums.size() - 1; i > idx; i--)\n {\n while (s.size() > 0 && nums[i] >= s.top()) s.pop();\n greater[i] = s.size() == 0 ? -1 : s.top();\n s.push(nums[i]);\n }\n return greater;\n}\n};\n```
| 5 | 0 |
[]
| 2 |
next-greater-element-ii
|
Python-time & space - O(n) New interesting solution using hashmap w/thought process & explanation
|
python-time-space-on-new-interesting-sol-ky1d
|
I came with a solution that is a good candidate to be considered as a new approach. At least it would definitely help train our mind to think of data structures
|
mystic13
|
NORMAL
|
2021-06-25T12:08:16.162282+00:00
|
2021-06-25T12:09:16.638165+00:00
| 880 | false |
I came with a solution that is a good candidate to be considered as a new approach. At least it would definitely help train our mind to think of data structures in ingenious ways at least for practice and training. So here goes.\n\nMy thought process started with finding the largest element (if many, then the last such element) and its index (assume max_el_idx), because from then I can start setting the next greater element for all by iterating to the left starting with max_el_idx - 1. So for max_el_idx will have the max_val as the greater element w/o doubt. Then for any new element the options are the prev_element or any one of the prev_elements\' greater elements. For example, [.... 10, 7, 9, 11....] subarray, when 10 is reached while iterating to the left, these are the answers 7 -> 9, 9 -> 11 , 11-> NA ... So for 10 , the prev element 7 is lesser so we go through the links of 7 to see where 10 would find its greater element and it will be in 9-> 11. And we will not be going through this link again (i.e. 7 to 11 ) because the subsequent numbers if they are smaller will have 10 as answer, if not then we go to the greater element of 10 and then keep linking up from there. And overall we will not be having more than O(n) ops for the linking checks as well. So we can find the greater element for entire array in O(n) itself.\n ```\n[.... 12, 10 -> 7 -> 9 -> 11....]\n |--->|-------->------^ (proceeds to search after 11)\n```\n\nNote: I know that if we break it down into fundamentals then it might have a resemblance to the stack strategy, but the thought process I think is a bit different.\n\nLet me know what you think..\n```\ndef nextGreaterElements(self, nums: List[int]) -> List[int]:\n max_el_idx = max_val = -2<<31\n for i, val in enumerate(nums):\n if val >= max_val:\n max_el_idx = i; max_val = val\n ite = max_el_idx-1; prev_el = max_val\n res =[-1 for i in range(len(nums))]\n hm={}\n while len(nums) + ite != max_el_idx:\n if nums[ite] != max_val:\n if nums[ite] < prev_el:\n hm[nums[ite]] = res[ite] = prev_el\n else:\n while prev_el<=nums[ite]:\n prev_el = hm[prev_el]\n hm[nums[ite]] = res[ite] = prev_el\n prev_el = nums[ite]\n ite-=1\n return res\n```\nI have used hashmap to store the greater element for the prev element and that is used to chain through till the greatest element to find out where the greater element for the current element stands.\nTime complexity - O(n)\nSpace complexity - O(n) for the hashmap
| 5 | 0 |
['Python', 'Python3']
| 0 |
next-greater-element-ii
|
python easy solution | beats 99.43% | using stack operation
|
python-easy-solution-beats-9943-using-st-dqo8
|
\nclass Solution(object):\n def nextGreaterElements(self, nums):\n\n n=len(nums)\n stack= []\n\t\tnext_g=[-1] * n\n \n \n
|
Abhishen99
|
NORMAL
|
2021-06-17T18:13:53.876956+00:00
|
2021-06-17T18:14:28.747318+00:00
| 482 | false |
```\nclass Solution(object):\n def nextGreaterElements(self, nums):\n\n n=len(nums)\n stack= []\n\t\tnext_g=[-1] * n\n \n \n for i in range(n):\n \n while stack and (nums[stack[-1]] < nums[i]):\n \n next_g[stack.pop()] = nums[i]\n \n \n stack.append(i)\n \n \n for i in range(n):\n \n while stack and (nums[stack[-1]] < nums[i]):\n \n next_g[stack.pop()] = nums[i]\n \n if stack == []:\n \n break\n \n return next_g\n```\n\n**if you like do upvote !**
| 5 | 0 |
['Python']
| 0 |
next-greater-element-ii
|
Java basic easy to understand O(N) stack solution
|
java-basic-easy-to-understand-on-stack-s-wlzh
|
\nclass Solution {\n public int[] nextGreaterElements(int[] nums) {\n int n = nums.length;\n int[] result = new int[n];\n Stack<Integer>
|
zeldox
|
NORMAL
|
2020-10-13T21:26:02.250434+00:00
|
2020-10-13T21:26:02.250475+00:00
| 149 | false |
```\nclass Solution {\n public int[] nextGreaterElements(int[] nums) {\n int n = nums.length;\n int[] result = new int[n];\n Stack<Integer> stack = new Stack<>();\n \n for(int i=n-1;i>=0;i--)\n stack.push(nums[i]);\n for(int i=n-1;i>=0;i--){\n while(!stack.empty() && stack.peek()<=nums[i])\n stack.pop();\n\n if(stack.empty())\n result[i] = -1;\n else\n result[i] = stack.peek();\n \n stack.push(nums[i]);\n }\n \n return result;\n \n }\n}\n```\nif u like it please upvote
| 5 | 0 |
[]
| 1 |
next-greater-element-ii
|
python stack
|
python-stack-by-jefferyzzy-a74v
|
\ndef nextGreaterElements(self, nums: List[int]) -> List[int]:\n size = len(nums)\n nums+=nums\n res = [-1] * size\n stack = []\n
|
jefferyzzy
|
NORMAL
|
2019-11-28T21:26:07.692489+00:00
|
2019-12-06T19:35:01.976463+00:00
| 1,091 | false |
```\ndef nextGreaterElements(self, nums: List[int]) -> List[int]:\n size = len(nums)\n nums+=nums\n res = [-1] * size\n stack = []\n for i in list(range(size))*2:\n while stack and (nums[stack[-1]] < nums[i]):\n res[stack.pop()] = nums[i]\n stack.append(i)\n return res\n```
| 5 | 0 |
['Python', 'Python3']
| 1 |
next-greater-element-ii
|
java simple solution
|
java-simple-solution-by-averillzheng-o9ow
|
```\nclass Solution {\n public int[] nextGreaterElements(int[] nums) {\n \n Stack value = new Stack<>();\n for(int i = nums.length - 1;
|
averillzheng
|
NORMAL
|
2018-07-03T00:50:01.303366+00:00
|
2018-09-24T20:59:24.545667+00:00
| 1,051 | false |
```\nclass Solution {\n public int[] nextGreaterElements(int[] nums) {\n \n Stack<Integer> value = new Stack<>();\n for(int i = nums.length - 1; i >= 0; --i) {\n value.push(nums[i]);\n }\n \n int[] result = new int[nums.length];\n for(int i = nums.length - 1; i >= 0; --i) {\n while(!value.isEmpty() && value.peek() <= nums[i]) {\n value.pop(); \n }\n \n int right = (value.isEmpty()) ? -1 : value.peek();\n result[i] = right;\n value.push(nums[i]);\n }\n return result;\n }\n}
| 5 | 0 |
[]
| 0 |
next-greater-element-ii
|
Next Greater Element II || Stack Approach || Complete and Easy Explanation 🔥🔥
|
next-greater-element-ii-stack-approach-c-nd89
|
NOTE: First try to solve Next Greater Element I\n\n# Intuition\nIn this problem, the goal is to find the next greater element for each number in a circular arra
|
Ayush_Singh2004
|
NORMAL
|
2024-10-03T07:05:00.967869+00:00
|
2024-10-03T07:05:00.967890+00:00
| 969 | false |
***NOTE:*** First try to solve [Next Greater Element I](https://leetcode.com/problems/next-greater-element-i/)\n\n# Intuition\nIn this problem, the goal is to find the next greater element for each number in a circular array. Since the array is circular, we need to consider the array elements in a "wrapped around" manner, meaning if we don\'t find a next greater element before reaching the end of the array, we should continue searching from the beginning. We can approach this problem using a stack to efficiently keep track of potential "next greater elements" while iterating through the array.\n\n# Approach\n**Reverse the array:** \n- We reverse the input array nums to traverse it from the end to the start. This allows us to keep track of the next greater elements as we iterate, without the need to circle back explicitly.\n\n**Use two stacks:**\n- The first stack st helps track the numbers we\'ve processed so far while looking for the next greater element.\nThe second stack `st1` holds the elements of the reversed array, and helps in finding the next greater element in the circular manner.\n\n**Traverse the array:**\n- For each element, we check both stacks:\n- If the stack st contains elements smaller than or equal to the current element, we pop those elements, as they can\'t be the next greater for the current element.\n- If `st` becomes empty, we then check st1 (which acts as our circular extension of the array). If `st1` has a greater element, we use that as the answer; otherwise, we `return -1`.\n\n**Push elements to stacks:**\n- After determining the next greater element, push the current element to stack st, which will be used for the next iteration.\n\n**Reverse the result:**\n- Since we processed the reversed array, the final result `ans` must be reversed to match the original input order.\n\n# Complexity\n**Time complexity:**\nWe traverse the array twice: once to build the second stack st1 and once to calculate the next greater elements. For each element, we may push or pop from the stacks at most once. This results in an overall time complexity of $$O(n)$$, where n is the size of the array\n\n**Space complexity:**\nWe use two stacks `(st and st1)` and a result vector ans, each of which may store up to n elements. Thus, the space complexity is $$O(n)$$.\n\n# Code\n```cpp []\nclass Solution {\npublic:\n vector<int> nextGreaterElements(vector<int>& nums) {\n \n stack<int> st;\n stack<int> st1;\n st1.push(-1);\n \n vector<int> ans;\n reverse(nums.begin(), nums.end());\n int n=nums.size();\n for(int i=0; i<n; i++){\n st1.push(nums[i]);\n }\n \n for(int i=0; i<n; i++){\n if(st.empty()){\n while(!st1.empty() && st1.top()<=nums[i]){\n st1.pop();\n }\n if(st1.empty()) ans.push_back(-1);\n else\n ans.push_back(st1.top());\n \n st.push(nums[i]);\n }\n else{\n while(!st.empty() && st.top()<=nums[i]){\n st.pop();\n } \n if(st.empty()){\n while(!st1.empty() && st1.top()<=nums[i]){\n st1.pop();\n }\n if(st1.empty()) ans.push_back(-1);\n else\n ans.push_back(st1.top());\n \n } \n else{\n ans.push_back(st.top());\n cout<<ans[i]; \n }\n st.push(nums[i]);\n }\n }\n reverse(ans.begin(),ans.end());\n return ans;\n\n }\n};\n```
| 4 | 0 |
['Array', 'Stack', 'C++']
| 0 |
next-greater-element-ii
|
🎇 [MONOTONIC STACK] INTUITION & APPROACH
|
monotonic-stack-intuition-approach-by-ra-5l2t
|
\uD83D\uDCA5 PLEASE CONSIDER UPVOTING\n\n# Intuition\n\nSince the array is circular, we need to consider elements that are at the beginning of the array as poss
|
ramitgangwar
|
NORMAL
|
2024-09-30T16:54:22.348443+00:00
|
2024-09-30T16:54:22.348477+00:00
| 755 | false |
* \uD83D\uDCA5 _**PLEASE CONSIDER UPVOTING**_\n***\n# Intuition\n\nSince the array is circular, we need to consider elements that are at the beginning of the array as possible "next greater elements" for elements at the end. Using a stack helps us efficiently track and find the next greater element as we traverse the array, but we need to handle the circular nature by treating the array as though it\'s repeated twice.\n\n# Approach\n\n1. We traverse the array from right to left twice (to simulate the circular nature of the array). This is achieved by iterating over the range `2 * size - 1` down to `0`.\n2. For each element at index `i % size` (to handle circular indexing), we pop from the stack while the top of the stack is less than or equal to the current element (since it cannot be the next greater element for the current element).\n3. If the stack is not empty, the top of the stack is the next greater element for the current element. Otherwise, we store `-1` as there is no next greater element.\n4. If the current index `i` is less than `size`, we are processing an element in the first pass over the array and update the answer array accordingly.\n5. Push the current element onto the stack for future comparisons.\n6. Finally, return the answer array.\n\n# Complexity\n- **Time complexity**:\n\n The time complexity is $$O(n)$$, where `n` is the length of the array. We traverse the array twice (due to the circular nature), and each element is pushed and popped from the stack at most once.\n\n- **Space complexity**:\n\n The space complexity is $$O(n)$$ because we use a stack to store elements, and in the worst case, all elements could be on the stack simultaneously.\n\n# Code\n```java\nclass Solution {\n public int[] nextGreaterElements(int[] arr) {\n int size = arr.length;\n int[] ans = new int[size];\n Stack<Integer> stack = new Stack<>();\n\n for(int i = 2 * size - 1; i >= 0; i--) {\n while(!stack.isEmpty() && arr[i % size] >= stack.peek()) {\n stack.pop();\n }\n\n if(i < size) {\n if(!stack.isEmpty()) {\n ans[i] = stack.peek();\n } else {\n ans[i] = -1;\n }\n }\n\n stack.push(arr[i % size]);\n }\n\n return ans;\n }\n}\n```
| 4 | 0 |
['Array', 'Stack', 'Monotonic Stack', 'Java']
| 1 |
next-greater-element-ii
|
Brute Force Approach|| Easy Understandable but ugly TC :(
|
brute-force-approach-easy-understandable-gz40
|
Approach\n - We know always rotation = len(nums) - 1\n - Pick 1 no from the list in the outer loop\n - Check from the very next element in the inner loop\n - -
|
Gourav_Sinha
|
NORMAL
|
2023-04-21T20:19:19.229764+00:00
|
2023-04-21T20:22:22.993316+00:00
| 595 | false |
# Approach\n - We know always ```rotation = len(nums) - 1```\n - Pick 1 no from the list in the outer loop\n - Check from the very next element in the inner loop\n - -```if nums[i] < nums[j]:``` then add ```nums[j]```\n - -```else``` add ```-1``` at the outer loop\n# Complexity\n- Space complexity:\nBeats 95%\n# Code\n```\nclass Solution:\n def nextGreaterElements(self, nums: List[int]) -> List[int]:\n ans = []\n flag = False\n for i in range(len(nums)):\n j = i + 1\n rotation = len(nums) - 1\n while rotation > 0:\n if j >= len(nums):\n j = 0\n if nums[i] < nums[j]:\n ans.append(nums[j])\n flag = True\n break\n else:\n rotation -= 1\n j += 1\n flag = False\n if flag == False:\n ans.append(-1)\n return ans\n```
| 4 | 0 |
['Python3']
| 1 |
next-greater-element-ii
|
Super Easy JAVA Sol.(Stack)
|
super-easy-java-solstack-by-harsh_tiwari-bg23
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
harsh_tiwari_
|
NORMAL
|
2023-04-04T05:50:51.274983+00:00
|
2023-04-04T05:50:51.275031+00:00
| 1,012 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int[] nextGreaterElements(int[] nums) {\n int n = nums.length;\n int[] res = new int[n];\n Stack<Integer> s = new Stack<>();\n // we double the length of loop to imitate a circular array\n // just remember to use i%n for indexing\n for (int i = 2*n; i>=0; i--) {\n while (!s.isEmpty() && s.peek() <= nums[i%n]) {\n s.pop();\n }\n res[i%n] = s.isEmpty() ? -1 : s.peek();\n s.push(nums[i%n]);\n }\n return res;\n\n }\n}\n```
| 4 | 0 |
['Java']
| 0 |
next-greater-element-ii
|
Easy java approach
|
easy-java-approach-by-saikatdass-5vo9
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\nAssume there are two array one by one.\n Describe your approach to solvin
|
SaikatDass
|
NORMAL
|
2023-03-27T17:43:20.025704+00:00
|
2023-03-27T17:43:20.025749+00:00
| 673 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nAssume there are two array one by one.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n- $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n- $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int[] nextGreaterElements(int[] nums) {\n int n = nums.length;\n Stack<Integer> s = new Stack<>();\n int[] arr = new int[n];\n for(int i = 2 * n - 1; i >= 0 ; i--){\n while(!s.isEmpty() && s.peek() <= nums[i % n]){\n s.pop();\n }\n if(s.isEmpty()){\n arr[i % n] = -1;\n }\n else{\n arr[i % n] = s.peek();\n }\n s.push(nums[i % n]);\n }\n return arr;\n }\n}\n```
| 4 | 0 |
['Java']
| 0 |
next-greater-element-ii
|
JS Solution ✅|| Explained with Intuition & Approach ✅
|
js-solution-explained-with-intuition-app-5b7y
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n- It is a two loops solution.\n\n# Approach\n Describe your approach to solving the p
|
Rajat310
|
NORMAL
|
2023-03-03T07:28:33.003080+00:00
|
2023-03-03T07:28:33.003127+00:00
| 327 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n- It is a two loops solution.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nThe approach used in the below code is :- \n\n1. To iterate over each element in the array and then for each element, iterate over all the other elements until it finds the next greater element. \n\n2. To handle the circular nature of the array, the index is taken modulo n (the length of the array) to wrap around to the beginning of the array.\n\n3. If a greater element is found, it is stored in the answer array at the current index. \n\n4. If no greater element is found after iterating over all the other elements, then -1 is stored in the answer array at the current index.\n\n5. Finally, the answer array is returned, which contains the next greater element for each element in the circular array.\n\n\n# Complexity\n- Time complexity: $$O(n^2)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n1. Here n is the length of the input array.\n\n2. This is because for each element in the array, the algorithm iterates over all the other elements until it finds the next greater element.\n\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n1. Here n is the length of the input array. \n\n2. This is because the algorithm creates an array to store the result, which has the same length as the input array.\n\n\n\n# Code\n```\n/**\n * @param {number[]} nums\n * @return {number[]}\n */\nvar nextGreaterElements = function(nums) {\n \n let n = nums.length;\n \n let ans = new Array(n);\n \n for (let i=0; i<n; i++) {\n \n let j = i+1;\n \n while (j % n !== i) {\n \n if (nums[j % n] > nums[i]) {\n \n ans[i] = nums[j % n];\n \n break;\n }\n \n j++;\n }\n \n if (j % n == i) {\n \n ans[i] = -1;\n }\n }\n \n return ans;\n};\n```\n\n\n\n
| 4 | 0 |
['Array', 'Stack', 'Monotonic Stack', 'JavaScript']
| 0 |
next-greater-element-ii
|
💥💡 Next Greater Element II - A Brilliant Algorithmic Solution in Java! 💻💪
|
next-greater-element-ii-a-brilliant-algo-il6o
|
\uD83D\uDCA1 Intuition\nWe can use a stack to find the next greater element of each element in the given array. We loop through the array twice to compare each
|
artistgreedy15
|
NORMAL
|
2023-02-26T12:25:13.493805+00:00
|
2023-02-26T12:25:13.493836+00:00
| 1,051 | false |
## \uD83D\uDCA1 Intuition\nWe can use a stack to find the next greater element of each element in the given array. We loop through the array twice to compare each element with every other element. For each element, we push its index onto the stack. If the current element is greater than the top element of the stack, we pop the stack and update the result array with the current element for the popped index. We continue this process until the stack is empty or the top element of the stack is greater than or equal to the current element. Finally, we return the result array.\n\n## \uD83C\uDFAF Approach\n1. Create an array of size n to store the result.\n2. Fill the result array with -1 initially.\n3. Create a stack using ArrayDeque.\n4. Loop through the array twice, because we need to compare each element with every other element.\n5. Get the current element by taking modulus with n.\n6. While the stack is not empty and the top element of the stack is less than the current element, update the result array with the current element for the popped index.\n7. If the current index is less than n, push it onto the stack.\n8. Return the result array.\n\n\n## \u23F0 Time Complexity\nThe time complexity of this algorithm is `O(n)`, where n is the length of the input array.\n\n## \uD83D\uDCBE Space Complexity\nThe space complexity of this algorithm is `O(n)`, because we are using a stack of size n and an array of size `n` to store the result.\n\n## \uD83D\uDCDD Code\n```\nclass Solution {\n public int[] nextGreaterElements(int[] nums) {\n int n = nums.length; // get the length of the array nums\n int[] res = new int[n]; // create an array of size n to store the result\n Arrays.fill(res, -1); // fill the result array with -1 initially\n Deque<Integer> stack = new ArrayDeque<>(); // create a stack using ArrayDeque since its efficient\n \n // loop through the array twice, because we need to compare each element with every other element\n for (int i = 0; i < 2 * n; i++) {\n int num = nums[i % n]; // get the current element by taking modulus with n\n while (!stack.isEmpty() && nums[stack.peek()] < num) {\n // while stack is not empty and top element of stack is less than current element\n res[stack.pop()] = num; // update result array with current element for top element of stack\n }\n if (i < n) {\n stack.push(i); // push the current index onto the stack if i < n\n }\n }\n return res; // return the result array\n }\n}\n```\n\n#### Please Upvote if it helped !!
| 4 | 0 |
['Array', 'Stack', 'Java']
| 1 |
next-greater-element-ii
|
JAVA | 2 approaches | Brute + Optimal (Stack) ✅
|
java-2-approaches-brute-optimal-stack-by-oai0
|
Please Upvote :D\n##### 1. Brute force approach:\n\nclass Solution {\n public int[] nextGreaterElements(int[] nums) {\n int n = nums.length;\n
|
sourin_bruh
|
NORMAL
|
2022-10-21T17:44:38.973530+00:00
|
2022-10-21T17:44:38.973569+00:00
| 627 | false |
### **Please Upvote** :D\n##### 1. Brute force approach:\n```\nclass Solution {\n public int[] nextGreaterElements(int[] nums) {\n int n = nums.length;\n int[] ans = new int[n];\n\n for (int i = 0; i < n; i++) {\n ans[i] = -1;\n\n for (int j = 0; j < n; j++) {\n if (nums[(i + j) % n] > nums[i]) {\n ans[i] = nums[(i + j) % n];\n break;\n }\n }\n }\n\n return ans;\n }\n}\n\n// TC: O(n ^ 2), SC: O(n)\n```\n##### 2. Optimal approach (Stack):\n```\nclass Solution {\n public int[] nextGreaterElements(int[] nums) {\n int n = nums.length;\n Stack<Integer> stack = new Stack<>();\n\n int[] ans = new int[n];\n Arrays.fill(ans, -1);\n\n for (int i = 0; i < 2 * n; i++) {\n while (!stack.isEmpty() && nums[stack.peek()] < nums[i % n]) {\n ans[stack.pop()] = nums[i % n];\n }\n\n if (i < n) stack.push(i);\n }\n\n return ans;\n }\n}\n\n// TC: O(n), SC: O(n)\n```
| 4 | 0 |
['Stack', 'Java']
| 0 |
next-greater-element-ii
|
✔️ Java 100% Fastest - Easy Solution using Stack
|
java-100-fastest-easy-solution-using-sta-04ua
|
\nclass Solution {\n public int[] nextGreaterElements(int[] nums) {\n int[] ans = new int[nums.length];\n Stack<Integer> stack = new Stack<Inte
|
andrewspourgeon
|
NORMAL
|
2022-10-10T11:51:40.983304+00:00
|
2022-10-10T11:51:40.983344+00:00
| 1,416 | false |
```\nclass Solution {\n public int[] nextGreaterElements(int[] nums) {\n int[] ans = new int[nums.length];\n Stack<Integer> stack = new Stack<Integer>();\n int len = nums.length;\n for(int i = (2*len)-1 ; i >= 0 ; i--){\n while(stack.size() != 0 && stack.peek() <= nums[i%len]){\n stack.pop();\n }\n if(i < len){\n if(stack.size() != 0){\n ans[i%len] = stack.peek();\n }\n else{\n ans[i%len] = -1;\n }\n }\n stack.push(nums[i%len]);\n }\n return ans;\n }\n}\n```
| 4 | 0 |
['Stack', 'Monotonic Stack', 'Java']
| 1 |
next-greater-element-ii
|
Check it..........
|
check-it-by-sharmahimanshu65018-a41t
|
Comment it\'s time complexity...\n\nvector<int> nextGreaterElements(vector<int>& v) \n {\n vector<int>ans(n,-1);\n int n=v.size();\n \n
|
sharmahimanshu65018
|
NORMAL
|
2022-08-01T05:22:11.075536+00:00
|
2022-08-01T05:23:51.697273+00:00
| 133 | false |
Comment it\'s time complexity...\n```\nvector<int> nextGreaterElements(vector<int>& v) \n {\n vector<int>ans(n,-1);\n int n=v.size();\n \n //Initialize stack \n stack<int>s;\n for(int i=n-1;i>=0;i--)\n {\n s.push(v[i]);\n }\n \n \n // next greater element \n for(int i=n-1;i>=0;i--)\n {\n while((!(s.empty()))&&(s.top()<=v[i]))\n s.pop();\n \n if(s.empty())\n {\n ans[i]=-1;\n }\n else\n {\n ans[i]=s.top();\n }\n s.push(v[i]);\n }\n \n return ans;\n }\n```
| 4 | 0 |
['Stack']
| 0 |
next-greater-element-ii
|
Java Solution using Monotonic decreasing stack
|
java-solution-using-monotonic-decreasing-5b55
|
\nclass Solution {\n public int[] nextGreaterElements(int[] nums) {\n int len = 2 * nums.length - 1;\n int[] result = new int[nums.length];\n
|
abhinandan1981
|
NORMAL
|
2022-07-31T15:21:31.967483+00:00
|
2022-07-31T15:21:31.967524+00:00
| 806 | false |
```\nclass Solution {\n public int[] nextGreaterElements(int[] nums) {\n int len = 2 * nums.length - 1;\n int[] result = new int[nums.length];\n Arrays.fill(result, -1);\n Stack<Integer> stack = new Stack<>();\n for (int i = 0; i < len; i++) {\n int index = i % nums.length;\n while(!stack.isEmpty() && nums[stack.peek()] < nums[index]) {\n int pop = stack.pop();\n result[pop] = nums[index];\n }\n stack.push(index);\n }\n return result;\n }\n}\n```
| 4 | 0 |
['Array', 'Monotonic Stack', 'Java']
| 1 |
next-greater-element-ii
|
C++||Stack
|
cstack-by-roshann07-wl5g
|
\nclass Solution {\npublic:\n vector<int> nextGreaterElements(vector<int>& nums) {\n stack<int>s;\n vector<int>v;\n int n = nums.size();
|
Roshann07
|
NORMAL
|
2022-06-16T14:58:57.742777+00:00
|
2022-06-16T14:58:57.742809+00:00
| 374 | false |
```\nclass Solution {\npublic:\n vector<int> nextGreaterElements(vector<int>& nums) {\n stack<int>s;\n vector<int>v;\n int n = nums.size();\n for(int i=n-2;i>=0;i--){\n while(s.size()>0&&s.top()<=nums[i])s.pop();\n s.push(nums[i]);\n }\n for(int i=n-1;i>=0;i--){\n while(s.size()>0&&s.top()<=nums[i])s.pop();\n v.push_back(s.size()==0?-1:s.top()); //if no greater element push -1.\n s.push(nums[i]);\n \n }\n reverse(v.begin(),v.end());\n return v;\n }\n};\n```
| 4 | 0 |
['Stack', 'C']
| 0 |
next-greater-element-ii
|
Simple Python Solution with Detailed Explanation (easy to understand)
|
simple-python-solution-with-detailed-exp-3ndx
|
using dp, setup save with len(nums) of -1, then create a list newn in which it includes two nums lists. Iterate through nums, and then newn. If newn[j] > nums[i
|
wulalawulalawu
|
NORMAL
|
2022-06-01T17:45:39.904607+00:00
|
2022-06-02T21:27:30.010938+00:00
| 614 | false |
using dp, setup save with len(nums) of -1, then create a list newn in which it includes two nums lists. Iterate through nums, and then newn. If newn[j] > nums[i], change save[i] to newn[j] and then break the inner loop. \n\n\n```\n\n```def nextGreaterElements(self, nums: List[int]) -> List[int]:\n \n save = [-1] * len(nums)\n newn = nums + nums\n \n for i in range(len(nums)):\n for j in range(i+1, len(newn)):\n if newn[j] > nums[i]:\n save[i] = newn[j]\n break\n \n return save
| 4 | 0 |
['Dynamic Programming', 'Python']
| 0 |
next-greater-element-ii
|
[Stack] JS Solution
|
stack-js-solution-by-hbjorbj-fnxf
|
\n/*\nWe are looking for the first number greater than current number. It doesn\'t matter if the\nposition of Next Greater Number (NGN) is before or after posit
|
hbjorbj
|
NORMAL
|
2020-11-02T14:40:22.116537+00:00
|
2021-05-22T21:30:26.004370+00:00
| 482 | false |
```\n/*\nWe are looking for the first number greater than current number. It doesn\'t matter if the\nposition of Next Greater Number (NGN) is before or after position of current number because\nthe array is circular.\n\nWe will use a Stack. We start iterating given array from the start.\nAt each number, we check if stack has a number smaller than current number. If so,\ncurrent number is the Next Greater Number for that element in the stack. Hence,\nwe keep popping smaller elements from stack and be their NGN. \n\nThen, we push current number into stack so that we can find our NGN (or not if there isn\'t one).\n\nWe will push index instead of number into stack so that we can fill our result array.\n\nAlso, we will iterate through the array twice so that for every number we can scan elements on both the left side and the right side.\n*/\n\nvar nextGreaterElements = function(nums) {\n let res = new Array(nums.length).fill(-1);\n let stack = [];\n for (let i = 0; i < nums.length * 2; i++) {\n let j = i % nums.length;\n while (stack.length > 0 && nums[stack[stack.length-1]] < nums[j]) {\n // current element is NGN for popped element\n res[stack.pop()] = nums[j];\n }\n stack.push(j);\n }\n return res;\n // T.C: O(N)\n // S.C: O(N)\n};\n```
| 4 | 1 |
['JavaScript']
| 1 |
next-greater-element-ii
|
Concise Java Solution
|
concise-java-solution-by-nikemafia-5y2m
|
\nclass Solution {\n public int[] nextGreaterElements(int[] nums) {\n Stack<Integer> stack = new Stack<>();\n int [] result = new int[nums.leng
|
nikeMafia
|
NORMAL
|
2020-05-30T19:54:06.058510+00:00
|
2020-05-30T19:54:06.058556+00:00
| 334 | false |
```\nclass Solution {\n public int[] nextGreaterElements(int[] nums) {\n Stack<Integer> stack = new Stack<>();\n int [] result = new int[nums.length];\n int size = nums.length;\n Arrays.fill(result,-1);\n for(int i=2*size-1; i>=0; i--){\n while(!stack.isEmpty() && nums[stack.peek()]<=nums[i%size])\n stack.pop();\n \n if(stack.isEmpty()){\n stack.push(i%size);\n }else{\n result[i%size]=nums[stack.peek()];\n stack.push(i%size);\n }\n }\n return result;\n }\n}\n```
| 4 | 0 |
[]
| 0 |
next-greater-element-ii
|
Next Greater Element II Java Solution
|
next-greater-element-ii-java-solution-by-ecnz
|
\tclass Solution {\n\t\tpublic int[] nextGreaterElements(int[] nums) {\n\t\t\tint len = nums.length;\n\t\t\tint[] res = new int[len];\n\t\t\tArrays.fill(res, -1
|
saito-asuka
|
NORMAL
|
2019-07-23T05:07:16.879925+00:00
|
2019-07-23T05:07:16.879979+00:00
| 452 | false |
\tclass Solution {\n\t\tpublic int[] nextGreaterElements(int[] nums) {\n\t\t\tint len = nums.length;\n\t\t\tint[] res = new int[len];\n\t\t\tArrays.fill(res, -1);\n\t\t\tStack<Integer> stack = new Stack<>();\n\n\t\t\tfor (int i = 0; i < len * 2; i++) {\n\t\t\t\tint num = nums[i % len];\n\t\t\t\twhile (!stack.isEmpty() && nums[stack.peek()] < num) {\n\t\t\t\t\tres[stack.pop()] = num;\n\t\t\t\t}\n\t\t\t\tif (i < len) stack.push(i);\n\t\t\t}\n\n\t\t\treturn res;\n\t\t}\n\t}
| 4 | 0 |
[]
| 3 |
next-greater-element-ii
|
concise c++ solution using stack that beats 98%
|
concise-c-solution-using-stack-that-beat-6ead
|
\n vector<int> nextGreaterElements(vector<int>& nums) {\n int n = nums.size();\n vector<int> vec(n, -1);\n stack<int> stack;\n for(i
|
caihao0727mail
|
NORMAL
|
2017-05-10T23:47:01.087000+00:00
|
2018-09-18T06:37:19.455119+00:00
| 1,162 | false |
``` \n vector<int> nextGreaterElements(vector<int>& nums) {\n int n = nums.size();\n vector<int> vec(n, -1);\n stack<int> stack;\n for(int i=0, j=0; i<2*n-1; i++){\n j = (i<n)?i:i-n;\n while(!stack.empty() && nums[stack.top()]<nums[j]){\n vec[stack.top()] = nums[j];\n stack.pop();\n }\n if(i<n)stack.push(i);\n }\n return vec;\n }\n```
| 4 | 0 |
[]
| 0 |
next-greater-element-ii
|
Easy and simple solution with analogy || understand the concept
|
easy-and-simple-solution-with-analogy-un-ir84
|
Problem DescriptionGiven a circular array nums (the next element after the last one is the first element), find the next greater element for each element. The n
|
VishalKumar10
|
NORMAL
|
2025-03-15T14:21:39.458520+00:00
|
2025-03-15T14:21:39.458520+00:00
| 436 | false |
## Problem Description
Given a circular array `nums` (the next element after the last one is the first element), find the next greater element for each element. The next greater element for a number `x` is the first number to its right in the circular array that is greater than `x`. If no such element exists, return -1. Return an array of these results.
---
## Intuition
We use a stack to find the next greater element for each number in a circular array by simulating two passes over the array and tracking larger elements.
---
## Analogy
Imagine `nums` as a circular row of streetlights of different heights around a park. For each streetlight, we want to find the next taller one as we walk around the circle (even wrapping around to the start). The stack acts like a spotlight, keeping only the taller lights in view and discarding shorter ones as we go.
---
## Approach
1. **Simulate Circular Behavior:**
- Since the array is circular, process it twice (2 * n elements) using modulo (`i % n`) to wrap around.
- Iterate from right to left (2n-1 to 0) to mimic the circular nature.
2. **Use a Stack:**
- For each element:
- Pop all smaller or equal elements from the stack (they can’t be the "next greater").
- If the stack has an element left and we’re in the first pass (i < n), it’s the next greater element.
- Push the current element onto the stack.
3. **Build Result:**
- Initialize a result vector with -1 (default if no greater element exists).
- Update the result only during the first pass (i < n) with the stack’s top element.
---
## Code
```cpp []
class Solution {
public:
vector<int> nextGreaterElements(vector<int>& nums) {
int n = nums.size();
stack<int> st;
vector<int> result(n, -1);
for(int i=2*n-1; i>=0; i--){
while(!st.empty() &&
st.top() <= nums[i%n]) st.pop();
if(i < n && !st.empty()) result[i] = st.top();
st.push(nums[i%n]);
}
return result;
}
};
```
## Dry Run
Let’s take `nums = [1, 2, 1]`.
| Index (i) | Current Element (nums[i % n]) | Stack (Top to Bottom) | Result Updates | Action |
|-----------|-------------------------------|-----------------------|----------------------|---------------------------------------------|
| 5 | 1 | [1] | - | Stack empty → push 1 |
| 4 | 2 | [2] | - | Pop 1 (1 ≤ 2), push 2 |
| 3 | 1 | [2, 1] | - | 2 > 1, no pop, push 1 |
| 2 | 1 | [2, 1] | [?, ?, 2] | Pop 1 (1 ≤ 1), result[2] = 2, push 1 |
| 1 | 2 | [2] | [?, 2, 2] | Pop 1 (1 ≤ 2), result[1] = 2, push 2 |
| 0 | 1 | [2, 1] | [-1, 2, 2] | 2 > 1, no pop, result[0] = -1, push 1 |
**Final Result:** `[-1, 2, 2]`
---
## Time and Space Complexity Analysis
- **Time Complexity: O(n)**
- We process 2n elements, but each element is pushed and popped from the stack at most once → O(n).
- **Space Complexity: O(n)**
- Stack: At most stores n elements → O(n).
- Result vector: O(n) for output.
---

| 3 | 0 |
['Array', 'Stack', 'Monotonic Stack', 'C++']
| 0 |
next-greater-element-ii
|
EASY BEGINNER|| JAVA C++ PYTHON || STEPWISE
|
easy-beginner-java-c-python-stepwise-by-4eqda
|
THE QUESTION IS SAME AS "THE NEXTGREATER ELEMENT" ON LEETCODE , I WILL RECOMMEND YOU TO TRY THAT FIRST THEN THIS IS GOING TO BE A CAKEWALK. AS CLICHE AS IT SOUN
|
Abhishekkant135
|
NORMAL
|
2024-11-13T18:40:15.221559+00:00
|
2024-11-13T18:40:15.221579+00:00
| 714 | false |
# THE QUESTION IS SAME AS "THE NEXTGREATER ELEMENT" ON LEETCODE , I WILL RECOMMEND YOU TO TRY THAT FIRST THEN THIS IS GOING TO BE A CAKEWALK. AS CLICHE AS IT SOUNDS , SERIOUSLY.\n\n**1. Stack Initialization:**\n - A stack `st` is created to store elements in decreasing order.\n\n**2. Iterating Through the Array Twice:**\n - The code iterates through the array twice, effectively treating it as a circular array.\n - For each element `nums[i]`:\n - While the stack is not empty and the top element is less than or equal to the current element, pop elements from the stack.\n - If the stack is empty, it means there\'s no greater element to the right of the current element, so -1 is assigned to the corresponding index in the `ans` array.\n - Otherwise, the top element of the stack is the next greater element, so it\'s assigned to the corresponding index in the `ans` array.\n - The current element is pushed onto the stack.\n\n**3. Return Result:**\n - The `ans` array containing the next greater elements for each element in the circular array is returned.\n\n\n\n\n# Code\n```java []\nclass Solution {\n public int[] nextGreaterElements(int[] nums) {\n int [] ans=new int[nums.length];\n Stack<Integer> st=new Stack<>();\n for(int i=nums.length*2-2;i>=0;i--){\n while(!st.isEmpty() && st.peek()<=nums[i%nums.length]){\n st.pop();\n }\n if(st.isEmpty()) ans[i%nums.length]=-1;\n else ans[i%nums.length]=st.peek();\n st.push(nums[i%nums.length]);\n }\n return ans;\n }\n}\n```\n```C++ []\n#include <vector>\n#include <stack>\nusing namespace std;\n\nclass Solution {\npublic:\n vector<int> nextGreaterElements(vector<int>& nums) {\n int n = nums.size();\n vector<int> ans(n, -1);\n stack<int> st;\n\n for(int i = 2 * n - 2; i >= 0; i--) {\n while(!st.empty() && st.top() <= nums[i % n]) {\n st.pop();\n }\n if(!st.empty()) {\n ans[i % n] = st.top();\n }\n st.push(nums[i % n]);\n }\n\n return ans;\n }\n};\n```\n```python []\nfrom typing import List\n\nclass Solution:\n def nextGreaterElements(self, nums: List[int]) -> List[int]:\n n = len(nums)\n ans = [-1] * n\n st = []\n\n for i in range(2 * n - 2, -1, -1):\n while st and st[-1] <= nums[i % n]:\n st.pop()\n if st:\n ans[i % n] = st[-1]\n st.append(nums[i % n])\n\n return ans\n```\n\n
| 3 | 0 |
['Stack', 'Python', 'C++', 'Java']
| 0 |
next-greater-element-ii
|
Easy C++ Solution | Step-wise Approach Explained | Beats 92.38% | Stacks
|
easy-c-solution-step-wise-approach-expla-us9u
|
Intuition and Approach\n Describe your first thoughts on how to solve this problem. \nImagine a scenario where you have a circular arrangement of numbers, like
|
darkaadityaa
|
NORMAL
|
2024-01-28T04:30:40.710578+00:00
|
2024-01-29T02:55:27.131812+00:00
| 465 | false |
# Intuition and Approach\n<!-- Describe your first thoughts on how to solve this problem. -->\nImagine a scenario where you have a **circular arrangement** of numbers, like a loop, and for each number, you want to find the next greater number in the loop. The catch is that the loop wraps around, meaning the next greater element for the last number might be at the beginning of the loop.\n\nWe can use a $$stack$$ to keep track of potential candidates for the next greater element. We traverse the **circular array** twice to ensure that we consider elements in a circular manner. For each element:\n\n1) If the stack is not empty and the current element is greater than the element at the top of the stack, we **update** the $$result$$ for the top element.\n2) Push the current element onto the stack.\n3) After the two passes, the result array contains the next greater element for each element in the circular array. Two passes are considered here, because we are interested to know from double sized array (in order to make sure there is a greater element previously in array which can be accessed further).\n\n--------------------------------------------------------------------\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n---------------------------------------------------------------------\n**If you find this solution helpful, consider giving it an upvote!**\n\n----------------------------------------------------------------------\n\n#### Do check out all other solutions posted by me here: https://github.com/adityajamwal02/Leetcode-Community-Solutions\n\n-------------------------------------------------------------------\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> nextGreaterElements(vector<int>& nums) {\n int n=nums.size();\n vector<int> result(n,-1);\n stack<int> st;\n for(int i=2*n-1;i>=0;i--){ // Circular array (double size)\n while(!st.empty() and st.top()<=nums[i%n]){\n st.pop();\n }\n if(i<n){\n if(!st.empty()) result[i]=st.top();\n }\n st.push(nums[i%n]);\n }\n return result; \n }\n};\n```
| 3 | 0 |
['Array', 'Stack', 'C++']
| 0 |
next-greater-element-ii
|
Easy Solution ✅ || Explained || C++ || Stack
|
easy-solution-explained-c-stack-by-under-kud1
|
Code\n\nclass Solution {\npublic:\n vector<int> nextGreaterElements(vector<int>& nums) {\n int n=nums.size();\n vector<int> ans(n,-1);\n
|
underdog13
|
NORMAL
|
2023-12-20T05:39:11.962054+00:00
|
2023-12-20T05:39:11.962088+00:00
| 651 | false |
# Code\n```\nclass Solution {\npublic:\n vector<int> nextGreaterElements(vector<int>& nums) {\n int n=nums.size();\n vector<int> ans(n,-1);\n stack<int> s;\n for(int i=2*n-1;i>=0;i--)\n {\n // we pop out all elements smaller than current element\n while(!s.empty() && s.top()<=nums[i%n]){\n s.pop();\n }\n // if stack is empty means no greater element is there\n // if not empty we make answer at that index equal to top element\n if(!s.empty() && i<n)\n ans[i]=s.top();\n s.push(nums[i%n]);\n }\n return ans;\n }\n};\n```\n\n**Do Upvote \uD83D\uDC4D and Comment \uD83D\uDCAC**
| 3 | 0 |
['Stack', 'C++']
| 0 |
next-greater-element-ii
|
3
|
3-by-naive-key-m766
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Naive-Key
|
NORMAL
|
2023-09-10T09:26:31.488215+00:00
|
2023-09-10T09:26:31.488234+00:00
| 181 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n#include <stack>\nclass Solution {\npublic:\n vector<int> nextGreaterElements(vector<int>& nums) {\n stack<int> s;\n vector<int> x(nums);\n int h=nums.size();\n s.push(-1);\n for(int i=2*h-1;i>=0;i--){\n while(!s.empty() && s.top()<=nums[i%h]){\n s.pop();\n }\n if(s.empty()){s.push(-1);}\n x[i%h]=s.top();\n s.push(nums[i%h]);\n }\n return x;\n }\n};\n```
| 3 | 0 |
['C++']
| 0 |
next-greater-element-ii
|
Simple C++ Solution using two loops || Begginers Friendly
|
simple-c-solution-using-two-loops-beggin-n9hp
|
Code\n\nclass Solution {\npublic:\n vector<int> nextGreaterElements(vector<int>& nums) {\n vector<int> res;\n int y=0,x=-1;\n for (int i
|
abhijeet5000kumar
|
NORMAL
|
2023-08-02T15:57:38.535013+00:00
|
2023-08-05T20:48:04.635227+00:00
| 66 | false |
# Code\n```\nclass Solution {\npublic:\n vector<int> nextGreaterElements(vector<int>& nums) {\n vector<int> res;\n int y=0,x=-1;\n for (int i=0;i<nums.size();i++){\n y=nums[i];\n for(int j=i+1;j<nums.size()+i;j++){\n if(nums[j%nums.size()]>y){x=0;res.push_back(nums[j%nums.size()]);break;}\n }\n if(x!=0){res.push_back(-1);}\n x=-1;\n }\n return res;\n }\n};\n```
| 3 | 0 |
['C++']
| 1 |
next-greater-element-ii
|
c++ solution without using stack | beginner friendly
|
c-solution-without-using-stack-beginner-63o64
|
Intuition\n Describe your first thoughts on how to solve this problem. \ncreate a new array of double size of nums. so that we can iterate over the array twice\
|
yash_jain26
|
NORMAL
|
2023-07-29T21:08:51.766266+00:00
|
2023-09-16T13:13:35.587256+00:00
| 1,437 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\ncreate a new array of double size of nums. so that we can iterate over the array twice\n# Approach\n<!-- Describe your approach to solving the problem. -->\niterate over the first n elements of temp and find the next greater element of each element if no greater element was found push back -1 to ans vector.\n# Complexity\n- Time complexity: O(N^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> nextGreaterElements(vector<int>& nums) {\n int n = nums.size();\n vector<int> temp;\n vector<int> ans;\n temp = nums;\n for(int i = 0; i < nums.size();i++){\n temp.push_back(nums[i]);\n }\n for(int i = 0; i < n; i++){\n int x = temp[i];\n int j = i + 1;\n while(j < temp.size()){\n if(temp[j] > x){\n x = temp[j];\n break;\n }\n j++;\n }\n if(x != temp[i]) ans.push_back(x);\n else ans.push_back(-1);\n }\n return ans;\n }\n};\n```
| 3 | 0 |
['Array', 'C++']
| 2 |
next-greater-element-ii
|
Unlock the Circular Puzzle: Find Next Greater Elements!
|
unlock-the-circular-puzzle-find-next-gre-1gp5
|
Intuition:\nThe approach to solving this problem involves using a stack to find the next greater element for each value in the circular array nums. We traverse
|
himanshu__mehra__
|
NORMAL
|
2023-07-20T07:01:55.600414+00:00
|
2023-07-20T07:01:55.600443+00:00
| 591 | false |
# Intuition:\nThe approach to solving this problem involves using a stack to find the next greater element for each value in the circular array nums. We traverse the array in reverse order (from right to left) to account for the circular nature. For each element, we pop elements from the stack until we find an element that is greater than the current element. If there is no such element, we assign -1 as the next greater element for the current element. Otherwise, we assign the greater element as the next greater element for the current element. Finally, we reverse the result to maintain the original order of elements in the array.\n\n# Algorithm:\n\nInitialize an empty stack st to store elements while traversing the circular array in reverse order and an empty vector nqe to store the next greater elements for each value in nums.\nTraverse the circular array nums in reverse order (from right to left) using a loop starting from 2*nums.size()-1 and decrementing by 1 in each iteration. This is done to handle the circular nature of the array, as the last element\'s next greater element can be at the beginning of the array.\nWhile traversing, for each element nums[i], do the following:\na. While the stack is not empty and the current element nums[i%n] is greater than or equal to the top of the stack, pop elements from the stack. This step ensures that the stack only contains elements that are greater than nums[i%n], as we want to find the next greater element.\nb. If the index i is less than n, it means we are in the original array, and we can directly access the top of the stack to find the next greater element. If the stack becomes empty after the while loop, it means there is no next greater element for the current element nums[i%n], so we assign -1 as the next greater element for this element in the vector nqe.\nc. Otherwise, we are in the circular part of the array, and we need to search circularly for the next greater element. In this case, we push the next greater element\'s value (found at the top of the stack) into the vector nqe.\nd. Push the current element nums[i%n] onto the stack.\nAfter completing the loop, the vector nqe will contain the next greater elements for each value in the circular array, taking the circular nature into account.\nReverse the vector nqe to maintain the original order of elements in the array.\nReturn the modified vector nqe as the final result.\nComplexity Analysis:\n\n# Time Complexity:\n The algorithm traverses the circular array once, which takes O(n) time, where n is the length of nums.\n# Space Complexity:\n The algorithm uses a stack to store at most n elements and a vector nqe to store the next greater elements, each of which takes O(n) extra space.\n\nOverall, the algorithm has a linear time complexity of O(n) and a linear space complexity of O(n). It efficiently finds the next greater element for each element in the circular array nums using a stack.\n\n\n\n\n\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> nextGreaterElements(vector<int>& nums) {\n vector<int> nqe;\n stack<int> st;\n \n int n=nums.size();\n for(int i=2*nums.size()-1; i>=0; i--){\n while(!st.empty() && nums[i%n]>=st.top()){\n st.pop();\n }\n if(i<n){\n if(st.empty()==false){ \n nqe.push_back(st.top());\n } else nqe.push_back(-1);\n }\n st.push(nums[i%n]); \n }\n reverse(nqe.begin(),nqe.end());\n return nqe;\n }\n};\n```\nIf you found my solution helpful, please consider upvoting it to show your appreciation! Your support motivates me to provide more helpful answers. Thank you!\n
| 3 | 0 |
['C++']
| 0 |
next-greater-element-ii
|
Java Solution with-out traversing array till 2*N times and without using mod operator:)
|
java-solution-with-out-traversing-array-bt7wm
|
Intuition\nUse same logic that we have already used in Next Greater Element-I\n\n# Approach\n\nHere is mine Solution with-out traversing array till 2*N times an
|
gurupreet-singh
|
NORMAL
|
2023-07-14T14:47:10.069403+00:00
|
2023-07-14T16:13:59.312532+00:00
| 1,079 | false |
# Intuition\nUse same logic that we have already used in Next Greater Element-I\n\n# Approach\n\n**Here is mine Solution with-out traversing array till 2*N times and without using mod operator to mimic array as a circular one!**\n\nJust take N extra space for result array named result[], use stack to store all the elements of given array named arr[] into it(traverse array from end)\nand use same logic that we have already used in Next Greater Element-I\n\nGot all the test cased Successfully Passed!! :) \n# Complexity\n- Time complexity:\nOverall TC would be O(N)\n\n- Space complexity:\nOverall SC would be O(N)\n\n# Code\n```\nclass Solution {\n public int[] nextGreaterElements(int[] arr) {\n if(arr.length == 1) {\n\t\t\treturn new int[] {-1};\n\t\t}\n\t\t\n\t\tint result[] = new int[arr.length];\n\t\tint resultPointer=result.length-1;\n\t\tStack<Integer> stack = new Stack<>();\n\t\t\n\t\tfor (int i = arr.length-1; i >=0 ; i--) {\n\t\t\t/**\n\t\t\t * just traverse the array from end and store all the greater element into it,\n\t\t\t * because we don\'t need to store smallest element i.e\n\t\t\t * if array has 5,4,3,2,1 than stack should have only 5 after end of the loop\n\t\t\t * \n\t\t\t * i.e if array has 1,2,3,4,3 than stack should have 4,3,2,1 after end of the loop\n\t\t\t * rather 3,4,3,2,1 because when we add 3 into stack , next time when we got 4 which\n\t\t\t * is greater than 3 we popped-out 3 from stack and store 4 and so on...\n\t\t\t */\n\t\t\tif(!stack.isEmpty() && stack.peek() <= arr[i]) {\n\t\t\t\tstack.pop();\n\t\t\t}\n\t\t\tstack.push(arr[i]);\n\t\t}\n\n ** // below code snippet of for loop is as same as \n // the logic used in Next Greater Element-I solution\n **\t\t\n for (int i = arr.length-1; i >=0 ; i--) {\n\t\t\t\n\t\t\twhile(!stack.isEmpty() && stack.peek() <= arr[i]) {\n\t\t\t\tstack.pop();\n\t\t\t}\n\t\t\t\n\t\t\tif(stack.isEmpty()) {\n\t\t\t\tresult[resultPointer--] = -1;\n\t\t\t\tstack.push(arr[i]);\n\t\t\t}\n\t\t\telse {\n\t\t\t\tresult[resultPointer--] = stack.peek();\n\t\t\t\tstack.push(arr[i]);\n\t\t\t}\n\t\t}\n\t\t** //this code snippet specific to this problem only, \n // pop all the element from stack until stack \n // become empty or \n // we found greater element form arr[arr.length-1]\n **\n\t\twhile(!stack.empty() && stack.peek() <= arr[arr.length-1]) {\n\t\t\tstack.pop();\n\t\t}\n\n\t\t** // when if stack is not empty that means we have found\n // at-least one greater element from arr[arr.length-1]\n // , pop it and store into result[]\n **\n\t\tif(!stack.empty()) {\n\t\t\tresult[result.length-1] = stack.pop();\n\t\t}\n\t\t\n\t\treturn result;\n }\n}\n```
| 3 | 0 |
['Array', 'Monotonic Stack', 'Java']
| 3 |
next-greater-element-ii
|
Next Greater Element II - [C++]
|
next-greater-element-ii-c-by-haneelkumar-n4ou
|
\nclass Solution {\npublic:\n vector<int> nextGreaterElements(vector<int>& nums) {\n int n = nums.size();\n vector<int> ans(n,-1),stack;\n
|
haneelkumar
|
NORMAL
|
2023-06-20T17:57:16.135391+00:00
|
2023-06-20T17:57:16.135409+00:00
| 580 | false |
```\nclass Solution {\npublic:\n vector<int> nextGreaterElements(vector<int>& nums) {\n int n = nums.size();\n vector<int> ans(n,-1),stack;\n for(int i=0;i<2*n;i++){\n while(stack.size() && nums[stack.back()] < nums[i%n]){\n ans[stack.back()] = nums[i%n];\n stack.pop_back();\n }\n stack.push_back(i%n);\n }\n return ans;\n }\n};\n```\n\n\n\nplease upvote! if you like.\nComment below \uD83D\uDC47
| 3 | 0 |
['Stack', 'C']
| 0 |
next-greater-element-ii
|
❇ next-greater-element-ii👌 🏆O(N)❤️ Javascript❤️ Memory👀95.45%🕕 Meaningful Vars✍️ 🔴❇ ✅ 👉 💪🙏
|
next-greater-element-ii-on-javascript-me-q288
|
\nvar nextGreaterElements = function (nums2) {\n const slicedArrayButLast = nums2.slice(0, nums2.length - 1)\n const updatedArray = [...nums2, ...slicedArrayB
|
anurag-sindhu
|
NORMAL
|
2023-04-02T06:22:45.208344+00:00
|
2023-04-02T06:22:45.208409+00:00
| 1,380 | false |
```\nvar nextGreaterElements = function (nums2) {\n const slicedArrayButLast = nums2.slice(0, nums2.length - 1)\n const updatedArray = [...nums2, ...slicedArrayButLast]\n const store = [updatedArray[updatedArray.length - 1]]\n const nextGreatElements = [-1]\n for (let index = updatedArray.length - 1 - 1; index >= 0; index--) {\n const tempStore = store[store.length - 1] > updatedArray[index]\n if (tempStore) {\n nextGreatElements.push(store[store.length - 1])\n } else {\n while (store[store.length - 1] <= updatedArray[index]) {\n store.pop()\n if (!store.length) {\n break\n }\n }\n if (!store.length) {\n nextGreatElements.push(-1)\n } else {\n nextGreatElements.push(store[store.length - 1])\n }\n }\n store.push(updatedArray[index])\n }\n nextGreatElements.reverse()\n return nextGreatElements.slice(0, nums2.length)\n}\n```
| 3 | 0 |
['Stack', 'Queue', 'JavaScript']
| 0 |
next-greater-element-ii
|
C++ solution in O(n) Time Complexity
|
c-solution-in-on-time-complexity-by-skum-7i66
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \nFirstly, we initialize
|
Skumar_2001
|
NORMAL
|
2023-03-23T12:25:43.380057+00:00
|
2023-03-23T12:25:43.380108+00:00
| 292 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFirstly, we initialize the vector<int> ans by -1, ans then initialize empty stack. Then we will iterate through the array twice and store the next larger element for the first iterator and then as i > n, we will store the index and then as the next larger element will come by comparision then we will store in the ans vector.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> nextGreaterElements(vector<int>& nums) {\n int n = nums.size();\n\n vector<int> ans(n,-1);\n stack<int> st;\n\n for(int i = 0 ; i<2*n;i++){\n int x = nums[i%n];\n while(!st.empty() && nums[st.top()] < x){\n ans[st.top()] = x;\n st.pop();\n }\n if(i<n)\n st.push(i);\n }\n\n return ans;\n }\n};\n```
| 3 | 0 |
['C++']
| 0 |
next-greater-element-ii
|
Simple approach using stack || O(N) time ||
|
simple-approach-using-stack-on-time-by-s-38wg
|
\n\n# Code\n\nclass Solution {\npublic:\n vector<int> nextGreaterElements(vector<int>& nums) {\n //idea is to go for next gtreater in nums+nums\n
|
Shristha
|
NORMAL
|
2023-01-18T14:07:19.817336+00:00
|
2023-01-18T14:07:19.817385+00:00
| 2,231 | false |
\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> nextGreaterElements(vector<int>& nums) {\n //idea is to go for next gtreater in nums+nums\n int n=nums.size();\n nums.resize(2*n);\n for(int i=n;i<2*n;i++){\n nums[i]=nums[i-n];\n }\n vector<int>res(n);\n stack<int>st;\n for(int i=nums.size()-1;i>=0;i--){\n while(!st.empty() && nums[i]>=nums[st.top()]){\n st.pop();\n }\n int idx=i%n;\n res[idx]=st.empty()?-1:nums[st.top()];\n st.push(i);\n }\n return res;\n }\n};\n```
| 3 | 0 |
['Stack', 'C++']
| 1 |
next-greater-element-ii
|
✅ Easy and Optimal Solution || TC : O(N) || SC: O(N) ||
|
easy-and-optimal-solution-tc-on-sc-on-by-85oh
|
Prerequisite\n\nThis problem is similar to Find next greater element-1.\n# Approach\n Describe your approach to solving the problem. \n- Finding next greater el
|
sathwik_karne
|
NORMAL
|
2023-01-02T19:06:22.093637+00:00
|
2023-01-02T19:06:22.093695+00:00
| 931 | false |
# Prerequisite\n\nThis problem is similar to [Find next greater element-1](https://leetcode.com/problems/next-greater-element-i/description/).\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Finding next greater element in an array is similar to this problem.\n- The only change here is the next greater elements can be found in circular fashion too from end to starting of array.\n- So for elements at end of array, we can look at startin of array for it\'s nge. SO BASICALLY THIS IS A CIRCULAR ARRAY.\n- Notice one thing, *if we just append this array to end of this array, this problem can be solved directly using nge approach*.\n\n- So repeat the same process except keep in mind the indices we need for result.\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> nextGreaterElements(vector<int>& nums) {\n int n=nums.size();\n vector<int> res(n,-1);\n stack<int> st;\n //assume appending nums to it again but it can be done using index manipulation without actually appending\n for(int i=2*n-1;i>=0;--i){\n while(!st.empty() and st.top()<=nums[i%n]) st.pop();//remove all smaller elements\n if(i<n){\n if(!st.empty()) res[i]=st.top();\n }\n st.push(nums[i%n]);\n }\n return res;\n }\n};\n```
| 3 | 0 |
['Stack', 'Monotonic Stack', 'C++']
| 0 |
next-greater-element-ii
|
Java Solution || Easy to Understand
|
java-solution-easy-to-understand-by-janh-49iq
|
\npublic class Solution {\n public int[] nextGreaterElements(int[] nums) {\n int[] result = new int[nums.length];\n Stack<Integer> stack = new
|
Janhvi__28
|
NORMAL
|
2022-10-28T07:00:48.978986+00:00
|
2022-10-28T07:00:48.979024+00:00
| 787 | false |
```\npublic class Solution {\n public int[] nextGreaterElements(int[] nums) {\n int[] result = new int[nums.length];\n Stack<Integer> stack = new Stack<Integer>();\n for (int i = 0; i < result.length; i ++) {\n result[i] = -1;\n }\n for (int i = 0; i < 2 * result.length; i ++) {\n int num = nums[i % result.length];\n while (!stack.isEmpty() && nums[stack.peek()] < num) {\n result[stack.pop()] = num;\n }\n if (i < result.length) {\n stack.push(i);\n }\n }\n return result;\n }\n}\n```
| 3 | 0 |
['Java']
| 0 |
next-greater-element-ii
|
USING O(n) EXTRA SPACE WITHIN TIME O(n) SIMPLE AND EASY TO UNDERSTAND C++ SOLUTION
|
using-on-extra-space-within-time-on-simp-2glo
|
\nclass Solution {\npublic:\n vector<int> nextGreaterElements(vector<int>& nums) {\n int i = 0, n = nums.size();\n int k = n;\n for(i =
|
abhay_12345
|
NORMAL
|
2022-10-07T18:54:40.815058+00:00
|
2022-10-07T18:54:40.815095+00:00
| 732 | false |
```\nclass Solution {\npublic:\n vector<int> nextGreaterElements(vector<int>& nums) {\n int i = 0, n = nums.size();\n int k = n;\n for(i = 0; i < n-1; i++){\n nums.push_back(nums[i]);\n }\n stack<int> s;\n n = nums.size();\n vector<int> ans(n,-1);\n for(i = n-1; i >= 0; i--){\n while(!s.empty() && s.top()<=nums[i]){\n s.pop();\n }\n if(!s.empty()){\n ans[i] = s.top();\n }\n s.push(nums[i]);\n }\n return vector(ans.begin(),ans.begin()+k);\n }\n};\n```
| 3 | 0 |
['Stack', 'C', 'Monotonic Stack', 'C++']
| 0 |
next-greater-element-ii
|
java | easy solution | stack | 100% faster
|
java-easy-solution-stack-100-faster-by-s-bldz
|
\nclass Solution {\n public int[] nextGreaterElements(int[] nums) {\n \n int n = nums.length;\n int[] output = new int[n];\n Stac
|
Shubham_Awasthi__07
|
NORMAL
|
2022-10-02T15:37:43.263840+00:00
|
2022-10-02T15:37:43.263881+00:00
| 344 | false |
```\nclass Solution {\n public int[] nextGreaterElements(int[] nums) {\n \n int n = nums.length;\n int[] output = new int[n];\n Stack<Integer> st = new Stack<Integer>();\n Arrays.fill(output , -1);\n \n for(int i = 0 ; i < 2*n ; i++){\n int idx = i%n;\n \n while(!st.empty() && nums[idx] > nums[st.peek()]){\n output[st.peek()] = nums[idx];\n st.pop();\n }\n st.push(idx); \n }\n return output;\n }\n```
| 3 | 0 |
['Stack', 'Java']
| 0 |
next-greater-element-ii
|
C++ || Monotonic Stack || 503
|
c-monotonic-stack-503-by-iamshreyash28-3ycr
|
\n vector<int> nextGreaterElements(vector<int>& nums) {\n stack<int> ele;\n vector<int> ans1;\n int i,x;\n int n=nums.size();\n
|
iamshreyash28
|
NORMAL
|
2022-09-23T10:30:23.203677+00:00
|
2022-09-23T10:32:45.059480+00:00
| 55 | false |
```\n vector<int> nextGreaterElements(vector<int>& nums) {\n stack<int> ele;\n vector<int> ans1;\n int i,x;\n int n=nums.size();\n for(i=0;i<n;i++)\n {\n int j=(i+1)%n;\n while((j)%n!=i)\n {\n if(nums[j]>nums[i])\n {\n \n ele.push(nums[j]);\n break;\n }\n j=(j+1)%n;\n }\n if(!ele.empty())\n {\n x=ele.top();\n ele.pop();\n ans1.push_back(x);\n }\n else\n {\n ans1.push_back(-1);\n } \n }\n return ans1;\n \n```
| 3 | 0 |
['Monotonic Stack']
| 0 |
next-greater-element-ii
|
Python Monotonic Stack O(n) Approach
|
python-monotonic-stack-on-approach-by-ma-ov4x
|
Monotonic Decreasing Stack : reference from here\n\n| next greater | decreasing (equal allowed) | stackTop < current | inside while loop |\n\nc
|
maj3r
|
NORMAL
|
2022-07-30T21:17:27.553577+00:00
|
2022-07-30T21:18:36.971329+00:00
| 377 | false |
Monotonic Decreasing Stack : reference from [here](https://leetcode.com/discuss/study-guide/2347639/a-comprehensive-guide-and-template-for-monotonic-stack-based-problems)\n\n| next greater | decreasing (equal allowed) | stackTop < current | inside while loop |\n\nconcept : same as [496. Next Greater Element I\n](https://leetcode.com/problems/next-greater-element-i/) but perform it twice.\n```\nclass Solution:\n def nextGreaterElements(self, nums: List[int]) -> List[int]:\n stack = []\n res = [-1] * len(nums)\n \n for _ in range(2):\n for i in range(len(nums)):\n while stack and nums[stack[-1]] < nums[i]:\n idx = stack.pop()\n res[idx] = nums[i]\n stack.append(i)\n \n return res\n \n```
| 3 | 0 |
['Monotonic Stack', 'Python']
| 0 |
next-greater-element-ii
|
[JAVA] self explanatory O(n)
|
java-self-explanatory-on-by-jugantar2020-391k
|
```\nclass Solution {\n public int[] nextGreaterElements(int[] nums) {\n Stack st = new Stack<>();\n for(int i = nums.length - 1; i >= 0; i --) {\n
|
Jugantar2020
|
NORMAL
|
2022-07-07T06:55:32.260720+00:00
|
2022-07-07T06:55:32.260772+00:00
| 314 | false |
```\nclass Solution {\n public int[] nextGreaterElements(int[] nums) {\n Stack<Integer> st = new Stack<>();\n for(int i = nums.length - 1; i >= 0; i --) {\n st.push(nums[i]); \n }\n \n int ans[] = new int[nums.length];\n for(int i = nums.length - 1; i >= 0; i --) {\n while(!st.isEmpty() && st.peek() <= nums[i]) {\n st.pop();\n }\n ans[i] = st.empty() ? -1 : st.peek();\n st.push(nums[i]);\n }\n return ans;\n }\n}
| 3 | 0 |
['Stack', 'Monotonic Stack', 'Java']
| 0 |
next-greater-element-ii
|
Extending Next Greater Element 1 Solution | Java Solution
|
extending-next-greater-element-1-solutio-f934
|
\nclass Solution {\n public int[] nextGreaterElements(int[] nums) {\n \n Stack<Integer> stack = new Stack<>();\n int[] ans= new int[nums
|
user7247jp
|
NORMAL
|
2022-07-05T13:23:05.263982+00:00
|
2022-07-05T13:23:27.833808+00:00
| 223 | false |
```\nclass Solution {\n public int[] nextGreaterElements(int[] nums) {\n \n Stack<Integer> stack = new Stack<>();\n int[] ans= new int[nums.length];\n \n\t\t//For Circular array adding elements from n-2 to 0\n //As for nth element first element is 0th element\n //So when we check for next greater for nth element\n //We should start looking from 0 to n-2\n for(int i=nums.length-2;i>=0;i--)\n stack.push(nums[i]);\n \n\t //Next Greater Element 1 Solution\n for(int i=nums.length-1;i>=0;i--)\n {\n while(!stack.isEmpty()&&nums[i]>=stack.peek())\n stack.pop();\n \n if(stack.isEmpty())\n ans[i] = -1;\n else\n ans[i] = stack.peek();\n \n stack.push(nums[i]);\n }\n \n return ans;\n }\n}\n```
| 3 | 0 |
['Stack', 'Java']
| 0 |
next-greater-element-ii
|
Python Simple O(n) Solution (Monotonic Stack)
|
python-simple-on-solution-monotonic-stac-v3uc
|
\nclass Solution:\n def nextGreaterElements(self, nums: List[int]) -> List[int]:\n n = len(nums)\n ans = n * [-1]\n nums += nums\n
|
oim8
|
NORMAL
|
2022-04-29T21:43:21.704561+00:00
|
2022-04-29T21:43:21.704607+00:00
| 502 | false |
```\nclass Solution:\n def nextGreaterElements(self, nums: List[int]) -> List[int]:\n n = len(nums)\n ans = n * [-1]\n nums += nums\n \n stack = []\n for i, num in enumerate(nums):\n while stack and stack[-1][1] < num:\n ans[stack.pop()[0]] = num\n if i < n: stack.append((i, num))\n \n return ans\n```\n\nn = length of nums\nTime complexity: O(2 * n) = O(n)\nSpace complexity: O(n)
| 3 | 0 |
['Monotonic Stack', 'Python']
| 0 |
next-greater-element-ii
|
✅ [Solution] Swift: Next Greater Element II
|
solution-swift-next-greater-element-ii-b-73wr
|
swift\nclass Solution {\n func nextGreaterElements(_ nums: [Int]) -> [Int] {\n let len = nums.count\n var arr = Array(repeating: -1, count: len
|
AsahiOcean
|
NORMAL
|
2022-03-22T16:24:16.809099+00:00
|
2022-03-22T16:24:16.809135+00:00
| 833 | false |
```swift\nclass Solution {\n func nextGreaterElements(_ nums: [Int]) -> [Int] {\n let len = nums.count\n var arr = Array(repeating: -1, count: len)\n var stack: [Int] = []\n for i in 0..<len*2 {\n while !stack.isEmpty, nums[stack.last!] < nums[i % len] {\n arr[stack.removeLast()] = nums[i % len]\n }\n stack.append(i % len)\n }\n return arr\n }\n}\n```\n\n<hr>\n\n<details>\n<summary><img src="https://git.io/JDblm" height="24"> <b>TEST CASES</b></summary>\n\n<pre>\nResult: Executed 2 tests, with 0 failures (0 unexpected) in 0.016 (0.018) seconds\n</pre>\n\n```swift\nimport XCTest\n\nclass Tests: XCTestCase {\n\n private let solution = Solution()\n \n // Explanation: The first 1\'s next greater number is 2;\n // The number 2 can\'t find next greater number.\n // The second 1\'s next greater number needs to search circularly, which is also 2.\n func test0() {\n let value = solution.nextGreaterElements([1,2,1])\n XCTAssertEqual(value, [2,-1,2])\n }\n \n func test1() {\n let value = solution.nextGreaterElements([1,2,3,4,3])\n XCTAssertEqual(value, [2,3,4,-1,4])\n }\n}\n\nTests.defaultTestSuite.run()\n```\n\n</details>
| 3 | 0 |
['Swift']
| 0 |
next-greater-element-ii
|
C++ || Stack || Easy to understand
|
c-stack-easy-to-understand-by-priyanshup-ori6
|
\nclass Solution {\npublic:\n vector<int> nextGreaterElements(vector<int>& nums) {\n int n = nums.size();\n vector<int> ans(n);\n stack<
|
PriyanshuPundhir
|
NORMAL
|
2022-03-12T17:25:32.050797+00:00
|
2022-03-12T17:25:32.050844+00:00
| 199 | false |
```\nclass Solution {\npublic:\n vector<int> nextGreaterElements(vector<int>& nums) {\n int n = nums.size();\n vector<int> ans(n);\n stack<int> st;\n for(int i=n-2;i>=0;i--)\n {\n // if current element is greater than stack top then insert it and pop top of stack\n while(st.size()>0 && st.top() <=nums[i]) \n {\n st.pop();\n }\n st.push(nums[i]);\n }\n for(int i=n-1;i>=0;i--)\n {\n while(st.size()>0 && st.top() <=nums[i]) \n {\n st.pop();\n }\n // if stack is empty then no greater element then add -1 else stack top\n ans[i] = st.size() == 0?-1 : st.top();\n st.push(nums[i]);\n }\n return ans;\n }\n};\n```
| 3 | 0 |
['Stack', 'C', 'C++']
| 0 |
next-greater-element-ii
|
Java easy Solution beats 94% submission 6 ms
|
java-easy-solution-beats-94-submission-6-p1s0
|
\n class Solution {\n public int[] nextGreaterElements(int[] a) {\n\n\n // List<Integer> l=new ArrayList<>();\n\n int n=a.length
|
aadishjain__
|
NORMAL
|
2021-09-13T09:44:05.197585+00:00
|
2021-09-13T09:44:05.197632+00:00
| 119 | false |
```\n class Solution {\n public int[] nextGreaterElements(int[] a) {\n\n\n // List<Integer> l=new ArrayList<>();\n\n int n=a.length; \n int max=a[0];\n int cur=0;\n for(int i=0;i<n;i++)\n {\n if(max<a[i])\n {\n max=a[i];\n cur=i;\n }\n }\n int []res= new int[a.length];\n Stack<Integer> s=new Stack<>();\n s.push(a[cur]);\n res[cur]=-1;\n for(int i=cur-1;i>=0;i--)\n {\n while(s.size()>0 && a[i]>=s.peek())\n {\n s.pop();\n }\n if(s.size()>0)\n {\n res[i]=s.peek();\n }\n else\n {\n res[i]=-1;\n }\n s.push(a[i]);\n }\n\n\n\n for(int i=n-1;i>cur;i--)\n {\n while(s.size()>0 && a[i]>=s.peek())\n {\n s.pop();\n }\n if(s.size()>0)\n {\n res[i]=s.peek();\n }\n else\n {\n res[i]=-1;\n }\n s.push(a[i]);\n }\n\n return res;\n }\n }\n\n\n```
| 3 | 0 |
[]
| 0 |
next-greater-element-ii
|
Find the Max Element, and use Stack to keep track O(2n) complexity
|
find-the-max-element-and-use-stack-to-ke-8lqo
|
First find the maximum element in the array, it will always have a -1 for the answer to it\'s next greater element because no element is greater than that in th
|
goelaya1998
|
NORMAL
|
2021-08-10T08:21:55.392091+00:00
|
2021-08-10T08:25:14.806382+00:00
| 437 | false |
First find the maximum element in the array, it will always have a -1 for the answer to it\'s next greater element because no element is greater than that in the array.\nThen, start a loop from that index till the same index in a backward direction, and fill the stack accordingly, if stack contains any lesser elements remove them, then check if stack is empty the answer will be -1 or else the top element of stack.\n\nTC: O(n) for finding the max element + O(n) for finding next greater elements of every element\nSC: O(n) at max the stack may contain n elements.\n\nJAVA:\n```class Solution {\n public int[] nextGreaterElements(int[] nums) {\n int pm = -1;\n int max = Integer.MIN_VALUE;\n for (int i = 0; i < nums.length; i++)\n if (max < nums[i]) {\n max = nums[i];\n pm = i;\n }\n int[] res = new int[nums.length];\n Stack<Integer> stk = new Stack<>();\n int i = pm;\n res[i] = -1;\n stk.push(nums[i]);\n i--;\n if (i < 0)\n i = nums.length - 1;\n \n while (i != pm) {\n while (!stk.isEmpty() && stk.peek() <= nums[i]) \n stk.pop();\n if (stk.isEmpty())\n res[i] = -1;\n else\n res[i] = stk.peek();\n stk.push(nums[i]);\n i--;\n if (i < 0)\n i = nums.length - 1;\n }\n return res;\n }\n}
| 3 | 0 |
[]
| 1 |
next-greater-element-ii
|
c++ | Simple | Single loop | stack
|
c-simple-single-loop-stack-by-anujsingh3-dab8
|
Simple solution with TC: O(2*n) , just using single loop.\n\n\nclass Solution {\npublic:\n vector<int> nextGreaterElements(vector<int>& nums) {\n int
|
anujsingh35788
|
NORMAL
|
2021-07-28T07:22:22.007357+00:00
|
2021-07-28T07:24:35.028534+00:00
| 283 | false |
Simple solution with TC: O(2*n) , just using single loop.\n\n```\nclass Solution {\npublic:\n vector<int> nextGreaterElements(vector<int>& nums) {\n int n = nums.size();\n vector<int>res(n,-1);\n stack<int>s;\n \n\t\t//in worst case we have to traverse array 2n times\n for(int i=0;i<n*2;i++){\n\t\t // if we reach end just change the index to 0\n int ind = (i>=n)?i-n:i;\n while(!s.empty() && nums[s.top()]<nums[ind]){\n res[s.top()] = nums[ind];\n s.pop();\n }\n s.push(ind); \n }\n return res;\n }\n};\n```\n\nif found helpful please upvote!!!
| 3 | 0 |
['Stack', 'C']
| 0 |
next-greater-element-ii
|
C++ Neat
|
c-neat-by-shtanriverdi-ezjt
|
\nclass Solution {\npublic:\n vector<int> nextGreaterElements(vector<int>& nums) {\n int n = nums.size();\n stack<int> s;\n vector<int>
|
shtanriverdi
|
NORMAL
|
2021-04-27T16:33:21.271707+00:00
|
2021-04-27T16:33:21.271744+00:00
| 207 | false |
```\nclass Solution {\npublic:\n vector<int> nextGreaterElements(vector<int>& nums) {\n int n = nums.size();\n stack<int> s;\n vector<int> result(n, -1);\n for (int i = 0; i < n * 2; i++) {\n while (!s.empty() && nums[i % n] > nums[s.top()]) {\n result[s.top()] = nums[i % n];\n s.pop();\n }\n s.push(i % n);\n }\n return result;\n }\n};\n```
| 3 | 2 |
['Stack', 'C']
| 1 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
A better Python solution
|
a-better-python-solution-by-yuxiong-8ot7
|
Here I copied the previous top voted Python solution:\n\nclass Solution:\n def buildTree(self, inorder, postorder):\n if not inorder or not postorder:
|
yuxiong
|
NORMAL
|
2019-01-19T18:22:41.196249+00:00
|
2022-01-03T18:34:24.349643+00:00
| 37,740 | false |
Here I copied the previous top voted Python solution:\n```\nclass Solution:\n def buildTree(self, inorder, postorder):\n if not inorder or not postorder:\n return None\n \n root = TreeNode(postorder.pop())\n inorderIndex = inorder.index(root.val) # Line A\n\n root.right = self.buildTree(inorder[inorderIndex+1:], postorder) # Line B\n root.left = self.buildTree(inorder[:inorderIndex], postorder) # Line C\n\n return root\n```\n\nThe code is clean and short. However, if you give this implementation during an interview, there is a good chance you will be asked, "can you improve/optimize your solution?"\n\nWhy? Take a look at Line A, Line B and Line C.\nLine A takes O(N) time.\nLine B and C takes O(N) time and extra space.\nThus, the overall running time and extra space is O(N^2).\nSo this implementation has a very bad performance, and you can avoid it.\n\nHere is my solution which has O(N) time and extra space.\n```\nclass Solution:\n def buildTree(self, inorder, postorder):\n map_inorder = {}\n for i, val in enumerate(inorder): map_inorder[val] = i\n def recur(low, high):\n if low > high: return None\n x = TreeNode(postorder.pop())\n mid = map_inorder[x.val]\n x.right = recur(mid+1, high)\n x.left = recur(low, mid-1)\n return x\n return recur(0, len(inorder)-1)\n```
| 498 | 6 |
[]
| 61 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
[ C++ ] Detail Explain | Diagram
|
c-detail-explain-diagram-by-suman_buie-sfiu
|
The Idea is As They Given us Inorder and Postorder\n\n \xA0 \xA0as we Know Inorder Fallow --> Left_subtree => Root_Node => Right_subtree Traverse\n \xA0 \xA0ans
|
suman_buie
|
NORMAL
|
2020-07-27T08:23:52.394465+00:00
|
2020-07-29T05:20:13.134506+00:00
| 26,794 | false |
The Idea is As They Given us ```Inorder and Postorder```\n\n \xA0 \xA0as we Know Inorder Fallow --> ```Left_subtree => Root_Node => Right_subtree ``` Traverse\n \xA0 \xA0ans \xA0 Postorder Fallow --> ```Left_subtree => Right_subtree =>Root_Node ```traverse\n using Postorder_array We can Find Root_Node Which always lay in Postorder_array last Possition\n After Finding That Root_Node ,First we are going to divide Inorder_array Into Two Part and Postorder Array \n into Two part .\n\n Then We are going to use Both of the arrays left part to Figur Out Left_subtree\n and Both of the arraysRigth Part to Figur out Right_subtree\n\n We are going to recursively do so until One Of the array dose not got empty\n\nLet\'s take an Example \n```\n inorder = [4 2 5 1 6 3 7]\n postorder = [4 5 2 6 7 3 1]\n\n So root would be 1 here and Left array which lay left of 1 is [4 2 5] and Right of 1 is [6 3 7]\n so left_inorder_array = [4 2 5] and right_inorder_arry = [6 3 7]\n\n using 6 [ which is just rigth of 1] we are going to devide Postorder_array into two part\n [4 5 2] and [6 7 3]\n\n\n 1st Phase=> \n\t 1\n\n / \\\n\n [4 2 5] [6 3 7] <= inorder array\n [4 5 2] [6 7 3] <= postorder array\n\nNow we have new freash problem like need to make tree by using inorder = [4 2 5] && postorder = [4 5 2] for left subtree \nAND inorder = [6 3 7] && postorder = [6 7 3] for right subtree \n**now same process we need to do again and again until One Of the array dose not got empty\nRest of the Process show in a diagram Form :)\n\n 2nd Phase =>\n 1\n\n / \\\n 2 3\n [4] [5] [6] [7] <= inorder array\n [4] [5] [6] [7] <= postorder array\n\n\n3rd Phase => \n\t 1\n\n / \\\n 2 3\n \n / \\ / \\ <==== Answer\n \n 4 5 6 7 \n```\n\n```\nclass Solution {\npublic:\n TreeNode *Tree(vector<int>& in, int x, int y,vector<int>& po,int a,int b){\n if(x > y || a > b)return nullptr;\n TreeNode *node = new TreeNode(po[b]);\n int SI = x; \n while(node->val != in[SI])SI++;\n node->left = Tree(in,x,SI-1,po,a,a+SI-x-1);\n node->right = Tree(in,SI+1,y,po,a+SI-x,b-1);\n return node;\n }\n TreeNode* buildTree(vector<int>& in, vector<int>& po){\n return Tree(in,0,in.size()-1,po,0,po.size()-1);\n }\n};\n```\nIf You Really Like It please **upvote**\nAny doubt Comments Bellow\n**happy Coding :)**
| 403 | 8 |
[]
| 28 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
🔥Easy Solutions in Java 📝, Python 🐍, and C++ 🖥️🧐Look at once 💻
|
easy-solutions-in-java-python-and-c-look-71ia
|
Intuition\n Describe your first thoughts on how to solve this problem. \nTo construct a binary tree from inorder and postorder traversal arrays, we first need t
|
Vikas-Pathak-123
|
NORMAL
|
2023-03-16T00:37:47.784404+00:00
|
2023-03-16T00:37:47.784435+00:00
| 31,092 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo construct a binary tree from inorder and postorder traversal arrays, we first need to understand what each of these traversals represents.\nInorder traversal visits the nodes in ascending order of their values, i.e., left child, parent, and right child. On the other hand, postorder traversal visits the nodes in the order left child, right child, and parent.\nKnowing this, we can say that the last element in the postorder array is the root node, and its index in the inorder array divides the tree into left and right subtrees. We can recursively apply this logic to construct the entire binary tree.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Start with the last element of the postorder array as the root node.\n2. Find the index of the root node in the inorder array.\n3. Divide the inorder array into left and right subtrees based on the index of the root node.\n4. Divide the postorder array into left and right subtrees based on the number of elements\nin the left and right subtrees of the inorder array.\n5. Recursively construct the left and right subtrees.\n\n\n\n\n\n# Complexity\n- Time complexity:\nThe time complexity of this algorithm is O(n), where n is the number of nodes in the tree. We visit each node only once.\n\n- Space complexity:\nThe space complexity of this algorithm is O(n). We create a hashmap to store the indices of the inorder traversal, which takes O(n) space. Additionally, the recursive call stack can go up to O(n) in the worst case if the binary tree is skewed.\n\n\n\n\n\n\n\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n```\nThanks for visiting my solution.\uD83D\uDE0A Keep Learning\nPlease give my solution an upvote! \uD83D\uDC4D\nIt\'s a simple way to show your appreciation and\nkeep me motivated. Thank you! \uD83D\uDE0A\n```\n# Code\n``` Java []\nlass Solution {\n public TreeNode buildTree(int[] inorder, int[] postorder) {\n // Call the recursive function with full arrays and return the result\n return buildTree(inorder, 0, inorder.length - 1, postorder, 0, postorder.length - 1);\n }\n \n private TreeNode buildTree(int[] inorder, int inStart, int inEnd, int[] postorder, int postStart, int postEnd) {\n // Base case\n if (inStart > inEnd || postStart > postEnd) {\n return null;\n }\n \n // Find the root node from the last element of postorder traversal\n int rootVal = postorder[postEnd];\n TreeNode root = new TreeNode(rootVal);\n \n // Find the index of the root node in inorder traversal\n int rootIndex = 0;\n for (int i = inStart; i <= inEnd; i++) {\n if (inorder[i] == rootVal) {\n rootIndex = i;\n break;\n }\n }\n \n // Recursively build the left and right subtrees\n int leftSize = rootIndex - inStart;\n int rightSize = inEnd - rootIndex;\n root.left = buildTree(inorder, inStart, rootIndex - 1, postorder, postStart, postStart + leftSize - 1);\n root.right = buildTree(inorder, rootIndex + 1, inEnd, postorder, postEnd - rightSize, postEnd - 1);\n \n return root;\n }\n}\n\n\n```\n```Python []\nclass Solution(object):\n def buildTree(self, inorder, postorder):\n """\n :type inorder: List[int]\n :type postorder: List[int]\n :rtype: TreeNode\n """\n # Base case\n if not inorder:\n return None\n \n # The last element of postorder list is the root\n root_val = postorder.pop()\n root = TreeNode(root_val)\n \n # Find the position of the root in the inorder list\n inorder_index = inorder.index(root_val)\n \n # Recursively build the left and right subtrees\n root.right = self.buildTree(inorder[inorder_index+1:], postorder)\n root.left = self.buildTree(inorder[:inorder_index], postorder)\n \n return root\n\n```\n```C++ []\nclass Solution {\npublic:\n TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {\n unordered_map<int, int> index;\n for (int i = 0; i < inorder.size(); i++) {\n index[inorder[i]] = i;\n }\n return buildTreeHelper(inorder, postorder, 0, inorder.size() - 1, 0, postorder.size() - 1, index);\n }\n \n TreeNode* buildTreeHelper(vector<int>& inorder, vector<int>& postorder, int inorderStart, int inorderEnd, int postorderStart, int postorderEnd, unordered_map<int, int>& index) {\n if (inorderStart > inorderEnd || postorderStart > postorderEnd) {\n return nullptr;\n }\n int rootVal = postorder[postorderEnd];\n TreeNode* root = new TreeNode(rootVal);\n int inorderRootIndex = index[rootVal];\n int leftSubtreeSize = inorderRootIndex - inorderStart;\n root->left = buildTreeHelper(inorder, postorder, inorderStart, inorderRootIndex - 1, postorderStart, postorderStart + leftSubtreeSize - 1, index);\n root->right = buildTreeHelper(inorder, postorder, inorderRootIndex + 1, inorderEnd, postorderStart + leftSubtreeSize, postorderEnd - 1, index);\n return root;\n }\n};\n\n\n```\n# Please Comment\uD83D\uDC4D\uD83D\uDC4D\n```\nThanks for visiting my solution comment below if you like it.\uD83D\uDE0A\n```
| 328 | 2 |
['Divide and Conquer', 'Tree', 'Python', 'C++', 'Java']
| 14 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
✅ [C++/Python] 2 Simple Solutions w/ Images and Detailed Explanation | Recursion + Hashmap
|
cpython-2-simple-solutions-w-images-and-3d248
|
\u2714\uFE0F Solution - I (Recursive)\n\nFirst, we need to observe that we cant form exact binary tree with only 1 traversal. \n For eg. inorder = [9,3,15,20,7]
|
archit91
|
NORMAL
|
2021-11-21T05:20:33.018337+00:00
|
2021-11-21T05:25:47.087653+00:00
| 12,207 | false |
\u2714\uFE0F ***Solution - I (Recursive)***\n\nFirst, we need to observe that we cant form exact binary tree with only 1 traversal. \n* For eg. `inorder = [9,3,15,20,7]`, here we dont know which is the root node of tree and their children. It could start with any node as root and form a valid binary tree. \n* Similarly, `postorder = [9,15,7,20,3]`, here we know `3` is the root node since traversal ended with it, however we are not sure of its children. It could have been all rest nodes on right side as `(root)3 -> 20 -> 7 -> 15 -> 9` or all on left side as `9 <- 15 <- 7 <- 20 <- 3(root)` or any intermediate of these.\n\nBut, when we consider both traversals, we can form a unique tree. Since the postorder traversal ends with root node, we know the root node of tree is last node of `postorder`. At the same time, we can search for that node in `inorder` and we know that the nodes that occur to its left form its left sub-tree and nodes occuring to the right of it form its right sub-tree. We recursively repeat the same process - \n* Next node in the line from last from `postorder` forms the root node, we search it in `inorder` and see what its left and right subtree are, then recurse for right subtree first, then the left one...until all nodes are traversed.\n\n\n\n\n<table>\n<tr>\n<th>\n<p align=middle><b>Step</b></p>\n</th>\n<th>\n<p align=middle><b>Description</b></p>\n</th>\n</tr>\n<tr></tr>\n<tr>\n<td><img src="https://assets.leetcode.com/users/images/90e76a97-9d03-4d51-b6d5-cb0409a67736_1637459119.542401.png" width=600 /></td>\n<td>The red node-3 denotes current root node</br>The blue nodes on left and right of red node denotes its left & right-subtrees respectively</br>We recursively construct the right subtree and then left subtree</td>\n</tr>\n<tr></tr>\n<tr>\n<td><img src="https://assets.leetcode.com/users/images/86ac3f2b-c0ce-49b7-b537-f87ae555a5dc_1637459304.2370312.png" width=600 /></td>\n<td>We have recursed to form the right subtree of previous root node-3</br>20 is the next node from end in postorder traversal and so it forms the current node</br>Again, the blue nodes on left & right of 20 denote its left & right-subtrees respectively</br>We again recursively construct the right subtree and then left subtree</td>\n</tr>\n<tr></tr>\n<tr>\n<td><img src="https://assets.leetcode.com/users/images/505ebc42-7713-4fa7-9110-ea5edc82fc9c_1637459360.4169023.png" width=600 /></td>\n<td>We have recursed to form the right subtree of previous root node-20</br>7 is next node in postorder which forms current node</br>There are no left and right subtrees for 7</br>So just create node-7 and return</td>\n</tr>\n<tr></tr>\n<tr>\n<td><img src="https://assets.leetcode.com/users/images/c881ffb6-5c85-4e06-a195-e506b30d3272_1637459438.2325265.png" width=600 /></td>\n<td>Now, we recurse from step-2 to form left subtree of root node-20</br>Again, 15 is next node in postorder and it forms the current node</br>Again, there are no left and right subtrees</br> So just create node-15 and return</td>\n</tr>\n<tr></tr>\n<tr>\n<td><img src="https://assets.leetcode.com/users/images/075935ae-9ceb-4c2d-8d72-b9bb530dcbf7_1637459480.7908006.png" width=600 /></td>\n<td>Now, we recurse from step-1 to form left subtree of root node-3</br>9 is the next node in postorder and it forms current node</br>We dont have any left and right subtree for 9</br> So just create node-9 and return</td>\n</tr>\n<tr></tr>\n<tr>\n<td><img src="https://assets.leetcode.com/users/images/2ae430ac-ac5b-4886-a4e8-1859f7e6c7de_1637461160.3626633.png" width=600 /></td>\n<td>All the nodes have been traversed</br>The recursion stops here and we return the final tree</td>\n</tr>\n</table>\n\nSo to summarize the algorithm can be stated as -\n1. We start by initializing `postIdx = n-1`, where `n` is the number of nodes. `postIdx` denotes the index of postorder traversal that we are at. It will give us the root node for each point of recursion\n2. We also initialize `inStart = 0` and `inEnd = n-1` which denotes the current range in `inorder` that the subtree will lie in. \n3. At each recursion, we choose `postorder[postIdx]` as current root node. We search that index of that node in `inorder` as well. Then all nodes to the left of that index (till the previous root) are part of current root\'s left sub-tree and all nodes to the right of it are part of its right sub-tree.\n3. We decrement `postIdx` and recurse to build the right sub-tree and then left sub-tree. \n **Why right first**? Because postorder goes as `left->right->root` and we are traversing it from end. So we consider in order `root->right->left`)\n 4. The process is continued till all nodes are traversed.\n\n**C++**\n```cpp\nclass Solution {\npublic:\n TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {\n int n = size(inorder), postIdx = n-1;\n return build(inorder, postorder, 0, n-1, postIdx);\n }\n\n TreeNode* build(vector<int>& in, vector<int>& post, int inStart, int inEnd, int& postIdx) {\n if(inStart > inEnd) return nullptr;\n TreeNode* root = new TreeNode(post[postIdx--]);\n int inIdx = find(begin(in), end(in), root -> val) - begin(in);\n root -> right = build(in, post, inIdx+1, inEnd, postIdx);\n root -> left = build(in, post, inStart, inIdx-1, postIdx);\n return root;\n }\n};\n```\n\n**Python**\n```python\nclass Solution:\n def buildTree(self, inorder, postorder):\n self.postIdx = len(postorder)-1\n def build(inStart, inEnd):\n if inStart > inEnd: return None\n root = TreeNode(postorder[self.postIdx])\n self.postIdx -= 1\n root.right = build(inorder.index(root.val)+1, inEnd)\n root.left = build(inStart, inorder.index(root.val)-1)\n return root \n return build(0, len(inorder)-1)\n```\n\n***Time Complexity :*** **<code>O(N<sup>2</sup>)</code>** where `N` is the number of nodes in the tree. At each recursion, we are choosing `post[postIdx]` and searching it in `inorder`. This may take `O(N)` for each search and we are building a tree with `N` such nodes. So total time complexity is <code>O(N<sup>2</sup>)</code>\n***Space Complexity :*** **<code>O(N)</code>**, required by implicit recursive stack. In worst case of skewed tree, the recursion depth might go upto `N`.\n\n---\n\n\u2714\uFE0F ***Solution - II (Recursive w/ Hashmap)***\n\nIn the previous approach, we had to search a node in the `inorder` array everytime which cost us `O(N)` and led to higher time complexity. However, we can reduce this cost if we maintain a mapping of node\'s value to `inorder` node index in a hashmap. This allows us to fetch index of a node in `inorder` array in `O(1)` time at each recursion.\n\n**C++**\n```cpp\nclass Solution {\npublic:\n unordered_map<int, int> mp;\n TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {\n for(int i = 0; i < size(inorder); i++) mp[inorder[i]] = i;\n int n = size(inorder), postIdx = n-1;\n return build(inorder, postorder, 0, n-1, postIdx);\n }\n\n TreeNode* build(vector<int>& in, vector<int>& post, int inStart, int inEnd, int& postIdx) {\n if(inStart > inEnd) return nullptr;\n TreeNode* root = new TreeNode(post[postIdx--]);\n int inIdx = mp[root -> val];\n root -> right = build(in, post, inIdx+1, inEnd, postIdx);\n root -> left = build(in, post, inStart, inIdx-1, postIdx);\n return root;\n }\n};\n```\n\n**Python**\n```python\nclass Solution:\n def buildTree(self, inorder, postorder):\n self.postIdx, mp = len(postorder)-1, {val: idx for idx, val in enumerate(inorder)}\n def build(inStart, inEnd):\n if inStart > inEnd: return None\n root = TreeNode(postorder[self.postIdx])\n self.postIdx -= 1\n root.right = build(mp[root.val]+1, inEnd)\n root.left = build(inStart, mp[root.val]-1)\n return root \n return build(0, len(inorder)-1)\n```\n\n***Time Complexity :*** `O(N)`, now we can find `inIdx` in `O(1)` time. So the time required to build the tree out of `N` nodes each taking `O(1)` comes out to be `O(N)`\n***Space Complexity :*** `O(N)`, requried by recursive stack and to maintain hashmap.\n\n\n\n---\n---\n\n\uD83D\uDCBBIf there are any suggestions / questions / mistakes in my post, comment below \uD83D\uDC47 \n\n---\n---
| 318 | 1 |
[]
| 24 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
My recursive Java code with O(n) time and O(n) space
|
my-recursive-java-code-with-on-time-and-j7bye
|
The the basic idea is to take the last element in postorder array as the root, find the position of the root in the inorder array; then locate the range for lef
|
lurklurk
|
NORMAL
|
2014-09-13T00:04:21+00:00
|
2018-10-17T14:16:18.077954+00:00
| 82,427 | false |
The the basic idea is to take the last element in postorder array as the root, find the position of the root in the inorder array; then locate the range for left sub-tree and right sub-tree and do recursion. Use a HashMap to record the index of root in the inorder array.\n\n public TreeNode buildTreePostIn(int[] inorder, int[] postorder) {\n \tif (inorder == null || postorder == null || inorder.length != postorder.length)\n \t\treturn null;\n \tHashMap<Integer, Integer> hm = new HashMap<Integer,Integer>();\n \tfor (int i=0;i<inorder.length;++i)\n \t\thm.put(inorder[i], i);\n \treturn buildTreePostIn(inorder, 0, inorder.length-1, postorder, 0, \n postorder.length-1,hm);\n }\n \n private TreeNode buildTreePostIn(int[] inorder, int is, int ie, int[] postorder, int ps, int pe, \n HashMap<Integer,Integer> hm){\n \tif (ps>pe || is>ie) return null;\n \tTreeNode root = new TreeNode(postorder[pe]);\n \tint ri = hm.get(postorder[pe]);\n \tTreeNode leftchild = buildTreePostIn(inorder, is, ri-1, postorder, ps, ps+ri-is-1, hm);\n \tTreeNode rightchild = buildTreePostIn(inorder,ri+1, ie, postorder, ps+ri-is, pe-1, hm);\n \troot.left = leftchild;\n \troot.right = rightchild;\n \treturn root;\n }
| 263 | 17 |
[]
| 56 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
✅[C++] EASY Intuitive Sol | Clean Recursive Code w/ Explanation (Dry Run) | T.C:O(N)
|
c-easy-intuitive-sol-clean-recursive-cod-8wxb
|
Hello everyone! I hope you all are doing great.\n\nNote: Please do upvote if you find this post helpful!\nNote: Some people are unethically downvoting my post,
|
riemeltm
|
NORMAL
|
2021-11-21T01:58:32.764638+00:00
|
2021-11-21T08:25:09.570518+00:00
| 6,617 | false |
Hello everyone! I hope you all are doing great.\n\n***Note: Please do upvote if you find this post helpful!***\n**Note: Some people are unethically downvoting my post, please do upvote and save this post from disappearing**\n\nNow, we want to create our binary tree with given postorder and inorder traversals.\n\n**Observations:**\n1. *Inorder* is `LEFT ROOT RIGHT`. So for any node lets say current node is at index `i` in inorder array, if you think it as a root of its subtree, then all the nodes at indices less than `i` will be on the left subtree of the current node and all the nodes at indices greater than `i` will be on the right subtree of the current node.\n\n2. *Postorder* is `LEFT RIGHT ROOT`. So the **last element** of our postorder array will always be our `root`, and then we will move backwards in our postorder array to find the next root.\n\n**My Approach:**\n1. Since Post Order traversal is like `LEFT RIGHT ROOT`, therefore we will traverse the postorder array from backwards and will construct our tree like `ROOT RIGHT LEFT`.\n\n2. Take our node from postorder array, let say it is at index `idx` (We came from `postorder.size()-1` to `idx`) and this will be our root in current recursive call, then decrement the `idx` for our next upcoming root.\n\n3. Now find our current node (from step 2) in our inorder array (let say we found it at `i`), then we will have nodes in left subtree of current node who are at position less than `i` and nodes in right subtree of current node who are at position greater than `i`.\n\n4. So we make a recursive call to construct the right subtree first, then we make a recursive call to construct the left subtree of our current node. (Since we are building our Binary Tree in `ROOT RIGHT LEFT`).\n\n**DRY RUN for algo explained above:**\n\n**Initial Situtation: (Step 1)** \n```\nInorder array: [9,3,15,20,7]\nPostorder array: [9,15,7,20,3]\n\nHence 3 will be our root and inorder range for left subtree will be [9] and inorder range for right subtree will be [15, 20, 7]\n\n\t\t\t3\n\t\t /\t \\\n\t [9] [15, 20, 7] -> Inorder\n\t [9] [15, 7, 20] -> Postorder\n```\n\n**Step 2:**\n```\n\t\t\t3\n\t\t /\t \\\n\t\t9\t 20\n\t / \\\t / \\\n\t * * [15] [7] -> Inorder\n\t\t\t [15] [7] -> Postorder\n```\n\n**Step 3:**\n```\n\t\t\t3\n\t\t /\t \\\n\t\t9\t 20\n\t / \\\t / \\\n\t * * 15 7\n\t\t\t / \\ / \\\n\t\t\t * * * *\n```\n\n**Below is the code for the approach I gave above:**\n\n```\nclass Solution {\npublic:\n unordered_map<int, int>mp; // Stores (node -> index in inorder array)\n \n TreeNode* make_tree(int start, int end, int &idx, vector<int>& postorder, vector<int>& inorder){\n \n\t\t// If range for inorder is NOT valid then return NULL\n if(start > end) return NULL;\n \n\t\t// Create a node for our root node of current subtree\n TreeNode* root = new TreeNode(postorder[idx]);\n \n\t\t// Find position of current root in inorder array\n int i = mp[root->val];\n\t\t\n\t\t// Decrement our pointer to postorder array for our next upcoming root if any\n idx--;\n\t\t\n\t\t// Make a call to create right subtree, inorder range [i+1, end]\n root->right = make_tree(i+1, end, idx, postorder, inorder);\n\t\t\n\t\t// Make a call to create left subtree, inorder range [start, i-1]\n root->left = make_tree(start, i-1, idx, postorder, inorder);\n \n return root;\n }\n \n TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {\n int idx=postorder.size()-1;\n \n\t\t// Create (nodes -> index of inorder array) mapping\n for(int i{}; i<inorder.size(); ++i){\n \n mp[inorder[i]] = i;\n }\n\t\t// Create tree starting from root at position (n-1) in postorder array\n\t\t// Range for current inirder array : [0, n-1]\n return make_tree(0, inorder.size()-1, idx, postorder, inorder);\n }\n};\n```\n\n**Time Complexity:** ***O(N)*** since we are visiting every node from postorder array at once and creating a node for it.\n\n**Space Complexity:** ***O(N)*** since we are creating a mapping for every node that will contain its index for a node in inorder array.\n\n***NOTE: Please do \u2705 Upvote if you like my solution!***
| 147 | 36 |
[]
| 15 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
A Python recursive solution
|
a-python-recursive-solution-by-google-6qbd
|
# Definition for a binary tree node\n # class TreeNode:\n # def __init__(self, x):\n # self.val = x\n # self.left = None\n #
|
google
|
NORMAL
|
2015-03-21T05:06:08+00:00
|
2018-10-08T14:21:44.215468+00:00
| 22,418 | false |
# Definition for a binary tree node\n # class TreeNode:\n # def __init__(self, x):\n # self.val = x\n # self.left = None\n # self.right = None\n \n class Solution:\n # @param inorder, a list of integers\n # @param postorder, a list of integers\n # @return a tree node\n # 12:00\n def buildTree(self, inorder, postorder):\n if not inorder or not postorder:\n return None\n \n root = TreeNode(postorder.pop())\n inorderIndex = inorder.index(root.val)\n \n root.right = self.buildTree(inorder[inorderIndex+1:], postorder)\n root.left = self.buildTree(inorder[:inorderIndex], postorder)\n \n return root
| 107 | 12 |
['Python']
| 20 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
Sharing my straightforward recursive solution
|
sharing-my-straightforward-recursive-sol-gv0n
|
TreeNode *buildTree(vector<int> &inorder, vector<int> &postorder) {\n return create(inorder, postorder, 0, inorder.size() - 1, 0, postorder.size() - 1);\
|
zxyperfect
|
NORMAL
|
2014-12-09T05:58:57+00:00
|
2018-10-17T06:51:12.156506+00:00
| 23,397 | false |
TreeNode *buildTree(vector<int> &inorder, vector<int> &postorder) {\n return create(inorder, postorder, 0, inorder.size() - 1, 0, postorder.size() - 1);\n }\n \n TreeNode* create(vector<int> &inorder, vector<int> &postorder, int is, int ie, int ps, int pe){\n if(ps > pe){\n return nullptr;\n }\n TreeNode* node = new TreeNode(postorder[pe]);\n int pos;\n for(int i = is; i <= ie; i++){\n if(inorder[i] == node->val){\n pos = i;\n break;\n }\n }\n node->left = create(inorder, postorder, is, pos - 1, ps, ps + pos - is - 1);\n node->right = create(inorder, postorder, pos + 1, ie, pe - ie + pos, pe - 1);\n return node;\n }\n\nActually, this problem is pretty similar as the previous one. \n\n[Here is a like to that solution. ][1]\n\n\n [1]: https://oj.leetcode.com/discuss/18101/sharing-my-straightforward-recursive-solution
| 93 | 2 |
['C++']
| 10 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
Java | Recursive | Most Intutive | Intution Explanation Using Image
|
java-recursive-most-intutive-intution-ex-ul1k
|
Intution: Firstly observe both the arrays and think how they are formed from a tree...which index contain which part from the tree.\n * Inorder Traversal: After
|
Chaitanya1706
|
NORMAL
|
2021-11-21T03:21:10.753535+00:00
|
2022-06-04T07:50:21.684367+00:00
| 7,236 | false |
**Intution:** Firstly observe both the arrays and think how they are formed from a tree...which index contain which part from the tree.\n * *Inorder Traversal*: After storing the inorder traversal of tree u can see that root will always come in between and left of root will be all the nodes of left subtree and in right will be nodes of right subtree.\n* *Postorder Traversal*: Here u can see that in the array firstly there will be all the left subtree nodes then all the righgt subtree nodes and then at last will be root;\n ##### So now u can say that you have the root node confirmed that is at last index of postorder traversal array\n\t Now u have to just recursively update the left and right subtree of the root using your two arrays.\n\t \n\t \n\n\n```\nclass Solution {\n public TreeNode buildTree(int[] inorder, int[] postorder) {\n return build(inorder,0,inorder.length-1,postorder,0,postorder.length-1);\n }\n \n public TreeNode build(int[] inorder, int inS, int inE, int[] postorder, int posS, int posE){\n if(inS>inE || posS>posE) return null;\n \n TreeNode root = new TreeNode(postorder[posE]);\n \n int rootI=0;\n for(int i=0;i<inorder.length;i++){\n if(inorder[i]==root.val){\n rootI = i;\n break;\n }\n }\n \n root.left = build(inorder,inS,rootI-1,postorder,posS,posS+rootI-inS-1);\n root.right = build(inorder,rootI+1,inE,postorder,posS+rootI-inS,posE-1);\n \n return root;\n }\n}
| 90 | 7 |
['Recursion', 'Java']
| 12 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
Java iterative solution with explanation
|
java-iterative-solution-with-explanation-bwag
|
\n public TreeNode buildTree(int[] inorder, int[] postorder) {\n if (inorder.length == 0 || postorder.length == 0) return null;\n int ip = inor
|
mayijie88
|
NORMAL
|
2015-01-31T18:35:24+00:00
|
2018-10-13T14:15:18.192743+00:00
| 23,719 | false |
\n public TreeNode buildTree(int[] inorder, int[] postorder) {\n if (inorder.length == 0 || postorder.length == 0) return null;\n int ip = inorder.length - 1;\n int pp = postorder.length - 1;\n \n Stack<TreeNode> stack = new Stack<TreeNode>();\n TreeNode prev = null;\n TreeNode root = new TreeNode(postorder[pp]);\n stack.push(root);\n pp--;\n \n while (pp >= 0) {\n while (!stack.isEmpty() && stack.peek().val == inorder[ip]) {\n prev = stack.pop();\n ip--;\n }\n TreeNode newNode = new TreeNode(postorder[pp]);\n if (prev != null) {\n prev.left = newNode;\n } else if (!stack.isEmpty()) {\n TreeNode currTop = stack.peek();\n currTop.right = newNode;\n }\n stack.push(newNode);\n prev = null;\n pp--;\n }\n \n return root;\n }\n\nThis is my iterative solution, think about "Constructing Binary Tree from inorder and preorder array", the idea is quite similar. Instead of scanning the preorder array from beginning to end and using inorder array as a kind of mark, in this question, the key point is to scanning the postorder array from end to beginning and also use inorder array from end to beginning as a mark because the logic is more clear in this way. ***The core idea is: Starting from the last element of the postorder and inorder array, we put elements from postorder array to a stack and each one is the right child of the last one until an element in postorder array is equal to the element on the inorder array. Then, we pop as many as elements we can from the stack and decrease the mark in inorder array until the peek() element is not equal to the mark value or the stack is empty. Then, the new element that we are gonna scan from postorder array is the left child of the last element we have popped out from the stack.***
| 90 | 0 |
['Java']
| 11 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
Awesome Logic Python3
|
awesome-logic-python3-by-ganjinaveen-idch
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
GANJINAVEEN
|
NORMAL
|
2023-03-16T02:53:55.733957+00:00
|
2023-03-16T02:53:55.734018+00:00
| 4,050 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:90%\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:80%\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:\n if not inorder or not postorder:\n return None\n root=TreeNode(postorder[-1])\n index=inorder.index(postorder[-1])\n root.left=self.buildTree(inorder[:index],postorder[:index])\n root.right=self.buildTree(inorder[index+1:],postorder[index:-1])\n return root\n #please upvote me it would encourage me alot\n\n```
| 80 | 0 |
['Python3']
| 2 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
Simple and clean Java solution with comments, recursive.
|
simple-and-clean-java-solution-with-comm-1zzo
|
\n public TreeNode buildTree(int[] inorder, int[] postorder) {\n return buildTree(inorder, inorder.length-1, 0, postorder, postorder.length-1);\n }
|
jinwu
|
NORMAL
|
2015-09-18T06:20:53+00:00
|
2015-09-18T06:20:53+00:00
| 13,647 | false |
\n public TreeNode buildTree(int[] inorder, int[] postorder) {\n return buildTree(inorder, inorder.length-1, 0, postorder, postorder.length-1);\n }\n\n\tprivate TreeNode buildTree(int[] inorder, int inStart, int inEnd, int[] postorder,\n\t\t\tint postStart) {\n\t\tif (postStart < 0 || inStart < inEnd)\n\t\t\treturn null;\n\t\t\n\t\t//The last element in postorder is the root.\n\t\tTreeNode root = new TreeNode(postorder[postStart]);\n\t\t\n\t\t//find the index of the root from inorder. Iterating from the end.\n\t\tint rIndex = inStart;\n\t\tfor (int i = inStart; i >= inEnd; i--) {\n\t\t\tif (inorder[i] == postorder[postStart]) {\n\t\t\t\trIndex = i;\n\t\t\t\tbreak;\n\t\t\t}\n\t\t}\n\t\t//build right and left subtrees. Again, scanning from the end to find the sections.\n\t\troot.right = buildTree(inorder, inStart, rIndex + 1, postorder, postStart-1);\n\t\troot.left = buildTree(inorder, rIndex - 1, inEnd, postorder, postStart - (inStart - rIndex) -1);\n\t\treturn root;\n\t}
| 73 | 5 |
['Java']
| 12 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
[Python] O(n) recursion, explained with diagram
|
python-on-recursion-explained-with-diagr-si8q
|
To solve this problem we need to understand, what is inorder and what is postorder traversal of tree. Let me remind you:\n\n1. inorder traversal is when you vis
|
dbabichev
|
NORMAL
|
2020-07-27T11:28:27.963808+00:00
|
2020-07-27T12:23:14.173835+00:00
| 3,312 | false |
To solve this problem we need to understand, what is `inorder` and what is `postorder` traversal of tree. Let me remind you:\n\n1. `inorder` traversal is when you visit `left, root, right`, where `left` is left subtree, `root` is root node and `right` is right subtree.\n2. `postorder` traversal is when you visit `left, right, root`.\n\nWe can see that in `postorder` traverasl `root` will be in the end, so we take this element and we need to find it in `inorder` array. Then we need to call function recursively on the `left` subtree and `right` subtree. It is easier said that done, so let us introduce function `helper(post_beg, post_end, in_beg, in_end)`, which has `4` parameters:\n1. `post_beg` and `post_end` are indices in original `postorder` array of current window. Note, that we use python notation, so `post_end` points to one element after the end.\n2. `in_beg` and `in_end` are indices in original `inorder` array of current window. We again use python notation, where `in_end` points to one element after the end.\n\nThen what we need to do is to find indices of left part and right part. First of all, evaluate `ind = dic[postorder[post_end-1]]`, where we create `dic = {elem: it for it, elem in enumerate(inorder)}` for fast access to elements. Now, look at the next two images:\n\nOn the first one `1, 2, 3, 4` in circles are equal to `post_beg, post_beg + ind - in_beg, in_beg, ind`. Why? `1` should point to beginning of `left` in postorder, so it is equal to `post_beg`. `2` should point to one element after the end of `left`, so we need to know the length of `left`, we can find it from `inorder` array, it is `ind - in_beg`. So, finally, point `2` is equal to `post_beg + ind - in_beg`. Point `3` should point to start of `left` in `inorder` array, that is `in_beg` and point `4` should point to element after the end of `left` in `inorder` array, that is `ind`.\n\nOn the second one `1, 2, 3, 4` in circles are equal to `post_end - in_end + ind, post_end - 1, ind + 1, in_end`. The logic is similar as for `left` parts, but here we look into `right` arrays.\n\n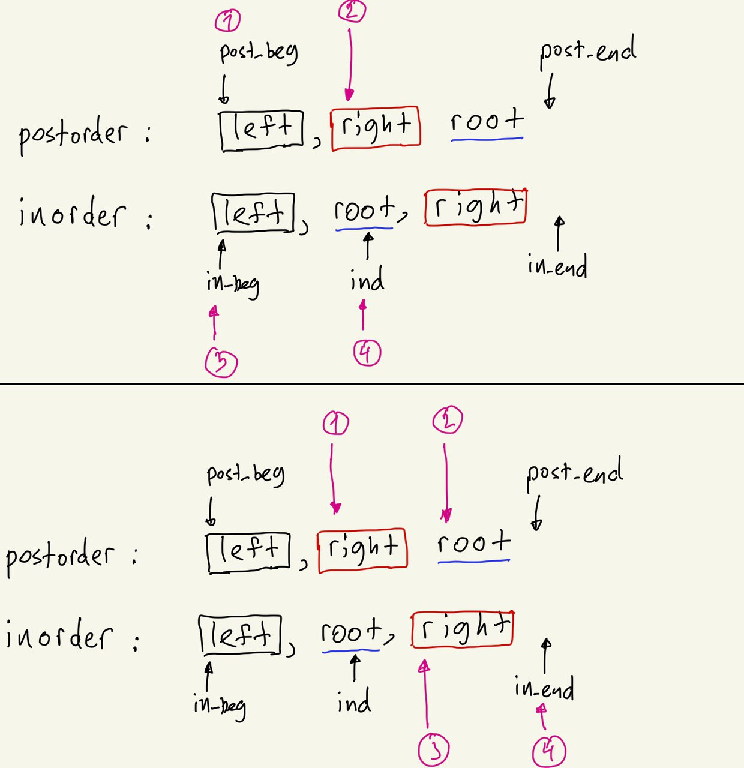\n\n**Complexity**: Time complexity is `O(n)`, because we traverse each element only once and we have `O(1)` complexity to find element in `dic`. Space complexity is also `O(n)`, because we keep additional `dic` with this size.\n\n```\nclass Solution:\n def buildTree(self, inorder, postorder):\n def helper(post_beg, post_end, in_beg, in_end):\n if post_end - post_beg <= 0: return None\n ind = dic[postorder[post_end-1]]\n\n root = TreeNode(inorder[ind]) \n root.left = helper(post_beg, post_beg + ind - in_beg, in_beg, ind)\n root.right = helper(post_end - in_end + ind, post_end - 1, ind + 1, in_end)\n return root\n \n dic = {elem: it for it, elem in enumerate(inorder)} \n return helper(0, len(postorder), 0, len(inorder))\n```\n\nIf you have any questoins, feel free to ask. If you like the solution and explanation, please **upvote!**
| 66 | 2 |
['Recursion']
| 3 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
C++ Simple and Clean Recursive Solution, With Explanation, No Map
|
c-simple-and-clean-recursive-solution-wi-41u7
|
Explanation:\nWhen we do an inorder traversal, we have the left subtree, then somewhere in the middle the root, then the right subtree.\nWhen we do postorder tr
|
yehudisk
|
NORMAL
|
2021-11-21T00:11:21.512562+00:00
|
2021-11-21T00:12:36.876035+00:00
| 3,701 | false |
**Explanation:**\nWhen we do an inorder traversal, we have the left subtree, then somewhere in the middle the root, then the right subtree.\nWhen we do postorder traversal, we have the root at the end.\n\nSo we have `m_curr` to go from the end of `m_postorder` - this will be the root at each iteration.\nNow, we have the value of the root, we try to find that value in `m_inorder`.\nOnce we found the index of the root in `m_inorder`, we know that the subarray in the left belongs to the left subtree and the right subarray is the right subtree.\nSo all we need to do is create the current root from that value and send to a recursive call with the right indices.\nWe also decrease `m_curr` to have the next subtree\'s root.\n```\nclass Solution {\npublic:\n TreeNode* rec(int l, int r) {\n if (l > r) return NULL;\n \n int i = 0;\n while (m_inorder[i] != m_postorder[m_curr]) {\n i++;\n }\n \n m_curr--;\n TreeNode* node = new TreeNode(m_inorder[i]);\n node->right = rec(i+1, r);\n node->left = rec(l, i-1);\n return node;\n \n }\n \n TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {\n m_postorder = postorder, m_inorder = inorder, m_curr = inorder.size()-1;\n return rec(0, postorder.size()-1);\n }\n \nprivate:\n int m_curr;\n vector<int> m_postorder, m_inorder;\n};\n```\n**Like it? please upvote!**
| 60 | 19 |
['C']
| 5 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
C++ solution Using Recursion and Map with Explanation(90.33% faster)
|
c-solution-using-recursion-and-map-with-bhkuj
|
Explanation:\nWe Using Unorder map to know the index of the ROOT element in INORDER element. that\'s why,we have to iterate all over the INORDER element and sav
|
markkais129
|
NORMAL
|
2021-08-07T18:29:00.236602+00:00
|
2021-08-07T19:40:17.631980+00:00
| 3,957 | false |
**Explanation:**\nWe Using Unorder map to know the index of the ROOT element in INORDER element. that\'s why,we have to iterate all over the INORDER element and save their value and index in our **UNORDERED_MAP**; \nIt makes the solution **O(n)** instead of O(n^2).\n\n\nWe know that, the last element of **POSTORDER** array contains main **ROOT** Node. and In **INORDER** array we see that the left side of the **ROOT** element contains the **LEFT** side element and **Right** side contains all the **RIGHT** side element.\nSo, we have to find out the index of **ROOT** element in **INORDER** Element. \nSo, \n```int inorderIndex = m[postorder[postIndex]];```\nand Make ROOT =\n```TreeNode *root =new TreeNode(inorder[inorderIndex]);```\nand postIndex decreament by 1 for the next purpose.\nAnd then we go to the **Right side** first and make the **Right side** of the **ROOT**. Here the start index is inorderIndex+1 cause all Right Part is in the Right Side of the inorder Array.\n```root->right=solve(inorder,postorder,inorderIndex+1,end,postIndex);```\n\nAnd then we go to the **Left Side** and make the Left side of the **ROOT**. Here the end index is inorderIndex-1 cause all left Part is in the left Side of the inorder Array.\n```root->left=solve(inorder,postorder,start,inorderIndex-1,postIndex);```\n\nAnd Now the **base case**, when we stop our Recursion:\nWe all know when, start> end, we return NULL;\n``` if(start>end) return NULL;```\n\nAnd Last we return ROOT;\n\n**N:B: If you recurse Left Side first , it cause Runtime Error, cursed the code**\nCause,when you call left first the postindex got decreased in every call until left part finishes off but we are comparing from the last so need to get the last indexes for right part too that we will not be able to get it if we called for left part first.\nIf we call right part eventually postindex should decrease till left part so that we will be able to access parent node for every left tree element.\nHope this helps:)\n\n**Code:**\n\n```\nclass Solution {\npublic:\n unordered_map<int,int>m;\n TreeNode* solve(vector<int>& inorder,vector<int>& postorder,int start,int end,int &postIndex){\n if(start>end) return NULL;\n int inorderIndex = m[postorder[postIndex]];\n\n TreeNode* root = new TreeNode(inorder[inorderIndex]); \n \n (postIndex)--;\n root->right=solve(inorder,postorder,inorderIndex+1,end,postIndex);\n root->left=solve(inorder,postorder,start,inorderIndex-1,postIndex);\n \n return root;\n }\n \n \n TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {\n\n for(int i=0;i<inorder.size();i++){\n m[inorder[i]] = i;\n \n }\n int postIndex=postorder.size()-1;\n return solve(inorder,postorder,0,postorder.size()-1,postIndex);\n }\n};\n```\n**If you helped by this Explanation or Code or learn something from this, PLEASE UPVOTE**\nif I make any mistake , please comment and If you have better Idea please Comment. Thank you for Reading.
| 53 | 2 |
['Recursion', 'C', 'C++']
| 7 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
💡JavaScript Solution
|
javascript-solution-by-aminick-apjy
|
The idea\n1. Inorder: <LEFT><ROOT><RIGHT>, postorder: <LEFT><RIGHT><ROOT>\n2. The last element of postorder will always be the root of a subtree. We can furter
|
aminick
|
NORMAL
|
2020-01-27T07:40:56.199493+00:00
|
2020-01-27T07:40:56.199527+00:00
| 3,027 | false |
### The idea\n1. Inorder: `<LEFT><ROOT><RIGHT>`, postorder: `<LEFT><RIGHT><ROOT>`\n2. The last element of postorder will always be the root of a subtree. We can furter determine its left and right subtree by finding its position in the inorder array. \n<img src="https://assets.leetcode.com/users/aminick/image_1580110093.png" width=600px>\n\n``` javascript\n/**\n * @param {number[]} inorder\n * @param {number[]} postorder\n * @return {TreeNode}\n */\nvar buildTree = function(inorder, postorder) { \n let hash = {};\n for (let i=0;i<inorder.length;i++) hash[inorder[i]] = i; \n \n let recur = function(start, end) {\n if (start > end) return null;\n let val = postorder.pop();\n let root = new TreeNode(val);\n root.right = recur(hash[val] + 1, end);\n root.left = recur(start, hash[val] - 1);\n return root;\n }\n \n return recur(0, inorder.length - 1); \n};\n```
| 52 | 1 |
['JavaScript']
| 4 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
Python easy to understand recursive solution
|
python-easy-to-understand-recursive-solu-enxh
|
\nclass Solution(object):\n def buildTree1(self, inorder, postorder):\n if not inorder:\n return None\n idx = inorder.index(postorde
|
oldcodingfarmer
|
NORMAL
|
2015-08-13T16:53:10+00:00
|
2020-10-15T15:05:55.167075+00:00
| 6,714 | false |
```\nclass Solution(object):\n def buildTree1(self, inorder, postorder):\n if not inorder:\n return None\n idx = inorder.index(postorder.pop())\n root = TreeNode(inorder[idx])\n root.left = self.buildTree(inorder[:idx], postorder[:idx])\n root.right = self.buildTree(inorder[idx+1:], postorder[idx:])\n return root\n \n def buildTree(self, inorder, postorder): \n if inorder:\n ind = inorder.index(postorder.pop())\n root = TreeNode(inorder[ind])\n root.right = self.buildTree(inorder[ind+1:], postorder)\n root.left = self.buildTree(inorder[:ind], postorder)\n return root\n```
| 48 | 1 |
['Recursion', 'Python']
| 5 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
My comprehension of O(n) solution from @hongzhi
|
my-comprehension-of-on-solution-from-hon-jsqr
|
Below is the O(n) solution from @hongzhi but that discuss is closed now 'cause @hongzhi says little about his code. \n\nhttps://oj.leetcode.com/discuss/6334/her
|
lancelod_liu
|
NORMAL
|
2014-11-04T06:59:44+00:00
|
2014-11-04T06:59:44+00:00
| 19,794 | false |
Below is the O(n) solution from @hongzhi but that discuss is closed now 'cause @hongzhi says little about his code. \n\nhttps://oj.leetcode.com/discuss/6334/here-is-my-o-n-solution-is-it-neat\n\nI've modified some of and tried this code and got AC.\nJust share about some comprehension about his code.\n\nI've modified vtn(vector) to stn(stack) in that **stack** is probably what this algs means and needs.\n\nWhat matters most is the meaning of *stn*. \n\nOnly nodes whoes left side **hasn't been** handled will be pushed into *stn*.\n\nAnd inorder is organized as (inorder of left) root (inorder of right),\n\nAnd postorder is as (postorder of left) (postorder of right) root.\n\nSo at the very begin, we only have root in stn and we check if *inorder.back() == root->val* and in most cases it's **false**(see Note 1). Then we make this node root's right sub-node and push it into stn. \n\n**Note 1: this is actually *(inorder of right).back() == (postorder of right).back()*, so if only there's no right subtree or the answer will always be false.**\n\n**Note 2: we delete one node from *postorder* as we push one into stn.**\n\nNow we have [root, root's right] as stn and we check *inorder.back() == stn.top()->val* again. \n\n - **true** means *inorder.back()* is the root node and needs handled left case.\n - **false** means *inorder.back()* is the next right sub-node\n\nSo when we encounter a true, we will cache *stn.top()* as p and **delete both nodes from inorder and stn**. \n\nThen we check inorder.size(), if there's no nodes left, it means p has no left node. \n\nElse the next node in inorder could be *p's left node* or *p's father* which equals to the now *stn.top()* (remember we popped *p* from *stn* above). \n\nIf the latter happens, it means *p* has **no left node** and we need to move on to *p's father(stn.top())*.\n\nIf the former happens, it means *p* has one left node and it's *postorder.back()*, so we put it to p's left and delete it from the *postorder* and push the left node into *stn* 'cause **it** should be the next check node as the *postorder* is organized as above.\n\nThat's all of it. The algs just build a binary tree. :)\n\nInform me if there's anything vague or wrong, I'm open to any suggestions.\n\n class Solution {\n public:\n TreeNode *buildTree(vector<int> &inorder, vector<int> &postorder) {\n if(inorder.size() == 0)return NULL;\n TreeNode *p;\n TreeNode *root;\n stack<TreeNode *> stn;\n \n root = new TreeNode(postorder.back()); \n stn.push(root); \n postorder.pop_back(); \n \n while(true)\n {\n if(inorder.back() == stn.top()->val) \n {\n p = stn.top();\n stn.pop(); \n inorder.pop_back(); \n if(inorder.size() == 0) break;\n if(stn.size() && inorder.back() == stn.top()->val)\n continue;\n p->left = new TreeNode(postorder.back()); \n postorder.pop_back();\n stn.push(p->left);\n }\n else \n {\n p = new TreeNode(postorder.back());\n postorder.pop_back();\n stn.top()->right = p; \n stn.push(p); \n }\n }\n return root;\n }\n };
| 43 | 3 |
[]
| 7 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
My C++ Solution
|
my-c-solution-by-hellogdut-lgmt
|
class Solution {\n \n public:\n TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {\n \n return helper(inorde
|
hellogdut
|
NORMAL
|
2015-06-23T12:36:01+00:00
|
2015-06-23T12:36:01+00:00
| 9,501 | false |
class Solution {\n \n public:\n TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {\n \n return helper(inorder,0,inorder.size(),postorder,0,postorder.size());\n }\n private:\n TreeNode* helper(vector<int>& inorder,int i,int j,vector<int>& postorder,int ii,int jj)\n {\n // \u6bcf\u6b21\u53d6postorder\u7684\u6700\u540e\u4e00\u4e2a\u503cmid\uff0c\u5c06\u5176\u4f5c\u4e3a\u6811\u7684\u6839\u8282\u70b9\n // \u7136\u540e\u4eceinroder\u4e2d\u627e\u5230mid\uff0c\u5c06\u5176\u5206\u5272\u6210\u4e3a\u4e24\u90e8\u5206\uff0c\u5de6\u8fb9\u4f5c\u4e3amid\u7684\u5de6\u5b50\u6811\uff0c\u53f3\u8fb9\u4f5c\u4e3amid\u7684\u53f3\u5b50\u6811\n // tree: 8 4 10 3 6 9 11\n // Inorder [3 4 6] 8 [9 10 11]\n // postorder [3 6 4] [9 11 10] 8\n \n if(i >= j || ii >= jj)\n return NULL;\n \n int mid = postorder[jj - 1];\n \n auto f = find(inorder.begin() + i,inorder.begin() + j,mid);\n \n int dis = f - inorder.begin() - i;\n \n TreeNode* root = new TreeNode(mid);\n root -> left = helper(inorder,i,i + dis,postorder,ii,ii + dis);\n root -> right = helper(inorder,i + dis + 1,j,postorder,ii + dis,jj - 1);\n \n return root;\n \n }\n };
| 38 | 1 |
[]
| 9 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
Clean Codes🔥🔥|| Full Explanation✅|| Using Stack✅|| C++|| Java|| Python3
|
clean-codes-full-explanation-using-stack-7buz
|
Intuition :\n- Given two integer arrays inorder and postorder ,construct and return the binary tree.\n Describe your first thoughts on how to solve this problem
|
N7_BLACKHAT
|
NORMAL
|
2023-03-16T02:25:15.058053+00:00
|
2023-03-16T02:25:15.058091+00:00
| 10,218 | false |
# Intuition :\n- Given two integer arrays inorder and postorder ,construct and return the binary tree.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach : Iterative Approach using Stack\n- Use the last element in the postorder traversal as the root node, then iterate over the rest of the postorder traversal from right to left. \n- For each element, we create a new node and add it to the stack. We then check if the new node is the left or right child of the previous node. \n- If it\'s the left child, we simply attach it to the previous node. \n- If it\'s the right child, we pop the stack until we find the parent node whose left child is the previous node, and attach the new node to its right child. \n- We repeat this process until we\'ve processed all the nodes in the postorder traversal.\n<!-- Describe your approach to solving the problem. -->\n**Credits to @mayijie88 for helping me out**\n# Let\'s See an Example :\n- Let\'s take the following inorder and postorder traversals as an example:\n```\ninorder = [9,3,15,20,7]\npostorder = [9,15,7,20,3]\n```\n- So we want to use these traversals to build a binary tree. \n# Steps to be followed :\n- Both the inorder and postorder traversals are non-empty, so we can continue.\n\n```\nip = 4 (the index of the last element in the inorder traversal), \npp = 4 (the index of the last element in the postorder traversal).\n```\n- We create an empty `stack` and initialize `prev` to `null`.\n- We create the root node using the last element in the postorder traversal, which is 3. We push the root node onto the stack and decrement pp to 3.\n\n```\nStack:\n| 3 |\n```\n\n- We iterate over the rest of the postorder traversal from right to left. The next element is 20. \n- We create a new node for 20 and push it onto the stack. We check if 20 is the left or right child of the previous node (which is 3). \n- Since it\'s the right child, we pop the stack until we find the parent node whose left child is 3, which is null. \n- We attach 20 as the right child of 3, and push 20 onto the stack. prev is set to null.\n\n```\nStack:\n| 20 |\n| 3 |\n```\n\n- The next element is 7. We create a new node for 7 and push it onto the stack. We check if 7 is the left or right child of the previous node (which is 20). \n- Since it\'s the right child, we pop the stack until we find the parent node whose left child is 20, which is 3. \n- We attach 7 as the right child of 20, and push 7 onto the stack. prev is set to null.\n\n```\nStack:\n| 7 |\n| 20 |\n| 3 |\n```\n\n- The next element is 15. We create a new node for 15 and push it onto the stack. We check if 15 is the left or right child of the previous node (which is 7). \n- Since it\'s the left child, we attach 15 as the left child of 7, and push 15 onto the stack. prev is set to null.\n\n```\nStack:\n| 15 |\n| 7 |\n| 20 |\n| 3 |\n```\n\n- The next element is 9. We create a new node for 9 and push it onto the stack. We check if 9 is the left or right child of the previous node (which is 15). \n- Since it\'s the left child, we attach 9 as the left child of 15, and push 9 onto the stack. prev is set to null.\n\n```\nStack:\n| 9 |\n| 15 |\n| 7 |\n| 20 |\n| 3 |\n```\n\n- We\'ve processed all the elements in the postorder traversal, so we can return the root node of the binary tree, which is 3.\n- The resulting binary tree looks like this:\n```\n 3\n / \\\n 9 20\n / \\\n 15 7\n\n```\n# Complexity :\n- Time complexity : O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity : O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n```\nThanks for visiting my solution.\uD83D\uDE0A\n```\n# Codes [C++ |Java |Python3] : With Comments\n```Java []\nclass Solution \n{\n public TreeNode buildTree(int[] inorder, int[] postorder) {\n // If either of the input arrays are empty, the tree is empty, so return null\n if (inorder.length == 0 || postorder.length == 0) return null;\n \n // Initialize indices to the last elements of the inorder and postorder traversals\n int ip = inorder.length - 1;\n int pp = postorder.length - 1;\n\n // Create an empty stack to help us build the binary tree\n Stack<TreeNode> stack = new Stack<TreeNode>();\n // Initialize prev to null since we haven\'t processed any nodes yet\n TreeNode prev = null;\n // Create the root node using the last element in the postorder traversal\n TreeNode root = new TreeNode(postorder[pp]);\n // Push the root onto the stack and move to the next element in the postorder traversal\n stack.push(root);\n pp--;\n\n // Process the rest of the nodes in the postorder traversal\n while (pp >= 0) {\n // While the stack is not empty and the top of the stack is the current inorder element\n while (!stack.isEmpty() && stack.peek().val == inorder[ip]) {\n // The top of the stack is the parent of the current node, so pop it off the stack and update prev\n prev = stack.pop();\n ip--;\n }\n // Create a new node for the current postorder element\n TreeNode newNode = new TreeNode(postorder[pp]);\n // If prev is not null, the parent of the current node is prev, so attach the node as the left child of prev\n if (prev != null) {\n prev.left = newNode;\n // If prev is null, the parent of the current node is the current top of the stack, so attach the node as the right child of the current top of the stack\n } else if (!stack.isEmpty()) {\n TreeNode currTop = stack.peek();\n currTop.right = newNode;\n }\n // Push the new node onto the stack, reset prev to null, and move to the next element in the postorder traversal\n stack.push(newNode);\n prev = null;\n pp--;\n }\n\n // Return the root of the binary tree\n return root;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {\n // If either of the input vectors are empty, the tree is empty, so return null\n if (inorder.size() == 0 || postorder.size() == 0) return nullptr;\n\n // Initialize indices to the last elements of the inorder and postorder traversals\n int ip = inorder.size() - 1;\n int pp = postorder.size() - 1;\n\n // Create an empty stack to help us build the binary tree\n stack<TreeNode*> st;\n // Initialize prev to null since we haven\'t processed any nodes yet\n TreeNode* prev = nullptr;\n // Create the root node using the last element in the postorder traversal\n TreeNode* root = new TreeNode(postorder[pp]);\n // Push the root onto the stack and move to the next element in the postorder traversal\n st.push(root);\n pp--;\n\n // Process the rest of the nodes in the postorder traversal\n while (pp >= 0) {\n // While the stack is not empty and the top of the stack is the current inorder element\n while (!st.empty() && st.top()->val == inorder[ip]) {\n // The top of the stack is the parent of the current node, so pop it off the stack and update prev\n prev = st.top();\n st.pop();\n ip--;\n }\n // Create a new node for the current postorder element\n TreeNode* newNode = new TreeNode(postorder[pp]);\n // If prev is not null, the parent of the current node is prev, so attach the node as the left child of prev\n if (prev != nullptr) {\n prev->left = newNode;\n // If prev is null, the parent of the current node is the current top of the stack, so attach the node as the right child of the current top of the stack\n } else if (!st.empty()) {\n TreeNode* currTop = st.top();\n currTop->right = newNode;\n }\n // Push the new node onto the stack, reset prev to null, and move to the next element in the postorder traversal\n st.push(newNode);\n prev = nullptr;\n pp--;\n }\n\n // Return the root of the binary tree\n return root;\n }\n};\n```\n```Python []\nclass Solution:\n def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:\n # If either of the input lists are empty, the tree is empty, so return None\n if not inorder or not postorder:\n return None\n\n # Initialize indices to the last elements of the inorder and postorder traversals\n ip = len(inorder) - 1\n pp = len(postorder) - 1\n\n # Create an empty stack to help us build the binary tree\n st = []\n # Initialize prev to None since we haven\'t processed any nodes yet\n prev = None\n # Create the root node using the last element in the postorder traversal\n root = TreeNode(postorder[pp])\n # Push the root onto the stack and move to the next element in the postorder traversal\n st.append(root)\n pp -= 1\n\n # Process the rest of the nodes in the postorder traversal\n while pp >= 0:\n # While the stack is not empty and the top of the stack is the current inorder element\n while st and st[-1].val == inorder[ip]:\n # The top of the stack is the parent of the current node, so pop it off the stack and update prev\n prev = st.pop()\n ip -= 1\n # Create a new node for the current postorder element\n new_node = TreeNode(postorder[pp])\n # If prev is not None, the parent of the current node is prev, so attach the node as the left child of prev\n if prev:\n prev.left = new_node\n # If prev is None, the parent of the current node is the current top of the stack, so attach the node as the right child of the current top of the stack\n elif st:\n curr_top = st[-1]\n curr_top.right = new_node\n # Push the new node onto the stack, reset prev to None, and move to the next element in the postorder traversal\n st.append(new_node)\n prev = None\n pp -= 1\n\n # Return the root of the binary tree\n return root\n```\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\n\n
| 35 | 1 |
['Stack', 'Python', 'C++', 'Java', 'Python3']
| 3 |
construct-binary-tree-from-inorder-and-postorder-traversal
|
Super simple Java solution // beat 100%
|
super-simple-java-solution-beat-100-by-c-re0x
|
\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode(int x)
|
charlie11
|
NORMAL
|
2018-09-02T23:57:16.206541+00:00
|
2021-04-30T02:52:27.425808+00:00
| 4,755 | false |
```\n/**\n * Definition for a binary tree node.\n * public class TreeNode {\n * int val;\n * TreeNode left;\n * TreeNode right;\n * TreeNode(int x) { val = x; }\n * }\n */\nclass Solution {\n \n private int idx;\n \n public TreeNode buildTree(int[] inorder, int[] postorder) {\n if (inorder.length != postorder.length) return null;\n if (inorder.length == 0) return null;\n idx = postorder.length-1;\n TreeNode root = build(inorder, postorder, 0, idx);\n return root;\n }\n \n private TreeNode build(int[] inorder, int[] postorder, int start, int end) {\n if (start>end) return null;\n TreeNode node = new TreeNode(postorder[idx--]);\n if (start==end) return node;\n \n int index = findIdx(inorder, node.val, end);\n node.right = build(inorder, postorder, index+1, end);\n node.left = build(inorder, postorder, start, index-1);\n return node;\n }\n \n private int findIdx(int[] inorder, int val, int end) {\n for (int i=end; i>=0; i--) {\n if (inorder[i]==val) return i;\n }\n return 0;\n }\n}\n// TC: O(N^2)\n// AS: O(N)\n// The worst case falls into the case when tree is a skew tree\n```
| 31 | 0 |
['Tree', 'Java']
| 14 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.