question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
check-if-it-is-a-good-array
|
[Go] GCD
|
go-gcd-by-harotobira-6p5k
|
Runtime: 36 ms, faster than 100.00% of Go online submissions for Check If It Is a Good Array.\nMemory Usage: 8.8 MB, less than 100.00% of Go online submissions
|
harotobira
|
NORMAL
|
2020-11-08T18:13:27.451866+00:00
|
2020-11-08T18:13:27.451899+00:00
| 153 | false |
Runtime: 36 ms, faster than 100.00% of Go online submissions for Check If It Is a Good Array.\nMemory Usage: 8.8 MB, less than 100.00% of Go online submissions for Check If It Is a Good Array.\n\n```\nfunc isGoodArray(nums []int) bool {\n t := nums[0]\n \n for _, num := range nums{\n t = gcd(num, t)\n if t == 1{\n return true\n }\n }\n \n return false\n}\n\nfunc gcd (a,b int) int{\n if a < b{\n return gcd(b,a)\n }\n \n if a % b == 0{\n return b\n }\n \n return gcd(b, a%b)\n}
| 1 | 0 |
['Go']
| 1 |
check-if-it-is-a-good-array
|
C++ just find two co-primes, (Bezout's identity) explained
|
c-just-find-two-co-primes-bezouts-identi-mrrc
|
\n// Bezout\'s identity\n// Let a and b be integers with greatest common divisor d.\n// Then, there exist integers x and y such that ax + by = d.\n// In our cas
|
ishanrai05
|
NORMAL
|
2020-10-15T13:03:51.312626+00:00
|
2020-10-15T13:03:51.312658+00:00
| 244 | false |
```\n// Bezout\'s identity\n// Let a and b be integers with greatest common divisor d.\n// Then, there exist integers x and y such that ax + by = d.\n// In our case, we just have two find two numbers such that they are co-prime, i.e. their gcd=1\nclass Solution {\npublic:\n bool isGoodArray(vector<int>& nums) {\n int n=nums.size();\n int g=nums[0];\n for (int i=1;i<n;i++){\n g=__gcd(g,nums[i]);\n\t\t\t// If there are two co-primes then the entire array is co-prime\n if (g==1) return true;\n }\n return g==1;\n }\n};\n```
| 1 | 0 |
[]
| 1 |
check-if-it-is-a-good-array
|
C solution with gcd, short and easy with brief explanation
|
c-solution-with-gcd-short-and-easy-with-4zxoz
|
If anyone wants mathematical proof just comment below\n\nint gcd(int a, int b)\n{\n if (a == 0) return (b);\n return (gcd(b % a , a));\n}\n\nbool isGoodAr
|
leofu
|
NORMAL
|
2020-09-10T18:36:43.665442+00:00
|
2020-09-10T18:36:43.665498+00:00
| 171 | false |
If anyone wants mathematical proof just comment below\n```\nint gcd(int a, int b)\n{\n if (a == 0) return (b);\n return (gcd(b % a , a));\n}\n\nbool isGoodArray(int* nums, int numsSize)\n{\n if (numsSize == 1) return (nums[0] == 1);\n int flag = gcd(nums[0],nums[1]);\n for(int i = 2 ; i < numsSize ; i++) flag = gcd(flag, nums[i]);\n return (flag == 1);\n}\n//if there exists one integer greater than 1 that can divide all the numbers, return false\n//else return true\n```
| 1 | 1 |
[]
| 1 |
check-if-it-is-a-good-array
|
Python. 3 Lines.
|
python-3-lines-by-nag007-aimj
|
\nclass Solution:\n def isGoodArray(self, x: List[int]) -> bool:\n g=x[0]\n for i in x:g=gcd(i,g)\n return g==1\n
|
nag007
|
NORMAL
|
2020-07-28T17:19:14.608491+00:00
|
2020-07-28T17:22:37.755057+00:00
| 326 | false |
```\nclass Solution:\n def isGoodArray(self, x: List[int]) -> bool:\n g=x[0]\n for i in x:g=gcd(i,g)\n return g==1\n```
| 1 | 2 |
[]
| 1 |
check-if-it-is-a-good-array
|
Very Easy Solution C++ [With Explanation]
|
very-easy-solution-c-with-explanation-by-w3vg
|
Firstly if we have a subset with gcd 1 then we can find the proper multiplicand which will make that subset equal to 1, so we need to check whether there exists
|
peeyushbh1998
|
NORMAL
|
2020-06-02T04:24:48.266090+00:00
|
2020-06-02T04:24:48.266131+00:00
| 366 | false |
Firstly if we have a subset with gcd 1 then we can find the proper multiplicand which will make that subset equal to 1, so we need to check whether there exists a subset with gcd equal to 1 or not... Now if a subset has gcd 1 then if we add an element to it, it\'s gcd remains 1 so that means if a subset has gcd 1 then whole array has also gcd 1, so check the gcd of whole array if it\'s 1 then possible otherwise not possible..\n```\nclass Solution {\npublic:\n int gcd(int a,int b){\n if(b==0) return a;\n return gcd(b,a%b);\n }\n bool isGoodArray(vector<int>& nums) {\n if(!nums.size()) return false;\n if(nums.size()==1) return nums[0]==1;\n int g=nums[0];\n for(int i=1;i<nums.size();i++){\n g=gcd(g,nums[i]);\n }\n return g==1;\n }\n};\n```
| 1 | 0 |
['C', 'C++']
| 0 |
check-if-it-is-a-good-array
|
Javascript and C++ solutions
|
javascript-and-c-solutions-by-claytonjwo-0ll4
|
Thoughts and Intuition:\n\nWhen I first read this problem, I thought there\'s no way I can check every possible combination without TLE. So I started looking f
|
claytonjwong
|
NORMAL
|
2020-04-21T14:12:30.920015+00:00
|
2020-04-21T14:12:30.920071+00:00
| 173 | false |
**Thoughts and Intuition:**\n\nWhen I first read this problem, I thought there\'s no way I can check every possible combination without TLE. So I started looking for a pattern for a potential math solution. I first noticed example 1 results in `true` with prime numbers `5` and `7` as input, and example 3 results in `false` with non-prime numbers `3` and `6` as input. However, example 2 results in `true` with non-prime numbers also. So I thought maybe GCD would work, and indeed it did! After I solved this problem, I read about [Bezout\'s Identity in this post](https://leetcode.com/problems/check-if-it-is-a-good-array/discuss/419324/Bezout\'s-Identity).\n\n---\n\n*Javascript*\n```\nlet isGoodArray = (A, gcd = (a, b) => !b ? a : gcd(b, a % b)) => {\n let x = A.shift();\n A.forEach(y => x = gcd(x, y));\n return x == 1;\n};\n```\n\n---\n\n*C++*\n```\nclass Solution {\npublic:\n using VI = vector<int>;\n bool isGoodArray(VI& A, bool good = false) {\n auto x = A.back(); A.pop_back();\n for_each(A.begin(), A.end(), [&](auto y) { x = gcd(x, y); });\n return x == 1;\n }\nprivate:\n int gcd(int a, int b) { return !b ? a : gcd(b, a % b); }\n};\n```
| 1 | 0 |
[]
| 0 |
check-if-it-is-a-good-array
|
C++ gcd(98%)
|
c-gcd98-by-antimelee-h2rm
|
```\nint gcd(int a, int b)\n { \n int t;\n if(b>a){\n t=a;\n a=b;b=t;\n }\n while (b != 0)\n {\n t = a %
|
antimelee
|
NORMAL
|
2020-03-24T08:24:42.366310+00:00
|
2020-03-24T08:24:42.366361+00:00
| 239 | false |
```\nint gcd(int a, int b)\n { \n int t;\n if(b>a){\n t=a;\n a=b;b=t;\n }\n while (b != 0)\n {\n t = a % b;\n a = b;\n b = t;\n }\n return a;\n }\n bool isGoodArray(vector<int>& nums) {\n if(nums.size()<1)return false;\n int gbs=nums[0];\n for(int i=1;i<nums.size();i++)\n {\n gbs=gcd(gbs,nums[i]);\n }\n if(gbs==1)return true;\n else return false;\n }\n\t\'\'\'
| 1 | 1 |
[]
| 0 |
check-if-it-is-a-good-array
|
Java 100% time and space, with solution explanation.
|
java-100-time-and-space-with-solution-ex-ns2c
|
Let a[] be the array of values and b[] be the array of constants such that\nsigma( a[i]b[i] ) =1 for 0 <= i < n.\n\nThis is equivalent to solving gcd( a[0], a[1
|
okeke
|
NORMAL
|
2020-03-14T14:04:32.170841+00:00
|
2020-03-14T14:04:32.170873+00:00
| 304 | false |
Let a[] be the array of values and b[] be the array of constants such that\nsigma( a[i]*b[i] ) =1 for 0 <= i < n.\n\nThis is equivalent to solving gcd( a[0], a[1] )*Y + sigma( a[i]*b[i]) = 1 for 2 <= i < n for some constant Y.\n\nWe simply reduced the problem from N to N-1. You can apply this recursively to solve the problem.\n\n```\nclass Solution {\n public boolean isGoodArray(int[] a) {\n int ans=a[0];\n for(int t : a){\n if(ans==1) break;\n ans = gcd(ans, t);\n }\n return ans==1 ? true: false;\n }\n \n private int gcd( int a, int b) {\n if( a < b) return gcd(b,a);\n if( b == 0 ) return a;\n return gcd(b,a%b);\n }\n}\n```
| 1 | 0 |
[]
| 1 |
check-if-it-is-a-good-array
|
Scala, Explained by by Chinese remainder theorem additive property
|
scala-explained-by-by-chinese-remainder-yveq4
|
Additive property: if a==f (mod d), b==f (mod d), then it must be true that (xa + yb)==f (mod d)\n\nSo when we think of (xa + yb) mod d, and set the f ==0, then
|
qiuqiushasha
|
NORMAL
|
2020-01-24T15:28:20.959801+00:00
|
2020-01-24T15:28:20.959852+00:00
| 163 | false |
Additive property: if a==f (mod d), b==f (mod d), then it must be true that (x*a + y*b)==f (mod d)\n\nSo when we think of (x*a + y*b) mod d, and set the f ==0, then, there must be k=[1...d-1] ranges, which can map (x*a + y*b)/k to this range. Thus there must be a (x\'*a + y\'*b)==1 always existed. \n\n\n```\n def isGoodArray(nums: Array[Int]): Boolean = {\n var res = nums(0)\n\n def gcd(a: Int, b: Int): Int = {\n if (b == 0) return a\n gcd(b, a % b)\n }\n\n for (i <- 1 to nums.length - 1) res = gcd(res, nums(i))\n res == 1\n }\n```
| 1 | 0 |
[]
| 0 |
check-if-it-is-a-good-array
|
Easy and fast solution with mathematical explaination (beats > 99.7%)
|
easy-and-fast-solution-with-mathematical-ky8x
|
Theorem. A necessary and sufficient condition for that the greatest common divisor (gcd) of n positive integers a_1, a_2, ..., a_n is 1 is that there exist n in
|
jinghuayao
|
NORMAL
|
2019-12-09T05:21:25.166114+00:00
|
2019-12-09T05:23:20.048308+00:00
| 365 | false |
Theorem. A necessary and sufficient condition for that the *greatest common divisor* (gcd) of n positive integers a_1, a_2, ..., a_n is 1 is that there exist n integers b_1, b_2, ..., b_n such that\n* b_1*a_1 + b_2*a_2 + ... + b_n*a_n = 1. (The proof is elementary.)\n\nTherefore, the problem here is equivalent to that if the gcd of the nums in the array is 1 or not. If it is 1, it is a good array; otherwise, not.\n\nMethod 1. Write the functions directly\n```\nclass Solution:\n def isGoodArray(self, nums: List[int]) -> bool:\n if not nums:\n return False\n if len(nums) == 1:\n if nums[0] == 1:\n return True\n else:\n return False\n factor = self.gcd(nums[0], nums[1])\n for num in nums[2:]:\n factor = self.gcd(factor, num)\n if factor == 1:\n return True\n else:\n return False \n \n def gcd(self, m, n):\n if m > n:\n m, n = n, m\n if n % m == 0:\n return m\n else:\n return self.gcd(n%m, m)\n```\nMethod 2. Use the built-in functions\n```\nfrom math import gcd\nfrom functools import reduce\nclass Solution:\n def isGoodArray(self, nums: List[int]) -> bool:\n return reduce(gcd, nums) == 1\n```
| 1 | 1 |
[]
| 0 |
check-if-it-is-a-good-array
|
C# short, GCD
|
c-short-gcd-by-serpol-1ohl
|
Here d is a GCD for first i numbers.\n\n\tpublic bool IsGoodArray(int[] nums) {\n int d = nums[0];\n for(int i = 1; i < nums.Length; i++) {\n
|
serpol
|
NORMAL
|
2019-11-21T06:40:47.156613+00:00
|
2019-11-21T06:42:17.986846+00:00
| 167 | false |
Here d is a GCD for first i numbers.\n```\n\tpublic bool IsGoodArray(int[] nums) {\n int d = nums[0];\n for(int i = 1; i < nums.Length; i++) {\n if(d == 1) break;\n int r = nums[i];\n while((r %= d) > 0) {\n int t = d;\n d = r;\n r = t;\n }\n }\n return d == 1;\n }\n```
| 1 | 1 |
[]
| 0 |
check-if-it-is-a-good-array
|
Java
|
java-by-master_alcy-cuxl
|
\n// O(n)\n// O(1)\nclass Solution {\n public boolean isGoodArray(int[] nums) {\n int n = nums.length;\n if (n == 0 || nums == null) {\n
|
master_alcy
|
NORMAL
|
2019-11-07T05:27:03.442592+00:00
|
2019-11-07T05:27:47.499696+00:00
| 348 | false |
```\n// O(n)\n// O(1)\nclass Solution {\n public boolean isGoodArray(int[] nums) {\n int n = nums.length;\n if (n == 0 || nums == null) {\n return false;\n }\n \n int k = nums[0];\n for (int i = 0; i < nums.length; i++) {\n k = GCD(k, nums[i]);\n if (k == 1) {\n return true;\n }\n }\n return false;\n }\n \n public int GCD(int m, int n) {\n if (m < n) {\n return GCD(n, m);\n }\n \n while (n != 0) {\n int k = m % n;\n m = n;\n n = k; \n }\n return m;\n }\n}\n```
| 1 | 0 |
['Java']
| 0 |
check-if-it-is-a-good-array
|
Python3 one line
|
python3-one-line-by-xuhuiwang-b444
|
Calculate the GCD of all numbers in this array.\n\nfrom math import gcd\nfrom functools import reduce\nclass Solution:\n def isGoodArray(self, nums: List[int
|
xuhuiwang
|
NORMAL
|
2019-11-03T18:46:52.964533+00:00
|
2019-11-03T18:46:52.964598+00:00
| 183 | false |
Calculate the GCD of all numbers in this array.\n```\nfrom math import gcd\nfrom functools import reduce\nclass Solution:\n def isGoodArray(self, nums: List[int]) -> bool:\n return reduce(gcd, nums) == 1\n\t\t\n```
| 1 | 0 |
[]
| 1 |
check-if-it-is-a-good-array
|
Check if GCD is 1
|
check-if-gcd-is-1-by-gagandeepahuja09-ehvt
|
\nclass Solution {\npublic:\n bool isGoodArray(vector<int>& nums) {\n int gcd = nums[0];\n if(gcd == 1)\n return true;\n for(
|
gagandeepahuja09
|
NORMAL
|
2019-11-03T04:02:11.811722+00:00
|
2019-11-03T04:02:11.811771+00:00
| 259 | false |
```\nclass Solution {\npublic:\n bool isGoodArray(vector<int>& nums) {\n int gcd = nums[0];\n if(gcd == 1)\n return true;\n for(int i = 1; i < nums.size(); i++) {\n gcd = __gcd(gcd, nums[i]);\n if(gcd == 1)\n return true;\n }\n return false;\n }\n};\n```
| 1 | 1 |
[]
| 0 |
check-if-it-is-a-good-array
|
easy solution
|
easy-solution-by-ester45764-jukx
|
IntuitionApprocherComplexité
Complexité temporelle :
o(log(min(n)))
Complexité de l’espace :
Code
|
ester45764
|
NORMAL
|
2025-03-23T22:16:45.342677+00:00
|
2025-03-23T22:16:45.342677+00:00
| 10 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->o(log(min(n)))
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def isGoodArray(self, nums: List[int]) -> bool:
if gcd(*nums)==1:
return True
else:
return False
```
| 0 | 0 |
['Array', 'Math', 'Number Theory', 'Python3']
| 0 |
check-if-it-is-a-good-array
|
Python Hard
|
python-hard-by-lucasschnee-nc3m
| null |
lucasschnee
|
NORMAL
|
2025-02-08T23:02:42.772931+00:00
|
2025-02-08T23:02:42.772931+00:00
| 8 | false |
```python3 []
class Solution:
def isGoodArray(self, nums: List[int]) -> bool:
if 1 in nums:
return True
N = len(nums)
x = nums[0]
for y in nums:
x = math.gcd(x, y)
if x == 1:
return True
return False
```
| 0 | 0 |
['Python3']
| 0 |
check-if-it-is-a-good-array
|
1250. Check If It Is a Good Array
|
1250-check-if-it-is-a-good-array-by-g8xd-rzr4
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
G8xd0QPqTy
|
NORMAL
|
2025-01-04T04:20:11.993306+00:00
|
2025-01-04T04:20:11.993306+00:00
| 10 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public boolean isGoodArray(int[] nums) {
int gcd = nums[0];
for (int num : nums) {
gcd = gcd(gcd, num);
if (gcd == 1) return true;
}
return gcd == 1;
}
private int gcd(int a, int b) {
while (b != 0) {
int temp = b;
b = a % b;
a = temp;
}
return a;
}
}
```
| 0 | 0 |
['Java']
| 0 |
check-if-it-is-a-good-array
|
Check If It Is a Good Array Solved (Explanation)- beats 100%(Java,c#,c++,JS,TypeScript,Python)
|
check-if-it-is-a-good-array-solved-expla-b2mz
|
Intuition
The problem requires us to determine if we can generate the number 1 by taking a subset of the numbers in the array and multiplying them by integers.
|
ayanLeet-99
|
NORMAL
|
2024-12-20T19:49:35.123811+00:00
|
2024-12-20T19:49:35.123811+00:00
| 14 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
- The problem requires us to determine if we can generate the number 1 by taking a subset of the numbers in the array and multiplying them by integers.
- This boils down to finding if the greatest common divisor (GCD) of all the numbers in the array is 1, because if the GCD of all the numbers is 1, then we can find integer multiples that sum to 1.
- If the GCD is greater than 1, it's impossible to make 1, because all multiples of any number that shares a GCD greater than 1 will be divisible by that GCD.
# Approach
<!-- Describe your approach to solving the problem. -->
- Initialize the gcd with the first number in the array.
- Traverse the array, updating the gcd with each number using the Euclidean algorithm.
- If at any point, the gcd becomes 1, we can immediately return true since we know it's possible to form 1 from the array.
- If after iterating through all the numbers the GCD is still greater than 1, return false.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
$$O(n * log(max(nums)))$$, where n is the length of the array, and max(nums) is the largest number. The gcd() function takes logarithmic time relative to the smaller of the two numbers.
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
$$O(1)$$, because we're using a constant amount of extra space
# Code
```java []
//Not Recomended
<!-- class Solution {
public boolean isGoodArray(int[] nums) {
int x =nums[0],y;
for(int a: nums){
while( a> 0){
y=x%a;
x=a;
a=y;
}
}
return x ==1;
}
} -->
class Solution {
public boolean isGoodArray(int[] nums) {
int gcd = nums[0];
for (int i = 1; i < nums.length; i++) {
gcd = gcd(gcd, nums[i]);
if (gcd == 1) {
return true; // Early exit if GCD becomes 1
}
}
return gcd == 1;
}
// Helper function to compute GCD of two numbers using Euclidean algorithm
private int gcd(int a, int b) {
while (b != 0) {
int temp = b;
b = a % b;
a = temp;
}
return a;
}
}
```
```C# []
// C# Solution
public class Solution {
public bool IsGoodArray(int[] nums) {
int gcd = nums[0];
for (int i = 1; i < nums.Length; i++) {
gcd = Gcd(gcd, nums[i]);
if (gcd == 1) {
return true; // Early exit if GCD becomes 1
}
}
return gcd == 1;
}
// Helper function to compute GCD of two numbers using Euclidean algorithm
private int Gcd(int a, int b) {
while (b != 0) {
int temp = b;
b = a % b;
a = temp;
}
return a;
}
}
```
```Python []
# Python Solution
from math import gcd
from functools import reduce
def isGoodArray(nums):
gcd_value = nums[0]
for num in nums[1:]:
gcd_value = gcd(gcd_value, num)
if gcd_value == 1:
return True # Early exit if GCD becomes 1
return gcd_value == 1
```
```JS []
// JavaScript Solution
var isGoodArray = function(nums) {
let gcd = nums[0];
for (let i = 1; i < nums.length; i++) {
gcd = getGCD(gcd, nums[i]);
if (gcd === 1) {
return true; // Early exit if GCD becomes 1
}
}
return gcd === 1;
};
// Helper function to compute GCD of two numbers using Euclidean algorithm
function getGCD(a, b) {
while (b !== 0) {
let temp = b;
b = a % b;
a = temp;
}
return a;
}
```
```C++ []
// C++ Solution
class Solution {
public:
bool isGoodArray(vector<int>& nums) {
int gcd_value = nums[0];
for (int i = 1; i < nums.size(); i++) {
gcd_value = gcd(gcd_value, nums[i]);
if (gcd_value == 1) {
return true; // Early exit if GCD becomes 1
}
}
return gcd_value == 1;
}
// Helper function to compute GCD of two numbers using Euclidean algorithm
int gcd(int a, int b) {
while (b != 0) {
int temp = b;
b = a % b;
a = temp;
}
return a;
}
};
```
```TypeScript []
// TypeScript Solution
function isGoodArray(nums: number[]): boolean {
let gcd_value = nums[0];
for (let i = 1; i < nums.length; i++) {
gcd_value = getGCD(gcd_value, nums[i]);
if (gcd_value === 1) {
return true; // Early exit if GCD becomes 1
}
}
return gcd_value === 1;
}
// Helper function to compute GCD of two numbers using Euclidean algorithm
function getGCD(a: number, b: number): number {
while (b !== 0) {
let temp = b;
b = a % b;
a = temp;
}
return a;
}
```
| 0 | 0 |
['Array', 'Python', 'C++', 'Java', 'TypeScript', 'JavaScript', 'C#']
| 0 |
check-if-it-is-a-good-array
|
beats 100%
|
beats-100-by-surya0224-s88b
| null |
surya0224
|
NORMAL
|
2024-12-12T19:40:59.814384+00:00
|
2024-12-12T19:40:59.814384+00:00
| 8 | false |
# Intuition\nWent through the hints and figured out an approach.First thought need **to use subarrays but then realized that the solution using the GCD of the entire array is still valid because the concept of a linear combination of numbers works for any subset of the array. If the GCD of all the elements in the array is 1, then it\'s possible to form 1 from some subset of those numbers, regardless of whether the elements are contiguous or not.**\n\n# Approach\nax+by=1;\ngcd(a,b)=1\n\n# Complexity\n- Time complexity:O(nlogM)\nn is the number of elements in the array nums.\nM is the maximum value in the array nums.\n- Space complexity:\nO(1)\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int gcd(int a,int b){\n if (b>a){\n return gcd(b,a);\n \n }\n if (b==0) return a;\n return gcd(b,a%b);\n \n }\n bool isGoodArray(vector<int>& nums) {\n int gcd_=nums[0];\n for (int i=1;i<=nums.size()-1;i++){\n gcd_=gcd(gcd_,nums[i]);\n if (gcd_==1){\n return true;\n }\n }\n return gcd_==1;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
check-if-it-is-a-good-array
|
Simple C++ Solution Beats 100%
|
simple-c-solution-beats-100-by-dakshg-y4a1
|
Code\ncpp []\nclass Solution {\npublic:\n bool isGoodArray(vector<int>& nums) {\n int a = nums[0];\n for(int i : nums)\n a = gcd(a,
|
dakshg
|
NORMAL
|
2024-12-07T06:51:00.431804+00:00
|
2024-12-07T06:51:00.431836+00:00
| 4 | false |
# Code\n```cpp []\nclass Solution {\npublic:\n bool isGoodArray(vector<int>& nums) {\n int a = nums[0];\n for(int i : nums)\n a = gcd(a, i);\n return a == 1;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
check-if-it-is-a-good-array
|
Super Easy solution C# | Math | GCD | O(N)
|
super-easy-solution-c-math-gcd-on-by-bog-tyik
|
\n# Complexity\n- Time complexity: O(N)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(1)\n Add your space complexity here, e.g. O(n) \n\n
|
bogdanonline444
|
NORMAL
|
2024-12-01T09:54:29.461117+00:00
|
2024-12-01T09:54:29.461159+00:00
| 3 | false |
\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```csharp []\npublic class Solution {\n public bool IsGoodArray(int[] nums) {\n int num = nums[0];\n for(int i = 1; i < nums.Length; i++)\n {\n num = GCD(nums[i], num);\n }\n if(num == 1)\n {\n return true;\n }\n return false;\n }\n public int GCD(int a, int b)\n {\n if(a % b == 0)\n {\n return b;\n }\n return GCD(b, a % b);\n }\n}\n```\n\n
| 0 | 0 |
['Array', 'Math', 'C#']
| 0 |
check-if-it-is-a-good-array
|
simple solution
|
simple-solution-by-bhavitha_reddy78-7vny
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Bhavitha_Reddy78-
|
NORMAL
|
2024-11-09T15:01:46.566389+00:00
|
2024-11-09T15:01:46.566431+00:00
| 1 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n static int gcd(int n,int m){\n if(m==0)\n return n;\n else\n return gcd(m,n%m);\n }\n public boolean isGoodArray(int[] nums) {\n int res=nums[0];\n for(int i=1;i<nums.length;i++)\n res=gcd(res,nums[i]);\n return res==1;\n }\n}\n```
| 0 | 0 |
['Array', 'Math', 'Number Theory', 'Java']
| 0 |
check-if-it-is-a-good-array
|
Swift Solution
|
swift-solution-by-khaledkamal-usbu
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
khaledkamal
|
NORMAL
|
2024-10-14T13:04:28.850492+00:00
|
2024-10-14T13:04:28.850528+00:00
| 2 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```swift []\nclass Solution {\n func isGoodArray(_ nums: [Int]) -> Bool {\n func gcd(_ a: Int, _ b: Int) -> Int {\n return b == 0 ? a : gcd(b, a % b)\n }\n \n var result = nums[0]\n \n for num in nums {\n result = gcd(result, num)\n \n if result == 1 {\n return true\n }\n }\n \n return result == 1\n }\n}\n```
| 0 | 0 |
['Swift']
| 0 |
check-if-it-is-a-good-array
|
python3 1liner
|
python3-1liner-by-0icy-1het
|
\n\n# Code\npython3 []\nclass Solution:\n def isGoodArray(self, nums: List[int]) -> bool:\n return reduce(gcd,nums) == 1\n
|
0icy
|
NORMAL
|
2024-09-25T11:14:52.556306+00:00
|
2024-09-25T11:14:52.556333+00:00
| 9 | false |
\n\n# Code\n```python3 []\nclass Solution:\n def isGoodArray(self, nums: List[int]) -> bool:\n return reduce(gcd,nums) == 1\n```
| 0 | 0 |
['Python3']
| 0 |
check-if-it-is-a-good-array
|
1250. Check If It Is a Good Array.cpp
|
1250-check-if-it-is-a-good-arraycpp-by-2-8ss0
|
Code\n\nclass Solution {\npublic:\n bool isGoodArray(vector<int>& nums) {\n int gd=nums[0];\n for(int i=0;i<nums.size();i++)\n gd=__gcd(
|
202021ganesh
|
NORMAL
|
2024-09-20T09:43:16.341961+00:00
|
2024-09-20T09:43:16.341998+00:00
| 0 | false |
**Code**\n```\nclass Solution {\npublic:\n bool isGoodArray(vector<int>& nums) {\n int gd=nums[0];\n for(int i=0;i<nums.size();i++)\n gd=__gcd(nums[i],gd);\n return (gd==1);\n }\n};\n```
| 0 | 0 |
['C']
| 0 |
check-if-it-is-a-good-array
|
Easiest Solution CPP beats 90% Easy Maths
|
easiest-solution-cpp-beats-90-easy-maths-b9d6
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
kingsenior
|
NORMAL
|
2024-09-16T10:40:34.395805+00:00
|
2024-09-16T10:40:34.395832+00:00
| 1 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n bool isGoodArray(vector<int>& nums) {\n int n=nums.size();\n if(n==1){\n if(nums[0]==1) return true;\n return false;\n }\n int g=nums[0];\n for(int i=1;i<n;i++) g=__gcd(nums[i],g);\n if(g>1) return false;\n return true;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
check-if-it-is-a-good-array
|
check-if-it-is-a-good-array
|
check-if-it-is-a-good-array-by-syed_abdu-aovr
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
syed_abdulbasit
|
NORMAL
|
2024-09-04T15:17:25.568716+00:00
|
2024-09-04T15:17:25.568743+00:00
| 2 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(nlog(max(nums)))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python []\nfrom functools import reduce\n\nclass Solution(object):\n def gcd(self, a, b):\n # Custom GCD function using the Euclidean algorithm\n while b:\n a, b = b, a % b\n return a\n \n def isGoodArray(self, nums):\n """\n :type nums: List[int]\n :rtype: bool\n """\n # Compute the GCD of the entire array using the custom gcd function\n array_gcd = reduce(self.gcd, nums)\n \n # Check if the GCD is 1\n return array_gcd == 1\n\nsol = Solution()\nprint(sol.isGoodArray([12, 5, 7, 23])) \nprint(sol.isGoodArray([29, 6, 10])) \nprint(sol.isGoodArray([3, 6])) \n\n```
| 0 | 0 |
['Python']
| 0 |
check-if-it-is-a-good-array
|
Bezout's Identity Theorem
|
bezouts-identity-theorem-by-laithy_uchih-e8dn
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Laithy_uchiha
|
NORMAL
|
2024-09-02T02:42:28.781346+00:00
|
2024-09-02T02:42:28.781365+00:00
| 2 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n\n int gcd(int a,int b){\n if(b==0) return a;\n else return gcd(b,a%b);\n }\n\n bool isGoodArray(vector<int>& arr) {\n int n=arr.size();\n int ans=0;\n for(int i=0;i<n;i++) ans=gcd(ans,arr[i]);\n return ans==1 ? true : false;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
check-if-it-is-a-good-array
|
Easy Java Solution 🔥 Beats 94 % of Java Users .
|
easy-java-solution-beats-94-of-java-user-zwv9
|
\n# gcd(A,B,C) = GCD( GCD(A,B) , C ) = GCD(A,GCD(B,C))\n\n## If gcd(a,b,c...d) = 1 , According to the Bezout lemma :\n ### Sum( a , b , c , ... , d ) = 1 \n###
|
zzzz9
|
NORMAL
|
2024-08-26T14:41:14.247818+00:00
|
2024-08-26T14:41:14.247849+00:00
| 11 | false |
\n# gcd(A,B,C) = GCD( GCD(A,B) , C ) = GCD(A,GCD(B,C))\n\n## If gcd(a,b,c...d) = 1 , According to the Bezout lemma :\n ### Sum( a , b , c , ... , d ) = 1 \n### That\'s The Response . \n\n\n# Code\n```java []\nclass Solution {\n public int pgcd( int a , int b ){\n while( b!=0 ){\n int temp = a ; \n a = b ; \n b = temp%b ; \n }\n return a ; \n }\n public boolean isGoodArray(int[] nums) {\n int n = nums.length ; \n if( n==1){\n return nums[0] == 1 ; \n }\n int curr = pgcd( nums[0] , nums[1] ) ; \n if( curr == 1 ) return true ; \n for(int i=2 ; i<n ; ++i){\n curr = pgcd( nums[i] , curr ) ; \n if( curr == 1 ) return true ;\n }\n return false ; \n }\n}\n```
| 0 | 0 |
['Array', 'Math', 'Number Theory', 'Java']
| 0 |
check-if-it-is-a-good-array
|
Clean and easiest solution
|
clean-and-easiest-solution-by-vishalshar-k4q7
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\nWe will iterate till we get gcd 1\n\n# Complexity\n- Time complexity:\n A
|
vishalsharmab46
|
NORMAL
|
2024-08-24T08:04:22.859346+00:00
|
2024-08-24T08:04:22.859384+00:00
| 5 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nWe will iterate till we get gcd 1\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n bool isGoodArray(vector<int>& nums) {\n int n = nums.size();\n int GCD = nums[0];\n\n for (int i = 1; i < n; i++) {\n GCD = __gcd(GCD, nums[i]);\n\n if (GCD == 1) {\n return true;\n }\n }\n return GCD == 1;\n }\n};\n```
| 0 | 0 |
['Number Theory', 'C++']
| 0 |
check-if-it-is-a-good-array
|
Check If It Is a Good Array
|
check-if-it-is-a-good-array-by-shaludroi-l74a
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Shaludroid
|
NORMAL
|
2024-08-19T20:08:54.085930+00:00
|
2024-08-19T20:08:54.085955+00:00
| 4 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public boolean isGoodArray(int[] nums) {\n int gcd = nums[0]; // Start with the first element\n for (int i = 1; i < nums.length; i++) {\n gcd = gcd(gcd, nums[i]); // Compute GCD of the current GCD and the next element\n if (gcd == 1) {\n return true; // If at any point GCD becomes 1, return true\n }\n }\n return gcd == 1; // Final check, return true if GCD is 1\n }\n\n // Helper function to compute GCD of two numbers using Euclidean algorithm\n private int gcd(int a, int b) {\n while (b != 0) {\n int temp = b;\n b = a % b;\n a = temp;\n }\n return a;\n }\n\n public static void main(String[] args) {\n Solution solution = new Solution();\n System.out.println(solution.isGoodArray(new int[]{12, 5, 7, 23})); // Output: true\n System.out.println(solution.isGoodArray(new int[]{29, 6, 10})); // Output: true\n System.out.println(solution.isGoodArray(new int[]{3, 6, 9})); // Output: false\n }\n}\n\n```
| 0 | 0 |
['Java']
| 0 |
check-if-it-is-a-good-array
|
Euclid's algorithm to find common factor, with proof
|
euclids-algorithm-to-find-common-factor-pvbir
|
TLDR - The array is good if and only if the array\'s elements do not share a common factor. Use Eulcid\'s algorithm iteratively to find if there is a common fac
|
louisjaeckle1
|
NORMAL
|
2024-08-15T18:53:56.045460+00:00
|
2024-09-17T02:41:22.330048+00:00
| 7 | false |
TLDR - The array is good if and only if the array\'s elements do not share a common factor. Use Eulcid\'s algorithm iteratively to find if there is a common factor or not.\n\n# Intuition\nThe first approach I thought about was bad.\n\nThe second approach followed from the realization that if all the numbers shared a common factor, the array would not be "good" since any combination of them would also share that factor. I then realized that if there was no common factor to all the elements, then the array must be good (a mathematical proof follows the code below). Thus the question "is the array good?" reduces to "is there no factor common to all the elements?"\n\n# Approach\nWe need to find if there is a common factor to all the elements. A variable `factor` keeps track of the largest factor common to all the elements up to the current point in iteration. `factor` is initialized to nums[0], then as we iterate through the array, we update it to be the greatest common factor between the old `factor` and the current array element using Euclid\'s algorithm. If at any point `factor` is 1, then there is no common factor between the previously inspected elements; Thus the array is good and we return `true`. Otherwise, there is a common factor, the array is not good, and we return `false`.\n\n# Complexity\n- Time complexity: $O(nlogm)$\n\nEuclid\'s algorithm is logarithmic in the size of the elements. Since this algorithm has to be run for every array element (in the worst case), the overall complexity is $O(nlogm)$, where $n$ and $m$ are the size and maximum of `nums`, respectively\n\n- Space complexity: $O(1)$\n\nOnly one variable is used.\n\n# Code\n```\nclass Solution {\npublic:\n bool isGoodArray(vector<int>& nums) {\n int factor = nums[0];\n for(int num:nums){\n factor = euclid_gcd(factor,num);\n if(factor==1){\n return true;\n }\n }\n return false;\n }\n\n int euclid_gcd(int a, int b){\n if(b<a){\n int temp = a;\n a=b;\n b=temp;\n }\n if(b%a==0){\n return a;\n }\n return euclid_gcd(b%a,a);\n }\n};\n```\n# Proof\nSuppose there is a prime factor, $p$, common to all elements. Then any integer combination of these elements, $a\\cdot nums[0]+b\\cdot nums[1]+...$ will be divisible by $p$. Since one is not divisible by $p$, this means that this sum will never equal one, thus in this case the array is not "good". \n\nOn the other hand, suppose no such prime factor exists. First, a lemma:\n\nLemma: For any positive coprime integers $x$ and $y$, there are integers $j$ and $k$ such that $jx-ky=1$.\nProof: Let $x$ and $y$ be positive coprime integers, i.e. integers which share no common factors. Consider the sequence $x\\%y,2x\\%y,...(y-1)x\\%y$. Each member of this sequence can take on integer values from 1 to y-1. \nSuppose two members $ax\\%y$ and $bx\\%y$ are equal, with $0<b<a<y$. Then there exist integers $c$ and $d$ such that $ax-cy=bx-dy$, with $(a-b)x = (c-d)y$. But $a-b<y$, thus the least common multiple of $x$ and $y$ is less than $x\\cdot y$. But $x$ and $y$ are coprime, so their least common multiple is $x\\cdot y$. This is a contradiction. Thus all member of the sequence are unique.\nSince all $y-1$ members of the sequence are unique, and there are $y-1$ possible values for them to take, every value from $1$ to $y=1$ appears in the sequence. Thus there exists some integer $j$ such that $jx\\%y=1$. Therefore there is some integer $k$ such that $jx-ky=1$.\n\nNow, suppose there is no prime factor common to all the elements. If there is only one element, then that element must be one (otherwise any factor of that element would be common to "all the elements"), and then the array is good under the combination $1*1=1$. Otherwise, there is more than one element. Let $a=nums[0]$. Consider the subset $nums[1],nums[2], . . . nums[n-1]$, where $n$ is the size of nums. Call the greatest common factor of this subset $b$. If $b$ shares a prime factor with $a$, then that factor is shared between all of the elements of the subset and $a$, and is therefore common to all of the elements - contradicting the assumption. Therefore, $a$ and $b$ are coprime. $b$ can be built as an integer combination of the elements of the subset, via the following method- start with $c = nums[1]$. For each of the elements of the subset $nums[2], nums[3]. . . nums[n-1]$, set $d = nums[i]$. Now, at the beginning of the each step, $c$ and $d$ should be positive integer combinations of the subsets. (This is the case for the first step- the inductive case will be proven below). Iteratively update $c$ and $d$ according to the steps of Euclid\'s algorithm, i.e. subtract the smaller number from the larger until one of them is 0. Since this alorithm involves iteratively taking differences of integer combinations of the subset, the resulting $c$ and $d$ are integer combinations of the subset, and the larger is greatest common factor to the original numbers. Set $c$ to the larger of these numbers. Since $c$ is the greatest common factor to $gcf(nums[1]. . . nums[i-1])$ and $nums[i]$, it is the greatest common factor to $nums[1]...nums[i]$. Once the process is complete, $c=gcf(nums[1]. ..nums[n-1])=b$, and $c$ is an integer combination of this subset. Therefore $b$ is an integer combination of the subset. By the above lemma and the fact that $a$ and $b$ are coprime, there is an integer combination of $a$ and $b$ which is equal to one. This combination of $a$ and $b$ is an integer combination of $nums[0]$ and an integer combination of $nums[1]...nums[n-1]$, and therefore and integer combination of $nums[0]...nums[n-1]$. Therefore, there is an integer combination of $nums$ which is equal to one, and therefore the array is good.\n\nThus, the array is good if and only if there is no prime factor common to all elements.
| 0 | 0 |
['C++']
| 0 |
check-if-it-is-a-good-array
|
Good Array
|
good-array-by-sanjaym-3rsm
|
Here\u2019s a concise version for the problem:\n\n### Intuition\nTo determine if a list of integers nums has a GCD of 1, we need to check if all numbers in the
|
SanjayM_
|
NORMAL
|
2024-08-15T15:21:44.116032+00:00
|
2024-08-15T15:21:44.116105+00:00
| 20 | false |
Here\u2019s a concise version for the problem:\n\n### Intuition\nTo determine if a list of integers `nums` has a GCD of 1, we need to check if all numbers in the list are coprime. This means their only common divisor is 1.\n\n### Approach\nUse the `reduce` function with `gcd` to compute the GCD of all numbers in the list. Check if the final GCD equals 1.\n\n### Complexity\n- **Time complexity:** \\(O(n \\log(\\text{max}(nums)))\\), where \\(n\\) is the number of elements in `nums`.\n- **Space complexity:** \\(O(1)\\).\n\n### Code\n```python\nfrom functools import reduce\nfrom math import gcd\nfrom typing import List\n\nclass Solution:\n def isGoodArray(self, nums: List[int]) -> bool:\n return reduce(gcd, nums) == 1\n```\n\nThis code efficiently determines if the numbers in `nums` are pairwise coprime.
| 0 | 0 |
['Python3']
| 0 |
check-if-it-is-a-good-array
|
C Code
|
c-code-by-saras-5epa
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
saras_
|
NORMAL
|
2024-07-28T10:02:29.535511+00:00
|
2024-07-28T10:02:29.535543+00:00
| 3 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nint gcd(int a, int b)\n{\n while(b != 0)\n {\n int temp = b;\n b = a % b;\n a = temp;\n }\n return a;\n}\nbool isGoodArray(int* nums, int numsSize) {\n int result = nums[0];\n for(int i = 0;i<numsSize;i++)\n {\n result = gcd(result, nums[i]);\n }\n if(result == 1)\n {\n return true;\n }\n return false;\n}\n```
| 0 | 0 |
['C']
| 0 |
check-if-it-is-a-good-array
|
Check If an Array Can Produce Sum of 1 Using Linear Combinations
|
check-if-an-array-can-produce-sum-of-1-u-5w2x
|
Intuition\nThe problem requires checking if you can create a sum of 1 using any subset of given integers, each of which can be multiplied by any integer. The co
|
codewithsom
|
NORMAL
|
2024-07-24T04:23:24.656849+00:00
|
2024-07-24T04:23:24.656880+00:00
| 8 | false |
# Intuition\nThe problem requires checking if you can create a sum of `1` using any subset of given integers, each of which can be multiplied by any integer. The core idea relies on number theory. Specifically, if you can express `1` as a combination of the numbers in the array, then their greatest common divisor (GCD) must be `1`. This is because the GCD of a set of numbers is the smallest positive integer that can be expressed as a linear combination of those numbers. Therefore, if the GCD is `1`, it means that `1` can be expressed using some combination of those numbers.\n# Approach\n1. Compute the GCD:\n\n- Calculate the GCD of all numbers in the array. This can be done iteratively using the `std::gcd` function from the C++ Standard Library.\n- If at any point during the GCD calculation, the GCD becomes `1`, we can immediately conclude that the array is good because `1` can be expressed as a linear combination of these numbers.\n\n2. Early Exit:\n\n- As soon as the GCD becomes `1`, we can exit early, optimizing the solution by avoiding further unnecessary calculations.\n\n3. Final Check:\n\n- If the final GCD after processing all elements is `1`, then return `true`. Otherwise, return `false`.\n# Complexity\n- Time complexity: `O(n)`\n - The time complexity is `O(n)` because we traverse the array once and compute the GCD in each iteration. The `std::gcd` function operates in logarithmic time relative to the values involved, making the overall complexity linear with respect to the number of elements.\n- Space complexity: `O(1)`\nThe space complexity is `O(1)` because we use only a few extra variables for storing the GCD value and iterating through the array.\n# Code\n```\n#include <vector>\n#include <algorithm> // for std::gcd\n\nclass Solution {\npublic:\n bool isGoodArray(std::vector<int>& nums) {\n int gcd_value = nums[0];\n \n // Compute the GCD of the entire array\n for (int num : nums) {\n gcd_value = std::gcd(gcd_value, num);\n if (gcd_value == 1) {\n return true; // Early exit if GCD becomes 1\n }\n }\n \n // Final check if GCD is 1\n return gcd_value == 1;\n }\n};\n\n```
| 0 | 0 |
['Array', 'Math', 'Number Theory', 'C++']
| 0 |
check-if-it-is-a-good-array
|
java best solution
|
java-best-solution-by-anoopchaudhary1-8y4s
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Anoopchaudhary1
|
NORMAL
|
2024-07-11T07:43:31.889307+00:00
|
2024-07-11T07:43:31.889326+00:00
| 4 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public boolean isGoodArray(int[] nums) {\n int g = nums[0];\n for(int i =1 ; i< nums.length ;i++){\n g = gcd(g ,nums[i]);\n if(g==1) break;\n }\n if(g==1) return true;\n return false;\n }\n\n public static int gcd(int a, int b) {\n while(a > 0 && b > 0) {\n if(a > b) {\n a = a % b;\n }\n else {\n b = b % a;\n }\n }\n if(a == 0) {\n return b;\n }\n return a;\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
check-if-it-is-a-good-array
|
[Python3] just wanna pass(Runtime 98.60, Memory 36.28%)
|
python3-just-wanna-passruntime-9860-memo-lmqz
|
\n\n\n# Code\n\nimport math\nfrom functools import reduce\nclass Solution:\n def isGoodArray(self, nums: List[int]) -> bool:\n # Compute the GCD of th
|
stefanj
|
NORMAL
|
2024-07-10T17:03:06.521201+00:00
|
2024-07-10T17:03:06.521237+00:00
| 17 | false |
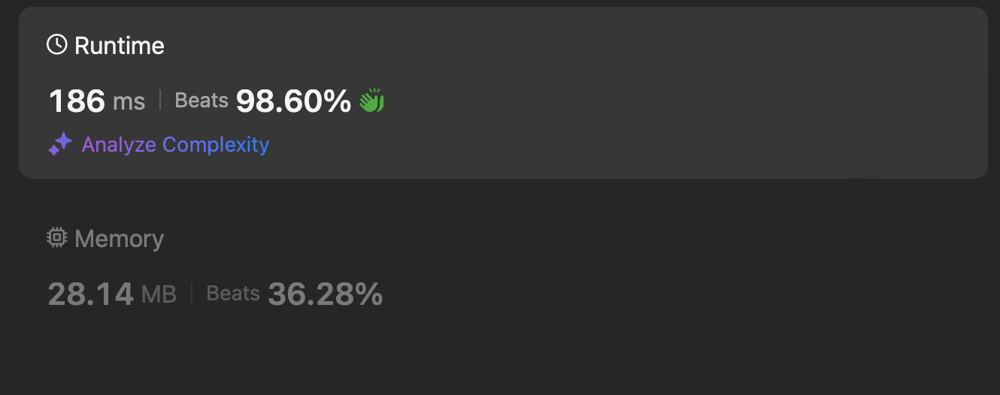\n\n\n# Code\n```\nimport math\nfrom functools import reduce\nclass Solution:\n def isGoodArray(self, nums: List[int]) -> bool:\n # Compute the GCD of the entire array\n # gcd_all=math.gcd(*nums)\n # If the GCD of the entire array is 1, the array is good\n return math.gcd(*nums) == 1\n \n```
| 0 | 0 |
['Python3']
| 0 |
check-if-it-is-a-good-array
|
C++ Solution | GCD
|
c-solution-gcd-by-mhasan01-g31a
|
Just check whether the GCD of all the numbers is equal to $1$, if so then we can prove that there is always a way that makes the array good according to Diophan
|
mhasan01
|
NORMAL
|
2024-07-02T19:43:44.380061+00:00
|
2024-07-02T19:43:44.380097+00:00
| 3 | false |
Just check whether the GCD of all the numbers is equal to $1$, if so then we can prove that there is always a way that makes the array good according to [Diophantine Equation](https://en.wikipedia.org/wiki/Diophantine_equation)\n\n# Code\n```\nclass Solution {\npublic:\n bool isGoodArray(vector<int>& a) {\n int g = 0;\n for (int x : a) {\n g = __gcd(g, x);\n }\n return g == 1;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
check-if-it-is-a-good-array
|
Brute Force Approach || C++ ||
|
brute-force-approach-c-by-akshitkansal01-eh35
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
AkshitKansal01
|
NORMAL
|
2024-06-26T19:15:28.492105+00:00
|
2024-06-26T19:15:28.492136+00:00
| 11 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n\nint gcd(int a, int b) {\n while (b != 0) {\n int temp = b;\n b = a % b;\n a = temp;\n }\n return a;\n}\n\n// Function to calculate GCD of an array of elements\nint findGCD(vector<int>& nums) {\n int result = nums[0];\n for (int i = 1; i < nums.size(); i++) {\n result = gcd(result, nums[i]);\n // If at any point the GCD becomes 1, we can stop early\n if (result == 1) {\n break;\n }\n }\n return result;\n}\n\npublic:\n bool isGoodArray(vector<int>& nums) {\n //vector<int> subset = subsets(nums);\n return findGCD(nums)==1;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
check-if-it-is-a-good-array
|
Good Array
|
good-array-by-tehreemfatima-j34x
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
tehreemfatima
|
NORMAL
|
2024-06-26T14:35:20.426808+00:00
|
2024-06-26T14:35:20.426834+00:00
| 1 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public boolean isGoodArray(int[] nums) {\n int temp = nums[0];\n \n for(int i=0;i<nums.length;i++){\n temp = func(temp, nums[i]);\n if(temp == 1){\n return true;\n }\n }\n return false;\n }\n\n int func(int x, int y){\n if(y == 0){\n return x; \n }\n else{\n return func(y, (x%y));\n }\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
check-if-it-is-a-good-array
|
easy solution
|
easy-solution-by-dhruvmohanty15-yt3w
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
dhruvmohanty15
|
NORMAL
|
2024-06-26T03:51:09.890205+00:00
|
2024-06-26T03:51:09.890245+00:00
| 7 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public boolean isGoodArray(int[] nums) {\n int x = nums[0],y;\n for(int a: nums){\n while(a>0){\n y=x%a;\n x=a;\n a=y;\n }\n }\n return x == 1; \n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
random-pick-with-blacklist
|
Java O(B) / O(1), HashMap
|
java-ob-o1-hashmap-by-cafebaby-o51o
|
Suppose N=10, blacklist=[3, 5, 8, 9], re-map 3 and 5 to 7 and 6.\n\n\n\nclass Solution {\n \n // N: [0, N)\n // B: blacklist\n // B1: < N\n // B2
|
cafebaby
|
NORMAL
|
2018-07-03T22:49:51.012088+00:00
|
2018-10-25T03:15:54.697622+00:00
| 17,050 | false |
Suppose N=10, blacklist=[3, 5, 8, 9], re-map 3 and 5 to 7 and 6.\n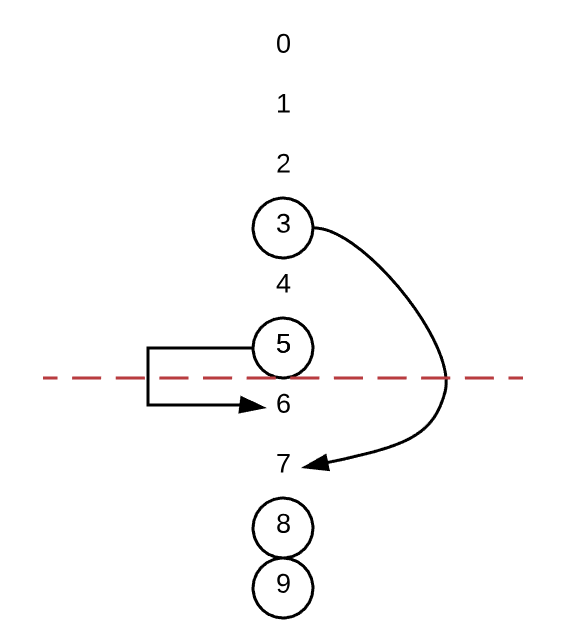\n\n```\nclass Solution {\n \n // N: [0, N)\n // B: blacklist\n // B1: < N\n // B2: >= N\n // M: N - B1\n int M;\n Random r;\n Map<Integer, Integer> map;\n\n public Solution(int N, int[] blacklist) {\n map = new HashMap();\n for (int b : blacklist) // O(B)\n map.put(b, -1);\n M = N - map.size();\n \n for (int b : blacklist) { // O(B)\n if (b < M) { // re-mapping\n while (map.containsKey(N - 1))\n N--;\n map.put(b, N - 1);\n N--;\n }\n }\n \n r = new Random();\n }\n \n public int pick() {\n int p = r.nextInt(M);\n if (map.containsKey(p))\n return map.get(p);\n return p;\n }\n}\n```\n
| 370 | 3 |
[]
| 37 |
random-pick-with-blacklist
|
Super Simple Python AC w/ Remapping
|
super-simple-python-ac-w-remapping-by-au-8orw
|
Treat the first N - |B| numbers as those we can pick from. Iterate through the blacklisted numbers and map each of them to to one of the remaining non-blacklist
|
ele0999
|
NORMAL
|
2018-07-07T16:58:13.484534+00:00
|
2018-08-27T13:49:01.820912+00:00
| 7,027 | false |
Treat the first N - |B| numbers as those we can pick from. Iterate through the blacklisted numbers and map each of them to to one of the remaining non-blacklisted |B| numbers\n\nFor picking, just pick a random uniform int in 0, N - |B|. If its not blacklisted, return the number. If it is, return the number that its mapped to\n```\nimport random\n\nclass Solution:\n def __init__(self, N, blacklist):\n blacklist = sorted(blacklist)\n self.b = set(blacklist)\n self.m = {}\n self.length = N - len(blacklist)\n j = 0\n for i in range(self.length, N):\n if i not in self.b:\n self.m[blacklist[j]] = i\n j += 1\n\n def pick(self):\n i = random.randint(0, self.length - 1)\n return self.m[i] if i in self.m else i\n```
| 75 | 2 |
[]
| 15 |
random-pick-with-blacklist
|
[C++] DO NOT use rand() after C++11 !
|
c-do-not-use-rand-after-c11-by-zhoubowei-v5ly
|
It is not recommand to use rand() when N is large.\nhttps://en.cppreference.com/w/cpp/numeric/random/uniform_int_distribution\n\nOther solutions which use rand(
|
zhoubowei
|
NORMAL
|
2018-07-07T05:57:57.767498+00:00
|
2018-10-21T13:46:56.127927+00:00
| 6,769 | false |
It is not recommand to use `rand()` when N is large.\nhttps://en.cppreference.com/w/cpp/numeric/random/uniform_int_distribution\n\nOther solutions which use `rand()/M` are wrong. \n`rand()` generates random numbers in [0, RAND_MAX], where `RAND_MAX` depends on the complier.\nUsually, `RAND_MAX` is 32767 (in leetcode it is 2147483647), which could not generate numbers larger than it. In this problem, `N` could be 1000000000, so we cannot directly use `rand()/M` here.\n\nAnother problem is, even if N is less than 10000, it is also not accurate to use `rand()/M`.\nFor example, use `rand()/10000` to generate numbers in [0,9999]. It is more likely to generate a number in [0, 2767] than in [2868, 9999]:\n```\n[0,2767] % 10000->[0,2767]\n[2768,9999] % 10000->[2768,9999]\n[10000,12767] % 10000->[0,2767]\n[12768,19999] % 10000->[2768,9999]\n[20000,22767] % 10000->[0,2767]\n[22768,29999] % 10000->[2768,9999]\n[30000,32767] % 10000->[0,2767]\n```\n\nHere is my code, O(b log b) construction and O(log b) pick. (not the fastest, see other solutions)\n\n```\nclass Solution {\npublic:\n vector<int> v;\n std::mt19937 gen;\n std::uniform_int_distribution<> dis;\n Solution(int N, vector<int> blacklist) {\n v = blacklist;\n sort(v.begin(), v.end());\n v.push_back(N);\n for (int i = 0; i < v.size(); i++) v[i] -= i;\n \n std::random_device rd; //Will be used to obtain a seed for the random number engine\n gen = std::mt19937(rd()); //Standard mersenne_twister_engine seeded with rd()\n dis = std::uniform_int_distribution<>(0, N - v.size());\n }\n \n int pick() {\n int rnd = dis(gen);\n auto it = upper_bound(v.begin(), v.end(), rnd) - 1;\n int idx = it - v.begin();\n return idx + rnd + 1;\n }\n};\n\n/**\n * Your Solution object will be instantiated and called as such:\n * Solution obj = new Solution(N, blacklist);\n * int param_1 = obj.pick();\n */\n```
| 48 | 2 |
[]
| 8 |
random-pick-with-blacklist
|
[Python3] hash solution using dict (92.28%)
|
python3-hash-solution-using-dict-9228-by-dwzd
|
Hash map blacklisted value in [0, N-len(blacklist)) to whitelisted value in [N-len(blacklist), N), and then randomly pick number in [0, N-len(blacklist)). \n\nf
|
ye15
|
NORMAL
|
2019-12-02T04:56:25.834359+00:00
|
2019-12-02T04:56:25.834407+00:00
| 4,249 | false |
Hash map blacklisted value in `[0, N-len(blacklist))` to whitelisted value in `[N-len(blacklist), N)`, and then randomly pick number in `[0, N-len(blacklist))`. \n```\nfrom random import randint\n\nclass Solution:\n\n def __init__(self, N: int, blacklist: List[int]):\n blacklist = set(blacklist) #to avoid TLE\n self.N = N - len(blacklist) #to be used in pick()\n key = [x for x in blacklist if x < N-len(blacklist)]\n val = [x for x in range(N-len(blacklist), N) if x not in blacklist]\n self.mapping = dict(zip(key, val))\n\n def pick(self) -> int:\n i = randint(0, self.N-1)\n return self.mapping.get(i, i)\n```\n
| 36 | 1 |
['Python3']
| 6 |
random-pick-with-blacklist
|
Java Binary Search Solution O(BlogB) for constructor and O(logB) for pick()
|
java-binary-search-solution-oblogb-for-c-i79o
|
Constructor: Sort the blacklist then build the intervals list. e.g. N = 10, blacklist = [3, 8, 7, 6], we will have intervals: [0, 2], [4, 5], [9, 9]. Because of
|
wangzi6147
|
NORMAL
|
2018-07-03T07:44:36.175300+00:00
|
2018-08-25T04:58:38.862986+00:00
| 4,764 | false |
`Constructor`: Sort the blacklist then build the intervals list. e.g. `N = 10`, `blacklist = [3, 8, 7, 6]`, we will have intervals: `[0, 2], [4, 5], [9, 9]`. Because of the sorting, time complexity is `O(BlogB)`, where `B` is the length of blacklist.\n\n`pick()`: Use one time `random.nextInt(l)` to get the `index` of the number, where `l = N - B`. Then use binary search to search for the interval which contains the `indexth` number. The process will take `O(logB)` time.\n\nSpace complexity: `O(B)` for the interval list.\n\nUse one time `random.nextInt()` for each `pick()`.\n\n```\nclass Solution {\n \n class Interval {\n int low;\n int high;\n int preCount;\n Interval(int low, int high, int preCount) {\n this.low = low;\n this.high = high;\n this.preCount = preCount;\n }\n }\n \n private List<Interval> intervals;\n private Random r;\n private int l;\n\n public Solution(int N, int[] blacklist) {\n Arrays.sort(blacklist);\n intervals = new ArrayList<>();\n r = new Random();\n l = N - blacklist.length;\n int pre = 0, count = 0;\n for (int b : blacklist) {\n if (pre != b) {\n intervals.add(new Interval(pre, b - 1, count));\n count += b - pre;\n }\n pre = b + 1;\n }\n intervals.add(new Interval(pre, N - 1, count));\n }\n \n public int pick() {\n int index = r.nextInt(l);\n int low = 0, high = intervals.size() - 1;\n while (low <= high) {\n int mid = low + (high - low) / 2;\n Interval cur = intervals.get(mid);\n if (cur.preCount <= index && index < cur.preCount + cur.high - cur.low + 1) {\n return cur.low + index - cur.preCount;\n } else if (cur.preCount > index) {\n high = mid - 1;\n } else {\n low = mid + 1;\n }\n }\n return -1;\n }\n}\n```
| 25 | 0 |
[]
| 8 |
random-pick-with-blacklist
|
✅ C++ | Simple Solution
|
c-simple-solution-by-bahubaii-46od
|
\n// idea is to map blacklist numbers with non blacklist numbers\n// now i will generate a random number if that number is in the \n// blacklist i will return a
|
BahubaIi
|
NORMAL
|
2022-03-05T01:54:00.620632+00:00
|
2022-07-13T16:31:26.790748+00:00
| 1,535 | false |
```\n// idea is to map blacklist numbers with non blacklist numbers\n// now i will generate a random number if that number is in the \n// blacklist i will return a number mapped to this number \n// that is not in our blacklist \n// ex :- n = 7 , blacklist = {2,3,5}\n// 2 -> 4\n// 3 -> 6\n\n//5 -> 7 this case will never happen because i am limiting\n// the random generated values from 0 - 4 ( n - number of blacklisted)\n\n// now i will pick random numbers from 0 , 4 if\n// that random number is in blacklist i will return the \n// mapped value to that blackedlisted number and the \n// mapped value is not in blacklist \n\n\n\nunordered_map<int,int> mp;\n int valid_nums=0;\n Solution(int n, vector<int>& blacklist) {\n \n set<int> st;\n \n for(auto &x : blacklist) st.insert(x);\n\t\t\n valid_nums = n-st.size();\n int idx = valid_nums; \n \n for(auto &x:st)\n {\n if(x<valid_nums)\n {\n while(st.count(idx)) idx++; \n\t\t\t\tmp[x] = idx++;\n } \n } \n }\n \n int pick() {\n int ans = rand()%valid_nums;\n \n if(mp.count(ans))\n return mp[ans];\n \n return ans;\n \n }\n```
| 16 | 0 |
['C']
| 2 |
random-pick-with-blacklist
|
Simple Java solution with Binary Search
|
simple-java-solution-with-binary-search-c21ei
|
We need to first sort B. Let L denote its length.\nLet M = N-L. We will generate numbers from the interval [0, M). Possible cases for a random value r are as fo
|
ramazan_yilmaz
|
NORMAL
|
2018-07-07T17:38:08.530040+00:00
|
2018-09-14T11:46:30.264597+00:00
| 2,983 | false |
We need to first sort `B`. Let `L` denote its length.\nLet `M = N-L`. We will generate numbers from the interval `[0, M)`. Possible cases for a random value `r` are as follows;\n* If it is in `[0,B[0])`, we can return `r` as it is.\n* If it is in `[B[0], B[1]-1)`, we can return `r+1`.\n* If it is in `[B[1]-1, B[2]-2)`, we can return `r+2`.\n* ...\n* If it is in `[B[i]-i, B[i+1]-(i+1))`, we can return `r+i+1`. Note that `B[i] < r+i+1 < B[i+1]`, so it is safe.\n* ...\n* If it is in `[B[L-1]-(L-1), M)`, we can return `r+L`. Note that `B[L-1] < r+L < N`, so it is safe.\n\nSo we will make a binary search on the interval boundaries (i.e. `B[i]-(i+1)`) and apply an offset according the the interval that the random number falls into.\n\n```\nclass Solution {\n\n int[] b;\n int M;\n \n public Solution(int N, int[] blacklist) {\n b = blacklist;\n this.M = N - b.length;\n \n Arrays.sort(b);\n for (int i = 0; i < b.length; i++) {\n b[i] -= (i+1);\n }\n }\n \n public int pick() {\n int r = (int) Math.floor(Math.random()*M);\n int index = Arrays.binarySearch(b, r);\n if (index < 0) {\n return r - (index+1);\n } else {\n // here is a bit tricky. we need to select the first boundary that \n // matches, because the intervals degenerate if B[i+1]=B[i]+1.\n while (index > 0 && b[index-1] == r)\n index--;\n return r + index;\n }\n }\n}\n```
| 16 | 0 |
[]
| 3 |
random-pick-with-blacklist
|
python | solution faster than 97.79% using hashmap with detailed explanation
|
python-solution-faster-than-9779-using-h-d638
|
Imagine we had a list generated by list(range(n-1)), and consider numbers in blacklist as "black numbers" and the rest as "white numbers". We are required to ra
|
KiraCodingBot
|
NORMAL
|
2022-06-08T22:50:27.896655+00:00
|
2022-06-08T22:50:27.896686+00:00
| 1,129 | false |
Imagine we had a list generated by `list(range(n-1))`, and consider numbers in blacklist as "black numbers" and the rest as "white numbers". We are required to randomly pick white numbers with equal probability and minimum built-in random operation.\nThe idea is to partition the list into 2 parts: interval [0,`n-len(blacklist)` ) is "white part" and the rest [`n-len(blacklist)`, n-1] is "black part". We swap the black numbers in white part with white numbers in black part one by one, and mark those white numbers coming from black part in a hashmap in the form of `black number being swapped : white number`, because the black number swapped with the white number is exactly the index of the white number in white part. In this way, after iterating through the blacklist and having all the numbers adjusted, in `pick()` we can simply randomize a number from 0 to `n-len(blacklist)` as an index and return the white number at that index.\nI hope words like "white number", "black number", "white part", "black part" in my explanation might not sound too confusing to you, since it is the most straightforward way I find so far to see into this question :)\n```\nclass Solution:\n\n def __init__(self, n: int, blacklist: List[int]):\n self.hashmap={}\n for b in blacklist:\n self.hashmap[b]=-1\n self.length=n-len(blacklist)\n flag=n-1\n for b in blacklist:\n if b<self.length: \n while flag in self.hashmap:\n flag-=1\n self.hashmap[b]=flag\n flag-=1\n \n def pick(self) -> int:\n seed=random.randrange(self.length)\n return self.hashmap.get(seed,seed)
| 13 | 0 |
['Python']
| 2 |
random-pick-with-blacklist
|
Python
|
python-by-satwik95-1v4p
|
Split [0,N) into [0,N-len(blacklist)) and [N-len(blacklist), N). The number of black items in left half == no. of whitelist items on right half. Hence just map
|
satwik95
|
NORMAL
|
2021-02-09T02:32:06.127005+00:00
|
2021-02-09T02:33:47.496242+00:00
| 1,664 | false |
Split [0,N) into [0,N-len(blacklist)) and [N-len(blacklist), N). The number of black items in left half == no. of whitelist items on right half. Hence just map the blacklist item on left side to a whitelist item on the right side. \n```\n def __init__(self, N: int, blacklist: List[int]):\n self.blacklist = blacklist\n self.B = len(blacklist)\n self.N = N\n self.mapping = {}\n \n second_hlf_wl = iter(set([i for i in range(N-self.B, N)]).difference(self.blacklist))\n\n for n in blacklist:\n if n<self.N-self.B:\n self.mapping[n] = next(second_hlf_wl) \n \n def pick(self) -> int:\n x = random.randint(0, self.N - self.B-1) \n if x in self.mapping:\n return self.mapping[x]\n return x\n```
| 7 | 0 |
['Ordered Set', 'Python']
| 2 |
random-pick-with-blacklist
|
Python Simplest Binary Search Explanation
|
python-simplest-binary-search-explanatio-j241
|
I haven\'t seen an easy to understand binary search solution, so here is mine. It took me a while of staring at it to figure this out, so hopefully this is help
|
andrewkho
|
NORMAL
|
2022-03-11T07:52:19.272743+00:00
|
2022-03-11T08:08:57.648006+00:00
| 597 | false |
I haven\'t seen an easy to understand binary search solution, so here is mine. It took me a while of staring at it to figure this out, so hopefully this is helpful for someone else. For an interview, I think the hashmap solution is more intuitive and easier to implement.\n\nThere are 2 key ideas for this problem:\n1) sample uniformly from the interval `[ 0, n - len(blacklist) )`. This ensures every valid response has the same probability of being drawn.\n2) the index in the sorted blacklist tells you how many elements are skipped before the blacklisted element, so if you add the index to the random draw, you\'ll get the result you want. Imagine doing a linear scan through the sorted blacklist for `draw`, you won\'t stop until `blacklist[i] > draw + i`. This is the same condition you want for your binary search. \n\nAs an example:\n```\nn = 7, blacklist = [2, 3, 5]\nRandomly draw from the interval [0, n - len(blacklist) ) -> [0, 4)\n\nBlacklist: 2, 3, 5\nDraw: 0, 1, 2, 3\nOutput: 0, 1, 2, 3, 4, 5, 6\n\nExample: draw = 2\nBlacklist idx: 0, 1, 2\nBlacklist: 2, 3, 5\nDraw + idx: 2, 3, 4\n```\n\n\nThe cleanest flavour of binary search for this problem is the same as `bisect.bisect_right`.\nExplanation of `bisect.bisect_right`: If you have an array of `arr = [0, 0, 2, 2, 4, 4]` `bisect_right` will return the index `i` that splits this array in two, so that if you did `arr[:i]` and `arr[i:]`, the value you\'re searching for would appear on the left array. Searching for value `2` would return index `4`. (If the value doesn\'t appear, it splits where that element would insert, for example searching for value `3` would return index `4`). \n\nGeneric Bisect-right binary search: the same as binary-searching for the right most insertion point, but adding 1 to the output.\n```\ndef bisect_right(arr: List[int], target: int) -> int:\n\tl, r = 0, len(arr)-1\n\twhile l <= r:\n\t\tm = (l+r)//2\n\t\tif arr[m] <= target:\n\t\t\tl = m+1\n\t\telse:\n\t\t\tr = m-1\n\treturn r+1\n```\n\n\nHere is the full solution, `O(B logB)` construction and `O(logB)` to pick.\n\n```\nclass Solution:\n def __init__(self, n: int, blacklist: List[int]):\n self.blacklist = sorted(blacklist)\n self.max = n - len(blacklist)\n\n def pick(self) -> int:\n v = random.randint(0, self.max-1)\n l, r = 0, len(self.blacklist) - 1\n while l <= r:\n m = (l+r)//2\n if self.blacklist[m] <= v+m:\n l = m+1\n else:\n r = m-1\n return v + r + 1\n```\n\nNote that you could also convert `arr[m] <= draw + m` to `arr[m] - m <= draw` which gives the pre-processed blacklist solution: `blacklist = [b - i for i, b in enumerate(blacklist]`. For this case, the solution is simplified if you are willing to use the builtin `bisect` library:\n\n```\nclass Solution:\n def __init__(self, n: int, blacklist: List[int]):\n self.blacklist = [b-i for i, b in enumerate(sorted(blacklist))]\n self.max = n - len(blacklist)\n\n def pick(self) -> int:\n v = random.randint(0, self.max-1)\n\t\treturn v + bisect.bisect_right(self.blacklist, v)\n```\n\nOne caveat is that I don\'t think this will work if there are duplicates in `blacklist`. In that case you\'d want to de-dupe in the constructor with something like: `self.blacklist = sorted(set(blacklist))`.
| 6 | 0 |
['Binary Tree', 'Python']
| 0 |
random-pick-with-blacklist
|
19 lines C++, O(B) constructor & O(log B) for pick.
|
19-lines-c-ob-constructor-olog-b-for-pic-4jwz
|
\nclass Solution {\n vector<int> prefix;\n mt19937 gen;\n uniform_int_distribution<> dis;\npublic:\n Solution(int N, vector<int> blacklist): dis(0,
|
plus2047
|
NORMAL
|
2019-03-29T13:04:36.966702+00:00
|
2019-03-29T13:04:36.966767+00:00
| 1,087 | false |
```\nclass Solution {\n vector<int> prefix;\n mt19937 gen;\n uniform_int_distribution<> dis;\npublic:\n Solution(int N, vector<int> blacklist): dis(0, N - int(blacklist.size()) - 1) {\n sort(blacklist.begin(), blacklist.end());\n for(int i = 0; i < blacklist.size(); i++) {\n prefix.push_back(blacklist[i] - i);\n }\n prefix.push_back(N - blacklist.size());\n }\n int pick() {\n int idx = dis(gen);\n return idx + (upper_bound(prefix.begin(), prefix.end(), idx) - prefix.begin());\n }\n};\n```\n\nKey point: `prefix` vector keep the prefix sum of range length for each serial range.\n\nFor example, `N = 10, B = [4, 6, 7]`. So the serial range is: `[0,1,2,3], [5], [], [8,9]` (Keep the empty range). So the prefix range is: `[4, 5, 5, 7]`. \n\nAs for the `pick` function, it get the index of the number to generate (only `N - len(B)` number left), than it use binary search to find the index of the range this number is in, than the number is it\'s index in the blocked list plus it\'s range index.\nFor example, for `N = 10, B = [4, 6, 7]`, we try to get the 5th numer, as for the blocked list is `[0,1,2,3], [5], [], [8,9]`, this number is in the 3rd range, so it is 8.\n\nI think use Map for this question (the TOP answer) is better, but this solution is not so bad and is much shorter.
| 6 | 0 |
[]
| 2 |
random-pick-with-blacklist
|
Map blacklisted numbers, create map elegantly in single pass
|
map-blacklisted-numbers-create-map-elega-8g9u
|
Intuition\nWe want to only call Math.random() once, we want to be able to check the blacklist once to figure out the actual output to return, and we want to be
|
cepheids
|
NORMAL
|
2023-04-06T14:21:47.278407+00:00
|
2023-04-06T18:00:40.975801+00:00
| 575 | false |
# Intuition\nWe want to only call Math.random() once, we want to be able to check the blacklist once to figure out the actual output to return, and we want to be able to process the blacklist quickly. \n\n# Approach\nAt `pick` time, we generate a random number in the range `[0, n - blacklist.length]` as that reflects the actual number of valid outputs. However, that number may be in the blacklist, so, we refer to a map to figure out what to transform that number into.\n\nTo build that map, we go through the blacklist and assign each blacklisted number to a new map-to value that starts right after `n - blacklist.length` incrementing by one each time.\n\nHowever, the map-to values we assign are not guaranteed to be valid outputs as they may also be in the blacklist. To fix this, everytime we process a blacklisted number, we also need to check if another blacklisted number has already been mapped to it.\n\nBecause of this, we need to process the blacklisted numbers in ascending order. At each blacklisted number, we will be able to determine if it is a brand new number, or if it has already been assigned as a map-to value for another blacklisted number.\n\nFor brand new numbers, we simply assign the next map-to number. For those that have already been referenced, we need to go back and update the entry that referenced it.\n\n# Optimization\nNow, it is possible to avoid sorting with a little bit of acrobatics. Instead of simply tacking on a new tail segment and updating the head entry on each iteration, we make the code a bit complex to handle the possibility of attaching head segments and joining chains.\n\nIt turns out that this can be elegantly done, most of the acrobatics is in determine the head and tail indices.\n\n# Complexity\n- Time complexity:\n- - Solution: $$O(b)$$\n- - Pick: $$O(1)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n- - Solution: $$O(b)$$\n- - Pick: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * @param {number} n\n * @param {number[]} blacklist\n */\nvar Solution = function(n, blacklist) {\n this.space = n - blacklist.length;\n this.map = {};\n\n blacklist.forEach((b, i) => {\n const next = this.space + i;\n\n const head = this.map[b] === undefined ? b : this.map[b];\n const tail = this.map[next] === undefined ? next : this.map[next];\n\n this.map[head] = tail;\n this.map[tail] = head;\n });\n};\n\n/**\n * @return {number}\n */\nSolution.prototype.pick = function() {\n const result = Math.floor(Math.random() * this.space);\n return this.map[result] || result;\n};\n\n/** \n * Your Solution object will be instantiated and called as such:\n * var obj = new Solution(n, blacklist)\n * var param_1 = obj.pick()\n */\n```
| 5 | 0 |
['JavaScript']
| 0 |
random-pick-with-blacklist
|
Java solution with HashSet 100% fast - logic explained
|
java-solution-with-hashset-100-fast-logi-tmsg
|
Idea : If count of banned elements is greater than or equal to N/3, then simply create a list of allowed elements, and return a random item from allowed list.\n
|
cpp_to_java
|
NORMAL
|
2020-01-25T03:17:48.702358+00:00
|
2020-02-26T02:50:40.167906+00:00
| 725 | false |
**Idea :** If count of banned elements is greater than or equal to N/3, then simply create a list of allowed elements, and return a random item from allowed list.\nIf count of banned elements is less than N/3, then this makes p = 2/3 probability that any randomly selected element will NOT be in the banned list.\n\n**Expected** number of trials for first success when sucess probability is p = 1/p\n\nSo, **expected** number of calls to Random = 3/2 (practically 2).\n\n```\nclass Solution {\n HashSet<Integer> banned;\n List<Integer> allowed;\n Random r;\n int N;\n \n public Solution(int N, int[] blacklist) {\n this.N = N;\n banned = new HashSet<Integer>();\n allowed = new ArrayList<Integer>();\n \n for(int x : blacklist){\n banned.add(x);\n }\n \n int M = banned.size();\n if(M >= (N/3)){\n for(int i = 0; i < N; i++){\n if(!banned.contains(i)){\n allowed.add(i);\n }\n }\n }\n \n r = new Random();\n }\n \n public int pick() {\n if(allowed.size() > 0){\n // too many blacklisted elements\n int index = r.nextInt(allowed.size());\n return allowed.get(index);\n }else{\n while(true){\n int index = r.nextInt(N);\n if(!banned.contains(index))\n return index;\n }\n }\n }\n}\n\n/**\n * Your Solution object will be instantiated and called as such:\n * Solution obj = new Solution(N, blacklist);\n * int param_1 = obj.pick();\n */\n\n```
| 5 | 0 |
[]
| 0 |
random-pick-with-blacklist
|
Python HashMap O(B) and O(1)
|
python-hashmap-ob-and-o1-by-arizonatea-6jzw
|
\nclass Solution:\n\n def __init__(self, N, blacklist):\n """\n :type N: int\n :type blacklist: List[int]\n """\n self.N,
|
arizonatea
|
NORMAL
|
2019-01-17T05:23:14.880709+00:00
|
2019-01-17T05:23:14.880756+00:00
| 1,100 | false |
```\nclass Solution:\n\n def __init__(self, N, blacklist):\n """\n :type N: int\n :type blacklist: List[int]\n """\n self.N, self.N_b = N, len(blacklist)\n self.map = {}\n self.black = set(blacklist)\n cur_white = self.N - self.N_b\n for b in self.black:\n if b < self.N - self.N_b:\n while cur_white in self.black:\n cur_white += 1\n self.map[b] = cur_white\n cur_white += 1\n\n def pick(self):\n """\n :rtype: int\n """\n k = random.randint(0, self.N-self.N_b - 1) \n return self.map[k] if k in self.black else k\n\n \n \n\n\n# Your Solution object will be instantiated and called as such:\n# obj = Solution(N, blacklist)\n# param_1 = obj.pick()\n```
| 5 | 0 |
[]
| 0 |
random-pick-with-blacklist
|
simple and easy C++ solution 😍❤️🔥
|
simple-and-easy-c-solution-by-shishirrsi-v1du
|
\n# if it\'s help, please up \u2B06 vote! \u2764\uFE0F\n\n###### Let\'s Connect on LinkedIn: www.linkedin.com/in/shishirrsiam\n###### Let\'s Connect on Facebook
|
shishirRsiam
|
NORMAL
|
2024-08-23T05:57:11.286825+00:00
|
2024-08-23T05:57:11.286876+00:00
| 367 | false |
\n# if it\'s help, please up \u2B06 vote! \u2764\uFE0F\n\n###### Let\'s Connect on LinkedIn: www.linkedin.com/in/shishirrsiam\n###### Let\'s Connect on Facebook: www.fb.com/shishirrsiam\n\n# Complexity\n- Time complexity: O(n log m)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int sz;\n vector<int>nums;\n Solution(int n, vector<int>& blacklist) \n {\n n = min(100000, n);\n set<int>st(begin(blacklist), end(blacklist));\n for(int i=0;i<n;i++)\n if(not (st.count(i)))\n nums.push_back(i);\n sz = nums.size();\n }\n \n int pick() \n {\n int idx = rand() % sz; \n return nums[idx];\n }\n};\n```
| 4 | 0 |
['Array', 'Hash Table', 'Math', 'Binary Search', 'Sorting', 'Ordered Set', 'Randomized', 'C++']
| 4 |
random-pick-with-blacklist
|
Java HashMap solution with explanation
|
java-hashmap-solution-with-explanation-b-3s5k
|
\nimport java.util.*;\n\nclass Solution {\n\n /** Idea is to shift the whitelisted number up and \n take the random index from 0 to whitelisted.length
|
vchoudhari
|
NORMAL
|
2019-11-19T00:26:00.847438+00:00
|
2019-11-19T00:26:15.728153+00:00
| 496 | false |
```\nimport java.util.*;\n\nclass Solution {\n\n /** Idea is to shift the whitelisted number up and \n take the random index from 0 to whitelisted.length\n \n For e.g. N = 6\n blacklist = {2, 3, 4}\n \n 1, 2, 3, 4, 5, 6\n w b b b w w\n \n Only 3 whitelisted, \n so swap 2 with 5 & swap 3 with 6\n \n which make the arr \n 1, 5, 6, 4, 2, 3\n w w w b b b\n \n And then take random number from 0 - whitelisted.lenth\n */\n Random r = new Random();\n HashMap<Integer, Integer> map = new HashMap<Integer, Integer>();\n int wlen = 0;\n public Solution(int N, int[] blacklist) {\n int blen = blacklist.length;\n wlen = N - blen;\n \n HashSet<Integer> set = new HashSet<Integer>();\n //4, 5, 6\n int from = wlen;\n while(from <= N) {\n set.add(from);\n from++;\n }\n //System.out.println(set);\n \n //5, 6\n for(int i = 0; i < blen; i++) {\n set.remove(blacklist[i]);\n }\n //System.out.println(set);\n \n //Iterator over whitelist & blacklist and map\n Iterator<Integer> itr = set.iterator();\n for(int i = 0; i < blen; i++) {\n //System.out.println("BlackList: "+blacklist[i]);\n if(blacklist[i] < wlen) {\n int e = itr.next();\n //System.out.println("BlackList: "+blacklist[i]+" WhiteListing with "+e);\n map.put(blacklist[i], e);\n }\n }\n //System.out.println(map);\n }\n \n public int pick() {\n int rIndex = r.nextInt(wlen);\n return map.getOrDefault(rIndex, rIndex);\n }\n}\n \n/**\n * Your Solution object will be instantiated and called as such:\n * Solution obj = new Solution(N, blacklist);\n * int param_1 = obj.pick();\n */\n```
| 4 | 0 |
[]
| 0 |
random-pick-with-blacklist
|
Python Simple Intuitive Solution
|
python-simple-intuitive-solution-by-zou_-7ss8
|
\nfrom random import randint\nclass Solution(object):\n\n def __init__(self, N, blacklist):\n """\n :type N: int\n :type blacklist: List
|
zou_zheng
|
NORMAL
|
2019-07-26T03:24:37.252645+00:00
|
2019-07-26T03:24:37.252681+00:00
| 552 | false |
```\nfrom random import randint\nclass Solution(object):\n\n def __init__(self, N, blacklist):\n """\n :type N: int\n :type blacklist: List[int]\n """\n self.dic = {} \n self.black_set = set(blacklist)\n self.threshold = N - 1 - len(blacklist)\n j = self.threshold + 1\n for num in blacklist:\n if num <= self.threshold:\n while j < N and j in self.black_set:\n j += 1\n self.dic[num] = j\n j += 1\n\n def pick(self):\n """\n :rtype: int\n """\n num = randint(0,self.threshold)\n if num in self.dic:\n return self.dic[num]\n else:\n return num\n```
| 4 | 0 |
[]
| 1 |
random-pick-with-blacklist
|
Intuitive approach - Choosing between 2 easy approaches on runtime
|
intuitive-approach-choosing-between-2-ea-uaaf
|
Intuition\n Describe your first thoughts on how to solve this problem. \nThere can be 2 approaches to solve this.\nApproach 1\nGenerate random integers until a
|
segment-tree
|
NORMAL
|
2023-07-22T10:19:18.131564+00:00
|
2023-07-22T10:19:18.131588+00:00
| 317 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThere can be 2 approaches to solve this.\nApproach 1\nGenerate random integers until a whitelisted number is generated.\nApproach 2\nMaintain a list of whitelisted numnbers and pick one randomly from it.\n\nApproach 1 will not work if most numbers are blacklisted\nApproach 2 will not work if most numbers are whitelisted (MLE)\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nDecide between Approach 1 and Approach 2 dynamically based on number of whitelisted and blacklisted numbers\n\n# Complexity\n- Time complexity: O(m) to iniitialise\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n- Space complexity: O(m) to maintain list of whitelisted / blacklisted\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n- Number of calls to rand() : O(1)\n\n# Code\n```\n/*\nApproach 1\ngenerate random integer in range (0, n - 1), generate again if blacklisted\nE = 1 + m / n * E\nE (n - m) / n = 1\nE = n / (n - m)\n\nif m is < n/2 this approach works as E = 2, which means we only call generate twice\n\nTime O(1) per pick\nMemory O(M) for maintainng blackisted hash table\n\nApproach 2\n\nMaintain a list of non-blacklisted numbers and pick each of them randomly.\n\nTime O(1) per pick\nMemory O(N - M) for maintaining list of whitelisted numbers\n\nThis solution does not work when N is large\n\n*/\n\nclass Solution {\npublic:\n\n int approach;\n\n int n, m;\n\n unordered_set<int> hash_set;\n\n vector<int> whitelist;\n\n\n Solution(int nn, vector<int>& blacklist) {\n n = nn;\n m = blacklist.size();\n for(auto it : blacklist) {\n hash_set.insert(it);\n }\n if(m * 2 < n) {\n approach = 1;\n }\n else {\n approach = 2;\n for(int i = 0; i < n; i++) {\n if(hash_set.find(i) == hash_set.end()) {\n whitelist.push_back(i);\n }\n }\n }\n }\n \n int pick() {\n if(approach == 1) {\n while(true) {\n int val = rand() % n;\n if(hash_set.find(val) == hash_set.end()) {\n return val;\n }\n }\n }\n else {\n int idx = rand() % whitelist.size();\n return whitelist[idx];\n }\n }\n};\n\n/**\n * Your Solution object will be instantiated and called as such:\n * Solution* obj = new Solution(n, blacklist);\n * int param_1 = obj->pick();\n */\n```
| 3 | 0 |
['C++']
| 0 |
random-pick-with-blacklist
|
Four lines of Python
|
four-lines-of-python-by-trentono-ag0j
|
\nfrom random import randint\nfrom bisect import bisect_right\n\nclass Solution:\n\n def __init__(self, N: int, blacklist: List[int]):\n self.num_choi
|
trentono
|
NORMAL
|
2021-04-12T08:08:38.191742+00:00
|
2021-04-12T08:58:49.964916+00:00
| 481 | false |
```\nfrom random import randint\nfrom bisect import bisect_right\n\nclass Solution:\n\n def __init__(self, N: int, blacklist: List[int]):\n self.num_choices = N - len(blacklist)\n self.search_list = [b - i for i, b in enumerate(sorted(blacklist))]\n \n def pick(self) -> int:\n rand_n = randint(0, self.num_choices-1)\n \n return rand_n + bisect_right(self.search_list, rand_n)\n\n```
| 3 | 0 |
[]
| 2 |
random-pick-with-blacklist
|
binary search c++ standard
|
binary-search-c-standard-by-neal_yang-k0kz
|
\n// you are try to find the k + 1 th white\n\nclass Solution {\nprivate:\n int N;\n int b;\n vector<int> blackList;\npublic:\n Solution(int N, vect
|
neal_yang
|
NORMAL
|
2019-09-27T05:02:57.792089+00:00
|
2019-09-27T05:49:22.626942+00:00
| 738 | false |
```\n// you are try to find the k + 1 th white\n\nclass Solution {\nprivate:\n int N;\n int b;\n vector<int> blackList;\npublic:\n Solution(int N, vector<int>& blacklist) : b(blacklist.size()), N(N), blackList(blacklist) {\n sort(blackList.begin(), blackList.end());\n cout<<RAND_MAX<<endl;\n }\n \n int pick() {\n int k = rand() % (N - b);\n if (b == 0)\n return k;\n if (blackList[0] > k)\n return k;\n int start = 0, end = b - 1;\n while (start <= end) {\n int mid = (start + end) / 2;\n int wc = blackList[mid] - mid;\n if (wc <= k && (mid == b-1 || mid != b-1 && blackList[mid+1] - mid - 1 > k)) {\n return k + 1 - wc + blackList[mid];\n } else if (wc > k) {\n end = mid - 1;\n } else {\n start = mid + 1;\n }\n }\n return -1;\n \n }\n};\n\n/**\n * Your Solution object will be instantiated and called as such:\n * Solution* obj = new Solution(N, blacklist);\n * int param_1 = obj->pick();\n */\n```
| 3 | 1 |
[]
| 0 |
random-pick-with-blacklist
|
Python AC solution with a very simple approach
|
python-ac-solution-with-a-very-simple-ap-6v0s
|
Firstly make blacklist as set instead of list to O(1) check for forbidden\n Then create another empty set for pre-used numbers\n Define current number (self.cur
|
cenkay
|
NORMAL
|
2018-07-03T10:25:25.956479+00:00
|
2018-07-03T10:25:25.956479+00:00
| 1,275 | false |
* Firstly make blacklist as set instead of list to O(1) check for forbidden\n* Then create another empty set for pre-used numbers\n* Define current number (self.cur) as 0\n* And then in each pick, iterate from current number (self.cur) if possible\n* If current number is within [0, N) return it\n* Else return random number from pre-used numbers\n* In total it is O(N + B) time for setting B set and iterating from 0 to N in the worst case\n```\nclass Solution:\n\n def __init__(self, N, blacklist):\n self.forbidden = set(blacklist)\n self.n = N\n self.used = set()\n self.cur = 0\n def pick(self):\n while self.cur in self.forbidden:\n self.cur += 1\n if self.cur < self.n:\n num = self.cur\n self.cur += 1\n else:\n num = self.used.pop()\n self.used.add(num)\n return num\n```\n* Compressed\n```\nclass Solution:\n\n def __init__(self, N, blacklist):\n self.forbidden, self.n, self.used, self.cur = set(blacklist), N, set(), 0\n def pick(self):\n while self.cur in self.forbidden: self.cur += 1\n if self.cur < self.n: num, self.cur = self.cur, self.cur + 1\n else: num = self.used.pop()\n self.used.add(num)\n return num\n```
| 3 | 1 |
[]
| 5 |
random-pick-with-blacklist
|
Java O(B) constructor and O(1) pick, HashMap
|
java-ob-constructor-and-o1-pick-hashmap-5uigm
|
The idea is very simple, we have elements in the blacklist which we should not pick, so we need to remap these elements to some other values.\n\nFor the first l
|
danyfang7
|
NORMAL
|
2018-07-03T10:08:58.500163+00:00
|
2018-07-03T10:08:58.500163+00:00
| 1,201 | false |
The idea is very simple, we have elements in the blacklist which we should not pick, so we need to remap these elements to some other values.\n\nFor the first loop, we make a set that records all elements from blacklist that are smaller than N, these elements should not be picked, the set has size count.\nWe then know the uniform random distribution interval, which is \\[0,M) where M = N-count. (In other words, there are M uniform-randomly distributed elements), and we initialize our random key to be in this interval.\n\nFor the second loop, we remap all elements from blacklist that are in range \\[0, M), we just need to remap them to values in \\[M, N). But we need to be careful as there may be some elements in \\[M, N) that are also in the blacklist, we just need to skip them.\n```\nclass Solution {\n private Map<Integer, Integer> map;\n private int key;\n private int M;\n public Solution(int N, int[] b) {\n Set<Integer> set = new HashSet<>();\n for(int c : b){\n if(c < N){\n set.add(c);\n }\n }\n M = N - set.size();\n Random r = new Random();\n key = r.nextInt(M);\n map = new HashMap<>();\n int count = 0;\n for(int c : b){\n if(c < M){\n while(set.contains(M + count)){\n count++;//skip elements in blacklist\n }\n map.put(c, M+count++);\n }\n }\n } \n public int pick() {\n int k = key;\n key = (k+1) % M;\n return map.getOrDefault(k, k);\n }\n}\n```
| 3 | 0 |
[]
| 3 |
random-pick-with-blacklist
|
✅✅Easy to Understand || Cpp Solution || Beats 100% with 8ms of runtime 🔥🔥
|
easy-to-understand-cpp-solution-beats-10-kf20
|
Approach
Calculate Valid Range: The total number of valid integers is m = n - len(blacklist). This is because we exclude all blacklisted integers from the tota
|
Gaurav_Chandola2023
|
NORMAL
|
2025-01-31T04:02:50.545277+00:00
|
2025-01-31T04:02:50.545277+00:00
| 258 | false |
# Approach
1. Calculate Valid Range: The total number of valid integers is m = n - len(blacklist). This is because we exclude all blacklisted integers from the total count.
2. Partition the Range: Divide the range [0, n-1] into two parts:
(i) The first part [0, m-1] which includes some valid integers and some blacklisted integers.
(ii) The second part [m, n-1] which includes the remaining integers.
3. Mapping Blacklisted Integers: For each blacklisted integer in the first part, find a corresponding valid integer in the second part. This mapping ensures that every number in the range [0, m-1] can be translated to a valid integer either directly (if it's valid) or via the mapped value (if it's blacklisted).
# Code
```cpp []
class Solution {
private:
int m;
unordered_map<int, int> mapping;
unordered_set<int> black_set;
public:
Solution(int n, vector<int>& blacklist) {
m = n - blacklist.size();
black_set = unordered_set<int>(blacklist.begin(), blacklist.end());
vector<int> first_part_black;
for (int num : blacklist) {
if (num < m) {
first_part_black.push_back(num);
}
}
int candidate = m;
for (int b : first_part_black) {
while (black_set.count(candidate)) {
++candidate;
}
mapping[b] = candidate;
++candidate;
}
}
int pick() {
int r = rand() % m;
if (mapping.find(r) != mapping.end()) {
return mapping[r];
}
return r;
}
};
/**
* Your Solution object will be instantiated and called as such:
* Solution* obj = new Solution(n, blacklist);
* int param_1 = obj->pick();
*/
```
| 2 | 0 |
['C++']
| 0 |
random-pick-with-blacklist
|
Java | 39ms | beats 99% | randomly pick up numbers from all or only from allowed
|
java-39ms-beats-99-randomly-pick-up-numb-uln4
|
Intuition\nFirst of all, let\'s forget about random calls minimization requirement, this problem can be interesting even without this requirement.\n\nAssume tha
|
avasiukevich
|
NORMAL
|
2023-11-17T00:37:47.447205+00:00
|
2023-11-17T00:39:15.203027+00:00
| 111 | false |
# Intuition\nFirst of all, let\'s forget about random calls minimization requirement, this problem can be interesting even without this requirement.\n\nAssume that we need to pick up random integer $x$ such that $0 \\leq x < n$ and we have $k$ blocked integers. So, we have $n - k$ allowed integers.\nWe have 2 cases:\n1. if $n - k < k$ then we can find all allowed integers and then just randomly pick up them\n2. if $n - k >= k$ then number of allowed integers can be too large (e.g when $n = 1e9$). But when we\'ll randomly pick up integers from range $[0, n)$ then probability to pick up blocked number will be equal to $k/n \\leq 1/2$. So, we can randomly pick up numbers, and ***on average*** it will require only constant number of random calls ($\\mathrm{avg} \\leq 2$, see proof below)\n\n# Approach\nOne can easiliy implement solution using algorithm description from the Intuition section.\n\nBut we need to prove that case 2 will have average pick time $O(1)$.\nLet\'s assume that $q$ is blocked numbers fraction ($q = k/n \n\\leq 1/2$)\nWhat will be probability of the event: we called random generator $i$ times in single `pick` in order to generate allowed number?\nIt will be $p(i) = q^{i-1} (1-q)$ (we randomly selected blocked numbers for the first $i-1$ attempts, and on $i$-th attempt we picked up allowed number). Let\'s calculate expected time for `pick` procedure:\n$$\n\\mathsf{E} [\\mathrm{pick \\; time }]\n = \\sum\\limits_{i = 1}^{\\infty} i \\; p(i)\n = \\sum\\limits_{i = 1}^{\\infty} i \\; q^{i-1} (1 - q)\n = \\frac{1}{(1-q)^2} (1 - q)\n = \\frac{1}{1-q}\n \n$$\n$$\n\\;\\;\\;\\;\\;\\; \\left| \\; \n\\sum\\limits_{i = 1}^{\\infty} i \\; q^{i-1}\n = \\frac{\\partial}{\\partial q}\\left( \n \\sum\\limits_{i = 0}^{\\infty} q^{i} \\right)\n = \\frac{\\partial}{\\partial q}\\left( \\frac{1}{1-q} \\right)\n = \\frac{1}{(1-q)^2}\n\\right.\n$$\nSo, on average we will use $\\frac{1}{1-q}$ random calls in case 2, and because $q \\leq 1/2$ in this case we\'ll use on average no more than $2$ random calls.\n\n# Complexity\n- Time complexity: init - $O(k)$, pick - $O(1)$\n\n- Space complexity: $O(k)$\n\n# Code\n```\nclass Solution {\n private final Random random = new Random();\n\n private final boolean useBlocked;\n\n private final int n;\n private final Set<Integer> blocked;\n\n private final List<Integer> allowed;\n\n public Solution(int n, int[] blacklist) {\n this.n = n;\n int blSize = blacklist.length;\n useBlocked = (blSize * 2 <= n);\n blocked = new HashSet<>(blSize);\n allowed = new ArrayList<>();\n for (int val : blacklist) {\n blocked.add(val);\n }\n if (!useBlocked) {\n for (int val = 0; val < n; ++val) {\n if (!blocked.contains(val)) {\n allowed.add(val);\n }\n }\n }\n }\n \n public int pick() {\n if (useBlocked) {\n int val = random.nextInt(0, n);\n while (blocked.contains(val)) {\n val = random.nextInt(0, n);\n }\n return val;\n } else {\n int idx = random.nextInt(0, allowed.size());\n return allowed.get(idx);\n }\n }\n}\n\n/**\n * Your Solution object will be instantiated and called as such:\n * Solution obj = new Solution(n, blacklist);\n * int param_1 = obj.pick();\n */\n \n```
| 2 | 0 |
['Randomized', 'Java']
| 0 |
random-pick-with-blacklist
|
C++ || Simplest Solution || No hashmap || No binary search
|
c-simplest-solution-no-hashmap-no-binary-0zqz
|
\nclass Solution {\npublic:\n vector<vector<int>> v;\n \n Solution(int n, vector<int>& b) {\n sort(b.begin(),b.end());\n int pre=0;\n
|
vermastra
|
NORMAL
|
2022-07-10T11:35:34.522946+00:00
|
2022-07-10T11:35:34.522993+00:00
| 383 | false |
```\nclass Solution {\npublic:\n vector<vector<int>> v;\n \n Solution(int n, vector<int>& b) {\n sort(b.begin(),b.end());\n int pre=0;\n for(auto &i:b){\n if(i-1>=pre){\n v.push_back({pre,i-1});\n }\n pre=i+1;\n }\n if(pre<=n-1)v.push_back({pre,n-1});\n }\n \n int pick() {\n int idx=rand()%(v.size());\n int ans=rand()%(v[idx][1]-v[idx][0]+1)+v[idx][0];\n return ans;\n }\n};\n\n```
| 2 | 0 |
[]
| 1 |
random-pick-with-blacklist
|
[Java] Solution using weighted intervals
|
java-solution-using-weighted-intervals-b-lryq
|
Algorithm:\nPreprocessing: \n1. Generate all whitelisted intervals in form [start, end];\n2. Generate array of weights of these intervals, where weight is the l
|
maxmironov
|
NORMAL
|
2022-04-29T16:40:45.565549+00:00
|
2022-04-29T16:40:45.565591+00:00
| 112 | false |
**Algorithm:**\nPreprocessing: \n1. Generate all whitelisted intervals in form `[start, end]`;\n2. Generate array of weights of these intervals, where weight is the length of interval;\n3. Calculate prefix sum for the weights, so each sum is the number of elements in this and all previous intervals (required for picking interval with weight)l.\n\nPick:\n1. Choose a random number from `[0, number of whitelisted numbers)`;\n2. Find an interval where that number falls in (as intervals are weighted, probability of chosing an interval is equal to the number of elements in it);\n3. Choose a random number from that interval.\n\nI used binary search for finding weighted interval. I simply searched for the first interval with prefixed weight (i.e. sum of its weight and all previous ones) is greater than chosen number.\n\n```\nclass Solution {\n \n List<int[]> intervals;\n int[] a;\n\n public Solution(int n, int[] blacklist) {\n Arrays.sort(blacklist);\n int min = 0, max = n - 1;\n intervals = new ArrayList<>();\n for (int i: blacklist) {\n if (i - min > 0) {\n intervals.add(new int[] {min, i - 1});\n max = i - 1;\n }\n \n min = i + 1;\n }\n \n if (min < n) {\n intervals.add(new int[] {min, n - 1});\n max = n - 1;\n }\n \n a = new int[intervals.size()];\n a[0] = intervals.get(0)[1] - intervals.get(0)[0] + 1;\n for (int i = 1; i < a.length; ++i) {\n a[i] = intervals.get(i)[1] - intervals.get(i)[0] + 1 + a[i - 1];\n }\n }\n \n public int pick() {\n int n = (int)(Math.random() * a[a.length - 1]);\n int l = 0, r = a.length - 1;\n while (l < r) {\n int m = (l + r) / 2;\n if (n < a[m]) {\n r = m;\n } else {\n l = m + 1;\n }\n }\n \n int[] interval = intervals.get(l);\n return (int)(Math.random() * (interval[1] - interval[0] + 1) + interval[0]);\n }\n}\n\n/**\n * Your Solution object will be instantiated and called as such:\n * Solution obj = new Solution(n, blacklist);\n * int param_1 = obj.pick();\n */\n```
| 2 | 0 |
['Binary Tree', 'Java']
| 0 |
random-pick-with-blacklist
|
710. Random Pick with Blacklist via Hash map
|
710-random-pick-with-blacklist-via-hash-7xotc
|
Here we create the hash map to map elements in the blacklist into the whitelist. Suppose the length of the whitelist is whiteSize. We randomly generate an integ
|
zwang198
|
NORMAL
|
2022-01-11T23:34:57.805586+00:00
|
2022-01-11T23:34:57.805623+00:00
| 382 | false |
Here we create the hash map to map elements in the blacklist into the whitelist. Suppose the length of the whitelist is **whiteSize**. We randomly generate an integer **index** in the interval **[0, whiteSize)** at first. If the integer **index** is in the hash map we created before, we can use this map to transform this **index** to another index corresponding to an element in the whitelist.\n```\nclass Solution:\n\tdef __init__(self, n, blacklist):\n\t\tself.whiteSize = n - len(blacklist)\n\t\tself.hmap = {ele: 1 for ele in blacklist}\n\t\t\n\t\tidx = n - 1\n\t\tfor ele in self.hmap:\n\t\t\tif ele >= self.whiteSize:\n\t\t\t\tcontinue\n\t\t\t\n\t\t\twhile idx in self.hmap:\n\t\t\t\tidx -= 1\n\t\t\tself.hmap[ele] = idx\n\t\t\tidx -= 1\n\t\t\t\n\tdef pick(self):\n\t\tindex = randint(0, self.whiteSize - 1)\n\t\tif index in self.hmap:\n\t\t\treturn self.hmap[index]\n\t\treturn index\n```\nThe idea is to divide **[0, n)** into two parts at the partition point **whiteSize**, where **[0, whiteSize]** ideally is used to store indices of whitelist. However, if there are some elements in the blacklist appearing in **[0, whiteSize]** (which implies definitely there are some elements in the whitelist showing in **[whiteSize, n)**), we use a hash map to construct a connection (a map) between elements incorrectly falling into above 2 sub-intervals around.\n\nOur goal is to map all blacklist elements into the tail of the list [0, n). So for each element in the blacklist, if it is already located at the tail (implies this element is >= **whiteSize**), we do not bother it. However, if it is before **whiteSize**, we want to map it to a value as far back as possible. This is the reason we initialize a reference **idx = n - 1**, and keep decreasing it by 1 after each mapping. However, if this **idx** actually is the element in the blacklist (use **hmap** to make search/check efficient), we need to give up this and decrease it (by using while loop) until it is not a blacklist element any more (mapping a blacklist element to a blacklist element does not make sense).\n\nOnce we finish creating this map, we are ready for multiple downstream jobs -- pick. If the number we generate is exactly the whitelist element, we directly return it. Otherwise, call the hash map.\n\nSuppose the length of the blacklist is n. Then the time complexity is O(n) since we are trying to construct a map for each blacklist element, and hence the space complexity is O(n).\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n
| 2 | 0 |
['Hash Table', 'Python3']
| 0 |
random-pick-with-blacklist
|
Python solution using hashmap
|
python-solution-using-hashmap-by-gswe-y44k
|
\nfrom random import randint\nclass Solution:\n\n def __init__(self, n: int, blacklist: List[int]):\n self.n = n\n self.hm = {}\n blackl
|
GSWE
|
NORMAL
|
2021-08-08T21:10:15.858494+00:00
|
2021-08-08T21:10:15.858524+00:00
| 280 | false |
```\nfrom random import randint\nclass Solution:\n\n def __init__(self, n: int, blacklist: List[int]):\n self.n = n\n self.hm = {}\n blacklist.sort()\n self.blacklist = set(blacklist)\n blacklistIndex = 0\n for i in range(n-len(blacklist), n):\n if i not in self.blacklist:\n self.hm[blacklist[blacklistIndex]] = i\n blacklistIndex+= 1\n \n # validIndex = n-1\n # for i in range(len(blacklist)):\n # while validIndex >= 0:\n # if validIndex not in self.blacklist: break\n # validIndex -= 1\n # if blacklist[i] >= validIndex: break\n # self.hm[blacklist[i]] = validIndex\n # self.blacklist.remove(blacklist[i])\n # validIndex -=1\n # self.validIndex = validIndex\n\n def pick(self) -> int:\n randomNum = randint(0,self.n-len(self.blacklist)-1)\n # randomNum = randint(0,max(0,self.validIndex))\n if randomNum not in self.hm: return randomNum\n return self.hm[randomNum]\n \n\n```
| 2 | 0 |
[]
| 0 |
random-pick-with-blacklist
|
Python3 one random() and one bisect() for each pick
|
python3-one-random-and-one-bisect-for-ea-8j4x
|
\nfrom random import random\nfrom bisect import bisect\n\nclass Solution:\n\n def __init__(self, n: int, blacklist: List[int]):\n blacklist.sort()\n
|
vsavkin
|
NORMAL
|
2021-06-25T13:51:12.536260+00:00
|
2021-06-25T13:51:12.536291+00:00
| 411 | false |
```\nfrom random import random\nfrom bisect import bisect\n\nclass Solution:\n\n def __init__(self, n: int, blacklist: List[int]):\n blacklist.sort()\n delta = 0\n self.offsets = []\n for v in blacklist:\n self.offsets.append(v-delta)\n delta += 1\n self.randmax = n-delta\n assert(self.randmax>=1)\n \n\n def pick(self) -> int:\n rnd = int(random()*self.randmax)\n ind = bisect(self.offsets, rnd)\n return rnd+ind\n```
| 2 | 0 |
['Python']
| 1 |
random-pick-with-blacklist
|
Easy C# Solution With Explanation
|
easy-c-solution-with-explanation-by-maxp-7s4y
|
1) Get Ranges of available numbers\n2) Choose weighted range randomly (see https://leetcode.com/problems/random-pick-with-weight/). Weight = size of range\n3) P
|
maxpushkarev
|
NORMAL
|
2020-01-11T07:32:36.185037+00:00
|
2020-01-11T07:32:36.185090+00:00
| 196 | false |
1) Get Ranges of available numbers\n2) Choose weighted range randomly (see https://leetcode.com/problems/random-pick-with-weight/). Weight = size of range\n3) Pick any number in choosen range\n\n```\n public class Solution\n {\n private readonly IList<(int from, int to)> _ranges;\n private readonly int[] _weightdRangesIndices;\n private readonly Random _rnd;\n\n public Solution(int n, int[] blacklist)\n {\n _rnd = new Random();\n _ranges = new List<(int @from, int to)>();\n\n Array.Sort(blacklist);\n\n int from = 0;\n int to = 0;\n\n for (int i = 0; i < blacklist.Length; i++)\n {\n to = blacklist[i];\n\n if (from < to)\n {\n _ranges.Add((from, to));\n }\n\n from = to + 1;\n }\n\n to = n;\n\n if (from < to)\n {\n _ranges.Add((from, to));\n }\n\n _weightdRangesIndices = new int[_ranges.Count];\n int sumWeight = 0;\n for (int i = 0; i < _ranges.Count; i++)\n {\n sumWeight += (_ranges[i].to - _ranges[i].from);\n _weightdRangesIndices[i] = sumWeight;\n }\n }\n\n //https://leetcode.com/problems/random-pick-with-weight/\n private int PickRangeIndex()\n {\n int weight = _rnd.Next(0, _weightdRangesIndices.Last()) + 1;\n int res = Array.BinarySearch(_weightdRangesIndices, weight);\n return res >= 0 ? res : -res - 1;\n }\n\n public int Pick()\n {\n int rangeIdx = PickRangeIndex();\n return _rnd.Next(_ranges[rangeIdx].from, _ranges[rangeIdx].to);\n }\n }\n```
| 2 | 0 |
[]
| 1 |
random-pick-with-blacklist
|
Easy to understand re-mapping.
|
easy-to-understand-re-mapping-by-ygoop-ffus
|
\nclass Solution {\n Map<Integer, Integer> map;\n Random random = new Random();\n int bound;\n public Solution(int N, int[] blacklist) {\n ma
|
ygoop
|
NORMAL
|
2019-06-11T01:49:02.809855+00:00
|
2019-06-11T01:49:02.809892+00:00
| 511 | false |
```\nclass Solution {\n Map<Integer, Integer> map;\n Random random = new Random();\n int bound;\n public Solution(int N, int[] blacklist) {\n map = new HashMap<Integer, Integer>();\n bound = N-blacklist.length;\n \n Set<Integer> set = new HashSet<>();\n for (int i: blacklist){\n set.add(i);\n }\n int idx = N-1;\n for (int i: blacklist){\n if (i < N-blacklist.length){\n while(set.contains(idx)){\n idx--;\n }\n map.put(i, idx);\n idx--;\n }\n }\n }\n \n public int pick() {\n int r = random.nextInt(bound);\n return map.getOrDefault(r, r);\n }\n}\n```
| 2 | 1 |
[]
| 2 |
random-pick-with-blacklist
|
c++ solution, O(1) extra space, O(log(blacklist.size)) pick time
|
c-solution-o1-extra-space-ologblacklists-hqzq
|
```\nclass Solution \n{\n vector bl;\n std::default_random_engine generator;\n std::uniform_int_distribution distribution;\npublic:\n Solution(int N
|
magaiti
|
NORMAL
|
2018-11-23T11:58:49.573452+00:00
|
2018-11-23T11:58:49.573491+00:00
| 685 | false |
```\nclass Solution \n{\n vector<int> bl;\n std::default_random_engine generator;\n std::uniform_int_distribution<int> distribution;\npublic:\n Solution(int N, vector<int> blacklist)\n {\n swap(bl, blacklist);\n sort(bl.begin(), bl.end());\n for (int i = 0, e = bl.size(); i < e; ++i)\n bl[i] -= i;\n \n distribution = std::uniform_int_distribution<int>(0, N - 1 - bl.size());\n }\n \n int pick() {\n auto r = distribution(generator);\n return r + (upper_bound(bl.begin(), bl.end(), r) - bl.begin());\n }\n};\n
| 2 | 1 |
[]
| 3 |
random-pick-with-blacklist
|
Python O(BlogB) construction and O(logB*logB) pick
|
python-oblogb-construction-and-ologblogb-ex4q
|
Read some good solutions to achieve O(1) time pick with pre-processing. Here is another choice of trade-off. If the banned numbers are 1 and 4 in 0123456, the m
|
luxy622
|
NORMAL
|
2018-08-20T02:34:08.521764+00:00
|
2018-08-20T02:34:08.521810+00:00
| 313 | false |
Read some good solutions to achieve O(1) time pick with pre-processing. Here is another choice of trade-off. If the banned numbers are `1` and `4` in `0123456`, the mapping would be \n```\n B=[1,4]\n \n012345\n0_12_3\n```\nso if we generate a random index 3, which should be mapped to 5, the third number that is not in B.\n\nLet `p(i)` denote the number of banned numbers in `B`. We have `5 - p(5) == 3` in this case.\nNote that `i - p(i)` is a monotonic array, we can binary search for the smallest `i` such that `i - p(i) == 3`.\nNote that ` 3<= i <= 3 + len(B)`, and it takes `O(log B)` time to compute each `p(i)`, so the time complexity is `O(log B * log B)` because we call `p(i)` for at most `O(log B)` times.\n```\nclass Solution:\n\n def __init__(self, N, blacklist):\n self.b = sorted(list(set(blacklist)))\n self.N = N\n\n def pick(self):\n l = x = random.randint(0, self.N-len(self.b)-1)\n h = x + len(self.b)\n while l < h:\n m = (l + h) // 2\n if m - bisect.bisect_right(self.b, m) < x: \n l = m + 1\n else:\n h = m\n return l\n```
| 2 | 0 |
[]
| 0 |
random-pick-with-blacklist
|
C++ O(B)/O(1), beats 95%, uses whitelist when B>N/2
|
c-obo1-beats-95-uses-whitelist-when-bn2-v7fos
|
Make blackset in O(B), then\n1. B<=N/2, uses rejection sampling. O(1) average per sample because the probability of rejection is at most 1/2.\n2. B>N/2, make wh
|
cai_lw
|
NORMAL
|
2018-08-05T02:59:12.871059+00:00
|
2018-08-05T02:59:12.871059+00:00
| 478 | false |
Make blackset in `O(B)`, then\n1. `B<=N/2`, uses rejection sampling. `O(1)` average per sample because the probability of rejection is at most 1/2.\n2. `B>N/2`, make whitelist in `O(N)` (which equals `O(B)` since `N/B` is bounded by a constant factor 2), and sample from whitelist.\n```\nclass Solution {\n int n;\n vector<int> whitelist;\n unordered_set<int> blackset;\npublic:\n Solution(int N, vector<int> blacklist) {\n n=N;\n blackset=unordered_set<int>(blacklist.begin(),blacklist.end());\n whitelist=vector<int>();\n if(blacklist.size()>N/2)\n for(int i=0;i<N;i++)\n if(!blackset.count(i))whitelist.push_back(i);\n }\n \n int pick() {\n if(!whitelist.empty())return whitelist[rand()%whitelist.size()];\n else while(true){\n int r=rand()%n;\n if(!blackset.count(r))return r;\n }\n }\n};\n```
| 2 | 0 |
[]
| 0 |
random-pick-with-blacklist
|
Java using Interval with Explanation
|
java-using-interval-with-explanation-by-31wcx
|
The idea is simple as follows:\nBased on the given black list, create a range pick for Random.next() as follows:\nFor example: Black List is [2,3,5] and N is 7,
|
bmask
|
NORMAL
|
2018-08-01T00:01:32.935378+00:00
|
2018-08-01T00:01:32.935378+00:00
| 567 | false |
The idea is simple as follows:\nBased on the given black list, create a range pick for Random.next() as follows:\nFor example: Black List is [2,3,5] and N is 7, so our range pick will be;\n[0,2], [4,5], and [6,7]. This is gonna be our Range Pick List. \n\nThen all we need to do is call Random.Next to pick the next Index (range) from our Range Pick List like Random.Next(list.size())\nand after that based on the range we use this formula:\nRandom.nextInt(EndRange-StartRange)+StartRange\n\n```\n Random random; int listSize=0; List<int[]> list;\n public Solution(int N, int[] blacklist) {\n \trandom = new Random();\n Arrays.sort(blacklist); //Sort the BlackList \n list = new ArrayList<>();\n int start=0; int i=0;\n int len=blacklist.length;\n while(i<len){ \t// create the Range Pick List\n \tif(start==blacklist[i]){start++; i++; continue;} \n \tlist.add(new int[]{start,blacklist[i]});\n \tstart=blacklist[i]+1;\n \ti++;\n }\n if(start<N) list.add(new int[]{start,N});\n listSize=list.size(); \n }\n \n public int pick() {\n int index = random.nextInt(listSize); //Pick the Range Pick List Index First\n int[] next = list.get(index); // Pick the Range from the list\n return random.nextInt(next[1]-next[0])+next[0]; //Call any number in the range\n }\n```
| 2 | 0 |
[]
| 2 |
random-pick-with-blacklist
|
Python swap solution
|
python-swap-solution-by-rogerfederer-7l8q
|
\nclass Solution(object):\n\n def __init__(self, N, blacklist):\n """\n :type N: int\n :type blacklist: List[int]\n """\n
|
rogerfederer
|
NORMAL
|
2018-07-05T03:56:01.393996+00:00
|
2020-10-14T18:42:55.012920+00:00
| 310 | false |
```\nclass Solution(object):\n\n def __init__(self, N, blacklist):\n """\n :type N: int\n :type blacklist: List[int]\n """\n self.bmap = {}\n for num in blacklist:\n if num <= N-1:\n self.bmap[num] = -1\n\n self.M = N - len(self.bmap)\n i = N-1\n for bn in self.bmap:\n while i in self.bmap:\n i -= 1\n if bn < self.M:\n self.bmap[bn] = i\n i -= 1\n\n def pick(self):\n """\n :rtype: int\n """\n idx = random.randint(0, self.M-1)\n\n if idx not in self.bmap:\n return idx\n else:\n return self.bmap[idx]\n```
| 2 | 1 |
[]
| 0 |
random-pick-with-blacklist
|
Simple O(1) design with detailed explanation
|
simple-o1-design-with-detailed-explanati-g9yk
|
IntuitionFirst, We can think of a number line with numbers from 0 to n. Now, we can divide this number line into some divisions where we can look for a number.T
|
demonX7292
|
NORMAL
|
2025-02-23T13:04:19.726772+00:00
|
2025-02-23T13:04:19.726772+00:00
| 42 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
First, We can think of a number line with numbers from 0 to n. Now, we can divide this number line into some divisions where we can look for a number.
These divisions are created by removing the blacklisted numbers from the number line.
Each of this division covers a range of numbers. Now we can assign an id to each of this division. Now, if we want to pick a random number, we first call random function to pick a division, we want to look for a number, then again call the random function to pick a number from the range of the chosen division.
For example : n = 10, blackList = [2, 3, 7]
Original number line :
```[0, 1, 2, 3, 4, 5, 6, 8, 9]```
Modified number line with divisions:
```[0, 1] , [4, 5, 6] , [8, 9]```
each of these divisions can be represented by their range like :
```[0 - 1] , [4 - 6] , [8 - 9]```
The id of each of these division is their index in the list.
# Approach
<!-- Describe your approach to solving the problem. -->
To implement this in code, we traverse the blacklist list and maintain a start and end pointer, marking the start and end of a range. When we process a blacklisted number, we add a corresponding range into our dividedRange list
Now, when we want to pick a number, we choose a random division by doing random() call on the size of dividedRange list. Then we again call random() to pick a random number from the range of picked division.
# Complexity
- Time complexity:
- O(n) one-time for precomputing the divisions.
- O(1) for picking the random number
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
- O(n) for storing the divisons list
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
List <int[]> dividedRange;
int numberOfDivisions = 0;
Random rand;
public Solution(int n, int[] arr) {
Arrays.sort(arr);
rand = new Random();
dividedRange = new ArrayList <>();
int start = 0, end = 0;
for (int i = 0; i < arr.length; i++) {
end = arr[i] - 1;
if (start > end) {
start = arr[i] + 1;
continue;
}
dividedRange.add(new int[]{start, end});
start = arr[i] + 1;
}
if (start < n) {
dividedRange.add(new int[]{start, n-1});
}
numberOfDivisions = dividedRange.size();
}
public int pick() {
int pickedDivision = rand.nextInt(numberOfDivisions);
int start = dividedRange.get(pickedDivision)[0];
int end = dividedRange.get(pickedDivision)[1];
return rand.nextInt(end - start + 1) + start;
}
}
/**
* Your Solution object will be instantiated and called as such:
* Solution obj = new Solution(n, blacklist);
* int param_1 = obj.pick();
*/
```
| 1 | 0 |
['Java']
| 0 |
random-pick-with-blacklist
|
O(1) allowed and forbidden partition
|
o1-allowed-and-forbidden-partition-by-mi-n29v
|
We calculate the count of allowed numbers; and create a "logical partition".Upper partition numbers are excluded from being picked directly. Some might be vali
|
michelusa
|
NORMAL
|
2025-02-21T01:24:13.366933+00:00
|
2025-02-21T01:24:13.366933+00:00
| 93 | false |
We calculate the count of allowed numbers; and create a "logical partition".
Upper partition numbers are excluded from being picked directly. Some might be valid or invalid.
Invalid numbers from the lower partition are mapped 1:1 to valid numbers from the upper partition.
The rest of the upper partition is composed of any invalid numbers that already belonged there.
Pick is O(1) time complexity [hash table lookup]
# Code
```cpp []
class Solution {
unordered_map<int, int> disallowed_to_allowed;
int n_;
public:
Solution(int n, vector<int>& forbidden) : n_(n - forbidden.size()) {
unordered_set<int> disallowed_all(cbegin(forbidden), cend(forbidden));
disallowed_to_allowed.reserve(forbidden.size());
int last_allowed = n - 1;
for (int val : forbidden) {
// Already in upper partition.
if (val >= this->n_) {
continue;
}
// Find next valid number in upper partition.
for (; disallowed_all.contains(last_allowed); --last_allowed)
;
disallowed_to_allowed[val] = last_allowed;
--last_allowed;
}
}
int pick() {
const int random_num = rand() % (n_);
if (auto it = disallowed_to_allowed.find(random_num);
it != disallowed_to_allowed.end()) {
return it->second;
} else {
return random_num;
}
}
};
/**
* Your Solution object will be instantiated and called as such:
* Solution* obj = new Solution(n, blacklist);
* int param_1 = obj->pick();
*/
```
| 1 | 0 |
['C++']
| 0 |
random-pick-with-blacklist
|
C# Binary Search
|
c-binary-search-by-ilya-a-f-nizz
|
csharp\npublic class Solution\n{\n List<int> weights = new();\n List<int> starts = new();\n List<int> ends = new();\n\n public Solution(int n, int[]
|
ilya-a-f
|
NORMAL
|
2024-06-11T17:32:48.932262+00:00
|
2024-11-08T23:33:58.585799+00:00
| 25 | false |
```csharp\npublic class Solution\n{\n List<int> weights = new();\n List<int> starts = new();\n List<int> ends = new();\n\n public Solution(int n, int[] blacklist)\n {\n var weight = 0;\n var start = 0;\n\n foreach (var end in blacklist.Append(n).Order())\n {\n if (end > start)\n {\n weight += end - start;\n weights.Add(weight);\n starts.Add(start);\n ends.Add(end);\n }\n\n start = end + 1;\n }\n }\n\n public int Pick()\n {\n var random = Random.Shared.Next(weights[^1]);\n var index = Math.Abs(weights.BinarySearch(random) + 1);\n return Random.Shared.Next(starts[index], ends[index]);\n }\n}\n```
| 1 | 0 |
['Binary Search', 'C#']
| 0 |
random-pick-with-blacklist
|
cpp easy solution with queue
|
cpp-easy-solution-with-queue-by-vinamra-u1pk0
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
vinamra-123
|
NORMAL
|
2024-04-23T12:56:56.424397+00:00
|
2024-04-23T12:56:56.424427+00:00
| 200 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n queue<int>ans;\n Solution(int n, vector<int>& blacklist) {\n\n set<int> res(blacklist.begin(),blacklist.end());\n for(int i=0;i<n;i++){\n if(res.find(i)==res.end()){\n ans.push(i);\n }\n if(ans.size() == 1e5) break; \n }\n }\n \n int pick() {\n int f= ans.front();\n ans.pop();\n ans.push(f);\n return f;\n }\n};\n\n/**\n * Your Solution object will be instantiated and called as such:\n * Solution* obj = new Solution(n, blacklist);\n * int param_1 = obj->pick();\n */\n## please upvote
| 1 | 0 |
['Queue', 'C++']
| 2 |
random-pick-with-blacklist
|
✅Beginner friendly explanation with comments - beats 100% - C++✅
|
beginner-friendly-explanation-with-comme-vx73
|
Explanation\ntrick ye hai manle ki 20 numbers hai aur unme se 5 tere blacklist number h toh\nnon-backlist tere hue 20 - 5 = 15 toh 15 non-blacklist ho gaye. m k
|
bhishu
|
NORMAL
|
2024-03-02T05:02:29.855751+00:00
|
2024-03-02T05:02:29.855788+00:00
| 28 | false |
# Explanation\ntrick ye hai manle ki 20 numbers hai aur unme se 5 tere blacklist number h toh\nnon-backlist tere hue 20 - 5 = 15 toh 15 non-blacklist ho gaye. m kya karunga 0-15 numbers tak jaunga, ab 15 ke baad toh 5 number bachege. m kya karunga ki\nuss 15 numbers ke andar jo blacklist number h usko m 15 ke baad wale\nnon-blacklist number se map karwa dunga. ye m map lekr karunga toh kya hoga ki\nrandom number toh tu non-blacklit ke liye hi nikalega kyuki tujhe chahiye toh\nnon blacklist hi, bole toh 0 - 15 ke beech toh agr jo tunne random number nikala\nagr ye tera blacklist h toh m kya karunga ki uske corresponding jo non blacklist\nh vo return kardunga ni toh jo number generate kiya that will be a non-blacklist\ntoh I\'ll return that.\n\n# Complexity\n- Time complexity: O(B)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n unordered_map<int, int> mp;\n int valid_range;\n Solution(int n, vector<int>& blacklist) {\n // set le liya h toh sort karne ki need ni, iske andar automatically\n // sorted hi milega\n set<int> st;\n for (auto numbers : blacklist) {\n st.insert(numbers);\n }\n\n // kis range tak hi number niklege ki kitne non-blacklist h\n valid_range = n - blacklist.size();\n\n int lastNum = valid_range;\n\n for (auto number : st) {\n // jo range ke andar ho aur blacklist ho, toh aise number se map\n // karunga jo range ke bahar ho par non-blacklist ho\n // sabse pehle check karunga ki range ke andar hai vo blacklist\n // number...then range ke bahar ka number mapk karwaunga jo st ke\n // andar na ho bole toh blacklist na ho\n if (number < valid_range) {\n while (st.count(lastNum)) {\n lastNum++;\n }\n mp[number] = lastNum;\n lastNum++;\n }\n }\n }\n\n int pick() {\n int random = rand() % valid_range;\n if (mp.count(random)) {\n return mp[random];\n }\n return random;\n }\n};\n/*\ntrick ye hai manle ki 20 numbers hai aur unme se 5 tere blacklist number h toh\nnon-backlist tere hue 20 - 5 = 15 toh 15 non-blacklist ho gaye. m kya karunga 0\n- 15 numbers tak jaunga, ab 15 ke baad toh 5 number bachege. m kya karunga ki\nuss 15 numbers ke andar jo blacklist number h usko m 15 ke baad wale\nnon-blacklist number se map karwa dunga. ye m map lekr karunga toh kya hoga ki\nrandom number toh tu non-blacklit ke liye hi nikalega kyuki tujhe chahiye toh\nnon blacklist hi, bole toh 0 - 15 ke beech toh agr jo tunne random number nikala\nagr ye tera blacklist h toh m kya karunga ki uske corresponding jo non blacklist\nh vo return kardunga ni toh jo number generate kiya that will be a non-blacklist\ntoh I\'ll return that.\n\n*/\n\n```
| 1 | 0 |
['C++']
| 0 |
random-pick-with-blacklist
|
710. Random Pick with Blacklist - Beats 100%
|
710-random-pick-with-blacklist-beats-100-b3v7
|
Complexity\n- Time complexity:\n Add your time complexity here, e.g. O(n) \n O(1) \n\n---\n\n- Space complexity:\n Add your space complexity here, e.g. O(n) \nO
|
amit_rk
|
NORMAL
|
2023-11-26T06:17:35.299409+00:00
|
2023-11-26T06:17:35.299440+00:00
| 128 | false |
# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n ***$$O(1)$$*** \n\n---\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n\n---\n\n# Code\n```\nk = 10\nclass Solution:\n def __init__(self, n: int, blacklist: List[int]):\n self.data = []\n black = {}\n if len(blacklist) == 1:\n n = min(n, k)\n if len(blacklist) != 0 and min(blacklist) > k:\n n = min(n, k)\n for ele in blacklist:\n black[ele] = True\n for i in range(0, n):\n if black.get(i) is None:\n self.data.append(i)\n self.index = 0\n def pick(self) -> int:\n k = self.data[self.index]\n self.index += 1\n if self.index == len(self.data):\n self.index = 0\n return k\n \n```
| 1 | 1 |
['Array', 'Hash Table', 'Randomized', 'Python3']
| 1 |
random-pick-with-blacklist
|
[Python] pick from list of valid ranges
|
python-pick-from-list-of-valid-ranges-by-nsdu
|
\n"""\nStore array of valid ranges, then pick random range, and random\nvalue from that range.\n"""\nclass Solution:\n\n def __init__(self, n: int, blacklist
|
pbelskiy
|
NORMAL
|
2023-11-16T15:01:01.669000+00:00
|
2023-11-16T15:01:01.669043+00:00
| 188 | false |
```\n"""\nStore array of valid ranges, then pick random range, and random\nvalue from that range.\n"""\nclass Solution:\n\n def __init__(self, n: int, blacklist: List[int]):\n self.n = n\n self.r = []\n\n if not blacklist:\n self.r.append((0, n - 1))\n return\n\n b = sorted(blacklist)\n if b[0] != 0:\n self.r.append((0, b[0] - 1))\n\n for i in range(len(b) - 1):\n if b[i] + 1 != b[i + 1]:\n self.r.append((b[i] + 1, b[i + 1] - 1))\n\n if b[-1] != n - 1:\n self.r.append((b[-1] + 1, n - 1))\n\n def pick(self) -> int:\n left, right = random.choice(self.r)\n return random.randint(left, right)\n```
| 1 | 0 |
['Sorting', 'Python', 'Python3']
| 1 |
random-pick-with-blacklist
|
Using Queue. Simple approach.
|
using-queue-simple-approach-by-drhadenst-0n6d
|
Complexity\n- Time complexity:\nPreprocessing - O(n)\nQueries - O(1)\n\n- Space complexity:\nO(n)\n\n# Code\n\nclass Solution {\n queue<int> q;\npublic:\n
|
DrHadenstein
|
NORMAL
|
2023-09-25T01:42:05.381983+00:00
|
2023-09-25T01:42:05.382004+00:00
| 29 | false |
# Complexity\n- Time complexity:\nPreprocessing - O(n)\nQueries - O(1)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution {\n queue<int> q;\npublic:\n Solution(int n, vector<int>& blacklist) {\n unordered_set<int> list(blacklist.begin(), blacklist.end());\n for(int i = 0; i < n; i++){\n if(list.find(i) == list.end()) q.push(i);\n if(q.size() == 1e5) break; \n/* As the queries may be upto 2*1e4 then it is wise to just make a queue containing these many numbers. Still 1e5 is just for simplicity. Required because n can be 1e9 which cannot be stored in queue due to MLE. */\n } \n }\n \n int pick() {\n int front = q.front();\n q.pop();\n q.push(front);\n return front;\n }\n};\n```
| 1 | 0 |
['C++']
| 0 |
random-pick-with-blacklist
|
Simple approach - no HashMap, no rand calls
|
simple-approach-no-hashmap-no-rand-calls-3gyu
|
Split the main [0, n - 1] range into a list of valid ranges, by excluding the blacklist numbers.\nThen, just pick an index from the list, and a number from the
|
Bogdan-Dinu
|
NORMAL
|
2023-07-26T14:16:33.237592+00:00
|
2023-07-26T14:18:22.214082+00:00
| 57 | false |
Split the main `[0, n - 1]` range into a list of valid ranges, by excluding the blacklist numbers.\nThen, just pick an index from the list, and a number from the range associated with the chosen item. I used the current time **ticks** information to induce the randomness factor.\n\nPlease press **upvote** below if you liked this solution. **Thank you!**\n\n# Code\n```\npublic class Solution {\n\n List<(int start, int end)> l = new();\n\n public Solution(int n, int[] blacklist) \n {\n Array.Sort(blacklist);\n\n var start = 0;\n for(int i = 0; i < blacklist.Length; i++)\n {\n var end = blacklist[i] - 1;\n if (start <= end)\n l.Add(new (start, end));\n\t\t\tstart = blacklist[i] + 1;\n } \n\t\tif (start < n)\n\t\t\tl.Add(new (start, n - 1)); \n }\n \n public int Pick() \n {\n int i = (int)(DateTime.Now.Ticks % l.Count);\n var count = l[i].end - l[i].start + 1;\n return l[i].start + (int)(DateTime.Now.Ticks % count);\n }\n}\n\n```
| 1 | 0 |
['C#']
| 0 |
random-pick-with-blacklist
|
C++ BEATS 100 %
|
c-beats-100-by-antony_ft-bg2n
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
antony_ft
|
NORMAL
|
2023-07-19T16:38:00.580036+00:00
|
2023-07-19T16:38:00.580134+00:00
| 29 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nstatic const auto init = []{\n cin.tie(nullptr);\n ios::sync_with_stdio(false);\n return false;\n}();\nint prefsum[100005];\nint psz = 0;\n\nclass Solution {\npublic:\n Solution(int n, vector<int>& blacklist) {\n ::sort(begin(blacklist), end(blacklist));\n psz = 0;\n int pre = 0;\n int sz = blacklist.size();\n for (int i = 0; i < sz;) {\n int j = i+1;\n while (j < sz && blacklist[j] == blacklist[j-1] + 1) {++j;}\n if (blacklist[i] != 0) {\n intv.push_back({pre, blacklist[i]-1});\n }\n pre = blacklist[j-1] + 1;\n i = j;\n }\n if (pre <= n-1) {\n intv.push_back({pre, n-1});\n }\n total = 0;\n for (int i = 0; i < intv.size(); ++i) {\n int length = intv[i].second - intv[i].first + 1;\n prefsum[psz++] = total;\n total += length;\n }\n }\n int pick() {\n int r = rand()%total;\n int idx = upper_bound(prefsum, prefsum+psz, r) - prefsum - 1;\n int offset = r - prefsum[idx];\n return intv[idx].first + offset;\n }\n vector<pair<int,int>> intv;\n int total;\n};\n```
| 1 | 0 |
['C++']
| 0 |
random-pick-with-blacklist
|
Java
|
java-by-gadmo-w7xd
|
\n\n# Code\n\nclass Solution {\n\n int len,n;\n Map <Integer, Integer> map; \n Random r;\n public Solution(int n, int[] blacklist) {\n // ma
|
gadmo
|
NORMAL
|
2023-07-02T13:28:43.502467+00:00
|
2023-07-02T13:28:43.502497+00:00
| 359 | false |
\n\n# Code\n```\nclass Solution {\n\n int len,n;\n Map <Integer, Integer> map; \n Random r;\n public Solution(int n, int[] blacklist) {\n // map blacklist into the cells {n - blacklist.length : n}, call random(0:n - blacklist.length) and if we land on blacklist return the mapping instead\n len = blacklist.length;\n this.n = n; \n map = new HashMap();\n for (int i = 0; i < len ; i++) map.put(blacklist[i] , n - len + i);\n for (int i = 0; i < len ; i++) map.put(blacklist[i] , find(map.get(blacklist[i]))); // remove chains optimization\n r = new Random();\n }\n\n private int find(int x){ \n if (!map.containsKey(x) || map.get(x) <= x) return x;\n return find(map.get(x));\n }\n \n public int pick() {\n int rand = r.nextInt(n - len);\n while (map.containsKey(rand)) rand = map.get(rand);\n return rand;\n }\n}\n\n/**\n * Your Solution object will be instantiated and called as such:\n * Solution obj = new Solution(n, blacklist);\n * int param_1 = obj.pick();\n */\n```
| 1 | 0 |
['Java']
| 0 |
random-pick-with-blacklist
|
Java, from two-pointer to MLE to remapping solution
|
java-from-two-pointer-to-mle-to-remappin-430k
|
from two-pointer to MLE to remapping solution \n\nIf we want to pick uniformly random, the underlying API would be something like Random.nextInt(bound). So how
|
eigenvector0
|
NORMAL
|
2023-06-30T21:12:09.481192+00:00
|
2023-06-30T21:12:09.481212+00:00
| 247 | false |
<h1>from two-pointer to MLE to remapping solution</h1>\n\nIf we want to pick uniformly random, the underlying API would be something like `Random.nextInt(bound)`. So how could we use this API to pick non-blacklist numbers? We can store those numbers in some random access data structure like array `pool`, then `Random.nextInt(pool.length)` would do the trick.\n\nHow could we end up with such a `pool`? One way is to partition an array with length `n`, such that all blacklisted numbers are at the end of the array. How can we do that? We can use two-pointers `i` `j`, where `i` is always `0`, and maintain the loop invariant that `pool[j+1..]` are all blacklist numbers. In particular we init `pool` with identity mapping, i.e. `pool[i] = i;`. We process `blacklist` in **descending** order, for each `b` swapping `pool[b]` with `pool[j]` then decrement `j`.\n``` java\nclass Solution {\n\tint[] pool;\n int poolLen;\n Random seed;\n \n public Solution(int n, int[] blacklist) {\n \tArrays.sort(blacklist);\n \tthis.seed = new Random();\n \tthis.pool = new int[n];\n\t\tthis.poolLen = n - blacklist.length;\n \t/* init as id map */\n \t\tfor (int i = 0; i < this.pool.length; i++) {\n \t\t\tthis.pool[i] = i;\n \t\t}\n \t\t/* two pointer to partition blacklist at pool end */\n \t\tint poolEnd = this.pool.length-1;\n \t\tfor (int i = blacklist.length-1; i >= 0; i--) {\n \t\t\tfinal int val = blacklist[i];\n \t\t\t/* still in id map => index pool[val] */\n \t\t\t/* swap with the other pointer */\n \t\t\tint temp = this.pool[poolEnd];\n \t\t\tthis.pool[poolEnd] = this.pool[val];\n \t\t\tthis.pool[val] = temp;\n \t\t\tpoolEnd--;\n \t\t}\n \t}\n \n \tpublic int pick() {\n \t\tint i = this.seed.nextInt(this.poolLen);\n \t\treturn this.pool[i];\n \t}\n}\n```\n\nThis is all good until I got **Memory Limit Exceeded**. The test case is roughly like no. 66/68: [n=1e9, blacklist=[6838038]]. So `pool` uses too much memory.\n\nHow could we space optimization on such cases? I noticed that for all "untouched" indices in `pool`, they remain identity mapping (`pool[i] == i`). These are non-blacklisted numbers. So rather than maintaining a mapping for those numbers, we could instead maintain the mapping for blacklist numbers, which uses max space `1e5` as indicated by input size constraints.\n\nBelow are final accepted solution. The algorithm is the same, just that I did mapping of blacklist numbers instead to save memory.\n\n``` java\nclass Solution {\n\tHashMap<Integer,Integer> map;\n\tint poolLen;\n\tRandom seed;\n\n\tpublic Solution(int n, int[] blacklist) {\n\t\tArrays.sort(blacklist);\n\t\tthis.seed = new Random();\n\t\tthis.map = new HashMap<>();\n\t\tthis.poolLen = n - blacklist.length;\n\t\t/* two pointer to partition blacklist at pool end */\n\t\tint poolEnd = n-1;\n\t\tfor (int i = blacklist.length-1; i >= 0; i--) {\n\t\t\tfinal int val = blacklist[i];\n\t\t\t/* swapping */\n\t\t\tif (!this.map.containsKey(poolEnd)) {\n\t\t\t\t/* `poolEnd` is id map */\n\t\t\t\tthis.map.put(val, poolEnd);\n\t\t\t} else {\n\t\t\t\t/* `flatten\' chain map */\n\t\t\t\tthis.map.put(val, this.map.get(poolEnd));\n\t\t\t\t/* no need this key */\n\t\t\t\tthis.map.remove(poolEnd);\n\t\t\t}\n\t\t\tpoolEnd--;\n\t\t}\n\t}\n\n\tpublic int pick() {\n\t\tint i = this.seed.nextInt(this.poolLen);\n\t\tif (this.map.containsKey(i)) {\n\t\t\t/* blacklist */\n\t\t\treturn this.map.get(i);\n\t\t}\n\t\t/* whitelist: id map */\n\t\treturn i;\n\t}\n}\n```\n\n<h2>Complexity</h2>\nTime Complexity\n\n`O(nlogn)`\n\nSpace Complexity\n`O(blacklist.length)`\n
| 1 | 0 |
['Java']
| 0 |
random-pick-with-blacklist
|
С++ || simple and tasteful
|
s-simple-and-tasteful-by-sibedir-43un
|
Solution() time complexity: O(m\xD7log(m))\n- pick() time complexity: O(log(m))\n\nm - size of blacklist\n\nclass Solution {\nprivate:\n\tvector<int>& _blacklis
|
sibedir
|
NORMAL
|
2023-06-03T05:17:25.515577+00:00
|
2023-06-03T05:17:25.515611+00:00
| 75 | false |
- Solution() time complexity: $$O(m\xD7log(m))$$\n- pick() time complexity: $$O(log(m))$$\n\n$$m$$ - size of blacklist\n```\nclass Solution {\nprivate:\n\tvector<int>& _blacklist;\n\tint total;\npublic:\n\tSolution(int n, vector<int>& blacklist) : _blacklist(blacklist), total(n - blacklist.size()) {\n \tsort(_blacklist.begin(), _blacklist.end());\n\t}\n\n\tint pick() {\n\t\tint desired = rand() % total;\n\t\tint left = -1;\n\t\tint right = _blacklist.size();\n\t\twhile ((left + 1) < right) {\n\t\t\tint mid = (left + right) / 2;\n\t\t\tif (_blacklist[mid] - mid > desired)\n\t\t\t\tright = mid;\n\t\t\telse\n\t\t\t\tleft = mid;\n\t\t}\n\t\treturn desired + left + 1;\n\t}\n};\n```
| 1 | 0 |
['C++']
| 0 |
random-pick-with-blacklist
|
Solution
|
solution-by-deleted_user-05el
|
C++ []\nstatic const auto init = []{\n cin.tie(nullptr);\n ios::sync_with_stdio(false);\n return false;\n}();\nint prefsum[100005];\nint psz = 0;\n\ncl
|
deleted_user
|
NORMAL
|
2023-05-08T06:20:50.007534+00:00
|
2023-05-08T07:05:28.927888+00:00
| 1,372 | false |
```C++ []\nstatic const auto init = []{\n cin.tie(nullptr);\n ios::sync_with_stdio(false);\n return false;\n}();\nint prefsum[100005];\nint psz = 0;\n\nclass Solution {\npublic:\n Solution(int n, vector<int>& blacklist) {\n ::sort(begin(blacklist), end(blacklist));\n psz = 0;\n int pre = 0;\n int sz = blacklist.size();\n for (int i = 0; i < sz;) {\n int j = i+1;\n while (j < sz && blacklist[j] == blacklist[j-1] + 1) {++j;}\n if (blacklist[i] != 0) {\n intv.push_back({pre, blacklist[i]-1});\n }\n pre = blacklist[j-1] + 1;\n i = j;\n }\n if (pre <= n-1) {\n intv.push_back({pre, n-1});\n }\n total = 0;\n for (int i = 0; i < intv.size(); ++i) {\n int length = intv[i].second - intv[i].first + 1;\n prefsum[psz++] = total;\n total += length;\n }\n }\n int pick() {\n int r = rand()%total;\n int idx = upper_bound(prefsum, prefsum+psz, r) - prefsum - 1;\n int offset = r - prefsum[idx];\n return intv[idx].first + offset;\n }\n vector<pair<int,int>> intv;\n int total;\n};\n```\n\n```Python3 []\nimport random\n\nclass Solution:\n def __init__(self, n, blacklist):\n bLen = len(blacklist)\n self.blackListMap = {}\n blacklistSet = set(blacklist)\n\n for b in blacklist:\n if b >= (n-bLen):\n continue\n self.blackListMap[b] = None\n \n start = n-bLen\n for b in self.blackListMap.keys():\n while start < n and start in blacklistSet:\n start += 1\n self.blackListMap[b] = start\n start += 1\n self.numElements = n - bLen\n\n def pick(self):\n randIndex = int(random.random() * self.numElements)\n return self.blackListMap[randIndex] if randIndex in self.blackListMap else randIndex\n```\n\n```Java []\nclass Solution {\n Map<Integer, Integer> map;\n Random rand = new Random();\n int size;\n\n public Solution(int n, int[] blacklist) {\n map = new HashMap<>();\n size = n - blacklist.length;\n int last = n - 1;\n for (int b: blacklist) {\n map.put(b, -1);\n }\n for (int b: blacklist) {\n if (b >= size) {\n continue;\n }\n while (map.containsKey(last)) {\n last--;\n }\n map.put(b, last);\n last--;\n }\n }\n public int pick() {\n int idx = rand.nextInt(size);\n if (map.containsKey(idx)) {\n return map.get(idx);\n }\n return idx;\n }\n}\n```\n
| 1 | 0 |
['C++', 'Java', 'Python3']
| 0 |
random-pick-with-blacklist
|
710题解
|
710ti-jie-by-zhuangms-l28j
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\u5173\u952E\u662F\u4F1A\u62A5MLE,\u6240\u4EE5\u53EA\u80FD\u7528\u6620\u5C04\u7684\u529
|
zhuangms
|
NORMAL
|
2023-04-05T09:53:19.967835+00:00
|
2023-04-05T09:53:19.967868+00:00
| 182 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\u5173\u952E\u662F\u4F1A\u62A5MLE,\u6240\u4EE5\u53EA\u80FD\u7528\u6620\u5C04\u7684\u529E\u6CD5\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/*\n * @lc app=leetcode.cn id=710 lang=cpp\n *\n * [710] \u9ED1\u540D\u5355\u4E2D\u7684\u968F\u673A\u6570\n */\n\n// @lc code=start\n#include<bits/stdc++.h>\nusing namespace std;\n\nclass Solution {\npublic:\n int sz;\n unordered_map<int,int> map;\n Solution(int n, vector<int>& blacklist) {\n sz = n-blacklist.size();\n int last = n-1;\n for(int b:blacklist) map[b] = 666;\n for(int b:blacklist){\n if(b>=sz) continue;\n while(map.count(last)) last--;\n map[b] = last;\n last--; \n }\n }\n \n int pick() {\n int tmp = rand()%sz;\n if(map.count(tmp)){\n return map[tmp];\n }\n return tmp;\n }\n};\n\n/**\n * Your Solution object will be instantiated and called as such:\n * Solution* obj = new Solution(n, blacklist);\n * int param_1 = obj->pick();\n */\n// @lc code=end\n\n\n```
| 1 | 0 |
['C++']
| 0 |
random-pick-with-blacklist
|
Java Solution using a HashMap
|
java-solution-using-a-hashmap-by-momosun-ypsc
|
Code\n\nclass Solution {\n HashMap<Integer, Integer> blacklistMap;\n int whiteSize;\n public Solution(int n, int[] blacklist) {\n blacklistMap =
|
momosunny
|
NORMAL
|
2023-03-12T04:43:23.128955+00:00
|
2023-03-12T04:43:23.129001+00:00
| 112 | false |
# Code\n```\nclass Solution {\n HashMap<Integer, Integer> blacklistMap;\n int whiteSize;\n public Solution(int n, int[] blacklist) {\n blacklistMap = new HashMap<>();\n whiteSize = n - blacklist.length;\n\n for(int b: blacklist) {\n blacklistMap.put(b, -1);\n }\n //\u5C06whitesize\u8303\u56F4\u91CC\u7684\u9ED1\u540D\u5355\u6620\u5C04\u5230whitesize\u4E4B\u540E\u7684\u767D\u540D\u5355\n int last = n - 1;\n for(int b: blacklist) {\n if(b < whiteSize) {\n while(blacklistMap.containsKey(last)) {\n last--;\n }\n blacklistMap.put(b, last);\n last--;\n }\n }\n\n }\n \n public int pick() {\n int rand = (int)(Math.random() * whiteSize);\n if(blacklistMap.containsKey(rand)) {\n return blacklistMap.get(rand);\n }\n return rand;\n }\n}\n\n/**\n * Your Solution object will be instantiated and called as such:\n * Solution obj = new Solution(n, blacklist);\n * int param_1 = obj.pick();\n */\n```
| 1 | 0 |
['Java']
| 0 |
random-pick-with-blacklist
|
Simple O(1) pick 97.7% time 86.34% space with explanation
|
simple-o1-pick-977-time-8634-space-with-iex25
|
Intuition\n Describe your first thoughts on how to solve this problem. \nWe need a random number that is not in the blacklist. This may seem difficult, but onc
|
DrNotGood
|
NORMAL
|
2023-03-07T04:52:42.961972+00:00
|
2023-03-07T04:52:42.962031+00:00
| 94 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe need a random number that is not in the blacklist. This may seem difficult, but once you realize that we need a number that is **between** the numbers in that blacklist, it becomes simple\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nWe keep a list of intervals.\n\nIf the blacklist is empty, then we simply add the interval [ 0,n ) to our intervals;\n\nOtherwise, we sort the numbers in the blacklist. We add intervals [0, min_blacklist) ans [max_blacklist+1, n) to our list, but only if those intervals are non-empty. We then the intervals between blacklist numbers to our list, only if they are non-empty.\n\nIn pick(), we pick a random interval, and then a random number in that interval.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(nlog(n)) for constructor, O(1) for pick.\n\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n) for constructor, O(1) for pick.\n\n# Code\n```\nclass Solution {\n vector<pair<int, int>> intervals;\npublic:\n Solution(int n, vector<int>& blacklist) {\n if(!blacklist.size()) {\n intervals.push_back({0, n});\n } else {\n sort(blacklist.begin(), blacklist.end());\n\n //Add intervals outside the bounds of the blacklist\n int mn = blacklist.front();\n int mx = blacklist.back();\n if(mn > 0) {\n intervals.push_back({0, mn});\n }\n\n if(mx < n-1) {\n intervals.push_back({mx+1, n});\n }\n\n //Add intervals between bounds of the blacklist\n for(size_t i = 1; i < blacklist.size(); ++i) {\n if(blacklist[i] - blacklist[i-1] > 1) {\n intervals.push_back({blacklist[i-1]+1, blacklist[i]});\n }\n }\n }\n }\n \n int pick() {\n //Pick random interval\n int idx = rand() % intervals.size();\n int a = intervals[idx].first;\n int b = intervals[idx].second;\n\n //Pick random number in that interval\n return a + (rand() % (b-a));\n }\n};\n\n/**\n * Your Solution object will be instantiated and called as such:\n * Solution* obj = new Solution(n, blacklist);\n * int param_1 = obj->pick();\n */\n```
| 1 | 0 |
['C++']
| 1 |
random-pick-with-blacklist
|
Java || HashMap || Random Set
|
java-hashmap-random-set-by-xiandong127-2m3l
|
If the number from blacklist set has already in the [sz, N), there is no need to map the connection between them. \n\n\n\nclass Solution {\n\n Map<Integer, I
|
xiandong127
|
NORMAL
|
2022-07-21T03:22:44.923341+00:00
|
2022-07-21T03:22:44.923378+00:00
| 408 | false |
If the number from blacklist set has already in the [sz, N), there is no need to map the connection between them. \n\n\n```\nclass Solution {\n\n Map<Integer, Integer> m;\n Random r;\n int wlen;\n\n public Solution(int n, int[] b) {\n m = new HashMap<>();\n r = new Random();\n wlen = n - b.length;\n Set<Integer> w = new HashSet<>();\n for (int i = wlen; i < n; i++) w.add(i);\n for (int x : b) w.remove(x);\n Iterator<Integer> wi = w.iterator();\n for (int x : b)\n if (x < wlen)\n m.put(x, wi.next());\n }\n\n public int pick() {\n int k = r.nextInt(wlen);\n return m.getOrDefault(k, k);\n }\n}\n```
| 1 | 0 |
['Java']
| 0 |
random-pick-with-blacklist
|
JAVA Without Using HashSet
|
java-without-using-hashset-by-daizhengge-mwwe
|
Simplfied version:\n```\n class Solution {\n Random random; \n HashMap map;\n int size;\n public Solution(int n, int[] blacklist) {\n map =
|
daizhengge
|
NORMAL
|
2022-07-20T00:07:11.420945+00:00
|
2022-07-20T00:07:11.420972+00:00
| 167 | false |
Simplfied version:\n```\n class Solution {\n Random random; \n HashMap<Integer, Integer> map;\n int size;\n public Solution(int n, int[] blacklist) {\n map = new HashMap<>();\n size = n - blacklist.length;\n random = new Random();\n //We put the blacklist\'s elements into the map first.\n for(int i : blacklist){\n map.put(i, -1);\n }\n int last = n - 1;\n for(int i : blacklist){\n //If current element exceed the size, we do not need to switch it with the last element.\n if(i >= size){\n continue;\n }\n //If map contains the last element, it means it is in the blacklist, so we need to skip it.\n while(map.containsKey(last)){\n last--;\n }\n map.put(i, last);\n last--;\n }\n }\n \n //We can use getOrDefault method to get the value or the current number\n public int pick() {\n int index = random.nextInt(size);\n return map.getOrDefault(index, index);\n }\n}
| 1 | 0 |
[]
| 0 |
random-pick-with-blacklist
|
Python Remapping
|
python-remapping-by-xvv-edmy
|
Find the blacklist elements need to remap(not in the tailpart);\nFind the available tail elements to remap and remap with the previous blacklist elements in a d
|
xvv
|
NORMAL
|
2022-06-12T04:43:07.899094+00:00
|
2022-06-12T04:43:07.899128+00:00
| 193 | false |
Find the blacklist elements need to remap(not in the tailpart);\nFind the available tail elements to remap and remap with the previous blacklist elements in a dict\n\n\n```\nclass Solution:\n\n def __init__(self, n: int, blacklist: List[int]):\n blacklist = set(blacklist)\n self.length = n - len(blacklist)\n self.remap = {}\n need_remap = []\n \n for x in blacklist:\n if x < self.length:\n need_remap.append(x)\n \n j = 0\n for i in range(self.length, n):\n if i not in blacklist:\n self.remap[need_remap[j]] = i\n j += 1\n \n\n def pick(self) -> int:\n idx = random.randrange(self.length)\n return self.remap[idx] if idx in self.remap else idx\n\n\n\n```
| 1 | 0 |
[]
| 0 |
random-pick-with-blacklist
|
[Python] use either Whitelist or Blacklist, simple
|
python-use-either-whitelist-or-blacklist-azil
|
The idea is simple, if there are too many blacklisted numbers (more than a third of all possible numbers), then just make a whitelist and randomly choose from i
|
z1bbo
|
NORMAL
|
2022-05-29T09:23:49.607660+00:00
|
2022-06-02T06:46:45.133546+00:00
| 191 | false |
The idea is simple, if there are too many blacklisted numbers (more than a third of all possible numbers), then just make a whitelist and randomly choose from it.\n\nElse we know that only 1/3 of possible random choices are blacklisted, so we can just do a few random draws and the probability of continously choosing blacklisted numbers decreases exponentially, e.g. for 12 draws `(1/3) ** 12` it is less than 2 in a million.\n\n```\nimport random\n\nclass Solution:\n def __init__(self, n: int, blacklist: List[int]):\n self.n = n\n if len(blacklist) > n//3:\n self.whitelist = list(set(range(0, n)) - set(blacklist))\n else:\n self.blacklist = set(blacklist)\n\n def pick(self) -> int:\n if hasattr(self, \'whitelist\'):\n return random.choice(self.whitelist)\n while (rand:= random.randint(0, self.n - 1)) in self.blacklist:\n continue\n return rand\n```
| 1 | 0 |
['Python']
| 0 |
random-pick-with-blacklist
|
Easy C++ solution || 0(B) time complexity
|
easy-c-solution-0b-time-complexity-by-th-fedj
|
\nclass Solution {\npublic:\n int idx;\n unordered_map<int, int>mp;\n set<int> s;\n Solution(int n, vector<int>& blacklist) {\n idx = n - blac
|
thanoschild
|
NORMAL
|
2022-05-27T14:50:48.704813+00:00
|
2022-05-27T14:50:48.704848+00:00
| 348 | false |
```\nclass Solution {\npublic:\n int idx;\n unordered_map<int, int>mp;\n set<int> s;\n Solution(int n, vector<int>& blacklist) {\n idx = n - blacklist.size();\n n--;\n for(int i = 0; i<blacklist.size(); i++) s.insert(blacklist[i]);\n for(int i = 0; i<blacklist.size(); i++){\n if(blacklist[i] < idx){\n while(s.find(n) != s.end())n--;\n mp[blacklist[i]] = n;\n n--; \n }\n } \n }\n \n int pick() {\n int ans = rand()%(idx);\n if(mp.count(ans)) return mp[ans];\n return ans;\n }\n};\n```
| 1 | 0 |
['C', 'C++']
| 0 |
random-pick-with-blacklist
|
Simple Python Solution | Dictionary/Map | O(n) time O(1) space
|
simple-python-solution-dictionarymap-on-hxi1b
|
\nimport random\nclass Solution:\n # hashmap to represent reflected value \n # to simulate pushing elements to the end (to enhance intimacy of group of el
|
Kiyomi_
|
NORMAL
|
2022-05-01T05:00:09.573106+00:00
|
2022-05-01T05:00:09.573139+00:00
| 87 | false |
```\nimport random\nclass Solution:\n # hashmap to represent reflected value \n # to simulate pushing elements to the end (to enhance intimacy of group of elements)\n def __init__(self, n: int, blacklist: List[int]):\n # [0, self.white - 1] is whitelist, [white, n - 1] is blacklist\n self.white = n - len(blacklist)\n self.dict = {}\n last = n - 1\n\n for b in blacklist:\n self.dict[b] = -1 # mark blacklist\n \n for b in blacklist:\n if b >= self.white: # in the range of blacklist, leave it, as we won\'t pick a rand in the range of blacklist\n continue\n \n while last in self.dict: # last is in blacklist\n last -= 1 # reduce last so the element won\'t repeat\n\n self.dict[b] = last # reflect blacklist to the white\n last -= 1 # reduce last so the element won\'t repeat\n\n def pick(self) -> int:\n rand = random.randint(0, self.white - 1) # only pick in the range of [0, self.white - 1]\n if rand in self.dict:\n return self.dict[rand] # return the reflected value\n return rand\n\n\n# Your Solution object will be instantiated and called as such:\n# obj = Solution(n, blacklist)\n# param_1 = obj.pick()\n```
| 1 | 0 |
[]
| 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.