question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
minimum-remove-to-make-valid-parentheses
|
C➕➕ Solution with explanation || T.C. -> O(n) & S.C -> O(n) || Stack
|
c-solution-with-explanation-tc-on-sc-on-nvtw6
|
Intuition\nJust guessing which bracket is wrongly placed makes the problem more difficult as it can be anywhere.\n\nSo basic intuition could be, finding the wro
|
tripathiharish2001
|
NORMAL
|
2023-05-23T11:24:51.250306+00:00
|
2023-05-23T11:24:51.250350+00:00
| 343 | false |
# Intuition\nJust guessing which bracket is wrongly placed makes the problem more difficult as it can be anywhere.\n\nSo basic intuition could be, finding the wrong bracket\'s or we can say unwanted bracket\'s indices in the string.\n\n# Approach\nApproach is very similar to that of finding valid parenthesis.\n\nSuppose we have ( ( ) ( ( ) ) ) ) ) (.\n\nNow lets try to find valid parenthesis using stack : - \n- ( - pushed , idx = 0\n- ( - pushed , idx = 1\n- ) - valid match as top of stack \'(\' ,so popped last \'(\', idx = 2\n\nwe can continue this way and at the end we would be having only unwanded bracket.\n\n\nIf you find a pair, that is valid one else it is invalid.\n\n# Complexity\n- Time complexity:\n O(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution {\npublic:\n string minRemoveToMakeValid(string s) {\n \n stack<pair<char,int>> st;\n\n for(int i = 0 ; i < s.length() ; i++){\n if(s[i]==\'(\'){\n st.push({s[i],i});\n }else if(s[i]==\')\'){\n if(!st.empty() && st.top().first==\'(\')st.pop();\n else st.push({s[i],i});\n }\n }\n\n string str = "";\n\n for(int i = s.length()-1; i>=0 ; i--){\n if(!st.empty() && st.top().second == i){\n st.pop();\n continue;\n }else str+=s[i];\n \n }\n\n reverse(str.begin(),str.end());\n return str;\n }\n};\n```
| 5 | 0 |
['C++']
| 0 |
minimum-remove-to-make-valid-parentheses
|
Swift Stack
|
swift-stack-by-duyetnt-sa98
|
From what I can see, most of the parenthesis problems can be solved using Stack.\n\n*1. Maintain invalid indices that shouldn\'t be included in the final result
|
duyetnt
|
NORMAL
|
2022-03-15T19:02:11.418843+00:00
|
2022-03-15T19:32:40.767779+00:00
| 327 | false |
From what I can see, most of the parenthesis problems can be solved using Stack.\n\n****1. Maintain invalid indices that shouldn\'t be included in the final result****\nThe idea is to maintain a `stack` consisting of indices of `(` and `invalidIndices` set donating the indices we shouldn\'t include in the final result. \n* Iterate over every index `i` of the input string, we have to handle **3 cases**:\n\t* If `arr[i] == "("`, append `i` to `stack`\n\t* If `arr[i] == ")"`, there are **2 sub-cases**:\n\t\t* If `stack is empty` --> `i` is an invalid index --> insert into `invalidIndices`\n\t\t* If `stack is not empty` --> `i` can make a balanced pair with any index inside `stack` --> remove the last element from `stack`\n\t* If `arr[i] is other character`, `i` is indeed a valid index --> don\'t need to do anything.\n* Every remaining index inside `stack` is invalid --> insert all into `invalidIndices`\n* Finally, iterate over every index `i` again, if `i` doesn\'t exist in the `invalidIndices`, append `arr[i]` to the final result.\n```swift\nclass Solution {\n func minRemoveToMakeValid(_ s: String) -> String {\n let arr = Array(s)\n let n = arr.count\n \n var invalidIndices = Set<Int>()\n var stack = [Int]()\n for i in 0..<n {\n let c = arr[i]\n switch c {\n case "(": stack.append(i)\n case ")":\n if stack.isEmpty {\n invalidIndices.insert(i)\n } else {\n stack.popLast()\n }\n default: break\n }\n }\n \n invalidIndices.formUnion(stack)\n \n var res = ""\n for i in 0..<n where !invalidIndices.contains(i) {\n res.append(arr[i])\n }\n \n return res\n }\n}\n// Time complexity: O(n) where n is length of s\n// Space complexity: O(n)\n```\n\n****2. Maintain valid indices that need to be included in the final result****\nAnother way is to maintain `validIndices` set donating the indices we must include in the final result. It requires some small tweaks from the approach #1 above.\n* Iterate over every index `i` of the input string, we have to handle **3 cases**:\n\t* If `arr[i] == "("`, append `i` to `stack`\n\t* If `arr[i] == ")"`, there are **2 sub-cases**:\n\t\t* If `stack is empty` --> `i` is an invalid index --> do nothing\n\t\t* If `stack is not empty` --> `i` can make a balanced pair with any index inside `stack` --> remove the last element from `stack` and insert it as well as `i` into `validIndices`\n\t* If `arr[i] is other character`, `i` is indeed a valid index --> insert into `validIndices`\n* Finally, iterate over every index `i` again, if `i` exists in the `validIndices`, append `arr[i]` to the final result.\n\nI find this approach is slightly better than approach #1, especially when `s` only contains `(`.\n```swift\nclass Solution {\n func minRemoveToMakeValid(_ s: String) -> String {\n let arr = Array(s)\n let n = arr.count \n \n var validIndices = Set<Int>()\n var stack = [Int]()\n for i in 0..<n {\n switch arr[i] {\n case "(": stack.append(i)\n case ")": \n if let last = stack.popLast() {\n validIndices.formUnion([last, i])\n }\n default: validIndices.insert(i)\n }\n }\n \n var res = ""\n for i in 0..<n where validIndices.contains(i) {\n res.append(arr[i])\n }\n \n return res\n }\n}\n// Time complexity: O(n) where n is length of s\n// Space complexity: O(n)\n```
| 5 | 0 |
['Stack', 'Swift']
| 0 |
minimum-remove-to-make-valid-parentheses
|
[ Python ] ✔✔ Simple Python Solution Using Stack and Iterative Approach 🔥✌
|
python-simple-python-solution-using-stac-y67a
|
If It is Useful to Understand Please Upvote Me \uD83D\uDE4F\uD83D\uDE4F\n\n\tclass Solution:\n\t\tdef minRemoveToMakeValid(self, s: str) -> str:\n\n\t\t\ts=list
|
ashok_kumar_meghvanshi
|
NORMAL
|
2022-03-15T03:46:19.331721+00:00
|
2022-03-15T03:46:19.331763+00:00
| 528 | false |
# If It is Useful to Understand Please Upvote Me \uD83D\uDE4F\uD83D\uDE4F\n\n\tclass Solution:\n\t\tdef minRemoveToMakeValid(self, s: str) -> str:\n\n\t\t\ts=list(s)\n\n\t\t\tstack = []\n\n\t\t\tfor i in range(len(s)):\n\n\t\t\t\tif s[i]==\'(\':\n\n\t\t\t\t\tstack.append(i)\n\n\t\t\t\telif s[i]==\')\':\n\n\t\t\t\t\tif len(stack)>0:\n\n\t\t\t\t\t\tstack.pop()\n\n\t\t\t\t\telse:\n\n\t\t\t\t\t\ts[i] = \'\'\n\n\t\t\twhile len(stack)>0:\n\n\t\t\t\ts[stack[-1]]=\'\'\n\n\t\t\t\tstack.pop()\n\n\t\t\treturn \'\'.join(s)\n
| 5 | 1 |
['Stack', 'Python', 'Python3']
| 0 |
minimum-remove-to-make-valid-parentheses
|
Facebook followup: without using stack
|
facebook-followup-without-using-stack-by-lctb
|
\n # without stack\n s = list(s)\n count = 0\n for i, char in enumerate(s):\n if char == \'(\':\n count += 1\n
|
asakhala
|
NORMAL
|
2021-10-18T00:21:32.857535+00:00
|
2021-10-18T00:21:32.857561+00:00
| 404 | false |
```\n # without stack\n s = list(s)\n count = 0\n for i, char in enumerate(s):\n if char == \'(\':\n count += 1\n elif char == \')\':\n if count: count -= 1\n else: s[i] = \'\'\n if count:\n for i in range(len(s)-1, -1, -1):\n if count and s[i] == \'(\':\n s[i] = \'\'\n count -= 1\n if not count: break\n return \'\'.join(s)\n```
| 5 | 0 |
[]
| 1 |
minimum-remove-to-make-valid-parentheses
|
fastest solution in python using stack | easy
|
fastest-solution-in-python-using-stack-e-q82i
|
\nclass Solution:\n def minRemoveToMakeValid(self, s: str) -> str:\n s= list(s)\n stack= []\n \n \n for i in range(len(s))
|
Abhishen99
|
NORMAL
|
2021-06-23T05:29:34.457142+00:00
|
2021-06-23T05:29:34.457186+00:00
| 311 | false |
```\nclass Solution:\n def minRemoveToMakeValid(self, s: str) -> str:\n s= list(s)\n stack= []\n \n \n for i in range(len(s)):\n \n if s[i]==\'(\':\n stack.append(i)\n elif s[i]==\')\':\n \n if stack:\n stack.pop()\n else:\n s[i]=\'\'\n \n for i in stack:\n s[i]=\'\'\n \n return \'\'.join(s)\n```
| 5 | 0 |
['Python', 'Python3']
| 0 |
minimum-remove-to-make-valid-parentheses
|
[C++] Array-based, Less-than-2-pass Solution Explained, ~100% Time, ~90% Space
|
c-array-based-less-than-2-pass-solution-n2q05
|
So, the problem of the valid parentheses is a classic declined in several variations - like this one that has filler characters - nothing too complex, but still
|
Ajna2
|
NORMAL
|
2021-02-19T23:11:14.033726+00:00
|
2024-04-06T09:47:28.244963+00:00
| 325 | false |
So, the problem of the valid parentheses is a classic declined in several variations - like this one that has filler characters - nothing too complex, but still a minor hindrance to consider.\n\nTo solve this problem, we will first of all declare a few support variables:\n* `tmp` is an array of chars, with the same size of `s`;\n* `p` will count how many parentheses we opened, while `pos` will be the pointer we will use to work on `tmp` - both will be set to `0`.\n\nIn our first pass through all the characters in the input string, we will have 3 base case:\n* `c == \'(\'` will make it add to `tmp` (and increase `pos`), on top of increasing the dedicated `p` counter;\n* `c == \')\'` will add the character to `tmp` only if `p > 0` and we will do nothing otherwise (ie: the character is ignored);\n* we will add any other character to `tmp`.\n\nOnce done, we will have stored `pos` character to compose a new, filtered string; but we might also have potentially `p` open parentheses that need to be removed.\n\nTo do so, we will generate out result variable `res` to be `pos - p` characters long and then proceed to fill it from the right, always adding each character that is not an opened parentheses, decreasing `p` otherwise and actually adding `\'(\'` only after `p` is `<= 0` - meaning we got rid of the extra `p` open parentheses we collected before (whereas we can be sure that `tmp` will never have any extra closed parentheses).\n\nOnce done, we can return `res` :)\n\nThe code:\n\n```cpp\nclass Solution {\npublic:\n string minRemoveToMakeValid(string &s) {\n // support variables\n char tmp[s.size()];\n int p = 0, pos = 0;\n for (char c: s) {\n switch(c) {\n case \'(\':\n p++;\n tmp[pos++] = c;\n break;\n case \')\':\n // inserting closing parentheses only with p > 0\n if (p > 0) {\n p--;\n }\n else break;\n default:\n tmp[pos++] = c;\n }\n }\n // properly sizing res\n string res(pos - p, \'*\');\n for (int i = pos - 1, j = pos - p - 1; i >= 0; i--) {\n if (tmp[i] != \'(\' || p-- <= 0) res[j--] = tmp[i];\n }\n return res;\n }\n};\n```\n\nWant to save even more memory? Okay, then overwrite directly `s`:\n\n```cpp\nclass Solution {\npublic:\n string minRemoveToMakeValid(string &s) {\n // support variables\n char tmp[s.size()];\n int p = 0, pos = 0;\n for (char c: s) {\n switch(c) {\n case \'(\':\n p++;\n tmp[pos++] = c;\n break;\n case \')\':\n // inserting closing parentheses only with p > 0\n if (p > 0) {\n p--;\n }\n else break;\n default:\n tmp[pos++] = c;\n }\n }\n // properly sizing s\n s.resize(pos - p);\n for (int i = pos - 1, j = pos - p - 1; i >= 0; i--) {\n if (tmp[i] != \'(\' || p-- <= 0) s[j--] = tmp[i];\n }\n return s;\n }\n};\n```
| 5 | 0 |
['String', 'C', 'C++']
| 1 |
minimum-remove-to-make-valid-parentheses
|
Detailed C++ solution with Stack and without Stack | Easy to Understand |
|
detailed-c-solution-with-stack-and-witho-r6s4
|
Solution Without stack\niterative soultion ----->\n==> if whenever the string is not valid we replace it with (*) so that we do not add that character to out re
|
super_cool123
|
NORMAL
|
2021-02-19T12:13:15.031725+00:00
|
2021-02-19T12:25:56.936519+00:00
| 490 | false |
**Solution Without stack**\n**iterative soultion ----->\n==> if whenever the string is not valid we replace it with (*) so that we do not add that character to out result.\n==> we do the above operation from left side and than right side and finally return the string.\n```\nclass Solution {\npublic:\n string minRemoveToMakeValid(string s) {\n int cnt = 0;\n // starting from left to right \n // check if string is valid or not\n // if not valid replace * with string\n for(int i=0; i<s.size(); i++) {\n if(s[i] == \'(\') cnt++;\n else if(s[i] == \')\') {\n cnt--;\n if(cnt < 0) {\n s[i] = \'*\';\n cnt = 0;\n }\n }\n }\n \n cnt = 0;\n // starting from right to left\n for(int i=s.size()-1; i>=0; i--) {\n if(s[i] == \')\') cnt++;\n else if(s[i] == \'(\') {\n cnt--;\n if(cnt < 0) {\n s[i] = \'*\';\n cnt = 0;\n }\n }\n }\n string ans = "";\n for(int i=0; i<s.size(); i++) {\n if(s[i] != \'*\') ans += s[i];\n }\n return ans;\n }\n};\n```\n**Solution With Stack**\n==>Push \'(\' into a stack and whenever \')\' appears in the string, try to pop \'(\' from stackif exists.\n==> If \'(\' does not exist, then erase \')\' from string.\n==> After parsing the entire string, erase extra \'(\' present in stack from string.\n```\nclass Solution {\npublic:\n string minRemoveToMakeValid(string s) {\n stack<int> box;\n int n = s.size();\n \n for(int i=0; i<n; i++) {\n if(s[i] == \')\'){\n if(!box.empty() && s[box.top()] == \'(\'){\n box.pop();\n }else{\n s.erase(i,1);\n i--;\n }\n }\n else if(s[i] == \'(\'){\n box.push(i);\n }\n }\n \n while(!box.empty()) {\n s.erase(box.top(),1);\n box.pop();\n }\n \n return s;\n }\n};\n```\n\nupvote if u like
| 5 | 0 |
['Stack', 'C', 'Iterator', 'C++']
| 1 |
minimum-remove-to-make-valid-parentheses
|
[go] stack
|
go-stack-by-iamslash-avv4
| ERROR: type should be string, got "https://github.com/iamslash/learntocode/blob/master/leetcode/MinimumRemovetoMakeValidParentheses/a.go\\n\\n\\n// 4ms 98.97% 6MB 100.00%\\n// stack\\n// O(N) O(N)\\nfu" |
iamslash
|
NORMAL
|
2020-02-29T13:18:57.744146+00:00
|
2020-02-29T13:18:57.744180+00:00
| 145 | false | ERROR: type should be string, got "https://github.com/iamslash/learntocode/blob/master/leetcode/MinimumRemovetoMakeValidParentheses/a.go\\n\\n```\\n// 4ms 98.97% 6MB 100.00%\\n// stack\\n// O(N) O(N)\\nfunc minRemoveToMakeValid(s string) string {\\n\\tstck := []int{}\\n\\tbs := []byte(s)\\n\\tfor i, b := range bs {\\n\\t\\tif b == \\'(\\' {\\n\\t\\t\\tstck = append(stck, i)\\n\\t\\t} else if b == \\')\\' {\\n\\t\\t\\tif len(stck) > 0 {\\n\\t\\t\\t\\tstck = stck[:len(stck)-1]\\n\\t\\t\\t} else {\\n\\t\\t\\t\\tbs[i] = \\'*\\'\\n\\t\\t\\t}\\n\\t\\t}\\n\\t}\\n\\tfor len(stck) > 0 {\\n\\t\\tbs[stck[len(stck)-1]] = \\'*\\'\\n\\t\\tstck = stck[:len(stck)-1]\\n\\t}\\n\\treturn strings.ReplaceAll(string(bs), \"*\", \"\")\\n}\\n```" | 5 | 0 |
[]
| 1 |
minimum-remove-to-make-valid-parentheses
|
No Stack | No Hashmap | Two pass solution | Python
|
no-stack-no-hashmap-two-pass-solution-py-7vzq
|
\nclass Solution(object):\n def minRemoveToMakeValid(self, s): \n out = []\n left, right = 0,0\n include = [True] * len(s)\n fo
|
incomingoogle
|
NORMAL
|
2020-01-04T21:08:31.129094+00:00
|
2020-01-05T00:20:49.823762+00:00
| 743 | false |
```\nclass Solution(object):\n def minRemoveToMakeValid(self, s): \n out = []\n left, right = 0,0\n include = [True] * len(s)\n for i in range(len(s)):\n if s[i] ==\'(\':\n left = left + 1\n elif s[i] ==\')\':\n right = right + 1\n \n if(right>left):\n left,right = 0,0\n include[i] = False\n \n left, right = 0,0\n for i in range(len(s)-1,-1,-1):\n if s[i] ==\'(\':\n left = left + 1\n elif s[i] ==\')\':\n right = right + 1\n \n if(left>right):\n left,right = 0,0\n include[i] = False\n \n if include[i]==True:\n out.append(s[i])\n \n\t \n return reversed(out)\n```
| 5 | 0 |
[]
| 0 |
minimum-remove-to-make-valid-parentheses
|
[Beats 100%🔥] Stack Approach | Beginner Friendly🚀
|
beats-100-stack-approach-beginner-friend-cdsj
|
IntuitionTo determine how to make the string valid with minimal removals, we need to identifyunmatched parentheses.
Using astackis a natural choice, as it allow
|
PradhumanGupta
|
NORMAL
|
2025-02-22T13:54:44.315876+00:00
|
2025-02-22T13:54:44.315876+00:00
| 327 | false |
# Intuition
To determine how to make the string valid with minimal removals, we need to identify **unmatched parentheses**.
- Using a **stack** is a natural choice, as it allows us to track unmatched opening parentheses `(`.
- When encountering `)`, we check if there's a matching `(` in the stack. If not, it's unmatched and should be removed.
- Any leftover `(` in the stack after processing the string are also unmatched and should be removed.
# Approach
1. **First Pass:**
- Iterate through the string and use a stack to store indices of unmatched `(`.
- If `)` appears and no matching `(` exists, mark it for removal.
2. **Second Pass:**
- Remove remaining unmatched `(` from the stack.
3. **Final Step:**
- Construct the valid string by removing marked characters.
# Complexity
- **Time Complexity:** $$O(n)$$
- **Space Complexity:** $$O(n)$$
# Code
```java []
class Solution {
public String minRemoveToMakeValid(String s) {
Stack<Integer> stack = new Stack<>();
StringBuilder valid = new StringBuilder(s);
// First pass to find unmatched closing parentheses ')'
for (int i = 0; i < s.length(); i++) {
if (s.charAt(i) == '(') {
stack.push(i); // Push index of '(' onto the stack
} else if (s.charAt(i) == ')') {
if (stack.isEmpty()) {
valid.setCharAt(i, ' '); // Mark unmatched ')' as ' '
} else {
stack.pop(); // Valid match found, pop '(' from stack
}
}
}
// Second pass to remove unmatched opening parentheses '('
while (!stack.isEmpty()) {
valid.setCharAt(stack.pop(), ' '); // Mark unmatched '(' as ' '
}
// Remove all spaces (marked invalid characters)
return valid.toString().replace(" ", "");
}
}
```
**Please Upvote⬆️**

| 4 | 0 |
['String', 'Stack', 'Java']
| 1 |
minimum-remove-to-make-valid-parentheses
|
Simple Solution with Diagrams in Video - JavaScript, C++, Java, Python
|
simple-solution-with-diagrams-in-video-j-5g2e
|
VideoPlease upvote here so others save time too!Like the video on YouTube if you found it usefulClick here to subscribe on YouTube:
https://www.youtube.com/@may
|
danieloi
|
NORMAL
|
2025-01-10T12:54:02.869375+00:00
|
2025-01-10T12:54:02.869375+00:00
| 433 | false |
# Video
Please upvote here so others save time too!
Like the video on YouTube if you found it useful
Click here to subscribe on YouTube:
https://www.youtube.com/@mayowadan?sub_confirmation=1
Thanks!
https://youtu.be/Lruz_Tp4DtQ?si=2R9QottyEFRi8XSd
```Javascript []
/**
* @param {string} s
* @return {string}
*/
var minRemoveToMakeValid = function (s) {
let stack = [];
let s_list = Array.from(s);
for (let i = 0; i < s.length; i++) {
let val = s[i];
// if stack is not empty and top element of stack is an opening parenthesis
// and the current element is a closing parenthesis
if (stack.length > 0 && stack[stack.length - 1][0] === '(' && val === ')') {
// pop the opening parenthesis as it makes a valid pair
// with the current closing parenthesis
stack.pop();
}
// if the current value is an opening or a closing parenthesis
else if (val === '(' || val === ')') {
// push onto stack
stack.push([val, i]);
}
}
// Remove the invalid parentheses
for (let p of stack) {
s_list[p[1]] = "";
}
// convert the list to string
let result = s_list.join('');
return result;
};
```
```Python []
class Solution:
def minRemoveToMakeValid(self, s: str) -> str:
stack = []
to_remove = set()
# First pass: Identify the positions of invalid parentheses
for i, char in enumerate(s):
if char == "(":
stack.append(i)
elif char == ")":
if stack:
stack.pop()
else:
to_remove.add(i)
# Add remaining unmatched '(' positions to the set
while stack:
to_remove.add(stack.pop())
# Build the result string by skipping invalid parentheses
result = []
for i, char in enumerate(s):
if i not in to_remove:
result.append(char)
return "".join(result)
```
```Java []
class Solution {
public String minRemoveToMakeValid(String s) {
Stack<Integer> stack = new Stack<>();
Set<Integer> toRemove = new HashSet<>();
// First pass: Identify the positions of invalid parentheses
for (int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
if (c == '(') {
stack.push(i);
} else if (c == ')') {
if (!stack.isEmpty() && s.charAt(stack.peek()) == '(') {
stack.pop();
} else {
toRemove.add(i);
}
}
}
// Add remaining unmatched '(' positions to the set
while (!stack.isEmpty()) {
toRemove.add(stack.pop());
}
// Build the result string by skipping invalid parentheses
StringBuilder result = new StringBuilder();
for (int i = 0; i < s.length(); i++) {
if (!toRemove.contains(i)) {
result.append(s.charAt(i));
}
}
return result.toString();
}
}
```
```C++ []
class Solution {
public:
string minRemoveToMakeValid(string s) {
stack<int> stk;
vector<bool> toRemove(s.size(), false);
// First pass: Identify the positions of invalid parentheses
for (int i = 0; i < s.size(); ++i) {
if (s[i] == '(') {
stk.push(i);
} else if (s[i] == ')') {
if (!stk.empty() && s[stk.top()] == '(') {
stk.pop();
} else {
toRemove[i] = true;
}
}
}
// Mark remaining unmatched '(' as invalid
while (!stk.empty()) {
toRemove[stk.top()] = true;
stk.pop();
}
// Build the result string by skipping invalid parentheses
string result;
for (int i = 0; i < s.size(); ++i) {
if (!toRemove[i]) {
result += s[i];
}
}
return result;
}
};
```
| 4 | 0 |
['Python', 'C++', 'Java', 'Python3', 'JavaScript']
| 0 |
minimum-remove-to-make-valid-parentheses
|
Easy to follow approach using Stack - O(n) Time and Space
|
easy-to-follow-approach-using-stack-on-t-s7l1
|
Approach using Stack\n\nStep 1: Iterate through the string to identify and mark invalid closing parentheses and remember the positions of unmatched opening pare
|
kev_codes
|
NORMAL
|
2024-07-28T23:52:39.248906+00:00
|
2024-07-28T23:52:39.248923+00:00
| 120 | false |
# Approach using Stack\n\n**Step 1:** Iterate through the string to identify and mark invalid closing parentheses and remember the positions of unmatched opening parentheses using a stack.\n\n**Step 2:** Remove any unmatched opening parentheses recorded in the stack. \n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n```python\nclass Solution:\n def minRemoveToMakeValid(self, s: str) -> str:\n s = list(s)\n stack = []\n for i, c in enumerate(s):\n if c == "(":\n stack.append(i)\n elif c == ")":\n if not stack:\n s[i] = ""\n else:\n stack.pop()\n while stack:\n s[stack.pop()] = ""\n return "".join(s)\n \n```
| 4 | 0 |
['Stack', 'Python3']
| 1 |
minimum-remove-to-make-valid-parentheses
|
The parenthesis template Question || Brute intuitive || interview
|
the-parenthesis-template-question-brute-7nuon
|
Get to solve the best parenthesis question in brute and optimised way\n\nunderstanding problem solving\n\n\n1541. Minimum Insertions to Balance a Parentheses St
|
Dixon_N
|
NORMAL
|
2024-06-21T19:00:45.221129+00:00
|
2024-06-21T19:02:31.221914+00:00
| 44 | false |
Get to solve the best parenthesis question in brute and optimised way\n\nunderstanding problem solving\n\n\n[1541. Minimum Insertions to Balance a Parentheses String](https://leetcode.com/problems/minimum-insertions-to-balance-a-parentheses-string/solutions/5348641/the-parenthesis-template-question-brute-intuitive-interview/)\n[921. Minimum Add to Make Parentheses Valid](https://leetcode.com/problems/minimum-add-to-make-parentheses-valid/solutions/5348632/brute-intuitive-solution-with-and-without-stack-beast-time-and-space/)\n[20. Valid Parentheses](https://leetcode.com/problems/valid-parentheses/solutions/5159895/brute-intuitive-solution-beats-98/) --> *simple yet tricky*\n[301. Remove Invalid Parentheses](https://leetcode.com/problems/remove-invalid-parentheses/solutions/5305306/have-fun-solving-this-easy-problem/) -> **Important**\n[32. Longest Valid Parentheses](https://leetcode.com/problems/longest-valid-parentheses/solutions/5348623/simple-solution-in-java-must-read/)\n[1614. Maximum Nesting Depth of the Parentheses](https://leetcode.com/problems/maximum-nesting-depth-of-the-parentheses/solutions/5304994/the-parenthesis-problems/)\n[282. Expression Add Operators](https://leetcode.com/problems/expression-add-operators/solutions/5348619/brute-intuitive-recursive-solution-must-read/) --> **Important**\n[2232. Minimize Result by Adding Parentheses to Expression](https://leetcode.com/problems/minimize-result-by-adding-parentheses-to-expression/solutions/5304516/beats-98/)\n[241. Different Ways to Add Parentheses](https://leetcode.com/problems/different-ways-to-add-parentheses/solutions/5304322/java-simple-solution/)\n[856. Score of Parentheses](https://leetcode.com/problems/score-of-parentheses/solutions/5203496/scoreofparentheses/) --> **unique**\n[678. Valid Parenthesis String]()\n[1003. Check If Word Is Valid After Substitutions]()\n[1963. Minimum Number of Swaps to Make the String Balanced]()\n\n# Code\n```\nclass Solution {\n public String minRemoveToMakeValid(String s) {\n int openCount = 0, closeCount = 0;\n StringBuilder stringBuilder = new StringBuilder();\n\n // First pass: remove excess closing parentheses\n for (char c : s.toCharArray()) {\n if (c == \'(\') {\n openCount++;\n stringBuilder.append(c);\n } else if (c == \')\') {\n if (openCount > closeCount) {\n closeCount++;\n stringBuilder.append(c);\n }\n } else {\n stringBuilder.append(c);\n }\n }\n\n // If the counts are balanced, return the result directly\n if (openCount == closeCount) {\n return stringBuilder.toString();\n }\n\n StringBuilder result = new StringBuilder();\n openCount = 0;\n closeCount = 0;\n\n // Second pass: remove excess opening parentheses from the end\n for (int i = stringBuilder.length() - 1; i >= 0; i--) {\n char currentChar = stringBuilder.charAt(i);\n if (currentChar == \'(\') {\n if (openCount < closeCount) {\n result.append(currentChar);\n openCount++;\n }\n } else if (currentChar == \')\') {\n closeCount++;\n result.append(currentChar);\n } else {\n result.append(currentChar);\n }\n }\n\n return result.reverse().toString();\n }\n}\n\n```\n\n\n## -----------------------------------------------\n\n\ninitially I came up with seperate count for \'*\' and if the count if \'*\' is greater than the difference in count of open and close bracket the return true, but this passed 55 test cases , but that let to the intuitiion of below solution!!\n\nDry run yourself if will make a better understanding for these probelms\n\n\n\n\n# Code\n```\nclass Solution {\n public boolean checkValidString(String s) {\n int cmin = 0, cmax = 0; // open parentheses count in range [cmin, cmax]\n for (char c : s.toCharArray()) {\n if (c == \'(\') {\n cmax++;\n cmin++;\n } else if (c == \')\') {\n cmax--;\n cmin--;\n } else if (c == \'*\') {\n cmax++; // if `*` become `(` then openCount++\n cmin--; // if `*` become `)` then openCount--\n // if `*` become `` then nothing happens\n // So openCount will be in new range [cmin-1, cmax+1]\n }\n if (cmax < 0) return false; // Currently, don\'t have enough open parentheses to match close parentheses-> Invalid\n // For example: ())(\n cmin = Math.max(cmin, 0); // It\'s invalid if open parentheses count < 0 that\'s why cmin can\'t be negative\n }\n return cmin == 0; // Return true if can found `openCount == 0` in range [cmin, cmax]\n }\n}\n```
| 4 | 0 |
['Java']
| 5 |
minimum-remove-to-make-valid-parentheses
|
JAVA Solution Explained in HINDI(4 Approaches)
|
java-solution-explained-in-hindi4-approa-ponx
|
https://youtu.be/UwIcJm_-9L8\n\nFor explanation, please watch the above video and do like, share and subscribe the channel. \u2764\uFE0F Also, please do upvote
|
The_elite
|
NORMAL
|
2024-04-06T16:39:00.438012+00:00
|
2024-04-08T06:57:06.711549+00:00
| 287 | false |
https://youtu.be/UwIcJm_-9L8\n\nFor explanation, please watch the above video and do like, share and subscribe the channel. \u2764\uFE0F Also, please do upvote the solution if you liked it.\n\nSubscribe link:- [ReelCoding](https://www.youtube.com/@reelcoding?sub_confirmation=1)\n\nSubscribe Goal:- 300\nCurrent Subscriber:- 293\n\n# Approach 1\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public String minRemoveToMakeValid(String s) {\n HashSet<Integer> badIndex = new HashSet<>();\n ArrayDeque<Integer> st = new ArrayDeque<>();\n\n for (int i = 0; i < s.length(); i++) {\n if (s.charAt(i) == \'(\') {\n st.push(i);\n } else if (s.charAt(i) == \')\') {\n if (st.isEmpty()) {\n badIndex.add(i);\n } else {\n st.pop();\n }\n }\n }\n\n while (!st.isEmpty()) {\n badIndex.add(st.pop());\n }\n\n StringBuilder ans = new StringBuilder();\n for (int i = 0; i < s.length(); i++) {\n if (!badIndex.contains(i)) {\n ans.append(s.charAt(i));\n }\n }\n \n return ans.toString();\n }\n}\n\n```\n\n# Approach 2\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n```\nclass Solution {\n public String minRemoveToMakeValid(String s) {\n HashSet<Integer> badIndex = new HashSet<>();\n int diff = 0;\n\n for (int i = 0; i < s.length(); i++) {\n if (s.charAt(i) == \'(\') {\n diff++;\n } else if (s.charAt(i) == \')\') {\n if (diff == 0) {\n badIndex.add(i);\n } else {\n diff--;\n }\n }\n }\n\n for (int i = s.length() - 1; i >= 0 && diff > 0; i--) {\n if (s.charAt(i) == \'(\') {\n diff--;\n badIndex.add(i);\n }\n }\n\n StringBuilder ans = new StringBuilder();\n for (int i = 0; i < s.length(); i++) {\n if (!badIndex.contains(i)) {\n ans.append(s.charAt(i));\n }\n }\n \n return ans.toString();\n }\n}\n```\n# Approach 3\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n```\nclass Solution {\n public String removeWhYouCan(String s, char open, char close) {\n StringBuilder ans = new StringBuilder();\n int diff = 0;\n\n for (int i = 0; i < s.length(); i++) {\n char c = s.charAt(i);\n if (c == open) {\n diff++;\n ans.append(c);\n } else if (c == close) {\n if (diff == 0) {\n continue;\n }\n diff--;\n ans.append(c);\n } else {\n ans.append(c);\n }\n }\n\n return ans.toString();\n }\n\n public String minRemoveToMakeValid(String s) {\n String ans = removeWhYouCan(s, \'(\', \')\');\n ans = new StringBuilder(ans).reverse().toString();\n ans = removeWhYouCan(ans, \')\', \'(\');\n return new StringBuilder(ans).reverse().toString();\n }\n}\n```\n\n# Approach 4\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n```\nclass Solution {\n public String minRemoveToMakeValid(String s) {\n StringBuilder ans = new StringBuilder();\n int diff = 0;\n int countOpen = 0;\n\n // First pass to remove invalid closing parentheses and count open parentheses\n for (int i = 0; i < s.length(); i++) {\n char c = s.charAt(i);\n if (c == \'(\') {\n diff++;\n countOpen++;\n ans.append(c);\n } else if (c == \')\') {\n if (diff == 0) {\n continue;\n }\n diff--;\n ans.append(c);\n } else {\n ans.append(c);\n }\n }\n\n // Second pass to remove extra open parentheses\n StringBuilder res = new StringBuilder();\n int times = countOpen - diff;\n for (int i = 0; i < ans.length(); i++) {\n char c = ans.charAt(i);\n if (c == \'(\') {\n times--;\n if (times < 0) {\n continue;\n }\n }\n res.append(c);\n }\n \n return res.toString();\n }\n}\n```\n
| 4 | 0 |
['Java']
| 0 |
minimum-remove-to-make-valid-parentheses
|
C++ || Beats 93% 🔥|| ✅Easy Solution with Explanation || Stack
|
c-beats-93-easy-solution-with-explanatio-1v6g
|
Approach\n\n- If opening parenthesis \'(\':\n - Push its index into stack.\n- If closing parenthesis \')\' , then two cases arises:\n - stack is not empty {me
|
roligautam118
|
NORMAL
|
2024-04-06T11:09:55.396903+00:00
|
2024-04-06T11:09:55.396927+00:00
| 162 | false |
# Approach\n\n- If opening parenthesis \'(\':\n - Push its index into stack.\n- If closing parenthesis \')\' , then two cases arises:\n - stack is not empty {means there is a matching opening parenthesis}, pop the top index from the stack.\n - stack is empty, means there is no matching opening parenthesis for this closing parenthesis, so erase it from the string and decrement the loop index.\n- After processing all parentheses, remove any remaining unmatched opening parentheses by erasing them from the string.\n- Return the modified string.\n\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n string minRemoveToMakeValid(string s) {\n stack<int> st;\n for (int i = 0; i < s.length(); i++) {\n if(s[i] == \'(\'){\n st.push(i);\n }else if(s[i] == \')\'){\n if(!st.empty()) st.pop();\n else{\n s.erase(i, 1);\n i--;\n }\n }\n }\n while (!st.empty()) {\n int pos = st.top();\n st.pop();\n s.erase(pos,1);\n }\n return s;\n }\n};\n```
| 4 | 0 |
['String', 'Stack', 'C++']
| 1 |
minimum-remove-to-make-valid-parentheses
|
STACK || Solution of minimum remove to make valid parentheses problem
|
stack-solution-of-minimum-remove-to-make-0g7b
|
This was a daily challenge for April 6th 2024.\n# Stack\nTo solve this problem we use the stack structure\n## Definition \nA stack is a linear data structure th
|
tiwafuj
|
NORMAL
|
2024-04-06T08:36:48.867509+00:00
|
2024-04-07T19:13:16.692871+00:00
| 383 | false |
# This was a daily challenge for April 6th 2024.\n# Stack\n**To solve this problem we use the stack structure**\n## Definition \nA stack is a linear data structure that stores items in a Last-In/First-Out (LIFO) or First-In/Last-Out (FILO) manner. In stack, a new element is added at one end and an element is removed from that end only. The insert and delete operations are often called push and pop.\n## Usage\nThe functions associated with stack are:\n- `empty()` \u2013 Returns whether the stack is empty \u2013 Time Complexity: $$O(1)$$\n- `size()` \u2013 Returns the size of the stack \u2013 Time Complexity: $$O(1)$$\n- `top()` / `peek()` \u2013 Returns a reference to the topmost element of the stack \u2013 Time Complexity: $$O(1)$$\n- `pop()` \u2013 Deletes the topmost element of the stack \u2013 Time Complexity: $$O(1)$$\n# Approach\n- First step: \n**if current char is `"("`:** add `"("` to the stack and to the answer\n**if current char is `")"`:** if stack has `"("` then add `")"` to the answer and pop `"("` from the stack\n**if current char is not `"("` or `")"`:** add char to the answer\n- Second step:\nif stack has any amount of `"("` then replace them with `""`\n# Complexity\n- Time complexity:\n$$O(n)$$ - as loop takes linear time\n- Space complexity:\n$$O(n)$$ - as we use extra space for stack and answer \n\n# Code\n```\nclass Solution:\n def minRemoveToMakeValid(self, s: str) -> str:\n stack = []\n answer = ""\n for idx in range(len(s)):\n if s[idx] == "(":\n stack.append((s[idx], idx))\n answer += s[idx]\n elif s[idx] == ")":\n if len(stack) > 0:\n stack.pop()\n answer += s[idx]\n else:\n answer += s[idx]\n pre_answer = answer[::-1]\n answer = pre_answer.replace(\'(\', \'\', len(stack))\n return answer[::-1]\n\n```
| 4 | 0 |
['String', 'Stack', 'Python3']
| 0 |
minimum-remove-to-make-valid-parentheses
|
easy code in c++
|
easy-code-in-c-by-shobhit_panuily-vi1q
|
\n# Code\n\nclass Solution {\npublic:\n string minRemoveToMakeValid(string s) {\n stack<char> st;\n int n=s.size();\n string ans="";\n
|
Shobhit_panuily
|
NORMAL
|
2024-04-06T06:15:57.384087+00:00
|
2024-04-06T06:15:57.384119+00:00
| 189 | false |
\n# Code\n```\nclass Solution {\npublic:\n string minRemoveToMakeValid(string s) {\n stack<char> st;\n int n=s.size();\n string ans="";\n for(int i=0;i<n;i++) {\n if(s[i] == \'(\') {\n st.push(s[i]);\n }\n else if(s[i] == \')\') {\n if( !st.empty() ) {\n st.pop();\n }\n else {\n continue;\n }\n }\n ans.push_back(s[i]);\n }\n int i=ans.size()-1;\n while(!st.empty() && i>=0) {\n if(ans[i] == \'(\') {\n ans.erase(ans.begin()+i);\n st.pop();\n }\n i--;\n }\n return ans;\n }\n};\n```
| 4 | 0 |
['C++']
| 0 |
minimum-remove-to-make-valid-parentheses
|
Easy Solution with Explanation 🔥🔥🔥 | Beats 96.23% 🔥🔥🔥 | Python | Python3
|
easy-solution-with-explanation-beats-962-nitl
|
Intuition\n Describe your first thoughts on how to solve this problem. \nThe core idea here is to make sure every opening parenthesis \'(\' finds a matching clo
|
KrishSukhani23
|
NORMAL
|
2024-04-06T01:40:32.496717+00:00
|
2024-04-06T01:40:32.496740+00:00
| 924 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe core idea here is to make sure every opening parenthesis \'(\' finds a matching closing parenthesis \')\' and vice versa. However, if there\'s an imbalance\u2014too many opening or closing parentheses\u2014we need to remove the minimum number to correct this imbalance. We focus on ensuring the string becomes valid by having each parenthesis pair properly matched from left to right.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTrack Open Parentheses: We use a stack to keep track of parentheses as we scan through the string. The stack helps us understand the current state of open and closed parentheses.\nScan and Build: As we go through each character in the string:\n- If it\'s an opening parenthesis \'(\', we add it to the stack and note that we have one more unmatched \'(\'.\n- If it\'s a closing parenthesis \')\', we check if we have an unmatched \'(\' earlier. If we do, this \')\' is a valid match, and we add it to the stack. \n- If not, we ignore this \')\' because it doesn\'t have a pair.\n- For any other character, we just add it to the stack since they don\'t affect the validity of the parentheses.\n\nRemove Excess Opening Parentheses: After the first pass, we might have some \'(\' left without a match. We then make a backward pass through the stack to remove these excess \'(\' characters, ensuring we don\'t leave any unmatched \'(\'.\n\nReconstruct the String: Finally, we join the characters left in the stack to form the modified string, which now has valid parentheses.\n\n\n# Complexity\nTime complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n- O(N): We traverse the string twice\u2014once to build the stack and once to remove any unmatched \'(\'. Since each pass is linear with respect to the length of the string (N), the overall time complexity is linear.\n\n\nSpace complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n- O(N): In the worst case, we might need to store all characters of the string in the stack (for example, if all characters are opening parentheses). Thus, the space complexity is linear with respect to the input string\'s length.\n\n# Code\n```\nclass Solution:\n def minRemoveToMakeValid(self, s: str) -> str:\n stack = [] # Keep track of valid characters.\n array = list(s) \n\n paranthesisCount = 0 # Number of open parentheses.\n\n for char in array:\n if char == \'(\':\n # If the char is (, increment the count and add it to the stack.\n paranthesisCount += 1\n stack.append(char)\n elif char == \')\':\n # If the char is a ), check if there is an unmatched open parenthesis.\n if paranthesisCount > 0:\n # If there is, decrement the count and add the closing parenthesis to the stack.\n paranthesisCount -= 1\n stack.append(char)\n else:\n # If there isn\'t, ignore this closing parenthesis as it\'s invalid.\n continue\n else:\n # If the character is not a parenthesis, add it to the stack as it is.\n stack.append(char)\n \n # Now, we need to remove any unmatched open parentheses from the stack.\n # We iterate in reverse to start from the end of the string.\n for i in range(len(stack)-1, -1, -1):\n if paranthesisCount > 0 and stack[i] == \'(\':\n # If we still have unmatched open parentheses, remove them from the stack.\n stack.pop(i)\n paranthesisCount -= 1\n \n # Convert the stack back to a string and return it.\n return \'\'.join(stack)\n\n```
| 4 | 0 |
['Stack', 'Python', 'Python3']
| 4 |
minimum-remove-to-make-valid-parentheses
|
C++ Solution || Stack || Very Easy Understanding
|
c-solution-stack-very-easy-understanding-p67d
|
Intuition\n Describe your first thoughts on how to solve this problem. \nfind an invalid bracket index and store in stack.\nwhile traversing stack remove that b
|
sunnyjha1512002
|
NORMAL
|
2023-01-04T06:24:53.268397+00:00
|
2023-01-04T06:24:53.268441+00:00
| 827 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nfind an invalid bracket index and store in stack.\nwhile traversing stack remove that bracket from string.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nstack\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$o(n)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$o(n)$$\n\n# Code\n```\nclass Solution {\npublic:\n string minRemoveToMakeValid(string s) {\n stack<pair<char,int>> st;\n int n = s.size();\n for(int i=0;i<n;i++){\n if(s[i]==\'(\'){\n st.push({s[i],i});\n }else if(s[i]==\')\') {\n if(!st.empty()&&st.top().first==\'(\'){\n st.pop();\n }else{\n st.push({s[i],i});\n }\n }\n }\n while(!st.empty()){\n int top = st.top().second;\n s.erase(s.begin()+top);\n st.pop();\n }\n return s;\n }\n};\n```
| 4 | 0 |
['String', 'Stack', 'C++']
| 1 |
minimum-remove-to-make-valid-parentheses
|
9-line Simple C++ Solution No Stack No Deque!!!
|
9-line-simple-c-solution-no-stack-no-deq-dbi6
|
Please upvote if you find the code helpful!!!\nThis solution is sort of a simili to a stack, but I am not using stack here.\n\n// Without explanation -- for tho
|
pieceofpie
|
NORMAL
|
2022-08-20T19:42:09.296827+00:00
|
2022-08-20T19:42:09.296891+00:00
| 369 | false |
Please ***upvote*** if you find the code helpful!!!\nThis solution is sort of a simili to a stack, but I am not using stack here.\n```\n// Without explanation -- for those who want to copy-paste my solution ;)\nclass Solution {\npublic:\n string minRemoveToMakeValid(string s) {\n int C = 0; string ans; vector<char> hehe;\n for (int i = 0; i < s.size(); i++) {\n if (s[i] == \'(\') { C++; hehe.push_back(s[i]); } \n else if (s[i] == \')\') {if (C > 0) { C--; hehe.push_back(s[i]); }}\n else hehe.push_back(s[i]); \n }\n if (C > 0) for (int i = hehe.size() - 1; i >= 0; i--) if (hehe[i] == \'(\') { hehe.erase(hehe.begin() + i); C--; if (C == 0) break; }\n for (int i = 0; i < hehe.size(); i++) ans += hehe[i];\n return ans;\n }\n};\n```\n```\n// With explanation\nclass Solution {\npublic:\n string minRemoveToMakeValid(string s) {\n\t\t// Defining the variables\n int C = 0; string ans; vector<char> hehe;\n for (int i = 0; i < s.size(); i++) {\n\t\t\t // add a \'(\' every time we encounter one\n if (s[i] == \'(\') { C++; hehe.push_back(s[i]); }\n\t\t\t// make sure that the number of \'(\' is equal to the number of \')\'; if there are more \')\' than \'(\', skip\n else if (s[i] == \')\') {if (C > 0) { C--; hehe.push_back(s[i]); }}\n // if char is a lowercase letter just add the letter\n\t\t\telse hehe.push_back(s[i]);\n }\n\t\t// If there are more \'(\' than \')\' at the end, delete the \'(\' from right to left\n\t\t// until when the number of \'(\' is equal to the number of \')\' (i.e. when C == 0)\n if (C > 0) for (int i = hehe.size() - 1; i >= 0; i--) if (hehe[i] == \'(\') { hehe.erase(hehe.begin() + i); C--; if (C == 0) break; }\n\t\t// Add the remaining chars in the answer since we need to return a string\n for (int i = 0; i < hehe.size(); i++) ans += hehe[i];\n\t\t// Return da answer!\n return ans;\n }\n};\n```\n```\n// Readable Version With explanation\nclass Solution {\npublic:\n string minRemoveToMakeValid(string s) {\n\t\t// Defining the variables\n int C = 0;\n string ans;\n vector<char> hehe;\n for (int i = 0; i < s.size(); i++) {\n\t\t\t// add a \'(\' every time we encounter one\n if (s[i] == \'(\') {\n C++;\n hehe.push_back(s[i]);\n }\n\t\t\t// make sure that the number of \'(\' is equal to the number of \')\'; if there are more \')\' than \'(\', skip\n else if (s[i] == \')\') {\n if (C > 0) {\n C--;\n hehe.push_back(s[i]);\n }\n }\n\t\t\t// if char is a lowercase letter just add the letter\n else hehe.push_back(s[i]);\n }\n\t\t// If there are more \'(\' than \')\' at the end, delete the \'(\' from right to left\n\t\t// until when the number of \'(\' is equal to the number of \')\' (i.e. when C == 0)\n if (C > 0) {\n for (int i = hehe.size() - 1; i >= 0; i--) {\n if (hehe[i] == \'(\') {\n hehe.erase(hehe.begin() + i); C--;\n if (C == 0) break;\n }\n }\n }\n\t\t// Add the remaining chars in the answer since we need to return a string\n for (int i = 0; i < hehe.size(); i++) ans += hehe[i];\n\t\t// Return da answer!\n return ans;\n }\n};\n```\nPlease ***upvote*** if you find the code helpful!!!
| 4 | 0 |
['C', 'C++']
| 0 |
minimum-remove-to-make-valid-parentheses
|
Python Easy understanding
|
python-easy-understanding-by-hardernhard-pwt6
|
2 arrays to store the 1) index of ( and 2) charactors of str\n```\nclass Solution:\n def minRemoveToMakeValid(self, s: str) -> str:\n\t\tstack = []\n
|
hardernharder
|
NORMAL
|
2022-05-17T02:16:15.857231+00:00
|
2022-05-17T02:24:06.626498+00:00
| 139 | false |
2 arrays to store the 1) index of `(` and 2) charactors of `str`\n```\nclass Solution:\n def minRemoveToMakeValid(self, s: str) -> str:\n\t\tstack = []\n res = []\n for i,v in enumerate(s):\n res.append(v) # save the charactors to final resutls\n if v == \'(\':\n stack.append(i) # always save left \'(\' index, to decided if this need to remove or not \n if v == \')\':\n if stack:\n stack.pop() # as stack saved left \'(\', so here is good to pop one no matter the index value, just pop the left as a pair\n else:\n res[-1] = \'\' # as stack is empty, now we see additional right \')\', need replace res[-1] with a empty str, \n\t\t\t\t\t # why not pop out? \n\t\t\t\t\t\t\t\t\t\t# if we do pop, once we loop to the end of the string\n\t\t\t\t\t\t\t\t\t\t# if we still have some left \'(\' in stack, \n\t\t\t\t\t\t\t\t\t\t# while we do replace array value, it may mess up. \n\t\t\t\t\t\t\t\t\t\t# here, we need keep our res index consistent with the original str \'s\'.\n\t\t\n\t\t# if we have some left \'(\' index stack, which means not paired ones, let\'s remove these ones\n while stack:\n res[stack.pop()] = \'\'\n\t\t\n return "".join(res)\n\t\t\t\t\t\n\t\t\t\t\t\n\t\t\t\t\t\n\t\t\t\t\t\n\t\t\t\t\t\n\t\t\t\t\t\n\t\t\t\t\t\n\t\t\t\t\t
| 4 | 0 |
['Stack', 'Python']
| 0 |
minimum-remove-to-make-valid-parentheses
|
C++ | Sharing my O(1) Space Complexity
|
c-sharing-my-o1-space-complexity-by-edua-n0fx
|
The ideia here it\'s to do all the operations in-place of the string s. \n\nLet\'s divide the problem in three steps:\n\t1. Mark all the extra closing parenthe
|
eduardocesb
|
NORMAL
|
2022-04-17T17:23:24.128065+00:00
|
2022-04-17T17:23:24.128104+00:00
| 93 | false |
The ideia here it\'s to do all the operations in-place of the string `s`. \n\nLet\'s divide the problem in three steps:\n\t1. Mark all the extra closing parenthesis to be removed in the future, changing the values to a space.\n\t2. Mark all the extra opening parenthesis to be remover in the future, changing the values to a space.\n\t3. Erase the spaces in the string `s`, moving the non-space chars to the left.\n\n\n```\nclass Solution {\nprivate:\n void removeInvalid(string &s, char open, char close)\n {\n int count = 0;\n\n for (auto &curr : s)\n {\n if (curr == open)\n count++;\n else if (curr != close)\n continue;\n else if (count == 0)\n curr = \' \';\n else\n count--;\n }\n }\npublic:\n string& minRemoveToMakeValid(string &s) {\n //"Removing" the extra closing parenthesis.\n removeInvalid(s, \'(\', \')\');\n reverse(s.begin(), s.end());\n\n //"Removing" the extra opening parenthesis.\n removeInvalid(s, \')\', \'(\');\n reverse(s.begin(), s.end());\n\n //Removing the extra spaces in the string\n int lastIndex = 0;\n for (auto curr : s)\n if (curr != \' \')\n s[lastIndex++] = curr;\n\n //Removing the extra chars remaing in the end\n s.resize(lastIndex);\n\n return s;\n }\n};\n```
| 4 | 0 |
[]
| 1 |
minimum-remove-to-make-valid-parentheses
|
✅ Python Easy prefix count
|
python-easy-prefix-count-by-dhananjay79-xga5
|
The approach is quite simple\n1. To add the opening (, we have to see the future, how many closing ) are at right side in order to make it valid, so we count it
|
dhananjay79
|
NORMAL
|
2022-03-15T14:51:36.259141+00:00
|
2022-03-15T15:12:05.223879+00:00
| 161 | false |
The approach is quite simple\n1. To add the opening ```(```, we have to see the future, how many closing ```)``` are at right side in order to make it valid, so we count it. if we have some closing at right then only we can add the opening.\n2. To add the closing ```)``` we have to count how many opening```(``` we had at left side waiting for closing ```)```. If no one is waiting why would we add it.\n```\nclass Solution:\n def minRemoveToMakeValid(self, s: str) -> str:\n closing, opening, ans = s.count(\')\'), 0, \'\'\n for i in s:\n if i == \'(\':\n opening += 1\n if opening <= closing: ans += \'(\'\n elif i == \')\':\n if opening > 0: ans += \')\'\n closing -= 1; opening -= 1\n if opening < 0: opening = 0\n else: ans += i\n return ans\n```
| 4 | 0 |
['Python', 'Python3']
| 0 |
minimum-remove-to-make-valid-parentheses
|
Stack Solution using Python || Intuition + Code || Easy-to-understand
|
stack-solution-using-python-intuition-co-99tp
|
Intuition:\n\n\nSolution:\n\n def minRemoveToMakeValid(self, s: str) -> str:\n string = list(s)\n stack = []\n for i in range(len(string
|
deleted_user
|
NORMAL
|
2022-03-15T14:17:51.545464+00:00
|
2022-03-15T14:17:51.545494+00:00
| 136 | false |
# Intuition:\n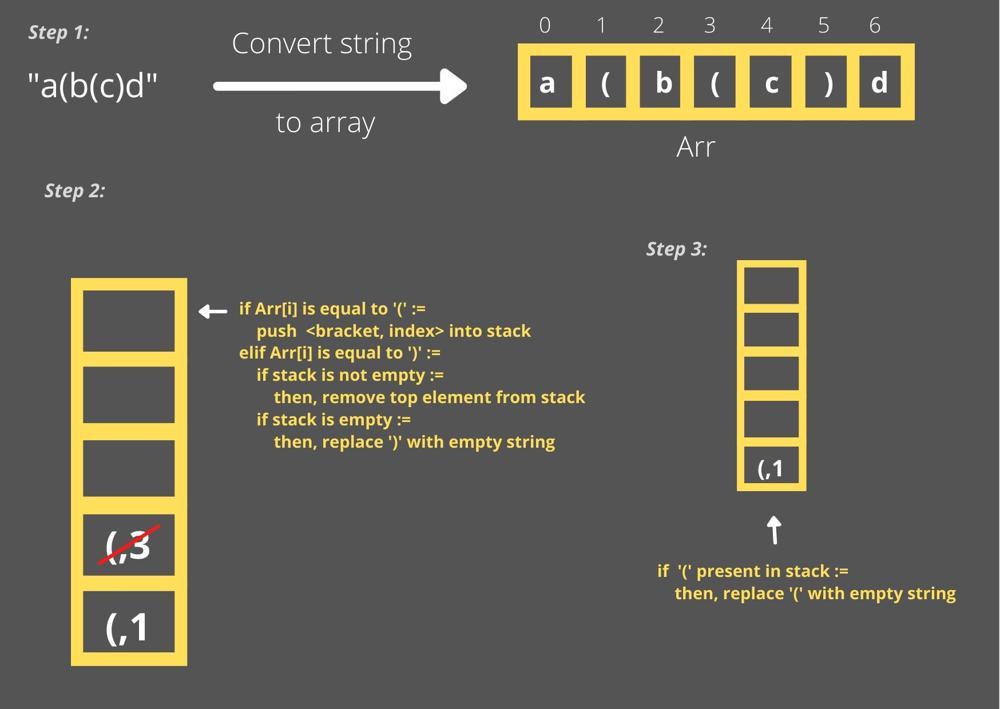\n\n**Solution:**\n```\n def minRemoveToMakeValid(self, s: str) -> str:\n string = list(s)\n stack = []\n for i in range(len(string)):\n if string[i] == \'(\':\n stack.append((\'(\',i))\n elif string[i] == \')\':\n if stack:\n stack.pop()\n else:\n string[i] = ""\n for i in range(len(stack)):\n string[stack[i][1]] = ""\n \n return "".join(string)\n```\n\n- Hope you find this helpful. Feel free to comment your approachs and intuition.\n
| 4 | 0 |
['Stack', 'Python']
| 2 |
minimum-remove-to-make-valid-parentheses
|
Minimum Remove to make Valid parentheses
|
minimum-remove-to-make-valid-parentheses-72ub
|
//Input: s = "lee(t(c)o)de)"\nOutput: "lee(t(c)o)de"\nExplanation: "lee(t(co)de)" , "lee(t(c)ode)" would also be accepted.//\n******Explanations*****\n-->In the
|
shrutikumariagrahari
|
NORMAL
|
2022-03-15T13:08:06.264041+00:00
|
2022-04-02T07:08:51.583223+00:00
| 194 | false |
//Input: s = "lee(t(c)o)de)"\nOutput: "lee(t(c)o)de"\nExplanation: "lee(t(co)de)" , "lee(t(c)ode)" would also be accepted.//\n*********************************************Explanations************************************\n-->In the given que we need to remove the extra \'(\' & \')\' (brackets).\n-->first apporach in my mind that we use string , stack , map and so on.\n-->so , I m using the string .\n-->firstly iterate the loop from the starting and the secondly iterate the loop from the ending.\n--> so , my apporach is that we iterate the loop from the starting and if we find the "("(opening bracket) , then increment it , and if we find the ")"(closing bracket) is more then the "(" then we need to decrement it .(no. closing> no.opening)\n--> thats why we are using the s[i]==\'@\', and decrement the count --;\n--> second loop started from the end . \n--> if no. opening > the no. closing , then decrement the \'(\' (opening)\n--> at last run the loop \n\n```\nclass Solution {\npublic:\n string minRemoveToMakeValid(string s) {\n int n=s.length();\n int count=0;\n\t\t// first loop from the starting \n for(int i=0;i<n;i++){\n if(s[i]==\'(\'){\n count++;\n }\n else if(s[i]==\')\'){\n if(count==0){\n s[i]=\'@\';\n }\n else{\n count--;\n }\n }\n }\n\t\t// second loop from the ending\n count=0;\n for(int i=n-1;i>=0;i--){\n if(s[i]==\')\'){\n count++;\n }\n else if(s[i]==\'(\'){\n if(count==0){\n s[i]=\'@\';\n }\n else{\n count--;\n }\n }\n }\n string ans="";\n for(int i=0;i<n;i++){\n if(s[i]!=\'@\'){\n ans.push_back(s[i]);\n }\n }\n return ans;\n }\n};\n```\n**If this code is helpful then please upvote my solution and if any query then feel free to ask \nTHANKU**
| 4 | 1 |
['String', 'C', 'C++']
| 0 |
minimum-remove-to-make-valid-parentheses
|
1249 | C++ | Easy O(N) solution with explanation
|
1249-c-easy-on-solution-with-explanation-8rtl
|
Please upvote if you find this solution helpful :)\n\nAlgorithm:\n initialize count = 0 and result string\n\nStart traversing from beginning\n if we find open p
|
Yash2arma
|
NORMAL
|
2022-03-15T06:20:17.869981+00:00
|
2022-03-15T06:31:14.733976+00:00
| 57 | false |
**Please upvote if you find this solution helpful :)**\n\n**Algorithm:**\n* initialize count = 0 and result string\n\n**Start traversing from beginning**\n* if we find open parenthesis then we increase the count by 1 that helps in find valid pair.\n* if we find close parenthesis there may be 2 cases.\n* \tif count==0 it means there is no open parenthesis and this close parenthesis is invalid so we replace s[i] with \'_\'.\n* \telse decrease the count by 1 because we find one valid pair.\n\nNow, again initialze count = 0\n\n**and start traversing from the end.**\n* \tif we find close parenthesis then we increase the count by 1that helps in find valid pair.\n* \tif we find open parenthesis there may be 2 cases.\n* \tif count==0 it means this open parenthesis is invalid so we replace s[i] with \'_\'.\n* \telse decrease the count by 1 becuase we find valid pair.\n\t\t\n\t\t\n**Now, we again traverse through string from beginning and if s[i] != \'_ \' we put that char into the result string.**\n\n**Time Complexity - O(N)\nSpace Complexity - O(1).**\n\n```\nclass Solution {\npublic:\n string minRemoveToMakeValid(string s) \n {\n string res = "";\n int n = s.size(), count = 0;\n \n //iterate from beginning\n for(int i=0; i<n; i++)\n {\n //if get \'(\' increase count by 1\n if(s[i] == \'(\')\n count++;\n \n else if(s[i] == \')\')\n {\n // if count=0 replace \')\' with \'_\'\n if(count==0)\n s[i] = \'_\';\n \n else \n count--;\n }\n }\n \n count = 0;\n //Now iterate from end\n for(int i=n-1; i>=0; i--)\n {\n //if get \')\' increase count by 1\n if(s[i] == \')\')\n count++;\n \n else if(s[i] == \'(\')\n {\n //if count=0 replace \'(\' with \'_\'\n if(count==0)\n s[i] = \'_\';\n else \n count--;\n }\n }\n \n //add all the char into res string except \'_\'\n for(int i=0; i<n; i++)\n {\n if(s[i] != \'_\')\n {\n res.push_back(s[i]);\n }\n }\n return res;\n }\n};\n```\n\n\n**Please upvote if you find this solution helpful :)**
| 4 | 0 |
[]
| 0 |
minimum-remove-to-make-valid-parentheses
|
Simple | JAVA | Using Stack
|
simple-java-using-stack-by-anantashutosh-ze3q
|
\nclass Solution {\n public String minRemoveToMakeValid(String s) {\n \n \n Stack<Integer> st= new Stack<>(); //to check for valid pare
|
anantashutosh
|
NORMAL
|
2022-03-15T01:57:04.561518+00:00
|
2022-03-15T01:57:04.561559+00:00
| 285 | false |
```\nclass Solution {\n public String minRemoveToMakeValid(String s) {\n \n \n Stack<Integer> st= new Stack<>(); //to check for valid parentheses\n char[] ch=s.toCharArray(); \n \n //this for loop make valid ch array and containing \'.\' you can use anything for flag\n for(int i=0;i<ch.length;i++){\n \n if(ch[i]==\'(\'){\n st.push(i);\n }else if(ch[i] == \')\'){\n if(st.size()==0){\n ch[i]=\'.\';\n }else\n st.pop();\n }\n \n \n }\n \n \n //remaining elements in stack\n while(st.size()>0){\n ch[st.pop()] =\'.\';\n }\n \n \n //store arrays ch int string for returning the valid string\n StringBuilder str = new StringBuilder();\n for(char c : ch){\n if(c!=\'.\'){\n str.append(c);\n }\n }\n \n \n return str.toString();\n }\n}\n```
| 4 | 1 |
['String', 'Stack', 'Java']
| 1 |
minimum-remove-to-make-valid-parentheses
|
C++ | Without using stack | Easy to Understand
|
c-without-using-stack-easy-to-understand-pf7j
|
Intution\n 1. Add closing bracket to answer string when count of open bracket is greater than closing bracket.\n 2. Remove the extra open bracket from the answe
|
__aditya45__
|
NORMAL
|
2022-02-03T05:11:53.977222+00:00
|
2022-02-03T05:19:54.359454+00:00
| 115 | false |
**Intution**\n **1.** Add closing bracket to answer string when count of open bracket is greater than closing bracket.\n **2.** Remove the extra open bracket from the answer string.\n \n```\nclass Solution {\npublic:\n string minRemoveToMakeValid(string s) {\n string ans=""; // Create Empty string to store characters \n int c1=0; // store Count of open brackets\n int c2=0; //Store count of closing bracket\n for(int i=0;i<s.size();i++)\n {\n if(s[i]==\'(\')\n {\n c1++;\n ans+=s[i];\n }\n else if(s[i]==\')\')\n {\n if(c1>c2) //Adding closing bracket to asnwer string when count of opening bracket greater than the closing bracket\n {\n ans+=s[i];\n c2++;\n }\n }\n else{\n ans+=s[i];\n }\n }\n\t\t/* Answer string may contain extra open brackets so we have to remove the extra open brackets*/\n string p=""; \n c1=0;\n for(int i=0;i<ans.size();i++) //For Example answer string may be ans="(a(a(b)vd)"\n {\n if(ans[i]==\'(\' && c1<c2) // Add only c2 no. of open brackets to the final string\n {\n p+=ans[i];\n c1++;\n }\n else if(ans[i]!=\'(\')\n {\n p+=ans[i];\n }\n \n }\n return p;\n }\n};\n```
| 4 | 0 |
['String']
| 0 |
minimum-remove-to-make-valid-parentheses
|
C++ | Stack | O(N)
|
c-stack-on-by-vaman644-9r6u
|
\nstring minRemoveToMakeValid(string s) {\n\tstack<int> st;\n\tfor (int i = 0; i < s.length(); i++) {\n\t\tif (s[i] == \'(\') {\n\t\t\tst.push(i);\n\t\t} else i
|
vaman644
|
NORMAL
|
2022-01-02T10:50:16.436077+00:00
|
2022-01-02T10:50:16.436108+00:00
| 199 | false |
```\nstring minRemoveToMakeValid(string s) {\n\tstack<int> st;\n\tfor (int i = 0; i < s.length(); i++) {\n\t\tif (s[i] == \'(\') {\n\t\t\tst.push(i);\n\t\t} else if (s[i] == \')\') {\n\t\t\tif (!st.empty())\n\t\t\t\tst.pop();\n\t\t\telse\n\t\t\t\ts[i] = \'*\';\n\t\t}\n\t}\n\n\twhile (!st.empty()) {\n\t\ts[st.top()] = \'*\';\n\t\tst.pop();\n\t}\n\n\tstring ans;\n\tfor (auto ch : s) {\n\t\tif (ch != \'*\') {\n\t\t\tans += ch;\n\t\t}\n\t}\n\treturn ans;\n}\n```
| 4 | 0 |
['Stack', 'C']
| 1 |
minimum-remove-to-make-valid-parentheses
|
js stack
|
js-stack-by-soley-eon6
|
\nvar minRemoveToMakeValid = function(s) {\n let op = []\n s = s.split(\'\')\n for(let i=0; i<s.length; i++){\n if(s[i]===\'(\') op.push(i)\n
|
soley
|
NORMAL
|
2021-03-12T16:22:29.926912+00:00
|
2021-03-12T16:22:29.926951+00:00
| 183 | false |
```\nvar minRemoveToMakeValid = function(s) {\n let op = []\n s = s.split(\'\')\n for(let i=0; i<s.length; i++){\n if(s[i]===\'(\') op.push(i)\n if(s[i]===\')\') {\n if(op.length) op.pop(); else s[i]=\'\'\n }\n }\n while(op.length) s[op.pop()]=\'\';\n return s.join(\'\')\n};\n```
| 4 | 1 |
['JavaScript']
| 0 |
minimum-remove-to-make-valid-parentheses
|
Minimum Remove to Make Valid Parentheses | JS, Python, Java, C++ | Stack Solution w/ Explanation
|
minimum-remove-to-make-valid-parentheses-ysy0
|
(Note: This is part of a series of Leetcode solution explanations. If you like this solution or find it useful, please upvote this post.)\n\n---\n\nIdea:\n\nVal
|
sgallivan
|
NORMAL
|
2021-02-19T13:03:51.414279+00:00
|
2021-02-19T18:22:13.122992+00:00
| 254 | false |
*(Note: This is part of a series of Leetcode solution explanations. If you like this solution or find it useful,* ***please upvote*** *this post.)*\n\n---\n\n***Idea:***\n\nValid parentheses follow the **LIFO method** (last in, first out), so we should automatically be thinking of some kind of **stack** solution.\n\nTo check for valid parentheses, you push any **"("** onto **stack**, then pop off the top stack element every time you find a matching **")"**. If you find a **")"** when **stack** is empty, that **")"** must be invalid. At the end of **S**, any leftover **"("**\'s left in **stack** must be invalid, as well. Since we\'ll want to remove those **"("**\'s by index at the end, **stack** should contain said indexes, rather than just the **"("**.\n\nNow that we\'ve identified all the invalid parentheses, that leaves us with the problem of removing them from **S**. We could perform a lot of string slices and copies, but those are typically very slow and memory intensive, so we should probably find a data type that can be directly modified by index access and use that as an intermediary.\n\nThe most effective method varies by language, so I\'ll discuss those in the *Implementation* section.\n\nThen we can make our removals and re-form and **return** our answer.\n\n---\n\n***Implementation:***\n\nJavascript has basic arrays, Python has lists, and Java has char arrays that will perform the job of a more flexible data type for this problem. C++ alone of the four languages has mutable strings, so we can just leave **S** as is.\n\nWhile Java has stack/deque/list structures, they\'re not always terribly efficient, so we can just use a more basic int[] with a length fixed to the size of **S**, along with an index variable (**stIx**).\n\nJavascript conveniently allows us to directly delete an array element without screwing up our iteration, so we can use that on the initial pass for invalid **"("**\'s. Python can\'t do that, but we can easily replace each character we want to delete with an empty string, which effectively does the same thing once the string has been joined again.\n\nJava and C++ won\'t allow us to replace characters with empty strings, so we can just mark those characters with a **character mask** for later removal.\n\nOn the second pass through Javascript and Python can just repeat the same method while going through the remaining **stack**. Python is very fast with its appends and pops, so we can use that to our advantage.\n\nFor Java and C++, things are more difficult. We can\'t change the length of the intermediary, but we *can* alter its contents by index assignment. That means we can use a two-pointer approach to rewrite the beginning portion of the intermediary before ultimately returning a subsection of it.\n\nSince we want to iterate through **stack** in opposite order (**FIFO**) this time, we can just tag a **-1** onto the end of the stack to avoid issues with going out-of-bounds, and then use **stIx** starting at **0**.\n\nThen, for every iteration, **j** will increment, but **i** will only increment if it\'s not a character we want to remove (either by matching the character mask or the next stack entry), and we\'ll overwrite the intermediary at **i** with **j**\'s value.\n\nAt the end, the substring between **0** and **i** will represent the "squeezed" string with all invalid parentheses removed, so we should **return** it.\n\n---\n\n***Javascript Code:***\n\nThe best result for the code below is **76ms / 44.7MB** (beats 100% / 96%).\n```javascript\nvar minRemoveToMakeValid = function(S) {\n S = S.split("")\n let len = S.length, stack = []\n for (let i = 0, c = S[0]; i < len; c = S[++i])\n if (c === ")")\n if (stack.length) stack.pop()\n else delete S[i]\n else if (c === "(") stack.push(i)\n for (let i = 0; i < stack.length; i++)\n delete S[stack[i]]\n return S.join("")\n};\n```\n\n---\n\n***Python Code:***\n\nThe best result for the code below is **72ms / 15.8MB** (beats 100% / 91%).\n```python\nclass Solution:\n def minRemoveToMakeValid(self, S: str) -> str:\n S, stack = list(S), []\n for i, c in enumerate(S):\n if c == ")":\n if stack: stack.pop()\n else: S[i] = ""\n elif c == "(": stack.append(i)\n for i in stack: S[i] = ""\n return "".join(S)\n```\n\n---\n\n***Java Code:***\n\nThe best result for the code below is **5ms / 39.1MB** (beats 100% / 99%).\n```java\nclass Solution {\n public String minRemoveToMakeValid(String S) {\n char[] ans = S.toCharArray();\n int len = S.length(), stIx = 0, i = 0, j = 0;\n int[] stack = new int[len+1];\n for (; i < len; i++)\n if (ans[i] == \')\')\n if (stIx > 0) stIx--;\n else ans[i] = \'_\';\n else if (ans[i] == \'(\') stack[stIx++] = i;\n for (i = 0, stack[stIx] = -1, stIx = 0; j < len; j++)\n if (j == stack[stIx]) stIx++;\n else if (ans[j] != \'_\') ans[i++] = ans[j];\n return new String(ans, 0, i);\n }\n}\n```\n\n---\n\n***C++ Code:***\n\nThe best result for the code below is **16ms / 10.2MB** (beats 99% / 91%).\n```c++\nclass Solution {\npublic:\n string minRemoveToMakeValid(string S) {\n int len = S.size(), i = 0, j = 0, stIx = 0;\n vector<int> stack;\n for (; i < len; i++)\n if (S[i] == \')\')\n if (stack.size() > 0) stack.pop_back();\n else S[i] = \'_\';\n else if (S[i] == \'(\') stack.push_back(i);\n stack.push_back(-1);\n for (i = 0; j < len; j++)\n if (j == stack[stIx]) stIx++;\n else if (S[j] != \'_\') S[i++] = S[j];\n return S.substr(0, i);\n }\n};\n```
| 4 | 6 |
[]
| 1 |
minimum-remove-to-make-valid-parentheses
|
[Python] Minimum Remove to Make Valid Parentheses Solution | easy way
|
python-minimum-remove-to-make-valid-pare-hheq
|
Easy if else conditions\n\n\nclass Solution:\n def minRemoveToMakeValid(self, s: str) -> str:\n s = list(s)\n left_parr = 0\n left_ind =
|
arunrathi201
|
NORMAL
|
2021-02-19T09:39:58.108348+00:00
|
2021-02-19T09:39:58.108385+00:00
| 146 | false |
Easy if else conditions\n\n```\nclass Solution:\n def minRemoveToMakeValid(self, s: str) -> str:\n s = list(s)\n left_parr = 0\n left_ind = []\n for i in range(len(s)):\n if s[i] == \')\' and left_parr == 0:\n s[i] = \'\'\n elif s[i] == \'(\':\n left_parr += 1\n left_ind.append(i)\n elif s[i] == \')\' and left_parr > 0:\n left_parr -= 1\n left_ind.pop()\n\n if len(left_ind) > 0:\n for j in left_ind:\n s[j] = \'\'\n\n return \'\'.join(s)\n```
| 4 | 0 |
['Python']
| 0 |
minimum-remove-to-make-valid-parentheses
|
c++ solution || faster than 98% || using stack
|
c-solution-faster-than-98-using-stack-by-dsyd
|
\n string minRemoveToMakeValid(string s) \n {\n stack<int >st; // stack to store the index to each paranthesis\n for(int i=0;i<s.size();i++)\
|
skjaiswal
|
NORMAL
|
2021-01-21T18:16:01.633248+00:00
|
2021-01-21T18:19:16.748746+00:00
| 101 | false |
```\n string minRemoveToMakeValid(string s) \n {\n stack<int >st; // stack to store the index to each paranthesis\n for(int i=0;i<s.size();i++)\n {\n if(s[i]==\'(\')\n {\n st.push(i);\n }\n else if(s[i]==\')\')\n {\n if(!st.empty())\n st.pop();\n else\n s[i]=\'@\';\n }\n }\n while(!st.empty()) \n {\n int temp=st.top(); st.pop();\n s[temp]=\'@\'; // updating the unbalanced paranthesis with \'@\'\n }\n s.erase(remove(s.begin(),s.end(),\'@\'),s.end()); // removing all occurence of \'@\'\n return s;\n }\n```
| 4 | 0 |
[]
| 0 |
minimum-remove-to-make-valid-parentheses
|
Two approaches - Stack & Without Stack O(1) space
|
two-approaches-stack-without-stack-o1-sp-79sx
|
1. Solution with Stack\nAdd ( to stack index corresponding to the current length of res and skip adding of ) if the stack is empty\n\n\nvar minRemoveToMakeValid
|
ratiboi
|
NORMAL
|
2020-11-07T07:06:23.725015+00:00
|
2021-02-19T21:37:17.860073+00:00
| 285 | false |
**1. Solution with Stack**\nAdd `(` to stack index corresponding to the current length of `res` and skip adding of `)` if the stack is empty\n\n```\nvar minRemoveToMakeValid = function(s) {\n let res = []\n let stack = []\n\t\n for(let i=0; i<s.length; i++){\n if(s[i] == \'(\') stack.push(res.length)\n else if(s[i] == \')\'){\n if(stack.length) stack.pop()\n else continue\n }\n res.push(s[i])\n }\n \n while(stack.length){\n res[stack.pop()] = \'\'\n }\n\n return res.join(\'\')\n};\n```\n\n**2. Solution without Stack**\nThis approach is O(1) space without considering the ouptput array\n\n```\nvar minRemoveToMakeValid = function(s) {\n let res = []\n let r = 0\n let open = 0\n \n for(let char of s){\n if(char == \')\') r++\n }\n \n for(let i=0; i<s.length; i++){\n if(s[i] == \')\'){\n if(open > 0){\n res.push(s[i])\n open--\n }\n else r--\n } else if(s[i] == \'(\'){\n if(r>0){\n res.push(s[i])\n open++\n r--\n }\n } else res.push(s[i])\n }\n \n return res.join(\'\')\n};\n```
| 4 | 0 |
['Stack', 'JavaScript']
| 0 |
minimum-remove-to-make-valid-parentheses
|
C++ very easy solution using stack, Commented
|
c-very-easy-solution-using-stack-comment-8r87
|
\n\nclass Solution {\n\tpublic:\n string minRemoveToMakeValid(string s) {\n //to store value and its index\n\t\t\tstack<pair<int, int>> st;\n s
|
niteshsingh
|
NORMAL
|
2020-08-11T09:26:28.270270+00:00
|
2020-09-07T10:52:34.758918+00:00
| 535 | false |
```\n\nclass Solution {\n\tpublic:\n string minRemoveToMakeValid(string s) {\n //to store value and its index\n\t\t\tstack<pair<int, int>> st;\n string temp;\n for(int i = 0;i<s.size();i++)\n {\n //if we have to remove symbol, store some other symbol instead of this:\n if(s[i] == \')\' && st.empty())\n s[i] = \'{\';\n else if(s[i] == \')\' && !st.empty())\n st.pop();\n else if(s[i] == \'(\')\n st.push({s[i], i});\n \n }\n \n while(!st.empty())\n {\n s[st.top().second] = \'{\';\n st.pop();\n }\n //store required string into some temp,don\'t include symbols which we have to remove.\n for(int i = 0;i<s.size();i++)\n {\n if(s[i] != \'{\')\n temp.push_back(s[i]);\n }\n return temp;\n }\n};\n\n```
| 4 | 0 |
['Stack', 'C', 'C++']
| 1 |
minimum-remove-to-make-valid-parentheses
|
Java Stack of Pairs Solution
|
java-stack-of-pairs-solution-by-ryud54-bhfi
|
\nclass Solution {\n public String minRemoveToMakeValid(String s) {\n Stack<Pair<Character,Integer>> validStack = new Stack<>();\n for(int i =
|
ryud54
|
NORMAL
|
2020-07-23T20:42:18.283457+00:00
|
2020-07-23T20:42:18.283506+00:00
| 4,270 | false |
```\nclass Solution {\n public String minRemoveToMakeValid(String s) {\n Stack<Pair<Character,Integer>> validStack = new Stack<>();\n for(int i = 0; i < s.length(); i++){\n if(s.charAt(i) == \'(\' || s.charAt(i) == \')\'){\n char top = s.charAt(i);\n if(!validStack.isEmpty()) top = validStack.peek().getKey();\n char curr = s.charAt(i);\n if(validStack.isEmpty() || curr == top || (curr == \'(\' && top == \')\')){\n Pair p = new Pair(curr,i);\n validStack.add(p);\n }\n else if(curr == \')\' && top == \'(\'){\n validStack.pop();\n } \n }\n }\n StringBuilder sb = new StringBuilder(s);\n while(!validStack.isEmpty()){\n int index = validStack.peek().getValue();\n sb.deleteCharAt(index);\n validStack.pop();\n }\n return sb.toString();\n }\n}\n```
| 4 | 0 |
[]
| 1 |
minimum-remove-to-make-valid-parentheses
|
C# beats 98.66% using Stack
|
c-beats-9866-using-stack-by-pawel753-n5sa
|
Runtime: 88 ms, faster than 98.66% of C# online submissions for Minimum Remove to Make Valid Parentheses.\nMemory Usage: 34.8 MB, less than 100.00% of C# online
|
pawel753
|
NORMAL
|
2020-05-29T21:19:56.550415+00:00
|
2020-05-29T21:19:56.550447+00:00
| 668 | false |
Runtime: 88 ms, faster than 98.66% of C# online submissions for Minimum Remove to Make Valid Parentheses.\nMemory Usage: 34.8 MB, less than 100.00% of C# online submissions for Minimum Remove to Make Valid Parentheses.\n```\npublic class Solution\n{\n public string MinRemoveToMakeValid(string s)\n {\n var res = new StringBuilder();\n var openPos = new Stack<int>();\n int i = 0;\n foreach (var c in s)\n switch (c)\n {\n case \'(\':\n res.Append(c);\n openPos.Push(i++);\n break;\n case \')\':\n if (openPos.Any())\n {\n res.Append(c);\n openPos.Pop();\n i++;\n }\n break;\n default:\n res.Append(c);\n i++;\n break;\n }\n\n while (openPos.Any())\n {\n var pos = openPos.Pop();\n res.Remove(pos, 1);\n }\n\n return res.ToString();\n }\n}\n```
| 4 | 0 |
['C#']
| 1 |
minimum-remove-to-make-valid-parentheses
|
Java, two scans, no stack, explained
|
java-two-scans-no-stack-explained-by-gth-5dj8
|
We can find invalid paretheses in two scans - first one from left to right we\'re finding ")" without proper opening "(", remove those immidiately. On the secon
|
gthor10
|
NORMAL
|
2020-02-14T05:57:24.375966+00:00
|
2020-02-17T15:58:51.658700+00:00
| 635 | false |
We can find invalid paretheses in two scans - first one from left to right we\'re finding ")" without proper opening "(", remove those immidiately. On the second pass go from right to left and search for invalid "(" without proper ")". \nAs we need to return string we already have to create a new DS to store that result. It\'s possible to use StringBuilder to append and remove characters.\nO(n) time - two string scans. O(n) space - need a StringBuilder of length up to n.\n\n```\n public String minRemoveToMakeValid(String s) {\n StringBuilder sb = new StringBuilder();\n int c = 0;\n for (char ch : s.toCharArray()) {\n if (ch == \')\') {\n if (c == 0) continue;\n --c;\n }\n else if (ch == \'(\') ++c;\n sb.append(ch);\n }\n c = 0; int i = sb.length();\n while (--i >= 0) {\n if (sb.charAt(i) == \')\') ++c;\n else if (sb.charAt(i) == \'(\') {\n if (c == 0) {\n sb.deleteCharAt(i);\n continue;\n }\n --c;\n } \n }\n return sb.toString();\n }\n```
| 4 | 0 |
['String', 'Java']
| 2 |
minimum-remove-to-make-valid-parentheses
|
c# First practice in 2020
|
c-first-practice-in-2020-by-jianminchen-vnxg
|
January 8, 2020\n1249. Minimum Remove to Make Valid Parentheses\n\nI took a more than three weeks break and it is the first algorithm I like to solve in 2020. I
|
jianminchen
|
NORMAL
|
2020-01-08T20:10:18.902385+00:00
|
2020-10-06T06:30:37.575982+00:00
| 5,462 | false |
January 8, 2020\n1249. Minimum Remove to Make Valid Parentheses\n\nI took a more than three weeks break and it is the first algorithm I like to solve in 2020. I like to solve 240 algorithms in 2020. This is my first one. \n\n**Case study**\nIn order for me to solve the algorithm, I learn that I have to put two test cases into consideration. \nCase 1: lee(t(c)o)de)\nThe idea is to use stack to store all indexes of open paretheses, and if there is \')\', then remove matched open parethese. Otherwise replace stringbuilder temporary variable **copy** - a copy of string - using placeholder char * at index of \')\'. We can name it "replace unmatched close parenthese with wildchar *". \n\nlee(t(c)o)de) -> lee(t(c)o)de* -> remove * in the string. \nput \'(\' in stack, and if there is matched \')\', then pop \'(\' otherwise replace stringBuilder index position with \'*\'.\n\nCase 2: ))((\nDo not forget to pop out all chars in the stack, remove open parenthese \'(\' at the index position in **copy** variable. \n\nHere are my C# practice highlights:\n1. C# string is immutable, so declare a StringBuilder variable to make a copy of string. \n2. Get familiar with C# StringBuilder.Replace and Remove API, empty char has issue to use Replace, so empty string "" works. \n3. Always work on my weakness, come out test cases to fully test the code by myself first. This time I missed test case ))((. I quickly fixed the bug after online judge showed me the bug with the test case ))((. \n\n```\nusing System;\nusing System.Collections.Generic;\nusing System.Linq;\nusing System.Text;\nusing System.Threading.Tasks;\n\nnamespace _1249_minimumToRemove\n{\n class Program\n {\n static void Main(string[] args)\n {\n var result = MinRemoveToMakeValid("lee(t(c)o)d)e"); \n }\n\n /// <summary>\n /// lee(t(c)o)de) -> lee(t(c)o)de* -> remove * in the string\n /// put ( in stack, and if there is matched ), then pop ( otherwise replace stringBuilder index position with *\n /// </summary>\n /// <param name="s"></param>\n /// <returns></returns>\n public static String MinRemoveToMakeValid(String s)\n {\n var sb = new StringBuilder(s);\n var stack = new Stack<int>();\n\n var length = s.Length;\n for (int i = 0; i < length; i++)\n {\n var current = s[i];\n var isOpen = current == \'(\';\n var isClose = current == \')\';\n\n if (isOpen)\n {\n stack.Push(i); \n }\n\n if (isClose)\n {\n if (stack.Count > 0)\n {\n stack.Pop();\n }\n else\n {\n sb.Replace(\')\',\'*\',i,1);\n }\n }\n }\n\n // remove extract ((, for example ))((\n while (stack.Count > 0)\n { \n sb.Remove(stack.Pop(), 1); \n }\n\n return sb.Replace("*","",0,sb.Length).ToString();\n }\n }\n}\n```
| 4 | 0 |
[]
| 2 |
minimum-remove-to-make-valid-parentheses
|
swift: stack
|
swift-stack-by-zijia-p3rj
|
\nclass Solution {\n \n func minRemoveToMakeValid(_ s: String) -> String {\n var arr = Array(s)\n var stack = [Int]()\n for (i, c) in
|
zijia
|
NORMAL
|
2019-11-13T00:06:59.232727+00:00
|
2019-11-13T00:06:59.232758+00:00
| 551 | false |
```\nclass Solution {\n \n func minRemoveToMakeValid(_ s: String) -> String {\n var arr = Array(s)\n var stack = [Int]()\n for (i, c) in arr.enumerated() {\n if c == "(" {\n stack.append(i)\n } else if c == ")" {\n if !stack.isEmpty {\n stack.removeLast()\n } else {\n arr[i] = "*"\n }\n }\n }\n while !stack.isEmpty {\n let i = stack.removeLast()\n arr[i] = "*"\n }\n \n return String(arr).replacingOccurrences(of: "*", with: "")\n \n }\n}\n```
| 4 | 0 |
[]
| 0 |
minimum-remove-to-make-valid-parentheses
|
O(n) time using HashSet and Stack Java Solution
|
on-time-using-hashset-and-stack-java-sol-qbg0
|
```\nclass Solution {\n public String minRemoveToMakeValid(String s) {\n \n int n = s.length();\n if(n == 0) return s;\n StringBu
|
manrajsingh007
|
NORMAL
|
2019-11-03T04:03:22.643286+00:00
|
2019-11-03T04:03:22.643342+00:00
| 375 | false |
```\nclass Solution {\n public String minRemoveToMakeValid(String s) {\n \n int n = s.length();\n if(n == 0) return s;\n StringBuilder sb = new StringBuilder();\n \n HashSet<Integer> set = new HashSet<>();\n Stack<Integer> stack = new Stack<>();\n \n for(int i = 0; i < n; i++){\n \n char curr = s.charAt(i);\n \n if(curr == \'(\'){\n stack.push(i);\n }\n \n else if(curr == \')\'){\n if(stack.size() > 0){\n stack.pop();\n }\n else{\n set.add(i);\n }\n }\n \n else continue;\n }\n \n while(stack.size() > 0){\n set.add(stack.pop());\n }\n \n for(int i = 0; i < n; i++){\n if(!set.contains(i)){\n sb.append("" + s.charAt(i));\n }\n }\n \n return sb.toString();\n \n }\n}
| 4 | 0 |
[]
| 0 |
check-if-it-is-a-good-array
|
[Java/C++/Python] Chinese Remainder Theorem
|
javacpython-chinese-remainder-theorem-by-o0cx
|
Intuition\nThis problem is realated a Chinese theorem:\nChinese remainder theorem, created in 5th centry.\nAlso well known as Hanson Counting.\n\n\n## Explanati
|
lee215
|
NORMAL
|
2019-11-03T04:03:56.833684+00:00
|
2021-07-16T02:44:14.656423+00:00
| 13,950 | false |
## **Intuition**\nThis problem is realated a Chinese theorem:\nChinese remainder theorem, created in 5th centry.\nAlso well known as Hanson Counting.\n<br>\n\n## **Explanation**\nIf `a % x = 0` and `b % x = 0`,\nappareantly we have `(pa + qb) % x == 0`\nIf `x > 1`, making it impossible `pa + qb = 1`.\n\nWell, I never heard of Bezout\'s identity.\nEven though the intuition only proves the necessary condition,\nit\'s totally enough.\n\nThe process of gcd,\nis exactly the process to get the factor.\nThe problem just doesn\'t ask this part.\n<br>\n\n## **Complexity**\nOf course you can return true as soon as `gcd = 1`\nI take gcd calculate as `O(1)`.\n\nTime `O(N)`\uFF0C\nSpace `O(1)`\n\n<br>\n\n**Java:**\n```java\n public boolean isGoodArray(int[] A) {\n int x = A[0], y;\n for (int a: A) {\n while (a > 0) {\n y = x % a;\n x = a;\n a = y;\n }\n }\n return x == 1;\n }\n```\n\n**C++:**\n```cpp\n bool isGoodArray(vector<int>& A) {\n int res = A[0];\n for (int a: A)\n res = gcd(res, a);\n return res == 1;\n }\n```\n\n**Python:**\n```python\n def isGoodArray(self, A):\n gcd = A[0]\n for a in A:\n while a:\n gcd, a = a, gcd % a\n return gcd == 1\n```\n\n**Python, 1-line using fractions**\n```python\nimport fractions\nclass Solution(object):\n def isGoodArray(self, A):\n return reduce(fractions.gcd, A) < 2\n```
| 123 | 10 |
[]
| 22 |
check-if-it-is-a-good-array
|
Bezout's Identity
|
bezouts-identity-by-songsari-w30v
|
Read (https://brilliant.org/wiki/bezouts-identity/, https://en.wikipedia.org/wiki/B\xE9zout%27s_identity)\n\nThe basic idea is that for integers a and b, if gcd
|
songsari
|
NORMAL
|
2019-11-03T04:01:33.545610+00:00
|
2019-11-03T04:08:56.001509+00:00
| 4,609 | false |
Read (https://brilliant.org/wiki/bezouts-identity/, https://en.wikipedia.org/wiki/B\xE9zout%27s_identity)\n\nThe basic idea is that for integers a and b, if gcd(a,b) = d, then there exist integers x and y, s.t a * x + b * y = d;\n\nThis can be generalized for (n >= 2) . e.g. if gcd(a,b,c) = d, then there exist integers x, y, and z, s.t, a* x + b*y + c * z = d.\n\nNow this problem is just asking if gcd(x1, ......, xn) = 1\n\n```\nclass Solution {\n\npublic:\n bool isGoodArray(vector<int>& nums) {\n if (nums.size() == 1) return nums[0] == 1;\n \n int a = nums[0];\n \n for (int i = 1; i < nums.size(); i++) {\n if (__gcd(a, nums[i]) == 1) return true;\n a = __gcd(a, nums[i]);\n }\n \n return false;\n }\n};\n```
| 45 | 1 |
[]
| 4 |
check-if-it-is-a-good-array
|
The whole logic
|
the-whole-logic-by-liketheflower-xkwi
|
The solution should be clear at this point. Here I\'d like to tidy up the whole logic to have a better understanding of the solution.\n1. "B\xE9zout\'s identity
|
liketheflower
|
NORMAL
|
2019-11-06T20:57:40.731188+00:00
|
2022-06-21T01:47:28.493759+00:00
| 1,731 | false |
The solution should be clear at this point. Here I\'d like to tidy up the whole logic to have a better understanding of the solution.\n1. "B\xE9zout\'s identity: (the GCD of a and b) is the smallest positive linear combination of non-zero a and b"[1]\n2. For this problem, if we can find any subset, which can generate gcd(subset) = 1, it is true. Otherwise, the gcd will be greater than 1, it is obvious that it is false.\n3. If **any subset** of the whole nums list has a gcd(subset)=1, then gcd(nums)=1 as:\n a) The gcd is a commutative function: gcd(a, b) = gcd(b, a) [2]\n b) The gcd is an associative function: gcd(a, gcd(b, c)) = gcd(gcd(a, b), c). [2]\n c) If none of a1, a2, . . . , ar is zero, then gcd( a1, a2, . . . , ar ) = gcd( gcd( a1, a2, . . . , ar-1 ), ar ) [2]\n d) It should be trival that gcd(1, n) where n is a non negative interger to be 1.\n4. based on 3, we change check \'whether we have gcd of **any subset** to be 1\' to \'check whether the gcd of the whole nums list is 1\' as: if we have a subset {**a, e, f**} and gcd(a, e, f)=1, and the whole list contains {**a,** b, c, d, **e, f**}. Based on 3a), we will have gcd(a, b, c) = gcd( gcd(a,b), c) based on 3b) gcd(a,gcd(b,c))=gcd(gcd(a,b),c). Based on 3a)and 3b) gcd(gcd(a,b),c) = gcd(c, gcd(a,b)) = gcd(gd(c, a), b). We can get general assocation by changing gcd(**a,** b, c, d, **e, f**) to gcd(gcd(b,c,d), gcd(a,e,f))=1.\n\n**Reference**\n[1] https://eli.thegreenplace.net/2009/07/10/the-gcd-and-linear-combinations\n[2] https://en.wikipedia.org/wiki/Greatest_common_divisor
| 30 | 0 |
[]
| 2 |
check-if-it-is-a-good-array
|
C++ 3 lines
|
c-3-lines-by-votrubac-nuzt
|
\nbool isGoodArray(vector<int>& nums) {\n auto gcd = nums[0];\n for (auto n : nums) gcd = __gcd(gcd, n);\n return gcd == 1;\n}\n
|
votrubac
|
NORMAL
|
2019-11-03T07:13:15.590722+00:00
|
2019-11-03T07:13:15.590763+00:00
| 2,520 | false |
```\nbool isGoodArray(vector<int>& nums) {\n auto gcd = nums[0];\n for (auto n : nums) gcd = __gcd(gcd, n);\n return gcd == 1;\n}\n```
| 20 | 3 |
[]
| 3 |
check-if-it-is-a-good-array
|
trivial is the new hard
|
trivial-is-the-new-hard-by-stefanpochman-g7s7
|
\ndef is_good_array(nums)\n nums.reduce(:gcd) == 1\nend\n
|
stefanpochmann
|
NORMAL
|
2019-11-26T20:51:25.356110+00:00
|
2019-11-26T20:51:25.356143+00:00
| 1,449 | false |
```\ndef is_good_array(nums)\n nums.reduce(:gcd) == 1\nend\n```
| 16 | 5 |
[]
| 0 |
check-if-it-is-a-good-array
|
A Rigorous Proof For Solving The Problem: Why The Solution Works, From Proof to Pseudocode
|
rigorous-proof-for-solving-the-problem-b-yn0p
|
Note: In this proof, a notable amount of subscript is used. However since it is not exactly feasible to properly format the subscript, instead array index is us
|
macgaussian
|
NORMAL
|
2022-05-25T09:16:17.298706+00:00
|
2025-02-22T07:46:03.718562+00:00
| 748 | false |
Note: In this proof, a notable amount of subscript is used. However since it is not exactly feasible to properly format the subscript, instead array index is used in place of subscript. For example, `t[i]` will be used instead of t<sub>i</sub>.
The explanation in this proof will be divided into the following parts:
**Section 1: Foundation**
**Section 2: Proof for Solution to The Problem**
**Section 3: Pseudocode to Solution**
> Note:
> - If you got the solution but wondering why it works like that, Section 2(b) explains why the solution works
> - If you solved the problem with some intuition and you found it worked but can't put a finger why, Section(c) explains the more "feel"-y approach.
_Jump to the end of the post to see the TLDR version._
# **Section 1: Foundation**
___
To begin, the foundation for the proof is to be laid out. First, the congruence relation (`≡`) and some of its properties are presented
**Definition:** `a ≡ r (mod d)` is an expression equivalent to the equation `a = qd + r` where:
- `q` (quotient) is an integer that follows `q = floor(a / d)`,
- `d` (divisor) is a variable integer
- `r` (remainder) is an integer that follows `r = a modulo d`, `0 ≤ r, < d`
- `a` is variable integer, particularly serves as dividend.
This expression and equation stems from a division operation: `a / d`.
**Example:** Suppose a division operation is given as follows:
```c
29 / 8
```
By definition, the quotient and remainder can be found:
```c
q = floor(29 / 8)
q = 3
r = 29 modulo 8
r = 5
```
Equivalently, this can be represented as:
```c
29 = 3(q) * 8(d) + 5(r)
```
or
```
29 ≡ 5 (mod 8)
```
**Definition:** Addition, subtraction, and multiplication operation on integers preserves their congruence relation.
**Example:** Addition. Suppose the following equation in a congruence system of 4 (i.e. `... ≡ ... (mod 4)`:
```c
5 + 10
```
The congruence relation of the equation's outcome is equal to adding each of the element's congruence in the equation.
```
The congruence relation of the equation's outcome
5 + 10 = 15
15 ≡ 3 (mod 4)
Adding each of the element's congruence
5 ≡ 1 (mod 4)
10 ≡ 2 (mod 4)
1 (mod 4) + 2 (mod 4) = 3 (mod 4)
```
**Example:** Subtraction. Suppose the following equation in a congruence system of 7 i.e. (`... ≡ ... (mod 7)`:
```c
16 - 3
```
The congruence relation of the equation's outcome is equal to subtracting the element's congruence in the equation.
```
The congruence relation of the equation's outcome
16 - 3 = 13
13 ≡ 6 (mod 7)
Subtracting each of the element's congruence
16 ≡ 2 (mod 7)
3 ≡ 3 (mod 7)
2 (mod 7) - 3 (mod 7) = -1 (mod 7)
2 (mod 7) - 3 (mod 7) = 6 (mod 7)
```
In the last line, the equation underflows back to positive because `r` is limited to be `0 ≤ r < d`.
**Example:** Multiplication. Suppose the following equation in a congruence system of 9 i.e. (... ≡ ... (mod 9)`):
```c
20 * 16
```
The congruence relation of the equation's outcome is equal to multiplying each of the element's congruence in the equation.
```c
The congruence relation of the equation's outcome
20 * 16 = 320
320 ≡ 5 (mod 9)
Multiplying each of the element's congruence in the equation.
20 ≡ 2 (mod 9)
16 ≡ 7 (mod 9)
2 (mod 9) * 7 (mod 9) = 14 (mod 9)
2 (mod 9) * 7 (mod 9) = 5 (mod 9)
```
In the last line, the answer is reduced down so that 14 is under 9, because `r` is limited to be `0 ≤ r < d)`.
**Theorem I: Bezout Identity (special case, reworded).** There exists some pair of integer `(p, q)` such that given two integer `a` and `b` where both are coprime (i.e. `gcd(a, b) = 1`), the equation `1 = ab + pq` can be made. [1, with modification]
*Proof*
First, the following equation is formally presented, By definition,
```
gcd(a, b) = 1
1 = ab + pq, for some integer pair (p, q)
```
Therefore,
```
gcd(a, b) = ab + pq, for some integer pair (p, q) -- (1)
```
The only time two positive integers namely `a` and `b`, and for the sake of proof, `a > b`, can result in 1 by following the equation `ap + bq` for some variable `p` and `q`, is when `a` and `b` are coprime i.e. `gcd(a, b) = 1`. It is impossible to create 1 if this condition is not met, because when `g = gcd(a, b)` and `g != 1` that means `a ≡ 0 (mod g)` and `b ≡ 0 (mod g)`. It follows that when a number `n ≡ 0 (mod g)`, its multiple will also be `0 (mod g)` i.e.
```
n ≡ 0 (mod g)
n * x ≡ 0 * x (mod g), for some integer x
nx ≡ 0 (mod g), for some integer x
```
Therefore both `a` and `b` will not have any multiple that when divided by `g` will result in some remainder.
Adding (and subtracting) `a` and `b` will also result in `0 (mod g)` i.e.
```
a + b ≡ (0 + 0) (mod g)
a + b ≡ 0 (mod g)
```
```
a - b ≡ (0 - 0) (mod g)
a - b ≡ 0 (mod g)
```
All of this lead to the conclusion that all arithmetical operation except division using `a` and `b` all will result in a number multiple of `g`. This implies that it is impossible to generate a number other than `g` and its multiple. And since `g != 1` it is impossible to generate an integer 1 altogether. Therefore, it is necessary for `g = 1`, where `g = gcd(a, b)`, holds true to generate 1. ■
# Section 2: Proof for Solution to The Problem
___
We will split this section into the following parts:
Part (a) - Establishing Problem Function Statement
Part (b) - Proving Hypothesis I: Finding the relation between solving `gcd` functions to the original problem statement
Part (c) - Proving Hypothesis II: Figuring out if nesting `gcd` function will result in a highest common factor between all parameters used.
## Part A - Problem Function Statement
To start, the following statement in the problem will be formulated into mathematical expression:
> ...multiply each element by an integer and add all these numbers...
The above statement is equal to:

where `c` are free variables and `i` are some selected number from `nums`.
## Part B - Hypothesis I:
> Solving for nested `gcd` function(s) is equivalent to solving the problem.
### *Proof*
To prove the hypothesis, this section attempts to figure out whether solving for `gcd` function will end up with the problem function statement (equation (2)).
The following parts will explain the cases needed to prove the hypothesis.
*Case 1: Supplying one `gcd` function as a `gcd` argument.*
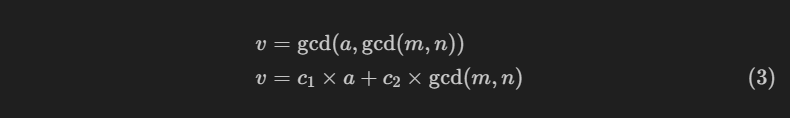
where `c` are free variable.
Equation (3) can be expanded into the following.
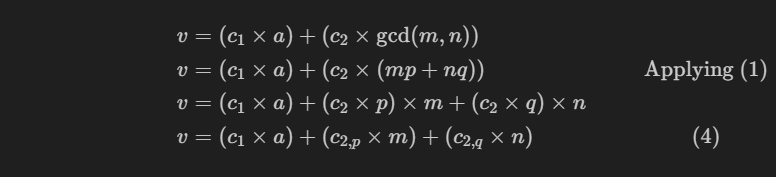
where `c`, `p`, `q` are some free variables. It can be seen easily that **equation (4) follows the form of problem function statement (equation (2)).**
**Corollary I:** The variation where the `gcd`-as-argument is supplied into the first position of the outer `gcd` follows the same reasoning, and will end up with the same conclusion stated above.
*Case 2: Supplying two `gcd` function as a `gcd` argument.*
(Note: I kinda forgot why I explain this in the first place, but I'll leave this as is because why not lol.)
Consider the following equation.
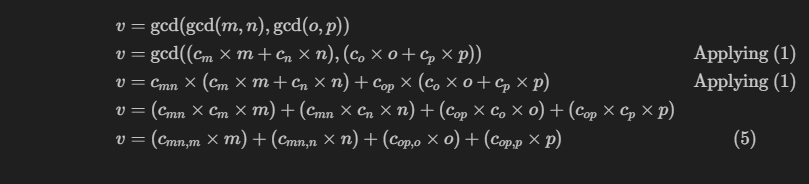
where `c` is a free variable. Once again, **equation (5) follows the form of problem function statement (equation (2)).** This shows that solving `gcd(gcd(m, n), gcd(o, p))` for some `m`, `n`, `o`, and `p` is equivalent to solving the problem function statement (equation (2)).
Therefore, solving a nested `gcd` function will result in the problem function statement. The hypothesis is proven true. ■
**Corollary II:** `gcd` of two number can be used as an intermediary value for some next iteration of `gcd` function when solving the problem.
___
It has been established that the solution to the problem can be reduced to whether it is possible to find any set of number in `nums` such that their `gcd` is 1.
It should be relatively easy to intuitively deduce that the value `v` from equation (5) is in fact the `gcd` to all input in question. Nevertheless, the next part will discuss the correctness of the following hypothesis. This is for the sake of completeness of the proof along with providing the correctness of the algorithm to solve the problem.
___
## Part C - Hypothesis II
> `gcd` function with more than two parameters can be built on `gcd` function with two parameters:
$$
\begin{align}
\gcd(a, b, c) = \gcd(\gcd(a, b), c)
\end{align}
$$
### *Proof*
The hypothesis will be proved using two lemmata:
#### *Lemma I - Common divisibility*
> Given $w = \gcd(\gcd(a,\ b),\ c)$, `w` divides `a`, `b`, and `c`.
Corollary II states that the `gcd` of two input can be used as the input of another `gcd` function. This corollary can be utilized to find the `gcd` of a set of number (instead of only two).
Consider the following equation.
$$
\begin{align}
\gcd(a, b) = v
\end{align}
$$
By definition, this means that:
(1) `v` divides `a`
(2) `v ≤ a` as direct consequence of (1)
(3) `v` divides `b`
(4) `v ≤ b` as direct consequence of (2)
(5) There is no arbitrary `n` where `n > v` such that `n` divides both `a` and `b`
Next, consider the following equation.
$$
\begin{align}
\gcd(v, c) = w
\end{align}
$$
By definition, this means that:
(6) `w` divides `v`
(7) `w ≤ v` as direct consequence of (6)
(8) `w` divides `c`
(9) `w ≤ c` as direct conseuquence of (9)
(10) There is no arbitrary `n` where `n > w` such that `n` divides both `v` and `c`
Divisibility is transitive. Meaning, if `x` divides `y` and `y` divides `z`, then `x` divides `z` (for additional reading material, see [2]). Returning to the previous findings,
(6) `w` divides `v` + (1) `v` divides `a` → (11) `w` divides `a`
(6) `w` divides `v` + (3) `v` divides `b` → (12) `w` divides `b`
Therefore, given
$$
\begin{align}
\gcd(a, b) &= v \\
\gcd(v, c) &= w
\end{align}
$$
We have the following properties:
(8) `w` divides `c`
(11) `w` divides `a`
(12) `w` divides `b`
This proves that `w` is a common divisor of `a`, `b`, and `c`.
#### *Lemma II - No higher solution possible*
> Given $w = \gcd(\gcd(a,\ b),\ c)$, there can be no arbitrary `x` where `x > w` such that `x` divides `a`, `b`, and `c`.
What is left to do now is to show that `w` is in fact the greatest value possible for `a`, `b`, and `c`. This easily follows using the definition of `gcd` (meaning, the below statements hold true by definition)
(5) There is no arbitrary `n` where `n > v` such that `n` divides both `a` and `b`
(7) `w ≤ v` as direct consequence of (6)
(10) There is no arbitrary `n` where `n > w` such that `n` divides both `v` and `c`
Using these statements, the following premises can be derived:
##### First Derived Premise
Since (7) `w ≤ v` and (5) there is no arbitrary `n` where `n > v` such that `n` divides both `a` and `b`, that means:
(13) There is no arbitrary `n` where `n > w` such that `n` divides both `a` and `b`.
##### Second Derived Premise
We have these two premises:
(10) There is no arbitrary `n` where `n > w` such that `n` divides both `v` and `c`
(13) There is no arbitrary `n` where `n > w` such that `n` divides both `a` and `b`.
Combining the two, we can obtain:
(14) **There is no arbitrary `n` where `n > w` such that `n|v`, `n|a`, `n|b`, and `n|c`**
Therefore, `w` is in fact the biggest value possible that can factor `a`, `b`, and `c`. ■
#### Wrap-up
By combining the two lemma:
Lemma I: Given $w = \gcd(\gcd(a,\ b),\ c)$, `w` divides `a`, `b`, and `c`.
Lemma II: Given $w = \gcd(\gcd(a,\ b),\ c)$, there can be no arbitrary `x` where `x > w` such that `x` divides `a`, `b`, and `c`.
it can be concluded that chaining 2-ary `gcd` function will output the greatest common divisor for all the input in question. That is,
$$
\begin{align}
\gcd(a, b, \cdots, z) = \gcd(a, \gcd(b, \gcd(\cdots, z)))
\end{align}
$$
# Section 3: Pseudocode to Solution
Using Hypothesis II, the core algorithm to solve the problem can be constructed by means of the following pseudocode,
```c++
Input: nums - an array of integers
let hcf ← gcd(nums[1], nums[2])
for i from 3 to nums.length:
hcf ← gcd(hcf, nums[i])
if hcf equal to 1:
return true
else:
return false
```
Variation can be made, for example, to quit early when at one point it has been established that `hcf` is 1. The `gcd` function implementation can use the Euclidean Algorithm [4].
___
# TLDR version:
1. The problem boils down to finding out if the GCD of any combination of elements in `nums` is equal to 1
- Why:
- The Euclidean Algorithm gives GCD of two numbers
- In doing so, if we have `a` and `b`, Euclidean Algorithm guarantees the existence `p` and `q` that gives `gcd(a, b)` like so: $ap + bq = \gcd(a,\ b)$
- Put the other way: if we know the value of $\gcd(a,\ b)$, it is guaranteed that there exists value pair `p` and `q` that gives $ap + bq = \gcd(a,\ b)$
- If we can find certain `a` and `b` that yields $\gcd(a,\ b) = 1$, we automatically solve the problem.
- Isn't it great? We don't have to find the `p` and `q` themselves to solve the problem! Just need to find the right `a` and `b`.
- Key takeaway: forget the problem statement and just solve for GCD. Solving one will solve the other.
2. GCD function classically accepts only two parameters. Will it work if the function accepts many parameters?
- Yes.
- Do it like so: `gcd(a, b, c) = gcd(gcd(a, b), c)`.
- We can do it like this too if we want: `gcd(a, b, c) = gcd(a, gcd(b, c))`
- Why:
- GCD function returns a value `v` that has this properties:
1. `v` divides all of the parameter.
2. There is no integer bigger than `v` that can do point (a).
- Division is transitive: if `a` divides `b`, and `b` divides `c`, then `a` divides `c`.
- Example: 10 divides 200, and 200 divides 2400. Therefore 10 divides 2400.
- Given `v = gcd(a, b)`, what happen if we set `a = gcd(x, y)`?
- First, we have `v` divides `a` and `b`.
- Then we have `a` divides `x` and `y`.
- Division is transitive, meaning: `v` divides `x` and `y`.
- Therefore:
1. `v` divides `x`, `y`, and `b`
2. There is no integer bigger than `v` that can do point (a)
- This is the very same properties of GCD isn't it? See the first point of "Why?".
- Therefore: chaining GCD function inside it gives the highest common factor for all inputs used.
3. In conclusion the following step will yield the correct answer:
1. Put all value in `nums` into GCD function (point 2)
2. Check if the result is 1 (point 1)
Reference:
[1] Bezout's Identity, https://en.wikipedia.org/wiki/Bézout%27s_identity (accessed at 24th May 2022)
[2] Properties of Divisibility, https://ccssmathanswers.com/properties-of-divisibility/ (accessed at 24th May 2022)
[3] Greatest Common Divisor, https://en.wikipedia.org/wiki/Greatest_common_divisor (accessed at 25th May 2022)
[4] Euclidean Algorithm, https://en.wikipedia.org/wiki/Euclidean_algorithm#Procedure (accessed at 25th May 2022)
<small>Here's hoping for LaTeX typesetting support</small>
| 10 | 0 |
['Math', 'Number Theory']
| 4 |
check-if-it-is-a-good-array
|
Bézout's identity (GCD calculation)
|
bezouts-identity-gcd-calculation-by-chri-9fq3
|
Based on B\xE9zout\'s identity,\nFor ints a and b, if gcd(a,b) = d, then there exists some x, y with a * x + b * y = d;\n\ncsharp\npublic bool IsGoodArray(int[]
|
christris
|
NORMAL
|
2019-11-03T05:24:53.026338+00:00
|
2019-11-03T05:24:53.026383+00:00
| 926 | false |
Based on [B\xE9zout\'s identity](https://en.wikipedia.org/wiki/B%C3%A9zout%27s_identity),\nFor ints a and b, if gcd(a,b) = d, then there exists some x, y with a * x + b * y = d;\n\n```csharp\npublic bool IsGoodArray(int[] nums) \n{\n\tif(nums == null || nums.Length == 0)\n\t{\n\t\treturn true;\n\t}\n\n\tif(nums.Length == 1)\n\t{\n\t\treturn nums[0] == 1;\n\t}\n\n\tint gcdResult = nums[0]; \n\tfor(int i = 1; i < nums.Length; i++)\n\t{\n\t\tgcdResult = gcd(nums[i], gcdResult);\n\t\tif(gcdResult == 1)\n\t\t{\n\t\t\treturn true;\n\t\t}\n\t}\n\n\treturn false; \n}\n\nint gcd(int a, int b)\n{\n\twhile(b != 0)\n\t{\n\t\tint t = b;\n\t\tb = a % b;\n\t\ta = t; \n\t}\n\n\treturn a;\n}\n```
| 8 | 0 |
[]
| 0 |
check-if-it-is-a-good-array
|
[Python] Diophantine Equation
|
python-diophantine-equation-by-pony1999-qcch
|
This is a multivariate linear Diophantine equation with 1 on the right hand side. It has solution if and only if the gcd of all the numbers in nums divides 1, w
|
pony1999
|
NORMAL
|
2021-07-04T00:20:57.877637+00:00
|
2021-07-23T00:01:00.199059+00:00
| 862 | false |
This is a multivariate linear [Diophantine equation](https://en.wikipedia.org/wiki/Diophantine_equation) with 1 on the right hand side. It has solution if and only if the gcd of all the numbers in nums divides 1, which means it must be 1. See [this math stack exchange post](https://math.stackexchange.com/questions/145346/diophantine-equations-with-multiple-variables) for detailed proof.\n```\nclass Solution:\n def isGoodArray(self, nums: List[int]) -> bool:\n return gcd(*nums) == 1\n```
| 7 | 0 |
['Math', 'Python']
| 0 |
check-if-it-is-a-good-array
|
💥💥TypeScript | 100% beats runtime and memory [EXPLAINED]
|
typescript-100-beats-runtime-and-memory-f8smy
|
\n\n# Intuition\nTo solve the problem, I realized that if I can find a common factor among all numbers in the array, it tells me something about whether I can m
|
r9n
|
NORMAL
|
2024-09-19T19:41:29.259498+00:00
|
2024-09-19T19:41:29.259518+00:00
| 77 | false |
\n\n# Intuition\nTo solve the problem, I realized that if I can find a common factor among all numbers in the array, it tells me something about whether I can make the number 1 from these numbers. If the greatest common divisor (GCD) of the entire array is 1, then it means I can indeed form the number 1 using some combination of these numbers and their multipliers.\n\n\n# Approach\nCalculate the GCD: Start with the first number and iteratively find the GCD of it with each subsequent number in the array.\n\n\nCheck the Result: If the GCD ever becomes 1, I know it\'s possible to form the number 1, so I return true. If the loop finishes and the GCD is still greater than 1, return false.\n\n\n# Complexity\n- Time complexity:\nO(n * log(max)) where n is the number of elements in the array and max is the maximum number in the array. This is because computing the GCD takes O(log(max)) time, and I do this for each element.\n\n- Space complexity:\nO(1). I only need a few extra variables to store the GCD and perform calculations, so the space used doesn\u2019t depend on the size of the input.\n\n# Code\n```typescript []\nfunction isGoodArray(nums: number[]): boolean {\n const gcd = (a: number, b: number): number => {\n while (b !== 0) {\n const temp = b;\n b = a % b;\n a = temp;\n }\n return a;\n };\n\n let currentGCD = nums[0];\n for (let i = 1; i < nums.length; i++) {\n currentGCD = gcd(currentGCD, nums[i]);\n if (currentGCD === 1) {\n return true;\n }\n }\n return currentGCD === 1;\n}\n\n```
| 6 | 0 |
['TypeScript']
| 0 |
check-if-it-is-a-good-array
|
Java GCD Solution
|
java-gcd-solution-by-hiteshprajapati8895-3nfx
|
```\nclass Solution {\n public boolean isGoodArray(int[] nums) {\n int gcd = nums[0];\n for(int i = 1; i<nums.length; i++){\n gcd =
|
hiteshprajapati8895
|
NORMAL
|
2022-01-25T08:22:59.759184+00:00
|
2022-01-25T08:22:59.759226+00:00
| 892 | false |
```\nclass Solution {\n public boolean isGoodArray(int[] nums) {\n int gcd = nums[0];\n for(int i = 1; i<nums.length; i++){\n gcd = gcd(gcd, nums[i]);\n if(gcd == 1)\n return true;\n }\n return gcd==1;\n }\n public int gcd(int a, int b){\n if(b==0)\n return a;\n return gcd(b,a%b);\n }\n}
| 6 | 0 |
['Java']
| 1 |
check-if-it-is-a-good-array
|
Simple C++ with Explanation
|
simple-c-with-explanation-by-basushibam-tmwq
|
According to Euclid\'s Theorem,\nIf the GCD of two integers (a,b) is d, then there exists two integers x and y such that ax + by = d.\n\nIf a,b,c... are the ele
|
basushibam
|
NORMAL
|
2021-02-18T18:18:59.388021+00:00
|
2021-02-18T18:18:59.388061+00:00
| 468 | false |
According to Euclid\'s Theorem,\n***If the GCD of two integers (a,b) is d, then there exists two integers x and y such that ax + by = d.***\n\nIf a,b,c... are the elements of the array we are calculating ax + by + cz...which gives hint that we have to use the above theorem.\n\nNow in this problem the d is given to be 1, which means the GCD should be 1.\nSo instead of checking for all posiible subsets of the given array it is enough to check every pair (a,b).\n***"Does the array contain two integers a and b such that ax + by = 1 for some integers x,y ?"***\nOr the same question can be asked as\n***"Does the array contain two co-prime integers?"***\n\nBut checking all pairs will have quadratic time complexity. We have to optimize it.\n\nNow what happens if we calculate the GCD of all the integers in the array ?\nIf the array contains co-prime integers then the GCD of those two will become 1 and the GCD of 1 with the remaining n-2 integers will be 1 only.\nBut if the array does not contain coprime integers then the GCD of all the integers will be greater than 1.\n\nSo the question reduces to\n***"Is the GCD of all the number in the array equal to 1?"***\n```\nclass Solution {\npublic:\n bool isGoodArray(vector<int>& nums)\n {\n int GCD = nums[0];\n \n for (int i = 1; i < nums.size(); i++)\n {\n GCD = __gcd(GCD, nums[i]);\n }\n \n return GCD == 1;\n }\n};\n```
| 6 | 0 |
[]
| 1 |
check-if-it-is-a-good-array
|
C++ explained briefly
|
c-explained-briefly-by-chase_master_kohl-90cx
|
\nclass Solution {\npublic:\n /* \n Read (https://brilliant.org/wiki/bezouts-identity/, https://en.wikipedia.org/wiki/B\xE9zout\'s_identity)\n\nThe basic i
|
chase_master_kohli
|
NORMAL
|
2019-11-04T07:06:10.222081+00:00
|
2019-11-04T07:06:10.222114+00:00
| 519 | false |
```\nclass Solution {\npublic:\n /* \n Read (https://brilliant.org/wiki/bezouts-identity/, https://en.wikipedia.org/wiki/B\xE9zout\'s_identity)\n\nThe basic idea is that for integers a and b, if gcd(a,b) = d, then there exist integers x and y, s.t a * x + b * y = d;\n\nThis can be generalized for (n >= 2) . e.g. if gcd(a,b,c) = d, then there exist integers x, y, and z, s.t, a* x + b*y + c * z = d.\n\nNow this problem is just asking if gcd(x1, ......, xn) = 1\n */ \n bool isGoodArray(vector<int>& A) {\n int res = A[0];\n for (int a: A)\n res = gcd(res, a);\n return res == 1;\n }\n};\n```
| 6 | 0 |
[]
| 0 |
check-if-it-is-a-good-array
|
[C++] | Explained | Faster than 90%
|
c-explained-faster-than-90-by-mkhasib1-oyxx
|
In order to solve the problem, we need to search more about the first hint:\n\nEq. ax+by=1 has solution x, y if gcd(a,b) = 1.\n\nif we found ANY two numbers tha
|
mkhasib1
|
NORMAL
|
2021-04-22T03:12:12.370868+00:00
|
2021-04-22T03:14:17.808453+00:00
| 258 | false |
In order to solve the problem, we need to search more about the **first** hint:\n```\nEq. ax+by=1 has solution x, y if gcd(a,b) = 1.\n```\nif we found **ANY two numbers** that has a ` gcd(a,b)=1`, then ANY added numbers won\'t change the fact that gcd will results at max of 1! \nthat is :`gcd(a,b,c,d,e)=1 if gcd(a,e)=1`\nSo find If that\'s possible and **return if that\'s possible**.\n```\nint gcd(int a, int b)\n{\n if (a == 0)\n return b;\n return gcd(b%a, a);\n}\npublic:\n bool isGoodArray(vector<int>& nums) {\n int n=nums.size();\n int prevGCD=nums[0];\n for(int i=1;i<n;i++)\n {prevGCD=gcd(prevGCD,nums[i]);\n }\n return prevGCD==1;\n }\n```\nIf you **like** my explanation, **hit** the **Upvote** button and If you **don\'t**, **hit** the **Downvote** \uD83E\uDD73\nand If you have ANY questions, feel free to ask them down below \uD83D\uDC47
| 5 | 1 |
[]
| 0 |
check-if-it-is-a-good-array
|
easy 3 line solution //C++ code //BEATS 100%
|
easy-3-line-solution-c-code-beats-100-by-lxgq
|
ApproachLet's walk through a dry run of the provided code with the input nums = [12, 5, 7, 23].Initialization:cpp
auto gcd = nums[0]; // gcd = 12
First iterati
|
s4abi
|
NORMAL
|
2025-03-10T14:44:58.174720+00:00
|
2025-03-10T14:44:58.174720+00:00
| 132 | false |
# Approach
Let's walk through a dry run of the provided code with the input nums = [12, 5, 7, 23].
Initialization:
cpp
auto gcd = nums[0]; // gcd = 12
First iteration:
n = 12
Update gcd:
cpp
gcd = __gcd(12, 12); // gcd = 12
Second iteration:
n = 5
Update gcd:
cpp
gcd = __gcd(12, 5); // gcd = 1
Third iteration:
n = 7
Update gcd:
cpp
gcd = __gcd(1, 7); // gcd = 1
Fourth iteration:
n = 23
Update gcd:
cpp
gcd = __gcd(1, 23); // gcd = 1
After iterating through all the elements in the nums array, the final value of gcd is 1.
Return value:
cpp
return gcd == 1; // return true
So, the function will return true for the input nums = [12, 5, 7, 23]
# Complexity
- Time complexity: O(N)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:O(N)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
bool isGoodArray(vector<int>& nums) {
auto gcd = nums[0];
for (auto n : nums) gcd = __gcd(gcd, n);
return gcd == 1;
}
};
```
| 4 | 0 |
['Array', 'Math', 'Number Theory', 'C++']
| 0 |
check-if-it-is-a-good-array
|
🔥🔥JAVA SOLUTION 🔥🔥|| 🔥🔥SIMPLE AND EASY🔥🔥
|
java-solution-simple-and-easy-by-darshan-hwdh
|
\n# Approach\nGretest Comman Divisor\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n\nclass Solution {\n public boolean is
|
darshan_anghan
|
NORMAL
|
2024-05-23T07:24:45.258207+00:00
|
2024-05-23T07:24:45.258241+00:00
| 924 | false |
\n# Approach\nGretest Comman Divisor\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution {\n public boolean isGoodArray(int[] nums) {\n int tempGCD = nums[0];\n int i=0;\n while(i<nums.length){\n tempGCD=gcd(tempGCD , nums[i]);\n i++;\n if(tempGCD ==1 )return true;\n }\n return false;\n }\n\n int gcd(int a , int b){\n if(b==0)return a;\n else return gcd(b , (a%b));\n }\n}\n```
| 4 | 0 |
['Java']
| 1 |
check-if-it-is-a-good-array
|
return GCD(nums)==1 || C++
|
return-gcdnums1-c-by-ganeshkumawat8740-7t5c
|
Code\n\nclass Solution {\npublic:\n bool isGoodArray(vector<int>& nums) {\n int g = 0;\n for(auto &i: nums){\n g = __gcd(i,g);\n
|
ganeshkumawat8740
|
NORMAL
|
2023-06-10T08:52:51.515641+00:00
|
2023-06-10T08:52:51.515682+00:00
| 842 | false |
# Code\n```\nclass Solution {\npublic:\n bool isGoodArray(vector<int>& nums) {\n int g = 0;\n for(auto &i: nums){\n g = __gcd(i,g);\n if(g==1)return true;\n }\n return false;\n }\n};\n```
| 4 | 0 |
['C++']
| 0 |
check-if-it-is-a-good-array
|
C++ solution | simple and easy
|
c-solution-simple-and-easy-by-ajiteshgau-pstk
|
class Solution {\npublic:\n\n // if we choose any two elements from the array:\n\t// if the gcd is 1 then the required condition is true and\n\t// if gcd is
|
ajiteshgautam4
|
NORMAL
|
2022-08-07T14:51:28.451728+00:00
|
2022-08-07T14:51:28.451775+00:00
| 1,433 | false |
class Solution {\npublic:\n\n // if we choose any two elements from the array:\n\t// if the gcd is 1 then the required condition is true and\n\t// if gcd is not equal to 1 then the condition will never satisfy\n\t// its an observation, so don\'t get confused ( like an AXIOM )\n\t// you can dry run the given test cases to confirm\n\t\n int gcd(int a, int b){\n while (a%b != 0){\n int rem=a%b;\n a=b;\n b=rem;\n }\n return b;\n }\n bool isGoodArray(vector<int>& nums) {\n int n = nums.size();\n int a = 0;\n for(int i=0; i<n; i++){\n a = gcd(a,nums[i]);\n if(a==1)\n return true;\n }\n return false;\n }\n};
| 4 | 0 |
['C', 'C++']
| 0 |
check-if-it-is-a-good-array
|
C++ Simple Soln. || 4 lines
|
c-simple-soln-4-lines-by-vikal__009-f3p1
|
\n //aX + bY = k has __integer solution__ (X, Y) if k is multiple of gcd(a, b)\n //here k=1 so __gcd should be 1\n //Subset has gcd 1 == whole array shou
|
vikal__009
|
NORMAL
|
2021-08-01T09:53:18.705975+00:00
|
2021-08-01T09:53:18.706005+00:00
| 225 | false |
```\n //aX + bY = k has __integer solution__ (X, Y) if k is multiple of gcd(a, b)\n //here k=1 so __gcd should be 1\n //Subset has gcd 1 == whole array should have 1\n bool isGoodArray(vector<int>& nums) {\n int k=nums[0];\n for(auto i:nums){\n k=__gcd(k,i);\n }\n return k==1;\n }\n```
| 4 | 0 |
[]
| 0 |
check-if-it-is-a-good-array
|
Hand Written Easy Explanation with Bézout's Lemma
|
hand-written-easy-explanation-with-bezou-x55p
|
\n\n\n\n# Code\n\nclass Solution:\n def isGoodArray(self, nums: List[int]) -> bool:\n ans=nums[0]\n for i in range (1,len(nums)):\n
|
_helios
|
NORMAL
|
2023-04-15T04:24:03.457749+00:00
|
2023-04-15T04:25:47.471351+00:00
| 850 | false |
\n\n\n\n# Code\n```\nclass Solution:\n def isGoodArray(self, nums: List[int]) -> bool:\n ans=nums[0]\n for i in range (1,len(nums)):\n ans=math.gcd(ans,nums[i])\n return ans==1\n```\n\nPlease Upvote the solution is you like it.
| 3 | 0 |
['Python3']
| 0 |
check-if-it-is-a-good-array
|
Java Solution || Easy to understand
|
java-solution-easy-to-understand-by-vish-s6ck
|
\nclass Solution {\n public boolean isGoodArray(int[] nums) {\n int result=nums[0];\n for(int i=1;i<nums.length;i++){\n result=G
|
vishaal351
|
NORMAL
|
2022-10-18T05:28:14.294145+00:00
|
2022-10-18T05:28:14.294171+00:00
| 723 | false |
```\nclass Solution {\n public boolean isGoodArray(int[] nums) {\n int result=nums[0];\n for(int i=1;i<nums.length;i++){\n result=GCD(nums[i],result);\n }\n return result==1;\n }\n static int GCD(int i,int j){\n if(j==0) return i;\n return GCD(j,i%j);\n }\n}\n```\n**Please upvote if u like it**
| 3 | 0 |
['Math', 'Java']
| 0 |
check-if-it-is-a-good-array
|
Math fact - C++
|
math-fact-c-by-iamssuraj-eew7
|
```\nclass Solution {\npublic:\n int gcd(int a, int b)\n {\n if(b == 0)\n return a;\n return gcd(b, a%b);\n }\n bool isGood
|
iamssuraj
|
NORMAL
|
2022-09-09T14:36:24.216728+00:00
|
2022-09-09T14:36:45.512196+00:00
| 350 | false |
```\nclass Solution {\npublic:\n int gcd(int a, int b)\n {\n if(b == 0)\n return a;\n return gcd(b, a%b);\n }\n bool isGoodArray(vector<int>& nums) {\n // if there are 2 integers, a and b such that gcd(a, b) = d, then there exists integers x, y, such that a*x + b*y = d;\n int g = nums[0];\n for(auto it:nums)\n g = gcd(g, it);\n return g == 1;\n }\n};
| 3 | 0 |
[]
| 0 |
check-if-it-is-a-good-array
|
Solution with derivation and explaination
|
solution-with-derivation-and-explainatio-ix4n
|
consider ax + by = 1\nAssuming integer solution exists then \n\nwe can take out the common divisor of a and b. \nThe gcf is the greatest common divisor of a and
|
ani1998ket
|
NORMAL
|
2021-08-06T14:13:43.802699+00:00
|
2021-08-06T14:14:25.237282+00:00
| 218 | false |
consider ax + by = 1\nAssuming integer solution exists then \n\nwe can take out the common divisor of a and b. \nThe gcf is the greatest common divisor of a and b.\n\ntherefor ax + by = gcf(a,b) * ( (a/gcf) * x + (b/gcf) * y ) = 1\n\nsince gcf divides a we can rewrite a as a = gcf * a1 .. where a1 is some integer\nsimilarly b = gcf * b1.. where b1 is some integer\n\nso ax + by = gcf * ( a1 * x + b1 * y ) = 1\n\ndividing both sides by gcf we get\n\na1 * x + b1 * y = 1 / gcf\n\nNow LHS is a integer because (a1, b1, x, y ) are all integer values. and LHS = RHS. Therefore 1/gcf should also be an integer. This is only possible when gcf = 1. For all other values 1/gcf will not be an integer.\nAlso if (x,y) integer solutions don\'t exist the condition won\' t be valid.\n\nTherefor ax + by = 1 only if gcf(a,b) = 1\n\nFor n variables as given in the question similar logic can be used to take out gcf( a, b, c , d .... ) common from LHS and we get gcf(a,b,c,d ... ) = 1 as the condition.\n\nOne must realise that the subarray simply means taking the 0 as the multiplicative coefficients for number not included.\n\n```\nclass Solution {\npublic:\n bool isGoodArray(vector<int>& nums) {\n int gcd = nums[0];\n for( auto e : nums ){\n gcd = __gcd( gcd, e );\n }\n \n return gcd == 1;\n }\n};\n```
| 3 | 0 |
[]
| 0 |
check-if-it-is-a-good-array
|
1250 - true if gcd(array) is 1, use co-primes existence for early exit
|
1250-true-if-gcdarray-is-1-use-co-primes-5abb
|
---\n\nHard to see at first, and its pure math\nA long one coming, below :)\n\n---\n\nAlgo\n\n- 1 <= nums[i] <= 10^9 So array elements are always +ve\n- For [1]
|
pgmreddy
|
NORMAL
|
2021-07-01T12:59:49.775133+00:00
|
2021-07-01T14:19:06.772598+00:00
| 284 | false |
---\n\nHard to see at first, and its pure math\nA long one coming, below :)\n\n---\n\n**Algo**\n\n- `1 <= nums[i] <= 10^9` So array elements are always +ve\n- For `[1]` or `[1,2,3]` or `[1,5,10,15,20]` array is good\n - because we have subset as `[ 1 ]` & multiplicand as `1`, so our sum (after multiplying with each element of array with some multiplicand is `1*1`) is `1`\n- For `[5,10,15,20]`, array is not good\n - because we dont have 1 as element\n - so some of elements must have `-ve` numbers as `multiplicand`\n - but even after having them, for example `5*-2 + 10*1`, it comes to `0`\n - this is because they are all multiples of a number (`5` in this case)\n - but we need `1`\n - so picking multiples of number won\'t help\n - and picking `co-primes` will help\n - Now we know `co-primes` will help\n - Some exampels are `[5,7]` , `[5,11]` , `[7,37]`\n - It\'s easy to see that the gcd of 1st two is `1`, also it is also for last one\n - But is it working really? `5*3 + 7*-2 = 1`, `5*-2 + 11*1 = 1`, `-7*21 + 4*37 = 1`, yes, it is working\n - So, we know that if `gcd` is 1 then it is working\n- But what about `[5,10,15,20, 7]`?\n - Here there some numbers are multiples of `5`, also `5 & 7` are `co-prime`\n - Since we can take subset, we can take `[5,7]` and they are co-prime (`gcd = 1`), we its good\n - How? Same as above `5*3 + 7*-2 = 1`\n - So, effectively both `[5,10,15,20, 7]` and `[5,7]` are same\n - In other words, if we have 2 prime numbers, then we are done, or if we have two co-primes we are good\n - Is `[5,7]` is good - yes, why? `5 & 7 are co-prime` (that is `gcd = 1`)\n - Is `[3,4]` is good - yes, why? `3 & 4 are co-prime` (that is `gcd = 1`)\n - Is `[10,8]` is good - No, why? `10 & 8 are Not co-prime`, because they have a prime number `2` as common factor (that is `gcd = 2`)\n- So can I stop going ahead once I found 2 co-primes? yes\n - `[8,9,100,200,300,400,500,600]` is same as `[8,9]`, as 8 & 9 are co-prime we don\'t need to look at `100, 200..`\n - [9,100,200,300,400,500,600] is same as `[9,100]` yes they are `3*3` and `2*2*5*5` but there are no common factors with each other (`co-prime`), their only common factor is `1` (`gcd=1`), (`gcf=hcf=gcd=1`)\n - So we can exit as soon as we find `two co-primes` (`gcd=1`)\n - see last solution below for early exit\n- Why is `[6,10,15]` a kind of special test case?\n - But `6*1 + 10*-2 + 15*1 = 1`\n - gcd of 6, 10, and 15 is 1\n - but there are no `co-primes`\n - `co-primes` if present then good, but may not present too but good array for our question\n - so `gcd is 1` can be trusted always, use and `co-primes` existence can be used for early exit\n- Want more? :)\n - Check gcd properties here - https://en.wikipedia.org/wiki/Greatest_common_divisor#Properties\n - Especially, see the closest one - 2nd property in above link - `B\xE9zout\'s identity`\n\nHope it is simple to understand.\n\n---\n\n```\nvar isGoodArray = function (A) {\n const gcd = (a, b) => (b ? gcd(b, a % b) : a);\n return A.reduce((g, n) => gcd(g, n)) === 1;\n};\n```\n\n\n\n---\n\n```\nvar isGoodArray = function (A) {\n return A.reduce((gcd = (a, b) => (b ? gcd(b, a % b) : a))) === 1;\n};\n```\n\n\n\n---\n\n```\nvar isGoodArray = (A) => A.reduce((gcd = (a, b) => (b ? gcd(b, a % b) : a))) === 1;\n```\n\n\n\n---\n\n```\nvar isGoodArray = function (A) {\n const gcd = (a, b) => (b ? gcd(b, a % b) : a);\n\n let g = A[0];\n for (let n of A) {\n g = gcd(g, n);\n if (g === 1)\n return true; // early exit\n }\n return false;\n};\n```\n\n\n\n---\n
| 3 | 0 |
['JavaScript']
| 0 |
check-if-it-is-a-good-array
|
Java solution | 0ms
|
java-solution-0ms-by-atthezoo-3su5
|
```\nclass Solution {\n public boolean isGoodArray(int[] nums) {\n int t = nums[0];\n for (int i = 0; i < nums.length; i++) {\n t =
|
atthezoo
|
NORMAL
|
2020-06-04T07:28:07.515011+00:00
|
2020-06-04T07:28:07.515062+00:00
| 351 | false |
```\nclass Solution {\n public boolean isGoodArray(int[] nums) {\n int t = nums[0];\n for (int i = 0; i < nums.length; i++) {\n t = gcd(nums[i], t);\n if (t == 1)\n return true;\n \n }\n return false;\n }\n\n public int gcd(int a, int b) {\n if (a < b)\n return gcd(b, a);\n return a % b == 0 ? b : gcd(b, a % b);\n }\n}
| 3 | 0 |
[]
| 0 |
check-if-it-is-a-good-array
|
C++ Simple GCD Solution (60%)
|
c-simple-gcd-solution-60-by-uds5501-pfr8
|
Uses inbuilt GCD function and checks if the gcd of array is 1 or not.\n\nbool isGoodArray(vector<int>& nums) {\n if (nums.size() == 0) return false;\n
|
uds5501
|
NORMAL
|
2020-06-01T18:20:01.965540+00:00
|
2020-06-01T18:20:01.965573+00:00
| 253 | false |
Uses inbuilt GCD function and checks if the gcd of array is 1 or not.\n```\nbool isGoodArray(vector<int>& nums) {\n if (nums.size() == 0) return false;\n else {\n int g = nums[0];\n for(int i=1; i<nums.size(); i++) {\n g = __gcd(g, nums[i]);\n }\n if (g == 1) return true;\n }\n return false;\n }\n```
| 3 | 0 |
['C++']
| 0 |
check-if-it-is-a-good-array
|
O(n) solution
|
on-solution-by-coder206-jqx2
|
Any linear combination of some subset of numbers is divisible by their greatest common divisor and GCD can be obtained as some linear combination. Thus, an arra
|
coder206
|
NORMAL
|
2019-11-03T04:01:43.906146+00:00
|
2019-11-03T04:21:08.171328+00:00
| 473 | false |
Any linear combination of some subset of numbers is divisible by their greatest common divisor and GCD can be obtained as some linear combination. Thus, an array is good if and only if GCD of its values is 1.\n\n\n```\n bool isGoodArray(vector<int>& nums)\n {\n if (nums.empty()) return false;\n int d = nums[0];\n for (int i = 1; i < nums.size(); i++)\n d = gcd(d, nums[i]);\n return d == 1;\n }\n```
| 3 | 2 |
[]
| 2 |
check-if-it-is-a-good-array
|
2 line code 0ms 100% beat
|
2-line-code-0ms-100-beat-by-gautamtushar-r0wq
|
Approach
`Let's walk through a dry run of the provided code with the input nums = [12, 5, 7, 23].Initialization:cpp
auto gcd = nums[0]; // gcd = 12
First iterat
|
gautamtushar00011
|
NORMAL
|
2025-03-11T05:32:20.099678+00:00
|
2025-03-11T05:32:20.099678+00:00
| 85 | false |
Approach
`Let's walk through a dry run of the provided code with the input nums = [12, 5, 7, 23].
Initialization:
cpp
auto gcd = nums[0]; // gcd = 12
First iteration:
n = 12
Update gcd:
cpp
gcd = __gcd(12, 12); // gcd = 12
Second iteration:
n = 5
Update gcd:
cpp
gcd = __gcd(12, 5); // gcd = 1
Third iteration:
n = 7
Update gcd:
cpp
gcd = __gcd(1, 7); // gcd = 1
Fourth iteration:
n = 23
Update gcd:
cpp
gcd = __gcd(1, 23); // gcd = 1
After iterating through all the elements in the nums array, the final value of gcd is 1.
Return value:
cpp
return gcd == 1; // return true
So, the function will return true for the input nums = [12, 5, 7, 23]
Complexity
Time complexity: O(N)
Space complexity:O(N)`
Code
```
class Solution {
public:
bool isGoodArray(vector<int>& nums) {
auto gcd = nums[0];
for (auto n : nums) gcd = __gcd(gcd, n);
return gcd == 1;
}
};```
| 2 | 0 |
['Array', 'Math', 'Iterator', 'Number Theory', 'C++']
| 0 |
check-if-it-is-a-good-array
|
Java, Simple Using GCD🌻
|
java-simple-using-gcd-by-ravithemore-b3b8
|
Intuition\nThe problem seems to involve finding the greatest common divisor (GCD) of elements in the given array.\n\n# Approach\nThe code defines a gcd method t
|
ravithemore
|
NORMAL
|
2023-11-15T06:12:21.646280+00:00
|
2023-11-15T06:12:21.646309+00:00
| 421 | false |
# Intuition\nThe problem seems to involve finding the greatest common divisor (GCD) of elements in the given array.\n\n# Approach\nThe code defines a gcd method to calculate the GCD of two numbers using recursion. Then, the isGoodArray method initializes a variable result with the first element of the array and iteratively calculates the GCD of result and the next element in the array. If at any point the GCD becomes 1, it returns true. Finally, the method checks if the final GCD is 1 and returns true if so, otherwise false.\n\n# Complexity\n- Time complexity:\nThe time complexity of the gcd function is typically O(log(min(a, b))), and the loop in the isGoodArray method iterates through the array once. So, the overall time complexity is O(n log(min(a, b))), where n is the length of the array.\n\n- Space complexity:\nThe space complexity is O(1) as there is no additional space used that scales with the input.\n\n# Code\n```\nclass Solution {\n\n public int gcd(int a, int b)\n {\n if (b==0) return a;\n\n if (a>b)\n return gcd(b , a%b);\n\n else \n return gcd(a, b%a);\n }\n\n\n public boolean isGoodArray(int[] nums) {\n \n int result = nums[0];\n\n for (int i=1;i<nums.length;i++)\n {\n if (result==1) return true;\n\n else result = gcd(result, nums[i]);\n }\n\n if (result==1) return true;\n return false;\n }\n}\n```
| 2 | 0 |
['Java']
| 0 |
check-if-it-is-a-good-array
|
JAVA || beginner friendly || GCD
|
java-beginner-friendly-gcd-by-deepakajay-ngeo
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
deepakajay77
|
NORMAL
|
2023-03-07T11:39:11.799994+00:00
|
2023-03-07T11:39:11.801384+00:00
| 922 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public boolean isGoodArray(int[] nums) {\n //gcd of numbers\n if(nums.length == 0){\n return false;\n }\n int ans = nums[0];\n for(int i = 1;i < nums.length;i++){\n ans = gcd(ans, nums[i]);\n }\n if(ans == 1) return true;\n else return false;\n }\n public int gcd(int a, int b){\n if(a == 0){\n return b;\n }\n return gcd(b % a, a);\n }\n}\n```
| 2 | 0 |
['Java']
| 0 |
check-if-it-is-a-good-array
|
JAVA solution || easy to understand code
|
java-solution-easy-to-understand-code-by-tgii
|
\nSimple gcd calculation program.\n\n\n\nclass Solution {\n static int gcd(int n,int m){\n if(m==0)\n return n;\n else\n
|
saurabh-huh
|
NORMAL
|
2022-11-30T21:58:56.344130+00:00
|
2022-11-30T21:58:56.344171+00:00
| 873 | false |
\nSimple gcd calculation program.\n\n\n```\nclass Solution {\n static int gcd(int n,int m){\n if(m==0)\n return n;\n else\n return gcd(m,n%m);\n }\n public boolean isGoodArray(int[] nums) {\n int res=nums[0];\n for(int i=1;i<nums.length;i++)\n res=gcd(res,nums[i]);\n return res==1;\n }\n}\n```
| 2 | 0 |
['Java']
| 1 |
check-if-it-is-a-good-array
|
Java Sol using Bezout's Identity
|
java-sol-using-bezouts-identity-by-rimmi-jyzl
|
Explanation:\n\nBezout\'s Identity\n \n let a and b be integers with greatest common divisor as d\n then there exist integers x and y such
|
rimmisharma
|
NORMAL
|
2022-10-11T09:03:39.510549+00:00
|
2022-10-11T09:03:39.510573+00:00
| 819 | false |
# Explanation:\n\n*Bezout\'s Identity*\n \n let a and b be integers with greatest common divisor as d\n then there exist integers x and y such that ax + by = d\n \n In Example 1,\n\n a=5, x=3, b=7, y=-2\n So, 5*3 + 7*(-2) = 1\n \n \n\n\n\n\n# Code\n```\nclass Solution {\n public boolean isGoodArray(int[] nums) {\n \n\n //Basically check for GCD and return true if its 1\n\n int x = nums[0], y;\n for(int a : nums){\n while(a > 0){\n y = x%a;\n x = a;\n a = y;\n }\n }\n\n return x == 1;\n }\n}\n```
| 2 | 0 |
['Java']
| 1 |
check-if-it-is-a-good-array
|
Linear Diophantine Equation
|
linear-diophantine-equation-by-karany-selg
|
Read the first answer and you can solve this problem.\nhttps://math.stackexchange.com/questions/145346/diophantine-equations-with-multiple-variables\n\nAs a sid
|
KaranY
|
NORMAL
|
2022-08-24T14:42:01.043679+00:00
|
2022-09-11T17:09:51.586104+00:00
| 356 | false |
Read the first answer and you can solve this problem.\nhttps://math.stackexchange.com/questions/145346/diophantine-equations-with-multiple-variables\n\nAs a side note, this equation is also used in the two water jars problem (https://leetcode.com/problems/water-and-jug-problem/). Also, this is one of the most frequently used mathematics concept (along with sieve) in Codeforces/coding contests in general, so it\'s worth learning. \n\n```\nbool isGoodArray(vector<int>& nums) {\n int hcf = nums[0];\n for (auto x: nums)\n hcf = gcd(x, hcf);\n return hcf == 1;\n }\n```
| 2 | 0 |
['Math']
| 1 |
check-if-it-is-a-good-array
|
Not to worry about !!
|
not-to-worry-about-by-diyora13-68ue
|
\nclass Solution {\npublic:\n bool isGoodArray(vector<int>& a) \n {\n int g=0;\n for(int i=0;i<(int)a.size();i++)\n g=__gcd(g,a[i
|
diyora13
|
NORMAL
|
2022-05-27T16:42:31.361501+00:00
|
2022-05-27T16:42:31.361560+00:00
| 399 | false |
```\nclass Solution {\npublic:\n bool isGoodArray(vector<int>& a) \n {\n int g=0;\n for(int i=0;i<(int)a.size();i++)\n g=__gcd(g,a[i]);\n if(g>1) return 0;\n else return 1;\n }\n};\n```
| 2 | 0 |
['Math', 'C', 'C++']
| 0 |
check-if-it-is-a-good-array
|
C++ One Line O(n) Bezout's Lemma
|
c-one-line-on-bezouts-lemma-by-safwankdb-imkk
|
We just need to check that GCD of all numbers is 1 (follows from Bezout\'s Lemma).\nC++\nbool isGoodArray(vector<int>& nums) {\n return accumulate(nums.b
|
safwankdb
|
NORMAL
|
2022-03-15T12:20:15.652852+00:00
|
2022-04-20T06:07:16.457538+00:00
| 337 | false |
We just need to check that GCD of all numbers is 1 (follows from Bezout\'s Lemma).\n```C++\nbool isGoodArray(vector<int>& nums) {\n return accumulate(nums.begin(), nums.end(), 0, [] (int a, int b) {return __gcd(a, b);}) == 1;\n}\n```
| 2 | 0 |
['Math', 'C']
| 1 |
check-if-it-is-a-good-array
|
Java Solution || GCD approach
|
java-solution-gcd-approach-by-kanikatyag-srcn
|
\nclass Solution {\n \n public int gcd(int a, int b) {\n if(b==0)\n return a;\n return gcd(b,a%b);\n }\n \n public boole
|
kanikatyagi
|
NORMAL
|
2022-02-25T03:33:20.884337+00:00
|
2022-02-25T03:33:20.884370+00:00
| 322 | false |
```\nclass Solution {\n \n public int gcd(int a, int b) {\n if(b==0)\n return a;\n return gcd(b,a%b);\n }\n \n public boolean isGoodArray(int[] nums) {\n int ans = nums[0];\n for (int element: nums){\n ans = gcd(ans, element);\n if(ans == 1){\n return true;\n }\n }\n return false;\n }\n}\n```
| 2 | 0 |
['Java']
| 0 |
check-if-it-is-a-good-array
|
simple explanation for noobs like me
|
simple-explanation-for-noobs-like-me-by-ybxm7
|
in this problem i simply thought that we have to select some elements and after some interger multipication my result should be 1 now let say we have selected
|
coderVip007
|
NORMAL
|
2021-12-20T17:38:22.730087+00:00
|
2021-12-20T17:49:43.860261+00:00
| 252 | false |
in this problem i simply thought that we have to select some elements and after some interger multipication my result should be 1 now let say we have selected some elements\n\n\n\n\n\nnow we have 2 cases\ncase1: -hcf of selected elements==1\n\ncase2:- hcf of selected elements!=1\n\nin case 2 we can take some intezer common let set we select \n(a,b,c,d)\nafter taking hcf common let say h\nh(a1,b1,c1,d1) here h !=1(case2) \'\nwe can easily say that whatever multiplication(with int) we make on a1,b1,c1,d1 we can\'t make it a fraction (as the result is always intezer) so the expression we can,t make it 1 as h>1 \n\nlow let say we are given an arr\narr={ 6, 8, 12, 14, 3, 9, 15}\'\n\'\nnow let say we select element 6 8 and 12 we can easily see hcf is 2\nso we can write it as 2( 3 , 4, 6) now whatever operation we make on 3,4,6 we can,t make it 1/2 for sure so we can\'t make the expression as 1\n\n\n\n\nbut in case 1 we can make it 1 i don\'t know the reason for this !!\n\n\n```\nclass Solution {\npublic:\n \n int hcf(int a,int b)\n {\n if(a==0)return b;\n \n if(a>b)return hcf(b,a);\n \n return hcf(b%a,a); \n }\n \n bool isGoodArray(vector<int>& nums) {\n \n bool ans=false;\n \n if(nums.size()==1)\n {\n return nums[0]==1;\n }\n \n \n \n \n int h=hcf(nums[0],nums[1]);\n \n if(h==1)return true;\n \n for(int i=2;i<nums.size();i++)\n {\n h=hcf(h,nums[i]);\n \n if(h==1)\n {\n ans=true;\n break;\n }\n \n }\n \n \n return ans;\n \n \n }\n};\n```
| 2 | 0 |
['C']
| 0 |
check-if-it-is-a-good-array
|
c++ O(n) with explanations
|
c-on-with-explanations-by-sjaubain-gah4
|
Since the GCD is an associative function, we have\n* gcd(a0, a1,...,an - 1) = gcd(a0, gcd(a1,...,an-1) = gcd(gcd(a0, a1), gcd(a2,...,an-1)) = ...\n\nand so on,
|
sjaubain
|
NORMAL
|
2021-11-14T13:15:08.950823+00:00
|
2021-11-14T14:43:23.009389+00:00
| 251 | false |
Since the GCD is an associative function, we have\n* gcd(a<sub>0</sub>, a<sub>1</sub>,...,a<sub>n - 1</sub>) = gcd(a<sub>0</sub>, gcd(a<sub>1</sub>,...,a<sub>n-1</sub>) = gcd(gcd(a<sub>0</sub>, a<sub>1</sub>), gcd(a<sub>2</sub>,...,a<sub>n-1</sub>)) = ...\n\nand so on, every possible combination is included. So we just have to iterate through `nums` until we find a gcd of `1`. In other world, if gcd(a<sub>0</sub>, a<sub>1</sub>,...,a<sub>n - 1</sub>) = 1, there exist a subsequence a<sub>i<sub>j</sub></sub> with #{a<sub>i<sub>0</sub></sub>,...,a<sub>i<sub>k</sub></sub>} = k, 1 <= k <= n, that give a gcd of `1.`\n\n```\nclass Solution {\n \npublic:\n \n bool isGoodArray(vector<int>& nums) {\n if(nums.size() == 1 and nums[0] == 1) return true;\n int gcd = 0;\n for(int i = 0; i < nums.size(); ++i) {\n if(i == 0) gcd = nums[i];\n else {\n gcd = __gcd(gcd, nums[i]);\n if(gcd == 1) return true;\n }\n }\n return false;\n }\n};\n```
| 2 | 0 |
['C']
| 0 |
check-if-it-is-a-good-array
|
This problem is about chinese remainder theorem.
|
this-problem-is-about-chinese-remainder-pfwk6
|
If gcd(a1, a2, ..., an) =1, there exist integers x1, ..., xn such that a1x1 + .... + an xn = 1\nhttps://en.wikipedia.org/wiki/Chinese_remainder_theorem\n\n\ncla
|
byuns9334
|
NORMAL
|
2021-09-27T14:09:38.236978+00:00
|
2021-09-27T14:09:38.237027+00:00
| 554 | false |
If gcd(a1, a2, ..., an) =1, there exist integers x1, ..., xn such that a1*x1 + .... + an *xn = 1\nhttps://en.wikipedia.org/wiki/Chinese_remainder_theorem\n\n```\nclass Solution:\n def isGoodArray(self, nums: List[int]) -> bool:\n import math \n n = len(nums)\n if n ==1:\n return nums[0] ==1\n d = math.gcd(nums[0], nums[1])\n for i in range(n):\n d = math.gcd(nums[i], d)\n return d ==1\n```
| 2 | 0 |
['Python', 'Python3']
| 0 |
check-if-it-is-a-good-array
|
Solution in Java | 100% Faster
|
solution-in-java-100-faster-by-s34-9gcl
|
hint - Finding gcd of numbers in the given array, if (gcd==1) then return true.(i.e. it is a good array); else return false.\n\nclass Solution {\n public int
|
s34
|
NORMAL
|
2021-02-25T01:31:17.388753+00:00
|
2021-02-25T01:31:17.388793+00:00
| 159 | false |
hint - Finding gcd of numbers in the given array, if (gcd==1) then return true.(i.e. it is a good array); else return false.\n```\nclass Solution {\n public int gcd(int a, int b){\n if(a==0)\n return b;\n return gcd(b%a,a);\n }\n public boolean isGoodArray(int[] nums) {\n if(nums.length==1){\n if(nums[0]!=1)\n return false;\n else\n return true;\n }\n int res=gcd(nums[0],nums[1]);\n for(int i=2;i<nums.length;i++){\n res=gcd(res,nums[i]);\n }\n return (res==1)?true:false;\n }\n}\n```\nPlease **upvote**, if you like the solution:)
| 2 | 0 |
[]
| 1 |
check-if-it-is-a-good-array
|
Python sol by G.C.D. & Bézout Lemma 90%+ [w/ Hint]
|
python-sol-by-gcd-bezout-lemma-90-w-hint-lxdx
|
Python sol by Greatest Common Divisor & B\xE9zout Lemma\n\n---\n\nHint:\n\nRecall that for integer a, b\naX + bY = k has integer solution (X, Y) if k is multipl
|
brianchiang_tw
|
NORMAL
|
2020-03-02T02:51:44.301148+00:00
|
2020-03-02T02:54:55.491991+00:00
| 433 | false |
Python sol by Greatest Common Divisor & B\xE9zout Lemma\n\n---\n\n**Hint**:\n\nRecall that for integer a, b\naX + bY = k has integer solution (X, Y) if k is multiple of gcd(a, b) from **[B\xE9zout lemma](https://proofwiki.org/wiki/B\xE9zout\'s_Lemma)**\n\nIn addition, [description](https://leetcode.com/problems/check-if-it-is-a-good-array/) sets k = 1, which means gcd(a,b) | 1.\ngcd(a,b) | 1\n=> gcd(a,b) = 1\n=> **a, b** is **co-prime**.\n\nNow, back to question itself.\n\nIf **gcd( all integers in given array) = 1**, then there exist at least one subset (a, b) satisfies aX + bY = 1. \nTherefore, input is a **good array**.\n\nOtherwise, there is no solution.\nAnd input is Not a good Array.\n\n---\n\n**Bezout Lemma**:\n\n\n\n---\n\n**Implementation**:\n\n```\nfrom math import gcd\n\nclass Solution:\n def isGoodArray(self, nums: List[int]) -> bool:\n \n \n # ax + by = 1 has integer solution only when gcd(a, b) == 1\n \n x = nums[0]\n \n\t\t# compute the greatest common divisor for all input integers\n for number in nums:\n \n x = gcd(x, number)\n \n \n return x == 1\n```\n\n---\n\nReference:\n\n[1] [Wiki Proof: B\xE9zout\'s Lemma](https://proofwiki.org/wiki/B\xE9zout\'s_Lemma)\n\n[2] [Python official docs about math.gcd()](https://docs.python.org/3/library/math.html?highlight=gcd#math.gcd)
| 2 | 0 |
['Math', 'Python']
| 0 |
check-if-it-is-a-good-array
|
[C++] gcd of all numbers
|
c-gcd-of-all-numbers-by-orangezeit-kyd6
|
[Small Improvement] As long as we the gcd becomes 1, we can return true.\n\nclass Solution {\npublic:\n bool isGoodArray(vector<int>& nums) {\n int g(
|
orangezeit
|
NORMAL
|
2019-11-03T04:09:14.585643+00:00
|
2019-11-03T15:14:57.061342+00:00
| 544 | false |
[Small Improvement] As long as we the gcd becomes 1, we can return true.\n```\nclass Solution {\npublic:\n bool isGoodArray(vector<int>& nums) {\n int g(nums[0]);\n for (const int& n: nums)\n if ((g = gcd(g, n)) == 1)\n return true;\n return false;\n }\n};\n```
| 2 | 1 |
[]
| 0 |
check-if-it-is-a-good-array
|
easy sol^n || beats 98% || Linear Diophantine Equation
|
easy-soln-beats-98-linear-diophantine-eq-b4sy
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \nIterate over the whole
|
abhinav6859
|
NORMAL
|
2024-10-11T16:44:01.718722+00:00
|
2024-10-11T16:44:01.718758+00:00
| 190 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nIterate over the whole array and calculate gcd\nIf gcd is 1 then return true, otherwise false\n# Complexity\n- Time complexity:0(n\u2217log(c))\n- where c= min(a,b)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:0(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int kcd1(int a,int b){\n if(b==0) return a;\n return kcd1(b,a%b);\n }\n bool isGoodArray(vector<int>& nums) {\n ios_base::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n int k=0;\n \n for(auto it:nums){\n k= kcd1(k,it);\n \n }\n return k==1;\n }\n};\n```
| 1 | 0 |
['Array', 'Math', 'Number Theory', 'C++']
| 1 |
check-if-it-is-a-good-array
|
Very Simple || C++ || Math
|
very-simple-c-math-by-akash92-svu9
|
Intuition\n Describe your first thoughts on how to solve this problem. \nIf we can find some numbers whose gcd is 1, then we can multiply each with some multipl
|
akash92
|
NORMAL
|
2024-09-06T06:23:12.930507+00:00
|
2024-09-06T06:23:12.930538+00:00
| 187 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIf we can find some numbers whose gcd is 1, then we can multiply each with some multiplicand and add or subtract from each others, to get 1\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nIterate over the whole array and calculate gcd\nIf gcd is 1 then return true, otherwise false\n\n# Complexity\n- Time complexity: $$O(n*log(n))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n bool isGoodArray(vector<int>& nums) {\n int g = 0;\n for(auto it: nums){\n g = gcd(g, it);\n }\n\n return g==1;\n }\n};\n```
| 1 | 0 |
['Array', 'Math', 'Number Theory', 'C++']
| 0 |
check-if-it-is-a-good-array
|
1250. | OPTIMISED CODE | BEATS 94% | UNDERSTAND THE INTUITION
|
1250-optimised-code-beats-94-understand-arqc4
|
Intuition\n\n## Problem Statement\n\nLet\'s say I have an array {a1,a2,a3}. Now we want to find out if there exists a subset that can yield us 1. This means, do
|
intbliss
|
NORMAL
|
2024-07-11T16:40:16.898664+00:00
|
2024-07-11T16:40:16.898711+00:00
| 320 | false |
# Intuition\n\n## Problem Statement\n\nLet\'s say I have an array `{a1,a2,a3}`. Now we want to find out if there exists a subset that can yield us 1. This means, does the equation `a1x + a2y + a3z = 1` (where x, y, z are integers) have a solution? \n\n## Bezout\'s Theorem\n\nThere is a direct mathematical identity called Bezout\'s Theorem which states:\n\nFor integers a, b, there exist integers x, y such that `ax + by = gcd(a,b)`.\n\nWe can use this theorem to address our question. Specifically, `a1x + a2y + a3z = 1` is true if `gcd(a1, a2, a3) == 1`.\n\n## Solution Approach\n\nTherefore, all we need to do now is calculate the gcd of all the elements in the array and check if the gcd is 1 or not. If you want to understand how this method works, look for the proof of Bezout\'s theorem.\n\n### Intuition Example\n\nConsider the example array `{3, 6}`. Now,\n\n`3x + 6y = 1`\n\nSimplifying further,\n\n`3(x + 2y) = 1`\n\n`x + 2y = 1/3`\n\nIt\'s clear that there are no integer values of x and y that can satisfy `x + 2y = 1/3`.\n\n### Tip\n\nWhile iterating over the array and calculating the gcd, if we find that the gcd is 1 at any point, there\'s no need to continue iterating further.\n\n\n# Approach\n1. **Initialization:**\n - Initialize `x` with the first element of `nums`. This assumes `nums` is non-empty.\n\n2. **Iterate through array:**\n - Iterate through each `num` in `nums`.\n\n3. **Reduce `num` to 1:**\n - Use a `while` loop to repeatedly compute the modulo (`temp = x % num`) and update `x` and `num` until `num` becomes 0. This effectively reduces `num` to the greatest common divisor (gcd) of `x` and `num`.\n\n4. **Check condition:**\n - After the `while` loop, check if `x` equals 1 (`if (x == 1)`). If true, return `true` indicating there exists a number `x` such that all elements in `nums` can be reduced to 1.\n\n5. **Return false:**\n - If the loop completes without finding `x` equal to 1 for any `num`, return `false`.\n\n\n# Complexity\n- Time complexity:\n$$O(n)$$ \n\n- Space complexity:\n $$O(1)$$ \n\n# Code\n```\nclass Solution {\n public boolean isGoodArray(int[] nums) {\n\n int x = nums[0] ;\n int temp ;\n\n for(int num : nums)\n {\n while(num > 0)\n {\n temp = x%num ;\n x = num ;\n num = temp ;\n }\n if(x == 1) return true ;\n }\n\n return false ;\n \n }\n}\n```
| 1 | 0 |
['Java']
| 2 |
check-if-it-is-a-good-array
|
Simple setwise coprimality check
|
simple-setwise-coprimality-check-by-burk-u84m
|
Intuition\nWe need to determine if the numbers are setwise coprime.\n\n# Code\n\nclass Solution:\n def isGoodArray(self, nums: List[int]) -> bool:\n r
|
burkh4rt
|
NORMAL
|
2023-12-12T03:47:15.573934+00:00
|
2024-01-28T05:08:32.721186+00:00
| 118 | false |
# Intuition\nWe need to determine if the numbers are setwise coprime.\n\n# Code\n```\nclass Solution:\n def isGoodArray(self, nums: List[int]) -> bool:\n return reduce(gcd, nums) == 1\n```
| 1 | 0 |
['Python3']
| 0 |
check-if-it-is-a-good-array
|
5 lines of Solution , Simple
|
5-lines-of-solution-simple-by-abagul200-5k3j
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
abagul200
|
NORMAL
|
2023-12-04T10:43:10.773515+00:00
|
2023-12-04T10:43:10.773537+00:00
| 46 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n bool isGoodArray(vector<int>& nm) {\n int n=nm.size();\n int it=0;\n for(int i=0; i<n; i++){\n it=__gcd(it, nm[i]);\n }\n return (it==1);\n }\n};\n```
| 1 | 0 |
['C++']
| 0 |
check-if-it-is-a-good-array
|
C# Solution using Gcd
|
c-solution-using-gcd-by-mohamedabdelety-u5y6
|
\n# Complexity\n- Time complexity:\nO(N log max)\n- Space complexity:\nO(1)\n# Code\n\npublic class Solution {\n public bool IsGoodArray(int[] nums) {\n
|
mohamedAbdelety
|
NORMAL
|
2023-05-13T12:02:02.525723+00:00
|
2023-05-13T12:02:02.525761+00:00
| 47 | false |
\n# Complexity\n- Time complexity:\nO(N log max)\n- Space complexity:\nO(1)\n# Code\n```\npublic class Solution {\n public bool IsGoodArray(int[] nums) {\n int gcd(int a,int b) => (a == 0) ? b : gcd(b % a, a);\n int curGcd = nums[0];\n for(int i = 1; i < nums.Length;i++){\n curGcd = gcd(curGcd,nums[i]);\n if(curGcd == 1) return true;\n } \n return curGcd == 1;\n }\n}\n```
| 1 | 0 |
['Number Theory', 'C#']
| 0 |
check-if-it-is-a-good-array
|
Easiest One-Liner || Easy to understand.
|
easiest-one-liner-easy-to-understand-by-o8fmm
|
Approach\n Describe your approach to solving the problem. \nIf the GCD of all the elements of the array is equal to 1, return True\n\n# Complexity\n- Time compl
|
Abhishek004
|
NORMAL
|
2022-12-20T04:24:32.758169+00:00
|
2022-12-20T04:24:32.758214+00:00
| 150 | false |
# Approach\n<!-- Describe your approach to solving the problem. -->\nIf the GCD of all the elements of the array is equal to 1, return **True**\n\n# Complexity\n- Time complexity: **O(n)**\n\n- Space complexity: **O(1)**\n\n# Code\n```\nclass Solution:\n def isGoodArray(self, nums: List[int]) -> bool:\n return True if math.gcd(*nums)==1 else False\n```
| 1 | 0 |
['Python', 'Python3']
| 0 |
check-if-it-is-a-good-array
|
C++ || gcd || Easy to understand
|
c-gcd-easy-to-understand-by-anil_gtm-w4tz
|
\nclass Solution {\npublic:\n bool isGoodArray(vector<int>& nums) {\n //using diophantine equation approach\n //we have to select subset which
|
ANIL_GTM
|
NORMAL
|
2022-08-28T17:45:39.855783+00:00
|
2022-08-28T17:45:39.855848+00:00
| 402 | false |
```\nclass Solution {\npublic:\n bool isGoodArray(vector<int>& nums) {\n //using diophantine equation approach\n //we have to select subset which has gcd of 1\n //so we have to give only whether we are able to select such subset that has gcd=1\n //so if such subset has gcd = 1 so the all element has also gcd having 1. if all element having gcd than only can return true otherwise return false\n int g = nums[0];\n for(auto i:nums){\n g = __gcd(g,i);\n }\n if(g==1) return true;\n else return false;\n }\n};\n```
| 1 | 0 |
['C']
| 0 |
check-if-it-is-a-good-array
|
C++ || GCD
|
c-gcd-by-geetesh_pandey-ne6h
|
\nclass Solution {\npublic:\n bool isGoodArray(vector<int>& nums) {\n int n = 0;\n for(int i=0;i<nums.size();i++)\n {\n n = _
|
Geetesh_Pandey
|
NORMAL
|
2022-07-07T10:31:38.255510+00:00
|
2022-07-07T10:31:38.255541+00:00
| 203 | false |
```\nclass Solution {\npublic:\n bool isGoodArray(vector<int>& nums) {\n int n = 0;\n for(int i=0;i<nums.size();i++)\n {\n n = __gcd(n,nums[i]);\n if(n == 1)\n return true;\n }\n return false;\n }\n};\n```
| 1 | 0 |
['C']
| 0 |
check-if-it-is-a-good-array
|
Fully explained || GCD || CO-Prime || CPP
|
fully-explained-gcd-co-prime-cpp-by-anuk-idsz
|
Intuition here is to get a set from nums whose gcd=1 as if gcd(a,b)==1 then there exist atleast one multiple of a & b whose difference is 1:)\n\nSo in order to
|
anukul1325
|
NORMAL
|
2022-07-06T02:30:46.411338+00:00
|
2022-07-06T04:08:50.010338+00:00
| 235 | false |
Intuition here is to get a set from nums whose gcd=1 as if gcd(a,b)==1 then there exist atleast one multiple of a & b whose difference is 1:)\n\nSo in order to check this, we can simply check the gcd of whole list because if there exist a single co-prime pair then gcd of list will be 1.\n\nPFB my code for your reference:\n```\nclass Solution {\npublic:\n bool isGoodArray(vector<int>& nums) {\n int n=nums.size();\n \xA0 \xA0 \xA0 \xA0/// if(n==1) return nums[0]==1;\n int ans=nums[0];\n for(int i=1;i<n;i++)\n ans=__gcd(ans,nums[i]);\n return ans==1;\n }\n};\n```
| 1 | 0 |
[]
| 1 |
check-if-it-is-a-good-array
|
Bezout's algorithm C++
|
bezouts-algorithm-c-by-vibhanshu2001-v8xb
|
\nclass Solution {\npublic:\n //bezout\'s algorithm\n bool isGoodArray(vector<int>& nums) {\n if(nums.size()==1 && nums[0]==1){\n return
|
vibhanshu2001
|
NORMAL
|
2022-06-21T16:40:58.195875+00:00
|
2022-06-21T16:40:58.195917+00:00
| 91 | false |
```\nclass Solution {\npublic:\n //bezout\'s algorithm\n bool isGoodArray(vector<int>& nums) {\n if(nums.size()==1 && nums[0]==1){\n return true;\n }\n int num = nums[0];\n for(int i=1;i<nums.size();i++){\n num = __gcd(num,nums[i]);\n if(num==1){\n return true;\n }\n }\n return false;\n }\n};\n```
| 1 | 0 |
[]
| 0 |
check-if-it-is-a-good-array
|
✅ Java best approach :-)
|
java-best-approach-by-devilabhi-6c16
|
\nclass Solution {\n public boolean isGoodArray(int[] nums) {\n int gcd=nums[0];\n for(int i=1; i<nums.length; i++){\n gcd=gcd(gcd, nums
|
devilabhi
|
NORMAL
|
2022-04-17T16:33:35.694719+00:00
|
2022-04-17T16:33:35.694755+00:00
| 215 | false |
```\nclass Solution {\n public boolean isGoodArray(int[] nums) {\n int gcd=nums[0];\n for(int i=1; i<nums.length; i++){\n gcd=gcd(gcd, nums[i]);\n if(gcd==1)return true;\n }\n return gcd==1;\n}\n public int gcd(int a, int b) {\n if (b==0) return a;\n return gcd(b,a%b);\n }\n}\n\n```\n
| 1 | 0 |
['Java']
| 1 |
check-if-it-is-a-good-array
|
Linear Combination possible if subset with GCD 1 exists
|
linear-combination-possible-if-subset-wi-awlr
|
\nclass Solution:\n def gcd(self, a, b):\n while b:\n a, b = b, a % b\n return a\n \n def isGoodArray(self, nums: List[int]) -
|
theabbie
|
NORMAL
|
2022-01-23T15:30:26.109973+00:00
|
2022-01-23T15:53:16.461528+00:00
| 113 | false |
```\nclass Solution:\n def gcd(self, a, b):\n while b:\n a, b = b, a % b\n return a\n \n def isGoodArray(self, nums: List[int]) -> bool:\n n = len(nums)\n curr = nums[0]\n for i in range(1, n):\n curr = self.gcd(curr, nums[i])\n if curr == 1:\n return True\n return curr == 1\n```
| 1 | 0 |
['Python']
| 0 |
check-if-it-is-a-good-array
|
Java Solution
|
java-solution-by-hawtsauce-iwnl-6pmn
|
\nclass Solution {\n // O(N) Time | O(1) Space\n // If GCD of all the elements is 1, the array is a good array\n \n public boolean isGoodArray(int[]
|
hawtsauce-iwnl
|
NORMAL
|
2021-12-26T12:06:37.555721+00:00
|
2021-12-26T12:06:37.555752+00:00
| 158 | false |
```\nclass Solution {\n // O(N) Time | O(1) Space\n // If GCD of all the elements is 1, the array is a good array\n \n public boolean isGoodArray(int[] nums) {\n int result = 0;\n for (int element: nums){\n result = gcd(result, element);\n if(result == 1)\n {\n return true;\n }\n }\n return false;\n }\n \n int gcd(int a, int b) {\n if(a == 0) {\n return b;\n }\n return gcd(b % a, a);\n }\n}\n```
| 1 | 0 |
[]
| 0 |
check-if-it-is-a-good-array
|
Python3 one liner
|
python3-one-liner-by-pradhyumnjain10-seo9
|
The minimum difference that can be created by manipulating two numbers in a way given by the question is equal to the greatest common divisor of the two numbers
|
pradhyumnjain10
|
NORMAL
|
2021-12-15T00:24:43.530710+00:00
|
2021-12-15T00:24:43.530737+00:00
| 103 | false |
The minimum difference that can be created by manipulating two numbers in a way given by the question is equal to the greatest common divisor of the two numbers. \n\nFor example : \n```\nnums = [12,18]\ngcd(12,18) = 6\n```\nTherefore the minimum difference after manipulating the numbers would be 6.\n\nFor this problem, we need to find whether the gcd of any two numbers in `nums` is 1\n--> gcd(nums) == 1\n\n**Python3 One Liner:**\n```\nclass Solution:\n def isGoodArray(self, nums: List[int]) -> bool:\n return reduce(gcd,nums) == 1\n```
| 1 | 0 |
[]
| 0 |
check-if-it-is-a-good-array
|
[C++] | Easy solution | Space lesser than 97%
|
c-easy-solution-space-lesser-than-97-by-tmboa
|
We know there exists a solution for ax+by =1 when there exists a , b such that their hcf is 1.\nIf we find 2 nums whose hcf is 1 we return true; else return fal
|
dexter_2000
|
NORMAL
|
2021-09-12T16:50:11.493417+00:00
|
2021-09-12T16:50:11.493465+00:00
| 221 | false |
We know there exists a solution for `ax+by =1` when there exists a , b such that their hcf is 1.\nIf we find 2 nums whose hcf is 1 we `return true;` else `return false;` .\n```\nbool isGoodArray(vector<int>& nums) {\n int n=nums.size();\n if(!n) return false;\n int hcf=nums[0];\n\t\t\n for(int i=1;i<n;i++){\n hcf=__gcd(hcf,nums[i]);\n }\n\t\t\n return hcf==1;\n }
| 1 | 0 |
['C', 'C++']
| 0 |
check-if-it-is-a-good-array
|
C++ 1 line
|
c-1-line-by-sanzenin_aria-hd0a
|
```\n bool isGoodArray(vector& nums) {\n return accumulate(nums.begin(), nums.end(), nums[0], gcd) == 1;\n }
|
sanzenin_aria
|
NORMAL
|
2021-01-09T06:08:35.610331+00:00
|
2021-01-09T06:11:31.281376+00:00
| 147 | false |
```\n bool isGoodArray(vector<int>& nums) {\n return accumulate(nums.begin(), nums.end(), nums[0], gcd<int,int>) == 1;\n }
| 1 | 0 |
[]
| 1 |
check-if-it-is-a-good-array
|
Python 3.9 solution
|
python-39-solution-by-charlesqwu-4yns
|
Python 3.9 allows math.gcd() to take an iterable: \nmath.gcd(*integers)\nReturn the greatest common divisor of the specified integer arguments. If any of the ar
|
charlesqwu
|
NORMAL
|
2020-12-21T06:22:14.624806+00:00
|
2020-12-21T06:22:14.624836+00:00
| 237 | false |
Python 3.9 allows math.gcd() to take an iterable: \nmath.gcd(*integers)\nReturn the greatest common divisor of the specified integer arguments. If any of the arguments is nonzero, then the returned value is the largest positive integer that is a divisor of all arguments. If all arguments are zero, then the returned value is 0. gcd() without arguments returns 0.\n\nNew in version 3.5.\nChanged in version 3.9: Added support for an arbitrary number of arguments. Formerly, only two arguments were supported.\n\nLeetcode has been using Python 3.9 since 2020-10-20.\n\nSo, Python 3.9 solution is the simplest code that you may have for a "hard" problem:\n```\n def isGoodArray(self, nums: List[int]) -> bool:\n return math.gcd(*nums) == 1\n```
| 1 | 0 |
[]
| 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.