question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
maximum-population-year
|
✅C++ || Brute force
|
c-brute-force-by-abhinav_0107-mbu7
|
\n\nn==log.size()\nT->O((j-i) * n ) && S->O(1)\n\n\tclass Solution {\n\tpublic:\n\t\tint maximumPopulation(vector>& logs) {\n\t\t\tint i=INT_MAX,j=INT_MIN;\n\t\
|
abhinav_0107
|
NORMAL
|
2022-07-08T19:54:47.154851+00:00
|
2022-07-08T19:54:47.154894+00:00
| 462 | false |
\n\n**n==log.size()\nT->O((j-i) * n ) && S->O(1)**\n\n\tclass Solution {\n\tpublic:\n\t\tint maximumPopulation(vector<vector<int>>& logs) {\n\t\t\tint i=INT_MAX,j=INT_MIN;\n\t\t\tfor(int k=0;k<logs.size();k++){\n\t\t\t\ti=min(logs[k][0],i);\n\t\t\t\tj=max(logs[k][1],j);\n\t\t\t}\n\t\t\tint maxpop=INT_MIN,count;\n\t\t\tint a=i,b=j;\n\t\t\twhile(i<j){\n\t\t\t\tcount=0;\n\t\t\t\tfor(int k=0;k<logs.size();k++){\n\t\t\t\t\tif(logs[k][0]<=i && i<logs[k][1])count++;\n\t\t\t\t}\n\t\t\t\tmaxpop=max(maxpop,count);\n\t\t\t\ti++;\n\t\t\t}\n\t\t\twhile(a<b){\n\t\t\t\tcount=0;\n\t\t\t\tfor(int k=0;k<logs.size();k++){\n\t\t\t\t\tif(logs[k][0]<=a && a<logs[k][1])count++;\n\t\t\t\t}\n\t\t\t\tif(maxpop==count)return a;\n\t\t\t\ta++;\n\t\t\t}\n\t\t\treturn -1;\n\t\t}\n\t};
| 2 | 0 |
['C', 'C++']
| 0 |
maximum-population-year
|
Java 100% faster solution ✅ O(N) time
|
java-100-faster-solution-on-time-by-chir-m76g
|
class Solution {\n public int maximumPopulation(int[][] logs) {\n \n int [] arr = new int[101];\n for(int i = 0;i<logs.length ;i++)\n
|
chiragvohra
|
NORMAL
|
2022-05-18T23:32:55.007356+00:00
|
2022-05-18T23:32:55.007381+00:00
| 399 | false |
class Solution {\n public int maximumPopulation(int[][] logs) {\n \n int [] arr = new int[101];\n for(int i = 0;i<logs.length ;i++)\n {\n \n \n arr[logs[i][0]-1950]++;\n arr[logs[i][1]-1950]--;\n \n }\n for(int i = 1;i<101;i++)\n {\n arr[i]=arr[i-1]+arr[i];\n }\n int max=0,year=1950;\n for(int i = 0;i<101;i++)\n {\n if(arr[i]>max){\n max = arr[i];\n year=i+1950;\n }\n }\n return year;\n }\n \n}
| 2 | 0 |
['Java']
| 1 |
maximum-population-year
|
Python One-Liner
|
python-one-liner-by-lrnx-sfdu
|
\ndef maximumPopulation(self, logs: List[List[int]]) -> int:\n return max(accumulate(sorted(zip(chain(*logs), cycle((1, -1)))), lambda x, y: (y[0], y[1] +
|
Lrnx
|
NORMAL
|
2022-04-18T08:52:36.906085+00:00
|
2022-04-18T08:52:36.906113+00:00
| 184 | false |
```\ndef maximumPopulation(self, logs: List[List[int]]) -> int:\n return max(accumulate(sorted(zip(chain(*logs), cycle((1, -1)))), lambda x, y: (y[0], y[1] + x[1])), key=itemgetter(1))[0] \n```\n\nRoughly equivalent to (but here we do max and accumulate together in one for loop):\n```\ndef maximumPopulation(self, logs: List[List[int]]) -> int:\n events = []\n for start, end in logs:\n\tevents += (start, 1), (end, -1)\n events.sort()\n maxi = 0\n max_year = 0\n count = 0\n for year, effect in events:\n\tcount += effect\n\tif count > maxi:\n\t maxi = count\n\t max_year = year\n return max_year\n```
| 2 | 0 |
['Python']
| 0 |
maximum-population-year
|
Java| Easy Solution
|
java-easy-solution-by-pranav_bobade-ko8z
|
class Solution {\n public int maximumPopulation(int[][] logs) {\n int a[]=new int [101];\n for (int i = 0; i < logs.length ; i++) \n {\n
|
pranav_bobade
|
NORMAL
|
2022-04-16T16:54:47.263926+00:00
|
2022-04-16T16:54:47.263956+00:00
| 128 | false |
class Solution {\n public int maximumPopulation(int[][] logs) {\n int a[]=new int [101];\n for (int i = 0; i < logs.length ; i++) \n {\n for (int j = logs[i][0]; j <logs[i][1] ; j++)\n { // to traverse from birth year to death year\n a[j-1950]++; \n // store population from oth position of a[] i.e a[0]=1.......\n }\n }\n int maxVal=0;\n int maxYear=1950;\n for (int i = 0; i < 101; i++)\n {\n if(a[i]>maxVal)\n {\n maxVal=a[i];\n maxYear=i+1950;\n }\n }\n return maxYear;\n }\n}
| 2 | 0 |
[]
| 0 |
maximum-population-year
|
4 liner, hash map solution
|
4-liner-hash-map-solution-by-sushmitha01-ik44
|
\ncount = {}\nfor i in logs:\n for v in range(i[0],i[1]):\n count[v] = count.get(v,0) + 1\n m = max(count.values())\n return min([i for i in count i
|
sushmitha0127
|
NORMAL
|
2022-03-23T02:42:21.509956+00:00
|
2022-03-23T02:42:21.509991+00:00
| 608 | false |
```\ncount = {}\nfor i in logs:\n for v in range(i[0],i[1]):\n count[v] = count.get(v,0) + 1\n m = max(count.values())\n return min([i for i in count if count[i] == m])\n```
| 2 | 0 |
['Python', 'Python3']
| 0 |
maximum-population-year
|
Java Sol | 0ms | 100% faster | with explanation
|
java-sol-0ms-100-faster-with-explanation-mh92
|
\nclass Solution {\n public int maximumPopulation(int[][] logs) {\n\n int[] arr = new int[101]; \n //1950-2050 +1\n // brute force -> O(
|
tohellwith
|
NORMAL
|
2022-03-01T20:16:27.809961+00:00
|
2022-03-01T20:16:27.810030+00:00
| 270 | false |
```\nclass Solution {\n public int maximumPopulation(int[][] logs) {\n\n int[] arr = new int[101]; \n //1950-2050 +1\n // brute force -> O(n^2)\n // optimized -> O(n)\n \n int max=Integer.MIN_VALUE;\n int count=0, year=0;\n \n for(int[] log:logs) {\n arr[log[0]-1950]++;\n arr[log[1]-1950]--;\n }\n \n for(int i=1950; i<=2050; i++) {\n // IMP -> count will be the running sum of the array \n \n // example - [[1993,1999],[2000,2010]]\n // arr = [0,0......,1,0,0,..0,-1,...]\n // arr[1993 -1950] will have value 1 \n // so count = 1 from 1993 to 1949 \n // count =0 at 1950 \n // so the only instance max<count is when i=1993\n // next time max=1 so for [2000,2010] year will not be updated\n \n count += arr[i-1950];\n \n year = max < count ? i : year;\n max=Math.max(max,count);\n }\n \n return year;\n \n }\n}\n```
| 2 | 0 |
['Array', 'Java']
| 0 |
maximum-population-year
|
Java || 100% || Straightforward
|
java-100-straightforward-by-summi_r-panf
|
Array size as per declared constraints and adjusting array indexes while referencing it...\n\nThanks for dropping by...Pls upvote if it\'s useful to you... :-)\
|
summi_r
|
NORMAL
|
2022-02-20T08:49:21.646931+00:00
|
2022-02-20T08:49:21.646965+00:00
| 158 | false |
Array size as per declared constraints and adjusting array indexes while referencing it...\n\nThanks for dropping by...Pls upvote if it\'s useful to you... :-)\n\n\n```\nclass Solution {\n public int maximumPopulation(int[][] logs) {\n int[] alive = new int[101]; //1950-2050+1\n int max=Integer.MIN_VALUE;\n int count=0, year=0;\n \n for(int[] log:logs) {\n alive[log[0]-1950]++;\n alive[log[1]-1950]--;\n }\n \n for(int i=1950; i<=2050; i++) {\n count += alive[i-1950];\n \n year = max < count ? i : year;\n max=Math.max(max,count);\n }\n \n return year;\n }\n}\n```
| 2 | 0 |
['Array']
| 0 |
maximum-population-year
|
More intuitive Java code
|
more-intuitive-java-code-by-dahaejeon-uqen
|
\nclass Solution {\n public int maximumPopulation(int[][] logs) {\n int[] countArr = new int[2051];\n int res = 0;\n for (int[] log : lo
|
dahaejeon
|
NORMAL
|
2021-12-31T01:12:31.596331+00:00
|
2021-12-31T01:12:31.596368+00:00
| 154 | false |
```\nclass Solution {\n public int maximumPopulation(int[][] logs) {\n int[] countArr = new int[2051];\n int res = 0;\n for (int[] log : logs) {\n for (int i = log[0]; i < log[1]; i++) {\n countArr[i]++;\n }\n }\n\n for (int i = 1950; i < 2050; i++) {\n if (countArr[res] < countArr[i]) {\n res = i;\n }\n }\n\n return res;\n }\n}\n\n```
| 2 | 0 |
['Java']
| 0 |
maximum-population-year
|
JAVA O(n)
|
java-on-by-user5386he-kbng
|
Note: So the logic is to increment the every year value if there is someone born.\nfor example if someone birth year and deadth year is 1950,1962 then the year
|
user5386HE
|
NORMAL
|
2021-11-28T15:05:52.137430+00:00
|
2021-11-28T15:05:52.137463+00:00
| 314 | false |
Note: So the logic is to increment the every year value if there is someone born.\nfor example if someone birth year and deadth year is 1950,1962 then the year from 1950 to 1961 will have count of 1 this will identify the no of persons present in a particular in this way the value of every year will vary based on the birth year and deadth year and at the end the year having maximum count will have maximum popullation.\n\n\n\n\npublic int maximumPopulation(int[][] logs) {\n int[] years=new int[101];\n int max=0,ans=1950;\n for(int[] a:logs){\n for(int i=a[0];i<a[1];i++){\n years[(i)-1950]++;\n }\n }\n for(int i=0;i<years.length;i++){\n if(years[i]>max){\n max=years[i];\n ans=1950+i;\n }\n }\n return ans;\n }
| 2 | 0 |
['Java']
| 0 |
maximum-population-year
|
Difference Array | Space Optimization with Explanation
|
difference-array-space-optimization-with-pdeg
|
You might have seen many solutions using array of size 2050 for difference array / line sweep. But we can do better than that.\n\nFrom constraints 1950 <= bir
|
bitmasker
|
NORMAL
|
2021-11-28T13:12:58.132054+00:00
|
2021-11-28T13:19:30.740541+00:00
| 211 | false |
<br/> You might have seen many solutions using array of size 2050 for difference array / line sweep. <br/> But we can do better than that.\n\nFrom constraints `1950 <= birth[i] < death[i] <= 2050` we can see that number of years will be at max 101 (1950 - 2050). <br/>So we can use an array of size 101 in which `the index i will represent the year i + 1950`\n<br/> Then we can follow the typical Difference array approach\n\n* Initially make population count in all years as 0\n* For each log in logs, **increment count for birth[i] year (log[0]) and decrement count for death[i] year (log[1])**\n* Calculate prefix sum of the array and you will get the population count in each year\n* Keep track of the index i which has maximum population\n* **Return i + 1950** (The year with maximum population)\n<br/>\n\n```cpp\nint maximumPopulation(vector<vector<int>>& logs) {\n \n vector<int> years(101, 0);\n \n for(auto &log: logs) {\n years[log[0] - 1950]++;\n years[log[1] - 1950]--;\n }\n \n int maxPopulation = years[0];\n int year = 1950;\n \n for(int i = 1; i <= 100; i++) {\n years[i] += years[i - 1];\n \n if(years[i] > maxPopulation) {\n maxPopulation = years[i];\n year = i + 1950;\n }\n }\n \n return year;\n }\n```\n<br/>
| 2 | 0 |
['C', 'C++']
| 0 |
maximum-population-year
|
Simple java solution
|
simple-java-solution-by-siddhant_1602-20yf
|
class Solution {\n\n public int maximumPopulation(int[][] l) {\n int a[]=new int[151];\n int k=l.length;\n for(int i=0;i<k;i++)\n
|
Siddhant_1602
|
NORMAL
|
2021-11-25T16:47:25.729651+00:00
|
2022-03-08T07:00:25.072270+00:00
| 172 | false |
class Solution {\n\n public int maximumPopulation(int[][] l) {\n int a[]=new int[151];\n int k=l.length;\n for(int i=0;i<k;i++)\n {\n for(int j=l[i][0];j<l[i][1];j++)\n {\n a[j-1950]++;\n }\n }\n int s=Integer.MIN_VALUE,p=0;\n for(int i=0;i<151;i++)\n {\n if(a[i]>s)\n {\n s=a[i];\n p=i+1950;\n }\n }\n return p;\n }\n}
| 2 | 1 |
['Java']
| 0 |
maximum-population-year
|
Java with Simle Approach | With Comments
|
java-with-simle-approach-with-comments-b-0y4j
|
\n\n\n\nimport java.util.Arrays;\nclass Solution {\n public int maximumPopulation(int[][] logs) {\n int start , end;\n int[] years = new int[20
|
gaurav89830
|
NORMAL
|
2021-09-16T07:23:20.987742+00:00
|
2021-09-16T07:31:09.625207+00:00
| 307 | false |
\n\n\n```\nimport java.util.Arrays;\nclass Solution {\n public int maximumPopulation(int[][] logs) {\n int start , end;\n int[] years = new int[2051];\n \n for(int i=0;i<logs.length;i++){\n start = logs[i][0]; //Birth year\n end = logs[i][1]; //Death year\n for(int x=start;x<end;x++){ // +1 in each year between Birth and ( Death - 1 ) year\n years[x]++;\n }\n }\n int max=0;int ans=0;\n for(int i=1950;i<=2050;i++){ //to find maximum polulation year\n if(max<years[i]){\n max = years[i];\n ans = i;\n }\n }\n return ans;\n }\n}\n\n\n\n\n```\nAfter optimization\n```\n\n\nimport java.util.Arrays;\nclass Solution {\n public int maximumPopulation(int[][] logs) {\n int start , end;\n int[] years = new int[101];\n \n for (int i = 0; i < logs.length; i++) {\n start = logs[i][0];\n end = logs[i][1];\n for (int x = start; x < end; x++) {\n years[x - 1950]++;\n }\n }\n int max = 0;\n int ans = 0;\n for (int i = 1950; i <= 2050; i++) {\n if (max < years[i - 1950]) {\n max = years[i - 1950];\n ans = i;\n }\n }\n\n\n return ans;\n }\n}\n\n\n\n```\n
| 2 | 0 |
[]
| 1 |
maximum-population-year
|
C++ Solution || brute Force || Line Sweep Algo || Comment for help !!
|
c-solution-brute-force-line-sweep-algo-c-hgup
|
\n// brute force solution\n\nclass Solution\n{\npublic:\n int maximumPopulation(vector<vector<int>> &logs)\n {\n int n = logs.size();\n map<
|
raj1999gupta
|
NORMAL
|
2021-06-27T09:46:44.192524+00:00
|
2021-06-27T09:46:44.192555+00:00
| 139 | false |
```\n// brute force solution\n\nclass Solution\n{\npublic:\n int maximumPopulation(vector<vector<int>> &logs)\n {\n int n = logs.size();\n map<int, int> mp;\n int max = 0;\n int ans;\n if (n == 1)\n return logs[0][0];\n for (auto i : logs)\n {\n for (int j = i[0]; j < i[1]; j++)\n mp[j - 1950]++;\n }\n for (auto i : mp)\n {\n if (max < i.second)\n {\n max = i.second;\n ans = i.first;\n }\n }\n return ans + 1950;\n }\n};\n\n// Line swipe algorithm\n\nclass Solution\n{\npublic:\n int maximumPopulation(vector<vector<int>> &logs)\n {\n map<int, int> mp;\n for (vector<int> log : logs)\n {\n mp[log[0] - 1950]++;\n mp[log[1] - 1950]--;\n }\n int ans, count = 0, year;\n for (auto i : mp)\n {\n count += i.second;\n if (ans < count)\n {\n ans = count;\n year = i.first;\n }\n }\n return year + 1950;\n }\n};\n\n```
| 2 | 0 |
[]
| 0 |
maximum-population-year
|
Python simple!!
|
python-simple-by-meganath-1xl3
|
\tclass Solution:\n\t\tdef maximumPopulation(self, logs: List[List[int]]) -> int:\n\t\t\tx=[0]*2050\n\t\t\tfor start,end in logs:\n\t\t\t\tfor i in range(start,
|
meganath
|
NORMAL
|
2021-06-05T14:08:24.491647+00:00
|
2021-06-05T14:08:24.491677+00:00
| 153 | false |
\tclass Solution:\n\t\tdef maximumPopulation(self, logs: List[List[int]]) -> int:\n\t\t\tx=[0]*2050\n\t\t\tfor start,end in logs:\n\t\t\t\tfor i in range(start,end):\n\t\t\t\t\tx[i]+=1\n\t\t\treturn(x.index(max(x)))\nUpvote if u lyk it :)\t\t\t
| 2 | 0 |
[]
| 0 |
maximum-population-year
|
C++ using Prefix Sum || O(n) Solution
|
c-using-prefix-sum-on-solution-by-hd-hit-3iu7
|
\nclass Solution {\npublic:\n int maximumPopulation(vector<vector<int>>& logs) {\n int n=logs.size();\n int pre[2055]={0};\n for(int i=0
|
hd-hitesh
|
NORMAL
|
2021-06-03T11:57:51.040819+00:00
|
2021-06-03T11:57:51.040850+00:00
| 156 | false |
```\nclass Solution {\npublic:\n int maximumPopulation(vector<vector<int>>& logs) {\n int n=logs.size();\n int pre[2055]={0};\n for(int i=0;i<n;i++){\n pre[logs[i][0]]++; pre[logs[i][1]]--;\n }\n for(int i=1950;i<=2051;i++){\n pre[i]=pre[i-1]+pre[i];\n }\n int mx= max_element(pre,pre+2055)-pre;\n return mx;\n }\n};\n```
| 2 | 0 |
['C', 'Binary Tree', 'Prefix Sum']
| 0 |
maximum-population-year
|
Simple Approach | 0(n) | C++
|
simple-approach-0n-c-by-ankitdhariwal-z5z3
|
class Solution {\npublic:\n int maximumPopulation(vector>& logs) {\n vector countPep(101);\n int n = logs.size();\n \n for(int i=
|
ankitdhariwal
|
NORMAL
|
2021-05-29T21:29:35.757117+00:00
|
2021-05-29T21:29:35.757149+00:00
| 111 | false |
class Solution {\npublic:\n int maximumPopulation(vector<vector<int>>& logs) {\n vector<int> countPep(101);\n int n = logs.size();\n \n for(int i=0;i<n;i++) {\n int st = logs[i][0];\n int ed = logs[i][1];\n \n while(st<ed){\n countPep[st-1950]++; st++;\n }\n }\n int maxPep=0,ans=0;\n \n for(int i=0;i<=100;i++) {\n\t\t\n if (countPep[i] > maxPep){\n ans = i;\n maxPep = countPep[i];\n }\n }\n return ans+1950;\n }\n};
| 2 | 0 |
[]
| 0 |
maximum-population-year
|
python 3 easy solution
|
python-3-easy-solution-by-sadman022-ggyc
|
last year I solved this problem from hackerrank, \nhttps://www.hackerrank.com/challenges/crush/problem\nI just used the exact same idea with slight modification
|
sadman022
|
NORMAL
|
2021-05-27T07:26:55.685541+00:00
|
2021-05-27T07:26:55.685593+00:00
| 457 | false |
last year I solved this problem from hackerrank, \nhttps://www.hackerrank.com/challenges/crush/problem\nI just used the exact same idea with slight modification. \nWell frankly speaking I couldn\'t figure out that this approach could be followed to solve this leetcode problem, after looking at a video tutorial I suddenly remembered. \nhope you like the solution\n\n```\ndef maximumPopulation(self, logs: List[List[int]]) -> int:\n\tminy, maxy = 2051, 1949\n\tdic = {}\n\n\tfor l in logs:\n\t\tif l[0] in dic:\n\t\t\tdic[l[0]]+=1\n\t\telse:\n\t\t\tdic[l[0]]=1\n\t\tif l[1] in dic:\n\t\t\tdic[l[1]]-=1\n\t\telse:\n\t\t\tdic[l[1]]=-1\n\t\tminy, maxy = min(miny, l[0]), max(maxy, l[1])\n\n\tmaxb, b = 0, 0\n\tfor i in range(miny, maxy+1):\n\t\tif i in dic:\n\t\t\tb+=dic[i]\n\t\tif b>maxb:\n\t\t\tmaxb = b\n\t\t\tres = i\n\treturn res\n```
| 2 | 0 |
['Python3']
| 0 |
maximum-population-year
|
Python straightforward solution
|
python-straightforward-solution-by-user7-l7cm
|
class Solution:\n def maximumPopulation(self, logs: List[List[int]]) -> int:\n \n d = {}\n # use a dictionary to keep track of year:popu
|
user7867e
|
NORMAL
|
2021-05-16T06:23:28.472336+00:00
|
2021-05-16T18:49:19.390793+00:00
| 395 | false |
class Solution:\n def maximumPopulation(self, logs: List[List[int]]) -> int:\n \n d = {}\n # use a dictionary to keep track of year:population size pair\n for i in range(len(logs)):\n for j in range(logs[i][0], logs[i][1]):\n if j in d:\n d[j] += 1\n else:\n d[j] = 1\n # go over the dictionary to find out the earliest year with max population\n max_pop = -1\n max_pop_year = -1\n #\n for x in d:\n if d[x] > max_pop:\n max_pop = d[x]\n max_pop_year = x\n elif d[x] == max_pop:\n if x < max_pop_year:\n max_pop_year = x\n #\n return(max_pop_year)
| 2 | 1 |
['Python', 'Python3']
| 1 |
maximum-population-year
|
python solution
|
python-solution-by-_light-11vg
|
\nclass Solution:\n def maximumPopulation(self, logs: List[List[int]]) -> int:\n b=[logs[i][0] for i in range(len(logs))]\n d=[logs[i][1] for i
|
_light_
|
NORMAL
|
2021-05-13T10:09:02.898645+00:00
|
2021-05-13T10:09:02.898678+00:00
| 318 | false |
```\nclass Solution:\n def maximumPopulation(self, logs: List[List[int]]) -> int:\n b=[logs[i][0] for i in range(len(logs))]\n d=[logs[i][1] for i in range(len(logs))]\n m=0 #max population\n a=0 #alive\n r=1950\n for i in range(1950,2051):\n a+=b.count(i)-d.count(i)\n if a>m:\n m=a\n r=i \n return r\n \n```
| 2 | 0 |
['Python', 'Python3']
| 0 |
maximum-population-year
|
JAVA | Range Addition | 100% faster
|
java-range-addition-100-faster-by-archit-ulyr
|
Objective - You have to calculate for every year, how many people are alive.\nAlgorithm\n- Make an array of size max_year possible according to constraints an
|
architaapandey
|
NORMAL
|
2021-05-09T15:19:32.551289+00:00
|
2021-05-09T15:22:00.069768+00:00
| 251 | false |
**Objective** - You have to calculate for every year, how many people are alive.\n***Algorithm***\n- Make an array of size max_year possible according to constraints and traverse the logs.\n- Increment all the years in the year array which lie in the born -> die range for every entry in the log by 1.\n- Find the year with the maximum number of people alive and return it.\n\nDo upvote the solution if you like it and comment optimizations if any.\n\n```\npublic int maximumPopulation(int[][] logs) {\n int year[] = new int[2051], i, max = Integer.MIN_VALUE, j;\n for(i=0;i<logs.length;i++)\n for(j=logs[i][0];j<logs[i][1];j++)\n year[j]++;\n j = 1949;\n for(i=1950;i<=2050;i++)\n if(year[i] > max) {\n j = i;\n max = year[i];\n }\n return j;\n}\n```\nThank You!
| 2 | 0 |
['Java']
| 0 |
maximum-population-year
|
C# | O(N Log N) | Sort the census log | Sorting
|
c-on-log-n-sort-the-census-log-sorting-b-exh0
|
Intuition: List down all the years on ascending ordering then count the population based on event Birth / Death, when it is death population increases when it i
|
crackthebig
|
NORMAL
|
2021-05-09T08:10:49.401513+00:00
|
2021-05-09T08:18:31.514829+00:00
| 457 | false |
**Intuition:** List down all the years on ascending ordering then count the population based on event Birth / Death, when it is death population increases when it is death poulation decreases, track the maximum population year. \n\n**Algo:**\n* \tProcess all logs and make it plan list with sorted in year by tracking whether that year is birth (0) or death (1)\n* \tSort the records and calculate population for each year based on the log type.\n* \tTrack the maximum and its year would be our solution\n\n\n**time:** ```O(n logn)```\n**space:** ```O(n)```\n\n```\npublic class Solution {\n public int MaximumPopulation(int[][] logs) {\n int n = logs.Length;\n \n List<(int year, int type)> years = new List<(int, int)>();\n \n for(int i=0; i<n; i++){\n years.Add((logs[i][0], 0));\n years.Add((logs[i][1]-1, 1)); // "logs[i][1] - 1" here reducing 1 as per problem description death year should not be considered living\n }\n \n years = years.OrderBy(x=>x.year)\n .ThenBy(y=>y.type)\n .ToList();\n \n int maxYear = 0, maxPop =0, pop = 0;\n foreach(var rec in years){\n if(rec.type == 0)\n pop++;\n else\n pop--;\n \n if(maxPop < pop)\n {\n maxPop = pop;\n maxYear = rec.year;\n }\n }\n return maxYear;\n }\n}\n```
| 2 | 1 |
['Sorting']
| 0 |
maximum-population-year
|
JavaScript O(n) solution, line sweep variant
|
javascript-on-solution-line-sweep-varian-qyaw
|
I didn\'t remember / didn\'t come up with the line sweep algorithm while solving this problem, but managed to get some variant of it.\n\nThe basic idea is to ma
|
user4125zi
|
NORMAL
|
2021-05-09T05:55:42.276756+00:00
|
2021-05-09T05:55:42.276800+00:00
| 636 | false |
I didn\'t remember / didn\'t come up with the line sweep algorithm while solving this problem, but managed to get some variant of it.\n\nThe basic idea is to maintain 2 arrays:\n- no of people born in a given year;\n- no of people dead in a given year;\n\nThen, we can go over years 1950 - 2050 and calculate no of people still alive by adding ones that were born and substracting ones that were dead.\n\nHere is the complete code:\n\n```\nvar maximumPopulation = function(logs) {\n const s = new Uint8Array(101);\n const e = new Uint8Array(101);\n \n for (const [rs, re] of logs) {\n s[rs - 1950]++;\n e[re - 1950]++;\n }\n \n let noOfPeople = 0, maxNoOfPeople = 0, maxYear = undefined;\n for (let i = 0; i <= 100; i++) {\n noOfPeople += s[i];\n noOfPeople -= e[i];\n \n if (noOfPeople > maxNoOfPeople) {\n maxNoOfPeople = noOfPeople;\n maxYear = i;\n }\n }\n \n return maxYear + 1950;\n};\n```\n\nImplementation note: I\'m using JS typed arrays of size 101 to limit memory usage (additional bonus: those arrays are intitialised with 0 by default).
| 2 | 0 |
['JavaScript']
| 1 |
maximum-population-year
|
Using priority queue
|
using-priority-queue-by-arun432-b7tw
|
\npublic int maximumPopulation(int[][] logs) {\n int len=logs.length;\n PriorityQueue<int[]> pq = new PriorityQueue<>(len,(n1,n2)->n1[1]-n2[1]);\n
|
Arun432
|
NORMAL
|
2021-05-09T04:28:21.747210+00:00
|
2021-05-09T04:47:48.482005+00:00
| 96 | false |
```\npublic int maximumPopulation(int[][] logs) {\n int len=logs.length;\n PriorityQueue<int[]> pq = new PriorityQueue<>(len,(n1,n2)->n1[1]-n2[1]);\n int max_count=0,ans=0;\n Arrays.sort(logs,(n1,n2)->n1[0]-n2[0]);\n for(int i=0;i<len;i++){\n \n while(!pq.isEmpty() && pq.peek()[1]-1<logs[i][0]){\n \n pq.poll();\n }\n pq.add(logs[i]);\n if(pq.size()>max_count){\n max_count=pq.size();\n ans=logs[i][0];\n }\n }\n return ans;\n}\n```
| 2 | 1 |
[]
| 0 |
maximum-population-year
|
using simple map clear code Best solution
|
using-simple-map-clear-code-best-solutio-htrs
|
class Solution {\npublic:\n int maximumPopulation(vector>& logs) {\n \n map mp;\n for(int i = 0;i<logs.size();i++){\n \n
|
kkeshav60_be18
|
NORMAL
|
2021-05-09T04:15:55.760527+00:00
|
2021-05-09T04:19:03.452680+00:00
| 126 | false |
class Solution {\npublic:\n int maximumPopulation(vector<vector<int>>& logs) {\n \n map<int,int> mp;\n for(int i = 0;i<logs.size();i++){\n \n int b = logs[i][0];\n int d = logs[i][1];\n for(int j = b;j<d;j++){\n mp[j]++;\n }\n }\n int ans = 1950;\n int mx = 0;\n for(auto i : mp){\n if(i.second>mx){\n mx = i.second;\n ans = i.first;\n }\n }\n \n cout<<ans;\n return ans;\n }\n};
| 2 | 1 |
['C']
| 0 |
maximum-population-year
|
javascript ordered map 92ms
|
javascript-ordered-map-92ms-by-henrychen-216m
|
\nconst maximumPopulation = (logs) => {\n let m = new Map();\n for (const [b, d] of logs) {\n for (let y = b; y < d; y++) {\n m.set(y, m
|
henrychen222
|
NORMAL
|
2021-05-09T04:12:53.813071+00:00
|
2021-05-09T04:13:59.000753+00:00
| 321 | false |
```\nconst maximumPopulation = (logs) => {\n let m = new Map();\n for (const [b, d] of logs) {\n for (let y = b; y < d; y++) {\n m.set(y, m.get(y) + 1 || 1);\n }\n }\n m = new Map([...m].sort((x, y) => {\n if (x[1] == y[1]) return x[0] - y[0]; // if population same, smaller year comes first\n return y[1] - x[1]; // sort by population decreasing\n }));\n return m.keys().next().value;\n};\n```
| 2 | 0 |
['JavaScript']
| 0 |
maximum-population-year
|
Javascript line sweep algo
|
javascript-line-sweep-algo-by-1709abhish-3r16
|
Intuitionline sweep algorithmApproachmake an array line of 2052 (constraint) length. sweep through it and remember the end year is not inclusive. record the max
|
1709abhishek
|
NORMAL
|
2025-03-12T18:35:09.976010+00:00
|
2025-03-12T18:35:09.976010+00:00
| 22 | false |
# Intuition
line sweep algorithm
# Approach
make an array line of 2052 (constraint) length. sweep through it and remember the end year is not inclusive. record the maximum.
# Complexity
- Time complexity:
O(n)
- Space complexity:
O(n)
# Code
```javascript []
/**
* @param {number[][]} logs
* @return {number}
*/
var maximumPopulation = function(logs) {
let line=new Array(2052).fill(0);
for(let i=0;i<logs.length;i++){
line[logs[i][0]]++;
line[logs[i][1]]--;
}
for(let i=1;i<line.length;i++){
line[i]+=line[i-1];
}
let max=0;
let fin=0;
for(let i=0;i<line.length;i++){
if(line[i]>max){
max=line[i];
fin=i;
}
}
return fin;
};
```
| 1 | 0 |
['Line Sweep', 'JavaScript']
| 1 |
maximum-population-year
|
Solution Using Prefix Sum
|
solution-using-prefix-sum-by-prateeksuth-gnle
|
IntuitionApproachComplexity
Time complexity : O ( N )
Space complexity : O ( N )
Code
|
prateeksuthar2hzar
|
NORMAL
|
2025-02-05T07:04:07.161706+00:00
|
2025-02-05T07:04:07.161706+00:00
| 187 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity : O ( N )
- Space complexity : O ( N )
# Code
```java []
class Solution {
public int maximumPopulation(int[][] logs) {
int[] arr = new int[101];
for(int log[] : logs){
int by = log[0], dy = log[1];
arr[by-1950]++;
arr[dy-1950]--;
}
int max = arr[0];
int maxYear = 1950;
for(int i = 1; i < 101; i++){
arr[i] += arr[i-1];
if(max < arr[i]){
max = arr[i];
maxYear = i + 1950;
}
}
return maxYear;
}
}
```
| 1 | 0 |
['Java']
| 0 |
maximum-population-year
|
Easy to understand solution using constraints with 0ms beats 100%.
|
easy-to-understand-solution-using-constr-3jfi
|
IntuitionApproachWe track population changes using an array.
We compute cumulative population for each year.
We return the earliest year with the maximum popula
|
anshgupta1234
|
NORMAL
|
2025-02-04T10:42:42.319468+00:00
|
2025-02-04T10:42:42.319468+00:00
| 143 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
We track population changes using an array.
We compute cumulative population for each year.
We return the earliest year with the maximum population.
# Complexity
- Time complexity:
0(n)
- Space complexity:
0(1)
# Code
```java []
class Solution {
public int maximumPopulation(int[][] logs) {
int[] years = new int[101];
for (int[] log : logs) {
years[log[0] - 1950]++;
years[log[1] - 1950]--;
}
int maxPopulation = 0, maxYear = 1950;
int currentPopulation = 0;
for (int i = 0; i < years.length; i++) {
currentPopulation = currentPopulation + years[i];
if (currentPopulation > maxPopulation) {
maxPopulation = currentPopulation;
maxYear = 1950 + i;
}
}
return maxYear;
}
}
```
| 1 | 0 |
['Java']
| 0 |
maximum-population-year
|
Easiest Solution in Java
|
easiest-solution-in-java-by-sathurnithy-puds
|
Code
|
Sathurnithy
|
NORMAL
|
2025-01-29T04:52:58.389348+00:00
|
2025-01-29T04:52:58.389348+00:00
| 147 | false |
# Code
```java []
class Solution {
public int maximumPopulation(int[][] logs) {
int[] yearFreq = new int[101];
for(int i=0; i<logs.length; i++){
for(int j=logs[i][0]; j<logs[i][1]; j++){
yearFreq[j - 1950]++;
}
}
int max = yearFreq[0], ind = 0;
for(int i=1; i<101; i++){
if(yearFreq[i] > max){
max = yearFreq[i];
ind = i;
}
}
return ind + 1950;
}
}
```
| 1 | 0 |
['Array', 'Counting', 'Prefix Sum', 'Java']
| 0 |
maximum-population-year
|
Easiest Solution in C
|
easiest-solution-in-c-by-sathurnithy-tjcu
|
Code
|
Sathurnithy
|
NORMAL
|
2025-01-29T04:46:34.764838+00:00
|
2025-01-29T04:46:34.764838+00:00
| 44 | false |
# Code
```c []
int maximumPopulation(int** logs, int logsSize, int* logsColSize) {
int yearFreq[101] = {0};
for(int i=0; i<logsSize; i++){
for(int j=logs[i][0]; j<logs[i][1]; j++){
yearFreq[j - 1950]++;
}
}
int max = yearFreq[0], ind = 0;
for(int i=1; i<101; i++){
if(yearFreq[i] > max){
max = yearFreq[i];
ind = i;
}
}
return ind + 1950;
}
```
| 1 | 0 |
['Array', 'C', 'Counting', 'Prefix Sum']
| 0 |
maximum-population-year
|
Easy Solution Using Frequency array in Java
|
easy-solution-using-frequency-array-in-j-3qle
|
Code
|
Pradeep5377
|
NORMAL
|
2025-01-26T08:48:24.031164+00:00
|
2025-01-26T08:48:24.031164+00:00
| 59 | false |
# Code
```java []
class Solution {
public int maximumPopulation(int[][] logs) {
int[] freq = new int[101];
for(int[] array : logs){
for(int i=array[0];i<array[1];i++){
freq[i-1950]++;
}
}
int max = freq[0];
int j=0;
for(int i=1;i<101;i++){
if(max < freq[i]){
max = freq[i];
j = i;
}
}
return j+1950;
}
}
```
| 1 | 0 |
['Array', 'Counting', 'Java']
| 0 |
maximum-population-year
|
JAVA BEATS 100% || EASY AND SIMPLE SOLUTION WITH APPROACH
|
java-beats-100-easy-and-simple-solution-ypp6i
|
Intuition1. Tracking Changes with a Difference Array:Instead of iterating over every year for every person (which would be inefficient), the solution uses a dif
|
Yashvendra
|
NORMAL
|
2025-01-25T16:42:51.783139+00:00
|
2025-01-25T16:42:51.783139+00:00
| 90 | false |
# Intuition
#### 1. Tracking Changes with a Difference Array:
Instead of iterating over every year for every person (which would be inefficient), the solution uses a **difference array** approach:
- Increment the population count for the birth year (`arr[birthYear]++`).
- Decrement the population count for the death year (`arr[deathYear]--`).
- This marks the start and end of a person's lifespan.
This ensures that we only record the **net change in population** at specific years. Later, we can calculate the actual population for each year using a cumulative sum.
---
#### 2. Finding the Year with Maximum Population:
After populating the `arr` array:
1. Compute the cumulative population using a running total (`temp`).
2. Track the year with the highest cumulative population using a variable (`max`).
3. If the current year's population (`temp`) exceeds `max`, update `max` and store the corresponding year.
# Approach
1. **Initialize a Population Array**:
- Create an array `arr` of size 2051 (to cover years from 1950 to 2050).
- Initialize all values in `arr` to `0`.
2. **Update the Array for Births and Deaths**:
- For every `log` entry `[birthYear, deathYear]`:
- Increment `arr[birthYear]` to denote a birth.
- Decrement `arr[deathYear]` to denote the end of life.
3. **Calculate Cumulative Population**:
- Iterate through the years from `1950` to `2050`.
- Maintain a running total (`temp`) to compute the cumulative population.
- Keep track of the maximum population (`max`) and the corresponding year (`year`).
4. **Return the Year**:
- Return the year with the maximum population.
# Complexity
- Time complexity:
O(N) where N is the size of the given array logs.
- Space complexity:
Constant space complextity O(1).
# Code
```java []
class Solution {
public int maximumPopulation(int[][] logs) {
int[] arr = new int[2051];
for(int[] pop: logs){
arr[pop[0]]++;
arr[pop[1]]--;
} int max=0,year=0,temp=0;
for(int i=1950;i<2051;i++){
temp+=arr[i];
if(temp>max){
max=temp;
year=i;
}
}
return year;
}
}
```
| 1 | 0 |
['Array', 'Counting', 'Prefix Sum', 'Java']
| 0 |
maximum-population-year
|
Solution in C
|
solution-in-c-by-vickyy234-ebbm
|
Code
|
vickyy234
|
NORMAL
|
2025-01-21T09:04:37.411341+00:00
|
2025-01-21T09:04:37.411341+00:00
| 63 | false |
# Code
```c []
int maximumPopulation(int** logs, int logsSize, int* logsColSize) {
int* arr = calloc(sizeof(int), 101);
for (int i = 0; i < logsSize; i++) {
int x = logs[i][0];
int y = logs[i][1];
for (int a = x - 1950; a < y - 1950; a++) {
arr[a]++;
}
}
int max = arr[0], index = 0;
for (int i = 1; i < 101; i++) {
if (max < arr[i]) {
max = arr[i];
index = i;
}
}
return index + 1950;
}
```
| 1 | 0 |
['Array', 'C', 'Counting']
| 0 |
maximum-population-year
|
BEAT 100%
|
beat-100-by-runningfalcon-dnl5
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
runningfalcon
|
NORMAL
|
2025-01-11T12:57:33.675591+00:00
|
2025-01-11T12:57:33.675591+00:00
| 106 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int maximumPopulation(int[][] logs) {
int[] ar = new int[101];
int pop = 0;
int maxPop = 0;
int maxY = 0;
for (var x : logs) {
int b = x[0];
int d = x[1];
ar[b - 1950]++;
ar[d - 1950]--;
}
int runpop = 0;
for (int i = 0; i < 101; i++) {
runpop += ar[i]; //At any time people alive in that particular year
if (runpop > maxPop) { //If curr exceed max pop then updat maxpop
maxPop = runpop;
maxY = i + 1950; //now it means that max year will change
}
}
return maxY;
}
}
```
| 1 | 0 |
['Java']
| 0 |
maximum-population-year
|
Python, clean solution
|
python-clean-solution-by-arif-kalluru-4r87
|
Complexity
Time complexity:
O(n)
Space complexity:
O(1)
Code
|
Arif-Kalluru
|
NORMAL
|
2025-01-05T14:15:54.838180+00:00
|
2025-01-05T14:15:54.838180+00:00
| 74 | false |
# Complexity
- Time complexity:
$$O(n)$$
- Space complexity:
$$O(1)$$
# Code
```python3 []
class Solution:
def maximumPopulation(self, logs: List[List[int]]) -> int:
base = 1950 # base year
n = 101
population = [0] * n # 1950 to 2050
year = 0
max_pop = 0
for [birth, death] in logs:
birth -= base
death -= base
population[birth] += 1
population[death] -= 1 # end of range is death-1; marking end of range
for i in range(1, n):
population[i] += population[i-1]
for i, pop in enumerate(population):
if pop > max_pop:
year = i
max_pop = pop
return year + base
```
| 1 | 0 |
['Array', 'Counting', 'Prefix Sum', 'Python3']
| 0 |
maximum-population-year
|
Best SOlution 👌👇
|
best-solution-by-ram_saketh-apio
|
Complexity
Time complexity:O(n)
Space complexity:O(1)
Code
|
Ram_Saketh
|
NORMAL
|
2025-01-03T19:38:22.540932+00:00
|
2025-01-03T19:38:22.540932+00:00
| 130 | false |
# Complexity
- Time complexity:O(n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int maximumPopulation(int[][] logs) {
int pop[] = new int[2051], res = 0;
for (var l : logs) {
++pop[l[0]];
--pop[l[1]];
}
for (int i = 1950; i < 2050; ++i) {
pop[i] += pop[i - 1];
res = pop[i] > pop[res] ? i : res;
}
return res;
}
}
```
| 1 | 0 |
['Array', 'Counting', 'Prefix Sum', 'Java']
| 0 |
maximum-population-year
|
medley of prefix sum & frequency array for intersection of handling ranges:
|
medley-of-prefix-sum-frequency-array-for-52vk
|
Code
|
KAAL_KIN
|
NORMAL
|
2024-12-28T12:30:21.537903+00:00
|
2024-12-28T12:30:21.537903+00:00
| 142 | false |
# Code
```cpp []
class Solution {
public:
int maximumPopulation(vector<vector<int>>& logs) {
vector<int> population(101, 0);
for (const auto& log : logs) {
population[log[0]-1950] += 1; // Increment for birth year
population[log[1]-1950] -= 1; // Decrement for death year
}
int maxp = 0;
int max=0;
int currp= 0;
for (int i=0; i<101; ++i) {
currp +=population[i]; // Add population change
if (currp>maxp) {
maxp = currp;
max=i;
}
}
return max+1950;
}
};
```
| 1 | 0 |
['Prefix Sum', 'C++']
| 0 |
maximum-population-year
|
Easy Solution | 1ms | Java
|
easy-solution-1ms-java-by-sundarkarthiks-tjd7
|
1msCode
|
sundarkarthiks
|
NORMAL
|
2024-12-23T00:49:06.577608+00:00
|
2024-12-23T00:49:06.577608+00:00
| 159 | false |
# 1ms
# Code
```java []
class Solution {
public int maximumPopulation(int[][] logs) {
int[] arr = new int[101];
for(int[] l: logs){
int birth = l[0];
int death = l[1];
arr[birth - 1950]++;
arr[death - 1950]--;
}
int max = arr[0];
int year = 1950;
for(int i =1; i< arr.length; i++){
arr[i] = arr[i - 1] + arr[i];
if(arr[i] > max){
max = arr[i];
year = 1950 + i;
}
}
return year;
}
}
```
| 1 | 0 |
['Java']
| 1 |
maximum-population-year
|
Simple Solution in C...Beats 100%
|
simple-solution-in-cbeats-100-by-ronit_0-683h
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Ronit_0109
|
NORMAL
|
2024-06-24T16:18:14.744293+00:00
|
2024-06-24T16:18:14.744330+00:00
| 18 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nint maximumPopulation(int** logs, int n, int* logsColSize) {\n int *freq=(int*)malloc(101*sizeof(int));\n for(int i=0;i<100;i++)freq[i]=0;\n for(int i=0;i<n;i++){\n int birth=logs[i][0],death=logs[i][1];\n while(birth<death){\n freq[birth-1950]++;\n birth++;\n }\n }\n int max=0,ans=0;\n for(int i=0;i<=100;i++){\n if(max<freq[i]){\n max=freq[i];\n ans=i;\n }\n }\n free(freq);\n return 1950+ans;\n}\n```
| 1 | 0 |
['C']
| 0 |
maximum-population-year
|
✅ ✅ Python Easiest Solution Beats 99% 🔥🔥🔥
|
python-easiest-solution-beats-99-by-priy-xbtj
|
image.png\n\n\n# Intuition\nThe idea here is to use prefix sum to count the number of people alive in a particular year. Each time we encounter a year which is
|
priyanshuJain-32
|
NORMAL
|
2024-03-16T06:47:19.908872+00:00
|
2024-03-16T06:47:19.908892+00:00
| 64 | false |
image.png\n\n\n# Intuition\nThe idea here is to use prefix sum to count the number of people alive in a particular year. Each time we encounter a year which is a death year we substract the population by 1 and increament if it is a birth year.\n\nTo do this we need to keep a count of death years. For this I am using a dictionary.\n\nIn first loop we create a dictionary of deaths with count of each death year. We will use this later to give priority to reduction of population first as compared to incrementing it. As if the death and birth are in same year for different person we count them as 1 and not 2.\n\nNext we sort the years and calculate running total of population in a given year. If a year is present in dictionary we simply substract the population by 1 if the count of death years is more than 0.\n\nIf the year is not in deaths than we increment the count.\n\nNow all we need to do is find the year when prefix array had maximum value.\n\n# Complexity\n- Time complexity: nlogn due to sorting\n\n- Space complexity: O(n)\n\n# Find me on LinkedIn\n****[CLICK HERE](https://www.linkedin.com/in/priyanshu-jain-iim/)**\n\n# Find me on GitHub\n****[CLICK HEREEE...](https://github.com/priyanshuJain-32)**\n\n# PLEASE UPVOTE. HELPS MY MOTIVATION.\n\n\n\n# Code\n```\nclass Solution:\n def maximumPopulation(self, logs: List[List[int]]) -> int:\n deaths = defaultdict(int)\n all_years = []\n for b,d in logs:\n deaths[d] += 1\n all_years.extend([b,d])\n all_years.sort()\n \n n = len(all_years)\n prefix = [0]*(n+1)\n for i in range(n):\n if all_years[i] in deaths:\n if deaths[all_years[i]]>0:\n prefix[i+1] = prefix[i]-1\n deaths[all_years[i]]-=1\n else:\n prefix[i+1] = prefix[i]+1\n else:\n prefix[i+1] = prefix[i]+1\n \n max_pop = -1\n for pop, year in zip(prefix[1:], all_years):\n if pop>max_pop:\n max_pop = pop\n max_year = year\n\n return max_year\n```\n
| 1 | 0 |
['Prefix Sum', 'Python', 'Python3']
| 0 |
maximum-population-year
|
Simple java code 0 ms beats 100 %
|
simple-java-code-0-ms-beats-100-by-arobh-1adl
|
\n# Complexity\n- \n\n# Code\n\nclass Solution {\n public int maximumPopulation(int[][] logs) {\n int[] year = new int[2051];\n for(int[] log :
|
Arobh
|
NORMAL
|
2024-01-07T16:28:50.685121+00:00
|
2024-01-07T16:28:50.685153+00:00
| 9 | false |
\n# Complexity\n- \n\n# Code\n```\nclass Solution {\n public int maximumPopulation(int[][] logs) {\n int[] year = new int[2051];\n for(int[] log : logs){\n year[log[0]] += 1;\n year[log[1]] -= 1;\n }\n \n int maxNum = year[1950], maxYear = 1950;\n \n for(int i = 1951; i < year.length; i++){\n year[i] += year[i - 1]; \n \n if(year[i] > maxNum){\n maxNum = year[i];\n maxYear = i;\n }\n }\n \n return maxYear;\n }\n}\n```
| 1 | 0 |
['Java']
| 0 |
maximum-population-year
|
Python Simple Brute Force Solution | O(n)
|
python-simple-brute-force-solution-on-by-m1uu
|
Intuition\nThe given code aims to determine the year with the maximum population based on a list of birth and death year intervals (logs). The goal is to iterat
|
Lucad4
|
NORMAL
|
2023-08-30T11:49:04.861949+00:00
|
2023-08-30T12:09:46.153956+00:00
| 24 | false |
# Intuition\nThe given code aims to determine the year with the maximum population based on a list of birth and death year intervals (logs). The goal is to iterate through the intervals to find the earliest year (birth year) with the highest number of people alive.\n\n# Approach\n Initialize _min and _max to 2050 and 1950 respectively. These variables will store the minimum and maximum years found in the logs, acting as bounds for the birth years\' range.\n\n Iterate through the logs list to find the actual minimum and maximum years. This ensures that we know the range within which the birth years can fall.\n\n Initialize earliest as _min and ans as 0. These variables will keep track of the year with the highest population and the maximum population count, respectively.\n\n Loop through each year in the range _min to _max + 1 (inclusive). For each year:\n a. Initialize a people counter to 0. This counter will keep track of the number of people alive during the current year.\n b. Iterate through each log in the logs list. If the current year falls within the birth and death year interval of a log, increment the people counter.\n c. Compare the people counter with the current maximum population count (ans). If the people counter is greater, update ans to people and earliest to the current year.\n\n Return earliest, which will represent the year with the highest population count.\n\n# Complexity\n- Time complexity:\n$$O(n * 100)$$ -> $$O(n)$$\n\n- Space complexity:\n$$O(1)$$\n\n# Code\n```\nclass Solution:\n def maximumPopulation(self, logs: List[List[int]]) -> int:\n _min, _max = 2050, 1950\n for log in logs:\n if log[0] < _min:\n _min = log[0]\n if log[1] > _max:\n _max = log[1]\n earliest, ans = _min, 0\n for year in range(_min, _max + 1):\n people = 0\n for log in logs:\n if log[0] <= year < log[1]:\n people += 1 \n if people > ans:\n ans = people\n earliest = year\n return earliest\n```
| 1 | 0 |
['Array', 'Counting', 'Python3']
| 0 |
maximum-population-year
|
TC : O(N*LogN) | SC : O(N) | C++ | Line Sweep Algo
|
tc-onlogn-sc-on-c-line-sweep-algo-by-omk-nr4b
|
Code\n\nclass Solution {\npublic:\n int maximumPopulation(vector<vector<int>>& logs) {\n int n = logs.size();\n\n int maxPopulation = INT_MIN,
|
omkarsase
|
NORMAL
|
2023-06-29T14:34:46.389520+00:00
|
2023-06-29T15:16:41.673737+00:00
| 146 | false |
# Code\n```\nclass Solution {\npublic:\n int maximumPopulation(vector<vector<int>>& logs) {\n int n = logs.size();\n\n int maxPopulation = INT_MIN, maxPopulationYear = 0;\n\n map<int, int> tracker;\n\n for (int idx = 0; idx < n; idx++) {\n tracker[logs[idx][0]]++;\n tracker[logs[idx][1]]--;\n }\n \n int sum = 0;\n\n for (auto it : tracker) {\n sum += it.second;\n\n if (sum > maxPopulation) {\n maxPopulation = sum;\n maxPopulationYear = it.first; \n } \n }\n\n return maxPopulationYear;\n }\n};\n```
| 1 | 0 |
['Line Sweep', 'C++']
| 0 |
redundant-connection
|
From DFS to Union Find
|
from-dfs-to-union-find-by-gracemeng-2t44
|
DFS\nalready_connected[x] indicates reachable nodes from x that are known so far.\nWhile we iterate through edges, for a new edge [x, y], if y is in already_con
|
gracemeng
|
NORMAL
|
2018-04-15T02:46:21.450675+00:00
|
2021-08-30T02:58:48.708551+00:00
| 68,682 | false |
# DFS\n`already_connected[x]` indicates reachable nodes from x that are known so far.\nWhile we iterate through edges, for a new edge `[x, y]`, if `y` is in `already_connected[x]`, the edge `[x, y]` is redundant.\n```\nclass Solution:\n def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:\n self.already_connected = defaultdict(list)\n for edge in edges:\n self.visited = defaultdict(bool)\n x, y = edge[0], edge[1]\n if self.is_already_connected(x, y):\n return edge\n self.already_connected[x].append(y)\n self.already_connected[y].append(x)\n \n def is_already_connected(self, x, y):\n if x == y:\n return True\n for x_adjacent in self.already_connected[x]:\n if not self.visited[x_adjacent]:\n self.visited[x_adjacent] = True\n if self.is_already_connected(x_adjacent, y):\n return True\n return False\n```\n# Union Find\nAn edge will connect two nodes into one connected component.\n\nWhen we count an edge in, if two nodes have already been in the same connected component, the edge will result in a cycle. That is, the edge is redundant. \n\nWe can make use of **Disjoint Sets (Union Find)**.\n\nIf we regard a node as an element, a connected component is actually a disjoint set.\n\n>For example,\n```\nGiven edges [1, 2], [1, 3], [2, 3],\n 1\n / \\\n2 - 3\n```\n>Initially, there are 3 disjoint sets: 1, 2, 3.\nEdge [1,2] connects 1 to 2, i.e., 1 and 2 are winthin the same connected component.\nEdge [1,3] connects 1 to 3, i.e., 1 and 3 are winthin the same connected component.\nEdge [2,3] connects 2 to 3, but 2 and 3 have been winthin the same connected component already, so [2, 3] is redundant.\n\n****\n```\nclass Solution:\n def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:\n parent = [-1] * (len(edges) + 1)\n rank = [0] * (len(edges) + 1)\n\n def find(x):\n if parent[x] == -1:\n return x\n parent[x] = find(parent[x])\n return parent[x]\n\n def union(x, y):\n root_x = find(x)\n root_y = find(y)\n if root_x == root_y:\n return False\n elif rank[root_x] < rank[root_y]:\n parent[root_x] = root_y\n rank[root_y] += 1\n return True\n else:\n parent[root_y] = root_x\n rank[root_x] += 1\n return True\n\n for x, y in edges:\n if not union(x, y): \n return [x, y]\n \n raise ValueError("Illegal input.")\n```\nThe **Union by Rank** and **Path Compression (in find)** can optimize the time complexity from O(n) to O(logn) (even smaller).\n\n**(\u4EBA \u2022\u0348\u1D17\u2022\u0348)** Thanks for voting!
| 462 | 4 |
[]
| 58 |
redundant-connection
|
✅ Easy Solution w/ Explanation | All Possible Approaches with comments
|
easy-solution-w-explanation-all-possible-ccyc
|
\u2714\uFE0F Solution - I (Multiple DFS Traversals)\n\nThis solution is similar to that mentioned in the offical solution. We will construct the graph by adding
|
archit91
|
NORMAL
|
2021-06-25T09:38:43.786818+00:00
|
2021-11-23T16:29:10.162023+00:00
| 25,966 | false |
\u2714\uFE0F ***Solution - I (Multiple DFS Traversals)***\n\nThis solution is similar to that mentioned in the offical solution. We will construct the graph by adding edges one after another. After each addition of a new edge, we will do a `dfs` traversal to check if any cycle has formed. If a cycle is detected, we know that the last edge addition has led to the formation of cycle and hence we will simply return that edge.\n\n```\nvector<int> findRedundantConnection(vector<vector<int>>& e) {\n\tint n = size(e);\n\tvector<vector<int>> graph(n+1);\n\tvector<bool> vis(n+1); \n\tfor(auto& E : e) {\n fill(begin(vis), end(vis), false); // reset the vis array\n graph[E[0]].push_back(E[1]), graph[E[1]].push_back(E[0]);\n if(dfs(graph, vis, E[0])) return E;\n }\n\treturn { }; // un-reachable\n}\nbool dfs(vector<vector<int>>& graph, vector<bool>& vis, int cur, int par = -1) {\n if(vis[cur]) return true; // reached already visited node - cycle detected\n vis[cur] = true;\n for(auto child : graph[cur]) \n if(child != par && dfs(graph, vis, child, cur)) return true;\n return false; // no cycle found\n}\n```\n\n***Time Complexity :*** **<code>O(n<sup>2</sup>)</code>**, In worst case, we may need `n` dfs calls with each taking `O(n)` time complexity.\n***Space Complexity :*** **<code>O(n)</code>**, to maintain `graph`\n\n---\n\n\u2714\uFE0F ***Solution - II (Single DFS Traversal)***\n\nI didn\'t get the first idea and solved the question using this solution instead. Suprisingly, I don\'t see anyone solving the question using a similar approach as this.\n\nWe need to find a cycle in the given graph and return an edge in that cycle that occurs last in input *`edges`*. We are given that a cycle always exist in the given graph and hence an answer will always exist. So, we only need to find the cycle and the edges involved in that cycle of the graph. We will store these edges in a set called *`cycle`*. \n\nFor this we can use **DFS traversal** with small modification. We will start the dfs on the given graph from node `1` and maintain a *`vis`* array denoting the nodes that are visited. We will also keep a *`par`* variable to denote the parent of current node *`cur`*. In each dfs. we will iterate over the `child` nodes of `cur`. If we ever visit an already visited node, we know that we are in a cycle. So, we will mark this node as the `cycleStart` and return. We will start pushing all nodes from the recursion stack until we reach `cycleStart` node (its first visit recursive call)\n\nWe have the following cases:\n\n1. **`child == par`** : The child node of *`cur`* is it\'s parent. So, skip it.\n2. **`cycle.empty() == true`**: We haven\'t yet detected any cycle. So we will continue exploring the graph with recursive `dfs` calls.\n3. **`cycleStart != -1`**: We have detected a cycle and marked the starting node of it. We will stop further dfs calls as cycle is found. We push all the nodes till we reach back to node numbered - `cycleStart` since they are all part of the cycle.\n4. **`cur == cycleStart`**: We have reached back to the start of cycle. By now, we have pushed all nodes in the cycle. So, just mark cycleStart as -1 denoting we don\'t need to further push any nodes and return.\n\nFinally, *`cycle`* contains all the nodes of cycle in the graph. We will iterate over the input edges in the reverse order to find the last edge in it that\'s part of cycle. If both node of an edge is in *`cycle`*, then we will return that edge.\n\n```\nunordered_set<int> cycle; // will store all nodes of cycle\nint cycleStart = -1; // used to mark start node of cycle\nvector<int> findRedundantConnection(vector<vector<int>>& e) {\n\tint n = size(e);\n\tvector<vector<int>> graph(n+1);\n\tvector<bool> vis(n+1); \n\t// constructing the graph from the edges\n\tfor(auto& edge : e) graph[edge[0]].push_back(edge[1]), graph[edge[1]].push_back(edge[0]);\n\tdfs(graph, vis, 1); // dfs traveral to detect cycle and fill the those nodes in cycle set.\n\tfor(int i = n-1; ~i; i--)\n\t\tif(cycle.count(e[i][0]) && cycle.count(e[i][1])) return e[i]; // last edge of input having both nodes in cycle\n\treturn { }; // un-reachable\n}\nvoid dfs(vector<vector<int>>& graph, vector<bool>& vis, int cur, int par = -1) {\n\tif(vis[cur]) { cycleStart = cur; return; } // reached an visited node - mark it as start of cycle and return\n\tvis[cur] = true; // not visited earlier - mark it as visited\n\tfor(auto child : graph[cur]) { // iterate over child / adjacents of current node\n\t\tif(child == par) continue; // dont visit parent again - avoids back-and-forth loop\n\t\tif(cycle.empty()) dfs(graph, vis, child, cur); // cycle not yet detected - explore graph further with dfs\n\t\tif(cycleStart != -1) cycle.insert(cur); // cycle detected - keep pushing nodes till we reach start of the cycle\n\t\tif(cur == cycleStart) { cycleStart = -1; return; } // all nodes of cycle taken - now just return\n\t}\n}\n```\n\n<blockquote>\n<details>\n<summary>Alternate Implementation (Faster Runtime ~4ms)</summary>\n\n```\nint cycleStart = -1;\nbool *cycle, *vis, found{};\nvoid dfs(vector<int> graph[], int cur, int par = -1) {\n\tif(vis[cur]) { cycleStart = cur; found = true; return; } \n\tvis[cur] = true; \n\tfor(auto child : graph[cur]) { \n\t\tif(child == par) continue; \n\t\tif(!found) dfs(graph, child, cur); \n\t\tif(cycleStart != -1) cycle[cur]=true; \n\t\tif(cur == cycleStart) { cycleStart = -1; return; } \n\t}\n}\nvector<int> findRedundantConnection(vector<vector<int>>& e) {\n\tint n = size(e);\n\tvector<int> graph[n+1];\n\tcycle = (bool*)calloc(n+1, sizeof(bool));\n vis = (bool*)calloc(n+1, sizeof(bool));\n\tfor(auto& edge : e) graph[edge[0]].push_back(edge[1]), graph[edge[1]].push_back(edge[0]);\n\tdfs(graph, 1); \n\tfor(int i = n-1; ~i; i--)\n\t\tif(cycle[e[i][0]] && cycle[e[i][1]]) return e[i]; \n\treturn { }; \n}\n```\n\n</details>\n</blockquote>\n\n\n***Time Complexity :*** **`O(n)`**, where *`n`* is the number of nodes in the graph. We need `O(n)` for *`dfs`* and another `O(n)` for iterating through the input for finding the last edge in it that occurs in the cycle.\n***Space Complexity :*** **`O(n)`**, for maintaining *`graph`* and *`cycle`*\n\n\n---\n\n\u2714\uFE0F ***Solution - III (Union-Find)***\n\n\nWe can solve this using a Disjoint Subset Union (DSU). It involes two operations -\n* **`find(x)`**: finds the id which represents the component that a node belongs to\n* **`union(x, y)`**: joins the two components into a single component. This involves finding the representative of x-component (by `find(x)`) and y-component (by `find(y)`) and assigning them a common representative (same parent).\n\n\nWe are given various edges of the graph. These can be consider as different disconnected components. We will join these one by one. A component will be represented as a tree with all its members linked to some parent and the top parent will be considered that component\'s representative. When we find an edge that joins two nodes which are already in the same component, we will return that edge as answer. Otherwise, we will just **Union** it, i.e, connect the two components by picking that edge.\n\n```\nclass DSU {\n vector<int> par, rank;\npublic:\n DSU(int n) : par(n), rank(n) {\n iota(begin(par), end(par), 0); // initializes each node\'s parent to be itself - fills as [0,1,2,3,...,n]\n }\n int find(int x) {\n if(x == par[x]) return x; // x is itself the parent of this component\n return find(par[x]); // recurse for parent of x\n }\n bool Union(int x, int y) {\n auto xp = find(x), yp = find(y); // find parents of x and y, i.e, representatives of components that x and y belong to\n if(xp == yp) return false; // x and y already belong to same component - not possible to union\n return par[xp] = yp; // union x and y by making parent common\n }\n // iterative implementation of find\n // int find(int x) { \n // while(x != par[x]) x = par[x];\n // return par[x];\n // }\n};\nclass Solution {\npublic:\n vector<int> findRedundantConnection(vector<vector<int>>& e) {\n DSU ds(size(e)+1);\n for(auto& E : e) \n if(!ds.Union(E[0], E[1])) return E;\t// not possible to union - adding this edge was causing the cycle\n return { }; // un-reachable\n }\n};\n```\n\n---\n\n***Time Complexity :*** **<code>O(n<sup>2</sup>)</code>**, In this naive implementation, the worst case may lead to a scenario where we get a single component with a long lopsided chain and each `find` call will take `O(n)` for a total of `n` calls.\n***Space Complexity :*** **<code>O(n)</code>**, to maintain `par` array\n\n---\n\n\u2714\uFE0F ***Solution - IV (Union and Find with Path Compression)***\n\nThere\'s a very small change here from `Solution - II` in the *`find()`* function. We update the *`par[x]`* as the result returned by *`find(par[x])`* before returning from each recursive call. This will ensure that any future calls to *`find(x)`* won\'t require us to re-iterate all the way till the base `par[x]`. This effectively, **compresses the path** to parent of `x` (for future calls), as the name suggests.\n\n```\nclass DSU {\n vector<int> par, rank;\npublic:\n DSU(int n) : par(n), rank(n) {\n iota(begin(par), end(par), 0);\n }\n int find(int x) {\n if(x == par[x]) return x; // x is itself the parent of this component\n return par[x] = find(par[x]); // update parent of x before returning for each call\n }\n bool Union(int x, int y) {\n auto xp = find(x), yp = find(y); // find parents of x and y, i.e, representatives of components that x and y belong to\n if(xp == yp) return false; // x and y already belong to same component - not possible to union\n return par[xp] = yp; // union x and y by making parent common\n }\n};\nclass Solution {\npublic:\n vector<int> findRedundantConnection(vector<vector<int>>& e) {\n DSU ds(size(e)+1);\n for(auto& E : e) \n if(!ds.Union(E[0], E[1])) return E;\t// not possible to union - adding this edge was causing the cycle\n return { }; // un-reachable\n }\n};\n```\n\n***Time Complexity :*** **<code>\u0398(nlogn)</code>** , `find` may take `O(n)` for first few calls but since we are using path compression, each one makes subsequent searches faster and hence the amortized time complexity over a set of calls to `find` operation is `O(logn)`\n***Space Complexity :*** **<code>O(n)</code>**\n\n---\n\n\u2714\uFE0F ***Solution - V (Union By Rank and Find with path Compression)***\n\nThis optimization involves doing the union based on the rank (or size) of parents / representative of a component instead of just attaching one to the other randomly. This will ensure that even in the worst-case, we don\'t end up in a scenario where the *`par`* forms a skewed tree (all nodes on one-side) and we wouldn\'t need to iterate all nodes on each *`find`* call. Performing the union based on rank will keep the components/tree balanced in size.\n\n```\nclass DSU {\n vector<int> par, rank;\npublic:\n DSU(int n) : par(n), rank(n) {\n iota(begin(par), end(par), 0);\n }\n int find(int x) {\n if(x == par[x]) return x; // x is itself the parent of this component\n return par[x] = find(par[x]); // update parent of x before returning for each call\n }\n bool Union(int x, int y) {\n int xp = find(x), yp = find(y); // find parents of x and y, i.e, representatives of components that x and y belong to\n if(xp == yp) return false; // x and y already belong to same component - not possible to union\n if(rank[xp] > rank[yp]) par[yp] = par[xp]; // union by rank - join smaller ranked to bigger one\n else if(rank[yp] > rank[xp]) par[xp] = par[yp];\n else par[xp] = yp, rank[yp]++; // same rank - join either to other and increment rank of final parent\n return true;\n }\n};\nclass Solution {\npublic:\n vector<int> findRedundantConnection(vector<vector<int>>& e) {\n DSU ds(size(e) + 1);\n for(auto& E : e) \n if(!ds.Union(E[0], E[1])) return E;\t// not possible to union - adding this edge was causing the cycle\n return { }; // un-reachable\n }\n};\n```\n\n<blockquote>\n<details>\n<summary>Union by Size Implementation</summary>\n\nJust using the size of trees instead of rank while doing the union. Both should give same performance on average.\n\n```\nclass DSU {\n vector<int> par, Size;\npublic:\n DSU(int n) : par(n), Size(n,1) {\n iota(begin(par), end(par), 0);\n }\n int find(int x) {\n if(x == par[x]) return x; \n return par[x] = find(par[x]); \n }\n bool Union(int x, int y) {\n int xp = find(x), yp = find(y); \n if(xp == yp) return false; \n if(Size[xp] > Size[yp]) par[yp] = par[xp], Size[xp] += Size[yp]; // union by size\n else par[xp] = par[yp], Size[yp] += Size[xp];\n return true;\n }\n};\nclass Solution {\npublic:\n vector<int> findRedundantConnection(vector<vector<int>>& e) {\n DSU ds(size(e) + 1);\n for(auto& E : e) \n if(!ds.Union(E[0], E[1])) return E;\t\n return { }; \n }\n};\n```\n\n</details>\n</blockquote>\n\n***Time Complexity :*** **<code>O(n*\u03B1(n)) \u2248 O(n)</code>**, the time complexity of each `find` call after union-by-rank and path compression comes out to be `O(\u03B1(n))`, where `\u03B1(n)` is the inverse Ackermann function. It doesn\'t exceed 4 for any <code>n < 10<sup>600</sup></code> and hence is practically constant. We make `O(n)` calls in total.\n***Space Complexity :*** **<code>O(n)</code>**\n\n\n---\n---\n\n\uD83D\uDCBB\uD83D\uDC31\u200D\uD83D\uDCBBIf there are any suggestions / questions / mistakes in my post, please do comment below \uD83D\uDC47 \n\n---\n---\n\n
| 389 | 23 |
['Depth-First Search', 'C']
| 24 |
redundant-connection
|
[C++/Java/Python] Union Find - Feel free to reuse! - Clean & Concise - O(N)
|
cjavapython-union-find-feel-free-to-reus-vw0p
|
Idea\n- A valid tree is an undirected graph which has exactly N-1 edges to connect N vertices in the tree.\n- Since the given tree has a redundant edge, so ther
|
hiepit
|
NORMAL
|
2021-06-25T09:59:56.687296+00:00
|
2021-08-19T03:41:24.928091+00:00
| 12,679 | false |
**Idea**\n- A valid tree is an undirected graph which has exactly `N-1` edges to connect `N` vertices in the tree.\n- Since the given tree has a redundant edge, so there is `N` edges in the given input.\n- Number of vertices `N = len(edges)`.\n- There is a data structure called [UnionFind or Disjoint-set](https://en.wikipedia.org/wiki/Disjoint-set_data_structure) which has 2 basic operations:\n\t- `uf.find(u)`, which outputs a unique id so that two nodes have the same id if and only if they are in the same connected component.\n\t- `uf.union(u, v)`, which connects the components with id `find(u)` and `find(v)` together. If it already connected then return False, else return True.\n- Then we iterate edge `[u, v]` in `edges`, if `u` and `v` is already connected in the UnionFind then we return that redundant edge.\n\n**Implementation**\n<iframe src="https://leetcode.com/playground/j33hRwjo/shared" frameBorder="0" width="100%" height="720"></iframe>\n\n**Complexity**\n- Time: `O(N * \u03B1(N))`, where `N` is number of vertices in the graph.\n Explanation: Using both **path compression** and **union by size** ensures that the **amortized time** per **UnionFind** operation is only `\u03B1(n)`, which is optimal, where `\u03B1(n)` is the inverse Ackermann function. This function has a value `\u03B1(n) < 5` for any value of n that can be written in this physical universe, so the disjoint-set operations take place in essentially constant time.\nReference: https://en.wikipedia.org/wiki/Disjoint-set_data_structure or https://www.slideshare.net/WeiLi73/time-complexity-of-union-find-55858534 for more information.\n- Space: `O(N)`\n\n**Practice more on UnionFind topics**\n- [1319. Number of Operations to Make Network Connected](https://leetcode.com/problems/number-of-operations-to-make-network-connected/discuss/477660)\n- [721. Accounts Merge](https://leetcode.com/problems/accounts-merge/)\n- [1627. Graph Connectivity With Threshold](https://leetcode.com/problems/graph-connectivity-with-threshold/)\n\nIf you **have any questions, feel free to comment below**, I will try my best to answer. If you think this post is useful, I\'m happy if you **give it a vote**. Thanks.
| 184 | 8 |
[]
| 10 |
redundant-connection
|
DFS Java Solution With Explanation
|
dfs-java-solution-with-explanation-by-na-q7gr
|
Idea\nWe build adjList progressevily as we go on adding edges. Say we are trying to add the edge [u,v] and want to know if that will form a cyle. We do not add
|
naveen_kothamasu
|
NORMAL
|
2019-04-18T04:49:54.868212+00:00
|
2019-04-18T04:49:54.868296+00:00
| 15,553 | false |
**Idea**\nWe build `adjList` progressevily as we go on adding edges. Say we are trying to add the edge `[u,v]` and want to know if that will form a cyle. We do not add the edge yet but we do `dfs` on the existing graph to see if we can reach `v` from `u`. If we can, then adding `[u,v]` will form a cycle. But we need the last possible edge that will form a cycle, so we can just set it to `ret` and move on without adding it.\n\nAlso since it is a `dfs` on an undirected graph, we have `v` in `u`\'s children and `u` in `v`\'s. So to avoid exploring the same edge from both the ends, we can pass in the current parent `pre` down the stack calls. \n\n```\npublic int[] findRedundantConnection(int[][] edges) {\n int[] ret = null;\n int n = edges.length;\n List<Set<Integer>> adjList = new ArrayList<>(1001);\n for(int i=0; i < 1001; i++)\n adjList.add(new HashSet<>());\n \n for(int[] edge : edges){\n int u = edge[0], v = edge[1];\n if(dfs(u, v, 0, adjList)){\n ret = edge;\n }else{\n adjList.get(u).add(v);\n adjList.get(v).add(u);\n }\n }\n return ret;\n }\n \n private boolean dfs(int u, int v, int pre, List<Set<Integer>> adjList){\n if(u == v)\n return true;\n for(int w : adjList.get(u)){\n if(w == pre) continue;\n boolean ret = dfs(w, v, u, adjList);\n if(ret) return true;\n }\n return false;\n }\n```
| 142 | 1 |
[]
| 22 |
redundant-connection
|
10 line Java solution, Union Find.
|
10-line-java-solution-union-find-by-shaw-s75c
|
\nclass Solution {\n public int[] findRedundantConnection(int[][] edges) {\n int[] parent = new int[2001];\n for (int i = 0; i < parent.length;
|
shawngao
|
NORMAL
|
2017-09-24T03:20:59.296000+00:00
|
2018-10-17T20:40:27.013472+00:00
| 33,143 | false |
```\nclass Solution {\n public int[] findRedundantConnection(int[][] edges) {\n int[] parent = new int[2001];\n for (int i = 0; i < parent.length; i++) parent[i] = i;\n \n for (int[] edge: edges){\n int f = edge[0], t = edge[1];\n if (find(parent, f) == find(parent, t)) return edge;\n else parent[find(parent, f)] = find(parent, t);\n }\n \n return new int[2];\n }\n \n private int find(int[] parent, int f) {\n if (f != parent[f]) {\n parent[f] = find(parent, parent[f]); \n }\n return parent[f];\n }\n}\n```
| 141 | 9 |
[]
| 40 |
redundant-connection
|
Unicode-Find (5 short lines)
|
unicode-find-5-short-lines-by-stefanpoch-up1t
|
def findRedundantConnection(self, edges):\n tree = ''.join(map(chr, range(1001)))\n for u, v in edges:\n if tree[u] == tree[v]:\n
|
stefanpochmann
|
NORMAL
|
2017-09-24T03:02:46.653000+00:00
|
2018-10-23T04:42:22.935521+00:00
| 15,182 | false |
def findRedundantConnection(self, edges):\n tree = ''.join(map(chr, range(1001)))\n for u, v in edges:\n if tree[u] == tree[v]:\n return [u, v]\n tree = tree.replace(tree[u], tree[v])\n\nStart with each node being its own tree, then combine trees by adding the edges. The first (and only) edge closing a loop is the last edge in that loop, which is the edge we must return.\n\nMy `tree[u]` denotes the tree of node `u`. I use a string because it has a convenient and fast `replace` method. My title is of course a pun on [Union-Find](https://en.wikipedia.org/wiki/Disjoint-set_data_structure).
| 106 | 17 |
[]
| 14 |
redundant-connection
|
C++ solution using union find
|
c-solution-using-union-find-by-fancy1984-qtov
|
O(n) time union find solution\n```\nclass Solution {\npublic:\n vector findRedundantConnection(vector>& edges) {\n vector p(2000, 0);\n for(int
|
fancy1984
|
NORMAL
|
2017-09-25T00:01:22.949000+00:00
|
2018-10-22T05:10:41.208332+00:00
| 13,838 | false |
O(n) time union find solution\n```\nclass Solution {\npublic:\n vector<int> findRedundantConnection(vector<vector<int>>& edges) {\n vector<int> p(2000, 0);\n for(int i = 0; i < p.size(); i++ )\n p[i] = i;\n \n vector<int> res;\n for(auto v : edges ){\n int n1 = v[0], n2 = v[1];\n while(n1 != p[n1]) n1 = p[n1];\n while(n2 != p[n2]) n2 = p[n2];\n if( n1 == n2 )\n res = v;\n else\n p[n1] = n2;\n }\n return res;\n }\n};\n````
| 100 | 8 |
['Union Find']
| 14 |
redundant-connection
|
JS, Python, Java, C++ | Simple Union-Find Solution w/ Explanation
|
js-python-java-c-simple-union-find-solut-5j3q
|
(Note: This is part of a series of Leetcode solution explanations. If you like this solution or find it useful, please upvote this post.)\n\n---\n\n#### Idea:\n
|
sgallivan
|
NORMAL
|
2021-06-25T07:54:14.621274+00:00
|
2021-06-25T08:40:00.875955+00:00
| 8,082 | false |
*(Note: This is part of a series of Leetcode solution explanations. If you like this solution or find it useful,* ***please upvote*** *this post.)*\n\n---\n\n#### ***Idea:***\n\nIn this problem, the redundant edge will be the one that links together an already-linked graph. To determine whether already-seen segments of the graph have been connected, we can use a simple **union-find** (**UF**) implementation to keep track of the different segments.\n\nWith **UF**, we must define two functions: **union** and **find**. The **find** function will **recursively** trace a node\'s lineage back to its ultimate parent and update its value in the parent array (**par**), providing a shortcut for the next link.\n\nThe **union** function merges two segments by assigning the ultimate parent of one segment to another.\n\nWe can iterate through **edges** and **find** both vertices of the edge to see if they belong to the same segment. If so, we\'ve located our redundant edge and can **return** it. If not, we should merge the two different segments with **union**.\n\n - _**Time Complexity: O(N)** where **N** is the length of **edges**_\n - _**Space Complexity: O(N)** for **par** and the recursion stack_\n\n---\n\n#### ***Javascript Code:***\n\nThe best result for the code below is **76ms / 41.2MB** (beats 98% / 44%).\n```javascript\nvar findRedundantConnection = function(edges) {\n let par = Array.from({length: edges.length + 1}, (_,i) => i)\n const find = x => x === par[x] ? par[x] : par[x] = find(par[x])\n const union = (x,y) => par[find(y)] = find(x)\n for (let [a,b] of edges)\n if (find(a) === find(b)) return [a,b]\n else union(a,b)\n};\n```\n\n---\n\n#### ***Python Code:***\n\nThe best result for the code below is **44ms / 14.6MB** (beats 99% / 95%).\n```python\nclass Solution:\n def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:\n par = [i for i in range(len(edges) + 1)]\n def find(x: int) -> int:\n if x != par[x]: par[x] = find(par[x])\n return par[x]\n def union(x: int, y: int) -> None:\n par[find(y)] = find(x)\n for a,b in edges:\n if find(a) == find(b): return [a,b]\n else: union(a,b)\n```\n\n---\n\n#### ***Java Code:***\n\nThe best result for the code below is **0ms / 39.2MB** (beats 100% / 70%).\n```java\nclass Solution {\n public int[] findRedundantConnection(int[][] edges) {\n par = new int[edges.length+1];\n for (int i = 0; i < par.length; i++)\n par[i] = i;\n for (int[] e : edges)\n if (find(e[0]) == find(e[1])) return e;\n else union(e[0],e[1]);\n return edges[0];\n }\n private int[] par;\n private int find(int x) {\n if (x != par[x]) par[x] = find(par[x]);\n return par[x];\n }\n private void union(int x, int y) {\n par[find(y)] = find(x);\n }\n}\n```\n\n---\n\n#### ***C++ Code:***\n\nThe best result for the code below is **4ms / 8.7MB** (beats 98% / 83%).\n```c++\nclass Solution {\npublic:\n vector<int> findRedundantConnection(vector<vector<int>>& edges) {\n par.resize(edges.size()+1);\n for (int i = 0; i < par.size(); i++)\n par[i] = i;\n for (auto& e : edges)\n if (find(e[0]) == find(e[1])) return e;\n else uniun(e[0],e[1]);\n return edges[0];\n }\nprivate:\n vector<int> par;\n int find(int x) {\n if (x != par[x]) par[x] = find(par[x]);\n return par[x];\n }\n void uniun(int x, int y) {\n par[find(y)] = find(x);\n }\n};\n```
| 83 | 14 |
['C', 'Python', 'Java', 'JavaScript']
| 5 |
redundant-connection
|
Python: Easy to understand: GRAPH - DFS
|
python-easy-to-understand-graph-dfs-by-m-asqg
|
As we read the question, it is clearly a Graph related question that emphasizes on finding a cycle in the graph. \n\nIt differs from other graph-cycle finding p
|
meaditya70
|
NORMAL
|
2021-06-25T10:38:43.536835+00:00
|
2021-06-25T10:38:43.536864+00:00
| 4,744 | false |
As we read the question, it is clearly a Graph related question that emphasizes on finding a cycle in the graph. \n\nIt differs from other graph-cycle finding problem in a way that, in general graph cycle finding problem we just need to say that whether a cycle exists or not. But in this problem we need to **return the edge that caused the cycle** and if multiple edges caused the cycle then we need to return the later occuring edge.\n\n**Note:** *The question says the edge was added later, and did not exist earlier. So, in my view, we should keep developing the graph by adding edges one by one and performing cycle check simultanesouly.*\n\n***Cycle Check can be performed using a standard DFS algorithm using visited sets.***\n\nThe basic flow of code:\n```\n\t\tn = len(edges) # the number of nodes == number of edges, in this question (Given) \n \n\t\t"""\n\t\tThe graph for [[2,1],[1,3],[2,3]] will look like:\n\t\t\tgraph [1] = [2,3]\n\t\t\tgraph [2] = [1,3]\n\t\t\tgraph [3] = [1,2]\n\t\tAs the graph is undirected.\n\t\t\n\t\t"""\n\t\t\n\t\tgraph = defaultdict(list) \n \n ans = []\n\t\t# for each edge in edges\n for u, v in edges:\n visited = set()\n\t\t\t# perform dfs every time you add an edge\n\t\t\t# so that we if a cycle is formed we know exactly this edge has caused the cycle\n if dfs(u, v):\n\t\t\t\t# do not return the edge directly here\n\t\t\t\t# as we want the last possible edge that caused the cycle\n ans = [u,v]\n\t\t\t# add the edge and reverse edge in graph as it is undirected\n graph[u].append(v)\n graph[v].append(u)\n return ans\n```\n\nNow the simple Cycle Detection Algorithm using DFS:\nIdea: If u, v is already an edge and through DFS we found v can be reached from u, then a cycle exists. We can say that DFS will find a different path because, we have not yet added [u,v] in the graph. Only after we return from DFS we add it to graph.\n\n```\n\t\tdef dfs(u,v):\n\t\t\t# if a node is visited we cannot find a path through it as it itself formed a cycle which we do not want\n if u in visited:\n return False\n\t\t\t# if dfs finally reached to the node \'v\' means it has found path from \'u\' to \'v\'.\n if u == v:\n return True\n \n\t\t\t# mark the node of dfs as visited.\n visited.add(u)\n \n\t\t\t# each node connected to u, split the different dfs recurssion path\n for i in graph[u]:\n if dfs(i, v):\n return True\n return False\n```\n\nI hope this made it clear!\n\nTime = O(n) for DFS and O(n) for preparing the graph simultanesouly = O(n^2).\nSpace = O(n) for recurssion stack.\n\n**The FULL CODE:**\n```\nclass Solution:\n def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:\n \n def dfs(u,v):\n if u in visited:\n return False\n if u == v:\n return True\n \n visited.add(u)\n \n for i in graph[u]:\n if dfs(i, v):\n return True\n return False\n \n \n n = len(edges)\n graph = defaultdict(list)\n \n \n ans = []\n for u, v in edges:\n visited = set()\n if dfs(u, v):\n ans = [u,v]\n graph[u].append(v)\n graph[v].append(u)\n return ans\n```\n
| 61 | 2 |
['Depth-First Search', 'Graph', 'Python']
| 5 |
redundant-connection
|
Very well explained 4ms C++ solution (disjoint set) with an example
|
very-well-explained-4ms-c-solution-disjo-3yef
|
This solution uses disjoint set or union-find method. \n\nLet\'s take the following example and see how the code works.\n\n\n[[1,2], [1,3], [2,3]]\n\n\t 1\
|
tktripathy
|
NORMAL
|
2019-10-14T18:58:16.589409+00:00
|
2019-10-14T19:01:47.095974+00:00
| 3,215 | false |
This solution uses disjoint set or union-find method. \n\nLet\'s take the following example and see how the code works.\n\n```\n[[1,2], [1,3], [2,3]]\n\n\t 1\n\t\t / \\\n\t\t2 - 3\n```\n\nThe parent subset array created is as follows. The 0 slot is not used. By -1 we mean that each vertex stands on its own and parents have not been determined yet.\n\n```\n 0 1 2 3 \n-1 -1 -1 -1\n```\n\nFor edge [1,2] - find(ss, 1) returns 1, find(ss, 2) returns 2. Since both are not equal, we unionize them as follows:\n\n```\n 0 1 2 3 \n-1 -1 1 -1\n\nIt means, "we made the vertex 1 a parent of 2"\n```\n\nFor edge [1,3] - find(ss, 1) returns 1, find(ss, 3) returns 3. Since both are not equal, we unionize them as follows:\n\n```\n 0 1 2 3 \n-1 -1 1 1\n\nIt means, "we made the vertex 1 a parent of 3"\n```\n\nNow comes the edge [2, 3] - find(ss, 2) returns 1 and find(ss, 3) returns 1. Both are equal => this edge is causing the cycle and it must be the answer.\n\n```\n/* LeetCode: tktripathy */\nclass Solution {\npublic:\n /*\n * Find the subset a vertex belongs to.\n */\n int find(vector<int> &ss, int x) {\n if (ss[x] == -1) return x;\n return find(ss, ss[x]);\n }\n \n /*\n * Unionize two subsets. \n */\n void _union(vector<int> &ss, int x, int y) {\n int xp = find(ss, x);\n int yp = find(ss, y);\n if (xp != yp) ss[yp] = xp;\n }\n \n /*\n * We use disjoint set (or Union-Find) to detect a cycle in\n * an undirected graph.\n */\n vector<int> findRedundantConnection(vector<vector<int> >& e/*dges*/) {\n \n /* Create parent subsets and initialize them to -1 - this means\n * the subsets contain only one item - i.e ss[i] only contains\n * vertex i.\n */\n vector<int> ss; ss.push_back(-1);\n for (int i = 0; i < e.size(); i++) ss.push_back(-1);\n \n /*\n * We go through each edge one by one. We find the subset\n * that the vertices of an edge belongs to. If they belong\n * to two different subsets, we merge them into one set \n * using Union. Now, if both vertices are in the same \n * subset, we got a cycle - we return it.\n *\n */\n for (int i = 0; i < e.size(); ++i) {\n int x = find(ss, e[i][0]), y = find(ss, e[i][1]); \n if (x == y) return { e[i][0], e[i][1] };\n _union(ss, x, y);\n }\n \n /* No redundant edge found */\n return vector<int>();\n }\n};\n```
| 51 | 0 |
[]
| 10 |
redundant-connection
|
Java Union Find + DFS + BFS
|
java-union-find-dfs-bfs-by-a_love_r-uae5
|
DFS\n~~~java\n\n public int[] findRedundantConnection(int[][] edges) {\n int m = edges.length;\n Map> map = new HashMap<>();\n for (int
|
a_love_r
|
NORMAL
|
2019-07-11T01:49:05.241087+00:00
|
2019-07-11T01:49:05.241118+00:00
| 4,270 | false |
* DFS\n~~~java\n\n public int[] findRedundantConnection(int[][] edges) {\n int m = edges.length;\n Map<Integer, Set<Integer>> map = new HashMap<>();\n for (int i = 1; i <= m; i++) {\n map.put(i, new HashSet<>());\n }\n \n for (int[] edge : edges) {\n if (dfs(new HashSet<>(), map, edge[0], edge[1])) return edge;\n map.get(edge[0]).add(edge[1]);\n map.get(edge[1]).add(edge[0]);\n }\n \n return new int[]{-1,-1};\n }\n \n private boolean dfs(Set<Integer> visited, Map<Integer, Set<Integer>> map,\n int src, int target) {\n if (src == target) return true;\n visited.add(src);\n for (int next : map.get(src)) {\n if (!visited.contains(next)) {\n if (dfs(visited, map, next, target)) return true;\n }\n }\n return false;\n }\n\n~~~\n\n* BFS\n\n~~~java\n\n public int[] findRedundantConnection(int[][] edges) {\n int m = edges.length;\n Map<Integer, Set<Integer>> map = new HashMap<>();\n for (int i = 1; i <= m; i++) {\n map.put(i, new HashSet<>());\n }\n \n for (int[] edge : edges) {\n if (bfs(map, edge[0], edge[1])) return edge;\n map.get(edge[0]).add(edge[1]);\n map.get(edge[1]).add(edge[0]);\n }\n \n return new int[]{-1,-1};\n }\n \n private boolean bfs(Map<Integer, Set<Integer>> map,\n int src, int target) {\n Queue<Integer> q = new LinkedList<>();\n q.offer(src);\n Set<Integer> visited = new HashSet<>();\n visited.add(src);\n \n while (!q.isEmpty()) {\n int cur = q.poll();\n if (cur == target) return true;\n for (int next : map.get(cur)) {\n if (visited.add(next)) {\n q.offer(next);\n }\n }\n }\n \n return false;\n }\n\n~~~\n\n* Union Find\n\n~~~java\n\n int[] parent;\n \n public int[] findRedundantConnection(int[][] edges) {\n int m = edges.length;\n parent = new int[m + 1];\n for (int i = 0; i < m; i++) parent[i] = i;\n \n for (int[] edge : edges) {\n if (!union(edge[0], edge[1])) return edge;\n }\n \n return new int[]{-1,-1};\n }\n \n private boolean union(int x, int y) {\n int p1 = find(x), p2 = find(y);\n if (p1 == p2) return false;\n parent[p1] = p2;\n return true;\n }\n \n private int find(int x) {\n while (x != parent[x]) {\n x = parent[x];\n parent[x] = parent[parent[x]];\n }\n return x;\n }\n\n\n~~~
| 48 | 0 |
[]
| 4 |
redundant-connection
|
✅ Redundant Connection | Easy Solution w/ Explanation |All Possible Approaches w/ Comments
|
redundant-connection-easy-solution-w-exp-d5jh
|
\u2714\uFE0F Solution - I (Multiple DFS Traversals)\n\nThis solution is similar to that mentioned in the offical solution. We will construct the graph by adding
|
archit91
|
NORMAL
|
2021-06-25T09:39:35.260609+00:00
|
2021-06-26T04:38:14.116095+00:00
| 2,720 | false |
\u2714\uFE0F ***Solution - I (Multiple DFS Traversals)***\n\nThis solution is similar to that mentioned in the offical solution. We will construct the graph by adding edges one after another. After each addition of a new edge, we will do a `dfs` traversal to check if any cycle has formed. If a cycle is detected, we know that the last edge addition has led to the formation of cycle and hence we will simply return that edge.\n\n```\nvector<int> findRedundantConnection(vector<vector<int>>& e) {\n\tint n = size(e);\n\tvector<vector<int>> graph(n+1);\n\tvector<bool> vis(n+1); \n\tfor(auto& E : e) {\n fill(begin(vis), end(vis), false); // reset the vis array\n graph[E[0]].push_back(E[1]), graph[E[1]].push_back(E[0]);\n if(dfs(graph, vis, E[0])) return E;\n }\n\treturn { }; // un-reachable\n}\nbool dfs(vector<vector<int>>& graph, vector<bool>& vis, int cur, int par = -1) {\n if(vis[cur]) return true; // reached already visited node - cycle detected\n vis[cur] = true;\n for(auto child : graph[cur]) \n if(child != par && dfs(graph, vis, child, cur)) return true;\n return false; // no cycle found\n}\n```\n\n***Time Complexity :*** **<code>O(n<sup>2</sup>)</code>**, In worst case, we may need `n` dfs calls with each taking `O(n)` time complexity.\n***Space Complexity :*** **<code>O(n)</code>**, to maintain `graph`\n\n---\n\n\u2714\uFE0F ***Solution - II (Single DFS Traversal)***\n\nI didn\'t get the first idea and solved the question using this solution instead. Suprisingly, I don\'t see anyone solving the question using a similar approach as this.\n\nWe need to find a cycle in the given graph and return an edge in that cycle that occurs last in input *`edges`*. We are given that a cycle always exist in the given graph and hence an answer will always exist. So, we only need to find the cycle and the edges involved in that cycle of the graph. We will store these edges in a set called *`cycle`*. \n\nFor this we can use **DFS traversal** with small modification. We will start the dfs on the given graph from node `1` and maintain a *`vis`* array denoting the nodes that are visited. We will also keep a *`par`* variable to denote the parent of current node *`cur`*. In each dfs. we will iterate over the `child` nodes of `cur`. If we ever visit an already visited node, we know that we are in a cycle. So, we will mark this node as the `cycleStart` and return. We will start pushing all nodes from the recursion stack until we reach `cycleStart` node (its first visit recursive call)\n\nWe have the following cases:\n\n1. **`child == par`** : The child node of *`cur`* is it\'s parent. So, skip it.\n2. **`cycle.empty() == true`**: We haven\'t yet detected any cycle. So we will continue exploring the graph with recursive `dfs` calls.\n3. **`cycleStart != -1`**: We have detected a cycle and marked the starting node of it. We will stop further dfs calls as cycle is found. We push all the nodes till we reach back to node numbered - `cycleStart` since they are all part of the cycle.\n4. **`cur == cycleStart`**: We have reached back to the start of cycle. By now, we have pushed all nodes in the cycle. So, just mark cycleStart as -1 denoting we don\'t need to further push any nodes and return.\n\nFinally, *`cycle`* contains all the nodes of cycle in the graph. We will iterate over the input edges in the reverse order to find the last edge in it that\'s part of cycle. If both node of an edge is in *`cycle`*, then we will return that edge.\n\n```\nunordered_set<int> cycle; // will store all nodes of cycle\nint cycleStart = -1; // used to mark start node of cycle\nvector<int> findRedundantConnection(vector<vector<int>>& e) {\n\tint n = size(e);\n\tvector<vector<int>> graph(n+1);\n\tvector<bool> vis(n+1); \n\t// constructing the graph from the edges\n\tfor(auto& edge : e) graph[edge[0]].push_back(edge[1]), graph[edge[1]].push_back(edge[0]);\n\tdfs(graph, vis, 1); // dfs traveral to detect cycle and fill the those nodes in cycle set.\n\tfor(int i = n-1; ~i; i--)\n\t\tif(cycle.count(e[i][0]) && cycle.count(e[i][1])) return e[i]; // last edge of input having both nodes in cycle\n\treturn { }; // un-reachable\n}\nvoid dfs(vector<vector<int>>& graph, vector<bool>& vis, int cur, int par = -1) {\n\tif(vis[cur]) { cycleStart = cur; return; } // reached an visited node - mark it as start of cycle and return\n\tvis[cur] = true; // not visited earlier - mark it as visited\n\tfor(auto child : graph[cur]) { // iterate over child / adjacents of current node\n\t\tif(child == par) continue; // dont visit parent again - avoids back-and-forth loop\n\t\tif(cycle.empty()) dfs(graph, vis, child, cur); // cycle not yet detected - explore graph further with dfs\n\t\tif(cycleStart != -1) cycle.insert(cur); // cycle detected - keep pushing nodes till we reach start of the cycle\n\t\tif(cur == cycleStart) { cycleStart = -1; return; } // all nodes of cycle taken - now just return\n\t}\n}\n```\n\n<blockquote>\n<details>\n<summary>Alternate Implementation (Faster Runtime ~4ms)</summary>\n\n```\nint cycleStart = -1;\nbool *cycle, *vis, found{};\nvoid dfs(vector<int> graph[], int cur, int par = -1) {\n\tif(vis[cur]) { cycleStart = cur; found = true; return; } \n\tvis[cur] = true; \n\tfor(auto child : graph[cur]) { \n\t\tif(child == par) continue; \n\t\tif(!found) dfs(graph, child, cur); \n\t\tif(cycleStart != -1) cycle[cur]=true; \n\t\tif(cur == cycleStart) { cycleStart = -1; return; } \n\t}\n}\nvector<int> findRedundantConnection(vector<vector<int>>& e) {\n\tint n = size(e);\n\tvector<int> graph[n+1];\n\tcycle = (bool*)calloc(n+1, sizeof(bool));\n vis = (bool*)calloc(n+1, sizeof(bool));\n\tfor(auto& edge : e) graph[edge[0]].push_back(edge[1]), graph[edge[1]].push_back(edge[0]);\n\tdfs(graph, 1); \n\tfor(int i = n-1; ~i; i--)\n\t\tif(cycle[e[i][0]] && cycle[e[i][1]]) return e[i]; \n\treturn { }; \n}\n```\n\n</details>\n</blockquote>\n\n\n***Time Complexity :*** **`O(n)`**, where *`n`* is the number of nodes in the graph. We need `O(n)` for *`dfs`* and another `O(n)` for iterating through the input for finding the last edge in it that occurs in the cycle.\n***Space Complexity :*** **`O(n)`**, for maintaining *`graph`* and *`cycle`*\n\n\n---\n\n\u2714\uFE0F ***Solution - III (Union-Find)***\n\n\nWe can solve this using a Disjoint Subset Union (DSU). It involes two operations -\n* **`find(x)`**: finds the id which represents the component that a node belongs to\n* **`union(x, y)`**: joins the two components into a single component. This involves finding the representative of x-component (by `find(x)`) and y-component (by `find(y)`) and assigning them a common representative (same parent).\n\n\nWe are given various edges of the graph. These can be consider as different disconnected components. We will join these one by one. A component will be represented as a tree with all its members linked to some parent and the top parent will be considered that component\'s representative. When we find an edge that joins two nodes which are already in the same component, we will return that edge as answer. Otherwise, we will just **Union** it, i.e, connect the two components by picking that edge.\n\n```\nclass DSU {\n vector<int> par, rank;\npublic:\n DSU(int n) : par(n), rank(n) {\n iota(begin(par), end(par), 0); // initializes each node\'s parent to be itself - fills as [0,1,2,3,...,n]\n }\n int find(int x) {\n if(x == par[x]) return x; // x is itself the parent of this component\n return find(par[x]); // recurse for parent of x\n }\n bool Union(int x, int y) {\n auto xp = find(x), yp = find(y); // find parents of x and y, i.e, representatives of components that x and y belong to\n if(xp == yp) return false; // x and y already belong to same component - not possible to union\n return par[xp] = yp; // union x and y by making parent common\n }\n // iterative implementation of find\n // int find(int x) { \n // while(x != par[x]) x = par[x];\n // return par[x];\n // }\n};\nclass Solution {\npublic:\n vector<int> findRedundantConnection(vector<vector<int>>& e) {\n DSU ds(size(e)+1);\n for(auto& E : e) \n if(!ds.Union(E[0], E[1])) return E;\t// not possible to union - adding this edge was causing the cycle\n return { }; // un-reachable\n }\n};\n```\n\n---\n\n***Time Complexity :*** **<code>O(n<sup>2</sup>)</code>**, In this naive implementation, the worst case may lead to a scenario where we get a single component with a long lopsided chain and each `find` call will take `O(n)` for a total of `n` calls.\n***Space Complexity :*** **<code>O(n)</code>**, to maintain `par` array\n\n---\n\n\u2714\uFE0F ***Solution - IV (Union and Find with Path Compression)***\n\nThere\'s a very small change here from `Solution - II` in the *`find()`* function. We update the *`par[x]`* as the result returned by *`find(par[x])`* before returning from each recursive call. This will ensure that any future calls to *`find(x)`* won\'t require us to re-iterate all the way till the base `par[x]`. This effectively, **compresses the path** to parent of `x` (for future calls), as the name suggests.\n\n```\nclass DSU {\n vector<int> par, rank;\npublic:\n DSU(int n) : par(n), rank(n) {\n iota(begin(par), end(par), 0);\n }\n int find(int x) {\n if(x == par[x]) return x; // x is itself the parent of this component\n return par[x] = find(par[x]); // update parent of x before returning for each call\n }\n bool Union(int x, int y) {\n auto xp = find(x), yp = find(y); // find parents of x and y, i.e, representatives of components that x and y belong to\n if(xp == yp) return false; // x and y already belong to same component - not possible to union\n return par[xp] = yp; // union x and y by making parent common\n }\n};\nclass Solution {\npublic:\n vector<int> findRedundantConnection(vector<vector<int>>& e) {\n DSU ds(size(e)+1);\n for(auto& E : e) \n if(!ds.Union(E[0], E[1])) return E;\t// not possible to union - adding this edge was causing the cycle\n return { }; // un-reachable\n }\n};\n```\n\n***Time Complexity :*** **<code>\u0398(nlogn)</code>** , `find` may take `O(n)` for first few calls but since we are using path compression, each one makes subsequent searches faster and hence the amortized time complexity over a set of calls to `find` operation is `O(logn)`\n***Space Complexity :*** **<code>O(n)</code>**\n\n---\n\n\u2714\uFE0F ***Solution - V (Union By Rank and Find with path Compression)***\n\nThis optimization involves doing the union based on the rank (or size) of parents / representative of a component instead of just attaching one to the other randomly. This will ensure that even in the worst-case, we don\'t end up in a scenario where the *`par`* forms a skewed tree (all nodes on one-side) and we wouldn\'t need to iterate all nodes on each *`find`* call. Performing the union based on rank will keep the components/tree balanced in size.\n\n```\nclass DSU {\n vector<int> par, rank;\npublic:\n DSU(int n) : par(n), rank(n) {\n iota(begin(par), end(par), 0);\n }\n int find(int x) {\n if(x == par[x]) return x; // x is itself the parent of this component\n return par[x] = find(par[x]); // update parent of x before returning for each call\n }\n bool Union(int x, int y) {\n int xp = find(x), yp = find(y); // find parents of x and y, i.e, representatives of components that x and y belong to\n if(xp == yp) return false; // x and y already belong to same component - not possible to union\n if(rank[xp] > rank[yp]) par[yp] = par[xp]; // union by rank - join smaller ranked to bigger one\n else if(rank[yp] > rank[xp]) par[xp] = par[yp];\n else par[xp] = yp, rank[yp]++; // same rank - join either to other and increment rank of final parent\n return true;\n }\n};\nclass Solution {\npublic:\n vector<int> findRedundantConnection(vector<vector<int>>& e) {\n DSU ds(size(e) + 1);\n for(auto& E : e) \n if(!ds.Union(E[0], E[1])) return E;\t// not possible to union - adding this edge was causing the cycle\n return { }; // un-reachable\n }\n};\n```\n\n<blockquote>\n<details>\n<summary>Union by Size Implementation</summary>\n\nJust using the size of trees instead of rank while doing the union. Both should give same performance on average.\n\n```\nclass DSU {\n vector<int> par, Size;\npublic:\n DSU(int n) : par(n), Size(n) {\n iota(begin(par), end(par), 0);\n }\n int find(int x) {\n if(x == par[x]) return x; \n return par[x] = find(par[x]); \n }\n bool Union(int x, int y) {\n int xp = find(x), yp = find(y); \n if(xp == yp) return false; \n if(Size[xp] > Size[yp]) par[yp] = par[xp], Size[xp] += Size[yp]; // union by size\n else par[xp] = par[yp], Size[yp] += Size[xp];\n return true;\n }\n};\nclass Solution {\npublic:\n vector<int> findRedundantConnection(vector<vector<int>>& e) {\n DSU ds(size(e) + 1);\n for(auto& E : e) \n if(!ds.Union(E[0], E[1])) return E;\t\n return { }; \n }\n};\n```\n\n</details>\n</blockquote>\n\n***Time Complexity :*** **<code>O(n*\u03B1(n)) \u2248 O(n)</code>**, the time complexity of each `find` call after union-by-rank and path compression comes out to be `O(\u03B1(n))`, where `\u03B1(n)` is the inverse Ackermann function. It doesn\'t exceed 4 for any <code>n < 10<sup>600</sup></code> and hence is practically constant. We make `O(n)` calls in total.\n***Space Complexity :*** **<code>O(n)</code>**\n\n\n---\n---\n\n\uD83D\uDCBB\uD83D\uDC31\u200D\uD83D\uDCBBIf there are any suggestions / questions / mistakes in my post, please do comment below \uD83D\uDC47 \n\n---\n---\n\n
| 45 | 8 |
['Depth-First Search', 'C']
| 2 |
redundant-connection
|
A completely difference approach: recursively remove leaf nodes to uncover the cycle in the graph
|
a-completely-difference-approach-recursi-cgog
|
Although union-find is a natural fit to this problem, I find there is another way to tackle this problem which is also intuitive and easy to understand. That is
|
imsure
|
NORMAL
|
2017-11-16T03:23:14.464000+00:00
|
2018-08-22T18:53:03.163196+00:00
| 4,583 | false |
Although union-find is a natural fit to this problem, I find there is another way to tackle this problem which is also intuitive and easy to understand. That is, `we can recursively remove leaf nodes from the graph to uncover the cycle existing in the graph.` A leaf node in an undirected graph is defined as `a node that is has only one adjacent neighbor.` For example, consider the following graph:\n \n 1 \u2014\u2014\u2014 2 \n \\ /\n 3 \u2014\u2014 4\n`node 4` would be a leaf node.\nBefore removing the leaf node, the graph is:\n1: 2, 3\n2: 1,3\n3: 1,2,4\n4: 3\nBefore removing the leaf node, the graph becomes:\n1: 2, 3\n2: 1,3\n3: 1,2\n\nSince now the graph only contains cycle, it's straightforward to find the answer.\nBelow is my C++ code to implement this:\n```\nclass Solution {\nprivate:\n void uncoverCycle(unordered_map<int, unordered_set<int>>& graph) {\n int n = graph.size();\n vector<int> remove = {};\n for (auto& kv : graph) {\n int node = kv.first;\n auto& adjlist = kv.second;\n if (adjlist.size() == 1) { // leaf node\n remove.push_back(node);\n auto it = adjlist.begin();\n graph[*it].erase(node);\n }\n }\n\n if (remove.empty()) return;\n else {\n for (int node : remove) graph.erase(node);\n uncoverCycle(graph);\n }\n }\n\npublic:\n vector<int> findRedundantConnection(vector<vector<int>>& edges) {\n int n = edges.size();\n unordered_map<int, unordered_set<int>> graph;\n for (int i = 0; i < n; ++i) { // undirected graph\n graph[edges[i][0]].insert(edges[i][1]);\n graph[edges[i][1]].insert(edges[i][0]);\n }\n\n // recursively remove leaf nodes to uncover the cycle\n uncoverCycle(graph);\n\n for (int i = n - 1; i >= 0; --i) {\n if (graph.count(edges[i][0]) && graph.count(edges[i][1])) return edges[i];\n }\n\n return {};\n }\n};\n```
| 44 | 3 |
['Graph', 'C']
| 10 |
redundant-connection
|
Redundant Connection | JS, Python, Java, C++ | Simple Union-Find Solution w/ Explanation
|
redundant-connection-js-python-java-c-si-x46d
|
(Note: This is part of a series of Leetcode solution explanations. If you like this solution or find it useful, please upvote this post.)\n\n---\n\n#### Idea:\n
|
sgallivan
|
NORMAL
|
2021-06-25T07:54:47.864873+00:00
|
2021-06-25T08:40:13.521779+00:00
| 1,875 | false |
*(Note: This is part of a series of Leetcode solution explanations. If you like this solution or find it useful,* ***please upvote*** *this post.)*\n\n---\n\n#### ***Idea:***\n\nIn this problem, the redundant edge will be the one that links together an already-linked graph. To determine whether already-seen segments of the graph have been connected, we can use a simple **union-find** (**UF**) implementation to keep track of the different segments.\n\nWith **UF**, we must define two functions: **union** and **find**. The **find** function will **recursively** trace a node\'s lineage back to its ultimate parent and update its value in the parent array (**par**), providing a shortcut for the next link.\n\nThe **union** function merges two segments by assigning the ultimate parent of one segment to another.\n\nWe can iterate through **edges** and **find** both vertices of the edge to see if they belong to the same segment. If so, we\'ve located our redundant edge and can **return** it. If not, we should merge the two different segments with **union**.\n\n - _**Time Complexity: O(N)** where **N** is the length of **edges**_\n - _**Space Complexity: O(N)** for **par** and the recursion stack_\n\n---\n\n#### ***Javascript Code:***\n\nThe best result for the code below is **76ms / 41.2MB** (beats 98% / 44%).\n```javascript\nvar findRedundantConnection = function(edges) {\n let par = Array.from({length: edges.length + 1}, (_,i) => i)\n const find = x => x === par[x] ? par[x] : par[x] = find(par[x])\n const union = (x,y) => par[find(y)] = find(x)\n for (let [a,b] of edges)\n if (find(a) === find(b)) return [a,b]\n else union(a,b)\n};\n```\n\n---\n\n#### ***Python Code:***\n\nThe best result for the code below is **44ms / 14.6MB** (beats 99% / 95%).\n```python\nclass Solution:\n def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:\n par = [i for i in range(len(edges) + 1)]\n def find(x: int) -> int:\n if x != par[x]: par[x] = find(par[x])\n return par[x]\n def union(x: int, y: int) -> None:\n par[find(y)] = find(x)\n for a,b in edges:\n if find(a) == find(b): return [a,b]\n else: union(a,b)\n```\n\n---\n\n#### ***Java Code:***\n\nThe best result for the code below is **0ms / 39.2MB** (beats 100% / 70%).\n```java\nclass Solution {\n public int[] findRedundantConnection(int[][] edges) {\n par = new int[edges.length+1];\n for (int i = 0; i < par.length; i++)\n par[i] = i;\n for (int[] e : edges)\n if (find(e[0]) == find(e[1])) return e;\n else union(e[0],e[1]);\n return edges[0];\n }\n private int[] par;\n private int find(int x) {\n if (x != par[x]) par[x] = find(par[x]);\n return par[x];\n }\n private void union(int x, int y) {\n par[find(y)] = find(x);\n }\n}\n```\n\n---\n\n#### ***C++ Code:***\n\nThe best result for the code below is **4ms / 8.7MB** (beats 98% / 83%).\n```c++\nclass Solution {\npublic:\n vector<int> findRedundantConnection(vector<vector<int>>& edges) {\n par.resize(edges.size()+1);\n for (int i = 0; i < par.size(); i++)\n par[i] = i;\n for (auto& e : edges)\n if (find(e[0]) == find(e[1])) return e;\n else uniun(e[0],e[1]);\n return edges[0];\n }\nprivate:\n vector<int> par;\n int find(int x) {\n if (x != par[x]) par[x] = find(par[x]);\n return par[x];\n }\n void uniun(int x, int y) {\n par[find(y)] = find(x);\n }\n};\n```
| 43 | 14 |
[]
| 1 |
redundant-connection
|
Simple First Cycle/Union Find Two Solution First Connection
|
simple-stackunordered-map-first-connecti-gyte
|
IntuitionThe problem asks us to find a redundant connection in a graph formed by edges. A "redundant connection" is the edge that, when added, creates a cycle.
|
Sumeet_Sharma-1
|
NORMAL
|
2025-01-29T00:50:00.467720+00:00
|
2025-01-29T02:47:16.756418+00:00
| 9,934 | false |
# Intuition
The problem asks us to find a redundant connection in a graph formed by edges. A "redundant connection" is the edge that, when added, creates a cycle. We are tasked with finding the **first such edge** in the given list. Since the graph initially has no cycles, our goal is to detect the first edge that completes a cycle.
# --------------------------------------------------------


# --------------------------------------------------------- #
To achieve this, we maintain a representation of the graph using an adjacency list. We can then determine if adding a new edge forms a cycle by checking if there is already a path between the two nodes of that edge. If a path exists, the edge forms a cycle, and we return it.
# Approach
1. **Graph Representation**:
Use an `unordered_map<int, vector<int>>` to represent the graph as an adjacency list. This data structure allows us to dynamically store the connections between nodes and efficiently traverse the graph.
2. **Cycle Detection Without DFS/BFS**:
Instead of a standard DFS or BFS, implement a custom iterative path-checking mechanism:
- Use a stack to simulate traversal starting from one node.
- Use an `unordered_set` to track visited nodes during this process.
- If the target node is found during traversal, it indicates that adding the current edge would form a cycle.
3. **Processing Edges**:
- Iterate through each edge in the input.
- Before adding an edge, check if there is already a path between the two nodes using the path-checking function (`isConnected`).
- If a path exists, return the current edge as it forms the first cycle.
- If no path exists, add the edge to the graph by updating the adjacency list.
4. **Termination**:
Once we find the first edge forming a cycle, return it. Otherwise, if no cycles are detected (which won't happen based on the problem constraints), return an empty result.
# Complexity
- **Time Complexity**:
- For each edge, we check if there is a path between two nodes using an iterative traversal.
- In the worst case, this traversal can visit all nodes \(O(V)\), and we repeat this for each edge \(O(E)\).
- Hence, the overall time complexity is \(O(E+ V)\), where \(E\) is the number of edges and \(V\) is the number of nodes.
- **Space Complexity**:
- The adjacency list requires \(O(V + E)\) space.
- The stack and visited set for traversal require \(O(V)\) space during path checking.
- Therefore, the total space complexity is \(O(V + E)\).
# ✨✨


# Code
```C++_STACK+UNORDERMAP []
class Solution {
public:
vector<int> findRedundantConnection(vector<vector<int>>& edges) {
unordered_map<int, vector<int>> graph;
auto isConnected = [&](int u, int v) {
unordered_set<int> visited;
stack<int> stack;
stack.push(u);
while (!stack.empty()) {
int node = stack.top();
stack.pop();
if (visited.count(node)) continue;
visited.insert(node);
if (node == v) return true;
for (int neighbor : graph[node]) {
stack.push(neighbor);
}
}
return false;
};
for (const auto& edge : edges) {
int u = edge[0], v = edge[1];
if (graph.count(u) && graph.count(v) && isConnected(u, v)) {
return edge;
}
graph[u].push_back(v);
graph[v].push_back(u);
}
return {};
}
};
```
```C++_UNION_FIND []
class DisjointSet {
vector<int> parent, depth;
public:
DisjointSet(int n) : parent(n), depth(n) {
depth.assign(n, 1);
iota(parent.begin(), parent.end(), 0);
}
int getRoot(int x) {
if (x == parent[x])
return x;
return parent[x] = getRoot(parent[x]);
}
bool merge(int x, int y) {
int rootX = getRoot(x), rootY = getRoot(y);
if (rootX == rootY)
return false;
if (depth[rootX] > depth[rootY])
swap(rootX, rootY);
parent[rootX] = rootY;
if (depth[rootX] == depth[rootY])
depth[rootY]++;
return true;
}
};
class Solution {
public:
vector<int> findRedundantConnection(vector<vector<int>>& edges) {
int n = edges.size();
DisjointSet ds(n + 1);
for (auto& edge : edges)
if (!ds.merge(edge[0], edge[1])) return edge;
return {};
}
};
```
| 42 | 0 |
['Stack', 'Union Find', 'Graph', 'Ordered Map', 'C++']
| 7 |
redundant-connection
|
Python | Simple Union-Find | O(n), O(n) | Beats 100%
|
python-simple-union-find-on-on-beats-100-rurz
|
CodeComplexity
Time complexity: O(n). Iterating over edges is O(n). Find_root uses path compression and is α(n), simplifies to constant.
Space complexity: O(
|
2pillows
|
NORMAL
|
2025-01-29T01:41:50.055350+00:00
|
2025-01-29T02:12:56.636872+00:00
| 5,124 | false |
# Code
```python3 []
class Solution:
def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:
root = list(range(len(edges) + 1)) # each node is root of own subtree
def find_root(node):
if root[node] != node:
root[node] = find_root(root[node]) # set root for node as root of subtree
return root[node] # found root of subtree
for node1, node2 in edges:
root1, root2 = find_root(node1), find_root(node2)
if root1 == root2:
return [node1, node2] # both nodes are already in same subtree
root[root2] = root1 # found new connection between nodes / subtrees
# root[root1] = root2 also works
```
# Complexity
- Time complexity: $$O(n)$$. Iterating over edges is O(n). Find_root uses path compression and is α(n), simplifies to constant.
- Space complexity: $$O(n)$$. Root is O(n). Maximum recursion depth is each node or O(n).
# Performance
| 31 | 0 |
['Depth-First Search', 'Union Find', 'Python3']
| 6 |
redundant-connection
|
[faster than 100.00% ][C++][beginner friendly]
|
faster-than-10000-cbeginner-friendly-by-f9gdv
|
Runtime: 0 ms, faster than 100.00% of C++ online submissions \nMemory Usage: 9.1 MB, less than 92.16% of C++ online submissions\n\nclass Solution {\npublic:\n
|
rajat_gupta_
|
NORMAL
|
2021-01-16T19:45:15.910176+00:00
|
2021-01-16T19:45:15.910204+00:00
| 3,468 | false |
**Runtime: 0 ms, faster than 100.00% of C++ online submissions \nMemory Usage: 9.1 MB, less than 92.16% of C++ online submissions**\n```\nclass Solution {\npublic:\n vector<int> parent;\n vector<int> findRedundantConnection(vector<vector<int>>& edges) {\n if(edges.size()==0) return{};\n parent.resize(edges.size()+1);\n for(int i=1;i<edges.size()+1;i++){\n parent[i]=i;\n }\n for(vector<int> edge : edges){\n int f1=find(edge[0]);\n int f2=find(edge[1]);\n if(f1!=f2)\n parent[f1]=f2;\n else\n return edge;\n }\n return {};\n }\n int find(int x){\n return parent[x]==x ? x : find(parent[x]);\n }\n \n};\n```\n**Feel free to ask any question in the comment section.**\nI hope that you\'ve found the solution useful.\nIn that case, **please do upvote and encourage me** to on my quest to document all leetcode problems\uD83D\uDE03\nHappy Coding :)\n
| 31 | 1 |
['Union Find', 'C', 'C++']
| 3 |
redundant-connection
|
Python 52ms DFS Algorithm with Explanations (compared with 52ms union-find)
|
python-52ms-dfs-algorithm-with-explanati-7fr2
|
The algorithm based on the following fact in graph theory:\n\na simple connected graph with no cycle is a tree.\n\nThe statement of the problem guarantees that
|
flamesofmoon
|
NORMAL
|
2017-09-24T07:44:34.148000+00:00
|
2018-10-13T21:51:57.465743+00:00
| 10,067 | false |
The algorithm based on the following fact in graph theory:\n\n**a simple connected graph with no cycle is a tree**.\n\nThe statement of the problem guarantees that by deleting one and only one edge the graph is a tree, so we know it is connected and has one cycle. Our goal is to find the edge in this cycle with the largest index and return it.\n\nHow? DFS!\n\nWe store the graph in a dictionary `e` so that we can easily find adjacent vertices. `indices` helps me keep track of the original indices of edges in `edges`. `path` is to record the fact that we arrive at a vertex `v` from `path[v]`.\n\nWhen constructing `e`, we already get rid of the 2-cycle case by\n```\n if p[1] in e[p[0]]:\n return p\n```\nso in DFS, we only focus on cycles whose length >= 3. Since the graph is connected, we will find the cycle wherever we start. Pick one randomly (i.e., `e.keys()[0]`) and set off!\n\nIn `DFS(v)`: \n1) Look at all vertices 'w' adjacent to v such that the predecessor of `v` in DFS path is not `w` (otherwise it would be a two-vertex infinite loop, and we know there is no 2-cycle).\n\n2) If `path[w] != 0`, means `w` is on the current DFS path! The cycle is found and just need to make the change `path[w] = v` to complete the cycle and return the result.\n\n3) Standard DFS things: we record down the path in `path` and after DFS change it back to 0 state.\n\n4) It is possible that the DFS path goes into a dead end, so in a branch of DFS, it is possible that nothing is returned. We respect this possibility and do the check\n```\n temp = DFS(w)\n if temp:\n return temp\n```\nThe function `Result` is just a practice of typing once we have `indices` which indicates the corresponding indices for edges.\n\nMy thought is pretty natural besides the fact that for this problem union-find is a method much easier to type up (and could be as fast). Anyway, here is my DFS algorithm:\n\n```\n def Result(w): # given w is a vertex in a cycle, find the edge with the largest index in this cycle\n prev, curr =w, path[w]\n M = indices[(curr, prev)]\n while curr != w:\n prev, curr = curr, path[curr]\n M = max(M,indices[(curr, prev)])\n\n return edges[M]\n \n def DFS(v):\n for w in e[v]:\n if path[v] == w: # if predecessor of v is w, it's bad\n continue\n\n if path[w] != 0: # the cycle is found\n path[w] = v # complete the cycle\n return Result(w)\n\n path[w] = v\n temp = DFS(w)\n if temp: # in case it is a dead end and returns nothing\n return temp\n path[w] = 0\n \n e = collections.defaultdict(set) # e[x] is the set of all vertices adjacent to x\n indices = {} # key is edge, value is indices in the list 'edges'\n for i,p in enumerate(edges):\n if p[1] in e[p[0]]:\n return p # if one edge appears twice in 'edges', return tha latter one\n e[p[0]].add(p[1])\n e[p[1]].add(p[0])\n indices[(p[0],p[1])] = indices[(p[1],p[0])] = i\n\n path = {x:0 for x in e} # record the path in DFS\n return DFS(e.keys()[0])\n```\nMy union-find algorithm with best time performance:\n```\n def find(v): # find the root of the tree\n return find(parent[v]) if v in parent else v\n\n parent = {} # record the child: parent relation in the forest\n for i,p in enumerate(edges):\n r1, r2 = map(find, p)\n if r1 == r2:\n return p\n else:\n parent[r1] = parent[r2] = str(i) # use str(i) as the tree label\n```
| 31 | 0 |
['Depth-First Search', 'Union Find', 'Python']
| 2 |
redundant-connection
|
Cases Explained | DSU | 100% BEATS | C++ | JAVA | Python
|
cases-explained-dsu-100-beats-c-java-pyt-2wnk
|
Intuition:
Think of building a tree by adding edges one by one.
If a new edge connects two nodes that are already connected, it creates a cycle.
To track connec
|
shubham6762
|
NORMAL
|
2025-01-29T01:48:21.576792+00:00
|
2025-01-29T01:48:21.576792+00:00
| 9,894 | false |
**Intuition:**
1. Think of building a tree by adding edges one by one.
2. If a new edge connects two nodes that are *already connected*, it creates a cycle.
3. To track connections efficiently, we use **DSU (Disjoint Set Union)**.
4. DSU groups nodes into sets, where each set represents a connected component.
5. When adding an edge, if the nodes are in the same set, the edge is redundant—it forms a cycle.
6. The last such edge in the input is the answer.
---
**Why Return the Last Edge?**
The problem specifies that if multiple answers exist, return the **last occurrence** in the input. DSU processes edges in order, and the **first detected cycle-causing edge** during this traversal is the one that appears last in the input (since it’s the final piece needed to close the cycle).
---
**How DSU Works with Examples:**
Let’s break it down with symbolic scenarios (`A->B` means connecting nodes A and B):
1. **Case 1: No Cycle (Normal Tree Growth)**
- **Edges:** `A-B`, `B-C`, `C-D`
- Add `A-B`: A and B are now connected.
- Add `B-C`: B (connected to A) and C merge.
- Add `C-D`: C (connected to A-B) and D merge.
- **Result:** All nodes form a single chain. No cycles.
2. **Case 2: Cycle Detected (Redundant Edge)**
- **Edges:** `A-B`, `B-C`, `C-A`
- Add `A-B`: Connected.
- Add `B-C`: Connected (A-B-C).
- Add `C-A`: A and C are already connected! This edge **creates a cycle**.
- **Result:** `C-A` is redundant. Return it.
3. **Case 3: Multiple Components Merged**
- **Edges:** `X-Y`, `Y-Z`, `W-V`, `V-W` (typo: should be `V-U`?), `Y-W`
- Add `X-Y`: Connected.
- Add `Y-Z`: Connected (X-Y-Z).
- Add `W-V`: New component (W-V).
- Add `V-W`: Already connected. Redundant!
- **Result:** Return `V-W` (last redundant edge).
4. **Real Example from Problem:**
- **Input:** `[[1,2],[1,3],[2,3]]`
- Add `1-2`: Connected.
- Add `1-3`: Connected (1-2-3).
- Add `2-3`: 2 and 3 are already connected via 1. **Cycle formed!**
- **Output:** `[2,3]` (last edge in input causing the cycle).
---
**Solution Code:**
```cpp []
class Solution {
vector<int> parent;
vector<int> rank;
int find(int i) {
if (parent[i] != i)
parent[i] = find(parent[i]); // Path compression
return parent[i];
}
void join(int u, int v) {
int rootU = find(u), rootV = find(v);
if (rootU != rootV) {
// Union by rank to balance trees
if (rank[rootU] > rank[rootV]) parent[rootV] = rootU;
else if (rank[rootU] < rank[rootV]) parent[rootU] = rootV;
else {
parent[rootV] = rootU;
rank[rootU]++;
}
}
}
public:
vector<int> findRedundantConnection(vector<vector<int>>& edges) {
int n = edges.size();
parent.resize(n + 1);
rank.resize(n + 1, 0);
// Initialize each node as its own parent
for (int i = 1; i <= n; i++) parent[i] = i;
for (auto& edge : edges) {
int u = edge[0], v = edge[1];
if (find(u) == find(v)) return edge; // Cycle detected!
join(u, v); // Merge sets
}
return {}; // Unreachable for valid inputs
}
};
```
``` Java []
class Solution {
private int[] parent;
private int[] rank;
public int[] findRedundantConnection(int[][] edges) {
int n = edges.length;
parent = new int[n + 1];
rank = new int[n + 1];
// Initialize each node as its own parent
for (int i = 1; i <= n; i++) {
parent[i] = i;
}
for (int[] edge : edges) {
int u = edge[0];
int v = edge[1];
if (find(u) == find(v)) {
return edge; // Cycle detected
}
join(u, v); // Merge sets
}
return new int[0]; // Unreachable for valid inputs
}
private int find(int i) {
if (parent[i] != i) {
parent[i] = find(parent[i]); // Path compression
}
return parent[i];
}
private void join(int u, int v) {
int rootU = find(u);
int rootV = find(v);
if (rootU != rootV) {
// Union by rank
if (rank[rootU] > rank[rootV]) {
parent[rootV] = rootU;
} else if (rank[rootU] < rank[rootV]) {
parent[rootU] = rootV;
} else {
parent[rootV] = rootU;
rank[rootU]++;
}
}
}
}
```
``` Python []
class Solution(object):
def findRedundantConnection(self, edges):
"""
:type edges: List[List[int]]
:rtype: List[int]
"""
n = len(edges)
parent = [i for i in range(n + 1)] # Initialize each node as its own parent
rank = [0] * (n + 1) # Rank for union by rank
def find(i):
if parent[i] != i:
parent[i] = find(parent[i]) # Path compression
return parent[i]
def join(u, v):
rootU = find(u)
rootV = find(v)
if rootU != rootV:
# Union by rank
if rank[rootU] > rank[rootV]:
parent[rootV] = rootU
elif rank[rootU] < rank[rootV]:
parent[rootU] = rootV
else:
parent[rootV] = rootU
rank[rootU] += 1
for u, v in edges:
if find(u) == find(v):
return [u, v] # Cycle detected
join(u, v) # Merge sets
return [] # Unreachable for valid inputs
```
**How the Code Works:**
1. **Initialization:** Every node starts as its own parent.
2. **For each edge:**
- Check if the two nodes are already connected (`find(u) == find(v)`).
- If yes: this edge is redundant. Return it immediately.
- If no: merge their sets (`join(u, v)`).
3. **Union-Find Optimizations:**
- **Path Compression:** Flattens the structure for faster future queries.
- **Union by Rank:** Keeps the tree shallow to optimize `find` operations.
### **Time Complexity**
The solution efficiently detects the redundant edge in **O(n α(n))** time, which is near-linear. Here, **α(n)** is the inverse Ackermann function, a very slow-growing function that is practically constant for most inputs. This ensures the algorithm is highly efficient even for large graphs.
| 30 | 6 |
['Union Find', 'Python', 'C++', 'Java']
| 4 |
redundant-connection
|
Python3 | DFS | with clear explanation
|
python3-dfs-with-clear-explanation-by-sh-vmal
|
Intuition\nRedundant edge will always be the one which is responsible for forming a cycle within graph. And we can be ensured that a cycle will be formed becaus
|
shib00
|
NORMAL
|
2023-08-07T12:42:33.162653+00:00
|
2023-08-07T12:42:33.162676+00:00
| 3,962 | false |
# Intuition\nRedundant edge will always be the one which is responsible for forming a cycle within graph. And we can be ensured that a cycle will be formed because number of edges >= number of nodes. \n\n\nLet\'s consider the input -\n[[1,2],[1,3],[2,3]]\n\nLet\'s form the graph - \n\n\n# Pseudo Code\n1. keep track of graph constructed so far\n2. for each pair of nodes (u,v) provided in input\n - check if path exists between u and v using dfs\n - if it exists it means that adding the current edge will create a cycle hence return (u,v) as answer\n - else add that to graph\n\n# Complexity\n- Time complexity:\n$$O(n^2)$$ because for each pair of nodes we run dfs.\n=> $$O(n)$$ during **for loop** and $$O(n)$$ during **dfs** \n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\ndef findRedundantConnection(self, edges: List[List[int]]) -> List[int]:\n # variable to keep track of graph constructed so far\n graph_so_far = collections.defaultdict(lambda: [])\n \n # dfs function to check if path exists between nodes u and v\n def path_exists(u, v):\n # we reached to v from u\n if u == v:\n return True\n\n # mark u as visited\n visited.add(u)\n\n # iterate through all the neighbors of u and if they are not visited call dfs on them\n for neighbor in graph_so_far[u]:\n if neighbor not in visited:\n if path_exists(neighbor, v):\n return True\n \n return False\n\n # iterate through all the pairs of edges\n for u, v in edges:\n # we make a fresh visited because we call dfs for every pair of edges\n visited = set()\n # if path exists between u and v return that\'s the answer\n if path_exists(u,v):\n return [u,v]\n else:\n # if path does not exist we add edges to graph\n graph_so_far[u].append(v)\n graph_so_far[v].append(u)\n\n return None\n```
| 30 | 1 |
['Depth-First Search', 'Python3']
| 9 |
redundant-connection
|
C++ | Simple DSU Implementation with explanation
|
c-simple-dsu-implementation-with-explana-aavm
|
Approach: (Disjoint Set Union)\n\nWe are given with the edges as an input. As every edge connection can be considered as union operation, we do it for every edg
|
cyber-venom003
|
NORMAL
|
2021-10-06T22:30:34.683627+00:00
|
2021-10-06T22:30:34.683659+00:00
| 2,546 | false |
### Approach: (Disjoint Set Union)\n\nWe are given with the edges as an input. As every edge connection can be considered as union operation, we do it for every edge.\n\nAs soon as we encounter an edge between two nodes, which have same parents, that means those nodes are contributing to cycle, hence we got our redundant connection. \n\nMy submission:\n\n```\nclass Solution {\npublic:\n vector<int> parents;\n int find_parent(int a){\n if(parents[a] == a){\n return a;\n } else {\n return parents[a] = find_parent(parents[a]); //Finding parents using path compression\n }\n }\n void do_union(int node1 , int node2){ \n node1 = find_parent(node1);\n node2 = find_parent(node2);\n if(node1 == node2){ // If they have same parents, do nothing\n return;\n } else { //Else, connect node1 to node2 by assigning the parent of node1 to node2\n parents[node2] = node1;\n return;\n }\n }\n vector<int> findRedundantConnection(vector<vector<int>>& edges) {\n parents = vector<int>(1001);\n for(int i = 0 ; i < 1001 ; ++i){ //Self initializing the parents, because every node is disconnected at first.\n parents[i] = i;\n }\n vector<int> answer(2 , 0);\n for(int i = 0 ; i < edges.size() ; ++i){\n if(find_parent(edges[i][0]) == find_parent(edges[i][1])){ //If parents of these nodes are same, means they already visited/connected, hence contributing in cycle.\n answer[0] = edges[i][0];\n answer[1] = edges[i][1];\n break;\n } else {\n do_union(edges[i][0] , edges[i][1]);\n }\n }\n return answer;\n }\n};\n```\n**PLEASE UPVOTE IT IF YOU LIKED IT, IT REALLY MOTIVATES!! :)**\n
| 29 | 0 |
['Union Find', 'C', 'C++']
| 0 |
redundant-connection
|
[Pyhon] DSU solution, explained
|
pyhon-dsu-solution-explained-by-dbabiche-8nn9
|
Actually, what we need to do in this problem is to find loop. We can do it, using dfs or we can use Union Find idea. Let us add edges one by one and when we see
|
dbabichev
|
NORMAL
|
2021-06-25T07:55:13.117220+00:00
|
2021-06-25T15:48:33.154450+00:00
| 1,262 | false |
Actually, what we need to do in this problem is to find loop. We can do it, using dfs or we can use Union Find idea. Let us add edges one by one and when we see that we have a loop, that is two ends of our connection were already in the same component, we return it immedietly. Note, that because nodes enumerated from `1`, not `0`, we need to deal with this as well.\n\n#### Complexity\nIn this problem we have tree with one edge added, so there will be both `n` nodes and edges. So, if we assume that operations for our union find structure can be done in `O(1)`, total complexity will be `O(n)`. (In fact in my code I use dsu without ranks and with paths compression for simplicity, but due to small tests it works almost the same, in theory it is `O(log n)` complexity). Space complexity is `O(n)` as well.\n\n\n```python\nclass DSU:\n def __init__(self, N):\n self.p = list(range(N))\n\n def find(self, x):\n if self.p[x] != x:\n self.p[x] = self.find(self.p[x])\n return self.p[x]\n\n def union(self, x, y):\n xr = self.find(x)\n yr = self.find(y)\n self.p[xr] = yr\n\nclass Solution:\n def findRedundantConnection(self, edges):\n N = len(set(chain(*edges)))\n dsu = DSU(N)\n for i, j in edges:\n if dsu.find(i-1) == dsu.find(j-1):\n return([i,j])\n else:\n dsu.union(i-1,j-1)\n```\n\nIf you have any question, feel free to ask. If you like the explanations, please **Upvote!**
| 28 | 1 |
['Union Find']
| 2 |
redundant-connection
|
✅✅ Cycle detection || C++ solution || Easy to understand 🔥🔥| DFS
|
cycle-detection-c-solution-easy-to-under-wpvn
|
Intuition\nCheck if adding the edge in a graph is causing to form a cycle.\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n1. Crea
|
PrathameshLohar
|
NORMAL
|
2024-02-07T19:56:35.871787+00:00
|
2024-02-07T19:56:35.871806+00:00
| 1,847 | false |
# Intuition\nCheck if adding the edge in a graph is causing to form a cycle.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Create adjcency list for given graph\n2. Start adding edges and every time check its forming a cycle after addition of that edge.\n3. if yes then return that edge.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n * (V + E))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. -->\n\n# Code\n```\nclass Solution {\npublic:\n bool dfs(int src, int parent, vector<int> adj[], vector<bool>& vis) {\n vis[src] = true;\n for (auto adjnode : adj[src]) {\n if (!vis[adjnode]) {\n if (dfs(adjnode, src, adj, vis))\n return true;\n } else if (adjnode != parent)\n return true;\n }\n return false;\n }\n\n vector<int> findRedundantConnection(vector<vector<int>>& edges) {\n int n = edges.size();\n vector<int> adj[n + 1];\n for (int i = 0; i < n; i++) {\n adj[edges[i][0]].push_back(edges[i][1]);\n adj[edges[i][1]].push_back(edges[i][0]);\n vector<bool> vis(n + 1, false);\n if (dfs(edges[i][0], -1, adj, vis)) {\n return edges[i];\n }\n }\n return {};\n }\n};\n```\n\n\n
| 26 | 0 |
['Depth-First Search', 'Breadth-First Search', 'C++']
| 0 |
redundant-connection
|
Python by union-find [w/ Visualization]
|
python-by-union-find-w-visualization-by-mx8nh
|
Python by union-find (also known as disjoint set data structure)\n\n---\n\nHint:\n\nFind the redudant connection by picking the edge which forms a cycle in grap
|
brianchiang_tw
|
NORMAL
|
2020-09-18T06:32:09.994324+00:00
|
2020-09-18T06:37:28.201507+00:00
| 3,176 | false |
Python by **[union-find](https://en.wikipedia.org/wiki/Disjoint-set_data_structure)** (also known as **[disjoint set](https://en.wikipedia.org/wiki/Disjoint-set_data_structure)** data structure)\n\n---\n\n**Hint**:\n\nFind the redudant connection by **picking the edge which forms a cycle** in graph G\n\n---\n\n**Visualization and Diagram**:\n\n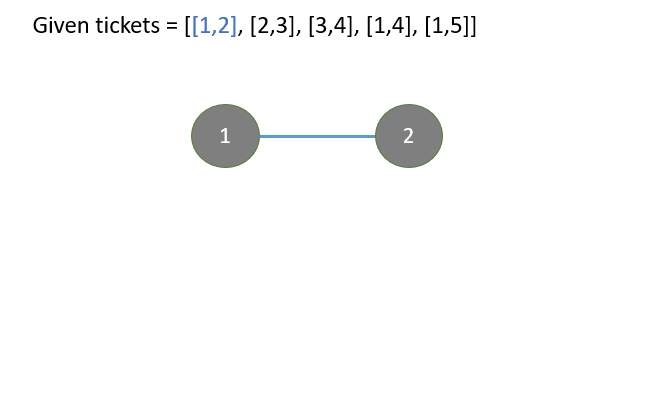\n\n---\n\n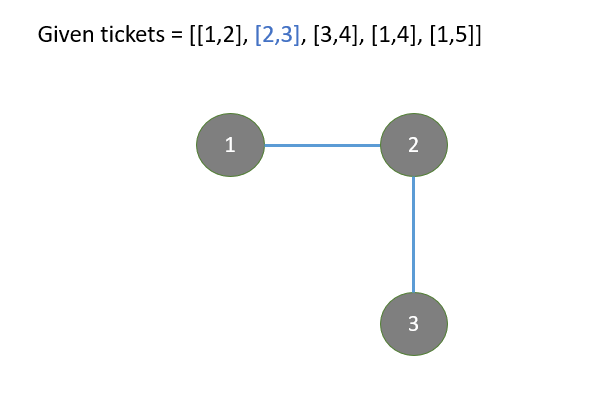\n\n---\n\n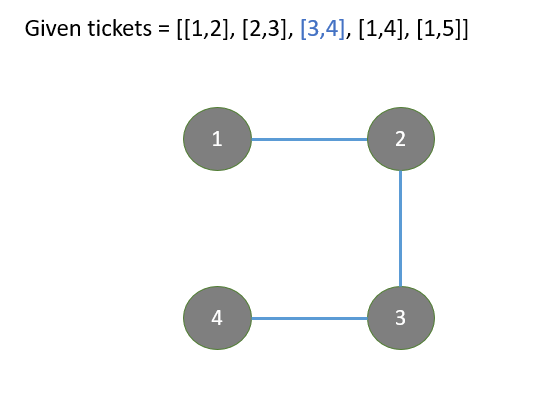\n\n---\n\n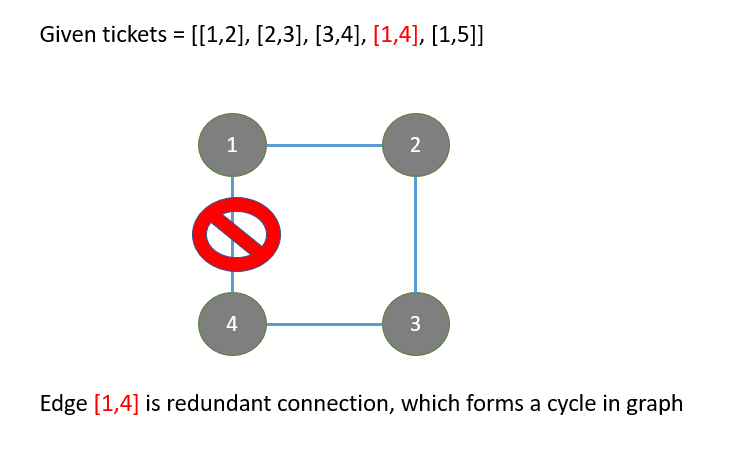\n\n\n---\n\n**Implementation** by union-find:\n\n```\nclass Solution:\n def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:\n \n parent = {v:-1 for v in range(1, len(edges)+1)}\n \n # ---------------------------------\n \n def find(u):\n \n if parent[u] != -1:\n # find root with path compression\n parent[u] = find(parent[u])\n return parent[u]\n \n else:\n # root node must be with -1\n return u\n \n \n # ---------------------------------\n \n def union(u, v):\n\n \n parent_of_u = find(u)\n parent_of_v = find(v)\n \n if parent_of_u == parent_of_v:\n \n # u and v has the same parent node\n # this edges froms a cycle in graph\n return True\n \n \n else:\n \n # after adding edge(u, v)\n # graph is still a tree without cycle\n parent[parent_of_u] = parent_of_v\n return False\n \n \n # ---------------------------------\n \n redundant = None\n for u, v in edges:\n \n if union(u, v):\n # check if edge (u, v) forms a cycle\n redundant = [u, v]\n return redundant\n \n \n```
| 26 | 0 |
['Union Find', 'Graph', 'Iterator', 'Python', 'Python3']
| 5 |
redundant-connection
|
UnionFind is good vs DFS+ bitset for cycle||beats 100%
|
unionfind-is-goodbeats-100-by-anwendeng-nhlh
|
IntuitionUse UnionFind to solve in quick.
2nd approach uses DFS+ bitset for vertices on cycle.Approach
Define the UnionFind class with rank optimization
In find
|
anwendeng
|
NORMAL
|
2025-01-29T00:40:11.841506+00:00
|
2025-01-29T16:03:40.033514+00:00
| 2,453 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Use UnionFind to solve in quick.
2nd approach uses DFS+ bitset for vertices on cycle.
# Approach
<!-- Describe your approach to solving the problem. -->
1. Define the UnionFind class with rank optimization
2. In `findRedundantConnection(vector<vector<int>>& edges)` let `n=|edges|`
3. Declare the Unionfind object `G(n+1)`
4. Procced a single loop `if (!G.Union(e[0], e[1])) return e` for `e in edges`
5. If the whole loop is though, return `{}`, but according to LC's description it will never reach.
> Given a graph that started as a tree with n nodes labeled from 1 to n, with one additional edge added.
# UnionFind makes some quesitions easier
the usual Union Find class with members `root`, `rank`, `Find`, `Union`, `connected`! The very crucial fact is that **every vertex in a connected component shares a common root, i.e. x is connected to y** $\iff$ Find(x)==Find(y) $\iff$ root[x]==root[y]
Some problems can be solved by used UnionFind
[2658. Maximum Number of Fish in a Grid](https://leetcode.com/problems/maximum-number-of-fish-in-a-grid/solutions/6337415/ez-dfsc-beats-100-by-anwendeng-nd07/)
[959. Regions Cut By Slashes](https://leetcode.com/problems/regions-cut-by-slashes/solutions/5614770/unionfind-dfs-euler-theorem-v-e-f-2-beats-100/)
[1971. Find if Path Exists in Graph](https://leetcode.com/problems/find-if-path-exists-in-graph/solutions/5052126/union-find-is-good-vs-dfs-vs-bfs-193ms-beats-99-93/)
[Please turn English subtitles if necessary]
[https://youtu.be/B1GQlUN08lk?si=DpfxrPBWc-t5eSPi](https://youtu.be/B1GQlUN08lk?si=DpfxrPBWc-t5eSPi)
```
class UnionFind { // usual UnionFind class
vector<int> root, rank;
public:
UnionFind(int n) : root(n), rank(n) {
rank.assign(n, 1);
iota(root.begin(), root.end(), 0);
}
int Find(int x) {//Path compression
if (x == root[x])
return x;
else
return root[x] = Find(root[x]);
}
bool Union(int x, int y) {//Union by rank with connecting info
int rX = Find(x), rY = Find(y);
//they have same root, already in same component
if (rX == rY)
return 0;// does not affect the components
if (rank[rX] > rank[rY])
swap(rX, rY);
root[rX] = rY;
if (rank[rX] == rank[rY])
rank[rY]++;
return 1;// connect 2 disjoint components
}
};
```
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
$O((V+E)\alpha(V))$ where $\alpha(.)$ is the inverse Ackermann function which growths very slowly.
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
$O(V)$
# Code||C++ 0ms beats 100%
```cpp []
class Solution {
public:
vector<int> findRedundantConnection(vector<vector<int>>& edges) {
const int n=edges.size();
UnionFind G(n+1);
for(auto& e: edges)
if (!G.Union(e[0], e[1])) return e;
return {};
}
};
```
# DFS + bitset for cycle|0ms
```
class Solution {
public:
bitset<1001> viz;
vector<vector<short>> adj;
vector<int> parent;
int found = -1;
void dfs(int i) {
viz[i] = 1;
for (int j : adj[i]) {
if (!viz[j]) {
parent[j] = i;
dfs(j);
} else if (j != parent[i] && found == -1) {
found = j;
parent[j] = i;
}
}
}
vector<int> findRedundantConnection(vector<vector<int>>& edges) {
int n = edges.size();
adj.resize(n + 1);
parent.assign(n + 1, -1);
for (auto& e : edges) {
short u = e[0], v = e[1];
adj[u].push_back(v);
adj[v].push_back(u);
}
dfs(edges[0][0]);
// cout<<found<<endl;
bitset<1001> cycle = 0;
int j = found;
do {
cycle[j] = 1;
j = parent[j];
} while (j != found);
for (int i = n - 1; i >= 0; i--) {
int u = edges[i][0], v = edges[i][1];
if (cycle[u] && cycle[v])
return edges[i];
}
return {};
}
};
```
# Relationship to Minimal Spanning Tree
It's to remove the edge with the maximal edge index which makes a cycle; in other words, the remaining edges build a spanning tree.
If putting the edge index as the edge weight, it is to find the mininimal spanning tree; ie. the spanning tree with minimal summation of weights. There are several kinds of algorithms dealing with. One is Prim's algorithm which is very similar to Dijkstra's Algorithm finding shortest path; the other using Union-Find is called Krusal's Algorithm.
The 1st solution can be reguarded as a special case for Krusal's algorithm; it doesn't need to sort the edges, the rest is very similar to.
LC has few questions on this topic, can ref.
[1584. Min Cost to Connect All Points](https://leetcode.com/problems/min-cost-to-connect-all-points/solutions/4046658/c-prim-s-algorithm-vs-kruskal-s-algorithm-beats-96-09/)
[1489. Find Critical and Pseudo-Critical Edges in Minimum Spanning Tree
](https://leetcode.com/problems/find-critical-and-pseudo-critical-edges-in-minimum-spanning-tree/solutions/3930534/c-kruskal-s-algorithm-beats-95-26-math/)
| 20 | 6 |
['Depth-First Search', 'Union Find', 'Graph', 'C++']
| 4 |
redundant-connection
|
[C++] Simple C++ Code || 99.63% time || 89% space
|
c-simple-c-code-9963-time-89-space-by-pr-bz34
|
\n# If you like the implementation then Please help me by increasing my reputation. By clicking the up arrow on the left of my image.\n\nclass Solution {\n v
|
_pros_
|
NORMAL
|
2022-08-18T08:22:25.762066+00:00
|
2022-08-18T08:22:25.762104+00:00
| 2,492 | false |
\n# **If you like the implementation then Please help me by increasing my reputation. By clicking the up arrow on the left of my image.**\n```\nclass Solution {\n vector<int> parent;\n int find_set(int v)\n {\n if(v == parent[v])\n return v;\n return parent[v] = find_set(parent[v]);\n }\n bool union_set(int a, int b)\n {\n a = find_set(a);\n b = find_set(b);\n if(a == b)\n return true;\n parent[b] = a;\n return false;\n }\npublic:\n vector<int> findRedundantConnection(vector<vector<int>>& edges) {\n int n = edges.size();\n for(int i = 0; i <= n; i++)\n parent.push_back(i);\n for(vector<int> &edge : edges)\n {\n if(union_set(edge[0], edge[1]))\n return {edge[0], edge[1]};\n }\n return {-1,-1};\n }\n};\n```
| 20 | 0 |
['Union Find', 'C', 'C++']
| 3 |
redundant-connection
|
C++ (4 approaches, DFS -> BFS -> UNION Find -> Union Find with rank) with Comments
|
c-4-approaches-dfs-bfs-union-find-union-qdj1s
|
Know more about interview questions : https://github.com/MAZHARMIK/Interview_DS_Algo\n\n//Approach-1 (DFS)\nclass Solution {\npublic:\n bool dfs(map<int, vec
|
mazhar_mik
|
NORMAL
|
2021-06-25T11:47:52.711458+00:00
|
2021-06-25T11:51:08.779137+00:00
| 1,285 | false |
Know more about interview questions : https://github.com/MAZHARMIK/Interview_DS_Algo\n```\n//Approach-1 (DFS)\nclass Solution {\npublic:\n bool dfs(map<int, vector<int>>& mp, int start, int end, vector<bool>& visited) {\n visited[start] = true;\n if(start == end)\n return true;\n \n for(int &x : mp[start]) {\n if(!visited[x] && dfs(mp, x, end, visited)) {\n return true;\n }\n }\n return false;\n }\n \n vector<int> findRedundantConnection(vector<vector<int>>& edges) {\n map<int, vector<int>> mp;\n \n int n = edges.size();\n vector<bool> visited(n+1, false);\n \n for(int i = 0; i<n; i++) {\n int u = edges[i][0];\n int v = edges[i][1];\n \n fill(begin(visited), end(visited), false);\n \n //if u and v are already in graph, then we check\n //if this current edge connects them again ?\n //If yes, this edge is unwanted (redundant)\n if(mp.find(u) != mp.end() && mp.find(v) != mp.end()\n && dfs(mp, u, v, visited))\n return edges[i];\n \n //Else, add them to graph\n mp[u].push_back(v);\n mp[v].push_back(u);\n }\n \n return {};\n }\n};\n```\n\n```\n//Approach-2 (BFS)\nclass Solution {\npublic:\n int n;\n bool bfs(map<int, vector<int>>& mp, int start, int end) {\n vector<bool> visited(n+1, false);\n queue<int> que;\n que.push(start);\n \n while(!que.empty()) {\n int curr = que.front();\n que.pop();\n visited[curr] = true;\n if(curr == end)\n return true;\n \n for(int &x : mp[curr]) {\n if(!visited[x]) {\n que.push(x);\n }\n }\n }\n return false;\n }\n vector<int> findRedundantConnection(vector<vector<int>>& edges) {\n map<int, vector<int>> mp;\n n = edges.size();\n \n for(int i = 0; i<n; i++) {\n int u = edges[i][0];\n int v = edges[i][1];\n \n //if u and v are already in graph, then we check\n //if this current edge connects them again ?\n //If yes, this edge is unwanted (redundant)\n if(mp.find(u) != mp.end() && mp.find(v) != mp.end() && bfs(mp, u, v))\n return edges[i];\n \n //Else add them to graph\n mp[u].push_back(v);\n mp[v].push_back(u);\n }\n \n return {};\n }\n};\n```\n\n```\n//Approach-3 (Union Find with Path compression)\nclass Solution {\npublic:\n int find(int x, vector<int>& parent) {\n if(parent[x] != x)\n return parent[x] = find(parent[x], parent); //Path compression\n \n return parent[x];\n }\n \n void Union(int u, int v, vector<int>& parent) {\n parent[u] = v;\n }\n \n vector<int> findRedundantConnection(vector<vector<int>>& edges) {\n int n = edges.size();\n vector<int> parent(n+1);\n for(int i = 1; i<=n; i++)\n parent[i] = i;\n for(int i = 0; i<n; i++) {\n int u = edges[i][0];\n int v = edges[i][1];\n \n int set_u = find(u, parent);\n int set_v = find(v, parent);\n \n if(set_u == set_v) {\n //means they were already connected before\n //So, this edge is redundant\n return edges[i];\n }\n \n //Else, bring them in one subset\n Union(set_u, set_v, parent);\n }\n return {};\n }\n};\n```\n\n```\n//Approach-4 (Union Find with Rank and Path Compression)\nclass Solution {\npublic:\n int find(int x, vector<vector<int>>& parent) {\n if(parent[x][0] != x)\n return parent[x][0] = find(parent[x][0], parent); //Path Compression\n \n return parent[x][0];\n }\n \n void Union(int u, int v, vector<vector<int>>& parent) {\n\t\t//Union by Rank\n //put node of lower rank under node of higher rank\n if(parent[u][1] < parent[v][1]) {\n parent[u][0] = v;\n } else if(parent[u][1] > parent[v][1]) {\n parent[v][0] = u;\n } else {\n parent[u][0] = v;\n parent[u][1]++; //increase rank of v\n }\n }\n \n vector<int> findRedundantConnection(vector<vector<int>>& edges) {\n int n = edges.size();\n vector<vector<int>> parent(n+1, vector<int>(2, 0));\n //parent[i][0] = parent of i\n //parent[i][1] = rank of i\n \n for(int i = 1; i<=n; i++) {\n parent[i][0] = i;\n parent[i][1] = 0; //initially rank = 0\n }\n \n for(int i = 0; i<n; i++) {\n int u = edges[i][0];\n int v = edges[i][1];\n \n int set_u = find(u, parent);\n int set_v = find(v, parent);\n \n if(set_u == set_v) {\n //means they were already connected before\n //So, this edge is redundant\n return edges[i];\n }\n \n //Else, bring them in one subset\n Union(set_u, set_v, parent);\n }\n return {};\n }\n};\n```\n
| 20 | 1 |
[]
| 2 |
redundant-connection
|
Why does this(Input: [[2,3],[5,2],[1,5],[4,2],[4,1]] Output: [4,2] Expected: [4,1] ) happens?
|
why-does-thisinput-2352154241-output-42-u0q2h
|
@administrators \n@contributors \nAs the title says, my solution is not accepted. Why does this happen? I think we should remove [4,2] as my solution. What is w
|
yanchao_hust
|
NORMAL
|
2017-09-24T03:08:50.445000+00:00
|
2017-09-24T03:08:50.445000+00:00
| 5,052 | false |
@administrators \n@contributors \nAs the title says, my solution is not accepted. Why does this happen? I think we should remove [4,2] as my solution. What is wrong?\n\nInput: [[2,3],[5,2],[1,5],[4,2],[4,1]]\nOutput: [4,2]\nExpected: [4,1]\n\n```\nclass Solution {\npublic:\n vector<int> findRedundantConnection(vector<vector<int>>& edges) {\n map<int, int> parent;\n for (auto e : edges) {\n if (parent.find(e[1]) != parent.end()) {\n return e; \n }\n if (parent.find(e[0]) != parent.end()) {\n if (parent[e[0]] == e[1])\n return e;\n }\n parent[e[1]] = e[0];\n } \n set<int> root;\n for (auto e : edges) {\n if (root.find(e[1]) != root.end())\n return e;\n root.insert(e[0]);\n }\n return edges.back();\n }\n};\n```
| 18 | 2 |
[]
| 10 |
redundant-connection
|
Cycle detection in undirected graph
|
cycle-detection-in-undirected-graph-by-a-qjzo
|
\nclass UnionFind {\n private:\n vector<int> parent;\n public: \n UnionFind(int n){\n parent = vector<int>(n+1,-1);\n }\n \n int find(i
|
Aadi_Yogi
|
NORMAL
|
2021-05-20T14:59:50.885064+00:00
|
2021-05-20T14:59:50.885107+00:00
| 59,360 | false |
```\nclass UnionFind {\n private:\n vector<int> parent;\n public: \n UnionFind(int n){\n parent = vector<int>(n+1,-1);\n }\n \n int find(int x){\n if(parent[x]==-1) return x;\n return find(parent[x]);\n }\n \n void Union(int x,int y){\n int X = find(x);\n int Y = find(y);\n parent[X]=Y;\n }\n \n};\n\nclass Solution {\npublic:\n vector<int> findRedundantConnection(vector<vector<int>>& edges) {\n int n = edges.size();\n UnionFind *uf = new UnionFind(n);\n \n for(auto x:edges){\n int a = uf->find(x[0]);\n int b = uf->find(x[1]);\n if(a==b) return {x[0],x[1]};\n \n uf->Union(x[0],x[1]);\n }\n return {};\n }\n};\n```
| 17 | 0 |
['Union Find', 'C']
| 1 |
redundant-connection
|
Python DFS with explanation
|
python-dfs-with-explanation-by-zuu-4hlf
|
Solution explanation is pretty vague, I think this is a better explanation for the DFS solution. \n\nclass Solution:\n \'\'\'\n Tree Properties\n 1) On
|
zuu
|
NORMAL
|
2020-07-08T02:45:34.616301+00:00
|
2020-07-08T02:45:34.616351+00:00
| 842 | false |
Solution explanation is pretty vague, I think this is a better explanation for the DFS solution. \n```\nclass Solution:\n \'\'\'\n Tree Properties\n 1) Only 1 edge between two vertices\n 2) Every child can have only one parent\n 3) No cycles\n 4) Must have n-1 edges where n is the number of vertices \n \n In a valid tree, there is a unique path from each node to every other\n node in the tree:\n \n 1 1 -> 2: (1,2)\n / \\ 1 -> 3: (1,3)\n 2 3 2 -> 3: (2,1,3)\n 3 -> 2: (3,1,2)\n\n If we add one more edge to this tree, then the tree would be invalid:\n \n 1 1 -> 2: (1,2), (1,3,2)\n / \\ 1 -> 3: (1,3), (1,2,3)\n 2 - 3 2 -> 3: (2,1,3), (2,3)\n 3 -> 2: (3,1,2), (3,2)\n \n To find the redundant connection we can iterate through the list of edges\n and create the graph as we go along the list. For each node u,v in the list\n of edges if both u and v exist as nodes in the graph, then we can try and \n form a path from u to v. \n \n If the u -> v path already exists then adding another edge from u to v would \n make our tree invalid.\n \'\'\' \n def dfs(self, graph, src, dest, visited):\n if src not in visited:\n visited.add(src)\n neighbors = graph[src]\n \n # We have found a path from src to dest\n if src == dest:\n return True\n \n for neighbor in neighbors:\n path = self.dfs(graph, neighbor, dest, visited)\n if path:\n return True\n \n # No path from src to dest\n return False\n \n def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:\n graph = collections.defaultdict(set)\n \n for edge in edges:\n u,v = edge\n # If we can reach edge u from edge v already then this edge is redundant\n if u in graph and v in graph and self.dfs(graph, u, v, set()):\n return edge\n # No path from u to v, this edge is valid\n graph[u].add(v)\n graph[v].add(u)\n \n return graph\n```
| 16 | 0 |
[]
| 2 |
redundant-connection
|
c++ solution using dfs
|
c-solution-using-dfs-by-shweta_k-dvh4
|
\nWe will create unordered map to store the edges, and for each nnode we will visit the other nodes from map and check if that is already visited using dfs. If
|
shweta_k
|
NORMAL
|
2021-04-30T06:34:02.272664+00:00
|
2021-04-30T06:34:02.272705+00:00
| 3,348 | false |
\nWe will create unordered map to store the edges, and for each nnode we will visit the other nodes from map and check if that is already visited using dfs. If it already is visited means it creates a cycle.\n \nWe add edges one by one in graph and as soon as adding any edge creates the cycle, we will return the result.\n\n\n```\nclass Solution {\npublic:\n\nbool dfs(unordered_map<int, vector<int>> &m, int node, vector<int> visited, int parent)\n{\n if(find(visited.begin(),visited.end(),node)!=visited.end())\n return true;\n visited.push_back(node);\n // cout<<node<<" "<<visited.size()<<endl;\n for(int v: m[node]){\n if(v==parent)\n continue;\n if(dfs(m,v,visited,node)){\n return true;\n }\n }\n \n return false;\n}\n\nvector<int> findRedundantConnection(vector<vector<int>>& A)\n {\n int n = A.size();\n vector<int> visited;\n \n unordered_map<int, vector<int>> m;\n \n for(int i=0;i<n;i++)\n {\n int f = A[i][0];\n int s = A[i][1];\n \n m[f].push_back(s);\n m[s].push_back(f); \n // cout<<"***** "<<f<<" *****\\n";\n if(dfs(m,f,visited,-1)) \n {\n return {f,s};\n }\n visited.clear();\n }\n \n return {};\n }\n};\n```\n\n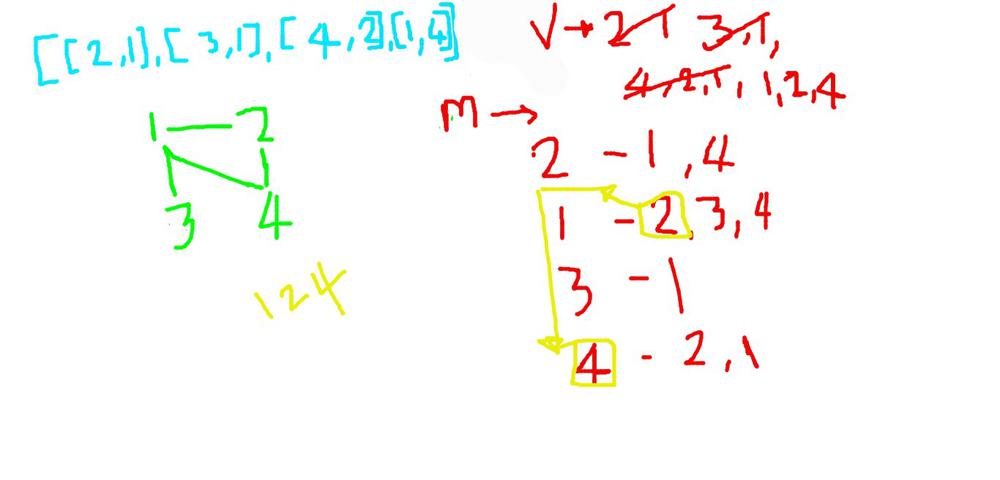\n
| 15 | 1 |
['Depth-First Search', 'C', 'C++']
| 1 |
redundant-connection
|
My DFS and BSF solutions
|
my-dfs-and-bsf-solutions-by-23sweet-ujen
|
share my DFS and BFS solution, although there are not effcient\n\npublic int[] bfs(List<Set<Integer>> adj, int[][]edges){\n \n for(int[] e: edges){\n
|
23sweet
|
NORMAL
|
2018-01-24T10:48:56.311000+00:00
|
2018-10-23T20:03:48.422223+00:00
| 7,593 | false |
share my DFS and BFS solution, although there are not effcient\n```\npublic int[] bfs(List<Set<Integer>> adj, int[][]edges){\n \n for(int[] e: edges){\n int from = e[0], to = e[1];\n \n Queue<Integer> q = new ArrayDeque<>();\n Set<Integer> visited = new HashSet<>();\n q.add(from);\n visited.add(from);\n while( !q.isEmpty() ){\n \n int p = q.poll();\n if(adj.get(p).contains(to))\n return e;\n \n for(int w: adj.get(p)){\n if(visited.contains(w)) // avoid visit the last adj node\n continue;\n q.add(w);\n visited.add(w);\n }\n }\n \n adj.get(from).add(to);\n adj.get(to).add(from);\n }\n return new int[]{-1,-1};\n }\n\n\n public int[] dfs(List<Set<Integer>> adj, int[][]edges){\n for(int[] e: edges){\n int from = e[0], to = e[1];\n if(dfsR(adj, edges, from, to, from)) // \u6709\u73af\n return e;\n adj.get(from).add(to);\n adj.get(to).add(from);\n }\n return new int[]{-1,-1};\n }\n```\n``` \n// return true if has cycle\n public boolean dfsR(List<Set<Integer>> adj, int[][]edges, int cur, int target, int pre){\n \n if(adj.get(cur).contains(target)) \n return true;\n \n for(int w: adj.get(cur)){\n if(w == pre) // skip the last adj node\n continue;\n if( dfsR(adj,edges,w,target,cur) )\n return true;\n }\n \n return false;\n }\n```
| 15 | 2 |
[]
| 4 |
redundant-connection
|
dfs and union find
|
dfs-and-union-find-by-huakaihuaxie-i46t
|
dfs \n\nclass Solution {\n public int[] findRedundantConnection(int[][] edges) {\n List<List<Integer>> adjList = new ArrayList<>();\n for(int i = 0
|
huakaihuaxie
|
NORMAL
|
2018-08-27T17:27:27.211343+00:00
|
2018-10-18T20:52:39.316684+00:00
| 3,282 | false |
dfs \n```\nclass Solution {\n public int[] findRedundantConnection(int[][] edges) {\n List<List<Integer>> adjList = new ArrayList<>();\n for(int i = 0; i < edges.length + 1; i++){\n adjList.add(new ArrayList<>());\n }\n for(int[] edge : edges){\n int v = edge[0];\n int u = edge[1];\n \n HashSet<Integer> visited = new HashSet<>();\n \n if(dfs(visited, u, v, adjList)){ // return true if there\'s a path between u and v already\n // connect u and v directly make it a graph from tree\n return edge;\n }\n // if the path doesnt exist \n \n adjList.get(u).add(v);\n adjList.get(v).add(u);\n }\n return null;\n }\n private boolean dfs(HashSet<Integer> visited, int u, int v, List<List<Integer>> adjList){\n // base case , when u and v are the same pos \n if(u == v) return true;\n \n // else, mark u as visited\n visited.add(u);\n \n \n // check every nei, dfs on nei\n for(int nei : adjList.get(u)){\n if(visited.contains(nei)) continue;\n if(dfs(visited, nei, v, adjList)) return true;\n }\n return false;\n }\n}\n \n```\nuf \n```\nclass Solution {\n public int[] findRedundantConnection(int[][] edges) {\n int n = edges.length;\n UnionFind uf = new UnionFind(n);\n \n for(int[] edge : edges){\n int u = edge[0];\n int v = edge[1];\n \n if(uf.find(u) == uf.find(v)){\n return edge;\n }else{\n uf.union(u, v);\n }\n }\n return null;\n }\n \n class UnionFind{\n int[] parent;\n \n public UnionFind(int n){\n parent = new int[n + 1];\n for(int i = 1; i < n + 1; i++){\n parent[i] = i;\n }\n }\n \n public void union(int a, int b){\n int pa = find(a);\n int pb = find(b);\n parent[pa] = pb;\n }\n \n public int find(int x){\n while(parent[x] != x){\n x = parent[x];\n }\n return x;\n }\n }\n\n}\n```
| 14 | 0 |
[]
| 4 |
redundant-connection
|
Union Find concept and multiple solutions - Java
|
union-find-concept-and-multiple-solution-efa1
|
Hello Guys, \n\nList of all Union Find related problems:\n1. https://leetcode.com/problems/redundant-connection/\n2. https://leetcode.com/problems/redundant-con
|
letsdoitthistime
|
NORMAL
|
2022-07-13T22:15:22.585880+00:00
|
2024-02-14T01:31:10.276138+00:00
| 1,564 | false |
Hello Guys, \n\nList of all Union Find related problems:\n1. https://leetcode.com/problems/redundant-connection/\n2. https://leetcode.com/problems/redundant-connection-ii/\n3. https://leetcode.com/problems/most-stones-removed-with-same-row-or-column/\n4. https://leetcode.com/problems/number-of-operations-to-make-network-connected/\n5. https://leetcode.com/problems/number-of-provinces/\n6. https://leetcode.com/problems/accounts-merge/description/\n\nThere is a similar code for the simple concept. I hope this Helps:\n\n**1. 684. Redundant Connection**\n```\n// Union Find\nclass Solution {\n \n int[] parent;\n public int[] findRedundantConnection(int[][] edges) {\n parent = new int[edges.length+1];\n \n for(int i=0; i<parent.length; i++) {\n parent[i] = i;\n }\n \n for(int[] edge : edges) {\n if(find(edge[0]) == find(edge[1])) {\n return edge;\n }\n \n union(edge[0], edge[1]);\n }\n \n return new int[]{-1,-1};\n }\n \n \n // Find Operation\n private int find(int node) {\n while(parent[node] != node) {\n node = parent[node];\n }\n \n return node;\n }\n \n //Find Union Operation\n private void union(int i, int j) {\n int iRoot = find(i);\n int jRoot = find(j);\n \n if(iRoot != jRoot) {\n parent[jRoot] = iRoot;\n }\n }\n}\n```\n\n**2. 685. Redundant Connection II**\n\n```\n/*\nTo detect a cycle in Directed graph, there are two possible cases.\n\nCase 1: There is a cycle but every node has a single parent\nCase 2: These is no cycle but a single node has two or more parents\n\n1) 5<-----1----->2 2) 5<-----1----->2\n ^ | | | \n | | | |\n | V V V \n 4<-----3 4<-----3 \n*/\t\t\t \nclass Solution {\n \n int[] parent;\n \n public int[] findRedundantDirectedConnection(int[][] edges) {\n parent = new int[edges.length+1];\n \n int[] ans1 = null;\n int[] ans2 = null;\n \n\t\t// checking that how many parents are possible for each node\n for(int[] edge : edges) {\n int u = edge[0];\n int v = edge[1];\n \n if(parent[v] > 0) {\n ans1 = new int[]{parent[v], v};\n ans2 = edge; // Last possible edge which is creating the cycle - need to return this of we have multiple answer\n }\n \n parent[v] = u;\n }\n \n// System.out.println(Arrays.toString(parent)+" "+Arrays.toString(ans1)+" "+Arrays.toString(ans2));\n parent = new int[edges.length+1];\n \n for(int i=0; i<parent.length; i++) {\n parent[i] = i;\n }\n \n for(int[] edge: edges) {\n \n if(edge == ans2) continue;\n \n if(find(edge[0]) == find(edge[1])) {\n return ans1 == null ? edge : ans1; \n }\n union(edge[0], edge[1]);\n }\n \n return ans2;\n }\n \n private int find(int node) {\n while(parent[node] != node) {\n node = parent[node];\n }\n \n return node;\n }\n \n private void union(int i, int j) {\n int iRoot = find(i);\n int jRoot = find(j);\n \n if(iRoot!=jRoot) {\n parent[jRoot] = iRoot;\n }\n \n }\n}\n```\n\n**3. 947. Most Stones Removed with Same Row or Column**\n```\nclass Solution {\n public int removeStones(int[][] stones) {\n int[] parent = new int[stones.length];\n \n Arrays.fill(parent, -1);\n \n for(int i=0; i<stones.length; i++) {\n for(int j=i+1; j<stones.length; j++) {\n int[] stone1 = stones[i];\n int[] stone2 = stones[j];\n \n if(stone1[0] == stone2[0] || stone1[1] == stone2[1]) {\n union(i, j, parent);\n }\n }\n }\n \n int component = 0;\n for(int i=0; i<parent.length; i++) {\n if(parent[i] == -1) {\n component++;\n }\n }\n \n return stones.length-component;\n }\n \n private int find(int node, int[] parent) {\n while(parent[node]!=-1) {\n node = parent[node];\n }\n \n return node;\n }\n \n private void union(int A, int B, int[] parent) {\n int parentA = find(A, parent);\n int parentB = find(B, parent);\n \n if(parentA != parentB) {\n parent[parentB] = parentA;\n }\n }\n}\n```\n\n**4. 1319. Number of Operations to Make Network Connected**\n\n```\nclass Solution {\n public int makeConnected(int n, int[][] connections) {\n int[] parent = new int[n];\n int extraCable = 0;\n \n Arrays.fill(parent, -1);\n \n for(int[] connection : connections) {\n \n if(find(connection[0], parent) == find(connection[1], parent)) {\n extraCable++;\n } else {\n union(connection[0], connection[1], parent);\n }\n }\n \n int component = 0;\n \n for(int i=0; i<parent.length; i++) {\n if( parent[i] == -1) {\n component++;\n }\n }\n \n return extraCable >= (component-1) ? component-1 : -1;\n }\n \n private int find(int node, int[] parent) {\n while(parent[node] != -1) {\n node = parent[node];\n }\n \n return node;\n }\n \n private void union(int a, int b, int[] parent) {\n int parentA = find(a, parent);\n int parentB = find(b, parent);\n \n if(parentA != parentB) {\n parent[parentB] = parentA;\n }\n }\n}\n```\n\n**5. 547. Number of Provinces**\n\n```\n/*\n// Same as https://leetcode.com/problems/number-of-connected-components-in-an-undirected-graph/\n\nclass Solution {\n \n int ans = 0;\n public int findCircleNum(int[][] isConnected) {\n \n BFS(isConnected);\n \n return ans;\n }\n \n private void BFS(int[][] isConnected) {\n boolean[] visited = new boolean[isConnected.length];\n \n for(int i=0; i<isConnected.length; i++) {\n if(visited[i] == false) {\n ans++;\n BFSHelper(isConnected, visited, i);\n }\n }\n }\n \n private void BFSHelper(int[][] isConnected, boolean[] visited, int start) {\n Queue<Integer> queue = new LinkedList<>();\n queue.add(start);\n visited[start] = true;\n \n while(!queue.isEmpty()) {\n int node = queue.poll();\n \n for(int i=0; i<isConnected.length; i++) {\n if(isConnected[node][i] == 1 && visited[i] != true) {\n queue.add(i);\n visited[i] = true;\n }\n }\n }\n }\n}\n*/\nclass Solution {\n int[] parent;\n public int findCircleNum(int[][] isConnected) {\n parent = new int[isConnected.length];\n int result = 0;\n \n Arrays.fill(parent, -1);\n \n for(int i=0; i<isConnected.length; i++) {\n for(int j=0; j<isConnected[0].length; j++) {\n if(isConnected[i][j] == 1) {\n union(i,j);\n }\n }\n }\n \n for(int i=0; i<parent.length; i++) {\n if(parent[i] == -1) {\n result++;\n }\n }\n \n return result;\n }\n \n private int find(int node) {\n while(parent[node] != -1) {\n node = parent[node];\n }\n \n return node;\n }\n \n private void union(int a, int b) {\n int parentA = find(a);\n int parentB = find(b);\n \n if(parentA != parentB) {\n parent[parentB] = parentA;\n }\n }\n}\n```\n**6. 721. Accounts Merge**\n\n```\n/* This problem is simple concept as we have to use the union find concept here but code is slightly heavy.\n\nInput:\n[["John","J1@mail","J2@mail"],["John","J1@mail","J3@mail"],["Mary","m1@mail"],["John","[email protected]"]]\n\n\n emailToIdx emailToName Parent\n\n J1@mail 0 J1@mail John 0 1 2 3 (Indexes)\n J2@mail 0 J2@mail John 0 0 2 3 \n J3@mail 1 J3@mail John\n m1@mail 2 m1@mail Mary\n J4@mail 3 J4@mail John\n\n\n Groups\n 0 -> [J1@mail, J2@mail, J3@mail]\n 1 -> []\n 2 -> [m1@mail]\n 3 -> [J4@mail]\n\n\n*/\n\nclass Solution {\n int[] parent;\n public List<List<String>> accountsMerge(List<List<String>> accounts) {\n \n Map<String, Integer> emailToIdx = new HashMap<>();\n\n Map<String, String> emailToName = new HashMap<>();\n\n parent = new int[accounts.size()];\n\n for(int i=0; i<parent.length; i++) {\n parent[i] = i;\n }\n\n int idx = 0;\n\n for(List<String> account : accounts) {\n String name = account.get(0);\n\n for(int i=1; i<account.size(); i++) {\n String curEmail = account.get(i);\n\n if(!emailToIdx.containsKey(curEmail)) {\n emailToIdx.put(curEmail, idx);\n emailToName.put(curEmail, name);\n }\n\n // Union the first email with the current email\n int firstEmailIdx = emailToIdx.get(account.get(1));\n int curEmailIdx = emailToIdx.get(curEmail);\n\n union(firstEmailIdx, curEmailIdx);\n }\n idx++;\n }\n\n // Grouping emails that belong to the same set\n Map<Integer, TreeSet<String>> groups = new HashMap<>();\n\n for(String email : emailToIdx.keySet()) {\n int root = find(emailToIdx.get(email));\n groups.computeIfAbsent(root, x -> new TreeSet<>()).add(email);\n }\n\n // Constructing the answer\n List<List<String>> result = new ArrayList<>();\n\n for(TreeSet<String> group : groups.values()) {\n List<String> account = new ArrayList<>();\n account.add(emailToName.get(group.first())); // add name\n account.addAll(group); // add emails\n result.add(account);\n }\n\n return result;\n }\n\n // Find operation with path compression\n private int find(int node) {\n while(parent[node] != node) {\n node = parent[node];\n }\n return node;\n }\n\n // Union operation\n private void union(int i, int j) {\n int parentA = find(i);\n int parentB = find(j);\n\n if(parentA != parentB) {\n parent[parentA] = parentB;\n }\n }\n}\n```\n\nPlease upvoe if you find it useful.\nHappy coding!
| 13 | 0 |
['Java']
| 2 |
redundant-connection
|
Very Short, Clean, and Simple Solution
|
very-short-clean-and-simple-solution-by-k8xkq
|
IntuitionWe simply remove all the leaves from the graph one by one. And when only a cycle remains we take the last element.Code
|
charnavoki
|
NORMAL
|
2025-01-29T00:18:49.105806+00:00
|
2025-01-29T00:18:49.105806+00:00
| 1,375 | false |
# Intuition
We simply remove all the leaves from the graph one by one. And when only a cycle remains we take the last element.
# Code
```javascript []
const findRedundantConnection = (edges) => {
const leaves = edges.flat().filter((v, i, a) => a.indexOf(v) === a.lastIndexOf(v));
if (leaves.length) {
return findRedundantConnection(edges.filter(([a, b]) => !leaves.includes(a) && !leaves.includes(b)));
}
return edges.at(-1);
};
```
| 11 | 1 |
['JavaScript']
| 3 |
redundant-connection
|
✅ One Line Solution
|
one-line-solution-by-mikposp-uirf
|
(Disclaimer: this is not an example to follow in a real project - it is written for fun and training mostly)Code #1.1 - One LineTime complexity: O(n2). Space co
|
MikPosp
|
NORMAL
|
2025-01-29T11:29:58.055912+00:00
|
2025-01-29T11:30:35.252817+00:00
| 960 | false |
(Disclaimer: this is not an example to follow in a real project - it is written for fun and training mostly)
# Code #1.1 - One Line
Time complexity: $$O(n^2)$$. Space complexity: $$O(n)$$.
```python3
class Solution:
def findRedundantConnection(self, e: List[List[int]]) -> List[int]:
return (t:=''.join(map(chr,range(1001)))) and next([u,v] for u,v in e if (t[u]==t[v],t:=t.replace(t[u],t[v]))[0])
```
[Ref](https://leetcode.com/problems/redundant-connection/solutions/108002/unicode-find-5-short-lines)
# Code #1.2 - Unwrapped
```python3
class Solution:
def findRedundantConnection(self, e: List[List[int]]) -> List[int]:
t = ''.join(map(chr, range(1001)))
for u,v in e:
if t[u] == t[v]:
return [u, v]
t = t.replace(t[u], t[v])
```
(Disclaimer 2: code above is just a product of fantasy packed into one line, it is not claimed to be 'true' oneliners - please, remind about drawbacks only if you know how to make it better)
| 10 | 0 |
['Tree', 'Union Find', 'Graph', 'Python', 'Python3']
| 1 |
redundant-connection
|
Union Find. Simple solution (+ Topological sort, DFS)
|
union-find-simple-solution-by-xxxxkav-twn0
|
Union Find
Time: O(n∗alpha(n)) where alpha(n) is the inverse Ackermann function
Space: O(n)
Topological sort
Time: O(n). Space: O(n)
DFS
Time: O(n). Space: O
|
xxxxkav
|
NORMAL
|
2025-01-29T00:41:15.714444+00:00
|
2025-01-29T10:48:52.400231+00:00
| 1,593 | false |
1. Union Find
Time: $O(n*alpha(n))$ where $alpha(n)$ is the inverse Ackermann function
Space: $O(n)$
```
class UnionFind:
def __init__(self, n: int):
self.parent = [*range(n)]
self.rank = [1] * n
def find(self, x: int) -> int:
if self.parent[x] != x:
self.parent[x] = self.find(self.parent[x])
return self.parent[x]
def union(self, x: int, y: int) -> None:
x, y = self.find(x), self.find(y)
if x == y:
return True
if self.rank[x] < self.rank[y]:
self.parent[x] = y
else:
self.parent[y] = x
if self.rank[x] == self.rank[y]:
self.rank[x] += 1
return False
class Solution:
def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:
uf = UnionFind(len(edges)+1)
for u, v in edges:
if uf.union(u, v):
return [u, v]
```
2. Topological sort
Time: $O(n)$. Space: $O(n)$
```
class Solution:
def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:
graph = [[] for _ in range(len(edges)+1)]
for u, v in edges:
graph[v].append(u)
graph[u].append(v)
indegree = [len(neighbors) for neighbors in graph]
queue = deque(node for node in range(len(edges)+1) if indegree[node] == 1)
while queue:
next_node = queue.popleft()
for neighbor in graph[next_node]:
indegree[neighbor] -= 1
if indegree[neighbor] == 1:
queue.append(neighbor)
for u, v in reversed(edges):
if indegree[u] == 2 and indegree[v] == 2:
return [u, v]
```
3. DFS
Time: $O(n)$. Space: $O(n)$
```
class Solution:
def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:
def find_cycle(node, parent):
if visited[node] == 1:
visited[parent] = 2
cycle_nodes.add(node)
return
visited[node] = 1
for neighbor in graph[node]:
if neighbor != parent:
find_cycle(neighbor, node)
if node in cycle_nodes:
return
if visited[node] == 2:
visited[parent] = 2
cycle_nodes.add(node)
return
graph = [[] for _ in range(len(edges)+1)]
for u, v in edges:
graph[v].append(u)
graph[u].append(v)
cycle_nodes, visited = set(), [0] * (len(edges)+1)
find_cycle(1, 0)
for u, v in reversed(edges):
if u in cycle_nodes and v in cycle_nodes:
return [u, v]
```
| 10 | 1 |
['Depth-First Search', 'Topological Sort', 'Python3']
| 1 |
redundant-connection
|
⭐ JS | Simple & Explained | Union Find
|
js-simple-explained-union-find-by-shinch-tnew
|
684. Redundant Connection \uD83D\uDE80\n\n### Solution Developed In:\n\n\n## The Question\nFor this article we will be covering Leetcode\'s \'684. Redundant Con
|
shinchliffe
|
NORMAL
|
2022-07-14T14:57:33.075624+00:00
|
2022-07-14T14:57:33.075670+00:00
| 505 | false |
# 684. Redundant Connection \uD83D\uDE80\n***\n### Solution Developed In:\n\n\n## The Question\nFor this article we will be covering Leetcode\'s \'[684. Redundant Connection](https://leetcode.com/problems/redundant-connection/)\' question. Knowing how to solve this problem with UnionFind will be vital to solving [1584. Min Cost to Connect All Points](https://leetcode.com/problems/min-cost-to-connect-all-points/)\' with [Kruskal\'s Algorithm](https://leetcode.com/problems/kruskal-algorithm/).\n\nQuestion:\n\n> In this problem, a tree is an **undirected graph** that is connected and has no cycles.\n> You are given a graph that started as a tree with n nodes labeled from `1` to `n`, with one additional edge added. The added edge has two **different** vertices chosen from `1` to `n`, and was not an edge that already existed. The graph is represented as an array edges of length n where edges`[i] = [ai, bi]` indicates that there is an `edge` between nodes ai and bi in the graph.\n> Return an edge that can be removed so that the resulting graph is a tree of `n` nodes. If there are multiple answers, return the answer that occurs last in the input.\n\n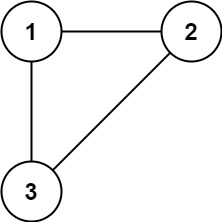\n\n>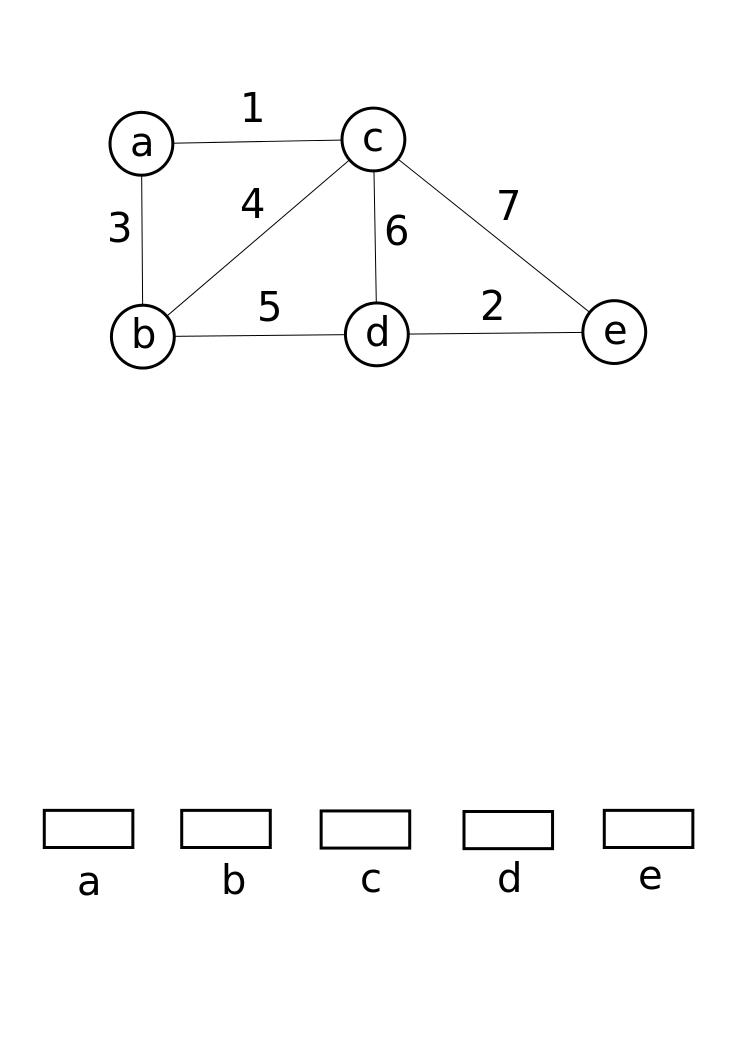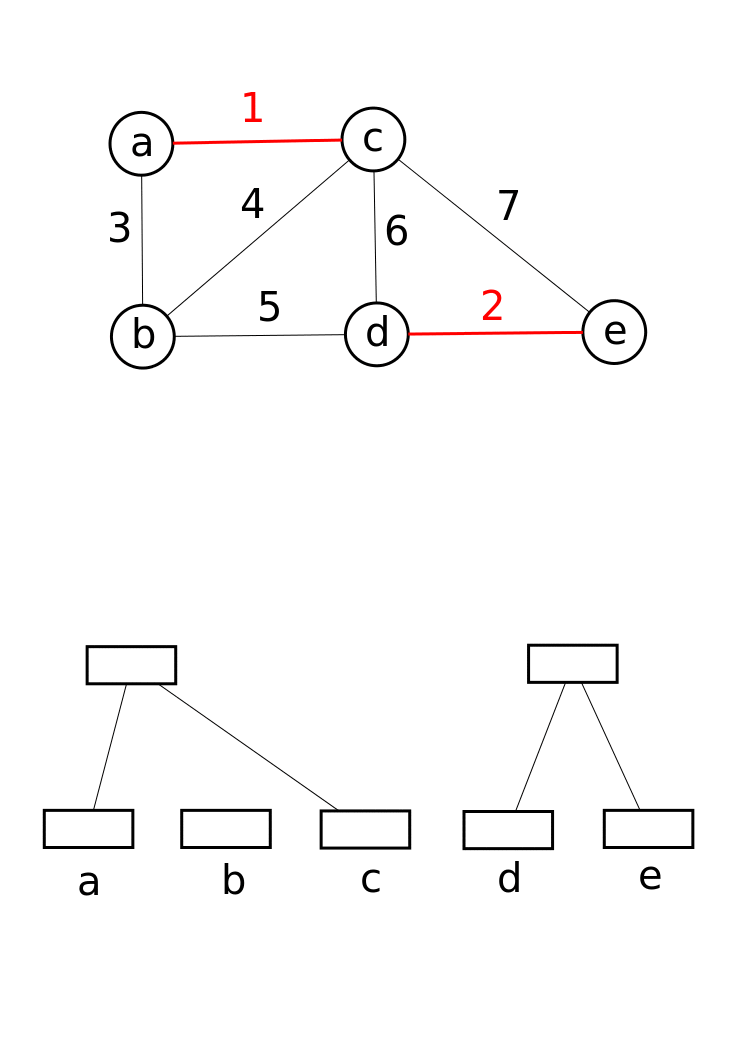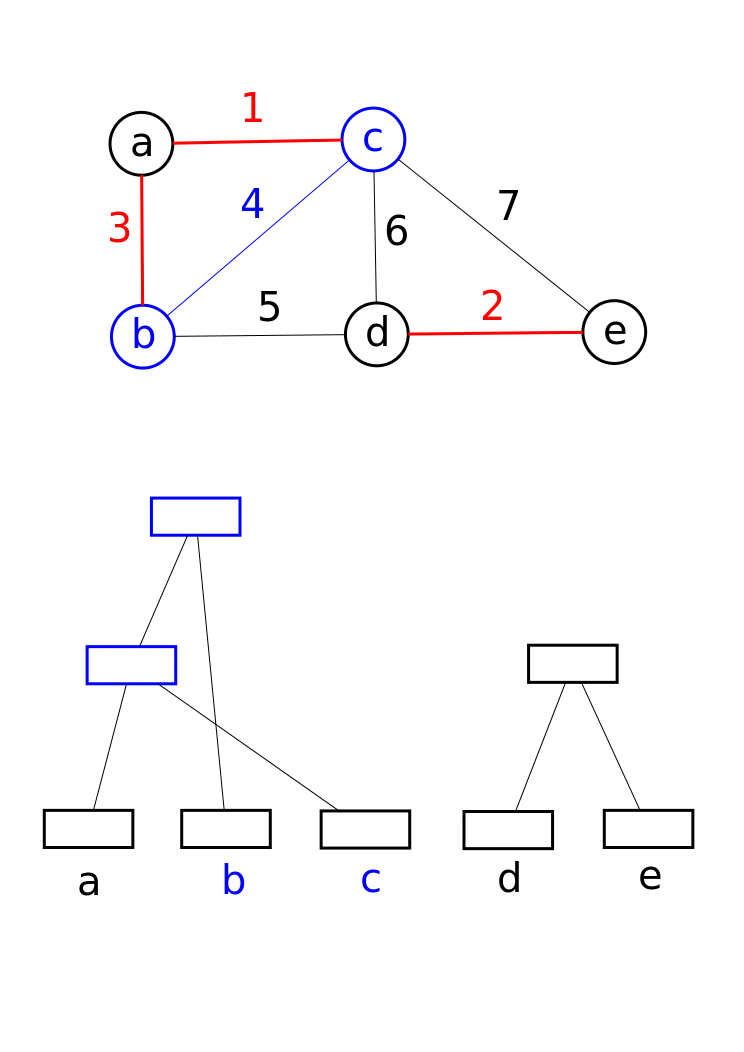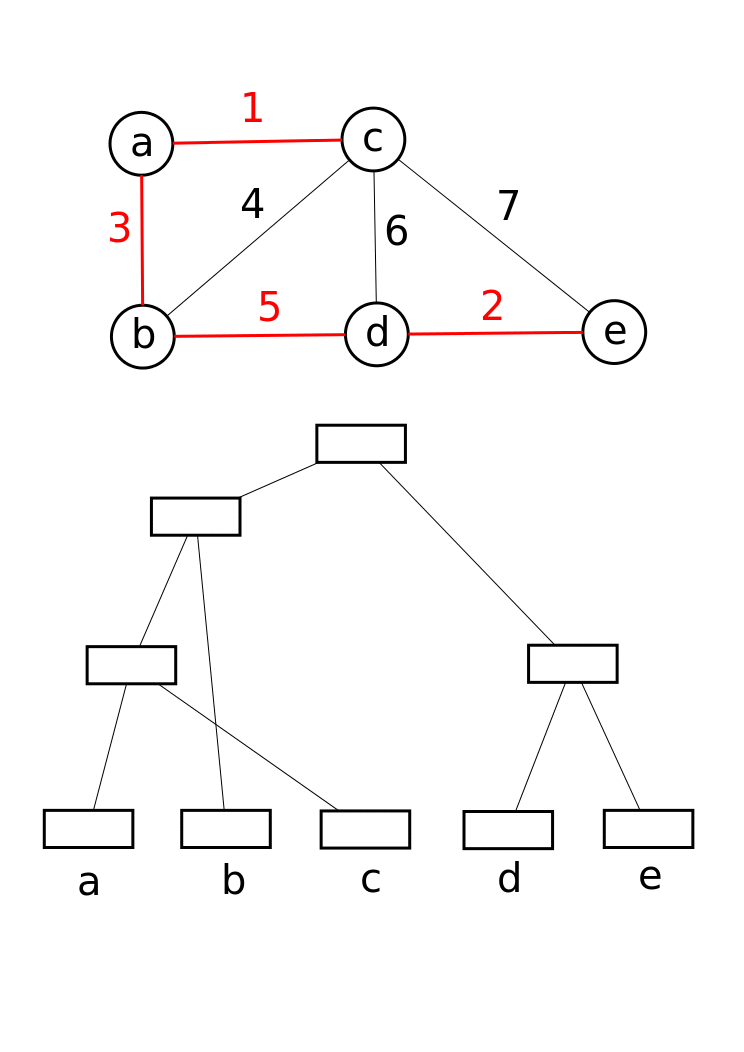\n\n```\nInput: edges = [[1,2],[1,3],[2,3]]\nOutput: [2,3]\n```\n\n## Explaining The Question\nThis Question is rated **Medium**. Which is for the most part accurate. This question is kinda of a trick question, if you\'re like me you\'ll probably think \'Greedy Depth First Search on all nodes until we find out last loop\'. Which works, but is not the best way to solve this problem.\n\nWhat\'s expected of you is to use [Union Find](https://en.wikipedia.org/wiki/Disjoint-set_data_structure) to solve this problem. Specifically, [Union Find by Rank](https://en.wikipedia.org/wiki/Disjoint-set_data_structure#Union-find_by_rank) is expected.\n\nThis question is only **Medium** if you know how to use [Union Find](https://en.wikipedia.org/wiki/Disjoint-set_data_structure) with [Union Find by Rank](https://en.wikipedia.org/wiki/Disjoint-set_data_structure#Union-find_by_rank).\n\nWe have been given a list of Nodes and Edges ([Node -> Edge]). Which forms a [Graph](https://en.wikipedia.org/wiki/Graph_(abstract)), we need to find the [Redundant Edge](https://en.wikipedia.org/wiki/Redundant_edge). Which is the last connection between two nodes that forms a [Cycle](https://en.wikipedia.org/wiki/Cycle_(graph_theory)).\n\n***\n\n## Recommended Knowledge\n1. [Graph Theory](https://en.wikipedia.org/wiki/Graph_theory#:~:text=In%20mathematics%2C%20graph%20theory%20is,also%20called%20links%20or%20lines)\n2. [Union Find](https://en.wikipedia.org/wiki/Disjoint-set_data_structure)\n3. [Union Find by Rank](https://en.wikipedia.org/wiki/Disjoint-set_data_structure#Union-find_by_rank)\n4. [Path Compression](https://en.wikipedia.org/wiki/Disjoint-set_data_structure#Path_compression)\n5. [Amortized Analysis](https://en.wikipedia.org/wiki/Amortized_analysis)\n\n## What do we know?\n1. We have a 2D Array of `\'1\'`s and `\'0\'`s.\n2. It\'s a *M x N* Matrix\n3. Neighbors are left, right, top, and bottom.\n4. We need to find the max area of an island. Meaning, the number of cells in the island.\n\n## How we\'re going to do it:\n\nWe\'re going to find this [Redundant Edge](https://en.wikipedia.org/wiki/Redundant_edge) by using a [Union Find](https://en.wikipedia.org/wiki/Disjoint-set_data_structure) data structure. We\'ll be creating a Tree from the provided Node & Edge array. The reasons this will work is because within a tree, there are no cycles. So when we\'re creating the tree, we\'ll be checking if the 2 given nodes have the same parent. What that mean\'s their was an attempt to create a connection in what was once a perfect tree. \n\nOnce we detect that attempted connection, we can identify the Node Edge that would\'ve created a redundant connection. \n\n1. We\'re going to firstly define our Ranks and Parents. A rank is the number of nodes that tree has. A parent is the node that is the parent of the current node. With this information, we know the size and structure of the tree. \n2. We\'re going to define our `Find()` function. When we\'re Unioning two nodes, we need to find the parents of the given node. We implement this function by asking the parents array, \'Who this nodes parent?\' and we keep asking this question until the parent of a node is itself (Meaning, it\'s the root). We also implement a [Path Compression](https://en.wikipedia.org/wiki/Disjoint-set_data_structure#Path_compression) technique to speed up this process to achieve an Amortized O(1) time complexity.\n3. We\'re going to define our `Union()` function. The purpose of this function is to merge 2 trees together. Firstly, we need to `Find()` the root nodes of the 2 supplied nodes. We check if they\'re of the same parent, meaning it\'s a redundant connection and we need to stop execution. If they\'re not, we need to merge the 2 trees. We do this by setting the parent of the 2 nodes to the same parent. As well as updating their ranks\n4. Now we have all of our functions for a UnionFind structure, we will now attempt to Union all the supplied nodes. If at any point our Union connection returns false (Found a redundant connection), we can stop execution and return that edge.\n\n## Big O Notation:\n* Time Complexity: *O(**V * E**)* / *O(**n**)* | Where ***n*** is the number of nodes in the Graph. As we\'re going to visit every node in the matrix. Where ***V*** is the number of nodes in the graph and ***E*** is the number of edges in the graph. As in the worst case, the last node will attempt a redundant connection. \n\n* Space Complexity: *O(**h**)* | Where ***h*** is the largest number of nodes within our graph. As we\'re going to create a tree from the graph. Which will be the same as the number of nodes in the graph.\n\nWe did although implemented a [Path Compression](https://en.wikipedia.org/wiki/Disjoint-set_data_structure#Path_compression) and [Union by Rank](https://en.wikipedia.org/wiki/Disjoint-set_data_structure#Union-find_by_rank) technique to achieve a Amortized O(1) time complexity on our Union and Find functions. But as we will still need to iterate through the Nodes, we will still have a O(**n**) time complexity.\n## Leetcode Results:\n\nSee Submission Link: \n\n* Runtime: 78 ms, faster than ***85.83%*** of JavaScript online submissions for Max Area of Island\n* Memory Usage: 45.1 MB, less than ***67.24%*** of JavaScript online submissions for Max Area of Island.\n\n[](https://leetcode.com/submissions/detail/716824590/)\n\n\n***\n\n# The Solution\n```\nclass UnionFind {\n \n /**\n\t * @summary We\'re going to generate a UnionFind data structure.\n\t * Union Find is a special data-structure that can be used to form\n\t * a disjoint set (A tree). For this solution, we\'re going to use\n\t * the Rank variant of Union Find. All this mean\'s is that we keep\n\t * track the number of nodes a given tree has. It allows us to merge\n\t * trees that will require the minimal amount of work (Increases\n\t * the Amortized Complexity).\n\t *\n\t * @param {Array} edges [[node, edge_to_connect_to], [node, edge_to_connect_to]]\n\t */\n constructor(edges) {\n\n // Create a array of Ranks (Index -> Tree Size)\n // Looks Like: [1,1,1,1]\n // (Each node is a tree of size 1 by default)\n this.ranks = new Array(edges.length).fill(1);\n\n // Create a array of Parents (Index -> Index of Parent)\n // If we keep following the parent, we\'ll eventually find\n // the root of the tree.\n // Looks Like: [0,1,2,3]\n // (Each node\'s parent is itself by default, as it\'s the root of it\'s tree)\n this.parents = Array.from(Array(edges.length).keys());\n }\n\n /**\n\t * @summary Find the root of a given node, we do this by asking the parents\n\t * list \'Who\'s the parent of this node\'s index?\', we repeat this until the parent\n\t * of the node is itself. Meaning, we have reached the root of the tree.\n\t * We have also utilized a concept called \'Path Compression\'. This mean\'s\n\t * instead of going up the tree one node at a time, we go up the tree 2 nodes\n\t * at a time. Tree height should be very small due to the \'rank\' concept.\n\t *\n\t * Time Complexity: Amortized O(1) (Best, tree height is small)\n\t * : O(log n) (Average)\n\t * : O(n) (Worst, linked list tree)\n\t *\n\t * Space Complexity: O(1) (Finding allocated no space)\n\t *\n\t * Technically, we rate an algorithm by it\'s worst case. Thus this is\n\t * O(n) in time. But it\'s such a rare case that we don\'t care, so it\'s better\n\t * to use the amortized case of O(1)\n\t *\n\t * @param {Number} index (Index of node in [Parents, Ranks, Edges])\n\t * @return {Number} (Index of parent, the root node of the tree)\n\t */\n find(index) {\n // Get parent of node\n let parent = this.parents[index];\n\n // Keep getting parents until we reach the root of the tree\n while (parent != this.parents[parent]) {\n // Path Compression\n parent = this.parents[this.parents[parent]];\n }\n return parent;\n }\n\n /**\n\t * @summary Merge two trees by connecting the root of the tree by rank.\n\t * What this mean\'s, is we\'re going to find the parents of both of the supplied\n\t * nodes, and then figure out which tree is larger. We then connect the root of\n\t * the smaller tree to the root of the larger tree.\n\t * Why? Because, during the Find() operation, we want to reduce the number of\n\t * steps required to get to the root of a given tree. By merging smaller into larger\n\t * we won\'t need as many steps to find the root of a given parent.\n\t *\n\t * This is called Union by Rank. Rank meaning, size of a given tree. When you combine\n\t * Path Compression and Union by Rank, you get a amortized O(1) time complexity.\n\t *\n\t * Time and Space Complexity is the same as Find() as we utilise that function.\n\t *\n\t * @param {Number} n1 (Index of node 1)\n\t * @param {Number} n2 (Index of node 2)\n\t * @return {Boolean} (False if nodes are already in the same tree)\n\t */\n union(n1, n2) {\n\n // Find the parents of each node.\n const n1_parent = this.find(n1);\n const n2_parent = this.find(n2);\n\n // Are the nodes already in the same tree?\n // REDUNDANT CONNECTION!!!\n if (n1_parent === n2_parent) return false;\n\n // Union by rank, merge smallest into largest.\n if (this.ranks[n1_parent] > this.ranks[n2_parent]) {\n // Update parent and ranks\n this.parents[n2_parent] = n1_parent;\n this.ranks [n2_parent] += this.ranks[n1_parent];\n } else {\n // Merge n1 into n2\n this.parents[n1_parent] = n2_parent;\n this.ranks [n1_parent] += this.ranks[n2_parent];\n }\n\n // Successfully merged. Ranks and parents updated\n return true;\n }\n}\n\n/**\n * @param {number[][]} edges\n * @return {number[]}\n */\nvar findRedundantConnection = function (edges) {\n // The basic premise of this solution is\n // to use UnionFind to find the redundant edge.\n // UnionFind will attempt to create a tree by merging nodes\n // together. If at any point, two nodes are already connected,\n // meaning, they\'re in the same tree, we have found the redundant connection.\n\n // We\'re going to initialize a Union Find data structure\n // so we can attempt to build our tree.\n const Union_Find = new UnionFind(edges);\n\n // Let\'s build our tree.\n // Union each node and their edges together.\n // If at any point, a node and edge are already in the same Tree.\n // END loop, we found the redundant connection.\n for (const [node, edge] of edges) {\n if (!Union_Find.union(node, edge)) return [node, edge];\n }\n};\n\n```
| 10 | 0 |
['Depth-First Search', 'Union Find', 'JavaScript']
| 0 |
redundant-connection
|
Java Simple and easy to understand solution, 0 ms, faster than 100.00% , clean code with comments
|
java-simple-and-easy-to-understand-solut-iah3
|
PLEASE UPVOTE IF YOU LIKE THIS SOLUTION\n\n\n\nclass Solution {\n public int[] findRedundantConnection(int[][] edges) {\n \n int n = edges.leng
|
satyaDcoder
|
NORMAL
|
2021-04-03T07:51:24.287378+00:00
|
2021-04-03T07:51:24.287409+00:00
| 2,255 | false |
**PLEASE UPVOTE IF YOU LIKE THIS SOLUTION**\n\n\n```\nclass Solution {\n public int[] findRedundantConnection(int[][] edges) {\n \n int n = edges.length;\n \n DSU dsu = new DSU(n);\n \n for(int[] edge : edges){\n int nodeX = edge[0] - 1;\n int nodeY = edge[1] - 1;\n \n \n int parentX = dsu.find(nodeX);\n int parentY = dsu.find(nodeY);\n \n if(parentX == parentY){\n //same parent means, they are in the same set,\n //same set means, all nodde already added, we can remove this one\n return edge;\n }\n \n //merge this two different set\n dsu.unionSet(nodeX, nodeY);\n }\n \n return new int[0];\n }\n}\n\n//Disjoint Set Union\nclass DSU {\n int[] parent;\n \n public DSU(int size){\n parent = new int[size];\n \n //intially every element are in their set,\n //and respresentative of their set\n for(int i = 0; i < size; i++){\n parent[i] = i;\n }\n }\n \n //find set of x, (Representative of set)\n public int find(int x){\n if(x == parent[x])\n return x;\n \n parent[x] = find(parent[x]);\n \n return parent[x];\n }\n \n public void unionSet(int x, int y){\n //set X\n int parentX = find(x);\n \n //set Y\n int parentY = find(y);\n \n //now merge the set X with set Y\n //make parent of parent of X, with parent of y\n parent[parentX] = parentY;\n \n }\n}\n```
| 10 | 0 |
['Union Find', 'Java']
| 2 |
redundant-connection
|
DFS approach with Cycle detection - intuitive approach
|
dfs-approach-with-cycle-detection-intuit-ne5e
|
Basically am adding edges one by one in graph and as soon as adding any edge creates the cycle, I will return the result.\n\n\n public int[] findRedundantCon
|
neham
|
NORMAL
|
2020-11-24T22:16:31.520448+00:00
|
2020-11-24T22:17:49.008217+00:00
| 960 | false |
Basically am adding edges one by one in graph and as soon as adding any edge creates the cycle, I will return the result.\n\n\n public int[] findRedundantConnection(int[][] edges) {\n Map<Integer, Set<Integer>> gp = new HashMap<>(); \n\t\tSet<Integer> visited = new HashSet<>();\n for (int[] edge: edges) {\n gp.putIfAbsent(edge[0], new HashSet<>());\n gp.putIfAbsent(edge[1], new HashSet<>());\n gp.get(edge[0]).add(edge[1]);\n gp.get(edge[1]).add(edge[0]);\n \n if (isCycle(gp, edge[0], visited, -1)) {\n return new int[] {edge[0], edge[1]};\n }\n\t\t\tvisited.clear();\n }\n \n return new int[] {}; //shouldnt happen\n }\n \n private boolean isCycle(Map<Integer, Set<Integer>> gp, int node, Set<Integer> visited, int pre) {\n if (visited.contains(node)) {\n return true;\n }\n visited.add(node);\n if (gp.get(node) != null) {\n for (int child: gp.get(node)) {\n if (child == pre) {\n continue;\n }\n if (isCycle(gp, child, visited, node)) {\n return true;\n } \n } \n }\n return false;\n }
| 10 | 0 |
[]
| 1 |
redundant-connection
|
Simple Implementation in python using union find
|
simple-implementation-in-python-using-un-0zl6
|
Hi guys. hope you are safe and healthy !\nThis is a simple code \nHere i have found something interesting\nWhen i initialise my self.parent = [0] len it is givi
|
2699amruthap
|
NORMAL
|
2020-08-25T18:04:23.935870+00:00
|
2020-08-25T18:04:23.935902+00:00
| 1,539 | false |
Hi guys. hope you are safe and healthy !\nThis is a simple code \nHere i have found something interesting\nWhen i initialise my self.parent = [0]* len it is giving me 40% while when i do this [-1]* len then i am getting 98% in time\n[-1] idea given by @arnav3\nHope this will help\n\n```\n def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:\n # using union find\n \n self.parent = [-1]*(len(edges)+1) # -1 is giving me 98% time \n\t\t# self.parent = [0]*(len(edges)+1) # 0 is giving me 40% time \t\n \n def find(x):\n while self.parent[x] > 0:\n x = self.parent[x]\n return x \n \n def union(x,y):\n root_x = find(x)\n root_y = find(y)\n \n if root_x == root_y:\n return False\n else:\n self.parent[root_x] = root_y\n return True\n \n for u,v in edges:\n if not union(u,v):\n return [u,v]\n \n```
| 10 | 1 |
['Union Find', 'Python', 'Python3']
| 1 |
redundant-connection
|
[Python] Two DFS approaches with detailed explanation
|
python-two-dfs-approaches-with-detailed-3zyqp
|
Approach -1- Brute Force [34/39]\nO(E) * O(E+V)\n\nMy Approach\n- Iterate over the edges of the graph and remove an edge one at a time\n- for each edge that is
|
Hieroglyphs
|
NORMAL
|
2019-08-08T13:31:14.124817+00:00
|
2020-02-24T01:15:15.719092+00:00
| 1,513 | false |
**Approach -1- Brute Force [34/39]**\n**O(E) * O(E+V)**\n\n**My Approach**\n- Iterate over the edges of the graph and remove an edge one at a time\n- for each edge that is removed:\n - check if the resulting graph is a tree\n - (problem magically transfomred into (isGraphValidTree)\n - we know 3 properties of a tree:\n 1 - Acyclic\n 2 - connected\n 3 - nodes = edges + 1\n \n\t- Howeverbecause we know an edge was inserted between two different, already-exiting nodes,\n\t\twe know for fact that porperties (2 and 3) are true which only leaves property 1 (detec a cycle)\n\t\tThe problem has been simplified even further to (detec a cycle in an undirected graph)\n\t\t\t\t\n**Code**\n\n```\ndef findRedundantConnection(self, edges: List[List[int]]) -> List[int]:\n \n # helper - hasCycle - #\n def hasCycle(node):\n \'\'\'DFS - detec cycle in undirected graph using visited set\'\'\'\n stack = [node]\n visited = set()\n while stack:\n node = stack.pop()\n for n in treeDict[node]:\n if n not in visited:\n stack.append(n)\n visited.add(n)\n treeDict[n].remove(node)\n else: # n is in visit -> cycel\n return True\n del treeDict[node]\n return False\n \n # main function #\n # 1 - convert edges to adjlist dict:\n from collections import defaultdict\n d = defaultdict(list)\n for edge in edges:\n k, v = edge\n d[k].append(v)\n d[v].append(k) # undirected\n \n for i in reversed(range(len(edges))): # reversed becuz we are told to give priority to edges near the end\n # copies:\n candidateTree = copy.deepcopy(edges)\n treeDict = copy.deepcopy(d)\n # mutate edges (edge list)\n candidateTree.pop(i)\n # mutate (adj list) dict - remove symmetric edge:\n treeDict[edges[i][0]].remove(edges[i][1])\n treeDict[edges[i][1]].remove(edges[i][0])\n \n # now check if candidateTree is acyclic\n startNode = candidateTree[0][0] # random choice\n if not hasCycle(startNode):\n print(edges[i])\n return edges[i]\n return [0]\n \n \n```\n\n**THE REASON WHY MY APPROACH WON\'T GENERALIZE WELL**\n- Consider the following test-case:\n\n-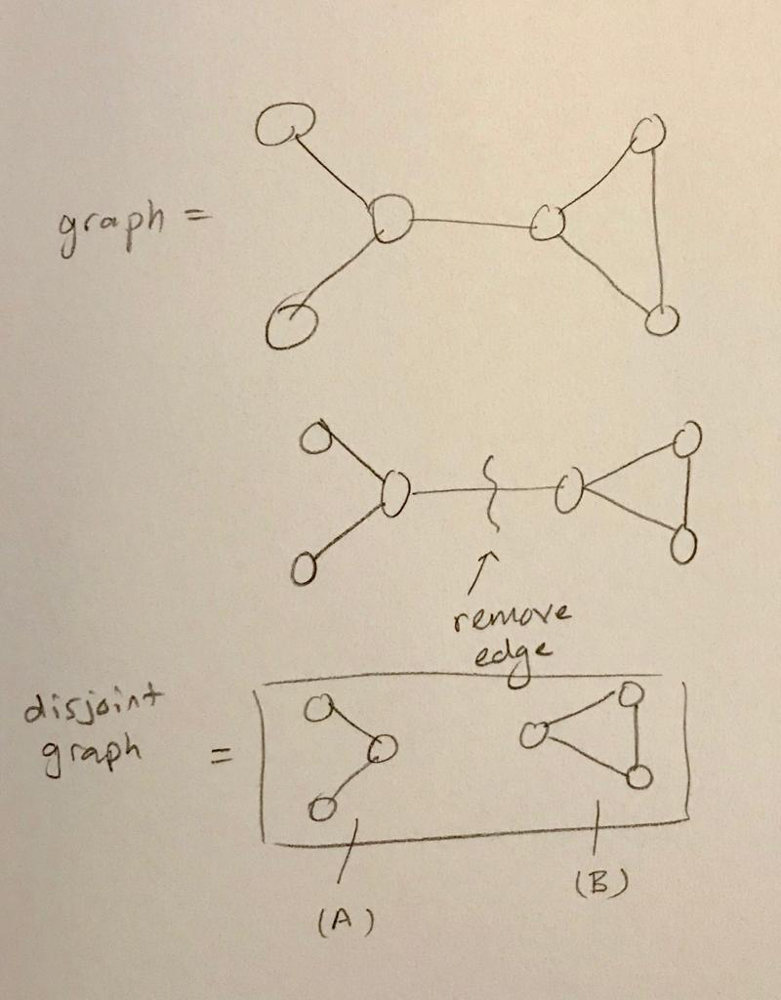\n- By removing the intermediate edge shown in the sketch, we get a disjoint graph. This can be specially problematic if one part (connected component)(for example part A) of the graph is a tree while the other part (part B) is a graph. \n- So even if you iterate over the nodes, you might find yourself applying DFS on part(A) which will obviosuly return (no cycle found) and thus the algorithm will return the removed edge as the desired edge while in fact it didn\'t successfuly convert the input graph into a tree (but instead converted only a portion of it to a tree).\n\n\n\n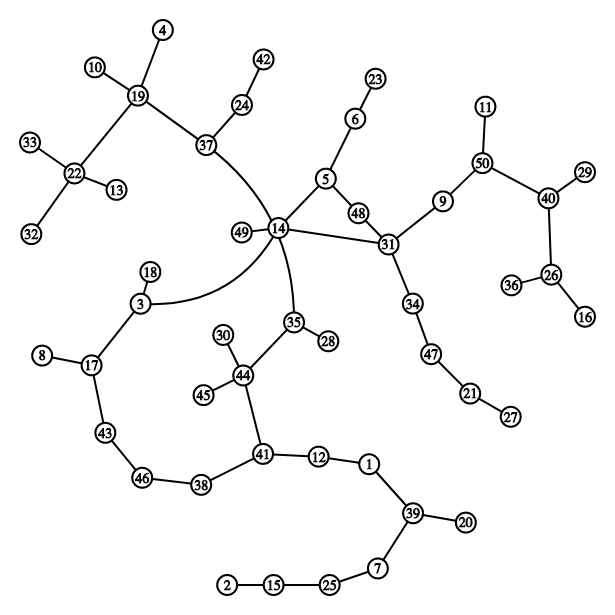\n\n\n**Approach -2- Intutive**\n**time: O(E) * O(E+V)**\n\n- iterate over edges -> add one edge at a time to graph\n- for the edge at hand, check if:\n\t\t1- the two nodes represented by the edge already exit in the graph\n\t\t2- the above mentioned nodes are already connected undirectly (via a longer route)\n\t- if 1 & 2 -> then edge at hand (the one you\'re about to insert into the graph) is \n\tredundant. Mark it as such and proceed to add it to graph\n\n\n```\n# - helper - #\ndef dfs(k, v):\n\tstack = [k] # start at k and see if you can reach v\n\tvisited = set()\n\twhile stack:\n\t\tnode = stack.pop()\n\t\tif node == v:\n\t\t\treturn True\n\t\tvisited.add(node)\n\n\t\tfor nei in d[node]:\n\t\t\tif nei not in visited:\n\t\t\t\tstack.append(nei)\n\treturn False\n\n\n# - main logic - #\nif not edges:\n\treturn []\n\nfrom collections import defaultdict\nd = defaultdict(list)\n\nredundant = []\nfor k, v in edges:\n\t# 1 - check if nodes exist already\n\tif k in d and v in d:\n\t\t# 2 - check if k and v are connected:\n\t\tif dfs(k, v):\n\t\t\tredundant.append(k)\n\t\t\tredundant.append(v)\n\n\n\td[k].append(v)\n\td[v].append(k) # undirected\n\nreturn redundant\n```\n
| 10 | 0 |
['Depth-First Search', 'Python']
| 1 |
redundant-connection
|
Using Bridges and Articulation Points | Explained
|
using-bridges-and-articulation-points-ex-i28z
|
While it\'s a lesser known topic than Union Find and DFS, this can actually be modelled perfectly by Tarjan\'s Bridge finding algorithm.\nWe capture low and dis
|
thaicurry
|
NORMAL
|
2020-07-12T10:53:30.477405+00:00
|
2020-07-12T10:58:27.438172+00:00
| 1,557 | false |
While it\'s a lesser known topic than Union Find and DFS, this can actually be modelled perfectly by Tarjan\'s Bridge finding algorithm.\nWe capture low and disc for each node in the traversal, and then we check if any of them are a bridge.\n\nIn this question, we need to find the last edge which is *not* a bridge. I had to add an awkward bit of swap logic since I\'m checking for bridges after the fact, but otherwise this is a classic implementation of the Bridge finding algorithm.\n\n```\nclass Solution {\n \n int time = 1;\n public int[] findRedundantConnection(int[][] edges) {\n\n int n = edges.length;\n int[] low = new int[n + 1];\n int[] disc = new int[n + 1];\n \n List<List<Integer>> adjList = buildGraph(edges);\n dfs(adjList, 1, low, disc, -1);\n \n for (int i = n - 1; i >= 0; i--) {\n int[] edge = edges[i];\n int u = edge[0];\n int v = edge[1];\n \n // Swap since u must always be the earlier node during our check\n if (disc[u] > disc[v]) {\n int temp = u;\n u = v;\n v = temp;\n }\n \n if (low[v] > disc[u]){\n // We have bridge\n continue;\n } else {\n return edge;\n }\n }\n \n return null;\n }\n \n private List<List<Integer>> buildGraph(int[][] edges) {\n int n = edges.length;\n List<List<Integer>> adjList = new ArrayList<>();\n for (int i = 0; i <= n; i++) {\n adjList.add(new ArrayList<>());\n }\n \n for (int[] edge: edges) {\n int src = edge[0];\n int dst = edge[1];\n adjList.get(src).add(dst);\n adjList.get(dst).add(src);\n }\n \n return adjList;\n }\n \n private void dfs(List<List<Integer>> adjList, int u, int[] low, int[] disc, int parent) {\n if (disc[u] != 0) {\n return;\n }\n \n disc[u] = time;\n low[u] = time;\n time++;\n \n for (int v: adjList.get(u)) {\n if (v == parent) {\n continue;\n }\n if (disc[v] == 0) {\n dfs(adjList, v, low, disc, u);\n low[u] = Math.min(low[u], low[v]);\n } else {\n low[u] = Math.min(low[u], disc[v]);\n }\n }\n }\n}\n```\n
| 9 | 0 |
['Java']
| 0 |
redundant-connection
|
Javascript Union Find Solution
|
javascript-union-find-solution-by-0618-629p
|
js\nvar findRedundantConnection = function(edges) {\n let uf = {};\n for(let edge of edges){\n let u = edge[0];\n let v = edge[1];\n
|
0618
|
NORMAL
|
2019-04-01T17:44:38.962769+00:00
|
2019-04-01T17:44:38.962815+00:00
| 920 | false |
```js\nvar findRedundantConnection = function(edges) {\n let uf = {};\n for(let edge of edges){\n let u = edge[0];\n let v = edge[1];\n if(find(u) === find(v)){\n return edge;\n } else {\n union(u, v);\n }\n }\n \n function union(a, b){\n uf[find(a)] = uf[find(b)];\n }\n \n function find(x){\n if(!uf[x]) uf[x] = x;\n if(uf[x] === x) return x;\n return find(uf[x]);\n }\n};\n```
| 9 | 0 |
['Union Find', 'JavaScript']
| 1 |
redundant-connection
|
Redundant Connection [C++]
|
redundant-connection-c-by-moveeeax-k2gi
|
IntuitionThe problem requires us to find an extra edge in a connected undirected graph that makes it cyclic. This means that all nodes are already connected, an
|
moveeeax
|
NORMAL
|
2025-01-29T08:11:03.691084+00:00
|
2025-01-29T08:11:03.691084+00:00
| 249 | false |
### **Intuition**
The problem requires us to find an extra edge in a connected undirected graph that makes it cyclic. This means that all nodes are already connected, and adding one more edge creates a cycle.
A **Disjoint Set Union (DSU) / Union-Find** structure is well-suited for detecting cycles in an undirected graph. The key observation is:
- If two nodes are already connected (i.e., belong to the same component), then adding an edge between them will form a cycle.
### **Approach**
We use the **Union-Find** data structure with **Path Compression** and **Union by Rank** to efficiently detect cycles in the graph:
1. **Initialize** the parent array where each node is its own parent and the rank array to manage tree depth.
2. **Iterate through the edges** and perform `union` operations:
- If both nodes of an edge are already in the same connected component (i.e., they have the same root in the DSU structure), we have found the redundant edge.
- Otherwise, merge the sets using `union by rank`.
3. **Return the first edge that causes a cycle**.
### **Complexity Analysis**
- **Time Complexity**: \(O(N \alpha(N)) \approx O(N)\)
- Each `find()` and `union()` operation runs in almost **constant time** \(O(\alpha(N))\), where \(\alpha(N)\) is the **inverse Ackermann function**, which grows extremely slowly.
- We iterate over all edges, so the total complexity is close to **O(N)**.
- **Space Complexity**: \(O(N)\)
- We store two arrays (`parent` and `rank`), each of size \(O(N)\).
---
### **Code**
```cpp
class Solution {
public:
vector<int> parent, rank;
int find(int x) {
return parent[x] == x ? x : parent[x] = find(parent[x]);
}
bool unionSet(int x, int y) {
int rootX = find(x), rootY = find(y);
if (rootX == rootY) return false;
if (rank[rootX] > rank[rootY]) swap(rootX, rootY);
parent[rootX] = rootY;
if (rank[rootX] == rank[rootY]) rank[rootY]++;
return true;
}
vector<int> findRedundantConnection(vector<vector<int>>& edges) {
int n = edges.size();
parent.resize(n + 1);
rank.resize(n + 1, 0);
iota(parent.begin(), parent.end(), 0);
for (const auto& edge : edges) {
if (!unionSet(edge[0], edge[1])) {
return edge;
}
}
return {};
}
};
```
### **Why This Works Well**
✅ **Path compression in `find()`** makes lookups faster by flattening the tree.
✅ **Union by rank** keeps the tree shallow, reducing unnecessary merging.
✅ **Iterating over edges once** ensures we return the first redundant edge in **O(N) time**.
🚀 **This is an optimal solution for cycle detection in an undirected graph using DSU!**
| 8 | 0 |
['C++']
| 0 |
redundant-connection
|
DSU || ACKERMAN Concept with Time and Space Complexity Explained ||Beats 100% CPP Users ||
|
dsu-ackerman-concept-with-time-and-space-r0sy
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
Heisenberg_wc
|
NORMAL
|
2025-01-29T01:44:58.494788+00:00
|
2025-01-29T01:44:58.494788+00:00
| 742 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Disjoint_set{
public:
vector<int>parent;
vector<int>rank;
Disjoint_set(int n){
parent.resize(n+1);
rank.resize(n+1);
parent[0]=0;
rank[0]=0;
for(int i=1 ;i <=n;i++){//O(N) Time Complexity
parent[i]=i;
rank[i]=0;
}
}
int find_parent(int n){
if(parent[n]==n){return n;}
return parent[n]=find_parent(parent[n]);//Path Compression to reduce further call s
}
void union_(int u, int v){
int a=find_parent(u);
int b=find_parent(v);
if(rank[a]<rank[b]){
parent[a]=b;
}
else if(rank[b]<rank[a]){
parent[b]=a;
}
else{
parent[a]=b;
rank[b]++;
}
}
};
class Solution {
public:
vector<int> findRedundantConnection(vector<vector<int>>& edges) {
int n=edges.size();
Disjoint_set ds(n);//Create the Disjoint Set data structure
for(int i=0;i<n;i++){
int u=ds.find_parent(edges[i][0]);// Finding the parent of each node or vertices
int v=ds.find_parent(edges[i][1]);
if(u!=v){// if bouth doesnot have same parent , means are not connected yet
ds.union_(u,v);
}
else{return {edges[i][0],edges[i][1]};// it means they are connected beforehand and this the edge is an extra edge. // And thus can conclude this two verties are our answer
}
}
return {};
//Overall Time Complexity :O(αlogn) : α: Ackermann Constant and is close to Linearity
//Space Complexity :O(N)+O(N) :: One for parent array and the other for maintaining the rank array
}
};
```
| 8 | 0 |
['Union Find', 'Graph', 'C++']
| 0 |
redundant-connection
|
🚀🚀684. Redundant Connection🔥🔥|| ✅Efficient Solution by Kanishka✅|| 🔥🔥Beats 75% in Java🚀🚀
|
684-redundant-connection-efficient-solut-80lr
|
🧠IntuitionWe need to find an edge that, when removed, allows all nodes to be connected without any cycles. This means we need to detect a cycle in the graph.🔍 A
|
kanishka21535
|
NORMAL
|
2025-01-29T00:20:05.956960+00:00
|
2025-01-29T00:20:05.956960+00:00
| 1,759 | false |
# 🧠Intuition
We need to find an edge that, when removed, allows all nodes to be connected without any cycles. This means we need to detect a cycle in the graph.
# 🔍 Approach
We'll use the Union-Find data structure to help detect cycles. As we add each edge, we'll use the Union-Find operations to check if adding the edge would form a cycle. If it does, then that's the redundant connection.
# ⏳Complexity
- Time complexity:
$$O(E \cdot \alpha(V))$$, where $$E$$ is the number of edges and $$\alpha$$ is the inverse Ackermann function. This is almost constant time.
- Space complexity:
$$O(V)$$, where $$V$$ is the number of nodes.
# 📜Code
```java []
class Solution {
public int[] findRedundantConnection(int[][] edges) {
UnionFind uf = new UnionFind(edges.length);
for (int[] edge : edges) {
int first = uf.find(edge[0] - 1);
int second = uf.find(edge[1] - 1);
if (first == second) {
return new int[] {edge[0], edge[1]};
} else {
uf.union(first, second);
}
}
return null;
}
static class UnionFind {
private final int[] parent;
private final int[] rank;
public UnionFind(int size) {
parent = new int[size];
rank = new int[size];
for (int i = 0; i < size; i++) {
parent[i] = i;
rank[i] = 1;
}
}
public int find(int x) {
if (parent[x] != x) {
parent[x] = find(parent[x]);
}
return parent[x];
}
public void union(int x, int y) {
int rootX = find(x);
int rootY = find(y);
if (rootX != rootY) {
if (rank[rootX] > rank[rootY]) {
parent[rootY] = rootX;
} else if (rank[rootX] < rank[rootY]) {
parent[rootX] = rootY;
} else {
parent[rootY] = rootX;
rank[rootX]++;
}
}
}
}
}
```
##### I hope this helps! Feel free to reach out if you need more assistance. Happy coding! 🚀✨
| 8 | 1 |
['Java']
| 1 |
redundant-connection
|
C++ solution using dfs
|
c-solution-using-dfs-by-server-monk-17-edc4
|
\nclass Solution {\n bool dfs(int node, int parent, vector<vector<int>>& adj, vector<bool>& vis) {\n vis[node] = true;\n for(auto it : adj[node
|
Server-monk-17
|
NORMAL
|
2022-01-27T04:22:19.419177+00:00
|
2022-01-27T04:22:19.419222+00:00
| 1,052 | false |
```\nclass Solution {\n bool dfs(int node, int parent, vector<vector<int>>& adj, vector<bool>& vis) {\n vis[node] = true;\n for(auto it : adj[node]) {\n if(!vis[it]){\n if(dfs(it, node, adj, vis)) return true;\n }else if(it!=parent) return true;\n }\n return false;\n }\npublic:\n vector<int> findRedundantConnection(vector<vector<int>>& edge) {\n int n = edge.size();\n vector<vector<int>> adj(n+1);\n vector<bool> vis(n+1, 0); \n for(auto i : edge) {\n fill(begin(vis), end(vis), 0);\n adj[i[0]].push_back(i[1]);\n adj[i[1]].push_back(i[0]);\n if(dfs(i[0], -1, adj, vis)) return i;\n }\n return {};\n }\n\n};\n```
| 8 | 0 |
['Depth-First Search', 'C']
| 1 |
redundant-connection
|
100% beats ... Simple solution ... cycle Detection ... happy coding 🌞
|
100-beats-simple-solution-cycle-detectio-ujhn
|
Intuitionwe are required to make the graph as tree, therefore we need to detect the cycle.ApproachUsing DSU we can easily find the node which contribute to the
|
sourav12345singhpraval
|
NORMAL
|
2025-01-29T01:26:46.948044+00:00
|
2025-01-29T01:26:46.948044+00:00
| 1,307 | false |
# Intuition
we are required to make the graph as tree, therefore we need to detect the cycle.
# Approach
Using DSU we can easily find the node which contribute to the cycle detection i.e. if in the union function we get the parent of different nodes equal that means, they form a cycle.
# Complexity
- Time complexity:
O(n)
- Space complexity:
O(n)
# Code
```cpp []
class Solution {
public:
int find(vector<int> &parent,int x){
if(parent[x]==x){
return x;
}
return parent[x]=find(parent,parent[x]);
}
bool Union(vector<int>&parent,vector<int>&size,int a,int b){
int pa=find(parent,a);
int pb=find(parent,b);
if(pa==pb){
return true;
}
if(size[pa]>=size[pb]){
size[pa]+=size[pb];
parent[pb]=pa;
}
else{
size[pb]+=size[pa];
parent[pa]=pb;
}
return false;
}
vector<int> findRedundantConnection(vector<vector<int>>& edges) {
int n=edges.size();
vector<int> parent(n+1);
vector<int> size(n+1,1);
for(int i=0;i<=n;i++){
parent[i]=i;
}
for(int i=0;i<n;i++){
if(Union(parent,size,edges[i][0],edges[i][1])){
return {edges[i][0],edges[i][1]};
}
}
return {};
}
};
```
| 7 | 1 |
['Union Find', 'Graph', 'C++']
| 1 |
redundant-connection
|
💡 | O(n) | C++ 0ms Beats 100.00% | Disjoint Set Union (DSU) 🧠
|
on-c-0ms-beats-10000-disjoint-set-union-kdqhp
|
Problem Overview 🎯In this problem, we are given a graph that started as a tree with n nodes labeled from 1 to n, with one additional edge added. The task is to
|
user4612MW
|
NORMAL
|
2025-01-29T01:15:30.338788+00:00
|
2025-01-29T01:31:45.761210+00:00
| 285 | false |
---
### **Problem Overview** 🎯
In this problem, we are given a graph that started as a tree with $$n$$ nodes labeled from $$1$$ to $$n$$, with one additional edge added. The task is to find and return the redundant edge that, when removed, will restore the graph to a tree structure.
---
### **Intuition** 🧩
A tree is an acyclic connected graph. Adding an extra edge to a tree creates exactly one cycle. To identify this redundant edge, we can utilize the **Union-Find** data structure, which efficiently tracks connected components and detects cycles in an undirected graph.
---
### **Approach** 🎯
1. **Union-Find Initialization**
Initialize the $$parent$$ array where each node is its own parent.
- Initialize the $$rank$$ array to keep track of the tree depth for union by rank optimization.
2. **Processing Edges**
- Iterate through each edge in the graph.
- For each edge $$(u, v)$$, perform the union operation:
- If $$u$$ and $$v$$ are already connected (i.e., they have the same root), then adding this edge would form a cycle, making it the redundant edge.
- If they are not connected, unite them by updating their parent and rank accordingly.
3. **Cycle Detection**
- If a cycle is detected during the union operation, return the current edge as the redundant connection.
---
### **Complexity Analysis** 📊
- **Time Complexity** Each $$find$$ and $$union$$ operation has an amortized time complexity of $$O(\alpha(n))$$, where $$\alpha$$ is the inverse Ackermann function, which grows very slowly and is practically constant for all reasonable n. Therefore, processing all edges results in a time complexity of $$O(n \cdot \alpha(n))$$, which is effectively $$O(n)$$.
- **Space Complexity** The space complexity is $$O(n)$$ due to the storage required for the $$parent$$ and $$rank$$ arrays.
---
### **Code Implementation** 💻
```cpp []
class UnionFind {
vector<int> parent, rank;
public:
UnionFind(int n) : parent(n), rank(n, 0) {
iota(parent.begin(), parent.end(), 0);
}
int find(int x) {
return x == parent[x] ? x : parent[x] = find(parent[x]);
}
bool unite(int u, int v) {
int rootU = find(u), rootV = find(v);
if (rootU == rootV) return false;
if (rank[rootU] < rank[rootV]) swap(rootU, rootV);
parent[rootV] = rootU;
if (rank[rootU] == rank[rootV]) rank[rootU]++;
return true;
}
};
class Solution {
public:
vector<int> findRedundantConnection(vector<vector<int>>& edges) {
UnionFind uf(edges.size() + 1);
for (const auto& edge : edges) {
if (!uf.unite(edge[0], edge[1])) {
return edge;
}
}
return {};
}
};
```
---
> **C++**
> 

---
---
| 7 | 5 |
['C++']
| 4 |
redundant-connection
|
🚀🚀684. Redundant Connection🔥🔥|| ✅Efficient Solution by Dhandapani✅|| 🔥🔥Beats 100% in Java🚀🚀
|
684-redundant-connection-efficient-solut-269h
|
🧠IntuitionWe need to find an edge that, when removed, allows all nodes to be connected without any cycles. This means we need to detect a cycle in the graph.🔍 A
|
Dhandapanimaruthasalam
|
NORMAL
|
2025-01-29T00:19:57.611992+00:00
|
2025-01-29T00:19:57.611992+00:00
| 772 | false |
# 🧠Intuition
We need to find an edge that, when removed, allows all nodes to be connected without any cycles. This means we need to detect a cycle in the graph.
# 🔍 Approach
We'll use the Union-Find data structure to help detect cycles. As we add each edge, we'll use the Union-Find operations to check if adding the edge would form a cycle. If it does, then that's the redundant connection.
# ⏳Complexity
- Time complexity:
$$O(E \cdot \alpha(V))$$, where $$E$$ is the number of edges and $$\alpha$$ is the inverse Ackermann function. This is almost constant time.
- Space complexity:
$$O(V)$$, where $$V$$ is the number of nodes.
# 📜Code
```java []
class Solution {
public int[] findRedundantConnection(int[][] edges) {
UnionFind uf = new UnionFind(edges.length);
for (int[] edge : edges) {
int first = uf.find(edge[0] - 1);
int second = uf.find(edge[1] - 1);
if (first == second) {
return new int[] {edge[0], edge[1]};
} else {
uf.union(first, second);
}
}
return null;
}
static class UnionFind {
private final int[] parent;
private final int[] rank;
public UnionFind(int size) {
parent = new int[size];
rank = new int[size];
for (int i = 0; i < size; i++) {
parent[i] = i;
rank[i] = 1;
}
}
public int find(int x) {
if (parent[x] != x) {
parent[x] = find(parent[x]);
}
return parent[x];
}
public void union(int x, int y) {
int rootX = find(x);
int rootY = find(y);
if (rootX != rootY) {
if (rank[rootX] > rank[rootY]) {
parent[rootY] = rootX;
} else if (rank[rootX] < rank[rootY]) {
parent[rootX] = rootY;
} else {
parent[rootY] = rootX;
rank[rootX]++;
}
}
}
}
}
```
##### I hope this helps! Feel free to reach out if you need more assistance. Happy coding! 🚀✨
| 7 | 0 |
['Java']
| 1 |
redundant-connection
|
Python BFS, Kahn's algorithm and Time Complexity O(N)
|
python-bfs-kahns-algorithm-and-time-comp-m2zi
|
Intuition\n Describe your first thoughts on how to solve this problem. \nUse Kahn\'s algorithm to drop out each node with indegree == 1, and check the first edg
|
ychanc2104
|
NORMAL
|
2022-11-09T04:32:00.803119+00:00
|
2022-11-09T04:33:42.577605+00:00
| 731 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUse Kahn\'s algorithm to drop out each node with indegree == 1, and check the first edge with both indegree == 2.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Build a undirected graph and indegree\n2. Find initial value of queue for dropping out\n3. Do BFS and drop out each neighboring node with indegree == 1\n4. There are a cycle in remaining nodes, and check each edge from the end with \n```\nindegree[a] == 2 and indegree[b] and return [a, b]\n```\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(|V|+|E|) = O(N), N is number of edges\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(|V|+|E|) = O(N)\n# Code\n```\nclass Solution:\n def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:\n # drop out indegree == 1, and check from the bottom return first indegree==2\n n = len(edges)\n indegree = collections.defaultdict(int) # SC: O(|V|)\n graph = collections.defaultdict(list) # SC: O(|V|+|E|)\n for a,b in edges:\n graph[a].append(b)\n graph[b].append(a)\n indegree[a] += 1\n indegree[b] += 1\n # find indegree == 1\n queue = collections.deque([i for i,v in indegree.items() if v==1])\n while queue: # TC: O(|V|+|E|), explore all vertices and edges\n node = queue.popleft()\n indegree[node] -= 1\n for nei in graph[node]:\n indegree[nei] -= 1\n if indegree[nei] == 1:\n queue.append(nei)\n # find first indegree == 2 edges from the end\n for a, b in edges[::-1]:\n if indegree[a] == 2 and indegree[b]:\n return [a,b]\n\n```
| 7 | 0 |
['Breadth-First Search', 'Graph', 'Python3']
| 1 |
redundant-connection
|
97 % using recursion and iterative Union find ,simple and easy in python
|
97-using-recursion-and-iterative-union-f-4nbt
|
Method 1.1: Recursive Union Find\n\n\nclass Solution:\n def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:\n n = len(edges)\n
|
Bivas-Biswas
|
NORMAL
|
2021-05-09T23:54:14.889315+00:00
|
2021-05-10T00:09:46.984211+00:00
| 332 | false |
# Method 1.1: Recursive Union Find\n\n```\nclass Solution:\n def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:\n n = len(edges)\n self.parent = [ i for i in range(n+1)]\n \n for v, e in edges:\n p1 = self.get_parent(v)\n p2 = self.get_parent(e)\n \n if p1 == p2:\n return [v,e]\n \n self.parent[p2] = p1\n \n # for get parent of any node \n def get_parent(self, node):\n \n if self.parent[node] == node:\n return node\n else:\n return self.get_parent(self.parent[node])\n```\n\n\n# Method 1.2: Iterative Union Find\n```\nclass Solution:\n def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:\n n = len(edges)\n parent = [i for i in range(n+1)]\n \n count = n\n \n for e in edges:\n \n pari, parj = e\n\n while parent[pari] != pari:\n pari = parent[pari]\n\n while parent[parj] != parj:\n parj = parent[parj]\n\n if pari == parj:\n return e\n \n parent[parj] =pari\n```\n\n
| 7 | 0 |
['Union Find', 'Recursion', 'Iterator', 'Python']
| 0 |
redundant-connection
|
[c++][runtime beats 98.89 %][union find]
|
cruntime-beats-9889-union-find-by-rajat_-rekt
|
\nclass Solution {\npublic:\n int find(int x, vector<int>& parents) {\n return parents[x] == x ? x : find(parents[x], parents);\n }\n vector<int
|
rajat_gupta_
|
NORMAL
|
2020-10-14T05:41:43.035571+00:00
|
2020-10-14T05:41:43.035604+00:00
| 584 | false |
```\nclass Solution {\npublic:\n int find(int x, vector<int>& parents) {\n return parents[x] == x ? x : find(parents[x], parents);\n }\n vector<int> findRedundantConnection(vector<vector<int>>& edges) {\n vector<int> res(edges.size()+1);\n for(int i=1;i<edges.size()+1;i++) res[i]=i;\n vector<int> ans;\n for(auto edge: edges){\n int a1=find(edge[0],res);\n int a2=find(edge[1],res);\n if(a1!=a2) res[a1]=a2;\n else ans={edge[0],edge[1]};\n }\n return ans;\n }\n};\n```\n**Feel free to ask any question in the comment section.**\nI hope that you\'ve found the solution useful.\nIn that case, **please do upvote and encourage me** to on my quest to document all leetcode problems\uD83D\uDE03\nHappy Coding :)\n
| 7 | 1 |
['Union Find', 'C', 'C++']
| 2 |
redundant-connection
|
JavaScript DFS Solution
|
javascript-dfs-solution-by-hiitsherby-4wxh
|
\n/**\n * @param {number[][]} edges\n * @return {number[]}\n */\nvar findRedundantConnection = function(edges) {\n let map = {};\n let currRedundant = nul
|
hiitsherby
|
NORMAL
|
2019-06-30T09:03:35.570093+00:00
|
2019-06-30T09:03:43.156623+00:00
| 1,047 | false |
```\n/**\n * @param {number[][]} edges\n * @return {number[]}\n */\nvar findRedundantConnection = function(edges) {\n let map = {};\n let currRedundant = null;\n \n const dfs = (u, v, visited) => {\n visited.add(u);\n \n if (u in map){\n if (map[u].has(v)) return true;\n for (let w of map[u]){\n if (!visited.has(w)){\n visited.add(w);\n if (dfs(w, v, visited)) return true;\n }\n }\n return false;\n }\n return false;\n }\n \n for (let edge of edges){\n let [u, v] = edge;\n \n if (dfs(u, v, new Set())) currRedundant = edge;\n \n if (!(u in map)) map[u] = new Set();\n if (!(v in map)) map[v] = new Set();\n \n map[u].add(v);\n map[v].add(u);\n }\n \n return currRedundant;\n};\n```
| 7 | 0 |
['Depth-First Search', 'JavaScript']
| 1 |
redundant-connection
|
Union find python (general approach) beats 99%
|
union-find-python-general-approach-beats-egzr
|
Similar approach can be followed for \n\n1. Number of Islands II\n2. Couples Holding Hands\n3. Most Stones Removed\n4. Redundant Connection\npython\nclass Unio
|
rarara
|
NORMAL
|
2019-03-02T05:18:39.494665+00:00
|
2019-03-02T05:18:39.494707+00:00
| 1,046 | false |
Similar approach can be followed for \n\n1. [ Number of Islands II](https://leetcode.com/problems/number-of-islands-ii/discuss/246928/Union-find-(general-approach))\n2. [Couples Holding Hands](https://leetcode.com/problems/couples-holding-hands/discuss/246929/Python-union-find-beats-100)\n3. [Most Stones Removed](https://leetcode.com/problems/most-stones-removed-with-same-row-or-column/discuss/246931/Python-union-find-(general-approach))\n4. [Redundant Connection](https://leetcode.com/problems/redundant-connection/discuss/246972/Union-find-python-(general-approach)-beats-99)\n```python\nclass UnionFind(object):\n def __init__(self):\n self.parents = {}\n \n def make_set(self, x):\n self.parents[x] = x\n \n def find(self, x):\n if x not in self.parents:\n self.make_set(x)\n return x\n elif self.parents[x] == x:\n return x\n self.parents[x] = self.find(self.parents[x])\n return self.parents[x]\n \n def union(self, x, y):\n x_set = self.find(x)\n y_set = self.find(y)\n if x_set != y_set:\n self.parents[x_set] = y_set\n return True\n return False\n\n\nclass Solution(object):\n def findRedundantConnection(self, edges):\n """\n :type edges: List[List[int]]\n :rtype: List[int]\n """\n n=len(edges)\n uf = UnionFind()\n for x, y in edges:\n if not uf.union(x, y):\n return ((x,y))\n```
| 7 | 1 |
[]
| 1 |
redundant-connection
|
Easiest solution available in solutions. 100% faster (0ms) using union find
|
easiest-solution-available-in-solutions-p36of
|
IntuitionIf while iterating the edges vector, we check the node is connected or not we can easily find the solution, here comes union find (dsu). just get the u
|
madhavgarg2213
|
NORMAL
|
2025-01-29T04:22:27.081920+00:00
|
2025-01-29T04:22:27.081920+00:00
| 492 | false |
# Intuition
If while iterating the edges vector, we check the node is connected or not we can easily find the solution, here comes union find (dsu). just get the union finds template from gfg.
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
After getting the union find code. just iterate through the edges and check if it is connected before than this edge will lead to form a closed curve hence that edge will be the answer.
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: O(n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(n)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class UnionFind {
vector<int> parent, rank;
public:
UnionFind(int size) {
parent.resize(size);
rank.resize(size, 0);
for (int i = 0; i < size; i++) {
parent[i] = i;
}
}
int find(int i) {
if (parent[i] != i) {
parent[i] = find(parent[i]);
}
return parent[i];
}
void unite(int i, int j) {
int rootI = find(i);
int rootJ = find(j);
if (rootI != rootJ) {
if (rank[rootI] > rank[rootJ]) {
parent[rootJ] = rootI;
} else if (rank[rootI] < rank[rootJ]) {
parent[rootI] = rootJ;
} else {
parent[rootJ] = rootI;
rank[rootI]++;
}
}
}
};
class Solution {
public:
vector<int> findRedundantConnection(vector<vector<int>>& edges) {
int n = edges.size();
UnionFind uf(n+1);
for(auto i : edges){
int p1 = uf.find(i[0]);
int p2 = uf.find(i[1]);
if(p1==p2){
return i;
}else{
uf.unite(i[0], i[1]);
}
}
return {};
}
};
```
| 6 | 0 |
['Union Find', 'Graph', 'C++']
| 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.