question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
redundant-connection
|
Functional JavaScript 1-liner DSU 0ms
|
functional-javascript-1-liner-by-serhii_-q44b
|
IntuitionWe can use edges.find to return edge that creates a cycle in a graph.
Edge creates cycle if both ends already belong to the same connected component (g
|
Serhii_Hrynko
|
NORMAL
|
2025-01-29T02:07:21.707676+00:00
|
2025-01-29T22:44:27.246127+00:00
| 279 | false |
# Intuition
We can use `edges.find` to return edge that creates a cycle in a graph.
Edge creates cycle if both ends already belong to the same connected component (group of connected nodes).
Initially all nodes are in their own group which we will give number equal to node's number.
We can use mapping to merge groups. For every new edge, one group number becomes base number for merged group and we map other group's number to this base number.
```
findRedundantConnection = (
edges,
$ = x => $[x] ? $[x] = $($[x]) : x
) => edges.find(([a, b]) => (a = $(a)) == ($[a] = $(b)))
```
Time: $$O(n)$$
Space: $$O(n)$$
| 6 | 0 |
['Union Find', 'Recursion', 'JavaScript']
| 2 |
redundant-connection
|
Incredibly short solution
|
incredibly-short-solution-by-jacek_pizde-f496
|
IntuitionIt is called "union find"Code
|
Jacek_Pizdecki
|
NORMAL
|
2025-01-29T00:39:47.109441+00:00
|
2025-01-29T00:41:15.890877+00:00
| 234 | false |
# Intuition
It is called "**union find**"
# Code
```javascript []
const findRedundantConnection = (edges) => {
const u = {};
const find = a => !u[a] || u[a] === a ? u[a] = a : find(u[a]);
for (let [a, b] of edges){
if (find(a) - find(b)) {
u[find(a)] = u[find(b)];
} else {
return [a, b];
}
}
};
```
| 6 | 0 |
['JavaScript']
| 2 |
redundant-connection
|
Fast and Intuitive solution in C++ !
|
fast-and-intuitive-solution-in-c-by-divy-k0lh
|
Intuition\nDelete every edge one by one and check for cycle.\n Describe your first thoughts on how to solve this problem. \n\n# Approach\nFrom the last , delete
|
divyansh-xz
|
NORMAL
|
2023-01-09T06:47:26.223162+00:00
|
2023-01-09T06:47:26.223212+00:00
| 1,705 | false |
# Intuition\nDelete every edge one by one and check for cycle.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nFrom the last , delete edge from graph one by one and run dfs to check for cycle. If cycle no longer exists on both node where edge was deleted then that deleted edge is answer. Also insert edge back into graph is that edge is not the answer.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n^2)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n bool dfs(vector<unordered_set<int>> &gr, vector<bool> &vis, int s, int p)\n {\n // cout<<s;\n if(vis[s]) return true;\n vis[s] = true;\n for(auto e: gr[s])\n { \n if(e!=p and dfs(gr, vis, e, s)) \n return true;\n }\n return false;\n }\n vector<int> findRedundantConnection(vector<vector<int>>& edges) {\n int n = edges.size();\n vector<unordered_set<int>> gr(n+1);\n for(auto &v:edges)\n {\n gr[v[0]].insert(v[1]);\n gr[v[1]].insert(v[0]);\n }\n\n for(int i = n-1; i>=0;i--)\n {\n auto ed = edges[i];\n vector<bool> vis1(n+1, false);\n vector<bool> vis2(n+1, false);\n gr[ed[0]].erase(ed[1]);\n gr[ed[1]].erase(ed[0]);\n\n if(!dfs(gr, vis1, ed[0], 0) and !dfs(gr, vis2, ed[1], 0))\n return ed;\n\n gr[ed[0]].insert(ed[1]);\n gr[ed[1]].insert(ed[0]);\n }\n return {0,0};\n }\n};\n```
| 6 | 0 |
['Depth-First Search', 'Graph', 'C++']
| 0 |
redundant-connection
|
Java dfs solution with explain
|
java-dfs-solution-with-explain-by-dkfg20-05lz
|
Since the question require us to remove the redundant edge, when we constructing the graph, we do dfs on each edge to see is it redundant, if yes return the edg
|
dkfg2012
|
NORMAL
|
2022-05-19T03:39:19.359412+00:00
|
2022-05-19T03:39:19.359453+00:00
| 2,311 | false |
Since the question require us to remove the redundant edge, when we constructing the graph, we do dfs on each edge to see is it redundant, if yes return the edge, if no add the edge into the graph. \n\n\nWhy dfs can find redundant. Actually a redundant edge means after we add this edge, the graph will contain a cycle. So, when we came across a new edge, we do dfs from its start and its end, if there already exist a path from start to end, this new edge is redundant. \n\n```\n boolean[] visited;\n\n public int[] findRedundantConnection(int[][] edges) {\n HashMap<Integer, List<Integer>> hashMap = new HashMap<Integer, List<Integer>>();\n for(int i = 0; i < edges.length; i++){\n hashMap.put(i + 1, new ArrayList<>());\n }\n\n int[] res = new int[2];\n for(int i = 0; i < edges.length; i++){\n int[] edge = edges[i];\n visited = new boolean[edges.length + 1];\n if(!hashMap.get(edge[0]).isEmpty() && !hashMap.get(edge[1]).isEmpty() && dfs(edge[0], edge[1], hashMap)){\n return edge;\n }\n hashMap.get(edge[0]).add(edge[1]);\n hashMap.get(edge[1]).add(edge[0]);\n }\n return res;\n }\n\n public boolean dfs(int src, int target, HashMap<Integer, List<Integer>> hashMap){\n if(src == target){\n return true;\n }\n visited[src] = true;\n List<Integer> edgeList = hashMap.get(src);\n\n for(Integer next: edgeList){\n if(!visited[next]){\n if(dfs(next, target, hashMap)){\n return true;\n }\n }\n }\n\n return false;\n }\n```
| 6 | 0 |
['Depth-First Search', 'Java']
| 2 |
redundant-connection
|
C++ Clean & Concise DFS Backtracking & Cycle Detection
|
c-clean-concise-dfs-backtracking-cycle-d-o3h4
|
\nclass Solution {\npublic:\n vector<int> findRedundantConnection(vector<vector<int>>& edges) {\n int n = edges.size() + 1;\n vector<vector<int
|
shtanriverdi
|
NORMAL
|
2021-08-03T18:31:56.495825+00:00
|
2021-08-03T18:32:11.953724+00:00
| 699 | false |
```\nclass Solution {\npublic:\n vector<int> findRedundantConnection(vector<vector<int>>& edges) {\n int n = edges.size() + 1;\n vector<vector<int>> graph(n);\n vector<bool> seen(n, false);\n for (vector<int> &edge : edges) {\n graph[edge[0]].push_back(edge[1]);\n graph[edge[1]].push_back(edge[0]);\n if (hasCycle(edge[0], -1, graph, seen)) {\n return edge;\n }\n }\n return { 1, 4, 5, 3 };\n }\n \n bool hasCycle(int node, int parent, vector<vector<int>> &graph, vector<bool> &seen) {\n seen[node] = true;\n bool cycleFound = false;\n for (int &neighbor : graph[node]) {\n if (!seen[neighbor]) {\n cycleFound |= hasCycle(neighbor, node, graph, seen);\n }\n else if (neighbor != parent) {\n return true;\n }\n }\n seen[node] = false;\n return cycleFound;\n }\n};\n```
| 6 | 0 |
['Backtracking', 'Depth-First Search', 'C']
| 0 |
redundant-connection
|
[Python] RECURSION Easy & short
|
python-recursion-easy-short-by-aatmsaat-tpw0
|
Redundant Connection\nIdea\n We assume there is a tree, we add nodes from the edges one by one \n We check for edge u & v :-\n 1. If both have same root then i
|
aatmsaat
|
NORMAL
|
2021-06-25T12:58:30.867205+00:00
|
2021-06-26T07:29:11.573749+00:00
| 355 | false |
# Redundant Connection\n**Idea**\n* We assume there is a tree, we add nodes from the **edges** one by one \n* We check for **edge** `u & v` :-\n* 1. If both have same root then it forms a loop and we have to return this **edge**\n* 2. If not have then add that edge to tree\n\n[Note] Here `recur` function will return the root for every node `u & v`. \nIn for loop :-\n* Storing roots of u & v in x & y respectively\n* if both u & v have same roots then return u & v\n* if u node is not already added then connect v to u\n* if v node in not already added then connect u to v\n* if both nodes are added but have different roots then connect root of v to root of u\n\n\n**Complexity**\n* `Time Complexity` -> `O(n*n)` , where n is number of **edges**\n* `Space Complexity` -> `O(n)`, for storing tree path in `w`\n\n```\nclass Solution:\n def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:\n w = [*range(len(edges)+1)]\n def recur(x):\n if w[x] == x:\n return x\n return recur(w[x])\n for u, v in edges:\n x, y = recur(u), recur(v)\n if x == y: return [u, v]\n elif w[u] == u: w[u] = v\n elif w[v] == v: w[v] = u\n else: w[x] = y\n```\n\n*please upvote if you like the solution and comment if have queries*
| 6 | 0 |
['Recursion', 'Python']
| 2 |
redundant-connection
|
C++ union find solution
|
c-union-find-solution-by-ag_piyush-grxh
|
\n```\nclass Solution {\npublic:\n vector findRedundantConnection(vector>& edges) {\n \n //Since we have 1 based index for nodes\n //Thi
|
ag_piyush
|
NORMAL
|
2020-08-06T13:45:40.197065+00:00
|
2020-08-06T13:45:40.197115+00:00
| 722 | false |
\n```\nclass Solution {\npublic:\n vector<int> findRedundantConnection(vector<vector<int>>& edges) {\n \n //Since we have 1 based index for nodes\n //This vector represents the parent of each node\n\t\t\n vector<int> parent(edges.size()+1, 0); \n vector<int> redundantEdge;\n \n for(int i=0;i<parent.size();i++)\n parent[i] = i;\n \n for(auto e : edges) {\n int u = e[0];\n int v = e[1];\n \n while(u!=parent[u])\n u = parent[u];\n while(v!=parent[v])\n v = parent[v];\n \n if(u==v)\n redundantEdge = e;\n else\n parent[v] = u;\n }\n return redundantEdge;\n }\n};
| 6 | 0 |
['Union Find', 'C']
| 0 |
redundant-connection
|
[JAVA] Union Find is cool !!
|
java-union-find-is-cool-by-miyamura-etfr
|
I would highly suggest you to first watch this video before looking at solution.\nhttps://www.youtube.com/watch?v=wU6udHRIkcc\n\nclass Solution {\n public in
|
miyamura
|
NORMAL
|
2020-06-25T15:41:02.494251+00:00
|
2020-07-16T12:03:55.354194+00:00
| 1,027 | false |
I would highly suggest you to first watch this video before looking at solution.\nhttps://www.youtube.com/watch?v=wU6udHRIkcc\n```\nclass Solution {\n public int[] findRedundantConnection(int[][] edges) {\n int n = edges.length;\n int[] parent = new int[n+1];\n \n Arrays.fill(parent,-1);\n \n for(int[] e : edges){\n int p1 = find(e[0],parent);\n int p2 = find(e[1],parent);\n if(p1 != p2)\n union(p1,p2,parent);\n else\n return new int[]{e[0],e[1]};\n }\n \n return new int[]{};\n }\n \n private int find(int vertex,int[] parent){\n while(parent[vertex] > -1)\n vertex = parent[vertex];\n \n return vertex;\n }\n \n private void union(int p1,int p2,int[] parent){\n int totalNodes = parent[p2] + parent[p1];\n if(parent[p1] <= parent[p2]){\n parent[p2] = p1;\n parent[p1] = totalNodes;\n }else{\n parent[p1] = p2;\n parent[p2] = totalNodes;\n }\n }\n}\n```
| 6 | 0 |
['Union Find', 'Java']
| 1 |
redundant-connection
|
python 10 line union find solution, beat 90%+
|
python-10-line-union-find-solution-beat-7zglr
|
python\nclass Solution:\n def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:\n p = list(range(len(edges) + 1))\n def find(
|
jason003
|
NORMAL
|
2019-03-09T13:12:44.178333+00:00
|
2019-03-09T13:12:44.178362+00:00
| 602 | false |
```python\nclass Solution:\n def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:\n p = list(range(len(edges) + 1))\n def find(x):\n while p[x] != x:\n p[x] = p[p[x]]\n x = p[x]\n return p[x]\n for a, b in edges:\n pa, pb = find(a), find(b)\n if pa == pb: return [a, b]\n p[pa] = p[pb]\n```
| 6 | 0 |
[]
| 0 |
redundant-connection
|
Java BFS Edge Removal
|
java-bfs-edge-removal-by-cheng_coding_at-ahim
|
Find the node that has only edge, remove that edge and node, then look again to find node with one edge. Remove all of them until can\'t find node with one edge
|
cheng_coding_attack
|
NORMAL
|
2018-09-16T00:26:42.150669+00:00
|
2018-09-30T04:27:49.034599+00:00
| 563 | false |
Find the node that has only edge, remove that edge and node, then look again to find node with one edge. Remove all of them until can\'t find node with one edge anymore. Now what\'s left in the graph is a circle, all the edges (connections) remaining will be a valid choice.\n\n```\n1 - 2 - 3 - 4\n | |\n 5 - 6\n\t\t\t\t\n 2 - 3 - 4\n | |\n 5 - 6\n\t\t\t\t\n 3 - 4\n | |\n 5 - 6\n```\n\n```\nclass Solution {\n \n public int[] findRedundantConnection(int[][] edges) {\n Map<Integer, Set<Integer>> map = new HashMap<>();\n for (int[] edge : edges) {\n if (!map.containsKey(edge[0])) map.put(edge[0], new HashSet<>());\n if (!map.containsKey(edge[1])) map.put(edge[1], new HashSet<>());\n map.get(edge[0]).add(edge[1]);\n map.get(edge[1]).add(edge[0]);\n }\n Queue<Integer> q = new LinkedList<>();\n for (int key : map.keySet()) {\n if (map.get(key).size() == 1) q.offer(key);\n }\n while (!q.isEmpty()) {\n int node = q.poll();\n Set<Integer> set = map.get(node);\n map.remove(node);\n for (int neighbor : set) {\n map.get(neighbor).remove(node);\n if (map.get(neighbor).size() == 1) q.offer(neighbor);\n }\n }\n for (int i = edges.length - 1; i >= 0; i--) {\n int[] edge = edges[i];\n if (map.containsKey(edge[0]) && map.containsKey(edge[1])) return edge;\n }\n return new int[]{};\n }\n \n}\n```
| 6 | 0 |
[]
| 0 |
redundant-connection
|
Interesting C++ DFS Solution with o(n) time complexity (Approach #1 DFS is o(N^2))
|
interesting-c-dfs-solution-with-on-time-b32gx
|
Using DFS to detect whether a graph has a circle or not is very classic, just use a vector visited to record three different status of node (0 means not visited
|
woaidabomei
|
NORMAL
|
2018-07-24T23:32:26.865738+00:00
|
2018-10-01T10:28:46.548814+00:00
| 1,427 | false |
Using DFS to detect whether a graph has a circle or not is very classic, just use a vector visited<int> to record three different status of node (0 means not visited, 1 means visiting, 2 means already visited and there\'s no circle), so when we are running the dfs, we found out a node visited value is 1, then it means there\'s a circle.\n\nWell, the solution for this problem is similiar, the only difference is we need to mark all nodes inside the circle to 1 and ends the recursion to stop it from changing to 2, while marking all nodes outside the circle to 2.\n\nThe problem is, assume parent node is outside of the circle and we set it to 1 and keep running the dfs with one of it\'s children node, what if that children node is inside a circle and the dfs returns false? If we terminate dfs immediately, then the parent node value will always be 1; but if we don\'t terminate dfs, then all nodes inside the circle will become 2 eventually. \n\nSo instead, we need to record that specific node to a different value to let the parent node know. Imagine we encounter the first node of the circle, we mark it to 1, and run the dfs and encounter that node again, we will see that node visited value already becomes 1, we set it to 4; and recursively when we are back from the stack to that node, if it\'s 4, we set it to 3(make it even); after that it will go back to parent node. If the parent node knows one of it\'s children node visited value is 3, it keeps traversing other children node even if the dfs returns false.\n\nEventually, all the nodes visited value will be 1 or 2 or 3; we choose those nodes with odd value to make then a circle.\n\n\n```\nclass Solution {\npublic:\n vector<int> findRedundantConnection(vector<vector<int>>& edges) {\n vector<int> result;\n vector<vector<int>> graph(edges.size() + 1);\n for (auto e:edges) {\n graph[e[0]].push_back(e[1]);\n graph[e[1]].push_back(e[0]);\n }\n vector<int> visited(edges.size() + 1, 0);\n //start dfs from node 1\n dfs(graph, visited, 1, 0);\n for (int i = edges.size() - 1; i >= 0; i--) {\n //if the visited[node] is odd, then it means the node is inside the cicle\n if (visited[edges[i][0]]%2 && visited[edges[i][1]]%2) {\n result = edges[i];\n break;\n }\n }\n return result;\n }\n //false means this node is in a circle, we want to keep the value to odd (most case would be 1)\n //true means this node is not in a circle, we want to keep the value to 2\n bool dfs(vector<vector<int>>& graph, vector<int>& visited, int node, int parent) {\n if (visited[node] == 2) return true;\n if (visited[node] == 1) {\n // this node is the beginning node of the circle while traversing the graph, record it with 4 for the first time\n visited[node] = 4;\n return false;\n }\n visited[node] = 1;\n for (int i = 0; i < graph[node].size(); i++) {\n if (graph[node][i] != parent) {\n if (!dfs(graph, visited, graph[node][i], node)) {\n if (visited[graph[node][i]] == 3) {//that children node graph[node][i] is the beginning of the circle\n continue;\n }\n //if this node value becomes 4, then mark it to 3 and let it\'s parent\n //node recognize that it is the beginning of a circle and continue bfs even if it returns false \n if (visited[node] == 4) \n visited[node] = 3;\n return false;\n }\n }\n }\n visited[node] = 2;\n return true;\n }\n};\n```\n\n\n\n
| 6 | 0 |
[]
| 4 |
redundant-connection
|
Redundant Connection in RUBY!
|
redundant-connection-in-ruby-by-quantumm-vimo
|
IntuitionWhen I first saw this problem, I realized it's about finding a cycle in an undirected graph. Since we need to find the last edge that creates a cycle,
|
quantummaniac609
|
NORMAL
|
2025-01-29T11:11:48.075804+00:00
|
2025-01-29T11:11:48.075804+00:00
| 46 | false |
# Intuition
When I first saw this problem, I realized it's about finding a cycle in an undirected graph. Since we need to find the last edge that creates a cycle, Union-Find (Disjoint Set) would be perfect as we can process edges in order and detect when an edge connects two already-connected components.
# Approach
I implemented the solution using Union-Find with path compression:
1. **Initialize Union-Find**:
- Create parent array where each node is its own parent initially
- Size is n+1 since nodes are 1-indexed
2. **Process Each Edge**:
- For each edge [x,y]:
- Find parents of both nodes
- If parents are same, we found a cycle
- Otherwise, union the components
3. **Path Compression**:
- Implement find with path compression
- Makes subsequent operations more efficient
# Complexity
- Time complexity: $$O(N\alpha(N))$$
- N is number of nodes
- α is inverse Ackermann function
- Nearly constant time per operation
- Space complexity: $$O(N)$$
- Parent array stores N elements
- Recursion stack for find operations
# Code
```ruby
def find_redundant_connection(edges)
n = edges.length
parent = Array.new(n + 1) { |i| i }
def find(parent, x)
if parent[x] != x
parent[x] = find(parent, parent[x])
end
parent[x]
end
def union(parent, x, y)
parent[find(parent, x)] = find(parent, y)
end
edges.each do |x, y|
px, py = find(parent, x), find(parent, y)
if px == py
return [x, y]
end
union(parent, x, y)
end
end
```
| 5 | 0 |
['Ruby']
| 0 |
redundant-connection
|
Easy solution 🚀🚀🚀🚀🚀🚀🚀🚀🚀🚀🚀
|
easy-solution-by-sharvil_karwa-fbrj
|
Code
|
Sharvil_Karwa
|
NORMAL
|
2025-01-29T04:21:48.927544+00:00
|
2025-01-29T04:21:48.927544+00:00
| 1,508 | false |
# Code
```cpp []
class Solution {
public:
int fp(int node, vector<int> &par){
if(node==par[node]) return node;
return fp(par[node], par);
}
vector<int> findRedundantConnection(vector<vector<int>>& edges) {
vector<int> ans, par(edges.size()+1);
for(int i=0;i<par.size();i++) par[i] = i;
for(auto i:edges){
int n1 = i[0];
int n2 = i[1];
int p1 = fp(n1, par);
int p2 = fp(n2, par);
if(p1==p2) ans = {n1, n2};
else par[p2] = p1;
}
return ans;
}
};
```
| 5 | 0 |
['Depth-First Search', 'Breadth-First Search', 'Union Find', 'Graph', 'Python', 'C++', 'Java']
| 0 |
redundant-connection
|
Beginner Friendly || DSU || Union Find || C++ || Simple Explanation
|
beginner-friendly-dsu-union-find-c-simpl-e76c
|
Intuition\nIf two nodes are already connected then this edge is redundant\n\n# Approach\n- Use union find\n- If the nodes of edge are not already connected, con
|
mAniket
|
NORMAL
|
2023-08-06T05:34:46.686361+00:00
|
2023-08-06T05:34:46.686383+00:00
| 799 | false |
# Intuition\nIf two nodes are already connected then this edge is redundant\n\n# Approach\n- Use union find\n- If the nodes of edge are not already connected, connect them (UNION)\n- If they are already connected, it means the current edge is redundant, return this edge\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n```\nclass Solution {\npublic:\n\nint parent[3002]; //to store parent of each node\nint size[3002]; //to store the size of component\n\nvoid make(int v) { // initializing a component with one node\n parent[v] = v;\n size[v] = 1;\n}\n\nint findPar(int a) { // returns parent of node a\n if (a == parent[a]) return a;\n else return parent[a] = findPar(parent[a]);\n}\n\nvoid Union(int a, int b) { // connects two nodes in one component\n a = findPar(a);\n b = findPar(b);\n\n if (a == b) return;\n\n if (size[a] < size[b]) {\n swap(a, b);\n }\n\n parent[b] = a;\n size[a] += size[b];\n}\n vector<int> findRedundantConnection(vector<vector<int>>& edges) {\n vector<int> ans;\n int n = edges.size();\n for (int i = 1; i <= n; i++) make(i);\n for (int i = 0; i < n; i++) {\n int u = edges[i][0], v = edges[i][1];\n int a = findPar(u), b = findPar(v);\n if (a == b) { // u and v are already connected, return current edge as it is redundant\n return {u, v};\n } else {\n Union(u, v); // connects u and v\n }\n }\n return ans;\n }\n};\n```
| 5 | 0 |
['Union Find', 'Graph', 'C++']
| 0 |
redundant-connection
|
Very Simple and clean DSU Solution || JAVA
|
very-simple-and-clean-dsu-solution-java-n569q
|
Approach\n- Simply performing the union operation to the edges until the vertex from the same component is found \n- As that same component is responsible in fo
|
Kshitij_Pandey
|
NORMAL
|
2023-06-01T18:46:51.832631+00:00
|
2023-06-01T18:46:51.832656+00:00
| 355 | false |
# Approach\n- Simply performing the union operation to the edges until the vertex from the same component is found \n- As that same component is responsible in formation of the graph from the tree.\n- Perform simply union-find algorithm I have used union by size as I find it more intuitive. \n\n# Code\n```\nclass Solution {\n public int[] findRedundantConnection(int[][] edges) {\n int n = edges.length;\n int[] parent = new int[n+1];\n int[] size = new int[n+1];\n\n for(int i=0; i<= n; i++){\n parent[i] =i;\n size[i] = 1;\n }\n int i=0;\n for(; i< n; i++){\n int[] edge = edges[i];\n int u = edge[0];\n int v = edge[1];\n\n int ul = find(parent, u);\n int vl = find(parent, v);\n\n if(ul == vl) break;\n else{\n union(ul, vl, parent, size);\n }\n }\n return edges[i];\n \n }\n private int find(int[] parent, int i){\n if(parent[i] == i){\n return parent[i];\n }\n return parent[i] = find(parent, parent[i]);\n }\n\n private void union(int ul, int vl, int[] parent, int[] size){\n if(ul < vl){\n parent[ul] = vl;\n size[ul] += size[vl];\n }\n else{\n parent[vl] = ul;\n size[vl] += size[ul]; \n }\n }\n}\n```
| 5 | 0 |
['Java']
| 0 |
redundant-connection
|
Simple Commented Javascript DFS Solution
|
simple-commented-javascript-dfs-solution-cmph
|
Intuition\nWe are performing cycle prevention not cycle detection\n\n# Approach\nFor each edge [a,b] that is addded to the graph / adjacency list\nPerform a DFS
|
user4026j
|
NORMAL
|
2023-02-03T08:03:07.373361+00:00
|
2023-12-05T07:57:48.301420+00:00
| 415 | false |
# Intuition\nWe are performing **cycle prevention** not cycle detection\n\n# Approach\nFor each edge `[a,b]` that is addded to the graph / adjacency list\nPerform a DFS to check if you can traverse from `b` to `a`\n\n# Complexity\nwhere e is the number of edges\n- Time complexity:\n$$O(e^2)$$ --> For each edge that is traversed in the graph\n\n- Space complexity:\n$$O(e)$$ --> The adjacency list contains all the edges and the DFS call stack will traverse each edge\n\n# Code\n```\n/**\n * @param {number[][]} edges\n * @return {number[]}\n\n Intuition to solve this problem is that we need to build the graph and then check if there is a cycle\n */\nvar findRedundantConnection = function(edges) {\n\n const adjacencyList = {}\n const dfs = (node, target, prev) =>{\n if (node === target) return true \n for (let subnode of adjacencyList[node]){\n if (subnode !== prev && dfs(subnode, target, node)) return true\n }\n return false\n }\n\n // Build graph one edge at a time\n for (let edge of edges){\n const [a,b] = edge\n if (!adjacencyList[a]) adjacencyList[a] = []\n if (!adjacencyList[b]) adjacencyList[b] = []\n\n adjacencyList[a].push(b)\n adjacencyList[b].push(a)\n\n // Traverse the graph and check for a cycle for each new edge\n if (dfs(b,a,a)) return [a,b]\n }\n};\n```
| 5 | 0 |
['Depth-First Search', 'Graph', 'JavaScript']
| 0 |
redundant-connection
|
C++ solution | union find | easy short code
|
c-solution-union-find-easy-short-code-by-zr6p
|
\n\n\tclass Solution {\n\tpublic:\n \n int parent(int i, vector &p)\n {\n if(p[i]==i)\n {\n return i;\n }\n \n
|
bhavyrastogi2002
|
NORMAL
|
2022-01-21T09:46:32.645549+00:00
|
2022-01-21T09:46:32.645575+00:00
| 128 | false |
\n\n\tclass Solution {\n\tpublic:\n \n int parent(int i, vector<int> &p)\n {\n if(p[i]==i)\n {\n return i;\n }\n \n return parent(p[i],p);\n }\n vector<int> findRedundantConnection(vector<vector<int>>& edges) {\n \n int n = edges.size();\n vector<int> p(n+1);\n vector<int> ans;\n \n for(int i=0;i<n+1;i++)\n {\n p[i]=i;\n }\n \n for(int i=0;i<n+1;i++)\n {\n int a = parent(edges[i][0], p);\n int b = parent(edges[i][1], p);\n \n if(a != b)\n {\n p[a] = b;\n }\n else\n {\n ans.push_back(edges[i][0]);\n ans.push_back(edges[i][1]);\n break;\n }\n \n }\n \n return ans;\n \n }\n};\n\n\nEasy and very short code , Using union-find algorithm \nstep 1 : make a parent array having ith node as its own parent \nstep 2: iterate over the array of edges one by one \nstep 3: for ith edge , find parent of both the node and if both the parents are not equal make any one, parent of other. repeat that until u find the edge having same parent which means that edge is making a cycle and to make the graph a tree , we have to remove that node which is our ans.
| 5 | 0 |
['Graph']
| 1 |
redundant-connection
|
Java Simple and easy Union find video explanation
|
java-simple-and-easy-union-find-video-ex-6ngs
|
Java Simple and easy Union find video explanation -\nLanguage- english/hindi\n\nhttps://www.youtube.com/watch?v=rzRsU5EVFYM&t=168s\n\n\n\n\n
|
abhishekbabbar1989
|
NORMAL
|
2020-06-01T06:19:30.475446+00:00
|
2020-06-01T06:29:42.531560+00:00
| 132 | false |
Java Simple and easy Union find video explanation -\nLanguage- english/hindi\n\nhttps://www.youtube.com/watch?v=rzRsU5EVFYM&t=168s\n\n\n\n\n
| 5 | 0 |
[]
| 1 |
redundant-connection
|
C++ O(N) Union with Rank and Find with Path Compression with clear comments in code.
|
c-on-union-with-rank-and-find-with-path-qi50y
|
First, lets talk about why we need to do this with Union-Find in the context of an interview ? \nUnion Find is required for follow-ups like what if the graph
|
pradosh
|
NORMAL
|
2020-05-12T20:53:22.862467+00:00
|
2020-05-12T20:53:22.862521+00:00
| 1,399 | false |
First, lets talk about why we need to do this with Union-Find in the context of an interview ? \nUnion Find is required for **follow-ups** like what if the graph is large (cant use DFS) , OR what if the components (edge connections) dynamically change etc ? . \n\nI believe this question teaches us the basic nitty-gritties of **Union Find (with Rank and Path compression)**. If you do normal UF without Rank and Path compression, then the TC will be the same as DFS or BFS and interviewer will ask you to implement Rank and Path Compression so minimize the TC to O(N). So better to learn it with Rank and Path Compression at the get go !\n\n**PRE_REQUISITE** : [ Disjoint Sets Data Structure - Weighted Union and Collapsing Find](https://www.youtube.com/watch?v=wU6udHRIkcc)\n\n**Once youve understood the video completely above**, my code is fairly readable with comments. \n\n **Time Complexity** \n \n it is **O(N alpha(N))**, where **alpha(N**) is called the "*Inverse Ackermann Function*", which is basically a fancy way of saying that **alpha(N) grows VERY SLOWLY** (in practise alpha(N) is <= 4). So, the complexity reduces O( N ), *where N is the number of Nodes in the graph*. \n \nIntuitively thinking, we can say in an interiview that we make AT MOST N queries to our **Union** Function, so TC is bounded by N queries i.e O(N) . \n\n```\nclass DisjointDS{\npublic:\n vector<int> parent; // Stores the parent of ith node\n vector<int> rank; //Stores the rank of ith node\n \n DisjointDS(int n){ //n is the number of nodes in the graph\n parent.resize(n + 1); \n rank.resize(n + 1); \n rank.clear(); //Initialize the rank of every node as 0\n \n for(int i = 0; i < n+1; i++){ //Inititalize the parent of node i as i itself. Meaning they are a set on their own\n parent[i] = i;\n }\n }\n \n bool Union(int u, int v){ //Union by Rank . Returns TRUE if UNION can be performed without introducing any cycle\n //Get the representatives of the vertices\n int ru = Find(u);\n int rv = Find(v);\n \n //an edge between them will create a loop since they both belong to the same set/component\n if(ru == rv) return false; \n \n if(rank[ru] > rank[rv]){\n parent[rv] = parent[ru];\n }else if (rank[rv] > rank[ru]){\n parent[ru] = parent[rv];\n }else{\n parent[rv] = parent[ru];\n rank[ru]++;\n }\n return true;\n }\n \n int Find(int node){ //Returns the representative of this node\n if(parent[node] == node) return node; //If i am my own parent/rep\n //Find with Path compression, meaning we update the parent for this node once recursion returns\n parent[node] = Find(parent[node]); \n return parent[node];\n }\n};\n\nclass Solution {\npublic:\n vector<int> findRedundantConnection(vector<vector<int>>& edges) {\n int numOfNodes = edges.size();\n DisjointDS dds(numOfNodes);\n \n for(auto& edge: edges){\n int u = edge[0];\n int v = edge[1];\n \n if(dds.Union(u, v) == false) return {u, v}; // If we cannot unionize these 2 edges, means they must beling to the same\n //connected component, hence adding them will create a cycle. so we found our Redundant Edge\n }\n \n return {-1, -1};\n }\n};\n```\n
| 5 | 0 |
['Union Find', 'C', 'C++']
| 1 |
redundant-connection
|
100 % beats --> Efficient & Easy to Understand Java code 🔥🔥
|
100-beats-efficient-easy-to-understand-j-bll1
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
THAKUR_GAURAV_14
|
NORMAL
|
2025-02-02T07:29:10.507639+00:00
|
2025-02-02T07:29:10.507639+00:00
| 127 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
// Performs DFS and returns true if there's a path between src and target.
private boolean isConnected(
int src,
int target,
boolean[] visited,
List<Integer>[] adjList
) {
visited[src] = true;
if (src == target) {
return true;
}
boolean isFound = false;
for (int adj : adjList[src]) {
if (!visited[adj]) {
isFound = isFound || isConnected(adj, target, visited, adjList);
}
}
return isFound;
}
public int[] findRedundantConnection(int[][] edges) {
int N = edges.length;
List<Integer>[] adjList = new ArrayList[N];
for (int i = 0; i < N; i++) {
adjList[i] = new ArrayList<>();
}
for (int[] edge : edges) {
boolean[] visited = new boolean[N];
// If DFS returns true, we will return the edge.
if (isConnected(edge[0] - 1, edge[1] - 1, visited, adjList)) {
return new int[] { edge[0], edge[1] };
}
adjList[edge[0] - 1].add(edge[1] - 1);
adjList[edge[1] - 1].add(edge[0] - 1);
}
return new int[] {};
}
}
```
| 4 | 0 |
['Depth-First Search', 'Breadth-First Search', 'Union Find', 'Graph', 'Java']
| 0 |
redundant-connection
|
💢Faster✅💯 Lesser C++✅Python3🐍✅Java✅C✅Python🐍✅C#✅💥🔥💫Explained☠💥🔥 Beats 💯
|
faster-lesser-cpython3javacpythoncexplai-6tfv
|
IntuitionThis is a reference vedio for the Solution. I tried to explain the solution in best way i can, please watch out the solution.
Approach
JavaScript Code
|
Edwards310
|
NORMAL
|
2025-01-29T19:27:10.925047+00:00
|
2025-01-29T19:27:10.925047+00:00
| 202 | false |

# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
***This is a reference vedio for the Solution. I tried to explain the solution in best way i can, please watch out the solution.***
https://youtu.be/WzEv-yni6MM?si=NA2l-91vNrK2ZlqT
# Approach
<!-- Describe your first thoughts on how to solve this problem. -->
- ***JavaScript Code -->*** https://leetcode.com/problems/redundant-connection/submissions/1524713565
- ***C++ Code -->*** https://leetcode.com/problems/redundant-connection/submissions/1524689978
- ***Python3 Code -->*** https://leetcode.com/problems/redundant-connection/submissions/1524701459
- ***Java Code -->*** https://leetcode.com/problems/redundant-connection/submissions/1524695773
- ***C Code -->*** https://leetcode.com/problems/redundant-connection/submissions/1524710881
- ***Python Code -->*** https://leetcode.com/problems/redundant-connection/submissions/1524700190
- ***C# Code -->*** https://leetcode.com/problems/redundant-connection/submissions/1524711651
- ***Go Code -->*** https://leetcode.com/problems/redundant-connection/submissions/1524714131
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(N)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(N)
# Code

| 4 | 0 |
['Union Find', 'Graph', 'C', 'Python', 'C++', 'Java', 'Go', 'Python3', 'JavaScript', 'C#']
| 0 |
redundant-connection
|
✅ Easy to Understand | 100% Faster | Disjoint Set Union | Detailed Video explanation 🔥
|
easy-to-understand-100-faster-disjoint-s-o84o
|
IntuitionThe problem requires us to find a redundant edge in a connected undirected graph. A redundant edge means that if we remove it, the graph remains connec
|
sahilpcs
|
NORMAL
|
2025-01-29T18:06:10.987386+00:00
|
2025-01-29T18:06:10.987386+00:00
| 146 | false |
# Intuition
The problem requires us to find a redundant edge in a connected undirected graph. A redundant edge means that if we remove it, the graph remains connected.
Since the graph initially forms a tree (which has **n nodes and n-1 edges**), adding an extra edge will always create a **cycle**.
Thus, the problem boils down to detecting the first edge that forms a cycle in the given sequence.
A **Union-Find (Disjoint Set)** data structure is an efficient way to detect cycles in an undirected graph.
By iterating through all edges and checking whether two nodes are already connected, we can determine the redundant edge.
---
# Approach
1. **Use Union-Find (Disjoint Set) to track connected components.**
2. **For each edge \([u, v]\):**
- Use the **find()** function to determine the root parent of `u` and `v`.
- If `find(u) == find(v)`, adding this edge creates a cycle → **Return the edge**.
- Otherwise, use the **union()** function to merge the components.
3. **Return the redundant edge that caused a cycle.**
### **Union-Find Implementation**
- **Find with Path Compression**: This optimizes the `find()` function by flattening the tree structure, making future lookups faster.
- **Union without Rank Optimization**: This version only assigns the parent but does not balance the tree depth.
---
# Complexity
- **Time Complexity**:
- The **find()** and **union()** operations are nearly **constant time** \( O(\alpha(n)) \), where \( \alpha(n) \) is the inverse Ackermann function.
- Since we process **n edges**, the total complexity is **\( O(n) \)**.
- **Space Complexity**:
- We maintain a **parent array** of size \( O(n) \).
- No extra space is used apart from this, so the overall space complexity is **\( O(n) \)**.
# Code
```java []
class Solution {
public int[] findRedundantConnection(int[][] edges) {
int n = edges.length;
UnionFind uf = new UnionFind(n);
for(int[] edge: edges){
if( ! uf.union(edge[0]-1, edge[1]-1) ){
return edge;
}
}
return new int[]{}; // won't reach here as per problem.
}
static class UnionFind {
int[] parent;
public UnionFind(int n) {
parent = new int[n];
Arrays.fill(parent, -1); // no parent, single node currently in component, khud ka parent
}
public int find(int x) {
if (parent[x] == -1) {
return x;
}
return parent[x] = find(parent[x]); // pruning , path compression
}
public boolean union(int a, int b) {
a = find(a);
b = find(b);
if (a != b) {
parent[a] = b;
return true;
}
return false; // already part of one component.
}
}
}
```
LeetCode 684 Redundant Connection | Disjoint Set Union | Graph Theory Essential
https://youtu.be/oHNaJFk6qdg
| 4 | 0 |
['Union Find', 'Graph', 'Java']
| 1 |
redundant-connection
|
⬆️ Beats 100% | C++ | Python | Simplified | Union-Find | Seperate Modular Class
|
beats-100-simplified-union-find-approach-7t1u
|
IntuitionThe problem requires identifying an extra edge in a graph that, when added, results in a cycle. This "redundant connection" is the first edge in the gi
|
durjoydutta
|
NORMAL
|
2025-01-29T10:10:37.913346+00:00
|
2025-02-06T03:05:37.096226+00:00
| 228 | false |
# Intuition
The problem requires identifying an extra edge in a graph that, when added, results in a cycle. This "redundant connection" is the first edge in the given list that **causes the graph to become cyclic**. Since the initial graph has no cycles, our goal is to **detect the earliest edge that completes a cycle**.
We are going to utilize a Disjoint Set (Union-Find) data structure. By maintaining disjoint sets of connected nodes, we can efficiently determine whether adding an edge would form a cycle. **If two nodes in an edge already belong to the same set, then adding that edge would create a cycle, making it redundant.**
# Approach
1. **Disjoint Set Representation:**
We initialize a Disjoint Set (also known as Union-Find) where each node is its own parent. This structure helps in keeping track of connected components in the graph.
2. **Union-Find with Path Compression:**
Find operation: This method retrieves the root representative of a node, utilizing path compression to optimize future queries.
Union operation: This method merges two sets, connecting two previously unlinked components. If the nodes are already in the same set, it means adding the edge creates a cycle.
3. **Processing Edges:**
Iterate through each edge in the input. Use the Union operation to merge sets. If merging fails (i.e., both nodes are already connected), return the current edge as it is the first one forming a cycle.
4. **Termination:**
Once a redundant edge is found, return it immediately. If no cycle is detected (which is guaranteed not to happen per the problem constraints), return an empty result.
# Complexity Analysis
- **Time Complexity:**
Each find operation has nearly constant time complexity due to path compression **(O(α(N))**, where α is the inverse Ackermann function).
We perform find and union for each edge, leading to an overall time complexity of **O(E α(V))**, which is almost linear in practice.
- **Space Complexity:**
No extra space apart from a few integer variables is used, making the total space complexity O(V).
# Code
```cpp []
// Simplified DS implementation for easy understanding, can be optimized further by using Union by Size/ Rank
class DisjointSet {
private:
vector<int> parent;
public:
DisjointSet(int n) {
parent.resize(n+1);
for (int i = 0; i < n + 1; ++i) {
parent[i] = i; //initially all nodes are set as independent
}
}
int find(int u) {
if (parent[u] == u) return u;
return parent[u] = find(parent[u]);
}
bool Union(int u, int v) {
int parU = find(u);
int parV = find(v);
if (parU != parV) { // not part of the set yet
parent[parV] = parU;
return true;
} else return false; // already part of the set
}
};
class Solution {
public:
vector<int> findRedundantConnection(vector<vector<int>>& edges) {
int n = edges.size(); //here graphs with n nodes have n edges
DisjointSet ds(n);
for (const auto &edge : edges) {
int u = edge[0], v = edge[1];
if (!ds.Union(u, v)) return edge;
}
return {};
}
};
```
```python []
class DisjointSet:
def __init__(self, n):
self.parent = list(range(n + 1)) # Initialize each node as its own parent
def find(self, u):
if self.parent[u] == u:
return u
self.parent[u] = self.find(self.parent[u]) # Path compression
return self.parent[u]
def union(self, u, v):
root_u = self.find(u)
root_v = self.find(v)
if root_u != root_v:
self.parent[root_v] = root_u # Merge sets
return True
return False # redundant edge detected
class Solution:
def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:
n = len(edges) # Number of nodes (since n edges for n nodes)
ds = DisjointSet(n)
for u, v in edges:
if not ds.union(u, v):
return [u, v] # Return the first redundant edge
return []
```
| 4 | 0 |
['Union Find', 'Graph', 'C++', 'Python3']
| 0 |
redundant-connection
|
C# Solution for Redundant Connection Problem
|
c-solution-for-redundant-connection-prob-exeu
|
IntuitionThe problem requires us to find the redundant edge in a given tree with an extra edge, which means the graph initially had no cycles, but adding one ed
|
Aman_Raj_Sinha
|
NORMAL
|
2025-01-29T03:55:41.848291+00:00
|
2025-01-29T03:55:41.848291+00:00
| 220 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The problem requires us to find the redundant edge in a given tree with an extra edge, which means the graph initially had no cycles, but adding one edge created exactly one cycle.
To efficiently detect this extra edge, we use the Union-Find (Disjoint Set) data structure. The key idea is:
1. A tree is an acyclic connected graph with (n - 1) edges.
2. Adding an extra edge creates exactly one cycle.
3. Union-Find helps efficiently track connected components and detect cycles.
By processing edges one by one:
• If two nodes of an edge already belong to the same connected component, adding the edge creates a cycle → this is the redundant edge.
• Otherwise, we merge the sets (connect the nodes) using Union-Find with path compression and union by rank.
# Approach
<!-- Describe your approach to solving the problem. -->
Step 1: Initialize Union-Find Data Structures
• Create a parent[] array where each node is its own parent initially (parent[i] = i).
• Create a rank[] array initialized to 1 for all nodes to keep track of tree height.
Step 2: Process Each Edge in edges[]
• For each edge (u, v):
• Use Find to get the roots of u and v.
• If Find(u) == Find(v), it means u and v are already connected → Cycle detected → return [u, v].
• Otherwise, perform Union by Rank to merge the sets efficiently.
Step 3: Find with Path Compression
• When searching for the root of a node, we recursively update its parent to point directly to the root, flattening the tree.
• This optimizes future queries, making them nearly constant time O(α(n)).
Step 4: Union by Rank
• Attach the smaller tree under the larger tree to keep the height minimal.
• If both trees have the same rank, arbitrarily choose one as the root and increase its rank.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
• Find operation with path compression runs in O(α(n)), where α(n) is the inverse Ackermann function (grows extremely slow, practically constant).
• Union operation with rank also runs in O(α(n)).
• Since we perform n union operations, the overall complexity is **O(n * α(n))`, which simplifies to O(n) for practical purposes.
Worst-Case Time Complexity: O(n)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
• Parent array (parent[]) → O(n)
• Rank array (rank[]) → O(n)
• No extra recursive calls or data structures beyond these.
Worst-Case Space Complexity: O(n)
# Code
```csharp []
public class Solution {
public int[] FindRedundantConnection(int[][] edges) {
int n = edges.Length;
int[] parent = new int[n + 1];
int[] rank = new int[n + 1];
for (int i = 1; i <= n; i++) {
parent[i] = i;
rank[i] = 1;
}
foreach (var edge in edges) {
int u = edge[0], v = edge[1];
if (!Union(u, v, parent, rank)) {
return edge;
}
}
return new int[0];
}
private int Find(int node, int[] parent) {
if (parent[node] != node) {
parent[node] = Find(parent[node], parent);
}
return parent[node];
}
private bool Union(int u, int v, int[] parent, int[] rank) {
int rootU = Find(u, parent);
int rootV = Find(v, parent);
if (rootU == rootV) return false;
if (rank[rootU] > rank[rootV]) {
parent[rootV] = rootU;
} else if (rank[rootU] < rank[rootV]) {
parent[rootU] = rootV;
} else {
parent[rootV] = rootU;
rank[rootU]++;
}
return true;
}
}
```
| 4 | 0 |
['C#']
| 0 |
redundant-connection
|
This One Trick with Union-Find Will Blow Your Mind! 🚀| beats 100% |
|
this-one-trick-with-union-find-will-blow-f29k
|
IntuitionThe problem requires us to find the redundant edge in a graph that forms a cycle. A cycle in a graph means there is an edge that connects two vertices
|
typecaster99
|
NORMAL
|
2025-01-29T03:29:49.548141+00:00
|
2025-01-29T03:29:49.548141+00:00
| 406 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The problem requires us to find the redundant edge in a graph that forms a cycle. A cycle in a graph means there is an edge that connects two vertices that are already connected through some other path. Using Union-Find (Disjoint Set Union - DSU), we can efficiently detect cycles by checking if two vertices of an edge are already in the same set. If they are, the edge is redundant.
# Approach
<!-- Describe your approach to solving the problem. -->
1. Initialize DSU:
- Create a parent array to keep track of the root parent of each vertex.
- Create a size array to implement union by size for optimization.
2. Process Each Edge:
- For each edge, find the root parent of both vertices using the find function.
- If the root parents are the same, the edge is redundant and forms a cycle.
- If the root parents are different, perform a union operation to merge the two sets.
3. Return the Redundant Edge:
- The last edge that forms a cycle is the redundant edge.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
$$O(Nα(N))$$
Here,
N is the number of edges.
The find and union operations in DSU are nearly constant time due to path compression and union by size, where $α(N)$ is the inverse Ackermann function.
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
$$O(N)$$
We use two arrays (parent and size) of size N+1 to store the DSU information.
# Code
```cpp []
class Solution {
class DSU{
vector<int> parent;
vector<int> sz;
public:
DSU(int n){
for(int i=0; i<=n; i++){
parent.push_back(i);
sz.push_back(1);
}
}
int find(int u){
if(parent[u] != u){
parent[u] = find(parent[u]);
}
return parent[u];
}
void unionBySize(int u, int v){
int pu = find(u);
int pv = find(v);
if(pu!=pv){
if(sz[pu]>= sz[pv]){
parent[pv] = pu;
sz[pu]+=sz[pv];
}
else{
parent[pu] = pv;
sz[pv]+=sz[pu];
}
}
}
};
public:
vector<int> findRedundantConnection(vector<vector<int>>& edges) {
int n = edges.size();
DSU dsu(n);
vector<int> ans;
for(int i=0; i<n; i++){
int x = edges[i][0];
int y = edges[i][1];
int px = dsu.find(x);
int py = dsu.find(y);
if(px == py){
ans = edges[i];
}
else{
dsu.unionBySize(px,py);
}
}
return ans;
}
};
```
```java []
import java.util.*;
class Solution {
class DSU {
int[] parent;
int[] size;
public DSU(int n) {
parent = new int[n + 1];
size = new int[n + 1];
for (int i = 0; i <= n; i++) {
parent[i] = i; // Each node is its own parent initially
size[i] = 1; // Each set has size 1 initially
}
}
// Find the root parent of a node with path compression
public int find(int u) {
if (parent[u] != u) {
parent[u] = find(parent[u]); // Path compression
}
return parent[u];
}
// Union two sets by size
public void unionBySize(int u, int v) {
int pu = find(u);
int pv = find(v);
if (pu != pv) {
if (size[pu] >= size[pv]) {
parent[pv] = pu;
size[pu] += size[pv];
} else {
parent[pu] = pv;
size[pv] += size[pu];
}
}
}
}
public int[] findRedundantConnection(int[][] edges) {
int n = edges.length;
DSU dsu = new DSU(n);
int[] result = new int[2];
for (int[] edge : edges) {
int x = edge[0];
int y = edge[1];
int px = dsu.find(x);
int py = dsu.find(y);
if (px == py) {
// If both nodes are in the same set, this edge is redundant
result[0] = x;
result[1] = y;
} else {
// Otherwise, union the two sets
dsu.unionBySize(x, y);
}
}
return result;
}
}
```
```python []
from typing import List
class DSU:
def __init__(self, n: int):
self.parent = list(range(n + 1)) # Each node is its own parent initially
self.size = [1] * (n + 1) # Each set has size 1 initially
def find(self, u: int) -> int:
if self.parent[u] != u:
self.parent[u] = self.find(self.parent[u]) # Path compression
return self.parent[u]
def union_by_size(self, u: int, v: int) -> None:
pu, pv = self.find(u), self.find(v)
if pu != pv:
if self.size[pu] >= self.size[pv]:
self.parent[pv] = pu
self.size[pu] += self.size[pv]
else:
self.parent[pu] = pv
self.size[pv] += self.size[pu]
class Solution:
def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:
n = len(edges)
dsu = DSU(n)
for x, y in edges:
px, py = dsu.find(x), dsu.find(y)
if px == py:
return [x, y] # This edge is redundant
else:
dsu.union_by_size(x, y)
return []
```
Please upvote if you found this useful.
| 4 | 0 |
['Union Find', 'Python', 'C++', 'Java']
| 0 |
redundant-connection
|
Union-Find ✅ | Beats 100%🔥| Detailed Explanation Solution ✅
|
union-find-beats-100-detailed-explanatio-1f83
|
🔗 Redundant Connection - Java Solution 🏗️📜 Problem StatementGiven a graph with N nodes, we have N edges forming an undirected tree. However, there's one extra e
|
___shubh404
|
NORMAL
|
2025-01-29T01:13:21.161668+00:00
|
2025-01-29T01:13:21.161668+00:00
| 522 | false |
---
# 🔗 **Redundant Connection** - Java Solution 🏗️
---
## 📜 **Problem Statement**
Given a graph with **N** nodes, we have `N` edges forming an **undirected tree**. However, there's **one extra edge**, making the graph **cyclic**.
Your task is to **find and remove that extra edge** so that the remaining graph is a **tree**.
✅ The graph consists of **N nodes labeled from `1` to `N`**.
✅ There will always be **exactly one redundant connection**.
✅ Return the **edge that, when removed, leaves a tree**.
✅ If multiple answers exist, return the edge **that appears last** in the input.
---
## 🧠 **Understanding the Problem with an Example**
### **Input**
```plaintext
edges = [[1,2], [1,3], [2,3]]
```
### **Graph Representation**
Before removing any edge, the graph looks like this:
```
1
/ \
2 - 3
```
### **Expected Output**
```plaintext
[2,3]
```
Removing `[2,3]` makes it a valid **tree**.
---
## 🔥 **Approach: Union-Find (Disjoint Set)**
### ✨ **Why Use Union-Find?**
Union-Find is a **powerful** data structure used to detect **cycles** in an **undirected graph** efficiently.
### ✅ **Key Idea**
- If **two nodes are already connected** and we try to add an edge **between them**, it **creates a cycle**. 🚨
- The first such edge in the list is our **answer**!
### 🔑 **Steps to Solve the Problem**
1️⃣ **Initialize a Parent Array**:
- `p[i]` stores the parent of node `i`.
- Initially, each node is its **own parent** (`p[i] = i`).
2️⃣ **Use Path Compression for Union-Find**:
- For every edge `[u, v]`, **find their root parents**.
- If they have the **same root**, the edge is **redundant**.
- Otherwise, **union** them by making one parent of the other.
---
## 💻 **Java Code**
```java
class Solution {
public int[] findRedundantConnection(int[][] edges) {
int n = edges.length;
int[] parent = new int[n + 1]; // Parent array
// Initialize parent array: each node is its own parent
for (int i = 1; i <= n; i++) {
parent[i] = i;
}
int[] ans = {0, 0}; // Store the redundant edge
for (int[] edge : edges) {
int p1 = find(parent, edge[0]); // Find root of first node
int p2 = find(parent, edge[1]); // Find root of second node
if (p1 == p2) {
ans = edge; // If they have the same root, this edge is redundant
} else {
parent[p2] = p1; // Union: connect p2 to p1
}
}
return ans;
}
// Union-Find with Path Compression
private int find(int[] parent, int node) {
while (parent[node] != node) {
parent[node] = parent[parent[node]]; // Path compression
node = parent[node];
}
return node;
}
}
```
---
## 🧩 **Step-by-Step Execution**
Let’s walk through an example to see how this works!
### **Example**
```plaintext
edges = [[1,2], [1,3], [2,3]]
```
### **Initialization**
```plaintext
parent[] = [0, 1, 2, 3] (Each node is its own parent)
```
### **Processing Edges**
1️⃣ **Processing `[1,2]`**
- Find `parent(1) = 1`, `parent(2) = 2`.
- Since they have **different parents**, merge them.
- `parent[2] = 1`.
- **Updated Parent Array**: `[0, 1, 1, 3]`.
2️⃣ **Processing `[1,3]`**
- Find `parent(1) = 1`, `parent(3) = 3`.
- Merge them: `parent[3] = 1`.
- **Updated Parent Array**: `[0, 1, 1, 1]`.
3️⃣ **Processing `[2,3]`**
- Find `parent(2) = 1`, `parent(3) = 1`.
- **They have the same root!** 🚨 **Cycle detected!**
- **Redundant edge is `[2,3]`**.
### **Final Output**
```plaintext
[2,3]
```
---
## 📊 **Time and Space Complexity**
| Complexity | Value |
|------------|-------|
| 🕒 Time Complexity | **O(N α(N)) ≈ O(N)** *(Almost linear due to path compression)* |
| 🗄 Space Complexity | **O(N)** *(For parent array storage)* |
---
## 🔥 **Why is This Approach Efficient?**
✅ **Avoids building an explicit graph** (no adjacency list).
✅ **Path compression ensures** nearly constant time `find()` operations.
✅ **Runs in almost linear time**: **O(N)** (because of the inverse Ackermann function `α(N)`).
---
## 🎯 **Summary**
- ✅ Used **Union-Find** to detect cycles efficiently.
- ✅ **Path Compression** ensures optimal time complexity.
- ✅ **Finds the last redundant edge**, which, when removed, leaves a valid tree.
- ✅ Works in **O(N)** time.
---
## 🎉 **Final Thoughts**
💡 **Mastering Union-Find is crucial for graph problems!**
📌 This problem is a great **practice for cycle detection** and **graph connectivity**.
---
**🙌🏻 If this solution and explanation helped, consider upvoting! Let’s ace those coding challenges together!** ✨
| 4 | 0 |
['Union Find', 'Graph', 'Java']
| 4 |
redundant-connection
|
DFS based O(N^2) solution w comments
|
dfs-based-on2-solution-w-comments-by-sur-s1qh
|
Complexity\n- Time complexity:\nO(n^2)\n\n- Space complexity:\nO(n)\n\n# Code\n\nclass Solution {\n\n public int[] findRedundantConnection(int[][] edges) {\n
|
surbhisharma_2
|
NORMAL
|
2023-07-19T20:01:29.497577+00:00
|
2023-07-19T20:03:55.183890+00:00
| 993 | false |
# Complexity\n- Time complexity:\nO(n^2)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution {\n\n public int[] findRedundantConnection(int[][] edges) {\n\n int n = edges.length;\n\n ArrayList<ArrayList<Integer>> graph = new ArrayList<>();\n\n for (int i = 0; i < n; i++) {\n graph.add(new ArrayList<>());\n }\n\n for (int[] edge : edges) {\n int u = edge[0] - 1;\n int v = edge[1] - 1;\n\n boolean[] visited = new boolean[n]; //reinitializing the `visited` array before we start exploring again\n/*\nChecking if there is already a path between the two nodes before adding an edge, this way we can identify the additional edge that needs to be removed.\n*/\n if (dfs(graph, u, v, visited)) {\n return edge;\n }\n\n graph.get(u).add(v); //otherwise add to the graph\n graph.get(v).add(u);\n }\n \n return new int[0]; // returning empty list\n }\n\n private boolean dfs(ArrayList<ArrayList<Integer>> graph, int u, int v, boolean[] visited) {\n\n if (u == v) { // if src(u) reaches dest(v), then stop thr DFS\n return true;\n }\n\n visited[u] = true;\n\n for (int next : graph.get(u)) {\n if (!visited[next]) {\n if (dfs(graph, next, v, visited)) {\n return true;\n }\n }\n }\n return false;\n }\n}\n\n\n```
| 4 | 0 |
['Depth-First Search', 'Java']
| 2 |
redundant-connection
|
Union-Find | Cycle-detection | C++ Solution
|
union-find-cycle-detection-c-solution-by-qyn3
|
Algorithm\n1. The edge wich joins nodes of same set is a redundent edge\n\nclass DisjointSet {\n vector<int> parent, size;\npublic:\n DisjointSet(int n) {
|
solvedORerror
|
NORMAL
|
2023-06-01T09:10:30.110957+00:00
|
2023-06-01T09:10:30.111000+00:00
| 1,547 | false |
**Algorithm**\n1. The edge wich joins nodes of same set is a redundent edge\n```\nclass DisjointSet {\n vector<int> parent, size;\npublic:\n DisjointSet(int n) {\n parent.resize(n + 1);\n size.resize(n + 1);\n for (int i = 0; i <= n; i++) {\n parent[i] = i;\n size[i] = 1;\n }\n }\n\n int find(int node) {\n if (node == parent[node])\n return node;\n return parent[node] = find(parent[node]);\n }\n bool unionBySize(int u, int v) {\n int ulp_u = find(u);\n int ulp_v = find(v);\n if (ulp_u == ulp_v) return false;\n if (size[ulp_u] < size[ulp_v]) {\n parent[ulp_u] = ulp_v;\n size[ulp_v] += size[ulp_u];\n }\n else {\n parent[ulp_v] = ulp_u;\n size[ulp_u] += size[ulp_v];\n }\n return true;\n }\n};\nclass Solution {\npublic:\n vector<int> findRedundantConnection(vector<vector<int>>& edges) {\n int mx=edges.size();\n DisjointSet ds(mx);\n for(auto &edge:edges){\n int u=edge[0];int v=edge[1];\n if(!ds.unionBySize(u,v)){\n return {u,v};\n }\n }\n return {-1,-1};\n }\n};\n```
| 4 | 0 |
['Union Find', 'C']
| 0 |
redundant-connection
|
✅[Python] Simple and Clean, beats 88%✅
|
python-simple-and-clean-beats-88-by-_tan-9brd
|
Please upvote if you find this helpful. \u270C\n\n\nThis is an NFT\n# Intuition\nThe problem asks us to find an edge in a graph that can be removed to make it a
|
_Tanmay
|
NORMAL
|
2023-05-22T19:21:04.214937+00:00
|
2023-05-22T19:24:09.348631+00:00
| 1,271 | false |
### Please upvote if you find this helpful. \u270C\n<img src="https://assets.leetcode.com/users/images/b8e25620-d320-420a-ae09-94c7453bd033_1678818986.7001078.jpeg" alt="Cute Robot - Stable diffusion" width="200"/>\n\n*This is an NFT*\n# Intuition\nThe problem asks us to find an edge in a graph that can be removed to make it a tree. A tree is an undirected graph that is connected and has no cycles. So, we need to find an edge that creates a cycle in the graph. One way to detect cycles in an undirected graph is to use the `Union-Find algorithm.`\n\n# Approach\n1. Initialize the `parent` array with each node being its own parent and the `rank` array with all elements set to 1.\n2. Define the `find` function that takes a node as input and returns its root parent using path compression.\n3. Define the `union` function that takes two nodes as input and merges their sets if they are not already in the same set. The function returns `False` if the two nodes are already in the same set (i.e., there is a cycle), otherwise it returns `True`.\n4. Iterate over each edge in the `edges` array and call the `union` function with the two nodes of the edge as input.\n5. If the `union` function returns `False`, return the current edge as it creates a cycle in the graph.\n\n# Complexity\n- Time complexity: $$O(n \\alpha(n))$$ where $$n$$ is the number of nodes in the graph and $$\\alpha(n)$$ is the inverse Ackermann function which grows very slowly and can be considered a constant for all practical purposes.\n- Space complexity: $$O(n)$$ where $$n$$ is the number of nodes in the graph.\n\n# Code\n```\nclass Solution:\n def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:\n # Initialize the parent array with each node being its own parent\n # and the rank array with all elements set to 1\n parent = [i for i in range(len(edges)+1)]\n rank = [1]*(len(edges)+1)\n \n # Define the find function that takes a node as input\n # and returns its root parent using path compression\n def find(n):\n p = parent[n]\n while p != parent[p]:\n parent[p] = parent[parent[p]]\n p = parent[p]\n return p\n \n # Define the union function that takes two nodes as input\n # and merges their sets if they are not already in the same set\n # The function returns False if the two nodes are already in the same set (i.e., there is a cycle)\n # otherwise it returns True\n def union(n1,n2):\n p1,p2 = find(n1),find(n2)\n if p1==p2:\n return False\n if rank[p1]>rank[p2]:\n parent[p2]=p1\n rank[p1]+=rank[p2]\n else:\n parent[p1]=p2\n rank[p2]+=rank[p1]\n return True\n \n # Iterate over each edge in the edges array and call the union function with the two nodes of the edge as input\n for n1,n2 in edges:\n if not union(n1,n2):\n # If the union function returns False, return the current edge as it creates a cycle in the graph\n return [n1,n2]\n```
| 4 | 0 |
['Union Find', 'Graph', 'Python', 'Python3']
| 0 |
redundant-connection
|
C++ Solution. || Using DFS
|
c-solution-using-dfs-by-shubhammishrabst-ulsf
|
\nclass Solution {\npublic:\n bool dfs(vector<vector<int>> &adj,vector<int> &visited,int v,int parent){\n visited[v]=1;\n for(int i=0;i<adj[v].
|
shubhammishrabst
|
NORMAL
|
2022-10-14T16:34:48.177063+00:00
|
2022-10-14T16:34:48.177107+00:00
| 1,508 | false |
```\nclass Solution {\npublic:\n bool dfs(vector<vector<int>> &adj,vector<int> &visited,int v,int parent){\n visited[v]=1;\n for(int i=0;i<adj[v].size();i++){\n if(!visited[adj[v][i]]){\n if(dfs(adj,visited,adj[v][i],v)){\n return true;\n }\n }else if(parent!=adj[v][i]){\n return true;\n }\n }\n return false;\n }\n vector<int> findRedundantConnection(vector<vector<int>>& edges) {\n vector<int> res;\n int n=edges.size();\n int minV=INT_MAX;\n vector<vector<int>> adj(n+1);\n for(int i=0;i<n;i++){\n adj[edges[i][0]].push_back(edges[i][1]);\n adj[edges[i][1]].push_back(edges[i][0]);\n vector<int> visited(n+1,0);\n if(dfs(adj,visited,edges[i][0],-1)){\n res={edges[i][0],edges[i][1]};\n break;\n }\n }\n return res;\n }\n};\n```
| 4 | 0 |
['Depth-First Search', 'C', 'C++']
| 4 |
redundant-connection
|
CPP || For each insertion checking whether cycle is formed
|
cpp-for-each-insertion-checking-whether-8lyyw
|
```\nclass Solution {\npublic:\n\n bool iscycle(int i,int parent,vector>&ans,vector&visited){\n \n visited[i]=1;\n \n for(auto el
|
Sanket_Jadhav
|
NORMAL
|
2022-09-07T03:49:34.048556+00:00
|
2022-09-07T03:49:34.048600+00:00
| 1,074 | false |
```\nclass Solution {\npublic:\n\n bool iscycle(int i,int parent,vector<vector<int>>&ans,vector<int>&visited){\n \n visited[i]=1;\n \n for(auto ele:ans[i]){\n if(!visited[ele]){\n if(iscycle(ele,i,ans,visited))return true;\n }\n \n else if(parent!=ele)return true;\n }\n \n visited[i]=0;\n return false;\n }\n \n vector<int> findRedundantConnection(vector<vector<int>>& edges) {\n \n vector<vector<int>>ans(edges.size()+1);\n vector<int>visited(edges.size()+1);\n \n for(int i=0;i<edges.size();i++){\n \n ans[edges[i][0]].push_back(edges[i][1]);\n ans[edges[i][1]].push_back(edges[i][0]);\n\n \n if(iscycle(edges[i][0],-1,ans,visited))return edges[i];\n \n }\n \n return {};\n }\n};
| 4 | 0 |
['C++']
| 0 |
redundant-connection
|
Best Java Solution 1ms | Union Find Notes
|
best-java-solution-1ms-union-find-notes-zco0v
|
\nclass Solution {\n int[] parent;\n int x,y;\n int[] res;\n public int[] findRedundantConnection(int[][] edges) {\n int n = edges.length;\n
|
vishalrajput__
|
NORMAL
|
2022-05-11T16:51:26.400485+00:00
|
2022-05-11T16:52:16.014317+00:00
| 90 | false |
```\nclass Solution {\n int[] parent;\n int x,y;\n int[] res;\n public int[] findRedundantConnection(int[][] edges) {\n int n = edges.length;\n parent = new int[n+1];\n res = new int[2];\n for(int i=1; i <= n; ++i){\n parent[i] = i;\n }\n for(int i = 0; i < n;++i){\n x = find_parent(edges[i][0]);\n y = find_parent(edges[i][1]);\n if(x == y){\n res[0] = edges[i][0];\n res[1] = edges[i][1];\n break;\n }\n Union(x,y);\n }\n return res;\n }\n public void Union(int x, int y){\n parent[x] = y;\n }\n \n public int find_parent(int a){\n if(a == parent[a]){\n return a;\n }\n else{\n return find_parent(parent[a]);\n }\n }\n}\n```\n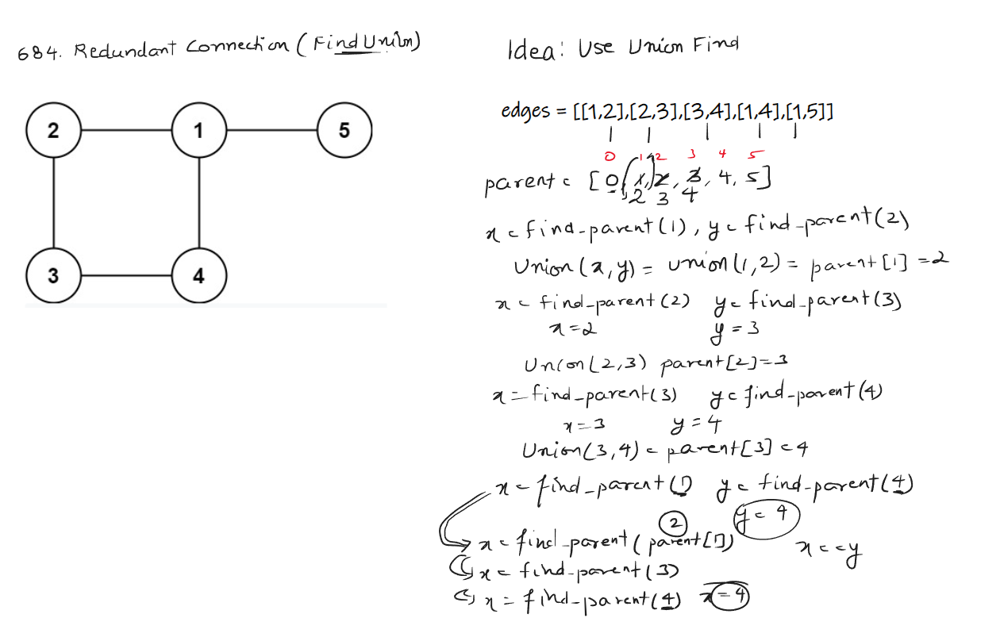\n
| 4 | 0 |
['Union Find', 'Graph']
| 0 |
redundant-connection
|
DSU | Java | Explained with Comments
|
dsu-java-explained-with-comments-by-sora-q4xq
|
Every line of code is explained using comments (hope I didn\'t go overboard with comments \uD83D\uDE05)\n\nclass Solution {\n \n // "parents" and "ranks"
|
sorabhtomar
|
NORMAL
|
2022-03-02T01:19:36.668234+00:00
|
2022-03-02T01:24:46.461497+00:00
| 396 | false |
Every line of code is explained using comments (hope I didn\'t go overboard with comments \uD83D\uDE05)\n```\nclass Solution {\n \n // "parents" and "ranks" arrays required for applying DSU\n int[] parents;\n int[] ranks;\n \n // v: vertex\n private int find(int v) {\n // using recursion, we\'ll find the "ultimate" leader after going from parent to parent (until v is its parent i.e. parents[v] == v), which will be the base case\n if(parents[v] == v) {\n return v;\n }\n \n // we got our leader\n int leader = find(parents[v]);\n // for efficiency, now we\'ll update our parent with leader directly (so that next time we won\'t have to travel that long). This step is called "path compression"\n parents[v] = leader;\n \n return leader;\n }\n \n public int[] findRedundantConnection(int[][] edges) {\n // tree: a connected, acyclic graph. Here, it is also "undirectional". \n // no. of "edges" for this tree = no. of "vertices" - 1\n \n // vc: vertices count\n int vc = edges.length;\n \n // We\'ll find the "redundant edge" using DSU (disjoint set union). For DSU, we actually need "edges" which are convenient given (instead of graph) \n // looking at the input, we observe that the vertices are 1-indexed (will take care of that)\n parents = new int[vc];\n ranks = new int[vc];\n \n // initialization of parents and ranks\n for(int i = 0; i < vc; i++) {\n // initially, for each vertex parent is itself and rank is 0\n parents[i] = i;\n ranks[i] = 0;\n }\n \n // preparation done for applying DSU: done using union() and find(). If we write a separate function union() for DSU (here done below), the above preparatory steps are done in there\n \n // now, we\'ll loop through each edge and check to see if it is redundant using DSU\n for(int i = 0; i < edges.length; i++) {\n // since vertices of the edges are given to be 1-indexed, we\'ll assume 1 as 0 (by subtracting u and v by 1 below)\n int u = edges[i][0]; u--;\n int v = edges[i][1]; v--;\n \n // lu: leader (group leader) of u, lv: leader (group leader) of v\n int lu = find(u);\n int lv = find(v);\n \n if(lu != lv) {\n // u and v belong to different groups \n // i.e. merging of those groups will take place (based on ranks of lu and lv)\n // smaller rank vertex will go into the group of larger rank vertex\n if(ranks[lu] < ranks[lv]) {\n // lu will make lv its parent\n parents[lu] = lv;\n \n } else if(ranks[lu] > ranks[lv]) {\n // lv will make lu its parent\n parents[lv] = lu;\n \n } else {\n // ranks[lu] == ranks[lv]\n // anyone can go in any group; but whoever\'s group it goes will increase its rank by 1\n parents[lu] = lv;\n ranks[lv]++; // increasing rank of lv by 1 (since lu merged its group under lv)\n \n }\n \n } else {\n // we found our redundant edge\n return edges[i];\n }\n }\n \n // some invalid edge (will not hit this case)\n return new int[] {-1, -1}; \n }\n}\n```
| 4 | 0 |
['Union Find', 'Graph', 'Java']
| 0 |
redundant-connection
|
C++ Soln. Union By Rank and Path Compression
|
c-soln-union-by-rank-and-path-compressio-q4uh
|
If You Like it Please Upvote. If you have any doubts feel free to ask in the comments.\n\nclass Solution {\npublic:\n int find(int parent[],int s){\n
|
AvaraKedavra
|
NORMAL
|
2021-05-30T14:33:06.866019+00:00
|
2021-05-30T14:34:07.626745+00:00
| 87 | false |
**If You Like it Please Upvote. If you have any doubts feel free to ask in the comments.**\n```\nclass Solution {\npublic:\n int find(int parent[],int s){\n if(parent[s]!=s){\n parent[s]=find(parent,parent[s]);\n }\n return parent[s];\n }\n void Union(int parent[],int rank[],int x,int y){\n if(rank[x]>rank[y]){\n parent[y]=x;\n }\n else if(rank[y]>rank[x]){\n parent[x]=y;\n }\n else{\n parent[x]=y;\n rank[y]++;\n } \n }\n vector<int> findRedundantConnection(vector<vector<int>>& edges) {\n vector<int>ans;\n int n=edges.size();\n int parent[n+1];\n int rank[n+1];\n for(int i=1;i<=n;++i){\n parent[i]=i;\n rank[i]=0;\n }\n for(int i=0;i<edges.size();++i){\n int x=find(parent,edges[i][0]);\n int y=find(parent,edges[i][1]);\n if(x==y){\n ans.push_back(edges[i][0]);\n ans.push_back(edges[i][1]);\n break;\n }\n else{\n Union(parent,rank,x,y);\n }\n }\n return ans;\n }\n};\n```
| 4 | 0 |
[]
| 0 |
redundant-connection
|
Two solutions - Disjoint Sets & DFS | Ruby
|
two-solutions-disjoint-sets-dfs-ruby-by-gxhso
|
\nUnion find\ndef find_redundant_connection(edges)\n @parent = Array.new(edges.size + 1, -1)\n edges.each do |u, v|\n return [u, v] if union(u, v)\n end\n
|
piyushsawaria
|
NORMAL
|
2021-01-29T15:55:48.634401+00:00
|
2021-01-29T17:43:17.081705+00:00
| 180 | false |
```\nUnion find\ndef find_redundant_connection(edges)\n @parent = Array.new(edges.size + 1, -1)\n edges.each do |u, v|\n return [u, v] if union(u, v)\n end\nend\n\ndef union(u, v)\n p1 = find(u)\n p2 = find(v)\n @parent[p2] = p1\n p1 == p2\nend\n\ndef find(x)\n return x if @parent[x] == -1\n @parent[x] = find(@parent[x])\n @parent[x]\nend\n\n```\n\n```\nDFS\ndef find_redundant_connection(edges)\n @graph = {}\n edges.each do |u, v|\n return [u, v] if dfs(u, v, Set.new)\n \n @graph[u] = @graph[u] ? @graph[u].push(v) : [v]\n @graph[v] = @graph[v] ? @graph[v].push(u) : [u]\n end\nend\n\ndef dfs(u, v, visited)\n visited.add(u)\n if @graph[u]\n return true if @graph[u].include?(v)\n @graph[u].each do |neighbour|\n unless visited.include?(neighbour)\n visited.add(neighbour)\n return true if dfs(neighbour, v, visited)\n end\n end\n end\n false\nend
| 4 | 0 |
['Depth-First Search', 'Union Find', 'Ruby']
| 1 |
redundant-connection
|
Union Find (Disjoint Set) | Explanation + Visual | [Python]
|
union-find-disjoint-set-explanation-visu-yeu6
|
TL;DR (visuals + explanation below) this problem can be solved by finding the minimum cost spanning tree with kruskal\'s algorithm via a disjoint set data stru
|
gtshepard
|
NORMAL
|
2020-12-27T22:15:52.470582+00:00
|
2020-12-28T21:02:55.987147+00:00
| 672 | false |
***TL;DR*** (visuals + explanation below) this problem can be solved by finding the ***minimum cost spanning tree*** with ***kruskal\'s algorithm*** via a ***disjoint set*** data structure. Our problem deals with special case of the *minimum cost spanning tree problem* where ***edge weights*** have a value of ```1``` and ties are broken by a predefined ordering. \n\n```python\nclass DisjointSet:\n def __init__(self, n):\n self.disjoint_set = [-1 for _ in range(n + 1)]\n self.disjoint_set[0] = float(\'-inf\')\n self.cycle = None\n \n def find(self, vertex):\n while self.disjoint_set[vertex] > 0:\n vertex = self.disjoint_set[vertex]\n return vertex, self.disjoint_set[vertex]\n \n def union(self, edge):\n u, v = edge\n s1, r1 = self.find(u)\n s2, r2 = self.find(v)\n if s1 != s2:\n if r1 <= r2:\n self.disjoint_set[s1] -= 1\n self.disjoint_set[s2] = s1\n else:\n self.disjoint_set[s2] -= 1\n self.disjoint_set[s1] = s2 \n else:\n self.cycle = edge \n \nclass Solution:\n def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:\n vertices = set()\n for u, v in edges:\n vertices.add(u)\n vertices.add(v)\n \n # number of dsitinct vertices \n n = len(vertices)\n disjoint_set = DisjointSet(n)\n \n for edge in edges:\n disjoint_set.union(edge)\n \n return disjoint_set.cycle\n```\n\n\n### Overview \n\nThe ***key observation*** to sovling this problem is to recognize that the ***tree*** we are asked to find is actually a ***spanning tree***.\n\na ***spanning tree*** of an undirected graph ```G``` is a subgraph of ```G``` that is a ***tree*** , ***contains all vertices*** of ```G```, and has the ***minimum possible number of edges***. (we define a tree as an undirected graph with no cycles for this problem). \n\nObserve the following graph.\n\n\n\nif we remove edge ```(1, 6)``` from the above graph, we get a spanning tree. becuase the graph is now ***acyclic*** (contains no cycles) , and still ***contains all vertices*** and does so with the ***minimum possible number of edges***. (their is more than one spanning tree for ```G``` this is just one).\n\n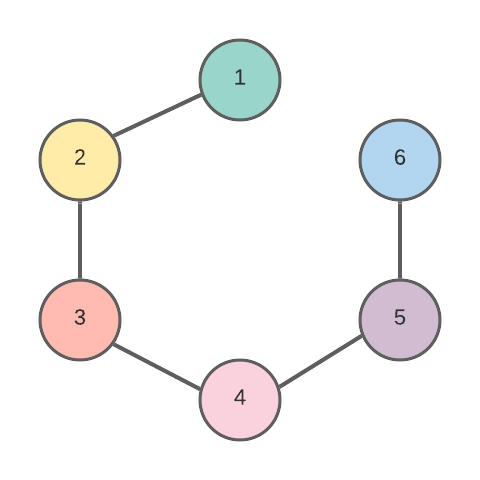\n\n\n ***Kruskal\'s Algorithm*** is a well known algorithm for finding the ***minimum cost spanning tree***. This problem is asking us to find the *minimum cost spanning tree* for the special case where all edge weights are```1``` and ties are broken by a predefined ordering. \n\n### Kruskal\'s Algorithm (Intuition) \n\nKruskal\'s is a greedy algoritm and says, start building a spanning tree by always taking the minimum cost edge, and keep going until all ```n``` vertices are included. \n\nif one keeps building our spanning tree in such a manner eventually we may choose an edge that results in a graph with a ***cycle***, in this event, do not include this edge in the ***spanning tree***.\n\nSince all edges in this problem have a weight of ```1```, take the edges in any order. Thus the order the edges are given will suffice. \n\n***Constructing the graph based on the order the edges are given...***\n\n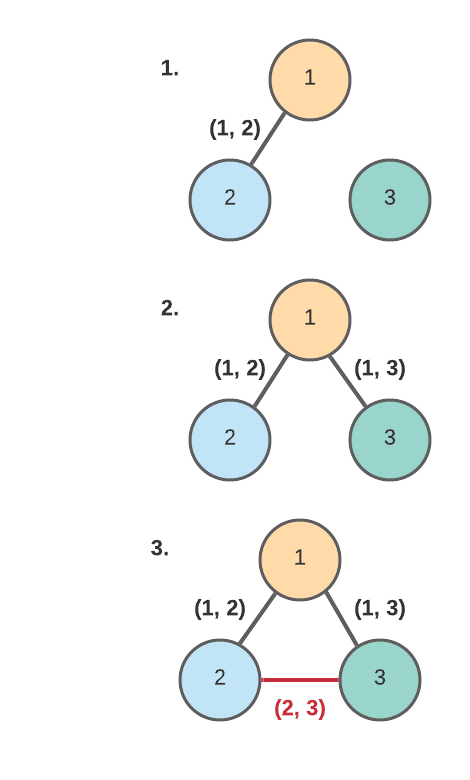\n\nAdding Edge ```(2, 3)``` in step 3 results in a cycle, thus it should not be included in the spanning tree. \n\nStep 2 in the diagram above is a minimum spanning tree, because it is an ***acyclic connected graph*** that includes all vertices with the ***minimum possible number of edges***. it is a minimum cost spanning tree because all edge weights added together have the lowest cost (there is an implicit weight of ```1```) there are other spanning trees with the same cost. any will suffice. \n\n\n### Kruskals (Implementation)\n\nA [disjoint set data structure](https://en.wikipedia.org/wiki/Disjoint_sets) makes implementing kruskal\'s algorithm straightforward.\n\n\nbelow is a visual walkthrough of kruskal\'s using an array based disjoint set implementation for this graph\n\n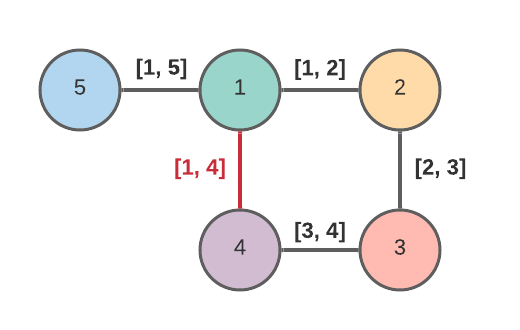\n\n\nHere is the walk through. \n\n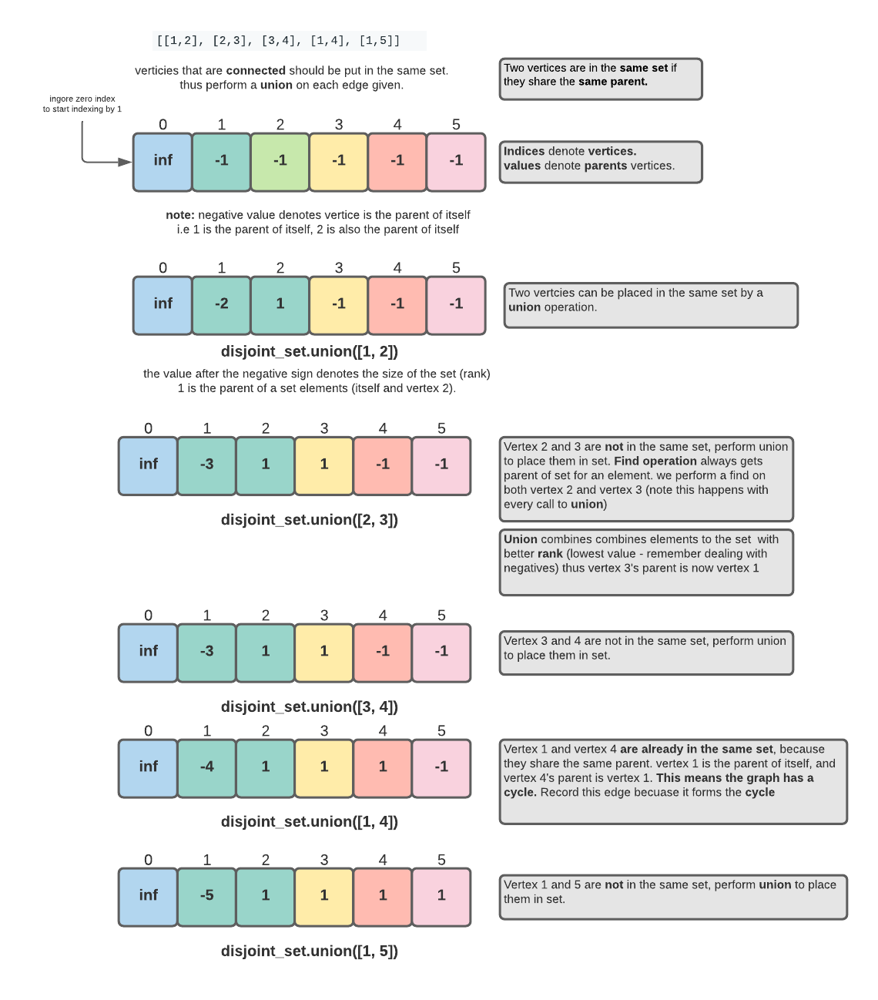\n\nNote that if the graph contains more than one cycle, just continue in the same fashion keeping track of the most recent cycle. the most recent cycle after all edges have been seen is the answer.\n\nFor an indepth of video walkthough of kruskals and disjoint sets \n[Disjoint Set](https://www.youtube.com/watch?v=wU6udHRIkcc&list=PLDN4rrl48XKpZkf03iYFl-O29szjTrs_O&index=17)\n
| 4 | 0 |
['Union Find', 'Python']
| 2 |
redundant-connection
|
JavaScript Clean Union Find
|
javascript-clean-union-find-by-control_t-jkz0
|
javascript\nvar findRedundantConnection = function(edges) {\n \n class UnionFind {\n constructor(n) {\n this.graph = [...Array(n)].map((
|
control_the_narrative
|
NORMAL
|
2020-07-23T06:41:35.869500+00:00
|
2020-07-23T06:41:35.869548+00:00
| 433 | false |
```javascript\nvar findRedundantConnection = function(edges) {\n \n class UnionFind {\n constructor(n) {\n this.graph = [...Array(n)].map((_, i) => i);\n this.extra = null;\n }\n \n find(id) {\n if(this.graph[id] === id) return id;\n this.graph[id] = this.find(this.graph[id]);\n return this.graph[id];\n }\n \n union(x, y) {\n const rootX = this.find(x);\n const rootY = this.find(y);\n if(rootX !== rootY) this.graph[rootY] = rootX;\n else this.extra = [x, y]\n }\n }\n \n const unionfind = new UnionFind(edges.length+1);\n \n for(let [u, v] of edges) {\n unionfind.union(u, v);\n }\n return unionfind.extra; \n};\n```
| 4 | 0 |
['Union Find', 'JavaScript']
| 0 |
redundant-connection
|
Python Union-Find (+ path compression)
|
python-union-find-path-compression-by-th-mbwz
|
Words are redundant\n\nclass Solution:\n def findRedundantConnection(self, edges):\n """\n :type edges: List[List[int]]\n :rtype: List[i
|
the_islander
|
NORMAL
|
2018-12-30T04:32:49.010317+00:00
|
2018-12-30T04:32:49.010365+00:00
| 266 | false |
Words are redundant\n```\nclass Solution:\n def findRedundantConnection(self, edges):\n """\n :type edges: List[List[int]]\n :rtype: List[int]\n """\n N = len(edges)\n parent = [i for i in range(N+1)]\n\n def find(node):\n if parent[node] == node:\n return node\n parent[node] = find(parent[node])\n return parent[node]\n \n def union(node1, node2):\n root1 = find(node1)\n root2 = find(node2)\n if root1 == root2:\n return False\n parent[root1] = root2\n return True\n \n for n1, n2 in edges:\n if not union(n1, n2):\n return [n1, n2]\n\n```
| 4 | 0 |
[]
| 0 |
redundant-connection
|
JavaScript Union Find and DFS solutions
|
javascript-union-find-and-dfs-solutions-tbgh5
|
\nvar findRedundantConnection = function(edges) {\n const dsu = new UnionFind(edges.length);\n for(let edge of edges) {\n const [u,v] = edge;\n
|
slkuo230
|
NORMAL
|
2018-11-29T17:37:01.892639+00:00
|
2018-11-29T17:37:01.892711+00:00
| 1,014 | false |
```\nvar findRedundantConnection = function(edges) {\n const dsu = new UnionFind(edges.length);\n for(let edge of edges) {\n const [u,v] = edge;\n if(!dsu.union(u, v)) {\n return edge;\n }\n }\n return [];\n};\n\nclass UnionFind {\n \n constructor(size) {\n this.parent = new Array(size);\n for(let i = 0; i < size; i++) {\n this.parent[i] = i;\n }\n this.rank = new Array(size);\n }\n \n find(x) {\n if(this.parent[x] !== x) {\n this.parent[x] = this.find(this.parent[x]);\n }\n return this.parent[x];\n }\n \n union(x,y) {\n let xr = this.find(x);\n let yr = this.find(y);\n if(xr === yr) {\n return false; // already have the same parent\n } else if(this.rank[xr] < this.rank[yr]) {\n this.parent[xr] = yr;\n } else if(this.rank[xr] > this.rank[yr]) {\n this.parent[yr] = xr;\n } else {\n // same height\n this.parent[yr] = xr;\n this.rank[xr]++;\n }\n return true;\n }\n}\n```\n\nDFS speed at 0% percentile lmao :D\n```\nconst adjList = {};\n\nfunction dfs(source, target, visited) {\n\n\tif(source === target) {\n\t\treturn true;\n\t}\n\n\tif(!visited[source]) {\n\t\tvisited[source] = true;\n\t}\n\n\tif(adjList[source] === undefined) return false;\n\n\tfor(let nei of adjList[source]) {\n\t\tif(visited[nei]) {\n\t\t\tcontinue;\n\t\t}\n\t\tif(dfs(nei, target, {...visited})) {\n\t\t\treturn true;\n\t\t}\n\t}\n\treturn false;\n} \n\nfor(let edge of edges) { \n\tconst [u,v] = edge;\n\tif(dfs(u,v,{})) {\n\t\treturn [u,v];\n\t}\n\tif(!adjList[u]) {\n\t\tadjList[u] = [];\n\t}\n\tif(!adjList[v]) {\n\t\tadjList[v] = [];\n\t}\n\tadjList[u].push(v);\n\tadjList[v].push(u);\n}\n```
| 4 | 0 |
[]
| 0 |
redundant-connection
|
C++ Solution || DSU Solution || Detailed Explanation
|
c-solution-dsu-solution-detailed-explana-nvck
|
IntuitionThe problem requires us to find an edge in a graph that, if removed, results in a tree. A tree is an acyclic connected graph, meaning that the addition
|
Rohit_Raj01
|
NORMAL
|
2025-01-29T07:31:28.976826+00:00
|
2025-01-29T07:31:28.976826+00:00
| 248 | false |
# Intuition
The problem requires us to find an edge in a graph that, if removed, results in a tree. A tree is an acyclic connected graph, meaning that the additional edge creates a cycle. The problem can be solved using **Disjoint Set Union (DSU)** or **Union-Find**.
# Approach
1. **Use DSU (Disjoint Set Union)**: We will maintain a **parent** and **size** array to keep track of connected components.
2. **Find the parent of each node**: Using path compression, we efficiently find the representative of the set a node belongs to.
3. **Union by size**: We merge smaller sets into larger ones to keep the DSU operations efficient.
4. **Detect cycle**: If both nodes of an edge have the same parent, then that edge creates a cycle and is the redundant connection.
5. **Return the redundant edge**: The first edge that creates a cycle is our answer.
# Complexity Analysis
- **Time Complexity**: $$O(n \alpha(n))$$, where $$\alpha(n)$$ is the inverse Ackermann function, which is nearly constant.
- **Space Complexity**: $$O(n)$$ for storing the parent and size arrays.
# Code
```cpp
class dsu {
public:
vector<int> parent, size;
dsu(int n) {
parent.resize(n + 1, 0);
size.resize(n + 1, 1);
for (int i = 0; i < n; i++) {
parent[i] = i;
size[i] = 1;
}
}
int findparent(int node) {
if (node == parent[node]) {
return node;
}
return parent[node] = findparent(parent[node]); // Path compression
}
void unionbysize(int u, int v) {
int ulp = findparent(u);
int vlp = findparent(v);
if (ulp == vlp) return;
if (size[ulp] < size[vlp]) {
parent[ulp] = vlp;
size[vlp] += size[ulp];
} else {
parent[vlp] = ulp;
size[ulp] += size[vlp];
}
}
};
class Solution {
public:
vector<int> findRedundantConnection(vector<vector<int>>& edges) {
int n = edges.size();
dsu ds(n);
for (auto it : edges) {
if (ds.findparent(it[0]) == ds.findparent(it[1])) {
return {it[0], it[1]};
}
ds.unionbysize(it[0], it[1]);
}
return {};
}
};
```
## Explanation with Example
**Input:**
```cpp
edges = {{1,2}, {1,3}, {2,3}}
```
**Processing:**
1. `1-2` → No cycle, so we union `1` and `2`.
2. `1-3` → No cycle, so we union `1` and `3`.
3. `2-3` → Both nodes belong to the same set → Cycle detected!
**Output:**
```cpp
{2,3}
```
## Edge Cases Considered
- A graph with no redundant connections (already a tree).
- A graph where the last edge forms the cycle.
- A case with multiple cycles (only the first redundant edge is returned).

| 3 | 0 |
['Union Find', 'Graph', 'C++']
| 0 |
redundant-connection
|
BEATS 100% USERS
|
beats-100-users-by-shahivaibhav16-f5bj
|
IntuitionThe intuition was to return the edge which was already connected to the component.Example:-Input: edges = [[1,2],[1,3],[2,3]]
Output: [2,3]Let's say a
|
shahivaibhav16
|
NORMAL
|
2025-01-29T04:03:20.929191+00:00
|
2025-01-29T04:03:20.929191+00:00
| 254 | false |
# Intuition
The intuition was to return the edge which was already connected to the component.Example:-
**Input**: edges = [[1,2],[1,3],[2,3]]
**Output**: [2,3]
**Let's say a = [1, 2], b = [1, 3], c = [2, 3]**
Starting from "a" 1 gets connected to 2, then in "b" 1 gets connected to 3, so 3 is also connected to 2, then coming to "c" as 2 is already connected to 3 we return this edge.
# Approach
As we are using the concept of connecting components we will be using Disjoint Sets.
In this particular problem i have used **Union by Size**
# Complexity
- Time complexity:
Find: α(n) is the Inverse Ackermann function (almost constant).
Union: O(α(n)) due to Union by Size.
**Overall Time Complexity = O(n)**
- Space complexity:
O(n)
# Code
```cpp []
class Solution {
public:
vector<int> parent;
vector<int> size;
int findParent(int x){
if(parent[x] == x) return x;
return parent[x] = findParent(parent[x]);
}
void UnionBySize(int x, int y){//Join components on based of size
int parent_x = findParent(x);
int parent_y = findParent(y);
if(size[parent_x] > size[parent_y]){
parent[parent_y] = parent_x;
size[parent_x] += size[parent_y];
}
else{
parent[parent_x] = parent_y;
size[parent_y] += size[parent_x];
}
}
vector<int> findRedundantConnection(vector<vector<int>>& edges) {
int n = edges.size();
parent.resize(n);
size.resize(n, 1);
for(int i = 0; i < n; i++){
parent[i] = i;
}
for(const auto&edge : edges){
//As Edges are from 1 to n , for our indexing we will subtract 1
int x = edge[0] - 1;
int y = edge[1] - 1;
int parent_x = findParent(x);
int parent_y = findParent(y);
if(parent_x == parent_y){//Component is already connected
return edge;
}else{//Join the Components
UnionBySize(x, y);
}
}
return {};
}
};
```
| 3 | 0 |
['Union Find', 'Graph', 'C++']
| 1 |
redundant-connection
|
✅✅Beats 100%🔥C++🔥Python|| 🚀🚀Super Simple and Efficient Solution🚀🚀||🔥Python🔥C++✅✅
|
beats-100cpython-super-simple-and-effici-9eo2
|
Complexity
Time complexity: O(n)
Space complexity: O(n)
⬆️👇⬆️UPVOTE it⬆️👇⬆️Code⬆️👇⬆️UPVOTE it⬆️👇⬆️
|
shobhit_yadav
|
NORMAL
|
2025-01-29T03:01:26.852922+00:00
|
2025-01-29T03:01:26.852922+00:00
| 639 | false |
# Complexity
- Time complexity: $$O(n)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(n)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
⬆️👇⬆️UPVOTE it⬆️👇⬆️
# Code
```cpp []
class UnionFind {
public:
UnionFind(int n) : id(n), rank(n) {
iota(id.begin(), id.end(), 0);
}
bool unionByRank(int u, int v) {
const int i = find(u);
const int j = find(v);
if (i == j)
return false;
if (rank[i] < rank[j]) {
id[i] = j;
} else if (rank[i] > rank[j]) {
id[j] = i;
} else {
id[i] = j;
++rank[j];
}
return true;
}
private:
vector<int> id;
vector<int> rank;
int find(int u) {
return id[u] == u ? u : id[u] = find(id[u]);
}
};
class Solution {
public:
vector<int> findRedundantConnection(vector<vector<int>>& edges) {
UnionFind uf(edges.size() + 1);
for (const vector<int>& edge : edges) {
const int u = edge[0];
const int v = edge[1];
if (!uf.unionByRank(u, v))
return edge;
}
throw;
}
};
```
```python []
class UnionFind:
def __init__(self, n: int):
self.id = list(range(n))
self.rank = [0] * n
def unionByRank(self, u: int, v: int) -> bool:
i = self._find(u)
j = self._find(v)
if i == j:
return False
if self.rank[i] < self.rank[j]:
self.id[i] = j
elif self.rank[i] > self.rank[j]:
self.id[j] = i
else:
self.id[i] = j
self.rank[j] += 1
return True
def _find(self, u: int) -> int:
if self.id[u] != u:
self.id[u] = self._find(self.id[u])
return self.id[u]
class Solution:
def findRedundantConnection(self, edges: list[list[int]]) -> list[int]:
uf = UnionFind(len(edges) + 1)
for edge in edges:
u, v = edge
if not uf.unionByRank(u, v):
return edge
```
⬆️👇⬆️UPVOTE it⬆️👇⬆️
| 3 | 0 |
['Depth-First Search', 'Breadth-First Search', 'Union Find', 'Graph', 'C++', 'Python3']
| 0 |
minimum-remove-to-make-valid-parentheses
|
Super simple Python solution with explanation. Faster than 100%, Memory Usage less than 100%
|
super-simple-python-solution-with-explan-g0la
|
Convert string to list, because String is an immutable data structure in Python and it\'s much easier and memory-efficient to deal with a list for this task.\n2
|
dreamcoder21
|
NORMAL
|
2020-05-31T17:51:07.298920+00:00
|
2020-05-31T17:52:22.421239+00:00
| 35,199 | false |
1. Convert string to list, because String is an immutable data structure in Python and it\'s much easier and memory-efficient to deal with a list for this task.\n2. Iterate through list\n3. Keep track of indices with open parentheses in the stack. In other words, when we come across open parenthesis we add an index to the stack.\n4. When we come across close parenthesis we pop an element from the stack. If the stack is empty we replace current list element with an empty string\n5. After iteration, we replace all indices we have in the stack with empty strings, because we don\'t have close parentheses for them.\n6. Convert list to string and return\n\n```\ndef minRemoveToMakeValid(self, s: str) -> str:\n s = list(s)\n stack = []\n for i, char in enumerate(s):\n if char == \'(\':\n stack.append(i)\n elif char == \')\':\n if stack:\n stack.pop()\n else:\n s[i] = \'\'\n while stack:\n s[stack.pop()] = \'\'\n return \'\'.join(s)\n```\n\nTime complexity is O(n)\nMemory complexity is O(n)
| 611 | 0 |
['Python', 'Python3']
| 42 |
minimum-remove-to-make-valid-parentheses
|
Java/C++ Stack
|
javac-stack-by-votrubac-4aqo
|
Intuition\nTo make the string valid with minimum removals, we need to get rid of all parentheses that do not have a matching pair.\n\n1. Push char index into th
|
votrubac
|
NORMAL
|
2019-11-03T04:06:48.610846+00:00
|
2019-12-02T20:35:57.660559+00:00
| 69,244 | false |
#### Intuition\nTo make the string valid with minimum removals, we need to get rid of all parentheses that do not have a matching pair.\n\n1. Push char index into the stack when we see `\'(\'`.\n\n2. Pop from the stack when we see `\')\'`.\n\n\t- If the stack is empty, then we have `\')\'` without the pair, and it needs to be removed.\n\n3. In the end, the stack will contain indexes of `\'(\'` without the pair, if any. We need to remove all of them too. \n\n**Update:** check out the new approach 2 that collects indexes of all mismatched parentheses, and removes them right-to-left.\n\n#### Approach 1: Stack and Placeholder\n\nWe mark removed parentheses with `\'*\'`, and erase all of them in the end.\n\n**Java**\n```Java\npublic String minRemoveToMakeValid(String s) {\n StringBuilder sb = new StringBuilder(s);\n Stack<Integer> st = new Stack<>();\n for (int i = 0; i < sb.length(); ++i) {\n if (sb.charAt(i) == \'(\') st.add(i);\n if (sb.charAt(i) == \')\') {\n if (!st.empty()) st.pop();\n else sb.setCharAt(i, \'*\');\n }\n }\n while (!st.empty())\n sb.setCharAt(st.pop(), \'*\');\n return sb.toString().replaceAll("\\\\*", "");\n}\n```\n**C++**\n```CPP\nstring minRemoveToMakeValid(string s) {\n stack<int> st;\n for (auto i = 0; i < s.size(); ++i) {\n if (s[i] == \'(\') st.push(i);\n if (s[i] == \')\') {\n if (!st.empty()) st.pop();\n else s[i] = \'*\';\n }\n }\n while (!st.empty()) {\n s[st.top()] = \'*\';\n st.pop();\n }\n s.erase(remove(s.begin(), s.end(), \'*\'), s.end());\n return s;\n}\n```\n#### Approach 2: Stack with Tracking\n\nInstead of using placeholders, we can track indexes of all mismatched parentheses, and erase them in the end going right-to-left. This idea was inspired by [dibdidib](https://leetcode.com/dibdidib/).\n\nWe can introduce another stack to collect indexes of mismatched `\')\'`, or we can use the same stack and mark mismatched `\')\'` somehow. Here, we just negate the index to indicate `\')\'`.\n\n> Note that I am adding `1` to make the index `1`-based. You cannot tell if zero is negated :)\n\n**Java**\n```Java\npublic String minRemoveToMakeValid(String s) {\n StringBuilder sb = new StringBuilder(s);\n Stack<Integer> st = new Stack();\n for (int i = 0; i < sb.length(); ++i) {\n if (sb.charAt(i) == \'(\') st.add(i + 1);\n if (sb.charAt(i) == \')\') {\n if (!st.empty() && st.peek() >= 0) st.pop();\n else st.add(-(i + 1));\n }\n }\n while (!st.empty())\n sb.deleteCharAt(Math.abs(st.pop()) - 1);\n return sb.toString();\n}\n```\nIf we want to optimize for the worst-case scenario, we should avoid `deleteCharAt` inside the loop. Instead, we can copy characters that do not appear in the stack into another string builder. Since characters in the stack are naturally sorted, we can use two-pointer technique to do it in the linear time.\n> Note that for the OJ test cases, the runtime of this solution is a bit worse than for `deleteCharAt`.\n```\npublic String minRemoveToMakeValid(String s) {\n StringBuilder sb = new StringBuilder(s), sb1 = new StringBuilder();\n Stack<Integer> st = new Stack();\n for (int i = 0; i < sb.length(); ++i) {\n if (sb.charAt(i) == \'(\') st.add(i + 1);\n if (sb.charAt(i) == \')\') {\n if (!st.empty() && st.peek() >= 0) st.pop();\n else st.add(-(i + 1));\n }\n }\n for(int i = 0, j = 0; i < sb.length(); ++i) {\n if (j >= st.size() || i != Math.abs(st.elementAt(j)) - 1) {\n sb1.append(sb.charAt(i));\n } else ++j;\n }\n return sb1.toString();\n}\n```\n**Complexity Analysis**\n- Time: O(n). We process each character once, or twice for \'single\' `\'(\'`.\n- Memory: O(n) for the stack.
| 541 | 4 |
[]
| 76 |
minimum-remove-to-make-valid-parentheses
|
100% Beat | Easy 2 Approaches Stack & Without Stack || Detailed Explanation
|
100-beat-easy-2-approaches-stack-without-qzsw
|
Note: Code is Re Formatted using chatgpt for bettter Comments and variable names so that you can better understand..\n# Personal opinion\nLeetcode is trying to
|
ashimkhan
|
NORMAL
|
2024-04-06T00:10:29.940343+00:00
|
2024-04-06T13:57:41.944723+00:00
| 50,202 | false |
*Note: Code is Re Formatted using chatgpt for bettter Comments and variable names so that you can better understand..*\n# Personal opinion\nLeetcode is trying to teach us Stack DS so before doing this you should try the daily problem of day before yesterday\nhttps://leetcode.com/problems/maximum-nesting-depth-of-the-parentheses/description/ and then yesterday \nhttps://leetcode.com/problems/make-the-string-great/description/\nand then this problem. \ni hope next day we will get another problem of stack DS.\n# Intuition\n\n<!-- Describe your first thoughts on how to solve this problem. -->\nImagine a shoe store where each customer needs a matching pair of shoes.\n\n**Preparing:**\n\n- The store manager sets up empty shelves for left and right shoes (startPart and endPart).\n- They get a list of all customers\' shoe requests (char[] arr).\n- They have a counter to track the number of customers who still need a left shoe (openParenthesesCount).\n\n**First Pass: Finding Extra Right Shoes:**\n\n- The manager goes through the list one customer at a time.\n- If a customer needs a left shoe (arr[i] == \'(\'), they increase the counter.\n- If a customer needs a right shoe (`arr[i] == \')\'), they check:\n- If no customers need left shoes (openParenthesesCount == 0), the right shoe is extra (arr[i] = \'*\'). They mark it for return.\n- If there are customers needing left shoes, a pair is made, and the counter goes down.\n\n**Second Pass: Finding Extra Left Shoes:**\n\n- The manager starts from the end of the list, looking for extra left shoes.\n- If a customer needs a left shoe (arr[i] == \'(\') and there are still customers needing right shoes (openParenthesesCount > 0), the left shoe is extra. They mark it for return.\n\n **Arranging the Shelves:**\n\n- The manager takes all non-marked shoes (arr[i] != \'*\') and puts them neatly on the shelves.\n\n**Displaying the Shoes:**\n\n- They beautifully display the matching pairs from the shelves (result).\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n**Initialization:**\n- Initialize pointers for the start and end of the string, variables to store the start and end parts of the string, and the final result. Convert the input string into a character array for easier manipulation.\n\n**First Pass:** \n- Iterate through the string from left to right. Track the count of open parentheses encountered. If an excess closing parenthesis is encountered (i.e., a closing parenthesis with no matching opening parenthesis), mark it with \'*\'. Keep track of the count of open parentheses encountered.\n\n**Second Pass:** \n- Iterate through the string from right to left. If there are excess opening parentheses remaining (i.e., opening parentheses with no matching closing parenthesis), mark them with \'*\'.\n\n**Filtering:** \n- Filter out the marked characters (\'*\') from the character array, leaving only the valid parentheses.\n\n**Construct Result:** \n- Construct the result string from the filtered character array.\n\n**Return Result:** \n- Return the final result string, which contains the minimum number of parentheses required to make the input string valid.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n# Approach -1 Without Stack\n```java []\n\nclass Solution {\n public String minRemoveToMakeValid(String s) {\n // Initialize pointers for the start and end of the string\n int startPointer = 0;\n int endPointer = s.length() - 1;\n\n String result;\n\n // Convert input string to character array for easier manipulation\n char[] arr = s.toCharArray();\n \n // Counter for open parentheses\n int openParenthesesCount = 0;\n\n // First pass: mark excess closing parentheses with \'*\'\n for (int i = 0; i < arr.length; i++) {\n if (arr[i] == \'(\')\n openParenthesesCount++;\n else if (arr[i] == \')\') {\n if (openParenthesesCount == 0)\n arr[i] = \'*\'; // Mark excess closing parentheses\n else\n openParenthesesCount--;\n }\n }\n\n // Second pass: mark excess opening parentheses from the end\n for (int i = arr.length - 1; i >= 0; i--) {\n if (openParenthesesCount > 0 && arr[i] == \'(\') {\n arr[i] = \'*\'; // Mark excess opening parentheses\n openParenthesesCount--;\n }\n }\n \n // Filter out marked characters and store the result in the character array\n int p = 0; // Pointer for updating the character array\n for (int i = 0; i < arr.length; i++) {\n if (arr[i] != \'*\')\n arr[p++] = arr[i];\n }\n\n // Construct the result string from the filtered character array\n result = new String(arr).substring(0, p);\n\n return result;\n }\n}\n```\n```C++ []\n\nclass Solution {\npublic:\n string minRemoveToMakeValid(string s) {\n // Initialize variables\n int openParenthesesCount = 0;\n vector<char> arr(s.begin(), s.end()); // Convert string to character array\n\n // First pass: mark excess closing parentheses with \'*\'\n for (int i = 0; i < arr.size(); i++) {\n if (arr[i] == \'(\')\n openParenthesesCount++;\n else if (arr[i] == \')\') {\n if (openParenthesesCount == 0)\n arr[i] = \'*\'; // Mark excess closing parentheses\n else\n openParenthesesCount--;\n }\n }\n\n // Second pass: mark excess opening parentheses from the end\n for (int i = arr.size() - 1; i >= 0; i--) {\n if (openParenthesesCount > 0 && arr[i] == \'(\') {\n arr[i] = \'*\'; // Mark excess opening parentheses\n openParenthesesCount--;\n }\n }\n \n // Filter out marked characters and store the result in a new string\n string result = "";\n for (char c : arr) {\n if (c != \'*\')\n result += c;\n }\n\n return result;\n }\n};\n\n```\n```Python []\nclass Solution:\n def minRemoveToMakeValid(self, s: str) -> str:\n # Initialize variables\n openParenthesesCount = 0\n arr = list(s)\n\n # First pass: mark excess closing parentheses with \'*\'\n for i in range(len(arr)):\n if arr[i] == \'(\':\n openParenthesesCount += 1\n elif arr[i] == \')\':\n if openParenthesesCount == 0:\n arr[i] = \'*\' # Mark excess closing parentheses\n else:\n openParenthesesCount -= 1\n\n # Second pass: mark excess opening parentheses from the end\n for i in range(len(arr) - 1, -1, -1):\n if openParenthesesCount > 0 and arr[i] == \'(\':\n arr[i] = \'*\' # Mark excess opening parentheses\n openParenthesesCount -= 1\n \n # Filter out marked characters and construct the result string\n result = \'\'.join(c for c in arr if c != \'*\')\n\n return result\n\n```\n\n# Approach -2 With Stack\n```java []\nclass Solution {\n public String minRemoveToMakeValid(String s) {\n // Initialize counts for left and right parentheses\n int leftCount = 0;\n int rightCount = 0;\n\n // Use a stack to keep track of valid parentheses\n Stack<Character> stack = new Stack<>();\n\n // Pass 1: Iterate through the string and process parentheses\n for (int i = 0; i < s.length(); i++) {\n char currentChar = s.charAt(i);\n\n // Increment count for left parentheses\n if (currentChar == \'(\') {\n leftCount++;\n }\n // Increment count for right parentheses\n if (currentChar == \')\') {\n rightCount++;\n }\n\n // If there are more right parentheses than left, skip the current right parenthesis\n if (rightCount > leftCount) {\n rightCount--; // Decrease right count\n continue; // Skip processing this right parenthesis\n } else {\n stack.push(currentChar); // Add valid parentheses to the stack\n }\n }\n\n // Pass 2: Reconstruct the string using the valid parentheses in the stack\n StringBuilder result = new StringBuilder();\n while (!stack.isEmpty()) {\n char currentChar = stack.pop();\n // If there are more left parentheses than right, skip the current left parenthesis\n if (leftCount > rightCount && currentChar == \'(\') {\n leftCount--; // Decrease left count\n // Do nothing, skip this left parenthesis\n } else {\n result.append(currentChar); // Add valid parentheses to the result\n }\n }\n\n // Reverse the result string and return\n return result.reverse().toString();\n }\n}\n\n```\n```python []\nclass Solution:\n def minRemoveToMakeValid(self, s: str) -> str:\n left_count = 0\n right_count = 0\n stack = []\n\n # Pass 1\n for ch in s:\n if ch == \'(\':\n left_count += 1\n elif ch == \')\':\n right_count += 1\n if right_count > left_count:\n right_count -= 1\n else:\n stack.append(ch)\n\n result = ""\n\n # Pass 2\n while stack:\n current_char = stack.pop()\n if left_count > right_count and current_char == \'(\':\n left_count -= 1\n else:\n result += current_char\n\n # Reverse the result string\n return result[::-1]\n\n```\n```C++ []\n\nclass Solution {\npublic:\n std::string minRemoveToMakeValid(std::string s) {\n int leftCount = 0;\n int rightCount = 0;\n std::stack<char> stack;\n\n // Pass 1\n for (char ch : s) {\n if (ch == \'(\') {\n leftCount++;\n } else if (ch == \')\') {\n rightCount++;\n }\n if (rightCount > leftCount) {\n rightCount--;\n continue;\n } else {\n stack.push(ch);\n }\n }\n\n std::string result = "";\n \n // Pass 2\n while (!stack.empty()) {\n char currentChar = stack.top();\n stack.pop();\n if (leftCount > rightCount && currentChar == \'(\') {\n leftCount--;\n } else {\n result += currentChar;\n }\n }\n\n // Reverse the result string\n std::reverse(result.begin(), result.end());\n return result;\n }\n};\n```\n\n\n\n
| 281 | 6 |
['Python', 'C++', 'Java', 'Python3']
| 19 |
minimum-remove-to-make-valid-parentheses
|
[Python , Javascript] Easy solution with very clear Explanation
|
python-javascript-easy-solution-with-ver-7cbr
|
Please dont downvote guys if cannot support,We are putting lot of effort in it\uD83D\uDE42\n\n\nWhat the Question asking us to do \uD83E\uDD14 ?\nYour task is t
|
mageshyt
|
NORMAL
|
2022-03-15T03:41:10.072604+00:00
|
2022-03-15T04:57:02.354691+00:00
| 18,124 | false |
**Please dont downvote guys if cannot support,We are putting lot of effort in it\uD83D\uDE42**\n\n```\nWhat the Question asking us to do \uD83E\uDD14 ?\nYour task is to remove the minimum number of parentheses ( \'(\' or \')\', in any positions )\nso that the resulting parentheses string is valid and return any valid string\n```\n\n\n\n\n\n\n\n\n\n```\nBig o:\n n-->size of the s\n Time: O(n)\n Space: O(n)\n```\n\n`Javascript`\n\n```\nconst minRemoveToMakeValid = (str)=> {\n const stack = [];\n const splitted_str = str.split("");\n for (let i = 0; i < str.length; i++) {\n const char = str[i];\n if (char === "(") stack.push(i); // if curr char is ( then we will push into our stack\n else if (char === ")") {\n if (stack.length === 0) {\n // if out stack is empty then we will make ) as \'\'\n splitted_str[i] = "";\n } else {\n //! if stack is not empty then we will pop top of the stack\n stack.pop();\n }\n }\n }\n // if we have extra ( bracket we will remove it by making it as \'\'\n for (let i = 0; i < stack.length; i++) {\n const char = stack[i];\n splitted_str[char] = "";\n }\n\n return splitted_str.join(""); // at last we will join the splitted_str\n};\n```\n\n`Python`\n\n```\nclass Solution:\n def minRemoveToMakeValid(self, s) :\n stack=[]\n split_str=list(s)\n for i in range(len(s)):\n if s[i]==\'(\':\n # if current char is \'(\' then push it to stack\n stack.append(i)\n elif s[i]==\')\':\n # if current char is \')\' then pop top of the stack\n if len(stack) !=0:\n stack.pop()\n else:\n # if our stack is empty then we can\'t pop so make current char as \'\'\n split_str[i]=""\n for i in stack:\n split_str[i]=""\n return \'\' .join(split_str)\n```\n\n```\nUPVOTE if you like \uD83D\uDE03 , If you have any question, feel free to ask.\n```
| 250 | 5 |
['Python', 'JavaScript']
| 28 |
minimum-remove-to-make-valid-parentheses
|
C++ | 2 Approaches | O(n), Beats 100% | No Extra Space (Best) | Explanation
|
c-2-approaches-on-beats-100-no-extra-spa-cs4v
|
APPROACH 1\nHere, we will use a stack for checking the validity of parentheses, and later remove the indexes of invalid parentheses from the string s. Thanks @h
|
akash2099
|
NORMAL
|
2021-02-19T17:38:45.105790+00:00
|
2021-03-01T07:03:19.545848+00:00
| 15,046 | false |
**APPROACH 1**\nHere, we will use a **stack** for checking the validity of parentheses, and later remove the indexes of invalid parentheses from the string `s`. Thanks [@harmxnkhurana](https://leetcode.com/harmxnkhurana) for the suggestion of directly marking the invalid parentheses in string `s` rather than redundant storing it in a different vector. \n- First, iterate the string `s` and mark the index of those characters which need to be removed to make it *parentheses string* using a special symbol **`\'#\'`**.\n- Here, a **stack** is used for finding the **valid** pair of parentheses, and while doing so also **mark** the indexes of **invalid parentheses** in ```s```.\n- Finally, iterate `s` again and append **non-marked symbol** (`#`) to `ans`.\n\n**COMPLETE CODE**\n```\nclass Solution {\npublic:\n string minRemoveToMakeValid(string s) {\n \n stack<int>st; // helper stack for finding matching parentheses\n \n for(int i=0;i<s.length();++i){\n if(s[i]==\'(\'){ // for open parentheses push into stack\n st.push(i);\n }\n else if(s[i]==\')\'){ // for closing parentheses\n // if no matching previous open parentheses found, we need to remove the index of that open parentheses from "s" so for now we are marking it with special character \'#\'\n if(st.empty()){ \n s[i]=\'#\';\n }\n else{\n // if matching open parentheses found remove that from the stack\n st.pop();\n }\n }\n }\n\n // if stack is not empty, that means it contains open parentheses indexes which don\'t have any matching closing parentheses\n while(!st.empty()){\n s[st.top()]=\'#\';\n st.pop();\n }\n \n string ans="";\n for(int i=0;i<s.length();++i){\n if(s[i]!=\'#\'){ // append not marked character to the end of "ans"\n ans.push_back(s[i]);\n }\n }\n \n return ans;\n }\n};\n```\n\n**TIME COMPLEXITY**\n**O(n)**\n\n**SPACE COMPLEXITY**\n**O(n)** [ *For stack* ]\n\n---\n\n**APPROACH 2 ( Better Approach )**\nIn this approach, we don\'t need a stack so **no extra space** will be used. Thanks [@Ajna2](https://leetcode.com/Ajna2) for the suggestion of keeping a count variable instead of using a stack.\n- First, create a `count` variable for storing the number of **opening** or **closing** brackets as per our need.\n- **STEP 1:**\n\t- Initialize `count=0`. For this step, we will use `count` for storing the number of **open** brackets.\n\t- Then, iterate the string `s` from **start** and at each iteration:\n\t\t- if **open bracket** found, then **increase** `count`.\n\t\t- if **close bracket** found, then check *if* **no. of close brackets > no. of open brackets**, then mark that character in `s` by *replacing* it by **`#`**, *else* **decrease** the `count` ( as **matching parentheses** found ).\n\t```\n\tint count=0; \n\tfor(int i=0;i<n;++i){\n\t\tif(s[i]==\'(\'){ // for open bracket\n\t\t\t++count;\n\t\t}\n\t\telse if(s[i]==\')\'){ // for close bracket\n\t\t\tif(count==0){ // if no. of close brackets > no. of open brackets\n\t\t\t\ts[i]=\'#\';\n\t\t\t}\n\t\t\telse{\n\t\t\t\t// if matching parentheses found decrease count\n\t\t\t\t--count;\n\t\t\t}\n\t\t}\n\t}\n\t```\n- **STEP 2 ( Reverse of STEP 1 )**\n\t- Again, make `count=0`. For this step, we will use `count` for storing the number of **close** brackets.\n\t- Then, iterate the string `s` from the **end** and at each iteration:\n\t\t- if **close bracket** found, then **increase** `count`.\n\t\t- if **open bracket** found, then check *if* **no. of open brackets > no. of close brackets**, then mark that character in `s` by *replacing* it by **`#`**, *else* **decrease** the `count` ( as **matching parentheses** found ). \n\t```\n\tcount=0;\n\tfor(int i=n-1;i>=0;--i){\n\t\tif(s[i]==\')\'){ // for close bracket\n\t\t\t++count;\n\t\t}\n\t\telse if(s[i]==\'(\'){ // for open bracket\n\t\t\tif(count==0){ // if no. of open brackets > no. of close brackets\n\t\t\t\ts[i]=\'#\';\n\t\t\t}\n\t\t\telse{\n\t\t\t\t// if matching parentheses found decrease count\n\t\t\t\t--count;\n\t\t\t}\n\t\t}\n\t}\n\t```\n- **STEP 3:**\n\t- Iterate the string `s` and append each non - marked character (`#`) to `ans` string.\n\t- return `ans`.\n\t```\n\tstring ans="";\n\tfor(int i=0;i<n;++i){\n\t\tif(s[i]!=\'#\'){ \n\t\t\tans.push_back(s[i]);\n\t\t}\n\t}\n\treturn ans;\n\t```\n\n**COMPLETE CODE**\n```\nclass Solution {\npublic:\n string minRemoveToMakeValid(string s) {\n int n=s.length();\n // Step 1 : Iterate from start\n int count=0; \n for(int i=0;i<n;++i){\n if(s[i]==\'(\'){ // for open bracket\n ++count;\n }\n else if(s[i]==\')\'){ // for close bracket\n if(count==0){ // if no. of close brackets > no. of open brackets\n s[i]=\'#\';\n }\n else{\n // if matching parentheses found decrease count\n --count;\n }\n }\n }\n \n // Step 2 : Iterate from end\n count=0;\n for(int i=n-1;i>=0;--i){\n if(s[i]==\')\'){ // for close bracket\n ++count;\n }\n else if(s[i]==\'(\'){ // for open bracket\n if(count==0){ // if no. of open brackets > no. of close brackets\n s[i]=\'#\';\n }\n else{\n // if matching parentheses found decrease count\n --count;\n }\n }\n }\n \n // Step 3 : Create "ans" by ignoring the special characters \'#\'\n string ans="";\n for(int i=0;i<n;++i){\n if(s[i]!=\'#\'){ \n ans.push_back(s[i]);\n }\n }\n return ans;\n }\n};\n```\n\n**TIME COMPLEXITY**\n**O(n+n+n) = O(n)** [ *Each step takes O(n) time* ]\n\n**SPACE COMPLEXITY**\n**O(1)** [ *No extra space used, ignoring "ans"* ]
| 247 | 3 |
['Stack', 'C']
| 26 |
minimum-remove-to-make-valid-parentheses
|
Stack Based | Easy to Understand | Faster than 99% | JavaScript Solution
|
stack-based-easy-to-understand-faster-th-tj3r
|
\nvar minRemoveToMakeValid = function(str) {\n str = str.split("");\n\tlet stack = [];\n for(let i = 0; i<str.length; i++){\n if(str[i]==="(")\n
|
mrmagician
|
NORMAL
|
2020-01-08T15:25:01.334117+00:00
|
2020-08-08T04:57:13.669073+00:00
| 16,163 | false |
```\nvar minRemoveToMakeValid = function(str) {\n str = str.split("");\n\tlet stack = [];\n for(let i = 0; i<str.length; i++){\n if(str[i]==="(")\n stack.push(i);\n else if(str[i]===")"){\n if(stack.length) stack.pop();\n else str[i]="";\n }\n }\n \n for(let i of stack) str[i] = "";\n \n return str.join("");\n\t\n}\n```\n\n**I hope that you\'ve found the solution useful.**\n*In that case, please do upvote and encourage me to on my quest to document all leetcode problems\uD83D\uDE03*\nPS: Search for **mrmagician** tag in the discussion, if I have solved it, You will find it there\uD83D\uDE38\n\n**This is by far my most upvoted solution \uD83C\uDF89 ! Thanks Guys \uD83D\uDC9A**
| 222 | 3 |
['JavaScript']
| 18 |
minimum-remove-to-make-valid-parentheses
|
Constant Space Solution
|
constant-space-solution-by-balla_musa-8f30
|
\n public String minRemoveToMakeValid(String s) {\n\t\tint openCloseCount = 0;\n\t\tint close = 0;\n\t\tfor (int i = 0; i < s.length(); i++) if (s.charAt(i)
|
balla_musa
|
NORMAL
|
2019-11-03T04:28:00.088411+00:00
|
2019-11-03T04:28:00.088444+00:00
| 10,800 | false |
```\n public String minRemoveToMakeValid(String s) {\n\t\tint openCloseCount = 0;\n\t\tint close = 0;\n\t\tfor (int i = 0; i < s.length(); i++) if (s.charAt(i) == \')\') close++;\n\t\t\n StringBuilder sb = new StringBuilder();\n\t\t\n\t\tfor (char c: s.toCharArray()) {\n\t\t\tif (c == \'(\') {\n\t\t\t\tif (openCloseCount == close) continue;\n\t\t\t\topenCloseCount++;\n\t\t\t} else if (c == \')\') {\n\t\t\t\tclose--;\n\t\t\t\tif (openCloseCount == 0) continue;\n\t\t\t\topenCloseCount--;\n\t\t\t} \n\n\t\t\t\tsb.append(c);\n\t\t}\n\t\treturn sb.toString();\n }\n```
| 137 | 11 |
[]
| 24 |
minimum-remove-to-make-valid-parentheses
|
✅ C++ || 2 Appraches || Explained With Algorithm || Easy & Simple
|
c-2-appraches-explained-with-algorithm-e-avch
|
1249. Minimum Remove to Make Valid Parentheses\nKNOCKCAT\n\n1. Easy C++\n2. Line by Line Explanation with Comments.\n3. Detailed Explanation \u2705\n4. 2 Apprao
|
knockcat
|
NORMAL
|
2022-03-15T01:56:09.838234+00:00
|
2022-12-31T07:03:45.394939+00:00
| 8,426 | false |
# 1249. Minimum Remove to Make Valid Parentheses\n**KNOCKCAT**\n```\n1. Easy C++\n2. Line by Line Explanation with Comments.\n3. Detailed Explanation \u2705\n4. 2 Appraoches with initution.\n5. Please Upvote if it helps\u2B06\uFE0F\n6. Link to my Github Profile contains a repository of Leetcode with all my Solutions. \u2B07\uFE0F\n\t// \uD83D\uDE09If you Like the repository don\'t foget to star & fork the repository\uD83D\uDE09\n```\n[LeetCode](http://github.com/knockcat/Leetcode) **LINK TO LEETCODE REPOSITORY**\n\nPlease upvote my comment so that i get to win the 2022 giveaway and motivate to make such discussion post.\n**Happy new Year 2023 to all of you**\n**keep solving keep improving**\nLink To comment\n[Leetcode Give away comment](https://leetcode.com/discuss/general-discussion/2946993/2022-Annual-Badge-and-the-Giveaway/1734919)\n\n``` ```\n**APPROACH 1 O(n) & O(1)**\n\n* **ALGORITHM**\n* **Iterating the string from beginning.**\n\t* **take a cnt variable**, and **increase the cnt when you find an open parenthesis \'(\'.**\n\t* when you **find a close parenthiesis**, **2 cases were checked.**\n\t* i**f cnt is 0** , that **means no open parenthesis has occured earlier**.\n\t* therefore **replace the string index with \'#\'.**\n\t* **otherwise decrease the cnt**, as a **valid pair has found**.\n\t\n* Now **iterate the string from behind** and **repeat the same steps** , but **this time check for closing parenthisis**.\n\t* if **closing parenthesis occur increase the cnt**.\n\t* if **open parenthesis occur**, now **again 2 cases are need to check.**\n\t* if the **cnt == 0, that means no closing parenthisis occur** before **therfore replace that string index with \'#\'.**\n\t* Otherwise **decrease the cnt.**\n* **At end make the resultant string by excluding \'#\'**\n* **Time Complexity** is O(n+n+n) = **O(n)** for each 3 steps\n* **Space Complexity** is **O(1)** , No extra space taken excluding result string.\n```\n```\n\n**CODE WITH EXPLANATION**\n```\n\t\t\t\t\t// \uD83D\uDE09\uD83D\uDE09\uD83D\uDE09\uD83D\uDE09Please upvote if it helps \uD83D\uDE09\uD83D\uDE09\uD83D\uDE09\uD83D\uDE09\nclass Solution\n{\npublic:\n string minRemoveToMakeValid(string s)\n {\n int n = s.length();\n string res = "";\n\n int cnt = 0;\n // iterating from beginnning\n for (int i = 0; i < s.length(); ++i)\n {\n // if we find and open parenthesis increase the cnt\n if (s[i] == \'(\')\n ++cnt;\n // if we found an close parenthisis\n // check if cnt == 0 , that means we have no earlier open parenthesis,\n // therefore replace that index by \'#\'\n else if (s[i] == \')\')\n {\n if (cnt == 0)\n s[i] = \'#\';\n // else decrease the cnt beacuse a valid pair is found\n else\n --cnt;\n }\n }\n\n cnt = 0;\n // iterating from the end\n for (int i = n - 1; i >= 0; --i)\n {\n // if we find and close parenthesis increase the cnt\n if (s[i] == \')\')\n ++cnt;\n // if we found an open parenthisis\n // check if cnt == 0 , that means we have no earlier close parenthesis,\n // therefore replace that index by \'#\'\n else if (s[i] == \'(\')\n {\n if (cnt == 0)\n s[i] = \'#\';\n // else decrease the cnt beacuse a valid pair is found\n else\n --cnt;\n }\n }\n\n // making the resultant string by excluding \'#\'\n for (int i = 0; i < s.length(); ++i)\n {\n if (s[i] != \'#\')\n res.push_back(s[i]);\n }\n\n return res;\n }\n};\n```\n\n**APPROACH 2 USING STACK**\n\n* **ALGORITHM**\n``` ```\n* **Using Stack** for **checking valadity of parenthesis**.\n* first it**erate the string** and when you **find a open parenthesis push it into the stack**.\n* if You **find and close parenthesis** , then **check if the stack is not empty**, if **stack is not empt**y that m**eans open parenthesis exist** **therefore pop the open parenthesis from the stack.**\n* **if the stack is empty** that **means no open parenthesis exist first** therefore **replace that string index with \'#\'.**\n* Now there **may be a case that string contain only open parenthesis** that is also an **invalid parenthesis.**\n* therefore **while stack doesn\'t become empty** **marked the indexes from the stack top with \'#\'.**\n* **pop that parenthesis from the stack.**\n* Now **at end** **create the resultant string excluding \'#\'**\n* **Time Complexity** is = **O(n)** \n* **Space Complexity** is **O(n)** , stack used.\n```\n```\n\n**CODE WITH EXPLANATION**\n\n```\n\t\t\t\t\t\t// \uD83D\uDE09\uD83D\uDE09\uD83D\uDE09\uD83D\uDE09Please upvote if it helps \uD83D\uDE09\uD83D\uDE09\uD83D\uDE09\uD83D\uDE09\nclass Solution\n{\npublic:\n string minRemoveToMakeValid(string s)\n {\n stack<int> st;\n string res = "";\n\n for (int i = 0; i < s.length(); ++i)\n {\n // if we find open parenthesis push it to stack\n if (s[i] == \'(\')\n st.push(i);\n // if we find close parenthisis check\n // if there is a open parenthisis or the stack is empty\n else if (s[i] == \')\')\n {\n // if stack is empty then we need to remove that index from string\n // replacing it with \'#\' for our convenience\n if (st.empty())\n s[i] = \'#\';\n else\n // if there is an open parenthesis than remove that from the stack\n st.pop();\n }\n }\n\n // now , if stack is not empty that means it has open parenthesis\n // which have no closing parenthesis.\n // so we have to replace that index of string with \'#\' for our convenience\n while (!st.empty())\n {\n s[st.top()] = \'#\';\n st.pop();\n }\n\n // making the resultant string by excluding \'#\'\n for (int i = 0; i < s.length(); ++i)\n {\n if (s[i] != \'#\')\n res.push_back(s[i]);\n }\n\n return res;\n }\n};\n```
| 133 | 9 |
['Stack', 'C', 'C++']
| 8 |
minimum-remove-to-make-valid-parentheses
|
[Java/Python] Stack solution - O(N) - Clean & Concise
|
javapython-stack-solution-on-clean-conci-v49z
|
Idea\n- Use stack to remove invalid mismatching parentheses, that is:\n\t- Currently, meet closing-parentheses but no opening-parenthesis in the previous -> rem
|
hiepit
|
NORMAL
|
2019-11-03T04:02:28.020137+00:00
|
2021-09-28T04:35:28.275081+00:00
| 7,414 | false |
**Idea**\n- Use stack to remove invalid mismatching parentheses, that is:\n\t- Currently, meet closing-parentheses but no opening-parenthesis in the previous -> remove current closing-parenthesis. For example: `s = "())"`.\n\t- If there are redundant opening-parenthesis at the end, for example: `s = "((()"`.\n\n<iframe src="https://leetcode.com/playground/R22sMX7c/shared" frameBorder="0" width="100%" height="500"></iframe>\n\n**Complexity**\n- Time: `O(N)`, where `N <= 10^5` is length of string `s`.\n- Space: `O(N)`
| 99 | 4 |
[]
| 10 |
minimum-remove-to-make-valid-parentheses
|
📌 [Java] 4 Solutions with slight optimisations
|
java-4-solutions-with-slight-optimisatio-rsec
|
\uD83D\uDCCE A similar question to this is :\n\nMin swaps to make string balanced\n\n*\n\n\u2318 Given statement : \n Your task is to remove the minimum number
|
Kaustubh_22
|
NORMAL
|
2022-03-15T01:50:32.054124+00:00
|
2024-04-06T07:49:51.263882+00:00
| 19,377 | false |
\uD83D\uDCCE A similar question to this is :\n\n[Min swaps to make string balanced](https://leetcode.com/problems/minimum-number-of-swaps-to-make-the-string-balanced/discuss/1676045/Java-4-Solutions-or-Intuition-or-O(n)-or-O(1)-Solutions)\n\n****\n\n\u2318 Given statement : \n* Your task is to remove the minimum number of parentheses.\n* return any valid string.\n\n\u2318 Observations : \n\nIt is quite obvious to get a hunch of using stack when we see a parenthesis problem but we can for sure optimise the space in such a case where the input is limited. [ eg: `here s[i] is either\'(\' , \')\', or lowercase English letter` ].\n\n****\n# Solution 1 : Stack\n```\nclass Solution {\n public String minRemoveToMakeValid(String s) {\n Stack<Integer> stack = new Stack<>();\n for(int i=0;i<s.length();i++) {\n char ch = s.charAt(i);\n if(Character.isAlphabetic(ch))\n continue;\n if(ch == \'(\')\n stack.push(i);\n else {\n if(!stack.isEmpty() && s.charAt(stack.peek()) == \'(\')\n stack.pop();\n else stack.push(i);\n }\n }\n \n // if(stack.size() == 0) return "";\n \n StringBuilder result = new StringBuilder();\n HashSet<Integer> set = new HashSet<>(stack);\n for(int i=0;i<s.length();i++)\n if(!set.contains(i))\n result.append(s.charAt(i));\n \n return result.toString();\n }\n}\n```\n\n****\n# Solution 2 : Using Deque\n```\nclass Solution {\n public String minRemoveToMakeValid(String s) {\n\t\tif (s == null || s.length() == 0) {\n return s;\n }\n \n char[] chars = s.toCharArray();\n Deque<Integer> deque = new ArrayDeque<>();\n\t\t\n\t\t// push invalid indices in deque\n for (int i = 0; i < chars.length; i++) {\n char c = chars[i];\n if (c == \'(\') {\n deque.push(i);\n } else if (c == \')\') {\n if (deque.isEmpty()) {\n chars[i] = \'#\';\n } else {\n deque.pop();\n }\n } \n }\n // mark invalid indices\n while (!deque.isEmpty()) {\n chars[deque.pop()] = \'#\';\n }\n \n StringBuilder ans = new StringBuilder();\n for (char c : chars) {\n if (c != \'#\') {\n ans.append(c);\n }\n }\n return ans.toString();\n }\n}\n```\n\n# Constant Solutions : [ Naive -> Optimal ]\n\u2318 Constant Solution 1 : [ ` Slow as we are using insert() function ` ]\n\n\u2714\uFE0F Logic : [ `2 steps` ]\n * remove invalid close parenthesis\n * remove invalid open parenthesis\n\n```\nclass Solution {\n public String minRemoveToMakeValid(String s) {\n StringBuilder R = new StringBuilder();\n int open = 0, close = 0;\n \n // remove invalid close parenthesis\n for(char ch : s.toCharArray()) {\n if(Character.isAlphabetic(ch)) {\n R.append(ch);\n }\n else if(ch==\'(\') {\n open++;\n R.append(ch);\n }\n else {\n if(open > close) { // if there is an \'(\' to be considered for a valid pair\n R.append(ch);\n close++;\n }\n else {\n open = open < 0 ? 0 : open--;\n }\n }\n }\n\n s = R.toString();\n R.setLength(0); // reset ans\n int n = s.length();\n open = close = 0;\n\t\t\n\t\t// remove invalid open parenthesis\n\t\t\n for(int i=n-1;i>=0;i--) {\n char ch = s.charAt(i);\n if(Character.isAlphabetic(ch)) {\n R.insert(0, ch);\n }\n else if(ch == \')\') {\n R.insert(0, ch);\n close++;\n }\n else {\n if(close > open) {\n R.insert(0, ch);\n open++;\n }\n else {\n close = close < 0 ? 0 : close--;\n }\n }\n } \n return R.toString();\n }\n}\n```\n****\n\n\u2318 Optimal / Refactored Code : \n```\nclass Solution {\n public String minRemoveToMakeValid(String s) {\n int n = s.length();\n StringBuilder ans = removeInvalid(s, \'(\' , \')\');\n ans = removeInvalid(ans.reverse(), \')\', \'(\');\n return ans.reverse().toString();\n }\n \n private StringBuilder removeInvalid(CharSequence s, char open_char, char close_char) {\n StringBuilder answer = new StringBuilder();\n int open = 0, close = 0, n = s.length();\n for(int i=0;i<n;i++) {\n char ch = s.charAt(i);\n if(Character.isAlphabetic(ch)) answer.append(ch);\n else if(ch == open_char) {\n open++;\n answer.append(ch);\n }\n else {\n if(open > close) {\n open--; // found a pair\n answer.append(ch);\n } else {\n // we did not find a ( to pair with )\n }\n }\n }\n return answer;\n }\n}\n```
| 78 | 1 |
['Stack', 'Queue', 'Java']
| 15 |
minimum-remove-to-make-valid-parentheses
|
[Java] Clean StringBuilder solution
|
java-clean-stringbuilder-solution-by-wal-7qkk
|
O(N) Solution:\n\nA pair of parentheses is consist of an open and a close. The open has to be before the close.\nSo, we can remove the extra close parenthese th
|
wall__e
|
NORMAL
|
2019-11-03T04:17:14.912691+00:00
|
2021-09-28T16:26:46.950460+00:00
| 8,661 | false |
**O(N) Solution:**\n\nA pair of parentheses is consist of an open and a close. The open has to be before the close.\nSo, we can remove the extra close parenthese then remove extra open parenthese\n\n the fist iteration, we remove the unwanted )\n the second iteration, we remove the unwanted (\n \n```\npublic String minRemoveToMakeValid(String s) {\n StringBuilder sb = new StringBuilder();\n int open = 0;\n for (char c : s.toCharArray()) {\n if (c == \'(\') \n open++;\n else if (c == \')\') {\n if (open == 0) continue; // remove invalid close parenthese\n open--;\n }\n sb.append(c);\n }\n \n StringBuilder result = new StringBuilder();\n for (int i = sb.length() - 1; i >= 0; i--) {\n if (sb.charAt(i) == \'(\' && open-- > 0) continue; // remove invalid open parenthese\n result.append(sb.charAt(i));\n }\n \n return result.reverse().toString();\n}\n```\n\n\nCredit to @Sithis and @hamlet_fiis pointing out the time comlexity of `deleteCharAt(i)` being O(N) which makes this a O(N2) solution. \nEdited the code to append all characters except those invalid open parentheses, then reverse the stringbuilder. This will achieve O(N) with slight headache.\nA new `StringBuilder` is created for the result, but you could reuse the first one by replacing the `(` in place and prune the starting `open` number of chars.\n\n**Original O(N2) Solution:**\n\nThe intuition is counting the number of invalid `(` and removing the invalid `)` in the first pass.\nIf there are `open` number of invalid `(` left, we just need to remove them from the end in the second pass.\n\n```\npublic String minRemoveToMakeValid(String s) {\n StringBuilder sb = new StringBuilder();\n int open = 0;\n for (char c : s.toCharArray()) {\n if (c == \'(\') {\n open++;\n } else if (c == \')\') {\n if (open == 0) continue;\n open--;\n }\n sb.append(c);\n }\n \n for (int i = sb.length() - 1; i >= 0 && open > 0; i--) {\n if (sb.charAt(i) == \'(\') {\n sb.deleteCharAt(i);\n open--;\n }\n }\n \n return sb.toString();\n}\n```\n
| 57 | 1 |
[]
| 9 |
minimum-remove-to-make-valid-parentheses
|
C++ inplace removal, O(n) time, O(1) space
|
c-inplace-removal-on-time-o1-space-by-co-xl7q
|
\n string minRemoveToMakeValid(string s)\n {\n int i = s.size();\n int balance = 0;\n for (int j = s.size() - 1; j >= 0; j--) {\n
|
coder206
|
NORMAL
|
2019-11-03T06:15:41.698703+00:00
|
2019-11-03T06:15:41.698753+00:00
| 5,387 | false |
```\n string minRemoveToMakeValid(string s)\n {\n int i = s.size();\n int balance = 0;\n for (int j = s.size() - 1; j >= 0; j--) {\n if (s[j] == \')\') balance++;\n else if (s[j] == \'(\') {\n if (balance == 0) continue;\n balance--;\n }\n s[--i] = s[j];\n }\n int len = 0;\n balance = 0;\n for (; i < s.size(); i++) {\n if (s[i] == \'(\') balance++;\n else if (s[i] == \')\') {\n if (balance == 0) continue;\n balance--;\n }\n s[len++] = s[i];\n }\n s.erase(len);\n return s;\n }\n```
| 54 | 1 |
[]
| 7 |
minimum-remove-to-make-valid-parentheses
|
python stack O(N)
|
python-stack-on-by-shuuchen-u6gl
|
\nclass Solution:\n def minRemoveToMakeValid(self, s: str) -> str:\n \n stack, cur = [], \'\'\n for c in s:\n if c == \'(\':\
|
shuuchen
|
NORMAL
|
2019-11-13T06:42:03.986749+00:00
|
2022-04-13T03:33:06.953467+00:00
| 6,273 | false |
```\nclass Solution:\n def minRemoveToMakeValid(self, s: str) -> str:\n \n stack, cur = [], \'\'\n for c in s:\n if c == \'(\':\n stack += [cur]\n cur = \'\'\n elif c == \')\':\n if stack:\n cur = stack.pop() + \'(\' + cur + \')\' \n else:\n cur += c\n \n while stack:\n cur = stack.pop() + cur\n \n return cur\n```\n\n@licaiuu also provided a good solution, which is really easy to understand. It is simplified as following:\n```\nclass Solution:\n def minRemoveToMakeValid(self, s: str) -> str:\n \n stack, res = [], [\'\'] * len(s)\n \n for i, x in enumerate(s):\n \n if x == \'(\':\n stack += [i]\n \n elif x == \')\':\n if stack:\n res[stack.pop()] = \'(\'\n res[i] = \')\'\n \n else:\n res[i] = x\n return \'\'.join(res)\n```\n\t\t
| 43 | 0 |
[]
| 9 |
minimum-remove-to-make-valid-parentheses
|
Beats 90%🔥||Easy Stack ✅and Naive ✅ with explanation😊😊..
|
beats-90easy-stack-and-naive-with-explan-1759
|
The short form of the question is to print the paranthesis only if it is possible to form a pair..\n\nif a paranthesis is ( then we would have to iterate throug
|
21eca01
|
NORMAL
|
2024-04-06T01:32:55.886173+00:00
|
2024-04-06T02:17:35.278818+00:00
| 13,847 | false |
**The short form of the question is to print the paranthesis only if it is possible to form a pair..**\n\n**if a paranthesis is ```(``` then we would have to iterate throughout the array till we found ```)``` but it is not the optimal one.**\n\n**Approach 1:\nwhy cant we just iterate the array and take the ```min of open and close``` parnthesis, thus only ```min(open,close) pairs``` is possible.**\n**we can just define the ```)``` only when open ```(``` is used and the count is greater than zero.**\n\n**similarly we can only use the ```(``` only when count>0**\n\n**thus it would take O(n) time..**\n\n\n# Code\n``` Java []\nclass Solution {\n public String minRemoveToMakeValid(String s) {\n int open=0,close=0,flag=0;\n for(int i=0;i<s.length();i++){\n if(s.charAt(i)==\'(\') {\n open++;\n flag+=1;\n }\n else if(s.charAt(i)==\')\'&&flag>0) {\n close++;\n flag--;\n }\n }\n int k=Math.min(open,close);\n String ans="";\n open=k;\n close=k;\n for(int i=0;i<s.length();i++){\n if(s.charAt(i)==\'(\'){\n if(open>0) {\n ans+=\'(\';\n open--;\n }\n continue;\n } \n if(s.charAt(i)==\')\') {\n if(close>0&&close>open) {\n ans+=\')\'; \n close--;\n }\n continue;\n }\n else ans+=s.charAt(i);\n }\n return ans;\n }\n}\n```\n\n``` Python3 []\nclass Solution:\n def minRemoveToMakeValid(self, s: str) -> str:\n open_count = 0\n close_count = 0\n flag = 0\n ans = ""\n \n for char in s:\n if char == \'(\':\n open_count += 1\n flag += 1\n elif char == \')\' and flag > 0:\n close_count += 1\n flag -= 1\n \n k = min(open_count, close_count)\n open_count = k\n close_count = k\n \n for char in s:\n if char == \'(\':\n if open_count > 0:\n ans += \'(\'\n open_count -= 1\n continue\n if char == \')\':\n if close_count > 0 and close_count > open_count:\n ans += \')\'\n close_count -= 1\n continue\n else:\n ans += char\n \n return ans\n\n```\n\n``` C++ []\n#include <string>\n#include <algorithm>\n\nclass Solution {\npublic:\n std::string minRemoveToMakeValid(std::string s) {\n int open = 0, close = 0, flag = 0;\n for (char c : s) {\n if (c == \'(\') {\n open++;\n flag++;\n } else if (c == \')\' && flag > 0) {\n close++;\n flag--;\n }\n }\n \n int k = std::min(open, close);\n std::string ans = "";\n open = k;\n close = k;\n for (char c : s) {\n if (c == \'(\') {\n if (open > 0) {\n ans += \'(\';\n open--;\n }\n continue;\n }\n if (c == \')\') {\n if (close > 0 && close > open) {\n ans += \')\';\n close--;\n }\n continue;\n } else {\n ans += c;\n }\n }\n return ans;\n }\n};\n\n```\n``` JavaScript []\n/**\n * @param {string} s\n * @return {string}\n */\nvar minRemoveToMakeValid = function(s) {\n \n\n\n\n let open = 0, close = 0, flag = 0;\n for (let i = 0; i < s.length; i++) {\n if (s[i] === \'(\') {\n open++;\n flag++;\n } else if (s[i] === \')\' && flag > 0) {\n close++;\n flag--;\n }\n }\n \n let k = Math.min(open, close);\n let ans = \'\';\n open = k;\n close = k;\n for (let i = 0; i < s.length; i++) {\n if (s[i] === \'(\') {\n if (open > 0) {\n ans += \'(\';\n open--;\n }\n continue;\n }\n if (s[i] === \')\') {\n if (close > 0 && close > open) {\n ans += \')\';\n close--;\n }\n continue;\n } else {\n ans += s[i];\n }\n }\n return ans;\n}\n\n\n```\n\n\n**Approach 2:\nYeah we can just use stack to peep() whether there is any trailing \n```(``` before addng ```)``` so that we can just pop() that thing out of it**\n\n\n**so basically youre going to add the indexes on the stack whenever you realize a ```close )``` does not have any ```open(``` ,if there is a pair availbale just pop() the pair.This can be done,whenever you see a close with trailing open just pop() open and move further**\n\n**then just append the whole string except the indexes which are present inside the stack they are the indexes which do not form a pair**\n\n``` Java []\nclass Solution {\n public String minRemoveToMakeValid(String s) {\n Stack <Integer> st=new Stack<>();\n for(int i=0;i<s.length();i++){\n if(s.charAt(i)==\'(\') st.push(i);\n else if(s.charAt(i)==\')\'){\n if(!st.isEmpty()&&s.charAt((int)st.peek())==\'(\'){\n st.pop();\n }\n else st.push(i);\n }\n else continue;\n }\n StringBuilder sb=new StringBuilder();\n for(int i=s.length()-1;i>=0;i--){\n if(!st.isEmpty()&&(int)st.peek()==i) {\n st.pop();\n continue;\n }\n else sb.append(s.charAt(i));\n }\n return sb.reverse().toString();\n }\n}\n```\n```Python3 []\nclass Solution:\n def minRemoveToMakeValid(self, s: str) -> str:\n stack = []\n for i, char in enumerate(s):\n if char == \'(\':\n stack.append(i)\n elif char == \')\':\n if stack and s[stack[-1]] == \'(\':\n stack.pop()\n else:\n stack.append(i)\n \n result = []\n for i, char in enumerate(s):\n if stack and i == stack[0]:\n stack.pop(0)\n continue\n result.append(char)\n \n return \'\'.join(result)\n\n```\n\n```JavaScript []\nclass Solution {\n minRemoveToMakeValid(s) {\n const stack = [];\n for (let i = 0; i < s.length; i++) {\n if (s[i] === \'(\') {\n stack.push(i);\n } else if (s[i] === \')\') {\n if (stack.length && s[stack[stack.length - 1]] === \'(\') {\n stack.pop();\n } else {\n stack.push(i);\n }\n }\n }\n \n let result = \'\';\n for (let i = 0; i < s.length; i++) {\n if (stack.length && i === stack[0]) {\n stack.shift();\n continue;\n }\n result += s[i];\n }\n \n return result;\n }\n}\n```\n\n
| 42 | 1 |
['String', 'Stack', 'C++', 'Java', 'Python3', 'JavaScript']
| 10 |
minimum-remove-to-make-valid-parentheses
|
3 Interview Approaches with Video Explanation 🔥 ||(Stack+Visited)->(Only Stack)->(No Stack) ✅
|
3-interview-approaches-with-video-explan-ij8t
|
Intuition\n Describe your first thoughts on how to solve this problem. \nParentheses (think about stacks). \nIn Interviews you need to follow this pattern. Firs
|
ayushnemmaniwar12
|
NORMAL
|
2024-04-06T02:52:00.600193+00:00
|
2024-04-06T04:11:16.319841+00:00
| 6,146 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n**Parentheses (think about stacks). \nIn Interviews you need to follow this pattern. First you need to explain Brute Force and you can optimize in the subsequent approaches.**\n\n\n# ***Easy Video Explanation***\n\n***Most of you knows the solution but approaches are important.\n(This video helps you, how to approach this types of problems in interviews)***\n\nhttps://youtu.be/mIypvv75WJ4\n \n\n# Code (Stack + Visited)\n\n\n```C++ []\nclass Solution {\npublic:\n string minRemoveToMakeValid(string s) {\n int n=s.size();\n vector<bool>vis(n,1);\n stack<int>st;\n for(int i=0;i<n;i++) {\n if(s[i]>=\'a\' && s[i]<=\'z\')\n continue;\n if(s[i]==\'(\') {\n st.push(i);\n } else {\n if(!st.empty()) {\n st.pop();\n } else {\n vis[i]=0;\n }\n }\n }\n while(!st.empty()) {\n vis[st.top()]=0;\n st.pop();\n }\n string ans="";\n for(int i=0;i<n;i++) {\n if(vis[i]==1)\n ans.push_back(s[i]);\n }\n return ans;\n }\n};\n```\n```python []\nclass Solution:\n def minRemoveToMakeValid(self, s: str) -> str:\n n = len(s)\n vis = [False] * n\n st = []\n for i in range(n):\n if s[i].islower():\n continue\n if s[i] == \'(\':\n st.append(i)\n else:\n if st:\n st.pop()\n else:\n vis[i] = True\n while st:\n vis[st.pop()] = True\n ans = ""\n for i in range(n):\n if not vis[i]:\n ans += s[i]\n return ans\n\n```\n```Java []\nimport java.util.Stack;\n\nclass Solution {\n public String minRemoveToMakeValid(String s) {\n int n = s.length();\n boolean[] vis = new boolean[n];\n Stack<Integer> st = new Stack<>();\n for (int i = 0; i < n; i++) {\n if (Character.isLowerCase(s.charAt(i)))\n continue;\n if (s.charAt(i) == \'(\') {\n st.push(i);\n } else {\n if (!st.isEmpty()) {\n st.pop();\n } else {\n vis[i] = true;\n }\n }\n }\n while (!st.isEmpty()) {\n vis[st.pop()] = true;\n }\n StringBuilder ans = new StringBuilder();\n for (int i = 0; i < n; i++) {\n if (!vis[i])\n ans.append(s.charAt(i));\n }\n return ans.toString();\n }\n}\n\n```\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(N)\n \n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(N)\n\n \n\n# Code (Only Stack)\n\n\n```C++ []\nclass Solution {\npublic:\n string minRemoveToMakeValid(string s) {\n int n=s.size();\n stack<int>st;\n for(int i=0;i<n;i++) {\n if(s[i]>=\'a\' && s[i]<=\'z\')\n continue;\n if(s[i]==\'(\') {\n st.push(i);\n } else {\n if(!st.empty()) {\n st.pop();\n } else {\n s[i]=\'#\';\n }\n }\n }\n while(!st.empty()) {\n s[st.top()]=\'#\';\n st.pop();\n }\n string ans="";\n for(int i=0;i<n;i++) {\n if(s[i]!=\'#\')\n ans.push_back(s[i]);\n }\n return ans;\n }\n};\n```\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(N)\n \n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(N)\n\n\n# Code (No Stack O(1) space)\n\n\n```C++ []\nclass Solution {\npublic:\n std::string minRemoveToMakeValid(std::string s) {\n int open = 0, close = 0, flag = 0;\n for (char c : s) {\n if (c == \'(\') {\n open++;\n flag++;\n } else if (c == \')\' && flag > 0) {\n close++;\n flag--;\n }\n }\n \n int k = std::min(open, close);\n std::string ans = "";\n open = k;\n close = k;\n for (char c : s) {\n if (c == \'(\') {\n if (open > 0) {\n ans += \'(\';\n open--;\n }\n continue;\n }\n if (c == \')\') {\n if (close > 0 && close > open) {\n ans += \')\';\n close--;\n }\n continue;\n } else {\n ans += c;\n }\n }\n return ans;\n }\n};\n```\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(N)\n \n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(1)\n\n# ***If you like the solution Please Upvote and subscribe to my youtube channel***\n***It Motivates me to record more videos***\n\n*Thank you* \uD83D\uDE00
| 39 | 1 |
['String', 'Stack', 'Python', 'C++', 'Java']
| 6 |
minimum-remove-to-make-valid-parentheses
|
[Java] Both runtime and memory beats 100.00% submissions
|
java-both-runtime-and-memory-beats-10000-10vd
|
\nclass Solution {\n public String minRemoveToMakeValid(String s) {\n\n char[] arr = s.toCharArray();\n int open = 0;\n\n for (int i = 0
|
Jami20
|
NORMAL
|
2020-04-05T08:12:18.571381+00:00
|
2020-04-05T08:12:18.571446+00:00
| 3,893 | false |
```\nclass Solution {\n public String minRemoveToMakeValid(String s) {\n\n char[] arr = s.toCharArray();\n int open = 0;\n\n for (int i = 0; i < arr.length; i++) {\n if (arr[i] == \'(\')\n open++;\n else if (arr[i] == \')\') {\n if (open == 0)\n arr[i] = \'*\';\n else\n open--;\n }\n }\n\n for (int i = arr.length - 1; i >= 0; i--) {\n if (open > 0 && arr[i] == \'(\') {\n arr[i] = \'*\';\n open--;\n }\n }\n\n int p = 0;\n for (int i = 0; i < arr.length; i++) {\n if (arr[i] != \'*\')\n arr[p++] = arr[i];\n }\n\n return new String(arr).substring(0, p);\n }\n}\n```
| 36 | 0 |
['Java']
| 7 |
minimum-remove-to-make-valid-parentheses
|
Python - Memory Usage Less Than 100%, Faster than 100%
|
python-memory-usage-less-than-100-faster-1hm4
|
\nclass Solution:\n def minRemoveToMakeValid(self, s: str) -> str:\n \n open = 0\n s = list(s)\n \n for i, c in enumerate(
|
mmbhatk
|
NORMAL
|
2020-02-09T06:14:32.896440+00:00
|
2020-02-09T06:14:32.896492+00:00
| 4,188 | false |
```\nclass Solution:\n def minRemoveToMakeValid(self, s: str) -> str:\n \n open = 0\n s = list(s)\n \n for i, c in enumerate(s):\n if c == \'(\': open += 1\n elif c == \')\':\n if not open: s[i] = ""\n else: open -= 1\n \n for i in range(len(s)-1, -1, -1):\n if not open: break\n if s[i] == \'(\': s[i] = ""; open -= 1\n \n return "".join(s)\n```
| 30 | 2 |
['Python', 'Python3']
| 5 |
minimum-remove-to-make-valid-parentheses
|
[Java] O(n) solution without Stack
|
java-on-solution-without-stack-by-sithis-dni7
|
Time complexity: O(n).\nSpace complexity: O(n).\n\n\npublic String minRemoveToMakeValid(String str) {\n int n = str.length();\n StringBuilder sb = new Str
|
sithis
|
NORMAL
|
2019-11-03T09:27:35.127574+00:00
|
2024-02-27T17:25:00.895823+00:00
| 2,770 | false |
Time complexity: O(n).\nSpace complexity: O(n).\n\n```\npublic String minRemoveToMakeValid(String str) {\n int n = str.length();\n StringBuilder sb = new StringBuilder(n);\n boolean[] remove = new boolean[n];\n int open = 0;\n for (int i = 0; i < n; i++) {\n if (str.charAt(i) == \'(\') {\n open++;\n } else if (str.charAt(i) == \')\') {\n if (open > 0) {\n open--;\n } else {\n remove[i] = true;\n }\n }\n }\n\n int close = 0;\n for (int i = n - 1; i >= 0; i--) {\n if (str.charAt(i) == \')\') {\n close++;\n } else if (str.charAt(i) == \'(\') {\n if (close > 0) {\n close--;\n } else {\n remove[i] = true;\n }\n }\n }\n\n for (int i = 0; i < n; i++) {\n if (!remove[i]) sb.append(str.charAt(i));\n }\n\n return sb.toString();\n}\n```
| 24 | 0 |
['Java']
| 4 |
minimum-remove-to-make-valid-parentheses
|
✅With stack. ~100% Easy ✅
|
with-stack-100-easy-by-husanmusa-x3p0
|
Intuition\nPlease upvt if you found it useful\n\n# Complexity\n- Time complexity: O(N)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(N)\n
|
husanmusa
|
NORMAL
|
2024-04-06T00:51:20.256711+00:00
|
2024-04-06T00:51:20.256730+00:00
| 2,556 | false |
# Intuition\nPlease **upvt** if you found it useful\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\ntype stack struct {\n top int\n v []byte\n index []int\n}\n\nfunc minRemoveToMakeValid(s string) string {\n stc := stack{top: -1}\n\n // collect bad brackets\n for i, v := range s {\n if v == \'(\' {\n stc.v = append(stc.v, \'(\')\n stc.index = append(stc.index, i)\n stc.top++\n } else if v == \')\' {\n if stc.top > -1 && stc.v[stc.top] == \'(\' {\n stc.v = stc.v[:stc.top]\n stc.index = stc.index[:stc.top]\n stc.top--\n } else {\n stc.v = append(stc.v, \')\')\n stc.index = append(stc.index, i)\n stc.top++\n }\n }\n }\n\n // remove them\n res := []byte{}\n i := 0\n for _, v := range stc.index {\n res = append(res, s[i:v]...)\n i = v + 1\n }\n\n // checking of end\n if len(res) + len(stc.index) < len(s) {\n res = append(res, s[i:]...)\n }\n\n return string(res)\n}\n```
| 21 | 0 |
['Stack', 'Go']
| 9 |
minimum-remove-to-make-valid-parentheses
|
🔥 BEATS ~100% | ✅ [ C++ / Java / Py / C / C# / JS / GO ]
|
beats-100-c-java-py-c-c-js-go-by-neoni_7-44u2
|
\nC++ []\nclass Solution {\npublic:\n string minRemoveToMakeValid(string s) {\n int open = 0;\n for (int i = 0; i < s.size(); ++i) {\n
|
Neoni_77
|
NORMAL
|
2024-04-06T05:40:41.293812+00:00
|
2024-04-12T05:56:45.526097+00:00
| 2,915 | false |
\n```C++ []\nclass Solution {\npublic:\n string minRemoveToMakeValid(string s) {\n int open = 0;\n for (int i = 0; i < s.size(); ++i) {\n if (s[i] == \'(\') {\n ++open;\n } else if (s[i] == \')\') {\n if (open == 0) {\n s.erase(i, 1);\n --i; // Adjust index after erasing\n } else {\n --open;\n }\n }\n }\n\n // Remove excessive \'(\'\n for (int i = s.size() - 1; open > 0 && i >= 0; --i) {\n if (s[i] == \'(\') {\n s.erase(i, 1);\n --open;\n }\n }\n\n return s;\n }\n};\n\n```\n```python []\nclass Solution:\n def minRemoveToMakeValid(self, s: str) -> str:\n stack = []\n s = list(s)\n \n # First pass: track indices of \'(\' and mark \')\' for removal\n for i, char in enumerate(s):\n if char == \'(\':\n stack.append(i)\n elif char == \')\':\n if stack:\n stack.pop()\n else:\n s[i] = \'\' # Mark \')\' for removal\n \n # Mark remaining \'(\' for removal\n while stack:\n s[stack.pop()] = \'\' # Mark \'(\' for removal\n \n return \'\'.join(s)\n\n```\n```Java []\nimport java.util.Stack;\n\nclass Solution {\n public String minRemoveToMakeValid(String s) {\n StringBuilder sb = new StringBuilder(s);\n Stack<Integer> stack = new Stack<>();\n\n // First pass: remove excessive \')\' and track \'(\' indices\n for (int i = 0; i < sb.length(); ++i) {\n if (sb.charAt(i) == \'(\') {\n stack.push(i);\n } else if (sb.charAt(i) == \')\') {\n if (!stack.isEmpty()) {\n stack.pop();\n } else {\n sb.setCharAt(i, \'*\'); // Mark \')\' for removal\n }\n }\n }\n\n // Mark excessive \'(\' for removal\n while (!stack.isEmpty()) {\n sb.setCharAt(stack.pop(), \'*\');\n }\n\n // Construct result string\n StringBuilder result = new StringBuilder();\n for (int i = 0; i < sb.length(); ++i) {\n if (sb.charAt(i) != \'*\') {\n result.append(sb.charAt(i));\n }\n }\n\n return result.toString();\n }\n}\n\n```\n```C []\n\nchar* minRemoveToMakeValid(char* s) {\n int len = strlen(s);\n char* result = (char*)malloc((len + 1) * sizeof(char));\n int* stack = (int*)malloc(len * sizeof(int));\n int top = -1;\n\n // First pass: track indices of \'(\' and mark \')\' for removal\n for (int i = 0; i < len; i++) {\n if (s[i] == \'(\') {\n stack[++top] = i;\n } else if (s[i] == \')\') {\n if (top >= 0) {\n top--;\n } else {\n s[i] = \'\\0\'; // Mark \')\' for removal\n }\n }\n }\n\n // Mark remaining \'(\' for removal\n while (top >= 0) {\n s[stack[top--]] = \'\\0\'; // Mark \'(\' for removal\n }\n\n // Construct result string\n int resultIndex = 0;\n for (int i = 0; i < len; i++) {\n if (s[i] != \'\\0\') {\n result[resultIndex++] = s[i];\n }\n }\n result[resultIndex] = \'\\0\';\n\n free(stack);\n return result;\n}\n\n```\n```C# []\npublic class Solution {\n public string MinRemoveToMakeValid(string s) {\n Stack<int> stack = new Stack<int>();\n StringBuilder result = new StringBuilder(s);\n\n // First pass: track indices of \'(\' and mark \')\' for removal\n for (int i = 0; i < result.Length; i++) {\n if (result[i] == \'(\') {\n stack.Push(i);\n } else if (result[i] == \')\') {\n if (stack.Count > 0) {\n stack.Pop();\n } else {\n result[i] = \'*\'; // Mark \')\' for removal\n }\n }\n }\n\n // Mark remaining \'(\' for removal\n while (stack.Count > 0) {\n result[stack.Pop()] = \'*\'; // Mark \'(\' for removal\n }\n\n // Construct result string\n StringBuilder finalResult = new StringBuilder();\n foreach (char c in result.ToString()) {\n if (c != \'*\') {\n finalResult.Append(c);\n }\n }\n\n return finalResult.ToString();\n }\n}\n\n```\n```Javascript []\nvar minRemoveToMakeValid = function(s) {\n const stack = [];\n const chars = s.split(\'\');\n\n // First pass: track indices of \'(\' and mark \')\' for removal\n for (let i = 0; i < chars.length; i++) {\n if (chars[i] === \'(\') {\n stack.push(i);\n } else if (chars[i] === \')\') {\n if (stack.length > 0) {\n stack.pop();\n } else {\n chars[i] = \'\'; // Mark \')\' for removal\n }\n }\n }\n\n // Mark remaining \'(\' for removal\n while (stack.length > 0) {\n chars[stack.pop()] = \'\'; // Mark \'(\' for removal\n }\n\n // Construct result string\n var minRemoveToMakeValid = function(s) {\n const stack = [];\n const chars = s.split(\'\');\n\n // First pass: track indices of \'(\' and mark \')\' for removal\n for (let i = 0; i < chars.length; i++) {\n if (chars[i] === \'(\') {\n stack.push(i);\n } else if (chars[i] === \')\') {\n if (stack.length > 0) {\n stack.pop();\n } else {\n chars[i] = \'\'; // Mark \')\' for removal\n }\n }\n }\n\n // Mark remaining \'(\' for removal\n while (stack.length > 0) {\n chars[stack.pop()] = \'\'; // Mark \'(\' for removal\n }\n\n // Construct result string\n return chars.join(\'\');\n};\n\n};\n\n```\n```Go []\nfunc minRemoveToMakeValid(s string) string {\n var stack []int\n chars := []rune(s)\n\n // First pass: track indices of \'(\' and mark \')\' for removal\n for i, char := range chars {\n if char == \'(\' {\n stack = append(stack, i)\n } else if char == \')\' {\n if len(stack) > 0 {\n stack = stack[:len(stack)-1]\n } else {\n chars[i] = 0 // Mark \')\' for removal\n }\n }\n }\n\n // Mark remaining \'(\' for removal\n for _, index := range stack {\n chars[index] = 0 // Mark \'(\' for removal\n }\n\n // Construct result string\n result := make([]rune, 0, len(chars))\n for _, char := range chars {\n if char != 0 {\n result = append(result, char)\n }\n }\n\n return string(result)\n}\n\n```\n\n\n```\n// ------------------- UPVOTE PLZ IF HELPFULL -------------------//\n```
| 20 | 0 |
['C', 'Python', 'C++', 'Java', 'Go', 'Python3', 'JavaScript', 'C#']
| 4 |
minimum-remove-to-make-valid-parentheses
|
Simple and short C++ solution
|
simple-and-short-c-solution-by-divyaraok-pmox
|
Approach:\nPush every occurrence of \'(\' into a stack and whenever \')\' appears in the string, try to pop \'(\' from stack if exists. If \'(\' does not exist,
|
divyaraok29
|
NORMAL
|
2020-07-30T13:55:31.062326+00:00
|
2020-07-30T13:55:31.062358+00:00
| 1,645 | false |
**Approach:**\nPush every occurrence of \'(\' into a stack and whenever \')\' appears in the string, try to pop \'(\' from stack if exists. If \'(\' does not exist, then erase \')\' from string. After parsing the entire string, erase extra \'(\' present in stack from string.\n\n***Note***\n*Store indices of string in stack instead of the character for easy access and less iteration.*\n\n```\nclass Solution {\npublic:\n string minRemoveToMakeValid(string s) {\n stack<int> box;\n int n = s.length();\n \n for(int i=0; i<n; i++) {\n if(s[i] == \')\'){\n if(!box.empty() && s[box.top()] == \'(\'){\n box.pop();\n }else{\n s.erase(i,1);\n i--;\n }\n }\n else if(s[i] == \'(\'){\n box.push(i);\n }\n }\n \n while(!box.empty()) {\n s.erase(box.top(),1);\n box.pop();\n }\n \n return s;\n }\n};\n```\n\n***Hope it helps. :)***
| 20 | 0 |
['C']
| 4 |
minimum-remove-to-make-valid-parentheses
|
deque +string vs string+ reverse vs string||6ms Beats 99.97%
|
deque-string-vs-string-reverse-vs-string-a42y
|
IntuitionA several pass solution. 1st pass is to remove the redundant ')'; 2nd pass is an inverse trasversal which removes the redundant '('.Later try other app
|
anwendeng
|
NORMAL
|
2024-04-06T00:36:12.329138+00:00
|
2025-04-01T10:50:13.463032+00:00
| 1,876 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
A several pass solution. 1st pass is to remove the redundant ')'; 2nd pass is an inverse trasversal which removes the redundant '('.
Later try other approaches.
2nd approach uses just string & reverse.
3rd approach uses only string with SC O(1); thanks to the suggestion by @ Sergei, 1st pass is backward, 2nd pass is a forward trasversal. The C++ implementation :6ms Beats 99.97%, C implementation is faster only 2ms & & beats 98.08%
# Approach
<!-- Describe your approach to solving the problem. -->
[Please turn on English subtitles if necessary]
[https://youtu.be/527BNZYm6aE?si=h0hrcDHFx-Q3t6Vl](https://youtu.be/527BNZYm6aE?si=h0hrcDHFx-Q3t6Vl)
Since the depth of any char c in a VPS=(# of `'('` before c)-(# of '`)'` before c),
transverse do the following
```
p+=(c=='(')-(c==')');//count the current depth for the char c
```
1. 1st pass needs a container like stack, a string `t` is good for this task; when p>=0, the parenthesis string is valid by `push_back(c)`, otherwise reset p=0.
2. 2nd pass needs a container which has O(1)-time for `push_front`( `appendleft` in Python); a deque `q` is used for this task. When p<=0, the parenthesis string is valid by `push_front(c)`, otherwise reset p=0.
3. Convert deque `q` to string and return
Let's see the process for the testcase `"lee(t(c))o)de))())("` which is adding some outputs for submitted code
```
1st transverse:
l : p= 0 t= l
e : p= 0 t= le
e : p= 0 t= lee
( : p= 1 t= lee(
t : p= 1 t= lee(t
( : p= 2 t= lee(t(
c : p= 2 t= lee(t(c
) : p= 1 t= lee(t(c)
) : p= 0 t= lee(t(c))
o : p= 0 t= lee(t(c))o
) : removing
d : p= 0 t= lee(t(c))od
e : p= 0 t= lee(t(c))ode
) : removing
) : removing
( : p= 1 t= lee(t(c))ode(
) : p= 0 t= lee(t(c))ode()
) : removing
( : p= 1 t= lee(t(c))ode()(
---
t= lee(t(c))ode()(
transverse reversely:
( : removing
) : p= -1 q= )
( : p= 0 q= ()
e : p= 0 q= e()
d : p= 0 q= de()
o : p= 0 q= ode()
) : p= -1 q= )ode()
) : p= -2 q= ))ode()
c : p= -2 q= c))ode()
( : p= -1 q= (c))ode()
t : p= -1 q= t(c))ode()
( : p= 0 q= (t(c))ode()
e : p= 0 q= e(t(c))ode()
e : p= 0 q= ee(t(c))ode()
l : p= 0 q= lee(t(c))ode()
```
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
$$O(n)$$
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
$$O(n)\to O(1)$$
# Code||C++ 14ms Beats 95.19%
```C++ []
#pragma GCC optimize("O3", "unroll-loops")
class Solution {
public:
string minRemoveToMakeValid(string& s) {
string t;//Temporary string to store valid parentheses
int p=0;// p is the balance of '(' and ')'
// Forward pass to remove excess ')' and ensure balance
for(char c: s){
p+=(c=='(')-(c==')');//find the depth for c
if (p>=0) t.push_back(c);// depth>=0, valid
else p=0;// ')' too many, reset p
}
p=0;// Reset balance for backward pass
deque<char> q;// Using deque for efficient push_front
//Backward pass to remove excess '('
for(int i=t.size()-1; i>=0; i--){
char c=t[i];
p+=(c=='(')-(c==')');//find the depth for c
if (p<=0)q.push_front(c); // depth<=0, valid
else p=0; // '(' too many, reset p
}
//Convert deque to string and return
return string(q.begin(), q.end());
}
};
auto init = []()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
return 'c';
}();
```
```python []
class Solution:
def minRemoveToMakeValid(self, s: str) -> str:
t=[]
p=0
for c in s:
p+=(c=='(')-(c==')')
if p>=0: t.append(c)
else: p=0
p=0
q=deque()
for c in t[::-1]:
p+=(c=='(')-(c==')')
if p<=0: q.appendleft(c)
else: p=0
return ''.join(q)
```
# 2nd C++ using string & reverse||C++ 14ms Beats 95.19%
Almost the same as the 1st one. Just use reverse & reuse `s` to replace the role played by deque `q`.
```
#pragma GCC optimize("O3", "unroll-loops")
class Solution {
public:
string minRemoveToMakeValid(string& s) {
string t;
int p=0, n=s.size();
for(char c: s){
p+=(c=='(')-(c==')');
if (p>=0) t.push_back(c);
else p=0;
}
p=0;
s="";
for(int i=t.size()-1; i>=0; i--){
char c=t[i];
p+=(c=='(')-(c==')');
if (p<=0) s.push_back(c);
else p=0;
}
reverse(s.begin(), s.end());
return s;
}
};
```
# Codes using only string with SC O(1)||C: 2ms Beats 98.08% C++:6ms Beats 99.97%
__Less containers less elapsed time!__
Thanks to suggestions by @Sergei. Try to construct a 2 pass solution.
Resue string `s`, it doesn't need other containers. 1st backward transverse marks excess '('s with '@'.
The 2nd forward transverse obtains the valid parentheses string. C++ is really a 2 pass solution. The coresponding C code uses strlen function, & hence a 3 pass solution.
```C++ []
#pragma GCC optimize("O3", "unroll-loops")
class Solution {
public:
string minRemoveToMakeValid(string& s) {
int p=0, n=s.size();
for(int i=n-1; i>=0; i--){
char& c=s[i];
p+=(c=='(')-(c==')');
if (p>0) c='@', p=0;
}
// cout<<s<<endl;
int sz=n;
p=0;
for(int i=0, j=0; i<n; i++){
char c=s[i];
p+=(c=='(')-(c==')');
if (c!='@' && p>=0) s[j++]=c;
else sz--, p=0;
}
s.resize(sz, '\0');
return s;
}
};
auto init = []()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
return 'c';
}();
```
```C []
#pragma GCC optimize("O3", "unroll-loops")
char* minRemoveToMakeValid(char* s) {
int p=0, n=strlen(s);
for(register int i=n-1; i>=0; i--){
char c=s[i];
p+=(c=='(')-(c==')');
if (p>0) s[i]='@', p=0;
}
int sz=n;
p=0;
for(register int i=0, j=0; i<n; i++){
char c=s[i];
p+=(c=='(')-(c==')');
if (c!='@' && p>=0) s[j++]=c;
else sz--, p=0;
}
s[sz]='\0';
return s;
}
```
| 19 | 0 |
['String', 'Queue', 'C', 'C++', 'Python3']
| 6 |
minimum-remove-to-make-valid-parentheses
|
Beginner friendly [Java/JavaScript/Python] solution
|
beginner-friendly-javajavascriptpython-s-o5jp
|
Time Complexity : O(n)\nJava\n\nclass Solution {\n public String minRemoveToMakeValid(String s) {\n StringBuilder sb = new StringBuilder(s);\n
|
HimanshuBhoir
|
NORMAL
|
2022-03-15T00:42:06.717057+00:00
|
2022-08-06T07:02:42.059068+00:00
| 1,672 | false |
**Time Complexity : O(n)**\n**Java**\n```\nclass Solution {\n public String minRemoveToMakeValid(String s) {\n StringBuilder sb = new StringBuilder(s);\n Stack<Integer> stack = new Stack<>();\n for(int i=0; i<s.length(); i++){\n if(sb.charAt(i) == \'(\') stack.push(i);\n else if (sb.charAt(i) == \')\'){\n if(!stack.isEmpty()) stack.pop();\n else sb.setCharAt(i, \'*\');\n }\n }\n while(!stack.isEmpty()) sb.setCharAt(stack.pop(), \'*\');\n return sb.toString().replaceAll("\\\\*", "");\n }\n}\n```\n**JavaScript**\n```\nvar minRemoveToMakeValid = function(s) {\n s = s.split("")\n let stack = []\n for(let i=0; i<s.length; i++){\n if(s[i] == "(") stack.push(i)\n else if (s[i] == ")"){\n if(stack.length) stack.pop()\n else s[i] = ""\n }\n }\n for(let i of stack) s[i] = ""\n return s.join("")\n};\n```\n**Python**\n```\nclass Solution(object):\n def minRemoveToMakeValid(self, s):\n s = list(s)\n stack = []\n for i in range(len(s)):\n if s[i] == "(":\n stack.append(i)\n elif s[i] == ")":\n if len(stack):\n stack.pop()\n else:\n s[i] = ""\n for i in stack:\n s[i] = ""\n return "".join(s)\n\n```
| 19 | 0 |
['Python', 'Java', 'JavaScript']
| 1 |
minimum-remove-to-make-valid-parentheses
|
JS, Python, Java, C++ | Stack Solution w/ Explanation | beats 100%
|
js-python-java-c-stack-solution-w-explan-zyd6
|
(Note: This is part of a series of Leetcode solution explanations. If you like this solution or find it useful, please upvote this post.)\n\n---\n\nIdea:\n\nVal
|
sgallivan
|
NORMAL
|
2021-02-19T13:05:50.876951+00:00
|
2021-02-19T18:55:11.628080+00:00
| 1,640 | false |
*(Note: This is part of a series of Leetcode solution explanations. If you like this solution or find it useful,* ***please upvote*** *this post.)*\n\n---\n\n***Idea:***\n\nValid parentheses follow the **LIFO method** (last in, first out), so we should automatically be thinking of some kind of **stack** solution.\n\nTo check for valid parentheses, you push any **"("** onto **stack**, then pop off the top stack element every time you find a matching **")"**. If you find a **")"** when **stack** is empty, that **")"** must be invalid. At the end of **S**, any leftover **"("**\'s left in **stack** must be invalid, as well. Since we\'ll want to remove those **"("**\'s by index at the end, **stack** should contain said indexes, rather than just the **"("**.\n\nNow that we\'ve identified all the invalid parentheses, that leaves us with the problem of removing them from **S**. We could perform a lot of string slices and copies, but those are typically very slow and memory intensive, so we should probably find a data type that can be directly modified by index access and use that as an intermediary.\n\nThe most effective method varies by language, so I\'ll discuss those in the *Implementation* section.\n\nThen we can make our removals and re-form and **return** our answer.\n\n---\n\n***Implementation:***\n\nJavascript has basic arrays, Python has lists, and Java has char arrays that will perform the job of a more flexible data type for this problem. C++ alone of the four languages has mutable strings, so we can just leave **S** as is.\n\nWhile Java has stack/deque/list structures, they\'re not always terribly efficient, so we can just use a more basic int[] with a length fixed to the size of **S**, along with an index variable (**stIx**).\n\nJavascript conveniently allows us to directly delete an array element without screwing up our iteration, so we can use that on the initial pass for invalid **"("**\'s. Python can\'t do that, but we can easily replace each character we want to delete with an empty string, which effectively does the same thing once the string has been joined again.\n\nJava and C++ won\'t allow us to replace characters with empty strings, so we can just mark those characters with a **character mask** for later removal.\n\nOn the second pass through Javascript and Python can just repeat the same method while going through the remaining **stack**. Python is very fast with its appends and pops, so we can use that to our advantage.\n\nFor Java and C++, things are more difficult. We can\'t change the length of the intermediary, but we *can* alter its contents by index assignment. That means we can use a two-pointer approach to rewrite the beginning portion of the intermediary before ultimately returning a subsection of it.\n\nSince we want to iterate through **stack** in opposite order (**FIFO**) this time, we can just tag a **-1** onto the end of the stack to avoid issues with going out-of-bounds, and then use **stIx** starting at **0**.\n\nThen, for every iteration, **j** will increment, but **i** will only increment if it\'s not a character we want to remove (either by matching the character mask or the next stack entry), and we\'ll overwrite the intermediary at **i** with **j**\'s value.\n\nAt the end, the substring between **0** and **i** will represent the "squeezed" string with all invalid parentheses removed, so we should **return** it.\n\n---\n\n***Javascript Code:***\n\nThe best result for the code below is **76ms / 44.7MB** (beats 100% / 96%).\n```javascript\nvar minRemoveToMakeValid = function(S) {\n S = S.split("")\n let len = S.length, stack = []\n for (let i = 0, c = S[0]; i < len; c = S[++i])\n if (c === ")")\n if (stack.length) stack.pop()\n else delete S[i]\n else if (c === "(") stack.push(i)\n for (let i = 0; i < stack.length; i++)\n delete S[stack[i]]\n return S.join("")\n};\n```\n\n---\n\n***Python Code:***\n\nThe best result for the code below is **72ms / 15.8MB** (beats 100% / 91%).\n```python\nclass Solution:\n def minRemoveToMakeValid(self, S: str) -> str:\n S, stack = list(S), []\n for i, c in enumerate(S):\n if c == ")":\n if stack: stack.pop()\n else: S[i] = ""\n elif c == "(": stack.append(i)\n for i in stack: S[i] = ""\n return "".join(S)\n```\n\n---\n\n***Java Code:***\n\nThe best result for the code below is **5ms / 39.1MB** (beats 100% / 99%).\n```java\nclass Solution {\n public String minRemoveToMakeValid(String S) {\n char[] ans = S.toCharArray();\n int len = S.length(), stIx = 0, i = 0, j = 0;\n int[] stack = new int[len+1];\n for (; i < len; i++)\n if (ans[i] == \')\')\n if (stIx > 0) stIx--;\n else ans[i] = \'_\';\n else if (ans[i] == \'(\') stack[stIx++] = i;\n for (i = 0, stack[stIx] = -1, stIx = 0; j < len; j++)\n if (j == stack[stIx]) stIx++;\n else if (ans[j] != \'_\') ans[i++] = ans[j];\n return new String(ans, 0, i);\n }\n}\n```\n\n---\n\n***C++ Code:***\n\nThe best result for the code below is **16ms / 10.2MB** (beats 99% / 91%).\n```c++\nclass Solution {\npublic:\n string minRemoveToMakeValid(string S) {\n int len = S.size(), i = 0, j = 0, stIx = 0;\n vector<int> stack;\n for (; i < len; i++)\n if (S[i] == \')\')\n if (stack.size() > 0) stack.pop_back();\n else S[i] = \'_\';\n else if (S[i] == \'(\') stack.push_back(i);\n stack.push_back(-1);\n for (i = 0; j < len; j++)\n if (j == stack[stIx]) stIx++;\n else if (S[j] != \'_\') S[i++] = S[j];\n return S.substr(0, i);\n }\n};\n```
| 19 | 0 |
['C', 'Python', 'Java', 'JavaScript']
| 5 |
minimum-remove-to-make-valid-parentheses
|
Explained With Images. Commented Solution.
|
explained-with-images-commented-solution-thwd
|
Approach\nIn this solution, we will use a stack with its method, LIFO, to remove all the extra parentheses from the input string. We traverse the input string,
|
Kunal_Tajne
|
NORMAL
|
2024-08-12T21:12:19.165207+00:00
|
2024-08-12T21:12:19.165230+00:00
| 312 | false |
# Approach\nIn this solution, we will use a stack with its method, LIFO, to remove all the extra parentheses from the input string. We traverse the input string, and every time we encounter an opening parenthesis, we push it, along with its index, onto the stack and keep traversing. Meanwhile, whenever we find a closing parenthesis, we decide whether to push it onto the stack or not.\n\n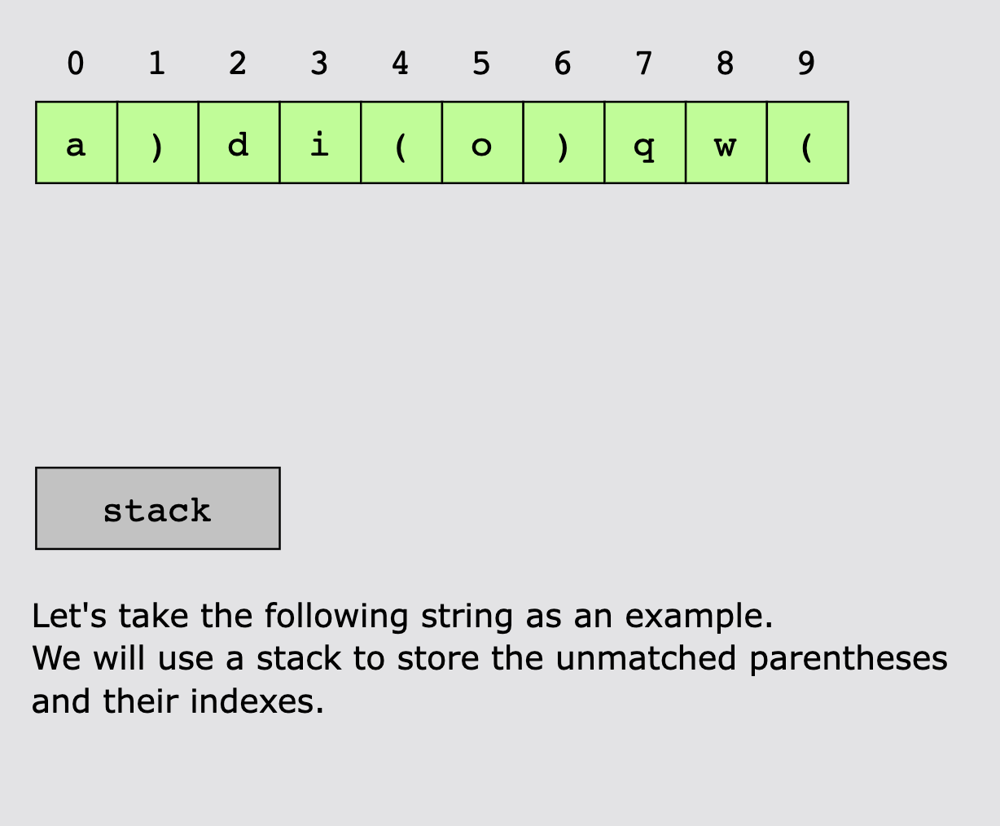\n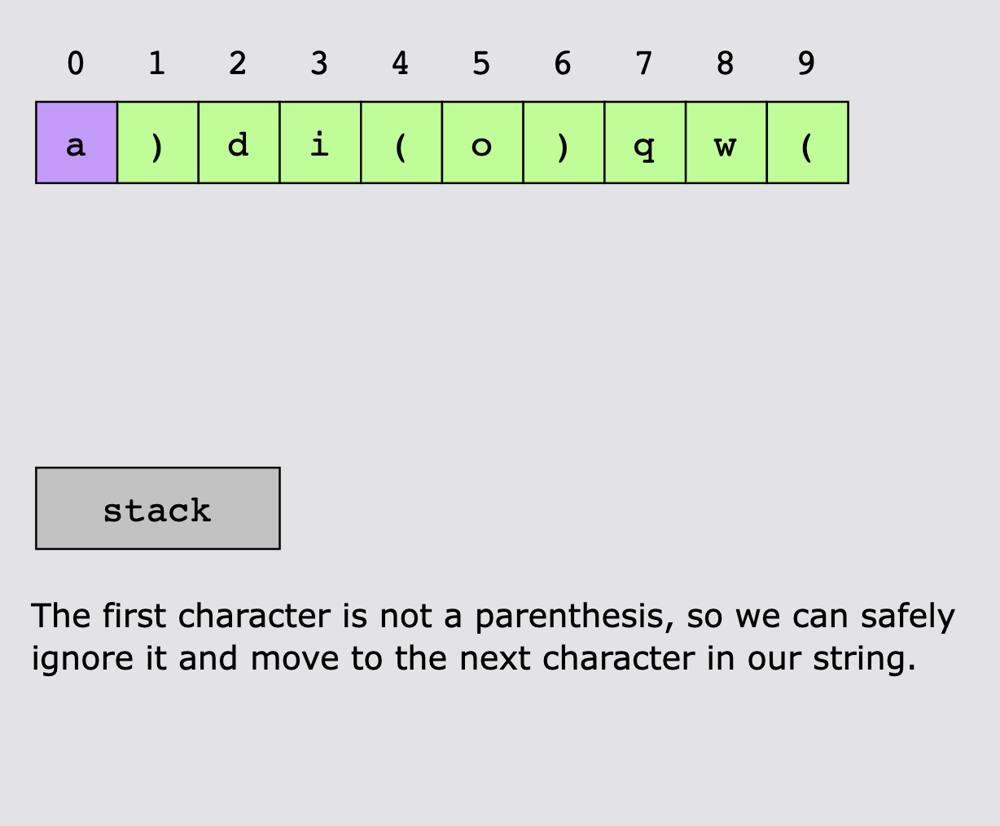\n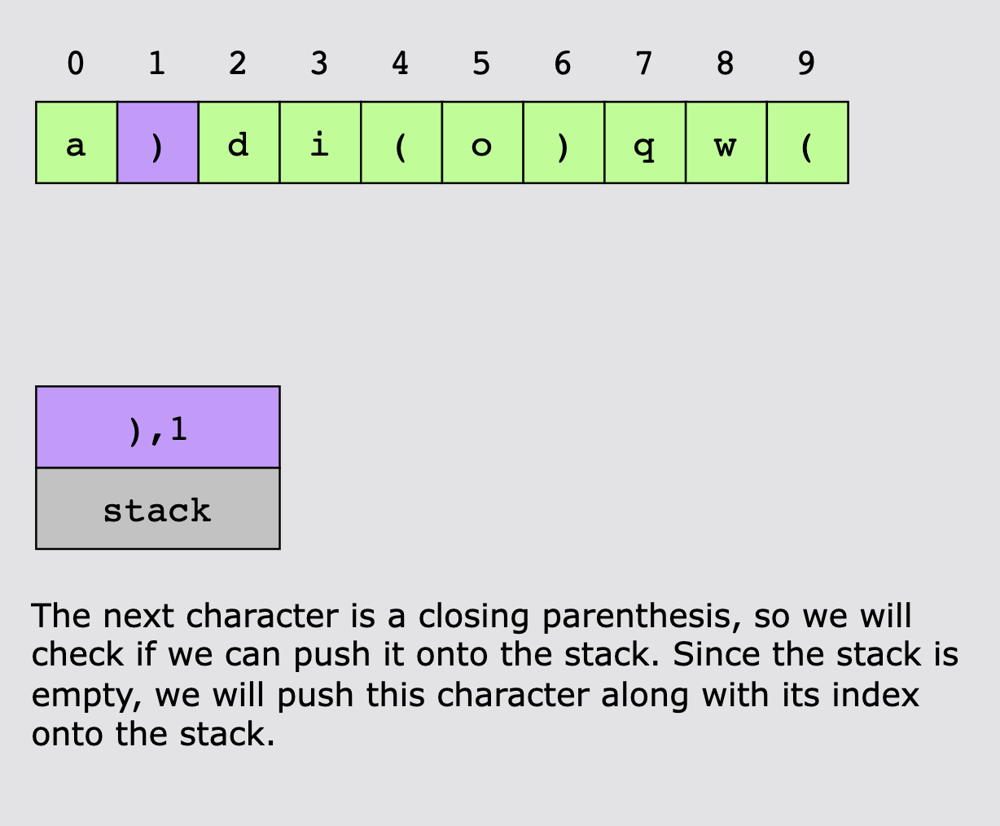\n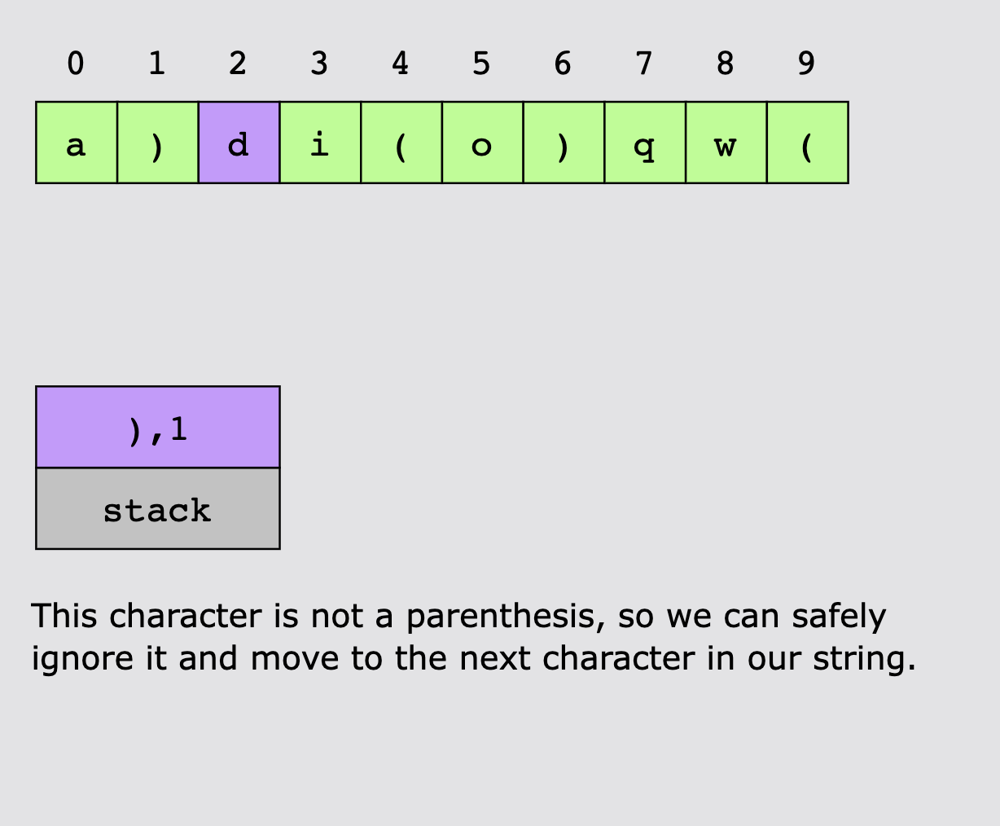\n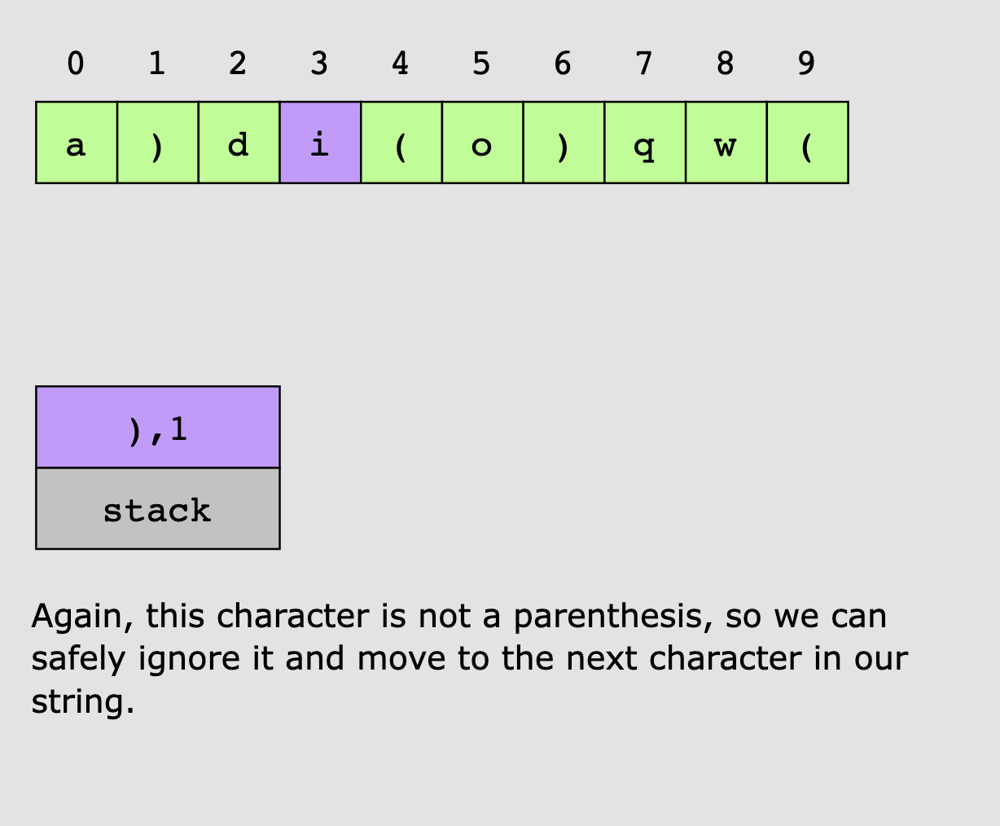\n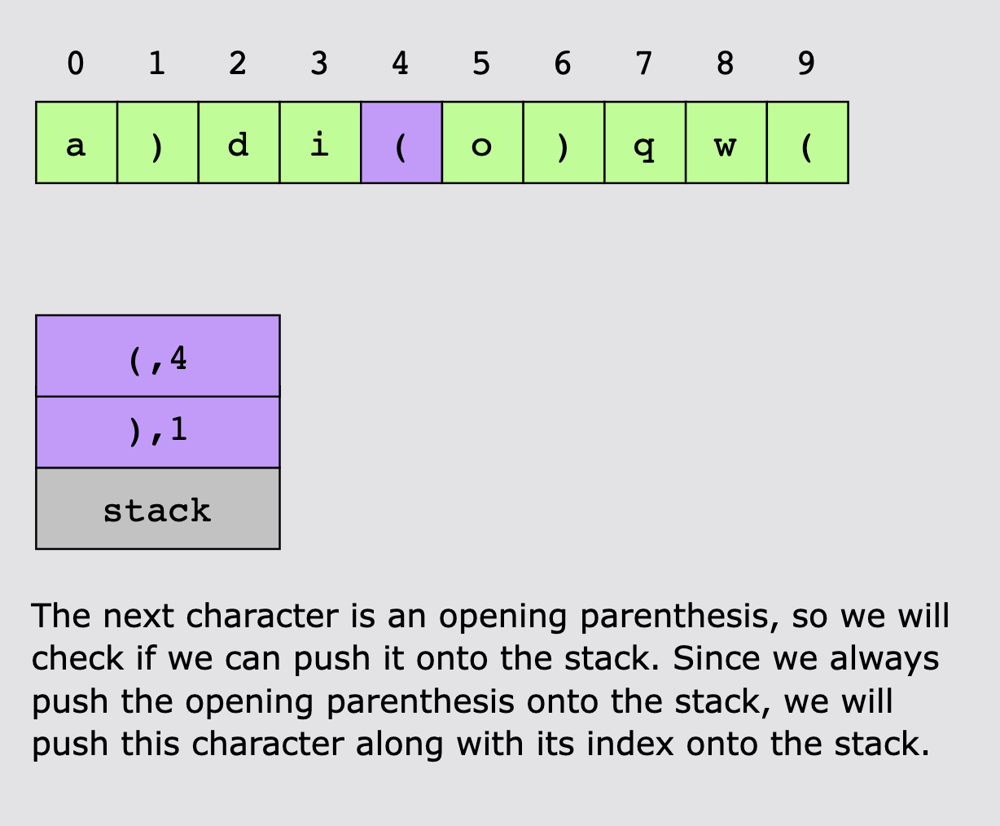\n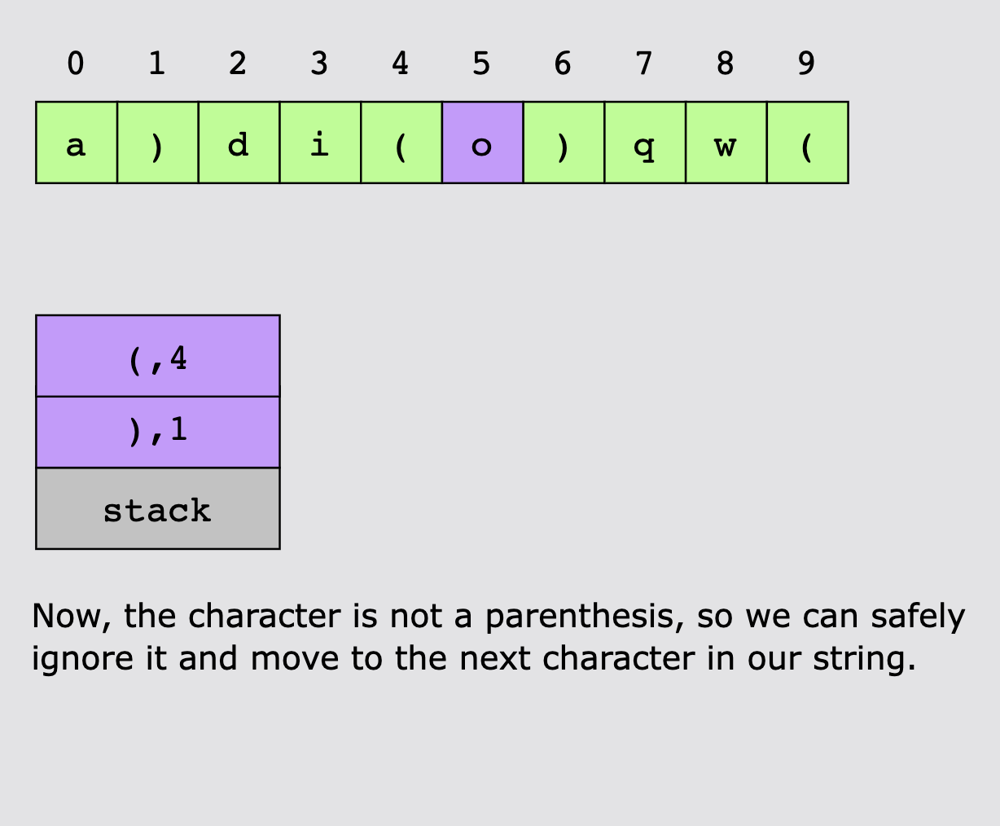\n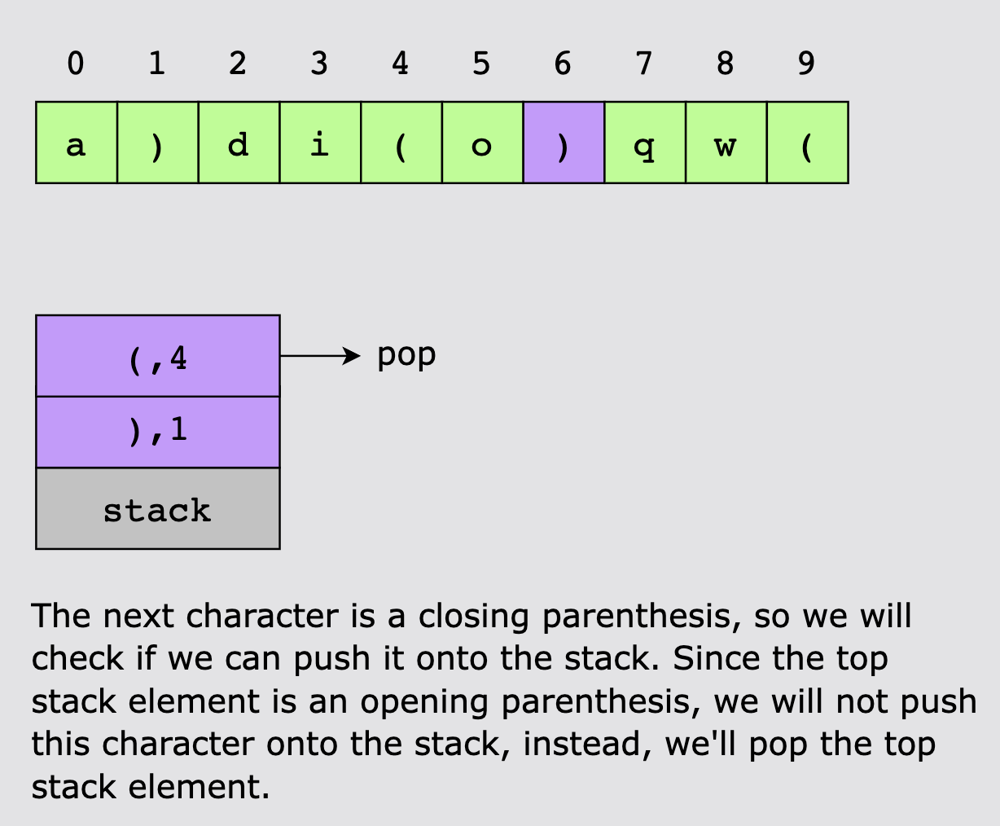\n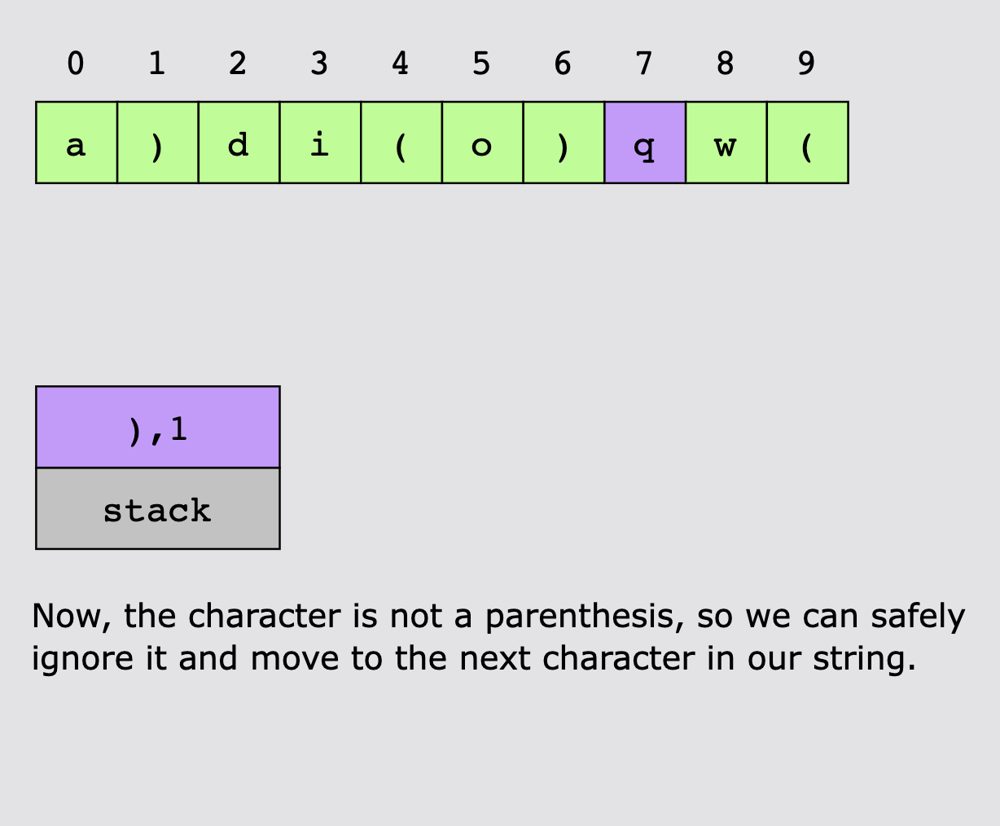\n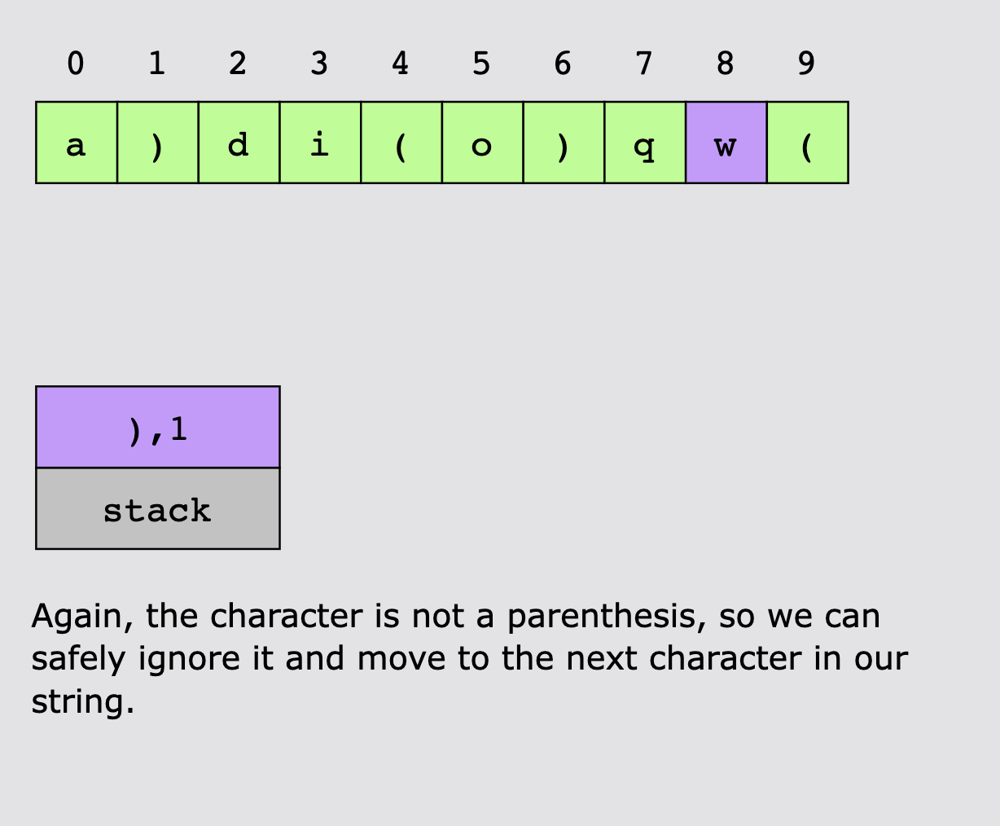\n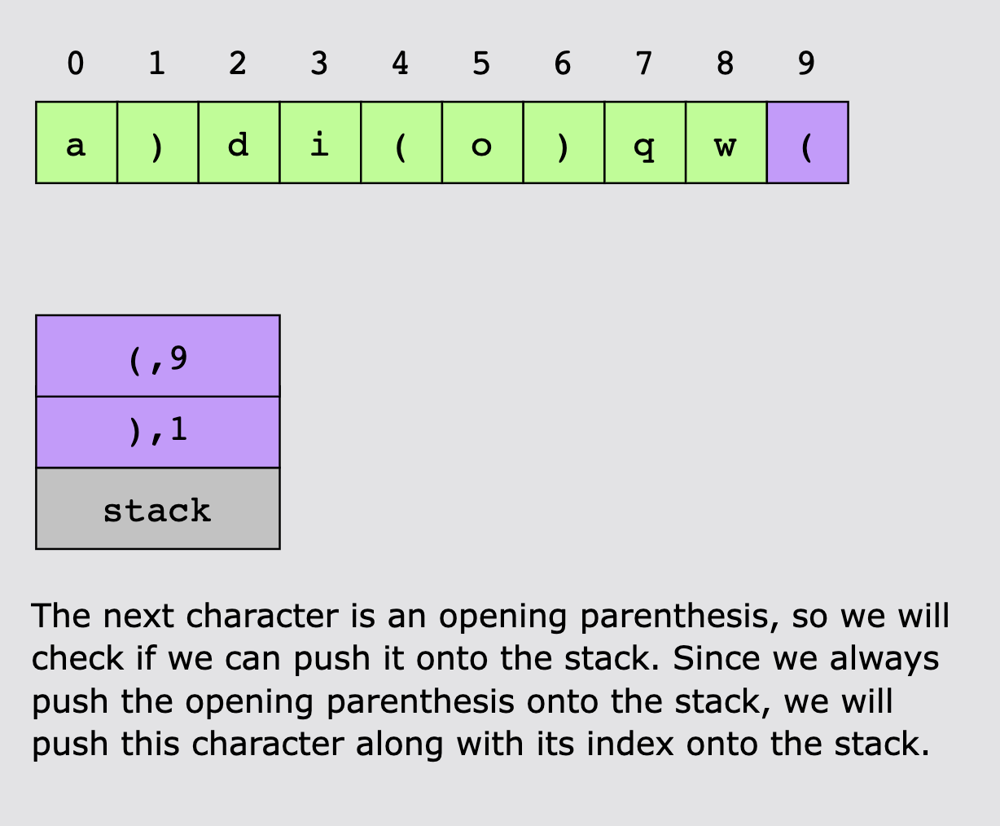\n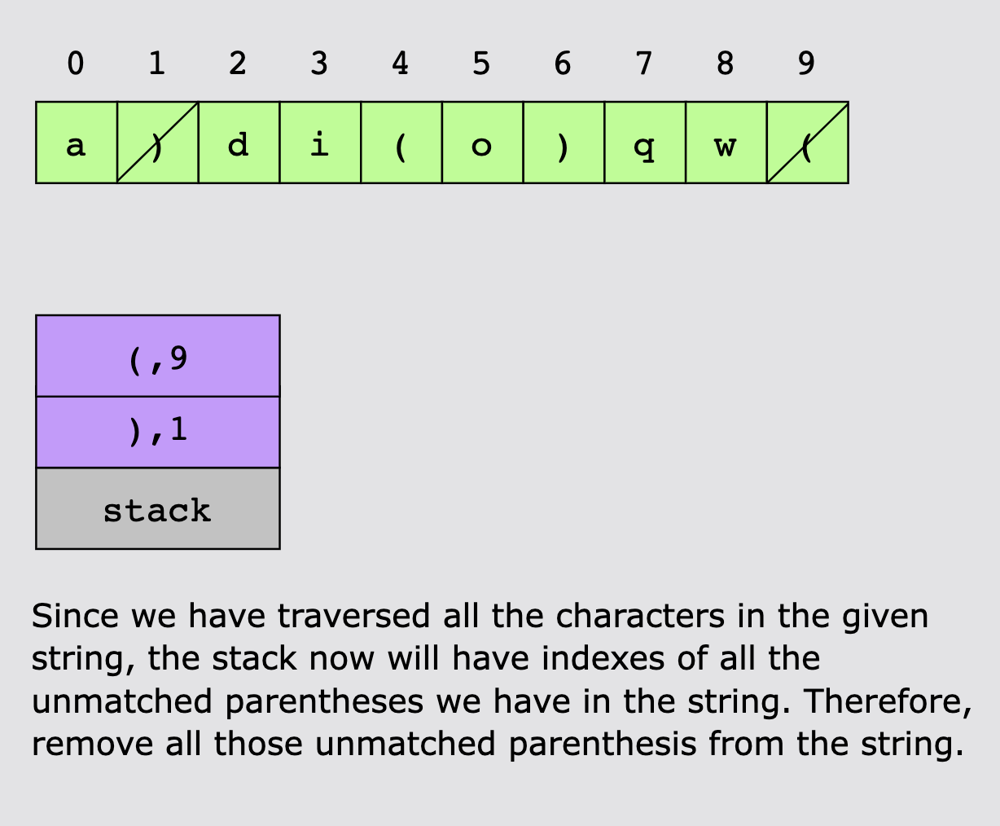\n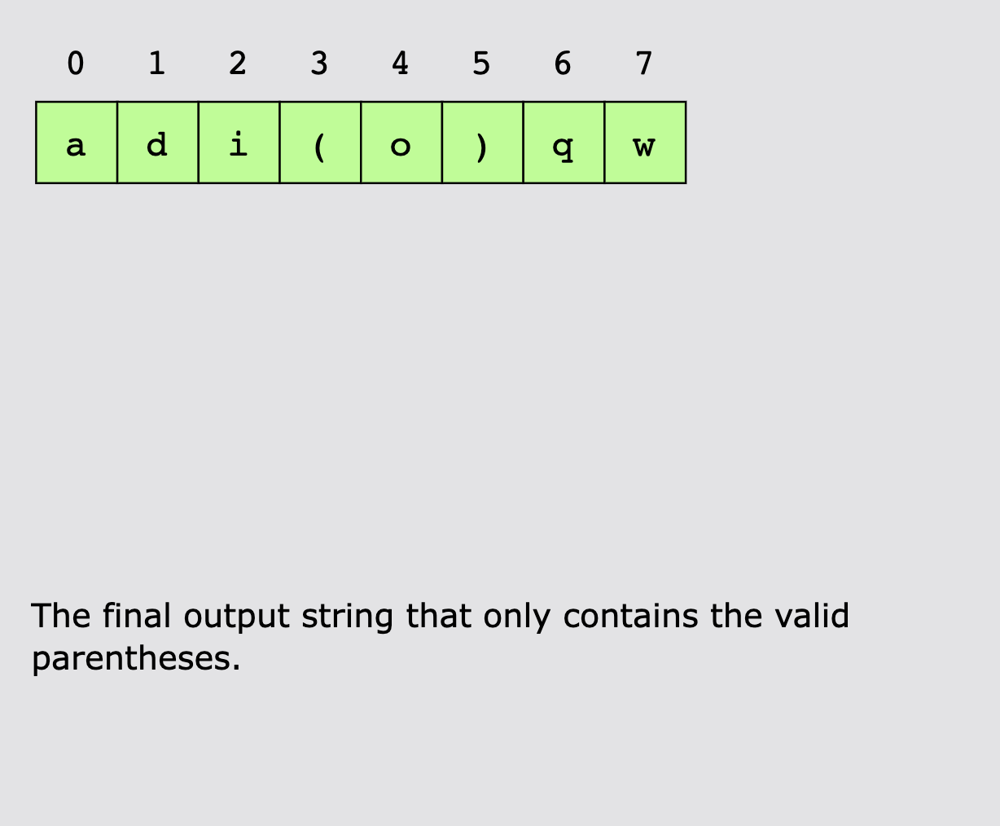\n\n\n# Time Complexity $$O(N)$$\n\n# Space Complexity $$O(N)$$\n\n# Code\n```\nclass Solution {\n public String minRemoveToMakeValid(String s) {\n\n Stack<int[]> stack = new Stack<>();\n char[] sArray = s.toCharArray();\n\n for (int i = 0; i < s.length(); i++) {\n char val = s.charAt(i);\n // if stack is not empty and top element of stack is an opening parenthesis\n // and the current element is a closing parenthesis\n if (!stack.isEmpty() && stack.peek()[0] == \'(\' && val == \')\') {\n // pop the opening parenthesis as it makes a valid pair \n // with the current closing parenthesis\n stack.pop();\n }\n // if the current value is an opening or a closing parenthesis \n else if (val == \'(\' || val == \')\') {\n // push onto stack\n stack.push(new int[]{val, i});\n }\n }\n\n // Remove the invalid parentheses\n while (!stack.isEmpty()) {\n sArray[stack.pop()[1]] = \' \';\n }\n\n // Convert the char array to a string\n StringBuilder result = new StringBuilder();\n for (char c : sArray) {\n if (c != \' \') {\n result.append(c);\n }\n }\n\n return result.toString();\n }\n}\n```\n\n# A single upvote is all it takes :)\nIf found helpful, give a upvote. Keeps me motivated to post more solutions. Thanks!\n\n\n\n\n\n\n
| 16 | 0 |
['String', 'Stack', 'C++', 'Java', 'Python3']
| 0 |
minimum-remove-to-make-valid-parentheses
|
java easy to understand |using stack & stringBuilder
|
java-easy-to-understand-using-stack-stri-w4vk
|
\nclass Solution {\n public String minRemoveToMakeValid(String s) {\n Stack<Integer> st = new Stack<>();\n StringBuilder ans = new StringBuilde
|
rmanish0308
|
NORMAL
|
2021-09-21T14:28:56.784455+00:00
|
2021-09-21T14:28:56.784503+00:00
| 1,258 | false |
```\nclass Solution {\n public String minRemoveToMakeValid(String s) {\n Stack<Integer> st = new Stack<>();\n StringBuilder ans = new StringBuilder(s);\n \n for(int i=0;i<s.length();i++)\n {\n if(s.charAt(i) == \'(\')\n st.push(i);\n else if(s.charAt(i) == \')\')\n {\n if(st.size() > 0 && s.charAt(st.peek()) == \'(\')\n st.pop();\n else\n st.push(i);\n }\n }\n \n while(st.size()>0)\n ans.deleteCharAt(st.pop());\n \n return ans.toString();\n }\n}\n```\nPlease upvote if u find my code easy to understand
| 16 | 1 |
['Stack', 'Java']
| 4 |
minimum-remove-to-make-valid-parentheses
|
Python | Easy
|
python-easy-by-khosiyat-cgqf
|
see the Successfully Accepted Submission\n\n# Code\n\nclass Solution:\n def minRemoveToMakeValid(self, s: str) -> str:\n stack = []\n to_remove
|
Khosiyat
|
NORMAL
|
2024-04-06T05:34:21.808578+00:00
|
2024-04-06T05:34:21.808610+00:00
| 819 | false |
[see the Successfully Accepted Submission](https://leetcode.com/problems/minimum-remove-to-make-valid-parentheses/submissions/1224541327/?envType=daily-question&envId=2024-04-06)\n\n# Code\n```\nclass Solution:\n def minRemoveToMakeValid(self, s: str) -> str:\n stack = []\n to_remove = set()\n \n for i, char in enumerate(s):\n if char == \'(\':\n stack.append(i)\n elif char == \')\':\n if stack:\n stack.pop()\n else:\n to_remove.add(i)\n \n # Add remaining unmatched opening parentheses to to_remove\n to_remove.update(stack)\n \n # Construct the resulting string excluding characters to be removed\n result = \'\'\n for i, char in enumerate(s):\n if i not in to_remove:\n result += char\n \n return result\n\n```\n\n
| 15 | 0 |
['Python3']
| 4 |
minimum-remove-to-make-valid-parentheses
|
Python | Fast & Easy | Beats 98%
|
python-fast-easy-beats-98-by-slavaherasy-2nwr
|
Time complexity: O(n)\n\nBrief description:\n\nThere is one loop of searching parentheses in the string. It\'s important to use a stack to store the positions
|
slavaherasymov
|
NORMAL
|
2021-02-19T15:28:59.603059+00:00
|
2021-02-19T21:04:10.159341+00:00
| 1,450 | false |
Time complexity: O(n)\n\nBrief description:\n\nThere is one loop of searching parentheses in the string. It\'s important to use a stack to store the positions of open parentheses, because during iteration open parentheses are added and popped from the top of this data collection . In python the best implementation of the stack is using a list.\n\nThere are 2 reasons to remove parentheses:\n1) If there is a valid parentheses string before a close parenthesis, remove this parenthesis. This removal is done during the loop, so the string was converted to a list at the beginning.\n2) If there are extra open parentheses (the stack is not empty), these parantheses should be deleted.\n\n\nSolution:\n```\nclass Solution:\n def minRemoveToMakeValid(self, s: str) -> str:\n stack = []\n s = list(s)\n for i in range(len(s)):\n if s[i] == "(": stack.append(i)\n elif s[i] == ")":\n if stack: stack.pop()\n else: s[i] = ""\n for i in stack:\n s[i] = ""\n return "".join(s)\n```
| 14 | 0 |
['Stack', 'Python', 'Python3']
| 2 |
minimum-remove-to-make-valid-parentheses
|
[Python] Two-pass O(n) solution, explained
|
python-two-pass-on-solution-explained-by-3cj1
|
When you see in problem formulation, that it is something about valid parantheses, you should immedietly thing about stack, because the very classical problems
|
dbabichev
|
NORMAL
|
2021-02-19T09:17:00.844070+00:00
|
2021-02-19T10:12:28.869239+00:00
| 1,026 | false |
When you see in problem formulation, that it is something about valid parantheses, you should immedietly thing about **stack**, because the very classical problems in this topic uses stack.\n\nLet us traverse our string from left to right and make sure, that we do not have any problems with balance:\n1. If symbol is `(`, then we increase balance by `1` and add this symbol to `ans`.\n2. If symbol is `)`, then we can add this symbol only if balance is positive: if it is `0`, then we can not recover our string if we continue.\n3. If symbol not `(` and not `)`, we add it to `ans`.\n\nHowever, it is not enough to do only one traverse: so far when we finished, we can say that:\n1. Balance is never negative\n2. But balance in the end should be equal to `0`.\n\nThese `2` conditions and **sufficient** and **enough** to have valid parentheses and at the moment only the fist one is fulfilled. What we can do now is to traverse string from the end and keep removing symbols until balance becomes equal to `0`. Or we can use our `clean` function and apply it to reversed string.\n\n**Complexity**: time complexity is `O(n)`, we traverse our string twice. Space complexity is also `O(n)`.\n\n```\nclass Solution:\n def minRemoveToMakeValid(self, s):\n def clean(s, op, cl):\n balance, ans = 0, ""\n for i in s:\n if i == op:\n balance += 1\n ans += i\n elif i == cl and balance > 0:\n balance -= 1\n ans += i\n elif i not in "()":\n ans += i \n return ans\n \n return clean(clean(s, "(", ")")[::-1], ")", "(")[::-1]\n```\n\nIf you have any question, feel free to ask. If you like the explanations, please **Upvote!**
| 14 | 3 |
['Stack']
| 4 |
minimum-remove-to-make-valid-parentheses
|
a few solutions
|
a-few-solutions-by-claytonjwong-n4zx
|
Perform a linear scan of the input string s and use a stack S to store each the index of each \'(\' character. Whenever a \')\' character is seen, pop the inde
|
claytonjwong
|
NORMAL
|
2019-11-03T23:33:45.411776+00:00
|
2022-03-15T19:51:59.775886+00:00
| 2,236 | false |
Perform a linear scan of the input string `s` and use a stack `S` to store each the index of each `\'(\'` character. Whenever a `\')\'` character is seen, pop the index of the nearest corresponding match (if possible), otherwise if the stack is empty, then mark the current index to be deleted, ie. we add the index onto the set `X`. Upon completion of the linear scan, we append "leftover" indices of the stack `S` onto `X` to be deleted.\n\nIn summary:\n\n1. we mark indices of `\')\'` to be deleted **during** the linear scan of the input string `s`\n2. we mark indices of `\'(\'` to be deleted **after** the linear scan of the input string `s`\n\n---\n\n*Kotlin*\n```\nclass Solution {\n fun minRemoveToMakeValid(s: String): String {\n var X = mutableSetOf<Int>()\n var S = mutableListOf<Int>()\n for ((i, c) in s.toCharArray().withIndex()) {\n if (c == \'(\')\n S.add(i)\n if (c == \')\') {\n if (0 < S.size)\n S.removeAt(S.lastIndex)\n else\n X.add(i)\n }\n }\n for (i in S) X.add(i)\n return s.toCharArray().withIndex().filter{ (i, c) -> !X.contains(i) }.map{ (_, c) -> c }.joinToString("")\n }\n}\n```\n\n*Javascript*\n```\nlet minRemoveToMakeValid = (s, S = [], X = new Set()) => {\n for (let i = 0; i < s.length; ++i) {\n let c = s[i];\n if (c == \'(\')\n S.push(i);\n if (c == \')\') {\n if (S.length)\n S.pop();\n else\n X.add(i);\n }\n }\n S.forEach(i => X.add(i));\n return s.split(\'\').filter((_, i) => !X.has(i)).join(\'\');\n};\n```\n\n*Python3*\n```\nclass Solution:\n def minRemoveToMakeValid(self, s: str, cnt = 0) -> str:\n S = []\n X = set()\n for i, c in enumerate(s):\n if c == \'(\':\n S.append(i)\n if c == \')\':\n if len(S):\n S.pop()\n else:\n X.add(i)\n [X.add(i) for i in S]\n return \'\'.join(c for i, c in enumerate(s) if i not in X)\n```\n\n*Rust*\n```\nuse std::collections::HashSet;\nimpl Solution {\n pub fn min_remove_to_make_valid(s: String) -> String {\n let mut S = vec![];\n let mut R = HashSet::new();\n for (i, c) in s.chars().enumerate() {\n if c == \'(\' {\n S.push(i);\n }\n if c == \')\' {\n if 0 < S.len() {\n S.pop();\n } else {\n R.insert(i);\n }\n }\n }\n let L: HashSet<usize> = S.drain(..).collect();\n return s.chars().enumerate().filter(|(i, c)| !L.contains(i) && !R.contains(i)).map(|(i, c)| c).collect();\n }\n}\n```\n\n*C++*\n```\nclass Solution {\npublic:\n using Set = unordered_set<int>;\n using VI = vector<int>;\n string minRemoveToMakeValid(string s, string t = {}, VI S = {}, Set X = {}) {\n for (auto i{ 0 }; i < s.size(); ++i) {\n auto c = s[i];\n if (c == \'(\')\n S.push_back(i);\n if (c == \')\') {\n if (S.size())\n S.pop_back();\n else\n X.insert(i);\n }\n }\n X.insert(S.begin(), S.end());\n copy_if(s.begin(), s.end(), back_inserter(t), [&X, i = -1](auto c) mutable { return X.find(++i) == X.end(); });\n return t;\n }\n};\n```\n\n---\n\n**Legacy Solutions November 4, 2019:**\nLet ```t``` be ```s``` transformed with minimum parens removed to make a valid paren string. ```t``` is generated by iterating over each index ```i``` of ```s```:\n* **Case 1:** if ```s[i]``` is ```(```, then push index ```i``` onto the stack since ```s[i]``` contains a potentially a "leftover" ```(```\n* **Case 2:** if ```s[i]``` is ```)```, then the next step depends on the current stack state:\n\t* **either** the stack is empty and the ```)``` is superfluous and it\'s index ```i``` is immediately marked for deletion\n\t* **or** the stack contains a matching ```(``` and it\'s index ```i``` is popped off the stack [ie. the last seen ```(``` matches the current ```)```, thus the last seen ```(``` is *not* a potential "leftover"]\n* **Case 3:** if ```s[i]``` is an alpha char, then no additional processing is needed [ie. it will be copied from ```s``` to ```t``` "as is"]\n\n**Notes:**\n* For *case 1*, we do *not* know if each potential "leftover" ```(``` is actual "leftover" until ```s``` is completely processed since each potential future corresponding ```)``` found causes the index ```i``` associated with each potential "leftover" ```(``` to be popped off the stack.\n* After ```s``` is completely processed all indices remaining in the stack are associated with "leftover" ```(```. Mark all these indices for deletion.\n\n*Javascript*\n```\nvar minRemoveToMakeValid = (s, t=[], del=new Set(), stack=[]) => {\n for (let i=0; i < s.length; ++i) {\n if (s[i] == \'(\')\n stack.push(i);\n if (s[i] == \')\') {\n if (stack.length == 0)\n del.add(i);\n else\n stack.pop();\n }\n }\n stack.forEach(i => del.add(i));\n for (let i=0; i < s.length; ++i)\n if (!del.has(i))\n t.push(s[i]);\n return t.join(\'\');\n};\n```\n\n*C++*\n```\nclass Solution {\npublic:\n string minRemoveToMakeValid(string s, string t={}, unordered_set<int> del={}, vector<int> stack={}) {\n for (auto i=0; i < s.size(); ++i) {\n if (s[i] == \'(\')\n stack.push_back(i);\n if (s[i] == \')\') {\n if (stack.empty())\n del.insert(i);\n else\n stack.pop_back();\n }\n }\n del.insert(stack.begin(), stack.end());\n for (auto i=0; i < s.size(); ++i)\n if (del.find(i) == del.end())\n t.push_back(s[i]);\n return t;\n }\n};\n```
| 14 | 0 |
[]
| 3 |
minimum-remove-to-make-valid-parentheses
|
~8ms🔰Unable to beats100% ||BUT||😔 only 97.%~ |🔰| JAVA USERS🔰Parentheses Removal Approach 🔰
|
8msunable-to-beats100-but-only-97-java-u-vsgo
|
By employing this two-pass optimization technique and directly modifying the input string, the code achieves efficient removal of parentheses while minimizing m
|
Shakaal_ya
|
NORMAL
|
2024-04-06T01:44:05.646199+00:00
|
2024-04-06T01:52:18.261892+00:00
| 1,654 | false |
> By employing this two-pass optimization technique and directly modifying the input string, the code achieves efficient removal of parentheses while minimizing memory usage and runtime overhead.\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public String minRemoveToMakeValid(String s) {\n char[] chars = s.toCharArray();\n int openCount = 0;\n \n // Forward pass: mark invalid closing parentheses and count open parentheses\n for (int i = 0; i < chars.length; i++) {\n char c = chars[i];\n if (c == \'(\') {\n openCount++;\n } else if (c == \')\') {\n if (openCount == 0) {\n chars[i] = \'*\'; // Mark invalid closing parenthesis\n } else {\n openCount--;\n }\n }\n }\n \n // Backward pass: mark extra open parentheses\n for (int i = chars.length - 1; i >= 0 && openCount > 0; i--) {\n if (chars[i] == \'(\') {\n chars[i] = \'*\'; // Mark extra open parenthesis\n openCount--;\n }\n }\n \n // Construct result string\n StringBuilder result = new StringBuilder();\n for (char c : chars) {\n if (c != \'*\') {\n result.append(c);\n }\n }\n \n return result.toString();\n }\n}\n\n\n```
| 13 | 0 |
['Java']
| 11 |
minimum-remove-to-make-valid-parentheses
|
c++ | without stack
|
c-without-stack-by-rajat_gupta-zka6
|
\nclass Solution {\npublic:\n string minRemoveToMakeValid(string s){\n int cnt=0;\n for(char &c: s){\n if(c==\'(\') cnt++;\n
|
rajat_gupta_
|
NORMAL
|
2021-05-24T17:03:16.280452+00:00
|
2021-05-24T17:03:16.280499+00:00
| 775 | false |
```\nclass Solution {\npublic:\n string minRemoveToMakeValid(string s){\n int cnt=0;\n for(char &c: s){\n if(c==\'(\') cnt++;\n else if(c==\')\')\n if(cnt==0) c=\'*\';\n else cnt--;\n }\n cnt=0;\n for(int i=s.size()-1;i>=0;i--){\n if(s[i]==\')\') cnt++;\n else if(s[i]==\'(\')\n if(cnt==0) s[i]=\'*\';\n else cnt--;\n }\n s.erase(remove(s.begin(),s.end(),\'*\'),s.end());\n return s;\n }\n};\n```\n**Feel free to ask any question in the comment section.**\nI hope that you\'ve found the solution useful.\nIn that case, **please do upvote and encourage me** to on my quest to document all leetcode problems\uD83D\uDE03\nHappy Coding :)\n
| 13 | 0 |
['C', 'C++']
| 4 |
minimum-remove-to-make-valid-parentheses
|
C++ Super Simple O(n) Solution Using Stack
|
c-super-simple-on-solution-using-stack-b-zsi5
|
\nclass Solution {\npublic:\n string minRemoveToMakeValid(string s) {\n stack<int> stack;\n int n = s.size();\n \n for (int i = 0
|
yehudisk
|
NORMAL
|
2021-02-19T09:47:16.638453+00:00
|
2021-02-19T09:47:16.638484+00:00
| 1,040 | false |
```\nclass Solution {\npublic:\n string minRemoveToMakeValid(string s) {\n stack<int> stack;\n int n = s.size();\n \n for (int i = 0; i < n; i++) {\n if (s[i] == \'(\') \n stack.push(i);\n \n else if (s[i] == \')\') {\n \n if (!stack.empty()) {\n stack.pop();\n }\n \n else {\n s.erase(i, 1);\n i--;\n }\n }\n }\n \n while (!stack.empty()) {\n s.erase(stack.top(), 1);\n stack.pop();\n }\n return s;\n }\n};\n```\n**Like it? please upvote...**
| 13 | 2 |
['C']
| 7 |
minimum-remove-to-make-valid-parentheses
|
Simply Simple Python Solution - with comments
|
simply-simple-python-solution-with-comme-pd4k
|
\ndef minRemoveToMakeValid(self, s: str) -> str:\n status_dict = {}\n stack = []\n \n # keep indexe\'s status in status_dict. If a pa
|
limitless_
|
NORMAL
|
2019-11-03T16:38:19.717456+00:00
|
2019-11-03T16:38:19.717498+00:00
| 3,907 | false |
```\ndef minRemoveToMakeValid(self, s: str) -> str:\n status_dict = {}\n stack = []\n \n # keep indexe\'s status in status_dict. If a parenthesis is valid\n # mark it as True else False. use stack to check it\'s validity\n for idx, ch in enumerate(s):\n if ch == "(":\n stack.append(idx)\n elif ch == ")" and len(stack) > 0:\n status_dict[idx] = True\n status_dict[stack[-1]] = True\n stack.pop()\n \n res = []\n for idx, ch in enumerate(s):\n if ch == "(" or ch == ")":\n if idx in status_dict: # only append the parenthesis which are valid\n res.append(ch)\n else:\n res.append(ch)\n \n return "".join(res)\n```
| 13 | 0 |
['Python', 'Python3']
| 5 |
minimum-remove-to-make-valid-parentheses
|
👏Beats 96.03% of users with Java || ✅Simple & Easy Without Space Well Explained Solution 🔥💥
|
beats-9603-of-users-with-java-simple-eas-t9k0
|
Intuition\ncount variable is counting parentheses and we make changes in stringbuilder sb.\nKeep counting the opening parentheses and when the closing parenthes
|
Rutvik_Jasani
|
NORMAL
|
2024-04-06T06:57:12.101240+00:00
|
2024-04-06T06:57:12.101267+00:00
| 830 | false |
# Intuition\ncount variable is counting parentheses and we make changes in stringbuilder sb.\nKeep counting the opening parentheses and when the closing parentheses comes, ignore it and decrement the count.\nThen if count is greater than 0, then remove as many opening parentheses from the back as count.\n\n# I Think This Can Help You(For Proof Click on the Image)\n[](https://leetcode.com/problems/minimum-remove-to-make-valid-parentheses/submissions/1224581986/?envType=daily-question&envId=2024-04-06)\n\n# Approach\n1. Initilize string builder sb, because string is immutable we can not change anything in the string.\n ```\n StringBuilder sb = new StringBuilder(s);\n ```\n2. Initilize count variable to count parentheses.\n ```\n int count = 0;\n ```\n3. Iterate the loop from 0 to sb\'s length.(Below code in the loop)\n - Check if ith charcter is opening parentheses then increase count by 1.\n ```\n if(sb.charAt(i)==\'(\'){\n count++;\n }\n ```\n - Check if ith character is closing parentheses and count is more than 0 then decrease count by 1.\n ```\n else if(sb.charAt(i) == \')\' && count>0){\n count--;\n }\n ```\n - Check if ith character is closing parentheses and count will be 0 then delete ith character and i decreased by 1, because one character will be removed from the string builder, so its length will be reduced by one and a new index will be created in which the middle character will not be forgotten, so we have to decrease i.\\\n ```\n else if(sb.charAt(i) == \')\' && count==0){\n sb.delete(i,i+1);\n i--;\n }\n ```\n- Completed loop look like this\n ```\n for(int i=0;i<sb.length();i++){\n if(sb.charAt(i)==\'(\'){\n count++;\n } else if(sb.charAt(i) == \')\' && count>0){\n count--;\n } else if(sb.charAt(i) == \')\' && count==0){\n sb.delete(i,i+1);\n i--;\n }\n }\n ```\n4. After that if we have extra opening parentheses we remove extra opening parentheses from back of the string builder.\n ```\n for(int i=sb.length()-1;i>=0;i--){\n if(count==0){\n break;\n }\n if(sb.charAt(i)==\'(\'){\n sb.delete(i,i+1);\n count--;\n }\n }\n ```\n5. our return type is string so we convert string builder to string and return it.\n ```\n return sb.toString();\n ```\n\n# Complexity\n- Time complexity:\nO(n) --> We go linearlly.\n\n- Space complexity:\nO(1) --> we do not uise any extra space.\n\n# Code\n```\nclass Solution {\n public String minRemoveToMakeValid(String s) {\n StringBuilder sb = new StringBuilder(s);\n int count = 0;\n for(int i=0;i<sb.length();i++){\n if(sb.charAt(i)==\'(\'){\n count++;\n } else if(sb.charAt(i) == \')\' && count>0){\n count--;\n } else if(sb.charAt(i) == \')\' && count==0){\n sb.delete(i,i+1);\n i--;\n }\n }\n for(int i=sb.length()-1;i>=0;i--){\n if(count==0){\n break;\n }\n if(sb.charAt(i)==\'(\'){\n sb.delete(i,i+1);\n count--;\n }\n }\n return sb.toString();\n }\n}\n```\n\n\n
| 11 | 0 |
['String', 'Stack', 'Java']
| 2 |
minimum-remove-to-make-valid-parentheses
|
Counting Open and Closed Parentheses
|
counting-open-and-closed-parentheses-by-nbhhf
|
Intuition\nThe task is to remove the minimum number of parentheses to make the string valid. The approach taken in this code is to traverse the string twice. In
|
CS_MONKS
|
NORMAL
|
2024-04-06T01:19:47.250474+00:00
|
2024-04-06T10:21:22.814195+00:00
| 2,815 | false |
# Intuition\nThe task is to remove the minimum number of parentheses to make the string valid. The approach taken in this code is to traverse the string twice. In the first loop, we count the opening parentheses encountered and maintain a valid string by appending characters accordingly. If a closing parenthesis is encountered and there are unmatched opening parentheses, we include it in the resulting string and decrement the count of unmatched opening parentheses. In the second loop, if there are still unmatched opening parentheses, we traverse the string backward to remove any extra opening parentheses.\n\n# Approach\n1. Initialize variables `open` and `close` to track the counts of opening and closing parentheses, respectively, and an empty string `ans` to store the resulting valid string.\n2. Iterate through the string:\n - If the character is not a parenthesis, append it to `ans`.\n - If the character is an opening parenthesis, increment the `open` count and append it to `ans`.\n - If the character is a closing parenthesis and there are unmatched opening parentheses (`open > 0`), decrement the `open` count and append the closing parenthesis to `ans`.\n3. If there are still unmatched opening parentheses (`open > 0`), indicating extra opening parentheses, traverse the string backward to remove them:\n - Iterate through the reversed string:\n - If the character is not a parenthesis, append it to a new string.\n - If the character is a closing parenthesis, increment the `close` count and append it to the new string.\n - If the character is an opening parenthesis and there are unmatched closing parentheses (`close > 0`), decrement the `close` count and append the opening parenthesis to the new string.\n - Reverse the new string to obtain the final valid string.\n4. Return the final valid string.\n\n# Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(n)$$\n# without stack \n```c++ []\nclass Solution {\npublic:\n string minRemoveToMakeValid(string s) {\n int open = 0, close = 0;\n string ans;\n //traverse from start to end to eleminate extra closing braces\n for (const char& c : s) {\n if (c != \'(\' && c != \')\') {\n ans += c;\n } else if (c == \'(\') {\n open++;\n ans += c;\n } else if (open > 0) {\n ans += c;\n open--;\n }\n }\n\n //traverse from end to start to remove extra opening braces\n if (open > 0) {\n int n = ans.length();\n s = ans;\n ans = "";\n open = 0, close = 0;\n for (int i = n - 1; i >= 0; i--) {\n char c = s[i];\n if (c != \'(\' && c != \')\') {\n ans += c;\n } else if (c == \')\') {\n close++;\n ans += c;\n } else if (close > 0) {\n ans += c;\n close--;\n }\n }\n }\n else{\n return ans;\n }\n reverse(ans.begin(), ans.end());\n return ans;\n }\n};\n```\n# with stack\n```c++ []\nclass Solution {\npublic:\n string minRemoveToMakeValid(string s) {\n int open = 0, close = 0;\n stack<char>st;\n //traverse from start to end to eleminate extra closing braces\n for (const char& c : s) {\n if (c != \'(\' && c != \')\') {\n st.push(c);\n } else if (c == \'(\') {\n open++;\n st.push(c);\n } else if (open > 0) {\n st.push(c);\n open--;\n }\n }\n string ans;\n //traverse from left to right to remove extra opening braces\n open = 0, close = 0;\n while(!st.empty()) {\n char c = st.top();\n st.pop();\n if (c != \'(\' && c != \')\') {\n ans += c;\n } else if (c == \')\') {\n close++;\n ans += c;\n } else if (close > 0) {\n ans += c;\n close--;\n }\n }\n \n reverse(ans.begin(), ans.end());\n return ans;\n }\n};\n```
| 10 | 0 |
['C++']
| 8 |
minimum-remove-to-make-valid-parentheses
|
Easy understanding solution using Stack and Stringbuilder
|
easy-understanding-solution-using-stack-hrtdm
|
```\nclass Solution {\n public String minRemoveToMakeValid(String s) {\n Stack st = new Stack<>();\n StringBuilder ans = new StringBuilder(s);\n
|
Jugantar2020
|
NORMAL
|
2022-03-15T13:14:42.960835+00:00
|
2022-03-15T13:14:42.960879+00:00
| 585 | false |
```\nclass Solution {\n public String minRemoveToMakeValid(String s) {\n Stack<Integer> st = new Stack<>();\n StringBuilder ans = new StringBuilder(s);\n for(int i = 0; i < s.length(); i ++)\n {\n if(s.charAt(i) == \'(\')\n st.push(i);\n else if(s.charAt(i) == \')\')\n {\n if(st.size() > 0 && s.charAt(st.peek()) == \'(\')\n st.pop();\n else\n st.push(i);\n }\n }\n while(st.size() > 0)\n ans.deleteCharAt(st.pop());\n \n return ans.toString();\n }\n}
| 10 | 0 |
['String', 'Stack', 'Java']
| 0 |
minimum-remove-to-make-valid-parentheses
|
Min remove to make valid parantheses | C++ | Stack | Code explained
|
min-remove-to-make-valid-parantheses-c-s-g325
|
\nclass Solution {\npublic:\n string minRemoveToMakeValid(string s) {\n\t\n\t\t// define a stack which holds the parantheses along with the position\n
|
tonystark_3000
|
NORMAL
|
2021-02-19T08:17:21.919974+00:00
|
2021-02-24T05:56:32.113244+00:00
| 264 | false |
```\nclass Solution {\npublic:\n string minRemoveToMakeValid(string s) {\n\t\n\t\t// define a stack which holds the parantheses along with the position\n stack<pair<int, char> > stk;\n\t\t\n for(int i=0; i<s.length(); i++){\n if(s[i] == \'(\'){\n\t\t\t // if opening braces, push into the stack\n stk.push(make_pair(i, \'(\'));\n }else if(s[i] == \')\'){\n\t\t\t // If closing braces, check if opening present or not. If yes, pop it.\n\t\t\t\t// Else mark that position of closing brace with \'1\' in the string.\n\t\t\t\t// 1 suggest that it should get removed.\n if(stk.empty()){\n s[i] = \'1\';\n }else{\n stk.pop();\n }\n }\n }\n \n\t\t// Now check for any leftover opening braces in the stack.\n\t\t// Mark those position with \'1\'.\n\t\t// That is they should get removed.\n while(!stk.empty()){\n pair<int, char> TOP = stk.top();\n s[TOP.first] = \'1\';\n stk.pop();\n }\n \n\t\t\n\t\t// Now push all the characters in a string which aren\'t marked as \'1\'.\n\t\tstring output = "";\n for(int i=0; i<s.length(); i++){\n if(s[i] != \'1\'){\n output.push_back(s[i]);\n }\n }\n \n return output;\n }\n};\n```\n\nWhy am using 1 to mark position?\nCause it is previously said to us that input string will only contain \'(\' and \')\' and lower-case letters.\n\nPlease *upvote* if you like the solution.
| 10 | 2 |
[]
| 1 |
minimum-remove-to-make-valid-parentheses
|
Python in 12 lines to solve the classic parentheses problem
|
python-in-12-lines-to-solve-the-classic-965ia
|
1st approach\n\nHere was my first approach using the way I solved #921 \nNot the best but easy to come up with if you solved similar problem e.g. #921 #20 \n\n
|
calvinchankf
|
NORMAL
|
2019-12-04T15:48:16.751219+00:00
|
2019-12-04T15:48:16.751265+00:00
| 1,098 | false |
#### 1st approach\n\nHere was my first approach using the way I solved [#921](https://leetcode.com/problems/minimum-add-to-make-parentheses-valid) \nNot the best but easy to come up with if you solved similar problem e.g. [#921](https://leetcode.com/problems/minimum-add-to-make-parentheses-valid) [#20](https://leetcode.com/problems/valid-parentheses) \n\n```py\n"""\n 1st: stack + hashtable\n - similar to lc921 but save the indices of the redundant opens & closes\n - construct the result by removing the characters at redundant indices\n - 12 lines\n \n Time O(3N)\n Space O(N)\n 164 ms, faster than 79.33%\n"""\nclass Solution(object):\n def minRemoveToMakeValid(self, s):\n opens, closes = [], []\n for i in range(len(s)):\n c = s[i]\n if c == \'(\':\n opens.append(i)\n elif c == \')\':\n if len(opens) == 0:\n closes.append(i)\n else:\n opens.pop()\n hs = set(opens+closes)\n return \'\'.join(s[i] for i in range(len(s)) if i not in hs)\n```\n\n#### 2nd approach\n\nIf you don\'t like hashtable, we can just construct an array to save the redundant parentheses and solve the problem in the same way\n\n```py\n"""\n 2nd: similar logic without using a hashtable\n\t- 17 lines\n\n Time O(3N)\n Space O(N)\n 244 ms, faster than 45.31%\n"""\n\n\nclass Solution(object):\n def minRemoveToMakeValid(self, s):\n res, opens = [], []\n for i in range(len(s)):\n c = s[i]\n if c == \'(\':\n opens.append(i)\n res += c\n elif c == \')\':\n if len(opens) == 0:\n res += \'*\'\n else:\n opens.pop()\n res += c\n else:\n res += c\n for x in opens:\n res[x] = \'*\'\n return \'\'.join(c for c in res if c != \'*\')\n```
| 10 | 0 |
[]
| 0 |
minimum-remove-to-make-valid-parentheses
|
Easiest and Clean C++ Sol | No stack-Direct sol | Beats 97.2% Users | Easiest Explanation
|
easiest-and-clean-c-sol-no-stack-direct-gf2sp
|
Intuition\n\n\n Describe your first thoughts on how to solve this problem. \nWe remove unnecessary parentheses by iterating through the string twice: first loop
|
vipulbhardwaj279
|
NORMAL
|
2024-04-06T06:12:07.527582+00:00
|
2024-04-06T06:12:07.527606+00:00
| 638 | false |
# Intuition\n\n\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe remove unnecessary parentheses by iterating through the string twice: first loop to remove excess closing parentheses,second loop to remove extra opening parentheses.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n - Initialize an empty string `temp`, which will store the processed string without unnecessary closing parentheses, and a counter `open` for tracking open parentheses.\n - Iterate through each character in the input string `s`.\n - If the character is \'(\', add it to `temp` and increment `open`.\n - If the character is \')\' and there are open parentheses (i.e., `open > 0`), add it to `temp` and decrement `open`.\n - If the character is neither \'(\' nor \')\', add it directly to `temp`.\n - After the first pass, `temp` contains a string with balanced parentheses and no extra closing parentheses.\n - Iterate through `temp` in reverse order (so that the opening parenthesis without having corresponding closing parenthesis come first ):\n - If an opening parentheses \'(\' is encountered and there are still unmatched open parentheses (`open > 0`), decrement `open`.\n - Otherwise, add the character to the final answer string `ans`.\n - Reverse `ans` and return it as the result.\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n# Please UPVOTE if you like it : )\n\n# Code\n```\nclass Solution {\npublic:\n string minRemoveToMakeValid(string s) {\n ios_base::sync_with_stdio(false), cin.tie(NULL), cout.tie(NULL);\n\n string temp="",ans="";\n int open=0;\n for(int i=0;i<s.size();i++){\n if(s[i]==\'(\')temp+=s[i],open++;\n else if(s[i]==\')\' && open>0)temp+=s[i],open--;\n else if(s[i]!=\'(\' && s[i]!=\')\')temp+=s[i];\n }\n for(int i=temp.size()-1;i>=0;i--){\n if(temp[i]==\'(\' && open>0)open--;\n else ans+=temp[i];\n }\n reverse(ans.begin(),ans.end());\n return ans; \n }\n};\n\n```\n\n
| 9 | 0 |
['C++']
| 8 |
minimum-remove-to-make-valid-parentheses
|
✅C++ solution using STACK in O(n) time complexity with explanation
|
c-solution-using-stack-in-on-time-comple-zqli
|
\n> If you\u2019re interested in coding you can join my Discord Server, link in the comment section. Also if you find any mistake please let me know. Thank you!
|
dhruba-datta
|
NORMAL
|
2022-02-06T10:14:13.311511+00:00
|
2022-04-14T15:33:17.799467+00:00
| 781 | false |
\n> **If you\u2019re interested in coding you can join my Discord Server, link in the comment section. Also if you find any mistake please let me know. Thank you!\u2764\uFE0F**\n> \n\n---\n\n## Explanation:\n\n### Solution 01\n\n- Here we\u2019re using a stack to store the position of parentheses.\n- If it is an open parenthesis then increase the count and push the index to stack.\n- else if it\u2019s a close parenthesis then check if the count is not 0 then decrease the count and pop the last element from the stack. if count=0 then push the index to stack.\n- now iterate the stack and remove the elements from the index present in the stack\n- **Time complexity:** O(n^2).\n\n---\n\n## Code:\n\n```cpp\n//Solution 01:\nclass Solution {\npublic:\n string minRemoveToMakeValid(string s) {\n int n = s.size();\n stack<int> st;\n int i=0, count=0;\n while(i<n){\n if(s[i] == \'(\'){\n count++;\n st.push(i);\n }\n else if(s[i] == \')\'){\n if(count > 0){\n count--;\n st.pop();\n }\n else\n st.push(i);\n }\n i++;\n }\n int m = st.size();\n while(m--){\n int temp= st.top();\n s.erase(temp,1);\n st.pop();\n }\n return s;\n }\n};\n```\n\n---\n\n> **Please upvote this solution**\n>
| 9 | 1 |
['Stack', 'C', 'C++']
| 4 |
minimum-remove-to-make-valid-parentheses
|
✅Easy✨||C++|| Beats 100% || With Explanation ||
|
easyc-beats-100-with-explanation-by-olak-o3s4
|
Intuition\n Describe your first thoughts on how to solve this problem. \nWe remove unnecessary parentheses by iterating through the string twice: first loop to
|
olakade33
|
NORMAL
|
2024-04-06T08:36:23.897472+00:00
|
2024-04-06T08:36:23.897495+00:00
| 1,310 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe remove unnecessary parentheses by iterating through the string twice: first loop to remove excess closing parentheses,second loop to remove extra opening parentheses.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialize an empty string temp, which will store the processed string without unnecessary closing parentheses, and a counter open for tracking open parentheses.\n2. Iterate through each character in the input string s.\n. If the character is \'(\', add it to temp and increment open.\n. If the character is \')\' and there are open parentheses (i.e., open > 0), add it to temp and decrement open.\n. If the character is neither \'(\' nor \')\', add it directly to temp.\n3. After the first pass, temp contains a string with balanced parentheses and no extra closing parentheses.\n4. Iterate through temp in reverse order (so that the opening parenthesis without having corresponding closing parenthesis come first ):\n. If an opening parentheses \'(\' is encountered and there are still unmatched open parentheses (open > 0), decrement open.\n. Otherwise, add the character to the final answer string ans.\n5. Reverse ans and return it as the result.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n# Code\n```\nclass Solution {\npublic:\n string minRemoveToMakeValid(string s) {\n ios_base::sync_with_stdio(false), cin.tie(NULL), cout.tie(NULL);\n\n string temp="",ans="";\n int open=0;\n for(int i=0;i<s.size();i++){\n if(s[i]==\'(\')temp+=s[i],open++;\n else if(s[i]==\')\' && open>0)temp+=s[i],open--;\n else if(s[i]!=\'(\' && s[i]!=\')\')temp+=s[i];\n }\n for(int i=temp.size()-1;i>=0;i--){\n if(temp[i]==\'(\' && open>0)open--;\n else ans+=temp[i];\n }\n reverse(ans.begin(),ans.end());\n return ans; \n }\n};\n```
| 8 | 0 |
['C++']
| 0 |
minimum-remove-to-make-valid-parentheses
|
Easy Java Solution | O(N) time
|
easy-java-solution-on-time-by-himanshura-7off
|
Upvote if you Got It \uD83D\uDE42\nclass Solution {\n\n public String minRemoveToMakeValid(String s) {\n Stack st = new Stack<>();\n StringBuil
|
himanshuramranjan
|
NORMAL
|
2021-12-08T05:23:33.007484+00:00
|
2021-12-08T05:23:33.007536+00:00
| 721 | false |
**Upvote if you Got It** \uD83D\uDE42\nclass Solution {\n\n public String minRemoveToMakeValid(String s) {\n Stack<Integer> st = new Stack<>();\n StringBuilder sb = new StringBuilder(s);\n\t\t\n for(int i=0;i<s.length();i++){\n if(s.charAt(i)==\'(\')\n st.push(i);\n else if(s.charAt(i)==\')\'){\n if(!st.isEmpty() && s.charAt(st.peek())==\'(\')\n st.pop();\n else\n st.push(i);\n }\n }\n while(!st.isEmpty())\n sb.deleteCharAt(st.pop());\n return sb.toString();\n }\n}
| 8 | 0 |
['Stack', 'Java']
| 2 |
minimum-remove-to-make-valid-parentheses
|
[JAVA] [STACK / STRINGBUILDER]
|
java-stack-stringbuilder-by-trevor-aksha-6dya
|
```\nclass Solution {\n public String minRemoveToMakeValid(String s) {\n Stack stack = new Stack<>();\n StringBuilder stringBuilder = new Strin
|
trevor-akshay
|
NORMAL
|
2021-02-11T06:26:06.697765+00:00
|
2021-02-11T06:26:06.697803+00:00
| 632 | false |
```\nclass Solution {\n public String minRemoveToMakeValid(String s) {\n Stack<Integer> stack = new Stack<>();\n StringBuilder stringBuilder = new StringBuilder(s); //a)b(c)d"\n for(int i = 1;i<=s.length();i++){\n if(s.charAt(i-1) == \'(\')\n stack.push(i);\n else if(s.charAt(i-1) == \')\' && !stack.empty())\n stack.pop();\n else if(s.charAt(i-1) ==\')\' && stack.empty()){//))((\n stringBuilder.replace(i-1,i, "0");\n }\n }\n \n while (!stack.empty()){\n stringBuilder.deleteCharAt(stack.pop()-1);\n }\n return stringBuilder.toString().\n replace(\'0\',\' \').\n replaceAll("\\\\s+","");\n }\n}
| 8 | 0 |
['Stack', 'Java']
| 1 |
minimum-remove-to-make-valid-parentheses
|
C++ O(n) explanation
|
c-on-explanation-by-leodicap99-d71n
|
\nThe way to tackle this question is to keep a varial lets say open that increments for every opening braces and decrements for every closing\nbraces.\nWe will
|
leodicap99
|
NORMAL
|
2020-04-28T15:28:04.579512+00:00
|
2020-04-28T15:28:04.579553+00:00
| 696 | false |
```\nThe way to tackle this question is to keep a varial lets say open that increments for every opening braces and decrements for every closing\nbraces.\nWe will first be considering mismatches of the closing brackets \')\'.\nif open is equal to 0 and a closing bracket occurs ignore it.\ns = "lee(t(c)o)de)" open=0\n ^\n |\n i\nopen = 1\ns = "lee(t(c)o)de)"\n ^\n |\n i \nopen = 2\n\ns = "lee(t(c)o)de)"\n ^\n |\n i\nopen is not 0 \nopen = 1\n\ns = "lee(t(c)o)de)"\n ^\n |\n i \nopen not 0 \nopen = 0\n\ns = "lee(t(c)o)de)"\n ^\n |\n i \nopen is 0 so ignore\n\nBut what if there are more opening braces than closing to handle this we first make sure the closing braces are taken care of\n then with the same open we start from behind and check if open is > 0 if so we skip it and decremnt open.\n\n\n string minRemoveToMakeValid(string s) {\n int open=0;\n string t;\n for(int i=0;i<s.size();i++)\n {\n if(s[i]==\'(\')open++;\n else if(s[i]==\')\')\n {\n if(open==0)continue;\n open--;\n }\n t+=s[i];\n }\n string ans;\n for(int i=t.size()-1;i>=0;i--)\n {\n if(t[i]==\'(\' && open>0)\n {\n open--;\n continue;\n }\n ans+=t[i];\n }\n reverse(ans.begin(),ans.end());\n return ans;\n } \n\n```
| 8 | 0 |
['C', 'C++']
| 0 |
minimum-remove-to-make-valid-parentheses
|
Kotlin solution
|
kotlin-solution-by-lihaiyang-vevw
|
Code\n\nclass Solution {\n fun minRemoveToMakeValid(s: String) = buildString {\n val indexes = mutableListOf<Int>()\n s.forEach {\n
|
lihaiyang
|
NORMAL
|
2024-01-14T08:40:51.928749+00:00
|
2024-01-14T08:40:51.928802+00:00
| 230 | false |
# Code\n```\nclass Solution {\n fun minRemoveToMakeValid(s: String) = buildString {\n val indexes = mutableListOf<Int>()\n s.forEach {\n when (it) {\n \'(\' -> indexes.add(length)\n \')\' -> if (!indexes.isEmpty()) indexes.removeLast()\n else return@forEach\n }\n append(it)\n }\n indexes.reversed().forEach {\n deleteAt(it)\n }\n }\n}\n```\n\nLet me know if you have any suggestions. Thanks!
| 7 | 0 |
['Kotlin']
| 2 |
minimum-remove-to-make-valid-parentheses
|
😎💥
|
by-doaaosamak-tvt6
|
Code\n\nclass Solution {\n public String minRemoveToMakeValid(String s) {\n int startPointer = 0;\n int endPointer = s.length() - 1;\n\n
|
DoaaOsamaK
|
NORMAL
|
2024-04-06T17:37:53.103489+00:00
|
2024-04-06T17:37:53.103527+00:00
| 66 | false |
# Code\n```\nclass Solution {\n public String minRemoveToMakeValid(String s) {\n int startPointer = 0;\n int endPointer = s.length() - 1;\n\n String result;\n char[] arr = s.toCharArray();\n int openParenthesesCount = 0;\n for (int i = 0; i < arr.length; i++) {\n if (arr[i] == \'(\')\n openParenthesesCount++;\n else if (arr[i] == \')\') {\n if (openParenthesesCount == 0)\n arr[i] = \'*\'; \n else\n openParenthesesCount--;\n }\n }\n for (int i = arr.length - 1; i >= 0; i--) {\n if (openParenthesesCount > 0 && arr[i] == \'(\') {\n arr[i] = \'*\'; \n openParenthesesCount--;\n }\n }\n int p = 0; \n for (int i = 0; i < arr.length; i++) {\n if (arr[i] != \'*\')\n arr[p++] = arr[i];\n }\n result = new String(arr).substring(0, p);\n\n return result;\n }\n}\n```
| 6 | 0 |
['Java']
| 0 |
minimum-remove-to-make-valid-parentheses
|
Intuitive stack approach 😮 | O(N) run time ⏱️
|
intuitive-stack-approach-on-run-time-by-y38sw
|
\n# Approach\n- Create a vector of size "s" and initialize all the values to be zero, representing whether each character in the input string is to be added to
|
HarishbarathiS
|
NORMAL
|
2024-04-06T16:35:11.575262+00:00
|
2024-04-06T16:35:51.280446+00:00
| 487 | false |
\n# Approach\n- Create a vector of size "s" and initialize all the values to be zero, representing whether each character in the input string is to be added to the resultant string or not. (0 - ignore, 1 - add).\n- Use a stack which stores only the parentheses and their indices in the string so that it will be easy for us to locate and eliminate.\n- Iterate through the string, pushing only the parentheses onto the stack while checking if there is an opening parentheses ( \' ( \' ) at the top of the stack when encountering a closing parentheses( \' ) \' ). If such a pair exists, pop the top element of the stack as we got a valid pair of parentheses and mark the corresponding indices in the vector as 1 to indicate inclusion in the resultant string.\n- This way we can identify the parentheses that doesn\'t have a pair.\n- If a character is encountered just set the value as 1 in the vector.\n- Finally, add all the characters that are marked as 1 in the vector to form the resultant string.\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n string minRemoveToMakeValid(string s) {\n stack<pair<char,int>> stk;\n vector<int> vec(s.size(),0);\n for(int i=0;i<s.size();i++){\n if(!stk.empty() && stk.top().first == \'(\' && s[i] == \')\'){\n int num = stk.top().second; \n vec[num] = 1;\n stk.pop();\n vec[i] = 1;\n }else if(s[i] == \')\' || s[i] == \'(\'){\n stk.push(make_pair(s[i],i));\n }else{\n vec[i] = 1;\n }\n }\n string res = "";\n for(int i=0;i<s.size();i++){\n if(vec[i]){\n res += s[i];\n }\n }\n return res;\n }\n};\n```
| 6 | 0 |
['C++']
| 2 |
minimum-remove-to-make-valid-parentheses
|
✅ One Line Solution
|
one-line-solution-by-mikposp-qztp
|
(Disclaimer: this is not an example to follow in a real project - it is written for fun and training mostly)\n\n# Code #1.1 - One Line\nTime complexity: O(n). S
|
MikPosp
|
NORMAL
|
2024-04-06T10:17:51.755951+00:00
|
2024-04-06T13:41:36.844515+00:00
| 2,388 | false |
(Disclaimer: this is not an example to follow in a real project - it is written for fun and training mostly)\n\n# Code #1.1 - One Line\nTime complexity: $$O(n)$$. Space complexity: $$O(n)$$.\n```\nclass Solution:\n def minRemoveToMakeValid(self, s: str) -> str:\n return (q:=0) or \'\'.join(\'\'.join((q:=q+(c==\'(\')-(c==\')\'),c)[1] for c in s if q or c!=\')\').rsplit(\'(\',q))\n```\n\n# Code #1.2 - Unwrapped\n```\nclass Solution:\n def minRemoveToMakeValid(self, s: str) -> str:\n result, q = [], 0\n for c in s:\n if q or c != \')\':\n q += (c == \'(\') - (c == \')\')\n result.append(c)\n\n return \'\'.join(\'\'.join(result).rsplit(\'(\', q))\n```\n\n# Code #2 - [Regular Solution](https://leetcode.com/problems/minimum-remove-to-make-valid-parentheses/solutions/3410191/elegant-and-fast-approach/)\n\n(Disclaimer 2: all code above is just a product of fantasy, it is not claimed to be pure impeccable oneliners - please, remind about drawbacks only if you know how to make it better. PEP 8 is violated intentionally)
| 6 | 0 |
['String', 'Python', 'Python3']
| 1 |
minimum-remove-to-make-valid-parentheses
|
[C++] || No stack || Beginner friendly || Fastest
|
c-no-stack-beginner-friendly-fastest-by-emmso
|
you can shorter this code i have written in easiet way so that everyone can understand \uD83D\uDE0A\n\n1. Make a variable count \n2. increase count everytime we
|
4byx
|
NORMAL
|
2022-03-15T03:57:46.939337+00:00
|
2022-03-15T04:05:29.295912+00:00
| 539 | false |
*you can shorter this code i have written in easiet way so that everyone can understand \uD83D\uDE0A*\n```\n1. Make a variable count \n2. increase count everytime we get \'(\' \n3. decrease count everytime we get \')\'\n4. if count == 0 and we get \')\' this means there is no opening bracket dont do anywork else store\ncharacters\n5. if extra opening are found we can handle it after this work by removing from last and\n decreasing count\n```\n**CODE**\n```\nclass Solution {\npublic:\n string minRemoveToMakeValid(string s) {\n int n = s.size();\n int cnt = 0;\n string ans = "";\n for(int i = 0 ; i < n ; i++){\n\t\t\n\t\t// if we get opening bracket increase count as we get same number of \n\t\t// closing bracket in a valid \n if(s[i] == \'(\'){\n cnt++;\n ans += s[i];\n }\n\t\t\t\n\t\t// we get closing bracket now there can be 2 cases if count is 0 which means there is no \n\t\t// opening found then dont do any work\n else if(s[i] == \')\'){\n if(cnt == 0){\n \n }\n\t\t\t\t\n\t\t// 2nd case when cnt > 0 then decrease count and add char to ans\n else{\n cnt--;\n ans += s[i];\n }\n }\n\t\t\t\n\t// else lowercase found\n else{\n ans += s[i];\n }\n }\n \n\t\n\t\n\t// this is case when count > 0 which means only opening found\n\t\n\t// like s = "abc((" then after upper loop we get ans = "abc((" and cnt == 2 now we have to do some work to \n\t// remove opening brackets according to count\n if(cnt > 0){\n for(int i = ans.size()-1 ; i >= 0 ; i--){\n if(ans[i] == \'(\' and cnt > 0){\n cnt--;\n }\n else{\n res += ans[i];\n }\n }\n reverse(res.begin(),res.end());\n return res;\n }\n return ans;\n }\n};\n```\n\n*just code no comments*\n```\nclass Solution {\npublic:\n string minRemoveToMakeValid(string s) {\n int n = s.size();\n int cnt = 0;\n string ans = "";\n for(int i = 0 ; i < n ; i++){\n if(s[i] == \'(\'){\n cnt++;\n ans += s[i];\n }\n else if(s[i] == \')\'){\n if(cnt == 0){\n \n }\n else{\n cnt--;\n ans += s[i];\n }\n }\n else{\n ans += s[i];\n }\n }\n \n if(cnt > 0){\n for(int i = ans.size()-1 ; i >= 0 ; i--){\n if(ans[i] == \'(\' and cnt > 0){\n cnt--;\n }\n else{\n res += ans[i];\n }\n }\n reverse(res.begin(),res.end());\n return res;\n }\n return ans;\n }\n};\n```
| 6 | 1 |
['C']
| 1 |
minimum-remove-to-make-valid-parentheses
|
Buidling_Intuition_step_by_step | Comments | Stack_Based | c++ | proper_Intuition
|
buidling_intuition_step_by_step-comments-dou7
|
take the first taste case: "lee(t(c)o)de)"\n answer should be : "lee(t(c)o)de"\n \n intuition: \n 1) if we observe, the one who opens later need to close
|
Mohit_Smash
|
NORMAL
|
2022-03-15T02:12:27.532310+00:00
|
2022-03-15T03:17:26.325073+00:00
| 234 | false |
take the first taste case: "lee(t(c)o)de)"\n answer should be : "lee(t(c)o)de"\n \n intuition: \n 1) if we observe, the one who opens later need to closed first so stack comes into picture \n 2) so here \'(\' at index 5 needs to closed first and then \'(\' at index 3 needs to closed subsequently\n 3) simalarly we maintain the count for open_brackets and closed_brackets \n 4) if (count of closed brackets becomes) > (the open_brackets) that means we don\'t have any open bracket before this closed bracket so we need to eleminate this closed bracket from answer string\n \n\tso here in this first tast case \n\t1)closed bracket at index 7 will be satisfy with open bracket at index 5\n\t2)closed bracket at index 9 will be satisfy with open bracket at index 3\n\t3)but closed bracket at index 12 does not have any open bracket so we will not take that one in our answer\n\t\nNow take second test case: "a)b(c)d"\nanswer should be : "ab(c)d"\n```\nso here in second test case:\n \n 1)here closed bracket at index 1 does not have any open bracket before it so we will not take that in our answer\n 2)but closed bracket at index 5 have open brakcet before it to satisfy so we will take it\n```\n\nNow take 3rd test case : "))(("\nanswer: ""\n\n```\nSo here int 3rd test case:\n1)here closed brackets at index 0 and 1 are out from our answer\n2)but open brackets at index 2 and 3 does not have any closed brackets to satisfy them so no need to take them in answer \n```\n\n\n```\nso Approach:\n1. we will create empty stack\n2. then tarverse the string from left to right\n 1. if s[i]!=\'(\' && s[i]!=\')\' then add it into our stack\n 2. else if s[i]==\'(\' then add into stack and increase the count of open_brackets++\n 3. else means closed bracket add it to stack increase the count of closed_brackets but \n 1. if closed_brackets>open_brackets then remove the closed bracket from the stack and \n decrese the count of closed bracket\n3.so uptil now we have taken care of closed brackets but how to takel open brackets\n4. so we have count of open_brackets and closed_brackets\n5. if open_brackets are more then closed_brackets means their are more (open_brackets - closed_brackest) open brackets so to handle them we will remove first (open_bracket - closed_brackets) open brackest from stack \n```\n \n \n\nThanks and if you liked please upvote\n\n```\nstring minRemoveToMakeValid(string s) {\n \n int length_s=s.size(); //getting the length of string \n stack<char> stk; //creating the empty stack for storing the characters\n \n int open_brackets=0; //initizing the count for open_brackets\n int close_brackets=0; ////initizing the count for close_brackets\n \n for(int i=0;i<length_s;i++) //traversing the string from left to right\n {\n if(s[i]!=\'(\' && s[i]!=\')\') // if it character not equal to open and closed bracket \n {\n stk.push(s[i]); //then add it to stack\n }\n else\n {\n if(s[i]==\'(\') //if it is open bracket\n {\n open_brackets++; //increase the count of open_bracket\n stk.push(s[i]); //add it to stack \n }\n else\n {\n close_brackets++; //if it is closed bracket\n stk.push(s[i]); //add it to satck \n if(close_brackets>open_brackets) //if closed brackets are more than open brackets then \n {\n stk.pop(); //pop the closed bracket which we have added\n close_brackets--; //and decrease the count og close_bracket\n }\n }\n }\n }\n string ans=""; //initilizing the answer string\n if(open_brackets>close_brackets) //we have already taken care of closed brackets now need to handle open brackets\n {\n int diff=open_brackets-close_brackets; //number of open brackets more than closed brackets need to remove from answer string\n while(stk.empty()==false)\n {\n char top=stk.top();\n stk.pop();\n \n if(top==\'(\' && diff!=0) \n {\n diff--;\n }\n else\n {\n ans+=top;\n }\n }\n }\n else\n {\n while(stk.empty()==false)\n {\n char top=stk.top();\n stk.pop();\n ans+=top;\n }\n }\n reverse(ans.begin(),ans.end()); //reversing the string \n return(ans);\n }\n```\n
| 6 | 0 |
['Stack', 'C']
| 3 |
minimum-remove-to-make-valid-parentheses
|
C++,Easy to understand with Proper Explanation.
|
ceasy-to-understand-with-proper-explanat-bbot
|
Daily Challenge:-15/03/2022.\nConcept:-We have to remove total of those braces which are invalid.\n-->Step1:- With the Help of stack store the indices of invali
|
bnb_2001
|
NORMAL
|
2022-03-15T01:32:10.024717+00:00
|
2022-03-15T01:32:10.024747+00:00
| 463 | false |
# Daily Challenge:-15/03/2022.\n**Concept:**-We have to remove total of those braces which are invalid.\n-->**Step1:-** With the Help of stack store the indices of invalid braces.\n-->**Step2:-** Calculation to calculate the output result,by neglecting invalid braces indices which will present in stack.\n```\nclass Solution {\npublic:\n string minRemoveToMakeValid(string s) {\n /*Step1:-With the Help of Stack we are storing Indices of invalid braces.*/\n stack<pair<char,int>>st;\n string result="";\n for(int i=0;i<s.size();i++)\n {\n if(s[i]==\'(\'||s[i]==\')\')\n {\n if(st.size()>0&&(st.top().first==\'(\'&&s[i]==\')\'))\n st.pop();\n else\n st.push({s[i],i});\n }\n }\n \n/*Step2:-As we know after the step 1 calculation,Stack will store the indices of invalid braces from right to left. Means stack top have indices of invalid braces which is in right most.\nThat\'s why itrating from right to left in string.\nIn side this Loop ,we are checking,wheather the ith index is invalid or not by comparing with stack top.\nif it is invalid then we didn\'t store it in our result,and we pop it from stack.\nOtherwise we store it in our resut.*/\n for(int i=s.size()-1;i>=0;i--)\n {\n if(st.size()>0&&st.top().second==i)\n {\n st.pop();\n continue;\n }\n else\n result.push_back(s[i]);\n }\n \n reverse(result.begin(),result.end()); //At the end reverse the answer.\n return result; //return result \n }\n};\n```\nIf you Find it helpful,please Upvote.
| 6 | 0 |
['Stack', 'C']
| 0 |
minimum-remove-to-make-valid-parentheses
|
Easy and Fast JavaScript Solution (faster than 90%)
|
easy-and-fast-javascript-solution-faster-ev9t
|
javascript\nvar minRemoveToMakeValid = function(s) {\n let result = [...s];\n let open = [];\n \n for (let i = 0; i < s.length; i++) {\n if (s[i] === "("
|
Cookie_Ryu
|
NORMAL
|
2021-07-08T13:08:29.835647+00:00
|
2021-07-08T13:08:29.835692+00:00
| 569 | false |
```javascript\nvar minRemoveToMakeValid = function(s) {\n let result = [...s];\n let open = [];\n \n for (let i = 0; i < s.length; i++) {\n if (s[i] === "(") open.push(i);\n else if (s[i] === ")") {\n if (open.length > 0) open.pop();\n else result[i] = "";\n }\n }\n\n while (open.length > 0) result[open.pop()] = "";\n \n return result.join("");\n};\n```
| 6 | 0 |
['JavaScript']
| 0 |
minimum-remove-to-make-valid-parentheses
|
Simple Java Solution using stack
|
simple-java-solution-using-stack-by-_anu-ncdq
|
\nclass Solution {\n public String minRemoveToMakeValid(String s) {\n if(s.length() == 0 || s == null){\n return "";\n }\n St
|
_anusharma
|
NORMAL
|
2021-03-28T07:11:29.662997+00:00
|
2021-03-28T07:11:29.663024+00:00
| 524 | false |
```\nclass Solution {\n public String minRemoveToMakeValid(String s) {\n if(s.length() == 0 || s == null){\n return "";\n }\n StringBuilder sb = new StringBuilder(s);\n \n Stack<Integer> st = new Stack<>();\n \n for(int i = 0; i < s.length(); ++i){\n \n char ch = s.charAt(i);\n \n if(ch == \'(\'){\n st.push(i);\n }else if(ch == \')\'){\n if(st.size() == 0){\n st.push(i);\n }else{\n if(s.charAt(st.peek()) == \'(\'){\n st.pop();// this makes a pair of valid parenthesis\n }else{\n st.push(i); // this makes "))"\n }\n }\n }\n }\n \n while(st.size() > 0){\n sb.deleteCharAt(st.pop()); // remove invalid at the indices\n }\n \n return sb.toString();\n \n }\n}\n```\n\n
| 6 | 0 |
['Stack', 'Java']
| 1 |
minimum-remove-to-make-valid-parentheses
|
General Parantheses Problem | Python | Interview Prep
|
general-parantheses-problem-python-inter-xx7r
|
Minimum Remove to Make Valid Parentheses\nhttps://leetcode.com/problems/minimum-remove-to-make-valid-parentheses/\n\n\nclass Solution(object):\n def minRemov
|
pakilamak
|
NORMAL
|
2020-09-07T00:24:59.057899+00:00
|
2020-09-07T01:57:04.599476+00:00
| 497 | false |
1249. Minimum Remove to Make Valid Parentheses\nhttps://leetcode.com/problems/minimum-remove-to-make-valid-parentheses/\n\n```\nclass Solution(object):\n def minRemoveToMakeValid(self, s):\n """\n :type s: str\n :rtype: str\n """\n stack =[]\n \n s =list(s)\n for i, char in enumerate(s):\n if char == "(":\n stack.append(i)\n else:\n if char == ")":\n if stack:\n stack.pop()\n else:\n s[i] = ""\n \n while stack:\n s[stack.pop()] = "" \n return "".join(s)\n```\n\n921. Minimum Add to Make Parentheses Valid\nhttps://leetcode.com/problems/minimum-add-to-make-parentheses-valid/\n\n```\nclass Solution(object):\n def minAddToMakeValid(self, S):\n """\n :type S: str\n :rtype: int\n """\n stack =[]\n for i in S:\n if i=="(":\n stack.append(i)\n \n else:\n if i == ")":\n \n if stack and stack[-1]=="(":\n stack.pop()\n else:\n stack.append(i)\n \n return len(stack)\n```\n\n20. Valid Parentheses\nhttps://leetcode.com/problems/valid-parentheses/\n\n```\nclass Solution(object):\n def isValid(self, s):\n """\n :type s: str\n :rtype: bool\n """\n dic ={"{":"}",\n "[":"]",\n "(":")"}\n \n stack = []\n \n for i in s:\n if i in dic:\n stack.append(i)\n \n # if there is input as "]", then we need to \n # check the if the length of stack is empty or not.\n elif len(stack) == 0 or dic[stack.pop()]!=i:\n return False\n return len(stack)==0\n```\n\n32. Longest Valid Parentheses\nhttps://leetcode.com/problems/longest-valid-parentheses/\n```\nclass Solution(object):\n def longestValidParentheses(self, s):\n """\n :type s: str\n :rtype: int\n """\n stack =[]\n \n cur_long = 0\n max_long = 0\n \n for i in s:\n if i == "(":\n stack.append(cur_long)\n cur_long =0\n else:\n if stack:\n cur_long += stack.pop() + 2\n max_long = max(cur_long, max_long)\n else:\n cur_long = 0\n \n return max_long\n```
| 6 | 1 |
['Python']
| 0 |
minimum-remove-to-make-valid-parentheses
|
Just easy JS code
|
just-easy-js-code-by-nbekweb-ipyx
|
\n\n# Code\n\n/**\n * @param {string} s\n * @return {string}\n */\n\nvar minRemoveToMakeValid = function(s) {\n const stack = []; // Initialize a stack to ho
|
Nbekweb
|
NORMAL
|
2024-04-06T08:37:07.385143+00:00
|
2024-04-06T08:37:07.385182+00:00
| 172 | false |
\n\n# Code\n```\n/**\n * @param {string} s\n * @return {string}\n */\n\nvar minRemoveToMakeValid = function(s) {\n const stack = []; // Initialize a stack to hold indices of opening parentheses\n const str = s.split(\'\'); // Convert the string to an array for efficient modification\n \n // Iterate through each character of the string\n for (let i = 0; i < s.length; i++) {\n const ch = s[i]; // Current character\n \n // If an opening parenthesis is encountered, push its index onto the stack\n if (ch == \'(\')\n stack.push(i);\n else {\n // If a closing parenthesis is encountered\n if (ch == \')\') {\n // If there\'s a matching opening parenthesis in the stack, pop it\n if (stack.length)\n stack.pop();\n // If there\'s no matching opening parenthesis, \n // remove the current closing parenthesis by setting it to an empty string\n else\n str[i] = \'\';\n }\n }\n }\n \n // Remove any remaining unmatched opening parentheses by setting their corresponding characters to an empty string\n for (let i of stack) {\n str[i] = \'\';\n }\n \n return str.join(\'\');\n};\n```
| 5 | 0 |
['JavaScript']
| 3 |
minimum-remove-to-make-valid-parentheses
|
Without STACK .. Beginner Friendly Solution ..Beats no one..
|
without-stack-beginner-friendly-solution-40xu
|
Intuition\n Describe your first thoughts on how to solve this problem. \nAs there are only one type of brackets we don\'t need any stack to balance them .. we c
|
kalpit04
|
NORMAL
|
2024-04-06T05:52:04.502115+00:00
|
2024-04-06T05:52:04.502148+00:00
| 210 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAs there are only one type of brackets we don\'t need any stack to balance them .. we can just maintain a count variable .. For eg if cnt==3 it means we have encountered 3 more opening brackets than closing brackets..something like this .. "()()(()(("\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSo firstly we will try to balance the closing brackets.. Balancing them means removing those \')\' which come before \'(\' .. we can do this just maintain a cnt variable and increment and decrement it when we encounter opening and closing bracket respectively .. \n\nAfter removing those extra closing brackets we store the string in new string temp .. Rest of the string remains same .. \nFor eg -> "))()()(" gets changed to "()()(" (we have removed first two closing brackets)\n\nnow we check how many extra opening brackets we have .. after the first step we are sure that no extra closing brackets only we can have extra opening brackets .. \n\nAnd to remove them we should not remove them from beginning as they would imbalance the closing brackets .. we should remove from the last to balance them ..\n\nTo do this .. just count how many extra opening brackets we have and just remove them from last .. and at last reverse the string and return \n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n# Code\n```\nclass Solution {\npublic:\n string minRemoveToMakeValid(string s) {\n int cnt=0;\n \n string temp="";\n // temp string stores the string after removing extra closing brackets \n for(auto ch:s){\n if(ch==\')\'&&cnt==0){\n cnt=0;\n continue;\n\n }\n if(ch==\'(\') cnt++;\n if(ch==\')\') cnt--;\n temp+=ch;\n }\n \n cnt=0;\n // now cnt stores the extra opening brackets..\n for(auto c:temp){\n if(c==\'(\') cnt++;\n if(c==\')\') cnt--;\n }\n // if 0 it is balanced already \n if(cnt==0) return temp;\n string rev="";\n \n // traverse from end and remove cnt number of opening brackets\n for(int i=temp.length()-1;i>=0;i--){\n if(temp[i]==\'(\'&&cnt>0){\n cnt--;\n continue;\n }\n rev+=temp[i];\n\n\n }\n // reverse it and return \n\n reverse(rev.begin(),rev.end());\n \n return rev;\n \n }\n};\n```
| 5 | 0 |
['C++']
| 3 |
minimum-remove-to-make-valid-parentheses
|
C++ || O(n) TIME AND SPACE || Apr 6 2024 Daily
|
c-on-time-and-space-apr-6-2024-daily-by-23oi3
|
Intuition\nThe problem involves removing the minimum number of parentheses from a string to make it a valid parentheses string. A valid parentheses string must
|
praneelpa
|
NORMAL
|
2024-04-06T00:31:12.377168+00:00
|
2024-04-06T00:31:26.287052+00:00
| 1,278 | false |
# Intuition\nThe problem involves removing the minimum number of parentheses from a string to make it a valid parentheses string. A valid parentheses string must have balanced parentheses, meaning each opening parenthesis \'(\' must have a corresponding closing parenthesis \')\', and they must be properly nested. One might think of using a stack to keep track of the indices of opening parentheses and removing excess closing parentheses.\n\n# Approach\nThe provided code utilizes a stack to keep track of the indices of opening parentheses encountered in the string. It iterates through the string s character by character. Whenever an opening parenthesis \'(\' is encountered, its index is pushed onto the stack. If a closing parenthesis \')\' is encountered and the stack is empty, indicating there is no matching opening parenthesis, the closing parenthesis is marked for removal by replacing it with \'\'. Otherwise, the topmost index on the stack is popped, indicating that the current closing parenthesis matches with an opening parenthesis. After iterating through the entire string, any remaining opening parentheses on the stack are marked for removal by replacing them with \'\'. Finally, all \'*\' characters are removed from the string, and the resulting string is returned.\n\n# Complexity\n- Time complexity:\nO(n), where n is the length of the string s. The code iterates through the string once to process each character.\n\n- Space complexity:\nO(n), where n is the length of the string s. The space complexity arises from the stack, which can potentially store up to n/2 indices in the worst case if all characters are opening parentheses. Additionally, the code utilizes extra space to store the resulting string after removal of \'*\' characters.\n\n# Code\n```\nclass Solution {\npublic:\n string minRemoveToMakeValid(string s) {\n stack<int> stack;\n\n for (int i = 0; i < s.length(); ++i)\n if (s[i] == \'(\') {\n stack.push(i);\n } else if (s[i] == \')\') {\n if (stack.empty())\n s[i] = \'*\';\n else\n stack.pop();\n }\n\n while (!stack.empty())\n s[stack.top()] = \'*\', stack.pop();\n\n s.erase(remove(s.begin(), s.end(), \'*\'), s.end());\n return s;\n }\n};\n```
| 5 | 0 |
['String', 'Stack', 'C++']
| 5 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.