question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
find-the-original-array-of-prefix-xor
|
C# Solution for Find the Original Array of the Prefix XOR Problem
|
c-solution-for-find-the-original-array-o-6ak1
|
Intuition\n Describe your first thoughts on how to solve this problem. \nThe intuition behind the given solution lies in the property of the XOR operation and h
|
Aman_Raj_Sinha
|
NORMAL
|
2023-10-31T03:24:25.815076+00:00
|
2023-10-31T03:24:25.815104+00:00
| 154 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition behind the given solution lies in the property of the XOR operation and how it can be used to reconstruct the original array by performing XOR operations in reverse order on the \u2018pref\u2019 array.\n\nThe XOR operation is reversible. Given two numbers A and B, if we perform an XOR operation between them (A ^ B), the result can be used to recover either A or B by performing another XOR operation with the other number (A ^ (A ^ B) = B and B ^ (A ^ B) = A). Using this property, the solution works backward, gradually reconstructing the \u2018arr\u2019 array by reversing the XOR operations carried out on \u2018pref\u2019. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1.\tIterative XOR Operations in Reverse: The solution iterates through the \u2018pref\u2019 array in reverse (from the last element towards the first).\n2.\tXOR Operation: At each step, it computes the XOR of \u2018pref[i]\u2019 and \u2018pref[i-1]\u2019 and stores the result in \u2018pref[i]\u2019. This process continues until the first element is reached.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of this solution is O(n), where \u2018n\u2019 is the number of elements in the \u2018pref\u2019 array. The algorithm processes each element in the array only once, performing XOR operations, which takes constant time.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(1) as the algorithm operates in place without utilizing any extra space in proportion to the input size. The operations are performed directly on the \u2018pref\u2019 array without using any additional data structures.\n\n# Code\n```\npublic class Solution {\n public int[] FindArray(int[] pref) {\n int n = pref.Length;\n\n for (int i = n - 1; i > 0; i--) {\n pref[i] = pref[i] ^ pref[i - 1];\n }\n\n return pref;\n }\n}\n```
| 2 | 0 |
['C#']
| 1 |
find-the-original-array-of-prefix-xor
|
C++ Solution
|
c-solution-by-pranto1209-hls8
|
Complexity\n- Time complexity:\n Add your time complexity here, e.g. O(n) \n O(N)\n\n- Space complexity:\n Add your space complexity here, e.g. O(n) \n O(
|
pranto1209
|
NORMAL
|
2023-10-31T03:10:38.584587+00:00
|
2023-10-31T03:10:38.584647+00:00
| 7 | false |
# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(N)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(N)\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> findArray(vector<int>& pref) {\n int n = pref.size();\n vector<int> ans;\n ans.push_back(pref[0]);\n for (int i = 1; i < n; i++) {\n ans.push_back(pref[i] ^ pref[i - 1]);\n }\n return ans;\n }\n};\n```
| 2 | 0 |
['C++']
| 0 |
find-the-original-array-of-prefix-xor
|
Python simple solution with easy explanation
|
python-simple-solution-with-easy-explana-6tqa
|
Intuition\n\npref = \begin{matrix}[a_1 & a_2 & a_3 & a_4 & a_5]\end{matrix} \n\nLet \space result = \begin{matrix}[r_1 & r_2 & r_3 & r_4 & r_5]\end{matrix}.\n\
|
pilsungdev
|
NORMAL
|
2023-10-31T03:10:00.552456+00:00
|
2023-10-31T04:57:46.361493+00:00
| 60 | false |
# Intuition\n$$\npref = \\begin{matrix}[a_1 & a_2 & a_3 & a_4 & a_5]\\end{matrix} \n$$\nLet $$ \\space result = \\begin{matrix}[r_1 & r_2 & r_3 & r_4 & r_5]\\end{matrix}.\n$$\n\nFYI) $$ \\oplus$$ is XOR symbol\n\n$$\na_1 = r_1 \\space \\oplus \\space 0\n\\newline\na_2 = r_1 \\space \\oplus \\space r_2 \n\\newline\na_3 = r_1 \\space \\oplus \\space r_2 \\space \\oplus \\space r_3\n\\newline\na_4 = r_1 \\space \\oplus \\space r_2 \\space \\oplus \\space r_3 \\space \\oplus \\space r_4\n\\newline\na_5 = r_1 \\space \\oplus \\space r_2 \\space \\oplus \\space r_3 \\space \\oplus \\space r_4 \\space \\oplus \\space r_5\n\\newline\n$$\ncan be rewriteen as\n$$\na_1 = r_1 \\space \\oplus \\space 0\n\\newline\na_2 = a_1 \\space \\oplus \\space r_2 \n\\newline\na_3 = a_2 \\space \\oplus \\space r_3\n\\newline\na_4 = a_3 \\space \\oplus \\space r_4\n\\newline\na_5 = a_4 \\space \\oplus \\space r_5\n\\newline\n$$\n\nWhen $$ a \\space \\oplus \\space b = c$$, also $$ c \\space \\oplus \\space a = b$$ is true.\nThus,\n\n$$\nr_1 = a_1 \\oplus 0\n\\newline\nr_2 = a_1 \\space \\oplus \\space a_2 \n\\newline\nr_3 = a_2 \\space \\oplus \\space a_3\n\\newline\nr_4 = a_3 \\space \\oplus \\space a_4\n\\newline\nr_5 = a_4 \\space \\oplus \\space a_5\n\\newline\n$$\n\n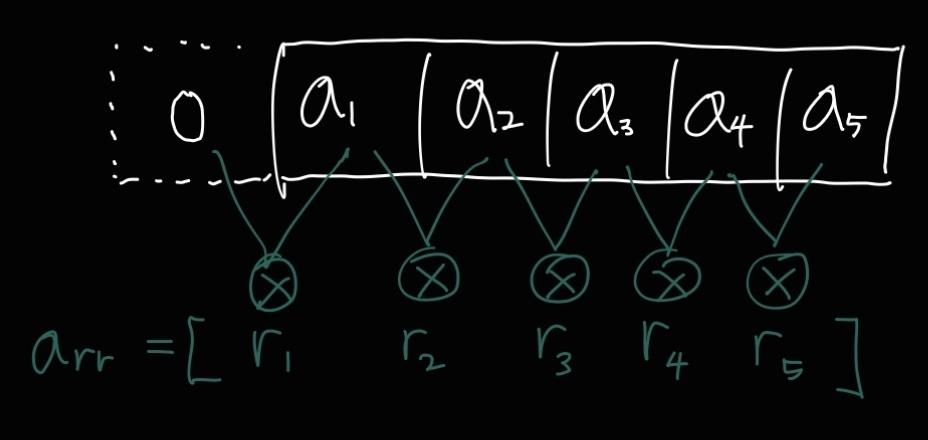\n\n\n\n# Code\n```\nclass Solution:\n def findArray(self, pref: List[int]) -> List[int]:\n pref.insert(0,0)\n return [pref[idx]^pref[idx+1] for idx in range(len(pref)-1)]\n```
| 2 | 0 |
['Python3']
| 2 |
find-the-original-array-of-prefix-xor
|
Python3 Solution
|
python3-solution-by-motaharozzaman1996-7u75
|
\n\nclass Solution:\n def findArray(self, pref: List[int]) -> List[int]:\n N=len(pref)\n arr=[pref[0]]\n \n for i in range(1,N):\
|
Motaharozzaman1996
|
NORMAL
|
2023-10-31T02:50:04.311468+00:00
|
2023-10-31T02:50:04.311503+00:00
| 347 | false |
\n```\nclass Solution:\n def findArray(self, pref: List[int]) -> List[int]:\n N=len(pref)\n arr=[pref[0]]\n \n for i in range(1,N):\n arr.append(pref[i-1]^pref[i])\n \n return arr \n```
| 2 | 0 |
['Python', 'Python3']
| 1 |
find-the-original-array-of-prefix-xor
|
EASY - BEGINNER FRIENDLY CODE || Prefix xor
|
easy-beginner-friendly-code-prefix-xor-b-768i
|
Intuition\nThe code essentially transforms the input vector by XORing each element with the previous one.\n\n# Approach\n1. Initialize a variable prev with the
|
calm_porcupine
|
NORMAL
|
2023-10-31T02:07:55.060195+00:00
|
2023-10-31T02:07:55.060220+00:00
| 236 | false |
# Intuition\nThe code essentially transforms the input vector by XORing each element with the previous one.\n\n# Approach\n1. Initialize a variable prev with the value of the first element in the pref vector.\n2. Create an auxiliary variable aux to temporarily store the result of the XOR operation.\n3. Iterate through the pref vector starting from the second element (index 1).\n3. For each element at index i, calculate auxiliary/temporary value by performing a bitwise XOR operation (^) between prev and the current element pref[i]. Update the prev variable to be the current element pref[i] for the next iteration. Update the current element in the pref vector with the calculated aux value, effectively modifying the vector in place.\n4. Repeat step 3 for all elements in the pref vector.\nFinally, return the modified pref vector.\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(1)$$\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> findArray(vector<int>& pref) {\n int prev = pref[0];// prev -- store the (i-1)th value of original vector\n int aux; // temporary variable\n for(int i = 1;i<pref.size();i++){\n aux=prev^pref[i];\n prev = pref[i];\n pref[i] = aux;\n }\n return pref;\n }\n};\n```
| 2 | 0 |
['Bit Manipulation', 'C++']
| 1 |
find-the-original-array-of-prefix-xor
|
1-Line Javascript/Typescript Solution
|
1-line-javascripttypescript-solution-by-p1jbo
|
Complexity\n- Time complexity: O(n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(n)\n Add your space complexity here, e.g. O(n) \n\n# Co
|
wentland
|
NORMAL
|
2023-10-31T01:45:27.400815+00:00
|
2023-10-31T01:45:27.400833+00:00
| 21 | false |
# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nconst findArray = (arr: number[]) => arr.map((num, i) => num ^ arr[i - 1]);\n\n```
| 2 | 0 |
['TypeScript', 'JavaScript']
| 0 |
find-the-original-array-of-prefix-xor
|
[C++] XOR again
|
c-xor-again-by-awesome-bug-vudd
|
Intuition\n Describe your first thoughts on how to solve this problem. \n- pref[i] = arr[0] ^ arr[1] ^ ... ^ arr[i - 1] ^ arr[i]\n- pref[i - 1] = arr[0] ^ arr[1
|
pepe-the-frog
|
NORMAL
|
2023-10-31T01:29:34.149110+00:00
|
2023-10-31T03:55:13.711909+00:00
| 822 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- `pref[i] = arr[0] ^ arr[1] ^ ... ^ arr[i - 1] ^ arr[i]`\n- `pref[i - 1] = arr[0] ^ arr[1] ^ ... ^ arr[i - 1]`\n- To get `arr[i]` we can biwise-xor `pref[i]` and `pref[i - 1]`\n - `pref[i] ^ pref[i - 1]`\n - ` = (arr[0] ^ arr[0]) ^ (arr[1] ^ arr[1]) ^ ... ^ (arr[i - 1] ^ arr[i - 1]) ^ arr[i]`\n - ` = 0 ^ 0 ^ ... ^ 0 ^ arr[i]`\n - ` = arr[i]` \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Base case: `i = 0`\n - `arr[0] = pref[0]`\n- Normal case: `i = [1, n)`\n - `arr[i] = pref[i - 1] ^ pref[i]`\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$ -> $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n // time/space: O(n)/O(n)\n vector<int> findArray(vector<int>& pref) {\n const int n = pref.size();\n vector<int> arr(pref);\n for (int i = 1; i < n; i++) arr[i] = pref[i - 1] ^ pref[i];\n return arr;\n }\n};\n```\n```\nclass Solution {\npublic:\n // time/space: O(n)/O(1)\n vector<int> findArray(vector<int>& pref) {\n for (int i = pref.size() - 1; i > 0; i--) pref[i] ^= pref[i - 1];\n return pref;\n }\n};\n```
| 2 | 0 |
['Bit Manipulation', 'C++']
| 3 |
find-the-original-array-of-prefix-xor
|
[C++] Straightforward & Clean Solution
|
c-straightforward-clean-solution-by-makh-6127
|
Complexity\n- Time complexity:\nO(n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity:\nO(n)\n Add your space complexity here, e.g. O(n) \n\n#
|
makhonya
|
NORMAL
|
2023-10-31T00:13:21.804727+00:00
|
2023-10-31T00:13:21.804756+00:00
| 1,826 | false |
# Complexity\n- Time complexity:\n$$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n$$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> findArray(vector<int>& p) {\n int n = p.size(), cur = p[0];\n vector<int> result(n, cur);\n for(int i = 1; i < n; i++)\n result[i] = cur ^ p[i], cur = p[i];\n return result;\n }\n};\n```
| 2 | 0 |
['C++']
| 4 |
find-the-original-array-of-prefix-xor
|
Simple Approach, C++ Beats 90% ✅✅
|
simple-approach-c-beats-90-by-deepak_591-fwnv
|
Approach\n Describe your approach to solving the problem. \nin problem statement it is given that :-\npref[i] = arr[0]^arr[1]^arr[2]......arr[i-1]^arr[i]\nwe ca
|
Deepak_5910
|
NORMAL
|
2023-07-04T06:34:05.682713+00:00
|
2023-07-04T06:34:05.682734+00:00
| 176 | false |
# Approach\n<!-- Describe your approach to solving the problem. -->\nin problem statement it is given that :-\n**pref[i] = arr[0]^arr[1]^arr[2]......arr[i-1]^arr[i]**\nwe can write the statement in another way :-\n**arr[i] = arr[0]^arr[1].....arr[i-2]^arr[i-1]^pref[i]**\n# Complexity\n- Time complexity:O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> findArray(vector<int>& pref) {\n int n = pref.size(),xorvalue = pref[0];\n for(int i = 1;i<pref.size();i++)\n {\n int tmp = xorvalue^pref[i];\n pref[i] = tmp;\n xorvalue = xorvalue^pref[i];\n }\n return pref;\n }\n};\n```\n\n
| 2 | 0 |
['Bit Manipulation', 'C++']
| 0 |
find-the-original-array-of-prefix-xor
|
JAVA | VERY EASY SOLUTION✅💯
|
java-very-easy-solution-by-dipesh_12-tqdb
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
dipesh_12
|
NORMAL
|
2023-06-13T07:07:06.858097+00:00
|
2023-06-13T07:07:06.858115+00:00
| 85 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int[] findArray(int[] pref) {\n int n=pref.length;\n int ans[]=new int[n];\n ans[0]=pref[0];\n for(int i=1;i<n;i++){\n ans[i]=pref[i]^pref[i-1];\n }\n return ans;\n }\n}\n```
| 2 | 0 |
['Java']
| 0 |
find-the-original-array-of-prefix-xor
|
Simple Java Solution
|
simple-java-solution-by-ololx-eamy
|
Simple Java Solution\n\n# Code\n\nclass Solution {\n public int[] findArray(int[] pref) {\n int[] originArray = new int[pref.length];\n originA
|
ololx
|
NORMAL
|
2023-05-14T09:34:10.387467+00:00
|
2023-05-14T09:34:10.387500+00:00
| 231 | false |
Simple Java Solution\n\n# Code\n```\nclass Solution {\n public int[] findArray(int[] pref) {\n int[] originArray = new int[pref.length];\n originArray[0] = pref[0];\n\n for (int elementIndex = 1; elementIndex < pref.length; elementIndex++) {\n originArray[elementIndex] = pref[elementIndex] ^ pref[elementIndex - 1];\n }\n\n return originArray;\n }\n}\n```
| 2 | 0 |
['Java']
| 0 |
find-the-original-array-of-prefix-xor
|
Find The Original Array of Prefix Xor Solution in C++
|
find-the-original-array-of-prefix-xor-so-6zfs
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
The_Kunal_Singh
|
NORMAL
|
2023-04-15T04:38:45.477235+00:00
|
2023-04-27T16:34:40.579518+00:00
| 628 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n# Code\n```\nclass Solution {\npublic:\n vector<int> findArray(vector<int>& pref) {\n int i;\n vector<int> arr;\n arr.push_back(pref[0]);\n for(i=1 ; i<pref.size() ; i++)\n {\n arr.push_back(pref[i-1]^pref[i]);\n }\n return arr;\n }\n};\n```\n
| 2 | 0 |
['C++']
| 0 |
find-the-original-array-of-prefix-xor
|
✅ Easy approach
|
easy-approach-by-pg99285-sy3f
|
Intuition\nRecall the concepts of XOR.\n\n# Approach\n\na ^ b = c\n\nThen the following relations will also be true,\n\na ^ c = b\nb ^ c = a\n\n\n# Complexity\n
|
pg99285
|
NORMAL
|
2023-02-19T19:25:56.305196+00:00
|
2023-02-19T19:25:56.305223+00:00
| 28 | false |
# Intuition\nRecall the concepts of XOR.\n\n# Approach\n```\na ^ b = c\n```\nThen the following relations will also be true,\n```\na ^ c = b\nb ^ c = a\n```\n\n# Complexity\nO(n)\n\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> findArray(vector<int>& pref) {\n int n = pref.size();\n vector<int> res;\n\n res.push_back(pref[0]);\n for(int i=1; i<n; i++){\n res.push_back(pref[i-1]^pref[i]);\n }\n \n return res;\n }\n};\n```
| 2 | 0 |
['Bit Manipulation', 'C++']
| 0 |
find-the-original-array-of-prefix-xor
|
JAVA | 100% fast solution
|
java-100-fast-solution-by-firdavs06-gns4
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Firdavs06
|
NORMAL
|
2023-02-19T16:25:14.574531+00:00
|
2023-02-19T16:25:14.574576+00:00
| 29 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int[] findArray(int[] pref) {\n int len = pref.length;\n for(int i = len - 1; i > 0; i--){\n pref[i] = pref[i - 1] ^ pref[i];\n }\n return pref;\n }\n}\n```
| 2 | 0 |
['Array', 'Java']
| 0 |
find-the-original-array-of-prefix-xor
|
Easy cpp solution(a^b=c then a^c=b)
|
easy-cpp-solutionabc-then-acb-by-chalobe-gfa2
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n(a^b=c then a^c=b)\n\n# Complexity\n- Time complexity:\n Add your time co
|
prathamesh45_
|
NORMAL
|
2023-02-07T02:12:53.121304+00:00
|
2023-02-07T02:12:53.121347+00:00
| 84 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n(a^b=c then a^c=b)\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> findArray(vector<int>& nums) {\n vector<int>arr;\n arr.push_back(nums[0]);\n for(int i =0; i<nums.size()-1; i++){\n arr.push_back(nums[i]^nums[i+1]);\n }\n return arr;\n }\n};\n```
| 2 | 0 |
['C++']
| 0 |
find-the-original-array-of-prefix-xor
|
Simple c++ O(n) solution || Beats others
|
simple-c-on-solution-beats-others-by-shr-1n2y
|
\n\n# Code\n\nclass Solution {\npublic:\n vector<int> findArray(vector<int>& pref) {\n vector<int>org;\n org.push_back(pref[0]);\n for(i
|
Shristha
|
NORMAL
|
2023-01-14T17:31:37.364648+00:00
|
2023-01-14T17:31:37.364693+00:00
| 874 | false |
\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> findArray(vector<int>& pref) {\n vector<int>org;\n org.push_back(pref[0]);\n for(int i=1;i<pref.size();i++){\n org.push_back(pref[i]^pref[i-1]);\n }\n return org;\n \n }\n};\n```
| 2 | 0 |
['C++']
| 0 |
find-the-original-array-of-prefix-xor
|
Easy Solution | Python3 Beats 99%
|
easy-solution-python3-beats-99-by-lalith-35xl
|
\n# Code\n\nclass Solution:\n def findArray(self, pref: List[int]) -> List[int]:\n lst=[pref[0]]\n for i in range(len(pref)-1):\n ls
|
Lalithkiran
|
NORMAL
|
2023-01-08T16:46:54.187125+00:00
|
2023-01-08T16:46:54.187171+00:00
| 174 | false |
\n# Code\n```\nclass Solution:\n def findArray(self, pref: List[int]) -> List[int]:\n lst=[pref[0]]\n for i in range(len(pref)-1):\n lst.append(pref[i]^pref[i+1])\n return lst\n\n\n```
| 2 | 0 |
['Python3']
| 0 |
find-the-original-array-of-prefix-xor
|
ONE LINER PYTHON-3 SIMPLE SOLUTION EASY TO UNDERSTAND
|
one-liner-python-3-simple-solution-easy-q5fjz
|
```class Solution:\n def findArray(self, p: List[int]) -> List[int]:\n return [p[0]] +[p[i]^p[i-1]for i in range(1,len(p))]
|
thezealott
|
NORMAL
|
2022-11-15T08:59:38.296196+00:00
|
2022-11-15T08:59:38.296259+00:00
| 620 | false |
```class Solution:\n def findArray(self, p: List[int]) -> List[int]:\n return [p[0]] +[p[i]^p[i-1]for i in range(1,len(p))]
| 2 | 0 |
['Python']
| 0 |
find-the-original-array-of-prefix-xor
|
Java 2ms Fast And Easy Solution
|
java-2ms-fast-and-easy-solution-by-humam-tq79
|
\n\t\tint n=pref.length;\n int[] arr=new int [n];\n arr[0]=pref[0];\n \n for(int i=(n-1);i>0;i--){\n arr[i]=pref[i]^pref[
|
humam_saeed_ansari
|
NORMAL
|
2022-10-27T22:25:47.235287+00:00
|
2022-10-28T18:53:35.456850+00:00
| 1,162 | false |
```\n\t\tint n=pref.length;\n int[] arr=new int [n];\n arr[0]=pref[0];\n \n for(int i=(n-1);i>0;i--){\n arr[i]=pref[i]^pref[i-1];\n }\n return arr;\n```
| 2 | 0 |
['Bit Manipulation', 'Java']
| 0 |
find-the-original-array-of-prefix-xor
|
Ruby one-liner, beats 100%/100%
|
ruby-one-liner-beats-100100-by-dnnx-by0u
|
\n# @param {Integer[]} pref\n# @return {Integer[]}\ndef find_array(pref)\n [0, *pref].each_cons(2).map { _1 ^ _2 }\nend\n
|
dnnx
|
NORMAL
|
2022-10-10T08:26:36.393490+00:00
|
2022-10-10T08:26:36.393521+00:00
| 18 | false |
```\n# @param {Integer[]} pref\n# @return {Integer[]}\ndef find_array(pref)\n [0, *pref].each_cons(2).map { _1 ^ _2 }\nend\n```
| 2 | 0 |
['Ruby']
| 0 |
find-the-original-array-of-prefix-xor
|
Easy
|
easy-by-telugu_coder-9ems
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Telugu_Coder
|
NORMAL
|
2022-10-09T18:45:20.131173+00:00
|
2022-10-18T02:26:48.071408+00:00
| 221 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * @param {number[]} pref\n * @return {number[]}\n */\nvar findArray = function(pref) {\nlet arr = [];\narr[0] = pref[0];\nfor(i=1;i<pref.length;i++){\n arr[i] = pref[i] ^ pref[i-1]\n}\nreturn arr\n};\n```
| 2 | 0 |
['JavaScript']
| 0 |
find-the-original-array-of-prefix-xor
|
1-liner ^^
|
1-liner-by-andrii_khlevniuk-x3l1
|
time: O(N); space: O(1)\n\nvector<int> findArray(vector<int>& p)\n{\n\treturn {begin(p), adjacent_difference(begin(p), end(p), begin(p), bit_xor{})};\n}\n
|
andrii_khlevniuk
|
NORMAL
|
2022-10-09T17:38:09.325928+00:00
|
2022-10-10T09:20:26.334310+00:00
| 714 | false |
**time: `O(N)`; space: `O(1)`**\n```\nvector<int> findArray(vector<int>& p)\n{\n\treturn {begin(p), adjacent_difference(begin(p), end(p), begin(p), bit_xor{})};\n}\n```
| 2 | 0 |
['C', 'C++']
| 1 |
find-the-original-array-of-prefix-xor
|
✅✅Faster || Easy To Understand || C++ Code
|
faster-easy-to-understand-c-code-by-__kr-j2ch
|
Using Bit Manipulation\n\n Time Complexity :- O(N)\n\n Space Complexity :- O(N)\n\n\nclass Solution {\npublic:\n vector<int> findArray(vector<int>& pref) {\n
|
__KR_SHANU_IITG
|
NORMAL
|
2022-10-09T07:49:28.515822+00:00
|
2022-10-09T07:49:28.515859+00:00
| 116 | false |
* ***Using Bit Manipulation***\n\n* ***Time Complexity :- O(N)***\n\n* ***Space Complexity :- O(N)***\n\n```\nclass Solution {\npublic:\n vector<int> findArray(vector<int>& pref) {\n \n int n = pref.size();\n \n // we know that (x ^ x == 0)\n \n // let say pref[i] = (a ^ b ^ c ^ d) and pref[i - 1] = (a ^ b ^ c), when we will do (pref[i] ^ pref[i - 1]) i.e. (a ^ b ^ c ^ d ^ a ^ b ^ c) club the pairs like (a ^ a ^ b ^ b ^ c ^ c ^ d) it will become (d)\n \n // perform the same operation to find every element of array\n \n vector<int> arr(n);\n \n arr[0] = pref[0];\n \n for(int i = 1; i < n; i++)\n {\n arr[i] = (pref[i] ^ pref[i - 1]);\n }\n \n return arr;\n }\n};\n```
| 2 | 0 |
['Bit Manipulation', 'C', 'C++']
| 1 |
find-the-original-array-of-prefix-xor
|
Explained Intuition for XOR || 2 Line Solution
|
explained-intuition-for-xor-2-line-solut-wjxa
|
XOR PROPERTY : \n\n\tFor a,b,c if (a ^ b = c) then (a ^ c = b), (b ^ c = a) \n let variable XOR store ,xor of all previous elements of our ans array.\n le
|
theomkumar
|
NORMAL
|
2022-10-09T06:29:21.080958+00:00
|
2022-10-09T06:36:53.720703+00:00
| 232 | false |
**XOR PROPERTY :** \n```\n\tFor a,b,c if (a ^ b = c) then (a ^ c = b), (b ^ c = a) \n let variable XOR store ,xor of all previous elements of our ans array.\n let ans[i] be x. //we have to find ans[i].\n =>XOR ^ x = p[i] //XOR property\n => x = p[i] ^ XOR \n```\nWe have to insert p[i] ^ XOR in our ans array!\n \nApproach 1: forward iteration\n```\nvector<int> findArray(vector<int>& p) { \n\tint n = p.size();\n\tint XOR = 0;\n\n\tfor(int i = 0; i < n; i++) \n\t{\n\t\tp[i] ^= XOR; //ans[i] = p[i] ^ XOR\n\t\tXOR ^= p[i]; //update XOR to include curr element as well\n\t}\n\treturn p;\n}\n```\n 2 lines! - we know p[0] will be 1 so we can save one iteration!\n \n vector<int> findArray(vector<int>& p) {\n for(int i=1,XOR=p[0]; i<size(p); XOR^=p[i++]) p[i] ^= XOR;\n return p;\n }\nAPPROACH 2 : backward itertion without XOR variable! : [@lee215](https://leetcode.com/problems/find-the-original-array-of-prefix-xor/discuss/2678904/JavaC%2B%2BPython-Easy-and-Concise-with-Explantion) discussion: same intuition.\n
| 2 | 0 |
['C']
| 1 |
find-the-original-array-of-prefix-xor
|
java || 3 ms ||100%faster || simplest solution
|
java-3-ms-100faster-simplest-solution-by-8tdr
|
class Solution {\n public int[] findArray(int[] pre) {\n int[] ans=new int[pre.length];\n ans[0]=pre[0];\n for(int i=1;i<pre.length;i++)
|
arpit_9565
|
NORMAL
|
2022-10-09T06:22:44.509894+00:00
|
2022-10-09T06:22:44.509936+00:00
| 103 | false |
# class Solution {\n public int[] findArray(int[] pre) {\n int[] ans=new int[pre.length];\n ans[0]=pre[0];\n for(int i=1;i<pre.length;i++)\n {\n ans[i]=pre[i-1]^pre[i];\n }\n return ans;\n }\n}
| 2 | 0 |
['Java']
| 0 |
find-the-original-array-of-prefix-xor
|
2 Solutions, one liner & beginner friendly
|
2-solutions-one-liner-beginner-friendly-hoq89
|
\nclass Solution {\npublic:\n vector<int> findArray(vector<int>& pref) {\n \n // beginner friendly\n // time -> O(N) space -> O(N)\n \n
|
NextThread
|
NORMAL
|
2022-10-09T04:39:14.083155+00:00
|
2022-10-09T04:39:14.083188+00:00
| 23 | false |
```\nclass Solution {\npublic:\n vector<int> findArray(vector<int>& pref) {\n \n // beginner friendly\n // time -> O(N) space -> O(N)\n \n vector<int>ans;\n ans.push_back(pref[0]);\n int xr = pref[0];\n for(int i = 1 ; i < pref.size() ; i++) {\n xr = pref[i]^pref[i-1];\n ans.push_back(xr);\n }\n return ans;\n \n // one liner\n // time -> O(N) space -> O\n for (int i = pref.size() - 1; i > 0; --i) pref[i] = pref[i]^pref[i - 1];\n return pref;\n }\n};\n```
| 2 | 0 |
['C']
| 0 |
find-the-original-array-of-prefix-xor
|
Java | 2ms beats 100%
|
java-2ms-beats-100-by-rishabh_raghuwansh-tf54
|
Simple observation:\n\nIf c = a^b then we know a = b^c\n5 ^ 2 = 7 can be written as 5 = 7 ^ 2\n5 ^ 7 = 2 can be written as 7 = 2 ^ 5\nBasic maths LHS = RHS\n\n\
|
Rishabh_Raghuwanshi
|
NORMAL
|
2022-10-09T04:37:52.130149+00:00
|
2022-10-09T04:37:52.130185+00:00
| 65 | false |
Simple observation:\n\nIf c = a^b then we know a = b^c\n5 ^ 2 = 7 can be written as 5 = 7 ^ 2\n5 ^ 7 = 2 can be written as 7 = 2 ^ 5\nBasic maths LHS = RHS\n\n```\nclass Solution {\n public int[] findArray(int[] pref) {\n int xor = pref[0];\n for(int i = 1;i<pref.length;i++)\n {\n int temp = xor ^ pref[i];\n xor = pref[i];\n pref[i] = temp;\n }\n return pref;\n }\n}\n```
| 2 | 0 |
['Bit Manipulation', 'Java']
| 0 |
find-the-original-array-of-prefix-xor
|
2 Solution, one liner & beginner friendly
|
2-solution-one-liner-beginner-friendly-b-enou
|
\nclass Solution {\npublic:\n vector<int> findArray(vector<int>& pref) {\n \n // beginner friendly\n \n vector<int>ans;\n ans.push_b
|
NextThread
|
NORMAL
|
2022-10-09T04:36:53.303805+00:00
|
2022-10-09T04:36:53.303841+00:00
| 15 | false |
```\nclass Solution {\npublic:\n vector<int> findArray(vector<int>& pref) {\n \n // beginner friendly\n \n vector<int>ans;\n ans.push_back(pref[0]);\n int xr = pref[0];\n for(int i = 1 ; i < pref.size() ; i++) {\n xr = pref[i]^pref[i-1];\n pref[i] = xr;\n }\n return ans;\n \n // one liner\n \n for (int i = pref.size() - 1; i > 0; --i) pref[i] = pref[i]^pref[i - 1];\n return pref;\n }\n};\n```
| 2 | 0 |
['C']
| 0 |
find-the-original-array-of-prefix-xor
|
Easy Java Solution
|
easy-java-solution-by-devkd-am08
|
Find The Original Array of Prefix Xor\n# Easy Java Solution\n\nApproach:\n1.) The resultant array can be found by doing the Xor of the prev ans with current pre
|
DevKD
|
NORMAL
|
2022-10-09T04:10:45.579928+00:00
|
2022-10-09T04:10:45.579972+00:00
| 507 | false |
# Find The Original Array of Prefix Xor\n# Easy Java Solution\n\n**Approach:**\n1.) The resultant array can be found by doing the Xor of the prev ans with current pref[i].\n2.) Initially prev would be 0.\n\n```\nclass Solution {\n public int[] findArray(int[] pref) {\n //Creating an ans array\n int[] ans=new int[pref.length];\n int prev=0;\n for(int i=0;i<pref.length;i++){\n //Getting the prev XOR pref[i] as our current answer\n ans[i]=prev^pref[i];\n //Storing pref[i] as prev\n prev=pref[i];\n }\n return ans;\n }\n}\n```
| 2 | 0 |
['Java']
| 1 |
find-the-original-array-of-prefix-xor
|
C++ Simple and easiest approach 3 line code
|
c-simple-and-easiest-approach-3-line-cod-k5e0
|
\nvector findArray(vector& pref) {\n \n vectorans;\n ans.push_back(pref[0]);\n for(int i = 0 ; i < pref.size()-1 ;i++){\n
|
flexsloth
|
NORMAL
|
2022-10-09T04:05:33.378677+00:00
|
2022-10-09T04:10:15.892844+00:00
| 58 | false |
\nvector<int> findArray(vector<int>& pref) {\n \n vector<int>ans;\n ans.push_back(pref[0]);\n for(int i = 0 ; i < pref.size()-1 ;i++){\n int yes = pref[i] xor pref[i+1];\n ans.push_back(yes);\n }\n return\xA0ans;\n\xA0\xA0\xA0\xA0}
| 2 | 1 |
['C']
| 2 |
find-the-original-array-of-prefix-xor
|
Simple Adj XOR | C++
|
simple-adj-xor-c-by-gourav0sharma1-m43b
|
\nvector<int> findArray(vector<int>& pref) {\n vector<int> ans = pref;\n for(int i = 1; i < pref.size();i++){\n ans[i]=pref[i] ^ pref[i
|
gourav0sharma1
|
NORMAL
|
2022-10-09T04:01:13.077484+00:00
|
2022-10-09T04:01:13.077522+00:00
| 188 | false |
```\nvector<int> findArray(vector<int>& pref) {\n vector<int> ans = pref;\n for(int i = 1; i < pref.size();i++){\n ans[i]=pref[i] ^ pref[i-1];\n }\n return ans;\n }\n```
| 2 | 0 |
['C']
| 1 |
find-the-original-array-of-prefix-xor
|
100% Beat || Java code || small and super easy
|
100-beat-java-code-small-and-super-easy-d76w9
|
Complexity
Time complexity: O(n)
Space complexity: O(1)
Code
|
DeepBit-X
|
NORMAL
|
2025-04-10T20:12:40.829507+00:00
|
2025-04-10T20:12:40.829507+00:00
| 5 | false |
# Complexity
- Time complexity: O(n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int[] findArray(int[] pref) {
for(int i=pref.length-1;i>0;i--)
{
pref[i] ^= pref[i-1];
}
return pref;
}
}
```
| 1 | 0 |
['Java']
| 0 |
find-the-original-array-of-prefix-xor
|
Beat 100% of other submissions runtime.
|
beat-100-of-other-submissions-runtime-by-h5r9
|
IntuitionFirstly, we need to know what are the basic properties of xor operator, In xor operation, if x^y=z will always implies x^z=y and y^z=x. we will use thi
|
vivek_ydv99
|
NORMAL
|
2025-04-08T11:16:34.348171+00:00
|
2025-04-08T11:16:34.348171+00:00
| 12 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Firstly, we need to know what are the basic properties of xor operator, In xor operation, if x^y=z will always implies x^z=y and y^z=x. we will use this property to solve this problem.
# Approach
<!-- Describe your approach to solving the problem. -->
Using above property we can simply solve this question, by traversing the array one by one index,
As you can see in the solution in we will keep a xr variable which will keep xor of all the numbers in the new answer array which is helping at each index to calculate the answer of next index.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(N)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(N)
# Code
```cpp []
class Solution {
public:
vector<int> findArray(vector<int>& pref) {
vector<int>ans(pref.size(),0);
ans[0]=pref[0];
int xr=ans[0];
for(int ind=1;ind<pref.size();ind++){
ans[ind]=xr^pref[ind];
xr=xr^ans[ind];
}
return ans;
}
};
```
| 1 | 0 |
['C++']
| 0 |
find-the-original-array-of-prefix-xor
|
Optimized In-Place Solution | Beats 100% | O(1) Space
|
optimized-in-place-solution-beats-100-o1-idun
|
Intuition
The given pref array represents the prefix XOR of an original array.
We need to reconstruct the original array directly within the pref array itsel
|
Abhilash_Mishra
|
NORMAL
|
2025-03-23T17:51:13.834792+00:00
|
2025-03-23T17:58:27.086749+00:00
| 72 | false |
# Intuition
- The given `pref` array represents the prefix XOR of an original array.
- We need to reconstruct the original array directly within the `pref` array itself to optimize space usage.
- Observing the properties of XOR, we can derive the original elements using:
arr[i] = pref[i] ^ pref[i-1]
- By modifying `pref` in place, we eliminate the need for extra space.
# Approach
1. Iterate from the last index down to `1`, updating `pref[i]` using:
pref[i] = pref[i - 1] ^ pref[i]
2. Return `pref`, which now holds the reconstructed array in place.
# Complexity
- **Time Complexity:**
O(n) — We iterate through the array once.
- **Space Complexity:**
O(1) — In-place modification without extra space.
# Code
```java []
class Solution {
public int[] findArray(int[] pref) {
//Optimized approach: Modifying the input array in place to avoid extra space
int n = pref.length;
// Computing the original array in-place
for(int i = n - 1; i > 0;i--){
pref[i] = pref[i - 1] ^ pref[i];
}
return pref;// answer
}
}
```
```python []
def findArray(pref):
n = len(pref)
# Compute the original array in-place
for i in range(n - 1, 0, -1):
pref[i] = pref[i - 1] ^ pref[i]
return pref # The modified pref now represents the original array
```
```C++ []
#include <vector>
class Solution {
public:
std::vector<int> findArray(std::vector<int>& pref) {
int n = pref.size();
// Computing the original array in-place
for (int i = n - 1; i > 0; i--) {
pref[i] = pref[i - 1] ^ pref[i];
}
// The modified pref now represents the original array
return pref;
}
};
```
```javascript []
var findArray = function(pref) {
let n = pref.length;
// Compute the original array in-place
for (let i = n - 1; i > 0; i--) {
pref[i] = pref[i - 1] ^ pref[i];
}
return pref; // The modified pref now represents the original array
};
```
| 1 | 0 |
['Array', 'Bit Manipulation', 'C++', 'Java', 'JavaScript']
| 0 |
find-the-original-array-of-prefix-xor
|
C++✅ || Beats 50%💯|| 2 Lines Code💀💯|| Bit Manipulation🔥💯
|
c-beats-50-2-lines-code-bit-manipulation-77jr
|
💡 IntuitionThe given pref array represents the prefix XOR of the original array. We need to reconstruct the original array using the property:
[
arr[i] = pref[i
|
yashm01
|
NORMAL
|
2025-03-07T16:31:43.675325+00:00
|
2025-03-07T16:31:43.675325+00:00
| 36 | false |
# 💡 Intuition
The given `pref` array represents the prefix XOR of the original array. We need to reconstruct the original array using the property:
\[
arr[i] = pref[i] \oplus pref[i-1]
\]
where `arr[0] = pref[0]`.
# 🔍 Approach
1. **Initialize the result array `ans`** with the first element of `pref`.
2. **Iterate from index 1 to n-1** and compute `arr[i]` using:
\[
arr[i] = pref[i] \oplus pref[i-1]
\]
3. **Return the `ans` array** as the final result.
# ⏳ Complexity
- **Time Complexity:** \( O(n) \)
- We iterate through the `pref` array once.
- **Space Complexity:** \( O(n) \)
- We store the reconstructed array.
# 📝 Code
```cpp
class Solution {
public:
vector<int> findArray(vector<int>& pref) {
vector<int> ans;
int n = pref.size();
ans.push_back(pref[0]);
for(int i = 1; i < n; i++) {
ans.push_back(pref[i-1] ^ pref[i]);
}
return ans;
}
};
```

| 1 | 0 |
['Array', 'Bit Manipulation', 'C++']
| 0 |
find-the-original-array-of-prefix-xor
|
Simple XOR Approach
|
simple-xor-approach-by-sairangineeni-43ul
|
IntuitionWe are given a pref array, which represents prefix XOR values of some original array arr. Our goal is to find the original array.ApproachInitialize an
|
Sairangineeni
|
NORMAL
|
2025-03-02T07:47:11.485988+00:00
|
2025-03-02T07:47:11.485988+00:00
| 40 | false |
# Intuition
We are given a pref array, which represents prefix XOR values of some original array arr. Our goal is to find the original array.
# Approach
Initialize an array arr of the same size as pref.
Set arr[0] = pref[0] (since pref[0] is already the first value).
We can do this = ans[i] = pref[i] ^ pref[i-1];
# Code
```java []
class Solution {
public static int[] findArray(int[] pref) {
int n = pref.length;
int ans[] = new int[n];
ans[0] = pref[0];
for (int i = 1; i < ans.length; i++) {
ans[i] = pref[i] ^ pref[i-1];
}
return ans;
}
}
```
| 1 | 0 |
['Java']
| 0 |
find-the-original-array-of-prefix-xor
|
easy solution c++
|
easy-solution-c-by-anandgoyal0810-uc83
|
IntuitionApproachComplexity
Time complexity:
O(N)
Space complexity:
o(N)
Code
|
anandgoyal0810
|
NORMAL
|
2025-02-15T16:16:31.958514+00:00
|
2025-02-15T16:16:31.958514+00:00
| 39 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
- O(N)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
- o(N)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
vector<int> findArray(vector<int>& pref) {
int n=pref.size();
vector<int> ans( n , 0 );
if (n==0) return {};
ans[0]=pref[0];
for (int i=1; i<n;i++){
ans[i]=pref[i-1]^pref[i];
}
return ans;
}
};
```
| 1 | 0 |
['C++']
| 0 |
find-the-original-array-of-prefix-xor
|
Easy solution
|
easy-solution-by-harshulgarg-k16e
|
IntuitionEach element in the original array can be derived using the property:
a[i]=pref[i]⊕pref[i−1]
where the first element remains the same.ApproachInitializ
|
harshulgarg
|
NORMAL
|
2025-02-13T15:43:31.896261+00:00
|
2025-02-13T15:43:31.896261+00:00
| 43 | false |
# Intuition
Each element in the original array can be derived using the property:
a[i]=pref[i]⊕pref[i−1]
where the first element remains the same.
# Approach
Initialize a with pref[0].
Iterate from i = 1 to len(pref) - 1 and compute:
a[i]=pref[i]⊕pref[i−1]
Return a.
# Complexity
- Time complexity:
O(n)
- Space complexity:
O(n)
# Code
```python3 []
class Solution:
def findArray(self, pref: List[int]) -> List[int]:
a=[]
a.append(pref[0])
for i in range(1,len(pref)):
a.append(pref[i-1]^pref[i])
return a
```
| 1 | 0 |
['Array', 'Python3']
| 0 |
find-the-original-array-of-prefix-xor
|
2433. Find The Original Array of Prefix Xor
|
2433-find-the-original-array-of-prefix-x-gwse
|
IntuitionThe problem involves reconstructing an original array from a given prefix XOR array. The prefix XOR array is defined such that each element at index i
|
Vaibhav_Mangla
|
NORMAL
|
2025-02-12T17:07:55.393875+00:00
|
2025-02-12T17:07:55.393875+00:00
| 19 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The problem involves reconstructing an original array from a given prefix XOR array. The prefix XOR array is defined such that each element at index i in the prefix array is the XOR of all elements from the original array up to index i. The goal is to derive the original array from this prefix XOR array.
# Approach
<!-- Describe your approach to solving the problem. -->
1. **Understanding Prefix XOR:** The prefix XOR array is defined as:
- pref[i] = arr[0] ^ arr[1] ^ ... ^ arr[i]
- To find the original array, we can use the property of XOR:
- If a = b ^ c, then b = a ^ c and c = a ^ b.
- From the prefix XOR, we can derive:
- arr[i] = pref[i] ^ pref[i - 1] for i > 0
- For the first element, arr[0] = pref[0] since there is no previous element to XOR with.
1. **Iterate Backwards:** We can iterate through the prefix array from the end to the beginning, updating the prefix array in place to derive the original array:
- Start from the last element and move towards the first element, applying the XOR operation to reconstruct the original values.
1. **Return the Result:** After processing, the modified pref array will contain the original values.
# Complexity
- Time complexity: **O(n).**
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: **O(1).**
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
vector<int> findArray(vector<int>& pref) {
int n = pref.size();
for(int i = n - 1; i > 0; i--) {
pref[i] ^= pref[i - 1];
}
return pref;
}
};
```
| 1 | 0 |
['C++']
| 0 |
longest-square-streak-in-an-array
|
✅ Clean and fully Explained Code🔥|| Step by Step breakdown
|
clean-and-fully-explained-code-step-by-s-a0lo
|
Intuition\nThe problem involves finding the longest "square streak" in a list of numbers, where each number in a streak is the square of the previous number. Ob
|
uk07
|
NORMAL
|
2024-10-28T00:41:59.942119+00:00
|
2024-10-28T00:41:59.942142+00:00
| 25,940 | false |
# Intuition\nThe problem involves finding the longest "square streak" in a list of numbers, where each number in a streak is the square of the previous number. Observing the problem, one might realize that if we can store and reference each square root\'s streak length, we can build up streaks efficiently by iterating over a sorted list of numbers.\n\n# Approach\n1. **Sort the Array**: Sorting the input list of numbers in ascending order ensures that smaller numbers and their squares appear before the larger squares in the list.\n2. **Initialize a Map**: Use a map `mp` to keep track of the streak length for each number.\n3. **Iterate Through Numbers**: For each number in the sorted list, calculate its integer square root.\n - If the number is a perfect square (i.e., the square of the square root equals the number) and the square root exists in the map, we can extend a streak.\n - Update the map entry for the current number to `mp[_sqrt] + 1` to indicate it\'s part of an extended streak.\n4. **Track the Longest Streak**: Update the result with the maximum streak length found during the iteration.\n\nFinally, return the result, which represents the longest square streak.\n\n# Complexity\n- Time complexity: \n Sorting takes $$O(n \\log n)$$, and iterating over the list to calculate the square root and update the map takes $$O(n)$$, making the overall complexity $$O(n \\log n)$$.\n\n- Space complexity: \n The map `mp` may store up to $$O(n)$$ entries (for each unique number in `nums`), giving a space complexity of $$O(n)$$.\n\n# Code Breakdown:\n- **Sorting**: Sorts the array in $$O(n \\log n)$$ to ensure that smaller squares are processed before larger ones.\n- **Map Setup**: A map `mp` tracks the length of streaks associated with each number.\n- **Square Check and Update**: For each number, we check if it\u2019s a perfect square and if its square root has a streak in the map, extending that streak if both conditions are met. Otherwise, we initialize a new streak.\n- **Result Calculation**: The maximum streak length is updated continuously, so at the end, `res` contains the length of the longest square streak.\n\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int longestSquareStreak(vector<int>& nums) {\n map<int, int>mp;\n sort(nums.begin(), nums.end());\n int res = -1;\n for(int num: nums) {\n int _sqrt = sqrt(num);\n if(_sqrt*_sqrt == num && mp.find(_sqrt)!=mp.end()) {\n mp[num] = mp[_sqrt]+1;\n res = max(res, mp[num]);\n } else mp[num] = 1;\n }\n return res;\n }\n};\n```\n```java []\nclass Solution {\n public int longestSquareStreak(int[] nums) {\n Map<Integer, Integer> mp = new HashMap<>();\n Arrays.sort(nums);\n int res = -1;\n\n for (int num : nums) {\n int sqrt = (int) Math.sqrt(num);\n\n if (sqrt * sqrt == num && mp.containsKey(sqrt)) {\n mp.put(num, mp.get(sqrt) + 1);\n res = Math.max(res, mp.get(num));\n } else {\n mp.put(num, 1);\n }\n }\n return res;\n }\n}\n```\n```python []\nclass Solution:\n def longestSquareStreak(self, nums):\n mp = {}\n nums.sort()\n res = -1\n\n for num in nums:\n sqrt = isqrt(num)\n\n if sqrt * sqrt == num and sqrt in mp:\n mp[num] = mp[sqrt] + 1\n res = max(res, mp[num])\n else:\n mp[num] = 1\n\n return res\n```\n```javascript []\nfunction longestSquareStreak(nums) {\n const mp = new Map();\n nums.sort((a, b) => a - b);\n let res = -1;\n\n for (const num of nums) {\n const sqrt = Math.floor(Math.sqrt(num));\n\n if (sqrt * sqrt === num && mp.has(sqrt)) {\n mp.set(num, mp.get(sqrt) + 1);\n res = Math.max(res, mp.get(num));\n } else {\n mp.set(num, 1);\n }\n }\n\n return res;\n}\n```\n```golang []\nfunc longestSquareStreak(nums []int) int {\n mp := make(map[int]int)\n sort.Ints(nums)\n res := -1\n\n for _, num := range nums {\n sqrt := int(math.Sqrt(float64(num)))\n\n if sqrt*sqrt == num {\n if val, exists := mp[sqrt]; exists {\n mp[num] = val + 1\n if mp[num] > res {\n res = mp[num]\n }\n } else {\n mp[num] = 1\n }\n } else {\n mp[num] = 1\n }\n }\n\n return res\n}\n```\n```rust []\nimpl Solution {\n pub fn longest_square_streak(nums: Vec<i32>) -> i32 {\n let mut mp = HashMap::new();\n let mut nums = nums.clone();\n nums.sort();\n let mut res = -1;\n\n for &num in &nums {\n let sqrt = (num as f64).sqrt() as i32;\n\n if sqrt * sqrt == num {\n if let Some(&streak) = mp.get(&sqrt) {\n let new_streak = streak + 1;\n mp.insert(num, new_streak);\n res = res.max(new_streak);\n } else {\n mp.insert(num, 1);\n }\n } else {\n mp.insert(num, 1);\n }\n }\n\n res\n }\n}\n```\n\n\n
| 140 | 0 |
['Array', 'Hash Table', 'Dynamic Programming', 'Sorting', 'Python', 'C++', 'Java', 'Go', 'Python3', 'JavaScript']
| 14 |
longest-square-streak-in-an-array
|
Short DP (C++/Java) || LIS type
|
short-dp-cjava-lis-type-by-xxvvpp-8ipo
|
For every number we reach, we just check if its a perfect square:\n + If its a Perfect Square, we pair up with its Square Root.\n + Else, we keep it in dp a
|
xxvvpp
|
NORMAL
|
2022-12-11T04:27:59.408524+00:00
|
2022-12-11T06:54:43.199510+00:00
| 5,590 | false |
+ # For every number we reach, we just check if its a `perfect square`:\n + If its a `Perfect Square`, we pair up with its `Square Root`.\n + Else, we keep it in `dp` array with length as `1`, for pairing up its `square number` later.\n \n Similar Question : [1218. Longest Arithmetic Subsequence of Given Difference](https://leetcode.com/problems/longest-arithmetic-subsequence-of-given-difference/#:~:text=Input%3A%20arr%20%3D%20%5B1%2C,subsequence%20is%20any%20single%20element.)\n# C++ \n\tint longestSquareStreak(vector<int>& A) {\n unordered_map<int, int> dp;\n int res = 0;\n sort(begin(A), end(A));\n for(auto i : A){\n int root = sqrt(i);\n if(root * root == i)\n\t\t\t dp[i] = 1 + dp[root];\n\t\t\telse \n\t\t\t dp[i] = 1;\n res = max(res, dp[i]);\n }\n return res < 2 ? -1 : res;\n }\n# Java\n public int longestSquareStreak(int[] A) {\n HashMap<Integer, Integer> dp = new HashMap<>();\n int res = 0;\n Arrays.sort(A);\n for(var i : A){\n int root = (int)Math.sqrt(i);\n if(root * root == i) \n\t\t\t dp.put(i, dp.getOrDefault(root, 0) + 1);\n else \n\t\t\t dp.put(i, 1);\n res = Math.max(res, dp.get(i));\n }\n return res < 2 ? -1 : res;\n }\n> Time : O(nlogn)\n\n> Space - O(n)
| 62 | 3 |
['C', 'Java']
| 17 |
longest-square-streak-in-an-array
|
Bitset instead of unordered_set vs Counting sort||beats 100%
|
bitset-instead-of-unordered_set-vs-count-0zsq
|
Intuition\n Describe your first thoughts on how to solve this problem. \nLC gives a hint\n> With the constraints, the length of the longest square streak possib
|
anwendeng
|
NORMAL
|
2024-10-28T00:40:37.484536+00:00
|
2024-10-28T05:22:21.418272+00:00
| 4,557 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nLC gives a hint\n> With the constraints, the length of the longest square streak possible is 5.\n\nSince the constainst `2 <= nums[i] <= 10^5`, it\'s possible to use the bitset instead of unordered_set.\n\n2nd approach is similar to use counting sort which is also fast.\n\n3rd approach reconsider the upper bounds for max streak=5,4,3,2; that code optimizes the possiblity for the early stop. \n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Declare `long long N=100001` as a global variable\n2. Set `bitset<N> hasX=0`\n3. Set bit `hasX[x]=1` for x in nums\n4. Let `maxStreak=0`\n5. Proceed the loop\n```\nfor(long long x: nums){\n int streak=1;\n for(long long z=x*x; z<N; z*=z)// avoid of overflow\n if (hasX[z]) streak++;\n else break;\n maxStreak=max(maxStreak, streak);// update maxStreak\n if (maxStreak==5) break; //Early stop for 5 being the max\n}\n```\n6. if `maxStreak<2` return -1 otherwise return `maxStreak`\n7. The approach is using the argument in counting sort in which the used x in `nums` is unset avoiding of double computing. In 1st approach it\'s an unsorted array which can not be proceeded in such a way.\n# Why maxSreak<=5? Think how to furthermore optimize\nJust consider the small number 2. Just make squaring several times\n$$\n2, 2^2=4, 2^{2\\times 2}=2^4=16, 2^{4\\times 2}=2^8=256, 2^{8\\times 2}=2^{16}=65536\n$$\nThe square of $2^{16}=65536$ is $2^{32}$ which is $>10^5$\nThe upper bound for max streak beginning from 2 is 5\nIf $x=3$ then $3^8=6561$, the upper bound for max streak beginning from 3 is 4.\nIf $x=5$ then $3^8=390625$, the upper bound for max streak beginning from 5 is 3.\nIn fact, $\\sqrt[4]{100000}=17.782...$, when $x>=18$, the upper bound for max streak is just 2.\n\nA code using such facts is presented.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\nCounting sort: $O(n+N)$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(N)$$\n# revised Code||C++ 0ms beats 100% \nUsing the suggestion of @Sergei to find M=max(nums) during the 1st pass\n```cpp []\nconst long long N=100001;\nclass Solution {\npublic:\n int longestSquareStreak(vector<int>& nums) {\n bitset<N> hasX=0;\n int M=0;\n for(int x: nums){\n hasX[x]=1;\n M=max(M, x);\n }\n int maxStreak=0;\n for(long long x: nums){\n int streak=1;\n for(long long z=x*x; z<=M; z*=z)\n if (hasX[z]) streak++;\n else break;\n maxStreak=max(maxStreak, streak);\n if (maxStreak==5) break;\n }\n return maxStreak<2?-1:maxStreak;\n }\n};\n```\n# C++ using argument in Counting sort||0ms beats 100%\nThe outer loop tests up to sqrt(M) thanks to suggestion of @Sergei\n```\nconst long long N=100001;\nclass Solution {\npublic:\n int longestSquareStreak(vector<int>& nums) {\n bitset<N> hasX=0;\n int M=0;\n for(int x: nums){\n hasX[x]=1;\n M=max(M, x);\n }\n int maxStreak=0, Msqrt=sqrt(M);;\n for(long long x=2; x<=Msqrt; x++){\n if (hasX[x]==0) continue;\n int streak=1;\n for(long long z=x*x; z<=M; z*=z){\n if (hasX[z]) {\n streak++;\n hasX[z]=0;\n }\n else break;\n }\n maxStreak=max(maxStreak, streak);\n if (maxStreak==5) break;\n }\n return maxStreak<2?-1:maxStreak;\n }\n};\n\n\nauto init = []()\n{ \n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n```\n# 3rd C++ using upper bounds for max streak=5,4,3,2||0ms beats 100%\n```\nconst long long N=100001;\nconst int bound[]={2, 4, 17, 316};// bounds for early stop\nclass Solution {\npublic:\n int longestSquareStreak(vector<int>& nums) {\n bitset<N> hasX=0;\n int M=0;\n for(int x: nums){\n hasX[x]=1;\n M=max(M, x);\n }\n int lim=5, i=0;\n int maxStreak=0;\n for(long long x=2; x<=bound[3]; x++){\n if (hasX[x]==0) continue;\n if (x>bound[i]) {\n i++;\n lim--;\n }\n int streak=1;\n for(long long z=x*x; z<=M; z*=z){\n if (hasX[z]) {\n streak++;\n hasX[z]=0;\n }\n else break;\n }\n maxStreak=max(maxStreak, streak);\n if (maxStreak==lim) break;\n }\n return maxStreak<2?-1:maxStreak;\n }\n};\n\n\nauto init = []()\n{ \n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n```
| 33 | 0 |
['Array', 'Math', 'Bit Manipulation', 'Counting Sort', 'C++']
| 10 |
longest-square-streak-in-an-array
|
✅ [Python/C++] extract square root till death
|
pythonc-extract-square-root-till-death-b-k9qb
|
\u2705 IF YOU LIKE THIS SOLUTION, PLEASE UPVOTE.\n*\n\n*Python.\n\nclass Solution:\n def longestSquareStreak(self, nums: List[int]) -> int:\n \n
|
stanislav-iablokov
|
NORMAL
|
2022-12-11T04:02:18.143509+00:00
|
2022-12-11T04:40:32.780386+00:00
| 2,404 | false |
**\u2705 IF YOU LIKE THIS SOLUTION, PLEASE UPVOTE.**\n****\n\n**Python.**\n```\nclass Solution:\n def longestSquareStreak(self, nums: List[int]) -> int:\n \n sqr = Counter(sorted(set(nums)))\n \n for n in sqr:\n while (s:=isqrt(n))**2 == n and s in sqr:\n sqr[s] += 1\n n = s\n\n return c if (c:=max(sqr.values())) >= 2 else -1\n```\n\n**C++.**\n```\nclass Solution \n{\npublic:\n int longestSquareStreak(vector<int>& nums) \n {\n auto isqrt = [](int n) { return (int)floor(sqrt(n)); };\n \n sort(nums.begin(), nums.end());\n nums.erase(unique(nums.begin(), nums.end()), nums.end());\n \n int s, c = 0;\n unordered_map<int,int> sqr;\n \n for (int n : nums)\n {\n sqr[n] = 1;\n while ((s = isqrt(n)) && s*s == n && sqr.count(s))\n sqr[s] += 1, n = s;\n }\n \n for (auto[n,s] : sqr) c = max(c,s);\n return c > 1 ? c : -1;\n }\n};\n```
| 28 | 4 |
[]
| 10 |
longest-square-streak-in-an-array
|
✅C++ | ✅Hashmap & Sorting | ✅Easy Approach
|
c-hashmap-sorting-easy-approach-by-yash2-st75
|
Approach\nSort nums in decreasing order so that instead of finding square of elements, we can find square root of elements. Then, we store frequency of each ele
|
Yash2arma
|
NORMAL
|
2022-12-11T04:01:33.263558+00:00
|
2022-12-11T15:55:53.461876+00:00
| 3,236 | false |
# Approach\nSort nums in decreasing order so that instead of finding square of elements, we can find square root of elements. Then, we store frequency of each element in the hashmap. Then, we find perfect square root of each element (if exists) repeatedly until that element becomes a prime number.\n\n# Time Complexity\nO(N*log(N))\n\n# Space Complexity\nO(N) \n\n# Code\n```\nclass Solution \n{\npublic:\n int longestSquareStreak(vector<int>& nums) \n { \n sort(nums.begin(), nums.end(), greater<int>());\n \n unordered_map<int, int> mp;\n for(auto &it:nums)\n {\n mp[it]++;\n }\n \n int count;\n int maxi=1;\n \n for(int i=0; i<nums.size()-1; i++)\n {\n count=1;\n int x=nums[i];\n while(mp[sqrt(x)]>0)\n {\n int p=sqrt(x);\n //Since sqrt(x) can be a decimal number so we need to check perfect square condition\n if(p*p==x) count++;\n else break;\n mp[sqrt(x)]--;\n x = sqrt(x);\n }\n maxi = max(maxi, count);\n }\n return maxi==1?-1:maxi;\n }\n};\n```
| 22 | 1 |
['Hash Table', 'Sorting', 'C++']
| 5 |
longest-square-streak-in-an-array
|
C++ using set || DP not required || Very Simple and Easy to Understand
|
c-using-set-dp-not-required-very-simple-hdd1l
|
\n\nclass Solution {\npublic:\n int longestSquareStreak(vector<int>& nums) {\n int ans = 0;\n sort(nums.begin(), nums.end());\n unordere
|
kreakEmp
|
NORMAL
|
2022-12-11T04:02:26.283238+00:00
|
2022-12-11T04:14:03.759072+00:00
| 1,878 | false |
\n```\nclass Solution {\npublic:\n int longestSquareStreak(vector<int>& nums) {\n int ans = 0;\n sort(nums.begin(), nums.end());\n unordered_set<int> s;\n for(auto n: nums) s.insert(n);\n for(auto n: nums) {\n \n long long t = n;\n int c = 0;\n while(s.find(t) != s.end()){\n c++;\n s.erase(t);\n t = t*t;\n }\n ans = max(ans, c);\n }\n return ans<2?-1:ans;\n }\n};\n```
| 18 | 7 |
['C++']
| 14 |
longest-square-streak-in-an-array
|
Python 3 || 11 lines, mathematics, w/ brief comments || T/S: 92% / 81%
|
python-3-11-lines-mathematics-w-brief-co-shl1
|
Pretty much the same solution as others, except the set of potential squares has been pruned back to just those numbers n such that n%4 == 0 or n%4 == 1. \nPyt
|
Spaulding_
|
NORMAL
|
2022-12-12T23:43:43.654472+00:00
|
2024-10-28T07:32:03.975928+00:00
| 879 | false |
Pretty much the same solution as others, except the set of potential squares has been pruned back to just those numbers `n` such that `n%4 == 0` or `n%4 == 1`. \n```Python3 []\nclass Solution:\n def longestSquareStreak(self, nums: List[int]) -> int:\n\n nums = sorted(set(nums))\n cands = {n for n in nums if n%4 < 2}\n ans = 0\n\n for n in nums:\n square = n*n\n tally = 1\n\n while square in cands:\n cands.remove(square)\n tally+= 1\n square*= square\n\n ans = max(ans, tally)\n \n return ans if ans > 1 else -1\n```\n```C++ []\nclass Solution {\npublic:\n int longestSquareStreak(vector<int>& nums) {\n\n sort(nums.begin(), nums.end());\n nums.erase(unique(nums.begin(), nums.end()), nums.end());\n \n unordered_set<long long> cands;\n for (int n : nums) {\n if (n % 4 < 2) cands.insert(n); }\n\n int ans = 0;\n for (int n : nums) {\n long long square = (long long)n * n;\n int tally = 1;\n\n while (cands.find(square) != cands.end()) {\n cands.erase(square);\n tally++;\n square *= square;}\n\n ans = max(ans, tally);}\n\n return ans > 1 ? ans : -1;}\n};\n```\n[https://leetcode.com/problems/longest-square-streak-in-an-array/submissions/1290480480/](https://leetcode.com/problems/longest-square-streak-in-an-array/submissions/1290480480/)\n\nI could be wrong, but I think that time complexity is *O*(*N* log *N*) and space complexity is *O*(*N*), in which *N* ~ number of distinct integers in \'nums\'.\n
| 16 | 0 |
['C++', 'Python3']
| 2 |
longest-square-streak-in-an-array
|
🌟 Beats 100.00% 👏 || Explained with example
|
beats-10000-explained-with-example-by-sr-ymz7
|
Intuition\n Describe your first thoughts on how to solve this problem. \nThe goal of the function is to find the longest "square streak" in an array of integers
|
srinivas_bodduru
|
NORMAL
|
2024-10-28T06:36:24.202437+00:00
|
2024-10-28T06:36:24.202469+00:00
| 5,738 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe goal of the function is to find the longest "square streak" in an array of integers. A square streak begins with a number and follows the sequence of its squares until the square value no longer exists in the array. We are looking for the longest sequence among such square streaks. If the longest streak is 1 or fewer, we return -1 (as no square streak of length greater than 1 exists).\n\n# Approach\nConvert the array into a set to efficiently check the presence of elements.\nSort the unique elements to process them in increasing order.\nFor each unique number in the sorted array:\nStart counting a square streak by checking the square of the current number.\nKeep counting as long as each subsequent square exists in the set.\nTrack the maximum length of square streaks found.\nReturn the maximum length if it\u2019s greater than 1; otherwise, return -1.\n\n# Example\n\n\n# Complexity\n- Time complexity:O(NLOGN)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```javascript []\nvar longestSquareStreak = function(nums) {\n let max=-1\n let set = new Set(nums)\n let setarr = Array.from(set.values())\n setarr.sort((a,b)=>a-b)\n for(let i=0;i<setarr.length;i++){\n let curr = setarr[i]\n let count=0\n while(set.has(curr)){\n set.delete(curr)\n curr=curr**2\n count++\n }\n max = Math.max(max,count)\n \n }\n return max>1?max:-1\n};\n```\n```python []\nclass Solution(object):\n \n \n def longestSquareStreak(self , nums):\n max_len = -1\n num_set = set(nums)\n sorted_nums = sorted(num_set)\n \n for num in sorted_nums:\n count = 0\n curr = num\n while curr in num_set:\n num_set.remove(curr)\n curr = curr ** 2\n count += 1\n \n max_len = max(max_len, count)\n \n return max_len if max_len > 1 else -1\n \n```\n```java []\nimport java.util.*;\n\npublic class Solution {\n public int longestSquareStreak(int[] nums) {\n int max = -1;\n Set<Integer> set = new HashSet<>();\n for (int num : nums) {\n set.add(num);\n }\n List<Integer> setArr = new ArrayList<>(set);\n Collections.sort(setArr);\n \n for (int i = 0; i < setArr.size(); i++) {\n int curr = setArr.get(i);\n int count = 0;\n \n while (set.contains(curr)) {\n set.remove(curr);\n curr = curr * curr;\n count++;\n }\n \n max = Math.max(max, count);\n }\n \n return max > 1 ? max : -1;\n }\n}\n\n```\n```c []\n#include <stdio.h>\n#include <stdlib.h>\n#include <stdbool.h>\n\nint compare(const void *a, const void *b) {\n return (*(int *)a - *(int *)b);\n}\n\nbool set_contains(int *set, int setSize, int value) {\n for (int i = 0; i < setSize; i++) {\n if (set[i] == value) return true;\n }\n return false;\n}\n\nint longestSquareStreak(int *nums, int numsSize) {\n int max = -1;\n int set[numsSize];\n int setSize = 0;\n\n // Remove duplicates and add to set\n for (int i = 0; i < numsSize; i++) {\n bool exists = false;\n for (int j = 0; j < setSize; j++) {\n if (set[j] == nums[i]) {\n exists = true;\n break;\n }\n }\n if (!exists) set[setSize++] = nums[i];\n }\n\n qsort(set, setSize, sizeof(int), compare);\n\n for (int i = 0; i < setSize; i++) {\n int curr = set[i];\n int count = 0;\n \n while (set_contains(set, setSize, curr)) {\n for (int j = 0; j < setSize; j++) {\n if (set[j] == curr) {\n set[j] = -1; // Mark as removed\n break;\n }\n }\n curr = curr * curr;\n count++;\n }\n \n if (count > max) max = count;\n }\n \n return max > 1 ? max : -1;\n}\n\n```\n```c++ []\n#include <iostream>\n#include <vector>\n#include <unordered_set>\n#include <algorithm>\n\nclass Solution {\npublic:\n int longestSquareStreak(std::vector<int>& nums) {\n int max = -1;\n std::unordered_set<int> numSet(nums.begin(), nums.end());\n std::vector<int> sortedNums(numSet.begin(), numSet.end());\n \n std::sort(sortedNums.begin(), sortedNums.end());\n \n for (int num : sortedNums) {\n int curr = num;\n int count = 0;\n \n while (numSet.count(curr)) {\n numSet.erase(curr);\n curr *= curr;\n count++;\n }\n \n max = std::max(max, count);\n }\n \n return max > 1 ? max : -1;\n }\n};\n\n```
| 14 | 0 |
['Hash Table', 'Binary Search', 'Dynamic Programming', 'C', 'Sorting', 'Python', 'C++', 'Java', 'Python3', 'JavaScript']
| 5 |
longest-square-streak-in-an-array
|
C++ || Using Map
|
c-using-map-by-mayanksamadhiya12345-ueg2
|
\n\n# Code\n\nclass Solution {\npublic:\n int longestSquareStreak(vector<int>& nums) \n {\n map<long long,long long> mp;\n int n = nums.size
|
mayanksamadhiya12345
|
NORMAL
|
2022-12-11T04:04:26.515544+00:00
|
2022-12-11T04:19:37.238214+00:00
| 1,092 | false |
\n\n# Code\n```\nclass Solution {\npublic:\n int longestSquareStreak(vector<int>& nums) \n {\n map<long long,long long> mp;\n int n = nums.size();\n \n for(auto it : nums)\n {\n mp[it]++;\n }\n \n int mx = -1;\n bool flag = false;\n for(auto it : mp)\n {\n long long curr = it.first*it.first;\n int cnt = 1;\n while(mp.count(curr)==1)\n {\n cout<<curr<<" ";\n flag = true;\n cnt++;\n curr = curr*curr;\n }\n \n mx = max(cnt,mx);\n }\n \n if(!flag) return -1;\n \n return mx;\n }\n};\n```
| 14 | 1 |
['C++']
| 1 |
longest-square-streak-in-an-array
|
hashmap and sorting || java
|
hashmap-and-sorting-java-by-flyroko123-8w0p
|
Intuition \nusing hashmap to store array elements and sorting it\n Describe your first thoughts on how to solve this problem. \n\n\n# Complexity\n- Time complex
|
flyRoko123
|
NORMAL
|
2022-12-11T04:03:39.502572+00:00
|
2022-12-11T05:29:25.230242+00:00
| 1,463 | false |
# Intuition \nusing hashmap to store array elements and sorting it\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n\n# Complexity\n- Time complexity:o(NlogN)\n<!-- O(N) -->\n\n- Space complexity:O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int longestSquareStreak(int[] nums) {\n Arrays.sort(nums);\n Map<Integer,Integer> m=new HashMap<>();\n int res=-1;\n for(int x:nums){\n int perfect=(int)Math.sqrt(x);\n //check perfect int or not as there may be int which will not form perfect square\n \n if(perfect*perfect==x && m.containsKey(perfect)){\n m.put(x,m.get(perfect)+1);\n res=Math.max((m.get(perfect)+1),res); \n }\n else{\n m.put(x,1);\n }\n } \n return res;\n }\n}\n```
| 13 | 0 |
['Java']
| 2 |
longest-square-streak-in-an-array
|
✅ Explained step by step | Beats 100% | ✅ Working 28.10.2024
|
explained-step-by-step-beats-100-working-0wo3
|
\npython3 []\nclass Solution:\n def longestSquareStreak(self, nums: List[int]) ->int:\n # Convert nums to a sorted set to remove duplicates and have o
|
Piotr_Maminski
|
NORMAL
|
2024-10-28T00:39:26.983213+00:00
|
2024-10-28T00:57:17.515409+00:00
| 3,539 | false |
\n```python3 []\nclass Solution:\n def longestSquareStreak(self, nums: List[int]) ->int:\n # Convert nums to a sorted set to remove duplicates and have ordered numbers\n nums = sorted(set(nums))\n \n # Create a set for O(1) lookup time\n num_set = set(nums)\n \n # Track the maximum streak length found\n max_length = 0\n \n # Iterate through each number in sorted order\n for num in nums:\n # Initialize streak length for current number\n length = 0\n # Start with current number\n current = num\n \n # Keep squaring the number while it exists in our set\n while current in num_set:\n length += 1\n current = current ** 2\n \n # Only update max_length if we found a streak of length > 1\n if length > 1:\n max_length = max(max_length, length)\n \n # Return max_length if we found a valid streak, otherwise return -1\n return max_length if max_length > 1 else -1\n```\n```cpp []\nclass Solution {\npublic:\n int longestSquareStreak(vector<int>& nums) {\n // Convert nums to a sorted set to remove duplicates and have ordered numbers\n set<long long> num_set;\n for (int num : nums) {\n num_set.insert(num);\n }\n \n // Track the maximum streak length found\n int max_length = 0;\n \n // Iterate through each number in sorted order\n for (long long num : num_set) {\n // Initialize streak length for current number\n int length = 0;\n // Start with current number\n long long current = num;\n \n // Keep squaring the number while it exists in our set\n while (num_set.find(current) != num_set.end()) {\n length++;\n if (current > 100000) break; // Prevent overflow\n current = current * current;\n }\n \n // Only update max_length if we found a streak of length > 1\n if (length > 1) {\n max_length = max(max_length, length);\n }\n }\n \n // Return max_length if we found a valid streak, otherwise return -1\n return max_length > 1 ? max_length : -1;\n }\n};\n```\n```java []\nimport java.util.*;\n\nclass Solution {\n public int longestSquareStreak(int[] nums) {\n // Convert array to TreeSet to remove duplicates and have ordered numbers\n TreeSet<Integer> sortedSet = new TreeSet<>();\n for (int num : nums) {\n sortedSet.add(num);\n }\n \n // Create HashSet for O(1) lookup time\n HashSet<Integer> numSet = new HashSet<>(sortedSet);\n \n // Track the maximum streak length found\n int maxLength = 0;\n \n // Iterate through each number in sorted order\n for (int num : sortedSet) {\n // Initialize streak length for current number\n int length = 0;\n // Start with current number\n long current = num;\n \n // Keep squaring the number while it exists in our set\n while (current <= Integer.MAX_VALUE && numSet.contains((int)current)) {\n length++;\n current = current * current;\n }\n \n // Only update maxLength if we found a streak of length > 1\n if (length > 1) {\n maxLength = Math.max(maxLength, length);\n }\n }\n \n // Return maxLength if we found a valid streak, otherwise return -1\n return maxLength > 1 ? maxLength : -1;\n }\n}\n```\n```csharp []\npublic class Solution {\n public int LongestSquareStreak(int[] nums) {\n // Convert nums to a sorted set to remove duplicates and have ordered numbers\n var numSet = new HashSet<int>(nums);\n var sortedNums = numSet.OrderBy(x => x).ToList();\n \n // Track the maximum streak length found\n int maxLength = 0;\n \n // Iterate through each number in sorted order\n foreach (int num in sortedNums) {\n // Initialize streak length for current number\n int length = 0;\n // Start with current number\n long current = num;\n \n // Keep squaring the number while it exists in our set\n while (current <= int.MaxValue && numSet.Contains((int)current)) {\n length++;\n current = current * current;\n }\n \n // Only update maxLength if we found a streak of length > 1\n if (length > 1) {\n maxLength = Math.Max(maxLength, length);\n }\n }\n \n // Return maxLength if we found a valid streak, otherwise return -1\n return maxLength > 1 ? maxLength : -1;\n }\n}\n```\n```golang []\nfunc longestSquareStreak(nums []int) int {\n // Create a map for O(1) lookup time\n numSet := make(map[int]bool)\n \n // Remove duplicates and add to map\n for _, num := range nums {\n numSet[num] = true\n }\n \n // Track the maximum streak length found\n maxLength := 0\n \n // Iterate through each number\n for num := range numSet {\n length := 0\n current := num\n \n // Keep squaring the number while it exists in our map\n for numSet[current] {\n length++\n // Check if squaring would overflow int\n if current > 46340 { // sqrt(MaxInt32) \u2248 46340\n break\n }\n current *= current\n }\n \n // Only update maxLength if we found a streak of length > 1\n if length > 1 {\n maxLength = max(maxLength, length)\n }\n }\n \n // Return maxLength if we found a valid streak, otherwise return -1\n if maxLength > 1 {\n return maxLength\n }\n return -1\n}\n\n// Helper function for max\nfunc max(a, b int) int {\n if a > b {\n return a\n }\n return b\n}\n```\n```swift []\nclass Solution {\n func longestSquareStreak(_ nums: [Int]) -> Int {\n // Convert nums to a sorted set to remove duplicates and have ordered numbers\n let sortedNums = Array(Set(nums)).sorted()\n \n // Create a set for O(1) lookup time\n let numSet = Set(nums)\n \n // Track the maximum streak length found\n var maxLength = 0\n \n // Iterate through each number in sorted order\n for num in sortedNums {\n // Initialize streak length for current number\n var length = 0\n // Start with current number\n var current = num\n \n // Keep squaring the number while it exists in our set\n while numSet.contains(current) {\n length += 1\n // Need to handle potential integer overflow\n let nextSquare = current * current\n if nextSquare > Int.max {\n break\n }\n current = nextSquare\n }\n \n // Only update maxLength if we found a streak of length > 1\n if length > 1 {\n maxLength = max(maxLength, length)\n }\n }\n \n // Return maxLength if we found a valid streak, otherwise return -1\n return maxLength > 1 ? maxLength : -1\n }\n}\n```\n```javascript [JS]\n// JavaScript\n\n\n/**\n * @param {number[]} nums\n * @return {number}\n */\nvar longestSquareStreak = function(nums) {\n // Convert nums to a sorted set to remove duplicates and have ordered numbers\n const numSet = new Set(nums);\n \n // Track the maximum streak length found\n let maxLength = 0;\n \n // Iterate through each number in the set\n for (let num of numSet) {\n // Initialize streak length for current number\n let length = 0;\n // Start with current number\n let current = num;\n \n // Keep squaring the number while it exists in our set\n while (numSet.has(current)) {\n length++;\n if (current > 100000) break; // Prevent overflow\n current = current * current;\n }\n \n // Only update maxLength if we found a streak of length > 1\n if (length > 1) {\n maxLength = Math.max(maxLength, length);\n }\n }\n \n // Return maxLength if we found a valid streak, otherwise return -1\n return maxLength > 1 ? maxLength : -1;\n};\n```\n```typescript [TS]\n// TypeScript\n\n\n\nfunction longestSquareStreak(nums: number[]): number {\n // Convert nums to a sorted set to remove duplicates and have ordered numbers\n const numSet = new Set(nums);\n const sortedNums = Array.from(numSet).sort((a, b) => a - b);\n \n // Track the maximum streak length found\n let maxLength = 0;\n \n // Iterate through each number in sorted order\n for (const num of sortedNums) {\n // Initialize streak length for current number\n let length = 0;\n // Start with current number\n let current = num;\n \n // Keep squaring the number while it exists in our set\n while (numSet.has(current)) {\n length++;\n current = current ** 2;\n \n // Add safety check for numbers getting too large\n if (current > 100000) break;\n }\n \n // Only update maxLength if we found a streak of length > 1\n if (length > 1) {\n maxLength = Math.max(maxLength, length);\n }\n }\n \n // Return maxLength if we found a valid streak, otherwise return -1\n return maxLength > 1 ? maxLength : -1;\n}\n```\n```rust []\nuse std::collections::HashSet;\n\nimpl Solution {\n pub fn longest_square_streak(nums: Vec<i32>) -> i32 {\n // Convert to HashSet and sort\n let mut unique_nums: Vec<i64> = nums.into_iter()\n .map(|x| x as i64)\n .collect::<HashSet<_>>()\n .into_iter()\n .collect();\n unique_nums.sort_unstable();\n \n // Create HashSet for O(1) lookup\n let num_set: HashSet<i64> = unique_nums.iter().cloned().collect();\n \n // Track maximum streak length\n let mut max_length = 0;\n \n // Check each number\n for &num in &unique_nums {\n let mut length = 0;\n let mut current = num;\n \n // Keep squaring while number exists in set\n while num_set.contains(¤t) {\n length += 1;\n // Check if squaring would overflow\n if current > (1i64 << 31) {\n break;\n }\n current *= current;\n }\n \n // Update max_length if streak length > 1\n if length > 1 {\n max_length = max_length.max(length);\n }\n }\n \n if max_length > 1 {\n max_length\n } else {\n -1\n }\n }\n}\n```\n```ruby []\n# @param {Integer[]} nums\n# @return {Integer}\ndef longest_square_streak(nums)\n # Convert nums to a sorted set to remove duplicates and have ordered numbers\n nums = nums.uniq.sort\n \n # Create a set for O(1) lookup time\n num_set = nums.to_set\n \n # Track the maximum streak length found\n max_length = 0\n \n # Iterate through each number in sorted order\n nums.each do |num|\n # Initialize streak length for current number\n length = 0\n # Start with current number\n current = num\n \n # Keep squaring the number while it exists in our set\n while num_set.include?(current)\n length += 1\n current = current ** 2\n end\n \n # Only update max_length if we found a streak of length > 1\n if length > 1\n max_length = [max_length, length].max\n end\n end\n \n # Return max_length if we found a valid streak, otherwise return -1\n max_length > 1 ? max_length : -1\nend\n```\n\n\n### Complexity \n- Time complexity: O(n * log m)\n\n- Space complexity: O(n)\n\n\n\n\n\n## Explained step by step\n\n---\n\n1. Input Processing:\n```\nnums = sorted(set(nums))\nnum_set = set(nums)\n```\n\n- Converts input array to a sorted set to remove duplicates\n- Creates a separate set for O(1) lookups\n2. Initialization:\n```\nmax_length = 0\n```\n\n- Sets up a variable to track the longest valid streak found\n3. Main Logic:\n```\nfor num in nums:\n length = 0\n current = num\n while current in num_set:\n length += 1\n current = current ** 2\n```\n\n\n- Iterates through each number\n- For each number, keeps squaring it while the result exists in the set\n- Counts the length of the streak\n4. Streak Validation:\n```\nif length > 1:\n max_length = max(max_length, length)\n```\n- Only considers streaks with length > 1\n- Updates max_length if current streak is longer\n5. Final Result:\n```\nreturn max_length if max_length > 1 else -1\n```\n\n- Returns the longest streak if found (> 1)\n- Returns -1 if no valid streak exists\n\n---\n\n\n\n\n
| 12 | 1 |
['Swift', 'C++', 'Java', 'Go', 'TypeScript', 'Python3', 'Rust', 'Ruby', 'JavaScript', 'C#']
| 6 |
longest-square-streak-in-an-array
|
Python | Two-Pointer, Sliding Window & Set Lookup
|
python-two-pointer-sliding-window-set-lo-bknp
|
see the Successfully Accepted Submission\n\n# Code\npython3 []\nclass Solution:\n def longestSquareStreak(self, nums: List[int]) -> int:\n # Sort and
|
Khosiyat
|
NORMAL
|
2024-10-28T02:14:10.890999+00:00
|
2024-10-28T02:14:10.891029+00:00
| 1,486 | false |
[see the Successfully Accepted Submission](https://leetcode.com/problems/longest-square-streak-in-an-array/submissions/1435743887/?envType=daily-question&envId=2024-10-28)\n\n# Code\n```python3 []\nclass Solution:\n def longestSquareStreak(self, nums: List[int]) -> int:\n # Sort and convert list to a set for quick lookup\n nums.sort()\n num_set = set(nums)\n \n longest_streak = 0\n \n # Check for square streak starting with each number\n for num in nums:\n streak_length = 0\n current = num\n \n # Continue as long as we find the square in the set\n while current in num_set:\n streak_length += 1\n current = current * current # Square the current number\n \n # Update longest streak if this one is the longest so far\n if streak_length >= 2:\n longest_streak = max(longest_streak, streak_length)\n \n # If no streak of at least 2 was found, return -1\n return longest_streak if longest_streak >= 2 else -1\n\n```\n\n## Approach\n\n1. **Sort the Array**: \n - Sorting `nums` will make it easier to find sequences where each element is the square of the previous one.\n\n2. **Hash Set for Fast Lookup**: \n - Use a set to store elements from `nums` for constant-time lookup. This helps us quickly check if a number and its squares exist in `nums`.\n\n3. **Iterate and Check for Streaks**:\n - For each number in `nums`, attempt to build a "square streak" starting from that number.\n - Continuously check if the square of the current number exists in `nums`. If it does, add it to the streak, and update the current number to its square.\n - Keep track of the longest streak found during this process.\n\n4. **Return the Result**:\n - If the longest streak found is at least 2, return its length.\n - If no valid streak of at least 2 is found, return `-1`.\n\n## Explanation of the Code\n\n1. **Sorting and Set Initialization**:\n - `nums.sort()` and `num_set = set(nums)` allow us to search for square relationships more effectively.\n\n2. **Main Loop**:\n - For each `num` in `nums`, we initialize a potential streak and use a `while` loop to keep squaring `current` as long as `current` exists in `num_set`.\n\n3. **Updating the Longest Streak**:\n - If the length of the current streak (`streak_length`) is at least 2, we update `longest_streak` with the maximum length found so far.\n\n4. **Return Result**:\n - We return the longest streak if it\u2019s at least 2; otherwise, we return `-1`.\n\n## Complexity Analysis\n\n- **Time Complexity**: \\(O(n \\log n)\\) due to sorting, where \\(n\\) is the length of `nums`. The subsequent operations are \\(O(n)\\).\n- **Space Complexity**: \\(O(n)\\) for storing `nums` in a set.\n\n\n
| 11 | 0 |
['Python3']
| 5 |
longest-square-streak-in-an-array
|
Set with Optimizations
|
set-with-optimizations-by-votrubac-llh8
|
Many ways to solve this problem.\n\n## Set\nHere, we insert small values (< 317), and values with an integer square root, into a sorted set.\n\nThen, for each s
|
votrubac
|
NORMAL
|
2022-12-11T05:34:38.704890+00:00
|
2022-12-11T05:44:07.324630+00:00
| 919 | false |
Many ways to solve this problem.\n\n## Set\nHere, we insert small values (< 317), and values with an integer square root, into a sorted set.\n\nThen, for each small value, we check it\'s square root sequence.\n\n**C++**\n```cpp\nint longestSquareStreak(vector<int>& n) {\n int res = 0;\n set<int> s;\n for(int val : n)\n if (int sr = sqrt(val); val < 317 || sr * sr == val)\n s.insert(val);\n for (auto it = begin(s); it != end(s) && *it < 317; ++it) {\n int sz = s.size();\n for (int i = *it; i < 317 && s.count(i * i); i *= i)\n s.erase(i * i);\n res = max(res, sz - (int)s.size());\n }\n return res == 0 ? -1 : res + 1;\n}\n```
| 10 | 0 |
['C']
| 5 |
longest-square-streak-in-an-array
|
Python | 3 Solutions | DP | Union Find | While loop | Beats 100% 🚀
|
python-3-solutions-dp-union-find-while-l-yd4m
|
Intuition\n Describe your first thoughts on how to solve this problem. \nI have 3 solutions: \n\n1. Dynamic programming\n2. While loop and seen set\n3. Union Fi
|
shivamtld
|
NORMAL
|
2024-10-28T01:55:40.789996+00:00
|
2024-10-28T15:41:53.876839+00:00
| 1,039 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nI have 3 solutions: \n\n1. Dynamic programming\n2. While loop and seen set\n3. Union Find solution\n\n\n# Complexity\n- Time complexity:$$O(n)/ O(nlogm)$$\nwhere m=unique numbers\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Dynamic Programming Solution Beats 100% \uD83D\uDE80\n```python3 []\n\nclass Solution:\n def longestSquareStreak(self, nums: List[int]) -> int:\n nums = sorted(set(nums))\n dp={i:1 for i in nums}\n longest=1\n for i in nums:\n sq= i**2\n if sq in dp:\n dp[sq]= dp[i]+1\n if dp[sq]==5: return dp[sq]\n if dp[sq]>longest:\n longest=dp[sq]\n return longest if longest!=1 else -1\n \n```\n\n\n# Intuitive while loop solution, Calculates square and sqrt without sorting Beats 100% \uD83D\uDE80\n```python3 []\nclass Solution:\n def longestSquareStreak(self, nums: List[int]) -> int:\n nums = set(nums)\n maxcount=1\n while(nums):\n i= nums.pop()\n count=1\n sq= i**2\n sqroot = math.sqrt(i)\n while(sq in nums):\n count+=1\n nums.remove(sq)\n sq=sq**2\n while (sqroot in nums):\n count+=1\n nums.remove(sqroot)\n sqroot = math.sqrt(sqroot)\n if count==5: return count\n elif count>maxcount:\n maxcount= count \n return maxcount if maxcount>1 else -1 \n```\n\n\n\n# Union Find solution Beats 100% \uD83D\uDE80\n```python3 []\nclass UnionFind():\n def __init__(self):\n self.rank={}\n self.parent = {}\n self.maxrank = 0\n \n def add(self, node):\n self.parent[node] = node\n self.rank[node]=1\n \n def find(self, n1):\n if self.parent[n1]!=n1:\n self.parent[n1] = self.find(self.parent[n1])\n return self.parent[n1]\n \n def union (self, n1, n2):\n p1, p2= self.find(n1), self.find(n2)\n if p1==p2:\n return \n if self.rank[p1]>self.rank[p2]:\n self.parent[p2]=p1\n self.rank[p1]+=self.rank[p2]\n if self.rank[p1]> self.maxrank:\n self.maxrank = self.rank[p1]\n else:\n self.parent[p1]=p2\n self.rank[p2]+=self.rank[p1]\n if self.rank[p2]> self.maxrank:\n self.maxrank = self.rank[p2] \n if self.maxrank ==5:\n return 5\nclass Solution:\n def longestSquareStreak(self, nums: List[int]) -> int:\n nums= set(nums)\n uf = UnionFind()\n for i in nums:\n sq=i**2\n if sq in nums:\n if i not in uf.parent:\n uf.add(i)\n if sq not in uf.parent:\n uf.add(sq)\n if uf.union(i, sq):\n return 5\n return uf.maxrank if uf.maxrank!=0 else -1\n```\n\n\n
| 8 | 0 |
['Hash Table', 'Dynamic Programming', 'Union Find', 'Ordered Set', 'Python3']
| 7 |
longest-square-streak-in-an-array
|
C++ || DP || Binary Search
|
c-dp-binary-search-by-mohakharjani-0c2c
|
\nclass Solution {\npublic:\n int longestSquareStreak(vector<int>& nums) \n {\n sort(nums.begin(), nums.end());\n int n = nums.size();\n
|
mohakharjani
|
NORMAL
|
2022-12-11T04:10:24.577514+00:00
|
2022-12-11T04:10:24.577538+00:00
| 1,018 | false |
```\nclass Solution {\npublic:\n int longestSquareStreak(vector<int>& nums) \n {\n sort(nums.begin(), nums.end());\n int n = nums.size();\n vector<int>dp(n, 0);\n dp[n - 1] = 1;\n int mxLen = 1;\n for (int i = n - 2; i >= 0; i--)\n {\n long long target = (long long)nums[i] * nums[i];\n //======================================================\n int low = i + 1, high = n - 1;\n int pos = -1;\n while(low <= high)\n {\n int mid = low + (high - low) / 2;\n if (nums[mid] == target) { pos = mid; break; }\n else if (nums[mid] < target) low = mid + 1;\n else if (nums[mid] > target) high = mid - 1;\n }\n //=========================================================\n int currLen;\n if (pos == -1) currLen = 1;\n else currLen = 1 + dp[pos];\n dp[i] = currLen;\n mxLen = max(dp[i], mxLen);\n }\n if (mxLen == 1) return -1;\n return mxLen;\n \n }\n};\n\n```
| 8 | 0 |
['C', 'C++']
| 3 |
longest-square-streak-in-an-array
|
Java + HashMap || O(n*logn)
|
java-hashmap-onlogn-by-himanshubhoir-0c2y
|
\n# Complexity\n- Time complexity:\nO(n*logn)\n\n# Code\n\nclass Solution {\n public int longestSquareStreak(int[] nums) {\n Arrays.sort(nums);\n
|
HimanshuBhoir
|
NORMAL
|
2022-12-11T04:05:09.556362+00:00
|
2022-12-11T04:28:32.232080+00:00
| 1,027 | false |
\n# Complexity\n- Time complexity:\nO(n*logn)\n\n# Code\n```\nclass Solution {\n public int longestSquareStreak(int[] nums) {\n Arrays.sort(nums);\n HashMap<Integer, Integer> map = new HashMap<>();\n for(int i=nums.length-1; i>=0; i--) \n map.put(nums[i], map.getOrDefault(nums[i]*nums[i], 0) +1);\n int max = 0;\n for(int val : map.values())\n max = Math.max(max, val);\n return max == 1 ? -1 : max;\n }\n}\n```
| 8 | 0 |
['Java']
| 3 |
longest-square-streak-in-an-array
|
DFS Approach✅✅
|
dfs-approach-by-arunk_leetcode-w49u
|
Approach\n Describe your approach to solving the problem. \n1. First i made a graph using the conditions of square\n2. Did a simple dfs on the graph and found t
|
arunk_leetcode
|
NORMAL
|
2024-10-28T07:51:06.977241+00:00
|
2024-10-28T07:51:06.977272+00:00
| 507 | false |
# Approach\n<!-- Describe your approach to solving the problem. -->\n1. First i made a graph using the conditions of square\n2. Did a simple `dfs` on the graph and found the max length of the component in the graph\n3. For better understanding see the code->> \n\n# Complexity\n- Time complexity: `O(NLog(N))`\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: `O(n)`\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n bool isSquare(int n){\n int x = sqrt(n);\n return n == x*x;\n }\n void dfs(int node, map<int, int>& vis, map<int, int>& mp, int& cnt){\n vis[node] = 1;\n if(vis.find(mp[node]) == vis.end() && mp[node]!=0){\n cnt++;\n // cout<<mp[node]<<" ";\n dfs(mp[node], vis, mp, cnt);\n }\n }\n int longestSquareStreak(vector<int>& nums) {\n map<int, int> mp, mpp;\n for(auto it: nums) mpp[it]++;\n //build the graph->\n for(int i=0; i<nums.size(); i++){\n int n = sqrt(nums[i]);\n if(isSquare(nums[i]) && mpp.find(n)!=mpp.end()){\n mp[n] = nums[i];\n }\n }\n if(mp.size() == 0) return -1;\n int maxi=0;\n //do dfs on the graph\n map<int, int> vis;\n for(auto it: mp){\n int node = it.first;\n if(vis.find(node) == vis.end()){\n int cnt=1;\n // cout<<node<<endl;\n dfs(node, vis, mp, cnt);\n // cout<<endl;\n maxi = max(maxi, cnt);\n }\n }\n return maxi;\n }\n};\n```
| 7 | 0 |
['Depth-First Search', 'C++']
| 2 |
longest-square-streak-in-an-array
|
python/java sort + hashmap
|
pythonjava-sort-hashmap-by-akaghosting-0vyc
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
akaghosting
|
NORMAL
|
2022-12-11T04:01:49.024505+00:00
|
2022-12-11T04:01:49.024545+00:00
| 741 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def longestSquareStreak(self, nums: List[int]) -> int:\n square = {}\n nums.sort(reverse = True)\n res = -1\n for num in nums:\n if num * num in square:\n square[num] = square[num * num] + 1\n res = max(res, square[num])\n else:\n square[num] = 1\n return res\n\n\nclass Solution {\n public int longestSquareStreak(int[] nums) {\n Map<Integer, Integer> square = new HashMap<>();\n Arrays.sort(nums);\n int res = -1;\n for (int i = nums.length - 1; i > -1; i --) {\n int num = nums[i];\n if (square.containsKey(num * num)) {\n square.put(num, square.get(num * num) + 1);\n res = Math.max(res, square.get(num));\n } else {\n square.put(num, 1);\n }\n }\n return res;\n }\n}\n```
| 7 | 0 |
['Java', 'Python3']
| 2 |
longest-square-streak-in-an-array
|
🔥C++ || Brute->Better->Best->Optimal || 5 Approaches || Easy Beginner Friendly || Beats 100%✅
|
c-brute-better-best-optimal-5-approaches-kmpr
|
Approach-1 ---> Brute Force\n# Intuition\nThe problem involves finding the longest streak of squares within an array. We aim to start from each element and chec
|
aaradhyabansal
|
NORMAL
|
2024-10-28T09:12:31.390560+00:00
|
2024-10-28T11:24:47.245290+00:00
| 259 | false |
# Approach-1 ---> Brute Force\n# Intuition\nThe problem involves finding the longest streak of squares within an array. We aim to start from each element and check if the square of the current element exists in the array, extending the streak as long as each successive square can be found.\n\n# Approach\n##### Frequency Map Setup:\n Use an unordered map to store the occurrences of each element in the array. This helps to quickly check if a number\u2019s square exists in the array.\n#### Square Streak Calculation:\nFor each element in the array, set up a counter temp to track the current streak length and initialize num as the current element.\nUse a loop to calculate the square of num. If the square exists in the map, increment the streak counter, update num to this square, and continue. Otherwise, stop the streak.\n##### Track Maximum Streak: \nFor each element\'s square streak, keep track of the maximum streak encountered. If the longest streak found is 1, return -1; otherwise, return the longest streak.\n# Complexity\n##### Time Complexity: \nO(n log m), where n is the size of nums and m is the maximum element in nums. For each number, we calculate squares until the result exceeds the largest number in nums.\n##### Space Complexity:\n O(n), due to the space taken by the map to store each element\'s occurrence.\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int longestSquareStreak(vector<int>& nums) {\n unordered_map<long long,int>mp;\n int cnt=0;\n for(auto& it:nums)\n mp[it]++;\n\n for(auto& it:nums)\n {\n int temp=1,num=it;\n while(1)\n {\n long long mul=1LL*num*num;\n if(mp.find(mul)==mp.end())\n break;\n\n temp++;\n num=mul;\n }\n cnt=max(cnt,temp);\n }\n return cnt==1?-1:cnt;\n }\n};\n```\n# Approach-2 ---> Binary Search\n# Intuition\nThe goal is to find the longest "square streak" in an array, where a square streak is a sequence starting from an element and repeatedly squaring it to get the next element in the sequence. Using binary search helps us efficiently search for the square of the current element in a sorted array.\n\n# Approach\n##### Sort the Array: \nSorting allows us to use binary search for finding the squares efficiently.\n##### Binary Search for Square Streak:\nFor each element, we initialize mul to its square, representing the next element in the square streak.\nUsing binary search, we look for mul in the remaining elements. If mul is found, increment the streak count, square mul again, and search for the new square from the current position to the end of the array.\nIf mul is not found, break the loop and continue to the next element.\nTrack Maximum Streak: For each element\u2019s streak, update the maximum streak length (cnt).\n##### Edge Case:\n If the longest streak is 1, return -1, as a valid streak requires at least one square transformation.\n# Complexity \n##### Time Complexity:\n O(n log n) for sorting and O(n log n) for iterating through each element and performing binary search, making the total time complexity O(n log n).\n##### Space Complexity: \nO(1) (excluding input/output) since no additional data structures are used beyond primitive variables.\n# Code\n```\nclass Solution {\npublic:\nint cnt,n;\nvoid solveUsingBS(int i,vector<int>& nums)\n{\n int s=i,e=n-1,temp=1;\n long long mul=1LL*nums[i]*nums[i];\n\n while(s<=e)\n {\n int mid=s+(e-s)/2;\n if(nums[mid]==mul)\n {\n temp++;\n mul=1LL*nums[mid]*nums[mid];\n e=n-1;\n }\n else if(nums[mid]>mul)\n {\n e=mid-1;\n }\n else\n s=mid+1;\n }\n cnt=max(cnt,temp);\n}\n int longestSquareStreak(vector<int>& nums) {\n sort(nums.begin(),nums.end());\n\n cnt=0,n=nums.size();\n\n for(int i=0;i<n;i++)\n {\n solveUsingBS(i,nums);\n }\n return cnt==1?-1:cnt;\n }\n};\n```\n# Approach-3 ---> Recursion\n# Intuition\nThe goal is to find the longest "square streak" in an array where each consecutive element in the streak is the square of the previous one. This recursive approach allows us to evaluate all possible square streaks by including or excluding each element based on whether it can extend a valid streak.\n\n# Approach\n##### Sorting the Array:\n\nSort nums to ensure we can check elements in increasing order, which allows us to explore the square streaks more systematically.\n##### Recursive Backtracking:\n\nDefine a recursive function solve(idx, prev_idx) where:\nidx is the current element index in nums.\nprev_idx is the index of the last included element in the streak.\n##### For each element at idx, determine if it can be included in the current streak by checking:\nEither there\u2019s no previous element in the streak (prev_idx == -1), or\nThe current element (nums[idx]) is the square of the previous element (nums[prev_idx]).\n##### Include or Exclude the Element:\nIf nums[idx] can extend the streak, call solve(idx + 1, idx) to include it.\nCall solve(idx + 1, prev_idx) to exclude nums[idx].\nTrack the maximum streak length from either including or excluding each element.\n##### Edge Case:\n\nIf the longest streak is 1, return -1, as a valid square streak must contain at least one square transformation.\n# Complexity Analysis\n##### Time Complexity:\n This recursive solution has O(2^n) complexity as it explores both inclusion and exclusion possibilities for each element, which makes it inefficient for large inputs.\n##### Space Complexity\n O(n) for the recursion stack.\n\n# Code\n```\nclass Solution {\npublic:\n int n;\n // 2,3,4,6,8,16\n int solve(int idx,int prev_idx,vector<int>& nums)\n {\n if(idx>=n)\n return 0;\n int incl=0,excl=0;\n \n if( (prev_idx==-1 || (nums[idx]==(1LL*nums[prev_idx]*nums[prev_idx]))))\n {\n incl=1+solve(idx+1,idx,nums);\n }\n excl=solve(idx+1,prev_idx,nums);\n\n return max(incl,excl);\n }\n\n int longestSquareStreak(vector<int>& nums) {\n sort(nums.begin(),nums.end());\n n=nums.size();\n int ans=solve(0,-1,nums);\n return ans==1?-1:ans;\n }\n};\n```\n# Approach-4 ---> Memoization\n# Intuition\nTo find the longest "square streak" in an array where each consecutive element is the square of the previous one, we use a recursive approach with memoization. Memoization helps store previously computed results to avoid redundant calculations and optimize performance, especially when overlapping subproblems are involved.\n\n# Approach\n##### Sorting the Array:\n\nFirst, we sort nums to process elements in increasing order, enabling us to check if each element can extend a square streak.\nRecursive Function with Memoization:\n\n##### Define solveMemo(idx, prev_idx):\nidx is the current element index.\nprev_idx is the index of the last element in the current streak. A prev_idx of -1 indicates the start of a new streak.\nFor each idx, check if nums[idx] can extend the streak starting from nums[prev_idx]:\nInclude nums[idx] if prev_idx is -1 (new streak) or if it equals nums[prev_idx] squared.\nUse memoization with dp[idx][prev_idx+1] to store the result, where dp[idx][prev_idx+1] saves the longest streak length for the given indices.\n##### Edge Case:\n\nIf the longest streak is 1, return -1 as it doesn\'t qualify as a square streak without a transformation.\n# Complexity Analysis\nTime Complexity: O(n\xB2), where n is the size of nums. Each state (idx, prev_idx) is computed once and stored in dp.\nSpace Complexity: O(n\xB2) for the dp array, as it stores results for each possible combination of idx and prev_idx. Additionally, O(n) space is used for the recursion stack.\n# Code\n```\nclass Solution {\npublic:\n int n;\n // int solve(int idx,int prev_idx,vector<int>& nums)\n // {\n // if(idx>=n)\n // return 0;\n // int incl=0,excl=0;\n \n // if( (prev_idx==-1 || (nums[idx]==(1LL*nums[prev_idx]*nums[prev_idx]))))\n // {\n // incl=1+solve(idx+1,idx,nums);\n // }\n // excl=solve(idx+1,prev_idx,nums);\n // return max(incl,excl);\n // }\n int solveMemo(int idx,int prev_idx,vector<int>& nums,vector<vector<int>>& dp)\n {\n if(idx>=n)\n return 0;\n\n if(dp[idx][prev_idx+1]!=-1)\n return dp[idx][prev_idx+1];\n \n int incl=0,excl=0;\n \n if( (prev_idx==-1 || (nums[idx]==(1LL*nums[prev_idx]*nums[prev_idx]))))\n {\n incl=1+solveMemo(idx+1,idx,nums,dp);\n }\n excl=solveMemo(idx+1,prev_idx,nums,dp);\n return dp[idx][prev_idx+1]= max(incl,excl);\n }\n\n int longestSquareStreak(vector<int>& nums) {\n sort(nums.begin(),nums.end());\n n=nums.size();\n // int ans=solve(0,-1,nums);\n vector<vector<int>>dp(n+1,vector<int>(n+2,-1));\n int ans=solveMemo(0,-1,nums,dp);\n return ans==1?-1:ans;\n }\n};\n```\n# Approach-5 ---> Tabulation Space Optimized\n# Intuition\nTo optimize the previous memoized approach, we can apply tabulation (bottom-up dynamic programming) with space optimization. This approach avoids the recursive overhead by building the solution iteratively from smaller subproblems and reduces space complexity by keeping only two arrays for the current and next row.\n\n# Approach\n##### Sorting the Array:\n\nSorting nums helps in maintaining a sequence where we can check each element\u2019s "square streak" efficiently.\n##### Iterative DP with Space Optimization:\n\nWe create two 1D arrays, next_row and curr, to store results for each possible combination of idx and prev_idx.\nStarting from the last element in nums, we iterate backwards to fill our DP table from the bottom up.\n##### For each element nums[idx], we check two cases:\nInclude nums[idx] if it\u2019s the start of a new streak or a square of the previous number nums[prev_idx].\nExclude nums[idx], where we take the maximum streak length found so far.\nAt the end of each loop for idx, update next_row with curr to proceed to the next set of subproblems.\n##### Edge Case:\n\nIf the longest streak found is 1, we return -1 as there are no transformations.\n# Complexity Analysis\nTime Complexity: O(n\xB2), due to the nested loop where each element and each possible previous index is iterated.\nSpace Complexity: O(n), using two 1D arrays of size n + 2 for next_row and curr.\n# Code\n```\nclass Solution {\npublic:\n int n;\n // int solve(int idx,int prev_idx,vector<int>& nums)\n // {\n // if(idx>=n)\n // return 0;\n // int incl=0,excl=0;\n \n // if( (prev_idx==-1 || (nums[idx]==(1LL*nums[prev_idx]*nums[prev_idx]))))\n // {\n // incl=1+solve(idx+1,idx,nums);\n // }\n // excl=solve(idx+1,prev_idx,nums);\n // return max(incl,excl);\n // }\n // int solveMemo(int idx,int prev_idx,vector<int>& nums,vector<vector<int>>& dp)\n // {\n // if(idx>=n)\n // return 0;\n\n // if(dp[idx][prev_idx+1]!=-1)\n // return dp[idx][prev_idx+1];\n \n // int incl=0,excl=0;\n \n // if( (prev_idx==-1 || (nums[idx]==(1LL*nums[prev_idx]*nums[prev_idx]))))\n // {\n // incl=1+solveMemo(idx+1,idx,nums,dp);\n // }\n // excl=solveMemo(idx+1,prev_idx,nums,dp);\n // return dp[idx][prev_idx+1]= max(incl,excl);\n // }\n\n int solveTab(vector<int>& nums)\n{\n int n = nums.size();\n vector<int> next_row(n + 2, 0), curr(n + 2, 0);\n\n for (int idx = n - 1; idx >= 0; idx--)\n {\n for (int prev_idx = idx - 1; prev_idx >= -1; prev_idx--)\n {\n int incl = 0, excl = 0;\n\n if (prev_idx == -1 || nums[idx] == 1LL * nums[prev_idx] * nums[prev_idx])\n {\n incl = 1 + next_row[idx + 1];\n }\n excl = next_row[prev_idx + 1];\n\n curr[prev_idx + 1] = max(incl, excl);\n }\n next_row = curr; \n }\n return next_row[0];\n}\n\n\n int longestSquareStreak(vector<int>& nums) {\n sort(nums.begin(),nums.end());\n n=nums.size();\n // int ans=solve(0,-1,nums);\n // vector<vector<int>>dp(n+1,vector<int>(n+2,-1));\n // int ans=solveMemo(0,-1,nums,dp);\n int ans=solveTab(nums);\n return ans==1?-1:ans;\n }\n};\n```\n\n\n
| 6 | 0 |
['Array', 'Hash Table', 'Binary Search', 'Dynamic Programming', 'Recursion', 'Memoization', 'Sorting', 'C++']
| 2 |
longest-square-streak-in-an-array
|
Runtime beats 91.89%, memory beats 51.33% [EXPLAINED]
|
runtime-beats-9189-memory-beats-5133-exp-ubpc
|
Intuition\nFind the longest sequence in the array where each number is the square of the previous one. This means if we start with a number, the next number in
|
r9n
|
NORMAL
|
2024-10-28T05:24:41.998650+00:00
|
2024-10-28T05:24:41.998676+00:00
| 20 | false |
# Intuition\nFind the longest sequence in the array where each number is the square of the previous one. This means if we start with a number, the next number in the sequence must be its square, and we keep going as long as we can find the next square in the array.\n\n# Approach\nSort the array, use a dictionary to track the length of each sequence we start, and for each number, keep squaring it until it\u2019s not in the array, updating the longest sequence found if it\u2019s at least two.\n\n# Complexity\n- Time complexity:\nO(n log n) because we sort first and then check each number once.\n\n- Space complexity:\nO(n) because we store the length of each sequence in a dictionary.\n\n# Code\n```python3 []\nclass Solution:\n def longestSquareStreak(self, nums: list[int]) -> int:\n num_set = set(nums)\n max_streak = -1\n\n for num in nums:\n streak_len = 0\n current = num\n\n # Count the length of the streak by squaring each number\n while current in num_set:\n streak_len += 1\n current *= current # Square the current number\n\n # Only consider streaks of length >= 2\n if streak_len >= 2:\n max_streak = max(max_streak, streak_len)\n\n return max_streak\n\n```
| 6 | 0 |
['Array', 'Hash Table', 'Sorting', 'Python3']
| 0 |
longest-square-streak-in-an-array
|
Find max comp size using DSU | O(N)
|
find-max-comp-size-using-dsu-on-by-el_lu-4yei
|
Intuition\nWhile Traversing the array we store the value mapped to its index in an unorderd map\nWhenever we see a number, we find its\nsquare root,\nsquare\nIf
|
el_luchador
|
NORMAL
|
2024-10-28T02:44:51.604013+00:00
|
2024-10-28T02:53:12.064183+00:00
| 414 | false |
# Intuition\nWhile Traversing the array we store the value mapped to its index in an unorderd map\nWhenever we see a number, we find its\nsquare root,\nsquare\nIf we have seen any of the above before, we connect both the indices\nAt the end we just need to return the largest component in the dsu.\n\n# Approach\nDSU + Traversal\n\n# Complexity\n\n- Time complexity:\n\nO(N)\nSince in DSU, we can do union in almost constant time, So the time complexity is O(N)\n\n\n\n- Space complexity:\n\nO(N)\nTo store the DSU array of parent and size and the unordered map\n\n\n\n# Code\n```cpp []\nstruct _dsu{\n vector <int> _parent;\n vector <int> _size;\n\n _dsu(int n){\n _parent.resize(n);\n for( int i = 0 ; i < n ; i++ ){\n _parent[i] = i;\n }\n\n _size.resize(n,1);\n }\n\n int _find(int n){\n if( _parent[n] == n )\n return n;\n return _parent[n] = _find(_parent[n]);\n }\n\n void _union(int a,int b){\n a = _find(a);\n b = _find(b);\n if( a == b )\n return;\n if( _size[a] < _size[b])\n swap(a,b);\n \n _parent[b] = a;\n _size[a] += _size[b]; \n }\n\n int maxComp(){\n return *max_element(_size.begin(), _size.end());\n }\n};\n\nclass Solution {\npublic:\n int longestSquareStreak(vector<int>& nums) {\n int n = nums.size();\n _dsu dsu = _dsu(n);\n unordered_map <long long,int> mpp;\n\n for( int i = 0 ; i < n ; i++ ){\n if( mpp.count(nums[i]))\n continue;\n long long x = nums[i];\n long long sq = x*x;\n long long rt = sqrt(x);\n if( mpp.count(sq) > 0 ){\n dsu._union(i, mpp[sq]);\n }\n if( rt*rt == x && mpp.count(rt) > 0 ){\n dsu._union(i, mpp[rt]);\n }\n mpp[x] = i;\n }\n int ans = dsu.maxComp();\n return ans > 1 ? ans : -1;\n }\n};\n```
| 6 | 0 |
['Union Find', 'Graph', 'C++']
| 2 |
longest-square-streak-in-an-array
|
Simple Java Solution | HashSet
|
simple-java-solution-hashset-by-arunbiit-yt5g
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
arunbiits
|
NORMAL
|
2022-12-11T04:00:50.918880+00:00
|
2022-12-11T04:00:50.918923+00:00
| 1,172 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int longestSquareStreak(int[] nums) {\n int max = 0;\n Set<Integer> set = new HashSet<>();\n for(int i: nums) set.add(i);\n for(int i=0;i<nums.length;i++) {\n int num = nums[i];\n int count = 1;\n while(set.contains(num*num)) {\n num = num*num;\n count++;\n }\n if(count > 1 && count > max) max = count;\n }\n return max==0 ? -1 : max;\n }\n}\n```
| 6 | 1 |
['Java']
| 4 |
longest-square-streak-in-an-array
|
✅ One Line Solution
|
one-line-solution-by-mikposp-3i4h
|
(Disclaimer: this is not an example to follow in a real project - it is written for fun and training mostly)\n\n# Code #1.1 - One Line\nTime complexity: O(n*max
|
MikPosp
|
NORMAL
|
2024-10-28T08:47:58.870581+00:00
|
2024-10-28T20:55:55.071238+00:00
| 592 | false |
(Disclaimer: this is not an example to follow in a real project - it is written for fun and training mostly)\n\n# Code #1.1 - One Line\nTime complexity: $$O(n*maxStreakLen)$$. Space complexity: $$O(maxStreakLen)$$. maxStreakLen - a small number depending on constraints.\n```python3\nclass Solution:\n def longestSquareStreak(self, a: List[int]) -> int:\n return (-1,r:=max(map(f:=lambda v:1+(v*v in a and f(v*v)),a:={*a})))[r>1]\n```\n\n# Code #1.2 - Unwrapped\n```python3\nclass Solution:\n def longestSquareStreak(self, a: List[int]) -> int:\n def f(v):\n return 1 + (v*v in a and f(v*v))\n\n a = {*a}\n r = max(map(f, a))\n if r > 1:\n return r\n return -1\n```\n\n(Disclaimer 2: code above is just a product of fantasy packed into one line, it is not claimed to be \'true\' oneliners - please, remind about drawbacks only if you know how to make it better)
| 5 | 0 |
['Array', 'Hash Table', 'Dynamic Programming', 'Recursion', 'Memoization', 'Python', 'Python3']
| 2 |
longest-square-streak-in-an-array
|
C++ Solution || Easy Set Solution || Detailed Explanation
|
c-solution-easy-set-solution-detailed-ex-asuz
|
Intuition\nTo solve this problem, we need to find the longest streak of numbers in which each number is the square of the previous one. By converting the array
|
Rohit_Raj01
|
NORMAL
|
2024-10-28T04:55:28.014676+00:00
|
2024-10-28T04:55:28.014704+00:00
| 720 | false |
# Intuition\nTo solve this problem, we need to find the longest streak of numbers in which each number is the square of the previous one. By converting the array to a set, we can use its properties to check if the square of a number exists in constant time, thereby efficiently counting streaks.\n\n# Approach\n1. Convert the array `nums` to a set, `st`, to quickly check the existence of elements and to avoid duplicates.\n2. Initialize `maxcnt` as `-1` to keep track of the longest streak found.\n3. **For each unique number in `st`**:\n - Initialize `cnt` to count the length of the current streak.\n - Repeatedly square the number and check if the squared number exists in `st`. If it does, increment `cnt`.\n4. If the streak length is at least 2, update `maxcnt` with the maximum streak length found.\n5. Return `maxcnt`, which will be the length of the longest square streak.\n\n# Complexity\n- Time complexity: $$O(nlogn)$$\n\n- Space complexity: $$O(n)$$ \n\n# Code\n```cpp []\nclass Solution {\npublic:\n int longestSquareStreak(vector<int>& nums) {\n set<long long> st(nums.begin(), nums.end());\n int maxcnt = -1;\n for (auto num : st) {\n int cnt = 0;\n while (st.find(num) != st.end()) {\n cnt++;\n num *= num;\n }\n\n if (cnt >= 2) {\n maxcnt = max(maxcnt, cnt);\n }\n }\n return maxcnt;\n }\n};\n```\n\n# Quote of the Day\n> ***Persevere through the small gains. The longest streaks are built by staying consistent and pushing forward.***\n\n\n
| 5 | 0 |
['Array', 'Hash Table', 'C++']
| 2 |
longest-square-streak-in-an-array
|
java solution
|
java-solution-by-kthnode-88mn
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
kthNode
|
NORMAL
|
2023-05-28T06:29:20.238539+00:00
|
2023-05-28T06:29:20.238578+00:00
| 577 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int longestSquareStreak(int[] nums) {\n Arrays.sort(nums);\n Map<Integer,Integer> m=new HashMap<>();\n int res=-1;\n for(int x:nums){\n int perfect=(int)Math.sqrt(x);\n //check perfect int or not as there may be int which will not form perfect square\n \n if(perfect*perfect==x && m.containsKey(perfect)){\n m.put(x,m.get(perfect)+1);\n res=Math.max((m.get(perfect)+1),res); \n }\n else{\n m.put(x,1);\n }\n } \n return res;\n }\n}\n```
| 5 | 0 |
['Java']
| 0 |
longest-square-streak-in-an-array
|
Python Simple Sorting solution
|
python-simple-sorting-solution-by-vincen-mpha
|
\ndef longestSquareStreak(self, nums: List[int]) -> int:\n\tnums, used, ans = set(nums), set(), 1\n\tfor n in sorted(nums):\n\t\tif n in used:\n\t\t\tcontinue\n
|
vincent_great
|
NORMAL
|
2022-12-11T04:01:04.347662+00:00
|
2022-12-11T04:01:04.347702+00:00
| 1,440 | false |
```\ndef longestSquareStreak(self, nums: List[int]) -> int:\n\tnums, used, ans = set(nums), set(), 1\n\tfor n in sorted(nums):\n\t\tif n in used:\n\t\t\tcontinue\n\t\tused.add(n)\n\t\tcur = 1\n\t\twhile(n**2 in nums):\n\t\t\tused.add(n**2)\n\t\t\tn *= n \n\t\t\tcur += 1\n\t\tans = max(cur, ans)\n\treturn ans if ans>1 else -1\n```
| 5 | 0 |
[]
| 3 |
longest-square-streak-in-an-array
|
C++ | Simple Map and Sorting
|
c-simple-map-and-sorting-by-me356500-nzvx
|
Approach\nStore value, and sort the given vector.\nChecking longest Square Streak one by one and erase the number in map.\n\nThe range of nums[i] is small, so w
|
me356500
|
NORMAL
|
2022-12-11T04:00:40.892048+00:00
|
2023-10-16T04:36:47.857627+00:00
| 2,410 | false |
## Approach\nStore value, and sort the given vector.\nChecking longest Square Streak one by one and erase the number in map.\n\nThe range of ```nums[i]``` is small, so we can simply use vector instead of unordered_map.\n\n## Code\n```\nclass Solution {\npublic:\n int longestSquareStreak(vector<int>& nums) {\n\n vector<int> vis(1e5 + 1, 0);\n // build map\n for (const auto &i : nums)\n ++vis[i];\n\n sort(nums.begin(), nums.end());\n int ans = -1, cnt = 0, n = nums.size();\n\n for (int i = 0, len = 0; i < n && cnt < n; ++i, len = 0) {\n \n if (!vis[nums[i]])\n continue;\n\n for (long now = nums[i]; now <= 1e5 && vis[now]; \n ++len, vis[now] = 0, now *= now);\n\n // update valid ans\n if (len > 1)\n ans = max(ans, len);\n\n }\n\n return ans;\n }\n};\n```\n**Upvote** if you like this post : )
| 5 | 0 |
['Hash Table', 'Sorting', 'C++']
| 2 |
longest-square-streak-in-an-array
|
Solved...........🔥🔥🔥🔥
|
solved-by-pritambanik-th08
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
PritamBanik
|
NORMAL
|
2024-10-28T17:16:14.643926+00:00
|
2024-10-28T17:16:14.643946+00:00
| 60 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: 100%\u2705\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: 100%\u2705\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```c []\n#define maxN 100005\n\nint max(int a, int b) { return a > b ? a : b; }\n\nint cmp(const void *a, const void *b) { return *(int *)a - *(int *)b; }\n\nint biSearch(int *arr, int n, int target) {\n int left = 0;\n int right = n - 1;\n while (left <= right) {\n int mid = left + (right - left) / 2;\n if (arr[mid] == target) {\n return mid;\n } else if (arr[mid] < target) {\n left = mid + 1;\n } else {\n right = mid - 1;\n }\n }\n return -1;\n}\n\nint longestSquareStreak(int *nums, int numsSize) {\n int seen[maxN] = {0};\n int *set = (int *)malloc(maxN * sizeof(int));\n int setidx = 0;\n for (int i = 0; i < numsSize; i++) {\n if (!seen[nums[i]]) {\n seen[nums[i]] = 1;\n set[setidx++] = nums[i];\n } else {\n continue;\n }\n }\n qsort(set, setidx, sizeof(int), cmp);\n int ans = -1;\n for (int i = 0; i < setidx; i++) {\n int curr = set[i];\n if (curr >= 400) {\n continue;\n }\n int big = curr * curr;\n int currRes = -1;\n while (biSearch(set, setidx, big) != -1) {\n if (currRes == -1) {\n currRes = 2;\n } else {\n currRes++;\n }\n curr = big;\n if (curr >= 400) {\n break;\n }\n big = curr * curr;\n // printf("curr = %d, big = %d\\n", curr, big);\n }\n ans = max(ans, currRes);\n }\n return ans;\n}\n```
| 4 | 0 |
['Array', 'Hash Table', 'Binary Search', 'Dynamic Programming', 'C', 'Sorting']
| 0 |
longest-square-streak-in-an-array
|
For loop + Hashset Solution + Explanation ✅ | TC: O(n), SC: O(n) 🚀 (UPVOTE PLS)
|
for-loop-hashset-solution-explanation-tc-boma
|
Intuition\nThe problem is about finding the longest sequence of numbers such that each number in the sequence is the square of the previous one. Since a direct
|
LovinsonDieujuste
|
NORMAL
|
2024-10-28T16:39:07.686912+00:00
|
2024-10-28T16:39:07.686944+00:00
| 89 | false |
## Intuition\nThe problem is about finding the longest sequence of numbers such that each number in the sequence is the square of the previous one. Since a direct approach could involve a lot of redundant checks, it makes sense to store numbers in a set for efficient lookup. By focusing only on numbers that are the starting points of potential sequences, we avoid unnecessary calculations and improve the solution\u2019s efficiency.\n\n## Approach\n1. **Convert List to Set**: First, we convert the list `nums` into a set to allow O(1) time complexity for lookups, which makes it easy to check if the square of a number is present.\n2. **Identify Starting Points**: For each number, check if it is a potential start of a streak by verifying that its square root is not in the set (since if it was, the current number would be part of a previous streak).\n3. **Extend the Streak**: Starting from each identified base, keep squaring the number and incrementing the streak length until the squared number is no longer in the set.\n4. **Update the Longest Streak**: Track the longest streak encountered. If no streaks longer than 1 are found, return -1 as required by the problem statement.\n\n## Complexity\n- **Time Complexity**: $$O(n)$$, where \\( n \\) is the number of elements in `nums`. Each element is processed once as part of extending its streak or skipping when it\'s not a potential start.\n- **Space Complexity**: $$O(n)$$ due to the storage of `nums` in a set.\n\n\n# Code\n```python3 []\nclass Solution:\n def longestSquareStreak(self, nums: List[int]) -> int:\n \n\n nums = set(nums)\n\n max_streak = 0\n\n for num in nums:\n if (num ** .5) in nums:\n continue\n\n cur_streak = 1\n goal = num ** 2\n while True:\n if goal in nums:\n cur_streak +=1\n goal **= 2\n else:\n break\n\n max_streak = max(max_streak, cur_streak)\n \n if max_streak == 1:\n return -1\n\n return max_streak\n\n```
| 4 | 0 |
['Hash Table', 'Python3']
| 0 |
longest-square-streak-in-an-array
|
Find Longest Square Streak in Sequence Using Set Lookup Optimization | Java | C++ | Video Solution
|
find-longest-square-streak-in-sequence-u-dsdb
|
Intuition, approach, and complexity discussed in video solution in detail.\nhttps://youtu.be/U0qpuY6LGEs\n\n# Code\njava []\nclass Solution {\n public int lo
|
Lazy_Potato_
|
NORMAL
|
2024-10-28T13:19:22.522680+00:00
|
2024-10-28T13:19:22.522707+00:00
| 311 | false |
# Intuition, approach, and complexity discussed in video solution in detail.\nhttps://youtu.be/U0qpuY6LGEs\n\n# Code\n```java []\nclass Solution {\n public int longestSquareStreak(int[] nums) {\n Set<Long> unqNums = new HashSet<>();\n for(var num : nums){\n unqNums.add(num * 1l);\n }\n int maxSSLen = 0;\n for(var num : nums){\n int currSSLen = 1;\n long currNum = num * 1l;\n while(unqNums.contains(currNum * currNum)){\n currSSLen++;\n currNum = currNum * currNum;\n }\n maxSSLen = Math.max(maxSSLen, currSSLen);\n }\n return maxSSLen == 1 ? -1 : maxSSLen;\n }\n}\n```\n```cpp []\nclass Solution {\npublic:\n int longestSquareStreak(vector<int>& nums) {\n unordered_set<long long> unqNums;\n for (auto num : nums) {\n unqNums.insert(static_cast<long long>(num));\n }\n \n int maxSSLen = 0;\n for (auto num : nums) {\n int currSSLen = 1;\n long long currNum = static_cast<long long>(num);\n while (unqNums.count(currNum * currNum)) {\n currSSLen++;\n currNum = currNum * currNum;\n }\n maxSSLen = max(maxSSLen, currSSLen);\n }\n \n return maxSSLen == 1 ? -1 : maxSSLen;\n }\n};\n\n```
| 4 | 0 |
['Array', 'Hash Table', 'C++', 'Java']
| 1 |
longest-square-streak-in-an-array
|
Longest Square streak in an array- Easy Explanation and Unique Solution 👌🔜
|
longest-square-streak-in-an-array-easy-e-oqez
|
Intuition\nThe count of the square streak should be atleast 2, hence if there is no such streak found, we\'ll return -1.\n\nTraverse through the whole array and
|
RAJESWARI_P
|
NORMAL
|
2024-10-28T09:07:39.218181+00:00
|
2024-10-28T09:07:39.218219+00:00
| 241 | false |
# Intuition\nThe count of the square streak should be atleast 2, hence if there is no such streak found, we\'ll return -1.\n\nTraverse through the whole array and add that element into the hashset for easy retrieval.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n**Initialization**:\n 1. Initialize the hashset of the type long since it also holds the square of the current element.\n 1. Intialize the maxcnt to -1 if no such streak of length 2 is found and intialize the value of n as number of elements in the array.\n\n Set<Long> set=new HashSet<>();\n int maxcnt=-1;\n int n=nums.length;\n\n**Fill the Set**:\n Iterate through the whole array and store each element of the array as type long in the hashset.\n\n for(int num:nums)\n {\n set.add((long)num);\n }\n\n**Find the square repeatedly**:\n Iterate through the whole nums array, then at each iteration -> initialize the cnt as 1.\n Find if the square of the current element is in hashset or not , if so change that square as current element and increase the cnt.\n At the end of the loop , if the cnt is greater than 2, then that streak may be accepted and then replace the maximum length.\n\n for(int num:nums)\n {\n long current=num;\n int cnt=1;\n while(set.contains(current*current))\n {\n current=current*current;\n cnt++;\n }\n if(cnt>=2)\n maxcnt=Math.max(cnt,maxcnt);\n \n }\n\n**Returning the value**:\n Return the maxcnt which gives the longest square streak in an array.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- ***Time complexity***: **O(nlogM)**\n n -> number of elements in the array.\n M -> largest number in the streak of the square.\n\n**Initial Set Population**: **O(n)**.\n We iterate over nums and insert each element into the hashset.Iterating each element will take **O(1) time** and for iterating n elements will take **O(n) time**.\n\n**Outer loop**: **O(logM).**\n if every element leads to a lengthy streak (which is unlikely since numbers grow exponentially when squared), this could require \n**O(logM)** operations per element.\n\n**Finding Maximum Count**: **O(1)**.\n This operation is a simple operation and it takes **O(1) time**.\n\n**Overall Time Complexity**: **O(nlogM )**.\n Since the outerloop requires O(logM) operation per element and we have n elements.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- ***Space complexity***: **O(n)**.\n n -> number of elements in the array.\n \n**Set Storage** :**O(n)**.\n We use a HashSet to store up to n elements from nums, so the space complexity for the set is O(n).\n\n**Auxillary variables**: **O(1)**.\n The program uses a **constant amount of extra space** for integers like current, cnt, and maxcnt, making this **O(1)**.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int longestSquareStreak(int[] nums) {\n //Arrays.sort(nums);\n Set<Long> set=new HashSet<>();\n int maxcnt=-1;\n\n int n=nums.length;\n for(int num:nums)\n {\n set.add((long)num);\n }\n for(int num:nums)\n {\n long current=num;\n int cnt=1;\n while(set.contains(current*current))\n {\n current=current*current;\n cnt++;\n }\n if(cnt>=2)\n maxcnt=Math.max(cnt,maxcnt);\n \n }\n return maxcnt;\n }\n}\n```
| 4 | 0 |
['Array', 'Hash Table', 'Java']
| 1 |
longest-square-streak-in-an-array
|
C solution for Longest Square Streak
|
c-solution-for-longest-square-streak-by-8tyx1
|
Approach\nGiven a string of n integers, find the numbers which are in a streak where each number is the quare of the previous number.\nEg:- a={2,8,5,4,90,16}\nH
|
samarthag01
|
NORMAL
|
2024-10-28T09:07:00.444755+00:00
|
2024-10-28T09:07:00.444787+00:00
| 19 | false |
# Approach\nGiven a string of n integers, find the numbers which are in a streak where each number is the quare of the previous number.\nEg:- a={2,8,5,4,90,16}\nHere the streak is of 3 as after sorting {2,4,16} where each number is the sqaure of the previous number and there are only 3 such numbers present in the string given in the above example.\nThis is a very simple approach.\n\n# Complexity\n#### Time complexity\nO(logn)\n#### Space complexity: O(n)\nO(n)\n# PLEASE UPVOTE\n\n# Code\n```c []\nint cmp(const void* a, const void* b) {\n return (*(int*)a < *(int*)b);\n}\n\nint longestSquareStreak(int* nums, int numsSize) {\n int sqr[100001]={0};\n int chk[317]={0};\n bool exist[317]={0};\n int n=0;\n for (int i=0;i<numsSize;i++) {\n if (nums[i]>316) { \n sqr[nums[i]]=1;\n }\n else if (!exist[nums[i]]) { \n //only keep one number of each as they can appear multiple time\n chk[n++]=nums[i];\n exist[nums[i]]=true;\n }\n }\n int count=-1;\n qsort(chk, n, sizeof(int), cmp);\n for (int i=0;i<n;i++) {\n sqr[chk[i]]=sqr[chk[i]*chk[i]]+1;\n if (count<sqr[chk[i]]) {\n count=sqr[chk[i]];\n }\n \n }\n return (count<=1) ? -1 : count;\n}\n```
| 4 | 0 |
['C']
| 1 |
longest-square-streak-in-an-array
|
C++ | BEGINNER FRIENDLY | BINARY SEARCH | INTUITIVE
|
c-beginner-friendly-binary-search-intuit-74xf
|
\n# Intuition\nSince we are changing the order of final subsequence (i.e. Sort)\nWe can sort the whole vector initially for our benefit to use binary search(i.e
|
codman_1
|
NORMAL
|
2024-10-28T03:05:21.878872+00:00
|
2024-10-28T13:17:26.816958+00:00
| 1,356 | false |
\n# Intuition\nSince we are changing the order of final subsequence (i.e. Sort)\nWe can sort the whole vector initially for our benefit to use binary search(i.e. lower_bound for searching next element in the subsequence)\n\nSo what we can do , find all the subsequence starting from unique number , for that we can use a visited vector , to check whether it is not used in earlier subsequence , because longest will be the earlier one (Think yourself).\n\n# Approach\n1. Initialize vector<int>vis(n,0).\n2. sort(nums.begin(),nums.end()).\n3. For nums[i] not visited , get possible subsequence for this and mark the next subsequence element index (if found) through out the process.\n4. For finding next square of curr element we are using lower bound , and when we dont have next square of curr present in the array we are breaking the while(1) loop .\n5. After finding the longest possible sequence starting at index i , we update the longest variable that store the longest sequence according to problem . \n6. if (longest<2)return -1 . Said in problem statement\n\n# Complexity\n- Time complexity:\nO(NLOGN)\n\n- Space complexity:\nO(N)\n\n# Code\n```cpp []\nclass Solution {\npublic:\n void getSequence(vector<int>&nums,long long start,int &temp_long,vector<bool>&vis){\n start=start*start;\n while(1){\n auto it = lower_bound(nums.begin(),nums.end(),start);\n if(it!=nums.end() && start==(*it)){\n start*=start;vis[it-nums.begin()]=1;\n temp_long++;\n }\n else break;\n }\n }\n int longestSquareStreak(vector<int>& nums) {\n int n = nums.size();\n vector<bool>vis(n,0);\n int longest = 0 ,temp_long=0;\n sort(nums.begin(),nums.end());\n\n for(int i=0;i<n;i++){\n if(!vis[i] || (i>0 && nums[i]!=nums[i-1])){\n vis[i]=1;\n temp_long=1;\n getSequence(nums,nums[i],temp_long,vis);\n longest=max(longest,temp_long);\n }\n }\n if(longest<2)return -1;\n return longest;\n }\n};\n```
| 4 | 1 |
['Math', 'Binary Search', 'Sorting', 'C++']
| 4 |
longest-square-streak-in-an-array
|
Chasing Squares: Finding the Longest Square Streak in an Array!
|
chasing-squares-finding-the-longest-squa-b8wc
|
Intuition\n Describe your first thoughts on how to solve this problem. \nThe goal is to find the longest "square streak," where a sequence of elements in the ar
|
LalithSrinandan
|
NORMAL
|
2024-10-28T02:26:31.062550+00:00
|
2024-10-28T02:26:31.062584+00:00
| 165 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe goal is to find the longest "square streak," where a sequence of elements in the array each is a square of the previous one. The initial thought is to use a Set for constant-time membership checking, allowing us to verify each squared element\'s presence efficiently.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nStep1: Add all elements from nums into a Set for quick lookup.\nStep2: For each unique element in the set, try to build a streak by repeatedly squaring the element and checking if the result exists in the set.\nStep3: Track the longest streak found. Use a long type to avoid overflow when squaring.\nStep4: Return the longest streak, or -1 if the maximum streak length is 1.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n\u22C5logm)\nwhere\nn is the number of unique elements and \nm is the largest element. Each element might be squared multiple times until it exceeds Integer.MAX_VALUE.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nfor storing the elements in a Set\n\n# Code\n```java []\nclass Solution {\n public int longestSquareStreak(int[] nums) {\n Set<Integer> s= new LinkedHashSet<>();\n for(int i: nums) s.add(i);\n List<Integer> l= new ArrayList<>(s);\n long lon=0;\n for(int i=0; i<l.size(); i++){\n int lo=1;\n long ele= l.get(i);\n while(ele*ele<= Integer.MAX_VALUE && s.contains((int)(ele*ele))){\n ele= ele*ele;\n lo+=1;\n }\n lon= Math.max(lon, lo);\n }\n return lon==1? -1: (int)lon;\n }\n}\n```
| 4 | 0 |
['Java']
| 1 |
longest-square-streak-in-an-array
|
✅ C++ || 2 DP solutions || 4 Lines || Recursive + Iterative || Faster 94%
|
c-2-dp-solutions-4-lines-recursive-itera-2zge
|
Intuition\n- While traversing from backward, if current items i\'s square ( i * i ) does not exist store count 0 in DP[i]\n- If square ( i * i ) exists in DP,
|
t86
|
NORMAL
|
2023-03-15T19:08:30.076135+00:00
|
2023-03-24T19:48:48.796422+00:00
| 439 | false |
**Intuition**\n- While traversing from backward, if current items `i`\'s `square ( i * i )` does not exist store count 0 in `DP[i]`\n- If `square ( i * i )` exists in DP, store `DP[i] = DP[i * i] + 1`\n- Keep tracking the `max_value` for `DP[i]`\n- Return `max_value + 1` if `max_value != 0`, otherwise -1\n\n**Iterative Approach** ( Accepted \u2705 94.32 % )\n```c++\nclass Solution {\npublic:\n int longestSquareStreak(vector<int>& nums, int res = 0) {\n sort(nums.begin(), nums.end());\n unordered_map<long long, int> dp;\n for (int i = nums.size() - 1; i >= 0; i--) {\n long long curr = nums[i], next = curr * curr;\n dp[curr] = dp.count(next) ? dp[next] + 1: 0;\n res = max(res, dp[curr]);\n }\n return res ? res + 1: -1;\n }\n};\n```\n\n**Previous Attempt: Recursive Approach** ( Gets TLE \u274C )\n```c++\nclass Solution {\npublic:\n int longestSquareStreak(vector<int>& nums) {\n sort(nums.begin(), nums.end());\n auto gen_key = [](long long i, long long j) { return to_string(i) + "-" + to_string(j); };\n unordered_map<string, long long> cache;\n \n function<long long(long long, long long)> go = \n [&](auto idx, auto prev) -> long long {\n if (idx == nums.size()) return 0;\n \n auto key = gen_key(idx, prev);\n if (cache.count(key)) return cache[key];\n \n long long res = go(idx + 1, nums[idx]);\n if (prev) res = max(res, go(idx + 1, prev));\n if (prev * prev != (long long) nums[idx]) return res;\n return cache[key] = max(res, 1 + go(idx + 1, nums[idx]));\n };\n \n auto res = go(0LL, 0LL);\n return res ? res + 1: -1;\n }\n};\n```\n\n**For more solutions, check out this \uD83C\uDFC6 [GITHUB REPOSITORY](https://github.com/MuhtasimTanmoy/playground) with over 1500+ solutions.**
| 4 | 1 |
['Dynamic Programming', 'Recursion']
| 1 |
longest-square-streak-in-an-array
|
Why use long long || Solving Overflow using int only !!
|
why-use-long-long-solving-overflow-using-zciv
|
Overflow Solution : Since constraint is- 2 <= nums[i] <= 1e5\nSo finding squares of elements greater than 317 is useless.\n\n# Code\n\nclass Solution {\npublic:
|
yadivyanshu
|
NORMAL
|
2022-12-11T07:12:46.762451+00:00
|
2022-12-11T07:12:46.762489+00:00
| 153 | false |
Overflow Solution : Since constraint is- 2 <= nums[i] <= 1e5\nSo finding squares of elements greater than 317 is useless.\n\n# Code\n```\nclass Solution {\npublic:\n int longestSquareStreak(vector<int>& nums) {\n unordered_map<int, int>mp;\n for(auto& it : nums) mp[it] = 1;\n sort(begin(nums), end(nums));\n int r = -1;\n for(int i = 0; i < nums.size(); i++) {\n if(nums[i] >= 317) break;\n int cur = nums[i] * nums[i];\n int cnt = 1;\n while(mp[cur]) {\n cnt++;\n if(cur >= 317) break;\n cur = cur *cur;\n }\n r = max(r, cnt);\n }\n return r == 1 ? -1 : r;\n }\n};\n```
| 4 | 0 |
['C++']
| 0 |
longest-square-streak-in-an-array
|
6 lines with hashmap
|
6-lines-with-hashmap-by-her0e1c1-dowx
|
reversing nums is better because no need to take care of float\n\n# Code\n\nclass Solution:\n def longestSquareStreak(self, nums: List[int]) -> int:\n
|
her0e1c1
|
NORMAL
|
2022-12-11T06:31:21.044322+00:00
|
2022-12-11T06:31:21.044359+00:00
| 399 | false |
reversing nums is better because no need to take care of float\n\n# Code\n```\nclass Solution:\n def longestSquareStreak(self, nums: List[int]) -> int:\n ans, buf = -1, {}\n for n in reversed(sorted(nums)):\n buf[n] = buf.get(n*n, 0) + 1\n if buf[n] > 1:\n ans = max(ans, buf[n])\n return ans\n```
| 4 | 0 |
['Python3']
| 0 |
longest-square-streak-in-an-array
|
Map Traversal || simple solution || c++
|
map-traversal-simple-solution-c-by-diksh-vz32
|
Just store the value in map and traverse to find the square\nUpvote if it was helpful\n\nclass Solution\n{\npublic:\n int longestSquareStreak(vector<int> &nu
|
dikshant_sh
|
NORMAL
|
2022-12-11T04:12:41.580984+00:00
|
2022-12-11T04:27:41.530559+00:00
| 441 | false |
**Just store the value in map and traverse to find the square**\n**Upvote if it was helpful**\n```\nclass Solution\n{\npublic:\n int longestSquareStreak(vector<int> &nums)\n {\n unordered_map<long long, long long> mp;\n for (auto &it : nums)\n mp[it]++;\n\n int ans = INT_MIN;\n for (auto &it : mp)\n {\n long long to_search = it.first;\n int temp = 0;\n while (mp.find(to_search) != mp.end())\n {\n if (mp.find(to_search) != mp.end())\n {\n temp++;\n to_search = to_search * to_search;\n }\n }\n ans = max(temp, ans);\n }\n if (ans == 1 || ans == 0)\n return -1;\n else\n return ans;\n }\n};\n```
| 4 | 0 |
['Interactive']
| 0 |
longest-square-streak-in-an-array
|
Simple java solution
|
simple-java-solution-by-siddhant_1602-3xjt
|
\n\n# Complexity\n- Time complexity: O(n logn) for sorting + O(n) for traversing the loop\n\n- Space complexity: O(n) --> For storing elements in the hashmap\n\
|
Siddhant_1602
|
NORMAL
|
2022-12-11T04:01:14.140193+00:00
|
2022-12-11T04:14:18.922740+00:00
| 990 | false |
\n\n# Complexity\n- Time complexity: O(n logn) for sorting + O(n) for traversing the loop\n\n- Space complexity: O(n) --> For storing elements in the hashmap\n\n# Code\n```\nclass Solution {\n public int longestSquareStreak(int[] nums) {\n Arrays.sort(nums);\n Map<Integer,Integer> nm=new HashMap<>();\n int p=-1,s=-1;\n for(int i=0;i<nums.length;i++)\n {\n int m=(int)Math.sqrt(nums[i]);\n if(m*m == nums[i] && nm.containsKey(m))\n {\n nm.put(nums[i],nm.get(m)+1);\n if(nm.containsKey(m))\n {\n if(nm.get(m)+1>s)\n {\n s=nm.get(m)+1;\n }\n }\n }\n else\n {\n nm.put(nums[i],1);\n }\n }\n return s;\n }\n}\n\n```
| 4 | 0 |
['Hash Table', 'Java']
| 0 |
longest-square-streak-in-an-array
|
Simply py,JAVA code using 3Approaches(HashMap+sort,Sort+set,set)!!!
|
simply-pyjava-code-using-3approacheshash-ovlv
|
\n# Problem understanding\n Describe your first thoughts on how to solve this problem. \n- Let\'s understand the problem first,what they are asking is a subsequ
|
arjunprabhakar1910
|
NORMAL
|
2024-10-28T14:32:26.308783+00:00
|
2024-10-28T14:46:24.755060+00:00
| 13 | false |
\n# Problem understanding\n<!-- Describe your first thoughts on how to solve this problem. -->\n- Let\'s understand the problem first,what they are asking is a *subsequence* of numbers which are *squares of on another* continously.\n```\nnums=[2,4,16,256]\n\n```\n- The longest streak is for `2` here which is `2*2(4)->4*4(16)->16*16(256)` which is `4` including `2`.\n- \n\n---\n\n# Approach-1:sets+sorting\n# Intuition\n- My idea here is to use `2-SETS` one to to store visited numbers\n`visited` and our normal `nums`(given) in a set as `num_set` or `checker`.\n- why `visited` ? I felt we are going to compute the same number more than once,if it is true for the smallest number say `2` in our above example then we get our ans (`4`) till `256`,then the computaion of `4`,`16` is useless.\n- Because compuation of them is always going to lead to a smaller value of `maxlen`.\n- what I did is to choose an element and store it in `num` which is then *squared* each time and checked until it fails to exist in `num_set` or `checker`,while increasing `l` and adding `num*num` in `visited` to avoid future computation.\n- Sorting(`sort`) is must since I am traversing from small element,because starting from a large elment and then looking for even bigger number is pointless.\n\n\n# Complexity\n- Time complexity:$O(N*log(N))$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$O(N)$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def longestSquareStreak(self, nums: List[int]) -> int:\n nums.sort()\n nums_set=set(nums)\n visited=set([])\n print(nums)\n maxl=0\n for i in nums:\n num=i\n l=1\n while num*num in nums_set and num*num not in visited:\n visited.add(num*num)\n num=num*num\n l+=1\n maxl=max(maxl,l)\n #print(i,visited,maxl)\n #print(\'------------------\')\n return maxl if maxl>=2 else -1\n \n```\n```JAVA []\n//This fails last two test cases but the same logic!!(90/92)\nclass Solution {\n public int longestSquareStreak(int[] nums) {\n Arrays.sort(nums);\n int maxlen=0,len=0;\n Set<Integer> visited=new HashSet<>();\n Set<Integer> checker=new HashSet<>();\n for(int i:nums){\n checker.add(i);\n }\n for(int n:nums){\n int num=n;\n len=1;\n while(checker.contains(num*num) && !visited.contains(num*num)){\n visited.add(num*num);\n num=num*num;\n len++;\n }\n maxlen=Math.max(maxlen,len);\n }\n return maxlen>=2?maxlen:-1;\n }\n}\n```\n\n---\n\n# Approach-2:HashMap+sort\n# Intuition\n- This is a clever way to solve a problem.\n- We will `sort` as for the same reason stated above!\n- The `map` stores the previosly found *perfect squares\'s streak*\n- we will take square root of a current number `n` and store it in `sqroot` or `sqrt`.Magic happens here,if they are *perfect roots* and if they had any `prev` value in `map` which is `Dictionary or HashMap`,we increase the value(`val`) of stored `sqrt` and then map it from our current `num`.\n- else then we create *map(key,val)* for it in `map`\n```\nnums=[1,4,16,2,256,3,5]\n//after sort\nnums=[1,2,3,4,5,16,256]\n1->{1:1}\n2->{1:1,2:1} //sqrt(2)=1.414\n3->{1:1,2:1,3:1}\n4->{1:1,2:1,3:1,4:2} //sqrt(4)=2[2:1]....Hence maintains STREAK!!\n5->{1:1,2:1,3:1,4:2,5:1}\n16->{1:1,2:1,3:1,4:2,5:1,16:3} //sqrt(16)=4[4:2]....STREAK!!\n256->{1:1,2:1,3:1,4:2,5:1,16:3,256:4} //sqrt(256)=16[16:3]..STREAK!!\n```\n- This is optimised than previous code becuase `two loops are avoided!.`\n\n\n\n# Complexity\n- Time complexity:$O(N*log(N))$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$O(N)$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def longestSquareStreak(self, nums: List[int]) -> int:\n nums.sort()\n maxlen=0\n map=dict()\n for n in nums:\n sqroot=int(math.sqrt(n))\n if sqroot*sqroot==n and sqroot in map:\n map[n]=map[sqroot]+1\n maxlen=max(maxlen,map[n])\n else:\n map[n]=1\n return maxlen if maxlen>=2 else -1\n \n```\n```JAVA []\nclass Solution {\n public int longestSquareStreak(int[] nums) {\n Arrays.sort(nums);\n int maxlen=0,sqrt=0;\n HashMap<Integer,Integer> map=new HashMap<>();\n for(int n:nums){\n sqrt=(int)Math.sqrt(n);\n if(sqrt*sqrt==n && map.containsKey(sqrt)){\n map.put(n,map.get(sqrt)+1);\n maxlen=Math.max(maxlen,map.get(n));\n }\n else{\n map.put(n,1);\n }\n }\n return maxlen>=2?maxlen:-1;\n }\n}\n```\n\n---\n\n\n# Approach-3:set(Beats100%)\n# Intuition\n- This is kinda similar to *approach-1* but here we never mind about `visited`,just do the same logic and convert `nums` *list* into a `set(list)`\n- with help of a `set` DS(Data Structure),u can have $O(1)$\nlookup.\n\n# Complexity\n- Time complexity:$O(N)$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$O(N)$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def longestSquareStreak(self, nums: List[int]) -> int:\n nums=set(nums)\n maxlen=0\n for n in nums:\n num=n\n l=1\n while num*num in nums:\n l+=1\n num*=num\n maxlen=max(maxlen,l)\n return maxlen if maxlen>=2 else -1\n \n```\n```JAVA []\n//This fails last two test cases but the same logic!!(90/92)\nclass Solution {\n public int longestSquareStreak(int[] nums) {\n Arrays.sort(nums);\n int maxlen=0,len=0,num;\n Set<Integer> numss=new HashSet<>();\n for(int i:nums){\n numss.add(i);\n }\n for(int n:nums){\n num=n;\n len=1;\n while(numss.contains(num*num)){\n num*=num;\n len++;\n }\n maxlen=Math.max(maxlen,len);\n }\n return maxlen>=2?maxlen:-1;\n }\n}\n```\n[GithubCodes for same probelm with dry run!!](https://github.com/themysterysolver/LEET-AND-FUN/tree/main/2586-longest-square-streak-in-an-array)\n
| 3 | 0 |
['Array', 'Hash Table', 'Java', 'Python3']
| 0 |
longest-square-streak-in-an-array
|
easy solution | java clean code ✅
|
easy-solution-java-clean-code-by-somgest-zshf
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
somgester13
|
NORMAL
|
2024-10-28T07:20:19.646696+00:00
|
2024-10-28T07:20:19.646729+00:00
| 18 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int longestSquareStreak(int[] nums) {\n Arrays.sort(nums);\n int [] arr = new int[100001];\n int maxi = 0;\n for(int i: nums)\n {\n int root = (int)Math.sqrt(i);\n if(root * root != i) arr[i] = 1; //no predecessor\n else arr[i] = arr[root] + 1; // extend streak from root\n maxi = Math.max(maxi, arr[i]);\n }\n if(maxi == 1) return -1;\n else return maxi;\n }\n}\n```
| 3 | 0 |
['Array', 'Sorting', 'Java']
| 0 |
longest-square-streak-in-an-array
|
Beats 100% || 2 Extremely Easy DP Solution Detailed Explanation⭐🏆
|
beats-100-2-extremely-easy-dp-solution-d-169c
|
Longest Square Streak\n\n## Problem Description\nGiven an array of integers nums, you are required to find the length of the longest subsequence where each elem
|
_Rishabh_96
|
NORMAL
|
2024-10-28T05:47:01.396099+00:00
|
2024-10-28T05:47:01.396136+00:00
| 491 | false |
# Longest Square Streak\n\n## Problem Description\nGiven an array of integers `nums`, you are required to find the length of the longest subsequence where each element is a perfect square of its preceding element. If no such sequence with length greater than or equal to 2 exists, return `-1`.\n\n## Intuition\nThe initial intuition is to use a recursive approach with dynamic programming to keep track of the longest square streak that can be built with each element. By iterating through each element and using a hashmap to store square streak lengths, we can build the solution iteratively while minimizing the memory usage.\n\n## Approach\n1. **Sorting**: Sort the array to ensure that we only need to check for potential square sequences in one direction (from smaller to larger numbers).\n2. **HashMap for DP**: Use an `unordered_map` (hashmap) to store the length of the longest square streak ending at each element.\n3. **Square Check**: For each element, calculate its integer square root, and check if the square of that root equals the element. If it does, update the streak length by adding 1 to the value in the hashmap corresponding to that root.\n4. **Result**: Track the maximum streak length throughout, and if the maximum streak length is at least 2, return it. Otherwise, return `-1`.\n\n## Complexity\n- **Time complexity**: \\(O(n \\log n)\\) due to sorting the array, where \\(n\\) is the number of elements in `nums`.\n- **Space complexity**: \\(O(n)\\) for the hashmap that stores streak lengths for each element.\n\n## Code\n```cpp\nclass Solution {\npublic:\n int solve(vector<int>& nums, int index, int prevIndex, vector<vector<int>>& dp) {\n \n if (index == nums.size()) {\n return 0;\n }\n\n if (dp[index][prevIndex + 1] != -1) {\n return dp[index][prevIndex + 1];\n }\n\n int skip = solve(nums, index + 1, prevIndex, dp);\n\n int include = 0;\n if (prevIndex == -1 || nums[index] == nums[prevIndex] * nums[prevIndex]) {\n include = 1 + solve(nums, index + 1, index, dp);\n }\n\n return dp[index][prevIndex + 1] = max(include, skip);\n }\n\n // int longestSquareStreak(vector<int>& nums) {\n // sort(nums.begin(), nums.end());\n // // vector<vector<int>> dp(nums.size(), vector<int>(nums.size() + 1, -1));\n // // int maxLength = solve(nums, 0, -1, dp);\n // // return maxLength >= 2 ? maxLength : -1;\n\n // int n = nums.size();\n // vector<int> dp(n + 1, 0); \n // int maxLength = 0;\n\n // for (int index = n - 1; index >= 0; index--) {\n // int currentMax = 0;\n // for (int nextIndex = index + 1; nextIndex < n; nextIndex++) {\n // if (static_cast<long long>(nums[index]) * nums[index] == nums[nextIndex]) {\n // currentMax = max(currentMax, dp[nextIndex]);\n // }\n // }\n // dp[index] = 1 + currentMax;\n // maxLength = max(maxLength, dp[index]);\n // }\n\n // return maxLength >= 2 ? maxLength : -1;\n // }\n\n int longestSquareStreak(vector<int>& nums) {\n \n unordered_map<int, int> dp;\n int res = 0;\n sort(begin(nums), end(nums));\n\n for(auto i : nums){\n int root = sqrt(i);\n if(root * root == i)\n dp[i] = 1 + dp[root];\n else \n dp[i] = 1;\n res = max(res, dp[i]);\n }\n return res < 2 ? -1 : res;\n }\n};\n```
| 3 | 0 |
['Array', 'Hash Table', 'Binary Search', 'Dynamic Programming', 'Sorting', 'C++']
| 2 |
longest-square-streak-in-an-array
|
Best Solution Ever ❤️🔥❤️🔥!!!! Done ✅ !!!! No Sorting !!!! Easy Solution ✅ !!!!
|
best-solution-ever-done-no-sorting-easy-48t21
|
Intuition\nThe problem requires us to find the longest "square streak" in the input array. A "square streak" is a sequence of numbers where each number is the s
|
satyendra_s
|
NORMAL
|
2024-10-28T03:08:45.771837+00:00
|
2024-10-28T03:08:45.771878+00:00
| 472 | false |
# Intuition\nThe problem requires us to find the longest "square streak" in the input array. A "square streak" is a sequence of numbers where each number is the square of the previous one, starting from a number in the array.\n\n**The main idea is to:**\n- **Identify Starting Points:** For each number in the array, check if it can be the start of a square streak. We don\u2019t want to start from a number that is already a square of another number in the array, as that would be in the middle of a streak, not the start.\n- **Track and Count Streaks:** For each valid starting point, multiply it repeatedly by itself to see how many times you can continue this sequence within the set.\n- **Update the Maximum Streak:** Keep track of the maximum streak length encountered during the process.\n\n# Approach\n- **Store Elements in a Set:** First, insert all elements in an unordered set `(unordered_set)` for efficient lookup. This allows us to quickly check if the next number in a streak exists in the array.\n\n- **Iterate Over Each Number:** For each number in the array, check if it could be the beginning of a streak by confirming that its square root does not exist in the set (`st.find(sqrt(num)) == st.end()`).\n\n- **Count the Streak:** If it\u2019s a valid starting point, keep squaring the number and counting the streak length while each squared value is still in the set. To avoid overflow, break the loop if the squared number exceeds `INT_MAX`.\n\n- **Update the Answer:** Update the answer with the maximum streak length. If no streak of length 2 or more is found, return `-1`.\n\n# Complexity\n- Time complexity:\n1. **Initialization of the unordered_set**: The construction of the unordered_set from the vector `nums` takes O(n) time, where n is the number of elements in `nums`.\n\n2. **Outer loop**: The outer loop iterates over each element in `nums`, which takes O(n) time.\n\n3. **Inner while loop**: For each number in `nums`, the inner while loop checks if the current number (starting from `num` and then squaring it) exists in the set. In the worst case, this loop could run multiple times, but since the numbers grow exponentially (squaring), the number of iterations is limited. Specifically, the number of times you can square a number before it exceeds INT_MAX is logarithmic in relation to the size of the number. Therefore, the inner loop can be considered to run O(log m) times, where m is the maximum value in `nums`.\n\nCombining these, the overall time complexity can be approximated as `O(n log m)`.\n\n- **Space complexity:**\nThe space complexity is primarily determined by the unordered_set, which stores all unique elements from `nums`. Therefore, the space complexity is O(n) in the worst case, where all elements in `nums` are unique.\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int longestSquareStreak(vector<int>& nums) {\n unordered_set<long long> st(nums.begin(), nums.end());\n\n int ans = 0;\n for (int num : nums) {\n int count = 0;\n long long curr = num;\n while (st.find(curr) != st.end()) {\n count++;\n curr = curr * curr;\n if (curr > INT_MAX) break; // Avoid overflow\n }\n ans = max(ans, count);\n }\n return ans >= 2 ? ans : -1;\n }\n};\n\n```\n```Java []\nimport java.util.HashSet;\nimport java.util.Set;\n\nclass Solution {\n public int longestSquareStreak(int[] nums) {\n Set<Long> set = new HashSet<>();\n for (int num : nums) {\n set.add((long) num);\n }\n\n int maxStreak = 0;\n for (int num : nums) {\n int count = 0;\n long current = num;\n while (set.contains(current)) {\n count++;\n current = current * current;\n if (current > Integer.MAX_VALUE) break; // Avoid overflow\n }\n maxStreak = Math.max(maxStreak, count);\n }\n\n return maxStreak >= 2 ? maxStreak : -1;\n }\n}\n```\n```Python []\nclass Solution:\n def longestSquareStreak(self, nums):\n num_set = set(nums)\n max_streak = 0\n \n for num in nums:\n count = 0\n current = num\n while current in num_set:\n count += 1\n current = current * current\n if current > 2**31 - 1: # Avoid overflow (INT_MAX equivalent)\n break\n max_streak = max(max_streak, count)\n \n return max_streak if max_streak >= 2 else -1\n\n```\n```JavaScript []\nvar longestSquareStreak = function(nums) {\n const set = new Set(nums.map(num => BigInt(num)));\n let maxStreak = 0;\n\n for (let num of nums) {\n let count = 0;\n let current = BigInt(num);\n while (set.has(current)) {\n count++;\n current *= current;\n if (current > BigInt(Number.MAX_SAFE_INTEGER)) break; // Avoid overflow\n }\n maxStreak = Math.max(maxStreak, count);\n }\n\n return maxStreak >= 2 ? maxStreak : -1;\n};\n```
| 3 | 0 |
['Array', 'Hash Table', 'Binary Search', 'Dynamic Programming', 'Sorting', 'C++', 'Java', 'Python3', 'JavaScript']
| 2 |
longest-square-streak-in-an-array
|
must see || easy to understand || binary search
|
must-see-easy-to-understand-binary-searc-puqh
|
do binary serach for every element of the array and find its square; \ntime complexcity of binary serach is log(n);\nbinary search for every n elements is n*log
|
akshat0610
|
NORMAL
|
2023-01-08T06:22:32.048859+00:00
|
2023-01-08T06:22:32.048898+00:00
| 379 | false |
do binary serach for every element of the array and find its square; \ntime complexcity of binary serach is log(n);\nbinary search for every n elements is n*log(n);\n\n# Code\n```\nclass Solution \n{\npublic:\n int longestSquareStreak(vector<int>& nums) {\n \n int ans = -1;\n sort(nums.begin(),nums.end());\n for(int i=0;i<nums.size();i++)\n {\n long long int num = nums[i];\n long long int pwr = num*num;\n long long int len = 1;\n\n while(binary_search(nums.begin(),nums.end(),pwr) == true)\n {\n len++;\n long long int ele = pwr;\n pwr = ele * ele;\n }\n if(len!=1 and len > ans)\n ans = len;\n }\n return ans;\n }\n};\n```
| 3 | 0 |
['Array', 'Binary Search', 'Dynamic Programming', 'Sorting', 'C++']
| 0 |
longest-square-streak-in-an-array
|
[Python / JS] dont use expensive sqrt() function
|
python-js-dont-use-expensive-sqrt-functi-2fwz
|
Python\n\nclass Solution:\n def longestSquareStreak(self, nums: List[int]) -> int:\n nums.sort(reverse=True)\n seen = {}\n ans = -1\n\n
|
SmittyWerbenjagermanjensen
|
NORMAL
|
2022-12-11T15:54:58.544605+00:00
|
2022-12-11T15:54:58.544636+00:00
| 679 | false |
# Python\n```\nclass Solution:\n def longestSquareStreak(self, nums: List[int]) -> int:\n nums.sort(reverse=True)\n seen = {}\n ans = -1\n\n for n in nums:\n if n*n in seen:\n seen[n] = seen[n*n]+1\n ans = max(ans, seen[n])\n else:\n seen[n] = 1\n\n return ans\n```\n# JavaScript\n```\nconst longestSquareStreak = nums => {\n nums.sort((a,b) => b-a)\n const seen = new Map()\n let ans = -1\n\n for (let n of nums) {\n if (seen.has(n*n)) {\n seen.set(n, seen.get(n*n) + 1)\n ans = Math.max(ans, seen.get(n))\n } else {\n seen.set(n, 1)\n }\n }\n\n return ans\n}\n```
| 3 | 0 |
['Python', 'Python3', 'JavaScript']
| 0 |
longest-square-streak-in-an-array
|
JAVA | HashSet | Easy ✅
|
java-hashset-easy-by-sourin_bruh-fn1n
|
Please Upvote :D\n\n---\n\n\n\n---\n\njava []\nclass Solution {\n public int longestSquareStreak(int[] nums) {\n int maxLen = 0;\n\n Set<Intege
|
sourin_bruh
|
NORMAL
|
2022-12-11T10:04:31.716186+00:00
|
2022-12-11T10:04:31.716272+00:00
| 115 | false |
# Please Upvote :D\n\n---\n\n\n\n---\n\n``` java []\nclass Solution {\n public int longestSquareStreak(int[] nums) {\n int maxLen = 0;\n\n Set<Integer> set = new HashSet<>();\n for (int n : nums) {\n set.add(n);\n }\n\n for (int i = 0; i < nums.length; i++) {\n int n = nums[i];\n int len = 1;\n\n while (set.contains(n * n)) {\n n *= n;\n len++;\n }\n\n maxLen = Math.max(maxLen, len);\n }\n\n return maxLen > 1? maxLen : -1;\n }\n}\n\n// TC: O(n) + O(n) => O(n)\n// SC: O(n)\n```
| 3 | 0 |
['Hash Table', 'Java']
| 1 |
longest-square-streak-in-an-array
|
C++ || HAshing
|
c-hashing-by-pradipta_ltcode-ikc8
|
\n# Code\n\nclass Solution {\npublic:\n int longestSquareStreak(vector<int>& nums) {\n sort(nums.begin(), nums.end());\n unordered_map<long lon
|
pradipta_ltcode
|
NORMAL
|
2022-12-11T04:06:14.377249+00:00
|
2022-12-11T04:06:14.377282+00:00
| 600 | false |
\n# Code\n```\nclass Solution {\npublic:\n int longestSquareStreak(vector<int>& nums) {\n sort(nums.begin(), nums.end());\n unordered_map<long long, int> mp;\n long long res = -1;\n for(auto n : nums) mp[n]++;\n \n for(auto n : nums) {\n if(!mp.size())\n break;\n if(mp.count(n) != 0) {\n long long cnt = 1, cur = (long long)n * (long long)n;\n while(mp.size()) {\n if(mp.count(cur)) {\n mp.erase(cur);\n ++cnt;\n cur *= cur;\n }\n else\n break;\n }\n if(cnt > 1)\n res= max(res, cnt);\n }\n }\n return res;\n }\n};\n```
| 3 | 0 |
['C++']
| 1 |
longest-square-streak-in-an-array
|
[Python 3] Simple | Using set
|
python-3-simple-using-set-by-0xabhishek-f4vt
|
\nclass Solution:\n def longestSquareStreak(self, nums: List[int]) -> int:\n uniq = set(nums)\n res = 0\n \n for i in nums:\n
|
0xAbhishek
|
NORMAL
|
2022-12-11T04:04:15.206714+00:00
|
2022-12-11T04:04:15.206744+00:00
| 335 | false |
```\nclass Solution:\n def longestSquareStreak(self, nums: List[int]) -> int:\n uniq = set(nums)\n res = 0\n \n for i in nums:\n temp = i\n t = 0\n while temp * temp in uniq:\n temp *= temp\n t += 1\n \n res = max(res, t)\n \n return res + 1 if res else -1\n```
| 3 | 0 |
['Ordered Set', 'Python', 'Python3']
| 1 |
longest-square-streak-in-an-array
|
Simple O(n) solution
|
on-solution-exists-actually-by-serious7s-09cm
|
IntuitionPut all numbers into map with counter.For each number we calc it's double (next) and sqrt (previous) elements.If we already had previous or next number
|
serious7sam
|
NORMAL
|
2025-01-18T15:37:20.159622+00:00
|
2025-01-19T13:16:13.200212+00:00
| 52 | false |
# Intuition
Put all numbers into map with counter.
For each number we calc it's double (next) and sqrt (previous) elements.
If we already had previous or next numbers: we get their counts, sum and store back into map.
Resulting counter will always converge to needed sequence length no matter the order of when numbers appear.
*Note: this only works because max sequence length is 5*
# Complexity
- Time complexity: **O(n)**
- Space complexity: **O(n)**
# Code
```java []
class Solution {
public int longestSquareStreak(int[] nums) {
var map = new HashMap<Integer, Integer>(); // [number, sequenceLength]
int res = 0;
for (var num : nums) {
if (map.containsKey(num)) { // no need to evaluate already processed number
continue;
}
int numDouble = 0;
if ((long)num * num < 100001) { // prevent overflow
numDouble = num * num;
}
int sqrt = 0;
double tmp2 = Math.sqrt(num);
if (tmp2 == (int)tmp2) {
sqrt = (int)tmp2;
}
int count = 1;
if (numDouble != 0) count += map.getOrDefault(numDouble,0);
if (sqrt != 0) count += map.getOrDefault(sqrt,0);
map.put(num, count);
// store counter only for values that exist in map
if (numDouble != 0 && map.containsKey(numDouble)) map.put(numDouble, count);
if (sqrt != 0 && map.containsKey(sqrt)) map.put(sqrt, count);
res = Math.max(res, count);
}
return res == 1 ? -1 : res;
}
}
```
| 2 | 0 |
['Java']
| 1 |
longest-square-streak-in-an-array
|
Beat 100% O[nlogn] space complexity O[n]
|
beat-100-onlogn-space-complexity-on-by-e-v1fy
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
expon23_9
|
NORMAL
|
2024-10-29T05:25:35.912443+00:00
|
2024-10-29T05:25:35.912485+00:00
| 10 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int longestSquareStreak(vector<int>& nums) {\n unordered_map<int,int>container;\n sort(nums.begin(),nums.end());\n int rtrn = -1;\n for(auto n : nums)\n { \n int root = sqrt(n);\n //there is a problem comes eg: for n = 36,37 the value of root comes 6 \n //thus we must need cross check\n if(root*root==n && container.find(root)!=container.end())\n {\n container[n]=container[root]+1;\n rtrn = max(rtrn , container[n]);\n }\n else container[n]=1;\n } \n return rtrn;\n }\n};\n```
| 2 | 0 |
['C++']
| 0 |
longest-square-streak-in-an-array
|
Easy DP solution
|
easy-dp-solution-by-shark_shrimp-em1t
|
Intuition\n- Create a DP hashmap to store the maximum streak up to the current number and contains the current number (e.g. [2, 4, 16] then dp[16] = 3).\n- For
|
Shark_Shrimp
|
NORMAL
|
2024-10-28T15:45:28.567387+00:00
|
2024-10-28T15:45:28.567422+00:00
| 8 | false |
# Intuition\n- Create a DP hashmap to store the maximum streak up to the current number and contains the current number (e.g. [2, 4, 16] then dp[16] = 3).\n- For any number i, if its square root (sqrt) is already in the hashmap, its hash value will be DP[sqrt] + 1\n- Variable ans to keep track of the max so far.\n\n# Complexity\n- Time complexity:\nO(n)\n- Space complexity:\nO(n)\n# Code\n```python []\nclass Solution(object):\n def longestSquareStreak(self, nums):\n """\n :type nums: List[int]\n :rtype: int\n """\n nums.sort()\n ans = 0\n n = len(nums)\n for i in range(len(nums)):\n sqrt = math.sqrt(nums[i])\n if sqrt in dp:\n dp[nums[i]] = dp[sqrt]+1\n else:\n dp[nums[i]] = 1\n ans = max(ans, dp[nums[i]])\n if ans == 1:\n return -1\n return ans\n```
| 2 | 0 |
['Python']
| 1 |
longest-square-streak-in-an-array
|
Simple Approach - Beats 94.59% | Similar to LCS
|
simple-approach-beats-9459-similar-to-lc-h10g
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
user5113m
|
NORMAL
|
2024-10-28T12:39:42.623553+00:00
|
2024-10-28T12:39:42.623575+00:00
| 13 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n\u22C5logm)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def longestSquareStreak(self, nums: List[int]) -> int:\n\n nums_set = set(nums)\n\n Longest_string = 1\n\n for num in nums_set:\n\n square = num**2\n\n l=1\n\n while square in nums_set:\n square=square**2\n l+=1\n \n Longest_string = max(Longest_string,l)\n \n return Longest_string if Longest_string>1 else -1\n \n\n
| 2 | 0 |
['Python3']
| 0 |
longest-square-streak-in-an-array
|
O(N logN) DP + Sorting Solution (C++ code, beats 95%)
|
on-logn-dp-sorting-solution-c-code-beats-ozsp
|
Intuition\nMy first observation was that the order of the numbers in the array doesn\'t matter, since the subsequences are sorted anyways, so we can sort the ar
|
cristi_macovei
|
NORMAL
|
2024-10-28T11:32:47.823082+00:00
|
2024-10-28T11:32:47.823102+00:00
| 80 | false |
# Intuition\nMy first observation was that the order of the numbers in the array doesn\'t matter, since the subsequences are sorted anyways, so we can sort the array however we like.\nAfter we sort the array, all subsequences will be ordered correctly, for example: [**2**, 3, **4**, 6, 8, **16**].\nSo for each number, we can check if it\'s square exists after it in the array and if it does, we should always add it to our sequence.\nAlso another observation is that duplicates don\'t matter, for example if we had two values of 16 in the previous array, it\'s irrelevant which of the two we add to the subsequence.\n\n# Approach\n\nWe have established that for each number, we only need to check if it\'s square exists after it in the array, and duplicates don\'t matter, so it makes the most sense to store this result for every value.\nSince our values are all less than $10^5$, we can use a simple array to store this data. If we had bigger values, we would\'ve needed a hashmap or a similar container structure.\nSo for our dynamic programming we have the following recurrence:\n```\ndp[i] = length of the maximum subsequence that starts with the value i\ndp[i] = 1 + dp[i * i], if (i * i exists in the array)\n\t = 1 , otherwise\n```\nSince $dp[i]$ depends on $dp[i \\cdot i]$, which is always greater, it makes sense to sort the numbers non-increasingly (reverse order), to process the bigger numbers first and for every element $a$ in the array, we already know $dp[a \\cdot a]$.\n\n\n# Complexity\n- Time complexity: $O(n * log(n))$ because of sorting\n\n- Space complexity: \n\t- $O(max\\_value)$ in this approach\n\t- $O(n)$ for the hashmap approach\n\n# Code\n```cpp []\n#include <algorithm>\n#include <vector>\n#include <cstring>\n\nconst int VMAX = 1e5 + 8;\n\nint dp[VMAX];\n\nclass Solution {\n public:\n\tint longestSquareStreak(std::vector<int> &nums)\n\t{\n\t\t// sort in reverse order\n\t\tstd::sort(nums.begin(), nums.end(), std::greater<int>());\n\n\t\t// initialise the dp with zeroes for all values\n\t\tint max = nums[0];\n\t\tmemset(dp, 0, sizeof(int) * (1 + max));\n\n\t\tint ans = 0;\n\t\tfor (int i : nums) {\n\t\t\t// base case is that we can\'t extend the subsequence \n\t\t\tdp[i] = 1;\n\n\t\t\t// check if i * i doesn\'t overflow\n\t\t\t// and if dp[i * i] > 0\n\t\t\t// (ie. i * i exists before the current val)\n\t\t\tif (i <= max / i && dp[i * i] != 0) {\n\t\t\t\tdp[i] = 1 + dp[i * i];\n\t\t\t}\n\n\t\t\t// if we extended the subsequence more than prev. answer\n\t\t\t// update the answer\n\t\t\tif (dp[i] > ans) {\n\t\t\t\tans = dp[i];\n\t\t\t}\n\t\t}\n\n\t\t// if ans is < 2, we have no valid subsequence, so return -1\n\t\tif (ans < 2) {\n\t\t\tans = -1;\n\t\t}\n\t\treturn ans;\n\t}\n};\n```
| 2 | 0 |
['Array', 'Dynamic Programming', 'Sorting', 'C++']
| 0 |
longest-square-streak-in-an-array
|
C++ using array hashing easy to understand
|
c-using-array-hashing-easy-to-understand-45ku
|
Intuition\nOur task is to form a progression where each number is the square of the previous one, we need to find the longest chain of numbers where each elemen
|
sanyammahajan09
|
NORMAL
|
2024-10-28T10:36:19.588384+00:00
|
2024-10-28T10:36:19.588416+00:00
| 10 | false |
# Intuition\nOur task is to form a progression where each number is the square of the previous one, we need to find the longest chain of numbers where each element is the square of the preceding one. A straightforward but inefficient approach would involve looping through the array and, for each number, searching for its square in the remaining array. The longest sequence found this way would be our desired "square streak."\n\nHowever, performing a linear search across the entire array is too slow. To optimize, we can use a boolean array as a presence map, with a fixed size of (10^5) (the maximum possible value). This map allows us to check if an element is present by looking up the corresponding index: if the value is `1`, it\u2019s present; if `0`, it\u2019s absent.\n\nFor each test case, though, a fixed-size array of (10^5) would waste memory. Instead, we can optimize by setting the size of the array to `maxValue + 1`, where `maxValue` is the largest number in `nums`. This way, our presence map only covers the range necessary for each test case, balancing both efficiency and memory usage.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n \n<!-- Describe your approach to solving the problem. -->\n# Complexity\n- Time complexity: `O(N)`\nThe time complexity of the std::max_element function in C++ is `O(N)`\nThe Initialization of vector takes `O(N)`\nThe for loop that itrates over the numbers in nums takes `O(N)`\nFor each number it checks a sequence of squares until either the square reaches the `maxValue` making it `O(1)` making the effective time complexity of the main Loop to be `O(1)*O(N)` which is effectively `O(N)`\nThe overall time complexity becomes `O(N) + O(N) + O(N) + O(N)`\nwhich simplifies to ` O(N)`\n<!-- Add your time complexity here, e.g. $$O(N)$$ -->\n\n- Space complexity: `O(N)`\nLet\'s break down the space complexity for each component in the code:\n**`maxValue`**: This is a single integer, so it requires `O(1)` space.\n**`valuesMap`**: This is a boolean vector of size `maxValue + 1`. If the maximum element in `nums` is N, the vector will have (N + 1) elements, So it requires `O(N)` space.\n**`streak`**: This is also a single integer, so it requires `O(1)` space.\nThe overall time complexity becomes `O(1) + O(N) + O(1)`\nwhich simplifies to ` O(N)`\n<!-- Add your space complexity here, e.g. $$O(N)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int longestSquareStreak(vector<int>& nums) {\n\n int maxValue = *max_element(nums.begin(),nums.end());\n vector<bool>valuesMap(maxValue+1,0);\n\n for(int& num:nums){\n valuesMap[num]=1;\n }\n\n int streak = 0;\n\n for(int& num:nums){\n int curStreak = 0;\n long long cur = num;\n\n while(valuesMap[(int) cur]){\n curStreak++;\n if(cur*cur > maxValue){\n break;\n }\n cur*=cur;\n }\n streak = max(streak,curStreak);\n }\n\n return streak<2?-1:streak;\n }\n};\n```
| 2 | 0 |
['Array', 'Hash Table', 'C++']
| 0 |
longest-square-streak-in-an-array
|
Sort, map setup then check square and calculate result... <<< EASY TO UNDERSTAND >>>
|
sort-map-setup-then-check-square-and-cal-l0u9
|
Intuition\n1. Initially we find square streak in a list of numbers, where each number in a streak is the square of the previous number. \n2. Looking at the prob
|
Yourstruly_priyanshu
|
NORMAL
|
2024-10-28T09:26:09.467131+00:00
|
2024-10-28T09:26:09.467154+00:00
| 6 | false |
# Intuition\n1. Initially we find square streak in a list of numbers, where each number in a streak is the square of the previous number. \n2. Looking at the problem, one might realize that if we can store and reference each square root\'s streak length, we can build up streaks efficiently by iterating over a sorted list of numbers.\n\n# Approach\n1. Sort the Array\n2. Initialize a Map\n3. Iterate Through Numbers\n4. Track the Longest Streak\n\n# Complexity\n- Time complexity:\nO(nlogn)\n\n- Space complexity:\nO(n)\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int longestSquareStreak(vector<int>& nums) {\n map<int, int>a;\n sort(nums.begin(), nums.end());\n int r = -1;\n for(int n: nums) {\n int sq = sqrt(n);\n if(sq*sq == n && a.find(sq)!=a.end()) {\n a[n] = a[sq]+1;\n r = max(r, a[n]);\n } else a[n] = 1;\n }\n return r;\n }\n};\n```
| 2 | 0 |
['Array', 'Hash Table', 'Dynamic Programming', 'Sorting', 'C++']
| 0 |
longest-square-streak-in-an-array
|
Solution using SET | no DP | no two pointer | no sliding window | no hash map
|
solution-using-set-no-dp-no-two-pointer-8q4fz
|
Intuition\n Describe your first thoughts on how to solve this problem. \nTo solve this problem, we need a subsequence in nums where each element (after sorting)
|
skshanthakumar
|
NORMAL
|
2024-10-28T09:20:08.995284+00:00
|
2024-10-28T09:20:08.995317+00:00
| 46 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo solve this problem, we need a subsequence in nums where each element (after sorting) is the square of the previous one. Since sorting removes the need for a specific order, we can convert nums to a set, allowing efficient checks for squared relationships.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. **Set up a Pool**: We start by creating a set from the input list nums. This set, named pool, allows us to check for the presence of elements in constant time, which is efficient for our needs.\n\n2. **Iterate Through Each Element**: For each element in pool, we initiate a local count (localCount) to track the length of the current "square streak" subsequence.\n\n3. **Square Streak Check**:\n\n - We check if the square of the current element exists in pool.\n - If it does, we update the element to its square and increment localCount.\n - This process continues as long as the next square exists in the set, effectively building a chain of elements where each is the square of the previous.\n4. **Update Global Count**: After each subsequence chain ends (i.e., no further squares are found), we compare localCount to a global count, updating it if localCount is greater. This ensures we always have the longest square streak.\n\n5. **Return Result**: If count remains 1 (indicating no valid streak of length at least 2 was found), we return -1. Otherwise, we return count as the length of the longest square streak.\n\nThis approach ensures we efficiently find the longest square streak by leveraging the fast lookup times provided by a set.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity is O(n log n), where \uD835\uDC5B is the number of elements in nums. This complexity arises because:\n- We iterate through each unique element, and in the worst case, we may square each element multiple times, but this is limited to \nlog max(\uD835\uDC5B\uD835\uDC62\uD835\uDC5A\uD835\uDC60) squares, as squaring grows exponentially.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(n) due to storing elements in a set for efficient lookup.\n# Code\n```python3 []\nclass Solution:\n def longestSquareStreak(self, nums: List[int]) -> int:\n pool = set(nums)\n\n count = 1\n for element in pool:\n n = element\n localCount = 1\n while n*n in pool:\n n = n*n\n localCount += 1\n count = max(count, localCount)\n \n return count if count != 1 else -1\n```\n```java []\nclass Solution {\n public int longestSquareStreak(int[] nums) {\n Set<Long> pool = new HashSet<>();\n for (int num : nums) {\n long n = num;\n pool.add(n);\n }\n\n int count = 1;\n for(Long element: pool){\n long n = element;\n int localCount = 1;\n while (pool.contains(n*n)){\n n = n*n;\n localCount++;\n }\n count = Math.max(count, localCount);\n }\n return (count != 1)? count: -1;\n }\n}\n```
| 2 | 0 |
['Ordered Set', 'Python3']
| 1 |
longest-square-streak-in-an-array
|
Daily Problem 28th October | Using DP O(n^2) and HashMap O(n)
|
daily-problem-28th-october-using-dp-on2-3gy5d
|
Using map\n- Time Complexity: O(n)\n- Space Complexity: O(n)\n# Code\ncpp []\nclass Solution {\npublic:\n int longestSquareStreak(vector<int>& arr) {\n
|
kkunal_0919
|
NORMAL
|
2024-10-28T09:05:26.077255+00:00
|
2024-10-28T09:05:26.077295+00:00
| 47 | false |
# Using map\n- **Time Complexity: O(n)**\n- **Space Complexity: O(n)**\n# Code\n```cpp []\nclass Solution {\npublic:\n int longestSquareStreak(vector<int>& arr) {\n int n = arr.size();\n sort(arr.begin(), arr.end());\n int ans = 0;\n map<int, int> m;\n for(auto x : arr) {\n int sq = sqrt(x);\n if(sq * sq == x) {\n // now check if the value is present inside the map or not\n if(m.count(sq)) {\n m[x] = m[sq] + 1;\n } else {\n m[x] = 1;\n }\n } else m[x] = 1;\n }\n\n for(auto x : m) ans = max(x.second, ans);\n return ans == 1 ? -1 : ans;\n }\n};\n```\n\n# Using DP\n- **Time Complexity: O(n*n)**\n- **Space Complexity: O(n)**\n# Code\n```cpp []\nclass Solution {\npublic:\n int longestSquareStreak(vector<int>& arr) {\n int n = arr.size();\n sort(arr.begin(), arr.end());\n // 2 3 4 6 8 16\n // 1 1 2 1 \n int ans = 0;\n vector<int> dp(n + 1, 1);\n dp[0] = 0;\n for(int i = 1;i <= n;i++) {\n for(int j = 1;j < i;j++) {\n if(arr[j - 1] * arr[j - 1] == arr[i - 1]) {\n dp[i] = max(1 + dp[j], dp[i]);\n }\n }\n ans = max(ans, dp[i]);\n }\n // for(auto x: dp) cout << x << " ";\n // cout << endl;\n return ans == 1 ? -1 : ans;\n }\n};\n```
| 2 | 0 |
['Hash Table', 'Dynamic Programming', 'Sorting', 'C++']
| 0 |
longest-square-streak-in-an-array
|
🔥BEATS 💯 % 🎯 |✨SUPER EASY BEGINNERS 👏
|
beats-super-easy-beginners-by-codewithsp-i3pv
|
\n\n\n---\n\n# Intuition\nThe task requires finding the longest sequence of numbers where each number is the square of the previous one. By counting such sequen
|
CodeWithSparsh
|
NORMAL
|
2024-10-28T08:07:47.829499+00:00
|
2024-10-28T08:07:47.829534+00:00
| 17 | false |
\n\n\n---\n\n# Intuition\nThe task requires finding the longest sequence of numbers where each number is the square of the previous one. By counting such sequences for each number in the sorted list, we aim to identify the longest possible streak.\n\n# Approach\n1. **Sort the List**: Sorting `nums` allows binary search to efficiently check for subsequent square values.\n2. **Count Sequence for Each Number**: For each `n` in `nums`, call `getCounts` to calculate the streak length, squaring each time until the squared value is not found in the list.\n3. **Binary Search**: `binarySearch` locates target values within `nums`, optimizing search time with `O(log n)`.\n4. **Result**: Return the maximum count for all numbers or `-1` if no streak exceeds one element.\n\n# Complexity\n- **Time Complexity**: \\(O(n \\log n + n \\log m)\\), where \\(n\\) is the number of elements in `nums` and \\(m\\) is the number of streak elements for each number.\n- **Space Complexity**: \\(O(1)\\), no additional space is used apart from counters.\n\n---\n\n# Code\n\n\n```dart []\nclass Solution {\n int longestSquareStreak(List<int> nums) {\n nums.sort();\n int ans = -1;\n for (int n in nums) {\n int counts = getCounts(n, nums);\n if (counts > 1) {\n ans = max(ans, counts);\n }\n }\n return ans;\n }\n\n int getCounts(int target, List<int> arrays) {\n int found = 1;\n target = target * target;\n while (binarySearch(target, arrays)) {\n found++;\n target = target * target;\n }\n return found;\n }\n\n bool binarySearch(int target, List<int> arrays) {\n int start = 0;\n int end = arrays.length - 1;\n while (start <= end) {\n int mid = start + (end - start) ~/ 2;\n if (arrays[mid] == target) return true;\n if (arrays[mid] > target)\n end = mid - 1;\n else\n start = mid + 1;\n }\n return false;\n }\n}\n```\n\n\n```java []\nimport java.util.Arrays;\n\nclass Solution {\n public int longestSquareStreak(int[] nums) {\n Arrays.sort(nums);\n int ans = -1;\n for (int n : nums) {\n int counts = getCounts(n, nums);\n if (counts > 1) {\n ans = Math.max(ans, counts);\n }\n }\n return ans;\n }\n\n private int getCounts(int target, int[] arrays) {\n int found = 1;\n target *= target;\n while (binarySearch(target, arrays)) {\n found++;\n target *= target;\n }\n return found;\n }\n\n private boolean binarySearch(int target, int[] arrays) {\n int start = 0, end = arrays.length - 1;\n while (start <= end) {\n int mid = start + (end - start) / 2;\n if (arrays[mid] == target) return true;\n if (arrays[mid] > target) end = mid - 1;\n else start = mid + 1;\n }\n return false;\n }\n}\n```\n\n\n```javascript []\nfunction longestSquareStreak(nums) {\n nums.sort((a, b) => a - b);\n let ans = -1;\n for (let n of nums) {\n let counts = getCounts(n, nums);\n if (counts > 1) ans = Math.max(ans, counts);\n }\n return ans;\n}\n\nfunction getCounts(target, arrays) {\n let found = 1;\n target = target * target;\n while (binarySearch(target, arrays)) {\n found++;\n target = target * target;\n }\n return found;\n}\n\nfunction binarySearch(target, arrays) {\n let start = 0, end = arrays.length - 1;\n while (start <= end) {\n let mid = Math.floor((start + end) / 2);\n if (arrays[mid] === target) return true;\n if (arrays[mid] > target) end = mid - 1;\n else start = mid + 1;\n }\n return false;\n}\n```\n\n```python []\nfrom typing import List\n\nclass Solution:\n def longestSquareStreak(self, nums: List[int]) -> int:\n nums.sort()\n ans = -1\n for n in nums:\n counts = self.getCounts(n, nums)\n if counts > 1:\n ans = max(ans, counts)\n return ans\n\n def getCounts(self, target: int, arrays: List[int]) -> int:\n found = 1\n target *= target\n while self.binarySearch(target, arrays):\n found += 1\n target *= target\n return found\n\n def binarySearch(self, target: int, arrays: List[int]) -> bool:\n start, end = 0, len(arrays) - 1\n while start <= end:\n mid = (start + end) // 2\n if arrays[mid] == target:\n return True\n elif arrays[mid] > target:\n end = mid - 1\n else:\n start = mid + 1\n return False\n```\n\n\n```cpp []\n#include <vector>\n#include <algorithm>\n\nclass Solution {\npublic:\n int longestSquareStreak(std::vector<int>& nums) {\n std::sort(nums.begin(), nums.end());\n int ans = -1;\n for (int n : nums) {\n int counts = getCounts(n, nums);\n if (counts > 1) {\n ans = std::max(ans, counts);\n }\n }\n return ans;\n }\n\nprivate:\n int getCounts(int target, const std::vector<int>& arrays) {\n int found = 1;\n target *= target;\n while (binarySearch(target, arrays)) {\n found++;\n target *= target;\n }\n return found;\n }\n\n bool binarySearch(int target, const std::vector<int>& arrays) {\n int start = 0, end = arrays.size() - 1;\n while (start <= end) {\n int mid = start + (end - start) / 2;\n if (arrays[mid] == target) return true;\n if (arrays[mid] > target) end = mid - 1;\n else start = mid + 1;\n }\n return false;\n }\n};\n```\n\n\n```go []\nimport "sort"\n\nfunc longestSquareStreak(nums []int) int {\n sort.Ints(nums)\n ans := -1\n for _, n := range nums {\n counts := getCounts(n, nums)\n if counts > 1 {\n if counts > ans {\n ans = counts\n }\n }\n }\n return ans\n}\n\nfunc getCounts(target int, arrays []int) int {\n found := 1\n target = target * target\n for binarySearch(target, arrays) {\n found++\n target = target * target\n }\n return found\n}\n\nfunc binarySearch(target int, arrays []int) bool {\n start, end := 0, len(arrays)-1\n for start <= end {\n mid := start + (end - start) / 2\n if arrays[mid] == target {\n return true\n }\n if arrays[mid] > target {\n end = mid - 1\n } else {\n start = mid + 1\n }\n }\n return false\n}\n```\n {:style=\'width:250px\'}
| 2 | 0 |
['Array', 'C', 'Sorting', 'C++', 'Java', 'Go', 'Python3', 'JavaScript', 'Dart']
| 0 |
longest-square-streak-in-an-array
|
Basic Solution Time Complexity: O(Nlogn)
|
basic-solution-time-complexity-onlogn-by-u72v
|
Code\npython3 []\nimport math\nclass Solution:\n def longestSquareStreak(self, num: List[int]) -> int:\n nums = list(set(num))\n result = []\n
|
NurzhanSultanov
|
NORMAL
|
2024-10-28T07:42:46.695041+00:00
|
2024-10-28T07:42:46.695084+00:00
| 56 | false |
# Code\n```python3 []\nimport math\nclass Solution:\n def longestSquareStreak(self, num: List[int]) -> int:\n nums = list(set(num))\n result = []\n for i in nums:\n if i == math.isqrt(i) ** 2:\n result.append(i)\n total = 0\n nums.sort()\n num.sort()\n result.sort()\n for i in range(len(num)):\n curr = result[:]\n temp = num[i]\n length = [temp]\n while curr:\n if curr[0] == temp * temp:\n length.append(curr.pop(0))\n temp = length[-1]\n else:\n curr.pop(0)\n if len(length) > 1:\n total = max(total, len(length))\n return total if total > 0 else -1\n\n```
| 2 | 0 |
['Python3']
| 1 |
longest-square-streak-in-an-array
|
💡 C++ | O(nLogn) | Beginner Solution | Simple Logic | With Full Explanation ✏️
|
c-onlogn-beginner-solution-simple-logic-lh44f
|
Intuition\nTo find the longest streak where each number can be squared to get the next number in the sequence, we can leverage a sorted list and a hash map. The
|
Tusharr2004
|
NORMAL
|
2024-10-28T07:36:16.660479+00:00
|
2024-10-28T07:36:16.660501+00:00
| 8 | false |
# Intuition\nTo find the longest streak where each number can be squared to get the next number in the sequence, we can leverage a sorted list and a hash map. The sorted list allows us to start with the smallest numbers and try to build streaks by squaring them. Using a hash map for quick lookups ensures that we can efficiently check if the squared result exists in `nums`.\n\n# Approach\n1. **Sort the Array:** Sorting helps us to process numbers from smallest to largest, making it easier to find streaks that start with the smallest base number.\n\n2. **Store Frequencies in Hash Map:** Use a hash map (`mpp`) to store the frequency of each element in nums. This allows constant-time lookups to check if a squared number exists in the original array.\n\n3. **Iterate through Each Element:** For each number in the sorted nums array, treat it as the starting point of a potential square streak.\n\n - Initialize a counter (`cnt`) to keep track of the streak length.\n - Use a loop to repeatedly square the current number. If the squared value exists in `mpp`, increment the streak count (`cnt`). If the squared number is not found in the hash map, the streak ends for this starting point.\n4. Update the Longest Streak: After ending each streak, update `ans` with the maximum streak length encountered.\n\n5. Return the Result: After processing all elements, `ans` holds the longest streak length where each number in the streak can be squared to get the next. If no valid streak was found, `ans` will return -1.\n\n# Complexity\n- Time complexity:\n```O(nLogn)```\n\n- Space complexity:\n```O(n)```\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int longestSquareStreak(vector<int>& nums) {\n int ans = -1; // Variable to store the maximum streak length\n unordered_map<int, int> mpp; // Hash map to count occurrences \n sort(nums.begin(), nums.end()); \n for (int i : nums) {\n mpp[i]++;\n }\n for (int i = 0; i < nums.size(); i++) {\n long num = nums.at(i);\n int cnt = 0; // Variable to count the streak length \n // Continue multiplying num by itself until it exceeds the largest number in nums\n while (num <= nums.at(nums.size() - 1)) {\n num *= num; \n \n // If the squared value is not found in the map, break the streak\n if (mpp[num] == 0) {\n if (cnt != 0) { // Update ans if a streak has been counted\n cnt++; // Increment the streak count for the current number\n ans = max(ans, cnt); // Update the max streak length\n }\n break; \n } else {\n cnt++; // Increment the streak count if squared value exists in the map\n }\n }\n }\n \n return ans; \n }\n};\n\n```\n\n\n\n\n\n# Ask any doubt !!!\nReach out to me \uD83D\uDE0A\uD83D\uDC47\n\uD83D\uDD17 https://tushar-bhardwaj.vercel.app/
| 2 | 0 |
['C++']
| 0 |
longest-square-streak-in-an-array
|
Easy solution using Hash Table for "Longest Square Streak in Array"
|
easy-solution-using-hash-table-for-longe-92io
|
\n# Longest Square Streak Problem\n\n## Intuition\nTo solve this problem, we aim to find the longest sequence of numbers where each successive number in the seq
|
shivam_1817
|
NORMAL
|
2024-10-28T07:02:42.502416+00:00
|
2024-10-28T07:02:42.502443+00:00
| 37 | false |
\n# Longest Square Streak Problem\n\n## Intuition\nTo solve this problem, we aim to find the longest sequence of numbers where each successive number in the sequence is the square of the previous one. Observing that the numbers need to be sorted and processed only when they fit within bounds provides an efficient way to handle the problem. We keep track of counts using a hash table to facilitate easy access and counting of each number.\n\n## Approach\n1. **Sorting**: Start by sorting the array, which ensures that each number is processed in increasing order.\n2. **Hash Table for Frequency**: Store the frequency of each number in a hash table to track each occurrence and allow marking numbers as used without additional data structures.\n3. **Iterate and Count Streaks**: For each number in the sorted list:\n - Initialize a count for the streak (`ans`), starting with the current number.\n - Follow the sequence by continually squaring the current number and checking if it exists in the hash table and falls within bounds.\n - Continue until the squared number exceeds the limit or is unavailable.\n4. **Update Maximum Streak**: Track the longest streak found and return it if it\u2019s greater than 1; otherwise, return -1.\n\n## Complexity\n\n- **Time Complexity**: \n $$O(n \\log n)$$ due to sorting, where $$n$$ is the number of elements in `nums`.\n \n- **Space Complexity**: \n $$O(n)$$ for storing the hash table of frequencies.\n\n## Code\n```cpp\nclass Solution {\npublic:\n int longestSquareStreak(vector<int>& nums) {\n sort(nums.begin(), nums.end());\n int hash[100001] = {0};\n \n for (int i = 0; i < nums.size(); i++) {\n hash[nums[i]]++;\n }\n \n int cnt = 0;\n \n for (int i = 0; i < nums.size(); i++) {\n int current = nums[i];\n int temp = 0;\n \n while (current <= 100000 && hash[current] > 0) {\n temp++;\n hash[current]--;\n \n long long nextSquare = (long long)current * current;\n if (nextSquare > 100000) break;\n \n current = nextSquare;\n }\n \n cnt = max(cnt, temp);\n }\n \n return (cnt > 1 ? cnt : -1);\n }\n};\n```\n
| 2 | 0 |
['Array', 'Hash Table', 'Sorting', 'C++']
| 2 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.