question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
sum-of-beauty-in-the-array
|
Python3 | Brute Force (TLE) and O(n) solution with explanation | 86%ile runtime
|
python3-brute-force-tle-and-on-solution-i0kqx
|
Here is how I arrived at the solution to this problem:\n\n## Attempt #1 - Brute Force:\nEssentially the idea here is to compute the rolling maximum and minimum
|
aaditya47
|
NORMAL
|
2021-09-21T16:41:53.244148+00:00
|
2021-09-22T03:00:53.953431+00:00
| 170 | false |
Here is how I arrived at the solution to this problem:\n\n## Attempt #1 - Brute Force:\nEssentially the idea here is to compute the rolling maximum and minimum values in every iteration inside the ```for``` loop.\n\nBelow is the implementation of the above stated approach:\n```\nclass Solution:\n def sumOfBeauties(self, nums: List[int]) -> int:\n beauty=[0]*len(nums)\n for i in range(1,len(nums)-1):\n leftarr=nums[:i]\n rightarr=nums[i+1:]\n if(max(leftarr)<nums[i] and min(rightarr)>nums[i]):\n beauty[i]=2\n elif(nums[i-1]<nums[i] and nums[i+1]>nums[i]):\n beauty[i]=1\n else:\n beauty[i]=0\n return sum(beauty)\n```\n\nAs expected, this solution TLEd.\n\n## Attempt #2 - Optimized approach:\n\nEssentially what you need to do is use 2 arrays: ```left``` and ```right```.\n\n```left``` is used to store maximum value of the array in the domain ```[0,k)``` where k is any index of the array, the first element of which is initialized as ```a[0]```, the first element of the array.\n\n```right``` is used to store minimum value of the array in the domain ```[k+1,len(arr))``` where k is any index of the array, the last element of which is initialized as ```a[-1]```, the first element of the array.\n\nPre-computation of these values brings down the time complexity of the program from ```O(n**2)``` to ```O(n)``` because it helps us avoid computing the rolling maximum and minimum in every iteration.\n\nBelow is the implementation of the above stated approach:\n```\nclass Solution:\n def sumOfBeauties(self, a: List[int]) -> int:\n temp,temp2=a[0],a[-1]\n left=([a[0]]+[0]*(len(a)-1))\n right=[0]*(len(a)-1) + [a[-1]]\n for i in range(1,len(a)):\n left[i]=max(a[i-1],temp)\n temp=left[i]\n for i in range(len(a)-2,-1,-1):\n right[i]=min(a[i+1],temp2)\n temp2=right[i]\n res=0\n for i in range(1,len(a)-1):\n if(a[i]>left[i] and a[i]<right[i]):\n res+=2\n elif(a[i]>a[i-1] and a[i]<a[i+1]):\n res+=1\n return res\n```
| 1 | 0 |
['Python3']
| 0 |
sum-of-beauty-in-the-array
|
[C++] Clean & concise solution with detailed explaination !
|
c-clean-concise-solution-with-detailed-e-0jrf
|
Solution\nTo check if nums[j] < nums[i] < nums[k], for all 0 <= j < i and for all i < k <= nums.length - 1 in O(1) we will build two arrays : max and min. \nma
|
thodung
|
NORMAL
|
2021-09-19T18:03:44.716938+00:00
|
2021-09-20T13:19:50.612672+00:00
| 61 | false |
* **Solution**\nTo check if nums[j] < nums[i] < nums[k], for all 0 <= j < i and for all i < k <= nums.length - 1 in O(1) we will build two arrays : max and min. \nmax[i] = max value from 0 to i\nmin[i] = min value from i to n-1\nTherefore when we calculate the beauty of the nums[i] we can easily check\n if (nums[i]>max[i-1] && nums[i]<min[i+1]) then we add 2 to the result\n else if (nums[i]>nums[i-1] && nums[i]<nums[i+1]) then we add 1 to the result.\n \n* **Time Complexity**\nWe just go through the nums array so the time complexity is **O(n)**.\n\n* **Space Complexity**\nBecause we just use two array min and max to store min and max value so the space complexity is **O(n)**.\n\n* **Source Code**\n\n```\nclass Solution {\npublic:\n int sumOfBeauties(vector<int>& nums) {\n int n = nums.size();\n int max[n];\n int min[n];\n \n //max[i] = max value from 0 to i\n //min[i] = min value from i to n-1\n \n max[0] = nums[0];\n min[n-1] = nums[n-1];\n \n //build max array\n for (int i=1;i<n;++i) {\n if (nums[i]>max[i-1]) max[i]=nums[i];\n else max[i] = max[i-1];\n } \n \n //build min array\n for (int i=n-2;i>=0;--i) {\n if (nums[i]<min[i+1]) min[i]=nums[i];\n else min[i] = min[i+1];\n }\n \n int res = 0;\n \n //calculate the result\n for (int i=1;i<n-1;++i) {\n if (nums[i]>max[i-1] && nums[i]<min[i+1]) res +=2 ;\n else if (nums[i]>nums[i-1] && nums[i]<nums[i+1]) ++res;\n }\n return res;\n }\n};\n```
| 1 | 0 |
[]
| 0 |
sum-of-beauty-in-the-array
|
C solution
|
c-solution-by-stanley_wu_ntu-dnh8
|
\nint sumOfBeauties(int* nums, int numsSize){\n int sum = 0;\n int pre_max = nums[0];\n int suf_min = nums[numsSize-1];\n int* pre = (int*)malloc(si
|
stanley_wu_ntu
|
NORMAL
|
2021-09-19T15:33:49.805161+00:00
|
2021-09-19T15:33:49.805197+00:00
| 64 | false |
```\nint sumOfBeauties(int* nums, int numsSize){\n int sum = 0;\n int pre_max = nums[0];\n int suf_min = nums[numsSize-1];\n int* pre = (int*)malloc(sizeof(int)*numsSize);\n int* suf = (int*)malloc(sizeof(int)*numsSize);\n for(int i = 0 ; i < numsSize; i++){\n if(nums[i] > pre_max){\n pre_max = nums[i];\n }\n pre[i] = pre_max;\n }\n for(int i = numsSize - 1 ; i >= 0 ; i--){\n if(nums[i] < suf_min){\n suf_min = nums[i];\n }\n suf[i] = suf_min;\n }\n for(int i = 1; i <= numsSize - 2; i++){\n if(nums[i] > pre[i-1] && nums[i] < suf[i+1])sum+=2;\n else if(nums[i] > nums[i-1] && nums[i+1] > nums[i])sum+=1;\n }\n return sum;\n}\n```
| 1 | 0 |
['C']
| 0 |
sum-of-beauty-in-the-array
|
Simple Hashmap Solution
|
simple-hashmap-solution-by-abhishek_triv-7zfh
|
class Solution {\npublic:\n int sumOfBeauties(vector& nums) {\n \n mapmp,cp;\n int n=nums.size();\n int ans=0;\n for(int i=0;
|
abhishek_trivedi
|
NORMAL
|
2021-09-19T14:49:12.417690+00:00
|
2021-09-19T14:49:12.417806+00:00
| 64 | false |
class Solution {\npublic:\n int sumOfBeauties(vector<int>& nums) {\n \n map<int,int>mp,cp;\n int n=nums.size();\n int ans=0;\n for(int i=0;i<nums.size();i++)\n {\n cp[nums[i]]++;\n }\n cp[nums[0]]--;\n if(cp[nums[0]]==0)\n cp.erase(nums[0]);\n mp[nums[0]]++;\n for(int i=1;i<n-1;i++)\n { \n \n cp[nums[i]]--;\n if(cp[nums[i]]==0)\n cp.erase(nums[i]);\n auto j=*mp.rbegin();\n auto y=*cp.begin();\n if(y.first>nums[i] && j.first<nums[i])\n {\n ans+=2;\n \n }\n else if(nums[i]>nums[i-1] && nums[i]<nums[i+1])\n {\n ans+=1;\n }\n mp[nums[i]]++;\n \n }\n return ans;\n \n }\n};\n//Time Complexity-> Nlog(N)\n// Space Complexity->O(N)
| 1 | 0 |
[]
| 0 |
sum-of-beauty-in-the-array
|
100% java O(n) solution | easy understand
|
100-java-on-solution-easy-understand-by-ex0li
|
Explanation:\nFor condition1, we need to prepare two array which indicates the left max element and right minimum element. To generate this two array we will co
|
ly2015cntj
|
NORMAL
|
2021-09-19T10:04:30.906328+00:00
|
2021-09-19T10:04:30.906360+00:00
| 159 | false |
Explanation:\nFor condition1, we need to prepare two array which indicates the left max element and right minimum element. To generate this two array we will cost O(n) complexity.\nThen we just need one loop to get answer.\nHope it helps :)\n\n```java\n// AC: Runtime: 4 ms, faster than 100.00% of Java online submissions for Sum of Beauty in the Array.\n// Memory Usage: 55.5 MB, less than 83.33% of Java online submissions for Sum of Beauty in the Array.\n// .\n// T:O(n), S:O(n)\n// \nclass Solution {\n public int sumOfBeauties(int[] nums) {\n int size = nums.length, ret = 0;\n int[] leftMax = new int[size], rightMin = new int[size];\n int curLeftMax = nums[0];\n for (int i = 1; i < size; i++) {\n leftMax[i] = curLeftMax;\n if (nums[i] > curLeftMax) {\n curLeftMax = nums[i];\n }\n }\n int curRightMin = nums[size - 1];\n for (int i = size - 2; i >= 0; i--) {\n rightMin[i] = curRightMin;\n if (nums[i] < curRightMin) {\n curRightMin = nums[i];\n }\n }\n\n for (int i = 1; i < size - 1; i++) {\n if (nums[i] > leftMax[i] && nums[i] < rightMin[i]) {\n ret += 2;\n } else if (nums[i] > nums[i - 1] && nums[i] < nums[i + 1]) {\n ret += 1;\n }\n }\n\n return ret;\n }\n}\n```
| 1 | 0 |
['Array', 'Java']
| 0 |
sum-of-beauty-in-the-array
|
Simple easy to understand Java solution using PriorityQueue | Java
|
simple-easy-to-understand-java-solution-y4czi
|
\tclass Solution {\n\t\tpublic int sumOfBeauties(int[] nums) {\n\n\t\t\tint n = nums.length; //length of nums array\n\n\t\t\tPriorit
|
Seeker_108
|
NORMAL
|
2021-09-19T08:53:02.257687+00:00
|
2021-09-19T15:22:05.747358+00:00
| 44 | false |
\tclass Solution {\n\t\tpublic int sumOfBeauties(int[] nums) {\n\n\t\t\tint n = nums.length; //length of nums array\n\n\t\t\tPriorityQueue<Integer> left = new PriorityQueue<>(Comparator.reverseOrder()); //max heap\n\t\t\tPriorityQueue<Integer> right = new PriorityQueue<>(); //min heap\n\n\t\t\tleft.offer(nums[0]);\n\t\t\tfor(int i = 1; i < n; ++i) {\n\t\t\t\tright.offer(nums[i]);\n\t\t\t}\n\n\t\t\tHashSet<Integer> indices = new HashSet<>();\n\t\t\tint count = 0;\n\t\t\tfor(int i = 1; i < n - 1; ++i) {\n\t\t\t\tint leftTop = left.peek();\n\t\t\t\tleft.offer(nums[i]);\n\t\t\t\tright.poll();\n\n\t\t\t\tif(nums[i] > leftTop && nums[i] < right.peek()) {\n\t\t\t\t\tcount++;\n\t\t\t\t\tindices.add(i);\n\t\t\t\t}\n\t\t\t}\n\t\t\tint beauty = 2 * count; //beauty for each index that satifies the first conditon is 2\n\t\t\tfor(int i = 1; i < n - 1; ++i) {\n\t\t\t\tif(nums[i] > nums[i - 1] && nums[i] < nums[i + 1] && !indices.contains(i)) {\n\t\t\t\t\tbeauty++;\n\t\t\t\t}\n\t\t\t}\n\t\t\treturn beauty;\n\t\t}\n\t}
| 1 | 0 |
[]
| 1 |
sum-of-beauty-in-the-array
|
Java | 0(n)| 100% faster
|
java-0n-100-faster-by-anupam92402-pqs3
|
The logic behind is that we are maintaining two arrays leftmax and rightmin . leftmax array will store the max value for each index i from 0 to i-1 (both includ
|
anupam92402
|
NORMAL
|
2021-09-19T06:27:57.869279+00:00
|
2021-10-08T05:55:34.869333+00:00
| 76 | false |
The logic behind is that we are maintaining two arrays leftmax and rightmin . leftmax array will store the max value for each index i from 0 to i-1 (both included). Moreover, rightmin array will store the min value for each index i from i+1 to n (both included).We will traverse the array from 1<=i<= N -2, since 0 and last index will never contribute to answer.If the value at index i lies in the middle of its adjecent indexes ( ie nums[i-1]<nums[i]<nums[i+1] ) then we will increment the value of beauty by 1.\nAlso , if it is greater than leftmax[i] and rightmin[i] we will increment the value of beauty by 1.\n\nTime Complexity (TC) - 0(n)\nSpace Complexity (SC) - 0(n)\n\n**Better Approach:-** You can keep a variable leftmax instead of array.So, it can be done using one extra array only,instead of two.\n\n\'\'\'\n\n\tpublic int sumOfBeauties(int[] nums) {\n int[] leftmax = new int[nums.length];\n\t\tint max = nums[0];\n\t\tfor (int i = 1; i < nums.length-1; i++) {\n\t\t\tleftmax[i] = max;\n\t\t\tmax = Math.max(max, nums[i]);\n\t\t}*\n\n\t\tint[] rightmin = new int[nums.length];\n\t\tmax = nums[nums.length - 1];\n\t\tfor (int i = nums.length - 2; i >= 1; i--) {\n\t\t\trightmin[i] = max;\n\t\t\tmax = Math.min(max, nums[i]);\n\t\t}\n\n\t\tint beauty = 0;\n\n\t\tfor (int i = 1; i < nums.length - 1; i++) {\n\t\t\tif (nums[i] > nums[i - 1] && nums[i] < nums[i + 1]) {\n\t\t\t\tbeauty++;\n\t\t\t\tif (nums[i] > leftmax[i] && nums[i] < rightmin[i]) {\n\t\t\t\t\tbeauty++;\n\t\t\t\t}\n\t\t\t}\n\t\t}\n\t\treturn beauty;\n }\n\t\n\t\n\t
| 1 | 1 |
['Java']
| 0 |
sum-of-beauty-in-the-array
|
[C++] Simple Solution | Logic Explained
|
c-simple-solution-logic-explained-by-the-zmqk
|
During the contest I completely missed the point -> 2, if nums[j] < nums[i] < nums[k], for all 0 <= j < i and for all i < k <= nums.length - 1. i.e. I did not c
|
theGateway
|
NORMAL
|
2021-09-19T05:57:42.786511+00:00
|
2021-09-19T05:57:55.828452+00:00
| 75 | false |
During the contest I completely missed the point -> 2, if nums[j] < nums[i] < nums[k], for all 0 <= j < i and for all **i < k <= nums.length - 1.** i.e. I did not check whether the current element is the minimum element among the elements on its right.\n```\nint sumOfBeauties(vector<int>& a) {\n int n= a.size();\n //This vector will store the minimum element on right side of current element, now the current element could also be the minimum when compared to right side of it, so min(nums[i], minRight[i+1])\n vector<int> minRight(n,0);\n minRight[n-1] = a[n-1];\n \n for(int i=n-2; i>=0; i--){\n minRight[i] = min(a[i], minRight[i+1]);\n }\n //Now for beauty == 2, we need to check whether the current element is maximum element among the elements on its left, no need of seperate array for that, it can be maintained as we traverse through te array.\n int maxLeft = a[0], res = 0;\n for(int i=1; i<n-1; i++){\n if(a[i] > maxLeft && a[i] < minRight[i+1]) res += 2;\n else if(a[i] > a[i-1] && a[i] < a[i+1]) res += 1;\n maxLeft = max(a[i], maxLeft);\n }\n \n return res;\n }\n```
| 1 | 0 |
['C', 'C++']
| 0 |
sum-of-beauty-in-the-array
|
C++ , maps , priority queue .
|
c-maps-priority-queue-by-imvoldemort-rqr9
|
\nclass Solution {\npublic:\n int sumOfBeauties(vector<int>& nums) {\n priority_queue<int, vector<int>, \n greater<int> > ran;\n
|
imvoldemort
|
NORMAL
|
2021-09-19T05:44:21.073301+00:00
|
2021-09-19T05:44:21.073343+00:00
| 47 | false |
```\nclass Solution {\npublic:\n int sumOfBeauties(vector<int>& nums) {\n priority_queue<int, vector<int>, \n greater<int> > ran;\n map<int,int> mp;\n for(int i=0;i!=nums.size();i++) {int a=nums[i]; if(i!=0) {ran.push(a);if(mp.find(a)==mp.end()) mp.insert(pair<int,int>(a,1));else{mp[a]++;}} else{ if(mp.find(a)==mp.end()) mp.insert(pair<int,int>(a,0));}}\n \n int mx=nums[0];int min=0;int sum=0;\n for(int i=1;i!=nums.size()-1;i++){\n mp[nums[i]]--;\n while(mp[ran.top()]==0) ran.pop();\n if(nums[i]>mx&&nums[i]<ran.top()){\n sum+=2;\n mx=max(mx,nums[i]);\n \n }\n else{\n \n if(nums[i]>mx) mx=nums[i];\n if(nums[i]>nums[i-1]&&nums[i]<nums[i+1]) sum++;\n }\n }\n return sum;\n }\n};\n```
| 1 | 0 |
[]
| 0 |
sum-of-beauty-in-the-array
|
C++||O(n)||Prefix and Suffix arrays|| Detailed Explaination
|
conprefix-and-suffix-arrays-detailed-exp-abuv
|
Please upvote if found helpful\n\nIdea is simple, just maintain the prefixMax array and SuffixMix array which will store the maximum element in the range [0,i-1
|
notacodinggeek
|
NORMAL
|
2021-09-19T04:55:17.929263+00:00
|
2021-09-19T04:55:17.929291+00:00
| 69 | false |
**Please upvote if found helpful**\n\nIdea is simple, just maintain the prefixMax array and SuffixMix array which will store the maximum element in the range [0,i-1] and minimum element in the range [i+1,n-1] respectively.\nIf nums[i]>prefixMax[i] it implies its greater than all the elements to its left and if nums[i]<suffixMin[i] it implies its less than all the elemnts to its right. If this condition doesn\'t get satisfied then we\'ll check if nums[i-1]<nums[i]<nums[i+1] and increment the answer accordingly.\n```\nclass Solution {\npublic:\n int sumOfBeauties(vector<int>& nums) {\n int n=nums.size();\n vector<int> prefixMax(n);\n vector<int> suffixMin(n);\n prefixMax[0]=INT_MIN;\n suffixMin[n-1]=INT_MAX;\n int ans=0;\n \n for(int i=1;i<n;i++) prefixMax[i]=max(prefixMax[i-1],nums[i-1]);\n for(int i=n-2;i>=0;i--) suffixMin[i]=min(suffixMin[i+1],nums[i+1]);\n \n for(int i=1;i<n-1;i++){\n if(nums[i]>prefixMax[i]&&nums[i]<suffixMin[i]) ans+=2;\n else if(nums[i]>nums[i-1]&&nums[i]<nums[i+1]) ans+=1;\n }\n \n return ans;\n \n }\n};\n```
| 1 | 0 |
[]
| 0 |
sum-of-beauty-in-the-array
|
C++ | easy| with explanation
|
c-easy-with-explanation-by-aman282571-i44b
|
To calculate beauty for each index i (1 <= i <= nums.length - 2) \n1. For checking first condition we want max from 0 to i-1 and min of i+1 to nums.length - 1.
|
aman282571
|
NORMAL
|
2021-09-19T04:32:54.860484+00:00
|
2021-09-19T04:32:54.860522+00:00
| 104 | false |
To calculate beauty for each index i (1 <= i <= nums.length - 2) \n1. For checking first condition we want max from 0 to i-1 and min of i+1 to nums.length - 1. To calculate this precompute min backwards. And we will find max from left as we iterate.\n2. If first condition is false then we calculate 2nd condition which is straight forward.\n**Time-O(n)\nSpace:-O(n)**\n\n```\nclass Solution {\npublic:\n int sumOfBeauties(vector<int>& nums) {\n int ans=0,size=nums.size(),left_max=nums[0];\n vector<int>right(size,0);\n int mini=nums[size-1];\n for(int i=size-1;i>=0;i--)\n {\n right[i]=mini;\n mini=min(mini,nums[i]);\n }\n for(int i=1;i<size-1;i++)\n {\n if(nums[i]>left_max && nums[i]<right[i])\n ans+=2;\n else if(nums[i]>nums[i-1] && nums[i]<nums[i+1])\n ans+=1;\n left_max=max(left_max,nums[i]);\n }\n return ans;\n }\n};\n```\nDo **UPVOTE** if it helps :)
| 1 | 0 |
['C']
| 0 |
sum-of-beauty-in-the-array
|
Swift solution
|
swift-solution-by-yamironov-dncz
|
Swift solution\n\nclass Solution {\n func sumOfBeauties(_ nums: [Int]) -> Int {\n let n = nums.count\n guard n > 2 else { return 0 }\n v
|
yamironov
|
NORMAL
|
2021-09-19T04:13:22.686715+00:00
|
2021-09-19T04:13:22.686752+00:00
| 75 | false |
Swift solution\n```\nclass Solution {\n func sumOfBeauties(_ nums: [Int]) -> Int {\n let n = nums.count\n guard n > 2 else { return 0 }\n var preMax = nums, postMin = nums, result = 0\n for i in 1..<n {\n preMax[i] = max(preMax[i], preMax[i - 1])\n postMin[n - 1 - i] = min(postMin[n - 1 - i], postMin[n - i])\n }\n for i in 1..<(n - 1) {\n if nums[i] > preMax[i - 1] && nums[i] < postMin[i + 1] {\n result += 2\n } else if nums[i] > nums[i - 1] && nums[i] < nums[i + 1] {\n result += 1\n }\n }\n return result\n }\n}\n```
| 1 | 0 |
['Swift']
| 0 |
sum-of-beauty-in-the-array
|
[Python3] Beats 100% Solution
|
python3-beats-100-solution-by-leefycode-jxxj
|
python\nclass Solution:\n def sumOfBeauties(self, nums: List[int]) -> int:\n n = len(nums)\n ans = 0\n maxPre = nums[0]\n minNums
|
leefycode
|
NORMAL
|
2021-09-19T04:09:08.134456+00:00
|
2021-09-19T04:10:26.536688+00:00
| 97 | false |
```python\nclass Solution:\n def sumOfBeauties(self, nums: List[int]) -> int:\n n = len(nums)\n ans = 0\n maxPre = nums[0]\n minNums = nums[-1]\n minPost = [0]*(n-1)\n for i in range(n-2, 0, -1):\n minPost[i] = minNums\n if nums[i] < minNums:\n minNums = nums[i]\n for i in range(1, n-1):\n if nums[i] > maxPre and nums[i] < minPost[i]:\n ans += 2\n elif nums[i] > nums[i-1] and nums[i] < nums[i+1]:\n ans += 1\n if nums[i] > maxPre:\n maxPre = nums[i]\n return ans\n```\n\n\n
| 1 | 1 |
['Python3']
| 0 |
sum-of-beauty-in-the-array
|
Python [max/min heap]
|
python-maxmin-heap-by-gsan-4q7o
|
Max heap for left hand side.\nMin heap for right hand side. Also pop lazily.\n\nTime: O(N logN)\nSpace: O(N)\n\npython\nclass Solution:\n def sumOfBeauties(s
|
gsan
|
NORMAL
|
2021-09-19T04:07:13.974283+00:00
|
2021-09-19T04:07:13.974310+00:00
| 135 | false |
Max heap for left hand side.\nMin heap for right hand side. Also pop lazily.\n\nTime: `O(N logN)`\nSpace: `O(N)`\n\n```python\nclass Solution:\n def sumOfBeauties(self, A):\n if len(A) <= 2: return 0\n \n # max heap for left side\n max_heap = []\n heapq.heappush(max_heap, -A[0])\n \n #lazy min heap for right side\n #so you also need to keep track of counts\n min_heap = []\n counts = collections.defaultdict(int)\n for i in range(2, len(A)):\n heapq.heappush(min_heap, A[i])\n \n ans = 0\n for i in range(1, len(A) - 1):\n if -max_heap[0] < A[i] < min_heap[0]:\n ans += 2\n elif A[i - 1] < A[i] < A[i + 1]:\n ans += 1\n \n #left side\n heapq.heappush(max_heap, -A[i])\n \n #right side\n counts[A[i + 1]] += 1\n while min_heap and counts[min_heap[0]] > 0:\n counts[min_heap[0]] -= 1\n heapq.heappop(min_heap)\n \n return ans\n```
| 1 | 0 |
[]
| 0 |
sum-of-beauty-in-the-array
|
C# O(n)
|
c-on-by-shockho-ix45
|
```\npublic class Solution {\n public int SumOfBeauties(int[] nums) {\n int res = 0;\n int size = nums.Length;\n \n int[] minRigh
|
shockho
|
NORMAL
|
2021-09-19T04:04:22.603619+00:00
|
2021-09-19T04:04:46.683945+00:00
| 82 | false |
```\npublic class Solution {\n public int SumOfBeauties(int[] nums) {\n int res = 0;\n int size = nums.Length;\n \n int[] minRight = new int[size];\n minRight[size-1] = nums[size-1];\n for(int i = size-2; i >= 0 ; i--)\n {\n minRight[i] = Math.Min(minRight[i+1],nums[i] );\n }\n int[] maxLeft = new int[size];\n maxLeft[0] = nums[0];\n for(int i = 1; i < size; i ++)\n {\n maxLeft[i] = Math.Max(maxLeft[i-1], nums[i]);\n }\n \n int index= 1;\n while(index < size-1)\n {\n if(maxLeft[index-1]<nums[index] && minRight[index+1]>nums[index])\n res+=2;\n else if(nums[index-1]<nums[index] && nums[index]<nums[index+1])\n res+=1;\n index++;\n }\n \n \n return res;\n }\n}
| 1 | 0 |
[]
| 0 |
sum-of-beauty-in-the-array
|
O(n) | Using Max and Min so-far
|
on-using-max-and-min-so-far-by-shreyansh-n2ml
|
\nclass Solution {\n public int sumOfBeauties(int[] nums) {\n int n = nums.length;\n \n // We can use a boolean array instead.\n
|
shreyansh94
|
NORMAL
|
2021-09-19T04:03:04.975301+00:00
|
2021-09-19T04:03:04.975352+00:00
| 156 | false |
```\nclass Solution {\n public int sumOfBeauties(int[] nums) {\n int n = nums.length;\n \n // We can use a boolean array instead.\n int[] lr = new int[n];\n int[] rl = new int[n];\n int max = nums[0];\n int min = nums[n-1];\n \n // If the i-th element is max so far, all the elements before it are smaller than i-th element.\n for(int i = 1; i <= n - 2; ++i){\n if(nums[i] > max) {\n lr[i] = 1;\n max = nums[i];\n }\n }\n \n // If the i-th element is min so far, all the elements after it are bigger than i-th element.\n for(int i = n-2; i >= 1; --i){\n if(nums[i] < min) {\n rl[i] = 1;\n min = nums[i];\n }\n }\n // Stores the beauty count.\n int b = 0;\n for(int i = 1; i <= n-2; ++i) {\n if(lr[i] == 1 && rl[i] == 1) b+=2;\n else if(nums[i-1] < nums[i] && nums[i] < nums[i+1]) b+=1;\n }\n return b;\n }\n}\n```
| 1 | 0 |
['Java']
| 0 |
sum-of-beauty-in-the-array
|
Prefix Sum Concept.
|
prefix-sum-concept-by-harshilnavinpatel-ikba
|
Code
|
harshilnavinpatel
|
NORMAL
|
2025-04-05T07:21:23.139428+00:00
|
2025-04-05T07:21:23.139428+00:00
| 2 | false |
# Code
```cpp []
class Solution {
public:
int sumOfBeauties(vector<int>& nums) {
int n = nums.size() ;
vector <int> prevlargest(n,0) ;
prevlargest[0] = -1;
for (int i=1; i<n; i++) {
prevlargest[i] = max(prevlargest[i-1], nums[i-1]) ;
}
vector <int> nextsmallest(n,0) ;
nextsmallest[n-1] = INT_MAX;
for (int i=n-2; i>=0; i--) {
nextsmallest[i] = min(nextsmallest[i+1], nums[i+1]) ;
}
vector <int> beauty(n,0) ;
for (int i=1; i<n-1; i++) {
if (prevlargest[i] < nums[i] && nums[i] < nextsmallest[i]) {
beauty[i] = 2;
}
else if (nums[i-1]<nums[i] && nums[i]<nums[i+1]) {
beauty[i] = 1;
}
}
int res = 0 ;
for (int i=1; i<n-1; i++) {
res += beauty[i] ;
}
return res ;
}
};
```
| 0 | 0 |
['C++']
| 0 |
sum-of-beauty-in-the-array
|
⚡ Fast & Clean Java 🧼 | 💯 O(n) Two-Pass Solution | 🚀 Beats 80%+
|
fast-clean-java-on-two-pass-solution-bea-8oo0
|
IntuitionThis problem could be solved by prefix array approach. However, we might not require two prefix arrays, it can be done using a single prefix array. The
|
user2980Fc
|
NORMAL
|
2025-04-04T19:00:38.297967+00:00
|
2025-04-04T19:00:38.297967+00:00
| 2 | false |
# Intuition
This problem could be solved by prefix array approach. However, we might not require two prefix arrays, it can be done using a single prefix array. The prefix array can be used to track the maximum from left to right and while implementing our actual logic, we can start from the right end towards the left. We can store the minimum in a single variable to keep a track of the minimum element towards the right of an element. It would be used to check if the element at arr[j] is smaller than the smallest element towards its right, i.e., for all the values of k in arr[k].
# Approach
To efficiently calculate the sum of beauties for each element, I used a two-pass strategy:
1. First Pass (Left to Right):
I built a lMax array where lMax[i] stores the maximum value from the beginning up to index i. This helps in checking if the current element is greater than all elements to its left.
2. Second Pass (Right to Left):
I maintained a variable rMin to keep track of the minimum value from the end up to the current index. This helps in checking if the current element is smaller than all elements to its right.
3. Final Pass:
For each element (excluding the first and last), I checked:
• If it’s strictly greater than all elements on its left and strictly smaller than all elements on its right → add 2 to the beauty.
• Else if it’s greater than its previous element and smaller than the next → add 1 to the beauty.
# Complexity
- Time complexity:
O(n)
- Space complexity:
O(n)
# Code
```java []
class Solution {
public int sumOfBeauties(int[] nums) {
int lMax[] = new int[nums.length];
lMax[0] = nums[0];
for(int i = 1, j=nums.length-2 ; i < nums.length ; i++, j--){
lMax[i] = Math.max(lMax[i-1], nums[i]);
}
int rMin = nums[nums.length-1];
int beautyCount = 0;
for(int i = nums.length-2 ; i >=1 ; i--){
if(nums[i] > lMax[i-1] && nums[i] < rMin)
beautyCount += 2;
else if(nums[i] > nums[i-1] && nums[i] < nums[i+1])
beautyCount += 1;
rMin = Math.min(rMin, nums[i]);
}
return beautyCount;
}
}
```
| 0 | 0 |
['Java']
| 0 |
sum-of-beauty-in-the-array
|
Four Solutions | Brute➡️Optimal | ✅Clean CPP Code✅
|
four-solutions-bruteoptimal-clean-cpp-co-33ji
|
😊 ~ 𝙒𝙞𝙩𝙝 ❤️ 𝙗𝙮 𝙃𝙞𝙧𝙚𝙣IntuitionHello There It's Easy!
Just Take A Look At The Code And Comments Within It, You'll Get It!ApproachApproaches -
: Using Brute Force
|
hirenjoshi
|
NORMAL
|
2025-04-04T15:22:20.540097+00:00
|
2025-04-04T15:30:17.605326+00:00
| 5 | false |
😊 ~ 𝙒𝙞𝙩𝙝 ❤️ 𝙗𝙮 𝙃𝙞𝙧𝙚𝙣
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
***Hello There It's Easy!
Just Take A Look At The Code And Comments Within It, You'll Get It!***
# Approach
<!-- Describe your approach to solving the problem. -->
***Approaches -
: Using Brute Force
: Avoiding Redundancy In Brute Force
: Using Time Optimization In Brute Force
: Space Optimization In Previous Approach***
***Similiar Problems:
[Problem 1](https://leetcode.com/problems/minimum-sum-of-mountain-triplets-ii/solutions/6612689/three-solutions-bruteoptimal-clean-cpp-c-yaea/)
[Problem 2](https://leetcode.com/problems/maximum-value-of-an-ordered-triplet-ii/solutions/6611757/three-solutions-bruteoptimal-clean-cpp-c-wrff/)***
# Complexity
- ***Time complexity: Mentioned with the code***
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- ***Space complexity: Mentioned with the code***
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
**Approach 1 : Using Brute Force (TLE)**
```
class BruteForce_V1 {
public:
// O(N^2) & O(1)
int sumOfBeauties(vector<int>& nums) {
int n = nums.size();
int sumOfBeauty = 0;
for(int i = 1; i <= n-2; ++i) {
int maxAtLeft = nums[0];
for(int j = 0; j < i; ++j) { // Find the maximum element lying at the left side of ith index
maxAtLeft = max(maxAtLeft, nums[j]);
}
int minAtRight = nums[n - 1];
for(int k = i+1; k < n; ++k) { // Find the minimum element lying at the right side of ith index
minAtRight = min(minAtRight, nums[k]);
}
if(maxAtLeft < nums[i] && nums[i] < minAtRight) { // Calculate the sum of beauty
sumOfBeauty += 2;
} else if(nums[i - 1] < nums[i] && nums[i] < nums[i + 1]) {
sumOfBeauty += 1;
}
}
return sumOfBeauty;
}
};
```
**Approach 2 : Avoiding Redundancy In Brute Force (TLE)**
```
class BruteForce_V2 {
public:
// O(N^2) & O(1)
int sumOfBeauties(vector<int>& nums) {
int n = nums.size();
int sumOfBeauty = 0;
for(int i = 1; i <= n-2; ++i) {
int maxAtLeft = nums[0];
int minAtRight = nums[n - 1];
for(int j = 0; j < n; ++j) { // Find the maximum and minimum element lying at the left and right side of ith index
if(j < i) {
maxAtLeft = max(maxAtLeft, nums[j]);
} else if(j > i) {
minAtRight = min(minAtRight, nums[j]);
}
}
if(maxAtLeft < nums[i] && nums[i] < minAtRight) { // Calculate the sum of beauty
sumOfBeauty += 2;
} else if(nums[i - 1] < nums[i] && nums[i] < nums[i + 1]) {
sumOfBeauty += 1;
}
}
return sumOfBeauty;
}
};
```
**Approach 3 : Time Optimization In Brute Force (Accepted)**
```
class Precomputation {
public:
// O(3*N) & O(2*N)
int sumOfBeauties(vector<int>& nums) {
int n = nums.size();
vector<int> maxAtLeft(n), minAtRight(n);
int maxElement = nums[0];
for(int i = 1; i < n; ++i) { // Find the maximum element lying at the left side of each index
maxAtLeft[i] = maxElement;
maxElement = max(maxElement, nums[i]);
}
int minElement = nums[n - 1];
for(int i = n-2; i >= 0; --i) { // Find the minimum element lying at the right side of each index
minAtRight[i] = minElement;
minElement = min(minElement, nums[i]);
}
int sumOfBeauty = 0;
for(int i = 1; i <= n-2; ++i) { // Calculate the sum of beauty
if(maxAtLeft[i] < nums[i] && nums[i] < minAtRight[i]) {
sumOfBeauty += 2;
} else if(nums[i - 1] < nums[i] && nums[i] < nums[i + 1]) {
sumOfBeauty += 1;
}
}
return sumOfBeauty;
}
};
```
**Approach 4 : Space Optimization In Previous Approach (Accepted)**
```
class PrecomputationEnhanced {
public:
// O(2*N) & O(1*N)
int sumOfBeauties(vector<int>& nums) {
int n = nums.size();
vector<int> maxAtLeft(n);
int maxElement = nums[0];
for(int i = 1; i < n; ++i) { // Find the maximum element lying at the left side of each index
maxAtLeft[i] = maxElement;
maxElement = max(maxElement, nums[i]);
}
int minAtRight = nums[n - 1];
int sumOfBeauty = 0;
for(int i = n-1; i >= 0; --i) { // Find the minimum element at the right side of each index, calculate the sum of beauty
if(i >= 1 && i <= n-2) {
if(maxAtLeft[i] < nums[i] && nums[i] < minAtRight) {
sumOfBeauty += 2;
} else if(nums[i - 1] < nums[i] && nums[i] < nums[i + 1]) {
sumOfBeauty += 1;
}
}
minAtRight = min(minAtRight, nums[i]);
}
return sumOfBeauty;
}
};
```
𝗨𝗣𝗩𝗢𝗧𝗘 𝗜𝗙 𝗬𝗢𝗨 𝗟𝗜𝗞𝗘 𝗧𝗛𝗘 𝗦𝗢𝗟𝗨𝗧𝗜𝗢𝗡 👍
| 0 | 0 |
['Array', 'Prefix Sum', 'C++']
| 0 |
sum-of-beauty-in-the-array
|
Beats 100% of C++ Users || Solution using Simple Looping|{\
|
beats-100-of-c-users-solution-using-simp-5897
|
IntuitionTo efficiently check whether an element is:Greater than all previous elements, andLess than all next elements,You can precompute:The maximum to the lef
|
dk8818604
|
NORMAL
|
2025-04-04T03:47:27.768774+00:00
|
2025-04-04T03:47:27.768774+00:00
| 0 | false |
# Intuition
To efficiently check whether an element is:
Greater than all previous elements, and
Less than all next elements,
You can precompute:
The maximum to the left of each index (prefix max)
The minimum to the right of each index (suffix min)
With this info:
If nums[i] > premax[i - 1] and nums[i] < sufmin[i + 1] → beauty is 2.
Else if nums[i - 1] < nums[i] < nums[i + 1] → beauty is 1.
Else → beauty is 0.
# Approach
Understand What Makes a Number "Beautiful":
For each element in the array (excluding the first and last), we are asked to evaluate its "beauty" based on certain conditions:
It gets 2 points if it is greater than all elements before it and less than all elements after it.
It gets 1 point if it is simply greater than its immediate left neighbor and less than its immediate right neighbor, but doesn't satisfy the 2-point condition.
It gets 0 points otherwise.
Why Not Check All Elements Manually?
Checking all previous and next elements for every index would be too slow, especially for large arrays. So, we need a more efficient way to find:
The maximum value before each element.
The minimum value after each element.
Precompute Left Maximums (Prefix Maximums):
Create an array where each element stores the maximum value from the start of the array up to that index.
This helps us quickly check if the current element is greater than all previous elements.
Precompute Right Minimums (Suffix Minimums):
Create another array where each element stores the minimum value from that index to the end of the array.
This helps us quickly check if the current element is less than all future elements.
Evaluate Beauty for Each Middle Element:
Now loop through the array from index 1 to n-2, and for each element:
If it is greater than the prefix max (just before it) and less than the suffix min (just after it), add 2 points.
Else if it is just greater than the previous and less than the next element, add 1 point.
Else, add 0.
Return the Total Beauty Score.
✅ Why This Works Well:
This approach is efficient — we only loop through the array a few times.
It avoids nested loops and redundant comparisons.
We reduce the problem of "check all before/after" into quick lookups using precomputed values.
# Complexity
- Time complexity:
O(n)
- Space complexity:
O(1)
# Code
```cpp []
class Solution {
public:
int sumOfBeauties(vector<int>& nums) {
int n=nums.size();
vector<int> premax=nums;
vector<int> sufmin=nums;
int maxa=nums[0];
for(int i=0; i<n; i++){
if(maxa<nums[i]){
maxa=nums[i];
}
else{
premax[i]=maxa;
}
}
int mini=nums[n-1];
for(int i=n-1; i>=0; i--){
if(sufmin[i]<mini){
mini=sufmin[i];
}
else{
sufmin[i]=mini;
}
}
int ans=0;
for(int i=1; i<n-1; i++){
if(nums[i]>premax[i-1] && nums[i]<sufmin[i+1]) ans+=2;
else if(nums[i]>nums[i-1] && nums[i]<nums[i+1]) ans+=1;
}
return ans;
}
};
```
| 0 | 0 |
['Array', 'C++']
| 0 |
sum-of-beauty-in-the-array
|
Beats 100% of C++ Users || Solution using Simple Looping|{\
|
beats-100-of-c-users-solution-using-simp-jkiz
|
IntuitionTo efficiently check whether an element is:Greater than all previous elements, andLess than all next elements,You can precompute:The maximum to the lef
|
dk8818604
|
NORMAL
|
2025-04-04T03:47:16.173392+00:00
|
2025-04-04T03:47:16.173392+00:00
| 1 | false |
# Intuition
To efficiently check whether an element is:
Greater than all previous elements, and
Less than all next elements,
You can precompute:
The maximum to the left of each index (prefix max)
The minimum to the right of each index (suffix min)
With this info:
If nums[i] > premax[i - 1] and nums[i] < sufmin[i + 1] → beauty is 2.
Else if nums[i - 1] < nums[i] < nums[i + 1] → beauty is 1.
Else → beauty is 0.
# Approach
Understand What Makes a Number "Beautiful":
For each element in the array (excluding the first and last), we are asked to evaluate its "beauty" based on certain conditions:
It gets 2 points if it is greater than all elements before it and less than all elements after it.
It gets 1 point if it is simply greater than its immediate left neighbor and less than its immediate right neighbor, but doesn't satisfy the 2-point condition.
It gets 0 points otherwise.
Why Not Check All Elements Manually?
Checking all previous and next elements for every index would be too slow, especially for large arrays. So, we need a more efficient way to find:
The maximum value before each element.
The minimum value after each element.
Precompute Left Maximums (Prefix Maximums):
Create an array where each element stores the maximum value from the start of the array up to that index.
This helps us quickly check if the current element is greater than all previous elements.
Precompute Right Minimums (Suffix Minimums):
Create another array where each element stores the minimum value from that index to the end of the array.
This helps us quickly check if the current element is less than all future elements.
Evaluate Beauty for Each Middle Element:
Now loop through the array from index 1 to n-2, and for each element:
If it is greater than the prefix max (just before it) and less than the suffix min (just after it), add 2 points.
Else if it is just greater than the previous and less than the next element, add 1 point.
Else, add 0.
Return the Total Beauty Score.
✅ Why This Works Well:
This approach is efficient — we only loop through the array a few times.
It avoids nested loops and redundant comparisons.
We reduce the problem of "check all before/after" into quick lookups using precomputed values.
# Complexity
- Time complexity:
O(n)
- Space complexity:
O(1)

# Code
```cpp []
class Solution {
public:
int sumOfBeauties(vector<int>& nums) {
int n=nums.size();
vector<int> premax=nums;
vector<int> sufmin=nums;
int maxa=nums[0];
for(int i=0; i<n; i++){
if(maxa<nums[i]){
maxa=nums[i];
}
else{
premax[i]=maxa;
}
}
int mini=nums[n-1];
for(int i=n-1; i>=0; i--){
if(sufmin[i]<mini){
mini=sufmin[i];
}
else{
sufmin[i]=mini;
}
}
int ans=0;
for(int i=1; i<n-1; i++){
if(nums[i]>premax[i-1] && nums[i]<sufmin[i+1]) ans+=2;
else if(nums[i]>nums[i-1] && nums[i]<nums[i+1]) ans+=1;
}
return ans;
}
};
```
| 0 | 0 |
['Array', 'C++']
| 0 |
sum-of-beauty-in-the-array
|
Prefix Suffix Sum
|
prefix-suffix-sum-by-user6178c-u1ow
|
IntuitionPrefix Suffix SumCode
|
user6178c
|
NORMAL
|
2025-04-03T20:06:09.897578+00:00
|
2025-04-03T20:06:09.897578+00:00
| 4 | false |
# Intuition
Prefix Suffix Sum
# Code
```java []
class Solution {
public int sumOfBeauties(int[] nums) {
int[] prefix = new int[nums.length];
int[] suffix = new int[nums.length];
prefix[0] = nums[0];
suffix[suffix.length-1] = nums[nums.length-1];
for(int i=1;i<nums.length;i++) {
prefix[i] = Math.max(prefix[i-1], nums[i]);
}
for(int i=nums.length-2;i>=0;i--) {
suffix[i] = Math.min(suffix[i+1], nums[i]);
}
int sum = 0;
for(int i=1;i<=nums.length-2;i++) {
if(nums[i]>prefix[i-1] && nums[i]<suffix[i+1]) {
sum=sum+2;
} else if(nums[i]>nums[i-1] && nums[i]<nums[i+1]) {
sum=sum+1;
}
}
return sum;
}
}
```
| 0 | 0 |
['Java']
| 0 |
sum-of-beauty-in-the-array
|
Easy to understand solution for beginners
|
easy-to-understand-solution-for-beginner-5yfx
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
user2540Ie
|
NORMAL
|
2025-04-03T13:20:23.231878+00:00
|
2025-04-03T13:20:23.231878+00:00
| 4 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int sumOfBeauties(int[] nums) {
int[] arr1=new int[nums.length];
int[] arr2=new int[nums.length];
arr1[0]=nums[0];
arr2[nums.length-1]=nums[nums.length-1];
for(int i=1;i<nums.length;i++){
int gt= nums[i];
if(gt>arr1[i-1]){
arr1[i]=gt;
}else{
arr1[i]=arr1[i-1];
}
if(i==0){
continue;
}else{
int gt2=nums[nums.length-1-i];
if(gt2>arr2[nums.length-1-i+1]){
arr2[nums.length-1-i]=arr2[nums.length-1-i+1];
}else{
arr2[nums.length-1-i]=gt2;
}
}
}
int max=0;
for(int i=1;i<nums.length-1;i++){
int gt;
if(nums[i-1]<nums[i] && nums[i]<nums[i+1]){
if(arr1[i-1]<nums[i] && arr2[i+1]>nums[i]){
gt=2;
}else{
gt=1;
}
}else{
gt=0;
}
max+=gt;
}
return max;
}
}
```
| 0 | 0 |
['Java']
| 0 |
sum-of-beauty-in-the-array
|
maxPrefix and minSuffix | Beats 100% runtime
|
maxprefix-and-minsuffix-by-tanishachatur-guls
|
IntuitionIf an element is greater than the maximum value before it, then it is also greater than all its previous elements. Similarly, if the current element is
|
Taniiishaa
|
NORMAL
|
2025-04-03T09:53:02.721960+00:00
|
2025-04-03T10:00:15.222678+00:00
| 5 | false |
# Intuition
If an element is greater than the maximum value before it, then it is also greater than all its previous elements. Similarly, if the current element is smaller than the minimum element after it, then it is also smaller than all the elements that come after it.
# Approach
<!-- Describe your approach to solving the problem. -->
For every index find the max value before it and min value after it using prefix and suffix arrays. Now, check from i=1 till i<n-1,
if(maxPrefix[i]<nums[i] && nums[i]<minSuffix[i])sum+=2;
else if(nums[i-1]<nums[i] && nums[i]<nums[i+1])sum+=1;
# Complexity
- Time complexity:O(N)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:O(N)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int sumOfBeauties(vector<int>& nums) {
int n = nums.size();
int sum = 0;
vector <int> maxPrefix(n,INT_MIN),minSuffix(n,INT_MAX);
for(int i=1;i<n;i++){
maxPrefix[i]=max(maxPrefix[i-1],nums[i-1]);
minSuffix[n-i-1]=min(minSuffix[n-i],nums[n-i]);
}
for(int i=1;i<n-1;i++){
if(maxPrefix[i]<nums[i] && nums[i]<minSuffix[i])sum+=2;
else if(nums[i-1]<nums[i] && nums[i]<nums[i+1])sum+=1;
}
return sum;
}
};
```
| 0 | 0 |
['C++']
| 0 |
sum-of-beauty-in-the-array
|
Java Solution | Prefix Maximum | Suffix Minimum
|
java-solution-prefix-maximum-suffix-mini-d1a8
|
Code
|
nikitaaa_
|
NORMAL
|
2025-04-03T09:16:22.140450+00:00
|
2025-04-03T09:16:22.140450+00:00
| 2 | false |
# Code
```java []
class Solution {
public int sumOfBeauties(int[] nums) {
int n = nums.length;
int[] left = new int[n];
int[] right = new int[n];
left[0] = Integer.MIN_VALUE;
for(int i = 1;i<n;i++){
left[i] = Math.max(left[i-1], nums[i-1]);
}
right[n-1] = Integer.MAX_VALUE;
for(int i = n-2;i>=0;i--){
right[i] = Math.min(right[i+1], nums[i+1]);
}
int sum = 0;
for(int i = 1;i<n-1;i++){
if(left[i] < nums[i] && right[i] > nums[i]){
sum += 2;
}else if(nums[i-1] < nums[i] && nums[i] < nums[i+1]){
sum += 1;
}
}
return sum;
}
}
```
| 0 | 0 |
['Java']
| 0 |
sum-of-beauty-in-the-array
|
Java Solution | Prefix Maximum | Suffix Minimum
|
java-solution-prefix-maximum-suffix-mini-3it3
|
Code
|
nikitaaa_
|
NORMAL
|
2025-04-03T09:16:17.279975+00:00
|
2025-04-03T09:16:17.279975+00:00
| 4 | false |
# Code
```java []
class Solution {
public int sumOfBeauties(int[] nums) {
int n = nums.length;
int[] left = new int[n];
int[] right = new int[n];
left[0] = Integer.MIN_VALUE;
for(int i = 1;i<n;i++){
left[i] = Math.max(left[i-1], nums[i-1]);
}
right[n-1] = Integer.MAX_VALUE;
for(int i = n-2;i>=0;i--){
right[i] = Math.min(right[i+1], nums[i+1]);
}
int sum = 0;
for(int i = 1;i<n-1;i++){
if(left[i] < nums[i] && right[i] > nums[i]){
sum += 2;
}else if(nums[i-1] < nums[i] && nums[i] < nums[i+1]){
sum += 1;
}
}
return sum;
}
}
```
| 0 | 0 |
['Java']
| 0 |
sum-of-beauty-in-the-array
|
Python | C++ Prefix+Suffix Arrays
|
python-c-prefixsuffix-arrays-by-kaluginp-f4sv
|
Complexity
Time complexity: O(N)
Space complexity: O(N)
Code
|
kaluginpeter
|
NORMAL
|
2025-04-03T08:13:04.995475+00:00
|
2025-04-03T08:13:04.995475+00:00
| 7 | false |
# Complexity
- Time complexity: O(N)
- Space complexity: O(N)
# Code
```python3 []
class Solution:
def sumOfBeauties(self, nums: List[int]) -> int:
n: int = len(nums)
left_part: list[int] = [0]
left_max: int = 0
for right in range(1, n):
if nums[left_max] < nums[right]: left_part.append(2)
elif nums[right - 1] < nums[right]: left_part.append(1)
else: left_part.append(0)
if nums[left_max] < nums[right]: left_max = right
score: int = 0
right_part: list[int] = []
right_min: int = n - 1
for left in range(n - 2, 0, -1):
if nums[left] < nums[right_min]: right_part.append(2)
elif nums[left] < nums[left + 1]: right_part.append(1)
else: right_part.append(0)
if nums[left] < nums[right_min]: right_min = left
if left_part[left] == 2 and right_part[-1] == 2: score += 2
elif left_part[left] and right_part[-1]: score += 1
return score
```
```cpp []
class Solution {
public:
int sumOfBeauties(vector<int>& nums) {
int n = nums.size();
vector<int> leftPart = {0}, rightPart;
int leftMax = 0;
for (int right = 1; right < n; ++right) {
if (nums[leftMax] < nums[right]) leftPart.push_back(2);
else if (nums[right] > nums[right - 1]) leftPart.push_back(1);
else leftPart.push_back(0);
if (nums[right] > nums[leftMax]) leftMax = right;
}
int score = 0, rightMin = n - 1;
for (int left = n - 2; left > 0; --left) {
if (nums[rightMin] > nums[left]) rightPart.push_back(2);
else if (nums[left] < nums[left + 1]) rightPart.push_back(1);
else rightPart.push_back(0);
if (nums[left] < nums[rightMin]) rightMin = left;
if (leftPart[left] == 2 && rightPart.back() == 2) score += 2;
else if (leftPart[left] && rightPart.back()) ++score;
}
return score;
}
};
```
| 0 | 0 |
['Array', 'Suffix Array', 'Prefix Sum', 'C++', 'Python3']
| 0 |
sum-of-beauty-in-the-array
|
Simple With Explanation
|
simple-with-explanation-by-naman_gupta21-a36j
|
Intuitionfor every i index from 1 to n-1 including we just have to check two conditions in O(1) timeApproachfirst condition
if all the elements befor i is smal
|
Naman_gupta21
|
NORMAL
|
2025-04-03T06:03:39.891085+00:00
|
2025-04-03T06:03:39.891085+00:00
| 5 | false |
# Intuition
for every i index from 1 to n-1 including we just have to check two conditions in O(1) time
# Approach
first condition
if all the elements befor i is smaller then i th element and all the element after ith element are bigger than the ith element then add 2
second condition
if first condition is not true then we have to check if the element just before the ith element is smaller then ith element and the element just after the ith element is bigger then add 1 to answer
so second condition could be checked easily
for first condition we will make two arrays one that will calculate the biggest element till now from the left side we call if pref
and for that calculates smallest element till now from right and we call it suffix
now we have smallest element of right side and biggest element of left side now the first condition could be checked easily
# Complexity
- Time complexity:
O(n)
- Space complexity:
O(n)
# Code
```cpp []
class Solution {
public:
int sumOfBeauties(vector<int>& nums) {
int beauty = 0;
int n = nums.size();
vector<int>pref(n,0);
pref[0] = nums[0];
vector<int>suff(n,0);
suff[n-1] = nums[n-1];
for(int i = 1;i<n;i++){
pref[i] = max(pref[i-1],nums[i]);
suff[n-i-1] = min(suff[n-i],nums[n-i-1]);
}
for(int i = 1;i<n-1;i++){
if(pref[i-1] < nums[i] && suff[i+1] > nums[i])beauty+=2;
else if(nums[i-1] < nums[i] && nums[i] < nums[i+1])beauty+=1;
}
return beauty;
}
};
```
| 0 | 0 |
['Suffix Array', 'Prefix Sum', 'C++']
| 0 |
sum-of-beauty-in-the-array
|
Prefix sum solution🚀✔🔥🚀
|
prefix-sum-solution-by-abhay_mandal-xsv5
| null |
Abhay_mandal
|
NORMAL
|
2025-04-03T05:36:14.625953+00:00
|
2025-04-03T05:36:14.625953+00:00
| 2 | false |
```
class Solution {
public:
int sumOfBeauties(vector<int>& nums) {
int sz = nums.size();
vector<int> pre(sz);
int mini=INT_MAX;
for(int i=sz-1; i>=0; i--){
pre[i] = mini;
if(nums[i]<mini) mini=nums[i];
}
int maxi=nums[0];
int ans = 0;
for(int i=1; i<sz-1; i++){
if(nums[i]>maxi && nums[i]<pre[i]) ans+=2;
else if(nums[i]>nums[i-1] && nums[i]<nums[i+1]) ans+=1;
if(nums[i]>maxi) maxi=nums[i];
}
return ans;
}
};
```
| 0 | 0 |
['Array', 'C++']
| 0 |
sum-of-beauty-in-the-array
|
Solution using Prefix and Suffix Arrays (DP)
|
solution-using-prefix-and-suffix-array-d-6zod
|
IntuitionThe problem asks us to compute a "beauty" score for each element in the array (except the first and last). The score depends on how nums[i] compares to
|
bishoy_sedra
|
NORMAL
|
2025-04-03T04:49:26.159727+00:00
|
2025-04-03T04:49:39.106103+00:00
| 1 | false |
# Intuition
The problem asks us to compute a "beauty" score for each element in the array (except the first and last). The score depends on how `nums[i]` compares to elements before and after it.
- My first thought was that to efficiently determine if `nums[i]` is greater than all elements to its left and less than all elements to its right, we could **precompute** prefix maximums and suffix minimums.
- This helps avoid nested loops and reduces the time complexity to linear.
---
# Approach
1. **Prefix Maximum Array**:
- For each index `i`, store the maximum of all elements from `nums[0]` to `nums[i]`.
- This helps check if `nums[i]` is greater than all previous values.
2. **Suffix Minimum Array**:
- For each index `i`, store the minimum of all elements from `nums[i]` to the end.
- This helps check if `nums[i]` is less than all following values.
3. **Iterate from 1 to n-2**:
- If `nums[i]` is strictly greater than `prefix[i-1]` and strictly less than `suffix[i+1]`, add 2 to the score.
- Else if `nums[i-1] < nums[i] < nums[i+1]`, add 1.
- Else, add 0 (implicitly by doing nothing).
This approach ensures we check the required conditions efficiently for each relevant index.
---
# Complexity
- **Time complexity:**
$$O(n)$$
One pass for prefix, one for suffix, and one for final iteration → total linear time.
- **Space complexity:**
$$O(n)$$
For storing the prefix and suffix arrays. Can be optimized to $$O(1)$$ with in-place comparisons, but this version prioritizes clarity.
---
# Code
```cpp
class Solution {
public:
int sumOfBeauties(vector<int>& nums) {
int n = nums.size();
vector<int> prefix(n, 0);
prefix[0] = nums[0];
for(int i = 1; i < n; i++){
prefix[i] = max(prefix[i - 1], nums[i]);
}
vector<int> suffix(n, 0);
suffix[n - 1] = nums[n - 1];
for(int i = n - 2; i >= 0; i--){
suffix[i] = min(suffix[i + 1], nums[i]);
}
int answer = 0;
for(int i = 1; i < n - 1; i++){
if(nums[i] > prefix[i - 1] && nums[i] < suffix[i + 1]){
answer += 2;
} else if(nums[i - 1] < nums[i] && nums[i] < nums[i + 1]){
answer++;
}
}
return answer;
}
};
```
| 0 | 0 |
['Array', 'Dynamic Programming', 'C++']
| 0 |
sum-of-beauty-in-the-array
|
3 ms | Beats 76.33% | maxprefix | minsuffix
|
3-ms-beats-7633-maxprefix-minsuffix-by-p-vvj4
|
🔹 IntuitionWe need to calculate the beauty of each element nums[i] in an array based on the following rules:
If nums[i] is strictly greater than all elements b
|
prashantmahawar
|
NORMAL
|
2025-04-03T02:50:53.312615+00:00
|
2025-04-03T02:50:53.312615+00:00
| 15 | false |
# 🔹 Intuition
We need to calculate the beauty of each element nums[i] in an array based on the following rules:
- If `nums[i] is strictly greater` than all elements before it and strictly smaller than all elements after it, `add 2 to the sum`.
- If `nums[i] is greater than nums[i−1] and smaller than nums[i+1]`, `add 1 to the sum`.
- Otherwise, add `0`.
To efficiently find elements satisfying the first condition, we use:
- Prefix Maximum Array (pre[i]) → Stores the `maximum value` from `nums[0] to nums[i]`
- Suffix Minimum Array (suff[i]) → Stores the `minimum value` from `nums[i] to nums[n-1]`
This allows us to check conditions in` O(1)` time for each nums[i].
<!-- Describe your first thoughts on how to solve this problem. -->
# 🔹 Approach
1. Compute pre[i] (Prefix Maximum Array)
- `pre[i] = max(pre[i-1], nums[i])`
2. Compute suff[i] (Suffix Minimum Array)
- `suff[i] = min(suff[i+1], nums[i])`
3. Iterate through nums[i] (from 1 to n-2)
- If `pre[i-1] < nums[i] < suff[i+1],` add `2`.
- Else, if `nums[i-1] < nums[i] < nums[i+1]`, add `1`.
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: $$O(n)$$
<!-- Add your time complexity here, e.g.-->
- Space complexity:$$O(n)$$
<!-- Add your space complexity here, e.g. -->
# Code
```cpp []
class Solution {
public:
int sumOfBeauties(vector<int>& nums) {
int maxsum=0;
int n=nums.size();
vector<int> pre(n,0);
vector<int> suff(n,0);
int a=nums[0];
for(int i=0;i<n;i++){
if(nums[i]>a){
a=nums[i];
}
pre[i]=a;
}
a=nums[n-1];
for(int i=n-1;i>=0;i--){
if(nums[i]<a){
a=nums[i];
}
suff[i]=a;
}
for(int i=1;i<n-1;i++){
if(pre[i-1]<nums[i]&& nums[i]<suff[i+1])maxsum+=2;
else if(nums[i-1]<nums[i]&& nums[i]<nums[i+1])maxsum+=1;
}
return maxsum;
}
};
```
```java []
class Solution {
public int sumOfBeauties(int[] nums) {
int n = nums.length, maxsum = 0;
int[] pre = new int[n], suff = new int[n];
// Compute prefix max array
pre[0] = nums[0];
for (int i = 1; i < n; i++)
pre[i] = Math.max(pre[i - 1], nums[i]);
// Compute suffix min array
suff[n - 1] = nums[n - 1];
for (int i = n - 2; i >= 0; i--)
suff[i] = Math.min(suff[i + 1], nums[i]);
// Compute beauty sum
for (int i = 1; i < n - 1; i++) {
if (pre[i - 1] < nums[i] && nums[i] < suff[i + 1])
maxsum += 2;
else if (nums[i - 1] < nums[i] && nums[i] < nums[i + 1])
maxsum += 1;
}
return maxsum;
}
}
```
```py []
class Solution:
def sumOfBeauties(self, nums: List[int]) -> int:
n = len(nums)
pre = [0] * n
suff = [0] * n
# Compute prefix max array
pre[0] = nums[0]
for i in range(1, n):
pre[i] = max(pre[i - 1], nums[i])
# Compute suffix min array
suff[n - 1] = nums[n - 1]
for i in range(n - 2, -1, -1):
suff[i] = min(suff[i + 1], nums[i])
# Compute beauty sum
maxsum = 0
for i in range(1, n - 1):
if pre[i - 1] < nums[i] < suff[i + 1]:
maxsum += 2
elif nums[i - 1] < nums[i] < nums[i + 1]:
maxsum += 1
return maxsum
```
| 0 | 0 |
['Array', 'C++', 'Java', 'Python3']
| 0 |
sum-of-beauty-in-the-array
|
C++ | Easy to understand | Beats 100%
|
c-easy-to-understand-beats-100-by-sharma-pk7x
|
IntuitionApproachComplexity
Time complexity:O(n)
Space complexity:O(n)
Code
|
sharmashobhit1000
|
NORMAL
|
2025-03-27T11:48:32.424021+00:00
|
2025-03-27T11:48:32.424021+00:00
| 7 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:$$O(n)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:$$O(n)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int sumOfBeauties(vector<int>& nums) {
int n = nums.size();
vector<int> v(
n); // To track min element from right subarray for each index
int mini = INT_MAX;
for (int i = n - 1; i >= 0; i--) {
mini = min(mini, nums[i]);
v[i] = mini;
}
int ans = 0, maxi = nums[0];
for (int i = 1; i < n - 1; i++) {
int x = nums[i];
if (x > maxi && x < v[i + 1]) {
ans += 2;
} else if (x > nums[i - 1] && x < nums[i + 1]) {
ans += 1;
}
maxi = max(maxi, nums[i]);
}
return ans;
}
};
```
| 0 | 0 |
['C++']
| 0 |
sum-of-beauty-in-the-array
|
Easy C++ solution.
|
easy-c-solution-by-khushi_joshi-flwa
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
KHUSHI_JOSHI_
|
NORMAL
|
2025-03-18T17:05:09.857013+00:00
|
2025-03-18T17:05:09.857013+00:00
| 6 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int sumOfBeauties(vector<int>& nums) {
int n=nums.size();
int sum=0;
vector<int>maxi(n);
vector<int>mini(n);
maxi[0]=nums[0];
for(int i=1;i<n;i++){
maxi[i]=max(maxi[i-1],nums[i]);
}
mini[n-1]=nums[n-1];
for(int i=n-2;i>=0;i--){
mini[i]=min(mini[i+1],nums[i]);
}
for(int i=1;i<n-1;i++){
if(nums[i]>maxi[i-1] && nums[i]<mini[i+1]){
sum+=2;
}
else if(nums[i]>nums[i-1] && nums[i]<nums[i+1]){
sum+=1;
}
}
return sum;
}
};
```
| 0 | 0 |
['C++']
| 0 |
sum-of-beauty-in-the-array
|
Beats 90% easy cpp solution
|
beats-90-easy-cpp-solution-by-rapo_999-jb5j
|
IntuitionApproachComplexity
Time complexity:
O(n)
Space complexity:
Code
|
rapo_999
|
NORMAL
|
2025-03-03T21:16:40.155912+00:00
|
2025-03-03T21:16:40.155912+00:00
| 9 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
$$O(n)$$
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int sumOfBeauties(vector<int>& nums) {
int n=nums.size();
vector<int>maxarr(n,0);
vector<int>minarr(n,0);
int maxi=INT_MIN;
int mini=INT_MAX;
for(int i=0;i<n;i++)
{
maxarr[i]=max(maxi,nums[i]);
maxi=maxarr[i];
}
for(int i=n-1;i>=0;i--)
{
minarr[i]=min(mini,nums[i]);
mini=minarr[i];
}
int count=0;
for(int i=1;i<=n-2;i++)
{
if(nums[i]<minarr[i+1] && nums[i]>maxarr[i-1])
{
count=count+2;
}
else if(nums[i - 1] < nums[i] && nums[i] < nums[i + 1])
{
count=count+1;
}
}
return count;
}
};
```
| 0 | 0 |
['Prefix Sum', 'C++']
| 0 |
sum-of-beauty-in-the-array
|
simple in java for beginner
|
simple-in-java-for-beginner-by-firozmars-jobr
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
FirozMars
|
NORMAL
|
2025-02-26T04:49:46.572580+00:00
|
2025-02-26T04:49:46.572580+00:00
| 5 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int sumOfBeauties(int[] nums) {
int minOnRight[] = new int[nums.length];
minOnRight[nums.length-1]=nums[nums.length-1];
int maxOnLeft = nums[0];
int n = nums.length;
for(int i=n-1;i>0;i--)
{
minOnRight[i-1]= Math.min(minOnRight[i],nums[i-1]);
}
int beauty=0;
for(int i=1;i<n-1;i++)
{
if(nums[i]>maxOnLeft && nums[i]<minOnRight[i+1])
beauty+=2;
else if(nums[i]>nums[i-1] && nums[i]<nums[i+1])
beauty+=1;
maxOnLeft=Math.max(nums[i],maxOnLeft);
}
return beauty;
}
}
```
| 0 | 0 |
['Java']
| 0 |
sum-of-beauty-in-the-array
|
Having max prefix and min prefix || O(N) || Beats 100% || Python
|
having-max-prefix-and-min-prefix-on-beat-ep8n
|
Code
|
srinijammula
|
NORMAL
|
2025-02-24T04:26:03.748036+00:00
|
2025-02-24T04:26:18.381122+00:00
| 7 | false |
# Code
```python3 []
class Solution:
def sumOfBeauties(self, nums: List[int]) -> int:
m=[]
t=nums[0]
s=0
for i in range(1,len(nums)-1):
if nums[i]>t:
m.append(1)
t=nums[i]
else:
m.append(0)
t=nums[len(nums)-1]
for i in range(len(nums)-2,0,-1):
if nums[i]<t and m[i-1]:
s+=2
elif nums[i]>nums[i-1] and nums[i]<nums[i+1]:
s+=1
if nums[i]<t:
t=nums[i]
return s
```
| 0 | 0 |
['Python3']
| 0 |
sum-of-beauty-in-the-array
|
Easy Java || O(n) || Beats 97.87% || Memory 92%
|
easy-java-on-beats-9787-memory-92-by-dip-ufay
|
IntuitionApproachComplexity
Time complexity: O(n)
Space complexity: O(n)
Code
|
Dip143
|
NORMAL
|
2025-02-23T14:39:02.456987+00:00
|
2025-02-23T14:39:02.456987+00:00
| 7 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: O(n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(n)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int sumOfBeauties(int[] nums) {
int[] leftMax=new int[nums.length];
int[] rightMin=new int[nums.length];
int temp=nums[0];
for(int i=1;i<nums.length;i++){
leftMax[i]=temp;
if(temp<nums[i])temp=nums[i];
}
temp=nums[nums.length-1];
for(int i=nums.length-2;i>=0;i--){
rightMin[i]=temp;
if(temp>nums[i])temp=nums[i];
}
int ansC=0;
for(int i=1;i<=nums.length-2;i++){
if(leftMax[i]<nums[i] && nums[i]<rightMin[i]){
ansC+=2;
}else if(nums[i - 1] < nums[i] && nums[i] < nums[i + 1]){
ansC++;
}
}
return ansC;
}
}
```
| 0 | 0 |
['Java']
| 0 |
sum-of-beauty-in-the-array
|
C++: Efficient Calculation Using Prefix and Suffix Arrays
|
c-efficient-calculation-using-prefix-and-83x5
|
IntuitionWe need to determine the "beauty" of each element in nums (excluding the first and last elements) based on specific conditions. The conditions require
|
ashotpetrossian91
|
NORMAL
|
2025-02-12T06:46:24.694644+00:00
|
2025-02-12T06:46:24.694644+00:00
| 4 | false |
# Intuition
We need to determine the "beauty" of each element in nums (excluding the first and last elements) based on specific conditions. The conditions require checking whether an element is between all previous elements and all next elements (for beauty 2) or simply between its immediate neighbors (for beauty 1).
To efficiently check the first condition, we can precompute two arrays:
* prefix[i]: The maximum value from the start of the array up to index i.
* suffix[i]: The minimum value from index i to the end of the array.
Using these precomputed values, we can efficiently determine whether an element satisfies the beauty conditions.
# Approach
* Precompute prefix and suffix:
* prefix[i] stores the maximum value from nums[0] to nums[i].
* suffix[i] stores the minimum value from nums[i] to nums[n-1].
* Iterate through the array (1 ≤ i ≤ n-2) and determine beauty values:
* If prefix[i-1] < nums[i] < suffix[i+1], add 2 to the result.
* Else, if nums[i-1] < nums[i] < nums[i+1], add 1 to the result.
# Complexity
- Time complexity: $$O(n)$$
- Space complexity: $$O(n)$$
# Code
```cpp []
class Solution {
public:
int sumOfBeauties(vector<int>& nums) {
int n = nums.size();
std::vector<int> prefix(n), suffix(n);
prefix[0] = nums[0];
suffix[n - 1] = nums[n - 1];
for (int i{1}, j{n - 2}; i < n; ++i, --j) {
prefix[i] = std::max(prefix[i - 1], nums[i]);
suffix[j] = std::min(suffix[j + 1], nums[j]);
}
int res{};
for (int i{1}; i < n - 1; ++i) {
if (prefix[i - 1] < nums[i] && nums[i] < suffix[i + 1]) res += 2;
else if (nums[i - 1] < nums[i] && nums[i] < nums[i + 1]) ++res;
}
return res;
}
};
```
| 0 | 0 |
['C++']
| 0 |
concatenation-of-consecutive-binary-numbers
|
C++ | Diagram | Related Problems
|
c-diagram-related-problems-by-kiranpalsi-cwfk
|
\n\n\n\n\ncpp\nclass Solution {\npublic:\n \n int numberOfBits(int n) {\n\t\t return log2(n) + 1;\n }\n \n int concatenatedBinary(int n) {\n
|
kiranpalsingh1806
|
NORMAL
|
2022-09-23T03:02:16.176594+00:00
|
2022-09-23T10:16:30.122578+00:00
| 14,567 | false |
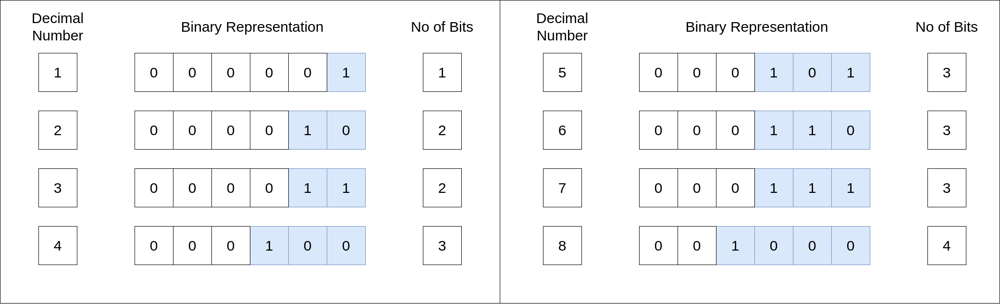\n\n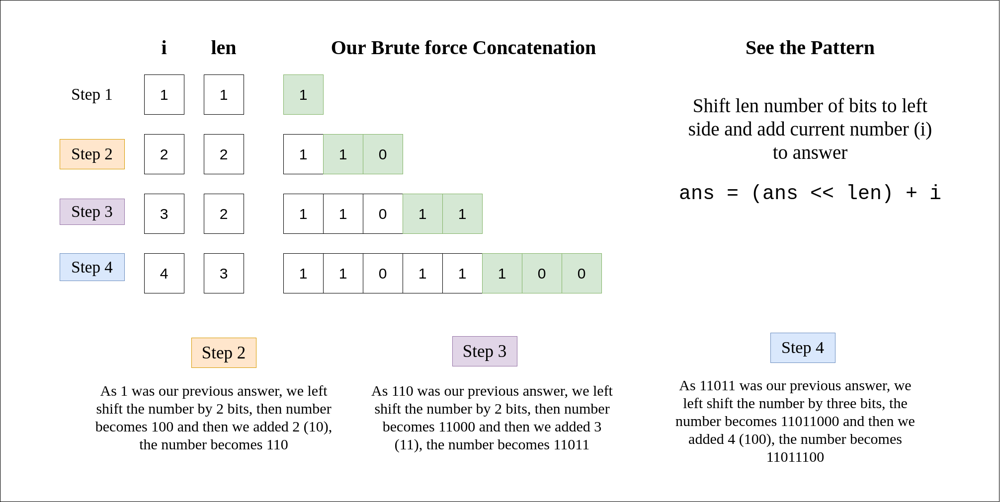\n\n\n```cpp\nclass Solution {\npublic:\n \n int numberOfBits(int n) {\n\t\t return log2(n) + 1;\n }\n \n int concatenatedBinary(int n) {\n long ans = 0, MOD = 1e9 + 7;\n \n for (int i = 1; i <= n; ++i) {\n int len = numberOfBits(i);\n ans = ((ans << len) % MOD + i) % MOD;\n }\n return ans;\n }\n};\n```\n\n**EDIT 1**\n**Optimization** in `numberOfBits` function\n```cpp\nint numberOfBits(int n) {\n int leadingZeros = __builtin_clz(n);\n return 32 - leadingZeros;\n}\n```\n\n**EDIT 2**\nAnother way of **calculating length of binary number** suggested by @CoolBud\n```cpp\nint numberOfBits(int n) {\n return log2(n) + 1;\n}\n```\n\n**EDIT 3**\nAnother way of **calculating length of binary number** suggested by @Sopindm\n```cpp\nint concatenatedBinary(int n) {\n long ans = 0, MOD = 1e9 + 7, len = 0;\n for (int i = 1; i <= n; ++i) {\n if(__builtin_popcount(i) == 1) ++len;\n ans = ((ans << len) % MOD + i) % MOD;\n }\n return ans;\n}\n```\n\n**Binary Representation Related Problems**\n[1. Add Binary ](https://leetcode.com/problems/add-binary/)\n[2. Add Two Numbers ](https://leetcode.com/problems/add-two-numbers/)\n[3. Counting Bits ](https://leetcode.com/problems/counting-bits/)\n[4. Binary Watch ](https://leetcode.com/problems/binary-watch/)\n[5. Reverse Bits ](https://leetcode.com/problems/reverse-bits/)\n[6. Binary Number with Alternating Bits ](https://leetcode.com/problems/binary-number-with-alternating-bits/)\n[7. Hamming Distance ](https://leetcode.com/problems/hamming-distance/)\n[8. Prime Number of Set Bits in Binary Representation ](https://leetcode.com/problems/prime-number-of-set-bits-in-binary-representation/)
| 341 | 1 |
['Bit Manipulation', 'C', 'C++']
| 39 |
concatenation-of-consecutive-binary-numbers
|
Java || 👍Explained in Detail👍|| Fast O(N) Solution✅|| Bit Manipulation & Math
|
java-explained-in-detail-fast-on-solutio-77sd
|
I do my best everyday to give a clear explanation, so to help everyone improve their skills.\n\nIf you find this helpful, please \uD83D\uDC4D upvote this post a
|
cheehwatang
|
NORMAL
|
2022-09-23T01:00:27.215526+00:00
|
2022-09-23T01:35:32.663292+00:00
| 7,347 | false |
I do my best everyday to give a clear explanation, so to help everyone improve their skills.\n\nIf you find this **helpful**, please \uD83D\uDC4D **upvote** this post and watch my [Github Repository](https://github.com/cheehwatang/leetcode-java).\n\nThank you for reading! \uD83D\uDE04 Comment if you have any questions or feedback.\n\n---\n\n**Java (Bit Manipulation) - Clean Code**\n\n```\nclass Solution {\n public int concatenatedBinary(int n) {\n final long modulo = (long) (1e9 + 7);\n long result = 0;\n int binaryDigits = 0;\n for (int i = 1; i <= n; i++) {\n if ((i & (i - 1)) == 0) binaryDigits++;\n result = ((result << binaryDigits) + i) % modulo;\n }\n return (int) result;\n }\n}\n```\n\n**Java (Bit Manipulation) - With Explanation**\n\n```\n// Time Complexity: O(N)\n// Space Complexity: O(1)\n// where N is n.\nclass Solution {\n\n // Approach:\n // Using bit manipulation as described below.\n // A bit of description for the bitwise operations used, if you are not familiar.\n // 1. & - Bitwise AND operation:\n // 0 & 0 = 0,\n // 1 & 0 = 0,\n // 1 & 1 = 1.\n // Example : 1101 & 1010 = 1000\n //\n // 2. << - Shift Left operation, by n position:\n // Example:\n // 11 (3) << 2 (n position) = 1100 (14)\n //\n\n public int concatenatedBinary(int n) {\n\n final long modulo = (long) (1e9 + 7);\n long result = 0;\n\n // This records the number of binaryDigits we need to shift left.\n int binaryDigits = 0;\n\n for (int i = 1; i <= n; i++) {\n\n // If i is a power of 2, we add one additional binaryDigits to shift.\n // Example:\n // i = 8 (1000), i-1 = 7 (111)\n // i & (i-1) = 1000 & 111 = 0\n // So we know we have increased the binaryDigits from 3 (in 111) to 4 (in 1000).\n if ((i & (i - 1)) == 0) {\n binaryDigits++;\n }\n\n // With the updated binaryDigits, we now can concatenate i to the result.\n // Each time get the remainder of the result % modulo.\n // Example:\n // i = 2\n // result = 1 (1) << 2 (n position) + 10 (2) = 100 (4) + 10 (2) = 110 (6).\n // i = 3\n // result = 110 (6) << 2 (n position) + 11 (3) = 11000 (24) + 11 (3) = 11011 (27).\n //\n result = ((result << binaryDigits) + i) % modulo;\n }\n return (int) result;\n }\n}\n```\n\n**Java (Math) - With Explanation**\n```\nclass Solution {\n \n // Approach:\n // We concatenate by shifting position of result with division and multiplication, then add the number.\n // As there are a lot of repetitions in shifting of positions, it is much less efficient than using bit manipulation.\n \n public int concatenatedBinary(int n) {\n final long modulo = (long) (1e9 + 7);\n long result = 0;\n for (int i = 1; i <= n; i++) {\n // For each i, we shift left the position of result with * 2,\n // while shifting right the position of i with / 2.\n int temp = i;\n while (temp > 0) {\n temp /= 2;\n result *= 2;\n }\n // Add the i to the result and get the remainder of modulo.\n result = (result + i) % modulo;\n }\n return (int) result;\n }\n}\n```\n
| 133 | 5 |
['Math', 'Bit Manipulation', 'Java']
| 11 |
concatenation-of-consecutive-binary-numbers
|
Detailed Thought Process with Steps Example | O(n) Time | Java 8 1-Liner
|
detailed-thought-process-with-steps-exam-nf2u
|
\nn = 3\n1 - 1\n2 - 10\n3 - 11\n\n123 -> 11011 --> \n\n(1 * 2^4) + (1 * 2 ^3 + 0 * 2 ^ 2) + (1 * 2^1 + 1 * 2^0)\n\n(1 * 2^4) + (2 * 2 ^2 + 0 * 2 ^ 2) + (2 * 2^0
|
poiuytrewq1as
|
NORMAL
|
2020-12-06T04:07:13.459828+00:00
|
2021-01-27T16:51:59.388756+00:00
| 9,562 | false |
```\nn = 3\n1 - 1\n2 - 10\n3 - 11\n\n123 -> 11011 --> \n\n(1 * 2^4) + (1 * 2 ^3 + 0 * 2 ^ 2) + (1 * 2^1 + 1 * 2^0)\n\n(1 * 2^4) + (2 * 2 ^2 + 0 * 2 ^ 2) + (2 * 2^0 + 1 * 2^0)\n\n(1 * 2^4) + (2 + 0) * 2 ^2 + (2 + 1)* 2^0\n\n(1)* 2^4 + (2) * 2 ^2 + (3)* 2^0\n\n((1)* 2^4 + (2) * 2 ^2) + (3)* 2^0\n\n((1)* 2^2 + (2)) * 2 ^2) + (3)* 2^0\n\n(4 + 2) * 2^2 + 3\n\n24 + 3 \n\n27\n\n```\n\n```\nclass Solution {\n public int concatenatedBinary(int n) {\n int MOD = 1_000_000_007;\n long sum = 0;\n for (int i = 1; i <= n; i++)\n sum = (sum * (int)Math.pow(2, Integer.toBinaryString(i).length()) + i) % MOD; // sum = ((sum << Integer.toBinaryString(i).length()) + i) % MOD;\n\n return (int)sum;\n }\n}\n```\n\n****************\n\n**Bitwise O(n) Time**\n\n```\nclass Solution {\n // TC - O(n)\n public int concatenatedBinary(int n) {\n int MOD = 1_000_000_007;\n long sum = 0;\n int length = 0;\n \n for(int i = 1; i <= n; i++) {\n if((i & (i - 1)) == 0)\n length++;\n sum = ((sum << length) | i) % MOD;\n }\n \n return (int) sum;\n }\n}\n```\n\n****************\n\nJava-8: 1 Liner using Long.range and reduce\n\n```\nclass Solution {\n public int concatenatedBinary(int n) {\n\t\treturn (int) LongStream.range(1, n + 1).reduce(0, (sum, i) -> (sum * (int) Math.pow(2, Long.toBinaryString(i).length()) + i) % 1_000_000_007);\n }\n}\n```\n\n\nIf you like solution - **upvote**.
| 106 | 14 |
[]
| 18 |
concatenation-of-consecutive-binary-numbers
|
[Python] O(n) and O(log^2 n) fast and short, explained
|
python-on-and-olog2-n-fast-and-short-exp-8kol
|
One way to solve this problem in competition is just create very long binary string and then find result of division by 10**9 + 7 and it will work fine. However
|
dbabichev
|
NORMAL
|
2021-01-27T09:32:51.521056+00:00
|
2021-01-27T13:11:58.106593+00:00
| 6,272 | false |
One way to solve this problem in competition is just create very long binary string and then find result of division by `10**9 + 7` and it will work fine. However in interview setup it is not the best idea and I prefer more honest way. Let us look at first several `n` to see how it works:\n`1`\n`110`\n`11011`\n`11011100`\n\nLet us try to find answer to `n`, using information about `n-1`. `110` = `1 * 100 + 10` (all in binary representation), `11011 = 110 * 100 + 11`, `11011100 = 11011 * 1000 + 100` and so on. We can see that on each step we need to multiply number by **lenght** of new number and add new number (and use `%M`) and that is all!\n\n**Complexity**: time complexity is `O(n)`, space is `O(1)`.\n\n```\nclass Solution:\n def concatenatedBinary(self, n):\n ans, M = 0, 10**9 + 7\n for x in range(n):\n ans = (ans * (1 << (len(bin(x+1)) - 2)) + x+1) % M\n return ans \n```\n\n**Further thoughts** When you found `O(n)` solution, you should ask a question, can you do better? Here I had very strong intuition that you can do it faster and I came up with `O(log^2 n)` solution. Then I checked discussions and there is in fact at least two solutions with this complexity: one uses idea of geometrical progressions: idea behind is the following: we can see that in binary representation of desired number there will be `O(log n)` sequences of ones with equal gaps for each of `O(log n)` lengths of numbers. You can find this solution in discussion, I will code my own version if I have time. Another solution using matrix multiplications and I was very impressed to see it.\n\n### Faster solution with O(log^2 n) complexity\n\nIt is easier to chose some `n` and go into details about this `n`. Let us choose `n = 54` and discuss how my algorithm works:\n\nFunction `bin_pow` will return powers of `2`, which sum to given number, for example `bin_pow(37) = [1, 4, 32]`, because `1 + 4 + 32 = 37`.\n\nNow, we have `n = 54`, and we have:\n1. `1` number with length `1`: just `1`\n2. `2` numbers with length `2`: `10, 11`\n3. `4` numbers with length `3`: `100, 101, 110, 111`.\n4. `8` numbers with length `4`: `1000, ..., 1111`\n5. `16` numbers with length `5`: `10000, ..., 11111`.\nNow, we have 23 more numbers and we keep to split them into groups:\n6. `16` numbers with lenght `6`, which **start with** `10....`, that is `100000, 100001, ... 101111`. Why we choose `16` of them? Because it is the biggest group we can take such that this group is full: given start we have all possible endings.\n7. `4` numbers with length `6`, which **start with** `1100`, that is `110000, 110001, 110010, 110011`\n8. `2` numbers with length `6`, which **start with** `11010`, that is `110100` and `110101`.\n9. `1` number with length `6`: `110110`, which is equal to `54`, our last number.\n\nWe will keep lenghts of our groups in list `B`, so we have:\n`B = [1, 2, 4, 8, 16, 16, 4, 2, 1`]\n\nWe will keep length of numbers in each group in list `C`, so we have:\n`C = [1, 2, 3, 4, 5, 6, 6, 6, 6]`\n\nSo far we have the following picture:\n\n`[1][10 11][100 101 110 111] ... [110000, 110001, 110010, 110011], [110100, 110101], [110110]`\n\nWe will keep starting places of each group in list `D`, in our case we have:\n`D = [266, 262, 250, 218, 138, 42, 18, 6, 0]`.\nLet us look from the end: last group we do not need to multiply by anything, previous group has `1` number with length `6`, so we need to multiply it by `2^6`. Next we have `2*6 + 1*6` shift, `4*6 + 2*6 + 1*6`, `16*6 + 4*6 + 2*6 + 1*6`, `16*5 + 16*6 + 4*6 + 2*6 + 1*6` and so on: it can be done efficiently, using `accumulate` function in python.\n\nFinal step is to iterate over our groups and evaluate number modulo `10**9 + 7` in each group:\n\nLet us look at group `[110000, 110001, 110010, 110011]` for better underastnding. This group will be somewhere in the middle of number, like `...[110000, 110001, 110010, 110011]...` and we need to understand what impact it has on our number, we need several values:\n1. Place, where this group is located, for this we use `D` list, `d` for given group.\n2. Lenth of elements in each group, for this we use `C` list, `c` for given group.\n3. Number of elements in our group, for this we use `B` list, `b` for given group.\n4. Also we need to now, from which element we start, in our case it is `110000`, we can evaluate it as `a - b + 1`, where `a` is corresponding element in `accumulate(B)`: here we have `accumulate(B) = [1, 3, 7, 15, 31, 47, 51, 53, 54]` and `51-4 + 1 = 48` is current number we start with, `a` for given group\n\nFinally, we need to do some mathematics: we need to evaluate sum:\n`[(a-b+1) * 2^(b*c) + (a-b+2)*2^(b*(c-1)) + ... + (a-b + c-1) * 2^(b*1) + (a-b + c) * 2^(b*0)]*2^d`.\n\nThis formula can be written in closed form! It is almost like sum of geometrical progression, but in fact, sum of several of them which lead us to closed form solution. We also need to work using modular arithmetic, so we use powerful `pow` python function. In my notation `t1 = [2^(bc) - 1] % MOD` and `t2 = [1/(2^c - 1)] % MOD`. Here we use Fermat\'s little theorem to evaluate inverse number in modular arithmetic. \n\n**Complexity**: time complexity of evaluating `B, C, D` lists is just `O(log n)`. However when we work with `pow` function, complexity to evaluate sum in each group will be also `O(log n)`, which leasd to `O(log^2 n)` time complexity. Space complexity is `O(log n)`.\n\n\n```\nclass Solution:\n def concatenatedBinary(self, n):\n def bin_pow(num): return [1<<i for i, b in enumerate(bin(num)[:1:-1]) if b == "1"]\n ans, MOD, q = 0, 10**9 + 7, len(bin(n)) - 3\n\n B = bin_pow((1<<q) - 1) + bin_pow(n - (1<<q) + 1)[::-1]\n C = list(range(1, q+1)) + [q+1]*(len(B) - q)\n D = list(accumulate(i*j for i,j in zip(B[::-1], C[::-1])))[::-1][1:] + [0]\n \n for a, b, c, d in zip(accumulate(B), B, C, D):\n t1 = pow(2, b*c, MOD) - 1\n t2 = pow(pow(2, c, MOD)-1, MOD - 2, MOD)\n ans += t2*((a-b+1+t2)*t1-b)*pow(2, d, MOD)\n\n return ans % MOD\n```\n\nIf you have any questions, feel free to ask. If you like solution and explanations, please **Upvote!**
| 90 | 6 |
[]
| 8 |
concatenation-of-consecutive-binary-numbers
|
🔥 [LeetCode The Hard Way] 🔥 Explained Line By Line
|
leetcode-the-hard-way-explained-line-by-k7np4
|
Please check out LeetCode The Hard Way for more solution explanations and tutorials. \nI\'ll explain my solution line by line daily and you can find the full li
|
__wkw__
|
NORMAL
|
2022-09-23T02:48:14.381437+00:00
|
2022-09-23T04:24:48.218396+00:00
| 4,193 | false |
Please check out [LeetCode The Hard Way](https://wingkwong.github.io/leetcode-the-hard-way/) for more solution explanations and tutorials. \nI\'ll explain my solution line by line daily and you can find the full list in my [Discord](https://discord.gg/Nqm4jJcyBf).\nIf you like it, please give a star, watch my [Github Repository](https://github.com/wingkwong/leetcode-the-hard-way) and upvote this post.\n\n---\n\n**Approach 1: Bit Manipulation**\n\n**C++**\n\n```cpp\n// Time Complexity: O(N)\n// Space Complexity: O(1)\nclass Solution {\npublic:\n // the idea is to use bit manipulation to set the current number based on the previous number\n // for example, \n // n = 1, ans = 0b1\n // n = 2 (10), we need to shift 2 bits of the previous ans to the left and add `n`\n // i.e. 1 -> 100 (shift 2 bits to the left) -> 110 (set `10`). ans = 0b110\n // n = 3 (11), we need to shift 2 bits of the previous ans to the left and add `n` \n // i.e 110 -> 11000 (shift 2 bits to the left) -> 11011 (set `11`). ans = 0b11011\n // n = 4 (100), we need to shift 3 bits of the previous ans to the left and add `n`\n // i.e. 11011 -> 11011000 (shift 3 bits to the left) -> 11011100 (set `100). ans = 0b11011100\n // so now we can see a pattern here\n // we need to shift `l` bits of the previous ans to the left and add the current `i` \n // how to know `l`? it is not difficult to see `x` only increases when we meet power of 2\n int concatenatedBinary(int n) {\n // `l` is the bit length to be shifted\n int M = 1e9 + 7, l = 0;\n // use long here as it potentially could overflow for int\n long ans = 0;\n for (int i = 1; i <= n; i++) {\n // i & (i - 1) means removing the rightmost set bit\n // e.g. 100100 -> 100000\n // 000001 -> 000000\n // 000000 -> 000000\n // after removal, if it is 0, then it means it is power of 2\n // as all power of 2 only contains 1 set bit\n // if it is power of 2, we increase the bit length `l`\n if ((i & (i - 1)) == 0) l += 1;\n // (ans << l) means shifting the orginal answer `l` bits to th left\n // (x | i) means using OR operation to set the bit\n // e.g. 0001 << 3 = 0001000\n // e.g. 0001000 | 0001111 = 0001111\n ans = ((ans << l) | i) % M;\n }\n return ans;\n }\n};\n```\n\n**Java**\n\n```java\n// Time Complexity: O(N)\n// Space Complexity: O(1)\nclass Solution {\n // the idea is to use bit manipulation to set the current number based on the previous number\n // for example, \n // n = 1, ans = 0b1\n // n = 2 (10), we need to shift 2 bits of the previous ans to the left and add `n`\n // i.e. 1 -> 100 (shift 2 bits to the left) -> 110 (set `10`). ans = 0b110\n // n = 3 (11), we need to shift 2 bits of the previous ans to the left and add `n` \n // i.e 110 -> 11000 (shift 2 bits to the left) -> 11011 (set `11`). ans = 0b11011\n // n = 4 (100), we need to shift 3 bits of the previous ans to the left and add `n`\n // i.e. 11011 -> 11011000 (shift 3 bits to the left) -> 11011100 (set `100). ans = 0b11011100\n // so now we can see a pattern here\n // we need to shift `l` bits of the previous ans to the left and add the current `i` \n // how to know `l`? it is not difficult to see `x` only increases when we meet power of 2\n public int concatenatedBinary(int n) {\n // `l` is the bit length to be shifted\n int M = 1000000007, l = 0;\n // use long here as it potentially could overflow for int\n long ans = 0;\n for (int i = 1; i <= n; i++) {\n // i & (i - 1) means removing the rightmost set bit\n // e.g. 100100 -> 100000\n // 000001 -> 000000\n // 000000 -> 000000\n // after removal, if it is 0, then it means it is power of 2\n // as all power of 2 only contains 1 set bit\n // if it is power of 2, we increase the bit length `l`\n if ((i & (i - 1)) == 0) l += 1;\n // (ans << l) means shifting the orginal answer `l` bits to th left\n // (x | i) means using OR operation to set the bit\n // e.g. 0001 << 3 = 0001000\n // e.g. 0001000 | 0001111 = 0001111\n ans = ((ans << l) | i) % M;\n }\n return (int) ans;\n }\n}\n```\n\n**Python**\n\n```py\n# Time Complexity: O(N)\n# Space Complexity: O(1)\nclass Solution:\n # the idea is to use bit manipulation to set the current number based on the previous number\n # for example, \n # n = 1, ans = 0b1\n # n = 2 (10), we need to shift 2 bits of the previous ans to the left and add `n`\n # i.e. 1 -> 100 (shift 2 bits to the left) -> 110 (set `10`). ans = 0b110\n # n = 3 (11), we need to shift 2 bits of the previous ans to the left and add `n` \n # i.e 110 -> 11000 (shift 2 bits to the left) -> 11011 (set `11`). ans = 0b11011\n # n = 4 (100), we need to shift 3 bits of the previous ans to the left and add `n`\n # i.e. 11011 -> 11011000 (shift 3 bits to the left) -> 11011100 (set `100). ans = 0b11011100\n # so now we can see a pattern here\n # we need to shift `l` bits of the previous ans to the left and add the current `i` \n # how to know `l`? it is not difficult to see `x` only increases when we meet power of 2\n def concatenatedBinary(self, n: int) -> int:\n M = 10 ** 9 + 7\n # `l` is the bit length to be shifted\n l, ans = 0, 0\n for i in range(1, n + 1):\n # i & (i - 1) means removing the rightmost set bit\n # e.g. 100100 -> 100000\n # 000001 -> 000000\n # 000000 -> 000000\n # after removal, if it is 0, then it means it is power of 2\n # as all power of 2 only contains 1 set bit\n # if it is power of 2, we increase the bit length `l`\n if i & (i - 1) == 0:\n l += 1\n # (ans << l) means shifting the orginal answer `l` bits to th left\n # (x | i) means using OR operation to set the bit\n # e.g. 0001 << 3 = 0001000\n # e.g. 0001000 | 0001111 = 0001111\n ans = ((ans << l) | i) % M\n return ans\n```\n\n**Go**\n\n```go\n// Time Complexity: O(N)\n// Space Complexity: O(1)\n\n// the idea is to use bit manipulation to set the current number based on the previous number\n// for example, \n// n = 1, ans = 0b1\n// n = 2 (10), we need to shift 2 bits of the previous ans to the left and add `n`\n// i.e. 1 -> 100 (shift 2 bits to the left) -> 110 (set `10`). ans = 0b110\n// n = 3 (11), we need to shift 2 bits of the previous ans to the left and add `n` \n// i.e 110 -> 11000 (shift 2 bits to the left) -> 11011 (set `11`). ans = 0b11011\n// n = 4 (100), we need to shift 3 bits of the previous ans to the left and add `n`\n// i.e. 11011 -> 11011000 (shift 3 bits to the left) -> 11011100 (set `100). ans = 0b11011100\n// so now we can see a pattern here\n// we need to shift `l` bits of the previous ans to the left and add the current `i` \n// how to know `l`? it is not difficult to see `x` only increases when we meet power of 2\nfunc concatenatedBinary(n int) int {\n // `l` is the bit length to be shifted\n ans, l, M := 0, 0, 1_000_000_007\n for i := 1; i <= n; i++ {\n // i & (i - 1) means removing the rightmost set bit\n // e.g. 100100 -> 100000\n // 000001 -> 000000\n // 000000 -> 000000\n // after removal, if it is 0, then it means it is power of 2\n // as all power of 2 only contains 1 set bit\n // if it is power of 2, we increase the bit length `l`\n if (i & (i - 1) == 0) {\n l += 1\n }\n // (ans << l) means shifting the orginal answer `l` bits to th left\n // (x | i) means using OR operation to set the bit\n // e.g. 0001 << 3 = 0001000\n // e.g. 0001000 | 0001111 = 0001111\n ans = ((ans << l) | i) % M\n } \n return ans\n}\n```
| 77 | 4 |
['Bit Manipulation', 'C', 'Python', 'C++', 'Java', 'Go', 'Python3']
| 10 |
concatenation-of-consecutive-binary-numbers
|
C++ O(N) time iterative
|
c-on-time-iterative-by-lzl124631x-kh2d
|
See my latest update in repo LeetCode\n\n## Solution 1. \n\nLet f(n) be the answer. sum_len(a, b) = sum( len(i) | a <= i <= b) and len(i) is the number of bits
|
lzl124631x
|
NORMAL
|
2020-12-06T04:00:38.718508+00:00
|
2020-12-06T09:57:18.546131+00:00
| 8,448 | false |
See my latest update in repo [LeetCode](https://github.com/lzl124631x/LeetCode)\n\n## Solution 1. \n\nLet `f(n)` be the answer. `sum_len(a, b) = sum( len(i) | a <= i <= b)` and `len(i)` is the number of bits in `i`.\n\nFor example: `len(1) = 1`, `len(3) = 2`, `len(6) = 3`. `sum_len(1,4) = len(1) + len(2) + len(3) + len(4) = 1 + 2 + 2 + 3 = 8`.\n\nSo we have\n\n```plaintext\nf(n) = (1 << sum_len(2, n)) + (2 << sum_len(3, n)) + ... + ((n - 1) << sum_len(n, n)) + (n << 0)\n\n// Example: f(4) = 11011100 = (1 << (2+2+3)) + (2 << (2+3)) + (3 << 3) + (4 << 0)\n\nf(n-1) = (1 << sum_len(2, n-1)) + (2 << sum_len(3, n-1)) + ... + ((n - 1) << 0)\n\nf(n) = (f(n-1) << len(n)) + n\n```\n\nSince `f(0) = 0`, we can iteratively build `f(n)`.\n\n```plaintext\nf(0) = 0\nf(1) = 1 = (f(0) << 1) + 1 // len(1) = 1\nf(2) = 110 = (f(1) << 2) + 2 // len(2) = 2\nf(3) = 11011 = (f(2) << 2) + 3 // len(3) = 2\n...\n```\n\n```cpp\n// OJ: https://leetcode.com/problems/concatenation-of-consecutive-binary-numbers/\n// Author: github.com/lzl124631x\n// Time: O(NlogN)\n// Space: O(1)\nclass Solution {\npublic:\n int concatenatedBinary(int n) {\n long ans = 0, mod = 1e9+7;\n for (int i = 1; i <= n; ++i) {\n int len = 0;\n for (int j = i; j; j >>= 1, ++len);\n ans = ((ans << len) % mod + i) % mod;\n }\n return ans;\n }\n};\n```\n\n## Solution 2.\n\nWe spent `O(logN)` time for calculating the `len`. We can reduce it to `O(1)` with the help of `__builtin_clz` which returns the number of leading zeros for a number, so `len = 32 - __builtin_clz(i)`. (Thanks 0xFFFFFFFF)\n\n```cpp\n// OJ: https://leetcode.com/problems/concatenation-of-consecutive-binary-numbers/\n// Author: github.com/lzl124631x\n// Time: O(N)\n// Space: O(1)\nclass Solution {\npublic:\n int concatenatedBinary(int n) {\n long ans = 0, mod = 1e9+7;\n for (int i = 1; i <= n; ++i) ans = ((ans << (32 - __builtin_clz(i))) % mod + i) % mod;\n return ans;\n }\n};\n```\n\nOr, with the observation that the `len` only increment when the `i` is a power of `2`, we can increment `len` only when `i` has a single bit `1`. We can check this via `(i & (i - 1)) == 0`. (Thanks @LVL99)\n\n```cpp\n// OJ: https://leetcode.com/problems/concatenation-of-consecutive-binary-numbers/\n// Author: github.com/lzl124631x\n// Time: O(N)\n// Space: O(1)\nclass Solution {\npublic:\n int concatenatedBinary(int n) {\n long ans = 0, mod = 1e9+7, len = 0;\n for (int i = 1; i <= n; ++i) {\n if ((i & (i - 1)) == 0) ++len;\n ans = ((ans << len) % mod + i) % mod;\n }\n return ans;\n }\n};\n```
| 66 | 3 |
[]
| 9 |
concatenation-of-consecutive-binary-numbers
|
C++ Super Simple, Short and Easy O(n) Solution
|
c-super-simple-short-and-easy-on-solutio-e2u9
|
\nclass Solution {\npublic:\n int concatenatedBinary(int n) {\n long res = 0, mod = 1e9+7, len_of_curr = 0;\n for (int i = 1; i <= n; i++) {\n\
|
yehudisk
|
NORMAL
|
2021-01-27T10:12:09.107613+00:00
|
2021-01-27T10:12:09.107640+00:00
| 3,715 | false |
```\nclass Solution {\npublic:\n int concatenatedBinary(int n) {\n long res = 0, mod = 1e9+7, len_of_curr = 0;\n for (int i = 1; i <= n; i++) {\n\t\t\n\t\t\t// the len increases every time we reach a number which is a power of two.\n if ((i & (i-1)) == 0)\n len_of_curr++;\n\t\t\t\t\n res = (res << len_of_curr) % mod;\n res += i % mod;\n }\n return res;\n }\n};\n```\n**Like it? please upvote...**
| 53 | 7 |
['C']
| 2 |
concatenation-of-consecutive-binary-numbers
|
✅Short || C++ || Explained Solution✔️ || Beginner Friendly ||🔥 🔥 BY MR CODER
|
short-c-explained-solution-beginner-frie-uj98
|
Watch this video \uD83E\uDC83 for the better explanation of the code.\n\nhttps://www.youtube.com/watch?v=yMwSJfpSYEo\n\nAlso you can SUBSCRIBE \uD83E\uDC81 \uD8
|
letternavodayan
|
NORMAL
|
2022-09-23T01:05:37.456210+00:00
|
2022-09-23T01:58:41.117612+00:00
| 3,526 | false |
**Watch this video \uD83E\uDC83 for the better explanation of the code.**\n\nhttps://www.youtube.com/watch?v=yMwSJfpSYEo\n\nAlso you can SUBSCRIBE \uD83E\uDC81 \uD83E\uDC81 \uD83E\uDC81 this channel for the daily leetcode challange solution.\nhttps://t.me/dsacoder \u2B05\u2B05 Telegram link to discuss leetcode daily questions and other dsa problems\n**C++**\n```\nclass Solution {\npublic:\n int concatenatedBinary(int n) {\n long ans = 0, mod = 1e9+7, length = 0;\n for (int i = 1; i <= n; ++i) {\n \n if ((i & (i - 1)) == 0) length++;\n ans = ((ans << length) + i) % mod;\n }\n return ans;\n }\n};\n```\n**Please do UPVOTE to motivate me to solve more daily challenges like this !!**
| 36 | 2 |
['C', 'C++']
| 3 |
concatenation-of-consecutive-binary-numbers
|
[c++][Beginner friendly][easy understanding]
|
cbeginner-friendlyeasy-understanding-by-qal2k
|
\n#define mod 1000000007\nclass Solution {\npublic:\n \n int concatenatedBinary(int n) {\n string s=decimalToBinary(n);\n return binaryToDec
|
rajat_gupta_
|
NORMAL
|
2020-12-06T04:25:21.808683+00:00
|
2020-12-06T04:26:26.680952+00:00
| 2,638 | false |
```\n#define mod 1000000007\nclass Solution {\npublic:\n \n int concatenatedBinary(int n) {\n string s=decimalToBinary(n);\n return binaryToDecimal(s);\n }\n\t\n\tstring decimalToBinary(int n) { \n string str="";\n for(int i=n;i>=1;--i){\n int no=i;\n while(no){\n str+=(no%2)+\'0\';\n no/=2;\n }\n }\n return str;\n } \n \n int binaryToDecimal(string n){\n long long ans=0,powe=1;\n for(int j=0;j<n.size();++j){\n long long now=(n[j]-\'0\')*(powe);\n powe*=2;\n powe%=mod;\n ans+=now;\n }\n return ans%mod;\n }\n};\n```\n**Feel free to ask any question in the comment section.**\nI hope that you\'ve found the solution useful.\nIn that case, **please do upvote and encourage me** to on my quest to document all leetcode problems\uD83D\uDE03\nHappy Coding :)\n
| 35 | 6 |
['C', 'C++']
| 6 |
concatenation-of-consecutive-binary-numbers
|
python (log(n)) ^2 approach
|
python-logn-2-approach-by-rbx-zptu
|
\n\nO(logn) level to iterate \nin each level calculating result of power for O(logn)\n\n\nclass Solution(object):\n def concatenatedBinary(self, n):\n
|
rbx
|
NORMAL
|
2020-12-07T17:02:44.147705+00:00
|
2020-12-07T17:22:00.775317+00:00
| 2,031 | false |
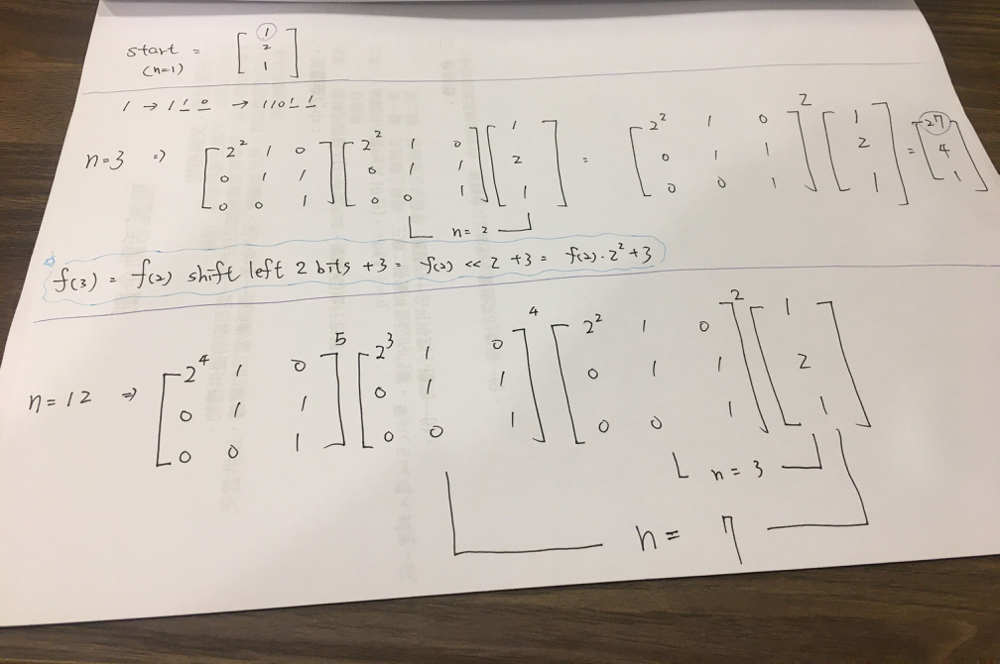\n\nO(logn) level to iterate \nin each level calculating result of power for O(logn)\n\n```\nclass Solution(object):\n def concatenatedBinary(self, n):\n """\n :type n: int\n :rtype: int\n """\n def multiply(X, Y):\n return [[sum(a*b for a,b in zip(X_row,Y_col)) % 1000000007 for Y_col in zip(*Y)] for X_row in X]\n \n ans, acc, level = [[1], [2], [1]], 1, 1\n while acc < n:\n M = 2 ** (level + 1)\n\t\t\t\n\t\t\t# number of matrix production in this level\n x = take = min(n, M - 1) - acc\n \n\t\t\tmat = [[M, 1, 0], [0, 1, 1], [0, 0, 1]]\n\t\t\t\n\t\t\t# for example\n\t\t\t# num^13 = num * num^4 * num^8\n\t\t\t# num^6 = num^2 * num^4\n while x > 0:\n if x & 1: ans = multiply(mat, ans)\n mat, x = multiply(mat, mat), x >> 1\n \n\t\t\tacc, level = acc + take, level + 1\n \n return ans[0][0]\n```\n\ncredit to @ckclark
| 30 | 1 |
[]
| 6 |
concatenation-of-consecutive-binary-numbers
|
C++ | Bit Manipulation Appraoch ✅
|
c-bit-manipulation-appraoch-by-prantik01-vjoh
|
If you like it, please give a star, to my Github Repository and upvote this post.\n\nIntuition:\nThe answer is the sum of the binary representations of the numb
|
prantik0128
|
NORMAL
|
2022-09-23T03:01:54.691740+00:00
|
2022-09-23T03:01:54.691780+00:00
| 2,892 | false |
**If you like it, please give a star, to my [Github](https://github.com/champmaniac/LeetCode) Repository and upvote this post.**\n\n**Intuition:**\nThe answer is the **sum** of the binary representations of the numbers from `1 to n`. The binary representation of a number is the sum of the **powers** of `2` that make up the number. The powers of `2` are the same as the **binary** representation of the number.\n\n**Approach:**\n* Iterate through the numbers from `1 to n` and add the `binary` representation of `each` number to the `answer`.\n* `ans` `= ans<<`(`number of bits in the binary representation of the current number`) + `binary representation of the current number.`\n\n**C++:**\n```\nclass Solution {\npublic:\n int concatenatedBinary(int n) {\n int mod = 1e9 + 7;\n long long ans = 0;\n int len = 0;\n for (int i = 1; i <= n; i++) {\n if ((i & (i - 1)) == 0) {\n len++;\n }\n ans = ((ans << len) + i) % mod;\n }\n return ans;\n }\n};\n```\n****\n**Time Complexity:** **O(n)**, where `n`: input number\n**Space Complexity:** **O(1)**\n****\n\n
| 24 | 1 |
['Bit Manipulation', 'C', 'C++']
| 2 |
concatenation-of-consecutive-binary-numbers
|
[Python 3] Bit manipulation, 4 solutions, 1 line, O(n), 44ms
|
python-3-bit-manipulation-4-solutions-1-0g936
|
Straightforward solution\n- Iteratively shift sum to the left by counter bit length and add the counter.\n- Iteratively get modulo 10\\9+7 to avoid slow big int
|
dpustovarov
|
NORMAL
|
2021-01-27T10:03:19.858656+00:00
|
2021-01-27T10:03:19.858681+00:00
| 1,358 | false |
# Straightforward solution\n- Iteratively shift sum to the left by counter bit length and add the counter.\n- Iteratively get modulo 10\\*\\*9+7 to avoid slow big int operations.\n- Time complexity is O(n), space complexity is O(1).\n```\nclass Solution:\n def concatenatedBinary(self, n: int) -> int:\n s = 0\n for i in range(1, n+1):\n s = (s << i.bit_length() | i) % 1000000007\n \n return s\n```\n# Functional approach\nThe same algorithm in 1 line.\n```\nclass Solution:\n def concatenatedBinary(self, n: int) -> int:\n return reduce(lambda s, i: (s << i.bit_length() | i) % 1000000007, range(1, n+1))\n```\n# Lazy memoization\n- Since task for small ```n``` is a subtask for big ```n``` we can cache all ```n``` to avoid duplicated calculations.\n- Time complexity is O(n), space complexity is O(n).\n```\nclass Solution:\n mem = [0]\n \n def concatenatedBinary(self, n: int) -> int:\n for i in range(len(Solution.mem), n+1):\n Solution.mem.append((Solution.mem[-1] << i.bit_length() | i) % 1000000007)\n \n return Solution.mem[n]\n```\n# Greedy memoization, 44ms\n- Since we know n <= 10\\*\\*5 we can precalculate all ```n```.\n- Time complexity is O(1) and initialization O(n), space complexity is O(n)\n```\nclass Solution:\n mem = list(accumulate(range(100001), lambda s, i: (s << i.bit_length() | i) % 1000000007))\n \n def concatenatedBinary(self, n: int) -> int:\n return Solution.mem[n]\n```\n\n
| 20 | 0 |
['Bit Manipulation', 'Memoization', 'Python']
| 2 |
concatenation-of-consecutive-binary-numbers
|
Python - Easiest Solution - Brute-Force - Beats 95%
|
python-easiest-solution-brute-force-beat-eize
|
Things I learnt which might benefit everyone :\n The bin() function in python returns the binary value prefixed with 0b, for our solution we use the format() to
|
rjrockzz
|
NORMAL
|
2022-09-23T05:17:22.557816+00:00
|
2022-09-23T05:17:22.557859+00:00
| 2,107 | false |
Things I learnt which might benefit everyone :\n* The `bin()` function in python returns the binary value **prefixed with 0b**, for our solution we use the `format()` to get rid of those prefixes.\n* To convert a binary to an integer equivalent, which can actually be done using `int()` , by passing in 2 as the second parameter\n```\nclass Solution:\n def concatenatedBinary(self, n: int) -> int:\n string = ""\n for i in range(1,n+1):\n string+=format(i,"b")\n return int(string,2)%(10**9 + 7)\n```
| 19 | 0 |
['Python']
| 4 |
concatenation-of-consecutive-binary-numbers
|
[Java] Bit manipulation without any library function O(n) time, O(1) space
|
java-bit-manipulation-without-any-librar-vcj7
|
\n```\n\tpublic int concatenatedBinary(int n) {\n int digits = 0, MOD = 1000000007;\n long result = 0;\n for(int i = 1; i <= n; i++){\n\t\t
|
dark_warlord
|
NORMAL
|
2021-01-27T10:03:17.837516+00:00
|
2021-01-27T10:14:10.372610+00:00
| 968 | false |
\n```\n\tpublic int concatenatedBinary(int n) {\n int digits = 0, MOD = 1000000007;\n long result = 0;\n for(int i = 1; i <= n; i++){\n\t\t\t/* if "i" is a power of 2, then we have one additional digit in\n\t\t\t its the binary equivalent compared to that of i-1 */\n if((i & (i - 1)) == 0) digits++; \n result = ((result << digits) + i) % MOD;\n }\n \n return (int) result;\n }
| 16 | 1 |
[]
| 6 |
concatenation-of-consecutive-binary-numbers
|
Java - Simple & Easy O(N) solution.
|
java-simple-easy-on-solution-by-popeye_t-pler
|
The idea is to add powers of 2 if the last bit is 1.\n\n```\n public int concatenatedBinary(int n) {\n long res = 0, mul = 1;\n int mod = 1_000
|
popeye_the_sailort
|
NORMAL
|
2020-12-06T04:01:35.205026+00:00
|
2020-12-06T04:04:53.517819+00:00
| 1,421 | false |
The idea is to add powers of 2 if the last bit is 1.\n\n```\n public int concatenatedBinary(int n) {\n long res = 0, mul = 1;\n int mod = 1_000_000_007;\n for(int i = n; i > 0; --i){\n int no = i;\n while(no > 0){\n if(no % 2 == 1) res = (res + mul) % mod;\n no >>= 1;\n mul = (mul<<1) % mod;\n }\n }\n \n return (int)res;\n }
| 14 | 5 |
[]
| 2 |
concatenation-of-consecutive-binary-numbers
|
[Python] clean solution using lowbit - O(N) / O(1)
|
python-clean-solution-using-lowbit-on-o1-gzrf
|
Idea\n\nWe simply go through every number from 1 to n and update ans. The idea is somewhat similar to rolling hash.\n\nIn Python, bin() comes in handy. The bin
|
alanlzl
|
NORMAL
|
2020-12-06T04:00:52.950843+00:00
|
2020-12-06T04:21:43.031843+00:00
| 1,562 | false |
**Idea**\n\nWe simply go through every number from `1` to `n` and update `ans`. The idea is somewhat similar to rolling hash.\n\nIn Python, `bin()` comes in handy. The `bin()` method converts and returns the binary equivalent string of a given integer. For example, `bin(3)` returns `0b11`.\n\nIf we are not using `bin()`, we can update the length of the binary representation, `l`, whenever we see `x & -x == x`. The idea of `x & -x` comes from Fenwick Tree, which gives us the low bit of `x`. And this condition checks if `x` is something like `100...0`.\n\n</br>\n\n**Complexity**\n\n- Time complexity: `O(N)`\n- Space complexity: `O(1)`\n\n</br>\n\n**Python**\n\nusing lowbit (`x & -x`):\n\n```Python\nclass Solution:\n def concatenatedBinary(self, n: int) -> int:\n ans, l, MOD = 0, 0, 10 ** 9 + 7\n for x in range(1, n + 1):\n if x & (-x) == x: l += 1\n ans = (ans * (1 << l) + x) % MOD\n return ans \n```\n\nusing `bin()`:\n\n\n```Python\nclass Solution:\n def concatenatedBinary(self, n: int) -> int:\n ans, MOD = 0, 10 ** 9 + 7\n for x in range(1, n + 1):\n ans = (ans * (1 << (len(bin(x)) - 2)) + x) % MOD\n return ans \n```\n
| 13 | 1 |
[]
| 8 |
concatenation-of-consecutive-binary-numbers
|
✔ Java || Simple || Using log() function
|
java-simple-using-log-function-by-coder4-p0n0
|
\nclass Solution {\n public int concatenatedBinary(int n) {\n long result=1;\n int length=0;\n for(int i=2;i<=n;i++) {\n // l
|
coder481
|
NORMAL
|
2022-09-23T02:19:21.372830+00:00
|
2022-09-23T02:19:21.372871+00:00
| 1,271 | false |
```\nclass Solution {\n public int concatenatedBinary(int n) {\n long result=1;\n int length=0;\n for(int i=2;i<=n;i++) {\n // length of number in binary form\n length=((int)(Math.log(i)/Math.log(2)))+1;\n result=((result<<length)+i)%1000000007;\n }\n return (int)result;\n }\n}\n```
| 12 | 1 |
['Java']
| 1 |
concatenation-of-consecutive-binary-numbers
|
JAVA|| Single Line Solution|| 90% Faster Code || Beginner Friendly
|
java-single-line-solution-90-faster-code-27e8
|
\tPLEASE UPVOTE IF YOU LIKE.\n\nclass Solution {\n public int concatenatedBinary(int n) {\n int modulo = 1000000007;\n \n long ans =0;\n
|
shivrastogi
|
NORMAL
|
2022-09-23T02:10:38.608655+00:00
|
2022-09-23T02:10:38.608692+00:00
| 1,675 | false |
\tPLEASE UPVOTE IF YOU LIKE.\n```\nclass Solution {\n public int concatenatedBinary(int n) {\n int modulo = 1000000007;\n \n long ans =0;\n for(int i=1; i<=n; i++){\n ans = (((ans<<(1+(int)(Math.log(i) / Math.log(2))))%modulo)+i)%modulo;\n }\n return (int)ans;\n }\n}\n```
| 11 | 1 |
['Java']
| 4 |
concatenation-of-consecutive-binary-numbers
|
[Python\C++] simple 4 liner. (Inbuilt and bitwise)
|
pythonc-simple-4-liner-inbuilt-and-bitwi-0utd
|
Using Python Inbuilt bin method:\nPython\n\n def concatenatedBinary(self, n: int) -> int:\n res = ""\n for i in range(1,n+1):\n res+=bi
|
anupbs
|
NORMAL
|
2020-12-06T04:07:13.704673+00:00
|
2020-12-11T07:32:37.955475+00:00
| 844 | false |
Using Python Inbuilt bin method:\nPython\n```\n def concatenatedBinary(self, n: int) -> int:\n res = ""\n for i in range(1,n+1):\n res+=bin(i)[2:]\n return int(res,2)%(10**9 + 7)\n```\n\nUsing bitwise operation:\nC++\n\n```\nint concatenatedBinary(int n) {\n long int res = 0, shift = 0 ;\n long int mod = 1e9 + 7;\n for (long int i = 1; i<=n; i++){\n if( (i & (i-1)) == 0)\n shift+=1;\n res = ((res<<shift)|i )%mod;\n \n }\n return res;\n }\n```
| 11 | 4 |
['Python3']
| 5 |
concatenation-of-consecutive-binary-numbers
|
[C++] 4 Solutions Compared and Explained, ~80% Time, ~100% Space
|
c-4-solutions-compared-and-explained-80-0w5e5
|
So, for the first one I wanted to give me the extra challenge of not using long (more on that later) and so I decided to count from 1 to n, get the bits right a
|
ajna
|
NORMAL
|
2021-01-27T22:28:35.729134+00:00
|
2021-01-27T23:22:19.757571+00:00
| 707 | false |
So, for the first one I wanted to give me the extra challenge of not using `long` (more on that later) and so I decided to count from `1` to `n`, get the bits right and religiously add one bit at a time.\n\nTo do so I declared a sole support variable `res` in the main scope of the function, and a few more in our main loop:\n* `i` will be our main pointer, going from `1` to `n`, as mentioned;\n* `j` will take the value of `i` and copy it, just to be disassembled, bit by bit;\n* `bits` is going to be our storage for the bits of each number initially stored in `j` - given the maximum input size, we are fine with just `17` bits;\n* `pos` is the pointer we will use to work on `bits`, initially set to `0` (first cell).\n\nNow, in our main loop we will:\n* assign the value of `i` to `j`, as mentioned;\n* extract all the bits and store them in `bits`, with the added convenience of storing them in reverse order;\n* we will then reverse all the bits in `bits` into `res`, resetting `pos` to `0` again and at each step updating `res` to be double its previous value modulo `1000000007`, plus the current bit.\n\nOnce done, we can return `res` :)\n\nThe code, running at around 30% time, with significantly low memory consumption (arrays, what would we do without them?):\n\n```cpp\nclass Solution {\npublic:\n int concatenatedBinary(int n) {\n // support variables\n int res = 0;\n for (int i = 1, j, bits[17], pos = 0; i <= n; i++) {\n j = i;\n // extracting the bits\n while (j) {\n bits[pos++] = j % 2;\n j >>= 1;\n }\n // applying the bits\n while (pos) {\n res = (res * 2) % 1000000007 + bits[--pos];\n }\n }\n return res;\n }\n};\n```\n\nNow, can we do better?\n\nBut of course, starting with removing the modulo operation, which is notoriously rather expensive, and changing the solution to this (bumped up to 40%):\n\n```cpp\nclass Solution {\npublic:\n int concatenatedBinary(int n) {\n // support variables\n int res = 0;\n for (int i = 1, j, bits[17], pos = 0; i <= n; i++) {\n j = i;\n // extracting the bits\n while (j) {\n bits[pos++] = j % 2;\n j >>= 1;\n }\n // applying the bits\n while (pos) {\n res <<= 1;\n res = (res > 1000000007 ? res - 1000000007 : res) + bits[--pos];\n }\n }\n return res;\n }\n};\n```\n\nCan we do even better? Sure.\n\nI admit I did not want to go there not to add extra complexity, but we really do not need to store the bit in `bits` if we "read" them from the left, so here is some further optimisation\n\nTo do so, we will add an extra support variable, `hasSeenBit`, and in our main loop we will change things a bit and have `j` be our binary pointer (is that even a term? Well, let\'s pretend it is), being initialised to `1 << bitLmt`, with `bitLmt` expressing the maximum amount of bits we will ever need - for example for `n == 20`, `bitLmt` will be set to `5` (`20` is `10100` in binary representation).\n\nWe will, in each loop:\n* reset `j` to be `1 << bitLmt` and `hasSeenBit` to be `false`;\n* we will then extract each bit with `bool(i & j)`, which in our previous example will give us `1`, `0`, `1`, `0` and `0`, as expected;\n* update `hasSeenBit`, so that it will be and stay `true` as soon as the first bit is found;\n* once a bit has been found, update `res` with the logic discussed above.\n\nThe code, which bumped with this change alone to almost 60%:\n\n```cpp\nclass Solution {\npublic:\n int concatenatedBinary(int n) {\n // support variables\n int res = 0;\n bool hasSeenBit;\n for (int i = 1, j, bit, bitLmt = ceil(log2(n)); i <= n; i++) {\n // preparing for a new loop\n j = 1 << 17;\n hasSeenBit = false;\n // extracting the bits\n while (j) {\n // getting the next bit, from the left\n bit = bool(i & j);\n // updating hasSeenBit\n hasSeenBit |= bit;\n // updating res, only after we have found at least a bit\n if (hasSeenBit) {\n res <<= 1;\n res = (res > 1000000007 ? res - 1000000007 : res) + bit;\n }\n j >>= 1;\n }\n }\n return res;\n }\n};\n```\n\nAnd finally the last "cheap" one - computing the length in bits of each number, shifting `res` (a `long`, not to risk overflows) by that amount and applying the same logic with modulo and, this time, the whole number in one go.\n\nThe last part in particular - not having to split the number into single bits, had the time jump over 80%:\n\n```cpp\nclass Solution {\npublic:\n int concatenatedBinary(int n) {\n // support variables\n long res = 0;\n for (int i = 1, j, bitLen; i <= n; i++) {\n j = i;\n bitLen = 0;\n // computing the length in bits of i\n while (j) {\n bitLen++;\n j >>= 1;\n }\n // shifting res by bitLen bits\n res = (res << bitLen) % 1000000007 + i;\n }\n return res;\n }\n};\n```
| 10 | 0 |
['Bit Manipulation', 'C', 'C++']
| 1 |
concatenation-of-consecutive-binary-numbers
|
JavaScript Short 4-Liner Simple Solution
|
javascript-short-4-liner-simple-solution-uynx
|
javascript\nvar concatenatedBinary = function(n) {\n let num = 0;\n \n for(let i = 1; i <= n; i++) {\n //OR num *= (1 << i.toString(2).length)\n
|
control_the_narrative
|
NORMAL
|
2021-01-27T10:27:38.248932+00:00
|
2021-01-27T10:27:38.248968+00:00
| 570 | false |
```javascript\nvar concatenatedBinary = function(n) {\n let num = 0;\n \n for(let i = 1; i <= n; i++) {\n //OR num *= (1 << i.toString(2).length)\n num *= (2 ** i.toString(2).length) \n num += i;\n num %= (10 ** 9 + 7)\n }\n return num;\n};\n```
| 10 | 0 |
['Bit Manipulation', 'JavaScript']
| 1 |
concatenation-of-consecutive-binary-numbers
|
C# Truly O(N) solution, 4 lines
|
c-truly-on-solution-4-lines-by-leoooooo-b8eg
|
f(n) = f(n-1) * m(n) + n\n\nm(1)=2\nm(2)=4\nm(3)=4\nm(4)=8\n....\nm(n) increases only when (n & n - 1) == 0\n\n\npublic class Solution\n{\n public int Concat
|
leoooooo
|
NORMAL
|
2020-12-06T04:51:39.845087+00:00
|
2020-12-06T05:30:29.243493+00:00
| 409 | false |
f(n) = f(n-1) * m(n) + n\n\nm(1)=2\nm(2)=4\nm(3)=4\nm(4)=8\n....\nm(n) increases only when (n & n - 1) == 0\n\n```\npublic class Solution\n{\n public int ConcatenatedBinary(int n)\n {\n long m = 1, res = 0, mod = (long)Math.Pow(10, 9) + 7;\n for (int i = 1; i <= n; i++)\n {\n if (i == m) // or ((i & i - 1) == 0)\n m <<= 1;\n res = (res * m + i) % mod;\n }\n return (int)res;\n }\n}\n```\n\n\nShorter version\n```\npublic class Solution\n{\n public int ConcatenatedBinary(int n)\n {\n long m = 1, res = 0, mod = (long)Math.Pow(10, 9) + 7;\n for (int i = 1; i <= n; i++)\n res = (res * (i == m ? m <<= 1 : m) + i) % mod;\n return (int)res;\n }\n}\n```
| 10 | 0 |
[]
| 0 |
concatenation-of-consecutive-binary-numbers
|
Python, O(n), O((log n)^2) Follow-up, with Explanation
|
python-on-olog-n2-follow-up-with-explana-x9ik
|
O(n) Solution\n### Idea\nGo from 1 to n. For each i, shift the answer left for the length of the binary of i, plus i and mod p=10**9+7.\n\nOptimizations include
|
sjoin
|
NORMAL
|
2021-01-27T15:50:14.428968+00:00
|
2021-01-27T15:50:14.428997+00:00
| 222 | false |
## **O(n) Solution**\n### Idea\nGo from 1 to `n`. For each `i`, shift the answer left for the length of the binary of `i`, plus `i` and mod `p=10**9+7`.\n\nOptimizations include: \n1) Maintain the length of current `i` with `cur_ibit` and use `next_bit` to detect when to increase. I bet this would be faster than calling `int.bit_length()` on every `i`.\n2) Use `ans |= i` instead of `ans += i` as the last bits that fit `i` will always be zeros.\n\n```python\nclass Solution:\n def concatenatedBinary(self, n: int, p: int = 10 ** 9 + 7) -> int:\n ans = 0\n next_bit = 1\n cur_ibit = 0\n for i in range(1, n+1):\n if i >= next_bit:\n next_bit <<= 1\n cur_ibit += 1\n ans <<= cur_ibit\n ans |= i\n ans %= p\n return ans\n```\n\n#### Complexity\n- O(n) time. Going over through `1..n`. \n- O(1) space. Only a few extra variables.\n\n#### Submission stats\nRuntime: 972 ms (beats 94.60 %)\nMemory Usage: 14.1 MB (beats 84.51 %)\n\n## **O((log n)^2) Solution**\nWe can achieve better time complexity with some math -- more specifically, matrix multiplication. \n \n #### Idea\n When processing with `i`, the accumulation of `ans` goes as `ans = (ans << i.bit_length()) + i`. If we use a vector of `v[i] = [ans[i], i+1, 1]`, we can write this process as matrix operation `v[i+1] = M_B @ v[i]`: \n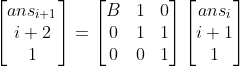,\nwhere `B = 1 << i.bit_length()` and it is the same for all `2^k <= i < 2^(k+1)`.\n\nThe good thing now is that we can fast compute the accumulative effect of those `2^k <= i < 2^(k+1)` (`2^k` of them) that share the same `B` using matrix power 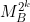, which takes O(k) time (see `matpowv()`).\n\nNow for a given `n`. Say `n = 25`. We start with `v[0] = [0, 1, 1]`. Then we do this matrix power thing for `i` in `[1, 2)`, `[2, 4)`, `[4, 8)`, `[8, 16)`, `[16, 26)`. That is, we calculate 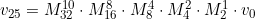 for `B, k = 2, 0`; `4, 1`; `8, 2`; `16, 3`; `32, 4`. In code, we do not explicitly keep `k` but instead use `min(bit, n - bit)` to get the power term. The final answer is `v[25][0]`.\n\nOptimizations:\n1) Same as before, use `bit` to keep track of the most significant bit instead of calculate it every time.\n2) Collapse matrices into the vector (`matpowv()`) every time to reduce the number of multiplication and additions from 3^3 (matrix multiplies matrix, `matmul()`) to 3^2 (matrix multiplies vector, `mv()`).\n\n\n```python\ndef matmul(X, Y, p):\n return [[sum(a * b for a, b in zip(X_row, Y_col)) % p for Y_col in zip(*Y)] for X_row in X]\n\ndef mv(X, v, p):\n return [sum(a * b for a, b in zip(X_row, v)) % p for X_row in X]\n\ndef matpowv(X, n, v, p):\n while n > 0:\n if n & 1: v = mv(X, v, p)\n X, n = matmul(X, X, p), n >> 1\n return v\n\nclass Solution:\n def concatenatedBinary(self, n: int, p: int = 10 ** 9 + 7) -> int:\n n += 1\n v = [0, 1, 1]\n bit = 1\n while bit < n:\n M = bit << 1\n mat = [\n [M, 1, 0],\n [0, 1, 1],\n [0, 0, 1],\n ]\n npow = min(bit, n - bit)\n v = matpowv(mat, npow, v, p)\n bit = M\n return v[0]\n```\n\n### Complexity\n- O((log n)^2) time. O(log n) for going up bit by bit from 1 to n. For each bit, O(log bit) ~ O(log n) for calculating the matrix pow. The size of matrices are irrelavent of n and are always 3x3 and thus the time complexity for matmul is O(1).\n- O(1) space. The matrices involved take up O(1) space (irrelavent of n). \n\n### Submission stats\nRuntime: 292 ms (beats 97.66 %)\nMemory Usage: 14.3 MB (beats 53.67 %)\n\n---\nIf you find this helpful, please **upvote**! Thank you!!! :-)\n\nAcknowledgement: The idea of the matrix solution comes from [@rbx](https://leetcode.com/rbx)\'s [post](https://leetcode.com/problems/concatenation-of-consecutive-binary-numbers/discuss/963549/python-(log(n))-2-approach).
| 9 | 0 |
['Math', 'Bit Manipulation']
| 2 |
concatenation-of-consecutive-binary-numbers
|
Concatenation of Consecutive Binary Numbers: Python, O(n), O((log n)^2) Follow-up, with Explanation
|
concatenation-of-consecutive-binary-numb-pj4o
|
O(n) Solution\n### Idea\nGo from 1 to n. For each i, shift the answer left for the length of the binary of i, plus i and mod p=10**9+7.\n\nOptimizations include
|
sjoin
|
NORMAL
|
2021-01-27T15:31:10.076743+00:00
|
2021-01-27T15:49:03.965406+00:00
| 462 | false |
## **O(n) Solution**\n### Idea\nGo from 1 to `n`. For each `i`, shift the answer left for the length of the binary of `i`, plus `i` and mod `p=10**9+7`.\n\nOptimizations include: \n1) Maintain the length of current `i` with `cur_ibit` and use `next_bit` to detect when to increase. I bet this would be faster than calling `int.bit_length()` on every `i`.\n2) Use `ans |= i` instead of `ans += i` as the last bits that fit `i` will always be zeros.\n\n```python\nclass Solution:\n def concatenatedBinary(self, n: int, p: int = 10 ** 9 + 7) -> int:\n ans = 0\n next_bit = 1\n cur_ibit = 0\n for i in range(1, n+1):\n if i >= next_bit:\n next_bit <<= 1\n cur_ibit += 1\n ans <<= cur_ibit\n ans |= i\n ans %= p\n return ans\n```\n\n#### Complexity\n- O(n) time. Going over through `1..n`. \n- O(1) space. Only a few extra variables.\n\n#### Submission stats\nRuntime: 972 ms (beats 94.60 %)\nMemory Usage: 14.1 MB (beats 84.51 %)\n\n## **O((log n)^2) Solution**\nWe can achieve better time complexity with some math -- more specifically, matrix multiplication. \n \n #### Idea\n When processing with `i`, the accumulation of `ans` goes as `ans = (ans << i.bit_length()) + i`. If we use a vector of `v[i] = [ans[i], i+1, 1]`, we can write this process as matrix operation `v[i+1] = M_B @ v[i]`: \n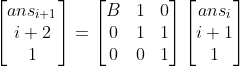,\nwhere `B = 1 << i.bit_length()` and it is the same for all `2^k <= i < 2^(k+1)`.\n\nThe good thing now is that we can fast compute the accumulative effect of those `2^k <= i < 2^(k+1)` (`2^k` of them) that share the same `B` using matrix power 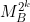, which takes O(k) time (see `matpowv()`).\n\nNow for a given `n`. Say `n = 25`. We start with `v[0] = [0, 1, 1]`. Then we do this matrix power thing for `i` in `[1, 2)`, `[2, 4)`, `[4, 8)`, `[8, 16)`, `[16, 26)`. That is, we calculate 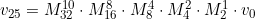 for `B, k = 2, 0`; `4, 1`; `8, 2`; `16, 3`; `32, 4`. In code, we do not explicitly keep `k` but instead use `min(bit, n - bit)` to get the power term. The final answer is `v[25][0]`.\n\nOptimizations:\n1) Same as before, use `bit` to keep track of the most significant bit instead of calculate it every time.\n2) Collapse matrices into the vector (`matpowv()`) every time to reduce the number of multiplication and additions from 3^3 (matrix multiplies matrix, `matmul()`) to 3^2 (matrix multiplies vector, `mv()`).\n\n\n```python\ndef matmul(X, Y, p):\n return [[sum(a * b for a, b in zip(X_row, Y_col)) % p for Y_col in zip(*Y)] for X_row in X]\n\ndef mv(X, v, p):\n return [sum(a * b for a, b in zip(X_row, v)) % p for X_row in X]\n\ndef matpowv(X, n, v, p):\n while n > 0:\n if n & 1: v = mv(X, v, p)\n X, n = matmul(X, X, p), n >> 1\n return v\n\nclass Solution:\n def concatenatedBinary(self, n: int, p: int = 10 ** 9 + 7) -> int:\n n += 1\n v = [0, 1, 1]\n bit = 1\n while bit < n:\n M = bit << 1\n mat = [\n [M, 1, 0],\n [0, 1, 1],\n [0, 0, 1],\n ]\n npow = min(bit, n - bit)\n v = matpowv(mat, npow, v, p)\n bit = M\n return v[0]\n```\n\n### Complexity\n- O((log n)^2) time. O(log n) for going up bit by bit from 1 to n. For each bit, O(log bit) ~ O(log n) for calculating the matrix pow. The size of matrices are irrelavent of n and are always 3x3 and thus the time complexity for matmul is O(1).\n- O(1) space. The matrices involved take up O(1) space (irrelavent of n). \n\n### Submission stats\nRuntime: 292 ms (beats 97.66 %)\nMemory Usage: 14.3 MB (beats 53.67 %)\n\n---\nIf you find this helpful, please **upvote**! Thank you!!! :-)\n\nAcknowledgement: The idea of the matrix solution comes from [@rbx](https://leetcode.com/rbx)\'s [post](https://leetcode.com/problems/concatenation-of-consecutive-binary-numbers/discuss/963549/python-(log(n))-2-approach).
| 9 | 0 |
['Math', 'Bit Manipulation', 'Python']
| 0 |
concatenation-of-consecutive-binary-numbers
|
Javascript | Easy Solution | beats 95%
|
javascript-easy-solution-beats-95-by-sga-knvw
|
(Note: This is part of a series of Leetcode solution explanations (index). If you like this solution or find it useful, please upvote this post.)\n\n---\n\nIdea
|
sgallivan
|
NORMAL
|
2021-01-27T09:14:31.254979+00:00
|
2021-02-03T20:56:24.820517+00:00
| 532 | false |
*(Note: This is part of a series of Leetcode solution explanations ([**index**](https://dev.to/seanpgallivan/leetcode-solutions-index-57fl)). If you like this solution or find it useful,* ***please upvote*** *this post.)*\n\n---\n\n***Idea:***\n\nThere are less efficient solutions which involve converting numbers to strings, or calculating the binary length each time, but the most efficient solution is actually even more basic, since we know precisely when a binary number will increase its length by 1.\n\nSo we can just iterate through while using **len** to keep track of how much you need to multiply **ans** by in order to fit **i** into the new **ans**. Don\'t forget to mod by **1e9+7**.\n\n---\n\n***Javascript Code:***\n\nThe best result for the code below is **148ms / 39.8MB** (95% / 84%).\n```javascript\nvar concatenatedBinary = function(n) {\n let ans = 1, len = 0b100\n for (let i = 2; i <= n; i++) {\n if (i === len) len <<= 1\n ans = (ans * len + i) % 1000000007\n }\n return ans\n};\n```\nThe same code but with decimal instead of binary for **len**:\n```javascript\nvar concatenatedBinary = function(n) {\n let ans = 1, len = 4\n for (let i = 2; i <= n; i++) {\n if (i === len) len *= 2\n ans = (ans * len + i) % 1000000007\n }\n return ans\n};\n```
| 9 | 0 |
['JavaScript']
| 1 |
concatenation-of-consecutive-binary-numbers
|
[Java/Python 3] Bit Manipulations.
|
javapython-3-bit-manipulations-by-rock-h6g6
|
java\n private static final List<Integer> table = new ArrayList<>(Arrays.asList(0));\n public int concatenatedBinary(int n) {\n if (table.size() <=
|
rock
|
NORMAL
|
2020-12-06T04:03:01.948418+00:00
|
2022-09-23T13:12:52.108480+00:00
| 471 | false |
```java\n private static final List<Integer> table = new ArrayList<>(Arrays.asList(0));\n public int concatenatedBinary(int n) {\n if (table.size() <= n) {\n long num = table.get(table.size() - 1);\n for (int i = table.size(); i <= n; ++i) {\n num <<= 32 - Integer.numberOfLeadingZeros(i);\n num |= i;\n num %= 1_000_000_007;\n table.add((int)num);\n }\n }\n return table.get(n);\n }\n```\n```python\n def concatenatedBinary(self, n: int) -> int:\n return int(\'\'.join(bin(i)[2 :] for i in range(1, n + 1)), 2) % (10 ** 9 + 7)\n```
| 9 | 2 |
[]
| 2 |
concatenation-of-consecutive-binary-numbers
|
c++ || bit manipulation || fully explained solution
|
c-bit-manipulation-fully-explained-solut-9e8c
|
Countbits function returns the number of bits in the number n\nLet\'s understand this with an example, \n\nWe will take the example of a decimal number(base 10)
|
harshitpanwar
|
NORMAL
|
2022-09-23T03:26:20.246315+00:00
|
2022-09-23T03:43:17.776260+00:00
| 673 | false |
Countbits function returns the number of bits in the number n\nLet\'s understand this with an example, \n\nWe will take the example of a decimal number(base 10).\nIf we take log10(n)+1 it will return the number of digits in the base 10.\n\nFor example, \n\nlog10(121)+1 = 3\nlog10(87)+1 = 2\nlog10(2)+1 = 1\n\nNow, the same goes for a log base 2 in a binary system.\nlog2(5)+1 = 3\nlog2(3)+1 = 2\nlog2(1)+1 = 2\n\nOnce we have the number of bits, we can continue ahead\n\n1. we just left shift our temp variable by the number of bits in ith number\n2. then we xor temp with i\n\nFor example,\n\ntemp=0;\nn=2;\ni->1 to 2;\nFor i=1,\n(temp<<1)^i -> (0<<1)^1 -> (00)^01 -> 01\ntemp = 01\n\nnext ,\n\nFor i=2,\n(temp<<2)^i -> (01<<2)^2 -> (0100)^10 -> 0110\ntemp = 110 -> 6\nso 6 will be the answer in this way\n\n```\nclass Solution {\npublic:\n \n long long int MOD = 1e9+7;\n \n int countbits(int n){\n return log2(n)+1;\n }\n \n int concatenatedBinary(int n) {\n \n long long temp = 0;\n for(int i=1;i<=n;i++) temp = ((temp<<countbits(i))^i)%MOD;\n return temp%MOD;\n \n }\n};\n```
| 8 | 0 |
['Bit Manipulation', 'C']
| 4 |
concatenation-of-consecutive-binary-numbers
|
[C++] from TLE to 40ms.
|
c-from-tle-to-40ms-by-lovebaonvwu-onws
|
inituitive brute force. We add each number bit by bit. But this will be TLE.\n\nclass Solution {\n public:\n int concatenatedBinary(int n) {\n int ans = 0;\
|
lovebaonvwu
|
NORMAL
|
2021-01-27T08:55:50.663847+00:00
|
2021-01-28T02:17:51.206596+00:00
| 676 | false |
inituitive brute force. We add each number bit by bit. But this will be TLE.\n```\nclass Solution {\n public:\n int concatenatedBinary(int n) {\n int ans = 0;\n\t\n\tstack<int> stk;\n\n for (int i = 1; i <= n; ++i) {\n int x = i;\n\n while (x > 0) {\n stk.push(x % 2);\n x /= 2;\n }\n\n while (!stk.empty()) {\n ans = ans * 2 + stk.top();\n stk.pop();\n\n ans %= 1000000007;\n }\n }\n\n return ans;\n }\n};\n```\n\nWe can optimize the following part to reduce the cost.\n```\n while (!stk.empty()) {\n ans = ans * 2 + stk.top();\n stk.pop();\n\n ans %= 1000000007;\n }\n```\nupdate it to\n```\nans = (ans << len) % mod + i;\n```\n\nWhat happend here is with the second solution we add the whole number with one ```<<``` operation instead of multiple ```<<``` operations with the first solution.\n```len``` is the binary length of a number which is equal to stack length of the first solution.\nIn another words, we recude ```<<``` operator from ```len``` times to 1 time.\n\nSolution 2,\n```\nclass Solution {\n public:\n int concatenatedBinary(int n) {\n long ans = 0;\n const int mod = 1000000007;\n\n for (int i = 1; i <= n; ++i) {\n int x = i, len = 0;\n\n while (x > 0) {\n ++len;\n x /= 2;\n }\n\n ans = (ans << len) % mod + i;\n }\n\n return ans % mod;\n }\n};\n```\n\nThanks to @jitendragupta1981, we could make it more reasonable.\n```\nclass Solution {\npublic:\n int concatenatedBinary(int n) {\n long ans = 0;\n const int mod = 1000000007;\n \n for (int i = 1; i <= n; ++i) {\n int x = i, len = 0;\n \n while (x > 0) {\n ++len;\n x /= 2;\n }\n \n ans = ((ans << len) + i) % mod; // or ans = ((ans << len) | i) % mod;\n }\n \n return ans % mod;\n }\n};\n```
| 8 | 0 |
[]
| 2 |
concatenation-of-consecutive-binary-numbers
|
🗓️ Daily LeetCoding Challenge September, Day 23
|
daily-leetcoding-challenge-september-day-ybh9
|
This problem is the Daily LeetCoding Challenge for September, Day 23. Feel free to share anything related to this problem here! You can ask questions, discuss w
|
leetcode
|
OFFICIAL
|
2022-09-23T00:00:11.076735+00:00
|
2022-09-23T00:00:11.076787+00:00
| 2,600 | false |
This problem is the Daily LeetCoding Challenge for September, Day 23.
Feel free to share anything related to this problem here!
You can ask questions, discuss what you've learned from this problem, or show off how many days of streak you've made!
---
If you'd like to share a detailed solution to the problem, please create a new post in the discuss section and provide
- **Detailed Explanations**: Describe the algorithm you used to solve this problem. Include any insights you used to solve this problem.
- **Images** that help explain the algorithm.
- **Language and Code** you used to pass the problem.
- **Time and Space complexity analysis**.
---
**📌 Do you want to learn the problem thoroughly?**
Read [**⭐ LeetCode Official Solution⭐**](https://leetcode.com/problems/concatenation-of-consecutive-binary-numbers/solution) to learn the 3 approaches to the problem with detailed explanations to the algorithms, codes, and complexity analysis.
<details>
<summary> Spoiler Alert! We'll explain these 3 approaches in the official solution</summary>
**Approach 1:** Change to Binary String
**Approach 2:** Math
**Approach 3:** Math (Bitwise Operation)
</details>
If you're new to Daily LeetCoding Challenge, [**check out this post**](https://leetcode.com/discuss/general-discussion/655704/)!
---
<br>
<p align="center">
<a href="https://leetcode.com/subscribe/?ref=ex_dc" target="_blank">
<img src="https://assets.leetcode.com/static_assets/marketing/daily_leetcoding_banner.png" width="560px" />
</a>
</p>
<br>
| 7 | 0 |
[]
| 41 |
concatenation-of-consecutive-binary-numbers
|
C++ Easy solution || Bit manipulation
|
c-easy-solution-bit-manipulation-by-sait-4yen
|
\nclass Solution {\npublic:\n int concatenatedBinary(int n) {\n \n //start from n to 1\n long long ans=1;\n for(int i=2;i<=n;i++)
|
saiteja_balla0413
|
NORMAL
|
2021-08-01T13:57:20.915334+00:00
|
2021-08-01T13:57:20.915400+00:00
| 436 | false |
```\nclass Solution {\npublic:\n int concatenatedBinary(int n) {\n \n //start from n to 1\n long long ans=1;\n for(int i=2;i<=n;i++)\n {\n //calculate the bits in the current number (i)\n long long num=(log(i)/log(2)) + 1;\n //left shift the bits as we need to append the i\n ans=ans<<num;\n ans|=i;\n ans%=1000000007;\n }\n return ans;\n }\n};\n```\n**upvote if this helps you :)**
| 6 | 0 |
['C']
| 0 |
concatenation-of-consecutive-binary-numbers
|
java with explaination | o(n) time | o(1) space | minimum lines | bitwise
|
java-with-explaination-on-time-o1-space-5zirs
|
if it is asked to make a decimal number how would concatenation work?\nfor example ->\nsuppose 1 is first number and we want to concate it with 2. it can be wri
|
kushguptacse
|
NORMAL
|
2021-01-28T06:58:21.571039+00:00
|
2021-01-28T07:02:27.606832+00:00
| 417 | false |
1. if it is asked to make a decimal number how would concatenation work?\nfor example ->\nsuppose 1 is first number and we want to concate it with 2. it can be written as 1* 10+2=12\nsuppose 1 is first number and we want to concate it with 21. it can be written as 1* 100+21=121\nsuppose 1 is first number and we want to concate it with 342. it can be written as 1* 1000+341=1341\nso what we can deduce is the result of append is like = original_num* pow(10,lengthOfSecondString) + secondString.\nin case of 1 and 341. length of 341 is 3 so, res= 1* pow(10,3) + 341\n2. so we just need to run loop from 2 to n and start applying above logic to build the answer.\n3. second observation. since above example is in decimal system that is why we are multiplying by 10 power. if it is binary me need to multiply by power (2,lengthOfSecondNumber).\n4. Now question is we need to find length of number in binary format. log of a number in base 2 will give the length of number in binary format +1. just like log of a number base 10 +1 gives length in decimal format. In java log base 2 method is not available only base 10 is available. so we can use below log property. \n5. for this we could use below formula - \nMath.log2(n) = Math.log10(n)/Math.log10(2);\n6.now we have length. we can using power method to multiply firstNumber* pow(2,lengthOfSecond) or we can use left shift operator. as we know left shift by 1 is multiply by 2. and left shift of length will be multiply by 2^length.\n\n\n```\nclass Solution {\n public int concatenatedBinary(int n) {\n long result=1;\n int length=0;\n for(int i=2;i<=n;i++) {\n length=((int)(Math.log(i)/Math.log(2)))+1;\n result=((result<<length)+i)%1000000007;\n }\n return (int)result;\n }\n}\n```
| 6 | 0 |
['Java']
| 3 |
concatenation-of-consecutive-binary-numbers
|
C++ O(n) Solution
|
c-on-solution-by-sairakesh-z69p
|
Left shift the answer every time by len and add the number, and then increment the length value at powers of 2.\n\n int concatenatedBinary(int n) {\n long a
|
sairakesh
|
NORMAL
|
2021-01-27T10:33:39.582081+00:00
|
2021-01-27T10:33:39.582107+00:00
| 500 | false |
Left shift the answer every time by len and add the number, and then increment the length value at powers of 2.\n```\n int concatenatedBinary(int n) {\n long ans=0;\n int mod=1e9+7,len=1;\n for(int i=1;i<=n;++i){\n ans=(ans<<len)%mod+i;\n if((i&(i+1))==0)\n len++;\n }\n\treturn ans % mod;\n }\n```
| 6 | 1 |
['C', 'C++']
| 0 |
concatenation-of-consecutive-binary-numbers
|
Very simple Java solution with explanation
|
very-simple-java-solution-with-explanati-tu6a
|
Here is the process how you can derive recurrent formula\n\nresult(n) = result(n - 1) * 2^binaryDigitsOf(n) + n\n\nwhere binaryDigitsOf(n) is the number of bina
|
jedipredator
|
NORMAL
|
2021-01-16T14:56:11.802062+00:00
|
2021-01-16T15:49:20.981657+00:00
| 283 | false |
Here is the process how you can derive recurrent formula\n\nresult(n) = result(n - 1) * 2^binaryDigitsOf(n) + n\n\nwhere binaryDigitsOf(n) is the number of binary digits needed to write number n. \n\ni = 1:\n1 -> "1" = 1\nresult is 1\n\ni = 2:\n2 -> "1""10" = (110) = (1 10) = 1 * 4 + 2 = result * 2^binaryDigitsOf(2) + 2 = result * 2^binaryDigitsOf(i) + i = 6\nresult is 6\n\ni = 3:\n3 -> "110""11" = (11011) = (110 11) = 6 * 4 + 3 = result * 2^binaryDigitsOf(3) + 3 = result * 2^binaryDigitsOf(i) + i = 27\nresult is 27\n\ni = 4:\n4 -> "11011""100" = (11011100) = (11011 100) = 27 * 8 + 4 = result * 2^binaryDigitsOf(4) + 4 = result * 2^binaryDigitsOf(i) + i = 220\nresult is 220\n\nAnd so on until n. We just need to take care of overflow, because of that we use long instead of int and do modulo operation. At the end we convert it to the int. That\'s it. Enjoy in code!\n\n```\nclass Solution {\n public int concatenatedBinary(int n) {\n \n\t\tint MOD = 1_000_000_007;\n\t\t\n\t\tlong[] powersOf2 = getPowersOf2();\n\t\t\n\t\tlong result = 0;\n\t\t\n\t\tfor (int i = 1; i <= n; i++) {\n\t\t\tresult = (result * powersOf2[getNumberOfBinaryDigits(i, powersOf2)] + i) % MOD;\n\t\t}\n\t\t\n\t\treturn (int) (result % MOD);\n }\n\t\n\tprivate int getNumberOfBinaryDigits(int n, long[] powersOf2) {\n\t\t\n\t\tfor (int i = 1; i < 32; i++) {\n\t\t\tif (powersOf2[i] > n) {\n\t\t\t\treturn i;\n\t\t\t} else if (powersOf2[i] == n) {\n\t\t\t\treturn i + 1;\n\t\t\t}\n\t\t}\n\t\t\n\t\treturn 1000; // never will come here\n\t}\n\n\tprivate long[] getPowersOf2() {\n\t\tlong[] powersOf2 = new long[32];\n\t\t\n\t\tpowersOf2[0] = 1;\n\t\t\n\t\tfor (int i = 1; i < 32; i++) {\n\t\t\tpowersOf2[i] = 2 * powersOf2[i - 1];\n\t\t}\n\t\t\n\t\treturn powersOf2;\n\t}\n}\n```
| 6 | 0 |
[]
| 0 |
concatenation-of-consecutive-binary-numbers
|
The O(log(n) * log(n)) you need to know
|
the-ologn-logn-you-need-to-know-by-lc_co-3d7y
|
The following is the O(log(n) * log(n)) solution which is faster than the O(n) and can work for very large n.\n\nMOD = pow(10, 9) + 7\n\ndef modInverse(n):\n
|
LC_Contest
|
NORMAL
|
2020-12-07T23:35:25.820941+00:00
|
2020-12-07T23:35:25.820972+00:00
| 772 | false |
The following is the `O(log(n) * log(n))` solution which is faster than the `O(n)` and can work for very large `n`.\n```\nMOD = pow(10, 9) + 7\n\ndef modInverse(n):\n return pow(n, MOD - 2, MOD)\n\ndef sumGeometricSeries(r, n):\n return (pow(r, n, MOD) - 1) * modInverse(r - 1)\n\ndef sumBinaryOfLength(n, r):\n res = pow(2, n - 1, MOD) * sumGeometricSeries(pow(2, n, MOD), r - pow(2, n - 1, MOD) + 1)\n res %= MOD\n res += (sumGeometricSeries(pow(2, n, MOD), r - pow(2, n - 1, MOD) + 1) - 1 - (r - pow(2, n - 1, MOD))) * modInverse(pow(2, n, MOD) - 1)\n return res % MOD\n\nclass Solution(object):\n def concatenatedBinary(self, n):\n curr_size = 1\n res = 0\n for b in range(n.bit_length(), 0, -1):\n res += sumBinaryOfLength(b, min(n, pow(2, b) - 1)) * curr_size\n res %= MOD\n curr_size *= pow(2, (min(n, pow(2, b) - 1) - pow(2, b - 1) + 1) * b, MOD)\n curr_size %= MOD\n return (res + MOD) % MOD\n```
| 6 | 2 |
[]
| 4 |
concatenation-of-consecutive-binary-numbers
|
python one line solution 94% beats
|
python-one-line-solution-94-beats-by-ben-831j
|
```\nclass Solution:\n def concatenatedBinary(self, n: int) -> int:\n return int("".join([bin(i)[2:] for i in range(1,n+1)]),2)%(10**9+7)\n \n
|
benon
|
NORMAL
|
2022-09-23T04:57:58.121388+00:00
|
2022-09-24T07:12:27.274862+00:00
| 1,004 | false |
```\nclass Solution:\n def concatenatedBinary(self, n: int) -> int:\n return int("".join([bin(i)[2:] for i in range(1,n+1)]),2)%(10**9+7)\n \n \n
| 5 | 0 |
['Python', 'Python3']
| 3 |
concatenation-of-consecutive-binary-numbers
|
C++ | Must Know Method ✔ | Explained ✔
|
c-must-know-method-explained-by-brijesha-skhe
|
Understanding: In a binary represenatation, 1110 = 14 can be written as: 1100 + 10 = (11<<2) + (10<<0) = 12+2 = 14.\n(All Binary Notation are in Bold.) \nExamp
|
brijeshagal
|
NORMAL
|
2022-09-23T01:49:46.527067+00:00
|
2022-09-23T01:49:46.527105+00:00
| 1,040 | false |
Understanding: In a **binary represenatation**, **1110** = 14 can be written as: **1100** + **10** = (**11**<<*2*) + (**10**<<*0*) = *12+2 = 14*.\n(All Binary Notation are in Bold.) \nExample:\nLets say n = *3*.\nSo, concatenation would be: **1 10 11 100**\nEach time we concatenate, we left shift our previous number by length of binary representation of that number.\nSo, at *1*, we have *1*.\nAt *2*, we have **1** **10**, (**1**<<*2*) + **10** = *4 + 2 = 6*,One left shifts twice to create space for the new number which has *2* bits in it. \nAt *3*, similarly, **110** **11**, 6 is left shifted twice, so* 6x2x2 = 24 + 3*(the new number) = *27*.\n\n```\nclass Solution {\npublic:\n const int mod = 1e9+7;\n int concatenatedBinary(int n) {\n long ans = 0;\n int length = 0;\n for (int i = 1; i <= n; ++i) {\n //Length increases on each power of two.\n if ((i&(i - 1)) == 0) \n ++length;\n //Left shift by that length.\n ans = ((ans << length) % mod + i) % mod;\n cout << length << endl;\n }\n return ans;\n }\n};\n```\n
| 5 | 0 |
['Math', 'Bit Manipulation', 'C', 'C++']
| 1 |
concatenation-of-consecutive-binary-numbers
|
BruteForce Faster than 100% | No Formula | Fooling Leetcode Judge | Static | Accepted
|
bruteforce-faster-than-100-no-formula-fo-7hs5
|
No Formula, No Nothing, Plain brute force with a twist. \n\nSo my first idea to run a bruteforce gave me TLE. I tried to think but did not get any clever solut
|
__tapatap__
|
NORMAL
|
2022-09-23T00:53:17.445597+00:00
|
2022-09-23T01:36:36.361227+00:00
| 638 | false |
No Formula, No Nothing, Plain brute force with a twist. \n\nSo my first idea to run a bruteforce gave me TLE. I tried to think but did not get any clever solutions, so being lazy to think i fooled leetcode judge like this.\n\nPrecomputed all the binary strings using a static array. This array will only be computed once and will be used commonly by all the testcases and the bruteforce solution passes.\n\n```\nclass Solution {\n\nstatic String arr[] = new String[100001];\n\npublic void build() {\n\tfor(int i=1; i<=100000; i++) {\n\t\tarr[i] = Integer.toBinaryString(i);\n\t}\n}\n\nint mod = 1000000007;\n\npublic int getVal(int n) {\n\tint val = 0;\n\tfor(int i=1; i<=n; i++) {\n\t\tfor(int j=0; j<arr[i].length(); j++) {\n\t\t\tint x = arr[i].charAt(j)-\'0\';\n\t\t\tval = (val*2 + x)%mod;\n\t\t}\n\t}\n\treturn val;\n}\n\npublic int concatenatedBinary(int n) {\n\tif(arr[1]==null) {\n\t\tbuild();\n\t}\n\treturn getVal(n);\n}\n}\n```\n\nUpdate : Faster than 100%\n\nNow along with computing binary string I added 3 line modification to calculate the answers as well. This makes the solution faster than 100% of the submissions, taking run time from 1600 ms to 24 ms\n\n\n\nCode \n\nclass Solution {\n \n static String arr[] = new String[100001];\n \n static int ans[] = new int[100001];\n \n public void build() {\n for(int i=1; i<=100000; i++) {\n arr[i] = Integer.toBinaryString(i);\n }\n }\n \n int mod = 1000000007;\n \n public int getVal(int n) {\n int val = 0;\n for(int i=1; i<=n; i++) {\n for(int j=0; j<arr[i].length(); j++) {\n int x = arr[i].charAt(j)-\'0\';\n val = (val*2 + x)%mod;\n }\n ans[i] = val;\n }\n return val;\n }\n \n public int concatenatedBinary(int n) {\n if(arr[1]==null) {\n build();\n getVal(100000);\n }\n return ans[n];\n }\n}\n
| 5 | 1 |
[]
| 4 |
concatenation-of-consecutive-binary-numbers
|
C++ | Easy to Understand with explanation
|
c-easy-to-understand-with-explanation-by-dxzv
|
\nclass Solution {\npublic:\n\t// get number of bits in a number\n int getBinary(int n) {\n int count = 0;\n while(n > 0) {\n n = n
|
ajayking9627
|
NORMAL
|
2020-12-06T04:11:47.562681+00:00
|
2020-12-06T04:11:47.562707+00:00
| 416 | false |
```\nclass Solution {\npublic:\n\t// get number of bits in a number\n int getBinary(int n) {\n int count = 0;\n while(n > 0) {\n n = n / 2;\n count++;\n }\n return count;\n }\n int concatenatedBinary(int n) {\n long long ans = 1;\n int mod = 1e9 + 7;\n for(int i = 2; i <= n; i++) {\n int bits = getBinary(i); // number of bits in i\n ans = ((ans << bits) % mod + i) % mod; // left shift the answer by number of bits and add current element into it\n }\n return (int)ans;\n }\n};\n```
| 5 | 1 |
[]
| 3 |
concatenation-of-consecutive-binary-numbers
|
Python O(n) 100% faster easy to understand
|
python-on-100-faster-easy-to-understand-n15df
|
\n#Try to understand this without using any Brute-force approach. (Its Competitive Programming, Learn as much as you can) :-)\nclass Solution:\n def concaten
|
jatindscl
|
NORMAL
|
2020-12-06T04:08:22.345986+00:00
|
2020-12-06T04:17:09.315943+00:00
| 318 | false |
```\n#Try to understand this without using any Brute-force approach. (Its Competitive Programming, Learn as much as you can) :-)\nclass Solution:\n def concatenatedBinary(self, n: int) -> int:\n l,ans =0,0\n for i in range(1,n+1): \n if i & (i - 1) == 0:\n l+=1\n ans=((ans <<l)|i)%(10**9+7)\n return(ans)\n```
| 5 | 2 |
['Python', 'Python3']
| 3 |
concatenation-of-consecutive-binary-numbers
|
[Java] Simple
|
java-simple-by-allenjue-q8yw
|
1680. Concatenation of Consecutive Binary Numbers\n\nclass Solution {\n public int concatenatedBinary(int n) {\n int i=1;\n int mod = (int)Math
|
allenjue
|
NORMAL
|
2020-12-06T04:05:38.672798+00:00
|
2022-09-23T04:04:34.899008+00:00
| 488 | false |
**1680. Concatenation of Consecutive Binary Numbers**\n```\nclass Solution {\n public int concatenatedBinary(int n) {\n int i=1;\n int mod = (int)Math.pow(10,9) + 7;\n StringBuilder sb = new StringBuilder();\n while(i<=n){\n sb.append(Integer.toBinaryString(i)); // Build string with integers\n i++;\n }\n String binary = sb.toString();\n int current = 0;\n for(i=0; i<binary.length();i++){\n current += binary.charAt(i) ==\'1\'? 1:0; // add 1 if it is a 1\n if(i+1 != binary.length()) // only multiply if it is not the last place or else it will be too big!\n current = ((current % mod) * 2) % mod; // modular multiplication to avoid overflow\n }\n return current;\n }\n}\n```\n**PROBLEM OVERVIEW**\nGiven an int, n, concatenate all numbers from 1 to n in binary. Convert this binary number into decimal. Numbers may be large so return the answer mod 10^9 + 7.\n\n**SOLUTION ANALYSIS**\nUse a StringBuilder for efficient String concatenation. For each decimal value 1 to n, we can use Java\'s inbuilt function Integer.toBinaryString(int i) to concatenate the binary representation.\n\nAfter that, we need to use modular multiplication to avoid overflow. To convert binary to decimal, we typically add 1 if it is a 1 at that place value and then multiply the sum by 2. However, bcause the number may be too large, we take the remainder of the current number and mod (10^9 + 7) before and after multiplying. By doing so, we prevent overflow.\n\nFor modular multiplication, the typical code is like this :\n```\npublic int modularMultiplication(int a, int b, int mod){\n\treturn ((a%mod) * (b%mod)) % mod;\n}\n```\n\n
| 5 | 0 |
[]
| 0 |
concatenation-of-consecutive-binary-numbers
|
Java binary strings solution
|
java-binary-strings-solution-by-olsh-dmg2
|
\nclass Solution {\n public int concatenatedBinary(int n) {\n int MOD = 1000000007;\n int res = 1;\n for (int i=2;i<=n;i++){\n
|
olsh
|
NORMAL
|
2022-09-23T19:01:38.693533+00:00
|
2022-09-23T19:01:38.693572+00:00
| 21 | false |
```\nclass Solution {\n public int concatenatedBinary(int n) {\n int MOD = 1000000007;\n int res = 1;\n for (int i=2;i<=n;i++){\n String s = Integer.toBinaryString(i);\n for (char c: s.toCharArray()){\n res=(res*2+c-48)%MOD;\n }\n }\n return res;\n }\n}\n```
| 4 | 0 |
[]
| 0 |
concatenation-of-consecutive-binary-numbers
|
✅ C++ | Hand Written Explanation | O(n) | ✅
|
c-hand-written-explanation-on-by-ritik_p-l17t
|
\n\n\n\nclass Solution {\npublic:\n int concatenatedBinary(int n) {\n \n long long int i=1, k=1, z, sum = 1, bit, M = 1e9+7;\n \n wh
|
ritik_pcl
|
NORMAL
|
2022-09-23T18:41:03.341680+00:00
|
2023-01-17T11:33:22.281550+00:00
| 171 | false |
\n\n\n```\nclass Solution {\npublic:\n int concatenatedBinary(int n) {\n \n long long int i=1, k=1, z, sum = 1, bit, M = 1e9+7;\n \n while(i != n)\n {\n z = pow(2,k);\n bit = pow(2,k+1);\n k++;\n \n while(z-- && i != n)\n {\n i++;\n sum = ((sum*bit)%M + i)%M;\n }\n }\n return sum%M;\n }\n}; \n```\n\uD83D\uDC47 Please Upvote if you find helpful \u2764
| 4 | 0 |
['C']
| 0 |
concatenation-of-consecutive-binary-numbers
|
Go | Bit manipulation
|
go-bit-manipulation-by-sprkweb-lna9
|
Let\'s say n = 3. To concatenate numbers 1, 2, 3 (binary: 1, 10, 11), we do the following:\n1. Add 1 to the result; ans = 1\n2. Move the result two bits left to
|
sprkweb
|
NORMAL
|
2022-09-23T09:40:45.782564+00:00
|
2022-09-23T09:40:45.782605+00:00
| 95 | false |
Let\'s say `n = 3`. To concatenate numbers 1, 2, 3 (binary: `1`, `10`, `11`), we do the following:\n1. Add `1` to the result; `ans = 1`\n2. Move the result two bits left to make a space for the next number; `ans = 100`\n3. Add `10`; `ans = 110`\n4. Move the result two more bits left; `ans = 11000`\n5. Add `11`; `ans = 11011`.\n \nTo understand, how much do we need to move `ans` to the left, we create variable `power`, which is incremented every time when `i` is increased twice.\n\n```\nfunc concatenatedBinary(n int) int {\n ans := 0\n threshold := 1\n power := 0\n for i := 1; i <= n; i++ {\n if i >= threshold {\n threshold = threshold << 1\n power += 1 \n }\n ans = (ans << power + i) % 1000000007\n }\n return ans\n}\n```
| 4 | 0 |
['Bit Manipulation', 'Go']
| 1 |
concatenation-of-consecutive-binary-numbers
|
C++ | Using Bit manipulation, Explained 100% !!
|
c-using-bit-manipulation-explained-100-b-70yh
|
Using BitManipulation...\n\nWell, we have to concatente the binary presentation of a consective numbers; Okey that\'s all until now\nLet\'s create a new problem
|
ychaaibi
|
NORMAL
|
2022-09-23T09:36:27.508918+00:00
|
2022-09-23T14:15:44.361225+00:00
| 169 | false |
Using BitManipulation...\n\nWell, we have to concatente the binary presentation of a consective numbers; Okey that\'s all until now\nLet\'s create a new problem using this problem which simple than this one instead of concatenting the the binary presentation Let\'s concatente the numbers their self :\nso for example **n = 9** so our numbers are **1, 2, 3, 4, 5, 6, 7, 8, 9** and we should get ***123456789***\nto do so :\nIt\'s simple **sum = 1**\nnext step we should get **12** : how would we do that ?? it\'s obvious that we should multiply the sum by 10 to be come 10 in this case then add our next number which is 2 to be become **sum = 12** (why we multiply by **10** ? we\'ll answer that lately)\n**sum = 12** and the next num is **3** so we should get **123** we do the same **sum = sum * 10** which will get us **sum = 120 **then add **3 **easily we will have **123**\nand so on until we get **123456789**\n```\n1-2 (e1) - 0\n0-0-3\n```\nto make this give us **123** it\'s obvious that we need to add 0 in (e1)\nOkey but the max number here is not 9\nos let\'s take **11** for example **(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11)**\nwe should get **[123456789]1011** the **123456789** which is the part one, we already explained it what about **1011** how can we add it, so :\n**sum = 123456789**\n**for i = 10**\nshould we multiply by 10, Let\'s do so\n```\n1-2-3-4-5-6-7-8-9-0\n0-0-0-0-0-0-0-0-1-0\n................0-0 we can stop here obviously not our solution the number was ruined !!\n```\nI think we should reserve a two new places for the current number to get its place\nso We have something like :\n```\n1-2-3-4-5-6-7-8-9-0-0\n0-0-0-0-0-0-0-0-0-1-0\n```\nit\'s clear that we wil get our answer\nso here we multiply by 100 not 10\nif n = 120 when we\'ll reach 100 for **(100, 101, 102, ..., 120)** we should start to multiply by 1000 (3 zeroes = digit count) so we can handle digits count in number...\nit\'s simple we should start mult = 10\nso we can always do this until `i = mult then mult should be multiplied by 10 to become mult = 100`\nand so one when `i = mult again (mult = 100) mult *= 10` to become mult = 1000 so we can reserve three spots for the new number **(100 - 999)** and so on\nLet\'s go back to our problem, I think now it looks a little more simple !!!\nSo it\'s the same as decimal.... we should concatenate **12 and 13** we should reserve two empty spots (0) beside 12 for 13 means whe should multiply by 100 **(10 ^ (number of spots we need))**\nIn binary we have 1001 and 111 it\'s simple we just need to reserve 3 empty spots (0) for 111 beside 1001 so we should make 1001 become **[1001]000** then easly add **111** to have `[1001]111 := 1001111`\nso we need only to know the length of the number that we\'re gonna concatenate and reserve the spots for it\nin decimal we multiply to reserve spots but in binary we shoud shift right to reserve spot\n`12 and 13 :: 12 * 100 = 1200 `**(we got two empty spots = 2 trailing zeroes)** we add 13 to become **1213**\n`1001 and 111 ::: 1001 << 3` **(digits count in the number [111 in this case])** = 1001000 then add **111** to become **1001111** we will just add number in decimal system and surely that will what we get in binary presentation or if we did a binary addition opperation\nso **for n = 5** we have **1, 10, 11, 100, 101**\n**result = 0**\n**digit_count = 1**\nsign_that_digit_count_increased = 2 (means if we reach 2 than 2 - 3 numbers will have 2 digits, and so one `"{ i in [2 ^ n, 2 ^ (n + 1) - 1] ::: digits count of i is n }"`\n\nwe should do simply\n```\nfor i = 0 ------> n;\n\tif (i == sign_that_digit_count_increased)\n\t\tsign_that_digit_count_increased *= 2 (2 = 10(binary), 4 = 100(binary), 8 = 1000, 16 = 10000, 32 = 100000, ...)\n\t\tdigit_count += 1\n\tresult = result << digit_count (to reserve for the new number);\n\tresult += i;\n```\n\nor instead of " sign_that_digit_count_increased " we just have to check if (i & i + 1) is zero for example 100 and 11, 1000 and 111, 10000 and 1111; cause every consective numbers have at least one bit active commun between them expect (2 ^ n and 2 ^ n - 1) for every n\nI hope It\'s all clear\n\n```\nclass Solution {\npublic:\n long long sum = 0;\n long long MOD = 1000000007;\n\n int concatenatedBinary(int n) {\n int length_b = 0;\n \n for (int i=1; i<=n; i++)\n {\n if ((i & (i - 1)) == 0)\n length_b++;\n sum = ((sum << length_b) + i) % MOD;\n }\n return (sum);\n }\n};\n```
| 4 | 0 |
['Bit Manipulation', 'C', 'C++']
| 1 |
concatenation-of-consecutive-binary-numbers
|
C++ || Nothing fancy || Clean and simple solution
|
c-nothing-fancy-clean-and-simple-solutio-do0w
|
\n int concatenatedBinary(int n) {\n int ans=0;\n long long bit=1;\n for(int i=n;i>0;i--)\n {\n int num=i;\n w
|
ashay028
|
NORMAL
|
2022-09-23T05:01:58.825596+00:00
|
2022-09-23T05:01:58.825641+00:00
| 32 | false |
```\n int concatenatedBinary(int n) {\n int ans=0;\n long long bit=1;\n for(int i=n;i>0;i--)\n {\n int num=i;\n while(num)\n {\n if(num%2) ans= (ans+bit)%1000000007;\n num/=2;\n bit= (bit*2)%1000000007;\n }\n }\n return ans;\n }\n```
| 4 | 0 |
[]
| 0 |
concatenation-of-consecutive-binary-numbers
|
Simple & Easy | O(n log n) | O(n)
|
simple-easy-on-log-n-on-by-megamind-mhts
|
Since we are concatenating binary numbers from left to right , for every number we have to left shift our result floor[ log(n)+1] times and add our current numb
|
megamind_
|
NORMAL
|
2022-09-23T04:29:45.402240+00:00
|
2022-09-23T04:41:02.464250+00:00
| 386 | false |
Since we are concatenating binary numbers from left to right , for every number we have to **left shift our result floor[ log(n)+1]** times and **add our current number** .\n```\nE.g. Consider 3\nres = 0 1 (1) 110 ( 1<<2 (i.e.log(2)+1) + 2) 11011 ( 110<<2 (i.e. log(3)+1) + 3) \n1 to N 1 2 3\n```\n\n```\nclass Solution {\npublic:\n int log2(int n ){\n int c = 0;\n while(n>1){\n n /=2;\n c++;\n }\n return c;\n }\n \n int concatenatedBinary(int n) {\n \n int mod = 1e9+7;\n long long ans = 0;\n for(int i =1;i<=n;i++){\n \n int a = log2(i)+1; \n ans = ans << a;\n ans = ans + i;\n if(ans>mod){\n ans = ans%mod;\n }\n \n }\n \n return ans%mod;\n }\n};\n```\n**Time Complexity : O(n logn)\nSpace Complexity : O(1)**\n\n**Note :** This can be easily reduced to **O(n)** if we keep the count of bits from the start of the loop .
| 4 | 0 |
['C']
| 1 |
concatenation-of-consecutive-binary-numbers
|
100% faster c++ solution | 24ms runtime | 10 lines of code
|
100-faster-c-solution-24ms-runtime-10-li-xwj3
|
Kindly Upvote \uD83D\uDC4D the solution if you like it...\n\n\nclass Solution {\npublic:\n int concatenatedBinary(int n) {\n int next = 1, length = 1;
|
Yaduttam_Pareek
|
NORMAL
|
2022-09-23T00:39:25.096085+00:00
|
2022-09-23T00:39:25.096124+00:00
| 474 | false |
## Kindly Upvote \uD83D\uDC4D the solution if you like it...\n\n```\nclass Solution {\npublic:\n int concatenatedBinary(int n) {\n int next = 1, length = 1;\n long max_n = pow(10, 9) + 7, result = 0;\n for (int i = 0; i <= n; i++) {\n if (i == next) {\n next *= 2;\n length++;\n }\n \n result = (result * next + i) % max_n;\n }\n return result;\n }\n};\n```\n\n\n## If you reached here and the solution worked for you please upvote its free \uD83D\uDC4D
| 4 | 0 |
['C++']
| 3 |
concatenation-of-consecutive-binary-numbers
|
javascript solutions
|
javascript-solutions-by-henrychen222-lp1y
|
\n/////////////////////////////// Solution 1 //////////////////////////////////\n// 1260ms\nconst mod = BigInt(1e9 + 7);\nconst concatenatedBinary = (n) => {\n
|
henrychen222
|
NORMAL
|
2020-12-06T11:34:20.671858+00:00
|
2020-12-06T11:39:50.013799+00:00
| 318 | false |
```\n/////////////////////////////// Solution 1 //////////////////////////////////\n// 1260ms\nconst mod = BigInt(1e9 + 7);\nconst concatenatedBinary = (n) => {\n let res = 0n;\n let shift = 1n;\n for (let i = 1n; i <= n; i++) {\n if (i == (1n << shift)) shift++;\n res <<= shift;\n res += i;\n res %= mod;\n }\n return Number(res);\n};\n\n// 664ms\nconst MOD = 1e9 + 7;\nconst concatenatedBinary = (n) => {\n let res = 0;\n let shift = 1;\n for (let i = 1; i <= n; i++) {\n if (i == (1 << shift)) shift++;\n res *= (2 ** shift); // difference, don\'t know what the hack: res << shift cause Number overflow while res * (2 ** shift) not, both should work the same\n res += i;\n res %= MOD;\n }\n return res;\n};\n\n\n/////////////////////////////// Solution 2 //////////////////////////////////\n// reference: https://leetcode.com/problems/concatenation-of-consecutive-binary-numbers/discuss/961350/C%2B%2B-O(N)-time-iterative\n// 1396ms\nconst mod = BigInt(1e9 + 7);\nconst concatenatedBinary = (n) => {\n let res = 0n;\n for (let i = 1n, shift = 0n; i <= n; i++) {\n let singleBit = (i & (i - 1n)) == 0n;\n if (singleBit) shift++;\n res <<= shift;\n res += i;\n res %= mod;\n }\n return Number(res);\n};\n\n// 672ms\nconst MOD = 1e9 + 7;\nconst concatenatedBinary = (n) => {\n let res = 0;\n for (let i = 1, shift = 0; i <= n; i++) {\n let singleBit = (i & (i - 1)) == 0;\n if (singleBit) shift++;\n res *= (2 ** shift); // difference\n res += i;\n res %= MOD;\n }\n return res;\n};\n\n/////////////////////////////// Solution 3 //////////////////////////////////\n// 2400ms\nconst mod = 1e9 + 7;\nconst concatenatedBinary = (n) => {\n let res = 0;\n for (let i = 1; i <= n; i++) {\n let bin = i.toString(2);\n let shift = bin.length;\n res *= (2 ** shift);\n res += i;\n res %= mod;\n }\n return res;\n};\n\n/////////////////////////////// Solution 4 //////////////////////////////////\n// 180ms\nconst mod = 1e9 + 7;\nconst concatenatedBinary = (n) => {\n let t = 2;\n let res = 0;\n for (let i = 1; i <= n; i++) {\n if (i == t) {\n t *= 2;\n }\n res = res * t + i;\n res %= mod;\n }\n return res;\n};\n```
| 4 | 0 |
[]
| 2 |
concatenation-of-consecutive-binary-numbers
|
C# - Simple O(N) using Binary Length
|
c-simple-on-using-binary-length-by-chris-j210
|
csharp\npublic int ConcatenatedBinary(int n)\n{\n\tlong result = 0;\n\tint MOD = (int)(1E9) + 7;\n\tint binaryLength = 0;\n\n\tfor (int i = 1; i <= n; i++)\n\t{
|
christris
|
NORMAL
|
2020-12-06T04:37:40.343175+00:00
|
2020-12-06T04:38:18.552478+00:00
| 183 | false |
```csharp\npublic int ConcatenatedBinary(int n)\n{\n\tlong result = 0;\n\tint MOD = (int)(1E9) + 7;\n\tint binaryLength = 0;\n\n\tfor (int i = 1; i <= n; i++)\n\t{\n\t\tif ((i & (i - 1)) == 0)\n\t\t{\n\t\t\tbinaryLength++;\n\t\t}\n\n\t\tresult = ((result << binaryLength) + i) % MOD;\n\t}\n\n\treturn (int)(result % MOD); \n}\n```
| 4 | 0 |
[]
| 0 |
concatenation-of-consecutive-binary-numbers
|
✅ One Line Solution
|
one-line-solution-by-mikposp-ec4k
|
(Disclaimer: this is not an example to follow in a real project - it is written for fun and training mostly)Code #1.1 - One LineTime complexity: O(n). Space com
|
MikPosp
|
NORMAL
|
2024-04-07T13:55:12.415065+00:00
|
2025-04-03T12:12:22.365605+00:00
| 24 | false |
(Disclaimer: this is not an example to follow in a real project - it is written for fun and training mostly)
# Code #1.1 - One Line
Time complexity: $$O(n)$$. Space complexity: $$O(1)$$.
```python3
class Solution:
def concatenatedBinary(self, n: int) -> int:
return reduce(lambda q,k:(q<<k.bit_length()|k)%(10**9+7),range(n+1))
```
# Code #1.2 - Unwrapped
```python3
class Solution:
def concatenatedBinary(self, n: int) -> int:
MOD = 10**9 + 7
q = 0
for k in range(1, n+1):
q = (q << k.bit_length() | k)%MOD
return q
```
(Disclaimer 2: all code above is just a product of fantasy, it is not considered to be 'true' oneliners - please, remind about drawbacks only if you know how to make it better)
| 3 | 0 |
['Bit Manipulation', 'Simulation', 'Python', 'Python3']
| 0 |
concatenation-of-consecutive-binary-numbers
|
Asymptomatic O(1) || Constant Time Solution || using static
|
asymptomatic-o1-constant-time-solution-u-dgc9
|
\nclass Solution {\n static final int N = 100001, mod = 1000000007;\n static int res[];\n Solution(){\n if(res==null){\n res=new int[
|
Lil_ToeTurtle
|
NORMAL
|
2022-09-23T18:00:56.475333+00:00
|
2022-09-23T18:00:56.475369+00:00
| 329 | false |
```\nclass Solution {\n static final int N = 100001, mod = 1000000007;\n static int res[];\n Solution(){\n if(res==null){\n res=new int[N];\n for(int i=1,n=0,pow=1;i<N;i++){\n if(i==pow){\n pow<<=1;\n n++;\n }\n res[i]=(int)((((long)res[i-1]<<n)|i)%mod);\n }\n }\n }\n public int concatenatedBinary(int n) {\n return res[n];\n }\n}\n```
| 3 | 0 |
['Java']
| 4 |
concatenation-of-consecutive-binary-numbers
|
Java | String | Straight Forward Solution | Easy to Understand
|
java-string-straight-forward-solution-ea-83wf
|
\nclass Solution {\n public int concatenatedBinary(int n) {\n StringBuilder str = new StringBuilder();\n for(int i = 1; i <= n; i++)\n
|
inferno_xo
|
NORMAL
|
2022-09-23T17:00:00.320741+00:00
|
2022-09-23T17:00:00.320793+00:00
| 145 | false |
```\nclass Solution {\n public int concatenatedBinary(int n) {\n StringBuilder str = new StringBuilder();\n for(int i = 1; i <= n; i++)\n str.append(Integer.toBinaryString(i));\n int MAX = 1000000007;\n int res = 0;\n String s = str.reverse().toString();\n int c = 1;\n for(int i = 0; i < s.length(); i++){\n res += (s.charAt(i)-\'0\')*c;\n res %= MAX;\n c *= 2;\n c %= MAX;\n }\n return res;\n }\n}\n\n```
| 3 | 0 |
['String', 'Java']
| 1 |
concatenation-of-consecutive-binary-numbers
|
Python very easy to understand
|
python-very-easy-to-understand-by-khan_b-xjl3
|
Complexity: time complexity is O(n), space is O(1). \n\nn=1 1\nn=2 110\nn=3 11011\nn=4 11011100\n\nLet us try to find answer to n by using the value of n-1
|
Khan_Baba
|
NORMAL
|
2022-09-23T13:02:07.937338+00:00
|
2022-09-23T13:03:21.672771+00:00
| 188 | false |
**Complexity: time complexity is O(n), space is O(1). **\n\nn=1 1\nn=2 110\nn=3 11011\nn=4 11011100\n\nLet us try to find answer to n by using the value of n-1 \n\nn=3\n\nWe have to calculate the value of 3 (11011) by using the value of 2\n n=2 (3-1) \nvalue =110\n\nBinary of 3=11(length 2)\nSo we multiply the initial value by 100 (1+ 2 zeroes)\nvalue_3 = value_2 *(100) +3\n\t 110 * 100 + 11\n\t 11000 + 11\n\t 11011\n\n\nSimilarly\n\nn=4\nbinary of 4=100(lenth 3)\nSo we multiply the initial value by 1000 (1+ 3 zeroes)\nvalue_4 = value_3 *(1000) + 4\n\t 11011 * 1000 + 100\n\t 11011000 + 100\n\t 11011100\n\n```\nclass Solution:\n def concatenatedBinary(self, n):\n ans, M = 0, 10**9 + 7\n for x in range(1,n+1):\n ans= (ans*(1<<(len(bin(x))-2))+x)%M\n return ans\n\t\t\n```\n\t\t\n\n# **Try to understand the below line:**\n **ans= (ans*(1<<(len(bin(x))-2))+x)%M**\n \n1. Since we have to return modulus of 10^9 +7\n\tans= (-------) %M\n\t\n2. We have to multiply the ans of previous value by power of 10 and have to add value of x\n\tans = ( ans*(----) + x) %M\n\t\n3. left shift of integer easily give us the value like 10,100,1000,1000,...\n\tans= ( ans*(1<< (-------)) + x) %M\n\t\n4. we have to do left shift of 1 by the binary length of x \n\tans= ( ans*(1<< (len(bin(x)) + x) %M\n\t\n5. But the binary form of any number always start with 0B or 0b. So we have to reduce the lenth by 2\n\tans= ( ans*(1<< (len(bin(x))-2)) + x) %M\n
| 3 | 0 |
[]
| 2 |
concatenation-of-consecutive-binary-numbers
|
[ Python ] ✅✅ Simple Python Solution Using Bin Function 🥳✌👍
|
python-simple-python-solution-using-bin-471s6
|
If You like the Solution, Don\'t Forget To UpVote Me, Please UpVote! \uD83D\uDD3C\uD83D\uDE4F\n# Runtime: 3110 ms, faster than 38.58% of Python3 online submissi
|
ashok_kumar_meghvanshi
|
NORMAL
|
2022-09-23T11:16:17.027077+00:00
|
2022-09-23T11:16:40.791050+00:00
| 354 | false |
# If You like the Solution, Don\'t Forget To UpVote Me, Please UpVote! \uD83D\uDD3C\uD83D\uDE4F\n# Runtime: 3110 ms, faster than 38.58% of Python3 online submissions for Concatenation of Consecutive Binary Numbers.\n# Memory Usage: 15.9 MB, less than 22.05% of Python3 online submissions for Concatenation of Consecutive Binary Numbers.\n\n\tclass Solution:\n\t\tdef concatenatedBinary(self, n: int) -> int:\n\n\t\t\tbinary = \'\'\n\n\t\t\tfor num in range(1, n+1):\n\n\t\t\t\tbinary = binary + bin(num)[2:]\n\n\t\t\tresult = int(binary, 2)\n\n\t\t\treturn result % (10**9 + 7)\n\n# Thank You \uD83E\uDD73\u270C\uD83D\uDC4D
| 3 | 0 |
['Python', 'Python3']
| 1 |
concatenation-of-consecutive-binary-numbers
|
python O(n) simple solution
|
python-on-simple-solution-by-namanxk-uhp0
|
\nclass Solution:\n def concatenatedBinary(self, n: int) -> int:\n arr = []\n \n\t\t# append each binary to arr\n for i in range(1, n +
|
namanxk
|
NORMAL
|
2022-09-23T07:58:56.048967+00:00
|
2022-09-23T15:52:11.120054+00:00
| 62 | false |
```\nclass Solution:\n def concatenatedBinary(self, n: int) -> int:\n arr = []\n \n\t\t# append each binary to arr\n for i in range(1, n + 1):\n arr.append(bin(i)[2:])\n \n return int(\'\'.join(arr), 2) % (pow(10, 9) + 7)\n```
| 3 | 0 |
['Python']
| 0 |
concatenation-of-consecutive-binary-numbers
|
Python || Bit Manipulation || O(N) || Easy to Understand
|
python-bit-manipulation-on-easy-to-under-3pd4
|
suppose we have two integers A and B with binary(a1,a2,..,an) and (b1,b2,..,bm) and we need to add the binary of both the digits\nthen what we can do is shift t
|
bhavsarpriyang9999
|
NORMAL
|
2022-09-23T06:40:05.190087+00:00
|
2022-09-23T06:55:51.095487+00:00
| 189 | false |
suppose we have two integers A and B with binary(a1,a2,..,an) and (b1,b2,..,bm) and we need to add the binary of both the digits\nthen what we can do is shift the bits of A to the left side m times which is the length of the second integer and add the second integer to the value like : ` A<<m + B`\n\nfor example A = 1 and B = 2 the binary representaions will be 1 and 10\nto add A and B binary strings we will have do a leftshift operation 2 times on 1(bin - 1) and the result will be 4(bin -100) and after that we will add 2 to the result that will be 6(bin - 110)\n\nfor this particular problem we can keep track of number of digits in B like if B is a power of 2 then we will increase number of digits \n\nif a number n is a power of 2 then the value n&(n-1) will always be 0 because there will be no matching set bits in n and (n-1) numbers\n\n\n\n```\n\nclass Solution: \n def concatenatedBinary(self, n: int) -> int:\n\t mod = 10**9 + 7\n digitsToLeftShift = 1 # number of digits to leftshift\n curr = 1 # current value to return\n for i in range(2,n+1):\n if not i&(i-1): # if i is power of 2 then increment digits to leftshift\n digitsToLeftShift += 1\n curr = ((curr<<digitsToLeftShift) + i) % mod # append the binary and assign to curr\n return curr\n \n\t \n\t Time Complexity : O(N)\n\t Space Complexity: O(1)\n\t \n```\n\t \n\t \n\t \n\n\n\n
| 3 | 0 |
['Bit Manipulation', 'Python']
| 1 |
concatenation-of-consecutive-binary-numbers
|
TODAYS solution
|
todays-solution-by-sohan507-r5c6
|
class Solution {\n public int concatenatedBinary(int n) {\n final long modulo = (long) (1e9 + 7);\n long result = 0;\n int binaryDigits
|
SOHAN507
|
NORMAL
|
2022-09-23T04:16:32.307964+00:00
|
2022-09-23T04:16:32.308003+00:00
| 337 | false |
class Solution {\n public int concatenatedBinary(int n) {\n final long modulo = (long) (1e9 + 7);\n long result = 0;\n int binaryDigits = 0;\n for (int i = 1; i <= n; i++) {\n if ((i & (i - 1)) == 0) binaryDigits++;\n result = ((result << binaryDigits) + i) % modulo;\n }\n return (int) result;\n }\n}
| 3 | 0 |
['Java']
| 1 |
concatenation-of-consecutive-binary-numbers
|
✅✅Faster || Easy To Understand || C++ Code
|
faster-easy-to-understand-c-code-by-__kr-lw9k
|
Bit Manipulation\n\n Time Complexity :- O(NlogN)\n\n Space Complexity :- O(N)\n\n\nclass Solution {\npublic:\n int concatenatedBinary(int n) {\n \n
|
__KR_SHANU_IITG
|
NORMAL
|
2022-09-23T03:55:31.810918+00:00
|
2022-09-23T03:55:31.810982+00:00
| 135 | false |
* ***Bit Manipulation***\n\n* ***Time Complexity :- O(NlogN)***\n\n* ***Space Complexity :- O(N)***\n\n```\nclass Solution {\npublic:\n int concatenatedBinary(int n) {\n \n long long mod = 1e9 + 7;\n \n long long res = 0;\n \n for(int i = 1; i <= n; i++)\n {\n // find the length of curr num\n \n int len = 0;\n \n int num = i;\n \n while(num)\n {\n len++;\n \n num = num >> 1;\n }\n \n // left shift the res by len\n \n res = (res << len) % mod;\n \n // add the curr num to the res\n \n res = (res % mod + i % mod) % mod;\n }\n \n return res % mod;\n }\n};\n```
| 3 | 0 |
['Bit Manipulation', 'C', 'C++']
| 0 |
concatenation-of-consecutive-binary-numbers
|
Javascript Solution
|
javascript-solution-by-kml_soni-5rsa
|
```\nvar concatenatedBinary = function(n) {\n let number = 0; \n for(let i = 1; i <= n; i++) {\n number *= (1 << i.toString(2).length)\n num
|
kml_soni
|
NORMAL
|
2022-09-23T03:10:07.751858+00:00
|
2022-09-23T03:10:07.751893+00:00
| 155 | false |
```\nvar concatenatedBinary = function(n) {\n let number = 0; \n for(let i = 1; i <= n; i++) {\n number *= (1 << i.toString(2).length)\n number += i;\n number %= (10 ** 9 + 7)\n }\n return number;\n};
| 3 | 0 |
['JavaScript']
| 0 |
concatenation-of-consecutive-binary-numbers
|
Using Long && Easy Logic without need of Explanation
|
using-long-easy-logic-without-need-of-ex-83x2
|
\nclass Solution {\n\tpublic int concatenatedBinary(int n) {\n\t\tlong res = 0;\n\t\tfor (int i = 1; i <= n; i++) {\n\t\t\tres = (res * (int) Math.pow(2, Intege
|
Aditya_jain_2584550188
|
NORMAL
|
2022-07-15T05:26:37.578739+00:00
|
2022-07-15T05:26:37.578789+00:00
| 178 | false |
```\nclass Solution {\n\tpublic int concatenatedBinary(int n) {\n\t\tlong res = 0;\n\t\tfor (int i = 1; i <= n; i++) {\n\t\t\tres = (res * (int) Math.pow(2, Integer.toBinaryString(i).length()) + i) % 1000000007;\n\t\t}\n\t\treturn (int) res;\n\t}\n}\n```
| 3 | 1 |
['Java']
| 1 |
concatenation-of-consecutive-binary-numbers
|
Python 1 liner solution
|
python-1-liner-solution-by-chris_cc-0n8i
|
\nclass Solution:\n def concatenatedBinary(self, n: int) -> int:\n return int(\'\'.join([str(bin(i))[2:] for i in range(1, n+1)]), 2)%(10**9+7) \n
|
chris_cc
|
NORMAL
|
2021-01-28T04:22:27.788270+00:00
|
2021-01-28T04:22:27.788319+00:00
| 100 | false |
```\nclass Solution:\n def concatenatedBinary(self, n: int) -> int:\n return int(\'\'.join([str(bin(i))[2:] for i in range(1, n+1)]), 2)%(10**9+7) \n```
| 3 | 0 |
[]
| 0 |
concatenation-of-consecutive-binary-numbers
|
JAVA - Only 6 lines of code very easy solution
|
java-only-6-lines-of-code-very-easy-solu-4iay
|
Complexity
Time complexity: O(N)
Space complexity: O(1)
Code
|
gs12051999
|
NORMAL
|
2021-01-27T17:29:15.977879+00:00
|
2025-02-10T05:14:13.246686+00:00
| 346 | false |
****
# Complexity
- Time complexity: O(N)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
public int concatenatedBinary(int n) {
long res = 0;
int mod = 1_000_000_007 , size = 0;
for(int i = 1 ; i <= n ; i++ ){
if((i & (i - 1)) == 0) size++;
res = (res << size | i) % mod;
}
return (int)res;
}
```
| 3 | 2 |
['Java']
| 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.