question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
number-of-bit-changes-to-make-two-integers-equal
|
0ms Shifting operator and "& operator
|
0ms-shifting-operator-and-operator-by-ja-6h3b
|
IntuitionTo transform n into k, we can only unset bits in n. This means:
If a bit in n is set (1), we can change it to unset (0).
If a bit in n is already unset
|
jacobjebaraj01
|
NORMAL
|
2025-01-31T16:50:42.460406+00:00
|
2025-01-31T16:50:42.460406+00:00
| 3 | false |
## **Intuition**
To transform `n` into `k`, we can only **unset** bits in `n`. This means:
1. If a bit in `n` is **set** (`1`), we can change it to **unset** (`0`).
2. If a bit in `n` is already **unset** (`0`), we **cannot** change it to `1`.
3. Our goal is to determine the **minimum** number of bit unsets needed to make `n` equal to `k`.
4. If it's **impossible** to achieve `k` using this operation, return `-1`.
---
## **Approach**
We process `n` and `k` bit by bit, starting from the least significant bit (LSB):
1. **Bitwise Right Shift:**
- Keep shifting `n` and `k` to the right until they become equal.
2. **Bitwise Comparison:**
- If the current bit of `n` is `1` and the corresponding bit in `k` is `0`, we **unset** this bit (increment `count`).
- If the current bit of `n` is `0` and the corresponding bit in `k` is `1`, we **cannot** convert `n` into `k`, so return `-1`.
3. **Repeat until `n == k`**, keeping track of the number of changes required.
---
## **Complexity Analysis**
- **Time Complexity:** \( O(\text{position of leftmost set bit}) \)
- The worst case is proportional to the number of bits in `n`, as we keep right-shifting until `n` and `k` match.
- **Space Complexity:** \( O(1) \)
- Only a few integer variables are used, making the space usage constant.
---
## **Code Implementation**
```cpp
class Solution {
public:
int minChanges(int n, int k) {
int count = 0;
while (n != k) {
if ((n & 1) && !(k & 1)) {
count++; // Unset this bit
} else if (!(n & 1) && (k & 1)) {
return -1; // Impossible case
}
n = n >> 1;
k = k >> 1;
}
return count;
}
};
| 0 | 0 |
['Bit Manipulation', 'C++']
| 0 |
number-of-bit-changes-to-make-two-integers-equal
|
🚨 Found a Bug on LeetCode Platform! 🚨
|
found-a-bug-on-leetcode-platform-by-suja-8hoy
|
Hey LeetCode community,I encountered a strange issue while solving Problem 3226: Number of Bit Changes to Make Two Integers Equal (Problem Link).Here’s the situ
|
sujalmehta328
|
NORMAL
|
2025-01-27T06:30:37.232209+00:00
|
2025-01-27T06:30:37.232209+00:00
| 8 | false |
## Hey LeetCode community,
I encountered a strange issue while solving **Problem 3226: Number of Bit Changes to Make Two Integers Equal** ([Problem Link](https://leetcode.com/problems/number-of-bit-changes-to-make-two-integers-equal/)).
Here’s the situation:
- When I **run the code**, the output is **correct** and matches the expected results. ✅
- However, when I **submit the code**, it throws an error or fails on certain test cases. ❌
Here’s the code I used:
```cpp
class Solution {
public:
int minChanges(int n, int k) {
string ns;
int temp = n;
while (temp) {
ns += to_string(temp % 2);
temp /= 2;
}
string ks;
temp = k;
while (temp) {
ks += to_string(temp % 2);
temp /= 2;
}
if (ns.length() < ks.length()) return -1;
int ans = 0;
for (int i = 0; i < ns.length(); i++) {
if (ns[i] == '1' && (i >= ks.length() || ks[i] == '0')) ans++;
else if (ns[i] == '0' && ks[i] == '1') return -1;
}
return ans;
}
};
```
### Steps to Reproduce:
1. Copy-paste the above code into the solution editor for the problem.
2. **Run the code** – it works as expected and produces correct outputs.
3. **Submit the code** – it fails on some test cases unexpectedly.
It seems like there’s a discrepancy between how test cases are being handled during runtime and during submission.
I’d encourage others to try this out and see if the same issue arises. If enough of us report it, the LeetCode team can investigate and resolve it.
Tagging LeetCode support for visibility: @LeetCode @LeetCodeAdmin
Let’s work together to make the platform better! 😊
| 0 | 0 |
['Bit Manipulation', 'C++']
| 0 |
number-of-bit-changes-to-make-two-integers-equal
|
🚨 Found a Bug on LeetCode Platform! 🚨
|
found-a-bug-on-leetcode-platform-by-suja-w5al
|
Hey LeetCode community,I encountered a strange issue while solving Problem 3226: Number of Bit Changes to Make Two Integers Equal (Problem Link).Here’s the situ
|
sujalmehta328
|
NORMAL
|
2025-01-27T06:22:32.563079+00:00
|
2025-01-27T06:22:32.563079+00:00
| 5 | false |
## Hey LeetCode community,
I encountered a strange issue while solving **Problem 3226: Number of Bit Changes to Make Two Integers Equal** ([Problem Link](https://leetcode.com/problems/number-of-bit-changes-to-make-two-integers-equal/)).
Here’s the situation:
- When I **run the code**, the output is **correct** and matches the expected results. ✅
- However, when I **submit the code**, it throws an error or fails on certain test cases. ❌
Here’s the code I used:
```cpp
class Solution {
public:
int minChanges(int n, int k) {
string ns;
int temp = n;
while (temp) {
ns += to_string(temp % 2);
temp /= 2;
}
string ks;
temp = k;
while (temp) {
ks += to_string(temp % 2);
temp /= 2;
}
if (ns.length() < ks.length()) return -1;
int ans = 0;
for (int i = 0; i < ns.length(); i++) {
if (ns[i] == '1' && (i >= ks.length() || ks[i] == '0')) ans++;
else if (ns[i] == '0' && ks[i] == '1') return -1;
}
return ans;
}
};
```
### Steps to Reproduce:
1. Copy-paste the above code into the solution editor for the problem.
2. **Run the code** – it works as expected and produces correct outputs.
3. **Submit the code** – it fails on some test cases unexpectedly.
It seems like there’s a discrepancy between how test cases are being handled during runtime and during submission.
I’d encourage others to try this out and see if the same issue arises. If enough of us report it, the LeetCode team can investigate and resolve it.
Tagging LeetCode support for visibility: @LeetCode @LeetCodeAdmin
Let’s work together to make the platform better! 😊
| 0 | 0 |
['Bit Manipulation', 'C++']
| 0 |
number-of-bit-changes-to-make-two-integers-equal
|
fundamental approach ,using (if...else statement only) python
|
fundamental-approach-using-ifelse-statem-9hhj
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
saber842
|
NORMAL
|
2025-01-26T07:22:31.529671+00:00
|
2025-01-26T07:22:31.529671+00:00
| 5 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def minChanges(self, n: int, k: int) -> int:
# 1 can change to 0 only.
count=0
s=""
m=""
if(n !=k):
while(n>0):
r=n%2
s=s+str(r)
n=n//2
s=s[::-1]
while(k>0):
r=k%2
m=m+str(r)
k=k//2
m=m[::-1]
if(len(m)==len(s)):
for i in range(0,len(s)):
if(m[i]!=s[i] and s[i]=="1"):
count=count+1
elif(m[i]!=s[i] and s[i]=="0"):
return -1
break
else:
if(len(m)<len(s)):
while(len(m)<len(s) ):
m="0"+m
for i in range(0,len(m)):
if(m[i]!=s[i] and s[i]=="1"):
count=count+1
elif(m[i]!=s[i] and s[i]=="0"):
return -1
break
else:
while(len(s)<len(m)):
s="0"+s
for i in range(0,len(m)):
if(m[i]!=s[i] and s[i]=="1"):
count=count+1
elif(m[i]!=s[i] and s[i]=="0"):
return -1
break
return count
```
| 0 | 0 |
['Python3']
| 0 |
number-of-bit-changes-to-make-two-integers-equal
|
[Java] ✅ 0MS ✅ 100% ✅ BIT ✅ FASTEST ✅ BEST ✅ CLEAN CODE
|
java-0ms-100-bit-fastest-best-clean-code-hyyr
|
Approach
Loop while n > 0 OR k > 0
if their last bit is different, return -1 if lastBitOfN is 0, else increment changes (as last bit of n is 1 and last bit of k
|
StefanelStan
|
NORMAL
|
2025-01-22T10:11:15.377443+00:00
|
2025-01-22T10:11:15.377443+00:00
| 9 | false |
# Approach
1. Loop while n > 0 OR k > 0
2. if their last bit is different, return -1 if lastBitOfN is 0, else increment changes (as last bit of n is 1 and last bit of k is 0)
# Complexity
- Time complexity:$$O(k)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:$$O(1)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int minChanges(int n, int k) {
int lastNBit, lastKBit;
int minChanges = 0;
while (n > 0 || k > 0) {
lastNBit = (n & 1);
lastKBit = (k & 1);
if (lastNBit != lastKBit) {
if (lastNBit == 0) {
return -1;
} else {
minChanges++;
}
}
n = n >> 1;
k = k >> 1;
}
return minChanges;
}
}
```
| 0 | 0 |
['Java']
| 0 |
number-of-bit-changes-to-make-two-integers-equal
|
Fast and Efficient Python Solution Beats 100% 🔥🔥
|
fast-and-efficient-python-solution-beats-goin
|
IntuitionI immediately thought of converting both numbers into binary, and proceeding from there.ApproachSimply checking all i where n[i] = 1 and k[i] = 0 is a
|
Gayathri_1711
|
NORMAL
|
2025-01-21T02:58:14.286237+00:00
|
2025-01-21T02:58:14.286237+00:00
| 3 | false |
# Intuition
I immediately thought of converting both numbers into binary, and proceeding from there.
# Approach
Simply checking all i where n[i] = 1 and k[i] = 0 is a perfectly valid and efficient solution. For all i that meet this condition, it suffices to increment the answer by 1 and set n[i] = 0. But this approach doesn't cover the case where the len(n) != len(k). If this is the case, just add their absolute difference number of zeroes to the shorter length number, which would yield in them being the same length.
# Complexity
- Time complexity:
$$O(n)$$
- Space complexity:
$$O(n)$$
# Code
```python3 []
class Solution:
def minChanges(self, n: int, k: int) -> int:
bn = " ".join(str(bin(n)).replace("0b", "")).split()
kn = " ".join(str(bin(k)).replace("0b", "")).split()
if len(bn) < len(kn):
bn = ["0"] * (len(kn) - len(bn)) + bn
elif len(kn) < len(bn):
kn = ["0"] * (len(bn) - len(kn)) + kn
ans = 0
for i in range(len(bn)):
if bn[i] == "1" and kn[i] == "0":
ans += 1
bn[i] = "0"
return ans if bn == kn else -1
```
| 0 | 0 |
['Python3']
| 0 |
number-of-bit-changes-to-make-two-integers-equal
|
scala twoliner
|
scala-twoliner-by-vititov-8xbm
| null |
vititov
|
NORMAL
|
2025-01-17T20:35:05.073885+00:00
|
2025-01-17T20:35:05.073885+00:00
| 1 | false |
```scala []
object Solution {
def minChanges(n: Int, k: Int): Int =
val (ns,ks) = LazyList.unfold((n,k)){case (n1,k1) =>
Option.when(n1!=0 || k1!=0) {((n1&1,k1&1), (n1>>1,k1>>1))}
}.collect{case (a,b) if a!=b => a-b}.partition(_ > 0)
if(ks.nonEmpty) -1 else ns.sum
}
```
| 0 | 0 |
['Bit Manipulation', 'Scala']
| 0 |
number-of-bit-changes-to-make-two-integers-equal
|
Easy solution
|
easy-solution-by-akshayya_ru-ui7r
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
Akshayya_RU
|
NORMAL
|
2025-01-16T06:05:06.909282+00:00
|
2025-01-16T06:05:06.909282+00:00
| 4 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int minChanges(int n, int k) {
//if(n==k)
// return 0;
bitset<32> b1(n),b2(k);
string N=b1.to_string(),K=b2.to_string();
int c=0;
for(int i=0;i<32;i++)
if(N[i]=='1' && K[i]=='0')
c++;
else if(N[i]=='0' && K[i]=='1')
return -1;
return c;
}
};
```
| 0 | 0 |
['C++']
| 0 |
number-of-bit-changes-to-make-two-integers-equal
|
Unique Answer
|
unique-answer-by-nyilinnhtin-3hgs
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
NyiLinnHtin
|
NORMAL
|
2025-01-15T01:05:27.243689+00:00
|
2025-01-15T01:05:27.243689+00:00
| 3 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def minChanges(self, n: int, k: int) -> int:
nbit = str("{0:b}".format(n))
kbit = str("{0:b}".format(k))
l = max(len(nbit), len(kbit))
nbit = nbit.zfill(l)
kbit = kbit.zfill(l)
count = 0
for i in range(l):
if nbit[i] == "1" and kbit[i] == "0":
count += 1
if nbit[i] == "0" and kbit[i] == "1":
return -1
return count
```
| 0 | 0 |
['Python3']
| 0 |
number-of-bit-changes-to-make-two-integers-equal
|
Simple C code with XOR operation solutions
|
simple-c-code-with-xor-operation-solutio-2vhx
|
Code
|
ggandrew1218
|
NORMAL
|
2025-01-13T08:53:01.576507+00:00
|
2025-01-13T08:53:01.576507+00:00
| 21 | false |
# Code
```c []
int minChanges(int n, int k) {
int tmp = n ^ k;
int ans = 0;
if( (tmp & k) == 0)
{
while(tmp>0)
{
if(tmp&1)
{
ans++;
}
tmp=tmp>>1;
}
return ans;
}
return -1;
}
```
| 0 | 0 |
['C']
| 0 |
number-of-bit-changes-to-make-two-integers-equal
|
JavaScript - JS
|
javascript-js-by-mlienhart-odou
| null |
mlienhart
|
NORMAL
|
2025-01-12T11:05:38.522547+00:00
|
2025-01-12T11:05:38.522547+00:00
| 5 | false |
```javascript []
/**
* @param {number} n
* @param {number} k
* @return {number}
*/
var minChanges = function (n, k) {
let binaryRepresentationOfN = n.toString(2);
let binaryRepresentationOfK = k.toString(2);
let result = 0;
const maximumLength = Math.max(
binaryRepresentationOfN.length,
binaryRepresentationOfK.length
);
binaryRepresentationOfN = binaryRepresentationOfN.padStart(
maximumLength,
"0"
);
binaryRepresentationOfK = binaryRepresentationOfK.padStart(
maximumLength,
"0"
);
for (let i = 0; i < binaryRepresentationOfN.length; i++) {
if (
binaryRepresentationOfN[i] === "1" &&
binaryRepresentationOfK[i] === "0"
) {
result++;
}
if (
binaryRepresentationOfN[i] === "0" &&
binaryRepresentationOfK[i] === "1"
) {
return -1;
}
}
return result;
};
```
| 0 | 0 |
['JavaScript']
| 0 |
number-of-bit-changes-to-make-two-integers-equal
|
Java Solution with explanation to Beat 100% | if you Like | Upvote Me!**
|
java-solution-with-explanation-to-beat-1-kr70
|
IntuitionJava Solution with explanation to Beat 100% | if you Like | Upvote Me!ApproachSteps:
k ^= n (XOR operation):
The XOR operation results in a value where
|
NavnathGutte
|
NORMAL
|
2025-01-10T18:26:52.114635+00:00
|
2025-01-10T18:26:52.114635+00:00
| 8 | false |
# Intuition
**Java Solution with explanation to Beat 100% | if you Like | Upvote Me!**
# Approach
Steps:
1) k ^= n (XOR operation):
The XOR operation results in a value where each bit is 1 if the corresponding bits of k and n are different, and 0 otherwise.
Integer.bitCount(k) (Count 1 bits):
2)The bitCount method returns the number of 1 bits in the binary representation of k.
3) k &= n (AND operation):
The AND operation updates k to include only the bits that are 1 in both k and n.
Comparison:
If the bit count of the modified k (after k &= n) matches the original cnt (from the XOR operation), return cnt. Otherwise, return -1.
Examples:
Let’s evaluate this with an example:
Input: n = 13 (binary 1101), k = 4 (binary 0100).
k ^= n:
Binary XOR:
1101 ->13
^ 0100 ->4
__________
K= 1001
Now k = 9 (binary 1001).
count = Integer.bitCount(k):
k = 9 (binary 1001), bitCount = 2.
k &= n:
Binary AND:
1001 ->9
& 1101 ->13
__________
K= 1001 number of 1-bit in binary no is 2 so count=2
Now k = 9 (binary 1001).
Comparison:
bitCount(k) = 2, count = 2. They are equal, so the method returns 2.
# Complexity
- Time complexity:
O(1)
- Space complexity:
O(1)
# Code
```java []
class Solution {
public int minChanges(int n, int k) {
k ^= n;
/*
1101 ->13
^ 0100 ->4
__________
K= 1001
*/
int count = Integer.bitCount(k);
/* count number of 1 in binary which is 2 in k*/
k &= n;
/*
1001 ->9
& 1101 ->13
__________
K= 1001 number of 1-bit 2 so count=2
*/
return count == Integer.bitCount(k) ? count : -1; //count=2
}
}
```
| 0 | 0 |
['Bit Manipulation', 'Java']
| 0 |
number-of-bit-changes-to-make-two-integers-equal
|
3226. Number of Bit Changes to Make Two Integers Equal
|
3226-number-of-bit-changes-to-make-two-i-2o99
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
G8xd0QPqTy
|
NORMAL
|
2025-01-08T07:50:34.550844+00:00
|
2025-01-08T07:50:34.550844+00:00
| 3 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def minChanges(self, n: int, k: int) -> int:
# If n has 0 where k has 1, it's impossible to convert n to k
if (n & k) != k:
return -1
# Count how many 1's are in n where k has 0
return bin(n & ~k).count('1')
```
| 0 | 0 |
['Python3']
| 0 |
number-of-bit-changes-to-make-two-integers-equal
|
Python Easy Solution
|
python-easy-solution-by-thanshir_md-5k5s
|
Code
|
Thanshir_Md
|
NORMAL
|
2025-01-04T15:50:09.739994+00:00
|
2025-01-04T15:50:09.739994+00:00
| 5 | false |
# Code
```python3 []
class Solution:
def minChanges(self, n: int, k: int) -> int:
max_bits = max(n.bit_length(), k.bit_length())
t=0
if n==k:
return 0
else:
nb=str(format(n, f'0{max_bits}b'))
kb=str(format(k, f'0{max_bits}b'))
for i in range(max_bits):
if nb[i]=='1' and kb[i]=='0':
nb=nb[:i]+'0'+nb[i+1:]
t+=1
return t if nb==kb else -1
```
| 0 | 0 |
['Array', 'Bit Manipulation', 'Python', 'Python3']
| 0 |
number-of-bit-changes-to-make-two-integers-equal
|
Simple Method || Bit Manipulation
|
simple-method-bit-manipulation-by-prajwa-wexq
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
prajwalkanade648
|
NORMAL
|
2025-01-01T14:08:02.059103+00:00
|
2025-01-01T14:08:02.059103+00:00
| 6 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int minChanges(int n, int k) {
int count = 0;
while(n > 0 || k > 0){
int Bitn = n & 1;
int Bitk = k & 1;
if(Bitn == 1 && Bitk== 0){
count++;
}
if(Bitn == 0 && Bitk == 1){
return -1;
}
n >>= 1;
k >>= 1;
}
return count;
}
}
```
| 0 | 0 |
['Java']
| 0 |
number-of-bit-changes-to-make-two-integers-equal
|
Bitwise
|
bitwise-by-j22qidyza7-8dw5
|
Code
|
J22qIDYZa7
|
NORMAL
|
2024-12-28T22:38:34.569374+00:00
|
2024-12-28T22:38:34.569374+00:00
| 3 | false |
# Code
```php []
class Solution
{
/**
* @param Integer $n
* @param Integer $k
* @return Integer
*/
function minChanges($n, $k)
{
$count = 0;
while ($n) {
$bitN = $n & 1;
$bitK = $k & 1;
if ($bitK && !$bitN)
return -1;
if (!$bitK && $bitN)
$count++;
$k >>= 1;
$n >>= 1;
}
if($k) return -1;
return $count;
}
}
```
| 0 | 0 |
['PHP']
| 0 |
number-of-bit-changes-to-make-two-integers-equal
|
beats 100% 0ms c++ easy solution([email protected])
|
beats-100-0ms-c-easy-solutionaunikverma3-or85
|
Complexity
Time complexity:O(N)
Space complexity:O(N)
Code
|
aunik36
|
NORMAL
|
2024-12-24T05:01:07.535648+00:00
|
2024-12-24T05:01:07.535648+00:00
| 3 | false |
# Complexity
- Time complexity:O(N)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:O(N)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int minChanges(int n, int k) {
if ((n & k) != k) return -1; // if its impossible to make them equal
string n1 = bitset<32>(n).to_string();
string k1 = bitset<32>(k).to_string();
int count = 0;
for (int i = 0; i < n1.size(); i++) {
if (n1[i] - k1[i] == 1) {
count++;
}
}
return count;
}
};
```
| 0 | 0 |
['C++']
| 0 |
number-of-bit-changes-to-make-two-integers-equal
|
Easy Solution
|
easy-solution-by-koushik_55_koushik-3ih0
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
Koushik_55_Koushik
|
NORMAL
|
2024-12-20T06:17:16.887983+00:00
|
2024-12-20T06:17:16.887983+00:00
| 2 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def minChanges(self, n: int, k: int) -> int:
if n==k:
return 0
if k>n:
return -1
k1=bin(n)[2:]
k2=bin(k)[2:]
max_length = max(len(k1), len(k2))
k1 = k1.zfill(max_length)
k2 = k2.zfill(max_length)
c=0
for i in range(max_length):
if k1[i]=='0' and k2[i]=='1':
return -1
elif k1[i]=='1' and k2[i]=='0':
c+=1
return c
```
| 0 | 0 |
['Python3']
| 0 |
number-of-bit-changes-to-make-two-integers-equal
|
The best solve in python
|
the-best-solve-in-python-by-shoxruxnorqo-ores
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
shoxruxnorqoziyev2004
|
NORMAL
|
2024-12-19T02:59:42.876066+00:00
|
2024-12-19T02:59:42.876066+00:00
| 2 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def minChanges(self, n: int, k: int) -> int:\n n=bin(n)[2:].zfill(20)\n k=bin(k)[2:].zfill(20)\n c=0\n for i in range(len(n)):\n if n[i]=="0" and k[i]=="1":\n return -1\n elif n[i]=="1" and k[i]=="0":\n c+=1\n return c\n```
| 0 | 0 |
['Python3']
| 0 |
number-of-bit-changes-to-make-two-integers-equal
|
✅🐍 Easy python solution 🐍✅
|
easy-python-solution-by-ninise-o92t
|
Code
|
Ninise
|
NORMAL
|
2024-12-16T18:53:43.229336+00:00
|
2024-12-16T18:53:43.229336+00:00
| 3 | false |
\n# Code\n```python3 []\nclass Solution:\n def minChanges(self, n: int, k: int) -> int:\n if n & k != k: return -1\n n_b, n_k = bin(n)[2:], bin(k)[2:]\n return n_b.count(\'1\') - n_k.count(\'1\')\n\n```
| 0 | 0 |
['Bit Manipulation', 'Python3']
| 0 |
number-of-bit-changes-to-make-two-integers-equal
|
minChanges: easy solution. BEAT 100% ✅
|
minchanges-easy-solution-beat-100-by-rti-phd5
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\nSimply extract one bit at a time from the two numbers.\nif bit_n is 1 and
|
rTIvQYSHLp
|
NORMAL
|
2024-12-08T09:38:31.409292+00:00
|
2024-12-08T09:38:31.409319+00:00
| 14 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nSimply extract one bit at a time from the two numbers.\nif bit_n is 1 and bit_k is 0, we increment by one the number of changes. if bit_n is 0 and bit_k is 1, return -1 because it is not possible to make n equal to k.\n\n# Complexity\n- Time complexity:\nO(1)\n\n- Space complexity:\nO(1)\n\n# Code\n```c []\nint minChanges(int n, int k) {\n int bit_n;\n int bit_k;\n int number_of_changes=0;\n for(int i=20;i>=0;i--){\n bit_n=(n >> i) & 1;\n bit_k=(k >> i) & 1;\n if(bit_n && !bit_k) number_of_changes++;\n else if(!bit_n && bit_k) return -1;\n }\n return number_of_changes;\n}\n```
| 0 | 0 |
['Bit Manipulation', 'C']
| 0 |
number-of-bit-changes-to-make-two-integers-equal
|
Most Optimal Solution (Bitwise Operations C++)
|
most-optimal-solution-bitwise-operations-h5u1
|
Intuition\n Describe your first thoughts on how to solve this problem. \nStraight forward thinking, check last bit if N (use n & 1) and check adj bit in K if we
|
pratikkedar
|
NORMAL
|
2024-12-08T05:11:12.040280+00:00
|
2024-12-08T05:11:12.040307+00:00
| 1 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nStraight forward thinking, check last bit if N (use n & 1) and check adj bit in K if we get 1 in n we can toggle to 0 if the need persist, increment count else if we get 0 return -1 as 0 cant be changed to 1.\n\nOptimized thinking : bit difference can be found using xor operation (n ^ k), rather than traversing in diff(xor diff) bit by bit (log n TC) we can only check the set bits in diff ! and check the corrosponding bit of n \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nTC better than log N, where N is bit difference ! \n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int minChanges(int n, int k) {\n int diff = n ^ k;\n unsigned int cnt = 0;\n \n while(diff)\n {\n // For every set bit in diff, check the adj bit in n\n unsigned int mask = diff & (-diff);\n\n // int ans = n & \n // We can only change 1s to 0 and not 0s to 1, if at mask location \n if((n & mask) == 0) return -1;\n else ++cnt;\n\n // unset the last set bit\n diff &= (diff - 1);\n }\n\n return cnt;\n }\n};\n```
| 0 | 0 |
['Bit Manipulation', 'C++']
| 0 |
number-of-bit-changes-to-make-two-integers-equal
|
simple solution with bitmask beats 100%
|
simple-solution-with-bitmask-beats-100-b-08ly
|
Code\ncpp []\nclass Solution {\npublic:\n int minChanges(int n, int k) {\n int ans = 0;\n\n for (int i = 0; i < 32; i++) {\n int n_i
|
oyetanishq
|
NORMAL
|
2024-12-05T15:18:27.995286+00:00
|
2024-12-05T15:18:27.995329+00:00
| 0 | false |
# Code\n```cpp []\nclass Solution {\npublic:\n int minChanges(int n, int k) {\n int ans = 0;\n\n for (int i = 0; i < 32; i++) {\n int n_ith_bit = (n & (1 << i));\n int k_ith_bit = (k & (1 << i));\n\n if ((n_ith_bit ^ k_ith_bit)) {\n if (n_ith_bit) ans++;\n else return -1;\n }\n \n }\n\n return ans;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
number-of-bit-changes-to-make-two-integers-equal
|
0ms | Java Solution | Bit Manipulation
|
0ms-java-solution-bit-manipulation-by-ha-65es
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Harsha2580
|
NORMAL
|
2024-12-04T05:22:10.342361+00:00
|
2024-12-04T05:22:10.342397+00:00
| 5 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public boolean check(int n, int i){\n return ((n>>i) & 1) == 1 ;\n }\n public int minChanges(int n, int k) {\n int c=0;\n for(int i=0;i<31;i++){\n if(check(n,i)==check(k,i)){}\n else if(check(n,i) & !check(k,i)) c++;\n else return -1;\n }\n return c;\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
number-of-bit-changes-to-make-two-integers-equal
|
Implicit type conversion, bit manipulation and addition (for answer) solution
|
implicit-type-conversion-bit-manipulatio-478q
|
\n# Code\ncpp []\nclass Solution {\npublic:\n int minChanges(int n, int k) {\n int ans = 0;\n while(n&&k)\n {\n ans+=(n&1)^(k
|
1jsd
|
NORMAL
|
2024-12-02T21:17:27.549856+00:00
|
2024-12-02T21:17:27.549881+00:00
| 1 | false |
\n# Code\n```cpp []\nclass Solution {\npublic:\n int minChanges(int n, int k) {\n int ans = 0;\n while(n&&k)\n {\n ans+=(n&1)^(k&1);\n if(!(n&1)&&(k&1)) return -1;\n n>>=1;\n k>>=1;\n }\n if(!n&&k) return -1;\n while(n)\n {\n ans+=n&1;\n n>>=1;\n }\n return ans;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
number-of-bit-changes-to-make-two-integers-equal
|
easy python solution
|
easy-python-solution-by-ramyasreekannan-l60x
|
\n\n# Code\npython3 []\nclass Solution:\n def minChanges(self, n: int, k: int) -> int:\n count =0\n for i in range(32):\n nb=n%2\n
|
ramyasreekannan
|
NORMAL
|
2024-12-02T04:42:14.501175+00:00
|
2024-12-02T04:42:14.501212+00:00
| 1 | false |
\n\n# Code\n```python3 []\nclass Solution:\n def minChanges(self, n: int, k: int) -> int:\n count =0\n for i in range(32):\n nb=n%2\n kb=k%2\n if (nb==1 and kb==0):\n count+=1\n if (nb==0 and kb==1):\n return -1\n\n\n n//=2\n k//=2\n return count \n```
| 0 | 0 |
['Python3']
| 0 |
number-of-bit-changes-to-make-two-integers-equal
|
EASY PYTHON SOLUTION
|
easy-python-solution-by-juantorrenegra-79nn
|
\n\npython []\nclass Solution(object):\n def minChanges(self, n, k):\n nbinario=bin(n)[2:] # 1101\n kbinario=bin(k)[2:] # 100\n largo=ma
|
juantorrenegra
|
NORMAL
|
2024-12-01T23:59:43.392342+00:00
|
2024-12-01T23:59:43.392361+00:00
| 3 | false |
\n\n```python []\nclass Solution(object):\n def minChanges(self, n, k):\n nbinario=bin(n)[2:] # 1101\n kbinario=bin(k)[2:] # 100\n largo=max(len(nbinario),len(kbinario) )# 4\n tes=[]\n nbin=nbinario.zfill(largo) # 1101\n kbin=kbinario.zfill(largo) # 0100\n\n count = 0\n for i in range(largo):\n if nbin[i]==kbin[i]:\n tes.append(nbin[i])\n else:\n if nbin[i]=="1":\n tes.append("0")\n count+=1\n else:\n tes.append(nbin)\n\n res="".join(tes) \n if res==kbin:\n return count \n else:\n return -1 \n```
| 0 | 0 |
['Python']
| 0 |
number-of-bit-changes-to-make-two-integers-equal
|
Bitwise operations
|
bitwise-operations-by-evgenysh-ejqn
|
Code\npython3 []\nclass Solution:\n def minChanges(self, n: int, k: int) -> int:\n changes = 0\n while n or k:\n n1, k1 = n & 1, k &
|
evgenysh
|
NORMAL
|
2024-11-27T20:10:12.287618+00:00
|
2024-11-27T20:10:12.287644+00:00
| 0 | false |
# Code\n```python3 []\nclass Solution:\n def minChanges(self, n: int, k: int) -> int:\n changes = 0\n while n or k:\n n1, k1 = n & 1, k & 1\n if n1 > k1:\n changes += 1\n elif n1 < k1:\n return -1\n n >>= 1\n k >>= 1\n return changes\n```
| 0 | 0 |
['Python3']
| 0 |
number-of-bit-changes-to-make-two-integers-equal
|
Simple solution, O(n)
|
simple-solution-on-by-ayonmondal-dn3r
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
ayonmondal
|
NORMAL
|
2024-11-24T05:33:27.201847+00:00
|
2024-11-24T05:33:27.201873+00:00
| 2 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int minChanges(int n, int k) {\n String nStr = Integer.toBinaryString(n);\n String kStr = Integer.toBinaryString(k);\n\n int nStrLen = nStr.length();\n int kStrLen = kStr.length();\n\n int operationCount = 0;\n\n if (n == k) return 0;\n\n if (nStrLen > kStrLen) {\n for (int i=1; i<=(nStrLen - kStrLen); i++) {\n kStr = "0" + kStr;\n }\n }\n else if (nStrLen < kStrLen) {\n for (int i=1; i<=(kStrLen - nStrLen); i++) {\n nStr = "0" + nStr;\n }\n }\n\n for (int i=0; i<nStrLen; i++) {\n if (nStr.charAt(i) != kStr.charAt(i)) {\n if (nStr.charAt(i) != \'1\') {\n return -1;\n }\n else operationCount++;\n }\n }\n\n return operationCount;\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
number-of-bit-changes-to-make-two-integers-equal
|
Simple String solution -> 1 ms
|
simple-string-solution-1-ms-by-developer-xjo4
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
DevelopersUsername
|
NORMAL
|
2024-11-19T18:36:17.057074+00:00
|
2024-11-19T18:36:17.057103+00:00
| 3 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```java []\nclass Solution {\n public int minChanges(int n, int k) {\n\n if (n == k) return 0;\n\n String nBits = Integer.toBinaryString(n);\n String kBits = Integer.toBinaryString(k);\n\n if (nBits.length() < kBits.length()) return -1;\n\n int ans = 0;\n for (int i = kBits.length() - 1, j = nBits.length() - 1; i >= 0; i--, j--)\n if (nBits.charAt(j) == \'1\' && kBits.charAt(i) == \'0\')\n ans++;\n else if (nBits.charAt(j) == \'0\' && kBits.charAt(i) == \'1\')\n return -1;\n\n for (int i = 0; i < nBits.length() - kBits.length(); i++)\n if (nBits.charAt(i) == \'1\') ans++;\n\n return ans;\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
number-of-bit-changes-to-make-two-integers-equal
|
Easy Solution
|
easy-solution-by-vemohan15-7h8d
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
vemohan15
|
NORMAL
|
2024-11-17T08:10:18.961875+00:00
|
2024-11-17T08:10:18.961906+00:00
| 2 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```csharp []\npublic class Solution {\n public int MinChanges(int n, int k) {\n int bitn,bitk;\n int count=0;\n while(n!=0 || k!=0){\n bitn=n&1;\n bitk=k&1; \n //Console.WriteLine(bitn+"*"+bitk); \n if(bitk==1 && bitn==0)return -1;\n if(bitk==0 && bitn==1)count++;\n n=n>>1; \n k=k>>1;\n //Console.WriteLine(n+"*"+k);\n }\n return count;\n }\n}\n```
| 0 | 0 |
['C#']
| 0 |
number-of-bit-changes-to-make-two-integers-equal
|
Swift💯
|
swift-by-upvotethispls-014i
|
Bit Logic (accepted answer)\nn | k == n ensures that k has no bit set that is not already set in n. If k has a bit set that is not in n, then it is impossible t
|
UpvoteThisPls
|
NORMAL
|
2024-11-16T06:55:05.155089+00:00
|
2024-11-16T07:01:05.028147+00:00
| 5 | false |
**Bit Logic (accepted answer)**\n`n | k == n` ensures that `k` has no bit set that is not already set in `n`. If `k` has a bit set that is not in `n`, then it is impossible to transform `n` into `k` by turning off bits. Once we know it\'s possible, `n ^ k` returns all the bits that are different between `n` and `k` (these should be 1 in `n` and 0 in `k`). Report a count of those bits.\n```\nclass Solution {\n func minChanges(_ n: Int, _ k: Int) -> Int {\n (n|k) == n ? (n^k).nonzeroBitCount : -1\n }\n}\n```
| 0 | 0 |
['Swift']
| 0 |
number-of-bit-changes-to-make-two-integers-equal
|
3226. Number of Bit Changes to Make Two Integers Equal
|
3226-number-of-bit-changes-to-make-two-i-wy35
|
Intuition\n Describe your first thoughts on how to solve this problem. \nEasy one, if you are good at bit manipulation!\n# Approach\n Describe your approach to
|
SPD-LEGEND
|
NORMAL
|
2024-11-15T16:27:51.521491+00:00
|
2024-11-15T16:27:51.521547+00:00
| 2 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nEasy one, if you are good at bit manipulation!\n# Approach\n<!-- Describe your approach to solving the problem. -->\nBit Manipulation => Checking if i\'th bit of \'n\' is set(1) && i\'th bit of \'k\' is unset(0) -> toggle i\'th bit of \'n\' using XOR(^) -> after altering all bits, if "n==k" return count of toggles, otherwise return -1.\n# Complexity\n- Time complexity: O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int minChanges(int n, int k) {\n int c = 0;\n for(int i=0;i<32;++i)\n {\n if(((n & (1<<i)) > 0) && ((k & (1<<i)) == 0 ))\n {\n n = (n^(1<<i));\n c++;\n }\n }\n if(n==k)\n return c;\n return -1;\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
number-of-bit-changes-to-make-two-integers-equal
|
Beats 100% || XOR || OR || Bit Manipulation
|
beats-100-xor-or-bit-manipulation-by-dev-tmyz
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
devansh_dubey
|
NORMAL
|
2024-11-13T21:12:27.526990+00:00
|
2024-11-13T21:12:27.527014+00:00
| 2 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int minChanges(int n, int k) {\n if(__builtin_popcount(~k|n)!=32){\n return -1;\n }\n return __builtin_popcount(n^k);\n }\n};\n```
| 0 | 0 |
['Bit Manipulation', 'C++']
| 0 |
number-of-bit-changes-to-make-two-integers-equal
|
Beat 100% with c++
|
beat-100-with-c-by-psieu8t8iu-j8c8
|
Intuition\nUsing bit manipulation to solve this problem.\n\n# Approach\nThis solution uses bit manipulation to determine the minimum number of changes needed to
|
psIeU8t8iu
|
NORMAL
|
2024-11-12T12:49:45.079749+00:00
|
2024-11-12T12:49:45.079781+00:00
| 0 | false |
# Intuition\nUsing bit manipulation to solve this problem.\n\n# Approach\nThis solution uses bit manipulation to determine the minimum number of changes needed to make integer n equal to integer k by only turning 1 bits in n to 0. Here\'s the approach:\n\n1. Bitwise OR Check: First, it checks if k can be derived from n by turning some of n\'s 1 bits to 0. If k has any 1 bits that n does not, it\u2019s impossible to make n equal to k, so we return -1. This is done by checking (n | k) != n.\n\n2. XOR Operation: If k can be obtained from n, we compute n ^ k, which highlights the differing bits between n and k.\n\n3. Counting Set Bits: Finally, we count the number of 1 bits in the result of n ^ k, representing the positions where n has 1s that need to be turned to 0s to match k.\n\nThe time complexity is O(log n) due to the bit counting, and the space complexity is O(1) since only a few variables are used.\n\n# Complexity\n- Time complexity:\n O(log n)\n\n- Space complexity:\n O(1)\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int minChanges(int n, int k) \n {\n if ((n | k) != n) \n {\n return -1;\n }\n\n int xored = n ^ k;\n int count = 0;\n while(xored)\n {\n if(xored & 1)\n {\n count++;\n }\n xored = xored >> 1; \n }\n return count;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
most-beautiful-item-for-each-query
|
C++ Solution | Sorting
|
c-solution-sorting-by-invulnerable-y63d
|
Solution\n\n Brute force approach would be : For each query, traverse the items and check the ones having price less than or equal to queries[i] and find the ma
|
invulnerable
|
NORMAL
|
2021-11-13T16:01:57.907787+00:00
|
2021-11-13T16:01:57.907826+00:00
| 6,906 | false |
**Solution**\n\n* Brute force approach would be : For each query, traverse the items and check the ones having price less than or equal to `queries[i]` and find the maximum beauty among these items - *O(QN)*.\n* Drawback of previous approach is, we have to traverse items multiple times. If we have found the answer for query say 80, we can find the answer for query 100 by only traversing the item with price in the range (80, 100] instead of checking all items in price range [0, 100].\n\n* If the items are sorted in increasing order of their price, then in the above example, for query 80 we will traverse the items only upto price 80 and then for 100 we will continue from the item where we would have left for 80.\n\n* The only problem is that the above method need the queries to be in increasing order. If query 80 comes after 100 then we don\'t have a way to use result for 100 to find the result for 80.\n\n* Hence, we will sort the queries, keeping their original index with them. Then process them in the same order.\n\n**Algorithm**\n\n1. Store each query `queries[i]` as a pair of {`queries[i]`, `i`} into the vector `queriesPair`.\n2. Sort `queriesPair` and `items` in ascending order.\n3. Iterate over `queriesPair`, find the maximum beauty of item having price less than `queriesPair[i].first`\n4. Store it in the `maxBeauty`.\n5. Store `maxBeauty` in the answer vector `ans` at index `queriesPair[i].second`.\n\n**Time Complexity**: \n\n- Sorting items takes NlogN\n- Sorting queries takes QlogQ\n- Iterating over each Item and query takes (N + Q)\n- Time Complexity : O(NlogN + QlogQ)\n\n```\nclass Solution {\npublic:\n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n vector<int> ans(queries.size());\n \n vector<pair<int ,int>> queriesPair;\n for (int i = 0; i < queries.size(); i++) {\n queriesPair.push_back({queries[i], i});\n }\n \n sort(queriesPair.begin(), queriesPair.end());\n sort(items.begin(), items.end());\n \n int itemIndex = 0, maxBeauty = 0;\n for (int i = 0; i < queriesPair.size(); i++) {\n int maxPriceAllowed = queriesPair[i].first;\n int queryOriginalIndex = queriesPair[i].second;\n \n // Iterate over items, stop when the price exceeds query price or no item left\n while (itemIndex < items.size() && items[itemIndex][0] <= maxPriceAllowed) {\n maxBeauty = max(maxBeauty, items[itemIndex][1]);\n itemIndex++;\n }\n \n ans[queryOriginalIndex] = maxBeauty;\n }\n \n return ans;\n }\n};\n```
| 93 | 3 |
[]
| 8 |
most-beautiful-item-for-each-query
|
🌟 Beats 100.00% 👏 || For loop || Explained with example
|
beats-10000-for-loop-explained-with-exam-pp9d
|
\n\n# Intuition\n Describe your first thoughts on how to solve this problem. \nThe goal of this algorithm is to find the maximum "beauty" of items a person can
|
srinivas_bodduru
|
NORMAL
|
2024-11-12T02:28:51.747445+00:00
|
2024-11-12T02:28:51.747492+00:00
| 26,766 | false |
\n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe goal of this algorithm is to find the maximum "beauty" of items a person can afford, given an array of items, where each item is represented as [price, beauty], and an array of queries, where each query represents an available budget.\n\nTo do this efficiently:\n\nWe preprocess the items to build a "price-beauty bracket" where each entry stores the highest possible beauty value achievable up to a certain price.\nFor each query, we quickly look up the maximum beauty achievable within that budget by consulting our preprocessed data.\nThis allows us to answer each query in constant time after the preprocessing step.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe algorithm is divided into two main parts: preprocessing the items and processing the queries.\n\nPart 1: Preprocessing\nSort the Items by Price: We first sort the items array by price in ascending order. Sorting helps ensure that each processed item has a price greater than or equal to previous items, allowing us to build a cumulative "price-beauty bracket."\n\nConstruct Price-Beauty Brackets:\n\nWe create a list res to store "price-beauty brackets." Each bracket is represented as [min_price, max_beauty, max_price].\nStarting with a bracket [0, 0, \u221E], which represents zero budget, we iterate over each item in sorted order:\nIf the current item\'s beauty is higher than the last recorded beauty in res, we add a new bracket with the current item\'s price and beauty, updating the last bracket\u2019s max_price to the current price.\nResult of Preprocessing: At the end of preprocessing, res will contain cumulative price-beauty brackets, allowing us to check the maximum beauty for any budget by examining the highest bracket we can afford.\n\nPart 2: Processing the Queries\nFor each budget in queries, we iterate backward through res (from the most expensive bracket to the least) and find the first bracket with a minimum price that fits within the query budget.\nWe record the corresponding beauty value in the result array.\n\n# Example\nSuppose we have:\n\nitems = [[1, 2], [3, 4], [5, 6], [6, 8]] (price-beauty pairs)\nqueries = [2, 3, 5, 7] (budgets)\nStep-by-Step Execution\nSorting Items by Price\n\nAfter sorting (already sorted here), we have items = [[1, 2], [3, 4], [5, 6], [6, 8]].\nBuilding the Price-Beauty Brackets (res)\n\nInitialize res with [0, 0, \u221E].\nProcess each item:\nItem [1, 2]: Since 2 > 0 (last bracket\'s beauty), add a new bracket [1, 2, \u221E] and set the last bracket\u2019s max_price to 1.\nItem [3, 4]: Since 4 > 2, add [3, 4, \u221E] and update the previous bracket\u2019s max_price to 3.\nItem [5, 6]: Since 6 > 4, add [5, 6, \u221E] and update the previous bracket\u2019s max_price to 5.\nItem [6, 8]: Since 8 > 6, add [6, 8, \u221E] and update the previous bracket\u2019s max_price to 6.\nFinal res: [[0, 0, 1], [1, 2, 3], [3, 4, 5], [5, 6, 6], [6, 8, \u221E]].\nAnswering Queries\n\nFor each query in queries, find the maximum beauty that can be afforded.\nQuery 2: Find the last bracket with min_price <= 2. Result: bracket [1, 2, 3], so beauty is 2.\nQuery 3: Last bracket with min_price <= 3. Result: bracket [3, 4, 5], so beauty is 4.\nQuery 5: Last bracket with min_price <= 5. Result: bracket [5, 6, 6], so beauty is 6.\nQuery 7: Last bracket with min_price <= 7. Result: bracket [6, 8, \u221E], so beauty is 8.\nOutput\nThe final output for the queries [2, 3, 5, 7] would be [2, 4, 6, 8].\n\n# Complexity\n- Time complexity:O(N log N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(M)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```javascript []\nvar maximumBeauty = function (items, queries) {\n const maxI = Number.MAX_SAFE_INTEGER;\n let res = [[0, 0, maxI]]\n\n items.sort((a, b) => a[0] - b[0])\n\n for (let item of items) {\n let price = item[0]\n let beauty = item[1]\n let lastBracket = res.at(-1)\n\n if (beauty > lastBracket[1]) {\n res[res.length - 1][2] = price\n res.push([price, beauty, maxI])\n }\n }\n\n let ans = []\n\n for (let x of queries) {\n for (let i = res.length - 1; i > -1; i--) {\n if (res[i][0] <= x) {\n ans.push(res[i][1])\n break\n }\n }\n }\n\n return ans\n\n};\n```\n```python []\nclass Solution(object):\n def maximumBeauty(self, items, queries):\n \n maxI = float(\'inf\')\n res = [[0, 0, maxI]]\n \n items.sort(key=lambda x: x[0])\n\n for price, beauty in items:\n lastBracket = res[-1]\n if beauty > lastBracket[1]:\n res[-1][2] = price\n res.append([price, beauty, maxI])\n\n ans = []\n\n for x in queries:\n for i in range(len(res) - 1, -1, -1):\n if res[i][0] <= x:\n ans.append(res[i][1])\n break\n\n return ans\n\n```\n```java []\nimport java.util.*;\n\npublic class Solution {\n public int[] maximumBeauty(int[][] items, int[] queries) {\n int maxI = Integer.MAX_VALUE;\n List<int[]> res = new ArrayList<>();\n res.add(new int[] {0, 0, maxI});\n\n Arrays.sort(items, Comparator.comparingInt(a -> a[0]));\n\n for (int[] item : items) {\n int price = item[0];\n int beauty = item[1];\n int[] lastBracket = res.get(res.size() - 1);\n\n if (beauty > lastBracket[1]) {\n lastBracket[2] = price;\n res.add(new int[] {price, beauty, maxI});\n }\n }\n\n int[] ans = new int[queries.length];\n\n for (int j = 0; j < queries.length; j++) {\n int x = queries[j];\n for (int i = res.size() - 1; i >= 0; i--) {\n if (res.get(i)[0] <= x) {\n ans[j] = res.get(i)[1];\n break;\n }\n }\n }\n\n return ans;\n }\n}\n\n```\n```c++ []\n#include <vector>\n#include <algorithm>\n#include <climits>\n\nusing namespace std;\n\nclass Solution {\npublic:\n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n int maxI = INT_MAX;\n vector<vector<int>> res = {{0, 0, maxI}};\n\n sort(items.begin(), items.end());\n\n for (const auto& item : items) {\n int price = item[0];\n int beauty = item[1];\n if (beauty > res.back()[1]) {\n res.back()[2] = price;\n res.push_back({price, beauty, maxI});\n }\n }\n\n vector<int> ans;\n\n for (int x : queries) {\n for (int i = res.size() - 1; i >= 0; i--) {\n if (res[i][0] <= x) {\n ans.push_back(res[i][1]);\n break;\n }\n }\n }\n\n return ans;\n }\n};\n```\n
| 58 | 2 |
['Array', 'Binary Search', 'C', 'Sorting', 'Python', 'C++', 'Java', 'Python3', 'JavaScript']
| 10 |
most-beautiful-item-for-each-query
|
[Python] 4-lines Solution
|
python-4-lines-solution-by-lee215-blqt
|
Explanation\nStep 1. Sort the items by price, O(nlog)\nStep 2. Iterate items, find maximum value up to now, O(n)\nStep 3. For each queries, binary search the ma
|
lee215
|
NORMAL
|
2021-11-13T16:27:31.785027+00:00
|
2021-11-13T16:28:11.294938+00:00
| 3,453 | false |
# **Explanation**\nStep 1. Sort the items by price, `O(nlog)`\nStep 2. Iterate items, find maximum value up to now, `O(n)`\nStep 3. For each queries, binary search the maximum `beauty`, `O(qlog)`\nStep 3 can be doen in `O(q+n)` though.\n<br>\n\n# **Complexity**\nTime `O(nlogn + qlogn)`\nSpace `O(n)`\n<br>\n\n\n**Python**\n```py\n def maximumBeauty(self, A, queries):\n A = sorted(A + [[0, 0]])\n for i in xrange(len(A) - 1):\n A[i + 1][1] = max(A[i][1], A[i + 1][1])\n return [A[bisect.bisect(A, [q + 1]) - 1][1] for q in queries]\n```\n
| 38 | 3 |
[]
| 7 |
most-beautiful-item-for-each-query
|
Sort + binary search||23ms Beats 100%
|
sort-binary-search23ms-beats-100-by-anwe-5pkf
|
Intuition\n Describe your first thoughts on how to solve this problem. \nSort the items w.r.t. default ordering.\nConstruct the array mostBeauty for which mostB
|
anwendeng
|
NORMAL
|
2024-11-12T00:17:38.062011+00:00
|
2024-11-12T06:08:46.765230+00:00
| 7,436 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSort the `items` w.r.t. default ordering.\nConstruct the array `mostBeauty` for which `mostBeauty[i]` is the max beauty up to index `i` for the sorted `items`. Do binary search for each query in `queries`\n\n1st C++ is slow.\n2nd C++ uses bit manipulation to pack vector to an uint64 which becomes a fast code.\n3rd C++ uses C++ STL sort, partial_sum with lambda, for_each with lamda & upper_bound which is the fastest one & a good exercise for using STL\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. sort `items` w.r.t. default ordering.\n2. Construct the array `mostBeauty` for which `mostBeauty[i] = max(mostBeauty[i-1], items[i][1])`\n3. Transverse the loop, for each query in queries as follows\n```\nint query = queries[i];\nvector<int>&& target={query, INT_MAX};\n// Use upper_bound to find the first item with a price > query\nint j = upper_bound(items.begin(), items.end(), target)-items.begin();\n\n// If j is 0, no items have price <= query\nif (j == 0) ans[i] = 0;\nelse ans[i] = mostBeauty[j - 1];\n```\n4. 2nd C++ uses bit manipulation to pack vector to an uint64;`priceIdx[i]=((unsigned long long)items[i][0]<<32)+i;`\n5. The binary search part is as follws\n```\nunsigned long long target=((unsigned long long)query<<32)+UINT_MAX;\n// Use upper_bound to find the first item with a price > query\nint j = upper_bound(priceIdx.begin(), priceIdx.end(), target)-priceIdx.begin();\n```\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O((n+m)\\log n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n# Code slow 76ms\n```cpp []\nclass Solution {\npublic:\n static vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n sort(items.begin(), items.end()); // Sort items by price\n const int n = items.size(), m = queries.size();\n\n vector<int> mostBeauty(n);\n mostBeauty[0] = items[0][1];\n\n // Build up the mostBeauty array\n for (int i = 1; i < n; i++)\n mostBeauty[i] = max(mostBeauty[i-1], items[i][1]);\n\n vector<int> ans(m);\n for (int i = 0; i < m; i++) {\n int query = queries[i];\n vector<int>&& target={query, INT_MAX};\n // Use upper_bound to find the first item with a price > query\n int j = upper_bound(items.begin(), items.end(), target)-items.begin();\n // If j is 0, no items have price <= query\n if (j == 0) ans[i] = 0;\n else ans[i] = mostBeauty[j - 1];\n }\n\n return ans;\n }\n};\n\n```\n# C++ ||23ms Beats 100%\n```\nclass Solution {\npublic:\n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n const int n = items.size(), m = queries.size();\n vector<unsigned long long> priceIdx(n);\n for(int i=0; i<n; i++)\n priceIdx[i]=((unsigned long long)items[i][0]<<32)+i;\n sort(priceIdx.begin(), priceIdx.end());\n\n vector<int> mostBeauty(n);\n mostBeauty[0] = items[priceIdx[0]&UINT_MAX][1];\n // Build up the mostBeauty array\n for (int i = 1; i < n; i++)\n mostBeauty[i] = max(mostBeauty[i-1], items[priceIdx[i]&UINT_MAX][1]);\n\n vector<int> ans(m);\n for (int i = 0; i < m; i++) {\n int query = queries[i];\n unsigned long long target=((unsigned long long)query<<32)+UINT_MAX;\n // Use upper_bound to find the first item with a price > query\n int j = upper_bound(priceIdx.begin(), priceIdx.end(), target)-priceIdx.begin();\n // If j is 0, no items have price <= query\n if (j == 0) ans[i] = 0;\n else ans[i] = mostBeauty[j-1];\n }\n return ans;\n }\n};\n\n \nauto init = []() {\n ios::sync_with_stdio(false);\n cin.tie(nullptr);\n cout.tie(nullptr);\n return \'c\';\n}();\n```\n# 3rd C++ STL solution||21ms beats 100%\n```\nclass Solution {\npublic:\n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n const int n = items.size(), m = queries.size();\n vector<unsigned long long> PB(n);\n for(int i=0; i<n; i++)\n PB[i]=((unsigned long long)items[i][0]<<32)+items[i][1];\n sort(PB.begin(), PB.end());\n\n vector<int> mostBeauty(n);\n partial_sum(PB.begin(), PB.end(), mostBeauty.begin(), [&](int sum, auto x){\n return sum=max(sum, (int)(x&INT_MAX));\n });\n\n vector<int> ans(m);\n for_each(queries.begin(), queries.end(), [&, i=0](int query) mutable{\n unsigned long long target=((unsigned long long)query<<32)+UINT_MAX;\n // Use upper_bound to find the first item with a price > query\n int j = upper_bound(PB.begin(), PB.end(), target)-PB.begin();\n // If j is 0, no items have price <= query\n ans[i++]= (j == 0) ?0: mostBeauty[j-1];\n });\n return ans;\n }\n};\n\n \nauto init = []() {\n ios::sync_with_stdio(false);\n cin.tie(nullptr);\n cout.tie(nullptr);\n return \'c\';\n}()\n```
| 33 | 5 |
['Array', 'Binary Search', 'Bit Manipulation', 'Sorting', 'C++']
| 11 |
most-beautiful-item-for-each-query
|
Java | TreeMap | BinarySearch | similar problems
|
java-treemap-binarysearch-similar-proble-ax3t
|
similar problems:\n1235. Maximum Profit in Job Scheduling https://leetcode.com/problems/maximum-profit-in-job-scheduling/\n2008. Maximum Earnings From Taxi http
|
qin10
|
NORMAL
|
2021-11-13T16:03:40.525815+00:00
|
2021-11-13T22:46:17.809140+00:00
| 2,881 | false |
similar problems:\n1235. Maximum Profit in Job Scheduling https://leetcode.com/problems/maximum-profit-in-job-scheduling/\n2008. Maximum Earnings From Taxi https://leetcode.com/problems/maximum-earnings-from-taxi/\n1353. Maximum Number of Events That Can Be Attended https://leetcode.com/problems/maximum-number-of-events-that-can-be-attended/\n2054. Two Best Non-Overlapping Events https://leetcode.com/problems/two-best-non-overlapping-events/\n\nTreeMap\n```\nclass Solution {\n public int[] maximumBeauty(int[][] items, int[] queries) {\n int[] result = new int[queries.length];\n Arrays.sort(items, (a, b) -> (a[0] - b[0]));\n \n TreeMap<Integer, Integer> map = new TreeMap<>(){{put(0, 0);}};\n int currMax = 0;\n for(int[] item : items) {\n currMax = Math.max(currMax, item[1]); //maintain largerst beauty so far\n map.put(item[0], currMax); //store in treeMap\n }\n \n for(int i = 0; i < queries.length; ++i)\n result[i] = map.floorEntry(queries[i]).getValue();\n \n return result;\n }\n}\n```\n\nBinarySearch:\n\n```\nclass Solution {\n public int[] maximumBeauty(int[][] items, int[] queries) {\n int[] result = new int[queries.length];\n Arrays.sort(items, (a, b) -> (a[0] - b[0]));\n \n for(int i = 1; i < items.length; ++i)\n items[i][1] = Math.max(items[i][1], items[i - 1][1]);\n\n for(int j = 0; j < queries.length; ++j)\n result[j] = binarySearch(items, queries[j]);\n \n return result;\n }\n \n private int binarySearch(int[][] items, int target) {\n int lo = 0, hi = items.length - 1;\n while(lo < hi) {\n int mid = (lo + hi + 1) >> 1; //find rightmost item\n if(items[mid][0] > target)\n hi = mid - 1;\n else\n lo = mid;\n }\n return items[lo][0] <= target ? items[lo][1] : 0;\n }\n}\n
| 33 | 2 |
[]
| 10 |
most-beautiful-item-for-each-query
|
C++ Offline Query
|
c-offline-query-by-lzl124631x-8tna
|
See my latest update in repo LeetCode\n## Offline Query\n\nA common trick for solving problems related to a series of queries. \n\nWhen we know all the queries
|
lzl124631x
|
NORMAL
|
2021-11-13T16:33:20.707627+00:00
|
2021-11-13T16:50:05.863129+00:00
| 1,854 | false |
See my latest update in repo [LeetCode](https://github.com/lzl124631x/LeetCode)\n## Offline Query\n\nA common trick for solving problems related to a series of queries. \n\nWhen we know all the queries upfront, we can sort the query and the original data in some order so that we can scan the query and the original data simultaneously (which takes `O(N + Q)` time), instead of scanning all original data for each query (which takes `O(N * Q)` time).\n\nThe name "offline" signifies the fact that we know all the queries upfront/offline. If the queries keep streaming in (i.e. online), we can\'t reorder the queries to get a better time complexity.\n\n**Problems**:\n* [1707. Maximum XOR With an Element From Array (Hard)](https://leetcode.com/problems/maximum-xor-with-an-element-from-array/)\n* [1847. Closest Room (Hard)](https://leetcode.com/problems/closest-room/)\n* [2070. Most Beautiful Item for Each Query (Medium)](https://leetcode.com/problems/most-beautiful-item-for-each-query/)\n\n## Solution 1. Offline Query\n\nSort both `items` and `queries` in ascending order of `price`. Traverse `queries`. Use a pointer `i` to cover all the items with a price `<=` the current query, and compute the maximum beauty among them. In this way, we traverse both array only once.\n\n```cpp\n// OJ: https://leetcode.com/problems/most-beautiful-item-for-each-query/\n// Author: github.com/lzl124631x\n// Time: O(NlogN + MlogM + M + N) where `N`/`M` is the length of `items`/`queries`.\n// Space: O(M)\nclass Solution {\npublic:\n vector<int> maximumBeauty(vector<vector<int>>& A, vector<int>& Q) {\n vector<pair<int, int>> queries;\n for (int i = 0; i < Q.size(); ++i) queries.push_back({Q[i],i});\n sort(begin(queries), end(queries));\n sort(begin(A), end(A));\n int i = 0, N = A.size(), maxBeauty = 0;\n vector<int> ans(Q.size());\n for (auto q : queries) {\n auto &[query, index] = q;\n for (; i < N && A[i][0] <= query; ++i) maxBeauty = max(maxBeauty, A[i][1]);\n ans[index] = maxBeauty;\n }\n return ans;\n }\n};\n```
| 26 | 0 |
[]
| 5 |
most-beautiful-item-for-each-query
|
C++ | Easy Sorting + Binary Search Solution | QlogN + NlogN
|
c-easy-sorting-binary-search-solution-ql-9s60
|
1) Sort in ascending order of price and beauty\n2) Now set the prefix max Beauty for each pair\n\nBefore Sorting \n1 2\t\n3 2\t\n2 4\t\n5 6\t\n3 5\t\n\n\nAfter
|
chandanagrawal23
|
NORMAL
|
2021-11-13T16:01:43.618603+00:00
|
2021-11-13T16:58:09.430212+00:00
| 2,430 | false |
1) Sort in ascending order of price and beauty\n2) Now set the prefix max Beauty for each pair\n\nBefore Sorting \n1 2\t\n3 2\t\n2 4\t\n5 6\t\n3 5\t\n\n\nAfter sorting \n1 2 \n2 4 \n3 2 \n3 5 \n5 6 \n\n\nPrefix Max\n\n1 2\n2 4\n3 4\n3 5\n5 6\n\n\nFor each query , find the largest last pair whose price is less than equal to given value , and print the correspoding prefix max beauty.\n\n\n```\nclass Solution {\npublic:\n\n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n sort(items.begin(),items.end());\n int maxi = items[0][1];\n // for(auto xt : items)\n // {\n // cout<<xt[0]<<" "<<xt[1]<<endl;\n // }\n for(auto &xt : items)\n {\n maxi = max(maxi , xt[1]);\n xt[1] = maxi;\n }\n // for(auto xt : items)\n // {\n // cout<<xt[0]<<" "<<xt[1]<<endl;\n // }\n vector<int>ans;\n int n = items.size();\n \n for(int key : queries){\n int left = 0;\n int right = n - 1;\n\n int count = 0;\n\n while (left <= right) {\n int mid = (right + left) / 2;\n if (items[mid][0] <= key) {\n count = mid + 1;\n left = mid + 1;\n }\n else\n right = mid - 1;\n }\n \n if(count==0)\n ans.push_back(0);\n else\n ans.push_back(items[count-1][1]);\n }\n return ans;\n }\n};\n\n```\n
| 25 | 2 |
['Binary Search', 'C']
| 9 |
most-beautiful-item-for-each-query
|
Easy & Simple Approach --> Most Beautiful Item for Each Query ✅ || Beats 100 % 🔥
|
easy-simple-approach-most-beautiful-item-s2z2
|
Intuition\n Describe your first thoughts on how to solve this problem. \nThe goal is to find the maximum beauty of an item for each query, such that the item\'s
|
Ashis2024
|
NORMAL
|
2024-11-12T05:06:07.695436+00:00
|
2024-11-12T05:06:07.695472+00:00
| 2,642 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe goal is to find the maximum beauty of an item for each query, such that the item\'s price is less than or equal to the query value. Given that each query should ideally search among items priced within a certain range, we can make this process efficient by sorting both items and queries. This allows us to process items in increasing order of price and answer queries in increasing order of their values, minimizing redundant checks.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1.\tSort Items by Price: We first sort items based on their prices. This helps us easily find items within any given query\'s price limit without having to repeatedly look through all items.\n2.\tSort Queries with Original Indices: Since we need to return results in the original order of queries, we store each query alongside its index, then sort the queries by their values. Sorting queries allows us to answer them efficiently by working from the lowest query value to the highest.\n3.\tIterate Through Items and Track Max Beauty:\n\u2022\tInitialize maxBeauty to keep track of the maximum beauty seen so far.\n\u2022\tFor each query in sorted order, check items that are affordable (i.e., items with prices <= current query).\n\u2022\tFor each affordable item, update maxBeauty if that item\u2019s beauty is higher than maxBeauty.\n4.\tAnswer Each Query:\n\u2022\tFor each query, after processing all affordable items, set the maxBeauty value for that query.\n\u2022\tStore the result for each query in ans, indexed by the original position of the query.\n5.\t Return Result: After processing all queries, ans contains the maximum beauty values for each query in their original order.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(NlogN+QlogQ), sorting items by price takes + sorting the queries by their values\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(Q), Q is elements\n# Code\n```cpp []\nclass Solution {\npublic:\n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n sort(items.begin(), items.end());\n vector<pair<int, int>> queryIndex; // {query, index} \n int n = queries.size();\n //Store the queries with indices\n for(int i = 0; i < n; i++)\n {\n queryIndex.push_back({queries[i], i});\n }\n sort(queryIndex.begin(), queryIndex.end());\n vector<int> ans(n, 0);\n int maxBeauty = 0;\n int i = 0;\n int m = items.size();\n //To check out every items price as compare to the queries\n for(auto& [query, index] : queryIndex)\n {\n while(i < m && items[i][0] <= query)\n {\n maxBeauty = max(maxBeauty, items[i][1]);\n i++;\n }\n ans[index] = maxBeauty; // Store the max beauty for this query\n }\n return ans;\n }\n};\n```\n```Java []\nclass Solution {\n public int[] maximumBeauty(int[][] items, int[] queries) {\n Arrays.sort(items, Comparator.comparingInt(a -> a[0]));\n\n // Step 2: Sort queries with their original indices\n int[][] queriesWithIndex = new int[queries.length][2];\n for (int i = 0; i < queries.length; i++) {\n queriesWithIndex[i][0] = queries[i];\n queriesWithIndex[i][1] = i;\n }\n Arrays.sort(queriesWithIndex, Comparator.comparingInt(a -> a[0]));\n\n int[] result = new int[queries.length];\n int maxBeauty = 0;\n int i = 0;\n\n for (int[] queryWithIndex : queriesWithIndex) {\n int query = queryWithIndex[0];\n int index = queryWithIndex[1];\n\n // Move through items that are within the current query\'s price range\n while (i < items.length && items[i][0] <= query) {\n maxBeauty = Math.max(maxBeauty, items[i][1]);\n i++;\n }\n\n // Store the max beauty for this query\n result[index] = maxBeauty;\n }\n return result;\n }\n}\n```\n\n\n
| 20 | 0 |
['Binary Search', 'Sorting', 'C++', 'Java']
| 2 |
most-beautiful-item-for-each-query
|
Simple Java Solution Using TreeMap
|
simple-java-solution-using-treemap-by-pa-cm89
|
\nclass Solution {\n public int[] maximumBeauty(int[][] items, int[] queries) {\n Arrays.sort(items,(a,b)->a[0]-b[0]); // Sort items by price in ascen
|
pavankumarchaitanya
|
NORMAL
|
2021-11-13T16:01:08.397423+00:00
|
2021-11-13T16:04:06.694099+00:00
| 1,074 | false |
```\nclass Solution {\n public int[] maximumBeauty(int[][] items, int[] queries) {\n Arrays.sort(items,(a,b)->a[0]-b[0]); // Sort items by price in ascending order\n int maxBeauty = 0;\n TreeMap<Integer, Integer> tm = new TreeMap<>();\n for(int[] item: items){\n maxBeauty = Math.max(maxBeauty,item[1]); // rolling max of beauty seen\n tm.put(item[0],maxBeauty);\n }\n int result[] = new int[queries.length];\n int index=0;\n for(int query: queries){\n Integer key = tm.floorKey(query); // if entry for a price exists, value should have max beauty seen else pick floor price entry\n result[index++] = (key==null)?0:tm.get(key); \n }\n return result;\n }\n}\n```
| 20 | 1 |
[]
| 5 |
most-beautiful-item-for-each-query
|
🤔Beats 99%💥 || 💸3 Approaches💡 || 🔌Unique😅
|
beats-99-3-approaches-unique-by-garv_vir-wytm
|
3 Approaches:\n\n# Approach-1\n# Code\ncpp []\nclass Solution {\npublic:\n int solve(vector<pair<int,int>>&v,int query){\n int s=0,e=v.size()-1;\n
|
Garv_Virmani
|
NORMAL
|
2024-11-12T03:34:09.800406+00:00
|
2024-11-12T05:56:16.306466+00:00
| 4,050 | false |
# 3 Approaches:\n\n# Approach-1\n# Code\n```cpp []\nclass Solution {\npublic:\n int solve(vector<pair<int,int>>&v,int query){\n int s=0,e=v.size()-1;\n int ans=0;\n while(s<=e){\n int mid=s+(e-s)/2;\n if(v[mid].first<=query){\n ans=v[mid].second;\n s=mid+1;\n }\n else{\n e=mid-1;\n }\n }\n return ans;\n }\n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n int n=queries.size();\n unordered_map<int,int>mp;\n for(auto item:items){\n if(mp.count(item[0])){\n if(item[1]>mp[item[0]]){\n mp[item[0]]=item[1];\n }\n }\n else{\n mp[item[0]]=item[1];\n }\n }\n vector<pair<int,int>>v;\n for(auto it:mp){\n v.push_back(it);\n }\n sort(v.begin(),v.end());\n for(int i=1;i<v.size();i++){\n v[i].second=max(v[i-1].second,v[i].second);\n }\n vector<int>ans;\n for(int i=0;i<n;i++){\n ans.push_back(solve(v,queries[i]));\n }\n return ans;\n }\n};\n```\n\n# Approach-2\n# Code\n```cpp []\nclass Solution {\npublic:\n int solve(vector<vector<int>>&v,int query){\n int s=0,e=v.size()-1;\n int ans=0;\n while(s<=e){\n int mid=s+(e-s)/2;\n if(v[mid][0]<=query){\n ans=v[mid][1];\n s=mid+1;\n }\n else{\n e=mid-1;\n }\n }\n return ans;\n }\n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n int n=queries.size();\n sort(items.begin(),items.end());\n for(int i=1;i<items.size();i++){\n items[i][1]=max(items[i-1][1],items[i][1]);\n }\n vector<int>ans;\n for(int i=0;i<n;i++){\n ans.push_back(solve(items,queries[i]));\n }\n return ans;\n }\n};\n```\n# Approach-3\n# Code\n```cpp []\nclass Solution {\npublic:\n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n int n=queries.size();\n vector<pair<int,int>>v;\n for(int i=0;i<n;i++){\n v.push_back({queries[i],i});\n }\n sort(v.begin(),v.end());\n sort(items.begin(),items.end());\n for(int i=1;i<items.size();i++){\n items[i][1]=max(items[i-1][1],items[i][1]);\n }\n vector<int>ans(n);\n int j=0,maxi=0;\n for(int i=0;i<n;i++){\n while(j<items.size() && items[j][0]<=v[i].first){\n maxi=max(maxi,items[j][1]);\n j++;\n }\n ans[v[i].second]=maxi;\n }\n return ans;\n }\n};\n```\n\n
| 19 | 8 |
['Array', 'Binary Search', 'C', 'Sorting', 'Prefix Sum', 'Python', 'C++', 'Java', 'Python3', 'JavaScript']
| 4 |
most-beautiful-item-for-each-query
|
Sort and Sweep
|
sort-and-sweep-by-votrubac-5tjd
|
Rhymes with short and sweet :)\n\nWe sort items cheap-to-expensive, and then sweep the array and assign maximum beauty so far.\n\nThen, use a binary search to f
|
votrubac
|
NORMAL
|
2021-11-14T21:52:38.229928+00:00
|
2021-11-14T21:52:38.229962+00:00
| 1,054 | false |
Rhymes with short and sweet :)\n\nWe sort items cheap-to-expensive, and then sweep the array and assign maximum beauty so far.\n\nThen, use a binary search to find the maximum beauty for the price.\n\n**C++**\n```cpp\nvector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& qs) {\n sort(begin(items), end(items));\n for (int i = 1; i < items.size(); ++i)\n items[i][1] = max(items[i][1], items[i - 1][1]);\n for (int i = 0; i < qs.size(); ++i) {\n auto it = upper_bound(begin(items), end(items), vector<int>{qs[i], INT_MAX});\n qs[i] = it == begin(items) ? 0 : (*prev(it))[1];\n }\n return qs;\n}\n```
| 19 | 0 |
[]
| 3 |
most-beautiful-item-for-each-query
|
Optimized Query-Based Maximum Beauty Retrieval Using Sorted Items
|
optimized-query-based-maximum-beauty-ret-m1ci
|
Problem Explanation :\n Given:\n\n- items: A list of pairs [price, beauty] representing products with their respective prices and beauty values.\n- queries:
|
anand_shukla1312
|
NORMAL
|
2024-11-12T04:42:11.958564+00:00
|
2024-11-12T04:42:11.958603+00:00
| 597 | false |
# Problem Explanation :\n Given:\n\n- `items:` A list of pairs [price, beauty] representing products with their respective prices and beauty values.\n- `queries:` A list of integers representing price limits for each query.\n\nObjective: For each query, we want to find the highest beauty value of any item that has a price less than or equal to the query\u2019s price limit.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach :\n<!-- Describe your approach to solving the problem. -->\n1. **Sort `items` by Beauty in Descending Order**:\n\n - First, we sort items by the second element (beauty) in descending order. This sorting ensures that when we search through items for each query, we encounter the highest beauty value first, which optimizes our search.\n - Sorting line: sorted_items = sorted(items, key=lambda x: x[1], reverse=True)\n2. **Iterate through Queries:**\n\n - We create an empty list ans to store the results for each query.\n - For each price limit in queries, we need to find the highest beauty value from sorted_items where the item price is within the query\u2019s price limit.\n3. **Find Maximum Beauty for Each Query:**\n\n - For each query:\n - Iterate through sorted_items.\n - Check if the price of the current item is less than or equal to the current query\'s price.\n - If it is, append the beauty of that item to ans and break out of the loop. This way, we get the highest beauty value that meets the price condition (since sorted_items is ordered by beauty).\n - If no item meets the price limit, append 0 to ans.\n- **Return the Result List:**\n\n - After processing all queries, ans will contain the maximum beauty values for each query (or 0 if no item meets a query\u2019s price limit).\n Return ans.\n# Complexity\n- Time complexity: $$O(nlogn)$$\n<!-- Add your time complexity here, e.g. -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def maximumBeauty(self, items: List[List[int]], queries: List[int]) -> List[int]:\n sorted_items = sorted(items, key = lambda x: x[1], reverse = True)\n ans = []\n for query in queries:\n for item in sorted_items:\n if item[0] <= query:\n ans.append(item[1])\n break\n else:\n ans.append(0)\n return ans\n \n```\n# SMALL REQUEST : If you found this post even remotely helpful, be kind enough to smash a upvote. I will be grateful.I will be motivated\uD83D\uDE0A\uD83D\uDE0A
| 17 | 0 |
['Array', 'Sorting', 'Iterator', 'Python3']
| 4 |
most-beautiful-item-for-each-query
|
✅ Tutorial Video | Simple and Short | Working 12.11.2024
|
tutorial-video-simple-and-short-working-xai7i
|
\n\nhttps://youtu.be/kybir7n8JJg?si=9bsPxiEvtf3d-YqM\n# #1 Sorting + Two Pointers - Most simple solution\n\n\n\npython3 []\nclass Solution:\n def maximumBeau
|
Piotr_Maminski
|
NORMAL
|
2024-11-12T00:22:01.473254+00:00
|
2024-11-13T09:58:01.340923+00:00
| 1,033 | false |
\n\nhttps://youtu.be/kybir7n8JJg?si=9bsPxiEvtf3d-YqM\n# #1 Sorting + Two Pointers - Most simple solution\n\n\n\n```python3 []\nclass Solution:\n def maximumBeauty(self, items: List[List[int]], queries: List[int]) -> List[int]:\n items.sort() \n queries = sorted([(q, i) for i, q in enumerate(queries)]) \n\n res = [0] * len(queries)\n max_bea = 0\n j = 0\n for q, i in queries:\n while j < len(items) and items[j][0] <= q:\n max_bea = max(max_bea, items[j][1])\n j += 1\n\n res[i] = max_bea\n\n return res\n\n\n```\n```cpp []\nclass Solution {\npublic:\n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n sort(items.begin(), items.end());\n vector<pair<int, int>> queriesWithIndex;\n for (int i = 0; i < queries.size(); i++) {\n queriesWithIndex.push_back({queries[i], i});\n }\n sort(queriesWithIndex.begin(), queriesWithIndex.end());\n \n vector<int> res(queries.size());\n int maxBea = 0;\n int j = 0;\n for (auto [q, i] : queriesWithIndex) {\n while (j < items.size() && items[j][0] <= q) {\n maxBea = max(maxBea, items[j][1]);\n j++;\n }\n res[i] = maxBea;\n }\n return res;\n }\n};\n```\n```java []\nclass Solution {\n public int[] maximumBeauty(int[][] items, int[] queries) {\n Arrays.sort(items, (a, b) -> a[0] - b[0]);\n int[][] queriesWithIndex = new int[queries.length][2];\n for (int i = 0; i < queries.length; i++) {\n queriesWithIndex[i] = new int[]{queries[i], i};\n }\n Arrays.sort(queriesWithIndex, (a, b) -> a[0] - b[0]);\n \n int[] res = new int[queries.length];\n int maxBea = 0;\n int j = 0;\n for (int[] query : queriesWithIndex) {\n while (j < items.length && items[j][0] <= query[0]) {\n maxBea = Math.max(maxBea, items[j][1]);\n j++;\n }\n res[query[1]] = maxBea;\n }\n return res;\n }\n}\n```\n```csharp []\npublic class Solution {\n public int[] MaximumBeauty(int[][] items, int[] queries) {\n Array.Sort(items, (a, b) => a[0].CompareTo(b[0]));\n var queriesWithIndex = queries.Select((q, i) => new { Query = q, Index = i })\n .OrderBy(x => x.Query)\n .ToArray();\n \n int[] res = new int[queries.Length];\n int maxBea = 0;\n int j = 0;\n foreach (var query in queriesWithIndex) {\n while (j < items.Length && items[j][0] <= query.Query) {\n maxBea = Math.Max(maxBea, items[j][1]);\n j++;\n }\n res[query.Index] = maxBea;\n }\n return res;\n }\n}\n```\n```golang []\nfunc maximumBeauty(items [][]int, queries []int) []int {\n sort.Slice(items, func(i, j int) bool {\n return items[i][0] < items[j][0]\n })\n \n type Query struct {\n val, idx int\n }\n queriesWithIndex := make([]Query, len(queries))\n for i, q := range queries {\n queriesWithIndex[i] = Query{q, i}\n }\n sort.Slice(queriesWithIndex, func(i, j int) bool {\n return queriesWithIndex[i].val < queriesWithIndex[j].val\n })\n \n res := make([]int, len(queries))\n maxBea := 0\n j := 0\n for _, q := range queriesWithIndex {\n for j < len(items) && items[j][0] <= q.val {\n if items[j][1] > maxBea {\n maxBea = items[j][1]\n }\n j++\n }\n res[q.idx] = maxBea\n }\n return res\n}\n```\n```swift []\nclass Solution {\n func maximumBeauty(_ items: [[Int]], _ queries: [Int]) -> [Int] {\n let sortedItems = items.sorted { $0[0] < $1[0] }\n let queriesWithIndex = queries.enumerated().map { ($1, $0) }.sorted { $0.0 < $1.0 }\n \n var res = Array(repeating: 0, count: queries.count)\n var maxBea = 0\n var j = 0\n \n for (query, index) in queriesWithIndex {\n while j < sortedItems.count && sortedItems[j][0] <= query {\n maxBea = max(maxBea, sortedItems[j][1])\n j += 1\n }\n res[index] = maxBea\n }\n return res\n }\n}\n```\n```javascript [JS]\n// JavaScript\n\nvar maximumBeauty = function(items, queries) {\n items.sort((a, b) => a[0] - b[0]);\n const queriesWithIndex = queries.map((q, i) => [q, i])\n .sort((a, b) => a[0] - b[0]);\n \n const res = new Array(queries.length).fill(0);\n let maxBea = 0;\n let j = 0;\n \n for (const [query, index] of queriesWithIndex) {\n while (j < items.length && items[j][0] <= query) {\n maxBea = Math.max(maxBea, items[j][1]);\n j++;\n }\n res[index] = maxBea;\n }\n return res;\n};\n```\n```typescript [TS]\n// TypeScript\n\nfunction maximumBeauty(items: number[][], queries: number[]): number[] {\n items.sort((a, b) => a[0] - b[0]);\n const queriesWithIndex = queries.map((q, i) => [q, i])\n .sort((a, b) => a[0] - b[0]);\n \n const res = new Array(queries.length).fill(0);\n let maxBea = 0;\n let j = 0;\n \n for (const [query, index] of queriesWithIndex) {\n while (j < items.length && items[j][0] <= query) {\n maxBea = Math.max(maxBea, items[j][1]);\n j++;\n }\n res[index] = maxBea;\n }\n return res;\n}\n```\n```rust []\nimpl Solution {\n pub fn maximum_beauty(items: Vec<Vec<i32>>, queries: Vec<i32>) -> Vec<i32> {\n let mut items = items;\n items.sort_by_key(|x| x[0]);\n \n let mut queries_with_index: Vec<(i32, usize)> = queries.iter()\n .enumerate()\n .map(|(i, &q)| (q, i))\n .collect();\n queries_with_index.sort_by_key(|&(q, _)| q);\n \n let mut res = vec![0; queries.len()];\n let mut max_bea = 0;\n let mut j = 0;\n \n for (query, index) in queries_with_index {\n while j < items.len() && items[j][0] <= query {\n max_bea = max_bea.max(items[j][1]);\n j += 1;\n }\n res[index] = max_bea;\n }\n res\n }\n}\n\n\n```\n```ruby []\ndef maximum_beauty(items, queries)\n items.sort!\n queries_with_index = queries.each_with_index.map { |q, i| [q, i] }.sort\n \n res = Array.new(queries.size, 0)\n max_bea = 0\n j = 0\n \n queries_with_index.each do |query, index|\n while j < items.size && items[j][0] <= query\n max_bea = [max_bea, items[j][1]].max\n j += 1\n end\n res[index] = max_bea\n end\n \n res\nend\n```\n\n- Complexy: Time O(n log n) and Space O(n)\n\n\n# #2 Sorting + Binary Search (almost all beats 100%)\n\n```python3 []\nclass Solution:\n def maximumBeauty(self, items: List[List[int]], queries: List[int]) -> List[int]:\n sorted_items = sorted(items, key=lambda item: item[0]) # Step 1: Sort items by price\n\n prices = [item[0] for item in sorted_items] # Step 2: Extract prices and beauties\n beauties = [item[1] for item in sorted_items]\n \n max_beauties = list(accumulate(beauties, max, initial=0)) # Step 3: Create running maximum beauty array\n \n result = [] # Step 4: Find maximum beauty for each query price\n for query_price in queries:\n index = bisect_right(prices, query_price)\n result.append(max_beauties[index]) \n return result\n```\n```cpp []\nclass Solution {\npublic:\n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n // Step 1: Sort items by price in ascending order\n sort(items.begin(), items.end());\n \n // Step 2: Extract prices and beauties into separate vectors\n vector<int> prices, beauties;\n for (const auto& item : items) {\n prices.push_back(item[0]);\n beauties.push_back(item[1]);\n }\n \n // Step 3: Create running maximum beauty array\n vector<int> max_beauties(1, 0);\n int curr_max = 0;\n for (int beauty : beauties) {\n curr_max = max(curr_max, beauty);\n max_beauties.push_back(curr_max);\n }\n \n // Step 4: Process each query using binary search\n vector<int> result;\n for (int query_price : queries) {\n auto index = upper_bound(prices.begin(), prices.end(), query_price) - prices.begin();\n result.push_back(max_beauties[index]);\n }\n \n return result;\n }\n};\n\n```\n```java []\nclass Solution {\n public int[] maximumBeauty(int[][] items, int[] queries) {\n // Step 1: Sort items by price in ascending order\n Arrays.sort(items, (a, b) -> Integer.compare(a[0], b[0]));\n \n int n = items.length;\n // Step 2: Extract prices and beauties into separate arrays\n int[] prices = new int[n];\n int[] beauties = new int[n];\n for (int i = 0; i < n; i++) {\n prices[i] = items[i][0];\n beauties[i] = items[i][1];\n }\n \n // Step 3: Create running maximum beauty array\n int[] maxBeauties = new int[n + 1];\n for (int i = 0; i < n; i++) {\n maxBeauties[i + 1] = Math.max(maxBeauties[i], beauties[i]);\n }\n \n // Step 4: Process each query using binary search\n int[] result = new int[queries.length];\n for (int i = 0; i < queries.length; i++) {\n int index = upperBound(prices, queries[i]);\n result[i] = maxBeauties[index];\n }\n \n return result;\n }\n \n // Helper method for binary search\n private int upperBound(int[] arr, int target) {\n int left = 0, right = arr.length;\n while (left < right) {\n int mid = left + (right - left) / 2;\n if (arr[mid] <= target) left = mid + 1;\n else right = mid;\n }\n return left;\n }\n}\n```\n```csharp []\npublic class Solution {\n public int[] MaximumBeauty(int[][] items, int[] queries) {\n // Step 1: Sort items by price in ascending order\n Array.Sort(items, (a, b) => a[0].CompareTo(b[0]));\n \n int n = items.Length;\n // Step 2: Extract prices and beauties into separate arrays\n int[] prices = new int[n];\n int[] beauties = new int[n];\n for (int i = 0; i < n; i++) {\n prices[i] = items[i][0];\n beauties[i] = items[i][1];\n }\n \n // Step 3: Create running maximum beauty array\n int[] maxBeauties = new int[n + 1];\n for (int i = 0; i < n; i++) {\n maxBeauties[i + 1] = Math.Max(maxBeauties[i], beauties[i]);\n }\n \n // Step 4: Process each query using binary search\n int[] result = new int[queries.Length];\n for (int i = 0; i < queries.Length; i++) {\n int index = Array.BinarySearch(prices, queries[i]);\n if (index < 0) index = ~index;\n result[i] = maxBeauties[index];\n }\n \n return result;\n }\n}\n```\n```golang []\nfunc maximumBeauty(items [][]int, queries []int) []int {\n // Step 1: Sort items by price in ascending order\n sort.Slice(items, func(i, j int) bool {\n return items[i][0] < items[j][0]\n })\n \n n := len(items)\n // Step 2: Extract prices and beauties into separate slices\n prices := make([]int, n)\n beauties := make([]int, n)\n for i, item := range items {\n prices[i] = item[0]\n beauties[i] = item[1]\n }\n \n // Step 3: Create running maximum beauty array\n maxBeauties := make([]int, n+1)\n for i := 0; i < n; i++ {\n maxBeauties[i+1] = max(maxBeauties[i], beauties[i])\n }\n \n // Step 4: Process each query using binary search\n result := make([]int, len(queries))\n for i, query := range queries {\n index := sort.SearchInts(prices, query+1)\n result[i] = maxBeauties[index]\n }\n \n return result\n}\n\nfunc max(a, b int) int {\n if a > b {\n return a\n }\n return b\n}\n```\n```swift []\nclass Solution {\n func maximumBeauty(_ items: [[Int]], _ queries: [Int]) -> [Int] {\n // Step 1: Sort items by price in ascending order\n let sortedItems = items.sorted { $0[0] < $1[0] }\n \n // Step 2: Extract prices and beauties into separate arrays\n let prices = sortedItems.map { $0[0] }\n let beauties = sortedItems.map { $0[1] }\n \n // Step 3: Create running maximum beauty array\n var maxBeauties = [0]\n var currentMax = 0\n for beauty in beauties {\n currentMax = max(currentMax, beauty)\n maxBeauties.append(currentMax)\n }\n \n // Step 4: Process each query using binary search\n return queries.map { query in\n let index = prices.firstIndex(where: { $0 > query }) ?? prices.count\n return maxBeauties[index]\n }\n }\n}\n```\n```javascript [JS]\n// JavaScript\n\nvar maximumBeauty = function(items, queries) {\n // Step 1: Sort items by price\n items.sort((a, b) => a[0] - b[0]);\n \n // Step 2: Extract prices and beauties\n const prices = items.map(item => item[0]);\n const beauties = items.map(item => item[1]);\n \n // Step 3: Create running maximum beauty array\n const maxBeauties = [0];\n let currentMax = 0;\n for (const beauty of beauties) {\n currentMax = Math.max(currentMax, beauty);\n maxBeauties.push(currentMax);\n }\n \n // Step 4: Find maximum beauty for each query price using binary search\n return queries.map(query => {\n let left = 0, right = prices.length;\n while (left < right) {\n const mid = Math.floor((left + right) / 2);\n if (prices[mid] <= query) {\n left = mid + 1;\n } else {\n right = mid;\n }\n }\n return maxBeauties[left];\n });\n};\n```\n```typescript [TS]\n// TypeScript\n\nfunction maximumBeauty(items: number[][], queries: number[]): number[] {\n // Step 1: Sort items by price in ascending order\n items.sort((a, b) => a[0] - b[0]);\n \n // Step 2: Extract prices and beauties into separate arrays\n const prices: number[] = items.map(item => item[0]);\n const beauties: number[] = items.map(item => item[1]);\n \n // Step 3: Create running maximum beauty array\n const maxBeauties: number[] = [0];\n let currentMax = 0;\n for (const beauty of beauties) {\n currentMax = Math.max(currentMax, beauty);\n maxBeauties.push(currentMax);\n }\n \n // Step 4: Process each query using binary search\n return queries.map(query => {\n const index = upperBound(prices, query);\n return maxBeauties[index];\n });\n}\n\n// Helper function for binary search\nfunction upperBound(arr: number[], target: number): number {\n let left = 0, right = arr.length;\n while (left < right) {\n const mid = Math.floor((left + right) / 2);\n if (arr[mid] <= target) left = mid + 1;\n else right = mid;\n }\n return left;\n}\n```\n```rust []\nimpl Solution {\n pub fn maximum_beauty(mut items: Vec<Vec<i32>>, queries: Vec<i32>) -> Vec<i32> {\n // Step 1: Sort items by price in ascending order\n items.sort_by_key(|item| item[0]);\n \n // Step 2: Extract prices and beauties into separate vectors\n let prices: Vec<i32> = items.iter().map(|item| item[0]).collect();\n let beauties: Vec<i32> = items.iter().map(|item| item[1]).collect();\n \n // Step 3: Create running maximum beauty array\n let mut max_beauties = vec![0];\n let mut current_max = 0;\n for &beauty in beauties.iter() {\n current_max = current_max.max(beauty);\n max_beauties.push(current_max);\n }\n \n // Step 4: Process each query using binary search\n queries.iter().map(|&query| {\n let index = prices.partition_point(|&x| x <= query);\n max_beauties[index]\n }).collect()\n }\n}\n```\n```ruby []\ndef maximum_beauty(items, queries)\n # Step 1: Sort items by price\n items.sort_by! { |item| item[0] }\n \n # Step 2: Extract prices and beauties\n prices = items.map { |item| item[0] }\n beauties = items.map { |item| item[1] }\n \n # Step 3: Create running maximum beauty array\n max_beauties = [0]\n current_max = 0\n beauties.each do |beauty|\n current_max = [current_max, beauty].max\n max_beauties << current_max\n end\n \n # Step 4: Find maximum beauty for each query price using binary search\n queries.map do |query|\n left = 0\n right = prices.length\n while left < right\n mid = (left + right) / 2\n if prices[mid] <= query\n left = mid + 1\n else\n right = mid\n end\n end\n max_beauties[left]\n end\nend\n```\n- Complexy: Time O(n log n) and Space O(n)\n\n\n\n# Step by Step\n\n---\n\n1. Sort all items by price in ascending order making it easier to find items within price ranges\n\n```\nsorted_items = sorted(items, key=lambda item: item[0])\n```\n2. Create two sorted lists\n- `prices`\n- `beauties`\n\n```\nprices = [item[0] for item in sorted_items]\nbeauties = [item[1] for item in sorted_items]\n```\n3. Track Maximum Beauty\n- Create a running maximum beauty array where each position i contains the maximum beauty value seen up to index i. `initial=0` In case when no items are affordable.\n```\nmax_beauties = list(accumulate(beauties, max, initial=0))\n```\n4. Query Processing\n- Use binary search (bisect_right) to find where the query price woud fit in the sorted prices\n- Looks up the maximum beauty achievable at that price point using the [pre-computed](https://en.wikipedia.org/wiki/Precomputation) `max_beauties` array\n\n```\nfor query_price in queries:\n index = bisect_right(prices, query_price)\n result.append(max_beauties[index])\n```\n\n---\n\n# Still dont understand binary search\n- IMO Best explained Binary Search: google "topcoder Binary Search" first \n- Video:\n https://www.youtube.com/watch?v=GU7DpgHINWQ\n\n\n---\n\n\n\n\n\n\n\n# Most common Array Interview Problems\nList based on my research (interviews, reddit, github) Probably not 100% accurate but very close to my recruitments. Leetcode Premium is probably more accurate [I don\'t have]\n\n\n**Easy:** [[1. Two Sum]](https://leetcode.com/problems/two-sum/solutions/5999466/beats-100-explained-step-by-step-list-most-common-array-inverview) **(common warm-up)** [[121. Best Time to Buy and Sell Stock]](https://leetcode.com/discuss/topic/6027720/solution/) [[88. Merge Sorted Array]](https://leetcode.com/problems/merge-sorted-array/solutions/6031394/beats-100-explained-step-by-step-list-most-common-string-interview-problems) [[27. Remove Element]](https://leetcode.com/problems/remove-element/solutions/6031528/beats-100-explained-step-by-step-list-most-common-array-interview-problems) [[929. Unique Email Addresses]](https://leetcode.com/problems/unique-email-addresses/solutions/6031687/explained-step-by-step-video-list-most-common-array-interview-problems) \n\n\n**Medium/Hard:** [[15. 3Sum]](https://leetcode.com/problems/3sum/description/) [[42. Trapping Rain Water]](https://leetcode.com/problems/trapping-rain-water/?envType=problem-list-v2&envId=atbyk0mj) [[56. Merge Intervals]](https://leetcode.com/problems/merge-intervals/description/) [[57. Insert Interval]](https://leetcode.com/problems/insert-interval/description/) [[46. Permutations]](https://leetcode.com/problems/permutations/description/) [[53. Maximum Subarray]](https://leetcode.com/problems/maximum-subarray/description/) [[73. Set Matrix Zeroes]](https://leetcode.com/problems/set-matrix-zeroes/description/) [[284. Peeking Iterator]](https://leetcode.com/problems/peeking-iterator/description/)\n\n\n#### [Interview Questions and Answers Repository](https://github.com/RooTinfinite/Interview-questions-and-answers)\n\n\n\n\n\n\n\n
| 13 | 0 |
['Swift', 'C++', 'Java', 'Go', 'TypeScript', 'Python3', 'Rust', 'Ruby', 'JavaScript', 'C#']
| 1 |
most-beautiful-item-for-each-query
|
Python 3 || 3 lines, binary search, w/ example || T/S: 80% / 58%
|
python-3-3-lines-binary-search-w-example-mf6q
|
\nclass Solution:\n def maximumBeauty(self, items: List[List[int]], queries: List[int]) -> List[int]:\n\n
|
Spaulding_
|
NORMAL
|
2022-11-17T19:48:08.613389+00:00
|
2024-06-11T23:20:35.366962+00:00
| 1,032 | false |
```\nclass Solution:\n def maximumBeauty(self, items: List[List[int]], queries: List[int]) -> List[int]:\n\n # Ex: items = [[1,2],[3,2],[2,4],[5,6],[3,5]]\n\t\t\t\t\t\t\t\t\t\t\t\t\t# queries = [1,2,3,4,5,6]\n\n price, beauty = zip(*sorted(items)) # sorted(items = [[1,2],[2,4],[3,2],[3, 5],[5, 6]]\n # price = [1,2,3,3,5], beauty = [2,4,2,5,6]\n\n beauty = list(accumulate(beauty,lambda x,y: max(x,y)))\n\t\t\n # beauty = [2,4,4,5,6] \n return [0 if q < price[0] else \n beauty[bisect_right(price, q)-1] for q in queries]\n\t\t\t\t\n # q price[i] beauty[i]\n # \u2013\u2013\u2013\u2013 \u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013 \u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\u2013\n # 1 [ /1\\ ,2,3,3,5] [ /2\\ ,4,4,5,6]\n # 2 [1, /2\\, 3,3,5] [2, /4\\ ,4,5,6]\n # 3 [1,2,3, /3\\ 5] [2,4,4, /5\\ ,6]\n # 4 [1,2,3, /3\\ ,5] [2,4,4, /5\\ ,6]\n # 5 [1,2,3,3, /5\\ ] [2,4,4,5, /6\\ ]\n # 6 [1,2,3,3, /5\\ ] [2,4,4,5, /6\\ ]\n\n # return [2,4,5,5,6,6]\n\n```\n[https://leetcode.com/problems/most-beautiful-item-for-each-query/submissions/1285375407/](https://leetcode.com/problems/most-beautiful-item-for-each-query/submissions/1285375407/)\n\nI could be wrong, but I think that time complexity is *O*((*N* + *M*) log *N*) and space complexity is *O*(*N*), in which *N* ~ `len(items)` and *M* ~ `len(queries)`.
| 13 | 0 |
['Python', 'Python3']
| 0 |
most-beautiful-item-for-each-query
|
Python | Two-Pointer & Binary Search
|
python-two-pointer-binary-search-by-khos-8xfh
|
see the Successfully Accepted Submission\n\n# Code\npython3 []\nclass Solution:\n def maximumBeauty(self, items: List[List[int]], queries: List[int]) -> List
|
Khosiyat
|
NORMAL
|
2024-11-12T01:57:59.866138+00:00
|
2024-11-12T01:57:59.866167+00:00
| 1,992 | false |
[see the Successfully Accepted Submission](https://leetcode.com/problems/most-beautiful-item-for-each-query/submissions/1450113444/?envType=daily-question&envId=2024-11-12)\n\n# Code\n```python3 []\nclass Solution:\n def maximumBeauty(self, items: List[List[int]], queries: List[int]) -> List[int]:\n # Sort items by price (first element in each sublist)\n items.sort()\n \n # Precompute the maximum beauty at each price level\n max_beauty_at_price = []\n current_max_beauty = 0\n \n for price, beauty in items:\n current_max_beauty = max(current_max_beauty, beauty)\n max_beauty_at_price.append((price, current_max_beauty))\n \n # Sort queries with indices to map results back to original order\n sorted_queries = sorted((q, i) for i, q in enumerate(queries))\n \n # Prepare result array\n result = [0] * len(queries)\n \n # Process each query\n for query, original_index in sorted_queries:\n # Binary search to find the largest price <= query\n idx = bisect_right(max_beauty_at_price, (query, float(\'inf\'))) - 1\n if idx >= 0:\n result[original_index] = max_beauty_at_price[idx][1]\n else:\n result[original_index] = 0\n \n return result\n\n```\n# Solution Approach\n\n### 1. Sort the Items by Price:\n- **Objective**: Sort `items` based on price in ascending order. If two items have the same price, the order doesn\'t matter, as we will take the maximum beauty at each price level.\n- **Benefit**: This sorting allows us to answer each query more efficiently by reducing the search space.\n\n### 2. Optimize Beauty Up to Each Price:\n- As we iterate through the sorted `items`, maintain the maximum beauty seen so far.\n- For each unique price level, store the maximum beauty up to that price. This lets us quickly reference the maximum beauty available for any price without recalculating.\n\n### 3. Binary Search for Each Query:\n- After sorting and creating a cumulative maximum beauty array, sort the `queries`.\n- For each query, use binary search to find the largest price that is less than or equal to the query price.\n- Use this position to get the precomputed maximum beauty for that price.\n\n### 4. Result Matching:\n- Since we sorted `queries`, we must match the results back to the original query order.\n\n# Time Complexity Analysis\n- Sorting `items` takes \\(O(N \\log N)\\).\n- Sorting `queries` also takes \\(O(Q \\log Q)\\).\n- Processing each query with a binary search on `items` takes \\(O(Q \\log N)\\).\n \nOverall complexity: \\(O((N + Q) \\log N)\\), which is efficient within the given constraints.\n\n#Code Explanation:\nSorting items:\n\nSorting makes it easy to process prices in increasing order and maintain a cumulative maximum beauty.\nBuilding max_beauty_at_price:\n\nFor each item, update current_max_beauty if the beauty of the item is higher. Append (price, current_max_beauty) so we have each price level\'s max beauty.\nSorting and Processing queries:\n\nSorting queries avoids redundant computations and lets us easily pair results back to the original order.\nBinary Search:\n\nFor each query, use bisect_right to find the rightmost price that is \u2264 the query value, then access the corresponding max beauty from max_beauty_at_price.\n\n#Edge Cases\nNo items with price \u2264 query: The answer for that query should be 0.\nMultiple items with the same price: Handled by taking the maximum beauty at each price.\nAll queries are smaller than the minimum item price: All query results should be 0.\n\n\n
| 11 | 0 |
['Python3']
| 4 |
most-beautiful-item-for-each-query
|
[C++] Simple C++ Code || O(NlogN)
|
c-simple-c-code-onlogn-by-prosenjitkundu-nkk9
|
\n# If you like the implementation then Please help me by increasing my reputation. By clicking the up arrow on the left of my image.\n\nclass Solution {\n i
|
_pros_
|
NORMAL
|
2022-08-11T09:05:52.623153+00:00
|
2022-08-11T09:05:52.623264+00:00
| 779 | false |
\n# **If you like the implementation then Please help me by increasing my reputation. By clicking the up arrow on the left of my image.**\n```\nclass Solution {\n int BinarySearch(vector<vector<int>>& items, int q, vector<int> &Beauty)\n {\n int start = 0, end = items.size()-1;\n int val = 0;\n while(start <= end)\n {\n int mid = start + (end-start)/2;\n if(q >= items[mid][0])\n {\n val = Beauty[mid];\n start = mid+1;\n }\n else\n end = mid-1;\n }\n return val;\n }\npublic:\n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) \n {\n int n = items.size();\n sort(items.begin(), items.end());\n vector<int> ans, mxBeauty(n);\n mxBeauty[0] = items[0][1];\n for(int i = 1; i < n; i++)\n {\n mxBeauty[i] = max(mxBeauty[i-1],items[i][1]);\n }\n for(int &q : queries)\n {\n ans.push_back(BinarySearch(items, q, mxBeauty));\n }\n return ans;\n }\n};\n```
| 11 | 0 |
['Binary Search', 'C', 'Sorting', 'Binary Tree', 'C++']
| 5 |
most-beautiful-item-for-each-query
|
Rust with sort, dedup & partition_point | 9ms, beats 100%
|
rust-with-sort-dedup-partition_point-9ms-u1q4
|
Intuition\nIf we sort the items by price (ascending) and then remove all the items for which the beauty is not higher than the previous highest beauty we can us
|
andriamanitra
|
NORMAL
|
2024-11-12T02:25:32.811097+00:00
|
2024-11-12T02:25:32.811126+00:00
| 224 | false |
# Intuition\nIf we sort the items by price (ascending) and then remove all the items for which the beauty is not higher than the previous highest beauty we can use binary search.\n\n# Code\n```rust []\nimpl Solution {\n pub fn maximum_beauty(mut items: Vec<Vec<i32>>, queries: Vec<i32>) -> Vec<i32> {\n items.sort_unstable();\n items.dedup_by(|right, left| right[1] <= left[1]);\n queries.into_iter().map(|q|\n match items.partition_point(|it| it[0] <= q) {\n 0 => 0,\n i => items[i - 1][1]\n }\n ).collect()\n }\n}\n```\n\n# Implementation notes\n* We don\'t need to use a key for sorting because the default comparison for `Vec` does elementwise comparison (starting from the price, which is what we want to sort by).\n* `.sort_unstable()` is typically a bit faster than `.sort()`.\n* After sorting the `.dedup_by(F)` method can be used to remove items for which there exists a cheaper item with the same or higher beauty to the left of it. Note that the elements are passed to `F` in opposite order from their order in the slice.\n* `partition_point(F)` uses binary search to find the first index for which the predicate `F` returns *false* (all elements for which `F` returns true must be at the start of the slice) so we need to subtract one from it to find the last element for which it returned *true*.\n\n# Complexity\n- Time complexity: $O((N + M) \\log M)$ where $N$ is the number of queries, and $M$ is the length of items\n\n- Space complexity: $O(N)$\n
| 10 | 0 |
['Array', 'Binary Search', 'Sorting', 'Rust']
| 4 |
most-beautiful-item-for-each-query
|
let's understand it in a crispy way, simple explanation with YouTube Video
|
lets-understand-it-in-a-crispy-way-simpl-aogl
|
YouTube explanation https://youtu.be/Lyssy7pJLE4\n# Intuition and approach\nlets keep it simple with below steps:-\n \n1) sort the items array based on price\n2
|
vinod_aka_veenu
|
NORMAL
|
2024-11-12T07:12:36.630895+00:00
|
2024-11-12T08:45:52.327323+00:00
| 2,059 | false |
# YouTube explanation https://youtu.be/Lyssy7pJLE4\n# Intuition and approach\nlets keep it simple with below steps:-\n \n**1)** sort the items array based on price\n**2)** make a **queryIndex[][] = new int[n][2]**, where n = queries.length\n**queryIndex[i][0] == price, queryIndex[i][1] == index** in queires array\n\n**why should make this??** ===> because we want to sort the array based on price in increasing order, but also want to keep track their orginal index otherwise we will loose the index info to put it in array.\n\nNOW we will also sort the **queryIndex array based on price**.\n\nnow we will create an answer array **ans[] = new int[n]**\n\nnow we will start with **itemIndex = 0 , and a variable say maxBeauty =0**\n\n\nso for **i = to i = n-1** \ncurrPrice = queryIndex[i][0]\ncurrIndex = queryIndex[i][1]\nnow we will search the value in Items array till we get the price that is smaller or equal to **currPrice** and we will record the max value during this loop.\n\nassign the maxvalue ans[currIndex] = maxVal;\n\nrepeat it till the for loop ends and return ans.\n\n**will relase a youtube video soon to explain everything in details**\n\n\n\n# Code\n```java []\n\nclass Solution {\n public int[] maximumBeauty(int[][] items, int[] queries) {\n int n = queries.length;\n int ans[] = new int[n]; \n\n int[][]queryIndex = new int[n][2];\n for(int i=0; i<n; i++)\n {\n queryIndex[i][0] = queries[i];\n queryIndex[i][1] = i; \n }\n Arrays.sort(queryIndex, (a, b)->a[0]-b[0]);\n Arrays.sort(items, (a, b)-> a[0]-b[0]);\n\n \n int maxBeauty = 0; \n int itemIndex = 0; \n\n for(int i=0; i<n; i++)\n {\n int currIndex = queryIndex[i][1];\n int currPrice = queryIndex[i][0];\n while(itemIndex<items.length && currPrice>=items[itemIndex][0])\n {\n maxBeauty = Math.max(maxBeauty, items[itemIndex][1]);\n itemIndex++;\n }\n ans[currIndex] = maxBeauty;\n }\n \n return ans;\n \n }\n}\n```
| 9 | 0 |
['Array', 'Math', 'Binary Search', 'Sorting', 'Java']
| 2 |
most-beautiful-item-for-each-query
|
[C++] - Sorting || Simple and easy || Comprehensive Test Cases and Explanation
|
c-sorting-simple-and-easy-comprehensive-nc876
|
IntuitionThe goal is to find the most beautiful item that costs less than or equal to a given price for each query. We need to efficiently determine the maximum
|
nitishhsinghhh
|
NORMAL
|
2024-11-12T07:12:17.864150+00:00
|
2025-01-25T19:01:39.923439+00:00
| 375 | false |
# Intuition
The goal is to find the most beautiful item that costs less than or equal to a given price for each query. We need to efficiently determine the maximum beauty for each query.
# Approach
1. Store Maximum Beauty for Each Price:
- Use a map to store the maximum beauty for each price. If multiple items have the same price, keep the one with the highest beauty.
2. Sort Prices:
- Convert the map to a list of pairs and sort it by price. This helps in quickly finding the maximum beauty for any given price.
3. Update Maximum Beauty:
- Ensure that for each price, the beauty is the maximum possible up to that price. This means if a higher price has a lower beauty, update it to the maximum beauty seen so far.
4. Binary Search for Queries:
- For each query, use binary search to find the highest price that is less than or equal to the query. Return the corresponding beauty.
# Complexity
- Time Complexity:
- Building the map takes O(n), where n is the number of items.
- Sorting the list of prices takes O(nlogn). Each query is processed in O(logn) due to binary search.
- Overall, the time complexity is O(nlogn+mlogn), where m is the number of queries.
- Space Complexity:
- The space complexity is O(n) for storing the map and the list of prices.
# Code
```cpp []
// GCC 13.1 (C++ 23)
#include <iostream>
#include <vector>
#include <algorithm>
#include <unordered_map>
#include <cassert>
#include <chrono>
using std::vector;
using std::pair;
using std::unordered_map;
using std::cout;
using std::endl;
using std::chrono::high_resolution_clock;
using std::chrono::duration_cast;
using std::chrono::milliseconds;
class Solution {
public:
/**
* @brief Finds the maximum beauty for a given query using binary search.
*
* This function performs a binary search on a sorted vector of pairs to find the maximum beauty
* value that is less than or equal to the given query.
*
* @param v A sorted vector of pairs where the first element is the price and the second element is the beauty.
* @param query The query value to find the maximum beauty for.
* @return The maximum beauty value for the given query.
*/
int solve(const vector<pair<int, int>>& v, int query) {
int s = 0, e = v.size() - 1;
int ans = 0;
while (s <= e) {
int mid = s + (e - s) / 2;
if (v[mid].first <= query) {
ans = v[mid].second;
s = mid + 1;
} else {
e = mid - 1;
}
}
return ans;
}
/**
* @brief Computes the maximum beauty for each query.
*
* This function processes a list of items and queries to determine the maximum beauty value for each query.
* It uses a hash map to store the maximum beauty for each price, sorts the items, and then uses binary search
* to find the maximum beauty for each query.
*
* @param items A vector of vectors where each inner vector contains two integers: price and beauty.
* @param queries A vector of integers representing the queries.
* @return A vector of integers representing the maximum beauty for each query.
*/
vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {
unordered_map<int, int> mp;
for (const auto& item : items) {
mp[item[0]] = std::max(mp[item[0]], item[1]);
}
vector<pair<int, int>> v(mp.begin(), mp.end());
std::sort(v.begin(), v.end());
for (size_t i = 1; i < v.size(); ++i) {
v[i].second = std::max(v[i - 1].second, v[i].second);
}
vector<int> ans;
ans.reserve(queries.size());
for (const int query : queries) {
ans.push_back(solve(v, query));
}
return ans;
}
};
// Unit Test: Basic functionality tests
void testBasicFunctionality() {
Solution sol;
// Test case 1
vector<vector<int>> items1 = {{1, 2}, {3, 2}, {2, 4}, {5, 6}, {3, 5}};
vector<int> queries1 = {1, 2, 3, 4, 5, 6};
vector<int> result1 = sol.maximumBeauty(items1, queries1);
vector<int> expected1 = {2, 4, 5, 5, 6, 6};
assert(result1 == expected1); // Expected result: {2, 4, 5, 5, 6, 6}
cout << "Basic functionality test 1 passed!" << endl;
// Test case 2
vector<vector<int>> items2 = {{1, 2}, {1, 2}, {1, 3}, {1, 4}};
vector<int> queries2 = {1};
vector<int> result2 = sol.maximumBeauty(items2, queries2);
vector<int> expected2 = {4};
assert(result2 == expected2); // Expected result: {4}
cout << "Basic functionality test 2 passed!" << endl;
// Test case 3
vector<vector<int>> items3 = {{10, 1000}};
vector<int> queries3 = {5};
vector<int> result3 = sol.maximumBeauty(items3, queries3);
vector<int> expected3 = {0};
assert(result3 == expected3); // Expected result: {0}
cout << "Basic functionality test 3 passed!" << endl;
}
// Edge Case: Single element array
void testEdgeCases() {
Solution sol;
vector<vector<int>> items4 = {{5, 10}};
vector<int> queries4 = {5, 10};
vector<int> result4 = sol.maximumBeauty(items4, queries4);
vector<int> expected4 = {10, 10}; // Expected result: {10, 10}
assert(result4 == expected4);
cout << "Edge case test passed!" << endl;
}
// Stress/Performance Test: Large input array with increasing values
void testPerformance() {
Solution sol;
vector<vector<int>> items5;
for (int i = 1; i <= 1000; ++i) {
items5.push_back({i, i * 2});
}
vector<int> queries5(1000);
for (int i = 0; i < 1000; ++i) {
queries5[i] = i + 1;
}
auto start = high_resolution_clock::now();
vector<int> result5 = sol.maximumBeauty(items5, queries5);
auto end = high_resolution_clock::now();
auto duration = duration_cast<milliseconds>(end - start).count();
cout << "Performance test duration: " << duration << " ms" << endl;
bool performanceTestPassed = true;
for (int i = 0; i < 1000; ++i) {
if (result5[i] != (i + 1) * 2) {
performanceTestPassed = false;
break;
}
}
assert(performanceTestPassed); // Expected result: true for all queries
cout << "Performance test passed!" << endl;
}
// Consistency Test: Run the function multiple times with the same input
void testConsistency() {
Solution sol;
vector<vector<int>> items6 = {{4, 9}, {6, 10}, {2, 5}};
vector<int> queries6 = {4, 6, 2};
vector<int> firstResult = sol.maximumBeauty(items6, queries6);
for (int i = 0; i < 10; ++i) {
vector<int> result = sol.maximumBeauty(items6, queries6);
assert(result == firstResult); // Expected result: true for all iterations
}
cout << "Consistency test passed!" << endl;
}
// Additional Integration Tests
void testIntegrationCases() {
Solution sol;
// Case 1: Already strictly increasing array
vector<vector<int>> items7 = {{1, 2}, {2, 3}, {3, 4}, {4, 5}, {5, 6}};
vector<int> queries7 = {1, 2, 3, 4, 5};
vector<int> result7 = sol.maximumBeauty(items7, queries7);
vector<int> expected7 = {2, 3, 4, 5, 6}; // Expected result: {2, 3, 4, 5, 6}
assert(result7 == expected7);
cout << "Integration test 1 passed!" << endl;
// Case 2: Array with large gaps
vector<vector<int>> items8 = {{10, 20}, {20, 30}, {30, 40}, {40, 50}, {50, 60}};
vector<int> queries8 = {10, 20, 30, 40, 50};
vector<int> result8 = sol.maximumBeauty(items8, queries8);
vector<int> expected8 = {20, 30, 40, 50, 60}; // Expected result: {20, 30, 40, 50, 60}
assert(result8 == expected8);
cout << "Integration test 2 passed!" << endl;
// Case 3: Array with no possible item to satisfy the query
vector<vector<int>> items9 = {{10, 100}, {20, 200}, {30, 300}};
vector<int> queries9 = {5, 15, 25};
vector<int> result9 = sol.maximumBeauty(items9, queries9);
vector<int> expected9 = {0, 100, 200}; // Expected result: {0, 100, 200}
assert(result9 == expected9);
cout << "Integration test 3 passed!" << endl;
// Case 4: Array with multiple items having the same price
vector<vector<int>> items10 = {{10, 100}, {10, 200}, {10, 300}};
vector<int> queries10 = {10};
vector<int> result10 = sol.maximumBeauty(items10, queries10);
vector<int> expected10 = {300}; // Expected result: {300}
assert(result10 == expected10);
cout << "Integration test 4 passed!" << endl;
}
int main() {
// Running all tests for maximumBeauty
testBasicFunctionality(); // Basic functionality tests
testEdgeCases(); // Edge case tests
testPerformance(); // Performance test
testConsistency(); // Consistency test
testIntegrationCases(); // Additional integration tests
return 0;
}
```
| 9 | 0 |
['Array', 'Binary Search', 'Sorting', 'C++']
| 0 |
most-beautiful-item-for-each-query
|
C++ O(nlogn) || Map || Binary Search
|
c-onlogn-map-binary-search-by-abhay5349s-jmut
|
Connect with me on LinkedIn: https://www.linkedin.com/in/abhay5349singh/\n\n\nclass Solution {\npublic:\n\n vector<int> maximumBeauty(vector<vector<int>>& it
|
abhay5349singh
|
NORMAL
|
2021-11-13T16:02:51.625932+00:00
|
2023-07-14T04:17:11.481949+00:00
| 685 | false |
**Connect with me on LinkedIn**: https://www.linkedin.com/in/abhay5349singh/\n\n```\nclass Solution {\npublic:\n\n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n int n=items.size(), m=queries.size();\n \n map<int,int> mp;\n \n for(int i=0;i<n;i++){\n int p=items[i][0], b=items[i][1];\n if(mp.find(p)==mp.end()){\n mp[p]=b;\n }else{\n int prev=mp[p];\n mp[p]=max(prev,b);\n }\n }\n map<int,int> :: iterator it;\n int maxb=-1;\n for(it=mp.begin();it!=mp.end();it++){\n int p=it->first;\n int b=mp[p];\n maxb=max(maxb,b);\n mp[p]=maxb; // maximum beauty possible till price [1,p]\n }\n \n vector<int> ans(m,0);\n for(int i=0;i<m;i++){\n int p=queries[i];\n \n if(mp.find(p)!=mp.end()){\n ans[i]=mp[p];\n }else{\n auto it = mp.lower_bound(p); // checking beauty for price just lower than for given query\n if(it!=mp.begin()){\n --it;\n ans[i]=it->second;\n }\n }\n }\n \n return ans;\n }\n};\n```\n\n**Do Upvote If it Helps**
| 9 | 1 |
['Binary Tree', 'C++']
| 4 |
most-beautiful-item-for-each-query
|
Java O(nLogn) + O(qLogn) | Sort + Binary Search
|
java-onlogn-oqlogn-sort-binary-search-by-jhgt
|
\nclass Solution {\n public int[] maximumBeauty(int[][] items, int[] q) {\n \n Arrays.sort(items,(a,b)->a[0]-b[0]); // sort on the basis of pri
|
surajthapliyal
|
NORMAL
|
2021-11-13T16:01:08.212260+00:00
|
2021-11-13T18:03:06.208939+00:00
| 658 | false |
```\nclass Solution {\n public int[] maximumBeauty(int[][] items, int[] q) {\n \n Arrays.sort(items,(a,b)->a[0]-b[0]); // sort on the basis of prices.\n \n for(int i = 1; i < items.length; i++){\n items[i][1] = Math.max( items[i][1], items[i-1][1] ); // ith item will store max beauty till now.\n }\n \n int n = q.length;\n int ans[] = new int[n];\n \n for(int i = 0; i < n; i++){\n \n int s = 0, e = items.length - 1;\n \n while(s <= e){ // perform binary search to find the last price <= queries[i].\n int mid = s + (e - s) / 2;\n \n if(items[mid][0] <= q[i]) {\n s = mid + 1;\n ans[i] = Math.max( ans[i], items[mid][1] ); // update ans[i] for max value.\n }else{\n e = mid - 1;\n }\n \n }\n \n }\n \n return ans;\n \n }\n}\n```
| 9 | 0 |
[]
| 3 |
most-beautiful-item-for-each-query
|
Beats 95% || C++ || Sorting || Offline Queries
|
beats-95-c-sorting-offline-queries-by-ak-ffdl
|
Intuition\n Describe your first thoughts on how to solve this problem. \nTo maximize beauty for each query efficiently, sorting both the queries and the items b
|
akash92
|
NORMAL
|
2024-11-12T04:16:08.442397+00:00
|
2024-11-12T04:16:08.442425+00:00
| 839 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo maximize beauty for each query efficiently, sorting both the queries and the items by price in ascending order is key. By doing this, we can iterate through items and update the maximum beauty value for all queries whose price threshold has been reached.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1.\tPair each query with its original index and sort the queries by their price.\n2.\tSort the items by price.\n3.\tUse a two-pointer approach: iterate over the items, updating the maximum beauty whenever the item price is less than or equal to the query price.\n4.\tStore the results in the answer array at the corresponding indices from the original queries.\n# Complexity\n- Time complexity: $$O(n*log(n) + m*log(m))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n+m)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n int n = items.size(), m = queries.size();\n vector<pair<int,int>> vp;\n for(int j=0; j<m; j++){\n vp.push_back({queries[j], j});\n }\n sort(vp.begin(), vp.end());\n sort(items.begin(), items.end());\n\n int maxi = 0, i = 0;\n vector<int> ans(m);\n for(auto it: vp){\n int price = it.first, ind = it.second;\n while(i<n && items[i][0] <= price){\n maxi = max(maxi, items[i][1]);\n i++;\n }\n ans[ind] = maxi;\n }\n return ans;\n }\n};\n```
| 8 | 0 |
['Array', 'Sorting', 'C++']
| 0 |
most-beautiful-item-for-each-query
|
[Python3] sorting + binary search
|
python3-sorting-binary-search-by-shaad94-0uom
|
\nclass Solution:\n def maximumBeauty(self, items: List[List[int]], queries: List[int]) -> List[int]:\n items.sort()\n maxArr = [items[0][1]] *
|
shaad94
|
NORMAL
|
2021-11-13T16:09:48.756293+00:00
|
2021-11-13T16:36:37.090220+00:00
| 1,984 | false |
```\nclass Solution:\n def maximumBeauty(self, items: List[List[int]], queries: List[int]) -> List[int]:\n items.sort()\n maxArr = [items[0][1]] * len(items)\n\t\t# for each cell calculate maximum beautifulnes\n for i in range(1, len(items)):\n maxArr[i] = max(maxArr[i-1], items[i][1])\n \n onlyKeys = list(map(lambda x:x[0], items)) # since 3.9 python doesn\'t have `key` in bisect\n \n res = []\n for q in queries:\n # if minimum price is greated than query, no items can be found for query\n notPossible = items[0][0] > q\n if notPossible:\n res.append(0)\n else:\n # otherwise find last cell with value less or equals to query\n i = bisect.bisect_right(onlyKeys, q)\n # lookup result in our maximum array by index\n res.append(maxArr[i-1])\n \n return res\n```\t\t
| 8 | 0 |
[]
| 1 |
most-beautiful-item-for-each-query
|
[Python3] - Sort + Binary Search - Easy to understand
|
python3-sort-binary-search-easy-to-under-ii50
|
Intuition\n Describe your first thoughts on how to solve this problem. \nProblem said price is less than or equal so it means we can think about sorting by pric
|
dolong2110
|
NORMAL
|
2023-03-14T18:07:41.438985+00:00
|
2023-08-10T15:13:15.913277+00:00
| 663 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nProblem said `price is less than or equal` so it means we can think about sorting by `price` and then do binary search to find `price is less than or equal` to the `queries[j]`. But it is not only that simple. In here we have to find the maximum `beauty` for all the price less than or equal to `queries[j]`. Assume the highest `price` in `items` that is <= `queries[j]` is at index `i`. we can easily get that `max beauty = items[k][1] for 0 <= k <= i` \n- So we must find the max beauty in range from 0 to i for the `queries[j]`\n \n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Sort items by price - $O(nlogn)$\n- update the beauty for index i in items = `max(items[x] for x in range(i + 1))` - $O(n)$\n- for each query, binary search for the highest item which has price `<=` this query\'s value, then add to final result the `max beauty` in range `first query to current querry` - $O(nlogn)$\n\n# Complexity\n- Time complexity: $O(nlogn + n + nlogn)$ ~ $O(nlogn)$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(1)$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maximumBeauty(self, items: List[List[int]], queries: List[int]) -> List[int]:\n items.sort()\n n = len(items)\n res = []\n for i in range(1, n):\n items[i][1] = max(items[i][1], items[i - 1][1])\n\n for q in queries:\n l, r = 0, n - 1\n while l <= r:\n m = (l + r) >> 1\n p, b = items[m]\n if p > q: r = m - 1\n else: l = m + 1\n res.append(items[r][1] if r >= 0 else 0)\n return res\n```
| 7 | 0 |
['Binary Search', 'Sorting', 'Python3']
| 1 |
most-beautiful-item-for-each-query
|
java || binary search
|
java-binary-search-by-rakshitachoudhary2-9ds6
|
Approach\n-Sort items by price.\n-Precompute the maximum beauty up to each price level in maxBeauty.\n-For each query, use binary search to find the largest pri
|
rakshitachoudhary2000
|
NORMAL
|
2024-11-12T15:29:42.297941+00:00
|
2024-11-12T15:29:42.297974+00:00
| 218 | false |
# Approach\n-Sort items by price.\n-Precompute the maximum beauty up to each price level in maxBeauty.\n-For each query, use binary search to find the largest price in items that is less than or equal to the query and return the corresponding maximum beauty from maxBeauty.\n\n# Code\n```java []\nclass Solution {\n public int[] maximumBeauty(int[][] items, int[] queries) {\n Arrays.sort(items,(a,b)->a[0]-b[0]);\n int n=items.length;\n int[] maxbeauty=new int[n];\n maxbeauty[0]=items[0][1];\n for(int i=1;i<n;i++){\n maxbeauty[i]=Math.max(maxbeauty[i-1],items[i][1]);\n }\n for(int i=0;i<queries.length;i++){\n int q=queries[i];\n int left=0;int right=n-1;\n while (left <= right) {\n int mid = left + (right - left) / 2;\n if (items[mid][0] <= q) {\n left = mid + 1;\n } else {\n right = mid - 1;\n }\n }if(right>=0){queries[i]=maxbeauty[right];}\n else{queries[i]=0;}\n }\n return queries;\n }\n}\n```
| 6 | 0 |
['Java']
| 0 |
most-beautiful-item-for-each-query
|
JAVA || EASY TO UNDERSTAND || BEATS 92% 🚀 || O(nlogn)
|
java-easy-to-understand-beats-92-onlogn-hx2eu
|
Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem is essentially to find, for each query price, the maximum beauty of items t
|
user6791FW
|
NORMAL
|
2024-11-12T07:57:04.887962+00:00
|
2024-11-12T07:57:04.887998+00:00
| 299 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem is essentially to find, for each query price, the maximum beauty of items that have a price less than or equal to that query price. This suggests a combination of sorting and binary search:\n1. **Sorting** helps organize items by price, making it easier to find the maximum beauty for any given price threshold.\n2. **Binary Search** allows efficient searching within this sorted list for each query price.\n\nBy sorting the items by price and then using binary search for each query, we can efficiently determine the maximum beauty available under or equal to each query price.\n\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. **Sort the Items by Price**:\n - First, sort `items` based on their price in ascending order. This ensures that for any price threshold, the items we need to consider are sequentially arranged.\n\n2. **Process Each Query Using Binary Search**:\n - For each query, we perform a binary search on the sorted `items` array.\n - The goal is to find the largest price in `items` that is less than or equal to the current query price.\n - **Binary Search Steps**:\n - Initialize `low` and `high` pointers.\n - Calculate the middle point `mid` and check if `items[mid][0] <= queryPrice`.\n - If yes, update `maxBeauty` to be the maximum of `maxBeauty` and `items[mid][1]`, and continue searching in the right half (`low = mid + 1`).\n - If not, search in the left half (`high = mid - 1`).\n - After the binary search completes, `maxBeauty` will hold the maximum beauty for the current query, and we update `queries[i]` directly.\n\n3. **Return the Updated `queries` Array**:\n - The function modifies the `queries` array in place to store the maximum beauty for each query price, and this modified array is returned as the final result.\n\n# Complexity\n- **Time complexity:**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n1. **Sorting** the `items` array takes \\(O(m \\log m)\\), where \\(m\\) is the number of items.\n2. **Binary Search** for each query takes \\(O(\\log m)\\), and since we have \\(n\\) queries, this part contributes \\(O(n \\log m)\\).\n\nOverall, the time complexity is: \\[O(m \\log m + n \\log m)\\]\nwhere:\n- \\(m\\) is the number of items.\n- \\(n\\) is the number of queries.\n\n- **Space complexity:** The space complexity is \\(O(1)\\) if we ignore the input and output storage, as the algorithm modifies `queries` in place without needing extra space for intermediate results.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```java []\nclass Solution {\n public int[] maximumBeauty(int[][] items, int[] queries) {\n Arrays.sort(items, (a,b) -> a[0]-b[0]);\n\n for (int i = 1; i < items.length; i++) {\n items[i][1] = Math.max(items[i][1], items[i - 1][1]);\n }\n\n for (int i = 0; i < queries.length; i++) {\n int queryPrice = queries[i];\n int low = 0, high = items.length - 1;\n int maxBeauty = 0;\n\n // Binary search for the highest price <= queryPrice\n while (low <= high) {\n int mid = low + (high - low) / 2;\n if (items[mid][0] <= queryPrice) {\n maxBeauty = items[mid][1];\n low = mid + 1;\n } else {\n high = mid - 1;\n }\n }\n // Update queries[i] with the maximum beauty found\n queries[i] = maxBeauty;\n }\n return queries;\n }\n}\n```
| 6 | 0 |
['Array', 'Binary Search', 'Sorting', 'Java']
| 1 |
most-beautiful-item-for-each-query
|
Super Simple Beginner Friendly Java/C SolutionO(n(logn)+k(logn))
|
super-simple-beginner-friendly-javac-sol-pmke
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n1. Sort the items array
|
rajnarayansharma110
|
NORMAL
|
2024-11-12T07:07:57.378288+00:00
|
2024-11-12T07:07:57.378315+00:00
| 169 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Sort the items array using 1st elem(price) and if 1st elem is same then sort according to 2nd elem(beauty) in ascending order to use binary search.\n2. Store the maxBeauty for each price(say two items are {1,3} and {1,5} the maxPrice will hold beauty 5 for price 1)\n3. Simply binary search to find the best beautiful item.\n# Complexity\n- Time complexity:O(nlogn+klogn). {k is size of query and n is size of items}\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n+k)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int[] maximumBeauty(int[][] items, int[] queries) {\n Arrays.sort(items, (a, b) -> {\n if(a[0]==b[0]) return a[1]-b[1];\n return a[0] - b[0];\n });\n int n = items.length;\n int[] maxBeauty = new int[n];\n maxBeauty[0] = items[0][1];\n for (int i = 1; i < n; i++) {\n maxBeauty[i] = Math.max(maxBeauty[i - 1], items[i][1]);\n }\n\n int[] res = new int[queries.length];\n for (int i = 0; i < queries.length; i++) {\n int q = queries[i];\n int left = 0, right = n - 1;\n while (left <= right) {\n int mid = (left + right) / 2;\n if (items[mid][0] <= q) left = mid + 1;\n else right = mid - 1;\n }\n res[i] = right >= 0 ? maxBeauty[right] : 0;\n }\n\n return res;\n }\n}\n```\n```C []\nint compare(const void *a, const void *b) {\n int *item1 = *(int **)a;\n int *item2 = *(int **)b;\n if (item1[0] == item2[0]) return item1[1] - item2[1];\n return item1[0] - item2[0];\n}\n\nint* maximumBeauty(int** items, int itemsSize, int* itemsColSize, int* queries, int queriesSize, int* returnSize) {\n qsort(items, itemsSize, sizeof(int*), compare);\n\n int* maxBeauty = (int*)malloc(itemsSize * sizeof(int));\n maxBeauty[0] = items[0][1];\n for (int i = 1; i < itemsSize; i++) {\n maxBeauty[i] = (maxBeauty[i - 1] > items[i][1]) ? maxBeauty[i - 1] : items[i][1];\n }\n\n int* res = (int*)malloc(queriesSize * sizeof(int));\n *returnSize = queriesSize;\n \n for (int i = 0; i < queriesSize; i++) {\n int q = queries[i];\n int left = 0, right = itemsSize - 1;\n while (left <= right) {\n int mid = (left + right) / 2;\n if (items[mid][0] <= q) left = mid + 1;\n else right = mid - 1;\n }\n res[i] = (right >= 0) ? maxBeauty[right] : 0;\n }\n\n free(maxBeauty);\n return res;\n}\n```
| 6 | 0 |
['Binary Search', 'C', 'Sorting', 'Java']
| 0 |
most-beautiful-item-for-each-query
|
Most Beauty Item for each query - Easy Explanation - 🌟Beats 100%🌟
|
most-beauty-item-for-each-query-easy-exp-9206
|
Intuition\n1. Sort the items array based on the prices and if the prices are same, sort the items based on beauty in descending order.\n\n1. Use of TreeMap for
|
RAJESWARI_P
|
NORMAL
|
2024-11-12T01:24:44.094596+00:00
|
2024-11-12T01:24:44.094623+00:00
| 484 | false |
# Intuition\n1. Sort the items array based on the prices and if the prices are same, sort the items based on beauty in descending order.\n\n1. Use of TreeMap for efficient computation of key-value pair.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n\n**Custom sorting of items array**:\n \nSort the items based on the prices in ascending order and if the prices are same, sort the items based on beauty in descending .\n\nHence for the item with same prices , the item with maximum prices will appear first and so on..\n\n Arrays.sort(items,(a,b)-> a[0]==b[0]? b[1]-a[1] : a[0]-b[0]);\n\n**Initialization**:\n\nInitialize the currMaxBeauty to 0 to keep track of the maximum beauty till now.\n\nInitialize TreeMap with key and value as integer for efficient storing and computation purpose.\n\n int currMaxBeauty=0;\n TreeMap<Integer,Integer> map=new TreeMap<>();\n\n**Storing values in TreeMap**:\n\nIterate through the whole items array \n\n for(int[] item:items) {\n int price=item[0];\n int beauty=item[1];\n\ncheck if the beauty is less than currMaxBeauty,If so continue to the next iteration.\n\n if(currMaxBeauty>=beauty)\n continue;\n\nOtherwise , store the price and currMaxBeauty to the TreeMap as key->value pair.\n\n currMaxBeauty=beauty;\n map.put(price,currMaxBeauty);\n\n**Finding the maximum beauty**:\n \n**Initialization**:\n\nInitialize no_queries with the total length of the query.\n\nanswer as an Integer array of size no_queries to store maximum beauty that has price less than or equal to queries[i].\n\n int no_queries=queries.length;\n int[] answer=new int[no_queries];\n\n**Iteration**:\n\nIterate through the whole queries array.\n\n for(int i=0;i<no_queries;i++){\n\nFind entry in TreeMap with price less than or equal to price in queries array using map.floorEntry().\n\n Map.Entry<Integer,Integer> entry=map.floorEntry(queries[i]);\n\nIf the function returns an entry, then the value at the entry is stored in the answer array.\n\n if(entry!=null)\n {\n answer[i]=entry.getValue();\n }\n\n\nIf it is null, then in the answer array, the result for the query is stored as 0.\n\n else\n {\n answer[i]=0;\n }\n\n**Returning the value**:\n\n Return answer array which contains the result for each query if exists .Otherwise, it\'s zero.\n\n return answer;\n\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- ***Time complexity***: **O(nlogn + (m+n) log k)**. \n n -> number of items.\n m -> number of queries.\n k -> number of unique prices.\n\n**Sorting** : **O(nlogn)**.\n\n The first step sorts the items array by price in ascending order, and if two items have the same price, it sorts by beauty in descending order.Sorting of n items take **O(nlogn) time**.\n\n**Building the TreeMap**: **O(nlogk)**.\n\n Inserting the TreeMap takes **O(log k) times** , k is the number of unique prices in the items array.\n\n Thus loop runs in **O(nlogk) time** in worst case for n items.\n\n**Processing Queries**: **O(mlogk)**.\n\nEach query involves a floorEntry lookup in the TreeMap, which takes **O(logk) time**.\n\nWith m queries, this loop runs in **O(mlogk) time**.\n\n**Overall Time Complexity**: **O(nlogn + (n+m) logk)**.\n\n Combining the above steps, the overall time complexity is **O(nlogn)+O(nlogk)+O(mlogk)**.\n\n Since **O(nlogn)** is generally the dominant term when sorting a large array, the overall time complexity simplifies to **O(nlogn+(n+m)logk)**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- ***Space complexity***: **O(n+m)**.\n n -> number of items.\n m -> number of queries.\n\n**TreeMap Storage**: **O(n)**.\n\nThe TreeMap stores at most n entries (if each item has a unique price). This takes **O(n) space**.\n\n**Answer array**: **O(m)**.\n\nThe answer array stores m integers, taking **O(m) space**.\n\n**Overall Space Complexity**: **O(n+m)**.\n Hence the overall space complexity:\n **O(n) + O(m) = O(n+m)**.\n\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\npublic class Solution {\n public int[] maximumBeauty(int[][] items, int[] queries) {\n // Sort items by price ,\n // if they have same price -> then sort by beauty in descending order\n\n Arrays.sort(items,(a,b)-> a[0]==b[0]? b[1]-a[1] : a[0]-b[0]);\n int currMaxBeauty=0;\n\n\n TreeMap<Integer,Integer> map=new TreeMap<>();\n for(int[] item:items)\n {\n int price=item[0];\n int beauty=item[1];\n\n if(currMaxBeauty>=beauty)\n continue;\n currMaxBeauty=beauty;\n map.put(price,currMaxBeauty);\n \n }\n\n int no_queries=queries.length;\n int[] answer=new int[no_queries];\n\n for(int i=0;i<no_queries;i++)\n {\n Map.Entry<Integer,Integer> entry=map.floorEntry(queries[i]);\n if(entry!=null)\n {\n answer[i]=entry.getValue();\n }\n else\n {\n answer[i]=0;\n }\n }\n return answer;\n \n }\n}\n```
| 6 | 0 |
['Array', 'Sorting', 'Java']
| 1 |
most-beautiful-item-for-each-query
|
Binary Search Solution.
|
binary-search-solution-by-1mknown-01i9
|
Sort the array by its price and then modify the items array in such a way that each item contains the maximum value that we can get within that price.\n\nfor ex
|
1mknown
|
NORMAL
|
2021-11-13T19:57:21.644324+00:00
|
2021-11-19T12:14:04.772262+00:00
| 430 | false |
Sort the array by its price and then modify the items array in such a way that each item contains the maximum value that we can get within that price.\n\nfor example if we have items=[[2,5], [3,2], [4,4]]\nthen modified items=[[2,5], [3,5], [4,5]]\nhere the values of items[1] and items[2] is 5 because that is the maximum value we can get within price=4, price=3 and price=2.\n\nNow the items array contains the maximum value that we can get within price p. So for each query we just need to find the index of the item for which price<=queries[i].**\n\nQuestion with similar concept : https://leetcode.com/problems/two-best-non-overlapping-events/\n\n```\nvector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n sort(items.begin(), items.end());\n int cur=0;\n for(int i=0;i<items.size();i++){\n cur=max(items[i][1], cur);\n items[i][1]=cur;\n }\n vector<int>ans;\n for(int i=0;i<queries.size();i++){\n int x=queries[i];\n int low=0, high=items.size()-1, mid=0, a=-1;\n while(low<high){\n mid=low+(high-low)/2;\n if(items[mid][0]<=x){\n a=mid;\n low=mid+1;\n }else{\n high=mid-1;\n }\n }\n if(items[low][0]<=x)a=low;\n if(a==-1)ans.push_back(0);\n else\n ans.push_back(items[a][1]);\n }\n return ans;\n }\n```
| 6 | 0 |
['Sorting', 'Binary Tree', 'C++']
| 0 |
most-beautiful-item-for-each-query
|
✅✅ C++ | Easy Solution | Sorting & Binary Search | Clean Code
|
c-easy-solution-sorting-binary-search-cl-jcte
|
This question is based on binary search.\n\nApproach:\n1. First sort the items vector.\n2. Now store the maximum value of beauty till the current index i ( i >=
|
avijuneja2007
|
NORMAL
|
2021-11-13T17:55:00.871112+00:00
|
2021-12-27T06:07:29.448086+00:00
| 425 | false |
This question is based on **binary search**.\n\n**Approach:**\n1. First **sort** the items vector.\n2. Now store the maximum value of beauty till the current index i ( i >=0 && i <= n-1)\n3. Now iterate on the queries vector and **find the greatest index of the q[i] in the items vector using binary search.**\n4. **If the index is -1** then there is no such value in items vector. Simply put 0 in ans[i]. \n5. Store the value corresponding to this index in ans[i].\n\n**Code:**\n\n\n int binary_s(vector<vector<int>>&items, int val){\n \n int lo = 0;\n int hi = items.size() - 1;\n \n int ans = -1;\n while(lo <= hi){\n int mid = lo + (hi - lo)/2;\n if(items[mid][0] <= val){\n ans = mid;\n lo = mid + 1;\n }\n else{\n hi = mid - 1;\n }\n }\n \n return ans;\n }\n \n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& q) {\n \n int n = items.size();\n sort(items.begin() , items.end());\n \n vector<int>a(n);\n int max_val = 0;\n for(int i = 0 ; i < n ; i++){\n int val = items[i][1];\n max_val = max(max_val , val);\n a[i] = max_val;\n }\n \n int m = q.size();\n \n vector<int>ans(m);\n for(int i = 0 ; i < m ; i++){\n int idx = binary_s(items, q[i]);\n if(idx == -1){\n ans[i] = 0;\n }\n else{\n ans[i] = a[idx]; \n }\n }\n \n return ans;\n }\n\t\n\tPlease upvote the post if this helped you!
| 6 | 0 |
['C', 'Binary Tree']
| 1 |
most-beautiful-item-for-each-query
|
Easy to understand c++ solution
|
easy-to-understand-c-solution-by-himansh-cnmb
|
\nclass Solution {\npublic:\n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n sort(items.begin(),items.end());\n
|
himanshugupta14
|
NORMAL
|
2021-11-13T16:04:06.850208+00:00
|
2021-11-13T16:04:06.850254+00:00
| 372 | false |
```\nclass Solution {\npublic:\n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n sort(items.begin(),items.end());\n vector<int> arr1,arr2;\n \n for(int i=0;i<items.size();i++){\n arr1.push_back(items[i][0]);\n arr2.push_back(items[i][1]);\n }\n \n vector<int> ret;\n \n vector<int>narr;\n int maxm = 0;\n \n // creating a new array which stores maximum value till ith term;\n for(int i=0;i<arr2.size();i++){\n maxm = max(maxm,arr2[i]);\n narr.push_back(maxm);\n }\n \n for(int i =0;i<queries.size();i++){\n int x = queries[i];\n \n auto l = lower_bound(arr1.begin(),arr1.end(),x+1);\n int dis = l-1-arr1.begin();\n \n if(dis == -1) ret.push_back(0);\n else ret.push_back(narr[dis]); // directly putting maximum value using the array which we created earlier\n }\n return ret;\n }\n};\n```
| 6 | 0 |
[]
| 1 |
most-beautiful-item-for-each-query
|
Kotlin | Rust
|
kotlin-rust-by-samoylenkodmitry-1usf
|
\n\n\nhttps://youtu.be/BnRaBTepoqI\n\n#### Join me on Telegram\n\nhttps://t.me/leetcode_daily_unstoppable/798\n\n#### Problem TLDR\n\nQueries of max beauty for
|
SamoylenkoDmitry
|
NORMAL
|
2024-11-12T08:04:29.655861+00:00
|
2024-11-12T08:24:39.611426+00:00
| 89 | false |
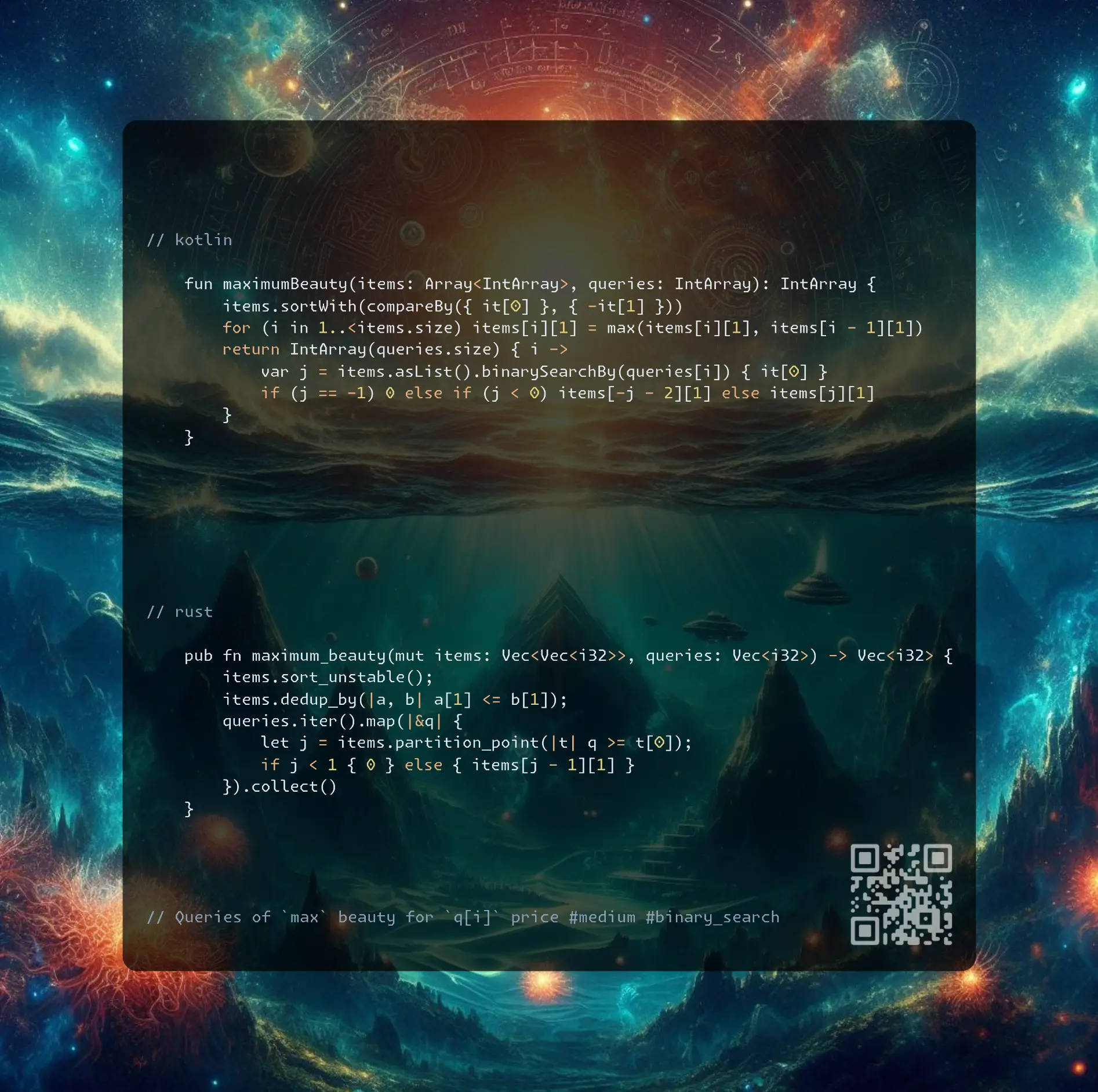\n\n\nhttps://youtu.be/BnRaBTepoqI\n\n#### Join me on Telegram\n\nhttps://t.me/leetcode_daily_unstoppable/798\n\n#### Problem TLDR\n\nQueries of `max` beauty for `q[i]` price #medium #binary_search\n\n#### Intuition\n\nIf we sort everything, we can do a line sweep: for each increasing `query` price move `items` pointer and pick `max` beauty.\n\nMore shorter solution is to do a BinarySearch for each query. But we should precompute `max beauty` for each item price range.\n\n#### Approach\n\n* Kotlin has a `binarySearchBy` but only for `List`\n* Rust & C++ has a more elegant `partition_point`\n\n#### Complexity\n\n- Time complexity:\n$$O(nlog(n))$$ for the Line Sweep and for the Binary Search\n\n- Space complexity:\n$$O(n)$$\n\n#### Code\n\n```kotlin []\n\n fun maximumBeauty(items: Array<IntArray>, queries: IntArray): IntArray {\n items.sortWith(compareBy({ it[0] }, { -it[1] }))\n for (i in 1..<items.size) items[i][1] = max(items[i][1], items[i - 1][1])\n return IntArray(queries.size) { i ->\n var j = items.asList().binarySearchBy(queries[i]) { it[0] }\n if (j == -1) 0 else if (j < 0) items[-j - 2][1] else items[j][1]\n }\n }\n\n```\n```rust []\n\n pub fn maximum_beauty(mut items: Vec<Vec<i32>>, queries: Vec<i32>) -> Vec<i32> {\n items.sort_unstable();\n items.dedup_by(|a, b| a[1] <= b[1]);\n queries.iter().map(|&q| {\n let j = items.partition_point(|t| q >= t[0]);\n if j < 1 { 0 } else { items[j - 1][1] }\n }).collect()\n }\n\n```\n```c++ []\n\n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n sort(begin(items), end(items));\n for (int i = 1; i < items.size(); ++i) items[i][1] = max(items[i][1], items[i - 1][1]);\n vector<int> res;\n for (int q: queries) {\n auto it = partition_point(begin(items), end(items), \n [q](const auto& x) { return q >= x[0];});\n res.push_back(it == begin(items) ? 0 : (*(it - 1))[1]);\n }\n return res;\n }\n\n```
| 5 | 0 |
['Binary Search', 'C++', 'Rust', 'Kotlin']
| 2 |
most-beautiful-item-for-each-query
|
Easy C++ Solution With Small Explanation
|
easy-c-solution-with-small-explanation-b-e5x1
|
Intuition\nHere we have to do two things - first we have to find the price that is closest to the given query and then we have to find the maximum beauty.\n\n#
|
itsme_S
|
NORMAL
|
2024-11-12T05:17:17.535372+00:00
|
2024-11-12T05:17:17.535404+00:00
| 202 | false |
# Intuition\nHere we have to do two things - first we have to find the price that is closest to the given query and then we have to find the maximum beauty.\n\n# Approach\nWe will sort the items first so that we can easily find the beauty for each index and then to apply binary search.\nFor the first part i.e. to search for the prices that is closest to the given query we can use binary search and then for finding the maximum beauty, we can store the maximum beauty till each index in a different array or in the same items array which will optimize memory.\n\n# Complexity\n- Time complexity:\nO(nlogn + mlogn)\n\n- Space complexity:\nO(1)\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int binSearch(int num, vector<vector<int>>& items) {\n int low = 0, high = items.size() - 1;\n int ans = -1;\n \n while (low <= high) {\n int mid = low + (high - low) / 2;\n if (items[mid][0] <= num) {\n ans = mid;\n low = mid + 1;\n } else {\n high = mid - 1;\n }\n }\n \n return ans;\n }\n \n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n sort(items.begin(), items.end());\n \n int maxBeauty = 0;\n for (int i = 0; i < items.size(); ++i) {\n maxBeauty = max(maxBeauty, items[i][1]);\n items[i][1] = maxBeauty;//finding the beauty and placing them inplace without using extra memory\n }\n \n vector<int> ans;\n ans.reserve(queries.size()); \n for (int query : queries) {\n int index = binSearch(query, items);\n if (index != -1) {\n ans.push_back(items[index][1]);\n } else {\n ans.push_back(0);\n }\n }\n \n return ans;\n }\n};\n```
| 5 | 0 |
['C++']
| 1 |
most-beautiful-item-for-each-query
|
3-Line C++ Easy Solution without Loops
|
3-line-c-easy-solution-without-loops-by-41d7w
|
Intuition\nTo maximize efficiency, we can sort the items by price and compute the maximum beauty at each price threshold. By precomputing these values, we can a
|
benjami4n
|
NORMAL
|
2024-11-12T01:13:04.370634+00:00
|
2024-11-12T01:13:04.370661+00:00
| 1,017 | false |
# Intuition\nTo maximize efficiency, we can sort the items by price and compute the maximum beauty at each price threshold. By precomputing these values, we can answer each query in logarithmic time by finding the highest price that doesn\'t exceed the query price.\n\n# Approach\n1. **Sort Items**: Add a dummy item `{0, 0}` and sort items by price.\n2. **Compute Cumulative Maximum Beauty**: Use `partial_sum` to ensure each item at price `p` has the maximum beauty for prices up to `p`.\n3. **Answer Queries with Binary Search**: For each query, find the largest price less than or equal to the query using `upper_bound` and retrieve the corresponding maximum beauty.\n\n# Complexity\n- **Time complexity**: O((n + m) log n), where n is the number of items and m is the number of queries.\n- **Space complexity**: O(n + m), for storing sorted items and query results.\n\n\n# Code\n```cpp []\nclass Solution {\npublic:\n vector<int> maximumBeauty(vector<vector<int>> v, vector<int> q) {\n v.push_back({0, 0}); sort(begin(v), end(v));\n partial_sum(begin(v), end(v), begin(v), [](auto p, auto& c) { c[1] = max(p[1], c[1]); return c; });\n transform(begin(q), end(q), begin(q), [&](int i) { return v[upper_bound(begin(v), end(v), vector{i, INT_MAX}) - begin(v) - 1][1]; });\n return q;\n }\n};\n\n```\n\n\n\n\n
| 5 | 0 |
['Sorting', 'C++']
| 3 |
most-beautiful-item-for-each-query
|
[JavaScript] 2070. Most Beautiful Item for Each Query
|
javascript-2070-most-beautiful-item-for-ceg6o
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n. binary search in items for each queryPrice\n\n# Complexity\n- Time comp
|
pgmreddy
|
NORMAL
|
2023-12-01T16:03:28.375075+00:00
|
2023-12-01T16:08:54.589397+00:00
| 384 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n. binary search in `items` for each `queryPrice`\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n\n---\n\n```\nvar maximumBeauty = function (items, queries) {\n items.sort((a, b) => a[0] - b[0]);\n let maxBeauty = 0;\n let prefixMaxBeauty = [];\n for (let [price, beauty] of items) {\n prefixMaxBeauty.push((maxBeauty = Math.max(maxBeauty, beauty)));\n }\n let answer = [];\n for (let queryPrice of queries) {\n let low = 0;\n let high = items.length - 1;\n while (low <= high) {\n let mid = ~~(low / 2 + high / 2);\n if (items[mid][0] <= queryPrice) {\n low = mid + 1;\n } else {\n high = mid - 1;\n }\n }\n answer.push(high >= 0 ? prefixMaxBeauty[high] : 0);\n }\n return answer;\n};\n```\n\n\n\n---\n
| 5 | 0 |
['JavaScript']
| 1 |
most-beautiful-item-for-each-query
|
Most Beautiful item for Each Query(using Binary Search)
|
most-beautiful-item-for-each-queryusing-oq5il
|
Most Beautiful item for Each Query \n// all steps \n->>>>> \n // items - > [[2,4], [4,5], [2,1] ,[3,6] ,[1,3]] another example i take\n // quries-> [1,3,2
|
BibhabenduMukherjee
|
NORMAL
|
2021-12-05T13:10:38.610180+00:00
|
2021-12-05T13:12:03.537499+00:00
| 207 | false |
**Most Beautiful item for Each Query **\n// all steps \n->>>>> \n // items - > [[2,4], [4,5], [2,1] ,[3,6] ,[1,3]] another example i take\n // quries-> [1,3,2]\n\n // fill the answer array \n // ans = [3,6,4]\n\n\n // sort the items array\n // [[1,3] , [2,1] ,[2,4] ,[3,6] ,[4,5]]\n // store prefix max in items[i][1]\n\n // [[1,3], [2,3], [2,4], [3,6], [4,6]]\n\n // loop over each quries \n // price req is quries[i]\n\n // find a index in items array where items[i][0] > priceRequired\n\n // the previous ind is the ans and the beauty is store over\n // items[ind][1] \n\t \n\t \n\t \n# code -> using binary search\nclass Solution {\npublic:\n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n \n \n sort(items.begin() , items.end());\n\n // calculate the prefix max array\n \n int n = items.size();\n for(int i =0 ; i<n ; i++){\n if(i==0) continue;\n\n items[i][1] = max(items[i-1][1] , items[i][1] );\n }\n\n\n // [[1,3], [2,3], [2,4], [3,6], [4,6]] are formed now\n\nvector<int> ans;\n\n for(auto &priceReq : queries){\n vector<int> dummy(2);\n\n dummy[0] = priceReq;\n dummy[1] = INT_MAX;\n\n int ind = upper_bound(items.begin() , items.end() , dummy) - items.begin();\n\n ind--;\n\n if(ind>=0){\n ans.push_back(items[ind][1]);\n }else\n {\n ans.push_back(0);\n } \n }\n\n\n \n return ans;\n }\n};\n\n\n
| 5 | 0 |
[]
| 0 |
most-beautiful-item-for-each-query
|
📌📌 Well-Explained || 99% faster || Mainly for Beginners 🐍
|
well-explained-99-faster-mainly-for-begi-300y
|
IDEA :\n\n Step 1. Sort the items by price, O(nlog)\n\n Step 2. Iterate items, find maximum value up to now, O(n) and store the max value in dictionary(MAP) her
|
abhi9Rai
|
NORMAL
|
2021-11-26T07:08:51.293978+00:00
|
2021-11-26T07:08:51.294005+00:00
| 537 | false |
## IDEA :\n\n* Step 1. Sort the items by price, O(nlog)\n\n* Step 2. Iterate items, find maximum value up to now, O(n) and store the max value in dictionary(MAP) here `dic`.\n* Step 3. For each queries, binary search the maximum beauty, O(log k) in key of the map which we formed and append the max value of the query from dictionary in O(1) .\n* Step 4. Whole process is doen in `O(q+n)` though.\n\n**Impementation :**\n\'\'\'\n\n\tclass Solution:\n\t\tdef maximumBeauty(self, items: List[List[int]], queries: List[int]) -> List[int]:\n\n\t\t\titems.sort()\n\t\t\tdic = dict()\n\t\t\tres = []\n\t\t\tgmax = 0\n\t\t\tfor p,b in items:\n\t\t\t\tgmax = max(b,gmax)\n\t\t\t\tdic[p] = gmax\n\n\t\t\tkeys = sorted(dic.keys())\n\t\t\tfor q in queries:\n\t\t\t\tind = bisect.bisect_left(keys,q)\n\t\t\t\tif ind<len(keys) and keys[ind]==q:\n\t\t\t\t\tres.append(dic[q])\n\t\t\t\telif ind==0:\n\t\t\t\t\tres.append(0)\n\t\t\t\telse:\n\t\t\t\t\tres.append(dic[keys[ind-1]])\n\n\t\t\treturn res\n\t\n### \tThanks and Upvote if you like the Idea !!\u270C
| 5 | 0 |
['Binary Search Tree', 'Sorting', 'Python', 'Python3']
| 0 |
most-beautiful-item-for-each-query
|
100% faster [Sorting and Map] [C++]
|
100-faster-sorting-and-map-c-by-vaibhavs-3g0g
|
```\nvector maximumBeauty(vector>& items, vector& queries) {\n sort(items.begin(),items.end());\n map mp;\n int maxbeauty=INT_MIN;\n
|
vaibhavshekhawat
|
NORMAL
|
2021-11-13T18:05:33.832776+00:00
|
2021-11-15T06:19:53.493362+00:00
| 402 | false |
```\nvector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n sort(items.begin(),items.end());\n map<int,int> mp;\n int maxbeauty=INT_MIN;\n for(auto i:items){\n maxbeauty=max(maxbeauty,i[1]);\n mp[i[0]]=maxbeauty;\n }\n vector<int> ans(queries.size());\n \n for(int i=0;i<queries.size();i++){\n\t\t\n if(mp.find(queries[i])!=mp.end()){\n ans[i]=mp[queries[i]];\n }\n\t\t\t\n else{\n auto it = mp.lower_bound(queries[i]); // In, it=mp.lower_bound(value), it always points on key which is higher than value\n if(it!=mp.begin()){\n it--;\n ans[i]=(*it).second;\n }\n else ans[i]=0;\n }\n }\n return ans;\n }
| 5 | 0 |
['C']
| 1 |
most-beautiful-item-for-each-query
|
[C++] Sorting + Map + Concept of Prefix Sum (Designing FloorKey in C++)
|
c-sorting-map-concept-of-prefix-sum-desi-gtpm
|
\nclass Solution {\npublic:\n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n map<int,int> m;\n vector<int> ans
|
debanjan2002
|
NORMAL
|
2021-11-13T17:30:39.844340+00:00
|
2021-11-13T17:30:39.844376+00:00
| 449 | false |
```\nclass Solution {\npublic:\n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n map<int,int> m;\n vector<int> ans;\n sort(items.begin(),items.end());\n int maxBeauty = 0;\n \n\t\t// I am filling the map in such a way that every element has the following parts - \n\t\t// First element of a map element (it->first) : Contains PRICE\n\t\t// Second element of a map element (it->second) : Contains Maximum BEAUTY till that PRICE (i.e till it->first)\n\t\t// In this way we are keeping prefix price-beauty map \n\t\t// Since it is a map, it is sorted in terms of the first element, i.e in terms of PRICE.\n for(int i=0; i<items.size(); i++){\n int currMaxPrice = items[i][0];\n int currBeauty = items[i][1];\n maxBeauty = max(maxBeauty,currBeauty);\n m[currMaxPrice] = maxBeauty;\n }\n for(int i=0; i<queries.size(); i++){\n int maxAllowedPrice = queries[i];\n auto begin = m.begin();\n auto end = --m.end();\n\t\t\t\n\t\t\t// If the current query PRICE is less that the smallest PRICE in the map, \n\t\t\t// then there are no PRICE which are less than query[i]\n if(begin->first > maxAllowedPrice)\n ans.push_back(0);\n\t\t\t\t\n\t\t\t// If the current query price is more than the maximum PRICE in the map \n\t\t\t// (i.e it is greater than the last element PRICE in the map), \n\t\t\t// then it is obviously greater than all other PRICE values in the map. \n\t\t\t// In this case we add the last elements BEAUTY, which is the cummulative maximum BEAUTY.\n else if(end->first < maxAllowedPrice){\n ans.push_back(end->second);\n }\n else{\n auto find = m.find(maxAllowedPrice);\n\t\t\t\t\n\t\t\t\t// If the exact PRICE is there in the map, then that element will contain the maximum BEAUTY till that PRICE.\n\t\t\t\t// So we can simply add that BEAUTY\n if(find != m.end())\n ans.push_back(find->second);\n\t\t\t\t\n\t\t\t\t// Else we find the lower_bound (please read about lower_bound, incase you don\'t know).\n\t\t\t\t// And we add the immediate previous BEAUTY value.\n else{\n auto lower = m.lower_bound(maxAllowedPrice);\n --lower;\n ans.push_back(lower->second);\n }\n }\n \n }\n return ans;\n }\n};\n```
| 5 | 1 |
['Binary Search', 'C', 'Sorting', 'Binary Tree', 'Prefix Sum', 'C++']
| 0 |
most-beautiful-item-for-each-query
|
Solved.......🔥🔥🔥
|
solved-by-pritambanik-87s0
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
PritamBanik
|
NORMAL
|
2024-11-12T17:19:58.974992+00:00
|
2024-11-12T17:19:58.975065+00:00
| 45 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: 100%\u2705\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: 100%\u2705\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```c []\n/**\n * Note: The returned array must be malloced, assume caller calls free().\n */\nint compare(const void *a, const void *b) {\n int *item1 = *(int **)a;\n int *item2 = *(int **)b;\n if (item1[0] == item2[0]) return item1[1] - item2[1];\n return item1[0] - item2[0];\n}\n\nint* maximumBeauty(int** items, int itemsSize, int* itemsColSize, int* queries, int queriesSize, int* returnSize) {\n qsort(items, itemsSize, sizeof(int*), compare);\n\n int* maxBeauty = (int*)malloc(itemsSize * sizeof(int));\n maxBeauty[0] = items[0][1];\n for (int i = 1; i < itemsSize; i++) {\n maxBeauty[i] = (maxBeauty[i - 1] > items[i][1]) ? maxBeauty[i - 1] : items[i][1];\n }\n\n int* res = (int*)malloc(queriesSize * sizeof(int));\n *returnSize = queriesSize;\n \n for (int i = 0; i < queriesSize; i++) {\n int q = queries[i];\n int left = 0, right = itemsSize - 1;\n while (left <= right) {\n int mid = (left + right) / 2;\n if (items[mid][0] <= q) left = mid + 1;\n else right = mid - 1;\n }\n res[i] = (right >= 0) ? maxBeauty[right] : 0;\n }\n\n free(maxBeauty);\n return res;\n}\n```
| 4 | 0 |
['Array', 'Binary Search', 'C', 'Sorting']
| 0 |
most-beautiful-item-for-each-query
|
🌟 Beats 75.41 % 👏 || Easy and Step-by-Step Breakdown 🔥💯
|
beats-7541-easy-and-step-by-step-breakdo-28uk
|
\n\n## \uD83C\uDF1F Access Daily LeetCode Solutions Repo : click here\n\n---\n\n\n\n---\n\n# Intuition\nWhen I first looked at this problem, I noticed that we n
|
withaarzoo
|
NORMAL
|
2024-11-12T02:13:42.456121+00:00
|
2024-11-12T02:13:42.456147+00:00
| 879 | false |
\n\n## **\uD83C\uDF1F Access Daily LeetCode Solutions Repo :** [click here](https://github.com/withaarzoo/LeetCode-Solutions)\n\n---\n\n\n\n---\n\n# Intuition\nWhen I first looked at this problem, I noticed that we needed to answer multiple queries by finding the "most beautiful" item within a certain price range for each query. This means we need to efficiently compare items and quickly determine the maximum beauty within each price range. My initial thought was that sorting the items by price and precomputing maximum beauty values would allow us to answer each query in constant time.\n\nBy keeping a running maximum of beauty values for each unique price, we can use binary search on the sorted list to find the maximum beauty for any price constraint given in the queries.\n\n---\n\n# Approach\nHere\'s a breakdown of my approach:\n\n1. **Sort the Items by Price**: I sorted the items by price to ensure that we can easily find items with prices less than or equal to any given query.\n\n2. **Create a Running Maximum of Beauty Values**: As I iterate through the sorted items, I keep track of the maximum beauty seen so far and store it alongside each price. This allows us to know the highest beauty achievable for any price range.\n\n3. **Binary Search for Each Query**: For each query, I used binary search to find the largest price that does not exceed the query price. Using this position, I could quickly get the maximum beauty value for that price. If no such price exists, we return 0.\n\nThis approach combines sorting and binary search to ensure efficient processing of both the items and the queries.\n\n---\n\n# Complexity\n- **Time complexity**: Sorting the items takes \\(O(N \\log N)\\), where \\(N\\) is the number of items. Each query takes \\(O(\\log N)\\) to binary search through the sorted list, making the total complexity \\(O(N \\log N + Q \\log N)\\), where \\(Q\\) is the number of queries.\n- **Space complexity**: We use \\(O(N)\\) space for storing the precomputed prices and beauty values.\n\n---\n\n# Code\n```C++ []\n#include <vector>\n#include <algorithm>\nusing namespace std;\n\nclass Solution {\npublic:\n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n // Sort items by price\n sort(items.begin(), items.end());\n\n // Prepare price-beauty pairs with running max beauty\n vector<pair<int, int>> priceBeauty;\n int maxBeauty = 0;\n for (auto& item : items) {\n maxBeauty = max(maxBeauty, item[1]);\n priceBeauty.push_back({item[0], maxBeauty});\n }\n\n // Process each query\n vector<int> result;\n for (int query : queries) {\n auto it = upper_bound(priceBeauty.begin(), priceBeauty.end(), make_pair(query, INT_MAX)) - 1;\n result.push_back(it >= priceBeauty.begin() ? it->second : 0);\n }\n return result;\n }\n};\n\n```\n```Java []\nimport java.util.*;\n\nclass Solution {\n public int[] maximumBeauty(int[][] items, int[] queries) {\n Arrays.sort(items, Comparator.comparingInt(a -> a[0]));\n\n List<int[]> priceBeauty = new ArrayList<>();\n int maxBeauty = 0;\n for (int[] item : items) {\n maxBeauty = Math.max(maxBeauty, item[1]);\n priceBeauty.add(new int[]{item[0], maxBeauty});\n }\n\n int[] result = new int[queries.length];\n for (int i = 0; i < queries.length; i++) {\n int query = queries[i];\n int idx = binarySearch(priceBeauty, query);\n result[i] = idx != -1 ? priceBeauty.get(idx)[1] : 0;\n }\n return result;\n }\n\n private int binarySearch(List<int[]> priceBeauty, int query) {\n int left = 0, right = priceBeauty.size() - 1;\n while (left <= right) {\n int mid = left + (right - left) / 2;\n if (priceBeauty.get(mid)[0] <= query) left = mid + 1;\n else right = mid - 1;\n }\n return right;\n }\n}\n\n```\n```JavaScript []\n/**\n * @param {number[][]} items\n * @param {number[]} queries\n * @return {number[]}\n */\nvar maximumBeauty = function(items, queries) {\n items.sort((a, b) => a[0] - b[0]);\n let priceBeauty = [];\n let maxBeauty = 0;\n\n for (let [price, beauty] of items) {\n maxBeauty = Math.max(maxBeauty, beauty);\n priceBeauty.push([price, maxBeauty]);\n }\n\n return queries.map(query => {\n let left = 0, right = priceBeauty.length - 1;\n while (left <= right) {\n let mid = left + Math.floor((right - left) / 2);\n if (priceBeauty[mid][0] <= query) left = mid + 1;\n else right = mid - 1;\n }\n return right >= 0 ? priceBeauty[right][1] : 0;\n });\n};\n\n```\n```Python []\nfrom bisect import bisect_right\nfrom typing import List\n\nclass Solution:\n def maximumBeauty(self, items: List[List[int]], queries: List[int]) -> List[int]:\n items.sort()\n price_beauty = []\n max_beauty = 0\n\n for price, beauty in items:\n max_beauty = max(max_beauty, beauty)\n price_beauty.append((price, max_beauty))\n\n result = []\n for query in queries:\n idx = bisect_right(price_beauty, (query, float(\'inf\'))) - 1\n result.append(price_beauty[idx][1] if idx >= 0 else 0)\n \n return result\n\n```\n```Go []\nimport (\n "sort"\n)\n\nfunc maximumBeauty(items [][]int, queries []int) []int {\n sort.Slice(items, func(i, j int) bool {\n return items[i][0] < items[j][0]\n })\n\n priceBeauty := make([][2]int, 0)\n maxBeauty := 0\n for _, item := range items {\n price, beauty := item[0], item[1]\n maxBeauty = max(maxBeauty, beauty)\n priceBeauty = append(priceBeauty, [2]int{price, maxBeauty})\n }\n\n result := make([]int, len(queries))\n for i, query := range queries {\n idx := sort.Search(len(priceBeauty), func(j int) bool {\n return priceBeauty[j][0] > query\n }) - 1\n if idx >= 0 {\n result[i] = priceBeauty[idx][1]\n } else {\n result[i] = 0\n }\n }\n return result\n}\n\nfunc max(a, b int) int {\n if a > b {\n return a\n }\n return b\n}\n\n```\n\n---\n\n# Step-by-Step Detailed Explanation\n\n1. **Sort the Items**: We first sort the items by price. This allows us to maintain an increasing sequence of prices, making it easier to find items that fall within any price range.\n\n2. **Compute Running Maximum Beauty**: By iterating over the sorted items and keeping track of the maximum beauty encountered so far, we create a list of pairs `[price, maxBeauty]`. For each price, we store the highest beauty achievable at or below that price.\n\n3. **Binary Search on Queries**: For each query, we perform a binary search on the `priceBeauty` list to find the highest price that does not exceed the query price. Using this index, we can directly retrieve the maximum beauty for that price range.\n\nThis approach ensures that each query is handled efficiently by leveraging sorting and binary search. It\u2019s a practical and optimized solution to handle large inputs.\n\n---\n\n\n
| 4 | 0 |
['Array', 'Binary Search', 'Sorting', 'C++', 'Java', 'Go', 'Python3', 'JavaScript']
| 3 |
most-beautiful-item-for-each-query
|
Two solutions: Binary search and Sorting
|
two-solutions-binary-search-and-sorting-0700i
|
Binary search: time $O((M+N)\u22C5logM)$\n\nclass Solution:\n def maximumBeauty(self, items: List[List[int]], queries: List[int]) -> List[int]:\n item
|
xxxxkav
|
NORMAL
|
2024-11-12T00:04:25.384086+00:00
|
2024-11-12T01:11:59.059141+00:00
| 799 | false |
1. Binary search: time $O((M+N)\u22C5logM)$\n```\nclass Solution:\n def maximumBeauty(self, items: List[List[int]], queries: List[int]) -> List[int]:\n items.sort(key = itemgetter(0))\n max_beauty = [*accumulate(map(itemgetter(1), items), max, initial = 0)]\n return [max_beauty[bisect_right(items, q, key = itemgetter(0))] for q in queries]\n```\n> More readable\n```\nclass Solution:\n def maximumBeauty(self, items: List[List[int]], queries: List[int]) -> List[int]:\n items.sort(key = itemgetter(0))\n max_beauty, curr_max_beauty = [0], 0\n for price, beauty in items:\n curr_max_beauty = max(curr_max_beauty, beauty)\n max_beauty.append(curr_max_beauty)\n ans = []\n for q in queries:\n i = bisect_right(items, q, key = itemgetter(0))\n ans.append(max_beauty[i])\n return ans\n```\n2. Sorting: time $O(M\u22C5logM+N\u22C5logN)$\n```\nclass Solution:\n def maximumBeauty(self, items: List[List[int]], queries: List[int]) -> List[int]:\n items.sort(key = lambda n: -n[0])\n ans, max_beauty = [0] * len(queries), 0\n for i in sorted(range(len(queries)), key = lambda i: queries[i]):\n while items and items[-1][0] <= queries[i]:\n max_beauty = max(max_beauty, items.pop()[1])\n ans[i] = max_beauty\n return ans\n```
| 4 | 0 |
['Binary Search', 'Sorting', 'Python3']
| 1 |
most-beautiful-item-for-each-query
|
Easy and simple approach
|
easy-and-simple-approach-by-krushna_yesh-mdb5
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach : Prefix and Binary\n Describe your approach to solving the problem. \n\n#
|
Krushna_Yeshwante
|
NORMAL
|
2024-09-10T18:37:14.400124+00:00
|
2024-09-10T18:37:14.400140+00:00
| 180 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach : Prefix and Binary\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(nlogn+mlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n+m)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\npublic int[] maximumBeauty(int[][] items, int[] queries) {\n // Sort the items based on price\n Arrays.sort(items, (a, b) -> Integer.compare(a[0], b[0]));\n \n int n = items.length;\n int[] maxBeauty = new int[n];\n int[] prices = new int[n];\n \n // Fill maxBeauty with the maximum beauty seen so far and prices with item prices\n maxBeauty[0] = items[0][1];\n prices[0] = items[0][0];\n \n for (int i = 1; i < n; i++) {\n prices[i] = items[i][0];\n maxBeauty[i] = Math.max(maxBeauty[i - 1], items[i][1]);\n }\n \n // Array to store the results for the queries\n int m = queries.length;\n int[] answer = new int[m];\n \n // For each query, find the maximum beauty with price <= query using binary search\n for (int i = 0; i < m; i++) {\n int idx = binarySearch(prices, queries[i]);\n if (idx == -1) {\n answer[i] = 0; // No item has price <= queries[i]\n } else {\n answer[i] = maxBeauty[idx]; // Maximum beauty up to price queries[i]\n }\n }\n \n return answer;\n }\n\n // Binary search to find the largest price <= target\n private int binarySearch(int[] prices, int target) {\n int low = 0, high = prices.length - 1;\n int result = -1;\n \n while (low <= high) {\n int mid = low + (high - low) / 2;\n if (prices[mid] <= target) {\n result = mid; // Save the index of this valid price\n low = mid + 1; // Try to find a larger price within the limit\n } else {\n high = mid - 1;\n }\n }\n \n return result;\n}\n}\n```
| 4 | 0 |
['Array', 'Binary Search', 'Sorting', 'Prefix Sum', 'Java']
| 0 |
most-beautiful-item-for-each-query
|
C++ || SORT
|
c-sort-by-ganeshkumawat8740-5mho
|
Code\n\nclass Solution {\npublic:\n vector<int> maximumBeauty(vector<vector<int>>& v1, vector<int>& v) {\n int n = v.size(),i;\n vector<vector<
|
ganeshkumawat8740
|
NORMAL
|
2023-06-20T01:42:13.496576+00:00
|
2023-06-20T01:42:13.496601+00:00
| 445 | false |
# Code\n```\nclass Solution {\npublic:\n vector<int> maximumBeauty(vector<vector<int>>& v1, vector<int>& v) {\n int n = v.size(),i;\n vector<vector<int>> v2;\n for(i=0;i<n;i++){\n v2.push_back({v[i],i});\n }\n vector<int> ans(n,0);\n sort(v1.begin(),v1.end());\n sort(v2.begin(),v2.end());\n // for(auto &i: v1)cout<<i[0]<<" "<<i[1]<<" # ";cout<<endl;\n // for(auto &i: v2)cout<<i[0]<<" "<<i[1]<<" # ";cout<<endl;\n int j = 0, x = 0, a = v1.size(),b=v2.size();\n i = 0;\n while(j<b){\n while(i<a&&v2[j][0]>=v1[i][0]){\n x = max(v1[i][1],x);\n i++;\n }\n ans[v2[j][1]] = x;\n j++;\n }\n return ans;\n }\n};\n```
| 4 | 0 |
['Array', 'Sorting', 'C++']
| 0 |
most-beautiful-item-for-each-query
|
C++||Most Easy Binary Search Solution
|
cmost-easy-binary-search-solution-by-ark-5geb
|
\nclass Solution {\npublic:\n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n sort(items.begin(),items.end());\n
|
Arko-816
|
NORMAL
|
2023-03-10T04:53:20.798137+00:00
|
2023-03-10T04:53:20.798170+00:00
| 258 | false |
```\nclass Solution {\npublic:\n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n sort(items.begin(),items.end());\n map<int,int> mp;\n int maxi=INT_MIN;\n int n=items.size();\n mp[0]=0;\n for(int i=0;i<n;i++)\n {\n maxi=max(maxi,items[i][1]);\n mp[items[i][0]]=maxi;\n }\n vector<int> ans;\n for(int i=0;i<queries.size();i++)\n {\n auto it=mp.lower_bound(queries[i]);\n if(mp.find(queries[i])!=mp.end())\n ans.push_back((*it).second);\n else\n {\n *it--;\n ans.push_back((*it).second);\n }\n }\n return ans;\n }\n};\n```
| 4 | 0 |
['Binary Tree']
| 0 |
most-beautiful-item-for-each-query
|
C++ | MAP |SORTING | WITH EXPLANATION
|
c-map-sorting-with-explanation-by-chikzz-taff
|
PLEASE UPVOTE IF U LIKE MY SOLUTION AND EXPLANATION\n\n\nclass Solution {\npublic:\n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queri
|
chikzz
|
NORMAL
|
2021-11-26T05:34:21.424639+00:00
|
2021-11-26T05:34:21.424668+00:00
| 171 | false |
***PLEASE UPVOTE IF U LIKE MY SOLUTION AND EXPLANATION***\n\n```\nclass Solution {\npublic:\n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n \n //map of the price and the maximum beauty of all the items below the price\n map<int,int>mp2;\n \n //sort the items vector\n sort(items.begin(),items.end());\n \n mp2[items[0][0]]=items[0][1];\n for(int i=1;i<items.size();i++)\n {\n //just store the max_beauty(curr_it)=max(beauty(curr_it),beauty(prev_it));\n //mp2[prev_it] stores the max beauty of all the items whose price are below prev_it(price)\n mp2[items[i][0]]=max(items[i][1],mp2[items[i-1][0]]);\n }\n vector<int>res;\n for(auto &it:queries)\n {\n //for each query we find the price<=query in the map\n auto x=mp2.upper_bound(it);\n \n //if all prices are greater than the query then we return 0\n if(x==mp2.begin()){res.push_back(0);continue;}\n \n //as upper_bound returns the next greater ele even if there is the el present \n\t\t\t//in the map so x-- points to the iterator<=query\n x--;\n \n //just return the beauty associated with the iterator\n res.push_back((*x).second);\n }\n return res;\n }\n};\n```
| 4 | 0 |
['Sorting']
| 0 |
most-beautiful-item-for-each-query
|
[Python3] greedy
|
python3-greedy-by-ye15-etoy
|
Please check out this commit for solutions of biweekly 65. \n\nclass Solution:\n def maximumBeauty(self, items: List[List[int]], queries: List[int]) -> List[
|
ye15
|
NORMAL
|
2021-11-13T22:15:09.198116+00:00
|
2021-11-14T01:47:43.226677+00:00
| 279 | false |
Please check out this [commit](https://github.com/gaosanyong/leetcode/commit/e61879b77928a08bb15cc182a69259d6e2bce59a) for solutions of biweekly 65. \n```\nclass Solution:\n def maximumBeauty(self, items: List[List[int]], queries: List[int]) -> List[int]:\n items.sort()\n ans = [0]*len(queries)\n prefix = ii = 0 \n for x, i in sorted((x, i) for i, x in enumerate(queries)): \n while ii < len(items) and items[ii][0] <= x: \n prefix = max(prefix, items[ii][1])\n ii += 1\n ans[i] = prefix\n return ans \n```
| 4 | 0 |
['Python3']
| 1 |
most-beautiful-item-for-each-query
|
[C++] || Map - Multiset || Simple - Easy to Understand
|
c-map-multiset-simple-easy-to-understand-m1k6
|
class Solution {\npublic:\n \n \n vector maximumBeauty(vector>& items, vector& v) {\n mapm;\n sort(items.begin(), items.end());\n in
|
kukreti____________
|
NORMAL
|
2021-11-13T16:05:51.177638+00:00
|
2021-11-13T16:05:51.177669+00:00
| 101 | false |
class Solution {\npublic:\n \n \n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& v) {\n map<int,int>m;\n sort(items.begin(), items.end());\n int max_val = 0;\n for(int i=0;i<items.size();i++){\n int s= items[i][0];\n int d = items[i][1];\n max_val = max(max_val , d); /// store the max_val , at that point\n m[s] = max(m[s] , max_val); \n }\n \n multiset <int, greater <int> > iammultiset;\n for(auto i : m){\n iammultiset.insert(i.first);\n }\n \n for(int i=0;i<v.size();i++){\n if(m.find(v[i])!=m.end()){ // if v[i] is present in map , simply that number will be maximum\n v[i] = m[v[i]];\n }\n else{ /// else the maximum will me lower_bound of v[i] in map \n v[i] = m[ *iammultiset.lower_bound(v[i]) ];\n }\n }\n \n return v;\n \n }\n};
| 4 | 1 |
[]
| 0 |
most-beautiful-item-for-each-query
|
[C++] Sorting Queries | Explanation | Concise Code + Comments
|
c-sorting-queries-explanation-concise-co-awih
|
Idea\nThe idea is to process the queries in the increasing order. I construct a 2D queries array of dimentions q * 2 which has the index of the query as the sec
|
astroash
|
NORMAL
|
2021-11-13T16:03:04.802842+00:00
|
2021-11-13T16:03:04.802868+00:00
| 166 | false |
**Idea**\nThe idea is to process the queries in the increasing order. I construct a 2D queries array of dimentions *q * 2* which has the index of the query as the second element of each query. This array is sorted on the basis of the first element i.e *the actual query value not its index*. The items array is sorted on the basis of price. Then the queries are processed in increasing order and using a *two-pointer approach*, I maintain an iterator which traverses items in increasing order and it points to the first item whose price is greater than the current query. While doing so, I also determine the maximum beauty encountered. This is the answer for the present query. \n\n**C++**\n```\nclass Solution {\npublic:\n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& qry) {\n int n = items.size();\n int q = qry.size();\n vector<int> op(q);\n\t\t\n\t\t// Creating a 2D queries array to maintain the orginal indices of queries after sorting\n vector<vector<int>> queries(q, vector<int>(2));\n for(int i = 0; i < q; i++) {\n queries[i] = {qry[i], i};\n }\n sort(queries.begin(), queries.end());\n sort(items.begin(), items.end());\n \n int j = 0;\n int ans = 0;\n\t\t\n\t\t// Traversing the queries in increasing order\n for(int i = 0; i < q; i++) {\n\t\t\n\t\t\t// Finding the first item whose price is greater than the query\n\t\t\t// The maximum beauty encountered before this element \n\t\t\t// is the answer for the present query\n while(j < n && items[j][0] <= queries[i][0]) {\n ans = max(ans, items[j][1]);\n j++;\n }\n op[queries[i][1]] = ans;\n }\n \n return op;\n }\n};\n```\n\n**Complexity Analysis**\n*Space Complexity (Auxiliary): O(q), where q is the number of queries.*\n*Time Complexity: O(nlogn + qlogq)*
| 4 | 0 |
[]
| 0 |
most-beautiful-item-for-each-query
|
Java | TreeMap | Simple | No Sorting | Explanation
|
java-treemap-simple-no-sorting-explanati-vksi
|
Approach:\n Create TreeMap[price, max beauty of a product].\n Iterate through tree map and update the max beauty of a product with max beauty to so far.\n For e
|
gnaby
|
NORMAL
|
2021-11-13T16:02:07.653611+00:00
|
2021-11-13T16:39:15.045028+00:00
| 378 | false |
**Approach:**\n* Create TreeMap[price, max beauty of a product].\n* Iterate through tree map and update the max beauty of a product with max beauty to so far.\n* For each query use built in floorEntry method to find the greatest price less than or equal to a query.\n\n**Complexities:**\nTime Complexity: O(N log N + Q log N)\nSpace Complexity: O(N)\n\n**Solution:**\n```\nimport java.util.*;\nclass Solution {\n public int[] maximumBeauty(int[][] items, int[] queries) {\n NavigableMap<Integer, Integer> map = new TreeMap<>();\n \n for (int[] item: items) {\n if (map.containsKey(item[0])) {\n map.put(item[0], Math.max(item[1], map.get(item[0])));\n } else {\n map.put(item[0], item[1]);\n }\n }\n \n int maxSoFar = Integer.MIN_VALUE;\n for (Map.Entry<Integer, Integer> entry : map.entrySet()) {\n maxSoFar = Math.max(maxSoFar, entry.getValue());\n entry.setValue(maxSoFar);\n } \n \n for (int i = 0; i < queries.length; ++ i) {\n Map.Entry<Integer, Integer> entry = map.floorEntry(queries[i]);\n if (entry == null) {\n queries[i] = 0;\n } else {\n queries[i] = entry.getValue();\n }\n }\n \n return queries;\n }\n}\n```
| 4 | 0 |
['Java']
| 1 |
most-beautiful-item-for-each-query
|
simple upper bound binary search approach
|
simple-upper-bound-binary-search-approac-h10z
|
Code\ncpp []\nclass Solution {\npublic:\n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n sort(items.begin(),items.end
|
shashwat1915
|
NORMAL
|
2024-11-12T16:43:09.051330+00:00
|
2024-11-12T16:43:09.051363+00:00
| 51 | false |
# Code\n```cpp []\nclass Solution {\npublic:\n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n sort(items.begin(),items.end());\n vector<int>ans;\n int maxi=INT_MIN;\n for(auto & x:items){\n if(x[1]>maxi) maxi=x[1];\n else x[1]=maxi;\n }\n // for(int i=items.size()-2;i>=0;i--){\n // if(items[i+1][0]!=items[i][0]) continue;\n // items[i][1]=max(items[i][1],items[i+1][1]);\n // }\n // for(auto x:items) cout<<x[0]<<","<<x[1]<<" ";\n for(int i=0;i<queries.size();i++){\n if(items[0][0]>queries[i]){\n ans.push_back(0);\n continue;\n }\n else{\n int start=0,end=items.size();\n while(start<end){\n int mid=start+(end-start)/2;\n if(items[mid][0]<=queries[i]) start=mid+1;\n else end=mid;\n }\n ans.push_back(items[end-1][1]);\n }\n }\n return ans;\n }\n};\n```
| 3 | 0 |
['Array', 'Binary Search', 'Sorting', 'C++']
| 3 |
most-beautiful-item-for-each-query
|
4 ms -> 100% | 91.44 MB -> 95.95% | Readable with Comments (map)
|
4-ms-100-9144-mb-9595-readable-with-comm-tbiv
|
\n\n# Code\ncpp []\nclass Solution {\npublic:\n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n int itemsLen = items.s
|
Ununheks
|
NORMAL
|
2024-11-12T15:33:43.705377+00:00
|
2024-11-12T16:57:38.913184+00:00
| 82 | false |
\n\n# Code\n```cpp []\nclass Solution {\npublic:\n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n int itemsLen = items.size();\n int queriesLen = queries.size();\n\n map<int, int> beautyMap;\n\n int i = 0;\n std::map<int, int>::iterator it;\n\n for (; i < itemsLen; ++i) {\n // We try to find in map element with lower price\n it = beautyMap.upper_bound(items[i][0]);\n it = (it != beautyMap.begin()) ? --it : it;\n\n // Then we add it to map if the price we found is bigger\n // might happen when there is only 1 element in map\n // or we add when the beauty is higher\n if (it->first > items[i][0] || it->second < items[i][1]) {\n beautyMap[items[i][0]] = items[i][1];\n\n // after adding the item to map we iterate over the \n // map and update the beauty for higher prices\n // with higher beauties of lower prices\n for (it = std::next(beautyMap.begin()); it != beautyMap.end(); ++it) {\n if (std::prev(it)->second > it->second)\n it->second = std::prev(it)->second;\n }\n }\n }\n\n // we change the values in queries to beauties you can \n // buy for those prices by ussing upper_bound and --it\n // to find the beauty we can get with that price\n for (i = 0; i < queriesLen; ++i) {\n if (queries[i] < beautyMap.begin()->first) queries[i] = 0;\n else {\n it = beautyMap.upper_bound(queries[i]);\n --it;\n queries[i] = it->second;\n }\n }\n\n return queries;\n }\n};\n```
| 3 | 0 |
['C++']
| 2 |
most-beautiful-item-for-each-query
|
Optimal Approach to Maximum Beauty Queries Using Price Mapping and Binary Search | Python3
|
optimal-approach-to-maximum-beauty-queri-oem3
|
Intuition\nThe goal is to answer each query by finding the maximum beauty of items that have a price less than or equal to the query price. This involves both f
|
Jahnavi_S_Umarji
|
NORMAL
|
2024-11-12T14:42:11.228333+00:00
|
2024-11-12T14:45:31.150221+00:00
| 26 | false |
### Intuition\nThe goal is to answer each query by finding the maximum beauty of items that have a price less than or equal to the query price. This involves both finding the highest beauty value up to a certain price threshold and being able to efficiently retrieve this value for each query. \n\nTo achieve this, we can take advantage of sorting and use a binary search to quickly find the maximum beauty for prices that do not exactly match any given query. By sorting the items based on price and storing the cumulative maximum beauty for each price, we can ensure that we access the best possible beauty values without re-calculating for each query.\n\n### Approach\n1. **Sort Items by Price**: First, sort the `items` list in ascending order of price. This allows us to process items in increasing order, ensuring that each price has the maximum beauty recorded up to that point.\n\n2. **Create a Mapping of Price to Maximum Beauty**:\n - Initialize a dictionary, `fmap`, to store each price along with the maximum beauty achievable at that price or any lower price.\n - Iterate through the sorted `items` list. For each item, update `mx` to be the maximum beauty encountered so far, and map the current price to this maximum beauty in `fmap`.\n\n3. **Process Queries Using Binary Search**:\n - For each query, check if the query price exists directly in `fmap`. If it does, retrieve the beauty value directly.\n - If the query price does not exist in `fmap`, perform a binary search on the sorted list of `fmap` keys to find the largest price that is less than or equal to the query price. Use this price to retrieve the corresponding maximum beauty.\n - Append the beauty value for each query to the `ans` list, returning `0` if no valid price was found.\n\n4. **Return Results**: After processing all queries, return the `ans` list containing the maximum beauty for each query price.\n\n### Complexity\n- **Time Complexity**:\n - Sorting the `items` array takes \\(O(n \\log n)\\), where \\(n\\) is the number of items.\n - Creating the `fmap` dictionary takes \\(O(n)\\), as we iterate through the sorted items.\n - Each query requires \\(O(\\log n)\\) time for a binary search on `fmap` keys, and with \\(q\\) queries, this part takes \\(O(q \\log n)\\).\n - Overall, the time complexity is \\(O((n + q) \\log n)\\).\n\n- **Space Complexity**:\n - Storing the `fmap` dictionary requires \\(O(n)\\) space for the maximum beauties mapped to unique prices.\n - The `ans` array requires \\(O(q)\\) space.\n - Thus, the total space complexity is \\(O(n + q)\\).\n\n# Code\n```python3 []\nclass Solution:\n def maximumBeauty(self, items: List[List[int]], queries: List[int]) -> List[int]:\n items.sort()\n fmap = dict()\n n = len(items)\n mx = float(\'-inf\')\n for lst in items:\n mx = max(mx,lst[1])\n fmap[lst[0]] = mx\n ans = []\n k = list(fmap.keys())\n for ele in queries:\n if ele in fmap:\n ans.append(fmap[ele])\n else:\n l = 0\n r = len(k)-1 \n idx = -1\n while l<=r:\n mid = (l+r)//2\n if k[mid]<ele:\n idx = mid\n l = mid+1\n else:\n r = mid-1\n if idx!=-1:\n ans.append(fmap[k[l-1]])\n else:\n ans.append(0)\n return ans\n\n\n```
| 3 | 0 |
['Array', 'Binary Search', 'Sorting', 'Python3']
| 1 |
most-beautiful-item-for-each-query
|
Python Elegant & Short | Sorting & Prefix Max & Binary Search
|
python-elegant-short-sorting-prefix-max-0jfvi
|
Complexity\n- Time complexity: O((n + m) * \log_2 {n}), where m - length of queries\n- Space complexity: O(n)\n\n# Code\npython3 []\nclass Solution:\n def ma
|
Kyrylo-Ktl
|
NORMAL
|
2024-11-12T08:39:11.618797+00:00
|
2024-11-12T08:39:11.618823+00:00
| 146 | false |
# Complexity\n- Time complexity: $$O((n + m) * \\log_2 {n})$$, where $$m$$ - length of queries\n- Space complexity: $$O(n)$$\n\n# Code\n```python3 []\nclass Solution:\n def maximumBeauty(self, items: list[list[int]], queries: list[int]) -> list[int]:\n prices = []\n beauties = [0]\n\n for price, beauty in sorted(items):\n prices.append(price)\n beauties.append(max(beauties[-1], beauty))\n\n max_beauty = []\n\n for max_price in queries:\n idx = bisect(prices, max_price)\n max_beauty.append(beauties[idx])\n\n return max_beauty\n```\n
| 3 | 0 |
['Binary Search', 'Sorting', 'Prefix Sum', 'Python', 'Python3']
| 0 |
most-beautiful-item-for-each-query
|
STANDARD BINARY SEARCH || C++
|
standard-binary-search-c-by-shahivaibhav-riq3
|
Intuition\n--items[i][0] indicates price and items[i][1] indicates beauty.\n--We want to return ans vector containing maximum beauty for particular query.\n--Th
|
shahivaibhav16
|
NORMAL
|
2024-11-12T07:40:33.635672+00:00
|
2024-11-12T07:40:33.635701+00:00
| 33 | false |
# Intuition\n--items[i][0] indicates price and items[i][1] indicates beauty.\n--We want to return ans vector containing maximum beauty for particular query.\n--The query vector has list of prices for which we want to find maximum beauty from items.\n--The maximum beauty can be of a lower price.\n\nFor eg:- items = [[1,100], [2, 8]], query[1, 2] \nFor this our ans = [100, 100] as upto price 2 our maximum beauty is 100.\n\nSo for this we can precalculate the maximum value upto certain points.\nFor this purpose we will sort the items vector.\n\n# Approach\n1. Sort the items vector.\n2. Precalculate the maximum beauty for every price.\n3. Using standard binary search for optimally finding maximum beauty for each query.\n\n# Complexity\nm -> size of item vector, n -> size of query vector\n\n# Time complexity:- \nO(mlogm)[Sorting]\nO(m)[Finding max Beauty before calculating ans]\nO(nlogm)[Binary Search for each query]\n\n\n### Overall Time Complexity :- \nO((n+m)logm)\n\n# Space Complexity:- \nO(n)[Storing ans]\n\n# Code\n```cpp []\n\n\nclass Solution {\npublic:\n\n int binarySearch(vector<vector<int>>& items, int query){\n \n int n = items.size();\n\n int start = 0;\n int end = n - 1;\n\n int ans = 0;\n\n while(start <= end){\n int mid = start + (end - start)/2;\n\n if(items[mid][0] <= query){\n ans = items[mid][1];\n start = mid+1;\n }\n else{\n end = mid - 1;\n }\n }\n\n return ans;\n }\n\n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n\n //Step1:- Sorting\n sort(items.begin(), items.end());\n\n //Step2: Precalculate maxBeauty \n for (int i = 1; i < items.size(); i++) {\n items[i][1] = max(items[i][1], items[i - 1][1]);\n }\n\n> //Stepr:- Finding our ans by B.S\n int n = queries.size();\n vector<int> maxBeauty(n, 0);\n\n for(int i = 0; i < n; i++){\n int temp = binarySearch(items, queries[i]);\n\n maxBeauty[i] = temp;\n }\n\n return maxBeauty;\n \n }\n};\n\n//Please upvote**\n```
| 3 | 0 |
['Array', 'Binary Search', 'Sorting', 'C++']
| 1 |
most-beautiful-item-for-each-query
|
BEATS 100%.
|
beats-100-by-tejasupadhyay-v4gm
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
tejasupadhyay
|
NORMAL
|
2024-11-12T06:42:40.241080+00:00
|
2024-11-12T06:42:40.241110+00:00
| 75 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution(object):\n def maximumBeauty(self, items, queries):\n \n maxI = float(\'inf\')\n res = [[0, 0, maxI]]\n \n items.sort(key=lambda x: x[0])\n\n for price, beauty in items:\n lastBracket = res[-1]\n if beauty > lastBracket[1]:\n res[-1][2] = price\n res.append([price, beauty, maxI])\n\n ans = []\n\n for x in queries:\n for i in range(len(res) - 1, -1, -1):\n if res[i][0] <= x:\n ans.append(res[i][1])\n break\n\n return ans\n```
| 3 | 0 |
['Python3']
| 0 |
most-beautiful-item-for-each-query
|
Easiest Solution !! Beats 82% (Optimized)
|
easiest-solution-beats-82-optimized-by-n-h6l8
|
Problem Analysis\nThe problem asks us to find the maximum beauty of an item that has a price less than or equal to a given query price. Each item is represented
|
NikhileshGoswami
|
NORMAL
|
2024-11-12T06:41:46.402597+00:00
|
2024-11-12T06:41:46.402631+00:00
| 84 | false |
# Problem Analysis\nThe problem asks us to find the maximum beauty of an item that has a price less than or equal to a given query price. Each item is represented as [price, beauty]. For each price in queries, we need to return the maximum beauty of items that have a price less than or equal to the query.\n# Intuition\n**1.** ***Sorting and Preprocessing:***\n\nIf we sort items by price, we can preprocess to find the maximum beauty seen so far for any given price.\n\nThis allows us to quickly determine the maximum beauty for any price limit using binary search.\n\n**2.** ***Efficient Querying:***\n\nOnce we preprocess the maximum beauty for increasing prices, we can use binary search to quickly answer each query.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n**1.** ***Sort items by price:***\n\nSorting the items helps us to build a list of prices and corresponding maximum beauties in increasing order.\n\n**2.** ***Preprocess Maximum Beauty:***\n\nIterate through the sorted items and maintain the highest beauty encountered so far.\nStore each unique price and its corresponding maximum beauty in a list v (as a pair of (price, max_beauty)).\n\n**3.** ***Answer Queries Using Binary Search:***\n\nFor each query, use lower_bound (binary search) to find the maximum price that is less than or equal to the query price.\nIf such a price is found, return the associated maximum beauty; otherwise, return 0.\n<!-- Describe your approach to solving the problem. -->\n\n# Explanation of the Code\n**1.** ***Sorting Items:***\n\nSorting the items based on price allows us to efficiently find the maximum beauty up to any price.\n\n**2.** ***Building the Preprocessed List (v):***\n\nWe keep track of the maximum beauty encountered so far.\n\nWe only add a new entry if the price changes, ensuring the list remains compact.\n\n**3.** ***Binary Search for Each Query:***\n\nFor each query, use lower_bound to find the smallest element greater than query + 1.\n\nIf the iterator points to the beginning, it means there is no item with a price \u2264 query, so return 0.\n\nOtherwise, return the beauty of the largest item with a price \u2264 query.\n\n# Complexity\n- **Time complexity**: O(n log n + m log n) *where m is the length of queries* \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- **Space complexity:** O(n + m)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n\n\n# Code\n```cpp []\nclass Solution {\npublic:\n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n sort(items.begin(), items.end());\n\n vector<pair<int, int>> v;\n int maxBeauty = 0;\n\n for (const auto& item : items) {\n int price = item[0];\n int beauty = item[1];\n maxBeauty = max(maxBeauty, beauty);\n\n if (v.empty() || v.back().first != price) {\n v.push_back({price, maxBeauty});\n }\n if(v.back().first == price){\n v.back().second = maxBeauty;\n }\n }\n\n vector<int> ans;\n for (int i = 0 ; i < queries.size() ; i++) {\n auto it = lower_bound(v.begin(), v.end(), make_pair(queries[i]+1 , 0));\n if (it == v.begin()) {\n ans.push_back(0);\n } else {\n ans.push_back(prev(it)->second);\n }\n }\n\n return ans;\n }\n};\n\n```\n\n\n\n\n\n
| 3 | 0 |
['Array', 'Binary Search', 'C', 'Sorting', 'C++']
| 0 |
most-beautiful-item-for-each-query
|
Beats 100% simple code using Sorting and Forloop
|
beats-100-simple-code-using-sorting-and-fi8ju
|
Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem requires finding the maximum beauty for each query, where beauty values are
|
Dilpreet1206
|
NORMAL
|
2024-11-12T06:02:59.060070+00:00
|
2024-11-12T06:12:57.139398+00:00
| 174 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem requires finding the maximum beauty for each query, where beauty values are associated with items of certain prices. To achieve this efficiently, we should consider sorting the items by their beauty values in descending order. This way, we can iterate through the items and quickly find the maximum beauty available within a given price constraint.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. **Sort Items by Beauty:** First, sort the items array by beauty values in descending order. This allows us to prioritize higher beauty values when searching for an item that meets the price constraint of each query.\n\n2. **Process Each Query:** For each query:\nInitialize maxi to 0. This variable stores the maximum beauty for items within the price limit of the current query.\nTraverse the sorted items array and check if an item\u2019s price is less than or equal to the query price. If so, set maxi to the beauty value of that item (since it is the highest beauty value encountered so far) and break out of the loop.\n\n3. **Store Results:** For each query, store the maximum beauty found in the ans array and return it as the result.\n\n# Complexity\n- Time Complexity:\nSorting the `items` array takes \\( O(m \\log m) \\), where \\( m \\) is the number of items. For each query, we might traverse all items, resulting in a time complexity of \\( O(m + q \\cdot m) \\), where \\( q \\) is the number of queries. Future optimizations, like binary search, could reduce the inner loop complexity.\n\n- Space Complexity:\nWe use \\( O(q) \\) additional space to store the `ans` array, where \\( q \\) is the number of queries. Other than this, there\u2019s no significant extra auxiliary space required.\n\n# Code\n```java []\nclass Solution {\n public int[] maximumBeauty(int[][] items, int[] queries) {\n Arrays.sort(items,(a,b)-> b[1]-a[1]);\n int ans[] = new int[queries.length];\n for(int i=0;i<queries.length;i++){\n int maxi=0;\n for(int j=0;j<items.length;j++){\n if(items[j][0]<= queries[i]){\n maxi = items[j][1];\n break;\n }\n }\n ans[i] = maxi;\n }\n return ans;\n }\n}\n```\n``` python []\ndef maximumBeauty(items, queries):\n items.sort(key=lambda x: -x[1])\n ans = []\n\n for query in queries:\n maxi = 0\n for price, beauty in items:\n if price <= query:\n maxi = beauty\n break\n ans.append(maxi)\n \n return ans\n```\n``` c++ []\n#include <algorithm>\n#include <vector>\nusing namespace std;\n\nclass Solution {\npublic:\n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n sort(items.begin(), items.end(), [](vector<int>& a, vector<int>& b) {\n return b[1] - a[1];\n });\n\n vector<int> ans(queries.size());\n \n for (int i = 0; i < queries.size(); i++) {\n int maxi = 0;\n for (const auto& item : items) {\n if (item[0] <= queries[i]) {\n maxi = item[1];\n break;\n }\n }\n ans[i] = maxi;\n }\n \n return ans;\n }\n};\n```\n``` javascript []\nfunction maximumBeauty(items, queries) {\n items.sort((a, b) => b[1] - a[1]);\n let ans = [];\n\n for (let query of queries) {\n let maxi = 0;\n for (let [price, beauty] of items) {\n if (price <= query) {\n maxi = beauty;\n break;\n }\n }\n ans.push(maxi);\n }\n\n return ans;\n}\n```
| 3 | 0 |
['Array', 'Binary Search', 'Sorting', 'Python', 'C++', 'Java', 'JavaScript']
| 1 |
most-beautiful-item-for-each-query
|
Find Maximum Beauty within Budget 💸✨ | Efficient Solution for Query-Based Item Search 🕵️♀️
|
find-maximum-beauty-within-budget-effici-54ei
|
Intuition \uD83D\uDCA1\n\nTo find the most beautiful item within a budget for each query, we can leverage a sorted mapping of prices to their maximum achievable
|
lasheenwael9
|
NORMAL
|
2024-11-12T05:06:05.783040+00:00
|
2024-11-12T05:06:05.783077+00:00
| 160 | false |
# Intuition \uD83D\uDCA1\n\nTo find the most beautiful item within a budget for each query, we can leverage a sorted mapping of prices to their maximum achievable beauty. This allows us to quickly answer each query using binary search on price limits.\n\n---\n\n# Approach \uD83D\uDEE0\uFE0F\n\n1. **Build Maximum Beauty Map**:\n - First, map each price to its highest possible beauty using a dictionary (`mp`).\n - For each price in sorted order, we ensure that the beauty at a given price is at least the beauty of any lower-priced items.\n\n2. **Precompute Cumulative Maximums**:\n - Convert the mapping into a list of keys (`keys`), where each position reflects cumulative maximum beauty up to that price.\n\n3. **Answer Each Query Efficiently**:\n - For each query, use binary search (`upper_bound`) on `keys` to find the closest price less than or equal to the query budget. This enables quick access to the maximum achievable beauty within the budget.\n\n---\n\n# Complexity \u23F3\n\n- **Time Complexity**: $$O(n \\log n + m \\log n)$$, where $$n$$ is the number of items and $$m$$ is the number of queries.\n- **Space Complexity**: $$O(n)$$ for the `map` and `keys` array.\n\n---\n\n\n\n# Code \uD83D\uDCBB\n\n```cpp\nclass Solution {\npublic:\n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n // Step 1: Map each price to its maximum beauty\n map<int, int> mp;\n for (vector<int> item : items) {\n mp[item[0]] = max(mp[item[0]], item[1]);\n }\n\n // Step 2: Precompute maximum beauty up to each price point\n vector<int> keys(mp.size() + 1, 0);\n int it = 1;\n for (auto item : mp) {\n keys[it] = item.first;\n mp[keys[it]] = max(mp[keys[it]], mp[keys[it - 1]]);\n it++;\n }\n\n // Step 3: Answer each query using binary search\n vector<int> res(queries.size());\n it = 0;\n for (int q : queries) {\n int i = upper_bound(keys.begin(), keys.end(), q) - keys.begin() - 1;\n res[it] = mp[keys[i]];\n it++;\n }\n\n return res;\n }\n};\n```\n\n---\n\n# Explanation \uD83D\uDCD8\n\n1. **Mapping Price to Maximum Beauty**: This ensures that at any price point, we only consider the most beautiful item.\n2. **Binary Search for Fast Query Resolution**: Each query is resolved in $$O(\\log n)$$ time by finding the closest price within the budget using `upper_bound`.\n\n---\n\n> # Found this solution helpful? **Upvote and Share!** \uD83D\uDC4D\n\n\n
| 3 | 0 |
['Array', 'Binary Search', 'Sorting', 'C++']
| 0 |
most-beautiful-item-for-each-query
|
C# Solution for Most Beautiful Item For Each Query Problem
|
c-solution-for-most-beautiful-item-for-e-qeix
|
Intuition\n Describe your first thoughts on how to solve this problem. \nThe goal is to find the maximum beauty of items available within the price limits speci
|
Aman_Raj_Sinha
|
NORMAL
|
2024-11-12T03:22:35.511434+00:00
|
2024-11-12T03:22:35.511457+00:00
| 211 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe goal is to find the maximum beauty of items available within the price limits specified by each query. A brute-force approach would involve scanning all items for each query, but this would be inefficient for large inputs. Instead, by grouping items by price and precomputing the maximum beauty up to each price, we can efficiently retrieve the required maximum beauty for each query using binary search.\n\nBy first sorting the prices and accumulating maximum beauties, we can handle each query in logarithmic time by searching for the largest price that does not exceed the query\u2019s price.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1.\tGroup and Maximize Beauties by Price:\n\t\u2022\tWe use a dictionary priceToBeauty to store the maximum beauty for each unique price. If multiple items share the same price, only the highest beauty for that price is stored.\n2.\tSort Prices and Accumulate Maximum Beauties:\n\t\u2022\tWe sort the unique prices. After sorting, we accumulate the maximum beauty up to each price. This cumulative process ensures that each entry in priceToBeauty represents the maximum beauty achievable at that price or any lower price.\n\t\u2022\tThis cumulative maximum allows us to answer queries efficiently by providing the highest possible beauty for any affordable price.\n3.\tAnswer Queries Using Binary Search:\n\t\u2022\tFor each query, we perform a binary search over the sorted prices to find the largest price that is less than or equal to the query price. The corresponding beauty at this price gives the maximum beauty available for that query.\n\t\u2022\tIf no such price exists (i.e., all items are too expensive), the answer is 0 for that query.\n4.\tReturn Results:\n\t\u2022\tStore each query\u2019s result in the output array and return it as the final answer.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\u2022\tBuilding the Dictionary: O(n), where n is the number of items, as we iterate through items once to populate priceToBeauty.\n\u2022\tSorting Prices: Sorting the unique prices takes O(k log k), where k is the number of unique prices. In the worst case, k <= n.\n\u2022\tAccumulating Maximum Beauties: This requires a single traversal of the sorted prices, which takes O(k).\n\u2022\tBinary Search for Each Query: For each query, we perform a binary search on the sorted list of prices, which takes O(log k) per query. With m queries, this step requires O(m log k) time.\n\u2022\tOverall Time Complexity: The total time complexity is O(n + k log k + m log k). In the worst case where k = n, this simplifies to O(n log n + m log n).\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\u2022\tDictionary: The priceToBeauty dictionary requires O(k) space, where k is the number of unique prices.\n\u2022\tSorted List of Prices: The sortedPrices list requires O(k) space.\n\u2022\tResult Array: We need O(m) space to store the results for each query.\n\u2022\tOverall Space Complexity: The total space complexity is O(k + m), which, in the worst case, is O(n + m) when k = n.\n\n# Code\n```csharp []\npublic class Solution {\n public int[] MaximumBeauty(int[][] items, int[] queries) {\n var priceToBeauty = new Dictionary<int, int>();\n foreach (var item in items) {\n int price = item[0], beauty = item[1];\n if (!priceToBeauty.ContainsKey(price)) {\n priceToBeauty[price] = beauty;\n } else {\n priceToBeauty[price] = Math.Max(priceToBeauty[price], beauty);\n }\n }\n\n var sortedPrices = new List<int>(priceToBeauty.Keys);\n sortedPrices.Sort();\n\n for (int i = 1; i < sortedPrices.Count; i++) {\n priceToBeauty[sortedPrices[i]] = Math.Max(priceToBeauty[sortedPrices[i]], priceToBeauty[sortedPrices[i - 1]]);\n }\n\n int[] results = new int[queries.Length];\n for (int i = 0; i < queries.Length; i++) {\n int queryPrice = queries[i];\n int maxBeauty = GetMaxBeauty(sortedPrices, priceToBeauty, queryPrice);\n results[i] = maxBeauty;\n }\n\n return results;\n }\n private int GetMaxBeauty(List<int> sortedPrices, Dictionary<int, int> priceToBeauty, int queryPrice) {\n int left = 0, right = sortedPrices.Count - 1;\n int result = 0; \n\n while (left <= right) {\n int mid = left + (right - left) / 2;\n if (sortedPrices[mid] <= queryPrice) {\n result = priceToBeauty[sortedPrices[mid]]; \n left = mid + 1; \n } else {\n right = mid - 1; \n }\n }\n\n return result;\n }\n}\n```
| 3 | 0 |
['C#']
| 0 |
most-beautiful-item-for-each-query
|
C++ || SORT
|
c-sort-by-ganeshkumawat8740-3t3y
|
Code\n\nclass Solution {\npublic:\n vector<int> maximumBeauty(vector<vector<int>>& v1, vector<int>& v) {\n int n = v.size(),i;\n vector<vector<
|
ganeshkumawat8740
|
NORMAL
|
2023-06-20T01:42:41.338320+00:00
|
2023-06-20T01:42:41.338349+00:00
| 660 | false |
# Code\n```\nclass Solution {\npublic:\n vector<int> maximumBeauty(vector<vector<int>>& v1, vector<int>& v) {\n int n = v.size(),i;\n vector<vector<int>> v2;\n for(i=0;i<n;i++){\n v2.push_back({v[i],i});\n }\n vector<int> ans(n,0);\n sort(v1.begin(),v1.end());\n sort(v2.begin(),v2.end());\n // for(auto &i: v1)cout<<i[0]<<" "<<i[1]<<" # ";cout<<endl;\n // for(auto &i: v2)cout<<i[0]<<" "<<i[1]<<" # ";cout<<endl;\n int j = 0, x = 0, a = v1.size(),b=v2.size();\n i = 0;\n while(j<b){\n while(i<a&&v2[j][0]>=v1[i][0]){\n x = max(v1[i][1],x);\n i++;\n }\n ans[v2[j][1]] = x;\n j++;\n }\n return ans;\n }\n};\n```
| 3 | 0 |
['Array', 'Sorting', 'C++']
| 1 |
most-beautiful-item-for-each-query
|
By BinarySearch Using Hashing Technique [JAVA] [Optimized Approach]
|
by-binarysearch-using-hashing-technique-jzos6
|
Binary Search using Hashing technique\n\n Sort the items (2D array) By making a pair class and sort it,\n make another beauty array that store the maximum beaut
|
hemant-singh1811
|
NORMAL
|
2022-04-30T11:48:49.486239+00:00
|
2022-04-30T12:32:03.101004+00:00
| 470 | false |
**Binary Search** using **Hashing** technique\n\n* Sort the items (2D array) By making a pair class and sort it,\n* make another beauty array that store the maximum beauty of every index till now (According to the sorted items array indexing) (that will us to achive to get maximum beauty of any index in O(1).\n* now starts traversing on queries ,and on each iteration apply binary search on it.\n\n```\nclass pair {\n\tint p;\n\tint b;\n\n\tpair(int p, int b) {\n\t\tthis.p = p;\n\t\tthis.b = b;\n\t}\n}\n\nclass Solution {\n\tpublic int[] maximumBeauty(int[][] items, int[] q) {\n\n\t\tint n = items.length,i=0;\n\n\t\tpair[] p = new pair[n];\n \n\t\tfor (int[] x : items) {\n\t\t\tint pii = x[0];\n\t\t\tint b = x[1];\n\t\t\tpair pi = new pair(pii, b);\n\t\t\tp[i] = pi;\n\n\t\t\tbe[i] = maxb;\n\t\t\ti++;\n\t\t}\n\n\t\tArrays.sort(p, (a, b) -> {\n\t\t\treturn a.p - b.p;\n\t\t});\n\n\t\ti = 0;\n\t\tint[] be = new int[n];\n\t\tint maxb = Integer.MIN_VALUE;\n\t\t\n\t\tfor (pair x : p) {\n\n\t\t\tmaxb = Integer.max(maxb, x.b);\n\t\t\tbe[i] = maxb;\n\t\t\ti++;\n\t\t}\n\n\t\ti = 0;\n\t\tint[] ans = new int[q.length];\n\n\t\tfor (int x : q) {\n\t\t\tans[i] = search(p, x, be);\n\t\t\ti++;\n\t\t}\n\n\t\treturn ans;\n\t}\n\n\tpublic int search(pair[] p, int el, int[] b) {\n\n\t\tint l = 0, h = p.length - 1, i = -1;\n\n\t\twhile (l <= h) {\n\n\t\t\tint mid = (l + h) / 2;\n\n\t\t\tif (p[mid].p <= el) {\n\t\t\t\ti = mid;\n\t\t\t\tl = mid + 1;\n\t\t\t} else\n\t\t\t\th = mid - 1;\n\t\t}\n\n\t\tif (i == -1) return 0;\n\t\t\n\t\treturn b[i];\n\t}\n}\n```\n
| 3 | 0 |
['Array', 'Sorting', 'Binary Tree', 'Java']
| 0 |
most-beautiful-item-for-each-query
|
Runtime: 264 ms, faster than 100.00% of JavaScript online submissions
|
runtime-264-ms-faster-than-10000-of-java-u7mv
|
\nvar maximumBeauty = function(items, queries) {\n items.sort((a,b) => a[0]-b[0]);\n const n = items.length;\n \n \n let mx = items[0][1];\n \
|
masha-nv
|
NORMAL
|
2022-04-28T20:34:05.928397+00:00
|
2022-04-28T20:34:05.928427+00:00
| 143 | false |
```\nvar maximumBeauty = function(items, queries) {\n items.sort((a,b) => a[0]-b[0]);\n const n = items.length;\n \n \n let mx = items[0][1];\n \n for (let i = 0; i<n; i++) {\n mx = Math.max(mx, items[i][1]);\n items[i][1] = mx;\n }\n \n \n const ans = [];\n \n for (const q of queries) {\n let l = 0, r = n-1, a = 0;\n while (l<=r) {\n let mid = Math.floor(l+(r-l)/2);\n if (items[mid][0]<=q) {\n a = items[mid][1]\n l = mid+1;\n } else r = mid-1;\n }\n ans.push(a)\n }\n \n return ans;\n};\n```
| 3 | 0 |
['Binary Tree', 'JavaScript']
| 0 |
most-beautiful-item-for-each-query
|
Optimized Binary Search with Monotonic Stack
|
optimized-binary-search-with-monotonic-s-xk27
|
Intuition\nThe key insight is that for any given price query, we only care about the item with maximum beauty among all items with prices less than or equal to
|
hisyamsk
|
NORMAL
|
2024-11-24T08:32:39.146784+00:00
|
2024-11-24T08:32:39.146815+00:00
| 11 | false |
# Intuition\nThe key insight is that for any given price query, we only care about the item with maximum beauty among all items with prices less than or equal to the query. We can optimize this by:\n\n1. First sorting items by price\n2. Keeping only items that could potentially be the answer (items with higher beauty for same/lower price)\n3. Using binary search to efficiently find the answer for each query\n\n# Approach\n1. Sort items by price to establish price order\n2. Build an optimized list `max_items` using monotonic stack principle:\n\n - Keep only items where **increasing price leads to increasing beauty**\n - Remove items with same price but lower beauty\n - This ensures `max_items` maintains strictly increasing beauty\n\n\n3. For each query, use binary search to find the rightmost item with `price` <= `query`\n\n# Complexity\n- Time complexity: $O(n \\log n + m \\log n)$, where $n$ is length of items and $m$ is length of queries\n\n - $O(n \\log n)$ for sorting items\n - $O(n)$ for building `max_items` list\n - $O(\\log n)$ for each query\'s binary search\n - Total $O(m \\log n)$ for processing all queries\n\n\n- Space complexity: $O(n)$ for storing `max_items` list\n\n In worst case, all items could be in `max_items` if each has higher beauty than previous\n\n# Code\n```python3 []\nclass Solution:\n def maximumBeauty(self, items: List[List[int]], queries: List[int]) -> List[int]:\n items.sort()\n max_items = []\n for price, beauty in items:\n while (\n max_items and\n max_items[-1][0] == price and\n max_items[-1][1] <= beauty\n ):\n max_items.pop()\n if not max_items or max_items[-1][1] < beauty:\n max_items.append((price, beauty))\n\n return [self.bin_search(max_items, query) for query in queries]\n\n def bin_search(self, items: List[List[int]], query: int) -> int:\n left, right = 0, len(items)-1\n while left <= right:\n mid = left + ((right - left) // 2)\n if items[mid][0] > query:\n right = mid - 1\n else:\n left = mid + 1\n\n return items[right][1] if right != -1 else 0\n```
| 2 | 0 |
['Binary Search', 'Sorting', 'Monotonic Stack', 'Python3']
| 0 |
most-beautiful-item-for-each-query
|
Python | 83ms | Beats 100% | Greedy
|
python-83ms-beats-100-greedy-by-shivamtl-00ib
|
Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem is about finding the maximum beauty for each given query where the price of
|
shivamtld
|
NORMAL
|
2024-11-12T19:57:38.897857+00:00
|
2024-11-12T20:52:00.767558+00:00
| 47 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem is about finding the maximum beauty for each given query where the price of the item is less than or equal to the query price. Given that both the items and queries can be very large, a brute force approach (checking each query against all items) would be inefficient. The goal is to use sorting and efficient look-up techniques to optimize the process.\n\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n**Sort Items:** \nStart by sorting the items based on their price. This allows us to efficiently process the maximum beauty up to any given price point.\n\n**Initialize Variables:**\n\nmaxB: To keep track of the maximum beauty encountered as we process each item. This value is updated whenever an item with higher beauty is found.\ni and j: Two pointers used to iterate through the queries and items, respectively.\n\n**Sort Queries:** \nSort the queries to align the processing of queries with the sorted items, enabling efficient computation of results.\n\n**Process Queries with Two Pointers:**\n\nUsing the two pointers (i for queries and j for items), iterate through the sorted queries.\nFor each query, check whether the current item\'s price is less than or equal to the query. If it is, update maxB (if the current item\'s beauty is greater than maxB), and move to the next item by incrementing j.\nIf the current item\'s price is greater than the query price or if all items have been processed, just move to the next query by incrementing i.\nStore the maximum beauty found for each query price in a dictionary.\n\n**Build Result:**\n After processing all queries, construct the output list using the dictionary values corresponding to the original queries. This step ensures that each query gets the correct maximum beauty value based on its original order, not the sorted order.\n\n# Complexity\n- Time complexity:$$O(Nlogn+Qlogq)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(n+q)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Sanitized Code\n```python3 []\nclass Solution:\n def maximumBeauty(self, items: List[List[int]], queries: List[int]) -> List[int]:\n # Sort items based on their price in ascending order\n items.sort(key=lambda x: x[0])\n \n # Dictionary to store the maximum beauty for each query\n dict1 = {}\n \n # Variables to keep track of the maximum beauty, and indices for items and queries\n max_beauty = 0\n item_index = 0\n query_index = 0\n \n # Sort the queries to process them in order\n sorted_queries = sorted(queries)\n \n # Process each query\n while query_index < len(sorted_queries):\n current_query = sorted_queries[query_index]\n \n # Update the maximum beauty as long as there are items that can be bought within current_query price\n while item_index < len(items) and current_query >= items[item_index][0]:\n max_beauty = max(max_beauty, items[item_index][1])\n item_index += 1\n \n # Store the maximum beauty for the current query price\n dict1[current_query] = max_beauty\n query_index += 1\n \n # Return the results for the original order of queries\n return [dict1[query] for query in queries]\n```\n\n# Original Code\n\n```python3 []\nclass Solution:\n def maximumBeauty(self, items: List[List[int]], queries: List[int]) -> List[int]:\n items.sort(key = lambda x: x[0])\n dict1 = {}\n maxB = i = j = 0\n q= sorted(queries)\n while i<len(q):\n while j<len(items) and q[i]>=items[j][0]:\n maxB = max(maxB, items[j][1] )\n j+=1 \n dict1[q[i]] = maxB\n i+=1\n return [dict1[i] for i in queries]\n```\n\n\n\n\n
| 2 | 0 |
['Array', 'Sorting', 'Python3']
| 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.