question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
most-beautiful-item-for-each-query
|
My solution....
|
my-solution-by-yourstruly_priyanshu-urnx
|
Explanation \n\n1. Sorting the Items:\n - The items list is sorted by price, so we can keep track of the maximum beauty for each price threshold as we iterate
|
Yourstruly_priyanshu
|
NORMAL
|
2024-11-12T17:58:28.844922+00:00
|
2024-11-12T17:58:28.844949+00:00
| 7 | false |
# Explanation \n\n1. **Sorting the Items**:\n - The `items` list is sorted by price, so we can keep track of the maximum beauty for each price threshold as we iterate.\n\n2. **Tracking Maximum Beauty**:\n - `maxb` keeps the maximum beauty seen so far as we iterate through `items`. This allows us to record the best beauty achievable at each price level.\n - Each `(price, max beauty so far)` tuple is appended to the list `b`.\n\n3. **Binary Search on Queries**:\n - For each query price, `bisect_right` is used on `b` to find the index of the highest price that does not exceed the query price.\n - `b[idx][1]` retrieves the maximum beauty at that index. If no prices are less than or equal to the query price, we return `0`.\n\n# Complexity\n- Time complexity:\nO(nlogn+mlogn)\n\n- Space complexity:\nO(n+m)\n\n# Code\n```python3 []\nclass Solution:\n def maximumBeauty(self, items: List[List[int]], queries: List[int]) -> List[int]:\n items.sort()\n b = []\n maxb = 0\n for price, beauty in items:\n maxb = max(maxb, beauty)\n b.append((price, maxb))\n \n res = []\n for q in queries:\n idx = bisect_right(b, (q, float(\'inf\'))) - 1\n res.append(b[idx][1] if idx >= 0 else 0)\n return res\n\n```
| 2 | 0 |
['Python3']
| 0 |
most-beautiful-item-for-each-query
|
Simple and easy solution
|
simple-and-easy-solution-by-yash_visavad-4ik6
|
Code\npython3 []\nclass Solution:\n def maximumBeauty(self, items: List[List[int]], queries: List[int]) -> List[int]:\n mapp = defaultdict(int)\n\n
|
yash_visavadia
|
NORMAL
|
2024-11-12T17:46:20.351741+00:00
|
2024-11-12T17:46:20.351780+00:00
| 4 | false |
# Code\n```python3 []\nclass Solution:\n def maximumBeauty(self, items: List[List[int]], queries: List[int]) -> List[int]:\n mapp = defaultdict(int)\n\n for p, b in items:\n mapp[p] = max(mapp[p], b)\n\n data = sorted(mapp.items())\n i = 0\n ans = [0] * len(queries)\n\n max_beauty = 0\n for q, ind in sorted([(q, i) for i, q in enumerate(queries)]):\n while i < len(data) and data[i][0] <= q:\n max_beauty = max(max_beauty, data[i][1])\n i += 1\n\n ans[ind] = max_beauty\n\n return ans\n```
| 2 | 0 |
['Python3']
| 0 |
most-beautiful-item-for-each-query
|
Java || Easy
|
java-easy-by-saanvi_sonker-labs
|
\n\n# Code\njava []\nclass Solution {\n public int[] maximumBeauty(int[][] items, int[] queries) {\n Arrays.sort(items,(a,b)->a[0]-b[0]);\n int
|
Saanvi_Sonker
|
NORMAL
|
2024-11-12T15:34:21.709652+00:00
|
2024-11-12T15:34:21.709679+00:00
| 39 | false |
\n\n# Code\n```java []\nclass Solution {\n public int[] maximumBeauty(int[][] items, int[] queries) {\n Arrays.sort(items,(a,b)->a[0]-b[0]);\n int n=items.length;\n int[] maxbeauty=new int[n];\n maxbeauty[0]=items[0][1];\n for(int i=1;i<n;i++){\n maxbeauty[i]=Math.max(maxbeauty[i-1],items[i][1]);\n }\n for(int i=0;i<queries.length;i++){\n int q=queries[i];\n int left=0;int right=n-1;\n while (left <= right) {\n int mid = left + (right - left) / 2;\n if (items[mid][0] <= q) {\n left = mid + 1;\n } else {\n right = mid - 1;\n }\n }if(right>=0){queries[i]=maxbeauty[right];}\n else{queries[i]=0;}\n }\n return queries;\n }\n}\n```
| 2 | 0 |
['Java']
| 1 |
most-beautiful-item-for-each-query
|
✅Simple Loop Solution Beats 100% 🔥35ms 🎯
|
simple-loop-solution-beats-100-35ms-by-i-0qbd
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \nC++\n\n\nPython\n\n\n\n
|
Iamorphouz
|
NORMAL
|
2024-11-12T15:25:56.992752+00:00
|
2024-11-12T15:51:10.273176+00:00
| 14 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nC++\n\n\nPython\n\n\n\n# Complexity\n- Time complexity:\n$$O(n^2)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```cpp []\nclass Solution {\npublic:\n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n int maxi = INT_MAX;\n\n sort(items.begin(), items.end());\n\n vector<vector<int>> res = {{0, 0, maxi}}; // minprice beauty maxprice\n\n for(auto& item : items){\n int price = item[0];\n int beauty = item[1];\n if(beauty > res.back()[1]){\n if(price == res.back()[0]){\n res.back()[1] = beauty;\n }\n else{\n res.back()[2] = price;\n res.push_back({price, beauty, maxi});\n }\n }\n }\n\n vector<int> ans;\n\n for(int q : queries){\n for(int i = res.size() - 1; i >= 0; i--){\n if(res[i][0] <= q){\n ans.push_back(res[i][1]);\n break;\n }\n }\n }\n\n return ans;\n }\n};\n```\n```python3 []\nclass Solution:\n def maximumBeauty(self, items: List[List[int]], queries: List[int]) -> List[int]:\n \n maxi = float(\'inf\')\n res = [[0, 0, maxi]] # minprice, beauty, maxprice\n**Bold**\n items.sort(key = lambda x: x[0])\n\n for price, beauty in items:\n \n if beauty > res[-1][1]:\n if price == res[-1][0]:\n res[-1][1] = beauty\n else:\n res[-1][2] = price\n res.append([price, beauty, maxi])\n\n ans = []\n\n for q in queries:\n for i in range(len(res) - 1, -1, -1):\n if res[i][0] <= q:\n ans.append(res[i][1])\n break\n \n return ans\n```
| 2 | 0 |
['Array', 'Sorting', 'C++', 'Python3']
| 0 |
most-beautiful-item-for-each-query
|
Easy Java Solution
|
easy-java-solution-by-priyanshi_chauhan2-s22y
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
priyanshi_chauhan209
|
NORMAL
|
2024-11-12T15:19:13.190679+00:00
|
2024-11-12T15:19:13.190715+00:00
| 35 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int[] maximumBeauty(int[][] items, int[] queries) {\n int []result= new int [queries.length];\n int []prices = new int [items.length];\n int[] max= new int[items.length +1];\n Arrays.sort(items,(a,b) -> Integer.compare(a[0],b[0]));\n\n for (int i=0;i<items.length;i++){\n max[i+1]=Math.max(max[i],items[i][1]);\n\n }\n for (int i=0;i<queries.length;i++){\n int a= binarySearch(items,queries[i]);\n result[i]=max[a];\n }\n return result;\n }\n\n private int binarySearch(int[][] items, int b) {\n int l = 0;\n int r = items.length;\n while (l < r) {\n final int mid = (l + r) / 2;\n if (items[mid][0] > b)\n r = mid;\n else\n l = mid+ 1;\n }\n return l;\n }\n}\n```
| 2 | 0 |
['Java']
| 0 |
most-beautiful-item-for-each-query
|
Beats 100 || C++ || Java || Python || with explanation🔥🔥
|
beats-100-c-java-python-with-explanation-56hm
|
Intuition\nThe key idea behind this solution is to precompute the maximum beauty for each price. This allows us to quickly answer the queries without having to
|
saurabh_bhandariii
|
NORMAL
|
2024-11-12T15:02:56.622036+00:00
|
2024-11-12T15:02:56.622075+00:00
| 18 | false |
# Intuition\nThe key idea behind this solution is to precompute the maximum beauty for each price. This allows us to quickly answer the queries without having to search through all the items every time.\n\nBy sorting the items, we can ensure that the maximum beauty for a given price is the maximum beauty of all items with a price less than or equal to that price. This allows us to efficiently build the maxBeauty vector.\n\nOnce we have the maxBeauty vector, we can simply look up the maximum beauty for each query, which takes constant time.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nSorting the items: We start by sorting the items vector based on the price of the items in ascending order. This will help us efficiently find the maximum beauty for each price.\n\nPrecomputing the maximum beauty: We then iterate through the sorted items and keep track of the maximum beauty seen so far. We store this maximum beauty for each price in a maxBeauty vector.\n\nAnswering the queries: For each query in queries, we need to find the maximum beauty of the items whose price is less than or equal to the current query. To do this, we use the maxBeauty vector to efficiently look up the maximum beauty for each query.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution { \npublic: \n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) { \n int maxi = INT_MAX; \n vector<vector<int>> res = {{0, 0, maxi}}; \n sort(items.begin(), items.end(), [](const vector<int>& a, const vector<int>& b) { \n return a[0] < b[0]; \n }); \n for (const auto& item : items) { \n auto& lastBracket = res.back(); \n if (item[1] > lastBracket[1]) { \n lastBracket[2] = item[0]; \n res.push_back({item[0], item[1], maxi}); \n } \n } \n vector<int> ans; \n for (int x : queries) { \n for (int i = res.size() - 1; i >= 0; i--) { \n if (res[i][0] <= x) { \n ans.push_back(res[i][1]); \n break; \n } \n } \n } \n return ans; \n } \n};\n\n```\n```python []\nclass Solution:\n def maximumBeauty(self, items: List[List[int]], queries: List[int]) -> List[int]:\n maxi = float(\'inf\')\n res = [[0,0,maxi]]\n items.sort(key=lambda x: x[0])\n for price,beauty in items:\n lastbracket = res[-1]\n if beauty > lastbracket[1]:\n res[-1][2] = price\n res.append([price,beauty,maxi])\n ans = []\n for x in queries:\n for i in range(len(res)-1,-1,-1):\n if res[i][0] <= x:\n ans.append(res[i][1])\n break\n return\n```\n```Java []\nclass Solution { \n public int[] maximumBeauty(int[][] items, int[] queries) { \n // Sort the items based on price in ascending order \n Arrays.sort(items, (a, b) -> a[0] - b[0]); \n\n // Precompute the maximum beauty for each price \n int[] maxBeauty = new int[1000001]; \n int maxSoFar = 0; \n for (int[] item : items) { \n maxSoFar = Math.max(maxSoFar, item[1]); \n maxBeauty[item[0]] = maxSoFar; \n } \n\n // Compute the answer for each query \n int[] answer = new int[queries.length]; \n for (int i = 0; i < queries.length; i++) { \n int query = queries[i]; \n int idx = findUpperBound(items, query); \n if (idx == 0) { \n answer[i] = 0; \n } else { \n answer[i] = maxBeauty[items[idx - 1][0]]; \n } \n } \n\n return answer; \n } \n\n private int findUpperBound(int[][] items, int target) { \n int left = 0; \n int right = items.length - 1; \n while (left <= right) { \n int mid = left + (right - left) / 2; \n if (items[mid][0] <= target) { \n left = mid + 1; \n } else { \n right = mid - 1; \n } \n } \n return left; \n } \n}\n```\n
| 2 | 0 |
['C++']
| 1 |
most-beautiful-item-for-each-query
|
Simple and easy java solution
|
simple-and-easy-java-solution-by-apoorvm-w99g
|
Intuition\nThe code is a method designed to find the maximum beauty of items that can be purchased within a given budget defined by the queries. Each item has a
|
Apoorvmittal
|
NORMAL
|
2024-11-12T13:15:24.249907+00:00
|
2024-11-12T13:15:24.249947+00:00
| 40 | false |
# Intuition\nThe code is a method designed to find the maximum beauty of items that can be purchased within a given budget defined by the queries. Each item has a price and a beauty value, and the goal is to return an array of maximum beauty values corresponding to each query.\n\n# Approach\nThe items are sorted in descending order based on their beauty value \n****(b[1] - a[1])**.** This means that the item with the highest beauty will be considered first. \n\nans[] is an integer array initialized to store the final answer.\nThe outer loop iterates over each query in the queries array.\n******## **max** is initialized to zero for each query.******\n\nThe inner loop iterates over all items to find the first item whose price (items[j][0]) is less than or equal to the current query value (queries[i]).\nIf such an item is found, max is updated to the beauty of that item (items[j][1]), and the loop is exited with break.\n\n# After checking all items for the current query, the value of max is stored in the ans array at index i.\n\nFinally, return the ans array.\n\n- Time complexity:\nO(N^2)\n\n- Space complexity:\nO(N)\n\n# Code\n```java []\nclass Solution {\n public int[] maximumBeauty(int[][] items, int[] queries) {\n Arrays.sort(items, (a, b) -> b[1] - a[1]);\n int m = queries.length;\n int ans[] = new int[m];\n for (int i = 0; i < queries.length; i++) {\n int max = 0;\n for (int j = 0; j < items.length; j++) {\n if (items[j][0] <= queries[i]) {\n max = items[j][1];\n break;\n }\n }\n ans[i] = max;\n }\n return ans;\n }\n}\n```
| 2 | 0 |
['Java']
| 0 |
most-beautiful-item-for-each-query
|
simple py solution
|
simple-py-solution-by-noam971-myyb
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
noam971
|
NORMAL
|
2024-11-12T12:06:05.084417+00:00
|
2024-11-12T21:42:32.346623+00:00
| 15 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(nlog(n))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def maximumBeauty(self, items: List[List[int]], queries: List[int]) -> List[int]:\n items.sort(key= lambda x: -x[1]) # sort by beauty\n res = []\n for q in queries:\n for x in items:\n if x[0] <= q:\n res.append(x[1])\n break\n else:\n res.append(0)\n \n return res\n\n\n```
| 2 | 0 |
['Python3']
| 0 |
most-beautiful-item-for-each-query
|
price is key..beauty is value....hello again hashmaps!!
|
price-is-keybeauty-is-valuehello-again-h-kurq
|
Intuition\nFigured that for a corresponding price let\'s just store the max value of the key(less than equal to) in the map.\n\n# Approach\nIntution was correct
|
arnav2000agr
|
NORMAL
|
2024-11-12T06:56:45.887545+00:00
|
2024-11-12T06:56:45.887580+00:00
| 55 | false |
# Intuition\nFigured that for a corresponding price let\'s just store the max value of the key(less than equal to) in the map.\n\n# Approach\nIntution was correct, I managed to make a map that could give me the best beauty value for a key and rest was just plain binary search. Hashtables are too valuable!!\n\n# Code\n```cpp []\nclass Solution {\npublic:\n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) \n {\n unordered_map<int,int> a;\n vector<int> b;\n int n=items.size();\n sort(items.begin(),items.end());\n int m=0;\n for(int i=0;i<n;i++)\n {\n b.push_back(items[i][0]);\n m=max(m,items[i][1]);\n a[items[i][0]]=max(m,items[i][1]);\n }\n vector<int> ans;\n for(int i=0;i<queries.size();i++)\n {\n int l=0,u=n-1,res=0;\n while(l<=u)\n {\n int mid=l+(u-l)/2;\n if(b[mid]>queries[i])\n {\n u=mid-1;\n }\n else if(b[mid]<=queries[i])\n {\n l=mid+1;\n res=max(res,a[b[mid]]);\n }\n }\n ans.push_back(res);\n }\n return ans;\n\n }\n};\n```
| 2 | 0 |
['Array', 'Hash Table', 'Binary Search', 'Sorting', 'C++']
| 0 |
most-beautiful-item-for-each-query
|
(Beat 55%) Easy Approach & Easy to understand 😊😊
|
beat-55-easy-approach-easy-to-understand-1cnf
|
Intuition\n Describe your first thoughts on how to solve this problem. \nThe code uses sorting and a prefix maximum transformation to efficiently answer each qu
|
patelaviral
|
NORMAL
|
2024-11-12T06:33:25.750042+00:00
|
2024-11-12T06:35:42.550057+00:00
| 61 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe code uses sorting and a prefix maximum transformation to efficiently answer each query with binary search. By preprocessing items so that each entry stores the highest achievable beauty up to that price, the binarySearch can quickly find the maximum beauty value for any given target price.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Sort items: The items array is sorted by price in ascending order. This allows us to efficiently find items priced up to a certain value, using binary search later on.\n\n2. Optimize beauty values: As we iterate through the sorted items, we maintain the maximum beauty encountered so far. This allows us to update each item\u2019s beauty value to be the maximum beauty for all items with a price up to that item\u2019s price. This transformation prepares the data so that for any price point, the maximum beauty value up to that price is already computed.\n\n3. Binary search on queries: For each query, the binary search function (binarySearch) helps us find the maximum beauty for items priced up to the query\u2019s target price.\n\n- The binary search finds the highest index in items such that items[mid][0] <= target price.\n- If an item meets this criterion, the corresponding beauty is returned. Otherwise, if no such item is found, we return 0 since no item meets the target price.\n\n# Complexity\n- Time complexity: the overall complexity is \uD835\uDC42((\uD835\uDC5B+\uD835\uDC5A)log \uD835\uDC5B).\n\n# Code\n```java []\nclass Solution {\n public int[] maximumBeauty(int[][] items, int[] queries) {\n int len = queries.length;\n int val = Integer.MIN_VALUE;\n Arrays.sort(items,Comparator.comparingInt(a -> a[0]));\n for(int i = 0;i < items.length;i++){\n val = Math.max(val,items[i][1]);\n items[i][1] = val;\n }\n for(int i = 0;i < len;i++){\n queries[i] = binarySearch(items,queries[i]);\n }\n return queries;\n }\n public int binarySearch(int[][] items, int tar){\n int end = items.length-1;\n int start = 0;\n while(start <= end){\n int mid = start+((end-start)/2);\n if(items[mid][0] <= tar){\n start = mid+1;\n }\n else{\n end = mid-1;\n }\n }\n return start-1 == -1 ? 0 : items[start-1][1];\n }\n}\n```
| 2 | 0 |
['Binary Search', 'Sorting', 'Java']
| 0 |
most-beautiful-item-for-each-query
|
🔥BEATS 💯 % 🎯 | 2 SOLUTIONS | 2nd one is SIMPLE| ✨SUPER EASY BEGINNERS 👏
|
beats-2-solutions-2nd-one-is-simple-supe-9p29
|
\n\n---\n\n### Intuition\nTo find the maximum beauty of an item within a given price, we can use a sorted list of items by price and then determine the highest
|
CodeWithSparsh
|
NORMAL
|
2024-11-12T05:38:34.666025+00:00
|
2024-11-12T16:13:55.968049+00:00
| 29 | false |
\n\n---\n\n### Intuition\nTo find the maximum beauty of an item within a given price, we can use a sorted list of items by price and then determine the highest beauty available for each query price.\n\n### Approach\n1. **Sort Items**: Sort items by price in ascending order.\n2. **Filter and Build a Result List**: Build a list where each entry is a unique price with the highest beauty up to that price.\n3. **Query Search**: For each query, use binary search to find the maximum beauty available within the given budget.\n\n### Complexity\n- **Time Complexity**: Sorting items takes \\(O(n \\log n)\\), and answering each query takes \\(O(q \\log n)\\) due to binary search.\n- **Space Complexity**: \\(O(n + q)\\) for storing the results and answers.\n\n---\n\n\n```dart []\nclass Solution {\n List<int> maximumBeauty(List<List<int>> items, List<int> queries) {\n items.sort((a, b) => a[0].compareTo(b[0]));\n List<List<int>> res = [\n [0, 0, double.maxFinite.toInt()]\n ];\n\n for (List<int> item in items) {\n int price = item[0], beauty = item[1];\n if (beauty > res.last[1]) {\n res.last[2] = price;\n res.add([price, beauty, double.maxFinite.toInt()]);\n }\n }\n\n List<int> ans = List.filled(queries.length, 0);\n for (int j = 0; j < queries.length; j++) {\n int x = queries[j];\n for (int i = res.length - 1; i >= 0; i--) {\n if (res[i][0] <= x) {\n ans[j] = res[i][1];\n break;\n }\n }\n }\n return ans;\n }\n}\n```\n\n\n```python []\nfrom bisect import bisect_right\n\nclass Solution:\n def maximumBeauty(self, items, queries):\n items.sort()\n res = [(0, 0)]\n \n for price, beauty in items:\n if beauty > res[-1][1]:\n res.append((price, beauty))\n \n ans = []\n for x in queries:\n i = bisect_right(res, (x, float(\'inf\'))) - 1\n ans.append(res[i][1])\n \n return ans\n```\n\n\n```javascript []\nclass Solution {\n maximumBeauty(items, queries) {\n items.sort((a, b) => a[0] - b[0]);\n const res = [[0, 0]];\n \n for (const [price, beauty] of items) {\n if (beauty > res[res.length - 1][1]) {\n res.push([price, beauty]);\n }\n }\n \n return queries.map(x => {\n let i = 0;\n while (i < res.length && res[i][0] <= x) i++;\n return res[i - 1][1];\n });\n }\n}\n```\n\n\n```java []\nimport java.util.*;\n\nclass Solution {\n public int[] maximumBeauty(int[][] items, int[] queries) {\n Arrays.sort(items, (a, b) -> Integer.compare(a[0], b[0]));\n List<int[]> res = new ArrayList<>();\n res.add(new int[]{0, 0});\n\n for (int[] item : items) {\n int price = item[0], beauty = item[1];\n if (beauty > res.get(res.size() - 1)[1]) {\n res.add(new int[]{price, beauty});\n }\n }\n\n int[] ans = new int[queries.length];\n for (int i = 0; i < queries.length; i++) {\n int x = queries[i];\n int idx = Collections.binarySearch(res, new int[]{x + 1, 0},\n Comparator.comparingInt(a -> a[0])) - 1;\n if (idx < 0) idx = -idx - 2;\n ans[i] = res.get(idx)[1];\n }\n return ans;\n }\n}\n```\n\n\n```cpp []\n#include <vector>\n#include <algorithm>\nusing namespace std;\n\nclass Solution {\npublic:\n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n sort(items.begin(), items.end());\n vector<pair<int, int>> res = {{0, 0}};\n \n for (auto &item : items) {\n int price = item[0], beauty = item[1];\n if (beauty > res.back().second) {\n res.push_back({price, beauty});\n }\n }\n\n vector<int> ans;\n for (int x : queries) {\n int idx = upper_bound(res.begin(), res.end(), make_pair(x, INT_MAX)) - res.begin() - 1;\n ans.push_back(res[idx].second);\n }\n return ans;\n }\n};\n```\n\n\n```go []\nimport (\n "sort"\n)\n\nfunc maximumBeauty(items [][]int, queries []int) []int {\n sort.Slice(items, func(i, j int) bool {\n return items[i][0] < items[j][0]\n })\n \n res := [][]int{{0, 0}}\n for _, item := range items {\n price, beauty := item[0], item[1]\n if beauty > res[len(res)-1][1] {\n res = append(res, []int{price, beauty})\n }\n }\n \n ans := make([]int, len(queries))\n for i, x := range queries {\n idx := sort.Search(len(res), func(j int) bool { return res[j][0] > x }) - 1\n ans[i] = res[idx][1]\n }\n \n return ans\n}\n```\n\n---\n\n# 2nd Simple Solution\n\nHere\'s the solution in multiple programming languages.\n\n---\n\n### Intuition\nThe task involves finding the maximum beauty of an item within a given price range for each query. Sorting and binary searching for the maximum beauty within budget is a straightforward approach.\n\n### Approach\n1. **Sort Items by Price**: Sort the items by price and then iterate to keep track of the maximum beauty for each price.\n2. **Binary Search for Queries**: Use binary search to find the maximum beauty available for each query price by searching through the sorted list.\n\n### Complexity\n- **Time Complexity**: Sorting the items takes \\(O(n \\log n)\\) time. Each query is processed in \\(O(\\log n)\\) due to binary search, making it \\(O((n + q) \\log n)\\) overall.\n- **Space Complexity**: \\(O(n)\\) for storing the intermediate maximum beauty at each price point.\n\n---\n\n### Code Implementation\n\n```dart []\nclass Solution {\n List<int> maximumBeauty(List<List<int>> items, List<int> queries) {\n items.sort((a, b) => a[0].compareTo(b[0]));\n List<List<int>> sortedBeauty = [];\n sortedBeauty.add(items.first);\n int maxBeauty = items.first[1];\n\n for (int i = 1; i < items.length; i++) {\n int newPrice = items[i][0];\n int newBeauty = items[i][1];\n maxBeauty = max(maxBeauty, newBeauty);\n if (newPrice != sortedBeauty.last[0]) {\n sortedBeauty.add([newPrice, maxBeauty]);\n } else {\n sortedBeauty.last[1] = maxBeauty;\n }\n }\n\n return queries.map((query) => _getMaxBeauty(sortedBeauty, query)).toList();\n }\n\n int _getMaxBeauty(List<List<int>> sortedBeauty, int query) {\n int res = 0, start = 0, end = sortedBeauty.length - 1;\n while (start <= end) {\n int mid = start + (end - start) ~/ 2;\n if (sortedBeauty[mid][0] <= query) {\n res = sortedBeauty[mid][1];\n start = mid + 1;\n } else {\n end = mid - 1;\n }\n }\n return res;\n }\n}\n```\n\n```python []\nfrom bisect import bisect_right\n\nclass Solution:\n def maximumBeauty(self, items, queries):\n items.sort()\n sorted_beauty = [[items[0][0], items[0][1]]]\n max_beauty = items[0][1]\n\n for price, beauty in items[1:]:\n max_beauty = max(max_beauty, beauty)\n if price != sorted_beauty[-1][0]:\n sorted_beauty.append([price, max_beauty])\n else:\n sorted_beauty[-1][1] = max_beauty\n\n def get_max_beauty(query):\n idx = bisect_right(sorted_beauty, [query, float(\'inf\')]) - 1\n return sorted_beauty[idx][1] if idx >= 0 else 0\n\n return [get_max_beauty(query) for query in queries]\n```\n\n```javascript []\nclass Solution {\n maximumBeauty(items, queries) {\n items.sort((a, b) => a[0] - b[0]);\n const sortedBeauty = [[items[0][0], items[0][1]]];\n let maxBeauty = items[0][1];\n\n for (let i = 1; i < items.length; i++) {\n const [price, beauty] = items[i];\n maxBeauty = Math.max(maxBeauty, beauty);\n if (price !== sortedBeauty[sortedBeauty.length - 1][0]) {\n sortedBeauty.push([price, maxBeauty]);\n } else {\n sortedBeauty[sortedBeauty.length - 1][1] = maxBeauty;\n }\n }\n\n return queries.map(query => this.getMaxBeauty(sortedBeauty, query));\n }\n\n getMaxBeauty(sortedBeauty, query) {\n let res = 0, start = 0, end = sortedBeauty.length - 1;\n while (start <= end) {\n const mid = Math.floor((start + end) / 2);\n if (sortedBeauty[mid][0] <= query) {\n res = sortedBeauty[mid][1];\n start = mid + 1;\n } else {\n end = mid - 1;\n }\n }\n return res;\n }\n}\n```\n\n```java []\nimport java.util.*;\n\nclass Solution {\n public int[] maximumBeauty(int[][] items, int[] queries) {\n Arrays.sort(items, Comparator.comparingInt(a -> a[0]));\n List<int[]> sortedBeauty = new ArrayList<>();\n sortedBeauty.add(new int[] {items[0][0], items[0][1]});\n int maxBeauty = items[0][1];\n\n for (int i = 1; i < items.length; i++) {\n int price = items[i][0];\n int beauty = items[i][1];\n maxBeauty = Math.max(maxBeauty, beauty);\n if (price != sortedBeauty.get(sortedBeauty.size() - 1)[0]) {\n sortedBeauty.add(new int[] {price, maxBeauty});\n } else {\n sortedBeauty.get(sortedBeauty.size() - 1)[1] = maxBeauty;\n }\n }\n\n int[] result = new int[queries.length];\n for (int i = 0; i < queries.length; i++) {\n result[i] = getMaxBeauty(sortedBeauty, queries[i]);\n }\n return result;\n }\n\n private int getMaxBeauty(List<int[]> sortedBeauty, int query) {\n int start = 0, end = sortedBeauty.size() - 1, res = 0;\n while (start <= end) {\n int mid = start + (end - start) / 2;\n if (sortedBeauty.get(mid)[0] <= query) {\n res = sortedBeauty.get(mid)[1];\n start = mid + 1;\n } else {\n end = mid - 1;\n }\n }\n return res;\n }\n}\n```\n\n```cpp []\n#include <vector>\n#include <algorithm>\nusing namespace std;\n\nclass Solution {\npublic:\n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n sort(items.begin(), items.end());\n vector<pair<int, int>> sortedBeauty;\n sortedBeauty.push_back({items[0][0], items[0][1]});\n int maxBeauty = items[0][1];\n\n for (int i = 1; i < items.size(); i++) {\n int price = items[i][0];\n int beauty = items[i][1];\n maxBeauty = max(maxBeauty, beauty);\n if (price != sortedBeauty.back().first) {\n sortedBeauty.push_back({price, maxBeauty});\n } else {\n sortedBeauty.back().second = maxBeauty;\n }\n }\n\n vector<int> result;\n for (int query : queries) {\n result.push_back(getMaxBeauty(sortedBeauty, query));\n }\n return result;\n }\n\nprivate:\n int getMaxBeauty(const vector<pair<int, int>>& sortedBeauty, int query) {\n int res = 0, start = 0, end = sortedBeauty.size() - 1;\n while (start <= end) {\n int mid = start + (end - start) / 2;\n if (sortedBeauty[mid].first <= query) {\n res = sortedBeauty[mid].second;\n start = mid + 1;\n } else {\n end = mid - 1;\n }\n }\n return res;\n }\n};\n```\n\n```go []\nimport (\n "sort"\n)\n\nfunc maximumBeauty(items [][]int, queries []int) []int {\n sort.Slice(items, func(i, j int) bool {\n return items[i][0] < items[j][0]\n })\n \n sortedBeauty := [][]int{{items[0][0], items[0][1]}}\n maxBeauty := items[0][1]\n\n for i := 1; i < len(items); i++ {\n price, beauty := items[i][0], items[i][1]\n maxBeauty = max(maxBeauty, beauty)\n if price != sortedBeauty[len(sortedBeauty)-1][0] {\n sortedBeauty = append(sortedBeauty, []int{price, maxBeauty})\n } else {\n sortedBeauty[len(sortedBeauty)-1][1] = maxBeauty\n }\n }\n\n res := make([]int, len(queries))\n for i, query := range queries {\n res[i] = getMaxBeauty(sortedBeauty, query)\n }\n return res\n}\n\nfunc getMaxBeauty(sortedBeauty [][]int, query int) int {\n res, start, end := 0, 0, len(sortedBeauty)-1\n for start <= end {\n mid := start + (end-start)/2\n if sortedBeauty[mid][0] <= query {\n res = sortedBeauty[mid][1]\n start = mid + 1\n } else {\n end = mid - 1\n }\n }\n return res\n}\n\nfunc max(a, b int) int {\n if a > b {\n return a\n }\n return b\n}\n```\n\n\n\n\n\n\n---\n\n {:style=\'width:250px\'}
| 2 | 0 |
['Array', 'Binary Search', 'C', 'Sorting', 'C++', 'Java', 'Go', 'Python3', 'JavaScript', 'Dart']
| 0 |
most-beautiful-item-for-each-query
|
Java Clean TM Solution
|
java-clean-tm-solution-by-shree_govind_j-xs7x
|
Complexity\n- Time complexity:O(sorting+n+m)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity:O(n)\n Add your space complexity here, e.g. O(n)
|
Shree_Govind_Jee
|
NORMAL
|
2024-11-12T04:24:16.629422+00:00
|
2024-11-12T04:24:16.629487+00:00
| 145 | false |
# Complexity\n- Time complexity:$$O(sorting+n+m)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\n// TC:O(2n+SORTING)\n// SC:O(items.length)\nclass Solution {\n public int[] maximumBeauty(int[][] items, int[] queries) {\n Arrays.sort(items, (a, b) -> a[0] - b[0]);\n\n int currMax = Integer.MIN_VALUE;\n TreeMap<Integer, Integer> tm = new TreeMap<>();\n tm.put(0, 0);\n for (int[] item : items) {\n currMax = Math.max(currMax, item[1]);\n tm.put(item[0], currMax);\n }\n\n int[] res = new int[queries.length];\n for (int i = 0; i < queries.length; i++) {\n res[i] = tm.floorEntry(queries[i]).getValue();\n }\n return res;\n }\n}\n```
| 2 | 0 |
['Array', 'Hash Table', 'Binary Search', 'Sorting', 'Hash Function', 'Java']
| 0 |
most-beautiful-item-for-each-query
|
Rust | 7ms | beats 100%
|
rust-7ms-beats-100-by-jsusi-lopr
|
Code\nrust []\nimpl Solution {\n pub fn maximum_beauty(mut items: Vec<Vec<i32>>, queries: Vec<i32>) -> Vec<i32> {\n items.sort_unstable_by_key(|k| (-k
|
JSusi
|
NORMAL
|
2024-11-12T04:03:03.033697+00:00
|
2024-11-12T07:26:59.407915+00:00
| 38 | false |
# Code\n```rust []\nimpl Solution {\n pub fn maximum_beauty(mut items: Vec<Vec<i32>>, queries: Vec<i32>) -> Vec<i32> {\n items.sort_unstable_by_key(|k| (-k[1], k[0]));\n items.dedup_by(|a, b| a[0] >= b[0]);\n queries\n .into_iter()\n .map(|q| match items.binary_search_by_key(&-q, |k| -k[0]) {\n Ok(i) | Err(i) => items.get(i).map_or(0, |k| k[1]),\n })\n .collect()\n }\n}\n```
| 2 | 0 |
['Rust']
| 1 |
most-beautiful-item-for-each-query
|
Java Solution for Most Beautiful Item For Each Query Problem
|
java-solution-for-most-beautiful-item-fo-pqu9
|
Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem requires finding the maximum beauty of items that are affordable given a ce
|
Aman_Raj_Sinha
|
NORMAL
|
2024-11-12T03:17:03.642841+00:00
|
2024-11-12T03:17:03.642875+00:00
| 179 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem requires finding the maximum beauty of items that are affordable given a certain price limit in each query. Since we want to efficiently determine this maximum beauty for multiple queries, we can utilize sorting and a cumulative maximum array to avoid redundant calculations.\n\nBy sorting items by price, we can pre-compute the maximum beauty available at each price point. Then, for each query, we use binary search to quickly locate the highest affordable price index and retrieve the corresponding maximum beauty. This approach allows each query to be processed in logarithmic time.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1.\tSort Items by Price:\n\t\u2022\tFirst, we sort the items array based on price in ascending order. Sorting helps ensure that as we move through the items, each item\u2019s price will always be greater than or equal to the previous item\u2019s price.\n2.\tPrecompute Maximum Beauty Up to Each Price:\n\t\u2022\tAfter sorting, we initialize an array maxBeauty where maxBeauty[i] will store the maximum beauty of any item with a price less than or equal to the price of items[i].\n\t\u2022\tWe traverse through the sorted items, maintaining the highest beauty seen so far, and update maxBeauty accordingly.\n\t\u2022\tThis array allows us to look up the maximum beauty for any price threshold efficiently.\n3.\tAnswer Queries Using Binary Search:\n\t\u2022\tFor each query price, we want to find the maximum beauty of an item that does not exceed this price. Using binary search, we locate the rightmost index in items where the price is less than or equal to the query price.\n\t\u2022\tIf such an index is found, maxBeauty[idx] provides the maximum beauty up to that price; otherwise, the answer is 0 if no items are affordable.\n4.\tReturn the Results:\n\t\u2022\tWe store each result for the queries in an output array and return it.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\u2022\tSorting the Items: Sorting items by price takes O(n log n), where n is the number of items.\n\u2022\tBuilding maxBeauty Array: This step requires a single traversal through items, taking O(n).\n\u2022\tProcessing Queries: For each query, we perform a binary search over items, which takes O(log n). Since there are m queries, the total time for processing all queries is O(m log n).\n\u2022\tOverall Time Complexity: The total time complexity is O(n log n + m log n).\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\u2022\tStorage for maxBeauty Array: This array requires O(n) space to store the cumulative maximum beauties up to each price.\n\u2022\tOutput Array: We need O(m) space to store the results for each query.\n\u2022\tOverall Space Complexity: The total space complexity is O(n + m).\n\n# Code\n```java []\nclass Solution {\n public int[] maximumBeauty(int[][] items, int[] queries) {\n Arrays.sort(items, (a, b) -> Integer.compare(a[0], b[0]));\n\n int n = items.length;\n int[] maxBeauty = new int[n];\n maxBeauty[0] = items[0][1];\n for (int i = 1; i < n; i++) {\n maxBeauty[i] = Math.max(maxBeauty[i - 1], items[i][1]);\n }\n int[] result = new int[queries.length];\n for (int i = 0; i < queries.length; i++) {\n int queryPrice = queries[i];\n int idx = binarySearch(items, queryPrice);\n result[i] = (idx == -1) ? 0 : maxBeauty[idx];\n }\n \n return result;\n }\n private int binarySearch(int[][] items, int price) {\n int left = 0, right = items.length - 1;\n int result = -1;\n \n while (left <= right) {\n int mid = left + (right - left) / 2;\n if (items[mid][0] <= price) {\n result = mid; \n left = mid + 1;\n } else {\n right = mid - 1;\n }\n }\n \n return result;\n }\n}\n```
| 2 | 0 |
['Java']
| 0 |
most-beautiful-item-for-each-query
|
✅ Simple Java Solution
|
simple-java-solution-by-harsh__005-uwk6
|
CODE\nJava []\npublic int[] maximumBeauty(int[][] items, int[] queries) {\n\tint n = items.length;\n\tArrays.sort(items, (a,b)->{\n\t\tif(a[0] == b[0]) return b
|
Harsh__005
|
NORMAL
|
2024-11-12T03:10:00.063432+00:00
|
2024-11-12T03:10:00.063468+00:00
| 7 | false |
## **CODE**\n```Java []\npublic int[] maximumBeauty(int[][] items, int[] queries) {\n\tint n = items.length;\n\tArrays.sort(items, (a,b)->{\n\t\tif(a[0] == b[0]) return b[1]-a[1];\n\t\treturn a[0]-b[0];\n\t});\n\n\tfor(int i=1; i<n; i++) {\n\t\titems[i][1] = Math.max(items[i-1][1], items[i][1]);\n\t}\n\n\tint res[] = new int[queries.length];\n\tfor(int i=0; i<queries.length; i++) {\n\t\tint l = 0, r = n-1;\n\t\twhile(l <= r) {\n\t\t\tint mid = l + (r-l)/2;\n\t\t\tif(items[mid][0] <= queries[i]) {\n\t\t\t\tres[i] = items[mid][1];\n\t\t\t\tl = mid+1;\n\t\t\t} else {\n\t\t\t\tr = mid-1;\n\t\t\t}\n\t\t}\n\t}\n\n\treturn res;\n}\n```
| 2 | 0 |
['Sorting', 'Binary Tree']
| 1 |
most-beautiful-item-for-each-query
|
Unique Beginner-Friendly Intuitive Solution (HashMap + Sorting)
|
unique-beginner-friendly-intuitive-solut-huh6
|
Intuition\nTried Brute Force and Worked up on it.\n\n# Approach\nBrute Force but the searching for the max beauty for a particular query becomes easier with the
|
sarthakvs
|
NORMAL
|
2024-11-12T02:17:56.465774+00:00
|
2024-11-12T10:33:27.758908+00:00
| 127 | false |
# Intuition\nTried Brute Force and Worked up on it.\n\n# Approach\nBrute Force but the searching for the max beauty for a particular query becomes easier with the STL.\n\n# Complexity\n- Time complexity:\nO(nlogn + mlogn)\n\n- Space complexity:\nO(n)\n\n# Code\n```cpp []\nclass Solution {\npublic:\n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n // Sort items by price first, then by beauty\n sort(items.begin(), items.end());\n \n // Create a map to store the maximum beauty for each price\n map<int, int> priceToBeauty;\n int maxBeauty = 0;\n for (const auto& item : items) {\n // Update maxBeauty if the current item\'s beauty is greater\n maxBeauty = max(maxBeauty, item[1]);\n priceToBeauty[item[0]] = maxBeauty;\n }\n // Result vector to store the results for each query\n vector<int> res;\n for (const auto& query : queries) {\n // Find the max beauty for any price less than or equal to the query\n auto it = priceToBeauty.upper_bound(query);\n if (it == priceToBeauty.begin()) {\n res.push_back(0); // No items available within the price range\n } else {\n res.push_back(prev(it)->second); // Previous max beauty\n }\n }\n \n return res;\n }\n};\n\n```
| 2 | 0 |
['Array', 'Ordered Map', 'Sorting', 'Ordered Set', 'C++']
| 1 |
most-beautiful-item-for-each-query
|
KOTLIN and JAVA solution - beats 100%
|
kotlin-and-java-solution-beats-100-by-an-jkk1
|
\u2618\uFE0F\u2618\uFE0F\u2618\uFE0F If this solution was helpful, please consider upvoting! \u2705\n\n# Intuition\nThis problem requires finding the maximum be
|
anlk
|
NORMAL
|
2024-11-12T00:10:34.690826+00:00
|
2024-11-12T00:10:34.690853+00:00
| 206 | false |
\u2618\uFE0F\u2618\uFE0F\u2618\uFE0F If this solution was helpful, please consider upvoting! \u2705\n\n# Intuition\nThis problem requires finding the maximum beauty of items that meet a price constraint, given multiple queries. \n\nSorting the items by price can simplify the task, allowing us to efficiently track the highest available beauty for each query using binary search.\n\n# Approach\n- Sort and Track Maximum Beauty:\n\n - Sort items by price and sort queries while keeping track of their original indices.\n - Traverse the sorted items to build a cumulative list of maximum beauty values up to each price, so we can easily know the maximum beauty available for any price constraint.\n- Binary Search with Queries:\n\n - For each query (sorted in ascending order), use binary search to find the highest price that\u2019s within the query price.\n - Retrieve the corresponding maximum beauty for that price from the precomputed list.\n- Efficiency with Binary Search:\n\n - Using binary search on the sorted prices reduces the complexity for each query, making the solution efficient for large inputs.\n\n\n# Code\n```Kotlin []\nclass Solution {\n fun maximumBeauty(items: Array<IntArray>, queries: IntArray): IntArray {\n items.sortBy { it[0] }\n \n val maxBeautyByPrice = TreeMap<Int, Int>()\n var maxBeauty = 0\n \n for ((price, beauty) in items) {\n maxBeauty = maxOf(maxBeauty, beauty)\n maxBeautyByPrice[price] = maxBeauty\n }\n \n return queries.map { query ->\n maxBeautyByPrice.floorEntry(query)?.value ?: 0\n }.toIntArray() \n }\n}\n```\n\n```Java []\nclass Solution {\n public int[] maximumBeauty(int[][] items, int[] queries) {\n Arrays.sort(items, (a, b) -> Integer.compare(a[0], b[0]));\n \n TreeMap<Integer, Integer> maxBeautyByPrice = new TreeMap<>();\n int maxBeauty = 0;\n for (int[] item : items) {\n maxBeauty = Math.max(maxBeauty, item[1]);\n maxBeautyByPrice.put(item[0], maxBeauty);\n }\n \n int[] result = new int[queries.length];\n for (int i = 0; i < queries.length; i++) {\n Integer price = maxBeautyByPrice.floorKey(queries[i]);\n result[i] = (price == null) ? 0 : maxBeautyByPrice.get(price);\n }\n \n return result;\n }\n}\n```
| 2 | 0 |
['Array', 'Binary Search', 'Sorting', 'Java', 'Kotlin']
| 2 |
most-beautiful-item-for-each-query
|
SORTNG || SIMPLE || EASY UNDERSTAND C++ SOLUTION
|
sortng-simple-easy-understand-c-solution-cilt
|
\nclass Solution {\npublic:\n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n vector<vector<int>> v;\n int n = q
|
yash___sharma_
|
NORMAL
|
2023-02-08T14:10:43.414241+00:00
|
2023-02-08T14:10:43.414285+00:00
| 857 | false |
```\nclass Solution {\npublic:\n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n vector<vector<int>> v;\n int n = queries.size();\n for(int i = 0; i < n; i++){\n v.push_back({queries[i],i});\n }\n sort(v.begin(),v.end());\n sort(items.begin(),items.end());\n vector<int> ans(n);\n int j=0;\n n = items.size();\n int mx = 0;\n for(auto &i: v){\n while(j<n && items[j][0]<=i[0]){\n mx = max(mx,items[j][1]);\n j++;\n }\n ans[i[1]] = mx;\n }\n return ans;\n }\n};\n```
| 2 | 0 |
['C', 'Sorting', 'C++']
| 0 |
most-beautiful-item-for-each-query
|
[JAVA] BEATS 100.00% MEMORY/SPEED 0ms // APRIL 2022
|
java-beats-10000-memoryspeed-0ms-april-2-ncx5
|
\nclass Solution {\n public int[] maximumBeauty(int[][] items, int[] queries) {\n int n = queries.length, m = items.length;\n Arrays.sort(items
|
darian-catalin-cucer
|
NORMAL
|
2022-04-23T20:54:51.667344+00:00
|
2022-04-23T20:54:51.667387+00:00
| 431 | false |
```\nclass Solution {\n public int[] maximumBeauty(int[][] items, int[] queries) {\n int n = queries.length, m = items.length;\n Arrays.sort(items, Comparator.comparingInt(o -> o[0]));\n int[] ans = new int[n];\n\n for (int i = 0; i < m; i++)\n items[i][1] = Math.max(items[i][1], items[i > 0? i - 1 : 0][1]);\n\n int j = 0;\n for (int q : queries){\n int lo = -1, hi = m - 1; //pad lo = -1 to mark no result\n while(lo < hi){\n int mid = lo + (hi - lo) / 2 + 1;\n if (q >= items[mid][0]) lo = mid;\n else hi = mid - 1;\n }\n ans[j++] = lo == -1? 0 : items[lo][1];\n }\n\n return ans;\n }\n}\n```\n\n***Consider upvote if usefull!***
| 2 | 0 |
['Java']
| 0 |
most-beautiful-item-for-each-query
|
Python sort / dict / bisect - 90% / 75%
|
python-sort-dict-bisect-90-75-by-andydte-pfay
|
```\nclass Solution:\n\n def floorSearch(self, array: List[int], target: int) -> int:\n\t\n idx = bisect_left(array,target)\n return array[idx-
|
andydtest
|
NORMAL
|
2022-02-15T21:51:04.158812+00:00
|
2022-02-15T22:33:20.538296+00:00
| 76 | false |
```\nclass Solution:\n\n def floorSearch(self, array: List[int], target: int) -> int:\n\t\n idx = bisect_left(array,target)\n return array[idx-1]\n \n def maximumBeauty(self, items: List[List[int]], queries: List[int]) -> List[int]:\n \n items.sort()\n dic = {}\n curr_max_beauty = items[0][1]\n keys = []\n for price,beauty in items:\n keys.append(price)\n curr_max_beauty = max(beauty,curr_max_beauty)\n dic[price] = curr_max_beauty\n res = []\n for q in queries:\n if q < keys[0]:\n res.append(0)\n elif q in dic:\n res.append(dic[q])\n else:\n res.append(dic[self.floorSearch(keys,q)])\n return res
| 2 | 0 |
[]
| 1 |
most-beautiful-item-for-each-query
|
Java | using Map and Binary Search | O(QlogN+NlogN) | beats 73%
|
java-using-map-and-binary-search-oqlognn-q5hr
|
\nclass Solution {\n\tMap<Integer, Integer> map;\n\tint[] res;\n\tint[] maxTillNow;\n\n\tpublic int[] maximumBeauty(int[][] items, int[] q) {\n\t\tmap = new Has
|
bruceBane26
|
NORMAL
|
2022-02-09T17:56:21.544098+00:00
|
2022-02-09T17:56:21.544135+00:00
| 73 | false |
```\nclass Solution {\n\tMap<Integer, Integer> map;\n\tint[] res;\n\tint[] maxTillNow;\n\n\tpublic int[] maximumBeauty(int[][] items, int[] q) {\n\t\tmap = new HashMap<>();\n\t\tres = new int[q.length];\n\n\t\tint x = 0;\n\t\tfor (int[] a : items)\n\t\t\tmap.put(a[0], Math.max(map.getOrDefault(a[0], 0), a[1]));\n\n\t\tmaxTillNow = new int[map.size()];\n\t\tint[] ar = new int[map.size()];\n\n\t\tfor (Map.Entry<Integer, Integer> e : map.entrySet()) {\n\t\t\tar[x++] = (int) e.getKey();\n\t\t}\n\t\tArrays.sort(ar);\n\n\t\tint max = 0;\n\t\tfor (int i = 0; i < ar.length; i++) {\n\t\t\tmax = Math.max(max, map.get(ar[i]));\n\t\t\tmaxTillNow[i] = max;\n\t\t}\n\n\t\tint i = 0;\n\t\tfor (int val : q)\n\t\t\tres[i++] = find(ar, val, ar.length);\n\t\t\n\t\treturn res;\n\t}\n\n\tint find(int[] ar, int val, int n) {\n\t\tint l = 0, r = n - 1, mid = l + (r - l) / 2;\n\t\tint lastLess = -1;\n\t\twhile (l <= r) {\n\t\t\tmid = l + (r - l) / 2;\n\t\t\tif (ar[mid] == val)\n\t\t\t\treturn maxTillNow[mid];\n\t\t\tif (val > ar[mid]) {\n\t\t\t\tlastLess = mid;\n\t\t\t\tl = mid + 1;\n\t\t\t} else\n\t\t\t\tr = mid - 1;\n\t\t}\n\n\t\treturn lastLess >= 0 ? maxTillNow[lastLess] : 0;\n\t}\n}\n```
| 2 | 0 |
['Binary Search']
| 0 |
most-beautiful-item-for-each-query
|
Multiple Approaches Explained || Sorting , Binary Search & Offline Query || C++ Clean Code
|
multiple-approaches-explained-sorting-bi-ibtc
|
-----------------------------------------------------\n# Approach 1: Sorting + Binary Search\n-----------------------------------------------------\n\n---------
|
i_quasar
|
NORMAL
|
2021-11-27T04:03:10.673235+00:00
|
2021-12-11T02:34:00.565257+00:00
| 153 | false |
-----------------------------------------------------\n# **Approach 1: Sorting + Binary Search**\n-----------------------------------------------------\n\n-----------------------------------------------------\n * **Code :**\n\n\t\tvector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n\n\t\t\tint n = items.size();\n\n\t\t\tsort(items.begin(), items.end());\n\n\t\t\tvector<int> maxBeautyTillNow(n, 0);\n\n\t\t\tfor(int i=0; i<n; i++) {\n\t\t\t\tmaxBeautyTillNow[i] = (i == 0) ? items[i][1] : max(maxBeautyTillNow[i-1], items[i][1]);\n\t\t\t}\n\n\t\t\tvector<int> answer;\n\t\t\tfor(auto& query : queries) {\n\t\t\t\tint idx = upper_bound(items.begin(), items.end(), vector<int>({query, INT_MAX})) - items.begin();\n\n\t\t\t\tif(idx >= n || items[idx][0] > query) idx--;\n\n\t\t\t\tif(idx < 0) answer.push_back(0);\n\t\t\t\telse answer.push_back(maxBeautyTillNow[idx]);\n\t\t\t}\n\n\t\t\treturn answer;\n\t\t}\n\n-----------------------------------------------------\n\n* **Complexity :**\n\n\t* Time : `O(N logN) + O(N) + O(Q logN)` \n\t\t* `O(N logN)` : sorting `items` list, \n\t\t* `O(N)` : building prefix max i.e `maxBeautyTillNow` array and \n\t\t* `O(Q logN)` : searching index for each query in `queries`\n\n\n\t* Space : `O(N)`, N is size of `items` list\n\t\t* N : Size of `items` list\n\t\t* Q : Size of `queries` list\n-----------------------------------------------------\n-----------------------------------------------------\n# **Approach 2 : Sorting + Offline Query**\n-----------------------------------------------------\n\n-----------------------------------------------------\n * **Code :**\n\n\t\tvector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n\n\t\t\tint n = items.size();\n\t\t\tint m = queries.size();\n\n\t\t\tsort(begin(items), end(items));\n\n\t\t\tvector<pair<int, int>> newQueries;\n\t\t\tint i=0; \n\t\t\tfor(auto& q : queries) {\n\t\t\t\tnewQueries.push_back({q, i++});\n\t\t\t}\n\n\t\t\tsort(begin(newQueries), end(newQueries));\n\n\t\t\tint idx = 0, maxBeauty = 0;\n\t\t\tvector<int> answer(m, 0);\n\n\t\t\tfor(auto& [query, index] : newQueries) {\n\n\t\t\t\twhile(idx < n && items[idx][0] <= query) {\n\t\t\t\t\tmaxBeauty = max(maxBeauty, items[idx][1]);\n\t\t\t\t\tidx++;\n\t\t\t\t}\n\n\t\t\t\tanswer[index] = maxBeauty;\n\t\t\t}\n\n\t\t\treturn answer;\n\t\t}\n-----------------------------------------------------\n\n* **Complexity :**\n\n\t* Time : `O(N logN) + O(Q + Q log Q) + O(Q + N)` \n\t\t* `O(N log N)` : sorting `items` list, \n\t\t* `O(Q + Q logQ )` : creating and sorting `newQueries` list, \n\t\t* `O(Q + N)` : processing query in `newQueries`\n\n\t* Space : `O(Q)`, Q is size of `queries` list\n\t\t* N : Size of `items` list\n\t\t* Q : Size of `queries` list\n-----------------------------------------------------\n\n***If you find this helpful, do give it a like :)***
| 2 | 0 |
['C', 'Sorting', 'Binary Tree']
| 0 |
most-beautiful-item-for-each-query
|
Python faster than 99.78% (1124ms)
|
python-faster-than-9978-1124ms-by-rjmcmc-bj2c
|
```\nclass Solution:\n def maximumBeauty(self, items: List[List[int]], queries: List[int]) -> List[int]:\n to_check = queries.copy()\n to_check
|
rjmcmc
|
NORMAL
|
2021-11-20T20:45:15.636492+00:00
|
2021-11-20T20:45:15.636519+00:00
| 102 | false |
```\nclass Solution:\n def maximumBeauty(self, items: List[List[int]], queries: List[int]) -> List[int]:\n to_check = queries.copy()\n to_check = sorted(to_check)[::-1]\n items = sorted(items, key=lambda x:x[0])\n items = items[::-1]\n max_beauty = 0\n ans_lookup = dict()\n while to_check:\n while items and items[-1][0] <= to_check[-1]:\n max_beauty = max(max_beauty,items.pop()[1])\n ans_lookup[to_check.pop()] = max_beauty\n return [ans_lookup[x] for x in queries]
| 2 | 0 |
[]
| 0 |
most-beautiful-item-for-each-query
|
java solution with binary search(80.32% faster)
|
java-solution-with-binary-search8032-fas-25fv
|
\nclass Solution {\n public int[] maximumBeauty(int[][] items, int[] queries) {\n int m = items.length;\n Arrays.sort(items, (a, b) -> Double.co
|
abhipantdev8
|
NORMAL
|
2021-11-18T16:26:14.193750+00:00
|
2021-11-18T16:27:10.002835+00:00
| 70 | false |
```\nclass Solution {\n public int[] maximumBeauty(int[][] items, int[] queries) {\n int m = items.length;\n Arrays.sort(items, (a, b) -> Double.compare(a[0], b[0]));\n int n = queries.length;\n int[] mxLeft = new int[m];\n\n mxLeft[0]= items[0][1];\n for(int i=1;i<m;i++)\n mxLeft[i] = Math.max(mxLeft[i-1],items[i][1]);\n\n int[] ans = new int[n];\n for(int i=0;i<n;i++){\n int curr= queries[i];\n int l=0,r=m-1;\n int profit = -1;\n\n while(l<=r){\n int mid = l+(r-l)/2;\n if(items[mid][0]>curr){\n r=mid-1;\n }\n else{\n profit=mid;\n l=mid+1;\n }\n }\n if(profit==-1) continue;\n ans[i]=mxLeft[profit];\n }\n\n\n return ans;\n }\n}\n```
| 2 | 0 |
[]
| 0 |
most-beautiful-item-for-each-query
|
C++ | Easy to understand | Sorting + Map | 100% faster | 356 MS Solution
|
c-easy-to-understand-sorting-map-100-fas-oj9p
|
\n\nstatic const auto Initialize = []{\n ios::sync_with_stdio(false); cin.tie(nullptr);\n return nullptr;\n}();\nclass Solution {\npublic:\n vector<int
|
int_float_double
|
NORMAL
|
2021-11-13T18:47:18.877396+00:00
|
2021-11-13T18:47:18.877422+00:00
| 58 | false |
\n```\nstatic const auto Initialize = []{\n ios::sync_with_stdio(false); cin.tie(nullptr);\n return nullptr;\n}();\nclass Solution {\npublic:\n vector<int> maximumBeauty(vector<vector<int>>& it, vector<int>& q) {\n int n=it.size();\n int m=q.size();\n sort(it.begin(),it.end());\n map<int,int>mp;\n mp[0]=0;\n mp[it[0][0]]=it[0][1];\n int ma=0;\n for(int i=1;i<n;i++){\n it[i][1]=it[i][1]>it[i-1][1]?it[i][1]:it[i-1][1];\n mp[it[i][0]]=it[i][1];\n }\n vector<int>ans;\n for(int i=0;i<m;i++){\n if(!mp.count(q[i])){\n mp[q[i]]=0;\n }\n }\n for(auto it=mp.begin();it!=mp.end();it++){\n auto it1=it;\n it1--;\n if(it->second==0){\n it->second=it1->second;\n }\n }\n for(auto x:q){\n ans.push_back(mp[x]);\n }\n return ans;\n }\n};\n```\n\nIf u Like the Solution Please Do Upvote
| 2 | 0 |
['Sorting']
| 0 |
most-beautiful-item-for-each-query
|
Thinking Process behind Binary Search and Sort with Pictures, C++ implementation
|
thinking-process-behind-binary-search-an-yhty
|
Thinking Process\nYou must have seen many different solution in the discussion tab, everyone is saying that Sort + Binary Search!. But wait, from where did that
|
usurperhk
|
NORMAL
|
2021-11-13T16:51:18.136152+00:00
|
2021-11-13T16:52:38.363787+00:00
| 111 | false |
# Thinking Process\nYou must have seen many different solution in the discussion tab, everyone is saying that **Sort + Binary Search!**. But wait, from where did that even came from?\nLet me explain it to you in depth the thinking process behind this approach.\n\n* I am hoping that you know how to solve this with brute force approach. Let\'s start with something new.\n* The problem want us to find the maximum beauty out of all items for each query such that the price of each item is `<= query` itself.\n* So that\'s mean, the answer for query `q = 5` depends on items whose price is `<= 5`. ***And this also implies that we don\'t give a shit about items whose price value is greater than the query***. when you get this thought you probably got the idea of sorting.\n* With sorting we can optimise the brute force by avoiding unnecessary iterations over items.\n* But again, in worst case we might end up having the same time complexity as of brute force. So that\'s mean sorting alone is not enough.\n* Now let\'s write the items in sorted order first, than think of how to optimise it. I am using pen and paper, you can use whatever you like.\n\n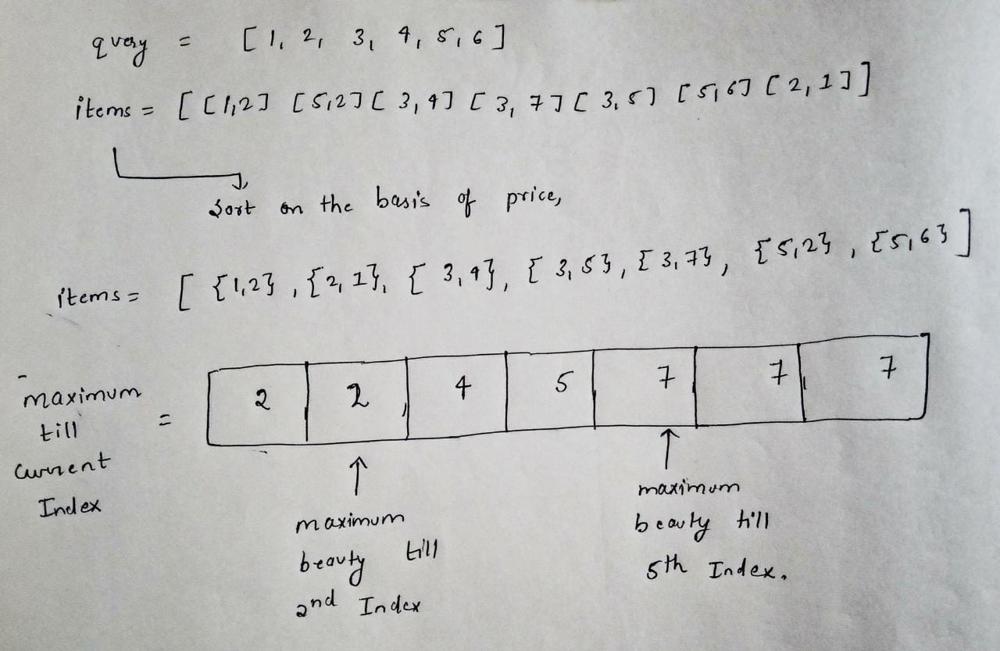\n\n* Now, in the image I have shared above only one thing you may found new that is the rectangular box I have made. It is nothing but the maximum beauty available till the current index in the available items. \n* Let\'s say we are looking for maximum beauty for query `q = 3`. You can easily see that the answer for this is` 7`. \n* If you closely look to the sorted array of items, you will realize that if you have that rectangular box with you than you just need the last index of query in the list of sorted items. If you have that you can easily find the maximum beauty for the current query in constant time. \n* And also finding the last index of an item in a sorted array is a standard binary search problem. ***That\'s is how we finally reach to Sorting + Binary Search solution.***\n\nSo, the answer for the queries shown in image is : [2, 2, 7, 7, 7, 7]. And yes don\'t forget to handle the edge case when the query do not exists in the items array.\n\n# C++ Implementation\n```\nclass Solution {\npublic:\n int findLastIndex(vector<vector<int>>& items, int& q) {\n // as usual binary search\n int lo = 0, hi = items.size()-1, res = -1;\n while(lo <= hi) {\n int mid = lo+(hi-lo)/2;\n \n // if the current item price <= required item price\n // than this might be our answer, so update answer \n // and look for the right half for higher values\n if(items[mid][0] <= q) {\n res = mid;\n lo = mid+1;\n }\n \n // else we need to search in lower half\n else {\n hi = mid-1;\n }\n }\n return res;\n }\n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n int n = items.size();\n \n // sort on the basis of first price\n sort(begin(items), end(items));\n \n // maxBeauty store the max beauty till the current index, \n // it will always be in increasing order\n vector<int> maxBeauty(n);\n vector<int> res;\n \n // assign the maximum beauty to each index\n maxBeauty[0] = items[0][1];\n for(int i=1; i<n; i++) {\n maxBeauty[i] = max(maxBeauty[i-1], items[i][1]);\n }\n \n // now for every query binary seach the last index in the pairs\n // whose price <= current query price\n for(auto q: queries) {\n auto i = findLastIndex(items, q);\n \n // if we do not find this item in the items list\n res.push_back(i == -1 ? 0 : maxBeauty[i]);\n }\n \n return res;\n }\n};\n```\n\n# Time Complexity\n* I leave this to you, let me know in the comments. \n* Thanks for reading and Happy coding!.\n
| 2 | 0 |
[]
| 1 |
most-beautiful-item-for-each-query
|
[Python3] Binary Search
|
python3-binary-search-by-expensiveac-zd2w
|
\nclass Solution:\n def maximumBeauty(self, items: List[List[int]], queries: List[int]) -> List[int]:\n \n items.sort(key=lambda x: x[0])\n
|
ExpensiveAC
|
NORMAL
|
2021-11-13T16:44:19.624462+00:00
|
2021-11-13T16:44:19.624495+00:00
| 83 | false |
```\nclass Solution:\n def maximumBeauty(self, items: List[List[int]], queries: List[int]) -> List[int]:\n \n items.sort(key=lambda x: x[0])\n a = []\n b = []\n \n for i in range(len(items)):\n a.append(items[i][0])\n \n for i in range(len(items)):\n b.append(items[i][1])\n \n for i in range(1,len(b)):\n if b[i] < b[i-1]:\n b[i] = b[i-1]\n\n idx = 0\n \n res = []\n \n for i in range(len(queries)):\n \n idx = bisect.bisect_right(a,queries[i])\n \n if idx == 0:\n res.append(0)\n else:\n res.append(b[idx-1])\n \n return res\n```
| 2 | 0 |
[]
| 0 |
most-beautiful-item-for-each-query
|
✅ C++ || Sorting || Binary Search
|
c-sorting-binary-search-by-99notout_half-jeuv
|
Approach\n\nSteps\n\t(1) Sort the items on the basis of their price\n\t(2) prepare answer for every price in prefix\n\t(3) use binary search to find a price val
|
99NotOut_half_dead
|
NORMAL
|
2021-11-13T16:25:16.979950+00:00
|
2021-11-13T16:30:03.487640+00:00
| 125 | false |
# ***Approach***\n```\nSteps\n\t(1) Sort the items on the basis of their price\n\t(2) prepare answer for every price in prefix\n\t(3) use binary search to find a price value in items which is closest to query price\n\t(4) take answer from prefix to answer a query\n\tTime : O(nlog(n) + qlog(n))\n```\n# ***Code***\n```\nclass Solution {\npublic:\n static bool comparator(vector<int> &a , vector<int> &b)\n {\n return a[0] < b[0];\n }\n vector<int> maximumBeauty(vector<vector<int>> &nums, vector<int> &queries) {\n vector<int> prefix;\n sort(nums.begin() , nums.end() , comparator);\n \n int max_beauty = 0;\n for(auto v : nums)\n {\n max_beauty = max(max_beauty , v[1]);\n prefix.push_back(max_beauty);\n }\n \n vector<int> res;\n for(int q : queries)\n { \n int x = bin_search(nums , q);\n if(x < 0)\n res.push_back(0);\n else\n res.push_back(prefix[x]);\n }\n return res;\n }\n int bin_search(vector<vector<int>> &nums , int target)\n {\n int left = 0 , right = nums.size() - 1;\n while(left <= right)\n {\n int mid = left + (right - left) / 2;\n if(nums[mid][0] > target)\n right = mid - 1;\n else\n left = mid + 1;\n }\n return right;\n }\n};\n```\n# ***If you liked the Solution, Give it an Upvote :)***
| 2 | 0 |
[]
| 1 |
most-beautiful-item-for-each-query
|
Lessons learned
|
lessons-learned-by-vyshnavkr-hnjd
|
Code:\n\nclass Solution {\n public int[] maximumBeauty(int[][] items, int[] queries) {\n \n int m = items.length;\n int n = queries.leng
|
vyshnavkr
|
NORMAL
|
2021-11-13T16:15:30.668297+00:00
|
2021-11-13T16:15:30.668350+00:00
| 80 | false |
**Code**:\n```\nclass Solution {\n public int[] maximumBeauty(int[][] items, int[] queries) {\n \n int m = items.length;\n int n = queries.length;\n \n // SORT FOR BINARY SEARCH\n Arrays.sort(items, (a, b) -> a[0] - b[0]);\n \n // AUXILLARY ARRAY FOR FINDING MAX IN O(1) \n int[] maxBeauty = new int[m];\n maxBeauty[0] = items[0][1];\n for (int i = 1; i < m; ++i) {\n int beauty = items[i][1];\n maxBeauty[i] = Math.max(maxBeauty[i - 1], beauty);\n }\n \n // BUILD ANSWER\n int[] ans = new int[n];\n for (int i = 0; i < n; ++i) {\n int val = binarySearch(queries[i], items, maxBeauty);\n ans[i] = val;\n }\n \n return ans;\n }\n \n // BINARY SEARCH\n private int binarySearch(int maxPrice, int[][] items, int[] maxBeauty) {\n int m = items.length;\n int ans = 0;\n int left = 0, right = m - 1;\n while (left <= right) {\n int mid = left + (right - left) / 2;\n int price = items[mid][0];\n if (price <= maxPrice) {\n ans = maxBeauty[mid];\n left = mid + 1;\n } else {\n right = mid - 1;\n }\n }\n return ans;\n }\n}\n```
| 2 | 0 |
[]
| 0 |
most-beautiful-item-for-each-query
|
[C++] Binary Search and HashMap
|
c-binary-search-and-hashmap-by-ykv749-i3fn
|
\nclass Solution {\npublic:\n \n int next(vector<vector<int>>& arr, int target, int end){\n \n if(end==0) return -1;\n if(target>arr[en
|
ykv749
|
NORMAL
|
2021-11-13T16:03:55.482153+00:00
|
2021-11-13T16:03:55.482192+00:00
| 63 | false |
```\nclass Solution {\npublic:\n \n int next(vector<vector<int>>& arr, int target, int end){\n \n if(end==0) return -1;\n if(target>arr[end-1][0]) return end-1;\n \n int start=0;\n \n int ans=-1;\n while (start<=end){\n int mid=(start+end)/2;\n\n if (arr[mid][0]>=target){\n end=mid-1;\n }\n\n else{\n ans=mid;\n start=mid+1;\n }\n }\n \n return ans;\n }\n \n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n \n map<int,int>mp;\n sort(items.begin(),items.end());\n int mx=INT_MIN;\n for(auto x:items){\n mx=max(mx,x[1]);\n mp[x[0]]=mx;\n }\n \n /*\n for(auto x:items){\n cout<<x[0]<<" "<<x[1]<<\'\\n\';\n }*/\n \n vector<int>res;\n for(auto x:queries){\n if(!(mp[x])){\n \n if(x<items[0][0]) mp[x]=0;\n else if(x>=items[items.size()-1][0]) mp[x]=mp[items[items.size()-1][0]];\n else {\n int k=next(items,x,items.size());\n mp[x]=mp[items[k][0]];\n }\n \n }\n \n res.push_back(mp[x]);\n }\n \n return res;\n \n }\n};\n```
| 2 | 0 |
[]
| 0 |
most-beautiful-item-for-each-query
|
Solution with Beats 97% 🥳
|
solution-with-beats-97-by-asifar-2few
|
Intuition\n Describe your first thoughts on how to solve this problem. \nSo if we sort the array we can easily get the value\n# Approach\n Describe your approac
|
Asifar
|
NORMAL
|
2024-11-12T20:32:17.588944+00:00
|
2024-11-12T20:32:17.588977+00:00
| 2 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSo if we sort the array we can easily get the value\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nfirst I sorted the array and then finded the neartest greatest value if its checksu will be false or else 0 will be added\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\no(n<sup>2</sup>)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n# Code\n```python3 []\nclass Solution:\n def maximumBeauty(self, items: List[List[int]], queries: List[int]) -> List[int]:\n\n items=sorted(items,key=lambda x : x[1],reverse=True)\n\n \n res=[]\n for i in queries:\n check=True\n for j in items:\n if j[0]<=i:\n res.append(j[1])\n check=False\n break\n if check:\n res.append(0)\n return res\n \n\n \n \n```
| 1 | 0 |
['Python3']
| 0 |
most-beautiful-item-for-each-query
|
Binary Search Tree Solution (Runtime: 4ms, Beats 100%)
|
binary-search-tree-solution-runtime-4ms-055v6
|
\n# Intuition\n Describe your first thoughts on how to solve this problem. \nThe goal is to find the item with the highest beauty value within a given price ran
|
bytewise
|
NORMAL
|
2024-11-12T19:27:08.014740+00:00
|
2024-11-12T20:00:17.822905+00:00
| 5 | false |
\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe goal is to find the item with the highest beauty value within a given price range for each query. Since items can be inserted in any order and need to be queried based on price, a binary search tree (BST) structure can efficiently store the items, allowing us to search by price in \\(O(\\log N)\\) time on average.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. **Insert items into a Binary Search Tree (BST):** Each item is added based on its price, and for each price, we only keep the maximum beauty. We recursively add each item, building a tree where nodes with higher prices go to the right and nodes with lower prices go to the left.\n2. **Search for the maximum beauty in the BST for each query:** For each query, traverse the tree to find nodes with prices less than or equal to the query price, and keep track of the highest beauty encountered.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n - **Average case:** \\(O(N \\log N + Q \\log N)\\), where \\(N\\) is the number of items, and \\(Q\\) is the number of queries.\n - **Worst case:** \\(O(N^2 + Q \\cdot N)\\) if the BST is unbalanced.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n - \\(O(N + Q)\\), where \\(N\\) is the space for the BST, and \\(Q\\) is for the result array.\n\n# Code\n```java []\nclass Solution {\n public int[] maximumBeauty(int[][] items, int[] queries) {\n // Initialize the root node of the binary search tree (BST) to store items based on price\n Node root = null;\n\n // Insert each item into the BST\n for (int[] item : items) {\n int price = item[0];\n int beauty = item[1];\n if (root == null) {\n root = new Node(price, beauty); // Initialize root with the first item\n } else {\n root.add(price, beauty); // Insert subsequent items into the BST\n }\n }\n\n int[] result = new int[queries.length];\n\n // For each query, find the maximum beauty for items priced at or below the query value\n for (int i = 0; i < queries.length; i++) {\n int query = queries[i];\n result[i] = root != null ? root.find(query) : 0;\n }\n\n return result;\n }\n\n // Define a nested Node class to represent each node in the binary search tree\n private static class Node {\n Node left; // Left child node\n Node right; // Right child node\n int price; // Price of the item\n int beauty; // Beauty value of the item\n\n public Node(int price, int beauty) {\n this.price = price;\n this.beauty = beauty;\n }\n\n // Finds the maximum beauty of an item\n int find(int price) {\n Node node = this;\n int maxBeauty = 0;\n\n // Traverse the tree to find the maximum beauty for items\n while (node != null) {\n if (node.price <= price) {\n // update maxBeauty if needed\n maxBeauty = Math.max(maxBeauty, node.beauty);\n node = node.right; // Move to the right child to find potentially higher prices within the range\n } else {\n node = node.left;\n }\n }\n return maxBeauty;\n }\n\n // Adds a new item to the BST based on its price and beauty\n void add(int price, int beauty) {\n // If price is greater than current node\'s price, consider adding it to the right\n if (price > this.price) {\n // It doesn\'t make sense to add the node with higher price if it\'s beauty is less than current node\'s beauty\n if (beauty > this.beauty) {\n if (this.right != null) {\n this.right.add(price, beauty); // Recursive call to add to the right child\n } else {\n this.right = new Node(price, beauty); // Create new right child if null\n }\n }\n }\n // If price is less than or equal to current price, add to the left or update current node\n else {\n if (beauty >= this.beauty) {\n // Update current node if the new beauty is greater or equal\n this.price = price;\n this.beauty = beauty;\n } else {\n // Otherwise, add to the left subtree if beauty is not the highest for this price range\n if (this.left != null) {\n this.left.add(price, beauty);\n } else {\n this.left = new Node(price, beauty);\n }\n }\n }\n }\n }\n}\n```
| 1 | 0 |
['Java']
| 0 |
most-beautiful-item-for-each-query
|
easy cpp solution to understand
|
easy-cpp-solution-to-understand-by-prati-vb9q
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
pratik5722
|
NORMAL
|
2024-11-12T18:18:16.459497+00:00
|
2024-11-12T18:18:16.459526+00:00
| 14 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n vector<int> maximumBeauty(vector<vector<int>>& items, vector<int>& queries) {\n ios_base ::sync_with_stdio(false), cin.tie(0), cout.tie(0);\n int n = items.size();\n int m = queries.size();\n vector<int>v;\n\n sort(items.begin(), items.end());\n\n for(int i = 1;i < n;i++){\n items[i][1] = max(items[i][1], items[i - 1][1]);\n }\n\n for(auto i : queries){\n int low = 0;\n int high = n - 1;\n int ans = 0;\n while(low <= high){\n int mid = (low + high) / 2;\n if(i >= items[mid][0]){\n ans = items[mid][1];\n low = mid + 1;\n }\n else high = mid - 1;\n }\n v.push_back(ans);\n }\n return v;\n }\n};\n```
| 1 | 0 |
['Binary Search', 'C++']
| 0 |
most-beautiful-item-for-each-query
|
FP: Single expression, 7 lines, 196ms, beats 100%. Sort, scan, to SortedMap, look up queries in map
|
fp-single-expression-7-lines-196ms-beats-y3jw
|
Intuition\nSort by price, walk the array assigning each price the maximum beauty found so far.\n\nLook up each query in a sorted map of (price, beauty). \n\nThe
|
tpdi
|
NORMAL
|
2024-11-12T18:08:17.333334+00:00
|
2024-11-12T18:40:18.461522+00:00
| 7 | false |
# Intuition\nSort by price, walk the array assigning each price the maximum beauty found so far.\n\nLook up each query in a sorted map of (price, beauty). \n\nThe sorted map allows us to find the greatest key less than or equal to the query: this key\'s value is the maximum beauty for the query.\n\n# Approach\nSort the (price, beauty) pairs by price ascending, beauty descending: this orders the prices from lowest to highhesy, and within each price, the first beauty is the ximum for that price.\n\nScan over the sorted pairs, and for each, map it to a pair of (price, maximum beauty seen so far). This is why within each price, the maximum beauty for that price comes first.\n\nSince the list returned by scan starts with scan\'s seed value, which we make Pair(0, 0), this ensures we return zero for a query less than the minimum price.\n\nTurn the pairs into a Map, then turn the Map into a SortedMap.\n\nFor each query, get the headMap for the query plus 1, and take the headMap\'s maximum key. This gives us the maximum key less than or equal to the query.\n\nMap the query to the value of that key.\n\n# Complexity\n- Time complexity:\n$$O(n*log(n)) + O(m * log (n))$$ \n\n- Space complexity:\n$$O(n + m)$$ \n\n# Code\n```kotlin []\nclass Solution {\n fun maximumBeauty(items: Array<IntArray>, queries: IntArray): IntArray {\n return items\n .sortedWith(compareBy({ it[0] }, { -it[1] }))\n .scan(Pair(0, 0)) { (a1, a2), (e1, e2) -> Pair(e1, max(a2, e2)) }\n .toMap()\n // or we could .associate { it }\n .toSortedMap()\n .let { m -> queries.map { m[m.headMap(it + 1).lastKey()]!! }}\n .toIntArray()\n }\n}\n```
| 1 | 0 |
['Ordered Map', 'Sorting', 'Kotlin']
| 0 |
process-restricted-friend-requests
|
C++ Union Find
|
c-union-find-by-lzl124631x-re15
|
See my latest update in repo LeetCode\n## Solution 1. Union Find\n\nGiven the constraints, a solution with O(R * B) is acceptable -- for each request, check if
|
lzl124631x
|
NORMAL
|
2021-11-14T04:01:43.345945+00:00
|
2021-11-14T04:32:26.262128+00:00
| 5,622 | false |
See my latest update in repo [LeetCode](https://github.com/lzl124631x/LeetCode)\n## Solution 1. Union Find\n\nGiven the constraints, a solution with `O(R * B)` is acceptable -- for each request, check if it obeys all the bans.\n\nFor the check, we can do it in `O(1)` time using UnionFind. For each prior valid requests, we connect the two friends. For a new request, we just need to check if the leaders of the two parties are in any of those bans.\n\n```cpp\n// OJ: https://leetcode.com/problems/process-restricted-friend-requests/\n// Author: github.com/lzl124631x\n// Time: O(R * B) where `R`/`B` is the length of `requests`/`bans`\n// Space: O(N)\nclass UnionFind {\n vector<int> id;\npublic:\n UnionFind(int n) : id(n) {\n iota(begin(id), end(id), 0);\n }\n void connect(int a, int b) {\n id[find(a)] = find(b);\n }\n int find(int a) {\n return id[a] == a ? a : (id[a] = find(id[a]));\n }\n int connected(int a, int b) {\n return find(a) == find(b);\n }\n};\nclass Solution {\npublic:\n vector<bool> friendRequests(int n, vector<vector<int>>& bans, vector<vector<int>>& requests) {\n vector<bool> ans;\n UnionFind uf(n);\n for (auto &r : requests) {\n int p = uf.find(r[0]), q = uf.find(r[1]); // the leaders of the two parties\n bool valid = true;\n if (!uf.connected(p, q)) { // Only need to check the bans if the two parties are not already connected\n for (auto &b : bans) {\n int x = uf.find(b[0]), y = uf.find(b[1]); // the leaders of the two banned parties\n if ((x == p && y == q) || (x == q && y == p)) {\n valid = false;\n break;\n }\n }\n }\n ans.push_back(valid);\n if (valid) uf.connect(p, q); // connect two parties if request is valid\n }\n return ans;\n }\n};\n```
| 66 | 0 |
[]
| 6 |
process-restricted-friend-requests
|
[Python] Usual union find, explained.
|
python-usual-union-find-explained-by-dba-nqhf
|
The idea is that given problem constraints, we can allow to use union find. The idea is to traverse x, y in requests and check if we can make these persons frie
|
dbabichev
|
NORMAL
|
2021-11-14T04:00:41.840178+00:00
|
2022-01-03T14:19:44.256507+00:00
| 4,032 | false |
The idea is that given problem constraints, we can allow to use union find. The idea is to traverse `x, y in requests` and check if we can make these persons friends or not. We can make them if we do not have restrictions: we go through all restrictions and check that we do not have restriction for two given connected components.\n\n#### Complexity\nIt is `O(n * m * log(n))` for time and `O(n)` for space, where `m = len(requests)`.\n\n```python\nclass DSU:\n def __init__(self, N):\n self.p = list(range(N))\n\n def find(self, x):\n if self.p[x] != x:\n self.p[x] = self.find(self.p[x])\n return self.p[x]\n\n def union(self, x, y):\n xr = self.find(x)\n yr = self.find(y)\n self.p[xr] = yr\n\nclass Solution:\n def friendRequests(self, n, restr, requests):\n dsu, ans = DSU(n), []\n for x, y in requests:\n x_p, y_p = dsu.find(x), dsu.find(y)\n bad = True\n for a, b in restr:\n a_p, b_p = dsu.find(a), dsu.find(b)\n if set([a_p, b_p]) == set([x_p, y_p]):\n bad = False\n break\n \n ans += [bad]\n if bad: dsu.union(x, y)\n \n return ans\n```\n\nIf you have any questoins, feel free to ask. If you like the solution and explanation, please **upvote!**
| 56 | 4 |
['Union Find']
| 9 |
process-restricted-friend-requests
|
[Python] Union-Friends
|
python-union-friends-by-lee215-89ry
|
Explanation\nUse union-found to union friends.\nFor each request, check if doesn\'t obey any restrictions.\n\n\n# Complexity\nUnion-find operation with rank and
|
lee215
|
NORMAL
|
2021-11-14T04:06:53.342497+00:00
|
2021-11-14T04:06:53.342526+00:00
| 3,410 | false |
# **Explanation**\nUse union-found to union friends.\nFor each request, check if doesn\'t obey any restrictions.\n<br>\n\n# **Complexity**\nUnion-find operation with rank and path comression,has amotized `O(1)`\nTime `O(requests * restrictions)`\nSpace `O(n)`\n<br>\n\n**Python**\n```py\n def friendRequests(self, n, restrictions, requests):\n uf = {i: i for i in xrange(n)}\n res = []\n\n def find(i):\n if i != uf[i]:\n uf[i] = find(uf[i])\n return uf[i]\n\n for i, j in requests:\n success = True\n pi, pj = find(i), find(j)\n if pi != pj:\n for x, y in restrictions:\n px, py = find(x), find(y)\n if (px, py) == (pi, pj) or (px, py) == (pj, pi):\n success = False\n break\n if success:\n uf[pj] = pi\n res.append(success)\n return res\n```\n
| 38 | 7 |
[]
| 6 |
process-restricted-friend-requests
|
[C++] | Union Find | Simple Straightforward Idea Explained
|
c-union-find-simple-straightforward-idea-fc4y
|
\n\nThis problem is generous in terms of constraints and we can leverage that to come up with an easily understandable solution!\n\nUnion Find\nA Union Find dat
|
astroash
|
NORMAL
|
2021-11-14T04:00:35.583121+00:00
|
2021-11-14T04:01:23.039382+00:00
| 2,515 | false |
\n\nThis problem is generous in terms of constraints and we can leverage that to come up with an easily understandable solution!\n\n**Union Find**\nA Union Find data structure, also known as the Disjoint Set data structure, stores a collection of disjoint (non overlapping) sets. It mainly has two operations:\n* Union(x, y): It unifies the two arguments into a single set\n* Find(x): It finds the root or the parent of the set which the argument belongs to.\n\nThis data structure is perfect for our current problem as we can group all the friends in disjoint sets and make use of the operations to efficiently do so. I also employ something known as path compression which makes the complexity of both *union* and *find* operations to be amortized O(1). You can learn more about Union Find on Hackerearth and GFG. In fact, I have prepared my template from these sites. \n\n**Idea**\nNow that it is clear we are going to use Union Find here, let us proceed to discussing about how exactly are we planning to do so. \nThe idea is simple and straightforward. We maintain a Union Find data structure which stores all the friends. When we encounter a new friend request, we *accept* it but not really! What I mean is we temporarily accept to check whether it causes any violation of the restrictions or not. \nHow do we do so? \nBy making a copy of our Union Find data structure and unifying the participants of the request in the copy. Then we traverse the list of restrictions and individually check if we are violating any. This is done by checking that the roots/parents of the members of the restriction are same or not. If they are, then they belong to the same friend group which is a violation. If we face no violations, then we can *accept* this friend request in our original data structure as well.\n\nThat\'s it!\n\nThe code might look big, but that is only because of the template. \n\n**C++**\n```\nclass UnionFind {\npublic:\n vector<int> parent;\n\n UnionFind(int n) {\n parent.resize(n + 1, -1);\n }\n\n int find(int x) {\n int root = x;\n while (parent[root] >= 0) {\n root = parent[root];\n }\n\n // Path Compression\n while (parent[x] >= 0) {\n int next = parent[x];\n parent[x] = root;\n x = next;\n }\n\n return root;\n }\n\n void unionz(int x, int y) {\n int root1 = find(x);\n int root2 = find(y);\n\n if (root1 == root2)\n return;\n\n if (parent[root1] < parent[root2]) {\n parent[root1] += parent[root2];\n parent[root2] = root1;\n } else {\n parent[root2] += parent[root1];\n parent[root1] = root2;\n }\n }\n};\n\nclass Solution {\npublic:\n vector<bool> friendRequests(int n, vector<vector<int>>& restrictions, vector<vector<int>>& requests) {\n int m = requests.size();\n vector<bool> ans(m, 0);\n \n UnionFind UF(n);\n \n for(int i = 0; i < m; i++) {\n UnionFind temp = UF;\n temp.unionz(requests[i][0], requests[i][1]);\n bool flag = true;\n for(vector<int>& v : restrictions) {\n if(temp.find(v[0]) == temp.find(v[1])) {\n flag = false;\n break;\n }\n }\n \n if(flag) {\n ans[i] = true;\n UF.unionz(requests[i][0], requests[i][1]);\n }\n }\n \n return ans;\n }\n};\n```\n\n**Complexity Analysis**\n*Space Complexity (Auxiliary): O(n)*\n*Time Complexity: O(m * n)*
| 35 | 1 |
['Union Find']
| 7 |
process-restricted-friend-requests
|
[Python] Union-find, beat 100% by updating restrictions
|
python-union-find-beat-100-by-updating-r-d164
|
\nclass Solution:\n def friendRequests(self, n: int, restrictions: List[List[int]], requests: List[List[int]]) -> List[bool]:\n parents = [i for i in
|
hukenneth
|
NORMAL
|
2021-11-14T06:26:39.517459+00:00
|
2021-11-14T06:26:39.517496+00:00
| 1,026 | false |
```\nclass Solution:\n def friendRequests(self, n: int, restrictions: List[List[int]], requests: List[List[int]]) -> List[bool]:\n parents = [i for i in range(n)]\n ranks = [0] * n\n forbidden = collections.defaultdict(set)\n for i, j in restrictions:\n forbidden[i].add(j)\n forbidden[j].add(i)\n \n def find(i):\n if i != parents[i]:\n parents[i] = find(parents[i])\n return parents[i]\n \n def union(p1, p2):\n if ranks[p1] > ranks[p2]:\n parents[p2] = p1\n elif ranks[p1] < ranks[p2]:\n parents[p1] = p2\n p1, p2 = p2, p1\n else:\n ranks[p1] += 1\n parents[p2] = p1\n \n forbidden[p1] |= forbidden[p2]\n for i in forbidden[p2]:\n forbidden[i].remove(p2)\n forbidden[i].add(p1)\n del forbidden[p2]\n \n ans = []\n for i, j in requests:\n p1 = find(i)\n p2 = find(j)\n if p1 == p2:\n ans.append(True) \n elif p2 in forbidden[p1]:\n ans.append(False)\n else:\n union(p1, p2)\n ans.append(True)\n\n return ans\n \n```
| 23 | 0 |
[]
| 4 |
process-restricted-friend-requests
|
Java Clean and Commented Code With Explanation | Union-Find Algorithm
|
java-clean-and-commented-code-with-expla-jjkk
|
PREREQUISITE: UNION-FIND ALGORITHM\n\nThis problem is pretty straightforwad. Basically they are saying that two people can be friends if they have no restrictio
|
rajarshisg
|
NORMAL
|
2021-11-14T18:56:18.455646+00:00
|
2021-11-16T08:18:47.096656+00:00
| 1,894 | false |
**PREREQUISITE: UNION-FIND ALGORITHM**\n\nThis problem is pretty straightforwad. Basically they are saying that two people can be friends if they have no restrictions or any of their mutual friends have no restriction.\n\nThe simplest way to solve this would be to use the union-find technique to link all the persons with mutual friends to one common ancestor. Now for every request we simply check that whether those ancestors have any restrictions or not. If they do they can\'t be friends or else they can be.\n\n**EDIT - There is a nice optimization that could be done inside findParent, check @chinghsuanwei0206\'s comment for explanation.**\n\nHere is the code for the same,\n\n```\nclass Solution {\n \n //Classic Union-Find Algorithm to find Common Ancestor\n private int findParent(int[] parent, int index) {\n if(parent[index] == index) return index;\n return findParent(parent, parent[index]);\n }\n \n public boolean[] friendRequests(int n, int[][] restrictions, int[][] requests) {\n int resLength = restrictions.length, reqLength = requests.length;\n boolean[] result = new boolean[reqLength];\n int[] parent = new int[n];\n \n //Initially ith person\'s parent is i itself\n for(int i = 0; i < n; i++) parent[i] = i;\n \n\n for(int i = 0; i < reqLength; i++) {\n //finding the parents of the first person and second person of ith request\n int firstParent = findParent(parent, requests[i][0]);\n int secondParent = findParent(parent, requests[i][1]);\n \n //if they have same parents i.e. mutual friends they can be friends\n if(firstParent == secondParent) {\n result[i] = true;\n continue;\n }\n \n //iterating through the restrictions array to find whether the parents of first ans second person have a conflict \n boolean flag = true;\n for(int j = 0; j < resLength; j++) {\n //finding parents of the restriction persons\n int firstRestriction = findParent(parent, restrictions[j][0]);\n int secondRestriction = findParent(parent, restrictions[j][1]);\n \n //if any of the parents are matching i.e. if the parents of first and second person have a mutual conflict they can\'t be friend\n if((firstRestriction == firstParent && secondRestriction == secondParent) || (secondRestriction == firstParent && firstRestriction == secondParent)) {\n flag = false;\n break;\n }\n }\n \n if(flag) {\n result[i] = true;\n parent[firstParent] = secondParent; //setting the common ancestor -> classic union find technique\n }\n }\n \n return result;\n }\n}\n```
| 22 | 0 |
['Java']
| 5 |
process-restricted-friend-requests
|
Union Find
|
union-find-by-votrubac-5np4
|
I thought there is some clever way to track enemies, and wasted a lot of time. Should have looked at constraints closelly - 1000 is not a big number for a n * m
|
votrubac
|
NORMAL
|
2021-11-14T06:33:03.589300+00:00
|
2021-11-14T07:28:49.472477+00:00
| 1,790 | false |
I thought there is some clever way to track enemies, and wasted a lot of time. Should have looked at constraints closelly - `1000` is not a big number for a `n * m` solution. \n\nSo we join frieds using union-find. But before we do, we scan through all `restrictions`, to make sure that sets of friends that we are joining do not include any restricted pair.\n\n**C++**\n```cpp\nint find(vector<int> &ds, int i) {\n return ds[i] < 0 ? i : ds[i] = find(ds, ds[i]);\n}\nvector<bool> friendRequests(int n, vector<vector<int>>& enemies, vector<vector<int>>& requests) {\n vector<bool> res;\n vector<int> ds(n, -1);\n for (auto &req : requests) {\n int i = find(ds, req[0]), j = find(ds, req[1]);\n bool friends = i == j;\n if (!friends) {\n friends = true;\n for (int k = 0; friends && k < enemies.size(); ++k) {\n int x = find(ds, enemies[k][0]), y = find(ds, enemies[k][1]);\n friends = (x != i || y != j) && (x != j || y != i);\n }\n if (friends)\n ds[j] = i;\n }\n res.push_back(friends);\n }\n return res;\n}\n```
| 14 | 0 |
[]
| 3 |
process-restricted-friend-requests
|
💥Beats 100% on runtime [EXPLAINED]
|
beats-100-on-runtime-explained-by-r9n-8pe6
|
Intuition\nDetermine if two people can be friends based on a list of restrictions, where some pairs of people cannot be friends due to prior conditions. The key
|
r9n
|
NORMAL
|
2024-10-28T05:54:23.363732+00:00
|
2024-10-28T05:54:23.363765+00:00
| 138 | false |
# Intuition\nDetermine if two people can be friends based on a list of restrictions, where some pairs of people cannot be friends due to prior conditions. The key insight is that if two people belong to the same restricted pair, they cannot be friends, so we need to manage relationships dynamically while respecting these restrictions.\n\n# Approach\nUse a Disjoint Set Union (DSU) to group friends and check requests; for each request, temporarily union the two people, then verify against restrictions, restoring the state if invalid.\n\n# Complexity\n- Time complexity:\nO((R+Q)\u22C5\u03B1(N)), where \uD835\uDC45 R is the number of restrictions, \uD835\uDC44 Q is the number of requests, \uD835\uDC41 N is the number of people, and \uD835\uDEFC \u03B1 is the inverse Ackermann function, which grows very slowly, making this efficient in practice.\n\n- Space complexity:\nO(N) due to the storage of the parent and rank arrays in the DSU.\n\n# Code\n```csharp []\nusing System;\nusing System.Collections.Generic;\n\npublic class DSU\n{\n public List<int> parent;\n public List<int> rank;\n\n public DSU(int n)\n {\n parent = new List<int>(new int[n]);\n rank = new List<int>(new int[n]);\n\n for (int i = 0; i < n; i++)\n {\n parent[i] = -1; // Initialize each node as its own parent\n rank[i] = 0; // Initialize rank to 0\n }\n }\n\n public int Find(int i)\n {\n if (parent[i] == -1)\n {\n return i; // If it\'s its own parent, return itself\n }\n return parent[i] = Find(parent[i]); // Path compression\n }\n\n public void Union(int a, int b)\n {\n int s1 = Find(a);\n int s2 = Find(b);\n\n if (s1 != s2) // If they are not already in the same set\n {\n // Union by rank\n if (rank[s1] >= rank[s2])\n {\n parent[s2] = s1; // Make s1 the parent of s2\n rank[s1] += rank[s2]; // Update the rank of s1\n }\n else\n {\n parent[s1] = s2; // Make s2 the parent of s1\n rank[s2] += rank[s1]; // Update the rank of s2\n }\n }\n }\n}\n\npublic class Solution\n{\n public bool[] FriendRequests(int n, IList<IList<int>> restrictions, IList<IList<int>> requests)\n {\n DSU dsu = new DSU(n); // Create an instance of DSU\n List<bool> ans = new List<bool>(); // To store the result of each request\n \n // Process each friend request\n foreach (var request in requests)\n {\n int u = request[0];\n int v = request[1];\n bool canBeFriends = true;\n\n // Backup the current state of the DSU\n var backupParent = new int[n];\n var backupRank = new int[n];\n Array.Copy(dsu.parent.ToArray(), backupParent, n);\n Array.Copy(dsu.rank.ToArray(), backupRank, n);\n \n dsu.Union(u, v); // Temporarily union the friends\n \n // Check all restrictions\n foreach (var restriction in restrictions)\n {\n // If both people in the restriction are in the same connected component\n if (dsu.Find(restriction[0]) == dsu.Find(restriction[1]))\n {\n canBeFriends = false; // They cannot be friends due to restriction\n break;\n }\n }\n\n if (canBeFriends)\n {\n ans.Add(true); // If no restrictions were violated, the request is successful\n }\n else\n {\n ans.Add(false); // If restrictions were violated, reject the request\n // Restore the backup if the request is rejected\n dsu.parent = new List<int>(backupParent);\n dsu.rank = new List<int>(backupRank);\n }\n }\n\n return ans.ToArray(); // Convert List<bool> to bool[] and return\n }\n}\n\n```
| 10 | 0 |
['Union Find', 'Graph', 'C#']
| 0 |
process-restricted-friend-requests
|
[c++] bitset & union find [50ms]
|
c-bitset-union-find-50ms-by-lyronly-7dom
|
This problem is the perfect one to use bitset. since # is less than 1000.\nwe have 2 bitset array \nvector<bitset<1000>> hate;\nvector<bitset<1000>> g;\nreprese
|
lyronly
|
NORMAL
|
2021-11-14T05:57:55.283196+00:00
|
2021-11-16T00:18:49.633152+00:00
| 576 | false |
This problem is the perfect one to use bitset. since # is less than 1000.\nwe have 2 bitset array \nvector<bitset<1000>> hate;\nvector<bitset<1000>> g;\nrepresent a group\'s member, and a group\'s members\'s hate-list(can not be friend with).\n\n```\nclass Solution {\npublic:\n vector<int> parent;\n vector<bitset<1000>> hate;\n vector<bitset<1000>> g;\n int findp(int p) {\n return (parent[p] == p) ? p : parent[p]=findp(parent[p]);\n }\n bool tryun(int a, int b) {\n int pa = findp(a);\n int pb = findp(b);\n if (pa == pb) return true;\n if ((hate[pa] & g[pb]).any()) return false;\n g[pa] |= g[pb];\n hate[pa] |= hate[pb];\n parent[pb] = pa;\n return true;\n }\n vector<bool> friendRequests(int n, vector<vector<int>>& restrictions, vector<vector<int>>& requests) {\n parent.resize(n);\n hate.resize(n);\n g.resize(n);\n for (int i = 0; i < n; i++) { parent[i] = i; g[i][i] = 1;} \n for (auto& r : restrictions) { hate[r[0]][r[1]] = 1; hate[r[1]][r[0]] = 1;}\n vector<bool> ans;\n for (auto& r : requests) ans.push_back(tryun(r[0], r[1]));\n return ans;\n }\n};\n```
| 8 | 0 |
[]
| 1 |
process-restricted-friend-requests
|
Intuition Explained || Straight Forward DSU || C++ Clean Code
|
intuition-explained-straight-forward-dsu-dor6
|
Code: \n\n\n// Standard DSU Class\nclass DSU {\n vector<int> parent, size;\npublic: \n \n DSU(int n) {\n for(int i=0; i<=n; i++) {\n
|
i_quasar
|
NORMAL
|
2021-11-27T04:24:33.081543+00:00
|
2021-11-27T04:25:00.711386+00:00
| 667 | false |
# Code: \n\n```\n// Standard DSU Class\nclass DSU {\n vector<int> parent, size;\npublic: \n \n DSU(int n) {\n for(int i=0; i<=n; i++) {\n parent.push_back(i);\n size.push_back(1);\n }\n }\n \n int findParent(int num) {\n if(parent[num] == num) return num;\n return parent[num] = findParent(parent[num]);\n }\n \n\t// Directly getting parents of u and v\n\t// To avoid finding parent multiple times\n void unionBySize(int parU, int parV) {\n \n if(size[parU] < size[parV]) {\n size[parV] += size[parU];\n parent[parU] = parV;\n }\n else {\n size[parU] += size[parV];\n parent[parV] = parU;\n }\n }\n};\n\nclass Solution {\npublic:\n vector<bool> friendRequests(int n, vector<vector<int>>& restrictions, vector<vector<int>>& requests) {\n \n DSU dsu(n);\n \n vector<bool> successful;\n \n for(auto& request : requests) {\n \n int u = request[0], v = request[1];\n \n int parU = dsu.findParent(u), parV = dsu.findParent(v);\n \n bool flag = true;\n \n if(parU != parV) {\n \n\t\t\t\t// Check if current friend requested is restricted or not.\n for(auto& restriction : restrictions) {\n int restricted_U = restriction[0], restricted_V = restriction[1];\n \n int restricted_parU = dsu.findParent(restricted_U);\n int restricted_parV = dsu.findParent(restricted_V);\n \n if((parU == restricted_parU && parV == restricted_parV) || (parU == restricted_parV && parV == restricted_parU)) {\n flag = false;\n break;\n }\n }\n \n\t\t\t\t// Union u and v by passing parents\n\t\t\t\t// Since it is already calculated above\n if(flag) {\n dsu.unionBySize(parU, parV);\n }\n }\n \n successful.push_back(flag);\n }\n \n return successful;\n }\n};\n```
| 6 | 0 |
['Union Find', 'C']
| 0 |
process-restricted-friend-requests
|
[JAVA] beats 98% with comments and complexity analysis
|
java-beats-98-with-comments-and-complexi-8tm1
|
time complexity:\nnumber of persons: n\nnumber of restrictions: m\nnumber of requests: k\n\ninitialize friends and enemies: O(n + m)\nCollaping find: O(n)\nmerg
|
jiajiasheen
|
NORMAL
|
2021-11-14T21:31:21.356621+00:00
|
2021-11-15T23:38:05.494895+00:00
| 831 | false |
time complexity:\nnumber of persons: n\nnumber of restrictions: m\nnumber of requests: k\n\ninitialize friends and enemies: O(n + m)\nCollaping find: O(n)\nmerge enemies set: O(m)\n\nin total: n + m + k * (n + m) = O (k * (n + m))\n\n\nSpace: O(n + m)\n\n```\nclass Solution {\n public boolean[] friendRequests(int n, int[][] restrictions, int[][] requests) {\n boolean[] res = new boolean[requests.length];\n \n Set<Integer>[] enemies = new Set[n];\n int[] friends = new int[n];\n \n for (int i = 0; i < n; i++) {\n friends[i] = i;\n enemies[i] = new HashSet<>();\n }\n \n for (int i = 0; i < restrictions.length; i++) {\n //add person A to person B\'s enmey circle.\n //add person B to person A\'s enemy circle.\n enemies[restrictions[i][0]].add(restrictions[i][1]);\n enemies[restrictions[i][1]].add(restrictions[i][0]);\n }\n \n for (int i = 0; i < requests.length; i++) {\n int personA = findRootFriend(friends, requests[i][0]);\n int personB = findRootFriend(friends, requests[i][1]);\n Set<Integer> personAEnemies = enemies[personA];\n Set<Integer> personBEnemies = enemies[personB]; \n \n if (personA == personB) {\n res[i] = true;\n } else if (!personAEnemies.contains(personB) && !personBEnemies.contains(personA)) {\n //can merge. update personB\'s root to be person A\n friends[personB] = personA;\n \n // add all B\'s enemies to A\'s enemyies\n personAEnemies.addAll(personBEnemies);\n \n // inform all B\'s enemies that A is a new enemy\n for (int k : personBEnemies) {\n enemies[k].add(personA);\n }\n \n res[i] = true;\n } else {\n res[i] = false;\n }\n } \n \n return res;\n }\n \n private int findRootFriend(int[] friends, int i) {\n if (friends[i] == i) {\n return i;\n }\n \n return findRootFriend(friends, friends[i]);\n }\n}\n```
| 6 | 0 |
[]
| 1 |
process-restricted-friend-requests
|
Java, Union Find
|
java-union-find-by-qingqi_lei-gq1j
|
\nclass Solution {\n public boolean[] friendRequests(int n, int[][] re, int[][] requests) {\n UnionFind uf = new UnionFind();\n boolean[] res =
|
qingqi_lei
|
NORMAL
|
2021-11-14T04:03:52.418532+00:00
|
2021-11-14T04:03:52.418604+00:00
| 617 | false |
```\nclass Solution {\n public boolean[] friendRequests(int n, int[][] re, int[][] requests) {\n UnionFind uf = new UnionFind();\n boolean[] res = new boolean[requests.length];\n Arrays.fill(res,true);\n for(int i = 0; i < requests.length; i++){\n int[] r =requests[i];\n int a = r[0], b = r[1];\n int a1 = uf.find(a), b1 = uf.find(b);\n for(int[] t: re){\n int t1 = uf.find(t[0]), t2 = uf.find(t[1]);\n if(t1 == a1 && b1 == t2 || a1 == t2 && b1 == t1){\n res[i] = false;\n break;\n }\n }\n if(res[i]) uf.union(a,b);\n }\n return res;\n }\n \n}\n\nclass UnionFind{\n Map<Integer, Integer> map = new HashMap<>();\n int find(int n){\n map.putIfAbsent(n,n);\n while(n != map.get(n)){\n map.put(n, map.get(map.get(n)));\n n = map.get(n);\n }\n return n;\n }\n void union(int a, int b){\n map.put(find(a), find(b));\n }\n}\n```
| 6 | 0 |
[]
| 1 |
process-restricted-friend-requests
|
[C++] Simple C++ Code || 90% time || union find
|
c-simple-c-code-90-time-union-find-by-pr-cje0
|
\n# If you like the implementation then Please help me by increasing my reputation. By clicking the up arrow on the left of my image.\n\nclass Solution {\n v
|
_pros_
|
NORMAL
|
2022-08-21T10:54:25.544900+00:00
|
2022-08-21T10:54:25.544943+00:00
| 916 | false |
\n# **If you like the implementation then Please help me by increasing my reputation. By clicking the up arrow on the left of my image.**\n```\nclass Solution {\n vector<int> parents;\n int find_set(int v)\n {\n if(v == parents[v])\n return v;\n return parents[v] = find_set(parents[v]);\n }\n void union_set(int a, int b)\n {\n a = find_set(a);\n b = find_set(b);\n if(a == b)\n return;\n if(a != b)\n parents[b] = a;\n return;\n }\npublic:\n vector<bool> friendRequests(int n, vector<vector<int>>& restrictions, vector<vector<int>>& requests) {\n for(int i = 0; i < n; i++)\n parents.push_back(i);\n vector<bool> ans;\n for(vector<int> &req : requests)\n {\n int v = 1;\n int a = find_set(req[0]);\n int b = find_set(req[1]);\n for(vector<int> &res : restrictions)\n {\n int r1 = find_set(res[0]);\n int r2 = find_set(res[1]);\n if((a == r1 && b == r2) || (b == r1 && a == r2))\n {\n v = 0;\n break;\n }\n }\n ans.push_back(v);\n if(v)\n {\n union_set(a,b);\n }\n }\n return ans;\n }\n};\n```
| 4 | 0 |
['Union Find', 'C', 'C++']
| 0 |
process-restricted-friend-requests
|
[Python] Union find beats 98% runtime and 34% space
|
python-union-find-beats-98-runtime-and-3-9lfr
|
I think it is easy for everyone to see this problem requires union find. \nThe key point is about how to detect if the friend request is restricted or not. \nWe
|
watashij
|
NORMAL
|
2021-12-09T21:03:36.565901+00:00
|
2021-12-19T21:21:40.010117+00:00
| 351 | false |
I think it is easy for everyone to see this problem requires union find. \nThe key point is about how to detect if the friend request is restricted or not. \nWe can of course iterate through all restricted ones and check, but that will be too expensive. \nHere I have maintained a map called `excluded`, which is `{people => { set of restricted peoples } }`.\nThis map is updated whenever a successful union happens.\nWe use `DisjointSet` to keep the information of friend circles, like everyone would do.\n\nSo the algorithm has only 3 conditions for people1 trying to make friend with people2:\n1. people1 and people2 are already in the same group (directly or indirectly), that is just fine. `res = True`\n2. people2 is in people1\'s excluding list, then they cannot be friends. `res = False`\n3. people1 and people2 are not in the same friend circle, and they are not mutually excluded, then we just merge their friend circles. The merge happens by updating the excluded map (more details in the next paragraph) and DisjointSet. `res = True`\n\nThe excluded map update is straight forward, it does 2 things to update:\n1. Merge names from people2\'s list to people1\'s list. Because people1 and people2 are in the same group now, and the excluded people should be merged.\n2. For every people excluded by people2, they also exclude people2, and we need them to exclude people1 as well\n\nHere is the code:\n```python\nclass DisjointSet:\n def __init__(self, n):\n self.parent = list(range(n))\n def find(self, x):\n if self.parent[x] != x:\n self.parent[x] = self.find(self.parent[x])\n return self.parent[x]\n\nclass Solution:\n def friendRequests(self, n: int, restrictions: List[List[int]], requests: List[List[int]]) -> List[bool]:\n from collections import defaultdict\n excluded = defaultdict(set)\n for people1, people2 in restrictions: # exclusion is mutual\n excluded[people1].add(people2) \n excluded[people2].add(people1)\n\t\t\t\n def update_exclusion(from_p, to_p): # update exclusion map\n targets = excluded.pop(from_p, [])\n for people in targets: # people being excluded by people2 should now also exclude people1\n excluded[people].remove(from_p)\n excluded[people].add(to_p)\n excluded[to_p].update(targets) # people1 should exclude people that are excluded by people2\n\t\t\t\n res = []\n disjoint_set = DisjointSet(n)\n for people1, people2 in requests:\n circle1 = disjoint_set.find(people1)\n circle2 = disjoint_set.find(people2)\n if circle1 == circle2: \n res.append(True)\n elif circle2 in excluded[circle1]:\n res.append(False)\n else:\n update_exclusion(circle2, circle1)\n disjoint_set.parent[circle2] = circle1\n res.append(True)\n return res\n \n```
| 4 | 0 |
['Union Find']
| 0 |
process-restricted-friend-requests
|
✅ [Python] UnionFind || Easy to Understand with Explanation
|
python-unionfind-easy-to-understand-with-9ev7
|
\nclass UnionFindSet(object):\n def __init__(self, n):\n self.data = range(n)\n\n def find(self, x):\n while x <> self.data[x]:\n
|
linfq
|
NORMAL
|
2021-11-17T11:19:30.365763+00:00
|
2021-11-17T11:19:30.365799+00:00
| 398 | false |
```\nclass UnionFindSet(object):\n def __init__(self, n):\n self.data = range(n)\n\n def find(self, x):\n while x <> self.data[x]:\n x = self.data[x]\n return x\n\n def union(self, x, y):\n self.data[self.find(x)] = self.find(y)\n\n def speedup(self):\n for i in range(len(self.data)):\n self.data[i] = self.find(i)\n\n\nclass Solution(object):\n def friendRequests(self, n, restrictions, requests):\n uf = UnionFindSet(n)\n ret = [True] * len(requests)\n for k, [x, y] in enumerate(requests): # Process Requests Sequentially\n xh = uf.find(x) # backup the head of x for undo\n uf.union(x, y) # link [x, y] and verify if any restriction triggers\n for [i, j] in restrictions:\n if uf.find(i) == uf.find(j):\n ret[k] = False\n break\n if not ret[k]: # if any restriction triggers, undo\n uf.data[xh] = xh\n else:\n uf.speedup()\n return ret\n```\n**If you have any questoins, feel free to ask. If you like the solution and explanation, please upvote!**
| 4 | 0 |
['Union Find', 'Python']
| 0 |
process-restricted-friend-requests
|
C++ || DSU || 2 Approaches
|
c-dsu-2-approaches-by-anshul_07-jf70
|
Approach 1\n\nclass DSU {\nprivate: \n\tvector<int> parent, size, rank; \n \n\tpublic:\n DSU(int n) {\n\t\tfor(int i=0; i<n; i++) {\n\t\t\tparent.push_back(i
|
Anshul_07
|
NORMAL
|
2021-11-15T22:04:14.157243+00:00
|
2021-11-19T18:43:02.476748+00:00
| 280 | false |
# **Approach 1**\n```\nclass DSU {\nprivate: \n\tvector<int> parent, size, rank; \n \n\tpublic:\n DSU(int n) {\n\t\tfor(int i=0; i<n; i++) {\n\t\t\tparent.push_back(i); \n\t\t\tsize.push_back(1); \n\t\t\trank.push_back(0); \n\t\t}\n\t}\n \n \npublic: \n\tint findPar(int node) {\n\t\tif(parent[node] == node) {\n\t\t\treturn node; \n\t\t}\n\t\treturn parent[node] = findPar(parent[node]); \n\t}\n \npublic:\n\tvoid unionSize(int u, int v) {\n\t\tint pu = findPar(u); \n\t\tint pv = findPar(v); \n\t\tif(pu == pv) {\n\t\t\treturn; \n\t\t}\n\t\tif(size[pu] < size[pv]) {\n\t\t\tparent[pu] = pv; \n\t\t\tsize[pv] += size[pu]; \n\t\t}\n\t\telse {\n\t\t\tparent[pv] = pu; \n\t\t\tsize[pu] += size[pv]; \n\t\t}\n\t}\npublic:\n\tvoid unionRank(int u, int v) {\n\t\tint pu = findPar(u); \n\t\tint pv = findPar(v); \n\t\tif(pu == pv) {\n\t\t\treturn; \n\t\t}\n\t\tif(rank[pu] < rank[pv]) {\n\t\t\tparent[pu] = pv; \n\t\t}\n\t\telse if(rank[pv] < rank[pu]){\n\t\t\tparent[pv] = pu; \n\t\t}\n\t\telse {\n\t\t\tparent[pu] = pv;\n\t\t\trank[pv]++; \n\t\t}\n\t}\n};\n\nclass Solution {\npublic:\n vector<bool> friendRequests(int n, vector<vector<int>>& restrictions, vector<vector<int>>& requests) {\n DSU dsu(n);\n vector<bool> ans;\n \n for(auto it: requests){\n int x = it[0];\n int y = it[1];\n \n DSU temp = dsu;\n \n temp.unionRank(x, y);\n \n bool flag = true;\n for(auto itr: restrictions){\n int x1 = itr[0];\n int y1 = itr[1];\n \n if(temp.findPar(x1)==temp.findPar(y1)){\n flag=false; \n break;\n }\n }\n \n if(flag==true){\n ans.push_back(true);\n dsu.unionRank(x, y);\n }\n else{\n ans.push_back(false);\n }\n }\n return ans;\n }\n};\n```\n\n# **Approach 2**\n**(with better space complexity)**\n\n```\nclass DSU {\nprivate: \n\tvector<int> parent, size, rank; \n \n\tpublic:\n DSU(int n) {\n\t\tfor(int i=0; i<n; i++) {\n\t\t\tparent.push_back(i); \n\t\t\tsize.push_back(1); \n\t\t\trank.push_back(0); \n\t\t}\n\t}\n \n \npublic: \n\tint findPar(int node) {\n\t\tif(parent[node] == node) {\n\t\t\treturn node; \n\t\t}\n\t\treturn parent[node] = findPar(parent[node]); \n\t}\n \npublic:\n\tvoid unionSize(int u, int v) {\n\t\tint pu = findPar(u); \n\t\tint pv = findPar(v); \n\t\tif(pu == pv) {\n\t\t\treturn; \n\t\t}\n\t\tif(size[pu] < size[pv]) {\n\t\t\tparent[pu] = pv; \n\t\t\tsize[pv] += size[pu]; \n\t\t}\n\t\telse {\n\t\t\tparent[pv] = pu; \n\t\t\tsize[pu] += size[pv]; \n\t\t}\n\t}\npublic:\n\tvoid unionRank(int u, int v) {\n\t\tint pu = findPar(u); \n\t\tint pv = findPar(v); \n\t\tif(pu == pv) {\n\t\t\treturn; \n\t\t}\n\t\tif(rank[pu] < rank[pv]) {\n\t\t\tparent[pu] = pv; \n\t\t}\n\t\telse if(rank[pv] < rank[pu]){\n\t\t\tparent[pv] = pu; \n\t\t}\n\t\telse {\n\t\t\tparent[pu] = pv;\n\t\t\trank[pv]++; \n\t\t}\n\t}\n};\n\nclass Solution {\npublic:\n vector<bool> friendRequests(int n, vector<vector<int>>& restrictions, vector<vector<int>>& requests) {\n DSU dsu(n);\n vector<bool> ans;\n \n for(auto &it: requests){\n int x = it[0];\n int y = it[1];\n int px = dsu.findPar(x);\n int py = dsu.findPar(y);\n \n bool flag=true;\n if(px!=py){\n for(auto &itr: restrictions){\n int pu = dsu.findPar(itr[0]);\n int pv = dsu.findPar(itr[1]);\n \n if((pu==px && pv==py) || pu==py && pv==px){\n flag=false;\n break;\n }\n }\n }\n if(flag==false){\n ans.push_back(false);\n }\n else{\n ans.push_back(true);\n dsu.unionRank(x, y);\n }\n }\n return ans;\n }\n};\n```
| 4 | 0 |
[]
| 1 |
process-restricted-friend-requests
|
Easy to follow Java Code, 12 ms time (beats 100%)
|
easy-to-follow-java-code-12-ms-time-beat-q0qd
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
topoGraphKing
|
NORMAL
|
2023-08-02T11:35:56.897912+00:00
|
2023-08-02T11:40:47.009684+00:00
| 138 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe runtime of the code is O(n * m). where n is the number of restrictions (restrictions.length) and m is the number of queries (requests.length).\n\nThe first loop in the DisjoinSet class takes O(n) time to initialize the parent and rank arrays. The second loop takes O(n) time to add each restriction to the appropriate set. The notRestricted() method takes O(1) time to check if two roots are restricted from being in the same set.\n\nThe union() method takes O(1) time to find the roots of the two nodes being unioned. If the two roots are not restricted from being in the same set, then the union() method takes O(1) time to union the two sets. If the two roots are restricted from being in the same set, then the union() method takes O(n) time to update the restrictions of the two sets.\n\nThe friendRequests() method takes O(m) time to iterate through the queries and call the union() method for each query.\n\nTherefore, the overall runtime of the code is O(n * m).\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n//Idea and code from \n// https://leetcode.com/problems/process-restricted-friend-requests/solutions/3814592/union-find-disjoint-sets-solution-faster-than-90-java/\n\nclass DisjoinSet {\n private final int [] parent;\n private final int [] rank;\n private final List<Set<Integer>> restrictions;\n\n DisjoinSet(int size, int[][] restrictions){\n this.parent = new int [size];\n this.rank = new int [size]; \n this.restrictions = new ArrayList<>(size);\n\n for(int i =0; i <size; i++) {\n this.parent[i] = i;\n this.rank[i] = 1;\n this.restrictions.add(new HashSet<>());\n }\n\n for (int [] restriction: restrictions){\n this.restrictions.get(restriction[0]).add(restriction[1]);\n this.restrictions.get(restriction[1]).add(restriction[0]);\n }\n }\n\n private int find(int node){\n int root=node;\n while(parent[root]!=root){\n root=parent[root];\n }\n\n while (parent[node]!=root){\n int next = parent[node];\n parent[node]=root;\n node = next;\n }\n return root;\n }\n\n public boolean union (int n1, int n2){\n int p1 = find(n1);\n int p2 = find(n2);\n\n if (p1==p2){\n return true;\n }\n \n if (notRestricted(p1,p2)){\n if (rank[p1]>rank[p2]){\n rank[p1]+=rank[p2];\n parent[p2]=p1;\n // Combine the restrictions list\n //Add all parent Nodes from other list \n for (int node: restrictions.get(p2)){\n restrictions.get(p1).add(find(node) );\n }\n } else{\n rank[p2]+=rank[p1];\n parent[p1]= p2;\n // Combine the restrictions list\n //Add all parent Nodes from other list \n for (int node: restrictions.get(p1)){\n restrictions.get(p2).add(find(node) );\n }\n }\n return true;\n }\n return false;\n }\n \n private boolean notRestricted(int root1, int root2) {\n if (restrictions.get(root1).contains(root2))\n return false;\n if (restrictions.get(root2).contains(root1))\n return false;\n return true;\n }\n}\n\nclass Solution {\n public boolean[] friendRequests(int n, int[][] restrictions, int[][] requests) {\n if (restrictions.length==0){\n boolean [] queries = new boolean [requests.length];\n Arrays.fill(queries,true);\n return queries;\n }\n DisjoinSet set = new DisjoinSet(n,restrictions);\n boolean [] queries = new boolean [requests.length];\n for (int i =0; i<requests.length ;i++){\n queries[i] = set.union(requests[i][0],requests[i][1] );\n }\n return queries;\n }\n}\n```
| 3 | 0 |
['Java']
| 1 |
process-restricted-friend-requests
|
C++ Make Friends
|
c-make-friends-by-changoi-k6p5
|
Hint/Thought Process\n- If x is a friend of y, and y is a friend of z, then x will be a friend of z. So, we can say, friends will form a connected component.\n\
|
changoi
|
NORMAL
|
2021-11-14T04:00:32.022077+00:00
|
2021-11-14T04:00:32.022129+00:00
| 583 | false |
**Hint/Thought Process**\n- If x is a friend of y, and y is a friend of z, then x will be a friend of z. So, we can say, friends will form a connected component.\n\t- => Hint for using disjoint set union.\n\n**Algorithm**\n- We process requests sequentially.\n\t- Let\'s say we are processing request[ i ] = [u,v]\n\t\n\t- Then, from previous requests, we know u & v will be part of some components.\n\t- Let say u\'s component contains: [u1,u2,u3,..., ux] and v\'s component contains: [v1,v2,v3,...,vy]\n\t\t- Now, after processing the current request, every pair (u_i, v_j) will be friends, for all i<=x and j<=y\n\t\t- Thus, if any of such pairs is restricted, i.e. (u_i, v_j) can\'t be friends \n\t\t\t- => We can\'t process the current request i.\n\t- Hence, we iterate over the Restrictions array for every request and check if any of the restriction is violated.\n\t\t- If no restriction is violated, we can process the current request.\n\t\t- Otherwise, we can\'t process the current request.\n\n\n**Time Complexity**\n- Let N = requests.size(), M = restrictions.size(), n = # people\n- O(N*M)\n\n**Code**\n```\nint find(vector<int> &ds, int i) {\n return ds[i] < 0 ? i : ds[i] = find(ds, ds[i]);\n}\n\nbool Union(vector<int> &ds, int i, int j){\n\t i = find(ds, i), j = find(ds, j);\n\t if(i==j) return false;\n\t if(abs(ds[i]) < abs(ds[j])) swap(i,j); \n\t ds[i]+=ds[j]; \n\t ds[j]=i;\n\t return true;\n}\n\nclass Solution {\npublic:\n vector<bool> friendRequests(int n, vector<vector<int>>& restrictions, vector<vector<int>>& requests) {\n vector<bool> res;\n vector<int> ds(n, -1);\n for(auto &r : requests){\n int u = find(ds,r[0]), v = find(ds,r[1]), can = 1;\n\t\t\t\n for(auto &rt : restrictions){\n int u1 = find(ds,rt[0]), v1 = find(ds, rt[1]);\n if((u1==u && v1 == v) || (u1==v && v1==u)){ \n //restricted pair will be connected!! => Do not process the request\n can = 0;\n break;\n }\n }\n if(can) Union(ds,u,v);\n res.push_back(can); \n }\n return res;\n }\n};\n```
| 3 | 0 |
[]
| 2 |
process-restricted-friend-requests
|
[C++] O(1) to check all restrictions Beats 100.00%
|
c-o1-to-check-all-restrictions-beats-100-006z
|
Intuition\nUse DisJoinSet to check circle. Maintain likes and unlikes for each node;\n\n# Approach\n Describe your approach to solving the problem. \n1. If we c
|
andrewfu
|
NORMAL
|
2023-10-31T04:31:32.600848+00:00
|
2023-10-31T04:32:24.269754+00:00
| 354 | false |
# Intuition\nUse DisJoinSet to check circle. Maintain likes and unlikes for each node;\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. If we can know the like and unlike nodes, we can process all restrictions at once.\n2. Before union (making friend), we need to check no conflic beteen unlikes and likes.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n class DJS {\n public:\n vector<int> parent, size;\n vector<bitset<1000>> like, unlike;\n DJS(int n, const vector<vector<int>>& restrictions) {\n parent.resize(n); \n like.resize(n);\n unlike.resize(n); \n size.resize(n);\n fill(size.begin(), size.end(), 1);\n for (int i = 0; i < n; i++) {\n parent[i] = i;\n like[i][i] = true;\n }\n for (auto& r : restrictions) {\n unlike[r[0]][r[1]] = true;\n unlike[r[1]][r[0]] = true;\n }\n }\n int find(int a) {\n int node = a;\n while (node != parent[node]) {\n node = parent[node];\n }\n return parent[a] = node;\n }\n bool unionBySize(int a, int b) {\n int pa = find(a), pb = find(b);\n if (pa == pb) return true;\n // we need to check no conflic beteen unlikes and likes.\n if ((unlike[pa] & like[pb]).any() || (unlike[pb] & like[pa]).any()) {\n return false;\n }\n int lead = pb, follow = pa;\n if (size[pa] > size[pb]) {\n lead = pa;\n follow = pb;\n } \n parent[follow] = lead;\n size[lead] += size[follow];\n like[lead] |= like[follow];\n unlike[lead] |= unlike[follow];\n return true;\n }\n };\n vector<bool> friendRequests(int n, vector<vector<int>>& restrictions, vector<vector<int>>& requests) {\n DJS djs(n, restrictions);\n int m = requests.size();\n vector<bool> ans(m);\n for (int i = 0; i < m; i++) {\n ans[i] = djs.unionBySize(requests[i][0], requests[i][1]);\n }\n return ans;\n }\n};\n\n\n\n```
| 2 | 0 |
['C++']
| 2 |
process-restricted-friend-requests
|
c++ | easy | short
|
c-easy-short-by-venomhighs7-ks87
|
\n# Code\n\nclass Solution {\n vector<int> parents;\n int find_set(int v)\n {\n if(v == parents[v])\n return v;\n return parents
|
venomhighs7
|
NORMAL
|
2022-10-20T04:16:44.163588+00:00
|
2022-10-20T04:16:44.163629+00:00
| 604 | false |
\n# Code\n```\nclass Solution {\n vector<int> parents;\n int find_set(int v)\n {\n if(v == parents[v])\n return v;\n return parents[v] = find_set(parents[v]);\n }\n void union_set(int a, int b)\n {\n a = find_set(a);\n b = find_set(b);\n if(a == b)\n return;\n if(a != b)\n parents[b] = a;\n return;\n }\npublic:\n vector<bool> friendRequests(int n, vector<vector<int>>& restrictions, vector<vector<int>>& requests) {\n for(int i = 0; i < n; i++)\n parents.push_back(i);\n vector<bool> ans;\n for(vector<int> &req : requests)\n {\n int v = 1;\n int a = find_set(req[0]);\n int b = find_set(req[1]);\n for(vector<int> &res : restrictions)\n {\n int r1 = find_set(res[0]);\n int r2 = find_set(res[1]);\n if((a == r1 && b == r2) || (b == r1 && a == r2))\n {\n v = 0;\n break;\n }\n }\n ans.push_back(v);\n if(v)\n {\n union_set(a,b);\n }\n }\n return ans;\n }\n};\n```
| 2 | 0 |
['C++']
| 0 |
process-restricted-friend-requests
|
Java Solution | Union Find | Disjoint Sets | Without rank
|
java-solution-union-find-disjoint-sets-w-0sju
|
```\nclass Solution {\n public boolean[] friendRequests(int n, int[][] restrictions, int[][] requests) {\n int[] arr=new int[n];\n for(int i=0;
|
20250301.mohdnisab
|
NORMAL
|
2022-08-27T08:46:54.344758+00:00
|
2022-08-27T08:51:15.578719+00:00
| 371 | false |
```\nclass Solution {\n public boolean[] friendRequests(int n, int[][] restrictions, int[][] requests) {\n int[] arr=new int[n];\n for(int i=0;i<n;i++){\n arr[i]=i;\n }\n int j=0;\n boolean[] ret=new boolean[requests.length];\n for(int[] a:requests){\n int x=find(a[0],arr);\n int y=find(a[1],arr);\n boolean flag=true;\n for(int i=0;i<restrictions.length;i++){\n int l=find(restrictions[i][0],arr);\n int r=find(restrictions[i][1],arr);\n if(((l==x && r==y) || (l==y && r==x))){\n flag=false;\n break;\n }\n }\n ret[j++]=flag;\n if(flag){\n union(x,y,arr);\n }\n }\n return ret;\n }\n private void union(int a,int b,int[] arr){\n int x=find(a,arr);\n int y=find(b,arr);\n if(x==y) return;\n arr[y]=x;\n }\n private int find(int x,int[] arr){\n if(arr[x]==x) return x;\n return find(arr[x],arr);\n }\n}
| 2 | 0 |
['Union Find', 'Java']
| 0 |
process-restricted-friend-requests
|
JavaScript Union Find
|
javascript-union-find-by-anna_f-a8oz
|
This solution uses a boilerplate for DSU that can be reused for other problems. Approach is based on other solutions posted on the discussion section. Please le
|
anna_F
|
NORMAL
|
2022-04-13T02:20:41.130387+00:00
|
2022-04-13T14:19:09.413108+00:00
| 107 | false |
This solution uses a boilerplate for DSU that can be reused for other problems. Approach is based on other solutions posted on the discussion section. Please let me know if you have improvements or comments on time complexity.\n\n**Friend request function:**\n\t1. Add nodes 0 to n - 1 to DSU instance\n\t2. For each friend request [f1, f2], check each restriction pair [e1, e2]. \n\t3. Perform find on each of the four persons (f1, f2, e1, e2). \n\t4. If unionFind(f1) = unionFind(e1) and unionFind(f2) = unionFind(e2) OR viceversa, request is not valid.\n\n**Time complexity** \nI believe is O(N + MK). Step 1 takes O(N) where N is number of friends. Steps 2 - 4 take O(MK) where M are number of requests and K are number of restrictions.\nDSU finds and unions take an amortized time of O(1) because we are using path compression and union by rank.\n\n\n```\n/*\nDSU Class Template\n*/\nclass DSU {\n constructor() {\n this.parents = new Map();\n this.rank = new Map();\n }\n \n add(x) {\n this.parents.set(x, x);\n this.rank.set(x, 0);\n }\n \n find(x) {\n const parent = this.parents.get(x);\n if (parent === x) return x;\n const setParent = this.find(parent);\n this.parents.set(x, setParent);\n return setParent;\n }\n \n union(x, y) {\n const xParent = this.find(x), yParent = this.find(y);\n const xRank = this.rank.get(xParent), yRank = this.rank.get(yParent);\n if (xParent === yParent) return;\n if (xRank > yRank) {\n this.parents.set(yParent, xParent);\n } else if (yRank > xRank) {\n this.parents.set(xParent, yParent);\n } else {\n this.parents.set(xParent, yParent);\n this.rank.set(yParent, yRank + 1);\n } \n }\n}\n\n/*\nFriend Requests\n*/\nvar friendRequests = function(n, restrictions, requests) {\n const dsu = new DSU(), result = [];\n for (let i = 0; i < n; i++) dsu.add(i);\n \n for (let [friend1, friend2] of requests) {\n const parent1 = dsu.find(friend1), parent2 = dsu.find(friend2);\n let friendshipPossible = true;\n for (let [enemy1, enemy2] of restrictions) {\n const enemyParent1 = dsu.find(enemy1), enemyParent2 = dsu.find(enemy2);\n const condition1 = (enemyParent1 === parent1 && enemyParent2 === parent2);\n const condition2 = (enemyParent1 === parent2 && enemyParent2 === parent1);\n if (condition1 || condition2) {\n friendshipPossible = false;\n break;\n }\n }\n if (friendshipPossible) dsu.union(friend1, friend2);\n result.push(friendshipPossible);\n }\n return result;\n};\n```
| 2 | 0 |
['Union Find', 'JavaScript']
| 0 |
process-restricted-friend-requests
|
Python Union Find & Bitmask,O(M+N)
|
python-union-find-bitmaskomn-by-cava-balj
|
uni.rep means friends in one group, uni.cnf means this group cannot make friends with these people.\n\nclass UniSet:\n def __init__(self, n):\n self.u
|
cava
|
NORMAL
|
2022-03-24T07:49:06.798011+00:00
|
2022-03-24T07:53:43.208055+00:00
| 92 | false |
*uni.rep* means friends in one group, *uni.cnf* means this group cannot make friends with these people.\n```\nclass UniSet:\n def __init__(self, n):\n self.uni = list(range(n))\n self.rep = [1 << i for i in range(n)]\n self.cnf = [0] * n\n \n def find(self, x):\n if self.uni[x] != x: self.uni[x] = self.find(self.uni[x])\n return self.uni[x]\n \n def same(self, x, y):\n return self.find(x) == self.find(y)\n\n def check_merge(self, x, y):\n x, y = self.find(x), self.find(y)\n if self.cnf[x] & self.rep[y] | self.rep[x] & self.cnf[y]: return False\n x, y = min(x, y), max(x, y)\n self.uni[y] = x\n self.rep[x] |= self.rep[y]\n self.cnf[x] |= self.cnf[y]\n return True\n\nclass Solution:\n def friendRequests(self, n: int, restrictions: List[List[int]], requests: List[List[int]]) -> List[bool]:\n uni = UniSet(n)\n for x, y in restrictions:\n uni.cnf[x] |= 1 << y\n uni.cnf[y] |= 1 << x\n return [uni.check_merge(x, y) for x, y in requests]\n```
| 2 | 0 |
[]
| 0 |
process-restricted-friend-requests
|
Simple Union Find in Java
|
simple-union-find-in-java-by-blue_bubble-xd69
|
Before using union, go through all restrictions, and make sure they are not in the same group as the two nodes currently being connnected. \nSay, current reques
|
blue_bubble
|
NORMAL
|
2021-12-24T16:44:20.824325+00:00
|
2021-12-24T16:44:20.824354+00:00
| 150 | false |
Before using union, go through all restrictions, and make sure they are not in the same group as the two nodes currently being connnected. \nSay, current request is n1 - n2. \nAnd there is a restriction s1 - s2 \nIf s1 is connected to n1 and s2 is connected to n2. \nWhen n1 and n2 are connected, s1 and s2 get connected indirectly too. \nTherefore we make sure that there is no pair of restriction that gets connected on accepting the request. \nIf there is no pair of restriction for the same, then we do union. \n\n```\n\nclass Solution {\n public boolean[] friendRequests(int n, int[][] restrictions, int[][] requests) {\n int[] parent = new int[n];\n boolean[] ans = new boolean[requests.length];\n int[] rank = new int[requests.length];\n for (int i = 0; i < n; i++){parent[i] = i;} \n \n for (int i = 0; i < requests.length; i++){\n int t1 = find(parent, requests[i][0]);\n int t2 = find(parent, requests[i][1]);\n boolean vis = true;\n for (int j = 0; j < restrictions.length; j++){\n int a1 = find(parent, restrictions[j][0]);\n int a2 = find(parent, restrictions[j][1]);\n if (a1 == t1 && a2 == t2){\n vis = false; break;\n }\n else if (a1 == t2 && a2 == t1){\n vis = false; break;\n }\n else if (a1 == t1 && a2 == t1){\n vis = false; break;\n }\n else if (a1 == t2 && a2 == t2){vis = false; break;}\n \n }\n if (vis == true){ans[i] = true; union(parent, requests[i][0], requests[i][1]);}\n \n }\n \n return ans; \n \n }\n public int find(int[] parents, int i){\n if (parents[i] == i) return i; \n return find(parents, parents[i]);\n }\n \n public void union(int[] parent, int a1, int a2){\n if (find(parent, a1) == find(parent, a2)) return; \n int s1 = find(parent, a1); int s2 = find(parent, a2);\n parent[s2] = s1; \n \n }\n \n \n \n}\n```
| 2 | 0 |
['Graph']
| 0 |
process-restricted-friend-requests
|
Java Union Find Solution With Comment
|
java-union-find-solution-with-comment-by-l4do
|
\nclass Solution {\n int[] parent;\n boolean[] result;\n \n public boolean[] friendRequests(int n, int[][] restrictions, int[][] requests) {\n
|
stevenbooke
|
NORMAL
|
2021-12-14T20:31:34.133184+00:00
|
2021-12-14T20:31:34.133213+00:00
| 313 | false |
```\nclass Solution {\n int[] parent;\n boolean[] result;\n \n public boolean[] friendRequests(int n, int[][] restrictions, int[][] requests) {\n parent = new int[n];\n for (int i = 0; i < n; i++) {\n parent[i] = i;\n }\n result = new boolean[requests.length];\n \n for (int i = 0; i < requests.length; i++) {\n // personA and personB can become friends if for all restrictions\n // person x_i and person y_i are not in the same set as personA and personB\n // and vice versa\n int personA = requests[i][0];\n int personB = requests[i][1];\n int personASetRepresentative = find(personA);\n int personBSetRepresentative = find(personB);\n boolean flag = true;\n for (int[] restriction : restrictions) {\n int blackListPersonARepresentative = find(restriction[0]);\n int blackListPersonBRepresentative = find(restriction[1]);\n if (personASetRepresentative == blackListPersonARepresentative && personBSetRepresentative == blackListPersonBRepresentative) {\n flag = false;\n }\n if (personASetRepresentative == blackListPersonBRepresentative && personBSetRepresentative == blackListPersonARepresentative) {\n flag = false;\n }\n }\n if (flag) {\n union(personA, personB);\n }\n result[i] = flag;\n }\n return result;\n }\n \n private int find(int node) {\n int root = node;\n while (parent[root] != root) {\n root = parent[root];\n }\n \n //path compression\n int curr = node;\n while (parent[curr] != root) {\n int next = parent[curr];\n parent[curr] = root;\n curr = next;\n }\n return root;\n }\n \n private boolean union(int node1, int node2) {\n int root1 = find(node1);\n int root2 = find(node2);\n if (root1 == root2) {\n return false;\n }\n parent[root2] = root1;\n return true;\n }\n}\n```
| 2 | 0 |
['Union Find', 'Java']
| 0 |
process-restricted-friend-requests
|
JAVA DISJOINT SET SOLUTION
|
java-disjoint-set-solution-by-harsh__005-ubce
|
Here, used "rank" means height of tree\nalways join smaller set with larger set\nusing that it becomes more efficient\nand take less time to find parent\n\nclas
|
Harsh__005
|
NORMAL
|
2021-11-16T12:35:34.472018+00:00
|
2021-11-16T12:36:15.116496+00:00
| 84 | false |
**Here, used "rank" means height of tree\nalways join smaller set with larger set\nusing that it becomes more efficient\nand take less time to find parent**\n```\nclass dsu{\n int rank[],parent[];\n dsu(int len){\n rank = new int[len];\n parent = new int[len];\n for(int i=0; i<len; i++) parent[i] = i;\n }\n \n private int findparent(int v){\n if(parent[v] == v) return v;\n \n return parent[v] = findparent(parent[v]);\n }\n \n private void union(int u, int v){\n if(u == v) return;\n \n if(rank[u]==rank[v]){\n parent[u] = v;\n rank[v]++;\n }else{\n if(rank[u] > rank[v]){\n parent[v] = u;\n }else{\n parent[u] = v;\n }\n }\n }\n }\n public boolean[] friendRequests(int n, int[][] restrictions, int[][] requests) {\n dsu obj = new dsu(n);\n boolean ans[] = new boolean[requests.length];\n int i=0;\n for(int arr[] : requests){\n int u=arr[0],v=arr[1];\n u = obj.findparent(u);\n v = obj.findparent(v);\n \n boolean flag = true;\n for(int r[] : restrictions){\n int p1 = obj.findparent(r[0]);\n int p2 = obj.findparent(r[1]);\n if((p1==u&&p2==v) || (p1==v&&p2==u)){\n flag = false;\n break;\n }\n }\n \n ans[i++] = flag;\n if(flag){\n obj.union(u,v); \n }\n }\n return ans;\n }\n```
| 2 | 0 |
['Java']
| 0 |
process-restricted-friend-requests
|
JAVA | DSU direct application
|
java-dsu-direct-application-by-sharmashi-cm4v
|
\n\nclass Solution {\n int[] parent, rank;\n \n public boolean[] friendRequests(int n, int[][] restrictions, int[][] requests) {\n parent = new
|
sharmashivang1999
|
NORMAL
|
2021-11-16T11:52:01.823028+00:00
|
2021-11-16T11:52:01.823057+00:00
| 104 | false |
\n```\nclass Solution {\n int[] parent, rank;\n \n public boolean[] friendRequests(int n, int[][] restrictions, int[][] requests) {\n parent = new int[n];\n rank = new int[n];\n \n for(int i = 0; i < n; i++)\n parent[i] = i;\n \n boolean[] ans = new boolean[requests.length]; \n \n for(int i = 0; i < requests.length; i++) {\n int u = requests[i][0];\n int v = requests[i][1];\n \n u = find(u);\n v = find(v);\n \n boolean flag = true;\n \n for(int j = 0; j < restrictions.length; j++) {\n int u_ = restrictions[j][0];\n int v_ = restrictions[j][1];\n \n u_ = find(u_);\n v_ = find(v_);\n \n if((u_ == u && v_ == v) || (u_ == v && v_ == u)) {\n flag = false;\n break;\n }\n }\n \n if(flag == true)\n union(u, v);\n \n ans[i] = flag;\n }\n \n return ans;\n }\n \n // Time complexity = O(n^2)\n // Space complexity = O(n)\n \n private int find(int x) {\n if(parent[x] == x)\n return x;\n \n return parent[x] = find(parent[x]);\n }\n \n private void union(int u, int v) {\n u = find(u);\n v = find(v);\n \n if(rank[u] > rank[v])\n parent[v] = u;\n\n else if(rank[u] < rank[v])\n parent[u] = v;\n\n else {\n parent[u] = v;\n rank[v]++;\n }\n }\n}\n```
| 2 | 0 |
[]
| 0 |
process-restricted-friend-requests
|
[Python] [272 ms,36 MB] Maintain connected components of the graph
|
python-272-ms36-mb-maintain-connected-co-bufe
|
Maintain two lists of sets connected_components and banned_by_comps to store the connected components the restrictions of nodes in each connected component. Mai
|
lonelyquantum
|
NORMAL
|
2021-11-14T05:10:24.979712+00:00
|
2021-11-14T05:14:33.758954+00:00
| 472 | false |
Maintain two lists of sets ```connected_components``` and ```banned_by_comps``` to store the connected components the restrictions of nodes in each connected component. Maintain a dictionary ```connected_comp_dict``` to map each node to its connected compoent. Update them when a new edge is added.\n```\nclass Solution:\n def friendRequests(self, n: int, restrictions: List[List[int]], requests: List[List[int]]) -> List[bool]: \n result = [False for _ in requests]\n \n connected_components = [{i} for i in range(n)]\n \n connected_comp_dict = {}\n for i in range(n):\n connected_comp_dict[i] = i\n \n banned_by_comps = [set() for i in range(n)]\n for res in restrictions:\n banned_by_comps[res[0]].add(res[1])\n banned_by_comps[res[1]].add(res[0])\n for i,r in enumerate(requests):\n n1, n2 = r[0], r[1]\n c1, c2 = connected_comp_dict[n1], connected_comp_dict[n2]\n if c1 == c2:\n result[i] = True\n else:\n if not (connected_components[c1].intersection(banned_by_comps[c2]) or connected_components[c2].intersection(banned_by_comps[c1])):\n connected_components[c1].update(connected_components[c2])\n banned_by_comps[c1].update(banned_by_comps[c2])\n for node in connected_components[c2]:\n connected_comp_dict[node] = c1\n result[i] = True\n \n return result\n\n```
| 2 | 0 |
['Graph', 'Ordered Set', 'Python', 'Python3']
| 2 |
process-restricted-friend-requests
|
C++ || Union-Find || Easy to Understand
|
c-union-find-easy-to-understand-by-jk20-yjpo
|
Algorithm ( Union Find with modification ) \n\n Process the request first \n Store Parent Array in some other temporary data structure.\n Merge the vertices/no
|
jk20
|
NORMAL
|
2021-11-14T05:02:54.937758+00:00
|
2021-11-14T05:07:00.559525+00:00
| 244 | false |
#### Algorithm ( Union Find with modification ) \n\n* Process the request first \n* Store Parent Array in some other temporary data structure.\n* Merge the vertices/nodes \n* Check in the requests array if we have violated the conditions\n* If conditions are violated rollback the requests by updating parent array to the one stored in temporary data structure.\n\n\n```\nclass Solution {\npublic:\n vector<int>parent;\n int find(int node)\n {\n \n if(node==parent[node])\n return node;\n \n return parent[node]=find(parent[node]);\n }\n void merge(int u,int v)\n {\n int pu=find(u);\n int pv=find(v);\n parent[pu]=pv;\n }\n vector<bool> friendRequests(int n, vector<vector<int>>& restrictions, vector<vector<int>>& requests) {\n \n \n \n int i;\n \n parent.resize(n);\n for(i=0;i<n;i++)\n parent[i]=i;\n \n vector<bool>ans(requests.size());\n \n for(i=0;i<requests.size();i++)\n {\n int u=requests[i][0];\n int v=requests[i][1];\n \n \n auto temp_copy=parent;\n ans[i]=true;\n merge(u,v);\n for(auto &it:restrictions)\n {\n \n int p=it[0];\n int q=it[1];\n \n if(find(p)==find(q))\n {\n ans[i]=false;\n break;\n }\n }\n if(!ans[i])\n parent=temp_copy;\n \n }\n \n return ans;\n \n }\n};\n\n```\n \n### Pls upvote if you found helpful
| 2 | 0 |
['Union Find', 'C', 'C++']
| 0 |
process-restricted-friend-requests
|
(C++) 2076. Process Restricted Friend Requests
|
c-2076-process-restricted-friend-request-biqn
|
\n\nclass UnionFind {\npublic: \n vector<int> parent, rank; \n UnionFind(int n) {\n parent.resize(n); \n iota(begin(parent), end(parent), 0)
|
qeetcode
|
NORMAL
|
2021-11-14T04:06:01.008411+00:00
|
2021-11-14T04:06:01.008447+00:00
| 176 | false |
\n```\nclass UnionFind {\npublic: \n vector<int> parent, rank; \n UnionFind(int n) {\n parent.resize(n); \n iota(begin(parent), end(parent), 0); \n rank.resize(n); \n fill(rank.begin(), rank.end(), 1); \n } \n \n int find(int p) {\n /* find with path compression */\n if (parent[p] != p) \n parent[p] = find(parent[p]); \n return parent[p]; \n }\n \n bool connect(int p, int q) {\n /* union with rank */\n int prt = find(p), qrt = find(q); \n if (prt == qrt) return false; \n if (rank[prt] > rank[qrt]) swap(prt, qrt);\n parent[prt] = qrt; \n rank[qrt] += rank[prt]; \n return true; \n }\n};\n\n\nclass Solution {\npublic:\n vector<bool> friendRequests(int n, vector<vector<int>>& restrictions, vector<vector<int>>& requests) {\n vector<bool> ans; \n UnionFind *uf = new UnionFind(n); \n for (auto& request : requests) {\n int u = uf->find(request[0]), v = uf->find(request[1]); \n bool found = false; \n for (auto& restriction : restrictions) {\n int x = uf->find(restriction[0]), y = uf->find(restriction[1]); \n if ((u == x && v == y) || (u == y && v == x)) {\n found = true; \n break; \n }\n }\n ans.push_back(!found); \n if (!found) uf->connect(u, v); \n }\n delete uf; \n return ans; \n }\n};\n```
| 2 | 0 |
['C']
| 0 |
process-restricted-friend-requests
|
[Python3] union-find
|
python3-union-find-by-ye15-dzdg
|
Please check out this commit for solutions of weekly 267.\n\nclass UnionFind:\n\n\tdef __init__(self, n: int):\n\t\tself.parent = list(range(n))\n\t\tself.rank
|
ye15
|
NORMAL
|
2021-11-14T04:04:17.729534+00:00
|
2021-11-14T04:07:43.660111+00:00
| 214 | false |
Please check out this [commit](https://github.com/gaosanyong/leetcode/commit/8d693371fa97ea3b0717d02448c77201b15e5d12) for solutions of weekly 267.\n```\nclass UnionFind:\n\n\tdef __init__(self, n: int):\n\t\tself.parent = list(range(n))\n\t\tself.rank = [1] * n\n\n\tdef find(self, p: int, halving: bool=True) -> int:\n\t\tif p != self.parent[p]:\n\t\t\tself.parent[p] = self.find(self.parent[p]) \n\t\treturn self.parent[p]\n\n\tdef union(self, p: int, q: int) -> bool:\n\t\tprt, qrt = self.find(p), self.find(q)\n\t\tif prt == qrt: return False \n\t\tif self.rank[prt] > self.rank[qrt]: prt, qrt = qrt, prt \n\t\tself.parent[prt] = qrt\n\t\tself.rank[qrt] += self.rank[prt]\n\t\treturn True\n\n\nclass Solution:\n def friendRequests(self, n: int, restrictions: List[List[int]], requests: List[List[int]]) -> List[bool]:\n ans = []\n uf = UnionFind(n)\n for u, v in requests: \n uu = uf.find(u)\n vv = uf.find(v)\n for x, y in restrictions: \n xx = uf.find(x)\n yy = uf.find(y)\n if uu == xx and vv == yy or uu == yy and vv == xx: \n ans.append(False)\n break \n else: \n ans.append(True)\n uf.union(u, v)\n return ans \n```
| 2 | 0 |
['Python3']
| 0 |
process-restricted-friend-requests
|
Java | Sets with Communities | Easy to Understand
|
java-sets-with-communities-easy-to-under-ol84
|
Idea: Create a list of sets of communities (List<Set<Integer>> communities) and check whether can be they joined or not based on restrictions.\n\nAlgorithm: Let
|
akezhr
|
NORMAL
|
2021-11-14T04:03:12.324811+00:00
|
2021-11-14T04:06:05.471534+00:00
| 195 | false |
**Idea**: Create a list of sets of communities (`List<Set<Integer>> communities`) and check whether can be they joined or not based on restrictions.\n\n**Algorithm**: Let\'s take example from the problem. `n = 3, restrictions = [[0,1]], requests = [[0,2],[2,1]]`. You will firstly create such communities` [ {0}, {1}, {2} ]`. Furthermore, we will maintain restrictions in hashmap for quick access.\nThen, in each request we check whether we are able to merge these communities together or not. After first iteration (`[0,2]`), we will get `[ {0,2}, {1} ]`. In the second request, we see that `{1}` cannot be inside the set with `0` and `2`, becase `2` has `0` in its community. Please, check the code for additional conditions of comparing the sets with each other.\n\n\n```\nclass Solution {\n public boolean[] friendRequests(int n, int[][] restrictions, int[][] requests) {\n boolean[] res = new boolean[requests.length];\n List<Integer>[] restricted = new List[n];\n for (int i = 0; i < n; i++)\n restricted[i] = new ArrayList<Integer>();\n \n for (int[] r : restrictions) {\n restricted[r[0]].add(r[1]);\n restricted[r[1]].add(r[0]);\n }\n \n List<HashSet<Integer>> communities = new ArrayList();\n for (int i = 0; i < n; i++) {\n HashSet<Integer> s = new HashSet<Integer>();\n s.add(i);\n communities.add(s);\n }\n \n int k = 0;\n for (int[] req : requests) {\n int x = req[0];\n int y = req[1];\n int xi = 0, yi = 0; // Indices of sets in which there people belong to\n \n for (int i = 0; i < communities.size(); i++) {\n if (communities.get(i).contains(x)) {\n xi = i;\n }\n if (communities.get(i).contains(y)) {\n yi = i;\n }\n }\n \n if (xi == yi) { // they are both already in one community\n res[k++] = true;\n continue;\n }\n \n int flag = -1;\n for (int node : communities.get(xi)) {\n if (flag >= 0) break;\n for (int other : communities.get(yi)) {\n if (restricted[node].contains(other)) {\n flag = 0;\n break;\n } else if (communities.get(xi).contains(other)) {\n flag = 1;\n break;\n }\n }\n }\n if (flag == 0) {\n res[k++] = false;\n } else {\n mergeSets(communities, xi, yi);\n res[k++] = true;\n }\n } \n \n return res;\n }\n \n public void mergeSets(List<HashSet<Integer>> communities, int xi, int yi) {\n HashSet<Integer> a = communities.get(xi);\n HashSet<Integer> b = communities.get(yi);\n if (xi > yi) {\n communities.remove(xi);\n communities.remove(yi);\n } else {\n communities.remove(yi);\n communities.remove(xi);\n }\n for (int val : b) {\n a.add(val);\n }\n communities.add(a);\n }\n}\n```
| 2 | 0 |
[]
| 0 |
process-restricted-friend-requests
|
[JavaScript] Union Find 2 Solutions
|
javascript-union-find-2-solutions-by-ste-6h0g
|
javascript\nvar friendRequests = function(numPeople, restrictions, requests) {\n // base union find data structure\n const friendships = [...new Array(num
|
stevenkinouye
|
NORMAL
|
2021-11-14T04:01:53.398172+00:00
|
2021-11-14T22:51:37.020073+00:00
| 305 | false |
```javascript\nvar friendRequests = function(numPeople, restrictions, requests) {\n // base union find data structure\n const friendships = [...new Array(numPeople).keys()];\n // this is equivalent to find in union find\n const findRootFriend = (x) => friendships[x] = friendships[x] === x ? x : findRootFriend(friendships[x]);\n // this is equivalent to union in union find\n const createFriendship = (x, y) => friendships[findRootFriend(x)] = findRootFriend(y);\n \n const isInSameFriendshipGroup = (person1, person2) => findRootFriend(person1) === findRootFriend(person2);\n const findFriendsInGroup = (friend) => {\n const friendsInGroup = [];\n for (let person = 0; person < numPeople; person++) {\n if (isInSameFriendshipGroup(person, friend)) {\n friendsInGroup.push(person);\n }\n }\n return friendsInGroup;\n }\n \n const mappedRestrictions = mapRestrictions(numPeople, restrictions);\n \n return requests.map(([friend1, friend2], i) => {\n const friendsOfFriend1 = findFriendsInGroup(friend1);\n \n for (let person = 0; person < numPeople; person++) {\n if (isInSameFriendshipGroup(person, friend2)) {\n\n // check all the friends in friend1\'s group to see if\n // person can be friends with friend of friend1\n for (let friendOfFriend1 of friendsOfFriend1) {\n if (mappedRestrictions[person].has(friendOfFriend1)) {\n return false;\n }\n }\n }\n }\n // create the friendship\n createFriendship(friend1, friend2);\n return true;\n })\n};\n\nfunction mapRestrictions(numPeople, restrictions) {\n const mappedRestrictions = new Array(numPeople).fill(0).map(() => new Set());\n for (const [person1, person2] of restrictions) {\n mappedRestrictions[person1].add(person2);\n mappedRestrictions[person2].add(person1);\n }\n return mappedRestrictions;\n}\n\n\n\n//////////////////////////////////////////////////////////\n//////////////////////////////////////////////////////////\n//////////////////////////////////////////////////////////\n// Credit to: lee215\n\n\nvar friendRequests = function(numPeople, restrictions, requests) {\n // base union find data structure\n const friendships = [...new Array(numPeople).keys()];\n // this is equivalent to find in union find\n const findRootFriend = (x) => friendships[x] = friendships[x] === x ? x : findRootFriend(friendships[x]);\n // this is equivalent to union in union find\n const createFriendship = (x, y) => friendships[findRootFriend(x)] = findRootFriend(y);\n const isInSameFriendshipGroup = (person1, person2) => findRootFriend(person1) === findRootFriend(person2);\n \n return requests.map(([friend1, friend2], i) => {\n if (isInSameFriendshipGroup(friend1, friend2)) return true;\n \n for (const [person1, person2] of restrictions) {\n if ((isInSameFriendshipGroup(person1, friend1) && isInSameFriendshipGroup(person2, friend2)) ||\n (isInSameFriendshipGroup(person1, friend2) && isInSameFriendshipGroup(person2, friend1))) {\n return false;\n }\n }\n createFriendship(friend1, friend2);\n return true;\n })\n};\n```
| 2 | 0 |
['Union Find', 'JavaScript']
| 0 |
process-restricted-friend-requests
|
C++ Solution. union-find and brute-force.
|
c-solution-union-find-and-brute-force-by-99ur
|
\n\n### Idea\n- Try to make a connection for each request, after making this connection and if one of the restrictions is violated, then the answer is false and
|
11235813
|
NORMAL
|
2021-11-14T04:01:38.061210+00:00
|
2021-11-14T04:01:38.061247+00:00
| 251 | false |
\n\n### Idea\n- Try to make a connection for each request, after making this connection and if one of the restrictions is violated, then the answer is false and recover the union-find array to the previous status.\n \n```\nclass Solution {\npublic:\n vector<int> arr;\n vector<int> vis;\n int find(int x) {\n if(arr[x] == 0) return arr[x] = x;\n if(arr[x] == x) return x;\n return arr[x] = find(arr[x]);\n }\n void combine(int a, int b) {\n a = find(a);\n b = find(b);\n arr[a] = b;\n }\n vector<bool> friendRequests(int n, vector<vector<int>>& restrictions, vector<vector<int>>& requests) {\n arr.resize(n + 2);\n vector<bool> ans(requests.size());\n for(int i = 0; i < requests.size(); i++) {\n int a = requests[i][0] + 1, b = requests[i][1] + 1;\n auto src = arr;\n combine(a, b);\n ans[i] = true;\n for(auto &r : restrictions) {\n int a = r[0] + 1, b = r[1] + 1;\n if(find(a) == find(b)) {\n ans[i] = false;\n break;\n }\n }\n if(!ans[i]) arr = src;\n }\n return ans;\n }\n};\n```
| 2 | 0 |
[]
| 0 |
process-restricted-friend-requests
|
Modified DSU with Restrictions - Friend Request Management [TC: O(α(N)) | SC: O(N)]
|
modified-dsu-with-restrictions-friend-re-u5mk
|
IntuitionThe problem is a unique modification of the classic Disjoint Set Union (DSU) data structure, where we need to track not just connections between elemen
|
holdmypotion
|
NORMAL
|
2025-01-26T21:29:43.204016+00:00
|
2025-01-26T21:29:43.204016+00:00
| 93 | false |
# Intuition
The problem is a unique modification of the classic Disjoint Set Union (DSU) data structure, where we need to track not just connections between elements but also maintain restrictions on which elements cannot be connected. The core challenge is managing these restrictions efficiently while performing unions.
The key insight is that restrictions between elements can be propagated through unions - if A cannot connect with B, and we unite B with C, then A also cannot connect with C. This leads to the idea of maintaining a set of restrictions for each parent node.
# Approach
1. **Enhanced DSU Structure**:
- Traditional DSU implementation with parent array (`p`) and size array for union by size
- Additional `restrictions` array where each element maintains a set of parent nodes it cannot unite with
2. **Restriction Management**:
- When adding a restriction between elements A and B:
- Find their parents (pA, pB)
- Add each parent to the other's restriction set
- During union, merge restriction sets and update all affected nodes
3. **Union Operation Enhancement**:
- Before uniting elements:
- Check if their parents are already in each other's restriction sets
- If not restricted, perform union and merge restrictions
- Union by size optimization to keep tree height minimal
4. **Main Algorithm Flow**:
- Initialize DSU with N elements
- Process all restrictions first
- Handle each friend request by attempting to unite the elements
# Key Implementation Details
1. **Restriction Propagation**:
```python
self.restrictions[pa].update(self.restrictions[pb])
for other_parent in self.restrictions[pb]:
self.restrictions[other_parent].remove(pb)
self.restrictions[other_parent].add(pa)
```
This ensures all restrictions are properly maintained after union.
2. **Union Safety Check**:
```python
def can_unite(self, a, b):
pa, pb = self.find(a), self.find(b)
if pa == pb:
return True
return pb not in self.restrictions[pa]
```
Verifies if union is allowed before performing it.
# Complexity
- Time complexity: **O(α(N))** per operation
- Find operation with path compression: O(α(N))
- Union operation: O(α(N)) amortized
- Restriction management: O(R) where R is number of restrictions
- α(N) is the inverse Ackermann function, which grows extremely slowly
- Space complexity: **O(N + R)**
- Parent array: O(N)
- Size array: O(N)
- Restrictions sets: O(N + R) where R is total number of restrictions
# Code
```python3 []
class DSU:
def __init__(self, n):
self.n = n
self.p = list(range(n+1))
self.size = [1]*(n+1)
self.restrictions = [set() for _ in range(n+1)]
def find(self, u):
if self.p[u] == u:
return u
self.p[u] = self.find(self.p[u])
return self.p[u]
def add_restriction(self, a, b):
pa, pb = self.find(a), self.find(b)
if pa != pb:
self.restrictions[pa].add(pb)
self.restrictions[pb].add(pa)
def can_unite(self, a, b):
pa, pb = self.find(a), self.find(b)
if pa == pb:
return True
return pb not in self.restrictions[pa]
def unite(self, a, b):
if not self.can_unite(a, b):
return False
pa, pb = self.find(a), self.find(b)
if pa != pb:
if self.size[pa] < self.size[pb]: pa, pb = pb, pa
self.restrictions[pa].update(self.restrictions[pb])
for other_parent in self.restrictions[pb]:
self.restrictions[other_parent].remove(pb)
self.restrictions[other_parent].add(pa)
self.size[pa] += self.size[pb]
self.p[pb] = pa
return True
class Solution:
def friendRequests(self, n: int, restrictions: List[List[int]], requests: List[List[int]]) -> List[bool]:
dsu = DSU(n)
for u, v in restrictions:
dsu.add_restriction(u, v)
return [dsu.unite(u, v) for u, v in requests]
```
| 1 | 0 |
['Union Find', 'Ordered Set', 'Python3']
| 1 |
process-restricted-friend-requests
|
✅DSU + reversal | JAVA | 80% better | Easy One!!
|
dsu-reversal-java-80-better-easy-one-by-nwwza
|
Hi
So this approach uses simple DSU Application
we will be making the requests happen that is
each request will be made successfull and then it will be checked
|
Orangjustice777
|
NORMAL
|
2025-01-14T12:07:28.714149+00:00
|
2025-01-14T12:07:28.714149+00:00
| 64 | false |
Hi
So this approach uses simple DSU Application
we will be making the requests happen that is
each request will be made successfull and then it will be checked whther that request voilates the restrictions condition
- if yes then we remove the friendship
- if no then we let them be friends
simple!!
Just simply Dive into the code you'll understand the reversal of the DSU
by having the parent and rank arrays as backups then union the friends and then check for the restrictions
# Code
```java []
class Solution {
int[] parent ;
int[] rank ;
public boolean[] friendRequests(int n, int[][] restrictions, int[][] requests) {
boolean[] ans = new boolean[requests.length];
int count = 0 ;
init(n);
for(int[] req : requests){
int u = req[0];
int v = req[1];
boolean canBeFrnd = true ;
int[] backupParent = Arrays.copyOf(parent , parent.length);
int[] backupRank = Arrays.copyOf(rank , n);
union(u , v);
for(int[] res : restrictions){
int U = res[0];
int V = res[1];
if(find(U) == find(V)){
canBeFrnd = false ;
break ;
}
}
if(canBeFrnd){
ans[count] = true ;
}else{
ans[count] = false ;
parent = Arrays.copyOf(backupParent , n);
rank = Arrays.copyOf(backupRank , n);
}
count++ ;
}
return ans;
}
public void init(int n){
parent = new int[n];
rank = new int[n];
for(int i = 0 ; i < n ; i++) parent[i] = i ;
}
public int find(int x){
if(parent[x] == x){
return x ;
}
return parent[x] = find(parent[x]);
}
public void union(int u , int v){
int parU = find(u);
int parV = find(v);
if(rank[parU] == rank[parV]){
parent[parU] = parV ;
rank[parV]++ ;
}else if(rank[parU] > rank[parV]){
parent[parV] = parU ;
}else{
parent[parU] = parV ;
}
}
}
```
| 1 | 0 |
['Union Find', 'Graph', 'Java']
| 0 |
process-restricted-friend-requests
|
python3 simple union find
|
python3-simple-union-find-by-0icy-t0fi
|
\n\n# Code\n\nclass Solution:\n def friendRequests(self, n: int, restrictions: List[List[int]], requests: List[List[int]]) -> List[bool]:\n res = []\n
|
0icy
|
NORMAL
|
2023-11-01T07:32:04.535148+00:00
|
2023-11-01T07:32:04.535178+00:00
| 96 | false |
\n\n# Code\n```\nclass Solution:\n def friendRequests(self, n: int, restrictions: List[List[int]], requests: List[List[int]]) -> List[bool]:\n res = []\n self.parent = list(range(n))\n for a,b in requests:\n temp = self.parent.copy()\n self.union(a,b)\n flag = True\n for x,y in restrictions:\n if self.find(x)==self.find(y):\n flag = False\n break\n if flag:\n res.append(True)\n else:\n res.append(False)\n self.parent = temp\n \n return res\n\n def find(self, a):\n acopy = a\n while a != self.parent[a]:\n a = self.parent[a]\n while acopy != a:\n self.parent[acopy], acopy = a, self.parent[acopy]\n return a\n \n def union(self, a, b):\n self.parent[self.find(b)] = self.find(a)\n\n```
| 1 | 0 |
['Python3']
| 0 |
process-restricted-friend-requests
|
UnionFind beats 100%. Simple and intuitive explanation.
|
unionfind-beats-100-simple-and-intuitive-bw3d
|
Intuition\n Describe your first thoughts on how to solve this problem. \nThis is just an extension of UnionFind alorithm (Disjoint set)\n# Approach\n Describe y
|
vijay_narayanan
|
NORMAL
|
2023-10-22T14:20:47.648124+00:00
|
2023-10-22T14:20:47.648142+00:00
| 18 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis is just an extension of UnionFind alorithm (Disjoint set)\n# Approach\n<!-- Describe your approach to solving the problem. -->\nLets consider we have a restriction A-C\nNow when we\'ve a request connecting D to C, there are 2 possibilities.\n 1. C will be the parent of D\n 2. D will be the parent of C\n\nCase 1: C will be the parent of D\n The restrictions of D will be added to restrictions of C. For our case, D does not have any restrictions. \n\nCase 2: D will be the parent of C\n In this case, the restrictions Set[C] will have A. The restrictions of C will be added to restrictions of D. That is, A is also added to D. Now when A is getting unionized to this component with A-D, we will check if we have any restrictions. Yes, D is the parent and it has restrictions on A. As restrictions of C were added to D.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(\u03B1(N)) \n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N)\n\n# Code\n```\n class UnionFind {\n int[] root;\n int[] size;\n Set<Integer>[] restrictions;\n\n public UnionFind(int n) {\n root = new int[n];\n size = new int[n];\n restrictions = new Set[n];\n\n for (int i = 0; i < n; i++) {\n root[i] = i;\n size[i] = 1;\n restrictions[i] = new HashSet<>();\n }\n }\n\n public void addRestrictions(int[][] restricts) {\n for (int[] r : restricts) {\n restrictions[r[0]].add(r[1]);\n restrictions[r[1]].add(r[0]);\n }\n }\n\n\n public int find(int x) {\n if (x == root[x]) return x;\n return root[x] = find(root[x]);\n }\n\n public boolean union(int x, int y) {\n int rootX = find(x);\n int rootY = find(y);\n\n if (rootX == rootY) return true;\n if (restrictions[rootX].contains(rootY) || restrictions[rootY].contains(rootX)) return false;\n\n // Lets consider we have a restriction A-C\n // Now when we\'re connecting D to C, there are 2 possibilities.\n // 1. C will be the parent of D\n // 2. D will be the parent of C\n\n // Case 1: C will be the parent of D\n // The restrictions of D will be added to restrictions of C. For our case, D does not have any restrictions. \n\n // Case 2: D will be the parent of C\n // In this case, the restrictions Set[C] will have A. The restrictions of C will be added to restrictions of D. That is, A is also added to D. Now when A is getting unionized to this component with A-D, we will check in the line above if we have any restrictions. Yes, D is the parent and it has restrictions on A. As restrictions of C were added to D.\n if (size[rootX] > size[rootY]) {\n root[rootY] = rootX;\n for (Integer r : restrictions[rootY]) {\n restrictions[rootX].add(find(r));\n }\n } else if (size[rootX] < size[rootY]) {\n root[rootX] = rootY;\n for (Integer r : restrictions[rootX]) {\n restrictions[rootY].add(find(r));\n }\n } else {\n root[rootY] = rootX;\n for (Integer r : restrictions[rootY]) {\n restrictions[rootX].add(find(r));\n }\n size[rootX]++;\n }\n return true;\n }\n\n }\n\nclass Solution {\n\n\n\n public boolean[] friendRequests(int n, int[][] restrictions, int[][] requests) {\n UnionFind uf = new UnionFind(n);\n uf.addRestrictions(restrictions);\n boolean[] result = new boolean[requests.length];\n\n for (int i = 0; i < requests.length; i++) {\n result[i] = uf.union(requests[i][0], requests[i][1]);\n }\n return result;\n\n }\n\n \n}\n```
| 1 | 0 |
['Java']
| 0 |
process-restricted-friend-requests
|
Union-find / Disjoint sets Solution || Faster than 90% || Java
|
union-find-disjoint-sets-solution-faster-2qh2
|
Code\n\nclass DisjointSet {\n private final int[] root;\n private final int[] rank;\n private final List<Set<Integer>> restrictions;\n\n DisjointSet
|
youssef1998
|
NORMAL
|
2023-07-25T12:51:35.192342+00:00
|
2023-07-25T12:51:35.192365+00:00
| 272 | false |
# Code\n```\nclass DisjointSet {\n private final int[] root;\n private final int[] rank;\n private final List<Set<Integer>> restrictions;\n\n DisjointSet(int size, int[][] restrictions) {\n root = new int[size];\n rank = new int[size];\n this.restrictions = new ArrayList<>();\n for (int i = 0; i < size; i++) {\n root[i] = i;\n rank[i] = 1;\n this.restrictions.add(new HashSet<>());\n }\n for (int[] restriction: restrictions) {\n this.restrictions.get(restriction[0]).add(restriction[1]);\n this.restrictions.get(restriction[1]).add(restriction[0]);\n }\n }\n\n private int find(int vertex) {\n if(root[vertex] == vertex) return vertex;\n return root[vertex] = find(root[vertex]);\n }\n\n public boolean union(int vertex1, int vertex2) {\n int root1 = find(vertex1);\n int root2 = find(vertex2);\n if(root1 == root2) return true;\n if(notRestricted(root1, root2)) {\n if(rank[root1] > rank[root2]) {\n root[root2] = root1;\n restrictions.get(root1).addAll(restrictions.get(root2));\n addRoots(root1);\n } else if(rank[root2] > rank[root1]) {\n root[root1] = root2;\n restrictions.get(root2).addAll(restrictions.get(root1));\n addRoots(root2);\n } else {\n root[root2] = root1;\n rank[root1]++;\n restrictions.get(root1).addAll(restrictions.get(root2));\n addRoots(root1);\n }\n return true;\n }\n return false;\n }\n\n private void addRoots(int index) {\n Set<Integer> added = new HashSet<>();\n for (int node: restrictions.get(index)) \n added.add(find(node));\n restrictions.get(index).addAll(added); \n }\n\n private boolean notRestricted(int root1, int root2) {\n for (int node: restrictions.get(root1)) if(node == root2) return false;\n for (int node: restrictions.get(root2)) if(node == root1) return false;\n return true;\n }\n}\n\nclass Solution {\n public boolean[] friendRequests(int n, int[][] restrictions, int[][] requests) {\n DisjointSet set = new DisjointSet(n, restrictions);\n boolean[] queries = new boolean[requests.length];\n for (int i = 0; i < requests.length; i++) \n queries[i] = set.union(requests[i][0], requests[i][1]);\n return queries;\n }\n}\n```
| 1 | 0 |
['Java']
| 2 |
process-restricted-friend-requests
|
C++ || EASY TO UNDERSTAND || DSU IMPLEMENTATION
|
c-easy-to-understand-dsu-implementation-d5xo3
|
\nclass dsu {\n int *rank, *parent, n;\n \npublic:\n dsu(int n)\n {\n rank = new int[n];\n parent = new int[n];\n this->n = n;\n
|
jatinbansal1179
|
NORMAL
|
2022-06-29T17:32:36.471179+00:00
|
2022-06-29T17:32:36.471227+00:00
| 350 | false |
```\nclass dsu {\n int *rank, *parent, n;\n \npublic:\n dsu(int n)\n {\n rank = new int[n];\n parent = new int[n];\n this->n = n;\n makeSet();\n }\n void makeSet()\n {\n for (int i = 0; i < n; i++) {\n parent[i] = i;\n }\n }\n \n int par(int x)\n {\n if (parent[x] != x) {\n parent[x] = par(parent[x]);\n }\n return parent[x];\n }\n void unions(int x, int y)\n {\n int xset = par(x);\n int yset = par(y);\n if (xset == yset)\n return;\n if (rank[xset] < rank[yset]) {\n parent[xset] = yset;\n }\n else if (rank[xset] > rank[yset]) {\n parent[yset] = xset;\n }\n else {\n parent[yset] = xset;\n rank[xset] = rank[xset] + 1;\n }\n }\n};\n \n\nclass Solution {\npublic:\n vector<bool> friendRequests(int n, vector<vector<int>>& res, vector<vector<int>>& req) {\n dsu obj(n);\n obj.makeSet();\n vector<bool> ans;\n for(int i = 0; i < req.size();i++){\n int x= obj.par(req[i][0]);\n int y = obj.par(req[i][1]);\n bool b = true;\n for(int j = 0; j < res.size();j++){\n int x1 = obj.par(res[j][0]);\n int y1 = obj.par(res[j][1]);\n if((x==x1&&y==y1)||(x==y1&&y==x1)){\n b = false;\n break;\n }\n }\n if(b){\n ans.push_back(true);\n obj.unions(req[i][0],req[i][1]);\n }\n else{\n ans.push_back(false);\n }\n }\n return ans;\n }\n};\n```
| 1 | 0 |
['Union Find', 'C', 'C++']
| 0 |
process-restricted-friend-requests
|
Better than 100% of Solns
|
better-than-100-of-solns-by-user7203i-sxd3
|
Plain union find - 323 ms\n\nclass Solution(object):\n def friendRequests(self, n, restrictions, requests):\n """\n :type n: int\n :type
|
user7203i
|
NORMAL
|
2022-06-22T17:11:29.908374+00:00
|
2022-06-22T17:11:29.908410+00:00
| 107 | false |
Plain union find - `323 ms`\n```\nclass Solution(object):\n def friendRequests(self, n, restrictions, requests):\n """\n :type n: int\n :type restrictions: List[List[int]]\n :type requests: List[List[int]]\n :rtype: List[bool]\n """\n p = {i:i for i in range(n)}\n \n def find(x):\n ox = x\n while p[x] != x:\n x = p[x]\n p[ox] = x\n return x\n \n bl = defaultdict(set)\n ans = []\n for ri, rj in restrictions:\n bl[ri].add(rj)\n bl[rj].add(ri)\n for ri, rj in requests:\n rpi, rpj = find(ri), find(rj)\n if rpi == rpj:\n ans.append(True)\n else:\n cc = rpj not in bl[rpi]\n if cc:\n p[rpj] = rpi\n bl[rpi] = bl[rpi].union(bl[rpj])\n for i in bl[rpj]:\n bl[i].add(rpi)\n ans.append(cc)\n \n return ans\n```
| 1 | 0 |
['Union Find', 'Python']
| 1 |
process-restricted-friend-requests
|
Java solution with Union Find
|
java-solution-with-union-find-by-forhapp-5ai2
|
\nclass Solution {\n public boolean[] friendRequests(int n, int[][] restrictions, int[][] requests) {\n UnionFind uf = new UnionFind(n);\n \n
|
forhappy
|
NORMAL
|
2022-05-22T23:58:19.432428+00:00
|
2022-05-22T23:58:19.432469+00:00
| 65 | false |
```\nclass Solution {\n public boolean[] friendRequests(int n, int[][] restrictions, int[][] requests) {\n UnionFind uf = new UnionFind(n);\n \n boolean[] result = new boolean[requests.length];\n Arrays.fill(result, false);\n \n int i = 0;\n for (int[] request: requests) {\n int x = request[0];\n int y = request[1];\n \n result[i] = uf.union(x, y, restrictions);\n \n i += 1;\n }\n \n return result;\n }\n}\n\nclass UnionFind {\n int[] parents;\n int[] ranks;\n\n public UnionFind(int n) {\n this.parents = new int[n];\n this.ranks = new int[n];\n\n for (int i = 0; i < n; i++) {\n this.parents[i] = i;\n this.ranks[i] = 1;\n }\n }\n\n public int find(int x) {\n if (parents[x] != x) parents[x] = find(parents[x]);\n\n return parents[x];\n }\n\n public boolean union(int x, int y, int[][] restrictions) {\n int xRoot = find(x);\n int yRoot = find(y);\n\n // Skip union if they already in the same group.\n if (xRoot == yRoot) return true;\n \n for (int[] restriction: restrictions) {\n int u = restriction[0];\n int v = restriction[1];\n int uRoot = find(u);\n int vRoot = find(v);\n \n if ((uRoot == yRoot && vRoot == xRoot) || (uRoot == xRoot && vRoot == yRoot)) {\n return false;\n }\n }\n\n if (ranks[xRoot] < ranks[yRoot]) {\n parents[xRoot] = yRoot;\n } else {\n parents[yRoot] = xRoot;\n }\n\n if (ranks[xRoot] == ranks[yRoot]) {\n ranks[xRoot]++;\n }\n \n return true;\n }\n}\n```
| 1 | 0 |
[]
| 0 |
process-restricted-friend-requests
|
c++||Union Find||Easy to Understand
|
cunion-findeasy-to-understand-by-return_-i03o
|
```\nclass Solution {\npublic:\n int find(vector &par,int u)\n {\n if(u==par[u])\n return u;\n return par[u]=find(par,par[u]);\n
|
return_7
|
NORMAL
|
2022-05-16T10:17:15.943744+00:00
|
2022-05-16T10:17:15.943778+00:00
| 112 | false |
```\nclass Solution {\npublic:\n int find(vector<int> &par,int u)\n {\n if(u==par[u])\n return u;\n return par[u]=find(par,par[u]);\n }\n void merge(vector<int> &par,int u,int v)\n {\n int pu=find(par,u);\n int pv=find(par,v);\n \n par[pv]=pu;\n }\n vector<bool> friendRequests(int n, vector<vector<int>>& restrictions, vector<vector<int>>& requests)\n {\n int m=requests.size();\n vector<bool> ans(m,true);\n vector<int> par(n);\n for(int i=0;i<n;i++)\n {\n par[i]=i;\n }\n for(int i=0;i<requests.size();i++)\n {\n int p=find(par,requests[i][0]);\n int q=find(par,requests[i][1]);\n if(!(find(par,p)==find(par,q)))\n {\n for(auto &rs:restrictions )\n {\n int x=find(par,rs[0]),y=find(par,rs[1]);\n {\n if((x==p&&y==q)||(x==q&&y==p))\n {\n ans[i]=false;\n break;\n }\n }\n }\n if(ans[i])\n {\n merge(par ,p,q);\n }\n }\n \n }\n return ans;\n \n }\n};\n// if you like the solution plz upvote.
| 1 | 0 |
['Union Find', 'C']
| 0 |
process-restricted-friend-requests
|
[Python] Union Find [BEST SOLUTION]
|
python-union-find-best-solution-by-seafm-lmi0
|
\nclass Solution:\n def friendRequests(self, n: int, restrictions: List[List[int]], requests: List[List[int]]) -> List[bool]:\n uf = {i:i for i in ran
|
seafmch
|
NORMAL
|
2022-04-10T04:47:27.098627+00:00
|
2022-04-10T04:47:27.098657+00:00
| 83 | false |
```\nclass Solution:\n def friendRequests(self, n: int, restrictions: List[List[int]], requests: List[List[int]]) -> List[bool]:\n uf = {i:i for i in range(n)}\n ans = [None] * len(requests)\n \n def find(i):\n if uf[i] != i:\n uf[i] = find(uf[i])\n return uf[i]\n \n def union(i, j):\n uf[find(i)] = uf[find(j)]\n \n for i, (p1, p2) in enumerate(requests):\n foundSet = set([find(p1), find(p2)])\n ans[i] = not any(find(r1) in foundSet and find(r2) in foundSet \\\n for (r1, r2) in restrictions)\n \n if ans[i] == True:\n union(p1, p2)\n \n return ans\n```
| 1 | 0 |
[]
| 0 |
process-restricted-friend-requests
|
Python union find with detailed explanation
|
python-union-find-with-detailed-explanat-76xl
|
Use the union find algorithm. The critical part is all about the restrictions. When there are too many people and too many restrictions, it will be time-consumi
|
KC19920313
|
NORMAL
|
2022-01-26T19:42:44.596753+00:00
|
2022-01-26T19:43:30.049817+00:00
| 108 | false |
Use the union find algorithm. The critical part is all about the restrictions. When there are too many people and too many restrictions, it will be time-consuming to check each restriction, before answering a request. We know that union is kind of a hierarchy system, where everyone has a supervisor (better than the usually known "parent").\n\nIt would good to let the supervisors to handle the restrictions. If A dislike B, let A\'s supervisor dislike B\'s supervisor. Since initially everyone supervises oneself, the given restrictions are a good start. We build a Hash map to handle the restrictions. \n\nFor a coming request, we only check the two supervisors. If they do not dislike each other, the relation can be built\nand call union()! During the union process, one supervisor SA retires and the other supervisor SB remains, and also supervises SA. In addition to the union itself, there are two important things to do:\n1) Go through everyone that SA dislikes, let each dislike SB (, who now supervises SA), instead of SA.\n2) SB should take all the restrictions that SA are involved in. One can pop SA from the map, since he does not bother this kind of nonsense any more. \n\n```\nclass Solution:\n def friendRequests(self, n: int, restrictions: List[List[int]], requests: List[List[int]]) -> List[bool]:\n rst = defaultdict(set)\n for a, b in restrictions:\n rst[a].add(b)\n rst[b].add(a)\n del restrictions\n ans = []\n supervisor = [i for i in range(n)]\n def find(x):\n if supervisor[x] == x:\n return x\n else:\n supervisor[x] = find(supervisor[x])\n return supervisor[x]\n\n def union(x, y): # the method is more than the conventional union() method\n x, y = find(x), find(y)\n if x > y:\n x, y = y, x\n supervisor[y] = x # "y", who was a supervisor, retires. "x" becomes his supervisor.\n rst[y] = rst.get(y, set()) # persons who "y", as well as his group, does not like\n for z in rst[y]: # for each of those persons\n rst[z].remove(y) # stop hating "y"\n rst[z].add(x) # hate his supervisor instead\n if x not in rst: # "x" consider everyone who "y" and his group do not like\n rst[x] = set()\n rst[x] |= rst.pop(y)\n return\n\t\t\t\n for a, b in requests: # process each request\n sa, sb = find(a), find(b) # approach the two supervisors\n if sa == sb: # they are the same, meaning that a and b are already friends\n ans.append(True)\n elif sb in rst.get(sa, set()): # if the supervisors do not permit\n ans.append(False)\n else: # if the supervisors permit\n ans.append(True)\n union(a, b) # build the relation\n return ans\n```
| 1 | 0 |
[]
| 0 |
process-restricted-friend-requests
|
Python UnionFind 87% faster avg O(E+R) with Explaination
|
python-unionfind-87-faster-avg-oer-with-7ovyp
|
Correct me if I am wrong but the time complexity I think would be O(N + ER) on worst case and O(N+E+R) on average case where E is number of requests and R is nu
|
palisade
|
NORMAL
|
2022-01-13T22:01:29.601008+00:00
|
2022-01-13T22:16:42.689226+00:00
| 231 | false |
Correct me if I am wrong but the time complexity I think would be O(N + ER) on worst case and O(N+E+R) on average case where E is number of requests and R is number of restrictions. And the space complexity is O(N+R). Basically we will keep track of all the root of restrictions from in each root node in union find. \n\nWhen we are adding (x, y) the request we will check if there is restriction between root_of_x and root_of_y. If there are restrictions we will return False.\n\nIf nodes can be friends, we will add those nodes by union by rank and keep track of root and child between those root_of_x and root_of_y.\n\nSuppose when we did the union root = root_of_x and child = root_of_y, then, we will loop through all the restrictions in root_of_y and try to find their root in the graph and add that root to the restriction of root_of_x. Then we will delete the restriction of root_of_y.\n\nThis way when we are doing union, the restrictions will be merged. \n```\nclass Solution:\n def friendRequests(self, n: int, restrictions: List[List[int]], requests: List[List[int]]) -> List[bool]:\n \n union_find = UnionFind(n, restrictions)\n result = []\n for u, v in requests:\n if union_find.union(u, v):\n result.append(True)\n else:\n result.append(False)\n return result\n \nclass UnionFind:\n def __init__(self, n, restricts):\n self.root = [i for i in range(n)]\n self.rank = [1 for i in range(n)]\n self.restrictions = {}\n for u, v in restricts:\n if u not in self.restrictions:\n self.restrictions[u] = set()\n if v not in self.restrictions:\n self.restrictions[v] = set()\n self.restrictions[u].add(v)\n self.restrictions[v].add(u)\n \n def find(self, x):\n if self.root[x] != x:\n self.root[x] = self.find(self.root[x])\n return self.root[x]\n def union(self, x, y):\n root_x = self.find(x)\n root_y = self.find(y)\n if (root_x in self.restrictions and root_y in self.restrictions[root_x]) or (root_y in self.restrictions and root_x in self.restrictions[root_y]):\n return False\n \n if root_x != root_y:\n root, child = root_y, root_x\n if self.rank[root_x] < self.rank[root_y]:\n self.root[root_x] = root_y\n elif self.rank[root_y] < self.rank[root_x]:\n self.root[root_y] = root_x\n root, child = root_x, root_y\n else:\n self.root[root_x] = root_y\n self.rank[root_y] += 1\n if child in self.restrictions:\n for rest in self.restrictions[child]:\n if root not in self.restrictions:\n self.restrictions[root] = set()\n self.restrictions[root].add(self.find(rest))\n del self.restrictions[child]\n return True\n```
| 1 | 0 |
['Union Find', 'Python']
| 0 |
process-restricted-friend-requests
|
C++ | DSU | Check in restriction before allowing them to be friends
|
c-dsu-check-in-restriction-before-allowi-9rm8
|
cpp\nclass DSU {\npublic:\n vector<int> parent, rank;\n DSU(int N) {\n for (int i = 0; i < N + 5; ++i) {\n parent.push_back(i);\n
|
ajay_5097
|
NORMAL
|
2021-12-29T08:55:26.162302+00:00
|
2021-12-29T08:55:26.162344+00:00
| 142 | false |
```cpp\nclass DSU {\npublic:\n vector<int> parent, rank;\n DSU(int N) {\n for (int i = 0; i < N + 5; ++i) {\n parent.push_back(i);\n rank.push_back(1);\n }\n }\n \n int find(int u) {\n if (parent[u] == u) return u;\n return parent[u] = find(parent[u]);\n }\n \n void merge(int x, int y) {\n int rootX = find(x);\n int rootY = find(y);\n if (rootX == rootY) return ;\n if (rank[rootX] >= rank[rootY]) {\n parent[rootY] = rootX;\n rank[rootX] += rank[rootY];\n } else {\n parent[rootX] = rootY;\n rank[rootY] += rank[rootX];\n }\n }\n \n bool isConnected(int x, int y) {\n return find(x) == find(y);\n }\n};\n\nclass Solution {\npublic:\n vector<bool> friendRequests(int n, vector<vector<int>>& restrictions, vector<vector<int>>& requests) {\n DSU dsu(n);\n vector<bool> res;\n for (const auto &req: requests) {\n int p1 = dsu.find(req[0]);\n int p2 = dsu.find(req[1]);\n //If they are friends, then they will always be friends\n if(p1 == p2) {\n res.push_back(true);\n continue;\n }\n bool flag = true;\n for(const auto &rest : restrictions) {\n int x1 = dsu.find(rest[0]);\n int x2 = dsu.find(rest[1]);\n\t\t\t\t//Since in DSU, parents can also be reversed\n\t\t\t\t//hence we check for the reverse as well\n if(p1 == x1 && p2 == x2 || p1 == x2 && p2 == x1) {\n flag = false;\n break;\n } \n }\n if(flag) {\n dsu.merge(req[0], req[1]);\n }\n res.push_back(flag);\n }\n return res;\n }\n};\n```
| 1 | 0 |
[]
| 0 |
process-restricted-friend-requests
|
Python UnionFind Concise Solution
|
python-unionfind-concise-solution-by-che-aqio
|
\nclass Solution:\n def friendRequests(self, n: int, restrictions: List[List[int]], requests: List[List[int]]) -> List[bool]:\n size = [1] * (n + 1)\n
|
chenchenchenchenchen111
|
NORMAL
|
2021-11-20T10:11:37.321074+00:00
|
2021-11-20T10:15:07.165212+00:00
| 103 | false |
```\nclass Solution:\n def friendRequests(self, n: int, restrictions: List[List[int]], requests: List[List[int]]) -> List[bool]:\n size = [1] * (n + 1)\n uf = [i for i in range(n+1)]\n \n def union(f, s):\n root_f, root_s = find(f), find(s)\n \n\t\t\t# loop over restrictions and return False if find any.\n for item in restrictions:\n cur_root = (find(item[0]), find(item[1]))\n if cur_root == (root_f, root_s) or cur_root == (root_s, root_f):\n return False\n\t\t\t\t\t\n # does not find any rstriction, union input and return True.\n if size[root_f] >= size[root_s]:\n uf[root_s] = root_f\n size[root_f] += size[root_s]\n else:\n uf[root_f] = root_s\n size[root_s] += size[root_f]\n \n return True\n \n def find(node):\n while uf[node] != node:\n node = uf[node]\n \n return node\n \n res = []\n for s, t in requests:\n res.append(union(s, t))\n \n return res\n \n```
| 1 | 0 |
[]
| 0 |
process-restricted-friend-requests
|
DSU UNION by SIZE || JAVA
|
dsu-union-by-size-java-by-gourav02-fnxs
|
\nclass Solution {\n public boolean[] friendRequests(int n, int[][] restrictions, int[][] requests) {\n Dsu dsu = new Dsu(n);\n \n boole
|
gourav02
|
NORMAL
|
2021-11-16T12:52:18.418760+00:00
|
2021-11-16T12:52:18.418802+00:00
| 159 | false |
```\nclass Solution {\n public boolean[] friendRequests(int n, int[][] restrictions, int[][] requests) {\n Dsu dsu = new Dsu(n);\n \n boolean[] ans = new boolean[requests.length];\n int i=0;\n \n for(int[]x : requests){\n int pu = dsu.findpar(x[0]);\n int pv= dsu.findpar(x[1]);\n boolean fl = true;\n if(pu!=pv){\n for(int[] x2:restrictions){\n int pu1 = dsu.findpar(x2[0]);\n int pv1 = dsu.findpar(x2[1]);\n \n if((pu == pu1 && pv == pv1) || (pu == pv1 && pv ==pu1)){\n fl = false;\n break;\n }\n }\n if(fl){\n dsu.union(pu,pv);\n }\n \n }\n ans[i++] = fl;\n }\n return ans;\n }\n}\nclass Dsu{\n int[] parent = new int[1000];\n int[]size = new int[1000];\n \n Dsu(int n){\n \n for(int i=0;i<n;i++){\n parent[i] = i;\n size[i] = 0;\n }\n }\n \n public int findpar(int n){\n if(parent[n] == n)return n;\n return parent[n] = findpar(parent[n]);\n }\n \n public void union(int u ,int v){\n int pu = findpar(u);\n int pv = findpar(v);\n \n if(pu==pv)return;\n \n if(size[pu]<size[pv]){\n parent[pu]=pv;\n size[pv] += size[pu];\n }else{\n parent[pv] = pu;\n size[pu] += size[pv];\n }\n }\n}\n```
| 1 | 0 |
['Java']
| 1 |
process-restricted-friend-requests
|
[Java] Unin Find, try to connect then find violation
|
java-unin-find-try-to-connect-then-find-7boqh
|
This is a regular union find set approach, try to connect two persons in each request, then check if the new connection violates the restrictions array.\n\nclas
|
brickman
|
NORMAL
|
2021-11-15T23:52:23.818991+00:00
|
2021-11-16T00:22:58.026651+00:00
| 89 | false |
This is a regular `union find set` approach, try to connect two persons in each request, then check if the new connection violates the `restrictions` array.\n```\nclass Solution {\n public boolean[] friendRequests(int n, int[][] restrictions, int[][] requests) {\n boolean[] res = new boolean[requests.length];\n \n int[] friends = new int[n];\n \n for (int i = 0; i < n; i++) {\n friends[i] = i;\n }\n \n for (int i = 0; i < requests.length; i++) {\n int rootA = friends[requests[i][0]];\n int rootB = friends[requests[i][1]];\n \n if (rootA == rootB) {\n res[i] = true;\n continue;\n }\n \n int[] friendsCopy = tryConnect(friends, rootA, rootB);\n \n if (isValid(friendsCopy, restrictions)) {\n res[i] = true;\n friends = friendsCopy;\n } else {\n res[i] = false;\n }\n } \n \n return res;\n }\n \n private int[] tryConnect(int[] friends, int rootA, int rootB) {\n // try on a cloned array rather than in place\n\t\tint n = friends.length;\n int[] friendsCopy = new int[n];\n \n for (int i = 0; i < n; i++) {\n if(friends[i] == rootA) {\n friendsCopy[i] = rootB;\n } else {\n friendsCopy[i] = friends[i];\n }\n }\n \n return friendsCopy;\n }\n \n private boolean isValid(int[] friends, int[][] restrictions) {\n for (int[] restriction: restrictions) {\n int personA = restriction[0];\n int personB = restriction[1];\n if (friends[personA] == friends[personB]) {\n return false;\n }\n }\n return true;\n }\n}\n```
| 1 | 0 |
[]
| 0 |
process-restricted-friend-requests
|
C++ || DSU || with comments || easy to understand
|
c-dsu-with-comments-easy-to-understand-b-9cdv
|
\nclass DSU{\nprivate:\n vector<int> parent,rank;\n\npublic:\n DSU(int n){\n for(int i=0; i<n; i++){\n parent.push_back(-1); //can show
|
is720463
|
NORMAL
|
2021-11-15T22:21:44.013346+00:00
|
2021-11-15T22:21:44.013381+00:00
| 149 | false |
```\nclass DSU{\nprivate:\n vector<int> parent,rank;\n\npublic:\n DSU(int n){\n for(int i=0; i<n; i++){\n parent.push_back(-1); //can show seg fault if written like this parent[i] = -1;\n rank.push_back(0); // same goes for this\n }\n }\n\n int find(int i){\n if(parent[i]==-1){\n return i;\n }\n return parent[i] = find(parent[i]);\n }\n\n void Union(int a, int b){\n int s1 = find(a);\n int s2 = find(b);\n\n if(s1!=s2){\n if(rank[s1] >= rank[s2]){\n parent[s2] = s1;\n rank[s1] += rank[s2];\n }\n else{\n parent[s1] = s2;\n rank[s2] += rank[s1];\n }\n }\n }\n};\n\nclass Solution {\npublic:\n vector<bool> friendRequests(int n, vector<vector<int>>& restrictions, vector<vector<int>>& requests) {\n DSU d(n);\n vector<bool> ans;\n \n //CONCEPT:- My enemy\'s enemy is my friend\n for(int i=0; i<requests.size(); i++){\n DSU t = d; //copy the previous dsu to check that the current request will be accepted or not\n t.Union(requests[i][0],requests[i][1]);\n bool flag = false;\n \n for(auto &it: restrictions){\n if(t.find(it[0]) == t.find(it[1])){ //check that would there be any restriction which we had \n flag = true; //accepted but not supposed to be accepted\n break;\n }\n }\n \n if(flag==false){\n d.Union(requests[i][0],requests[i][1]); //request approved -> true/ change in main dsu\n ans.push_back(true);\n }\n else{\n ans.push_back(false); //request rejected -> false/ no need to change main dsu\n }\n }\n \n return ans;\n \n }\n};\n```
| 1 | 0 |
['Backtracking', 'C']
| 2 |
process-restricted-friend-requests
|
If anyone gets TLE ,make sure to do this optimization.
|
if-anyone-gets-tle-make-sure-to-do-this-bvmcd
|
If someone is getting tle ,make sure to iterate using refrence in for each loop.\n\nclass union_find\n{\n\tvector<int>par;\n\tvector<int>sz;\npublic:\n\tunion_f
|
codifier_69
|
NORMAL
|
2021-11-15T15:14:23.879554+00:00
|
2021-11-15T20:13:34.131896+00:00
| 74 | false |
If someone is getting tle ,make sure to iterate using refrence in for each loop.\n```\nclass union_find\n{\n\tvector<int>par;\n\tvector<int>sz;\npublic:\n\tunion_find(int n){\n par.resize(n);\n sz.resize(n);\n for(int i=0;i<n;i++){\n \tpar[i]=i;\n \tsz[i]=1;\n }\n\t}\n\tint find(int x){\n\t\tif(par[x]==x)\n\t\t\treturn x;\n\t\treturn par[x]=find(par[x]);\n\t}\n\tvoid unite(int u,int v){\n\t\tint a=find(u);\n\t\tint b=find(v);\n\t\tif(not (a==b)){\n\t\t\tif(sz[a]<sz[b]){\n\t\t\t\tpar[a]=b;\n\t\t\t\tsz[b]+=sz[a];\n\t\t\t}else {\n\t\t\t\tpar[b]=a;\n\t\t\t\tsz[a]+=sz[b];\n\t\t\t}\n\t\t}\n\t}\n};\nclass Solution {\npublic:\n vector<bool> friendRequests(int n, vector<vector<int>>& restrictions, vector<vector<int>>& requests) {\n union_find un(n);\n vector<bool>res;\n for(auto &i:requests){ // & (refrence) is making the code faster, without using this i was getting tle on the same code.\n int u=un.find(i[0]);\n int v=un.find(i[1]);\n bool val=true;\n if(not (u==v)){\n for(auto &j:restrictions){ // & (refrence) is making the code faster\n int x=un.find(j[0]),y=un.find(j[1]);\n if((u==x&&v==y)||(u==y&&v==x)){\n val=false;\n break;\n }\n }\n }\n if(val){\n un.unite(u,v);\n }\n res.push_back(val);\n }\n return res;\n }\n};\n\n\n\n\n\n\n\n\n```
| 1 | 0 |
[]
| 2 |
process-restricted-friend-requests
|
Java Union Find O(N)
|
java-union-find-on-by-the-traveller-28qb
|
```\nclass Solution {\n class UF{\n int[] parent;\n public UF(int n){\n parent = new int[n];;\n for(int i=0;i<n;++i)\n
|
the-traveller
|
NORMAL
|
2021-11-14T22:13:52.310469+00:00
|
2021-11-14T22:13:52.310495+00:00
| 69 | false |
```\nclass Solution {\n class UF{\n int[] parent;\n public UF(int n){\n parent = new int[n];;\n for(int i=0;i<n;++i)\n parent[i] = i;\n }\n \n public int find(int x){\n while(x != parent[x]){\n parent[x] = parent[parent[x]];\n x = parent[x];\n }\n return x;\n }\n \n public boolean union(int x, int y, int[][] rest){\n int rootX = find(x);\n int rootY = find(y);\n \n if(rootX != rootY){\n for(int[] res : rest){\n int px = find(res[0]), py = find(res[1]);\n if((px == rootX && py == rootY) || (px == rootY && py == rootX))\n return false;\n }\n parent[rootY] = rootX;\n }\n \n return true;\n }\n }\n public boolean[] friendRequests(int n, int[][] restrictions, int[][] requests) {\n UF uf = new UF(n);\n boolean[] res = new boolean[requests.length];\n int i = 0;\n for(int[] req : requests){\n if(uf.union(req[0], req[1], restrictions))\n res[i] = true;\n i++;\n }\n return res;\n }\n}
| 1 | 1 |
[]
| 0 |
process-restricted-friend-requests
|
[Python] Union Find [350ms, 15MB]
|
python-union-find-350ms-15mb-by-huytq000-528y
|
python\nclass UnionFind:\n def __init__(self, bans, n):\n self.bans = bans # people that are banned inside union\n self.people = [set([i]) for
|
huytq000605
|
NORMAL
|
2021-11-14T06:01:39.272789+00:00
|
2021-11-18T07:00:56.018946+00:00
| 121 | false |
``` python\nclass UnionFind:\n def __init__(self, bans, n):\n self.bans = bans # people that are banned inside union\n self.people = [set([i]) for i in range(n)] # people inside union\n self.parent = [i for i in range(n)] # parent of each person \n self.r = [1 for i in range(n)] # rank in union\n \n def find(self, x):\n if self.parent[x] != x:\n self.parent[x] = self.find(self.parent[x])\n return self.parent[x]\n \n def union(self, x, y):\n x_p = self.find(x)\n y_p = self.find(y)\n if x_p == y_p:\n return True\n if self.r[y_p] > self.r[x_p]: # Path compression by rank\n x_p, y_p = y_p, x_p\n \n\t\t# Check if does union x_p, y_p have people in ban\n\t\t\n for person in self.bans[y_p]: \n if person in self.people[x_p]:\n return False\n \n for person in self.bans[x_p]:\n if person in self.people[y_p]:\n return False\n \n\t\t# Update all people, rank, ban, parent in y_p to x_p\n self.r[x_p] += self.r[y_p]\n self.people[x_p].update(self.people[y_p])\n self.bans[x_p].update(self.bans[y_p])\n self.parent[y_p] = x_p\n return True\n \n\nclass Solution:\n def friendRequests(self, n: int, bans: List[List[int]], requests: List[List[int]]) -> List[bool]:\n banGraph = [set() for i in range(n)]\n for x, y in bans:\n banGraph[x].add(y)\n banGraph[y].add(x)\n uf = UnionFind(banGraph, n)\n result = []\n for x,y in requests:\n result.append(uf.union(x, y))\n return result\n```\n
| 1 | 1 |
['Union Find', 'Python']
| 2 |
process-restricted-friend-requests
|
[Python3] Concise Union Find
|
python3-concise-union-find-by-shaad94-rkp9
|
Time - O(len(requests) * len(restrictions) * (log len(requests))\nSpace - O(len(n)\n\nclass Solution:\n def friendRequests(self, n: int, restrictions: List[L
|
shaad94
|
NORMAL
|
2021-11-14T04:40:54.601606+00:00
|
2021-11-14T04:41:23.048980+00:00
| 82 | false |
Time - O(len(requests) * len(restrictions) * (log len(requests))\nSpace - O(len(n)\n```\nclass Solution:\n def friendRequests(self, n: int, restrictions: List[List[int]], requests: List[List[int]]) -> List[bool]:\n parent = [i for i in range(n)] # create parent array\n \n def findParent(i):\n p = parent[i] # iteratively groing through parent table until cell is a parent of itself\n while p!=parent[p]: p = parent[p]\n return p\n \n res = []\n for l, r in requests:\n lParent, rParent = findParent(l), findParent(r) # searching parent for both cells\n \n parent[lParent] = parent[rParent] = min(lParent, rParent) # applying change request\n \n blocked = False\n for rl, rr in restrictions:\n pl, pr = findParent(rl), findParent(rr) # searching the parent for both parts of restriction\n \n if pl == pr: # if for any restriction parent is the same, rollback the request and mark as False\n blocked = True\n parent[lParent], parent[rParent] = lParent, rParent\n break\n res.append(not blocked)\n \n return res\n```
| 1 | 0 |
[]
| 0 |
process-restricted-friend-requests
|
Why did my C++ union find solution get TLE?
|
why-did-my-c-union-find-solution-get-tle-vfwy
|
My solution during the contest is similar to several solutions which got accepted. Is my Union find implementation slow?\n\n//------DSU---------------------//\n
|
isocyanide7
|
NORMAL
|
2021-11-14T04:10:28.444245+00:00
|
2021-11-14T04:25:03.085869+00:00
| 109 | false |
My solution during the contest is similar to several solutions which got accepted. Is my Union find implementation slow?\n```\n//------DSU---------------------//\n#define ll int\nclass DSU\n{\n public:\n vector <ll> parent,rnk;\n DSU(ll n)\n {\n parent.resize(n+5,0);\n rnk.resize(n+5,0);\n for(ll i=0;i<n+5;i++)\n parent[i]=i;\n }\n ll find_set(ll v)\n {\n if(parent[v]==v)\n return v;\n return parent[v]=find_set(parent[v]); \n }\n void union_sets(ll a,ll b)\n {\n a=find_set(a);\n b=find_set(b);\n if(a!=b)\n {\n if(rnk[a]<rnk[b])\n swap(a,b);\n parent[b]=a; \n if(rnk[a]==rnk[b])\n rnk[a]++; \n }\n }\n};\n//------DSU---------------------//\nclass Solution {\npublic:\n vector<bool> friendRequests(int n, vector<vector<int>>& restrictions, vector<vector<int>>& requests) {\n DSU ds(n);\n vector <bool> ans;\n for(auto u:requests){\n int x=u[0],y=u[1];\n x=ds.find_set(x);\n y=ds.find_set(y);\n if(x==y){\n ans.push_back(true);\n continue;\n }\n bool flag=true;\n for(auto uu:restrictions){\n int p=ds.find_set(uu[0]);\n int q=ds.find_set(uu[1]);\n if((p==x and q==y) or (p==y and q==x)){\n flag=false;\n break;\n }\n }\n ans.push_back(flag);\n if(flag){\n ds.union_sets(x,y);\n }\n }\n return ans;\n }\n};\n\n```\n\nEdit: I found why I am getting TLE. I was creating copies of the vectors in restrictions everytime, because I was not iterating by reference.
| 1 | 0 |
[]
| 1 |
process-restricted-friend-requests
|
Java | Clean | Union Find
|
java-clean-union-find-by-ping_pong-5aoe
|
```\nclass Solution {\n public boolean[] friendRequests(int n, int[][] restrictions, int[][] requests) {\n DSU dsu = new DSU(n, restrictions);\n
|
ping_pong
|
NORMAL
|
2021-11-14T04:01:08.245517+00:00
|
2021-11-14T04:01:08.245556+00:00
| 178 | false |
```\nclass Solution {\n public boolean[] friendRequests(int n, int[][] restrictions, int[][] requests) {\n DSU dsu = new DSU(n, restrictions);\n int r = requests.length;\n boolean res[] = new boolean[r];\n for(int i = 0; i < r; i++) {\n int req[] = requests[i];\n res[i] = dsu.union(req[0], req[1]);\n }\n return res;\n }\n \n static class DSU {\n \n Map<Integer, Set<Integer>> cmpToNodes = new HashMap<>();\n int parent[];\n int[][] restrictions;\n DSU(int n, int[][] restrictions) {\n parent = new int[n];\n for(int i = 0; i < n; i++) {\n Set s = new HashSet<>();\n s.add(i);\n cmpToNodes.put(i, s);\n parent[i] = i;\n }\n this.restrictions = restrictions;\n }\n \n int find(int u) {\n if(u == parent[u]) return u;\n return parent[u] = find(parent[u]);\n }\n \n boolean union(int u, int v) {\n int pu = find(u);\n int pv = find(v);\n \n if(pu != pv) {\n Set<Integer> setU = cmpToNodes.get(pu);\n Set<Integer> setV = cmpToNodes.get(pv);\n for(int restrict[] : restrictions) {\n int x = restrict[0];\n int y = restrict[1];\n boolean foundX = setU.contains(x) || setV.contains(x);\n boolean foundY = setU.contains(y) || setV.contains(y);\n if(foundX && foundY) return false;\n }\n setV.addAll(setU);\n parent[pu] = parent[pv];\n }\n return true;\n }\n }\n}
| 1 | 0 |
[]
| 0 |
process-restricted-friend-requests
|
C++ Union solution
|
c-union-solution-by-jbakin-zck6
|
IntuitionApproachUnion Find data structure for quick identifying of which group friend belongs toComplexity
Time complexity:
O(N * M * α(n)) (worst case)
Space
|
jbakin
|
NORMAL
|
2025-02-22T09:55:24.070399+00:00
|
2025-02-22T10:02:13.277499+00:00
| 7 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
Union Find data structure for quick identifying of which group friend belongs to
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(N * M * α(n)) (worst case)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(n + N)
N - number of requests
M - number of restrictions
n - total number of friends/users
α(n) - inverse Ackermann function
# Code
```cpp []
class UnionFind {
public:
// initialise union
UnionFind(int n) : parents(n, 0), size(n, 0) {
for(int i = 0; i < n; ++i) {
parents[i] = i;
size[i] = 1;
}
}
// find root parent of some node
int find(int id) {
if(parents[id] == id) return id;
// find a root and rewrite it's root for each parent
parents[id] = find(parents[id]);
return parents[id];
}
// connect 2 groups of connected graph/tree
void connect(int a, int b) {
int rootA = find(a);
int rootB = find(b);
if(size[rootA] > size[rootB]) {
swap(rootA, rootB);
}
parents[rootA] = rootB;
size[rootB] += size[rootA];
}
bool isConnected(int a, int b) {
// if their root parent is the same, they are connected
return find(a) == find(b);
}
private:
vector<int> parents;
vector<long long> size;
};
class Solution {
public:
vector<bool> friendRequests(int n, vector<vector<int>>& restrictions, vector<vector<int>>& requests) {
// N number of requests
int N = requests.size();
vector<bool> ans(N);
UnionFind uf(n);
// process all requests in turn
for(int i = 0; i < N; ++i) {
// find parent of each friend, to see if they are connected
int a = uf.find(requests[i][0]);
int b = uf.find(requests[i][1]);
// allowed to set a friendship
bool allowed = true;
// only continue if friends are not connected
if(a != b) {
// check their restrictions
for(int j = 0; j < restrictions.size(); ++j) {
// p and q are groups of friends which are not allowed to be connected together
int p = uf.find(restrictions[j][0]);
int q = uf.find(restrictions[j][1]);
// make sure we check a for both groups and b for both groups
if((a == p && b == q) || (a == q && b == p)) {
allowed = false;
}
}
}
// create a friendship between a and b if it's allowed
if(allowed) {
uf.connect(a, b);
}
// add to answer
ans[i] = allowed;
}
return ans;
}
};
```
| 0 | 0 |
['C++']
| 0 |
process-restricted-friend-requests
|
Python Hard
|
python-hard-by-lucasschnee-alza
| null |
lucasschnee
|
NORMAL
|
2025-02-08T23:15:12.252996+00:00
|
2025-02-08T23:15:12.252996+00:00
| 7 | false |
```python3 []
class UnionFind:
def __init__(self, N):
self.count = N
self.parent = [i for i in range(N)]
self.rank = [1] * N
def find(self, p):
if p != self.parent[p]:
self.parent[p] = self.find(self.parent[p])
return self.parent[p]
def union(self, p, q):
prt, qrt = self.find(p), self.find(q)
if prt == qrt: return False
if self.rank[prt] >= self.rank[qrt]:
self.parent[qrt] = prt
self.rank[prt] += self.rank[qrt]
else:
self.parent[prt] = qrt
self.rank[qrt] += self.rank[prt]
self.count -= 1
return True
class Solution:
def friendRequests(self, n: int, restrictions: List[List[int]], requests: List[List[int]]) -> List[bool]:
'''
we can handle requests in any oder, not sure if thats helpful
we can
'''
N = n
A = []
UF = UnionFind(N)
for u, v in requests:
pu, pv = UF.find(u), UF.find(v)
if pu == pv:
A.append(True)
continue
check = True
for uu, vv in restrictions:
puu, pvv = UF.find(uu), UF.find(vv)
if puu == pu and pvv == pv:
check = False
break
if puu == pv and pvv == pu:
check = False
break
if check:
A.append(True)
UF.union(u, v)
else:
A.append(False)
return A
```
| 0 | 0 |
['Python3']
| 0 |
process-restricted-friend-requests
|
Root Method
|
root-method-by-binary_mutex-36bb
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
Binary_Mutex
|
NORMAL
|
2025-02-04T10:26:54.421333+00:00
|
2025-02-04T10:26:54.421333+00:00
| 4 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def friendRequests(self, n: int, restrictions: List[List[int]], requests: List[List[int]]) -> List[bool]:
p = [i for i in range(n)]
def find(x):
if x!=p[x]:
p[x] = find(p[x])
return p[x]
res = []
for u,v in requests:
pu,pv = sorted([find(u),find(v)])
possible = True
for a,b in restrictions:
pa,pb = sorted([find(a),find(b)])
if (pa,pb) in [(pu,pv),(pu,pu),(pv,pv)]:
possible = False
break
res.append(possible)
if possible: p[pv] = pu
return res
```
| 0 | 0 |
['Python3']
| 0 |
process-restricted-friend-requests
|
Check if possible
|
check-if-possible-by-theabbie-z488
| null |
theabbie
|
NORMAL
|
2025-01-26T07:15:17.882052+00:00
|
2025-01-26T07:15:17.882052+00:00
| 10 | false |
```python3 []
class DSU:
def __init__(self, n):
self.p = list(range(n))
self.sz = [1] * n
self.history = []
self.components = n
def find(self, x):
return x if self.p[x] == x else self.find(self.p[x])
def union(self, a, b):
a = self.find(a)
b = self.find(b)
if self.sz[a] < self.sz[b]:
a, b = b, a
self.history.append((self.sz, a, self.sz[a]))
self.history.append((self.p, b, self.p[b]))
self.history.append((self, "components", self.components))
if a != b:
self.p[b] = a
self.sz[a] += self.sz[b]
self.components -= 1
def rollback(self):
for _ in range(3):
arr, index, old_value = self.history.pop()
if isinstance(arr, DSU):
setattr(arr, index, old_value)
else:
arr[index] = old_value
class Solution:
def friendRequests(self, n: int, restrictions: List[List[int]], requests: List[List[int]]) -> List[bool]:
dsu = DSU(n)
g = [[] for _ in range(n)]
for u, v in restrictions:
g[u].append(v)
g[v].append(u)
res = []
for u, v in requests:
dsu.union(u, v)
allowed = True
for x, y in restrictions:
if dsu.find(x) == dsu.find(y):
allowed = False
break
res.append(allowed)
if not allowed:
dsu.rollback()
return res
```
| 0 | 0 |
['Python3']
| 0 |
process-restricted-friend-requests
|
Modified DSU
|
modified-dsu-by-kamalrathore7060-blet
|
Complexity
Time complexity: req*rest*log(people)
Space complexity: O(people)
Code
|
kamalrathore7060
|
NORMAL
|
2025-01-20T20:23:21.773812+00:00
|
2025-01-20T20:23:21.773812+00:00
| 15 | false |
# Complexity
- Time complexity: req\*rest\*log(people)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(people)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
vector<bool> friendRequests(int n, vector<vector<int>>& restrictions, vector<vector<int>>& requests) {
vector<int> parent(n, -1);
function<int(int)> findP= [&](int a) -> int{
if(parent[a]<0)
return a;
return parent[a]= findP(parent[a]);
};
function<bool(int, int)> unionP= [&](int a, int b) -> bool{
int pa= findP(a);
int pb= findP(b);
if(pa== pb)
return true;
for(auto rest: restrictions){
int pc= findP(rest[0]);
int pd= findP(rest[1]);
if((pc== pa && pd== pb)||(pc== pb && pd== pa))
return false;
}
if(abs(parent[pa])>=abs(parent[pb])){
parent[pa]+= parent[pb];
parent[pb]= pa;
}
else{
parent[pb]+= parent[pa];
parent[pa]= pb;
}
return true;
};
vector<bool> ans;
for(auto r: requests)
ans.push_back(unionP(r[0], r[1]));
return ans;
}
};
```
| 0 | 0 |
['C++']
| 0 |
process-restricted-friend-requests
|
2076. Process Restricted Friend Requests
|
2076-process-restricted-friend-requests-b0h3i
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
G8xd0QPqTy
|
NORMAL
|
2025-01-17T16:08:53.688299+00:00
|
2025-01-17T16:08:53.688299+00:00
| 6 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public boolean[] friendRequests(int n, int[][] restrictions, int[][] requests) {
boolean[] response = new boolean[requests.length];
Set<Integer>[] blockList = new Set[n];
int[] leader = new int[n];
for (int i = 0; i < n; i++) {
leader[i] = i;
blockList[i] = new HashSet<>();
}
for (int[] pair : restrictions) {
blockList[pair[0]].add(pair[1]);
blockList[pair[1]].add(pair[0]);
}
for (int i = 0; i < requests.length; i++) {
int user1 = findLeader(leader, requests[i][0]);
int user2 = findLeader(leader, requests[i][1]);
Set<Integer> blockedUser1 = blockList[user1];
Set<Integer> blockedUser2 = blockList[user2];
if (user1 == user2) {
response[i] = true;
} else if (!blockedUser1.contains(user2) && !blockedUser2.contains(user1)) {
leader[user2] = user1;
blockedUser1.addAll(blockedUser2);
for (int blocked : blockedUser2) {
blockList[blocked].add(user1);
}
response[i] = true;
} else {
response[i] = false;
}
}
return response;
}
private int findLeader(int[] leader, int person) {
if (leader[person] != person) {
leader[person] = findLeader(leader, leader[person]);
}
return leader[person];
}
}
```
| 0 | 0 |
['Java']
| 0 |
process-restricted-friend-requests
|
Union Find
|
union-find-by-smal-m5q4
|
Complexity
|
smal
|
NORMAL
|
2025-01-17T02:55:29.895392+00:00
|
2025-01-17T02:55:29.895392+00:00
| 8 | false |
# Complexity
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
```python3 []
class UnionFind:
def __init__(self, n, restrictions):
self.n = n
self.parent = [i for i in range(n)]
self.rank = [0] * n
self.restrictions = defaultdict(list)
for x, y in restrictions:
self.restrictions[x].append(y)
self.restrictions[y].append(x)
def find(self, i):
if self.parent[i] != i:
self.parent[i] = self.find(self.parent[i])
return self.parent[i]
def union(self, i, j):
i = self.find(i)
j = self.find(j)
# update the parents
for x in range(self.n):
self.find(x)
# check for each of the nodes in the same set as i
# if any of the restrictions of that node are in j
# symmetrical so only need to run once
for x in range(self.n):
if self.parent[x] == i:
for k in self.restrictions[x]:
if self.find(k) == j:
return False
if i == j:
return True
if self.rank[i] > self.rank[j]:
self.parent[j] = i
elif self.rank[i] < self.rank[j]:
self.parent[i] = j
else:
self.parent[i] = j
self.rank[j] += 1
return True
class Solution:
def friendRequests(self, n: int, restrictions: List[List[int]], requests: List[List[int]]) -> List[bool]:
dsu = UnionFind(n, restrictions)
ans = []
for x, y in requests:
ans.append(dsu.union(x,y))
return ans
```
| 0 | 0 |
['Python3']
| 0 |
process-restricted-friend-requests
|
DSU based approach
|
dsu-based-approach-by-vats_lc-1lb2
|
Code
|
vats_lc
|
NORMAL
|
2024-12-29T11:00:54.026870+00:00
|
2024-12-29T11:00:54.026870+00:00
| 11 | false |
# Code
```cpp []
class Solution {
public:
int findParent(int node, vector<int>& parent) {
if (node == parent[node])
return node;
return parent[node] = findParent(parent[node], parent);
}
void Union(int a, int b, vector<int>& parent, vector<int>& size) {
a = findParent(a, parent);
b = findParent(b, parent);
if (a == b)
return;
if (size[a] < size[b])
swap(a, b);
parent[b] = a;
size[a] += size[b];
}
bool violationFound(vector<vector<int>>& restrictions,
vector<int>& parent) {
for (auto i : restrictions)
if (findParent(i[0], parent) == findParent(i[1], parent))
return true;
return false;
}
vector<bool> friendRequests(int n, vector<vector<int>>& restrictions,
vector<vector<int>>& requests) {
int r = requests.size();
vector<int> parent(n, 0), size(n, 1);
for (int i = 0; i < n; i++)
parent[i] = i;
vector<bool> ans(r, true);
for (int i = 0; i < r; i++) {
vector<int> newParent = parent, newSize = size;
Union(requests[i][0], requests[i][1], newParent, newSize);
if (violationFound(restrictions, newParent))
ans[i] = false;
else
parent = newParent, size = newSize;
}
return ans;
}
};
```
| 0 | 0 |
['C++']
| 0 |
process-restricted-friend-requests
|
Straight forward union find
|
straight-forward-union-find-by-maxorgus-tm74
|
Code
|
MaxOrgus
|
NORMAL
|
2024-12-16T08:31:15.604648+00:00
|
2024-12-16T08:31:15.604648+00:00
| 9 | false |
# Code\n```python3 []\nclass Solution:\n def friendRequests(self, n: int, restrictions: List[List[int]], requests: List[List[int]]) -> List[bool]:\n p = [i for i in range(n)]\n def find(x):\n if x!=p[x]:\n p[x] = find(p[x])\n return p[x]\n res = []\n for u,v in requests:\n pu,pv = sorted([find(u),find(v)])\n possible = True\n for a,b in restrictions:\n pa,pb = sorted([find(a),find(b)])\n if (pa,pb) in [(pu,pv),(pu,pu),(pv,pv)]:\n possible = False\n break\n res.append(possible)\n if possible: p[pv] = pu\n return res\n```
| 0 | 0 |
['Union Find', 'Python3']
| 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.