question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
design-browser-history
|
Easy JS solution Using DLL || Beats 89% online submissions
|
easy-js-solution-using-dll-beats-89-onli-idv1
|
By using Node\n\nWe will create a Node class. Each node in the linked list represents a visited URL, and has a "val" (URL string), "prev" (previous node) and "n
|
Viraj_Patil_092
|
NORMAL
|
2023-03-18T04:45:10.208390+00:00
|
2023-03-18T04:45:10.208428+00:00
| 668 | false |
# **By using Node**\n\nWe will create a Node class. Each node in the linked list represents a visited URL, and has a "val" (URL string), "prev" (previous node) and "next" (next node) field.\n\nThe "visit" method adds a new URL to the history by creating a new node and setting its "prev" field to the current "root" node, and the "next" field of the current "root" node to the new node. The "root" variable is then updated to point to the new node.\n\nThe "back" method navigates the history backward by following the "prev" pointers of nodes until the desired number of steps is reached, or until the beginning of the history is reached. The "root" variable is then updated to point to the current node, and its "val" field is returned.\n\nThe "forward" method navigates the history forward by following the "next" pointers of nodes until the desired number of steps is reached, or until the end of the history is reached. The "root" variable is then updated to point to the current node, and its "val" field is returned.\n\n# By using List\n\nThe current URL is represented by the index "curr", which starts at 1 (since the first visited URL is at index 0). The total number of visited URLs is stored in the "total" variable.\n\nThe "visit" method adds a new URL to the history by either setting the element at index "curr" to the new URL (if there are already visited URLs after the current position), or by adding the new URL to the end of the list. The "curr" and "total" variables are updated accordingly.\n\nThe "back" method navigates the history backward by decrementing "curr" by the specified number of steps, but ensuring that it never goes below 1 (the beginning of the history). The URL at index "curr-1" is then returned.\n\nThe "forward" method navigates the history forward by incrementing "curr" by the specified number of steps, but ensuring that it never goes above the "total" number of visited URLs. The URL at index "curr-1" is then returned.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(1)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N)\n# Code\n```\nclass BrowserHistory {\n \n constructor(homepage) {\n this.history = [homepage];\n this.curr = 0;\n this.limit = 0;\n }\n \n visit(url) {\n this.curr++;\n if(this.curr == this.history.length) this.history.push(url);\n else this.history[this.curr] = url;\n this.limit = this.curr;\n }\n \n back(steps) {\n this.curr = Math.max(0, this.curr-steps);\n return this.history[this.curr];\n }\n \n forward(steps) {\n this.curr = Math.min(this.limit, this.curr+steps);\n return this.history[this.curr];\n }\n}\n```
| 3 | 0 |
['Linked List', 'Design', 'Doubly-Linked List', 'Data Stream', 'JavaScript']
| 0 |
design-browser-history
|
Java | ArrayList | Clean code
|
java-arraylist-clean-code-by-judgementde-b8cq
|
Code\n\nclass BrowserHistory {\n private List<String> list;\n private int currIdx;\n private int lastIdx;\n\n public BrowserHistory(String homepage) {\n
|
judgementdey
|
NORMAL
|
2023-03-18T03:21:58.330719+00:00
|
2023-03-18T03:22:23.587769+00:00
| 25 | false |
# Code\n```\nclass BrowserHistory {\n private List<String> list;\n private int currIdx;\n private int lastIdx;\n\n public BrowserHistory(String homepage) {\n list = new ArrayList<>(Arrays.asList(homepage));\n currIdx = lastIdx = 0;\n }\n \n public void visit(String url) {\n currIdx++;\n lastIdx = currIdx;\n\n if (currIdx < list.size())\n list.set(currIdx, url);\n else\n list.add(url);\n }\n \n public String back(int steps) {\n currIdx = Math.max(0, currIdx - steps);\n return list.get(currIdx);\n }\n \n public String forward(int steps) {\n currIdx = Math.min(currIdx + steps, lastIdx);\n return list.get(currIdx);\n }\n}\n```
| 3 | 0 |
['Java']
| 0 |
design-browser-history
|
Easy C++ Code | Detailed Explanation | Doubly Linked List
|
easy-c-code-detailed-explanation-doubly-opet8
|
\n# Approach\n Describe your approach to solving the problem. \nHi there, let\'s understand this code in detail. I have implemented the BrowserHistory using a d
|
anmolrajsoni15
|
NORMAL
|
2023-03-18T02:14:42.873218+00:00
|
2023-03-18T02:30:02.327258+00:00
| 188 | false |
\n# Approach\n<!-- Describe your approach to solving the problem. -->\nHi there, let\'s understand this code in detail. I have implemented the ```BrowserHistory``` using a **doubly linked list**. If you\'re not familiar with what a doubly linked list is, don\'t worry, I\'ll explain it along the way. Let\'s dive in!\n\nThe first thing we need to do is to define a class called ```Node```. A node is an object that represents an element of the list. It has three attributes: url, prev and next. The url is a string that stores the web address of the page that the node corresponds to. The prev and next are pointers to other nodes that indicate the previous and next elements in the list.\n\nThe constructor of the Node class takes a url as an argument and assigns it to the url attribute. It also sets the prev and next attributes to NULL, which means they point to nothing initially.\n\nNext, we need to define another class called BrowserHistory. This is the main class that will handle the operations of browsing history. It has one attribute: root. The root is a pointer to a node that represents the current page that we are on.\n\nThe constructor of the ```BrowserHistory``` class takes a homepage as an argument and creates a new node with that url. It then assigns it to the root attribute.\n\nNow let\'s look at the methods of the BrowserHistory class. The first one is visit, which takes a url as an argument and creates a new node with that url. It then links this new node after the current root node by setting its prev attribute to point to root and setting root\'s next attribute to point to it. Finally, it updates root to point to this new node.\n\nThe second method is back, which takes an integer steps as an argument and moves backward in history by steps number of times or until we reach the beginning of history (whichever comes first). It does this by updating root to point to its prev attribute repeatedly until either steps becomes zero or root\'s prev becomes NULL (meaning there is no previous node). It then returns root\'s url as output.\n\nThe third method is forward, which takes an integer steps as an argument and moves forward in history by steps number of times or until we reach the end of history (whichever comes first). It does this by updating root to point to its next attribute repeatedly until either steps becomes zero or root\'s next becomes NULL (meaning there is no next node). It then returns root\'s url as output.\n\nThat\'s it! We have implemented a browser history using a doubly linked list.\n\nA doubly linked list is basically a sequence of nodes that can be traversed in both directions by following their prev and next pointers. It allows us to easily insert and delete nodes at any position without shifting other elements. It also allows us to access any element in constant time given its pointer.\n\n---\n\n\n**I hope you enjoyed this post and learned something new today.\nIf you have any questions or feedback, feel free to leave them in\nthe comments section below. Thanks for reading!**\n\n### And yeah don\'t forget to upvote this post if you liked it.\n\n# Complexity\n- Time complexity:\n The time complexity of the visit method is O(1) because it involves constant time operations such as creating a new node and updating pointers. The time complexity of the back and forward methods is O(steps) because they involve traversing the linked list for a maximum of steps times.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n The space complexity of this code is O(n), where n is the number of nodes in the linked list. This is because we need to store each visited URL in a node.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Node{\npublic:\n string url;\n Node* prev;\n Node* next;\n\n Node(string url){\n this->url = url;\n prev = NULL;\n next = NULL;\n }\n};\n\nclass BrowserHistory {\nprivate:\n Node *root;\npublic:\n BrowserHistory(string homepage) {\n root = new Node(homepage);\n }\n \n void visit(string url) {\n Node* node = new Node(url);\n root->next = node;\n node->prev = root;\n root = root->next;\n }\n \n string back(int steps) {\n for(int i = 0; i<steps && root->prev != NULL; i++){\n root = root->prev;\n }\n return root->url;\n }\n \n string forward(int steps) {\n for(int i = 0; i<steps && root->next != NULL; i++){\n root = root->next;\n }\n return root->url;\n }\n};\n\n/**\n * Your BrowserHistory object will be instantiated and called as such:\n * BrowserHistory* obj = new BrowserHistory(homepage);\n * obj->visit(url);\n * string param_2 = obj->back(steps);\n * string param_3 = obj->forward(steps);\n */\n```
| 3 | 0 |
['Linked List', 'Doubly-Linked List', 'C++']
| 0 |
design-browser-history
|
LINKELIST JAVA APPROACH JAVA
|
linkelist-java-approach-java-by-amanagra-3zf6
|
\nclass BrowserHistory {\n\n LinkedList<String> list = new LinkedList<>();\n int index = 0;\n public BrowserHistory(String homepage) {\n list.add(
|
amanagrawal20156
|
NORMAL
|
2023-03-18T01:23:11.239825+00:00
|
2023-03-18T01:23:11.239859+00:00
| 345 | false |
```\nclass BrowserHistory {\n\n LinkedList<String> list = new LinkedList<>();\n int index = 0;\n public BrowserHistory(String homepage) {\n list.add(homepage);\n }\n \n public void visit(String url) {\n index++;\n list.add(index, url);\n while(index < list.size()-1){\n list.removeLast();\n }\n return;\n }\n \n public String back(int steps) {\n if(index-steps < 0){\n index = 0;\n return list.getFirst();\n } \n index -=steps;\n return list.get(index);\n }\n \n public String forward(int steps) {\n if(index+steps >= list.size()){\n index = list.size()-1;\n \n return list.getLast();\n } \n index+= steps;\n return list.get(index);\n}\n}\n```
| 3 | 0 |
['C', 'Java']
| 0 |
design-browser-history
|
[Rust] two stacks & stack + index
|
rust-two-stacks-stack-index-by-tmtappr-jip1
|
Intuition\nThe first thought anyone likely has is this is something that can be solved with a stack in some way.\n\n# Approach Two Stacks\nTwo stacks are create
|
tmtappr
|
NORMAL
|
2023-03-18T00:59:58.250525+00:00
|
2023-03-18T07:39:16.828450+00:00
| 214 | false |
# Intuition\nThe first thought anyone likely has is this is something that can be solved with a stack in some way.\n\n# Approach Two Stacks\nTwo stacks are created: a `backward` stack that can be used to navigate backward, and a `forward` stack that can be used to navigate forward.\n\nThere will always be at least one item on the `backward` stack, which will be the homepage URL.\n\nWhen going back to previous URL\'s, the items on the `backward` stack are popped and pushed onto the `forward` stack. Going forward is the opposite, assuming the `forward` stack isn\'t cleared by interjecting a new URL via `visit()`.\n\n# Complexity\n- Time complexity: $O(1)$ for `visit()`, and $O(steps)$ for `back()` and `forward()`.\n- Space complexity: $O(n)$ where $n$ the number of URL\'s visited.\n\n# Code\n```rust\nstruct BrowserHistory {\n backward : Vec<String>,\n forward : Vec<String>,\n}\n\nimpl BrowserHistory {\n\n fn new(homepage: String) -> Self {\n Self{ backward: vec![homepage], forward: vec![] }\n }\n \n fn visit(&mut self, url: String) {\n self.backward.push(url);\n self.forward.clear();\n }\n \n fn back(&mut self, steps: i32) -> String {\n for _ in 0..steps.min(self.backward.len() as i32 - 1) {\n self.forward.push(self.backward.pop().unwrap());\n }\n self.backward.last().unwrap().clone()\n }\n \n fn forward(&mut self, steps: i32) -> String {\n for _ in 0..steps.min(self.forward.len() as i32) {\n self.backward.push(self.forward.pop().unwrap());\n }\n self.backward.last().unwrap().clone()\n }\n}\n```\n\n# Approach Stack and Index\nThis approach is similar, but has better time-complexity for a couple methods. Instead of popping items off a stack to go backward, an index is decremented. Going forward it\'s incremented.\n\nWhenever a new URL is visited, the stack is truncated and the new URL is pushed.\n\nThe home page should always be at the bottom of the stack; so to prevent it from being popped, the value of `self.index` can\'t decrement any lower than `0`. And `index + 1` is used to determine where to truncate the stack when `visit()` is called.\n\n`usize::saturating_sub()` is conveniently used to ensure that no matter how many steps back we reduce `self.index` by, it can go no lower than `0` (it would actually roll over if allowed to decrement past 0).\n\n# Complexity\n- Time complexity: $O(1)$ for `visit()`, `back()` and `forward()`.\n- Space complexity: $O(n)$.\n\n# Code\n\n```rust\nstruct BrowserHistory {\n stack : Vec<String>,\n index : usize,\n}\n\nimpl BrowserHistory {\n\n fn new(homepage: String) -> Self {\n Self{ stack: vec![homepage], index: 0 }\n }\n \n fn visit(&mut self, url: String) {\n self.index += 1;\n self.stack.truncate(self.index);\n self.stack.push(url);\n }\n \n fn back(&mut self, steps: i32) -> String {\n self.index = self.index.saturating_sub(steps as usize);\n self.stack[self.index].clone()\n }\n \n fn forward(&mut self, steps: i32) -> String {\n self.index = (self.index + steps as usize).min(self.stack.len() - 1);\n self.stack[self.index].clone()\n }\n}\n```
| 3 | 0 |
['Rust']
| 1 |
design-browser-history
|
Swift | Two Stacks
|
swift-two-stacks-by-upvotethispls-1zto
|
Two Stacks (accepted answer)\n\nclass BrowserHistory {\n var history = [String]()\n\tvar future = [String]()\n \n init(_ homepage: String) {\n
|
UpvoteThisPls
|
NORMAL
|
2023-03-18T00:23:29.170924+00:00
|
2023-03-18T00:24:13.404046+00:00
| 118 | false |
**Two Stacks (accepted answer)**\n```\nclass BrowserHistory {\n var history = [String]()\n\tvar future = [String]()\n \n init(_ homepage: String) {\n visit(homepage)\n }\n \n func visit(_ url: String) {\n future = []\n history.append(url)\n }\n \n func back(_ steps: Int) -> String {\n for i in 0 ..< min(steps, history.count-1) {\n future.append(history.last!)\n history.removeLast()\n }\n return history.last!\n }\n \n func forward(_ steps: Int) -> String {\n for i in 0 ..< min(steps, future.count) {\n history.append(future.last!)\n future.removeLast()\n } \n return history.last!\n }\n}\n```
| 3 | 0 |
['Swift']
| 0 |
design-browser-history
|
🗓️ Daily LeetCoding Challenge March, Day 18
|
daily-leetcoding-challenge-march-day-18-hr90m
|
This problem is the Daily LeetCoding Challenge for March, Day 18. Feel free to share anything related to this problem here! You can ask questions, discuss what
|
leetcode
|
OFFICIAL
|
2023-03-18T00:00:21.411335+00:00
|
2023-03-18T00:00:21.411413+00:00
| 3,570 | false |
This problem is the Daily LeetCoding Challenge for March, Day 18.
Feel free to share anything related to this problem here!
You can ask questions, discuss what you've learned from this problem, or show off how many days of streak you've made!
---
If you'd like to share a detailed solution to the problem, please create a new post in the discuss section and provide
- **Detailed Explanations**: Describe the algorithm you used to solve this problem. Include any insights you used to solve this problem.
- **Images** that help explain the algorithm.
- **Language and Code** you used to pass the problem.
- **Time and Space complexity analysis**.
---
**📌 Do you want to learn the problem thoroughly?**
Read [**⭐ LeetCode Official Solution⭐**](https://leetcode.com/problems/design-browser-history/solution) to learn the 3 approaches to the problem with detailed explanations to the algorithms, codes, and complexity analysis.
<details>
<summary> Spoiler Alert! We'll explain this 0 approach in the official solution</summary>
</details>
If you're new to Daily LeetCoding Challenge, [**check out this post**](https://leetcode.com/discuss/general-discussion/655704/)!
---
<br>
<p align="center">
<a href="https://leetcode.com/subscribe/?ref=ex_dc" target="_blank">
<img src="https://assets.leetcode.com/static_assets/marketing/daily_leetcoding_banner.png" width="560px" />
</a>
</p>
<br>
| 3 | 0 |
[]
| 24 |
design-browser-history
|
Solution with LinkedList - TS/JS, faster than 90%
|
solution-with-linkedlist-tsjs-faster-tha-gw1w
|
Code\n\nclass ListNode2 {\n val: string;\n next: ListNode2 | null;\n prev: ListNode2 | null;\n\n constructor(value: string, next: ListNode2 | null =
|
nursultanbegaliev
|
NORMAL
|
2023-03-09T08:41:07.746907+00:00
|
2023-03-09T08:41:07.746946+00:00
| 419 | false |
# Code\n```\nclass ListNode2 {\n val: string;\n next: ListNode2 | null;\n prev: ListNode2 | null;\n\n constructor(value: string, next: ListNode2 | null = null, prev: ListNode2 | null = null) {\n this.val = value;\n this.next = next;\n this.prev = prev;\n }\n}\n\nclass BrowserHistory {\n list: ListNode2 | null;\n\n constructor(homepage: string) {\n this.list = new ListNode2(homepage);\n }\n\n visit(url: string): void {\n this.list.next = new ListNode2(url, null, this.list);\n this.list = this.list.next;\n }\n\n back(steps: number): string {\n while(steps && this.list.prev) {\n steps--;\n this.list = this.list.prev;\n }\n return this.list.val;\n }\n\n forward(steps: number): string {\n while(steps && this.list.next) {\n steps--;\n this.list = this.list.next;\n }\n return this.list.val;\n }\n}\n```
| 3 | 0 |
['TypeScript', 'JavaScript']
| 0 |
design-browser-history
|
Java || Doubly Linked List || Complete explanation
|
java-doubly-linked-list-complete-explana-2i3f
|
```\nclass BrowserHistory {\n // creating the structure for doubly linked list \n class Node {\n String val;\n Node prev;\n Node nex
|
kurmiamreet44
|
NORMAL
|
2023-01-26T17:43:48.982768+00:00
|
2023-01-26T17:43:48.982796+00:00
| 498 | false |
```\nclass BrowserHistory {\n // creating the structure for doubly linked list \n class Node {\n String val;\n Node prev;\n Node next;\n \n public Node(String val)\n {\n this.val = val;\n }\n }\n \n // the node which will be used to traverse \n Node curr;\n \n \n public BrowserHistory(String homepage) {\n // making the first node using homepage\n Node node = new Node(homepage);\n node.prev = null;\n node.next = null;\n curr = node;\n \n }\n // simple explanation of visit is that the new node to be visited from the curr is attched just to the next to it, \n // even if the url is already present in the linked still we need to create a new node of url and attach it next to curr,\n // imp-> if any other chain of nodes are present ahead of curr, they are removed and the new url node is added \n public void visit(String url) {\n Node node = new Node(url);\n curr.next = node;\n Node temp = curr;\n curr = curr.next;\n curr.prev = temp;\n \n \n }\n // go back and get the value , if we exceed the linked list then return the first value \n \n public String back(int steps) {\n \n while(curr.prev!=null && steps-->0)\n {\n curr = curr.prev; \n }\n \n return curr.val;\n \n }\n // same as back \n \n public String forward(int steps) {\n \n while(curr.next!=null && steps-->0)\n curr = curr.next;\n \n return curr.val;\n }\n}\n\n// leetcode google facebook \n// c
| 3 | 0 |
['Linked List', 'Java']
| 0 |
design-browser-history
|
✅ [C++] | Beginner Friendly Solutions | Stack & Doubly Linked List
|
c-beginner-friendly-solutions-stack-doub-buto
|
Using Stack\n Time Complexity = O(N)\n Space Complexity = O(N) + O(N)\n\nclass BrowserHistory {\npublic:\n stack<string> prev;\n stack<string> next;\n\n
|
psycho_programer
|
NORMAL
|
2023-01-10T09:11:05.656469+00:00
|
2023-01-10T09:11:05.656509+00:00
| 511 | false |
##### Using Stack\n* Time Complexity = `O(N)`\n* Space Complexity = `O(N) + O(N)`\n```\nclass BrowserHistory {\npublic:\n stack<string> prev;\n stack<string> next;\n\n BrowserHistory(string homepage) {\n prev.push(homepage);\n }\n \n void visit(string url) {\n prev.push(url);\n while(!next.empty()) next.pop();\n }\n \n string back(int steps) {\n string last;\n while(steps-- && !prev.empty()) {\n last = prev.top();\n next.push(last);\n prev.pop();\n }\n\n if(prev.empty()) {\n prev.push(last);\n next.pop();\n }\n\n return prev.top();\n }\n \n string forward(int steps) {\n string last;\n while(steps-- && !next.empty()) {\n last = next.top();\n prev.push(last);\n next.pop();\n }\n\n return prev.top();\n }\n};\n```\n\n##### Using Doubly Linked List\n* Time Complexity = `O(N)`\n* Spcace Complexity = `O(N)`\n\n```\nclass Node {\npublic:\n string str;\n Node* prev;\n Node* next;\n\n Node(string data) {\n str = data;\n prev = nullptr;\n next = nullptr;\n }\n};\n\nclass BrowserHistory {\npublic:\n Node* curr;\n\n BrowserHistory(string homepage) {\n curr = new Node(homepage);\n }\n \n void visit(string url) {\n Node* newNode = new Node(url);\n newNode -> prev = curr;\n curr -> next = newNode;\n curr = newNode;\n }\n \n string back(int steps) {\n while(steps-- && curr->prev) {\n curr = curr->prev;\n }\n return curr->str;\n }\n \n string forward(int steps) {\n while(steps-- && curr -> next) {\n curr = curr -> next;\n }\n return curr -> str;\n }\n};\n```\n
| 3 | 0 |
['C++']
| 0 |
design-browser-history
|
Python - 3 Easy Solutions (Array, Doubly Linked List) - O(1)
|
python-3-easy-solutions-array-doubly-lin-ffhr
|
Approach\n1. Doubly Linked List \n2. Array\n3. Array Optimised\n\n# Code - Doubly Linked List Solution\n\nclass ListNode:\n def __init__(self, val = "", next
|
PtrkH
|
NORMAL
|
2022-11-14T10:57:58.991884+00:00
|
2022-11-14T11:01:37.383784+00:00
| 553 | false |
# Approach\n1. Doubly Linked List \n2. Array\n3. Array Optimised\n\n# Code - Doubly Linked List Solution\n```\nclass ListNode:\n def __init__(self, val = "", next = None, prev = None):\n self.val = val\n self.next = next\n self.prev = prev\n\nclass BrowserHistory:\n # Space O(number_of_pages_visited)\n def __init__(self, homepage: str):\n self.current_page = ListNode(val=homepage)\n \n # Time O(1)\n def visit(self, url: str) -> None:\n if self.current_page.next:\n self.current_page.next.prev = None\n self.current_page.next = ListNode(val=url, prev=self.current_page)\n self.current_page = self.current_page.next\n \n # Time O(steps)\n def back(self, steps: int) -> str:\n while self.current_page.prev and steps > 0:\n steps -= 1\n self.current_page = self.current_page.prev\n return self.current_page.val\n\n # Time O(steps)\n def forward(self, steps: int) -> str:\n while self.current_page.next and steps > 0:\n steps -= 1\n self.current_page = self.current_page.next\n return self.current_page.val\n```\n# Code - Array \n```\nclass BrowserHistory:\n # Space O(number_of_pages_visited)\n def __init__(self, homepage: str):\n self.array = [homepage]\n self.cur_page_pointer = 0 \n\n # Time O(n) - Apparently del is O(n)\n def visit(self, url: str) -> None:\n if self.cur_page_pointer < len(self.array)-1:\n del self.array[self.cur_page_pointer+1:]\n self.array.append(url)\n self.cur_page_pointer += 1\n \n # Time O(1)\n def back(self, steps: int) -> str:\n self.cur_page_pointer = max(0, self.cur_page_pointer - steps)\n return self.array[self.cur_page_pointer]\n \n\n # Time O(1)\n def forward(self, steps: int) -> str:\n self.cur_page_pointer = min(len(self.array)-1, self.cur_page_pointer + steps)\n return self.array[self.cur_page_pointer]\n```\n# Code - Array Optimised\nTime O(1) - Achieved through writing over discarded values\n```\nclass BrowserHistory:\n # Space O(number_of_pages_visited)\n def __init__(self, homepage: str):\n self.array = [homepage]\n self.cur_page_pointer = 0 \n self.cur_boundary = 0\n\n # Time O(1)\n def visit(self, url: str) -> None:\n self.cur_page_pointer += 1\n if self.cur_page_pointer == len(self.array):\n self.array.append(url)\n else:\n self.array[self.cur_page_pointer] = url\n self.cur_boundary = self.cur_page_pointer\n \n # Time O(1)\n def back(self, steps: int) -> str:\n self.cur_page_pointer = max(0, self.cur_page_pointer - steps)\n return self.array[self.cur_page_pointer]\n \n\n # Time O(1)\n def forward(self, steps: int) -> str:\n self.cur_page_pointer = min(self.cur_boundary, self.cur_page_pointer + steps)\n return self.array[self.cur_page_pointer]\n\n```
| 3 | 0 |
['Array', 'Doubly-Linked List', 'Python', 'Python3']
| 0 |
design-browser-history
|
C++ Easy O(1) T.C. Faster than 96%
|
c-easy-o1-tc-faster-than-96-by-aryanshsi-35ga
|
\'\'\'\nclass BrowserHistory {\npublic:\n \n int c=0;\n int c_max=0;\n unordered_mapmp;\n BrowserHistory(string homepage) {\n mp[c]=homepa
|
aryanshsingla
|
NORMAL
|
2022-11-09T13:31:41.098670+00:00
|
2022-11-09T13:31:41.098702+00:00
| 448 | false |
\'\'\'\nclass BrowserHistory {\npublic:\n \n int c=0;\n int c_max=0;\n unordered_map<int,string>mp;\n BrowserHistory(string homepage) {\n mp[c]=homepage;\n }\n \n void visit(string url) {\n c++;\n mp[c]=url;\n c_max=c;\n }\n \n string back(int steps) {\n c=c-steps;\n if(c<0)c=0;\n return mp[c];\n }\n \n string forward(int steps) {\n c=c+steps;\n if(c>c_max)c=c_max;\n return mp[c];\n }\n};\n\n/**\n * Your BrowserHistory object will be instantiated and called as such:\n * BrowserHistory* obj = new BrowserHistory(homepage);\n * obj->visit(url);\n * string param_2 = obj->back(steps);\n * string param_3 = obj->forward(steps);\n */\n\'\'\'
| 3 | 0 |
['Design', 'C']
| 0 |
design-browser-history
|
c++|stack
|
cstack-by-ansh811-us73
|
class BrowserHistory {\npublic:\n stacka;\n stackb;\n BrowserHistory(string homepage) {\n a.push(homepage);\n }\n \n void visit(string
|
ansh811
|
NORMAL
|
2022-09-22T07:37:26.188356+00:00
|
2022-09-22T07:37:26.188405+00:00
| 506 | false |
class BrowserHistory {\npublic:\n stack<string>a;\n stack<string>b;\n BrowserHistory(string homepage) {\n a.push(homepage);\n }\n \n void visit(string url) {\n a.push(url);\n while(!b.empty()){\n b.pop();\n }\n }\n \n string back(int steps) {\n while(a.size()>1 && steps!=0){\n b.push(a.top());\n a.pop();\n steps--;\n }\n return a.top();\n }\n \n string forward(int steps) {\n while(b.size()>0 && steps!=0){\n a.push(b.top());\n b.pop();\n steps--;\n }\n return a.top();\n\n }\n};\n
| 3 | 0 |
['Stack', 'C']
| 0 |
design-browser-history
|
✅✅✅98% Faster C Code || Super Short/Concise ✅✅✅
|
98-faster-c-code-super-shortconcise-by-l-l266
|
\ntypedef struct BrowserHistory{\n char *val;\n struct BrowserHistory *next,*prev;\n} BrowserHistory;\n\nBrowserHistory *curr;\n\nBrowserHistory* browserH
|
Lil_ToeTurtle
|
NORMAL
|
2022-06-28T19:22:08.163074+00:00
|
2022-06-28T19:41:39.309762+00:00
| 162 | false |
```\ntypedef struct BrowserHistory{\n char *val;\n struct BrowserHistory *next,*prev;\n} BrowserHistory;\n\nBrowserHistory *curr;\n\nBrowserHistory* browserHistoryCreate(char * homepage) {\n BrowserHistory *p=(BrowserHistory*)malloc(sizeof(BrowserHistory));\n p->val=homepage;\n p->prev=p->next=NULL;\n return curr=p;\n}\n\nvoid browserHistoryVisit(BrowserHistory* obj, char * url) {\n obj=curr,obj->next=browserHistoryCreate(url),obj->next->prev=obj;\n}\n\nchar * browserHistoryBack(BrowserHistory* obj, int steps) {\n while(steps--) curr=(curr->prev==NULL)?curr:curr->prev;\n return curr->val;\n}\n\nchar * browserHistoryForward(BrowserHistory* obj, int steps) {\n while(steps--) curr=(curr->next==NULL)?curr:curr->next;\n return curr->val;\n}\n\nvoid browserHistoryFree(BrowserHistory* obj) {\n free(obj);\n}\n```
| 3 | 0 |
['Linked List', 'C']
| 1 |
design-browser-history
|
Python Easy Solution
|
python-easy-solution-by-jhansi_mns-0up9
|
\nclass BrowserHistory:\n\n def __init__(self, homepage: str):\n self.back_stack = []\n self.fw_stack = []\n self.back_stack.append(home
|
Jhansi_MNS
|
NORMAL
|
2022-05-11T11:24:29.509629+00:00
|
2022-05-11T11:24:29.509659+00:00
| 285 | false |
```\nclass BrowserHistory:\n\n def __init__(self, homepage: str):\n self.back_stack = []\n self.fw_stack = []\n self.back_stack.append(homepage)\n \n def visit(self, url: str) -> None:\n self.back_stack.append(url)\n self.fw_stack = []\n \n def back(self, steps: int) -> str:\n while steps != 0:\n len_back = len(self.back_stack)\n if len_back > 0 and len_back != 1:\n temp = self.back_stack.pop(-1)\n self.fw_stack.append(temp)\n steps = steps - 1\n return self.back_stack[-1]\n \n def forward(self, steps: int) -> str:\n while steps != 0:\n if len(self.fw_stack) > 0:\n temp = self.fw_stack.pop(-1)\n self.back_stack.append(temp)\n steps = steps - 1\n return self.back_stack[-1]\n\t\t\n```
| 3 | 0 |
['Python']
| 0 |
design-browser-history
|
🔴 Python Solution 🔴
|
python-solution-by-alekskram-3th4
|
Upvote if you like solution and feel free to ask If you have any question.\n\nclass LinkedList:\n def __init__(self, url: str, prev_page=None, next_page=None
|
alekskram
|
NORMAL
|
2022-05-05T12:02:21.893414+00:00
|
2022-05-05T12:02:21.893442+00:00
| 239 | false |
**Upvote** if you like solution and feel **free to ask** If you have any question.\n```\nclass LinkedList:\n def __init__(self, url: str, prev_page=None, next_page=None):\n self.page = url\n self.prev_page = prev_page\n self.next_page = next_page\n \nclass BrowserHistory:\n\n def __init__(self, homepage: str):\n self.here = LinkedList(homepage)\n\n def visit(self, url: str) -> None:\n place = LinkedList(url, self.here)\n self.here.next_page = place\n self.here = self.here.next_page\n\n def back(self, steps: int) -> str:\n while steps > 0 and self.here.prev_page is not None:\n steps -= 1\n self.here = self.here.prev_page\n return self.here.page\n\n def forward(self, steps: int) -> str:\n while steps > 0 and self.here.next_page is not None:\n steps -= 1\n self.here = self.here.next_page\n return self.here.page\n```
| 3 | 0 |
['Linked List', 'Python']
| 0 |
design-browser-history
|
Python using List | Easy | 99% faster
|
python-using-list-easy-99-faster-by-pkpr-qs0v
|
\nclass BrowserHistory:\n\n def __init__(self, homepage: str):\n self.urls = []\n self.urls.insert(0,"#")\n self.urls.insert(1,homepage)
|
pkprasad1996
|
NORMAL
|
2022-03-01T23:46:51.472641+00:00
|
2022-03-01T23:46:51.472684+00:00
| 238 | false |
```\nclass BrowserHistory:\n\n def __init__(self, homepage: str):\n self.urls = []\n self.urls.insert(0,"#")\n self.urls.insert(1,homepage)\n self.ptr = 1\n\n \n def visit(self, url: str) -> None:\n self.ptr += 1\n self.urls.insert(self.ptr,url)\n self.urls = self.urls [0:self.ptr+1]\n return None\n\n \n def back(self, steps: int) -> str:\n if steps >= self.ptr:\n self.ptr = 1\n else:\n self.ptr = self.ptr-steps\n return self.urls[self.ptr]\n \n \n def forward(self, steps: int) -> str:\n if (steps+self.ptr)<len(self.urls):\n self.ptr = steps+self.ptr\n else:\n self.ptr = len(self.urls)-1\n return self.urls[self.ptr]\n```
| 3 | 1 |
['Python', 'Python3']
| 0 |
design-browser-history
|
C++ || EASY TO UNDERSTAND || simple code
|
c-easy-to-understand-simple-code-by-aari-fjei
|
\nclass BrowserHistory {\nprivate:\n vector<string> v;\n int i;\npublic:\n BrowserHistory(string homepage) {\n v.push_back(homepage);\n i
|
aarindey
|
NORMAL
|
2022-01-15T04:48:00.636386+00:00
|
2022-01-15T04:48:00.636423+00:00
| 79 | false |
```\nclass BrowserHistory {\nprivate:\n vector<string> v;\n int i;\npublic:\n BrowserHistory(string homepage) {\n v.push_back(homepage);\n i=0;\n }\n \n void visit(string url) {\n v.erase(v.begin()+i+1,v.end());\n v.push_back(url);\n i++;\n }\n \n string back(int steps) {\n i=max(0,i-steps);\n return v[i];\n }\n \n string forward(int steps) {\n i=min((int)(v.size()-1),(int)(i+steps));\n return v[i];\n }\n};\n```\n**Please upvote to motivate me in my quest of documenting all leetcode solutions(to help the community). HAPPY CODING:)\nAny suggestions and improvements are always welcome**
| 3 | 0 |
[]
| 0 |
design-browser-history
|
[C++] clean code & creating linked list
|
c-clean-code-creating-linked-list-by-tur-hl3j
|
\nclass BrowserHistory {\npublic:\n struct Node {\n string data;\n Node* next;\n Node* prev;\n \n Node(string val) {\n
|
ihavehiddenmyid
|
NORMAL
|
2021-09-13T02:16:16.887727+00:00
|
2021-09-13T02:27:40.285943+00:00
| 231 | false |
```\nclass BrowserHistory {\npublic:\n struct Node {\n string data;\n Node* next;\n Node* prev;\n \n Node(string val) {\n data = val;\n next = nullptr;\n prev = nullptr;\n }\n };\n \n Node* current = nullptr;\n \t \n BrowserHistory(string homepage) {\n Node* nn = new Node(homepage);\n current = nn;\n }\n \n void visit(string url) {\n Node* nn = new Node(url);\n\t\tcurrent->next = nn;\n\t\tnn->prev = current;\n\t\tnn->next = nullptr;\n current = nn;\n }\n \n string back(int steps) {\n while (steps > 0 && current->prev != nullptr) {\n current = current->prev;\n steps--;\n }\n return current->data;\n }\n \n string forward(int steps) {\n while (steps > 0 && current->next != nullptr) {\n current = current->next;\n steps--;\n }\n return current->data;\n }\n};\n```
| 3 | 0 |
['Linked List', 'C', 'C++']
| 0 |
design-browser-history
|
Java || Doubly Linked List || 45ms || beats 90%
|
java-doubly-linked-list-45ms-beats-90-by-3bpq
|
\n\n\tclass ListNode {\n\n\t\tString url;\n\t\tListNode next;\n\t\tListNode prev;\n\n\t\tpublic ListNode(String url) {\n\t\t\tthis.url = url;\n\t\t\tthis.next =
|
LegendaryCoder
|
NORMAL
|
2021-07-27T14:44:02.442679+00:00
|
2021-07-27T14:44:02.442730+00:00
| 56 | false |
\n\n\tclass ListNode {\n\n\t\tString url;\n\t\tListNode next;\n\t\tListNode prev;\n\n\t\tpublic ListNode(String url) {\n\t\t\tthis.url = url;\n\t\t\tthis.next = null;\n\t\t\tthis.prev = null;\n\t\t}\n\t}\n\n\tclass BrowserHistory {\n\n\t\tListNode curr;\n\n\t\t// O(1)\n\t\tpublic BrowserHistory(String homepage) {\n\t\t\tcurr = new ListNode(homepage);\n\t\t}\n\n\t\t// O(1)\n\t\tpublic void visit(String url) {\n\t\t\tListNode temp = new ListNode(url);\n\t\t\tcurr.next = temp;\n\t\t\ttemp.prev = curr;\n\t\t\tcurr = temp;\n\t\t}\n\n\t\t// O(steps)\n\t\tpublic String back(int steps) {\n\t\t\twhile (curr.prev != null && steps >= 1) {\n\t\t\t\tcurr = curr.prev;\n\t\t\t\tsteps--;\n\t\t\t}\n\t\t\treturn curr.url;\n\t\t}\n\n\t\t// O(steps)\n\t\tpublic String forward(int steps) {\n\t\t\twhile (curr.next != null && steps >= 1) {\n\t\t\t\tcurr = curr.next;\n\t\t\t\tsteps--;\n\t\t\t}\n\t\t\treturn curr.url;\n\t\t}\n\t}
| 3 | 0 |
[]
| 0 |
design-browser-history
|
Python3 || Simplest solution using list (array) and two pointers || 99% faster || O(1)
|
python3-simplest-solution-using-list-arr-lwev
|
The solution is using a list (array) and two pointers (current and end) to maintain states.\nConstraint was max calls altogether is 5000. So maximum calls of vi
|
abhattad4
|
NORMAL
|
2021-07-26T05:11:02.817147+00:00
|
2021-07-26T05:12:53.186246+00:00
| 365 | false |
The solution is using a list (array) and two pointers (current and end) to maintain states.\nConstraint was max calls altogether is 5000. So maximum calls of visit is 5000 plus one __init__ in worst case. So maximum urls that can be there in one test case in 5001.\n\nJust my manipulating 2 pointers (current and end), we can do back(steps) and forward(steps) operation in O(1). Visit(url) operation is also O(1).\n\n**Kindly upvote if you like the simplest and easy solution.**\n\n\'\'\'\nclass BrowserHistory:\n\n def __init__(self, homepage: str):\n self.urlarr = [None]*5001\n \n self.curr = 0\n self.end = 0\n self.urlarr[self.curr] = homepage\n\n def visit(self, url: str) -> None:\n # print(self.curr,self.end,url)\n self.curr+=1\n self.urlarr[self.curr] = url\n self.end = self.curr\n\n def back(self, steps: int) -> str:\n if self.curr - steps <= 0:\n self.curr = 0\n return self.urlarr[0]\n else:\n self.curr = self.curr - steps\n return self.urlarr[self.curr]\n\n def forward(self, steps: int) -> str:\n if self.curr + steps >= self.end:\n self.curr = self.end\n return self.urlarr[self.end]\n else:\n self.curr = self.curr + steps\n return self.urlarr[self.curr]\n\'\'\'
| 3 | 0 |
['Python', 'Python3']
| 0 |
design-browser-history
|
[Python3] Browser History: Constant Time Operations
|
python3-browser-history-constant-time-op-3q6l
|
\nclass BrowserHistory:\n\n def __init__(self, homepage: str):\n self.history_stack = []\n self.current_url_index = -1\n self.visit(home
|
phoenix-2
|
NORMAL
|
2020-10-08T03:27:45.939229+00:00
|
2020-10-08T03:27:45.939261+00:00
| 353 | false |
```\nclass BrowserHistory:\n\n def __init__(self, homepage: str):\n self.history_stack = []\n self.current_url_index = -1\n self.visit(homepage)\n\n def visit(self, url: str) -> None:\n self.history_stack = self.history_stack[:self.current_url_index + 1]\n self.history_stack.append(url)\n self.current_url_index += 1\n\n def back(self, steps: int) -> str:\n if self.current_url_index - steps >= 0:\n self.current_url_index -= steps\n else:\n self.current_url_index = 0\n\n return self.history_stack[self.current_url_index]\n\n def forward(self, steps: int) -> str:\n if self.current_url_index + steps < len(self.history_stack):\n self.current_url_index = self.current_url_index + steps \n else:\n self.current_url_index = len(self.history_stack) - 1\n \n return self.history_stack[self.current_url_index]\n\n```
| 3 | 1 |
['Python3']
| 1 |
design-browser-history
|
Shortest And Cleanest code with( 100.00% space efficient of Python3)
|
shortest-and-cleanest-code-with-10000-sp-3ang
|
\n\nclass BrowserHistory:\n def __init__(self, homepage: str):\n self.hist=[homepage]\n self.curr=0\n\n def visit(self, url: str) -> None:\n
|
acloj97
|
NORMAL
|
2020-06-07T04:28:06.054950+00:00
|
2020-06-07T05:38:14.335015+00:00
| 91 | false |
\n```\nclass BrowserHistory:\n def __init__(self, homepage: str):\n self.hist=[homepage]\n self.curr=0\n\n def visit(self, url: str) -> None:\n self.hist=self.hist[:self.curr+1] #Deleting forward histories from current point and keeping the history until current point only before visiting any other url\n self.hist.append(url)\n self.curr+=1 #increasing self.curr to point to the current url in the history\n\n def back(self, steps: int) -> str:\n #we check if subtracting steps from current index results in index less than 0, then we just take the 0th element or else take (self.curr-steps)th\n stepback=max(self.curr-steps,0)\n self.curr=stepback\n return self.hist[self.curr]\n\n def forward(self, steps: int) -> str:\n\t#we check if adding stes to current index results in indexoutofboubds, then we just take thelast element or else take (self.curr+steps)th\n stepforw=min(self.curr+steps,len(self.hist)-1)\n self.curr=stepforw\n return self.hist[self.curr]\n```
| 3 | 0 |
[]
| 0 |
design-browser-history
|
Python - Two Stacks
|
python-two-stacks-by-cool_shark-tnvm
|
Use a back stack for navigating back and use forward stack for navigating forward.\n\npy\n\nclass BrowserHistory:\n\n def __init__(self, homepage: str):\n
|
cool_shark
|
NORMAL
|
2020-06-07T04:11:14.332629+00:00
|
2020-06-07T04:11:14.332681+00:00
| 270 | false |
Use a back stack for navigating back and use forward stack for navigating forward.\n\n```py\n\nclass BrowserHistory:\n\n def __init__(self, homepage: str):\n self.back_stack = [homepage]\n self.forward_stack = []\n\n def visit(self, url: str) -> None:\n self.forward_stack.clear() \n self.back_stack.append(url)\n\n def back(self, steps: int) -> str:\n while len(self.back_stack) >= 2 and steps > 0:\n top = self.back_stack.pop()\n self.forward_stack.append(top)\n steps -= 1\n return self.back_stack[-1]\n\n def forward(self, steps: int) -> str:\n while len(self.forward_stack) > 0 and steps > 0:\n top = self.forward_stack.pop()\n self.back_stack.append(top)\n steps -= 1\n return self.back_stack[-1]\n\n\n```
| 3 | 0 |
[]
| 1 |
design-browser-history
|
[C++] two stacks with comments and 3 variations
|
c-two-stacks-with-comments-and-3-variati-z8in
|
Intuition:\ntwo stacks are used to move backward into history and forward in to current again, which is the last visit.\n\nvector are used to simulate stack and
|
codedayday
|
NORMAL
|
2020-06-07T04:08:05.630597+00:00
|
2020-06-07T20:30:16.042740+00:00
| 347 | false |
**Intuition:**\ntwo stacks are used to move backward into history and forward in to current again, which is the last visit.\n\nvector are used to simulate stack and the rightmost is the top of stack:\n stack1: { backward2, backward1, cur}, \n stack2: {forward2, forward1}\n \n Version 1: use vector to simulate stack\n```\nclass BrowserHistory {\npublic: //Time/Space: O(N*steps), O(N); Coding cost: 34 Lines\n BrowserHistory(string homepage) {\n visit(homepage);\n }\n \n void visit(string url) {\n h_.emplace_back(url); \n if(!stk2_.empty()) stk2_.clear(); // future is zero\n }\n \n string back(int steps) { \n int new_cur = max(0, (int) h_.size() - 1 - steps); \n int diff = h_.size() - 1 - new_cur; \n while(diff-- > 0){\n stk2_.emplace_back(h_.back());\n h_.pop_back();\n } \n return h_.back();\n }\n \n string forward(int steps) { \n int diff= min((int) stk2_.size(), steps); \n while(diff-- > 0){\n h_.push_back(stk2_.back());\n stk2_.pop_back();\n } \n return h_.back(); \n }\n \nprivate:\n vector<string> h_; // history, backward\n vector<string> stk2_; // future, foward\n};\n```\n\n\nVersion 2: use stack \n```\nclass BrowserHistory { // 2 stack simulation of history & future\npublic: //Time/Space: O(N*steps), O(N); Coding cost: 31 Lines\n BrowserHistory(string homepage) {\n history_.push(homepage);\n }\n \n void visit(string url) {\n history_.push(url);\n future_=stack<string>();\n }\n \n string back(int steps) { \n while(steps-- > 0 && history_.size() >=2){\n future_.push(history_.top());\n history_.pop(); \n }\n return history_.top();\n }\n \n string forward(int steps) {\n while(steps-- > 0 && !future_.empty()){\n history_.push(future_.top());\n future_.pop();\n }\n return history_.top();\n }\n \nprivate:\n stack<string> history_;\n stack<string> future_;\n};\n\n```\n\nVersion 3: array + 2 points\n```\nclass BrowserHistory {\npublic: //Time/Space: O(N), O(N); Coding cost: 22 Lines\n string logs[5000];\n int p; // pointer to present\n int t; // pointer to top\n \n BrowserHistory(string homepage) {\n logs[p=t=0] = move(homepage); \n }\n \n void visit(string url) {\n logs[t=++p]=move(url);\n }\n \n string back(int steps) {\n return logs[p=max(0, p-steps)];\n }\n \n string forward(int steps) {\n return logs[p=min(t, p+steps)];\n }\n};\n\n```\n
| 3 | 0 |
['Stack', 'C']
| 0 |
design-browser-history
|
Python linked list
|
python-linked-list-by-aj_to_rescue-ff4f
|
\nclass Node:\n \n def __init__(self, val, prev=None, next=None):\n self.val = val\n self.next = next\n self.prev = prev\n \nc
|
aj_to_rescue
|
NORMAL
|
2020-06-07T04:03:10.142965+00:00
|
2020-06-07T04:04:09.469412+00:00
| 285 | false |
```\nclass Node:\n \n def __init__(self, val, prev=None, next=None):\n self.val = val\n self.next = next\n self.prev = prev\n \nclass BrowserHistory(object):\n\n def __init__(self, homepage):\n """\n :type homepage: str\n """\n self.head = Node(val=homepage)\n\n def visit(self, url):\n """\n :type url: str\n :rtype: None\n """\n self.head.next = Node(val=url, prev=self.head)\n self.head = self.head.next\n\n def back(self, steps):\n """\n :type steps: int\n :rtype: str\n """\n while steps and self.head.prev:\n self.head = self.head.prev\n steps -= 1\n return self.head.val\n \n\n def forward(self, steps):\n """\n :type steps: int\n :rtype: str\n """\n while steps and self.head.next:\n self.head = self.head.next\n steps -= 1\n return self.head.val\n```
| 3 | 0 |
['Python3']
| 0 |
design-browser-history
|
Python Stack Easy (self explanatory)
|
python-stack-easy-self-explanatory-by-so-58ct
|
```\nclass BrowserHistory:\n def init(self, homepage: str):\n self.stack = [homepage]\n self.curr = 0\n\n def visit(self, url: str) -> None:
|
sonaksh
|
NORMAL
|
2020-06-07T04:02:39.354737+00:00
|
2020-06-08T17:04:29.869707+00:00
| 389 | false |
```\nclass BrowserHistory:\n def __init__(self, homepage: str):\n self.stack = [homepage]\n self.curr = 0\n\n def visit(self, url: str) -> None:\n while len(self.stack) > self.curr+1:\n self.stack.pop()\n self.stack.append(url)\n self.curr = len(self.stack) - 1\n \n def back(self, steps: int) -> str:\n self.curr = max(0, self.curr - steps)\n return self.stack[self.curr]\n\n def forward(self, steps: int) -> str:\n \xA0 \xA0 \xA0 \xA0self.curr = min(self.curr + steps, len(self.stack) - 1)\n\t\treturn self.stack[self.curr]\n
| 3 | 0 |
['Stack', 'Python3']
| 1 |
design-browser-history
|
✅✅ Using Stacks || Beginner Friendly || Easy Solution
|
using-stacks-beginner-friendly-easy-solu-uw46
|
IntuitionTo simulate browser history behavior, we need to efficiently track pages visited before and after the current one. Two stacks make this easy — one for
|
Karan_Aggarwal
|
NORMAL
|
2025-04-10T12:52:57.578681+00:00
|
2025-04-10T12:52:57.578681+00:00
| 22 | false |
# Intuition
To simulate browser history behavior, we need to efficiently track pages visited before and after the current one. Two stacks make this easy — one for the past (back history) and one for the future (forward history). A separate `curr` string keeps track of the current page.
# Approach
- Use two stacks:
- `past` stack stores the history before the current page.
- `future` stack stores pages after the current page when the user goes back.
- On visiting a new URL:
- Push the current page to `past`.
- Clear the `future` stack.
- On going back:
- Pop from `past` and push the current page to `future`.
- Repeat until steps are 0 or `past` is empty.
- On going forward:
- Pop from `future` and push the current page to `past`.
- Repeat until steps are 0 or `future` is empty.
# Time Complexity
- `visit(url)`: O(1)
- `back(steps)`: O(steps)
- `forward(steps)`: O(steps)
# Space Complexity
- O(n), where n is the total number of pages visited.
Each visited page can be stored in either `past`, `future`, or `curr`.
# Code
```cpp []
class BrowserHistory {
public:
stack<string>past;
stack<string>future;
string curr;
BrowserHistory(string homepage) {
curr=homepage;
}
void visit(string url) {
past.push(curr);
curr=url;
future=stack<string>();
}
string back(int steps) {
while(!past.empty() && steps--){
future.push(curr);
curr=past.top();
past.pop();
}
return curr;
}
string forward(int steps) {
while(!future.empty() && steps--){
past.push(curr);
curr=future.top();
future.pop();
}
return curr;
}
};
```
# Have a Good Day 😊 UpVote?
| 2 | 0 |
['Array', 'Stack', 'Design', 'Data Stream', 'C++']
| 0 |
design-browser-history
|
C++ solution using Doubly Linked List
|
c-solution-using-doubly-linked-list-by-s-w1zn
|
IntuitionApproachThis implementation uses a doubly linked list to manage the browser history:Node Structure:
Each node stores a URL along with pointers to the p
|
Sachin_Kumar_Sharma
|
NORMAL
|
2025-03-27T05:14:41.049731+00:00
|
2025-03-27T05:14:41.049731+00:00
| 65 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
This implementation uses a doubly linked list to manage the browser history:
Node Structure:
Each node stores a URL along with pointers to the previous and next nodes.
Constructor:
The BrowserHistory constructor initializes the list with the homepage as the first node.
visit(string url):
When a new URL is visited, a new node is created, linked to the current node, and then set as the current node. This automatically discards any forward history.
back(int steps):
Moves the current pointer backwards up to the specified steps (or until no previous node exists) and returns the URL at the current node.
forward(int steps):
Moves the current pointer forward up to the specified steps (or until no next node exists) and returns the URL at the current node.
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: O(N)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(N)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class BrowserHistory {
public:
struct Node{
string url;
Node* next;
Node* prev;
Node(string url): url(url),next(NULL),prev(NULL){}
};
Node* curr;
BrowserHistory(string homepage) {
curr=new Node(homepage);
}
void visit(string url) {
Node* newNode=new Node(url);
curr->next=newNode;
newNode->prev=curr;
curr=newNode;
}
string back(int steps) {
while(steps-- > 0 && curr->prev){
curr=curr->prev;
}
return curr->url;
}
string forward(int steps) {
while(steps-- > 0 && curr->next){
curr=curr->next;
}
return curr->url;
}
};
/**
* Your BrowserHistory object will be instantiated and called as such:
* BrowserHistory* obj = new BrowserHistory(homepage);
* obj->visit(url);
* string param_2 = obj->back(steps);
* string param_3 = obj->forward(steps);
*/
```
| 2 | 0 |
['C++']
| 0 |
design-browser-history
|
Using Two Stacks
|
using-two-stacks-by-vibhutigoel27-4kwu
|
Intuition\nWhy use Stack ? \nStack is used when we used to maintain the history. Since here, we need to maintain both the back and forward history two stacks wi
|
vibhutigoel27
|
NORMAL
|
2024-11-29T16:24:06.079973+00:00
|
2024-11-29T16:24:06.080013+00:00
| 195 | false |
# Intuition\nWhy use Stack ? \nStack is used when we used to maintain the history. Since here, we need to maintain both the back and forward history two stacks will be used.\n\n# Approach\n1. We will keep on pushing urls in the back stack whenever visit function is called.\n2. We will keep a string variable which will keep track of our answer.\n3. In the back function, we will push the curr element into stack and pop the back array.\n\n# Complexity\n- Time complexity:\n1. for back function: O(no of steps)\n2. for forward function: O(no of steps)\n3. for visit function: O(n)\n\n# Code\n```java []\nclass BrowserHistory {\n Stack<String> back = new Stack<>();\n Stack<String> forward = new Stack<>();\n String curr;\n public BrowserHistory(String homepage) {\n curr = homepage;\n }\n \n public void visit(String url) {\n back.push(curr);\n curr = url;\n while(!forward.isEmpty()) {\n forward.pop();\n }\n }\n \n public String back(int steps) {\n for(int i=0;i<steps && !back.isEmpty();i++) {\n forward.push(curr);\n curr = back.peek();\n back.pop();\n }\n return curr;\n }\n \n public String forward(int steps) {\n for(int i=0;i<steps && !forward.isEmpty();i++) {\n back.push(curr);\n curr = forward.pop();\n }\n return curr;\n }\n}\n\n/**\n * Your BrowserHistory object will be instantiated and called as such:\n * BrowserHistory obj = new BrowserHistory(homepage);\n * obj.visit(url);\n * String param_2 = obj.back(steps);\n * String param_3 = obj.forward(steps);\n */\n```
| 2 | 0 |
['Stack', 'Java']
| 1 |
design-browser-history
|
Simple Solution || Using Vector C++
|
simple-solution-using-vector-c-by-orewa_-1pds
|
\n# Complexity\n- Time complexity:\nO(n)\n- Space complexity:\nO(n)\n# Code\n\nclass BrowserHistory {\n\n vector<string> list;\n int currIndex;\n\npublic:
|
Orewa_Abhi
|
NORMAL
|
2024-02-27T05:25:21.684226+00:00
|
2024-02-27T05:25:21.684251+00:00
| 17 | false |
\n# Complexity\n- Time complexity:\n$$O(n)$$\n- Space complexity:\n$$O(n)$$\n# Code\n```\nclass BrowserHistory {\n\n vector<string> list;\n int currIndex;\n\npublic:\n\n BrowserHistory(string homepage) {\n list.push_back(homepage);\n currIndex = 0;\n }\n \n void visit(string url) {\n // removing all the forward history until currIndex\n while(currIndex < list.size()-1)\n {\n list.pop_back();\n }\n list.push_back(url);\n currIndex++;\n }\n \n string back(int steps) {\n int newInd = currIndex - steps;\n if(newInd < 0) newInd = 0;\n currIndex = newInd;\n return list[currIndex];\n }\n \n string forward(int steps) {\n int newInd = currIndex + steps;\n if(newInd > list.size()-1) newInd = list.size()-1;\n currIndex = newInd;\n return list[currIndex];\n }\n};\n\n/**\n * Your BrowserHistory object will be instantiated and called as such:\n * BrowserHistory* obj = new BrowserHistory(homepage);\n * obj->visit(url);\n * string param_2 = obj->back(steps);\n * string param_3 = obj->forward(steps);\n */\n```
| 2 | 0 |
['C++']
| 0 |
design-browser-history
|
Using Doubly Linked Lists || C++
|
using-doubly-linked-lists-c-by-orewa_abh-zo2k
|
Complexity\n- Time complexity:\nO(n) \n- Space complexity:\nO(n) \n# Code\n\nclass BrowserHistory {\n \n struct list{\n string val;\n struct
|
Orewa_Abhi
|
NORMAL
|
2024-02-27T05:00:38.633519+00:00
|
2024-02-27T05:00:38.633555+00:00
| 155 | false |
# Complexity\n- Time complexity:\n$$O(n)$$ \n- Space complexity:\n$$O(n)$$ \n# Code\n```\nclass BrowserHistory {\n \n struct list{\n string val;\n struct list *next, *pre;\n };\n\npublic:\n list *head;\n BrowserHistory(string homepage) {\n head = new(struct list);\n head->val = homepage;\n head->next = NULL;\n head->pre = NULL;\n }\n \n void visit(string url) {\n // add a new node ie visiting a new site\n list *newNode = new (list);\n list *node = head->pre;\n\n newNode->val = url;\n newNode->next = head;\n head->pre = newNode;\n newNode->pre = NULL;\n head = newNode;\n }\n \n string back(int steps) {\n // going to the next node for steps number of times\n while(head->next && steps)\n {\n head = head->next;\n steps--;\n }\n return head->val;\n }\n \n string forward(int steps) {\n // going to the pre node for steps number of times\n while(head->pre and steps)\n {\n head = head->pre;\n steps--;\n }\n return head->val;\n }\n};\n\n/**\n * Your BrowserHistory object will be instantiated and called as such:\n * BrowserHistory* obj = new BrowserHistory(homepage);\n * obj->visit(url);\n * string param_2 = obj->back(steps);\n * string param_3 = obj->forward(steps);\n */\n```
| 2 | 0 |
['C++']
| 0 |
design-browser-history
|
🟩O(1) time beats 92.46% Nice and clear 🟩🟩🟩
|
o1-time-beats-9246-nice-and-clear-by-tek-galk
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\nThis problem simulates the behavior of a web browser history. We need to implement fu
|
teklumt
|
NORMAL
|
2024-01-29T16:34:43.848520+00:00
|
2024-01-29T16:34:43.848555+00:00
| 380 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nThis problem simulates the behavior of a web browser history. We need to implement functionalities to visit a new URL, go back a certain number of steps, and go forward a certain number of steps.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe can maintain a stack to keep track of visited URLs. Whenever we visit a new URL, we push it onto the stack. When we go back, we pop URLs from the stack according to the given steps. Similarly, when we go forward, we move forward in the stack according to the given steps.\n# Complexity\n- Time complexity:O(1)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass BrowserHistory:\n\n def __init__(self, homepage: str):\n self.stack=[homepage]\n self.cur=0\n\n def visit(self, url: str) -> None:\n \n self.stack=self.stack[:self.cur+1]\n self.cur+=1\n self.stack.append(url)\n \n \n\n def back(self, steps: int) -> str:\n \n if steps <= self.cur:\n self.cur-=steps\n else:\n self.cur=0\n \n return self.stack[self.cur]\n\n def forward(self, steps: int) -> str:\n if self.cur + steps < len(self.stack):\n self.cur +=steps\n else:\n self.cur = len(self.stack)-1\n return self.stack[self.cur]\n \n\n\n# Your BrowserHistory object will be instantiated and called as such:\n# obj = BrowserHistory(homepage)\n# obj.visit(url)\n# param_2 = obj.back(steps)\n# param_3 = obj.forward(steps)\n```
| 2 | 0 |
['Python3']
| 1 |
smallest-subarrays-with-maximum-bitwise-or
|
[Java/C++/Python] Bit Solution with Explanation 🔥
|
javacpython-bit-solution-with-explanatio-r6hi
|
Intuition\nAssume the array has only 0 and 1.\nThen the question changes:\nIf A[i] = 1, shortest array is [A[i]], length is 1.\nIf A[i] = 0, we need to find the
|
lee215
|
NORMAL
|
2022-09-17T16:05:45.525253+00:00
|
2022-09-17T16:24:38.979554+00:00
| 9,869 | false |
# **Intuition**\nAssume the array has only 0 and 1.\nThen the question changes:\nIf `A[i] = 1`, shortest array is `[A[i]]`, length is 1.\nIf `A[i] = 0`, we need to find the index `j` of next `1`,\nthen `j - i + 1` is the length of shortest subarray.\nIf no next 1, 1 is the length\n\nTo solve this problem,\nwe can iterate the array reversely\nand keep the index `j` of last time we saw 1.\n`res[i] = max(1, last - i + 1)`\n<br>\n\n# **Explanation**\nFor `0 <= A[i] <= 10^9`,\nwe simply do the above process for each bit.\n`res[i] = max(1, max(last) - i + 1)`\n<br>\n\n# **Complexity**\nTime `O(30n)`\nSpace `O(30)`\n<br>\n\n**Java**\n```java\n public int[] smallestSubarrays(int[] A) {\n int n = A.length, last[] = new int[30], res[] = new int[n];\n for (int i = n - 1; i >= 0; --i) {\n res[i] = 1;\n for (int j = 0; j < 30; ++j) {\n if ((A[i] & (1 << j)) > 0)\n last[j] = i;\n res[i] = Math.max(res[i], last[j] - i + 1);\n }\n }\n return res;\n }\n```\n\n**C++**\n```cpp\n vector<int> smallestSubarrays(vector<int>& A) {\n int last[30] = {}, n = A.size();\n vector<int> res(n, 1);\n for (int i = n - 1; i >= 0; --i) {\n for (int j = 0; j < 30; ++j) {\n if (A[i] & (1 << j))\n last[j] = i;\n res[i] = max(res[i], last[j] - i + 1);\n }\n }\n return res;\n }\n```\n\n**Python**\n```py\n def smallestSubarrays(self, A):\n last = [0] * 32\n n = len(A)\n res = [0] * n\n for i in range(n - 1, -1, -1):\n for j in range(32):\n if A[i] & (1 << j):\n last[j] = i\n res[i] = max(1, max(last) - i + 1)\n return res\n```\n
| 213 | 1 |
['C', 'Python', 'Java']
| 30 |
smallest-subarrays-with-maximum-bitwise-or
|
simple clean C++ code || O(N) solution || Bit-Manipulation
|
simple-clean-c-code-on-solution-bit-mani-2sa3
|
Idea -By looking at how OR works, we can see that bits can only be turned on with 1. So, start from the end and keep track of the minimum index that will keep t
|
bharat_bardiya
|
NORMAL
|
2022-09-17T19:04:16.516277+00:00
|
2022-09-18T20:23:38.387788+00:00
| 3,544 | false |
***Idea*** -*By looking at how OR works, we can see that bits can only be turned on with 1. So, start from the end and keep track of the minimum index that will keep the bit set. Then, take the maximum of all the indexes that contain set bits.*\nfor this purpose, we maintain an Array named nearest of 32 bits which indicate the index of the `nearest` array element which set the particular `jth` bit at that particular instance. then we find the farthest set bit we found so far.\nlet see an example -\n`nums[] = {9,13,55,48,56};`\nbit representation are as follow - \n```\ni j--> 5 4 3 2 1 0\n--------------------\n9 -> 0 0 1 0 0 1\n13 -> 0 0 1 1 0 1\n55 -> 1 1 0 1 1 1\n48 -> 1 1 0 0 0 0\n56 -> 1 1 1 0 0 0\n\nlet see how we get length for first element (for 9) let\'s find it manually.\nat bit position 0 -> what is the nearest element who is set to 1. the answer is 9 itself so nearest[0] = 0 (i position of 9)\nat bit position 1 -> what is the nearest element who is set to 1. the answer is 55(2nd element) nearest[1] = 2 (i position of 55)\nat bit position 2 -> what is the nearest element who is set to 1. the answer is 13(1st element) nearest[2] = 1 (i position of 13)\nat bit position 3 -> what is the nearest element who is set to 1. the answer is 9 itself so nearest[3] = 0 (i position of 9)\nat bit position 4 -> what is the nearest element who is set to 1. the answer is 55(2nd element) nearest[4] = 2 (i position of 55)\nat bit position 5 -> what is the nearest element who is set to 1. the answer is 55(2st element) nearest[5] = 2 (i position of 55)\n\nnearest[] = {0,2,1,0,2,2};\namong them the fathest nearest[j] = 2;\nso if we start OR operation from 0th index then first time we get our maximum value at 2nd index.\nso the smallest subset is nums[0..2] => of size 3;\n\nfor maintaining the nearest array we have to triverse nums from right to left\nand keep updating nearest[j] if current element have a set bit at jth position.\n```\n```\nclass Solution {\npublic:\n vector<int> smallestSubarrays(vector<int>& nums) {\n \n int n = nums.size();\n // for keeping track of last index of every bit till the ith index.\n // total bit in a data type int is 32.\n vector<int>nearest(32,-1);\n vector<int>ans(n);\n \n for(int i = n-1; i>=0; i--){\n for(int j = 0; j<32; j++){\n // 1<<j -> a number with only set bit at jth position.\n // nums[i]&(1<<j) checks whether jth bit is set or not of nums[i];\n \n // if jth bit of nums[i] is set then we update nearest[j] to i;\n if(nums[i]&(1<<j)){\n nearest[j] = i;\n }\n }\n \n // initially set lastSetBit to i because we have to start our set with ith element.\n int lastSetBit = i;\n\t\t\t\n // now we have to find which one is the bit seted most farthest among all 32 bits. we need the index i for this bit.\n for(int j = 0; j<32; j++){\n // we keep updating lastSetBit if we get any greater "i" of set bit.\n lastSetBit = max(nearest[j],lastSetBit);\n }\n // from last set bit only we can get smallest subarray.\n // after this we get same value but our subarray size will increase.\n ans[i] = lastSetBit-i+1;\n }\n \n \n return ans;\n }\n};\n```\nPLEASE UPVOTE IF YOU FOUND IT HELPFUL\uD83D\uDE22\uD83D\uDE36\u200D\uD83C\uDF2B\uFE0F\uD83D\uDE36\u200D\uD83C\uDF2B\uFE0F
| 72 | 0 |
['Bit Manipulation', 'C', 'C++']
| 8 |
smallest-subarrays-with-maximum-bitwise-or
|
Closest Position of Each Bit
|
closest-position-of-each-bit-by-votrubac-0pes
|
My first idea was to count occurrences each bit, and use this information for a sliding window. \n\nThe implementation was tricky, so I decided to just use a se
|
votrubac
|
NORMAL
|
2022-09-17T23:21:43.715747+00:00
|
2022-09-21T15:39:16.208541+00:00
| 2,343 | false |
My first idea was to count occurrences each bit, and use this information for a sliding window. \n\nThe implementation was tricky, so I decided to just use a segment tree for range bitwise OR queries (second solution below).\n\n> Even though the second solution is O(n log n), its runtime is a bit better. With `n` limited to `100,000`, `log2 n` is `~17`, So, it needs `17 * 100,000` operations, while the first solution takes `30 * 100,000` (30 bits to check for each number).\n\nLater, I realized that we do not need to count each bit if we process numbers right-to-left. We just need to track the closest position of each bit\n\n#### Closest Position of Each Bit\nWe go right-to-left, and use `closest` array to track the closest (or smallest) position of each bit.\n\nWe can then use the maximum position among all bits to find out the shortest subarrays with all bits set.\n\nHere is an example for `[4, 2, 1, 5, 3, 1, 2, 1]` case:\n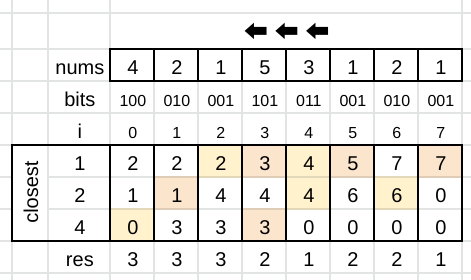\n\n**C++**\n```cpp\nvector<int> smallestSubarrays(vector<int>& nums) {\n vector<int> res(nums.size()), closest(30);\n for (int i = nums.size() - 1; i >= 0; --i) {\n for (int b = 0; b < 30; ++b)\n if (nums[i] & (1 << b))\n closest[b] = i;\n res[i] = max(1, *max_element(begin(closest), end(closest)) - i + 1);\n }\n return res;\n} \n```\n#### Segment Tree\nWe can use a segment tree to query bitwise XOR of any interval in O(log n).\n\n**C++**\n```cpp\nint st[2 * (1 << 17)] = {}; // 2 ^ 16 < 100000 < 2 ^ 17\nclass Solution {\npublic:\nint bit_or(int l, int r, int tl, int tr, int p = 1) {\n if (l > r) \n return 0;\n if (l == tl && r == tr)\n return st[p];\n int tm = (tl + tr) / 2;\n return bit_or(l, min(r, tm), tl, tm, p * 2) | bit_or(max(l, tm + 1), r, tm + 1, tr, p * 2 + 1);\n} \nint build(vector<int>& nums, int tl, int tr, int p = 1) {\n if (tl == tr)\n return st[p] = nums[tl];\n int tm = (tl + tr) / 2;\n return st[p] = build(nums, tl, tm, p * 2) | build(nums, tm + 1, tr, p * 2 + 1);\n} \nvector<int> smallestSubarrays(vector<int>& nums) {\n vector<int> res;\n build(nums, 0, nums.size() - 1);\n for (int i = 0, j = 0; i < nums.size(); j = max(++i, j)) {\n while (bit_or(i, j, 0, nums.size() - 1) < bit_or(i, nums.size() - 1, 0, nums.size() - 1))\n ++j;\n res.push_back(j - i + 1);\n } \n return res;\n}\n};\n```
| 28 | 1 |
[]
| 10 |
smallest-subarrays-with-maximum-bitwise-or
|
Java | O(n*31) time | Slide Backwards | In-depth Easy Explanation with Example
|
java-on31-time-slide-backwards-in-depth-5clfo
|
Let\'s take the example of nums = [6,2,1,3,0]\nIn binary notation, we have:\nindex - value - binary notation\n0 - 6 - 110\n1 - 2 - 010\n2 - 1 - 001\n3 - 3 - 011
|
yoshi_toad
|
NORMAL
|
2022-09-17T17:30:22.207539+00:00
|
2022-09-17T17:40:15.447417+00:00
| 1,100 | false |
Let\'s take the example of nums = [6,2,1,3,0]\nIn binary notation, we have:\nindex - value - binary notation\n0 - 6 - 110\n1 - 2 - 010\n2 - 1 - 001\n3 - 3 - 011\n4 - 0 - 000\n\nWe can get the maximum bitwise or value for each index by looping from end to start:\n0 - 7 (111) = 0 | 3 | 1 | 2 | 6\n1 - 3 (011) = 0 | 3 | 1 | 2\n2 - 3 (011) = 0 | 3 | 1\n3 - 3 (011) = 0 | 3 \n0 - 0 (000) = 0\n\nAn initial idea is to, for each index, loop from the index to the end of the array to find the minimum length yielding the value, but that is O(n^2) time, which is the brute-force approach. We want something better.\n\nAnother way of looking at the problem is to look at how the bits get set when iterating from a specific index ```i``` to ```n-1``` (where ```n == nums.length```). Looking at nums:\nFor index 0 (110), it has to reach index 2 (001) in order to get the rightmost bit set.\n=> smallest subarray for index 0 is length 2 - 0 + 1 = 3\n\nFor index 1 (010), it has to reach index 2 (001) in order to get the rightmost bit set.\n=> smallest subarray for index 1 is length 2 - 1 + 1 = 2\n\nFor index 2 (001), it has to reach index 3 (010) in order to get the 2nd rightmost bit set.\n=> smallest subarray for index 1 is length 3 - 2 + 1 = 2\n\nFor index 3 (011), it has to reach index 3 (011) in order to both the 1st and 2nd rightmost bit set.\n=> smallest subarray for index 1 is length 3 - 3 + 1 = 1\n\nFor index 4 (000), it has no indices to reach.\n=> smallest subarray for index 1 is length 3 - 3 + 1 = 1\n\nWe can then tabulate these "furthest indices" by iterating from ```n-1``` to ```0``` and by using array ```store``` to track them. ```store``` has size 31 since each array element represents a binary digit. We update store at index ```j``` on the iteration for index ```i``` when the jth rightmost binary digit of ```nums[i]``` is set (We\'ll just show the first three elements of ```store``` here for simplicity):\ni - nums[i] - store[0] store[1] store[2]\ni = 4 (nums[4] = 000): -1 -1 -1\ni = 3 (nums[3] = 011): 3 3 -1\ni = 2 (nums[2] = 001): 2 3 -1\ni = 1 (nums[1] = 010): 2 1 -1\ni = 0 (nums[0] = 110): 2 0 0\n\nAt iteration ```i```, max(store[0], ..., store[30]) then yields the furthest index we need to reach in order to get the max value.\nmax(store[0], ..., store[30]) - i + 1 then yields the minimum length needed.\nAn exception to this is when ```store[0] == ... == store[30] == -1```, then we set the minimum length to 1, since this only happens when the array is full of zeros from index ```i``` onwards.\nFor the example:\ni = 4: -1 (-1 means no bits have been set, we don\'t need nums[j] with j > i to set bits => min length = 1)\ni = 3: 3 (=> min length = 3 - 3 + 1 = 1)\ni = 2: 3 (=> min length = 3 - 2 + 1 = 2)\ni = 1: 2 (=> min length = 2 - 1 + 1 = 2)\ni = 0: 2 (=> min length = 2 - 0 + 1 = 3)\n\nFinally we put all of the above into some Java code:\n```\nclass Solution {\n public int[] smallestSubarrays(int[] nums) {\n int n = nums.length;\n int[] ans = new int[n];\n \n int[] store = new int[31];\n Arrays.fill(store, -1);\n for(int i = n-1; i >= 0; --i){\n int temp = nums[i];\n for(int j = 0; j < 31; ++j){\n if((temp & 1) == 1){\n store[j] = i;\n }\n temp >>= 1;\n }\n \n int maxVal = Integer.MIN_VALUE;\n for(int val: store){\n maxVal = Math.max(maxVal, val);\n }\n if(maxVal == -1){\n ans[i] = 1;\n }else{\n ans[i] = maxVal - i + 1; \n }\n }\n return ans;\n }\n}\n```
| 13 | 1 |
['Bit Manipulation', 'Sliding Window', 'Java']
| 2 |
smallest-subarrays-with-maximum-bitwise-or
|
python3 || 8 lines, bits || T/S: 53% / 38%
|
python3-8-lines-bits-ts-53-38-by-spauldi-9ovl
|
\nclass Solution:\n def smallestSubarrays(self, nums: List[int]) -> List[int]: \n\n n, ans, bits = len(nums), deque(), defaultdict(int)\n\n
|
Spaulding_
|
NORMAL
|
2022-11-30T01:16:03.665304+00:00
|
2024-06-14T19:30:01.273812+00:00
| 394 | false |
```\nclass Solution:\n def smallestSubarrays(self, nums: List[int]) -> List[int]: \n\n n, ans, bits = len(nums), deque(), defaultdict(int)\n\n for i in range(n-1, -1, -1:\n I = i\n\n for b in range(31):\n\n if nums[i] & (1 << b): bits[b] = i\n elif b in bits and I < bits[b]: I = bits[b] \n\n ans.appendleft(I+1-i)\n\n return ans\n```\t\n[https://leetcode.com/problems/smallest-subarrays-with-maximum-bitwise-or/submissions/1288445441/](https://leetcode.com/problems/smallest-subarrays-with-maximum-bitwise-or/submissions/1288445441/)\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(1), in which *N* ~ `len(nums)`. (We assume that *bit-count* <= 32)
| 9 | 0 |
['Python']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
[Python 3] [Binary Search] Solution with Intuition and Steps
|
python-3-binary-search-solution-with-int-vkw6
|
\n### Intuitition:\nWhile applying bitwise OR on an array from the beginning to the end, once a bit is set to 1, it will not be set back to 0 anymore, as 1|?=1.
|
leet_go
|
NORMAL
|
2022-09-17T16:03:24.077830+00:00
|
2022-09-17T16:05:31.106615+00:00
| 824 | false |
\n### Intuitition:\nWhile applying bitwise OR on an array from the beginning to the end, once a bit is set to 1, it will not be set back to 0 anymore, as `1|?=1`. \n\nTo find the smallest length array with maximum bitwise OR sum. we only need to find the first occurrence of the number since each index in the array with bit = 1 for each bit \n\n### Detailed Steps:\n- Limit in the problem indicates that each number n <= 10^9 which menas that n < 2^30 and there are at most 30 bits for numbers in the array.\n- For each bit, create a list to record the index of numbers in the array which has this bit equals to 1 `(n >> bit) % 2 == 1`. For example, for [0, 1, 3, 2], the index array for bit 0 is [0, 2] and the index array for bit 1 is [2.3]. This step has `Complexity = O(n * k)` where k = 30 in this problem.\n- For each index i in the number list, for each bit, find the first occurrence index of a number with this bit equals to 1. Put these occurrence index in the list IND. The smallest length array for index i is `max(IND) - i + 1`. For example,` for [1, 0, 3, 2], i = 1`, when i = 0, IND = [0, 2] and the result array should have `length = 2 - 0 + 1 = 3`, which is [1, 0, 3]. This step has` Complexity = O(nlogn * k)`\n\n\n### Solution:\n```\nclass Solution:\n def smallestSubarrays(self, nums: List[int]) -> List[int]:\n maximum_bits = int(log(10**9, 2)) + 1\n index_for_each_bit = [[] for _ in range(maximum_bits)]\n # Create lists to record the index of numbers in the array with each bit = 1\n for i in range(len(nums)):\n n = nums[i]\n for bit in range(maximum_bits):\n if n % 2 == 1:\n index_for_each_bit[bit].append(i)\n n >>= 1\n\n res = []\n for i in range(len(nums)):\n cur_idx = [i]\n n = nums[i]\n # Find the first occurrence index of the number with each bit equals to 1\n for bit in range(maximum_bits):\n bit_index = index_for_each_bit[bit]\n if n % 2 == 0:\n k = bisect_left(bit_index, i)\n if k < len(bit_index):\n cur_idx.append(bit_index[k])\n n >>= 1\n res.append(max(cur_idx) - i + 1)\n return res\n```
| 6 | 1 |
['Binary Tree']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
Simple Observation
|
simple-observation-by-godfather_010-gbrn
|
\nclass Solution {\npublic:\n vector<int> smallestSubarrays(vector<int>& nums) {\n int n = nums.size();\n vector<int> bit(32, -1);\n vec
|
godfather_010
|
NORMAL
|
2022-09-17T16:02:03.853861+00:00
|
2022-09-17T16:02:03.853901+00:00
| 1,594 | false |
```\nclass Solution {\npublic:\n vector<int> smallestSubarrays(vector<int>& nums) {\n int n = nums.size();\n vector<int> bit(32, -1);\n vector<int> dp(n, 0);\n dp[n-1] = nums[n-1];\n for(int i = n-2; i>=0; i--)\n {\n dp[i] = (dp[i+1]|nums[i]);\n }\n vector<int> ans;\n for(int i = n-1; i>=0; i--)\n {\n for(int b = 0; b <31; b++)\n {\n if((nums[i]&(1<<b)))\n {\n bit[b] = i;\n }\n }\n int maxi = i;\n for(int b = 0; b < 31; b++)\n {\n if((dp[i]&(1<<b)))\n maxi = max(maxi, bit[b]);\n }\n ans.push_back(maxi - i + 1);\n }\n reverse(ans.begin(), ans.end());\n return ans;\n }\n};\n```
| 6 | 0 |
[]
| 1 |
smallest-subarrays-with-maximum-bitwise-or
|
[C++] || Sliding Window || 100% faster
|
c-sliding-window-100-faster-by-4byx-gi05
|
Same as Last Contests\nhttps://leetcode.com/problems/longest-nice-subarray/discuss/2527311/c-sliding-window-bit\n\nCODE\n\nclass Solution {\npublic:\n\tbool che
|
4byx
|
NORMAL
|
2022-09-17T16:02:02.117613+00:00
|
2022-09-17T16:05:27.939282+00:00
| 3,417 | false |
**Same as Last Contests**\nhttps://leetcode.com/problems/longest-nice-subarray/discuss/2527311/c-sliding-window-bit\n\n**CODE**\n```\nclass Solution {\npublic:\n\tbool check(vector<int> &maxiv , int len , vector<int> &vis) {\n\t\tfor (int i = 0 ; i <= len ; i++) {\n\t\t\tif (maxiv[i] != 0 and vis[i] == 0) return false;\n\t\t}\n\t\treturn true;\n\t}\n\n\tvoid add(int a , int len , vector<int> &vis) {\n\t\tfor (int i = 0 ; i <= len ; i++) {\n\t\t\tif (((a >> i) & 1) == 1) vis[i]++;\n\t\t}\n\t}\n\tvoid addmaxi(int a , int len , vector<int> &maxiv) {\n\t\tfor (int i = 0 ; i <= len ; i++) {\n\t\t\tif (((a >> i) & 1) == 1) maxiv[i]++;\n\t\t}\n\t}\n\n\tvoid clear(int a , int len , vector<int> &vis) {\n\t\tfor (int i = 0 ; i <= len ; i++) {\n\t\t\tif (((a >> i) & 1) == 1) vis[i]--;\n\t\t}\n\t}\n\tvoid clearfrom(int a , int len , vector<int> &maxiv) {\n\t\tfor (int i = 0 ; i <= len ; i++) {\n\t\t\tif (((a >> i) & 1) == 1) maxiv[i]--;\n\t\t}\n\t}\n\n\tbool empty(vector<int> &maxiv , int len) {\n\t\tfor (int i = 0 ; i <= len ; i++) {\n\t\t\tif (maxiv[i] != 0) return false;\n\t\t}\n\t\treturn true;\n\t}\n\n\tvector<int> smallestSubarrays(vector<int>& nums) {\n \n // calc maximum bits in nums\n int maxi = 0;\n for(auto x : nums) maxi = maxi|x;\n\n\t\tint n = nums.size() , i =0 , j= 0 , len;\n\t\tif (maxi != 0) len = log2(maxi);\n\t\telse len = 0;\n\n\n\n\t\tvector<int> maxiv(len + 1, 0);\n\t\tfor (auto x : nums) {\n\t\t\taddmaxi(x, len, maxiv);\n\t\t}\n\n\n\t\t// checking visited bits\n\t\tvector<int> vis(len + 1, 0);\n\n\n\t\t//returning ans\n\t\tvector<int> ans(n, 0);\n\n\t\twhile (i < n and j < n) {\n\n\t\t\t// maxiv is empty then all elements after is 0\n\t\t\tif (empty(maxiv, len)) j++;\n\n\n\t\t\t// checking for window\n\t\t\twhile (!check(maxiv, len, vis) and j < n) {\n\t\t\t\tadd(nums[j], len, vis);\n\t\t\t\tj++;\n\t\t\t}\n\n\n\n\t\t\tif (j < n and check(maxiv, len, vis)) {\n\t\t\t\tans[i] = j - i;\n\t\t\t\tclear(nums[i], len, vis);\n\t\t\t\tclearfrom(nums[i], len, maxiv);\n\t\t\t\ti++;\n\t\t\t}\n\n\t\t}\n\n\n\t\t// remaining last elements which ended at n\n\t\twhile (i < j) {\n\t\t\tans[i] = j - i;\n\t\t\tclear(nums[i], len, vis);\n\t\t\ti++;\n\t\t}\n\n\t\treturn ans;\n\t}\n};\n\n```
| 6 | 0 |
['C']
| 1 |
smallest-subarrays-with-maximum-bitwise-or
|
C++ || bit wise index, transform from back || fast (100%, 116ms)
|
c-bit-wise-index-transform-from-back-fas-6hg1
|
Solution 1: index per bit, transform from the back\n\nFor each bit we keep track of the "nearst" index at which it is set and if we scan from the back we can re
|
heder
|
NORMAL
|
2022-09-18T19:49:46.693946+00:00
|
2022-09-18T19:49:46.693986+00:00
| 608 | false |
### Solution 1: index per bit, transform from the back\n\nFor each bit we keep track of the "nearst" index at which it is set and if we scan from the back we can rewrite ```nums``` as we go.\n\n```\n static vector<int> smallestSubarrays(vector<int>& nums) {\n array<int, 30> idx = {};\n for (int i = size(nums) - 1; i >= 0; --i) {\n const int num = nums[i];\n for (int j = 0; j < size(idx); ++j) {\n if (num & (1 << j)) {\n idx[j] = i;\n }\n }\n const int mx = *max_element(begin(idx), end(idx));\n nums[i] = max(mx, i) - i + 1;\n }\n return nums;\n }\n```\n\n_As always: Feedback, comments, and questions are welcome. Please upvote if you like the post._
| 5 | 0 |
[]
| 1 |
smallest-subarrays-with-maximum-bitwise-or
|
c++ solution using fenwink tree
|
c-solution-using-fenwink-tree-by-dilipsu-b73v
|
\nclass Solution {\npublic:\n int N=1e5+10;\n int bit[100005];\n void update(int i,int val)\n {\n i++;\n while(i<N)\n {\n
|
dilipsuthar17
|
NORMAL
|
2022-09-17T17:26:48.823181+00:00
|
2022-09-17T17:26:48.823224+00:00
| 371 | false |
```\nclass Solution {\npublic:\n int N=1e5+10;\n int bit[100005];\n void update(int i,int val)\n {\n i++;\n while(i<N)\n {\n bit[i]|=val;\n i+=(i&-i);\n }\n }\n int find(int i)\n {\n i++;\n int sum=0;\n while(i>0)\n {\n sum|=bit[i];\n i-=(i&-i);\n }\n return sum;\n }\n vector<int> smallestSubarrays(vector<int>& nums) \n {\n int n=nums.size();\n vector<int>ans(n,0);\n int total=0;\n for(int i=n-1;i>=0;i--)\n {\n total|=nums[i];\n update(i,nums[i]);\n int l=i;\n int r=n-1;\n int index=n-1;\n while(l<=r)\n {\n int mid=(l+r)/2;\n if(find(mid)==total)\n {\n index=mid;\n r=mid-1;\n }\n else\n {\n l=mid+1;\n }\n }\n ans[i]=(index-i+1);\n }\n return ans;\n }\n};\n```
| 4 | 0 |
['C', 'C++']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
JavaScript
|
javascript-by-blankzzz-y41f
|
\nvar smallestSubarrays = function (nums) {\n const n = nums.length;\n\n const res = Array(n).fill(0);\n\n const last = Array(32).fill(0);\n\n for (let i =
|
blankzzz
|
NORMAL
|
2022-09-17T16:21:17.309258+00:00
|
2022-09-17T16:41:53.961176+00:00
| 128 | false |
```\nvar smallestSubarrays = function (nums) {\n const n = nums.length;\n\n const res = Array(n).fill(0);\n\n const last = Array(32).fill(0);\n\n for (let i = n - 1; i >= 0; i--) {\n res[i] = 1;\n\n for (let j = 0; j < 32; j++) {\n if (nums[i] & (1 << j)) {\n last[j] = i;\n }\n res[i] = Math.max(res[i], last[j] - i + 1);\n }\n }\n\n return res;\n}\n```
| 4 | 0 |
['JavaScript']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
C++ | Binary Search + Segtree
|
c-binary-search-segtree-by-lukewu28-8q7a
|
First, precompute the maximum for each subarray starting at i.\nThen, initialize an OR segtree.\nFinally, for each i, binary search for the length and verify mi
|
lukewu28
|
NORMAL
|
2022-09-17T16:04:18.660689+00:00
|
2022-09-17T16:04:18.660739+00:00
| 856 | false |
First, precompute the maximum for each subarray starting at `i`.\nThen, initialize an OR segtree.\nFinally, for each `i`, binary search for the length and verify `mid` using the segtree.\n```\ntemplate<class T>\nclass stt{\n\tpublic:\n\tvector<T> t;\n\tint n;\n\tstt(int _n, vector<int>& a){\n\t\tn = _n;\n\t\tt = vector<T>(2*n, 0);\n\t\tfor(int i=0;i< n;i++) t[n+i] = a[i];\n\t\tfor (int i = n - 1; i > 0; --i) t[i] = t[i<<1] | t[i<<1|1];\n\t}\n\tT query(int l, int r){\n\t\tT res = 0;\n\t\tfor(l+=n, r+=n; l < r; l>>=1, r>>=1){\n\t\t\tif(l&1) res |= t[l++];\n\t\t\tif(r&1) res |= t[--r];\n\t\t}\n\t\treturn res;\n\t}\n};\n\nclass Solution {\npublic:\n vector<int> smallestSubarrays(vector<int>& nums) {\n int n = nums.size();\n int ma[n];\n int cur = 0;\n for (int i = n-1; i >= 0; i--){cur |= nums[i]; ma[i] = cur;}\n \n vector<int> re(n);\n stt<int> st(n, nums);\n for(int i = 0; i < n; i ++){\n int l = 1, r = n-i;\n while(l<r){\n int mid = (l+r)/2;\n int cure = st.query(i, i+mid);\n if(cure == ma[i]) r = mid;\n else l = mid+1;\n }\n re[i] = l;\n } \n return re;\n \n }\n};\n```
| 4 | 0 |
['Binary Search', 'Tree', 'C']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
Simple Map and Set that's it
|
simple-map-and-set-thats-it-by-bahubaii-t99w
|
\n// well idea to keep track of all the index array where \n// jth bit( where j is from 0 to 30) is set\n// now while traversing through the array\n// just che
|
BahubaIi
|
NORMAL
|
2022-09-17T16:03:52.677893+00:00
|
2022-09-17T17:14:13.293131+00:00
| 780 | false |
```\n// well idea to keep track of all the index array where \n// jth bit( where j is from 0 to 30) is set\n// now while traversing through the array\n// just check if jth bit is 0 if yes then find the next\n// closest index where jth bit is 1\n// similary check from all jth bits(0-30)\n// and out of all furthest is our answer\n// if jth bit is already 1 then we don\'t need to do anything\n\n vector<int> smallestSubarrays(vector<int>& nums) \n {\n vector<int>bits(32,0);\n int n = nums.size();\n vector<int>ans;\n map<int,int> mp;\n map<int,set<int>> mset;\n for(int i=0;i<n;i++)\n {\n for(int j=0;j<31;j++)\n {\n if(nums[i]&((int)pow(2,j)))\n {\n mp[j]++;\n mset[j].insert(i);\n }\n }\n }\n \n \n for(int i=0;i<n;i++)\n {\n int idx =i;\n for(int j=30;j>=0;j--)\n {\n if(mp.find(j)!=mp.end() && (nums[i]&((int)pow(2,j)))==0)\n idx = max(idx,*(mset[j].begin()));\n \n else if(nums[i]&((int)pow(2,j)))\n mset[j].erase(i);\n \n }\n ans.push_back(idx-i+1);\n }\n \n return ans;\n }\n```
| 4 | 0 |
['Ordered Set']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
C++ | Suffix array for bits for storing Bits position | Accepted
|
c-suffix-array-for-bits-for-storing-bits-grl9
|
class Solution {\npublic:\n vector smallestSubarrays(vector& nums) {\n \n \n vector temp = nums;\n int n=nums.size();\n \n
|
rajatk133
|
NORMAL
|
2022-09-17T16:01:12.036005+00:00
|
2022-09-17T16:05:11.330392+00:00
| 798 | false |
class Solution {\npublic:\n vector<int> smallestSubarrays(vector<int>& nums) {\n \n \n vector<int> temp = nums;\n int n=nums.size();\n \n \n vector<int> ans(n,-1);\n vector<vector<int>> bits(32,vector<int>(n,n));\n \n \n for(int i=0;i<32;i++)\n {\n \n for(int j=n-1;j>=0;j--){\n \n if(((nums[j] >> i)&1) == 1){\n bits[i][j] = j;\n }else{\n if(j!=(n-1))bits[i][j] = bits[i][j+1];\n }\n }\n \n }\n \n \n for(int j=0;j<n-1;j++)\n {\n int len=INT_MIN;\n for(int i=0;i<32;i++)\n {\n if(bits[i][j+1]!=n){\n len=max(len,bits[i][j]);\n }\n }\n \n if(len!=INT_MIN){\n ans[j]=len-j+1;\n }else{\n ans[j]=1;\n }\n }\n ans[n-1]=1;\n \n \n return ans;\n \n }\n};
| 4 | 0 |
['Suffix Array']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
C++ | Binary search | with comments
|
c-binary-search-with-comments-by-aman282-9ovv
|
\n\nclass Solution {\npublic:\n vector<int> smallestSubarrays(vector<int>& nums) {\n int sz=nums.size();\n vector<vector<int>>arr(31);\n
|
aman282571
|
NORMAL
|
2022-09-17T16:00:41.810122+00:00
|
2022-09-17T16:06:36.816179+00:00
| 967 | false |
```\n\nclass Solution {\npublic:\n vector<int> smallestSubarrays(vector<int>& nums) {\n int sz=nums.size();\n vector<vector<int>>arr(31);\n int j=0;\n // arr[i] will store the indices of values in which ith bit is on\n for(auto & ele:nums){\n for(int i=0;i<31;i++){\n if((ele>>i)&1)\n arr[i].push_back(j);\n }\n j++;\n }\n // suf[i] will store maximum or starting at this index\n vector<int>suf=nums;\n for(int i=sz-2;i>=0;i--)\n suf[i]=nums[i]|suf[i+1];\n vector<int>ans(sz,0);\n for(int i=0;i<sz;i++){\n // assume max OR value starting at this index is "x", then we will check if "kth" bit is on or off,\n // if its on then we want to find the minimum greater index which can set its bit on,we are doing this using binary search.\n int res=1;\n for(int k=0;k<31;k++){\n if((suf[i]>>k)&1){\n auto it=lower_bound(begin(arr[k]),end(arr[k]),i);\n int len=(*it)-i+1;\n res=max(res,len);\n }\n }\n ans[i]=res;\n }\n return ans;\n }\n};\n```\nDo **UPVOTE** is it helps:)\n
| 4 | 0 |
['C']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
C++ || SIMPLE || EASY TO UNDERSTAND
|
c-simple-easy-to-understand-by-ganeshkum-sdf9
|
Code\n\nclass Solution {\npublic:\n bool check(vector<int> &v1,int &x){\n for(int i = 0; i <=31; i++){\n if(!v1[i] && (x&(1<<i))){\n
|
ganeshkumawat8740
|
NORMAL
|
2023-05-22T04:58:26.880215+00:00
|
2023-05-22T04:58:26.880258+00:00
| 1,243 | false |
# Code\n```\nclass Solution {\npublic:\n bool check(vector<int> &v1,int &x){\n for(int i = 0; i <=31; i++){\n if(!v1[i] && (x&(1<<i))){\n return true;\n }\n }\n return false;\n }\n vector<int> smallestSubarrays(vector<int>& nums) {\n int n = nums.size();\n if(n==1)return {1};\n vector<int> v1(32,0);\n int i = 0, j = 0,k;\n vector<int> ans;\n vector<int> v2(n);\n v2[n-1] = nums[n-1];\n for(i = n-2; i >= 0; i--){\n v2[i] = (nums[i]|v2[i+1]);\n }\n // for(auto &i: v2)cout<<i<<" ";\n i = 0, j = 0;\n while(i<n){\n if(v2[i]==0){\n ans.push_back(1);\n i++;\n j++;\n continue;\n }\n while(j<n && check(v1,v2[i])){\n for(k = 0; k <= 31; k++){\n if(nums[j]&(1<<k)){\n v1[k]++;\n }\n }\n j++;\n }\n ans.push_back(j-i);\n for(k = 0; k <= 31; k++){\n if(nums[i]&(1<<k)){\n v1[k]--;\n }\n }\n i++;\n }\n return ans;\n }\n};\n```
| 3 | 0 |
['Array', 'Two Pointers', 'Bit Manipulation', 'Sliding Window', 'C++']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
Easy Bit Solution
|
easy-bit-solution-by-travanj05-kx23
|
cpp\nclass Solution {\npublic:\n vector<int> smallestSubarrays(vector<int> &nums) {\n int n = nums.size();\n vector<int> res, bit(32, -1);\n
|
travanj05
|
NORMAL
|
2022-09-17T17:05:19.390881+00:00
|
2022-09-17T17:05:19.390918+00:00
| 208 | false |
```cpp\nclass Solution {\npublic:\n vector<int> smallestSubarrays(vector<int> &nums) {\n int n = nums.size();\n vector<int> res, bit(32, -1);\n for (int i = n - 1; i >= 0; i--) {\n int idx = i;\n for (int j = 0; j < 32; j++) {\n if (nums[i] & (1 << j)) bit[j] = i;\n idx = max(idx, bit[j]);\n }\n res.push_back(idx - i + 1);\n }\n reverse(res.begin(), res.end());\n return res;\n }\n};\n```
| 3 | 0 |
['Bit Manipulation', 'C', 'C++']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
Tracking first occurrence of each set bit
|
tracking-first-occurrence-of-each-set-bi-ti8m
|
\nclass Solution {\npublic:\n vector<int> smallestSubarrays(vector<int>& nums) {\n vector<set<int>> bits_occurances(32);\n for(int i=0;i<32;i++
|
lambodara
|
NORMAL
|
2022-09-17T16:24:46.778818+00:00
|
2022-09-17T16:24:46.778862+00:00
| 123 | false |
```\nclass Solution {\npublic:\n vector<int> smallestSubarrays(vector<int>& nums) {\n vector<set<int>> bits_occurances(32);\n for(int i=0;i<32;i++){\n for(int j=0;j<nums.size();j++){\n if(nums[j] & (1<<i)) bits_occurances[i].insert(j);\n }\n }\n int n=nums.size();\n vector<int> ans(n,1);\n for(int i=0;i<n;i++){\n for(int j=0;j<32;j++){\n if(bits_occurances[j].size()>0){\n auto it=bits_occurances[j].begin();\n ans[i]= max(ans[i],(*it) - i +1);\n if(*it==i) bits_occurances[j].erase(it);\n }\n }\n }\n return ans;\n }\n};\n```
| 3 | 0 |
['Bit Manipulation', 'Ordered Set']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
🔥VERY SIMPLE LOGIC using only vector🔥🔥. Beginner friendly and easy to understand.
|
very-simple-logic-using-only-vector-begi-b1rn
|
\n\n# Approach\nFind the closest distance of the bit we are checking if it is set in subsequent positions using lower bound.\nWe take the max of all such distan
|
Saksham_Gulati
|
NORMAL
|
2024-06-19T10:13:30.420268+00:00
|
2024-06-19T10:13:30.420290+00:00
| 95 | false |
\n\n# Approach\nFind the closest distance of the bit we are checking if it is set in subsequent positions using lower bound.\nWe take the max of all such distances for that index in nums.\n\n# Complexity\n- Time complexity:\n $$O(n*32*logn)$$ \n\n- Space complexity:\n $$O(n*32)$$ \n\n# Code\n```\nclass Solution {\npublic:\n vector<int> smallestSubarrays(vector<int>& nums) {\n vector<vector<int>>v(32);\n int n=nums.size();\n for(int i=0;i<32;i++)\n {\n for(int j=0;j<n;j++)\n {\n if(nums[j]&(1ll<<i))v[i].push_back(j);\n }\n }\n vector<int>ans;\n for(int i=0;i<n;i++)\n {\n int mn=1;\n for(int j=0;j<32;j++)\n {\n if(!v[j].size())continue;\n int in=lower_bound(v[j].begin(),v[j].end(),i)-v[j].begin();\n if(in==v[j].size())continue;\n mn=max(mn,v[j][in]-i+1);\n }\n ans.push_back(mn);\n }\n return ans;\n }\n};\n```
| 2 | 0 |
['C++']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
C++ || O(n*32) || Bits Manipulation ||
|
c-on32-bits-manipulation-by-lovelesh26-7xwo
|
C++ Code:\n\n\n bool check(int &i,int &j,vector<vector<int>>&arr){\n for(int k=0;k<32;k++){\n if(arr[i][k]!=0 && arr[i][k]<=arr[j][k]){\n
|
Lovelesh26
|
NORMAL
|
2022-09-21T05:52:05.906419+00:00
|
2022-09-21T05:52:05.906457+00:00
| 367 | false |
**C++ Code:**\n\n```\n bool check(int &i,int &j,vector<vector<int>>&arr){\n for(int k=0;k<32;k++){\n if(arr[i][k]!=0 && arr[i][k]<=arr[j][k]){\n return false;\n }\n }\n return true; \n }\n vector<int> smallestSubarrays(vector<int>& nums) {\n int n = nums.size();\n vector<vector<int>>arr(n,vector<int>(32,0));\n \n // decimal to binary conversion \n for(int i=0;i<n;i++){\n int a = nums[i];\n int j = 31;\n while(a>0){\n if(a%2!=0) arr[i][j] = 1;\n j--;\n a = a/2;\n }\n }\n \n // calculating prefix sum\n for(int i=n-2;i>=0;i--){\n for(int j=0;j<32;j++){\n arr[i][j] += arr[i+1][j];\n }\n } \n \n vector<int>ans(n);\n ans[n-1]=1;\n int j=n-1;\n for(int i=n-2;i>=0;i--){\n while(i<j && check(i,j,arr)){\n j--;\n }\n cout<<j<<" ";\n ans[i] = j-i+1;\n }\n return ans; \n }\n```
| 2 | 0 |
['Bit Manipulation', 'C']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
Java Simple !!
|
java-simple-by-patelsajal2-1qp7
|
Step 1--> Firstly we have to check how many bits are set , it can be 1 ,2 ,3 or more .\nwe all know the table of bitwise OR\n0 0--> 0\n1 1-->1\n1 0-->1\n1 1
|
patelsajal2
|
NORMAL
|
2022-09-18T11:54:29.542156+00:00
|
2022-09-18T11:54:29.542202+00:00
| 243 | false |
Step 1--> Firstly we have to check how many bits are set , it can be 1 ,2 ,3 or more .\nwe all know the table of bitwise OR\n0 0--> 0\n1 1-->1\n1 0-->1\n1 1-->1\nFrom here we can easily conclude that by adding more and more elements the value will remain equal or can be increase \nTake an Example -> [1,0,2,1,3]\ncorresponding binary -->\n[01, 0, 10, 01, 11]\n0 1 2 3 4 index \nNow , execution of step 1\nno of bits | index\n1 -> | 0,3,4\n2 -> | 2,4\n3 ->\n4 ->\n5 ->\nHere we have to get the max from 0 ,2 here we get 2 so its the no. of bits are set we dont have to go further.\nWe can use TreeSet or PriorityQueue that will ultimately gives the maximum and then simply traverse the DS and get the maximum bit wise XOR of the smallest subarray .\n```\nclass Solution {\n\n public int[] smallestSubarrays(int[] nums) {\n TreeSet<Integer>[] sys = new TreeSet[32];\n for (int i = 0; i < 32; i++) sys[i] = new TreeSet<>();\n for (int i = 0; i < nums.length; i++) {\n for (int j = 0; j < 32; j++) {\n if ((nums[i] >> j & 1) == 1) sys[j].add(i);\n }\n }\n int ans[] = new int[nums.length];\n for (int i = 0; i < nums.length; i++) {\n int max = i;\n for (TreeSet<Integer> set : sys) {\n if (!set.isEmpty()) {\n max = Math.max(max, set.first());\n set.remove(i);\n }\n }\n ans[i] = (max - i + 1);\n }\n return ans;\n }\n}\n```\n
| 2 | 0 |
['Bit Manipulation', 'Java']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
Super Weird!!!!!!!!!
|
super-weird-by-lil_toeturtle-n7fz
|
\nclass Solution {\n public int[] smallestSubarrays(int[] nums) {\n int max[]=new int[33],i,j=-1,arr[]=new int[33],n=nums.length,x=0, res[]= new int[n
|
Lil_ToeTurtle
|
NORMAL
|
2022-09-17T16:20:26.267455+00:00
|
2022-09-17T16:20:26.267499+00:00
| 564 | false |
```\nclass Solution {\n public int[] smallestSubarrays(int[] nums) {\n int max[]=new int[33],i,j=-1,arr[]=new int[33],n=nums.length,x=0, res[]= new int[n];\n for(int num: nums){\n x=x|num;\n }\n or(max,x,1);\n for(i=0;i<n;i++){\n while(j<n && !isEqual(arr,max)){\n j++;\n if(j<n) or(arr,nums[j],1);\n if(j==n){\n for(int lp=0;lp<33;lp++){\n max[lp]=arr[lp];\n arr[lp]=0;\n }\n j=i-1;\n }\n }\n res[i]=Math.max(j-i+1,1);\n if(j==n) res[i]--;\n or(arr,nums[i],-1);\n }\n return res;\n }\n boolean isEqual(int arr[], int max[]){\n for(int i=0;i<arr.length;i++){\n if(arr[i]*max[i]==0 && arr[i]+max[i]!=0)return false;\n }\n return true;\n }\n void or(int arr[], int num, int val){\n int i=0;\n while(num>0){\n if((num&1)==1){\n arr[i]+=val;\n }\n i++;\n num=num>>1;\n }\n }\n}\n```
| 2 | 0 |
['Java']
| 2 |
smallest-subarrays-with-maximum-bitwise-or
|
Easy O(n*32) java solution
|
easy-on32-java-solution-by-ajithbabu-9c8j
|
\nclass Solution {\n public int[] smallestSubarrays(int[] nums) {\n int[] map = new int[32];\n int[] res = new int[nums.length];\n for (
|
ajithbabu
|
NORMAL
|
2022-09-17T16:20:19.491973+00:00
|
2022-09-17T16:20:19.492011+00:00
| 253 | false |
```\nclass Solution {\n public int[] smallestSubarrays(int[] nums) {\n int[] map = new int[32];\n int[] res = new int[nums.length];\n for (int i = nums.length - 1; i >= 0; i--) {\n int num = nums[i];\n for (int j = 0; j <= 31; j++) {\n int mask = 1 << (j);\n if ((num & mask) > 0) {\n map[j] = i;\n }\n }\n \n int max = i;\n for (int e : map) max = Math.max(e, max);\n res[i] = max - i + 1;\n }\n return res;\n }\n}\n```
| 2 | 0 |
['Java']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
OverKill | Used Segment Trees | Binary Search | C++
|
overkill-used-segment-trees-binary-searc-shsn
|
\n#include <bits/stdc++.h>\nusing namespace std;\n\nclass segTree {\n private:\n vector<int> tree, arr;\n int n;\n\n void build(int index, int low, in
|
yashberchha
|
NORMAL
|
2022-09-17T16:11:24.350360+00:00
|
2022-09-18T06:41:54.868302+00:00
| 193 | false |
```\n#include <bits/stdc++.h>\nusing namespace std;\n\nclass segTree {\n private:\n vector<int> tree, arr;\n int n;\n\n void build(int index, int low, int high)\n {\n if (low == high) {\n tree[index] = arr[low];\n return;\n }\n\n int mid = (low + high) >> 1;\n int left = 2 * index + 1;\n int right = 2 * index + 2;\n\n build(left, low, mid);\n build(right, mid + 1, high);\n\n tree[index] = tree[left] | tree[right];\n }\n\n void updateUtil(int index, int low, int high, int pos, int val)\n {\n if (low == high) {\n tree[index] = val;\n return;\n }\n\n int mid = (low + high) >> 1;\n int left = 2 * index + 1;\n int right = 2 * index + 2;\n\n if (pos <= mid)\n updateUtil(left, low, mid, pos, val);\n else\n updateUtil(right, mid + 1, high, pos, val);\n\n tree[index] = tree[left] + tree[right];\n }\n\n int queryUtil(int index, int low, int high, int qLeft, int qRight)\n {\n // (qLeft, qRight) [low, high] (qLeft, qRight)\n\n if (qRight < low || high < qLeft) {\n return 0;\n }\n\n // (qLeft (low, right) qRight)\n if (qLeft <= low and high <= qRight) {\n return tree[index];\n }\n\n int mid = (low + high) >> 1;\n int left = 2 * index + 1;\n int right = 2 * index + 2;\n\n int LeftSum = queryUtil(left, low, mid, qLeft, qRight);\n int RightSum = queryUtil(right, mid + 1, high, qLeft, qRight);\n\n return LeftSum | RightSum;\n }\n\n public:\n segTree(vector<int> &nums)\n {\n this->n = nums.size();\n this->arr = nums;\n tree.resize(4 * n + 1);\n\n build(0, 0, n - 1);\n }\n\n void update(int index, int val)\n {\n updateUtil(0, 0, n - 1, index, val);\n }\n\n int query(int left, int right)\n {\n return queryUtil(0, 0, n - 1, left, right);\n }\n};\nclass Solution {\npublic:\n vector<int> smallestSubarrays(vector<int>& nums) {\n int n = nums.size();\n segTree sgt(nums);\n \n vector<int> ans;\n for(int i = 0; i < n; i++) {\n int l = i, r = n - 1;\n int mx = sgt.query(i, n - 1);\n \n int ind = n - 1;\n while(l <= r) {\n int mid = (l + r) / 2;\n \n if ((nums[i] | sgt.query(i, mid)) == mx) {\n ind = mid;\n r = mid - 1;\n }\n else {\n l = mid + 1;\n }\n }\n \n ans.push_back(ind - i + 1);\n }\n \n return ans;\n }\n};\n```\n\n\n\n
| 2 | 0 |
['Tree', 'Binary Tree']
| 3 |
smallest-subarrays-with-maximum-bitwise-or
|
Bit solution
|
bit-solution-by-code_dev03-x3cb
|
Code
|
Code_Dev03
|
NORMAL
|
2025-04-09T05:24:24.740277+00:00
|
2025-04-09T05:24:24.740277+00:00
| 3 | false |
# Code
```cpp []
class Solution {
public:
vector<int> smallestSubarrays(vector<int>& nums) {
int n = nums.size();
vector<int> last(32, -1); // Last seen position of each bit
vector<int> ans(n);
for (int i = n - 1; i >= 0; --i) {
// Update the last seen positions for bits set in nums[i]
for (int b = 0; b < 32; ++b) {
if (nums[i] & (1 << b)) {
last[b] = i;
}
}
// Find the furthest index we need to include to match OR
int furthest = i;
for (int b = 0; b < 32; ++b) {
if (last[b] != -1) {
furthest = max(furthest, last[b]);
}
}
ans[i] = furthest - i + 1;
}
return ans;
}
};
```
| 1 | 0 |
['C++']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
O(N) || Easy and precise C++ solution
|
on-easy-and-precise-c-solution-by-gaurav-dbkk
|
\n# Approach\n Describe your approach to solving the problem. \nCount array will store the next occurence of each (1)bit\nJust keep traversing array from backsi
|
gaurav_ghidode
|
NORMAL
|
2024-09-14T11:03:07.404079+00:00
|
2024-09-14T11:03:07.404112+00:00
| 35 | false |
\n# Approach\n<!-- Describe your approach to solving the problem. -->\nCount array will store the next occurence of each (1)bit\nJust keep traversing array from backside and if any bit is 1, then store it\'s index in count array. Then find the maximum index stored in the count array. That will be anser for that index.\n\n# Complexity\n- Time complexity: O(32*n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(32)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n vector<int> smallestSubarrays(vector<int>& nums) {\n vector<int> ans;\n vector<int> count(32, 0);\n\n for(int i=nums.size()-1;i>=0;i--){\n int maxi=0;\n for(int j=0;j<32;j++){\n if ((1<<j) & nums[i]){\n count[j]=i;\n }\n }\n for(int j=0;j<32;j++){\n maxi=max(maxi, count[j]);\n }\n \n ans.push_back(max(maxi-i+1, 1));\n }\n reverse(ans.begin(), ans.end());\n return ans;\n }\n};\n```
| 1 | 0 |
['C++']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
bits + binary search || easy to understand || must see
|
bits-binary-search-easy-to-understand-mu-7u9h
|
Code\ncpp []\nclass Solution {\npublic:\n unordered_map<int,set<int>>mp;\n void preprocess(vector<int>&nums)\n {\n //pos --> {}\n for(i
|
akshat0610
|
NORMAL
|
2024-09-10T11:03:05.318362+00:00
|
2024-09-10T11:03:05.318397+00:00
| 116 | false |
# Code\n```cpp []\nclass Solution {\npublic:\n unordered_map<int,set<int>>mp;\n void preprocess(vector<int>&nums)\n {\n //pos --> {}\n for(int i = 0 ; i < nums.size() ; i++){\n for(int j = 0 ; j < 32 ; j++){\n if((nums[i] & (1 << j)) > 0){\n //this nums[i] has the jth bit set\n mp[j].insert(i); //jth bit kaun kaun se index m set h\n }\n }\n }\n }\n vector<int> smallestSubarrays(vector<int>& nums) {\n //lower_bound function give the iterator to the first position ele equal or greater than the value\n //upper_bound function give the iterator to the first position ele greater than the value\n preprocess(nums);\n\n vector<int>ans;\n for(int i = 0 ; i < nums.size() ; i++){\n int start = i;\n int end = i;\n int curror = 0;\n curror = curror | nums[i];\n for(int j = 31 ; j >= 0 ; j--){\n \n if((curror & (1 << j)) > 0) continue;\n\n int pos = fun(j,i); //get the min / nearest index of such element\n if(pos != -1) {\n curror = curror | nums[pos];\n end = max(end , pos);\n } \n }\n ans.push_back((end - start + 1));\n }\n return ans;\n }\n int fun(int pos , int idx){\n if(mp.find(pos) != mp.end()){ //if we have the pos bit set in any index\n //finding the index which is just greater then the ith index\n auto it = mp[pos].upper_bound(idx);\n if(it == mp[pos].end()) return -1;\n int ans = *(it);\n return ans;\n }\n return -1;\n }\n};\n```
| 1 | 0 |
['Array', 'Binary Search', 'Bit Manipulation', 'Sliding Window', 'C++']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
Kotlin | Sliding Window Beats 100%
|
kotlin-sliding-window-beats-100-by-jeffr-cahm
|
Intuition\n Describe your first thoughts on how to solve this problem. \nThe smallest subsequence of a or is the smallest possible one, where all bits that came
|
jeffreyntue
|
NORMAL
|
2024-07-04T09:00:58.568573+00:00
|
2024-07-04T09:00:58.568607+00:00
| 6 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe smallest subsequence of a or is the smallest possible one, where all bits that came before is at least included once. Since there are only 32 Bits in an Integer it can be calculated in linear time.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThis solution uses the slinding window technique. The bits are counted in an array dp. If a value in the array is zero, that means this bit wasn\'t used before. The algorithm goes from right to left in order to store the numbers.\n\nA number can be removed from the subsequence if all bits of the number are at least two times in the array. This can be used to check if the number of the outer right can be removed. If it is the case then remove the number and repeat the process. The smallest subsequence is the difference of the position of the number and the position of the right most number plus one. \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n\n# Code\n```\nclass Solution {\n fun addElement(num:Int, dp:IntArray){\n for(i:Int in 0..31) if((1 shl i) and num > 0) dp[i] += 1\n }\n \n fun removeElement(num:Int, dp:IntArray): Boolean {\n for(i:Int in 0..31) if(dp[i] == 1 && (1 shl i) and num > 0) return false\n for(i:Int in 0..31) if((1 shl i) and num > 0) dp[i] -= 1\n\n return true\n }\n\n fun smallestSubarrays(nums: IntArray): IntArray {\n val n:Int = nums.size\n val dp:IntArray = IntArray(32){0}\n var r:Int = n-1\n\n val sol:IntArray = IntArray(n){0}\n\n for(i:Int in n-1 downTo 0){\n addElement(nums[i], dp)\n\n while(i<r && removeElement(nums[r], dp)) r--\n \n sol[i] = r-i+1\n }\n\n return sol\n }\n}\n```
| 1 | 0 |
['Kotlin']
| 1 |
smallest-subarrays-with-maximum-bitwise-or
|
Easiest and most efficient solution using bit manipulation
|
easiest-and-most-efficient-solution-usin-cpv7
|
Intuition Assume the array has only 0 and 1.\nThen the question changes:\nIf A[i] = 1, shortest array is [A[i]], length is 1.\nIf A[i] = 0, we need to find the
|
vikas_singh_1999
|
NORMAL
|
2024-05-20T12:19:26.038305+00:00
|
2024-05-20T12:19:26.038339+00:00
| 9 | false |
# Intuition Assume the array has only 0 and 1.\nThen the question changes:\nIf A[i] = 1, shortest array is [A[i]], length is 1.\nIf A[i] = 0, we need to find the index j of next 1,\nthen j - i + 1 is the length of shortest subarray.\nIf no next 1, 1 is the length\n\nTo solve this problem,\nwe can iterate the array reversely\nand keep the index j of last time we saw 1.\nres[i] = max(1, last - i + 1)\n\n# Complexity\n- Time complexity:O(n*30)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> smallestSubarrays(vector<int>& nums) {\n int n=nums.size();\n vector<int> ans(n,1);\n vector<int> next_one(30);\n for(int i=n-1;i>=0;i--) {\n for(int j=0;j<30;j++) {\n if((nums[i] & (1<<j))) next_one[j]=i;\n ans[i]=max(ans[i],next_one[j]-i+1);\n }\n }\n return ans;\n }\n};\n```
| 1 | 0 |
['Bit Manipulation', 'C++']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
A Middle-Earth Tale of Smallest Subarrays and Maximum Bitwise OR
|
a-middle-earth-tale-of-smallest-subarray-ibll
|
Solution\n\n\nfrom typing import List\n\nclass Solution:\n def smallestSubarrays(self, nums: List[int]) -> List[int]:\n\n def update_last_seen_bits(nu
|
dinar
|
NORMAL
|
2023-06-08T18:02:17.880717+00:00
|
2023-06-08T18:08:08.331146+00:00
| 10 | false |
**Solution**\n\n```\nfrom typing import List\n\nclass Solution:\n def smallestSubarrays(self, nums: List[int]) -> List[int]:\n\n def update_last_seen_bits(num, index, last_seen_bits):\n """Updates the last seen indices of each bit in \'num\'."""\n bit_index = 0\n while (num >> bit_index):\n if (num >> bit_index) & 1:\n last_seen_bits[bit_index] = index\n bit_index += 1\n\n # Calculate the maximum bit length to cover all bits in \'nums\'.\n max_bit_length = max(1, max(n.bit_length() for n in nums))\n\n # Initialize the last seen bits array.\n last_seen_bits = [0] * max_bit_length\n\n # Initialize the result array.\n result = [0] * len(nums)\n\n # Iterate over \'nums\' in reverse order.\n for i in range(len(nums) - 1, -1, -1):\n update_last_seen_bits(nums[i], i, last_seen_bits)\n # The size of the smallest subarray with maximum bitwise OR \n # starting at \'i\' is the maximum last seen bit index - \'i\' + 1.\n result[i] = max(1, max(last_seen_bits) - i + 1)\n\n return result\n\n```\n\n\nIn the land of Middle-Earth, where shadows lie and algorithms thrive, we find ourselves on an epic quest. A quest not for the One Ring, but for an understanding of a powerful algorithmic problem - finding the smallest subarrays with maximum bitwise OR.\n\n## Setting Forth on the Quest\n\nThe brave fellowship of coders are given an array of non-negative integers, `nums`. Their task is to find, for each starting point in the array, the length of the smallest subarray which yields the maximum bitwise OR. The bitwise OR of an array is simply the bitwise OR of all its numbers. The output of their journey will be an array of integers, each representing the smallest subarray length with maximum bitwise OR, for each starting point in `nums`.\n\n## The Secret of the Last Seen Bits\n\nThe wise wizards of the fellowship devised a cunning strategy. They knew that to compute the maximum bitwise OR, they would need to understand the layout of the bits in each number. But they also knew that the bit length of any number, on most mortal and immortal computers, is limited to either 32 or 64 bits. Hence, they could create an array, `last_seen_bits`, to keep track of the last occurrence of each bit in the numbers from `nums`.\n\n```python\nmax_bit_length = max(1, max(n.bit_length() for n in nums))\nlast_seen_bits = [0] * max_bit_length\n```\nIn this part of the journey, the `max_bit_length` is calculated. This ensures that the `last_seen_bits` array covers all possible bits in `nums`. The `max(1, ...)` construction is used to handle the case where `nums` is an empty array.\n\n## The Journey Backwards\n\nThe wise wizards also knew that the smallest subarray with maximum bitwise OR, for each starting point in the array, can be found by traversing the array in reverse order. As they traverse `nums`, for each number, they go through its bits. For each bit that is set (1), they update the corresponding element in `last_seen_bits` to the current index. This enchantment is performed by the `update_last_seen_bits` function.\n\n```python\ndef update_last_seen_bits(num, index, last_seen_bits):\n\tbit_index = 0\n\twhile (num >> bit_index):\n\t\tif (num >> bit_index) & 1:\n\t\t\tlast_seen_bits[bit_index] = index\n\t\tbit_index += 1\n```\n\n## One Subarray to Rule Them All\n\nThe fellowship now understood that for each starting index `i`, the length of the smallest subarray with maximum bitwise OR is given by the maximum last seen bit index - `i` + 1. This is because the maximum bitwise OR starting at `i` must include all bits set in `nums[i]`, and hence must include all numbers up to the maximum last seen bit index. \n\n```python\nresult = [0] * len(nums)\nfor i in range(len(nums) - 1, -1, -1):\n\tupdate_last_seen_bits(nums[i], i, last_seen_bits)\n\tresult[i] = max(1, max(last_seen_bits) - i + 1)\nreturn result\n```\n\n## The Path to Mount Doom\n\nThis valiant strategy led the fellowship through their quest with both speed and precision. The time complexity of their journey is O(nm), where `n` is the number of elements in `nums` and `m` is the maximum bit length in `nums`. However, given that `m` is limited to either 32 or 64 on most machines, it can be treated as a constant factor, making the overall time complexity effectively O(n).\n\nTheir journey also left a small footprint. The space complexity of the solution is O(m), which arises from the need to store the result array and the `last_seen_bits` array. Again, given the constraints on `m`, it can be treated as a constant factor, yielding a space complexity of O(1).\n\n## Return of the King\n\nWith their quest completed, the fellowship has illuminated the path to understanding the smallest subarrays with maximum bitwise OR. Their tale serves as a reminder that even in the deepest darkness, there is a light that never goes out - the light of knowledge, of understanding, and of the joy of coding.
| 1 | 0 |
['Two Pointers', 'Python']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
The Jedi Path to Unraveling the Smallest Subarrays with Maximum Bitwise OR
|
the-jedi-path-to-unraveling-the-smallest-96ej
|
Solution\n\nfrom collections import defaultdict\nfrom typing import List\n\nclass Solution:\n def smallestSubarrays(self, nums: List[int]) -> List[int]:\n\n
|
dinar
|
NORMAL
|
2023-06-08T17:22:15.197315+00:00
|
2023-06-08T17:22:15.197359+00:00
| 14 | false |
**Solution**\n```\nfrom collections import defaultdict\nfrom typing import List\n\nclass Solution:\n def smallestSubarrays(self, nums: List[int]) -> List[int]:\n\n def add_to_dict(num, bit_dict):\n """Adds the bits of \'num\' to the dictionary \'bit_dict\'."""\n bit_index = 0\n while (num >> bit_index):\n if (num >> bit_index) & 1:\n bit_dict[bit_index] += 1\n bit_index += 1\n\n def remove_from_dict(num, bit_dict):\n """Removes the bits of \'num\' from the dictionary \'bit_dict\'."""\n bit_index = 0\n while (num >> bit_index):\n if (num >> bit_index) & 1:\n bit_dict[bit_index] -= 1\n if bit_dict[bit_index] == 0:\n del bit_dict[bit_index]\n bit_index += 1\n\n bit_counts = defaultdict(int)\n for num in nums:\n add_to_dict(num, bit_counts)\n\n current_bit_counts = defaultdict(int)\n right_ptr = 0\n ans = [0] * len(nums)\n \n for left_ptr, num in enumerate(nums):\n if len(bit_counts) == 0:\n for j in range(left_ptr, len(nums)):\n ans[j] = 1\n break\n \n while len(current_bit_counts) != len(bit_counts):\n add_to_dict(nums[right_ptr], current_bit_counts)\n right_ptr += 1\n \n ans[left_ptr] = right_ptr - left_ptr\n \n remove_from_dict(num, bit_counts)\n remove_from_dict(num, current_bit_counts)\n \n return ans\n\n```\n\nIn a galaxy far, far away, the Jedi Council of Data Structures and Algorithms has uncovered a new challenge, one that requires a deep understanding of the Force, also known as Bit Manipulation and Sliding Window techniques. This complex task involves finding the smallest subarrays within a given array, such that the bitwise OR of each subarray is maximized. Worry not, young padawans. The path may be treacherous, but the Force is with us. We shall embark on this quest and solve this enigma together.\n\n## The Task at Hand\n\nOur mission is to determine the size of the smallest subarray with maximum possible bitwise OR starting at each index i in a given array, `nums`. The bitwise OR of an array is the bitwise OR of all numbers within it. Our output shall be an array of equal size, where each element corresponds to the length of the smallest subarray starting at the respective index in `nums` that achieves this maximum bitwise OR.\n\n## The Force of Sliding Windows and Bit Manipulation\n\nOur Jedi solution calls upon two powerful techniques in the coding universe - the Sliding Window and Bit Manipulation. The Sliding Window approach harnesses the powers of two pointers, `left_ptr` and `right_ptr`, that define our current window within the array. As these pointers traverse the galaxy of our array, they uncover the smallest subarray size needed to reach the maximum bitwise OR at each index. \n\nBit Manipulation, our second tool, comes into play when we\'re calculating the bitwise OR for the numbers in our current window. We use it to track and manipulate the individual bits of our numbers, allowing us to reach the maximum bitwise OR with Jedi-like precision and efficiency.\n\n## The Path to the Solution\n\nNow, let\'s embark on our coding journey together. Remember, a Jedi\'s strength flows from the Force. \n\n```python\nfrom collections import defaultdict\nfrom typing import List\n\nclass Solution:\n def smallestSubarrays(self, nums: List[int]) -> List[int]:\n```\n\nThe first step in our journey is the creation of two helper functions, `add_to_dict` and `remove_from_dict`. These two functions use the power of Bit Manipulation to respectively add and remove the bits of a number to and from a dictionary:\n\n```python\n def add_to_dict(num, bit_dict):\n """Adds the bits of \'num\' to the dictionary \'bit_dict\'."""\n bit_index = 0\n while (num >> bit_index):\n if (num >> bit_index) & 1:\n bit_dict[bit_index] += 1\n bit_index += 1\n\n def remove_from_dict(num, bit_dict):\n """Removes the bits of \'num\' from the dictionary \'bit_dict\'."""\n bit_index = 0\n while (num >> bit_index):\n if (num >> bit_index) & 1:\n bit_dict[bit_index] -= 1\n if bit_dict[bit_index] == 0:\n del bit_dict[bit_index]\n bit_index += 1\n```\n\nHaving constructed our helper functions, we now create the `bit_counts` dictionary. This Jedi tool stores the count of each bit present in the bitwise OR of all numbers in `nums`:\n\n```python\n bit_counts = defaultdict(int)\n for num in nums:\n add_to_dict(num, bit_counts)\n```\n\nNext, we initialize `current_bit_counts`, a dictionary that will keep track of the bits in the bitwise OR of the numbers within our current window. We also set up `right_ptr`, the pointer that will slide across `nums` to extend our\n\n current window:\n\n```python\n current_bit_counts = defaultdict(int)\n right_ptr = 0\n ans = [0] * len(nums)\n```\n\nOur next task is to traverse the universe of our array with the `left_ptr` pointer. The current window starts at the `left_ptr` index, and we extend this window by moving `right_ptr` until the bitwise OR of the numbers in the window equals the maximum bitwise OR. This equality is checked by comparing `current_bit_counts` with `bit_counts`. \n\n```python\n for left_ptr, num in enumerate(nums):\n if len(bit_counts) == 0:\n for j in range(left_ptr, len(nums)):\n ans[j] = 1\n break\n \n while len(current_bit_counts) != len(bit_counts):\n add_to_dict(nums[right_ptr], current_bit_counts)\n right_ptr += 1\n \n ans[left_ptr] = right_ptr - left_ptr\n```\n\nThe last part of our journey involves moving the `left_ptr` to the right, effectively reducing the window size by one. The `num` at this index is removed from both `bit_counts` and `current_bit_counts` to reflect this change. This process continues until the entire array has been traversed:\n\n```python\n remove_from_dict(num, bit_counts)\n remove_from_dict(num, current_bit_counts)\n \n return ans\n```\n\n## The Computational Complexity of the Force\n\nThe path we have tread together is not just the way of the Jedi, but also the way of Optimal Algorithm Design. Our approach here is efficient and elegant, boasting a time complexity of O(n). Each number in the array is processed exactly once due to the nature of the sliding window technique, which results in a linear time complexity. \n\nIn terms of space complexity, our solution sits at O(n). This arises from the need to store the output array `ans` and the dictionaries for bit counts, which in the worst-case scenario could be as large as the input array.\n\n## In a Galaxy not so far away\u2026\n\nOur journey has now come to an end. We have successfully solved the problem with the wisdom of the Jedi, unraveling the secrets of Bit Manipulation and the Sliding Window technique. Remember, the Force will be with you. Always.\n\n
| 1 | 0 |
['Two Pointers', 'Python']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
Closest bit O(n) C++
|
closest-bit-on-c-by-josipdev-ihkl
|
Remember the last position you saw a \'1\' for each bit in 32 bits int.\nFor each element find the idx you found the \'1\' that it furthest appart. That is the
|
JosipDev
|
NORMAL
|
2022-09-21T10:54:17.064957+00:00
|
2022-09-21T10:54:17.064983+00:00
| 141 | false |
Remember the last position you saw a \'1\' for each bit in 32 bits int.\nFor each element find the idx you found the \'1\' that it furthest appart. That is the minimum length of the array.\n\n```\nvector<int> smallestSubarrays(vector<int>& nums) {\n\tint n = nums.size();\n\n\tvector<int> ans(n);\n\n\tunordered_map<int,int> idx;\n\tfor (int i = 0; i < 32; ++i) {\n\t\tidx[1 << i] = n;\n\t}\n\n\tfor (int i = n - 1, m = 0, j = 0; i >= 0; --i) {\n\t\tj = i;\n\t\tm |= nums[i];\n\t\tfor (int num = m; num; ) {\n\t\t\tint lsb = (num & -num);\n\t\t\tif (nums[i] & lsb) idx[lsb] = i; // closest satisfied \n\t\t\tj = max(j, idx[lsb]); // furthest j\n\t\t\tnum ^= lsb; // flip\n\t\t}\n\t\tans[i] = j - i + 1;\n\t}\n\n\treturn ans;\n}\n```
| 1 | 0 |
['C']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
✅ [Rust] 26 ms, fastest (100%) one-pass solution (with detailed comments)
|
rust-26-ms-fastest-100-one-pass-solution-aqvo
|
This solution employs a one-pass algorithm to update first-occurence positions of bits. It demonstrated 26 ms runtime (100.00%) and used 3.5 MB memory (80.29%).
|
stanislav-iablokov
|
NORMAL
|
2022-09-19T20:15:21.907865+00:00
|
2022-10-23T12:55:22.634933+00:00
| 42 | false |
This [**solution**](https://leetcode.com/submissions/detail/810097381/) employs a one-pass algorithm to update first-occurence positions of bits. It demonstrated **26 ms runtime (100.00%)** and used **3.5 MB memory (80.29%)**. Detailed comments are provided.\n\n**IF YOU LIKE THIS SOLUTION, PLEASE UPVOTE.**\n```\nimpl Solution \n{\n pub fn smallest_subarrays(nums: Vec<i32>) -> Vec<i32> \n {\n let mut ret: Vec<i32> = vec![1;nums.len()];\n \n // [1] when performing OR operation on an array, \n // we care only about the first occurence of each bit,\n // because all subsequent occurences do not change the result;\n // thus, we should arrange a storage \'bit_idx\' for the positions of \n // the first occurence of each bit; \n let mut bit_idx: [i32;30] = [0;30];\n\n let mut max_pos : i32;\n let mut bit : i32;\n \n // [2] for a one-pass solution, we iterate over \'nums\' from the end;\n // this allows us to dynamically update the first occurence of bits;\n // terminal zeros are skipped, their respective minimal subarray size is 1\n for (pos, &n) in nums.iter().enumerate().rev().skip_while(|(_,n)| **n == 0)\n {\n // [3] for each bit, update the earliest/first position it was seen at;\n // here we use an arithmetic way to update \'bit_idx\',\n // use of conditional statement is slower\n for b in 0..30\n {\n bit = (n >> b) & 1;\n bit_idx[b] = (1 - bit) * bit_idx[b] + bit * (pos as i32);\n }\n\n // [4] minimal subarray/window is the one that accounts for all bits\n // that were seen at least once \n max_pos = *bit_idx.iter().max().unwrap();\n ret[pos] = max_pos - pos as i32 + 1;\n }\n \n return ret;\n }\n}\n```
| 1 | 0 |
['Rust']
| 1 |
smallest-subarrays-with-maximum-bitwise-or
|
[C++] | Bitwise XOR
|
c-bitwise-xor-by-user0382o-m8g4
|
\nclass Solution {\npublic:\n vector<int> smallestSubarrays(vector<int>& nums) {\n vector<int> closed(30);\n vector<int> res(nums.size());\n
|
user0382o
|
NORMAL
|
2022-09-19T18:28:26.511495+00:00
|
2022-09-19T18:28:26.511544+00:00
| 94 | false |
```\nclass Solution {\npublic:\n vector<int> smallestSubarrays(vector<int>& nums) {\n vector<int> closed(30);\n vector<int> res(nums.size());\n for(int i = nums.size()- 1; i >= 0; i--){\n for(int j = 0; j < 30; j++)\n if(nums[i] & (1 << j))\n closed[j] = i;\n res[i] = max(1, *max_element(closed.begin(), closed.end()) - i + 1);\n }\n return res;\n }\n};\n```
| 1 | 0 |
[]
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
Python. Closest bit
|
python-closest-bit-by-nikamir-vmpe
|
\nclass Solution:\n def smallestSubarrays(self, nums: List[int]) -> List[int]:\n def get_bits(x):\n index = 0\n while x > 0:\n
|
nikamir
|
NORMAL
|
2022-09-19T10:55:29.277180+00:00
|
2022-09-19T10:55:29.277212+00:00
| 72 | false |
```\nclass Solution:\n def smallestSubarrays(self, nums: List[int]) -> List[int]:\n def get_bits(x):\n index = 0\n while x > 0:\n if x & 1:\n yield index\n index += 1\n x >>= 1\n \n nums_len = len(nums)\n last_bit_index = [nums_len] * 31\n result = [1] * nums_len\n cur_bits = set()\n for index in range(nums_len - 1, -1, -1):\n x = nums[index]\n x_bits = list(get_bits(x))\n for b in x_bits:\n last_bit_index[b] = index + 1\n cur_bits.update(x_bits)\n for b in cur_bits:\n result[index] = max(result[index], last_bit_index[b] - index)\n \n return result\n \n \n```
| 1 | 0 |
[]
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
C# individual bits queue
|
c-individual-bits-queue-by-pawel753-ys4b
|
\npublic int[] SmallestSubarrays(int[] nums)\n{\n\tvar bits = Enumerable.Range(0, 32).Select(_ => new Queue<int>()).ToArray();\n\tfor (int i = 0; i < nums.Lengt
|
pawel753
|
NORMAL
|
2022-09-18T14:39:21.491976+00:00
|
2022-09-18T14:39:21.492024+00:00
| 16 | false |
```\npublic int[] SmallestSubarrays(int[] nums)\n{\n\tvar bits = Enumerable.Range(0, 32).Select(_ => new Queue<int>()).ToArray();\n\tfor (int i = 0; i < nums.Length; i++)\n\t{\n\t\tvar n = nums[i];\n\t\tint bidx = 0;\n\t\twhile (n > 0)\n\t\t{\n\t\t\tif ((n & 1) > 0)\n\t\t\t\tbits[bidx].Enqueue(i);\n\t\t\tn >>= 1;\n\t\t\tbidx++;\n\t\t}\n\t}\n\n\tfor (int i = 0; i < nums.Length; i++)\n\t{\n\t\tvar max = 1;\n\t\tfor (int j = 0; j < bits.Length; j++)\n\t\t{\n\t\t\twhile (bits[j].TryPeek(out var idx) && idx < i)\n\t\t\t\tbits[j].Dequeue();\n\t\t\tif (bits[j].Count > 0)\n\t\t\t\tmax = Math.Max(max, bits[j].Peek() - i + 1);\n\t\t}\n\t\tnums[i] = max;\n\t}\n\treturn nums;\n}\n```
| 1 | 0 |
[]
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
Faster than 100% and Memory usage less than 100%
|
faster-than-100-and-memory-usage-less-th-5ys0
|
class Solution {\npublic:\n vector smallestSubarrays(vector& v) {\n int n=v.size();\n vector ans;\n vector dp(31);\n for(int i=n-
|
void_talha
|
NORMAL
|
2022-09-18T11:34:10.869812+00:00
|
2022-09-18T11:34:10.869858+00:00
| 158 | false |
class Solution {\npublic:\n vector<int> smallestSubarrays(vector<int>& v) {\n int n=v.size();\n vector<int> ans;\n vector<int> dp(31);\n for(int i=n-1;i>=0;i--)\n {\n for(int j=0;j<31;j++)\n {\n if(v[i] & 1<<j)\n dp[j]=i;\n }\n int mx=0;\n for(int j=0;j<31;j++)\n mx=max(mx,dp[j]);\n ans.push_back(max(1,mx-i+1));\n }\n reverse(ans.begin(),ans.end());\n return ans;\n }\n};
| 1 | 0 |
[]
| 2 |
smallest-subarrays-with-maximum-bitwise-or
|
C++| O(N*30)
|
c-on30-by-kumarabhi98-0qyt
|
\nclass Solution {\npublic:\n vector<int> smallestSubarrays(vector<int>& nums) {\n vector<int> dp(32,INT_MAX);\n vector<int> re(nums.size(),1);
|
kumarabhi98
|
NORMAL
|
2022-09-18T07:19:04.671915+00:00
|
2022-09-18T07:19:04.671946+00:00
| 51 | false |
```\nclass Solution {\npublic:\n vector<int> smallestSubarrays(vector<int>& nums) {\n vector<int> dp(32,INT_MAX);\n vector<int> re(nums.size(),1);\n int sum = 0;\n for(int i = nums.size()-1;i>=0;--i){\n sum=sum|nums[i];\n int k = i;\n for(int j = 0; j<30;++j){ \n if(nums[i]&(1<<j)) dp[j] = min(dp[j],i);\n if(dp[j]!=INT_MAX) k = max(k,dp[j]);\n }\n re[i] = k-i+1;\n }\n return re;\n }\n};\n```
| 1 | 0 |
['Bit Manipulation', 'C']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
[C++] | Sliding Window | Explained with Comment
|
c-sliding-window-explained-with-comment-cxgax
|
//Just like sliding window, we do this code as well. We maintain a map, tha store , that which index has been repeated and how many time, Eg :- 101 and 110 , ma
|
sramlax72
|
NORMAL
|
2022-09-18T06:12:59.855782+00:00
|
2022-09-18T06:12:59.855870+00:00
| 203 | false |
//Just like sliding window, we do this code as well. We maintain a map, tha store , that which index has been repeated and how many time, Eg :- 101 and 110 , map will have(indices like 2nd , 1st,0th) , then 0th index:- 1 , 1st index :- 1 , 2nd index :- 2)\n\nkeep 2 pointers i and j , from end\n\nLogic, start from end and move to start, at each step , add the indices of jth index, now we try to remove indices of ith index if, the map size is still same , else stop removing. Length will be (i-j+1)\n\n\n \n \n **CODE :- ** \n \n \n void add(int n , unordered_map<int,int> & m)\n {\n int i = 0;\n while(n > 0)\n {\n int r = n%2;\n n/=2;\n if(r == 1)\n {\n m[i]++;\n }\n i++;\n }\n }\n \n void del(int n , unordered_map<int,int> & m)\n {\n int i = 0;\n while(n > 0)\n {\n int r = n%2;\n n/=2;\n if(r == 1)\n {\n m[i]--;\n if(m[i] == 0)\n {\n m.erase(i);\n }\n }\n i++;\n }\n }\n \n vector<int> smallestSubarrays(vector<int>& nums) {\n int n = nums.size();\n int i = n-1 , j = n-2 ;\n \n vector<int> ans(n,1);\n \n unordered_map<int,int> m ;\n int sum = nums[n-1];\n \n add(nums[n-1] , m);\n while(j >= 0)\n {\n \n add(nums[j] , m);\n \n while(i > j)\n {\n int prev = m.size();\n del(nums[i],m);\n int new_val = m.size();\n \n if(prev == new_val)\n {\n i--;\n }\n else\n {\n add(nums[i],m);\n break;\n }\n \n \n }\n \n ans[j] = i-j+1;\n \n j--;\n \n \n }\n \n return ans;\n }
| 1 | 0 |
['Bit Manipulation', 'C', 'Sliding Window']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
C++ | SEGMENT TREE | BINARY SEARCH
|
c-segment-tree-binary-search-by-chikzz-dj9f
|
PLEASE DO UPVOTE IF U FIND MY SOLUTION HELPFUL :)\n\nclass Solution {\n vector<int>seg_tree;\n void build(int node,int s,int e,vector<int>& nums)\n {\n
|
chikzz
|
NORMAL
|
2022-09-18T03:00:14.119328+00:00
|
2022-09-18T03:00:14.119366+00:00
| 107 | false |
**PLEASE DO UPVOTE IF U FIND MY SOLUTION HELPFUL :)**\n```\nclass Solution {\n vector<int>seg_tree;\n void build(int node,int s,int e,vector<int>& nums)\n {\n if(s>e)return;\n if(s==e){seg_tree[node]=nums[s];return;}\n int mid=s+(e-s)/2;\n build(2*node,s,mid,nums);\n build(2*node+1,mid+1,e,nums);\n seg_tree[node]=seg_tree[2*node]|seg_tree[2*node+1];\n }\n int range_OR(int node,int s,int e,int l,int r)\n {\n if(s>e||e<l||s>r)\n return 0;\n if(s>=l&&e<=r||s==e)return seg_tree[node];\n \n int mid=s+(e-s)/2;\n int left_OR=range_OR(2*node,s,mid,l,r);\n int right_OR=range_OR(2*node+1,mid+1,e,l,r);\n return left_OR|right_OR;\n }\npublic:\n vector<int> smallestSubarrays(vector<int>& nums) {\n int n=nums.size();\n vector<int>v(n);\n v[n-1]=nums[n-1];\n for(int i=n-2;i>=0;i--)v[i]=nums[i]|v[i+1];\n \n seg_tree=vector<int>(4*n);\n build(1,0,n-1,nums);\n vector<int>res(n);\n for(int i=0;i<n;i++)\n {\n int max_OR=v[i];\n int lo=i,hi=n-1;\n while(lo<=hi)\n {\n int mid=lo+(hi-lo)/2;\n int rangeOR=range_OR(1,0,n-1,i,mid);\n if(rangeOR<max_OR)\n lo=mid+1;\n else\n hi=mid-1;\n }\n res[i]=lo-i+1;\n }\n return res;\n }\n};\n```
| 1 | 0 |
['Tree', 'Binary Tree']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
C++ | Bit Operation | No binary search
|
c-bit-operation-no-binary-search-by-adbm-va1v
|
\nclass Solution {\npublic:\n void dec2bin(int n, vector<int>& binbits) {\n for (int i = 0; i < 30; i++) {\n binbits[i] = n % 2;\n
|
adbmdzbsy
|
NORMAL
|
2022-09-17T19:39:56.767807+00:00
|
2022-09-17T19:39:56.767841+00:00
| 118 | false |
```\nclass Solution {\npublic:\n void dec2bin(int n, vector<int>& binbits) {\n for (int i = 0; i < 30; i++) {\n binbits[i] = n % 2;\n n /= 2;\n }\n }\n \n vector<int> smallestSubarrays(vector<int>& nums) {\n vector<deque<int>> contibutes(30);\n vector<int> ans(nums.size());\n vector<int> binbits(30);\n for (int i = 0; i < nums.size(); i++) {\n dec2bin(nums[i], binbits);\n for (int j = 0; j < 30; j++) \n if (binbits[j] == 1) contibutes[j].push_back(i);\n }\n \n for (int i = 0; i < nums.size(); i++) {\n vector<int> onesIdx;\n for (int i = 0; i < 30; i++) if (contibutes[i].size()) onesIdx.push_back(i);\n int tmax = -1;\n for (int& idx : onesIdx) tmax = max(tmax, contibutes[idx][0]);\n ans[i] = max(tmax-i+1, 1);\n for (int j = 0; j < 30; j++) if (contibutes[j][0] == i) contibutes[j].pop_front();\n\n }\n \n return ans;\n }\n};\n```
| 1 | 0 |
['Bit Manipulation', 'C']
| 1 |
smallest-subarrays-with-maximum-bitwise-or
|
Python || Bitmasking || O(31*n)
|
python-bitmasking-o31n-by-in_sidious-8lou
|
Keep track of all bits which have been set by latest index from right.Your answer is maximum of those.If that bit is never set anytime, don\'t consider that ind
|
iN_siDious
|
NORMAL
|
2022-09-17T18:35:52.341309+00:00
|
2022-09-18T16:08:37.578212+00:00
| 74 | false |
Keep track of all bits which have been set by latest index from right.Your answer is maximum of those.If that bit is never set anytime, don\'t consider that index for answer.\n```\nclass Solution:\n def smallestSubarrays(self, nums: List[int]) -> List[int]:\n n=len(nums)\n ans=[1]*n\n arr=[-1]*31\n for i in range(n-1,-1,-1):\n mmax=-1\n for idx in range(31):\n if (nums[i] & (1<<idx))!=0:\n arr[idx]=i\n mmax=max(mmax,arr[idx])\n if mmax!=-1:\n ans[i]=mmax-i+1\n return ans\n```\n
| 1 | 0 |
[]
| 1 |
smallest-subarrays-with-maximum-bitwise-or
|
🤯 100% TC 100% SC | Bit Manipuation | Explained | Python | Super fast
|
100-tc-100-sc-bit-manipuation-explained-zebvp
|
\n\nLogic: When we do an OR operation, once a bit becomes 1, it stays 1 afterwards no matter how many OR operations you do. So when we iterate from left to righ
|
ramsudharsan
|
NORMAL
|
2022-09-17T17:57:25.510732+00:00
|
2022-09-17T21:18:55.129871+00:00
| 113 | false |
\n\nLogic: When we do an OR operation, once a bit becomes 1, it stays 1 afterwards no matter how many OR operations you do. So when we iterate from left to right, as soon as a bit becomes 1, that is the best index (least possible) we will need to travel to make that bit 1. \n\n**We need to start from the end and update the least index required for making each bit 1. Once we update, the max index needed to make any bit 1 is the answer for the current index.**\n\nEg: [1, **3**] -> bitform = [01, **11**]\n**We iterate from right to left**\ncurrIndex = 1\nmax index to make LSB (rightmost bit) 1 = 1\nmax index to make MSB (leftmost bit) 1 = 1\nbestBitIndex = [1, 1]\n\n[**1**, 3] -> bitform = [**01**, 11]\ncurrIndex = 0\nmax index to make LSB (rightmost bit) 1 = 0 (we dont need to go till index 1 now, this bit will stay 1 starting from index 0)\nmax index to make MSB (leftmost bit) 1 = 1 (in order to make this bit 1, we still have to travel till index 1)\nbestBitIndex = [1, 0]\n\nUpvote if you understood the logic :) \n\n```\nclass Solution:\n def smallestSubarrays(self, nums: List[int]) -> List[int]:\n ans = [None] * len(nums)\n n = len(nums)\n bestBitIndices = [0] * 32\n\n for numIndex in range(len(nums) - 1, -1, -1):\n \n for bitIndex in range(32):\n if nums[numIndex] & (1 << bitIndex):\n\t\t\t\t # if 0 we need to atleast travel till the current index\n if bestBitIndices[bitIndex] == 0:\n bestBitIndices[bitIndex] = numIndex\n else:\n bestBitIndices[bitIndex] = min(bestBitIndices[bitIndex], numIndex)\n \n ans[numIndex] = max(1, max(bestBitIndices) - numIndex + 1)\n \n return ans\n```
| 1 | 0 |
['Python']
| 1 |
smallest-subarrays-with-maximum-bitwise-or
|
Sliding Window Intuitive
|
sliding-window-intuitive-by-user7381t-f1jg
|
First find the maximum OR of the array arr and then search for the maximum or from the start. Once the maximum OR is found update the maximum OR if required and
|
user7381t
|
NORMAL
|
2022-09-17T16:56:07.901302+00:00
|
2022-09-17T16:58:01.930817+00:00
| 246 | false |
First find the maximum OR of the array arr and then search for the maximum or from the start. Once the maximum OR is found update the maximum OR if required and remove the leftmost element of the array from the current OR.\n```\nclass Solution {\n public int[] smallestSubarrays(int[] nums) {\n int[] res=new int[nums.length];\n int freq[]=new int[32];\n int or=0;\n for(int i:nums){\n or|=i;\n addFreq(i,freq);\n }\n int l=0;\n int r=0;\n int cur=0;\n int cFreq[]=new int[32];\n while(r<nums.length){\n if(or==0){\n res[l]=1;\n l++;\n r++;\n continue;\n }\n cur|=nums[r];\n addFreq(nums[r],cFreq);\n while(l<nums.length&&cur==or&&cur!=0){\n res[l]=r-l+1;\n dFreq(nums[l],freq);\n or=update(freq);\n dFreq(nums[l],cFreq);\n cur=update(cFreq);\n l++;\n }\n \n r++;\n }\n res[nums.length-1]=1;\n return res;\n }\n \n public void addFreq(int i,int[] freq){\n int j=0;\n while(i>0){\n int bit=i&1;\n i=i>>1;\n if(bit==1) freq[j]++;\n j++;\n }\n \n }\n \n public void dFreq(int i,int[] freq){\n int j=0;\n while(i>0){\n int bit=i&1;\n i=i>>1;\n if(bit==1) freq[j]--;\n j++;\n }\n }\n \n public int update(int[] freq){\n int ans=0;\n for(int i=0;i<32;i++){\n if(freq[i]>0)\n ans|=(1<<i);\n }\n return ans;\n }\n \n \n}\n````
| 1 | 0 |
['Two Pointers', 'Sliding Window', 'Java']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
[C++| Bit Maipulation
|
c-bit-maipulation-by-mysterious_lord-y9uk
|
\nclass Solution {\npublic:\n vector<int> smallestSubarrays(vector<int>& a) \n {\n vector<int> ans(a.size(),1);\n vector<int> temp(30,0);\n
|
mysterious_lord
|
NORMAL
|
2022-09-17T16:44:42.681517+00:00
|
2022-09-17T16:44:42.681542+00:00
| 215 | false |
```\nclass Solution {\npublic:\n vector<int> smallestSubarrays(vector<int>& a) \n {\n vector<int> ans(a.size(),1);\n vector<int> temp(30,0);\n for(int i=a.size()-1; i>=0; i--)\n {\n int maxval=0;\n for(int j=0;j<30;j++)\n {\n if(((1<<j) & a[i])==0)\n maxval=max(maxval,temp[j]);\n ans[i]=max(maxval-i+1,1); \n }\n \n for(int j=0;j<30;j++)\n {\n if((1<<j) & a[i])\n temp[j]=i;\n }\n }\n return ans;\n }\n};\n```
| 1 | 0 |
['Two Pointers', 'Bit Manipulation', 'C', 'C++']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
O(n) Binary Search + bit manipulation solution
|
on-binary-search-bit-manipulation-soluti-7s1y
|
\nclass Solution {\npublic:\n vector<int> smallestSubarrays(vector<int>& v) {\n unordered_map<int,vector<int>> mp;\n for(int i=0 ; i<v.size() ;
|
mandysingh150
|
NORMAL
|
2022-09-17T16:40:59.974608+00:00
|
2022-09-17T16:40:59.974645+00:00
| 137 | false |
```\nclass Solution {\npublic:\n vector<int> smallestSubarrays(vector<int>& v) {\n unordered_map<int,vector<int>> mp;\n for(int i=0 ; i<v.size() ; ++i) {\n for(int j=0 ; j<31 ; ++j) {\n if(v[i]&(1<<j)) {\n mp[j].push_back(i);\n }\n }\n }\n vector<int> ans(v.size());\n for(int i=0 ; i<v.size() ; ++i) {\n int mx=i;\n for(int j=0 ; j<31 ; ++j) {\n auto len = lower_bound(begin(mp[j]), end(mp[j]), i);\n if(len != mp[j].end()) {\n mx = max(mx, *len);\n }\n }\n ans[i] = mx-i+1;\n }\n return ans;\n }\n};\n```
| 1 | 0 |
['Bit Manipulation', 'Binary Tree']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
C++ || DP || Bitmasking
|
c-dp-bitmasking-by-igloo11-579o
|
\nclass Solution {\npublic:\n vector<int> smallestSubarrays(vector<int>& nums) {\n int n = nums.size();\n vector<vector<int>> dp(n, vector<int>
|
Igloo11
|
NORMAL
|
2022-09-17T16:31:37.276728+00:00
|
2022-09-17T16:31:37.276771+00:00
| 106 | false |
```\nclass Solution {\npublic:\n vector<int> smallestSubarrays(vector<int>& nums) {\n int n = nums.size();\n vector<vector<int>> dp(n, vector<int>(31));\n \n for(int i = 0; i < 31; i++) {\n if(nums[n-1] & (1<<i)) \n dp[n-1][i] = n-1;\n }\n \n for(int i = n-2; i >= 0; i--) {\n dp[i] = dp[i+1];\n for(int j = 0; j < 31; j++) {\n if(nums[i] & (1<<j))\n dp[i][j] = i;\n }\n }\n \n vector<int> ans(n, 1);\n for(int i = 0; i < n; i++) {\n for(int j = 0; j < 31; j++)\n ans[i] = max(ans[i], dp[i][j]-i+1);\n }\n \n return ans;\n }\n};\n\n```
| 1 | 0 |
['Dynamic Programming', 'Bit Manipulation', 'C']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
[C++] Brute Force solution using map
|
c-brute-force-solution-using-map-by-skat-16yd
|
Approach: \n For every index i, starting from the end, we are using all the Bitwise OR results from index i + 1 along with the size of the subarray. \n If two s
|
skate1512
|
NORMAL
|
2022-09-17T16:31:15.417415+00:00
|
2022-09-17T16:31:15.417459+00:00
| 62 | false |
Approach: \n* For every index i, starting from the end, we are using all the Bitwise OR results from index i + 1 along with the size of the subarray. \n* If two subarrays have same Bitwise OR result then we keep only the shorter subarray. For this we are using a map. \n* For index i, we find the maximum Bitwise OR result having the smallest size.\n\n\nCode:\n```\nclass Solution {\npublic:\n vector<int> smallestSubarrays(vector<int>& nums) {\n int n = nums.size();\n vector<unordered_map<int, int>> ops(n);\n ops[n - 1][nums.back()] = 1;\n \n vector<int> res(n, 1); \n \n for(int i = n - 2; i >= 0; i--){\n int mx = nums[i], mxs = 1;\n for(auto [v, s]: ops[i + 1]){\n int x = nums[i] | v;\n if(ops[i].count(x))\n ops[i][x] = min(ops[i][x], s + 1);\n else ops[i][x] = s + 1;\n if(x >= mx){\n if(mx == x){\n mxs = min(mxs, s + 1);\n }\n else {\n mx = x;\n mxs = s + 1;\n } \n }\n } \n ops[i][nums[i]] = 1;\n res[i] = mxs;\n }\n return res;\n }\n};\n```\n
| 1 | 0 |
['C']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
solved by two pointers
|
solved-by-two-pointers-by-shojin_pro-9gcf
|
\nclass Solution {\n public int[] smallestSubarrays(int[] nums) {\n int n = nums.length;\n int[] max = new int[n];\n int now = 0;\n\t\t/
|
shojin_pro
|
NORMAL
|
2022-09-17T16:31:01.702745+00:00
|
2022-09-17T16:31:01.702787+00:00
| 179 | false |
```\nclass Solution {\n public int[] smallestSubarrays(int[] nums) {\n int n = nums.length;\n int[] max = new int[n];\n int now = 0;\n\t\t//1. The maximum value is calculated first (going back from N-1)\n for(int i = n-1; i >= 0; i--){\n now |= nums[i];\n max[i] = now;\n }\n int[] bit = new int[31];\n int right = 0;\n now = 0;\n int[] cnt = new int[n];\n for(int i = 0; i < n; i++){\n\t\t //2. Keep adding until the maximum value is reached.\n while(right < n && now < max[i]){\n for(int j = 0; j < 31; j++){\n if((nums[right] >> j) % 2 == 1){\n bit[j]++;\n\t\t\t\t\t\t//3. OR value increases when that bit goes 0 => 1\n if(bit[j] == 1){\n now += (1 << j);\n }\n }\n }\n right++;\n }\n cnt[i] = Math.max(1,right-i);\n\t\t\t// 4. Remove nums[i] from the OR value\n for(int j = 0; j < 31; j++){\n if((nums[i] >> j) % 2 == 1){\n bit[j]--;\n if(bit[j] == 0){\n\t\t\t\t\t // 5. OR value decreases when the bit becomes 1 => 0\n now -= (1 << j);\n }\n }\n }\n }\n return cnt;\n }\n}\n```
| 1 | 0 |
['Two Pointers', 'Java']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
[C++ / Cpp] | Bit Solution | Explaination | O(30)
|
c-cpp-bit-solution-explaination-o30-by-y-x3vf
|
\n\t\t// jai shri ram\n\t\t//we are using the or property if the ith idx is one then it will not change further.\n\t\t// we are checking the min idx from cur id
|
yashbansal24
|
NORMAL
|
2022-09-17T16:18:01.827593+00:00
|
2022-09-17T16:33:59.277100+00:00
| 198 | false |
```\n\t\t// jai shri ram\n\t\t//we are using the or property if the ith idx is one then it will not change further.\n\t\t// we are checking the min idx from cur idx that is responsible for set the ith bit and updating it from right to left \n\t\tvector<int>mp(31,-1);\n vector<int>ans;\n int n=nums.size();\n for(int i=n-1;i>=0;i--){\n for(int j=0;j<=30;j++){\n int mask=(1<<j); \n if((mask & nums[i])){ //checking the jth bit is set or not\n mp[j]=i; // if the bit is set then update the jth bit to cur idx means this jth bit can be set by this idx;\n }\n }\n int res=-1;\n for(auto x:mp){\n res=max(res,x); // finding the max idx which are contributing to max or\n }\n if(res!=-1) ans.push_back(res-i+1);\n else if(res==-1 && nums[i]==0) ans.push_back(1); // if there are zeroes to the right side then no bit is set then the ans will be 1.\n }\n reverse(ans.begin(),ans.end());\n return ans;\n```
| 1 | 0 |
['Bit Manipulation', 'C', 'C++']
| 1 |
smallest-subarrays-with-maximum-bitwise-or
|
[Secret Python Answer🤫🐍👌😍] Sliding Window with Double Dictionary of Binary Count
|
secret-python-answer-sliding-window-with-cqoh
|
\nclass Solution:\n def smallestSubarrays(self, nums: List[int]) -> List[int]:\n\n def create(m):\n t = 0\n for n in m:\n
|
xmky
|
NORMAL
|
2022-09-17T16:12:36.820515+00:00
|
2022-09-17T20:37:52.680877+00:00
| 441 | false |
```\nclass Solution:\n def smallestSubarrays(self, nums: List[int]) -> List[int]:\n\n def create(m):\n t = 0\n for n in m:\n if m[n] > 0:\n t = t | (1 << n)\n return t\n \n def add(a,m):\n ans = bin( a )\n s = str(ans)[2:]\n for i, b in enumerate( s[::-1]):\n if b == \'1\':\n m[i] += 1\n\n def remove(a,m):\n ans = bin( a )\n s = str(ans)[2:]\n for i, b in enumerate( s[::-1]):\n if b == \'1\':\n m[i] -= 1\n \n res = []\n\n \n n = defaultdict(int)\n for i in nums:\n add(i,n)\n\n \n m = defaultdict(int)\n r = 0\n c = 0\n\n for i,v in enumerate(nums):\n # The last check is for if nums[i] == 0, in that case we still want to add to the map\n while r < len(nums) and (create(m) != create(n) or (c==0 and nums[i] ==0)):\n add(nums[r],m)\n r+=1\n c+=1\n\n res.append(c)\n\n remove(nums[i],m)\n remove(nums[i],n)\n c-=1\n\n return res\n```
| 1 | 0 |
['Python', 'Python3']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
EXPLAINED: REVERSE SLIDING WINDOW WITH BIT MANIPULATION,COUNTING
|
explained-reverse-sliding-window-with-bi-a522
|
Do sliding window in reverse.\nAdd the set bits from the L index element to the bits array , meaning if L element is 2 then add one to 1st index of bits array s
|
narutoobito
|
NORMAL
|
2022-09-17T16:09:59.597286+00:00
|
2022-09-18T14:54:50.758267+00:00
| 269 | false |
Do sliding window in reverse.\nAdd the set bits from the L index element to the bits array , meaning if L element is 2 then add one to 1st index of bits array since 2=(10) in binary.\nthen try to remove the right elements by removing its set bits from bits array. if any bit you are removing has only 1 value that means if you remove right element the it would decrease the OR result so we will not remove that right element \nthe we will save r-l+1 as the as for L index.\n\nTime Complexity is linear meaning O(N) where N is the size of the nums array.\nSpace complexity is O{1), because we are just using an array of size 32 irrespective of nums array size.\n\nTime complexity is linear because it is just a normal sliding window and l and r can at max traverse the array once . the Inner loops will just run 32 times so they won\'t add any extra complexity to our solution.\n\n```\nvector<int> smallestSubarrays(vector<int>& nums) {\n vector<int>bits(32,0);\n \n int r=nums.size()-1;\n int l=nums.size()-1;\n vector<int>ans;\n \n while(l>=0){\n \n int temp=nums[r];\n \n for(int i=0;i<32;i++){\n if(nums[l]&(1<<i)){\n bits[i]++;\n }\n }\n \n \n bool notchange=false;\n while(r>l and !notchange){;\n notchange=false;\n vector<int>temp=bits;\n for(int i=0;i<32;i++){\n if(nums[r]&(1<<i)){\n if(bits[i]==1){\n notchange=true;\n break;\n }\n temp[i]--;\n }\n }\n if(notchange)break;\n r--;\n bits=temp;\n }\n ans.push_back(r-l+1);\n l--;\n }\n \n \n reverse(ans.begin(),ans.end());\n return ans;\n }\n```
| 1 | 0 |
['Bit Manipulation', 'C', 'Sliding Window']
| 2 |
smallest-subarrays-with-maximum-bitwise-or
|
PrefixSum + Binary Search | Java
|
prefixsum-binary-search-java-by-virendra-yllt
|
\nclass Solution {\n public int[] smallestSubarrays(int[] nums) {\n int n = nums.length;\n int[][] prefix = new int[n+1][32];\n for(int
|
virendra115
|
NORMAL
|
2022-09-17T16:03:57.010865+00:00
|
2022-09-17T16:05:45.675011+00:00
| 200 | false |
```\nclass Solution {\n public int[] smallestSubarrays(int[] nums) {\n int n = nums.length;\n int[][] prefix = new int[n+1][32];\n for(int i=0;i<n;i++){\n for(int j=0;j<32;j++){\n prefix[i+1][j] = prefix[i][j];\n if(((1<<j)&nums[i])!=0) prefix[i+1][j]++;\n }\n }\n int[] ans = new int[n];\n for(int i=0;i<n;i++){\n int l = i+1,r = n;\n while(l<r){\n int mid = (l+r)/2;\n boolean f = true;\n for(int j=0;j<32;j++){\n if((prefix[r][j]-prefix[i][j])!=0&&(prefix[mid][j]-prefix[i][j])==0) {\n f = false;\n break;\n }\n }\n if(f) r = mid;\n else l = mid+1;\n }\n ans[i] = r - i;\n }\n return ans;\n }\n}\n```
| 1 | 0 |
[]
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
Sliding Window on Bits | C++
|
sliding-window-on-bits-c-by-riddle_7-thvz
|
The key idea is to start fom the end and keep removing the element which do not alter the value of the maximum bitwise OR.\n\n\nclass Solution {\npublic:\n \
|
riddle_7
|
NORMAL
|
2022-09-17T16:02:54.586928+00:00
|
2022-09-17T16:09:00.157523+00:00
| 150 | false |
The key idea is to start fom the end and keep removing the element which do not alter the value of the maximum bitwise OR.\n\n```\nclass Solution {\npublic:\n \n bool isOk(vector<int> &crt, vector<int> &last){\n vector<int> temp(crt);\n for(int i = 0; i<64; i++){\n temp[i] = temp[i] - last[i];\n }\n for(int i = 0; i<64; i++){\n if(!temp[i]&&crt[i])return false;\n }\n return true;\n }\n \n vector<int> smallestSubarrays(vector<int>& nums) {\n vector<int> ans(nums.size());\n vector<vector<int>> bits(nums.size(), vector<int>(64, 0));\n for(int i = 0; i<nums.size(); i++){\n int temp = nums[i];\n int k = 0;\n while(temp){\n bits[i][k++] = temp%2;\n temp = temp/2;\n }\n }\n ans[nums.size()-1] = 1;\n vector<int> crt = bits[nums.size()-1];\n int last = nums.size()-1;\n for(int i = nums.size()-2; i>=0; i--){\n for(int j = 0; j<64; j++){\n crt[j] += bits[i][j];\n }\n while(last>i&&isOk(crt, bits[last])){\n for(int k = 0; k<64; k++){\n crt[k] = crt[k] - bits[last][k];\n }\n last--;\n }\n ans[i] = last-i+1;\n }\n return ans;\n }\n};\n```
| 1 | 0 |
[]
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
[Python] Segment tree and sliding window/two pointers
|
python-segment-tree-and-sliding-windowtw-l5pj
|
Explanation:\n1. Create a segment tree to calculate the bitwise OR for the intervals in the array.\n2. Starting from the end of the array and traversing back, w
|
stilleholz
|
NORMAL
|
2022-09-17T16:02:21.565629+00:00
|
2022-09-21T00:53:40.309414+00:00
| 174 | false |
**Explanation:**\n1. Create a segment tree to calculate the bitwise OR for the intervals in the array.\n2. Starting from the end of the array and traversing back, we can apply the sliding window/two pointers method. \n3. Whenever we satisfy the condition: (bitwise OR between[left, right-1] == bitwise OR between[left, right]), that means we don\'t need the num at the right pointer to get a larger bitwise OR value. We can then greedily shrink the window by decreasing the right pointer to get a smaller length of the subarray.\n\n```\nclass SegTree:\n\n def __init__(self, nums):\n self.n = n = len(nums)\n self.tree = [0] * (2 * n)\n for i in range(n):\n self.tree[i + n] = nums[i]\n for i in range(n-1, 0, -1):\n self.tree[i] = self.tree[2 * i] | self.tree[2 * i + 1]\n \n def orRange(self, left, right):\n left += self.n\n right += self.n + 1\n orRes = 0\n while left < right:\n if left % 2 == 1:\n orRes |= self.tree[left]\n left += 1\n \n if right % 2 == 1:\n right -= 1\n orRes |= self.tree[right]\n \n left //= 2\n right //= 2\n return orRes\n\nclass Solution:\n def smallestSubarrays(self, nums: List[int]) -> List[int]:\n \n segtree = SegTree(nums)\n \n ans = [1] * len(nums)\n l = len(nums) - 1\n r = len(nums) - 1\n \n while l >= 0:\n\n while r > l and segtree.orRange(l, r-1) == segtree.orRange(l, r):\n r -= 1\n \n ans[l] = r - l + 1\n l -= 1\n \n return ans\n```
| 1 | 0 |
['Tree', 'Sliding Window']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
a few solutions
|
a-few-solutions-by-claytonjwong-see4
|
Process the input array A from right-to-left.\n\n For each ith index, do we have what we need?\n * If not, we fulfill the need with the left-most jth index b
|
claytonjwong
|
NORMAL
|
2022-09-17T16:00:43.267291+00:00
|
2022-09-17T16:36:53.212422+00:00
| 233 | false |
Process the input array `A` from right-to-left.\n\n* For each `i`<sup>th</sup> index, do we `have` what we `need`?\n * If not, we fulfill the `need` with the left-most `j`<sup>th</sup> index based upon the `last` seen `k`<sup>th</sup> bit needed.\n\nNote: `need` is the running total of bitwise-OR of values of the input array `A`.\n\n---\n\n*Kotlin*\n```\nclass Solution {\n fun smallestSubarrays(A: IntArray): IntArray {\n var N = A.size\n var ans = IntArray(N)\n var last = IntArray(32) // last index of each 0..31 bit set (what we need to be added onto what we have)\n var (have, need) = Pair(0, 0)\n for (i in N - 1 downTo 0) {\n var j = i\n have = A[i]\n need = A[i] or need\n for (k in 0..31) {\n if (have and (1 shl k) != 0) last[k] = i\n if (need and (1 shl k) != 0) j = Math.max(j, last[k])\n }\n ans[i] = j - i + 1 // +1 for i..j inclusive\n }\n return ans\n }\n}\n```\n\n*Javascript*\n```\nlet smallestSubarrays = (A, have = 0, need = 0) => {\n let N = A.length;\n let ans = Array(N);\n let last = Array(32); // last index of each 0..31 bit set (what we need to be added onto what we have)\n for (let i = N - 1; 0 <= i; --i) {\n let j = i;\n have = A[i];\n need = A[i] | need;\n for (let k = 0; k < 32; ++k) {\n if (have & (1 << k)) last[k] = i;\n if (need & (1 << k)) j = Math.max(j, last[k]);\n }\n ans[i] = j - i + 1; // +1 for i..j inclusive\n }\n return ans;\n};\n```\n\n*Python3*\n```\nclass Solution:\n def smallestSubarrays(self, A: List[int], need = 0) -> List[int]:\n N = len(A)\n ans = [0] * N\n last = [0] * 32 # last index of each 0..31 bit set (what we need to be added onto what we have)\n for i in range(N - 1, -1, -1):\n j = i\n have = A[i]\n need = A[i] | need\n for k in range(32):\n if have & (1 << k): last[k] = i\n if need & (1 << k): j = max(j, last[k])\n ans[i] = j - i + 1 # +1 for i..j inclusive\n return ans\n```\n\n*Rust*\n```\ntype VI = Vec<i32>;\nuse std::cmp::max;\nimpl Solution {\n pub fn smallest_subarrays(A: VI) -> VI {\n let N = A.len();\n let mut ans = vec![0; N];\n let mut last = vec![0; 32]; // last index of each 0..31 bit set (what we need to be added onto what we have)\n let (mut have, mut need) = (0, 0);\n for i in (0..N).rev() {\n let mut j = i;\n have = A[i];\n need = A[i] | need;\n for k in 0..32 {\n if have & (1 << k) != 0 { last[k] = i; }\n if need & (1 << k) != 0 { j = max(j, last[k]) }\n }\n ans[i] = (j - i + 1) as i32; // +1 for i..j inclusive\n }\n ans\n }\n}\n```\n\n*C++*\n```\nclass Solution {\npublic:\n using VI = vector<int>;\n VI smallestSubarrays(VI& A, int have = 0, int need = 0) {\n int N = A.size();\n VI ans(N);\n VI last(32); // last index of each 0..31 bit set (what we need to be added onto what we have)\n for (auto i{ N - 1 }; 0 <= i; --i) {\n auto j = i;\n have = A[i];\n need = A[i] | need;\n for (auto k{ 0 }; k < 32; ++k) {\n if (have & (1 << k)) last[k] = i;\n if (need & (1 << k)) j = max(j, last[k]);\n }\n ans[i] = j - i + 1; // +1 for i..j inclusive\n }\n return ans;\n }\n};\n```
| 1 | 0 |
[]
| 1 |
smallest-subarrays-with-maximum-bitwise-or
|
Smallest Subarrays With Maximum Bitwise OR
|
smallest-subarrays-with-maximum-bitwise-8phqu
|
Code
|
srinivas_lingampelli
|
NORMAL
|
2025-03-25T15:14:19.202290+00:00
|
2025-03-25T15:14:19.202290+00:00
| 4 | false |
# Code
```java []
class Solution {
public int[] smallestSubarrays(int[] nums) {
int n = nums.length;
int[] ans = new int[n];
int []last=new int[30];
for (int i = n-1; i >=0; i--) {
ans[i]=1;
for(int j=0;j<30;j++)
{
if((nums[i] & (1<<j))>0)
{
last[j]=i;
}
ans[i]=Math.max(ans[i],last[j]-i+1);
}
}
return ans;
}
}
```
| 0 | 0 |
['Java']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
Segment Tree Solution
|
segment-tree-solution-by-sanjay2108-02uc
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
sanjay2108
|
NORMAL
|
2025-03-03T14:23:16.660995+00:00
|
2025-03-03T14:23:16.660995+00:00
| 3 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
struct SegmentTree {
int n;
vector<int> tree;
// Constructor: builds the tree from the given data vector.
SegmentTree(const vector<int>& data) {
n = data.size();
tree.resize(4 * n, 0);
build(data, 1, 0, n - 1);
}
// Recursively build the segment tree.
void build(const vector<int>& data, int node, int start, int end) {
if(start == end) {
tree[node] = data[start]; // Leaf node holds the original array element.
} else {
int mid = (start + end) / 2;
build(data, 2 * node, start, mid);
build(data, 2 * node + 1, mid + 1, end);
// Internal node holds the bitwise OR of its two children.
tree[node] = tree[2 * node] | tree[2 * node + 1];
}
}
// Utility function to query the tree for range [l, r].
int query(int node, int start, int end, int l, int r) {
// If current segment is completely outside the query range.
if(r < start || end < l)
return 0; // 0 is the identity for bitwise OR.
// If current segment is completely inside the query range.
if(l <= start && end <= r)
return tree[node];
// Otherwise, query both children and combine the results.
int mid = (start + end) / 2;
int left_query = query(2 * node, start, mid, l, r);
int right_query = query(2 * node + 1, mid + 1, end, l, r);
return left_query | right_query;
}
// Public query interface: returns the bitwise OR of elements in the range [l, r].
int query(int l, int r) {
return query(1, 0, n - 1, l, r);
}
};
public:
vector<int> smallestSubarrays(vector<int>& nums) {
SegmentTree segTree(nums);
int n=nums.size();
vector<int> suff(n);
suff[n-1]=nums[n-1];
for(int i=n-2;i>=0;--i){
suff[i]=suff[i+1]|nums[i];
}
vector<int> ans(n);
for(int i=0;i<n;++i){
int exp=suff[i];
int low=1,high=n-i;
while(low<=high){
int mid=(low+high)/2;
if(segTree.query(i, i+mid-1)<exp){
low=mid+1;
}
else{
high=mid-1;
}
}
ans[i]=low;
}
return ans;
}
};
```
| 0 | 0 |
['Array', 'Binary Search', 'Sliding Window', 'C++']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
2411. Smallest Subarrays With Maximum Bitwise OR
|
2411-smallest-subarrays-with-maximum-bit-yk2x
|
IntuitionDO ITApproachstick to BF forget opti for now!Complexity
Time complexity:O(n * 32)
Space complexity:o(32)
Code
|
vg15o2
|
NORMAL
|
2025-02-14T15:17:45.054860+00:00
|
2025-02-14T15:17:45.054860+00:00
| 11 | false |
# Intuition
DO IT
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
stick to BF forget opti for now!
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:O(n * 32)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:o(32)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def smallestSubarrays(self, nums: List[int]) -> List[int]:
n = len(nums)
last = [0] * 32 # Store last occurrence of each bit
ans = [1] * n # Initialize with minimum possible length
# Process from right to left
for i in range(n - 1, -1, -1):
# Update last occurrence for current number's bits
for j in range(32):
if nums[i] & (1 << j):
last[j] = i
# For current position, extend to rightmost bit needed
max_last = i
for j in range(32):
max_last = max(max_last, last[j])
ans[i] = max_last - i + 1
return ans
```
| 0 | 0 |
['Python3']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
Ruby O(n) counting last seen index for each bit
|
ruby-on-counting-last-seen-index-for-eac-jrna
|
ApproachGo through the nums array in reverse order. Save the last seen position of each bit. For each position, calculate the distance between the current posit
|
adrianov
|
NORMAL
|
2025-01-20T11:11:45.488250+00:00
|
2025-01-20T11:11:45.488250+00:00
| 2 | false |
# Approach
<!-- Describe your approach to solving the problem. -->
Go through the nums array in reverse order. Save the last seen position of each bit. For each position, calculate the distance between the current position and the index of each set bit. Use the maximum distance, when all bits are set, as the result for the current index.
# Code
```ruby []
# @param {Integer[]} nums
# @return {Integer[]}
def smallest_subarrays(nums)
n = nums.length
# Calculate the smallest subarray length for each position
result = Array.new(n, 1)
last_seen = Array.new(32, -1)
(n - 1).downto(0) do |i|
nums[i].bit_length.times do |bit|
last_seen[bit] = i if nums[i][bit] == 1
end
max_index = i
last_seen.each do |index|
max_index = [max_index, index].max if index != -1
end
result[i] = max_index - i + 1
end
result
end
```
| 0 | 0 |
['Ruby']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
Easy Python Solution
|
easy-python-solution-by-vidhyarthisunav-ay6y
|
Code
|
vidhyarthisunav
|
NORMAL
|
2025-01-16T22:38:20.260376+00:00
|
2025-01-16T22:38:20.260376+00:00
| 10 | false |
# Code
```python3 []
class Solution:
def smallestSubarrays(self, nums: List[int]) -> List[int]:
n = len(nums)
last_seen = [-1] * 32
res = [1] * n
for i in range(n - 1, -1, -1):
for bit in range(32):
if nums[i] & (1 << bit):
last_seen[bit] = i
farthest = i
for bit in range(32):
if last_seen[bit] != -1:
farthest = max(farthest, last_seen[bit])
res[i] = farthest - i + 1
return res
```
| 0 | 0 |
['Python3']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
Sliding Window + Array of Set Bits. Time: O(nlogM), Space: O(logM)
|
sliding-window-array-of-set-bits-time-on-d8yo
|
IntuitionThe maximum OR value starting at index, i, will be the subarray going till the end of the array. We will need to use a sliding window with an array of
|
iitjsagar
|
NORMAL
|
2024-12-19T23:26:14.411318+00:00
|
2024-12-19T23:26:14.411318+00:00
| 2 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The maximum OR value starting at index, i, will be the subarray going till the end of the array. We will need to use a sliding window with an array of set bits to ensure we are not losing any set bits when we reduce the window size by moving right side pointer left.
# Complexity
- Time complexity: $$O(nlogM)$$
- n: length of array
- M: OR value of all elements in the array. With the current approach, we will need to iterate through the bit array thrice for every element. Size of bit array will be log M.
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(logM)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
Size of bit array
# Code
```python []
class Solution(object):
def smallestSubarrays(self, nums):
"""
:type nums: List[int]
:rtype: List[int]
"""
max_num = 0
for num in nums:
max_num = max_num | num
if max_num == 0:
return [1]*len(nums)
#print max_num
cur = max_num
count = 0
while cur > 0:
count += 1
cur >>= 1
bit_arr = [0]*count
max_so_far = 0
r = len(nums)-1
res = [0]*len(nums)
for i in range(len(nums)-1,-1,-1):
cur = nums[i]
idx = 0
while cur > 0:
if cur & 1:
bit_arr[idx] += 1
cur >>= 1
idx += 1
while r > i:
cur = nums[r]
idx = 0
canSkip = True
while cur > 0:
if cur & 1:
if bit_arr[idx] <= 1:
canSkip = False
break
cur >>= 1
idx += 1
if canSkip:
cur = nums[r]
idx = 0
while cur > 0:
if cur & 1:
bit_arr[idx] -= 1
cur >>= 1
idx += 1
r -= 1
else:
break
res[i] = r-i+1
return res
```
| 0 | 0 |
['Python']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
C++ || Bitwise Sliding Window
|
c-bitwise-sliding-window-by-twilightfox-whe3
| null |
twilightfox
|
NORMAL
|
2024-12-12T22:34:32.440441+00:00
|
2024-12-12T22:34:32.440441+00:00
| 6 | false |
# Intuition\nThe Bitwise OR operation strictly increases in reverse order. e.g.\n``` \nInput: nums = [4,1,2]\nBitwise maximum OR: [7,3,2] \n```\nWe should iterate through the array `nums` in reverse, because if we also store the last index we see each bit, we can now find the right end of the subarray in O(1) time.\n\n# Approach\n\n n == nums.length\n 1 <= n <= 10 000\n 0 <= nums[i] <= 1 000 000 000\n1. Initialise a `largest` bitset with 31 bits, to store nums[i]\n2. Initialise a `bits` vector to store the last index we see any bit\n3. Iterate through the `nums` array backwards, updating `bits` and `largest` for each element, then checking the minimal subarray size using `bits`\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n\n\n# Code\n```cpp []\nclass Solution {\npublic:\n vector<int> smallestSubarrays(const vector<int>& nums) {\n vector<int> ans;\n ans.reserve(nums.size());\n bitset<31> largest;\n vector<int> bits(31, nums.size() - 1);\n\n // O(n)\n for (int i = nums.size() - 1; i >= 0; i--) {\n // O(1) \n int temp = nums[i], counter = 0;\n while (temp != 0) {\n if (temp & 1 == 1) {\n largest.set(counter);\n bits[counter] = i;\n }\n counter++;\n temp >>= 1;\n }\n \n // O(1)\n int right = 0;\n for (int j = 0; j < 31; j++) {\n if (largest.test(j)) {\n right = max(right, bits[j]);\n }\n }\n\n // O(1)\n ans.push_back(max(right - i + 1, 1));\n }\n\n // O(n)\n reverse(ans.begin(), ans.end());\n return ans;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
Most optimal O(N) - time and O(1) space solution NO Binary Search everything explained
|
most-optimal-on-time-and-o1-space-soluti-8rjp
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
ResilientWarrior
|
NORMAL
|
2024-11-22T08:49:09.547917+00:00
|
2024-11-22T08:49:09.547951+00:00
| 33 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def smallestSubarrays(self, nums: List[int]) -> List[int]:\n\n\n size = len(nums)\n minimum_subarr_size = [-1]*size \n\n # represent every set bits in your dictionary \n # to avoided checking every time if the ith \n # set bit is in our last_seen index or not \n last_seen = {i:-1 for i in range(32)} \n\n # an edge case where the end elements are zeros \n # since zero has no set bits \n size -= 1\n while size > -1 and nums[size] == 0: \n minimum_subarr_size[size] = 1 \n size -= 1\n\n # we start from the end and \n # traverse backwards \n # since we only care about values to the right of current index. \n for i in range(size,-1, -1): \n num = nums[i]\n j = 31 \n # find the set bits \n while num: \n if num & 1: \n last_seen[j] = i \n num >>= 1 \n j -= 1 \n \n # our minimum_subarr_size would be index of least recently seen \n # set bit plus one minus i or (i.e the length of subarray between)\n # i and least recently seen set bit index \n minimum_subarr_size[i] = (max(last_seen.values()) +1) - i\n return minimum_subarr_size\n\n\n\n # Time: O(N)\n # space: O(N) - used for minimum_subarr_size array \n # we can optimize the space complexity to O(1) \n # by updating the original array or (i.e)\n # nums[i] = (max(last_seen.values()) +1) - i\n # finally retrun nums \n```
| 0 | 0 |
['Array', 'Hash Table', 'Bit Manipulation', 'Sliding Window', 'Python', 'C++', 'Python3']
| 1 |
smallest-subarrays-with-maximum-bitwise-or
|
O(32N) C++ solution using hash map
|
o32n-c-solution-using-hash-map-by-mongli-b5x1
|
Intuition\nThe intuition in some of these bit related question is that we have a fixed number of bits (30 in this case as max value is 10^9). So storing a hashm
|
monglian_monkey
|
NORMAL
|
2024-11-17T14:37:08.525646+00:00
|
2024-11-17T14:37:08.525673+00:00
| 3 | false |
# Intuition\nThe intuition in some of these bit related question is that we have a fixed number of bits (30 in this case as max value is 10^9). So storing a hashmap might be a good idea.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe idea is to first get a vector maxor which stores max possible or for each element. Then we try to reach this max value in a single loop with the help of a hash map. We need the hash map to store the bit values after adding/removing each element. We remove the bits of the element when we remove it and we update our cur or value. \n\n\n# Complexity\n- Time complexity:\nO(32N)\n\n- Space complexity:\nO(N)\n\n# Code\n```cpp []\nclass Solution {\npublic:\n vector<int> smallestSubarrays(vector<int>& nums) {\n int n=nums.size();\n std::vector<int>maxor(n); \n std::vector<int>resArr(n,-1); \n int res; \n int curor=0; \n for(int i=n-1;i>=0;i--)\n {\n maxor[i]=curor | nums[i];\n curor=maxor[i];\n }\n\n int l=0;\n int r=0;\n std::unordered_map<int,int>map;\n int cur=0;\n\n while(resArr[n-1]==-1)\n {\n printf("in while; l= %d and r=%d\\n",l,r);\n if(r<n)\n {\n cur |= nums[r];\n std::bitset<32>bin(nums[r]);\n for(int j=0;j<32;j++)\n {\n map[j]+=bin[j];\n }\n }\n\n while(l<n && cur==maxor[l])\n {\n res=r-l+1;\n resArr[l]=res<=0?1:res;\n int toremove=nums[l];\n std::bitset<32>rem(toremove);\n for(int j=0;j<32;j++)\n {\n if(map[j]==1 && rem[j]==1)\n {\n printf("TO BE REMOVED!!!!!!!!!!! j = %d\\n",j);\n cur-=std::pow(2,j);\n }\n map[j]-=rem[j];\n }\n l+=1;\n }\n \n // for(const auto&pairs: map)\n // {\n // std::cout<<pairs.first<<":"<<pairs.second<<" ";\n // }\n // std::cout<<std::endl;\n // printf("curvalue: %d\\n",cur);\n // printf("resArr:\\n");\n // for(const auto&elem: resArr)\n // {\n // std::cout<<elem<<" ";\n // }\n if(l<n && cur<maxor[l])\n {\n r+=1;\n }\n }\n \n\n for(const auto&elem: maxor)\n {\n std::cout<<elem<<" ";\n }\n return resArr;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
Using vector | in 32*O(n) time complexity | O(n) SC
|
using-vector-in-32on-time-complexity-on-oxbd2
|
Intuition \n Describe your first thoughts on how to solve this problem. \nWe can count bits of every num in nums in a vector.\n\n# Approach \n Describe your app
|
Developer_Ashish_1234
|
NORMAL
|
2024-11-08T16:46:00.057058+00:00
|
2024-11-08T16:46:00.057084+00:00
| 1 | false |
## Intuition \n<!-- Describe your first thoughts on how to solve this problem. -->\nWe can count bits of every num in nums in a vector.\n\n# Approach \n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: 32 * O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n\nint f1(vector<int> &v,int x){\n int cntor = 0;\n for(int i = 0;i<32;i++){\n if(x & (1<<i)) v[i]++;\n }\n for(int i = 0;i<32;i++) {\n if(v[i]>0) cntor |= (1<<i);\n }\n return cntor;\n}\n\nint f2(vector<int> &v,int x){\n int cntor = 0;\n for(int i = 0;i<32;i++){\n if(x & (1<<i)) v[i]--;\n }\n for(int i = 0;i<32;i++) {\n if(v[i]>0) cntor |= (1<<i);\n }\n return cntor;\n}\n\n vector<int> smallestSubarrays(vector<int>& nums) {\n int n = nums.size();\n if(n==1) return {1};\n vector<int>ans(n,1);\n vector<int> arr(n);\n arr[n-1] = nums[n-1];\n for(int i = n-2;i>=0;i--){\n arr[i] = arr[i+1] | nums[i];\n }\n for(int i = 0;i<n;i++){\n cout<<arr[i]<<" ";\n }\n\n int maxor = 0;\n for(int n : nums) maxor = maxor | n;\n int i = 0,j = 0;\n int cntor = 0;\n vector<int> v(32,0);\n while(i<n){\n\n while(j<n){\n if(cntor == arr[i]) {\n \n break;\n }\n cntor = f1(v,nums[j]);\n j++;\n }\n ans[i] = j-i;\n if(arr[i]==0 ) ans[i] = 1;\n cntor = f2(v,nums[i]);\n\n i++;\n }\n return ans;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
Linear time solution without binary search and additional space
|
linear-time-solution-without-binary-sear-04or
|
Intuition\nFirstly i think how to reuse previous result. But starting from beginning gives only O(n^2) solution. Because i think about increasing sequnce of num
|
igoryan
|
NORMAL
|
2024-11-03T17:00:56.966086+00:00
|
2024-11-03T17:00:56.966115+00:00
| 1 | false |
# Intuition\nFirstly i think how to reuse previous result. But starting from beginning gives only $$O(n^2)$$ solution. Because i think about increasing sequnce of numbers after applying OR operation. And using binary search was helped to find nearest max number.\n\nAfter that i gave time limit exceeded and began thinnking about improving. And finally i think to use sliding window and reach linear time. I noticed that last number is trivial case and we can move window from back to the beginning.\n\n# Approach\nI count bits count in each position of numbers added to sliding window. Function starts from trivial case when last number is max and subarray starts from last position. In each step sliding window moved left and right border reduced if needed. Solution populated from the end.\n\n# Complexity\n- Time complexity:\n$$O(n)$$ moving window is has linear time\n\n- Space complexity:\n$$O(1)$$ we just store answer (it\'s included?) and sliding window stores array of bits positions\n\n# Code\n```cpp []\n#include <vector>\n#include <array>\n#include <algorithm>\n\nstruct SlidingWindow {\n std::array<int, 32> bit_count_in_pos{0};\n\n // returns true if increase number\n bool Add(int num) {\n bool res = false;\n int pos = 0;\n while (num) {\n if (num % 2) {\n res |= bit_count_in_pos[pos] == 0;\n ++bit_count_in_pos[pos];\n }\n ++pos;\n num >>= 1;\n }\n return res;\n }\n \n // returns true if we lost some bit\n bool Delete(int num) {\n bool res = false;\n int pos = 0;\n while (num) {\n if (num % 2) {\n --bit_count_in_pos[pos];\n res |= bit_count_in_pos[pos] == 0;\n }\n ++pos;\n num >>= 1;\n }\n return res;\n }\n};\n\nclass Solution {\npublic:\n std::vector<int> smallestSubarrays(std::vector<int>& nums) {\n std::vector<int> res(nums.size());\n res.back() = 1;\n SlidingWindow sw;\n sw.Add(nums.back());\n int right_border = nums.size() - 1;\n // we start from the end to dynamic programming approach\n for (int left_border = nums.size() - 2; left_border >= 0; --left_border) {\n sw.Add(nums[left_border]);\n while (left_border < right_border) {\n if (sw.Delete(nums[right_border])) {\n // don\'t move, we lost some bit\n sw.Add(nums[right_border]);\n break;\n }\n --right_border;\n }\n res[left_border] = right_border - left_border + 1;\n }\n return res;\n }\n};\n```
| 0 | 0 |
['Dynamic Programming', 'Sliding Window', 'C++']
| 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.