question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
maximum-distance-between-a-pair-of-values
|
Easy cpp,python code using two pointer approach
|
easy-cpppython-code-using-two-pointer-ap-qwz5
|
Intuition\n Describe your first thoughts on how to solve this problem. \nThe goal is to find the maximum distance j - i such that n1[i] <= n2[j]. Since both arr
|
sampath4292
|
NORMAL
|
2024-10-11T08:13:05.669725+00:00
|
2024-10-11T08:13:05.669759+00:00
| 33 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe goal is to find the maximum distance j - i such that n1[i] <= n2[j]. Since both arrays n1 and n2 are sorted in non-increasing order, we can utilize the two-pointer technique to efficiently compute the result.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Two Pointers (i and j):\n\n- i starts at the beginning of n1, representing the current element in n1.\n- j starts at the beginning of n2, representing the current element in n2.\n2. Condition Check:\n\n- For each i, if n1[i] > n2[j], increment i because this is not a valid pair (since n1[i] is greater than n2[j]).\n- If n1[i] <= n2[j], calculate the distance j - i and update the maximum distance x. \nThen increment j to try and find a larger distance.\n3. Termination:\n- The loop continues as long as both i and j are within the bounds of their respective arrays.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nSince both pointers traverse through the arrays once without backtracking, the time complexity is O(n), where n is the size of the arrays. This is efficient\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1), as we only use a few extra variables.\n\n# Code\n\n```python []\nclass Solution:\n def maxDistance(self, n1: List[int], n2: List[int]) -> int:\n x = 0\n i = 0\n j = 0\n \n while i < len(n1) and j < len(n2):\n if n1[i] > n2[j]:\n i += 1 \n else:\n x = max(x, j - i) \n j += 1 \n return x\n\n```\n\n```cpp []\nclass Solution {\npublic:\n int maxDistance(vector<int>& n1, vector<int>& n2) {\n int x=0,i=0,j=0;\n while(i<n1.size() && j<n2.size())\n {\n if(n1[i]>n2[j])\n {\n i++;\n }else\n {\n x=max(x,j-i);\n j++;\n }\n }\n return x;\n }\n};\n```
| 1 | 0 |
['Array', 'Two Pointers', 'C++', 'Python3']
| 0 |
maximum-distance-between-a-pair-of-values
|
SIMPLE TWO-POINTER C++ SOLUTION
|
simple-two-pointer-c-solution-by-jeffrin-ajxv
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Jeffrin2005
|
NORMAL
|
2024-07-23T12:38:53.496842+00:00
|
2024-07-23T12:39:15.171202+00:00
| 145 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:o(n+m)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:o(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n#define ll long long \nclass Solution {\npublic:\n int maxDistance(vector<int>& nums1, vector<int>& nums2) {\n int n = nums1.size();\n int m = nums2.size();\n int i=0;\n int j =0; \n int ans = 0; \n while(i < n && j < m){\n if(nums1[i] > nums2[j])\n i++;\n else{ // nums1[i] <= nums2[j]\n ans = max(ans ,j - i);\n j++;\n }\n }\n return ans;\n }\n};\n```
| 1 | 0 |
['C++']
| 0 |
maximum-distance-between-a-pair-of-values
|
C++ || EASY || Two Pointers || TC=O(n) && SC=O(1)
|
c-easy-two-pointers-tcon-sco1-by-flamexu-u8h4
|
Intuition\nAs both the array are in decreasing order;\nSo we know the that if we take an element form nums1 , and find its it\'s insertion point in array nums2
|
FlameXuser
|
NORMAL
|
2023-08-30T10:04:42.592154+00:00
|
2023-08-30T10:10:48.309886+00:00
| 43 | false |
# Intuition\nAs both the array are in decreasing order;\nSo we know the that if we take an element form nums1 , and find its it\'s insertion point in array nums2 without breaking sorting manner we can get the longest distance for that point;\nWhat i mean by insertion point i.e where it can be add to maintain sorting manner\nFor this we can go for 2 pointers; \n\n# Approach\nWe will take 2 pointer lets assume p1 & p2;\nif(nums1[p1]>nums2[p2]) p1++;\notherwise we will store the max value of p2-p1 and increase p2 by 1\nSo getting index upto which point its nums2[p2]>nums1[p1];\n\n# Complexity\n- Time complexity:\nO(n*m)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution {\npublic:\n int maxDistance(vector<int>& nums1, vector<int>& nums2) {\n int n=nums1.size();\n int ans=0,p1=0,p2=0;\n while(p1<nums1.size() && p2<nums2.size()){\n if(nums1[p1]>nums2[p2])\n p1++;\n else{\n ans=max(ans,p2-p1);\n p2++;\n }\n }\n return ans;\n }\n};\n```
| 1 | 0 |
['Two Pointers', 'C++']
| 0 |
maximum-distance-between-a-pair-of-values
|
Simple easy solution, beats 99% ✅✅
|
simple-easy-solution-beats-99-by-vaibhav-j75y
|
\n# Complexity\n- Time complexity: O(n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(1)\n Add your space complexity here, e.g. O(n) \n\n
|
vaibhav2112
|
NORMAL
|
2023-08-21T13:59:15.387130+00:00
|
2023-08-21T13:59:15.387157+00:00
| 136 | false |
\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int maxDistance(vector<int>& nums1, vector<int>& nums2) {\n int i = 0, j = 0, m = nums1.size(), n = nums2.size();\n int ans = 0;\n while(i<m && j<n){\n if(nums2[j] >= nums1[i]){\n ans = max(ans,(j-i));\n j++;\n }\n else{\n i++;\n }\n }\n return ans;\n }\n};\n```
| 1 | 0 |
['Two Pointers', 'C++']
| 0 |
maximum-distance-between-a-pair-of-values
|
100% BEATS Java Solutions🔥|| Clean and easy to understand code|| look at once
|
100-beats-java-solutions-clean-and-easy-6t4ev
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
L005er22
|
NORMAL
|
2023-03-27T14:25:17.761367+00:00
|
2023-03-27T14:25:17.761399+00:00
| 590 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int maxDistance(int[] nums1, int[] nums2) {\n int diff = 0;\n for(int i = 0;i<nums1.length;i++){\n int start = i;\n int end = nums2.length-1;\n while(start <= end){\n int mid = start+(end-start)/2;\n if(nums1[i] <= nums2[mid]){\n diff = Math.max(diff, mid-i);\n start = mid+1;\n }\n else{\n end = mid-1;\n }\n }\n }\n return diff;\n }\n}\n```\nplease upvote this for better solution of other questions\n
| 1 | 0 |
['Two Pointers', 'Binary Search', 'Java']
| 0 |
maximum-distance-between-a-pair-of-values
|
Easy Java Solution Using Two pointers
|
easy-java-solution-using-two-pointers-by-q3w4
|
\n\n# Code\n\nclass Solution {\n public int maxDistance(int[] nums1, int[] nums2) {\n int n = nums1.length;\n int n1 = nums2.length;\n i
|
agdarshit19
|
NORMAL
|
2023-03-15T08:49:05.638959+00:00
|
2023-03-15T08:49:05.639000+00:00
| 395 | false |
\n\n# Code\n```\nclass Solution {\n public int maxDistance(int[] nums1, int[] nums2) {\n int n = nums1.length;\n int n1 = nums2.length;\n if(n == 1 && n1 == 1)\n {\n return 0;\n }\n int i = 0;\n int j = 1;\n int max = 0;\n while(i < n && j < n1)\n {\n if(i <= j && nums1[i] <= nums2[j])\n {\n max = Math.max(max , j - i);\n System.out.println(j-i);\n }\n else\n {\n while(i < n && i <= j && nums1[i] > nums2[j])\n {\n i++;\n }\n }\n j++;\n }\n return max;\n }\n}\n```
| 1 | 0 |
['Java']
| 0 |
maximum-distance-between-a-pair-of-values
|
Simple C++ Solution
|
simple-c-solution-by-divyanshu_singh_cs-h7bh
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Divyanshu_singh_cs
|
NORMAL
|
2023-02-18T08:01:11.345161+00:00
|
2023-02-18T08:01:11.345194+00:00
| 673 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int maxDistance(vector<int>& nums1, vector<int>& nums2) {\n int n = nums1.size();\n int m = nums2.size();\n int c=0,i=0,j=0;\n \n while (i < n && j < m)\n if (nums1[i] > nums2[j])\n i++;\n else{\n c = max(c, j - i);\n j++;\n }\n return c;\n \n }\n};\n```
| 1 | 0 |
['C++']
| 0 |
maximum-distance-between-a-pair-of-values
|
C++/ Binary Search /O(nlog n)
|
c-binary-search-onlog-n-by-gagan012-luyz
|
Intuition\nSince both arrays are sorted in a non-increasing way this means that for each value in the first array. We can find the farthest value smaller than i
|
Gagan012
|
NORMAL
|
2023-02-14T12:57:31.893750+00:00
|
2023-02-14T13:02:49.995591+00:00
| 121 | false |
# Intuition\nSince both arrays are sorted in a non-increasing way this means that for each value in the first array. We can find the farthest value smaller than it using binary search.\n\n# Approach\nSimply we use binary search here, we take one by one element of nums1 array and search element greater and equal to in nums2 array. if we found that then we simply take difference of that index with nums1\'s index and store in maxi variable and continue this process and at last we return maxi.\n\n# Complexity\n- Time complexity:\n O(nlog n)\n\n# Code\n```\nclass Solution {\npublic:\n int maxDistance(vector<int>& nums1, vector<int>& nums2) {\n \n int maxi=0;\n for(int i=0;i<nums1.size();i++)\n { \n int l=0;\n int r=nums2.size()-1;\n int target=nums1[i];\n while(l<=r)\n {\n int mid=l+(r-l)/2;\n if(nums2[mid]<target)\n r=mid-1;\n else\n {\n l=mid+1;\n maxi=max(maxi,mid-i);\n }\n }\n }\n return maxi;\n }\n};\n```
| 1 | 0 |
['Binary Search', 'C++']
| 0 |
maximum-distance-between-a-pair-of-values
|
JAVA: 3 solutions : Maximum Distance Between a Pair of Values
|
java-3-solutions-maximum-distance-betwee-2uj6
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Nishant_219
|
NORMAL
|
2023-01-26T09:04:07.127169+00:00
|
2023-01-26T09:04:07.127214+00:00
| 29 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(n^2) --> O( maximum(n,m) ) --> O(nlogn)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(1)\n\n# Code\n```\nclass Solution {\n public int maxDistance(int[] nums1, int[] nums2) {\n\n // int diff=0;\n // for(int i=0 ;i<nums1.length; i++){\n // for(int j=i;j<nums2.length;j++){\n // if(nums1[i]<=nums2[j] && i<=j){\n // diff=Math.max(diff,(j-i));\n // }\n // }\n // }\n // return diff;\n\n//-----------------------------------------------------------\n\n // int i=0;\n // int j=0;\n // int res=0;\n // while(i<nums1.length && j<nums2.length ){\n // if(nums1[i]>nums2[j]){\n // i++;\n // }else{\n // res=Math.max(res,(j-i));\n // j++;\n // }\n // }\n // return res;\n\n//-----------------------------------------------------------\n\n int d = 0;\n for(int i=0;i<nums1.length;i++){\n int start = i;\n int end = nums2.length-1;\n while(start <= end){\n int mid = start + (end-start)/2;\n if(nums1[i] <= nums2[mid]){\n d = Math.max(d,mid-i);\n start = mid+1;\n } else {\n end = mid-1;\n }\n }\n }\n return d;\n\n\n }\n}\n```
| 1 | 0 |
['Two Pointers', 'Binary Search', 'Java']
| 0 |
maximum-distance-between-a-pair-of-values
|
Java Solution, 3 ms, Beats 95%
|
java-solution-3-ms-beats-95-by-abstractc-fevr
|
Code\n\nclass Solution {\n public int maxDistance(int[] nums1, int[] nums2) {\n int i = 0, j = 0, res = 0, n = nums1.length, m = nums2.length;\n
|
abstractConnoisseurs
|
NORMAL
|
2023-01-21T06:26:24.671481+00:00
|
2023-01-21T06:28:26.101126+00:00
| 175 | false |
# Code\n```\nclass Solution {\n public int maxDistance(int[] nums1, int[] nums2) {\n int i = 0, j = 0, res = 0, n = nums1.length, m = nums2.length;\n while (i < n && j < m) {\n if (nums1[i] > nums2[j]) {\n i++;\n }\n else {\n res = Math.max(res, j++ -i);\n }\n }\n return res;\n }\n}\n```
| 1 | 0 |
['Array', 'Two Pointers', 'Binary Search', 'Greedy', 'Java']
| 0 |
maximum-distance-between-a-pair-of-values
|
C++ Binary Search O(nlogm)
|
c-binary-search-onlogm-by-speedyy-b8e1
|
This Binary Search is giving the index of the last value from nums2 which is greater than or equal to nums[i]. Here left = the current i in nums1\n- Time comple
|
speedyy
|
NORMAL
|
2023-01-17T21:23:19.000925+00:00
|
2023-01-17T21:23:58.843799+00:00
| 26 | false |
This Binary Search is giving the index of the last value from nums2 which is greater than or equal to nums[i]. Here left = the current i in nums1\n- Time complexity : O(nlogm)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n```\n\nclass Solution \n{\npublic:\n int binary_search(vector<int> &nums2,int start,int target)\n {\n int left=start,right=nums2.size()-1,mid;\n while(left<=right)\n {\n mid=left+(right-left)/2;\n nums2[mid]>=target? left=mid+1 : right=mid-1;\n }\n return right;\n }\n int maxDistance(vector<int>& nums1, vector<int>& nums2) \n {\n int i=0,j,m=0,num=-1;\n for(i=0;i<nums1.size() && i<nums2.size();i++)\n {\n if(nums1[i]!=num) // IF nums[i]!=nums[i-1]\n {\n j = binary_search(nums2,i,nums1[i]);\n if(j>i) m = max(m,j-i);\n }\n num = nums1[i];\n }\n return m;\n }\n};\n```
| 1 | 0 |
['C++']
| 0 |
maximum-distance-between-a-pair-of-values
|
96% Faster | O(n^2) | Easy Solution✅
|
96-faster-on2-easy-solution-by-d0308-zob7
|
Code\n\nclass Solution:\n def maxDistance(self, nums1: List[int], nums2: List[int]) -> int:\n m, n = len(nums1), len(nums2)\n res = 0\n
|
D0308
|
NORMAL
|
2023-01-13T06:51:44.466841+00:00
|
2023-01-17T18:20:54.323350+00:00
| 31 | false |
# Code\n```\nclass Solution:\n def maxDistance(self, nums1: List[int], nums2: List[int]) -> int:\n m, n = len(nums1), len(nums2)\n res = 0\n j = 0\n for i in range(m):\n while j < n and nums1[i] <= nums2[j]:\n j += 1\n res = max(res, j - 1 - i)\n return res\n```
| 1 | 1 |
['Binary Search', 'Iterator', 'Python3']
| 1 |
maximum-distance-between-a-pair-of-values
|
TypeScript Solution: (Beats 100%) (Two Pointers) (O(M + N)) ✔📜
|
typescript-solution-beats-100-two-pointe-4p5g
|
Approach\nWe will mark the two arrays with p1, p2 then we will try to catch the max gap between i, j.\n\n# Complexity\n- Time complexity: O(n + m)\n\n- Space co
|
adhamniazy
|
NORMAL
|
2023-01-01T18:55:58.044352+00:00
|
2023-01-01T18:55:58.044389+00:00
| 38 | false |
# Approach\nWe will mark the two arrays with `p1`, `p2` then we will try to catch the max gap between `i`, `j`.\n\n# Complexity\n- Time complexity: $$O(n + m)$$\n\n- Space complexity: $$O(1)$$\n\n# Code\n```ts\nfunction maxDistance(nums1: number[], nums2: number[]): number {\n let p1 = 0, p2 = 0, ans = 0;\n while ( p1 < nums1.length && p2 < nums2.length ) {\n\n /* \n If nums1[p1] is larger then we need to go one step\n to decrease nums1[p1]\n */\n if ( nums1[p1] > nums2[p2] ) p1++;\n /*\n check if this diff is the max or not then take the max diff\n */\n else {\n ans = Math.max(ans, p2 - p1);\n p2++;\n }\n }\n\n return ans;\n};\n```
| 1 | 0 |
['Array', 'Two Pointers', 'Greedy', 'TypeScript']
| 1 |
maximum-distance-between-a-pair-of-values
|
c++ | easy to understand | short
|
c-easy-to-understand-short-by-venomhighs-uzqa
|
\n# Code\n\nclass Solution {\npublic:\n int maxDistance(vector<int>& nums1, vector<int>& nums2) {\n int n1 = nums1.size(),n2 = nums2.size(),ans = 0;\
|
venomhighs7
|
NORMAL
|
2022-10-05T12:40:27.487003+00:00
|
2022-10-05T12:40:27.487041+00:00
| 274 | false |
\n# Code\n```\nclass Solution {\npublic:\n int maxDistance(vector<int>& nums1, vector<int>& nums2) {\n int n1 = nums1.size(),n2 = nums2.size(),ans = 0;\n int i = n1-1,j = n2-1;\n while(j>=0 && nums2[j]<nums1[i]){\n j--;\n }\n while(j>=0){\n while(i>=0 && nums1[i]<=nums2[j]){\n i--;\n }\n ans = max(j-i-1,ans);\n j--;\n }\n return ans;\n }\n};\n```
| 1 | 0 |
['C++']
| 0 |
maximum-distance-between-a-pair-of-values
|
90% TIME AND 80% SPACE BEATS || C++ || SIMPLE || TIME O(n+m)
|
90-time-and-80-space-beats-c-simple-time-t6bq
|
\nclass Solution {\npublic:\n int maxDistance(vector<int>& nums1, vector<int>& nums2) {\n int n1 = nums1.size(),n2 = nums2.size(),ans = 0;\n in
|
abhay_12345
|
NORMAL
|
2022-09-30T15:47:25.904706+00:00
|
2022-09-30T15:47:25.904748+00:00
| 300 | false |
```\nclass Solution {\npublic:\n int maxDistance(vector<int>& nums1, vector<int>& nums2) {\n int n1 = nums1.size(),n2 = nums2.size(),ans = 0;\n int i = n1-1,j = n2-1;\n while(j>=0 && nums2[j]<nums1[i]){\n j--;\n }\n // cout<<1;\n while(j>=0){\n while(i>=0 && nums1[i]<=nums2[j]){\n i--;\n }\n ans = max(j-i-1,ans);\n j--;\n }\n return ans;\n }\n};\n```
| 1 | 0 |
['Two Pointers', 'C', 'C++']
| 0 |
maximum-distance-between-a-pair-of-values
|
C++ || Two-Pointers || Easy
|
c-two-pointers-easy-by-vibrant_coder-lwqi
|
\nint maxDistance(vector<int>& nums1, vector<int>& nums2) {\n int i=0,j=0,m=0;\n while(i<nums1.size() && j<nums2.size()){\n if(nums1[i]
|
vibrant_CoDeR
|
NORMAL
|
2022-09-25T18:47:29.390482+00:00
|
2022-09-25T18:47:29.390516+00:00
| 308 | false |
```\nint maxDistance(vector<int>& nums1, vector<int>& nums2) {\n int i=0,j=0,m=0;\n while(i<nums1.size() && j<nums2.size()){\n if(nums1[i]<=nums2[j]){\n m=max(m,j-i);\n j++;\n }\n else if(nums1[i]>nums2[j]){\n i++;\n while(i>j)\n j++; \n }\n }\n return m;\n```\t\t\n\t\t\n
| 1 | 0 |
['Two Pointers', 'C']
| 2 |
maximum-distance-between-a-pair-of-values
|
✅✅Faster || Easy To Understand || C++ Code
|
faster-easy-to-understand-c-code-by-__kr-9ziy
|
Approach 1 :- Using Binary Seacrh\n\n Time Complexity :- O(NlogN)\n\n Space Complexity :- O(1)\n\n\nclass Solution {\npublic:\n int maxDistance(vector<int>&
|
__KR_SHANU_IITG
|
NORMAL
|
2022-09-14T05:41:08.307259+00:00
|
2022-09-14T07:10:46.080149+00:00
| 80 | false |
* ***Approach 1 :- Using Binary Seacrh***\n\n* ***Time Complexity :- O(NlogN)***\n\n* ***Space Complexity :- O(1)***\n\n```\nclass Solution {\npublic:\n int maxDistance(vector<int>& nums1, vector<int>& nums2) {\n \n int n1 = nums1.size();\n \n int n2 = nums2.size();\n \n int maxi = 0;\n \n for(int i = 0; i < n1; i++)\n {\n // find the element from right side which is greater than equal to nums1[i]\n \n int idx = lower_bound(nums2.rbegin(), nums2.rend(), nums1[i]) - nums2.rbegin();\n \n // find the index of that number from right side\n \n idx = n2 - idx - 1;\n \n // update maxi\n \n if(idx >= i)\n {\n maxi = max(maxi, idx - i);\n }\n }\n \n return maxi;\n }\n};\n```\n\n* ***Approach 2 :- Using Two Pointer***\n\n* ***Time Complexity :- O(N)***\n\n* ***Space Complexity :- O(1)***\n\n```\nclass Solution {\npublic:\n int maxDistance(vector<int>& nums1, vector<int>& nums2) {\n \n int n1 = nums1.size();\n \n int n2 = nums2.size();\n \n int maxi = 0;\n \n int i = 0;\n \n int j = 0;\n \n while(i < n1 && j < n2)\n {\n // if element of nums1 is less than element of nums2\n \n // just increment the i\n \n if(nums1[i] > nums2[j])\n {\n i++;\n }\n else\n {\n j++;\n }\n \n // update maxi\n \n maxi = max(maxi, j - i - 1);\n }\n \n return maxi;\n }\n};\n```
| 1 | 0 |
['Two Pointers', 'C', 'Binary Tree', 'C++']
| 0 |
maximum-distance-between-a-pair-of-values
|
C++ || Easy ✅ || Two-Pointers✅ || Shortest and Fast 🔥
|
c-easy-two-pointers-shortest-and-fast-by-8uz1
|
\nclass Solution {\npublic:\n int maxDistance(vector<int>& nums1, vector<int>& nums2) {\n int ans = 0;\n int n = nums1.size(), m = nums2.size()
|
UjjwalAgrawal
|
NORMAL
|
2022-09-12T13:15:40.593952+00:00
|
2022-09-12T13:15:40.593999+00:00
| 62 | false |
```\nclass Solution {\npublic:\n int maxDistance(vector<int>& nums1, vector<int>& nums2) {\n int ans = 0;\n int n = nums1.size(), m = nums2.size();\n int i = n-1;\n \n for(int j = m - 1; j>=ans; j--){\n while(i>=0 && nums1[i] <= nums2[j])\n i--;\n \n if(i<n-1 && nums1[i+1] <= nums2[j])\n ans = max(ans, j-i-1);\n }\n \n return ans;\n }\n};\n```
| 1 | 0 |
['Two Pointers', 'C']
| 0 |
maximum-distance-between-a-pair-of-values
|
C++ || Easy Solution ✅🤷♂️
|
c-easy-solution-by-mahesh_1729-86wd
|
class Solution {\npublic:\n int maxDistance(vector& nums1, vector& nums2) {\n \n int i = 0, j = 0, ans = 0;\n while(i < nums1.size() &&
|
mahesh_1729
|
NORMAL
|
2022-09-07T17:40:36.678426+00:00
|
2022-09-07T17:40:36.678468+00:00
| 41 | false |
class Solution {\npublic:\n int maxDistance(vector<int>& nums1, vector<int>& nums2) {\n \n int i = 0, j = 0, ans = 0;\n while(i < nums1.size() && j < nums2.size()){\n if(nums1[i] > nums2[j])\n i++;\n else{\n ans = max(ans, j-i);\n j++;\n }\n }\n return ans;\n }\n};
| 1 | 0 |
['C', 'Binary Tree', 'C++']
| 0 |
maximum-distance-between-a-pair-of-values
|
[JAVA] 3ms two pointer easy solution
|
java-3ms-two-pointer-easy-solution-by-ju-qkx1
|
\nclass Solution {\n public int maxDistance(int[] nums1, int[] nums2) {\n int i = 0, j = 0, res = 0;\n while(i < nums1.length && j < nums2.length)
|
Jugantar2020
|
NORMAL
|
2022-08-22T15:41:43.140537+00:00
|
2022-08-22T15:41:43.140574+00:00
| 48 | false |
```\nclass Solution {\n public int maxDistance(int[] nums1, int[] nums2) {\n int i = 0, j = 0, res = 0;\n while(i < nums1.length && j < nums2.length) {\n if(nums1[i] > nums2[j])\n i ++;\n \n else \n res = Math.max(res, j++ - i);\n }\n return res;\n }\n}\n```\n# PLEASE UPVOTE IF IT WAS HELPFULL
| 1 | 0 |
['Two Pointers', 'Java']
| 0 |
maximum-distance-between-a-pair-of-values
|
Python Solution || Space complexity better than 98% of submissions
|
python-solution-space-complexity-better-bmka7
|
\nclass Solution:\n def maxDistance(self, nums1: List[int], nums2: List[int]) -> int:\n #\xA0Worst case, we walk through both arrays O(N + M) ~ Time c
|
sotiriG
|
NORMAL
|
2022-08-19T07:36:59.574202+00:00
|
2022-08-19T07:36:59.574244+00:00
| 23 | false |
```\nclass Solution:\n def maxDistance(self, nums1: List[int], nums2: List[int]) -> int:\n #\xA0Worst case, we walk through both arrays O(N + M) ~ Time complexity\n #\xA0Space complexity O(1) as we only allocate 3 free variables\n p1, p2 = 0, 0\n\n maxDiff = 0\n\n while p1 < len(nums1) and p2 < len(nums2):\n\n if nums1[p1] <= nums2[p2]:\n # Correct solution\n maxDiff = max(maxDiff, p2 - p1)\n #\xA0increment p2\n p2 += 1\n\n elif p1 == p2:\n # Event of nums2 being smaller, we need to walk both pointers\n p1 += 1\n p2 += 1\n elif p1 < p2:\n #\xA0walk only p1 because its behind\n p1 += 1\n\n return maxDiff\n```
| 1 | 0 |
['Two Pointers']
| 0 |
maximum-distance-between-a-pair-of-values
|
Java(Binary Search)-Self Explanatory
|
javabinary-search-self-explanatory-by-to-nysu
|
simplest way- Ask if you don\'t understand something\n\n\nclass Solution {\n public int maxDistance(int[] nums1, int[] nums2) {\n int n=nums1.length,m
|
toooolgod33
|
NORMAL
|
2022-08-14T14:10:56.907705+00:00
|
2022-08-14T14:10:56.907749+00:00
| 36 | false |
simplest way- Ask if you don\'t understand something\n\n```\nclass Solution {\n public int maxDistance(int[] nums1, int[] nums2) {\n int n=nums1.length,m=nums2.length,max=0;\n for(int i=0;i<n;i++){\n int l=i,r=m-1,mid=0,target=nums1[i],x=-1;\n while(l<=r){\n if(nums1[i]>nums2[i]) break;\n mid=l+(r-l)/2;\n if(nums2[mid]>=target){\n x=mid;\n l=mid+1;\n }\n else r=mid-1;\n }\n //System.out.println(x);\n max= Math.max(max,x-i);\n }\n return max;\n }\n}\n```
| 1 | 0 |
['Binary Search', 'Java']
| 0 |
maximum-distance-between-a-pair-of-values
|
Simple Python Solution || Beats 99.4%
|
simple-python-solution-beats-994-by-b160-mqfp
|
\n\n\nclass Solution:\n def maxDistance(self, nums1: List[int], nums2: List[int]) -> int:\n ptr1,ptr2, result = 0,0,0\n while ptr1 < len(nums1)
|
b160106
|
NORMAL
|
2022-08-14T09:17:56.253670+00:00
|
2022-08-14T09:17:56.253713+00:00
| 45 | false |
\n\n```\nclass Solution:\n def maxDistance(self, nums1: List[int], nums2: List[int]) -> int:\n ptr1,ptr2, result = 0,0,0\n while ptr1 < len(nums1) and ptr2 < len(nums2):\n while ptr2 < len(nums2) and nums1[ptr1] <= nums2[ptr2]:\n ptr2 += 1\n result = max(result,ptr2-ptr1-1)\n ptr1 += 1\n return result\n```
| 1 | 0 |
['Two Pointers', 'Python']
| 0 |
maximum-distance-between-a-pair-of-values
|
1855. Maximum Distance Between a Pair of Values || JAVA || Easy Understanding
|
1855-maximum-distance-between-a-pair-of-v7rrg
|
\nclass Solution {\n public int maxDistance(int[] nums1, int[] nums2) {\n int i=0,j=0,n=nums1.length,m=nums2.length;\n int max=0;\n while(i
|
Vishwa1909
|
NORMAL
|
2022-07-27T21:02:32.511211+00:00
|
2022-07-27T21:02:32.511248+00:00
| 33 | false |
```\nclass Solution {\n public int maxDistance(int[] nums1, int[] nums2) {\n int i=0,j=0,n=nums1.length,m=nums2.length;\n int max=0;\n while(i<n && j<m)\n {\n if(nums1[i]>nums2[j])\n i++;\n else\n {\n max=Math.max(max,j-i);\n j++;\n }\n }\n return max;\n }\n}\n```\n
| 1 | 0 |
['Java']
| 0 |
maximum-distance-between-a-pair-of-values
|
C++ Easy Solution
|
c-easy-solution-by-honey096-s6ue
|
class Solution {\npublic:\n int maxDistance(vector& nums1, vector& nums2) {\n int i=0,j=0,s,s1;\n s=nums1.size();\n s1=nums2.size();\n
|
honey096
|
NORMAL
|
2022-07-27T21:01:49.910171+00:00
|
2022-07-27T21:01:49.910206+00:00
| 40 | false |
class Solution {\npublic:\n int maxDistance(vector<int>& nums1, vector<int>& nums2) {\n int i=0,j=0,s,s1;\n s=nums1.size();\n s1=nums2.size();\n int max1=0;\n while(i<s && j<s1)\n {\n if(nums1[i]>nums2[j])\n i++;\n else\n {\n max1=max(max1,j-i);\n j++;\n }\n }\n return max1;\n }\n};
| 1 | 0 |
['C']
| 0 |
maximum-distance-between-a-pair-of-values
|
C++ Easy solution
|
c-easy-solution-by-krishgabani7-wjvn
|
\nclass Solution {\npublic:\n int maxDistance(vector<int>& nums1, vector<int>& nums2) {\n int i = 0, j = 0, ans = 0;\n while (i < nums1.size()
|
krishgabani7
|
NORMAL
|
2022-07-26T15:04:58.167291+00:00
|
2022-07-26T15:04:58.167336+00:00
| 19 | false |
```\nclass Solution {\npublic:\n int maxDistance(vector<int>& nums1, vector<int>& nums2) {\n int i = 0, j = 0, ans = 0;\n while (i < nums1.size() && j < nums2.size())\n if (nums1[i] > nums2[j])\n i++;\n else{\n ans = max(ans, j - i);\n j++;\n }\n return ans;\n }\n \n};\n```
| 1 | 0 |
[]
| 0 |
maximum-distance-between-a-pair-of-values
|
c++ code | pure binary search approach | easy to comprehend | short and to the point
|
c-code-pure-binary-search-approach-easy-ww54r
|
class Solution {\npublic:\n int maxDistance(vector& nums1, vector& nums2) {\n int ma_re=0;\n for(int i=0;i<nums1.size();i=i+1)\n {\n
|
prasb279
|
NORMAL
|
2022-07-25T10:07:30.594938+00:00
|
2022-07-25T10:07:30.594980+00:00
| 14 | false |
class Solution {\npublic:\n int maxDistance(vector<int>& nums1, vector<int>& nums2) {\n int ma_re=0;\n for(int i=0;i<nums1.size();i=i+1)\n {\n int low=i;\n int high=nums2.size()-1;\n while(low<=high)\n {\n int mid=low+(high-low)/2;\n if(nums1[i]>nums2[mid])\n {\n high=mid-1;\n }\n else\n if(nums1[i]<=nums2[mid])\n {\n low=mid+1;\n }\n else\n if(low==high)\n break;\n }\n if(low<nums2.size() && low>=0 && nums2[low]==nums1[i])\n {\n ma_re=max(ma_re,low-i);\n }\n else\n {\n ma_re=max(ma_re,low-i-1);\n }\n cout <<ma_re <<" ";\n }\n return ma_re;\n }\n};\n
| 1 | 0 |
['Binary Search']
| 0 |
maximum-distance-between-a-pair-of-values
|
Max Distance Between pair
|
max-distance-between-pair-by-rohit70705-jfa7
|
class Solution {\n public int maxDistance(int[] nums1, int[] nums2) {\n\t\n Brute FOrce Approach -----> Time Limit Exception for long input.\n\t\t\n
|
Rohit70705
|
NORMAL
|
2022-07-24T05:14:15.442736+00:00
|
2022-07-24T05:14:15.442781+00:00
| 38 | false |
class Solution {\n public int maxDistance(int[] nums1, int[] nums2) {\n\t\n Brute FOrce Approach -----> Time Limit Exception for long input.\n\t\t\n int mx =0;\n for(int i = 0;i<nums1.length; i++){\n int diff =0;\n for(int j = i; j<nums2.length; j++){\n if(i<=j && nums1[i]<=nums2[j]) diff = (j-i);\n mx = Math.max(mx,diff);\n } \n }\n return mx;\n//\n\n // Binary Search -----> \n\t\t \n int mx = 0;\n for(int i =0; i<nums1.length; i++){\n int lo = 0;\n int hi = nums2.length-1;\n while(lo<=hi){\n int mid = lo+(hi-lo)/2;\n if(nums2[mid]>=nums1[i]){\n lo = mid+1;\n }else hi = mid-1;\n }\n if(hi<0) continue;\n mx = Math.max(mx,hi-i);\n }\n return mx;\n \n// \n \n // Two Pointer\n\n int i = 0;\n int j = 0;\n int mx =0;\n while(i<nums1.length && j<nums2.length){\n if(nums1[i]>nums2[j])i++;\n else{\n mx = Math.max(mx,j-i);\n j++;\n }\n }\n return mx;\n }\n}\n***Please upvote if you like***
| 1 | 0 |
['Binary Search', 'Java']
| 0 |
maximum-distance-between-a-pair-of-values
|
C++ || Simple Binary Search || Easy to understand
|
c-simple-binary-search-easy-to-understan-4k5b
|
class Solution {\npublic:\n\n int maxDistance(vector& arr1, vector& arr2) {\n int n = arr1.size(), ans = 0;\n \n for(int i = 0; i < n; i
|
rosario1975
|
NORMAL
|
2022-07-22T15:38:09.310968+00:00
|
2022-07-22T15:38:09.311001+00:00
| 47 | false |
class Solution {\npublic:\n\n int maxDistance(vector<int>& arr1, vector<int>& arr2) {\n int n = arr1.size(), ans = 0;\n \n for(int i = 0; i < n; i++){\n int x = arr1[i];\n \n int l = i , h = arr2.size()-1, j = -1;\n \n while(l <= h){\n \n int m = l + (h-l)/2;\n \n if(x <= arr2[m]){\n j = m;\n l = m+1;\n }\n else h = m-1;\n }\n \n ans = max(ans,j-i);\n }\n return ans;\n }\n};
| 1 | 0 |
['C', 'Binary Tree', 'C++']
| 0 |
maximum-distance-between-a-pair-of-values
|
Cpp || Binary Search
|
cpp-binary-search-by-akhilesh_pokale-9ddg
|
Solving by binary search method\n\nc++\n int ans = 0;\n int m = nums1.size(), n = nums2.size();\n for (int i = 0; i < m; ++i) {\n
|
Akhilesh_Pokale
|
NORMAL
|
2022-07-22T04:58:25.173479+00:00
|
2022-07-22T04:58:25.173525+00:00
| 30 | false |
## Solving by binary search method\n\n``` c++\n int ans = 0;\n int m = nums1.size(), n = nums2.size();\n for (int i = 0; i < m; ++i) {\n int left = i, right = n - 1;\n while (left < right) {\n int mid = (left + right + 1) >> 1;\n if (nums2[mid] >= nums1[i]) {\n left = mid;\n } else {\n right = mid - 1;\n }\n }\n ans = max(ans, left - i);\n }\n return ans;\n```
| 1 | 0 |
['Binary Tree']
| 1 |
maximum-distance-between-a-pair-of-values
|
Python || Easy to understand || Binary Search || with extra func
|
python-easy-to-understand-binary-search-d5pxg
|
\ndef maxDistance(self, nums1: List[int], nums2: List[int]) -> int:\n \n \n def check(target, idx):\n l, r = 0, len(nums2
|
fattijenishbek
|
NORMAL
|
2022-07-21T06:42:00.376670+00:00
|
2022-07-21T06:42:00.376703+00:00
| 70 | false |
```\ndef maxDistance(self, nums1: List[int], nums2: List[int]) -> int:\n \n \n def check(target, idx):\n l, r = 0, len(nums2)\n while l<r:\n m=(l+r)//2\n if nums2[m]>=target:\n l=m+1\n else:\n r=m\n return l-1\n \n dic={}\n for i in range(len(nums1)):\n dic[i]=check(nums1[i],i)\n print(dic)\n \n res=0\n for i in range(len(dic)):\n if dic[i]-i>res:\n res=dic[i]-i\n return res\n \n```
| 1 | 0 |
['Binary Tree', 'Python']
| 0 |
maximum-distance-between-a-pair-of-values
|
60% TC and 67% SC easy python solution using binary search
|
60-tc-and-67-sc-easy-python-solution-usi-idvk
|
\ndef maxDistance(self, nums1: List[int], nums2: List[int]) -> int:\n\tdef binary(ele, i):\n\t\tj = len(nums2)-1\n\t\twhile(i < j):\n\t\t\tmid = i+(j-i)//2\n\t\
|
nitanshritulon
|
NORMAL
|
2022-07-12T07:47:19.468714+00:00
|
2022-07-12T07:47:19.468745+00:00
| 122 | false |
```\ndef maxDistance(self, nums1: List[int], nums2: List[int]) -> int:\n\tdef binary(ele, i):\n\t\tj = len(nums2)-1\n\t\twhile(i < j):\n\t\t\tmid = i+(j-i)//2\n\t\t\tif(nums2[mid] >= ele):\n\t\t\t\ti = mid+1\n\t\t\telse:\n\t\t\t\tj = mid-1\n\t\tif(nums2[i] < ele):\n\t\t\treturn i-1\n\t\treturn i\n\tans = 0\n\tfor i in range(len(nums1)):\n\t\tif(i+ans < len(nums2) and nums1[i] <= nums2[i+ans]):\n\t\t\tans = max(ans, binary(nums1[i], i) - i)\n\treturn ans\n```
| 1 | 0 |
['Binary Tree', 'Python', 'Python3']
| 0 |
create-maximum-number
|
Share my greedy solution
|
share-my-greedy-solution-by-dietpepsi-jm2d
|
Many of the posts have the same algorithm. In short we can first solve 2 simpler problem\n\n1. Create the maximum number of one array \n2. Create the maximum nu
|
dietpepsi
|
NORMAL
|
2015-12-24T03:15:47+00:00
|
2018-10-13T17:17:06.217330+00:00
| 80,888 | false |
Many of the posts have the same algorithm. In short we can first solve 2 simpler problem\n\n1. Create the maximum number of one array \n2. Create the maximum number of two array using all of their digits.\n\nFor an long and detailed explanation see my blog [here][1].\n\nThe algorithm is O((m+n)^3) in the worst case. It runs in 22 ms.\n\n**Java**\n\n public int[] maxNumber(int[] nums1, int[] nums2, int k) {\n int n = nums1.length;\n int m = nums2.length;\n int[] ans = new int[k];\n for (int i = Math.max(0, k - m); i <= k && i <= n; ++i) {\n int[] candidate = merge(maxArray(nums1, i), maxArray(nums2, k - i), k);\n if (greater(candidate, 0, ans, 0)) ans = candidate;\n }\n return ans;\n }\n private int[] merge(int[] nums1, int[] nums2, int k) {\n int[] ans = new int[k];\n for (int i = 0, j = 0, r = 0; r < k; ++r)\n ans[r] = greater(nums1, i, nums2, j) ? nums1[i++] : nums2[j++];\n return ans;\n }\n public boolean greater(int[] nums1, int i, int[] nums2, int j) {\n while (i < nums1.length && j < nums2.length && nums1[i] == nums2[j]) {\n i++;\n j++;\n }\n return j == nums2.length || (i < nums1.length && nums1[i] > nums2[j]);\n }\n public int[] maxArray(int[] nums, int k) {\n int n = nums.length;\n int[] ans = new int[k];\n for (int i = 0, j = 0; i < n; ++i) {\n while (n - i + j > k && j > 0 && ans[j - 1] < nums[i]) j--;\n if (j < k) ans[j++] = nums[i];\n }\n return ans;\n }\n\n\n [1]: http://algobox.org/create-maximum-number/
| 389 | 9 |
['Greedy', 'Java']
| 61 |
create-maximum-number
|
C++ 16ms, FASTEST, beats 97%.
|
c-16ms-fastest-beats-97-by-chellya-4ooy
|
The basic idea:\n\nTo create max number of length k from two arrays, you need to create max number of length i from array one and max number of length k-i from
|
chellya
|
NORMAL
|
2016-02-10T13:43:03+00:00
|
2018-10-07T13:34:03.061294+00:00
| 38,916 | false |
The basic idea:\n\nTo create max number of length k from two arrays, you need to create max number of length i from array one and max number of length k-i from array two, then combine them together. After trying all possible i, you will get the max number created from two arrays.\n\nOptimization: \n\n1. Suppose nums1 = [3, 4, 6, 5], nums2 = [9, 1, 2, 5, 8, 3], the maximum number you can create from nums1 is [6, 5] with length 2. For nums2, it's [9, 8, 3] with length 3. Merging the two sequence, we have [9, 8, 6, 5, 3], which is the max number we can create from two arrays without length constraint. If the required length k<=5, we can simply trim the result to required length from front. For instance, if k=3, then [9, 8, 6] is the result. \n\n2. Suppose we need to create max number with length 2 from num = [4, 5, 3, 2, 1, 6, 0, 8]. The simple way is to use a stack, first we push 4 and have stack [4], then comes 5 > 4, we pop 4 and push 5, stack becomes [5], 3 < 5, we push 3, stack becomes [5, 3]. Now we have the required length 2, but we need to keep going through the array in case a larger number comes, 2 < 3, we discard it instead of pushing it because the stack already grows to required size 2. 1 < 3, we discard it. 6 > 3, we pop 3, since 6 > 5 and there are still elements left, we can continue to pop 5 and push 6, the stack becomes [6], since 0 < 6, we push 0, the stack becomes [6, 0], the stack grows to required length again. Since 8 > 0, we pop 0, although 8 > 6, we can't continue to pop 6 since there is only one number, which is 8, left, if we pop 6 and push 8, we can't get to length 2, so we push 8 directly, the stack becomes [6, 8]. \n\n3. In the basic idea, we mentioned trying all possible length i. If we create max number for different i from scratch each time, that would be a waste of time. Suppose num = [4, 9, 3, 2, 1, 8, 7, 6], we need to create max number with length from 1 to 8. For i==8, result is the original array. For i==7, we need to drop 1 number from array, since 9 > 4, we drop 4, the result is [9, 3, 2, 1, 8, 7, 6]. For i==6, we need to drop 1 more number, 3 < 9, skip, 2 < 3, skip, 1 < 2, skip, 8 > 1, we drop 1, the result is [9, 3, 2, 8, 7, 6]. For i==5, we need to drop 1 more, but this time, we needn't check from beginning, during last scan, we already know [9, 3, 2] is monotonically non-increasing, so we check 8 directly, since 8 > 2, we drop 2, the result is [9, 3, 8, 7, 6]. For i==4, we start with 8, 8 > 3, we drop 3, the result is [9, 8, 7, 6]. For i==3, we start with 8, 8 < 9, skip, 7 < 8, skip, 6 < 7, skip, by now, we've got maximum number we can create from num without length constraint. So from now on, we can drop a number from the end each time. The result is [9, 8, 7], For i==2, we drop last number 7 and have [9, 8]. For i==1, we drop last number 8 and have [9].\n\n#\n\n class Solution {\n public:\n #define MIN(a,b) (a<b?a:b)\n #define MAX(a,b) (a>b?a:b)\n // create max number of length t from single non-empty vector\n void getMax(int* num, int& len, int* result, int& t, int& sortedLen)\n {\n \tint n, top = 0;\n \tresult[0] = num[0];\n \tconst int need2drop = len - t;\n \tfor (int i = 1; i < len; ++i){\n \t\tn = num[i];\n \t\twhile (top >= 0 && result[top] < n && (i - top) <= need2drop) --top; // i - top means already dropped i - top numbers\n \t\tif (i - top > need2drop){\n \t\t\tsortedLen = MAX(1,top);\n \t\t\twhile (++top < t) result[top] = num[i++];\n \t\t\treturn;\n \t\t}\n \t\tif (++top < t) result[top] = n;\n \t\telse top = t - 1;\n \t}\n }\n // create max number of different length from single vector\n void dp(int *num, int len, int&sortedLen, int& minL, int& maxL, int *res, int &k){\n \tint j, *head, *prevhead = res;\n \tconst int soi = sizeof(int);\n \tgetMax(num, len, res, maxL,sortedLen);\n \tfor (int l = maxL; l > MAX(minL,1); --l){\n \t\thead = prevhead + k;\n \t\tmemcpy(head, prevhead, l*soi);\n \t\tfor (j = sortedLen; j < l; ++j){\n \t\t\tif (head[j] > head[j - 1]){\n \t\t\t\tsortedLen = MAX(1, j - 1);\n \t\t\t\tmemcpy(head + j - 1, prevhead + j, soi*(l - j));\n \t\t\t\tbreak;\n \t\t\t}\n \t\t}\n \t\tif (j == l) sortedLen = l;\n \t\tprevhead = head;\n \t}\n }\n // merge max number created from single vector\n void merge(int* num1,int len1,int* num2,int len2,int* result,int& resSize){\n \tint i = 0, j = 0, k = 0;\n \twhile (i < resSize){\n \t\tif (j < len1 && k < len2){\n \t\t\tif (num1[j] > num2[k])\n \t\t\t\tresult[i++] = num1[j++];\n \t\t\telse if (num1[j] < num2[k])\n \t\t\t\tresult[i++] = num2[k++];\n \t\t\telse{\n \t\t\t\tint remaining1 = len1 - j, remaining2 = len2 - k, tmp = num1[j];\n \t\t\t\tint flag = memcmp(num1 + j, num2 + k, sizeof(int) * MIN(remaining1, remaining2));\n \t\t\t\tflag = (flag == 0 ? (remaining1>remaining2 ? 1 : -1) : flag);\n \t\t\t\tint * num = flag > 0 ? num1 : num2;\n \t\t\t\tint & cnt = flag > 0 ? j : k;\n \t\t\t\tint len = flag > 0 ? len1 : len2;\n \t\t\t\twhile (num[cnt]==tmp && cnt < len && i<resSize) result[i++] = num[cnt++];\n \t\t\t}\n \t\t}\n \t\telse if (j < len1) result[i++] = num1[j++];\n \t\telse result[i++] = num2[k++];\n \t}\n }\n \n vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k){\n \tint soi = sizeof(int), len1 = nums1.size(), len2 = nums2.size(), step = k*soi;\n \tint minL1 = MAX(0, k - len2), maxL1 = MIN(k, len1), minL2 = k - maxL1, maxL2 = k - minL1, range = maxL1 - minL1 + 1;\n \tint * res = new int[range * k * 2 + 2 * k], *dp1 = res + k, *dp2 = res + range*k+k, *tmp=res+range*2*k+k;\n \tmemset(res, 0, step);\n \tint sortedLen1 = 1, sortedLen2 = 1;\n \tif (len1 == 0 && len2 > 0) getMax(&nums2[0], len2, res, k, sortedLen2);\n \telse if (len1 > 0 && len2 == 0) getMax(&nums1[0], len1, res, k, sortedLen2);\n \telse if (len1 > 0 && len2 > 0){\n \t\tdp(&nums1[0], len1, sortedLen1, minL1, maxL1, dp1,k);\n \t\tdp(&nums2[0], len2, sortedLen2, minL2, maxL2, dp2,k);\n \t\tif (sortedLen1 + sortedLen2 > k){\n \t\t\tmerge(dp1 + k*(maxL1 - sortedLen1), sortedLen1, dp2 + k*(maxL2 - sortedLen2), sortedLen2, tmp, k);\n \t\t\tvector<int> resv(tmp, tmp + k);\n \t\t\tdelete[] res;\n \t\t\treturn resv;\n \t\t}\n \t\tfor (int i = minL1; i <= maxL1; ++i){\n \t\t\tmerge(dp1+k*(maxL1-i), i, dp2+k*(maxL2-k+i), (k-i), tmp,k);\n \t\t\tif (memcmp(res, tmp, step) < 0) memcpy(res, tmp, step);\n \t\t}\n \t}\n \tvector<int> resv(res, res + k);\n \tdelete[] res;\n \treturn resv;\n }\n };
| 248 | 6 |
[]
| 17 |
create-maximum-number
|
Short Python / Ruby / C++
|
short-python-ruby-c-by-stefanpochmann-b985
|
Python\n\n def maxNumber(self, nums1, nums2, k):\n\n def prep(nums, k):\n drop = len(nums) - k\n out = []\n for num i
|
stefanpochmann
|
NORMAL
|
2015-12-24T12:24:49+00:00
|
2018-10-09T07:57:41.266603+00:00
| 33,769 | false |
**Python**\n\n def maxNumber(self, nums1, nums2, k):\n\n def prep(nums, k):\n drop = len(nums) - k\n out = []\n for num in nums:\n while drop and out and out[-1] < num:\n out.pop()\n drop -= 1\n out.append(num)\n return out[:k]\n\n def merge(a, b):\n return [max(a, b).pop(0) for _ in a+b]\n\n return max(merge(prep(nums1, i), prep(nums2, k-i))\n for i in range(k+1)\n if i <= len(nums1) and k-i <= len(nums2))\n\nSolved it on my own but now I see others already posted this idea. Oh well, at least it's short, particularly my `merge` function.\n\nThe last two lines can be combined, but I find it rather ugly and not worth it: \n`for i in range(max(k-len(nums2), 0), min(k, len(nums1))+1))`\n\n---\n\n**Ruby**\n\n def prep(nums, k)\n drop = nums.size - k\n out = [9]\n nums.each do |num|\n while drop > 0 && out[-1] < num\n out.pop\n drop -= 1\n end\n out << num\n end\n out[1..k]\n end\n \n def max_number(nums1, nums2, k)\n ([k-nums2.size, 0].max .. [nums1.size, k].min).map { |k1|\n parts = [prep(nums1, k1), prep(nums2, k-k1)]\n (1..k).map { parts.max.shift }\n }.max\n end\n\n---\n\n**C++**\n\nTranslated it to C++ as well now. Not as short anymore, but still decent. And C++ allows different functions with the same name, so I chose to do that here to show how nicely the `maxNumber(nums1, nums2, k)` problem can be based on the problems `maxNumber(nums, k)` and `maxNumber(nums1, nums2)`, which would make fine problems on their own.\n\n vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {\n int n1 = nums1.size(), n2 = nums2.size();\n vector<int> best;\n for (int k1=max(k-n2, 0); k1<=min(k, n1); ++k1)\n best = max(best, maxNumber(maxNumber(nums1, k1),\n maxNumber(nums2, k-k1)));\n return best;\n }\n\n vector<int> maxNumber(vector<int> nums, int k) {\n int drop = nums.size() - k;\n vector<int> out;\n for (int num : nums) {\n while (drop && out.size() && out.back() < num) {\n out.pop_back();\n drop--;\n }\n out.push_back(num);\n }\n out.resize(k);\n return out;\n }\n\n vector<int> maxNumber(vector<int> nums1, vector<int> nums2) {\n vector<int> out;\n while (nums1.size() + nums2.size()) {\n vector<int>& now = nums1 > nums2 ? nums1 : nums2;\n out.push_back(now[0]);\n now.erase(now.begin());\n }\n return out;\n }\n\nAn alternative for `maxNumber(nums1, nums2)`:\n\n vector<int> maxNumber(vector<int> nums1, vector<int> nums2) {\n vector<int> out;\n auto i1 = nums1.begin(), end1 = nums1.end();\n auto i2 = nums2.begin(), end2 = nums2.end();\n while (i1 != end1 || i2 != end2)\n out.push_back(lexicographical_compare(i1, end1, i2, end2) ? *i2++ : *i1++);\n return out;\n }
| 217 | 9 |
['Python', 'C++', 'Ruby']
| 46 |
create-maximum-number
|
Share my Python solution with explanation
|
share-my-python-solution-with-explanatio-ghdl
|
To create the max number from num1 and nums2 with k elements, we assume the final result combined by i numbers (denotes as left) from num1 and j numbers (denote
|
caunion
|
NORMAL
|
2015-12-24T05:04:35+00:00
|
2018-10-10T01:54:50.741195+00:00
| 10,312 | false |
To create the max number from num1 and nums2 with k elements, we assume the final result combined by i numbers (denotes as **left**) from num1 and j numbers (denotes as **right**) from nums2, where i+j==k.\n\nObviously, left and right must be the maximum possible number in num1 and num2 respectively. i.e. num1 = [6,5,7,1] and i == 2, then left must be [7,1]. \n\nThe final result is the maximum possible merge of all left and right. \n\nSo there're 3 steps:\n\n 1. **iterate i from 0 to k.**\n 2. **find max number from num1, num2 by select i , k-i numbers, denotes as left, right**\n 3. **find max merge of left, right**\n\nfunction **maxSingleNumber** select i elements from num1 that is maximum. The idea find the max number one by one. i.e. assume nums [6,5,7,1,4,2], selects = 3.\n1st digit: find max digit in [6,5,7,1], the last two digits [4, 2] can not be selected at this moment.\n2nd digits: find max digit in [1,4], since we have already selects 7, we should consider elements after it, also, we should leave one element out.\n3rd digits: only one left [2], we select it. and function output [7,4,2]\n\nfunction **mergeMax** find the maximum combination of left, and right. \n\n\n class Solution(object):\n def maxNumber(self, nums1, nums2, k):\n """\n :type nums1: List[int]\n :type nums2: List[int]\n :type k: int\n :rtype: List[int]\n """\n n, m= len(nums1),len(nums2)\n ret = [0] * k\n for i in range(0, k+1):\n j = k - i\n if i > n or j > m: continue\n left = self.maxSingleNumber(nums1, i)\n right = self.maxSingleNumber(nums2, j)\n num = self.mergeMax(left, right)\n ret = max(num, ret)\n return ret\n\n\n def mergeMax(self, nums1, nums2):\n ans = []\n while nums1 or nums2:\n if nums1 > nums2:\n ans += nums1[0],\n nums1 = nums1[1:]\n else:\n ans += nums2[0],\n nums2 = nums2[1:]\n return ans\n\n def maxSingleNumber(self, nums, selects):\n n = len(nums)\n ret = [-1]\n if selects > n : return ret\n while selects > 0:\n start = ret[-1] + 1 #search start\n end = n-selects + 1 #search end\n ret.append( max(range(start, end), key = nums.__getitem__))\n selects -= 1\n ret = [nums[item] for item in ret[1:]]\n return ret
| 63 | 2 |
[]
| 13 |
create-maximum-number
|
divide to three subproblem solution, beat 98%
|
divide-to-three-subproblem-solution-beat-17xq
|
subproblem1: \nget the largest k numbers when keeping the relative order\n\nsubproblem2: \nmerge two arrays which are from subproblem1.\n\nsubproblem3: \ncompar
|
chaoyanghe
|
NORMAL
|
2017-01-15T11:53:19.963000+00:00
|
2018-10-10T01:49:00.381837+00:00
| 10,198 | false |
subproblem1: \nget the largest k numbers when keeping the relative order\n\nsubproblem2: \nmerge two arrays which are from subproblem1.\n\nsubproblem3: \ncompare two arrays.\n\n```\npublic class Solution {\n public int[] maxNumber(int[] nums1, int[] nums2, int k) {\n int len1 = nums1.length;\n int len2 = nums2.length;\n int[] result = new int[k];\n if(len1+len2 < k) {\n return result;//bad case\n }else if(len1+len2 == k){\n result = mergeTwoArrays(nums1, nums2, k);//edge case\n }else{\n for (int i = 0; i <= k; i++) {\n if(i<=len1 && (k-i)<=len2){\n int[] maxNumbers1 = maxNumberOfSingleArray(nums1, i);\n int[] maxNumbers2 = maxNumberOfSingleArray(nums2, k - i);\n int[] maxNumbers = mergeTwoArrays(maxNumbers1, maxNumbers2, k);\n if (compareTwoArrays(maxNumbers, 0, result, 0)) result = maxNumbers;\n }\n }\n }\n return result;\n }\n \n private int[] mergeTwoArrays(int[] nums1, int[] nums2, int k) {\n int[] result = new int[k];\n int idx1 = 0, idx2 = 0;\n int idx = 0;\n while(idx < k){\n //check the two remain arrays to see which one is larger.\n if(compareTwoArrays(nums1, idx1, nums2, idx2)){\n result[idx] = nums1[idx1++];\n }else{\n result[idx] = nums2[idx2++];\n }\n idx++;\n }\n return result;\n }\n \n //get the largest k numbers when keeping the relative order\n private int[] maxNumberOfSingleArray(int[] nums, int k){\n int[] result = new int[k];\n if(k == 0) return result;\n\n int len = nums.length;\n int idx = 0;\n for(int i = 0; i < len; i++){\n while((len-i-1) + (idx+1) > k && idx>0 && nums[i] > result[idx-1]) idx--;\n if(idx < k) result[idx++] = nums[i];\n }\n return result;\n }\n \n //compare two arrays at the "start" index\n public boolean compareTwoArrays(int[] nums1, int startIdx1, int[] nums2, int startIdx2) {\n int len1 = nums1.length - startIdx1;\n if(len1 <= 0) return false;\n int len2 = nums2.length - startIdx2;\n if(len2 <= 0) return true;\n int len = Math.max(len1, len2);\n for (int i = 0; i< len; i++) {\n \tint digit1 = startIdx1 + i < nums1.length ? nums1[startIdx1 + i] : 0;\n \tint digit2 = startIdx2 + i < nums2.length ? nums2[startIdx2 + i] : 0;\n \tif(digit1 != digit2){\n \t return digit1 > digit2;\n \t}\n }\n return true;//equal, choose either one is ok\n }\n}\n````
| 55 | 0 |
[]
| 7 |
create-maximum-number
|
Share my 21ms java solution with comments
|
share-my-21ms-java-solution-with-comment-q94o
|
To find the maximum ,we can enumerate how digits we should get from nums1 , we suppose it is i.\n\nSo , the digits from nums2 is K - i.\n\nAnd we can use a sta
|
murmured
|
NORMAL
|
2015-12-23T14:46:00+00:00
|
2015-12-23T14:46:00+00:00
| 18,894 | false |
To find the maximum ,we can enumerate how digits we should get from nums1 , we suppose it is i.\n\nSo , the digits from nums2 is K - i.\n\nAnd we can use a stack to get the get maximum number(x digits) from one array.\n\nOK, Once we choose two maximum subarray , we should combine it to the answer.\n\nIt is just like merger sort, but we should pay attention to the case: the two digital are equal.\n\nwe should find the digits behind it to judge which digital we should choose now.\n\nIn other words,we should judge which subarry is bigger than the other.\n\nThat's all.\n\nIf you have any question or suggest, I am happy you can comment on my blog : [Create Maximum Number][1].\n\nThanks, merry christmas :)\n\n *update:use stack to find max sub array and it runs 21ms now.( thanks to @dietpepsi )*\n\n \n\n /** * Created by hrwhisper on 2015/11/23. * http://www.hrwhisper.me/leetcode-create-maximum-number/ */\n \n \n public class Solution {\n public int[] maxNumber(int[] nums1, int[] nums2, int k) {\n int get_from_nums1 = Math.min(nums1.length, k);\n int[] ans = new int[k];\n for (int i = Math.max(k - nums2.length, 0); i <= get_from_nums1; i++) {\n int[] res1 = new int[i];\n int[] res2 = new int[k - i];\n int[] res = new int[k];\n res1 = solve(nums1, i);\n res2 = solve(nums2, k - i);\n int pos1 = 0, pos2 = 0, tpos = 0;\n \n while (res1.length > 0 && res2.length > 0 && pos1 < res1.length && pos2 < res2.length) {\n if (compare(res1, pos1, res2, pos2))\n res[tpos++] = res1[pos1++];\n else\n res[tpos++] = res2[pos2++];\n }\n while (pos1 < res1.length)\n res[tpos++] = res1[pos1++];\n while (pos2 < res2.length)\n res[tpos++] = res2[pos2++];\n \n if (!compare(ans, 0, res, 0))\n ans = res;\n }\n \n return ans;\n }\n \n public boolean compare(int[] nums1, int start1, int[] nums2, int start2) {\n for (; start1 < nums1.length && start2 < nums2.length; start1++, start2++) {\n if (nums1[start1] > nums2[start2]) return true;\n if (nums1[start1] < nums2[start2]) return false;\n }\n return start1 != nums1.length;\n }\n \n public int[] solve(int[] nums, int k) {\n int[] res = new int[k];\n int len = 0;\n for (int i = 0; i < nums.length; i++) {\n while (len > 0 && len + nums.length - i > k && res[len - 1] < nums[i]) {\n len--;\n }\n if (len < k)\n res[len++] = nums[i];\n }\n return res;\n } }\n\n\n [1]: http://www.hrwhisper.me/leetcode-create-maximum-number/
| 51 | 1 |
['Java']
| 5 |
create-maximum-number
|
Clean and easy to understand C++ solution
|
clean-and-easy-to-understand-c-solution-y7mwv
|
vector<int> maxVector(vector<int> nums, int k) {\n while (nums.size() > k) {\n int i = 0, n = nums.size();\n for (; i < n - 1; ++i)
|
lixuchen01
|
NORMAL
|
2015-12-24T15:36:56+00:00
|
2018-10-01T13:14:24.410978+00:00
| 8,411 | false |
vector<int> maxVector(vector<int> nums, int k) {\n while (nums.size() > k) {\n int i = 0, n = nums.size();\n for (; i < n - 1; ++i) {\n if (nums[i] < nums[i + 1]) {\n nums.erase(nums.begin() + i);\n break;\n }\n }\n if (i == n - 1) nums.erase(nums.begin() + i);\n }\n \n return nums;\n }\n \n bool compare(vector<int> &nums1, int i, vector<int> &nums2, int j) {\n while (i < nums1.size() && j < nums2.size() && nums1[i] == nums2[j]) {\n ++i;\n ++j;\n }\n if (j == nums2.size()) return true;\n if (i < nums1.size() && nums1[i] > nums2[j]) return true;\n return false;\n }\n \n vector<int> merge(vector<int> &nums1, vector<int> &nums2, int k) {\n vector<int> res(k, 0);\n for (int i = 0, j = 0, r = 0; r < k; ++r) {\n res[r] = compare(nums1, i, nums2, j) ? nums1[i++] : nums2[j++];\n }\n \n return res;\n }\n \n vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {\n int m = nums1.size(), n = nums2.size();\n vector<int> res(k, 0);\n \n for (int i = max(0, k - n); i <= min(k, m); ++i) {\n auto v1 = maxVector(nums1, i);\n auto v2 = maxVector(nums2, k - i);\n auto tmp = merge(v1, v2, k);\n if (compare(tmp, 0, res, 0)) res = tmp;\n }\n \n return res;\n }
| 27 | 3 |
['C++']
| 4 |
create-maximum-number
|
Greedy | Intuitive | Detailed Explanation
|
greedy-intuitive-detailed-explanation-by-sjkc
|
Intuition\n\nThis question is basically a combo of monotonic stack and merging two arrays.\n\nSo, to create a maximum number of k size array, we will iterate ov
|
Deepalisohane
|
NORMAL
|
2023-05-16T07:41:31.249604+00:00
|
2023-05-16T07:41:31.249628+00:00
| 4,638 | false |
# Intuition\n\nThis question is basically a combo of monotonic stack and merging two arrays.\n\nSo, to create a maximum number of k size array, we will iterate over the first array to take the size of largest possible number and correspondingly we will take the (k-i) size of largest possible number from the second array.\nAfter storing the largest arrays in n1 and n2 we are merging them using merge function and then taking maximum of all.\n\n```\n vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {\n int n = nums1.size(), m = nums2.size();\n string mx = "";\n for(int i = 0; i <= k && i <= n; i++){\n if((k-i) > m) continue; //If we are taking i size of largest array from nums1 then are we capable of building k-i size of largest array from num2 .\n vector<int> n1 = maxnum(nums1, i);\n vector<int> n2 = maxnum(nums2, k-i);\n string s = merge(n1, n2, k);\n mx = max(mx, s);\n }\n vector<int> res;\n for(int i = 0; i < mx.size(); i++) res.push_back(mx[i] - \'0\');\n return res;\n }\n```\n\nThis is the code to calculate the largest possible number of kth size from array nums. This is based on monotonic stack.\n\nSimilar question(Same logic): https://leetcode.com/submissions/detail/950762503/\n\n```\n vector<int> maxnum(vector<int> nums, int k){\n stack<int> st;\n int n = nums.size();\n for(int i = 0; i < n; i++){\n while(!st.empty() && nums[st.top()] < nums[i] && n - i + st.size() > k) st.pop();\n if(st.size() < k) st.push(i);\n }\n vector<int> ans;\n while(!st.empty()) ans.push_back(nums[st.top()]), st.pop();\n reverse(ans.begin(), ans.end());\n return ans;\n }\n\n\n\n``` \n\nSo, here we are merging both the arrays.\nIf element of n2 is greater then we will simply take its value in the ans array and vice versa (similar to merging of merge sort).\n\n**Most Important**\nWhen we will encounter equal values in n1 and n2 then we will simply increment both the indices.\n\n`nums1 = [5,0,2,1,0,1,0,3,9,1,2,8,0,9,8,1,4,7,3],\nnums2 = [7,6,7,1,0,1,0,5,6,0,5,0],\nk = 31`\n\nYou can dry run on this test case.\n\n```\n string merge(vector<int>& n1, vector<int>& n2, int k){\n vector<int> ans(k, 0);\n int i = 0, j = 0, x = 0;\n while(i < n1.size() && j < n2.size()){\n if(n2[j] > n1[i]) ans[x++] = n2[j], j++;\n else if(n2[j] == n1[i]){\n int indi=i, indj=j;\n while(indi < n1.size() && indj < n2.size() && n1[indi] == n2[indj]) indi++, indj++;\n if(indj == n2.size()) ans[x++] = n1[i], i++;\n else{\n if(indi < n1.size() && n1[indi] > n2[indj]) ans[x++] = n1[i], i++;\n else ans[x++] = n2[j], j++;\n }\n }\n\n else ans[x++] = n1[i], i++; \n }\n while(i < n1.size()) ans[x++] = n1[i], i++;\n while(j < n2.size()) ans[x++] = n2[j], j++;\n string s = "";\n for(auto it: ans) s += to_string(it);\n return s;\n }\n```\n\n\n\n# Complete Code\n```\nclass Solution {\npublic:\n\n vector<int> maxnum(vector<int> nums, int k){\n stack<int> st;\n int n = nums.size();\n for(int i = 0; i < n; i++){\n while(!st.empty() && nums[st.top()] < nums[i] && n - i + st.size() > k) st.pop();\n if(st.size() < k) st.push(i);\n }\n vector<int> ans;\n while(!st.empty()) ans.push_back(nums[st.top()]), st.pop();\n reverse(ans.begin(), ans.end());\n return ans;\n }\n\n string merge(vector<int>& n1, vector<int>& n2, int k){\n vector<int> ans(k, 0);\n int i = 0, j = 0, x = 0;\n while(i < n1.size() && j < n2.size()){\n if(n2[j] > n1[i]) ans[x++] = n2[j], j++;\n else if(n2[j] == n1[i]){\n int indi=i, indj=j;\n while(indi < n1.size() && indj < n2.size() && n1[indi] == n2[indj]) indi++, indj++;\n if(indj == n2.size()) ans[x++] = n1[i], i++;\n else{\n if(indi < n1.size() && n1[indi] > n2[indj]) ans[x++] = n1[i], i++;\n else ans[x++] = n2[j], j++;\n }\n }\n\n else ans[x++] = n1[i], i++; \n }\n while(i < n1.size()) ans[x++] = n1[i], i++;\n while(j < n2.size()) ans[x++] = n2[j], j++;\n string s = "";\n for(auto it: ans) s += to_string(it);\n return s;\n }\n\n vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {\n int n = nums1.size(), m = nums2.size();\n string mx = "";\n for(int i = 0; i <= k && i <= n; i++){\n if((k-i) > m) continue; //If we are taking i size of largest array from nums1 then are we capable of building k-i size of largest array from num2 .\n vector<int> n1 = maxnum(nums1, i);\n vector<int> n2 = maxnum(nums2, k-i);\n string s = merge(n1, n2, k);\n mx = max(mx, s);\n }\n vector<int> res;\n for(int i = 0; i < mx.size(); i++) res.push_back(mx[i] - \'0\');\n return res;\n }\n};\n\n```
| 26 | 0 |
['Greedy', 'Monotonic Stack', 'C++']
| 4 |
create-maximum-number
|
✅[C++] Intuition w/reference question | Stack and Merge sort Concept
|
c-intuition-wreference-question-stack-an-2bzh
|
\nThis question is a combination of multiple topics and also one of the best question i have encountered so far. \nBefore solving this question, you need have k
|
biT_Legion
|
NORMAL
|
2022-04-05T17:04:44.230934+00:00
|
2022-04-05T17:08:52.832546+00:00
| 3,798 | false |
\nThis question is a combination of multiple topics and also one of the best question i have encountered so far. \nBefore solving this question, you need have knowledge about merge sort technique and also you need to solve its prerequisite question ([1673. Find the Most Competitive Subsequence](https://leetcode.com/problems/find-the-most-competitive-subsequence/))\n\nFirst, Try that question and if you dont get any intuition, don\'t feel bad. Even i took some help. You can read its editorial from [here](https://leetcode.com/problems/find-the-most-competitive-subsequence/discuss/1903056/C%2B%2B-Stack-Solution-intuition-or-Monotonic-Stack)\n\n***Basic Idea*** of this problem is that we have two arrays, so we find the largest \'i\' digit number from nums1 and largest \'k-i\' digit number from nums2. After having these two, we merge them using merge sort algorithm. We use merge sort because it can be proved that largest number will always be sorted in descending order. The only thing to keep in mind while merging is the case where array elements are equal. In that case, we have to loop untill we find a greater element in one of the two arrays and then act accordingly.\n So after finding a i digit number from nums1 and k-i digit number from nums2, we merge them to form the maximum k digit number from these two arrays.\n\n\n```\nclass Solution {\npublic:\n vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {\n vector <int>res;\n\n for(int i = 0; i<=k; i++){\n vector <int> a = fun(nums1, i);\n vector <int> b = fun(nums2, k-i);\n\n vector <int> m;\n merge(a, b, m);\n\n if(m.size()==k) res = max(res,m);\n }\n return res;\n }\nprotected:\n // This function is the code of "Find most consecutive subsequence" problem, which finds the k digit maximum number possible\n vector <int> fun(vector <int>&nums, int k){\n if(k>nums.size()) return {};\n vector <int> res;\n stack <int> st;\n int rem = k, n = nums.size();\n for(int i = 0; i<n; i++){\n if(st.empty()) st.push(nums[i]), rem--;\n else{\n int avail = n-i;\n while(!st.empty() and st.top()<nums[i] and rem<k and avail>rem) st.pop(), rem++;\n st.push(nums[i]), rem--;\n }\n }\n while(st.size()>k) st.pop();\n while(!st.empty()) res.push_back(st.top()), st.pop();\n reverse(res.begin(), res.end());\n return res;\n }\n void merge(vector <int>&a, vector <int>&b, vector <int>&res){\n int i = 0, j = 0, k = 0;\n // This is the only case which we need to take care of. Here, we loop until we find a number greater than another number\n // in other array. When we do that, we push the element in result array accordingly. Note that i am not using the pointer\n // i and j to loop, instead i have creater a temporary pointers which finds the position where elements are different.\n while(i<a.size() and j<b.size()){\n if(a[i]==b[j]){\n int ti = i, tj = j;\n while(ti<a.size() and tj<b.size() and a[ti]==b[tj]) ti++, tj++;\n\n if(tj==b.size()) res.push_back(a[i]), i++;\n else\n if(ti<a.size() and a[ti]>b[tj]) res.push_back(a[i]), i++;\n else res.push_back(b[j]), j++;\n }\n else\n if(a[i]>b[j]) res.push_back(a[i]), i++;\n else res.push_back(b[j]), j++;\n }\n while(i<a.size()) res.push_back(a[i]), i++;\n while(j<b.size()) res.push_back(b[j]), j++;\n }\n};\n```
| 26 | 0 |
['Stack', 'C', 'C++']
| 5 |
create-maximum-number
|
Strictly O(NK) C++ Solution with detailed explanation
|
strictly-onk-c-solution-with-detailed-ex-r9go
|
\n\tclass list1\n {\n vector a;\n vector> f;\n public:\n list1() = delete;\n inline int size() {return a.size();}\n inl
|
syb3181
|
NORMAL
|
2015-12-23T13:58:02+00:00
|
2020-01-21T13:16:36.496780+00:00
| 9,358 | false |
\n\tclass list1\n {\n vector<int> a;\n vector<vector<int>> f;\n public:\n list1() = delete;\n inline int size() {return a.size();}\n inline int next(int x,int d) {return f[x][d];}\n list1(vector<int>& a0)\n {\n a = a0;\n f = vector<vector<int>>(a0.size() + 1,vector<int>(10,INT_MAX));\n for (int i = 0;i<a0.size();i++)\n {\n f[i][a[i]] = i;\n for (int j = i-1;j>=0;j--)\n {\n if (a[j] == a[i]) break;\n f[j][a[i]] = i;\n }\n }\n }\n };\n \n //dmd for detect_max_digit\n // dmd(a,x,rem) -> (max_digit, pos) , where a[pos-1] == max_digit\n // list a , from x, need rem numbers, x not included.\n \n pair<int,int> dmd(list1& a,int x,int rem)\n {\n for (int d = 9;d >= 0;d--)\n {\n int pos = a.next(x,d);\n if (pos == INT_MAX) continue;\n if (a.size() - (pos + 1) >= rem)\n return make_pair(d,pos + 1);\n }\n }\n \n \n class Solution {\n public:\n vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {\n list1 a1 = list1(nums1);\n int N1 = nums1.size();\n list1 a2 = list1(nums2);\n int N2 = nums2.size();\n \n auto ret = vector<int>(k,0);\n auto f = vector<int>(N1 + 1,0); \n //f[i] denote a1[0..i-1] need a2[0..f[i]-1] to reach the current maximal number, and can expand to length k\n // in other words, the state is : the number is current maximal and can be expanded, list1 begin with a1[i] and list2 with a2[f[i]] \n for (int d = 1;d <= k;d++)\n {\n int maxDigit = -1;\n auto tmpf = vector<int>(N1 + 1,INT_MAX);\n for (int x = 0;x<=N1;x++)\n {\n int y = f[x];\n if (y == INT_MAX) continue;\n auto m1 = dmd(a1,x,k-d-(N2-y)); \n auto m2 = dmd(a2,y,k-d-(N1-x));\n maxDigit = max(maxDigit,m1.first);\n maxDigit = max(maxDigit,m2.first);\n }\n ret[d-1] = maxDigit;\n for (int x = 0;x<=N1;x++)\n {\n int y = f[x];\n if (y == INT_MAX) continue;\n auto m1 = dmd(a1,x,k-d-(N2-y));\n if (m1.first == maxDigit)\n tmpf[m1.second] = min(tmpf[m1.second],y);\n auto m2 = dmd(a2,y,k-d-(N1-x));\n if (m2.first == maxDigit)\n tmpf[x] = min(tmpf[x],m2.second);\n }\n f = tmpf;\n }\n return ret;\n }\n };\n\nAny Question is welcome and will be answered as soon as possible.\nDetailed explanation is coming soon!\nYou may firstly read my code, it\'s quite easy to understand.\n\n## Detailed Solution ##\nLet a1,a2 be the two list from where we construct the maximal number.\nLet N1,N2 denote the size of a1,a2.\nWe construct the maximal number digit by digit.\n\nSuppose we are constructing the d-th digit(ret[0..d-1] is done) and we have a set of states S = {(a1,b1),(a2,b2),...(a_N,b_N)},For each state (x,y) in S, it means we use a1[0..(x-1)] and a2[0..(y-1)] to construct ret[0..d-1] and a1[x..N1] and a2[y..N2] are avaliabe to construct the remaining digits.\n\nIn the iteration, we need to construct the d-th digit as well as the set S\', that is from where we can construct the d+1-th digit.\n\nFor every state (x,y) in S, we use the function "dmd" to obtain the biggest d-th digit we can get from it. \nLet maxdigit = {max(dmd(x,y)[1])|(x,y) in S}, it is the d-th digit.\n\nAs we now the d-th digit,\nWe scan S again,\nFor every state (x,y) in S, we use the function "dmd" to obtain the (x\',y) and (x,y\') it extands to, \nif a1[x\'-1] == maxdigit, we add (x\',y) to S\'.\nif a2[y\'-1] == maxdigit, we add (x,y\') to S\'.\n\nNow we can construct the d+1-th digit from S\', note that the size of S\' is at most N1, for(x,y1) and (x,y2), y1 < y2, (x,y2) is needless to be recorded.\n\nFinally I\'d like to use an typical example to illustrate the process.\n\n> a1 = [8,1] a2 = [8,9] k = 4\n> \n> S = {(0,0)}\n\nthe first digit is 8,\n\n> S\' = {(0,1),(1,0)}\n\nthe second digit is 9, we construct it from (0,1)\n\n>S\'\' = {(0,2)}\n\nthe remain digits are 8 and 1,\nwe finally reach 8981.\n\nNow I use python and write a piece of much shorter and more readable code as follows:\n\n ```\nclass Solution:\n \n def maxNumber(self, nums1: List[int], nums2: List[int], k: int) -> List[int]:\n \n def calcnext(a):\n ret = [[-1] * 10 for i in range(len(a) + 1)]\n for i in reversed(range(len(a))):\n for d in range(0, 10):\n ret[i][d] = i if a[i] == d else ret[i + 1][d]\n return ret\n \n M, N = len(nums1), len(nums2)\n next1 = calcnext(nums1)\n next2 = calcnext(nums2)\n ret = []\n S = [(0, 0)]\n \n for i in range(k):\n rem = k - i - 1\n found, best = False, [N + 1] * (M + 1)\n for d in reversed(range(0, 10)):\n for (d1, d2) in S:\n n1 = next1[d1][d] + 1\n if n1 and M - n1 + N - d2 >= rem:\n found, best[n1] = True, min(best[n1], d2)\n n2 = next2[d2][d] + 1\n if n2 and M - d1 + N - n2 >= rem:\n found, best[d1] = True, min(best[d1], n2)\n if found:\n ret += [d]\n break\n S = [(i, best[i]) for i, x in enumerate(best) if best[i] <= N]\n\n return ret\n\n\n
| 22 | 5 |
[]
| 15 |
create-maximum-number
|
An Accepted Python Solution
|
an-accepted-python-solution-by-bookshado-02ld
|
This problem could be divided into 2 sub-problems:\n\n1. function getMax(nums, t):\n\n get t numbers from list nums to form one single maximized sub-list, with
|
bookshadow
|
NORMAL
|
2015-12-24T02:51:12+00:00
|
2015-12-24T02:51:12+00:00
| 3,776 | false |
This problem could be divided into 2 sub-problems:\n\n1. **function getMax(nums, t):**\n\n get t numbers from list *nums* to form one single maximized sub-list, with relative orders preserved\n\n2. **function merge(nums1, nums2):**\n\n merge *nums1* and *nums2* to form one single maximized list, with relative orders preserved\n\nThe final result could be solved by enumerate the length of sub-list *nums1* and *nums2*, and record the max merged list.\n\nPython Code:\n\n class Solution(object):\n def maxNumber(self, nums1, nums2, k):\n """\n :type nums1: List[int]\n :type nums2: List[int]\n :type k: int\n :rtype: List[int]\n """\n def getMax(nums, t):\n ans = []\n size = len(nums)\n for x in range(size):\n while ans and len(ans) + size - x > t and ans[-1] < nums[x]:\n ans.pop()\n if len(ans) < t:\n ans += nums[x],\n return ans\n \n def merge(nums1, nums2):\n ans = []\n while nums1 or nums2:\n if nums1 > nums2:\n ans += nums1[0],\n nums1 = nums1[1:]\n else:\n ans += nums2[0],\n nums2 = nums2[1:]\n return ans\n \n len1, len2 = len(nums1), len(nums2)\n res = []\n for x in range(max(0, k - len2), min(k, len1) + 1):\n tmp = merge(getMax(nums1, x), getMax(nums2, k - x))\n res = max(tmp, res)\n return res\n\nRef: [http://bookshadow.com/weblog/2015/12/24/leetcode-create-maximum-number/][1]\n\n\n [1]: http://bookshadow.com/weblog/2015/12/24/leetcode-create-maximum-number/
| 21 | 2 |
['Python']
| 4 |
create-maximum-number
|
Easy Understanding And Readable Code || Monotonic Stack || C++
|
easy-understanding-and-readable-code-mon-yw70
|
Intuition & Approach\n Describe your first thoughts on how to solve this problem. \nI will find lexographically greatest subsequence from both array and then me
|
anupamraZ
|
NORMAL
|
2023-06-03T07:26:21.800196+00:00
|
2023-06-03T07:26:21.800240+00:00
| 2,440 | false |
# Intuition & Approach\n<!-- Describe your first thoughts on how to solve this problem. -->\nI will find lexographically greatest subsequence from both array and then merge them.\nBut constraint is length=k must be satisfied. So have to find lexographically greater subsequence such that both combinedly have length k.\n\nBut how to decide how much length have to take from first array and how much from second array? --> This time go by bruteforce. So for possible {i, k-i} pair of length , we will find our answer.\n\nlet\'s divide the problem into subparts:\nsubpart-1: find out lexographically greatest subsequence from both array.\nsubpart-2: Merge them and keep taking maximum.\n\nImplemented stack logic through array. You can go through stack .\n# Complexity\n- Time complexity:O(K*N + K*N)= O(K*N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(K) => for this loop: for(int i=0;i<=k;i++) in maxNumber function.\nO(N) => for getGrtrSubseq function.\nO(K*N) => merge Function.\n- Space complexity: O(N) as all are linear vectors.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n // Function to calculate maximum number from nums of requiredLength.\n vector<int> getGrtrSubseq(vector<int> nums, int requiredLength)\n {\n vector<int> ans; // Store the resultant maximum\n int n = nums.size();\n // i will try to maximize initial digit as much as i can. If falling for shorter length, then i am forced to take last requiredLength-ans.size()\n //elements left. So, before popping any element check ((requiredLength-ans.size())<(n-i)) to ensure you have requiredLength of digits.\n for(int i=0;i<n;i++)\n {\n while(ans.size()>0 && ans.back()<nums[i] && ((requiredLength-ans.size())<(n-i))) // If true, then pop out the last element\n ans.pop_back();\n if(ans.size()<requiredLength)ans.push_back(nums[i]); \n }\n return ans;\n }\n void pop_front(std::vector<int> &v)\n {\n if (v.size() > 0)v.erase(v.begin());\n }\n vector<int> merge(vector<int> p1, vector<int>p2, int k)\n {\n vector<int> temp;\n for(int j=0;j<k;j++)\n { \n vector<int> temp2 = max(p1,p2);\n int fr = temp2.front();\n if(p1>p2)\n pop_front(p1);\n else\n pop_front(p2);\n temp.push_back(fr);\n }\n return temp;\n }\n vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) \n {\n int n1=nums1.size(), n2=nums2.size();\n vector<int>res;\n for(int i=0;i<=k;i++)\n {\n if(i>n1 || k-i>n2) continue;\n vector<int>grtrSubseq1=getGrtrSubseq(nums1,i);; \n vector<int>grtrSubseq2=getGrtrSubseq(nums2,k-i); \n vector<int>temp=merge(grtrSubseq1,grtrSubseq2,k); \n res = max(res, temp);\n }\n return res;\n }\n};\n```\n.\n\nCorrect me if i am wrong.\n
| 17 | 0 |
['Stack', 'Monotonic Stack', 'C++']
| 2 |
create-maximum-number
|
Java Self-explanatory Neat Code
|
java-self-explanatory-neat-code-by-grace-htvs
|
The final result res[] would be merged from res1[] and res2[], such that res1[] is max subsequence of nums1 of length ki, then res2[] is max subsequence of nums
|
gracemeng
|
NORMAL
|
2018-05-02T21:41:08.100877+00:00
|
2018-05-02T21:41:08.100877+00:00
| 1,589 | false |
The final result res[] would be merged from res1[] and res2[], such that res1[] is max subsequence of nums1 of length ki, then res2[] is max subsequence of nums2 with length k - ki.\nTo get max subsequence of length cnt, we use stack.\nTo do with merging and update final result, we use util method greater().\n```\n public int[] maxNumber(int[] nums1, int[] nums2, int k) {\n int[] result = new int[k];\n \n for (int ki = Math.max(0, k - nums2.length); ki <= Math.min(k, nums1.length); ki++) {\n int[] res1 = getMaxSubsequence(nums1, ki); // ki < nums1.length\n int[] res2 = getMaxSubsequence(nums2, k - ki); // k - ki < nums2.length\n int[] resTmp = new int[k];\n int p1 = 0, p2 = 0, pt = 0;\n while (p1 < res1.length || p2 < res2.length) {\n resTmp[pt++] = isGreater(res1, p1, res2, p2) ? res1[p1++] : res2[p2++];\n }\n if (!isGreater(result, 0, resTmp, 0)) {\n result = resTmp;\n }\n }\n return result;\n }\n \n private int[] getMaxSubsequence(int[] nums, int cnt){\n Stack<Integer> stack = new Stack<>();\n int remain = cnt;\n for (int i = 0; i < nums.length; i++) {\n while (!stack.isEmpty() && stack.peek() < nums[i] && nums.length - 1 - i >= remain) {\n stack.pop();\n remain++;\n }\n if (remain > 0) {\n stack.push(nums[i]);\n remain--;\n }\n }\n int[] maxSub = new int[cnt];\n int mi = maxSub.length - 1;\n while (!stack.isEmpty()) {\n maxSub[mi--] = stack.pop();\n }\n return maxSub;\n }\n \n private boolean isGreater(int[] nums1, int p1, int[] nums2, int p2) {\n for (; p1 < nums1.length && p2 < nums2.length; p1++, p2++) {\n if (nums1[p1] > nums2[p2]) {\n return true;\n }\n if (nums1[p1] < nums2[p2]) {\n return false;\n }\n }\n return p1 != nums1.length;\n }\n```
| 16 | 0 |
[]
| 0 |
create-maximum-number
|
Java | easy to understand | monotonic stack | 3 subproblems | same as Leetcode 16737
|
java-easy-to-understand-monotonic-stack-43ijd
|
1673. Find the Most Competitive Subsequence\n\n// TC-o(n)- Monotonously increasing stack\nclass Solution {\n public int[] mostCompetitive(int[] nums, int k)
|
arpan-banerjee7
|
NORMAL
|
2021-12-04T21:06:14.595179+00:00
|
2021-12-04T21:10:43.391333+00:00
| 2,517 | false |
# 1673. Find the Most Competitive Subsequence\n```\n// TC-o(n)- Monotonously increasing stack\nclass Solution {\n public int[] mostCompetitive(int[] nums, int k) {\n int n=nums.length;\n Stack<Integer> st=new Stack<>();\n int[] res=new int[k];\n int rem=n-k;\n for(int i=0;i<n;i++){\n while(!st.isEmpty() && st.peek()>nums[i] && rem>0){\n st.pop();\n rem--;\n }\n st.push(nums[i]);\n \n }\n while(rem>0){\n st.pop();\n rem--;\n }\n for(int i=k-1;i>=0;i--){\n res[i]=st.pop();\n }\n return res;\n }\n}\n```\n\n# 321. Create Maximum Number\n**3 Subproblems-**\n1. Find greatest numbers from nums1 and nums2 using the concept from leetcode 1673(monotonously decreasing stack here, that is the only change)\n2. Merge the two numbers(here they are in the form of arrays) such that it forms the greatest number\n3. Find the greatest among all the formed numbers.\nHere greatest means the number which is lexicographically greater.\n\n```\n// using the concept of 1673. Find the Most Competitive Subsequence\n// prob is we dn t know how many elements we will take from nums1 and nums2\n// so we will try for all combinations of k and find the max out of them\n\nclass Solution {\n \n // monotonic decreasing stack same as leetcode 1673 , only > changed to < \n\tpublic int[] findLexMax(int[] nums, int k) {\n\t\tint n = nums.length;\n\t\tStack<Integer> st = new Stack<>();\n\t\tint[] res = new int[k];\n \n /* we have to form a k digit number which is lexicographically greatest\n that gives some hint that we need to maintain a monotonic decreasing stack\n and rem=n-k means we will remove n-k smaller digits from stack\n lets say nums=[6,7,4,8,9] and k=3, we have to remove 5-3=2 digits from the stack,\n while we try to form monotonic decreasing satck\n o our max number will be [8,9]\n */\n\t\tint rem = n - k;\n\t\tfor (int i = 0; i < n; i++) {\n\t\t\twhile (!st.isEmpty() && st.peek() < nums[i] && rem > 0) {\n\t\t\t\tst.pop();\n\t\t\t\trem--;\n\t\t\t}\n\t\t\tst.push(nums[i]);\n\n\t\t}\n \n /* if still some elements can be removed, the best option would be to remove the\n elements from the top of the stack, as we are mainting a monotonic decreasing satck\n so elemets at the top would be smaller\n take this example arr-[6,4,2] k=2 ans would be [6,4]\n */\n\t\twhile (rem > 0) {\n\t\t\tst.pop();\n\t\t\trem--;\n\t\t}\n\t\tfor (int i = k - 1; i >= 0; i--) {\n\t\t\tres[i] = st.pop();\n\t\t}\n\t\treturn res;\n\t}\n \n\n\tprivate static boolean findMax(int[] arr1, int[] arr2, int p1,int p2) {\n\t\twhile (p1 < arr1.length && p2 < arr2.length) {\n\t\t\tif (arr1[p1] < arr2[p2]) {\n\t\t\t\treturn false;\n\t\t\t} else if (arr1[p1] > arr2[p2]) {\n\t\t\t\treturn true;\n\t\t\t} else {\n\t\t\t\tp1++;\n\t\t\t\tp2++;\n\t\t\t}\n\t\t}\n // when p1 is empty returns true, so that in merge function it picks up values of arr2\n // when p1==arr1.length, then returns false,so that we keep pn picking arr2 elements\n\t\treturn p1!=arr1.length; // tricky\n\t}\n\n \n\t// think of the case [6,0,4] and [6,7], can t do simple logic like merge two sorted arrays\n // we need to decide which pointer to move forward based on the rest of the array,\n // if both elements are same compare the next element, and then decide\n\tprivate int[] merge(int[] nums1, int[] nums2, int k) {\n\t\tint[] res = new int[k];\n\t\tint resIndex = 0;\n\t\tint p1 = 0;\n\t\tint p2 = 0;\n \n\t\twhile (resIndex<res.length) {\n\t\t\tres[resIndex++]=findMax(nums1,nums2,p1,p2)?nums1[p1++]:nums2[p2++];// tricky\n\t\t}\n\n\t\treturn res;\n\t}\n\n\tpublic int[] maxNumber(int[] nums1, int[] nums2, int k) {\n\t\tint len1 = nums1.length;\n\t\tint len2 = nums2.length;\n\t\tint[] maxRes = new int[k];\n\t\tfor (int i = 0; i <= k; i++) { \n\t\t\tint j = k - i;\n\t\t\tif (i <= len1 && (k - i) <= len2) { // skip invalid cases, imp step!\n\t\t\t\tint[] maxLex1 = findLexMax(nums1, i);\n\t\t\t\tint[] maxLex2 = findLexMax(nums2, j);\n\t\t\t\tint[] res = merge(maxLex1, maxLex2, k);\n\t\t\t\tboolean compareRes = findMax(res, maxRes,0,0);\n\t\t\t\tif (compareRes) {\n\t\t\t\t\tmaxRes = res;\n\t\t\t\t}\n\t\t\t}\n\t\t}\n\t\treturn maxRes;\n\t}\n \n}\n```
| 14 | 0 |
['Monotonic Stack', 'Java']
| 1 |
create-maximum-number
|
💥Memory beats 100.00%, Runtime beats 50.00% [EXPLAINED]
|
memory-beats-10000-runtime-beats-5000-ex-u8ii
|
Intuition\nThe intuition ensures that each subsequence is maximized independently and then combined optimally to form the largest number.\n\n# Approach\nHelper
|
r9n
|
NORMAL
|
2024-08-27T03:48:47.135997+00:00
|
2024-08-27T03:48:47.136039+00:00
| 770 | false |
# Intuition\nThe intuition ensures that each subsequence is maximized independently and then combined optimally to form the largest number.\n\n# Approach\nHelper Function for Maximum Number from Single Array: Define a function to get the maximum number of length length from a single array while preserving the order.\n\nMerge Function: Define a function to merge two arrays to form the maximum number by selecting the greatest number from the two at each step.\n\nMain Function: Iterate over all possible splits of k between the two arrays, use the helper function to get the maximum subsequence from each array for each split, and then merge them to get the maximum result.\n\n# Complexity\n- Time complexity:\nO(m+n)\n\n- Space complexity:\nO(k), due to storing intermediate results.\n\n# Code\n```typescript []\nfunction maxNumber(nums1: number[], nums2: number[], k: number): number[] {\n const getMaxSubsequence = (nums: number[], length: number): number[] => {\n const stack: number[] = [];\n let drop = nums.length - length; // Use \'let\' here to allow reassignment\n for (const num of nums) {\n while (drop && stack.length && stack[stack.length - 1] < num) {\n stack.pop();\n drop--;\n }\n stack.push(num);\n }\n return stack.slice(0, length);\n };\n\n const merge = (nums1: number[], nums2: number[]): number[] => {\n const result: number[] = [];\n while (nums1.length || nums2.length) {\n if (compare(nums1, nums2) > 0) {\n result.push(nums1.shift()!);\n } else {\n result.push(nums2.shift()!);\n }\n }\n return result;\n };\n\n const compare = (a: number[], b: number[]): number => {\n for (let i = 0; i < Math.min(a.length, b.length); i++) {\n if (a[i] !== b[i]) return a[i] - b[i];\n }\n return a.length - b.length;\n };\n\n let maxResult: number[] = [];\n for (let i = Math.max(0, k - nums2.length); i <= Math.min(k, nums1.length); i++) {\n const subseq1 = getMaxSubsequence(nums1, i);\n const subseq2 = getMaxSubsequence(nums2, k - i);\n const candidate = merge(subseq1, subseq2);\n if (compare(candidate, maxResult) > 0) maxResult = candidate;\n }\n\n return maxResult;\n}\n\n```
| 12 | 0 |
['TypeScript']
| 1 |
create-maximum-number
|
Python Solution | Greedy Search + Dynamic Programming
|
python-solution-greedy-search-dynamic-pr-h32b
|
```\nclass Solution:\n def maxNumber(self, nums1: List[int], nums2: List[int], k: int) -> List[int]: \n def merge(n1, n2):\n res = [
|
jmin3
|
NORMAL
|
2021-01-21T02:59:08.189131+00:00
|
2021-01-21T02:59:08.189170+00:00
| 3,180 | false |
```\nclass Solution:\n def maxNumber(self, nums1: List[int], nums2: List[int], k: int) -> List[int]: \n def merge(n1, n2):\n res = []\n while (n1 or n2) :\n if n1>n2:\n res.append(n1[0])\n n1 = n1[1:]\n else:\n res.append(n2[0])\n n2 = n2[1:]\n return res\n \n def findmax(nums, length):\n l = []\n maxpop = len(nums)-length\n for i in range(len(nums)):\n while maxpop>0 and len(l) and nums[i]>l[-1]:\n l.pop()\n maxpop -= 1\n l.append(nums[i])\n return l[:length]\n \n n1 = len(nums1)\n n2 = len(nums2)\n res = [0]*k\n for i in range(k+1):\n j = k-i\n if i>n1 or j>n2: continue\n l1 = findmax(nums1, i)\n l2 = findmax(nums2, j)\n res = max(res, merge(l1,l2))\n return res
| 9 | 0 |
['Dynamic Programming', 'Greedy', 'Python', 'Python3']
| 3 |
create-maximum-number
|
Greedy Solution | Time Complexity O(N^2) | Space Complexity O(N) | With Comments
|
greedy-solution-time-complexity-on2-spac-qjhv
|
Basic idea is to find best answer from nums1 with size i and from nums2 with size k-i. Then we merge the two arrays, the merge function has been optimized to b
|
satviksr
|
NORMAL
|
2019-07-08T07:43:20.026889+00:00
|
2019-07-08T07:43:20.026955+00:00
| 2,182 | false |
Basic idea is to find best answer from nums1 with size `i` and from `nums2` with size `k-i`. Then we merge the two arrays, the merge function has been optimized to be `O(N)` . Overall Complexity is `O(N^2)`\n\n```\nclass Solution {\npublic:\n vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {\n vector<int> answer(k);\n int n1 = nums1.size();\n int n2 = nums2.size();\n for(int i = 0; i <= k; i++) {\n int j = k - i;\n if (i <= n1 && j <= n2) {\n vector<int> ans1 = maxSingleNumber(nums1, i); // best of size i - O(n)\n vector<int> ans2 = maxSingleNumber(nums2, j); // best of size k - i - O(n)\n vector<int> ans = merge(ans1, ans2); // merging both - O(n)\n \n answer = max(ans, answer); // maximize answer - O(n)\n }\n }\n return answer;\n }\n \n vector<int> merge(vector<int>& nums1, vector<int>& nums2) {\n vector<int> ans; \n \n int i = 0;\n int j = 0;\n int k = 0; \n\n int n1 = nums1.size();\n int n2 = nums2.size();\n \n // Eventhough there are two nested loops, I believe this is linear as the second loop can only run once per element\n while(i<n1 && j<n2) {\n if (nums1[i] > nums2[j])\n ans.push_back(nums1[i++]);\n else if (nums1[i] < nums2[j])\n ans.push_back(nums2[j++]);\n else { // Both are equal, we need to pick the one that is better in the future\n int i1 = i + 1;\n int j1 = j + 1;\n int larger = 0; \n \n while(i1<n1 && j1 < n2 && !larger) {\n if(nums1[i1] == nums2[j1]) {\n if (nums1[i1] < nums1[i]) // This number is less than the current stopping position, so we would pick that instead \n break;\n i1++;\n j1++;\n }\n else if (nums1[i1] > nums2[j1]) // nums1 is better to pick \n larger = -1;\n else\n larger = 1; // nums2 is better to pick \n }\n \n if (i1 == n1)\n larger = 1;\n if (j1 == n2)\n larger = -1;\n \n if (larger == -1)\n ans.push_back(nums1[i++]);\n else \n ans.push_back(nums2[j++]);\n }\n }\n \n // Push Remaining elements\n while(i<n1)\n ans.push_back(nums1[i++]);\n \n while(j<n2)\n ans.push_back(nums2[j++]);\n \n return ans;\n \n \n }\n \n vector<int> maxSingleNumber(vector<int>& nums1, int k) {\n \n vector<int> stack; \n int n = nums1.size();\n for(int i = 0; i < n; i++) {\n // Pop elements from the stack if current element is greater than head of the stack\n // We can pop only if remaining elements in nums1 + remaining elements in stack \n // after popping is greater than or equal to k\n while(!stack.empty() && (stack.back() < nums1[i] && (stack.size() -1) + (n-i) >=k ))\n stack.pop_back();\n \n // Push if less than k elements\n if (stack.size() < k)\n stack.push_back(nums1[i]);\n }\n return stack;\n }\n \n};\n```
| 9 | 1 |
[]
| 2 |
create-maximum-number
|
[Java] Simple Code - DP
|
java-simple-code-dp-by-chipbk10-xgwe
|
dp[i][j][k] is denoted as the maximum string that takes a numbers from first i numbers from A, and b numbers from first j numbers from B to create a+b = k numbe
|
chipbk10
|
NORMAL
|
2020-05-08T15:06:54.252305+00:00
|
2020-05-08T15:06:54.252340+00:00
| 2,274 | false |
`dp[i][j][k]` is denoted as the maximum string that takes `a` numbers from first `i` numbers from `A`, and `b` numbers from first `j` numbers from `B` to create `a+b = k` numbers.\n\nedge case:\nif `(i+j < k)` then `dp[i][j][k] = empty`\nif `i = 0` or `j = 0`, the issue turns into `1 array`\nif `k = 0` then `dp[i][j][0] = empty`\n\n```\n public int[] maxNumber(int[] A, int[] B, int k) {\n int m = A.length, n = B.length;\n if (m+n < k) return new int[0];\n\n String[][][] dp = new String[m+1][n+1][k+1];\n for (int i = 0; i <= m; i++) {\n for (int j = 0; j <= n; j++) {\n for (int l = 0; l <= k; l++) {\n if (i+j < l) dp[i][j][l] = "";\n else {\n String chooseAi = (i == 0 || l == 0) ? "" : dp[i-1][j][l-1] + A[i-1];\n String chooseBj = (j == 0 || l == 0) ? "" : dp[i][j-1][l-1] + B[j-1];\n String maxChoose = max(chooseAi, chooseBj);\n\n String ignoreAi = (i == 0) ? "" : dp[i-1][j][l];\n String ignoreBj = (j == 0) ? "" : dp[i][j-1][l];\n String ignoreBoth = (i == 0 || j == 0) ? "" : dp[i-1][j-1][l];\n String maxIgnore = max(max(ignoreAi, ignoreBj), ignoreBoth);\n\n dp[i][j][l] = max(maxChoose, maxIgnore);\n }\n }\n }\n }\n\n return convert(dp[m][n][k]);\n }\n\n private String max(String s1, String s2) {\n return (s1.compareTo(s2) < 0) ? s2 : s1;\n }\n\n private int[] convert(String s) {\n int n = s.length(), res[] = new int[n];\n for (int i = 0; i < n; i++) {\n res[i] = s.charAt(i)-\'0\';\n }\n return res;\n }\n```\n\nTime complexity `O(mnk)`, Space complexity `O(mnk)`.\nthough `MLE`, but space complexity can be improved to `O(mn)` (good practice).
| 8 | 0 |
[]
| 5 |
create-maximum-number
|
Short python code with explanation (100% faster)
|
short-python-code-with-explanation-100-f-lzex
|
Step1: Create maximum numbers individually from nums1 and nums2. Store \'j\' digit max numbers in dictionary. (say dp1 and dp2) \nStep2: Combine dp1[i] + dp2[k
|
ihatevirus
|
NORMAL
|
2019-10-28T07:46:34.449138+00:00
|
2019-10-28T07:52:21.662015+00:00
| 1,269 | false |
Step1: Create maximum numbers individually from nums1 and nums2. Store \'j\' digit max numbers in dictionary. (say dp1 and dp2) \nStep2: Combine dp1[i] + dp2[k-i] to create maximum \'k\' digit number\n\n```\nclass Solution(object):\n def maxNumber(self, nums1, nums2, k):\n def maximize(nums,length):\n dp,i = {length:nums},0\n while (length):\n while (i+1<length and nums[i]>=nums[i+1]): i+=1\n nums,length = nums[:i]+nums[i+1:],length-1\n dp[length] = nums\n if i>0: i-=1\n return dp\n m,n,result = len(nums1),len(nums2),[]\n dp1,dp2 = maximize(nums1,m),maximize(nums2,n)\n for i in range(min(m+1,k+1)):\n if k-i not in dp2: continue\n\t\t\tresult = max(result,[max(dp1[i],dp2[k-i]).pop(0) for _ in range(k)])\n return result\n```
| 8 | 3 |
[]
| 0 |
create-maximum-number
|
C++ fast and elegant new idea, 12ms | 100% | time O(k(m+n)) | space O(m+n)
|
c-fast-and-elegant-new-idea-12ms-100-tim-p1xp
|
Iteratively (greedily) find the maximal number of x digits that could potentially be extended to k digits (i.e. there are at least k digits left). To determine
|
alreadydone
|
NORMAL
|
2018-12-29T01:20:12.145287+00:00
|
2018-12-29T01:20:12.145338+00:00
| 2,446 | false |
Iteratively (greedily) find the maximal number of x digits that could potentially be extended to k digits (i.e. there are at least k digits left). To determine whether the number can be extended, it suffices to record the index of the last used digit in both numbers (there can be multiple such pairs of indices leading to the same maximal number), and check that there are at least a total of k-x digits left in both numbers. In the following implementation, the indices following the last used digits are recorded in `list_indices`. (Using set instead of vector or list because it can has at most max(m,n) elements, but with repetition it can blow up to 2^x and TLE.)\nTo go from step x to x+1, for each pair of indices in `list_indices`, extend the maximum number by one digit chosen from the ranges starting from those indices. Depending on whether the added digit is from the first or the second number, we get two new pairs of indices (stored in `next_list_indices`). We can throw out those pairs whose corresponding added digits are not maximal.\nIf we index the elements in `list_indices` as (m1,n1), (m2, n2), ... then they can be shown to satisfy m1 > m2 > m3 > ... and n1 < n2 < n3 < ... which shows the size of `list_indices` can be at most max(m,n), so the space complexity is clearly O(m+n). (It helps to plot the indices in a 2D grid.) Further analysis shows that for set insertion we just need to check that the inserted element is not the same as the last inserted element, so we can get rid of a log(m+n) factor for insertion. There are k steps and for each step the total number of indices checked in `getBestIndex` doesn\'t exceed m+n (e.g. if you extend (m1,n1) by one digit from the first number, you get some (m1\',n1) with m1\' <= m2), so the time complexity is O(k(m+n)). With more reasoning you can avoid some of the `getBestIndex` calls under certain conditions, but that doesn\'t lead to improvement on the asymptotic complexity.\n\n```\nclass Solution {\npublic:\n pair<int,int> getBestIndex(vector<int>& nums, int start, int span) {\n\t// get index and maximum\n int max_idx = 0;\n int max_ = nums[start];\n int i = 1;\n while (i < span) {\n auto val = nums[start+i];\n if (val > max_) {\n max_idx = i;\n max_ = val;\n if (max_ == 9) break;\n }\n i++;\n }\n return pair<int,int>(max_idx, max_);\n }\n \n vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {\n vector<int> best_seq;\n set<pair<int,int>> list_indices = {{0,0}};\n while (k-- > 0) {\n set<pair<int,int>> next_list_indices;\n int max_ = -1;\n for (auto indices : list_indices) {\n auto n1 = indices.first;\n auto n2 = indices.second;\n auto remaining = nums1.size() + nums2.size() - n1 - n2 - k;\n int idx1, max1 = -1, idx2, max2 = -1;\n auto remaining1 = min(remaining, nums1.size() - n1);\n auto remaining2 = min(remaining, nums2.size() - n2);\n if (remaining1)\n tie(idx1, max1) = getBestIndex(nums1, n1, remaining1);\n if (remaining2)\n tie(idx2, max2) = getBestIndex(nums2, n2, remaining2);\n auto max12 = max(max1, max2);\n if (max12 < max_) continue;\n if (max12 > max_) { max_ = max12; next_list_indices.clear(); }\n if (max1 >= max2) next_list_indices.insert({n1+idx1+1, n2});\n if (max1 <= max2) next_list_indices.insert({n1, n2+idx2+1});\n }\n best_seq.emplace_back(max_);\n list_indices = move(next_list_indices);\n }\n return best_seq;\n }\n};\n```
| 7 | 0 |
[]
| 4 |
create-maximum-number
|
Share C++ 72ms with simple comments
|
share-c-72ms-with-simple-comments-by-lch-nndn
|
vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {\n const int size1 = nums1.size();\n const int size2 = nums2.size();\n
|
lchen77
|
NORMAL
|
2015-12-23T17:02:12+00:00
|
2015-12-23T17:02:12+00:00
| 2,867 | false |
vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {\n const int size1 = nums1.size();\n const int size2 = nums2.size();\n if (size1 + size2 < k) return vector<int>();\n vector<int> res(k, 0);\n vector<vector<int>> dp1(k+1, vector<int>()), dp2(k+1, vector<int>());\n getDp(nums1, k, dp1);\n getDp(nums2, k, dp2);\n for (int i = 0; i <= min(k, size1); i++) {\n int j = k - i;\n vector<int> temp_res(k, 0);\n myMerge(dp1[i].begin(), dp1[i].end(), dp2[j].begin(), dp2[j].end(), temp_res.begin());\n if (j <= size2 && compareVector(temp_res, res)) {\n res = temp_res;\n }\n }\n return res;\n }\n \n template <class container>\n bool compareVector ( container vec1, container vec2)\n {\n typename container::iterator first1 = vec1.begin(), last1 = vec1.end();\n typename container::iterator first2 = vec2.begin(), last2 = vec2.end();\n while (first1 != last1 && first2 != last2) {\n if (*first1 > *first2)\n return true;\n else if (*first1 < *first2) return false;\n ++first1; ++first2;\n }\n if (first1 == last1) return false;\n else return true;\n }\n \n void getDp(vector<int> nums, int k, vector<vector<int>> &dp) {\n while (nums.size() > k) {\n int j = 0;\n for (; j < nums.size() - 1; ++j) {\n if (nums[j] < nums[j + 1]) {\n nums.erase(nums.begin() + j); \n break;\n }\n }\n if (j == nums.size() - 1) nums.erase(nums.begin() + j); \n }\n dp[nums.size()] = nums;\n const int size1 = nums.size();\n for (int i = k; i > 0; i--) {\n if (i >= size1) continue; \n else {\n dp[i] = dp[i+1];\n int j = 0;\n const int size_dp = dp[i].size();\n for (; j < size_dp - 1; ++j) {\n if (dp[i][j] < dp[i][j + 1]) {\n dp[i].erase(dp[i].begin() + j); \n break;\n }\n }\n if (j == size_dp - 1) dp[i].erase(dp[i].begin() + j); \n }\n \n }\n }\n template <class InputIterator1, class InputIterator2, class OutputIterator>\n OutputIterator myMerge (InputIterator1 first1, InputIterator1 last1,\n InputIterator2 first2, InputIterator2 last2,\n OutputIterator result)\n {\n while (true) {\n if (first1==last1) return std::copy(first2,last2,result);\n if (first2==last2) return std::copy(first1,last1,result);\n if (*first2 > *first1) *result++ = *first2++;\n else if (*first2 < *first1) *result++ = *first1++;\n else { // *first1 == *first2\n auto pos1 = first1, pos2 = first2;\n while (true) {\n int f1 = (++pos1 != last1) ? *(pos1) : INT_MIN;\n int f2 = (++pos2 != last2) ? *(pos2) : INT_MIN;\n if (f1 > f2) { *result++ = *first1++; break;}\n else if (f1 < f2) {*result++ = *first2++; break;}\n }\n }\n }\n }
| 7 | 3 |
['Dynamic Programming']
| 3 |
create-maximum-number
|
C++ DP+greedy Solution should be easy to understand
|
c-dpgreedy-solution-should-be-easy-to-un-gfkj
|
Here is the idea:\n \nLet's consider a similar but simple version of this problem: if there is only one array arr of which length is m, ho
|
yular
|
NORMAL
|
2015-12-23T21:18:08+00:00
|
2015-12-23T21:18:08+00:00
| 4,435 | false |
Here is the idea:\n \nLet's consider a similar but simple version of this problem: if there is only one array arr of which length is m, how to find the k digits of it to create maximum number preserving the order?\nSo here comes to my DP solution: DP[ i ][ j ] means that the maximum number that has i digits we can get when the jth digits is the last one of this number. Thus the formula is as follows:\n\n dp[ i ] [ j ] = max(dp[ i ][ j ], max(dp[ i - 1 ][ 0 ... j - 1 ]))\n\nOk. We apply this formula to the two given arrays and then get two DP arrays DP1 and DP2 where DP[ i ] means the largest number with i digits. \n\nBack to our problem: Choose k digits of these two arrays/strings to create the maximum number. Now here is the greedy solution:\n\nFor every pair of i and j where i + j == k and i is the number of digits used from array1 and j is the number of digits used from array2, we have to combine to create a new number so that it is the largest of all combinations. Remember a similar greedy problem? The trick here is that we use two pointers for each array and in each iteration, pick up pointers pointing to the larger digit or the larger substring. Then the number created is the largest from the given two arrays/strings.\n \nStill confused? Plsz read the code below:\n \n \n \n class Solution {\n public:\n vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {\n vector<int> ans;\n if(!nums1.size() && !nums2.size() || !k)\n return ans;\n ans.resize(k);\n int n = nums1.size(), m = nums2.size();\n vector<string> dp1(min(k, n)), dp2(min(k, m));\n vector<string> dpprev1(n), dpcur1(n), dpprev2(m), dpcur2(m);\n \n for(int i = 0; i < dp1.size(); ++ i){\n string tmpval(i + 1, 0);\n dp1[i] = tmpval;\n if(!i){\n for(int j = 0; j < n; ++ j){\n dpprev1[j] = "";\n dpprev1[j] += (char)(nums1[j] + '0');\n dp1[i] = max(dp1[i], dpprev1[j]);\n if(j)\n dpprev1[j] = max(dpprev1[j], dpprev1[j - 1]);\n \n }\n }else{\n for(int j = i; j < n; ++ j){\n dpcur1[j] = tmpval;\n \n dpcur1[j] = max(dpcur1[j], dpprev1[j - 1] + (char)(nums1[j] + '0'));\n \n dp1[i] = max(dp1[i], dpcur1[j]);\n if(j >= i)\n dpcur1[j] = max(dpcur1[j], dpcur1[j - 1]);\n }\n dpprev1 = dpcur1;\n }\n \n }\n \n \n \n for(int i = 0; i < dp2.size(); ++ i){\n string tmpval(i + 1, 0);\n dp2[i] = tmpval;\n if(!i){\n for(int j = 0; j < m; ++ j){\n dpprev2[j] = "";\n dpprev2[j] += (char)(nums2[j] + '0');\n dp2[i] = max(dp2[i], dpprev2[j]);\n if(j)\n dpprev2[j] = max(dpprev2[j], dpprev2[j - 1]);\n }\n }else{\n for(int j = i; j < m; ++ j){\n dpcur2[j] = tmpval;\n \n dpcur2[j] = max(dpcur2[j], dpprev2[j - 1] + (char)(nums2[j] + '0'));\n \n dp2[i] = max(dp2[i], dpcur2[j]);\n if(j >= i)\n dpcur2[j] = max(dpcur2[j], dpcur2[j - 1]);\n }\n dpprev2 = dpcur2;\n }\n \n }\n \n \n string tmpans(k, 0), v = "";\n \n if(!dp1.size()){\n getAns(v, dp2[k - 1], ans, tmpans);\n }else{\n for(int i = 0; i <= min(k, (int)dp1.size()); ++ i){\n if(i == 0){\n if(dp2.size() >= k)\n getAns(v, dp2[k - 1], ans, tmpans);\n }else if(i < k){\n if(dp2.size() >= k - i)\n getAns(dp1[i - 1], dp2[k - i - 1], ans, tmpans);\n }else{\n if(dp1.size() >= k)\n getAns(dp1[k - 1], v, ans, tmpans);\n }\n }\n \n }\n \n return ans;\n }\n \n private:\n void getAns(string &s1, string &s2, vector<int> &ans, string &tmpans){\n string res;\n if(!s1.size())\n res = s2;\n else if(!s2.size())\n res = s1;\n else{\n int id1 = 0, id2 = 0;\n \n while(id1 < s1.size() && id2 < s2.size()){\n if(s1[id1] > s2[id2]){\n res += s1[id1 ++];\n }else if(s1[id1] < s2[id2]){\n res += s2[id2 ++];\n }else{\n if(s1.substr(id1) >= s2.substr(id2))\n res += s1[id1 ++];\n else\n res += s2[id2 ++];\n }\n }\n while(id1 < s1.size())\n res += s1[id1 ++];\n while(id2 < s2.size())\n res += s2[id2 ++];\n }\n \n if(res > tmpans){\n tmpans = res;\n for(int i = 0; i < res.size(); ++ i)\n ans[i] = (res[i] - '0');\n }\n }\n };
| 7 | 0 |
['Dynamic Programming', 'Greedy', 'C++']
| 2 |
create-maximum-number
|
C++ || Best and Easiest Solution || Monotonic Stack || vector merging
|
c-best-and-easiest-solution-monotonic-st-ca39
|
Approach\nTake ans = 0;\nfor every i from 0 to n-1, do the following : \n1. Take max number of i digits from nums1 and max number of k-i digits from nums2.\n2.
|
om_golhani
|
NORMAL
|
2023-01-13T02:23:46.140401+00:00
|
2023-01-13T02:30:24.679082+00:00
| 2,292 | false |
# Approach\nTake ans = 0;\nfor every i from 0 to n-1, do the following : \n1. Take max number of i digits from nums1 and max number of k-i digits from nums2.\n2. Merge the above generated numbers to get the maximum number temp of k digits.\n3. update our ans as ans = max(ans , temp);\n\n\n# Code\n```\nclass Solution {\npublic:\n\n // function to generate maximum number of k digits in the form of vector obtained using elements of array nums.\n vector<int> solve(int k , vector<int> &nums){\n int n = nums.size();\n if(k>n) return {};\n vector<int> ans;\n int rem = n-k;\n ans.push_back(nums[0]);\n // monotonic stack\n for(int i=1 ; i<n ; i++){\n while(!ans.empty() && nums[i]>ans.back() && rem>0){\n ans.pop_back();\n rem--;\n }\n ans.push_back(nums[i]);\n }\n while(rem--){\n ans.pop_back();\n }\n return ans;\n }\n\n // function to merge two numbers in the form of vectors (v1 and v2) to get the maximum possible number and store it in another vector temp\n void merge(vector<int> &ans , vector<int> &v1 , vector<int> &v2){\n int m = v1.size();\n int n = v2.size();\n int i=0;\n int j=0;\n \n while(i<m && j<n){\n // Case1:\n // ....5 5 5 5 5 7.... .... 5 5 5 5 5 5...\n // i j\n // tempi tempj\n if(v1[i] == v2[j]){\n int tempi= i;\n int tempj= j;\n while(tempi<m && tempj<n && v1[tempi]==v2[tempj]){\n tempi++;\n tempj++;\n }\n if(tempj == n){\n ans.push_back(v1[i]);\n i++;\n }else if(tempi == m){\n ans.push_back(v2[j]);\n j++;\n }else if(v1[tempi]>v2[tempj]){\n ans.push_back(v1[i]);\n i++;\n }else{\n ans.push_back(v2[j]);\n j++;\n } \n }\n // Case2 : ....5 6 7 3 4..... .....2 3 9 8 7....\n // i j\n else if(v1[i] > v2[j]){\n ans.push_back(v1[i]);\n i++;\n }\n // Case2 : ....2 6 7 3 4..... .....9 3 9 8 7....\n // i j\n else{\n ans.push_back(v2[j]);\n j++;\n }\n }\n // if ......8 9 7 ...3 5 2 8\n // i j\n while(i<m){\n ans.push_back(v1[i]);\n i++;\n }\n // if ......8 9 7 ...3 5 2 8\n // i j\n while(j<n){\n ans.push_back(v2[j]);\n j++;\n }\n }\n\n vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {\n // We consider every possible case:\n // eg.1 Take maximum number of 0 digits from nums1 and maximum number of k digits from nums2 and merge them to get a maximum number of k digits.\n // eg2. Take maximum number of 1 digits from nums1 and maximum number of k-1 digits from nums2 and merge them to get a maximum number of k digits.\n // eg3. Take maximum number of 2 digits from nums1 and maximum number of k-2 digits from nums2 and merge them to get a maximum number of k digits.\n // eg4. Take maximum number of 3 digits from nums1 and maximum number of k-3 digits from nums2 and merge them to get a maximum number of k digits.\n // and so on.................\n // Then take the maximum among all the above generated numbers as our answer.\n\n vector<int> ans;\n for(int i=0 ; i<=k ; i++){\n vector<int> temp1 = solve(i , nums1);\n vector<int> temp2 = solve(k-i , nums2);\n vector<int> temp;\n merge(temp , temp1 , temp2);\n if(temp.size() == k) ans = max(ans , temp);\n }\n return ans;\n }\n};\n```\n\n**Upvote if you understood the approach and the code!**
| 6 | 0 |
['C++']
| 0 |
create-maximum-number
|
java 100% 4ms
|
java-100-4ms-by-went_m-mopk
|
\nclass Solution {\n //\u6838\u5FC3\u5C31\u662F\u4E24\u4E2A\u6307\u9488\uFF0C\u4F9D\u6B21\u5BF9\u6BD4\uFF0C\u5728\u6EE1\u8DB3canSkip\u60C5\u51B5\u4E0B\uFF0C\
|
went_m
|
NORMAL
|
2019-09-18T05:42:36.308436+00:00
|
2019-09-18T05:45:51.257185+00:00
| 1,658 | false |
```\nclass Solution {\n //\u6838\u5FC3\u5C31\u662F\u4E24\u4E2A\u6307\u9488\uFF0C\u4F9D\u6B21\u5BF9\u6BD4\uFF0C\u5728\u6EE1\u8DB3canSkip\u60C5\u51B5\u4E0B\uFF0C\u627E\u6700\u5927\u7684\u503C\u3002\u96BE\u70B9\u662F\u5982\u679C\u6700\u5927\u503C\u76F8\u540C\uFF0C\u5219\u9700\u8981\u8FED\u4EE3\u5904\u7406\u3002\n public int[] maxNumber(int[] nums1, int[] nums2, int k) {\n //canSkip : \u6700\u591A\u53EF\u4EE5\u8DF3\u8FC7\u591A\u5C11\u4E2A\n int canSkip = nums1.length - 0 + nums2.length - 0 - k;\n return helper(nums1, 0, nums2, 0, k, canSkip, 1).result;\n }\n //\u6700\u540E\u4E00\u4E2A\u53C2\u6570ifSameThenWhich\u8868\u793A\u4E24\u8005\u7686\u53EF\u9009\u7684\u60C5\u51B5\u4E0B\uFF0C\u9009\u62E9\u54EA\u4E2A1\u8868\u793A\u9009\u7B2C\u4E00\u4E2A\u6570\u7EC4\uFF0C2\u8868\u793A\u9009\u7B2C\u4E8C\u4E2A\u6570\u7EC4\u3002\n public ResultInfo helper(int[] nums1, int start1, int[] nums2, int start2, int k, int canSkip, int ifSameThenWhich) {\n int[] result = new int[k];\n for (int index = 0; index < k; index++) {\n int max1Index = maxWithSkip(nums1, start1, canSkip);\n int max2Index = maxWithSkip(nums2, start2, canSkip);\n if (max1Index != -1 && max2Index != -1 && nums1[max1Index] > nums2[max2Index] || max1Index != -1 && max2Index == -1) {//\u7B2C\u4E00\u4E2A\u6570\u7EC4\u7684\u5927\uFF0C\u9009\u7B2C\u4E00\u4E2A\u6570\u7EC4\n result[index] = nums1[max1Index];\n canSkip = canSkip - (max1Index - start1);\n start1 = max1Index + 1;\n } else if (max1Index != -1 && max2Index != -1 && nums2[max2Index] > nums1[max1Index] || max2Index != -1 && max1Index == -1) {//\u7B2C\u4E8C\u4E2A\u6570\u7EC4\u7684\u5927\uFF0C\u9009\u7B2C\u4E8C\u4E2A\u6570\u7EC4\n result[index] = nums2[max2Index];\n canSkip = canSkip - (max2Index - start2);\n start2 = max2Index + 1;\n } else {//\u4E24\u503C\u76F8\u7B49\uFF0C\u5219\u5047\u8BBE\u90091\u6216\u90092\u540E\u7EED\u503C\u6BD4\u8F83\n boolean done = false;\n int newK = k - index - 1;//\u8FD8\u5269\u591A\u5C11\u4E2A\u6CA1\u9009\n int newStart1 = max1Index + 1;//\u5047\u8BBE\u90091\u52191\u65B0\u7684start1\u4E3AnewStart1\n int canSkip1 = canSkip - (max1Index - start1);//\u5047\u8BBE\u90091\u52191\u65B0\u7684canSkip\u4E3AcanSkip1\n int newStart2 = max2Index + 1;//\u5047\u8BBE\u90092\u52192\u65B0\u7684start2\u4E3AnewStart2\n int canSkip2 = canSkip - (max2Index - start2);//\u5047\u8BBE\u90092\u52192\u65B0\u7684canSkip\u4E3AcanSkip2\n ResultInfo resultInfo1 = new ResultInfo(null, newStart1, start2, canSkip1);\n ResultInfo resultInfo2 = new ResultInfo(null, start1, newStart2, canSkip2);\n for (int tmpK = 1; tmpK <= newK; tmpK++) {//\u6CE8\u610F\u4F18\u5316\uFF1A\u6BCF\u6B21\u53EA\u8BA1\u7B97\u957F\u5EA6\u4E3A1\u7684\u6570\u7EC4\uFF0C\u5982\u679C\u76F8\u540C\uFF0C\u518D\u8BA1\u7B97\u540E\u9762\u7684\n //\u5047\u8BBE\u90091\n resultInfo1 = helper(nums1, resultInfo1.start1, nums2, resultInfo1.start2, 1, resultInfo1.canSkip, 1);\n int result1 = resultInfo1.result[0];\n //\u5047\u8BBE\u90092\n resultInfo2 = helper(nums1, resultInfo2.start1, nums2, resultInfo2.start2, 1, resultInfo2.canSkip, 2);\n int result2 = resultInfo2.result[0];\n if (result1 > result2) {\n //\u90091\n result[index] = nums1[max1Index];\n canSkip = canSkip - (max1Index - start1);\n start1 = max1Index + 1;\n done = true;\n break;\n } else if (result1 < result2) {\n //\u90092\n result[index] = nums2[max2Index];\n canSkip = canSkip - (max2Index - start2);\n start2 = max2Index + 1;\n done = true;\n break;\n }\n }\n if (!done) {//\u90FD\u884C\uFF0C\u6839\u636EifSameThenWhich\u9009\n if (ifSameThenWhich == 1) {\n result[index] = nums1[max1Index];\n canSkip = canSkip - (max1Index - start1);\n start1 = max1Index + 1;\n } else {\n result[index] = nums2[max2Index];\n canSkip = canSkip - (max2Index - start2);\n start2 = max2Index + 1;\n }\n }\n }\n }\n return new ResultInfo(result, start1, start2, canSkip);\n }\n //\u5728\u6EE1\u8DB3canSkip\u6761\u4EF6\u4E0B\uFF0C\u627E\u6700\u5927\u503C\u3002\n public int maxWithSkip(int[] nums, int start, int canSkip) {//\u8FD4\u56DE\u6700\u5927\u503C\u4E0B\u6807\n if (start == nums.length) {\n return -1;\n }\n int index = start;\n for (int i = 1; i <= canSkip; i++) {\n if (start + i < nums.length && nums[start + i] > nums[index]) {\n index = start + i;\n }\n }\n return index;\n }\n}\nclass ResultInfo {//\u7ED3\u679C\u548C\u7ED3\u675F\u65F6\u7684\u72B6\u6001\u503C\uFF0C\u5176\u4E2D\u72B6\u6001\u503C\u7528\u4E8E\u8FED\u4EE3\u4F18\u5316\n int[] result;\n int start1;\n int start2;\n int canSkip;\n\n public ResultInfo(int[] result, int start1, int start2, int canSkip) {\n this.result = result;\n this.start1 = start1;\n this.start2 = start2;\n this.canSkip = canSkip;\n }\n}\n```
| 6 | 2 |
[]
| 1 |
create-maximum-number
|
321: Space 98.63%, Solution with step by step explanation
|
321-space-9863-solution-with-step-by-ste-yhdx
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n1. Define a function called "get_max_subseq" that takes two inputs: a lis
|
Marlen09
|
NORMAL
|
2023-03-01T05:05:44.666294+00:00
|
2023-03-07T13:33:11.951851+00:00
| 2,637 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Define a function called "get_max_subseq" that takes two inputs: a list of integers called "nums" and an integer "k" representing the length of the subsequence we want to extract from the list.\n2. Initialize an empty stack to hold the maximum subsequence and iterate through the input list "nums" using a for loop and the enumerate() function.\n3. For each element "num" in "nums", do the following:\na. While the stack is not empty AND the length of the remaining part of "nums" (i.e., len(nums) - i) plus the length of the stack is greater than "k" AND the last element in the stack is less than "num", pop the last element from the stack.\nb. If the length of the stack is less than "k", append "num" to the stack.\n4. Return the resulting stack, which contains the maximum subsequence of "nums" of length "k".\n5. Define a function called "merge" that takes two inputs: two lists of integers called "nums1" and "nums2".\n6. Initialize an empty list called "merged" to hold the merged list.\n7. Initialize two counters i and j to 0 to track the current index of "nums1" and "nums2", respectively.\n8. While i is less than the length of "nums1" OR j is less than the length of "nums2", do the following:\na. If i is greater than or equal to the length of "nums1", append the jth element of "nums2" to "merged" and increment j by 1.\nb. Else if j is greater than or equal to the length of "nums2", append the ith element of "nums1" to "merged" and increment i by 1.\nc. Else if the remaining part of "nums1" starting from the ith index is lexicographically greater than the remaining part of "nums2" starting from the jth index, append the ith element of "nums1" to "merged" and increment i by 1.\nd. Otherwise, append the jth element of "nums2" to "merged" and increment j by 1.\n9. Return the resulting merged list.\n10. Initialize an empty list called "ans" to hold the maximum subsequence of length "k" from "nums1" and "nums2".\n11. Loop through all possible lengths "i" of the subsequence from "nums1" ranging from max(0, k - len(nums2)) to min(len(nums1), k) + 1.\n12. Calculate the corresponding subsequence of "nums2" of length "j" by subtracting "i" from "k".\n13. Call the "get_max_subseq" function on "nums1" with "i" as the input "k" and store the result in "subseq1".\n14. Call the "get_max_subseq" function on "nums2" with "j" as the input "k" and store the result in "subseq2".\n15. Call the "merge" function on "subseq1" and "subseq2" and store the result in "merged".\n16. Update "ans" to be the maximum value between the current value of "ans" and "merged" using the max() function.\n17. Return the resulting maximum subsequence of length "k" from "nums1" and "nums2", which is stored in "ans".\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxNumber(self, nums1: List[int], nums2: List[int], k: int) -> List[int]:\n def get_max_subseq(nums, k):\n stack = []\n for i, num in enumerate(nums):\n while stack and len(nums) - i + len(stack) > k and stack[-1] < num:\n stack.pop()\n if len(stack) < k:\n stack.append(num)\n return stack\n \n def merge(nums1, nums2):\n merged = []\n i, j = 0, 0\n while i < len(nums1) or j < len(nums2):\n if i >= len(nums1):\n merged.append(nums2[j])\n j += 1\n elif j >= len(nums2):\n merged.append(nums1[i])\n i += 1\n elif nums1[i:] > nums2[j:]:\n merged.append(nums1[i])\n i += 1\n else:\n merged.append(nums2[j])\n j += 1\n return merged\n \n ans = []\n for i in range(max(0, k - len(nums2)), min(len(nums1), k) + 1):\n j = k - i\n subseq1 = get_max_subseq(nums1, i)\n subseq2 = get_max_subseq(nums2, j)\n merged = merge(subseq1, subseq2)\n ans = max(ans, merged)\n return ans\n\n```
| 5 | 0 |
['Stack', 'Greedy', 'Monotonic Stack', 'Python', 'Python3']
| 2 |
create-maximum-number
|
A very efficient solution accepted as best beating 98% 16ms in C++, well-commented
|
a-very-efficient-solution-accepted-as-be-wrnc
|
class Solution {\n public:\n // create max number of length t from single non-empty vector\n // @nums is the array of length @len \n //
|
lhearen
|
NORMAL
|
2016-05-04T12:22:36+00:00
|
2016-05-04T12:22:36+00:00
| 2,017 | false |
class Solution {\n public:\n // create max number of length t from single non-empty vector\n // @nums is the array of length @len \n // @result will be used to store the max number of length @t \n // @sortedLen indicates the prefix length which is in descending order;\n void getMax(int* nums, int& len, int* result, int& t, int& sortedLen)\n {\n int n, top = 0;\n result[0] = nums[0];\n const int need2drop = len - t;\n for (int i = 1; i < len; ++i){\n n = nums[i];\n while (top >= 0 && result[top] < n && (i - top) <= need2drop) --top; // i - top means already dropped i - top numsbers\n if (i - top > need2drop){\n sortedLen = max(1,top);\n while (++top < t) result[top] = nums[i++];\n return;\n }\n if (++top < t) result[top] = n;\n else top = t - 1;\n }\n }\n // create max number of different length from single vector\n // @nums is the original array of length @len\n // @sortedLen is the longest length of the descending prefix of the max number;\n // @minL and @maxL is the min and max length of the result max number\n // @res is a pointer which will record the max numbers of length ranging from minL to maxL\n // @k is the length of the final max number;\n void dp(int *nums, int len, int&sortedLen, int& minL, int& maxL, int *res, int &k)\n {\n int j, *head, *preHead = res;\n const int soi = sizeof(int);\n getMax(nums, len, res, maxL, sortedLen);\n for(int l = maxL; l > max(minL,1); --l) //according to the max number of length maxL to generate all the max numbers ranging from minL to maxL (exclusive) and append them;\n {\n head = preHead + k; //jump to the next max-number pointer;\n memcpy(head, preHead, l*soi); \n for(j = sortedLen; j < l; ++j)\n {\n if(head[j] > head[j - 1]) //remove the previous element encountering the first ascending pair;\n {\n sortedLen = max(1, j - 1); //update the sortedLen;\n memcpy(head + j - 1, preHead + j, soi*(l - j));\n break;\n }\n }\n if(j == l) sortedLen = l; //it's already descending, remove the last element updating sortedLen to l;\n preHead = head; //update preHead;\n }\n }\n // merge max number created from single vector\n // @nums1 is the first array of length @len1\n // @nums2 is the second array of length @len2\n // @result is the array of length @resSize which will contain the max number generated\n // by the both two arrays without changing the order in each array;\n void merge(int* nums1,int len1,int* nums2,int len2,int* result,int& resSize)\n {\n int i = 0, j = 0, k = 0; //i -> result, j -> nums1, k -> nums2;\n while (i < resSize)\n {\n if (j < len1 && k < len2) //normal case;\n {\n if (nums1[j] > nums2[k]) //collect the bigger element first;\n result[i++] = nums1[j++];\n else if (nums1[j] < nums2[k])\n result[i++] = nums2[k++];\n else //when they are equal, collect the one with bigger lexical order;\n {\n int remaining1 = len1-j, remaining2 = len2-k, tmp = nums1[j];\n int flag = memcmp(nums1+j, nums2+k, sizeof(int)*min(remaining1, remaining2));\n flag = (flag==0 ? (remaining1>remaining2 ? 1 : -1) : flag); //determine which is bigger in lexical order -> when the lexical order are the same the longer one will be bigger in order;\n int * nums = flag > 0 ? nums1 : nums2;\n int & cnt = flag > 0 ? j : k; //using reference to modify j or k;\n int len = flag > 0 ? len1 : len2;\n while (nums[cnt]==tmp && cnt < len && i<resSize) result[i++] = nums[cnt++];\n }\n }\n else if (j < len1) result[i++] = nums1[j++];\n else result[i++] = nums2[k++];\n }\n }\n \n //AC - 16ms - the most efficient solution;\n // Reference: https://leetcode.com/discuss/85603/c-16ms-fastest-beats-97%25\n vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k){\n int soi = sizeof(int), len1 = nums1.size(), len2 = nums2.size();\n int step = k*soi; //the space the final max number might take in memory;\n int minL1 = max(0, k-len2), maxL1 = min(k, len1), minL2 = k-maxL1, maxL2 = k-minL1, range = maxL1-minL1+1;\n int * res = new int[range*k*2 + 2*k], *dp1 = res+k, *dp2 = res+range*k+k, *tmp=res+range*2*k+k; //using one-dimension array to handle different arrays -> only using the necessary space without any waste;\n memset(res, 0, step);\n int sortedLen1=1, sortedLen2=1;\n if (len1 == 0 && len2 > 0) getMax(&nums2[0], len2, res, k, sortedLen2); //handle corner cases;\n else if (len1 > 0 && len2 == 0) getMax(&nums1[0], len1, res, k, sortedLen1);\n else if (len1 > 0 && len2 > 0) //the normal case;\n {\n dp(&nums1[0], len1, sortedLen1, minL1, maxL1, dp1,k);\n dp(&nums2[0], len2, sortedLen2, minL2, maxL2, dp2,k);\n if (sortedLen1+sortedLen2 > k) //special cases - needless to check each combination accelerating the process from 20ms to 16ms;\n merge(dp1 + k*(maxL1 - sortedLen1), sortedLen1, dp2 + k*(maxL2 - sortedLen2), sortedLen2, res, k);\n else for(int i = minL1; i <= maxL1; ++i)\n {\n merge(dp1+k*(maxL1-i), i, dp2+k*(maxL2-k+i), (k-i), tmp,k);\n if(memcmp(res, tmp, step) < 0) memcpy(res, tmp, step);\n }\n }\n vector<int> resv(res, res + k);\n delete[] res;\n return resv;\n }\n };
| 5 | 1 |
['C++']
| 0 |
create-maximum-number
|
O(k(m+n)). Python Solution with monotonically decreasing stack. Commented for clarity.
|
okmn-python-solution-with-monotonically-4g3b5
|
This solution is pretty efficient and intuitive.\nTime complexity is O(k(n+m)) where n and m is length of each list. \n\n\nTo understand this solution you must
|
saqibmubarak
|
NORMAL
|
2022-06-18T21:18:35.890443+00:00
|
2022-06-18T21:19:59.250304+00:00
| 1,424 | false |
This solution is pretty efficient and intuitive.\nTime complexity is **O(k(n+m))** where n and m is length of each list. \n\n\nTo understand this solution you must also do other problems concerning monotonic stack like LC-402 which are pre-requisites for this problem.\n\nDo give me a thumbs up if u like it.\n```\nclass Solution:\n def maxNumber(self, nums1: List[int], nums2: List[int], k: int) -> List[int]:\n def maximum_num_each_list(nums: List[int], k_i: int) -> List[int]:\n # monotonically decreasing stack\n s = []\n m = len(nums) - k_i\n for n in nums:\n while s and s[-1] < n and m > 0:\n s.pop()\n m -= 1\n s.append(n)\n s = s[:len(s)-m] # very important\n return s\n def greater(a, b, i , j): # get the number which is lexiographically greater\n while i< len(a) or j < len(b): \n if i == len(a): return False\n if j == len(b): return True\n if a[i] > b[j]: return True\n if a[i] < b[j]: return False\n i += 1 # we increment until each of their elements are same\n j += 1\n \n def merge(x_num, y_num):\n n = len(x_num)\n m = len(y_num)\n i = 0\n j = 0\n s = []\n while i < n or j < m:\n a = x_num[i] if i < n else float("-inf") \n b = y_num[j] if j < m else float("-inf") \n\n if a > b or greater(x_num, y_num, i , j):\n# greater(x_num, y_num, i , j): this function is meant for check which list has element lexicographically greater means it will iterate through both arrays incrementing both at the same time until one of them is greater than other.\n chosen = a\n i += 1\n else:\n chosen = b\n j += 1\n s.append(chosen)\n return s\n\n max_num_arr = []\n for i in range(k+1): # we check for all values of k and find the maximum number we can create for that value of k and we repeat this for all values of k and then at eacch time merge the numbers to check if arrive at optimal solution\n first = maximum_num_each_list(nums1, i)\n second = maximum_num_each_list(nums2, k-i)\n merged = merge(first, second)\n # these two conditions are required because list comparison in python only compares the elements even if one of their lengths is greater, so I had to add these conditions to compare elements only if length is equal.\n\t\t\t# Alternatively you can avoid this and convert them both to int and then compare, but I wanted to this as it is somewhat more efficient.\n if len(merged) == len(max_num_arr) and merged > max_num_arr:\n max_num_arr = merged\n elif len(merged) > len(max_num_arr):\n max_num_arr = merged\n return max_num_arr\n\n```\nFeel free to ask any questions in the comments.\nDo suggest improvements if any.
| 4 | 1 |
['Stack', 'Greedy', 'Monotonic Stack', 'Python', 'Python3']
| 2 |
create-maximum-number
|
360 ms python solution with detailed explanation
|
360-ms-python-solution-with-detailed-exp-n9le
|
The main idea: \n\n1 . get the maximum array with length of s1 from list nums1 called p1 and then get the maximum array with length of k-s1 from list nums2 call
|
yiweizhu0423
|
NORMAL
|
2020-09-26T17:07:32.484510+00:00
|
2020-09-26T17:07:32.484542+00:00
| 644 | false |
The main idea: \n\n1 . get the maximum array with length of s1 from list nums1 called p1 and then get the maximum array with length of k-s1 from list nums2 called p2\n2 . arrange p1 and p2 to make maximum rs \n\nTo get the maximum array with length of c_len and also reserve the relative order in that array:\n We use a helper function to get the maximum array with length of c_len\nas long as ans[-1]< current value and the remaining elements in list nums is enough to form ans with length c_len then we pop the last element in ans\n```\n\nclass Solution(object):\n def maxNumber(self, nums1, nums2, k):\n \n l1,l2 = len(nums1),len(nums2)\n rs = []\n \n \n def helper(nums,c_len):\n ans = []\n ln = len(nums)\n for idx,val in enumerate(nums):\n while ans and ans[-1]<val and ln-idx> c_len-len(ans):\n ans.pop(-1)\n if len(ans)<c_len:\n ans.append(val)\n return ans\n \n for s1 in range(max(0,k-l2),min(k,l1)+1):\n p1,p2 = helper(nums1,s1),helper(nums2,k-s1)\n rs = max(rs,[max(p1,p2).pop(0) for _ in range(k)])\n return rs\n```\n
| 4 | 1 |
[]
| 0 |
create-maximum-number
|
Java segment tree 3ms, unprecented 100%, O(klogn) + O(n) for best case
|
java-segment-tree-3ms-unprecented-100-ok-anbc
|
Basic idea is pick the maximum from nums1 and nums2, in a way that will ensure enough numbers for later picks. Two points cur1 and cur2 is maintained to ensure
|
tangentyh
|
NORMAL
|
2020-03-13T15:46:10.232345+00:00
|
2020-03-13T16:00:21.038209+00:00
| 654 | false |
Basic idea is pick the maximum from `nums1` and `nums2`, in a way that will ensure enough numbers for later picks. Two points `cur1` and `cur2` is maintained to ensure relative orders of picks.\n\nTo make picking a maximum *O(logn)*, segment tree is used, which stores indices and the query function, `reducer`, is max function.\n\n```java\nclass Solution {\n public int[] maxNumber(int[] nums1, int[] nums2, int k) {\n SegmentTreeMax st1 = new SegmentTreeMax(nums1), st2 = new SegmentTreeMax(nums2);\n int[] maxN = new int[k];\n int cur1 = 0, cur2 = 0, remained = nums1.length + nums2.length - k;\n for (int i = 0; i != k; ++i) {\n int to1 = remained - cur2 + i,\n to2 = remained - cur1 + i;\n int picked1 = st1.reduceClosedGuarded(cur1, to1);\n int picked2 = st2.reduceClosedGuarded(cur2, to2);\n int comparePicked = compareIdx(nums1, picked1, nums2, picked2);\n if (comparePicked == 0) {\n int p1 = picked1, p2 = picked2;\n for (int j = 1; comparePicked == 0; ++j) {\n p1 = st1.reduceClosedGuarded(p1 + 1, to1 + j);\n p2 = st2.reduceClosedGuarded(p2 + 1, to2 + j);\n comparePicked = compareIdx(nums1, p1, nums2, p2);\n }\n if (p1 == -1 && p2 == -1) {\n comparePicked = 0;\n p1 = picked1; p2 = picked2;\n while (comparePicked == 0) {\n p1 = st1.reduceClosedGuarded(cur1, p1 - 1);\n p2 = st2.reduceClosedGuarded(cur2, p2 - 1);\n comparePicked = -compareIdx(nums1, p1, nums2, p2);\n }\n }\n }\n if (comparePicked == 1) {\n maxN[i] = nums1[picked1];\n cur1 = picked1 + 1;\n }\n else {\n assert comparePicked == -1;\n maxN[i] = nums2[picked2];\n cur2 = picked2 + 1;\n }\n }\n return maxN;\n }\n private int compareIdx(int[] nums1, int i, int[] nums2, int j) {\n if (i == -1) return -1;\n if (j == -1) return 1;\n return Integer.compare(nums1[i], nums2[j]);\n }\n}\n\nclass SegmentTreeMax {\n private final int[] data;\n private final int[] origin;\n public SegmentTreeMax(int[] origin) {\n data = new int[origin.length << 1];\n this.origin = origin;\n for (int i = origin.length; i != data.length; ++i) data[i] = i - origin.length;\n for (int i = origin.length - 1; i > 0; --i) data[i] = reducer4Build(data[i << 1], data[(i << 1) | 1]);\n }\n private int reducer4Build(int a, int b) {\n return (origin[a] < origin[b]) ? b : a;\n }\n private int reducer(int a, int b) {\n if (a > b) {\n a = a ^ b;\n b = a ^ b;\n a = a ^ b;\n }\n return (origin[a] < origin[b]) ? b : a;\n }\n public int reduceClosedGuarded(int from, int to) {\n to = Math.min(to, origin.length - 1);\n if (from > to) return -1;\n int maxima = from;\n for (int i = from + origin.length, j = to + origin.length; i <= j; i >>= 1, j >>= 1) {\n if ((i & 1) == 1) maxima = reducer(maxima, data[i++]);\n if ((j & 1) == 0) maxima = reducer(maxima, data[j--]);\n }\n return maxima;\n }\n}\n```
| 4 | 0 |
[]
| 4 |
create-maximum-number
|
O(m*n*k) DP solution, TLE
|
omnk-dp-solution-tle-by-cfdream1-utqn
|
Now I find there are O(max(m, n) * k) greedy solution from the posts. My first idea is DP. Let f(i,j,k) represent maximum number of length k generated from nums
|
cfdream1
|
NORMAL
|
2016-01-03T17:57:00+00:00
|
2018-08-23T01:50:46.035163+00:00
| 2,984 | false |
Now I find there are O(max(m, n) * k) greedy solution from the posts. My first idea is DP. Let f(i,j,k) represent maximum number of length k generated from nums1[1:i] and nums2[1:j]. the formula is: f(i,j,k) = max{f(i-1,j,k), f(i,j-1,k), f(i-1,j,k-1) + [nums1[i]], f(i,j-1,k-1) + [nums2[j]] } The implementation is as follows,\n\n def maxNumber(self, nums1, nums2, k):\n """\n :type nums1: List[int]\n :type nums2: List[int]\n :type k: int\n :rtype: List[int]\n """\n m = len(nums1)\n n = len(nums2)\n if k > m + n or k <= 0:\n return []\n #kk = 0\n pre_dp = [[[] for _ in xrange(n + 1)] for __ in xrange(m + 1)]\n \n for kk in xrange(1, k + 1):\n #kk\n dp = [[[] for _ in xrange(n + 1)] for __ in xrange(m + 1)]\n #i >= kk, j = 0\n for i in xrange(kk, m + 1):\n dp[i][0] = max(pre_dp[i-1][0] + [nums1[i-1]], dp[i-1][0])\n \n #i = 0, j >= kk\n for j in xrange(kk, n + 1):\n dp[0][j] = max(pre_dp[0][j-1] + [nums2[j-1]], dp[0][j-1])\n \n #i > 0, j > 0\n for i in xrange(1, m + 1):\n for j in xrange(1, n + 1):\n if i + j < kk:\n continue\n dp[i][j] = max(dp[i-1][j], \\\n dp[i][j-1], \\\n pre_dp[i-1][j] + [nums1[i-1]], \\\n pre_dp[i][j-1] + [nums2[j-1]])\n pre_dp, dp = dp, pre_dp\n return pre_dp[m][n]
| 4 | 0 |
[]
| 5 |
create-maximum-number
|
C++ || Greedy || Commented || Easy to Understand
|
c-greedy-commented-easy-to-understand-by-24j8
|
\nclass Solution {\npublic:\n \n //function to find the maximum lexicographic sequence using monotonic stack implemented\n //via vector. It will give u
|
glock17
|
NORMAL
|
2022-11-28T11:06:54.481296+00:00
|
2022-11-28T11:07:38.448087+00:00
| 760 | false |
```\nclass Solution {\npublic:\n \n //function to find the maximum lexicographic sequence using monotonic stack implemented\n //via vector. It will give us maximum lexicographic sequence of length k.\n \n vector<int> maxLex(vector<int> nums, int k) {\n int N = nums.size();\n vector<int> res;\n \n for(int i=0; i<N; i++) {\n //condition to pop\n //the last condition ensures length k is returned\n while(!res.empty() and nums[i] > res.back() and k - (int)res.size() <= N - i - 1) {\n res.pop_back();\n }\n if(res.size() < k)\n res.push_back(nums[i]);\n }\n return res;\n }\n \n //function to return true if vector starting at a is lexicographically greater than nums2 starting at b\n \n bool greater(vector<int>& nums1, vector<int>& nums2, int a, int b) {\n while(a < nums1.size() or b < nums2.size()) {\n if(a >= nums1.size())\n return false;\n else if(b >= nums2.size())\n return true;\n else if(nums1[a] < nums2[b]) \n return false;\n else if(nums1[a] > nums2[b])\n return true;\n else \n ++a,++b;\n }\n return true;\n }\n \n vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {\n vector<int> ans;\n //we are trying to generate all possible max lexicographic sequences from the two vextors\n //of different lengths and then we merge them and compare for maximum result\n for(int i=0; i<=k; i++) {\n int j = k - i;\n \n if(i > nums1.size() or j > nums2.size())\n continue;\n \n vector<int> max1 = maxLex(nums1,i);\n vector<int> max2 = maxLex(nums2,j);\n \n //using merge sort technique\n vector<int> merged;\n \n int a = 0;\n int b = 0;\n \n while(a < max1.size() or b < max2.size()) {\n if(a >= max1.size())\n merged.push_back(max2[b++]);\n else if(b >= max2.size())\n merged.push_back(max1[a++]);\n else if(max1[a] < max2[b]) \n merged.push_back(max2[b++]);\n else if(max1[a] > max2[b])\n merged.push_back(max1[a++]);\n //if we have the case where we have got the same value then we have to consider \n //which of the two vectors have max lexicographic sequence beginning from a and b pointers\n //as a max sequence will affect the answer positively and we would be pushing the result\n //from the vector which has a max sequence\n else{\n if(greater(max1,max2,a,b)) {\n //if max1 is greater then we enter\n merged.push_back(max1[a++]);\n }\n else {\n merged.push_back(max2[b++]);\n }\n }\n }\n if(merged > ans)\n ans = merged;\n }\n return ans;\n }\n};\n```
| 3 | 0 |
['Stack', 'Greedy', 'C']
| 0 |
create-maximum-number
|
JAVA||Monotonic Stack
|
javamonotonic-stack-by-changxu_ren-8o4s
|
Please upvote if you find it useful! Thank you so much!!\n\n\nclass Solution {\n public int[] maxNumber(int[] nums1, int[] nums2, int k) {\n int len1
|
Changxu_Ren
|
NORMAL
|
2021-08-27T22:24:49.367936+00:00
|
2021-08-27T22:24:49.368051+00:00
| 656 | false |
Please upvote if you find it useful! Thank you so much!!\n\n```\nclass Solution {\n public int[] maxNumber(int[] nums1, int[] nums2, int k) {\n int len1 = nums1.length, len2 = nums2.length;\n int[] res = new int[k];\n int[] tempRes = null;\n \n // enumerate all the possible ways to construct an array with len k from two arrays\n // the length of the res is k \n // we assume that we pick k1 numbers from nums1, therefore we pick (k - k1) numbers\n // from nums2. The possible range of k1 is from Math.max(0, k-len2)\n // to Math.min(len1, k);\n for(int k1 = Math.max(0, k-len2); k1 <= Math.min(len1, k); k1++){\n int[] num1Max = findMaxSubsequence(nums1, k1);\n int[] num2Max = findMaxSubsequence(nums2, k - k1);\n tempRes = merge(num1Max, num2Max);\n if(isGreater(tempRes, 0, res, 0)){\n res = tempRes;\n }\n }\n return res;\n }\n \n // find the largest number that can be constructed from two arrays\n private int[] merge(int[] nums1, int[] nums2){\n int[] res = new int[nums1.length + nums2.length];\n int p1 = 0, p2 = 0, p3 = 0;\n \n while(p3 < res.length){\n res[p3++] = isGreater(nums1, p1, nums2, p2) ? nums1[p1++] : nums2[p2++]; \n }\n return res;\n }\n \n private boolean isGreater(int[] nums1, int p1, int[] nums2, int p2){\n while(p1 < nums1.length && p2 < nums2.length){\n if(nums1[p1] > nums2[p2]){\n return true;\n }else if(nums1[p1] < nums2[p2]){\n return false;\n }\n p1++;\n p2++;\n }\n return p1 != nums1.length;\n }\n \n // this subroutine is similar to leetcode 1673\n private int[] findMaxSubsequence(int[] num, int len){\n if(num.length == len){return num;}\n \n int[] stack = new int[len];\n int top = -1;\n int canRemoveCnt = num.length - len;\n \n for(int i = 0; i < num.length; i++){\n int curNum = num[i];\n \n while(top >= 0 && canRemoveCnt > 0 && curNum > stack[top]){\n top--;\n canRemoveCnt--;\n }\n \n if(top + 1 < stack.length){\n stack[++top] = curNum; \n }else{\n canRemoveCnt--;\n }\n }\n \n return stack;\n }\n}\n```
| 3 | 0 |
[]
| 0 |
create-maximum-number
|
C++ Solution - greedy, monotonic stack
|
c-solution-greedy-monotonic-stack-by-yuf-2qi7
|
\nclass Solution {\npublic:\n // pick k numbers from vector num\n vector<int> select(vector<int>& nums, int k){\n int n = nums.size();\n vec
|
yufeizheng
|
NORMAL
|
2021-07-22T03:16:13.211445+00:00
|
2021-07-22T03:16:13.211487+00:00
| 747 | false |
```\nclass Solution {\npublic:\n // pick k numbers from vector num\n vector<int> select(vector<int>& nums, int k){\n int n = nums.size();\n vector<int> res(k, INT_MIN);\n for(int i = 0, j = 0;i<nums.size();i++){\n int x = nums[i];\n // monotonic stack\n while(j>0&&x > res[j-1]&&i+k-j<n) j--;\n if(j<k) res[j++] = x;\n }\n return res;\n }\n vector<int> merge(vector<int>& a, vector<int> &b){\n vector<int> c;\n while(a.size()&&b.size()){\n // The time complexity of compare operation for two vector is order of n.\n // Greedy Algorithm:\n // If we meet two elements which have the same value, choose the vector which has the higher dictionary order first.\n // 1: ...xxxb , 2: ...xxxa, if a > b, then merge sequence 2 first. \n if(a > b)\n c.push_back(a[0]), a.erase(a.begin());\n else\n c.push_back(b[0]), b.erase(b.begin());\n }\n while(a.size())\n c.push_back(a[0]), a.erase(a.begin());\n while(b.size())\n c.push_back(b[0]), b.erase(b.begin());\n return c;\n }\n vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {\n vector<int> res(k, INT_MIN);\n int n = nums1.size(), m = nums2.size();\n // s1 => nums1.size(), s2 => nums2.size()\n // {0<=i<=k, i<=s1, 0<=k-i<=s2} => i>=max(0, k-s2), i<=min(k, n)\n for(int i = max(0, k-m);i<=min(k, n);i++){\n vector<int> a = select(nums1, i);\n vector<int> b = select(nums2, k - i);\n res = max(res, merge(a, b));\n }\n return res;\n }\n};\n```\n// yxc nb!
| 3 | 0 |
[]
| 0 |
create-maximum-number
|
CPP Simple Greedy solution.
|
cpp-simple-greedy-solution-by-user7634ri-9d7c
|
\n\nclass Solution {\npublic:\n vector<int> calc(vector<int> &v,int k,int n) {\n vector<int> v1;\n // IF I replace the current top or not.\n
|
user7634ri
|
NORMAL
|
2021-03-16T10:56:21.882649+00:00
|
2021-03-16T10:56:21.882679+00:00
| 639 | false |
```\n\nclass Solution {\npublic:\n vector<int> calc(vector<int> &v,int k,int n) {\n vector<int> v1;\n // IF I replace the current top or not.\n int i=-1,j,ind=-1,ans=-1;\n while(k) {\n j=i+1;ind=-1;ans=-1;\n while(j<n&&n-j>=k) {\n if(v[j]>ans) {\n ans=v[j];\n ind=j;\n }\n j++;\n }\n i=ind;\n v1.push_back(ans);\n k--;\n }\n return v1;\n }\n vector<int> merge(vector<int> &v1,vector<int> &v2,int n,int m) {\n vector<int> v;\n if(n>m) {\n swap(v1,v2);\n swap(n,m);\n }\n int i=0,j=0;\n while(i<n && j<m) {\n if(v1[i]>v2[j]) {\n v.push_back(v1[i]);\n i++;\n }\n else if(v1[i]<v2[j]) {\n v.push_back(v2[j]);\n j++;\n }\n else {\n int k=i+1,l=j+1,f=1;\n while(k<n && l<m) {\n if(v1[k]>v2[l]) { f=0;break; }\n else if(v1[k]<v2[l]) { f=1;break;}\n k++;\n l++;\n }\n \n if(f==0||l==m) { v.push_back(v1[i++]); }\n else { v.push_back(v2[j++]); }\n }\n }\n while(i<n) { v.push_back(v1[i]);i++; }\n while(j<m) { v.push_back(v2[j]);j++; }\n return v;\n }\n int comp(vector<int> v1,vector<int> v2,int k) {\n for(int i=0;i<k;i++) { \n if(v1[i]!=v2[i]) return v1[i]>v2[i];\n }\n return 0;\n }\n vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {\n int n=nums1.size(),m=nums2.size();\n // If I have to chose k greatest elements.\n // from a vector. how you are going to pick up.\n // this task is awesome.\n vector<int> ans(k,-1);\n for(int i=0;i<=min(n,k);i++) {\n int r=k-i;\n if(r<=m) { \n vector<int> v1=calc(nums1,i,n),v2=calc(nums2,r,m);\n vector<int> x=merge(v1,v2,i,r);\n if(comp(x,ans,k)>0) ans=x;\n }\n }\n return ans;\n }\n};\n\n```
| 3 | 0 |
[]
| 0 |
create-maximum-number
|
Help me understand the question
|
help-me-understand-the-question-by-csy99-xy77
|
I have a hard time understanding the question. \nFor the input:\n[5,5,4,1,1,6,2], [8,8], 4\nI think the expected output is [8,8,5,6], which still preserves the
|
csy99
|
NORMAL
|
2020-03-14T19:09:48.881093+00:00
|
2020-03-14T19:10:20.533246+00:00
| 275 | false |
I have a hard time understanding the question. \nFor the input:\n[5,5,4,1,1,6,2], [8,8], 4\nI think the expected output is [8,8,5,6], which still preserves the order of 2 arrays. \nHowever, the correct output is [8,8,6,2]\nAny comments will be helpful.
| 3 | 0 |
[]
| 1 |
create-maximum-number
|
C++ Solution based on @StefanPochmann's approach with very detailed explanation
|
c-solution-based-on-stefanpochmanns-appr-hf2j
|
@StefanPochmann solution is great but lacks detailed comments. Here is the solution that explains the process step by step. \n Idea - \n K elements can be
|
jayesch
|
NORMAL
|
2018-07-31T21:04:30.733619+00:00
|
2018-08-09T06:49:01.476653+00:00
| 693 | false |
@StefanPochmann solution is great but lacks detailed comments. Here is the solution that explains the process step by step. \n Idea - \n* K elements can be picked as i elements from nums1 and k-i elements from nums2. \n* We slice two lists nums1 and nums2 by choosing series of values for i\n* We create biggest number possible from each list for given value of i or k-i\n* We combine the two lists to get the biggest number for given slice.\n* We choose maximum number for all slices.\n\nCode below - \n```\nclass Solution {\n\nprivate:\n //Compare function for two generic collections.\n //if collection contains non primitive types then it must overload\n //operator \'<\'\n \n //returns true if second list is greater in value than first one\n //if all elements are equal then it returns true if second list is\n //larger in size\n \n template <class InputIterator1, class InputIterator2>\n bool lexicographical_compare (InputIterator1 first1, InputIterator1 last1,\n InputIterator2 first2, InputIterator2 last2)\n {\n while (first1!=last1)\n {\n if (first2==last2 || *first2<*first1) return false;\n else if (*first1<*first2) return true;\n ++first1; ++first2;\n }\n return (first2!=last2);\n }\npublic:\n \n //subproblem 1 = create the greatest number with K digits from a single list\n vector<int> maxNumber(vector<int> nums, int k) {\n int drop = nums.size()-k; //number of digits to be dropped\n vector<int> out;\n for(int num : nums) {\n //if there are digits left to be dropped and if we find\n //a digit that is greater than the digit we have in our \n //output array we drop the digits and add that digit\n while(drop > 0 && out.size() != 0 && out.back() < num) {\n drop--;\n out.pop_back();\n }\n out.push_back(num);\n }\n out.resize(k); // this is necessary if there are more than K digits in out\n return out;\n }\n \n /*\n subproblem 2 = create largest number from the two lists, containing\n digits [0-9]. The size of output number is sum of size of two\n lists\n */\n vector<int> maxNumber(vector<int> nums1, vector<int> nums2) {\n auto start1 = nums1.begin(), end1 = nums1.end(),\n start2 = nums2.begin(), end2 = nums2.end();\n vector<int> out;\n while(start1 != end1 || start2 != end2) {\n if(lexicographical_compare(start1,end1,start2,end2)) {\n out.push_back(*start2++);\n }\n else {\n out.push_back(*start1++);\n }\n }\n return out;\n }\n \n vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {\n int n1 = nums1.size(), n2 = nums2.size();\n vector<int> best;\n /* \n The start and end range of for the "for loop" is computed based on\n number of min elements we need to pick from nums1 and number of maximum\n elements we can pick from nums1. if k > n2 then we must at least pick up\n k-n2 elements from n1\n \n \n Example 1\n consider n1 = 4 and n2 = 6 and k = 5\n Result can be constructed in following ways \n (i:0, k-i:5), (i:1, k-i:4), (i:2, k-i:3), (i:3, k-i:2), (i:4, k-i:1)\n where i is number of elements picked from nums1 and k-i is number of elements\n picked from nums2. Please note\n --> (i:5, k-i:0) is not valid since n1=4\n \n Example 2\n Now consider n1 = 6 and n2 = 4 and k = 5\n (i:1, k-i:4), (i:2, k-i:3), (i:3, k-i:2), (i:4, k-i:1), (i:5, k-i:0)\n \n hence starting index for i that is associated with nums1 is \n max(0, k-n2) (in first example k-n2 = -1, in second example k-n2 = 1)\n \n end index for i associated with nums1 is \n min(k,n1) (in first example i can only go up to 4 since n1 = 4, in second example\n i can only go up to 5 since k = 5)\n \n Example 3\n n1 = 3, n2 = 4, k = 5\n we must pick at least 1 element from nums1 (k-n2 = 1) also i can only go up to 3 since\n n1 is capped at 3\n \n Example 4\n \n n1 = 5, n2=3, k = 4\n we must pick up at least 1 element from nums1 (k-n2 = 1) and i can go up to 4\n \n */\n for(int i = max(0,k-n2); i <= min(k,n1); i++) {\n \n if(best.size() == 0) {\n best = maxNumber(maxNumber(nums1,i),\n maxNumber(nums2,k-i));\n }\n else {\n vector<int> temp = maxNumber(maxNumber(nums1,i),\n maxNumber(nums2,k-i));\n if(lexicographical_compare(best.begin(), best.end(),\n temp.begin(),temp.end())) {\n best = temp;\n }\n }\n //vector class overloads "<" operator hence you could simply use the \n //statement below, above code is only to make things simple.\n //best = max(best,maxNumber(maxNumber(nums1,i),maxNumber(nums2,k-i)));\n }\n return best;\n } \n};\n```
| 3 | 0 |
[]
| 1 |
create-maximum-number
|
C++ implementation of the top voted answer without the compare function
|
c-implementation-of-the-top-voted-answer-i10b
|
class Solution {\n private:\n //get the max k-length number of array nums ...\n vector<int> helper(vector<int>& nums, int k){\n int
|
rainbowsecret
|
NORMAL
|
2015-12-27T07:43:56+00:00
|
2015-12-27T07:43:56+00:00
| 934 | false |
class Solution {\n private:\n //get the max k-length number of array nums ...\n vector<int> helper(vector<int>& nums, int k){\n int n=nums.size();\n int j=0; // the count of the stacked array \n vector<int> result(k,0);\n for(int i=0; i<n; i++){\n //result[j-1] stores the top of the stack \n while(j>0 && n-i+j>k && nums[i]>result[j-1]) j--;\n if(j<k) result[j++]=nums[i];\n }\n return result;\n }\n \n vector<int> merge(vector<int>& nums1, vector<int>& nums2, int k){\n vector<int> result(k, 0);\n ostringstream num_str1, num_str2;\n string str1, str2;\n for(auto num:nums1) num_str1 << num;\n for(auto num:nums2) num_str2 << num;\n str1=num_str1.str();\n str2=num_str2.str();\n for(int i=0, j=0, r=0; r<k; r++){\n result[r] = str1.substr(i).compare(str2.substr(j)) > 0 ? nums1[i++] : nums2[j++];\n }\n return result;\n }\n \n public:\n vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {\n int n=nums1.size(), m=nums2.size();\n vector<int> result(k, 0);\n string result_str;\n for(int i=max(0, k-m); i<=k && i<=n; i++){\n vector<int> sub_1 = helper(nums1, i);\n vector<int> sub_2 = helper(nums2, k-i);\n vector<int> candidate = merge(sub_1, sub_2, k);\n ostringstream str_c;\n for(auto number:candidate) str_c << number;\n if(result_str=="" || str_c.str().compare(result_str) > 0 ){\n result_str=str_c.str();\n result=candidate;\n }\n }\n return result;\n }\n };
| 3 | 0 |
['C++']
| 0 |
create-maximum-number
|
Java 17 ms O(n + m + k^2 or 3?) worst case merge with lazy computation
|
java-17-ms-on-m-k2-or-3-worst-case-merge-nsa1
|
I must admit I found this problem the most difficult so far, and I've solved more than 80 already.\n\nAt first my idea was very similar to [this solution][1], w
|
sergeytachenov
|
NORMAL
|
2016-01-06T12:38:24+00:00
|
2016-01-06T12:38:24+00:00
| 2,256 | false |
I must admit I found this problem the most difficult so far, and I've solved more than 80 already.\n\nAt first my idea was very similar to [this solution][1], which I think is the most awesome so far, but I wasn't able to get it right.\n\nSo in the end I had to look up solutions, and I usually don't do that. But once I saw the most common type of solutions so far, I was able to use some of my earlier ideas and came up with this:\n\n public int[] maxNumber(int[] nums1, int[] nums2, final int k) {\n if (k > nums1.length + nums2.length)\n throw new IllegalArgumentException("k=" + k + " n=" + nums1.length + " m=" + nums2.length);\n int[][] digitPositions1 = findDigitPositions(nums1);\n int[][] digitPositions2 = findDigitPositions(nums2);\n Merger best = null;\n final int l1start = nums2.length >= k ? 0 : k - nums2.length;\n final int l1end = Math.min(k, nums1.length);\n // Will now try to get the largest sequences of digits from nums1, nums2 of lengths l1, (k - l1)\n // and merge them. The largest merge result will be the answer.\n for (int l1 = l1start; l1 <= l1end; ++l1) {\n MaxFinder res1 = new MaxFinder(nums1, l1, k, digitPositions1);\n MaxFinder res2 = new MaxFinder(nums2, k - l1, k, digitPositions2);\n Merger merger = new Merger(res1, res2, k);\n if (best == null || merger.compareTo(best) > 0) {\n best = merger;\n }\n }\n assert best != null;\n return best.toIntArray();\n }\n\n private static int[][] findDigitPositions(int[] nums) {\n int[][] digitPositions = new int[nums.length][];\n int[] pos = new int[10];\n Arrays.fill(pos, -1);\n for (int i = nums.length - 1; i >= 0; --i) {\n pos[nums[i]] = i;\n digitPositions[i] = Arrays.copyOf(pos, pos.length);\n }\n return digitPositions;\n }\n \n private static class Merger implements Comparable<Merger> {\n private final MaxFinder seq1;\n private final MaxFinder seq2;\n private final int k; // total length\n private final int[] output;\n private int outPos = 0, inPos1 = 0, inPos2 = 0;\n\n Merger(MaxFinder seq1, MaxFinder seq2, int k) {\n this.seq1 = seq1;\n this.seq2 = seq2;\n this.k = k;\n this.output = new int[k];\n }\n \n int get(int i) {\n while (outPos <= i) {\n if (seq1.compareTo(seq2) >= 0) {\n output[outPos++] = seq1.get(inPos1++);\n } else {\n output[outPos++] = seq2.get(inPos2++);\n }\n }\n return output[i];\n }\n \n @Override\n public int compareTo(Merger that) {\n for (int i = 0; i < k; ++i) {\n int v1 = this.get(i), v2 = that.get(i);\n if (v1 > v2) {\n return +1;\n } else if (v1 < v2) {\n return -1;\n }\n }\n return 0;\n }\n \n int[] toIntArray() {\n get(k - 1); // complete generation\n return output;\n }\n }\n \n private static class MaxFinder implements Comparable<MaxFinder> {\n private final int[] input;\n private final int k; // total length of two sequences, needed for comparison caching\n private final int[][] digitPositions; // computed by findDigitPositions\n private final int[] output;\n private final int[] lastDiffPos;\n private int inPos = 0, outPos = 0;\n private int nextIndex = 0;\n \n MaxFinder(int[] nums, int length, int k, int[][] digitPositions) {\n this.input = nums;\n this.k = k;\n this.digitPositions = digitPositions;\n this.output = new int[length];\n this.lastDiffPos = new int[2 * k + 1];\n }\n \n int get(int i) {\n this.nextIndex = i + 1; // If we need to compare with the other sequence, here is where we should start.\n return compute(i);\n }\n \n // helper for get and compareTo\n private int compute(int i) {\n while (outPos <= i) {\n // Look for the next best digit.\n for (int d = 9; d >= 0; --d) {\n final int nextDigitPos = digitPositions[inPos][d];\n // The digit must satisfy two conditions:\n // 1. It must be out there somewhere (obviously).\n // 2. There must be enough digits after it, or we may end up running out of digits too soon.\n if (nextDigitPos != -1 && input.length - (nextDigitPos + 1) >= output.length - outPos - 1) {\n output[outPos++] = d;\n inPos = digitPositions[inPos][d] + 1;\n break;\n }\n }\n }\n return output[i];\n }\n \n @Override\n public int compareTo(MaxFinder that) {\n final int cacheIndex = k + (this.nextIndex - that.nextIndex);\n // We can use the cached position if there is one, but only if we haven't advanced past the last found\n // difference position (which is stored in the cache).\n if (lastDiffPos[cacheIndex] != 0 && lastDiffPos[cacheIndex] >= this.nextIndex) {\n int lastDiffPos1 = lastDiffPos[cacheIndex];\n int lastDiffPos2 = lastDiffPos1 + (that.nextIndex - this.nextIndex);\n if (lastDiffPos1 < this.output.length && lastDiffPos2 < that.output.length) {\n return Integer.compare(this.output[lastDiffPos1], that.output[lastDiffPos2]);\n } else {\n return Integer.compare(this.output.length - this.nextIndex, that.output.length - that.nextIndex);\n }\n }\n // No luck in the cache.\n final int end = Math.min(this.output.length - this.nextIndex, that.output.length - that.nextIndex);\n int result = 0;\n for (int i = 0; i < end; ++i) {\n result = this.compute(this.nextIndex + i) - that.compute(that.nextIndex + i);\n if (result != 0) {\n lastDiffPos[cacheIndex] = this.nextIndex + i;\n break;\n }\n }\n if (result == 0) {\n lastDiffPos[cacheIndex] = this.nextIndex + end;\n return Integer.compare(this.output.length - this.nextIndex, that.output.length - that.nextIndex);\n } else {\n return result;\n }\n }\n }\n\nThe code is quite verbose, but the ideas are pretty simple:\n\n1. Precompute the table of digit positions so we don't have to search for the next best digit (only have to try from 9 to 0).\n2. Compute everything lazily. We don't know in advance how many digits we need to compare two sequences, so why generate them fully? The same thing for merging.\n3. Cache comparison results. When we've already compared two sequences, we don't want to compare them again if we advance both positions by the same amount. Although some suffix tables would probably be better (maybe compute them lazily too).\n\nThe resulting code runs in 17 ms. The code without improvements 2\u20133 ran for 26 ms, but then I introduced classes and it was 37 ms (because local variables moved to heap?). So these improvements turned 37 to 17, actually. Moving back to local variables will probably improve a lot, but the code would be a real mess.\n\nP. S. I'm not exactly sure: doesn't this comparison caching technique essentially replaces the suffix array and reduces the complexity to O(n + m + k^2). On the 500/500/500 case `MaxFinder::get` is called 575356 times which is of order (500^2) * 2.\n\n [1]: https://leetcode.com/discuss/75655/strictly-o-nk-c-solution-with-detailed-explanation
| 3 | 1 |
['Java']
| 0 |
create-maximum-number
|
Very straight-forward solution yet still efficient in C++
|
very-straight-forward-solution-yet-still-x26c
|
If you prefer performance than anything else then check this post. The following solution is simplified for simplicity and readability, so the performance is re
|
lhearen
|
NORMAL
|
2016-06-21T07:20:10+00:00
|
2016-06-21T07:20:10+00:00
| 1,286 | false |
If you prefer performance than anything else then check this [post](https://leetcode.com/discuss/101043/efficient-solution-accepted-best-beating-16ms-well-commented). The following solution is simplified for simplicity and readability, so the performance is reduced.\n\n class Solution \n {\n public:\n //select the maximal number in certain length within one vector;\n vector<int> maxVector(vector<int> nums, int k) \n {\n while (nums.size() > k) \n {\n int i = 0, n = nums.size();\n for (; i < n - 1; ++i) //at least erase one element each time;\n {\n if (nums[i] < nums[i + 1]) \n {\n nums.erase(nums.begin() + i);\n break;\n }\n }\n if (i == n - 1) nums.erase(nums.begin() + i);\n }\n return nums;\n }\n \n //compare two vectors from certain index adopting lexical order;\n //if the first vector is bigger return true otherwise return false;\n bool compare(vector<int> &nums1, int i, vector<int> &nums2, int j) \n {\n while (i<nums1.size() && j<nums2.size() && nums1[i]==nums2[j]) ++i, ++j;\n if (i<nums1.size() && j<nums2.size()) return nums1[i]>nums2[j];\n else if(j == nums2.size()) return true;\n else return false;\n }\n \n //get the first k numbers which form the largest lexical sequence;\n vector<int> merge(vector<int> &nums1, vector<int> &nums2, int k) \n {\n vector<int> res(k, 0);\n for (int i=0, j=0, r=0; r < k; ++r) \n res[r] = compare(nums1, i, nums2, j) ? nums1[i++] : nums2[j++];\n return res;\n }\n \n //AC - 386ms - the most intuitive solution;\n vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) \n {\n int len1=nums1.size(), len2=nums2.size();\n vector<int> v(k, 0);\n for (int l1 = max(0, k-len2); l1 <= min(k, len1); ++l1) \n {\n auto v1 = maxVector(nums1, l1);\n auto v2 = maxVector(nums2, k-l1);\n auto tmp = merge(v1, v2, k);\n if (compare(tmp, 0, v, 0)) v = tmp;\n }\n return v;\n }\n };
| 3 | 0 |
['C++']
| 0 |
create-maximum-number
|
Easy to understand greedy C++ solution O(NMK)
|
easy-to-understand-greedy-c-solution-onm-ixr2
|
We pick optimal digit one by one. At each phase, let dp[sa] be the minimum number of elements we need to use\nin array b, if we use sa elements in array a, in o
|
imrusty
|
NORMAL
|
2017-12-01T01:16:41.681000+00:00
|
2017-12-01T01:16:41.681000+00:00
| 1,139 | false |
We pick optimal digit one by one. At each phase, let dp[sa] be the minimum number of elements we need to use\nin array b, if we use sa elements in array a, in order to obtain the optimal solution so far. We look ahead to find the next optimal digit then update dp accordingly.\n```\nclass Solution {\npublic:\n vector<int> maxNumber(vector<int>& a, vector<int>& b, int k) {\n int na = a.size(), nb =b.size();\n vector<int> dp(na+1);\n vector<int> ans;\n while (k) {\n int x = 0;\n for (int sa = 0; sa <= na; ++sa) if (dp[sa] <= nb && nb- dp[sa] + na - sa >=k) {\n for (int i = sa; i < na; ++i) if (na - i + nb- dp[sa] >= k) x = max(x,a[i]);\n for (int j = dp[sa]; j < nb; ++j) if (na - sa + nb - j >= k) x = max(x,b[j]);\n }\n vector<int> dp2(na+1,INT_MAX);\n for (int sa = 0; sa <= na; ++sa) if (dp[sa] <= nb && nb- dp[sa] + na - sa >=k) {\n for (int i = sa; i < na; ++i) if (na - i + nb- dp[sa] >= k) if (a[i] == x) dp2[i+1] = min(dp2[i+1], dp[sa]);\n for (int j = dp[sa]; j < nb; ++j) if (na - sa + nb - j >= k) if (b[j] == x) dp2[sa] = min(dp2[sa], j+1);\n }\n dp.swap(dp2);\n ans.push_back(x);\n --k;\n }\n \n return ans;\n }\n};\n```
| 3 | 0 |
[]
| 0 |
create-maximum-number
|
interesting problem
|
interesting-problem-by-iampilgrim-bgp1
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\nThe problem requires finding the largest possible number of length k formed by combin
|
IAmPilgrim_
|
NORMAL
|
2024-10-17T08:11:56.435126+00:00
|
2024-10-17T08:11:56.435160+00:00
| 615 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nThe problem requires finding the largest possible number of length `k` formed by combining two arrays while preserving the relative order of elements in each array. My intuition is to break the problem into smaller parts: select subsequences from both arrays and then merge them while maintaining the lexicographical order.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nHigh-Level Approach:\n1. **Determine the Number of Digits to Take from Each Array:**\n - Iterate over all possible ways to split `k` between `n1` (first array) and `n2` (second array). This means we decide how many elements to pick from `n1` and how many from `n2` such that the sum is equal to `k`.\n - For each split, we will attempt to pick the largest possible subsequence of digits from `n1` and `n2` using a helper function.\n \n2. **Select the Maximum Subsequence from an Array:**\n - To pick the maximum subsequence of a given length from a single array, we use a greedy approach with a stack. We iterate over the array and maintain a stack of the maximum digits by removing smaller digits that could be replaced by larger ones later in the array, while ensuring we select exactly the required number of digits.\n \n3. **Merge the Two Subsequences:**\n - After selecting subsequences from both arrays, we need to merge them into a single sequence. At each step, we pick the larger of the leading elements from the two subsequences. This ensures that the resulting sequence is as lexicographically large as possible.\n \n4. **Compare and Keep the Maximum Number:**\n - As we generate different combinations of subsequences and merge them, we compare the resulting numbers and keep the one that is lexicographically the largest. This ensures that by the end, we have the maximum possible number.\n\nLet\'s delve into each step in detail.\n\n# Complexity\n- **Time complexity:** \n The time complexity is $$O(k \\cdot (n + m))$$, where `n` and `m` are the lengths of the two input arrays. For each split of `k` (up to `k` times), we calculate subsequences from both arrays, which takes linear time with respect to the size of each array. Additionally, merging the subsequences also takes linear time.\n\n- **Space complexity:** \n The space complexity is $$O(n + m)$$ because we need space to store the subsequences and the merged results.\n\n# Code\n```cpp []\nclass Solution {\npublic:\n vector<int> maxSeq(vector<int>& n1, int n) {\n int del = n1.size() - n;\n stack<int> stc;\n\n for (int i = 0; i < n1.size(); i++) {\n while (del > 0 and !stc.empty() and stc.top() < n1[i]) {\n stc.pop();\n del--;\n }\n stc.push(n1[i]);\n }\n\n vector<int> ans;\n int extra = stc.size() - n;\n while (!stc.empty() and extra--)\n stc.pop();\n while (!stc.empty()) {\n ans.push_back(stc.top());\n stc.pop();\n }\n\n reverse(ans.begin(), ans.end());\n return ans;\n }\n\n bool isGreater(vector<int>& a, int i, vector<int>& b, int j) {\n while (i < a.size() && j < b.size()) {\n if (a[i] > b[j])\n return true;\n if (a[i] < b[j])\n return false;\n i++;\n j++;\n }\n return (a.size() - i) > (b.size() - j);\n }\n\n vector<int> merge(vector<int>& a, vector<int>& b) {\n int i = 0, j = 0;\n vector<int> merged;\n while (i < a.size() || j < b.size()) {\n if (isGreater(a, i, b, j)) {\n merged.push_back(a[i++]);\n } else {\n merged.push_back(b[j++]);\n }\n }\n return merged;\n }\n\n vector<int> maxNumber(vector<int>& n1, vector<int>& n2, int k) {\n int n = n1.size(), m = n2.size();\n vector<int> ans(k, -1), temp;\n\n for (int i = 0; i <= k; i++) {\n // sub-sequence from n1=i, from n2=k-i\n vector<int> s1 = maxSeq(n1, i);\n vector<int> s2 = maxSeq(n2, k - i);\n\n temp = merge(s1, s2);\n if (temp.size() < k)\n continue;\n\n if (isGreater(temp, 0, ans, 0))\n ans = temp;\n }\n\n return ans;\n }\n};\n```
| 2 | 0 |
['Array', 'Two Pointers', 'Stack', 'Greedy', 'Monotonic Stack', 'C++']
| 2 |
create-maximum-number
|
Monotonic Stack + Two Pointers | C++
|
monotonic-stack-two-pointers-c-by-coderp-ixow
|
Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem involves creating the maximum possible number by selecting a subsequence fr
|
coderpriest
|
NORMAL
|
2024-07-22T08:56:26.366040+00:00
|
2024-07-22T08:56:26.366074+00:00
| 306 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem involves creating the maximum possible number by selecting a subsequence from two given arrays while maintaining the relative order of elements. The idea is to use a greedy approach to find the maximum subsequence from each array independently and then merge them optimally to form the final result.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. **Extract Maximum Subsequences**: Use a greedy algorithm to find the maximum subsequence of a given length from each array.\n2. **Merge Subsequences**: Merge the two subsequences to form the maximum possible number by comparing elements and maintaining the relative order.\n3. **Iterate for All Combinations**: Iterate over all possible lengths of subsequences from both arrays to ensure we cover all combinations that sum up to `k`.\n\n# Complexity\n- **Time complexity:** The overall time complexity is $$O((n1 + n2) * k^2)$$ where `n1` and `n2` are the lengths of `nums1` and `nums2` respectively. This is due to the nested loops and the greedy subsequence extraction and merging steps.\n\n- **Space complexity:** The space complexity is $$O(k)$$, required to store the subsequences and the result.\n\n# Code\n```cpp\nint init = [](){\n ios_base::sync_with_stdio(0), cin.tie(0), cout.tie(0);\n return -1;\n}();\n\nclass Solution {\npublic: \n vector<int> getMaxSubsequence(vector<int>& nums, int k) {\n int n = nums.size();\n vector<int> ans;\n for (int i = 0; i < n; ++i) {\n while (!ans.empty() && ans.back() < nums[i] && ans.size() + n - i - 1 >= k) \n ans.pop_back();\n if (ans.size() < k) \n ans.push_back(nums[i]);\n }\n return ans;\n }\n \n bool isGreater(vector<int> &word1, vector<int> &word2, int i, int j) {\n while (i < word1.size() && j < word2.size()) {\n if (word1[i] > word2[j]) \n return true;\n else if (word1[i] < word2[j]) \n return false;\n i++, j++;\n }\n return i != word1.size();\n }\n\n vector<int> merge(vector<int> &a, vector<int> &b) {\n vector<int> ans;\n int i = 0, j = 0;\n while (i < a.size() && j < b.size()) {\n if (a[i] > b[j]) \n ans.push_back(a[i++]);\n else if (a[i] < b[j]) \n ans.push_back(b[j++]);\n else {\n if (isGreater(a, b, i, j)) \n ans.push_back(a[i++]);\n else \n ans.push_back(b[j++]); \n }\n }\n while (i < a.size()) \n ans.push_back(a[i++]);\n while (j < b.size()) \n ans.push_back(b[j++]);\n return ans;\n }\n\n vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {\n vector<int> ans(k, 0);\n int n1 = nums1.size(), n2 = nums2.size();\n for (int i = max(0, k - n2); i <= min(k, n1); ++i) {\n if (i > n1 || k - i > n2) \n continue;\n vector<int> a = getMaxSubsequence(nums1, i);\n vector<int> b = getMaxSubsequence(nums2, k - i);\n vector<int> tmp = merge(a, b);\n if (isGreater(tmp, ans, 0, 0)) \n ans = tmp;\n }\n return ans;\n }\n};\n```
| 2 | 0 |
['Array', 'Two Pointers', 'Stack', 'Greedy', 'Monotonic Stack', 'C++']
| 1 |
create-maximum-number
|
✅🔥 | Java Solution | Explained | ✅🔥
|
java-solution-explained-by-anushdubey01-yhzt
|
Intuition - \nThe problem requires finding the maximum number that can be formed by selecting k elements from two input arrays, nums1 and nums2. The elements sh
|
Chandrikasharma16
|
NORMAL
|
2023-07-10T17:51:37.317254+00:00
|
2023-07-10T17:51:37.317282+00:00
| 353 | false |
# Intuition - \nThe problem requires finding the maximum number that can be formed by selecting k elements from two input arrays, nums1 and nums2. The elements should maintain their relative order within each array. The solution involves dividing the problem into smaller subproblems, finding the maximum numbers that can be formed by selecting a certain number of elements from each array, and then merging those numbers to form the overall maximum number.\n\n# Approach - \n1. Initialize the result array of size k to store the maximum number.\n2. Iterate over the number of elements (i) to be selected from nums1, which ranges from 0 to the minimum of k and the length of nums1.\n - Calculate the corresponding number of elements (j) to be selected from nums2, which is equal to k - i.\n - Find the maximum subsequence of length i from nums1 using the `findMax` function.\n - Find the maximum subsequence of length j from nums2 using the `findMax` function.\n - Merge the two subsequences obtained from nums1 and nums2 using the `merge` function.\n - If the merged sequence is greater than the current result, update the result to the merged sequence.\n3. Return the resulting maximum number.\n\n# Complexity Analysis - \nLet n be the length of nums1 and m be the length of nums2.\n- The overall **time complexity of the solution is O((n + m)^3)** since we have three nested loops: one for iterating over the number of elements to be selected from nums1, one for iterating over the elements of nums1 and nums2 in the `merge` function, and one for iterating over the elements of nums in the `findMax` function.\n- The **space complexity is O(k)** since we are using a result array of size k to store the maximum number.\n\n# Code\n```\npublic class Solution {\n public int[] maxNumber(int[] nums1, int[] nums2, int k) {\n int[] result = new int[k];\n for (int i = Math.max(0, k - nums2.length); i <= Math.min(nums1.length, k); i++) {\n int j = k - i;\n int[] part1 = findMax(nums1, i);\n int[] part2 = findMax(nums2, j);\n int[] cand = merge(part1, part2);\n if (greater(cand, 0, result, 0)) {\n result = cand;\n }\n }\n return result;\n }\n\n private boolean greater(int[] nums1, int start1, int[] nums2, int start2) {\n while (start1 < nums1.length && start2 < nums2.length && nums1[start1] == nums2[start2]) {\n start1++;\n start2++;\n }\n return start2 == nums2.length || (start1 < nums1.length && nums1[start1] > nums2[start2]);\n }\n\n private int[] merge(int[] nums1, int[] nums2) {\n int[] result = new int[nums1.length + nums2.length];\n int i = 0, j = 0, k = 0;\n while (i < nums1.length && j < nums2.length) {\n if (greater(nums1, i, nums2, j)) {\n result[k++] = nums1[i++];\n } else {\n result[k++] = nums2[j++];\n }\n }\n while (i < nums1.length) {\n result[k++] = nums1[i++];\n }\n while (j < nums2.length) {\n result[k++] = nums2[j++];\n }\n return result;\n }\n\n private int[] findMax(int[] nums, int k) {\n int[] result = new int[k];\n int j = 0;\n for (int i = 0; i < nums.length; i++) {\n while (j > 0 && result[j - 1] < nums[i] && j + nums.length - i > k) {\n j--;\n }\n if (j < k) {\n result[j++] = nums[i];\n }\n }\n return result;\n }\n}\n```
| 2 | 0 |
['Stack', 'Greedy', 'Monotonic Stack', 'Java']
| 0 |
create-maximum-number
|
Easy Understanding And Readable Code || Monotonic Stack || C++
|
easy-understanding-and-readable-code-mon-9t15
|
Intuition & Approach\n Describe your first thoughts on how to solve this problem. \nI will find lexographically greatest subsequence from both array and then me
|
anupamraZ
|
NORMAL
|
2023-06-03T07:26:20.658479+00:00
|
2023-06-03T07:26:20.658520+00:00
| 368 | false |
# Intuition & Approach\n<!-- Describe your first thoughts on how to solve this problem. -->\nI will find lexographically greatest subsequence from both array and then merge them.\nBut constraint is length=k must be satisfied. So have to find lexographically greater subsequence such that both combinedly have length k.\n\nBut how to decide how much length have to take from first array and how much from second array? --> This time go by bruteforce. So for possible {i, k-i} pair of length , we will find our answer.\n\nlet\'s divide the problem into subparts:\nsubpart-1: find out lexographically greatest subsequence from both array.\nsubpart-2: Merge them and keep taking maximum.\n\nImplemented stack logic through array. You can go through stack .\n# Complexity\n- Time complexity:O(K*N + K*N)= O(K*N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(K) => for this loop: for(int i=0;i<=k;i++) in maxNumber function.\nO(N) => for getGrtrSubseq function.\nO(K*N) => merge Function.\n- Space complexity: O(N) as all are linear vectors.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n // Function to calculate maximum number from nums of requiredLength.\n vector<int> getGrtrSubseq(vector<int> nums, int requiredLength)\n {\n vector<int> ans; // Store the resultant maximum\n int n = nums.size();\n // i will try to maximize initial digit as much as i can. If falling for shorter length, then i am forced to take last requiredLength-ans.size()\n //elements left. So, before popping any element check ((requiredLength-ans.size())<(n-i)) to ensure you have requiredLength of digits.\n for(int i=0;i<n;i++)\n {\n while(ans.size()>0 && ans.back()<nums[i] && ((requiredLength-ans.size())<(n-i))) // If true, then pop out the last element\n ans.pop_back();\n if(ans.size()<requiredLength)ans.push_back(nums[i]); \n }\n return ans;\n }\n void pop_front(std::vector<int> &v)\n {\n if (v.size() > 0)v.erase(v.begin());\n }\n vector<int> merge(vector<int> p1, vector<int>p2, int k)\n {\n vector<int> temp;\n for(int j=0;j<k;j++)\n { \n vector<int> temp2 = max(p1,p2);\n int fr = temp2.front();\n if(p1>p2)\n pop_front(p1);\n else\n pop_front(p2);\n temp.push_back(fr);\n }\n return temp;\n }\n vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) \n {\n int n1=nums1.size(), n2=nums2.size();\n vector<int>res;\n for(int i=0;i<=k;i++)\n {\n if(i>n1 || k-i>n2) continue;\n vector<int>grtrSubseq1=getGrtrSubseq(nums1,i);; \n vector<int>grtrSubseq2=getGrtrSubseq(nums2,k-i); \n vector<int>temp=merge(grtrSubseq1,grtrSubseq2,k); \n res = max(res, temp);\n }\n return res;\n }\n};\n```\n.\n\nCorrect me if i am wrong.\n
| 2 | 0 |
['Stack', 'Monotonic Stack', 'C++']
| 0 |
create-maximum-number
|
✅ C++ | 94% Faster | Stack Solution | Merge Sort Variation
|
c-94-faster-stack-solution-merge-sort-va-mew6
|
321. Create Maximum Number\n\nTime Complexity : O(n2)\nSpace Complexity : O(n)\n\n\nvector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {\n
|
CodeMars
|
NORMAL
|
2022-10-17T09:26:49.080595+00:00
|
2022-10-17T09:26:49.080642+00:00
| 546 | false |
[**321. Create Maximum Number**](https://leetcode.com/problems/create-maximum-number/)\n\n**`Time Complexity : O(n2)`**\n**`Space Complexity : O(n)`**\n\n```\nvector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {\n int m=nums1.size(), n=nums2.size();\n vector<int>res(k);\n for(int i=0; i<=k; i++){\n if(i<=m and k-i<=n){\n vector<int>v1=maxArray(nums1, i), v2=maxArray(nums2, k-i);\n vector<int>v=merge(v1,v2 , k);\n res=max(res, v);\n }\n }\n return res;\n }\n\t\n vector<int>merge(vector<int>&nums1 , vector<int>&nums2, int k){\n vector<int>v(k);\n for(int i=0, j=0, t=0;t<k; t++){\n v[t]=cmp(nums1,i, nums2, j)?nums1[i++]:nums2[j++];\n }\n return v;\n }\n\t\n bool cmp(vector<int>&nums1, int i, vector<int>&nums2,int j){\n while(i<nums1.size() and j<nums2.size() and nums1[i]==nums2[j]){\n i++, j++;\n }\n return j==nums2.size() or (i<nums1.size() and nums1[i]>nums2[j]);\n }\n\t\n vector<int>maxArray(vector<int>&nums, int k){\n int n=nums.size();\n vector<int>v;\n for(int i=0; i<n; i++){\n while(v.size()+n-i>k and !v.empty() and v.back()<nums[i])v.pop_back();\n if(v.size()<k)v.push_back(nums[i]);\n }\n return v;\n }\n```\n***Happy Coding :)***\n```\nif(liked(\u2764\uFE0F)==true) Upvote(\u2B06\uFE0F);\nelse Comment(\uD83D\uDCDD);\nreturn Thank You\uD83D\uDE01;\n```\n\n
| 2 | 0 |
['Stack', 'C', 'Merge Sort']
| 1 |
create-maximum-number
|
Easy c++ solution with full explanation! | Two stacks with i & k-i sequences!
|
easy-c-solution-with-full-explanation-tw-e6ct
|
\nclass Solution {\npublic:\n vector<int> ans;\n vector<int> maxNumber(vector<int>& a, vector<int>& b, int k) {\n for(int i=0; i<=k; i++) {\n
|
rac101ran
|
NORMAL
|
2022-07-25T23:09:40.816896+00:00
|
2022-07-25T23:09:40.816942+00:00
| 589 | false |
```\nclass Solution {\npublic:\n vector<int> ans;\n vector<int> maxNumber(vector<int>& a, vector<int>& b, int k) {\n for(int i=0; i<=k; i++) {\n vector<int> s1 , s2;\n if(i>0) s1 = getBest(a,i); // make i length lexographically biggest sequence possible from stack 1 \n if(k-i>0) s2 = getBest(b,k-i); // make k-i length lexographically biggest sequence from stack 2\n vector<int> s3;\n int m = 0 , n = 0;\n \n // take the element from corresponding stack is is lexographically bigger!\n while(m<s1.size() && n<s2.size()) s3.push_back((cmp(s1,s2,m,n) ? s1[m++] : s2[n++]));\n \n while(m<s1.size()) s3.push_back(s1[m++]);\n while(n<s2.size()) s3.push_back(s2[n++]);\n \n if(s3.size()==k) ans=max(ans,s3);\n }\n return ans;\n }\n bool cmp(vector<int>&a,vector<int>&b,int i,int j) {\n while(i<a.size() && j<b.size() && a[i]==b[j]) i++,j++;\n return (j==b.size() || ((i<(int)a.size()) && (a[i] > b[j])));\n }\n vector<int> getBest(vector<int> &a,int k) {\n vector<int> stk;\n int n = a.size();\n for(int i=0; i<a.size(); i++) {\n // a bigger element is present than current maximum & you can make a sequence >= k !\n while(!stk.empty() && stk.back() < a[i] && (((int)stk.size() - 1) + (n - i)) >=k) stk.pop_back();\n stk.push_back(a[i]);\n }\n while(stk.size() > k) stk.pop_back();\n return stk;\n }\n};\n```
| 2 | 0 |
[]
| 0 |
create-maximum-number
|
C++, Not So Simple (Warning : Just run away, Don't Try This Problem)
|
c-not-so-simple-warning-just-run-away-do-e1rg
|
\nclass Solution {\npublic:\n vector<int> func(vector<int> &nums, int k)\n {\n vector<int> ret(k, 0);\n int n=nums.size();\n for(int
|
MrGamer2801
|
NORMAL
|
2022-07-05T20:49:23.440996+00:00
|
2022-07-05T20:49:23.441041+00:00
| 626 | false |
```\nclass Solution {\npublic:\n vector<int> func(vector<int> &nums, int k)\n {\n vector<int> ret(k, 0);\n int n=nums.size();\n for(int i=0; i<nums.size(); i++)\n {\n if(ret.empty() || ret.back()>=nums[i])\n {\n if(ret.size()<k)\n ret.push_back(nums[i]);\n }\n else{\n while(!ret.empty() && n-i>k-ret.size() && ret.back()<nums[i])\n ret.pop_back();\n ret.push_back(nums[i]);\n }\n }\n return ret;\n }\n bool isGreater(vector<int> &a, vector<int> &b)\n {\n for(int i=0; i<a.size(); i++)\n {\n if(b[i]>a[i])\n return false;\n else if(b[i]<a[i])\n return true;\n }\n return false;\n }\n vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {\n vector<vector<int>> v1, v2;\n vector<int> ret(k, 0);\n for(int i=0; i<=k; i++)\n {\n if(i>nums1.size() || k-i>nums2.size())\n continue;\n vector<int> x, y;\n if(i)\n x=func(nums1, i);\n if(k-i)\n y=func(nums2, k-i);\n vector<int> res;\n int p=0, q=0, m=x.size(), n=y.size();\n x.push_back(0);\n y.push_back(0);\n while(p<m && q<n)\n {\n if(x[p]>y[q])\n res.push_back(x[p++]);\n else if(x[p]<y[q])\n res.push_back(y[q++]);\n else\n {\n bool flag=true;\n int t=1;\n while(p+t<m && q+t<n && x[p+t]==y[q+t])\n t++;\n if(p+t>=m || (q+t<n && x[p+t]<y[q+t]))\n flag=false;\n if(flag)\n res.push_back(x[p++]);\n else\n res.push_back(y[q++]);\n }\n }\n while(p<m)\n res.push_back(x[p++]);\n while(q<n)\n res.push_back(y[q++]);\n if(isGreater(res, ret))\n ret=res;\n }\n return ret;\n }\n};\n\n```
| 2 | 0 |
['C']
| 1 |
create-maximum-number
|
[Python3] greedy
|
python3-greedy-by-ye15-5o06
|
\n\nclass Solution:\n def maxNumber(self, nums1: List[int], nums2: List[int], k: int) -> List[int]:\n \n def fn(arr, k):\n """Return
|
ye15
|
NORMAL
|
2021-09-16T16:50:03.641576+00:00
|
2021-09-16T16:50:03.641619+00:00
| 785 | false |
\n```\nclass Solution:\n def maxNumber(self, nums1: List[int], nums2: List[int], k: int) -> List[int]:\n \n def fn(arr, k):\n """Return largest sub-sequence of arr of size k."""\n ans = []\n for i, x in enumerate(arr): \n while ans and ans[-1] < x and len(ans) + len(arr) - i > k: ans.pop()\n if len(ans) < k: ans.append(x)\n return ans\n \n ans = [0] * k\n for i in range(k+1): \n if k - len(nums2) <= i <= len(nums1): \n val1 = fn(nums1, i)\n val2 = fn(nums2, k-i)\n cand = []\n i1 = i2 = 0\n while i1 < len(val1) or i2 < len(val2): \n if val1[i1:] >= val2[i2:]: \n cand.append(val1[i1])\n i1 += 1\n else: \n cand.append(val2[i2])\n i2 += 1\n ans = max(ans, cand)\n return ans \n```
| 2 | 1 |
['Python3']
| 0 |
create-maximum-number
|
Beginner Friendly Logic || Implementation in Java || Easy to understand
|
beginner-friendly-logic-implementation-i-ixld
|
Algorithm:\nLet the arrays be arr1 and arr2\n1. Find the maximum length of arr1 which is less than or equal to k. i.e. n <= k. Create a maximum array for this s
|
kartikeysemwal
|
NORMAL
|
2021-03-30T19:24:37.451827+00:00
|
2021-03-30T19:27:11.276973+00:00
| 716 | false |
Algorithm:\nLet the arrays be arr1 and arr2\n1. Find the maximum length of arr1 which is less than or equal to k. i.e. n <= k. Create a maximum array for this size using arr1.\n2. Now left length is k - n. Lets call it m, which will be the length for arr2. Create maximum array of this size using arr2.\n\nNow comes the main logic\n\n3. Start a loop \n4. At every step decrease the size of arr1 by one and increment the size of arr2 by one, so that the sum of both sizes of array is equal to k i.e. n-- and m++\n\nSo the loop condition will become (m <= k && n>=0 && m <= arr2.length)\n\n5. Generate the array and merge both the arrays and store in the form of String for easy lexicographical comparison \n\n```\nclass Solution {\n\n String str_ans;\n\n int[] build(int org[], int size) {\n\n // This function is for generating maximum array\n\n int res[] = new int[size];\n ArrayList<Integer> al = new ArrayList<>();\n\n for (int i = 0; i < org.length; i++) {\n al.add(i);\n }\n\n Collections.sort(al, (Integer a, Integer b) -> {\n return org[b] - org[a];\n });\n\n int index = 0;\n int count = 0;\n\n Arrays.fill(res, -1);\n\n while (count < size) {\n\n int cur_ind = al.get(index++);\n int smaller = org.length - cur_ind - 1;\n\n for (int i = Math.max(0, size - smaller - 1); i < size; i++) {\n if (res[i] == -1) {\n res[i] = cur_ind;\n count++;\n break;\n }\n if (res[i] > cur_ind) {\n break;\n }\n }\n }\n\n for (int i = 0; i < size; i++) {\n res[i] = org[res[i]];\n }\n\n return res;\n }\n\n int[] merge(int arr1[], int arr2[]) {\n int n = arr1.length;\n int m = arr2.length;\n\n int res[] = new int[n + m];\n\n int ind1 = 0;\n int ind2 = 0;\n\n for (int i = 0; i < n + m; i++) {\n int val1 = (ind1 >= n ? -1 : arr1[ind1]);\n int val2 = (ind2 >= m ? -1 : arr2[ind2]);\n\n if (val1 > val2) {\n res[i] = val1;\n ind1++;\n } else if (val2 > val1) {\n res[i] = val2;\n ind2++;\n } else {\n\n // As both the values are equal find the first unequal element\n\n int next_ind1 = ind1 + 1;\n int next_ind2 = ind2 + 1;\n while (next_ind1 < n && next_ind2 < m && arr1[next_ind1] == arr2[next_ind2]) {\n next_ind1++;\n next_ind2++;\n }\n if (next_ind1 == n) {\n res[i] = val2;\n ind2++;\n } else if (next_ind2 == m) {\n res[i] = val1;\n ind1++;\n } else if (arr1[next_ind1] > arr2[next_ind2]) {\n res[i] = val1;\n ind1++;\n } else {\n res[i] = val2;\n ind2++;\n }\n }\n }\n\n return res;\n }\n\n String toString(int arr[]) {\n StringBuilder sb = new StringBuilder();\n\n for (int i = 0; i < arr.length; i++) {\n sb.append(arr[i]);\n }\n\n return sb.toString();\n }\n\n public int[] maxNumber(int[] arr1, int[] arr2, int k) {\n int ans[] = new int[k];\n\n int n = Math.min(arr1.length, k);\n int m = k - n;\n\n str_ans = "";\n\n while (m <= k && n >= 0 && m <= arr2.length) {\n\n int cur_arr1[] = build(arr1, n);\n int cur_arr2[] = build(arr2, m);\n\n int res[] = merge(cur_arr1, cur_arr2);\n String str_res = toString(res);\n\n if (str_res.compareTo(str_ans) > 0) {\n str_ans = str_res;\n }\n\n n--;\n m++;\n }\n\n char c[] = str_ans.toCharArray();\n\n for (int i = 0; i < k; i++) {\n ans[i] = c[i] - \'0\';\n }\n\n return ans;\n }\n}\n\n```\n\nThe solution can be improved by using better logic for removing and adding of element from both the arrays in the loop avoiding the complexity to build maximum array
| 2 | 0 |
[]
| 0 |
create-maximum-number
|
dp + greedy faster than 80% c++ 36ms
|
dp-greedy-faster-than-80-c-36ms-by-henry-tofv
|
\nclass Solution {\npublic:\n vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {\n vector<int> ans;\n const int m = nums1.s
|
henrythu
|
NORMAL
|
2021-03-26T05:04:38.490158+00:00
|
2021-03-26T05:04:38.490202+00:00
| 768 | false |
```\nclass Solution {\npublic:\n vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {\n vector<int> ans;\n const int m = nums1.size(), n = nums2.size();\n \n for (int i = 0; i <= k; i++) {\n int j = k - i; \n if (i > m || j > n) continue;\n ans = max(ans, maxNumber(maxNumber(nums1,i),maxNumber(nums2,j)));\n }\n \n return ans;\n }\nprivate:\n \n vector<int> maxNumber(const vector<int>& nums, int k) {\n if (k == 0) return {};\n int to_pop = nums.size() - k;\n vector<int> ans;\n for (auto &num : nums) {\n while (!ans.empty() && ans.back() < num && 0 < to_pop--)\n ans.pop_back();\n ans.push_back(num);\n }\n ans.resize(k);\n return ans;\n }\n \n vector<int> maxNumber(const vector<int>& nums1,const vector<int>& nums2) {\n vector<int> ans;\n auto s1 = nums1.begin();\n auto e1 = nums1.end();\n auto s2 = nums2.begin();\n auto e2 = nums2.end();\n while (s1 != e1 || s2 != e2) {\n ans.push_back(lexicographical_compare(s1,e1,s2,e2)?*s2++:*s1++);\n }\n return ans;\n }\n \n};\n```
| 2 | 0 |
[]
| 0 |
create-maximum-number
|
C++ greedy easy to understand
|
c-greedy-easy-to-understand-by-bruce_cui-chgp
|
\nclass Solution {\npublic:\n vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {\n int n = nums1.size(), m = nums2.size();\n
|
bruce_cui
|
NORMAL
|
2021-03-02T12:13:15.412019+00:00
|
2021-03-02T12:13:15.412057+00:00
| 761 | false |
```\nclass Solution {\npublic:\n vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {\n int n = nums1.size(), m = nums2.size();\n vector<int>res(k, INT_MIN);\n \n for(int i=max(0, k-m);i<=min(k, n);i++)\n { \n auto a = maxarray(nums1, i);\n auto b = maxarray(nums2, k-i);\n auto c = merge(a, b);\n res = max(res, c);\n }\n return res;\n }\n \n vector<int>maxarray(vector<int>&nums, int k)\n {\n vector<int>res(k);\n int n = nums.size(), j = 0;\n for(int i=0;i<n;i++)\n {\n int x = nums[i];\n while(j && j + n-i > k && res[j-1] < x) j--;\n if(j < k) res[j++] = x;\n }\n return res;\n }\n \n vector<int>merge(vector<int>&a, vector<int>&b)\n {\n vector<int>res;\n while(a.size() && b.size())\n {\n if(a > b) res.push_back(a[0]), a.erase(a.begin());\n else res.push_back(b[0]), b.erase(b.begin());\n }\n while(a.size())\n res.push_back(a[0]), a.erase(a.begin());\n while(b.size())\n res.push_back(b[0]), b.erase(b.begin());\n return res;\n }\n};\n```
| 2 | 4 |
[]
| 1 |
create-maximum-number
|
C++: find all lenth combination of two, then merge them,
|
c-find-all-lenth-combination-of-two-then-trik
|
The idea is to \n1) find max number of each single array of lenght l1, l2 first. \n2) Then combine them to form the final largest one. \n3) Then select the l
|
alexl2008
|
NORMAL
|
2020-11-29T22:30:43.229971+00:00
|
2020-11-29T22:30:43.230017+00:00
| 686 | false |
The idea is to \n1) find max number of each single array of lenght l1, l2 first. \n2) Then combine them to form the final largest one. \n3) Then select the largest combined one. \n\nStep 1 and 2 are both quite tricky to get right.\n\n```\nclass Solution { \n \n \n // 54321 // find first bottom item: 3 \n // nums2 = [9, 1, 2, 5, 8, 3], k=3, remain 3 \n vector<int> maxNumber (vector<int>& nums1, int k)\n {\n int sz= nums1.size(), remove = sz-k;\n vector<int> res ;\n // best code structure: for + while\n // goal: generate an all decreasing sequence: remove bottom < next\n for (int i=0; i< nums1.size(); i++)\n {\n // when to pop the stack: back< current\n while (res.size()>0 && res.back()< nums1[i] && remove)\n {\n res.pop_back(); remove--; \n } \n res.push_back(nums1[i]); \n } \n\n // finished : res may be too many, we only need k element \n // the case of all decreasing, just remove from back\n while (remove)\n {\n res.pop_back(); remove--; \n } \n \n return res; \n }\n \n // merge linked list problem: but tricker to handle equal case\n // max len 2 : 6,5 \n // max len 3 : 9 8 3\n vector<int> combine (vector<int>& v1, vector<int>& v2)\n {\n vector<int> res; \n int p1=0, p2=0;\n \n while (p1<v1.size() && p2<v2.size())\n {\n // equal? look after until not equal, pick larger one next non equal one\n //nums1: {6, 7}\n // nums2: {6, 0, 4} : mistake: naive pick larger one won\'t work!!\n // look after until not equal \n if (v1[p1]==v2[p2])\n {\n int p1n=p1+1, p2n=p2+1;\n while (p1n<v1.size() && p2n<v2.size() && v1[p1n]==v2[p2n])\n {\n p1n++; p2n++; \n }\n // several conditions: p1n reach the end\n // either one reach the end, pick any of they, No! pick the one with remains!!\n if (p1n==v1.size() ) \n {\n res.push_back(v2[p2++]); \n }\n else if ( p2n==v2.size())\n res.push_back(v1[p1++]); \n else if (v1[p1n]>v2[p2n]) // first non equal element\n res.push_back(v1[p1++]); \n else\n res.push_back(v2[p2++]); \n }\n else if (v1[p1]>v2[p2])\n res.push_back(v1[p1++]);\n else\n res.push_back(v2[p2++]);\n }\n \n while (p1<v1.size())\n res.push_back(v1[p1++]);\n \n while (p2<v2.size())\n res.push_back(v2[p2++]); \n \n assert (res.size()== v1.size()+v2.size());\n return res;\n }\n\npublic:\n vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) { \n \n vector<int> max_res (k, 0); //min value \n for (int l1=0; l1<= nums1.size(); l1++) //select 0 to max from nums1\n { \n if (k-l1<0 ) break; // l1 too large, we stop \n if (k-l1> nums2.size()) continue; // l1 too small, we continue\t\t\t\n vector<int> m1= maxNumber (nums1, l1); \n vector<int> m2= maxNumber (nums2, k-l1); \n vector<int> merge1= combine (m1, m2); \n\n if (merge1>max_res)\n max_res= merge1; \n } \n return max_res; \n }\n};\n\n```\n\n
| 2 | 0 |
[]
| 1 |
create-maximum-number
|
C# faster than 75%, less then 100% Mem
|
c-faster-than-75-less-then-100-mem-by-ve-b482
|
Runtime: 316 ms\nMemory Usage: 32.1 MB\n\nWhat helped me was thinking in therms of elements that needed to be removed.\nSay you have 4 elements to remove to get
|
ve7545
|
NORMAL
|
2020-07-22T23:13:58.194728+00:00
|
2020-07-22T23:15:19.036634+00:00
| 558 | false |
Runtime: 316 ms\nMemory Usage: 32.1 MB\n\nWhat helped me was thinking in therms of elements that needed to be removed.\nSay you have 4 elements to remove to get to a total size of k.\nYou can remove 0 from nums1 and 4 to nums2 or 1-3, 2-2, 3-1 or 4-0.\nThen at each stage just merge the trimmed arrays taking care of the equal case (see code). Compare the resulting arrays to find the biggest number.\n\n```\n public int[] MaxNumber(int[] nums1, int[] nums2, int k) \n {\n nums1 = Trim(nums1, k);\n nums2 = Trim(nums2, k); \n \n int dif = (nums1.Length + nums2.Length) - k;\n\n if (dif == 0)\n {\n return Merge(nums1, nums2, k);\n }\n \n int[] new1;\n int[] new2;\n int[] crnt;\n int[] biggest = null;\n\n for (int i = dif, j = 0; i >= 0; i--, j++)\n {\n if (nums1.Length < i || nums2.Length < j) { continue; }\n\n new1 = Trim(nums1, nums1.Length - i);\n new2 = Trim(nums2, nums2.Length - j);\n\n crnt = Merge(new1, new2, k);\n\n if (biggest == null) \n { \n biggest = crnt; \n }\n else\n {\n for (int s = 0; s < k; s++)\n {\n if (biggest[s] < crnt[s]) { biggest = crnt; break; }\n else if (biggest[s] > crnt[s]) { break; }\n }\n }\n }\n\n return biggest;\n }\n \n private int[] Merge(int[] nums1, int[] nums2, int k)\n {\n int[] result = new int[k];\n\n int i = 0;\n int j = 0;\n int p = 0;\n\n int h;\n int g;\n\n while (i < nums1.Length && j < nums2.Length)\n {\n if (nums1[i] > nums2[j])\n {\n result[p++] = nums1[i++];\n }\n else if (nums1[i] < nums2[j])\n {\n result[p++] = nums2[j++];\n }\n else\n {\n //find next non equal pair.\n h = i + 1;\n g = j + 1;\n while (h < nums1.Length && g < nums2.Length && nums1[h] == nums2[g])\n {\n h++; g++;\n }\n\n if (h == nums1.Length) { result[p++] = nums2[j++]; }\n else if (g == nums2.Length) { result[p++] = nums1[i++]; }\n else if (nums1[h] > nums2[g]) { result[p++] = nums1[i++]; }\n else { result[p++] = nums2[j++]; }\n }\n }\n\n while (i < nums1.Length)\n {\n result[p++] = nums1[i++];\n }\n\n while (j < nums2.Length)\n {\n result[p++] = nums2[j++];\n }\n\n return result;\n }\n \n private int[] Trim(int[] nums, int k)\n {\n if (nums.Length <= k) { return nums; }\n \n int rem = nums.Length-k;\n \n Stack<int> stack = new Stack<int>();\n \n for(int i=0; i< nums.Length; i++)\n {\n if (stack.Count == 0 || rem == 0) { stack.Push(nums[i]); }\n else\n {\n while(stack.Count > 0 && stack.Peek() < nums[i] && rem > 0)\n {\n stack.Pop();\n rem--;\n }\n stack.Push(nums[i]);\n }\n }\n \n while (rem > 0) { stack.Pop(); rem--; }\n \n int[] result = new int[k];\n int j = k-1;\n while(stack.Count > 0)\n {\n result[j] = stack.Pop();\n j--;\n }\n \n return result;\n }
| 2 | 0 |
[]
| 1 |
create-maximum-number
|
Sharing my DP solution
|
sharing-my-dp-solution-by-kundan277-wutb
|
If you are going to calculate max in both array simultaneously, it is going to be order of (mnk) where m = arr1.length, n=arr2.length;\nIdea is calculate max i
|
kundan277
|
NORMAL
|
2020-07-12T09:33:06.860918+00:00
|
2020-07-12T09:33:06.860968+00:00
| 1,550 | false |
If you are going to calculate max in both array simultaneously, it is going to be order of (m*n*k) where m = arr1.length, n=arr2.length;\nIdea is calculate max in first array (m*k), calculate max in second array(n*k), then merge both max array to get final answer. complexity would be (m+n+k)*k;\n\n```\n// get max of two string\n private String max(String s1, String s2) {\n return (s1.compareTo(s2) < 0) ? s2 : s1;\n }\n \n // calculate max in one array\n public String[] helper1(int[] A, int k) {\n int m = A.length;\n String[][] dp = new String[m+1][k+1];\n for (int i = 0; i <= m; i++) {\n for (int l = 0; l <= k; l++) {\n String chooseAi = (i == 0 || l == 0) ? "" : dp[i - 1][l - 1] + A[i - 1];\n String ignoreAi = (i == 0) ? "" : dp[i - 1][l];\n dp[i][l] = max(chooseAi, ignoreAi);\n }\n }\n return dp[m];\n }\n\n \n public int[] maxNumber(int[] nums1, int[] nums2, int k) {\n\n String[] max1= helper1(nums1, Math.min(nums1.length,k)); // calculate max for num1\n String[] max2= helper1(nums2, Math.min(nums2.length,k)); // calculate max for num2\n \n // merge two max array \n String ans = "";\n for(int t=0;t<=k;t++) { // k*k*k\n int len1 = Math.min(nums1.length, t);\n int len2 = Math.min(nums2.length, k-t);\n if(len1+len2 != k) continue;\n String ans1 = max1[len1];\n String ans2 = max2[len2];\n StringBuilder tmp = new StringBuilder();\n while (tmp.length() < k) {\n char ch;\n if(ans1.compareTo(ans2)>=0){\n ch=ans1.charAt(0);\n ans1=ans1.substring(1);\n }\n else {\n ch=ans2.charAt(0);\n ans2=ans2.substring(1);\n }\n tmp.append(ch);\n }\n ans=max(ans,tmp.toString());\n\n }\n\n int[] tmp = new int[ans.length()];\n for(int i=0;i<tmp.length;i++){\n tmp[i]=ans.charAt(i)-\'0\';\n }\n return tmp;\n }\n```\n
| 2 | 2 |
['Dynamic Programming']
| 2 |
create-maximum-number
|
92ms cpp: try first biggest num, with index pre-process
|
92ms-cpp-try-first-biggest-num-with-inde-0ia8
|
The basic idea is to find the largest number in answer array's first position: try number from 9 to 0, firstly in nums1: if a number can be found, check if the
|
jwang42
|
NORMAL
|
2015-12-24T02:09:21+00:00
|
2015-12-24T02:09:21+00:00
| 654 | false |
The basic idea is to find the largest number in answer array's first position: try number from 9 to 0, firstly in nums1: if a number can be found, check if the left numbers (minus numbers before the found number) are sufficient for k.\n\nIf we can find a largest number in both nums1 and nums2, we should compare the two answers, and keep the bigger one.\n\nA fast pre-process for above solution: for i-th element in array nums1, lowPos1[i][num] is the smallest index of num in range [i, nums1.size()-1]. Since we have this helper, we can use O(1) time to find if num exists in nums1 or nums2 from a given position.\n\nAn important special case: when nums1.size() + nums2.size() = k, which means we have to use all elements in both arrays to produce the k-length answer. In such case, set two pointers pointing to the beginning of two arrays. Move the pointer with bigger number. Tricky part is when two pointers point to a same value, in this case we detect the values in two arrays behind the two pointers; we move the two pointers together until we find the values are different or one array is ended. The pointer with bigger value should go first, and if one pointer gets to end of array, the other pointer should go first.\n\n\n class Solution {\n public:\n unordered_map<string, vector<int>> store;\n deque<vector<int>> lowPos1, lowPos2;\n int len1, len2;\n \n vector<int> get(int p1, int p2, int k, vector<int>& nums1, vector<int>& nums2) {\n vector<int> ans;\n if (k==0)\n return ans;\n \n char buf[50];\n sprintf(buf, "%d.%d.%d", p1, p2, k);\n string key = buf;\n if (store.find(key) != store.end())\n return store[key];\n \n int rest = nums1.size()-p1 + nums2.size()-p2;\n if (k==rest) {\n while (p1<len1 || p2<len2)\n {\n if (p1==len1 || (p2<len2 && nums1[p1] < nums2[p2]))\n ans.push_back(nums2[p2++]);\n else if (p2==len2 || (p1<len1 && nums1[p1] > nums2[p2]))\n ans.push_back(nums1[p1++]);\n else {\n int i=0;\n while (p1+i<len1 && p2+i<len2) {\n if (nums1[p1+i] != nums2[p2+i])\n break;\n i++;\n }\n if (p1+i==len1 || (p2+i<len2 && nums2[p2+i]>nums1[p1+i]))\n ans.push_back(nums2[p2++]);\n else\n ans.push_back(nums1[p1++]);\n }\n }\n }\n else\n {\n for (int i=9; i>=0; i--) \n {\n vector<int> ans1, ans2;\n int j = p1==len1 ? -1 : lowPos1[p1][i];\n if (j!=-1 && rest-(j-p1)-1 >= k-1)\n {\n ans1.push_back(i);\n vector<int> temp = get(j+1, p2, k-1, nums1, nums2);\n ans1.insert(ans1.end(), temp.begin(), temp.end());\n }\n \n j = p2==len2 ? -1 : lowPos2[p2][i];\n if (j!=-1 && rest-(j-p2)-1 >= k-1)\n {\n ans2.push_back(i);\n vector<int> temp = get(p1, j+1, k-1, nums1, nums2);\n ans2.insert(ans2.end(), temp.begin(), temp.end());\n }\n \n if (ans1.size() + ans2.size())\n {\n if (ans1.size() < ans2.size())\n std::swap(ans1, ans2);\n bool use1=true;\n for (int i=0; i<min(ans1.size(), ans2.size()); i++)\n if (ans2[i] != ans1[i]) {\n use1 = ans1[i]>ans2[i];\n break;\n }\n ans = use1 ? ans1 : ans2;\n break;\n }\n }\n }\n \n store[key] = ans;\n return ans;\n }\n \n void preProcess(deque<vector<int>>& lowPos, const vector<int>& nums) {\n lowPos.push_back(vector<int> (10, -1));\n for (int i=(int)nums.size()-1; i>=0; i--) {\n lowPos.push_front(lowPos.front());\n lowPos.front()[nums[i]] = i;\n }\n lowPos.pop_back();\n }\n \n vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {\n len1=nums1.size(), len2=nums2.size();\n preProcess(lowPos1, nums1);\n preProcess(lowPos2, nums2);\n \n return get(0, 0, k, nums1, nums2);\n }\n };
| 2 | 0 |
[]
| 0 |
create-maximum-number
|
TLE Python DP Solution O(k*m*n*m*n)
|
tle-python-dp-solution-okmnmn-by-booksha-lfsw
|
Short but TLE... :P\n\nPython Code:\n\n class Solution(object):\n def maxNumber(self, nums1, nums2, k):\n len1 = len(nums1)\n le
|
bookshadow
|
NORMAL
|
2015-12-24T04:57:52+00:00
|
2015-12-24T04:57:52+00:00
| 1,043 | false |
Short but TLE... :P\n\nPython Code:\n\n class Solution(object):\n def maxNumber(self, nums1, nums2, k):\n len1 = len(nums1)\n len2 = len(nums2)\n dp = [[[[]] * (len2 + 1) for x in range(len1 + 1)] for y in range(k + 1)]\n for z in range(1, k + 1):\n for x in range(len1 + 1):\n for y in range(len2 + 1):\n for p in range(x):\n if len(dp[z-1][p][y]) == z - 1:\n dp[z][x][y] = max(dp[z][x][y], dp[z-1][p][y]+[nums1[p]])\n for q in range(y):\n if len(dp[z-1][x][q]) == z - 1:\n dp[z][x][y] = max(dp[z][x][y], dp[z-1][x][q]+[nums2[q]])\n return dp[k][len1][len2]
| 2 | 1 |
['Dynamic Programming', 'Python']
| 1 |
create-maximum-number
|
A 24 ms C++ solution with comments
|
a-24-ms-c-solution-with-comments-by-lhuo-csaa
|
// Get the max number from an array.\n void getMax(int num, // array. Should have capacity >= len\n int len, // array length\n
|
lhuo9876
|
NORMAL
|
2016-01-29T18:02:27+00:00
|
2016-01-29T18:02:27+00:00
| 777 | false |
// Get the max number from an array.\n void getMax(int* num, // array. Should have capacity >= len\n int len, // array length\n int* result, // buffer for getting back the result. Should have capacity >= t\n int t) // number of digit of the max number. t <= len.\n {\n int n;\n int top = 0; // Take the result as a stack and this is the top index of the stack. \n \n // Fill the first element\n result[0] = num[0];\n \n for(int i = 1; i < len; ++i)\n {\n n = num[i];\n // If top >= 0 AND result[top] is smaller than n AND there is enough remaining numbers to fill the result\n while(top >= 0 && result[top] < n && (t - top) <= (len - i) )\n {\n // Pop the top element.\n top--;\n }\n \n // Move to the new top\n top++;\n if(top < t)\n result[top] = n;\n else\n top = t - 1; // stay at the last element.\n }\n }\n \n // Merge two numbers so they generate the max number. This merge runs in linear time O(m + n)\n void merge(int* num1, // num1 with length of len1\n int len1, \n int* num2, // num2 with length of len2\n int len2, \n int* result) // result with length of (len1 + len2)\n {\n int i;\n int j, k;\n int t = len1 + len2;\n for(i = 0, j = 0, k = 0; i < t; ++i)\n {\n if(j < len1 && k < len2)\n {\n // Pick the larger number\n if(num1[j] > num2[k])\n result[i] = num1[j++];\n else if(num1[j] < num2[k])\n result[i] = num2[k++];\n else // if equal\n {\n int remaining1 = len1 - j;\n int remaining2 = len2 - k;\n if(remaining1 > remaining2)\n {\n // Compare remaining part. Pick the larger one.\n if(memcmp(num1 + j, num2 + k, sizeof(int) * remaining2) >= 0)\n result[i] = num1[j++];\n else\n result[i] = num2[k++];\n }\n else\n {\n if(memcmp(num2 + k, num1 + j, sizeof(int) * remaining1) >= 0)\n result[i] = num2[k++];\n else\n result[i] = num1[j++];\n }\n }\n }\n else if(j < len1 && k >= len2)\n {\n // Keep adding the remaining numbers\n result[i] = num1[j++];\n }\n else // if(j >= len1 && k < len2)\n {\n // Keep adding the remaining numbers\n result[i] = num2[k++];\n }\n }\n }\n \n vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {\n \n // Allocate memory\n int* num = new int[k * 4];\n int* buf1 = num + k;\n int* buf2 = num + k * 2;\n int* temp = num + k * 3;\n int memSize = sizeof(int) * k;\n memset(num, 0, memSize);\n \n int i;\n int t1, t2;\n int len1 = nums1.size();\n int len2 = nums2.size();\n if(len1 == 0 && len2 > 0)\n {\n getMax(&nums2[0], len2, num, k);\n }\n else if(len1 > 0 && len2 == 0)\n {\n getMax(&nums1[0], len1, num, k);\n }\n else if(len1 > 0 && len2 > 0)\n {\n if(len1 <= len2)\n {\n int smaller = len1 < k ? len1 : k;\n for(i = k - len2; i <= smaller; ++i)\n {\n // Tranverse the numbers with all possible combinations\n t1 = i;\n t2 = k - i;\n getMax(&nums1[0], len1, buf1, t1);\n getMax(&nums2[0], len2, buf2, t2);\n merge(buf1, t1, buf2, t2, temp);\n if(memcmp(num, temp, memSize) < 0)\n memcpy(num, temp, memSize);\n }\n }\n else\n {\n int smaller = len2 < k ? len2 : k;\n for(i = k - len1; i <= smaller; ++i)\n {\n // Tranverse the numbers with all possible combinations\n t2 = i;\n t1 = k - i;\n getMax(&nums1[0], len1, buf1, t1);\n getMax(&nums2[0], len2, buf2, t2);\n merge(buf1, t1, buf2, t2, temp);\n if(memcmp(num, temp, memSize) < 0)\n memcpy(num, temp, memSize);\n }\n }\n }\n \n vector<int> rev(num, num + k);\n delete [] num;\n \n return rev;\n\n }
| 2 | 2 |
[]
| 1 |
create-maximum-number
|
Beats 100.00% of python submissions surprisingly!
|
beats-10000-of-python-submissions-surpri-bj45
|
It's a tough way to solve this problem.\n\nMy solution is trying to construct the answer.\n\n1. At first, using dp[i][j][k] as a set to record the state, which
|
merrychris
|
NORMAL
|
2016-05-23T14:08:07+00:00
|
2016-05-23T14:08:07+00:00
| 1,240 | false |
It's a tough way to solve this problem.\n\nMy solution is trying to construct the answer.\n\n1. At first, using dp[i][j][k] as a set to record the state, which means the k-length result from arr1[i:] and arr[j:]. But got TLE.\n2. After that, trying to pre-process loc[i][x] to locate the digit x in arr[i:]. But still TLE.\n3. Finally, handling the case when l1+l2 == k. Got AC.\n\nI think the complexity maybe O((m+n+k)*10), since the number of answer is k*10.\n\nHere is my code. 128ms in py.\n\n ### 321. Create Maximum Number ###\n # @param {integer[]} nums1\n # @param {integer[]} nums2\n # @param {integer} k\n # @return {integer[]}\n def maxNumber(self, nums1, nums2, k):\n if not k or len(nums1)+len(nums2)<k: return []\n \n loc1 = [[-1]*10 for _ in range(len(nums1)+1)]\n loc2 = [[-1]*10 for _ in range(len(nums2)+1)]\n l12 = len(nums1)+len(nums2)\n vis, res = set(), [-1]*k\n \n def make(nums, loc):\n pos = [-1]*10\n for i in xrange(len(nums)-1,-1,-1):\n pos[nums[i]] = i\n for j in range(10):\n loc[i][j] = pos[j]\n \n make(nums1, loc1)\n make(nums2, loc2)\n \n def compare(p1, p2):\n if p2 == len(nums2): return 1\n if p1 == len(nums1): return 2\n if nums1[p1] > nums2[p2]: return 1\n if nums1[p1] < nums2[p2]: return 2\n return compare(p1+1, p2+1)\n \n def dfs(p1, p2, k):\n if k == 0 or (p1, p2, k) in vis: return\n \n if l12 == p1+p2+k:\n flag, update = True, False\n while flag and k>0:\n if compare(p1, p2) == 1:\n if res[-k] <= nums1[p1] or update:\n if res[-k] < nums1[p1]: update = True\n res[-k] = nums1[p1]\n p1 += 1\n else: flag = False\n else:\n if res[-k] <= nums2[p2] or update:\n if res[-k] < nums2[p2]: update = True\n res[-k] = nums2[p2]\n p2 += 1\n else: flag = False\n k -= 1\n else:\n flag = False\n for i in range(9,-1,-1):\n if loc1[p1][i] != -1:\n if l12-loc1[p1][i]-p2 >= k and res[-k] <= i:\n if res[-k] < i: res[-k:] = [-1]*k\n res[-k] = i\n dfs(loc1[p1][i]+1, p2, k-1)\n flag = True\n if loc2[p2][i] != -1:\n if l12-p1-loc2[p2][i] >= k and res[-k] <= i:\n if res[-k] < i: res[-k:] = [-1]*k\n res[-k] = i\n dfs(p1, loc2[p2][i]+1, k-1)\n flag = True\n if flag: break\n vis.add((p1, p2, k))\n \n dfs(0, 0, k)\n return res
| 2 | 0 |
['Python']
| 0 |
create-maximum-number
|
Java Solution With Comments (Inspired by @dietpepsi)
|
java-solution-with-comments-inspired-by-irr0j
|
It's almost the same with the solution by @dietpepsi. I changed some code and added comments to make it easier to understand.\n\n\npublic class Solution {\n
|
yuhao5
|
NORMAL
|
2016-09-01T10:12:31.883000+00:00
|
2016-09-01T10:12:31.883000+00:00
| 842 | false |
It's almost the same with the solution by @dietpepsi. I changed some code and added comments to make it easier to understand.\n\n```\npublic class Solution {\n public int[] maxNumber(int[] nums1, int[] nums2, int k) {\n int[] maxNum = new int[k];\n for (int i = 0; i <= k; i++) {\n if (nums1.length >= i && nums2.length >= k-i) {\n int[] merged = maxMerge(maxNumberSingleArray(nums1, i), maxNumberSingleArray(nums2, k-i));\n if (isGreater(merged, 0, maxNum, 0)) {\n maxNum = merged;\n }\n }\n }\n return maxNum;\n }\n \n // compute max number of a single array, given available numbers 'nums[]'' and length 'len'\n // assume len <= nums.length\n private int[] maxNumberSingleArray(int[] nums, int len) {\n int[] result = new int[len];\n int filledDigits = 0; // number of digits already filled\n for (int i = 0; i < nums.length; i++) {\n int j = filledDigits; // default position for current digit = index of last filled digit\n while (j > 0 && result[j-1] < nums[i] && nums.length-i >= len-(j-1)) {\n // want to place larger numbers to as high digit as possible\n j--;\n }\n if (j < len) {\n result[j] = nums[i];\n filledDigits = j+1;\n }\n }\n return result;\n }\n \n // merge two number arrays to create a maximum number array\n // want to use digits from the array with the higher lexicographical order\n private int[] maxMerge(int[] arr1, int[] arr2) {\n int len = arr1.length + arr2.length;\n int[] result = new int[len];\n int i = 0, j = 0, k = 0;\n while (k < len) {\n result[k++] = isGreater(arr1, i, arr2, j) ? arr1[i++] : arr2[j++];\n }\n return result;\n }\n \n // compare which array contains a larger number, returns < 0 if arr1 < arr2, == 0 if equal, > 0 if arr1 > arr2\n private boolean isGreater(int[] arr1, int i, int[] arr2, int j) {\n while (i < arr1.length && j < arr2.length && arr1[i] == arr2[j]) {\n i++;\n j++;\n }\n // arr1 is lexicographically greater if it has a longer length, or has a digit greater than the digit as same place in arr2\n return i < arr1.length && j == arr2.length || (i < arr1.length && j < arr2.length && arr1[i] > arr2[j]);\n }\n}\n```
| 2 | 0 |
[]
| 0 |
create-maximum-number
|
Python solution with detailed explanation
|
python-solution-with-detailed-explanatio-imej
|
Solution\n\nCreate Maximum Number https://leetcode.com/problems/create-maximum-number/\n\nDynamic Programming/Recursive Solution\n Sketch the recursion and thro
|
gabbu
|
NORMAL
|
2017-01-21T07:54:04.311000+00:00
|
2017-01-21T07:54:04.311000+00:00
| 663 | false |
**Solution**\n\n**Create Maximum Number** https://leetcode.com/problems/create-maximum-number/\n\n**Dynamic Programming/Recursive Solution**\n* Sketch the recursion and throw in a cache. The complexity will be O(i * j * k). \n* The recursion is interesting in terms of the number of cases. When you have i,j, you need to think in how many different ways you can advance i and j with and without choosing nums1[i] and nums2[j]. Refer to the code, especially:\n```\n self.max_number(i, j+1, k, nums1, nums2, so_far) \n self.max_number(i+1, j, k, nums1, nums2, so_far) \n self.max_number(i+1, j+1, k, nums1, nums2, so_far)\n```\n\n```\nclass Solution(object):\n def max_number(self, i, j, k, nums1, nums2, so_far):\n if len(so_far) == k:\n int_number = int("".join(map(str, so_far)))\n if int_number > self.maximum_number:\n self.maximum_number = int_number\n self.max_list = [x for x in so_far]\n elif 0<=i<len(nums1) and 0<=j<len(nums2):\n if nums1[i] > nums2[j]:\n so_far.append(nums1[i])\n self.max_number(i+1, j, k, nums1, nums2, so_far)\n so_far.pop()\n elif nums1[i] < nums2[j]:\n so_far.append(nums2[j])\n self.max_number(i, j+1, k, nums1, nums2, so_far)\n so_far.pop()\n elif nums1[i] == nums2[j]:\n so_far.append(nums1[i])\n self.max_number(i+1, j, k, nums1, nums2, so_far)\n so_far.pop() \n so_far.append(nums2[j])\n self.max_number(i, j+1, k, nums1, nums2, so_far)\n so_far.pop()\n # Ignore nums[i] \n self.max_number(i, j+1, k, nums1, nums2, so_far)\n # ignore nums[i]\n self.max_number(i+1, j, k, nums1, nums2, so_far)\n # Ignore both\n self.max_number(i+1, j+1, k, nums1, nums2, so_far)\n elif i == len(nums1) and 0<=j<len(nums2):\n so_far.append(nums2[j])\n self.max_number(i, j+1, k, nums1, nums2, so_far)\n so_far.pop()\n self.max_number(i, j+1, k, nums1, nums2, so_far)\n elif j == len(nums2) and 0<=i<len(nums1):\n so_far.append(nums1[i])\n self.max_number(i+1, j, k, nums1, nums2, so_far)\n so_far.pop()\n self.max_number(i+1, j, k, nums1, nums2, so_far)\n return\n \n def maxNumber(self, nums1, nums2, k):\n """\n :type nums1: List[int]\n :type nums2: List[int]\n :type k: int\n :rtype: List[int]\n """\n N, M = len(nums1), len(nums2)\n self.maximum_number, self.max_list = -2**31, None\n self.max_number(0, 0, k, nums1, nums2, [])\n return self.max_list\n```\n\n**Optimized Solution using Stacks**\n* There is a smarter solution to this problem which is a combination of 2 smaller problems. \n* The solution to this problem will comprise of k digits, i from nums1 and k-i from nums2. \n* Assume i were 2, then what would be the best candidate? Clearly, the answer is "maximum number of size 2 from nums1 while keeping the relative order of the digits". \n* So lets call that problem as P0: "Given an array nums and an integer n, return the maximum number of size n that can be formed from nums while keeping the relative order of digits". Now for i=2, we will have 2 lists from nums1 and nums2 of size i and K-1. \n* We can merge them to compute a candidate solution of size k. This will be problem P1\n* What can be all the possible candidate solutions? Clearly when i will range from 0 to K for nums1 we will have a corresponding pair from nums2 ranging in size K to 0. Merging each of these pairs will give us the K+1 candidates. We then choose the largest from this pool and we are done!\nhttps://discuss.leetcode.com/topic/32281/share-my-python-solution-with-explanation\n\nP1: Merge 2 arrays with size i and K-1 formed from nums1 and nums2 to return the maximum possible number array of size K.\n* This is just like merge-sort merging, except when the elements are same. In that case we need to look beyond the current element (skipping all equal elements) to find the first unequal element and then pick the one which has the higher unequal element. Notice that when nums1[i] (or nums2[j]) is the last element and the value is equal to nums2[j] (or nums1[i]), we always pick the from the sublist which has elements remaining since there is a possibility of finding a greater solution.\n```\n x,y = i, j\n while x < N and y < M and left[x] == right[y]:\n x,y = x+1, y+1\n if x != N and y != M and left[x] > right[y]:\n result.append(left[i])\n i += 1\n elif x != N and y != M and left[x] < right[y]:\n result.append(right[j])\n j += 1\n elif x == N:\n result.append(right[j])\n j += 1\n elif y == M:\n result.append(left[i])\n i += 1\n```\n* Notice that in Python we can compare 2 lists l1 > l2 (merge_solution function) which does the above.\n```\n if nums1 > nums2:\n ans += nums1[0],\n```\n\nP0: Given an array nums and an integer n, return the maximum number of size n that can be formed from nums while keeping the relative order of digits.\n\n**Method 1**\n* We can maintain a stack. As long as we get input in descending order, just keep pushing on the stack. if you get a number larger than top of stack, then pop till you find a smaller number.While doing this, make sure you do not pop so much that you cannot meet the constraint of K digits. Refer to the code in max_number_list.\n\n**Method 2**\n* Say the size of array is N = 10. Say K = 6. What is the maximum number that can be formed of size N = 10? Answer is the original array. What about K = 6?\n* This problem can be stated as: "Remove k1 (4) digits from the array to form the largest number". This is the opposite of https://leetcode.com/problems/remove-k-digits/ where we remove K digits to form the smallest number\n* The solution to the smallest number problem was to scan from left to right and remove the first peak element and then the next peak from the solution of previous.\n* The solution to this problem is opposite - remove the first trough element, i.e. element which is smaller than both its left and right side!\n\n```\nclass Solution(object):\n def max_number_list(self, nums, n):\n st, required_to_remove = [], len(nums)-n\n for idx, x in enumerate(nums):\n while required_to_remove and st and st[-1] < x:\n st.pop()\n required_to_remove = required_to_remove - 1\n st.append(x)\n while len(st) > n:\n st.pop()\n return st\n \n def merge(self, left, right):\n i, j = 0, 0\n N, M = len(left), len(right)\n result = []\n while i < N or j < M:\n if i == N:\n result.append(right[j])\n j += 1\n elif j == M:\n result.append(left[i])\n i += 1\n elif left[i] < right[j]:\n result.append(right[j])\n j += 1\n elif left[i] > right[j]:\n result.append(left[i])\n i += 1\n else:\n x,y = i, j\n while x < N and y < M and left[x] == right[y]:\n x,y = x+1, y+1\n if x != N and y != M and left[x] > right[y]:\n result.append(left[i])\n i += 1\n elif x != N and y != M and left[x] < right[y]:\n result.append(right[j])\n j += 1\n elif x == N:\n result.append(right[j])\n j += 1\n elif y == M:\n result.append(left[i])\n i += 1\n return result\n\n def merge_solution(self, nums1, nums2):\n ans = []\n while nums1 or nums2:\n if nums1 > nums2:\n ans += nums1[0],\n nums1 = nums1[1:]\n else:\n ans += nums2[0],\n nums2 = nums2[1:]\n return ans\n\n def maxNumber(self, nums1, nums2, k):\n """\n :type nums1: List[int]\n :type nums2: List[int]\n :type k: int\n :rtype: List[int]\n """\n N, M = len(nums1), len(nums2)\n self.max_list = [0]*k\n for i in range(k+1):\n if i <= N and k-i <= M:\n left, right = self.max_number_list(nums1, i), self.max_number_list(nums2, k-i)\n merged = self.merge(left, right)\n for i in range(k):\n if self.max_list[i] != merged[i]:\n if self.max_list[i] > merged[i]:\n break\n elif merged[i] > self.max_list[i]:\n self.max_list = merged\n break\n return self.max_list\n```
| 2 | 0 |
[]
| 0 |
create-maximum-number
|
My Easy C++ Code with comments
|
my-easy-c-code-with-comments-by-vaibhav1-7yqq
|
```\nclass Solution {\npublic:\n int n,m;\n vectorgreatest(vectornums, int k)\n {\n int leave=nums.size()-k;\n vectorgreat;\n for(
|
vaibhav15
|
NORMAL
|
2017-08-22T15:14:43.133000+00:00
|
2017-08-22T15:14:43.133000+00:00
| 460 | false |
```\nclass Solution {\npublic:\n int n,m;\n vector<int>greatest(vector<int>nums, int k)\n {\n int leave=nums.size()-k;\n vector<int>great;\n for(auto i : nums)\n {\n while(leave && great.size() && great.back()<i)\n {\n great.pop_back();\n leave--;\n }\n great.push_back(i); \n }\n great.resize(k);\n return great;\n }\n bool check(vector<int>nums1, int i, vector<int>nums2, int j)\n {\n while(i<nums1.size() && j<nums2.size() && nums1[i]==nums2[j])\n {\n i++;\n j++;\n }\n if(j==nums2.size()) return true;\n if(i<nums1.size() && nums1[i]>nums2[j]) return true;\n return false;\n }\n // merge the 2 big numbers we have got in 2 vectors into 1 big possible number of size k \n vector<int> merge(vector<int>nums1 , vector<int>nums2,int k)\n {\n int i=0,j=0;\n vector<int>great(k,0);\n for(int l=0;l<k;l++)\n {\n great[l]=check(nums1,i,nums2,j)?nums1[i++]:nums2[j++];\n }\n return great;\n }\n vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {\n n=nums1.size();\n m=nums2.size();\n vector<int>res;\n for(int i=max(0,k-m);i<=min(k,n);i++)\n {\n //v1 = greatest possible number stored in vector of length i\n //v2 = greatest possible number stored in vector of length k-i;\n auto v1 =greatest(nums1,i);\n auto v2=greatest(nums2,k-i);\n auto candidate=merge(v1,v2,k);\n if(check(candidate,0,res,0))\n res=candidate;\n }\n return res;\n }\n};\n````
| 2 | 0 |
[]
| 0 |
create-maximum-number
|
C++ | Greedy Approach
|
c-greedy-approach-by-kena7-kfve
|
Code
|
kenA7
|
NORMAL
|
2025-03-19T18:06:11.435017+00:00
|
2025-03-19T18:06:11.435017+00:00
| 218 | false |
# Code
```cpp []
class Solution {
vector<int> getLargestNum(vector<int> &nums, int k) {
int n=nums.size();
vector<int>res;
for(int i=0;i<n;i++) {
while(!res.empty() && nums[i]>res.back() && n-i-1>=k-res.size())
res.pop_back();
if(res.size()<k)
res.push_back(nums[i]);
}
return res;
}
vector<int> mergeNums(vector<int> &a, vector<int> &b) {
vector<int> res;
int i=0,j=0,m=a.size(),n=b.size();
while(i<m || j<n) {
if(i==m)
res.push_back(b[j++]);
else if(j==n || a[i]>b[j])
res.push_back(a[i++]);
else if(a[i]<b[j])
res.push_back(b[j++]);
else {
int k=0;
while(i+k<m && j+k<n && a[i+k]==b[j+k])
k++;
if(i+k>=m)
res.push_back(b[j++]);
else if(j+k>=n)
res.push_back(a[i++]);
else if(a[i+k]>b[j+k])
res.push_back(a[i++]);
else
res.push_back(b[j++]);
}
}
return res;
}
public:
vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k)
{
// Lets break k into k1 & k2 (k1 from nums1 & k2 from nums2)
vector<int>res(k,0);
for(int k1=0;k1<=k;k1++) {
int k2=k-k1;
if(k1>nums1.size() || k2>nums2.size())
continue;
auto num1 = getLargestNum(nums1, k1);
auto num2 = getLargestNum(nums2, k2);
auto merged = mergeNums(num1, num2);
if(merged>res)
res=merged;
}
return res;
}
};
```
| 1 | 0 |
['C++']
| 0 |
create-maximum-number
|
interesting tiny Python solution
|
interesting-tiny-python-solution-by-serg-qy3i
|
IntuitionIs it easy to merge two arrays to create the maximum number possible without the limit K? And what is the problem with the limit K?ApproachThe problem
|
SergioBear
|
NORMAL
|
2025-03-11T13:42:45.322056+00:00
|
2025-03-11T13:42:45.322056+00:00
| 187 | false |
# Intuition
Is it easy to merge two arrays to create the maximum number possible without the limit K? And what is the problem with the limit K?
# Approach
The problem is that we can basically skip digits if we don't like them, which means shifting the pointer during merging
`merge` function.

But how do we detect which numbers we need to skip and which ones to include? Easy — iterate from right to left and get the maximum number for the first place.
But are all numbers valid? No, a number is acceptable only if we have enough space for other digits.
Also, try to choose the leftmost number to have more choices
`largestk` function.
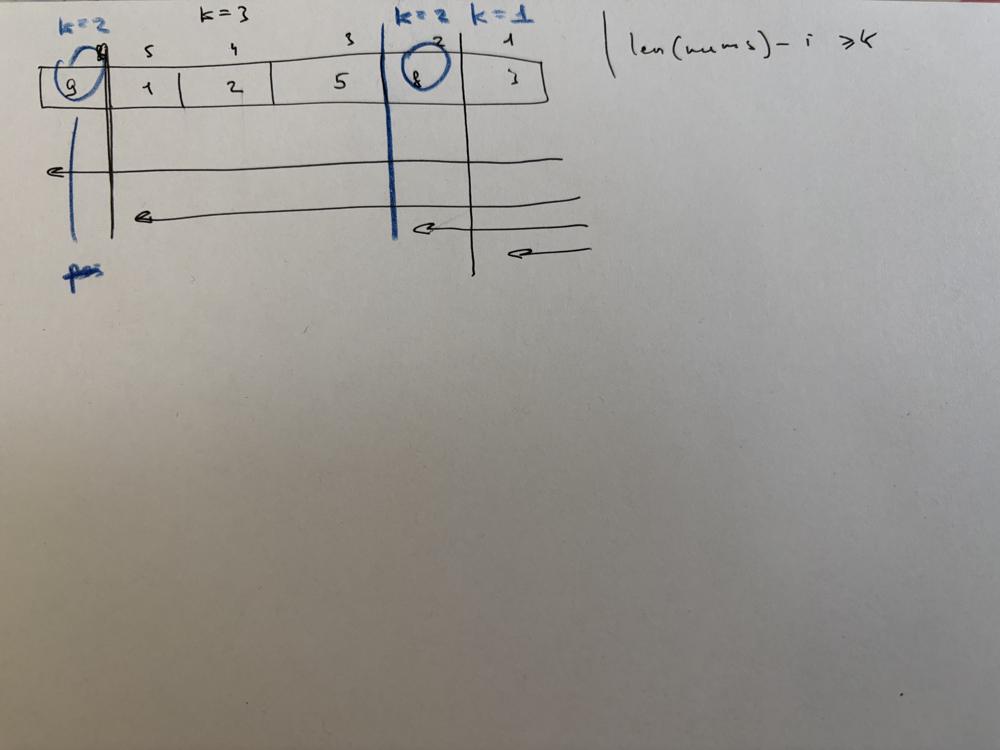
And how many elements do we need to choose from each array? all possible ranges.
for example, 5:
0,5
1,4
2,3
3,2
4,1
5,0
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
O(k*(n + m))
- Space complexity:
O(k*(n + m))
# Code
```python3 []
class Solution:
def maxNumber(self, nums1: List[int], nums2: List[int], k: int) -> List[int]:
# merge array
def merge(nums1, nums2):
n1, n2 = 0, 0
merge = []
while n1 < len(nums1) and n2 < len(nums2):
if nums1[n1:] > nums2[n2:]:
merge.append(nums1[n1])
n1 += 1
else:
merge.append(nums2[n2])
n2 += 1
if n1 < len(nums1):
merge.extend(nums1[n1:])
else:
merge.extend(nums2[n2:])
return merge
def largestk(nums, k):
# numbers left = len(nums) - i
l = -1
res = []
for _ in range(k):
maxx = float("-inf")
for r in range(len(nums) - 1, l, -1):
# check if the number is possible
if len(nums) - r >= k:
if maxx <= nums[r]:
maxx = nums[r]
l = r
k -= 1
res.append(maxx)
return res
res = []
for i in range(k + 1):
if i <= len(nums1) and k - i <= len(nums2):
largest1 = largestk(nums1, i)
largest2 = largestk(nums2, k - i)
res = max(res, merge(largest1, largest2))
return res
```
| 1 | 0 |
['Array', 'Two Pointers', 'Greedy', 'Python', 'Python3']
| 1 |
create-maximum-number
|
Lexicographically Largest Array based Answer
|
lexicographically-largest-array-based-an-8myt
|
IntuitionThe problem requires finding the lexicographically greatest subsequence of a given length from two arrays. The key idea is to leverage the greatest sub
|
PrashantSingh0110
|
NORMAL
|
2025-01-03T09:27:54.989330+00:00
|
2025-01-03T09:27:54.989330+00:00
| 51 | false |
### Intuition
The problem requires finding the lexicographically greatest subsequence of a given length from two arrays. The key idea is to leverage the greatest subsequence from each array and then merge them in a way that maintains the lexicographical order.
### Approach
1. **Greatest Subsequence Function**: Create a helper function to find the lexicographically greatest subsequence of a given length from a single array.
2. **Combination and Comparison**: For each possible split of the total length `k` between the two arrays, find the greatest subsequences from both arrays and merge them.
3. **Merge Logic**: Merge the two subsequences by comparing elements to maintain the lexicographical order.
4. **Result Update**: Keep track of the best result found during the merging process.
### Complexity
- **Time complexity**:
- The helper function `getGreatestSubsequence` runs in $$O(n)$$ time for each array.
- The merging process runs in $$O(k)$$ time for each combination.
- Overall, the time complexity is $$O(k \cdot (n + m))$$, where `n` and `m` are the lengths of the two input arrays.
- **Space complexity**:
- The space complexity is $$O(k)$$ for storing the result and intermediate arrays.
# Code
```java []
class Solution {
private static int[] getGreatestSubsequence(int[] array, int length) {
int n = array.length;
int[] result = new int[length];
int j = 0;
for (int i = 0; i < n; i++) {
while (j > 0 && result[j - 1] < array[i] && j + n - i > length) {
j--;
}
if (j < length) {
result[j++] = array[i];
}
}
return result;
}
public int[] maxNumber(int[] nums1, int[] nums2, int k) {
int[] res = new int[k];
for (int i = 0; i <= k; i++) {
if (i > nums1.length || k - i > nums2.length) continue;
int[] current = new int[k];
int[] res1 = getGreatestSubsequence(nums1, i);
int[] res2 = getGreatestSubsequence(nums2, k - i);
System.out.println(Arrays.toString(res1));
System.out.println(Arrays.toString(res2));
int l = 0, j = 0;
while (l < res1.length && j < res2.length) {
if (res1[l] > res2[j]) {
current[l + j] = res1[l];
l++;
} else if (res1[l] < res2[j]) {
current[l + j] = res2[j];
j++;
} else {
// Compare the remaining parts to decide
int[] remaining1 = Arrays.copyOfRange(res1, l, res1.length);
int[] remaining2 = Arrays.copyOfRange(res2, j, res2.length);
if (Arrays.compare(remaining1, remaining2) > 0) {
current[l + j] = res1[l];
l++;
} else {
current[l + j] = res2[j];
j++;
}
}
}
while (l < res1.length) {
current[l + j] = res1[l];
l++;
}
while (j < res2.length) {
current[l + j] = res2[j];
j++;
}
if (Arrays.compare(current, res) > 0) {
res = current;
}
}
return res;
}
}
```
| 1 | 0 |
['Array', 'Java']
| 0 |
create-maximum-number
|
Monotonic Stack and Lexicographical Merging
|
monotonic-stack-and-lexicographical-merg-pyal
|
Intuition\n Describe your first thoughts on how to solve this problem. \nTo form the largest possible number of length k from two arrays while maintaining their
|
orel12
|
NORMAL
|
2024-07-18T12:09:27.417513+00:00
|
2024-07-18T12:09:27.417543+00:00
| 38 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo form the largest possible number of length `k` from two arrays while maintaining their relative order, we need to explore all possible ways of picking elements from both arrays. This involves generating the largest subarrays of different lengths from both arrays and then merging these subarrays to form the largest number. The main challenge is efficiently selecting and merging these elements to achieve the optimal result.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. **Splitting the Selection**:\n - Iterate over all possible ways to split the selection of `k` elements between the two input arrays `nums1` and `nums2`. Specifically, for each `i` from `max(0, k - n)` to `min(k, m)`, `i` represents the number of elements taken from `nums1`, and `k - i` represents the number of elements taken from `nums2`.\n\n2. **Construct Maximum Subarrays**:\n - For each split, use the `getMaxSubarray` function to construct the maximum subarray of a given length from both `nums1` and `nums2`.\n\n - **`getMaxSubarray(array, subarrayLength)`**:\n - This function constructs the maximum subarray of length `subarrayLength` from the given array using a monotonic stack approach.\n - Traverse the array and use a stack to keep track of the maximum elements, ensuring that the remaining elements can still form a subarray of the required length.\n\n3. **Merge Subarrays**:\n - Merge the two maximum subarrays into a single array while maintaining their order using the `mergeSubarrays` function.\n - **`mergeSubarrays(subarray1, subarray2)`**:\n - This function merges two subarrays into one, ensuring the largest possible lexicographical order.\n - Traverse both subarrays and compare elements to construct the merged result, handling cases where elements are equal by comparing the remaining sequences.\n\n4. **Compare and Update**:\n - Compare each merged result with the current best result and update the best result if the new merged array is lexicographically larger.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity is $$O(k \\cdot (m + n))$$, where `m` and `n` are the lengths of `nums1` and `nums2`, respectively, and `k` is the number of elements to be selected. This accounts for iterating over all possible splits and constructing/merging the maximum subarrays.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is $$O(m + n + k)$$, which includes the space for the maximum subarrays and the result array.\n\n\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {\n int m = nums1.size();\n int n = nums2.size();\n vector<int> res;\n\n auto getMaxSubarray = [](const vector<int>& array, int subarrayLength) -> vector<int> {\n vector<int> stack;\n int remaining = array.size() - subarrayLength;\n for (int num : array) {\n while (!stack.empty() && remaining > 0 && stack.back() < num) {\n stack.pop_back();\n remaining--;\n }\n stack.push_back(num);\n }\n stack.resize(subarrayLength);\n return stack;\n };\n\n auto mergeSubarrays = [](const vector<int>& subarray1, const vector<int>& subarray2) -> vector<int> {\n vector<int> result;\n int i = 0, j = 0;\n while (i < subarray1.size() || j < subarray2.size()) {\n if (j == subarray2.size() || (i < subarray1.size() && subarray1[i] > subarray2[j])) {\n result.push_back(subarray1[i++]);\n } else if (i == subarray1.size() || (j < subarray2.size() && subarray2[j] > subarray1[i])) {\n result.push_back(subarray2[j++]);\n } else {\n if (lexicographical_compare(subarray1.begin() + i, subarray1.end(), subarray2.begin() + j, subarray2.end())) {\n result.push_back(subarray2[j++]);\n } else {\n result.push_back(subarray1[i++]);\n }\n }\n }\n return result;\n };\n\n for (int i = max(0, k - n); i <= min(k, m); i++) {\n vector<int> maxSubarray1 = getMaxSubarray(nums1, i);\n vector<int> maxSubarray2 = getMaxSubarray(nums2, k - i);\n vector<int> candidate = mergeSubarrays(maxSubarray1, maxSubarray2);\n if (lexicographical_compare(res.begin(), res.end(), candidate.begin(), candidate.end())) {\n res = candidate;\n }\n }\n\n return res;\n }\n};\n\n\n```
| 1 | 0 |
['C++']
| 0 |
create-maximum-number
|
A sweet Israeli solution:)
|
a-sweet-israeli-solution-by-e8hwn77klg-jni5
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
E8hwN77KLg
|
NORMAL
|
2024-07-08T19:05:51.835962+00:00
|
2024-07-08T19:05:51.835995+00:00
| 473 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n\npublic class Solution {\n public int[] maxNumber(int[] nums1, int[] nums2, int k) {\n int m = nums1.length, n = nums2.length;\n int[] maxSequence = new int[k];\n \n for (int i = Math.max(0, k - n); i <= Math.min(k, m); i++) {\n int[] seq1 = maxSubsequence(nums1, i);\n int[] seq2 = maxSubsequence(nums2, k - i);\n int[] candidate = merge(seq1, seq2);\n if (greater(candidate, 0, maxSequence, 0)) {\n maxSequence = candidate;\n }\n }\n \n return maxSequence;\n }\n\n private int[] maxSubsequence(int[] nums, int k) {\n int[] subsequence = new int[k];\n int len = 0;\n for (int i = 0; i < nums.length; i++) {\n while (len > 0 && len + nums.length - i > k && subsequence[len - 1] < nums[i]) {\n len--;\n }\n if (len < k) {\n subsequence[len++] = nums[i];\n }\n }\n return subsequence;\n }\n\n private int[] merge(int[] nums1, int[] nums2) {\n int[] merged = new int[nums1.length + nums2.length];\n int i = 0, j = 0, k = 0;\n while (i < nums1.length && j < nums2.length) {\n if (greater(nums1, i, nums2, j)) {\n merged[k++] = nums1[i++];\n } else {\n merged[k++] = nums2[j++];\n }\n }\n while (i < nums1.length) {\n merged[k++] = nums1[i++];\n }\n while (j < nums2.length) {\n merged[k++] = nums2[j++];\n }\n return merged;\n }\n\n private boolean greater(int[] nums1, int i, int[] nums2, int j) {\n while (i < nums1.length && j < nums2.length && nums1[i] == nums2[j]) {\n i++;\n j++;\n }\n return j == nums2.length || (i < nums1.length && nums1[i] > nums2[j]);\n }\n\n \n}\n\n```
| 1 | 0 |
['Java']
| 1 |
create-maximum-number
|
Intuitive | Beginner Friendly Explanation✅| C++ | Stack
|
intuitive-beginner-friendly-explanation-e7zxe
|
Intuition\nThe intuition idea is that to create a number of length k, we will take some subsequnce of length k1 from nums1, and of length k2 = ( k- k1 )from num
|
gauravY78
|
NORMAL
|
2024-04-12T13:08:21.014471+00:00
|
2024-04-12T13:08:21.014508+00:00
| 64 | false |
# Intuition\nThe intuition idea is that to create a number of length `k`, we will take some subsequnce of length `k1` from `nums1`, and of length `k2 = ( k- k1 ) `from `nums2`, since we have to preseve the order of digits from each array it is optimal to select the largest possible subsequnce from each array.\n\nNow we have the largest subsequence possible from both arrays (with `k1` and `k2` digits respectively)\nNow we will merge them to create the largest number possible of `k1 + k2 = k` digits.\n\nWe will try all possible combinations of `k1` and `k2` and return the maximum number encountered.\n\nNOTE: The above listed two sub-problems are separate problems on leetcode itself, i suggest to solve them first. The problem numbers are `1673` and `1754`.\n\nIf you are able to think how to do these two problems, great. if not please look at the following detailed explanations for each:\n\nhttps://leetcode.com/problems/find-the-most-competitive-subsequence/solutions/5012111/c-beginner-friendly-detailed-explantion-monotonic-stack/\n\nThe above problem is to give the smallest sub-sequence, i have done slight modification in the above code to use it to return largest sub-sequence.\n\nFor largest Merge Problem explanation:\nhttps://leetcode.com/problems/largest-merge-of-two-strings/solutions/5012449/clean-code-beginner-friendly-easy-explanation-two-pointers-c/\n\n\n# Approach\n1. To find the largest possible subsequnce from each array, i have used utility function `largestSubsequence` which takes paramters `nums` and `k` and returns the largest possible subsequnce of length `k` in `nums`\n\n2. After getting the largest subsequnce (of lengths `k1` and `k2`) from each array we will need to merge them to get our desired number of length `k`, the `largestMerge` function does the same\n\n3. Store the maximum of all the merged numbers encountered in the process and retutn it.\n\n\nSee the commented code for more clarity\n\n# Complexity\n- Time complexity:\n$$O(k*(m+n))$$\n\n- Space complexity:\n$$O(m+n)$$\n\n# Code\n```\nclass Solution {\n string largestSubsequence(vector<int>& nums, int k){\n string ans = "";\n int n = nums.size();\n for(int i = 0; i < n; i++){\n while( n - i > k - ans.size() && !ans.empty() && ans.back() - \'0\' < nums[i] )\n ans.pop_back(); \n if( ans.size() < k )\n ans += to_string(nums[i]);\n }\n return ans;\n }\n\n string largestMerge(string word1, string word2) {\n string ans = "";\n int i = 0, j = 0, m = word1.length(), n = word2.length();\n while( i < m && j < n ){\n if( word1[i] < word2[j] )\n ans += word2[j++];\n else if( word1[i] > word2[j] )\n ans += word1[i++];\n else{\n string w1 = word1.substr(i), w2 = word2.substr(j);\n if( w1 >= w2 )\n ans += word1[i++];\n else\n ans += word2[j++];\n }\n }\n\n if( i < m )\n ans += word1.substr(i);\n if( j < n )\n ans += word2.substr(j);\n\n return ans;\n }\n\n //NOTE: default max function does lexicogrphical comp. on strings\n //thus custom compare func for integer comparision\n string maxStr(string str1, string str2){\n if( str1.length() > str2.length() )\n return str1;\n if( str2.length() > str1.length() )\n return str2;\n \n return max(str1, str2);\n }\n\npublic:\n vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {\n int k1 = 0;\n string ans = "";\n //try out all possible combinations of k1 and k2\n while( k1 <= k ){\n string n1 = largestSubsequence(nums1, k1);\n string n2 = largestSubsequence(nums2, k - k1);\n\n ans = maxStr(ans, largestMerge(n1, n2));\n k1++;\n }\n\n //construct the vector from string\n vector<int> res(ans.begin(), ans.end());\n \n //As we create vector from string we get the ASCII values\n //of each character in our vector\n //convert it to integer by subtracting 48 as \'0\' = 48 in ASCII\n for(int i = 0; i < k; i++)\n res[i] -= 48;\n \n return res;\n }\n};\n```\n\nPLEASE UPVOTE IF THE EXPLANATION WAS HELPFULl\u2764\uFE0F\uD83E\uDD1E
| 1 | 0 |
['String', 'Greedy', 'Monotonic Stack', 'C++']
| 0 |
create-maximum-number
|
JAVA Solution
|
java-solution-by-raghu3696-rl1o
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Raghu3696
|
NORMAL
|
2024-02-11T18:15:04.655346+00:00
|
2024-02-11T18:15:04.655377+00:00
| 240 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int[] maxNumber(int[] nums1, int[] nums2, int k) {\n int m = nums1.length;\n int n = nums2.length;\n int[] maxNumber = new int[k];\n \n for (int i = Math.max(0, k - n); i <= k && i <= m; i++) {\n int[] candidate = merge(maxArray(nums1, i), maxArray(nums2, k - i), k);\n if (greater(candidate, 0, maxNumber, 0)) {\n maxNumber = candidate;\n }\n }\n \n return maxNumber;\n }\n \n private int[] maxArray(int[] nums, int k) {\n int[] result = new int[k];\n int len = 0;\n for (int i = 0; i < nums.length; i++) {\n while (len > 0 && len + nums.length - i > k && nums[i] > result[len - 1]) {\n len--;\n }\n if (len < k) {\n result[len++] = nums[i];\n }\n }\n return result;\n }\n \n private int[] merge(int[] nums1, int[] nums2, int k) {\n int[] result = new int[k];\n int i = 0, j = 0;\n for (int r = 0; r < k; r++) {\n if (greater(nums1, i, nums2, j)) {\n result[r] = nums1[i++];\n } else {\n result[r] = nums2[j++];\n }\n }\n return result;\n }\n \n private boolean greater(int[] nums1, int i, int[] nums2, int j) {\n while (i < nums1.length && j < nums2.length && nums1[i] == nums2[j]) {\n i++;\n j++;\n }\n return j == nums2.length || (i < nums1.length && nums1[i] > nums2[j]);\n }\n }\n\n```
| 1 | 0 |
['Java']
| 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.