question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
create-maximum-number
|
full commented solution py3
|
full-commented-solution-py3-by-borkiss-r37h
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
borkiss
|
NORMAL
|
2024-01-28T15:28:12.967490+00:00
|
2024-01-28T15:28:12.967506+00:00
| 113 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxNumber(self, nums1: List[int], nums2: List[int], k: int) -> List[int]:\n # Define a method to get the maximum subsequence of length k from the given nums\n def get_max_subseq(nums, k):\n stack = []\n for i, num in enumerate(nums):\n # While the stack is not empty, and removing elements from it\n # can create a larger subsequence, pop elements from the stack\n while stack and len(nums) - i + len(stack) > k and stack[-1] < num:\n stack.pop()\n # If the stack has fewer than k elements, or it can still accommodate more elements, append num to the stack\n if len(stack) < k:\n stack.append(num)\n return stack\n\n # Define a method to merge two lists into one, preserving the order to get the maximum number\n def merge(nums1, nums2):\n merged = []\n i, j = 0, 0\n # Iterate through both lists, comparing elements and appending the larger one to the merged list\n while i < len(nums1) or j < len(nums2):\n if i >= len(nums1):\n merged.append(nums2[j])\n j += 1\n elif j >= len(nums2):\n merged.append(nums1[i])\n i += 1\n elif nums1[i:] > nums2[j:]:\n merged.append(nums1[i])\n i += 1\n else:\n merged.append(nums2[j])\n j += 1\n return merged\n\n ans = []\n # Iterate through possible lengths of the subsequence from nums1\n for i in range(max(0, k - len(nums2)), min(len(nums1), k) + 1):\n j = k - i\n # Get the maximum subsequence of length i from nums1 and length j from nums2\n subseq1 = get_max_subseq(nums1, i)\n subseq2 = get_max_subseq(nums2, j)\n # Merge the two subsequences to get a single maximum subsequence\n merged = merge(subseq1, subseq2)\n # Keep track of the maximum subsequence seen so far\n ans = max(ans, merged)\n # Return the final maximum subsequence\n return ans\n\n```
| 1 | 0 |
['Python3']
| 0 |
create-maximum-number
|
Efficient solution using monotonic stack
|
efficient-solution-using-monotonic-stack-y9ad
|
Intuition\nWe need to consider some numbers from the first array and some from the second array, while maintaining relative ordering, and merge them together to
|
waxm
|
NORMAL
|
2023-12-30T14:46:04.607076+00:00
|
2023-12-30T14:46:04.607098+00:00
| 254 | false |
# Intuition\nWe need to consider some numbers from the first array and some from the second array, while maintaining relative ordering, and merge them together to get the result.\n\nTo do this, we need to calculate for all the possible combinations of the number of numbers that come from each array. Then we find the largest among them.\n\n# Approach\n1. Find the lexicographically largest sequence from the first array with x as the value of k, then find the largest sequence from the second array with y as the value of k using the constraint: `for any x & y where 0 < x \u2264 k and y = k - x;` \nExample: For k = 5.\n\n | x | y |\n | --- | --- |\n | 0 | 5 |\n | 1 | 4 |\n | 2 | 3 |\n | 3 | 2 |\n | 4 | 1 |\n | 5 | 0 |\n2. We will find the largest sequence for both the arrays individually and merge them together to get the final result by taking the largest element from each subsequence and incrementing the position.\n3. If we find that the number from both the sub-arrays are the same, we will take the number from the subarray that is lexicographically larger than the other.\n4. We can say that an array \'a\' is lexicographically larger than the array \'b\', if at the position they differ a[i] > b[i] or it could also be that they don\'t differ at any position but the length of a is larger than b. \n5. Once we have merged both the arrays, we compare it with the other possible combinations that will result from the iteration and we take the largest among them. \n\nIt\'s recommnded that you first solve this related problem which will teach you how to find the smallest subsequence from a single array for a given k: https://leetcode.com/problems/find-the-most-competitive-subsequence\n\n\n\n# Complexity\n- Time complexity:\nO(k * (m + n))\n\n# Code\n```\nfunction maxSingle(nums: number[], k: number): number[] {\n const stack: number[] = [];\n for (let i = 0; i < nums.length; ++i) {\n const num = nums[i];\n while (\n stack.length &&\n stack[stack.length - 1] < num &&\n nums.length - i > k - stack.length\n ) stack.pop();\n\n stack.push(num);\n }\n\n return stack.slice(0, k);\n}\n\nfunction lexGreater(nums1: number[], nums2: number[], i: number, j: number): boolean {\n while (i < nums1.length || j < nums2.length) {\n if (i >= nums1.length) return false;\n else if (j >= nums2.length) return true;\n else if (nums1[i] > nums2[j]) return true;\n else if (nums2[j] > nums1[i]) return false;\n else i++, j++;\n }\n\n return true;\n}\n\nfunction merge(nums1: number[], nums2: number[]): number[] {\n let i = 0;\n let j = 0;\n const merged: number[] = [];\n while (i < nums1.length || j < nums2.length) {\n if (i >= nums1.length) merged.push(nums2[j++]);\n else if (j >= nums2.length) merged.push(nums1[i++]);\n else if (nums1[i] < nums2[j]) merged.push(nums2[j++]);\n else if (nums1[i] > nums2[j]) merged.push(nums1[i++]);\n else {\n if (lexGreater(nums1, nums2, i, j)) merged.push(nums1[i++]);\n else merged.push(nums2[j++]);\n }\n }\n\n return merged;\n}\n\nfunction maxNumber(nums1: number[], nums2: number[], k: number): number[] {\n let res: number[] = [];\n for (let i = 0; i <= k; ++i) {\n let j = k - i;\n if (i > nums1.length || j > nums2.length) continue;\n const max1 = maxSingle(nums1, i);\n const max2 = maxSingle(nums2, j);\n\n const merged = merge(max1, max2);\n if (merged > res) {\n res = merged;\n }\n }\n\n return res; \n};\n```
| 1 | 0 |
['Stack', 'Monotonic Stack', 'TypeScript']
| 1 |
create-maximum-number
|
Solution
|
solution-by-deleted_user-jkcq
|
C++ []\nclass Solution {\npublic:\n #define MIN(a,b) (a<b?a:b)\n #define MAX(a,b) (a>b?a:b)\n void getMax(int* num, int& len, int* result, int& t, int&
|
deleted_user
|
NORMAL
|
2023-03-20T10:27:42.495375+00:00
|
2023-03-20T10:55:34.685517+00:00
| 218 | false |
```C++ []\nclass Solution {\npublic:\n #define MIN(a,b) (a<b?a:b)\n #define MAX(a,b) (a>b?a:b)\n void getMax(int* num, int& len, int* result, int& t, int& sortedLen)\n {\n \tint n, top = 0;\n \tresult[0] = num[0];\n \tconst int need2drop = len - t;\n \tfor (int i = 1; i < len; ++i){\n \t\tn = num[i];\n \t\twhile (top >= 0 && result[top] < n && (i - top) <= need2drop) --top;\n \t\tif (i - top > need2drop){\n \t\t\tsortedLen = MAX(1,top);\n \t\t\twhile (++top < t) result[top] = num[i++];\n \t\t\treturn;\n \t\t}\n \t\tif (++top < t) result[top] = n;\n \t\telse top = t - 1;\n \t}\n }\n void dp(int *num, int len, int&sortedLen, int& minL, int& maxL, int *res, int &k){\n \tint j, *head, *prevhead = res;\n \tconst int soi = sizeof(int);\n \tgetMax(num, len, res, maxL,sortedLen);\n \tfor (int l = maxL; l > MAX(minL,1); --l){\n \t\thead = prevhead + k;\n \t\tmemcpy(head, prevhead, l*soi);\n \t\tfor (j = sortedLen; j < l; ++j){\n \t\t\tif (head[j] > head[j - 1]){\n \t\t\t\tsortedLen = MAX(1, j - 1);\n \t\t\t\tmemcpy(head + j - 1, prevhead + j, soi*(l - j));\n \t\t\t\tbreak;\n \t\t\t}\n \t\t}\n \t\tif (j == l) sortedLen = l;\n \t\tprevhead = head;\n \t}\n }\n void merge(int* num1,int len1,int* num2,int len2,int* result,int& resSize){\n \tint i = 0, j = 0, k = 0;\n \twhile (i < resSize){\n \t\tif (j < len1 && k < len2){\n \t\t\tif (num1[j] > num2[k])\n \t\t\t\tresult[i++] = num1[j++];\n \t\t\telse if (num1[j] < num2[k])\n \t\t\t\tresult[i++] = num2[k++];\n \t\t\telse{\n \t\t\t\tint remaining1 = len1 - j, remaining2 = len2 - k, tmp = num1[j];\n \t\t\t\tint flag = memcmp(num1 + j, num2 + k, sizeof(int) * MIN(remaining1, remaining2));\n \t\t\t\tflag = (flag == 0 ? (remaining1>remaining2 ? 1 : -1) : flag);\n \t\t\t\tint * num = flag > 0 ? num1 : num2;\n \t\t\t\tint & cnt = flag > 0 ? j : k;\n \t\t\t\tint len = flag > 0 ? len1 : len2;\n \t\t\t\twhile (num[cnt]==tmp && cnt < len && i<resSize) result[i++] = num[cnt++];\n \t\t\t}\n \t\t}\n \t\telse if (j < len1) result[i++] = num1[j++];\n \t\telse result[i++] = num2[k++];\n \t}\n }\n vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k){\n \tint soi = sizeof(int), len1 = nums1.size(), len2 = nums2.size(), step = k*soi;\n \tint minL1 = MAX(0, k - len2), maxL1 = MIN(k, len1), minL2 = k - maxL1, maxL2 = k - minL1, range = maxL1 - minL1 + 1;\n \tint * res = new int[range * k * 2 + 2 * k], *dp1 = res + k, *dp2 = res + range*k+k, *tmp=res+range*2*k+k;\n \tmemset(res, 0, step);\n \tint sortedLen1 = 1, sortedLen2 = 1;\n \tif (len1 == 0 && len2 > 0) getMax(&nums2[0], len2, res, k, sortedLen2);\n \telse if (len1 > 0 && len2 == 0) getMax(&nums1[0], len1, res, k, sortedLen2);\n \telse if (len1 > 0 && len2 > 0){\n \t\tdp(&nums1[0], len1, sortedLen1, minL1, maxL1, dp1,k);\n \t\tdp(&nums2[0], len2, sortedLen2, minL2, maxL2, dp2,k);\n \t\tif (sortedLen1 + sortedLen2 > k){\n \t\t\tmerge(dp1 + k*(maxL1 - sortedLen1), sortedLen1, dp2 + k*(maxL2 - sortedLen2), sortedLen2, tmp, k);\n \t\t\tvector<int> resv(tmp, tmp + k);\n \t\t\tdelete[] res;\n \t\t\treturn resv;\n \t\t}\n \t\tfor (int i = minL1; i <= maxL1; ++i){\n \t\t\tmerge(dp1+k*(maxL1-i), i, dp2+k*(maxL2-k+i), (k-i), tmp,k);\n \t\t\tif (memcmp(res, tmp, step) < 0) memcpy(res, tmp, step);\n \t\t}\n \t}\n \tvector<int> resv(res, res + k);\n \tdelete[] res;\n \treturn resv;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def maxNumber(self, nums1: List[int], nums2: List[int], k: int) -> List[int]:\n \n def get_max_subarray(nums, k):\n stack = []\n drop = len(nums) - k\n for num in nums:\n while drop and stack and stack[-1] < num:\n stack.pop()\n drop -= 1\n stack.append(num)\n return stack[:k]\n\n max_num = []\n\n for i in range(max(0, k - len(nums2)), min(k, len(nums1)) + 1):\n max_subarray1 = get_max_subarray(nums1, i)\n max_subarray2 = get_max_subarray(nums2, k - i)\n\n candidate = []\n while max_subarray1 or max_subarray2:\n if max_subarray1 > max_subarray2:\n candidate.append(max_subarray1.pop(0))\n else:\n candidate.append(max_subarray2.pop(0))\n\n if candidate > max_num:\n max_num = candidate\n\n return max_num\n```\n\n```Java []\nclass Solution {\n public int[] maxNumber(int[] nums1, int[] nums2, int k) {\n\n int m = nums1.length, n = nums2.length;\n int[] ans = new int[k];\n \n for (int i = Math.max(0, k-n); i <= Math.min(k, m); i++) {\n int j = k - i;\n int[] maxNum1 = getMax(nums1, i);\n int[] maxNum2 = getMax(nums2, j);\n int[] merged = merge(maxNum1, maxNum2);\n if (compare(merged, 0, ans, 0) > 0) {\n ans = merged;\n }\n }\n return ans;\n}\nprivate int[] getMax(int[] nums, int k) {\n int n = nums.length;\n int[] stack = new int[k];\n int top = -1, remaining = n - k;\n \n for (int i = 0; i < n; i++) {\n int num = nums[i];\n while (top >= 0 && stack[top] < num && remaining > 0) {\n top--;\n remaining--;\n }\n if (top < k - 1) {\n stack[++top] = num;\n } else {\n remaining--;\n }\n }\n return stack;\n}\nprivate int[] merge(int[] nums1, int[] nums2) {\n int m = nums1.length, n = nums2.length;\n int[] merged = new int[m + n];\n int i = 0, j = 0, k = 0;\n \n while (i < m && j < n) {\n if (compare(nums1, i, nums2, j) > 0) {\n merged[k++] = nums1[i++];\n } else {\n merged[k++] = nums2[j++];\n }\n }\n while (i < m) {\n merged[k++] = nums1[i++];\n }\n while (j < n) {\n merged[k++] = nums2[j++];\n }\n return merged;\n}\nprivate int compare(int[] nums1, int i, int[] nums2, int j) {\n int m = nums1.length, n = nums2.length;\n while (i < m && j < n) {\n int diff = nums1[i] - nums2[j];\n if (diff != 0) {\n return diff;\n }\n i++;\n j++;\n }\n return (m - i) - (n - j);\n}\n}\n```\n
| 1 | 0 |
['C++', 'Java', 'Python3']
| 0 |
create-maximum-number
|
✅ C++ | DYNAMIC PROGRAMMING SOLUTION
|
c-dynamic-programming-solution-by-minhuc-502p
|
Complexity\n- Time complexity:\n Add your time complexity here, e.g. O(n) \nO(nm)\n- Space complexity:\n Add your space complexity here, e.g. O(n) \nO(nm)\n# Co
|
minhuchiha
|
NORMAL
|
2022-12-25T04:46:45.880261+00:00
|
2022-12-25T04:46:45.880306+00:00
| 895 | false |
# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(nm)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(nm)$$\n# Code\n```\nclass Solution {\npublic:\n string findMaxNum(vector<int>& nums1, vector<int>& nums2, int k, int x, int y, vector<vector<string>>& dp) {\n if (k == 0) return "";\n if (!dp[x][y].empty()) return dp[x][y];\n string res = "";\n int idx1 = x, idx2 = y, upperBound1 = nums2.size() + nums1.size() - y - k, upperBound2 = nums2.size() + nums1.size() - x - k;\n if (upperBound1 > nums1.size() - 1) upperBound1 = nums1.size() - 1;\n if (upperBound2 > nums2.size() - 1) upperBound2 = nums2.size() - 1;\n for (int i = x; i <= upperBound1; ++ i) if (nums1[i] > nums1[idx1]) idx1 = i;\n for (int i = y; i <= upperBound2; ++ i) if (nums2[i] > nums2[idx2]) idx2 = i;\n if (idx1 < nums1.size() && idx2 < nums2.size()) {\n if (nums1[idx1] >= nums2[idx2]) res = to_string(nums1[idx1]) + findMaxNum(nums1, nums2, k - 1, idx1 + 1, y, dp);\n if (nums1[idx1] <= nums2[idx2]) res = max(res, to_string(nums2[idx2]) + findMaxNum(nums1, nums2, k - 1, x, idx2 + 1, dp));\n } \n else if (idx1 < nums1.size()) res = to_string(nums1[idx1]) + findMaxNum(nums1, nums2, k - 1, idx1 + 1, y, dp);\n else if (idx2 < nums2.size()) res = to_string(nums2[idx2]) + findMaxNum(nums1, nums2, k - 1, x, idx2 + 1, dp);\n dp[x][y] = res;\n return res;\n\n }\n\n vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {\n vector<vector<string>> dp(nums1.size() + 1, vector<string>(nums2.size() + 1));\n string maxNum = findMaxNum(nums1, nums2, k, 0, 0, dp);\n vector<int> res;\n for (char c : maxNum) res.push_back(c - \'0\');\n return res;\n }\n};\n```\n**Please upvote if u like the solution :)**
| 1 | 0 |
['Dynamic Programming', 'Memoization', 'C++']
| 2 |
create-maximum-number
|
python 1 hard = 2 easy + 1 medium problems
|
python-1-hard-2-easy-1-medium-problems-b-yi8e
|
Intuition\n Describe your first thoughts on how to solve this problem. \nIf there is only one array, how to solve it, use monotonic stack.\nIf we can find subar
|
jasondecode
|
NORMAL
|
2022-11-30T12:24:14.571094+00:00
|
2022-11-30T12:24:14.571118+00:00
| 303 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIf there is only one array, how to solve it, use monotonic stack.\nIf we can find subarray in nums1 and nums2, then merge them.\nThe ans is all combinations of the merge\n# Approach\n<!-- Describe your approach to solving the problem. -->\nmonotonic stack is a medium problem\nmerge is an easy one\nfind combination should be an easy problem.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\nk* O(n^2)\n\nmonotonic stack is O(n)\nmerge is O(n)\nk loops\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n# Code\n```\nclass Solution:\n def maxNumber(self, nums1: List[int], nums2: List[int], k: int) -> List[int]:\n def getMaxOrder(nums, n, total, res): # monotonic stack\n for i, v in enumerate(nums):\n while res and len(res) + total - i > n and res[-1] < v:\n res.pop()\n if len(res) < n:\n res.append(nums[i])\n return res\n\n def merge(nums1, nums2, ans): # check lexicographically greater\n while nums1 or nums2:\n if nums1 > nums2:\n ans.append(nums1[0])\n nums1 = nums1[1:]\n else:\n ans.append(nums2[0])\n nums2 = nums2[1:]\n return ans\n\n n1, n2 = len(nums1), len(nums2)\n res = []\n for i in range(max(0, k - n2), min(k, n1) + 1): # find all combinations of nums1 and nums2\n ans = merge(getMaxOrder(nums1, i, n1, []), getMaxOrder(nums2, k - i, n2, []), [])\n res = max(ans, res)\n return res\n```
| 1 | 0 |
['Python3']
| 1 |
create-maximum-number
|
Java | Convert to string for easy comparison | Greedy
|
java-convert-to-string-for-easy-comparis-bjox
|
The merge operation is tricky because, say, we have the following 2 sequences\n\n0, 1, 8 ,5 (A)\n0, 1, 8 ,4 (B)\n\nIf both pointers are at 0, should we pick A o
|
Student2091
|
NORMAL
|
2022-07-04T20:13:29.762933+00:00
|
2022-07-04T20:13:29.762964+00:00
| 526 | false |
The merge operation is tricky because, say, we have the following 2 sequences\n```\n0, 1, 8 ,5 (A)\n0, 1, 8 ,4 (B)\n```\nIf both pointers are at 0, should we pick `A` or `B`? \nWe should pick `A` as the resulting sequence would be `0,1,8,5,0,1,8,4`\nWe can either advance both pointers and determine which to pick until they differ or meet the end, \nor we can just convert it to string and use `compareTo()`\n\n```Java\nclass Solution {\n public int[] maxNumber(int[] nums1, int[] nums2, int k) {\n String ans="";\n for (int i = Math.max(0, k-nums2.length); i <= Math.min(nums1.length, k); i++){ // try all possible lengths from each seq\n String one = solve(nums1, i); // find the best seq matching len of i\n String two = solve(nums2, k-i); // len of k-i\n StringBuilder sb = new StringBuilder();\n int a = 0, b = 0;\n while(a < i || b < k-i){ // merge it to the max\n sb.append(one.substring(a).compareTo(two.substring(b))>=0?one.charAt(a++):two.charAt(b++));\n }\n if (sb.toString().compareTo(ans)>0){ // if better, we replace.\n ans=sb.toString();\n }\n }\n int[] res = new int[k];\n for (int i = 0; i < k;++i){\n res[i]=ans.charAt(i)-\'0\';\n }\n return res;\n }\n\n private String solve(int[] arr, int k){\n Deque<Integer> stack = new ArrayDeque<>();\n for (int i = 0;i<arr.length;++i){\n while(!stack.isEmpty()&&arr.length-i+stack.size()>k&&stack.peek()<arr[i]){\n stack.pop();\n }\n stack.push(arr[i]);\n }\n StringBuilder sb = new StringBuilder();\n for (int i = 0; i < k;i++){\n sb.append(stack.pollLast());\n }\n return sb.toString();\n }\n}\n```
| 1 | 1 |
['Java']
| 1 |
create-maximum-number
|
C++ || BFS + HASH || T/S O((n1+n2)*k), 98.67% Fast, 89.12% Space || Notes
|
c-bfs-hash-ts-on1n2k-9867-fast-8912-spac-h6oo
|
\nclass Solution {\npublic:\n vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {\n vector<int> ans(k,0);\n\n int n1 = nums1
|
aholtzman
|
NORMAL
|
2022-06-27T16:19:14.576735+00:00
|
2022-06-28T18:40:41.584514+00:00
| 315 | false |
```\nclass Solution {\npublic:\n vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {\n vector<int> ans(k,0);\n\n int n1 = nums1.size();\n int n2 = nums2.size();\n vector<vector<int>> ind1(n1+1); // direct pointer for each digit for every ix\n vector<vector<int>> ind2(n2+1); // direct pointer for each digit for every ix\n vector<int> il(10,n1);\n ind1[n1] = il;\n int i;\n for(i=n1-1; i>=0; i--) \n { // Starting from the end, update the index for the next for each digit\n il[nums1[i]]=i;\n ind1[i] = il;\n }\n vector<int> ik(10,n2);\n ind2[n2] = ik;\n for(i=n2-1; i>=0; i--) \n { // Starting from the end, update the index for the next for each digit\n ik[nums2[i]]=i;\n ind2[i]=ik;\n }\n int ix = 0;\n queue<pair<int,int>> q1; // Double queues system to implement BFS\n queue<pair<int,int>> q2;\n queue<pair<int,int>> &q = q1; // Current queue\n queue<pair<int,int>> &q_next = q2; // Next queue\n q.push({0,0});\n\t\tunordered_map<int,int> hash; // Hash to avoid duplication\n while (ix < k)\n {\n while(!q.empty())\n {\n int ix1 = q.front().first;\n int ix2 = q.front().second;\n q.pop();\n if (hash.count(ix1*512+ix2)) continue; // Avoid duplication\n hash[ix1*512+ix2]++;\n for(int d = 9; d>=ans[ix]; d--)\n { // Checking the availebility from high to low (the current highest for this ix)\n int i =ind1[ix1][d];\n if (i<n1 && n1+n2-ix2-i>=k-ix) \n {\n // cout << d << ", " << i << endl;\n if (ans[ix] < d) \n { // if better than prev (same ix) clear prev\n while(!q_next.empty()) q_next.pop();\n ans[ix] = d;\n }\n q_next.push({i+1,ix2}); // add curent combination\n break;\n }\n }\n for(int d = 9; d>=ans[ix]; d--) \n { // Checking the availebility from high to low (the current highest for this ix)\n int i =ind2[ix2][d]; // Update the ix for next d (n2 means no next available)\n \n if (i<n2 && n1+n2-ix1-i>=k-ix) // Check if this ix allow leave enough digit to get to length k\n { // Yes - \n // cout << d << ",," << i << endl;\n if (ans[ix] < d) // Check if new max for this ix. \n { // If new max arase acumulated combination of the old max\n while(!q_next.empty()) q_next.pop();\n ans[ix] = d; // Save new max\n }\n q_next.push({ix1,i+1}); //\xA0Push current combination\n break;\n }\n }\n }\n swap(q,q_next); // prepare next queue (next become current)\n ix++;\n }\n return ans; \n }\n};\n\n```\n// Simple\n```\nclass Solution {\npublic:\n vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {\n vector<int> ans(k,0);\n\n int n1 = nums1.size();\n int n2 = nums2.size();\n vector<vector<int>> d1(10);\n vector<vector<int>> d2(10);\n for(int i=0; i<n1; i++) d1[nums1[i]].push_back(i);\n for(int i=0; i<n2; i++) d2[nums2[i]].push_back(i);\n int ix1[10]={0};\n int ix2[10]={0};\n int ix = 0;\n queue<pair<int,int>> q1;\n queue<pair<int,int>> q2;\n queue<pair<int,int>> &q = q1;\n queue<pair<int,int>> &q_next = q2;\n q.push({0,0});\n unordered_map<int,int> hash;\n while (ix < k)\n {\n while(!q.empty())\n {\n int ix1 = q.front().first;\n int ix2 = q.front().second;\n q.pop();\n if (hash.count(ix1*512+ix2)) continue; // Avoid duplication\n hash[ix1*512+ix2]++;\n for(int d = 9; d>=ans[ix]; d--)\n {\n int i;\n for (i=0; i<d1[d].size(); i++) \n {\n if (d1[d][i] < ix1) continue;\n if (n1+n2-ix2-d1[d][i]>=k-ix) break; // find largest available\n }\n if (i<d1[d].size()) \n {\n if (ans[ix] < d) \n { // if better than prev (same ix) clear prev\n while(!q_next.empty()) q_next.pop();\n ans[ix] = d;\n }\n q_next.push({d1[d][i]+1,ix2}); // add curent combination\n break;\n }\n }\n for(int d = 9; d>=ans[ix]; d--) \n {\n int i;\n for (i=0; i<d2[d].size(); i++) \n {\n if (d2[d][i] < ix2)continue;\n if (n1+n2-ix1-d2[d][i]>=k-ix) break;\n }\n if (i<d2[d].size()) \n { \n if (ans[ix] < d) \n {\n while(!q_next.empty()) q_next.pop();\n ans[ix] = d;\n }\n q_next.push({ix1,d2[d][i]+1});\n break;\n }\n }\n }\n swap(q,q_next); // prepare next queue\n ix++;\n }\n return ans;\n }\n};\n\n/*\n[3,4,6,5]\n[9,1,2,5,8,3]\n5\n\n[6,7]\n[6,0,4]\n5\n*/\n```
| 1 | 0 |
[]
| 0 |
create-maximum-number
|
Python 98% faster | Greedy + DP + Segment Tree for Range Query
|
python-98-faster-greedy-dp-segment-tree-mwgs9
|
\n\n\nfrom typing import List\nfrom collections import defaultdict\n\n\nclass Node(object):\n def __init__(self, beg, end):\n self.beg = beg\n
|
756143229
|
NORMAL
|
2022-06-07T15:14:21.042806+00:00
|
2022-06-07T15:15:13.949803+00:00
| 519 | false |
\n\n```\nfrom typing import List\nfrom collections import defaultdict\n\n\nclass Node(object):\n def __init__(self, beg, end):\n self.beg = beg\n self.end = end\n self.range_max = None\n self.left = None\n self.right = None\n\n def is_leaf(self):\n return self.beg == self.end\n\n def __repr__(self):\n if self.is_leaf():\n return f"{self.beg}: {self.range_max}"\n else:\n return f"{self.beg}~{self.end}: {self.range_max}"\n\n def query(self, beg, end):\n # Totally out of range\n if beg > self.end or end < self.beg:\n return float("-inf"), -1\n\n # Query range contains node range\n elif self.beg >= beg and self.end <= end:\n return self.range_max\n\n # Intersection\n else:\n return max(self.left.query(beg, end), self.right.query(beg, end))\n\n\ndef build_range_tree(a, beg, end):\n node = Node(beg, end)\n if beg == end:\n node.range_max = (a[beg], -beg)\n else:\n mid = (beg + end) // 2\n node.left = build_range_tree(a, beg, mid)\n node.right = build_range_tree(a, mid + 1, end)\n node.range_max = max(node.left.range_max, node.right.range_max)\n\n return node\n\n\ndef comp_array(a, b, beg_a, beg_b):\n for i, j in zip(range(beg_a, len(a)), range(beg_b, len(b))):\n if a[i] > b[j]:\n return 1\n elif a[i] < b[j]:\n return -1\n\n if len(a) - beg_a > len(b) - beg_b:\n return 1\n elif len(a) - beg_a < len(b) - beg_b:\n return -1\n else:\n return 0\n\n\ndef merge_2_arrays(a, b, beg_a, beg_b):\n ptr1 = beg_a\n ptr2 = beg_b\n\n while True:\n if ptr1 == len(a) or ptr2 == len(b):\n break\n comp_res = comp_array(a, b, ptr1, ptr2)\n if comp_res == 1:\n yield a[ptr1]\n ptr1 += 1\n else:\n yield b[ptr2]\n ptr2 += 1\n\n for i in range(ptr1, len(a)):\n yield a[i]\n\n for i in range(ptr2, len(b)):\n yield b[i]\n\n\ndef pick_k_numbers(a, tree_a, beg_a, k):\n if k == 0:\n return []\n len_a = len(a) - beg_a\n num_elements_to_drop = len_a - k\n if num_elements_to_drop == 0:\n return a[beg_a:]\n\n end_a = min(beg_a + num_elements_to_drop, len(a) - 1)\n\n max_val, max_idx = tree_a.query(beg_a, end_a)\n max_idx = -max_idx\n\n return [a[max_idx]] + pick_k_numbers(a, tree_a, max_idx + 1, k - 1)\n\n\ndef fetch_dp_table(a, b, tree_a, tree_b, beg_a, beg_b, k, dp_table):\n\n if k == 0:\n return []\n\n if (beg_a, beg_b, k) not in dp_table:\n\n len_a = len(a) - beg_a\n len_b = len(b) - beg_b\n\n num_elements_to_drop = len_a + len_b - k\n\n if num_elements_to_drop == 0:\n res = list(merge_2_arrays(a, b, beg_a, beg_b))\n\n elif len_b == 0:\n res = pick_k_numbers(a, tree_a, beg_a, k)\n\n elif len_a == 0:\n res = pick_k_numbers(b, tree_b, beg_b, k)\n\n else:\n end_a = min(beg_a + num_elements_to_drop, len(a) - 1)\n end_b = min(beg_b + num_elements_to_drop, len(b) - 1)\n\n max_val_a, max_idx_a = (\n tree_a.query(beg_a, end_a) if len_a > 0 else (float("-inf"), -1)\n )\n max_idx_a = -max_idx_a\n\n max_val_b, max_idx_b = (\n tree_b.query(beg_b, end_b) if len_b > 0 else (float("-inf"), -1)\n )\n max_idx_b = -max_idx_b\n\n if max_val_a > max_val_b:\n next_vals = fetch_dp_table(\n a, b, tree_a, tree_b, max_idx_a + 1, beg_b, k - 1, dp_table\n )\n res = [max_val_a] + next_vals\n elif max_val_b > max_val_a:\n next_vals = fetch_dp_table(\n a, b, tree_a, tree_b, beg_a, max_idx_b + 1, k - 1, dp_table\n )\n res = [max_val_b] + next_vals\n else:\n vala = fetch_dp_table(\n a, b, tree_a, tree_b, max_idx_a + 1, beg_b, k - 1, dp_table\n )\n valb = fetch_dp_table(\n a, b, tree_a, tree_b, beg_a, max_idx_b + 1, k - 1, dp_table\n )\n res = [max_val_a] + max(vala, valb)\n\n dp_table[(beg_a, beg_b, k)] = res\n else:\n pass\n\n return dp_table[(beg_a, beg_b, k)]\n\n\nclass Solution:\n def maxNumber(self, nums1: List[int], nums2: List[int], k: int) -> List[int]:\n tree_1 = build_range_tree(nums1, 0, len(nums1) - 1)\n tree_2 = build_range_tree(nums2, 0, len(nums2) - 1)\n dp_table = {}\n res = fetch_dp_table(nums1, nums2, tree_1, tree_2, 0, 0, k, dp_table)\n return res\n\n\nif __name__ == "__main__":\n nums1 = [3,4,6,5]\n nums2 = [9,1,2,5,8,3]\n k = 5\n # res = Solution().maxNumber(nums1, nums2, k)\n # print(res)\n```\n
| 1 | 0 |
['Dynamic Programming', 'Python']
| 0 |
create-maximum-number
|
Python | Easy to understand | Greedy + Dynamic Programminng
|
python-easy-to-understand-greedy-dynamic-3709
|
To solve the problem, we can define the subproblem "getMaxNumberString(i, j, length)": get the max number string with "length" from index "i" in nums1 and index
|
adairclo
|
NORMAL
|
2022-06-03T08:20:27.324166+00:00
|
2022-06-03T08:20:27.324196+00:00
| 384 | false |
To solve the problem, we can define the subproblem "getMaxNumberString(i, j, length)": get the max number string with "length" from index "i" in nums1 and index "j" in nums2.\n\ngetMaxNumberString(i, j, length)\n- if nums1 has bigger digit, getMaxNumberString(i, j, length) = str(nums1[index1]) + getMaxNumberString(index1 + 1, j, length - 1)\n- if nums2 has bigger digit, getMaxNumberString(i, j, length) = str(nums2[index2]) + getMaxNumberString(i, index2 + 1, length - 1)\n- if nums1 and nums2 have the same big digit, getMaxNumberString(i, j, length) = max(str(nums1[index1]) + getMaxNumberString(index1 + 1, j, length - 1), str(nums2[index2]) + getMaxNumberString(i, index2 + 1, length - 1))\n\n```\nclass Solution:\n def maxNumber(self, nums1: List[int], nums2: List[int], k: int) -> List[int]:\n m = len(nums1)\n n = len(nums2)\n dp = {}\n \n # get the max number string with "length" from index "i" in nums1 and index "j" in nums2\n # using number string to easy to compare\n def getMaxNumberString(i, j, length):\n if length == 0:\n return ""\n \n # using memoization to optimize for the overlapping subproblems\n key = (i, j, length)\n if key in dp:\n return dp[key]\n \n # greedy to find the possible max digit from nums1 and nums2\n # 1) bigger digit in the higher position of the number will get bigger number\n # 2) at the same time, we need to ensure that we still have enough digits to form a number with "length" digits\n \n # try to find the possible max digit from index i in nums1\n index1 = None\n for ii in range(i, m):\n if (m - ii + n - j) < length:\n break\n if index1 is None or nums1[index1] < nums1[ii]:\n index1 = ii\n \n # try to find the possible max digit from index j in nums2\n index2 = None\n for jj in range(j, n):\n if (m - i + n - jj) < length:\n break\n if index2 is None or nums2[index2] < nums2[jj]:\n index2 = jj\n \n maxNumberStr = None\n if index1 is not None and index2 is not None:\n if nums1[index1] > nums2[index2]:\n maxNumberStr = str(nums1[index1]) + getMaxNumberString(index1 + 1, j, length - 1)\n elif nums1[index1] < nums2[index2]:\n maxNumberStr = str(nums2[index2]) + getMaxNumberString(i, index2 + 1, length - 1)\n else:\n # get the same digit from nums1 and nums2, so need to try two cases and get the max one \n maxNumberStr = max(str(nums1[index1]) + getMaxNumberString(index1 + 1, j, length - 1), str(nums2[index2]) + getMaxNumberString(i, index2 + 1, length - 1))\n elif index1 is not None:\n maxNumberStr = str(nums1[index1]) + getMaxNumberString(index1 + 1, j, length - 1)\n elif index2 is not None:\n maxNumberStr = str(nums2[index2]) + getMaxNumberString(i, index2 + 1, length - 1)\n \n dp[key] = maxNumberStr\n return maxNumberStr\n\n result_str = getMaxNumberString(0, 0, k)\n \n # number string to digit array\n result = []\n for c in result_str:\n result.append(int(c))\n \n return result\n```
| 1 | 0 |
['Dynamic Programming', 'Greedy', 'Python3']
| 0 |
create-maximum-number
|
Python3 | Monotonic Stack | Greedy
|
python3-monotonic-stack-greedy-by-showin-9rlp
|
\nclass Solution:\n def maxNumber(self, nums1: List[int], nums2: List[int], k: int) -> List[int]:\n \n def find_k_max_number_in_an_array(nums,
|
showing_up_each_day
|
NORMAL
|
2022-04-25T18:13:59.473636+00:00
|
2022-04-25T18:13:59.473680+00:00
| 638 | false |
```\nclass Solution:\n def maxNumber(self, nums1: List[int], nums2: List[int], k: int) -> List[int]:\n \n def find_k_max_number_in_an_array(nums, k):\n drop_possible = len(nums) - k\n n = len(nums)\n stack = []\n for i, val in enumerate(nums):\n while stack and drop_possible and stack[-1] < val:\n drop_possible -= 1\n stack.pop()\n \n stack.append(val)\n \n return stack[:k]\n \n \n def merge_two_array(arr1, arr2):\n #print(arr1, arr2)\n return [max(arr1, arr2).pop(0) for _ in arr1 + arr2]\n\n def compare_two_array(arr1, arr2):\n """\n determine whether arr1 is greater than arr2\n """\n if not arr2:\n return True\n i = j = 0\n n = len(arr1)\n while i < n and j < n:\n if arr1[i] > arr2[j]:\n return True\n elif arr1[i] < arr2[j]:\n return False\n i += 1\n j += 1\n \n return True\n \n ans = 0\n for i in range(k + 1):\n p = k - i\n \n if i > len(nums1) or p > len(nums2):\n continue\n \n # get this two array by solving function find_k_max_number_in_an_array\n # using similar concept of 402. Remove K Digits\n first_arr = find_k_max_number_in_an_array(nums1, i)\n second_arr = find_k_max_number_in_an_array(nums2, p)\n \n # merge two array with everytime taking lexicographily larger list\n # https://leetcode.com/problems/create-maximum-number/discuss/77286/Short-Python-Ruby-C%2B%2B\n # see explanation\n curr_arr = merge_two_array(first_arr, second_arr)\n #print(curr_arr)\n \n # can be directly use python max function\n if compare_two_array(curr_arr, ans):\n ans = curr_arr\n # ans = max(ans, curr_arr) if ans else curr_arr\n \n #print(ans)\n \n return ans\n\n```
| 1 | 0 |
['Monotonic Stack', 'Python', 'Python3']
| 0 |
create-maximum-number
|
C++ solution, well explained.
|
c-solution-well-explained-by-slicedkiwis-lx92
|
Explanation:\n\nIdea 1: the first thing that popped into my head was to use recursion, the initial idea was to select an initial number and in each call stack h
|
slicedkiwis
|
NORMAL
|
2022-04-01T07:01:39.602679+00:00
|
2022-05-05T04:24:03.715738+00:00
| 622 | false |
**Explanation:**\n\nIdea 1: the first thing that popped into my head was to use recursion, the initial idea was to select an initial number and in each call stack have three different paths to take.\n1. \tchoose a number from array one\n2. \tchoose a number from array two\n3. \tdon\'t choose a number and move along \n\t\t\t* \tThe problem with this approach is that it is both time and memory expensive\n\t\t\nIdea 2: a greedy approach where i would take the lexigraphically greatest portion of array one merge it with the lexigraphically greatest portion of array two and collapse the arrays into themselves to be of size k, this idea works but we have to be careful.\n\nAlgorithm explained:\n\t1. \tpartition both arrays into a sub array of k, where each array contains the maximum lexigraphical order it can hold.\n\t\tThe subarrays are partitioned as such, (k - i) where i <= k would get you the first half and i gets the other half of that k sized array.\n* \t\t auto first = findMax(nums1, k - i);\n* \t\t auto second = findMax(nums2, i);\n\t\n2. \tThen merge those two arrays ( k - i) and i into an array of size k , where the array of size K respects the rule of being in the greatest lexigraphical order it can hold.\n* \t\t while (nP < n && mP < m)\n {\n if(nums1[nP] == nums2[mP]){ \n int i = nP; \n int j = mP;\n \n while( i < n && j < m && nums1[i] == nums2[j]){\n i++;\n j++;\n } \n \n if(i == n)\n res.push_back(nums2[mP++]);\n \n else if ( j == m)\n res.push_back(nums1[nP++]);\n \n else if(nums1[i] > nums2[j])\n res.push_back(nums1[nP++]); \n \n else\n res.push_back(nums2[mP++]); \n \n continue; \n } \n if (nums1[nP] > nums2[mP])\n res.push_back(nums1[nP++]);\n else if(nums2[mP] > nums1[nP]) \n res.push_back(nums2[mP++]);\n }\n3. Lastly compare with our answer derived from previous iterations and update if needed.\n\t\t*`ans = compare(ans, tmp);`\n\n```\nclass Solution\n{\npublic:\n void print(vector<int> & res){\n for(int x : res)\n cout << x << " ";\n cout << endl;\n }\n \n vector<int> findMax(vector<int> &nums, int k)\n {\n vector<int> res;\n int n = nums.size();\n for (int i = 0; i < n; i++)\n {\n int m = res.size();\n while (m && res.back() < nums[i])\n {\n if (((n - i) + m - 1) >= k)\n {\n res.pop_back();\n m--;\n }\n else\n break;\n }\n if (m < k)\n {\n m++;\n res.push_back(nums[i]);\n }\n }\n return res;\n }\n\n vector<int> compare(vector<int> &nums1, vector<int> &nums2)\n {\n int n = nums1.size();\n int m = nums2.size();\n if (n > m)\n return nums1;\n if (m > n)\n return nums2;\n for (int i = 0; i < n; i++)\n {\n if (nums1[i] > nums2[i])\n return nums1;\n else if (nums1[i] < nums2[i])\n return nums2;\n }\n return nums1;\n }\n vector<int> merge(vector<int> &nums1, vector<int> &nums2)\n {\n vector<int> res;\n int n = nums1.size();\n int m = nums2.size();\n int nP = 0;\n int mP = 0;\n while (nP < n && mP < m)\n {\n if(nums1[nP] == nums2[mP]){ \n int i = nP; \n int j = mP;\n \n while( i < n && j < m && nums1[i] == nums2[j]){\n i++;\n j++;\n } \n \n if(i == n)\n res.push_back(nums2[mP++]);\n \n else if ( j == m)\n res.push_back(nums1[nP++]);\n \n else if(nums1[i] > nums2[j])\n res.push_back(nums1[nP++]); \n \n else\n res.push_back(nums2[mP++]); \n \n continue; \n } \n if (nums1[nP] > nums2[mP])\n res.push_back(nums1[nP++]);\n else if(nums2[mP] > nums1[nP]) \n res.push_back(nums2[mP++]);\n }\n while (nP < n)\n res.push_back(nums1[nP++]);\n while (mP < m)\n res.push_back(nums2[mP++]);\n return res;\n }\n \n vector<int> maxNumber(vector<int> &nums1, vector<int> &nums2, int k)\n {\n vector<int> ans;\n for (int i = 0; i < k; i++)\n {\n auto first = findMax(nums1, k - i);\n auto second = findMax(nums2, i);\n auto tmp = merge(first, second);\n ans = compare(ans, tmp);\n }\n return ans;\n }\n};\n```
| 1 | 0 |
['Greedy', 'C', 'C++']
| 0 |
create-maximum-number
|
Java Simple Solution || Monotonic Stack || Merge || All Combinations
|
java-simple-solution-monotonic-stack-mer-ebbf
|
class Solution {\n \n public int[] largeNum(int[] nums,int k){\n int n = nums.length;\n Stack stack = new Stack<>();\n for(int i = 0;
|
Omkar_Alase
|
NORMAL
|
2022-03-18T08:07:59.536848+00:00
|
2022-03-18T08:07:59.536885+00:00
| 347 | false |
class Solution {\n \n public int[] largeNum(int[] nums,int k){\n int n = nums.length;\n Stack<Integer> stack = new Stack<>();\n for(int i = 0;i < n;i++){\n \n while(stack.size() > 0 && stack.peek() < nums[i] && k - stack.size() <= n - i - 1){\n stack.pop();\n }\n \n stack.push(nums[i]);\n }\n \n int[] ans = new int[stack.size()];\n int ptr = stack.size() - 1;\n \n while(!stack.isEmpty()){\n ans[ptr--] = stack.pop();\n }\n return ans;\n }\n \n boolean isGreater(int[] max1,int[] max2,int i,int j){\n \n while(i < max1.length || j < max2.length){\n \n if(i >= max1.length) return false;\n else if(j >= max2.length) return true;\n else if(max1[i] < max2[j]) return false;\n else if(max1[i] > max2[j]) return true;\n else{\n i++;\n j++;\n }\n }\n \n return true;\n \n }\n \n \n \n public int[] maxNumber(int[] nums1, int[] nums2, int k) {\n \n int[] ans = new int[k];\n \n for(int i = 0;i <= k;i++){\n \n if(i > nums1.length || k - i > nums2.length) continue;\n \n int[] max1 = largeNum(nums1,i);\n int[] max2 = largeNum(nums2,k - i);\n \n //merge\n int a = 0;\n int b = 0;\n int[] temp = new int[k];\n int ptr = 0;\n while(a < max1.length || b < max2.length){\n if(ptr >= k){\n break;\n }\n if(a >= max1.length) temp[ptr++] = max2[b++];\n else if(b >= max2.length) temp[ptr++] = max1[a++];\n else if(max1[a] < max2[b]) temp[ptr++] = max2[b++];\n else if(max1[a] > max2[b]) temp[ptr++] = max1[a++];\n else{\n if(isGreater(max1,max2,a,b)){\n temp[ptr++] = max1[a++];\n }\n else{\n temp[ptr++] = max2[b++];\n }\n }\n }\n // for(int j = 0;j < k;j++){\n // System.out.print(temp[j] + " ");\n // }\n //System.out.println();\n if(isGreater(temp,ans,0,0)){\n System.out.print("In");\n ans = temp;\n }\n \n }\n \n return ans;\n }\n}
| 1 | 0 |
['Monotonic Stack']
| 0 |
create-maximum-number
|
javascript greedy
|
javascript-greedy-by-henrychen222-at0v
|
\nconst maxNumber = (a, b, k) => {\n let m = a.length, n = b.length;\n let res = [];\n for (let i = Math.max(0, k - n); i <= Math.min(k, m); i++) {\n
|
henrychen222
|
NORMAL
|
2022-02-15T23:25:30.953214+00:00
|
2022-02-15T23:25:30.953263+00:00
| 318 | false |
```\nconst maxNumber = (a, b, k) => {\n let m = a.length, n = b.length;\n let res = [];\n for (let i = Math.max(0, k - n); i <= Math.min(k, m); i++) {\n let maxA = maxArray(a, i), maxB = maxArray(b, k - i);\n let merge = mergeArray(maxA, maxB);\n if (merge > res) res = merge;\n }\n return res;\n};\n\nconst maxArray = (a, k) => {\n let drop = a.length - k, res = [];\n for (const x of a) {\n while (drop > 0 && res.length && res[res.length - 1] < x) {\n res.pop();\n drop--;\n }\n res.push(x);\n }\n if (res.length >= k) {\n res = res.slice(0, k);\n } else {\n res = res.concat(Array(k - res.length).fill(0));\n }\n return res;\n};\n\nconst mergeArray = (a, b) => {\n let res = [];\n while (a.length + b.length) res.push(a > b ? a.shift() : b.shift())\n return res;\n};\n```
| 1 | 0 |
['Greedy', 'JavaScript']
| 0 |
create-maximum-number
|
Create Maximum Number
|
create-maximum-number-by-325803176-8z2p
|
c++solution\ntime and space surpass 90%+\n\n#include<bits/stdc++.h>\nusing namespace std;\n// #define DEBUG\nclass Solution {\npublic:\n vector<int> maxNumber(
|
325803176
|
NORMAL
|
2022-02-01T08:45:28.072604+00:00
|
2022-02-01T08:45:28.072636+00:00
| 242 | false |
c++solution\ntime and space surpass 90%+\n```\n#include<bits/stdc++.h>\nusing namespace std;\n// #define DEBUG\nclass Solution {\npublic:\n vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {\n int m = nums1.size(), n = nums2.size();\n int *ret = NULL;\n if(m > n) {\n return maxNumber(nums2, nums1, k);\n }\n // make sure that m is smaller than or equal to m\n int begin = max(0, k-n);\n int end = min(m, k);\n for(int i = begin; i <= end; i++) {\n int *maxSub1 = maxSubsequence(nums1, i);\n int *maxSub2 = maxSubsequence(nums2, k - i);\n #ifdef DEBUG\n cout << i << "---------------------------\\n";\n dump(maxSub1, i);\n dump(maxSub2, k-i);\n cout << "-------------------------\\n";\n #endif\n int *maxSub = merge(maxSub1, i, maxSub2, k-i);\n ret = comapreAndSwap(ret, maxSub, k);\n }\n return vector<int>(ret, ret + k);\n }\n void dump(int *sub, int size) {\n for(int i = 0; i < size; i++) {\n cout << sub[i] << " ";\n }\n cout << endl;\n return;\n }\n int *maxSubsequence(vector<int> &nums, int k) {\n int n = nums.size();\n int discard = n-k;\n int *ret = (int *)malloc(k * sizeof(int));\n int top = 0;\n for(auto i : nums) {\n while(top > 0 && ret[top-1] < i && discard > 0) {\n discard--;\n top--;\n }\n\n if(top < k) {\n ret[top++] = i;\n }else{\n discard--;\n }\n }\n return ret;\n }\n\n int *merge(int *sub1, int size1, int *sub2, int size2) {\n int idx1 = 0, idx2 = 0;\n int *ret = (int *)malloc((size1 + size2) * sizeof(int));\n for(int i = 0; i < size1 + size2; i++) {\n if(compare(sub1, size1, idx1, sub2, size2, idx2)) {\n ret[i] = sub1[idx1++];\n }else{\n ret[i] = sub2[idx2++];\n }\n }\n free(sub1);\n free(sub2);\n return ret;\n }\n\n int *comapreAndSwap(int *ret, int *sub, int k) {\n if(compare(ret, k, 0, sub, k, 0)) {\n free(sub);\n return ret;\n }else{\n free(ret);\n return sub;\n }\n }\n\n int compare(int *sub1, int size1, int idx1, int *sub2, int size2, int idx2) {\n if(size1 == idx1 || sub1 == NULL) {\n return 0;\n }else if(size2 == idx2) {\n return 1;\n }\n\n if(sub1[idx1] > sub2[idx2]) {\n return 1;\n }else if(sub1[idx1] < sub2[idx2]){\n return 0;\n }else{\n return compare(sub1, size1, idx1+1, sub2, size2, idx2+1);\n }\n }\n};\n\n```
| 1 | 0 |
[]
| 0 |
create-maximum-number
|
Merger of NearestGreaterElement and Lexicographical
|
merger-of-nearestgreaterelement-and-lexi-27xd
|
Do below problems before attempt this problem\n\nhttps://leetcode.com/problems/remove-k-digits/\nhttps://leetcode.com/problems/next-greater-element-ii/\nhttps:/
|
P_Khandal
|
NORMAL
|
2022-01-31T06:17:27.091438+00:00
|
2022-02-25T07:27:50.248491+00:00
| 237 | false |
**Do below problems before attempt this problem**\n\nhttps://leetcode.com/problems/remove-k-digits/\nhttps://leetcode.com/problems/next-greater-element-ii/\nhttps://leetcode.com/problems/remove-duplicate-letters/\n\n\tclass Solution {\n\t\tpublic:\n\n\n\t\t vector<int> maxNumber(vector<int> &nums1, vector<int> &nums2, int k)\n\t\t\t{\n\t\t\t\tvector<int> ans;\n\t\t\t\tfor (int i = 0; i <=k; i++)\n\t\t\t\t{\n\t\t\t\t\tint j = k - i;\n\t\t\t\t\t\n\t\t\t\t\tif(i>nums1.size()||j>nums2.size()) continue;\n\n\t\t\t\t\tvector<int> n1 = calculateNGEType(nums1, i);\n\t\t\t\t\tvector<int> n2 = calculateNGEType(nums2, j);\n\t\t\t\t\tvector<int> t = merge(n1, n2,k);\n\t\t\t\t\tif(t>ans)ans=t;\n\n\t\t\t\t}\n\n\t\t\t\treturn ans;\n\t\t\t}\n\n\n\t\t\tbool greater(vector<int> n1, vector<int> n2,int i,int j){\n\t\t\t\tint ns1 = n1.size();\n\t\t\t\tint ns2 = n2.size();\n\t\t\t\twhile (i < ns1 || j < ns2)\n\t\t\t\t{\n\t\t\t\t\tif (i >= ns1)\n\t\t\t\t\t\treturn false;\n\t\t\t\t\telse if (j >= ns2)\n\t\t\t\t\t\treturn true;\n\t\t\t\t\telse if (n1[i] > n2[j])\n\t\t\t\t\t\treturn true;\n\t\t\t\t\telse if (n1[i] < n2[j])\n\t\t\t\t\t\treturn false;\n\t\t\t\t\telse\n\t\t\t\t\t{\n\t\t\t\t\t\ti++,j++;\n\t\t\t\t\t}\n\t\t\t\t}\n\t\t\t\treturn true;\n\t\t\t}\n\n\t\t\tvector<int> merge(vector<int> n1, vector<int> n2,int k)\n\t\t\t{\n\t\t\t\tint ns1 = n1.size();\n\t\t\t\tint ns2 = n2.size();\n\t\t\t\tint i = 0, j = 0, l = 0;\n\t\t\t\tvector<int> ans;\n\t\t\t\twhile ((i < ns1 || j < ns2)&&k>0 )\n\t\t\t\t{\n\t\t\t\t\tif (i >= ns1)\n\t\t\t\t\t\tans.push_back(n2[j++]);\n\t\t\t\t\telse if (j >= ns2)\n\t\t\t\t\t\tans.push_back(n1[i++]);\n\t\t\t\t\telse if (n1[i] > n2[j])\n\t\t\t\t\t\tans.push_back(n1[i++]);\n\t\t\t\t\telse if (n1[i] < n2[j])\n\t\t\t\t\t\tans.push_back(n2[j++]);\n\t\t\t\t\telse \n\t\t\t\t\t{\n\t\t\t\t\t\tif(greater(n1,n2,i,j))\n\t\t\t\t\t\t\tans.push_back(n1[i++]);\n\t\t\t\t\t\telse\n\t\t\t\t\t\t\tans.push_back(n2[j++]);\n\t\t\t\t\t}\n\t\t\t\t\tk--;\n\t\t\t\t}\n\t\t\t\treturn ans;\n\t\t\t}\n\n\t\t\tvector<int> calculateNGEType(vector<int> &nums1, int k)\n\t\t\t{\n\t\t\t\tint removal = nums1.size() - k;\n\t\t\t\tvector<int> n1;\n\n\t\t\t\tfor (int i = 0; i < nums1.size(); i++)\n\t\t\t\t{\n\t\t\t\t\twhile (n1.size() > 0 && removal > 0 && n1.back() < nums1[i])\n\t\t\t\t\t{\n\t\t\t\t\t\tremoval--;\n\t\t\t\t\t\tn1.pop_back();\n\t\t\t\t\t}\n\t\t\t\t\tn1.push_back(nums1[i]);\n\t\t\t\t}\n\n\t\t\t\treturn n1;\n\t\t\t}\n\n\n\t\t};
| 1 | 0 |
['Stack', 'Greedy']
| 1 |
create-maximum-number
|
C# Recursion + Memo
|
c-recursion-memo-by-olegbelousov77-5el6
|
cs\npublic class Solution {\n\n public int[] MaxNumber(int[] nums1, int[] nums2, int k) {\n var lst = MaxNumber(GetMap(nums1), GetMap(nums2), nums1.Le
|
olegbelousov77
|
NORMAL
|
2021-11-30T16:43:15.769959+00:00
|
2021-11-30T16:43:15.770001+00:00
| 372 | false |
```cs\npublic class Solution {\n\n public int[] MaxNumber(int[] nums1, int[] nums2, int k) {\n var lst = MaxNumber(GetMap(nums1), GetMap(nums2), nums1.Length + nums2.Length, 0, 0, k); lst.Reverse();\n return lst.ToArray();\n }\n \n \n private IDictionary<(int,int,int),List<int>> memo = new Dictionary<(int,int,int),List<int>>();\n \n private List<int> MaxNumber(IReadOnlyDictionary<int,List<int>> map1, IReadOnlyDictionary<int,List<int>> map2, int count, int pos1, int pos2, int k) {\n \n if (k == 0)\n return new List<int>();\n \n var key = (pos1,pos2,k);\n if (memo.TryGetValue(key, out List<int> m))\n return new List<int>(m);\n \n var has1 = TryGetValue(map1, pos1, count - pos2 - k, out int val1, out int next1);\n var has2 = TryGetValue(map2, pos2, count - pos1 - k, out int val2, out int next2);\n \n if (!has1 || has2 && val2 > val1) {\n var list = MaxNumber(map1, map2, count, pos1, next2 + 1, k - 1); list.Add(val2);\n memo[key] = new List<int>(list);\n return list;\n }\n \n if (!has2 || has1 && val1 > val2) {\n var list = MaxNumber(map1, map2, count, next1 + 1, pos2, k - 1); list.Add(val1);\n memo[key] = new List<int>(list);\n return list;\n }\n \n var list1 = MaxNumber(map1, map2, count, next1 + 1, pos2, k - 1);\n var list2 = MaxNumber(map1, map2, count, pos1, next2 + 1, k - 1);\n \n var lst = IsLess(list1, list2) ? list2 : list1; lst.Add(val1);\n memo[key] = new List<int>(lst);\n return lst;\n }\n \n private IReadOnlyDictionary<int,List<int>> GetMap(int[] nums) {\n var dic = Enumerable.Range(0, 10).ToDictionary(i => i, i => new List<int>());\n for(var i = 0; i < nums.Length; i++)\n dic[nums[i]].Add(i);\n return dic;\n }\n \n private bool TryGetValue(IReadOnlyDictionary<int,List<int>> map, int from, int to, out int value, out int pos) {\n for(value = 9; value >= 0; value--) {\n var idx = map[value].BinarySearch(from);\n if (idx < 0)\n idx = ~idx;\n if (idx >= map[value].Count)\n continue;\n if (map[value][idx] > to)\n continue;\n pos = map[value][idx];\n return true;\n }\n pos = -1;\n return false;\n }\n \n private bool IsLess(List<int> lst1, List<int> lst2) {\n for(var i = lst1.Count - 1; i >= 0; i--) {\n if (lst1[i] < lst2[i])\n return true;\n if (lst1[i] > lst2[i])\n return false;\n }\n return false;\n }\n}\n```
| 1 | 0 |
['Recursion', 'Memoization', 'C#']
| 0 |
create-maximum-number
|
(C++) 321. Create Maximum Number
|
c-321-create-maximum-number-by-qeetcode-f8xl
|
\n\nclass Solution {\npublic:\n vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {\n vector<int> ans(k); \n \n auto
|
qeetcode
|
NORMAL
|
2021-09-16T18:30:11.523194+00:00
|
2021-09-16T18:30:11.523241+00:00
| 794 | false |
\n```\nclass Solution {\npublic:\n vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {\n vector<int> ans(k); \n \n auto fn = [](vector<int>& arr, int k) {\n vector<int> ans(k); \n for (int i = 0, n = 0; i < arr.size(); ++i) {\n while (n && ans[n-1] < arr[i] && n + arr.size() - i > k) --n; \n if (n < k) ans[n++] = arr[i]; \n }\n return ans; \n };\n \n auto cmp = [](vector<int>& val1, int i1, vector<int>& val2, int i2) {\n for (; i1 < val1.size() && i2 < val2.size(); i1++, i2++) {\n if (val1[i1] > val2[i2]) return true; \n if (val1[i1] < val2[i2]) return false; \n }\n return i2 == val2.size(); \n };\n \n for (int i = 0; i <= k; ++i) {\n if (i <= nums1.size() && k-i <= nums2.size()) {\n vector<int> val1 = fn(nums1, i), val2 = fn(nums2, k - i); \n vector<int> cand; \n for (int i1 = 0, i2 = 0; i1 < val1.size() || i2 < val2.size(); ) \n if (cmp(val1, i1, val2, i2)) cand.push_back(val1[i1++]);\n else cand.push_back(val2[i2++]); \n ans = max(ans, cand); \n }\n }\n return ans; \n }\n};\n```
| 1 | 0 |
['C']
| 0 |
create-maximum-number
|
c++ concise solution
|
c-concise-solution-by-anhongleetcode-nw4o
|
code comments itself.\n\ncpp\nclass Solution {\npublic:\n std::deque<int> getMax(const std::vector<int> &nums, int k)\n {\n if(k == 0){\n
|
anhongleetcode
|
NORMAL
|
2021-08-15T01:53:11.112134+00:00
|
2021-08-15T01:53:11.112167+00:00
| 421 | false |
code comments itself.\n\n```cpp\nclass Solution {\npublic:\n std::deque<int> getMax(const std::vector<int> &nums, int k)\n {\n if(k == 0){\n return {};\n }\n \n std::deque<int> result;\n const int drop = std::max<int>(0, nums.size() - k);\n\n for(int d = 0; const auto e: nums){\n while(!result.empty() && result.back() < e && d < drop){\n result.pop_back();\n d++;\n }\n result.push_back(e);\n }\n \n while(result.size() > k){\n result.resize(k);\n }\n return result;\n }\n \n std::vector<int> merge(std::deque<int> p, std::deque<int> q)\n {\n std::vector<int> result;\n while(!(p.empty() && q.empty())){\n if(p > q){\n result.push_back(p.front());\n p.pop_front();\n }\n else{\n result.push_back(q.front());\n q.pop_front();\n }\n }\n return result;\n }\n \n vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k)\n {\n std::vector<int> result;\n for(int i = 0; i <= k && i <= nums1.size(); ++i){\n if(int j = k - i; j <= nums2.size()){\n result = std::max(result, merge(getMax(nums1, i), getMax(nums2, j)));\n }\n }\n return result;\n }\n};\n```
| 1 | 0 |
[]
| 0 |
create-maximum-number
|
Concise commented DP+Greedy Soln
|
concise-commented-dpgreedy-soln-by-coder-en9y
|
\nclass Solution {\npublic:\n vector single_array(vector& arr1,int k)\n {\n int n = arr1.size();\n vector> dp(min(n,k),vector(n,""));//i+1 d
|
coder2765
|
NORMAL
|
2021-08-06T14:39:25.198761+00:00
|
2021-08-06T14:39:25.198792+00:00
| 239 | false |
\nclass Solution {\npublic:\n vector<string> single_array(vector<int>& arr1,int k)\n {\n int n = arr1.size();\n vector<vector<string>> dp(min(n,k),vector<string>(n,""));//i+1 digits and ending at j maintaining ordering\n vector<string> dp1(min(n,k),""); //max i-digit number formed maintaing ordering\n \n for(int j=0;j<n;j++)\n {\n dp[0][j].push_back((char)(arr1[j]+\'0\'));\n dp1[0] = max(dp1[0],dp[0][j]);\n if(j>0) dp[0][j] = max(dp[0][j],dp[0][j-1]);\n }\n \n for(int i=1;i<dp1.size();i++)\n {\n // num of digits required is i+1\n // we start at i, not before that\n for(int j=i;j<n;j++)\n {\n dp[i][j] = max(dp[i][j],dp[i-1][j-1]+(char)(arr1[j]+\'0\'));\n dp1[i] = max(dp[i][j],dp1[i]);\n if(j>i) dp[i][j] = max(dp[i][j],dp[i][j-1]); \n // beware : max on strings works as expected when both strings are of same size\n }\n }\n return dp1;\n \n }\n \n string merge(string r1,string r2)\n {\n string fin = "";\n int n = r1.size();\n int m = r2.size();\n int p1 = 0;\n int p2 = 0;\n while(p1<n && p2<m)\n {\n if(r1[p1]>r2[p2])\n {\n fin.push_back(r1[p1]);\n p1++;\n }\n else if(r1[p1]<r2[p2])\n {\n fin.push_back(r2[p2]);\n p2++;\n }\n else\n {\n if(r1.substr(p1)>=r2.substr(p2))\n {\n fin.push_back(r1[p1]);\n p1++;\n }\n else\n {\n fin.push_back(r2[p2]);\n p2++;\n }\n }\n }\n while(p1<n) \n {\n fin.push_back(r1[p1]);p1++;\n }\n while(p2<m) \n {\n fin.push_back(r2[p2]);p2++;\n }\n return fin;\n }\n \n vector<int> maxNumber(vector<int>& arr1, vector<int>& arr2, int k) \n {\n vector<int> ans;\n int n = arr1.size();\n int m = arr2.size();\n if(n==0 && m==0) return ans;\n if(k==0) return ans;\n \n vector<string> dp1 = single_array(arr1,k);\n vector<string> dp2 = single_array(arr2,k);\n \n string an = "";\n for(int i=0;i<=k;i++)\n {\n int sz1 = i;\n int sz2 = k-i;\n if(sz1==0 && sz2<=m) an = max(an,dp2[sz2-1]);\n else if(sz2==0 && sz1<=n) an = max(an,dp1[sz1-1]);\n else if(sz1<=n && sz2<=m) an = max(an,merge(dp1[sz1-1],dp2[sz2-1]));\n }\n \n \n for(auto c:an) ans.push_back(c-\'0\');\n return ans;\n \n }\n};
| 1 | 0 |
[]
| 0 |
create-maximum-number
|
Brute Force || pretty straight forward || less comments for explanation
|
brute-force-pretty-straight-forward-less-itw3
|
\nclass Solution {\n public int[] maxNumber(int[] a, int[] b, int k) {\n int n = a.length;\n int m = b.length;\n \n int x[][] = n
|
harshitgoel1110
|
NORMAL
|
2020-12-17T19:16:26.017263+00:00
|
2020-12-17T19:16:26.017303+00:00
| 789 | false |
```\nclass Solution {\n public int[] maxNumber(int[] a, int[] b, int k) {\n int n = a.length;\n int m = b.length;\n \n int x[][] = new int[n][];\n int y[][] = new int[m][];\n for(int i=0;i<n;i++)\n x[i] = new int[i+1];\n for(int i=0;i<m;i++)\n y[i] = new int[i+1];\n \n build(a , x);\n build(b , y);\n \n int ans[] = new int[k];\n \n for(int i=0;i<=k;i++){\n int count1 = i;\n int count2 = k-i;\n if(count1<=n && count2<=m){\n int left[] = new int[0];\n int right[] = new int[0];\n if(count1>0)\n left = x[count1-1];\n if(count2>0)\n right = y[count2-1];\n int now[] = max(left , right);\n if(less(ans , now)<0){\n ans = now;\n }\n }\n }\n return ans;\n }\n \n public int[] max(int a[] , int b[]){\n int c[] = new int[a.length+b.length];\n int i=0;\n int j=0;\n int k=0;\n while(i<a.length && j<b.length){\n if(a[i] == b[j]){\n int x = check(a , b , i , j);\n if(x == 0)\n c[k++] = a[i++];\n else\n c[k++] = b[j++];\n }\n else if(a[i]>b[j])\n c[k++] = a[i++];\n else\n c[k++] = b[j++];\n }\n while(i<a.length)\n c[k++] = a[i++];\n while(j<b.length)\n c[k++] = b[j++];\n return c;\n }\n \n public int check(int a[] , int b[] , int s1 , int s2){\n // 0 -> a 1 -> b\n int i=s1;\n int j=s2;\n while(i<a.length && j<b.length){\n if(a[i] == b[j]){\n i++;\n j++;\n continue;\n }\n if(a[i]<b[j])\n return 1;\n else\n return 0;\n }\n if(i == a.length)\n return 1;\n return 0;\n }\n \n public void build(int a[] , int x[][]){\n for(int i=0;i<a.length;i++){\n int num = a[i];\n if(i == 0){\n x[i][0] = num;\n continue;\n }\n for(int j=i;j>0;j--){\n int res = less(x[j] , x[j-1]);\n if(res>0);\n else if(res == 0){\n if(x[j][j]<num){\n x[j][j] = num;\n }\n }\n else{\n copy(x[j-1] , x[j]);\n x[j][j] = num;\n }\n }\n if(x[0][0]<num)\n x[0][0] = num;\n }\n }\n \n public void copy(int a[] , int b[]){\n for(int i=0;i<a.length;i++)\n b[i] = a[i];\n }\n \n public int less(int a[] , int b[]){\n // 0 -> equal -1 -> less 1 -> more\n for(int i=0;i<Math.min(a.length , b.length);i++){\n if(a[i] == b[i])\n continue;\n else if(a[i]<b[i])\n return -1;\n return 1;\n }\n return 0;\n }\n \n}\n```
| 1 | 1 |
['Dynamic Programming', 'Greedy', 'Java']
| 0 |
create-maximum-number
|
BFS Runtime: 112 ms, faster than 100.00% Current Python
|
bfs-runtime-112-ms-faster-than-10000-cur-oq6e
|
Runtime: 112 ms, faster than 100.00%\nMemory Usage: 14.4 MB, less than 63.64%\n# Explanation:\nLet N1 be the lenghth of nums1, and N2 the length of nums2.\nThe
|
jiangjixiang
|
NORMAL
|
2020-12-12T04:07:33.515570+00:00
|
2020-12-12T04:50:14.612473+00:00
| 403 | false |
Runtime: 112 ms, faster than 100.00%\nMemory Usage: 14.4 MB, less than 63.64%\n# Explanation:\nLet N1 be the lenghth of nums1, and N2 the length of nums2.\nThe `remain` is initialized to `k`, and reduced by 1 after choosed a candidate every time.\n\nThe 1st candidate must be in `nums1[0:min(len(nums1), max_skip+1)]` and `nums2[0:min(len(nums2), max_skip+1)]`, and the `max_skip` is the max number we can drop which equal to `N1 + N2 - remain`.\n\nAsume we get the 1st number at index `i1` in nums1.\nThe 2nd candidate must be in `nums1[i1+1:min(len(nums1), i1+1+max_skip+1)]` and `nums2[0:min(len(nums2), max_skip+1)]`. the `max_skip` is `N1-i1+N2-0-remain`\n....\nThe (k+1)th candidate must be in `nums1[i1+1:min(len(nums1), i1+1+max_skip+1)]` and `nums2[i2+1:min(len(nums2), i2+1+max_skip+1)]`. the `max_skip` is `N1-i1+N2-i2-remain`\n\nFor each level (represented by remain), we can we choose the best value for the current number.\n\nI hope this solution can help you.\n```\nclass Solution:\n def maxNumber(self, nums1: [int], nums2: [int], k: int) -> [int]:\n N1 = len(nums1)\n N2 = len(nums2)\n\n def _get_candidate(nums, start, max_skip):\n j = start\n v = -1\n for i in range(start, min(len(nums), start+max_skip+1)):\n if v < nums[i]:\n j = i\n v = nums[j]\n if nums[j] == 9:break\n return j,v\n \n next_candidates = {(0,0)}\n ret = [0]*k\n for remain in range(k,0,-1):\n candidates = next_candidates\n next_candidates = set()\n value_max = -1\n for (i1,i2) in candidates:\n if i1 >= N1 and i2 >= N2: continue\n r1 = N1 - i1\n r2 = N2 - i2\n max_skip = r1 + r2 - remain\n\n j1,v1 = _get_candidate(nums1, i1, max_skip)\n j2,v2 = _get_candidate(nums2, i2, max_skip)\n\n if v1 > value_max:\n next_candidates = {(j1+1, i2)}\n value_max = v1\n elif v1 == value_max:\n next_candidates.add((j1+1, i2))\n \n if v2 > value_max:\n next_candidates = {(i1, j2+1)}\n value_max = v2\n elif v2 == value_max:\n next_candidates.add((i1, j2+1))\n ret[-remain] = value_max\n \n return ret\n```
| 1 | 0 |
[]
| 1 |
create-maximum-number
|
Go divide and conquer
|
go-divide-and-conquer-by-dynasty919-yvvz
|
\nfunc maxNumber(nums1 []int, nums2 []int, k int) []int {\n res := make([]int, k)\n for i := 0; i <= k; i++ {\n if len(nums1) >= i && len(nums2) >=
|
dynasty919
|
NORMAL
|
2020-07-05T13:37:01.183061+00:00
|
2020-07-05T13:38:36.884793+00:00
| 502 | false |
```\nfunc maxNumber(nums1 []int, nums2 []int, k int) []int {\n res := make([]int, k)\n for i := 0; i <= k; i++ {\n if len(nums1) >= i && len(nums2) >= k - i {\n res1 := getMax(nums1, i)\n res2 := getMax(nums2, k - i)\n temp := merge(res1, res2)\n if isLarger(temp, res) {\n res = temp\n }\n }\n }\n return res\n}\n\nfunc getMax(nums []int, k int) []int {\n discard := len(nums) - k\n var stack []int\n for i := 0; i < len(nums); i++ {\n for len(stack) > 0 && discard > 0 && stack[len(stack) - 1] < nums[i] {\n stack = stack[:len(stack) - 1]\n discard--\n }\n stack = append(stack, nums[i])\n }\n return stack[:k]\n}\n\nfunc merge(a []int, b []int) []int {\n var res []int\n for len(a) > 0 && len(b) > 0 {\n if isLarger(a, b) {\n res = append(res, a[0])\n a = a[1:]\n } else {\n res = append(res, b[0])\n b = b[1:]\n }\n }\n \n if len(a) > 0 {\n res = append(res, a...)\n }\n \n if len(b) > 0 {\n res = append(res, b...)\n }\n \n return res\n}\n\nfunc isLarger(a []int, b []int) bool {\n l := min(len(a), len(b))\n for i := 0; i < l; i++ {\n if a[i] < b[i] {\n return false\n } else if a[i] > b[i] {\n return true\n }\n }\n return len(a) > len(b)\n}\n\nfunc min(a int, b int) int {\n if a < b {\n return a\n }\n return b\n}\n```
| 1 | 0 |
[]
| 0 |
create-maximum-number
|
10 lines with explanation
|
10-lines-with-explanation-by-jandk-ru1t
|
Gready + Merge Sort\nSince we need construct the maximum number from given arrays, the gready approach seems to be the core diea resovling this problem, which i
|
jandk
|
NORMAL
|
2020-07-05T12:22:53.099650+00:00
|
2020-07-05T12:22:53.099697+00:00
| 1,188 | false |
### Gready + Merge Sort\nSince we need construct the maximum number from given arrays, the gready approach seems to be the core diea resovling this problem, which is to select the maximum number and check if we can pick it. We can\'t pick the current number if the number of remaining elements are smaller than *K* as we don\'t have enough elements to pick *k* times. There are two different apparchs for us to select maximum elements. The first one is to find maximum between 2 arrays, namely we combine 2 arraysy and pick the maximum number to construct the global maximum result. The other one is to select maximum number for each array respectively, and merge it as local maximum and return the maximum one. As the local maximum is not always the global maximum in the first approach, we need go with second appraoch, which is much easier to implement as well.\nHence, the algorithm could be\n1. We pick the first `length` th maximum numbers from *nums1* and the other `k - length` th maximum numbers from *nums2*\n2. Construct the local maximum nubmer by merging and record it if it\'s the maximum so far\n3. Repeat the process for the `length` + 1 until it reaches the `min(k, nums1.length)`\n\nNote, we have variance on the `merge`, where we pick larger one if `nums1[i] != nums2[j]`, otherwise the one with larger successors.\n\n```python\n def maxNumber(self, nums1: List[int], nums2: List[int], k: int) -> List[int]:\n m = len(nums1)\n n = len(nums2)\n \n def getMax(nums, k):\n ans, i, n = [], 0, len(nums)\n while i < n:\n while ans and nums[i] > ans[-1] and n - i + len(ans) > k:\n ans.pop()\n ans.append(nums[i]) \n i += 1\n return ans[:k]\n \n def merge(nums1, nums2):\n return [max(nums1, nums2).popleft() for _ in range(len(nums1) + len(nums2))]\n \n return max(merge(deque(getMax(nums1, length)), deque(getMax(nums2, k - length))) for length in range(max(0, k - n), min(k, m) + 1))\n```\n\n*Time Complexity* = **O(k(n1 + n2)^2)**, *n1*, *n2* denotes the length of arrays respectively\n*Space Complexity* = **O(k)**
| 1 | 0 |
[]
| 0 |
create-maximum-number
|
java greedy solution
|
java-greedy-solution-by-66brother-jbn6
|
\nclass Solution {\n public int[] maxNumber(int[] A, int[] B, int k) {\n if(A.length==0)return get(B,k,true);\n if(B.length==0)return get(A,k,t
|
66brother
|
NORMAL
|
2020-06-19T08:12:43.054737+00:00
|
2020-06-19T08:13:28.702902+00:00
| 708 | false |
```\nclass Solution {\n public int[] maxNumber(int[] A, int[] B, int k) {\n if(A.length==0)return get(B,k,true);\n if(B.length==0)return get(A,k,true);\n int res[]=new int[k];\n for(int i=0;i<k;i++){\n int A1[]=get(A,i,false);\n int A2[]=get(B,k-i,false);\n if(A1==null||A2==null)continue;\n int newA[]=merge(A1,A2);\n if(compare(res,newA)){\n res=newA;\n }\n }\n return res;\n }\n \n public boolean compare(int A[],int B[]){\n for(int i=0;i<A.length;i++){\n if(B[i]==A[i])continue;\n if(B[i]>A[i])return true;\n else return false;\n }\n return false;\n }\n \n public int[] merge(int A[],int B[]){\n int res[]=new int[A.length+B.length-2];\n int i=0,j=0,k=0;\n while(i<A.length-1&&j<B.length-1){\n if(A[i]>B[j]){\n res[k++]=A[i++];\n }else if(B[j]>A[i]){\n res[k++]=B[j++];\n }else{//equal\n int ii=i,jj=j;\n int prei=i,prej=j;\n while(ii<A.length-1&&jj<B.length-1){\n while(ii<A.length-1&&A[ii]==A[prei])ii++;\n while(jj<B.length-1&&B[jj]==B[prej])jj++;\n if(ii<A.length-1&&jj<B.length-1&&A[ii]==B[jj]&&(ii-i==jj-j)){\n prei=ii;prej=jj;\n continue;\n }\n else break;\n }\n if(ii-i==jj-j){\n if(A[ii]>B[jj])res[k++]=A[i++];\n else res[k++]=B[j++];\n }else if(ii-i<jj-j){\n if(A[ii]>B[prej])res[k++]=A[i++];\n else res[k++]=B[j++];\n }else{\n if(B[jj]>A[prei])res[k++]=B[j++];\n else res[k++]=A[i++]; \n }\n \n }\n }\n while(i<A.length-1)res[k++]=A[i++];\n while(j<B.length-1)res[k++]=B[j++];\n return res;\n }\n \n public void print(int A[]){\n for(int i:A)System.out.print(i+" ");\n System.out.println();\n }\n \n public int[] get(int A[],int k,boolean flag){\n if(k>A.length)return null;\n Stack<Integer>stack=new Stack<>();\n int res[]=new int[k];\n for(int i=0;i<A.length;i++){\n int remain=A.length-(i+1);\n while(stack.size()!=0&&A[i]>stack.peek()&&stack.size()+remain>=k)stack.pop();\n stack.push(A[i]);\n }\n int index=res.length-1;\n while(stack.size()>k)stack.pop();\n while(stack.size()!=0){\n res[index--]=stack.pop();\n }\n if(flag)return res;\n int ans[]=new int[res.length+1];\n for(int i=0;i<res.length;i++)ans[i]=res[i];\n ans[ans.length-1]=Integer.MIN_VALUE;\n return ans;\n }\n}\n\n```
| 1 | 0 |
[]
| 0 |
create-maximum-number
|
C++ A horrible but efficient solution
|
c-a-horrible-but-efficient-solution-by-u-03ks
|
The idea is to build a binary tree based on sorted indices. The binary tree definition is as follows:\n\n\nstruct MyTreeNode{\n\xA0 \xA0 MyTreeNode(int idx, int
|
user9583e
|
NORMAL
|
2020-06-09T09:06:51.764818+00:00
|
2020-06-10T10:41:45.341303+00:00
| 575 | false |
The idea is to build a binary tree based on sorted indices. The binary tree definition is as follows:\n\n```\nstruct MyTreeNode{\n\xA0 \xA0 MyTreeNode(int idx, int val): idx(idx), val(val), left(nullptr), right(nullptr){}\n\xA0\n\xA0 \xA0 int idx;\n\xA0 \xA0 int val;\n\xA0 \xA0 \n\xA0 \xA0 MyTreeNode * left;\n\xA0 \xA0 MyTreeNode * right;\n};\n```\n\nTha property val holds the value and idx holds the corresponding inex.\nWe build a binary tree from each of the input arrays as follows. First we pick the largest element in the vector. Suppose it has index i. We create the root node from it. The index i splits the vector into two (not necessarily equal) parts. The right node of the root is the largest element on the right side, i.e. max(nums[j] ) j>i and the left one is the largest in the left side. \n\nThe code that builds the binary tree looks as follows:\n\n```\nMyTreeNode * getTree( const vector<int>& nums){\n\xA0 \xA0 \xA0 \xA0 if(nums.empty())\n\xA0 \xA0 \xA0 \xA0 \xA0 \xA0 return nullptr;\n\t\t\t\n\xA0 \xA0 \xA0 \xA0 vector<int> indices(nums.size());\n\xA0 \xA0 \xA0 \xA0 for(int i = 0; i < indices.size(); ++i)\n\xA0 \xA0 \xA0 \xA0 \xA0 \xA0 indices[i] = i;\n\xA0 \xA0 \xA0 \xA0 \n\t\t// after this the vector indices will hold the indices that sort nums in descending order\n\xA0 \xA0 \xA0 \xA0 sort(indices.begin(), indices.end(), [&](const int & a, const int &b){ if(nums[a] == nums[b]) return a <b; else return nums[a] > nums[b]; });\n\xA0 \xA0 \xA0 \xA0 \xA0 \xA0 \n\xA0 \xA0 \xA0 \xA0 MyTreeNode * head = new MyTreeNode(indices[0], nums[indices[0]]); \xA0 \xA0 \xA0\n\xA0 \xA0 \xA0 \xA0 for(int i = 1; i < indices.size(); ++i)\n\xA0 \xA0 \xA0 \xA0 \xA0 \xA0 insert(head, indices[i], nums[indices[i]]);\n\xA0 \xA0 \xA0 \xA0 return head;\n\xA0 \xA0 \xA0 \xA0 \xA0 \xA0 \n\xA0 \xA0 }\n\xA0 \xA0 \n\xA0 \xA0 void insert(MyTreeNode * head, int idx, int val){\n\xA0 \xA0 \xA0 \xA0 if(idx > head->idx) {\n\xA0 \xA0 \xA0 \xA0 \xA0 \xA0 if(head->right)\n\xA0 \xA0 \xA0 \xA0 \xA0 \xA0 \xA0 \xA0 insert(head->right, idx, val);\n\xA0 \xA0 \xA0 \xA0 \xA0 \xA0 else\n\xA0 \xA0 \xA0 \xA0 \xA0 \xA0 \xA0 \xA0 head->right = new MyTreeNode(idx, val);\n\xA0 \xA0 \xA0 \xA0 }\n\xA0 \xA0 \xA0 \xA0 else\n\xA0 \xA0 \xA0 \xA0 {\n\xA0 \xA0 \xA0 \xA0 \xA0 \xA0 if(head->left)\n\xA0 \xA0 \xA0 \xA0 \xA0 \xA0 \xA0 \xA0 insert(head->left, idx, val);\n\xA0 \xA0 \xA0 \xA0 \xA0 \xA0 else\n\xA0 \xA0 \xA0 \xA0 \xA0 \xA0 \xA0 \xA0 head->left = new MyTreeNode(idx, val);\n\xA0 \xA0 \xA0 \xA0 }\n\xA0 \xA0 }\n```\n\nHaving the corresponding tree it easy to find the next candidate element to pick. For each array we keep the last picked index idx1 ord idx2. \n\nWe start from the root of each tree. The candidate node should have idx value greater than the last picked index. So, if for any node *cur* this condition is not satisfyed we move to its right child. On the other hand, the element can be so much right in the array, that the number of the remaining items is not enough for filling the resulting vector with k elements. If this is the case then we move to the left. As soon as we arrive to a node, we can be sure that it is the largest node that satifies both requirements.\n\nThe code for this navigation reads:\n\n```\nMyTreeNode * \xA0getCandidate(MyTreeNode * node, int idx1, int remaining_items){\n\xA0 \xA0 while(node){\xA0 \xA0 \xA0 \xA0 \xA0 \n\xA0 \xA0 \xA0 \xA0 if(remaining_items \xA0- \xA0node->idx < 0)\n\xA0 \xA0 \xA0 \xA0 \xA0 \xA0 node = node->left;\n\xA0 \xA0 \xA0 \xA0 else if (node->idx <= idx1 )\n\xA0 \xA0 \xA0 \xA0 \xA0 \xA0 node = node->right;\n\xA0 \xA0 \xA0 \xA0 else \n\xA0 \xA0 \xA0 \xA0 \xA0 \xA0 break;\n \xA0 }\n\xA0 \xA0return node;\n}\n```\n\n**Solution with no collisions** (Attention: this one is not accepted).\n\n```\nclass Solution{\npublic:\n vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {\n MyTreeNode * t1 = getTree(nums1);\n\xA0 \xA0 \xA0 \xA0 MyTreeNode * t2 = getTree(nums2);\n\xA0 \xA0 \xA0 \xA0 vector<int> result;\n\t\t\n\t\tint idx1 = -1, idx2 = -1;\n\t\twhile(k > result.size()){\n\t\t MyTreeNode * cur1 = getCandidate(t1, idx1, nums1.size() \xA0+ nums2.size() - idx2 -1 - k + result.size());\n\xA0 \xA0 \xA0 \xA0 \xA0 \xA0 MyTreeNode * cur2 = getCandidate(t2, idx2, nums1.size() \xA0+ nums2.size() - idx1 -1 - k + result.size());\n\t\t\t\n\t\t\t// We then merge sort these trees into the result\n\t\t\tif(cur1 && cur2){\n\t\t\t if(cur1->val == cur2->val){\n\t\t\t\t // this one is tricky so let us for a moment assume that we do not encounter such cases\n\t\t\t\t}\n\t\t\t\telse if(cur1->val > cur2->val){\n\t\t\t\t // Move the last picked index of the first array \n\t\t\t\t idx1 = cur1->idx;\n\t\t\t\t\t// Append to the result\n\t\t\t\t\tresult.push_back(cur1->val);\n\t\t\t\t}\n\t\t\t\telse {\n\t\t\t\t idx2 = cur2->idx;\n\t\t\t\t\tresult.push_back(cur2->val);\n\t\t\t\t}\n\t\t\t}\n\t\t\telse if(cur1){\n\t\t\t idx1 = cur1->idx;\n\t\t\t result.push_back(cur1->val);\n\t\t\t}\n\t\t\telse{\n\t\t\t idx2 = cur2->idx;\n\t\t\t\tresult.push_back(cur2->val);\t\t\t\n\t\t\t}\n\t\t}\n\n }\n\n};\n```\n\nThe problem arises when the values of the candidate nodes are equal. I could not find a better solution to this rather than to maintain all possible paths until at some stage some of the paths give a smaller value to pick. For this reason let us introduce\n\n```\nstruct State{\n\xA0 \xA0 State(int idx1, int idx2, int value=numeric_limits<int>::min()): idx1(idx1), idx2(idx2), max_value(value){}\n\t\n\tint idx1;\n\xA0 \xA0 int idx2; \xA0 \n\xA0 \xA0 int max_value;\n\t\n bool operator ==(const State & other) const {\n return idx1 == other.idx1 && idx2 == other.idx2;\n }\n};\n```\n\n\nAnd the code becomes (ugly!!!):\n\n```\nclass Solution{\npublic:\n vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {\n MyTreeNode * t1 = getTree(nums1);\n\xA0 \xA0 \xA0 \xA0 MyTreeNode * t2 = getTree(nums2);\n\xA0 \xA0 \xA0 \xA0 vector<int> result;\n\t\t\n\t\tlist<State> states;\xA0 \xA0 \xA0 \xA0 \n\xA0 \xA0 \xA0 \xA0 states.push_front (State(-1,-1));\n\t\t\n\t\tint idx1 = -1, idx2 = -1;\n\t\twhile(k > result.size()){\n\t\t int max_value = numeric_limits<int>::min();\n\t\t\tlist<State> states_to_add;\n\t\t for(State & st: states){\n\n MyTreeNode * cur1 = getCandidate(t1, st.idx1, nums1.size() \xA0+ nums2.size() - st.idx2 -1 - k + result.size());\n\xA0 \xA0 \xA0 \xA0 \xA0 \xA0 MyTreeNode * cur2 = getCandidate(t2, st.idx2, nums1.size() \xA0+ nums2.size() - st.idx1 -1 - k + result.size());\n\t\t\t\n\t\t\t // We then merge sort these trees into the result\n\t\t\t if(cur1 && cur2){\n\t\t\t if(cur1->val == cur2->val){\n\t\t\t\t // We create 2 new states instead of one so that the comuptation will be done for both possible paths\n\t\t\t\t\t\tmax_value = max(max_value, cur1->val );\n\t\t\t\t\t\tstates_to_add.push_front(State(cur1->idx, st.idx2, cur1->value));\n\t\t\t\t\t\tstates_to_add.push_front(State(st.idx1, cur2->idx, cur2->value));\n\t\t\t\t\t\t\n\t\t\t\t\t\t// We set this so it is removed in below\n\t\t\t\t\t\tst.max_value = numeric_limits<int>::min();\n\t\t\t\t }\n\t\t\t\t else if(cur1->val > cur2->val){\t\t\t\t \n\t\t\t\t st.idx1 = cur1->idx;\t\t\t\t\t\n\t\t\t\t\t max_value = max(max_value, cur1->val );\n\t\t\t\t\t st.max_value = cur1->val;\n\t\t\t\t }\n\t\t\t\t else {\n\t\t\t\t st.idx2 = cur2->idx;\t\t\t\t\t\n\t\t\t\t\t max_value = max(max_value, cur2->val );\n\t\t\t\t\t st.max_value = cur2->val;\n\t\t\t\t }\n\t\t\t }\n\t\t\t else if(cur1){\n\t\t\t st.idx1 = cur1->idx;\t\t\t\t\t\n\t\t\t\t max_value = max(max_value, cur1->val );\n\t\t\t\t st.max_value = cur1->val;\n\t\t\t }\n\t\t\t else{\n\t\t\t st.idx2 = cur2->idx;\t\t\t\t\t\n\t\t\t\t max_value = max(max_value, cur2->val );\n\t\t\t\t st.max_value = cur2->val;\t\n\t\t\t }\n\t\t\t\n\t\t\t}\n\t\t result.push_back(max_value);\n\t\t\t// We should remove all the states which are doing worse than the best one\xA0 \xA0 \xA0 \xA0 \xA0 \xA0 \n states.remove_if([&](const State & st){return st.max_value < max_value;});\n\t\t\t\n\t\t\t// Add newly create states\n\t\t\tfor(State st: states_to_add)\n\xA0 \xA0 \xA0 \xA0 \xA0 \xA0 \xA0 \xA0 if(st.max_value == max_value)\n\xA0 \xA0 \xA0 \xA0 \xA0 \xA0 \xA0 \xA0 \xA0 \xA0 states.push_front(st);\n\t\t}\n\n }\n\n};\n```\n\nIt turns out, however, that the picking paths are not unique and states can merge later. I was lazy to find a good solution for this so just copy-pasted a similar code from one of my projects. We just add hashing function to the std namespace (outside any scope )\n\n```\nnamespace std{\ntemplate<>\nstruct hash<State> {\n std::size_t operator()(const State & state) const noexcept {\n std::hash<int> hasher;\n size_t seed = hasher(state.idx1);\n\t// from boost\n seed ^= hasher(state.idx2) + 0x9e3779b9 + (seed<<6) + (seed>>2);\n return seed;\n }\n};\n}\n```\n\nAnd at the very end of the while(k > result.size()) loop just add this stupid code \n\n```\nunordered_set<State> unique_states(states.begin(), states.end());\nif(unique_states.size()!= states.size()){\n states.clear();\n for(const State &st: unique_states)\n states.push_front(st);\n}\n```\n\n\nI will appretiate if someone points a good way to tackle the state problem and/or any other comments
| 1 | 0 |
[]
| 0 |
create-maximum-number
|
C++ solution
|
c-solution-by-wufengxuan1230-141n
|
\nclass Solution {\npublic:\n \nbool compare(vector<int>& nums1, vector<int>& nums2, int start_i, int start_j)\n{\n\tint loop_size = min(nums1.size() - start
|
wufengxuan1230
|
NORMAL
|
2019-12-17T16:00:21.628044+00:00
|
2019-12-18T19:13:14.890742+00:00
| 746 | false |
```\nclass Solution {\npublic:\n \nbool compare(vector<int>& nums1, vector<int>& nums2, int start_i, int start_j)\n{\n\tint loop_size = min(nums1.size() - start_i, nums2.size() - start_j);\n\n\tfor (int i = 0; i < loop_size; i++)\n\t{\n\t\tif (nums1[i + start_i] < nums2[i + start_j])\n\t\t\treturn true;\n\t\telse if (nums1[i + start_i] > nums2[i + start_j])\n\t\t\treturn false;\n\t}\n\treturn nums1.size() - start_i < nums2.size() - start_j;\n}\n\nvector<vector<int>> largetsNum(vector<int>& nums)\n{\n\tvector<vector<int>> res;\n\tres.resize(nums.size() + 1);\n\tres.back() = nums;\n\n\tfor (int i = res.size() - 2; i >= 0; i--)\n\t{\t\n\t\tint idx = 0;\n\t\twhile (idx + 1 < res[i + 1].size())\n\t\t{\n\t\t\tif (res[i + 1][idx] < res[i + 1][idx + 1])\n\t\t\t\tbreak;\n\t\t\tidx++;\n\t\t}\n\n\t\tfor (int j = 0; j < res[i + 1].size(); j++)\n\t\t{\n\t\t\tif (idx != j)\n\t\t\t\tres[i].push_back(res[i + 1][j]);\n\t\t}\n\t}\n\treturn res;\n}\n\nvector<int> merge(vector<int>& nums1, vector<int>& nums2)\n{\n\tvector<int> res;\n\tint i = 0, j = 0;\n\twhile (i < nums1.size() || j < nums2.size())\n\t{\n\t\t\tif (compare(nums1, nums2, i, j))\n\t\t\t\tres.push_back(nums2[j++]);\n\t\t\telse\n\t\t\t\tres.push_back(nums1[i++]);\n\t}\n\treturn res;\n}\n\nvector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, size_t k) \n{\n\tvector<vector<int>> largest_num1 = largetsNum(nums1);\n\tvector<vector<int>> largest_num2 = largetsNum(nums2);\n\n\tvector<int> res;\n\n\tint start = k > nums2.size() ? k - nums2.size() : 0;\n\n\tfor (int i = start; i < largest_num1.size() && i <= k; i++)\n\t{\n\t\tvector<int> tmp = merge(largest_num1[i], largest_num2[k - i]);\n\t\tif (res.empty() || compare(res, tmp, 0, 0))\n\t\t\tres = tmp;\n\t}\n\n\treturn res;\n}\n};\n```
| 1 | 0 |
[]
| 0 |
create-maximum-number
|
Python Simple Intuitive 3 Dimention Solution
|
python-simple-intuitive-3-dimention-solu-8rsp
|
\nclass Solution(object):\n def maxNumber(self, nums1, nums2, length):\n """\n :type nums1: List[int]\n :type nums2: List[int]\n
|
zou_zheng
|
NORMAL
|
2019-07-03T01:51:34.830017+00:00
|
2019-07-03T01:51:34.830061+00:00
| 504 | false |
```\nclass Solution(object):\n def maxNumber(self, nums1, nums2, length):\n """\n :type nums1: List[int]\n :type nums2: List[int]\n :type k: int\n :rtype: List[int]\n """\n if len(nums1) + len(nums2) < length:\n return []\n \n dp = [[[0 for _ in xrange(length + 1)] for _ in xrange(len(nums2) + 1)] for _ in xrange(len(nums1) + 1)]\n for k in xrange(1,length + 1):\n for j in xrange(k,len(nums2) + 1):\n dp[0][j][k] = max(dp[0][j - 1][k],10 * dp[0][j - 1][k - 1] + nums2[j - 1])\n for i in xrange(k,len(nums1) + 1):\n dp[i][0][k] = max(dp[i - 1][0][k],10 * dp[i - 1][0][k - 1] + nums1[i - 1])\n \n for i in xrange(1,len(nums1) + 1):\n for j in xrange(1,len(nums2) + 1):\n if i + j < k:\n continue\n dp[i][j][k] = max(dp[i][j][k],dp[i - 1][j][k],dp[i][j - 1][k])\n dp[i][j][k] = max(dp[i][j][k],dp[i - 1][j][k - 1] * 10 + nums1[i - 1])\n dp[i][j][k] = max(dp[i][j][k],dp[i][j - 1][k - 1] * 10 + nums2[j - 1])\n \n return map(int,list(str(dp[-1][-1][-1])))\n```
| 1 | 0 |
[]
| 0 |
create-maximum-number
|
C++ time complexity O(k * (m+n)), 24ms
|
c-time-complexity-ok-mn-24ms-by-dan0907-hd5a
|
\nclass Solution {\n void combine(std::vector<int> &res, std::vector<int> &v1, std::vector<int> &v2)\n {\n int len1 = v1.size();\n int len2
|
dan0907
|
NORMAL
|
2019-05-14T15:57:10.175228+00:00
|
2019-05-14T15:57:23.700584+00:00
| 1,171 | false |
```\nclass Solution {\n void combine(std::vector<int> &res, std::vector<int> &v1, std::vector<int> &v2)\n {\n int len1 = v1.size();\n int len2 = v2.size();\n int len = res.size();\n int left = 0;\n int right = 0;\n for (int i = 0; i < len;) {\n if (right == len2 || left != len1 && v1[left] > v2[right]) {\n res[i++] = v1[left++];\n } else if (left == len1 || v2[right] > v1[left]) {\n res[i++] = v2[right++];\n } else {\n int ori_left = left;\n int ori_right = right;\n int tar = left;\n int last_greater = right;\n res[i++] = v1[left];\n while (1) {\n ++left;\n ++right;\n if (left == len1 || right != len2 && v1[left] < v2[right]) {\n left = ori_left;\n break;\n } else if (right == len2 || v1[left] > v2[right]) {\n right = ori_right;\n break;\n }\n if (v1[left] < v1[tar]) {\n left = tar;\n right = last_greater + 1;\n break;\n } else if (v1[left] > v1[tar]) {\n last_greater = right;\n tar = ori_left;\n } else {\n ++tar;\n }\n res[i++] = v1[left];\n }\n }\n }\n }\n void max_num(std::vector<int> &res, std::vector<int> &nums, int k)\n {\n res.clear();\n int len = nums.size();\n int diff = len - k;\n for (int i = 0; i < len; ++i) {\n while (res.size() > std::max(i - diff, 0) && nums[i] > res.back()) {\n res.pop_back();\n }\n if (res.size() < k) {\n res.push_back(nums[i]);\n }\n }\n }\npublic:\n vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {\n std::vector<int> res(k);\n std::vector<int> cur(k);\n std::vector<int> temp1;\n std::vector<int> temp2;\n temp1.reserve(k);\n temp2.reserve(k);\n int len1 = nums1.size();\n int len2 = nums2.size();\n int max_len = std::min(len1, k);\n int min_len = std::max(k - len2, 0);\n for (int i = min_len; i <= max_len; ++i) {\n max_num(temp1, nums1, i);\n max_num(temp2, nums2, k - i);\n combine(cur, temp1, temp2);\n if (cur > res) {\n res.swap(cur);\n }\n }\n return res;\n }\n};\n```
| 1 | 1 |
['Greedy', 'C']
| 1 |
create-maximum-number
|
Python Greedy
|
python-greedy-by-arizonatea-bmdj
|
\nclass Solution:\n def maxNumber(self, nums1, nums2, k):\n """\n :type nums1: List[int]\n :type nums2: List[int]\n :type k: int\
|
arizonatea
|
NORMAL
|
2019-01-18T16:35:42.330182+00:00
|
2019-01-18T16:35:42.330224+00:00
| 557 | false |
```\nclass Solution:\n def maxNumber(self, nums1, nums2, k):\n """\n :type nums1: List[int]\n :type nums2: List[int]\n :type k: int\n :rtype: List[int]\n """\n n, m = len(nums1), len(nums2)\n ans = [0] * k\n for i in range(0, k+1):\n j = k - i\n if i > n or j > m: \n continue\n \n left = self.maxOneNumber(nums1, n, i)\n right = self.maxOneNumber(nums2, m, j)\n cur = self.merge(collections.deque(left), collections.deque(right))\n ans = max(ans, cur)\n\n return ans\n \n def maxOneNumber(self, nums, n, k):\n ans = [-1] * k\n j = 0\n for i in range(n):\n while n - i > k - j and j > 0 and ans[j-1] < nums[i]:\n j -= 1\n if j < k:\n ans[j] = nums[i]\n j += 1\n return ans\n \n def merge(self, nums1, nums2):\n ans = []\n while nums1 or nums2:\n if nums1 > nums2:\n ans.append(nums1.popleft())\n else:\n ans.append(nums2.popleft())\n return ans\n \n \n \n \n \n```
| 1 | 0 |
[]
| 0 |
create-maximum-number
|
the Basic/traditional DP solution?
|
the-basictraditional-dp-solution-by-rayd-er4j
|
Tips: Also this is not the final solution, As you need change the int to string , to solve the integer overload issue. but i think this is the basic DP. thanks
|
rayding007
|
NORMAL
|
2018-11-08T05:36:54.666667+00:00
|
2018-11-08T05:36:54.666709+00:00
| 610 | false |
Tips: Also this is not the final solution, As you need change the int to string , to solve the integer overload issue.
but i think this is the basic DP. thanks
DP[m][i][j] means the largest value when select m elements from A[0]-A[i] and B[0]- B[j]
Init:
DP[m][0][j] >> seleect 0-m from B[0]- B[j]
DP[m][i][0] >>seleect 0-m from A[0]- A[i]
DP:
DP[m][i][j] = Max(
++++ did not inlcude [i][j] in m elements+++++
res[m][i][j-1]; >> select m elements from [i][j-1]
res[m][i-1][j]; >> select m elements from [i-1][j]
++++ inlcude [i][j] in m elements+++++
res[m-1][i-1][j]*10+nums1[i-1]; >> end with nums1[i-1]
res[m-1][i][j-1]*10+nums2[j-1];
nums1[i-1]*10^m-1+res[m-1][0][j]; >> start with nums1[i-1]
nums2[j-1]*10^m-1+res[m-1][i][0];
)
'''
class Solution {
public:
vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {
int len1 = nums1.size();
int len2 = nums2.size();
vector<vector<vector<int> > > res (k+1,vector<vector<int>>(len1+1,vector<int>(len2+1,0)));
for(int m=1;m<=k;m++)
{
for(int j =1;j<=len2;j++)
{
if(j >=m)
{
res[m][0][j] = max(res[m][0][j-1],res[m-1][0][j-1]*10+nums2[j-1]);
}
}
}
for(int m=1;m<=k;m++)
{
for(int i =1;i<=len1;i++)
{
if(i >=m)
{
res[m][i][0] = max(res[m][i-1][0],res[m-1][i-1][0]*10+nums1[i-1]);
}
}
}
for(int m=1;m<=k;m++)
{
for(int i=1; i<=len1;i++)
{
for(int j =1;j<=len2;j++)
{
if(i+j >=m)
{
vector<int> tmp;
tmp.push_back(res[m][i][j-1]);
tmp.push_back(res[m][i-1][j]);
tmp.push_back(res[m-1][i-1][j]*10+nums1[i-1]);
tmp.push_back(res[m-1][i][j-1]*10+nums2[j-1]);
int dl = 0;
int dt = 0;
for(int p=0;p<m-1;p++)
{
dl = nums1[i-1]*10;
dt = nums2[j-1]*10;
}
tmp.push_back(dl+res[m-1][0][j]);
tmp.push_back(dt+res[m-1][i][0]);
sort(tmp.begin(),tmp.end());
res[m][i][j] = tmp[tmp.size()-1];
}
}
}
}
int ans = res[k][len1][len2];
vector<int> data;
while(ans!=0)
{
data.push_back(ans%10);
ans =ans/10;
}
reverse(data.begin(),data.end());
return data;
}
};
'''
| 1 | 0 |
[]
| 0 |
create-maximum-number
|
My readable Python solution
|
my-readable-python-solution-by-cenkay-hgtc
|
After struggling for awhile, i came with this solution and i think most of the solutions are similar.\n If we will make an array of length k, we can take some e
|
cenkay
|
NORMAL
|
2018-09-25T10:35:04.621491+00:00
|
2018-09-25T10:35:04.621556+00:00
| 1,005 | false |
* After struggling for awhile, i came with this solution and i think most of the solutions are similar.\n* If we will make an array of length k, we can take some elements from nums1, and complete rest from nums2.\n* Logic is simple. Get the max possible array from the targeted array in makeArr function.\n* Merge two array one by one to get merged max array.\n* Return max merged array from choices.\n```\nclass Solution:\n def maxNumber(self, nums1, nums2, k):\n def merge(arr1, arr2):\n res, i, j = [], 0, 0\n while i < len(arr1) and j < len(arr2):\n if arr1[i:] >= arr2[j:]:\n res.append(arr1[i])\n i += 1\n else: \n res.append(arr2[j])\n j += 1\n if i < len(arr1): res += arr1[i:]\n elif j < len(arr2): res += arr2[j:]\n return res \n \n def makeArr(arr, l):\n i, res = 0, []\n for r in range(l - 1, -1, -1):\n num, i = max(arr[i:-r] or arr[i:])\n i = -i + 1\n res.append(num)\n return res\n \n nums1, nums2, choices = [(num, -i) for i, num in enumerate(nums1)], [(num, -i) for i, num in enumerate(nums2)], []\n for m in range(k + 1):\n if m > len(nums1) or k - m > len(nums2): continue\n arr1, arr2 = makeArr(nums1, m), makeArr(nums2, k - m) \n choices.append(merge(arr1, arr2))\n return max(choices)\n```
| 1 | 0 |
[]
| 1 |
create-maximum-number
|
A Tip for C++ programmer
|
a-tip-for-c-programmer-by-liujiazzheng-stsm
|
The basic idea is sorts of like brute force, since we just pick 1 number from nums1, k-1 from nums2, \nnext we pick 2 from nums1, k-2 from nums2 , and so on....
|
liujiazzheng
|
NORMAL
|
2018-09-13T21:18:10.489278+00:00
|
2018-09-19T07:29:18.040917+00:00
| 1,403 | false |
The basic idea is sorts of like brute force, since we just pick 1 number from nums1, k-1 from nums2, \nnext we pick 2 from nums1, k-2 from nums2 , and so on........\nThanks to post "share my greedy solution"(ranking number 1 under this topic), I write a similiar one, but in C++.\nThe only thing I\'d like to share is, under such situation, it seems that we need to always copy a vector to another. And this will cost a lot. \nBut actually it shouldn\'t. Unlike Java, if you do something like`int a[] , int b[], a = b`, in java, the just a copy of **reference** , but in c++, it will automatically call the **copy** method, which indeed costs a lot.\nHowever we can still use assignment in term of reference by calling std::move. And if you do not know the method or the difference between rvalue and lvalue, please look up on C++ reference......\n```\npublic:\n vector<int> maxNumber(vector<int>& nums1, vector<int>& nums2, int k) {\n int n = nums1.size();\n int m = nums2.size();\n vector<int> ans(k,0);\n for (int i=std::max(0,k-m);i<=k && i<=n;i++){\n vector<int> candidate = std::move(merge(maxArray(nums1,i),maxArray(nums2,k-i)));\n if (greater(candidate,0,ans,0)) ans = std::move(candidate);\n }\n return ans;\n }\nprivate:\n bool greater(vector<int>& nums1, int i, vector<int>& nums2, int j){\n while (i<nums1.size() && j< nums2.size() && nums1[i] == nums2[j]){i++;j++;}\n return (j == nums2.size()) || (i<nums1.size() && nums1[i] > nums2[j]);\n }\n vector<int> merge(vector<int> && nums1, vector<int> && nums2){\n int k = nums1.size() + nums2.size();\n vector<int> ans(k);\n for (int r=0, i = 0 , j = 0; r < k ;r++)\n ans[r] = greater(nums1,i,nums2,j) ? nums1[i++] : nums2[j++];\n return ans;\n }\n vector<int> maxArray(vector<int> & nums, int k) {\n int n = nums.size();\n vector<int> ans(k);\n for (int i=0,j=0;i<n;i++){\n while (n-i+j > k && j > 0 && ans[j-1] < nums[i]) j--;\n if (j<k) ans[j++] = nums[i];\n }\n return ans;\n }\n```\nHope it helps.
| 1 | 0 |
[]
| 0 |
checking-existence-of-edge-length-limited-paths
|
[C++] DSU + Two Pointers
|
c-dsu-two-pointers-by-phoenixdd-huav
|
Observation\n\nThe key here is to notice that the queries are offline which means that we can reorganize them however we want.\n\nNow to answer the question, wh
|
phoenixdd
|
NORMAL
|
2020-12-20T04:00:39.907126+00:00
|
2020-12-20T06:07:08.935747+00:00
| 14,541 | false |
**Observation**\n\nThe key here is to notice that the queries are offline which means that we can reorganize them however we want.\n\nNow to answer the question, whether there is a path between any two nodes where the maximum edge length or weight is less than `limit`, we can join all the edges whose weight is less than `limit` and if we are still not able to reach one node from the other it essentially means that there is no path between them where edge weight is less than `limit`.\n\nWhich is the best data structure that can help us join edges as we want and answer whether in that structure, node `a` and node `b` are connected ? \nThat\'s right! **DSU**.\n\nLet\'s try and use these facts to solve the question.\n\n**Solution**\n\nFirst we need to sort the input `queries` and `edgeList` by edge length or `weight`.\n\nWe can now simply use a two pointer approach to `Union` all the nodes whose edges have `weight` less than `query[i]`.\n\nTo know if there is a path between them all we need is to know whether their parents (in DSU) are same.\n\n```c++\n// Standard Disjoint-set data structure implementation.\nstatic class DSU {\n vector<int> Parent, Rank;\n public:\n DSU(int n) {\n Parent.resize(n);\n Rank.resize(n, 0);\n for (int i = 0; i < n; i++) Parent[i] = i;\n }\n int Find(int x) {\n return Parent[x] = Parent[x] == x ? x : Find(Parent[x]);\n }\n bool Union(int x, int y) {\n int xset = Find(x), yset = Find(y);\n if (xset != yset) {\n Rank[xset] < Rank[yset] ? Parent[xset] = yset : Parent[yset] = xset;\n Rank[xset] += Rank[xset] == Rank[yset];\n return true;\n }\n return false;\n }\n};\nclass Solution {\npublic:\n vector<bool> distanceLimitedPathsExist(int n, vector<vector<int>>& edgeList, vector<vector<int>>& queries)\n {\n DSU dsu(n);\n\t\t\n\t\t//Add query indices to help with organizing/ordering results.\n for(int i=0;i<queries.size();i++)\n queries[i].push_back(i);\n\t\t\n\t\t//Sort inputs\n sort(queries.begin(), queries.end(), [](auto &l, auto &r) { return l[2] < r[2]; });\n sort(edgeList.begin(), edgeList.end(), [](auto &l, auto &r) { return l.back() < r.back(); });\n\t\t\n int i=0;\n vector<bool> result(queries.size());\n for (vector<int> &q:queries) \n {\n\t\t\t// Two pointer approach. Join the edges till their weight is less than the current query.\n while (i<edgeList.size()&&edgeList[i][2]<q[2]) \n dsu.Union(edgeList[i][0],edgeList[i++][1]);\n\t\t\t\n\t\t\t//If parents are same we know that their is a path.\n result[q.back()]=dsu.Find(q[0]) == dsu.Find(q[1]);\n }\n return result;\n }\n};\n```\n**Complexity**\nTime: `O(ElogE + QlogQ)`. Where `E` is the number of edges in `edgeList` and `Q` is the number of `queries`. This comes from sorting both inputs.\nSpace: `O(n)`. Where `n` is the number of nodes.
| 228 | 1 |
[]
| 18 |
checking-existence-of-edge-length-limited-paths
|
[Python3] Union-Find
|
python3-union-find-by-ye15-rc6d
|
Algo\nSort queries based on weight and sort edges based on weight as well. Scan through queries from lowest to highest weight and connect the edges whose weight
|
ye15
|
NORMAL
|
2020-12-20T04:15:02.165276+00:00
|
2020-12-22T17:20:09.168974+00:00
| 7,142 | false |
**Algo**\nSort queries based on weight and sort edges based on weight as well. Scan through queries from lowest to highest weight and connect the edges whose weight strictly fall below this limit. Check if the queried nodes `p` and `q` are connected in Union-Find structure. If so, put `True` in the relevant position; otherwise put `False`. \n\n**Implementation**\n```\nclass UnionFind:\n def __init__(self, N: int):\n self.parent = list(range(N))\n self.rank = [1] * N\n\n def find(self, p: int) -> int:\n if p != self.parent[p]:\n self.parent[p] = self.find(self.parent[p])\n return self.parent[p]\n\n def union(self, p: int, q: int) -> bool:\n prt, qrt = self.find(p), self.find(q)\n if prt == qrt: return False \n if self.rank[prt] > self.rank[qrt]: \n prt, qrt = qrt, prt \n self.parent[prt] = qrt \n self.rank[qrt] += self.rank[prt] \n return True \n\n\nclass Solution:\n def distanceLimitedPathsExist(self, n: int, edgeList: List[List[int]], queries: List[List[int]]) -> List[bool]:\n queries = sorted((w, p, q, i) for i, (p, q, w) in enumerate(queries))\n edgeList = sorted((w, u, v) for u, v, w in edgeList)\n \n uf = UnionFind(n)\n \n ans = [None] * len(queries)\n ii = 0\n for w, p, q, i in queries: \n while ii < len(edgeList) and edgeList[ii][0] < w: \n _, u, v = edgeList[ii]\n uf.union(u, v)\n ii += 1\n ans[i] = uf.find(p) == uf.find(q)\n return ans \n```\n\n**Analysis**\nTime complexity `O(NlogN) + O(MlogM)`\nSpace complexity `O(N)`
| 109 | 0 |
['Python3']
| 12 |
checking-existence-of-edge-length-limited-paths
|
Image Explanation🏆- [Easiest & Complete Intuition] - C++/Java/Python
|
image-explanation-easiest-complete-intui-32x5
|
Video Solution (Aryan Mittal) - Link in LeetCode Profile\nChecking Existence of Edge Length Limited Paths by Aryan Mittal\n\n\n\n# Approach & Intution\n\n\n\n\n
|
lc00701
|
NORMAL
|
2023-04-29T02:22:02.498070+00:00
|
2023-04-29T03:53:08.625192+00:00
| 15,223 | false |
# Video Solution (`Aryan Mittal`) - Link in LeetCode Profile\n`Checking Existence of Edge Length Limited Paths` by `Aryan Mittal`\n\n\n\n# Approach & Intution\n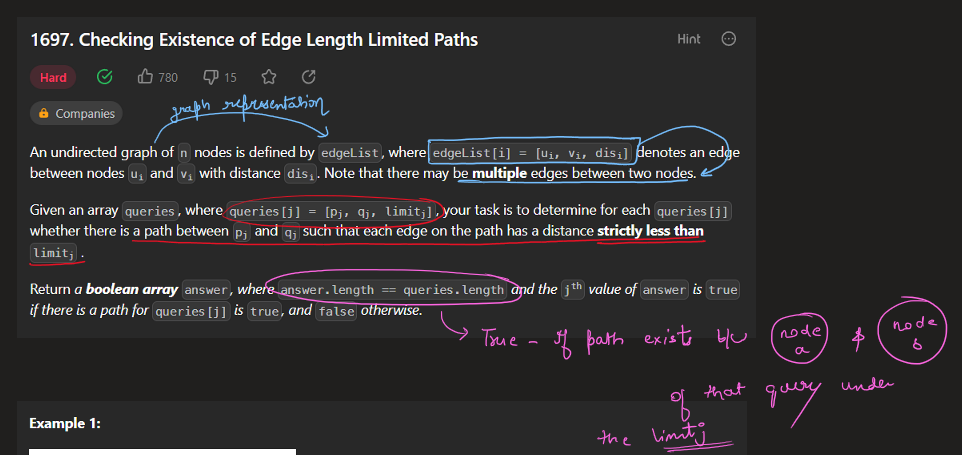\n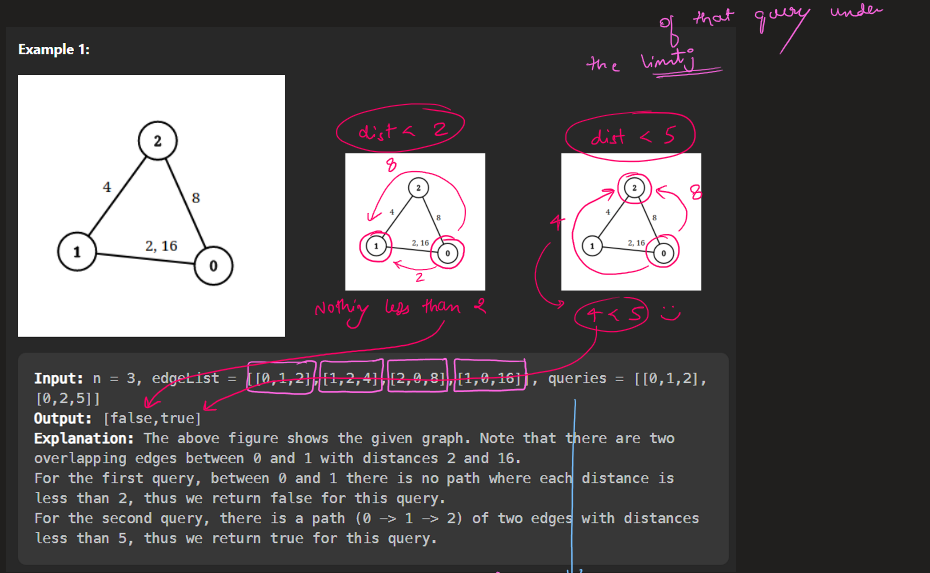\n\n\n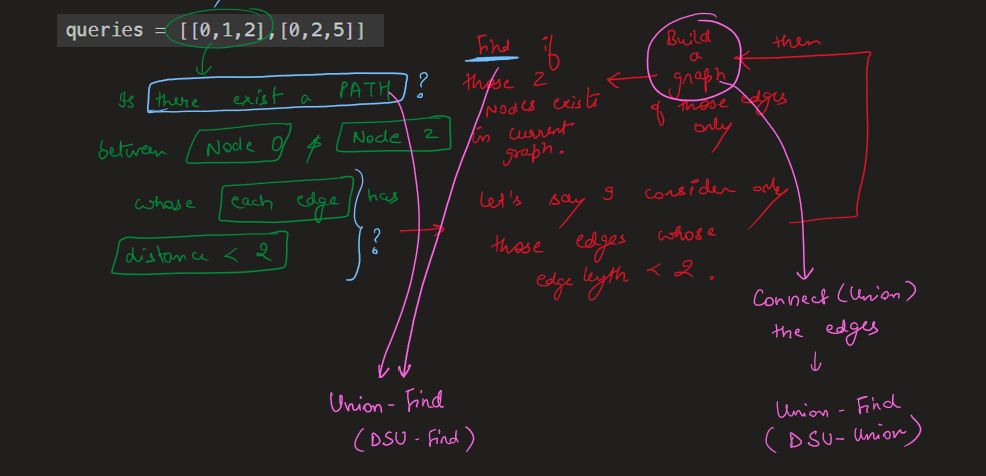\n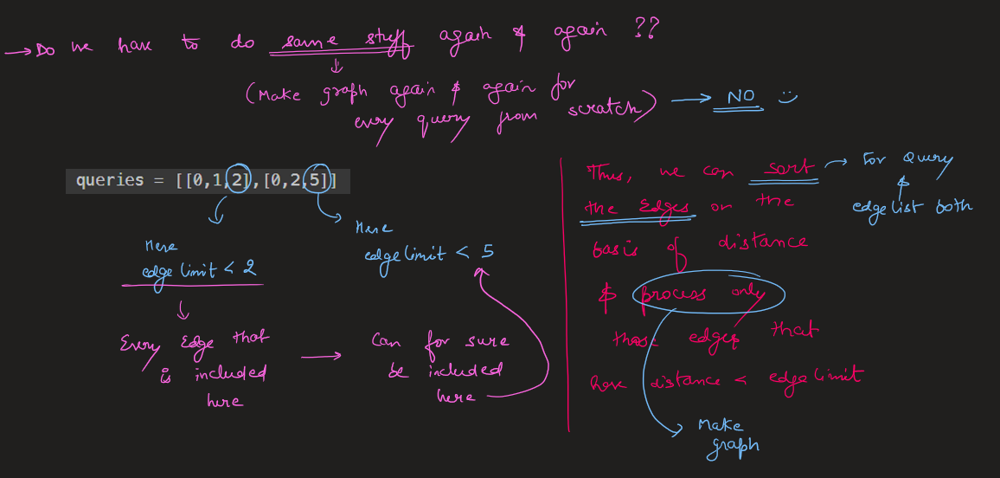\n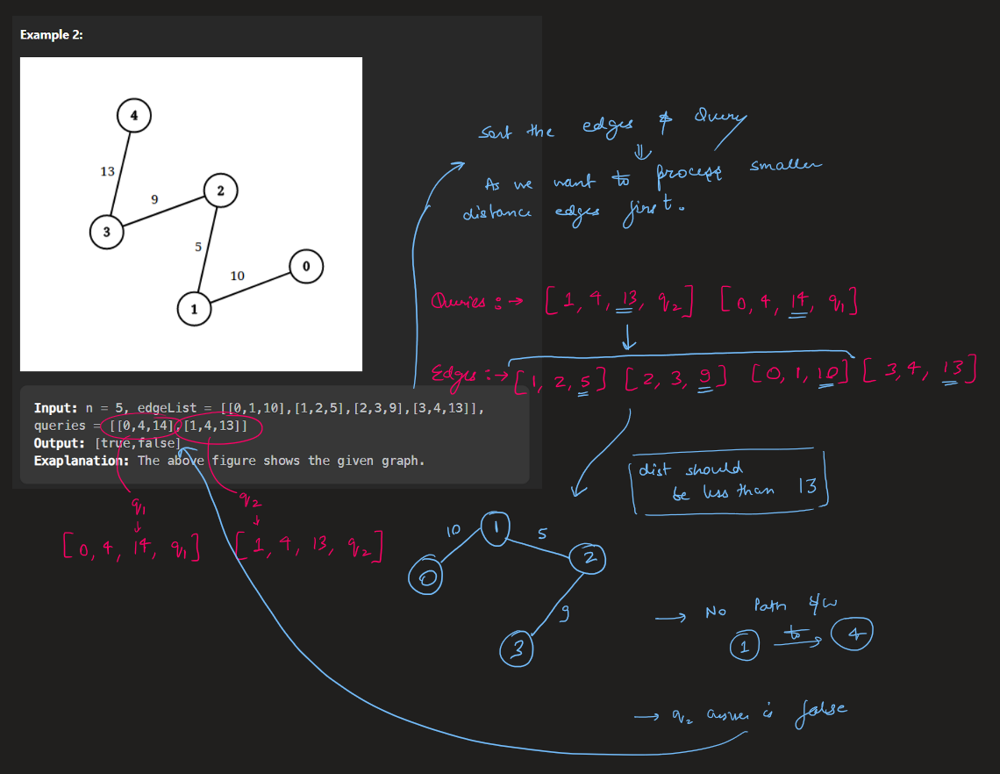\n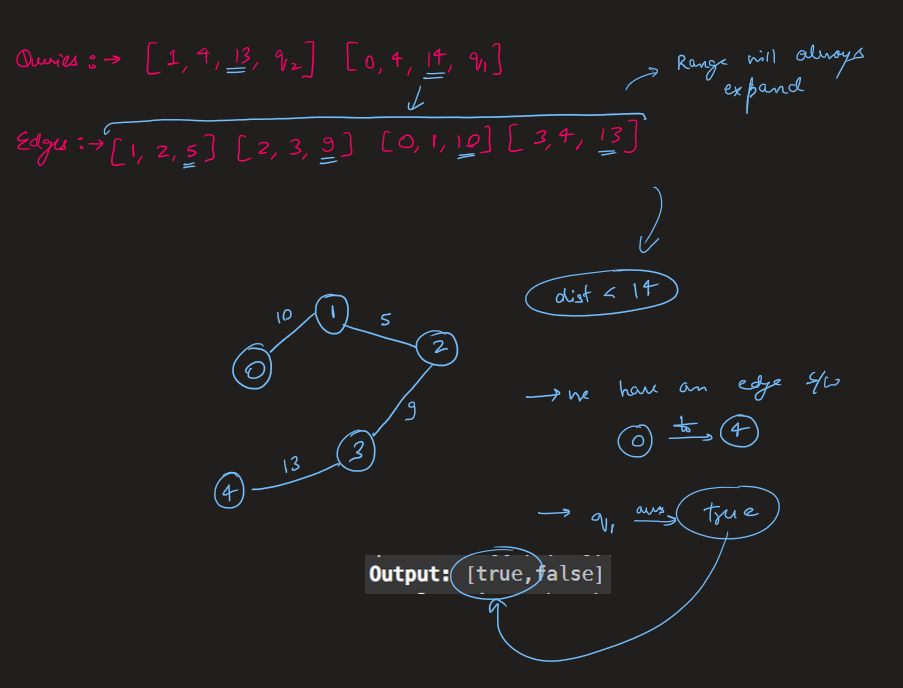\n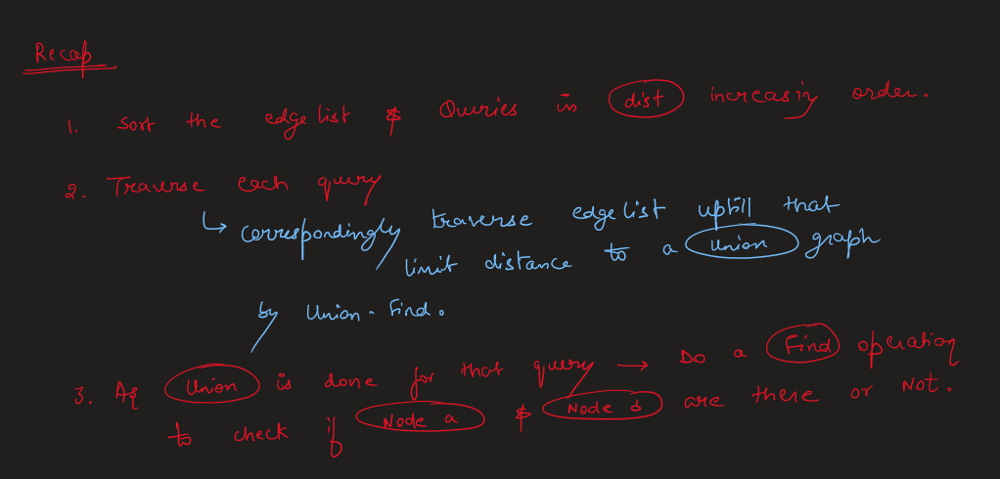\n\n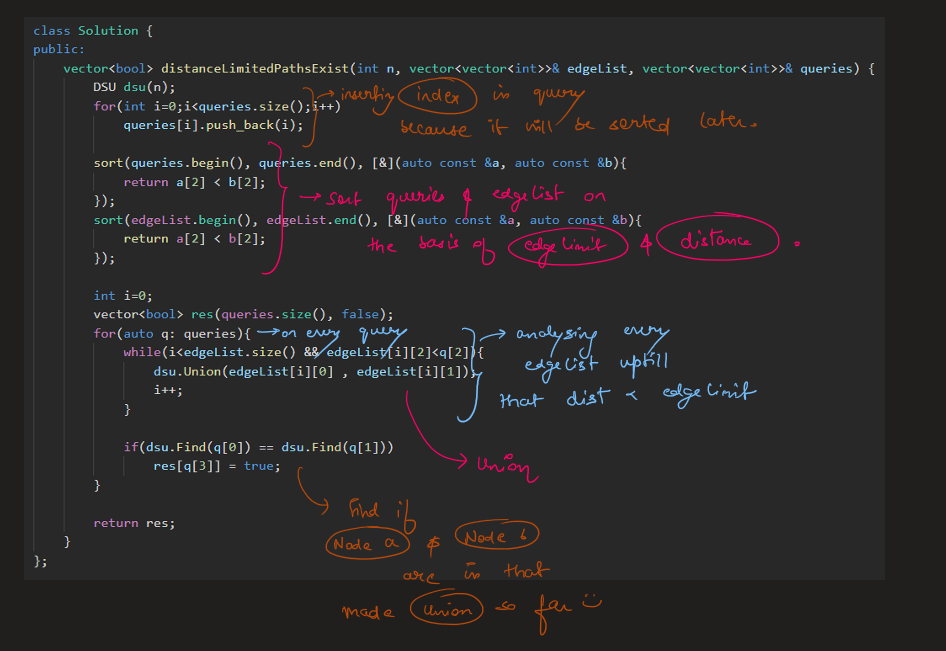\n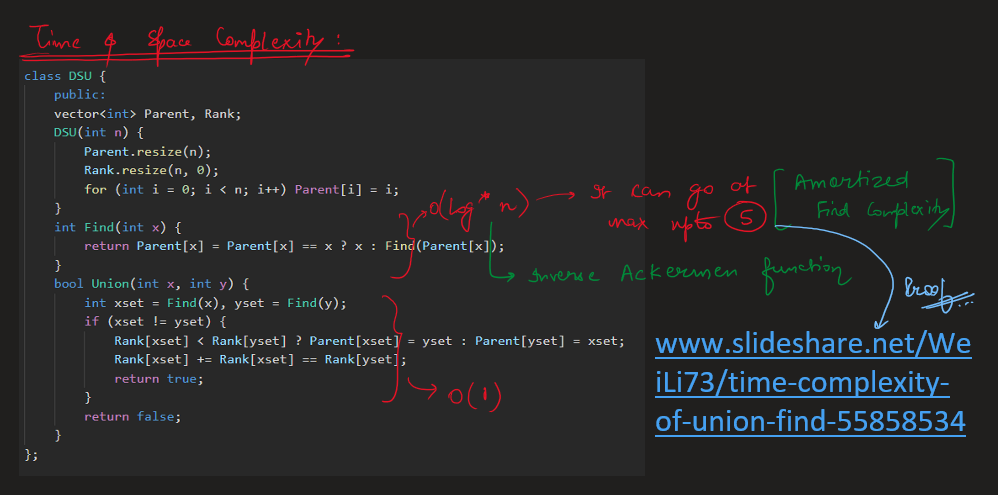\n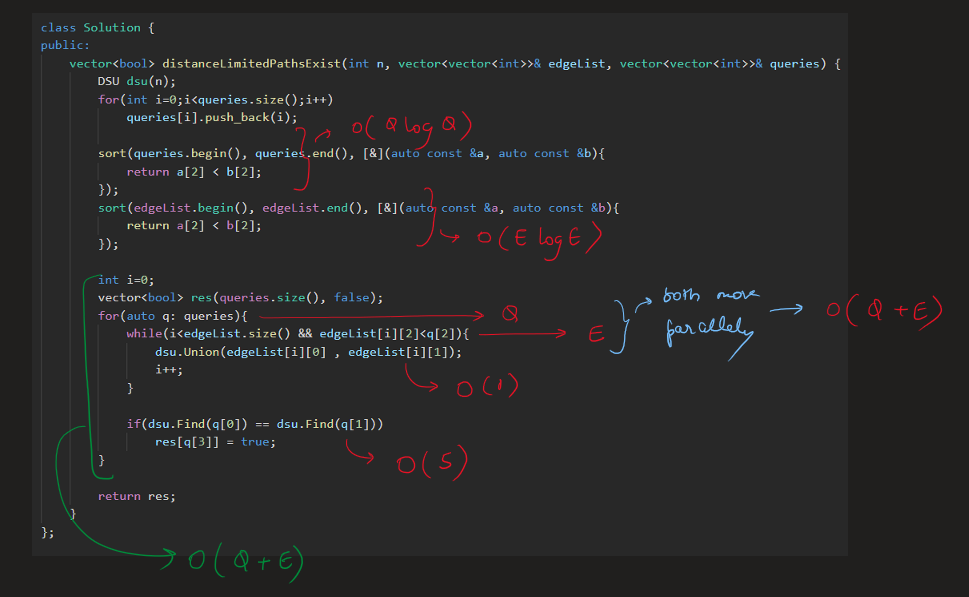\n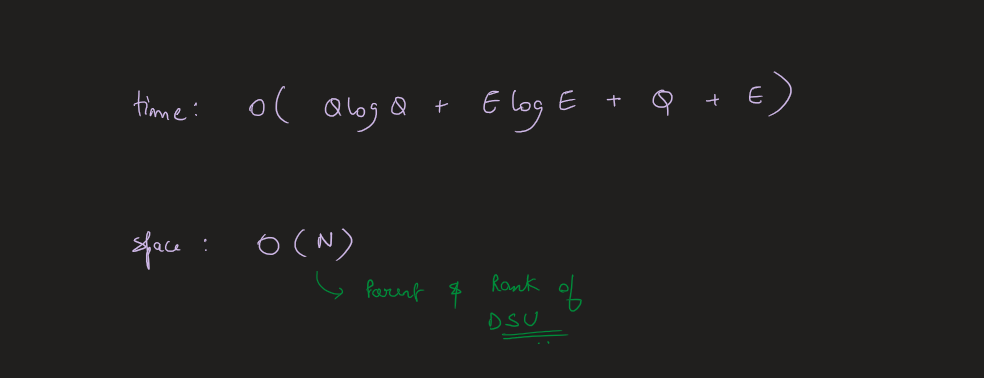\n\n\n# Code\n`Mark the DSU Code as the template [I always use this ONLY]`\n```C++ []\nclass DSU {\n public:\n vector<int> Parent, Rank;\n DSU(int n) {\n Parent.resize(n);\n Rank.resize(n, 0);\n for (int i = 0; i < n; i++) Parent[i] = i;\n }\n int Find(int x) {\n return Parent[x] = Parent[x] == x ? x : Find(Parent[x]);\n }\n bool Union(int x, int y) {\n int xset = Find(x), yset = Find(y);\n if (xset != yset) {\n Rank[xset] < Rank[yset] ? Parent[xset] = yset : Parent[yset] = xset;\n Rank[xset] += Rank[xset] == Rank[yset];\n return true;\n }\n return false;\n }\n};\n\nclass Solution {\npublic:\n vector<bool> distanceLimitedPathsExist(int n, vector<vector<int>>& edgeList, vector<vector<int>>& queries) {\n DSU dsu(n);\n for(int i=0;i<queries.size();i++)\n queries[i].push_back(i);\n \n sort(queries.begin(), queries.end(), [&](auto const &a, auto const &b){\n return a[2] < b[2];\n });\n sort(edgeList.begin(), edgeList.end(), [&](auto const &a, auto const &b){\n return a[2] < b[2];\n });\n \n int i=0;\n vector<bool> res(queries.size(), false);\n for(auto q: queries){\n while(i<edgeList.size() && edgeList[i][2]<q[2]){\n dsu.Union(edgeList[i][0] , edgeList[i][1]);\n i++;\n }\n \n if(dsu.Find(q[0]) == dsu.Find(q[1]))\n res[q[3]] = true;\n }\n \n return res;\n }\n};\n```\n```Java []\nclass DSU {\n private int[] parent;\n private int[] rank;\n\n public DSU(int n) {\n parent = new int[n];\n rank = new int[n];\n for (int i = 0; i < n; i++) {\n parent[i] = i;\n }\n }\n\n public int find(int x) {\n if (parent[x] == x) {\n return x;\n }\n return parent[x] = find(parent[x]);\n }\n\n public boolean union(int x, int y) {\n int xset = find(x), yset = find(y);\n if (xset != yset) {\n if (rank[xset] < rank[yset]) {\n parent[xset] = yset;\n } else {\n parent[yset] = xset;\n }\n if (rank[xset] == rank[yset]) {\n rank[xset]++;\n }\n return true;\n }\n return false;\n }\n}\n\nclass Solution {\n public boolean[] distanceLimitedPathsExist(int n, int[][] edgeList, int[][] queries) {\n DSU dsu = new DSU(n);\n for (int i = 0; i < queries.length; i++) {\n queries[i] = new int[] { queries[i][0], queries[i][1], queries[i][2], i };\n }\n\n Arrays.sort(queries, (a, b) -> Integer.compare(a[2], b[2]));\n Arrays.sort(edgeList, (a, b) -> Integer.compare(a[2], b[2]));\n\n int i = 0;\n boolean[] res = new boolean[queries.length];\n for (int[] q : queries) {\n while (i < edgeList.length && edgeList[i][2] < q[2]) {\n dsu.union(edgeList[i][0], edgeList[i][1]);\n i++;\n }\n\n if (dsu.find(q[0]) == dsu.find(q[1])) {\n res[q[3]] = true;\n }\n }\n\n return res;\n }\n}\n```\n```Python []\nclass DSU:\n def __init__(self, n):\n self.parent = list(range(n))\n self.rank = [0] * n\n\n def find(self, x):\n if self.parent[x] == x:\n return x\n self.parent[x] = self.find(self.parent[x])\n return self.parent[x]\n\n def union(self, x, y):\n xset, yset = self.find(x), self.find(y)\n if xset != yset:\n if self.rank[xset] < self.rank[yset]:\n self.parent[xset] = yset\n else:\n self.parent[yset] = xset\n if self.rank[xset] == self.rank[yset]:\n self.rank[xset] += 1\n return True\n return False\n\nclass Solution:\n def distanceLimitedPathsExist(self, n: int, edgeList: List[List[int]], queries: List[List[int]]) -> List[bool]:\n dsu = DSU(n)\n for i, q in enumerate(queries):\n queries[i].append(i)\n\n queries.sort(key=lambda q: q[2])\n edgeList.sort(key=lambda e: e[2])\n\n i = 0\n res = [False] * len(queries)\n for q in queries:\n while i < len(edgeList) and edgeList[i][2] < q[2]:\n dsu.union(edgeList[i][0], edgeList[i][1])\n i += 1\n\n if dsu.find(q[0]) == dsu.find(q[1]):\n res[q[3]] = True\n\n return res\n```\n
| 88 | 4 |
['Union Find', 'Graph', 'C++', 'Java', 'Python3']
| 8 |
checking-existence-of-edge-length-limited-paths
|
C++ Union Find
|
c-union-find-by-lzl124631x-wi0b
|
Solution 1. Union Find\n\nSort the edges from small distance to large distance.\n\nTraverse the queries from small limit to large limit. Given a limit, we union
|
lzl124631x
|
NORMAL
|
2020-12-20T04:00:47.380272+00:00
|
2021-01-18T18:30:56.942825+00:00
| 4,611 | false |
## Solution 1. Union Find\n\nSort the edges from small distance to large distance.\n\nTraverse the queries from small limit to large limit. Given a limit, we union the nodes that can be connected. \n\nIn this way, we just need to traverse the edges that are smaller than the limit. Since we are visiting the queries with increasing limit, we just need to visit the edges once from small distance to large distance.\n\n```cpp\n// OJ: https://leetcode.com/contest/weekly-contest-220/problems/checking-existence-of-edge-length-limited-paths/\n// Author: github.com/lzl124631x\n// Time: O(ElogE + QlogQ)\n// Space: O(N)\nclass UnionFind {\n vector<int> id;\npublic:\n UnionFind(int n) : id(n) {\n iota(begin(id), end(id), 0);\n }\n void connect(int a, int b) {\n int x = find(a), y = find(b);\n if (x == y) return;\n id[x] = y;\n }\n bool connected(int i, int j) { return find(i) == find(j); }\n int find(int a) {\n return id[a] == a ? a : (id[a] = find(id[a]));\n }\n};\nclass Solution {\npublic:\n vector<bool> distanceLimitedPathsExist(int n, vector<vector<int>>& E, vector<vector<int>>& Q) {\n vector<bool> ans(Q.size());\n for (int i = 0; i < Q.size(); ++i) Q[i].push_back(i);\n sort(begin(Q), end(Q), [&](auto &a, auto &b) { return a[2] < b[2]; });\n sort(begin(E), end(E), [&](auto &a, auto &b) { return a[2] < b[2]; });\n UnionFind uf(n);\n int i = 0;\n for (auto &q : Q) { // traverse the queries from small limit to large limit\n int u = q[0], v = q[1], limit = q[2], qid = q[3];\n for (; i < E.size() && E[i][2] < limit; ++i) uf.connect(E[i][0], E[i][1]); // visit the edges that are smaller than the limit\n ans[qid] = uf.connected(u, v);\n }\n return ans;\n }\n};\n```
| 45 | 1 |
[]
| 6 |
checking-existence-of-edge-length-limited-paths
|
✔💯 DAY 394 | Custom Union-Find | 100% 0ms | [PYTHON/JAVA/C++] | EXPLAINED | Approach 💫
|
day-394-custom-union-find-100-0ms-python-4y4b
|
Please Upvote as it really motivates me \uD83C\uDD99\uD83C\uDD99\uD83C\uDD99\n\n\n# Intuition & Approach\n Describe your approach to solving the problem. \n####
|
ManojKumarPatnaik
|
NORMAL
|
2023-04-29T03:44:29.820009+00:00
|
2023-04-29T10:27:56.838966+00:00
| 3,099 | false |
# Please Upvote as it really motivates me \uD83C\uDD99\uD83C\uDD99\uD83C\uDD99\n\n\n# Intuition & Approach\n<!-- Describe your approach to solving the problem. -->\n##### \u2022\tproblem is to determine if there is a path between two nodes in an undirected graph such that each edge on the path has a distance strictly less than a given limit.\n##### \u2022\tThe input consists of the number of nodes, the edge list, and the queries.\n##### \u2022\tThe edge list is an array of arrays, where each sub-array represents an edge between two nodes and the distance between them.\n##### \u2022\tThe queries are an array of arrays, where each sub-array represents a query with two nodes and a limit.\n##### \u2022\tThe using the union-find algorithm to determine if there is a path between two nodes.\n##### \u2022\tThe union-find algorithm is used to group nodes into connected components.\n##### \u2022\tFirst sorts the edges in the edge list by their distance in ascending order.\n##### \u2022 Then iterates over the sorted edges and performs a union operation on the nodes connected by the edge.\n##### \u2022\tThe union operation updates the parent and rank arrays to group the nodes into connected components.\n##### \u2022\tThen iterates over the queries and checks if the two nodes are connected and if the distance between them is less than the given limit.\n##### \u2022\tThe isConnectedAndWithinLimit method uses the find method to determine if the two nodes are connected and if the distance between them is less than the given limit.\n##### \u2022\tThe find method uses the parent and weight arrays to find the root of the connected component and checks if the weight of the edge is less than the given limit.\n##### \u2022\tThe union method updates the parent, rank, and weight arrays to group the nodes into connected components and store the weight of the edge.\n##### \u2022\tfinally returns a boolean array where each element represents if there is a path between the two nodes in the corresponding query with edges less than the given limit.\n\n\n\n# Code\n```java []\nclass Solution {\n private int[] parent;\n private int[] rank;\n private int[] weight;\n public boolean[] distanceLimitedPathsExist(int length, int[][] adjList, int[][] queries) {\n // Initialize parent, rank, and weight arrays\n parent = new int[length];\n rank = new int[length];\n weight = new int[length];\n for (int i = 0; i < length ; i++) parent[i] = i;\n\n // Sort edges in the adjacency list by distance\n Arrays.sort(adjList, Comparator.comparingInt(a -> a[2]));\n // Group nodes into connected components using union-find algorithm\n for (int[] edge : adjList) unionByRank(edge[0], edge[1], edge[2]);\n\n // Initialize answer array\n boolean[] answer = new boolean[queries.length];\n // Check if there is a path between two nodes with distance less than the given limit for each query\n for (int i = 0 ; i < queries.length; i++)\n answer[i] = isConnectedAndWithinLimit(queries[i][0], queries[i][1], queries[i][2]);\n\n return answer;\n }\n\n // Check if there is a path between two nodes with distance less than the given limit\n public boolean isConnectedAndWithinLimit(int p, int q, int limit) {\n return find(p, limit) == find(q, limit);\n }\n\n // Find the root of the connected component for a node with distance less than the given limit\n private int find (int x, int limit) {\n while (x != parent[x]) {\n // If the weight of the edge is greater than or equal to the given limit, break out of the loop\n if (weight[x] >= limit) {\n break;\n }\n x = parent[x];\n }\n return x;\n }\n\n // Union two nodes into the same connected component with the given limit as the weight of the edge\n private void unionByRank (int x, int y, int limit) {\n // Find the root of the connected component for each node\n int x_ref = find (x, Integer.MAX_VALUE);\n int y_ref = find (y, Integer.MAX_VALUE);\n if (x_ref != y_ref) {\n // If the rank of the root of x is less than the rank of the root of y, make y the parent of x\n if (rank[x_ref] < rank[y_ref]) {\n parent[x_ref] = y_ref;\n weight [x_ref] = limit;;\n } else {\n // Otherwise, make x the parent of y\n parent[y_ref] = x_ref;\n weight[y_ref] = limit;\n // If the ranks of the roots are equal, increment the rank of the root of x\n if (rank[x_ref] == rank[y_ref]) {\n rank[x_ref]++;\n }\n }\n }\n }\n}\n```\n```python []\nclass Solution:\n def distanceLimitedPathsExist(self, length: int, adjList: List[List[int]], queries: List[List[int]]) -> List[bool]:\n parent = [i for i in range(length)]\n rank = [0 for i in range(length)]\n weight = [0 for i in range(length)]\n\n adjList.sort(key=lambda x: x[2])\n for edge in adjList:\n self.unionByRank(edge[0], edge[1], edge[2], parent, rank, weight)\n\n answer = []\n for query in queries:\n answer.append(self.isConnectedAndWithinLimit(query[0], query[1], query[2], parent, weight))\n\n return answer\n\n def isConnectedAndWithinLimit(self, p: int, q: int, limit: int, parent: List[int], weight: List[int]) -> bool:\n return self.find(p, limit, parent, weight) == self.find(q, limit, parent, weight)\n\n def find(self, x: int, limit: int, parent: List[int], weight: List[int]) -> int:\n while x != parent[x]:\n if weight[x] >= limit:\n break\n x = parent[x]\n return x\n\n def unionByRank(self, x: int, y: int, limit: int, parent: List[int], rank: List[int], weight: List[int]) -> None:\n x_ref = self.find(x, float(\'inf\'), parent, weight)\n y_ref = self.find(y, float(\'inf\'), parent, weight)\n if x_ref != y_ref:\n if rank[x_ref] < rank[y_ref]:\n parent[x_ref] = y_ref\n weight[x_ref] = limit\n else:\n parent[y_ref] = x_ref\n weight[y_ref] = limit\n if rank[x_ref] == rank[y_ref]:\n rank[x_ref] += 1\n```\n\n```c++ []\nclass Solution {\npublic:\n vector<bool> distanceLimitedPathsExist(int length, vector<vector<int>>& adjList, vector<vector<int>>& queries) {\n vector<int> parent(length);\n vector<int> rank(length);\n vector<int> weight(length);\n for (int i = 0; i < length ; i++) parent[i] = i;\n\n sort(adjList.begin(), adjList.end(), [](const vector<int>& a, const vector<int>& b) {\n return a[2] < b[2];\n });\n for (vector<int>& edge : adjList) unionByRank(edge[0], edge[1], edge[2], parent, rank, weight);\n\n vector<bool> answer;\n for (vector<int>& query : queries)\n answer.push_back(isConnectedAndWithinLimit(query[0], query[1], query[2], parent, weight));\n\n return answer;\n }\n\n bool isConnectedAndWithinLimit(int p, int q, int limit, vector<int>& parent, vector<int>& weight) {\n return find(p, limit, parent, weight) == find(q, limit, parent, weight);\n }\n\n int find(int x, int limit, vector<int>& parent, vector<int>& weight) {\n while (x != parent[x]) {\n if (weight[x] >= limit) {\n break;\n }\n x = parent[x];\n }\n return x;\n }\n\n void unionByRank(int x, int y, int limit, vector<int>& parent, vector<int>& rank, vector<int>& weight) {\n int x_ref = find(x, INT_MAX, parent, weight);\n int y_ref = find(y, INT_MAX, parent, weight);\n if (x_ref != y_ref) {\n if (rank[x_ref] < rank[y_ref]) {\n parent[x_ref] = y_ref;\n weight[x_ref] = limit;\n } else {\n parent[y_ref] = x_ref;\n weight[y_ref] = limit;\n if (rank[x_ref] == rank[y_ref]) {\n rank[x_ref]++;\n }\n }\n }\n }\n};\n```\n```csharp []\npublic class Solution {\n public bool[] DistanceLimitedPathsExist(int length, int[][] adjList, int[][] queries) {\n int[] parent = Enumerable.Range(0, length).ToArray();\n int[] rank = new int[length];\n int[] weight = new int[length];\n\n Array.Sort(adjList, (a, b) => a[2].CompareTo(b[2]));\n foreach (int[] edge in adjList) {\n Union(edge[0], edge[1], edge[2], parent, rank, weight);\n }\n\n bool[] answer = new bool[queries.Length];\n for (int i = 0; i < queries.Length; i++) {\n answer[i] = IsConnectedAndWithinLimit(queries[i][0], queries[i][1], queries[i][2], parent, weight);\n }\n\n return answer;\n }\n\n private bool IsConnectedAndWithinLimit(int p, int q, int limit, int[] parent, int[] weight) {\n return Find(p, limit, parent, weight) == Find(q, limit, parent, weight);\n }\n\n private int Find(int x, int limit, int[] parent, int[] weight) {\n while (x != parent[x]) {\n if (weight[x] >= limit) {\n break;\n }\n x = parent[x];\n }\n return x;\n }\n\n private void Union(int x, int y, int limit, int[] parent, int[] rank, int[] weight) {\n int xRef = Find(x, int.MaxValue, parent, weight);\n int yRef = Find(y, int.MaxValue, parent, weight);\n if (xRef == yRef) {\n return;\n }\n if (rank[xRef] < rank[yRef]) {\n parent[xRef] = yRef;\n weight[xRef] = limit;\n } else {\n parent[yRef] = xRef;\n weight[yRef] = limit;\n if (rank[xRef] == rank[yRef]) {\n rank[xRef]++;\n }\n }\n }\n}\n```\n\n# Please Upvote as it really motivates me \uD83C\uDD99\uD83C\uDD99\uD83C\uDD99\n\n\n# 2nd union by size \n\n```java []\nclass Solution {\n private int[] parent;\n private int[] size;\n private int[] weight;\n public boolean[] distanceLimitedPathsExist(int length, int[][] adjList, int[][] queries) {\n // Initialize parent, size, and weight arrays\n parent = new int[length];\n size = new int[length];\n weight = new int[length];\n for (int i = 0; i < length ; i++) {\n parent[i] = i;\n size[i] = 1;\n }\n\n // Sort edges in the adjacency list by distance\n Arrays.sort(adjList, Comparator.comparingInt(a -> a[2]));\n // Group nodes into connected components using union-find algorithm\n for (int[] edge : adjList) unionBySize(edge[0], edge[1], edge[2]);\n\n // Initialize answer array\n boolean[] answer = new boolean[queries.length];\n // Check if there is a path between two nodes with distance less than the given limit for each query\n for (int i = 0 ; i < queries.length; i++)\n answer[i] = isConnectedAndWithinLimit(queries[i][0], queries[i][1], queries[i][2]);\n\n return answer;\n }\n\n // Check if there is a path between two nodes with distance less than the given limit\n public boolean isConnectedAndWithinLimit(int p, int q, int limit) {\n return find(p, limit) == find(q, limit);\n }\n\n // Find the root of the connected component for a node with distance less than the given limit\n private int find (int x, int limit) {\n while (x != parent[x]) {\n // If the weight of the edge is greater than or equal to the given limit, break out of the loop\n if (weight[x] >= limit) {\n break;\n }\n x = parent[x];\n }\n return x;\n }\n\n // Union two nodes into the same connected component with the given limit as the weight of the edge\n private void unionBySize (int x, int y, int limit) {\n // Find the root of the connected component for each node\n int x_ref = find (x, Integer.MAX_VALUE);\n int y_ref = find (y, Integer.MAX_VALUE);\n if (x_ref != y_ref) {\n // If the size of the root of x is less than the size of the root of y, make y the parent of x\n if (size[x_ref] < size[y_ref]) {\n parent[x_ref] = y_ref;\n weight [x_ref] = limit;\n size[y_ref] += size[x_ref];\n } else {\n // Otherwise, make x the parent of y\n parent[y_ref] = x_ref;\n weight[y_ref] = limit;\n size[x_ref] += size[y_ref];\n }\n }\n }\n}\n```\n# Complexity\n- Time complexity:\nSorting the adjacency list takes O(E log E) time, where E is the number of edges in the graph.\nThe union-find algorithm takes O(E \u03B1(V)) time, where \u03B1 is the inverse Ackermann function and V is the number of vertices in the graph. In practice, \u03B1(V) is a very small value, so we can consider the time complexity to be O(E).\nChecking if there is a path between two nodes with distance less than the given limit takes O(log V) time, where V is the number of vertices in the graph.\nWe perform this check for each query, so the total time complexity for all queries is O(Q log V), where Q is the number of queries.\nTherefore, the overall time complexity of the algorithm is O(E log E + Q log V).\n- Space Complexity:\nWe use three arrays of size V to store the parent, rank, and weight of each node in the graph, so the space complexity is O(V).\nWe also use a boolean array of size Q to store the answer for each query, so the space complexity is O(Q).\nTherefore, the overall space complexity of the algorithm is O(V + Q).\n\n\n# dry run \nFor the first: Input: n = 3, edgeList = [[0,1,2],[1,2,4],[2,0,8],[1,0,16]], queries = [[0,1,2],[0,2,5]]\nOutput: [false,true]\n\n\nWe have 3 nodes and the following edges: (0,1) with weight 2, (1,2) with weight 4, (2,0) with weight 8, and (1,0) with weight 16.\nWe have 2 queries: (0,1) with limit 2 and (0,2) with limit 5.\nWe initialize the parent, rank, and weight arrays to [0, 1, 2] and [0, 0, 0].\nWe sort the edges in the adjacency list by distance: (0,1) with weight 2, (1,2) with weight 4, (2,0) with weight 8, and (1,0) with weight 16.\nWe group the nodes into connected components using the union-find algorithm. First, we union nodes 0 and 1 with weight 2, then we union nodes 1 and 2 with weight 4, and finally we union nodes 2 and 0 with weight 8. The resulting parent array is [0, 0, 0].\nFor the first query (0,1) with limit 2, we check if there is a path between nodes 0 and 1 with distance less than 2. We find the root of node 0 with limit 2, which is 0, and the root of node 1 with limit 2, which is 0. Since the roots are the same, we return true.\nFor the second query (0,2) with limit 5, we check if there is a path between nodes 0 and 2 with distance less than 5. We find the root of node 0 with limit 5, which is 0, and the root of node 2 with limit 5, which is 0. Since the roots are the same, we return true.\nTherefore, the output is [false, true].\n\nFor the second input:\nInput: n = 5, edgeList = [[0,1,10],[1,2,5],[2,3,9],[3,4,13]], queries = [[0,4,14],[1,4,13]]\nOutput: [true,false]\n\nWe have 5 nodes and the following edges: (0,1) with weight 10, (1,2) with weight 5, (2,3) with weight 9, and (3,4) with weight 13.\nWe have 2 queries: (0,4) with limit 14 and (1,4) with limit 13.\nWe initialize the parent, rank, and weight arrays to [0, 1, 2, 3, 4] and [0, 0, 0, 0, 0].\nWe sort the edges in the adjacency list by distance: (1,2) with weight 5, (0,1) with weight 10, (2,3) with weight 9, and (3,4) with weight 13.\nWe group the nodes into connected components using the union-find algorithm. First, we union nodes 1 and 2 with weight 5, then we union nodes 0 and 1 with weight 10, then we union nodes 2 and 3 with weight 9, and finally we union nodes 3 and 4 with weight 13. The resulting parent array is [0, 0, 0, 2, 3].\nFor the first query (0,4) with limit 14, we check if there is a path between nodes 0 and 4 with distance less than 14. We find the root of node 0 with limit 14, which is 0, and the root of node 4 with limit 14, which is 3. Since the roots are not the same, we return false.\nFor the second query (1,4) with limit 13, we check if there is a path between nodes 1 and 4 with distance less than 13. We find the root of node 1 with limit 13, which is 0, and the root of node 4 with limit 13, which is 3. Since the roots are the same, we return true.\nTherefore, the output is [true, false].\n\n\n# FAQ \n\n# Why we want to merge the smaller tree into the larger tree?\n\nIn the Union-Find algorithm, the rank array is used to keep of the depth of each node in the tree. When performing the union operation, we want to merge the smaller tree into the larger tree to keep the depth of the tree as small as possible. This helps to improve the performance of the find operation, which is used to determine the root of the tree.\n\nIf we always merge the smaller tree into the larger tree, we can ensure that the depth of the tree does not increase significantly. This is because the depth of the tree is proportional to the logarithm of the number of nodes in the tree. By keeping the depth of the tree small, we can ensure that the find operation runs in O(log n) time, where n is the number of nodes in the tree.\n\nThe rank array is used to keep track of the depth of each node in the tree. When we merge two trees, we compare the rank of the root nodes of the two trees. If the rank of the root node of the first tree is less than the rank of the root node of the second tree, we make the root node of the first tree a child of the root node of the second tree. Otherwise, we make the root node of the second tree a child of the root node of the first tree. If the rank of the root nodes is the same, we arbitrarily choose one of the root nodes to be the parent and increment its rank by one.\n\nBy always merging the smaller tree into the larger tree, we can ensure that the depth of the tree does not increase significantly, which helps to improve the performance of the find operation.\n\n# How Path Compression will work in the Union-Find.\n\nPath is a technique used in the Union-Find algorithm to improve the performance the find operation The find operation is used to determine the root of the tree that a node belongs to. In the basic implementation of the Union-Find algorithm, the find operation traverses the tree from the node to the root to determine the root of the tree. This can take O(log n) time in the worst case, where n is the number of nodes in the tree.\n\nPath compression is a technique that can be used to reduce the depth of the tree during the find operation. When we perform the find operation on a node, we traverse the tree from the node to the root to determine the root of the tree. During this traversal, we can update the parent of each node along the path to the root to be the root itself. This can be done recursively or iteratively.\n\nBy updating the parent of each node along the path to the root to be the root itself, we can reduce the depth of the tree. This can help to improve the performance of the find operation, as subsequent find operations on the same node or its descendants will take less time.\n\n\n\n\n\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\nThanks for visiting my solution.\uD83D\uDE0A Keep Learning\nPlease give my solution an upvote! \uD83D\uDC4D \uD83C\uDD99\uD83C\uDD99\uD83C\uDD99\nhttps://leetcode.com/problems/checking-existence-of-edge-length-limited-paths/solutions/3465024/day-394-union-find-100-0ms-python-java-c-explained-approach/\nIt\'s a simple way to show your appreciation and\nkeep me motivated. Thank you! \uD83D\uDE0A
| 32 | 2 |
['Python', 'C++', 'Java', 'Python3', 'C#']
| 1 |
checking-existence-of-edge-length-limited-paths
|
C++ Union-Find and Multimap
|
c-union-find-and-multimap-by-votrubac-sajd
|
Did not see it... tried modified Floyd Warshall - too slow - and then BFS - faster but still too slow.\n\nThe key observation is that we can process queries in
|
votrubac
|
NORMAL
|
2020-12-20T05:14:39.647169+00:00
|
2020-12-20T05:14:39.647239+00:00
| 3,652 | false |
Did not see it... tried modified Floyd Warshall - too slow - and then BFS - faster but still too slow.\n\nThe key observation is that we can process queries in any order - e.g. from smallest to largest distance. When processing a query, we can use all edges with smaller distances. When processing the next query, we can add more edges, and so on.\n\nDisjoined set structure allows tracking connected sub-sets and joining them efficiently. \n\n```cpp\nint find(vector<int> &ds, int i) {\n return ds[i] < 0 ? i : ds[i] = find(ds, ds[i]);\n}\nvector<bool> distanceLimitedPathsExist(int n, vector<vector<int>>& edges, vector<vector<int>>& qs) {\n multimap<int, array<int, 3>> mm;\n for (auto i = 0; i < qs.size(); ++i)\n mm.insert({qs[i][2], {qs[i][0], qs[i][1], i}});\n sort(begin(edges), end(edges), [](vector<int> &a, vector<int> &b) { return a[2] < b[2]; });\n vector<int> ds(n, -1);\n vector<bool> res(qs.size());\n int ei = 0;\n for (auto &q : mm) {\n while (ei < edges.size() && edges[ei][2] < q.first) {\n int i = find(ds, edges[ei][0]), j = find(ds, edges[ei][1]);\n if (i != j) {\n if (ds[i] > ds[j])\n swap(i, j);\n ds[i] += ds[j];\n ds[j] = i;\n }\n ++ei;\n }\n res[q.second[2]] = find(ds, q.second[0]) == find(ds, q.second[1]);\n }\n return res;\n}\n```
| 30 | 1 |
[]
| 6 |
checking-existence-of-edge-length-limited-paths
|
Clean Java
|
clean-java-by-rexue70-wo0m
|
after sort edge, query by weight, we constract UnionFind from small to large\nwe use extra query[3] to save original index(position)\n\nclass Solution {\n pu
|
rexue70
|
NORMAL
|
2020-12-20T04:44:01.239963+00:00
|
2020-12-23T05:37:45.022747+00:00
| 2,949 | false |
after sort edge, query by weight, we constract UnionFind from small to large\nwe use extra query[3] to save original index(position)\n```\nclass Solution {\n public boolean[] distanceLimitedPathsExist(int n, int[][] edgeList, int[][] queries) {\n int M = edgeList.length, N = queries.length;\n DSU dsu = new DSU(n);\n for (int i = 0; i < queries.length; i++) \n queries[i] = new int[]{queries[i][0], queries[i][1], queries[i][2], i}; \n Arrays.sort(queries, (a, b) -> a[2] - b[2]);\n Arrays.sort(edgeList, (a, b) -> a[2] - b[2]);\n boolean[] res = new boolean[N];\n for (int i = 0, j = 0; i < N; i++) {\n int[] query = queries[i];\n while (j < M && edgeList[j][2] < queries[i][2])\n dsu.union(edgeList[j][0], edgeList[j++][1]);\n res[queries[i][3]] = dsu.find(queries[i][0]) == dsu.find(queries[i][1]);\n }\n return res;\n }\n}\n\nclass DSU {\n int[] parent;\n public DSU(int N) {\n this.parent = new int[N];\n for (int i = 0; i < N; i++) parent[i] = i;\n }\n public int find(int x) {\n if (parent[x] != x) parent[x] = find(parent[x]);\n return parent[x];\n }\n public void union(int x, int y) {\n parent[find(x)] = parent[find(y)];\n }\n}\n\n```
| 26 | 0 |
[]
| 7 |
checking-existence-of-edge-length-limited-paths
|
[Java] Clean Union-Find Solution || with detailed comments
|
java-clean-union-find-solution-with-deta-i145
|
This great question utilize the power of Union-Find which enables "constant" time query. The tricks are actually pretty straightforward: \n\n1. sort both querie
|
xieyun95
|
NORMAL
|
2021-05-05T06:32:58.019350+00:00
|
2021-06-14T05:43:46.191581+00:00
| 2,236 | false |
This great question utilize the power of **Union-Find** which enables "constant" time query. The tricks are actually pretty straightforward: \n\n1. sort both queries by increasing weight\n2. sort edges by increasing weight\n3. for each query, union all edges whose weight is less than this query\n4. check if two nodes in query belongs to the same group\n\nThis idea is pretty important (yet not unique). We may utilize similar tricks in these problems:\n* [1631. Path With Minimum Effort](https://leetcode.com/problems/path-with-minimum-effort/discuss/1192238/xieyun95)\n* [1102. Path With Maximum Minimum Value](https://leetcode.com/problems/path-with-maximum-minimum-value/)\n\n\n\n```\nclass Solution {\n private int[] parents;\n public boolean[] distanceLimitedPathsExist(int n, int[][] edgeList, int[][] queries) {\n this.parents = new int[n];\n for (int i = 0; i < n; i++) parents[i] = i;\n \n int m = queries.length;\n \n // storing {u, v, weight, original idx} by increasing weight\n int[][] sortedQueries = new int[m][4];\n for (int i = 0; i < m; i++) {\n sortedQueries[i] = new int[]{queries[i][0], queries[i][1], queries[i][2], i};\n }\n Arrays.sort(sortedQueries, (a,b) -> a[2] - b[2]);\n \n \n // sort edgeList by increasing weight \n Arrays.sort(edgeList, (a,b) -> a[2] - b[2]);\n int idx = 0;\n \n boolean[] res = new boolean[m];\n \n for (int i = 0; i < m; i++) {\n int[] q = sortedQueries[i];\n int w = q[2];\n \n // union all edges with weight less than current query\n while (idx < edgeList.length && edgeList[idx][2] < w) {\n int[] e = edgeList[idx++];\n int u = e[0], v = e[1];\n union(u, v);\n }\n \n int uQuery = q[0], vQuery = q[1], id = q[3];\n res[id] = (find(uQuery) == find(vQuery));\n }\n \n return res;\n }\n \n private void union(int u, int v) {\n int uParent = find(u);\n int vParent = find(v);\n parents[uParent] = vParent;\n }\n \n private int find(int u) {\n while (u != parents[u]) {\n parents[u] = parents[parents[u]];\n u = parents[u];\n }\n return u;\n } \n}\n```
| 22 | 0 |
['Union Find', 'Java']
| 4 |
checking-existence-of-edge-length-limited-paths
|
6 lines with Unicode-Find
|
6-lines-with-unicode-find-by-stefanpochm-ggvv
|
Accepted in 5064 ms. As long as LeetCode lets me, I\'m gonna use Unicode-Find every single time :-P\n\ndef distanceLimitedPathsExist(self, n, E, Q):\n s = \'
|
stefanpochmann
|
NORMAL
|
2020-12-22T03:52:51.599041+00:00
|
2020-12-22T05:55:00.633953+00:00
| 2,212 | false |
Accepted in 5064 ms. As long as LeetCode lets me, I\'m gonna use Unicode-Find every single time :-P\n```\ndef distanceLimitedPathsExist(self, n, E, Q):\n s = \'\'.join(map(chr, range(n)))\n *map(list.append, Q, count()),\n for u, v, d, *j in sorted(Q + E, key=itemgetter(2)):\n if j: Q[j[0]] = s[u] == s[v]\n else: s = s.replace(s[u], s[v])\n return Q\n```\n(This is Python3, I just didn\'t like the look of the long cluttered original function signature.)\n\nNo need to merge the sorted edges and queries on our own, we can just put the queries first and rely on Timsort\'s stability. I annotate the queries with their index, both to distinguish them from the edges and to know where to write their results.\n\nLOL, my results are *off the charts*. Literally. On opposite ends! My *time* of 5064 ms is off the time distribution chart\'s *right* end of about 3800 ms, and my *memory usage* of 53.1 MB is off the memory distribution\'s *left* end of 60.0 MB. Well, a string is a very compact data structure.\n\n
| 22 | 0 |
['Python']
| 5 |
checking-existence-of-edge-length-limited-paths
|
Easy Solution Of JAVA 🔥C++🔥Beginner Friendly With Comments🔥
|
easy-solution-of-java-cbeginner-friendly-y9bz
|
\n\n# Code\nPLEASE UPVOTE IF YOU LIKE.\n\nclass Solution {\n // union find\n // sort both edgeList and queries in increasing order of dist and limit, resp
|
shivrastogi
|
NORMAL
|
2023-04-29T01:10:13.966792+00:00
|
2023-04-29T01:35:46.694174+00:00
| 3,419 | false |
\n\n# Code\nPLEASE UPVOTE IF YOU LIKE.\n```\nclass Solution {\n // union find\n // sort both edgeList and queries in increasing order of dist and limit, respectively\n // two loops:\n // outer loop: for each query, if limit increases, than check to see if there is more edges that\n // can be added\n // inner loop: if dis is less than the new limit, add the edge\n\n // Runtime is bound by sorting: O(ElogE + NlogN + N + E);\n int[] up;\n \n public boolean[] distanceLimitedPathsExist(int n, int[][] edgeList, int[][] queries) {\n up = new int[n];\n Arrays.fill(up, -1);\n \n boolean[] res = new boolean[queries.length];\n Arrays.sort(edgeList, new arrComparator());\n \n \n int[][] temp = new int[queries.length][4];\n for (int i = 0; i < temp.length; i++) {\n temp[i][0] = queries[i][0];\n temp[i][1] = queries[i][1];\n temp[i][2] = queries[i][2];\n temp[i][3] = i;\n }\n queries = temp;\n Arrays.sort(queries, new arrComparator());\n \n int limit = 0;\n int j = 0;\n for (int i = 0; i < queries.length; i++) {\n int[] q = queries[i];\n if (q[2] > limit) {\n limit = q[2];\n while (j < edgeList.length && edgeList[j][2] < limit) {\n int x = edgeList[j][0];\n int y = edgeList[j][1];\n if (find(x) != find(y)) union(find(x), find(y));\n j++;\n }\n }\n res[q[3]] = find(q[0]) == find(q[1]);\n }\n return res;\n }\n \n private int find(int x) {\n int r = x;\n while (up[r] >= 0) {\n r = up[r];\n }\n \n if (r == x) return r;\n \n int p = up[x];\n while (p >= 0) {\n up[x] = r;\n x = p;\n p = up[x];\n }\n return r;\n }\n \n private void union(int x, int y) {\n if (up[x] > up[y]) {\n up[y] += up[x];\n up[x] = y;\n } else {\n up[x] += up[y];\n up[y] = x;\n }\n }\n \n class arrComparator implements Comparator<int[]> {\n public int compare(int[] a, int[] b) {\n return a[2] - b[2];\n } \n }\n}\n```\nC++\n```\nclass DSUnode{\n public:\n int parent,rank;\n DSUnode(int parent,int rank){\n this->parent=parent;\n this->rank=rank;\n }\n};\nclass DSU{\n private:\n vector<DSUnode>parents;\n void _merge(int parent,int child){\n this->parents[child].parent=parent;\n this->parents[parent].rank+=this->parents[child].rank;\n }\n int _find(int x){\n while(this->parents[x].parent!=x){\n x=this->parents[x].parent;\n }\n return x;\n }\n public:\n DSU(int n){\n for(int i=0;i<n;i++){\n DSUnode element(i,1);\n this->parents.push_back(element);\n }\n }\n void findUnion(int x,int y){\n int parx=this->_find(x);\n int pary=this->_find(y);\n if(parx!=pary){\n if(this->parents[parx].rank>=this->parents[pary].rank){\n this->_merge(parx,pary);\n } else {\n this->_merge(pary,parx);\n }\n }\n }\n bool isConnected(int start,int end){\n return this->_find(start)==this->_find(end);\n }\n};\nclass Solution {\nprivate:\n int determineEnd(vector<int>&weights,int limit){\n int end=lower_bound(weights.begin(),weights.end(),limit)-weights.begin();\n return end==weights.size()?end:end-1;\n }\n bool solve(DSU &dsu,int qs,int qe,int &start,int end,vector<vector<int>>&edges){\n if(dsu.isConnected(qs,qe)){\n return true;\n } else {\n while(start<=end){\n int s=edges[start][0];\n int e=edges[start][1];\n dsu.findUnion(s,e);\n if(dsu.isConnected(qs,qe)){\n return true;\n }\n start++;\n }\n return false;\n }\n }\npublic:\n vector<bool> distanceLimitedPathsExist(int n, vector<vector<int>>& edges, vector<vector<int>>& queries) {\n DSU dsu(n);\n for(int i=0;i<queries.size();i++){\n queries[i].push_back(i);\n }\n sort(edges.begin(),edges.end(),[](vector<int>&e1,vector<int>&e2){\n return e1[2]<e2[2];\n });\n sort(queries.begin(),queries.end(),[](vector<int>&q1,vector<int>&q2){\n return q1[2]<q2[2];\n });\n vector<int>weights;\n for(vector<int>edge:edges){\n weights.push_back(edge[2]);\n }\n vector<bool>ans(queries.size(),true);\n int start=0;\n for(vector<int>query:queries){\n int qs=query[0];\n int qe=query[1];\n int limit=query[2];\n int index=query[3];\n int end=determineEnd(weights,limit);\n ans[index]=solve(dsu,qs,qe,start,end,edges);\n }\n return ans;\n }\n};\n```
| 15 | 2 |
['Sorting', 'Java']
| 0 |
checking-existence-of-edge-length-limited-paths
|
✅[C++] Disjoin Set Union
|
c-disjoin-set-union-by-bit_legion-dplh
|
This question is so far one of the best problem of DSU. \n\nHow to identify DSU? \nWell, in questions where we are asked to reach one node from another, or wher
|
biT_Legion
|
NORMAL
|
2022-07-04T01:28:44.097757+00:00
|
2022-07-04T01:28:44.097786+00:00
| 1,578 | false |
This question is so far one of the best problem of DSU. \n\n**How to identify DSU?** \nWell, in questions where we are asked to reach one node from another, or where we need to attach nodes or form components of similiar types, we go with DSU. In DSU questions, most of the time, we are not given any extra conditions on the path, like shortest, longest, etc. We just need to find if we could reach from one node to another. \n\n**What to do after identifying?**\nThe only two functions in DSU are `join(Node1, Node2)`, to join two nodes, and `find(Node)` to find the godfather of the component to which `Node` belongs.\nNow we can use `Rank` to optimize the join function and `path-compression` to optimize the find function. I\'ve use path-compression only. \n\n**How to approach this question?**\nIn this question, we are given queries and edges. Now, in questions where we have to use DSU, we dont actually need to form the graph, we just have to join two nodes whose parents are not same. \nIn this problem, if we sort the queries and edges array based limits, then we would be able to use the precomputed answer. \n**How?** After sorting both of the arrays based on limits, for each query, we can loop in the edges vector and for each pair of node whose dist < limit, we can join them together. Joining them signifies that for the given limit, there exists a path between those two nodes which has all the edges < curr_limit.\n\n\n```\nvector <int> parent(100005,-1);\nclass Solution {\npublic:\n vector<bool> distanceLimitedPathsExist(int n, vector<vector<int>>& edges, vector<vector<int>>& queries) {\n for(int i = 0; i<=n; i++) parent[i] = i;\n \n\t\t// Sorting the edges array based on dist of each pair of node. \n sort(edges.begin(),edges.end(),[](vector<int>&a, vector<int>&b){\n if(a[2]<b[2]) return true;\n return false;\n });\n\n\t\t// We will need the indices of query elements coz after sorting, the order will change. \n\t\t// So we push the index in the same element vector of query.\n for(int i = 0; i<queries.size(); i++) queries[i].push_back(i);\n\t\t\t\n\t\t// Sorting queries based on limits. \n sort(queries.begin(),queries.end(),[](vector<int>&a,vector<int>&b){\n if(a[2]<b[2]) return true;\n return false;\n });\n \n vector <bool> ans(queries.size(),false);\n int idx = 0;\n for(int i = 0; i<queries.size(); i++){\n // Here we loop on edges vector and join the two nodes having dist < curr_limit.\n\t\t\twhile(idx<edges.size() and edges[idx][2]<queries[i][2]){\n join(edges[idx][0],edges[idx][1]);\n idx++;\n }\n\t\t\t// If the two nodes of current query has same godfather, we set this queries ans as true\n if(find(parent[queries[i][0]]) == find(parent[queries[i][1]])) ans[queries[i][3]] = true;\n }\n return ans;\n }\nprotected:\n int find(int x){\n if(parent[x]==x) return x;\n return parent[x] = find(parent[x]);\n }\n void join(int a, int b){\n a = find(a);\n b = find(b);\n \n if(a!=b) parent[b] = a;\n }\n};\n```
| 13 | 0 |
['Union Find', 'C', 'C++']
| 1 |
checking-existence-of-edge-length-limited-paths
|
C++ solution with disjoint set + two pointers, ~O(nlogn)
|
c-solution-with-disjoint-set-two-pointer-2mnu
|
\nclass disjoint_set {\npublic:\n\tvector<int> R;\n\tdisjoint_set(int n) : R(n) { iota(R.begin(), R.end(), 0); }\n\tint find(int i) { return R[i] == i ? i : R[i
|
mzchen
|
NORMAL
|
2020-12-20T04:00:24.360424+00:00
|
2020-12-20T04:06:19.461443+00:00
| 1,650 | false |
```\nclass disjoint_set {\npublic:\n\tvector<int> R;\n\tdisjoint_set(int n) : R(n) { iota(R.begin(), R.end(), 0); }\n\tint find(int i) { return R[i] == i ? i : R[i] = find(R[i]); }\n\tbool join(int i, int j) { i = find(i); j = find(j); if (i == j) return false; R[i] = j; return true; }\n};\nclass Solution {\npublic:\n vector<bool> distanceLimitedPathsExist(int n, vector<vector<int>>& el, vector<vector<int>>& qs) {\n disjoint_set ds(n);\n sort(el.begin(), el.end(), [](auto &a, auto &b){return a[2] < b[2];});\n\n vector<int> idx(qs.size()); // index sorting instead of data sorting\n iota(idx.begin(), idx.end(), 0);\n sort(idx.begin(), idx.end(), [&](int a, int b){return qs[a][2] < qs[b][2];});\n\n int x = 0;\n vector<bool> ans(qs.size());\n for (auto &i : idx) {\n for (; x < el.size() && el[x][2] < qs[i][2]; x++)\n ds.join(el[x][0], el[x][1]);\n ans[i] = ds.find(qs[i][0]) == ds.find(qs[i][1]);\n }\n return ans;\n }\n};\n```
| 11 | 1 |
[]
| 1 |
checking-existence-of-edge-length-limited-paths
|
✅ Java | DFS Approach - Just for Understanding
|
java-dfs-approach-just-for-understanding-5guq
|
\n// Approach 1: Depth First Search - TLE\n\n// Time complexity: O(n\xB2)\n// Space complexity: O(n\xB2)\t\n\nclass Solution {\n public boolean[] distanceLim
|
prashantkachare
|
NORMAL
|
2023-04-29T06:11:08.173543+00:00
|
2023-04-29T07:05:34.170547+00:00
| 1,352 | false |
```\n// Approach 1: Depth First Search - TLE\n\n// Time complexity: O(n\xB2)\n// Space complexity: O(n\xB2)\t\n\nclass Solution {\n public boolean[] distanceLimitedPathsExist(int n, int[][] edgeList, int[][] queries) {\n Map<Integer, List<Pair<Integer, Integer>>> adj = new HashMap<>();\n \n for (int[] edge : edgeList) {\n adj.computeIfAbsent(edge[0], k -> new ArrayList<>()).add(new Pair(edge[1], edge[2]));\n adj.computeIfAbsent(edge[1], k -> new ArrayList<>()).add(new Pair(edge[0], edge[2]));\n }\n \n boolean[] answer = new boolean[queries.length];\n int i = 0;\n \n for (int[] query : queries) {\n boolean[] visited = new boolean[n];\n answer[i++] = dfs(adj, query[0], query[1], query[2], visited); \n }\n \n return answer;\n }\n \n private boolean dfs(Map<Integer, List<Pair<Integer, Integer>>> adj, int curr, int dest, int limit, boolean[] visited) {\n if (curr == dest)\n return true;\n \n visited[curr] = true;\n \n if (!adj.containsKey(curr))\n return false;\n \n for (Pair<Integer, Integer> next : adj.get(curr)) {\n if (!visited[next.getKey()] && next.getValue() < limit) {\n if (dfs(adj, next.getKey(), dest, limit, visited))\n return true;\n }\n }\n \n return false;\n }\n}\n```\n**Note:-** This solution gives TLE. It\'s provided just for understanding purpose.\n**Please upvote if you find this solution useful. Happy Coding!**
| 10 | 1 |
['Depth-First Search', 'Graph', 'Java']
| 0 |
checking-existence-of-edge-length-limited-paths
|
[Java] Union-Find Solution
|
java-union-find-solution-by-marvinbai-j7lo
|
The trick is to sort the queries as well so that we could reuse the roots array.\n\nclass Solution {\n \n int curr = 0;\n \n public boolean[] distan
|
marvinbai
|
NORMAL
|
2020-12-20T04:38:25.326728+00:00
|
2020-12-20T07:56:55.017974+00:00
| 918 | false |
The trick is to sort the queries as well so that we could reuse the `roots` array.\n```\nclass Solution {\n \n int curr = 0;\n \n public boolean[] distanceLimitedPathsExist(int n, int[][] edges, int[][] queries) {\n Arrays.sort(edges, (a, b) -> (a[2] - b[2]));\n\t\t// Add another column to the queries so that we know the index after sorting.\n int[][] qs = new int[queries.length][4];\n for(int i = 0; i < queries.length; i++) {\n qs[i] = new int[]{queries[i][0], queries[i][1], queries[i][2], i};\n }\n Arrays.sort(qs, (a, b) -> (a[2] - b[2]));\n boolean[] res = new boolean[queries.length];\n int[] roots = new int[n];\n for(int i = 0; i < n; i++) roots[i] = i;\n for(int i = 0; i < queries.length; i++) {\n int[] q = qs[i];\n res[q[3]] = helper(edges, q[0], q[1], q[2], roots);\n }\n return res;\n }\n \n private boolean helper(int[][] edges, int start, int end, int limit, int[] roots) {\n for(int i = curr; i < edges.length; i++) {\n int[] e = edges[i];\n if(e[2] >= limit) {\n\t\t\t\t// \'curr\' is to mark until which step have we finished the union-find.\n curr = i;\n break;\n }\n int root1 = find(roots, e[0]);\n int root2 = find(roots, e[1]);\n if(root1 != root2) {\n roots[root1] = root2;\n }\n }\n return find(roots, start) == find(roots, end);\n }\n \n private int find(int[] roots, int i) {\n int j = i;\n while(roots[i] != i) {\n i = roots[i];\n }\n roots[j] = i;\n return i;\n }\n}\n```
| 8 | 1 |
['Java']
| 0 |
checking-existence-of-edge-length-limited-paths
|
Java - Sort and then Union Find / Disjoint Set
|
java-sort-and-then-union-find-disjoint-s-vkdy
|
The idea is to sort the queries/edges by distance, then build up a disjoint set with edges allowed for the current query and so on.\n\nRuntime is O(q log(q)) +
|
wilmol
|
NORMAL
|
2020-12-20T04:04:56.357025+00:00
|
2020-12-20T04:04:56.357068+00:00
| 1,173 | false |
The idea is to sort the queries/edges by distance, then build up a disjoint set with edges allowed for the current query and so on.\n\nRuntime is O(q log(q)) + O(e log(e))\n\n```\n public boolean[] distanceLimitedPathsExist(int n, int[][] edgeList, int[][] queries) {\n // DISJOINT SET\n\n Map<int[], Integer> original = new IdentityHashMap<>();\n for (int i = 0; i < queries.length; i++) {\n original.put(queries[i], i);\n }\n \n \n // start with smaller queries then union allowed edges and so on\n parent = IntStream.rangeClosed(0, n).toArray();\n\n Map<Integer, Boolean> result = new HashMap<>();\n Arrays.sort(queries, Comparator.comparingInt(a -> a[2]));\n Arrays.sort(edgeList, Comparator.comparingInt(a -> a[2]));\n int qI = 0;\n int eI = 0;\n for (; qI < queries.length; qI++){\n int[] query = queries[qI];\n while (eI < edgeList.length && edgeList[eI][2] < query[2]){\n union(edgeList[eI][0], edgeList[eI][1]);\n eI++;\n }\n result.put(qI, find(query[0]) == find(query[1]));\n }\n\n\n boolean[] r= new boolean[queries.length];\n for (int i = 0; i < queries.length; i++) {\n r[original.get(queries[i])] = result.get(i);\n }\n return r;\n\n }\n \n private int[] parent;\n\n private void union(int a, int b) {\n parent[find(a)] = find(b);\n }\n\n private int find(int a) {\n if (a != parent[a]) {\n parent[a] = find(parent[a]);\n }\n return parent[a];\n }\n```
| 8 | 0 |
[]
| 1 |
checking-existence-of-edge-length-limited-paths
|
[Python] Union-Find
|
python-union-find-by-forresty-1mh0
|
Intuition:\n\n- Since one of the constraints is 1 <= edgeList.length, queries.length <= 10^5 so O(N^2) solution won\'t pass, we need to be better than that\n- D
|
forresty
|
NORMAL
|
2020-12-20T04:04:42.969049+00:00
|
2020-12-20T04:04:42.969090+00:00
| 804 | false |
Intuition:\n\n- Since one of the constraints is `1 <= edgeList.length, queries.length <= 10^5` so `O(N^2)` solution won\'t pass, we need to be better than that\n- Disjoint Set Union is a great way to find if paths exist (if two nodes are connected)\n- To brute-force, for every query we can generate a DSU using edges smaller than the limit\n- To avoid repeated computation, if we can rearrange the queries from smaller limit to greater limit, we can build the DSU from the smaller distances to greater ones, and generate the desired answers iteratively.\n\n```python\nclass DSU:\n def __init__(self, N):\n self.root = list(range(N))\n def find(self, x):\n if self.root[x] != x:\n self.root[x] = self.find(self.root[x])\n return self.root[x]\n def union(self, x, y):\n x, y = self.find(x), self.find(y)\n self.root[x] = self.root[y] = min(x, y)\n def connected(self, x, y):\n x, y = self.find(x), self.find(y)\n return x == y\n\nclass Solution:\n def distanceLimitedPathsExist(self, N: int, edgeList: List[List[int]], queries: List[List[int]]) -> List[bool]:\n Q = len(queries)\n E = len(edgeList)\n edgeList.sort(key=lambda x: x[2])\n dsu = DSU(N)\n \n ans = [None] * Q\n j = 0\n \n for l, a, b, i in sorted(((l, a, b, i) for i, (a, b, l) in enumerate(queries))):\n while j < E and edgeList[j][2] < l:\n x, y, _ = edgeList[j]\n dsu.union(x, y)\n j += 1\n \n ans[i] = dsu.connected(a, b)\n \n return ans\n```
| 8 | 0 |
[]
| 2 |
checking-existence-of-edge-length-limited-paths
|
[ C++ ] [ Disjoint Set Union ]
|
c-disjoint-set-union-by-sosuke23-lw80
|
Code\n\nclass DisjointSet{\n public:\n vector<int>size;\n vector<int>parent;\n DisjointSet(int n){\n size.resize(n,1);\n parent.resize
|
Sosuke23
|
NORMAL
|
2023-04-29T02:33:19.169951+00:00
|
2023-04-29T02:33:19.169998+00:00
| 3,305 | false |
# Code\n```\nclass DisjointSet{\n public:\n vector<int>size;\n vector<int>parent;\n DisjointSet(int n){\n size.resize(n,1);\n parent.resize(n);\n for(int i=0;i<n;i++)parent[i]=i;\n }\n \n int findUpar(int node){\n if(node==parent[node])return node;\n\n return parent[node]=findUpar(parent[node]);\n }\n\n void UnionBySize(int u,int v){\n int ulp_u=findUpar(u);\n int ulp_v=findUpar(v);\n if(ulp_u==ulp_v)return ;\n if(size[ulp_u]<size[ulp_v]){\n parent[ulp_u]=ulp_v;\n size[ulp_v]+=size[ulp_u];\n }\n else{\n parent[ulp_v]=ulp_u;\n size[ulp_u]+=size[ulp_v];\n }\n \n }\n};\n\nclass Solution {\npublic:\n static bool cmp(vector<int>&a,vector<int>&b){\n return a[2]<b[2];\n }\n vector<bool> distanceLimitedPathsExist(int n, vector<vector<int>>& edgeList, vector<vector<int>>& queries) {\n DisjointSet ds(n);\n \n for(int i=0;i<queries.size();i++){\n queries[i].push_back(i);\n }\n vector<bool>ans(queries.size(),false);\n sort(queries.begin(),queries.end(),cmp);\n sort(edgeList.begin(),edgeList.end(),cmp);\n int j=0;\n for(int i=0;i<queries.size();i++){\n while(j<edgeList.size()&&edgeList[j][2]<queries[i][2]){\n ds.UnionBySize(edgeList[j][0],edgeList[j][1]);\n j++;\n }\n if(ds.findUpar(queries[i][0])==ds.findUpar(queries[i][1])){\n ans[queries[i][3]]=true;\n }\n }\n return ans;\n\n }\n};\n```
| 7 | 0 |
['C++']
| 2 |
checking-existence-of-edge-length-limited-paths
|
C# DisjointSet/UnionFind (DSU) + bonus - DisjointSet implementation
|
c-disjointsetunionfind-dsu-bonus-disjoin-p41q
|
Approach\n- Sort the inputs (queries and edgeList) by edge length (weight)\n- Use a two pointer approach to union all the nodes whose edges have length (weight
|
dmitriy-maksimov
|
NORMAL
|
2023-04-29T01:35:07.884409+00:00
|
2023-04-29T01:35:07.884441+00:00
| 455 | false |
# Approach\n- Sort the inputs (`queries` and `edgeList`) by edge length (weight)\n- Use a two pointer approach to union all the nodes whose edges have length (weight) less than $$query[i]$$\n- If there is a path between them than their parents (in DSU) are the same\n\n# Bonus\n`DisjointSet` implementation which is reusable for other problems.\n\n# Complexity\n- Time complexity: $$O(M \\times log(M) + N \\times log(N))$$ , where $$M$$ is the number of edges in `edgeList` and $$N$$ - the number of queries\n- Space complexity: $$O(n)$$\n\n# Code\n```\npublic class Solution\n{\n public class DisjointSet\n {\n private readonly int[] _parent;\n private readonly int[] _rank;\n\n public DisjointSet(int n)\n {\n _parent = new int[n];\n _rank = new int[n];\n for (var i = 0; i < n; i++)\n {\n _parent[i] = i;\n }\n }\n\n public int Find(int x)\n {\n // If `x` is the parent of itself then `x` is the representative of this set\n // Else we recursively call Find on its parent\n var xSet = _parent[x] == x ? x : Find(_parent[x]);\n\n // We cache the result by moving i\u2019s node directly under the representative of this set\n _parent[x] = xSet;\n\n return xSet;\n }\n\n public bool Union(int x, int y)\n {\n var xSet = Find(x);\n var ySet = Find(y);\n\n if (xSet == ySet)\n {\n // Elements are in same set, no need to unite anything.\n return false;\n }\n\n if (_rank[xSet] < _rank[ySet])\n {\n // If x\u2019s rank is less than y\u2019s rank then move x under y\n _parent[xSet] = ySet;\n }\n else if (_rank[xSet] > _rank[ySet])\n {\n // If y\u2019s rank is less than x\u2019s rank then move y under x\n _parent[xSet] = ySet;\n }\n else\n {\n // If their ranks are the same\n // Then move x under y (doesn\'t matter which one goes where)\n _parent[xSet] = ySet;\n\n // And increment the result tree\'s rank\n _rank[xSet]++;\n }\n\n return true;\n }\n }\n\n public bool[] DistanceLimitedPathsExist(int n, int[][] edgeList, int[][] queries)\n {\n var dsu = new DisjointSet(n);\n\n // Add query indices to help with ordering results\n for (var i = 0; i < queries.Length; i++)\n {\n queries[i] = new[] {queries[i][0], queries[i][1], queries[i][2], i};\n }\n\n Array.Sort(queries, (a, b) => a[2] - b[2]);\n Array.Sort(edgeList, (a, b) => a[2] - b[2]);\n\n var result = new bool[queries.Length];\n var j = 0;\n\n foreach (var query in queries)\n {\n // Two pointer => join the edges till their weight is less than the current query\n for (; j < edgeList.Length && edgeList[j][2] < query[2]; ++j)\n {\n dsu.Union(edgeList[j][0], edgeList[j][1]);\n }\n\n // If parents are the same than their is a path\n result[query[3]] = dsu.Find(query[0]) == dsu.Find(query[1]);\n }\n\n return result;\n }\n}\n```
| 7 | 0 |
['C#']
| 0 |
checking-existence-of-edge-length-limited-paths
|
Javascript | Union-Find Solution w/ Explanation | 100% / 100%
|
javascript-union-find-solution-w-explana-sorc
|
(Update: Small update to the code, streamlining the union/find process, using typed arrays for smaller overhead, and reusing queries as the answer array.)\n\nFo
|
sgallivan
|
NORMAL
|
2020-12-23T22:52:39.370661+00:00
|
2023-04-29T04:31:44.211638+00:00
| 600 | false |
_(**Update**: Small update to the code, streamlining the union/find process, using typed arrays for smaller overhead, and reusing_ **`queries`** _as the answer array.)_\n\nFor this solution, we\'re going to implement a Union-Find approach. The Union-Find approach involves keeping track of groups of linked objects and uses three main components: a parent array (**par**) in which to keep track of the parent of each of our elements, a **find** function used to find the parent of an element, and a **union** function used to merge two groups together under one parent.\n\nSo first, we build our intial **par** array, making each element its own parent by mapping each element\'s index to its value, such that **par[i] = i**.\n\nFor the **find** function, we want to return the ultimate parent, not simply the immediate parent, so we make it a recursive function that calls itself until it finds a parent which is its own parent. We can use this function to compress future processing time by rewriting the parent of each element along the chain to subsequently point to this ultimate parent.\n\nFor the **union** function, we simply **find** the parents of the two elements and make one a child to the other. (*You can use a weighting system in order to try to keep the subgroups balanced, but in this case it\'s not really necessary; the compression in the **find** function accomplishes much the same time-saving, making a weighting system more of a hindrance than a help.*)\n\nWe then need to sort the edge list (**e**) so that we can process the union of only those edges below the relative limit threshold of each of the queries (**q**).\n\nWe also should sort **q** so that we only have to process the edges once each instead of having to reset **par** between each query. But because our answer array (**ans**) needs to be in the same order as the original **q**, we should instead create an order key array (**ord**) of mapped out indexes and then sort it based on the limit values in **q**. This way we can keep our **q** in its original order but access its elements in sorted order.\n\nSo now we just iterate through our ordered queries and just before checking each query we process any edge unions up to the query\'s limit. We can use optional chaining when checking the next query\'s limit in order to account for reaching the end of **e**.\n\nThen we simply **find** the parent of each query\'s two nodes, and if they match, update the appropriate index in **ans** before finally rerturning **ans**.\n\n\n```\nvar distanceLimitedPathsExist = function(n, edgeList, queries) {\n const par = Uint32Array.from({length: n}, (_,i) => i),\n find = x => x === par[x] ? x : par[x] = find(par[x]),\n union = (x,y) => par[find(y)] = find(x)\n let ord = Uint32Array.from({length: queries.length}, (_,i) => i), j = 0\n edgeList.sort((a,b) => a[2] - b[2])\n ord.sort((a,b) => queries[a][2] - queries[b][2])\n for (let i of ord) {\n let [a,b,wt] = queries[i]\n while (edgeList[j]?.[2] < wt)\n union(edgeList[j][0], edgeList[j++][1])\n queries[i] = find(a) === find(b)\n }\n return queries\n};\n```
| 7 | 0 |
['Union Find', 'JavaScript']
| 3 |
checking-existence-of-edge-length-limited-paths
|
C++ || Solution using Union Find with approach and comments|| Faster than 95%
|
c-solution-using-union-find-with-approac-eghk
|
Intuition\n### Sort both the array weight wise and traverse until queries is smaller then edgeList\n Describe your first thoughts on how to solve this problem.
|
Rohan1808
|
NORMAL
|
2023-04-29T12:02:36.995645+00:00
|
2023-04-29T12:02:36.995678+00:00
| 1,146 | false |
# Intuition\n### **Sort both the array weight wise and traverse until queries is smaller then edgeList**\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Make a parent array and initialize it with themselves.\n2. Make a answer array and initislize it with false.\n3. Swap the first and third part of edgeList to sort it w.r.t weight.\n4. Sort edgeList.\n5. Make an array to store the weights of the queries vector and their index.\n6. Traverse in the edgeList until its weight is greater than queries weight.\n7. Make their parents same in the loop which has been traversed.\n8. Outside the loop check if they have same parents means they can be traversed so make them true.\n<!-- Describe your approach to solving the problem. -->\n\n<!-- # Complexity -->\n<!-- - Time complexity: -->\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n<!-- - Space complexity: -->\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int dsu(vector<int>& parent,int x)\n {\n //Base case\n if(parent[x] == x)\n return x;\n //Else check its parent\n else\n return parent[x] = dsu(parent,parent[x]);\n \n }\n vector<bool> distanceLimitedPathsExist(int n, vector<vector<int>>& edgeList, vector<vector<int>>& queries) \n {\n //A parent vector to store the parent of the elements\n vector<int> parent(n,-1);\n\n //Answer vector to store the answer\n vector<bool> ans(queries.size(),false);\n\n //Make every element its own parent\n for(int i=0;i<n;i++)\n parent[i]=i;\n \n //Swap the weight index with the first index so that we can sort it by weight\n for(int i=0;i<edgeList.size();i++)\n swap(edgeList[i][0],edgeList[i][2]);\n\n //Sort by Weight\n sort(edgeList.begin(),edgeList.end());\n\n //Store the queries weight and its index\n vector<pair<int,int>> arr;\n\n for(int i=0;i<queries.size();i++)\n arr.push_back({queries[i][2],i});\n \n //Sort the queries w.r.t weight\n sort(arr.begin(),arr.end());\n\n\n int j = 0;\n for(int i = 0; i < arr.size(); i++)\n {\n //Traverse until query weight is greater than the edge weight\n while(j < edgeList.size() && edgeList[j][0] < arr[i].first)\n { \n //Take the vertices of the edgelist\n int u = edgeList[j][1],v = edgeList[j][2];\n //Check their parents\n int pu = dsu(parent,u),pv = dsu(parent,v);\n //If not equal make them equal\n if(pu != pv)\n parent[pu] = pv;\n \n j++;\n }\n //Take the vertices of the query \n int x = queries[arr[i].second][0],y = queries[arr[i].second][1];\n //Check their parents\n int px = dsu(parent,x),py = dsu(parent,y);\n //If parents are equal then return true\n if(px == py)\n ans[arr[i].second] = true;\n \n }\n return ans;\n\n }\n};\n```\n# Please Upvote if helps!!!!!
| 5 | 0 |
['Array', 'Union Find', 'Graph', 'Sorting', 'C++']
| 0 |
checking-existence-of-edge-length-limited-paths
|
[C++] | SimpleDSU w/ DETAILED EXPLANATION & COMMENTED CODE | Easy To Understand
|
c-simpledsu-w-detailed-explanation-comme-grn3
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n1) We can apply BFS or DFS to find answer from moving one node\nto anothoer node. Obv
|
aryanttripathi
|
NORMAL
|
2023-04-29T07:59:53.925768+00:00
|
2023-04-29T07:59:53.925811+00:00
| 992 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n```\n1) We can apply BFS or DFS to find answer from moving one node\nto anothoer node. Obviously, traversing it queries number of time may \nlead to TLE.\n2) Instead of that we can apply DSU (Disjoint set Union) and why DSU ?\n3) In question we have to tell for each query that whether we are \nable to reach from one node to anthor node in less than limit value\nwhen we are given edges with distance values.\n4) So, for every queries[limit] value, we will try to find path in\nedges array that less than this limit value, how many nodes are \nwe able to travel.\n```\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n```\n5) Finally we will see that if in less than this limit we are able \nto make a group of nodes we can travel. \n6) If in this group both queries node also present than we answer \nwill be true for this index elsewise false.\n7) Now, why first: We will sort the edges array \nas will as the queries array.\n8) See, we will creating groups of nodes with the help of DSU that\nless than this limit value we are able to reach this number of nodes.\nIf we will sort the queries array on the basis of limit value then for\nith query limit we already know that less than this limit value,\nwe already group nodes, so by moving in increasing order we don\'t\nneed to create group again. There is much probaility that for covering\ncurrent ith value limit, maybe two of the nodes ask in queries already\ncovered with much less value and if it that, we already cover them \nin a group. \n9) Sorting edges array on the basis of weight help us in \nmoving linear increasing order as per by the queries limit values.\n```\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n```\nTime Complexity: O(n + q + szlogsz + qlogq + (sz + q) + n),\nsz: size of edges, q: size of queries\n\nwhere 1) n: no of nodes (intially making each node as parent of itslef)\n 2) q: holding up the exact/original indices for each query\n 3) szlogsz: sorting the edges array\n 4) qlogq: sorting the queries array \n 5) (sz + q): worst case for each query limit value \n there is only one edge array\n 6) n: recursive find function used to find parent\n```\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n```\nSpace Complexity: O(n + n + q) \n 1) defining parent array of size n\n 2) anthor n (recursive stack space used to find parent)\n 3) anthor q, to store answer\n```\n\n# Code\n```\nclass Solution {\npublic:\n// find function which is used to find parent of a node\n int find(int node, vector<int>& parent)\n {\n // if node is parent of itself return here\n if(node == parent[node])\n return node;\n \n // else go on in finding actual parent\n return parent[node] = find(parent[node], parent);\n }\n \n // union funtion to merge parents of two nodes\n void Union(int node0, int node1, vector<int>& parent)\n {\n int par0 = find(node0, parent); // find parent of node zero\n int par1 = find(node1, parent); // find parent of node one\n \n // if values of parents of node zero and one are equal \n // then we will return true from here\n if(par0 == par1)\n return;\n \n // make parent of one anothoer (parent[par1] = par0, also valid)\n parent[par0] = par1;\n }\n\n vector<bool> distanceLimitedPathsExist(int n, vector<vector<int>>& edges, vector<vector<int>>& queries) {\n int q = queries.size(); // defining size of queries array\n int sz = edges.size(); // defining size of edges array \n\n // Intiliaze parent array, which will take care of parent of every node\n vector<int> parent(n, 0); \n\n // intially make parent of everyone itself\n for(int i = 0; i < n; i++) parent[i] = i;\n\n // sort edges on the basis of distance weight\n sort(edges.begin(), edges.end(), [&](vector<int>& edge1, vector<int>& edge2){\n return edge1[2] < edge2[2];\n });\n\n // keep track of original indices\n for(int i = 0; i < q; i++) queries[i].push_back(i);\n \n // sort queries on the basis of weight\n sort(queries.begin(), queries.end(), [&](vector<int>& query1,vector<int>& query2) {\n \n return query1[2] < query2[2];\n });\n\n // declare answer array of size q, intially everything false\n vector<bool> ans(q, false);\n int edgeMoment = 0; // pointer to move in edges array\n\n // now, for each query we will calculate answer\n for(int eachQuery = 0; eachQuery < q; eachQuery++) {\n int currQueryWeight = queries[eachQuery][2]; // currentWeight in queries\n \n // move in edges till edge distane weight less than currQueryWeight \n // and map parents\n while(edgeMoment < sz && edges[edgeMoment][2] < currQueryWeight)\n Union(edges[edgeMoment][0], edges[edgeMoment][1], parent), edgeMoment++;\n\n // if for this currQueryWeight, queries nodes found in same group,\n // put answer true\n if(find(queries[eachQuery][0], parent) == \n find(queries[eachQuery][1], parent)) {\n\n ans[queries[eachQuery][3]] = true;\n }\n }\n \n // finally, return ans\n return ans;\n }\n};\n```
| 4 | 0 |
['Union Find', 'Graph', 'C++']
| 0 |
checking-existence-of-edge-length-limited-paths
|
JavaScript : With Explanation [100%, 100%] (Union Find)
|
javascript-with-explanation-100-100-unio-mz1a
|
Code\n\nvar distanceLimitedPathsExist = function(n, edgeList, queries) {\n const uf = new UnionFind(n), ans = [];\n\n // Create a list of index of queries
|
JayPokale
|
NORMAL
|
2023-04-29T04:39:56.611473+00:00
|
2023-04-29T04:39:56.611527+00:00
| 768 | false |
# Code\n```\nvar distanceLimitedPathsExist = function(n, edgeList, queries) {\n const uf = new UnionFind(n), ans = [];\n\n // Create a list of index of queries in incresing order of limit in each query\n const order = Array(queries.length).fill().map((_, i) => i);\n order.sort((a,b) => queries[a][2] - queries[b][2]);\n\n // Sort edgeList in incresing order of distances\n edgeList.sort((a,b) => a[2] - b[2]);\n\n let index=0;\n for(const i of order) {\n const [p, q, limit] = queries[i];\n\n // For each query, add all edges having distance less than limit\n while(edgeList[index]?.[2] < limit){\n uf.union(edgeList[index][0], edgeList[index][1]);\n index++;\n }\n\n // If all edges dis is less than limit then below condition return true\n ans[i] = uf.find(p) === uf.find(q);\n }\n return ans;\n};\n\n\n\n\n//////////////// Union Find Data Structure ////////////////\nclass UnionFind {\n constructor(n) {\n this.parent = Array(n).fill().map((_,i) => i);\n }\n\n find(i) {\n if(this.parent[i] !== i) this.parent[i] = this.find(this.parent[i]);\n return this.parent[i];\n }\n \n union(i, j) {\n this.parent[this.find(j)] = this.find(i);\n }\n}\n```
| 4 | 1 |
['JavaScript']
| 0 |
checking-existence-of-edge-length-limited-paths
|
✅✅C++ DSU/Union Find Easy
|
c-dsuunion-find-easy-by-heisenberg2003-ukgn
|
We Rearrange the Queries and EdgeLists so as to kind of precompute for future queries by DSU\n\n# Complexity\n- Time complexity:\n- O(N+Q)\n\n- Space complexity
|
Heisenberg2003
|
NORMAL
|
2023-01-15T09:58:26.297543+00:00
|
2023-01-15T09:58:26.297582+00:00
| 813 | false |
We Rearrange the Queries and EdgeLists so as to kind of precompute for future queries by DSU\n\n# Complexity\n- Time complexity:\n- O(N+Q)\n\n- Space complexity:\n- O(N+Q)\n\n# Code\n```\nclass Solution {\npublic:\n vector<int>parent,size;\n void make(int var)\n {\n parent[var]=var;\n size[var]=1;\n return;\n }\n int findparent(int var)\n {\n if(parent[var]==var)\n {\n return var;\n }\n parent[var]=findparent(parent[var]);\n return parent[var];\n }\n void Union(int var1,int var2)\n {\n var1=findparent(var1);\n var2=findparent(var2);\n if(var1==var2)\n {\n return;\n }\n if(size[var1]>size[var2])\n {\n parent[var2]=var1;\n size[var1]+=size[var2];\n }\n else\n {\n parent[var1]=var2;\n size[var2]+=size[var1];\n }\n return;\n }\n static bool comparator(vector<int>&a,vector<int>&b)\n {\n return (a[2]<=b[2]);\n }\n vector<bool> distanceLimitedPathsExist(int n,vector<vector<int>>&edgeList,vector<vector<int>>&queries) \n {\n parent.assign(n,0);\n size.assign(n,0);\n int i=0,j=0;\n for(i=0;i<n;i++)\n {\n make(i);\n }\n for(i=0;i<queries.size();i++)\n {\n queries[i].push_back(i);\n }\n vector<bool>ans(queries.size(),false);\n sort(edgeList.begin(),edgeList.end(),comparator);\n sort(queries.begin(),queries.end(),comparator);\n for(int i=0;i<queries.size();i++)\n {\n while(j<edgeList.size() && edgeList[j][2]<queries[i][2])\n {\n Union(edgeList[j][0],edgeList[j][1]);\n j++;\n }\n parent[queries[i][0]]=findparent(queries[i][0]);\n parent[queries[i][1]]=findparent(queries[i][1]);\n ans[queries[i][3]]=(parent[queries[i][0]]==parent[queries[i][1]]);\n }\n return ans;\n }\n};\n```
| 4 | 0 |
['C++']
| 0 |
checking-existence-of-edge-length-limited-paths
|
[Python/C++] Sort + Union Find
|
pythonc-sort-union-find-by-karutz-qkum
|
Idea\n Add edges to the graph from smallest to largest.\n Answer queries from smallest to largest.\n Use a Union-Find Data Structure to check connectivity.\n\n\
|
karutz
|
NORMAL
|
2020-12-20T04:05:33.991104+00:00
|
2020-12-21T15:47:18.318536+00:00
| 454 | false |
**Idea**\n* Add edges to the graph from smallest to largest.\n* Answer queries from smallest to largest.\n* Use a [Union-Find Data Structure](https://en.wikipedia.org/wiki/Disjoint-set_data_structure) to check connectivity.\n\n\n**Python**\n```python\nfrom collections import deque\n\nclass Solution:\n def distanceLimitedPathsExist(self, n, edgeList, queries):\n q = list(sorted((limit, p, q, i) for i, (p, q, limit) in enumerate(queries)))\n e = deque(sorted((d, u, v) for (u, v, d) in edgeList))\n \n uf = list(range(n))\n \n def find(x):\n if uf[x] != x:\n uf[x] = find(uf[x])\n return uf[x]\n \n def join(u, v):\n uf[find(u)] = find(v)\n \n def is_connected(u, v):\n return find(u) == find(v)\n \n ans = list(False for _ in range(len(q)))\n \n for limit, p, q, i in q:\n while e and e[0][0] < limit:\n _, u, v = e.popleft()\n join(u, v)\n ans[i] = is_connected(p, q)\n \n return ans\n```\n\n**C++**\n```c++\nclass Solution {\npublic:\n int uf[112345];\n \n int find(int x) {\n return uf[x] != x ? (uf[x] = find(uf[x])) : x;\n }\n \n void join(int x, int y) {\n uf[find(x)] = find(y);\n }\n \n bool is_connected(int x, int y) {\n return find(x) == find(y);\n }\n \n vector<bool> distanceLimitedPathsExist(\n int n, \n vector<vector<int>>& edges, \n vector<vector<int>>& queries) {\n iota(uf, uf + n, 0);\n \n for (int i = 0; i < queries.size(); i++) {\n queries[i].push_back(i);\n }\n \n auto by_weight = [](auto &a, auto &b) {\n return a[2] < b[2];\n };\n \n sort(queries.begin(), queries.end(), by_weight);\n sort(edges.begin(), edges.end(), by_weight);\n \n vector<bool> ans(queries.size());\n int j = 0;\n for (auto &q : queries) {\n for (; j < edges.size() && edges[j][2] < q[2]; j++) {\n join(edges[j][0], edges[j][1]);\n }\n ans[q[3]] = is_connected(q[0], q[1]);\n }\n \n return ans;\n }\n};\n```
| 4 | 0 |
[]
| 2 |
checking-existence-of-edge-length-limited-paths
|
C# Solution with Union find + Sort
|
c-solution-with-union-find-sort-by-maxpu-51lm
|
\n public class Solution\n {\n private class Unions\n {\n private readonly int[] _parents;\n private readonly int[] _rank
|
maxpushkarev
|
NORMAL
|
2020-12-20T04:00:48.460786+00:00
|
2020-12-20T04:00:48.460822+00:00
| 271 | false |
```\n public class Solution\n {\n private class Unions\n {\n private readonly int[] _parents;\n private readonly int[] _ranks;\n\n public Unions(int n)\n {\n _parents = new int[n];\n _ranks = new int[n];\n for (int i = 0; i < n; i++)\n {\n _parents[i] = i;\n }\n }\n\n public int Find(int x)\n {\n if (x != _parents[x])\n {\n x = Find(_parents[x]);\n }\n return _parents[x];\n }\n\n public bool Union(int x, int y)\n {\n int px = Find(x);\n int py = Find(y);\n if (px == py)\n {\n return false;\n }\n if (_ranks[px] > _ranks[py])\n {\n _parents[py] = px;\n _ranks[px]++;\n }\n else\n {\n _parents[px] = py;\n _ranks[py]++;\n }\n return true;\n }\n }\n\n\n public bool[] DistanceLimitedPathsExist(int n, int[][] edgeList, int[][] queries)\n {\n bool[] res = new bool[queries.Length];\n (int idx, int[] q)[] qData = new (int idx, int[] q)[queries.Length];\n\n for (int i = 0; i < queries.Length; i++)\n {\n qData[i] = (i, queries[i]);\n }\n\n //sort edges by length\n Array.Sort(edgeList, (e1, e2) => e1[2].CompareTo(e2[2]));\n //sort queries by limit\n Array.Sort(qData, (q1, q2) => q1.q[2].CompareTo(q2.q[2]));\n Unions dsu = new Unions(n);\n\n int edIdx = 0;\n\n for (int i = 0; i < qData.Length; i++)\n {\n //add edges accodring to current limit\n while (edIdx < edgeList.Length && edgeList[edIdx][2] < qData[i].q[2])\n {\n dsu.Union(edgeList[edIdx][0], edgeList[edIdx][1]);\n edIdx++;\n }\n\n res[qData[i].idx] = (dsu.Find(qData[i].q[0]) == dsu.Find(qData[i].q[1]));\n }\n\n return res;\n }\n }\n```
| 4 | 0 |
['Union Find']
| 1 |
checking-existence-of-edge-length-limited-paths
|
C++ DSU solution
|
c-dsu-solution-by-sachin_kumar_sharma-ikra
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Sachin_Kumar_Sharma
|
NORMAL
|
2024-07-24T06:05:29.571625+00:00
|
2024-07-24T06:05:29.571658+00:00
| 11 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass UnionFind {\npublic:\n UnionFind(int n) : parent(n), rank(n, 0) {\n for (int i = 0; i < n; ++i) {\n parent[i] = i;\n }\n }\n \n int find(int u) {\n if (parent[u] != u) {\n parent[u] = find(parent[u]);\n }\n return parent[u];\n }\n \n void unite(int u, int v) {\n int pu = find(u);\n int pv = find(v);\n if (pu != pv) {\n if (rank[pu] > rank[pv]) {\n parent[pv] = pu;\n } else if (rank[pu] < rank[pv]) {\n parent[pu] = pv;\n } else {\n parent[pv] = pu;\n rank[pu]++;\n }\n }\n }\n\nprivate:\n vector<int> parent;\n vector<int> rank;\n};\n\n\nclass Solution {\npublic:\n vector<bool> distanceLimitedPathsExist(int n, vector<vector<int>>& edgeList, vector<vector<int>>& queries) {\n sort(edgeList.begin(), edgeList.end(), [](const vector<int>& a, const vector<int>& b) {\n return a[2] < b[2];\n });\n\n // Add an index to each query to keep track of the original order\n for (int i = 0; i < queries.size(); ++i) {\n queries[i].push_back(i);\n }\n\n // Sort the queries by their limit\n sort(queries.begin(), queries.end(), [](const vector<int>& a, const vector<int>& b) {\n return a[2] < b[2];\n });\n\n // Initialize the Union-Find structure\n UnionFind uf(n);\n\n vector<bool> answer(queries.size());\n int edgeIndex = 0;\n\n // Process each query\n for (const auto& query : queries) {\n int p = query[0];\n int q = query[1];\n int limit = query[2];\n int queryIndex = query[3];\n\n // Add all edges with distance less than the current query limit to the Union-Find structure\n while (edgeIndex < edgeList.size() && edgeList[edgeIndex][2] < limit) {\n uf.unite(edgeList[edgeIndex][0], edgeList[edgeIndex][1]);\n edgeIndex++;\n }\n\n // Check if p and q are in the same connected component\n if (uf.find(p) == uf.find(q)) {\n answer[queryIndex] = true;\n } else {\n answer[queryIndex] = false;\n }\n }\n\n return answer;\n\n }\n};\n```
| 3 | 0 |
['C++']
| 0 |
checking-existence-of-edge-length-limited-paths
|
DSU solution || C++
|
dsu-solution-c-by-escaryninja17-v8ro
|
Intuition\n Describe your first thoughts on how to solve this problem. \nIn queries we have to find if there is a path from u to v such that maximum edgewt is l
|
eScaryNinja17
|
NORMAL
|
2023-05-03T09:58:55.258115+00:00
|
2023-05-03T09:58:55.258152+00:00
| 40 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIn queries we have to find if there is a path from u to v such that maximum edgewt is less that limit.This can be done through dsu . \nBut again we can\'t make graph for each queries , so we will reuse the graph made earlier through dsu. for this we will sort the queries on the basis of limit. \n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n \nclass DisjointSet\n{\npublic:\n vector<int> size, parent;\n DisjointSet(int n)\n {\n size.resize(n + 1, 1);\n parent.resize(n + 1);\n for (int i = 0; i <= n; i++)\n {\n parent[i] = i;\n }\n }\n int findUPar(int node)\n {\n if (node == parent[node])\n return node;\n return parent[node] = findUPar(parent[node]);\n }\n void unionBySize(int u, int v)\n {\n int ulp_u = findUPar(u), ulp_v = findUPar(v);\n if (ulp_u == ulp_v)\n return;\n if (size[ulp_u] >= size[ulp_v])\n {\n parent[ulp_v] = ulp_u;\n size[ulp_u] += size[ulp_v];\n }\n else if (size[ulp_u] < size[ulp_v])\n {\n parent[ulp_u] = ulp_v;\n size[ulp_v] += size[ulp_u];\n }\n }\n};\n\n vector<bool> distanceLimitedPathsExist(int n, vector<vector<int>>& edgeList, vector<vector<int>>& queries) {\n vector<vector<int>> edges;\n DisjointSet ds(n);\n for(auto it:edgeList)\n {\n int u=it[0],v=it[1],wt=it[2];\n edges.push_back({wt,u,v});\n }\n sort(edges.begin(),edges.end());\n vector<vector<int>> q;\n int i=0;\n for(auto it:queries)\n {\n int u=it[0],v=it[1],wt=it[2];\n q.push_back({wt,u,v,i++});\n }\n \n \n sort(q.begin(),q.end());\n i=0;\n vector<bool> ans(q.size());\n for(auto it:q)\n {\n int wt=it[0],u=it[1],v=it[2],ind =it[3];\n // cout<<wt<<" \\n";\n while(i<edges.size())\n {\n int dst=edges[i][0],x=edges[i][1],y=edges[i][2];\n if(dst>=wt)\n break;\n // cout<<wt<<" "<<dst<<endl;\n ds.unionBySize(x,y);\n i++;\n }\n if(ds.findUPar(u)==ds.findUPar(v))\n ans[ind]=1;\n else\n ans[ind]=0;\n\n }\n return ans;\n\n\n\n\n }\n};\n```
| 3 | 0 |
['C++']
| 0 |
checking-existence-of-edge-length-limited-paths
|
Sorting + Union Find | C++
|
sorting-union-find-c-by-tusharbhart-8cz8
|
\nclass Solution {\n static bool cmp(vector<int> &a, vector<int> &b) {\n return a[2] < b[2];\n }\n int find_prnt(int node, vector<int> &prnt) {\
|
TusharBhart
|
NORMAL
|
2023-04-29T13:21:23.107316+00:00
|
2023-04-29T13:21:23.107358+00:00
| 917 | false |
```\nclass Solution {\n static bool cmp(vector<int> &a, vector<int> &b) {\n return a[2] < b[2];\n }\n int find_prnt(int node, vector<int> &prnt) {\n if(node == prnt[node]) return node;\n return prnt[node] = find_prnt(prnt[node], prnt);\n }\n void unionn(int u, int v, vector<int> &prnt, vector<int> &rank) {\n int ulp_u = find_prnt(u, prnt), ulp_v = find_prnt(v, prnt);\n\n if(rank[ulp_u] > rank[ulp_v]) prnt[ulp_v] = ulp_u; \n else if(rank[ulp_u] < rank[ulp_v]) prnt[ulp_u] = ulp_v;\n else {\n prnt[ulp_v] = ulp_u;\n rank[ulp_u]++;\n }\n }\npublic:\n vector<bool> distanceLimitedPathsExist(int n, vector<vector<int>>& edgeList, vector<vector<int>>& queries) {\n int m = queries.size(), p = 0;\n for(int i=0; i<m; i++) queries[i].push_back(i);\n\n sort(edgeList.begin(), edgeList.end(), cmp);\n sort(queries.begin(), queries.end(), cmp);\n\n vector<bool> ans(m);\n vector<int> prnt(n), rank(n);\n for(int i=0; i<n; i++) prnt[i] = i;\n\n for(auto q : queries) {\n while(p < edgeList.size() && edgeList[p][2] < q[2]) {\n unionn(edgeList[p][0], edgeList[p][1], prnt, rank), p++;\n }\n ans[q[3]] = find_prnt(q[0], prnt) == find_prnt(q[1], prnt);\n }\n return ans;\n }\n};\n```
| 3 | 0 |
['Union Find', 'Sorting', 'C++']
| 0 |
checking-existence-of-edge-length-limited-paths
|
Deep and Step by Step Approach and Solution
|
deep-and-step-by-step-approach-and-solut-5l94
|
Intuition\n Describe your first thoughts on how to solve this problem. \nAfter reading the problem, the first approach that came to my mind was to try to find a
|
suyog_73
|
NORMAL
|
2023-04-29T08:14:14.196076+00:00
|
2023-04-29T08:14:14.196116+00:00
| 447 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAfter reading the problem, the first approach that came to my mind was to try to find an answer for each query using **Dijkstra**\'s algorithm. However, after analyzing the constraints, I realized that it would lead to a TLE (Time Limit Exceeded). As this approach takes O(Q*Nlog(E)) time.\n\nSince the problem requires us to check if a path exists between two nodes, I thought it could be solved using the **Disjoint Set Union (DSU)** data structure, as it helps to find the parent in nearly constant time.\n\n\n---\n\n\n\n# Approach\n1. Create a DisjointSet class to represent the graph, which will store the parent node for each node in the graph. Initially, each node is its own parent.\n2. Add a findParent method to the DisjointSet class, which finds the parent of a given node. If the parent of a node is itself, return the node, otherwise recursively call findParent on the parent of the node.\n3. Add a unionByRank method to the DisjointSet class, which takes two nodes and unions them together. The method finds the parent of each node, and if they are not the same, it merges the two sets by attaching the one with the smaller rank to the one with the larger rank.\n4. Add an isParentEqual method to the DisjointSet class, which checks if the parent of two nodes is the same. This method uses findParent to get the parent of each node and then checks if they are equal.\n5. Sort the edges by distance in non-decreasing order.\n6. Sort the queries by limit in non-decreasing order.\n7. For each query, loop through the edges until the distance is greater than the limit of the current query. For each edge, call the unionByRank method to merge the nodes together.\n8. After all edges less than the current query\'s limit have been processed, check if the parent of the source and destination nodes in the query are the same using the isParentEqual method. If they are, set the answer for the query to true, otherwise set it to false.\n9. Return the array of answers.\n\n\n---\n\n\n\n# Complexity\n- **Time complexity**:\n\n1. Sorting the edges takes O(ElogE) time.\n2. Sorting the queries takes O(QlogQ) time.\n3. For each query, we iterate through the edges up to limit distance. Therefore, for all queries, we iterate through all the edges at most once. So, iterating through all the edges takes O(E) time.\n4. Union-find operations take nearly O(1) time.\n5. Therefore, the total time complexity of the solution is O(ElogE + QlogQ + (O+E)).\n\n- **Space complexity**:\n\n1. We use a disjoint-set data structure to keep track of the connected components of the graph. The space required for this data structure is O(N).\n2.If we neglect space required to store answer, the total space complexity of the solution is O(N).\n\n\n---\n\n\n\n# Code\n```\nclass DisjointSet {\nprivate:\n vector<int> parent, rank;\n\npublic:\n DisjointSet(int n) {\n parent.resize(n+1, 0);\n rank.resize(n+1, 0);\n\n for(int i=0; i<n+1; i++) {\n parent[i] = i;\n }\n }\n\n int findParent(int node) {\n if(node == parent[node])\n return node;\n \n return parent[node] = findParent(parent[node]);\n }\n\n void unionByRank(int u, int v) {\n int upU = findParent(u);\n int upV = findParent(v);\n\n if(upU == upV)\n return;\n \n if(rank[upU] < rank[upV]) {\n parent[upU] = upV;\n }\n else {\n parent[upV] = upU;\n rank[upU]++;\n }\n }\n\n bool isParentEqual(int u, int v) {\n return (findParent(u) == findParent(v));\n }\n};\n\nclass Solution {\n bool static compare(const vector<int> &a, const vector<int> &b) {\n return (a[2] < b[2]);\n }\n\npublic:\n vector<bool> distanceLimitedPathsExist(int nodes, vector<vector<int>>& edges, vector<vector<int>>& queries) {\n int n = queries.size();\n\n vector<bool> ans(n, false);\n \n for(int i=0; i<n; i++) {\n queries[i].push_back(i);\n }\n\n sort(edges.begin(), edges.end(), compare);\n sort(queries.begin(), queries.end(), compare);\n\n DisjointSet ds(nodes);\n int i=0;\n\n for(auto &query : queries) {\n int u = query[0];\n int v = query[1];\n int limit = query[2];\n int qId = query[3];\n\n for(; (i < edges.size()) && (edges[i][2] < limit); i++) {\n ds.unionByRank(edges[i][0], edges[i][1]);\n }\n ans[qId] = ds.isParentEqual(u, v);\n }\n\n return ans;\n }\n};\n```\n\n\n---\n\n**Happy Coding...**\n\n
| 3 | 0 |
['Union Find', 'Graph', 'Sorting', 'C++']
| 0 |
checking-existence-of-edge-length-limited-paths
|
Rust + UnionFind
|
rust-unionfind-by-unknown-z94d
|
\nimpl Solution {\n pub fn distance_limited_paths_exist(n: i32, mut edge_list: Vec<Vec<i32>>, queries: Vec<Vec<i32>>) -> Vec<bool> {\n let mut idx: Ve
|
unknown-
|
NORMAL
|
2023-04-29T02:35:43.591821+00:00
|
2023-04-29T02:36:10.621249+00:00
| 93 | false |
```\nimpl Solution {\n pub fn distance_limited_paths_exist(n: i32, mut edge_list: Vec<Vec<i32>>, queries: Vec<Vec<i32>>) -> Vec<bool> {\n let mut idx: Vec<_> = (0..queries.len()).collect();\n idx.sort_by_key(|&i| queries[i][2]);\n edge_list.sort_by_key(|v| v[2]);\n\n let mut uf: Vec<usize> = (0..n as usize).collect();\n fn uf_find(i: usize, uf: &mut [usize]) -> usize {\n if (uf[i] != i) {\n uf[i] = uf_find(uf[i], uf);\n }\n uf[i]\n }\n fn uf_union(i: usize, j: usize, uf: &mut [usize]) {\n let i = uf_find(i, uf);\n let j = uf_find(j, uf);\n uf[i] = j;\n }\n\n let mut ret = vec![false; queries.len()];\n let mut j = 0;\n for i in idx {\n while j < edge_list.len() && edge_list[j][2] < queries[i][2] {\n uf_union(edge_list[j][0] as usize, edge_list[j][1] as usize, &mut uf);\n j += 1;\n }\n ret[i] = uf_find(queries[i][0] as usize, &mut uf) == uf_find(queries[i][1] as usize, &mut uf);\n }\n ret\n }\n}\n```
| 3 | 0 |
['Rust']
| 0 |
checking-existence-of-edge-length-limited-paths
|
Python3 beats 87.42% 🚀🚀 quibler7
|
python3-beats-8742-quibler7-by-quibler7-vjix
|
Code\n\nclass Solution:\n def distanceLimitedPathsExist(self, n: int, edgeList: List[List[int]], queries: List[List[int]]) -> List[bool]:\n \n
|
quibler7
|
NORMAL
|
2023-04-29T02:31:04.863291+00:00
|
2023-04-29T02:31:04.863323+00:00
| 621 | false |
# Code\n```\nclass Solution:\n def distanceLimitedPathsExist(self, n: int, edgeList: List[List[int]], queries: List[List[int]]) -> List[bool]:\n \n parent = [i for i in range(n+1)]\n \n rank = [0 for i in range(n+1)]\n\n def find(parent, x):\n\n if parent[x] == x:\n return x\n parent[x] = find(parent, parent[x])\n return parent[x]\n\n def union(parent, a, b):\n\n a = find(parent, a)\n b = find(parent, b)\n\n if a == b:\n return \n\n if rank[a] < rank[b]:\n parent[a] = b\n elif rank[a] > rank[b]:\n parent[b] = a\n else:\n parent[b] = a\n rank[a] += 1\n \n edgeList.sort(key = lambda x: x[2])\n res = [0] * len(queries)\n queries = [[i, ch] for i, ch in enumerate(queries)]\n queries.sort(key = lambda x: x[1][2])\n \n ind = 0\n for i, (a, b, w) in queries:\n \n while ind < len(edgeList) and edgeList[ind][2] < w:\n union(parent, edgeList[ind][0], edgeList[ind][1])\n ind += 1\n \n res[i] = find(parent, a) == find(parent, b)\n return res\n```
| 3 | 0 |
['Python3']
| 0 |
checking-existence-of-edge-length-limited-paths
|
minimum spanning tree ,disjoint set union
|
minimum-spanning-tree-disjoint-set-union-e293
|
\nclass Solution {\npublic:\n \n // darna mt bhai\n \n \n /* create a mst by given graph using krushkal\'s algorithm once mst is formed then we us
|
amitdnagar4
|
NORMAL
|
2022-10-19T18:26:56.329587+00:00
|
2022-10-19T18:26:56.329646+00:00
| 50 | false |
```\nclass Solution {\npublic:\n \n // darna mt bhai\n \n \n /* create a mst by given graph using krushkal\'s algorithm once mst is formed then we use binary lifting concept for finding lowest common ansestor is used for answering the query\n \n along with storing the parent array we also maintain a maxweight array \n where maxweight[i][j] tell that what is the maximum weight in path between \n node i and node (i+2^j) \n \n this can be calculated using dfs and once these vales are calculated then\n using lowest common anscestor method we can answer the query\n \n for better understanding look at my submission\n \n */\n // custom comparator used for sorting the edges array \n // helpful in kruskal\'s algorithm\n static bool comp(vector<int>&a,vector<int>&b){\n return a[2]<b[2];\n }\n \n // x=30 used for binary lifting\n int x=30;\n \n // different vectors used \n vector<vector<int>>parent,maxweight;\n vector<int>par,Size,vis,depth;\n vector<vector<pair<int,int>>>g;\n \n// union find to create mst\n void make(int i){\n par[i]=i;\n Size[i]=1;\n }\n int find(int a){\n if(par[a]==a)return a;\n return par[a]=find(par[a]);\n }\n void Union(int a,int b){\n a=find(a),b=find(b);\n if(a!=b){\n if(Size[a]<Size[b])swap(a,b);\n par[b]=a;\n Size[a]+=Size[b];\n return;\n }\n }\n \n //creating mst using kruskal\'s algorithm\n \n void create_mst(vector<vector<int>>&edge,int n){\n sort(edge.begin(),edge.end(),comp);\n par.clear(),Size.clear();\n par.resize(n),Size.resize(n);\n for(int i=0;i<n;++i)make(i);\n g.clear(),g.resize(n);\n for(auto e:edge){\n int a=e[0],b=e[1],w=e[2];\n if(find(a)!=find(b)){\n Union(a,b);\n g[a].push_back({b,w});\n g[b].push_back({a,w});\n }\n }\n return;\n }\n \n //run dfs for calculating (initial values of parent and maxweight)\n \n void dfs(int i){\n vis[i]=true;\n for(auto ch:g[i]){\n int v=ch.first,w=ch.second;\n if(!vis[v]){\n parent[v][0]=i;\n depth[v]=depth[i]+1;\n maxweight[v][0]=w;\n dfs(v);\n }\n }\n \n }\n \n // this function calculating all parent and maxweight values\n void cal(int n){\n parent.clear(),maxweight.clear(),depth.clear(),depth.resize(n,0);\nparent.resize(n,vector<int>(x+1,-1)),maxweight.resize(n,vector<int>(x+1,INT_MIN));\n vis.clear();\n vis.resize(n,false);\n for(int i=0;i<n;++i){\n if(!vis[i]){\n depth[i]=0;\n dfs(i);\n }\n }\n \n //calculating rest of parent and maxweight values\n \n for(int j=1;j<=x;++j){\n for(int i=0;i<n;++i){\n if(parent[i][j-1]!=-1){\n parent[i][j]=parent[parent[i][j-1]][j-1];\n maxweight[i][j]=max(maxweight[i][j-1],maxweight[parent[i][j-1]][j-1]);\n }\n }\n }\n }\n \n // modified method for finding k_Th ancestor\n \n pair<int,int> k_th_ancestor(int a,int k){\n int weight=INT_MIN;\n for(int i=x;i>=0;--i){\n if(k&(1<<i)){\n k-=(1<<i);\n weight=max(weight,maxweight[a][i]);\n a=parent[a][i];\n if(a==-1)return {-1,INT_MIN};\n }\n }\n return {a,weight};\n }\n \n //function for finding lca\n int lca(int a,int b){\n if(depth[a]>depth[b])swap(a,b);\n int d=depth[b]-depth[a];\n auto pr=k_th_ancestor(b,d);\n b=pr.first;\n int weight=pr.second;\n if(a==b)return weight;\n for(int i=x;i>=0;--i){\n if(parent[a][i]!=parent[b][i]){\n weight=max(weight,max(maxweight[a][i],maxweight[b][i]));\n a=parent[a][i];\n b=parent[b][i];\n }\n }\n weight=max(weight,max(maxweight[a][0],maxweight[b][0]));\n return weight;\n }\n \n vector<bool> distanceLimitedPathsExist(int n, vector<vector<int>>& edgeList, vector<vector<int>>& queries) {\n create_mst(edgeList,n);\n cal(n);\n vector<bool>ans(queries.size());\n for(int i=0;i<queries.size();++i){\n int a=queries[i][0],b=queries[i][1],limit=queries[i][2];\n if(find(a)!=find(b)){\n ans[i]=false;\n continue;\n }\n ans[i]=(lca(a,b)<limit);\n }\n return ans;\n }\n};\n```
| 3 | 0 |
[]
| 0 |
checking-existence-of-edge-length-limited-paths
|
Beginner LEVEL Intuition Development for any OFFLINE QUERY QUESTIONS
|
beginner-level-intuition-development-for-3xb7
|
In mostly every post in discuss everyone told the solution for this question.\nBut no one exactly has told the offline query concept. So i have tried to tell an
|
xxvvpp
|
NORMAL
|
2022-07-06T08:13:41.805912+00:00
|
2022-07-06T08:15:56.502619+00:00
| 328 | false |
In mostly every post in discuss everyone told the solution for this question.\nBut no one exactly has told the offline query concept. So i have tried to tell and highlight my approach of seeing and identifying offline query type questions.\n\nHope it helps. Plz upvote if u like!\n\n**Intuition for Solving OFFLINE QUERIES QUESTION**\n1. There will be first of all some `queries will be given`.\n2. Then we should first consider of `solving a single query in the best optimized way`.\n3. Then after applying the optimised approach found for a single querie in step2 , we will `apply it in every query and time complexity would be somewhat close to O(q.size() * N) because for every query we will be traversing whole array.`.\n4. Now we should think about applying **offline query** and we need to observe below written type of a scenario for offline query.\n\n ```\n```\n ```\nIn most of the case there would be some limit value would be given for every query.\nThen we will see that:\n\t For eg : <=7 will be also candidate for <=10 which will also be candidate for <=20 and so on.\nIf we observe above type of scenario in any query type question. Then we simply need to apply the offline query algorithm.\n```\n```\n```\n\n>> **OUR MAIN FOCUS SHOULD ONLY BE ON `How to solve a single query in most efficient way` and secondly, `identifying whether it is a offline query type question or not by observing above scenarios`, because after identifying the algorithm for any offline type qery is approx same as below**\n\n\n# Generic Algorithm for any OFFLINE QUERY TYPE QUESTION: \n\n //put indexes in the query\n\t\t for(int i=0;i<q.size();i++) q[i].push_back(i);\n\t\t //sort the queries and input\n sort(begin(a),end(a));\n sort(begin(q),end(q),[](auto &x,auto &y){ return x[1] < y[1]; });\n \n int i=0;\n vector<int> ans(q.size());\n \n for(auto j:q){\n int c= j[0], p=j[1], idx= j[2];\n for(;i<size(a) and a[i]<=p;i++) //call function for putting candidates of a single query\'\n\t\t\t\t//put answer of current query in its corresponding index number in the result array...\n if(i==0) ans[idx]=-1;\n else ans[idx]= //function for getting answer of single query \n } \n return ans;\n\n\n\n**Solution for this problem based on offline query concept** => C++\n \n class Solution {\n public:\n\n class DSU{\n vector<int> par,rank;\n public:\n \n DSU(int n){\n par.resize(n);\n rank.resize(n,1);\n iota(begin(par),end(par),0);\n }\n \n int find(int u){\n if(par[u]==u) return u;\n else return par[u]= find(par[u]);\n }\n \n void union_p(int u,int v){\n u= find(u);\n v= find(v);\n \n if(rank[u]<rank[v]) par[u]=v;\n else if(rank[u]>rank[v]) par[v]=u;\n else{\n par[v]=u;\n rank[u]++;\n }\n }\n };\n \n \n vector<bool> distanceLimitedPathsExist(int n, vector<vector<int>>&a, vector<vector<int>>& q) {\n \n DSU d(n);\n //Algofor offline queries\n for(int i=0;i<q.size();i++) q[i].push_back(i);\n //sort the queries and input\n sort(begin(a),end(a),[](auto &x,auto &y){ return x[2] < y[2]; });\n sort(begin(q),end(q),[](auto &x,auto &y){ return x[2] < y[2]; });\n \n int i=0;\n vector<bool> ans(q.size());\n \n for(auto j:q){\n int u= j[0], v=j[1], p=j[2], idx= j[3];\n for(;i<size(a) and a[i][2]<p;i++) d.union_p(a[i][0],a[i][1]);\n ans[idx]= (d.find(u)==d.find(v));\n } \n \n return ans;\n \n }\n };
| 3 | 0 |
['C']
| 1 |
checking-existence-of-edge-length-limited-paths
|
c++ solution using dsu
|
c-solution-using-dsu-by-dilipsuthar60-6jr1
|
\nclass union_find\n{\n private:\n vector<int>parent;\n vector<int>rank;\n public:\n union_find(int n)\n {\n parent=vector<int>(n,0);\n
|
dilipsuthar17
|
NORMAL
|
2021-11-25T05:54:09.886089+00:00
|
2021-11-25T11:53:21.184751+00:00
| 572 | false |
```\nclass union_find\n{\n private:\n vector<int>parent;\n vector<int>rank;\n public:\n union_find(int n)\n {\n parent=vector<int>(n,0);\n rank=vector<int>(n,1);\n iota(parent.begin(),parent.end(),0);\n }\n int find(int x)\n {\n if(x==parent[x])\n {\n return x;\n }\n return parent[x]=find(parent[x]);\n }\n void merge(int x,int y)\n {\n if(rank[x]>rank[y])\n {\n parent[y]=x;\n rank[x]+=rank[y];\n }\n else\n {\n parent[x]=y;\n rank[y]+=rank[x];\n }\n }\n bool is_connected(int x,int y)\n {\n return find(x)==find(y);\n }\n};\n\nclass Solution {\npublic:\n vector<bool> distanceLimitedPathsExist(int n, vector<vector<int>>&nums, vector<vector<int>>& q) \n { \n union_find dsu(n);\n sort(nums.begin(),nums.end(),[&](auto &a,auto &b)\n {return a[2]<b[2];});\n for(int i=0;i<q.size();i++)\n {\n q[i].push_back(i);\n }\n sort(q.begin(),q.end(),[&](auto &a,auto &b)\n {return a[2]<b[2];});\n int i=0;\n int X=nums.size();\n vector<bool>ans(q.size());\n for(auto it:q)\n {\n while(i<X&&nums[i][2]<it[2])\n {\n int p1=dsu.find(nums[i][0]);\n int p2=dsu.find(nums[i][1]);\n if(p1!=p2)\n {\n dsu.merge(p1,p2);\n }\n i++;\n }\n ans[it[3]]=dsu.is_connected(it[0],it[1]);\n }\n return ans;\n }\n};\n```
| 3 | 0 |
['Union Find', 'C', 'C++']
| 0 |
checking-existence-of-edge-length-limited-paths
|
C++ || Union-Find
|
c-union-find-by-amsv_24-ln9p
|
Sort all edges as well as queries in increasing order. To answer a query i.e. (qv1,qv2,weight) we connect all those edges whose weights are strictly less than \
|
amsv_24
|
NORMAL
|
2021-05-26T13:20:08.880112+00:00
|
2021-05-26T13:20:08.880143+00:00
| 359 | false |
Sort all edges as well as queries in increasing order. To answer a query i.e. (qv1,qv2,weight) we connect all those edges whose weights are strictly less than \'weight\'. After connecting those edges we check if the query nodes are connected or not which will be true only if edge weights smaller than \'weight\' were involved else it would be false as it requires extra edges having edge weights greater than \'weight\'.\n\n```\nclass Solution {\npublic:\n vector<int>parent,rank;\n \n void initialize(int n){\n for(int i=0;i<n;i++){\n parent[i]=i;\n rank[i]=0;\n }\n }\n \n int findPar(int v){\n if(v==parent[v]) return v;\n return parent[v]=findPar(parent[v]);\n }\n \n vector<bool> distanceLimitedPathsExist(int n, vector<vector<int>>& edgeList, vector<vector<int>>& queries) {\n int s=edgeList.size();\n int m=queries.size();\n parent.resize(n);\n rank.resize(n);\n initialize(n);\n \n vector<vector<int>>edges,q;\n for(int i=0;i<s;i++){\n vector<int>t;\n t.push_back(edgeList[i][2]); t.push_back(i);\n edges.push_back(t);\n }\n for(int i=0;i<m;i++){\n vector<int>t;\n t.push_back(queries[i][2]); t.push_back(i);\n q.push_back(t);\n }\n \n sort(edges.begin(),edges.end());\n sort(q.begin(),q.end());\n \n vector<bool>ans(m);\n int start=0;\n \n for(int i=0;i<m;i++){\n int weight=q[i][0];\n int qv1=queries[q[i][1]][0];\n int qv2=queries[q[i][1]][1];\n for(int j=start;j<s;j++){\n if(edges[j][0]<weight){\n int v1=edgeList[edges[j][1]][0];\n int v2=edgeList[edges[j][1]][1];\n int u=findPar(v1);\n int v=findPar(v2);\n if(u!=v){\n //union\n if(rank[u]<rank[v])\n parent[u]=v;\n else if(rank[v]<rank[u])\n parent[v]=u;\n else\n parent[v]=u,rank[u]++;\n }\n start++;\n \n }\n else\n break;\n \n }\n if(findPar(qv1)==findPar(qv2))\n ans[q[i][1]]=true;\n else\n ans[q[i][1]]=false;\n }\n return ans;\n }\n};\n```
| 3 | 0 |
['C']
| 0 |
checking-existence-of-edge-length-limited-paths
|
Edge Length Limited Paths - DSU & Sorting Solution 🔍
|
edge-length-limited-paths-dsu-sorting-so-l39s
|
IntuitionWhen I first saw this problem, I realized it's asking us to check if two nodes are connected using only edges with weights less than a given limit. Thi
|
ojasm777
|
NORMAL
|
2025-01-09T03:56:36.121988+00:00
|
2025-01-09T03:56:36.121988+00:00
| 58 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
When I first saw this problem, I realized it's asking us to check if two nodes are connected using only edges with weights less than a given limit. This naturally led me to think about using a Disjoint Set Union (DSU) data structure, which is perfect for keeping track of connected components in a graph.
Think of it like forming groups of friends - if A is friends with B, and B is friends with C, then A, B, and C are all in the same friend group. Here, we're doing the same with nodes, but only connecting them if the edge weight is less than our limit.
---
# Approach
<!-- Describe your approach to solving the problem. -->
Let's break this down into simple steps:
1. Preparation:
- Create a DSU to track connected components
- Add index to queries to remember original order
- Sort both queries and edges by weight/limit (ascending)
2. Main Logic:
- For each query in sorted order:
- Add all edges with weight < query limit to DSU
- Check if query nodes are in same component
The clever part is sorting queries by limit - this means we only need to process each edge once, and we can reuse the same DSU state for multiple queries.
---
# Complexity
- Time complexity: $$O((E + Q) \log(E + Q))$$ where E is number of edges and Q is number of queries
- Sorting takes O(E logE) and O(Q logQ)
- DSU operations are nearly constant time
- Space complexity: $$O(N + Q)$$
- N for DSU parent array
- Q for storing query indices
# Code
```cpp []
class DSU {
vector<int> parent, size;
int n;
public:
DSU(int n) {
this->n = n;
size.resize(n + 1, 1);
parent.resize(n + 1, 0);
iota(begin(parent), end(parent), 0);
}
int findParent(int x) {
return parent[x] = (parent[x] == x) ? x : findParent(parent[x]);
}
void Union(int a, int b) {
a = findParent(a);
b = findParent(b);
if(a == b) return;
if(size[a] >= size[b]) {
parent[b] = a;
size[a] += size[b];
} else {
parent[a] = b;
size[b] += size[a];
}
}
};
class Solution {
public:
vector<bool> distanceLimitedPathsExist(int n, vector<vector<int>>& edgeList, vector<vector<int>>& queries) {
int m = queries.size();
vector<bool> ans(m, false);
DSU dsu(n);
// I am thinking to use 1 dsu, sort the queries on the basis of limit and
// sort edgeList also on the basis of distance
// for each query go till limit and add those nodes in dsu simple
for(int i = 0; i < m; i++) {
queries[i].push_back(i);
}
sort(begin(queries), end(queries), [&](vector<int>& a, vector<int>& b) {
return a[2] < b[2]; // increasing order of limit
});
sort(begin(edgeList), end(edgeList), [&](vector<int>& a, vector<int>& b) {
return a[2] < b[2]; // increasing order of distance
});
int j = 0;
for(int i = 0; i < m; i++) {
int p = queries[i][0], q = queries[i][1], limit = queries[i][2];
while(j < edgeList.size() && edgeList[j][2] < limit){
dsu.Union(edgeList[j][0], edgeList[j][1]); // add them to the union
j++;
}
if(dsu.findParent(p) == dsu.findParent(q)) ans[queries[i][3]] = true;
}
return ans;
}
};
```
```python []
class DSU:
def __init__(self, n):
self.parent = list(range(n))
self.size = [1] * n
def find(self, x):
if self.parent[x] != x:
self.parent[x] = self.find(self.parent[x])
return self.parent[x]
def union(self, a, b):
pa, pb = self.find(a), self.find(b)
if pa == pb: return
if self.size[pa] >= self.size[pb]:
self.parent[pb] = pa
self.size[pa] += self.size[pb]
else:
self.parent[pa] = pb
self.size[pb] += self.size[pa]
class Solution:
def distanceLimitedPathsExist(self, n: int, edgeList: List[List[int]], queries: List[List[int]]) -> List[bool]:
# Add index to queries to remember original order
for i in range(len(queries)):
queries[i].append(i)
# Sort edges and queries by weight/limit
edgeList.sort(key=lambda x: x[2])
queries.sort(key=lambda x: x[2])
dsu = DSU(n)
ans = [False] * len(queries)
j = 0 # pointer for edgeList
# Process each query
for p, q, limit, original_index in queries:
# Add all edges with weight < limit
while j < len(edgeList) and edgeList[j][2] < limit:
dsu.union(edgeList[j][0], edgeList[j][1])
j += 1
# Check if nodes are connected
ans[original_index] = dsu.find(p) == dsu.find(q)
return ans
```
| 2 | 1 |
['Union Find', 'Graph', 'Sorting', 'C++', 'Python3']
| 0 |
checking-existence-of-edge-length-limited-paths
|
Simple DSU Solution Explained in Comments ✅
|
simple-dsu-solution-explained-in-comment-m21r
|
Complexity\n- Time complexity :\n- Space complexity :\n\n# Code\n\nclass DisjointSet {\npublic:\n vector<int> parent, rank;\n DisjointSet(int n) {\n
|
Sachin5115
|
NORMAL
|
2024-04-18T14:25:55.558376+00:00
|
2024-04-18T14:25:55.558407+00:00
| 28 | false |
# Complexity\n- Time complexity :\n- Space complexity :\n\n# Code\n```\nclass DisjointSet {\npublic:\n vector<int> parent, rank;\n DisjointSet(int n) {\n rank.resize(n + 1, 0); \n parent.resize(n + 1); \n // Initially, each element is its own parent\n for (int i = 0; i <= n; i++) {\n parent[i] = i; \n }\n }\n\n int findParent(int u) {\n if (u == parent[u]) return u; \n return parent[u] = findParent(parent[u]); \n }\n\n // Union operation by rank\n void unionByRank(int u, int v) {\n u = findParent(u);\n v = findParent(v);\n // If u and v are already in the same set, do nothing\n if (u == v) return; \n if (rank[u] < rank[v]) {\n parent[u] = v; \n } else if (rank[v] < rank[u]) {\n parent[v] = u;\n } else {\n parent[u] = v; \n rank[v]++;\n }\n }\n};\n\nclass Solution {\npublic:\n // Comparator function for sorting edgeList and queries based on distance/limit\n static bool cmp(vector<int>& a, vector<int>& b) {\n return a[2] < b[2]; \n }\n\n // Function to check if there exists a path between nodes within given distance limits\n vector<bool> distanceLimitedPathsExist(int n, vector<vector<int>>& edgeList, vector<vector<int>>& queries) {\n DisjointSet ds(n); \n int size = edgeList.size(); \n int k = queries.size(); \n\n // Add index to queries to keep track of their original position after sorting\n for (int i = 0; i < k; i++) queries[i].push_back(i);\n\n // Sort edgeList and queries based on distance limits so that processing done in a way that \n // edges are processed in increasing order of distance, and queries are processed accordingly\n sort(edgeList.begin(), edgeList.end(), cmp);\n sort(queries.begin(), queries.end(), cmp);\n\n // result vector\n vector<bool> ans(k, false); \n\n int i = 0; // Iterator over edgeList\n int j = 0; // Iterator over queries\n\n // Process queries\n while (j < k) {\n int u = queries[j][0];\n int v = queries[j][1];\n int lim = queries[j][2];\n int idx = queries[j][3]; // Index to update the answer\n\n // Add edges to Disjoint Set until reaching the current query\'s limit\n while (i < size && edgeList[i][2] < lim) {\n ds.unionByRank(edgeList[i][0], edgeList[i][1]);\n i++;\n }\n\n // Check if u and v belong to the same component in Disjoint Set i.e. we can move to any node from one to another so mark that as true\n if (ds.findParent(u) == ds.findParent(v)) ans[idx] = true;\n\n // Move to the next query\n j++; \n }\n\n // Return the result\n return ans; \n }\n};\n\n```
| 2 | 0 |
['Union Find', 'Sorting', 'C++']
| 0 |
checking-existence-of-edge-length-limited-paths
|
Java || 32ms 100% || 2 Sorts and Union-Find, Fastest, Beginner Friendly
|
java-32ms-100-2-sorts-and-union-find-fas-id1r
|
--- Algorithm ---\nThe code below has been optimized for speed, which sacrifices some simplicity. The code uses the following algorithm:\n\n1. Sort the edges i
|
dudeandcat
|
NORMAL
|
2023-04-29T20:06:32.892260+00:00
|
2023-08-23T23:49:38.687851+00:00
| 200 | false |
**--- Algorithm ---**\nThe code below has been optimized for speed, which sacrifices some simplicity. The code uses the following algorithm:\n\n1. Sort the edges in ascending distance order.\n2. Sort the queries in ascending distance order.\n3. Initialize a union-find for the nodes of the graph.\n4. Initialize boolean array to be returned, to all false.\n5. Initialize iterator for the sorted edges.\n6. Loop through the queries in sorted order.\n7. Add all edges with a distance shorter than the current queries limit distance, using iterator for the sorted edges, and using union-find to add those edges to the graph.\n8. If the two nodes of the query have the same union-find parent, then there must be a valid path between the query\'s two nodes, so set current query\'s entry in the boolean array to true.\n9. Loop back to step #6, until all queries have been processed.\n10. Return boolean array.\n\n**--- Union Find ---**\nIn this leetcode problem, the union-find is used to determine if any two nodes of the graph are connected by some path through the graph. As the queries are processed in ascending order sorted by their limit distance, we only partially build the graph, using only those edges that have a distance less than the current query\'s limit distance. Therefore, all edges that have been added to the graph, will always be valid edges for the current query. Determining if any path exists between the query\'s two nodes is done with a union-find.\n\nThe "**union-find**" is two operations. The "**find**" operation to find any node\'s "**root**" node in the graph. And the "**union**" operation to join any two nodes, which in this case is to add an edge between two nodes. The purpose of the union-find is to collect nodes into groups, where each group has a path or paths connecting all members of the group. a union-find group is identified by its root node. Another union-find group with a different root node, will NOT have any graph connections between the two groups. Union-find groups are connected within the group, but disconnected (or disjoint) from other groups.\n\nA union-find group\'s **root node has no special significance** in this leetcode problem. The root node has simply been arbitrarily chosen to be the union-find group\'s identifier. The root node of a group may change when the union operation merges two groups into a single group.\n\nTo implement the union-find data structure, we create an array `parents[]`. The `parents` array is indexed by a node\'s node number. The `parents` array contains each node\'s parent node number. A "**root**" node in the `parents` array is simply any node that is its own parent, or `parents[i]==i` for root nodes. For non-root nodes, which node is the parent node, has no special significance other than to find the path to that node\'s root node. The any node\'s parent node number may be modified by the union-find operations, so which node is currently the parent of another has little significance.\n\nTo create the `parents` array, we initialize each node to be its own parent, making each node a root node. Initially, no edges have been processed, so there are no connections between any nodes, and therefore each node is isolated in its own union-find group, with itself being the root node of its own group. The nodes will become connected later when performing union operations. To initialize the `parents` array, use the code:\n```\n int[] parents = new int[n];\n for (int i = n - 1; i >= 0; i--)\n parents[i] = i;\n```\nTo perform the union-find\'s find operation, call the `findRoot()` method. This method calls itself recursively to find the root of the union-find group. All nodes in the same union-find group have the same root node, and have edges that create paths between any two nodes in the same union-find group. The `findParent()` method will also update the nodes it recurses through, so next time they have a shorter path to the root node. The `parents[]` array contains the parent node number for every node. A node is the root of a union-find group if `parents[i]==i`.\n```\n private int findRoot(int[] parents, int node) {\n if (parents[node] == node) return node;\n return parents[node] = findRoot(parents, parents[node]);\n }\n```\nWe use the union-find\'s union operation to add an edge to the graph, using that edge\'s two nodes. The union operation is very simple. First we find the root node numbers for the edge\'s two nodes. If both nodes have the same root node, then some path between the two nodes already exists so nothing to do, because they are already in the same union-find group. If both nodes have different root nodes, then there was previously no path between the two nodes. But now this edge will directly connect the two nodes, so we need to merge the two union-find groups by setting the root node of one union-find group, to point to the root node of the other group, thereby demoting one of the root nodes a non-root node. For the root node that was demoted to a non-root node, any chain of parentage that led to that root node, will now continue that chain to the other root node, which is now the root node of the two groups that have been combined into a single group. When doing the union operation to merge two groups, it is arbitrary as to which root is demoted to non-root, and which root node becomes the root node for the new combined group. The union operation is performed with the following code:\n```\n int rootU = findRoot(parents, edge[0]);\n int rootV = findRoot(parents, edge[1]);\n if (rootU != rootV) parents[rootV] = rootU;\n```\nThis is a very simple implementation of union-find, but this simple implementation is enough for many leetcode problems. The union-find is also called "disjoint-set data structure", "merge-find set", or "union-find data structure". In this leetcode problem, the actual graph is NOT stored as edges are added to the graph. Only the union-find groupings of the graph\'s nodes is needed.\n\n**--- Sorting ---**\nSorting the edges and the queries does NOT modify the `edgeList` and `queries` arrays. Two sorted arrays are created. One sorted array for edges, and one sorted array for queries.\n\nTo sort, an array of `long` is created the same length of the array to be sorted. The distance and original index is written into each `long`. Then the array of `long` is sorted using `Arrays.sort()`, resulting in edges or queries in increasing distance order. Each `long` in the sorted array contains the original index back to the `edgeList` or `queries` arrays. An array of `long` is used for sorting because: 1) sorting an array of primitive types is faster than sorting more complex objects and this code has been optimized for speed, and 2) a `long` is needed to contain the values to be sorted.\n\nEach `long` value in the array to be sorted, is loaded with the distance value and the original index into the `edgeList` or `queries` arrays. The distance is placed in the more significant digits of the `long` to be able to sort by distance, and the original index is placed in the lowest digits of the `long`. Then the array is sorted using `Arrays.sort()`. \n\nThe first code example below has the sorted `long` values storing distance and index inside the `long` in binary bit positions, using SHIFT-LEFT to load the `long` values, and using AND to read the index value from the `long` value. These `long` values are stored as:\n```\n | Bit 63 Bit 0 |\n+V-------------+------------------------------+-------------------V+\n| (unused) | Bits 20..49 : distance | Bits 0..19 : index |\n+--------------+------------------------------+--------------------+\n\t\tAssigning value to long: long = distance << 20 + index\n\t\tReading index from long: index = long & 0xFFFFF\n\t\t\n```\nThe second code example below has the sorted `long` values storing distance and index inside the `long` in decimal digit positions, using MULTIPLY to load the `long` values, and MODULO to read the index from the `long` value. Storing the sorted values using binary operators, had runtimes as much as 12% faster as using decimal digit storage. These `long` values are stored as:\n```\nDecimal digits in 64-bit long: 00_00d_ddd_ddd_ddd_xxx_xxx\n\t\t\t\t\tx = Digits containing index value.\n\t\t\t\t\td = Digits containing distance value.\n\t\t\t\t\t0 = Unused decimal digits.\n\t\tAssigning value to long: long = distance * 1_000_000 + index\n\t\tReading index from long: index = long % 1_000_000\n```\n**--- Miscelaneous ---**\nThis code runs as fast as 32ms using binary stored data in the sorted `long` values, and 33ms using decimal stored data in the sorted `long` values, in August 2023.\n\nIf useful, please upvote.\n\n**--- Commented code with binary shift and mask for building and retrieving sorted values (faster) ---**\n\n```\nclass Solution {\n // These MASK and SHIFT values are used to build sort \n // arrays for the edges and for the queries. The arrays \n // to be sorted contain the higher binary digits, and \n // the index into the edges or the queries into the \n // lower binary digits. After sorting, only the index \n // in the lower part of the long value is used.\n static final long MASK = 0xFFFFFL;\n static final int SHIFT = 20;\n \n public boolean[] distanceLimitedPathsExist(int n, int[][] edgeList, \n int[][] queries) {\n int eCount = edgeList.length;\n int qCount = queries.length;\n\n // Sort the edges by distance.\n long[] eSort = new long[eCount];\n for (int i = eCount - 1; i >= 0; i--)\n eSort[i] = ((long)edgeList[i][2] << SHIFT) + i;\n Arrays.sort(eSort);\n \n // Sort the queries by limit distance.\n long[] qSort = new long[qCount];\n for (int i = qCount - 1; i >= 0; i--)\n qSort[i] = ((long)queries[i][2] << SHIFT) + i;\n Arrays.sort(qSort);\n \n // Build the parents array for the union find.\n int[] parents = new int[n];\n for (int i = n - 1; i >= 0; i--)\n parents[i] = i;\n \n boolean[] result = new boolean[qCount];\n int eSortIdx = 0;\n int[] e = edgeList[(int)(eSort[0] & MASK)];\n int eDist = e[2];\n // Loop through all of the queries, in increasing limit distance \n // order.\n for (int qSortIdx = 0; qSortIdx < qCount; qSortIdx++) {\n int qIdx = (int)(qSort[qSortIdx] & MASK);\n int[] q = queries[qIdx];\n int qDist = q[2];\n // Process all of the unprocessed edges that are within the \n // current query\'s limit distance. Because queries are processed \n // in low to high distance order, and edges are processed in low \n // to high distance order, we just process edged (i.e. connect \n // via union-find) until we hit an edge with larger or same \n // distance as the current query\'s limit distance.\n if (eSortIdx < eCount) {\n while (qDist > eDist) {\n int rootU = findRoot(parents, e[0]);\n int rootV = findRoot(parents, e[1]);\n if (rootU != rootV)\n parents[rootV] = rootU;\n eSortIdx++;\n if (eSortIdx >= eCount) break;\n e = edgeList[(int)(eSort[eSortIdx] & MASK)];\n eDist = e[2];\n }\n }\n // Use union-find roots to decide if the two query nodes \n // are connected by some path.\n if (findRoot(parents, q[0]) == findRoot(parents, q[1])) \n result[qIdx] = true;\n }\n return result;\n }\n \n \n private int findRoot(int[] parents, int node) {\n if (parents[node] == node) return node;\n return parents[node] = findRoot(parents, parents[node]);\n }\n}\n```\n**--- Clean Java code with decimal multiply and modulo for building and retrieving sorted values (slower) ---**\n```\nclass Solution {\n static final long MOD = 1_000_000L;\n \n public boolean[] distanceLimitedPathsExist(int n, int[][] edgeList, \n int[][] queries) {\n int eCount = edgeList.length;\n int qCount = queries.length;\n\n long[] eSort = new long[eCount];\n for (int i = eCount - 1; i >= 0; i--)\n eSort[i] = (long)edgeList[i][2] * MOD + i;\n Arrays.sort(eSort);\n \n long[] qSort = new long[qCount];\n for (int i = qCount - 1; i >= 0; i--)\n qSort[i] = (long)queries[i][2] * MOD + i;\n Arrays.sort(qSort);\n \n int[] parents = new int[n];\n for (int i = n - 1; i >= 0; i--)\n parents[i] = i;\n \n boolean[] result = new boolean[qCount];\n int eSortIdx = 0;\n int[] e = edgeList[(int)(eSort[0] % MOD)];\n int eDist = e[2];\n for (int qSortIdx = 0; qSortIdx < qCount; qSortIdx++) {\n int qIdx = (int)(qSort[qSortIdx] % MOD);\n int[] q = queries[qIdx];\n int qDist = q[2];\n if (eSortIdx < eCount) {\n while (qDist > eDist) {\n int rootU = findRoot(parents, e[0]);\n int rootV = findRoot(parents, e[1]);\n if (rootU != rootV)\n parents[rootV] = rootU;\n eSortIdx++;\n if (eSortIdx >= eCount) break;\n e = edgeList[(int)(eSort[eSortIdx] % MOD)];\n eDist = e[2];\n }\n }\n if (findRoot(parents, q[0]) == findRoot(parents, q[1])) \n result[qIdx] = true;\n }\n return result;\n }\n \n \n private int findRoot(int[] parents, int node) {\n if (parents[node] == node) return node;\n return parents[node] = findRoot(parents, parents[node]);\n }\n}\n```
| 2 | 0 |
['Union Find', 'Sorting', 'Java']
| 0 |
checking-existence-of-edge-length-limited-paths
|
Union Find python
|
union-find-python-by-sumanthn27-s6dt
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
SumanthN27
|
NORMAL
|
2023-04-29T16:23:34.599008+00:00
|
2023-04-29T16:23:34.599042+00:00
| 152 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass UnionFind:\n def __init__(self, N: int):\n self.parent = list(range(N))\n self.rank = [1] * N\n\n def find(self, p: int) -> int:\n if p != self.parent[p]:\n self.parent[p] = self.find(self.parent[p])\n return self.parent[p]\n\n def union(self, p: int, q: int) -> bool:\n prt, qrt = self.find(p), self.find(q)\n if prt == qrt: return False \n if self.rank[prt] > self.rank[qrt]: \n prt, qrt = qrt, prt \n self.parent[prt] = qrt \n self.rank[qrt] += self.rank[prt] \n return True \n\n\nclass Solution:\n def distanceLimitedPathsExist(self, n: int, edgeList: List[List[int]], queries: List[List[int]]) -> List[bool]:\n queries = sorted((w, p, q, i) for i, (p, q, w) in enumerate(queries))\n edgeList = sorted((w, u, v) for u, v, w in edgeList)\n \n uf = UnionFind(n)\n \n ans = [None] * len(queries)\n ii = 0\n for w, p, q, i in queries: \n while ii < len(edgeList) and edgeList[ii][0] < w: \n _, u, v = edgeList[ii]\n uf.union(u, v)\n ii += 1\n ans[i] = uf.find(p) == uf.find(q)\n return ans \n```
| 2 | 0 |
['Python3']
| 0 |
checking-existence-of-edge-length-limited-paths
|
Sorting + DSU
|
sorting-dsu-by-gauravgoyal_13-jffi
|
Complexity\n- Time complexity:O(ElogE + QlogQ + Q + E) = O(NlogN)\n\n- Space complexity:O(N)\n\n# Code\n\nclass DSU {\npublic:\n vector<int>Parent;\n vect
|
gauravgoyal_13
|
NORMAL
|
2023-04-29T08:14:26.486618+00:00
|
2023-04-29T08:14:26.486651+00:00
| 753 | false |
# Complexity\n- Time complexity:O(ElogE + QlogQ + Q + E) = O(NlogN)\n\n- Space complexity:O(N)\n\n# Code\n```\nclass DSU {\npublic:\n vector<int>Parent;\n vector<int>Rank;\n DSU(int n) {\n Parent.resize(n);\n Rank.resize(n, 0);\n for(int i = 0; i < n; i++) Parent[i] = i;\n }\n\n int Find(int x) {\n return Parent[x] = Parent[x] == x? x : Find(Parent[x]);\n }\n\n void Union(int a, int b) {\n a = Find(a);\n b = Find(b);\n if(Rank[a] == Rank[b]) Rank[a]++;\n if(Rank[a] > Rank[b]){\n Parent[b] = a;\n }\n else {\n Parent[a] = b;\n }\n }\n};\n\nclass Solution {\npublic:\n vector<bool> distanceLimitedPathsExist(int n, vector<vector<int>>& edgeList, vector<vector<int>>& q) {\n int nq = q.size();\n for(int i = 0; i < nq; i++) {\n q[i].push_back(i);\n }\n sort(begin(q), end(q), [&](auto const& a, auto const& b) {\n return a[2] < b[2];\n });\n sort(begin(edgeList), end(edgeList), [&](auto const& a, auto const& b) {\n return a[2] < b[2];\n });\n vector<bool>ans(nq, 0);\n int i = 0;\n DSU dsu(n);\n for(int j = 0; j < nq; j++) {\n while(i < edgeList.size() && edgeList[i][2] < q[j][2]) {\n dsu.Union(edgeList[i][0], edgeList[i][1]);\n i++;\n }\n if(dsu.Find(q[j][0]) == dsu.Find(q[j][1])) ans[q[j][3]] = 1;\n }\n return ans;\n }\n};\n```
| 2 | 0 |
['C++']
| 0 |
checking-existence-of-edge-length-limited-paths
|
Union Find | Python / JS Solution
|
union-find-python-js-solution-by-tfdleet-4sew
|
Hello Tenno Leetcoders, \nFor this problem, we have an undirected graph of n nodes defined by edgeList, where edgeList[i] = [ui, vi, disi]. denotes an edge betw
|
TFDLeeter
|
NORMAL
|
2023-04-29T02:51:51.989497+00:00
|
2023-04-29T02:51:51.989544+00:00
| 195 | false |
Hello **Tenno Leetcoders**, \nFor this problem, we have an undirected graph of `n` nodes defined by `edgeList`, where `edgeList[i] = [ui, vi, disi]`. denotes an edge between nodes `ui` and `v`i with distance `disi`.\n\nWe are given an `array queries`, where `queries[j] = [pj, qj, limitj]`, we want to determine for each `queries[i]`, whether there is a path between `pj` and `qj` such that each edge on the path has a distance strictly less than `limitj`.\n\n\nWe want to return a `boolean array answer`, where `answer.length == queries.length` and the `jth value` of answer is `true` if there is a `path` for `queries[j]` is `true`, and `false` otherwise.\n\n## Explanation\n\nThis problem want us to determine for each query in `queries` array, we want to know if there exists a path between node `pj` and `qj` in an undirected graph defined by `edgeList` such that each edge on the path has a distance stricly less than `limitj`\n\nSince, we want to determine if there is a path between two nodes such that each edges within the path has a distance strictly less than the given limit denoted as `limitj`\n\nWe can use `Union-find` to help us determine wether there is a path between two nodes that satisfy the given limit condition \n\nA basic usage of `Union-find` will be first, initializing each node as its own seperate component. \n\nAs we proceed each edge, we check whether the connection between two nodes are in the same component. \n\nWe can then determine the same two nodes belonging to the same component have the same root node.\n\nFor this problem though, we can use the same basic usage of`Union-find` with some modifications. We should first merge componenets by considering the weight of each edges. \n\nAs we merge two componenets, we want to choose the smallest edge weight between the parent and child.\n\nTo keep track of each parent node, we want to use an array and another array to keep track of distances betwen each node and its parent and set the starting distance as `0s`.\n\nWe will iterate our given `edgeList`. For each edge, we will find the parent nodes using `union-find`, comparing the distances between each node and its parent with their weight. If their weight is less than the distance, we can update the parent and the starting distances with the new parents distance.\n\nWe will need to check if there is a path between two nodes. by finding the root of the parent and child nodes using `union-find` again. We can then calculate the distance between each node and its root.\n\nIf their distance is less than the given limit denoted as `limitj` then we return `true` else `false`\n\n\n### Code\n\n**Python**\n```\nclass UnionFind:\n \n def __init__(self,n):\n self.parent = [i for i in range(n)]\n self.size = [0] * n\n \n def find(self, node):\n if self.parent[node] != node:\n self.parent[node] = self.find(self.parent[node])\n \n return self.parent[node]\n \n \n\n def union(self, node1, node2):\n root1 = self.find(node1)\n root2 = self.find(node2)\n \n if root1 == root2: return \n \n if self.size[root1] > self.size[root2]: self.parent[root2] = root1\n elif self.size[root1] < self.size[root2]: self.parent[root1] = root2\n else: \n self.parent[root1] = root2\n self.size[root2] += 1\n \n def connected(self, node1, node2):\n return self.find(node1) == self.find(node2)\n \nclass Solution: \n def distanceLimitedPathsExist(self, n: int, edgeList: List[List[int]], queries: List[List[int]]) -> List[bool]:\n uf = UnionFind(n)\n \n edgeList.sort(key=lambda x: x[2])\n \n queries_sorted = [(limit, i, p, q) for i, (p,q, limit) in enumerate(queries)]\n \n queries_sorted.sort()\n \n result = [False] * len(queries)\n \n edges_index = 0\n \n for limit, query_index, p, q in queries_sorted:\n while edges_index < len(edgeList) and edgeList[edges_index][2] < limit:\n uf.union(edgeList[edges_index][0], edgeList[edges_index][1])\n edges_index += 1\n \n if uf.connected(p,q):\n result[query_index] = True\n \n return result\n```\n\n**JavaScript**\n\n```\nclass UnionFind{\n \n constructor(n){\n this.parent = Array(n).fill().map((_, i) => i)\n this.size = Array(n).fill(0)\n }\n \n find(node){\n if(this.parent[node] !== node){\n this.parent[node] = this.find(this.parent[node])\n }\n return this.parent[node]\n } \n \n union(node1, node2){\n let root1 = this.find(node1)\n let root2 = this.find(node2)\n \n if (root1 === root2) return\n \n if(this.size[root1] > this.size[root2]) {\n this.parent[root2] = root1\n }\n else if(this.size[root1] < this.size[root2]){\n this.parent[root1] = root2\n }\n else{\n this.parent[root1] = root2\n this.size[root2] += 1\n }\n }\n \n connected(node1, node2){\n return this.find(node1) === this.find(node2)\n }\n \n}\n\nvar distanceLimitedPathsExist = function(n, edgeList, queries) {\n \n let uf = new UnionFind(n)\n \n edgeList.sort((a,b) => a[2] - b[2])\n \n let queries_sorted = queries.map((q,i) => [q[2], i, q[0], q[1]])\n queries_sorted.sort((a,b ) => a[0] - b[0])\n \n let result = Array(queries_sorted.length).fill(false)\n\n \n let edges_index = 0\n \n \n for(let [limit, query_index, p, q] of queries_sorted){\n \n while(edges_index < edgeList.length && edgeList[edges_index][2] < limit){\n \n uf.union(edgeList[edges_index][0], edgeList[edges_index][1])\n edges_index += 1\n }\n \n if(uf.connected(p,q)){\n result[query_index] = true\n }\n \n }\n \n return result\n};\n```\n\n***Warframe\'s Darvo wants you to upvote this post \uD83D\uDE4F\uD83C\uDFFB \u2764\uFE0F\u200D\uD83D\uDD25***\n\n
| 2 | 0 |
['Union Find', 'Python', 'JavaScript']
| 0 |
checking-existence-of-edge-length-limited-paths
|
✅ Swift Solution. Runtime beats 75% [2186 ms], Memory beats 100% [29.6 MB].
|
swift-solution-runtime-beats-75-2186-ms-qg1nx
|
Approach\nAs the backbone a variation of Floyd Warshall\'s algorithm is used, which is an all-pairs shortest path algorithm, to compute the shortest distance be
|
eleev
|
NORMAL
|
2023-04-29T00:18:07.387382+00:00
|
2023-05-04T16:39:12.496379+00:00
| 113 | false |
# Approach\nAs the backbone a variation of `Floyd Warshall\'s` algorithm is used, which is an all-pairs shortest path algorithm, to compute the shortest distance between all pairs of nodes in the graph considering only edges with distances less than the limit. A Union-Find data structure with path compression and union by rank was used for cases with large n.\n\n## Time Complexity\nThe time complexity of this solution is `O(E * log(E) + Q * log(Q))`, where E is the number of edges and Q is the number of queries. This complexity should work efficiently for large values of n.\n\n## Space Complexity\nThe space complexity is `O(n + E + Q)`, where n is the number of nodes, E is the number of edges, and Q is the number of queries. The space is used to store the `UnionFind` data structure, the sorted edges, the sorted queries, and the result array.\n\n# Solution\n```swift\nclass Solution {\n func distanceLimitedPathsExist(_ n: Int, _ edgeList: [[Int]], _ queries: [[Int]]) -> [Bool] {\n var edges = edgeList.sorted { $0[2] < $1[2] }\n var queriesWithIndex = queries.enumerated().sorted { $0.1[2] < $1.1[2] }\n var result = Array(repeating: false, count: queries.count)\n let uf = UnionFind(n)\n var edgeIndex = 0\n\n for (queryIndex, query) in queriesWithIndex {\n let p = query[0]\n let q = query[1]\n let limit = query[2]\n \n while edgeIndex < edges.count && edges[edgeIndex][2] < limit {\n let edge = edges[edgeIndex]\n uf.union(edge[0], edge[1])\n edgeIndex += 1\n }\n \n result[queryIndex] = uf.find(p) == uf.find(q)\n }\n \n return result\n }\n\n final class UnionFind {\n var parent: [Int]\n var rank: [Int]\n \n init(_ size: Int) {\n parent = Array(0..<size)\n rank = Array(repeating: 0, count: size)\n }\n \n func find(_ x: Int) -> Int {\n if parent[x] != x {\n parent[x] = find(parent[x])\n }\n return parent[x]\n }\n \n func union(_ x: Int, _ y: Int) {\n let rootX = find(x)\n let rootY = find(y)\n \n if rootX != rootY {\n if rank[rootX] > rank[rootY] {\n parent[rootY] = rootX\n } else if rank[rootX] < rank[rootY] {\n parent[rootX] = rootY\n } else {\n parent[rootY] = rootX\n rank[rootX] += 1\n }\n }\n }\n }\n}\n```
| 2 | 0 |
['Swift']
| 0 |
checking-existence-of-edge-length-limited-paths
|
🗓️ Daily LeetCoding Challenge April, Day 29
|
daily-leetcoding-challenge-april-day-29-rgr86
|
This problem is the Daily LeetCoding Challenge for April, Day 29. Feel free to share anything related to this problem here! You can ask questions, discuss what
|
leetcode
|
OFFICIAL
|
2023-04-29T00:00:19.221709+00:00
|
2023-04-29T00:00:19.221792+00:00
| 1,850 | false |
This problem is the Daily LeetCoding Challenge for April, Day 29.
Feel free to share anything related to this problem here!
You can ask questions, discuss what you've learned from this problem, or show off how many days of streak you've made!
---
If you'd like to share a detailed solution to the problem, please create a new post in the discuss section and provide
- **Detailed Explanations**: Describe the algorithm you used to solve this problem. Include any insights you used to solve this problem.
- **Images** that help explain the algorithm.
- **Language and Code** you used to pass the problem.
- **Time and Space complexity analysis**.
---
**📌 Do you want to learn the problem thoroughly?**
Read [**⭐ LeetCode Official Solution⭐**](https://leetcode.com/problems/checking-existence-of-edge-length-limited-paths/solution) to learn the 3 approaches to the problem with detailed explanations to the algorithms, codes, and complexity analysis.
<details>
<summary> Spoiler Alert! We'll explain this 1 approach in the official solution</summary>
**Approach 1:** Disjoint-Set Union
</details>
If you're new to Daily LeetCoding Challenge, [**check out this post**](https://leetcode.com/discuss/general-discussion/655704/)!
---
<br>
<p align="center">
<a href="https://leetcode.com/subscribe/?ref=ex_dc" target="_blank">
<img src="https://assets.leetcode.com/static_assets/marketing/daily_leetcoding_banner.png" width="560px" />
</a>
</p>
<br>
| 2 | 0 |
[]
| 8 |
checking-existence-of-edge-length-limited-paths
|
Online solution in O(M*logM+(N+Q)*logN)
|
online-solution-in-omlogmnqlogn-by-the_w-xl2o
|
We compute the minimum spanning trees (there can be multiple ones, we are not guaranteed that the graph is connected) using Kruskal\'s Algorithm. O(M*logM) fro
|
The_Winner
|
NORMAL
|
2022-11-30T17:43:03.927434+00:00
|
2022-11-30T17:43:03.927489+00:00
| 40 | false |
We compute the minimum spanning trees (there can be multiple ones, we are not guaranteed that the graph is connected) using Kruskal\'s Algorithm. ``O(M*logM)`` from sorting.\nWe then build Binary Lifting data structure on the trees. ``O(N*logN)``.\nFor each query we get LCA of the 2 nodes ``x`` and ``y`` using Binary Lifting data structure and we also get max edge cost on the path from ``x`` to LCA and from ``y`` to LCA. If the maximum edge cost on the path is less than the limit, the answer to query is true. ``O(logN)`` per query, ``O(Q*logN)`` total.\nAdding up the complexities ``O(M*logM+(Q+N)*logN)``.
| 2 | 1 |
[]
| 0 |
checking-existence-of-edge-length-limited-paths
|
Python| Union-Find| Sorting
|
python-union-find-sorting-by-zsun273-ftht
|
\n# Idea: \n# For a query [p, q, limit]\n# we can connect all edges with a weight less than limit -> union nodes u_i, v_i if dis_i < limit\n# after previous ste
|
zsun273
|
NORMAL
|
2022-08-21T03:29:07.592195+00:00
|
2022-08-21T03:29:07.592221+00:00
| 346 | false |
```\n# Idea: \n# For a query [p, q, limit]\n# we can connect all edges with a weight less than limit -> union nodes u_i, v_i if dis_i < limit\n# after previous step, simply check if p and q is connected ---> get answer for this query\n\n# Optimization: \n# we can sort the query in ASC by limit, so for query with larger limits, no need to connect small weight edges\n\n\nclass Solution:\n def distanceLimitedPathsExist(self, n: int, edgeList: List[List[int]], queries: List[List[int]]) -> List[bool]:\n \n # Dynamic union-find with path compression and union by rank\n class UnionFind:\n\t\t pass\n \n edgeList.sort(key=lambda x:x[2]) # sort all edges by weight("distance")\n for i in range(len(queries)):\n queries[i].append(i) # add original query index into query cuz we will sort it later\n # we still need original index to store answers\n \n queries.sort(key=lambda x:x[2]) # sort the query in ASC by limit\n uf = UnionFind()\n start = 0 # record start index of unvisited edge in edgeList\n ans = [False] * len(queries)\n \n for u, v, limit, index in queries:\n \n for i in range(start, len(edgeList)):\n a, b, weight = edgeList[i]\n if weight < limit:\n uf.union(a, b)\n else: # find an edge with weiight >= limit, stop here\n start = i # record current index, so we can resume more efficiently \n break\n \n if u in uf.parents and v in uf.parents and uf.find(u) == uf.find(v):\n ans[index] = True\n \n return ans \n```\n\nImplementation of UnionFind class in more details: \nWe don\'t always need path compression and union-by-rank, but it doesn\'t hurt if we implement that.\n\n```\n# Dynamic union-find with path compression and union by rank\n class UnionFind:\n def __init__(self):\n self.parents = {}\n self.ranks = {}\n \n def insert(self, x):\n if x not in self.parents:\n self.parents[x] = x\n self.ranks[x] = 0\n \n def find(self, x):\n if self.parents[x] != x:\n self.parents[x] = self.find(self.parents[x])\n return self.parents[x]\n \n def union(self, x, y):\n self.insert(x)\n self.insert(y)\n x, y = self.find(x), self.find(y)\n if x == y:\n return \n if self.ranks[x] > self.ranks[y]:\n self.parents[y] = x\n else:\n self.parents[x] = y\n if self.ranks[x] == self.ranks[y]:\n self.ranks[y] += 1\n```
| 2 | 0 |
['Union Find', 'Sorting', 'Python']
| 1 |
checking-existence-of-edge-length-limited-paths
|
DSU c++
|
dsu-c-by-vc8006-d93y
|
\nclass Solution {\npublic:\n static bool cmp(vector<int> &a,vector<int> &b)\n {\n return a[2]<b[2];\n }\n \n vector<int> parent;\n \n
|
vc8006
|
NORMAL
|
2022-08-11T12:44:32.206895+00:00
|
2022-08-11T12:44:32.206941+00:00
| 244 | false |
```\nclass Solution {\npublic:\n static bool cmp(vector<int> &a,vector<int> &b)\n {\n return a[2]<b[2];\n }\n \n vector<int> parent;\n \n int find(int x)\n {\n if(parent[x]==x)return x;\n return parent[x] = find(parent[x]);\n }\n \n void Union(int x,int y)\n {\n int lx = find(x);\n int ly = find(y);\n parent[lx] = ly;\n }\n \n vector<bool> distanceLimitedPathsExist(int n, vector<vector<int>>& edges, vector<vector<int>>& q) {\n int m = q.size();\n for(int i = 0;i<m;i++)\n {\n q[i].push_back(i);\n }\n \n parent.resize(n,0);\n for(int i = 0;i<n;i++)\n parent[i] = i;\n sort(edges.begin(),edges.end(),cmp);\n sort(q.begin(),q.end(),cmp);\n \n int i = 0;\n vector<bool> ans(m,0);\n \n for(auto it:q)\n {\n while(i<edges.size() and edges[i][2]<it[2])\n {\n Union(edges[i][0],edges[i][1]);\n i++;\n }\n ans[it[3]] = (find(it[0])==find(it[1]));\n }\n return ans; \n }\n};\n```
| 2 | 0 |
['C']
| 0 |
checking-existence-of-edge-length-limited-paths
|
C++,Union Find,Two pointer
|
cunion-findtwo-pointer-by-nideesh45-sw26
|
\n// custom comparator to sort based on weight\nbool comp(vector<int> &a,vector<int> &b){\n if(a[2] == b[2]){\n return a[1]<b[1];\n }\n return a
|
nideesh45
|
NORMAL
|
2022-07-25T07:13:12.053287+00:00
|
2022-07-25T07:13:12.053334+00:00
| 345 | false |
```\n// custom comparator to sort based on weight\nbool comp(vector<int> &a,vector<int> &b){\n if(a[2] == b[2]){\n return a[1]<b[1];\n }\n return a[2]<b[2];\n}\n\nclass Solution {\npublic:\n \n // Union Find data structure\n \n int parent[100005];\n int sz[100005];\n \n void makeset(int v){\n parent[v] = v;\n sz[v] = 1;\n }\n int find(int v){\n if(parent[v] == v) return v;\n return parent[v] = find(parent[v]);\n }\n void Union(int x,int y){\n x = find(x);\n y = find(y);\n if(x == y) return;\n if(sz[x]>sz[y]) swap(x,y);\n parent[y] = x;\n sz[y]+=sz[x];\n }\n \n vector<bool> distanceLimitedPathsExist(int n, vector<vector<int>>& edgeList, vector<vector<int>>& queries) {\n \n for(int i=0;i<n;i++) {\n makeset(i);\n }\n int m = queries.size();\n for(int i=0;i<queries.size();i++) {\n queries[i].push_back(i);\n }\n \n sort(queries.begin(),queries.end(),comp);\n sort(edgeList.begin(),edgeList.end(),comp);\n vector<bool> ans(queries.size(),false);\n int i=0;\n int j=0;\n // two pointer\n // building graph based on weights allowed by queries\n while(j<m){\n int wt = queries[j][2];\n \n while(i<edgeList.size() && edgeList[i][2]<wt){\n int a = edgeList[i][0];\n int b = edgeList[i][1];\n Union(a,b);\n i++;\n }\n if(find(queries[j][0]) == find(queries[j][1])){\n ans[queries[j][3]] = 1;\n }\n j++;\n }\n return ans;\n }\n};\n```
| 2 | 0 |
['Union Find', 'C', 'Sorting']
| 0 |
checking-existence-of-edge-length-limited-paths
|
Python | Union Find | Simple and Easy
|
python-union-find-simple-and-easy-by-ary-k6te
|
```\nclass Solution:\n def distanceLimitedPathsExist(self, n: int, edgeList: List[List[int]], queries: List[List[int]]) -> List[bool]:\n def find(v):\
|
aryonbe
|
NORMAL
|
2022-05-05T03:16:09.382657+00:00
|
2022-05-05T03:16:09.382688+00:00
| 238 | false |
```\nclass Solution:\n def distanceLimitedPathsExist(self, n: int, edgeList: List[List[int]], queries: List[List[int]]) -> List[bool]:\n def find(v):\n if parent[v] != v:\n parent[v] = find(parent[v])\n return parent[v]\n def union(v, w):\n parent[find(v)] = find(w)\n edgeList.sort(key = lambda e: e[2])\n queries = sorted(((v,w,limit,i) for i, (v, w, limit) in enumerate(queries)), key = lambda e:e[2])\n parent = [i for i in range(n)]\n j = 0\n res = [0]*len(queries)\n for v,w,limit,i in queries:\n while j < len(edgeList) and edgeList[j][2] < limit:\n p, q, _ = edgeList[j]\n union(p,q)\n j += 1\n res[i] = find(v) == find(w)\n return res
| 2 | 0 |
['Union Find', 'Python']
| 0 |
checking-existence-of-edge-length-limited-paths
|
[JAVA] Simple, Clear and Concise Solution with templated DSU
|
java-simple-clear-and-concise-solution-w-rh7i
|
\nclass Solution {\n public boolean[] distanceLimitedPathsExist(int n, int[][] edgeList, int[][] queries) {\n Arrays.sort(edgeList, (a, b) -> a[2] - b
|
unbrokenPanda
|
NORMAL
|
2022-04-13T11:18:04.482924+00:00
|
2022-04-13T11:18:04.482961+00:00
| 134 | false |
```\nclass Solution {\n public boolean[] distanceLimitedPathsExist(int n, int[][] edgeList, int[][] queries) {\n Arrays.sort(edgeList, (a, b) -> a[2] - b[2]);\n Map<int[], Integer> position = new HashMap<>();\n \n for (int i = 0; i < queries.length; i++) {\n position.put(queries[i], i);\n }\n \n Arrays.sort(queries, (a, b) -> a[2] - b[2]);\n \n DSU dsu = new DSU(n);\n boolean[] ans = new boolean[queries.length];\n int j = 0;\n \n for (int[] q : queries) {\n int limit = q[2];\n \n while(j < edgeList.length && edgeList[j][2] < limit) {\n dsu.union(edgeList[j][0], edgeList[j][1]);\n j++;\n }\n \n ans[position.get(q)] = dsu.isConnected(q[0], q[1]);\n }\n \n return ans;\n }\n\t\n```\n\n<br><br><br><br>\n\t\n\tHere\'s the standard DSU template used, I have solved most of the DSU problems using the below template :)\n\t\n<br><br><br><br><br>\n\n\n```\n \n class DSU {\n int[] root;\n int[] rank;\n \n public DSU (int n) {\n this.root = new int[n];\n this.rank = new int[n];\n \n for (int i = 0; i < n; i++) {\n root[i] = i;\n rank[i] = 1;\n }\n }\n \n public int find(int x) {\n if (root[x] == x) return x;\n return root[x] = find(root[x]);\n }\n \n public void union(int x, int y) {\n int rootX = find(x);\n int rootY = find(y);\n \n if (rootX == rootY) return;\n \n if (rank[rootX] > rank[rootY]) {\n root[rootY] = rootX;\n rank[rootX] += rank[rootY];\n \n } else {\n root[rootX] = rootY;\n rank[rootY] += rank[rootX];\n }\n }\n \n public boolean isConnected(int x, int y) {\n return find(x) == find(y);\n }\n }\n}\n```
| 2 | 0 |
[]
| 0 |
checking-existence-of-edge-length-limited-paths
|
Java | Passes all test cases | Union Find
|
java-passes-all-test-cases-union-find-by-fv3z
|
\nclass Solution {\n public boolean[] distanceLimitedPathsExist(int n, int[][] edgeList, int[][] queries) {\n int[] parent = new int[n];\n\n
|
prashantaxe
|
NORMAL
|
2021-08-10T18:20:12.374644+00:00
|
2021-08-10T18:20:12.374689+00:00
| 154 | false |
```\nclass Solution {\n public boolean[] distanceLimitedPathsExist(int n, int[][] edgeList, int[][] queries) {\n int[] parent = new int[n];\n\n for (int i = 0; i < n; ++i) {\n parent[i] = i;\n }\n\n // Sort the edges in the provided graph based on distance.\n Arrays.sort(edgeList, Comparator.comparing(a -> Integer.valueOf(a[2])));\n\n // Sort queries in increasing order of distance.\n List<int[]> q = new ArrayList<>();\n for (int i = 0; i < queries.length; ++i) {\n int[] entry = new int[4];\n entry[0] = queries[i][0]; // Start index\n entry[1] = queries[i][1]; // End Index\n entry[2] = queries[i][2]; // Threshold\n entry[3] = i; //\n\n q.add(entry);\n }\n\n q.sort(Comparator.comparing(a -> a[2]));\n\n int index = 0;\n boolean[] result = new boolean[q.size()];\n for (var entry : q) {\n int threshold = entry[2];\n //\n while (index < edgeList.length && edgeList[index][2] < threshold) {\n union(parent, edgeList[index][0], edgeList[index][1]);\n ++index;\n }\n\n result[entry[3]] = find(parent, entry[0]) == find(parent, entry[1]);\n }\n\n return result;\n }\n\n // O(Log(N))\n int find(int[] parent, int ind) {\n if (parent[ind] != ind) {\n return find(parent, parent[ind]);\n }\n\n return ind;\n }\n\n // O(Log(N))\n void union(int[] parent, int x, int y) {\n int p1 = find(parent, x);\n int p2 = find(parent, y);\n parent[p1] = p2;\n }\n }\n```
| 2 | 0 |
[]
| 1 |
checking-existence-of-edge-length-limited-paths
|
JAVA : Union Find
|
java-union-find-by-prashantharshi-l3ms
|
\nclass Solution {\n private static class DisJointSet{\n int val;\n DisJointSet par;\n public DisJointSet(int value){\n this.
|
prashantharshi
|
NORMAL
|
2021-02-05T04:22:22.746254+00:00
|
2021-02-05T04:22:22.746313+00:00
| 230 | false |
```\nclass Solution {\n private static class DisJointSet{\n int val;\n DisJointSet par;\n public DisJointSet(int value){\n this.val = value;\n this.par = this;\n }\n }\n\n private void union(DisJointSet set1, DisJointSet set2){ set1.par = set2; }\n\n private DisJointSet find(DisJointSet set){\n if(set.par == set) return set;\n return set.par = find(set.par);\n }\n\n private HashMap<Integer, DisJointSet> hashMap = new HashMap<>();\n private HashMap<DisJointSet, Set<Integer>> nodeMap = new HashMap();\n private int nodes;\n \n public boolean[] distanceLimitedPathsExist(int n, int[][] edgeList, int[][] queries) {\n nodes = n;\n for (int i = 0; i < nodes; i++)\n hashMap.put(i, new DisJointSet(i));\n //sort edges by weight - this is trivial thing to begin Kruskal\n Arrays.sort(edgeList, Comparator.comparingInt(arr -> arr[2]));\n \n //mark index along with query - not a better way as it use space ---use hashmap or something\n int[][] queriesWithIdx = new int[queries.length][];\n for (int idx = 0; idx < queries.length; idx++) {\n int[] query = queries[idx];\n int[] nquery = new int[]{query[0], query[1], query[2],idx};\n queriesWithIdx[idx] = nquery;\n }\n \n //sort queries by cost so that we will use edges only till that cost threshold to build MST\n Arrays.sort(queriesWithIdx, Comparator.comparingInt(arr -> arr[2]));\n boolean[] res = new boolean[queries.length];\n int prev = 0;\n for (int[] query : queriesWithIdx){\n int costThreshold = query[2];\n for (int i = prev; i < edgeList.length; i++){\n if(edgeList[i][2] >= costThreshold){\n //record the prev index , so that next run of kruskal should start from edge from that index\n prev = i;\n break;\n }\n int u = edgeList[i][0];\n int v = edgeList[i][1];\n union(find(hashMap.get(u)), find(hashMap.get(v)));\n }\n //after doing a kruskal on limites set of edges bound by constraint , check if the u and v are in same set or not\n if(find(hashMap.get(query[0])) == find(hashMap.get(query[1]))){\n res[query[3]] = true;\n }else\n res[query[3]] = false;\n }\n\n \n return res;\n }\n}\n```
| 2 | 0 |
[]
| 0 |
checking-existence-of-edge-length-limited-paths
|
[Javascript] Union Find
|
javascript-union-find-by-zachzwy-5wo7
|
Sort the query and edgeLists by limit. Start from the strictest limit.\n\n\nvar distanceLimitedPathsExist = function (n, edgeList, queries) {\n queries = queri
|
zachzwy
|
NORMAL
|
2020-12-20T04:55:29.939617+00:00
|
2020-12-20T17:42:55.478384+00:00
| 239 | false |
Sort the query and edgeLists by limit. Start from the strictest limit.\n\n```\nvar distanceLimitedPathsExist = function (n, edgeList, queries) {\n queries = queries.map((n, i) => [...n, i]).sort((a, b) => a[2] - b[2]);\n edgeList.sort((a, b) => a[2] - b[2]);\n \n const res = Array(queries.length);\n const ds = new DS(n);\n \n let j = 0;\n for (let [p, q, limit, i] of queries) {\n while (j < edgeList.length && edgeList[j][2] < limit) {\n const [u, v, dis] = edgeList[j];\n ds.union(u, v);\n j++;\n }\n res[i] = ds.find(p) === ds.find(q);\n }\n \n return res;\n};\n\nclass DS {\n constructor(n) {\n this.id = [...Array(n).keys()];\n this.rank = Array(n).fill(0);\n }\n \n find(i) {\n if (i !== this.id[i]) this.id[i] = this.find(this.id[i]);\n return this.id[i];\n }\n \n union(i, j) {\n const [I, J] = [this.find(i), this.find(j)];\n if (I === J) return false;\n const [rankI, rankJ] = [this.rank[I], this.rank[J]];\n if (rankI < rankJ) this.id[I] = J;\n else if (rankI > rankJ) this.id[J] = I;\n else {\n this.id[I] = J;\n this.rank[J]++;\n }\n return true;\n }\n}\n```
| 2 | 0 |
['Union Find', 'JavaScript']
| 0 |
checking-existence-of-edge-length-limited-paths
|
Python, Union-Find
|
python-union-find-by-warmr0bot-xo9h
|
The key idea is to populate the union-find data structure as we answer queries ordered by the allowed edge cost, from smallest to biggest. Any connection under
|
warmr0bot
|
NORMAL
|
2020-12-20T04:50:57.223765+00:00
|
2020-12-20T04:50:57.223792+00:00
| 447 | false |
The key idea is to populate the union-find data structure as we answer queries ordered by the allowed edge cost, from smallest to biggest. Any connection under that cost is allowed to go into our structure.\n```\nclass UnionFind:\n\n def __init__(self, size):\n self.size = size\n self.parents = list(range(size))\n self.sizes = [0] * size\n \n def union(self, x, y):\n rootx = self.find(x)\n rooty = self.find(y)\n if rootx == rooty: return\n small, big = (rootx, rooty) if self.sizes[rootx] < self.sizes[rooty] else (rooty, rootx)\n self.parents[small] = big\n \n def find(self, x):\n if self.parents[x] != x:\n self.parents[x] = self.find(self.parents[x])\n return self.parents[x]\n\nclass Solution:\n def distanceLimitedPathsExist(self, n: int, edgeList: List[List[int]], queries: List[List[int]]) -> List[bool]:\n uf = UnionFind(n)\n \n edgeList.sort(key=lambda x: x[2])\n answers = [None] * len(queries)\n queries = [(l, s, d, i) for i, (s, d, l) in enumerate(queries)]\n queries.sort(key=lambda x:x[0])\n \n eidx = 0\n for limit, src, dest, q_idx in queries:\n while eidx < len(edgeList) and edgeList[eidx][2] < limit:\n uf.union(edgeList[eidx][0], edgeList[eidx][1])\n eidx += 1\n \n answers[q_idx] = uf.find(src) == uf.find(dest)\n \n return answers\n```
| 2 | 0 |
['Union Find', 'Python', 'Python3']
| 0 |
checking-existence-of-edge-length-limited-paths
|
Simple Python | Union Find
|
simple-python-union-find-by-sushanthsama-qq5a
|
\nclass Solution:\n def distanceLimitedPathsExist(self, n: int, A: List[List[int]], B: List[List[int]]) -> List[bool]:\n par = {}\n A.sort(key
|
sushanthsamala
|
NORMAL
|
2020-12-20T04:12:04.902881+00:00
|
2020-12-21T18:55:29.354840+00:00
| 342 | false |
```\nclass Solution:\n def distanceLimitedPathsExist(self, n: int, A: List[List[int]], B: List[List[int]]) -> List[bool]:\n par = {}\n A.sort(key = lambda x: x[2])\n \n for i, query in enumerate(B):\n query.append(i)\n B.sort(key = lambda x: x[2])\n \n def find(a):\n par.setdefault(a, a)\n if par[a] != a:\n par[a] = find(par[a])\n return par[a]\n \n def union(a, b):\n par.setdefault(a, a)\n par.setdefault(b, b)\n par[find(a)] = par[find(b)]\n \n ans = [False]*len(B)\n i = 0\n for a, b, lim, idx in B:\n while i < len(A) and A[i][2] < lim:\n union(A[i][0], A[i][1])\n i += 1\n \n if find(a) == find(b):\n ans[idx] = True\n return ans\n ```
| 2 | 1 |
['Python3']
| 1 |
checking-existence-of-edge-length-limited-paths
|
Python [union-find]
|
python-union-find-by-gsan-hw23
|
Sort E.\nSort Q but only get indices.\nGradually add edges in sorted E based on sorted Q.\nCheck if the given query nodes are connected.\nEssentially union-find
|
gsan
|
NORMAL
|
2020-12-20T04:01:25.322819+00:00
|
2020-12-20T04:01:25.322856+00:00
| 353 | false |
Sort `E`.\nSort `Q` but only get indices.\nGradually add edges in sorted `E` based on sorted `Q`.\nCheck if the given query nodes are connected.\nEssentially union-find.\n\n```python\nclass Solution:\n def distanceLimitedPathsExist(self, n, E, Q):\n #this part is union-find\n def find(i):\n if i != root[i]:\n root[i] = find(root[i])\n return root[i]\n\n def uni(x, y):\n x, y = find(x), find(y)\n if x == y: return 0\n root[x] = y\n return 1\n \n root = list(range(n))\n \n #this will be the answer\n ans = [False]*len(Q)\n \n #sort edges based on cost\n i = 0\n E.sort(key=lambda x: x[2])\n \n #don\'t sort Q, but get the sorted list of queries in ix_all\n q = [x[2] for x in Q]\n ix_all = sorted(range(len(q)), key=q.__getitem__)\n for ix in ix_all: #loop over sorted indices of Q\n #add all edges that satisfy cost requirement\n while i<len(E) and E[i][2]<Q[ix][2]:\n x, y = E[i][0], E[i][1]\n i += 1\n uni(x,y)\n \n #check if the query nodes are connected\n if find(Q[ix][0]) == find(Q[ix][1]):\n ans[ix] = True\n \n return ans\n```
| 2 | 0 |
[]
| 0 |
checking-existence-of-edge-length-limited-paths
|
Python, solution with classic MST + DSU
|
python-solution-with-classic-mst-dsu-by-lq1nj
|
IntuitionBuilt MST incrementally, accoording to queries' theshold (preliminary presorted)
DSU structure used to check after each MST build step to verify either
|
dev_lvl_80
|
NORMAL
|
2025-02-10T19:03:27.249193+00:00
|
2025-02-10T19:03:27.249193+00:00
| 21 | false |
# Intuition
Built MST incrementally, accoording to queries' theshold (preliminary presorted)
DSU structure used to check after each MST build step to verify either vertes of current query belongs to the same set (path exists)
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
O(NlogN)
- Space complexity:
O(N)
# Code
```python3 []
class Solution:
def distanceLimitedPathsExist(self, n: int, edgeList: List[List[int]], queries: List[List[int]]) -> List[bool]:
q_len = len(queries)
# classic DSU - list PCH/representatives
r = list(range(n))
# DSU struct & methods
def get_repr(n)->int:
if r[n] != n:
r[n] = get_repr(r[n])
return r[n]
def unite(a, b)->None:
r_a = get_repr(a)
r_b = get_repr(b)
r[r_b] = r_a
# presort both, starting from least distance
queries = sorted([[*arr, pos] for pos, arr in enumerate(queries)], key = lambda x: x[2], reverse = True)
edgeList = sorted(edgeList, key = lambda x: x[2], reverse = True)
# we need preserve queries original positions, to return answer in the same order
ret = {}
while queries:
a, b, d, q_pos = queries.pop()
#print(f"query {a} {b} {d}. MST = {r}")
# build Min Spanning Tree, while distance is less than next query allows
while edgeList and edgeList[-1][2] < d:
e_from, e_to, _ = edgeList.pop()
#print(f"\tedge {e_from} {e_to} {e_d}.")
# check: no loops
if r[e_from] != r[e_to]:
unite(e_from, e_to)
#print(f"\tadding edge to MST {r}")
# check answer, either parent is same (united)
ret[q_pos] = get_repr(r[a]) == get_repr(r[b])
#print(f"\t answer {ret[q_pos]}")
# return answers in original order
return [ret[i] for i in range(q_len)]
```
| 1 | 0 |
['Python3']
| 0 |
checking-existence-of-edge-length-limited-paths
|
🔥 LeetCode Editorial-Style Solution 🔥 | DSU + Offline Queries | 🚀 Optimized Approach
|
leetcode-editorial-style-solution-dsu-of-1rv7
|
Intuition
The problem requires determining whether a path exists between two nodes with a weight limit.
A naive DFS/BFS approach would be too slow for large inp
|
kanchanlamba00
|
NORMAL
|
2025-02-10T07:23:13.537007+00:00
|
2025-02-10T07:23:13.537007+00:00
| 29 | false |
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
- The problem requires determining whether a path exists between two nodes with a weight limit.
- A naive DFS/BFS approach would be too slow for large inputs (O(N^2) worst case).
- Disjoint Set Union (DSU) efficiently tracks connectivity between nodes, making it an ideal choice.
- We process queries in increasing order of limit and edges in increasing order of weight, ensuring efficient connectivity checks.
# Approach
<!-- Describe your approach to solving the problem. -->
1. Sort Edges & Queries
- Sort edgeList by weight: We will only connect nodes with weight < limit for each query.
- Sort queries by limit: Ensures we only process relevant edges.
2. Process Queries Efficiently
- Maintain index i to track processed edges.
- For each query (u, v, limit), add edges where weight < limit to DSU.
- Check if u and v belong to the same component using DSU.
3. Store Results in Original Query Order
- Since queries are sorted by weight, we store their original index before sorting.
- This ensures that we return the results in the correct order.
# ⏳ Complexity Analysis
- Sorting Edges & Queries: O(E log E + Q log Q)
- Processing Queries with DSU: O(Q α(N)) (Inverse Ackermann function)
- Total Complexity: O((E + Q) log N) (Efficient for large inputs)
- Space Complexity: O(N) (For DSU arrays)
# Code
```cpp []
class disjoint{
public:
vector<int> size,parent;
disjoint(int n){
size.resize(n,1);
parent.resize(n);
for(int i=0;i<n;i++){
parent[i]=i;
}
}
int find(int node){
if(node==parent[node]){
return node;
}
return parent[node]=find(parent[node]);
}
void uNion(int u,int v){
int ult_u=find(u);
int ult_v=find(v);
if(ult_u==ult_v){
return ;
}
if(size[ult_u]<=size[ult_v]){
parent[ult_u]=ult_v;
size[ult_v]+=size[ult_u];
}
else{
parent[ult_v]=ult_u;
size[ult_u]+=size[ult_v];
}
}
};
class Solution {
public:
vector<bool> distanceLimitedPathsExist(int n, vector<vector<int>>& edgeList, vector<vector<int>>& queries) {
disjoint ds(n+1);
for(int i=0;i<queries.size();i++){
queries[i].push_back(i);
}
sort(edgeList.begin(),edgeList.end(),[](const vector<int>& a,const vector<int>& b){return a[2]<b[2];});
sort(queries.begin(),queries.end(),[](const vector<int>& a,const vector<int>& b){return a[2]<b[2];});
int i=0;
vector<bool> res(queries.size(),false);
for(auto& q:queries){
while(i<edgeList.size() && edgeList[i][2]<q[2]){
ds.uNion(edgeList[i][0],edgeList[i][1]);
i++;
}
if(ds.find(q[0])==ds.find(q[1])){
res[q[3]]=true;
}
}
return res;
}
};
```
| 1 | 0 |
['C++']
| 0 |
checking-existence-of-edge-length-limited-paths
|
Runtime beats 98.95%, Memory beats 88.07% [EXPLAINED]
|
runtime-beats-9895-memory-beats-8807-exp-fhhv
|
Intuition\nThe problem involves determining if there are paths between nodes in a graph where every edge on the path has a distance below a certain limit. Inste
|
r9n
|
NORMAL
|
2024-10-04T01:27:59.220479+00:00
|
2024-10-04T01:27:59.220513+00:00
| 8 | false |
# Intuition\nThe problem involves determining if there are paths between nodes in a graph where every edge on the path has a distance below a certain limit. Instead of checking each query independently, we can efficiently group the edges and queries based on their weights.\n\n# Approach\nWe sort the edges and queries by distance, then use a Union-Find structure to connect nodes while processing edges that meet the distance criteria, allowing us to quickly check if two nodes are connected for each query.v\n\n# Complexity\n- Time complexity:\nApproximately O((E + Q) * \u03B1(N)), where E is the number of edges, Q is the number of queries, N is the number of nodes, and \u03B1 is the Inverse Ackermann function, which grows very slowly.\n\n- Space complexity:\nO(N) for the Union-Find data structures (parent and rank arrays).\n\n# Code\n```python3 []\nclass Solution:\n def distanceLimitedPathsExist(self, n, edgeList, queries):\n # Step 1: Sort edges and queries\n edgeList.sort(key=lambda x: x[2]) # Sort edges by distance\n queries = sorted([(p, q, limit, i) for i, (p, q, limit) in enumerate(queries)], key=lambda x: x[2])\n \n # Step 2: Prepare Union-Find structure\n parent = list(range(n))\n rank = [1] * n\n\n def find(x):\n if parent[x] != x:\n parent[x] = find(parent[x])\n return parent[x]\n\n def union(x, y):\n rootX = find(x)\n rootY = find(y)\n if rootX != rootY:\n if rank[rootX] > rank[rootY]:\n parent[rootY] = rootX\n elif rank[rootX] < rank[rootY]:\n parent[rootX] = rootY\n else:\n parent[rootY] = rootX\n rank[rootX] += 1\n\n # Step 3: Process queries\n result = [False] * len(queries)\n edgeIndex = 0\n \n for p, q, limit, index in queries:\n # Union all edges with distance < limit\n while edgeIndex < len(edgeList) and edgeList[edgeIndex][2] < limit:\n u, v, d = edgeList[edgeIndex]\n union(u, v)\n edgeIndex += 1\n # Check if p and q are in the same component\n result[index] = find(p) == find(q)\n\n return result\n\n```
| 1 | 0 |
['Python3']
| 0 |
checking-existence-of-edge-length-limited-paths
|
[C++] Union Find using Template
|
c-union-find-using-template-by-lshigami-86rs
|
\n\n# Code\n\nclass DSU{\npublic:\n vector<int>Parent,Size;\npublic :\n\t// O(N)\n DSU(int n){\n Parent.resize(n);\n Size.resize(n);\n
|
lshigami
|
NORMAL
|
2024-04-21T15:30:38.120632+00:00
|
2024-04-21T15:30:38.120666+00:00
| 163 | false |
\n\n# Code\n```\nclass DSU{\npublic:\n vector<int>Parent,Size;\npublic :\n\t// O(N)\n DSU(int n){\n Parent.resize(n);\n Size.resize(n);\n for(int i=0;i<n;i++){\n Parent[i]=i;\n Size[i]=1;\n }\n }\n // O(N)\n int Find(int x){\n if(x==Parent[x]) return x;\n return Parent[x]=Find(Parent[x]);\n }\n //O(N)\n bool Union(int x,int y){\n x=Find(x);\n y=Find(y);\n if(x==y) return false;\n if(Size[x]<Size[y]){\n swap(x,y);\n }\n Parent[y] = x;\n Size[x] += Size[y];\n return true;\n }\n};\nclass Solution {\npublic:\n vector<bool> distanceLimitedPathsExist(int num, vector<vector<int>>& edgeList, vector<vector<int>>& queries) {\n int n=edgeList.size();\n int m=queries.size();\n vector<bool>ans(m);\n for(int i=0;i<m;i++){\n queries[i].push_back(i);\n }\n sort(edgeList.begin(),edgeList.end(),[](vector<int>a,vector<int>b)->bool{\n return a[2]<b[2];\n });\n sort(queries.begin(),queries.end(),[](vector<int>a,vector<int>b)->bool{\n return a[2]<b[2];\n });\n int eIdx=0;\n DSU dsu(num);\n for(int i=0;i<m;i++){\n for(;eIdx<n&& edgeList[eIdx][2]<queries[i][2];eIdx++ ){\n dsu.Union(edgeList[eIdx][0],edgeList[eIdx][1]);\n }\n ans[queries[i][3]]=(dsu.Find(queries[i][0])==dsu.Find(queries[i][1]));\n }\n return ans;\n }\n};\n```
| 1 | 0 |
['C++']
| 0 |
checking-existence-of-edge-length-limited-paths
|
Solution for a more general problem (answering queries online)
|
solution-for-a-more-general-problem-answ-uxsk
|
Intuition\n Describe your first thoughts on how to solve this problem. \nMST + biary lifting \n# Approach\n Describe your approach to solving the problem. \nBui
|
kalesnikauilya
|
NORMAL
|
2024-03-12T23:29:31.151688+00:00
|
2024-03-12T23:29:31.151708+00:00
| 2 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nMST + biary lifting \n# Approach\n<!-- Describe your approach to solving the problem. -->\nBuild MST, adding dummy edges with INF weight if initial graph is disconnected. Binary lifting to precompute max weight edges for every node to every other node at dost 2^i.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nMST Kruskal in O(NlogN) + precompute binary lifting in O(NlogN);\nquery in O(logN)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n#include <bits/stdc++.h>\n\n#include <algorithm>\n#include <cassert>\n#include <vector>\n\nnamespace atcoder {\n\nstruct dsu {\n public:\n dsu() : _n(0) {}\n explicit dsu(int n) : _n(n), parent_or_size(n, -1) {}\n\n int merge(int a, int b) {\n assert(0 <= a && a < _n);\n assert(0 <= b && b < _n);\n int x = leader(a), y = leader(b);\n if (x == y) return x;\n if (-parent_or_size[x] < -parent_or_size[y]) std::swap(x, y);\n parent_or_size[x] += parent_or_size[y];\n parent_or_size[y] = x;\n return x;\n }\n\n bool same(int a, int b) {\n assert(0 <= a && a < _n);\n assert(0 <= b && b < _n);\n return leader(a) == leader(b);\n }\n\n int leader(int a) {\n assert(0 <= a && a < _n);\n if (parent_or_size[a] < 0) return a;\n return parent_or_size[a] = leader(parent_or_size[a]);\n }\n\n int size(int a) {\n assert(0 <= a && a < _n);\n return -parent_or_size[leader(a)];\n }\n\n std::vector<std::vector<int>> groups() {\n std::vector<int> leader_buf(_n), group_size(_n);\n for (int i = 0; i < _n; i++) {\n leader_buf[i] = leader(i);\n group_size[leader_buf[i]]++;\n }\n std::vector<std::vector<int>> result(_n);\n for (int i = 0; i < _n; i++) {\n result[i].reserve(group_size[i]);\n }\n for (int i = 0; i < _n; i++) {\n result[leader_buf[i]].push_back(i);\n }\n result.erase(\n std::remove_if(result.begin(), result.end(),\n [&](const std::vector<int>& v) { return v.empty(); }),\n result.end());\n return result;\n }\n\n private:\n int _n;\n std::vector<int> parent_or_size;\n};\n\n} // namespace atcoder\n\n\nusing namespace std;\nusing namespace atcoder;\n\n\n// https://www.geeksforgeeks.org/maximum-weighted-edge-in-path-between-two-nodes-in-an-n-ary-tree-using-binary-lifting/\nconst int N = 100005;\n \n// Depths of Nodes\nvector<int> level(N);\nconst int LG = 20;\n \n// Parent at every 2^i level\nvector<vector<int> > dp(LG, vector<int>(N));\n \n// Maximum node at every 2^i level\nvector<vector<int> > mx(LG, vector<int>(N));\n \n \n// Function to traverse the nodes\n// using the Depth-First Search Traversal\nvoid dfs_lca(int a, int par, int lev, int n, vector<vector<pair<int, int>>> &g)\n{\n\n dp[0][a] = par;\n level[a] = lev;\n \n for (auto i : g[a]) {\n \n // Condition to check if its\n // equal to its parent then skip\n if (i.first == par)\n continue;\n mx[0][i.first] = i.second;\n \n // DFS Recursive Call\n dfs_lca(i.first, a, lev + 1, n, g);\n }\n}\n \n// Function to find the ancestor\nvoid find_ancestor(int n)\n{\n \n // Loop to set every 2^i distance\n for (int i = 1; i < LG; i++) {\n // Loop to calculate for\n // each node in the N-ary tree\n for (int j = 1; j <= n; j++) {\n dp[i][j]\n = dp[i - 1][dp[i - 1][j]];\n \n // Storing maximum edge\n mx[i][j]\n = max(mx[i - 1][j],\n mx[i - 1][dp[i - 1][j]]);\n }\n }\n}\n \nint getMax(int a, int b)\n{\n // Swapping if node a is at more depth\n // than node b because we will\n // always take at more depth\n if (level[b] < level[a])\n swap(a, b);\n \n int ans = 0;\n \n // Difference between the depth of\n // the two given nodes\n int diff = level[b] - level[a];\n while (diff > 0) {\n int log = log2(diff);\n ans = max(ans, mx[log][b]);\n \n // Changing Node B to its\n // parent at 2 ^ i distance\n b = dp[log][b];\n \n // Subtracting distance by 2^i\n diff -= (1 << log);\n }\n \n // Take both a, b to its\n // lca and find maximum\n while (a != b) {\n int i = level[a] == 0 ? 0 : log2(level[a]);\n \n // Loop to find the 2^ith\n // parent that is different\n // for both a and b i.e below the lca \n while (i > 0\n && dp[i][a] == dp[i][b])\n i--;\n \n // Updating ans\n ans = max(ans, mx[i][a]);\n ans = max(ans, mx[i][b]);\n \n // Changing value to its parent\n a = dp[i][a];\n b = dp[i][b];\n }\n return ans;\n}\n \n// Function to compute the Least\n// common Ancestor\nvoid compute_lca(int n, vector<vector<pair<int, int>>> &g)\n{\n dfs_lca(1, 0, 1, n, g);\n find_ancestor(n);\n}\n\n\nclass Solution {\npublic:\n vector<vector<pair<int, int>>> mst(int n, vector<vector<int>>& edgeList, dsu& dsu){\n sort(edgeList.begin(), edgeList.end(), [&](const vector<int> &le, const vector<int> &ri){\n return le[2] < ri[2];\n });\n \n\n vector<vector<pair<int, int>>> g(n + 1);\n int cnt = 0;\n for(auto &edge : edgeList){\n int u = edge[0] + 1;\n int v = edge[1] + 1;\n int dist = edge[2];\n if(!dsu.same(u, v)){\n g[u].push_back({v, dist});\n g[v].push_back({u, dist});\n dsu.merge(u, v);\n ++cnt;\n }\n }\n\n auto gr = dsu.groups();\n for(int i = 2; i < (int) gr.size(); ++i){\n if(!gr[0].empty() && !gr[i].empty()){\n g[gr[1][0]].push_back({gr[i][0], 2e9});\n g[gr[i][0]].push_back({gr[1][0], 2e9});\n }\n }\n return g;\n }\n\n vector<bool> distanceLimitedPathsExist(int n, vector<vector<int>>& edgeList, vector<vector<int>>& queries) {\n dsu dsu(n + 1);\n vector<vector<pair<int, int>>> g = mst(n, edgeList, dsu);\n compute_lca(n, g);\n vector<bool> ans;\n for(auto &q : queries){\n int u = q[0] + 1;\n int v = q[1] + 1;\n int limit = q[2];\n bool res = getMax(u, v) < limit;\n ans.push_back(res);\n }\n return ans;\n }\n};\n```
| 1 | 0 |
['C++']
| 0 |
checking-existence-of-edge-length-limited-paths
|
Concise and Clean 🧼🫧
|
concise-and-clean-by-lil_toeturtle-qod2
|
\n\nclass Solution {\n int p[];\n int find(int a) { return p[a]==a? a: (p[a]=find(p[a])); }\n void union(int a, int b) { p[find(b)]=p[find(a)]; }\n
|
Lil_ToeTurtle
|
NORMAL
|
2023-09-05T19:39:59.994251+00:00
|
2023-09-05T19:39:59.994285+00:00
| 178 | false |
\n```\nclass Solution {\n int p[];\n int find(int a) { return p[a]==a? a: (p[a]=find(p[a])); }\n void union(int a, int b) { p[find(b)]=p[find(a)]; }\n public boolean[] distanceLimitedPathsExist(int n, int[][] edgeList, int[][] queries) {\n p=new int[n]; for(int i=0;i<n;p[i]=i++);\n Arrays.sort(edgeList, (a,b)->a[2]-b[2]);\n for(int i=0;i<queries.length; queries[i]=new int[]{queries[i][0], queries[i][1], queries[i][2], i}, ++i); \n Arrays.sort(queries, (a,b)->a[2]-b[2]);\n\n boolean[] res=new boolean[queries.length];\n int i=0;\n for(int[] q: queries) {\n while(i<edgeList.length && edgeList[i][2] < q[2]) union(edgeList[i][0], edgeList[i++][1]);\n res[q[3]]=find(q[0])==find(q[1]);\n }\n return res;\n }\n}\n```
| 1 | 0 |
['Java']
| 1 |
checking-existence-of-edge-length-limited-paths
|
DSU | STRIVER Version!
|
dsu-striver-version-by-chatterjeeswastik-xz4a
|
\nclass DisjointSet {\n vector<int> rank, parent, size; \npublic: \n DisjointSet(int n) {\n rank.resize(n+1, 0); \n parent.resize(n+1);\n
|
chatterjeeswastik7772
|
NORMAL
|
2023-05-26T19:14:01.411092+00:00
|
2023-05-26T19:14:01.411138+00:00
| 20 | false |
```\nclass DisjointSet {\n vector<int> rank, parent, size; \npublic: \n DisjointSet(int n) {\n rank.resize(n+1, 0); \n parent.resize(n+1);\n size.resize(n+1); \n for(int i = 0;i<=n;i++) {\n parent[i] = i; \n size[i] = 1; \n }\n }\n\n int findUPar(int node) {\n if(node == parent[node])\n return node; \n return parent[node] = findUPar(parent[node]); \n }\n\n void unionByRank(int u, int v) {\n int ulp_u = findUPar(u); \n int ulp_v = findUPar(v); \n if(ulp_u == ulp_v) return; \n if(rank[ulp_u] < rank[ulp_v]) {\n parent[ulp_u] = ulp_v; \n }\n else if(rank[ulp_v] < rank[ulp_u]) {\n parent[ulp_v] = ulp_u; \n }\n else {\n parent[ulp_v] = ulp_u; \n rank[ulp_u]++; \n }\n }\n\n void unionBySize(int u, int v) {\n int ulp_u = findUPar(u); \n int ulp_v = findUPar(v); \n if(ulp_u == ulp_v) return; \n if(size[ulp_u] < size[ulp_v]) {\n parent[ulp_u] = ulp_v; \n size[ulp_v] += size[ulp_u]; \n }\n else {\n parent[ulp_v] = ulp_u;\n size[ulp_u] += size[ulp_v]; \n }\n }\n}; \n\n\nclass Solution {\nprivate:\n bool static comp(vector<int> &a, vector<int> &b){\n return a[2]<b[2];\n }\n bool static compQ(vector<int> &a, vector<int> &b){\n return a[2]<b[2];\n }\n \n \npublic:\n vector<bool> distanceLimitedPathsExist(int n, vector<vector<int>>& edgeList, vector<vector<int>>& q) {\n sort(edgeList.begin(),edgeList.end(),comp); //sorting according to dist\n DisjointSet ds(n);\n vector<bool> res(q.size());\n for(int i=0;i<q.size();i++){\n q[i].push_back(i); // pushing the index in each q so we don\'t loose track of its position\n }\n sort(q.begin(),q.end(),compQ); //sorting according to dist\n // for(auto it: edgeList) cout<<it[0]<<" ";\n \n int k=0;\n for(int i=0;i<q.size();i++){//for each q, traverse the edgelist and insert those edges into the DSU whose dist is\n\t\t//strictly less than the q_dist\n while(k<edgeList.size() && edgeList[k][2]<q[i][2]){\n if(ds.findUPar(edgeList[k][0])==ds.findUPar(edgeList[k][1])){ // they are connected\n }\n else{ // they are not connected\n ds.unionByRank(edgeList[k][0],edgeList[k][1]); \n \n }\n k++;\n }\n\t\t\t//after we are done connecting all the edges within our limit, we check if both the nodes from the q are from the same parent. If yes, insert true into the res or else insert false into the res vector.\n if(ds.findUPar(q[i][0])==ds.findUPar(q[i][1])){\n res[q[i][3]]=true;\n }\n else res[q[i][3]]=false;\n }\n \n return res;\n }\n};\n```\n\nPeace :-)
| 1 | 0 |
['C']
| 1 |
checking-existence-of-edge-length-limited-paths
|
EASY
|
easy-by-priyanka8d19-bd6v
|
\n# Code\n\nclass DisjointSet {\nprivate:\n vector<int> parent, rank;\n\npublic:\n DisjointSet(int n) {\n parent.resize(n+1, 0);\n rank.resi
|
priyanka8d19
|
NORMAL
|
2023-05-04T10:50:18.923429+00:00
|
2023-05-04T10:50:18.923457+00:00
| 158 | false |
\n# Code\n```\nclass DisjointSet {\nprivate:\n vector<int> parent, rank;\n\npublic:\n DisjointSet(int n) {\n parent.resize(n+1, 0);\n rank.resize(n+1, 0);\n\n for(int i=0; i<n+1; i++) {\n parent[i] = i;\n }\n }\n\n int findParent(int node) {\n if(node == parent[node])\n return node;\n \n return parent[node] = findParent(parent[node]);\n }\n\n void unionByRank(int u, int v) {\n int upU = findParent(u);\n int upV = findParent(v);\n\n if(upU == upV)\n return;\n \n if(rank[upU] < rank[upV]) {\n parent[upU] = upV;\n }\n else {\n parent[upV] = upU;\n rank[upU]++;\n }\n }\n\n bool isParentEqual(int u, int v) {\n return (findParent(u) == findParent(v));\n }\n};\n\nclass Solution {\n bool static compare(const vector<int> &a, const vector<int> &b) {\n return (a[2] < b[2]);\n }\n\npublic:\n vector<bool> distanceLimitedPathsExist(int nodes, vector<vector<int>>& edges, vector<vector<int>>& queries) {\n int n = queries.size();\n\n vector<bool> ans(n, false);\n \n for(int i=0; i<n; i++) {\n queries[i].push_back(i);\n }\n\n sort(edges.begin(), edges.end(), compare);\n sort(queries.begin(), queries.end(), compare);\n\n DisjointSet ds(nodes);\n int i=0;\n\n for(auto &query : queries) {\n int u = query[0];\n int v = query[1];\n int limit = query[2];\n int qId = query[3];\n\n for(; (i < edges.size()) && (edges[i][2] < limit); i++) {\n ds.unionByRank(edges[i][0], edges[i][1]);\n }\n ans[qId] = ds.isParentEqual(u, v);\n }\n\n return ans;\n }\n};\n```
| 1 | 0 |
['C++']
| 0 |
checking-existence-of-edge-length-limited-paths
|
Rub/Go: Disjoint-Set Union. Leetcode's solution translation.
|
rubgo-disjoint-set-union-leetcodes-solut-r346
|
Leetcode: 1697. Checking Existence of Edge Length Limited Paths.\n\nRuby/Go: Disjoint-Set Union. Leetcode\'s soltuoin translation.\n\nRuby and Go transltion of
|
user9697n
|
NORMAL
|
2023-04-30T15:43:58.600981+00:00
|
2023-04-30T15:43:58.601044+00:00
| 99 | false |
## Leetcode: 1697. Checking Existence of Edge Length Limited Paths.\n\n**Ruby/Go: Disjoint-Set Union. Leetcode\'s soltuoin translation.**\n\nRuby and Go transltion of the Leetcode\'s [solution](https://leetcode.com/problems/checking-existence-of-edge-length-limited-paths/solution/).\n\nRuby code:\n```Ruby\n# Leetcode: 1697. Checking Existence of Edge Length Limited Paths.\n# https://leetcode.com/problems/checking-existence-of-edge-length-limited-paths/\n# = = = = = = = = = = = = = =\n# Accepted.\n# Thanks God, Jesus Christ!\n# = = = = = = = = = = = = = =\n# Runtime: 726 ms, faster than 100.00% of Ruby online submissions for Checking\n# Existence of Edge Length Limited Paths.\n# Memory Usage: 247.5 MB, less than 100.00% of Ruby online submissions for\n# Checking Existence of Edge Length Limited Paths.\n# 2023.04.29 Daily Challenge.\n# @param {Integer} n\n# @param {Integer[][]} edge_list\n# @param {Integer[][]} queries\n# @return {Boolean[]}\nclass Uf\n def initialize(size)\n @g = Array.new(size).map.with_index{|x,i| i} \n @r = []\n end\n def find(n)\n if @g[n] != n\n @g[n] = find(@g[n])\n end\n @g[n]\n end\n def join(n1,n2)\n g1 = find(n1)\n g2 = find(n2)\n return if g1 == g2\n @r[g1] ||= 0\n @r[g2] ||= 0\n if @r[g1] > @r[g2]\n @g[g2] = g1\n elsif @r[g1] < @r[g2]\n @g[g1] = g2\n else\n @g[g1] = g2\n @r[g2] ||= 0\n @r[g2] += 1\n end\n end\n def con(n1,n2)\n g1 = find(n1)\n g2 = find(n2)\n g1 == g2\n end\nend\ndef distance_limited_paths_exist(n, edge_list, queries)\n # Based on:\n # https://leetcode.com/problems/checking-existence-of-edge-length-limited-paths/solution/\n uf = Uf.new(n)\n qc = queries.size\n ans = Array.new(qc,false)\n\n # Store original inicies with all queries.\n qwi = [] # Queries with index.\n qc.times do |i|\n qwi[i] = queries[i]\n qwi[i].push(i)\n end\n\n # Sort all edges in increasing order of their edge weights.\n edge_list.sort!{|a,b| a[2] - b[2]}\n # Sort all queries in increasing order of the limit of edge allowed.\n qwi.sort!{|a,b| a[2] - b[2]}\n\n # ei - edges index.\n ei = 0\n\n # qoi - Query original index.\n # l - limit.\n # Iterate on each query one by one.\n qwi.each do |pe,q,l,qoi|\n # We can attach edges with satisfy the limit given by the query.\n while ei < edge_list.size && edge_list[ei][2] < l\n n1 = edge_list[ei][0]\n n2 = edge_list[ei][1]\n uf.join(n1,n2)\n ei += 1\n end\n\n # If both nodes belong to the same component, it means we can reach them.\n ans[qoi] = uf.con(pe,q)\n end\n\n return ans\nend\n```\n\nGo code:\n```Go\n// Leetcode: 1697. Checking Existence of Edge Length Limited Paths.\n// https://leetcode.com/problems/checking-existence-of-edge-length-limited-paths/\n// = = = = = = = = = = = = = =\n// Accepted.\n// Thanks God, Jesus Christ!\n// = = = = = = = = = = = = = =\n// Runtime: 336 ms, faster than 66.67% of Go online submissions for Checking\n// Existence of Edge Length Limited Paths.\n// Memory Usage: 17.6 MB, less than 33.33% of Go online submissions for Checking\n// Existence of Edge Length Limited Paths.\n// 2023.04.30 Updated.\npackage main\n\n// import "sort"\n// Line 5: Char 8: sort redeclared in this block (solution.go)\n// Line -2: Char 2: other declaration of sort (solution.go)\n// Line 5: Char 8: imported and not used: "sort" (solution.go)\n\ntype unfn struct {\n\tg []int\n\tr []int\n}\n\nfunc (t *unfn) find(n int) int {\n\tif n != t.g[n] {\n\t\tt.g[n] = t.find(t.g[n])\n\t}\n\treturn t.g[n]\n}\n\nfunc (t *unfn) join(n1, n2 int) {\n\tg1, g2 := t.find(n1), t.find(n2)\n\tif g1 == g2 {\n\t\treturn\n\t}\n\tif t.r[g1] > t.r[g2] {\n\t\tt.g[g2] = g1\n\t} else if t.r[g1] < t.r[g2] {\n\t\tt.g[g1] = g2\n\t} else {\n\t\tt.g[g1] = g2\n\t\tt.r[g2] += 1\n\t}\n}\n\nfunc (t *unfn) con(n1, n2 int) bool {\n\tg1, g2 := t.find(n1), t.find(n2)\n\treturn g1 == g2\n}\n\nfunc newUn(n int) *unfn {\n\tx := unfn{}\n\tx.g = make([]int, n)\n\tx.r = make([]int, n)\n\tfor i := 0; i < n; i += 1 {\n\t\tx.g[i] = i\n\t}\n\treturn &x\n}\n\nfunc distanceLimitedPathsExist(n int, edgeList [][]int, queries [][]int) []bool {\n\n\t// Based on the Leetcode\'s solution.\n\n\tuf := newUn(n)\n\tqc := len(queries)\n\tans := make([]bool, qc)\n\n\t// Store original incides with all quieres.\n\tqwi := make([][]int, qc)\n\tfor i, _ := range qwi {\n\t\tqwi[i] = make([]int, len(queries[i])+1)\n\t\tfor j, v1 := range queries[i] {\n\t\t\tqwi[i][j] = v1\n\t\t}\n\t\tqwi[i][len(queries[i])] = i\n\t}\n\t// Sort all edges in increasing order of their edge weights.\n\tsort.Slice(edgeList, func(i, j int) bool {\n\t\ta, b := edgeList[i], edgeList[j]\n\t\treturn a[2] < b[2]\n\t})\n\t// Sort all queries in increasing orderof the limit of edge allowed.\n\tsort.Slice(qwi, func(i, j int) bool {\n\t\ta, b := qwi[i], qwi[j]\n\t\treturn a[2] < b[2]\n\t})\n\t// ei - edges index.\n\tei := 0\n\te := edgeList\n\tel := len(edgeList)\n\n\t// qoi - Query original index.\n\t// l - limit.\n\t// Iterate on each query one by one.\n\tfor _, v := range qwi {\n\t\tpe, q, l, qoi := v[0], v[1], v[2], v[3]\n\t\tfor ei < el && e[ei][2] < l {\n\t\t\tn1 := e[ei][0]\n\t\t\tn2 := e[ei][1]\n\t\t\tuf.join(n1, n2)\n\t\t\tei += 1\n\t\t}\n\t\t// If both nodes belong to the same component, it means we can reach\n\t\t// them.\n\t\tans[qoi] = uf.con(pe, q)\n\t}\n\n\treturn ans\n}\n```\n
| 1 | 0 |
['Go', 'Ruby']
| 0 |
checking-existence-of-edge-length-limited-paths
|
Simple Solution
|
simple-solution-by-rockstarpabitra-6vpk
|
\n\n# Complexity\n- Time complexity:\n Add your time complexity here, e.g. O(n) \nO(nlogn+qlogq)\n- Space complexity:\n Add your space complexity here, e.g. O(n
|
RockstarPabitra
|
NORMAL
|
2023-04-29T19:40:08.559470+00:00
|
2023-04-29T19:40:08.559522+00:00
| 58 | false |
\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(nlogn+qlogq)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n(n+q)\n# Code\n```\nclass UnionFind {\n public UnionFind(int n) {\n id = new int[n];\n rank = new int[n];\n for (int i = 0; i < n; ++i)\n id[i] = i;\n }\n\n public void unionByRank(int u, int v) {\n final int i = find(u);\n final int j = find(v);\n if (i == j)\n return;\n if (rank[i] < rank[j]) {\n id[i] = id[j];\n } else if (rank[i] > rank[j]) {\n id[j] = id[i];\n } else {\n id[i] = id[j];\n ++rank[j];\n }\n }\n\n public int find(int u) {\n return id[u] == u ? u : (id[u] = find(id[u]));\n }\n\n private int[] id;\n private int[] rank;\n}\n\nclass Solution {\n public boolean[] distanceLimitedPathsExist(int n, int[][] edgeList, int[][] queries) {\n boolean[] ans = new boolean[queries.length];\n int[][] qs = new int[queries.length][4];\n UnionFind uf = new UnionFind(n);\n\n for (int i = 0; i < queries.length; ++i) {\n qs[i][0] = queries[i][0];\n qs[i][1] = queries[i][1];\n qs[i][2] = queries[i][2];\n qs[i][3] = i;\n }\n\n Arrays.sort(qs, (a, b) -> a[2] - b[2]);\n Arrays.sort(edgeList, (a, b) -> a[2] - b[2]);\n\n int i = 0; // i := edgeList\'s index\n for (int[] q : qs) {\n // Union edges whose distances < limit (q[2])\n while (i < edgeList.length && edgeList[i][2] < q[2])\n uf.unionByRank(edgeList[i][0], edgeList[i++][1]);\n if (uf.find(q[0]) == uf.find(q[1]))\n ans[q[3]] = true;\n }\n\n return ans;\n }\n}\n```
| 1 | 0 |
['Java']
| 0 |
checking-existence-of-edge-length-limited-paths
|
Solution in C++
|
solution-in-c-by-ashish_madhup-wmsk
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
ashish_madhup
|
NORMAL
|
2023-04-29T17:15:16.708925+00:00
|
2023-04-29T17:15:16.708974+00:00
| 293 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int find(int node, vector<int>& parent)\n {\n if(node == parent[node])\n return node;\n return parent[node] = find(parent[node], parent);\n }\n void Union(int node0, int node1, vector<int>& parent)\n {\n int par0 = find(node0, parent); \n int par1 = find(node1, parent);\n if(par0 == par1)\n return;\n parent[par0] = par1;\n }\n vector<bool> distanceLimitedPathsExist(int n, vector<vector<int>>& edges, vector<vector<int>>& queries) {\n int q = queries.size();\n int sz = edges.size(); \n vector<int> parent(n, 0); \n for(int i = 0; i < n; i++) parent[i] = i;\n sort(edges.begin(), edges.end(), [&](vector<int>& edge1, vector<int>& edge2){\n return edge1[2] < edge2[2];\n });\n for(int i = 0; i < q; i++) queries[i].push_back(i);\n sort(queries.begin(), queries.end(), [&](vector<int>& query1,vector<int>& query2) \n {\n return query1[2] < query2[2];\n });\n vector<bool> ans(q, false);\n int edgeMoment = 0; \n for(int eachQuery = 0; eachQuery < q; eachQuery++) \n {\n int currQueryWeight = queries[eachQuery][2]; \n while(edgeMoment < sz && edges[edgeMoment][2] < currQueryWeight)\n Union(edges[edgeMoment][0], edges[edgeMoment][1], parent), edgeMoment++;\n if(find(queries[eachQuery][0], parent) == \n find(queries[eachQuery][1], parent)) {\n\n ans[queries[eachQuery][3]] = true;\n }\n }\n return ans;\n }\n};\n```
| 1 | 0 |
['C++']
| 0 |
checking-existence-of-edge-length-limited-paths
|
Swift Union Find
|
swift-union-find-by-tatianavol-kakl
|
Code\n\nclass Solution {\n \n var union: [Int] = []\n var ranks: [Int] = []\n\n func distanceLimitedPathsExist(_ n: Int, _ edgeList: [[Int]], _ queri
|
TatianaVol
|
NORMAL
|
2023-04-29T16:04:47.870165+00:00
|
2023-04-29T16:04:47.870192+00:00
| 22 | false |
# Code\n```\nclass Solution {\n \n var union: [Int] = []\n var ranks: [Int] = []\n\n func distanceLimitedPathsExist(_ n: Int, _ edgeList: [[Int]], _ queries: [[Int]]) -> [Bool] {\n\n union = Array(repeating: 0, count: n).enumerated().map { $0.offset }\n ranks = Array(repeating: 1, count: n)\n var answers = Array(repeating: false, count: queries.count)\n var edgeList = edgeList.sorted { $0[2] < $1[2] }.map { (from: $0[0], to: $0[1], limit: $0[2]) }\n\n var queries = queries.enumerated()\n .map { index, query in (index: index, from: query[0], to: query[1], limit: query[2]) }\n .sorted { $0.limit < $1.limit }\n\n var edgeListIndex = 0\n for i in (0..<answers.count) {\n let query = queries[i]\n while edgeListIndex < edgeList.count && edgeList[edgeListIndex].limit < query.limit {\n union(edgeList[edgeListIndex].from, edgeList[edgeListIndex].to)\n edgeListIndex += 1\n }\n answers[query.index] = areConnected(query.from, query.to)\n }\n\n return answers\n }\n\n func root(of node: Int) -> Int {\n var node = node\n while node != union[node] {\n node = union[node]\n }\n\n return node\n }\n\n func areConnected(_ p: Int, _ q: Int)-> Bool {\n root(of: p) == root(of: q)\n }\n\n func union(_ i: Int, _ j: Int) {\n if i == j { return }\n let jRoot = root(of: j)\n let iRoot = root(of: i)\n \n if jRoot == iRoot { return }\n if ranks[iRoot] < ranks[jRoot] {\n union[iRoot] = jRoot\n ranks[jRoot] += ranks[iRoot] \n } else {\n union[jRoot] = iRoot\n ranks[iRoot] += ranks[jRoot]\n }\n }\n}\n```
| 1 | 1 |
['Swift']
| 0 |
checking-existence-of-edge-length-limited-paths
|
Easy to Understand | optimized | Simple Approach
|
easy-to-understand-optimized-simple-appr-jz4p
|
\n\n# Code\n\nclass DSU {\n public:\n vector<int> Parent, Rank;\n DSU(int n) {\n Parent.resize(n);\n Rank.resize(n, 0);\n for (int
|
sagarbhadauriya
|
NORMAL
|
2023-04-29T14:38:26.849580+00:00
|
2023-04-29T14:38:26.849608+00:00
| 241 | false |
\n\n# Code\n```\nclass DSU {\n public:\n vector<int> Parent, Rank;\n DSU(int n) {\n Parent.resize(n);\n Rank.resize(n, 0);\n for (int i = 0; i < n; i++) Parent[i] = i;\n }\n int Find(int x) {\n return Parent[x] = Parent[x] == x ? x : Find(Parent[x]);\n }\n bool Union(int x, int y) {\n int xset = Find(x), yset = Find(y);\n if (xset != yset) {\n Rank[xset] < Rank[yset] ? Parent[xset] = yset : Parent[yset] = xset;\n Rank[xset] += Rank[xset] == Rank[yset];\n return true;\n }\n return false;\n }\n};\n\nclass Solution {\npublic:\n vector<bool> distanceLimitedPathsExist(int n, vector<vector<int>>& edgeList, vector<vector<int>>& queries) {\n DSU dsu(n);\n for(int i=0;i<queries.size();i++)\n queries[i].push_back(i);\n \n sort(queries.begin(), queries.end(), [&](auto const &a, auto const &b){\n return a[2] < b[2];\n });\n sort(edgeList.begin(), edgeList.end(), [&](auto const &a, auto const &b){\n return a[2] < b[2];\n });\n \n int i=0;\n vector<bool> res(queries.size(), false);\n for(auto q: queries){\n while(i<edgeList.size() && edgeList[i][2]<q[2]){\n dsu.Union(edgeList[i][0] , edgeList[i][1]);\n i++;\n }\n \n if(dsu.Find(q[0]) == dsu.Find(q[1]))\n res[q[3]] = true;\n }\n \n return res;\n }\n};\n```
| 1 | 0 |
['C++']
| 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.