question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
smallest-subarrays-with-maximum-bitwise-or
|
Easy Solution (Bit Manipulation) beats 100%
|
easy-solution-bit-manipulation-beats-100-tfie
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n youtube link - http
|
gopigaurav
|
NORMAL
|
2024-11-01T14:24:20.051400+00:00
|
2024-11-01T14:24:20.051437+00:00
| 9 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n youtube link - https://www.youtube.com/watch?v=PeouhGUGr7Q\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nfrom typing import List\n\nclass Solution:\n def smallestSubarrays(self, nums: List[int]) -> List[int]:\n n = len(nums)\n max_or_setbits = [-1] * 32\n ans = []\n\n for i in range(n - 1, -1, -1):\n cur = nums[i]\n pos = 0\n\n while cur:\n if cur & 1:\n max_or_setbits[pos] = i\n cur //= 2\n pos += 1\n\n max_index = max(max_or_setbits)\n ans.append(max_index - i + 1 if max_index != -1 else 1)\n\n return ans[::-1]\n\n```
| 0 | 0 |
['Python3']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
C++ Solution || Using BIT MANIPULATION
|
c-solution-using-bit-manipulation-by-vai-zohp
|
Code\ncpp []\nclass Solution {\npublic:\n vector<int> smallestSubarrays(vector<int>& nums) {\n int n=nums.size();\n vector<int> ans;\n v
|
Vaibhav_Arya007
|
NORMAL
|
2024-10-17T10:54:01.850447+00:00
|
2024-10-17T10:54:01.850478+00:00
| 1 | false |
# Code\n```cpp []\nclass Solution {\npublic:\n vector<int> smallestSubarrays(vector<int>& nums) {\n int n=nums.size();\n vector<int> ans;\n vector<int> set_bits(32,-1);\n\n int maxOR=0;\n\n for(int i=n-1; i>=0; i--){\n maxOR |=nums[i];\n int curr=nums[i];\n\n int setting_pos=0;\n while(curr){\n if(curr&1){\n set_bits[setting_pos]=i;\n\n }\n curr/=2;\n setting_pos++;\n \n }\n\n int max_ind=*max_element(set_bits.begin(), set_bits.end());\n\n if(max_ind==-1){\n ans.push_back(1);\n }\n else{\n ans.push_back(max_ind-i+1);\n }\n\n }\n\n reverse(ans.begin(), ans.end());\n return ans;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
Java Solution Time Complexity: O(N), Space Complexity: O(N)
|
java-solution-time-complexity-on-space-c-cu9d
|
Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(N)\n\n# Code\njava []\nclass Solution {\n\n public int[] smallestSubarrays(int[] nums) {\n
|
Hash17
|
NORMAL
|
2024-10-13T19:21:35.142633+00:00
|
2024-10-13T19:21:35.142659+00:00
| 6 | false |
# Complexity\n- Time complexity:\n$$O(N)$$\n\n- Space complexity:\n$$O(N)$$\n\n# Code\n```java []\nclass Solution {\n\n public int[] smallestSubarrays(int[] nums) {\n int[] maximumBitWiseOR = new int[nums.length];\n maximumBitWiseOR[nums.length - 1] = nums[nums.length - 1];\n for (int index = nums.length - 2; index >= 0; index--)\n maximumBitWiseOR[index] = nums[index] | maximumBitWiseOR[index + 1];\n int[] smallestSubArrays = new int[nums.length];\n int[] currentBitCounts = new int[32];\n int start = 0;\n for (int end = 0; end < nums.length; end++) {\n append(currentBitCounts, nums[end]);\n while (start <= end && value(currentBitCounts) == maximumBitWiseOR[start]) {\n smallestSubArrays[start] = end - start + 1;\n remove(currentBitCounts, nums[start++]);\n }\n }\n return smallestSubArrays;\n }\n\n private int value(int[] currentBitCounts) {\n int value = 0;\n for (int index = 0; index < currentBitCounts.length; index++)\n if (currentBitCounts[index] > 0) value |= (1 << index);\n return value;\n }\n\n private void append(int[] currentBitCounts, int value) {\n for (int index = 0; index < currentBitCounts.length; index++)\n if ((value & (1 << index)) > 0) currentBitCounts[index]++;\n }\n\n private void remove(int[] currentBitCounts, int value) {\n for (int index = 0; index < currentBitCounts.length; index++)\n if ((value & (1 << index)) > 0) currentBitCounts[index]--;\n }\n}\n```
| 0 | 0 |
['Bit Manipulation', 'Java']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
Brilliant use of data structures you could have ever seen! 🎀
|
brilliant-use-of-data-structures-you-cou-dfna
|
This is the first approach after brute force I came up with for this problem. Some times using nested data structures can come handy.\n\nTC: O(N x 32)\nSC: O(N
|
vedanty3
|
NORMAL
|
2024-10-02T19:26:38.299865+00:00
|
2024-10-02T19:26:38.299888+00:00
| 2 | false |
*This is the first approach after brute force I came up with for this problem. Some times using nested data structures can come handy.*\n\n*TC: O(N x 32)*\n*SC: O(N x 32)\nwhere 1e5 >= N >= 0*\n\n```\nclass Solution {\npublic:\n vector<int> smallestSubarrays(vector<int>& nums) {\n int n = nums.size();\n unordered_map<int, queue<int>>m;\n \n for(int i=0; i<n; ++i) {\n int bit = 0;\n int num = nums[i];\n \n while(num) {\n if(num&1) {\n m[bit].push(i);\n }\n \n num >>= 1;\n ++bit;\n }\n }\n \n vector<int>ans;\n \n for(int i=0; i<n; ++i) {\n int bit = 31;\n int max_len = 1;\n while(bit>=0) {\n if(m.find(bit)!=m.end()) {\n while(!m[bit].empty() and m[bit].front()<i) {\n m[bit].pop();\n }\n if(m[bit].empty()) {\n m.erase(bit);\n } else {\n max_len = max(max_len, m[bit].front()-i+1);\n }\n }\n --bit;\n }\n ans.push_back(max_len);\n }\n \n return ans;\n }\n};\n```
| 0 | 0 |
['Bit Manipulation', 'Queue']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
scala onleliner. bitmap suffixes
|
scala-onleliner-bitmap-suffixes-by-vitit-bwd3
|
scala []\nobject Solution {\n import scala.util.chaining._\n import collection.immutable.BitSet\n def smallestSubarrays(nums: Array[Int]): Array[Int] =\n
|
vititov
|
NORMAL
|
2024-09-14T12:39:20.123528+00:00
|
2024-09-14T12:39:20.123562+00:00
| 1 | false |
```scala []\nobject Solution {\n import scala.util.chaining._\n import collection.immutable.BitSet\n def smallestSubarrays(nums: Array[Int]): Array[Int] =\n nums.toList.zipWithIndex.reverseIterator.scanLeft((Map.empty[Int,Int],0)){case ((aMap,acc),(num,i))=>\n (aMap ++ BitSet.fromBitMask(Array(num)).map(_ -> i), acc | num)\n }.drop(1).toList.reverse.pipe(sfx => (nums.indices.toArray zip sfx).map{case (i,(bMap,mx)) =>\n if(mx == 0) 1 else BitSet.fromBitMask(Array(mx)).iterator.map(bMap).max - i + 1\n })\n}\n\n```
| 0 | 0 |
['Hash Table', 'Bit Manipulation', 'Prefix Sum', 'Scala']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
C++ | Sliding Window | Bit Manipulation
|
c-sliding-window-bit-manipulation-by-abh-ds5n
|
Intuition\n Describe your first thoughts on how to solve this problem. \nAs OR will always increase the value\nFor every index we find the maxOR value\nmaxOR va
|
abhishek10ghosh
|
NORMAL
|
2024-08-30T11:32:02.399189+00:00
|
2024-08-30T11:32:02.399223+00:00
| 15 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAs OR will always increase the value\nFor every index we find the maxOR value\nmaxOR value at every index (i) is OR of every number from i to n\nThis can be done via sliding window and keeping a 30 bit array\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nNow we have maxOR value every index i can take\nWe use sliding window to find the lenght of the shortest window which can make maxOR value at index i\n\nThe 30 bit size vector is used to check that do we still have a contributing 1 in current window, if no then remove the set bit at this position\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n vector<int> smallestSubarrays(vector<int>& nums) {\n // or always increases value\n int n=nums.size();\n int currOr = 0;\n vector<int> maxOr(n); // max OR value starting at index i\n vector<int> v(32,0);\n for(int i=0;i<n;i++){\n for(int j=0;j<31;j++){\n if(nums[i] & (1<<j)){\n v[j]++;\n }\n }\n \n currOr|=nums[i];\n }\n\n\n for(int i=0;i<n;i++){\n maxOr[i] = currOr;\n \n for(int j=0;j<31;j++){\n if(nums[i] & (1<<j)){\n v[j]--;\n }\n if(v[j]==0){\n currOr = (currOr & (~(1<<j)));\n }\n }\n }\n\n // sliding window to find smallest subarray size\n currOr=0;\n int j=0;\n vector<int> ans(n);\n vector<int> bit(32,0);\n for(int i=0;i<n;i++){\n while(currOr < maxOr[i]){\n for(int k=0;k<31;k++){\n if(nums[j] & (1<<k)){\n bit[k]++;\n }\n }\n currOr|=nums[j];\n j++;\n }\n ans[i] = j-i;\n ans[i] = max(ans[i],1); //min value can be 1\n for(int k=0;k<31;k++){\n if(nums[i] & (1<<k)){\n bit[k]--;\n }\n if(bit[k]==0){\n currOr = (currOr & (~(1<<k)));\n }\n }\n \n }\n\n return ans;\n }\n};\n```
| 0 | 0 |
['Bit Manipulation', 'Sliding Window', 'C++']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
lower_bound se kiya h
|
lower_bound-se-kiya-h-by-rohityadav2002-3ujf
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
RohitYadav2002
|
NORMAL
|
2024-07-31T06:34:08.345733+00:00
|
2024-07-31T06:34:08.345772+00:00
| 4 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> smallestSubarrays(vector<int>& nums) {\n int n = nums.size();\n vector<vector<int>> setBitIdx(31);\n for(int i = 0; i < n; i++) {\n int val = nums[i];\n int idx = 0;\n while(val) {\n if(val % 2) setBitIdx[idx].push_back(i);\n val = val / 2;\n idx++;\n }\n }\n\n // Debugging Output (Optional)\n <!-- for(int i = 0; i < 31; i++) {\n for(int j = 0; j < setBitIdx[i].size(); j++) {\n cout << setBitIdx[i][j] << " ";\n } cout << endl;\n } -->\n\n vector<int> ans(n, 1);\n for(int i = 0; i < n; i++) {\n int maxi = i;\n for(int j = 0; j < 31; j++) {\n auto it = lower_bound(setBitIdx[j].begin(), setBitIdx[j].end(), i);\n if (it != setBitIdx[j].end()) {\n maxi = max(maxi, *it);\n }\n }\n ans[i] = maxi - i + 1;\n }\n return ans;\n }\n};\n\n```
| 0 | 0 |
['C++']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
Simple Java Solution
|
simple-java-solution-by-sakshikishore-9o9b
|
Code\n\nclass Solution {\n public int[] smallestSubarrays(int[] nums) {\n int result[]=new int[nums.length];\n int max=0;\n for(int i=0;
|
sakshikishore
|
NORMAL
|
2024-07-27T02:34:56.832338+00:00
|
2024-07-27T02:34:56.832367+00:00
| 6 | false |
# Code\n```\nclass Solution {\n public int[] smallestSubarrays(int[] nums) {\n int result[]=new int[nums.length];\n int max=0;\n for(int i=0;i<nums.length;i++)\n {\n if(nums[i]>max)\n {\n max=nums[i];\n }\n }\n String str=Integer.toBinaryString(max);\n int ch[][]=new int[nums.length][str.length()];\n result[result.length-1]=1;\n int count=0;\n str=Integer.toBinaryString(nums[nums.length-1]);\n for(int i=str.length()-1;i>=0;i--)\n {\n if(str.charAt(i)==\'1\')\n {\n ch[nums.length-1][count]=1;\n }\n count++;\n }\n \n int start=nums.length-1;\n for(int i=nums.length-2;i>=0;i--)\n {\n int x=nums[i];\n count=0;\n while(x>0)\n {\n int p=( x & 1);\n if(p==1)\n {\n ch[i][count]=1;\n }\n x>>=1;\n count++;\n }\n for(int j=0;j<ch[i].length;j++)\n {\n ch[i][j]+=ch[i+1][j];\n }\n while(start!=i)\n {\n int flag=0;\n for(int j=0;j<ch[i].length;j++)\n {\n \n if(ch[i][j]!=0 && ch[i][j]-ch[start][j]==0)\n {\n \n flag=1;\n break;\n }\n }\n \n if(flag==0)\n {\n start--;\n }\n else\n {\n break;\n }\n }\n result[i]=start-i+1;\n\n }\n\n return result;\n\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
Rust Solution
|
rust-solution-by-rchaser53-fesv
|
Complexity\n- Time complexity:\nO(nm)\n\n- Space complexity:\nO(nm)\n\n# Code\n\nuse std::collections::*;\n\nimpl Solution {\n pub fn smallest_subarrays(nums:
|
rchaser53
|
NORMAL
|
2024-07-16T10:27:21.755269+00:00
|
2024-07-16T10:27:21.755299+00:00
| 0 | false |
# Complexity\n- Time complexity:\n$$O(n*m)$$\n\n- Space complexity:\n$$O(n*m)$$\n\n# Code\n```\nuse std::collections::*;\n\nimpl Solution {\n pub fn smallest_subarrays(nums: Vec<i32>) -> Vec<i32> {\n let n = nums.len();\n let mut result = vec![0;n];\n let mut memo = vec![VecDeque::new();35];\n\n for i in 0..n {\n let v = nums[i];\n for j in 0..35 {\n if v >> j & 1 == 1 {\n memo[j].push_back(i);\n }\n }\n }\n\n for i in 0..n {\n let mut max = i;\n for j in 0..35 {\n if !memo[j].is_empty() {\n max = max.max(memo[j][0]);\n\n if memo[j][0] == i {\n memo[j].pop_front();\n }\n }\n }\n\n result[i] = (max - i + 1) as i32;\n }\n\n result\n }\n}\n```
| 0 | 0 |
['Rust']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
JAVA
|
java-by-manu-bharadwaj-bn-ih8x
|
Code\n\nclass Solution {\n public int[] smallestSubarrays(int[] nums) {\n int[] map = new int[32];\n int[] ans = new int[nums.length];\n
|
Manu-Bharadwaj-BN
|
NORMAL
|
2024-07-15T12:22:42.205602+00:00
|
2024-07-15T12:22:42.205623+00:00
| 26 | false |
# Code\n```\nclass Solution {\n public int[] smallestSubarrays(int[] nums) {\n int[] map = new int[32];\n int[] ans = new int[nums.length];\n for (int i = nums.length - 1; i >= 0; i--) {\n int num = nums[i];\n for (int j = 0; j <= 31; j++) {\n int mask = 1 << (j);\n if ((num & mask) > 0) {\n map[j] = i;\n }\n }\n int max = i;\n for (int e : map)\n max = Math.max(e, max);\n ans[i] = max - i + 1;\n }\n return ans;\n }\n}\n```
| 0 | 0 |
['Java']
| 1 |
smallest-subarrays-with-maximum-bitwise-or
|
Easy C++ Solution | Most Basic Approach
|
easy-c-solution-most-basic-approach-by-v-q0m8
|
Code\n\nclass Solution {\npublic:\n bool canRemove(vector<int>& bits, int numberToInsert){\n vector<int> bitValues(32, 0);\n add(bitValues, num
|
vedantgarg2004
|
NORMAL
|
2024-07-06T07:18:16.135032+00:00
|
2024-07-06T07:18:39.248645+00:00
| 12 | false |
# Code\n```\nclass Solution {\npublic:\n bool canRemove(vector<int>& bits, int numberToInsert){\n vector<int> bitValues(32, 0);\n add(bitValues, numberToInsert);\n\n for(int i=0; i<32; i++){\n if(bits[i] > 0 && bits[i] - bitValues[i] == 0) return false;\n }\n for(int i=0; i<32; i++) bits[i] = max(0, bits[i] - bitValues[i]);\n return true;\n }\n void add(vector<int>& bits, int number){ //add Bit Value of new element:\n int bitPos = 0;\n while(number > 0){\n if(number&1) bits[bitPos]++;\n number = number>>1;\n bitPos++;\n }\n }\n vector<int> smallestSubarrays(vector<int>& nums) {\n vector<int> ans(nums.size(), -1);\n\n queue<int> q;\n vector<int> bits(32,0);\n for(int i=nums.size()-1; i>=0; i--){\n q.push(nums[i]);\n\n add(bits, nums[i]);\n while(!q.empty() && canRemove(bits, q.front())) q.pop();\n ans[i] = q.size() == 0 ? 1 : q.size();\n }\n\n return ans;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
C++ solution
|
c-solution-by-nguyenchiemminhvu-bpuw
|
\nclass Solution\n{\npublic:\n vector<int> smallestSubarrays(vector<int>& nums)\n {\n std::vector<int> res(nums.size(), 1);\n std::vector<in
|
nguyenchiemminhvu
|
NORMAL
|
2024-07-03T08:48:21.017909+00:00
|
2024-07-03T08:48:21.017933+00:00
| 0 | false |
```\nclass Solution\n{\npublic:\n vector<int> smallestSubarrays(vector<int>& nums)\n {\n std::vector<int> res(nums.size(), 1);\n std::vector<int> mask(32, -1);\n\n for (int i = nums.size() - 1; i >= 0; i--)\n {\n for (int imask = 0; imask < 32; imask++)\n {\n if (nums[i] & (1 << imask))\n {\n mask[imask] = i;\n }\n }\n\n int ifar = i;\n for (int imask = 0; imask < 32; imask++)\n {\n if (mask[imask] != -1)\n {\n ifar = std::max(ifar, mask[imask]);\n }\n }\n\n res[i] = ifar - i + 1;\n }\n\n return res;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
Java Bit Manipulation Memoization Sliding Window
|
java-bit-manipulation-memoization-slidin-smgq
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
mot882000
|
NORMAL
|
2024-06-11T07:07:55.183148+00:00
|
2024-06-11T07:07:55.183183+00:00
| 8 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int[] smallestSubarrays(int[] nums) {\n\n // 0. \uAC01 index\uC5D0\uC11C \uC2DC\uC791\uD574\uC11C or\uC5F0\uC0B0\uC744 \uD574\uB098\uAC14\uC744 \uB54C \uAC00\uC9C8 \uC218 \uC788\uB294 \uCD5C\uB300 \uAC12\uC774 \uC788\uACE0\n // \uADF8 \uCD5C\uB300\uAC12\uC744 \uB2EC\uC131\uD558\uAE30 \uC704\uD55C \uAC00\uC7A5 \uC9E7\uC740 subarray\n \n // 1. \uAC01 \uC790\uB9AC\uB9C8\uB2E4 \uAC00\uC9C8 \uC218 \uC788\uB294 max\uAC12\uB4E4\uC744 \uBBF8\uB9AC \uAD6C\uD574\uB193\uB294\uB2E4. \n // \u203B \uC2DC\uC791\uC810\uC774 \uB2E4\uB974\uAE30 \uB54C\uBB38\uC5D0 \uAC00\uC9C8 \uC218 \uC788\uB294 \uCD5C\uB300\uAC12\uC774 \uAC01\uAC01 \uB2E4\uB974\uB2E4. \n\n // 2. sliding windows \uB85C \uAD6C\uD55C\uB2E4. \n // \uD604\uC7AC\uC758 bitmask\uAC12\uC744 max[start] \uC640 \uBE44\uAD50\uD55C\uB2E4. \n // \u203B \uC2DC\uC791\uC810\uC774 start\uC774\uACE0 bitmask\uAC00 max[start]\uB791 \uAC19\uC73C\uBA74 \n // \uD574\uB2F9 \uAE38\uC774\uB97C result[start]\uC5D0 \uC800\uC7A5\n\n // \u203B bit\uC5F0\uC0B0 \uAC12\uC744 sliding window\uD560 \uB54C \uAC01 \uC790\uB9AC bit\uC758 \uAC1C\uC218\uB97C \uC720\uC9C0\uD574\uC8FC\uBA74\uC11C \uACC4\uC0B0\uD574\uC900\uB2E4.\n\n\n int n = nums.length;\n \n int result[] = new int[n];\n\n int max[] = new int[n];\n int m = 0;\n for(int i = n-1; i >= 0; i--) {\n m |= nums[i];\n max[i] = m;\n }\n\n\n int count[] = new int[30];\n int start = 0;\n int bitmask = 0;\n for(int i = 0; i < n; i++) {\n bitmask = add(count, nums[i]);\n\n while( start <= i && bitmask == max[start] ) {\n result[start] = i-start+1;\n bitmask = remove(count, nums[start]);\n start++;\n\n // for(int j = 0; j < result.length; j++) System.out.print(result[j] + ","); System.out.println();\n }\n\n // System.out.println(i + " " +bitmask);\n }\n\n return result;\n }\n\n private int add(int count[], int num) {\n \n int bitmask = 0;\n for(int i = 0; i < 30; i++) {\n if ( (num & ( 1 << i)) > 0 ) count[i]++;\n if (count[i] > 0 ) bitmask |= (1 << i);\n }\n\n return bitmask;\n }\n\n private int remove(int count[], int num) {\n int bitmask = 0;\n for(int i = 0; i < 30; i++) {\n if ( (num & ( 1 << i)) > 0 ) count[i]--;\n if ( count[i] > 0 ) bitmask |= (1 << i);\n }\n\n return bitmask;\n }\n\n}\n```
| 0 | 0 |
['Bit Manipulation', 'Memoization', 'Sliding Window', 'Java']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
C++ | 2 approaches | O(n * 32) | O(n * 32 * logn) | simple implementations
|
c-2-approaches-on-32-on-32-logn-simple-i-qyln
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
shubhamchandra01
|
NORMAL
|
2024-04-23T10:28:56.500216+00:00
|
2024-04-23T10:28:56.500234+00:00
| 4 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n\nBelow implementation is set + binary search (lower_bound)\n\nTime complexity: **O(n x 32 x logn)**\n\n```\nclass Solution {\npublic:\n vector<int> smallestSubarrays(vector<int>& nums) {\n\t\tint n = nums.size();\n\n\t\tvector<set<int>> idx(32);\n\t\tfor (int i = 0; i < n; i++) {\n\t\t\tfor (int j = 0; j < 32; j++) {\n\t\t\t\tif ((nums[i] >> j) & 1) {\n\t\t\t\t\tidx[j].insert(i);\n\t\t\t\t}\n\t\t\t}\n\t\t}\n\t\t\n\t\tvector<int> res(n);\n\t\tfor (int i = 0; i < n; i++) {\n\t\t\tint mn = i;\n\t\t\tfor (int j = 0; j < 32; j++) {\n\t\t\t\tset<int> &st = idx[j];\n\t\t\t\tauto it = st.lower_bound(i);\n\t\t\t\tif (it == st.end()) {\n\t\t\t\t\tst.clear();\n\t\t\t\t} else {\n\t\t\t\t\tmn = max(mn, *it);\n\t\t\t\t}\n\t\t\t}\n\t\t\tres[i] = mn - i + 1;\n\t\t}\n\t\treturn res;\n }\n};\n\n```\n\nImprovement: \nTime complexity **O(n x 32)**\n\n```\nclass Solution {\npublic:\n vector<int> smallestSubarrays(vector<int>& nums) {\n\t\tint n = nums.size();\n\n\t\tvector<queue<int>> idx(32);\n\t\tfor (int i = 0; i < n; i++) {\n\t\t\tfor (int j = 0; j < 32; j++) {\n\t\t\t\tif ((nums[i] >> j) & 1) {\n\t\t\t\t\tidx[j].push(i);\n\t\t\t\t}\n\t\t\t}\n\t\t}\n\t\t\n\t\tvector<int> res(n);\n\t\tfor (int i = 0; i < n; i++) {\n\t\t\tint mn = i;\n\t\t\tfor (int j = 0; j < 32; j++) {\n\t\t\t\tqueue<int> &q = idx[j];\n\t\t\t\twhile (!q.empty() && q.front() < i) q.pop();\n\t\t\t\tif (!q.empty()) {\n\t\t\t\t\tmn = max(mn, q.front());\n\t\t\t\t} \n\t\t\t}\n\t\t\tres[i] = mn - i + 1;\n\t\t}\n\t\treturn res;\n }\n};\n\n```\n\n\n\n
| 0 | 0 |
['C++']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
Python3 solution checking all possible OR values
|
python3-solution-checking-all-possible-o-7838
|
Intuition\n Describe your first thoughts on how to solve this problem. \nIdea from problem https://leetcode.com/problems/bitwise-ors-of-subarrays/description/\n
|
nguyenquocthao00
|
NORMAL
|
2024-04-22T09:31:28.935592+00:00
|
2024-04-22T09:36:47.405531+00:00
| 43 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIdea from problem https://leetcode.com/problems/bitwise-ors-of-subarrays/description/\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def smallestSubarrays(self, nums: List[int]) -> List[int]:\n n=len(nums)\n res=[0]*n\n m=defaultdict(lambda:n+1)\n for i in range(n-1,-1,-1):\n m2=defaultdict(lambda:n+1)\n m2[nums[i]]=1\n for k in m: \n x = k|nums[i]\n m2[x] = min(m2[x], m[k]+1)\n m=m2\n res[i] = m[max(m)]\n return res\n \n```
| 0 | 0 |
['Python3']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
Sliding window solution
|
sliding-window-solution-by-ulyx-q2sh
|
Intuition\n Describe your first thoughts on how to solve this problem. \nUsing an array to record the apprent times of every bit \ndon\'t know how to use bitmap
|
ulyx
|
NORMAL
|
2024-04-12T16:33:40.504183+00:00
|
2024-04-12T16:33:40.504209+00:00
| 3 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUsing an array to record the apprent times of every bit \ndon\'t know how to use bitmap, so using own code\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N)\n# Code\n```\nclass Solution {\n public int[] smallestSubarrays(int[] nums) {\n \n int len = nums.length;\n int r = 0;\n int b = len - 1;\n int e = len - 1;\n int[] res = new int[len];\n\n int[] count = new int[32];\n\n // b - e\n while (b >= 0) {\n\n r = r | nums[b];\n\n add(count, nums[b]);\n\n while (e > b && contains(count, nums[e])) {\n remove(count, nums[e]);\n e--;\n }\n\n res[b] = e - b + 1;\n\n b--;\n }\n\n return res;\n }\n\n boolean contains(int[] count, int a) {\n\n for (int i = 0; i < 32; i++) {\n if ((a & 1) == 1) {\n if (count[i] <= 1) {\n return false;\n }\n }\n a = a >> 1;\n }\n return true;\n }\n\n void remove(int[] count, int a) {\n for (int i = 0; i < 32; i++) {\n if ((a & 1) == 1) {\n count[i]--;\n }\n a = a >> 1;\n }\n }\n\n void add(int[] count, int a) {\n\n for (int i = 0; i < 32; i++) {\n if ((a & 1) == 1) {\n count[i]++;\n }\n a = a >> 1;\n }\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
Sliding window solution
|
sliding-window-solution-by-ulyx-eneh
|
Intuition\n Describe your first thoughts on how to solve this problem. \nUsing an array to record the apprent times of every bit \ndon\'t know how to use bitmap
|
ulyx
|
NORMAL
|
2024-04-12T16:33:39.445351+00:00
|
2024-04-12T16:33:39.445383+00:00
| 8 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUsing an array to record the apprent times of every bit \ndon\'t know how to use bitmap, so using own code\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N)\n# Code\n```\nclass Solution {\n public int[] smallestSubarrays(int[] nums) {\n \n int len = nums.length;\n int r = 0;\n int b = len - 1;\n int e = len - 1;\n int[] res = new int[len];\n\n int[] count = new int[32];\n\n // b - e\n while (b >= 0) {\n\n r = r | nums[b];\n\n add(count, nums[b]);\n\n while (e > b && contains(count, nums[e])) {\n remove(count, nums[e]);\n e--;\n }\n\n res[b] = e - b + 1;\n\n b--;\n }\n\n return res;\n }\n\n boolean contains(int[] count, int a) {\n\n for (int i = 0; i < 32; i++) {\n if ((a & 1) == 1) {\n if (count[i] <= 1) {\n return false;\n }\n }\n a = a >> 1;\n }\n return true;\n }\n\n void remove(int[] count, int a) {\n for (int i = 0; i < 32; i++) {\n if ((a & 1) == 1) {\n count[i]--;\n }\n a = a >> 1;\n }\n }\n\n void add(int[] count, int a) {\n\n for (int i = 0; i < 32; i++) {\n if ((a & 1) == 1) {\n count[i]++;\n }\n a = a >> 1;\n }\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
Simple For loop | TC - O(n*32)
|
simple-for-loop-tc-on32-by-aavvikk-xzp2
|
Idea - Traverse from right and check for each index i at what min index the the jth bit of nums[i] is set. Take the max of all these indices and subtract from
|
aavvikk__
|
NORMAL
|
2024-03-04T05:36:23.014308+00:00
|
2024-03-04T05:45:19.874237+00:00
| 3 | false |
**Idea** - Traverse from right and check for each index i at what min index the the jth bit of nums[i] is set. Take the max of all these indices and subtract from the curent index to get the answer for nums[i]. store it in a vector and return.\n\n```\nclass Solution {\npublic:\n vector<int> smallestSubarrays(vector<int>& nums) {\n \n vector<int> v;\n vector<int> minIndex(33, 0);\n \n for(int i = nums.size() - 1; i >= 0; --i) {\n \n for(int j = 31; j >= 0; --j) {\n \n // check if the jth bit is set or not\n if(nums[i]&(1<<j)) {\n \n minIndex[j] = i;\n }\n }\n \n int ans = i;\n for(int j = 31; j >= 0; --j) {\n ans = max(ans, minIndex[j]);\n }\n \n v.push_back(ans - i + 1);\n }\n \n reverse(v.begin(), v.end());\n return v;\n }\n};\n```
| 0 | 0 |
['C']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
JAVA | Bit-Array | Fastest | EasyToUnderStand | O(N)
|
java-bit-array-fastest-easytounderstand-xn3nh
|
Please VoteUp if you find the solution helpful :)\n\n# Intuition\n Describe your first thoughts on how to solve this problem. \nJust need to store the latest or
|
CodeS-Real
|
NORMAL
|
2024-02-25T14:47:37.269767+00:00
|
2024-02-25T14:47:37.269797+00:00
| 9 | false |
Please VoteUp if you find the solution helpful :)\n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nJust need to store the latest or most recent position any of the 32 bits are set for each value. If none are set answer is 1 else the max latest position which can set a bit .\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(N)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(N)\n# Code\n```\nclass Solution {\n public int[] smallestSubarrays(int[] nums) {\n int maxBit = 0, maxPos = nums.length;\n int bCntArr[] = new int[32];\n Arrays.fill(bCntArr, -1);\n int res[] = new int[nums.length];\n for(int i = nums.length - 1; i >= 0; i--) {\n int curCnt = getMinPos(nums[i], bCntArr, i);\n if(curCnt == -1)\n res[i] = 1;\n else\n res[i] = curCnt - i + 1;\n } \n return res;\n }\n\n int getMinPos(int n, int arr[], int pos) {\n int res = -1;\n for(int i = 0; i < 32; i++) {\n if((n & (1<<i)) > 0){\n arr[i] = pos;\n }\n res = Math.max(res, arr[i]);\n }\n return res;\n }\n}\n```
| 0 | 0 |
['Array', 'Bit Manipulation', 'Java']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
C++ | Bit Solution
|
c-bit-solution-by-pikachuu-cg1l
|
Code\n\nclass Solution {\npublic:\n vector<int> smallestSubarrays(vector<int>& nums) {\n int n = nums.size();\n vector<int> ans(n);\n ve
|
pikachuu
|
NORMAL
|
2024-02-22T21:12:06.763157+00:00
|
2024-02-22T21:12:06.763204+00:00
| 11 | false |
# Code\n```\nclass Solution {\npublic:\n vector<int> smallestSubarrays(vector<int>& nums) {\n int n = nums.size();\n vector<int> ans(n);\n vector<int> closestOne(32);\n for(int i = n - 1; i >= 0; i--) {\n for(int j = 0; j <= 31; j++) {\n if(nums[i] & (1 << j))\n closestOne[j] = i;\n }\n ans[i] = max(1, *max_element(closestOne.begin(), closestOne.end()) - i + 1);\n }\n return ans;\n }\n};\n```
| 0 | 0 |
['Bit Manipulation', 'C++']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
Simple java solution
|
simple-java-solution-by-masterdeniro-yv7t
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
masterdeniro
|
NORMAL
|
2023-12-10T05:22:31.539054+00:00
|
2023-12-10T05:22:31.539077+00:00
| 6 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int[] smallestSubarrays(int[] nums) {\n int[] bitsPositions = new int[32];\n int[] res = new int[nums.length];\n for(int i = nums.length -1;i >=0 ;i--) {\n var min = updateBitsAndGenMin(i, bitsPositions, nums[i]);\n res[i] = min;\n }\n return res; \n }\n private int updateBitsAndGenMin(int i, int[] bitsPositions, int num) {\n int bitPos = 0;\n while(num >0) {\n\n var newPos = num & 1;\n if (newPos == 1 ) {\n bitsPositions[bitPos] = i;\n\n }\n num = num >> 1; \n bitPos++;\n }\n\n int max = 0;\n for(int k =0; k < bitsPositions.length; k++) {\n if (bitsPositions[k] > 0) {\n max = Math.max(bitsPositions[k], max);\n }\n }\n\n return max == 0 ? 1 : max - i + 1;\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
[Java] Bit Solution with Explanation 🔥
|
java-bit-solution-with-explanation-by-sa-k37p
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
sahil_ansari98
|
NORMAL
|
2023-12-09T21:03:29.061297+00:00
|
2023-12-09T21:03:29.061328+00:00
| 5 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int[] smallestSubarrays(int[] nums) {\n int n = nums.length, last[] = new int[30], res[] = new int[n];\n for (int i = n - 1; i >= 0; --i) {\n res[i] = 1;\n for (int j = 0; j < 30; ++j) {\n if ((nums[i] & (1 << j)) > 0)\n last[j] = i;\n res[i] = Math.max(res[i], last[j] - i + 1);\n }\n }\n return res;\n }\n}\n```
| 0 | 0 |
['Java']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
bitmap mapping
|
bitmap-mapping-by-sisoj-35z0
|
Intuition\nWe have a set of bits that exists for the array, lets say we have \n1\n2\n4\n8\n16\netc. We are interested in the index where all these bits will be
|
sisoj
|
NORMAL
|
2023-11-01T20:59:29.781674+00:00
|
2023-11-01T20:59:29.781701+00:00
| 1 | false |
# Intuition\nWe have a set of bits that exists for the array, lets say we have \n1\n2\n4\n8\n16\netc. We are interested in the index where all these bits will be turned on the soonest. For this we will be tracking the list of indexes for each of the bits and the one that is maximum of the minimums will be the start position. Code might be easier to understand than the explanation.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n- O(N) * sizeof<INT>\n\n- Space complexity:\n- O(N) * sizeof<INT>\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> smallestSubarrays(vector<int>& nums) {\n int n = (int)nums.size();\n vector<vector<int>> bits(32);\n vector<int> indexes(32, -1);\n\n for (int i = 0; i<n; ++i) {\n for (int j = 0; j<31; j++) {\n if ((nums[i]>>j) & 1) {\n indexes[j] = 0;\n bits[j].push_back(i);\n }\n }\n }\n int last = 0;\n for (int i = 0; i<31; ++i) {\n if (!bits[i].size()) continue;\n if (bits[i][0] > last)\n last = bits[i][0];\n }\n vector<int> ans;\n for (int i = 0; i<n; ++i) {\n ans.push_back(max(1,last -i +1));\n for (int j =0; j<31; ++j) {\n if ((nums[i]>>j) & 1) {\n indexes[j]++;\n if (indexes[j] < (int)bits[j].size())\n last = max(last, bits[j][indexes[j]]);\n }\n }\n }\n\n return ans;\n\n\n\n \n \n \n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
python bit + hashmap + reverse traversal O(N*log(max(nums))) tc
|
python-bit-hashmap-reverse-traversal-onl-mt9w
|
a much more challenging problem than I expected, you need to spot some tricks.\n1. traverse in reversal\n2. the maximum_or must be or the whole array, hence, th
|
Pseudo_intelligent
|
NORMAL
|
2023-09-24T23:41:56.638657+00:00
|
2023-09-24T23:41:56.638674+00:00
| 2 | false |
a much more challenging problem than I expected, you need to spot some tricks.\n1. traverse in reversal\n2. the maximum_or must be or the whole array, hence, the right subarray max or must be \nthe \'suffing accumulative or\'\n3. hashmap goes into comparing current nums with current maximum suffix or. If cur num bit is 0 and cur or is 1 in this digit, mean we want to find a number with 1 at that digit to or with it. We use a hashmap to store the last index we encounter in that bit digit. Of all cases, we know the maximum last index we include all 1 digits we need.\n```\nclass Solution:\n def smallestSubarrays(self, nums: List[int]) -> List[int]:\n run_or = 0\n dp = []\n hashmap = {}\n for i in range(len(nums)-1,-1,-1):\n run_or |= nums[i]\n temp = 1\n minimax = i\n counts = 0\n while temp <= run_or:\n if nums[i] & temp:\n hashmap[counts] = i\n if run_or&temp and nums[i]&temp == 0:\n minimax = max(minimax,hashmap[counts])\n counts += 1\n temp <<=1\n dp.append(minimax-i+1)\n return dp[::-1]
| 0 | 0 |
[]
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
C++/Python, solution with explanation
|
cpython-solution-with-explanation-by-shu-drmp
|
Traverse nums reversely,\nuse an array to record which index is the latest 1 bit appears in 32 bits.\nAnd find furthest index of 1 bit, the length of subarray i
|
shun6096tw
|
NORMAL
|
2023-09-04T08:38:26.995816+00:00
|
2023-09-04T08:38:26.995847+00:00
| 3 | false |
Traverse nums reversely,\nuse an array to record which index is the latest 1 bit appears in 32 bits.\nAnd find furthest index of 1 bit, the length of subarray is furthest index - i + 1.\n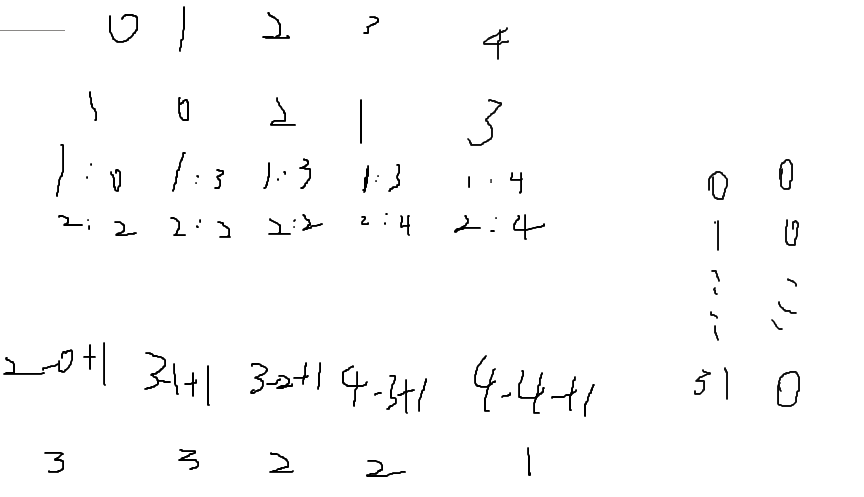\n\ntc isO(32n), sc is O(32).\n\n### python\n```python\nclass Solution:\n def smallestSubarrays(self, nums: List[int]) -> List[int]:\n cloest = [-1] * 32\n ans = [0] * len(nums)\n for i in range(len(nums)-1,-1,-1):\n furthest = i\n for j in range(32):\n if nums[i] >> j & 1:\n cloest[j] = i\n if cloest[j] > furthest: furthest = cloest[j]\n ans[i] = furthest - i + 1\n return ans\n```\n\n### c++\n```cpp\nclass Solution {\npublic:\n vector<int> smallestSubarrays(vector<int>& nums) {\n int closest [32] {0};\n vector<int> ans (nums.size());\n for (int i = nums.size() - 1, furthest; i >= 0; i-=1) {\n furthest = i;\n for (int j = 0; j < 32; j+=1) {\n if (nums[i] >> j & 1)\n closest[j] = i;\n if (closest[j] > furthest) furthest = closest[j];\n }\n ans[i] = furthest - i + 1;\n }\n return ans;\n }\n};\n```
| 0 | 0 |
['C', 'Python']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
C++ || Operation on each bit
|
c-operation-on-each-bit-by-gaurav_new-ebps
|
\n\n# Code\n\nclass Solution {\npublic:\n vector<int> smallestSubarrays(vector<int>& nums) {\n int orr=0;\n int n=nums.size();\n vector<
|
gaurav_new
|
NORMAL
|
2023-08-29T17:53:17.677784+00:00
|
2023-08-29T17:53:17.677803+00:00
| 33 | false |
\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> smallestSubarrays(vector<int>& nums) {\n int orr=0;\n int n=nums.size();\n vector<int>val(n,0);\n for(int i=n-1;i>=0;i--)\n {\n orr=orr|nums[i];\n val[i]=orr;\n }\n vector<int>ans;\n map<int,set<int>>bits;\n for(int i=0;i<n;i++)\n { \n \n for(int j=0;j<32;j++)\n { \n \n if(((nums[i])&(1<<j)))\n { \n bits[j].insert(i);\n }\n }\n }\n \n for(int i=0;i<nums.size();i++)\n {\n int maxxbit=val[i];\n int len=-1e9;\n for(int j=0;j<32;j++)\n {\n if((maxxbit&(1<<j)))\n {\n auto it=bits[j].lower_bound(i);\n int idx=*it;\n len=max(len,idx-i+1);\n }\n }\n if(len==-1e9) ans.push_back(1);\n else\n ans.push_back(len); \n }\n return ans;\n }\n};\n```
| 0 | 0 |
['Binary Search', 'Bit Manipulation', 'C++']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
bits
|
bits-by-shiva_rudra123-auij
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
shiva_rudra123
|
NORMAL
|
2023-08-12T04:43:30.801731+00:00
|
2023-08-12T04:43:30.801752+00:00
| 2 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<int> smallestSubarrays(vector<int>& arr) {\n int n=arr.size();\n vector<vector<int>>suffix(n);\n vector<int>suff(32,n);\n int sum=0;\n \n for(int i=n-1;i>=0;i--){\n for(int j=0;j<32;j++){\n if(arr[i]&(1<<j)){\n suff[j]=i;\n }\n }\n suffix[i]=suff;\n sum |=arr[i];\n }\n vector<int>ans;\n for(int i=0;i<n;i++){\n int right=i;\n for(int j=0;j<32;j++){\n if(suffix[i][j]!=n){\n right=max(right,suffix[i][j]);\n }\n }\n cout<<right<<endl;\n ans.push_back(right-i+1);\n }\n //cout<<endl;\n return ans;\n\n\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
C++ , Easy and precise , Sliding Window solution with BIT_COUNT,
|
c-easy-and-precise-sliding-window-soluti-f9vl
|
Intuition\n. \n\n\n# Approach\n Describe your approach to solving the problem. \n\nCreate a bit_vec (Vector) that stores tha count of bits that found till now\n
|
pranaynagpure
|
NORMAL
|
2023-07-08T15:46:13.764612+00:00
|
2023-07-08T15:46:13.764649+00:00
| 15 | false |
# Intuition\n<!--. -->\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nCreate a bit_vec (Vector) that stores tha count of bits that found till now\n\nExample\n\nn= [1,1,2,2,3,3] max_or = 3\n i=0,j=0;\n\nbit_vec[] = {0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0......32 times }\n\nnext\nn = [1,1,2,2,3,3] \n i=0, j =2 at this position we found or = 3 so increment i\n\nbit_vec[] = { 2 ,1, 0 ,0 ,0 ,0 ,0 .... 32 times}\n\nn = [1,1,2,2,3,3]\nres [3,0,0,0,0,0]\n i=1, j=2 still the or is => \'3\' so increment the i\nbit_vec[]= { 1,1,0,0,0,0,.... 32 times};\n\nnotice how bit_vec[0] changes from 2-1 becuse , as the i incremented we need to decrement the count of bits from the bit_vec;\n\nand if j reached the end bit i has not the recursively call the same fucntion\n\nPlease upvote the solution if you found helpful it helps me keep motivated\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\nO(32*N) not sure (please suggest as not sure about how many time reursion can go)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\nO(N) => for result vector\n\n# Code\n```\nclass Solution {\npublic:\n\n int getOR(vector<int> &bit_vec) // to convet the bit_vec into number example bit_vec[] = {2,3,4, 0 ,0,0,} => 7 as first 3 bits are set\n {\n int ans =0;\n for(int i =0 ; i<32 ; i++)\n if(bit_vec[i] >0)\n ans = ans | (1<<i); \n return ans;\n }\n vector<int> smallestSubarrays(vector<int>& nums) {\n \n vector<int> bit_vec(32,0);\n vector<int> res((int)nums.size(), 1);\n\n int OR =0;\n\n for(int &i : nums)\n OR = OR |i;\n\n int j =0 , i =0;\n\n for(j =0 ;j< nums.size(); ++j)\n {\n int a = nums[j];\n int k =0;\n while(a) // add bit count of current numebr to vector\n {\n if(a & 1)\n bit_vec[k]++;\n a >>=1;\n ++k;\n }\n\n while(i <=j and getOR(bit_vec) >= OR) // increment i uthil there is maximum or\n {\n res[i] = j-i+1;\n \n a= nums[i]; k=0;\n while(a) // remove the bit count from vector\n {\n if(a & 1)\n bit_vec[k]--;\n a >>=1;\n ++k;\n }\n i++;\n }\n }\n if(i< nums.size()) // if i is still less than nums size then recursively call the function \n {\n vector<int> t(nums.begin()+i,nums.end());\n auto v = smallestSubarrays( t);\n\n for(int k = i ;k< nums.size() ; k++)\n res[k] =v[k-i];\n }\n\n return res;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
C++ , Easy and precise , Sliding Window solution with BIT_COUNT,
|
c-easy-and-precise-sliding-window-soluti-5yz4
|
Intuition\n. \n\n\n# Approach\n Describe your approach to solving the problem. \n\nCreate a bit_vec (Vector) that stores tha count of bits that found till now\n
|
pranaynagpure
|
NORMAL
|
2023-07-08T15:46:11.419632+00:00
|
2023-07-08T15:46:11.419664+00:00
| 12 | false |
# Intuition\n<!--. -->\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\nCreate a bit_vec (Vector) that stores tha count of bits that found till now\n\nExample\n\nn= [1,1,2,2,3,3] max_or = 3\n i=0,j=0;\n\nbit_vec[] = {0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0......32 times }\n\nnext\nn = [1,1,2,2,3,3] \n i=0, j =2 at this position we found or = 3 so increment i\n\nbit_vec[] = { 2 ,1, 0 ,0 ,0 ,0 ,0 .... 32 times}\n\nn = [1,1,2,2,3,3]\nres [3,0,0,0,0,0]\n i=1, j=2 still the or is => \'3\' so increment the i\nbit_vec[]= { 1,1,0,0,0,0,.... 32 times};\n\nnotice how bit_vec[0] changes from 2-1 becuse , as the i incremented we need to decrement the count of bits from the bit_vec;\n\nand if j reached the end bit i has not the recursively call the same fucntion\n\nPlease upvote the solution if you found helpful it helps me keep motivated\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\nO(32*N) not sure (please suggest as not sure about how many time reursion can go)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\nO(N) => for result vector\n\n# Code\n```\nclass Solution {\npublic:\n\n int getOR(vector<int> &bit_vec) // to convet the bit_vec into number example bit_vec[] = {2,3,4, 0 ,0,0,} => 7 as first 3 bits are set\n {\n int ans =0;\n for(int i =0 ; i<32 ; i++)\n if(bit_vec[i] >0)\n ans = ans | (1<<i); \n return ans;\n }\n vector<int> smallestSubarrays(vector<int>& nums) {\n \n vector<int> bit_vec(32,0);\n vector<int> res((int)nums.size(), 1);\n\n int OR =0;\n\n for(int &i : nums)\n OR = OR |i;\n\n int j =0 , i =0;\n\n for(j =0 ;j< nums.size(); ++j)\n {\n int a = nums[j];\n int k =0;\n while(a) // add bit count of current numebr to vector\n {\n if(a & 1)\n bit_vec[k]++;\n a >>=1;\n ++k;\n }\n\n while(i <=j and getOR(bit_vec) >= OR) // increment i uthil there is maximum or\n {\n res[i] = j-i+1;\n \n a= nums[i]; k=0;\n while(a) // remove the bit count from vector\n {\n if(a & 1)\n bit_vec[k]--;\n a >>=1;\n ++k;\n }\n i++;\n }\n }\n if(i< nums.size()) // if i is still less than nums size then recursively call the function \n {\n vector<int> t(nums.begin()+i,nums.end());\n auto v = smallestSubarrays( t);\n\n for(int k = i ;k< nums.size() ; k++)\n res[k] =v[k-i];\n }\n\n return res;\n }\n};\n```
| 0 | 0 |
['C++']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
Dynamic programming approach with Python
|
dynamic-programming-approach-with-python-l40q
|
Intuition\n> We can iterate through nums in reverse order to find the maximum OR reachable from each index. After this we will iterate through nums from each in
|
FransV
|
NORMAL
|
2023-06-28T08:21:09.117612+00:00
|
2023-06-28T08:21:09.117645+00:00
| 77 | false |
# Intuition\n> We can iterate through nums in reverse order to find the maximum OR reachable from each index. After this we will iterate through nums from each index until we will reach the target OR. We will use dynamic programming to improve time efficiency.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport sys\n\nclass Solution:\n def smallestSubarrays(self, nums: List[int]) -> List[int]:\n\n def helper(i, item, target):\n\n #Dynamic programming\n if (i, item, target) in dp:\n return dp[i, item, target]\n \n #Has target been reached in the current index\n temp = item | nums[i]\n if temp == target:\n dp[i, item, target] = 1\n #Recursion call\n else:\n dp[i, item, target] = helper(i+1, temp, target) + 1\n\n return dp[i, item, target]\n\n #Increase recursion limit\n sys.setrecursionlimit(10**6)\n n = len(nums)\n\n #Find the maximum or reachable from each index\n item = 0\n max_or = []\n for i in range(n):\n item |= nums[-i-1]\n max_or.append(item) \n max_or.reverse()\n\n #Iterate through the array\n dp = {}\n output = []\n for i in range(n):\n output.append(helper(i, 0, max_or[i]))\n\n return output\n```
| 0 | 0 |
['Dynamic Programming', 'Bit Manipulation', 'Python3']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
very simple and Easy Solution using segment Tree+Two pointer+Prefix OR
|
very-simple-and-easy-solution-using-segm-1cuw
|
Intuition\nFirst find the maximum value for each subarray using reverse prefix or\nthen start from the right hand side and try to reduce the boundary \nsee the
|
51_KING
|
NORMAL
|
2023-06-21T06:10:59.263951+00:00
|
2023-06-21T06:10:59.263978+00:00
| 22 | false |
# Intuition\nFirst find the maximum value for each subarray using reverse prefix or\nthen start from the right hand side and try to reduce the boundary \nsee the solution you will easily understand.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(NlogN)\n\n- Space complexity:\nO(N)\n\n# Code\n```\n\nclass SegmentTree{\n vector <int> seg;\n public:\n SegmentTree(int n)\n {\n seg.resize(4*n,0);\n }\n void build(int node,int l,int r,vector <int> &nums)\n {\n if(l==r)\n {\n seg[node] = nums[l];\n return;\n }\n int mid = (l+r)>>1;\n build(2*node+1,l,mid,nums);\n build(2*node+2,mid+1,r,nums);\n \n seg[node] = seg[2*node+1]|seg[2*node+2];\n }\n \n int query(int node,int left,int right,int l,int r)\n {\n if(l>r||r<left||right<l) return 0;\n if(l>=left&&r<=right) return seg[node];\n \n int mid = (l+r)>>1;\n return query(2*node+1,left,right,l,mid) | query(2*node+2,left,right,mid+1,r);\n }\n};\nclass Solution {\npublic:\n vector<int> smallestSubarrays(vector<int>& nums) {\n int n = nums.size();\n SegmentTree segmentTree(n);\n segmentTree.build(0,0,n-1,nums);\n vector <int> maxOR(n);\n maxOR[n-1] = nums[n-1];\n for(int i=n-2;i>=0;i--)\n {\n maxOR[i] = maxOR[i+1] | nums[i];\n }\n int i=n-2,j=n-1;\n vector <int> ans(n);\n ans[n-1] = 1;\n \n while(i>=0)\n {\n while(i<j&&segmentTree.query(0,i,j-1,0,n-1)>=maxOR[i])\n j--;\n ans[i] = j-i+1;\n i--;\n }\n return ans;\n }\n};\n```
| 0 | 0 |
['Two Pointers', 'Segment Tree', 'Prefix Sum', 'C++']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
✅Simple solution using Binary Search
|
simple-solution-using-binary-search-by-r-cffv
|
\nclass Solution {\npublic:\n vector<int> smallestSubarrays(vector<int>& nums) {\n int n=nums.size();\n \n vector<vector<int>> list(n, v
|
realmmasterx
|
NORMAL
|
2023-05-27T15:15:10.167902+00:00
|
2023-05-27T15:15:10.167944+00:00
| 41 | false |
```\nclass Solution {\npublic:\n vector<int> smallestSubarrays(vector<int>& nums) {\n int n=nums.size();\n \n vector<vector<int>> list(n, vector<int>(30));\n for(int i=0;i<n;i++) {\n int temp = nums[i];\n for(int j=0;j<30;j++) {\n list[i][j]=temp%2;\n temp/=2;\n }\n }\n \n vector<vector<int>> prefix(n, vector<int>(30)), for_bi(30, vector<int>(n));\n prefix[0] = list[0];\n for(int i=1;i<n;i++) {\n for(int j=0;j<30;j++) {\n prefix[i][j]=prefix[i-1][j]+list[i][j];\n for_bi[j][i]=prefix[i][j];\n }\n }\n \n vector<int> compare(30);\n compare = prefix[n-1];\n \n vector<int> ans(n);\n ans[n-1] = 1;\n \n for(int i=0;i<n-1;i++) {\n int temp = 1;\n for(int j=0;j<30;j++) {\n if(prefix[i][j]<compare[j] && list[i][j]==0) {\n vector<int>::iterator fk=lower_bound(for_bi[j].begin()+i,for_bi[j].end(),prefix[i][j]+1);\n int x = (fk - (for_bi[j].begin()+i));\n temp = max(temp, x + 1);\n }\n }\n ans[i]=temp;\n }\n return ans;\n }\n};\n```
| 0 | 0 |
['Binary Search', 'C++']
| 0 |
smallest-subarrays-with-maximum-bitwise-or
|
[Python] find the largest distance for each bit of the maximum OR value
|
python-find-the-largest-distance-for-eac-mbuz
|
\nclass Solution:\n def smallestSubarrays(self, nums: List[int]) -> List[int]:\n # two sweeps\n len_n = len(nums)\n # sweep 1: find the
|
wangw1025
|
NORMAL
|
2023-04-07T05:59:42.797887+00:00
|
2023-04-07T05:59:42.797939+00:00
| 75 | false |
```\nclass Solution:\n def smallestSubarrays(self, nums: List[int]) -> List[int]:\n # two sweeps\n len_n = len(nums)\n # sweep 1: find the maximum OR value at each index\n max_or = [0] * len_n\n idx, c_or = len_n - 1, 0\n while idx >= 0:\n c_or |= nums[idx]\n max_or[idx] = c_or\n idx -= 1\n \n # sweep 2: starting from the last number, track the closest index for every bit\n ans = [1] * len_n\n bidx = [None] * 32\n idx = len_n - 1\n while idx >= 0:\n i = 0\n n = nums[idx]\n while n:\n if n & 1:\n bidx[i] = idx\n i += 1\n n >>= 1\n mor = max_or[idx]\n max_dist, i = 1, 0\n while mor:\n if mor & 1:\n max_dist = max(max_dist, bidx[i] - idx + 1)\n i += 1\n mor >>= 1\n ans[idx] = max_dist\n idx -= 1\n \n return ans\n```
| 0 | 0 |
['Python3']
| 0 |
maximum-distance-between-a-pair-of-values
|
O(n) 2 pointers
|
on-2-pointers-by-votrubac-85rc
|
Since our arrays are sorted, we can advance i while n1[i] is bigger than n2[j], and increment j otherwise.\n\nJava\njava\npublic int maxDistance(int[] n1, int[]
|
votrubac
|
NORMAL
|
2021-05-09T04:06:18.434244+00:00
|
2021-05-10T22:45:22.562993+00:00
| 9,085 | false |
Since our arrays are sorted, we can advance `i` while `n1[i]` is bigger than `n2[j]`, and increment `j` otherwise.\n\n**Java**\n```java\npublic int maxDistance(int[] n1, int[] n2) {\n int i = 0, j = 0, res = 0;\n while (i < n1.length && j < n2.length)\n if (n1[i] > n2[j])\n ++i;\n else\n res = Math.max(res, j++ - i);\n return res;\n}\n```\n**C++**\n```cpp\nint maxDistance(vector<int>& n1, vector<int>& n2) {\n int i = 0, j = 0, res = 0;\n while (i < n1.size() && j < n2.size())\n if (n1[i] > n2[j])\n ++i;\n else\n res = max(res, j++ - i);\n return res;\n}\n```\n**Python 3**\n```python\nclass Solution:\n def maxDistance(self, n1: List[int], n2: List[int]) -> int:\n i = j = res = 0\n while i < len(n1) and j < len(n2):\n if n1[i] > n2[j]:\n i += 1\n else:\n res = max(res, j - i)\n j += 1\n return res\n```
| 149 | 5 |
['C', 'Python', 'Java']
| 19 |
maximum-distance-between-a-pair-of-values
|
[Java/C++/Python] 2 Pointers, 3 Solutions
|
javacpython-2-pointers-3-solutions-by-le-vixv
|
Solution 1\nIterate on input array B\n\nTime O(n + m)\nSpace O(1)\n\nJava\njava\n public int maxDistance(int[] A, int[] B) {\n int res = 0, i = 0, n =
|
lee215
|
NORMAL
|
2021-05-09T04:09:48.597630+00:00
|
2021-05-09T04:18:34.214672+00:00
| 6,149 | false |
# Solution 1\nIterate on input array `B`\n\nTime `O(n + m)`\nSpace `O(1)`\n\n**Java**\n```java\n public int maxDistance(int[] A, int[] B) {\n int res = 0, i = 0, n = A.length, m = B.length;\n for (int j = 0; j < m; ++j) {\n while (i < n && A[i] > B[j])\n i++;\n if (i == n) break;\n res = Math.max(res, j - i);\n }\n return res;\n }\n```\n\n**C++**\n```cpp\n int maxDistance(vector<int>& A, vector<int>& B) {\n int res = 0, i = 0, n = A.size(), m = B.size();\n for (int j = 0; j < m; ++j) {\n while (i < n && A[i] > B[j])\n i++;\n if (i == n) break;\n res = max(res, j - i);\n }\n return res;\n }\n```\n\n**Python**\n```py\n def maxDistance(self, A, B):\n res = i = 0\n for j, b in enumerate(B):\n while i < len(A) and A[i] > b:\n i += 1\n if i == len(A): break\n res = max(res, j - i)\n return res\n```\n<br>\n\n# Solution 2\nIterate on input array `A`\n\nTime `O(n + m)`\nSpace `O(1)`\n\n**Java**\n```java\n public int maxDistance(int[] A, int[] B) {\n int res = 0, j = -1, n = A.length, m = B.length;\n for (int i = 0; i < n; ++i) {\n while (j + 1 < m && A[i] <= B[j + 1])\n j++;\n res = Math.max(res, j - i);\n }\n return res;\n }\n```\n**C++**\n```cpp\n int maxDistance(vector<int>& A, vector<int>& B) {\n int res = 0, j = -1, n = A.size(), m = B.size();\n for (int i = 0; i < n; ++i) {\n while (j + 1 < m && A[i] <= B[j + 1])\n j++;\n res = max(res, j - i);\n }\n return res;\n }\n```\n**Python**\n```py\n def maxDistance(self, A, B):\n res, j = 0, -1\n for i, a in enumerate(A):\n while j + 1 < len(B) and a <= B[j + 1]:\n j += 1\n res = max(res, j - i)\n return res\n```\n\n# Solution 3\nIterate on input array `A` and `B`\n\nTime `O(n + m)`\nSpace `O(1)`\n\n**Java**\n```java\n public int maxDistance(int[] A, int[] B) {\n int i = 0, j = 0, res = 0, n = A.length, m = B.length;\n while (i < n && j < m) {\n if (A[i] > B[j])\n i++;\n else\n res = Math.max(res, j++ - i);\n }\n return res;\n }\n```\n**C++**\n```cpp\n int maxDistance(vector<int>& A, vector<int>& B) {\n int i = 0, j = 0, res = 0, n = A.size(), m = B.size();\n while (i < n && j < m) {\n if (A[i] > B[j])\n i++;\n else\n res = max(res, j++ - i);\n }\n return res;\n }\n```
| 85 | 7 |
[]
| 15 |
maximum-distance-between-a-pair-of-values
|
7 Line c++ | Binary Search | STL
|
7-line-c-binary-search-stl-by-its_gupta_-ldyi
|
For any element nums1[i], we essentially need to find the farthest element nums2[j] with j>=i such that the nums2[j] element is not less than nums1[i].\n\nA bru
|
its_gupta_ananya
|
NORMAL
|
2021-05-09T07:08:03.218025+00:00
|
2021-05-09T07:29:25.397487+00:00
| 3,164 | false |
For any element nums1[i], we essentially need to find the farthest element nums2[j] with j>=i such that the nums2[j] element is not less than nums1[i].\n\nA brute force way of doing the same would be to iterate over every j in the range ```i <=j && j <n" ``` , but then we aren\'t using the fact that the two arrays are sorted in non-decreasing order. \n\nSo, what we instead do is, reverse the second array to make it non-increasing and then for every nums1[i], we find the first element which is either equal to or greater than it i.e. Lower_bound of the element (Note that for the original array this would be the same element which would be farther away satisfying the condition). \n\nIn the given code, j represents the index from the end (which would be it\'s index in the original array)\n``` \nclass Solution {\npublic:\n int maxDistance(vector<int>& nums1, vector<int>& nums2) {\n \n reverse(nums2.begin(),nums2.end());\n int ans = 0;\n for(int i=0;i<nums1.size();++i){\n auto it = lower_bound(nums2.begin(),nums2.end(),nums1[i]) - nums2.begin(); //Finds first element greater than or equal to nums1[i]\n int j = nums2.size() - 1 - it; //Index of the found element in the original array\n if(i<=j) ans = max(ans,j-i); //Update distance \n }\n return ans;\n \n }\n};\n```\n\n\nHope this helps!\nStay Safe.
| 36 | 4 |
['C', 'Binary Tree']
| 8 |
maximum-distance-between-a-pair-of-values
|
[C++] 2 pointers solution
|
c-2-pointers-solution-by-pankajgupta20-mjfp
|
\tclass Solution {\n\tpublic:\n\t\tint maxDistance(vector& nums1, vector& nums2) {\n\t\t\tint ans = 0;\n\t\t\tint i = 0;\n\t\t\tint j = 0;\n\t\t\twhile(i < nums
|
pankajgupta20
|
NORMAL
|
2021-05-09T05:21:45.800252+00:00
|
2021-05-09T05:21:45.800282+00:00
| 1,447 | false |
\tclass Solution {\n\tpublic:\n\t\tint maxDistance(vector<int>& nums1, vector<int>& nums2) {\n\t\t\tint ans = 0;\n\t\t\tint i = 0;\n\t\t\tint j = 0;\n\t\t\twhile(i < nums1.size() and j < nums2.size()){\n\t\t\t\tif(nums1[i] <= nums2[j]){\n\t\t\t\t\tif(i <= j){\n\t\t\t\t\t\tans = max(ans, j - i);\n\t\t\t\t\t}\n\t\t\t\t\tj++;\n\t\t\t\t}\n\t\t\t\telse{\n\t\t\t\t\ti++;\n\t\t\t\t}\n\t\t\t}\n\t\t\treturn ans;\n\t\t}\n\t};
| 19 | 0 |
['Two Pointers', 'C', 'C++']
| 3 |
maximum-distance-between-a-pair-of-values
|
Java Binary search
|
java-binary-search-by-zoey02-3svn
|
\nclass Solution {\n public int maxDistance(int[] nums1, int[] nums2) {\n int max = 0;\n for (int i = 0; i < nums1.length; i++) {\n
|
zoey02
|
NORMAL
|
2021-05-09T04:06:07.666366+00:00
|
2021-05-09T04:11:29.851898+00:00
| 1,417 | false |
```\nclass Solution {\n public int maxDistance(int[] nums1, int[] nums2) {\n int max = 0;\n for (int i = 0; i < nums1.length; i++) {\n int r = nums2.length - 1;\n int l = i;\n int m = i;\n while (l <= r) {\n m = l + (r - l) / 2;\n if (nums1[i] > nums2[m]) {\n r = m - 1;\n } else if (nums1[i] == nums2[m]) {\n l = m + 1;\n } else {\n l = m + 1;\n }\n }\n if (r < 0) {\n continue;\n }\n max = Math.max(max, r - i);\n }\n return max;\n }\n}\n```
| 15 | 1 |
['Binary Tree', 'Java']
| 3 |
maximum-distance-between-a-pair-of-values
|
O ( N ) || O ( N LOG N) || Both Approaches
|
o-n-o-n-log-n-both-approaches-by-karan_8-o38l
|
O ( N LOG N ) \n BINARY SEARCH in C++\n\n\nclass Solution {\npublic:\nint maxDistance(vector<int>& n1, vector<int>& n2) {\n\n int ans=0,k=min(n1.size(),n2.si
|
karan_8082
|
NORMAL
|
2022-05-28T05:49:40.848778+00:00
|
2022-05-28T05:49:40.848815+00:00
| 1,028 | false |
**O ( N LOG N ) \n BINARY SEARCH in C++**\n\n```\nclass Solution {\npublic:\nint maxDistance(vector<int>& n1, vector<int>& n2) {\n\n int ans=0,k=min(n1.size(),n2.size());\n for(int i=0; i<k;i++){\n int l=i,r=n2.size()-1,m;\n while(l<=r){\n m=l+(r-l)/2;\n int t= n1[i];\n if(n2[m]>=t){\n l=m+1;\n if(m-i>ans)ans=m-i;\n } \n else r=m-1;\n } \n }\n return ans;\n }\n};\n```\n\n\n**O ( N ) in PYTHON**\n```\nclass Solution:\n def maxDistance(self, nums1: List[int], nums2: List[int]) -> int:\n i=0\n j=0\n k=0\n while j<len(nums2):\n while i<len(nums1) and nums1[i]>nums2[j]:\n i+=1\n if (i<len(nums1)):\n k=max(k,j-i)\n j+=1\n if i==len(nums1):\n break\n return k\n```\n\n**O ( N ) in C++**\n```\nclass Solution {\npublic:\n int maxDistance(vector<int>& nums1, vector<int>& nums2) {\n int i=0;\n int j=0;\n int k=0;\n while (j<nums2.size()){\n while (i<nums1.size() && nums1[i]>nums2[j]){\n i++;\n }\n k = max(k,j-i);\n j++;\n if (i>=nums1.size()){\n break;\n }\n }\n return k;\n }\n};\n```\n\n
| 13 | 0 |
['Two Pointers', 'C', 'Binary Tree', 'Python', 'C++']
| 2 |
maximum-distance-between-a-pair-of-values
|
Easy C++| Detailed Explanation | 2 Pointers
|
easy-c-detailed-explanation-2-pointers-b-2m32
|
Problem Definition with Constraints :\n\nBoth the arrays are Non-Increasing.\nWe need to define a solution to find the Maximum distance j-i while maintaining t
|
saivenky031996
|
NORMAL
|
2021-05-17T05:20:28.401284+00:00
|
2021-05-18T14:30:34.616445+00:00
| 534 | false |
**Problem Definition with Constraints** :\n\nBoth the arrays are **Non-Increasing**.\nWe need to define a solution to find the **Maximum** distance `j-i` while maintaining the below 2 constraints.\n* i <= j\n* nums1[i] <= nums2[j]\n\n\n**Solution with Example** :\n \n```\nclass Solution {\npublic:\n int maxDistance(vector<int>& nums1, vector<int>& nums2) {\n int i=0, j=0;\n int dis=0;\n while(true) {\n \n\t\t// No more elements are left to process.\n if(i==nums1.size()||j==nums2.size()) break;\n \n\t\t// If the condition is not, then increment both.\n if(nums2[j]<nums1[i] ) {\n i++; \n j++;\n } else {\n\t\t // Calculate the current distance and try incrementing j to maximise the distance. \n dis = max(dis, j++ - i);\n }\n \n }\n return dis;\n }\n};\n```\n\n Consider the following 2 arrays.\n\n```\n[70,60,50,40,30,20,10]\n[80,77,74,71,68,65,62]\n```\n\n1. `i=0, j=0`\n`80>70, dist is j-i = 0, max = 0`\nTry incrementing j to maximise the distance. \n\n2. `i=0, j=1`\n`77>70, dist is j-i = 1, max = 1`\nTry incrementing j to maximise the distance. \n\n3. ` i=0, j=2`\n`74>70, dist is j-i = 2, max = 2`\nTry incrementing j to maximise the distance. \n\n4. `i=0, j=3`\n`71>70, dist is j-i = 3, max = 3`\nTry incrementing j to maximise the distance. \n\n5. `i=0, j=4`\n`68<70, max = 3`\nIncrement i and j. \n**Why j ? Cause we are trying to maintain this maximum. Incrementing i alone will anyways decrease the maximum only (4-1 < 5-1) .**\n\n6. `i=1, j=5`\n `60<65, dist is j-i = 4, max = 4`\nTry incrementing j to maximise the distance. \n7. ` i=1, j=6`\n`60<62, dist is j-i = 5, max = 5`\n\nReturn the maximum value of `5`.\n\n**Complexity**:\n\nTime: `O(maximum(nums1.size() , nums2.size())) `\nSpace: `O(1)`\nPl upvote if this was useful :).
| 11 | 0 |
['Two Pointers', 'C']
| 0 |
maximum-distance-between-a-pair-of-values
|
python binary search
|
python-binary-search-by-psean21c-akdk
|
Intuition\n\n\n1) nums1 = [30,29,19,5], nums2 = [25,25,25,25,25]\n2) convert to negative values\nnums1 = [-30,-29,-19,-5]\nnums2 = [-25,-25,-25,-25,-25]\n3) ite
|
psean21c
|
NORMAL
|
2021-05-09T04:23:18.785231+00:00
|
2021-05-09T04:55:51.115669+00:00
| 842 | false |
Intuition\n\n\n1) nums1 = [30,29,19,5], nums2 = [25,25,25,25,25]\n2) convert to negative values\nnums1 = [-30,-29,-19,-5]\nnums2 = [-25,-25,-25,-25,-25]\n3) iterate nums1 and compare each element with nums2\ni = 0: num1[0]= -30 => j = 0 because -30 is smaller than all nums2\ni = 1: num1[1]=-29 => j = 0 because -29 is smaller than all nums2\ni = 2: num1[2]=-19 => j = 5 because -19 is greater than all nums2\ni = 3 num1[3]=-5 => j = 5 because -5 is greater than all nums2\n\n\n```\n def maxDistance(self, nums1: List[int], nums2: List[int]) -> int:\n\n nums2 = [-1 * i for i in nums2]\n\n best = 0\n for i, n in enumerate(nums1):\n j = bisect.bisect_right(nums2, -n)\n if j >= i:\n best = max(best, j - i - 1)\n\n return best\n\n```
| 10 | 1 |
[]
| 1 |
maximum-distance-between-a-pair-of-values
|
📌 Python3 simple solution using two pointers
|
python3-simple-solution-using-two-pointe-kz3h
|
\nclass Solution:\n def maxDistance(self, nums1: List[int], nums2: List[int]) -> int:\n length1, length2 = len(nums1), len(nums2)\n i,j = 0,0\n
|
dark_wolf_jss
|
NORMAL
|
2022-06-28T12:57:30.958436+00:00
|
2022-06-28T12:57:30.958479+00:00
| 674 | false |
```\nclass Solution:\n def maxDistance(self, nums1: List[int], nums2: List[int]) -> int:\n length1, length2 = len(nums1), len(nums2)\n i,j = 0,0\n \n result = 0\n while i < length1 and j < length2:\n if nums1[i] > nums2[j]:\n i+=1\n else:\n result = max(result,j-i)\n j+=1\n \n return result\n```
| 8 | 0 |
['Two Pointers', 'Python3']
| 0 |
maximum-distance-between-a-pair-of-values
|
Easy Java solution || 2 Pointer
|
easy-java-solution-2-pointer-by-gau5tam-gwb3
|
Please UPVOTE if you like my solution!\n\n\nclass Solution {\n public int maxDistance(int[] nums1, int[] nums2) {\n int i = 0;\n int j = 0;\n
|
gau5tam
|
NORMAL
|
2023-04-20T16:50:20.857882+00:00
|
2023-04-20T16:50:20.857921+00:00
| 112 | false |
Please **UPVOTE** if you like my solution!\n\n```\nclass Solution {\n public int maxDistance(int[] nums1, int[] nums2) {\n int i = 0;\n int j = 0;\n int ans = 0;\n while(i<nums1.length && j<nums2.length){\n if(nums1[i] <= nums2[j]){\n ans = Math.max(ans,j-i);\n j++; \n }\n else{\n i++;\n } \n \n }\n return ans;\n }\n}\n```
| 7 | 0 |
['Two Pointers', 'Java']
| 0 |
maximum-distance-between-a-pair-of-values
|
Two Pointer solution in C++ and Java
|
two-pointer-solution-in-c-and-java-by-ka-p86r
|
Complexity\n- Time complexity:\n Add your time complexity here, e.g. O(n) \n O(n)\n\n- Space complexity:\n Add your space complexity here, e.g. O(n) \n O(
|
Kashif_Rahman
|
NORMAL
|
2022-10-14T16:17:45.470196+00:00
|
2022-10-14T16:17:45.470229+00:00
| 451 | false |
# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(1)\n\n# Code\nJava Solution \n```\nclass Solution {\n public int maxDistance(int[] nums1, int[] nums2) {\n int i = 0, j = 0, ans = 0;\n while(i < nums1.length&& j < nums2.length){\n if(nums1[i] > nums2[j])\n i++;\n else{\n ans = Integer.max(ans, j-i);\n j++;\n }\n }\n return ans;\n }\n}\n```\nC++ solution\n```\nclass Solution {\npublic:\n int maxDistance(vector<int>& nums1, vector<int>& nums2) {\n int i = 0, j = 0, ans = 0;\n while(i < nums1.size() && j < nums2.size()){\n if(nums1[i] > nums2[j])\n i++;\n else{\n ans = max(ans, j-i);\n j++;\n }\n }\n return ans;\n}\n};\n```\n
| 7 | 0 |
['Two Pointers', 'Binary Search', 'C++', 'Java']
| 1 |
maximum-distance-between-a-pair-of-values
|
JAVA 2 Pointer
|
java-2-pointer-by-himanshuchhikara-hmkt
|
CODE:\n\n public int maxDistance(int[] nums1, int[] nums2) {\n int i=0 , j=0;\n int result=0;\n while(i<nums1.length && j<nums2.length){
|
himanshuchhikara
|
NORMAL
|
2021-05-12T17:00:54.643337+00:00
|
2021-05-12T17:00:54.643383+00:00
| 523 | false |
**CODE:**\n```\n public int maxDistance(int[] nums1, int[] nums2) {\n int i=0 , j=0;\n int result=0;\n while(i<nums1.length && j<nums2.length){\n if(nums1[i]>nums2[j]){\n i++;\n }else{\n result=Math.max(j-i,result); //if(j<i , j-i will be negative and result will not get updated \n j++;\n }\n }\n return result;\n}\n```\n\n**Complexity:**\n`Time:O(maximum(n,m)) and Space:O(1)`\n\n
| 7 | 0 |
['Two Pointers', 'Java']
| 0 |
maximum-distance-between-a-pair-of-values
|
Easy 2-Pointer Solution
|
easy-2-pointer-solution-by-admin007-i701
|
\n def maxDistance(self, nums1: List[int], nums2: List[int]) -> int:\n m, n = len(nums1), len(nums2)\n i = j = 0\n ans = 0\n whil
|
admin007
|
NORMAL
|
2021-05-09T04:56:29.701702+00:00
|
2021-05-09T04:56:29.701730+00:00
| 478 | false |
```\n def maxDistance(self, nums1: List[int], nums2: List[int]) -> int:\n m, n = len(nums1), len(nums2)\n i = j = 0\n ans = 0\n while i < m and j < n:\n while j < n and nums1[i] <= nums2[j]:\n j += 1\n ans = max(ans, j - i - 1)\n while i < m and j < n and not (nums1[i] <= nums2[j]):\n i += 1\n return ans\n```
| 6 | 0 |
[]
| 0 |
maximum-distance-between-a-pair-of-values
|
python 2 pointers O(N)
|
python-2-pointers-on-by-tiantianluck-boo0
|
\tclass Solution(object):\n\t\tdef maxDistance(self, nums1, nums2):\n\t\t\t"""\n\t\t\t:type nums1: List[int]\n\t\t\t:type nums2: List[int]\n\t\t\t:rtype: int\n\
|
tiantianluck
|
NORMAL
|
2021-05-09T04:06:21.932973+00:00
|
2021-05-09T04:06:21.933001+00:00
| 468 | false |
\tclass Solution(object):\n\t\tdef maxDistance(self, nums1, nums2):\n\t\t\t"""\n\t\t\t:type nums1: List[int]\n\t\t\t:type nums2: List[int]\n\t\t\t:rtype: int\n\t\t\t"""\n\t\t\tret = 0\n\t\t\ti, j = 0, 0\n\t\t\twhile i < len(nums1) and j < len(nums2):\n\t\t\t\tif nums1[i] <= nums2[j]:\n\t\t\t\t\tret = max(ret, j-i)\n\t\t\t\t\tj += 1\n\t\t\t\telse:\n\t\t\t\t\ti += 1\n\t\t\t\t\tj += 1\n\t\t\treturn ret\n
| 6 | 1 |
[]
| 5 |
maximum-distance-between-a-pair-of-values
|
Python Binary Solution Shortest
|
python-binary-solution-shortest-by-manis-cgxf
|
```class Solution:\n def maxDistance(self, nums1: List[int], nums2: List[int]) -> int:\n distance = 0\n \n for i in range(len(nums1)):\n
|
manishchhipa
|
NORMAL
|
2022-05-07T10:34:25.842156+00:00
|
2022-05-07T10:35:48.450202+00:00
| 277 | false |
```class Solution:\n def maxDistance(self, nums1: List[int], nums2: List[int]) -> int:\n distance = 0\n \n for i in range(len(nums1)):\n start = i\n end = len(nums2)-1\n while start<= end:\n mid = (start+end)//2\n\t\t\t\t\n if nums2[mid] < nums1[i]:\n end = mid-1\n else:\n start = mid+1\n distance = max(distance, end -i)\n \n return distance
| 5 | 0 |
['Binary Tree', 'Python']
| 0 |
maximum-distance-between-a-pair-of-values
|
Binary Search||Lower_bound||C++
|
binary-searchlower_boundc-by-geekybits-q95v
|
EXPLANATION:The problem demands that for any element nums1[i], we have to find the farthest element nums2[j] with j>=i such that the nums2[j] element is not les
|
GeekyBits
|
NORMAL
|
2021-05-12T10:42:31.220397+00:00
|
2021-05-12T10:43:20.898125+00:00
| 310 | false |
**EXPLANATION:**The problem demands that for any element nums1[i], we have to find the farthest element nums2[j] with j>=i such that the nums2[j] element is not less than nums1[i].\n\nA brute force way of doing the same would be to iterate over every j in the range i <=j && j <n" , but then we aren\'t using the fact that the two arrays are sorted in non-increasing/decreasing order.\n\nSo, what we do is, reverse the second array to make it increasing and then for every nums1[i], we find the first element which is either equal to or greater than it i.e. Lower_bound of the element (Note that for the original array this would be the same element which would be farther away satisfying the condition).\n\n\n```\nclass Solution {\npublic:\n int maxDistance(vector<int>& nums1, vector<int>& nums2) {\n \n reverse(nums2.begin(),nums2.end());\n int ans = 0;\n for(int i=0;i<nums1.size();++i){\n auto it = lower_bound(nums2.begin(),nums2.end(),nums1[i]) - nums2.begin(); //Finds first element greater than or equal to nums1[i]\n int position= nums2.size() - 1 - it; //Index of the found element in the original array\n if(i<=position) ans = max(ans,position-i); //Update distance \n }\n return ans;\n \n }\n```\n**Feel free to ask any question in the comment section.**\nI hope that you\'ve found the solution useful.\nIn that case, please do upvote and encourage me to on my quest to document all leetcode problems\uD83D\uDE03\n**Happy Coding :)**\n};
| 5 | 1 |
[]
| 3 |
maximum-distance-between-a-pair-of-values
|
Python Solution- Simple -2 Pointer
|
python-solution-simple-2-pointer-by-sash-srxi
|
\nclass Solution:\n def maxDistance(self, nums1: List[int], nums2: List[int]) -> int:\n max_diff = 0\n i = 0\n j = 0\n while i<le
|
sasha59
|
NORMAL
|
2021-05-09T04:04:58.662895+00:00
|
2021-05-09T04:09:14.760753+00:00
| 256 | false |
```\nclass Solution:\n def maxDistance(self, nums1: List[int], nums2: List[int]) -> int:\n max_diff = 0\n i = 0\n j = 0\n while i<len(nums1) and j <len(nums2):\n if i <= j:\n if nums1[i] <= nums2[j]:\n max_diff=max(max_diff,j-i)\n j += 1\n else:\n i += 1\n else:\n j += 1\n return max_diff\n \n```
| 5 | 0 |
['Python', 'Python3']
| 2 |
maximum-distance-between-a-pair-of-values
|
2 ms faster than 99.57% Java solution of O(n) time and O(1) space
|
2-ms-faster-than-9957-java-solution-of-o-zlqb
|
Traversing from the right to the left, let \n i be the pointer in nums1 and \n j be the pointer of the rightmost index in nums2 that is larger than nums1[i].\n\
|
anf
|
NORMAL
|
2022-01-10T22:23:28.194406+00:00
|
2022-01-10T22:23:28.194459+00:00
| 272 | false |
Traversing from the right to the left, let \n* `i` be the pointer in `nums1` and \n* `j` be the pointer of the rightmost index in `nums2` that is larger than `nums1[i]`.\n\nWhile we move `i` from the right to the left, we adjust `j` accordingly. The difference of `j - i` is the furthest pair for the element `nums1[i]`.\n\nPlease upvote if you like it. Thank you! \uD83D\uDE0A\n\n```\nclass Solution {\n public int maxDistance(int[] nums1, int[] nums2) {\n int res = 0;\n int j = nums2.length - 1;\n for (int i = nums1.length - 1; i != -1; i--) {\n while (j >= i && nums2[j] < nums1[i])\n j--;\n res = Math.max(res, j - i);\n }\n return res;\n }\n}\n```
| 4 | 0 |
['Two Pointers', 'Java']
| 0 |
maximum-distance-between-a-pair-of-values
|
JavaScript O(n) time and O(1) space, 2 pointers solution
|
javascript-on-time-and-o1-space-2-pointe-5wit
|
To get the best answer we want to maximize j and minimize i, while maintaining 2 invariants:\n i <= j\n nums1[i] <= nums2[j]\n\nThis can be translated almost di
|
user4125zi
|
NORMAL
|
2021-05-09T06:21:42.402607+00:00
|
2021-05-09T06:21:42.402648+00:00
| 354 | false |
To get the best answer we want to maximize j and minimize i, while maintaining 2 invariants:\n* i <= j\n* nums1[i] <= nums2[j]\n\nThis can be translated almost directly to code:\n\n```javascript\nvar maxDistance = function(nums1, nums2) {\n let i = 0, j = 0;\n \n let ans = 0;\n while (i < nums1.length && j < nums2.length) {\n // maintain the i <= j invariant\n j = Math.max(j, i);\n \n // we want to maximize j so move it forward whenever possible\n while (nums1[i] <= nums2[j]) {\n ans = Math.max(ans, j - i);\n j++;\n }\n \n // we want to minimize i so move it forward only to maintain invariants\n i++;\n }\n \n return ans;\n};\n```
| 4 | 0 |
['Two Pointers', 'JavaScript']
| 1 |
maximum-distance-between-a-pair-of-values
|
C++ easy solution || binary search
|
c-easy-solution-binary-search-by-sriniva-myxu
|
\nint maxDistance(vector<int>& nums1, vector<int>& nums2) {\n int n = nums1.size();\n int maxi =0;\n for(int i=0;i<n;i++){\n int
|
srinivasteja18
|
NORMAL
|
2021-05-09T04:01:19.769449+00:00
|
2021-05-09T04:01:19.769471+00:00
| 262 | false |
```\nint maxDistance(vector<int>& nums1, vector<int>& nums2) {\n int n = nums1.size();\n int maxi =0;\n for(int i=0;i<n;i++){\n int num = nums1[i];\n int ind = binary_search(nums2,num);\n maxi = max(maxi,ind-i);\n }\n return maxi;\n }\n int binary_search(vector<int>&nums,int k){\n int i=0,j=nums.size()-1;\n while(i<j){\n int mid = (i+j)/2+1;\n if(nums[mid] < k) j = mid-1;\n else i = mid;\n }\n return j;\n }\n```
| 4 | 2 |
[]
| 0 |
maximum-distance-between-a-pair-of-values
|
Binary Search , Easy C++ ✅✅
|
binary-search-easy-c-by-deepak_5910-9e4i
|
Approach\n Describe your approach to solving the problem. \nHere both the Array are sorted, so we can solve this problem in O(N*Log(N)) time using binary search
|
Deepak_5910
|
NORMAL
|
2023-07-11T08:44:07.096575+00:00
|
2023-07-11T08:44:07.096596+00:00
| 103 | false |
# Approach\n<!-- Describe your approach to solving the problem. -->\nHere both the Array are **sorted**, so we can solve this problem in **O(N*Log(N))** time using **binary search**.\n\n**For example:- Array-1 = [55,30,5,4,2], Array-2 = [100,20,10,10,5]**\nFirst traverse the array from 0 to n and find the index value j **(such as j>=i and Array-2[j]>=Array-1[i])** using **binary search**.\n\n\n\n\n# Complexity\n- Time complexity:O(N*Log(N))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int maxDistance(vector<int>& arr1, vector<int>& arr2) {\n int n = arr1.size(),m = arr2.size(),ans = 0;\n for(int i = 0;i<n;i++)\n {\n int ind = -1,left = i,right = m-1;\n while(left<=right)\n {\n int mid = (left+right)/2;\n if(arr2[mid]>=arr1[i])\n {\n ind = mid;\n left = mid+1;\n }\n else\n right = mid-1;\n }\n if(ind!=-1) ans = max(ans,ind-i);\n }\n return ans;\n }\n};\n```\n\n
| 3 | 0 |
['C++']
| 0 |
maximum-distance-between-a-pair-of-values
|
Easy two pointer solution| JAVA | Beats 95% .
|
easy-two-pointer-solution-java-beats-95-wfwgx
|
Approach\n1. Initialize both pointers as 0 at first.\n2. Add a loop unti both the pointers are equal to the length of the array.\n3. For each value of the point
|
black_spade212
|
NORMAL
|
2023-06-23T04:57:19.749186+00:00
|
2023-06-23T04:57:19.749219+00:00
| 551 | false |
# Approach\n1. Initialize both pointers as 0 at first.\n2. Add a loop unti both the pointers are equal to the length of the array.\n3. For each value of the pointer check the condition given arr[i-1] >= arr[i]\n4. If the condition statisfies then increment pointer 2 and store the difference in max;\n5. Else increment the pointer 1.\n6. Return the max value.\n# Complexity\n- Time complexity:O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int maxDistance(int[] nums1, int[] nums2) {\n int max = 0;\n int diff =0;\n int p1 =0;\n int p2 = 0;\n while(p1<nums1.length && p2<nums2.length){\n if(nums2[p2] >= nums1[p1]){\n diff = p2 -p1;\n max = Math.max(max,diff);\n p2++;\n }\n else{\n p1++;\n }\n \n }\n return max;\n }\n}\n```
| 3 | 0 |
['Two Pointers', 'Java']
| 1 |
maximum-distance-between-a-pair-of-values
|
JAVA | Binary Search
|
java-binary-search-by-sarvesh33-llrm
|
Approach\nTraverse in nums1 and for each index use binary search to find the index of farthest equal element or greater element in nums2.\n\n# Code\n\nclass Sol
|
sarvesh33
|
NORMAL
|
2023-06-19T14:15:07.134012+00:00
|
2023-06-19T14:15:07.134048+00:00
| 62 | false |
# Approach\nTraverse in nums1 and for each index use binary search to find the index of farthest equal element or greater element in nums2.\n\n# Code\n```\nclass Solution {\n public int binarySearch(int[] arr, int i, int target){\n int low = i, high = arr.length-1;\n int res = -1;\n \n while(low<=high){\n int mid = high - (high-low)/2;\n if(arr[mid] >= target){\n res = Math.max(mid, res);\n low = mid+1;\n }\n else{\n high = mid-1;\n }\n }\n return res;\n }\n public int maxDistance(int[] nums1, int[] nums2) {\n int max = 0;\n for(int i=0; i<nums1.length; i++){\n int j = binarySearch(nums2, i, nums1[i]);\n max = Math.max(max, j-i);\n }\n return max;\n }\n}\n```
| 3 | 0 |
['Java']
| 0 |
maximum-distance-between-a-pair-of-values
|
||Beats 99%|| very easy java solution using two pointers ||
|
beats-99-very-easy-java-solution-using-t-jnq7
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
ammar_saquib
|
NORMAL
|
2023-05-02T19:17:34.337791+00:00
|
2023-05-02T19:17:34.337832+00:00
| 111 | false |
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int maxDistance(int[] nums1, int[] nums2) {\n int max=0;\n int i=0,j=0;\n while(i<nums1.length && j<nums2.length)\n {\n if(nums1[i]>nums2[j])\n i++;\n else\n max=Math.max(max,j++-i);\n \n }\n return max;\n }\n}\n```
| 3 | 0 |
['Two Pointers', 'Java']
| 0 |
maximum-distance-between-a-pair-of-values
|
[C++] Brute - Better - Optimal
|
c-brute-better-optimal-by-suren-yeager-mkyc
|
Brute Force (TLE):\n\n# Code\n\nclass Solution {\npublic:\n int maxDistance(vector<int>& nums1, vector<int>& nums2){\n int n1=size(nums1),n2=size(nums
|
suren-yeager
|
NORMAL
|
2023-03-15T15:25:16.794047+00:00
|
2023-03-15T15:25:16.794078+00:00
| 216 | false |
# Brute Force (TLE):\n\n# Code\n```\nclass Solution {\npublic:\n int maxDistance(vector<int>& nums1, vector<int>& nums2){\n int n1=size(nums1),n2=size(nums2),res=0;\n for(int i=0;i<n1;i++){\n for(int j=i;j<n2;j++) {\n if(nums1[i]<=nums2[j]) res=max(best,j-i);\n }\n }\n return res;\n }\n};\n```\n# Complexity\n- Time complexity: $$O(n*m)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n---\n\n# Better :\n\n# Code\n```\nclass Solution {\npublic:\n int maxDistance(vector<int>& nums1, vector<int>& nums2){\n int n1=size(nums1),n2=size(nums2),res=0; \n for(int i=0;i<n1;i++){\n int val=nums1[i];\n int l=i,r=n2-1;\n while(l<=r){\n int mid=l+(r-l)/2;\n if(nums2[mid]>=val){\n res=max(res,mid-i);\n l=mid+1;\n }\n else r=mid-1;\n }\n }\n return res;\n }\n};\n```\n# Complexity\n- Time complexity: $$O(n*log(m))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n---\n\n\n\n# Optimal :\n\n# Code\n```\nclass Solution {\npublic:\n int maxDistance(vector<int>& nums1, vector<int>& nums2){\n int n1=size(nums1),n2=size(nums2),res=0;\n for(int i=0,j=0;i<n1&&j<n2;){\n if(nums1[i]<=nums2[j]) res=max(res,(j++)-i);\n else i++;\n }\n return res;\n }\n};\n```\n# Complexity\n- Time complexity: $$O(n+m)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n\n
| 3 | 0 |
['Two Pointers', 'Binary Search', 'C++']
| 0 |
maximum-distance-between-a-pair-of-values
|
Python - O(N^2) ➜ O(NLogN) ➜ O(N) | EXPLAINED
|
python-on2-onlogn-on-explained-by-itsarv-yy06
|
1. BRUTE FORCE - O(N^2) - TLE\n\nThe Brute Force approach is pretty simple. For each element, go through each element in second list that is greater or equal an
|
itsarvindhere
|
NORMAL
|
2022-10-15T09:22:23.844491+00:00
|
2022-10-15T09:27:16.033728+00:00
| 423 | false |
# **1. BRUTE FORCE - O(N^2) - TLE**\n\nThe Brute Force approach is pretty simple. For each element, go through each element in second list that is greater or equal and keep calculating the maxDistance. Not efficient and will give TLE for large arrays. But from this, we can start thinking about optimizing our solution.\n\n```\ndef maxDistance(self, nums1: List[int], nums2: List[int]) -> int:\n # In Brute force approach, for each element in nums2\n # we go through each less or equal element in nums2\n # And we keep track of the maximum distance\n \n maxDistanceSoFar = 0\n \n for i,num1 in enumerate(nums1):\n for j in range(i, len(nums2)):\n if num1 <= nums2[j]: maxDistanceSoFar = max(maxDistanceSoFar, j - i) \n else: break\n \n return maxDistanceSoFar\n```\n\n# **2. BINARY SEARCH - O(NLogN)**\n\nBecause it is given that both the arrays are sorted in decreasing order, it means, instead of linear search on second array, we can perform Binary search. \n\t\n\tWhat do we have to search?\n\n\tWe have to search for the maximum possible value of "j" such that \n\tthe element at "j" index is >= particular element in the first list\n\t\nIf the element at mid satisfies the condition, it might be a possible solution but it is also possible that we may find an element after it that also satisfies the condition. In that case, we will get a larger distance. Hence, even if mid satisfies the condition, we continue searching on right side of mid.\n\t\n\tdef maxDistance(self, nums1: List[int], nums2: List[int]) -> int:\n # Because we are given that both arrays are sorted in decreasing order\n # We can use Binary search instead of linear search in the inner loop\n \n maxDistanceSoFar = 0\n \n for i,num1 in enumerate(nums1):\n # Binary search for the maximum index on right of i index at which element is >= num1\n start = i\n end = len(nums2) - 1\n \n while start <= end:\n mid = start + (end - start) // 2\n \n # If mid element is greater than num1, that\'s one possible solution\n # But we want to maximize the distance\n if nums2[mid] >= num1:\n maxDistanceSoFar = max(maxDistanceSoFar, mid - i)\n start = mid + 1\n else: end = mid - 1\n \n return maxDistanceSoFar\n\t\t\n# **3. TWO POINTERS - O(N)**\n\nUsing Two Pointers approach, we can do this problem in an O(N) time complexity which means this is the fastest solution among the three. \n\nWe start with both the pointers at the beginning of both lists as i <= j\n\nAnd now, we will compare the elements and check whether num2[j] >= num1[i]. If yes, calculate the distance and update the maxDistance if this distance is bigger than previous. And also, since we are looking for the maximum possible distance, we will also increment j. \n\nBut if num2[j] < num1[i], that means not only this element does not satisfy the condition, but no element after it will satisfy because array is sorted in decreasing order. Hence, it means we are done with nums1[i] and so, we can move on to the next ith index element.\n\n\tExample - nums1 = [55,30,5,4,2], nums2 = [100,20,10,10,5]\n\t\n\tInitially, i = 0, j = 0, maxDistance = 0\n\t\n\tSo, we see that num1[i] = 55 and num2[j] = 100\n\t\n\tSince 100 >= 50. We calculate the distance and it comes out to be 0 since j - i => 0 - 0 => 0\n\t\n\tSince we want to maximize the distance, we increment j. \n\t\n\tNow, i = 0, j = 1, num1[i] = 55 and num2[j] = 20\n\t\n\tIs 20 >= 55? NO! It means, no element after it is valid as well. So, for 55, we are done. Increment i.\n\t\n\tNow, i = 1, j = 1, num1[i] = 30 and num2[j] = 20\n\t\n\tIs 20 >= 30? NO. Again, increment i.\n\t\n\tWe see that here, i = 2 and j = 1. This violates the condition that says i <= j. \n\t\n\tHence, to make sure this condition is not violated, if i becomes > j when we increment it, we will also increment j.\n\t\n\tAnd this process continues till => i <len(nums1) and j < len(nums2\n\t\n**HERE IS THE CODE -**\n\n def maxDistance(self, nums1: List[int], nums2: List[int]) -> int:\n # Since both arrays are sorted in non-decreasing order\n # We can try two pointer approach here\n \n i = 0\n j = 0\n maxDistance = 0\n \n while i < len(nums1) and j < len(nums2): \n # If nums2[j] >= nums1[i] that means it is one possible solution\n # But because we want to maximize the distance, we increment j\n # Because if next element also satisfies this condition, then it will have a larger distance\n if nums2[j] >= nums1[i]: \n maxDistance = max(maxDistance, j - i)\n j += 1\n \n else: \n i += 1\n # We also want to make sure i is <= j\n if i > j: j += 1\n \n return maxDistance
| 3 | 0 |
['Two Pointers', 'Binary Search', 'Binary Tree', 'Python']
| 0 |
maximum-distance-between-a-pair-of-values
|
✔️Python, C++,Java|| Beginner level ||As Simple As U Think||Simple-Short-Solution✔️
|
python-cjava-beginner-level-as-simple-as-84z0
|
Please upvote to motivate me in my quest of documenting all leetcode solutions. HAPPY CODING:)\nAny suggestions and improvements are always welcome.\n___\n__\nQ
|
Anos
|
NORMAL
|
2022-08-17T18:03:53.616333+00:00
|
2022-08-17T18:03:53.616380+00:00
| 238 | false |
***Please upvote to motivate me in my quest of documenting all leetcode solutions. HAPPY CODING:)\nAny suggestions and improvements are always welcome*.**\n___________________\n_________________\n***Q1855. Maximum Distance Between a Pair of Values***\nYou are given two non-increasing 0-indexed integer arrays nums1 and nums2.\n\nA pair of indices` (i, j`), where` 0 <= i < nums1.length` and` 0 <= j < nums2.length`, is valid if both` i <= j` and `nums1[i] <= nums2[j]`. The distance of the pair is `j - i`.\n\nReturn the maximum distance of any valid `pair (i, j)`. If there are no valid pairs, return 0.\n\nAn array arr is non-increasing if `arr[i-1] >= arr[i]` for every` 1 <= i < arr.length`.\n____________________________________________________________________________________________________________________\n____________________________________________________________________________________________________________________\n\u2705 **Python Code** :\n```\nclass Solution:\n def maxDistance(self, nums1: List[int], nums2: List[int]) -> int:\n i,j,n,m,res=0,0,len(nums1),len(nums2),0\n while i<n and j<m:\n if nums1[i]>nums2[j]:\n i+=1\n else:\n res=max(res,j-i)\n j+=1\n return res\n```\n**Runtime:** 1627 ms\t\n**Memory Usage:** 31.1 MB\t\n____________________________________________________________________________________________________________________\n____________________________________________________________________________________________________________________\n\n\u2705 **Java Code** :\n```\nclass Solution {\n public int maxDistance(int[] nums1, int[] nums2) {\n int i=0,j=0,res=0,n=nums1.length,m=nums2.length;\n while(i<n && j<m)\n {\n if(nums1[i]>nums2[j])\n i++;\n else\n res=Math.max(res,j++-i);\n }\n return res; \n }\n}\n```\n**Runtime:** 2 ms\t\n**Memory Usage:** 48.6 MB\n____________________________________________________________________________________________________________________\n____________________________________________________________________________________________________________________\n\u2705 **C++ Code** :\n```\nclass Solution {\npublic:\n int maxDistance(vector<int>& nums1, vector<int>& nums2) {\n int i=0,j=0,res=0,n=nums1.size(),m=nums2.size();\n while(i<n && j<m)\n {\n if(nums1[i]>nums2[j])\n i++;\n else\n res=max(res,j++-i);\n }\n return res;\n }\n};\n```\n**Runtime:** 325 ms\t\n**Memory Usage:** 98.5 MB\t\t\n____________________________________________________________________________________________________________________\n____________________________________________________________________________________________________________________\n\nIf you like the solution, please upvote \uD83D\uDD3C\nFor any questions, or discussions, comment below. \uD83D\uDC47\uFE0F\n
| 3 | 0 |
['C', 'Binary Tree', 'Python', 'Java']
| 0 |
maximum-distance-between-a-pair-of-values
|
C++ O(N) Easy Solution Using two pointers
|
c-on-easy-solution-using-two-pointers-by-o818
|
\nclass Solution {\npublic:\n int maxDistance(vector<int>& nums1, vector<int>& nums2) {\n int i=0,j=0;\n int n=nums1.size(),m=nums2.size();\n
|
karan252
|
NORMAL
|
2022-06-29T21:24:02.045664+00:00
|
2022-06-29T21:24:02.045692+00:00
| 93 | false |
```\nclass Solution {\npublic:\n int maxDistance(vector<int>& nums1, vector<int>& nums2) {\n int i=0,j=0;\n int n=nums1.size(),m=nums2.size();\n int ans=0;\n while(i<n && j<m)\n {\n if(nums1[i]<=nums2[j]) \n {\n ans=max(j-i,ans);\n j++;\n }\n else\n {\n i++;\n }\n }\n return ans;\n }\n};\n```
| 3 | 0 |
['Two Pointers', 'C']
| 0 |
maximum-distance-between-a-pair-of-values
|
C++ Binary Search and Two Pointer Approach
|
c-binary-search-and-two-pointer-approach-anbc
|
Binary Search--->\n\n\nclass Solution {\npublic:\n int maxDistance(vector<int>& nums1, vector<int>& nums2) {\n int n=nums1.size();\n int m=nums
|
Yogesh02
|
NORMAL
|
2022-06-23T17:33:35.335990+00:00
|
2022-06-23T17:33:35.336038+00:00
| 179 | false |
`Binary Search--->`\n```\n\nclass Solution {\npublic:\n int maxDistance(vector<int>& nums1, vector<int>& nums2) {\n int n=nums1.size();\n int m=nums2.size();\n int maxi=INT_MIN;\n for(int i=0;i<n;i++){\n int l=i,h=m-1;\n while(l<=h){\n int mid=(l+h)/2;\n if(nums1[i]<=nums2[mid]){\n maxi=max(mid-i,maxi);\n l=mid+1;\n }\n else if(nums1[i]>nums2[mid]){\n h=mid-1;\n }\n \n }\n }\n return maxi==INT_MIN?0:maxi;\n }\n};\n```\n`Two Pointers--->`\n```\nclass Solution {\npublic:\n int maxDistance(vector<int>& nums1, vector<int>& nums2) {\n int n=nums1.size();\n int m=nums2.size();\n int maxi=0;\n int l=0,h=0;\n while(l<n && h<m){\n if(nums1[l]>nums2[h]) l++;\n else {\n maxi=max(h-l,maxi);\n h++;\n }\n \n }\n \n return maxi;\n }\n};\n```
| 3 | 0 |
['Two Pointers', 'C', 'Binary Tree', 'C++']
| 1 |
maximum-distance-between-a-pair-of-values
|
✅ [C++] Intuitive 2 pointers method
|
c-intuitive-2-pointers-method-by-bit_leg-487e
|
\nclass Solution {\npublic:\n int maxDistance(vector<int>& nums1, vector<int>& nums2) {\n int i = 0, j = 0;\n int ans = 0;\n\t\t// One pointer
|
biT_Legion
|
NORMAL
|
2022-05-27T05:35:35.064565+00:00
|
2022-05-27T05:35:35.064612+00:00
| 96 | false |
```\nclass Solution {\npublic:\n int maxDistance(vector<int>& nums1, vector<int>& nums2) {\n int i = 0, j = 0;\n int ans = 0;\n\t\t// One pointer is at first array, another is at 2nd array. \n while(i<nums1.size() and j<nums2.size()){\n\t\t\t// If i is greater than j, we move j to satisfy the conditions. \n if(i>j){ \n j++;\n continue;\n }\n\t\t\t// The above condition is already satisfied. If the below satisfies too, we update the answer AND move j\n\t\t\t// in the hope of finding a better answer for current i. NOTE we need to maximize the gap (j-i\n if(nums1[i]<=nums2[j]){\n ans = max(ans,j-i);\n j++;\n }\n else\n i++; // If the condition is not satisfied for current i, we move i\n }\n\t\t// If nums2 has not been fully traversed yet, we traverse it with the additional while loop and check our \n\t\t// answer with the last element of nums1.\n while(j<nums2.size()){\n if(nums1.back()<=nums2[j]){\n int temp = j-(nums1.size()-1);\n ans = max(ans,temp);\n }\n j++;\n }\n\t\t\n\t\t// NOTE that we are not doing this for nums1, because it would be of no good! If we finish nums2\n\t\t// before nums1, then j will always be less than i and thus our conditions will not be satisfied.\n return ans;\n }\n};\n```
| 3 | 0 |
['Two Pointers', 'C']
| 0 |
maximum-distance-between-a-pair-of-values
|
✅C++ | ✅Two Pointer |✅Binary Search|✅Easy O(N) and O(N*LogN)solution
|
c-two-pointer-binary-searcheasy-on-and-o-3whh
|
Just a few words to explain the solution a bit.\nThere is Three Approaches for this problem comes in my mind.\n1.Brute force : check for every element in array
|
aman_2_0_2_3
|
NORMAL
|
2022-05-20T19:17:55.212942+00:00
|
2022-05-20T19:17:55.212966+00:00
| 226 | false |
Just a few words to explain the solution a bit.\n**There is Three Approaches for this problem comes in my mind.**\n**1.Brute force : check for every element in array A to every element of array B then store the result in maxx variable. return it. But this will gives you TLE because of it\'s time complexity is much high i.e. O(n^2).**\n\n**2.Binary Search : Since both of the given array are sorted so take any one array iterate over it and try to upperbound of reverse array in second array. Time complexity O(N*LogM)**\n\n```\nclass Solution {\npublic:\n int maxDistance(vector<int>& nums1, vector<int>& nums2) {\n int maxx = 0;\n for(int i=0;i<nums1.size();i++){\n int target = nums1[i];\n vector<int>::iterator up;\n up = upper_bound(nums2.begin(),nums2.end(),target, greater<int>());\n int idx = up - nums2.begin();\n maxx = max(maxx,idx-1-i);\n }\n return maxx;\n }\n};\n```\n\n**3.Two pointer Approach. Time complexity is Linear. (Best Solution).**\n```\nclass Solution {\npublic:\n\tint maxDistance(vector<int>& nums1, vector<int>& nums2) {\n\t\tint ans = 0;\n\t\tint i = 0;\n\t\tint j = 0;\n\t\twhile(i < nums1.size() and j < nums2.size()){\n\t\t\tif(nums1[i] <= nums2[j]){\n\t\t\t\tif(i <= j){\n\t\t\t\t\tans = max(ans, j++ - i);\n\t\t\t\t}\n\t\t\t}\n\t\t\telse{\n\t\t\t\ti++;\n\t\t\t}\n\t\t}\n\t\treturn ans;\n\t}\n};\n```\n**PLEASE PLEASE..............UPVOTE ME**
| 3 | 0 |
['Binary Search', 'C', 'C++']
| 1 |
maximum-distance-between-a-pair-of-values
|
C++ binary search accepted solution #ACCEPTED😍😍
|
c-binary-search-accepted-solution-accept-uvbg
|
class Solution {\npublic:\n\n int maxDistance(vector& nums1, vector& nums2) {\n int ans = 0;\n \n int n = nums1.size();\n int m =
|
kinggaurav
|
NORMAL
|
2022-02-18T20:27:47.124667+00:00
|
2022-02-18T20:27:47.124711+00:00
| 271 | false |
class Solution {\npublic:\n\n int maxDistance(vector<int>& nums1, vector<int>& nums2) {\n int ans = 0;\n \n int n = nums1.size();\n int m = nums2.size();\n \n for(int i = 0 ; i < n ; i++){\n int low = i;\n int high = m - 1;\n int value = i;\n \n while(low <= high){\n int mid = (low + high) / 2;\n \n if(nums2[mid] >= nums1[i]){\n low = mid + 1;\n value = mid;\n }else{\n high = mid - 1;\n }\n }\n \n ans = max(ans , value - i);\n }\n \n return ans;\n }\n};
| 3 | 0 |
['C', 'Binary Tree']
| 0 |
maximum-distance-between-a-pair-of-values
|
Python Simple Two pointers
|
python-simple-two-pointers-by-solarbeam-m2vq
|
Extend j to the right as far as possible. Once we\'ve found a max distance we don\'t need to check any lengths smaller than that, so update i and j together.\n\
|
solarbeam
|
NORMAL
|
2021-05-09T04:29:51.223965+00:00
|
2021-05-09T04:31:56.046145+00:00
| 137 | false |
Extend j to the right as far as possible. Once we\'ve found a max distance we don\'t need to check any lengths smaller than that, so update i and j together.\n\n```\ndef maxDistance(self, nums1: List[int], nums2: List[int]) -> int:\n i,j = 0,0\n max_distance = 0\n \n while i < len(nums1) and j < len(nums2):\n if nums1[i] <= nums2[j]:\n max_distance = max(max_distance, j-i)\n j += 1\n else:\n j += 1\n i += 1\n\t\t\t\t\n return max_distance\n```
| 3 | 0 |
['Python']
| 0 |
maximum-distance-between-a-pair-of-values
|
C++ solution using lower_bound iterator with comments
|
c-solution-using-lower_bound-iterator-wi-gdwh
|
\nclass Solution\n{\npublic:\n //to return maximum among two elements\n int max(int a, int b)\n {\n if (a > b)\n return a;\n r
|
uzu86
|
NORMAL
|
2021-05-09T04:19:52.228327+00:00
|
2021-05-09T04:32:59.666751+00:00
| 189 | false |
```\nclass Solution\n{\npublic:\n //to return maximum among two elements\n int max(int a, int b)\n {\n if (a > b)\n return a;\n return b;\n }\n int maxDistance(vector<int> &nums1, vector<int> &nums2)\n {\n int dist = 0, n1 = nums1.size(), n2 = nums2.size();\n\n //sorting nums2 vector in ascending order\n sort(nums2.begin(), nums2.end());\n\n for (int i = 0; i < min(n1, n2); i++)\n {\n //lower_bound will return refernce to element >= nums[i]\n auto itr = lower_bound(nums2.begin(), nums2.end() - i, nums1[i]);\n\n //in case elemt found\n if (itr != nums2.end() - i)\n {\n //as previously sorted in decreasing order\n int original_index = n2 - 1 - (itr - nums2.begin());\n dist = max(dist, original_index - i);\n }\n }\n return dist;\n }\n};\n```
| 3 | 0 |
['Sorting', 'Binary Tree', 'Iterator']
| 0 |
maximum-distance-between-a-pair-of-values
|
Binary Search Python Explained
|
binary-search-python-explained-by-jiggly-0emi
|
Intuition\nThrough the given problem we have few conditions\n1. j >= i\n2. nums2[j] > nums1[i]\n\nNow to satisfy these conditions for every element in of nums1
|
JigglyyPuff
|
NORMAL
|
2023-04-18T15:08:58.485037+00:00
|
2023-04-18T15:09:19.877271+00:00
| 495 | false |
# Intuition\nThrough the given problem we have few conditions\n`1. j >= i`\n`2. nums2[j] > nums1[i]`\n\nNow to satisfy these conditions for every element in of nums1 we have to iterate over nums2(i, len(nums2))\n\nso we will use **binary search** having the above range always\nnow if we find *nums[mid] < nums1[i] => we can\'t consider* this thus shift ur right\n\nif *nums[mid] >= nums1[i] => we know the array is in descending order so store this mid index values as farthestSeen* now and shift left pointer.\n\n`why not return here?` Because to get the farthest position we have to find element > nums1[i] as far as possible from i\n\nCalculate the diff(j-i) and return the maxDiff as your ans :)\n\n# Code\n```\nclass Solution:\n def maxDistance(self, nums1: List[int], nums2: List[int]) -> int:\n def binary(left, right, num):\n farthestPos = 0\n while left < right:\n mid = (left + right) // 2\n if nums2[mid] < num:\n right = mid\n else:\n farthestPos = max(farthestPos, mid)\n left = mid + 1\n if nums2[left] >= num:\n farthestPos = max(farthestPos, left)\n return farthestPos\n maxDiff = 0\n for i in range(min(len(nums1), len(nums2))):\n if nums1[i] > nums2[i]:\n continue\n else:\n j = binary(i, len(nums2)-1, nums1[i])\n maxDiff = max(maxDiff, (j-i))\n return maxDiff\n```
| 2 | 0 |
['Array', 'Binary Search', 'Python3']
| 0 |
maximum-distance-between-a-pair-of-values
|
Easy C++ ✔|| Two Pointers || O(n+m)
|
easy-c-two-pointers-onm-by-snowflakes17-ilrr
|
\n# Approach\n Describe your approach to solving the problem. \n It first initializes two integer variables n and m with the sizes of nums1 and nums2, respectiv
|
snowflakes17
|
NORMAL
|
2023-04-03T17:37:22.663828+00:00
|
2023-04-03T17:37:22.663871+00:00
| 167 | false |
\n# Approach\n<!-- Describe your approach to solving the problem. -->\n* It first initializes two integer variables `n` and `m` with the **sizes of nums1 and nums2**, respectively.\n* It then initializes three integer variables `i, j,` and `ans to 0`. * The variable `i` will be used to **iterate over nums1**, the variable `j` will be used to `iterate over nums2`, and the variable` ans` will store the maximum distance found so far.\n* It enters a **while loop** that continues as long as `i < n` and \n`j < m`. Inside the loop, it checks if **nums1[i] is greater than nums2[j]**. If so, it increments i. Otherwise, it updates ans with the maximum of ans and the difference between j and i, and then increments j.\n* After the loop finishes, it **returns ans**.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n+m)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n\n# Code\n```\nclass Solution {\npublic:\n int maxDistance(vector<int>& nums1, vector<int>& nums2) {\n \n int n=nums1.size();\n int m=nums2.size();\n\n int i=0,j=0;\n int ans=0;\n\n while(i<n && j<m){\n if(nums1[i]>nums2[j]){\n i++;\n }\n else{\n ans=max(ans,j-i);\n j++;\n }\n }\n return ans;\n }\n};\n```
| 2 | 0 |
['C++']
| 0 |
maximum-distance-between-a-pair-of-values
|
simple binary search || must see
|
simple-binary-search-must-see-by-akshat0-jg7n
|
Code\n\nstatic int fast_io = []() \n{ \n std::ios::sync_with_stdio(false); \n cin.tie(nullptr); \n cout.tie(nullptr); \n return 0; \n}();\n\n#ifdef
|
akshat0610
|
NORMAL
|
2023-03-14T08:33:49.798129+00:00
|
2023-03-14T08:33:49.798170+00:00
| 192 | false |
# Code\n```\nstatic int fast_io = []() \n{ \n std::ios::sync_with_stdio(false); \n cin.tie(nullptr); \n cout.tie(nullptr); \n return 0; \n}();\n\n#ifdef LOCAL\n freopen("input.txt", "r" , stdin);\n freopen("output.txt", "w", stdout);\n#endif\n\nclass Solution {\npublic:\n int maxDistance(vector<int>& nums1, vector<int>& nums2) \n {\n //we will use i to iterate over the nums1\n \n int ans = 0;\n\n int i = 0;\n while(i < (nums1.size()))\n {\n int j = fun(nums1[i],i,nums2.size()-1,nums2);\n\n if(j != -1)\n {\n ans = max(ans,j-i);\n }\n\n i++;\n } \n return ans;\n }\n int fun(int &nums1,int start,int end,vector<int>&nums2)\n {\n int start_ = start;\n int end_ = end;\n\n int pos = -1;\n while(start <= end)\n {\n int mid = (start + ((end - start)/2));\n\n //either the nums[mid] could be smaller then the nums1\n //either the nums[mid] could be greater then the nums1\n\n if(nums2[mid] < nums1)\n {\n end = mid-1;\n }\n else if(nums2[mid] >= nums1)\n {\n pos = max(pos,mid);\n start = mid+1;\n }\n } \n if(start >= start_ and start <= end_ and nums2[start] >= nums1)\n pos = max(pos,start);\n\n if(end >= start_ and end <= end_ and nums2[end] >= nums1)\n pos = max(pos,end);\n\n return pos;\n }\n};\n```
| 2 | 1 |
['Array', 'Two Pointers', 'Binary Search', 'Greedy', 'C++']
| 0 |
maximum-distance-between-a-pair-of-values
|
C++ easy solution O(m*logn)
|
c-easy-solution-omlogn-by-hemant_1451-pukm
|
\n# Algorithm\nInitialize answer = 0.\nIterate over one array (let\'s say nums1), for each number nums1[i], we use binary search to find the insertion position
|
Hemant_1451
|
NORMAL
|
2023-01-11T06:57:39.143840+00:00
|
2023-01-11T06:57:39.143890+00:00
| 883 | false |
\n# Algorithm\nInitialize answer = 0.\nIterate over one array (let\'s say nums1), for each number nums1[i], we use binary search to find the insertion position j of nums1[i] to nums2.\nIf j < i, we move on to the next i by repeating the step 2.\nOtherwise, we find one valid pair, update answer as answer = max(answer, j - i).\n# Code\n```\nclass Solution {\npublic:\n int maxDistance(vector<int>& nums1, vector<int>& nums2) {\n int m = int(nums1.size()), n = int(nums2.size());\n int ans = 0;\n for (int i = 0; i < m; ++i) {\n int k = nums2.rend() - lower_bound(nums2.rbegin(), nums2.rend(), nums1[i]);\n if (k > 0) {\n ans = max(ans, k - i - 1);\n }\n }\n return ans;\n }\n};\n```
| 2 | 0 |
['C++']
| 0 |
maximum-distance-between-a-pair-of-values
|
Easy C++ Solution || Binary Search || O(nlogn) ✔
|
easy-c-solution-binary-search-onlogn-by-l7kes
|
\n## Code\n\nclass Solution {\npublic:\n int maxDistance(vector<int>& nums1, vector<int>& nums2) {\n int dis=0;\n for (int i=0; i<nums1.size();
|
akanksha984
|
NORMAL
|
2022-12-17T22:05:45.202791+00:00
|
2022-12-17T22:05:45.202813+00:00
| 608 | false |
\n## Code\n```\nclass Solution {\npublic:\n int maxDistance(vector<int>& nums1, vector<int>& nums2) {\n int dis=0;\n for (int i=0; i<nums1.size(); i++){\n int low= i+1; int high= nums2.size()-1;// int midi=i;\n while (low<=high){\n int mid= low+ (high-low)/2;\n if (nums1[i]>nums2[mid]){\n high= mid-1;\n }\n else {low= mid+1;}\n }\n dis= max(dis,low-1-i);\n }\n return dis;\n }\n};\n```\n### Complexity\n- Time complexity: $$O(nlogm),$$\n *n is the size of nums1\n m is the size of nums2*\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$ O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n
| 2 | 0 |
['C++']
| 0 |
maximum-distance-between-a-pair-of-values
|
Binary Search
|
binary-search-by-segnides-ahg1
|
Intuition\nWe just have to iterate over the first list and find the index of largest number in the second list using binary search.\n\n# Complexity\nm = len(num
|
segnides
|
NORMAL
|
2022-12-16T07:58:38.672077+00:00
|
2022-12-16T07:58:38.672109+00:00
| 209 | false |
# Intuition\nWe just have to iterate over the first list and find the index of largest number in the second list using binary search.\n\n# Complexity\nm = len(nums1)\nn = len(nums2)\n- Time complexity:\nO(m*log(n))\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def maxDistance(self, nums1: List[int], nums2: List[int]) -> int:\n max_d = 0\n l1, l2 = len(nums1), len(nums2)\n for i in range(l1):\n left, right = i, l2 - 1\n while left <= right:\n index = (left + right) // 2\n if nums2[index] >= nums1[i]:\n left = index + 1\n else:\n right = index - 1\n max_d = max(max_d, right - i)\n return max_d\n```
| 2 | 0 |
['Binary Search', 'Python3']
| 0 |
maximum-distance-between-a-pair-of-values
|
Binary Search Easy Solution || C++ || Beginner Friendly
|
binary-search-easy-solution-c-beginner-f-pv8u
|
\n# Time Complexity\nO(NLogM)\n\n# Code\n\nclass Solution {\n int helper(vector<int>&nums,int tar,int i){\n int st=i,en=nums.size()-1;\n int ma
|
Maxx_1007
|
NORMAL
|
2022-11-22T19:01:23.249275+00:00
|
2022-11-22T19:01:23.249325+00:00
| 448 | false |
\n# Time Complexity\nO(NLogM)\n\n# Code\n```\nclass Solution {\n int helper(vector<int>&nums,int tar,int i){\n int st=i,en=nums.size()-1;\n int maxi=INT_MIN;\n while(st<=en){\n int mid=st+(en-st)/2;\n if(nums[mid]>=tar){\n maxi=max(maxi,mid-i);\n st=mid+1;\n }\n else{\n en=mid-1;\n }\n }\n return maxi;\n }\npublic:\n int maxDistance(vector<int>& nums1, vector<int>& nums2) {\n int maxi=INT_MIN;\n for(int i=0;i<nums1.size();i++){\n maxi=max(maxi,helper(nums2,nums1[i],i));\n }\n return maxi==INT_MIN?0:maxi;\n }\n};\n```
| 2 | 0 |
['Array', 'Two Pointers', 'Binary Search', 'C++']
| 0 |
maximum-distance-between-a-pair-of-values
|
java | Brute Force | Two Pointers | Binary Search
|
java-brute-force-two-pointers-binary-sea-imjz
|
\nclass Solution {\n public int maxDistance(int[] nums1, int[] nums2) {\n \n //BinarySearch : TC=O(mlogn), SC=O(1)\n int d = 0;\n
|
gobindmishra23
|
NORMAL
|
2022-10-18T09:35:18.670129+00:00
|
2022-10-18T09:35:18.670167+00:00
| 87 | false |
```\nclass Solution {\n public int maxDistance(int[] nums1, int[] nums2) {\n \n //BinarySearch : TC=O(mlogn), SC=O(1)\n int d = 0;\n for(int i=0;i<nums1.length;i++){\n int start = i;\n int end = nums2.length-1;\n while(start <= end){\n int mid = start + (end-start)/2;\n if(nums1[i] <= nums2[mid]){\n d = Math.max(d,mid-i);\n start = mid+1;\n } else {\n end = mid-1;\n }\n }\n }\n return d;\n \n /*\n //Two Pointers Approach : TC=O(min(m,n)), SC=O(1)\n int i=0,j=0,d=0;\n while(i<nums1.length && j<nums2.length){\n if(i<=j && nums1[i]<=nums2[j]){\n d=Math.max(d,j-i);\n j++;\n \n } else if(nums1[i] > nums2[j]){\n i++;\n }else{\n j++;\n }\n }\n return d;\n */\n \n /*\n //BruteForce Approach : TC=O(m*n) , SC=O(1) -> TLE\n int d = 0;\n for(int i=0;i<nums1.length;i++){\n for(int j=0;j<nums2.length;j++){\n if(i<=j && nums1[i]<=nums2[j]){\n d = Math.max(d,j-i);\n }\n }\n }\n return d;\n */\n }\n}\n```
| 2 | 0 |
['Two Pointers', 'Binary Tree', 'Java']
| 1 |
maximum-distance-between-a-pair-of-values
|
Two pointers are 98% faster
|
two-pointers-are-98-faster-by-berryfur-h7he
|
\nclass Solution:\n def maxDistance(self, nums1: List[int], nums2: List[int]) -> int:\n i = maxdist = 0\n n = len(nums1)\n for j, number
|
BerryFur
|
NORMAL
|
2022-10-14T05:14:05.787451+00:00
|
2022-10-14T05:14:05.787493+00:00
| 415 | false |
```\nclass Solution:\n def maxDistance(self, nums1: List[int], nums2: List[int]) -> int:\n i = maxdist = 0\n n = len(nums1)\n for j, number2 in enumerate(nums2):\n while i < n and nums1[i] > number2:\n i += 1\n if i == n:\n return maxdist\n maxdist = max(maxdist, j - i)\n return maxdist\n```\n\n\n
| 2 | 0 |
['Two Pointers', 'Python']
| 0 |
maximum-distance-between-a-pair-of-values
|
Java Solution || Easy understanding ✔
|
java-solution-easy-understanding-by-mahe-xxno
|
class Solution {\n public int maxDistance(int[] nums1, int[] nums2) {\n \n int i = 0, j = 0, ans = 0;\n while(i < nums1.length && j < nu
|
mahesh_1729
|
NORMAL
|
2022-09-07T17:46:54.834468+00:00
|
2022-09-07T17:46:54.834510+00:00
| 309 | false |
class Solution {\n public int maxDistance(int[] nums1, int[] nums2) {\n \n int i = 0, j = 0, ans = 0;\n while(i < nums1.length && j < nums2.length){\n if(nums1[i] > nums2[j])\n i++;\n else{\n ans = Math.max(ans, j-i);\n j++;\n }\n }\n return ans;\n }\n}
| 2 | 0 |
['Binary Tree', 'Java']
| 0 |
maximum-distance-between-a-pair-of-values
|
Java solution | Brute force | Binary Search Solution | 2 approaches
|
java-solution-brute-force-binary-search-9duwo
|
Brute force approach: Gives TLE\n\n\npublic int maxDistance(int[] nums1, int[] nums2) {\n int maxDistance = 0;\n int len1 = nums1.length;\n
|
sankalpjadhav
|
NORMAL
|
2022-08-28T03:59:49.918466+00:00
|
2022-08-28T03:59:49.918495+00:00
| 244 | false |
Brute force approach: Gives TLE\n\n```\npublic int maxDistance(int[] nums1, int[] nums2) {\n int maxDistance = 0;\n int len1 = nums1.length;\n int len2 = nums2.length;\n for(int i=0;i<len1;i++){\n for(int j=i;j<len2;j++){\n if(nums1[i]<=nums2[j]){\n maxDistance = Math.max(maxDistance, j-i);\n }\n }\n }\n return maxDistance;\n }\n```\n\nBinary search solution:\n\n```\npublic int maxDistance(int[] nums1, int[] nums2) {\n int maxDistance = 0;\n int len1 = nums1.length;\n int len2 = nums2.length;\n for(int i=0;i<len1;i++){\n int low = i;\n int high = len2-1;\n while(low<=high){\n int mid = low+(high-low)/2;\n if(nums1[i] <= nums2[mid]){\n maxDistance = Math.max(maxDistance, mid-i);\n low = mid+1;\n }\n else{\n high = mid-1;\n }\n }\n }\n return maxDistance;\n }\n```\n\n
| 2 | 0 |
['Binary Tree', 'Java']
| 2 |
maximum-distance-between-a-pair-of-values
|
100% - 0ms - Dcode
|
100-0ms-dcode-by-devampanchasara-0zom
|
\nclass Solution {\n public int maxDistance(int[] nums1, int[] nums2) {\n int i=0,j=0;\n int n=nums1.length;\n int m=nums2.length;\n
|
DevamPanchasara
|
NORMAL
|
2022-07-27T21:02:34.120235+00:00
|
2022-07-27T21:02:34.120279+00:00
| 68 | false |
```\nclass Solution {\n public int maxDistance(int[] nums1, int[] nums2) {\n int i=0,j=0;\n int n=nums1.length;\n int m=nums2.length;\n int max=0;\n while(i<n && j<m){\n if(nums1[i]>nums2[j])\n i++;\n else{\n max=Math.max(max,j-i); \n j++;\n }\n }\n return max;\n }\n}\n```
| 2 | 0 |
['Java']
| 0 |
maximum-distance-between-a-pair-of-values
|
[C++] Binary Search nlogn
|
c-binary-search-nlogn-by-sandeep8381-9iu6
|
\nclass Solution {\npublic:\n \n int binarySearch(vector<int>& nums1, int val){\n int l = 0, h = nums1.size()-1;\n int ind = 1e9;\n w
|
sandeep8381
|
NORMAL
|
2022-07-12T07:45:07.009483+00:00
|
2022-07-12T07:45:07.009532+00:00
| 67 | false |
```\nclass Solution {\npublic:\n \n int binarySearch(vector<int>& nums1, int val){\n int l = 0, h = nums1.size()-1;\n int ind = 1e9;\n while(l<=h){\n int mid = l + (h-l)/2;\n if(nums1[mid] > val){\n l = mid+1;\n }else{\n ind = mid;\n h = mid-1;\n }\n }\n return ind;\n }\n \n int maxDistance(vector<int>& nums1, vector<int>& nums2) {\n int n = nums1.size();\n int m = nums2.size();\n int res = INT_MIN;\n for(int j=m-1; j>=0; j--){\n res = max(res,j - binarySearch(nums1,nums2[j]));\n }\n return res<0 ? 0:res;\n }\n};\n```
| 2 | 0 |
['C', 'Binary Tree']
| 0 |
maximum-distance-between-a-pair-of-values
|
Simple Binary Search Python Solution
|
simple-binary-search-python-solution-by-hd3ya
|
Approach: for each i in nums1, let\'s find the last j in nums2 (using binary search with initial limits left=i and right=len(nums2)) that satisfies nums1[i] <=
|
nordant
|
NORMAL
|
2022-06-15T07:14:36.009623+00:00
|
2022-06-15T07:14:36.009661+00:00
| 105 | false |
Approach: for each **i** in **nums1**, let\'s find the last **j** in **nums2** (using binary search with initial limits **left=i** and **right=len(nums2)**) that satisfies **nums1[i] <= nums2[j]** and then **count the distance (j-i)**. Return the maximum distance.\n\n```\nclass Solution:\n def maxDistance(self, nums1: List[int], nums2: List[int]) -> int:\n max_dist = 0\n for idx, i in enumerate(nums1):\n l=idx\n r=len(nums2)\n while r-l > 1:\n mid = (l+r)//2\n if nums2[mid] < i:\n r = mid\n else:\n l = mid\n if l-idx > max_dist:\n max_dist = l-idx\n return max_dist\n```\n\n**Thanks! Please, upvote if you find this solution useful.**
| 2 | 0 |
['Binary Tree', 'Python']
| 0 |
maximum-distance-between-a-pair-of-values
|
Simple java solution
|
simple-java-solution-by-siddhant_1602-o7o5
|
```\nclass Solution {\n public int maxDistance(int[] n1, int[] n2) {\n int m=n1.length,n=n2.length,s=0;\n for(int i=0,j=0;j<n&&in2[j])\n
|
Siddhant_1602
|
NORMAL
|
2022-06-14T18:15:41.786595+00:00
|
2022-06-14T18:15:41.786641+00:00
| 50 | false |
```\nclass Solution {\n public int maxDistance(int[] n1, int[] n2) {\n int m=n1.length,n=n2.length,s=0;\n for(int i=0,j=0;j<n&&i<m;)\n {\n if(n1[i]>n2[j])\n i++;\n else\n s=Math.max(s,j++-i);\n }\n return s;\n }\n}
| 2 | 0 |
['Two Pointers', 'Java']
| 0 |
maximum-distance-between-a-pair-of-values
|
Python | Binary Search
|
python-binary-search-by-sauravintheocean-066f
|
Approach:\n1. For each element in nums1, we perform binary search on nums2 to find the index of the right-most element which is greater than or equal to the cur
|
sauravintheocean
|
NORMAL
|
2022-06-09T14:22:18.028734+00:00
|
2022-06-09T14:47:45.849126+00:00
| 104 | false |
Approach:\n1. For each element in nums1, we perform binary search on nums2 to find the index of the right-most element which is greater than or equal to the current element in nums1.\n2. Since nums2 may contain duplicate elements, to move to the right-most element we need to make mid as right-biased by using mid = l + (r-l+1)/2\n3. We have three cases in binary search:\n* nums2[mid] < target: r = mid - 1\n* nums2[mid] > target: l = mid + 1\n* nums2[mid] = target: l = mid\nAfter Combining case 2 and case 3, we can say that if nums2[mid] >= target: l = mid\n4. Loop terminates when l and r become equal \n \n```\nclass Solution(object):\n def maxDistance(self, nums1, nums2):\n """\n :type nums1: List[int]\n :type nums2: List[int]\n :rtype: int\n """\n def binarySearch(start, target):\n l, r = start, len(nums2)-1\n while l < r:\n mid = l + (r-l+1)/2\n if nums2[mid] < target:\n r = mid - 1\n else:\n l = mid\n \n if nums2[r] >= target:\n return r\n else:\n return -1\n maxDistance = 0 \n for i in range(len(nums1)):\n j = binarySearch(i, nums1[i])\n if j != -1:\n maxDistance = max(maxDistance, j-i)\n return maxDistance \n```
| 2 | 0 |
['Binary Tree', 'Python']
| 0 |
maximum-distance-between-a-pair-of-values
|
Two Pointer | C++ | O(n)
|
two-pointer-c-on-by-salamnamaste-gizi
|
\nclass Solution {\npublic:\n int maxDistance(vector<int>& nums1, vector<int>& nums2) {\n int ans = 0;\n for(int i = 0, j = 0; i < nums1.size()
|
salamnamaste
|
NORMAL
|
2022-05-30T01:13:48.079899+00:00
|
2022-05-30T01:13:48.079960+00:00
| 48 | false |
```\nclass Solution {\npublic:\n int maxDistance(vector<int>& nums1, vector<int>& nums2) {\n int ans = 0;\n for(int i = 0, j = 0; i < nums1.size() && j < nums2.size(); i++) {\n while(j < nums2.size() && nums1[i] <= nums2[j]) j++;\n ans = max(ans, j-i-1);\n }\n return ans;\n }\n};\n```
| 2 | 0 |
[]
| 0 |
maximum-distance-between-a-pair-of-values
|
JavaScript Solution (Easy)
|
javascript-solution-easy-by-oneduck-up6x
|
\nvar maxDistance = function(nums1, nums2) {\n if(nums1[nums1.length - 1] > nums2[0]){\n return 0\n }\n \n let i = 0, j = 0, maxDistance = 0\
|
oneduck
|
NORMAL
|
2022-05-21T01:43:43.685602+00:00
|
2022-05-21T01:43:43.685633+00:00
| 75 | false |
```\nvar maxDistance = function(nums1, nums2) {\n if(nums1[nums1.length - 1] > nums2[0]){\n return 0\n }\n \n let i = 0, j = 0, maxDistance = 0\n \n while(i < nums1.length){\n if(j < nums2.length && nums1[i] <= nums2[j]){\n maxDistance = Math.max(maxDistance, j - i)\n j++\n }else{\n i++\n j++\n }\n }\n \n return maxDistance\n};\n```
| 2 | 0 |
[]
| 0 |
maximum-distance-between-a-pair-of-values
|
C++ solution
|
c-solution-by-peet_code-7bkx
|
\tclass Solution {\n\tpublic:\n int maxDistance(vector& nums1, vector& nums2) {\n int i = 0, j = 0, ans = 0;\n \n while(i<nums1.size() &
|
Peet_code_
|
NORMAL
|
2022-04-18T13:25:06.588494+00:00
|
2022-04-18T13:25:06.588546+00:00
| 84 | false |
\tclass Solution {\n\tpublic:\n int maxDistance(vector<int>& nums1, vector<int>& nums2) {\n int i = 0, j = 0, ans = 0;\n \n while(i<nums1.size() && j < nums2.size()){\n if(nums1[i] > nums2[j])\n i++;\n else\n ans = max(ans, j++ - i);\n }\n return ans;\n }\n\t};\n\n
| 2 | 0 |
['C', 'C++']
| 0 |
maximum-distance-between-a-pair-of-values
|
Python || Two Pointers
|
python-two-pointers-by-nashvenn-v3aw
|
Please upvote if it helps. Thank you!\n\nclass Solution:\n def maxDistance(self, nums1: List[int], nums2: List[int]) -> int:\n i, j, max_dist = 0, 0,
|
nashvenn
|
NORMAL
|
2022-04-11T13:33:08.283147+00:00
|
2022-04-11T13:33:08.283190+00:00
| 68 | false |
**Please upvote if it helps. Thank you!**\n```\nclass Solution:\n def maxDistance(self, nums1: List[int], nums2: List[int]) -> int:\n i, j, max_dist = 0, 0, 0\n for j in range(len(nums2)):\n if nums1[i] > nums2[j]:\n i += 1\n if i == len(nums1):\n break\n else:\n max_dist = max(max_dist, j - i)\n return max_dist\n```
| 2 | 0 |
['Two Pointers', 'Python']
| 0 |
maximum-distance-between-a-pair-of-values
|
Java solution | O(M + N)
|
java-solution-om-n-by-chinghsuanwei0206-q7av
|
\n public int maxDistance(int[] nums1, int[] nums2) {\n \n int i=0;\n int j=0;\n\n int diff = 0;\n while(i < nums1.length
|
chinghsuanwei0206
|
NORMAL
|
2022-01-27T14:47:07.840108+00:00
|
2022-01-27T14:47:14.665147+00:00
| 145 | false |
\n public int maxDistance(int[] nums1, int[] nums2) {\n \n int i=0;\n int j=0;\n\n int diff = 0;\n while(i < nums1.length && j < nums2.length)\n {\n \n if(nums2[j] >= nums1[i])\n {\n diff = Math.max(diff, j-i);\n j++;\n }\n else\n {\n i++;\n }\n \n }\n \n return diff;\n }
| 2 | 0 |
['Java']
| 0 |
maximum-distance-between-a-pair-of-values
|
two pointer js
|
two-pointer-js-by-cauld-j31h
|
\nvar maxDistance = function(nums1, nums2) {\n \n let maxDistance = Math.max();\n \n let ptr1 = 0;\n let ptr2 = 0;\n \n \n while
|
cauld
|
NORMAL
|
2021-09-17T19:20:56.764050+00:00
|
2021-09-17T19:20:56.764091+00:00
| 139 | false |
```\nvar maxDistance = function(nums1, nums2) {\n \n let maxDistance = Math.max();\n \n let ptr1 = 0;\n let ptr2 = 0;\n \n \n while(ptr2 < nums2.length){\n\n if(nums1[ptr1] <= nums2[ptr2]){\n maxDistance = Math.max(maxDistance, ptr2 - ptr1);\n ptr2++;\n } else {\n ptr1++;\n }\n \n while(ptr1 > ptr2){\n ptr2++;\n } \n \n }\n\n return maxDistance === Math.max() ? 0 : maxDistance;\n \n};\n```
| 2 | 0 |
['JavaScript']
| 0 |
maximum-distance-between-a-pair-of-values
|
c# : Easy Solution
|
c-easy-solution-by-rahul89798-4vy1
|
Solution 1:\n\n\n\npublic class Solution {\n public int MaxDistance(int[] nums1, int[] nums2) {\n int ans = 0, i = nums1.Length - 1, j = nums2.Length - 1;\n
|
rahul89798
|
NORMAL
|
2021-08-16T15:16:57.696847+00:00
|
2023-04-01T15:24:09.826496+00:00
| 70 | false |
**Solution 1:**\n\n```\n\npublic class Solution {\n public int MaxDistance(int[] nums1, int[] nums2) {\n int ans = 0, i = nums1.Length - 1, j = nums2.Length - 1;\n\n while(i >= 0 && j >= 0) {\n if(i > j) {\n i--;\n continue;\n }\n\n if(nums1[i] <= nums2[j]) {\n ans = Math.Max(ans, Math.Abs(j - i));\n i--;\n }\n else\n j--;\n }\n\n return ans;\n }\n}\n```\n\n**Solution 2:**\n\n```\npublic class Solution {\n public int MaxDistance(int[] nums1, int[] nums2) {\n int ans = 0, low = 0, high = nums2.Length;\n while(low <= high) {\n var mid = low + (high - low) / 2;\n if(IsPossible(nums1, nums2, mid)) {\n ans = Math.Max(ans, mid);\n low = mid + 1;\n }\n else\n high = mid - 1;\n }\n\n return ans;\n }\n\n private bool IsPossible(int[] nums1, int[] nums2, int dist) {\n for(int i = 0, j = dist; i < nums1.Length && j < nums2.Length; i++, j++) {\n if(nums1[i] <= nums2[j])\n return true;\n }\n\n return false;\n }\n}\n```
| 2 | 0 |
['Two Pointers', 'Binary Search']
| 0 |
maximum-distance-between-a-pair-of-values
|
Bisect whenever you can, 99% speed
|
bisect-whenever-you-can-99-speed-by-evge-hg1s
|
Runtime: 1048 ms, faster than 99.18% of Python3 online submissions for Maximum Distance Between a Pair of Values.\nMemory Usage: 31.8 MB, less than 89.90% of Py
|
evgenysh
|
NORMAL
|
2021-07-23T16:40:52.795865+00:00
|
2021-07-23T16:43:56.018824+00:00
| 117 | false |
Runtime: 1048 ms, faster than 99.18% of Python3 online submissions for Maximum Distance Between a Pair of Values.\nMemory Usage: 31.8 MB, less than 89.90% of Python3 online submissions for Maximum Distance Between a Pair of Values.\n```\nfrom bisect import bisect_left\nclass Solution:\n def maxDistance(self, nums1: List[int], nums2: List[int]) -> int:\n nums2.reverse()\n max_dist = 0\n len1 = len(nums2) - 1\n for i, n in enumerate(nums1):\n max_dist = max(max_dist, len1 - bisect_left(nums2, n) - i)\n if len1 - i <= max_dist:\n break\n return max_dist\n```
| 2 | 0 |
['Python', 'Python3']
| 0 |
maximum-distance-between-a-pair-of-values
|
Clear Explanation of O(nlogn) algorithm
|
clear-explanation-of-onlogn-algorithm-by-m8q6
|
Let\'s start selecting j index from the end of nums2 array, because our solution must satisfy the condition i < j. So it is more intuitive to select as large as
|
datoqobu
|
NORMAL
|
2021-05-30T09:12:24.321955+00:00
|
2021-07-01T14:21:38.228945+00:00
| 255 | false |
Let\'s start selecting `j` index from the end of `nums2` array, because our solution must satisfy the condition `i < j`. So it is more intuitive to select as large as possible `j` index and do the logic after that. As for `i` index, we must find the minimum `i` in `nums1` array, such that `nums1[i] <= nums2[j]`.\nNotice that both array are non-increasing (`arr` is non-increasing if `arr[i-1] >= arr[i]` for every `1 <= i < arr.length`), so they are decrease ordered. Thus we can use **binary search algorithm** to find `i` in `nums1` array.\n\nWhen we find appropriate `i` in `nums1` array, we must consider the difference `(j - i)` and compare it to previous difference value to select **max** between them. There is exist legitimate question: why we don\'t break finding process at this point? Why do we consider other pairs of indices `(i, j)`? Because it may happen that `nums2[j-k]` (where `k` is `0 <= k < j <= nums2.length`) would be too greater than `nums[j]`. So `i` index would be near of `0` index in `nums1` array. The example is:\n`nums1 = [20, 10, 6, 4, 2]` `nums2 = [80, 70, 60, 50, 5]` so when `j = 4 nums2[4] = 5` and `i = 3 nums1[3] = 4`. So `(j - i) = 4 - 3 = 1` but `j = 3 nums2[3] = 50` and `i = 0 nums1[0] = 30, (j - i) = 3`. Thus we would have found more valid pair `(j, i)` and its difference is `3`.\n\nProcess that is described above is main part of solution, but let\'s consider **edge cases**.\n 1. `elem` from `nums2` array is the smallest one in `nums1` array. So there is not exist `i` in `nums1` array. Then the difference `(j - i)` doesn\'t exist also.\n 2. `elem` from `nums2` array is the greatest one in `nums1` array, then `i` index must be `0`.\n 3. `nums1` and `nums2` arrays lengthes **are not equal** each other. Our algorithm must consider this edge case.\n\nSo there is java code:\n\n```java\npublic int maxDistance(int[] nums1, int[] nums2) {\n int res = 0;\n int start = 0, end = nums1.length - 1;\n for (int j = nums2.length - 1; j >= 0; j--) {\n int i = findAppropIndex(nums1, start, end, nums2[j]);\n\n if (i > end) continue;\n\n int diff = j - i;\n res = Math.max(res, diff);\n end = Math.min(j, i);\n }\n return res;\n }\n\n private int findAppropIndex(int[] arr, int start, int end, int elem) {\n if (elem < arr[end]) { // arr: [10, 9, 8, 7, 7] elem: 5\n return end + 1;\n }\n int low = start, high = end;\n while (low < high) {\n int mid = low + (high - low) / 2;\n if (arr[mid] > elem) {\n low = mid + 1;\n } else {\n high = mid;\n }\n }\n return high;\n }\n```\n\n***Notice:***\n\n**Binary search:** In general, it is better to compute mid as `low + (high - low) / 2` than `(low + high) / 2`, because `(low + high)` may be bigger than integer type capacity.\n\n**end = Math.min(j, i):** This is for better performance. We should not start to find `i` index always in the same range from `nums1` array. The range should be from `0` to `Math.min(j, i)`. We must select minimum value from `(j, i)` and do not assign `j` or `i` directly to the `end` variable (like: `end = j` or `end = i`). Because if we write `end = i`, what happens if `nums2.length` is smaller than `nums1.length`? Index `j` may be smaller than index `i`, so if `j < i` we could not have a valid pair even than `nums1[i] <= nums2[j]`. Second condition also must be satisfied: i <= j. And what happens if `end = j`? It may be **ArrayIndexOutOfBoundsException** when we select `arr[mid]` in binary search function. Because `mid = low + (high - low) / 2`. So if `nums2.length > nums1.length` mid index may be greater than `nums1.length` also. Thus we need minimum value from `j` and `i`.\n\nTime complexity is `O(nlogm)` where `m` is `nums1` array length and `n` is `nums2` array length. Ordering of `nums2` array is` O(n)` and in each step we do `O(logm)` operation for binary search in `nums1` array.\n\nI would love to have some sort of feedback from you. If you share me what can be improved in the article and what problems do you see currently, I\'ll correct them.\nThanks for reading.
| 2 | 1 |
['Binary Tree', 'Java']
| 0 |
maximum-distance-between-a-pair-of-values
|
[Python] Sliding Window - 5 Lines
|
python-sliding-window-5-lines-by-jump2fl-7kup
|
Iterate on input array \'nums1\'.\nStart with a size-1 shift on \'nums2\'\n\nTime O(n + m)\nSpace O(1)\n\n\nclass Solution:\n def maxDistance(self, nums1: Li
|
Jump2Fly
|
NORMAL
|
2021-05-10T10:23:05.414861+00:00
|
2021-05-10T10:27:16.222838+00:00
| 150 | false |
Iterate on input array \'nums1\'.\nStart with a size-1 shift on \'nums2\'\n\nTime O(n + m)\nSpace O(1)\n\n```\nclass Solution:\n def maxDistance(self, nums1: List[int], nums2: List[int]) -> int:\n shift = 1\n for i, num1 in enumerate(nums1):\n while i + shift < len(nums2) and num1 <= nums2[i + shift]:\n shift += 1\n return shift - 1\n```
| 2 | 0 |
[]
| 0 |
maximum-distance-between-a-pair-of-values
|
C++ 2 Pointers
|
c-2-pointers-by-aryanndhir-3ltl
|
\nint maxDistance(vector<int>& nums1, vector<int>& nums2) {\n \n int i = 0, j = 0;\n int n = nums1.size(), m = nums2.size(), maxlen = 0;\n
|
aryanndhir
|
NORMAL
|
2021-05-09T15:11:51.711745+00:00
|
2021-05-09T15:11:51.711790+00:00
| 54 | false |
```\nint maxDistance(vector<int>& nums1, vector<int>& nums2) {\n \n int i = 0, j = 0;\n int n = nums1.size(), m = nums2.size(), maxlen = 0;\n \n while(i < n && j < m){\n \n while(j < m && nums1[i] <= nums2[j])\n j++;\n\n maxlen = max(maxlen, j-i-1); \n \n while(i < n && j < m && nums1[i] > nums2[j])\n i++; \n }\n \n return maxlen;\n }\n}\n```
| 2 | 0 |
[]
| 0 |
maximum-distance-between-a-pair-of-values
|
[Python/C++] 2 Pointers - O(n)
|
pythonc-2-pointers-on-by-slough_10-98hg
|
Python3 \n\nclass Solution(object):\n\tdef maxDistance(self, nums1, nums2):\n\t\tresult = 0\n\t\ti, j = 0, 0\n\t\tn1,n2 = len(nums1), len(nums2)\n\t\t\n\t\twhil
|
slough_10
|
NORMAL
|
2021-05-09T04:35:28.630822+00:00
|
2021-05-09T04:35:52.747370+00:00
| 50 | false |
1. Python3 \n```\nclass Solution(object):\n\tdef maxDistance(self, nums1, nums2):\n\t\tresult = 0\n\t\ti, j = 0, 0\n\t\tn1,n2 = len(nums1), len(nums2)\n\t\t\n\t\twhile i < n1 and j < n2:\n\t\t\tif nums1[i] <= nums2[j]:\n\t\t\t\tresult = max(result, j-i)\n\t\t\t\tj += 1\n\t\t\telse:\n\t\t\t\ti += 1\n\t\t\t\tj += 1\n\t\treturn result\n```\n\n2. C++\n```\nint maxDistance(vector<int>& nums1, vector<int>& nums2) {\n int i = 0, j = 0, result = 0, n1 = nums1.size(), n2 = nums2.size();\n while (i < n1 && j < n2) {\n if (nums1[i] <= nums2[j]){\n result = max(result, j - i);\n\t\t\t\t j++;\n\t\t\t\t }\n else{\n\t\t\t\ti++;\n\t\t\t\tj++;\n\t\t\t} \n }\n return result;\n }\n```
| 2 | 0 |
[]
| 0 |
maximum-distance-between-a-pair-of-values
|
Two pointers O(N)
|
two-pointers-on-by-leetc1234-xf1d
|
class Solution {\n public int maxDistance(int[] nums1, int[] nums2) {\n \n int left = 0, right = 0, maxDist = 0;\n int len1 = nums1.length,
|
leetc1234
|
NORMAL
|
2021-05-09T04:08:51.426524+00:00
|
2021-05-10T19:57:58.174657+00:00
| 72 | false |
class Solution {\n public int maxDistance(int[] nums1, int[] nums2) {\n \n int left = 0, right = 0, maxDist = 0;\n int len1 = nums1.length, len2 = nums2.length;\n\n while(left < len1 && right < len2){\n \n if(nums1[left] > nums2[right]){\n left++;\n }else{\n maxDist = Math.max(maxDist, right - left);\n right++;\n }\n\n }\n\n return maxDist;\n \n }\n}\n\n\n
| 2 | 2 |
['Java']
| 0 |
maximum-distance-between-a-pair-of-values
|
[Python3] sliding window
|
python3-sliding-window-by-ye15-toon
|
\n\nclass Solution:\n def maxDistance(self, nums1: List[int], nums2: List[int]) -> int:\n ans = ii = 0 \n for i, x in enumerate(nums2): \n
|
ye15
|
NORMAL
|
2021-05-09T04:07:40.777825+00:00
|
2021-05-09T04:07:40.777858+00:00
| 134 | false |
\n```\nclass Solution:\n def maxDistance(self, nums1: List[int], nums2: List[int]) -> int:\n ans = ii = 0 \n for i, x in enumerate(nums2): \n while ii <= i and ii < len(nums1) and nums1[ii] > nums2[i]: ii += 1\n if ii < len(nums1) and nums1[ii] <= nums2[i]: ans = max(ans, i - ii)\n return ans \n```
| 2 | 0 |
['Python3']
| 0 |
maximum-distance-between-a-pair-of-values
|
python binary search
|
python-binary-search-by-cslzy-4pl9
|
\nclass Solution(object):\n def maxDistance(self, nums1, nums2):\n """\n :type nums1: List[int]\n :type nums2: List[int]\n :rtype
|
cslzy
|
NORMAL
|
2021-05-09T04:03:25.312081+00:00
|
2021-05-09T04:03:25.312130+00:00
| 149 | false |
```\nclass Solution(object):\n def maxDistance(self, nums1, nums2):\n """\n :type nums1: List[int]\n :type nums2: List[int]\n :rtype: int\n """\n res = 0\n n1 = len(nums1)\n n2 = len(nums2)\n \n \n for i in range(min(n1, n2)):\n if nums1[i] > nums2[i]:\n continue\n left = i\n right = n2 - 1\n \n iv = nums1[i]\n \n while left <= right:\n mid = (left + right) / 2\n if nums2[mid] >= iv:\n left = mid + 1\n elif nums2[mid] < iv:\n right = mid - 1\n \n res = max(res, left - i - 1)\n \n return res\n \n```
| 2 | 2 |
[]
| 0 |
maximum-distance-between-a-pair-of-values
|
C++ Easy and simple || 2 Pointer || O(N+M) time
|
c-easy-and-simple-2-pointer-onm-time-by-jxe3x
|
\nint maxDistance(vector<int>& nums1, vector<int>& nums2) {\n int n = nums1.size(), m = nums2.size(), i = 0, j = 0, total = 0;\n\n while (i < n && j < m)
|
faltu_admi
|
NORMAL
|
2021-05-09T04:01:59.122627+00:00
|
2021-05-09T04:03:49.256184+00:00
| 147 | false |
```\nint maxDistance(vector<int>& nums1, vector<int>& nums2) {\n int n = nums1.size(), m = nums2.size(), i = 0, j = 0, total = 0;\n\n while (i < n && j < m) {\n if (nums1[i] <= nums2[j]) {\n total = max(total, j - i);\n j++;\n } else if (i < j) {\n i++;\n } else {\n j++;\n }\n }\n return total;\n}\n```
| 2 | 0 |
[]
| 0 |
maximum-distance-between-a-pair-of-values
|
Java Binary Search Solution and two pointer solution
|
java-binary-search-solution-and-two-poin-vny6
|
O(nlogn) Solution\n\n\nclass Solution {\n public int maxDistance(int[] nums1, int[] nums2) {\n int res = 0;\n for(int i = nums2.length-1; i >=
|
ayush2332
|
NORMAL
|
2021-05-09T04:01:14.788189+00:00
|
2021-05-09T04:03:58.073554+00:00
| 178 | false |
**O(nlogn) Solution**\n\n```\nclass Solution {\n public int maxDistance(int[] nums1, int[] nums2) {\n int res = 0;\n for(int i = nums2.length-1; i >= 0; i--) {\n int start = 0, end = Math.min(nums1.length-1, i-1);\n while(start <= end) {\n int mid = start + (end - start) / 2;\n if(nums1[mid] <= nums2[i]) {\n res = Math.max(res, i - mid);\n end = mid - 1;\n }\n else {\n start = mid + 1;\n }\n \n }\n }\n return res;\n }\n}\n```\n\nO(n) Solution\n\n```\nclass Solution {\n public int maxDistance(int[] nums1, int[] nums2) {\n int i=0, j=0;\n int ans = 0;\n while(i<nums1.length && j<nums2.length){\n if(nums1[i]<=nums2[j]) ans = Math.max(j-i,ans);\n if(i==j || nums1[i]<=nums2[j]) j++;\n else i++;\n }\n return ans;\n }\n}\n```
| 2 | 0 |
[]
| 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.