question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
sort-by | One line solution JavaScript return arr.sort((a, b) => fn(a) - fn(b)); | one-line-solution-javascript-return-arrs-0j0r | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | yashdhameliya88 | NORMAL | 2024-11-16T18:18:07.937039+00:00 | 2024-11-16T18:18:07.937070+00:00 | 1 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```javascript []\nvar sortBy = function(arr, fn) {\n return arr.sort((a, b) => fn(a) - fn(b));\n};\n``` | 0 | 0 | ['JavaScript'] | 0 |
sort-by | sort-by | sort-by-by-jayesh0604-t9yr | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | jayesh0604 | NORMAL | 2024-11-16T16:21:19.899337+00:00 | 2024-11-16T16:21:19.899376+00:00 | 0 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```javascript []\n/**\n * @param {Array} arr\n * @param {Function} fn\n * @return {Array}\n */\nvar sortBy = function(arr, fn) {\n return arr.sort((a, b) => fn(a) - fn(b));\n};\n``` | 0 | 0 | ['JavaScript'] | 0 |
sort-by | Прикольные у вас тут задачки | prikolnye-u-vas-tut-zadachki-by-whitness-68pn | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Whitnessss | NORMAL | 2024-11-15T17:12:34.446666+00:00 | 2024-11-15T17:12:34.446706+00:00 | 1 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```javascript []\n/**\n * @param {Array} arr\n * @param {Function} fn\n * @return {Array}\n */\nvar sortBy = function(arr, fn) {\n return arr.sort((a,b) => fn(a) - fn(b));\n};\n``` | 0 | 0 | ['JavaScript'] | 0 |
sort-by | One line solution and detailed explanation. | one-line-solution-and-detailed-explanati-r5be | Intuition\n\nThe problem is about sorting an array arr based on a transformation function fn. Each element in arr is mapped to a numerical value through fn, and | 110208059 | NORMAL | 2024-11-15T02:56:48.416825+00:00 | 2024-11-15T02:56:48.416850+00:00 | 0 | false | ## Intuition\n\nThe problem is about sorting an array `arr` based on a transformation function `fn`. Each element in `arr` is mapped to a numerical value through `fn`, and the sorting order depends on these transformed values. The function `fn` is consistent and won\u2019t duplicate numbers for the same elements in `arr`, making it a stable transformation for sorting.\n\nThe core idea is:\n1. Map each element in `arr` to a value using `fn`.\n2. Use these values to determine the order of elements in `arr`.\n\n---\n\n## Approach\n\nThe steps to solve this problem are as follows:\n\n1. **Transform Each Element with `fn`**:\n Use the function `fn` to get a "key" (numerical value) for each element in `arr`. This key determines the order of the elements in the sorted array.\n\n2. **Use `.sort()` with Custom Comparator**:\n JavaScript\'s `.sort()` allows us to specify a custom comparator function that determines the sorting logic. Here\u2019s how:\n - For each pair of elements, `a` and `b`, in `arr`, we pass them to `fn`.\n - We compare `fn(a)` with `fn(b)` using `fn(a) - fn(b)`. This produces:\n - A negative result if `fn(a)` should appear before `fn(b)`.\n - Zero if `fn(a)` and `fn(b)` are equal (though in this problem, the prompt guarantees unique numbers).\n - A positive result if `fn(a)` should appear after `fn(b)`.\n\n3. **Return the Sorted Array**:\n By using `.sort()` in this way, we sort `arr` based on the transformation values from `fn`.\n\n---\n\n## Complexity\n\n- **Time Complexity**: \n The `.sort()` method has a time complexity of \\( O(n log n) \\), where \\( n \\) is the length of `arr`. Calculating `fn(a)` for each element is constant time \\( O(1) \\), so the overall time complexity remains \\( O(n log n) \\).\n\n- **Space Complexity**: \n Since we are sorting `arr` in-place, the space complexity is \\( O(1) \\), assuming `fn` does not add any additional memory usage. However, if `fn` has its own memory requirements, the space complexity could increase.\n\n---\n\n## Code\n\n\n```javascript\n/**\n * @param {Array} arr\n * @param {Function} fn\n * @return {Array}\n */\nvar sortBy = function(arr, fn) {\n return arr.sort((a, b) => fn(a) - fn(b));\n};\n```\n\n | 0 | 0 | ['JavaScript'] | 0 |
sort-by | JavaScript Easy Solution | One-linear | Beats 100% Faster :) | javascript-easy-solution-one-linear-beat-8v4t | Code \njavascript []\nconst sortBy = (arr, fn) => arr.sort((a, b) => fn(a) - fn(b));\n | Abhishek_Nayak_ | NORMAL | 2024-11-14T11:52:09.635908+00:00 | 2024-11-14T11:52:09.635944+00:00 | 1 | false | # Code \n```javascript []\nconst sortBy = (arr, fn) => arr.sort((a, b) => fn(a) - fn(b));\n``` | 0 | 0 | ['JavaScript'] | 0 |
sort-by | Custom Sort Function | custom-sort-function-by-bikash_kumar_gir-o7qk | Intuition\n Describe your first thoughts on how to solve this problem. \nThe intuition behind the sortBy function is to provide a flexible way to sort arrays ba | bikash_kumar_giri | NORMAL | 2024-11-13T16:59:32.769728+00:00 | 2024-11-13T16:59:32.769765+00:00 | 3 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition behind the sortBy function is to provide a flexible way to sort arrays based on any criterion defined by the user. By applying a callback function fn to each element in the array, we can determine the sort order dynamically. This approach leverages the built-in sort method but enhances its functionality with custom sorting logic.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFunction Definition: The sortBy function accepts an array and a callback function as arguments.\n\nSorting Logic: It uses the sort method, passing a comparator function that applies fn to each element.\n\nComparator Function: The comparator function (a, b) => fn(a) - fn(b) ensures the array is sorted according to the values returned by fn.\n\nFlexible Sorting: This method allows sorting arrays of various types, including numbers, strings, and objects, based on any criteria.\n\n\n# Complexity\n- Time complexity: The sort method in JavaScript typically has a time complexity of O(n log n), where n is the number of elements in the array. This is due to the efficient sorting algorithms (like Timsort) used under the hood.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: The space complexity is generally O(1) for in-place sorting. However, additional space may be used for temporary variables during sorting operations.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```javascript []\n/**\n * @param {Array} arr\n * @param {Function} fn\n * @return {Array}\n */\nvar sortBy = function(arr, fn) {\n return arr.sort((a, b) => fn(a) - fn(b));\n};\n``` | 0 | 0 | ['JavaScript'] | 0 |
sort-by | 2724. Sort By | 2724-sort-by-by-dhruvin_sorathiya-zkff | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | dhruvin_sorathiya | NORMAL | 2024-11-12T10:27:54.890508+00:00 | 2024-11-12T10:27:54.890534+00:00 | 1 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```javascript []\n/**\n * @param {Array} arr\n * @param {Function} fn\n * @return {Array}\n */\nvar sortBy = function (arr, fn) {\n return arr.sort((a, b) => fn(a) - fn(b));\n};\n``` | 0 | 0 | ['JavaScript'] | 0 |
sort-by | Sort By Function | sort-by-function-by-shanthibabu-sunt | Intuition\nThe task is to sort an array based on a given function\'s return values. This involves mapping each item to its sort value using the function fn and | shanthibabu | NORMAL | 2024-11-12T07:46:35.554156+00:00 | 2024-11-12T07:46:35.554177+00:00 | 0 | false | ## Intuition\nThe task is to sort an array based on a given function\'s return values. This involves mapping each item to its sort value using the function `fn` and then sorting based on these values.\n\n## Approach\n1. **Map the Items**: Use `map` to transform each item according to the function `fn`.\n2. **Sort**: Use `sort` to arrange the items in ascending order based on the values returned by `fn`.\n\n## Complexity\n- **Time complexity**: Sorting has a complexity of \\(O(n \\log n)\\), where \\(n\\) is the length of the array. Mapping the items to their transformed values has \\(O(n)\\) complexity, so the overall complexity is dominated by sorting: \\(O(n \\log n)\\).\n- **Space complexity**: \\(O(n)\\), due to the additional space needed to store the transformed array.\n\n## Code\n\n```javascript\n/**\n * @param {Array} arr\n * @param {Function} fn\n * @return {Array}\n */\nvar sortBy = function(arr, fn) {\n return arr.slice().sort((a, b) => fn(a) - fn(b));\n};\n | 0 | 0 | ['JavaScript'] | 0 |
sort-by | Simple sorted array | simple-sorted-array-by-fedwar-dvnw | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Fedwar | NORMAL | 2024-11-01T19:08:44.373730+00:00 | 2024-11-01T19:08:44.373759+00:00 | 3 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```javascript []\n/**\n * @param {Array} arr\n * @param {Function} fn\n * @return {Array}\n */\nvar sortBy = function(arr, fn) {\n return arr.toSorted((a,b) => fn(a) - fn(b));\n};\n``` | 0 | 0 | ['JavaScript'] | 0 |
sort-by | 30 days js 1-day | 30-days-js-1-day-by-deleted_user-pt96 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | deleted_user | NORMAL | 2024-10-30T11:53:49.717237+00:00 | 2024-10-30T11:53:49.717263+00:00 | 0 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```javascript []\n/**\n * @param {Array} arr\n * @param {Function} fn\n * @return {Array}\n */\nvar sortBy = function(arr, fn) {\n return arr.sort((a, b) => fn(a) - fn(b));\n};\n``` | 0 | 0 | ['JavaScript'] | 0 |
sort-by | Qick sort | qick-sort-by-leessonomy-1lho | Code\njavascript []\n\nvar sortBy = function (arr, fn) {\n if (arr.length <= 1) {\n return arr;\n }\n const pivot = arr[Math.floor(arr.length / 2)];\n | leessonomy | NORMAL | 2024-10-29T07:30:01.723508+00:00 | 2024-10-29T07:30:01.723533+00:00 | 4 | false | # Code\n```javascript []\n\nvar sortBy = function (arr, fn) {\n if (arr.length <= 1) {\n return arr;\n }\n const pivot = arr[Math.floor(arr.length / 2)];\n const left = [];\n const right = [];\n\n\n for(const o of arr) {\n const num = fn(o);\n const middle = fn(pivot);\n if (num < middle) {\n left.push(o)\n } else if (num > middle) {\n right.push(o)\n }\n }\n\n return [...sortBy(left, fn), pivot, ...sortBy(right, fn)]\n};\n\n``` | 0 | 0 | ['JavaScript'] | 0 |
sort-by | .toSorted() method | tosorted-method-by-phirimhel-oku0 | \n\n# Approach\nMethod toSorted() and sort() work about the same \n\nBut method toSorted(), unlike method sort(), returns a new array when sorting\n\n\n\n# Code | phirimhel | NORMAL | 2024-10-26T16:27:23.998241+00:00 | 2024-10-26T16:27:23.998262+00:00 | 4 | false | \n\n# Approach\nMethod toSorted() and sort() work about the same \n\nBut method **toSorted()**, unlike method sort(), returns a **new array when sorting**\n\n\n\n# Code\n```javascript []\n/**\n * @param {Array} arr\n * @param {Function} fn\n * @return {Array}\n */\nvar sortBy = (arr, fn) => arr.toSorted( (a,b) => fn(a) - fn(b) )\n``` | 0 | 0 | ['JavaScript'] | 0 |
sort-by | 2724. Sort By | 2724-sort-by-by-maimuna_javed-ditf | \n# Code\njavascript []\n\nvar sortBy = function (arr, fn) {\n return arr.sort((a, b) => fn(a) - fn(b));\n};\n\n | Maimuna_Javed | NORMAL | 2024-10-24T06:55:38.509568+00:00 | 2024-10-24T06:55:38.509598+00:00 | 7 | false | \n# Code\n```javascript []\n\nvar sortBy = function (arr, fn) {\n return arr.sort((a, b) => fn(a) - fn(b));\n};\n\n``` | 0 | 0 | ['JavaScript'] | 0 |
sort-by | Merge sort algorithm implementation! | merge-sort-algorithm-implementation-by-a-c7q0 | Intuition\nI didn\'t want to use sort function so I thought why not implement sorting algorithms for a change.\n# Approach\nBubble sort gave TLE, optimized bubb | arnav2000agr | NORMAL | 2024-10-15T06:34:38.385317+00:00 | 2024-10-15T06:36:12.415289+00:00 | 21 | false | # Intuition\nI didn\'t want to use sort function so I thought why not implement sorting algorithms for a change.\n# Approach\nBubble sort gave TLE, optimized bubble sort gave TLE, selection sort gave TLE, so ultimately went to merge sort to get the job done.\n\n\n# Code\n```javascript []\n/**\n * @param {Array} arr\n * @param {Function} fn\n * @return {Array}\n */\nvar sortBy = function(arr, fn) {\n let n = arr.length;\n function merge(left, right) {\n let result = [];\n let i = 0, j = 0;\n while (i < left.length && j < right.length) {\n if (fn(left[i]) <= fn(right[j])) {\n result.push(left[i]);\n i++;\n } else {\n result.push(right[j]);\n j++;\n }\n }\n while (i < left.length) {\n result.push(left[i]);\n i++;\n }\n while (j < right.length) {\n result.push(right[j]);\n j++;\n }\n\n return result;\n }\n for (let size = 1; size < n; size *= 2) {\n for (let leftStart = 0; leftStart < n; leftStart += 2 * size) {\n let mid = Math.min(leftStart + size, n);\n let rightEnd = Math.min(leftStart + 2 * size, n);\n let left = arr.slice(leftStart, mid);\n let right = arr.slice(mid, rightEnd);\n let merged = merge(left, right);\n\n for (let i = 0; i < merged.length; i++) {\n arr[leftStart + i] = merged[i];\n }\n }\n }\n\n return arr;\n};\n\n``` | 0 | 0 | ['Array', 'Merge Sort', 'JavaScript'] | 0 |
sort-by | Easy to Understand Code Day 24! | easy-to-understand-code-day-24-by-iamreh-sxkp | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | iamrehankhan21 | NORMAL | 2024-10-10T07:12:14.765793+00:00 | 2024-10-10T07:12:14.765831+00:00 | 0 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```javascript []\n/**\n * @param {Array} arr\n * @param {Function} fn\n * @return {Array}\n */\nvar sortBy = function(arr,fn){\n return arr.sort((a,b)=>{\n return fn(a)-fn(b) \n })\n}\n\n``` | 0 | 0 | ['JavaScript'] | 0 |
sort-by | #JS30: 18 (JSON - 4) | js30-18-json-4-by-darius0614-wnc8 | Intuition\n Describe your first thoughts on how to solve this problem. \n- Solve using the built-in array method - array.toSorted(compareFunction(a,b)) . the di | Darius0614 | NORMAL | 2024-10-08T12:24:48.286768+00:00 | 2024-10-08T12:24:48.286803+00:00 | 0 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- Solve using the built-in array method - `array.toSorted(compareFunction(a,b))` . the different between it and `array.sort(compareFunction(a,b))` is `toSorted` will return a new array and kept original array; While `sort` wil modify on the original array.\n\n- `compareFunction(a,b)` define, how the elements will be rearrange by compare pairs of elements in the array. \n\n- The function takes two arguments, `a` and `b`, which represent two elements from the array that are being compared.\n\n- The return value of the callback function determines the `order of a and b`:\n1. If the return value is less than 0: a comes before b.\n2. If the return value is greater than 0: b comes before a.\n3. If the return value is 0: The order of a and b remains unchanged.\n\n# Code\n```javascript []\n/**\n * @param {Array} arr\n * @param {Function} fn\n * @return {Array}\n */\nvar sortBy = function(arr, fn) {\n return arr.toSorted((a, b) => fn(a) - fn(b));\n};\n``` | 0 | 0 | ['JavaScript'] | 0 |
sort-by | fn(a) - fn(b), .sort automatically sorts based on the output | fna-fnb-sort-automatically-sorts-based-o-k742 | \n\n# Code\njavascript []\n/**\n * @param {Array} arr\n * @param {Function} fn\n * @return {Array}\n */\nvar sortBy = function(arr, fn) {\n return arr.sort(( | Z0TtKGNu7r | NORMAL | 2024-10-07T17:53:21.486433+00:00 | 2024-10-07T17:53:21.486462+00:00 | 0 | false | \n\n# Code\n```javascript []\n/**\n * @param {Array} arr\n * @param {Function} fn\n * @return {Array}\n */\nvar sortBy = function(arr, fn) {\n return arr.sort((a, b) => {\n let result = fn(a) - fn(b);\n return result;\n });\n};\n\n``` | 0 | 0 | ['JavaScript'] | 0 |
sort-by | Solution | solution-by-qqama-4vne | \n\n# Code\njavascript []\n/**\n * @param {Array} arr\n * @param {Function} fn\n * @return {Array}\n */\nvar sortBy = function(arr, fn) {\n return arr.sort(( | qqama | NORMAL | 2024-09-29T13:22:57.403575+00:00 | 2024-09-29T13:22:57.403613+00:00 | 0 | false | \n\n# Code\n```javascript []\n/**\n * @param {Array} arr\n * @param {Function} fn\n * @return {Array}\n */\nvar sortBy = function(arr, fn) {\n return arr.sort((a, b) => fn(a) - fn(b))\n};\n``` | 0 | 0 | ['JavaScript'] | 0 |
sort-by | Beats 99.5% | beats-995-by-jdszekeres-la8q | \n# Code\njavascript []\n/**\n * @param {Array} arr\n * @param {Function} fn\n * @return {Array}\n */\nvar sortBy = function(arr, fn) {\n return arr.sort((a, | jdszekeres | NORMAL | 2024-09-28T22:03:26.956870+00:00 | 2024-09-28T22:03:26.956887+00:00 | 2 | false | \n# Code\n```javascript []\n/**\n * @param {Array} arr\n * @param {Function} fn\n * @return {Array}\n */\nvar sortBy = function(arr, fn) {\n return arr.sort((a,b)=> {return fn(a) - fn(b)})\n};\n``` | 0 | 0 | ['JavaScript'] | 0 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | [C++ / Java] Textbook Union-Find Data Structure, Code with Explanation and comments | c-java-textbook-union-find-data-structur-nmlc | The idea here is to think that initially the graph is empty and now we want to add the edges into the graph such that graph is connected.\n\nUnion-Find is an ea | interviewrecipes | NORMAL | 2020-09-06T04:02:03.694455+00:00 | 2020-09-08T04:34:48.117824+00:00 | 20,293 | false | The idea here is to think that initially the graph is empty and now we want to add the edges into the graph such that graph is connected.\n\nUnion-Find is an easiest way to solve such problem where we start with all nodes in separate components and merge the nodes as we add edges into the graph.\n\nAs some edges are available to only Bob while some are available only to Alice, we will have two different union find objects to take care of their own traversability.\n\nKey thing to remember is that we should prioritize type 3 edges over type 1 and 2 because they help both of them at the same time.\n**C++**\n```\n/* You can simply plug in this class any many different codes. This class is a generic implementation of union-find. */\nclass UnionFind {\n vector<int> component;\n int distinctComponents;\npublic:\n /*\n * Initially all \'n\' nodes are in different components.\n * e.g. component[2] = 2 i.e. node 2 belong to component 2.\n */\n UnionFind(int n) {\n\t distinctComponents = n;\n for (int i=0; i<=n; i++) {\n component.push_back(i);\n }\n }\n \n /*\n * Returns true when two nodes \'a\' and \'b\' are initially in different\n * components. Otherwise returns false.\n */\n bool unite(int a, int b) { \n if (findComponent(a) == findComponent(b)) {\n return false;\n }\n component[findComponent(a)] = b;\n distinctComponents--;\n return true;\n }\n \n /*\n * Returns what component does the node \'a\' belong to.\n */\n int findComponent(int a) {\n if (component[a] != a) {\n component[a] = findComponent(component[a]);\n }\n return component[a];\n }\n \n /*\n * Are all nodes united into a single component?\n */\n bool united() {\n return distinctComponents == 1;\n }\n};\n\n\n\n// ----------------- Actual Solution --------------\nclass Solution {\n \npublic:\n int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {\n // Sort edges by their type such that all type 3 edges will be at the beginning.\n sort(edges.begin(), edges.end(), [] (vector<int> &a, vector<int> &b) { return a[0] > b[0]; });\n \n int edgesAdded = 0; // Stores the number of edges added to the initial empty graph.\n \n UnionFind bob(n), alice(n); // Track whether bob and alice can traverse the entire graph,\n // are there still more than one distinct components, etc.\n \n for (auto &edge: edges) { // For each edge -\n int type = edge[0], one = edge[1], two = edge[2];\n switch(type) {\n case 3:\n edgesAdded += (bob.unite(one, two) | alice.unite(one, two));\n break;\n case 2:\n edgesAdded += bob.unite(one, two);\n break;\n case 1:\n edgesAdded += alice.unite(one, two);\n break;\n }\n }\n \n return (bob.united() && alice.united()) ? (edges.size()-edgesAdded) : -1; // Yay, solved.\n }\n};\n```\n\n**Java** (Credits to @binlei)\n```\nclass Solution {\n public int maxNumEdgesToRemove(int n, int[][] edges) {\n Arrays.sort(edges, (a, b) -> b[0] - a[0]);\n \n int edgeAdd = 0;\n \n UnionFind alice = new UnionFind(n);\n UnionFind bob = new UnionFind(n);\n \n for (int[] edge : edges) {\n int type = edge[0];\n int a = edge[1];\n int b = edge[2];\n \n switch (type) {\n case 3:\n if (alice.unite(a, b) | bob.unite(a, b)) {\n edgeAdd++;\n }\n break;\n case 2:\n if (bob.unite(a, b)) {\n edgeAdd++;\n }\n break;\n case 1:\n if (alice.unite(a, b)) {\n edgeAdd++;\n } \n break;\n }\n }\n \n return (alice.united() && bob.united()) ? edges.length - edgeAdd : -1;\n }\n \n private class UnionFind {\n int[] component;\n int distinctComponents;\n \n public UnionFind(int n) {\n component = new int[n+1];\n for (int i = 0; i <= n; i++) {\n component[i] = i;\n }\n distinctComponents = n;\n }\n // unite. For example, if previously we have component {0, 4, 4, 4, 4, 6, 7, 7}, then invoke this method with a=1, b=5, then after invoke, {0, 4, 4, 4, 5, 7, 7, 7}\n private boolean unite(int a, int b) {\n if (findComponent(a) != findComponent(b)) {\n component[findComponent(a)] = b;\n distinctComponents--;\n return true;\n }\n \n return false;\n }\n \n // find and change component\n // for example, if previously we have component:{0, 2, 3, 4, 4, 6, 7, 7}, then after invoke this method with a=1, the component become {0, 4, 4, 4, 4, 6, 7, 7}\n private int findComponent(int a) {\n if (component[a] != a) {\n component[a] = findComponent(component[a]);\n }\n return component[a];\n }\n \n private boolean united() {\n return distinctComponents == 1;\n }\n \n }\n}\n``` | 249 | 5 | [] | 23 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | ✅Beats 100% -Explained with [ Video ] -C++/Java/Python/JS - Union Find | beats-100-explained-with-video-cjavapyth-p458 | \n\n\n# YouTube Video Explanation:\n\n ### To watch the video please click on "Watch On Youtube" option available the left bottom corner of the thumbnail. \n\n | lancertech6 | NORMAL | 2024-06-30T03:28:11.292445+00:00 | 2024-06-30T07:35:33.035489+00:00 | 27,537 | false | \n\n\n# YouTube Video Explanation:\n\n<!-- ### To watch the video please click on "Watch On Youtube" option available the left bottom corner of the thumbnail. -->\n\n<!-- **If you want a video for this question please write in the comments** -->\n\n\nhttps://youtu.be/LfaQjcE_LEM\n\n# The video doesn\'t have the code part today due to some failure. Please watch it from the solution below. Sorry for it.\n\n\n**\uD83D\uDD25 Please like, share, and subscribe to support our channel\'s mission of making complex concepts easy to understand.**\n\nSubscribe Link: https://www.youtube.com/@leetlogics/?sub_confirmation=1\n\n*Subscribe Goal: 2400 Subscribers*\n*Current Subscribers: 2357*\n\nFollow me on Instagram : https://www.instagram.com/divyansh.nishad/\n\n---\n\n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo solve this problem, we need to ensure that both Alice and Bob can traverse the entire graph independently. This can be achieved by ensuring each has a connected graph (spanning tree). Using the Union-Find data structure, we can efficiently manage the connectivity of the graph. The goal is to maximize the number of edges removed while ensuring both Alice and Bob can still traverse all nodes.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. **Initialize Union-Find Structures**: Create two separate Union-Find structures, one for Alice and one for Bob, to manage their connectivity.\n2. **Process Type 3 Edges First**: Type 3 edges are the most valuable because they can be used by both Alice and Bob. We iterate through these edges first and attempt to add them to both Alice\'s and Bob\'s graphs. If the edge successfully connects two previously unconnected components for either Alice or Bob, it is necessary.\n3. **Process Type 1 and Type 2 Edges**: After handling type 3 edges, we separately process type 1 edges for Alice and type 2 edges for Bob. These edges are only useful if they connect new components for Alice or Bob, respectively.\n4. **Check Full Connectivity**: After processing all edges, we check if both Alice\'s and Bob\'s graphs are fully connected.\n5. **Calculate Removable Edges**: The number of removable edges is the total number of edges minus the number of edges required to ensure full connectivity for both Alice and Bob.\n\n# Complexity\n- **Time Complexity**: \n - The Union-Find operations (find and union) are nearly constant time due to path compression and union by rank. \n - Processing all edges involves iterating through them twice, giving a complexity of \\(O(E)\\), where \\(E\\) is the number of edges.\n- **Space Complexity**: \n - We use extra space for the Union-Find data structures, each requiring \\(O(N)\\) space for representative and component size arrays, where \\(N\\) is the number of nodes.\n\n\n# Explanation\n\n1. **Initialization**:\n - Create two Union-Find instances: one for Alice and one for Bob.\n - Initialize the number of edges required to be included in the graph (`edgesRequired`).\n\n | Variable | Description |\n |-----------------|-----------------------------------------------------|\n | `alice` | Union-Find instance for Alice |\n | `bob` | Union-Find instance for Bob |\n | `edgesRequired` | Counter for edges that are required in the graph |\n\n2. **Processing Type 3 Edges**:\n - First, include all type 3 edges, which can be used by both Alice and Bob.\n\n | Edge Type | Operation |\n |-----------|-------------------------------------------------------------|\n | Type 3 | Try to union nodes in both `alice` and `bob` Union-Find |\n | | If successful in either, increment `edgesRequired` |\n\n3. **Processing Type 1 and Type 2 Edges**:\n - Process remaining edges: type 1 (Alice) and type 2 (Bob).\n\n | Edge Type | Operation |\n |-----------|-------------------------------------------------------------|\n | Type 1 | Try to union nodes in `alice` Union-Find |\n | | If successful, increment `edgesRequired` |\n | Type 2 | Try to union nodes in `bob` Union-Find |\n | | If successful, increment `edgesRequired` |\n\n4. **Final Check**:\n - Ensure both Alice and Bob can fully traverse the graph by checking if their respective Union-Find structures are fully connected.\n\n | Condition | Action |\n |------------------------------------------|---------------------------------|\n | Both `alice` and `bob` are connected | Return `len(edges) - edgesRequired` |\n | Either `alice` or `bob` is not connected | Return `-1` |\n\n#### Example Walkthrough\n\n**Example Input**:\n```python\nn = 4\nedges = [[3,1,2],[3,2,3],[1,1,3],[1,2,4],[1,1,2],[2,3,4]]\n```\n\n**Processing Steps**:\n\n1. **Initialize**:\n - `alice` and `bob` Union-Find instances.\n - `edgesRequired = 0`.\n\n2. **Type 3 Edges**:\n - Process `[3,1,2]`:\n - Union nodes 1 and 2 in both `alice` and `bob`.\n - Increment `edgesRequired` to 1.\n - Process `[3,2,3]`:\n - Union nodes 2 and 3 in both `alice` and `bob`.\n - Increment `edgesRequired` to 2.\n\n3. **Type 1 and Type 2 Edges**:\n - Process `[1,1,3]` for `alice`:\n - Union nodes 1 and 3.\n - Increment `edgesRequired` to 3.\n - Process `[1,2,4]` for `alice`:\n - Union nodes 2 and 4.\n - Increment `edgesRequired` to 4.\n - Process `[1,1,2]` for `alice`:\n - Union not needed (already connected), no increment.\n - Process `[2,3,4]` for `bob`:\n - Union nodes 3 and 4.\n - Increment `edgesRequired` to 5.\n\n4. **Final Check**:\n - Both `alice` and `bob` Union-Find structures are fully connected.\n - Total edges: 6, edges required: 5.\n - Edges removed: `6 - 5 = 1`.\n\n**Output**:\n```python\n1\n```\n\n# Code\n```java []\nclass Solution {\n public int maxNumEdgesToRemove(int n, int[][] edges) {\n UnionFind alice = new UnionFind(n);\n UnionFind bob = new UnionFind(n);\n\n \n int edgesRequired = 0;\n for(int[] edge : edges) {\n if(edge[0]==3) {\n edgesRequired+= (alice.preformUnion(edge[1], edge[2]) | bob.preformUnion(edge[1], edge[2]));\n }\n }\n\n for(int[] edge : edges) {\n if(edge[0]==2) {\n edgesRequired += bob.preformUnion(edge[1], edge[2]);\n } else if(edge[0]==1) {\n edgesRequired += alice.preformUnion(edge[1], edge[2]);\n }\n }\n\n if(alice.isConnected() && bob.isConnected()) {\n return edges.length - edgesRequired;\n }\n\n return -1;\n\n }\n\n class UnionFind {\n\n int[] representative;\n int[] componentSize;\n int components;\n\n UnionFind(int n) {\n components = n;\n representative = new int[n+1];\n componentSize = new int[n+1];\n\n for(int i=0;i<=n;i++) {\n representative[i] = i;\n componentSize[i] = i;\n }\n }\n\n int findRepresentative(int x) {\n if(representative[x] == x) {\n return x;\n }\n\n return representative[x] = findRepresentative(representative[x]);\n }\n\n int preformUnion(int x, int y) {\n x = findRepresentative(x); y = findRepresentative(y);\n\n if(x==y) {\n return 0;\n }\n\n if(componentSize[x]>componentSize[y]) {\n componentSize[x]+=componentSize[y];\n representative[y] = x;\n } else {\n componentSize[y]+=componentSize[x];\n representative[x] = y;\n }\n\n components--;\n return 1;\n }\n\n boolean isConnected() {\n return components==1;\n }\n } \n}\n```\n```C++ []\nclass Solution {\npublic:\n int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {\n class UnionFind {\n public:\n vector<int> parent, size;\n int components;\n UnionFind(int n) {\n components = n;\n parent.resize(n + 1);\n size.resize(n + 1, 1);\n for (int i = 0; i <= n; ++i) {\n parent[i] = i;\n }\n }\n\n int find(int x) {\n if (parent[x] != x) {\n parent[x] = find(parent[x]);\n }\n return parent[x];\n }\n\n bool unite(int x, int y) {\n int rootX = find(x), rootY = find(y);\n if (rootX == rootY) return false;\n if (size[rootX] < size[rootY]) swap(rootX, rootY);\n parent[rootY] = rootX;\n size[rootX] += size[rootY];\n components--;\n return true;\n }\n\n bool isConnected() {\n return components == 1;\n }\n };\n \n UnionFind alice(n), bob(n);\n int edgesRequired = 0;\n \n // Process type 3 edges first\n for (const auto& edge : edges) {\n if (edge[0] == 3) {\n if (alice.unite(edge[1], edge[2]) | bob.unite(edge[1], edge[2])) {\n edgesRequired++;\n }\n }\n }\n \n // Process type 1 and type 2 edges\n for (const auto& edge : edges) {\n if (edge[0] == 1) {\n if (alice.unite(edge[1], edge[2])) {\n edgesRequired++;\n }\n } else if (edge[0] == 2) {\n if (bob.unite(edge[1], edge[2])) {\n edgesRequired++;\n }\n }\n }\n \n // Check if both are fully connected\n if (alice.isConnected() && bob.isConnected()) {\n return edges.size() - edgesRequired;\n }\n \n return -1;\n }\n};\n```\n```Python []\nclass Solution(object):\n def maxNumEdgesToRemove(self, n, edges):\n # UnionFind class definition\n class UnionFind:\n def __init__(self, n):\n self.representative = list(range(n + 1))\n self.component_size = [1] * (n + 1)\n self.components = n\n \n def find_representative(self, x):\n if self.representative[x] == x:\n return x\n self.representative[x] = self.find_representative(self.representative[x])\n return self.representative[x]\n \n def perform_union(self, x, y):\n x = self.find_representative(x)\n y = self.find_representative(y)\n \n if x == y:\n return 0\n \n if self.component_size[x] > self.component_size[y]:\n self.component_size[x] += self.component_size[y]\n self.representative[y] = x\n else:\n self.component_size[y] += self.component_size[x]\n self.representative[x] = y\n \n self.components -= 1\n return 1\n \n def is_connected(self):\n return self.components == 1\n \n # Main function logic\n alice = UnionFind(n)\n bob = UnionFind(n)\n \n edges_required = 0\n \n for edge in edges:\n if edge[0] == 3:\n edges_required += (alice.perform_union(edge[1], edge[2]) | bob.perform_union(edge[1], edge[2]))\n \n for edge in edges:\n if edge[0] == 2:\n edges_required += bob.perform_union(edge[1], edge[2])\n elif edge[0] == 1:\n edges_required += alice.perform_union(edge[1], edge[2])\n \n if alice.is_connected() and bob.is_connected():\n return len(edges) - edges_required\n \n return -1\n```\n```JavaScript []\nvar maxNumEdgesToRemove = function(n, edges) {\n // UnionFind class definition\n class UnionFind {\n constructor(n) {\n this.representative = Array.from({ length: n + 1 }, (_, index) => index);\n this.componentSize = Array.from({ length: n + 1 }, () => 1);\n this.components = n;\n }\n\n findRepresentative(x) {\n if (this.representative[x] === x) {\n return x;\n }\n this.representative[x] = this.findRepresentative(this.representative[x]);\n return this.representative[x];\n }\n\n performUnion(x, y) {\n x = this.findRepresentative(x);\n y = this.findRepresentative(y);\n\n if (x === y) {\n return 0;\n }\n\n if (this.componentSize[x] > this.componentSize[y]) {\n this.componentSize[x] += this.componentSize[y];\n this.representative[y] = x;\n } else {\n this.componentSize[y] += this.componentSize[x];\n this.representative[x] = y;\n }\n\n this.components--;\n return 1;\n }\n\n isConnected() {\n return this.components === 1;\n }\n }\n\n // Main function logic\n let alice = new UnionFind(n);\n let bob = new UnionFind(n);\n\n let edgesRequired = 0;\n\n for (let edge of edges) {\n if (edge[0] === 3) {\n edgesRequired += (alice.performUnion(edge[1], edge[2]) | bob.performUnion(edge[1], edge[2]));\n }\n }\n\n for (let edge of edges) {\n if (edge[0] === 2) {\n edgesRequired += bob.performUnion(edge[1], edge[2]);\n } else if (edge[0] === 1) {\n edgesRequired += alice.performUnion(edge[1], edge[2]);\n }\n }\n\n if (alice.isConnected() && bob.isConnected()) {\n return edges.length - edgesRequired;\n }\n\n return -1;\n};\n```\n\n | 164 | 1 | ['Union Find', 'Graph', 'Python', 'C++', 'Java', 'JavaScript'] | 16 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | [Python] Union Find | python-union-find-by-lee215-20ct | Intuition\nAdd Type3 first, then check Type 1 and Type 2.\n\n\n# Explanation\nGo through all edges of type 3 (Alice and Bob)\nIf not necessary to add, increment | lee215 | NORMAL | 2020-09-06T04:06:21.366258+00:00 | 2020-09-06T06:28:39.127655+00:00 | 13,985 | false | # **Intuition**\nAdd Type3 first, then check Type 1 and Type 2.\n<br>\n\n# **Explanation**\nGo through all edges of type 3 (Alice and Bob)\nIf not necessary to add, increment `res`.\nOtherwith increment `e1` and `e2`.\n\nGo through all edges of type 1 (Alice)\nIf not necessary to add, increment `res`.\nOtherwith increment `e1`.\n\nGo through all edges of type 2 (Bob)\nIf not necessary to add, increment `res`.\nOtherwith increment `e2`.\n\nIf Alice\'s\'graph is connected, `e1 == n - 1` should valid.\nIf Bob\'s graph is connected, `e2 == n - 1` should valid.\nIn this case we return `res`,\notherwise return `-1`.\n<br>\n\n# Complexity\nTime O(E), if union find with compression and rank\nSpace O(E)\n<br>\n\n**Python:**\n```py\n def maxNumEdgesToRemove(self, n, edges):\n # Union find\n def find(i):\n if i != root[i]:\n root[i] = find(root[i])\n return root[i]\n\n def uni(x, y):\n x, y = find(x), find(y)\n if x == y: return 0\n root[x] = y\n return 1\n\n res = e1 = e2 = 0\n\n # Alice and Bob\n root = range(n + 1)\n for t, i, j in edges:\n if t == 3:\n if uni(i, j):\n e1 += 1\n e2 += 1\n else:\n res += 1\n root0 = root[:]\n\n # only Alice\n for t, i, j in edges:\n if t == 1:\n if uni(i, j):\n e1 += 1\n else:\n res += 1\n\n # only Bob\n root = root0\n for t, i, j in edges:\n if t == 2:\n if uni(i, j):\n e2 += 1\n else:\n res += 1\n\n return res if e1 == e2 == n - 1 else -1\n```\n | 160 | 5 | [] | 34 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Image Explanation🏆- [Easiest & Complete Intuition] - C++/Java/Python | image-explanation-easiest-complete-intui-vllm | Video Solution (Aryan Mittal) - Link in LeetCode Profile\nRemove Max Number of Edges to Keep Graph Fully Traversable by Aryan Mittal\n\n\n\n# Approach & Intutio | lc00701 | NORMAL | 2023-04-30T01:35:53.706797+00:00 | 2023-04-30T01:44:00.750617+00:00 | 16,838 | false | # Video Solution (`Aryan Mittal`) - Link in LeetCode Profile\n`Remove Max Number of Edges to Keep Graph Fully Traversable` by `Aryan Mittal`\n\n\n\n# Approach & Intution\n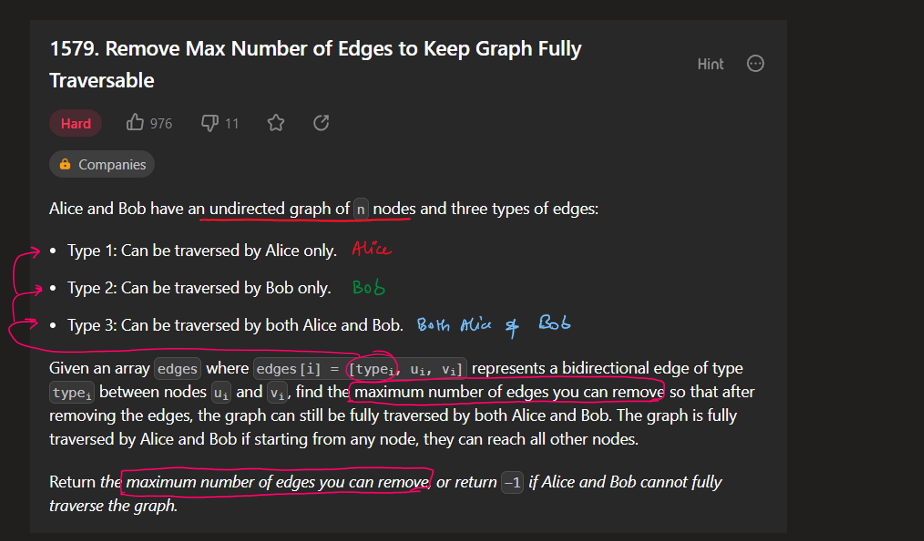\n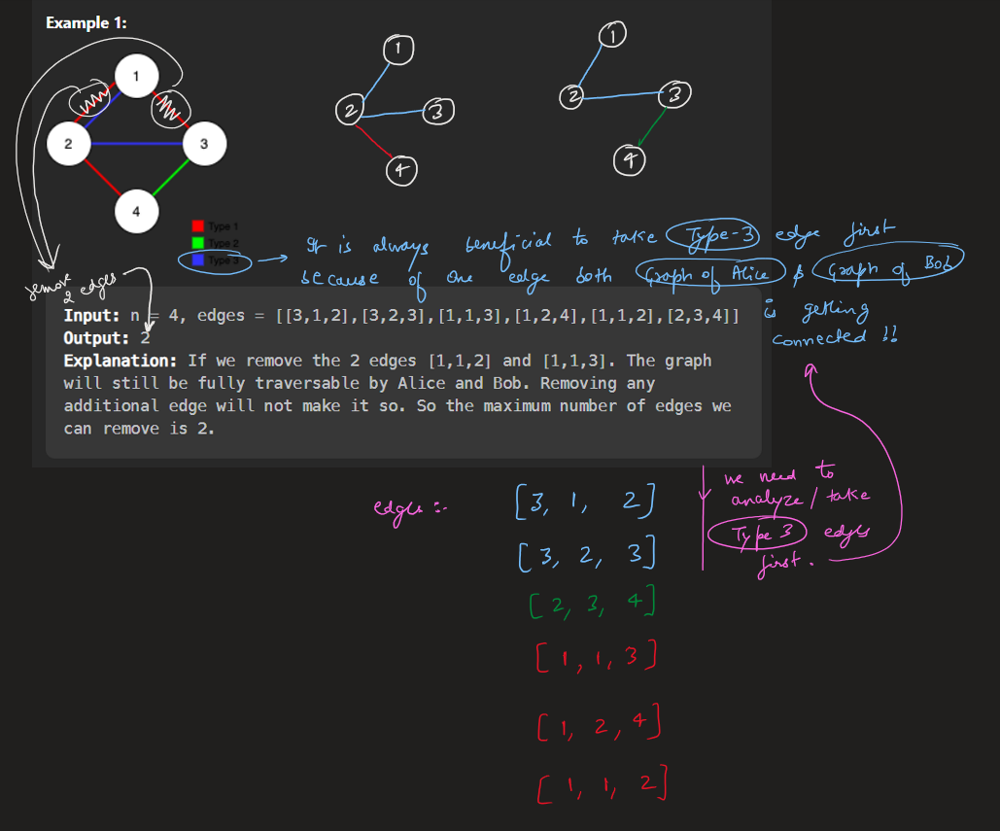\n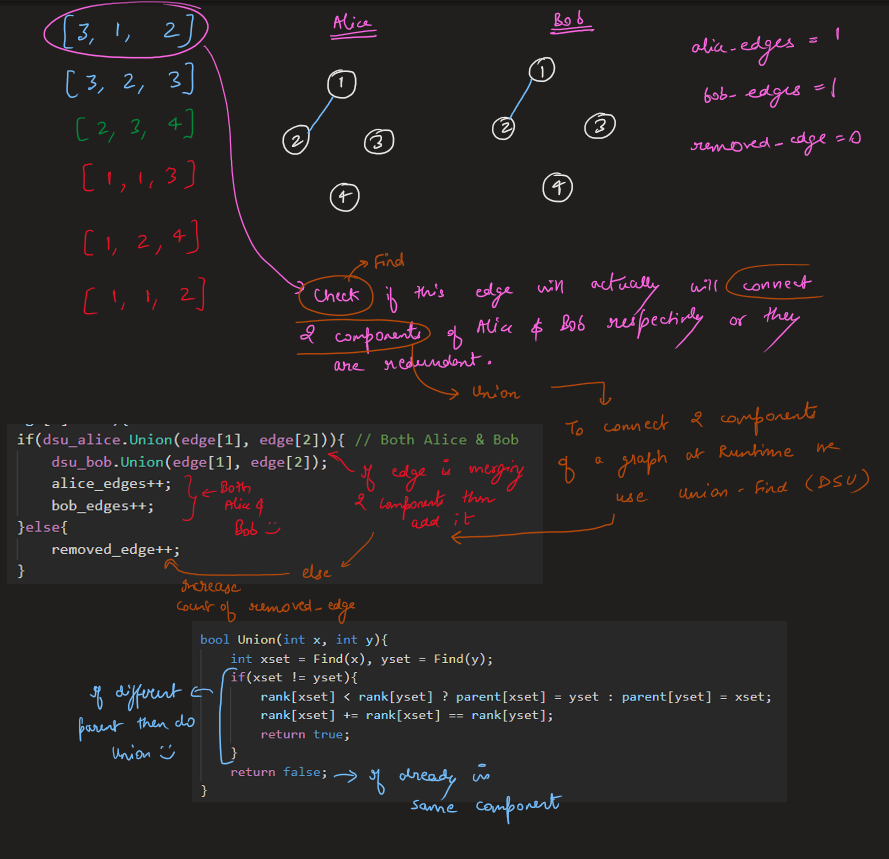\n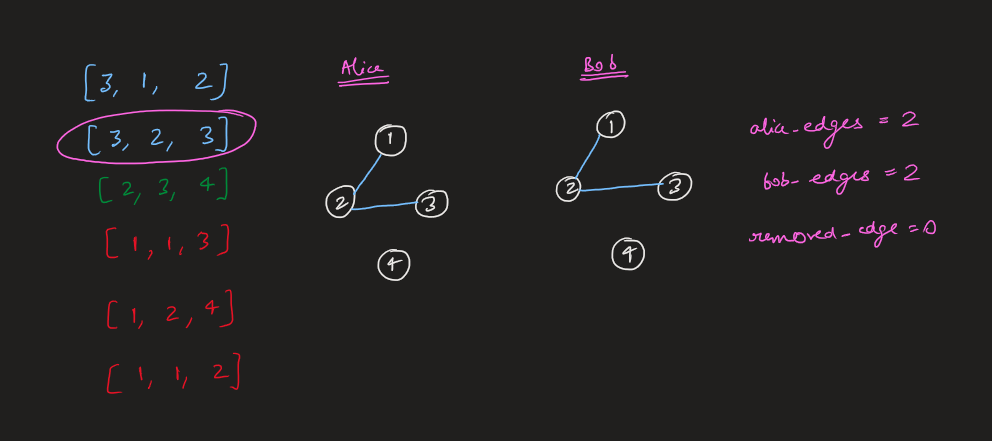\n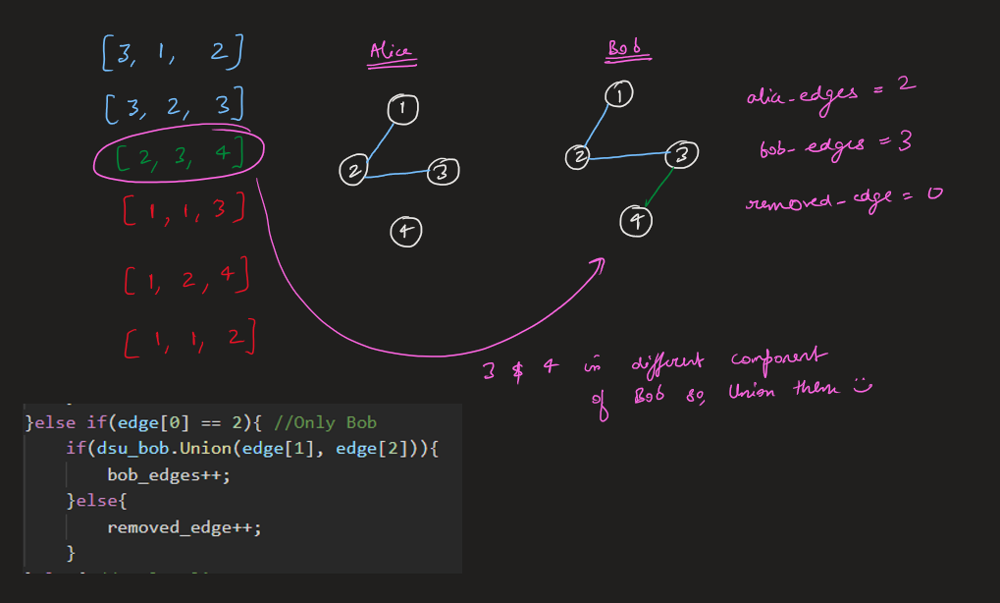\n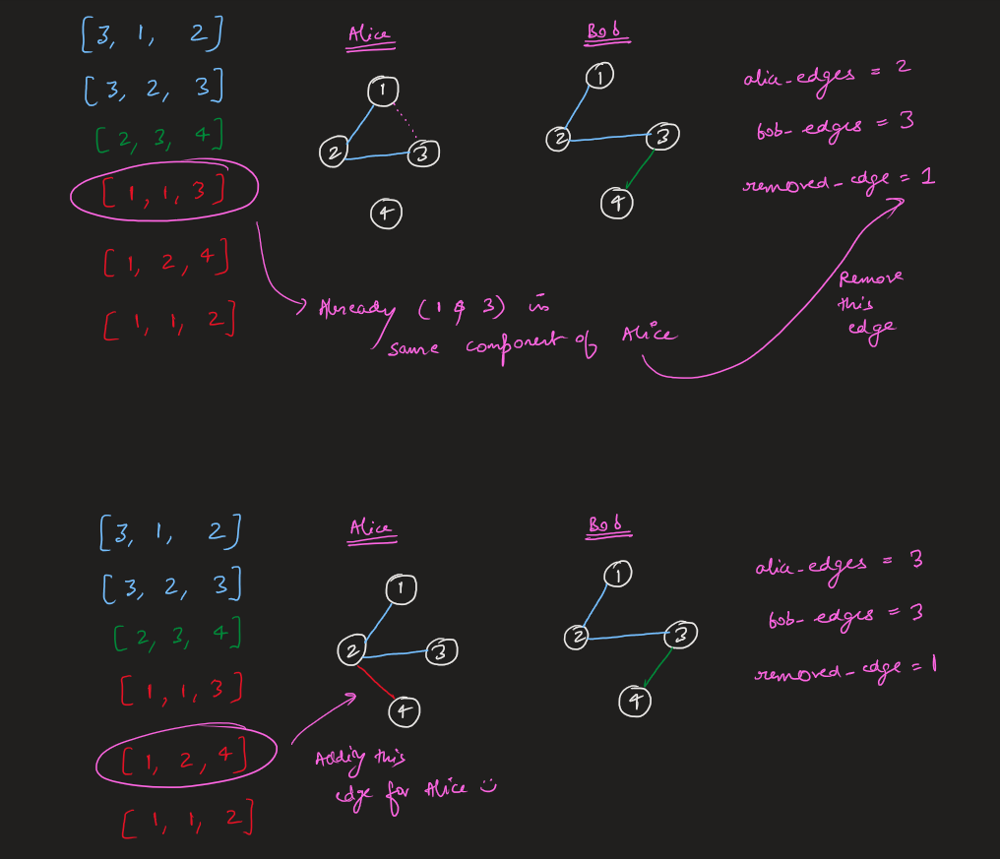\n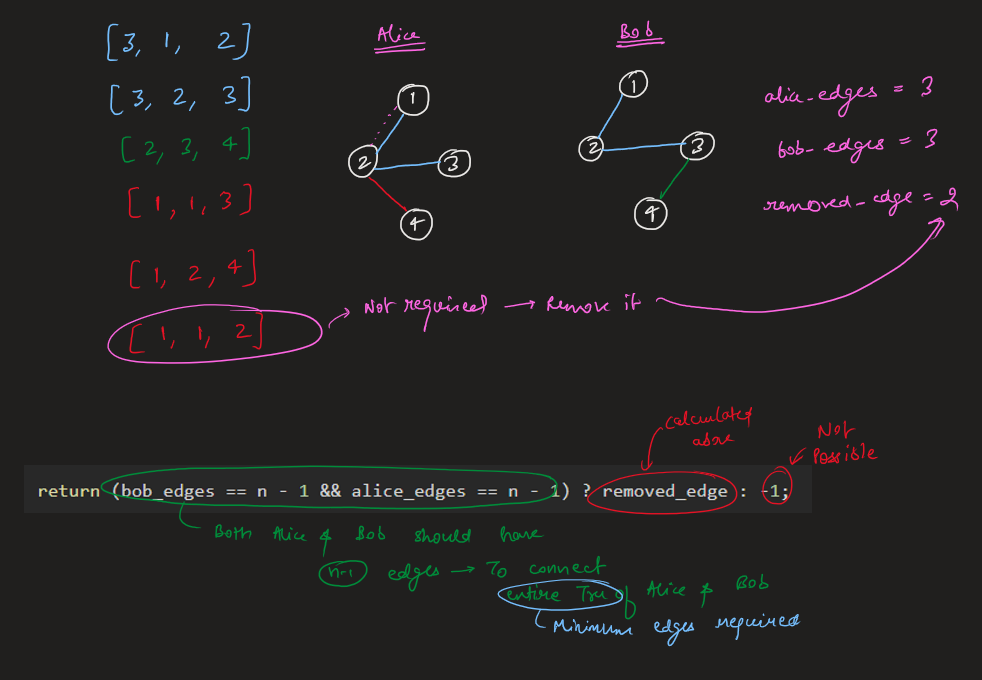\n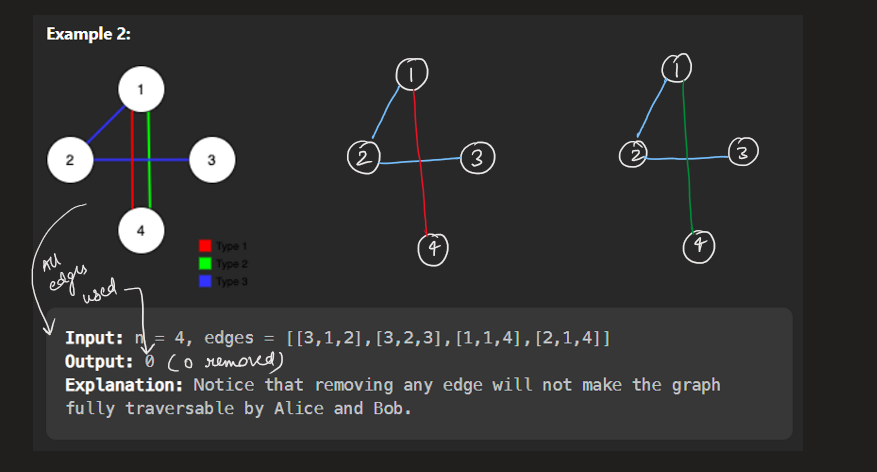\n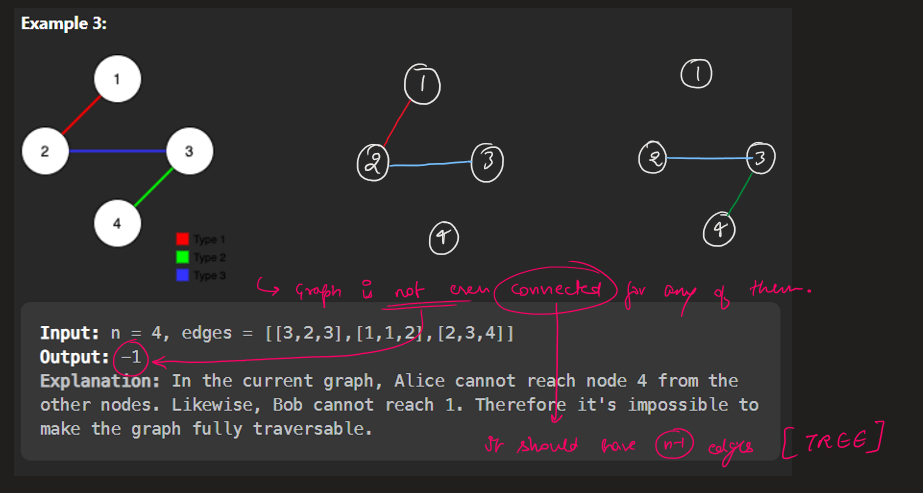\n\n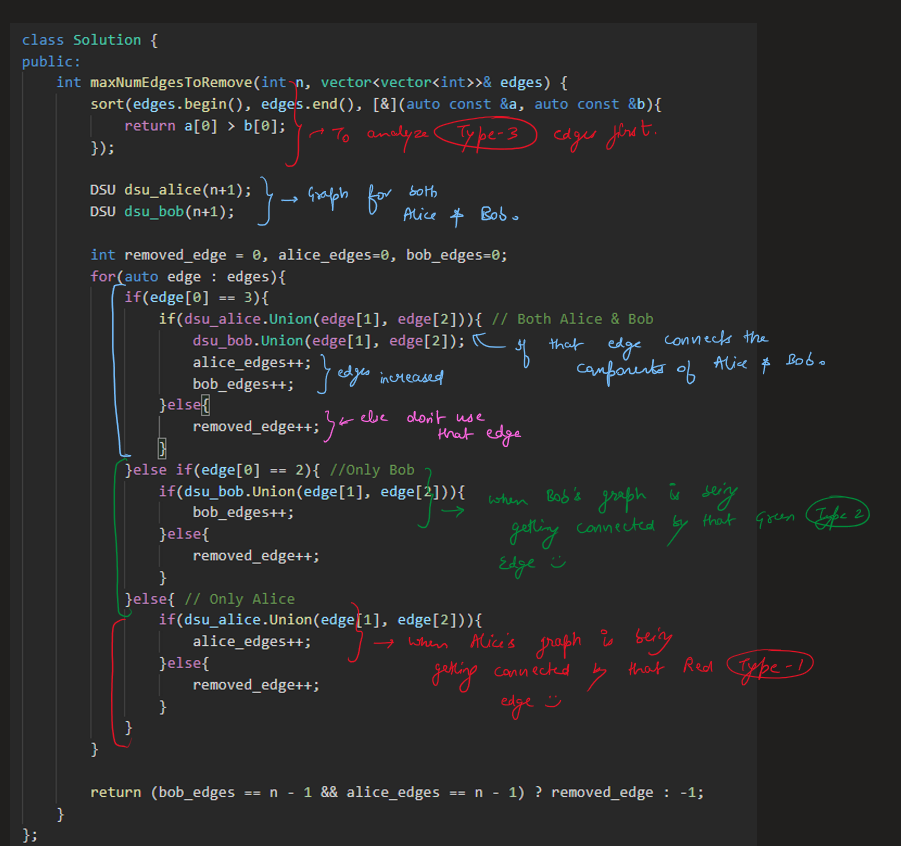\n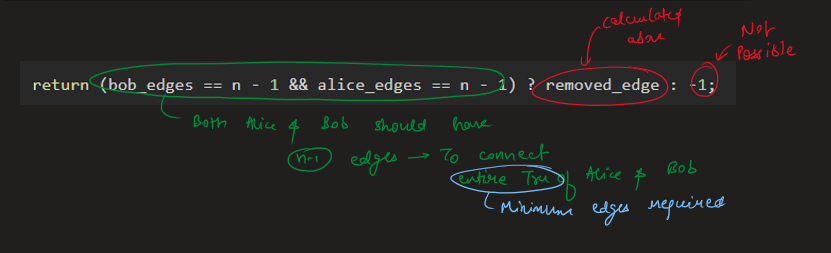\n\n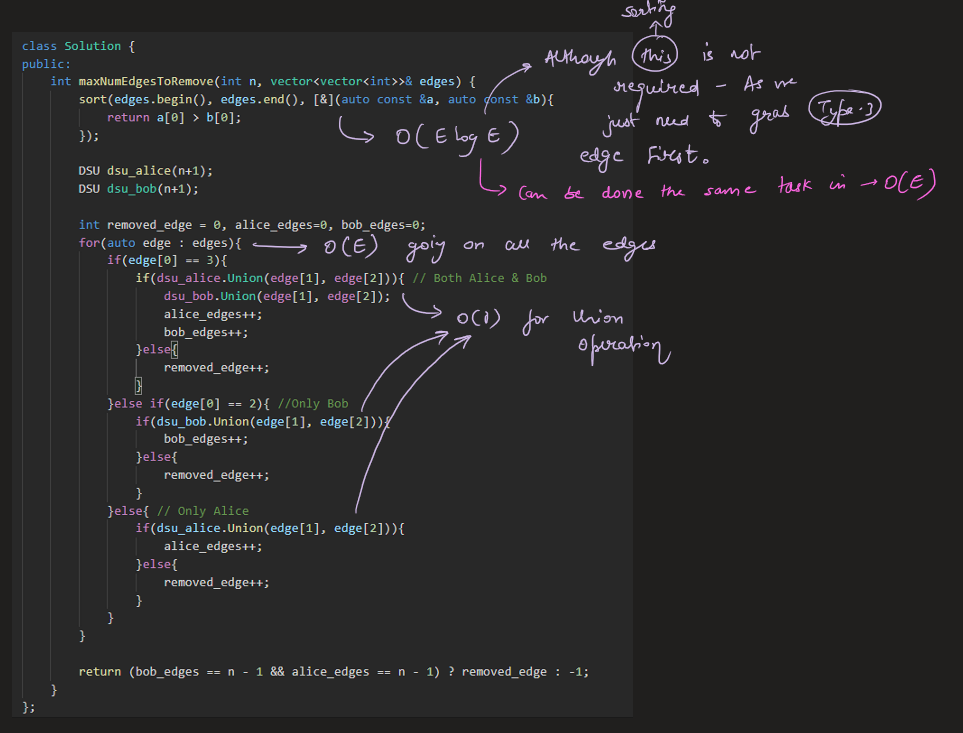\n\n\n# Code\n```C++ []\nclass DSU {\npublic:\n vector<int> parent, rank;\n DSU(int n){\n parent.resize(n, 0);\n rank.resize(n, 0);\n \n for(int i=0;i<n;i++) parent[i] = i;\n }\n \n int Find(int x){\n return parent[x] = parent[x] == x ? x : Find(parent[x]);\n }\n \n bool Union(int x, int y){\n int xset = Find(x), yset = Find(y);\n if(xset != yset){\n rank[xset] < rank[yset] ? parent[xset] = yset : parent[yset] = xset;\n rank[xset] += rank[xset] == rank[yset];\n return true;\n }\n return false;\n }\n};\n\nclass Solution {\npublic:\n int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {\n sort(edges.begin(), edges.end(), [&](auto const &a, auto const &b){\n return a[0] > b[0];\n });\n\n DSU dsu_alice(n+1);\n DSU dsu_bob(n+1);\n\n int removed_edge = 0, alice_edges=0, bob_edges=0;\n for(auto edge : edges){\n if(edge[0] == 3){\n if(dsu_alice.Union(edge[1], edge[2])){ // Both Alice & Bob\n dsu_bob.Union(edge[1], edge[2]);\n alice_edges++;\n bob_edges++;\n }else{\n removed_edge++;\n }\n }else if(edge[0] == 2){ //Only Bob\n if(dsu_bob.Union(edge[1], edge[2])){\n bob_edges++;\n }else{\n removed_edge++;\n }\n }else{ // Only Alice\n if(dsu_alice.Union(edge[1], edge[2])){\n alice_edges++;\n }else{\n removed_edge++;\n }\n }\n }\n\n return (bob_edges == n - 1 && alice_edges == n - 1) ? removed_edge : -1;\n }\n};\n```\n```Java []\nclass DSU {\n int[] parent;\n int[] rank;\n \n public DSU(int n) {\n parent = new int[n];\n rank = new int[n];\n for (int i = 0; i < n; i++) {\n parent[i] = i;\n }\n }\n \n public int find(int x) {\n if (parent[x] != x) {\n parent[x] = find(parent[x]);\n }\n return parent[x];\n }\n \n public boolean union(int x, int y) {\n int xset = find(x), yset = find(y);\n if (xset != yset) {\n if (rank[xset] < rank[yset]) {\n parent[xset] = yset;\n } else if (rank[xset] > rank[yset]) {\n parent[yset] = xset;\n } else {\n parent[xset] = yset;\n rank[yset]++;\n }\n return true;\n }\n return false;\n }\n}\n\nclass Solution {\n public int maxNumEdgesToRemove(int n, int[][] edges) {\n Arrays.sort(edges, (a, b) -> Integer.compare(b[0], a[0]));\n \n DSU dsu_alice = new DSU(n+1);\n DSU dsu_bob = new DSU(n+1);\n \n int removed_edge = 0, alice_edges = 0, bob_edges = 0;\n for (int[] edge : edges) {\n if (edge[0] == 3) {\n if (dsu_alice.union(edge[1], edge[2])) {\n dsu_bob.union(edge[1], edge[2]);\n alice_edges++;\n bob_edges++;\n } else {\n removed_edge++;\n }\n } else if (edge[0] == 2) {\n if (dsu_bob.union(edge[1], edge[2])) {\n bob_edges++;\n } else {\n removed_edge++;\n }\n } else {\n if (dsu_alice.union(edge[1], edge[2])) {\n alice_edges++;\n } else {\n removed_edge++;\n }\n }\n }\n \n return (bob_edges == n - 1 && alice_edges == n - 1) ? removed_edge : -1;\n }\n}\n```\n```Python []\nclass DSU:\n def __init__(self, n):\n self.parent = [i for i in range(n)]\n self.rank = [0] * n\n \n def find(self, x):\n if self.parent[x] != x:\n self.parent[x] = self.find(self.parent[x])\n return self.parent[x]\n \n def union(self, x, y):\n xset, yset = self.find(x), self.find(y)\n if xset != yset:\n if self.rank[xset] < self.rank[yset]:\n self.parent[xset] = yset\n elif self.rank[xset] > self.rank[yset]:\n self.parent[yset] = xset\n else:\n self.parent[xset] = yset\n self.rank[yset] += 1\n return True\n return False\n\nclass Solution:\n def maxNumEdgesToRemove(self, n: int, edges: List[List[int]]) -> int:\n edges.sort(reverse=True)\n dsu_alice = DSU(n+1)\n dsu_bob = DSU(n+1)\n removed_edge = 0\n alice_edges, bob_edges = 0, 0\n for edge in edges:\n if edge[0] == 3:\n if dsu_alice.union(edge[1], edge[2]):\n dsu_bob.union(edge[1], edge[2])\n alice_edges += 1\n bob_edges += 1\n else:\n removed_edge += 1\n elif edge[0] == 2:\n if dsu_bob.union(edge[1], edge[2]):\n bob_edges += 1\n else:\n removed_edge += 1\n else:\n if dsu_alice.union(edge[1], edge[2]):\n alice_edges += 1\n else:\n removed_edge += 1\n return removed_edge if bob_edges == n - 1 == alice_edges else -1\n``` | 112 | 0 | ['Union Find', 'Graph', 'C++', 'Java', 'Python3'] | 9 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | C++ Union-Find Both/One | c-union-find-bothone-by-votrubac-8q7x | Intuition\nWe would use union-find to solve this problem for one person. For two (or more) people, we first populate our "shared" disjoined set, using type 3 ed | votrubac | NORMAL | 2020-09-06T04:03:23.895281+00:00 | 2020-09-06T06:14:46.699340+00:00 | 7,535 | false | #### Intuition\nWe would use union-find to solve this problem for one person. For two (or more) people, we first populate our "shared" disjoined set, using type 3 edges.\n\nThen, we process Alice and Bob independently, using the "shared" disjoined set as a starting point.\n\nEvery time we find a non-redundant edge, we increment `used`. We also check that the graph is fully connected for each person.\n\nIn the end, we can remove `total - used` edges.\n\n**C++**\n```cpp\nint find(vector<int> &ds, int i) {\n return ds[i] < 0 ? i : ds[i] = find(ds, ds[i]);\n}\nint maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {\n vector<int> ds_both(n + 1, -1);\n int used = 0;\n for (int type = 3; type > 0; --type) {\n auto ds_one = ds_both;\n auto &ds = type == 3 ? ds_both : ds_one;\n for (auto &e : edges)\n if (e[0] == type) {\n int i = find(ds, e[1]), j = find(ds, e[2]);\n if (i != j) {\n ++used;\n if (ds[j] < ds[i])\n swap(i, j);\n ds[i] += ds[j];\n ds[j] = i;\n }\n }\n if (type != 3 && ds[find(ds, 1)] != -n)\n return -1;\n }\n return edges.size() - used;\n}\n```\n**Complexity Analysis**\n- Time: O(m), where m is the number of edges. We go through all edges 3 times. The complexity of the `find` operation is O(\uD835\uDEFC(n)) as we use both rank and path compression. \uD835\uDEFC(n) can be considered a constant for all practical purposes.\n- Memory: O(n) for a disjoined set. | 53 | 5 | [] | 12 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | 💯✅🔥Easy Java ,Python3 ,C++ Solution|| 32 ms ||≧◠‿◠≦✌ | easy-java-python3-c-solution-32-ms-_-by-5z0aj | Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem of "Maximum Number of Edges to Remove to Ensure Graph Connectivity" can be | suyalneeraj09 | NORMAL | 2024-06-30T02:41:15.075417+00:00 | 2024-06-30T02:41:15.075437+00:00 | 8,090 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem of "Maximum Number of Edges to Remove to Ensure Graph Connectivity" can be solved using a Union-Find data structure. The idea is to group the nodes into connected components and then remove the edges that are not necessary for maintaining the connectivity of the graph.\n\n---\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe approach taken in the provided code is as follows:\n1. Sort the edges in descending order of their type (type 3, then type 2, then type 1).\n1. Create two Union-Find data structures, one for Alice and one for Bob.\n1. Iterate through the sorted edges and process them as follows:\n - For type 3 edges, try to unite the nodes in both Alice\'s and Bob\'s Union-Find structures. If either of the unions is successful, increment the edgeAdd counter.\n - For type 2 edges, try to unite the nodes in Bob\'s Union-Find structure. If the union is successful, increment the edgeAdd counter.\n - For type 1 edges, try to unite the nodes in Alice\'s Union-Find structure. If the union is successful, increment the edgeAdd counter.\n1. After processing all the edges, check if both Alice and Bob have a single connected component (i.e., their Union-Find structures are united). If so, return the number of edges that were not added (edges.length - edgeAdd). Otherwise, return -1 to indicate that it\'s not possible to ensure connectivity for both Alice and Bob.\n---\n# Complexity\n- Time complexity:O(n log n).\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n---\n- Space complexity:O(n).\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n---\n# Code\n```java []\nclass Solution {\n public int maxNumEdgesToRemove(int n, int[][] edges) {\n Arrays.sort(edges, (a, b) -> b[0] - a[0]);\n \n int edgeAdd = 0;\n \n UnionFind alice = new UnionFind(n);\n UnionFind bob = new UnionFind(n);\n \n for (int[] edge : edges) {\n int type = edge[0];\n int a = edge[1];\n int b = edge[2];\n \n switch (type) {\n case 3:\n if (alice.unite(a, b) | bob.unite(a, b)) {\n edgeAdd++;\n }\n break;\n case 2:\n if (bob.unite(a, b)) {\n edgeAdd++;\n }\n break;\n case 1:\n if (alice.unite(a, b)) {\n edgeAdd++;\n } \n break;\n }\n }\n \n return (alice.united() && bob.united()) ? edges.length - edgeAdd : -1;\n }\n \n private class UnionFind {\n int[] component;\n int distinctComponents;\n \n public UnionFind(int n) {\n component = new int[n+1];\n for (int i = 0; i <= n; i++) {\n component[i] = i;\n }\n distinctComponents = n;\n }\n \n private boolean unite(int a, int b) {\n if (findComponent(a) != findComponent(b)) {\n component[findComponent(a)] = b;\n distinctComponents--;\n return true;\n }\n \n return false;\n }\n \n private int findComponent(int a) {\n if (component[a] != a) {\n component[a] = findComponent(component[a]);\n }\n return component[a];\n }\n \n private boolean united() {\n return distinctComponents == 1;\n }\n \n }\n}\n```\n```python3 []\nclass UnionFind:\n """A minimalist standalone union-find implementation."""\n def __init__(self, n):\n self.count = n # number of disjoint sets \n self.parent = list(range(n)) # parent of given nodes\n self.rank = [1]*n # rank (aka size) of sub-tree \n \n def find(self, p):\n """Find with path compression."""\n if p != self.parent[p]: \n self.parent[p] = self.find(self.parent[p]) # path compression \n return self.parent[p]\n \n def union(self, p, q):\n """Union with ranking."""\n prt, qrt = self.find(p), self.find(q)\n if prt == qrt: return False\n self.count -= 1 # one more connection => one less disjoint \n if self.rank[prt] > self.rank[qrt]: prt, qrt = qrt, prt # add small sub-tree to large sub-tree for balancing\n self.parent[prt] = qrt\n self.rank[qrt] += self.rank[prt] # ranking \n return True\n \n \nclass Solution:\n def maxNumEdgesToRemove(self, n: int, edges: List[List[int]]) -> int:\n ufa = UnionFind(n) # for Alice\n ufb = UnionFind(n) # for Bob\n \n ans = 0\n edges.sort(reverse=True) \n for t, u, v in edges: \n u, v = u-1, v-1\n if t == 3: ans += not (ufa.union(u, v) and ufb.union(u, v)) # Alice & Bob\n elif t == 2: ans += not ufb.union(u, v) # Bob only\n else: ans += not ufa.union(u, v) # Alice only\n return ans if ufa.count == 1 and ufb.count == 1 else -1 # check if uf is connected \n```\n```C++ []\nclass UnionFind {\n vector<int> component;\n int distinctComponents;\npublic:\n \n UnionFind(int n) {\n\t distinctComponents = n;\n for (int i=0; i<=n; i++) {\n component.push_back(i);\n }\n }\n \n bool unite(int a, int b) { \n if (findComponent(a) == findComponent(b)) {\n return false;\n }\n component[findComponent(a)] = b;\n distinctComponents--;\n return true;\n }\n \n int findComponent(int a) {\n if (component[a] != a) {\n component[a] = findComponent(component[a]);\n }\n return component[a];\n }\n \n bool united() {\n return distinctComponents == 1;\n }\n};\n\nclass Solution {\n \npublic:\n int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {\n // Sort edges by their type such that all type 3 edges will be at the beginning.\n sort(edges.begin(), edges.end(), [] (vector<int> &a, vector<int> &b) { return a[0] > b[0]; });\n \n int edgesAdded = 0; // Stores the number of edges added to the initial empty graph.\n \n UnionFind bob(n), alice(n); // Track whether bob and alice can traverse the entire graph,\n // are there still more than one distinct components, etc.\n \n for (auto &edge: edges) { // For each edge -\n int type = edge[0], one = edge[1], two = edge[2];\n switch(type) {\n case 3:\n edgesAdded += (bob.unite(one, two) | alice.unite(one, two));\n break;\n case 2:\n edgesAdded += bob.unite(one, two);\n break;\n case 1:\n edgesAdded += alice.unite(one, two);\n break;\n }\n }\n \n return (bob.united() && alice.united()) ? (edges.size()-edgesAdded) : -1; // Yay, solved.\n }\n};\n```\n---\n\n\n\n\n | 50 | 1 | ['Union Find', 'Graph', 'C++', 'Java', 'Python3'] | 4 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Beats 100% | beats-100-by-vigneshreddy06-cih2 | Intuition\n\n\n\n\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\ | vigneshreddy06 | NORMAL | 2024-06-30T06:57:13.008901+00:00 | 2024-06-30T06:57:13.008932+00:00 | 3,196 | false | # Intuition\n\n\n\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(E\u22C5\u03B1(n))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n+E)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code C++\n```\n#include <bits/stdc++.h>\nusing namespace std;\n\nclass DSU {\npublic:\n vector<int> parent, rank;\n \n DSU(int n) : parent(n+1), rank(n+1, 0) {\n iota(parent.begin(), parent.end(), 0);\n }\n\n int find(int u) {\n if (u != parent[u])\n parent[u] = find(parent[u]);\n return parent[u];\n }\n\n bool unite(int u, int v) {\n int root_u = find(u), root_v = find(v);\n if (root_u == root_v) return false;\n if (rank[root_u] > rank[root_v]) {\n parent[root_v] = root_u;\n } else if (rank[root_u] < rank[root_v]) {\n parent[root_u] = root_v;\n } else {\n parent[root_v] = root_u;\n rank[root_u]++;\n }\n return true;\n }\n};\n\nclass Solution {\npublic:\n int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {\n DSU dsuAlice(n), dsuBob(n);\n int removedEdges = 0;\n int usedEdgesAlice = 0, usedEdgesBob = 0;\n\n for (const auto& edge : edges) {\n if (edge[0] == 3) {\n bool aliceUnion = dsuAlice.unite(edge[1], edge[2]);\n bool bobUnion = dsuBob.unite(edge[1], edge[2]);\n if (!aliceUnion && !bobUnion) {\n removedEdges++;\n } else {\n if (aliceUnion) usedEdgesAlice++;\n if (bobUnion) usedEdgesBob++;\n }\n }\n }\n\n for (const auto& edge : edges) {\n if (edge[0] == 1) {\n if (dsuAlice.unite(edge[1], edge[2])) {\n usedEdgesAlice++;\n } else {\n removedEdges++;\n }\n }\n }\n\n for (const auto& edge : edges) {\n if (edge[0] == 2) {\n if (dsuBob.unite(edge[1], edge[2])) {\n usedEdgesBob++;\n } else {\n removedEdges++;\n }\n }\n }\n\n if (usedEdgesAlice == n-1 && usedEdgesBob == n-1) {\n return removedEdges;\n }\n return -1;\n }\n}; \n//if you upvote this you will get a good news in 1 hour \n```\n# Code Python3\n```\nclass Solution:\n def maxNumEdgesToRemove(self, n: int, edges: List[List[int]]) -> int:\n auf = UnionFind(n)\n buf = UnionFind(n)\n res = 0\n for edge in edges:\n if edge[0] == 3:\n if auf.union(edge[1], edge[2]) == 1:\n buf.union(edge[1], edge[2])\n res += 1\n if auf.is_connected() and buf.is_connected():\n return len(edges) - res\n for edge in edges:\n if edge[0] == 1:\n res += auf.union(edge[1], edge[2])\n if edge[0] == 2:\n res += buf.union(edge[1], edge[2])\n if auf.is_connected() and buf.is_connected():\n return len(edges) - res\n return -1\n\nclass UnionFind:\n def __init__(self, n):\n self.parent = [0] * (n + 1)\n self.node_count = n\n def find(self, x):\n if self.parent[x] == 0 or self.parent[x] == x:\n return x\n self.parent[x] = self.find(self.parent[x])\n return self.parent[x]\n def union(self, x, y):\n px = self.find(x)\n py = self.find(y)\n if px == py:\n return 0\n self.parent[py] = px\n self.node_count -= 1\n return 1\n def is_connected(self):\n return self.node_count == 1\n#if you upvote this you will get a good news in 1 hour \n```\n | 44 | 0 | ['C++', 'Python3'] | 5 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | [Java] Union-find solution | java-union-find-solution-by-marvinbai-8rsr | When iterating over each edge, we check if the roots of the two nodes are the same: \n\n If not, then this is a critical path which cannot be removed. And we co | marvinbai | NORMAL | 2020-09-06T04:00:50.037836+00:00 | 2020-09-06T19:12:26.788171+00:00 | 3,073 | false | When iterating over each edge, we check if the roots of the two nodes are the same: \n\n* If not, then this is a critical path which cannot be removed. And we connect these two nodes.\n\n* If yes, then this is a redundant path which can be removed. The result needs to increment by 1.\n\nHere order matters. Therefore we need to sort the edge by type. Type 3 comes first, then type 1 or 2. For type 3 edge, if and only if it is redundant for both players, then we can say that this path can be removed, otherwise not.\n\nAnother thing we need to check is whether the original graph is traversable for both players. So whenever we connect two new nodes, we decrease the total number of components in the graph by 1. The graph is only traversable when the total number of components is 1.\n\n```\nclass Solution {\n public int maxNumEdgesToRemove(int n, int[][] edges) {\n Arrays.sort(edges, (a, b) -> (b[0] - a[0]));\n int[] roots1 = new int[n + 1];\n int[] roots2 = new int[n + 1];\n for(int i = 1; i <= n; i++) {\n roots1[i] = i;\n roots2[i] = i;\n }\n int n1 = n, n2 = n; // Number of components for two players.\n int res = 0;\n for(int[] e : edges) {\n if(e[0] == 1) {\n int root_a = find(e[1], roots1);\n int root_b = find(e[2], roots1);\n if(root_a == root_b) { // If roots are the same, then this is a redundant edge and can be removed.\n res++;\n } else {\n roots1[root_a] = root_b; // If roots are different, we connect two different components.\n n1--;\n }\n } else if(e[0] == 2) {\n int root_a = find(e[1], roots2);\n int root_b = find(e[2], roots2);\n if(root_a == root_b) {\n res++;\n } else {\n roots2[root_a] = root_b;\n n2--;\n }\n } else {\n int root_a1 = find(e[1], roots1);\n int root_b1 = find(e[2], roots1);\n int root_a2 = find(e[1], roots2);\n int root_b2 = find(e[2], roots2);\n if(root_a1 != root_b1) {\n roots1[root_a1] = root_b1;\n n1--;\n }\n if(root_a2 != root_b2) {\n roots2[root_a2] = root_b2;\n n2--;\n }\n if(root_a1 == root_b1 && root_a2 == root_b2) {\n res++;\n }\n }\n }\n if(n1 != 1 || n2 != 1) return -1; // If total number of components is not one for either players, return -1.\n return res;\n }\n \n private int find(int i, int[] roots) {\n int j = i;\n while(roots[i] != i) {\n i = roots[i];\n }\n roots[j] = i;\n return i;\n }\n}\n``` | 35 | 1 | [] | 8 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | ✔💯 DAY 395 | DSU | 100% 0ms | [PYTHON/JAVA/C++] | EXPLAINED | Approach 🆙🆙🆙 | day-395-dsu-100-0ms-pythonjavac-explaine-qdrw | Please Upvote as it really motivates me \uD83C\uDD99\uD83C\uDD99\uD83C\uDD99\n\n\n# Intuition \n##### \u2022\tWe have a graph with N nodes and bidirectional edg | ManojKumarPatnaik | NORMAL | 2023-04-30T04:56:52.792118+00:00 | 2023-05-01T06:51:47.668118+00:00 | 3,436 | false | # Please Upvote as it really motivates me \uD83C\uDD99\uD83C\uDD99\uD83C\uDD99\n\n\n# Intuition \n##### \u2022\tWe have a graph with N nodes and bidirectional edges of three types: Type 1 (Alice only), Type 2 (Bob only), and Type 3 (both Alice and Bob).\n##### \u2022\tWe need to find the maximum number of edges that can be removed while still allowing both Alice and Bob to reach any node starting from any node via the remaining edges.\n##### \u2022\tWe can assume that there are two graphs, one for Alice and one for Bob, where the first graph has edges only of Type 1 and 3, and the second graph has edges only of Type 2 and 3.\n##### \u2022\tAn edge is useful only if it connects two nodes that are not already connected via some other edge or path.\n##### \u2022\tWe can use the Disjoint Set Union (DSU) data structure to detect if two nodes are connected via some path or not in O(\u03B1(N)), where \u03B1(N) is the extremely fast inverse Ackermann function.\n##### \u2022\tWe can use DSU to perform the union of two nodes for an edge, and if the nodes were not connected earlier (i.e., they have a different representative), then we know this edge is needed.\n##### \u2022\tFor every edge, if the two nodes were not connected earlier, we know this edge is required. To get the answer, we can subtract the number of required edges from the total number of edges.\n##### \u2022\tSince Type 3 edges are the most useful (as one Type 3 edge adds two edges, one for Alice and one for Bob), we will first iterate over the edges of Type 3 and add the edge to both graphs.\n##### \u2022\tIn the end, we need to check if the graph for both Alice and Bob is connected or not. If yes, we can say the edges that we didn\'t connect can be removed. To check if the individual graphs are connected, we will check if the number of components in the graph is 1 or not.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n##### \u2022\tDefine constants for edge types indices: TYPE U, V, ALICE, BOB, BOTH.\n##### \u2022\tDefine the maxNumEdgesToRemove function that takes in the number of nodes (n) and an array of edges (edges).\n##### \u2022\tMove all edges of type BOTH to the start of the array.\n##### \u2022\tCreate two UnionFind data structures, one for Alice and one for Bob.\n##### \u2022\tInitialize a variable added to 0.\n##### \u2022\tIterate over the edges and add them to the appropriate UnionFind data structure.\n##### \u2022\tIf the edge is of type BOTH, add it to both UnionFind data structures.\n##### \u2022\tIf the edge is of type ALICE, add it to the Alice UnionFind data structure.\n##### \u2022\tIf the edge is of type BOB, add it to the Bob UnionFind data structure.\n##### \u2022\tIf the two UnionFind data structures are united, return the number of edges that were not added (edges.length - added).\n##### \u2022\tIf both UnionFind data structures are not united, it is impossible to remove enough edges to make them united, so return -1.\n##### \u2022\tDefine the UnionFind class that takes in the number of elements (n).\n##### \u2022\tInitialize the parent array with n+1 elements and the groups variable to n.\n##### \u2022\tDefine the union function that takes in two elements (u and v) and returns 1 if they were not already in the same group, 0 otherwise.\n##### \u2022\tFind the parent of an element and perform path compression.\n##### \u2022\tDefine the isUnited function that checks if all elements are in the same group and returns true if they are, false otherwise.\n\n\n\n# Code\n```java []\nclass Solution {\n // constants for the edge types indices\n static final int \n TYPE = 0, U = 1, V = 2,\n ALICE = 1, BOB = 2, BOTH = 3;\n\n public int maxNumEdgesToRemove(final int n, final int[][] edges) {\n // Move all edges of type BOTH to the start of the array\n for (int i = 0, j = edges.length - 1; i < j; ) {\n if (edges[i][TYPE] == BOTH) {\n ++i;\n continue;\n }\n final var temp = edges[i];\n edges[i] = edges[j];\n edges[j] = temp;\n --j;\n }\n\n // Create two UnionFind data structures, one for Alice and one for Bob\n final UnionFind \n aliceUf = new UnionFind(n), \n bobUf = new UnionFind(n);\n private int added = 0;\n\n // Iterate over the edges and add them to the appropriate UnionFind data structure\n for (final var edge : edges) {\n final int type = edge[TYPE];\n final int u = edge[U];\n final int v = edge[V];\n\n // Add the edge to both UnionFind data structures if it is of type BOTH\n added += switch (type) {\n case BOTH -> \n aliceUf.union(u, v) | bobUf.union(u, v);\n case ALICE -> aliceUf.union(u, v);\n default -> bobUf.union(u, v);\n };\n\n // If both UnionFind data structures are united, return the number of edges that were not added\n if (aliceUf.isUnited() && bobUf.isUnited())\n return edges.length - added;\n }\n\n // If both UnionFind data structures are not united, it is impossible to remove enough edges to make them united\n return -1;\n }\n}\n\nclass UnionFind {\n static final int ZERO = 0;\n final int[] parent;\n int groups;\n\n // Initialize the UnionFind data structure with n groups\n UnionFind(final int n) {\n parent = new int[n + 1];\n groups = n;\n }\n\n // Union two elements and return 1 if they were not already in the same group, 0 otherwise\n int union(final int u, final int v) {\n final int uParent = find(u);\n final int vParent = find(v);\n if (uParent == vParent)\n return 0;\n parent[uParent] = vParent;\n --groups;\n return 1;\n }\n\n // Find the parent of an element and perform path compression\n int find(final int v) {\n if (parent[v] != ZERO)\n return parent[v] = find(parent[v]);\n return v;\n }\n\n // Check if all elements are in the same group\n boolean isUnited() {\n return groups == 1;\n }\n}\n```\n\n```c++ []\nclass Solution {\nprivate:\n // constants for the edge types indices\n static constexpr int \n TYPE = 0, U = 1, V =2,\n ALICE = 1, BOB = 2, BOTH = 3;\n\npublic:\n int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {\n // Move all edges of type BOTH to the end of the array\n for (int i = 0, j = edges.size() - 1; i < j; ) {\n if (edges[i][TYPE] == BOTH) {\n ++i;\n continue;\n }\n swap(edges[i], edges[j]);\n --j;\n }\n\n // Create two UnionFind data structures, one for Alice and one for Bob\n UnionFind alice_uf(n), bob_uf(n);\n int added = 0;\n\n // Iterate over the edges and add them to the appropriate UnionFind data structure\n for (const auto& edge : edges) {\n const int type = edge[TYPE];\n const int u = edge[U];\n const int v = edge[V];\n\n // Add the edge to both UnionFind data structures if it is of type BOTH\n added += (type == BOTH) ? \n alice_uf.union_(u, v) | bob_uf.union_(u, v) :\n (type == ALICE) ? alice_uf.union_(u, v) : bob_uf.union_(u, v);\n\n // If both UnionFind data structures are united, return the number of edges that were not added\n if (alice_uf.is_united() && bob_uf.is_united())\n return edges.size() - added;\n }\n\n // If both UnionFind data structures are united, return the number of edges that were not added\n if (alice_uf.is_united() && bob_uf.is_united())\n return edges.size() - added;\n\n // If both UnionFind data structures are not united, it is impossible to remove enough edges to make them united\n return -1;\n }\n};\n\nclass UnionFind {\nprivate:\n vector<int> parent;\n int groups;\n\npublic:\n // Initialize the UnionFind data structure with n groups\n UnionFind(int n) : parent(n + 1), groups(n) {\n iota(parent.begin(), parent.end(), 0);\n }\n\n // Union two elements and return 1 if they were not already in the same group, 0 otherwise\n int union_(int u, int v) {\n const int uParent = find_(u);\n const int vParent = find_(v);\n if (uParent == vParent)\n return 0;\n parent[uParent] = vParent;\n --groups;\n return 1;\n }\n\n // Find the parent of an element and perform path compression\n int find_(int v) {\n if (parent[v] != v)\n parent[v] = find_(parent[v]);\n return parent[v];\n }\n\n // Check if all elements are in the same group\n bool is_united() {\n return groups == 1;\n }\n};\n```\n```python []\nclass Solution:\n # constants for the edge types indices\n TYPE, U, V, ALICE, BOB, BOTH = range(6)\n\n def maxNumEdgesToRemove(self, n: int, edges: List[List[int]]) -> int:\n # Move all edges of type BOTH to the end of the array\n i, j = 0, len(edges) - 1\n while i < j:\n if edges[i][self.TYPE] == self.BOTH:\n i += 1\n continue\n edges[i], edges[j] = edges[j], edges[i]\n j -= 1\n\n # Create two UnionFind data structures, one for Alice and one for Bob\n alice_uf, bob_uf = UnionFind(n), UnionFind(n)\n added = 0\n\n # Iterate over the edges and add them to the appropriate UnionFind data structure\n for edge in edges:\n type_, u, v = edge[self.TYPE], edge[self.U], edge[self.V]\n\n # Add the edge to both UnionFind data structures if it is of type BOTH\n if type_ == self.BOTH:\n added += alice_uf.union(u, v) | bob_uf.union(u, v)\n elif type_ == self.ALICE:\n added += alice_uf.union(u, v)\n else:\n added += bob_uf.union(u, v)\n\n # If both UnionFind data structures are united, return the number of edges that were not added\n if alice_uf.is_united() and bob_uf.is_united():\n return len(edges) - added\n\n # If both UnionFind data structures are not united, it is impossible to remove enough edges to make them united\n if not alice_uf.is_united() or not bob_uf.is_united():\n return -1\n\n # If both UnionFind data structures are united, return the number of edges that were not added\n return len(edges) - added\n\n\nclass UnionFind:\n def __init__(self, n: int):\n self.parent = list(range(n + 1))\n self.groups = n\n\n def union(self, u: int, v: int) -> int:\n u_parent = self.find(u)\n v_parent = self.find(v)\n if u_parent == v_parent:\n return 0\n self.parent[u_parent] = v_parent\n self.groups -= 1\n return 1\n\n def find(self, v: int) -> int:\n if self.parent[v] != v:\n self.parent[v] = self.find(self.parent[v])\n return self.parent[v]\n\n def is_united(self) -> bool:\n return self.groups == 1\n```\n\n\n# Complexity\nTime Complexity:\n1 Moving all edges of type BOTH to the end of the array takes O(n) time.\n\nCreating two UnionFind data structures takes O(n) time.\nIterating over the edges takes O(m) time, where m is the number of edges.\nAdding an edge to a UnionFind data structure takes O(\u03B1(n)) time, where \u03B1(n) is the extremely fast inverse Ackermann function.\nChecking if both UnionFind data structures are united takes O(1) time.\nOverall, the time complexity of the code is O(m \u03B1(n)), where m is the number of edges and n is the number of nodes.\nSpace Complexity:\n\nCreating two UnionFind data structures takes O(n) space.\nCreating the parent array for the UnionFind data structures takes O(n) space.\nCreating the added variable takes O(1) space.\nOverall, the space complexity of the code is O(n).\n\n# Please Upvote as it really motivates me \uD83C\uDD99\uD83C\uDD99\uD83C\uDD99\n\n\n\n\n# Please Upvote\uD83D\uDC4D\uD83D\uDC4D\nThanks for visiting my solution.\uD83D\uDE0A Keep Learning\nPlease give my solution an upvote! \uD83D\uDC4D \uD83C\uDD99\uD83C\uDD99\uD83C\uDD99\nhttps://leetcode.com/problems/remove-max-number-of-edges-to-keep-graph-fully-traversable/solutions/3468567/day-395-dsu-100-0ms-python-java-c-explained-approach/\nIt\'s a simple way to show your appreciation and\nkeep me motivated. Thank you! \uD83D\uDE0A\n\n | 29 | 1 | ['Union Find', 'Python', 'C++', 'Java', 'Python3'] | 3 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Union Find with Size is good||284ms Beats 99.82% | union-find-with-size-is-good284ms-beats-3323l | Intuition\n Describe your first thoughts on how to solve this problem. \nA variant of UnionFind with component size is very suitible for solving this question.\ | anwendeng | NORMAL | 2024-06-30T00:55:56.321419+00:00 | 2024-06-30T13:26:04.285924+00:00 | 4,870 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nA variant of UnionFind with component size is very suitible for solving this question.\n\nFor comparison, a simple UnionFind without optimization with size is also implemented which is also fast & easily implemented.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Use UnionFind class with Size & components( count how many components it has)\n2. Construct 2 UnionFind objects Alice & Bob\n3. Process type 3 edges first\n4. Process type 1 and type 2 edges\n5. If the both of graphs for Alice and for Bob are connected, the answer is |edges|-edgesNeed, otherwise -1 \n# Why 2 passes? not 1 pass? not sorting?\nIn fact the solution is using Greedy algoirithm. The 1st loop processes type 3 edges; adding 1 type 3 edge has the effect of adding 1 edge in both Alice & Bob. Adding 1 type 1 edge just adding 1 edge in Alce, and adding 1 type 2 edge just adding 1 edge in Bob. \n\nThe problem is asking to obtain the maximal number of edges one can remove. In other words, the minimal number edges are needed to build both Alice & Bob connective. So type 3 edges must be treated firsly. **1 pass solution will go wrong.**\n\nOther correct method is to use sort, but it will increase the time complexity. 2 passes solution has less time than any kind of sorting.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n+\\alpha(n)|edges|)$$ where $\\alpha(n)$ is the inverse Ackermann function which grows very slow & almost constant.\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$O(n)$\n# Code UnionFind with Size||284ms Beats 99.82%\n```\n// union find class with Size & components\nclass UnionFind {\n vector<int> root, Size;\n int components;\npublic:\n //Constructor using initializer list\n UnionFind(int n): root(n+1), Size(n+1,1), components(n){\n iota(root.begin(), root.end(), 0);//[0,1,...,n] \n }\n \n int Find(int x) {//Path Compression O(alpha(n))\n if (x==root[x]) \n return x;\n return root[x] = Find(root[x]);\n }\n\n bool Union(int x, int y) { //Union by Size O(alpha(n)) \n x=Find(x), y=Find(y);\n \n if (x == y) return 0;\n \n if (Size[x] > Size[y]) {\n Size[x] +=Size[y];\n root[y] = x;\n } \n else {\n Size[y] += Size[x];\n root[x] = y;\n } \n components--;\n return 1;\n }\n\n bool isConnected() {\n return components == 1;\n }\n \n};\n\nclass Solution {\npublic:\n int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {\n UnionFind Alice(n), Bob(n);\n\n int edgesNeed=0;\n // Process type 3 edges first\n for (vector<int>& e: edges) {\n if (e[0]==3) {\n edgesNeed+=(Alice.Union(e[1], e[2]) | Bob.Union(e[1], e[2]));\n }\n }\n // Process type 1 and type 2 edges\n for (vector<int>& e: edges){\n if (e[0]==1) edgesNeed+=Alice.Union(e[1], e[2]);\n else if (e[0]==2) edgesNeed+=Bob.Union(e[1], e[2]);\n }\n\n if (Alice.isConnected() && Bob.isConnected())\n return edges.size()-edgesNeed;\n return -1;\n }\n};\n\nauto init = []() {\n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n\n```\n# C++ code using a simple UionFind class|| 289m Beats 99.82%\n```\nclass UnionFind { // simple version for UnionFind class\n vector<int> root;\n int components;\npublic:\n UnionFind(int n):root(n+1), components(n) {\n iota(root.begin(), root.end(), 0);\n }\n\n int Find(int x) {\n if (x == root[x])\n return x;\n else\n return root[x] = Find(root[x]);\n }\n\n bool Union(int x, int y) {//Without optimization\n x= Find(x), y= Find(y);\n if (x == y)\n return 0;\n else\n root[y]=x;\n components--;\n return 1;\n }\n\n\n bool isConnected() {\n return components == 1;\n }\n \n};\n\n```\nUnionFind is good for solving undirected graphical problem. The implemenations of it have several different versions, simple one, optimized by rank & optimized by size.\n1 easy application can be seen [1971. Find if Path Exists in Graph\n](https://leetcode.com/problems/find-if-path-exists-in-graph/solutions/5052126/union-find-is-good-vs-dfs-vs-bfs-193ms-beats-99-93/)\n[Please turn English subtitles if necessary]\n[https://youtu.be/B1GQlUN08lk?si=ty_sRVWJTrxO9CVG](https://youtu.be/B1GQlUN08lk?si=ty_sRVWJTrxO9CVG) | 26 | 1 | ['Greedy', 'Union Find', 'Graph', 'C++'] | 2 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | [Python] Union-Find 3 times - O(N) | python-union-find-3-times-on-by-alanlzl-z0j5 | Idea\n\nWe simply run Union-Find three times:\n\n- first on Type1 \n- then on Type2 and Type3 simultaneously\n\nIncrement ans whenever we find redundant edges. | alanlzl | NORMAL | 2020-09-06T04:00:58.794318+00:00 | 2020-09-06T20:52:38.488092+00:00 | 1,847 | false | **Idea**\n\nWe simply run Union-Find three times:\n\n- first on `Type1` \n- then on `Type2` and `Type3` simultaneously\n\nIncrement `ans` whenever we find redundant edges. Remember to check if the graph is fully connected at the end.\n\n<br />\n\n**Complexity**\n\nTime complexity: `O(N)`\nSpace complexity: `O(N)`\n\n<br />\n\n**Python**\n```Python\nclass UnionFindSet:\n def __init__(self, n):\n self.parents = list(range(n))\n self.ranks = [1] * n\n self.size = 1\n \n def find(self, u):\n if u != self.parents[u]:\n self.parents[u] = self.find(self.parents[u])\n return self.parents[u]\n \n def union(self, u, v):\n pu, pv = self.find(u), self.find(v)\n if pu == pv:\n return False\n if self.ranks[pu] > self.ranks[pv]:\n self.parents[pv] = pu\n elif self.ranks[pv] > self.ranks[pu]:\n self.parents[pu] = pv\n else:\n self.parents[pu] = pv\n self.ranks[pv] += 1\n self.size += 1\n return True\n \n \nclass Solution:\n def maxNumEdgesToRemove(self, n: int, edges: List[List[int]]) -> int:\n uf1, uf2, ans = UnionFindSet(n), UnionFindSet(n), 0\n\t\t\n for t, u, v in edges:\n if t != 3:\n continue\n if not uf1.union(u - 1, v - 1) or not uf2.union(u - 1, v - 1):\n ans += 1\n \n for t, u, v in edges:\n if t == 1 and not uf1.union(u - 1, v - 1):\n ans += 1\n elif t == 2 and not uf2.union(u - 1, v - 1):\n ans += 1\n \n return ans if uf1.size == n and uf2.size == n else -1\n``` | 19 | 0 | [] | 5 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Java || Easy Approach with Explanation || Union Find | java-easy-approach-with-explanation-unio-dj5c | \nclass Solution {\n public int maxNumEdgesToRemove(int n, int[][] edges) \n {\n Arrays.sort(edges, (a, b)->{\n return b[0]-a[0];\n | swapnilGhosh | NORMAL | 2021-09-25T06:19:09.839566+00:00 | 2021-09-25T06:19:09.839608+00:00 | 1,700 | false | ```\nclass Solution {\n public int maxNumEdgesToRemove(int n, int[][] edges) \n {\n Arrays.sort(edges, (a, b)->{\n return b[0]-a[0];\n });//giving the priority to third type of edge or the edge which Bob and Alice both can access\n \n //1-based indexing of nodes \n int []parentAlice= new int[n+1];//Graph 1 for Alice connectedness\n int []parentBob= new int[n+1];//Graph 2 for Bob connectedness\n \n for(int i= 0; i< n+1; i++){//every node is pointing to itself, at first no connection is considered all sets are independent(no dependency) \n parentAlice[i]= i;\n parentBob[i]= i;\n }\n \n //number of merged unique node for Alice and Bob that are required to maintain the connectedness of Alice and Bob graph nodes//intialised with one because merging happens in pair \n int mergeAlice= 1;\n int mergeBob= 1;\n \n //number of cyclic or the non dependent node, that are not required for the connectedness of Alice and Bob nodes \n int removeEdge= 0;\n \n for(int []edge: edges)\n {\n int cat= edge[0];//category of edge 1)edge Alice can only access 2)edge Bob can only access 3)edge both Alice and Bob can access\n int u= edge[1];\n int v= edge[2];\n \n if(cat == 3){//edge both Alice and Bob an access\n \n //creating dependency of nodes in graph 1 and 2 \n boolean tempAlice= union(u, v, parentAlice);\n boolean tempBob= union(u, v, parentBob);\n \n if(tempAlice == true)\n mergeAlice+= 1;\n \n if(tempBob == true)\n mergeBob+= 1;\n \n if(tempAlice == false && tempBob == false)//retundant or the cyclic non-dependent edge//both Alice and Bob don\'t rquire it connection is already there between these pair of nodes\n removeEdge+= 1;\n }\n else if(cat == 2){//edge Bob can only access \n \n //creating dependency of nodes in graph 2\n boolean tempBob= union(u, v, parentBob);\n \n if(tempBob == true)\n mergeBob+= 1;\n else//no merging of set is done, that means that this edge is not required because it will form cycle or the dependency \n removeEdge+= 1;\n }\n else{//edge Alice can only access \n \n //creating dependency of nodes in graph 1\n boolean tempAlice= union(u, v, parentAlice);\n \n if(tempAlice == true)\n mergeAlice+= 1; \n else//no merging of set is done, that means that this edge is not required because it will form cycle or the dependency \n removeEdge+= 1;\n }\n }\n if(mergeAlice != n || mergeBob != n)//all node are not connected, connectedness is not maintained \n return -1;\n return removeEdge;//number of edge removed by maintaining the connectedness \n }\n \n public int find(int x, int[] parent)\n {\n if(parent[x] == x)//when we found the absolute root or the leader of the set \n return x;\n \n int temp= find(parent[x], parent);\n \n parent[x]= temp;//Path Compression//child pointing to the absolute root or the leader of the set, while backtracking\n \n return temp;//returning the absolute root \n }\n \n public boolean union(int x, int y, int[] parent)\n {\n int lx= find(x, parent);//leader of set x or the absolute root\n int ly= find(y, parent);//leader of set y or the absolute root\n \n if(lx != ly){//belong to different set merging \n \n //Rank Compression is not done, but you can do it \n parent[lx]= ly;\n \n return true;//union done, dependency created\n }\n else\n return false;//no union done cycle is due to this edge \n }//Please do Upvote, it helps a lot \n}\n``` | 18 | 1 | ['Union Find', 'Graph', 'Java'] | 2 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | [Python3] union-find | python3-union-find-by-ye15-k2hs | Edited on 9/7/2020. \n\nAs practicing more on LC, we realize the importance of union-find data structure. Even though there isn\'t a builtin implementatin in Py | ye15 | NORMAL | 2020-09-06T04:02:11.290766+00:00 | 2020-09-07T15:57:09.188664+00:00 | 1,407 | false | Edited on 9/7/2020. \n\nAs practicing more on LC, we realize the importance of union-find data structure. Even though there isn\'t a builtin implementatin in Python, it is not difficult to do one from scratch. I have one [here](https://github.com/gaosanyong/algorithms/blob/master/unionfind.py) for reference. \n\nIn addition, I see lots of people taking part of union-find and mixing it along with the implementation of this problem. Personally, I prefer to start from a standard complete data structure. It is easier for developers to implment and easier for readers to understand. \n\n```\nclass UnionFind:\n """A minimalist standalone union-find implementation."""\n def __init__(self, n):\n self.count = n # number of disjoint sets \n self.parent = list(range(n)) # parent of given nodes\n self.rank = [1]*n # rank (aka size) of sub-tree \n \n def find(self, p):\n """Find with path compression."""\n if p != self.parent[p]: \n self.parent[p] = self.find(self.parent[p]) # path compression \n return self.parent[p]\n \n def union(self, p, q):\n """Union with ranking."""\n prt, qrt = self.find(p), self.find(q)\n if prt == qrt: return False\n self.count -= 1 # one more connection => one less disjoint \n if self.rank[prt] > self.rank[qrt]: prt, qrt = qrt, prt # add small sub-tree to large sub-tree for balancing\n self.parent[prt] = qrt\n self.rank[qrt] += self.rank[prt] # ranking \n return True\n \n \nclass Solution:\n def maxNumEdgesToRemove(self, n: int, edges: List[List[int]]) -> int:\n ufa = UnionFind(n) # for Alice\n ufb = UnionFind(n) # for Bob\n \n ans = 0\n edges.sort(reverse=True) \n for t, u, v in edges: \n u, v = u-1, v-1\n if t == 3: ans += not (ufa.union(u, v) and ufb.union(u, v)) # Alice & Bob\n elif t == 2: ans += not ufb.union(u, v) # Bob only\n else: ans += not ufa.union(u, v) # Alice only\n return ans if ufa.count == 1 and ufb.count == 1 else -1 # check if uf is connected \n``` | 16 | 0 | ['Python3'] | 3 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Easy Solution Of JAVA 🔥C++🔥With Comments 🔥Beginner Friendly 🔥 | easy-solution-of-java-cwith-comments-beg-l362 | \n\n# Code\n\nclass Solution {\n public int maxNumEdgesToRemove(int n, int[][] edges) {\n if (edges.length < n - 1) return -1; // if edges are less than n - | shivrastogi | NORMAL | 2023-04-30T01:09:59.807005+00:00 | 2023-04-30T01:09:59.807037+00:00 | 2,817 | false | \n\n# Code\n```\nclass Solution {\n public int maxNumEdgesToRemove(int n, int[][] edges) {\n if (edges.length < n - 1) return -1; // if edges are less than n - 1, then it\'s not a valid tree, not all nodes are accessible\n\n int[] parentAlice = new int[n + 1];\n for (int i = 0; i < parentAlice.length; i++) {\n parentAlice[i] = i;\n }\n\n // First process the type 3 nodes, this will help us to reduce number of edges required\n int numType3Edges = 0;\n for (int[] edge : edges) {\n if (edge[0] == 3) {\n if (union(parentAlice, edge[1], edge[2])) {\n numType3Edges++;\n }\n }\n }\n\n int[] parentBob = parentAlice.clone(); // as type 3 are for both alice and bob, clone it for bob as well\n\n // Process Alice\n int numType1Edges = 0;\n for (int[] edge : edges) {\n if (edge[0] == 1) {\n if (union(parentAlice, edge[1], edge[2])) {\n numType1Edges++;\n }\n }\n }\n if (numType1Edges + numType3Edges + 1 != n) return -1; // if edges are less than n - 1, then type 1 is not a valid tree, not all nodes are accessible\n\n // Process Bob\n int numType2Edges = 0;\n for (int[] edge : edges) {\n if (edge[0] == 2) {\n if (union(parentBob, edge[1], edge[2])) {\n numType2Edges++;\n }\n }\n }\n if (numType2Edges + numType3Edges + 1 != n) return -1; // if edges are less than n - 1, then type 1 is not a valid tree, not all nodes are accessible\n // return total edges - (number of type 3 + type 2 + type 1 edges required)\n return edges.length - numType1Edges - numType2Edges - numType3Edges;\n }\n\n int find(int[] parent, int node) {\n if (parent[node] != node) {\n parent[node] = find(parent, parent[node]);\n }\n return parent[node];\n }\n\n boolean union(int[] parent, int left, int right) {\n int leftParent = find(parent, left);\n int rightParent = find(parent, right);\n if (leftParent == rightParent) return false;\n parent[rightParent] = leftParent;\n return true;\n }\n}\n```\nC++\n```\nclass Solution {\npublic:\n int find(int x, vector<int> &parent, vector<int> &rank)\n {\n if(x==parent[x]) return x;\n return parent[x] = find(parent[x], parent, rank);\n }\n \n bool merge(int x, int y, vector<int> &parent, vector<int> &rank)\n {\n x = find(x, parent, rank); y = find(y, parent, rank);\n if(x!=y)\n {\n parent[x] = y;\n if(rank[x]<rank[y]) swap(x,y);\n rank[x] += rank[y];\n return true;\n }\n return false;\n }\n static bool comp(vector<int> &a, vector<int> &b){\n return a[0]>b[0];\n }\n int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {\n sort(edges.begin(), edges.end(), comp);\n vector<int> parentA(n+1,-1), rankA(n+1,1), parentB(n+1,-1), rankB(n+1,1);\n for(int i=1; i<n+1; i++)\n {\n parentA[i] = i;\n parentB[i] = i;\n }\n \n int mergedA = 1, mergedB = 1;\n int removed = 0;\n \n for(auto edge:edges)\n {\n int type = edge[0], u = edge[1], v = edge[2];\n if(type == 3){\n bool tempa = merge(u,v,parentA,rankA);\n bool tempb = merge(u,v, parentB, rankB);\n if(tempa) mergedA++;\n if(tempb) mergedB++;\n if(!tempa and !tempb) removed++;\n }\n else if(type==1){\n bool tempa = merge(u,v,parentA,rankA); \n if(tempa) mergedA++;\n else removed++;\n }\n else{\n bool tempb = merge(u,v, parentB, rankB); \n if(tempb) mergedB++;\n else removed++;\n }\n }\n \n if(mergedA != n || mergedB != n) return -1;\n return removed;\n }\n};\n\n``` | 13 | 4 | ['Java'] | 1 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | C++(Using Disjoint Set) | cusing-disjoint-set-by-amit_singhh-clag | Please Upvote if you like the Solution!\n\n class Solution {\n public:\n bool static comp(vector &a ,vector &b)//Compare according to type-3\n {\n | amit_singhh | NORMAL | 2021-10-06T07:24:34.681005+00:00 | 2022-01-05T05:04:24.048096+00:00 | 1,984 | false | **Please Upvote if you like the Solution!**\n\n class Solution {\n public:\n bool static comp(vector<int> &a ,vector<int> &b)//Compare according to type-3\n {\n return a[0]>b[0];\n }\n int findparent(int node,vector<int> &parent)//find parent function (fro disjoint set)\n {\n if(node==parent[node])\n return node;\n return parent[node]=findparent(parent[node],parent);\n }\n bool unionn(int u,int v,vector<int> &parent,vector<int> &rank)//Union function\n {\n u=findparent(u,parent);\n v=findparent(v,parent);\n \n if(u!=v)// when u and v are not equal return true else return false\n {\n if(rank[u]<rank[v])\n parent[u]=v;\n else if(rank[u]>rank[v])\n parent[v]=u;\n else\n {\n parent[v]=u;\n rank[u]++;\n }\n return true;\n }\n return false;\n }\n int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) \n {\n sort(edges.begin(),edges.end(),comp);//sort according to type 3, because type 3 solves problem of both alice and bob\n \n vector<int> parent_Alice(n+1);\n vector<int> parent_Bob(n+1);\n vector<int> rank_Alice(n+1);\n vector<int> rank_Bob(n+1);\n \n //Initialize the parent and rank Array\n for(int i=0;i<parent_Alice.size();i++)\n {\n parent_Alice[i]=i;//intially every node is their own parent and rank of all is 1\n parent_Bob[i]=i;\n rank_Alice[i]=1;\n rank_Bob[i]=1;\n }\n int merge_Alice=1;//to count how many nodes we already processed for alice\n int merge_Bob=1;//to count how many nodes we already processed for bob\n \n int remove_edges=0;//for counting how many edges we remove\n \n for(auto it:edges)\n {\n if(it[0]==3)//for type-3 edges,which is followed by both bob and Alice\n {\n bool temp_Alice=unionn(it[1],it[2],parent_Alice,rank_Alice);//unionn when it[0] is of type-3 for Alice\n bool temp_Bob=unionn(it[1],it[2],parent_Bob,rank_Bob);//unionnn when it[0] is of type-3 for Bob\n if(temp_Alice==true)//if it[0] and it[1] are not merged increase merge count\n merge_Alice++;\n \n if(temp_Bob==true)\n merge_Bob++;\n \n if(temp_Alice==false && temp_Bob==false)//when they are already merged,then increase count of removed edges\n remove_edges++;\n }\n else if(it[0]==1)//for type 1, path followed by Alice\n {\n bool temp_Alice=unionn(it[1],it[2],parent_Alice,rank_Alice);//unionn for Alice\n \n if(temp_Alice==true)//if unionn function is true, increase merge_ALice count\n merge_Alice++;\n else\n remove_edges++;//increase remove edges count, if unionn is false\n }\n else\n {\n bool temp_Bob=unionn(it[1],it[2],parent_Bob,rank_Bob);//for type2,which is followed by bob\n \n if(temp_Bob==true)\n merge_Bob++;\n else\n remove_edges++;\n }\n }\n if(merge_Alice!=n || merge_Bob!=n)//when merge count is not equal to number of nodes return -1\n {\n return -1;\n }\n return remove_edges;\n }\n }; | 13 | 0 | ['Union Find', 'C', 'C++'] | 2 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | C++ Union Find with explanation | c-union-find-with-explanation-by-lzl1246-2xwz | See my latest update in repo LeetCode\n\n## Solution 1. Union Find\n\nCreate two UnionFinds a and b for Alice and Bob respectively.\n\nWe should take type 3 edg | lzl124631x | NORMAL | 2020-09-06T04:02:00.856038+00:00 | 2020-09-10T09:01:43.153864+00:00 | 2,256 | false | See my latest update in repo [LeetCode](https://github.com/lzl124631x/LeetCode)\n\n## Solution 1. Union Find\n\nCreate two UnionFinds `a` and `b` for Alice and Bob respectively.\n\nWe should take type 3 edges first, then type 1 and 2.\n\nIf two nodes are already connected, we increment the answer `ans`. Otherwise we connect them.\n\nIn the end, if `a.getSize() == 1 && b.size() == 1` meaning that the graph is all connected for both Alice and Bob, we return `ans`; otherwise return `-1`.\n\n```cpp\n// OJ: https://leetcode.com/problems/remove-max-number-of-edges-to-keep-graph-fully-traversable/\n// Author: github.com/lzl124631x\n// Time: O(N + E)\n// Space: O(N)\nclass UnionFind{\n vector<int> id;\n int size;\npublic:\n UnionFind(int N ): id(N), size(N) {\n iota(begin(id), end(id), 0);\n }\n int find(int a) {\n return id[a] == a ? a : (id[a] = find(id[a]));\n }\n int connected(int a, int b) {\n return find(a) == find(b);\n }\n void connect(int a, int b) {\n int p = find(a), q = find(b);\n if (p == q) return;\n id[p] = q;\n --size;\n }\n int getSize() { return size; }\n};\nclass Solution {\npublic:\n int maxNumEdgesToRemove(int n, vector<vector<int>>& E) {\n UnionFind a(n), b(n);\n int ans = 0;\n for (auto &e : E) {\n if (e[0] != 3) continue;\n int u = e[1] - 1, v = e[2] - 1;\n if (a.connected(u, v)) {\n ++ans;\n continue;\n }\n a.connect(u, v);\n b.connect(u, v);\n }\n for (auto &e : E) {\n int u = e[1] - 1, v = e[2] - 1;\n if (e[0] == 1) {\n if (a.connected(u, v)) ++ans;\n else a.connect(u, v);\n } else if (e[0] == 2) {\n if (b.connected(u, v)) ++ans;\n else b.connect(u, v);\n }\n }\n return a.getSize() != 1 || b.getSize() != 1 ? -1 : ans;\n }\n};\n```\n\n---\n\nThe following code can beat 100% (~1000ms run time) but the idea is exactly the same.\n\n```cpp\n// OJ: https://leetcode.com/problems/remove-max-number-of-edges-to-keep-graph-fully-traversable/\n// Author: github.com/lzl124631x\n// Time: O(N + E)\n// Space: O(N)\n// The following block might trivially improve the exec time.\nstatic const auto __optimize__ = []() {\n std::ios::sync_with_stdio(false);\n std::cin.tie(NULL);\n return 0;\n}();\nclass UnionFind{\n vector<int> id;\n int size;\npublic:\n UnionFind(int N ): id(N), size(N) {\n iota(begin(id), end(id), 0);\n }\n int find(int a) {\n return id[a] == a ? a : (id[a] = find(id[a]));\n }\n int connected(int a, int b) {\n return find(a) == find(b);\n }\n void connect(int a, int b) {\n int p = find(a), q = find(b);\n if (p == q) return;\n id[p] = q;\n --size;\n }\n int getSize() { return size; }\n};\nclass Solution {\npublic:\n int maxNumEdgesToRemove(int n, vector<vector<int>>& E) {\n UnionFind a(n), b(n);\n int ans = 0;\n for (auto &e : E) {\n if (e[0] != 3) continue;\n int u = e[1] - 1, v = e[2] - 1;\n if (a.connected(u, v)) {\n ++ans;\n continue;\n }\n a.connect(u, v);\n b.connect(u, v);\n }\n for (auto &e : E) {\n if (e[0] != 1) continue;\n int u = e[1] - 1, v = e[2] - 1;\n if (a.connected(u, v)) ++ans;\n else a.connect(u, v);\n }\n if (a.getSize() != 1) return -1;\n for (auto &e : E) {\n if (e[0] != 2) continue;\n int u = e[1] - 1, v = e[2] - 1;\n if (b.connected(u, v)) ++ans;\n else b.connect(u, v);\n }\n return b.getSize() != 1 ? -1 : ans;\n }\n};\n``` | 13 | 1 | [] | 3 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Easy Peasy 💯 👍 | easy-peasy-by-raviparihar-asdq | Method: maxNumEdgesToRemove\nInitialization:\n\nTwo UnionFind instances are created: aliceUF and bobUF for Alice and Bob, respectively.\nAn addedEdges counter i | raviparihar_ | NORMAL | 2024-06-30T00:28:17.844827+00:00 | 2024-06-30T00:28:17.844847+00:00 | 3,174 | false | Method: maxNumEdgesToRemove\nInitialization:\n\nTwo UnionFind instances are created: aliceUF and bobUF for Alice and Bob, respectively.\nAn addedEdges counter is initialized to zero to keep track of the number of edges that have been added to the graph.\nProcessing Type 3 Edges:\n\nThe edges are processed in two passes. In the first pass, only type 3 edges (usable by both Alice and Bob) are considered.\nFor each type 3 edge, the union operation is performed on both aliceUF and bobUF.\nIf either union operation is successful, the edge is counted in addedEdges.\nProcessing Type 1 and Type 2 Edges:\n\nIn the second pass, type 1 and type 2 edges are processed separately.\nFor type 1 edges (usable by Alice only), the union operation is performed on aliceUF.\nFor type 2 edges (usable by Bob only), the union operation is performed on bobUF.\nIf the union operation is successful, the edge is counted in addedEdges.\nChecking Connectivity:\n\nAfter processing all edges, the connectivity of both Alice\'s and Bob\'s graphs is checked.\nIf either graph is not fully connected (i.e., the count of disjoint sets is more than 1), the method returns -1.\nCalculating Removable Edges:\n\nThe maximum number of edges that can be removed is calculated as the total number of edges minus the number of edges that have been added.\nExample Table for Clarification\nLet\'s consider an example with n = 4 and edges = {{3,1,2}, {3,2,3}, {1,1,3}, {1,2,4}, {1,1,2}, {2,3,4}}.\n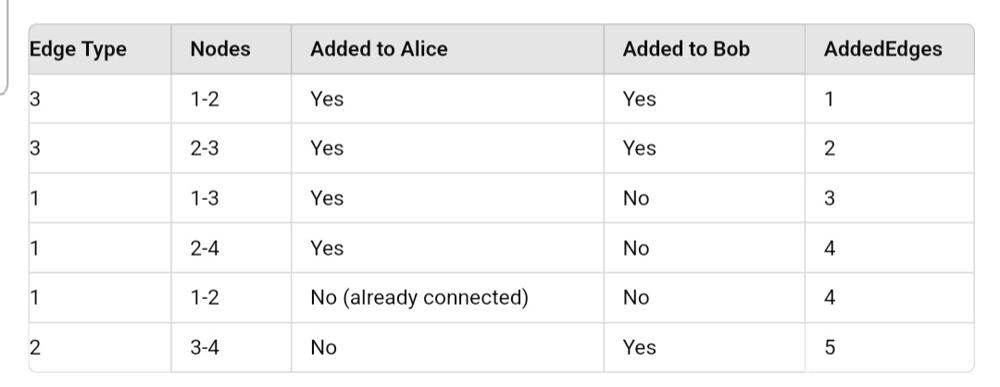\nFinal Check\naliceUF.getCount() > 1 or bobUF.getCount() > 1: Both are false since both graphs are fully connected.\nTotal edges = 6, addedEdges = 5.\nMaximum edges removable = 6 - 5 = 1.\n```\nclass Solution {\n class UnionFind {\n int[] parent;\n int[] rank;\n int count;\n public UnionFind(int n) {\n parent = new int[n];\n rank = new int[n];\n count = n;\n for (int i = 0; i < n; i++) {\n parent[i] = i;\n rank[i] = 0;\n }\n }\n\n public int find(int x) {\n if (parent[x] != x) {\n parent[x] = find(parent[x]);\n }\n return parent[x];\n }\n\n public boolean union(int x, int y) {\n int rootX = find(x);\n int rootY = find(y);\n\n if (rootX != rootY) {\n if (rank[rootX] > rank[rootY]) {\n parent[rootY] = rootX;\n } else if (rank[rootX] < rank[rootY]) {\n parent[rootX] = rootY;\n } else {\n parent[rootY] = rootX;\n rank[rootX]++;\n }\n count--;\n return true;\n }\n return false;\n }\n public int getCount() {\n return count;\n }\n }\n public int maxNumEdgesToRemove(int n, int[][] edges) {\n UnionFind aliceUF = new UnionFind(n);\n UnionFind bobUF = new UnionFind(n);\n int addedEdges = 0;\n Arrays.sort(edges, (a, b) -> b[0] - a[0]);\n for (int[] edge : edges) {\n int type = edge[0];\n int u = edge[1] - 1;\n int v = edge[2] - 1;\n\n if (type == 3) {\n boolean aliceConnected = aliceUF.union(u, v);\n boolean bobConnected = bobUF.union(u, v);\n if (aliceConnected || bobConnected) {\n addedEdges++;\n }\n } else if (type == 1) {\n if (aliceUF.union(u, v)) {\n addedEdges++;\n }\n } else if (type == 2) {\n if (bobUF.union(u, v)) {\n addedEdges++;\n }\n }\n }\n if (aliceUF.getCount() > 1 || bobUF.getCount() > 1) {\n return -1;\n }\n return edges.length - addedEdges;\n }\n\t}\n```\n```\nclass UnionFind:\n def __init__(self, n: int):\n self.parent = list(range(n))\n self.rank = [0] * n\n self.count = n\n\n def find(self, x: int) -> int:\n if self.parent[x] != x:\n self.parent[x] = self.find(self.parent[x])\n return self.parent[x]\n\n def union(self, x: int, y: int) -> bool:\n rootX = self.find(x)\n rootY = self.find(y)\n \n if rootX != rootY:\n if self.rank[rootX] > self.rank[rootY]:\n self.parent[rootY] = rootX\n elif self.rank[rootX] < self.rank[rootY]:\n self.parent[rootX] = rootY\n else:\n self.parent[rootY] = rootX\n self.rank[rootX] += 1\n self.count -= 1\n return True\n return False\n\nclass Solution:\n def maxNumEdgesToRemove(self, n: int, edges: List[List[int]]) -> int:\n aliceUF = UnionFind(n)\n bobUF = UnionFind(n)\n addedEdges = 0\n\n for edge in edges:\n if edge[0] == 3:\n u, v = edge[1] - 1, edge[2] - 1\n aliceConnected = aliceUF.union(u, v)\n bobConnected = bobUF.union(u, v)\n if aliceConnected or bobConnected:\n addedEdges += 1\n for edge in edges:\n if edge[0] == 1:\n u, v = edge[1] - 1, edge[2] - 1\n if aliceUF.union(u, v):\n addedEdges += 1\n elif edge[0] == 2:\n u, v = edge[1] - 1, edge[2] - 1\n if bobUF.union(u, v):\n addedEdges += 1\n if aliceUF.count > 1 or bobUF.count > 1:\n return -1\n return len(edges) - addedEdges\n```\n```\nclass UnionFind {\npublic:\n vector<int> parent;\n vector<int> rank;\n int count;\n\n UnionFind(int n) : parent(n), rank(n, 0), count(n) {\n for (int i = 0; i < n; ++i) {\n parent[i] = i;\n }\n }\n\n int find(int x) {\n if (parent[x] != x) {\n parent[x] = find(parent[x]);\n }\n return parent[x];\n }\n\n bool unionSets(int x, int y) {\n int rootX = find(x);\n int rootY = find(y);\n\n if (rootX != rootY) {\n if (rank[rootX] > rank[rootY]) {\n parent[rootY] = rootX;\n } else if (rank[rootX] < rank[rootY]) {\n parent[rootX] = rootY;\n } else {\n parent[rootY] = rootX;\n rank[rootX]++;\n }\n count--;\n return true;\n }\n return false;\n }\n\n int getCount() {\n return count;\n }\n};\n\nclass Solution {\npublic:\n int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {\n UnionFind aliceUF(n), bobUF(n);\n int addedEdges = 0;\n\n for (const auto& edge : edges) {\n if (edge[0] == 3) {\n int u = edge[1] - 1;\n int v = edge[2] - 1;\n bool aliceConnected = aliceUF.unionSets(u, v);\n bool bobConnected = bobUF.unionSets(u, v);\n if (aliceConnected || bobConnected) {\n addedEdges++;\n }\n }\n }\n\n for (const auto& edge : edges) {\n if (edge[0] == 1) {\n int u = edge[1] - 1;\n int v = edge[2] - 1;\n if (aliceUF.unionSets(u, v)) {\n addedEdges++;\n }\n } else if (edge[0] == 2) {\n int u = edge[1] - 1;\n int v = edge[2] - 1;\n if (bobUF.unionSets(u, v)) {\n addedEdges++;\n }\n }\n }\n\n if (aliceUF.getCount() > 1 || bobUF.getCount() > 1) {\n return -1;\n }\n\n return edges.size() - addedEdges;\n }\n};\n```\n\n\n | 12 | 1 | ['Java'] | 3 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | [Java] Detailed Explanation - (No Union-Find) Another Easy-Understand Thought | java-detailed-explanation-no-union-find-enin6 | Key Notes:\n- build a graph with type 3 only: then remove edges which form a cycle (they are not needed anyway in the future under ALL circumstances) and update | frankkkkk | NORMAL | 2020-09-06T19:23:37.815958+00:00 | 2020-09-06T19:23:37.816021+00:00 | 1,191 | false | **Key Notes:**\n- build a graph with **type 3 only**: then remove edges which form a cycle (they are not needed anyway in the future **under ALL circumstances**) and update in final "res"\n- count edges for Alice with **type 1 and type 3**. res += (totalEdges - (n - 1)), **BUT** if totalEdges < n - 1 or coverd nodes != n return -1.\n- count edges for Bob with **type 2 and type 3**. res += (totalEdges - (n - 1)), **BUT** if totalEdges < n - 1 or coverd nodes != n return -1.\n\n```java\npublic int maxNumEdgesToRemove(int n, int[][] edges) {\n \n\tint res = 0;\n\n\t// build type 3 only graph, and remove unnecessary edges which can form cycles\n\tSet<String> removedEdges = new HashSet<>();\n\tres += helper(edges, n, removedEdges);\n\n\t// count type 1 + 3 only edges for Alice: make sure: cover all nodes + edgesNum >= n - 1\n\tSet<Integer> nodes = new HashSet<>();\n\tint edgeCount = countEdges(2, removedEdges, nodes, edges);\n\tif (edgeCount < n - 1 || nodes.size() < n) return -1;\n\tres += (edgeCount - (n - 1));\n\n\t// count type 2 + 3 only edges for Bob: make sure: cover all nodes + edgesNum >= n - 1\n\tnodes = new HashSet<>();\n\tedgeCount = countEdges(1, removedEdges, nodes, edges);\n\tif (edgeCount < n - 1 || nodes.size() < n) return -1;\n\tres += (edgeCount - (n - 1));\n\n\treturn res;\n}\n\n// helper to build type 3 only graph, store in removedEdges set, return num of edges removed\nprivate int helper(int[][] edges, int n, Set<String> removedEdges) {\n\n\tint numEdgesRemoved = 0;\n\tMap<Integer, List<Integer>> map = new HashMap<>();\n\n\tfor (int[] edge : edges) {\n\t\tif (edge[0] != 3) continue;\n\t\tint a = edge[1], b = edge[2];\n\t\tmap.computeIfAbsent(a, f -> new ArrayList<>()).add(b);\n\t\tmap.computeIfAbsent(b, f -> new ArrayList<>()).add(a);\n\t}\n\n\n\tint[] visited = new int[n + 1]; // 0: not visited, > 0: depth\n\n\tfor (int i = 1; i <= n; ++i) {\n\t\tif (visited[i] != 0) continue;\n\t\tnumEdgesRemoved += dfs(map, visited, i, 1, removedEdges);\n\t}\n\n\treturn numEdgesRemoved;\n}\n\n// dfs for removing circle edges recursively\nprivate int dfs(Map<Integer, List<Integer>> map, int[] visited, int node, int depth, Set<String> removedEdges) {\n\n\tint count = 0;\n\tvisited[node] = depth;\n\n\tfor (int next : map.getOrDefault(node, new ArrayList<>())) {\n\n\t\tif (visited[next] == 0) { // keep going\n\t\t\tcount += dfs(map, visited, next, depth + 1, removedEdges);\n\t\t} else if (visited[next] == depth - 1) { // we ain\'t go back\n\t\t\tcontinue;\n\t\t} else if (!removedEdges.contains(node + "-" + next)) { // find cycle edge and not been removed\n\t\t\tremovedEdges.add(node + "-" + next); removedEdges.add(next + "-" + node);\n\t\t\tcount++;\n\t\t}\n\t}\n\n\treturn count;\n}\n\n// count edges without exclusiveType\nprivate int countEdges(int exclusiveType, Set<String> removedEdges, Set<Integer> nodes, int[][] edges) {\n\tint edgeCount = 0;\n\tfor (int[] edge : edges) {\n\t\tif (edge[0] == exclusiveType) continue;\n\t\tint a = edge[1], b = edge[2];\n\t\tnodes.add(a); nodes.add(b);\n\t\tif (edge[0] == 3 && removedEdges.contains(a + "-" + b)) continue;\n\t\tedgeCount++;\n\t}\n\treturn edgeCount;\n}\n``` | 12 | 2 | [] | 2 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Golang Solution ||| O(N) ||| DFS (No union find) ||| A lot of Explanations ||| Clean code | golang-solution-on-dfs-no-union-find-a-l-9r1n | Intuition\nCreate 3 graphs, find out the number of required edges for each graph and subtract them from the total number of edges.\n\n# Approach\n# Solution thr | https_whxyan | NORMAL | 2024-06-30T13:16:11.890900+00:00 | 2024-07-01T12:09:51.504551+00:00 | 441 | false | # Intuition\nCreate 3 graphs, find out the number of required edges for each graph and subtract them from the total number of edges.\n\n# Approach\n# Solution through connectivity components\n\nThe idea is that **we create separate connectivity components only from edges of type 3**, and depending on their number we see how many edges we need for alice and for bob.\n\n# Let me give an example of some graph consisting only of edges of type 3 and explain how we can use it to find the answer.\n\nThis is an example of a graph that consists of only 3 edges.\n\n**It has four components of cohesion:**\n\n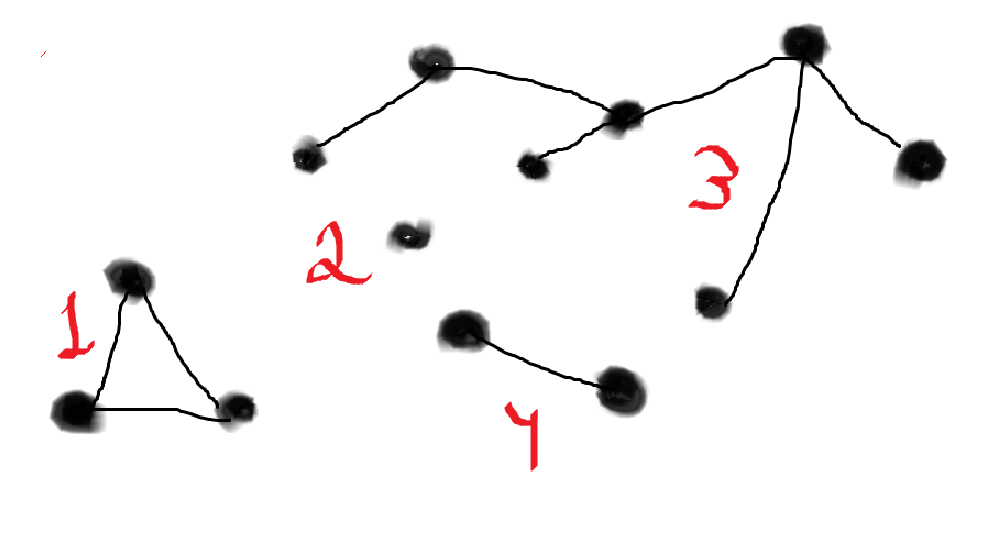\n\n# Recall that the minimum possible number of edges for a graph to be connected is n - 1, where n is the number of vertices.\n> Such a graph is called a tree.\n\n---\n\n\nTo make it possible for Alice, for example, to get from any vertex to any other vertex, **we need to connect all these connectivity components by a minimum number of edges.**\nThis number is equal to **4 - 1 = 3.**\nThe same logic applies to bean - **4 - 1 = 3.**\n\nExample:\n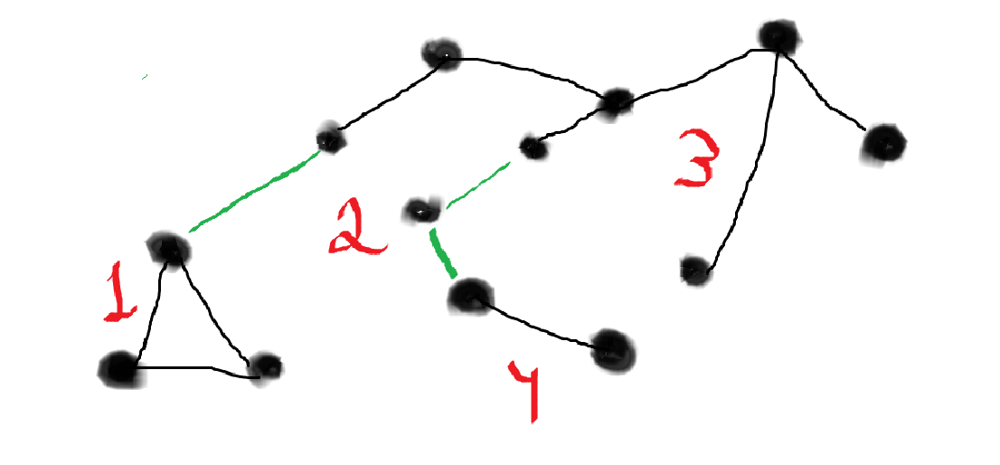\n\n# That is, for both alice and bean, the number of good edges is equal to the number of connectivity components of the graph of general type - 1.**\n\n\n---\n\n# Let\'s talk about the number of good type 3 ribs. \n\nWe have, say, **m connectivity components.**\nTry to understand, I tried to make it clear). \uD83D\uDE02\n1. For each of the m components, the number of edges it needs for the component to be connected is equal to the number of its vertices - 1.\n2. In total, we have n vertices. And m components.\n3. The sum of all vertices of all components is n.\n4. If we sum up all the numbers of good edges for each component, we have n - m, because for each of the m components we subtract 1.\n\n# So the total number of good edges of type 3 is n - m.\n\n---\n# Thus, the total number of ribs needed:\n**Find the number of connectivity components of the graph consisting only of edges of type 3. Let it be m.**\n\n1. Number of good edges of type 3: n - m\n2. Number of good edges of type 1: m - 1\n3. Number of good edges of type 2: m - 1 (sane as 1)\n4. Total number of good edges: \n (n - m) + (m - 1) + (m - 1) = \n n - m + 2 * m - 2 = \n n + m - 2\n# Total ans: nEdges - (n + m - 2)\n\n\n---\n\n\n# Let\'s deal with -1.\nWe return -1 **only if either Alice or Bob cannot pass the graph completely to any vertex.**\n\n**To check this**, we will create 2 graphs, one for Alice and one for Bob. \nFor alice we will add all edges whose type is either 1 or 3, and for bean either 2 or 3.\n\n**For them we** will also **find out the number of connectivity components. If it is not equal to 1**, then traversing the complete graph is impossible, **we return -1.**\n\n---\n# Code Explanation\n\n---\n```Golang []\ntype GraphType int\n\nconst (\n AliceType GraphType = 1\n BobType GraphType = 2\n CommonType GraphType = 3\n)\n\n// Graph Struct\n\ntype Graph struct {\n n int\n\n g map[int][]int\n graphType GraphType\n}\n```\n**The initialization methods are as follows:**\n```Golang []\nfunc NewGraph(graphType GraphType, n int, edges [][]int) *Graph {\n newG := &Graph{\n n: n,\n\n g: make(map[int][]int),\n graphType: graphType,\n }\n\n for _, edge := range edges {\n newG.addEdge(edge)\n }\n\n return newG\n}\n\nfunc (g *Graph) addEdge(edge []int) {\n edgeType, fromV, toV := edge[0], edge[1], edge[2]\n\n switch g.graphType {\n case AliceType:\n if edgeType == 1 || edgeType == 3 {\n g.g[fromV] = append(g.g[fromV], toV)\n g.g[toV] = append(g.g[toV], fromV)\n }\n case BobType:\n if edgeType == 2 || edgeType == 3 {\n g.g[fromV] = append(g.g[fromV], toV)\n g.g[toV] = append(g.g[toV], fromV)\n }\n case CommonType:\n if edgeType == 3 {\n g.g[fromV] = append(g.g[fromV], toV)\n g.g[toV] = append(g.g[toV], fromV)\n }\n }\n}\n```\n\n**The remaining 2 methods are used to find the number of connectivity components.**\n# How do you find the number of components of a connectivity?\nIn the graph structure we will add the used field - an array of boolean\'s.\n```Golang []\ntype Graph struct {\n //....\n\n used []bool\n}\n```\nIn a special method, where we will get the number of components of links, **we will try to call DFS from all vertices from 1 to n.**\n\n**If we succeed** *(i.e., the vertex has not yet been marked as used)*, **we increment the counter and start DFS from this vertex.** \n\n```Golang []\nfunc (g *Graph) GetComponentsCount() int {\n componentsCount := 0\n for startV := 1; startV <= g.n; startV++ {\n if !g.used[startV] {\n g.dfs(startV)\n componentsCount++\n }\n }\n\n return componentsCount\n}\n```\n**DFS is super standard, absolutely nothing new.**\n```Golang []\nfunc (g *Graph) dfs(v int) {\n if g.used[v] {\n return\n }\n g.used[v] = true\n for _, nextV := range g.g[v] {\n g.dfs(nextV)\n }\n}\n```\n\n# Because of the structure, it is now very easy for us to start a graph and count the number of good and necessary edges according to our solution.\n\n**The main method itself looks like this.** *I didn\'t comment the code, just made the names of the variables.*\n\n```Golang []\nfunc maxNumEdgesToRemove(n int, edges [][]int) int {\n aliceG := NewGraph(AliceType, n, edges)\n bobG := NewGraph(BobType, n, edges)\n\n\n aliceCompopentsCount := aliceG.GetComponentsCount()\n bobCompopentsCount := bobG.GetComponentsCount()\n\n if aliceCompopentsCount != 1 || bobCompopentsCount != 1 {\n return -1\n }\n\n commonG := NewGraph(CommonType, n, edges)\n commonCompopentsCount := commonG.GetComponentsCount()\n\n goodCommodEdges := n - commonCompopentsCount\n goodAliceEdges := commonCompopentsCount - 1\n goodBobEdges := goodAliceEdges // (commonCompopentsCount - 1)\n \n sumOfGoodEdges := goodCommodEdges + goodAliceEdges + goodBobEdges\n return len(edges) - sumOfGoodEdges\n}\n```\n\n\n\n# Complexity\n**- Time complexity:**\nThe graph creation itself takes at most $$O(N)$$.\nThe sum of execution time of the GetComponentsCount() method is $$O(N)$$, because we pass strictly over N vertices. total. \nCalculation of all variables in the main is $$O(1)$$.\n\n**Total time complexity -** $$O(N)$$\n\n# Code\n```\nfunc maxNumEdgesToRemove(n int, edges [][]int) int {\n aliceG := NewGraph(AliceType, n, edges)\n bobG := NewGraph(BobType, n, edges)\n\n\n aliceCompopentsCount := aliceG.GetComponentsCount()\n bobCompopentsCount := bobG.GetComponentsCount()\n\n if aliceCompopentsCount != 1 || bobCompopentsCount != 1 {\n return -1\n }\n\n commonG := NewGraph(CommonType, n, edges)\n commonCompopentsCount := commonG.GetComponentsCount()\n\n goodCommodEdges := n - commonCompopentsCount\n goodAliceEdges := commonCompopentsCount - 1\n goodBobEdges := goodAliceEdges // (commonCompopentsCount - 1)\n \n sumOfGoodEdges := goodCommodEdges + goodAliceEdges + goodBobEdges\n return len(edges) - sumOfGoodEdges\n}\n\n// ________________\n// Graph\n// ________________\n\ntype GraphType int\n\nconst (\n AliceType GraphType = 1\n BobType GraphType = 2\n CommonType GraphType = 3\n)\n\n// Graph Struct\n\ntype Graph struct {\n n int\n\n g map[int][]int\n graphType GraphType\n\n used []bool\n}\n\n// Initializators\n\nfunc NewGraph(graphType GraphType, n int, edges [][]int) *Graph {\n newG := &Graph{\n n: n,\n\n g: make(map[int][]int),\n graphType: graphType,\n\n used: make([]bool, n + 1),\n }\n\n for _, edge := range edges {\n newG.addEdge(edge)\n }\n\n return newG\n}\n\nfunc (g *Graph) addEdge(edge []int) {\n edgeType, fromV, toV := edge[0], edge[1], edge[2]\n\n switch g.graphType {\n case AliceType:\n if edgeType == 1 || edgeType == 3 {\n g.g[fromV] = append(g.g[fromV], toV)\n g.g[toV] = append(g.g[toV], fromV)\n }\n case BobType:\n if edgeType == 2 || edgeType == 3 {\n g.g[fromV] = append(g.g[fromV], toV)\n g.g[toV] = append(g.g[toV], fromV)\n }\n case CommonType:\n if edgeType == 3 {\n g.g[fromV] = append(g.g[fromV], toV)\n g.g[toV] = append(g.g[toV], fromV)\n }\n }\n}\n\n// ____________\n// DFS\n// ____________\n\nfunc (g *Graph) GetComponentsCount() int {\n componentsCount := 0\n for startV := 1; startV <= g.n; startV++ {\n if !g.used[startV] {\n g.dfs(startV)\n componentsCount++\n }\n }\n\n return componentsCount\n}\n\nfunc (g *Graph) dfs(v int) {\n if g.used[v] {\n return\n }\n g.used[v] = true\n for _, nextV := range g.g[v] {\n g.dfs(nextV)\n }\n}\n\n\n```\n\n | 11 | 0 | ['Depth-First Search', 'Graph', 'Design', 'Go'] | 4 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | [ C++ ] [ Union Find ] [ Implementation ] | c-union-find-implementation-by-sosuke23-7ptq | Code\n\nclass UnionFind {\n vector<int> representative;\n vector<int> componentSize;\n int components;\n \npublic:\n UnionFind(int n) {\n | Sosuke23 | NORMAL | 2023-04-30T02:24:51.454258+00:00 | 2023-04-30T02:24:51.454310+00:00 | 3,768 | false | # Code\n```\nclass UnionFind {\n vector<int> representative;\n vector<int> componentSize;\n int components;\n \npublic:\n UnionFind(int n) {\n components = n;\n for (int i = 0; i <= n; i++) {\n representative.push_back(i);\n componentSize.push_back(1);\n }\n }\n \n int findRepresentative(int x) {\n if (representative[x] == x) {\n return x;\n }\n return representative[x] = findRepresentative(representative[x]);\n }\n \n int performUnion(int x, int y) { \n x = findRepresentative(x); y = findRepresentative(y);\n \n if (x == y) {\n return 0;\n }\n \n if (componentSize[x] > componentSize[y]) {\n componentSize[x] += componentSize[y];\n representative[y] = x;\n } else {\n componentSize[y] += componentSize[x];\n representative[x] = y;\n }\n \n components--;\n return 1;\n }\n\n bool isConnected() {\n return components == 1;\n }\n};\n\nclass Solution {\npublic:\n int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {\n UnionFind Alice(n), Bob(n);\n\n int edgesRequired = 0;\n for (vector<int>& edge : edges) {\n if (edge[0] == 3) {\n edgesRequired += (Alice.performUnion(edge[1], edge[2]) | Bob.performUnion(edge[1], edge[2]));\n }\n }\n\n for (vector<int>& edge : edges) {\n if (edge[0] == 1) {\n edgesRequired += Alice.performUnion(edge[1], edge[2]);\n } else if (edge[0] == 2) {\n edgesRequired += Bob.performUnion(edge[1], edge[2]);\n }\n }\n\n if (Alice.isConnected() && Bob.isConnected()) {\n return edges.size() - edgesRequired;\n }\n \n return -1;\n }\n};\n``` | 11 | 0 | ['C++'] | 2 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Minimum Weight Spanning Tree, Prim's Algorithm | minimum-weight-spanning-tree-prims-algor-a2dm | The problem is essentially finding the minimum weight spanning tree for the graph for both Alice and Bob if we assign weights: say Type 3, 1, Type 1 and 2, 2.\ | yuhan-wang | NORMAL | 2020-09-06T05:10:14.518542+00:00 | 2020-09-06T05:10:14.518577+00:00 | 17,077 | false | The problem is essentially finding the minimum weight spanning tree for the graph for both Alice and Bob if we assign weights: say Type 3, 1, Type 1 and 2, 2.\n\nOne such algorithm is Prim\'s algorithm. (I learnt it during the contest since I didn\'t know any algo for weighted spanning trees.) The basic idea is simply (copied from wikipedia):\n1. Initialize a tree with a single vertex, chosen arbitrarily from the graph.\n2. Grow the tree by one edge: of the edges that connect the tree to vertices not yet in the tree, find the minimum-weight edge, and transfer it to the tree.\n3. Repeat step 2 (until all vertices are in the tree).\n\nMore details found here. [https://en.wikipedia.org/wiki/Prim%27s_algorithm](https://en.wikipedia.org/wiki/Prim%27s_algorithm)\n\nHere are my codes:\n```\nclass Solution:\n def maxNumEdgesToRemove(self, n: int, edges: List[List[int]]) -> int:\n\t\t# process graph\n graphs = [collections.defaultdict(list) for _ in range(3)]\n for c, i, j in edges:\n graphs[c-1][i].append((-c, j))\n graphs[c-1][j].append((-c, i))\n\t\t# build tree for Alice\n e = graphs[2][1] + graphs[0][1]\n heapq.heapify(e)\n treeset = set([1])\n type3 = 0\n while e:\n c, y = heapq.heappop(e)\n if y not in treeset:\n treeset.add(y)\n if c == -3:\n type3 += 1\n for item in graphs[2][y]:\n heapq.heappush(e, item)\n for item in graphs[0][y]:\n heapq.heappush(e, item)\n if len(treeset) != n:\n return -1\n\t\t# build tree for Bob\n e = graphs[2][1] + graphs[1][1]\n heapq.heapify(e)\n treeset = set([1])\n while e:\n c, y = heapq.heappop(e)\n if y not in treeset:\n treeset.add(y)\n for item in graphs[2][y]:\n heapq.heappush(e, item)\n for item in graphs[1][y]:\n heapq.heappush(e, item)\n if len(treeset) != n:\n return -1\n return len(edges) + type3 - 2 * (n - 1)\n```\n\nMy solution is by no means optimal. I think Prim\'s Algorithm in this case can be implemented using BFS (since we know what are the low weight edges):\n1. We don\'t care about the weights for Bob because if there exists a spanning tree for him, then there must be one with Type 3 edges precisely those in the one built for Alice (and it is also one with minimum weight for Bob). So we just need to check if there is a spanning tree for Bob and this can be done using BFS, DFS etc with time complexity ```O(E)```.\n2. The part for finding the MWSP for Alice can also be achieved in ```O(E)```. Starting from one node say ```1```, we build the spanning tree for the connected component containing ```1``` in the subgraph consisting of Type 3 edges using BFS and then do the same thing for Type 1 edges using BFS. \n\nIn short, BFS for the Type 3 edges, then BFS for the Type 1 edges. This get rids of the use of heap in my code, and improves performance. \n\n\nThere are many great solutions using Kruskal\'s algorithm with union-find implementation. Just want to point this out. \n | 11 | 0 | ['Breadth-First Search', 'Heap (Priority Queue)'] | 2 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Solution By Dare2Solve | Detailed Explanation | Union Find | Clean Code | solution-by-dare2solve-detailed-explanat-7rbb | Explanation []\nauthorslog.vercel.app/blog/O3ildCY4Uu\n\n\n# Code\n\ncpp []\nclass UnionFind {\npublic:\n vector<int> parent;\n int groups;\n\n UnionFi | JayPokale | NORMAL | 2023-04-30T03:58:22.586693+00:00 | 2024-06-30T06:07:43.445829+00:00 | 904 | false | ```Explanation []\nauthorslog.vercel.app/blog/O3ildCY4Uu\n```\n\n# Code\n\n```cpp []\nclass UnionFind {\npublic:\n vector<int> parent;\n int groups;\n\n UnionFind(int n) : parent(n), groups(n - 1) {\n for (int i = 0; i < n; ++i) {\n parent[i] = i;\n }\n }\n\n int find(int i) {\n if (parent[i] != i) {\n parent[i] = find(parent[i]);\n }\n return parent[i];\n }\n\n bool unionSets(int i, int j) {\n int x = find(i);\n int y = find(j);\n if (x == y) {\n return false;\n } else {\n parent[y] = x;\n --groups;\n return true;\n }\n }\n};\n\nclass Solution {\npublic:\n int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {\n UnionFind alice(n), bob(n);\n int count = 0;\n\n for (const auto& edge : edges) {\n int type = edge[0], u = edge[1] - 1, v = edge[2] - 1;\n if (type == 3 && alice.unionSets(u, v) && bob.unionSets(u, v)) {\n ++count;\n }\n }\n for (const auto& edge : edges) {\n int type = edge[0], u = edge[1] - 1, v = edge[2] - 1;\n if ((type == 1 && alice.unionSets(u, v)) || (type == 2 && bob.unionSets(u, v))) {\n ++count;\n }\n }\n\n if (alice.groups == 0 && bob.groups == 0) {\n return edges.size() - count;\n } else {\n return -1;\n }\n }\n};\n```\n\n```python []\nclass UnionFind:\n def __init__(self, n):\n self.parent = list(range(n))\n self.groups = n - 1\n \n def find(self, i):\n if self.parent[i] != i:\n self.parent[i] = self.find(self.parent[i])\n return self.parent[i]\n \n def union(self, i, j):\n x = self.find(i)\n y = self.find(j)\n if x == y:\n return False\n else:\n self.parent[y] = x\n self.groups -= 1\n return True\n\nclass Solution:\n def maxNumEdgesToRemove(self, n: int, edges: List[List[int]]) -> int:\n alice = UnionFind(n)\n bob = UnionFind(n)\n count = 0\n \n for edge in edges:\n type, u, v = edge[0], edge[1] - 1, edge[2] - 1\n if type == 3 and alice.union(u, v) and bob.union(u, v):\n count += 1\n \n for edge in edges:\n type, u, v = edge[0], edge[1] - 1, edge[2] - 1\n if (type == 1 and alice.union(u, v)) or (type == 2 and bob.union(u, v)):\n count += 1\n \n if alice.groups == 0 and bob.groups == 0:\n return len(edges) - count\n else:\n return -1\n```\n\n```java []\nclass UnionFind {\n int[] parent;\n int groups;\n\n UnionFind(int n) {\n parent = new int[n];\n for (int i = 0; i < n; ++i) {\n parent[i] = i;\n }\n groups = n - 1;\n }\n\n int find(int i) {\n if (parent[i] != i) {\n parent[i] = find(parent[i]);\n }\n return parent[i];\n }\n\n boolean union(int i, int j) {\n int x = find(i);\n int y = find(j);\n if (x == y) {\n return false;\n } else {\n parent[y] = x;\n groups--;\n return true;\n }\n }\n}\n\nclass Solution {\n public int maxNumEdgesToRemove(int n, int[][] edges) {\n UnionFind alice = new UnionFind(n);\n UnionFind bob = new UnionFind(n);\n int count = 0;\n\n for (int[] edge : edges) {\n int type = edge[0], u = edge[1] - 1, v = edge[2] - 1;\n if (type == 3 && alice.union(u, v) && bob.union(u, v)) {\n ++count;\n }\n }\n for (int[] edge : edges) {\n int type = edge[0], u = edge[1] - 1, v = edge[2] - 1;\n if ((type == 1 && alice.union(u, v)) || (type == 2 && bob.union(u, v))) {\n ++count;\n }\n }\n\n if (alice.groups == 0 && bob.groups == 0) {\n return edges.length - count;\n } else {\n return -1;\n }\n }\n}\n```\n\n```javascript []\n/**\n * @param {number} n\n * @param {number[][]} edges\n * @returns {number}\n */\nvar maxNumEdgesToRemove = function (n, edges) {\n const alice = new UnionFind(n), bob = new UnionFind(n);\n let count = 0;\n\n for (let [type, u, v] of edges) {\n if (type === 3 && alice.union(u, v) && bob.union(u, v)) count++;\n }\n for (let [type, u, v] of edges) {\n if (\n (type === 1 && alice.union(u, v)) ||\n (type === 2 && bob.union(u, v))\n )\n count++;\n }\n\n if (!bob.groups && !alice.groups) return edges.length - count;\n else return -1;\n};\n\n/**\n * @class UnionFind\n * @param {number} n\n */\nclass UnionFind {\n constructor(n) {\n this.parent = new Array(n).fill().map((_, i) => i);\n this.groups = n - 1;\n }\n\n /**\n * @param {number} i\n * @returns {number}\n */\n find(i) {\n if (this.parent[i] !== i) this.parent[i] = this.find(this.parent[i]);\n return this.parent[i];\n }\n\n /**\n * @param {number} i\n * @param {number} j\n * @returns {boolean}\n */\n union(i, j) {\n const x = this.find(i),\n y = this.find(j);\n if (x === y) return false;\n else {\n this.parent[y] = x;\n this.groups--;\n return true;\n }\n }\n}\n``` | 10 | 0 | ['Union Find', 'Graph', 'Python', 'C++', 'Java', 'Python3', 'JavaScript'] | 2 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Beats 93% users... Give my code a try and get accurate result | beats-93-users-give-my-code-a-try-and-ge-bfnm | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Aim_High_212 | NORMAL | 2024-06-30T02:33:25.663802+00:00 | 2024-06-30T02:33:25.663824+00:00 | 63 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass UnionFind:\n\n """A minimalist standalone union-find implementation."""\n\n def __init__(self, n):\n\n self.count = n # number of disjoint sets \n\n self.parent = list(range(n)) # parent of given nodes\n\n self.rank = [1]*n # rank (aka size) of sub-tree \n\n \n\n def find(self, p):\n\n """Find with path compression."""\n\n if p != self.parent[p]: \n\n self.parent[p] = self.find(self.parent[p]) # path compression \n\n return self.parent[p]\n\n \n\n def union(self, p, q):\n\n """Union with ranking."""\n\n prt, qrt = self.find(p), self.find(q)\n\n if prt == qrt: return False\n\n self.count -= 1 # one more connection => one less disjoint \n\n if self.rank[prt] > self.rank[qrt]: prt, qrt = qrt, prt # add small sub-tree to large sub-tree for balancing\n\n self.parent[prt] = qrt\n\n self.rank[qrt] += self.rank[prt] # ranking \n\n return True\n\n \n\n \n\nclass Solution:\n\n def maxNumEdgesToRemove(self, n: int, edges: List[List[int]]) -> int:\n\n ufa = UnionFind(n) # for Alice\n\n ufb = UnionFind(n) # for Bob\n\n \n\n ans = 0\n\n edges.sort(reverse=True) \n\n for t, u, v in edges: \n\n u, v = u-1, v-1\n\n if t == 3: ans += not (ufa.union(u, v) and ufb.union(u, v)) # Alice & Bob\n\n elif t == 2: ans += not ufb.union(u, v) # Bob only\n\n else: ans += not ufa.union(u, v) # Alice only\n\n return ans if ufa.count == 1 and ufb.count == 1 else -1 # check if uf is connected \n\n \n``` | 9 | 0 | ['Union Find', 'Graph', 'C', 'C++', 'Java', 'Python3', 'JavaScript'] | 0 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Java Solution, Beats 96.64% | java-solution-beats-9664-by-mohit-005-3rp8 | Intuition\n\nThe problem involves ensuring that Alice and Bob can both fully traverse the graph using the provided edges. The key insight is to maximize the num | Mohit-005 | NORMAL | 2024-06-30T00:31:28.029387+00:00 | 2024-06-30T00:31:28.029415+00:00 | 1,376 | false | # Intuition\n\nThe problem involves ensuring that Alice and Bob can both fully traverse the graph using the provided edges. The key insight is to maximize the number of edges that can be removed while ensuring that both Alice and Bob can still traverse the entire graph. This can be achieved by using a Union-Find data structure to manage the connectivity of the nodes for Alice and Bob separately.\n\n# Approach\n\n1. **Union-Find Data Structure**: \n - Use two separate Union-Find structures, one for Alice and one for Bob.\n - A Union-Find (also known as Disjoint Set Union, DSU) is used to manage the connected components of a graph efficiently.\n\n2. **Processing Edges**:\n - First, process all type 3 edges (shared by both Alice and Bob) and attempt to add them to both Alice\u2019s and Bob\u2019s graphs. These edges are essential for ensuring the connectivity of both graphs.\n - Then, process type 2 edges (only for Bob) and add them to Bob\u2019s graph.\n - Finally, process type 1 edges (only for Alice) and add them to Alice\u2019s graph.\n\n3. **Count Necessary Edges**:\n - Keep a count of all edges that are necessary for maintaining connectivity. This count will help in calculating the number of removable edges.\n\n4. **Check Full Connectivity**:\n - After processing all edges, check if both Alice\u2019s and Bob\u2019s graphs are fully connected.\n - If they are, the number of removable edges is the total number of edges minus the number of necessary edges.\n - If either graph is not fully connected, return -1 indicating it is impossible for both to fully traverse the graph.\n\n# Complexity\n\n## Time Complexity\n- The time complexity for processing edges is \\(O(N + E)\\), where \\(N\\) is the number of nodes and \\(E\\) is the number of edges. This is because the union-find operations are nearly constant time due to path compression and union by rank, making the total complexity linear in the number of nodes and edges.\n\n## Space Complexity\n- The space complexity is \\(O(N)\\), which is used for storing the representative and component size arrays in the Union-Find data structure.\n\n# Code\n```\nclass Solution {\n public int maxNumEdgesToRemove(int n, int[][] edges) {\n UnionFind alice = new UnionFind(n);\n UnionFind bob = new UnionFind(n);\n\n int edgesRequired = 0;\n // First process type 3 edges\n for (int[] edge : edges) {\n if (edge[0] == 3) {\n edgesRequired += (alice.preformUnion(edge[1], edge[2]) | bob.preformUnion(edge[1], edge[2]));\n }\n }\n\n // Process type 2 and type 1 edges\n for (int[] edge : edges) {\n if (edge[0] == 2) {\n edgesRequired += bob.preformUnion(edge[1], edge[2]);\n } else if (edge[0] == 1) {\n edgesRequired += alice.preformUnion(edge[1], edge[2]);\n }\n }\n\n // Check if both Alice\'s and Bob\'s graphs are fully connected\n if (alice.isConnected() && bob.isConnected()) {\n return edges.length - edgesRequired;\n }\n\n return -1;\n }\n\n class UnionFind {\n int[] representative;\n int[] componentSize;\n int components;\n\n UnionFind(int n) {\n components = n;\n representative = new int[n + 1];\n componentSize = new int[n + 1];\n\n for (int i = 0; i <= n; i++) {\n representative[i] = i;\n componentSize[i] = 1;\n }\n }\n\n int findRepresentative(int x) {\n if (representative[x] == x) {\n return x;\n }\n return representative[x] = findRepresentative(representative[x]);\n }\n\n int preformUnion(int x, int y) {\n x = findRepresentative(x);\n y = findRepresentative(y);\n\n if (x == y) {\n return 0;\n }\n\n if (componentSize[x] > componentSize[y]) {\n componentSize[x] += componentSize[y];\n representative[y] = x;\n } else {\n componentSize[y] += componentSize[x];\n representative[x] = y;\n }\n\n components--;\n return 1;\n }\n\n boolean isConnected() {\n return components == 1;\n }\n }\n}\n``` | 9 | 0 | ['Java'] | 2 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Python | Disjoint Set Union | python-disjoint-set-union-by-khosiyat-kyeq | see the Successfully Accepted Submission\n\n# Code\n\nclass Solution:\n def maxNumEdgesToRemove(self, n, edges):\n def find(x, parent):\n i | Khosiyat | NORMAL | 2024-06-30T06:18:08.553925+00:00 | 2024-06-30T06:18:08.553952+00:00 | 889 | false | [see the Successfully Accepted Submission](https://leetcode.com/problems/remove-max-number-of-edges-to-keep-graph-fully-traversable/submissions/1304542402/?envType=daily-question&envId=2024-06-30)\n\n# Code\n```\nclass Solution:\n def maxNumEdgesToRemove(self, n, edges):\n def find(x, parent):\n if parent[x] != x:\n parent[x] = find(parent[x], parent)\n return parent[x]\n\n def union(x, y, parent):\n parent[find(x, parent)] = find(y, parent)\n\n dsu1 = list(range(n + 1))\n dsu2 = list(range(n + 1))\n count = 0\n edges.sort(key=lambda x: x[0], reverse=True)\n\n for edge in edges:\n if edge[0] == 3:\n if find(edge[1], dsu1) == find(edge[2], dsu1) and find(edge[1], dsu2) == find(edge[2], dsu2):\n count += 1\n continue\n\n union(edge[1], edge[2], dsu1)\n union(edge[1], edge[2], dsu2)\n elif edge[0] == 1:\n if find(edge[1], dsu1) == find(edge[2], dsu1):\n count += 1\n\n union(edge[1], edge[2], dsu1)\n else:\n if find(edge[1], dsu2) == find(edge[2], dsu2):\n count += 1\n\n union(edge[1], edge[2], dsu2)\n\n for i in range(1, n + 1):\n find(i, dsu1)\n find(i, dsu2)\n\n for i in range(2, n + 1):\n if dsu1[i] != dsu1[1] or dsu2[i] != dsu2[1]:\n return -1\n\n return count\n```\n\n\n | 8 | 0 | ['Python3'] | 2 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Maximizing Removable Edges While Ensuring Full Traversability in Undirected Graphs for Alice and Bob | maximizing-removable-edges-while-ensurin-ntgu | Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem requires us to find the maximum number of edges that can be removed while e | iamanrajput | NORMAL | 2024-06-30T13:11:00.390214+00:00 | 2024-06-30T13:11:00.390248+00:00 | 170 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem requires us to find the maximum number of edges that can be removed while ensuring that the graph remains fully traversable by both Alice and Bob. The key insight is to use Union-Find (or Disjoint Set Union, DSU) to manage the connectivity of the graph for both Alice and Bob independently and together.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Union-Find Initialization:\n\n We create two Union-Find data structures, one for Alice and one for Bob.\nWe also create a counter to track the number of removed edges.\n2. Processing Type 3 Edges:\n\n These edges can be used by both Alice and Bob, so we attempt to union them in both Union-Find structures.\nIf a union operation fails (because the nodes are already connected), we increment the removed edges counter.\n3. Processing Type 1 and Type 2 Edges:\n\n Type 1 edges are only for Alice, so we try to union them in Alice\'s Union-Find.\nType 2 edges are only for Bob, so we try to union them in Bob\'s Union-Find.\nAgain, if a union operation fails, we increment the removed edges counter.\n4. Validation:\n\n After processing all edges, we check if both Union-Find structures have only one connected component (indicating full traversability).\nIf not, it means that either Alice or Bob (or both) cannot fully traverse the graph, and we return -1.\n# Complexity\n- Time complexity:The overall complexity is O(E\u22C5\u03B1(N)), where\nE is the number of edges and \u03B1 is the inverse Ackermann function, which is very slow-growing.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: The space complexity is O(N) due to the storage required for the Union-Find structures.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass UnionFind {\n private int[] p;\n private int[] size;\n public int cnt;\n\n public UnionFind(int n) {\n p = new int[n];\n size = new int[n];\n for (int i = 0; i < n; ++i) {\n p[i] = i;\n size[i] = 1;\n }\n cnt = n;\n }\n\n public int find(int x) {\n if (p[x] != x) {\n p[x] = find(p[x]);\n }\n return p[x];\n }\n\n public boolean union(int a, int b) {\n int pa = find(a - 1), pb = find(b - 1);\n if (pa == pb) {\n return false;\n }\n if (size[pa] > size[pb]) {\n p[pb] = pa;\n size[pa] += size[pb];\n } else {\n p[pa] = pb;\n size[pb] += size[pa];\n }\n --cnt;\n return true;\n }\n}\n\nclass Solution {\n public int maxNumEdgesToRemove(int n, int[][] edges) {\n UnionFind ufa = new UnionFind(n);\n UnionFind ufb = new UnionFind(n);\n int ans = 0;\n for (var e : edges) {\n int t = e[0], u = e[1], v = e[2];\n if (t == 3) {\n if (ufa.union(u, v)) {\n ufb.union(u, v);\n } else {\n ++ans;\n }\n }\n }\n for (var e : edges) {\n int t = e[0], u = e[1], v = e[2];\n if (t == 1 && !ufa.union(u, v)) {\n ++ans;\n }\n if (t == 2 && !ufb.union(u, v)) {\n ++ans;\n }\n }\n return ufa.cnt == 1 && ufb.cnt == 1 ? ans : -1;\n }\n}\n``` | 7 | 0 | ['Union Find', 'Graph', 'C++', 'Java'] | 0 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | [Python3] - Union Find - Easy to understand | python3-union-find-easy-to-understand-by-mvv1 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\nWith E | dolong2110 | NORMAL | 2023-04-30T15:59:28.950857+00:00 | 2024-06-30T09:26:52.022143+00:00 | 694 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\nWith `E` is number of edges and `V` is number of vertices\n- Time complexity: $$O(ElogE)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(V)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass UnionFind:\n\n def __init__(self, n: int):\n self.root = [i for i in range(n)]\n self.rank = [1 for _ in range(n)]\n self.group = n\n\n def find(self, x: int) -> int:\n if self.root[x] != x: self.root[x] = self.find(self.root[x])\n return self.root[x]\n\n def union(self, x: int, y: int) -> None:\n root_x, root_y = self.find(x), self.find(y)\n if root_x == root_y: return\n if self.rank[root_x] > self.rank[root_y]: self.root[root_y] = root_x\n elif self.rank[root_x] < self.rank[root_y]: self.root[root_x] = root_y\n else:\n self.root[root_y] = root_x\n self.rank[root_x] += 1\n self.group -= 1\n\n def are_connected(self, x: int, y: int) -> bool:\n return self.find(x) == self.find(y)\n\n\nclass Solution:\n def maxNumEdgesToRemove(self, n: int, edges: List[List[int]]) -> int:\n uf_a, uf_b = UnionFind(n), UnionFind(n)\n res = 0\n edges.sort(reverse=True)\n for t, u, v in edges:\n if t == 3:\n if uf_a.are_connected(u - 1, v - 1) or uf_b.are_connected(u - 1, v - 1): res += 1\n else:\n uf_a.union(u - 1, v - 1)\n uf_b.union(u - 1, v - 1)\n if t == 2:\n if uf_b.are_connected(u - 1, v - 1): res += 1\n else: uf_b.union(u - 1, v - 1)\n if t == 1:\n if uf_a.are_connected(u - 1, v - 1): res += 1\n else: uf_a.union(u - 1, v - 1)\n \n return res if uf_a.group == uf_b.group == 1 else -1\n``` | 7 | 0 | ['Union Find', 'Graph', 'Sorting', 'Python3'] | 2 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Clean Code || Easy to understand || Union Find | clean-code-easy-to-understand-union-find-sjpu | A BIT OF REDUNDANT CODE \uD83D\uDE05, JUST FOR SIMPLICITY\n### ALSO INCLUDED A \'NOT REDUNDANT\' CODE LATER \uD83D\uDC47\uD83D\uDC47\n\nclass Solution {\npublic | mohakharjani | NORMAL | 2023-04-30T01:05:45.539259+00:00 | 2023-04-30T01:08:32.218046+00:00 | 2,635 | false | ### A BIT OF REDUNDANT CODE \uD83D\uDE05, JUST FOR SIMPLICITY\n### ALSO INCLUDED A \'NOT REDUNDANT\' CODE LATER \uD83D\uDC47\uD83D\uDC47\n```\nclass Solution {\npublic:\n int findParent(vector<int>&parent, int node)\n {\n if (parent[node] == node) return node;\n else return findParent(parent, parent[node]);\n }\n bool merge(vector<int>&parent, vector<int>&rank, int node1, int node2)\n {\n int parent1 = findParent(parent, node1);\n int parent2 = findParent(parent, node2);\n if (parent1 == parent2) return false;\n else\n {\n //NON-OPTIMAL WAY => { parent[parent1] = parent2 or parent[parent2] = parent2; return; :)} \n //OPTIMAL WAY=> merge based on rank to reduce complexity in \'FINDING PARENT\' next time\n if (rank[parent1] == rank[parent2]) //both at same level\n {\n parent[parent1] = parent2; \n rank[parent2]++; \n }\n else if (rank[parent1] < rank[parent2]) //parent2 is at higher level\n parent[parent1] = parent2; \n else //parent1 is at higher level\n parent[parent2] = parent1;\n return true;\n }\n }\n int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) \n {\n int notUsed = 0, componentCount = n;\n vector<int>parent(n + 1);\n vector<int>rank(n + 1, 0);\n for (int i = 1; i <= n; i++) parent[i] = i;\n //===========================================================================\n //COMMON FOR BOTH\n for (vector<int>&edge : edges)\n {\n if (edge[0] != 3) continue;\n \n bool merged = merge(parent, rank, edge[1], edge[2]);\n if (!merged) notUsed++;\n else componentCount--;\n }\n //===========================================================================\n //ONLY FOR ALICE\n vector<int>aliceParent = parent, aliceRank = rank;\n int aliceComponentCount = componentCount;\n for (vector<int>&edge : edges)\n {\n if (edge[0] != 1) continue;\n bool merged = merge(aliceParent, aliceRank, edge[1], edge[2]);\n if (!merged) notUsed++;\n else aliceComponentCount--;\n }\n if (aliceComponentCount != 1) return -1; //still not connected, so return -1\n //==============================================================================\n //ONLY FOR BOB\n //could have used tha main \'parent\', \'rank\', \'componentCount\'...\n //made duplicate copies here also only to explain \n vector<int>bobParent = parent, bobRank = rank; \n int bobComponentCount = componentCount;\n for (vector<int>&edge : edges)\n {\n if (edge[0] != 2) continue;\n bool merged = merge(bobParent, bobRank, edge[1], edge[2]);\n if (!merged) notUsed++;\n else bobComponentCount--;\n }\n if (bobComponentCount != 1) return -1; //still not connected, so return -1\n //================================================================================\n return notUsed;//not used edges will be removed\n \n }\n};\n```\n//=======================================================================================================================\n## REDUCED DUPLICACY\n```\nclass Solution {\npublic:\n int notUsed = 0;\n int findParent(vector<int>&parent, int node)\n {\n if (parent[node] == node) return node;\n else return findParent(parent, parent[node]);\n }\n bool merge(vector<int>&parent, vector<int>&rank, int node1, int node2)\n {\n int parent1 = findParent(parent, node1);\n int parent2 = findParent(parent, node2);\n if (parent1 == parent2) return false;\n else\n {\n if (rank[parent1] == rank[parent2]) //both at same level\n {\n parent[parent1] = parent2; \n rank[parent2]++; \n }\n else if (rank[parent1] < rank[parent2]) //parent2 is at higher level\n parent[parent1] = parent2; \n else //parent1 is at higher level\n parent[parent2] = parent1;\n return true;\n }\n }\n void solve(vector<vector<int>>&edges, vector<int>&parent, vector<int>&rank, int& componentCount, int currType)\n {\n for (vector<int>&edge : edges)\n {\n if (edge[0] != currType) continue;\n \n bool merged = merge(parent, rank, edge[1], edge[2]);\n if (!merged) notUsed++; //declared global\n else componentCount--;\n }\n }\n int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) \n {\n //==============================================================================\n //COMMON FOR BOTH\n int componentCount = n;\n vector<int>parent(n + 1);\n vector<int>rank(n + 1, 0);\n for (int i = 1; i <= n; i++) parent[i] = i;\n solve(edges, parent, rank, componentCount, 3);\n //===============================================================================\n //ONLY FOR ALICE\n vector<int>aliceParent = parent, aliceRank = rank;\n int aliceComponentCount = componentCount;\n solve(edges, aliceParent, aliceRank, aliceComponentCount, 1);\n if (aliceComponentCount != 1) return -1; \n //==============================================================================\n //ONLY FOR BOB\n vector<int>bobParent = parent, bobRank = rank; \n int bobComponentCount = componentCount;\n solve(edges, bobParent, bobRank, bobComponentCount, 2);\n if (bobComponentCount != 1) return -1; \n //================================================================================\n return notUsed;//not used edges will be removed\n \n }\n};\n```\n | 7 | 0 | ['Union Find', 'C', 'C++'] | 1 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Somewhat Kruskal's Algo | Union-Find | somewhat-kruskals-algo-union-find-by-tan-c7dm | \nclass Solution {\npublic:\n\n // The idea is to connect type 3 vertices first, without forming any cycle. Then again do the same for type 1, and type 2. \n | tanyarajhans7 | NORMAL | 2022-05-29T07:10:11.829172+00:00 | 2022-05-29T07:10:11.829203+00:00 | 865 | false | ```\nclass Solution {\npublic:\n\n // The idea is to connect type 3 vertices first, without forming any cycle. Then again do the same for type 1, and type 2. \n\t\n vector<int> par;\n \n int find(int x){\n if(par[x]==x)\n return x;\n return par[x]=find(par[x]);\n }\n \n void merge(int x, int y){\n int a=find(x);\n int b=find(y);\n par[a]=b;\n }\n \n int isValid(int type, vector<vector<int>>& edges){\n int c=0;\n int m=edges.size();\n for(int i=0;i<m;i++){\n if(edges[i][0]==type && find(edges[i][1])!=find(edges[i][2])){\n c++;\n merge(edges[i][1], edges[i][2]);\n }\n }\n return c;\n }\n \n int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {\n int m=edges.size();\n for(int i=0;i<=n;i++){\n par.push_back(i);\n }\n int t3=isValid(3, edges);\n vector<int> p=par;\n int t1=isValid(1, edges);\n par=p;\n int t2=isValid(2, edges);\n if(t1+t3!=n-1 || t2+t3!=n-1)\n return -1;\n return m-t1-t2-t3;\n }\n};\n``` | 7 | 0 | ['C'] | 4 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | JAVA Solution Explained in HINDI | java-solution-explained-in-hindi-by-the_-9l0o | https://youtu.be/27uTv8PW7jw\n\nFor explanation, please watch the above video and do like, share and subscribe the channel. \u2764\uFE0F Also, please do upvote | The_elite | NORMAL | 2024-06-30T13:32:44.563132+00:00 | 2024-06-30T13:32:44.563157+00:00 | 202 | false | https://youtu.be/27uTv8PW7jw\n\nFor explanation, please watch the above video and do like, share and subscribe the channel. \u2764\uFE0F Also, please do upvote the solution if you liked it.\n\n# Subscribe:- [ReelCoding](https://www.youtube.com/@reelcoding?sub_confirmation=1)\n\nSubscribe Goal:- 500\nCurrent Subscriber:- 469\n\n# Complexity\n- Time complexity: O(mlogm)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n+m)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass DSU {\n int[] parent, rank;\n\n DSU(int n) {\n parent = new int[n];\n rank = new int[n];\n for (int i = 0; i < n; i++) {\n parent[i] = i;\n rank[i] = 0;\n }\n }\n\n int find(int x) {\n if (parent[x] != x) {\n parent[x] = find(parent[x]);\n }\n return parent[x];\n }\n\n boolean union(int x, int y) {\n int xRoot = find(x);\n int yRoot = find(y);\n if (xRoot != yRoot) {\n if (rank[xRoot] < rank[yRoot]) {\n parent[xRoot] = yRoot;\n } else if (rank[xRoot] > rank[yRoot]) {\n parent[yRoot] = xRoot;\n } else {\n parent[yRoot] = xRoot;\n rank[xRoot]++;\n }\n return true;\n }\n return false;\n }\n}\n\nclass Solution {\n public int maxNumEdgesToRemove(int n, int[][] edges) {\n Arrays.sort(edges, (a, b) -> b[0] - a[0]);\n\n DSU dsuAlice = new DSU(n + 1);\n DSU dsuBob = new DSU(n + 1);\n\n int removedEdges = 0, aliceEdges = 0, bobEdges = 0;\n\n for (int[] edge : edges) {\n if (edge[0] == 3) {\n if (dsuAlice.union(edge[1], edge[2])) {\n dsuBob.union(edge[1], edge[2]);\n aliceEdges++;\n bobEdges++;\n } else {\n removedEdges++;\n }\n } else if (edge[0] == 2) {\n if (dsuBob.union(edge[1], edge[2])) {\n bobEdges++;\n } else {\n removedEdges++;\n }\n } else {\n if (dsuAlice.union(edge[1], edge[2])) {\n aliceEdges++;\n } else {\n removedEdges++;\n }\n }\n }\n\n if (aliceEdges == n - 1 && bobEdges == n - 1) {\n return removedEdges;\n } else {\n return -1;\n }\n }\n}\n``` | 6 | 0 | ['Java'] | 0 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | 🗓️ Daily LeetCoding Challenge April, Day 30 | daily-leetcoding-challenge-april-day-30-clcfc | This problem is the Daily LeetCoding Challenge for April, Day 30. Feel free to share anything related to this problem here! You can ask questions, discuss what | leetcode | OFFICIAL | 2023-04-30T00:00:23.224604+00:00 | 2023-04-30T00:00:23.224688+00:00 | 2,942 | false | This problem is the Daily LeetCoding Challenge for April, Day 30.
Feel free to share anything related to this problem here!
You can ask questions, discuss what you've learned from this problem, or show off how many days of streak you've made!
---
If you'd like to share a detailed solution to the problem, please create a new post in the discuss section and provide
- **Detailed Explanations**: Describe the algorithm you used to solve this problem. Include any insights you used to solve this problem.
- **Images** that help explain the algorithm.
- **Language and Code** you used to pass the problem.
- **Time and Space complexity analysis**.
---
**📌 Do you want to learn the problem thoroughly?**
Read [**⭐ LeetCode Official Solution⭐**](https://leetcode.com/problems/remove-max-number-of-edges-to-keep-graph-fully-traversable/solution) to learn the 3 approaches to the problem with detailed explanations to the algorithms, codes, and complexity analysis.
<details>
<summary> Spoiler Alert! We'll explain this 1 approach in the official solution</summary>
**Approach 1:** Disjoint Set Union (DSU)
</details>
If you're new to Daily LeetCoding Challenge, [**check out this post**](https://leetcode.com/discuss/general-discussion/655704/)!
---
<br>
<p align="center">
<a href="https://leetcode.com/subscribe/?ref=ex_dc" target="_blank">
<img src="https://assets.leetcode.com/static_assets/marketing/daily_leetcoding_banner.png" width="560px" />
</a>
</p>
<br> | 6 | 0 | [] | 28 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Java Simple Union-FInd | java-simple-union-find-by-hobiter-dvu0 | Just use union-find to check if that is critical connect;\n1, if by find the root partent for the 2 nodes that one edge connected, it is not critical nonnect, c | hobiter | NORMAL | 2020-09-06T06:36:08.552991+00:00 | 2020-09-07T22:47:19.615931+00:00 | 560 | false | Just use union-find to check if that is critical connect;\n1, if by find the root partent for the 2 nodes that one edge connected, it is not critical nonnect, could be removed, res++;\nelse union it, islands--;\n2, union and count for type 3 first.\n\n\n```\nclass Solution {\n int res = 0, na, nb, psa[], psb[], es[][]; // na, islands of alice, nb, islands of bob, etc...\n public int maxNumEdgesToRemove(int n, int[][] edges) {\n na = nb = n; psa = new int[n + 1]; psb = new int[n + 1]; es = edges;\n for (int i = 1; i <= n; i++) {\n psa[i] = i; // init, single islands for each node;\n psb[i] = i;\n }\n count(3); // union and count for type 3 first.\n count(2);\n count(1);\n if (na != 1 || nb != 1) return -1; // either Alice or bob could not traverse\n return res;\n }\n \n private void count(int type) {\n for (int[] e : es) \n if (e[0] == type) {\n if (type == 3 && !union(1, e) && !union(2, e)) res++;\n else if (!union(type, e)) res++;\n }\n }\n \n private boolean union(int type, int[] e) {\n int ps[] = type == 1 ? psa : psb, up = find(e[1], ps), vp = find(e[2], ps);\n if (up == vp) return false; // don\'t need to union, non-critical edges, possible remove;\n ps[up] = vp;\n if (type == 1) na--;\n else nb--;\n return true;\n }\n \n private int find(int node, int[] ps) {\n int p = ps[node];\n if (node != p) ps[node] = find(ps[node], ps);\n return ps[node];\n }\n}\n``` | 6 | 0 | [] | 0 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Easiest Striver DSU Template Explained ✅🏆 | easiest-striver-dsu-template-explained-b-3hab | Max Number of Edges to Remove to Keep Graph Fully Traversable\n\n## Intuition\nTo solve the problem of determining the maximum number of edges we can remove whi | _Rishabh_96 | NORMAL | 2024-06-30T10:30:47.746069+00:00 | 2024-06-30T10:30:47.746093+00:00 | 819 | false | # Max Number of Edges to Remove to Keep Graph Fully Traversable\n\n## Intuition\nTo solve the problem of determining the maximum number of edges we can remove while still keeping the graph fully traversable by both Alice and Bob, we can utilize the Disjoint Set Union (DSU) data structure, also known as Union-Find. This data structure helps efficiently manage and merge sets.\n\n## Approach\n1. **Sort the edges**: \n - Sort the edges in descending order based on their types so that type 3 edges (usable by both Alice and Bob) are processed first. This allows us to maximize shared edges, which helps in minimizing the total number of edges used.\n \n2. **Initialize DSU for Alice and Bob**: \n - Create two instances of the DSU, one for Alice and one for Bob. This allows us to manage their connected components separately.\n\n3. **Process edges**:\n - Iterate through each edge and handle it based on its type:\n - **Type 3 (shared) edges**: Attempt to add them to both Alice\'s and Bob\'s DSU. If the edge results in a cycle in either DSU (i.e., the two nodes of the edge are already connected), it means the edge is redundant and can be removed. Increment the `removedEdges` counter for each such edge.\n - **Type 1 (Alice) edges**: Attempt to add them only to Alice\'s DSU. If the edge results in a cycle, it is redundant and can be removed. Increment the `removedEdges` counter for each such edge.\n - **Type 2 (Bob) edges**: Attempt to add them only to Bob\'s DSU. If the edge results in a cycle, it is redundant and can be removed. Increment the `removedEdges` counter for each such edge.\n\n4. **Check connectivity**:\n - After processing all edges, check if both Alice\'s and Bob\'s DSU are fully connected. This means checking if both DSUs have exactly one connected component spanning all nodes (i.e., all nodes are connected directly or indirectly).\n - If both Alice\'s and Bob\'s graphs are fully connected, return the count of removed edges. If not, return -1 indicating it\'s not possible to make both graphs fully traversable using the given edges.\n\n## Complexity\n- **Time complexity**:\n - Sorting the edges: \\(O(E \\log E)\\), where \\(E\\) is the number of edges.\n - Union-Find operations: nearly \\(O(1)\\) per operation, due to path compression and union by size/rank. So, the overall complexity for processing the edges is \\(O(E \\cdot \\alpha(N))\\), where \\(\\alpha\\) is the inverse Ackermann function.\n\n- **Space complexity**:\n - Storing the DSU data structures: \\(O(N)\\), where \\(N\\) is the number of nodes.\n\n## Code\n```cpp\nclass DisjointSet {\n vector<int> parent, size;\npublic:\n DisjointSet(int n) {\n parent.resize(n + 1);\n size.resize(n + 1);\n for (int i = 0; i <= n; i++) {\n parent[i] = i;\n size[i] = 1;\n }\n }\n\n int findUltimateParent(int node) {\n if (node == parent[node])\n return node;\n return parent[node] = findUltimateParent(parent[node]);\n }\n\n bool unionBySize(int u, int v) {\n int ulp_u = findUltimateParent(u);\n int ulp_v = findUltimateParent(v);\n if (ulp_u == ulp_v)\n return false;\n if (size[ulp_u] < size[ulp_v]) {\n parent[ulp_u] = ulp_v;\n size[ulp_v] += size[ulp_u];\n } else {\n parent[ulp_v] = ulp_u;\n size[ulp_u] += size[ulp_v];\n }\n return true;\n }\n};\n\nclass Solution {\npublic:\n int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {\n sort(edges.begin(), edges.end(), [&](auto const &a, auto const &b) {\n return a[0] > b[0];\n });\n\n DisjointSet dsAlice(n);\n DisjointSet dsBob(n);\n\n int removedEdges = 0, aliceEdges = 0, bobEdges = 0;\n for (auto edge : edges) {\n if (edge[0] == 3) {\n if (dsAlice.unionBySize(edge[1], edge[2])) {\n dsBob.unionBySize(edge[1], edge[2]);\n aliceEdges++;\n bobEdges++;\n } else {\n removedEdges++;\n }\n } else if (edge[0] == 2) {\n if (dsBob.unionBySize(edge[1], edge[2])) {\n bobEdges++;\n } else {\n removedEdges++;\n }\n } else {\n if (dsAlice.unionBySize(edge[1], edge[2])) {\n aliceEdges++;\n } else {\n removedEdges++;\n }\n }\n }\n return (bobEdges == n - 1 && aliceEdges == n - 1) ? removedEdges : -1;\n }\n};\n | 5 | 0 | ['Union Find', 'Graph', 'C++'] | 0 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | 🔥Very Easy✅|| Full Explanation || Union✅≧◠‿◠≦✅||🧠Less Memory || O(nlogn) Time | very-easy-full-explanation-union_less-me-ch26 | Intuition\nTo solve this problem, we can use the Union-Find (Disjoint Set Union, DSU) data structure. The goal is to ensure that both Alice and Bob can traverse | anand_shukla1312 | NORMAL | 2024-06-30T03:10:30.089197+00:00 | 2024-06-30T03:10:30.089220+00:00 | 336 | false | # Intuition\nTo solve this problem, we can use the Union-Find (Disjoint Set Union, DSU) data structure. The goal is to ensure that both Alice and Bob can traverse the entire graph while maximizing the number of edges removed.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n---\n\n\n# Approach \nThe steps are as follows:\n\n1. **Sort and Prioritize Edges**: Process type 3 edges first since they can be used by both Alice and Bob. Then, process type 1 and type 2 edges separately.\n\n2. **Union-Find Setup**: Maintain two separate Union-Find structures, one for Alice and one for Bob.\n\n3. **Union Operation**: Apply union operations to both Union-Find structures for type 3 edges. Then apply union operations for type 1 edges to Alice\'s Union-Find and type 2 edges to Bob\'s Union-Find.\n\n4. **Check Connectivity**: After processing all edges, check if both Alice and Bob can reach all nodes (i.e., the Union-Find structures should have exactly one connected component).\n\n5. **Count Removed Edges**: Keep track of the number of edges that were not used in the union operations.\n<!-- Describe your approach to solving the problem. -->\n\n---\n\n\n# Complexity\n- Time complexity: $$O(nlogn)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n+m)$$ \n - where n is the number of nodes and m is the number of edges.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n---\n\n\n# Code\n```\nfrom typing import List\n\nclass UnionFind:\n def __init__(self, n):\n self.parent = list(range(n))\n self.rank = [1] * n\n self.count = n\n\n def find(self, u):\n if self.parent[u] != u:\n self.parent[u] = self.find(self.parent[u]) # Path compression\n return self.parent[u]\n\n def union(self, u, v):\n root_u = self.find(u)\n root_v = self.find(v)\n if root_u != root_v:\n if self.rank[root_u] > self.rank[root_v]:\n self.parent[root_v] = root_u\n elif self.rank[root_u] < self.rank[root_v]:\n self.parent[root_u] = root_v\n else:\n self.parent[root_v] = root_u\n self.rank[root_u] += 1\n self.count -= 1\n return True\n return False\n\n def connected_components(self):\n return self.count\n\nclass Solution:\n def maxNumEdgesToRemove(self, n: int, edges: List[List[int]]) -> int:\n uf_alice = UnionFind(n)\n uf_bob = UnionFind(n)\n \n edges.sort(reverse=True, key=lambda x: x[0])\n \n used_edges = 0\n\n for edge_type, u, v in edges:\n u -= 1\n v -= 1\n if edge_type == 3:\n if uf_alice.union(u, v) | uf_bob.union(u, v):\n used_edges += 1\n elif edge_type == 1:\n if uf_alice.union(u, v):\n used_edges += 1\n elif edge_type == 2:\n if uf_bob.union(u, v):\n used_edges += 1\n \n if uf_alice.connected_components() > 1 or uf_bob.connected_components() > 1:\n return -1\n \n return len(edges) - used_edges\n \n```\n\n---\n\n\n# Explanation:\n- **Union-Find Initialization**: Two Union-Find structures are created, one for Alice and one for Bob.\n- **Processing Type 3 Edges**: These edges are used by both Alice and Bob. We perform the union operation on both Union-Finds.\n- **Processing Type 1 and Type 2 Edges**: Type 1 edges are used for Alice\'s Union-Find, and Type 2 edges are used for Bob\'s Union-Find.\n- **Connectivity Check**: After processing all edges, we check if both Alice and Bob can traverse all nodes by ensuring each Union-Find has exactly one connected component.\n- **Counting Removed Edges**: The difference between the total number of edges and the number of edges used gives the number of edges that can be removed.\n- \n---\n\n\n\n---\n\n> Thank You | 5 | 0 | ['Union Find', 'Graph', 'Python3'] | 2 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Easy Java Solution | DSU | Union Find | Beats 100 💯✅ | easy-java-solution-dsu-union-find-beats-afn4p | Max Number of Edges to Remove\n\n## Problem Statement\n\nGiven an undirected graph with n nodes and a list of edges, where each edge is of one of three types:\n | shobhitkushwaha1406 | NORMAL | 2024-06-30T01:48:03.732735+00:00 | 2024-06-30T01:48:03.732763+00:00 | 718 | false | # Max Number of Edges to Remove\n\n## Problem Statement\n\nGiven an undirected graph with `n` nodes and a list of `edges`, where each edge is of one of three types:\n\n- Type 1: Can be traversed by Alice.\n- Type 2: Can be traversed by Bob.\n- Type 3: Can be traversed by both Alice and Bob.\n\nOur goal is to remove the maximum number of edges such that both Alice and Bob can still traverse all nodes. If it\'s not possible to do so, return `-1`.\n\n## Intuition\n\nTo solve this problem, we need to ensure both Alice and Bob can traverse all the nodes in the graph using the fewest edges possible. The type 3 edges are the most valuable since they can be used by both Alice and Bob. By prioritizing these edges, we can potentially minimize the number of edges needed for both Alice and Bob.\n\nThe key steps are:\n1. Use type 3 edges first to build a common structure for both Alice and Bob.\n2. Then, use type 1 edges to connect Alice\'s graph.\n3. Lastly, use type 2 edges to connect Bob\'s graph.\n4. Check if both Alice and Bob can traverse all nodes. If not, return `-1`.\n\n## Approach\n\n1. **Union-Find Initialization:** We use a Union-Find data structure to manage the connectivity of nodes for both Alice and Bob.\n\n2. **Sort and Process Edges:** \n - Sort the edges based on type in descending order so that type 3 edges come first.\n - Iterate through the sorted edges:\n - For type 3 edges, try to connect the nodes for both Alice and Bob.\n - For type 1 edges, try to connect the nodes for Alice only.\n - For type 2 edges, try to connect the nodes for Bob only.\n - Count the number of edges added to the Union-Find structures.\n\n3. **Connectivity Check:** After processing all edges, check if both Alice and Bob\'s Union-Find structures have only one connected component each. If either does not, return `-1`.\n\n4. **Calculate Result:** The result is the total number of edges minus the number of edges used.\n\n## Complexity Analysis\n\n- **Time Complexity:** The algorithm mainly involves sorting the edges and performing union-find operations. Sorting takes `O(E log E)`, where `E` is the number of edges. Each union or find operation is nearly constant time, amortized to `O(alpha(N))`, where `(alpha)` is the inverse Ackermann function. Thus, the total time complexity is `(O(E log E + E alpha(N))`, which is `(O(E log E)` since `(alpha(N))` is very slow-growing.\n\n- **Space Complexity:** The space complexity is `(O(N + E))`, where `(N)` is the number of nodes and `(E)` is the number of edges. This includes the space for the Union-Find structures and the edges list.\n\n\n# Code\n```\nclass Solution {\n class UnionFind {\n int[] parent;\n int[] rank;\n int count;\n public UnionFind(int n) {\n parent = new int[n];\n rank = new int[n];\n count = n;\n for (int i = 0; i < n; i++) {\n parent[i] = i;\n rank[i] = 0;\n }\n }\n\n public int find(int x) {\n if (parent[x] != x) {\n parent[x] = find(parent[x]);\n }\n return parent[x];\n }\n\n public boolean union(int x, int y) {\n int rootX = find(x);\n int rootY = find(y);\n\n if (rootX != rootY) {\n if (rank[rootX] > rank[rootY]) {\n parent[rootY] = rootX;\n } else if (rank[rootX] < rank[rootY]) {\n parent[rootX] = rootY;\n } else {\n parent[rootY] = rootX;\n rank[rootX]++;\n }\n count--;\n return true;\n }\n return false;\n }\n public int getCount() {\n return count;\n }\n }\n public int maxNumEdgesToRemove(int n, int[][] edges) {\n UnionFind aliceUF = new UnionFind(n);\n UnionFind bobUF = new UnionFind(n);\n int addedEdges = 0;\n Arrays.sort(edges, (a, b) -> b[0] - a[0]);\n for (int[] edge : edges) {\n int type = edge[0];\n int u = edge[1] - 1;\n int v = edge[2] - 1;\n\n if (type == 3) {\n boolean aliceConnected = aliceUF.union(u, v);\n boolean bobConnected = bobUF.union(u, v);\n if (aliceConnected || bobConnected) {\n addedEdges++;\n }\n } else if (type == 1) {\n if (aliceUF.union(u, v)) {\n addedEdges++;\n }\n } else if (type == 2) {\n if (bobUF.union(u, v)) {\n addedEdges++;\n }\n }\n }\n if (aliceUF.getCount() > 1 || bobUF.getCount() > 1) {\n return -1;\n }\n return edges.length - addedEdges;\n }\n\t}\n``` | 5 | 0 | ['Union Find', 'Graph', 'Sorting', 'Java'] | 1 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Union Find Solution || optimal | union-find-solution-optimal-by-ankit_m15-xrq0 | \n# Approach\n Describe your approach to solving the problem. \n1. Firstly, make two disjointSet one for alice and one for bob.\n2. We will keep 3 counter, for | ankit_m15 | NORMAL | 2023-04-30T13:45:20.384247+00:00 | 2023-04-30T17:31:39.703960+00:00 | 592 | false | \n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Firstly, make two disjointSet one for alice and one for bob.\n2. We will keep 3 counter, for - alice, bob and both\n3. Now, first check for all the type 3 edges which is common for both alice and bob.\n4. If parents of nodes for Both alice and bob are already same so we will consider to remove it (both++).\n5. Else we will make there parents same.\n6. Now, similar step we will follow again for type 1 and type 2 edges.\n7. As we know, type 1 is for alice and type 2 is for bob\n8. so, if type 1 edge is there and the parent of nodes are already same so we can consider it to remove (alice++).else we will make there parent to be same.\n9. if type 2 edge is there and the parent of nodes are already same so we can consider it to remove (bob++).else we will make there parent to be same.\n10. Finally, before returning your you should check whether all nodes are connected or not (by checking if there parent is same or not) for both alice and bob.\n11. if all the nodes are connected for both of them. then, return ans as alice+bob+both. else return -1\n\n\n# Complexity\n- Time complexity: O(m \u03B1(n)), where m=no. of edges & n=no. of nodes\n \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass disjointSet{\n vector<int>parent,size;\n public:\n disjointSet(int n){\n parent.resize(n+1);\n size.resize(n+1,1);\n for(int i=0; i<=n; i++){\n parent[i]=i;\n }\n }\n int findParent(int node){\n if(node==parent[node]){\n return node;\n }\n return parent[node]=findParent(parent[node]);\n }\n void unionBySize(int u,int v){\n int parentOfU=findParent(u);\n int parentOfV=findParent(v);\n if(parentOfU==parentOfV) return;\n if(size[parentOfU] < size[parentOfV]){\n parent[parentOfU]=parentOfV;\n size[parentOfV]+=size[parentOfU];\n }\n else{\n parent[parentOfV]=parentOfU;\n size[parentOfU]+=size[parentOfV];\n }\n }\n bool check(int first,int second){\n if(findParent(first)==findParent(second)) \n return true;\n return false;\n }\n};\n\nclass Solution {\npublic:\n int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {\n disjointSet ds1(n);\n disjointSet ds2(n);\n int alice=0,bob=0,both=0;\n for(auto it:edges){\n int type=it[0];\n int node1=it[1];\n int node2=it[2];\n if(type==1 || type==2)continue;\n if(ds1.check(node1,node2) && ds2.check(node1,node2)){\n both++;\n }\n else{\n ds1.unionBySize(node1,node2);\n ds2.unionBySize(node1,node2);\n }\n }\n for(auto it:edges){\n int type=it[0];\n int node1=it[1];\n int node2=it[2];\n if(type==1){\n if(ds1.check(node1,node2))alice++;\n else ds1.unionBySize(node1,node2);\n }\n else if(type==2){\n if(ds2.check(node1,node2))bob++;\n else ds2.unionBySize(node1,node2);\n }\n }\n unordered_set<int>st1;\n unordered_set<int>st2;\n for(int i=1; i<=n; i++){\n st1.insert(ds1.findParent(i));\n if(st1.size()>1)break;\n }\n for(int i=1; i<=n; i++){\n st2.insert(ds2.findParent(i));\n if(st2.size()>1)break;\n }\n\n if(st1.size()==1 && st2.size()==1)\n return alice+bob+both;\n return -1;\n }\n};\n\n``` | 5 | 0 | ['Union Find', 'Graph', 'C++'] | 1 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | C++ DSU Application beats around 97% runtime | c-dsu-application-beats-around-97-runtim-mel3 | We give priority to third type of paths first. Essentially, we are connecting the nodes of different paths as seperate components and then adding/selecting edge | windrunner15 | NORMAL | 2022-08-29T10:57:06.546160+00:00 | 2022-08-29T10:57:06.546198+00:00 | 602 | false | We give priority to third type of paths first. Essentially, we are connecting the nodes of different paths as seperate components and then adding/selecting edges to connect them. \n```\nclass Solution {\npublic:\n vector<int> par, rank ; \n \n int find(int v){\n if(par[v] == v)\n return v ; \n return par[v] = find(par[v]) ; \n }\n \n void unionfn(int a, int b) {\n a = find(a) ; \n b = find(b) ; \n if(a!=b) {\n if(rank[a] < rank[b])\n swap(a, b) ; \n par[b] = a ; \n if(rank[b] == rank[a])\n rank[a]++ ; \n }\n }\n \n int calc(int type, vector<vector<int>>& e) {\n int ct = 0 ; \n for(int i = 0 ; i < e.size() ; i++) {\n if(e[i][0] == type and find(e[i][1]) != find(e[i][2])) {\n ct++ ; \n unionfn(e[i][1], e[i][2]) ; \n }\n }\n return ct ; \n }\n \n int maxNumEdgesToRemove(int n, vector<vector<int>>& e) {\n rank.assign(n+1, 0) ; \n for(int i =0 ; i <= n ; i++)\n par.push_back(i) ; \n int common = calc(3, e) ; \n vector<int> temp = par ; \n int alice = calc(1, e) ; \n par = temp ; \n int bob = calc(2, e) ; \n if((common + alice != n-1) or (common + bob != n-1))\n return -1 ; \n return (e.size()-common-alice-bob) ; \n }\n};\n``` | 5 | 0 | ['Union Find', 'C'] | 1 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | C# Union-Find O(n) concise code | c-union-find-on-concise-code-by-leoooooo-9mct | \npublic class Solution\n{\n public int MaxNumEdgesToRemove(int n, int[][] edges)\n {\n int res = 0;\n UnionFind alice = new UnionFind(n);\n | leoooooo | NORMAL | 2020-09-06T05:49:03.571403+00:00 | 2020-09-06T05:52:03.329855+00:00 | 163 | false | ```\npublic class Solution\n{\n public int MaxNumEdgesToRemove(int n, int[][] edges)\n {\n int res = 0;\n UnionFind alice = new UnionFind(n);\n UnionFind bob = new UnionFind(n);\n foreach (var edge in edges)\n {\n if(edge[0] == 3 && (!alice.Union(edge[1], edge[2]) || !bob.Union(edge[1], edge[2])))\n res++;\n }\n\n foreach (var edge in edges)\n {\n if (edge[0] == 1 && !alice.Union(edge[1], edge[2]))\n res++;\n if (edge[0] == 2 && !bob.Union(edge[1], edge[2]))\n res++;\n }\n\n return alice.Componets == 1 && bob.Componets == 1 ? res : -1;\n }\n}\n\npublic class UnionFind\n{\n private int[] parent;\n public int Componets { get; private set; }\n public UnionFind(int n)\n {\n Componets = n;\n parent = new int[n + 1];\n for (int i = 0; i <= n; i++)\n {\n parent[i] = i;\n }\n }\n\n public int Find(int x)\n {\n if (parent[x] != x)\n parent[x] = Find(parent[x]);\n return parent[x];\n }\n\n public bool Union(int x, int y)\n {\n int px = Find(x);\n int py = Find(y);\n if (px != py)\n {\n parent[px] = py;\n Componets--;\n return true;\n }\n return false;\n }\n}\n``` | 5 | 0 | [] | 0 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | [Python] Simple Union Find | python-simple-union-find-by-tomzy-zshn | Things we know:\n1. We know how to solve a problem if edges only contains type3 edges. The solusion will be: get a spanning tree, then all the other edges can b | tomzy | NORMAL | 2020-09-06T04:10:41.112028+00:00 | 2020-09-06T04:12:23.396266+00:00 | 423 | false | Things we know:\n1. We know how to solve a problem if edges only contains **type3** edges. The solusion will be: get a spanning tree, then all the other edges can be removed as the spanning tree already connected all nodes.\n2. We know **type3** edge is important becasues: **type3** edge can connect both for **Alice** and **Bob** in best case. But **type1** and **type2** edge can only connect **Alice** or **Bob** in best case.\n\nThen our idea will be:\n1. Use spanning tree algoritm to choose from **type3** edges first (**Union Find**): If two nodes are not from the same **union**, connect them\n2. Then use **type1** edges for **Alice**\n3. Use **type2** edges for Bob\n4. Finnaly if they are still not connected, return **-1**\n\n```\nclass UnionFind(object):\n def __init__(self, size):\n self.res = [i for i in range(size)]\n self.group = size\n self.size = [1] * size\n\n def find(self, child):\n if self.res[child] != child:\n idx = self.find(self.res[child])\n self.res[child] = idx\n return self.res[child]\n\n def union(self, a, b):\n pa = self.find(a)\n pb = self.find(b)\n if pa == pb:\n return\n if self.size[pa] > self.size[pb]:\n pa, pb = pb, pa\n self.group -= 1\n self.res[pa] = pb\n self.size[pb] += self.size[pa]\n \nclass Solution(object):\n def maxNumEdgesToRemove(self, n, edges):\n """\n :type n: int\n :type edges: List[List[int]]\n :rtype: int\n """\n\t\t# used edges count\n res = 0\n ua = UnionFind(n + 1)\n ub = UnionFind(n + 1)\n es = [[] for _ in range(4)]\n \n\t\t# group edges\n for edge in edges:\n es[edge[0]].append(edge)\n \n\t\t# use type 3 first\n for edge in es[3]:\n x = ua.find(edge[1])\n y = ua.find(edge[2])\n\t\t\t\n\t\t\t# if not from same union, add the edge and connect them\n if x != y:\n res += 1\n ua.union(x, y)\n ub.union(x, y)\n\n for edge in es[2]:\n x = ua.find(edge[1])\n y = ua.find(edge[2])\n if x != y:\n res += 1\n ua.union(x, y)\n \n for edge in es[1]:\n x = ub.find(edge[1])\n y = ub.find(edge[2])\n if x != y:\n res += 1\n ub.union(x, y)\n\t\t# if still not connected, return -1\n x = ua.find(1)\n if any(x != ua.find(i) for i in range(1, n + 1)):\n return -1\n \n\t\tx = ub.find(1)\n if any(x != ub.find(i) for i in range(1, n + 1)):\n return -1\n\n return len(edges) - res\n``` | 5 | 0 | ['Union Find', 'Python'] | 0 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Easy C++ Video Explanation | easy-c-video-explanation-by-prajaktakap0-7c71 | Video Explanation\nhttps://youtu.be/PmdyES1mtAw?si=b1KX0ivnRLEOq-Qg\n# Complexity\n\n- Time complexity:O(E *logE) \n Add your time complexity here, e.g. O(n) \n | prajaktakap00r | NORMAL | 2024-06-30T00:54:03.714763+00:00 | 2024-06-30T00:54:03.714792+00:00 | 1,660 | false | # Video Explanation\nhttps://youtu.be/PmdyES1mtAw?si=b1KX0ivnRLEOq-Qg\n# Complexity\n\n- Time complexity:$$O(E *logE)$$ \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(N+E)$$ \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nE is the number of edges\n\n# Code\n```\nclass Solution {\n bool static comp(vector<int>& a, vector<int>& b) { return a[0] > b[0]; }\n int findparent(int node, vector<int>& parent) {\n if (node == parent[node])\n return node;\n return parent[node] = findparent(parent[node], parent);\n }\n bool unionn(int u, int v, vector<int>& parent, vector<int>& rank) {\n u = findparent(u, parent);\n v = findparent(v, parent);\n\n if (u != v) {\n if (rank[u] < rank[v])\n parent[u] = v;\n else if (rank[u] > rank[v])\n parent[v] = u;\n else {\n parent[v] = u;\n rank[u]++;\n }\n return true;\n }\n return false;\n }\npublic:\n \n int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {\n vector<int>parent_alice(n+1);\n vector<int>parent_bob(n+1);\n vector<int>alice_rank(n+1);\n vector<int>bob_rank(n+1);\n\n sort(edges.begin(),edges.end(),comp);\n\n for(int i=0;i<parent_alice.size();i++){\n parent_alice[i]=i;\n parent_bob[i]=i;\n alice_rank[i]=1;\n bob_rank[i]=1;\n }\n int remove_edges=0;\n int merge_alice=1;\n int merge_bob=1;\n for(auto it:edges){\n if(it[0]==3){\n bool temp_alice=unionn(it[1],it[2],parent_alice,alice_rank);\n bool temp_bob=unionn(it[1],it[2],parent_bob,bob_rank);\n\n if(temp_alice==true){\n merge_alice++;\n }\n if(temp_bob==true){\n merge_bob++;\n }\n if(temp_alice==false && temp_bob==false){\n remove_edges++;\n }\n }else if(it[0]==1){\n bool temp_alice=unionn(it[1],it[2],parent_alice,alice_rank);\n if(temp_alice==true){\n merge_alice++;\n }else{\n remove_edges++;\n }\n }else{\n bool temp_bob=unionn(it[1],it[2],parent_bob,bob_rank);\n if(temp_bob==true){\n merge_bob++;\n }\n else{\n remove_edges++;\n }\n }\n\n }\n if(merge_alice!=n || merge_bob!=n) return -1;\n return remove_edges;\n }\n};\n``` | 4 | 0 | ['C++'] | 0 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | C++||Union Find|| Easy to Understand | cunion-find-easy-to-understand-by-return-0is1 | ```\nclass Solution {\npublic:\n int find(vector &par,int u)\n {\n if(u==par[u])\n return u;\n return par[u]=find(par,par[u]);\n | return_7 | NORMAL | 2022-05-16T14:00:23.464950+00:00 | 2022-05-16T14:00:23.465005+00:00 | 356 | false | ```\nclass Solution {\npublic:\n int find(vector<int> &par,int u)\n {\n if(u==par[u])\n return u;\n return par[u]=find(par,par[u]);\n }\n void unions(vector<int> &par,int u,int v)\n {\n int pu=find(par,u);\n int pv=find(par,v);\n par[pu]=pv;\n }\n int maxNumEdgesToRemove(int n, vector<vector<int>>& edges)\n {\n vector<int> a(n+1),b(n+1);\n int ans=0;\n for(int i=0;i<=n;i++)\n {\n a[i]=i;\n b[i]=i;\n }\n for(auto &e:edges)\n {\n if(e[0]!=3)\n continue;\n if(find(a,e[1])==find(a,e[2]))\n {\n ans++;\n continue;\n }\n unions(a,e[1],e[2]);\n unions(b,e[1],e[2]);\n }\n for(auto &e:edges)\n {\n int u=e[1],v=e[2];\n if(e[0]==1)\n {\n if(find(a,u)==find(a,v))\n {\n ans++;\n }\n else\n {\n unions(a,u,v);\n }\n }\n else if(e[0]==2)\n {\n if(find(b,u)==find(b,v))\n {\n ans++;\n }\n else\n {\n unions(b,u,v);\n }\n }\n }\n for(int i=1;i<=n;i++)\n {\n if(find(a,i)!=find(a,n)||find(b,i)!=find(b,n))\n {\n return -1;\n }\n }\n return ans;\n \n }\n};\n// if you like the solution plz upvote. | 4 | 0 | ['Union Find', 'C'] | 1 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Python, Union-Find two-pass | python-union-find-two-pass-by-yseeker-1gof | \nclass Solution(object):\n def maxNumEdgesToRemove(self, n, edges):\n\n ufa = UnionFind(n) # Graph for Alice\n ufb = UnionFind(n) # Graph for | yseeker | NORMAL | 2020-09-06T04:01:38.168742+00:00 | 2020-09-06T04:06:43.047906+00:00 | 299 | false | ```\nclass Solution(object):\n def maxNumEdgesToRemove(self, n, edges):\n\n ufa = UnionFind(n) # Graph for Alice\n ufb = UnionFind(n) # Graph for Bob\n cnt = 0 # number of removable edges\n \n for x, y, z in edges:\n if x == 3:\n flag1 = ufa.union(y, z)\n flag2 = ufb.union(y, z)\n if not flag1 or not flag2: cnt +=1\n\n for x, y, z in edges:\n if x == 1:\n flag = ufa.union(y, z)\n if not flag: cnt += 1\n if x == 2:\n flag = ufb.union(y, z)\n if not flag: cnt += 1\n\n return cnt if ufa.groups == 1 and ufb.groups == 1 else -1\n \n \nclass UnionFind():\n def __init__(self, n):\n self.parents = {i:i for i in range(1, n+1)}\n self.groups = n\n\n def find(self, x):\n if self.parents[x] == x:\n return x\n else:\n self.parents[x] = self.find(self.parents[x])\n return self.parents[x]\n\n def union(self, x, y):\n x = self.find(x)\n y = self.find(y)\n\n if x == y:\n return False\n\n self.parents[y] = x\n self.groups -= 1\n return True\n``` | 4 | 0 | ['Union Find', 'Python'] | 3 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Runtime beats 90.00%, Memory beats 100.00% [EXPLAINED] | runtime-beats-9000-memory-beats-10000-ex-jcs0 | Intuition\nThe problem involves managing connections in a graph where two people, Alice and Bob, can traverse different types of edges. The goal is to remove as | r9n | NORMAL | 2024-10-01T03:03:29.324644+00:00 | 2024-10-01T03:03:29.324681+00:00 | 14 | false | # Intuition\nThe problem involves managing connections in a graph where two people, Alice and Bob, can traverse different types of edges. The goal is to remove as many edges as possible while ensuring both can still reach all nodes. The key insight is that edges of type 3 are most beneficial because they connect both Alice and Bob.\n\n# Approach\nUse a union-find (or disjoint set) data structure to group connected nodes, processing type 3 edges first for both Alice and Bob, then type 1 edges for Alice, and finally type 2 edges for Bob, while counting how many edges were successfully used to maintain connectivity for both.\n\n# Complexity\n- Time complexity:\nO(m\u22C5\u03B1(n)), where m is the number of edges and \u03B1 is the inverse Ackermann function, which grows very slowly.\n\n- Space complexity:\nO(n) for the parent and rank arrays in the union-find structure.\n\n# Code\n```typescript []\ntype Edge = [number, number, number];\n\nclass DSU {\n private parent: number[];\n private components: number;\n\n constructor(n: number) {\n // Initialize the parent array and set components to 1\n this.parent = Array.from({ length: n + 1 }, (_, idx) => idx);\n this.components = 1;\n }\n\n // Find the root parent of a node with path compression\n private findParent(v: number): number {\n if (v === this.parent[v]) {\n return v;\n }\n return this.parent[v] = this.findParent(this.parent[v]);\n }\n\n // Union two nodes if they are in different components\n public union(v1: number, v2: number): boolean {\n const v1_parent = this.findParent(v1);\n const v2_parent = this.findParent(v2);\n\n if (v1_parent !== v2_parent) {\n this.parent[v1_parent] = v2_parent;\n this.components++; // Increase the component count\n return true; // Successful union\n }\n return false; // Already connected\n }\n\n // Check if all nodes are connected\n public isConnected(n: number): boolean {\n return this.components === n; // Compare components to the total number of nodes\n }\n}\n\n/**\n * @param {number} n - Number of nodes in the graph\n * @param {Edge[]} edges - List of edges with their types\n * @return {number} - Maximum number of edges that can be removed\n */\nfunction maxNumEdgesToRemove(n: number, edges: Edge[]): number {\n const alice = new DSU(n);\n const bob = new DSU(n);\n\n // Sort edges by type in descending order\n edges.sort((a, b) => b[0] - a[0]);\n\n let count = 0;\n\n // Process each edge based on its type\n for (let [type, v1, v2] of edges) {\n if (type === 1 || type === 3) {\n const isUnion = alice.union(v1, v2);\n if (isUnion) {\n count++; // Count the union if successful\n }\n }\n\n if (type === 2 || type === 3) {\n const isUnion = bob.union(v1, v2);\n if (type !== 3 && isUnion) {\n count++; // Count the union for Bob if successful\n }\n }\n }\n\n // Check if both Alice and Bob can traverse the graph fully\n if (alice.isConnected(n) && bob.isConnected(n)) {\n return edges.length - count; // Calculate removable edges\n }\n\n return -1; // Return -1 if full traversal is not possible\n}\n\n``` | 3 | 0 | ['TypeScript'] | 0 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | just a variant | just-a-variant-by-igormsc-z619 | Code\nKotlin []\nclass Solution {\n fun maxNumEdgesToRemove(n: Int, edges: Array<IntArray>): Int {\n val dsBoth = IntArray(n+1) {-1}\n var used | igormsc | NORMAL | 2024-06-30T08:18:21.731705+00:00 | 2024-06-30T08:18:21.731743+00:00 | 45 | false | # Code\n```Kotlin []\nclass Solution {\n fun maxNumEdgesToRemove(n: Int, edges: Array<IntArray>): Int {\n val dsBoth = IntArray(n+1) {-1}\n var used = 0\n\n fun find(ds: IntArray, i: Int): Int = if (ds[i] < 0) i else find(ds, ds[i]).also { ds[i] = it }\n\n (3 downTo 1).forEach { tp ->\n val ds = if (tp == 3) dsBoth else dsBoth.clone()\n edges.forEach { e ->\n if (e[0] == tp) {\n var i = find(ds, e[1])\n var j = find(ds, e[2])\n if (i != j) {\n used++\n if (ds[j] < ds[i]) i = j.also { j = i }\n ds[i] += ds[j]\n ds[j] = i\n }\n }\n }\n if (tp != 3 && ds[find(ds,1)] != -n) return -1\n }\n return edges.size - used\n }\n}\n``` | 3 | 0 | ['Kotlin'] | 0 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Using Disjoint Set | using-disjoint-set-by-gagan_kushwah25-4eb3 | Intuition\n Describe your first thoughts on how to solve this problem. \nSimple disjoint set use kiya hai, uske baad kuch for loops lagaye hai.\nSamajh aaye toh | gagan_kushwah25 | NORMAL | 2024-06-30T08:11:05.627593+00:00 | 2024-06-30T08:11:05.627628+00:00 | 355 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nSimple disjoint set use kiya hai, uske baad kuch for loops lagaye hai.\nSamajh aaye toh bdiya, warna \n\n\n\n\nThank for the view.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nApproch this question like you approch a girl on a date { I dont know how :( }\nAsk her what she wants, in this case she wants that alex and bob should traverse the graph completely after cutting unimportant edges.\nToo much demands. Either we can make seprate MST for both and check for unimportant edges, or we can say "Lets split the bill".\n\nSecond one is better. \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\npta nhi bhai, dekhlo tum , shyd O(n) hi hai\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Disjoint:\n def __init__(self, n):\n self.rank = [1]*n\n self.parents = [i for i in range(n)]\n def find(self, node):\n if self.parents[node] != node:\n self.parents[node] = self.find(self.parents[node])\n return self.parents[node]\n def union(self, u, v):\n uset = self.find(u)\n vset = self.find(v)\n\n if uset == vset:\n return \n if self.rank[uset] < self.rank[vset]:\n self.parents[uset] = vset\n elif self.rank[vset] < self.rank[uset]:\n self.parents[vset] = uset\n else:\n self.parents[vset] = uset\n self.rank[uset] += 1\n\nclass Solution:\n def maxNumEdgesToRemove(self, n: int, edges: List[List[int]]) -> int:\n edges3 = []\n wt1, wt2 = 0, 0\n ans1 = []\n ans2 = []\n ds1 = Disjoint(n+1)\n ds2 = Disjoint(n+1)\n for t, i,j in edges:\n if t==3:\n edges3.append((i,j))\n edges3.sort() \n for i, j in edges3:\n ii = ds1.find(i)\n jj = ds1.find(j)\n if ii != jj:\n wt1 += 1\n ans1.append((3,i,j))\n ds1.union(i,j)\n for i, j in edges3:\n ii = ds2.find(i)\n jj = ds2.find(j)\n if ii != jj:\n wt2 += 1\n ans2.append((3,i,j))\n ds2.union(i,j) \n\n\n for typee, i, j in edges:\n if typee == 1 or typee==3:\n ii = ds1.find(i)\n jj = ds1.find(j)\n if ii != jj:\n wt1 += 1\n ans1.append((typee,i,j))\n ds1.union(i,j)\n if typee == 2 or typee == 3:\n ii = ds2.find(i)\n jj = ds2.find(j)\n if ii != jj:\n wt2 +=1\n ans2.append((typee,i,j))\n ds2.union(i,j)\n #print(wt1, wt2) \n if wt1 != n-1 or wt2 != n-1:\n return -1\n #print(ans1)\n #print(ans2) \n a = set(ans1)\n for it in ans2:\n a.add(it)\n return len(edges) - len(a) \n\n\n\n \n``` | 3 | 0 | ['Python3'] | 3 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | C++ DFS + connected components | c-dfs-connected-components-by-atma-7opp | Intuition\nOnly scenario when answer is not possible is when either alice or bob are unable to visit any vertex from any source vertex with all edges present. E | Atma_ | NORMAL | 2024-06-30T06:50:10.864562+00:00 | 2024-06-30T06:50:10.864594+00:00 | 418 | false | # Intuition\nOnly scenario when answer is not possible is when either alice or bob are unable to visit any vertex from any source vertex with all edges present. Else, answer is always possible. To find the maximum edges that can be removed, traverse the graph with only edges of type 3 as much as possible. This will leave C disconnected components in graph, which can be connected with 2*(C-1) edges of type 1 and 2 each. \n\n# Approach\nMake 3 graphs : one which alice can traverse, one for bob and one with only type 3 edges (we can manage with a single graph too if needed). First check if the alice and bob graphs are connected using dfs. If not, then answer is not possible. \n\nThen, traverse the graph with type 3 edges using dfs only to make components of graph (each component needs to have only sz-1 edges if size of that component is sz, so we can remove rest of edges from each component). Now we can connect these C components with 2*(C-1) edges and can remove the rest of edges.\n\n# Complexity\n- Time complexity: O(V+E)\n\n- Space complexity: O(V+E)\n\n# Code\n```\nclass Solution {\npublic:\n \n void dfs(int node, vector<int>& vis, vector<vector<int>>& graph, \n int& sz, int& curedges){\n vis[node]=1;\n sz++;\n curedges+=graph[node].size();\n for(auto& g:graph[node]){\n if(!vis[g]){\n dfs(g,vis,graph,sz,curedges);\n }\n }\n }\n \n bool checkPossible(vector<vector<int>>& graph){\n int n=graph.size()-1;\n vector<int> vis(n+1,0);\n int sz=0,curedges=0;\n dfs(1,vis,graph,sz,curedges);\n for(int i=1;i<=n;++i){\n if(!vis[i]) return false;\n }\n return true;\n }\n \n int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {\n vector<vector<int>> graph(n+1),alice(n+1),bob(n+1);\n int total=edges.size(),type3=0;\n for(auto& e:edges){\n if(e[0]==3){\n graph[e[1]].push_back(e[2]);\n graph[e[2]].push_back(e[1]);\n alice[e[1]].push_back(e[2]);\n alice[e[2]].push_back(e[1]);\n bob[e[1]].push_back(e[2]);\n bob[e[2]].push_back(e[1]);\n type3++;\n }\n if(e[0]==1){\n alice[e[1]].push_back(e[2]);\n alice[e[2]].push_back(e[1]);\n }\n if(e[0]==2){\n bob[e[1]].push_back(e[2]);\n bob[e[2]].push_back(e[1]);\n }\n }\n if(!checkPossible(alice)) return -1;\n if(!checkPossible(bob)) return -1;\n total=total-type3;\n int components=0,ans=0;\n vector<int> vis(n+1,0);\n for(int i=1;i<=n;++i){\n if(!vis[i]){\n components++;\n int sz=0,curedges=0;\n dfs(i,vis,graph,sz,curedges);\n curedges/=2;\n ans+=curedges-(sz-1);\n }\n }\n total-=2*(components-1);\n ans+=total;\n return ans;\n }\n};\n``` | 3 | 0 | ['Depth-First Search', 'Graph', 'Recursion', 'C++'] | 1 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Python | Easy | Graph | Remove Max Number of Edges to Keep Graph Fully Traversable | python-easy-graph-remove-max-number-of-e-52kj | \nsee the Successfully Accepted Submission\nPython\nclass Solution:\n def maxNumEdgesToRemove(self, n, edges):\n def find(x, parent):\n if | Khosiyat | NORMAL | 2023-10-10T16:32:00.974591+00:00 | 2023-10-10T16:32:00.974609+00:00 | 81 | false | \n[see the Successfully Accepted Submission](https://leetcode.com/submissions/detail/1071110896/)\n```Python\nclass Solution:\n def maxNumEdgesToRemove(self, n, edges):\n def find(x, parent):\n if parent[x] != x:\n parent[x] = find(parent[x], parent)\n return parent[x]\n\n def union(x, y, parent):\n parent[find(x, parent)] = find(y, parent)\n\n dsu1 = list(range(n + 1))\n dsu2 = list(range(n + 1))\n count = 0\n edges.sort(key=lambda x: x[0], reverse=True)\n\n for edge in edges:\n if edge[0] == 3:\n if find(edge[1], dsu1) == find(edge[2], dsu1) and find(edge[1], dsu2) == find(edge[2], dsu2):\n count += 1\n continue\n\n union(edge[1], edge[2], dsu1)\n union(edge[1], edge[2], dsu2)\n elif edge[0] == 1:\n if find(edge[1], dsu1) == find(edge[2], dsu1):\n count += 1\n\n union(edge[1], edge[2], dsu1)\n else:\n if find(edge[1], dsu2) == find(edge[2], dsu2):\n count += 1\n\n union(edge[1], edge[2], dsu2)\n\n for i in range(1, n + 1):\n find(i, dsu1)\n find(i, dsu2)\n\n for i in range(2, n + 1):\n if dsu1[i] != dsu1[1] or dsu2[i] != dsu2[1]:\n return -1\n\n return count\n\n```\n\n**Intuituin**\n \n```\n def maxNumEdgesToRemove(self, n, edges):\n```\nDefine a helper function to find the parent of a set using path compression.\n```\n def find(x, parent):\n if parent[x] != x:\n parent[x] = find(parent[x], parent)\n return parent[x]\n```\n\n\nDefine a helper function to union two sets.\n```\n def union(x, y, parent):\n parent[find(x, parent)] = find(y, parent)\n```\n\nCreate two disjoint set arrays dsu1 and dsu2 for Alice and Bob.\n```\n dsu1 = list(range(n + 1))\n dsu2 = list(range(n + 1))\n count = 0 # Initialize a counter for the removed edges.\n```\n\n\nSort the edges in descending order so that we prioritize removing type-3 edges.\n```\n edges.sort(key=lambda x: x[0], reverse=True)\n\n for edge in edges:\n if edge[0] == 3:\n```\n\n Type-3 edge, check if the nodes are already in the same set for both Alice and Bob.\n ```\n if find(edge[1], dsu1) == find(edge[2], dsu1) and find(edge[1], dsu2) == find(edge[2], dsu2):\n```\n\n```\n count += 1 # Increment the count of removed edges.\n continue\n```\n\nUnion the nodes in both dsu1 and dsu2.\n```\n union(edge[1], edge[2], dsu1)\n union(edge[1], edge[2], dsu2)\n elif edge[0] == 1:\n```\n\nType-1 edge, check if the nodes are already in the same set for Alice.\n```\n if find(edge[1], dsu1) == find(edge[2], dsu1):\n```\n\n Increment the count of removed edges.\n```\n count += 1 \n```\n\nUnion the nodes in dsu1.\n```\n union(edge[1], edge[2], dsu1)\n else:\n```\n\nType-2 edge, check if the nodes are already in the same set for Bob.\n```\n if find(edge[1], dsu2) == find(edge[2], dsu2):\n count += 1 # Increment the count of removed edges.\n```\n\nUnion the nodes in dsu2.\n```\n union(edge[1], edge[2], dsu2)\n```\n\nEnsure that all nodes in dsu1 and dsu2 have the same parent (representing a single set).\n```\n for i in range(1, n + 1):\n find(i, dsu1)\n find(i, dsu2)\n```\n\n\nCheck if all nodes in both dsu1 and dsu2 belong to the same set.\n```\n for i in range(2, n + 1):\n if dsu1[i] != dsu1[1] or dsu2[i] != dsu2[1]:\n\t\t\t\n```\n\nIf not, it\'s not possible to remove all edges.\n```\n return -1 \n```\n\nReturn the count of removed edges, which represents the maximum possible.\n```\n return count \n```\n\n\n\n\n | 3 | 0 | ['Graph', 'Python'] | 0 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Simplest Python UF solution | simplest-python-uf-solution-by-tryingall-sa9z | \n# Code\n\nclass DSU():\n def __init__(self, n):\n self.par = list(range(n))\n self.rank = [1] * n\n self.size = 1\n \n def find( | tryingall | NORMAL | 2023-05-31T11:18:04.917813+00:00 | 2023-05-31T11:18:15.501134+00:00 | 588 | false | \n# Code\n```\nclass DSU():\n def __init__(self, n):\n self.par = list(range(n))\n self.rank = [1] * n\n self.size = 1\n \n def find(self, u):\n if u != self.par[u]:\n self.par[u] = self.find(self.par[u])\n return self.par[u]\n \n def union(self, u, v):\n uu, vv = self.find(u), self.find(v)\n if uu == vv:\n return False\n if self.rank[uu] > self.rank[vv]:\n self.par[vv] = self.par[self.par[vv]]\n self.par[vv] = uu\n elif self.rank[vv] > self.par[uu]:\n self.par[uu] = self.par[self.par[uu]]\n self.par[uu] = vv\n else:\n self.par[uu] = vv\n self.rank[vv] += 1\n self.size += 1\n return True\n\nclass Solution:\n def maxNumEdgesToRemove(self, n: int, edges: List[List[int]]) -> int:\n uf1, uf2, ans = DSU(n), DSU(n), 0\n\n for t, u, v in edges:\n if t == 3 and (not uf1.union(u-1, v-1) or not uf2.union(u-1, v-1)):\n ans += 1\n for t, u, v in edges:\n if t == 1 and not uf1.union(u-1, v-1):\n ans += 1\n elif t == 2 and not uf2.union(u-1, v-1):\n ans += 1\n return ans if uf1.size == n and uf2.size == n else -1\n``` | 3 | 0 | ['Python3'] | 1 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Python short and clean. DSU (Disjoint-Set-Union). Functional programming. | python-short-and-clean-dsu-disjoint-set-p0ick | Approach\nTL;DR, Similar to Editorial solution.\n\n# Complexity\n- Time complexity: O(e)\n\n- Space complexity: O(n)\n\nwhere,\nn is number of nodes,\ne is numb | darshan-as | NORMAL | 2023-04-30T19:17:57.462822+00:00 | 2023-04-30T19:18:12.065772+00:00 | 663 | false | # Approach\nTL;DR, Similar to [Editorial solution](https://leetcode.com/problems/remove-max-number-of-edges-to-keep-graph-fully-traversable/editorial/).\n\n# Complexity\n- Time complexity: $$O(e)$$\n\n- Space complexity: $$O(n)$$\n\nwhere,\n`n is number of nodes`,\n`e is number of edges`.\n\n# Code\n```python\nclass Solution:\n def maxNumEdgesToRemove(self, n: int, edges: list[list[int]]) -> int:\n es = reduce(lambda a, x: a[x[0]].append((x[1], x[2])) or a, edges, ([], [], [], []))\n\n def union_count(dsu: DSU, es: Iterable[tuple[T, T]]) -> int:\n return sum(dsu.union(u, v) or 1 for u, v in es if not dsu.is_connected(u, v))\n\n xs = range(1, n + 1)\n a_dsu, b_dsu = DSU(xs), DSU(xs)\n used = sum((\n union_count(a_dsu, es[3]) and\n union_count(b_dsu, es[3]),\n union_count(a_dsu, es[1]),\n union_count(b_dsu, es[2]),\n ))\n\n return len(edges) - used if a_dsu.ds_count() == b_dsu.ds_count() == 1 else -1\n\n\nT = Hashable\n\n\nclass DSU:\n def __init__(self, xs: Iterable[T] = ()) -> None:\n self.parents: Mapping[T, T] = {x: x for x in xs}\n self.sizes: Mapping[T, int] = {x: 1 for x in xs}\n self.count: int = len(self.parents)\n\n def find(self, u: T) -> T:\n self.parents[u] = u if self.parents[u] == u else self.find(self.parents[u])\n return self.parents[u]\n\n def union(self, u: T, v: T) -> None:\n ur, vr = self.find(u), self.find(v)\n if ur == vr:\n return\n low, high = (ur, vr) if self.sizes[ur] < self.sizes[vr] else (vr, ur)\n self.parents[low] = high\n self.sizes[high] += self.sizes[low]\n self.count -= 1\n\n def is_connected(self, u: T, v: T) -> bool:\n return self.find(u) == self.find(v)\n\n def ds_count(self) -> int:\n return self.count\n``` | 3 | 0 | ['Union Find', 'Graph', 'Python', 'Python3'] | 1 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | C++ || Union Find || using striver's template | c-union-find-using-strivers-template-by-oldln | Approach\n1. We have to find the maximum number of edges that can be removed from the graph while ensureing that both Alice and Bob able to construct a spanning | rajdip14 | NORMAL | 2023-04-30T16:44:34.972666+00:00 | 2023-04-30T17:33:57.230538+00:00 | 657 | false | **Approach**\n1. We have to find the maximum number of edges that can be removed from the graph while ensureing that both Alice and Bob able to construct a spanning tree. As spanning tree connects all the nodes in a graph, all nodes will be traversable in that case. we also know that there must be n-1 edges in the spanning tree.\n2. We can use the union-find data structure to keep track of which nodes are connected to each other in the spanning tree, so we have defined two dsu\'s for alice and bob. Initially, each node is its own parent. Also we defined alice_edge, bob_edge to track no of edges in their spanning tree and removed_edge for counting no of removable edges.\n3. At first we start by considering the edges that can be used by both Alice and Bob i.e. type 3 edges. Because If we can merge the two nodes of type 3 edge it contributes in construction of both alice and bobs spanning tree. so increase the count of edges of boths dsu\'s [alice_edge, bol_edge]. If not possible to merge them, it means they are already connected so the current edge is redundent and we can remove it.\n4. Next, we consider the edges that can only be used by Alice and Bob respectively. If a type 1 or type 2 edge can be used to connect two nodes in Alice\'s or Bob\'s respective connected components, then we know that only that user can use that edge to construct their spanning tree so increase their respcetive edge count. Otherwise, remove the edge same as type 3.\n5. Finally, check if both Alice and Bob were able to construct a spanning tree (i.e. they both have n-1 no of edges). If that possible then we can return the no of removed edge [removed_edge]. else return -1.\n\n**Disjoint Set class**\n```\nclass DisjointSet {\n vector<int> parent; \n vector<int> rank;\n public:\n DisjointSet(int n) {\n parent.resize(n+1,0);\n rank.resize(n+1,0);\n \n for(int i = 0; i < n; i++) {\n parent[i] = i;\n rank[i] = 1;\n }\n }\n \n int findUParent(int node) {\n if(node == parent[node])\n return node;\n return parent[node] = findUParent(parent[node]);\n }\n \n void unionByRank(int u, int v) {\n int uparentU = findUParent(u);\n int uparentV = findUParent(v);\n \n if(rank[uparentU] > rank[uparentV]) {\n parent[uparentV] = uparentU;\n\n } else if(rank[uparentU] < rank[uparentV]){\n parent[uparentU] = uparentV;\n\n } else {\n parent[uparentU] = uparentV;\n rank[uparentV]++;\n } \n }\n};\n```\n\n**Solution Class**\n```\nclass Solution {\npublic:\n int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {\n DisjointSet alice(n), bob(n);\n \n int removed_edge = 0, alice_edge = 0, bob_edge = 0;\n \n for(auto edge : edges) {\n if(edge[0] == 3) {\n if(alice.findUParent(edge[1]) != alice.findUParent(edge[2])) {\n alice.unionByRank(edge[1], edge[2]);\n bob.unionByRank(edge[1], edge[2]);\n alice_edge++;\n bob_edge++;\n } else {\n removed_edge++;\n }\n }\n }\n \n for(auto edge : edges) {\n if(edge[0] == 2) {\n if(bob.findUParent(edge[1]) != bob.findUParent(edge[2])) {\n bob.unionByRank(edge[1], edge[2]);\n bob_edge++;\n } else {\n removed_edge++;\n }\n } else if(edge[0] == 1) {\n if(alice.findUParent(edge[1]) != alice.findUParent(edge[2])) {\n alice.unionByRank(edge[1], edge[2]);\n alice_edge++;\n } else {\n removed_edge++;\n }\n }\n } \n \n return (alice_edge == n-1 && bob_edge == n-1) ? removed_edge : -1;\n }\n};\n```\n\n**TC : O(N)** [as we are using two loops and union find takes O(4\u03B1) which is approximately O(1)]\n**SC: O(N)** [as we taking two dsu objects means toatal 4 arrays i.e. O(N)]\n\n**Please upvote if you like the solution !!\uD83D\uDE0A** | 3 | 0 | ['Union Find', 'Graph', 'C'] | 0 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | python 3 - DSU + union by rank + path compression | python-3-dsu-union-by-rank-path-compress-6o1i | Intuition\nAs long as you know DSU, this question is quite straghtforward.\n\nProcess edges in 2 parts:\n- Join all type 3 edges and then type 1 edges. This den | markwongwkh | NORMAL | 2023-04-30T11:55:44.459094+00:00 | 2023-04-30T11:59:56.071308+00:00 | 493 | false | # Intuition\nAs long as you know DSU, this question is quite straghtforward.\n\nProcess edges in 2 parts:\n- Join all type 3 edges and then type 1 edges. This denotes all Alice edges. And edges with the same parent can be removed.\n- Same process will be done by using type 2 edges instead of type 1.\n\nCheck if all nodes belong to the same parent finally to see if any nodes cannot be reached.\n\n# Approach\nDSU\n\n# Complexity\n- Time complexity:\nO(n * alpha(n)) -> DSU operation on input edges list\n\n- Space complexity:\nO(n) -> DSU structure\'s sc\n\n# Code\n```\nclass DSU:\n def __init__(self, n):\n self.par = list(range(n))\n self.rank = [1] * n\n \n def find(self, node):\n if self.par[node] != node:\n self.par[node] = self.find(self.par[node])\n return self.par[node]\n \n def union(self, x, y):\n px, py = self.find(x), self.find(y)\n if self.rank[px] > self.rank[py]: # py to px\n self.par[py] = px\n self.rank[px] += self.rank[py]\n else: # px to py\n self.par[px] = py\n self.rank[py] += self.rank[px]\n\nclass Solution:\n def maxNumEdgesToRemove(self, n: int, edges: List[List[int]]) -> int:\n import collections\n type2edge = collections.defaultdict(list)\n for ty, u, v in edges:\n type2edge[ty].append([u, v])\n \n ans = 0\n\n # alice\n dsua = DSU(n+1)\n for u, v in type2edge[3]: # join common\n if dsua.find(u) == dsua.find(v):\n ans += 1\n else:\n dsua.union(u, v)\n for u, v in type2edge[1]:\n if dsua.find(u) == dsua.find(v):\n ans += 1\n else:\n dsua.union(u, v)\n \n for i in range(n):\n dsua.find(i)\n if len(set(dsua.par[1:])) > 1: # diff groups\n return -1\n \n # bob\n dsub = DSU(n+1)\n for u, v in type2edge[3]:\n if dsub.find(u) != dsub.find(v):\n dsub.union(u, v)\n for u, v in type2edge[2]:\n if dsub.find(u) == dsub.find(v):\n ans += 1\n else:\n dsub.union(u, v)\n \n for i in range(n):\n dsub.find(i)\n if len(set(dsub.par[1:])) > 1:\n return -1\n \n return ans\n``` | 3 | 0 | ['Union Find', 'Python3'] | 1 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Golang Go easy to follow Union find solution | golang-go-easy-to-follow-union-find-solu-j9mg | \n\n\nfunc maxNumEdgesToRemove(n int, edges [][]int) int {\n\n\tvar result int\n\n\tufAlice := NewUnionFind(n)\n\tufBob := NewUnionFind(n)\n\n\tfor _, edge := r | siboya | NORMAL | 2022-09-17T18:14:27.086433+00:00 | 2022-09-17T18:14:27.086480+00:00 | 415 | false | ```\n\n\nfunc maxNumEdgesToRemove(n int, edges [][]int) int {\n\n\tvar result int\n\n\tufAlice := NewUnionFind(n)\n\tufBob := NewUnionFind(n)\n\n\tfor _, edge := range edges {\n\t\t// When edge is 3, both Alice and Bob can use it\n\t\t// So we need to union both ufAlice and ufBob\n\t\t// If the union fails, it means that the two nodes are already connected\n\t\tif edge[0] == 3 {\n\t\t\tif !ufAlice.Union(edge[1]-1, edge[2]-1) {\n\t\t\t\t// Counting only once sice Alice and Bob are using the same edges\n\t\t\t\tresult++\n\t\t\t}\n\t\t\tufBob.Union(edge[1]-1, edge[2]-1)\n\t\t}\n\t}\n\n\tfor _, edge := range edges {\n\n\t\t// When edge is 1, only Alice can use it\n\t\tif edge[0] == 1 {\n\t\t\tif !ufAlice.Union(edge[1]-1, edge[2]-1) {\n\t\t\t\tresult++\n\t\t\t}\n\t\t}\n\n\t\t// When edge is 2, only Bob can use it\n\t\tif edge[0] == 2 {\n\t\t\tif !ufBob.Union(edge[1]-1, edge[2]-1) {\n\t\t\t\tresult++\n\t\t\t}\n\t\t}\n\t}\n\n\tfmt.Println("Count:", ufAlice.count, ufBob.count)\n\n\tif ufAlice.count != 1 || ufBob.count != 1 {\n\t\treturn -1\n\t}\n\treturn result\n\n}\n\n// Union Find Data Structure Implementation\ntype UnionFind struct {\n\tparent []int\n\tcount int\n}\n\nfunc NewUnionFind(num int) *UnionFind {\n\tarr := make([]int, num)\n\tfor i := 0; i < num; i++ {\n\t\tarr[i] = i\n\t}\n\treturn &UnionFind{\n\t\tarr,\n\t\tnum,\n\t}\n}\n\nfunc (u *UnionFind) Union(a, b int) bool {\n\n\tparentA := u.Find(a)\n\tparentB := u.Find(b)\n\tif parentA != parentB {\n\t\tu.parent[parentA] = parentB\n\t\tu.count--\n\t\treturn true\n\t}\n\treturn false\n\n}\n\nfunc (u *UnionFind) Find(a int) int {\n\n\tif u.parent[a] == a {\n\t\treturn a\n\t}\n\tu.parent[a] = u.Find(u.parent[a])\n\treturn u.parent[a]\n}\n``` | 3 | 0 | ['Union Find', 'Go'] | 0 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Union Find | union-find-by-empowered-pwtu | \nclass Solution {\npublic:\n static bool sortcol(vector<int> &a,vector<int> &b)\n {\n return a[0]>b[0]; \n }\n int extremeparent(vector<int> | Empowered | NORMAL | 2022-07-21T09:45:52.377016+00:00 | 2022-07-21T09:45:52.377069+00:00 | 186 | false | ```\nclass Solution {\npublic:\n static bool sortcol(vector<int> &a,vector<int> &b)\n {\n return a[0]>b[0]; \n }\n int extremeparent(vector<int> &parent,int x)\n {\n if(parent[x]==x)\n return x;\n parent[x]=extremeparent(parent,parent[x]);\n return parent[x]; \n }\n void changeparent(vector<int> &parent,int x,int y)\n {\n if(x>y)\n parent[x]=y;\n else\n parent[y]=x;\n return ; \n }\n int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {\n \n vector<int> parental(n+1,0);\n vector<int> parentbo(n+1,0);\n for(int i=0;i<n+1;i++) \n {\n parental[i]=i;\n parentbo[i]=i;\n }\n sort(edges.begin(),edges.end(),sortcol); \n vector<vector<int>> v=edges;\n int count=0; \n // cout<<count<<" "; \n for(int i=0;i<v.size();i++)\n {\n if(v[i][0]==3)\n {\n int flag=0; \n int x=extremeparent(parental,v[i][1]);\n int y=extremeparent(parental,v[i][2]);\n if(x!=y)\n changeparent(parental,x,y);\n else\n flag=1; \n x=extremeparent(parentbo,v[i][1]);\n y=extremeparent(parentbo,v[i][2]);\n if(x!=y)\n changeparent(parentbo,x,y);\n else\n flag++;\n if(flag==2)\n count++; \n }\n else if(v[i][0]==1)\n {\n int x=extremeparent(parental,v[i][1]);\n int y=extremeparent(parental,v[i][2]);\n if(x!=y)\n changeparent(parental,x,y);\n else\n count++; \n }\n else\n {\n int x=extremeparent(parentbo,v[i][1]);\n int y=extremeparent(parentbo,v[i][2]);\n if(x!=y)\n changeparent(parentbo,x,y); \n else\n count++; \n }\n // cout<<count<<" "; \n }\n int last=-1; \n for(int i=1;i<n+1;i++)\n {\n int x=extremeparent(parental,i);\n if(x==last||last==-1)\n {\n }\n else\n return -1;\n last=x; \n }\n for(int j=1;j<n+1;j++)\n {\n int x=extremeparent(parentbo,j);\n if(x==last||last==-1)\n {\n }\n else\n return -1;\n last=x; \n }\n return count;\n }\n};\n\n// \n// \n``` | 3 | 0 | [] | 0 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Easy C++ solution || Using Union Find Method | easy-c-solution-using-union-find-method-h5q83 | \nclass Solution\n{\npublic:\n class dsu{\n public:\n vector<int> parent, sz;\n dsu(int n){\n parent.resize(n);\n | thanoschild | NORMAL | 2022-05-14T19:48:49.795225+00:00 | 2022-05-14T19:48:49.795272+00:00 | 550 | false | ```\nclass Solution\n{\npublic:\n class dsu{\n public:\n vector<int> parent, sz;\n dsu(int n){\n parent.resize(n);\n sz.resize(n);\n for(int i = 0; i<n; i++){\n parent[i] = i;\n sz[i] = 1;\n }\n }\n\n int find_set(int x){\n if(parent[x] == x) return x;\n return parent[x] = find_set(parent[x]);\n }\n\n bool make_union(int x, int y){\n int a = find_set(x);\n int b = find_set(y);\n if(a == b) return false;\n if(sz[a] < sz[b]) swap(a, b);\n parent[b] = a;\n sz[a] += sz[b];\n return true;\n }\n\n int count(int x){\n return sz[x];\n }\n };\n int maxNumEdgesToRemove(int n, vector<vector<int>> &edges)\n {\n vector<pair<int,int>> alice, bob, both;\n for(int i = 0; i<edges.size(); i++){\n int t = edges[i][0];\n int x = edges[i][1]-1;\n int y = edges[i][2]-1;\n if(t == 3){\n both.push_back({x, y});\n }\n else if(t == 2){\n bob.push_back({x, y});\n }\n else{\n alice.push_back({x, y});\n }\n }\n\n dsu a(n), b(n);\n int ans = 0;\n for(auto it : both){\n ans += a.make_union(it.first, it.second);\n b.make_union(it.first, it.second);\n }\n for (auto it : alice){\n ans += a.make_union(it.first, it.second); \n }\n for (auto it : bob){\n ans += b.make_union(it.first, it.second); \n }\n if(a.count(a.find_set(0)) < n || b.count(b.find_set(0)) < n) return -1;\n return edges.size() - ans;\n }\n};\n``` | 3 | 0 | ['Union Find', 'C', 'C++'] | 2 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | [Python] Union Find by Rank w Path Compression (Beats 99%) | python-union-find-by-rank-w-path-compres-a3sf | First process the edges that both people can use. This has priority over Type 1 and Type 2 edges since the edge works for both Alice and Bob. After that, it\'s | srihariv | NORMAL | 2022-03-25T05:26:06.227634+00:00 | 2023-04-30T00:33:42.458606+00:00 | 225 | false | First process the edges that both people can use. This has priority over Type 1 and Type 2 edges since the edge works for both Alice and Bob. After that, it\'s textbook Union-Find for both Alice and Bob.\n\n```\nclass UnionFind:\n """\n Standard Union-Find data structure implementation\n with path compression and rank\n """\n def __init__(self, n):\n self.n = n\n self.uf = [i for i in range(n + 1)]\n self.rank = [0] * (n + 1)\n self.comp = n\n \n def root(self, u):\n if self.uf[u] != u:\n self.uf[u] = self.root(self.uf[u])\n return self.uf[u]\n\n def union(self, u, v):\n u, v = self.root(u), self.root(v)\n if u == v: return False\n if self.rank[u] > self.rank[v]:\n self.uf[v] = u\n elif self.rank[u] < self.rank[v]:\n self.uf[u] = v\n else:\n self.uf[v] = u\n self.rank[u] += 1\n \n self.comp -= 1\n return True\n\nclass Solution:\n def maxNumEdgesToRemove(self, n: int, edges: List[List[int]]) -> int:\n # initialize both data structures to keep track of connected components\n ufAlice = UnionFind(n)\n ufBob = UnionFind(n)\n\n numEdges = 0\n\n # Add all type 3 edges that don\'t create a cycle (i.e. have the same parent in the \n # data structure)\n for t, u, v in edges:\n if t == 3:\n numEdges += int(ufAlice.union(u, v))\n ufBob.union(u, v)\n \n # Unite all Alice / Bob edges that don\'t create a cycle\n for t, u, v in edges:\n if t == 1:\n numEdges += int(ufAlice.union(u, v))\n elif t == 2:\n numEdges += int(ufBob.union(u, v))\n \n # if there are multiple components in either alice / bob\'s graphs, then it is \n # disconnected and we return -1\n if ufAlice.comp != 1 or ufBob.comp != 1:\n return -1\n \n # otherwise, we can remove all edges that aren\'t chosen\n return len(edges) - numEdges\n\n```\n\n**Analysis**\nTime: $O(E * \\alpha(N))$ where E is the number of edges. We traverse the edges array twice, and the time complexity of Union-Find is the *Inverse Ackermann Function* ($\\alpha(N)$), which is near-constant but can be treated as $\\log(n)$.\n\nSpace: $O(N)$ To Store the Union-Find data structures | 3 | 0 | ['Python'] | 2 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | DSU c++ explained by comments | dsu-c-explained-by-comments-by-harshitsh-18e0 | \n\n\nclass Solution {\npublic:\n\n int alice[100001];\n int bob[100001];\n \nint finda(int a){\n\tif(alice[a]==-1)\n\treturn a;\n\treturn alice[a]=finda | harshitsharma007 | NORMAL | 2021-05-28T22:47:30.535606+00:00 | 2021-05-28T22:54:47.059481+00:00 | 275 | false | ```\n\n\nclass Solution {\npublic:\n\n int alice[100001];\n int bob[100001];\n \nint finda(int a){\n\tif(alice[a]==-1)\n\treturn a;\n\treturn alice[a]=finda(alice[a]);\n}\n int findb(int a){\n\tif(bob[a]==-1)\n\treturn a;\n\treturn bob[a]=findb(bob[a]);\n}\nvoid mergea (int a,int b){\n\talice[a]=b;\n}\n void mergeb (int a,int b){\n\tbob[a]=b;\n}\n int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {\n for(int i=0;i<100001;i++){\n\talice[i]=-1;\n bob[i]=-1;\n} \n int t3=0;//essential edges for both \n for(int i=0;i<edges.size();i++){\n if(edges[i][0]==3){\n if(finda(edges[i][1])!=finda(edges[i][2])){\n mergea(finda(edges[i][1]),finda(edges[i][2]));\n mergeb(findb(edges[i][1]),findb(edges[i][2]));\n t3++;\n }\n }\n }\n int t1=0; // essential edges for alice\n for(int i=0;i<edges.size();i++){\n if(edges[i][0]==1){\n if(finda(edges[i][1])!=finda(edges[i][2])){\n mergea(finda(edges[i][1]),finda(edges[i][2]));\n \n t1++;\n cout<<"I"<<i<<" ";\n }\n }\n }\n int t2=0; //essential edges for bob\n for(int i=0;i<edges.size();i++){\n if(edges[i][0]==2){\n if(findb(edges[i][1])!=findb(edges[i][2])){\n mergeb(findb(edges[i][1]),findb(edges[i][2]));\n \n t2++;\n }\n }\n }\n if(t1+t3<n-1||t3+t2<n-1)// if(t1+t3<n-1) then alice can not traverse the graph because tree requires n-1 edges to be spanned completely if(t2+t3<n-1)then bob can not traverse.\n return -1;\n \n cout<<t1<<" "<<t2<<" "<<t3<<endl;\n return edges.size()-t1-t2-t3; //(t1+t2+t3) are essential edges\n }\n};\n\n\n// below description in hindi vvvvvvvvvvvvvvvvvvvvvv//\n\n// yrrr agar yeh code smjhna he toh bsss sbse phle type third nodes count krrro jo essential he unse alice ka parent array aur bob ka parent array dono modify honge but in case of type 1 node we only modify alice array in second for loop then we run last loop for bob \n// so t1 +t2+t3 are all the essential edgess we can get \n//so answer is total -(essential);------------------:)\n\n\n``` | 3 | 0 | [] | 0 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Ruby - Union Find Kruskal's Algorithm with comments | ruby-union-find-kruskals-algorithm-with-fysi6 | Rephrase task\n\nAssume we do not have any edges initially: only some set of vertices (numbers from 1 to n). And some set of edges that we can use to make graph | shhavel | NORMAL | 2020-11-12T22:06:01.790585+00:00 | 2020-11-12T22:19:34.248777+00:00 | 144 | false | ## Rephrase task\n\nAssume we do not have any edges initially: only some set of vertices (numbers from 1 to n). And some set of edges that we can use to make graph traversable by both Alice and Bob. Number of edges in the set minus minimum number of edges to add (to make graph traversable by both Alice and Bob) equals to the initial value we need to calculate.\n\n## Observation\n\nEdges that are traversable by both Alice and Bob should be preoritasable over others edges. But only if any new age does not add a cycle in the graph. At the end we should have `n - 1` edges traversable by Alice and `n - 1` edges traversable by Bob. Some of them may be shared (if can by traversed by both Alice and Bob). So we need from `n - 1` upto ` 2(n - 1)` edges to make graph traversable by both.\n\n## Algorithm\n\nSplit edges by three groups (like in task description). Use `merge` method from Union Find algorithm to to check whether we can add next edge not adding cycles (vertices `u` and `v` should be in different groups). First use up to `n - 1` edges traversed by both Alice and Bob, then use up to `n - 1` edges traversed by Alice, and then use up to `n - 1` edges traversed by Bob. Return number not used edges if we have enough edges for Alice and Bob or `-1` if we ran out of edges.\n\n## Implementation\n\nRuby version\n\n```ruby\n# find with path compression\ndef find(par, x)\n par[x] == x ? x : (par[x] = find(par, par[x]))\nend\n\ndef merge(par, x, y)\n x = find(par, x)\n y = find(par, y)\n return false if x == y\n par[x] = y\n return true\nend\n\nALICE = 1\nBOB = 2\nBOTH = 3\n\ndef max_num_edges_to_remove(n, edges)\n res = edges.size # all minus min needed num of edges to make graph traversable\n # (remaining count after adding all nessasary edges)\n return res if n == 1\n return -1 if edges.size < n - 1 # not enough edges to make graph traversable\n\n edges_for = edges.group_by(&:first)\n return -1 if edges_for.keys.one? && edges_for.keys[0] != BOTH # not enough edges for Alice or Bob\n \n # Initially, each vertice is in its own single-vertice group where the vertice is the parent of that group.\n par_alice = *0..n\n need_alice = n - 1\n \n edges_for[BOTH]&.each do |_, u, v|\n if merge(par_alice, u, v)\n res -= 1\n need_alice -= 1\n return res if need_alice == 0\n end\n end\n \n par_bob = par_alice.dup\n need_bob = need_alice\n \n edges_for[ALICE]&.each do |_, u, v|\n if merge(par_alice, u, v)\n res -= 1\n need_alice -= 1\n break if need_alice == 0\n end\n end\n return -1 if need_alice > 0\n \n edges_for[BOB]&.each do |_, u, v|\n if merge(par_bob, u, v)\n res -= 1\n need_bob -= 1\n return res if need_bob == 0\n end\n end\n \n return -1\nend\n# Runtime: 216 ms\n```\n\n## Videos for Union Find (by William Fiset):\n- [Union Find Introduction](https://www.youtube.com/watch?v=ibjEGG7ylHk)\n- [Union Find Kruskal\'s Algorithm](https://www.youtube.com/watch?v=JZBQLXgSGfs)\n- [Union Find - Union and Find Operations](https://www.youtube.com/watch?v=0jNmHPfA_yE)\n- [Union Find Path Compression](https://www.youtube.com/watch?v=VHRhJWacxis)\n- [Union Find Code](https://www.youtube.com/watch?v=KbFlZYCpONw)\n\n[LeetCode Union Find Problems](https://leetcode.com/tag/union-find/)\n | 3 | 0 | ['Union Find', 'Ruby'] | 0 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | C++ | Union-Find | Code and Steps|Hinglish | c-union-find-code-and-stepshinglish-by-a-cdq8 | I am writing the steps in both English and Hinglish because I personally feel Hinglish makes it easier to understand for native Hindi speakers.\nSteps:-\n Make | akshay31verma | NORMAL | 2020-09-15T11:39:51.034530+00:00 | 2020-09-15T11:39:51.034574+00:00 | 353 | false | I am writing the steps in both English and Hinglish because I personally feel Hinglish makes it easier to understand for native Hindi speakers.\nSteps:-\n* Make all the components which you can reach from type 3 edges i.e traverserable for both Alice and Bob.(Sabse pehle saare components nikallo 3rd type ki edge use karke ,jisko Alice and Bob dono use kar sake).\n* Now using First go with alice and find if we can connect all the disconnected groups using the Alice edges.(uske baad yeh dekho ki kyaa alice apne edges use karke saare jagah jaa sakta hai ,toh isse humhe alice ke minimum required edges aajayenge).\n* And apply same for Bob.(Bob ke liye bhi check karlo)\n* Final answer will be \n\t*if(alice edges!=n-1 || bob edges!=-1){\n\t\tthen all the edges cannot be traversed.(Matlab Alice Bob nhi kar sakte saare destinations.)\n\t\treturn -1.\n\t}\n\totherwise (varna)\n\ttotaledges-(alice edges+bob edges-common edges(because we have added common edges with both alice and bob));(saare edges mein se alice ki requirement+bob ki requirement aur inmein se common edges jo 2 baar add hue hai unko total edges mein se subtract kardo.)\n\n\n\n\nclass Solution {\npublic:\n \n \n int findp(int x, vector<int> &par){\n if(par[x]!=x){\n par[x]=findp(par[x],par);\n }\n return par[x];\n }\n void unio(int x,int y, vector<int> &par){\n int p1=findp(x,par);\n int p2=findp(y,par);\n if(p1!=p2){\n par[p2]=p1;\n }\n }\n \n \n int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {\n unordered_map<int,vector<int>> gA;\n unordered_map<int,vector<int>> gB;\n unordered_map<int,vector<int>> gC;\n \n for(auto r:edges){\n if(r[0]==1){\n gA[r[1]].push_back(r[2]);\n gA[r[2]].push_back(r[1]);\n }else if(r[0]==2){\n gB[r[1]].push_back(r[2]);\n gB[r[2]].push_back(r[1]);\n }else{\n gC[r[1]].push_back(r[2]);\n gC[r[2]].push_back(r[1]);\n }\n }\n vector<int> par;\n par.resize(n+1,0);\n for(int i=1;i<=n;i++){\n par[i]=i;\n }\n \n int ed=0;\n int cnt=0;\n \n \n \n for(int i=1;i<=n;i++){\n for(int j:gC[i]){\n int p1=findp(i,par);\n int p2=findp(j,par);\n if(p1==p2){\n continue;\n }else{\n unio(i,j,par);\n ed++;\n }\n }\n }\n \n vector<int> pa=par;\n vector<int> pb=par;\n int ed1=ed;\n int ed2=ed;\n for(int i=1;i<=n;i++){\n int p1=findp(i,pa);\n \n for(auto j:gA[i]){\n int p2=findp(j,pa);\n if(p1==p2){\n continue;\n }else{\n unio(i,j,pa);\n ed1++;\n }\n }\n int p4=findp(i,pb);\n for(auto k:gB[i]){\n int p3=findp(k,pb);\n if(p4==p3){\n continue;\n }else{\n unio(i,k,pb);\n ed2++;\n }\n }\n }\n \n \n if(ed1!=n-1 || ed2!=n-1 ){\n return -1;\n }\n return edges.size()-(ed1+ed2-ed);\n \n }\n}; | 3 | 1 | ['Union Find', 'C'] | 0 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | [Javascript] Union Find easy and concise | javascript-union-find-easy-and-concise-b-u6cq | Intuition:\n\tUnion find appeals to problems related to paths that traverse the whole tree. Here we create two union finds, one for each player. The important t | George_Chrysochoou | NORMAL | 2020-09-06T23:34:09.577500+00:00 | 2020-09-06T23:34:09.577555+00:00 | 348 | false | **Intuition**:\n\tUnion find appeals to problems related to paths that traverse the whole tree. Here we create two union finds, one for each player. The important thing here is to always prefer type 3 edges over 2 or 1 because the latter are reduntant once the type 3 is chosen. So the whole idea is filling up my unionfinds with the components while keeping track of the edges I\'m using. In the end, the number of groups in each unionfind has to be 1 for each, meaning that both players can traverse the whole tree. If not, then the tree is not traversable and -1 has to be returned. The result is the total available edges minus the ones I actually used.\n\t\n```\nclass UnionFind {\n\n // Construction takes O(n)\n constructor(size){\n //the total count of different elements(not groups) in this union find\n this.count=size\n //tracks the sizes of each of the components(groups/sets)\n //groupsize[a] returns how many elements the component with root a has \n this.groupSize=[...Array(size)] \n //number of components(groups) in the union find\n this.numComponents=size\n //points to the parent of i, if parent[i]=i, i is a root node\n this.parent=[...Array(size)] //which is also the index of the group\n\n //put every element into its own group\n // rooted at itself\n for (let i = 0; i < size; i++) {\n this.groupSize[i]=i \n this.parent[i]=i \n }\n }\n\n\n\n //returns to which component (group) my element belongs to \n // \u03B1(n) --Amortized constant time \n // Update: Also compresses the paths so that each child points to its \n // parent\n find(element){\n let root=element\n //find the parent of the group the elemnt belongs to\n // When root===parent[root] is always the parent of that group (root)\n while(root!=this.parent[root])\n root=this.parent[root]\n\n // Compression, point the element to its parent if its not already pointed\n // Tldr: Not only do I point my element to its actual root, i point any\n // inbetween elements to that root aswell\n while(element!=root){\n let next=this.parent[element]\n this.parent[element]=root\n element=next\n }\n \n return root\n } \n\n //Unifies the sets containing A and B\n // \u03B1(n) --Amortized constant time \n union(A,B){\n let root1=this.find(A) //parent of A\n ,root2=this.find(B) //parent of B\n\n // I want to put the set with fewer elements \n // to the one with more elemenets\n if(this.groupSize[root1]<this.groupSize[root2]){\n this.groupSize[root2]+=this.groupSize[root1]\n this.parent[root1]=this.parent[root2]\n }\n else {\n this.groupSize[root1]+=this.groupSize[root2]\n this.parent[root2]=this.parent[root1]\n }\n\n this.numComponents-- //cos 1 less group, since i merged 2\n }\n\n //same parent=>samegroup\n sameGroup=(A,B)=>this.find(A)==this.find(B)\n\n //essentially the groupSize of its parent\'s group\n sizeOfGroup=(A)=>this.groupSize[this.find(A)]\n\n}\n\n//Main Function\n var maxNumEdgesToRemove = function(n, edges) {\n edges.sort((a,b)=>b[0]-a[0]) //sort to always prefer type 3 first\n let edgesUsed=0,Bob=new UnionFind(n),Alice=new UnionFind(n)\n \n for (const [type,f,to] of edges) {\n if((type==3||type==2)&&!Bob.sameGroup(f,to)){\n Bob.union(f,to)\n edgesUsed++\n }\n if((type==3||type==1)&&!Alice.sameGroup(f,to)){\n Alice.union(f,to)\n if(type==1)// I already incremented above for type 3s\n\t\t\t\tedgesUsed++\n }\n }\n\t\n\t//can they both traverse the whole tree?\n if(Bob.numComponents!=1||Alice.numComponents!==1)\n return -1\n return edges.length-edgesUsed\n };\n\n\t\n``` | 3 | 0 | ['Union Find', 'JavaScript'] | 1 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | What a crap test Cases and constraints...!! Same solution passing in practice and TLE in contest. | what-a-crap-test-cases-and-constraints-s-wfuv | Even it\'s showing better than 75% solutions. \nThis is my solution using BFS.\nFirst I used blue edges to mark nodes visited then tried using green and red edg | suri_kumkaran | NORMAL | 2020-09-06T07:20:00.237220+00:00 | 2020-09-06T07:24:31.774636+00:00 | 314 | false | Even it\'s showing better than 75% solutions. \nThis is my solution using BFS.\nFirst I used blue edges to mark nodes visited then tried using green and red edges to connect rest nodes and in last connecting different components of blue.\nI know there are so many scope of improvements even I have also submited a improved version but runtime is same for both still I was not able to pass the 82nd case in contest.\n\nLeetcode should do something for this kind of problems.\nTest cases and constraints should be consistent for all the solutions having similar complexity.\n\n\n```\nclass Solution {\npublic:\n \n int n;\n bool pos ;\n \n int seprateCount(vector<vector<int>> &gr,vector<vector<int>> goodBlue,vector<bool> vis)\n {\n int cnt=0;\n for(auto &x:goodBlue)\n {\n vector<int> ans;\n for(auto y:x)\n {\n \n for(auto z:gr[y])\n {\n if(vis[z]==false)\n {\n cnt++;\n queue<int> Q;\n Q.push(z);\n vis[z]=true;\n while(Q.size())\n {\n int cur = Q.front();\n Q.pop();\n ans.push_back(cur);\n for(auto xx: gr[cur])\n {\n if(vis[xx]==false)\n {\n vis[xx]=true;\n cnt++;\n Q.push(xx);\n }\n }\n }\n }\n }\n }\n for(auto y:ans)\n {\n x.push_back(y);\n }\n }\n \n for(auto x:vis)\n {\n if(x==false)\n {\n pos=false;\n return 0;\n }\n }\n \n vector<int> mark(n);\n int m = goodBlue.size();\n for(int i=0;i<m;i++)\n {\n for(auto x:goodBlue[i])\n {\n mark[x] = i;\n }\n }\n \n vector<vector<int>> newGraph(m);\n for(int i=0;i<n;i++)\n {\n int his = mark[i];\n for(auto x:gr[i])\n {\n if(mark[x]!=his)\n {\n newGraph[his].push_back(mark[x]);\n newGraph[mark[x]].push_back(his);\n }\n }\n }\n \n vector<bool> newVis(m,false);\n \n newVis[0]=true;\n queue<int> Q;\n Q.push(0);\n int cnt2 = 0;\n while(Q.size())\n {\n int cur = Q.front();\n Q.pop();\n for(auto xx: newGraph[cur])\n {\n if(newVis[xx]==false)\n {\n newVis[xx]=true;\n cnt2++;\n Q.push(xx);\n }\n }\n }\n \n if(cnt2<m-1)\n {\n pos=false;\n return 0;\n }\n \n \n return cnt+cnt2;\n }\n \n int goodBlueCount(vector<vector<int>> &gr,vector<vector<int>> &goodBlue,vector<bool> &vis)\n {\n int cnt=0,i;\n for(i=0;i<n;i++)\n {\n if(gr[i].size()&&vis[i]==false)\n {\n vector<int> emp;\n goodBlue.push_back(emp);\n vector<int> &ans = goodBlue.back();\n queue<int> Q;\n Q.push(i);\n vis[i]=true;\n while(Q.size())\n {\n int cur = Q.front();\n Q.pop();\n ans.push_back(cur);\n for(auto x: gr[cur])\n {\n if(vis[x]==false)\n {\n vis[x]=true;\n cnt++;\n Q.push(x);\n }\n }\n }\n }\n }\n return cnt;\n }\n \n\n bool BFS(vector<vector<int>> &newGraph,vector<bool> newVis)\n {\n \n newVis[0]=true;\n queue<int> Q;\n Q.push(0);\n int cnt2 = 0;\n while(Q.size())\n {\n int cur = Q.front();\n Q.pop();\n for(auto xx: newGraph[cur])\n {\n if(newVis[xx]==false)\n {\n newVis[xx]=true;\n cnt2++;\n Q.push(xx);\n }\n }\n }\n return cnt2==n-1;\n }\n \n int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {\n this-> n =n;\n int typeCnt[3] = {0,0,0};\n vector<vector<int>> blue(n);\n vector<vector<int>> red(n);\n vector<vector<int>> green(n);\n for(auto x:edges)\n {\n typeCnt[x[0]-1]++;\n \n //R\n if(x[0]==1)\n {\n red[x[2]-1].push_back(x[1]-1);\n red[x[1]-1].push_back(x[2]-1);\n }\n //G\n else if(x[0]==2)\n {\n green[x[2]-1].push_back(x[1]-1);\n green[x[1]-1].push_back(x[2]-1);\n }\n //B\n else\n {\n blue[x[2]-1].push_back(x[1]-1);\n blue[x[1]-1].push_back(x[2]-1);\n }\n }\n pos=true;\n vector<vector<int>> goodBlue;\n vector<bool> vis(n,false);\n int blueCnt = goodBlueCount(blue,goodBlue,vis);\n if(blueCnt)\n {\n int redCnt = seprateCount(red,goodBlue,vis);\n if(pos==false)\n return -1;\n\n int greenCnt = seprateCount(green,goodBlue,vis);\n if(pos==false)\n return -1;\n\n return typeCnt[0]+typeCnt[1]+typeCnt[2]-(blueCnt+redCnt+greenCnt);\n }\n else\n {\n if(BFS(red,vis)&&BFS(green,vis))\n {\n return 0;\n }\n return -1;\n }\n \n }\n};\n```\n\n\n\n | 3 | 1 | [] | 1 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | C++ | kruskal algorithm | easy to follow code | c-kruskal-algorithm-easy-to-follow-code-hi1b9 | Try to include Type 3 edges maximally (1.set)\n2. Count number of type1 edges that we can add to 1.set with out introducing any cycle.\n3. Count number of type2 | alibektu | NORMAL | 2020-09-06T04:16:27.417159+00:00 | 2020-09-06T04:21:24.011779+00:00 | 277 | false | 1. Try to include Type 3 edges maximally (1.set)\n2. Count number of type1 edges that we can add to 1.set with out introducing any cycle.\n3. Count number of type2 edges that we can add to 1.set with out introducing any cycle.\n\nthe answer will be (totoal_#_edges - size_of_set.1 - #_2 - #_3)\n\n```\nclass Solution {\npublic:\n vector<pair<long long, pair<int, int>>> p;\n vector<int> id;\n int N;\n\n void initialize() {\n id.resize(N);\n p.resize(N);\n for(int i = 0;i < N;++i)\n id[i] = i;\n }\n\n int root(int x) {\n while(id[x] != x) {\n id[x] = id[id[x]];\n x = id[x];\n }\n\n return x;\n }\n\n void union1(int x, int y) {\n int p = root(x);\n int q = root(y);\n id[p] = id[q];\n }\n\n int check_type(int type, int n, vector<vector<int>>& edges) {\n int x, y;\n int min_c = 0;\n for(int i = 0;i < edges.size();i++) {\n int x=edges[i][1];\n int y=edges[i][2];\n if (edges[i][0] == type && root(x) != root(y)) {\n min_c++;\n union1(x, y);\n }\n }\n \n return min_c;\n }\n\n int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {\n N=n+1;\n initialize();\n int t3 = check_type(3, n, edges);\n auto p_temp = p;\n auto id_temp = id;\n int t1 = check_type(1, n, edges);\n p=p_temp;\n id=id_temp;\n int t2 = check_type(2, n, edges);\n\n if (t3+t1 != n - 1 || t3+t2 != n - 1) {\n return -1;\n }\n \n return edges.size()-t3-t1-t2;\n }\n};\n``` | 3 | 0 | ['Union Find', 'C'] | 3 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Java, Union Find(compress path+rank) once, check type 3 edges, then check others | java-union-findcompress-pathrank-once-ch-ghxd | \nclass Solution {\n public int maxNumEdgesToRemove(int n, int[][] edges) {\n int[] componentsAlice=new int[n+1];\n int[] componentsBob=new int | fighting_for_flag | NORMAL | 2020-09-06T04:00:42.194853+00:00 | 2020-09-06T04:16:37.319989+00:00 | 438 | false | ```\nclass Solution {\n public int maxNumEdgesToRemove(int n, int[][] edges) {\n int[] componentsAlice=new int[n+1];\n int[] componentsBob=new int[n+1];\n // to make union find tree balance, avoid the worst case where the tree is a single linked list \n int[] sizeAlice=new int[n+1];\n int[] sizeBob=new int[n+1];\n int numsAlice=n,numsBob=n;\n int cycleAlice=0,cycleBob=0,commonCycle=0;\n // initialize union find related variables \n for(int i=1;i<=n;i++)\n { \n componentsAlice[i]=i;\n componentsBob[i]=i;\n sizeAlice[i]=1;\n sizeBob[i]=1;\n }\n // this step is very important!!!. we need to firstly check edges that can be traversed by Alice and Bob. \n // we use common edges to connect all nodes, then we use type 1/2 to connect nodes for Alice/Bob. So all edges that cause cycles in union find can be removed. \n Arrays.sort(edges,(a,b)->(b[0]-a[0]));\n for(int[] edge:edges){\n if(edge[0]==3){\n boolean resAlice=union(edge[1],edge[2],componentsAlice,sizeAlice);\n boolean resBob=union(edge[1],edge[2],componentsBob,sizeBob);\n if(resAlice&&resBob) commonCycle++;\n else {\n if(resAlice) cycleAlice++;\n else numsAlice--;\n if(resBob) cycleBob++;\n else numsBob--;\n } \n } else if(edge[0]==2){\n if(union(edge[1],edge[2],componentsBob,sizeBob))\n cycleBob++;\n else numsBob--;\n } else {\n if(union(edge[1],edge[2],componentsAlice,sizeAlice))\n cycleAlice++;\n else numsAlice--;\n }\n }\n if(numsAlice>1||numsBob>1) return -1;\n return cycleAlice+cycleBob+commonCycle;\n }\n \n int findParent(int n,int[] components){\n while(components[n]!=n){\n // compress path\n n=components[components[n]];\n }\n return n;\n }\n \n boolean union(int a,int b,int[] components,int[] size){\n int parentA=findParent(a,components);\n int parentB=findParent(b,components);\n // node a is already connected with node b. so this edge is redundant. \n if(parentA==parentB) return true;\n // use size to determine which node can be parent \n if(size[parentA]>size[parentB]){\n components[parentB]=parentA;\n size[parentA]+=size[parentB];\n } else{\n components[parentA]=parentB;\n size[parentB]+=size[parentA];\n }\n return false;\n }\n}\n``` | 3 | 0 | [] | 0 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Easy Explaination | Kid of 5 can understand | Penalty and DSUs | easy-explaination-kid-of-5-can-understan-nyc4 | 🚍 A Tale of Shared Roads: Alice, Bob, and the Government Bus 🚦Imagine a bustling city where Alice and Bob each have their own vehicles to commute. Alice prefers | JugalRShah | NORMAL | 2024-12-18T13:01:09.223647+00:00 | 2024-12-18T13:01:09.223647+00:00 | 48 | false | # \uD83D\uDE8D A Tale of Shared Roads: Alice, Bob, and the Government Bus \uD83D\uDEA6\n\nImagine a bustling city where Alice and Bob each have their own vehicles to commute. Alice prefers her routes, and Bob has his own. However, the government steps in with a unique initiative: free buses that run on shared paths for everyone to use. This initiative sparks a challenge: \n\n**How can we maximize the utilization of shared paths while keeping both Alice and Bob connected across the city?** \uD83E\uDD14\n\nLet\u2019s solve this intriguing problem together! \uD83D\uDEE0\uFE0F\n\n---\n\n## \uD83D\uDCA1 Intuition\n\nThe idea revolves around understanding **shared resources** (like the government bus routes) versus **exclusive resources** (paths only Alice or Bob can use). Shared paths are prioritized because they reduce redundancy and ensure efficient connectivity for both Alice and Bob. (Atleast that\'s how i got intuition like AMTS/BRTS(if you know you know\uD83E\uDD23\uD83D\uDE02) are cheaper than private vehicle petrol and other cost however sometimes you have to use no choice )\n\nHere\u2019s the plan:\n- **Shared paths (Type 3):** These are "free" in the sense that both Alice and Bob benefit, so we give them the highest priority (penalty = 0). \uD83D\uDE8C\n- **Exclusive paths (Type 1 or 2):** These come with a penalty (penalty = 1), as only Alice or Bob can use them. \uD83D\uDE97\uD83D\uDE99\n\nBy minimizing the number of redundant paths while keeping both Alice and Bob connected, we ensure an optimal solution. \uD83C\uDFAF\n\n---\n\n## \uD83D\uDEE0\uFE0F Approach\n\n### 1\uFE0F\u20E3 **Penalty-Based Sorting** \n- Assign a penalty to edges based on their type:\n - Shared paths (Type 3) are prioritized since they connect both Alice and Bob simultaneously (penalty = 0). \n - Exclusive paths (Type 1 or 2) come next (penalty = 1). \n- Sort the edges by penalty so shared paths are processed first.\n\n### 2\uFE0F\u20E3 **Union-Find (Disjoint Set Union)** \n- Use the **Union-Find** (or DSU) data structure to manage connectivity. \n- Maintain two separate DSUs:\n - One for Alice\'s network (Type 1 + Type 3 paths). \n - One for Bob\'s network (Type 2 + Type 3 paths). \n- Process each edge:\n - If the edge connects previously unconnected nodes, add it to the respective DSU. \n - If the edge is redundant, count it as "removable." \n\n### 3\uFE0F\u20E3 **Validation** \n- After processing all edges, check if both Alice and Bob are fully connected (i.e., they each have a single connected component). \n- If not, return `-1` (it\'s impossible to connect them fully). Otherwise, return the count of redundant edges.\n\n---\n\n## \u23F3 Complexity\n\n- **Time Complexity:** \n - Sorting the edges takes $$O(E \\log E)$$, where $$E$$ is the number of edges. \n - Union-Find operations are nearly constant time due to path compression, making the overall complexity approximately **$$O(E \\log E)$$**. \u2705\n\n- **Space Complexity:** \n - We store parent and size arrays for DSUs, requiring $$O(N)$$ space, where $$N$$ is the number of nodes. \n\n---\n\n## \uD83E\uDDD1\u200D\uD83D\uDCBB Code\n\nHere\u2019s the full implementation in C++: \n\n```cpp\nclass DJ {\nprivate:\n vector<int> parent, gSize;\n\npublic:\n DJ(int cap) {\n for (int i = 0; i < cap + 1; i++) {\n parent.push_back(i);\n gSize.push_back(1);\n }\n }\n\n bool unionBySize(int node1, int node2) {\n int ultP1 = getUltPar(node1), ultP2 = getUltPar(node2);\n if (ultP1 == ultP2) {\n return false;\n }\n\n if (gSize[ultP1] > gSize[ultP2]) {\n parent[ultP2] = ultP1;\n gSize[ultP1] += gSize[ultP2];\n } else {\n parent[ultP1] = ultP2;\n gSize[ultP2] += gSize[ultP1];\n }\n\n return true;\n }\n\n int getUltPar(int node) {\n if (parent[node] == node)\n return node;\n return parent[node] = getUltPar(parent[node]);\n }\n\n bool IsSingleComponent() {\n int ultP = getUltPar(1);\n for (int i = 1; i < parent.size(); i++) {\n if (getUltPar(i) != ultP) {\n return false;\n }\n }\n return true;\n }\n};\n\nclass Solution {\npublic:\n int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {\n int aliceSum = 0, bobSum = 0;\n for (auto& edge : edges) {\n if (edge[0] != 3)\n edge.push_back(1);\n else\n edge.push_back(0);\n }\n\n sort(edges.begin(), edges.end(), [&](vector<int>& a, vector<int>& b) {\n return a.back() < b.back();\n });\n\n DJ alice(n), bob(n);\n\n int count = 0;\n\n for (auto& edge : edges) {\n int from = edge[1], to = edge[2];\n bool used = false;\n\n if ((alice.getUltPar(from) != alice.getUltPar(to)) &&\n (edge[0] == 1 || edge[0] == 3)) {\n alice.unionBySize(from, to);\n used = true;\n }\n\n if ((bob.getUltPar(from) != bob.getUltPar(to)) &&\n (edge[0] == 2 || edge[0] == 3)) {\n bob.unionBySize(from, to);\n used = true;\n }\n\n if (!used) {\n count++;\n }\n }\n\n if (!alice.IsSingleComponent() || !bob.IsSingleComponent())\n return -1;\n return count;\n }\n};\n\n\n```\n# \uD83D\uDE80 Closing Thoughts\nThis problem is a great analogy for real-world optimization challenges, like city planning or resource allocation. By prioritizing shared resources (the government bus \uD83D\uDE8D) over costly private options (Alice\'s and Bob\'s vehicles \uD83D\uDE97\uD83D\uDE99), we ensure an efficient and cost-effective solution.\n\n\uD83D\uDCAC Did you enjoy this explanation? Let me know your thoughts, suggestions, or any alternate approaches in the comments below! \uD83D\uDC47\n\n\n\n\n# ***If you liked it a upvote will be high appreciated!*** | 2 | 0 | ['C++'] | 0 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Easy Explained Solution with comments||C++||Java | easy-explained-solution-with-commentscja-ca8d | Approach\n### DisjointSet Class Explanation\n\nThe DisjointSet class manages a collection of disjoint sets using two primary arrays: Parent and Rank. The Parent | Ashutosh_Kumar_0506 | NORMAL | 2024-06-30T14:09:40.408920+00:00 | 2024-06-30T14:09:40.408959+00:00 | 143 | false | # Approach\n### DisjointSet Class Explanation\n\nThe `DisjointSet` class manages a collection of disjoint sets using two primary arrays: `Parent` and `Rank`. The `Parent` array keeps track of the parent node for each element, while the `Rank` array helps to keep the tree flat by attaching smaller trees under the root of larger trees. The constructor initializes each node to be its own parent and sets the initial rank to zero. The `FindUltimateParent` method uses path compression to ensure that each node directly points to the root of its set, improving the efficiency of future queries. The `UnionByRank` method merges two sets by rank, ensuring that the tree remains balanced. The `isSingleComponent` method checks if all nodes are connected into a single component by verifying if there is only one component left.\n\n### Solution Class Explanation\n\nThe `Solution` class contains the `maxNumEdgesToRemove` method, which aims to maximize the number of removable edges while ensuring both Alice and Bob can still traverse the entire graph.\n\n1. **Edge Sorting:** Edges are sorted in descending order based on their type. Type 3 edges (usable by both Alice and Bob) are processed first, followed by type 2 (only for Bob) and type 1 (only for Alice). This ensures that edges which are most beneficial (type 3) are considered first.\n\n2. **Disjoint Sets for Alice and Bob:** Two separate `DisjointSet` instances are created for Alice and Bob to manage their respective graphs.\n\n3. **Processing Edges:** The method iterates over the sorted edges:\n - **Type 3 Edges:** If the edge connects two different components for either Alice or Bob, it is used and the components are united. The `edgeCount` is incremented if the edge is used by either Alice or Bob.\n - **Type 2 Edges:** If the edge connects two different components for Bob, it is used and the components are united. The `edgeCount` is incremented if the edge is used.\n - **Type 1 Edges:** If the edge connects two different components for Alice, it is used and the components are united. The `edgeCount` is incremented if the edge is used.\n\n4. **Checking Connectivity:** After processing all edges, the method checks if both Alice and Bob\'s graphs are fully connected using the `isSingleComponent` method. If both graphs are connected, the number of removable edges is calculated by subtracting `edgeCount` from the total number of edges. If either graph is not fully connected, the method returns `-1` to indicate that it\'s impossible to ensure full traversal for both Alice and Bob with the given edges.\n\n# Complexity\n### Space Complexity\n\n1. **DisjointSet Class:**\n - **Parent and Rank Arrays:** Each array has a size of \\(n + 1\\), where \\(n\\) is the number of nodes. Thus, the space complexity for these arrays is \\(O(n)\\).\n - **Components Variable:** This is an integer variable, so it has a space complexity of \\(O(1)\\).\n\n Overall, the space complexity of the `DisjointSet` class is \\(O(n)\\).\n\n2. **Solution Class:**\n - **Edges Storage:** The `edges` vector stores all the edges, and its space complexity is \\(O(E)\\), where \\(E\\) is the number of edges.\n - **Disjoint Sets for Alice and Bob:** Each `DisjointSet` instance requires \\(O(n)\\) space. Since there are two instances (one for Alice and one for Bob), this contributes \\(O(n) + O(n) = O(n)\\) space.\n\n Overall, the space complexity of the `Solution` class is \\(O(n + E)\\).\n\n### Time Complexity\n\n1. **DisjointSet Class:**\n - **FindUltimateParent:** The amortized time complexity of the `FindUltimateParent` method with path compression is \\(O(\\alpha(n))\\), where \\(\\alpha\\) is the inverse Ackermann function, which grows very slowly and is nearly constant for practical purposes.\n - **UnionByRank:** The time complexity for the `UnionByRank` method is \\(O(\\alpha(n))\\).\n\n2. **Solution Class:**\n - **Edge Sorting:** Sorting the edges takes \\(O(E \\log E)\\) time.\n - **Processing Each Edge:** For each edge, the `FindUltimateParent` and `UnionByRank` operations are performed. Each of these operations takes \\(O(\\alpha(n))\\) time. Since there are \\(E\\) edges, the total time for processing edges is \\(O(E \\cdot \\alpha(n))\\).\n\n Overall, the time complexity of the `maxNumEdgesToRemove` method is dominated by the sorting step and the processing of the edges, resulting in \\(O(E \\log E + E \\cdot \\alpha(n))\\). Given that \\(\\alpha(n)\\) is nearly constant, this can be simplified to \\(O(E \\log E)\\) for practical purposes.\n\n# Code\n```\nclass DisjointSet\n{\npublic:\n vector<int> Parent; // To store the parent of each node\n vector<int> Rank; // To store the rank (or depth) of each tree\n int components; // To keep track of the number of components\n\n // Constructor\n DisjointSet(int n)\n {\n Rank.resize(n + 1, 0); // Initialize rank to 0 for all nodes\n Parent.resize(n + 1); // Initialize parent array\n components = n; // Initially, each node is its own component\n for (int i = 0; i <= n; i++)\n {\n Parent[i] = i; // Each node is its own parent initially\n }\n }\n\n // Function to find the ultimate parent of a node with path compression\n int FindUltimateParent(int node)\n {\n if (node == Parent[node]) // If the node is its own parent, return the node\n {\n return node;\n }\n return (Parent[node] = FindUltimateParent(Parent[node])); // Path compression\n }\n\n // Union by rank\n void UnionByRank(int u, int v)\n {\n int Ult_U = FindUltimateParent(u); // Find the ultimate parent of u\n int Ult_V = FindUltimateParent(v); // Find the ultimate parent of v\n\n // If both nodes belong to the same component, do nothing\n if (Ult_U == Ult_V)\n {\n return;\n }\n\n // Else, unite the components\n if (Rank[Ult_U] < Rank[Ult_V])\n {\n Parent[Ult_U] = Ult_V; // Attach the tree with smaller rank to the root of the tree with larger rank\n }\n else if (Rank[Ult_U] > Rank[Ult_V])\n {\n Parent[Ult_V] = Ult_U; // Attach the tree with smaller rank to the root of the tree with larger rank\n }\n else\n {\n Parent[Ult_V] = Ult_U; // If ranks are equal, make one the parent and increase its rank\n Rank[Ult_U]++;\n }\n components--; // Decrease the component count since two components have been united\n }\n\n // Function to check if all nodes are in a single component\n bool isSingleComponent()\n {\n return components == 1;\n }\n};\n\nclass Solution {\nprivate:\n // Comparator function to sort edges\n static bool cmp(vector<int>&a, vector<int>&b)\n {\n return a[0] < b[0];\n }\n\npublic:\n int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {\n // Sort edges by type in descending order (type 3 first, then type 2, and type 1 last)\n sort(edges.rbegin(), edges.rend(), cmp);\n\n DisjointSet alice(n); // Disjoint set for Alice\n DisjointSet bob(n); // Disjoint set for Bob\n\n int edgeCount = 0; // Count of edges used\n\n for (auto &it : edges)\n {\n int type = it[0];\n int u = it[1];\n int v = it[2];\n\n if (type == 3)\n {\n bool flag = false;\n\n // For Alice\n if (alice.FindUltimateParent(u) != alice.FindUltimateParent(v))\n {\n alice.UnionByRank(u, v);\n flag = true;\n }\n\n // For Bob\n if (bob.FindUltimateParent(u) != bob.FindUltimateParent(v))\n {\n bob.UnionByRank(u, v);\n flag = true;\n }\n if (flag)\n {\n edgeCount++; // If the edge was used by either Alice or Bob, increase the count\n }\n }\n else if (type == 2)\n {\n bool flag = false;\n\n // For Bob\n if (bob.FindUltimateParent(u) != bob.FindUltimateParent(v))\n {\n bob.UnionByRank(u, v);\n flag = true;\n }\n if (flag)\n {\n edgeCount++; // If the edge was used by Bob, increase the count\n }\n }\n else\n {\n bool flag = false;\n\n // For Alice\n if (alice.FindUltimateParent(u) != alice.FindUltimateParent(v))\n {\n alice.UnionByRank(u, v);\n flag = true;\n }\n if (flag)\n {\n edgeCount++; // If the edge was used by Alice, increase the count\n }\n }\n }\n\n // If both Alice and Bob can traverse the entire graph, return the number of edges that can be removed\n if (alice.isSingleComponent() && bob.isSingleComponent())\n {\n return edges.size() - edgeCount; // Total edges minus used edges gives the removable edges\n }\n return -1; // If not, return -1 indicating it\'s not possible\n }\n};\n\n``` | 2 | 0 | ['Union Find', 'Graph', 'C++'] | 2 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Go HARD 62% | go-hard-62-by-ian_chechin-qj64 | \n\n# Code\n\ntype UnionFind struct {\n representative []int\n componentSize []int\n components int\n}\n\nfunc New(n int) *UnionFind {\n uf := Union | Ian_Chechin | NORMAL | 2024-06-30T07:48:19.285737+00:00 | 2024-06-30T07:48:19.285765+00:00 | 42 | false | \n\n# Code\n```\ntype UnionFind struct {\n representative []int\n componentSize []int\n components int\n}\n\nfunc New(n int) *UnionFind {\n uf := UnionFind{}\n uf.components = n\n uf.representative = make([]int, n+1)\n uf.componentSize = make([]int, n+1)\n for i := range uf.representative {\n uf.representative[i] = i\n uf.componentSize[i] = 1\n }\n return &uf\n}\n\nfunc (uf *UnionFind) findRepresentative(x int) int {\n if uf.representative[x] == x {\n return x\n }\n uf.representative[x] = uf.findRepresentative(uf.representative[x])\n return uf.representative[x]\n}\n\nfunc (uf *UnionFind) performUnion(x int, y int) int {\n x, y = uf.findRepresentative(x), uf.findRepresentative(y)\n\n if x == y {\n return 0\n }\n if uf.componentSize[x] > uf.componentSize[y] {\n uf.representative[y] = x\n uf.componentSize[x] += uf.componentSize[y]\n } else {\n uf.representative[x] = y\n uf.componentSize[y] += uf.componentSize[x]\n }\n uf.components--\n return 1\n}\n\nfunc (uf *UnionFind) isConnected() bool {\n return uf.components == 1\n}\n\nfunc maxNumEdgesToRemove(n int, edges [][]int) int {\n Alice, Bob := New(n), New(n)\n edgesRequired := 0\n for _, edge := range edges {\n if edge[0] == 3 {\n edgesRequired += Alice.performUnion(edge[1], edge[2]) | Bob.performUnion(edge[1], edge[2])\n }\n }\n\n for _, edge := range edges {\n if edge[0] == 1 {\n edgesRequired += Alice.performUnion(edge[1], edge[2])\n } else if edge[0] == 2 {\n edgesRequired += Bob.performUnion(edge[1], edge[2])\n }\n }\n\n if Alice.isConnected() && Bob.isConnected() {\n return len(edges) - edgesRequired\n }\n\n return -1\n}\n``` | 2 | 0 | ['Go'] | 0 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Union Find | Python | union-find-python-by-pragya_2305-0kbs | Complexity\n- Time complexity: O(E*A(n)) where E=len(edges) and A(n)=inverse ackerman function\n\n- Space complexity: O(n)\n\n# Code\n\nclass UnionFind:\n de | pragya_2305 | NORMAL | 2024-06-30T05:27:03.515336+00:00 | 2024-06-30T05:27:03.515385+00:00 | 245 | false | # Complexity\n- Time complexity: O(E*A(n)) where E=len(edges) and A(n)=inverse ackerman function\n\n- Space complexity: O(n)\n\n# Code\n```\nclass UnionFind:\n def __init__(self,n):\n self.par = [i for i in range(n+1)]\n self.rank = [1]*(n+1)\n\n def find(self,node):\n while node!=self.par[node]:\n self.par[node]=self.par[self.par[node]]\n node = self.par[node]\n return node\n\n def union(self,n1,n2):\n p1,p2 = self.find(n1),self.find(n2)\n\n if p1==p2:\n return 1\n \n if self.rank[p1]>self.rank[p2]:\n self.rank[p1]+=self.rank[p2]\n self.par[p2]=p1\n else:\n self.rank[p2]+=self.rank[p1]\n self.par[p1]=p2\n\n return 0\n\n\nclass Solution:\n def maxNumEdgesToRemove(self, n: int, edges: List[List[int]]) -> int:\n alice,bob = UnionFind(n),UnionFind(n)\n count = 0\n\n for t,v1,v2 in edges:\n if t==3:\n count+=(alice.union(v1,v2)|bob.union(v1,v2))\n\n for t,v1,v2 in edges:\n if t==1:\n count+=alice.union(v1,v2)\n elif t==2:\n count+=bob.union(v1,v2)\n \n return -1 if max(alice.rank)!=n or max(bob.rank)!=n else count\n``` | 2 | 0 | ['Union Find', 'Graph', 'Python', 'Python3'] | 1 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | 🌟 Maximize Removal of Edges for Optimal Connectivity! 🛠️ Beats 97%✨ | maximize-removal-of-edges-for-optimal-co-5a04 | \n\n# Intuition\nThe problem involves maximizing the number of edges that can be removed from a graph while ensuring connectivity based on specified edge types. | UDAY-SANKAR-MUKHERJEE | NORMAL | 2024-06-30T03:36:35.499775+00:00 | 2024-06-30T03:36:35.499800+00:00 | 330 | false | \n\n# Intuition\nThe problem involves maximizing the number of edges that can be removed from a graph while ensuring connectivity based on specified edge types. This requires understanding and manipulating the graph\'s connectivity using DFS (Depth-First Search) and component analysis.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Graph Representation: Represent the graph using adjacency lists for efficient traversal and\ncomponent identification.\n2. DFS for Component Identification: Use DFS to identify connected components of the graph\nand count the number of nodes in each component.\n3. Edge Removal Strategy: Separate edges based on their types (Type 1, Type 2, and Type 3) and\napply a strategy to maximize removals while maintaining connectivity:\n\u2022 For Type 3 edges, ensure all nodes in the same connected component.\n\u2022 For Type 1 and Type 2 edges, ensure connectivity between all nodes using these edges.\n# Detailed Steps\n1. Initialize Data Structures: Create adjacency lists for the graph and arrays to track visited nodes\nand connected components.\n2. DFS for Component Identification: Implement a DFS function to mark nodes with their\nrespective component numbers and count nodes in each component.\n3. Edge Categorization: Separate edges into Type 1, Type 2, and Type 3 based on their given\nspecifications.\n4. Ensure Connectivity: For Type 3 edges, ensure all nodes are in the same connected component.\nFor Type 1 and Type 2 edges, use DFS to ensure connectivity across the graph.\n5. Calculate Maximum Removals: Calculate the maximum number of edges that can be removed\nwhile maintaining connectivity and meeting the specified conditions.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n+m), where n is the number of nodes and m is the number of edges. This includes DFS operations and edge categorization.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n+m), for storing adjacency lists, visited arrays, and other data structures related to graph traversal.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n\n def dfs(self,vis,li,com,i):\n if(vis[i]):\n return 0\n vis[i]=com\n ans=1\n for j in li[i]:\n ans+=self.dfs(vis,li,com,j)\n return ans\n\n def maxNumEdgesToRemove(self, n: int, e: List[List[int]]) -> int:\n ans=0\n li=[[] for i in range(n)]\n for l in e:\n if(l[0]==3):\n li[l[1]-1].append(l[2]-1)\n li[l[2]-1].append(l[1]-1)\n vis=[0 for i in range(n)]\n com=0\n for i in range(n):\n if(vis[i]):\n continue\n else:\n com+=1\n temp=self.dfs(vis,li,com,i)\n ans+=(temp-1)\n lia=[[] for i in range(com)]\n lib=[[] for i in range(com)]\n for l in e:\n if(l[0]==1):\n a=vis[l[1]-1]-1\n b=vis[l[2]-1]-1\n if(a==b):\n continue\n lia[a].append(b)\n lia[b].append(a)\n elif(l[0]==2):\n a=vis[l[1]-1]-1\n b=vis[l[2]-1]-1\n if(a==b):\n continue\n lib[a].append(b)\n lib[b].append(a)\n visa=[0 for i in range(com)]\n coma=0\n comb=0\n for i in range(com):\n if(visa[i]):\n continue\n else:\n coma+=1\n if(coma>1):\n return -1\n self.dfs(visa,lia,coma,i)\n \n visb=[0 for i in range(com)]\n for i in range(com):\n if(visb[i]):\n continue\n else:\n comb+=1\n if(comb>1):\n return -1\n self.dfs(visb,lib,comb,i)\n if(coma>1 or comb>1):\n return -1\n ans+=(com-1)*2\n return len(e)-ans\n\n```\nIf you found this helpful, please upvote! \uD83D\uDC4D\n\n\n | 2 | 0 | ['Python3'] | 1 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | DIS-JOINTSET UNION | EASY | ✅✅ | IMPLEMENTATION | | dis-jointset-union-easy-implementation-b-n3va | Intuition\n- Using 2 separete disjoint set for both alice and bob.\n\n# Approach\n- Sort the edges.\n- First process type 3 edges and then connect u, v and incr | karthikeya48 | NORMAL | 2024-06-30T03:22:53.011091+00:00 | 2024-06-30T03:22:53.011121+00:00 | 45 | false | # Intuition\n- Using 2 separete disjoint set for both alice and bob.\n\n# Approach\n- Sort the edges.\n- First process type 3 edges and then connect u, v and increment the count if they have not unioned before\n- Simillarly process type 2 and type 1 edges and incremen the count of alice and bob and overall count.\n- if alice and bob != n - 1 return -1\n- else return edge.sz() - count\n\n\n# Code\n```\nclass DSU {\n\tvector<int>parent, size;\npublic:\n\n\tDSU(int n) {\n size.resize(n + 1, 0);\n\t\tparent.resize(n + 1, 0);\n\t\tfor(int i = 0; i <= n; i++) {\n\t\t\tparent[i] = i;\n\n\t\t}\n\t}\n\n\tbool isSame(int u, int v) {\n return findPar(u) == findPar(v);\n }\n\t\n\tint findPar(int node) {\n\t\tif(node == parent[node]) return node;\n\t\treturn parent[node] = findPar(parent[node]);\n\t}\n\n\tint unionBySize(int u, int v) {\n\t\tint ulp_u = findPar(u);\n\t\tint ulp_v = findPar(v);\n\t\tif(ulp_u == ulp_v) return 0;\n\t\tif(size[ulp_u] < size[ulp_v]) {\n\t\t\tparent[ulp_u] = ulp_v;\n\t\t\tsize[ulp_v] += size[ulp_u];\n\t\t} \n\t\telse {\n\t\t\tparent[ulp_v] = ulp_u;\n\t\t\tsize[ulp_u] += size[ulp_v];\n\t\t}\n return 1;\n\t}\n};\n\n\nclass Solution {\npublic:\n int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {\n\n DSU d1(n);\n DSU d2(n);\n\n int alice = 0, bob = 0, c = 0;\n\n sort(edges.rbegin(), edges.rend());\n\n for(auto it : edges) {\n int t = it[0], u = it[1], v = it[2];\n\n if(t == 3) {\n int f1 = d1.unionBySize(u, v);\n int f2 = d2.unionBySize(u, v);\n alice += f1;\n bob += f2;\n if(f1 | f2) c++;\n }\n else if(t == 2) {\n int f2 = d2.unionBySize(u, v);\n bob += f2;\n c += f2;\n }\n else {\n int f1 = d1.unionBySize(u, v);\n alice += f1;\n c += f1;\n }\n }\n\n if(alice != n- 1 || bob != n - 1) return -1;\n\n return edges.size() - c;\n }\n};\n``` | 2 | 0 | ['Union Find', 'C++'] | 2 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Solution using Prim's Minimum Spanning Tree | solution-using-prims-minimum-spanning-tr-gbqv | Intuition\nSince we need to find minimum edges with which graph is fully traversal for both alice and bob, it means we need to find MST possible for both alice | user9463Wq | NORMAL | 2023-07-29T10:49:47.667328+00:00 | 2023-07-29T10:49:47.667371+00:00 | 93 | false | # Intuition\nSince we need to find minimum edges with which graph is fully traversal for both alice and bob, it means we need to find MST possible for both alice and bob\n\n# Approach\n- We will apply prims algorithm to find minimum spanning tree for alice and bob \n- while picking edges we will give higher priority to edge with type 3\n- we will find MST for alice and bob separately and union their edges. This count is count of minimum edges we need to have graph fully travererable by both alice and bob\n- in priority queue, we will define sorting order first by type, then by src, and then by dest, because we can have mulitple type 3 edges to choose for same nodes, in such case we want to construct same mst for alice and bob both\n\n# Complexity\n- Time complexity:\nMST takes O(V*ElogV)\n\n# Code\n```\nclass Solution {\n static class Edge implements Comparable<Edge> {\n int s;\n int d;\n int t;\n\n Edge(int src, int dst, int type) {\n s = src;\n d = dst;\n t = type;\n }\n\n @Override\n public int compareTo(Edge e) {\n if(e.t != this.t)\n return e.t - this.t;\n\n if(e.s != this.s)\n return e.s - this.s;\n\n return e.d - this.d;\n }\n\n @Override\n public boolean equals(Object o) {\n Edge e = ((Edge)o);\n return e.t == this.t &&\n (\n (e.s == this.s && e.d == this.d) ||\n (e.s == this.d && e.d == this.s)\n );\n }\n\n @Override\n public int hashCode() {\n return 31 * t * s * d;\n }\n }\n\n private Set<Edge> getMST(List<Edge> adj[], int n, int type) {\n Set<Edge> out = new HashSet();\n PriorityQueue<Edge> q = new PriorityQueue();\n q.add(new Edge(0, 0, -1));\n\n boolean vis[] = new boolean[n];\n\n while(!q.isEmpty()) {\n Edge r = q.poll();\n\n if(vis[r.d])\n continue;\n\n vis[r.d] = true;\n\n if(r.t != -1)\n out.add(r);\n\n for(Edge e: adj[r.d]) {\n if(!vis[e.d] && (e.t == 3 || e.t == type)) {\n q.add(e);\n }\n }\n\n }\n\n for(int i=0;i<n;i++) {\n if(!vis[i])\n return Collections.emptySet();\n }\n\n return out;\n }\n\n public int maxNumEdgesToRemove(int n, int[][] edges) {\n\n List<Edge> adj[] = new List[n];\n for(int i=0;i<n;i++)\n adj[i] = new ArrayList();\n\n for(int i=0;i<edges.length;i++) {\n adj[edges[i][1]-1].add(new Edge(edges[i][1]-1, edges[i][2]-1, edges[i][0]));\n adj[edges[i][2]-1].add(new Edge(edges[i][2]-1, edges[i][1]-1, edges[i][0]));\n }\n\n Set<Edge> aliceMST = getMST(adj, n, 1);\n Set<Edge> bobMST = getMST(adj, n, 2);\n\n if(aliceMST.isEmpty() || bobMST.isEmpty())\n return -1;\n\n aliceMST.addAll(bobMST);\n\n return edges.length - aliceMST.size();\n }\n }\n``` | 2 | 0 | ['Minimum Spanning Tree', 'Java'] | 0 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Solution in C++ | solution-in-c-by-sejal7562-0mx7 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Sejal7562 | NORMAL | 2023-05-01T02:02:19.396163+00:00 | 2023-05-01T02:02:19.396200+00:00 | 459 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n struct DisjointUnionSets\n {\n int *rank,*parent;\n int x;\n DisjointUnionSets(int n)\n {\n rank=new int[n];\n parent=new int[n];\n x=n;\n for(int i=0;i<n;i++)\n parent[i]=i;\n }\n int find(int x)\n {\n if(parent[x]!=x)\n parent[x]=find(parent[x]);\n return parent[x];\n }\n bool Union(int x,int y)\n {\n int xRoot=find(x),yRoot=find(y);\n if(xRoot == yRoot)\n return false;\n if(rank[xRoot] < rank[yRoot])\n parent[xRoot]=yRoot;\n else if (rank[xRoot] > rank[yRoot])\n parent[yRoot]=xRoot;\n else\n {\n parent[yRoot]=xRoot;\n rank[xRoot]++;\n }\n return true;\n }\n};\n int maxNumEdgesToRemove(int n, vector<vector<int>>& edges)\n {\n int size=edges.size();\n vector<pair<int,int>> alice;\n vector<pair<int,int>> bob;\n vector<pair<int,int>> both;\n for(int i=0;i<size;i++)\n {\n int temp=edges[i][0];\n if(temp==1)\n alice.push_back(make_pair(edges[i][1]-1,edges[i][2]-1));\n else if(temp==2)\n bob.push_back(make_pair(edges[i][1]-1,edges[i][2]-1));\n else\n both.push_back(make_pair(edges[i][1]-1,edges[i][2]-1));\n }\n DisjointUnionSets a(n),b(n);\n int res=0,componentA=n,componentB=n;\n for(auto x:both){\n bool flag1=a.Union(x.first,x.second);\n bool flag2=b.Union(x.first,x.second);\n if(flag1)\n componentA--;\n if(flag2)\n componentB--;\n if(flag1 && flag2)\n res++;\n }\n for(auto x:alice){\n bool flag=a.Union(x.first,x.second);\n if(flag)\n {\n componentA--;\n res++;\n }\n }\n for(auto x:bob)\n {\n bool flag=b.Union(x.first,x.second);\n if(flag)\n {\n componentB--;\n res++;\n }\n }\n if(componentA!=1 ||componentB!=1)\n return -1;\n return size-res;\n }\n};\n``` | 2 | 0 | ['C++'] | 1 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Easy to understand C++ solution using DSU | easy-to-understand-c-solution-using-dsu-4drnj | Code\n\nclass DSU {\npublic:\n vector<int> parent;\n vector<int> rank;\n int components;\n\n DSU(int n) {\n parent.resize(n+1);\n for( | baquer | NORMAL | 2023-04-30T18:05:21.959485+00:00 | 2023-04-30T18:05:21.959520+00:00 | 352 | false | # Code\n```\nclass DSU {\npublic:\n vector<int> parent;\n vector<int> rank;\n int components;\n\n DSU(int n) {\n parent.resize(n+1);\n for(int i = 1; i <=n; i++) {\n parent[i] = i;\n }\n rank.resize(n+1);\n components = n;\n }\n\n int findParent(int node) {\n if(node == parent[node]) {\n return node;\n }\n return findParent(parent[node]);\n }\n\n void unionByRank(int node1, int node2) {\n int p1 = findParent(node1);\n int p2 = findParent(node2);\n\n if(p1 == p2) {\n return;\n }\n if(rank[p1] > rank[p2]) {\n parent[p2] = p1;\n } else if(rank[p2] > rank[p1]) {\n parent[p1] = p2;\n } else {\n parent[p1] = p2;\n rank[p2]++;\n }\n components--;\n }\n\n bool isSingle() {\n return components == 1;\n }\n\n};\n\nclass Solution {\npublic:\n \n int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {\n // Aaj bhi DSU ka question hai\n // 2 DSU Banao Alice and Bob k liye\n // aur edges ko traverse karo sorting order me type k 3,2,1\n // agr type 3 hai to u and v k parent check karo agr wo \n // alag hai to union karo aur edge++ karo ye kaam dono k liye karo\n // agr type 2 hai aur u and v ka parent same nahi to union karo aur\n // edge++ karo, same kaam type 1 k liye bhi\n // last me check karo ki agr components dono graph ka 1 hai to\n // return edges.size() - edge otherwise return -1;\n DSU Alice(n);\n DSU Bob(n);\n\n auto lambda = [](vector<int> &a, vector<int> &b) {\n return a[0] > b[0]; \n };\n sort(edges.begin(), edges.end(), lambda);\n\n int edge = 0;\n for(auto &ed: edges) {\n int type = ed[0];\n int u = ed[1];\n int v = ed[2];\n\n if(type == 3) {\n bool edgeAdded = false;\n if(Alice.findParent(u) != Alice.findParent(v)) {\n Alice.unionByRank(u,v);\n edgeAdded = true;\n }\n if(Bob.findParent(u) != Bob.findParent(v)) {\n Bob.unionByRank(u,v);\n edgeAdded = true;\n } \n if(edgeAdded == true) {\n edge++;\n } \n } else if (type == 2) {\n if(Bob.findParent(u) != Bob.findParent(v)) {\n Bob.unionByRank(u,v);\n edge++;\n }\n \n } else {\n if(Alice.findParent(u) != Alice.findParent(v)) {\n Alice.unionByRank(u,v);\n edge++;\n }\n }\n }\n if(Alice.isSingle() == true and Bob.isSingle() == true) {\n return edges.size() - edge;\n }\n return -1;\n }\n};\n``` | 2 | 0 | ['Graph', 'C++'] | 1 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | ✍ ✅ [PHP][JavaScript] 🚀Beats 100% | Using Union Find or Disjoint-set data structure | phpjavascript-beats-100-using-union-find-tuwy | This approach uses UnionFind to determine the number of edges to remove in order to disconnect a graph with edges of type 1, 2, and 3. \n\nThe union-find data s | akunopaka | NORMAL | 2023-04-30T17:14:50.196734+00:00 | 2023-04-30T17:14:50.196763+00:00 | 174 | false | This approach uses UnionFind to determine the number of edges to remove in order to disconnect a graph with edges of type 1, 2, and 3. \n\nThe union-find data structure helps to keep track of connected components in the graph. \n\nThe algorithm first iterates over all the edges of type 3 and uses the union-find data structure to union all the nodes connected by these edges. \nIt then iterates over the edges of type 1 and 2 for each one, it checks if the two nodes connected by this edge have been already connected (using union-find) or not. \nIf they are not connected, then the edge is added (using union-find) and the number of edges to keep is incremented. \n\nFinally, the algorithm checks if the graph is connected *isConnected* and if it is, it return the number of edges that need to be removed *(edges.length - resNumberOfEdgesToKeep)*, else it returns -1.\n\n# Complexity\n- Time complexity: $$O(m * log(n))$$ where *m* is the number of edges and *n* is the number of nodes. \n- Space complexity: $$O(N)$$, where N is the number of vertices.\n\n# JavaScript\n``` JavaScript\n/**\n * @param {number} n\n * @param {number[][]} edges\n * @return {number}\n */\nvar maxNumEdgesToRemove = function (n, edges) {\n let ufA = new UnionFind(n);\n let ufB = new UnionFind(n);\n let resNumberOfEdgesToKeep = 0;\n // Type 3\n for (let edge of edges) {\n if (edge[0] === 3) {\n resNumberOfEdgesToKeep += ufA.union(edge[1], edge[2]);\n ufB.union(edge[1], edge[2]);\n }\n }\n // Type 1 and 2\n for (let edge of edges) {\n if (edge[0] === 1) {\n resNumberOfEdgesToKeep += ufA.union(edge[1], edge[2]);\n } else if (edge[0] === 2) {\n resNumberOfEdgesToKeep += ufB.union(edge[1], edge[2]);\n }\n }\n return ufA.isConnected() && ufB.isConnected() ? edges.length - resNumberOfEdgesToKeep : -1;\n};\n\nclass UnionFind {\n constructor(n) {\n this.parent = {};\n this.rank = {};\n this.count = n;\n for (let i = 0; i <= n; i++) {\n this.parent[i] = i;\n this.rank[i] = 1;\n }\n }\n\n find(node) {\n while (node !== this.parent[node]) {\n this.parent[node] = this.parent[this.parent[node]];\n node = this.parent[node];\n }\n return node;\n }\n\n union(u, v) {\n let rootU = this.find(u);\n let rootV = this.find(v);\n if (rootU === rootV) return 0;\n if (this.rank[rootU] > this.rank[rootV]) {\n this.parent[rootV] = rootU;\n this.rank[rootU] += this.rank[rootV];\n } else {\n this.parent[rootU] = rootV;\n this.rank[rootV] += this.rank[rootU];\n }\n this.count--;\n return 1;\n }\n\n isConnected() {\n return this.count === 1;\n }\n}\n```\n\n# PHP\n``` PHP\nclass Solution\n{\n /**\n * @param Integer $n\n * @param Integer[][] $edges\n * @return Integer\n */\n function maxNumEdgesToRemove(int $n, array $edges): int {\n $ufA = new UnionFind($n);\n $ufB = new UnionFind($n);\n $resNumberOfEdgesToKeep = 0;\n // Type 3\n foreach ($edges as $edge) {\n if ($edge[0] == 3) {\n $resNumberOfEdgesToKeep += $ufA->union($edge[1], $edge[2]);\n $ufB->union($edge[1], $edge[2]);\n }\n }\n // Type 1 and 2\n foreach ($edges as $edge) {\n if ($edge[0] == 1) {\n $resNumberOfEdgesToKeep += $ufA->union($edge[1], $edge[2]);\n } else if ($edge[0] == 2) {\n $resNumberOfEdgesToKeep += $ufB->union($edge[1], $edge[2]);\n }\n }\n return $ufA->isConnected() && $ufB->isConnected() ? count($edges) - $resNumberOfEdgesToKeep : -1;\n }\n}\n\nclass UnionFind\n{\n private $parent = [];\n private $rank = [];\n private $count = 0;\n\n function __construct(int $n) {\n $this->count = $n;\n for ($i = 0; $i <= $n; $i++) {\n $this->parent[$i] = $i;\n $this->rank[$i] = 1;\n }\n }\n\n function find(int $node): int {\n while ($node != $this->parent[$node]) {\n $this->parent[$node] = $this->parent[$this->parent[$node]];\n $node = $this->parent[$node];\n }\n return $node;\n }\n\n function union(int $u, int $v): int {\n $rootU = $this->find($u);\n $rootV = $this->find($v);\n if ($rootU == $rootV) return 0;\n if ($this->rank[$rootU] > $this->rank[$rootV]) {\n $this->parent[$rootV] = $rootU;\n $this->rank[$rootU] += $this->rank[$rootV];\n } else {\n $this->parent[$rootU] = $rootV;\n $this->rank[$rootV] += $this->rank[$rootU];\n }\n $this->count--;\n return 1;\n }\n\n function isConnected(): bool {\n return $this->count == 1;\n }\n}\n```\n\n\n##### Thanks for reading! If you have any questions or suggestions, please leave a comment below. I would love to hear your thoughts! \uD83D\uDE0A\n### **Please upvote if you found this post helpful! \uD83D\uDC4D** | 2 | 0 | ['Union Find', 'Graph', 'PHP', 'JavaScript'] | 0 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | C# Solution | Union Find | O(nlogn) | c-solution-union-find-onlogn-by-anshulga-tnz5 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | anshulgarg904 | NORMAL | 2023-04-30T14:25:24.692010+00:00 | 2023-04-30T14:25:24.692057+00:00 | 201 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\npublic class Solution {\n public int MaxNumEdgesToRemove(int n, int[][] edges) {\n DSU dsu1 = new DSU(n);\n DSU dsu2 = new DSU(n);\n int count = 0;\n Array.Sort(edges, (a, b) => b[0] - a[0]);\n\n foreach(var edge in edges){\n if(edge[0] == 3){\n if(dsu1.find(edge[1]) == dsu1.find(edge[2]) && dsu2.find(edge[1]) == dsu2.find(edge[2])){\n count++;\n continue;\n }\n \n dsu1.union(edge[1], edge[2]);\n dsu2.union(edge[1], edge[2]);\n }\n else if(edge[0] == 1){\n if(dsu1.find(edge[1]) == dsu1.find(edge[2])){\n count++;\n }\n\n dsu1.union(edge[1], edge[2]);\n }\n else{\n if(dsu2.find(edge[1]) == dsu2.find(edge[2])){\n count++;\n }\n\n dsu2.union(edge[1], edge[2]);\n }\n }\n\n for(int i=1; i<=n; i++){\n dsu1.find(i);\n dsu2.find(i);\n }\n\n for(int i=2; i<=n; i++){\n if(dsu1.parent[i] != dsu1.parent[1] || dsu2.parent[i] != dsu2.parent[1]){\n return -1;\n }\n }\n\n return count;\n }\n\n class DSU {\n public int[] parent;\n\n public DSU(int n) {\n parent = new int[n+1];\n\n for (int i = 0; i <= n; i++) parent[i] = i;\n }\n\n public int find(int x) {\n if (parent[x] != x) parent[x] = find(parent[x]);\n return parent[x];\n }\n\n public void union(int x, int y) {\n parent[find(x)] = parent[find(y)];\n }\n }\n}\n``` | 2 | 0 | ['Union Find', 'Graph', 'C#'] | 1 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Swift UnionFind | swift-unionfind-by-tatianavol-vh8b | \n# Code\n\nclass Solution {\n \n enum UnType: Int {\n case alice = 1\n case bob = 2\n case both = 3\n }\n\n func maxNumEdgesTo | TatianaVol | NORMAL | 2023-04-30T14:07:20.798508+00:00 | 2023-04-30T19:16:36.269223+00:00 | 92 | false | \n# Code\n```\nclass Solution {\n \n enum UnType: Int {\n case alice = 1\n case bob = 2\n case both = 3\n }\n\n func maxNumEdgesToRemove(_ n: Int, _ edges: [[Int]]) -> Int {\n \n var edges = edges.map { (type: UnType(rawValue: $0[0])!, from: $0[1], to: $0[2]) }.sorted { $0.type.rawValue > $1.type.rawValue }\n var unionA = Union(n)\n var unionB = Union(n)\n \n var extra = 0\n for edge in edges {\n \n switch edge.type {\n case .both:\n let aConnected = unionA.wasConnected(edge.from, edge.to)\n let bConnected = unionB.wasConnected(edge.from, edge.to)\n if aConnected && bConnected { extra += 1 }\n case .alice:\n if unionA.wasConnected(edge.from, edge.to) { extra += 1 }\n case .bob:\n if unionB.wasConnected(edge.from, edge.to) { extra += 1 }\n }\n }\n \n return unionB.connected() && unionA.connected() ? extra : -1\n }\n}\n\nclass Union {\n \n private var union: [Int]\n private var ranks: [Int]\n \n init(_ n: Int) {\n union = Array(repeating: 0, count: n + 1).enumerated().map { $0.offset }\n ranks = Array(repeating: 1, count: n + 1)\n }\n \n // return true if i and j was connected previously\n func wasConnected(_ i: Int, _ j: Int) -> Bool {\n if areConnected(i, j) { return true }\n union(i, j)\n return false\n }\n \n func root(of node: Int) -> Int {\n var node = node\n while node != union[node] {\n node = union[node]\n }\n return node\n }\n \n func areConnected(_ i: Int, _ j: Int) -> Bool {\n root(of: i) == root(of: j)\n }\n \n func union(_ i: Int, _ j: Int) {\n if i == j { return }\n let iRoot = root(of: i)\n let jRoot = root(of: j)\n if iRoot == jRoot { return }\n \n if ranks[iRoot] < ranks[jRoot] {\n union[iRoot] = jRoot\n ranks[jRoot] += ranks[iRoot]\n } else {\n union[jRoot] = iRoot\n ranks[iRoot] += ranks[jRoot]\n }\n }\n \n func connected() -> Bool {\n Set(union.suffix(from: 1).map { root(of: $0) }).count == 1\n }\n}\n``` | 2 | 0 | ['Swift'] | 0 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | [Golang] UnionFind | golang-unionfind-by-vasakris-da4g | Complexity\n- Time complexity:\nO(N+E)\n\n- Space complexity:\nO(N)\n\n# Code\n\nfunc maxNumEdgesToRemove(n int, edges [][]int) int {\n // O(N)\n AliceUF | vasakris | NORMAL | 2023-04-30T10:53:22.132299+00:00 | 2023-04-30T10:53:22.132336+00:00 | 56 | false | # Complexity\n- Time complexity:\nO(N+E)\n\n- Space complexity:\nO(N)\n\n# Code\n```\nfunc maxNumEdgesToRemove(n int, edges [][]int) int {\n // O(N)\n AliceUF := NewUnionFind(n)\n BobUF := NewUnionFind(n)\n\n // O(E)\n edgesRequired := 0\n for _, edge := range edges {\n if edge[0] == 3 {\n // Check for both and increment edgesRequired if one of them required\n res1 := AliceUF.PerformUnion(edge)\n res2 := BobUF.PerformUnion(edge)\n if res1 || res2 {\n edgesRequired++\n }\n }\n }\n\n // O(E)\n for _, edge := range edges {\n if edge[0] == 1 && AliceUF.PerformUnion(edge) {\n edgesRequired++\n } else if edge[0] == 2 && BobUF.PerformUnion(edge) {\n edgesRequired++\n }\n }\n\n if AliceUF.isConnected() && BobUF.isConnected() {\n return len(edges) - edgesRequired\n }\n\n return -1\n}\n\ntype UnionFind struct {\n Parents []int\n Ranks []int\n Groups int\n}\n\nfunc NewUnionFind(n int) *UnionFind {\n parents := make([]int, n+1)\n for i := 1; i <= n; i++ {\n parents[i] = i\n }\n\n return &UnionFind{\n Parents : parents,\n Ranks : make([]int, n+1),\n Groups : n,\n }\n}\n\nfunc (uf *UnionFind) PerformUnion(edge []int) bool {\n p1 := uf.findParent(edge[1])\n p2 := uf.findParent(edge[2])\n\n if p1 == p2 {\n return false\n } \n\n if uf.Ranks[p1] > uf.Ranks[p2] {\n uf.Parents[p2] = p1\n } else if uf.Ranks[p2] > uf.Ranks[p1] {\n uf.Parents[p1] = p2\n } else {\n uf.Parents[p2] = p1\n uf.Ranks[p1]++\n }\n\n uf.Groups--\n return true\n}\n\nfunc (uf *UnionFind) findParent(idx int) int {\n if idx != uf.Parents[idx] {\n uf.Parents[idx] = uf.findParent(uf.Parents[idx])\n }\n return uf.Parents[idx]\n}\n\nfunc (uf *UnionFind) isConnected() bool {\n return uf.Groups == 1\n}\n``` | 2 | 0 | ['Go'] | 0 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Union Find | C++ | union-find-c-by-tusharbhart-ghis | \nclass Solution {\n int find_prnt(int node, vector<int> &prnt) {\n if(node == prnt[node]) return node;\n return prnt[node] = find_prnt(prnt[no | TusharBhart | NORMAL | 2023-04-30T10:15:54.785510+00:00 | 2023-04-30T10:15:54.785542+00:00 | 137 | false | ```\nclass Solution {\n int find_prnt(int node, vector<int> &prnt) {\n if(node == prnt[node]) return node;\n return prnt[node] = find_prnt(prnt[node], prnt);\n }\n void unionn(int u, int v, vector<int> &prnt, vector<int> &rank) {\n int ulp_u = find_prnt(u, prnt), ulp_v = find_prnt(v, prnt);\n\n if(rank[ulp_u] > rank[ulp_v]) prnt[ulp_v] = ulp_u; \n else if(rank[ulp_u] < rank[ulp_v]) prnt[ulp_u] = ulp_v;\n else {\n prnt[ulp_v] = ulp_u;\n rank[ulp_u]++;\n }\n }\n int solve(vector<pair<int, int>> &edges, vector<int> &prnt, vector<int> &rank) {\n int ans = 0;\n for(auto e : edges) {\n if(find_prnt(e.first, prnt) != find_prnt(e.second, prnt)) {\n unionn(e.first, e.second, prnt, rank);\n }\n else ans++;\n }\n int p = find_prnt(1, prnt);\n for(int i=1; i<prnt.size(); i++) {\n if(find_prnt(i, prnt) != p) return -1;\n }\n return ans;\n }\npublic:\n int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {\n vector<int> prnt1(n + 1), rank1(n + 1);\n vector<int> prnt2(n + 1), rank2(n + 1);\n for(int i=1; i<=n; i++) prnt1[i] = i, prnt2[i] = i;\n\n vector<pair<int, int>> alice, bob;\n int cntAlice = 0, cntBob = 0, ans = 0;\n\n for(auto e : edges) {\n if(e[0] == 3) {\n if(find_prnt(e[1], prnt1) != find_prnt(e[2], prnt1)) {\n unionn(e[1], e[2], prnt1, rank1);\n }\n else ans++;\n\n if(find_prnt(e[1], prnt2) != find_prnt(e[2], prnt2)) {\n unionn(e[1], e[2], prnt2, rank2);\n }\n }\n else if(e[0] == 2) bob.push_back({e[1], e[2]});\n else alice.push_back({e[1], e[2]});\n }\n\n int a = solve(alice, prnt1, rank1), b = solve(bob, prnt2, rank2);\n if(a == -1 || b == -1) return -1;\n return a + b + ans;\n }\n};\n``` | 2 | 0 | ['Union Find', 'C++'] | 0 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | 🌟C++ || DSU || Explained with detailed approach | c-dsu-explained-with-detailed-approach-b-5hxd | Intuition\nQuite a simple logic to solve this particular problem\n1. Intially sort the edges in descending order of their typessuch that the type 3 edges get th | yashamb444 | NORMAL | 2023-04-30T10:15:25.088180+00:00 | 2023-04-30T10:15:25.088224+00:00 | 328 | false | # Intuition\n***Quite a simple logic to solve this particular problem***\n1. Intially sort the edges in descending order of their typessuch that the type 3 edges get the highest priority\n2. Then simple create 2 objects one for Alice and one for Bob\n3. These DSU objects can be used to check whether both alice and bob can traverse the entire graph.\n4. Now start iterating the edges :- \n 4.1 if the edge is type 3 : add that edge for Alice and Bob;\n 4.2 if the edge is type 2 : add the edge to the Bob object;\n 4.3 if the edge is type 1 : add the edge to the Alice object;\n5. At the end check whether both Alice and Bob can traverse the Entire Graph\n\n# Code\n```\nclass dsu{\nprivate:\n vector<int>parent;\n int distinct_components;\npublic:\n \n dsu(int n){\n distinct_components = n;\n\n for(int i=0;i<=n;i++){\n parent.push_back(i);\n }\n }\n int find_parent(int u){\n if(parent[u] != u){\n parent[u] = find_parent(parent[u]);\n }\n return parent[u];\n }\n bool Union(int u, int v){\n if(find_parent(u) == find_parent(v)){\n return false;\n }\n\n parent[find_parent(u)] = v;\n distinct_components--;\n return true;\n }\n bool united(){\n return distinct_components == 1;\n }\n};\n\nclass Solution {\npublic:\n int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {\n\n sort(edges.begin(),edges.end(), [](auto& it, auto &it2){\n return it[0] > it2[0];\n });\n\n dsu *bob = new dsu(n);\n dsu *alice = new dsu(n);\n int edges_added = 0;\n\n for(auto &it : edges){\n int type = it[0];\n int u = it[1];\n int v = it[2];\n\n switch(type){\n case 3 : {\n edges_added += (bob->Union(u,v) | alice->Union(u,v));\n break;\n }\n case 2:{\n edges_added += bob->Union(u,v);\n break;\n }\n case 1 : {\n edges_added += alice->Union(u,v);\n break;\n }\n }\n }\n\n return (bob->united() && alice->united()) ? edges.size() - edges_added : -1;\n }\n};\n\n\n\n\n\n\n\n\n``` | 2 | 0 | ['C++'] | 1 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Easiest Code 🔥✅ Using Disjoint Set Data Structure | easiest-code-using-disjoint-set-data-str-15y7 | \tclass Solution {\n\tpublic:\n\n\tclass Disjoint\n\t{\n\tpublic:\n\t\tvector parent;\n\t\tvector size;\n\n\t\tDisjoint(int n)\n\t\t{\n\t\t\tparent.resize(n+1); | ritiktrippathi | NORMAL | 2023-04-30T07:40:47.508568+00:00 | 2023-04-30T07:40:47.508604+00:00 | 46 | false | \tclass Solution {\n\tpublic:\n\n\tclass Disjoint\n\t{\n\tpublic:\n\t\tvector<int> parent;\n\t\tvector<int> size;\n\n\t\tDisjoint(int n)\n\t\t{\n\t\t\tparent.resize(n+1);\n\t\t\tsize.resize(n+1, 1);\n\t\t\tfor(int i = 0; i <= n; i++)\n\t\t\t{\n\t\t\t\tparent[i] = i;\n\t\t\t}\n\t\t}\n\n\t\tint findParent(int u)\n\t\t{\n\t\t\tif(u == parent[u])\n\t\t\t\treturn u;\n\n\t\t\treturn parent[u] = findParent(parent[u]);\n\t\t}\n\n\n\t\tbool unionBySize(int u, int v)\n\t\t{\n\t\t\tint ultp_u = findParent(u);\n\t\t\tint ultp_v = findParent(v);\n\n\t\t\tif(ultp_u == ultp_v)\n\t\t\t\treturn false;\n\n\t\t\telse if (size[ultp_u] < size[ultp_v])\n\t\t\t{\n\t\t\t\tparent[ultp_u] = ultp_v;\n\t\t\t\tsize[ultp_v] += size[ultp_u];\n\t\t\t}\n\t\t\telse\n\t\t\t{\n\t\t\t\tparent[ultp_v] = ultp_u;\n\t\t\t\tsize[ultp_u] += size[ultp_v];\n\t\t\t}\n\t\t\treturn true;\n\t\t}\n\n\t};\n\n\t\tbool static cmp(vector<int> &v1, vector<int> &v2)\n\t\t{\n\t\t\treturn v1[0] > v2[0];\n\t\t}\n\n\n\t\tint maxNumEdgesToRemove(int n, vector<vector<int>>& e) \n\t\t{\n\t\t\tDisjoint bob(n);\n\t\t\tDisjoint alice(n);\n\n\n\t\t\tsort(e.begin(), e.end(), cmp);\n\t\t\tint count = 0;\n\t\t\tint bs = 0;\n\t\t\tint as = 0;\n\t\t\tfor(int i = 0; i < e.size(); i++)\n\t\t\t{\n\t\t\t\tint u = e[i][1];\n\t\t\t\tint v = e[i][2];\n\t\t\t\tint t = e[i][0];\n\n\t\t\t\tif(t == 3)\n\t\t\t\t{\n\t\t\t\t\tbool b1 = bob.unionBySize(u, v);\n\t\t\t\t\tbool b2 = alice.unionBySize(u, v);\n\t\t\t\t\tif(b1 == false && b1 == false)\n\t\t\t\t\t{\n\t\t\t\t\t\tcount++;\n\t\t\t\t\t}\n\t\t\t\t\tif(b1 == true)\n\t\t\t\t\t\tbs++;\n\t\t\t\t\tif(b2 == true)\n\t\t\t\t\t\tas++;\n\t\t\t\t}\n\t\t\t\telse if(t == 2)\n\t\t\t\t{\n\t\t\t\t\tbool b1 = bob.unionBySize(u, v);\n\t\t\t\t\tif(b1 == false)\n\t\t\t\t\t{\n\t\t\t\t\t\tcount++;\n\t\t\t\t\t}\n\t\t\t\t\tif(b1 == true)\n\t\t\t\t\t\tbs++;\n\t\t\t\t}\n\t\t\t\telse\n\t\t\t\t{\n\t\t\t\t\tbool b1 = alice.unionBySize(u, v);\n\t\t\t\t\tif(b1 == false)\n\t\t\t\t\t{\n\t\t\t\t\t\tcount++;\n\t\t\t\t\t}\n\t\t\t\t\tif(b1 == true)\n\t\t\t\t\t\tas++;\n\t\t\t\t}\n\t\t\t}\n\t\t\tif(bs != n-1 || as != n-1)\n\t\t\t\treturn -1;\n\n\t\t\treturn count;\n\t\t}\n\t}; | 2 | 0 | ['C++'] | 1 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Union Find | Python / JS Solution | union-find-python-js-solution-by-tfdleet-120a | Hello Tenno Leetcoders,\nFor this problem, Alice and Bob have an undirected graph with n nodes, where each node represents a point in the graph. The graph has t | TFDLeeter | NORMAL | 2023-04-30T05:36:31.741669+00:00 | 2023-04-30T05:37:15.318461+00:00 | 261 | false | Hello **Tenno Leetcoders**,\nFor this problem, Alice and Bob have an undirected graph with n nodes, where each node represents a point in the graph. The graph has three types of edges:\n\n1) Type 1: These edges can only be traversed by Alice.\n\n2) Type 2: These edges can only be traversed by Bob.\n\n3) Type 3: These edges can be traversed by both Alice and Bob.\n\nWe are asked to find the `maximum number of edges` that can be removed from the graph such that after removing the edges, Alice and Bob can still traverse the graph fully, meaning starting from any node, Alice and Bob can still reach all other nodes.\n\nYou are given an array edges, where `edges[i] = [typei, ui, vi]` represents a bidirectional edge of type `typei` between nodes `ui` and `vi`. \n\nif we have `edges[i] = [1, 2, 3]`, this represent that there is a `Type 1` edge between `nodes 2` and `3`, and Alice can traverse this edge.\n\nWe want to find `the maximum number of edges that can be removed` such that the graph can still be fully traversed by both Alice and Bob or return -1 if it is not possible to traverse the graph fully even after removing some edges\n\n### Explanation\n\nThe idea behind this problem is to keep track of which edges Alice and Bob can iterate separately and which edges both of them can iterate together. For this approach, we can use three different `Union Find`. For each of the three types of edges, we can create three different instances of Union Find\n\nWe will traverse through the edges and use these Union Find instances to keep track of the connected component for each type of edge separately.\n\nFor each `Type`, we will call `union() method`:\n\n- Type 1 will be called for Alice to merge componenet containing u and v\n\n- Type 2 will be called for Bob to merge corresponding components\n\n- Type 3 will be called for Alice and Bob to merge the componenets for both, since the edges can be traveled by both\n\nWith all the edges already processed, we need to check if Alice and Bob can traverse the entire graph by checking the number of connected components in both `Union Find` instance will be equal to one.\n\nIf both can travel the entire graph, we can start removing edges to see how many can be removed while still being able to traverse the graph\n\nThen we traverse through the edges counting type 3 edges that were merged by both Alice and Bob, and as well for type 1 and type 2 edges that was merged by either Alice or Bob\n\nWe can then check if both can traverse the graph by checking if they have more than one connected component\n\nIf either Alice or Bob has more than one connected component, then it means that there are some vertices that are not reachable by either Alice or Bob as the problem\'s requirement should be able to remove edges such that all vertices are reachable by both of them. \n\nTherefore, if there is more than one connected component for either Alice or Bob, we return -1 to indicate that it is not possible to remove edges to satisfy the requirement.\n\nThe `maximum number of edges that can be removed` while still being able to fully traversed by both will be the sum of the counts of `type1, type2 and type3 edges` denoted as `alice_remove, bob_remove, both_remove` or `return -1` as they were not able to traverse the whole graph\n\n\n### Code\n\n**Python**\n\n```\nclass UnionFind:\n def __init__(self, n):\n self.parent = [i for i in range(n + 1)]\n self.size = [1] * (n + 1)\n self.components = n\n\n def find(self, x):\n # If the parent of x is not x, recursively find the parent of x\n if self.parent[x] != x: self.parent[x] = self.find(self.parent[x])\n # Return the parent of x\n return self.parent[x]\n\n def union(self, x, y):\n # Find the parents of x and y\n x_root = self.find(x)\n y_root = self.find(y)\n # If the parents are the same, x and y are already in the same component\n if x_root == y_root: return False\n # Merge the smaller component into the larger component\n if self.size[x_root] < self.size[y_root]: x_root, y_root = y_root, x_root\n self.size[x_root] += self.size[y_root]\n self.parent[y_root] = x_root\n self.components -= 1\n return True\n\nclass Solution:\n def maxNumEdgesToRemove(self, n: int, edges: List[List[int]]) -> int:\n alice = UnionFind(n)\n bob = UnionFind(n)\n both = UnionFind(n)\n alice_remove = bob_remove = both_remove = 0\n\n # Process type 3 edges\n for t, u, v in edges:\n if t == 3:\n if both.union(u, v):\n alice.union(u, v)\n bob.union(u, v)\n else:\n both_remove += 1\n \n # Process type 1 edges\n for t, u, v in edges:\n if t == 1:\n if not alice.union(u, v):\n alice_remove += 1\n \n # Process type 2 edges\n for t, u, v in edges:\n if t == 2:\n if not bob.union(u, v):\n bob_remove += 1\n \n # Check if both Alice and Bob can traverse the graph\n if alice.components > 1 or bob.components > 1:\n return -1\n \n return alice_remove + bob_remove + both_remove\n```\n\n\n\n**JavaScript**\n\n```\n/**\n * @param {number} n\n * @param {number[][]} edges\n * @return {number}\n */\n\nclass UnionFind{\n \n constructor(n){\n this.parent = Array.from({length: n+1}, (_,i) => i)\n this.size = Array(n+1).fill(1);\n this.components = n\n }\n \n find(x) {\n return this.parent[x] !== x ? this.parent[x] = this.find(this.parent[x]) : this.parent[x];\n }\n \n union(x,y){\n const rootX = this.find(x)\n const rootY = this.find(y)\n \n if(rootX === rootY) return false\n const [smaller, bigger] = this.size[rootX] < this.size[rootY] ? [rootX, rootY] : [rootY, rootX];\n \n this.size[smaller] += this.size[bigger];\n this.parent[bigger] = smaller;\n this.components -= 1 \n return true\n }\n \n}\n\n\nvar maxNumEdgesToRemove = function(n, edges) {\n const alice = new UnionFind(n);\n const bob = new UnionFind(n);\n const both = new UnionFind(n);\n let aliceRemove = 0, bobRemove = 0, bothRemove = 0;\n\n // Process type 3 edges\n for(const [type, u, v] of edges){\n if(type === 3){\n both.union(u,v) ? (alice.union(u,v), bob.union(u,v) ): bothRemove +=1 \n }\n }\n\n // Process type 1 edges\n for(const[type, u,v] of edges){ \n if(type === 1)\n !alice.union(u, v) && aliceRemove++\n }\n\n // Process type 2 edges\n for(const[type, u,v] of edges){ \n if(type === 2){\n !bob.union(u, v) && bobRemove++ \n }\n }\n \n // Check if both Alice and Bob can traverse the graph\n if(alice.components > 1 || bob.components > 1) return -1\n \n return aliceRemove + bobRemove + bothRemove\n};\n```\n\n#### Time Complexity: O(m*\u03B1(n))\n\nUnion-Find algorithm with union-by-rank and path compression is `O(m\u03B1(n))` where n is the number of elements and m is the number of operations. `\u03B1(n)` is the inverse Ackermann function, which grows very slowly and is effectively constant for practical values of n.\n\n#### Space Complexity: O(n)\n\nwhere n is the number of vertices in the graph, because we need to store the parent and size arrays for each Union-Find data structure.\n\n \n***Warframe\'s Darvo wants you to upvote this post \uD83D\uDE4F\uD83C\uDFFB \u2764\uFE0F\u200D\uD83D\uDD25***\n\n | 2 | 0 | ['Union Find', 'Python', 'JavaScript'] | 0 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Best C++ Code... | best-c-code-by-prasad_bhoite-jdbb | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Prasad_Bhoite | NORMAL | 2023-04-30T04:20:38.782361+00:00 | 2023-04-30T04:20:38.782454+00:00 | 140 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n- The time complexity of this approach is O(E), where E is the number of edges, as we are using path compression and union by rank so the find and union function become O(1) on average.\n\n- Space complexity:\nThe space complexity is also O(N), where N is the number of nodes\n\n# Code\n```\nclass Solution {\npublic:\n int find(int i,vector<int> &par){\n if(par[i] == -1){\n return i;\n }\n return par[i] = find(par[i],par);\n //path compression.\n }\n bool union_set(int x,int y,vector<int> &par,vector<int> &rnk){\n int s1 = find(x,par);\n int s2 = find(y,par);\n \n if(s1 != s2){\n //union by rank.\n if(rnk[s1] > rnk[s2]){\n par[s2] = s1;\n rnk[s1] += rnk[s2];\n }\n else{\n par[s1] = s2;\n rnk[s2] += rnk[s1];\n }\n return true;\n }\n return false;\n }\n int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {\n \n sort(edges.begin(),edges.end(),[](vector<int> &a,vector<int> &b){\n return a[0] > b[0]; \n });\n // To process the edges of type 3 first we sort the edges vector.\n \n int rem = 0;\n \n vector<int> parAlice(n,-1);\n vector<int> parBob(n,-1);\n vector<int> rnkAlice(n,1);\n vector<int> rnkBob(n,1);\n \n for(int i=0;i<edges.size();i++){\n if(edges[i][0] == 3){\n bool fg1 = union_set(edges[i][1]-1,edges[i][2]-1,parAlice,rnkAlice);\n bool fg2 = union_set(edges[i][1]-1,edges[i][2]-1,parBob,rnkBob);\n if(fg1==false && fg2==false){\n //alice and bob are both connected to node x and node y so remove this edge.\n rem += 1;\n }\n }\n else if(edges[i][0] == 2){\n bool fg2 = union_set(edges[i][1]-1,edges[i][2]-1,parBob,rnkBob);\n if(fg2 == false){\n //bob is connected to node x and node y so remove this edge.\n rem += 1;\n }\n }\n else{\n bool fg1 = union_set(edges[i][1]-1,edges[i][2]-1,parAlice,rnkAlice);\n if(fg1 == false){\n //alice is connected to node x and node y so remove this edge.\n rem += 1;\n }\n }\n }\n \n int co1=0,co2=0;\n for(int i=0;i<n;i++){\n if(parAlice[i]==-1){co1++;}\n if(parBob[i]==-1){co2++;}\n //if the nodes can be connected then there will be only one parent in the parent array.\n }\n if(co1==1 && co2==1){return rem;}\n return -1;\n }\n};\n\n``` | 2 | 0 | ['C++'] | 0 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Swift | Union Find | Smallest & Fastest solution | swift-union-find-smallest-fastest-soluti-wrug | Union Find (accepted answer)\n\nclass Solution {\n func maxNumEdgesToRemove(_ n: Int, _ edges: [[Int]]) -> Int {\n var groups = [Array(0...n), Array(0 | UpvoteThisPls | NORMAL | 2023-04-30T01:39:40.617328+00:00 | 2023-04-30T01:57:46.025718+00:00 | 175 | false | **Union Find (accepted answer)**\n```\nclass Solution {\n func maxNumEdgesToRemove(_ n: Int, _ edges: [[Int]]) -> Int {\n var groups = [Array(0...n), Array(0...n)] // [0] = alice, [1] = bob\n var connectedCounts = [0,0], edgesNeeded = 0\n\n func find(_ x: Int, _ group: inout [Int]) -> Int {\n if x != group[x] { group[x] = find(group[x], &group) }\n return group[x]\n }\n\n func tryUnion(_ i:Int, _ j:Int, _ g:Int) -> Bool {\n let (x,y) = (find(i, &groups[g]), find(j, &groups[g]))\n groups[g][x] = y\n connectedCounts[g] += x != y ? 1 : 0\n return x != y\n }\n\n let ALICE = 1, BOB = 2, ALICE_OR_BOB = 3\n\n for e in edges where e[0] == ALICE_OR_BOB && tryUnion(e[1], e[2], 0) && tryUnion(e[1], e[2], 1) {\n edgesNeeded += 1 // Connect edges that both can use\n }\n\n for e in edges where (e[0] == ALICE && tryUnion(e[1], e[2], 0)) || (e[0] == BOB && tryUnion(e[1], e[2], 1)) {\n edgesNeeded += 1 // Connect edges that are not already joined for both\n }\n \n return connectedCounts.allSatisfy { $0 == n-1 } ? edges.count - edgesNeeded : -1\n }\n}\n``` | 2 | 0 | ['Swift'] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.