question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
remove-max-number-of-edges-to-keep-graph-fully-traversable | Python3 Solution | python3-solution-by-motaharozzaman1996-6fiy | \n\n\nclass Solution:\n\n def dfs(self,vis,li,com,i):\n if(vis[i]):\n return 0\n vis[i]=com\n ans=1\n for j in li[i]:\ | Motaharozzaman1996 | NORMAL | 2023-04-30T00:13:41.464471+00:00 | 2023-04-30T00:13:41.464505+00:00 | 1,157 | false | \n\n```\nclass Solution:\n\n def dfs(self,vis,li,com,i):\n if(vis[i]):\n return 0\n vis[i]=com\n ans=1\n for j in li[i]:\n ans+=self.dfs(vis,li,com,j)\n return ans\n\n def maxNumEdgesToRemove(self, n: int, e: List[List[int]]) -> int:\n ans=0\n li=[[] for i in range(n)]\n for l in e:\n if(l[0]==3):\n li[l[1]-1].append(l[2]-1)\n li[l[2]-1].append(l[1]-1)\n vis=[0 for i in range(n)]\n com=0\n for i in range(n):\n if(vis[i]):\n continue\n else:\n com+=1\n temp=self.dfs(vis,li,com,i)\n ans+=(temp-1)\n lia=[[] for i in range(com)]\n lib=[[] for i in range(com)]\n for l in e:\n if(l[0]==1):\n a=vis[l[1]-1]-1\n b=vis[l[2]-1]-1\n if(a==b):\n continue\n lia[a].append(b)\n lia[b].append(a)\n elif(l[0]==2):\n a=vis[l[1]-1]-1\n b=vis[l[2]-1]-1\n if(a==b):\n continue\n lib[a].append(b)\n lib[b].append(a)\n visa=[0 for i in range(com)]\n coma=0\n comb=0\n for i in range(com):\n if(visa[i]):\n continue\n else:\n coma+=1\n if(coma>1):\n return -1\n self.dfs(visa,lia,coma,i)\n \n visb=[0 for i in range(com)]\n for i in range(com):\n if(visb[i]):\n continue\n else:\n comb+=1\n if(comb>1):\n return -1\n self.dfs(visb,lib,comb,i)\n if(coma>1 or comb>1):\n return -1\n ans+=(com-1)*2\n return len(e)-ans\n\n\n``` | 2 | 0 | ['Python', 'Python3'] | 1 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | [C++] Simple C++ Code | c-simple-c-code-by-prosenjitkundu760-yxyi | \n# If you like the implementation then Please help me by increasing my reputation. By clicking the up arrow on the left of my image.\n\nclass Solution {\n v | _pros_ | NORMAL | 2022-08-21T16:10:21.463947+00:00 | 2022-08-21T16:10:21.463983+00:00 | 671 | false | \n# **If you like the implementation then Please help me by increasing my reputation. By clicking the up arrow on the left of my image.**\n```\nclass Solution {\n vector<int> alice, bob;\n static bool comp(vector<int> &a, vector<int> &b)\n {\n return a[0] > b[0];\n }\n int find_alice(int v)\n {\n if(v == alice[v])\n return v;\n return alice[v] = find_alice(alice[v]);\n }\n int find_bob(int v)\n {\n if(v == bob[v])\n return v;\n return bob[v] = find_bob(bob[v]);\n }\n void union_alice(int a, int b)\n {\n a = find_alice(a);\n b = find_alice(b);\n if(a == b)\n return;\n alice[b] = a;\n return;\n }\n void union_bob(int a, int b)\n {\n a = find_bob(a);\n b = find_bob(b);\n if(a == b)\n return;\n bob[b] = a;\n return;\n }\npublic:\n int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {\n sort(edges.begin(), edges.end(), comp);\n for(int i = 0; i <= n; i++)\n {\n alice.push_back(i);\n bob.push_back(i);\n }\n int ans = 0;\n for(vector<int> &v : edges)\n {\n if(v[0] == 3)\n {\n int xa = find_alice(v[1]);\n int ya = find_alice(v[2]);\n int xb = find_bob(v[1]);\n int yb = find_bob(v[2]);\n if(xa == ya && xb == yb)\n {\n ans++;\n }\n else\n {\n if(xa != ya)\n union_alice(xa, ya);\n if(xb != yb)\n union_bob(xb, yb);\n }\n }\n else if(v[0] == 2)\n {\n int xb = find_bob(v[1]);\n int yb = find_bob(v[2]);\n if(xb == yb)\n ans++;\n else\n {\n union_bob(xb, yb);\n }\n }\n else\n {\n int xa = find_alice(v[1]);\n int ya = find_alice(v[2]);\n if(xa == ya)\n ans++;\n else\n union_alice(xa, ya);\n }\n }\n int vala, valb;\n for(int i = 1; i <= n; i++)\n {\n if(i == 1)\n {\n vala = find_alice(i);\n valb = find_bob(i);\n }\n else\n {\n if(vala != find_alice(i))\n {\n return -1;\n }\n if(valb != find_bob(i))\n {\n return -1;\n }\n }\n }\n return ans;\n }\n};\n``` | 2 | 0 | ['Union Find', 'Graph', 'C', 'C++'] | 2 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Python Union Find Solution | python-union-find-solution-by-achal_jain-rxoe | As mentioned in many other solutions, the main idea is that we want to construct the graph from given edges rather than removing edges. \nYou need to argue and | Achal_Jain | NORMAL | 2022-08-16T15:26:05.264239+00:00 | 2022-08-16T15:26:05.264287+00:00 | 334 | false | As mentioned in many other solutions, the main idea is that we want to construct the graph from given edges rather than removing edges. \nYou need to argue and make yourself belive that it is always optimal to take blue colored edges and connect a red/green edge only if they aren\'t already connected ( part of same connected set), this is where the concept of DSU( Disjoing Set Union) comes in .\nBelow is the code.\n\n```\nclass UnionFind:\n def __init__(self, n):\n self.parent = [i for i in range(n + 1)]\n self.size = [1 for _ in range(n + 1)]\n self.count = n\n \n def find(self, x):\n if self.parent[x] == x:\n return x\n self.parent[x] = self.find(self.parent[x])\n return self.parent[x]\n\n def merge(self, a, b):\n pa = self.find(a)\n pb = self.find(b)\n if pa == pb:\n return False\n if self.size[pa]> self.size[pb]:\n self.size[pa] += self.size[pb]\n self.parent[pb] = pa\n else:\n self.size[pb] += self.size[pa]\n self.parent[pa] = pb\n\n return True\n \nclass Solution:\n def maxNumEdgesToRemove(self, n: int, edges: List[List[int]]) -> int:\n ufa = UnionFind(n)\n ufb = UnionFind(n)\n cnta = 0\n common = 0\n \n for edge in edges:\n if edge[0] == 3:\n if ufa.find(edge[1]) != ufa.find(edge[2]):\n ufa.merge(edge[1], edge[2])\n common += 1\n cnta += 1\n \n for edge in edges:\n if edge[0] == 1:\n if ufa.find(edge[1])!=ufa.find(edge[2]):\n ufa.merge(edge[1], edge[2])\n cnta += 1\n \n \n if cnta != n-1:\n return -1\n \n cntb = 0\n for edge in edges:\n if edge[0] == 3:\n if ufb.find(edge[1])!=ufb.find(edge[2]):\n ufb.merge(edge[1], edge[2])\n \n for edge in edges:\n if edge[0] == 2:\n if ufb.find(edge[1])!=ufb.find(edge[2]):\n ufb.merge(edge[1], edge[2])\n cntb += 1\n \n \n if cntb + common != n-1:\n return -1\n \n \n total = len(edges)\n print(total)\n return total - (cnta + cntb) \n``` | 2 | 0 | ['Union Find', 'Graph', 'Python3'] | 1 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | [Java] Union Find | java-union-find-by-anothercoderr-w9t1 | Sort the edges in non increasing order as we want to keep the edge with type 3 in the graph and try to remove the edges with type 1 and 2. This is due to we wan | anothercoderr | NORMAL | 2022-07-12T08:56:18.517088+00:00 | 2022-07-12T08:56:18.517117+00:00 | 426 | false | Sort the edges in non increasing order as we want to keep the edge with type 3 in the graph and try to remove the edges with type 1 and 2. This is due to we want to remove maximum number of edges.\n\nThen a simple Union Find separately for Alice and Bob for checking the connectivity of the graph.\n```\nclass Solution {\n public int maxNumEdgesToRemove(int n, int[][] edges) \n {\n Arrays.sort(edges , (a,b) -> b[0] - a[0]);\n \n int[] aparent = new int[n+1];\n int[] bparent = new int[n+1];\n \n int[] arank = new int[n+1];\n int[] brank = new int[n+1];\n \n for(int i=0;i<n+1;i++){\n aparent[i] = i;\n bparent[i] = i;\n arank[i] = 1;\n brank[i] = 1;\n }\n \n int amerged = 1;\n int bmerged = 1;\n int remove = 0;\n \n for(int[] edge : edges){\n if(edge[0] == 3){\n boolean aunion = union(edge[1] , edge[2] , aparent , arank);\n boolean bunion = union(edge[1] , edge[2] , bparent , brank);\n \n if(aunion == true)\n amerged++;\n if(bunion == true)\n bmerged++;\n if(aunion == false && bunion == false)\n remove++;\n }\n else if(edge[0] == 1){\n boolean aunion = union(edge[1] , edge[2] , aparent , arank);\n if(aunion == true)\n amerged++;\n else\n remove++;\n }\n else{\n boolean bunion = union(edge[1] , edge[2] , bparent , brank);\n if(bunion == true)\n bmerged++;\n else\n remove++;\n }\n \n }\n if(amerged != n || bmerged != n)\n return -1;\n return remove;\n }\n \n public int find(int x , int[] parent){\n if(parent[x] == x)\n return x;\n int temp = find(parent[x] , parent);\n parent[x] = temp;\n return temp;\n }\n \n public boolean union(int x , int y , int[] parent , int[] rank){\n int lx = find(x , parent);\n int ly = find(y , parent);\n \n if(lx != ly){\n if(rank[lx] > rank[ly])\n parent[ly] = lx;\n else if(rank[ly] > rank[lx])\n parent[lx] = ly;\n else{\n parent[ly] = lx;\n rank[lx]++;\n }\n return true;\n }\n return false;\n }\n}\n``` | 2 | 0 | ['Union Find', 'Java'] | 1 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | [Java] Mega easy solution to understand | java-mega-easy-solution-to-understand-by-amyh | The algorithm: \n0. Initialize count as number of total edges n\n1. Since the type 3 is applicable for both Alice and Bob, consider only those edges. It is opti | akezhr | NORMAL | 2022-05-28T07:09:00.218052+00:00 | 2022-05-28T07:09:00.218095+00:00 | 429 | false | The algorithm: \n0. Initialize `count` as number of total edges `n`\n1. Since the type 3 is applicable for both Alice and Bob, consider only those edges. It is optimal.\n2. Create a copy for `parent` and `rank`\n3. Continue merging only Bob edges. If they are already connected, do not consider them, decrement count.\n4. Use the copy to instantiate the DisjointSet\'s `parent` and `rank`.\n5. Continue merging only Alice edges. If they are already connected, do not consider them, decrement count. \n6. Return `n-cnt` which is the `total number of edges` - `necessary number of edges`\n\nP.S. Hope it helped, your likes would be appreciated)\n\n```\nclass Solution {\n class DisjointSet {\n int[] parent;\n int[] rank;\n int n;\n \n public DisjointSet(int n) {\n this.n = n;\n parent = new int[n+1];\n rank = new int[n+1];\n for (int i = 1; i <= n; i++) {\n parent[i] = i;\n }\n }\n \n public int find(int node) {\n while (node != parent[node])\n node = parent[node];\n \n return node;\n }\n \n public boolean merge(int a, int b) {\n int parentA = find(a);\n int parentB = find(b);\n \n if (parentA == parentB) return false;\n \n if (rank[parentA] >= rank[parentB]) {\n parent[parentB] = parentA;\n rank[parentA]++;\n } else {\n parent[parentA] = parentB;\n rank[parentB]++;\n }\n \n return true;\n }\n \n public int countSeparateComponents() {\n int cnt = 0;\n \n for (int i = 1; i <= n; i++) \n if (parent[i] == i) \n cnt++;\n \n return cnt;\n }\n }\n \n public int maxNumEdgesToRemove(int n, int[][] edges) {\n DisjointSet ds = new DisjointSet(n);\n int cnt = n;\n \n for (int[] e : edges) {\n if (e[0] == 3) {\n boolean status = ds.merge(e[1], e[2]);\n if (!status) cnt--;\n }\n }\n \n int[] parentCopy = new int[n+1];\n int[] rankCopy = new int[n+1];\n for (int i = 1; i <= n; i++) {\n parentCopy[i] = ds.parent[i];\n rankCopy[i] = ds.rank[i];\n }\n \n // Let\'s run for Bob only\n for (int[] e : edges) {\n if (e[0] == 2) {\n boolean status = ds.merge(e[1], e[2]);\n if (!status) cnt--;\n }\n }\n \n if (ds.countSeparateComponents() > 1) {\n return -1;\n } \n \n ds.parent = parentCopy;\n ds.rank = rankCopy;\n \n // Let\'s run for Alice only\n for (int[] e : edges) {\n if (e[0] == 1) {\n boolean status = ds.merge(e[1], e[2]);\n if (!status) cnt--;\n }\n }\n \n if (ds.countSeparateComponents() > 1) {\n return -1;\n } \n \n return n-cnt;\n }\n}\n``` | 2 | 0 | ['Union Find', 'Java'] | 2 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Modified DSU || C++ || Path Compression || Easy solution | modified-dsu-c-path-compression-easy-sol-2fub | Here, in1,in2 stores the true/false value for type1 and type2 respectively.\n\n\t\t\tclass Solution {\n\t\t\tpublic:\n\t\t\t\tint ans=0;\n\t\t\t\t\tint flag1=0, | svedant142 | NORMAL | 2022-02-26T12:36:56.577987+00:00 | 2023-04-30T13:19:57.797275+00:00 | 98 | false | Here, in1,in2 stores the true/false value for type1 and type2 respectively.\n\n\t\t\tclass Solution {\n\t\t\tpublic:\n\t\t\t\tint ans=0;\n\t\t\t\t\tint flag1=0,flag2=0;\n\t\t\t\tint find(int a,vector<int>& par)\n\t\t\t\t{\n\t\t\t\t\tif(par[a]==a) return a;\n\t\t\t\t\treturn par[a]=find(par[a],par);\n\t\t\t\t}\n\t\t\t\tvoid unionf(int a,int b,vector<int>& par,vector<int>& rank,int x,int in1,int in2)\n\t\t\t\t{\n\t\t\t\t\tint u=find(a,par);\n\t\t\t\t\tint v=find(b,par);\n\t\t\t\t\tif(u==v&&x==3)\n\t\t\t\t\t{ if(in1==1)\n\t\t\t\t\t\tflag1++;\n\t\t\t\t\t if(in2==1) flag2++;\n\t\t\t\t\t}\n\t\t\t\t\tif(u==v&&x!=3)\n\t\t\t\t\t{\n\t\t\t\t\t\tans++;\n\t\t\t\t\t}\n\t\t\t\t\tif(rank[u]<rank[v])\n\t\t\t\t\t\tpar[u]=v;\n\t\t\t\t\telse if(rank[u]>rank[v])\n\t\t\t\t\t{\n\t\t\t\t\t\tpar[v]=u;\n\t\t\t\t\t}\n\t\t\t\t\telse\n\t\t\t\t\t{\n\t\t\t\t\t\tpar[v]=u;\n\t\t\t\t\t\trank[u]++;\n\t\t\t\t\t}\n\t\t\t\t}\n\t\t\t\tint maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {\n\t\t\t\t\tvector<int> par1(n+1);\n\t\t\t\t\tvector<int> rank1(n+1);\n\t\t\t\t\t vector<int> par2(n+1);\n\t\t\t\t\tvector<int> rank2(n+1);\n\n\t\t\t\t\tfor(int i=1;i<=n;i++)\n\t\t\t\t\t{\n\t\t\t\t\t\tpar1[i]=i;\n\t\t\t\t\t\tpar2[i]=i;\n\t\t\t\t\t\trank1[i]=0;\n\t\t\t\t\t\trank2[i]=0;\n\t\t\t\t\t}\n\t\t\t\t\tfor(int i=0;i<edges.size();i++)\n\t\t\t\t\t{\n\t\t\t\t\t\tif(edges[i][0]==3)\n\t\t\t\t\t\t{\n\t\t\t\t\t\t\tunionf(edges[i][1],edges[i][2],par1,rank1,3,1,0);\n\t\t\t\t\t\t\tunionf(edges[i][1],edges[i][2],par2,rank2,3,0,1);\n\t\t\t\t\t\t\tif(flag1==1&&flag2==1) {\n\t\t\t\t\t\t\t\tflag1=flag2=0;\n\t\t\t\t\t\t\t\tans++;\n\t\t\t\t\t\t\t}\n\n\t\t\t\t\t\t}\n\t\t\t\t\t}\n\t\t\t\t\tfor(int i=0;i<edges.size();i++)\n\t\t\t\t\t{\n\t\t\t\t\t\tif(edges[i][0]==1)\n\t\t\t\t\t\t{\n\t\t\t\t\t\t\tunionf(edges[i][1],edges[i][2],par1,rank1,1,1,0);\n\t\t\t\t\t\t}\n\t\t\t\t\t\telse if(edges[i][0]==2)\n\t\t\t\t\t\t{\n\t\t\t\t\t\t\tunionf(edges[i][1],edges[i][2],par2,rank2,2,0,1);\n\t\t\t\t\t\t}\n\t\t\t\t\t}\n\t\t\t\t\tint c1=0,c2=0;\n\t\t\t\t\tfor(int i=1;i<=n;i++)\n\t\t\t\t\t{\n\t\t\t\t\t\tif(par1[i]==i) c1++;\n\t\t\t\t\t\tif(par2[i]==i) c2++;\n\t\t\t\t\t}\n\t\t\t\t\tif(c1>1||c2>1) return -1;\n\t\t\t\t\treturn ans;\n\t\t\t\t}\n\t\t\t};\n | 2 | 0 | ['Union Find', 'C'] | 0 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | [java] two union find for Alice and Bob | java-two-union-find-for-alice-and-bob-by-e0h5 | \nclass Solution {\n public int maxNumEdgesToRemove(int n, int[][] edges) {\n UF a = new UF(n + 1);\n UF b = new UF(n + 1);\n int extra | catamoose50 | NORMAL | 2022-02-08T13:40:55.416498+00:00 | 2022-02-08T13:40:55.416542+00:00 | 293 | false | ```\nclass Solution {\n public int maxNumEdgesToRemove(int n, int[][] edges) {\n UF a = new UF(n + 1);\n UF b = new UF(n + 1);\n int extra = 0;\n for (int[] e: edges) {\n if (e[0] != 3) continue;\n boolean ext = false;\n if (!a.add(e)) ext = true;\n if (!b.add(e)) ext = true;\n if (ext) extra++;\n }\n for (int[] e: edges) {\n if (e[0] == 1 && !a.add(e)) extra++;\n if (e[0] == 2 && !b.add(e)) extra++;\n }\n return a.isConnected() && b.isConnected() ? extra : -1;\n }\n}\n\nclass UF {\n int[] nodes;\n int edjCnt = 0;\n UF(int n) {\n nodes = new int[n];\n for(int i = 0; i < n; i++)\n nodes[i] = i;\n }\n \n boolean isConnected() {\n return (nodes.length - 1 - 1) == edjCnt;\n }\n \n boolean add(int[] edj) {\n int aHead = head(edj[1]);\n int bHead = head(edj[2]);\n if (aHead != bHead) {\n nodes[bHead] = aHead;\n edjCnt++;\n return true;\n }\n return false;\n }\n \n int head(int n) {\n if (n != nodes[n]) \n nodes[n] = head(nodes[n]);\n return nodes[n];\n }\n}\n``` | 2 | 0 | ['Union Find', 'Java'] | 0 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Java Union Find Beginner friendly Full Explanation 17ms | java-union-find-beginner-friendly-full-e-uh60 | Please upvote if u find useful\nCredits - A big thanks to @interviewrecipes and @akshay31verma\n\n\n The idea here is to think that initially the graph is empt | embrane | NORMAL | 2021-02-02T13:07:20.624852+00:00 | 2021-02-02T13:13:13.619638+00:00 | 387 | false | **Please upvote if u find useful**\nCredits - A big thanks to @interviewrecipes and @akshay31verma\n\n\n* The idea here is to think that initially the graph is empty and now we want to add the edges into the graph such that graph is connected. \n* As some edges are available to only Bob while some are available only to Alice, we will have two different union find objects to take care of their own traversability.\n* Make all the components which you can reach from type 3 edges i.e traverserable for both Alice and Bob\n* Now using First go with alice and find if we can connect all the disconnected groups using the Alice edges.\n* And apply same for Bob.\n* Also in Union Find DS i have made var comp. to calculate the no of independent Component in the graph of Alice and Bob\n* we cal. comp. for both alice and bob\n* ***if the graph is fully traversible then we must no. comp. = 2 (coz 0 is indept. node)***\n\nMy Simple Java Code:\n```\npublic int maxNumEdgesToRemove(int n, int[][] edges) {\n\t\t int nboth=0,nalice=0,nbob=0;\n\t\t List<int[]> both=new Vector<>();\n\t\t List<int[]> bob=new Vector<>();\n\t\t List<int[]> alice=new Vector<>();\n\t\t \n\t\t for(int[] t:edges) {\n\t\t\t if(t[0]==3) {nboth++;both.add(t);}\n\t\t\t else if(t[0]==2) {nbob++;bob.add(t);}\n\t\t\t else {nalice++;alice.add(t);}\n\t\t }\n\t\t \n\t\t Dsu dsu_bob=new Dsu(n+1);\n\t\t Dsu dsu_alice=new Dsu(n+1);\n\t\tint ans=0;\n\t\tint edge=0;\n\t\tfor(int[] t:both) {\n\t\t\tif(dsu_alice.union(t[1], t[2])==false&&dsu_bob.union(t[1], t[2])==false)\n\t\t\t\tedge++;\n\t\t}\n\t\tans+=nboth-edge;\n\t\tedge=0;\n\t\tfor(int[] t:alice) {\n\t\t\tif(dsu_alice.union(t[1], t[2])==false)\n\t\t\t\tedge++;\n\t\t}\n\t\tans+=nalice-edge;\n\t\tedge=0;\n\t\tfor(int[] t:bob) {\n\t\t\tif(dsu_bob.union(t[1], t[2])==false)\n\t\t\t\tedge++;\n\t\t}\n\t\tans+=nbob-edge;\n\t\tif(dsu_alice.comp>2|| dsu_bob.comp>2) return -1;\n\t\treturn ans;\n\t }\n\t static class Dsu{\n\t\t int[] parent;\n\t\t int[] rank;\n\t\t int comp;\n\t\t Dsu(int N){\n\t\t\t parent=new int[N];\n\t\t\t rank=new int[N];\n\t\t\t Arrays.fill(parent, -1);\n\t\t\t this.comp=N;\n\t\t }\n\t\t int find(int x) {\n\t\t\t if(parent[x]==-1)return x;\n\t\t\t return parent[x]=find(parent[x]);\n\t\t }\n\t\t boolean union(int u,int v) {\n\t\t\t int p1=find(u);\n\t\t\t int p2=find(v);\n\t\t\t if(p1==p2)return true;\n\t\t\t \n\t\t\t if(rank[p1] >rank[p2])\n\t\t\t\t parent[p2]=p1;\n\t\t\t else if(rank[p2] >rank[p1])\n\t\t\t\t parent[p1]=p2;\n\t\t\t else {\n\t\t\t\t parent[p2]=p1;\n\t\t\t\t rank[p1]++;\n\t\t\t }\n\t\t\t comp--;\n\t\t\t return false;\n\t\t }\n\t }\n\n```\n\nTime: O(m), where m is the number of edges.\nMemory: O(n) \n**Please upvote if u find useful** | 2 | 0 | [] | 0 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | A solution WITHOUT union-find. Just do at most 3 times of DFS/BFS | a-solution-without-union-find-just-do-at-a3dl | Almost all the solutions posted in Discuss are Union-Find solution. So I am providing a different solution without union-find here: Just do at most 3 times of g | decision | NORMAL | 2020-12-24T06:58:16.749725+00:00 | 2020-12-24T07:11:49.800718+00:00 | 168 | false | Almost all the solutions posted in Discuss are Union-Find solution. So I am providing a different solution without union-find here: Just do at most 3 times of graph traversal.\n1. First travel the graph by using only edge type 1 and type 3. If it can\'t visit all the nodes, then it means Alice can\'t visit all nodes. Return -1.\n2. Then travel the graph by using only edge type 2 and type 3. If it can\'t visit all the nodes, then it means Bob can\'t visit all nodes. Return -1.\n3. Finally travel the graph by using only edge type 3 and count the number of connected component, say x. Then the result is **edges.length - (n -1 + x -1)**.\n```\nclass Solution {\n public int maxNumEdgesToRemove(int n, int[][] edges) {\n ArrayList<Integer>[] als1=new ArrayList[n], als2=new ArrayList[n], als3=new ArrayList[n];\n for(int i=0;i<n;++i){\n als1[i]=new ArrayList();\n als2[i]=new ArrayList();\n als3[i]=new ArrayList();\n }\n for(int[] e : edges){\n if(e[0]==1){\n als1[e[1]-1].add(e[2]-1);\n als1[e[2]-1].add(e[1]-1);\n }else if(e[0]==2){\n als2[e[1]-1].add(e[2]-1);\n als2[e[2]-1].add(e[1]-1);\n }else{\n als3[e[1]-1].add(e[2]-1);\n als3[e[2]-1].add(e[1]-1);\n }\n }\n int[] kk=new int[1];\n check(als1,als3,new boolean[n],0,kk);\n if(kk[0]!=n)return -1;\n kk[0]=0;\n check(als2,als3,new boolean[n],0,kk);\n if(kk[0]!=n)return -1;\n boolean[] f=new boolean[n];\n int count=0;\n for(int i=0;i<n;++i){\n if(!f[i]){\n ++count;\n todo(als3,f,i);\n }\n }\n return edges.length - (n-1+(count-1));\n }\n \n private void todo(ArrayList<Integer>[] als, boolean[] f, int st){\n f[st]=true;\n for(int n : als[st]){\n if(!f[n])todo(als, f, n);\n }\n }\n \n private void check(ArrayList<Integer>[] als1, ArrayList<Integer>[] als2, boolean[] f, int st, int[] kk){\n f[st]=true;\n ++kk[0];\n for(int n : als1[st]){\n if(!f[n])check(als1, als2, f, n, kk);\n }\n for(int n : als2[st]){\n if(!f[n])check(als1, als2, f, n, kk);\n }\n }\n}\n``` | 2 | 0 | [] | 1 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Concise union-find python | concise-union-find-python-by-aimar88-up82 | ```\ndef maxNumEdgesToRemove(self, n: int, e: List[List[int]]) -> int:\n\tdef union(UF, u, v): \n\t\tUF[find(UF, v)] = find(UF, u)\n\tdef find(UF, u) | aimar88 | NORMAL | 2020-09-29T19:00:42.239785+00:00 | 2020-09-29T21:45:50.210368+00:00 | 154 | false | ```\ndef maxNumEdgesToRemove(self, n: int, e: List[List[int]]) -> int:\n\tdef union(UF, u, v): \n\t\tUF[find(UF, v)] = find(UF, u)\n\tdef find(UF, u):\n\t\tif UF[u] != u: UF[u] = find(UF, UF[u])\n\t\treturn UF[u] \n\tdef check(UF, t): \n\t\tUF = UF.copy()\n\t\tfor tp, u, v in e:\n\t\t\tif tp == t: \n\t\t\t\tif find(UF, u) == find(UF, v): self.ans += 1\n\t\t\t\telse: union(UF, u, v)\n\t\treturn len(set(find(UF, u) for u in UF)) == 1, UF\n\n\tself.ans, UF = 0, {u: u for u in range(1, n+1)} \n\tUF = check(UF, 3)[1]\n\tif not check(UF, 1)[0] or not check(UF, 2)[0]: return -1 \n\treturn self.ans | 2 | 0 | [] | 0 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Java - Easy To Understand UNION FIND | java-easy-to-understand-union-find-by-ha-q558 | \nclass Solution {\n\t// union-find structure\n class UnionFind {\n int count;\n int[] parent;\n int[] rank;\n public UnionFind(i | harin_mehta | NORMAL | 2020-09-06T09:55:50.007089+00:00 | 2020-09-06T09:58:02.903308+00:00 | 217 | false | ```\nclass Solution {\n\t// union-find structure\n class UnionFind {\n int count;\n int[] parent;\n int[] rank;\n public UnionFind(int n) {\n count = n;\n parent = new int[n+1];\n for(int i = 0; i < n+1; i++) {\n parent[i] = i;\n }\n rank = new int[n+1];\n }\n \n public int find(int a) {\n if(a != parent[a]) {\n parent[a] = find(parent[a]);\n }\n return parent[a];\n }\n // returns false if a and b are in same set, i.e., if both have already been reached\n public boolean union(int a, int b) {\n int parent_a = find(a);\n int parent_b = find(b);\n if(parent_a == parent_b) return false;\n if(rank[parent_a] >= rank[parent_b]) {\n parent[parent_b] = parent_a;\n if(rank[parent_a] == rank[parent_b])\n rank[parent_a]++;\n }\n else {\n parent[parent_a] = parent_b;\n }\n count--;\n return true;\n }\n \n \n }\n\t// real solution\n public int maxNumEdgesToRemove(int n, int[][] edges) {\n UnionFind uf_alice = new UnionFind(n);\n UnionFind uf_bob = new UnionFind(n);\n for(int[] edge : edges) {\n if(edge[0] == 1) {\n uf_alice.union(edge[1], edge[2]);\n }\n else if(edge[0] == 2) {\n uf_bob.union(edge[1], edge[2]);\n }\n else {\n uf_alice.union(edge[1], edge[2]);\n uf_bob.union(edge[1], edge[2]);\n }\n }\n\t\t// let\'s just make sure, if with given edges they can reach all nodes or not\n if(uf_alice.count != 1 || uf_bob.count != 1) return -1;\n \n\t\t/* okay, so they are reachable , now remove the redundant ones in following way :\n\t\t\t1. It\'s best to insert the type-3 edges, while removing the redundant ones.\n\t\t\t2. Once, above step is finished, we can remove the redundant type-1 and redundant type-2 edges. \n\t\t*/\n\t\t\n uf_alice = new UnionFind(n);\n uf_bob = new UnionFind(n);\n int ans = 0;\n for(int[] edge : edges) {\n if(edge[0] == 3) {\n if(!uf_alice.union(edge[1], edge[2]))\n ans++;\n uf_bob.union(edge[1], edge[2]);\n }\n }\n for(int[] edge : edges) {\n if(edge[0] == 1) {\n if(!uf_alice.union(edge[1], edge[2]))\n ans++;\n }\n else if(edge[0] == 2) {\n if(!uf_bob.union(edge[1], edge[2]))\n ans++;\n }\n }\n return ans;\n }\n}\n``` | 2 | 0 | ['Union Find', 'Java'] | 1 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | c++ | c-by-atulkumar1-8hcx | ``` \n\n//the idea is bascially union find // first do union find for type 3 edges and keep counter of extra edges \n//after that n using the previous union fi | ATulKumaR1 | NORMAL | 2020-09-06T06:40:46.013848+00:00 | 2020-09-06T06:40:46.013904+00:00 | 132 | false | ``` \n\n//the idea is bascially union find // first do union find for type 3 edges and keep counter of extra edges \n//after that n using the previous union find array do union find fortyep 1 and type 2 respecitvely and inceremnt the count of random edges \n\nclass Solution {\npublic: \n int find(vector<int>&p,int a)\n {\n if(p[a]==-1)\n {\n return a; \n }\n \n p[a]=find(p,p[a]); \n \n return p[a]; \n }\n int unionn(vector<int>&p,int a,int b)\n {\n int x,y; \n x=find(p,a); \n y=find(p,b); \n \n if(x==y)\n {\n return 1; \n }\n \n p[x]=y; \n return 0; \n \n } \n int find2(vector<int>&p,int a)\n {\n if(p[a]==-1)\n {\n return a; \n }\n \n p[a]=find(p,p[a]); \n \n return p[a]; \n }\n \n int unionn2(vector<int>&p,int a,int b)\n {\n int x,y; \n x=find2(p,a); \n y=find2(p,b); \n \n if(x==y)\n {\n return 1; \n }\n \n p[x]=y; \n return 0; \n \n } \n \n int solve(int n, vector<vector<int>>& e,int x,vector<int>p)\n {\n \n map<int,bool>vis; \n \n int i,j,k,l,ans=0; \n \n \n for(i=0;i<e.size();i++)\n {\n if(e[i][0]==x)\n { \n vis[e[i][1]]=true; \n vis[e[i][2]]=true; \n ans=ans+unionn2(p,e[i][1],e[i][2]); \n }\n if(e[i][0]==3)\n {\n vis[e[i][1]]=true; \n vis[e[i][2]]=true; \n }\n }\n \n \n for(i=1;i<=n;i++)\n {\n if(vis[i]==false)\n {\n return -1;\n }\n }\n \n\n \n return ans; \n }\n int maxNumEdgesToRemove(int n, vector<vector<int>>& e) {\n \n vector<int>p(n+1,-1); \n int i,j,k,l,ans; \n ans=0; \n \n for(i=0;i<e.size();i++)\n {\n if(e[i][0]==3)\n {\n ans+=unionn(p,e[i][1],e[i][2]); \n }\n \n }\n \n int alice,bob; \n \n alice=solve(n,e,1,p); \n \n if(alice==-1)\n {\n return -1; \n }\n \n bob=solve(n,e,2,p); \n \n if(bob==-1)\n {\n return -1;\n }\n \n return ans+alice+bob; \n \n \n } \n}; | 2 | 0 | [] | 0 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Java combine the MSTs O(n + e log e) easy to understand | java-combine-the-msts-on-e-log-e-easy-to-hqao | Algorithm:\n1. Calculate MSTs for both Alice and Bob.\n2. Combine these MSTs via intersection.\n3. Answer is total num edges - num combined MSTs edges.\n\nKey i | wilmol | NORMAL | 2020-09-06T04:43:56.240465+00:00 | 2020-09-06T07:12:27.275998+00:00 | 155 | false | Algorithm:\n1. Calculate MSTs for both Alice and Bob.\n2. Combine these MSTs via intersection.\n3. Answer is total num edges - num combined MSTs edges.\n\nKey idea:\n- When computing the MSTs, the shared edge has higher priority.\n\nUsed Kruskalls algorithm (union find) to calculate MSTs.\n\n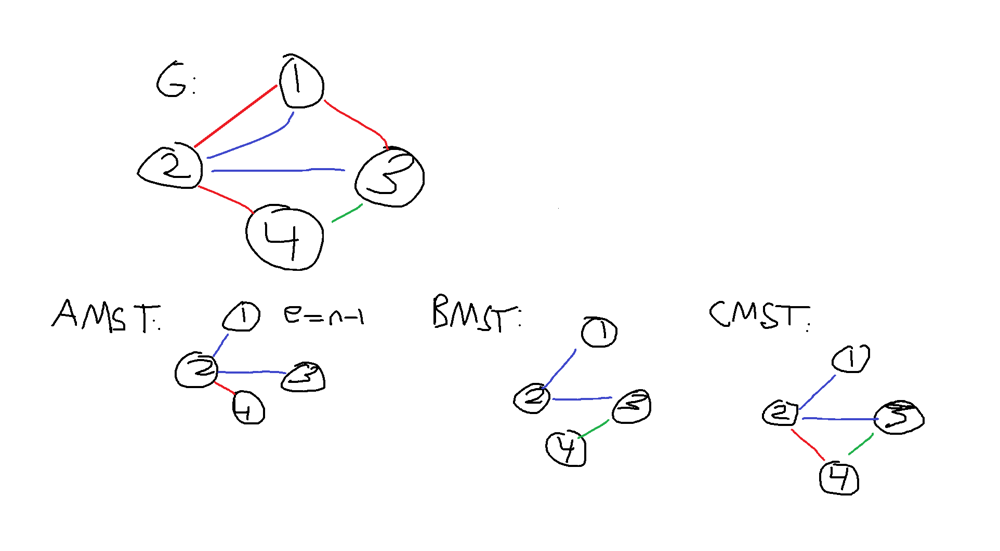\n\n```\nclass Solution {\n public int maxNumEdgesToRemove(int n, int[][] edges) {\n // solution: make MST for both bob and alice\n // combine MSTs by taking intersection\n // difference of total num edges - combined MST = num edges can be removed\n\n // {cost, src, dst}\n List<List<Integer>> aliceEdge = new ArrayList<>();\n List<List<Integer>> bobEdge = new ArrayList<>();\n for (int[] edge : edges) {\n if (edge[0] == 3) {\n // favour combined edge in MST calculation by making its cost cheaper\n aliceEdge.add(Arrays.asList(1, edge[1], edge[2]));\n bobEdge.add(Arrays.asList(1, edge[1], edge[2]));\n } else if (edge[0] == 1) {\n aliceEdge.add(Arrays.asList(2, edge[1], edge[2]));\n } else if (edge[0] == 2) {\n // use different cost to alice so combined mst considers them differently (i.e. in the Set.addAll)\n // wont have the unshared edges in same MST calculation so doesn\'t matter as long as > combined edge cost\n bobEdge.add(Arrays.asList(4, edge[1], edge[2]));\n }\n }\n\n Set<List<Integer>> aliceMst = mst(n, aliceEdge);\n if (aliceMst.size() != n - 1) {\n return -1;\n }\n Set<List<Integer>> bobMst = mst(n, bobEdge);\n if (bobMst.size() != n - 1) {\n return -1;\n }\n\n // intersection\n Set<List<Integer>> combinedMst = new HashSet<>();\n combinedMst.addAll(aliceMst);\n combinedMst.addAll(bobMst);\n\n return edges.length - combinedMst.size();\n }\n\n private int[] parent;\n\n // kruskals algorithm\n private Set<List<Integer>> mst(int n, List<List<Integer>> edges) {\n // make n sets\n parent = IntStream.rangeClosed(0, n).toArray();\n // sort so try cheapest edges first\n edges.sort(Comparator.comparing(list -> list.get(0)));\n\n Set<List<Integer>> mstEdges = new HashSet<>();\n\n // process edges until mst found or ran out of edges\n for (int i = 0; i < edges.size() && mstEdges.size() < n - 1; i++) {\n List<Integer> edge = edges.get(i);\n int src = edge.get(1);\n int dst = edge.get(2);\n\n int srcSet = find(src);\n int dstSet = find(dst);\n\n if (srcSet != dstSet) {\n // nodes in different tree, merge trees\n union(srcSet, dstSet);\n mstEdges.add(edge);\n }\n }\n return mstEdges;\n }\n\n private void union(int a, int b) {\n parent[find(a)] = find(b);\n }\n\n private int find(int a) {\n if (a != parent[a]) {\n parent[a] = find(parent[a]);\n }\n return parent[a];\n }\n}\n```\n\n | 2 | 0 | [] | 1 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | [Java] Union Find O(N) | java-union-find-on-by-yuhwu-f8nb | Let\nc1: number of connected components using type 1 edges only\nc2: number of connected components using type 1 and type 2 edges \nc3: number of connected com | yuhwu | NORMAL | 2020-09-06T04:02:15.035048+00:00 | 2020-09-06T04:03:17.827154+00:00 | 196 | false | Let\nc1: number of connected components using type 1 edges only\nc2: number of connected components using type 1 and type 2 edges \nc3: number of connected components using type 1 and type 3 edges \n=>\ncase 1: The graph is not connected for Alice or Bob, return -1\ncase 2: The graph is connected for Alice and Bob, return **number of edges - ((number of vertices - c3) + (c3 -1) + (c3 -1))**\n```\nclass Solution {\n public int maxNumEdgesToRemove(int n, int[][] edges) {\n DSU dsu3 = new DSU(n);\n DSU dsu2 = new DSU(n);\n DSU dsu1 = new DSU(n);\n for(int[] e : edges){\n int type = e[0];\n if(type==3){\n dsu3.union(e[1]-1, e[2]-1);\n dsu2.union(e[1]-1, e[2]-1);\n dsu1.union(e[1]-1, e[2]-1);\n }\n else if(type==2){\n dsu2.union(e[1]-1, e[2]-1);\n }\n else{\n dsu1.union(e[1]-1, e[2]-1);\n }\n }\n int c1 = dsu1.components;\n int c2 = dsu2.components;\n if(c1!=1 || c2!=1){\n return -1;\n }\n int c3 = dsu3.components;\n int need = n-c3 + c3-1 + c3-1;\n return edges.length-need;\n }\n \n class DSU{\n int[] parent;\n int[] size;\n int components;\n\n public DSU(int N){\n components = N;\n parent = new int[N];\n size = new int[N];\n for(int i=0; i<parent.length; i++){\n parent[i] = i;\n size[i] = 1;\n }\n }\n\n public int find(int x){\n if(parent[x]!=x){\n parent[x] = find(parent[x]);\n }\n return parent[x];\n }\n\n public int union(int x, int y){\n int xParent = find(x);\n int yParent = find(y);\n if(xParent==yParent) return size[xParent];\n components--;\n if(size[xParent]<=size[yParent]){\n parent[xParent] = yParent;\n size[yParent]+=size[xParent];\n return size[yParent];\n }\n else{\n parent[yParent] = xParent;\n size[xParent] += size[yParent];\n return size[xParent];\n }\n }\n }\n}\n``` | 2 | 0 | [] | 0 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | Simple solution using dsu in cpp | simple-solution-using-dsu-in-cpp-by-ashu-e8z9 | Data structure used : Dis joint set union.\nAlgorithm used : Cycle in undirected graph using dis joint set data structure and check if a graph is connected usin | ashu12_chi | NORMAL | 2020-09-06T04:01:31.403825+00:00 | 2020-09-06T04:01:31.403878+00:00 | 365 | false | Data structure used : Dis joint set union.\nAlgorithm used : Cycle in undirected graph using dis joint set data structure and check if a graph is connected using dis joint set data structure.\nTime complexity : O(n)\nSpace complexity : O(n)\n\nIn this problem we need to remove maximum number of edges so that our graph remains fully traversed by both Alice and Bob individually or tell that it is impossible to traverse graph completely.\n\nEdges are of three type here:\n\nType 1: Can be traversed by Alice only.\nType 2: Can be traversed by Bob only.\nType 3: Can by traversed by both Alice and Bob.\n\nWe can think greedly here that we should use maximum Type 3 edges, so that we can need to use less of Type 1 and Type 2 edges. So first we try to use Type 3 for both and then, Type 1 and Type 2 individually.\n\nWe will use the concept of cycle formation, we add an edge only when it is connecting two different components\nof graph otherwise increase our counter variable (for count of edge deletion).\n\nAt the end we check for both Alice and Bob if graph is fully connected for them, this can be done easily by\nfinding if all vertices have same parent in dis joint set structure.\n\nC++ implementation:\n\n```\nint find_set(int parent[],int v)\n{\n if(v == parent[v])\n return v;\n return parent[v] = find_set(parent,parent[v]);\n}\nvoid union_set(int parent[],int a,int b)\n{\n a = find_set(parent,a);\n b = find_set(parent,b);\n if(a != b)\n parent[b] = a;\n}\nclass Solution {\npublic:\n int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {\n int parent1[n+1];\n int parent2[n+1];\n for(int i=1;i<=n;i++)\n parent1[i] = parent2[i] = i;\n int ans = 0;\n for(int i=0;i<edges.size();i++)\n {\n if(edges[i][0] == 3)\n {\n int t1 = find_set(parent1,edges[i][1]);\n int t2 = find_set(parent1,edges[i][2]);\n if(t1 != t2)\n {\n union_set(parent1,edges[i][2],edges[i][1]);\n union_set(parent2,edges[i][2],edges[i][1]);\n }\n else\n ans++;\n }\n }\n for(int i=0;i<edges.size();i++)\n {\n if(edges[i][0] == 1)\n {\n int t1 = find_set(parent1,edges[i][1]);\n int t2 = find_set(parent1,edges[i][2]);\n if(t1 != t2)\n {\n union_set(parent1,edges[i][2],edges[i][1]);\n }\n else\n ans++;\n }\n else if(edges[i][0] == 2)\n {\n int t1 = find_set(parent2,edges[i][1]);\n int t2 = find_set(parent2,edges[i][2]);\n if(t1 != t2)\n {\n union_set(parent2,edges[i][2],edges[i][1]);\n }\n else\n ans++;\n }\n }\n int par1 = find_set(parent1,1);\n for(int i=1;i<=n;i++)\n {\n int t = find_set(parent1,i);\n if(t != par1)\n return -1;\n }\n int par2 = find_set(parent2,1);\n for(int i=1;i<=n;i++)\n {\n int t = find_set(parent2,i);\n if(t != par2)\n return -1;\n }\n return ans;\n }\n};\n``` | 2 | 1 | ['C++'] | 0 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | C# | c-by-adchoudhary-27ir | Code | adchoudhary | NORMAL | 2025-03-08T03:18:18.692435+00:00 | 2025-03-08T03:18:18.692435+00:00 | 4 | false | # Code
```csharp []
public class Solution {
public int MaxNumEdgesToRemove(int n, int[][] edges) {
DSU dsu1 = new DSU(n);
DSU dsu2 = new DSU(n);
int count = 0;
Array.Sort(edges, (a, b) => b[0] - a[0]);
foreach(var edge in edges){
if(edge[0] == 3){
if(dsu1.find(edge[1]) == dsu1.find(edge[2]) && dsu2.find(edge[1]) == dsu2.find(edge[2])){
count++;
continue;
}
dsu1.union(edge[1], edge[2]);
dsu2.union(edge[1], edge[2]);
}
else if(edge[0] == 1){
if(dsu1.find(edge[1]) == dsu1.find(edge[2])){
count++;
}
dsu1.union(edge[1], edge[2]);
}
else{
if(dsu2.find(edge[1]) == dsu2.find(edge[2])){
count++;
}
dsu2.union(edge[1], edge[2]);
}
}
for(int i=1; i<=n; i++){
dsu1.find(i);
dsu2.find(i);
}
for(int i=2; i<=n; i++){
if(dsu1.parent[i] != dsu1.parent[1] || dsu2.parent[i] != dsu2.parent[1]){
return -1;
}
}
return count;
}
class DSU {
public int[] parent;
public DSU(int n) {
parent = new int[n+1];
for (int i = 0; i <= n; i++) parent[i] = i;
}
public int find(int x) {
if (parent[x] != x) parent[x] = find(parent[x]);
return parent[x];
}
public void union(int x, int y) {
parent[find(x)] = parent[find(y)];
}
}
}
``` | 1 | 0 | ['C#'] | 0 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | 🔥 LeetCode Editorial-Style Solution 🔥 | Union-Find | DSU | Beats 100% 🚀 | leetcode-editorial-style-solution-union-v3yvq | 🧠 Intuition
The problem requires determining the maximum number of edges that can be removed while keeping both Alice and Bob's graphs fully connected.
Union-Fi | kanchanlamba00 | NORMAL | 2025-02-10T07:20:42.533562+00:00 | 2025-02-10T07:20:42.533562+00:00 | 26 | false | # 🧠 Intuition
- The problem requires determining the maximum number of edges that can be removed while keeping both Alice and Bob's graphs fully connected.
- Union-Find (Disjoint Set Union - DSU) is ideal for this problem to efficiently track components.
# 🔍 Approach
1️⃣ Union-Find Data Structure
- Parent Array: Helps in finding the root of a node.
- Size Array: Maintains the size of each connected component.
2️⃣ Process Edges in Decreasing Order of Type
- Type 3 (Common Edges): Used by both Alice & Bob (Process first to maximize sharing).
- Type 1 (Alice-Only Edges): Used only for Alice.
- Type 2 (Bob-Only Edges): Used only for Bob.
3️⃣ Count Edges Used & Remaining Components
- If Alice and Bob each form a single component, return the edges removed.
- Otherwise, return -1 (Impossible to connect both graphs).
-
# ⏳ Complexity Analysis
- Sorting Edges: O(E log E)
- Union-Find Operations: O(α(N)) ~ O(1) (Inverse Ackermann Function)
- Total Complexity: O(E log E + E) ≈ O(E log E) (Efficient for large inputs)
- Space Complexity: O(N) (For DSU arrays)
# 🔥 LeetCode Code | DSU | 🚀 Optimized
```cpp []
class disjoint{
public:
vector<int> size,parent;
disjoint(int n){
size.resize(n+1,1);
parent.resize(n+1);
for(int i=1;i<=n;i++){
parent[i]=i;
}
}
int find(int node){
if(node==parent[node]){
return parent[node];
}
return parent[node]=find(parent[node]);
}
void uNion(int u,int v){
int ulp_u=find(u);
int ulp_v=find(v);
if(ulp_v==ulp_u){
return ;
}
if(size[ulp_u]<=size[ulp_v]){
parent[ulp_u]=ulp_v;
size[ulp_v]+=size[ulp_u];
}
else{
parent[ulp_v]=ulp_u;
size[ulp_u]+=size[ulp_v];
}
}
};
class Solution {
public:
int maxNumEdgesToRemove(int n, vector<vector<int>>& edges) {
int count=0;
disjoint dsA(n);
disjoint dsB(n);
int componentA=n;
int componentB=n;
sort(edges.begin(),edges.end(),[](const vector<int>& a,const vector<int>& b){return a[0]>b[0];});
for(int i=0;i<edges.size();i++){
int e=edges[i][0];
int u=edges[i][1];
int v=edges[i][2];
if(e==3){
int ult_1=dsA.find(edges[i][1]);
int ult_2=dsA.find(edges[i][2]);
int ult_3=dsB.find(edges[i][1]);
int ult_4=dsB.find(edges[i][2]);
if(ult_1!=ult_2 && ult_3!=ult_4){
componentA--;
count++;
componentB--;
dsA.uNion(ult_1,ult_2);
dsB.uNion(ult_1,ult_2);
}
}
else if(e==1){
int ult_1=dsA.find(edges[i][1]);
int ult_2=dsA.find(edges[i][2]);
if(ult_1!=ult_2){
count++;
componentA--;
dsA.uNion(ult_1,ult_2);
}
}
else{
// e==2
int ult_1=dsB.find(edges[i][1]);
int ult_2=dsB.find(edges[i][2]);
if(ult_1!=ult_2){
count++;
componentB--;
dsB.uNion(ult_1,ult_2);
}
}
}
if(componentA==1 && componentB==1){
return edges.size()-count;
}
return -1;
}
};
``` | 1 | 0 | ['C++'] | 0 |
remove-max-number-of-edges-to-keep-graph-fully-traversable | take the common edge first || brute force || easy to understand || must see | take-the-common-edge-first-brute-force-e-uq1z | Code\ncpp []\nclass Solution {\npublic:\n int N;\n bool bobFlag = true;\n bool aliceFlag = true;\n set<vector<int>>bobSet;\n set<vector<int>>alic | akshat0610 | NORMAL | 2024-08-19T18:58:14.170374+00:00 | 2024-08-19T18:58:14.170415+00:00 | 5 | false | # Code\n```cpp []\nclass Solution {\npublic:\n int N;\n bool bobFlag = true;\n bool aliceFlag = true;\n set<vector<int>>bobSet;\n set<vector<int>>aliceSet;\n int maxNumEdgesToRemove(int n, vector<vector<int>>& arr) {\n N = n;\n sort(arr.begin(),arr.end());\n\n vector<vector<int>>bob;\n vector<vector<int>>alice;\n \n for(int i = arr.size()-1 ; i >=0 ; i--){\n if((arr[i][0] == 1) or (arr[i][0] == 3)){\n alice.push_back(arr[i]);\n }\n if((arr[i][0] == 2) or (arr[i][0] == 3)){\n bob.push_back(arr[i]);\n }\n }\n funAlice(alice); if(aliceFlag == false) return -1;\n funBob(bob); if(bobFlag == false) return -1;\n\n // cout<<"alice choise of the edges"<<endl;\n // for(auto v : aliceSet){\n // cout<<v[0]<<" "<<v[1]<<" "<<v[2]<<endl;\n // }\n // cout<<endl;\n // cout<<endl;\n // for(auto v : bobSet){\n // cout<<v[0]<<" "<<v[1]<<" "<<v[2]<<endl;\n // }\n // cout<<endl;\n return arr.size() - (aliceSet.size() + bobSet.size());\n \n }\n void funBob(vector<vector<int>>&Bob){\n vector<int>par(N+1,0);\n vector<int>rank(N+1,0);\n for(int i = 0 ; i < par.size() ; i++) par[i] = i;\n\n for(int i = 0 ; i < Bob.size() ; i++){\n \n int u = Bob[i][1];\n int v = Bob[i][2];\n if(union_rank(par,rank,u,v) == true){\n int a = u;\n int b = v;\n if(a > b) {\n int c=a;\n a=b;\n b=c;\n }\n if((Bob[i][0] == 2) or ((Bob[i][0] == 3) and (aliceSet.find({Bob[i][0] , a , b}) == aliceSet.end())))\n bobSet.insert({Bob[i][0] , a , b});\n }\n }\n unordered_set<int>st;\n for(int i = 1 ; i <= N ; i++) {\n par[i] = find_parent(i,par);\n st.insert(par[i]);\n }\n if(st.size() > 1) bobFlag = false; \n }\n void funAlice(vector<vector<int>>&alice){\n vector<int>par(N+1,0);\n vector<int>rank(N+1,0);\n for(int i = 0 ; i < par.size() ; i++) par[i] = i;\n\n for(int i = 0 ; i < alice.size() ; i++){\n \n int u = alice[i][1];\n int v = alice[i][2];\n if(union_rank(par,rank,u,v) == true){\n int a = u;\n int b = v;\n if(a > b) {\n int c=a;\n a=b;\n b=c;\n }\n aliceSet.insert({alice[i][0] , a , b});\n }\n }\n unordered_set<int>st;\n for(int i = 1 ; i <= N ; i++) {\n par[i] = find_parent(i,par);\n st.insert(par[i]);\n }\n if(st.size() > 1) aliceFlag = false; \n \n }\n int find_parent(int u , vector<int>&parent){\n if(parent[u] == u) return u;\n return parent[u] = find_parent(parent[u],parent);\n }\n bool union_rank(vector<int>&par,vector<int>&rank,int u,int v){\n int paru = find_parent(u,par);\n int parv = find_parent(v,par);\n\n if(paru == parv) return false;\n\n if(rank[paru] == rank[parv]){\n par[parv] = paru;\n rank[paru]++;\n }\n else if(rank[paru] < rank[parv]){\n par[paru] = parv;\n }\n else if(rank[parv] < rank[paru]){\n par[parv] = paru;\n }\n return true;\n }\n void print(vector<vector<int>>&arr){\n for(int i = 0 ; i < arr.size() ; i++){\n for(int j = 0 ; j < arr[i].size() ; j++){\n cout<<arr[i][j]<<" ";\n }\n cout<<" ";\n }\n return;\n }\n};\n``` | 1 | 0 | ['Union Find', 'Graph', 'C++'] | 0 |
max-chunks-to-make-sorted-ii | Java solution, left max and right min. | java-solution-left-max-and-right-min-by-873x6 | Algorithm: Iterate through the array, each time all elements to the left are smaller (or equal) to all elements to the right, there is a new chunck.\nUse two ar | shawngao | NORMAL | 2018-01-21T04:16:03.509000+00:00 | 2018-10-27T03:08:30.570352+00:00 | 23,115 | false | Algorithm: Iterate through the array, each time all elements to the left are smaller (or equal) to all elements to the right, there is a new chunck.\nUse two arrays to store the left max and right min to achieve O(n) time complexity. Space complexity is O(n) too.\nThis algorithm can be used to solve ver1 too.\n```\nclass Solution {\n public int maxChunksToSorted(int[] arr) {\n int n = arr.length;\n int[] maxOfLeft = new int[n];\n int[] minOfRight = new int[n];\n\n maxOfLeft[0] = arr[0];\n for (int i = 1; i < n; i++) {\n maxOfLeft[i] = Math.max(maxOfLeft[i-1], arr[i]);\n }\n\n minOfRight[n - 1] = arr[n - 1];\n for (int i = n - 2; i >= 0; i--) {\n minOfRight[i] = Math.min(minOfRight[i + 1], arr[i]);\n }\n\n int res = 0;\n for (int i = 0; i < n - 1; i++) {\n if (maxOfLeft[i] <= minOfRight[i + 1]) res++;\n }\n\n return res + 1;\n }\n}\n``` | 400 | 2 | [] | 35 |
max-chunks-to-make-sorted-ii | [C++] 9 lines, 15ms | c-9-lines-15ms-by-liuchuo-8rwc | \nint maxChunksToSorted(vector<int>& arr) {\n int sum1 = 0, sum2 = 0, ans = 0;\n vector<int> t = arr;\n sort(t.begin(), t.end());\n | liuchuo | NORMAL | 2018-01-28T08:30:40.478000+00:00 | 2018-10-14T23:15:25.263674+00:00 | 9,450 | false | ```\nint maxChunksToSorted(vector<int>& arr) {\n int sum1 = 0, sum2 = 0, ans = 0;\n vector<int> t = arr;\n sort(t.begin(), t.end());\n for(int i = 0; i < arr.size(); i++) {\n sum1 += t[i];\n sum2 += arr[i];\n if(sum1 == sum2) ans++;\n }\n\treturn ans;\n }\n``` | 187 | 1 | [] | 23 |
max-chunks-to-make-sorted-ii | [Java/Python] Easy and Straight Froward | javapython-easy-and-straight-froward-by-9xpff | Soluton 1\nCount numbers.\nO(nlogn) for sorting\nO(n^2) for check\nPython\npy\n def maxChunksToSorted(self, arr):\n res, c1, c2 = 0, collections.Count | lee215 | NORMAL | 2018-01-21T04:19:46.245000+00:00 | 2020-06-11T02:04:58.590237+00:00 | 12,249 | false | # Soluton 1\nCount numbers.\nO(nlogn) for sorting\nO(n^2) for check\n**Python**\n```py\n def maxChunksToSorted(self, arr):\n res, c1, c2 = 0, collections.Counter(), collections.Counter()\n for a, b in zip(arr, sorted(arr)):\n c1[a] += 1\n c2[b] += 1\n res += c1 == c2\n return res\n```\n<br>\n\n# Soluton 2\nCount prefix sum.\nO(nlogn) for sorting\nO(n) for check\n\n**Java**\nby @Chengyou0421\n```java\n public int maxChunksToSorted(int[] arr) {\n int[] sorted = arr.clone();\n Arrays.sort(sorted);\n int res = 0, sum1 = 0, sum2 = 0;\n for (int i = 0; i < arr.length; i++) {\n sum1 += arr[i];\n sum2 += sorted[i];\n if (sum1 == sum2) res += 1;\n }\n return res;\n }\n```\n**Python**\nSuggested by @here0007\n```py\n def maxChunksToSorted(self, A):\n res, s1, s2 = 0, 0, 0\n for a, b in zip(A, sorted(A)):\n s1 += a\n s2 += b\n res += s1 == s2\n return res\n```\n<br> | 129 | 8 | [] | 26 |
max-chunks-to-make-sorted-ii | Monotonic stack solution with detailed explanation | monotonic-stack-solution-with-detailed-e-kpf5 | If you are not familiar with monotonic stack, please refer to this first. \n\nUnderstanding how monotonic stack works (build an increasing or decreasing stack b | combat_shawn | NORMAL | 2020-04-24T22:49:57.283421+00:00 | 2020-04-24T22:50:11.794024+00:00 | 4,592 | false | If you are not familiar with **monotonic stack**, please refer to [this](https://leetcode.com/problems/sum-of-subarray-minimums/discuss/178876/stack-solution-with-very-detailed-explanation-step-by-step) first. \n\nUnderstanding how **monotonic stack** works (build an increasing or decreasing stack based on the input) and what it can do is relatively easy. Unfortunately the hardest part is solution based on monotonic stack is sometimes not intuitive. \n\nHere\'s the thought based on this question. \n\nFirst question, what is the largest number of chunks for an array given the length as `n`? it\'s simple, just `n`, namingly every single element makes up the single-element chunk. For a given array, the largest number of chunks happens when it is increasing and every element is already at the right place.\n`[0, 1, 3, 4]` => `[0, 1], [3], [4]`\n\nSo as long as we are seeing an array that has increasing order, we just keep counting the number of elements in the array. (If you are familiar with **monotonic stack**, have you already smelled that it could be something useful to solve this question?)\n\nLet\'s keeping counting, untill we see the next element `2`. So now the input is `[0, 1, 3, 4, 2]`\nWell what does a suddenly jumped out smaller number mean ?? It means, `2` is not at the right place in the sorted array (we can see `2` actually should sit at the 3rd place in the array right?), **and** **SOMETHING ELSE** before `2` is also at the wrong place, which we didn\'t realize until we see `2`. So we need to look back. \n\n(While, another hint, we are expecting an increasing order array and we have to look backwards when the order is broken. Does this smell like **monotonic stack** again?)\n\nSo what exactly are we looking for when we are looking back?\nWe want to find the correct place that `2` should sit at, which means: **We are looking for the largest number that is smaller than `2` in an ascending array**. Why we care about where `2` should be at? because anything between the current position and the should-be position for `2` is not at the correct position that it should be (otherwise how could the poor `2`\'s potion being occupied?). If we can find the elements (including `2`) that are not at the right position, they need to be put in a chunk, and sorting them inside the chunk is the only way to put them in right place. \n\nSo in this example: `[0, 1, 3, 4, 2]`, we found `1` is the largest number smaller than `2` given our monotonic stack `[0, 1, 3, 4]`. So everything between `3` and `2` (inclusive) is messed up and they `[3, 4, 2]` has to be put in a chunk, so we can sort them back to `[2, 3, 4]` and put them back to the right place. \n\nNormally, we rebuild the monotonic stack from `[0,1, 3, 4]` to `[0, 1, 2]` by poping out the elements larger than `2` and push `2` back to the queue. However this doesn\'t work for this question. \n\nLet\'s think about what exactly the meaning we want it to be for each element in the increasing stack.\n\nWe want it to mean: **The largest value in each chunk when the chunk cannot be partitioned to smaller ones**. So the number of elements in the stack is exactly the number we are looking for. \n\nSo now the stack became `[0, 1, 4]` instead of `[0, 1, 2]` and each `0` => `[0]`, `1` => `[1]`, `4` => `[3, 4, 2]`. \n\nAnd here\'s the short Python code:\n```\nclass Solution:\n def maxChunksToSorted(self, arr: List[int]) -> int:\n stack = []\n for num in arr:\n largest = num\n while stack and stack[-1] > num:\n largest = max(largest, stack.pop())\n stack.append(largest)\n \n return len(stack)\n```\n\n\n | 119 | 0 | [] | 16 |
max-chunks-to-make-sorted-ii | [c++] Using Stack with O(n) space and time complexity. With 7 lines. 4ms. Beats 100% | c-using-stack-with-on-space-and-time-com-946c | We can treat each chunk as a range with (max value, min value) as a pair. Because we want to find the longest chunks, we need to treat each number as a range at | joecruise | NORMAL | 2018-06-03T16:59:45.845438+00:00 | 2018-10-20T15:43:04.533502+00:00 | 5,042 | false | We can treat each chunk as a range with (max value, min value) as a pair. Because we want to find the longest chunks, we need to treat each number as a range at first. ( 5: treat as range(5,5) )We use a stack to store these ranges. We need to merge the current range and previous range when current range\'s min value < previous range\'s max value. The answer is the number of ranges stored in the stack.\n\n\nFor example: \n[2,1,3,4,4]\nWe first meet 2, set is as range with max and min value (2 , 2)\nWhen we encounter 1 as (1,1), current range (1,1), the min value 1 is smaller than previous (2,2) max value 2. So we need to merge these two ranges as (2,1). For (3,3), min value 3 is larger than (2,1) max value 2, so we keep it. In the same way, we keep (4,4) and (4,4). Finally, in our stack, it is (2,1),(3,3),(4,4),(4,4). So the answer is 4.\n\n```\nclass Solution {\npublic:\n int maxChunksToSorted(vector<int>& arr) {\n stack<pair<int,int>>st;\n for(int i=0;i<arr.size();i++) {\n pair<int,int> it=make_pair(arr[i],arr[i]);\n while( (!st.empty()) && (st.top().first>it.second) ) {\n auto pre=st.top();\n st.pop();\n it.second = min(pre.second,it.second);\n it.first = max(pre.first, it.first);\n }\n st.push(it);\n }\n return st.size()\n }\n};\n```\n\n\nThanks for @**einhorn** suggestion. We do not need to keep track of the min value. We just need to know the previous max value.\n```\n int maxChunksToSorted(vector<int>& arr) {\n stack<int>st;\n for(int i=0;i<arr.size();i++) {\n int curmax=st.empty() ? arr[i]: max(st.top(),arr[i]);\n while( (!st.empty()) && (st.top()>arr[i]) ) st.pop();\n st.push(curmax);\n }\n return st.size();\n }\n```\n\n | 78 | 0 | [] | 4 |
max-chunks-to-make-sorted-ii | Simple Java Solution with explanation | simple-java-solution-with-explanation-by-vcqw | In Ver 1, the basic idea is to use max[] array to keep track of the max value until the current position, and compare it to the sorted array. If the max[i] equa | lily4ever | NORMAL | 2018-01-21T04:03:05.013000+00:00 | 2018-10-14T23:10:38.831895+00:00 | 5,354 | false | In Ver 1, the basic idea is to use max[] array to keep track of the max value until the current position, and compare it to the sorted array. If the max[i] equals the element at index i in the sorted array, then the final count++.\nHere the only difference is that we need to a variable 'upperLimit' to help determine whether the current point is the correct division position.\n\nFor example,\n```\noriginal: 2, 1, 4, 4, 3, 5, 7, 6\nmax: 2, 2, 4, 4, 4, 5, 7, 7\nsorted: 1, 2, 3, 4, 4, 5, 6, 7\n```\nThe chunks are: 2, 1 | 4, 4, 3 | 5 | 7, 6\n\nIt needs to be noted that at index 3, although max[i] == sorted[i], this is not the right dividing point. Otherwise, the number after it (3) will be in the wrong chunk.\n\n```\n public int maxChunksToSorted(int[] arr) {\n if (arr == null || arr.length == 0) return 0;\n \n int[] sorted = arr.clone();\n Arrays.sort(sorted);\n \n int[] max = new int[arr.length];\n max[0] = arr[0];\n for (int i = 1; i < arr.length; i++) {\n max[i] = Math.max(max[i - 1], arr[i]);\n }\n \n int count = 0;\n int upperLimit = Integer.MAX_VALUE;\n for (int i = arr.length - 1; i >= 0; i--) {\n if (max[i] == sorted[i]) {\n if (sorted[i] > upperLimit) continue;\n \n count++;\n upperLimit = arr[i];\n }\n }\n \n return count;\n }\n``` | 31 | 1 | [] | 3 |
max-chunks-to-make-sorted-ii | C++ 7 lines, O (n * log n) / O(n) | c-7-lines-o-n-log-n-on-by-votrubac-himo | Same as Max Chunks To Make Sorted (ver. 1). We just need to normalize the input array so it contains the indexes. We use the sorting for the normalization, and | votrubac | NORMAL | 2018-01-21T04:03:16.666000+00:00 | 2018-08-20T15:34:12.855193+00:00 | 3,459 | false | Same as [Max Chunks To Make Sorted (ver. 1)](https://discuss.leetcode.com/topic/117837/c-4-lines-o-n-o-1). We just need to normalize the input array so it contains the indexes. We use the sorting for the normalization, and one trick here is to have a stable sort, so that if we have the same value, the index will be lowest for the value appearing first.\n```\nint maxChunksToSorted(vector<int>& v) {\n vector<int> arr(v.size());\n iota(arr.begin(), arr.end(), 0);\n sort(arr.begin(), arr.end(), [&v](int i1, int i2) {return v[i1] == v[i2] ? i1 < i2 : v[i1] < v[i2]; });\n\n for (auto i = 0, max_i = 0, ch = 0; i <= arr.size(); ++i) {\n if (i == arr.size()) return ch;\n max_i = max(max_i, arr[i]);\n if (max_i == i) ++ch;\n }\n}\n``` | 26 | 2 | [] | 4 |
max-chunks-to-make-sorted-ii | C++ Simple and with algorithm Solution O(n) time and space both. | c-simple-and-with-algorithm-solution-on-k3l0u | \nlet\'s take an example: \n || || ||\narr[] = 30 10 2 | aman_2_0_2_3 | NORMAL | 2022-02-17T10:56:50.083950+00:00 | 2022-02-17T10:57:09.567100+00:00 | 1,554 | false | ```\nlet\'s take an example: \n || || ||\narr[] = 30 10 20 || 40 || 60 50 || 75 70\nleft_max = 30 30 30 || 40 || 60 60 || 75 75\nright _min = 10 10 20 || 40 || 50 50 || 70 70\n || || ||\nhere we need a variable that will count the number of chunks.\nso take int count = 0;\n\nwhen we encounter (left_max[i] <= right_min) update count = count + 1.\nbut in the actual code i\'m taking only right_min vector not left_max,\nsince we can generate left_min value simultaneously within the loop.\n\nso that\'s it\n\n```\n**PLEASE UPVOTE if you like \uD83D\uDE01 If you have any question, feel free to ask.**\n```\nint maxChunksToSorted(vector<int>& arr) {\n \n int n = arr.size();\n vector<int> rightmin(n+1,INT_MAX);\n for(int i=n-1;i>=0;i--)\n {\n rightmin[i] = min(arr[i],rightmin[i+1]);\n }\n int count = 0;\n int leftmax = INT_MIN;\n for(int i=0;i<n;i++)\n {\n leftmax = max(leftmax,arr[i]);\n if(leftmax <= rightmin[i+1])\n {\n count++;\n }\n }\n return count++;\n \n }\n```\n**PLEASE UPVOTE if you like \uD83D\uDE01 If you have any question, feel free to ask.**\n | 20 | 0 | ['C', 'C++'] | 2 |
max-chunks-to-make-sorted-ii | 📌📌 Easy-to-Understand || 98% faster || Well-Explained 🐍 | easy-to-understand-98-faster-well-explai-pdc8 | IDEA:\nTake this [ 2, 1, 7, 6, 3, 5, 4, 9, 8 ] as an example and once try yourself to split it into maximum chunks using stack.\n\nYou will come to following co | abhi9Rai | NORMAL | 2021-10-02T12:18:08.660690+00:00 | 2021-10-02T12:20:24.514825+00:00 | 2,092 | false | ## IDEA:\n**Take this [ 2, 1, 7, 6, 3, 5, 4, 9, 8 ] as an example and once try yourself to split it into maximum chunks using stack.**\n\nYou will come to following conclusions : \n* The max number in the left chunk must always be <= the max number in the right chunk. \n\n* We only need to maintain the max number of each chunk in the stack. This is because if num[i] >= stack[-1], then num[i] must be bigger than all other elements in that chunk. \n* Otherwise if num[i] < stack[-1], then it must belong to the previous chunk regardless of whether num[i] is bigger than the other elements or not. Hence, only the max num in each chunk is relevant.\n\n**Implementation:**\n\n* So, we can loop through the array and maintain a stack. Each element in the stack represents a chunk.\n\n* Each time we encounter a num[i] that is bigger than or equal to the previous chunk max, we push it to the stack. If we encounter a smaller number, we must combine this number with the previous chunks. We do this by comparing with the top chunk in the stack and popping them off until we encounter a chunk with max number that is smaller than num[i]. \n* Then, we update the new combined chunk with the new max by pushing it back onto the stack. The number of elements in this stack at the end is the number of chunks.\n\n### CODE:\n\'\'\'\n\n\tclass Solution:\n def maxChunksToSorted(self, nums: List[int]) -> int:\n \n st = []\n for n in nums:\n if len(st)==0 or st[-1]<=n:\n st.append(n)\n else:\n ma = st[-1]\n while st and st[-1]>n:\n ma = max(ma,st.pop())\n st.append(ma)\n \n return len(st)\n\n**Thanks and *Upvote* if you like the idea!!\uD83E\uDD1E** | 20 | 0 | ['Stack', 'Python', 'Python3'] | 3 |
max-chunks-to-make-sorted-ii | Simple Stack O(n) Solution | simple-stack-on-solution-by-mehuljain53-l6ef | \n int maxChunksToSorted(vector& arr) {\n \n if(arr.size()==0)\n return 0;\n \n stack st;\n st.push(arr[0]);\n | mehuljain53 | NORMAL | 2018-11-25T08:05:27.777716+00:00 | 2018-11-25T08:05:27.777758+00:00 | 1,863 | false | \n int maxChunksToSorted(vector<int>& arr) {\n \n if(arr.size()==0)\n return 0;\n \n stack<int> st;\n st.push(arr[0]);\n for(int i=1;i<arr.size();i++){\n \n if(arr[i]>=st.top()){\n st.push(arr[i]);\n continue;\n }\n int temp = st.top();\n while(!st.empty() && arr[i] < st.top())\n st.pop();\n \n st.push(temp); \n }\n return st.size();\n } | 18 | 0 | [] | 4 |
max-chunks-to-make-sorted-ii | C++ O(N) solution with explanation | c-on-solution-with-explanation-by-varels-p0ql | If the range [L, R) is one of the chunks, than the values in range [L,R) should be the same after sorting. \nWe can extend this to say that the values in range | varelse | NORMAL | 2019-03-05T02:50:57.304937+00:00 | 2019-03-05T02:50:57.304994+00:00 | 891 | false | If the range [L, R) is one of the chunks, than the values in range [L,R) should be the same after sorting. \nWe can extend this to say that the values in range [0, R) should be the same after sorting(every chunk before [L, R) has the same property).\n\nTo check whether values in range [0, R) is the same after sorting, we only need to check \nif max of values in range [0,R) is smaller than or equal to the min of values in range [R, N). \nEach chunk is counted only once at its right boundary.\n```\nclass Solution {\npublic:\n int maxChunksToSorted(vector<int>& arr) {\n int N = arr.size();\n // Max[i]:Max value in range [0, i)\n vector<int> Max(N+1, INT_MIN);\n for(int i = 1 ; i <= N ; ++i)\n Max[i] = max(Max[i-1], arr[i-1]);\n \n // Min[i]:Min value in range [i,N)\n vector<int> Min(N+1, INT_MAX);\n for(int i = N - 1 ; i >= 0 ; --i)\n Min[i] = min(Min[i+1], arr[i]);\n \n // Calculate Chunks\n int nChunks = 0;\n for(int i = 1 ; i <= N ; ++i){\n // if max of range[0, i) <= min of range[i, N)\n // add 1 to number of chunks.\n nChunks += Max[i] <= Min[i];\n }\n return nChunks;\n }\n};\n``` | 14 | 0 | [] | 1 |
max-chunks-to-make-sorted-ii | Precise Python Stack 7 lines solution with explanation | precise-python-stack-7-lines-solution-wi-82qi | python\nclass Solution:\n def maxChunksToSorted(self, arr: List[int]) -> int:\n stack = [] # store a list of biggest element of each chunk\n fo | lyz1052 | NORMAL | 2019-10-06T02:44:42.986874+00:00 | 2019-10-06T02:45:40.177930+00:00 | 867 | false | ```python\nclass Solution:\n def maxChunksToSorted(self, arr: List[int]) -> int:\n stack = [] # store a list of biggest element of each chunk\n for n in arr:\n m = n # the biggest element from beginning to n\n while len(stack)>0 and stack[-1]>n:\n m = max(m, stack.pop())\n stack.append(m) # all element bigger than n was poped out of stack, so this is the biggest element\n return len(stack) # length of the chunks array\n```\n\nBecause no element will be visited over twice, this is a linear time complexity algorithm. | 13 | 0 | [] | 1 |
max-chunks-to-make-sorted-ii | Easy Solution || Greedy Approach || LeftMax And RightMin ||O(N) | easy-solution-greedy-approach-leftmax-an-q8ms | Intuition\nWe Cannot Make Chunk Untill Current Largest Element Doesn\'t Have Any element which are smaller than it on right hand side\n# Approach\nConsider the | brucewayne_5 | NORMAL | 2023-05-05T03:58:40.721776+00:00 | 2023-05-17T07:08:45.875562+00:00 | 644 | false | # Intuition\nWe Cannot Make Chunk Untill Current Largest Element Doesn\'t Have Any element which are smaller than it on right hand side\n# Approach\nConsider the arr=[3,2,1,5,4]\n**THOUGHT PROCESS**\nat i= 0 can we make a chunk here ?\nNo because there are smaller elements than 3 on its rhs\nat i= 1 can we make a chunk here ?\nNo because there are smaller elements than 2 on its rhs\nat i= 2 can we make a chunk here ?\nYes because there are no smaller elements than 1 on its rhs\nSo Number Of chunks=1;\nat i= 3 can we make a chunk here ?\nNo because there are smaller elements than 5 on its rhs\nat i= 4 can we make a chunk here ?\nYes because there are no smaller elements than 4 on its rhs\nSo Number Of chunks is equal to 2.\n**BUT** \nBut after thinking about more test cases i found that it will not work every testcase \nconsider array=[3,1,2,5,4]\nat i= 0 can we make a chunk here ?\nNo because there are smaller elements than 3 on its rhs\nat i= 1 can we make a chunk here ?\nYes because there are no smaller elements than 1 on its rhs\nBut it was Wrong , Because we have a 2 on the right of 1,\nSo if we break chunk as [3,1] and sorting it will doesn\'t ,make array as sorted.\n**So what should we track ?**\nThe Same Approach with Slight change :\nInstead Checking For every element ,we should track the larger elements from i=0 in the array.\n**How did it strike to me ?**\nconsider the same example where my first approach is failed\narr= [3,1,2,5,4]\nhere at i=1 and arr[i]=1 there no elements which are smaller than 1 on rhs.\nbut **we have a 3 on left of 1 and 2 on right of 1 where 3>2 which means even though we doesn\'t have any elements smaller than current element , we have elements which are smaller than its previous elements .\nso if we can track the maximum elements from the left and applying same logic will work here**\narr=[3,1,2,5,4]\nat i=0 currentmax=3 there are smaller elements than 3 on its rhs.\nat i=1 currentmax=3 there are smaller elements than 3 on its rhs.\nat i=2 currentmax=3 there are no smaller elements than 3 on its rhs\nhence we can make a chunk here.\nat i=3 currentmax=5 there are smaller elements than 5 on its rhs.\nat i=4 currentmax=5 there are no smaller elements than 5 on its rhs\nhence we can make a chunk here.\nso total number of chunks =2\nHope You understand the Solution\n**Please upvote if you understand the solution**\n\n\n\n\n\n\n# Complexity\n- Time complexity:\nO(N)\n- Space complexity:\'\nO(N)\n\n# Code\n```\nclass Solution {\npublic:\n int maxChunksToSorted(vector<int>& arr) {\n int n=arr.size();\n vector<int>rightmin(n);\n vector<int>leftmax(n);\n // calculate maximum elements from left side\n leftmax[0]=arr[0];\n for(int i=1;i<n;i++)\n {\n leftmax[i]=max(leftmax[i-1],arr[i]);\n }\n // calculate minimum elements from right side\n rightmin[n-1]=arr[n-1];\n for(int i=n-2;i>=0;i--)\n {\n rightmin[i]=min(arr[i],rightmin[i+1]);\n }\n /*atleast there will be one chunk \n the total array can be considered as a chunk */\n int chunks=1;\n for(int i=0;i<n-1;i++)\n {\n if(leftmax[i]<=rightmin[i+1]) chunks++;\n }\n return chunks;\n\n }\n};\n``` | 12 | 0 | ['Dynamic Programming', 'Greedy', 'Suffix Array', 'C++'] | 1 |
max-chunks-to-make-sorted-ii | TypeScript, simple solution | Runtime beats 100%, Memory beats 64.29% | typescript-simple-solution-runtime-beats-sjh2 | Intuition\n To split the array into the maximum number of chunks, each chunk should be sorted individually and then concatenated to form a fully sorted array.\n | r9n | NORMAL | 2024-09-05T16:02:54.131353+00:00 | 2024-09-05T16:06:35.522445+00:00 | 114 | false | # Intuition\n To split the array into the maximum number of chunks, each chunk should be sorted individually and then concatenated to form a fully sorted array.\n\n# Approach\nTrack Extremes: Record maximum values up to each index and minimum values from each index.\n\nCount Valid Chunks: Count positions where the maximum value to the left is \u2264 minimum value to the right.\n\n# Complexity\n- Time complexity:\nO(n) \u2014 Single pass for maxLeft and minRight, and another for counting.\n\n- Space complexity:\nO(n) \u2014 Arrays to store extremes.\n\n# Code\n```typescript []\nfunction maxChunksToSorted(arr: number[]): number {\n const n = arr.length;\n const maxLeft: number[] = new Array(n);\n const minRight: number[] = new Array(n);\n \n maxLeft[0] = arr[0];\n for (let i = 1; i < n; i++) {\n maxLeft[i] = Math.max(maxLeft[i - 1], arr[i]);\n }\n \n minRight[n - 1] = arr[n - 1];\n for (let i = n - 2; i >= 0; i--) {\n minRight[i] = Math.min(minRight[i + 1], arr[i]);\n }\n \n let chunks = 0;\n for (let i = 0; i < n - 1; i++) {\n if (maxLeft[i] <= minRight[i + 1]) {\n chunks++;\n }\n }\n \n return chunks + 1; // Include the last chunk\n}\n\n``` | 11 | 0 | ['TypeScript'] | 0 |
max-chunks-to-make-sorted-ii | Python solution using right min and current max | python-solution-using-right-min-and-curr-edt2 | Algorithm and Intuition: We have to maximize the number of chunks or partitions we can make. The idea is suppose we are at index i and we know that the minimum | siddharth4158 | NORMAL | 2022-03-06T11:33:09.938116+00:00 | 2022-03-06T11:33:09.938141+00:00 | 825 | false | **Algorithm and Intuition:** We have to maximize the number of chunks or partitions we can make. The idea is suppose we are at index i and we know that the minimum element from i+1 to last element is greater than or equal to the maximum element till index i then we can say that this partition between index i and i+1 is valid. Because in a sorted array, the elements present before index i will remain in the left part (0 to i) only and after index i will remain in right part (i+1 to n-1) only.\n\n**Steps:**\n\n* Create a **rightmin array** storing the **minimum element from i to n-1** (length of the array) by traversing the array backwards.\n* Iterate over the array from front and keep track of the **maximum element till current index** (maxele).\n* If **maxele** till index i is less than the **rightmin[i+1]** than it is a valid partition or chunk, so increment the answer variable.\n\n```\nans = 0\nn = len(arr)\nrightmin = [math.inf]*(n+1)\ncurrmin = math.inf\nmaxele = arr[0]\n\n# loop from backward of the array to get the minimum element from i to n\nfor j in range(n-1, -1, -1):\n\tif arr[j]<currmin:\n\t\tcurrmin = arr[j]\n\trightmin[j] = currmin\n\n#Forward loop to compare with current max element (maxele) and count the valid partitions\nfor i in range(len(arr)):\n\tif maxele<arr[i]:\n\t\tmaxele = arr[i]\n\tif maxele<=rightmin[i+1]:\n\t\tans+=1\nreturn ans\n```\n\nLet me know if there is any issue in understanding the solution. Please upvote if you find it useful :) | 11 | 0 | ['Greedy', 'Python', 'Python3'] | 1 |
max-chunks-to-make-sorted-ii | C++ solution O(N) Time complexity| With proper explaination | c-solution-on-time-complexity-with-prope-jk7q | Steps to follow:\n1) make a vector right of size arr.size() +1 which will having minimum from i th index to arr.size() -1;\n2) make a variable left_max and coun | kritika_12 | NORMAL | 2021-07-03T13:55:57.299855+00:00 | 2021-07-04T07:09:05.241679+00:00 | 863 | false | **Steps to follow:**\n1) make a vector right of size arr.size() +1 which will having minimum from i th index to arr.size() -1;\n2) make a variable left_max and count_chunks to calculate the maximum of chunks required to make the given array sorted.\n3) iterate from 0th index to arr.size()\n4) keep updating left_ max that is max of left_max and arr[i]\n5) if the left-max is smaller or equal to(why equal to also, because we want to have maximum chunks) right[i+1] than increment count_chunks\n6) count_chunks will return the maxium chunks required to make an array sorted\n\nThis solution has **O(N) time complexity**\n\n```\nclass Solution {\npublic:\n int maxChunksToSorted(vector<int>& arr) {\n vector<int>right(arr.size()+1);\n right[arr.size()] = INT_MAX;\n \n for(int i =arr.size()-1 ; i>= 0; i--){\n right[i] = min(right[i+1], arr[i]);\n }\n int left_max = INT_MIN;\n int count_chunks =0;\n for(int i =0; i<arr.size(); i++){\n left_max = max(left_max, arr[i]);\n if(left_max <= right[i+1]) count_chunks++; \n }\n return count_chunks;\n }\n};\n```\n**Please upvote if you like the solution and comment if have doubts** | 11 | 2 | ['C', 'C++'] | 0 |
max-chunks-to-make-sorted-ii | C++ O(n) greedy with proof | c-on-greedy-with-proof-by-imrusty-laf5 | Going from left to right, if there is a number to the right that is less than the current max of the chunk or if the chunk is empty, then the next number to the | imrusty | NORMAL | 2018-01-27T20:50:45.489000+00:00 | 2018-08-20T15:49:48.106142+00:00 | 1,631 | false | Going from left to right, if there is a number to the right that is less than the current max of the chunk or if the chunk is empty, then the next number to the right has to be included in the current chunk. Now if all the numbers to the right are at least as large as all numbers in the current chunk, then in an optimal solution, we can always split the current chunk out.\n```\nclass Solution {\npublic:\n int maxChunksToSorted(vector<int>& a) {\n int n = a.size();\n vector<int> b(n);\n b[n-1] = a[n-1];\n for( int i = n-2; i >=0; --i) b[i] = min(a[i],b[i+1]);\n int cnt = 1, ans = 1, mx = a[0];\n for (int i=1; i <n;++i) {\n if (b[i] < mx) ++cnt,mx = max(mx,a[i]);\n else cnt = 1, ++ans, mx = a[i];\n }\n return ans;\n }\n};\n``` | 11 | 0 | [] | 2 |
max-chunks-to-make-sorted-ii | Python 3 || 2 lines, accumulate || T/S: 97% / 40% | python-3-2-lines-accumulate-ts-97-40-by-eucc2 | Here\'s the plan:\nWe accumulate the sums of both arr and sorted(arr). A little thinking leads one to this conclusion: whenever the accumulated sums are equal, | Spaulding_ | NORMAL | 2024-01-18T21:27:13.559296+00:00 | 2024-05-29T19:28:12.932662+00:00 | 529 | false | Here\'s the plan:\nWe accumulate the sums of both `arr` and `sorted(arr)`. A little thinking leads one to this conclusion: whenever the accumulated sums are equal, we can break off a chunk. Thus, the problem reduces to counting the number of instances in which the respectives accumulated sums are equal.\n\n(Yes, I know it could be a one-liner, but I\'m not just that guy.)\n```\nclass Solution:\n def maxChunksToSorted(self, arr: List[int]) -> int:\n\n acc = zip(accumulate(arr), accumulate(sorted(arr)))\n\n return len(tuple(filter(lambda x: x[0] == x[1],acc)))\n```\n[https://leetcode.com/problems/max-chunks-to-make-sorted-ii/submissions/1150149800/](http://)\n\nI could be wrong, but I think that time complexity is *O*(*N*log*N*) and space complexity is *O*(*N*), in which *N* ~ `len(arr)`. | 9 | 0 | ['Python3'] | 0 |
max-chunks-to-make-sorted-ii | Python3 - stack O(n) 8 lines 56ms 100% | python3-stack-on-8-lines-56ms-100-by-yun-r0hk | Keep a non-decreasing stack, whenever a number is non-decreasing, add it to the stack. Note that the stack is actually keep the maximum value of each partition. | yunqu | NORMAL | 2021-04-14T21:39:46.847525+00:00 | 2021-04-14T21:42:18.097926+00:00 | 439 | false | Keep a non-decreasing stack, whenever a number is non-decreasing, add it to the stack. Note that the stack is actually keep the maximum value of each partition. \n\nWhenever there is a decreasing number, check if it is possible to merge with the immediate previous partition, i.e. stack[-1]; if it is even smaller than 2 groups before, we need to pop the stack and update the maximum value of that partition. \n\nFor example, let\'s go through the example 5,3,2,4,5,1\n* add 5 to stack, stack = [5]\n* 3 < 5, so ignore it since it can be merged with the previous partition, and stack = [5]; note it means that parition has maximum value 5 still.\n* 2 < 5 same as the previous iteration. stack = [5].\n* 4 < 5 same as before. stack = [5]\n* 6 >= 5, add to stack. stack = [5,6]. This means we can have up tp 2 paritions at this point.\n* stack has more than 2 elements, and 1 < stack[-2] = 5, this means we cannot simply merge 1 into the partition [6], so we need to pop 6; this also means we will merge this partition with partition [5]. After merging, the new parition will have maximum value 6. So finally stack = [6], indicating we have 1 parition with maximum value of 6. \n\nTime complexity O(n).\n\n```python\nclass Solution:\n def maxChunksToSorted(self, arr: List[int]) -> int:\n stack = []\n for a in arr:\n if not stack or a >= stack[-1]:\n stack += a,\n while len(stack) >= 2 and a < stack[-2]:\n j = stack.pop()\n stack[-1] = j\n return len(stack)\n``` | 8 | 1 | [] | 1 |
max-chunks-to-make-sorted-ii | n*lon(n) easy solution | 4 line logic | sorting | nlonn-easy-solution-4-line-logic-sorting-hgvk | ```\nint maxChunksToSorted(vector& v) \n {\n vector v1=v;\n\t\t\n sort(v1.begin(),v1.end());\n\t\t\n int n=v.size(),i,j,ans=0;\n\t\t//su | kevaljoshi2312 | NORMAL | 2021-02-26T05:42:23.877598+00:00 | 2021-02-26T05:42:23.877634+00:00 | 438 | false | ```\nint maxChunksToSorted(vector<int>& v) \n {\n vector<int> v1=v;\n\t\t\n sort(v1.begin(),v1.end());\n\t\t\n int n=v.size(),i,j,ans=0;\n\t\t//sum1 stores sum of original array while sum2 stores sum of sorted array\n long long sum1=0,sum2=0;\n for(i=0;i<n;i++)\n {\n sum1+=v[i];\n sum2+=v1[i];\n if(sum1==sum2)\n ans++;\n }\n return ans;\n } | 8 | 0 | ['C', 'Sorting', 'C++'] | 1 |
max-chunks-to-make-sorted-ii | Java O(n) Solution | java-on-solution-by-himanshuchhikara-rbyb | In general idea is maximum till now should be less than minimum from right then only we can make chunk .(minimum have place in right array itself because it is | himanshuchhikara | NORMAL | 2021-03-15T08:13:03.683934+00:00 | 2021-03-19T09:10:41.756459+00:00 | 631 | false | In **general idea** is maximum till now should be less than minimum from right then only we can make chunk .(minimum have place in right array itself because it is greater than maximum of left).\nIf minimum from right is less than maximum from left then in sorted array the position of minimum is in left part so therefore we cannot create chunk in that case.. \n \nSteps to follow:\n1. Always check for edge case if array length is 0 what to do.\n2. Make 2 arrays maximum from left and minimum from left.\n3. now check maximum till now <= minimum from right then chunk is possible(increase chunk count)\n\n```\nclass Solution {\n public int maxChunksToSorted(int[] arr) {\n \n if(arr.length==0) return 0;\n int[] maxfromstart=new int[arr.length];\n int[] minfromlast=new int[arr.length];\n \n maxfromstart[0]=arr[0];\n for(int i=1;i<arr.length;i++){\n if(arr[i]>maxfromstart[i-1]){\n maxfromstart[i]=arr[i];\n }else{\n maxfromstart[i]=maxfromstart[i-1];\n }\n }\n \n minfromlast[arr.length-1]=arr[arr.length-1];\n for(int i=arr.length-2;i>=0;i--){\n if(arr[i]<minfromlast[i+1]){\n minfromlast[i]=arr[i];\n }else{\n minfromlast[i]=minfromlast[i+1];\n }\n }\n \n int chunk=1; \n for(int i=0;i<arr.length-1;i++){\n if(maxfromstart[i]<=minfromlast[i+1]){\n chunk++;\n }\n }\n return chunk;\n }\n}\n```\nTime:O(N) and Space:O(N)\nPlease **upvote** if you find it helpful :) | 7 | 1 | ['Array', 'Java'] | 1 |
max-chunks-to-make-sorted-ii | [C++] multiset | c-multiset-by-alexander-c7ky | \nclass Solution {\npublic:\n int maxChunksToSorted(vector<int>& a) {\n int chunks = 0;\n multiset<int> cur;\n multiset<int> expect;\n | alexander | NORMAL | 2018-01-21T04:01:30.390000+00:00 | 2018-01-21T04:01:30.390000+00:00 | 957 | false | ```\nclass Solution {\npublic:\n int maxChunksToSorted(vector<int>& a) {\n int chunks = 0;\n multiset<int> cur;\n multiset<int> expect;\n vector<int> sorted = a;\n sort(sorted.begin(), sorted.end());\n for (int i = 0; i < a.size(); i++) {\n expect.insert(sorted[i]);\n cur.insert(a[i]);\n if (cur == expect) chunks++;\n }\n return chunks;\n }\n};\n``` | 7 | 1 | [] | 3 |
max-chunks-to-make-sorted-ii | Java Solution beats 99.9% with detailed example and explanation | java-solution-beats-999-with-detailed-ex-t9o6 | Problem Invariant: For an element, if all the numbers to its left are smaller or equal to all the numbers to its right, we can always insert a split point betwe | dibugger | NORMAL | 2019-05-24T22:03:30.261831+00:00 | 2019-05-24T22:03:30.261876+00:00 | 503 | false | Problem Invariant: For an element, if all the numbers to its left are smaller or equal to all the numbers to its right, we can always insert a split point between the element and its next element which separate the array into two parts and after we sort the two parts individually, the concatenation of them will be a sorted array.\n\nExample:\n\nindex: 0 1 2 3 4\narr[i] 2 1 3 4 4\nmaxLeft 2 2 3 4 4\nminRight 1 1 3 4 4\n\nwhen i = 1, maxLeft[i] <= minRight[i + 1] (maxLeft[i] includes the i-th number itself but minRight[i +1] only counts the numbers to its right), then we can insert a split point between index 1 and 2. This will generate two parts [2,1] and [3,4,4]. When we sort the two parts individually, the concatenation of the sorted arrays will also be a sorted array. [1,2] + [3,4,4] => [1,2,3,4,4].\n\nWhen i = 2, 3. The same analysis apply to them.\n\nCode:\n```\n public int maxChunksToSorted(int[] arr) {\n int n;\n if (arr == null || (n = arr.length) == 0) {\n return 0;\n }\n int[] maxLeft = new int[n];\n int[] minRight = new int[n];\n \n maxLeft[0] = arr[0];\n for (int i = 1; i < n; i++) {\n maxLeft[i] = Math.max(maxLeft[i - 1], arr[i]);\n }\n \n minRight[n - 1] = arr[n - 1];\n for (int i = n - 2; i >= 0; i--) {\n minRight[i] = Math.min(minRight[i + 1], arr[i]);\n }\n \n int numOfInsertion = 0;\n for (int i = 0; i < n - 1; i++) {\n if (maxLeft[i] <= minRight[i + 1]) {\n numOfInsertion++;\n }\n }\n return numOfInsertion + 1;\n }\n``` | 6 | 0 | [] | 0 |
max-chunks-to-make-sorted-ii | Simple 9 Lines C++, O(n) time, O(n) space using stack. | simple-9-lines-c-on-time-on-space-using-k8ykl | Approach\nKeep track of maximum element found, pop from stack till current element is less than top of stack. Finally push the current max onto the stack.\n\n# | JatinVijay | NORMAL | 2024-08-19T11:26:44.026669+00:00 | 2024-08-19T11:26:44.026690+00:00 | 416 | false | # Approach\nKeep track of maximum element found, pop from stack till current element is less than top of stack. Finally push the current max onto the stack.\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int maxChunksToSorted(vector<int>& arr) {\n stack<int> st;\n int n = arr.size();\n int curmax = -1;\n for(int i = 0;i<n;i++){\n curmax = max(curmax,arr[i]);\n while(st.size() && st.top()>arr[i]){\n st.pop();\n }\n st.push(curmax);\n }\n\n return st.size();\n\n\n }\n};\n``` | 5 | 1 | ['C++'] | 0 |
max-chunks-to-make-sorted-ii | Simple java using NGE | simple-java-using-nge-by-tryambak_trived-s4ha | \n\n# Code\n\nclass Solution {\n public int maxChunksToSorted(int[] arr) {\n Stack<Integer> a= new Stack<Integer>();\n\n for(int i=0;i<arr.leng | Tryambak_Trivedi | NORMAL | 2024-03-11T10:25:53.905249+00:00 | 2024-03-11T10:25:53.905280+00:00 | 372 | false | \n\n# Code\n```\nclass Solution {\n public int maxChunksToSorted(int[] arr) {\n Stack<Integer> a= new Stack<Integer>();\n\n for(int i=0;i<arr.length;i++)\n {\n int mx=arr[i];\n while(!a.isEmpty()&&arr[i]<a.peek())\n {\n mx= Math.max(mx,a.peek());\n a.pop();\n }\n\n a.push(mx);\n }\n return(a.size());\n }\n}\n``` | 5 | 0 | ['Java'] | 0 |
max-chunks-to-make-sorted-ii | C++ , with explanation and thought process | c-with-explanation-and-thought-process-b-i6pn | \n lets say we have something like this\n (a1----a2) | (a3-------a4) | (a5--------a6)\n part1 part2 part3\n these are the chunks | uttu_dce | NORMAL | 2021-08-12T14:00:16.169546+00:00 | 2021-08-12T14:00:16.169595+00:00 | 184 | false | \n lets say we have something like this\n (a1----a2) | (a3-------a4) | (a5--------a6)\n part1 part2 part3\n these are the chunks (sorting them individually sorts the entire array)\n lets say after sorting our new array becomes the following \n (b1----b2) | (b3-------b4) | (b5--------b6)\n part1 part2 part3\n so as the array is sorted , these properties should hold\n b1 <= b2\n b2 <= b3\n b3 <= b4\n b4 <= b5\n b5 <= b6\n\n so lets see what actually b1,b2,b3,b4,b5,b6 are\n \n b1 is the minimum element of the part1\n b2 is the maximum element of part1\n\n b3 is minimum element of part2\n b4 is maximum element of part2\n\n see these conditions b2 <= b3 and b4 <= b5\n these conditions tell us that whenever it is possible to create a partition here, the maximum of the current part should be less than \n or equal to the minimum of the next part\n\n so all we do is maintain leftMax and rightMin array and apply these checks\n\n \n\n\n```\nclass Solution {\npublic:\n \n \n int maxChunksToSorted(vector<int>& arr) {\n if(arr.size() == 1) return 1;\n if(arr.size() == 0) return 0;\n \n int n = arr.size();\n vector<int> leftMax(n+1);\n vector<int> rightMin(n+1);\n\n int maxTillHere = INT_MIN; \n for(int i=0; i<n; i++) {\n maxTillHere = max(maxTillHere , arr[i]);\n leftMax[i] = maxTillHere;\n }\n \n leftMax[n] = leftMax[n-1];\n \n int minTillHere = INT_MAX;\n for(int j=n-1; j>=0; j--) {\n minTillHere = min(minTillHere , arr[j]);\n rightMin[j] = minTillHere;\n }\n rightMin[n] = INT_MAX;\n\n int cnt = 0;\n for(int i=0; i<n; i++) \n {\n if(leftMax[i] <= rightMin[i+1]) cnt++;\n }\n return cnt;\n \n }\n};\n\n\n``` | 5 | 0 | [] | 0 |
max-chunks-to-make-sorted-ii | Python solution | python-solution-by-zitaowang-wfxj | Given an array [a_1, a_2, ..., a_n], we can make a split at some index i, such that sorting [a_1, ..., a_i] and [a_(i+1), ..., a_n] sorts the whole array, if an | zitaowang | NORMAL | 2019-01-03T13:10:40.783298+00:00 | 2019-01-03T13:10:40.783353+00:00 | 326 | false | Given an array `[a_1, a_2, ..., a_n]`, we can make a split at some index `i`, such that sorting `[a_1, ..., a_i]` and `[a_(i+1), ..., a_n]` sorts the whole array, if and only if `max(a_1,...,a_i) < min(a_(i+1),...a_n)`. Hence a simple algorithm would be to initialize an array `max_left` of length `n`, and iterate over `arr` from the left, and populate `max_left[i]` with the maximum in `[a_1, ..., a_i]`. Similarly, we initialize an array `min_right` of length `n`, and iterate over `arr` from the right, and populate `min_right[i]` with the minimum in `[a_i, ..., a_n]`. Finally, we initialize a `counter = 1`, and iterate `i` over `range(n-1)`, and compare `max_left[i]` with `min_right[i+1]`, if `max_left[i] <= min_right[i+1]`, we increment the counter by `1`. Finally, we return `counter`.\n\nTime complexity: `O(n)`, space complexity: `O(n)`.\n\n```\nclass Solution(object):\n def maxChunksToSorted(self, arr):\n """\n :type arr: List[int]\n :rtype: int\n """\n n = len(arr)\n min_right = [0]*n\n max_left = [0]*n\n \n for i in range(n):\n if i == 0:\n max_left[i] = arr[i]\n else:\n max_left[i] = max(arr[i], max_left[i-1])\n for i in range(n-1, -1, -1):\n if i == n-1:\n min_right[i] = arr[i]\n else:\n min_right[i] = min(arr[i], min_right[i+1])\n \n res = 1\n for i in range(n-1):\n if max_left[i] <= min_right[i+1]:\n res += 1\n return res\n``` | 5 | 0 | [] | 0 |
max-chunks-to-make-sorted-ii | Beats 100% 🔥 | Easy & Intuitive Solution 💡 | Clean Code Explained 🚀 | beats-100-easy-intuitive-solution-clean-l5jqz | IntuitionThe key to solving this problem is understanding that each "chunk" is a segment of the array where all elements can be sorted independently to form par | ayushku22 | NORMAL | 2024-12-19T22:44:12.054455+00:00 | 2024-12-19T22:44:12.054455+00:00 | 293 | false | # Intuition
The key to solving this problem is understanding that each "chunk" is a segment of the array where all elements can be sorted independently to form part of the sorted array. To determine when a chunk ends, we need to check if the cumulative difference between the sorted array and the original array is zero up to that point. If the difference becomes zero, it indicates that all elements up to that index can form a valid chunk.
# Approach
1. **Copy and Sort**: First, create a copy of the input array and sort it. This gives us the reference for the target order.
2. **Track Difference**: Use a variable `dif` to track the cumulative difference between the sorted and the original arrays at each index.
- For each element, update `dif` by adding the difference between the corresponding elements of the sorted array and the original array.
3. **Check for Chunks**: If `dif` becomes zero at any index, it means that all elements up to that index in the original array can be sorted independently to match the sorted array.
4. **Count Chunks**: Increment the `count` whenever `dif` is zero.
5. **Return Result**: At the end, `count` gives the maximum number of chunks.
# Complexity
- **Time complexity**:
Sorting the array takes $$O(n \log n)$$, and iterating through the array takes $$O(n)$$.
Therefore, the overall complexity is $$O(n \log n)$$.
- **Space complexity**:
The additional space used is $$O(n)$$ for storing the copy of the array. Thus, the space complexity is $$O(n)$$.
# Code
```cpp
class Solution {
public:
int maxChunksToSorted(vector<int>& arr) {
vector<int> dum = arr;
sort(arr.begin(), arr.end());
long long dif = 0;
int count = 0, n = arr.size();
for(int i=0; i<n; i++){
dif += (arr[i]-dum[i]);
count += (dif==0);
}
return count;
}
};
| 4 | 0 | ['C++'] | 2 |
max-chunks-to-make-sorted-ii | ✅✅Faster || Easy To Understand || C++ Code | faster-easy-to-understand-c-code-by-__kr-aib0 | Using Two Extra Arrays\n\n Time Complexity :- O(N)\n\n Space Complexity :- O(N)\n\n\nclass Solution {\npublic:\n int maxChunksToSorted(vector<int>& arr) {\n | __KR_SHANU_IITG | NORMAL | 2022-10-08T15:08:37.434713+00:00 | 2022-10-08T15:08:37.434750+00:00 | 1,538 | false | * ***Using Two Extra Arrays***\n\n* ***Time Complexity :- O(N)***\n\n* ***Space Complexity :- O(N)***\n\n```\nclass Solution {\npublic:\n int maxChunksToSorted(vector<int>& arr) {\n \n int n = arr.size();\n \n // left_max[i] will store the maximum till ith from left side\n \n vector<int> left_max(n, 0);\n \n // fill left_max\n \n left_max[0] = arr[0];\n \n for(int i = 1; i < n; i++)\n {\n left_max[i] = max(left_max[i - 1], arr[i]);\n }\n \n // right_min[i] will store the minimum till ith from right side\n \n vector<int> right_min(n, 0);\n \n // fill right_min array\n \n right_min[n - 1] = arr[n - 1];\n \n for(int i = n - 2; i >= 0; i--)\n {\n right_min[i] = min(right_min[i + 1], arr[i]);\n }\n \n // if at any index i we are having maximum till ith from left side is smaller than minimum till (i + 1)th from right side, then we found chunk\n \n int count = 0;\n \n for(int i = 0; i < n - 1; i++)\n {\n if(left_max[i] <= right_min[i + 1])\n {\n count++;\n }\n }\n \n // there will be always a partition at (n - 1)th index\n \n count++;\n \n return count;\n }\n};\n``` | 4 | 0 | ['Array', 'Greedy', 'C', 'C++'] | 1 |
max-chunks-to-make-sorted-ii | [Python] simple and faster than 96.5% | python-simple-and-faster-than-965-by-spa-8yyj | There is one rule to be maintained in any correct split to chunks\n The max number in every chunk should be <= than the max number in the following chunk\n\nThe | spandei | NORMAL | 2022-05-09T21:41:01.443186+00:00 | 2022-05-09T21:42:30.175890+00:00 | 549 | false | There is one rule to be maintained in any correct split to chunks\n* The max number in every chunk should be <= than the max number in the following chunk\n\nThen, we can build the greedy O(n) algorithm to iterate over nums in array and maintain the sequence of max numbers in chunks on each step (i.e. on step **i** we will have the sequence for elements with indices **0...i**)\nIn order to do that we will maintain a monotonic non-decreasing stack.\nFor each num in array:\n1. Initialize **m=num**\n2. Num is in the same chunk as all elements of stack for which **num < stack[i]**. Stack is monotonic non-decreasing (stack[0] <= stack[1] <= ... <= stack[-1]), so we can pop from the end of stack until we find that **num < stack[-1]**. Save max of the new last chunk to **m**.\n3. Append **m** to the stack\n\nThe algorithm is correct because:\nIf we popped any elements on step 2 - then **m** is the max element of the last chunk.\nOtherwise **m** is **num**, which is the max element of the new last chunk.\n\n```\nclass Solution:\n def maxChunksToSorted(self, arr: List[int]) -> int:\n stack = []\n for num in arr:\n m = num\n while stack and num < stack[-1]:\n m = max(m, stack.pop())\n stack.append(m)\n return len(stack)\n``` | 4 | 0 | ['Greedy', 'Monotonic Stack', 'Python'] | 0 |
max-chunks-to-make-sorted-ii | C++|Stack solution | cstack-solution-by-bit_legion1010-npiv | Please upvote if this will help you!!\uD83D\uDE0A\n\n\nclass Solution {\npublic:\n int maxChunksToSorted(vector<int>& arr) {\n stack<int>st;\n \n | bit_legion1010 | NORMAL | 2022-03-22T05:14:34.174027+00:00 | 2022-03-22T05:14:34.174079+00:00 | 531 | false | Please upvote if this will help you!!\uD83D\uDE0A\n\n```\nclass Solution {\npublic:\n int maxChunksToSorted(vector<int>& arr) {\n stack<int>st;\n \n for(int i=0;i<arr.size();i++){\n int num = arr[i];\n while(!st.empty()&& st.top()>arr[i]){\n num = max(num,st.top());\n st.pop();\n }\n st.push(num);\n }\n return st.size();\n }\n};\n``` | 4 | 0 | ['Stack', 'C', 'Monotonic Stack', 'C++'] | 0 |
max-chunks-to-make-sorted-ii | Java Solution, Beats 100%, left max and right min approach | java-solution-beats-100-left-max-and-rig-xmu1 | \nclass Solution {\n public int maxChunksToSorted(int[] arr) {\n\t \n\t // upvote if you like \n \n // Problem based on chaining techniq | kurmiamreet44 | NORMAL | 2022-03-21T18:28:53.482294+00:00 | 2022-03-21T18:29:33.356701+00:00 | 668 | false | ```\nclass Solution {\n public int maxChunksToSorted(int[] arr) {\n\t \n\t // upvote if you like \n \n // Problem based on chaining technique\n // First we will create a right minimum array\n \n int [] rmin = new int[arr.length+1];\n rmin[arr.length] = Integer.MAX_VALUE;\n \n for(int i=arr.length-1;i>=0;i--)\n {\n rmin[i] = Math.min(rmin[i+1], arr[i]);\n }\n // traversing through the left maximum array and checking if lmax <rmin \n \n int lmax = Integer.MIN_VALUE;\n \n int count = 0;\n for(int i=0;i<arr.length;i++)\n {\n lmax = Math.max(lmax,arr[i]);\n \n if(lmax<=rmin[i+1])\n {\n count++;\n }\n }\n return count;\n }\n}\n``` | 4 | 0 | ['Java'] | 2 |
max-chunks-to-make-sorted-ii | JAVA || 0 ms || full explanation using comments || faster than 100% submission || O(n) time | java-0-ms-full-explanation-using-comment-eq82 | \nclass Solution {\n public int maxChunksToSorted(int[] arr) {\n int[] leftMax=new int[arr.length]; // this array stores the max value from 0 to it | nandini29110 | NORMAL | 2021-12-02T15:11:38.993060+00:00 | 2021-12-02T15:11:38.993090+00:00 | 207 | false | ```\nclass Solution {\n public int maxChunksToSorted(int[] arr) {\n int[] leftMax=new int[arr.length]; // this array stores the max value from 0 to ith index at ith index\n leftMax[0]=arr[0]; \n int[] rightMin=new int[arr.length]; // this array stores the min value from i to arr.length-1 at ith index\n rightMin[arr.length-1]=arr[arr.length-1];\n for(int i=1;i<arr.length;i++){\n leftMax[i]=Math.max(leftMax[i-1],arr[i]);\n }\n for(int i=arr.length-2;i>=0;i--){\n rightMin[i]=Math.min(rightMin[i+1],arr[i]);\n }\n \n // now we traverse in leftMax array and rightMin array and compare the ith value of leftMax to (i+1)th value of rightMin array\n // if we find leftMax[i] <= rightMin[i+1] , then it means all the elements from 0 to i is less then or equal to all the elelemts from i+1 to arr.length-1 , and it means if we sort the left and right part separatly then also we got a perfectly sorted array.\n \n int i=0;\n int count=0; // count of number of partitions\n while(i<arr.length-1){\n if(leftMax[i]<=rightMin[i+1]){\n count++;\n }\n i++;\n }\n \n return count+1; // the number of chunks is one more than the number of partitions \n \n }\n}\n``` | 4 | 0 | [] | 1 |
max-chunks-to-make-sorted-ii | Max Chunks To make sorted II | max-chunks-to-make-sorted-ii-by-vk25-5ddf | Here we are using chaining technique but slight a different version of it. Firstly we have created a right min array which will store min element from right. Th | vk25 | NORMAL | 2021-07-28T15:31:10.180863+00:00 | 2021-07-28T15:31:10.180897+00:00 | 208 | false | Here we are using chaining technique but slight a different version of it. Firstly we have created a right min array which will store min element from right. Then we will generate left max array storing left max. While traversing whenever we encounterd a point where leftmax element becomes less than minimum of right max array. We will count it as a chunk and increment the value of count. We will keep doing this until array.length! \n```\nclass Solution {\n public int maxChunksToSorted(int[] arr) {\n //Form right min array\n int rmin[]=new int[arr.length+1];\n rmin[arr.length]=Integer.MAX_VALUE;\n for(int i=arr.length-1;i>=0;i--){\n rmin[i]=Math.min(rmin[i+1],arr[i]);\n }\n \n //Generating left max array and keeping track of count\n int lmax=Integer.MIN_VALUE;\n int c=0;\n for(int i=0;i<arr.length;i++){\n lmax=Math.max(lmax,arr[i]);\n if(lmax<=rmin[i+1])\n c++;\n }\n return c;\n }\n \n}\n``` | 4 | 0 | ['Java'] | 0 |
max-chunks-to-make-sorted-ii | C++ | Time Complexity 100 % | O(n) | c-time-complexity-100-on-by-divyam_sinha-h80e | Approach : A chunk can only be created when the maximum element in the left of the subarray is less than or equal to the smallest element in the right of the s | divyam_sinha | NORMAL | 2021-03-17T13:22:03.178882+00:00 | 2021-03-17T15:37:14.734902+00:00 | 228 | false | Approach : A chunk can only be created when the maximum element in the left of the subarray is less than or equal to the smallest element in the right of the sub array .\n\nEg : let nums = { 14 , 16 , 12 , 20 , 18 , 22 , 28 , 26 , 24 } ;\n\nhere we will compute max element so far from left to right as we have to check the maximum in the left subarray and compute min element so far from right to left as we have to check the min in the right subarray . \n\nmaxArr = { 14 , 16 , 16 , 20 , 20 , 22 , 28 , 28 , 28 }\nminArr = { 12 , 12 , 12 , 18 , 18 , 22 , 24 , 24 , 24 }\n\nhere we can see the at the 2nd idx the max element on the left is less than the min element on the right so , we have a chunk here \n\nhere n+1 length of vector and INT_MAX is used to handle the last chunk. \n\n\t\n\tint maxChunksToSorted(vector<int>& nums) {\n\t\t\tint n = nums.size() ;\n\t\t\tvector<int> minArr(n+1,INT_MAX) ; \n\t\t\tvector<int> maxArr(n+1,INT_MAX) ; \n\t\t\tint chunks = 0 ;\n\t\t\tmaxArr[0] = nums[0] ; \n\t\t\tminArr[n-1] = nums[n-1] ;\n\t\t\t// APPENDING MAX ELEMENTS \n\t\t\tfor(int i = 1 ; i < n ; i++){\n\t\t\t\tmaxArr[i] = max(maxArr[i-1] , nums[i]) ; \n\t\t\t}\n\t\t\t// APPENDING MIN ELEMENTS \n\t\t\tfor(int i = n-2 ; i >=0 ; i--){\n\t\t\t\tminArr[i] = min(minArr[i+1] , nums[i]) ; \n\t\t\t}\n\t\t\t// MAKING CHUNKS\n\t\t\tfor(int i = 0 ; i < n ; i++){\n\t\t\t\tif(maxArr[i] <= minArr[i+1]){ \n\t\t\t\t\tchunks++ ; \n\t\t\t\t}\n\t\t\t} \n\t\t\treturn chunks ; \n\t\t} | 4 | 0 | [] | 0 |
max-chunks-to-make-sorted-ii | [Java] O(n) time O(1) space. 9 lines beats 100% | java-on-time-o1-space-9-lines-beats-100-9ka7p | Based on monotonic stack approach well explained in this post.\n\n\n// 0 ms. 100%\npublic int maxChunksToSorted(int[] arr) {\n int top = 0;\n for(int a: a | shk10 | NORMAL | 2021-01-24T14:54:29.485892+00:00 | 2021-01-24T14:54:29.485923+00:00 | 565 | false | Based on monotonic stack approach well explained in [this post](https://leetcode.com/problems/max-chunks-to-make-sorted-ii/discuss/595713/Monotonic-stack-solution-with-detailed-explanation).\n\n```\n// 0 ms. 100%\npublic int maxChunksToSorted(int[] arr) {\n int top = 0;\n for(int a: arr) {\n int max = a;\n while(top > 0 && arr[top - 1] > a) {\n max = Math.max(max, arr[--top]);\n }\n arr[top++] = max;\n }\n return top;\n}\n```\n\nTime complexity: O(n)\nSpace complexity: O(1) | 4 | 0 | ['Java'] | 0 |
max-chunks-to-make-sorted-ii | Python left max & right min O(N) time & space | python-left-max-right-min-on-time-space-b16uk | \n def maxChunksToSorted(self, arr: List[int]) -> int:\n import math\n right_min = [math.inf] * len(arr)\n left_max = arr.copy()\n | etherwei | NORMAL | 2019-09-18T15:03:29.746778+00:00 | 2019-09-18T15:03:29.746828+00:00 | 328 | false | ```\n def maxChunksToSorted(self, arr: List[int]) -> int:\n import math\n right_min = [math.inf] * len(arr)\n left_max = arr.copy()\n for i in range(len(arr) - 2, -1, -1):\n right_min[i] = min(arr[i + 1], right_min[i + 1])\n for i in range(1, len(arr)):\n left_max[i] = max(left_max[i - 1], arr[i])\n chunks = 0\n for i in range(len(arr)):\n if right_min[i] >= left_max[i]:\n chunks += 1\n return chunks\n\n``` | 4 | 0 | [] | 2 |
max-chunks-to-make-sorted-ii | O(n) Java | on-java-by-weirongwang-ihyt | No difference between ver1 or 2. \n\n public int maxChunksToSorted(int[] arr) {\n \n int S = arr.length; \n int[] max = new int[S] | weirongwang | NORMAL | 2018-01-21T04:01:32.869000+00:00 | 2018-09-30T17:35:05.996590+00:00 | 563 | false | No difference between ver1 or 2. \n````\n public int maxChunksToSorted(int[] arr) {\n \n int S = arr.length; \n int[] max = new int[S];\n int[] min = new int[S];\n \n max[0] = arr[0];\n for (int i=1; i<S; i++)\n max[i] = Math.max(max[i-1], arr[i]);\n \n min[S-1] = arr[S-1];\n for (int i=S-2; i>=0; i--)\n min[i] = Math.min(min[i+1], arr[i]);\n \n int res = 0; \n for (int i=0; i<S-1; i++)\n if (max[i] <= min[i+1])\n res++; \n \n return res+1;\n }\n```` | 4 | 0 | [] | 1 |
max-chunks-to-make-sorted-ii | Simple Solution|| HashTable | simple-solution-hashtable-by-dhanushkodi-uzf3 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Dhanushkodi_S | NORMAL | 2024-01-26T09:14:54.038907+00:00 | 2024-01-26T09:14:54.038939+00:00 | 312 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int maxChunksToSorted(int[] arr) {\n int i,max=0,count=0;\n Map<Integer,Integer>map1=new HashMap<>();\n Map<Integer,Integer>map2=new HashMap<>();\n int nums[]=new int[arr.length];\n for(i=0;i<nums.length;i++)\n {\n nums[i]=arr[i];\n }\n Arrays.sort(nums);\n for(i=0;i<nums.length;i++)\n {\n map1.put(nums[i],map1.getOrDefault(nums[i],0)+1);\n map2.put(arr[i],map2.getOrDefault(arr[i],0)+1);\n if(map1.equals(map2))\n {\n count++;\n map1.clear();\n map2.clear();\n }\n }\n\n return count;\n }\n}\n``` | 3 | 0 | ['Hash Table', 'Java'] | 1 |
max-chunks-to-make-sorted-ii | Simple JAVA Solution || Beats 100% || O(N) | simple-java-solution-beats-100-on-by-sak-1ggo | Complexity\n- Time complexity: O(N)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(N)\n Add your space complexity here, e.g. O(n) \n\n# Co | Sakshi112 | NORMAL | 2023-07-25T12:16:14.779812+00:00 | 2023-07-25T12:16:14.779839+00:00 | 157 | false | # Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int maxChunksToSorted(int[] arr) {\n int n = arr.length;\n \n // Initialize two arrays to store the maximum elements from the left side\n // and the minimum elements from the right side for each index in the original array.\n int maxleftarr[] = new int[n];\n int minrightarr[] = new int[n];\n\n // Calculate the maximum elements from the left side of the array.\n maxleftarr[0] = arr[0];\n for (int i = 1; i < n; i++) {\n maxleftarr[i] = Math.max(maxleftarr[i - 1], arr[i]);\n }\n\n // Calculate the minimum elements from the right side of the array.\n minrightarr[n - 1] = arr[n - 1];\n for (int i = n - 2; i >= 0; i--) {\n minrightarr[i] = Math.min(minrightarr[i + 1], arr[i]);\n }\n\n int ans = 0;// keep track of the number of chunks found so far.\n\n // Compare the maximum element from the left side (maxleftarr[i]) with the minimum element\n // from the right side (minrightarr[i+1]) for each index i in the array.\n // If the maximum element from the left side is less than or equal to the minimum element\n // from the right side for a given index, it means we can split the array into chunks at that index.\n // Increment the ans variable to count the number of chunks.\n for (int i = 0; i < n - 1; i++) {\n if (maxleftarr[i] <= minrightarr[i + 1]) {\n ans++;\n }\n }\n\n // The ans variable will contain the number of chunks found, but we need to add 1 to get the final result,\n // as the initial array itself is a chunk.\n return ans + 1;\n }\n}\n\n``` | 3 | 0 | ['Java'] | 0 |
max-chunks-to-make-sorted-ii | 768. Max Chunks To Make Sorted II | 768-max-chunks-to-make-sorted-ii-by-pspr-18l6 | class Solution {\npublic: \n int maxChunksToSorted(vector& arr) {\n int n = arr.size(), i, j;\n vectormin_num(n, 0);\n min_num[n-1] = | pspraneetsehra08 | NORMAL | 2023-05-18T14:14:25.466561+00:00 | 2023-05-18T14:14:25.466620+00:00 | 140 | false | class Solution {\npublic: \n int maxChunksToSorted(vector<int>& arr) {\n int n = arr.size(), i, j;\n vector<int>min_num(n, 0);\n min_num[n-1] = arr[n-1];\n for (i = n-2; i >= 0; --i) min_num[i] = (arr[i] < min_num[i+1])? arr[i] : min_num[i+1];\n int maxv = 0, ans = 0;\n for(i = 0; i < n; ++i) {\n maxv = arr[i]; \n for (j = i+1; j < n; ++j) {\n if(maxv <= min_num[j]) break;\n if(maxv < arr[j]) maxv = arr[j];\n }\n ++ans;\n i = j - 1;\n }\n return ans;\n }\n}; | 3 | 0 | ['C', 'C++'] | 0 |
max-chunks-to-make-sorted-ii | Java || Runtime : 0ms || 100% || Easy | java-runtime-0ms-100-easy-by-yogesh_pand-wnra | If you love the solution please upvote\n\n\nclass Solution {\n public int maxChunksToSorted(int[] arr) {\n \n int[] rmin = new int[arr.length+1 | Yogesh_Pandey20 | NORMAL | 2022-07-26T13:12:10.790088+00:00 | 2022-07-26T13:12:10.790131+00:00 | 484 | false | **If you love the solution please upvote**\n\n```\nclass Solution {\n public int maxChunksToSorted(int[] arr) {\n \n int[] rmin = new int[arr.length+1];\n rmin[arr.length]=Integer.MAX_VALUE;\n for(int i=arr.length-1 ;i>=0;i--){\n rmin[i]=Math.min(rmin[i+1],arr[i]);\n }\n \n int lmax=Integer.MIN_VALUE, count=0;\n for(int i=0; i<arr.length; i++){\n lmax=Math.max(lmax,arr[i]);\n if(lmax<=rmin[i+1]){\n count++;\n }\n }return count;\n }\n}\n``` | 3 | 0 | ['Java'] | 1 |
max-chunks-to-make-sorted-ii | [Python3] Solution with using monotonic stack with comments | python3-solution-with-using-monotonic-st-7o8v | \n"""\nThe main idea is to get longest non-decreasing interval.\n\nFor decreasing interval (such an interval that we need to sort) we must the maximum of such i | maosipov11 | NORMAL | 2021-09-18T16:21:54.228116+00:00 | 2021-09-18T16:21:54.228168+00:00 | 389 | false | ```\n"""\nThe main idea is to get longest non-decreasing interval.\n\nFor decreasing interval (such an interval that we need to sort) we must the maximum of such interval.\n\nExample:\n\narr: [3,8,9,4,5]\n\n0. [] - empty stack\n1. [3] - it is non-decreasing interval\n2. [3,8] - it is non-decreasing interval\n3. [3,8,9] - it is non-decreasing interval\n4. [3,8,9,4] - it is decreasing interval (9 > 4)\n 4.1. need find position such we will have non-decreasing interval [3,4,8,9] - we need sort [8,9,4]\n while stack and stack[-1] > a\n 4.2. while we find begin of decreasing interval [8,9,4] we must find max value of such interval\n 4.3. why maximum ?\n 4.3.1. [3,8,9,4,5]. We can insert 5. Now decreasing interval - [8,9,4,5]. We must sort [8,9,4,5]. For [8,9,4] we can stay 9 in stack, and when we will consider element = 5 we will get decreasing interval again [9,5].\n\n"""\n\nclass Solution:\n def maxChunksToSorted(self, arr: List[int]) -> int:\n stack = []\n\n for a in arr:\n _max = a\n while stack and stack[-1] > a:\n top = stack.pop()\n _max = max(_max, top)\n \n \n stack.append(_max)\n \n return len(stack)\n``` | 3 | 0 | ['Stack', 'Python3'] | 0 |
max-chunks-to-make-sorted-ii | Python Solution - Monotonic queue O(N) | python-solution-monotonic-queue-on-by-ah-16a1 | I see a lot of solutions that are using one of these two approaches\n1. Using prefix arrays (O(N))\n2. Using a sorted set (O(NlogN))\nI think there is a simpler | ahujara | NORMAL | 2021-08-22T17:34:01.043340+00:00 | 2021-08-22T17:37:06.859352+00:00 | 254 | false | I see a lot of solutions that are using one of these two approaches\n1. Using prefix arrays (O(N))\n2. Using a sorted set (O(NlogN))\nI think there is a simpler approach, that can be solved with a monotonic queue(without any sorting)\nWe could store the entire array as sorted intervals. If we find any number that is lesser than any of these intervals, we would need to merge the intervals into one go. \nSimilar question - https://leetcode.com/problems/merge-intervals/\nHere is a run through\nExample\n[1,2,5,2,3,6,3]\ni = 0 S = [[1,1]]\ni = 1 S = [[1,1], [2,2]]\ni = 2 S = [[1,1], [2,2], [5,5]]\ni = 3 S = [[1,1], [2,2], [2, 5]]\ni = 4 S = [[1,1], [2,2], [2, 5]]\ni = 5 S = [[1,1], [2,2], [2, 5], [6,6]]\ni = 6 S = [[1,1], [2,2], [2, 6]]\n\n```\nclass Solution:\n def maxChunksToSorted(self, arr: List[int]) -> int:\n S = []\n for a in arr:\n min_i, max_i = a, a\n while S and a < S[-1][1]:\n start, end = S.pop()\n min_i, max_i = min(start, min_i), max(end, max_i)\n S.append([min_i, max_i])\n return len(S)\n``` | 3 | 0 | ['Python', 'Python3'] | 1 |
max-chunks-to-make-sorted-ii | [Python 3] | python-3-by-bakerston-du01 | \ndef maxChunksToSorted(self, arr: List[int]) -> int:\n d, s, n = collections.defaultdict(collections.deque), sorted(arr), len(arr)\n for i, x in | Bakerston | NORMAL | 2021-03-01T07:28:04.795616+00:00 | 2021-03-01T07:28:04.795665+00:00 | 112 | false | ```\ndef maxChunksToSorted(self, arr: List[int]) -> int:\n d, s, n = collections.defaultdict(collections.deque), sorted(arr), len(arr)\n for i, x in enumerate(s):\n d[x].append(i)\n idx, ans = 0, 0\n while idx < n:\n far = d[arr[idx]][0]\n d[arr[idx]].popleft()\n while far > idx:\n idx += 1\n far = max(far, d[arr[idx]][0])\n d[arr[idx]].popleft()\n ans += 1\n idx = far + 1\n return ans\n\t\t``` | 3 | 0 | [] | 0 |
max-chunks-to-make-sorted-ii | [C++] Simple NlogN Sorting + HashMap based solution. Updated O(n) Stack solution | c-simple-nlogn-sorting-hashmap-based-sol-xp32 | Time : O(nlogn) solution\n\nclass Solution {\npublic:\n int maxChunksToSorted(vector<int>& A) {\n unordered_map<int, int> mp;\n vector<int> exp | nicmit | NORMAL | 2020-01-15T11:16:18.774055+00:00 | 2020-01-15T11:19:32.217761+00:00 | 276 | false | Time : O(nlogn) solution\n```\nclass Solution {\npublic:\n int maxChunksToSorted(vector<int>& A) {\n unordered_map<int, int> mp;\n vector<int> expected(A); // this is the expected result after sorting\n sort(expected.begin(), expected.end());\n int n = A.size(), chunks = 0;\n for(int i = n - 1; i >= 0; i--)\n {\n mp[expected[i]]++;\n mp[A[i]]--;\n if(mp[A[i]] == 0)\n mp.erase(A[i]);\n if(mp[expected[i]] == 0)\n mp.erase(expected[i]);\n if(mp.empty()) // both the arrays have seen same elements in sorted as well as normal order, i.e. a chunk can be cut.\n chunks++;\n }\n return chunks;\n }\n};\n```\nUpdate : \nTime : O(n) solution\nThe stack stores the ranges of elements, when an overlap of range occurs, pop the previous range from stack and add the new range\n```\nclass Solution {\npublic:\n int maxChunksToSorted(vector<int>& A) {\n stack<int> s;\n int curMax = 0;\n for(int i = 0; i < A.size(); i++)\n {\n curMax = (s.empty() ? A[i] : max(s.top(), A[i])); // evaluate the current-Max element till now\n while(!s.empty() && s.top() > A[i]) // if the current element is smaller than previous max, \n // then it\'s a part of the previous chunk. Hence pop from stack and push later the updated range.\n s.pop();\n s.push(curMax);\n }\n return s.size();\n }\n};\n``` | 3 | 0 | ['C', 'Sorting'] | 0 |
max-chunks-to-make-sorted-ii | 100% Beat in Python Using Stack 🥇 | 100-beat-in-python-using-stack-by-fouzan-ypy2 | IntuitionThe problem involves partitioning the array into chunks such that when each chunk is sorted individually and then concatenated, the result is a fully s | fouzanm | NORMAL | 2024-12-19T13:58:56.205364+00:00 | 2024-12-19T13:58:56.205364+00:00 | 200 | false | # Intuition
The problem involves partitioning the array into chunks such that when each chunk is sorted individually and then concatenated, the result is a fully sorted array. This can be visualized as maintaining the order of elements in a stack-like structure. A stack can help keep track of chunks and manage conditions when merging is required.
# Approach
1. Stack-Based Approach: Use a stack to simulate chunk boundaries.
- Traverse the array and compare each element with the top of the stack.
- If the current element is greater than or equal to the top of the stack, it indicates that the current element can be part of the current chunk. Push it onto the stack.
- If the current element is less than the top of the stack, it indicates that merging of chunks is required. Pop elements from the stack until the stack top is smaller than or equal to the current element. This ensures that all elements in the merged chunk satisfy the sorting condition. Finally, push the maximum element from the merged chunk onto the stack.
2. Count Chunks: At the end of the traversal, the size of the stack gives the number of chunks, as each entry in the stack corresponds to a valid chunk.
# Complexity
- Time complexity:
$$O(n)$$
- Space complexity:
$$O(n)$$
# Code
```python3 []
class Solution:
def maxChunksToSorted(self, arr: List[int]) -> int:
stack = []
for num in arr:
if not stack or stack[-1] <= num:
stack.append(num)
else:
element = stack[-1]
while stack and stack[-1] > num:
stack.pop()
stack.append(element)
return len(stack)
``` | 2 | 0 | ['Array', 'Stack', 'Greedy', 'Monotonic Stack', 'Python3'] | 0 |
max-chunks-to-make-sorted-ii | C++ || Monotonic Stack | c-monotonic-stack-by-akash92-bss7 | Approach\n Describe your approach to solving the problem. \nWe iterate over the array and use a stack to keep track of the highest values encountered. If the cu | akash92 | NORMAL | 2024-09-24T12:12:46.236350+00:00 | 2024-09-24T12:12:46.236368+00:00 | 162 | false | # Approach\n<!-- Describe your approach to solving the problem. -->\nWe iterate over the array and use a stack to keep track of the highest values encountered. If the current element is less than the top of the stack, it means we cannot make a new chunk, and we need to merge previous chunks. We pop the stack until the current element is greater than or equal to the top, ensuring all merged chunks maintain order. We then push the maximum value from the merged chunks to preserve the sorting rule.\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int maxChunksToSorted(vector<int>& arr) {\n stack<int> st;\n for(int i=0; i<arr.size(); i++){\n int maxi = INT_MIN;\n while(!st.empty() && arr[i]<st.top()){\n maxi = max(maxi, st.top());\n st.pop();\n }\n if(maxi == INT_MIN) st.push(arr[i]);\n else st.push(maxi);\n }\n return st.size();\n }\n};\n``` | 2 | 0 | ['Array', 'Stack', 'Greedy', 'Monotonic Stack', 'C++'] | 0 |
max-chunks-to-make-sorted-ii | Go Simple solution || O(n logn) || 0ms || beats 100% | go-simple-solution-on-logn-0ms-beats-100-ob4q | Intuition\nWhen a partition is sorted, its sum should equal the sum of elements in original array, then we can make that partition. So just keep running sum of | user7454af | NORMAL | 2024-06-14T23:59:54.849006+00:00 | 2024-06-14T23:59:54.849031+00:00 | 118 | false | # Intuition\nWhen a partition is sorted, its sum should equal the sum of elements in original array, then we can make that partition. So just keep running sum of both original and sorted array and make partition when both sums are equal.\n\n# Complexity\n- Time complexity: $$O(nlogn)$$\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfunc maxChunksToSorted(arr []int) int {\n sarr := make([]int, len(arr))\n copy(sarr, arr)\n slices.Sort(sarr)\n sum, sorted_sum, ans := 0, 0, 0\n for i := 0; i < len(arr) ; i++ {\n sum += arr[i]\n sorted_sum += sarr[i]\n if sum == sorted_sum {\n ans++\n }\n }\n return ans\n}\n``` | 2 | 0 | ['Go'] | 0 |
max-chunks-to-make-sorted-ii | Solution | solution-by-deleted_user-j58r | C++ []\nclass Solution {\npublic:\n int maxChunksToSorted(vector<int>& arr) {\n int n=arr.size();\n vector<int> rightMin(n+1,0);\n right | deleted_user | NORMAL | 2023-04-27T08:39:19.792042+00:00 | 2023-04-27T08:56:04.475958+00:00 | 633 | false | ```C++ []\nclass Solution {\npublic:\n int maxChunksToSorted(vector<int>& arr) {\n int n=arr.size();\n vector<int> rightMin(n+1,0);\n rightMin[n]=INT_MAX;\n for(int i=n-1;i>=0;i--){\n rightMin[i]=min(arr[i],rightMin[i+1]);\n }\n int leftMax=-1;\n int chunks=0;\n for(int i=0;i<n;i++){\n leftMax=max(leftMax,arr[i]);\n if(leftMax<=rightMin[i+1]){\n chunks++;\n }\n }\n return chunks;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def maxChunksToSorted(self, A: List[int]) -> int:\n A_cp = A.copy()\n A_cp.sort()\n n = len(A)\n res, sum, sum_cp = 0, 0, 0\n for i in range(n):\n sum += A[i]\n sum_cp += A_cp[i]\n if sum == sum_cp:\n res += 1\n return res \n```\n\n```Java []\nclass Solution {\n public int maxChunksToSorted(int[] arr) {\n int n = arr.length;\n int[] maxOfLeft = new int[n];\n int[] minOfRight = new int[n];\n\n maxOfLeft[0] = arr[0];\n minOfRight[n-1]=arr[n-1];\n for (int i=1;i<n;i++)\n {\n maxOfLeft[i]=Math.max(maxOfLeft[i-1],arr[i]);\n }\n for (int i=n-2;i>=0;i--)\n {\n minOfRight[i]=Math.min(minOfRight[i+1],arr[i]);\n }\n int res=0;\n for (int i=0;i<n-1;i++)\n {\n if (maxOfLeft[i]<=minOfRight[i+1]) res++;\n }\n return res + 1;\n }\n}\n```\n | 2 | 0 | ['C++', 'Java', 'Python3'] | 0 |
max-chunks-to-make-sorted-ii | Javascriptc | Monotonic Stack with explanation | Time O(n) | Space O(n) | javascriptc-monotonic-stack-with-explana-w65u | Intuition\nTraverse the array from left to right, an element need to be arrange if there exists at least one element before it that greater than it. They have t | bahoang3105 | NORMAL | 2023-04-06T13:47:23.773195+00:00 | 2023-04-14T03:17:32.406252+00:00 | 470 | false | # Intuition\nTraverse the array from left to right, an element need to be arrange if there exists at least one element before it that greater than it. They have to be in the same chunk.\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n```\n/**\n * @param {number[]} arr\n * @return {number}\n */\nvar maxChunksToSorted = function(arr) {\n let stack = [arr[0]]; // stack[i] is the maximum element of chunk i\n for (let i = 1; i < arr.length; i++) {\n\n // if arr[i] greater than the last item in stack then arr[i] is a chunk.\n if (arr[i] > stack[stack.length - 1]) { \n stack.push(arr[i]);\n } \n\n // else arr[i] is a part of the chunk which is made up of all chunks whose maximum element is greater than arr[i]\n else { \n let maxElementOfAllChunks = stack[stack.length - 1];\n while (arr[i] < stack[stack.length - 1]) {\n stack.pop();\n }\n stack.push(maxElementOfAllChunks);\n }\n }\n return stack.length\n};\n``` | 2 | 0 | ['Monotonic Stack', 'JavaScript'] | 0 |
max-chunks-to-make-sorted-ii | 2 C++ Solution - Priority Queue and summation | 2-c-solution-priority-queue-and-summatio-dak4 | Priority Queue - O(n) space\n\nclass Solution {\npublic:\n int maxChunksToSorted(vector<int>& arr) {\n \n vector<int> v=arr;\n sort(v.be | ritvic-agg | NORMAL | 2023-01-26T11:44:08.595618+00:00 | 2023-01-26T11:44:08.595653+00:00 | 161 | false | # Priority Queue - O(n) space\n```\nclass Solution {\npublic:\n int maxChunksToSorted(vector<int>& arr) {\n \n vector<int> v=arr;\n sort(v.begin(),v.end());\n int i=0,j=0,ans=0;\n priority_queue<int,vector<int>,greater<int>>pq;\n while(i<v.size())\n {\n pq.push(arr[i++]);\n while(!pq.empty() && pq.top()==v[j])\n {\n pq.pop();\n j++;\n }\n if(pq.size()==0)ans++;\n }\n return ans;\n }\n};\n```\n\n\n# Using sum - O(1) space\n\n```\nint maxChunksToSorted(vector<int>& arr) {\n int sum1 = 0, sum2 = 0, ans = 0;\n vector<int> t = arr;\n sort(t.begin(), t.end());\n for(int i = 0; i < arr.size(); i++) {\n sum1 += t[i];\n sum2 += arr[i];\n if(sum1 == sum2) ans++;\n }\n\treturn ans;\n}\n``` | 2 | 0 | ['C++'] | 0 |
max-chunks-to-make-sorted-ii | C++ easy-to-understand solution | c-easy-to-understand-solution-by-dr_mash-jrxh | What we have to do is to look how far an element is from its position in the sorted array. Accordingly we decide. If in a range of array the sum of displacement | Dr_Mashoor_Gulati | NORMAL | 2023-01-19T11:14:40.272538+00:00 | 2023-01-19T11:14:40.272580+00:00 | 1,250 | false | What we have to do is to look how far an element is from its position in the sorted array. Accordingly we decide. If in a range of array the sum of displacement of elements from initial position is 0 then we can make them in a chunk.\n\n```\n static bool compare(pair<int,int> p1,pair<int,int> p2)\n{\n if(p1.first!=p2.first){return p1.first<p2.first;}\n return p1.second<p2.second;\n}\n\nint maxChunksToSorted(vector<int>& arr) \n{\n vector<pair<int,int> > a;\n for(int i=0;i<arr.size();i++)\n {\n a.push_back({arr[i],i});\n }\n sort(a.begin(),a.end(),compare);\n \n int ans=0;\n int sum=0;\n for(int i=0;i<a.size();i++)\n {\n sum+=(i-a[i].second);\n if(sum==0)\n {ans++;}\n }\n return ans;\n}\n``` | 2 | 0 | ['C', 'Sorting'] | 1 |
max-chunks-to-make-sorted-ii | [C++], 12ms, O(n) without sorting | c-12ms-on-without-sorting-by-shailesh_31-pjol | \n int maxChunksToSorted(vector<int>& arr) {\n int n = arr.size();\n \n vector<int> rightMin(n+1); rightMin[n] = INT_MAX;\n \n | Shailesh_3105 | NORMAL | 2022-09-18T06:46:05.815529+00:00 | 2022-11-28T14:48:44.193150+00:00 | 478 | false | ```\n int maxChunksToSorted(vector<int>& arr) {\n int n = arr.size();\n \n vector<int> rightMin(n+1); rightMin[n] = INT_MAX;\n \n for(int i=n-1;i>=0;i--) rightMin[i] = min(rightMin[i+1],arr[i]);\n \n int ans = 0, lmax = INT_MIN;\n \n for(int i=0;i<n;i++)\n {\n lmax = max(lmax, arr[i]);\n if(lmax <= rightMin[i+1]) ans++;\n }\n return ans;\n }\n``` | 2 | 0 | ['Array', 'C++'] | 0 |
max-chunks-to-make-sorted-ii | Java fast and easy with explanation. | java-fast-and-easy-with-explanation-by-r-vevd | This is observation based.\n\n1 2 3 4 | 5 6 7\n[1...4]..\nFor a increasing straight line , (Max till i) < (Min of I + 1)...\ni.e [1..4] max =4 , [5..7] min in 5 | Rupdeep | NORMAL | 2022-09-17T13:33:12.753922+00:00 | 2022-09-17T13:33:12.753965+00:00 | 749 | false | This is observation based.\n\n1 2 3 4 | 5 6 7\n[1...4]..\nFor a increasing straight line , (Max till i) < (Min of I + 1)...\ni.e [1..4] max =4 , [5..7] min in 5 ,\nSo , If MaxTillNow < MinOnRight , then there is no element on the right side , which belongs on the left side as per above observation.\nif MaxTillNow > MinOnRight, it means , there is some element on the right side, who belongs on the left, so we CANNOT create a chunk.\n\nSo we need to Iterate through the array, each time all elements till the index are smaller (or equal) to all elements on the right, there is a new chunck.\nWe use two arrays to store the maxTillNow and minOnRight to achieve O(n) time complexity. Space complexity is O(n) too.\n\n```\nclass Solution {\n public int maxChunksToSorted(int[] arr) {\n \n int n = arr.length;\n int[] maxTillNow = new int[n];\n int[] minOnRight = new int[n];\n \n maxTillNow[0] = arr[0];\n for(int i=1; i<n; i++){\n maxTillNow[i] = Math.max(arr[i], maxTillNow[i-1]);\n }\n \n minOnRight[n-1] = arr[n-1];\n for(int i=n-2; i>=0; i--){\n minOnRight[i] = Math.min(arr[i], minOnRight[i+1]);\n }\n \n int result = 0;\n for(int i = 0; i < n-1; i++){\n if(maxTillNow[i] <= minOnRight[i+1]){\n result++;\n }\n }\n return result+1;\n }\n}\n``` | 2 | 0 | ['Java'] | 0 |
max-chunks-to-make-sorted-ii | C++ Solutions, with small explanation, | c-solutions-with-small-explanation-by-ut-p2zo | \nclass Solution {\npublic:\n int maxChunksToSorted(vector<int>& a) {\n int n = a.size();\n if(n < 2) return 1;\n /*\n \n | uttu_dce | NORMAL | 2022-08-22T19:23:05.216445+00:00 | 2022-08-22T19:23:05.216474+00:00 | 287 | false | ```\nclass Solution {\npublic:\n int maxChunksToSorted(vector<int>& a) {\n int n = a.size();\n if(n < 2) return 1;\n /*\n \n after sorting the array should look like this:\n \n .....Max1 | Min2..........Max2 | Min3.........Max3 | Min4 ........... Max4|\n so Max1 <= Min2 , Max2 <= Min3 .... Max(n - 1) <= Min(n)\n \n so we just need to count them\n \n */\n \n vector<int> minR(n);\n vector<int> maxL(n);\n \n minR[n - 1] = a[n - 1];\n for(int i = n - 2; i >= 0; i--) minR[i] = min(minR[i + 1], a[i]);\n \n maxL[0] = a[0];\n for(int i = 1; i < n; i++) maxL[i] = max(maxL[i - 1], a[i]);\n \n int partitions = 0;\n for(int i = 0; i < n - 1; i++) {\n if(maxL[i] <= minR[i + 1]) partitions++;\n }\n \n int ans = partitions + 1;\n return ans;\n }\n};\n``` | 2 | 0 | [] | 0 |
max-chunks-to-make-sorted-ii | C++ || INTUITION | c-intuition-by-get_the_guns-d7qv | \nThis one was hard nailed it in 5 minutes >>>Power to u man\n\n\nclass Solution {\n\npublic:\n int maxChunksToSorted(vector<int>& arr) {\n int n=arr. | Get_the_Guns | NORMAL | 2022-07-25T10:50:39.463070+00:00 | 2022-07-25T10:50:39.463108+00:00 | 327 | false | ```\nThis one was hard nailed it in 5 minutes >>>Power to u man\n\n\nclass Solution {\n\npublic:\n int maxChunksToSorted(vector<int>& arr) {\n int n=arr.size(); \n vector<int> rmin(n+1); //rightmin array of size+1\n rmin[n]=INT_MAX;\n for(int i=n-1;i>=0;i--){\n rmin[i]=min(arr[i],rmin[i+1]); // prepare the rightmina array\n \n }\n int lmax=INT_MIN;\n int chunk=0;\n for(int i=0;i<n;i++){\n lmax=max(arr[i],lmax); //keep updating lmax array\n if(lmax<=rmin[i+1]){\n chunk++; // here u increment my chunks \n }\n }\n return chunk;\n }\n};\n\n``` | 2 | 0 | ['C++'] | 0 |
max-chunks-to-make-sorted-ii | why your code is so simple | why-your-code-is-so-simple-by-yudotle-m08p | Guys... I spent like two hours for this :( which is sad. I use RMQ to solve this prob.....\nAny idea to improve my code? I think I might doing it overkill with | YudoTLE | NORMAL | 2022-07-24T17:09:15.525050+00:00 | 2022-07-24T17:11:23.468617+00:00 | 115 | false | Guys... I spent like two hours for this :( which is sad. I use RMQ to solve this prob.....\nAny idea to improve my code? I think I might doing it overkill with less efective\n\n\'\'\'\n\n\t#include <bits/stdc++.h>\n\tusing namespace std;\n\t\n\tclass Solution {\n\tpublic:\n void generateTable (vector<vector<int>>& table) {\n int n = table[0].size();\n int p = 0;\n while (n - (1 << p) > 0) {\n vector<int> temp;\n int add = 1 << p;\n n -= add;\n for (int i = 0; i < n; i++) {\n temp.push_back(min(table[p][i], table[p][i + add]));\n } p++;\n table.push_back(temp);\n }\n }\n int getRMQ (int l, int r, vector<vector<int>>& table) {\n int n = r - l + 1;\n int p = log2(n);\n int k = 1 << p;\n return min(table[p][l], table[p][r - k + 1]);\n }\n \n int maxChunksToSorted(vector<int>& arr) {\n vector<vector<int>> table{arr};\n vector<int> arr2 = arr;\n sort(arr2.begin(), arr2.end());\n \n generateTable(table);\n \n int n = arr.size();\n int ans = 0, last = n;\n for (int i = n - 1; i >= 0; i--) for (int j = 0; j < last; j++) {\n if (arr[j] == arr2[i]) {\n int add = 0, red = 0;\n for (int k = last - 1; k > j; k--) {\n bool con1 = arr[k] == arr[j];\n bool con2 = arr[k] <= getRMQ(k, last - 1, table);\n if (con1) red++;\n if (con1 && con2)\n ++add;\n else\n break;\n }\n\t\t\t\tif ((last == n) || (arr[j] <= getRMQ(min(last, n - 1), n - 1, table))) ans += add + 1;\n\t\t\t\t\ti -= red;\n\t\t\t\t\tlast = j;\n\t\t\t\t\tbreak;\n\t\t\t\t}\n\t\t\t}\n return ans;\n\t\t}\n\t};\n\'\'\' | 2 | 0 | ['Two Pointers'] | 0 |
max-chunks-to-make-sorted-ii | Java | O(n) | A Stack Solution | java-on-a-stack-solution-by-student2091-r204 | Track the max and push it onto the stack if it is no less than the current max (meaning it is possible for it to be the start of a valid chuck).\n- If the curre | Student2091 | NORMAL | 2022-07-04T02:39:19.334361+00:00 | 2022-07-04T02:42:06.697727+00:00 | 97 | false | - Track the max and push it onto the stack if it is no less than the current max (meaning it is *possible* for it to be the start of a valid chuck).\n- If the current element is greater than the top of the stack, pop it off because it can\'t be a valid check (merge operation).\n- Initialize max to `-1` as the start.\n\n#### How does it work? \nLogically, the current element can **not** be less than the max recorded.\nBecause the size of stack is the number of valid chucks, we have to pop all invaild ones off.\nAlso, it is only possible for an element to be a start of a valid chuck when it is at least as large as the current max element, \nif it is not, then it belong to the previous chuck, so it shouldn\'t be pushed onto the stack.\n\n#### Commentary\nI think it is a pretty solution. Took me a bit of thinking to get it right. \n```Java\nclass Solution {\n public int maxChunksToSorted(int[] arr) {\n Deque<Integer> stack = new ArrayDeque<>();\n int max = -1;\n for (int i = 0; i < arr.length; i++){\n while(!stack.isEmpty() && arr[i]<stack.peek()){ // don\'t pop if they are ==\n stack.pop();\n }\n if (arr[i]>=max){\n stack.push(max);\n }\n max=Math.max(arr[i],max);\n }\n return stack.size();\n }\n}\n``` | 2 | 0 | ['Stack', 'Java'] | 0 |
max-chunks-to-make-sorted-ii | A very good question on stack | a-very-good-question-on-stack-by-kaushal-6k0g | \nclass Solution {\npublic:\n int maxChunksToSorted(vector<int>& arr) {\n stack<int>st;\n for(int i=0; i<arr.size(); i++){\n int cur | Kaushal_Kapoor | NORMAL | 2022-06-14T10:50:09.092529+00:00 | 2022-06-14T10:50:09.092572+00:00 | 130 | false | ```\nclass Solution {\npublic:\n int maxChunksToSorted(vector<int>& arr) {\n stack<int>st;\n for(int i=0; i<arr.size(); i++){\n int current_max;\n if(st.size()==0){\n current_max=arr[i];\n }\n else{\n current_max=max(arr[i],st.top());\n }\n while(st.size()>0&&arr[i]<st.top()){\n st.pop();\n }\n st.push(current_max);\n }\n return st.size();\n }\n};\n``` | 2 | 0 | ['Stack'] | 0 |
max-chunks-to-make-sorted-ii | C++ O(n) very easy solution,9 ms | c-on-very-easy-solution9-ms-by-rounak_sh-acr7 | we will maintain left max till i & right min till i+1,if(rmin[i]>=lmax[i]||i==arr.size()-1)ans++; \n\nclass Solution {\npublic:\n int maxChunksToSorted(vect | Rounak_sharma | NORMAL | 2022-06-04T07:34:34.992695+00:00 | 2022-06-04T07:34:34.992734+00:00 | 93 | false | # **we will maintain left max till i & right min till i+1,if(rmin[i]>=lmax[i]||i==arr.size()-1)ans++; \n```\nclass Solution {\npublic:\n int maxChunksToSorted(vector<int>& arr) {\n int ans=0;\n vector<int>lmax=arr;\n vector<int>rmin=arr;\n int maxi=INT_MIN;\n int mini=INT_MAX;\n for(int i=arr.size()-2;i>=0;i--){\n mini=min(arr[i+1],mini);\n rmin[i]=mini; \n }\n for(int i=0;i<arr.size();i++){\n maxi=max(maxi,arr[i]);\n lmax[i]=maxi;\n }\n for(int i=0;i<arr.size();i++){\n if(rmin[i]>=lmax[i]||i==arr.size()-1)ans++; \n }\n return ans;\n }\n};\n```\n# ***pls upvote this solution ,feel free to ask in comments | 2 | 0 | [] | 0 |
max-chunks-to-make-sorted-ii | Easy C++ solution using prefix sum concept | easy-c-solution-using-prefix-sum-concept-c92i | \nclass Solution {\npublic:\n int maxChunksToSorted(vector<int>& arr) {\n // vector \'v\' will be the sorted version of the original vector\n v | imran2018wahid | NORMAL | 2022-02-24T16:09:36.727862+00:00 | 2022-02-24T16:09:36.727899+00:00 | 154 | false | ```\nclass Solution {\npublic:\n int maxChunksToSorted(vector<int>& arr) {\n // vector \'v\' will be the sorted version of the original vector\n vector<int>v=arr;\n \n // sort vector \'v\'\n sort(v.begin(),v.end());\n \n // \'sum\' will be the running sum of the partitions\n long long sum=0;\n \n // prefix[i] = arr[0]+arr[1]+....+arr[i].\n vector<long long>prefix(arr.size());\n for(int i=0;i<v.size();i++) {\n prefix[i]=(i>0?prefix[i-1]+v[i]:v[i]);\n }\n \n // \'count\' will be our answer\n // \'low\' is the starting index of the current partition.\n int count=0,low=0;\n \n for(int i=0;i<arr.size();i++) {\n // calculate the running sum\n sum+=arr[i];\n \n // if at any index the running sum becomes equal to the prefix sum of that partition that means we\'ve reached the end of a valid partition\n if((low==0 && sum==prefix[i]) || (low>0 && sum==prefix[i]-prefix[low-1])) {\n \n // so increment the chunk count as we\'ve detected one more partition\n count++;\n \n // according to the definition of \'low\' , it should be set to the next index as it will be the starting index of the next partition.\n low=i+1;\n \n // set \'sum\' = 0 as we are going to start a fresh/new partition so it will cover the fresh sum of the next partition\n sum=0;\n }\n }\n \n // finally return the answer\n return count;\n }\n};\n```\n***Please upvote if you have got any help from my code. Thank you.*** | 2 | 0 | ['C', 'Prefix Sum'] | 0 |
max-chunks-to-make-sorted-ii | Simplest || With full Explanation || 100% fast || Comment if you have questions | simplest-with-full-explanation-100-fast-9xrbd | \nclass Solution {\n public int maxChunksToSorted(int[] arr) {\n //Basic logic - In a sorted array, at any point maximum number is lesser than the min | angePondu | NORMAL | 2022-01-02T08:26:22.608002+00:00 | 2022-01-02T08:26:22.608041+00:00 | 125 | false | ```\nclass Solution {\n public int maxChunksToSorted(int[] arr) {\n //Basic logic - In a sorted array, at any point maximum number is lesser than the minimum of all the numbers occuring after that. \n //eg in 1 2 4 7 9 11 15 || (7(max till that point) is less than 9( min till that point)) || (4(max till that point) is less than 7(min till that point))\n int len = arr.length;\n int ans = 1;// answer is set to 1 to count the last chunk as well\n \n //creating minimum value storing array\n int minArr[] = new int[len];\n minArr[len - 1] = arr[len - 1];// filling last value of array\n for( int i = len - 2; i>= 0; i--){\n //filling minimum of current(arr[i]) and next minimum (minarr[i+1]) in the array\n minArr[i] = Math.min(arr[i],minArr[i+1]);\n }\n \n //creating maximum value storing array\n int maxArr[] = new int[len];\n maxArr[0] = arr[0];// filling first value of array\n for( int i = 1; i<len; i++){\n //filling maximum of current(arr[i]) and previous maximum (maxArr[i+1]) in the array\n maxArr[i] = Math.max(arr[i],maxArr[i-1]);\n }\n \n for(int i = 0; i<len-1; i++){\n //using basic logic(given in the start)\n if(maxArr[i] <= minArr[i+1]) ans++;// if max till that point is less than the min after that point.. //this is chunk\n }\n return ans;\n }\n}\n``` | 2 | 0 | ['Java'] | 0 |
max-chunks-to-make-sorted-ii | C++ solution using chaining technique | c-solution-using-chaining-technique-by-r-ssnb | \n\nclass Solution {\npublic:\n int maxChunksToSorted(vector<int>& arr) {\n \n vector<int> rmin(arr.size() + 1);\n \n int val = I | ranveerraj248 | NORMAL | 2021-12-24T07:45:33.506458+00:00 | 2021-12-24T07:45:33.506490+00:00 | 149 | false | ```\n\nclass Solution {\npublic:\n int maxChunksToSorted(vector<int>& arr) {\n \n vector<int> rmin(arr.size() + 1);\n \n int val = INT_MAX;\n rmin[arr.size()] = val;\n for(int i = arr.size() - 1; i >= 0; i--) {\n val = min(val, arr[i]);\n rmin[i] = val;\n }\n \n int lmax = arr[0];\n int count = 0;\n for(int i = 0; i < arr.size(); i++) {\n lmax = max(lmax, arr[i]);\n \n if(lmax <= rmin[i + 1])\n count++;\n }\n \n return count;\n }\n};\n\n``` | 2 | 0 | ['C', 'C++'] | 0 |
max-chunks-to-make-sorted-ii | Easy C++ O(n) solution | easy-c-on-solution-by-shinchan_1207-crij | Please upvote if you like it\n\nclass Solution {\npublic:\n int maxChunksToSorted(vector<int>& arr) {\n //generate right min\n int n=arr.size(); | shinchan_1207 | NORMAL | 2021-10-12T07:17:55.726926+00:00 | 2021-10-12T07:18:59.995908+00:00 | 95 | false | **Please upvote if you like it**\n```\nclass Solution {\npublic:\n int maxChunksToSorted(vector<int>& arr) {\n //generate right min\n int n=arr.size();\n int rightMin[n+1];\n rightMin[n]=INT_MAX;\n for(int i=n-1;i>=0;i--)\n {\n rightMin[i]=min(rightMin[i+1],arr[i]);\n \n }\n\t\t\n int leftMax=INT_MIN;\n int count=0;\n\t\t//iterate an array and manage left max as well as count chunks\n for(int i=0;i<n;i++)\n {\n leftMax=max(leftMax,arr[i]);\n if(leftMax<=rightMin[i+1])\n {\n count++;\n }\n }\n return count;\n }\n};\n``` | 2 | 0 | [] | 0 |
max-chunks-to-make-sorted-ii | Simple Solution using maps:fun | simple-solution-using-mapsfun-by-return_-uaz4 | class Solution {\npublic:\n \n int maxChunksToSorted(vector& arr)\n {\n vectorp=arr;\n sort(p.begin(),p.end());\n int cnt=0;\n | return_45 | NORMAL | 2021-09-30T07:17:30.983934+00:00 | 2021-09-30T07:17:30.983961+00:00 | 80 | false | class Solution {\npublic:\n \n int maxChunksToSorted(vector<int>& arr)\n {\n vector<int>p=arr;\n sort(p.begin(),p.end());\n int cnt=0;\n map<int,int>a,b;//a for storing sorted values and b for original values\n for(int i=0;i<arr.size();i++)\n {\n a[p[i]]++;\n b[arr[i]]++;\n if(a==b)\n {\n cnt++;\n }\n }\n return cnt;\n }\n}; | 2 | 0 | ['C'] | 0 |
max-chunks-to-make-sorted-ii | c++ | easy to understand | c-easy-to-understand-by-loopless-1jri | We are keeping an array (mn) which stores from the back of array min value from last till that point.\nAfter that,we run a loop from the start of original array | loopless | NORMAL | 2021-09-10T06:31:57.261718+00:00 | 2021-09-10T06:31:57.261754+00:00 | 87 | false | We are keeping an array (mn) which stores from the back of array min value from last till that point.\nAfter that,we run a loop from the start of original array to check if the max value till a certain index is less than or equal to the value at array mn at the same index.If true,we increment c.\n```\nclass Solution {\npublic:\n int maxChunksToSorted(vector<int>& arr) {\n int n=arr.size();\n int mn[n];\n \n int c=1;\n mn[n-1]=arr[n-1];\n for(int i=n-2;i>=0;i--)\n {\n if(arr[i]<mn[i+1])\n mn[i]=arr[i];\n else\n mn[i]=mn[i+1];\n }\n int mx=arr[0];\n for(int i=0;i<n-1;i++)\n {\n \n mx=max(mx,arr[i]);\n if(mx<=mn[i+1])\n c++;\n \n }\n \n return c;\n }\n};\n``` | 2 | 0 | [] | 2 |
max-chunks-to-make-sorted-ii | Python solution using dictionary | python-solution-using-dictionary-by-flyi-3416 | from collections import defaultdict\nclass Solution:\n\n def maxChunksToSorted(self, arr: List[int]) -> int:\n sorted_list = sorted(arr)\n ans | flyingspa | NORMAL | 2021-07-22T10:51:11.299702+00:00 | 2021-07-22T10:51:11.299735+00:00 | 232 | false | from collections import defaultdict\nclass Solution:\n\n def maxChunksToSorted(self, arr: List[int]) -> int:\n sorted_list = sorted(arr)\n ans = 0\n s1 = defaultdict(int)\n s2 = defaultdict(int)\n # if sorted(arr[i:j]) == sorted_list[i:j]\n # then they must have the same elements and the number of occurences\n for i in range(len(arr)):\n s1[arr[i]]+=1\n s2[sorted_list[i]]+=1\n if s1==s2:\n s1 = defaultdict(int)\n s2 = defaultdict(int)\n ans+=1\n return ans | 2 | 0 | ['Python'] | 1 |
max-chunks-to-make-sorted-ii | C++ 3 approaches (each commented with intuition) | c-3-approaches-each-commented-with-intui-roct | \n//Approach-1 : Time - O(n), Space - O(n)\nclass Solution {\npublic:\n int maxChunksToSorted(vector<int>& arr) {\n int n = arr.size();\n \n | mazhar_mik | NORMAL | 2021-07-21T15:28:07.741921+00:00 | 2021-07-21T15:28:07.741963+00:00 | 176 | false | ```\n//Approach-1 : Time - O(n), Space - O(n)\nclass Solution {\npublic:\n int maxChunksToSorted(vector<int>& arr) {\n int n = arr.size();\n \n vector<int> rightMin(n);\n rightMin[n-1] = arr[n-1];\n \n for(int i = n-2; i>=0; i--)\n rightMin[i] = min(rightMin[i+1], arr[i]);\n \n int leftMax = arr[0];\n \n int count = 0;\n \n /*\n If current leftMax is less than or equal to\n minimum of all elements to its right,\n it means it can\'t have an impact further.\n It belongs to a chunk till this point only.\n And then, we move ahead.\n */\n \n for(int i = 0; i<n-1; i++) {\n leftMax = max(leftMax, arr[i]);\n if(leftMax <= rightMin[i+1])\n count++;\n }\n \n return count+1;\n }\n};\n```\n\n```\n//Approach-2 (Using similar concept of "Max Chunks To Make Sorted I"\nclass Solution {\npublic:\n int maxChunksToSorted(vector<int>& arr) {\n int n = arr.size();\n vector<int> sorted(arr);\n sort(begin(sorted), end(sorted));\n \n vector<int> MAX(n);\n MAX[0] = arr[0];\n for(int i = 1; i<n; i++)\n MAX[i] = max(MAX[i-1], arr[i]);\n \n int rightMax = MAX[n-1];\n int count = 0;\n for(int i = n-1; i>=0; i--) {\n if(sorted[i] == MAX[i]) {\n if(sorted[i] > rightMax)\n continue; //because we need to include this as well for being sorted correctly\n \n rightMax = arr[i];\n count++;\n }\n }\n \n return count;\n }\n};\n```\n\n```\n//Approach-3 (O(nlogn)) But smartest approach\n/*\n Why does this work ?\n Intuition -\n Let "sorted" be the input "arr" array after being sorted.\n A "chunk" is an interval [i, j] such that arr[i], ..., arr[j]\n is just a permutation of sorted[i], ..., sorted[j].\n \n Since each chunk is just a permutation, the sums of these\n two lists of numbers will be equal.\n And the point where cumulative sum gets equal, that\'s the\n point of partition of chunk.\n*/\nclass Solution {\npublic:\n int maxChunksToSorted(vector<int>& arr) {\n int n = arr.size();\n vector<int> sorted(arr);\n sort(begin(sorted), end(sorted));\n \n long long sum1 = 0, sum2 = 0;\n int count = 0;\n for(int i = 0; i<n; i++) {\n sum1 += arr[i];\n sum2 += sorted[i];\n \n if(sum1 == sum2)\n count++;\n }\n \n return count;\n }\n};\n``` | 2 | 0 | [] | 3 |
max-chunks-to-make-sorted-ii | Java O(N) Time and Space 100% Faster | java-on-time-and-space-100-faster-by-sun-8ll9 | ```\n\tpublic int maxChunksToSorted(int[] arr) {\n int[] temp= new int[arr.length+1];\n temp[arr.length]= Integer.MAX_VALUE;\n for(int i= a | sunnydhotre | NORMAL | 2021-05-21T14:32:20.039340+00:00 | 2021-05-21T14:42:38.530935+00:00 | 128 | false | ```\n\tpublic int maxChunksToSorted(int[] arr) {\n int[] temp= new int[arr.length+1];\n temp[arr.length]= Integer.MAX_VALUE;\n for(int i= arr.length-1; i>=0; i--){\n temp[i]= Math.min(arr[i],temp[i+1]);\n }\n int max= arr[0], chunks= 0;\n for(int i=0; i<arr.length; i++){\n max= Math.max(max,arr[i]);\n if(max <= temp[i+1]) chunks++;\n }\n return chunks;\n } | 2 | 0 | [] | 0 |
max-chunks-to-make-sorted-ii | Running Maximum and Minimum. O(N) with explanation | running-maximum-and-minimum-on-with-expl-w3da | Idea: We can create a partition in array at position i if max of [0..i] is less than min of [i+1..N-1]\nAlgorithm: Have two arrays max_left and min_right where | mukunddevulapalli | NORMAL | 2021-01-19T07:35:40.795272+00:00 | 2021-01-19T07:35:40.795333+00:00 | 261 | false | **Idea:** We can create a partition in array at position **i** if max of [0..i] is less than min of [i+1..N-1]\n**Algorithm**: Have two arrays max_left and min_right where max_left[i] is max of subarray [0..i] and min_right[i] is min of subarray [i, N-1]. For every i check if max_left[i] < min_left[i+1] and increment count\n**Complexity**: Time is O(N) and Space in O(N)\n\n```\nclass Solution:\n def maxChunksToSorted(self, arr: List[int]) -> int:\n \n N = len(arr)\n max_left = [0]*N\n min_right = [0]*N\n \n max_left[0] = arr[0]\n for i in range(1, N):\n max_left[i] = max(arr[i], max_left[i-1])\n \n min_right[N-1] = arr[N-1]\n for i in range(N-2, 0, -1):\n min_right[i] = min(min_right[i+1], arr[i])\n \n count = 0\n for i in range(N-1):\n \n if max_left[i] <= min_right[i+1]:\n count += 1\n \n return count+1\n \n``` | 2 | 0 | [] | 0 |
max-chunks-to-make-sorted-ii | C++ Easy Solution , O(n) time and O(n) space | c-easy-solution-on-time-and-on-space-by-9llur | \nclass Solution {\npublic:\n int maxChunksToSorted(vector<int>& arr) {\n int n = arr.size();\n int left[n],right[n];\n left[0] = arr[0] | mansibhardwaj50499 | NORMAL | 2020-10-29T12:41:22.954477+00:00 | 2020-10-29T12:41:22.954522+00:00 | 154 | false | ```\nclass Solution {\npublic:\n int maxChunksToSorted(vector<int>& arr) {\n int n = arr.size();\n int left[n],right[n];\n left[0] = arr[0];\n right[n-1] = arr[n-1];\n for(int i=1;i<n;i++)\n left[i] = max(arr[i],left[i-1]);\n for(int i = n-2;i>=0;i--)\n right[i] = min(arr[i],right[i+1]);\n int ans=1;\n for(int i=0;i<n-1;i++){\n if(left[i]<=right[i+1])\n ans++;\n }\n return ans;\n }\n};\n``` | 2 | 0 | [] | 0 |
max-chunks-to-make-sorted-ii | [Python] nlogn, faster than 97%, with detailed explanations and comments | python-nlogn-faster-than-97-with-detaile-zl74 | The idea is to build on Max Chunks to Make Sorted I, where the problem is easier with no repeats and all indexes present.\n\nThe solution to MCMS-I is simple on | kaijuml | NORMAL | 2020-05-05T08:03:38.517694+00:00 | 2020-05-06T07:41:05.371207+00:00 | 91 | false | The idea is to build on Max Chunks to Make Sorted I, where the problem is easier with no repeats and all indexes present.\n\nThe solution to MCMS-I is simple once you realize that each number represent an index, and in order for the array to be sorted at the end, each number should be in a chunk that includes its index (so that the sort operation will place it back at its correct position before the concatenation).\n\nFor instance, consider the example array [1, 0, 2, 3, 4]. In order for number 1 to be at the correct position (i.e. index 1) at the end of the operation, the chunk that includes number 1 should also includes index 1. That is, [1, 0] at the minimum. In the senario, number 0 is therefore also placed in this chunk, which also contains index 0 so we don\'t need to expand the chunk further. For number 2, we can simply use a chunk of size 1 because it is already place correctly, and so on, so forth until the end.\n\nConsider the second example array [4, 3, 2, 1, 0]. This time number 4 should be include in a chunk with index 4, that is at the minimum [4, 3, 2, 1, 0]. All other number are also include in this chunk, leaving solution equals 1.\n\nWe can solve this problem efficiently in O(N) with the following code:\n\n```python\ndef max_chunk_to_make_sorted_I(arr):\n\t"""\n\tWe define a target, which will be the index to include in the current chunk. \n\tWhile we parse the array, we either:\n\t\t- update the target because the current number is outside the range of the current chunk\n\t\t- close current chunk and start fresh at the next index\n\t"""\n \n target = 0 \n ret = 0\n for idx, num in enumerate(arr):\n\t\tif num > target:\n\t\t\t# in this case, this means that the current number represent an index outside the range of the chunk\n\t\t\t# we update the range of the chunk to be greater than (or equal to at least) this number\n\t\t\ttarget = num\n elif idx == target:\n\t\t\t# in this case we have reached the range of the chunk, without needing to expand it further\n\t\t\t# we "close" the chunk by counting +1 and move the target to the next index\n\t\t\tret += 1\n target = idx + 1\n\t\telse:\n\t\t\t# in this case, nothing happens.\n\t\t\t# We don\'t need to expand the range of the chunk, but we haven\'t reached it yet so we can\'t close it\n\t\t\tpass\n\t\t\n\treturn ret # we return the number of closed chunks\n```\n\nMCMS-II is more complicated because now, numbers don\'t necessarily represent indexes. We can not use the above strategy anymore. This is not a problem however because we can simply arg-sort the array and fall back to the previous case.\n\nConsider the example array [2,1,3,4,4]. The argsort operation will give us [1, 0, 2, 3, 4] because number 2 is the second smallest (i.e. index 1 because python is zero-indexed), number 1 is the smallest (i.e. index 0) and so on so forth.\n\nWe can now solve the problem with the previous code! The sorting operation is O(N logN) and solve operation is still O(N), resulting in total O(N logN)\n\n```python\ndef max_chunk_to_make_sorted_II(arr):\n\t"""\n\tWe argsort the array and solve the problem as with MCMS-I\n\t"""\n\t# we use built-in function \'enumerate\' which returns each number with its index, and sort with consideration on the number\n\tarr = sorted(enumerate(arr), key=lambda x: x[1])\n\t\n\t# we only care about the indexes\n\tarr = [idx for idx, num in arr]\n\t\n\t# we solve using the previous code!\n\treturn max_chunk_to_make_sorted_I(arr)\n```\n\nPlease let me know if this was useful to you, or if you need precision!\nCheers!\n\n\n\n\n | 2 | 0 | [] | 0 |
max-chunks-to-make-sorted-ii | C++ | O( N log(N) + N ) | With Picture explanation and Comments | c-o-n-logn-n-with-picture-explanation-an-haut | Credits to : https://leetcode.com/votrubac for the approach\nI will give my explanation to this approach .\nUPVOTE would be really appreciated !\n(Note : Steps | Might_Guy | NORMAL | 2020-04-24T20:12:30.048913+00:00 | 2020-04-24T20:18:33.527636+00:00 | 149 | false | Credits to : [https://leetcode.com/votrubac](http://) for the approach\nI will give my explanation to this approach .\nUPVOTE would be really appreciated !\n(Note : Steps will become clear by example )\n* Step 1 : Here we will make an array of indices and we will sort it (using a stable sort ) according to the values given in the input array.\n* Step 2: Traverse in the index array and increment count when the max-index-till-now reaches its index.\n\n EXAMPLE :\n\n\n\nNow when we traverse in the sorted index array , when then max index till now is equal to the current index we have reached end of a partition and we increment count.\nAt last return count !\n\nAlso,Lambda function is used in sorting beacuse we need access to the input vector while sorting.\n\n```\n\nclass Solution {\npublic:\n int maxChunksToSorted(vector<int>& arr) {\n int n = arr.size();\n \n// This will store indices from 0 to n-1\n vector<int> index_vector(n);\n for(int i=0;i<n;i++){\n index_vector[i] = i;\n }\n \n// place the indices as if they were the values themselves\n sort(index_vector.begin(),index_vector.end(),[&arr](int &a,int &b){\n if(arr[a]==arr[b])\n return a<b;\n return arr[a]<arr[b];\n });\n \n// When the max till now reaches to its position increment count\n int count = 0,max_index = 0;\n for(int i=0;i<n;i++){\n max_index = max(max_index,index_vector[i]);\n if(max_index == i)\n count++;\n }\n return count;\n }\n};\n``` | 2 | 0 | [] | 0 |
max-chunks-to-make-sorted-ii | JAVA O(n) solution, easy to understand | java-on-solution-easy-to-understand-by-s-ea6t | Max[i] is the max from begining to i (0 to i)\nMin[i] is the min from last to i (arr.length-1 to i)\ni can be a dividing point whenever max[i]<=min[i+1], don\'t | samuelwang1991 | NORMAL | 2020-04-18T23:18:16.484177+00:00 | 2020-04-18T23:18:41.171956+00:00 | 108 | false | Max[i] is the max from begining to i (0 to i)\nMin[i] is the min from last to i (arr.length-1 to i)\ni can be a dividing point whenever max[i]<=min[i+1], don\'t forget to add 1 to the last element since last element can always be a diving point.\n\nHere are the code:\n\n\n public int maxChunksToSorted(int[] arr) {\n int[] max = new int[arr.length];\n int[] min = new int[arr.length];\n max[0]=arr[0];\n min[arr.length-1]=arr[arr.length-1];\n for (int i=1;i<arr.length;i++) {\n max[i]=Math.max(max[i-1], arr[i]);\n }\n for (int i=arr.length-2;i>=0;i--) {\n min[i] = Math.min(min[i+1], arr[i]);\n }\n \n int count=0;\n for (int i=0;i<arr.length;i++) {\n if (i<arr.length-1&&max[i]<=min[i+1]) {\n count++;\n } \n }\n return ++count;\n } | 2 | 0 | [] | 0 |
max-chunks-to-make-sorted-ii | easy python solution nlogn | easy-python-solution-nlogn-by-medi-6fs7 | \nclass Solution(object):\n def maxChunksToSorted(self, arr):\n """\n :type arr: List[int]\n :rtype: int\n """\n if not ar | medi_ | NORMAL | 2020-01-31T21:27:02.676910+00:00 | 2020-01-31T21:27:21.712039+00:00 | 141 | false | ```\nclass Solution(object):\n def maxChunksToSorted(self, arr):\n """\n :type arr: List[int]\n :rtype: int\n """\n if not arr: return 0\n n=len(arr)\n temp=arr[::]\n temp.sort()\n chunks=0\n cum_sum_temp=cum_sum_arr=0\n\n for i in range(n):\n \tcum_sum_temp+=temp[i]\n \tcum_sum_arr+=arr[i]\n \tif cum_sum_temp==cum_sum_arr:\n \t\tchunks+=1\n return chunks\n``` | 2 | 0 | [] | 1 |
max-chunks-to-make-sorted-ii | Java o(nlogn) solution by used hashmap (769 solution is attatched) | java-onlogn-solution-by-used-hashmap-769-eirh | 769 solution:https://leetcode.com/problems/max-chunks-to-make-sorted/discuss/488014/Java-greedy-sol-100\n\nclass Solution {\n public int maxChunksToSorted(in | CUNY-66brother | NORMAL | 2020-01-23T03:09:09.067070+00:00 | 2020-01-23T03:11:52.429059+00:00 | 193 | false | 769 solution:https://leetcode.com/problems/max-chunks-to-make-sorted/discuss/488014/Java-greedy-sol-100\n```\nclass Solution {\n public int maxChunksToSorted(int[] arr) {\n int sort[]=new int[arr.length];\n int ans=0;\n Map<Integer,Integer>map=new HashMap<>();\n for(int i=0;i<arr.length;i++){\n sort[i]=arr[i];\n }\n Arrays.sort(sort);\n for(int i=0;i<arr.length;i++){\n if(map.containsKey(sort[i])){\n map.put(sort[i],map.get(sort[i])+1);\n }else{\n map.put(sort[i],1);\n }\n if(map.get(sort[i])==0){\n map.remove(sort[i]);\n }\n \n int num=arr[i];\n if(map.containsKey(num)){\n map.put(num,map.get(num)-1);\n if(map.get(num)==0){\n map.remove(num);\n }\n }else{\n map.put(num,-1);\n }\n if(map.size()==0){\n ans++;\n }\n //System.out.println(map);\n }\n return ans;\n }\n}\n``` | 2 | 0 | [] | 0 |
max-chunks-to-make-sorted-ii | C++ easy solution (beats 100%), recording min-max info for each chunk | c-easy-solution-beats-100-recording-min-4soke | \nclass Solution {\npublic:\n typedef pair<int,int> IntPair;\n int maxChunksToSorted(vector<int>& arr) {\n // we only need to maintain the {min, ma | kthtes | NORMAL | 2019-05-18T21:05:24.299337+00:00 | 2019-05-18T21:06:54.636964+00:00 | 253 | false | ```\nclass Solution {\npublic:\n typedef pair<int,int> IntPair;\n int maxChunksToSorted(vector<int>& arr) {\n // we only need to maintain the {min, max} info for each chunk\n vector<IntPair> minMax;\n \n // first, there\'s only one chunk: arr[0]\n minMax.push_back({arr[0], arr[0]});\n \n // starting from arr[1], we have 3 situations:\n for(int i=1;i<arr.size();i++){\n int last=minMax.size()-1;\n if(arr[i]>=minMax[last].second){\n // 1) if (arr[i] >= last chunk\'s largest number), we create a new chunk\n minMax.push_back({arr[i], arr[i]});\n }else if(arr[i]<minMax[last].first){\n // 2) if (arr[i] < last chunk\'s smallest number), we should look back\n int newMin=arr[i];\n int newMax=minMax[last].second;\n // because we must make sure arr[i] will be in a particular chunk[j],\n // so that chunk[j-1]\'s largest < arr[i] < chunk[j]\'s largest. \n minMax.pop_back();\n for(int j=last-1; j>=0 && arr[i]<minMax[j].second; j--){\n newMin=min(newMin, minMax[j].first);\n newMax=max(newMax, minMax[j].second);\n minMax.pop_back();\n }\n // once we found the chunk[j], we can pop_back all chunks after [j],\n // and push_back the new correct chunk we\'ve just found out.\n minMax.push_back({newMin, newMax});\n } // 3) otherwise, we do nothing\n }\n \n return minMax.size();\n }\n};\n``` | 2 | 0 | [] | 1 |
max-chunks-to-make-sorted-ii | 贪心的去找终点 | tan-xin-de-qu-zhao-zhong-dian-by-chris4f-yn53 | \u770B\u9898\u76EE\u7ED9\u76842\u4E2A\u4F8B\u5B50input1 = \u30104\uFF0C 3\uFF0C 2\uFF0C 1\uFF0C 0\u3011\uFF0Coutput1 = 1\uFF1Binput2 = \u30101\uFF0C0\uFF0C2\uFF | chris4fb | NORMAL | 2019-01-29T03:06:58.544143+00:00 | 2019-01-29T03:06:58.544214+00:00 | 243 | false | 1. \u770B\u9898\u76EE\u7ED9\u76842\u4E2A\u4F8B\u5B50input1 = \u30104\uFF0C 3\uFF0C 2\uFF0C 1\uFF0C 0\u3011\uFF0Coutput1 = 1\uFF1Binput2 = \u30101\uFF0C0\uFF0C2\uFF0C3\uFF0C4\u3011\uFF0Coutput2 = 4.\n2. \u5206\u6790\u9898\u76EE\u8981\u6C42\uFF0C\u95EE\u6700\u591A\u53EF\u4EE5\u5212\u5206\u4E3A\u51E0\u4E2Ablock\u3002\u663E\u7136\uFF0C\u6BCF\u4E00\u4E2Ablock\u5185\uFF0C\u5047\u8BBE\u4E3A\u3010i\uFF0Cj\u3011\uFF0C\u5373\u8D77\u70B9\u4E3Ai\uFF0C\u7EC8\u70B9\u4E3Aj\u3002\u4E0D\u7BA1\u8BE5block\u5185\u662F\u600E\u4E48\u6392\u5E8F\u7684\uFF0C\u4E00\u5B9A\u6709\u4E00\u4E2A\u6027\u8D28\uFF0C\u5373\u8BE5block\u7684\u957F\u5EA6j - i + 1\uFF0C\u5E76\u4E14\uFF0C\u5305\u542B\u4E86\u6240\u6709\u7684i\u5230j\u7684\u503C\uFF08\u7AEF\u70B9\u4E5F\u7B97\u5728\u5185\uFF09\u3002\n3. \u600E\u4E48\u4F7F\u7528\u5982\u4E0A\u6027\u8D28\uFF1A\u4ECE\u5F53\u524D\u4F4D\u7F6E\u5F80\u53F3\u8D70\uFF0C\u67E5\u770B\u5F53\u524D\u4F4D\u7F6E\u7684\u503C\u88AB\u5305\u542B\u7684block\u7684\u7EC8\u70B9\u5728\u54EA\u91CC\u3002\n\t\t3.1\u5982\u679Carr\u3010idx\u3011 = idx\uFF0C\u8BF4\u660Earr\u3010idx\u3011\u5728\u76F8\u5E94\u7684\u4F4D\u7F6E\uFF0C\u8D2A\u5FC3\u7684\u628A\u8BE5arr\u3010idx\u3011\u5F53\u505A\u4E00\u4E2Ablock\uFF0Ccnt++\u3002\n\t\t3.2\u5982\u679Carr\u3010idx\u3011\uFF01=idx\uFF0C\u8BF4\u660Earr\u3010idx\u3011\u4E0D\u5728\u76F8\u5E94\u7684\u4F4D\u7F6E\uFF0C\u5219\u770B\u5305\u542B\u8BE5arr\u3010idx\u3011\u7684block\u7684\u7EC8\u70B9\u5728\u54EA\u91CC\u3002\u6839\u636E\u5982\u4E0A\u6027\u8D28\uFF0C\u53EA\u8003\u8651\u5F53\u524D\u6570\u5B57arr\u3010idx\u3011\u7684\u8BDD\uFF0C\u7EC8\u70B9\u4E00\u5B9A\u662Farr\u3010idx\u3011\u548Cidx\u7684\u6700\u5927\u503C\u3002\u5219\uFF0C\u53E6\u8D77\u4E00\u4E2A\u5FAA\u73AF\uFF0C\u5411\u7EC8\u70B9\u8FDB\u884C\u904D\u5386\u3002\u5728\u904D\u5386\u8FC7\u7A0B\u4E2D\uFF0C\u7EC8\u70B9\u4F4D\u7F6E\u9700\u8981\u5B9E\u65F6\u66F4\u65B0\uFF0C\u5F53\u8D70\u5230\u6700\u7EC8\u7684\u7EC8\u70B9\u4F4D\u7F6E\u65F6\uFF0C\u8BF4\u660E\u8BE5block\u7ED3\u675F\uFF0Ccnt++\u3002\n4. \u6700\u540E\uFF0C\u522B\u5FD8\u4E86\u66F4\u65B0\u4E3B\u5FAA\u73AF\uFF0Ci=end\uFF0C\u5373\u4E0B\u4E00\u6B21\u4ECEend+1\u7684\u4F4D\u7F6E\u5F00\u59CB\u7EE7\u7EED\u627Eblock\u3002\n5. code\n```\nclass Solution {\n public int maxChunksToSorted(int[] arr) {\n if (arr == null || arr.length == 0) {\n return 0;\n }\n \n int cnt = 0;\n \n int end = 0;\n for (int i = 0; i < arr.length; i++) {\n if (arr[i] == i) {\n cnt++;\n } else {\n end = Math.max(i, arr[i]);\n for (int j = i; j <= end; j++) {\n end = Math.max(end, j);\n end = Math.max(end, arr[j]);\n \n }\n cnt++;\n i = end;\n }\n }\n \n return cnt;\n }\n}\n``` | 2 | 0 | [] | 1 |
max-chunks-to-make-sorted-ii | Two Java O(n) Solutions with Explanation, min array and stack | two-java-on-solutions-with-explanation-m-jci7 | If we know the smallest element at the right hand side and the current largest element, we can create a new chunk if largest element <= smallest element at the | crunner | NORMAL | 2018-09-06T03:45:15.340503+00:00 | 2018-09-06T03:45:15.340550+00:00 | 310 | false | If we know the smallest element at the right hand side and the current largest element, we can create a new chunk if largest element <= smallest element at the right hand side. The smallest element at the right hand side can be tracked by either an array or stack. The last element will always create a new chunk, either itself (if it\'s the largest one) or combine with the previous elements.\n\n```\n public int maxChunksToSorted(int[] arr) {\n int n = arr.length;\n Stack<Integer> smallest = new Stack<Integer>();\n for (int i = n-1; i >= 0; i--) {\n if (smallest.isEmpty() || arr[i] <= smallest.peek())\n smallest.push(arr[i]);\n }\n int largest = arr[0];\n int ret = 0;\n for (int i = 0; i < n-1; i++) {\n if (arr[i] == smallest.peek())\n smallest.pop();\n largest = Math.max(largest, arr[i]);\n if (largest <= smallest.peek()) {\n ret++;\n largest = arr[i+1];\n }\n }\n return ret+1;\n }\n\n public int maxChunksToSorted(int[] arr) {\n int n = arr.length;\n int[] smallest = new int[n];\n smallest[n-1] = arr[n-1];\n for (int i = n-2; i >= 0; i--) {\n smallest[i] = Math.min(smallest[i+1], arr[i]);\n }\n int largest = arr[0];\n int ret = 0;\n for (int i = 0; i < n-1; i++) {\n largest = Math.max(largest, arr[i]);\n if (largest <= smallest[i+1]) {\n ret++;\n largest = arr[i+1];\n }\n }\n return ret+1;\n }\n``` | 2 | 0 | [] | 0 |
max-chunks-to-make-sorted-ii | Easy to understand O(N) Java Solution | easy-to-understand-on-java-solution-by-t-yupx | In short we just need to confirm a new split when the smallest number on the right side for the current index is greater or equal to the current max number.\n\n | tongtong1990 | NORMAL | 2018-05-07T05:01:22.343505+00:00 | 2018-05-07T05:01:22.343505+00:00 | 144 | false | In short we just need to confirm a new split when the smallest number on the right side for the current index is greater or equal to the current max number.\n\n```\npublic int maxChunksToSorted(int[] arr) {\n int []rightMin = new int[arr.length];\n rightMin[arr.length - 1] = arr[arr.length - 1];\n for (int i = arr.length - 2; i >= 0; i--) rightMin[i] = Math.min(rightMin[i+1], arr[i]);\n int result = 0, max = 0;\n for (int i = 0; i < arr.length; i++) {\n max = Math.max(max, arr[i]);\n if (i == arr.length - 1 || max <= rightMin[i+1]) result++;\n }\n return result;\n }\n``` | 2 | 0 | [] | 0 |
max-chunks-to-make-sorted-ii | Two-pass Java O(n) time/space solution | two-pass-java-on-timespace-solution-by-f-8bei | Assume the input array is arr with length n. A subarray arr[i,j] can form a chunk if it satisfies the following two conditions simultaneously:\n\n1. Its maximum | fun4leetcode | NORMAL | 2018-01-21T23:25:09.639000+00:00 | 2018-01-21T23:25:09.639000+00:00 | 143 | false | Assume the input array is `arr` with length `n`. A subarray `arr[i,j]` can form a chunk if it satisfies the following two conditions simultaneously:\n\n1. Its maximum element is no greater than the minimum element of the subarray `arr[j+1, n-1]`.\n\n2. Its minimum element is no less than the maximum element of the subarray `arr[0, i-1]`. \n\nSince we want most number of chunks, we need to find as many such subarrays as possible -- we will build the chunks in a greedy manner, either from left to right or from right to left. For the former, the second condition will be met automatically for each chunk, while for the latter, the first condition will be met automatically for each chunk. \n\nHere we will take the first option and construct the chunks from left to right. All the information we need then is the minimum elements for each of the subarrays `arr[j+1, n-1]`. In the following code, we will use `min[j]` to denote the minimum element for the subarray `arr[j+1, n-1]` (for the special case `j == n-1`, we set `min[n-1] = Integer.MAX_VALUE`). To compute `min[j]`, we can use a simple recurrence relation: `min[j] = Math.min(min[j+1], arr[j+1])`, which entails a backward iteration of the `arr` array.\n\nWe then loop through `arr` in forward direction, where for each index `j`, we check if the first condition mentioned above is satisfied, that is, if the maximum element of the subarray `arr[0, j]` (which will also be the maximum element of the current chunk being searched) is no greater than the minimum element of the subarray `arr[j+1, n-1]`. If so, a chunk is found and we increase the result count by `1`. Here is the two-pass `O(n)` time/space solution:\n\n```\npublic int maxChunksToSorted(int[] arr) {\n int n = arr.length, res = 0;\n \n int[] min = new int[n];\n min[n - 1] = Integer.MAX_VALUE;\n \n for (int j = n - 2; j >= 0; j--) {\n min[j] = Math.min(min[j + 1], arr[j + 1]);\n }\n \n for (int j = 0, max = Integer.MIN_VALUE; j < n; j++) {\n max = Math.max(max, arr[j]);\n if (max <= min[j]) res++;\n }\n \n return res;\n}\n``` | 2 | 1 | [] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.