question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
number-of-ways-to-split-array | One Line Solution | one-line-solution-by-charnavoki-eaj1 | null | charnavoki | NORMAL | 2025-01-03T07:09:38.601727+00:00 | 2025-01-03T07:09:38.601727+00:00 | 19 | false |
```javascript []
const waysToSplitArray = ([a, ...nums], s = nums.reduce((x, y) => y + x)) =>
nums.reduce((w, v) => ([w, a, s] = [w + (a >= s), a + v, s - v])[0], 0);
``` | 2 | 0 | ['JavaScript'] | 0 |
number-of-ways-to-split-array | Step-by-Step Solution: Number of Ways to Split Array (100% Easy, 0ms) | step-by-step-solution-number-of-ways-to-8vc9g | IntuitionThe problem is about finding the number of ways to split an array into two non-empty parts such that the sum of the first part is greater than or equal | user1233nm | NORMAL | 2025-01-03T07:02:49.077530+00:00 | 2025-01-04T05:51:41.615688+00:00 | 26 | false | # Intuition
The problem is about finding the number of ways to split an array into two non-empty parts such that the sum of the first part is greater than or equal to the sum of the second part. The **prefix sum technique** provides an efficient way to calculate the cumulative sum and perform quick range queries.
# Approach
1. **Prefix Sum Calculation**:
- Compute the cumulative sum for the array using a `prefixSum` array, where `prefixSum[i]` represents the sum of elements from the start to the `i`th index.
2. **Iterate for Splits**:
- For each potential split index \( i \), check if the sum of the first part \( `prefixSum[i+1]` \) is greater than or equal to the sum of the second part \( `prefixSum[n]`- `prefixSum[i+1]` \).
- Count such splits.
3. **Return Count**:
- Return the total number of valid splits.
### TestCase:
`nums = [10, 4, -8, 7]`
### Step 1: Compute `prefixSum`
The prefix sum array stores the cumulative sum of elements in the array up to each index.
- **Initialization**: `prefixSum` is a vector of size `nums.size() + 1`, initialized to all zeros.
### Step 2: Check Valid Splits
For each split index \( i \), check if the sum of the first part (left) is greater than or equal to the sum of the second part (right).
- **Condition**:
\[
prefixSum[i + 1] >= prefixSum[n] - prefixSum[i + 1]
\]
where \( n \) is the size of `nums`.
#### Iteration:
1. \( i = 0 \):
- Left Sum: \( prefixSum[1] = 10 \)
- Right Sum: \( prefixSum[4] - prefixSum[1] = 13 - 10 = 3 \)
- \( 10 >= 3 \): **Valid split**
- Increment `count` → `count = 1`.
2. \( i = 1 \):
- Left Sum: \( prefixSum[2] = 14 \)
- Right Sum: \( prefixSum[4] - prefixSum[2] = 13 - 14 = -1 \)
- \( 14 >= -1 \): **Valid split**
- Increment `count` → `count = 2`.
3. \( i = 2 \):
- Left Sum: \( prefixSum[3] = 6 \)
- Right Sum: \( prefixSum[4] - prefixSum[3] = 13 - 6 = 7 \)
- \( 6 not >= 7 \): **Not a valid split**
- `count` remains unchanged.
### Final Output
**Total valid splits**: `2`
**Result**: `count = 2`
---
### Dry Run Summary
| Index \( i \) | Left Sum (\( prefixSum[i+1] \)) | Right Sum (\( prefixSum[n] - prefixSum[i+1] \)) | Condition ( >= \) | Valid Split |
|---------------|--------------------------------|-----------------------------------------------|------------------------|-------------|
| 0 | 10 | 3 | 10 >= 3 | Yes |
| 1 | 14 | -1 | 14 >= -1 | Yes |
| 2 | 6 | 7 | 6 !>= 7 | No |
**Output**: `2`
# Code ( Click on it !!!)
<details>
<summary><strong>C++</strong></summary>
```cpp
class Solution {
public:
int waysToSplitArray(vector<int>& nums) {
vector<long long> prefixSum(nums.size() + 1, 0);
int count = 0;
for (int i = 0; i < nums.size(); i++) {
prefixSum[i + 1] = prefixSum[i] + nums[i];
}
for (int i = 0; i < nums.size() - 1; i++) {
if (prefixSum[i + 1] >= prefixSum[nums.size()] - prefixSum[i + 1]) {
count++;
}
}
return count;
}
};
</details>
<details>
<summary><strong>Python</strong></summary>
```python
class Solution:
def waysToSplitArray(self, nums):
prefixSum = [0] * (len(nums) + 1)
count = 0
for i in range(len(nums)):
prefixSum[i + 1] = prefixSum[i] + nums[i]
for i in range(len(nums) - 1):
if prefixSum[i + 1] >= prefixSum[-1] - prefixSum[i + 1]:
count += 1
return count
```
</details>
<details>
<summary><strong>Java</strong></summary>
```java
class Solution {
public int waysToSplitArray(int[] nums) {
long[] prefixSum = new long[nums.length + 1];
int count = 0;
for (int i = 0; i < nums.length; i++) {
prefixSum[i + 1] = prefixSum[i] + nums[i];
}
for (int i = 0; i < nums.length - 1; i++) {
if (prefixSum[i + 1] >= prefixSum[nums.length] - prefixSum[i + 1]) {
count++;
}
}
return count;
}
}
```
</details>
<details>
<summary><strong>JavaScript</strong></summary>
```javascript
var waysToSplitArray = function(nums) {
const prefixSum = new Array(nums.length + 1).fill(0);
let count = 0;
for (let i = 0; i < nums.length; i++) {
prefixSum[i + 1] = prefixSum[i] + nums[i];
}
for (let i = 0; i < nums.length - 1; i++) {
if (prefixSum[i + 1] >= prefixSum[nums.length] - prefixSum[i + 1]) {
count++;
}
}
return count;
};
```
</details>
<details>
<summary><strong>Go</strong></summary>
```go
func waysToSplitArray(nums []int) int {
prefixSum := make([]int64, len(nums)+1)
count := 0
for i, num := range nums {
prefixSum[i+1] = prefixSum[i] + int64(num)
}
for i := 0; i < len(nums)-1; i++ {
if prefixSum[i+1] >= prefixSum[len(nums)]-prefixSum[i+1] {
count++
}
}
return count
}
```
</details>
<details>
<summary><strong>Rust</strong></summary>
```rust
impl Solution {
pub fn ways_to_split_array(nums: Vec<i32>) -> i32 {
let mut prefix_sum = vec![0i64; nums.len() + 1];
let mut count = 0;
for i in 0..nums.len() {
prefix_sum[i + 1] = prefix_sum[i] + nums[i] as i64;
}
for i in 0..nums.len() - 1 {
if prefix_sum[i + 1] >= prefix_sum[nums.len()] - prefix_sum[i + 1] {
count += 1;
}
}
count
}
}
```
</details>
# Complexity
- **Time Complexity**:
- Prefix sum calculation: \( O(n) \)
- Iterating through splits: \( O(n) \)
- Total: \( O(n) \)
- **Space Complexity**:
- \( O(n) \) for the prefix sum array.
Let's walk through the dry run for the input array `[10, 4, -8, 7]`, using the C++ implementation provided, and explain the process step by step.
<img src="https://media.tenor.com/WrG5Ar-qk5QAAAAM/upvote-give-this-man.gif" alt="Prefix Sum Visualization" style="max-width: 100%; width: 1000px; height: auto;">
| 2 | 0 | ['Array', 'Prefix Sum', 'C++', 'Java', 'Go', 'Python3', 'Rust', 'JavaScript'] | 1 |
number-of-ways-to-split-array | Beats 100% Easy C++ Using Prefix and Suffix -- Ways to Split Array into Two Parts | beats-100-easy-c-using-prefix-and-suffix-c9lb | Method 1 -- Optimized way of the second method given after thisIntuitionThe task is to split the array into two non-empty parts such that the sum of elements in | Abhishek-Verma01 | NORMAL | 2025-01-03T06:40:32.480841+00:00 | 2025-01-03T06:40:32.480841+00:00 | 27 | false | # Method 1 -- Optimized way of the second method given after this
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The task is to split the array into two non-empty parts such that the sum of elements in the left part `(lSum)` is greater than or equal to the sum of elements in the right part `(rSum)`. We aim to efficiently calculate the sums on both sides of the split for each potential index while minimizing memory usage.
Instead of recalculating sums repeatedly or precomputing all possible suffix sums, we use two variables (lSum and rSum) to keep track of the cumulative sums dynamically. This allows us to achieve the goal in a single pass with O(1) space complexity.
# Approach
<!-- Describe your approach to solving the problem. -->
1. Initial Total Sum (rSum):
* Compute the total sum of the array (rSum) in the first loop. This represents the initial value of the "right sum," assuming no elements are in the left part of the array.
2. Iterate Through the Array:
* Traverse the array from the beginning to the second-to-last element.
For each index:
* Add the current element to the left sum (lSum).
* Subtract the same element from the right sum (rSum).
3. Check Valid Split:
* Compare lSum and rSum for each split point. If lSum is greater than or equal to rSum, increment the validSplit counter.
4. Return the Count:
* Return the total number of valid splits stored in validSplit.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(n)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(1)
# Code
```cpp []
class Solution {
public:
int waysToSplitArray(vector<int>& nums) {
int n = nums.size(); // Number of elements in the array
long long rSum = 0; // Stores the cumulative sum of elements on the right side of the split
long long lSum = 0; // Stores the cumulative sum of elements on the left side of the split
int validSplit = 0; // Counter for valid splits
// Step 1: Calculate the total sum of the array (initial right sum)
for (int i : nums) {
rSum += i;
}
// Step 2: Iterate through the array to calculate left and right sums dynamically
for (int i = 0; i < n - 1; i++) {
lSum += nums[i]; // Add the current element to the left sum
rSum -= nums[i]; // Subtract the current element from the right sum
// Step 3: Check if the current split is valid
if (lSum >= rSum) {
validSplit++; // Increment the counter if the condition is satisfied
}
}
// Step 4: Return the total count of valid splits
return validSplit;
}
};
```
# Method 2 of Doing the same
# Intuition
To solve the problem of splitting an array into two non-empty parts such that the left sum `(lSum)` is greater than or equal to the right sum `(rSum)`, this approach precomputes and stores suffix sums for efficient access during the main loop.
Instead of recalculating the right sum `(rSum)` dynamically, we use an `unordered_map to store the suffix sums for all indices`. This ensures that for each split point, the right sum can be directly accessed in constant time. However, this approach trades memory usage for simplicity in accessing suffix sums.
# Approach
1. Precompute Suffix Sums:
* Use an unordered_map to store the suffix sum (rSum) for each index from the end of the array.
* Traverse the array from right to left and compute the cumulative sum, storing it in the map.
2. Calculate Left Sum Dynamically:
* Traverse the array from left to right, maintaining the cumulative left sum (lSum).
* For each split point, compare lSum with the precomputed rSum for the next index.
3. Count Valid Splits:
* Increment the validSplit counter whenever lSum is greater than or equal to rSum for a given split point.
4. Return the Count:
* Finally, return the total number of valid splits stored in validSplit.
# Complexity
- Time Complexity -
* O(n): One pass to compute the suffix sums and another pass to calculate the prefix sums and perform comparisons.
- Space Complexity -
* O(n): Additional storage for the suffix sums in the unordered_map.
## Code
```cpp []
class Solution {
public:
int waysToSplitArray(vector<int>& nums) {
// Edge case: If the array is empty, there are no valid splits
if (nums.size() == 0) {
return 0;
}
// Step 1: Precompute suffix sums and store them in a map
unordered_map<int, long long> mp; // Stores suffix sums with index as the key
long long sum = 0; // To compute the cumulative sum from the right
for (int i = nums.size() - 1; i >= 0; i--) {
sum += nums[i]; // Add the current element to the suffix sum
mp[i] = sum; // Store the suffix sum in the map with the current index as the key
}
// Step 2: Traverse the array to calculate prefix sums dynamically
int validSplit = 0; // Counter for valid splits
sum = 0; // Reset sum to calculate the left sum (prefix sum)
for (int i = 0; i < nums.size() - 1; i++) {
sum += nums[i]; // Add the current element to the left sum
// Check if the left sum is greater than or equal to the right sum
if (sum >= mp[i + 1]) {
validSplit++; // Increment the counter if the condition is satisfied
}
}
// Step 3: Return the total count of valid splits
return validSplit;
}
};
```
# Key Differences from Optimized Code
* Uses an unordered_map to store suffix sums, which requires extra space.
* Instead of dynamically updating the right sum (rSum), this approach precomputes and accesses it directly from the map.
* Trades memory usage for simplicity in accessing suffix sums.
# Takeaway
While this approach works efficiently for smaller arrays, it can become memory-intensive for larger inputs due to the additional storage required for the unordered_map. The dynamic sum update method (optimized approach) is generally preferred for space efficiency.
# Please UpVote If you like .... !!! | 2 | 0 | ['Array', 'Sliding Window', 'Suffix Array', 'Prefix Sum', 'C++'] | 0 |
number-of-ways-to-split-array | Simple prefixSum solution✅✅ | simple-prefixsum-solution-by-_shubham_22-67y1 | IntuitionThe task is to find the number of ways to split an array nums nums such that:
Both parts are non-empty.
The sum of the left part (prefixSum) is greater | _shubham_22 | NORMAL | 2025-01-03T06:11:34.107285+00:00 | 2025-01-03T06:11:34.107285+00:00 | 4 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The task is to find the number of ways to split an array nums nums such that:
1. Both parts are non-empty.
1. The sum of the left part (prefixSum) is greater than or equal to the sum of the right part (suffixSum).
By observing:
- prefixSum+suffixSum=totalSum,
- we can compute suffixSum=totalSum−prefixSum.
As we iterate through the array and keep track of prefixSum, suffixSum can be calculated directly. The problem reduces to checking whether prefixSum ≥ suffixSum for valid splits.
# Approach
<!-- Describe your approach to solving the problem. -->
1. Calculate Total Sum:
- Compute the total sum of the array once using a single pass. This will help in deriving suffixSum later.
1. Initialize Prefix Sum:
- Start with prefixSum=0.
- Use a variable count=0 to keep track of valid splits.
1. Iterate Through the Array:
- For each element (except the last one to ensure non-empty right part):
1. Update prefixSum by adding the current element.
1. Derive suffixSum as totalSum−prefixSum.
1. Check the condition prefixSum≥suffixSum:
- If true, increment the count.
1. Return Result:
- After iterating through the array, return count.
# Complexity
- Time complexity: O(n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int waysToSplitArray(vector<int>& nums) {
int n=nums.size();
long long totalSum = 0;
for (int num : nums) {
totalSum+=num;
}
long long prefixSum=0;
int count=0;
for(int i=0;i<n-1;i++){
prefixSum+=nums[i];
long long suffixSum=totalSum-prefixSum;
if(prefixSum>=suffixSum) count++;
}
return count;
}
};
``` | 2 | 0 | ['Array', 'Prefix Sum', 'C++'] | 0 |
number-of-ways-to-split-array | 🌟 Beat 100% | 🔥Optimized Approach 💡 | Beginner-Friendly 🐣 | Easy Solution ✅ | beat-100-optimized-approach-beginner-fri-62ra | Intuition 🧠
The goal is to find splits in the array such that the sum of the left part is greater than or equal to the sum of the right part. This involves calc | shubhamrajpoot_ | NORMAL | 2025-01-03T05:45:59.828286+00:00 | 2025-01-03T05:45:59.828286+00:00 | 52 | false | # Intuition 🧠
- The goal is to find splits in the array such that the sum of the left part is greater than or equal to the sum of the right part. This involves calculating prefix sums efficiently.
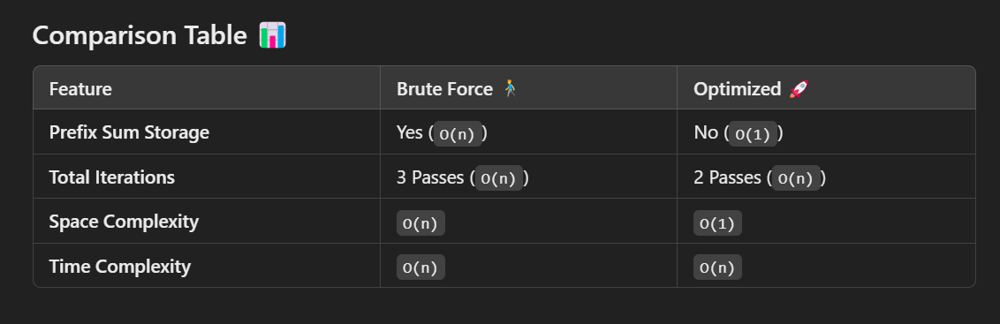
# *Brute Force Approach* 🚶♂️
## *Approach*:
- Compute two prefix sum arrays (left and right) for the left and right parts of the array.
- Iterate through all valid splits (i = 0 to n-2) and compare left[i] with right[i+1].
- Count the number of valid splits.
## Time Complexity (TC):
- O(n) for calculating left and right prefix sums.
- O(n) for iterating through the splits.
- Overall: O(n)
## Space Complexity (SC):
- O(n) for storing left and right prefix sum arrays.
# *Optimized Approach* 🚀
## *Approach*:
- Calculate the total sum of the array in one pass.
- Use a single variable (leftSum) to track the sum of the left part dynamically while iterating through the array.
- For each split, calculate the right part as totalSum - leftSum on the fly and compare.
- Count the number of valid splits.
## Time Complexity (TC):
- O(n) for calculating the total sum and iterating through the splits.
## Space Complexity (SC):
- O(1) since we don’t use any extra space for prefix sums.
# Code
```cpp []
class Solution {
public:
int waysToSplitArray(vector<int>& nums) {
//brute force
int n = nums.size() ;
vector<long long> left(n , 0) ;
vector<long long> right(n , 0) ;
//prefixsum left ka
long long sum = 0 ;
for(int i = 0 ; i < n ; i++)
{
sum += nums[i] ;
left[i] = sum ;
}
//prefixsum right ka
sum = 0 ;
for(int i = n-1 ; i >= 0 ; i--)
{
sum += nums[i] ;
right[i] = sum ;
}
int ans = 0 ;
for(int i = 0 ; i < left.size()-1 ; i++ )
{
if(left[i] >= right[i+1])
{
ans++ ;
}
}
return ans ;
//optimised solution
long long leftSum = 0 ;
long long totalSum = 0 ;
for(auto num : nums)
{
totalSum += num ;
}
int ans = 0 ;
for(int i = 0 ; i < nums.size() -1 ; i++ )
{
leftSum += nums[i] ;
long long rightSum = totalSum - leftSum ;
if(leftSum >= rightSum)
{
ans++ ;
}
}
return ans ;
}
};
```
```java []
class Solution {
public int waysToSplitArray(int[] nums) {
long totalSum = 0, leftSum = 0;
for (int num : nums) {
totalSum += num;
}
int ans = 0;
for (int i = 0; i < nums.length - 1; i++) {
leftSum += nums[i];
long rightSum = totalSum - leftSum;
if (leftSum >= rightSum) {
ans++;
}
}
return ans;
}
}
```
```python []
class Solution:
def waysToSplitArray(self, nums: list[int]) -> int:
totalSum = sum(nums)
leftSum = 0
ans = 0
for i in range(len(nums) - 1):
leftSum += nums[i]
rightSum = totalSum - leftSum
if leftSum >= rightSum:
ans += 1
return ans
```
```ruby []
def ways_to_split_array(nums)
total_sum = nums.sum
left_sum = 0
ans = 0
(0...nums.size - 1).each do |i|
left_sum += nums[i]
right_sum = total_sum - left_sum
ans += 1 if left_sum >= right_sum
end
ans
end
```
```typescript []
function waysToSplitArray(nums: number[]): number {
let totalSum = nums.reduce((a, b) => a + b, 0);
let leftSum = 0, ans = 0;
for (let i = 0; i < nums.length - 1; i++) {
leftSum += nums[i];
let rightSum = totalSum - leftSum;
if (leftSum >= rightSum) {
ans++;
}
}
return ans;
}
```
```C# []
public class Solution {
public int WaysToSplitArray(int[] nums) {
long totalSum = 0, leftSum = 0;
foreach (int num in nums) {
totalSum += num;
}
int ans = 0;
for (int i = 0; i < nums.Length - 1; i++) {
leftSum += nums[i];
long rightSum = totalSum - leftSum;
if (leftSum >= rightSum) {
ans++;
}
}
return ans;
}
}
```
```Go []
func waysToSplitArray(nums []int) int {
totalSum, leftSum := 0, 0
for _, num := range nums {
totalSum += num
}
ans := 0
for i := 0; i < len(nums)-1; i++ {
leftSum += nums[i]
rightSum := totalSum - leftSum
if leftSum >= rightSum {
ans++
}
}
return ans
}
```
| 2 | 0 | ['Prefix Sum', 'Python', 'C++', 'Java', 'Go', 'Rust', 'Ruby', 'JavaScript', 'C#', 'Dart'] | 0 |
number-of-ways-to-split-array | 2 ms🚀|| 100% Beats ✅ || JAVA || Simple Logic🌟 | 2-ms-100-beats-java-simple-logic-by-siva-p7w0 | IntuitionApproachComplexity
Time complexity: O(n + (n-1))
Space complexity:
Code | Sivaram11 | NORMAL | 2025-01-03T05:29:23.074767+00:00 | 2025-01-03T05:29:23.074767+00:00 | 27 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: O(n + (n-1))
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int waysToSplitArray(int[] nums) {
long sum = 0;
for(int i=0;i<nums.length;i++){
sum += nums[i];
}
int count = 0;
long val = nums[0];
for(int i=0;i<nums.length-1;i++){
if(val >= sum-val){
count++;
}
val += nums[i+1];
}
return count;
}
}
``` | 2 | 0 | ['Java'] | 1 |
number-of-ways-to-split-array | 🔥 Super Clean 4-Line C++ Solution | One-Pass Magic! | super-clean-4-line-c-solution-one-pass-m-2kr8 | IntuitionThe problem requires determining the number of valid ways to split the array such that the sum of elements on the left side is greater than or equal to | sachin1604 | NORMAL | 2025-01-03T05:24:59.669482+00:00 | 2025-01-03T05:24:59.669482+00:00 | 16 | false | # Intuition
The problem requires determining the number of valid ways to split the array such that the sum of elements on the left side is greater than or equal to the sum of elements on the right side. The key insight is that we can compute the prefix sum and suffix sum efficiently by traversing the array once and updating these values dynamically.
# Approach
1. Calculate the total sum of the array (suffixSum) initially using accumulate().
2. Traverse the array from left to right, updating: prefixSum by adding the current element. suffixSum by subtracting the current element.
3. After each update, check if prefixSum is greater than or equal to suffixSum. If true, increment the count (ans).
4. Return the count at the end of the traversal.
# Complexity
- Time complexity: $$O(n)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(1)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int waysToSplitArray(vector<int>& nums) {
long long ss = accumulate(nums.begin(), nums.end(), 0ll), ps = 0;
int ans = 0;
for (int i = 0; i < nums.size() - 1; i++) {
ps += nums[i];
ss -= nums[i];
if (ps >= ss) ans++;
}
return ans;
}
};
``` | 2 | 0 | ['Array', 'Prefix Sum', 'C++'] | 1 |
number-of-ways-to-split-array | Easy Solution || 2ms ✅ || Beats 100%👌|| Prefix Sum 👍 | easy-solution-2ms-beats-100-prefix-sum-b-fzwu | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | Sorna_Prabhakaran | NORMAL | 2025-01-03T05:22:12.752428+00:00 | 2025-01-03T05:22:12.752428+00:00 | 15 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution
{
public int waysToSplitArray(int[] nums)
{
long sum = 0;
long left = 0;
int count = 0;
for(int i = 0; i < nums.length; i++) sum += nums[i];
for(int i = 0; i < nums.length-1; i++)
{
left += nums[i];
sum -= nums[i];
if(left >= sum) count++;
}
return count;
}
}
``` | 2 | 0 | ['Java'] | 0 |
number-of-ways-to-split-array | Java and C++, Easy Solution | java-and-c-easy-solution-by-divyaaroraa-3lx7 | IntuitionThe problem asks for the number of valid splits of an array, where the sum of the left part is greater than or equal to the sum of the right part. This | divyaaroraa | NORMAL | 2025-01-03T05:18:36.918706+00:00 | 2025-01-03T05:18:36.918706+00:00 | 11 | false | # Intuition
The problem asks for the number of valid splits of an array, where the sum of the left part is greater than or equal to the sum of the right part. This can be efficiently solved using prefix sums.
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
1. First, calculate the total sum of the array, totalSum, which represents the sum of all elements.
2. Use a variable leftSum to keep track of the sum of the left part as we iterate through the array.
3. For every index i, compute the sum of the right part as:
rightSum=totalSum−leftSum
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: O(n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int waysToSplitArray(int[] nums) {
long totalSum = 0, leftSum = 0;
int count = 0;
for (int num : nums) {
totalSum += num;
}
for (int i = 0; i < nums.length - 1; i++) {
leftSum += nums[i];
long rightSum = totalSum - leftSum;
if (leftSum >= rightSum) {
count++;
}
}
return count;
}
}
```
```cpp []
class Solution {
public:
int waysToSplitArray(vector<int>& nums) {
long long totalSum = 0, leftSum = 0;
int count = 0;
for (int num : nums) {
totalSum += num;
}
for (int i = 0; i < nums.size() - 1; ++i) {
leftSum += nums[i];
long long rightSum = totalSum - leftSum;
if (leftSum >= rightSum) {
++count;
}
}
return count;
}
};
``` | 2 | 0 | ['C++'] | 0 |
number-of-ways-to-split-array | Beats 100% users in JAVA | beats-100-users-in-java-by-muskaan_1801-akyv | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | muskaan_1801 | NORMAL | 2025-01-03T05:12:29.978830+00:00 | 2025-01-03T05:12:29.978830+00:00 | 16 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int waysToSplitArray(int[] nums) {
int n = nums.length;
// Calculate the total sum of the array
long totalSum = 0;
for (int num : nums) {
totalSum += num;
}
// Initialize prefix sum and count of valid splits
long prefixSum = 0;
int validSplits = 0;
// Iterate through the array to count valid splits
for (int i = 0; i < n - 1; i++) { // We split at position `i`
prefixSum += nums[i];
long suffixSum = totalSum - prefixSum;
// If the prefix sum is greater than or equal to the suffix sum, it's a valid split
if (prefixSum >= suffixSum) {
validSplits++;
}
}
return validSplits;
}
}
``` | 2 | 0 | ['Java'] | 0 |
number-of-ways-to-split-array | Counting Valid Splits in an Array Based on Sum Comparison | counting-valid-splits-in-an-array-based-oen8t | IntuitionThe problem asks us to determine the number of valid splits in the array such that the sum of the left subarray is greater than or equal to the sum of | jasurbek_fm | NORMAL | 2025-01-03T05:05:34.492787+00:00 | 2025-01-03T05:05:34.492787+00:00 | 5 | false | # Intuition
The problem asks us to determine the number of valid splits in the array such that the sum of the left subarray is greater than or equal to the sum of the right subarray. A straightforward approach involves computing prefix sums and comparing them for each potential split.
# Approach
**1. Calculate Total Sum:**
- First, compute the total sum of the array to help calculate the right sum efficiently for any split.
**2. Iterate Over Possible Splits:**
- Maintain a ```left_sum``` variable to track the cumulative sum of the left subarray as we iterate through the array.
- For each index *i* (up to the second-to-last element), compute the right sum as ```total_sum - left_sum```.
- Check if ```left_sum >= right_sum```. If true, it's a valid split, so increment the counter.
**3. Return the Count:**
- At the end of the iteration, return the count of valid splits.
# Complexity
- Time complexity:
*O(n)*, where *n* is the size of the array. We iterate through the array twice: once to compute the total sum and once to check for valid splits.
- Space complexity:
*O(1)*, as we only use a few additional variables (```total_sum```, ```left_sum```, and ```right_sum```).
# Code
```cpp []
class Solution {
public:
int waysToSplitArray(vector<int>& nums) {
int valid_splits = 0;
long long total_sum = 0;
for (int num : nums){
total_sum += num;
}
// To keep track of the cumulative sum of the left part
long long left_sum = 0;
// Iterating through the array up to the second-to-last element
for (int i = 0; i < nums.size() - 1; i++) {
left_sum += nums[i];
// Calculating right sum as the remaining elements
long long right_sum = total_sum - left_sum;
if (left_sum >= right_sum) {
valid_splits++;
}
}
return valid_splits;
}
};
``` | 2 | 0 | ['Prefix Sum', 'C++'] | 0 |
number-of-ways-to-split-array | C++ solution using prefix sum and suffix sum. stay permission less | c-solution-using-prefix-sum-and-suffix-s-3yho | IntuitionApproachsimply create the prefix sum array and suffix sum array and then
if sum of prefix is grreater than equal to the next index of suffix sum then p | Gufrankhan | NORMAL | 2025-01-03T03:55:41.019573+00:00 | 2025-01-03T03:55:41.019573+00:00 | 17 | false | # Intuition
# Approach
simply create the prefix sum array and suffix sum array and then
if sum of prefix is grreater than equal to the next index of suffix sum then possible to split the array we count the number of ways and return it;
# Complexity
- Time complexity:
0(N) // size of nums
- Space complexity:
0(N)// prefix sum arr or suffix sum arr
# Code
```cpp []
#define ll long long
class Solution {
public:
int waysToSplitArray(vector<int>& nums) {
int n=nums.size(),cnt=0;
vector<ll>pre(n),suf(n);
// prefix sum
pre[0]=nums[0];
for(int i=1;i<n;i++)pre[i]+=pre[i-1]+nums[i];
// suffix sum
suf[n-1]=nums[n-1];
for(int i=n-2;i>=0;i--)suf[i]+=suf[i+1]+nums[i];
// checking if prefix(i) sum >=sufix(i+1)
for(int i=0;i<n-1;i++){
if(pre[i]>=suf[i+1])cnt++;
}
return cnt;
}
};
``` | 2 | 0 | ['C++'] | 0 |
number-of-ways-to-split-array | Number of Ways to Split Array- Two Approaches✅|| Beats 100% 🚀|| Prefix Sum & Single Pass || JAVA ☕ | number-of-ways-to-split-array-two-approa-5hoh | IntuitionThe problem asks us to find the number of valid splits in an array such that the sum of the left part is greater than or equal to the sum of the right | Megha_Mathur18 | NORMAL | 2025-01-03T03:50:33.506618+00:00 | 2025-01-03T03:50:33.506618+00:00 | 20 | false | # Intuition
The problem asks us to find the number of valid splits in an array such that the sum of the left part is greater than or equal to the sum of the right part. My initial thought was to maintain prefix sums for both left and right parts of the array, but I later realized that a single pass with cumulative sums can optimize the solution.
# Approach 1: Two-Prefix Arrays
In the first approach, we use two separate arrays to calculate the prefix sums for both the left and right parts of the array.
# Steps:
1. Compute a leftSum array where each element at index i stores the sum of elements from index 0 to i.
2. Compute a rightSum array where each element at index i stores the sum of elements from index i to the end of the array.
3. Iterate through the array, checking if the left sum at index i is greater than or equal to the right sum at index i+1.
# Complexity
- Time complexity: **O(N)**
- Space complexity: **O(N)**
# Code
```java []
class Solution {
public int waysToSplitArray(int[] nums) {
int n = nums.length;
int count = 0;
// Initialize leftSum array and set the first element
long leftSum[] = new long[n];
leftSum[0] = nums[0];
// Initialize rightSum array and set the last element
long rightSum[] = new long[n];
rightSum[n - 1] = nums[n - 1];
// Calculate the prefix sums for the left part
for (int i = 1; i < n; i++) {
leftSum[i] = leftSum[i - 1] + nums[i];
}
// Calculate the prefix sums for the right part
for (int i = n - 2; i >= 0; i--) {
rightSum[i] = rightSum[i + 1] + nums[i];
}
// Count valid splits where leftSum[i] >= rightSum[i+1]
for (int i = 0; i < n - 1; i++) {
if (leftSum[i] >= rightSum[i + 1]) {
count++;
}
}
return count;
}
}
```
# Approach 2: Single-Pass with Total Sum
The second approach is more efficient in terms of space usage. Instead of using additional arrays, we calculate the total sum of the array first and then keep a running sum for the left part of the array during a single pass.
# Steps:
1. Calculate the total sum of the array.
2. Use a variable leftSum to accumulate the sum of the left part of the array as you iterate through it.
3. At each step, calculate the right sum by subtracting leftSum from totalSum.
4. If the left sum is greater than or equal to the right sum, increment the count.
# Code
```java []
class Solution {
public int waysToSplitArray(int[] nums) {
int n = nums.length;
long totalSum = 0;
long leftSum = 0;
int count = 0;
// Calculate the total sum of the array
for (int i = 0; i < n; i++) {
totalSum += nums[i];
}
// Iterate through the array to count valid splits
for (int i = 0; i < n - 1; i++) {
leftSum += nums[i];
long rightSum = totalSum - leftSum;
// Check if the left sum is greater than or equal to the right sum
if (leftSum >= rightSum) {
count++;
}
}
return count;
}
}
```
# Complexity
- Time complexity: **O(N)**
- Space complexity: **O(1)**
# ⬆️⬆️⬆️⬆️⬆️⬆️⬆️UPVOTE ⬆️⬆️⬆️⬆️⬆️⬆
| 2 | 0 | ['Java'] | 0 |
number-of-ways-to-split-array | clear code with simple looping and tracking | 100% beats | clear-code-with-simple-looping-and-track-xe35 | Approach
Tracking the prefix sum and sufix sum with simple for loop and comparing prefix and sufix.
use long varible for prefix and sufix else we facing the err | keshavakumar_jr | NORMAL | 2025-01-03T03:37:57.567070+00:00 | 2025-01-03T03:37:57.567070+00:00 | 12 | false |
# Approach
<!-- Describe your approach to solving the problem. -->
1. Tracking the prefix sum and sufix sum with simple for loop and comparing prefix and sufix.
2. use long varible for prefix and sufix else we facing the error.
3. upvote if u like my approch and explanation.
# Complexity
- Time complexity:O(n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int waysToSplitArray(int[] nums) {
int count=0;
long sum=0;
for(int i:nums){
sum+=i;
}
long val=0;
for(int i=0;i<nums.length-1;i++){
val+=nums[i];
sum-=nums[i];
if(val>=sum) count++;
}
return count;
}
}
``` | 2 | 0 | ['Prefix Sum', 'Java'] | 0 |
number-of-ways-to-split-array | Simplest Code🚀 || Beat 100% || Complete Explanation | simplest-code-beat-100-complete-explanat-3lwn | Upvote if you find this helpful! 👍IntuitionThe problem involves finding the number of valid splits of an array such that the sum of the left part is greater tha | CodeNikET | NORMAL | 2025-01-03T03:31:39.807944+00:00 | 2025-01-03T03:31:39.807944+00:00 | 36 | false | # **Upvote if you find this helpful! 👍**
# Intuition
The problem involves finding the number of valid splits of an array such that the sum of the left part is greater than or equal to the sum of the right part. To achieve this, we can calculate prefix sums and suffix sums for efficient comparisons at each split point.
---
# Approach
1. **Prefix Sum Calculation**: Compute a cumulative sum from the start of the array (`sumFromStart`). This allows us to quickly calculate the sum of elements from the beginning to any index.
2. **Suffix Sum Calculation**: Similarly, compute a cumulative sum from the end of the array (`sumFromEnd`). This allows us to calculate the sum of elements from any index to the end.
3. **Validation of Splits**: Iterate through the array (excluding the last element) and compare the prefix sum at index `i` with the suffix sum starting at `i + 1`. If the prefix sum is greater than or equal, it represents a valid split.
4. **Count Valid Splits**: Maintain a counter to keep track of the number of valid splits.
---
# Complexity
- **Time complexity**:
The time complexity is $$O(n)$$ since we iterate over the array multiple times (once for prefix sums, once for suffix sums, and once to count valid splits).
- **Space complexity**:
The space complexity is $$O(n)$$ because we use two auxiliary vectors to store prefix and suffix sums.
---
# Code
```cpp
class Solution {
public:
int waysToSplitArray(vector<int>& nums) {
vector<long long int>sumFromStart(nums.size());
vector<long long int>sumFromEnd(nums.size());
sumFromStart[0] = nums[0];
for(int i=1;i<nums.size();i++){
sumFromStart[i] = nums[i] + sumFromStart[i-1];
}
sumFromEnd[nums.size()-1] = nums[nums.size()-1];
for(int i = nums.size()-2;i>=0;i--){
sumFromEnd[i] = nums[i] + sumFromEnd[i+1];
}
long long int ans=0;
for(int i=0;i<nums.size()-1;i++){
if(sumFromStart[i] >= sumFromEnd[i+1]) ans++;
}
return ans;
}
}; | 2 | 0 | ['Array', 'Math', 'Prefix Sum', 'C++'] | 1 |
number-of-ways-to-split-array | JAVA || 3MS 🚀🚀|| BEATS 60 % || EASY SOLUTION✅✅ || | java-3ms-beats-60-easy-solution-by-kavi_-yqn3 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | kavi_k | NORMAL | 2025-01-03T03:10:30.370528+00:00 | 2025-01-03T03:10:30.370528+00:00 | 18 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int waysToSplitArray(int[] arr) {
int count = 0;long sum = 0;
for(int i = 0 ; i< arr.length; i++)
{
sum += arr[i];
}
long temp = 0;
for(int i = 0; i < arr.length - 1; i++)
{
temp += arr[i];
if(temp >= sum - temp)
{
count++;
}
}
return count;
}
}
``` | 2 | 0 | ['Java'] | 0 |
largest-submatrix-with-rearrangements | [C++] Clean and Clear, With Intuitive Pictures, O(m * n * logn) | c-clean-and-clear-with-intuitive-picture-pcwo | This question is very similar to \n84. Largest Rectangle in Histogram\n85. Maximal Rectangle\n\nThey are both hard questions, so don\'t be frustrated if you can | aincrad-lyu | NORMAL | 2021-01-17T04:15:47.754131+00:00 | 2021-01-17T08:29:19.230247+00:00 | 13,659 | false | This question is very similar to \n[84. Largest Rectangle in Histogram](https://leetcode.com/problems/largest-rectangle-in-histogram/)\n[85. Maximal Rectangle](https://leetcode.com/problems/maximal-rectangle/)\n\nThey are both hard questions, so don\'t be frustrated if you cannot solve it in the contest.\n\nFirst think of what we can do with a collection of histograms ? What is the largest rectangle we can form?\n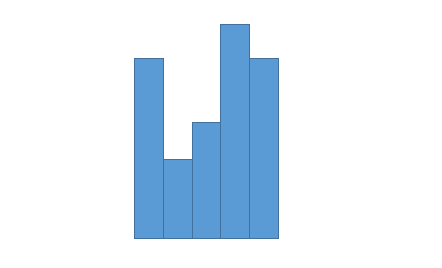\n\nUnlike [84. Largest Rectangle in Histogram](https://leetcode.com/problems/largest-rectangle-in-histogram/), the pillar in this question **can be rearranged !**\n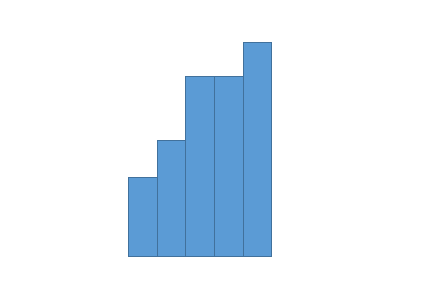\n\nFeel better now? Yes, for each pillar it can centainly form a rectangle with it\'s right neighbors.\n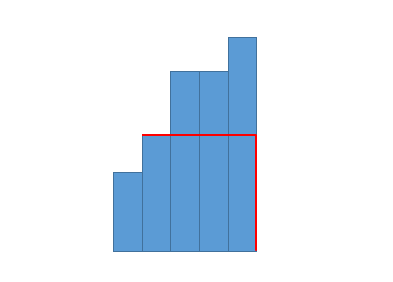\nSo we just iterate every pillar and calculate the maximum rectangle.\n\nNow comes the tricky part for this question, we can **view each row with its above as a collection of pillars!**\nAnd if the matrix[row][col] is 1 , we add the height of pillar in col by 1, ``height[row][col] = height[row - 1][col] + 1``, \nelse if matrix[row][col] is 0, we reset the height of pillar in col as 0, ``height[row][col] = 0``, because we can see it as broken pillar and hence useless.\n\n**Example**\n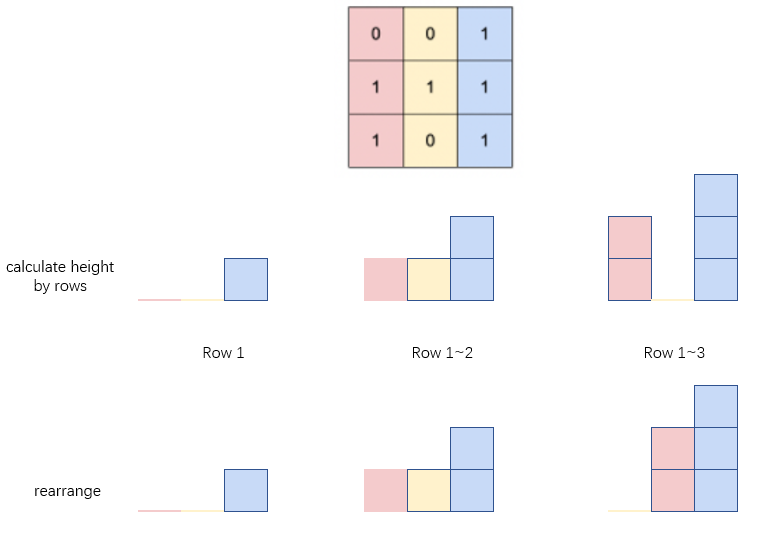\n\n\n**Code**\n*In code I just use one dimensional array height[col] to record heights of pillar*\n```\nclass Solution {\npublic:\n int largestSubmatrix(vector<vector<int>>& matrix) {\n int m = matrix.size(), n = matrix[0].size();\n int ans = 0;\n vector<int> height(n, 0);\n\t\t\n\t\t// view each row and its above as pillars \n for(int i = 0; i < m; ++i){\n\t\t\t// calculate heights\n for(int j = 0; j < n; ++j){\n if(matrix[i][j] == 0) height[j] = 0;\n else height[j] += 1;\n }\n\t\t\t\n\t\t\t// sort pillars\n vector<int> order_height = height;\n sort(order_height.begin(), order_height.end());\n\t\t\t\n\t\t\t// iterate to get the maxium rectangle\n for(int j = 0; j < n; ++j){\n ans = max(ans, order_height[j] * (n - j));\n }\n }\n return ans;\n }\n};\n``` | 821 | 19 | [] | 76 |
largest-submatrix-with-rearrangements | Java | 6ms | easy understanding with comments and images | java-6ms-easy-understanding-with-comment-sqoi | This is like this one https://leetcode.com/problems/maximal-rectangle/\nbut since each block can move, we cannot use that method (it will cause TLE).\nMy though | rioto9858 | NORMAL | 2021-01-17T04:10:11.353425+00:00 | 2021-01-17T13:59:57.508304+00:00 | 6,200 | false | This is like this one [https://leetcode.com/problems/maximal-rectangle/](http://)\nbut since each block can move, we cannot use that method (it will cause TLE).\nMy thought is like this : \n1. we need the rectangle for each column so we need to memorize that. --> change the matrix\n2. the columns can move ----> sort it!\n3. calculate the max --> from end (largest) to beginning (smallest) the larger would contain the smaller one. \n \nIf you like this solution, please leave your upvote :D\n```\n/* build the matrix to:\n\t\t\t\t [ [1, 0, 1, 1] [ [1, 0, 1, 1] \n\t\t\t\t [1, 0, 1, 0] --> [2, 0, 2, 0] \n\t\t\t\t [0, 1, 1, 0] ] [0, 1, 3, 0] ]\n*/\nclass Solution {\n public int largestSubmatrix(int[][] matrix) {\n for(int i = 1; i < matrix.length; i++){\n for(int j = 0; j < matrix[0].length; j++){\n if(matrix[i][j] == 1){\n matrix[i][j] = matrix[i - 1][j] + 1;\n }\n }\n }\n \n int count = 0;\n \n for(int i = 0; i < matrix.length; i++){\n Arrays.sort(matrix[i]); // sort the Array : e.g. from [2,3,0, 1, 2,3] to [0,1,2,2,3,3]\n for(int j = 1; j <= matrix[0].length; j++){\n count = Math.max(count, j * matrix[i][matrix[0].length - j]); // cauculate the max\n }\n }\n \n return count;\n }\n}\n```\n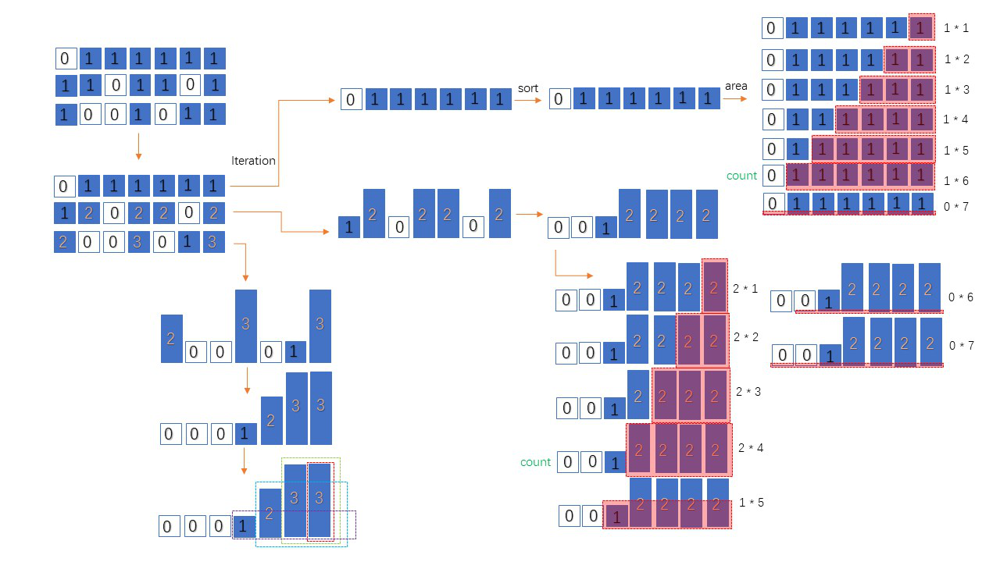\n\n\n | 206 | 5 | [] | 16 |
largest-submatrix-with-rearrangements | 【Video】Give me 10 minutes - how we think about a solution | video-give-me-10-minutes-how-we-think-ab-b8eb | Intuition\nUsing sort for width.\n\n---\n\n# Solution Video\n\nhttps://youtu.be/odAv92zWKqs\n\nThese days, many people watch my video more than 70% of whole tim | niits | NORMAL | 2023-11-26T07:49:27.916070+00:00 | 2023-11-28T20:00:39.302975+00:00 | 4,215 | false | # Intuition\nUsing sort for width.\n\n---\n\n# Solution Video\n\nhttps://youtu.be/odAv92zWKqs\n\nThese days, many people watch my video more than 70% of whole time, which is good to my channel reputation. Thank you!\n\nI\'m creating this video or post with the goal of ensuring that viewers, whether they read the post or watch the video, won\'t waste their time. I\'m confident that if you spend 10 minutes watching the video, you\'ll grasp the understanding of this problem.\n\n\u25A0 Timeline of the video\n\n`0:05` How we can move columns\n`1:09` Calculate height\n`2:48` Calculate width\n`4:10` Let\'s make sure it works\n`5:40` Demonstrate how it works\n`7:44` Coding\n`9:59` Time Complexity and Space Complexity\n`10:35` Summary of the algorithm with my solution code\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 3,225\nMy first goal is 10,000 (It\'s far from done \uD83D\uDE05)\nThank you for your support!\n\n**My channel reached 3,000 subscribers these days. Thank you so much for your support!**\n\n---\n\n# Approach\n## How we think about a solution\n\nWe should return the largest square in the metrix. Simply formula is\n\n```\nheight * width\n```\nLet\'s think about this.\n```\nInput: matrix = [[0,0,1],[1,1,1],[1,0,1]]\n```\nSince we can rearrange the matrix by entire columns, we can consider entire columns as a height.\n\n### How can we rearrange the matrix?\n\nFor example, we can move entire columns at index 2 to left.\n```\n \u2193 \u2193\n[0,0,1] [0,1,0]\n[1,1,1] \u2192 [1,1,1]\n[1,0,1] [1,1,0]\n```\nWe can\'t move part of columns like this.\n```\n[0,0,1] [0,0,1]\n[1,1,1] \u2192 [1,1,1]\n[1,0,1] [1,1,0]\u2190\n```\n### Calculate height at each column.\n```\nAt column index 0\n\n[0,0,1] [0,0,1]\n[1,1,1] \u2192 [1,1,1]\n[1,0,1] [2,0,1]\n\nmatrix[0][0] is 0 height.\nmatrix[1][0] is 1 height.\nmatrix[2][0] is 2 height.(= from matrix[1][0] to matrix[2][0])\n```\n```\nAt column index 1\n\n[0,0,1] [0,0,1]\n[1,1,1] \u2192 [1,1,1] \n[2,0,1] [2,0,1]\n\nmatrix[0][1] is 0 height.\nmatrix[1][1] is 1 height.\nmatrix[2][1] is 0 height.\n```\n```\nAt column index 2\n\n[0,0,1] [0,0,1]\n[1,1,1] \u2192 [1,1,2] \n[2,0,1] [2,0,3]\n\nmatrix[0][2] is 1 height.\nmatrix[1][2] is 2 height. (= from matrix[0][2] to matrix[1][2])\nmatrix[2][2] is 3 height. (= from matrix[0][2] to matrix[2][2])\n```\nIn the end\n```\nOriginal\n[0,0,1] [0,0,1]\n[1,1,1] \u2192 [1,1,2]\n[1,0,1]. [2,0,3]\n```\nIn my solution code, we iterate through each row one by one, then calculate heights. It\'s not difficult. When current number is `1`, add height from above row to current place. You can check it later in my solution code.\n\n### Calculate width at each row.\n\nNext, we need to think about width. We know that if each number is greater than `0`, it means that there is at least `1` in each position, so we can consider non zero position as `1` length for width.\n\nSince we can rearrange the matrix by entire columns, we can sort each row to move zero position to small index(left side).\n\nIn the solution code, we sort each row one by one but image of entire matrix after sorting is like this.\n```\n[0,0,1] [0,0,1]\n[1,1,2] \u2192 [1,1,2]\n[2,0,3] [0,2,3]\n```\nAfter sorting, all zeros in each row move to left side, that means we have some numbers on the right side, so we can consider right side as part of width.\n\nCalculation of each postion\nHeight is each number.\nWidth is length of row - current column index\n```\n[0,0,1]\n[1,1,2]\n[0,2,3]\n\n h w a\nmatrix[0][0]: 0 3 0\nmatrix[0][1]: 0 2 0\nmatrix[0][2]: 1 1 1\nmatrix[1][0]: 1 3 3\nmatrix[1][1]: 1 2 3\nmatrix[1][2]: 2 1 3\nmatrix[2][0]: 0 3 3\nmatrix[2][1]: 2 2 4\nmatrix[2][2]: 3 1 4\n\nh: height\nw: width\na: max area so far\n```\n```\nOutput: 4\n```\n### Are you sure sorting works?\n \nSomebody is wondering "Are you sure sorting works?"\n\nLet\'s focus on `[0,2,3]`. This means at `column index 1`, there is `2` heights and at `column index 2`(different column index from `column index 1`), there are `3` heights.\n\nSo we are sure that we can create this matrix.\n```\n[0,0,1] \n[1,1,1]\n[0,1,1]\n \u2191 \u2191\n 2 3\n```\nThat\'s why at `matrix[2][1]`, we calculate `2`(= height from `matrix[1][1]` to `matrix[2][1]`) * `2`(= width from `matrix[2][1]` to `matrix[2][2]`).\n\nSorting enables the creation of heights from right to left in descending order. In other words, we are sure after `column index 1`, we have `at least 2 height or more`(in this case, we have `3 heights`), so definitely we can calculate size of the square(in this case, `2 * 2`).\n\nThank you sorting algorithm!\nLet\'s wrap up the coding part quickly and grab a beer! lol\n\n---\n\n\n\n### Algorithm Overview:\n\n1. Calculate Heights:\n2. Calculate Maximum Area:\n\n### Detailed Explanation:\n\n1. **Calculate Heights:**\n```python\nclass Solution:\n def largestSubmatrix(self, matrix: List[List[int]]) -> int:\n row, col = len(matrix), len(matrix[0])\n\n # Calculate Heights for Each Column\n for i in range(1, row):\n for j in range(col):\n if matrix[i][j] == 1:\n matrix[i][j] += matrix[i - 1][j]\n```\n\n**Explanation:**\n- This part iterates through each row (starting from the second row) and each column.\n- If the current element is 1 (`matrix[i][j] == 1`), it adds the value from the previous row to the current element.\n- This creates a cumulative sum of heights for each column, forming a "height matrix."\n\n\n2. **Calculate Maximum Area:**\n\n```python\n res = 0\n\n # Calculate Maximum Area\n for i in range(row):\n # Sort the heights in ascending order\n matrix[i].sort()\n\n # Iterate through the sorted heights\n for j in range(col):\n height = matrix[i][j]\n width = col - j\n\n # Calculate the area using the current height and remaining width\n res = max(res, height * width)\n```\n\n**Explanation:**\n- This part initializes `res` to 0, which will store the maximum area.\n- It then iterates through each row of the matrix.\n- For each row, it sorts the heights in ascending order. This is crucial for calculating the maximum area.\n- It iterates through the sorted heights and calculates the area for each height and its corresponding width.\n- The maximum area is updated in the variable `res` if a larger area is found.\n\n\n---\n\n\n\n# Complexity\n- Time complexity: $$O(row * col * log(col))$$\nSort each row and each row has length of col.\n\n- Space complexity: $$O(log col)$$ or $$O(col)$$\nExcept matrix. The sort() operation on the heights array utilizes a temporary working space, which can be estimated as $$O(log col)$$ or $$O(col)$$ in the worst case.\n\n```python []\nclass Solution:\n def largestSubmatrix(self, matrix: List[List[int]]) -> int:\n row, col = len(matrix), len(matrix[0])\n\n # Calculate heights for each column\n for i in range(1, row):\n for j in range(col):\n if matrix[i][j] == 1:\n matrix[i][j] += matrix[i - 1][j]\n\n res = 0\n for i in range(row):\n # Sort the heights in ascending order\n matrix[i].sort()\n\n # Iterate through the sorted heights\n for j in range(col):\n height = matrix[i][j]\n width = col - j\n res = max(res, height * width)\n\n return res\n```\n```javascript []\nvar largestSubmatrix = function(matrix) {\n const row = matrix.length;\n const col = matrix[0].length;\n\n // Calculate heights for each column\n for (let i = 1; i < row; i++) {\n for (let j = 0; j < col; j++) {\n if (matrix[i][j] === 1) {\n matrix[i][j] += matrix[i - 1][j];\n }\n }\n }\n\n let res = 0;\n for (let i = 0; i < row; i++) {\n // Sort the heights in ascending order\n matrix[i].sort((a, b) => a - b);\n\n // Iterate through the sorted heights\n for (let j = 0; j < col; j++) {\n const height = matrix[i][j];\n const width = col - j;\n res = Math.max(res, height * width);\n }\n }\n\n return res; \n};\n```\n```java []\nclass Solution {\n public int largestSubmatrix(int[][] matrix) {\n int row = matrix.length;\n int col = matrix[0].length;\n\n // Calculate heights for each column\n for (int i = 1; i < row; i++) {\n for (int j = 0; j < col; j++) {\n if (matrix[i][j] == 1) {\n matrix[i][j] += matrix[i - 1][j];\n }\n }\n }\n\n int res = 0;\n for (int i = 0; i < row; i++) {\n // Sort the heights in ascending order\n Arrays.sort(matrix[i]);\n\n // Iterate through the sorted heights\n for (int j = 0; j < col; j++) {\n int height = matrix[i][j];\n int width = col - j;\n res = Math.max(res, height * width);\n }\n }\n\n return res; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int largestSubmatrix(vector<vector<int>>& matrix) {\n int row = matrix.size();\n int col = matrix[0].size();\n\n // Calculate heights for each column\n for (int i = 1; i < row; i++) {\n for (int j = 0; j < col; j++) {\n if (matrix[i][j] == 1) {\n matrix[i][j] += matrix[i - 1][j];\n }\n }\n }\n\n int res = 0;\n for (int i = 0; i < row; i++) {\n // Sort the heights in ascending order\n sort(matrix[i].begin(), matrix[i].end());\n\n // Iterate through the sorted heights\n for (int j = 0; j < col; j++) {\n int height = matrix[i][j];\n int width = col - j;\n res = max(res, height * width);\n }\n }\n\n return res; \n }\n};\n```\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n\u25A0 Twitter\nhttps://twitter.com/CodingNinjaAZ\n\n### My next daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/number-of-ways-to-divide-a-long-corridor/solutions/4340183/video-give-me-7-minutes-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/DF9NXNW0G6E\n\n\u25A0 Timeline of the video\n\n`0:05` Return 0\n`0:38` Think about a case where we can put dividers\n`4:44` Coding\n`7:18` Time Complexity and Space Complexity\n`7:33` Summary of the algorithm with my solution code\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/sum-of-absolute-differences-in-a-sorted-array/solutions/4329227/video-give-me-10-minutes-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/bwQh44GWME8\n\n\u25A0 Timeline of the video\n\n`0:05` How we can solve this question\n`1:56` Calculate left total\n`6:32` Calculate right total\n`11:12` Create answers\n`11:51` Coding\n`14:14` Time Complexity and Space Complexity\n`14:39` Summary of the algorithm with my solution code\n\n | 134 | 0 | ['C++', 'Java', 'Python3', 'JavaScript'] | 11 |
largest-submatrix-with-rearrangements | ✅ Beats 100% - Explained with [ Video ] - Simple Sorting - Visualized Too | beats-100-explained-with-video-simple-so-b8ia | \n\n # YouTube Video Explanation:\n\n<a href="https://youtu.be/biPaIwFMISI">https://youtu.be/biPaIwFMISI</a>\n\n**\uD83D\uDD25 Please like, share, and subscribe | lancertech6 | NORMAL | 2023-11-26T03:31:35.574328+00:00 | 2023-11-27T17:23:02.079063+00:00 | 11,200 | false | \n\n<!-- # YouTube Video Explanation:\n\n[https://youtu.be/biPaIwFMISI](https://youtu.be/biPaIwFMISI)\n\n**\uD83D\uDD25 Please like, share, and subscribe to support our channel\'s mission of making complex concepts easy to understand.**\n\nSubscribe Link: https://www.youtube.com/@leetlogics/?sub_confirmation=1\n\n*Subscribe Goal: 500 Subscribers*\n*Current Subscribers: 429*\n\n--- -->\n# Example Explanation\nLet\'s break down the process step by step using an example matrix:\n\n**Example Matrix:**\n```\n[\n [0, 0, 1],\n [1, 1, 1],\n [1, 0, 1]\n]\n```\n\n**Step 1: Preprocessing**\n```\n[\n [0, 0, 1],\n [1, 1, 2],\n [2, 0, 3]\n]\n```\n- For each cell `matrix[i][j] = 1`, update it with the height of consecutive 1s ending at this cell (`matrix[i][j] += matrix[i-1][j]`).\n\n**Step 2: Sorting Rows**\nSort each row in non-decreasing order.\n```\n[\n [0, 0, 1],\n [1, 1, 2],\n [0, 2, 3]\n]\n```\n\n**Step 3: Calculate Area**\nIterate through each row and calculate the area for each cell.\n```\n[\n [0, 0, 1], Area: row[j]*k = 1*1\n [1, 1, 2], Area: Max(row[j]*k) = Max(2x1,1x2,1x3)\n [0, 2, 3] Area: Max(row[j]*k) = Max(3x1,2x2)\n]\n```\n- For each cell, the area is the height * width. \n- For example in the last row, we are moving from backwards to forward, so j starts with n-1 and k=1.\n- In the first iteration row[j]= 3 but k = 1, so area becomes 3 but in the next iteration, row[j]=2 and k=2 so the area becomes 4, which is the maximum of all the areas of submatrix.\n\n**Step 4: Maximum Area**\nThe maximum area among all cells is 4.\n\n**Explanation:**\nThe maximum area of the submatrix containing only 1s after rearranging the columns optimally is 4, achieved at `matrix[2][2]`.\n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem asks for the area of the largest submatrix containing only 1s after rearranging the columns optimally. The solution involves preprocessing the matrix to store the height of consecutive 1s ending at each cell. Then, for each row, we sort the heights in non-decreasing order and calculate the area for each possible submatrix.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Iterate through the matrix starting from the second row (`i = 1`).\n2. For each cell `matrix[i][j]`:\n - If `matrix[i][j]` is 1, update it to store the height of consecutive 1s ending at this cell by adding the height of the previous row\'s corresponding cell (`matrix[i - 1][j]`).\n3. After preprocessing, for each row, sort the row in non-decreasing order.\n4. For each cell in the sorted row, calculate the area of the submatrix that ends at this cell, considering the consecutive 1s.\n - The area is given by `height * width`, where `height` is the height of consecutive 1s ending at this cell, and `width` is the position of the cell in the sorted row.\n - Update the maximum area accordingly.\n5. Return the maximum area as the result.\n\n# Complexity\n- Time Complexity: O(m * n * log(n)) - Sorting is done for each row.\n- Space Complexity: O(1) - No additional space is used except for variables.\n\n# Code\n\n```java []\nclass Solution {\n public int largestSubmatrix(int[][] matrix) {\n int m = matrix.length, n = matrix[0].length;\n for (int i = 1; i < m; ++i) {\n for (int j = 0; j < n; ++j) {\n if (matrix[i][j] == 1) {\n matrix[i][j] = matrix[i - 1][j] + 1;\n }\n }\n }\n int ans = 0;\n for (var row : matrix) {\n Arrays.sort(row);\n for (int j = n - 1, k = 1; j >= 0 && row[j] > 0; --j, ++k) {\n int s = row[j] * k;\n ans = Math.max(ans, s);\n }\n }\n return ans;\n }\n}\n```\n```cpp []\nclass Solution\n{\npublic:\n int largestSubmatrix(vector<vector<int>>& matrix)\n {\n int m = matrix.size(), n = matrix[0].size();\n int ans = 0;\n for(int j = 0; j < n; j++)\n for(int i = 1; i < m; i++)\n if(matrix[i][j] == 1)\n matrix[i][j] += matrix[i-1][j];\n for(int i = 0; i < m; i++)\n {\n sort(matrix[i].begin(), matrix[i].end());\n reverse(matrix[i].begin(), matrix[i].end());\n for(int j = 0; j < n; j++)\n ans = max(ans, matrix[i][j]*(j+1));\n }\n return ans;\n }\n};\n```\n```python []\nclass Solution(object):\n def largestSubmatrix(self, matrix):\n m, n = len(matrix), len(matrix[0])\n \n for i in range(1, m):\n for j in range(n):\n if matrix[i][j] == 1:\n matrix[i][j] += matrix[i - 1][j]\n \n ans = 0\n \n for row in matrix:\n row.sort(reverse=True)\n for j in range(n):\n ans = max(ans, row[j] * (j + 1))\n \n return ans\n```\n```javascript []\nvar largestSubmatrix = function(matrix) {\n const m = matrix.length;\n const n = matrix[0].length;\n\n for (let i = 1; i < m; ++i) {\n for (let j = 0; j < n; ++j) {\n if (matrix[i][j] === 1) {\n matrix[i][j] += matrix[i - 1][j];\n }\n }\n }\n \n let ans = 0;\n \n matrix.forEach(row => {\n row.sort((a, b) => b - a);\n for (let j = 0, k = 1; j < n && row[j] > 0; ++j, ++k) {\n const s = row[j] * k;\n ans = Math.max(ans, s);\n }\n });\n \n return ans;\n};\n```\n<!--  -->\n | 84 | 2 | ['Array', 'Greedy', 'Sorting', 'Matrix', 'Python', 'C++', 'Java', 'JavaScript'] | 13 |
largest-submatrix-with-rearrangements | C++ Solution | Easy Implementation | c-solution-easy-implementation-by-invuln-nbqp | \nint largestSubmatrix(vector<vector<int>>& matrix) {\n \n int i, j, ans = 0, n = matrix.size(), m = matrix[0].size();\n \n for(i = | invulnerable | NORMAL | 2021-01-17T04:00:49.698617+00:00 | 2021-01-17T13:43:38.351537+00:00 | 4,775 | false | ```\nint largestSubmatrix(vector<vector<int>>& matrix) {\n \n int i, j, ans = 0, n = matrix.size(), m = matrix[0].size();\n \n for(i = 0; i < m; i++)\n {\n for(j = 1; j < n; j++)\n {\n if(matrix[j][i] == 1)\n matrix[j][i] = matrix[j-1][i] + matrix[j][i];\n else\n matrix[j][i] = 0;\n }\n }\n\n for(i = 0; i < n; i++)\n {\n sort(matrix[i].begin(), matrix[i].end(), greater<int>());\n\n for(j = 0; j < m; j++)\n ans = max(ans, matrix[i][j] * (j + 1));\n }\n \n return ans;\n }\n```\n\nSolution:\n\n* Convert the matrix so that Matrix[i][j] is the sum of continous 1\'s upto ith row in the column number j.\n* If the element in that cell is 1 add it to the previous streak else make it 0.\n* Then find the maximum area upto ith row. To do this first sort the ith row in descending order.\n* Now minimum upto jth column * (j+1) will be the area, the maximum of all these is the final answer.\n\nFirst step is shown in the picture:\n\n **To** \n\nIf you are having problem in visualizing the solution please have a look at this article:\nhttps://leetcode.com/problems/largest-submatrix-with-rearrangements/discuss/1020710/C%2B%2B-Clean-and-Clear-With-Intuitive-Pictures-O(m-*-n-*-logn)\n | 82 | 4 | [] | 14 |
largest-submatrix-with-rearrangements | Optimal O(m*n) time, O(n) space, no sort :) | optimal-omn-time-on-space-no-sort-by-ale-lo45 | We first explain an O(m * n * log n) algorithm that, internally, uses an O(n * log n) sort for each row. That algorithm is similar to most other solutions for | alex_salcianu | NORMAL | 2021-01-17T04:43:49.992374+00:00 | 2021-01-18T09:47:08.263615+00:00 | 1,725 | false | We first explain an O(m * n * log n) algorithm that, internally, uses an O(n * log n) sort for each row. That algorithm is similar to most other solutions for this problem. It is good-enough for the current tests, but not optimal. Then, we explain how to remove that sort() and obtain an O(m * n) algorithm. Finally, we prove that our algorithm is asymptotically optimal.\n\n### **First try: O(m * n * log n) algorithm**\n\nThe algorithm processes the matrix row by row, starting from the top row. Each iteration r examines submatrices that "end" at the current row r (i.e., the max row for elements of that submatrix is r) and finds the one with the max area. Each such submatrix consists of a few contiguous "towers of 1s" truncated to their smallest height. Each "tower of 1s" corresponds to a column c where matrix[r\'][c] is 1 for all r\' in [r_start, r], for some r_start <= r.\n\nFor example, for the matrix from the picture below, assume we are currently examining row 3:\n\n\n\nIn row 3, we have 1 elements in columns 0, 2, 4, and 5. These 1 elements are part of some contiguous "towers of 1s". E.g., we have a tower of a single 1 in column 0, a tower of two 1s in column 2, a tower of four 1s in column 4, and a tower of two 1s in column 5. Notice that the 1s from position (0,0) and (1,0) are irrelevant, due to the 0 from (2,0), which separates them from the 1 at (3,0): when we examine row r (in this case row 3) we are interested in "towers of 1s" that end at row r (not earlier). We are also not interested in the continuation of these towers "downward" (e.g., the 1 from (4, 4)); those continuations will be examined when we examine later rows.\n\nThe heights of these "towers of 1s" are [1, 2, 4, 2] (towers of height zero are irrelevant). As we move from row to row, we can compute the heights of these towers in O(n) time per row: if matrix[r][c] is 1, we increment the height of the tower from column c; otherwise, we set it to 0.\n\nAny submatrix that "ends" in row 3 uses some of these "towers of 1s". As we can swap columns, it\'s irrelevant how far apart these towers are: we can always bring them together. E.g., we can bring columns 2, 4, and 5 together, and truncate them at height 2 to obtain a submatrix of size 3 * 2 = 6. In general, given a desired height h of the resulting submatrix, we can select all columns of height >= h.\n\nLet\'s rearrange the columns in decreasing order of the height of their towers of 1s:\n\n\n\nThe non-empty towers of 1s are [4, 2, 2, 1]. After this sort / rearrangement, if column i appears in the submatrix, then we should include all columns j <= i: due to the decresing order, they are at least as tall as column i; also, as we want the max-area submatrix, we include all columns that we can. I.e., we have i+1 columns (= the width of the submatrix) and the resulting submatrix has height equal to the height of the tower of 1s from column i.\n\nIn our example, if we select column 0, then we get a submatrix consisting of only this column, of area 1x4 = 4. If we select column 1, we get a submatrix consisting of the first 1+1=2 columns, and height 2, i.e., an area 2x2=4. If we select column 2, we get a submatrix consisting of the first 2+1=3 columns, and height 2, i.e., an area 3x2=6. Finally, if we select column 3, we end up with a submatrix of area 4x1=4. The maximum area of a matrix that ends at row 3 is 6.\n\nThese are the reasons most solutions (1) examine the input matrix row by row, (2) compute the tower heights, and (3) sort them (with equivalent variations: e.g., some sort them in increasing, some in decreasing order). This algorithm has complexity O(m * n * log n): for each of the O(m) rows, we scan all n row elements to update the tower heights, then sort the tower heights (in O(n * log n)) and next do another linear scan over the sorted vector to find the max-area submatrix.\n\nIn C++, we have\n\n```\n// Sub-optimal O(m * n * log n) solution:\nclass Solution {\npublic:\n int largestSubmatrix(vector<vector<int>>& matrix) {\n const int m = matrix.size(); // number of rows\n const int n = matrix[0].size(); // number of columns\n \n // tower[r][c] = height of the contiguous "tower\n // of 1s" that ends in (r, c). 0 if no such tower.\n vector<vector<int>> tower(m, vector<int>(n, 0));\n \n // Compute, in O(m * n), all elements of tower:\n // \n // Init first row, tower[0]:\n for (int c = 0; c < n; c++) {\n tower[0][c] = matrix[0][c];\n }\n \n // Compute each subsequent row, in order:\n for (int r = 1; r < m; r++) {\n for (int c = 0; c < n; c++) {\n if (matrix[r][c] == 1) {\n // 1 element => continue the tower in column c:\n tower[r][c] = tower[r-1][c] + 1;\n } else {\n // 0 element => reset the tower in column c:\n tower[r][c] = 0;\n }\n }\n }\n\n int max_area = 0;\n \n // Iterate over all rows:\n for (int r = 0; r < m; r++) {\n // Examine submatrices that end on row r:\n sort(tower[r].begin(), tower[r].end(), greater<int>());\n for (int c = 0; c < n; c++) {\n max_area = std::max(max_area, (c+1) * tower[r][c]);\n } \n }\n return max_area;\n }\n};\n```\n\nMany small optimizations are possible: e.g., one can store the tower heights in the original `matrix`, which avoids the need to allocate a new matrix. One can also merge the two traversals (the one that computes `tower` and the one that uses it), etc. In the next section, we present an optimization that reduces the asymptotic complexity.\n\n### **Better: O(m * n) algorithm**\n\n**Intuition #1**: very similar to the previous algorithm, but we maintain the list of the heights of the towers of 1s in a way that is always sorted in decreasing order. This means we do not need to do an explicit sort for each row.\n\n**Intuition #2**: The "tower height" information for row r (see previous paragraph) can be computed using the similar information for the previous row:\n* we increment the height of each existing "tower of 1s" that continues in this row: e.g., a tower in column c, such that matrix[r][c] is 1.\n* we drop other "towers of 1s": e.g., a tower in column c, such that matrix[r][c] == 0.\n* we possibly start new "towers of 1s" of height 1 if matrix[r][c] is 1 and there was no tower in that column for the previous row.\n\nAccordingly, given the list of "towers of 1s" that end on the previous row (in decreasing order of their heights), we selectively copy some of them (incrementing their heights), skip some other towers, and add some 1s at the end of the list. This can be done in O(n). If the previous list was in decreasing order, the resulting list is also in decreasing order.\n\nThe original list is empty, which is trivially sorted. Each subsequent step maintains the decreasing order, as explained by the previous paragraph.\n\nThe code below fills in the details.\n\n```\n// O(m * n) solution:\nclass Solution {\npublic:\n int largestSubmatrix(vector<vector<int>>& matrix) {\n const int m = matrix.size();\n const int n = matrix[0].size();\n int max_area = 0;\n\n // The loop below explores `matrix`, row by row, from the top.\n // After processing row r, `towers` contains pairs <h, c>,\n\t\t// where h is the height of the "contiguous tower of 1s" that\n\t\t// ends at matrix[r][c], for each c such that matrix[r][c] == 1.\n //\n // `towers` has O(n) elements: at most one pair for each column.\n //\n // The pairs from `towers` are sorted in decreasing order of\n // their first component (the tower height).\n vector<pair<int, int>> towers;\n for (int r = 0; r < m; r++) {\n // Updated version of towers, for the current row r.\n vector<pair<int, int>> next;\n \n // done[c] is true iff the "tower of 1s" that ends\n // in matrix[r][c] has already been considered and\n // a pair for it already exists in next.\n vector<bool> done(n, false);\n \n // Two ways to build "towers of 1s":\n // (1) Extend existing towers (if possible).\n for (const auto &p : towers) {\n const int c = p.second;\n if (matrix[r][c] == 1) {\n next.emplace_back(p.first + 1, c);\n done[c] = true;\n } else {\n // As matrix[r][c] == 0, there is no tower of 1s\n // ending at (r, c) => we drop this tower (= not\n // copy it into `next`).\n }\n }\n \n // (2) Start new towers (of height 1) for 1 elements\n // that did not have a tower above them:\n for (int c = 0; c < n; c++) {\n if (!done[c] && matrix[r][c] == 1) {\n next.emplace_back(1, c);\n }\n }\n\n towers = std::move(next);\n\t\t\t\n\t\t\t// Examine heights of the towers of 1s, in decreasing order.\n for (int i = 0; i < towers.size(); i++) {\n\t\t\t // Any max-area submatrix that includes tower i, also\n\t\t\t\t// includes all towers j <= i (i+1 towers in total).\n max_area = max(max_area, (i + 1) * towers[i].first);\n }\n }\n\n return max_area;\n }\n};\n```\n\n### **Optimality Proof**\n\nOur O(m * n) time-complexity algorithm is asymptotically optimal. \n\nProof: each correct algorithm must examine each element of the input matrix: e.g., consider an input matrix that is 1 everywhere, except in the one element that we don\'t read. Then, we have no way of knowing whether the correct answer is m * n or something strictly smaller that does not include that element. Hence, the asymptotic complexity of any correct algorithm is at least O(m * n), which means that our algorithm is asymptotically time optimal; "asymptotically" means that one can "fiddle" with the implementation, making it faster or slower, but the complexity is still big-O (m * n).\n | 32 | 0 | [] | 4 |
largest-submatrix-with-rearrangements | Explanation with Picture. Variation of Maximal Rectangle and Largest Rectangle in Histogram | explanation-with-picture-variation-of-ma-s9l3 | This problem is very similar to Maximum rectangular area and Largest Rectangle in Histogram. The only variation here is that we can swap the columns and put the | cut_me_half | NORMAL | 2021-01-17T04:01:00.137554+00:00 | 2021-01-18T04:57:20.524436+00:00 | 2,406 | false | This problem is very similar to Maximum rectangular area and Largest Rectangle in Histogram. The only variation here is that we can swap the columns and put the columns next to each other to optimize the answer.\n\nWell, we can just sort the current row in which we are and then can directly use `largestRectangularArea` function.\n\nHow i figured this out?\nI submitted WA first then I got that hint.\nConsider the current row to be [1,2,1,1,0,2,2]\nIf you solve it without sorting then you will calculate the wrong answer.\n\nWe need to do this for every row because it is possible that all the values in next row is zero then we will lose the sum we got so far from columns above the particular row.\n\nEvery cell will have cell_val (if cell value == 1) = 1 + sum of cell above it.\n\t\t\t\t\t\t\t\totherwise cell_val = 0 because we can\'t have empty cells in our submatrix.\n\n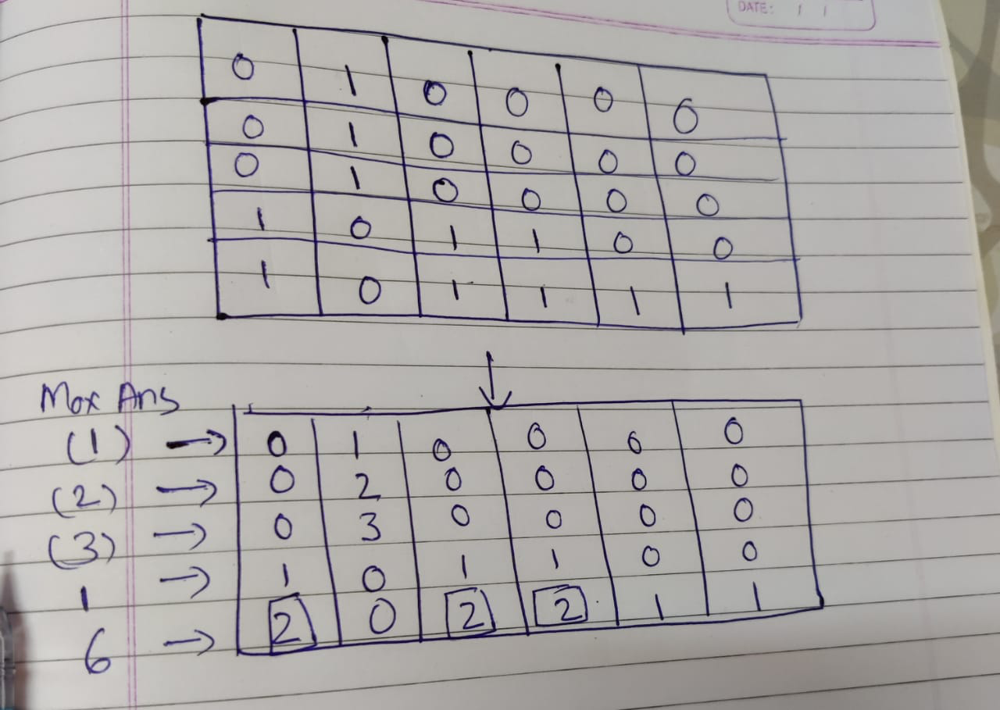\n\nEdit: Max ans in 4th row should be 3 not 1 as noticed by @mcclay. After sorting all 1s would come together.\n\nNotice that in the last row we used sorting so that columns ending up with value 2 are next to each other. If we don\'t do this then we are not taking the benefit of question statement to swap columns and put them next to each other.\n\nEdit: As suggested by @ArshadAQ there is no need to use stack to find largestRectangularArea as in maximal rectangle problem as we are allowed to reorder. \nSo, updating largestRectangleArea function.\n\nFinally, here is the code.\n```\nclass Solution {\npublic:\n int largestSubmatrix(vector<vector<int>>& matrix) {\n \n int rows = matrix.size();\n int cols = matrix[0].size();\n \n for(int i = 1; i < rows; i++)\n {\n for(int j = 0; j < cols; j++)\n {\n if(matrix[i-1][j] && matrix[i][j]) matrix[i][j] = matrix[i-1][j]+1;\n }\n }\n \n int maxval = INT_MIN;\n for(vector<int> v : matrix)\n maxval = max(maxval, largestRectangleArea(v));\n \n return maxval;\n }\n \n int largestRectangleArea(vector<int>& heights) {\n sort(heights.begin(), heights.end(), greater<int>());\n \n int res = INT_MIN;\n int minval = INT_MAX;\n \n for(int i = 0; i < heights.size(); i++)\n {\n minval = min(minval, heights[i]);\n res = max(res, minval*(i+1)); \n }\n \n return res;\n};\n```\n | 31 | 8 | [] | 7 |
largest-submatrix-with-rearrangements | Easy to Read || Beginner friendly || No Fluff || C++/Java/Python | easy-to-read-beginner-friendly-no-fluff-zu9q1 | Treat every column in the matrix as a height bar, where the base of that height represents total number of consecutives ones above it included himself. \n\n\n | Cosmic_Phantom | NORMAL | 2023-11-26T02:43:39.314790+00:00 | 2023-11-26T04:18:22.814244+00:00 | 3,460 | false | Treat every column in the matrix as a height bar, where the base of that height represents total number of consecutives ones above it included himself. \n\n```\n [[0,0,1],\n [1,1,1],\n [1,0,1]]\nheight->[2,0,3] -> sort -> [3,2,0] -> \n```\n\nNow iterate over this sorted row and consider the largest submatrix from it -> at col 0 height of 3. here the base is 3 but with that base we have only one col so area 3. \n\nNow check at col 1 with base height as 2. So we have two cols where base hight can be 2 so area=4. \n\nAt col 3 the base height should be 0 and thats the only col which has the base heght 0, so area =0. \n\nThus the max ans is 4.\n\n**C++:**\n```cpp\nclass Solution {\npublic:\n int largestSubmatrix(vector<vector<int>>& matrix) {\n int m = matrix.size(), n = matrix[0].size();\n int ans = 0;\n for (int row = 0; row<m; row++){\n for(int col = 0; col<n; col++){\n if(matrix[row][col] != 0 && row > 0){\n matrix[row][col] += matrix[row-1][col];\n }\n }\n \n vector<int> currRow = matrix[row];\n sort(currRow.begin(), currRow.end(), greater());\n for(int i=0; i<n;i++){\n ans = max(ans, currRow[i] * (i+1));\n }\n }\n return ans;\n }\n};\n```\n\n**Java:**\n```java\nclass Solution {\n public int largestSubmatrix(int[][] matrix) {\n int m = matrix.length;\n int n = matrix[0].length;\n int ans = 0;\n \n for (int row = 0; row < m; row++) {\n for (int col = 0; col < n; col++) {\n if (matrix[row][col] != 0 && row > 0) {\n matrix[row][col] += matrix[row - 1][col];\n }\n }\n \n int[] currRow = matrix[row].clone();\n Arrays.sort(currRow);\n for (int i = 0; i < n; i++) {\n ans = Math.max(ans, currRow[i] * (n - i));\n }\n }\n \n return ans;\n }\n}\n```\n\n**Python:**\n```python\nclass Solution(object):\n def largestSubmatrix(self, matrix):\n m, n = len(matrix), len(matrix[0])\n ans = 0\n \n for row in range(m):\n for col in range(n):\n if matrix[row][col] != 0 and row > 0:\n matrix[row][col] += matrix[row - 1][col]\n \n curr_row = sorted(matrix[row], reverse=True)\n \n for i in range(n):\n ans = max(ans, curr_row[i] * (i + 1))\n \n return ans\n``` | 26 | 0 | ['Array', 'Math', 'Sorting', 'Matrix'] | 5 |
largest-submatrix-with-rearrangements | [Python3] Concise solution | python3-concise-solution-by-kunqian-0-dcvw | Intuition\n\nFor each row, find the histogram height of each column. \nSort it and find the max rectangle you could find(refer to Question 84).\n\n# Complexity\ | kunqian-0 | NORMAL | 2021-01-17T04:03:20.569527+00:00 | 2021-01-17T07:18:56.342083+00:00 | 957 | false | # **Intuition**\n\nFor each row, find the histogram height of each column. \nSort it and find the max rectangle you could find(refer to [Question 84]( https://leetcode.com/problems/largest-rectangle-in-histogram/)).\n<br/>\n# **Complexity**\nTime: `O(m * n * log(n))`\nSpace: `O(n)`\n<br/>\n# **Python3**\n```python\ndef largestSubmatrix(self, A: List[List[int]]) -> int:\n\tm, n = len(A), len(A[0])\n\tH = [0] * n\n\tans = 0\n\tfor i in range(m):\n\t\tfor j in range(n):\n\t\t\tH[j] = H[j] + 1 if A[i][j] else 0\n\t\tans = max(ans, self.getMaxArea(H[:]))\n\treturn ans\n \ndef getMaxArea(self, heights):\n\theights.sort()\n\tarea = 0\n\tn = len(heights)\n\tfor i in range(n):\n\t\th = heights[i]\n\t\tarea = max(area, h * (n - i))\n\treturn area\n\n```\n\n\n | 21 | 7 | [] | 2 |
largest-submatrix-with-rearrangements | 🔥Beginner Friendly Solution with Detail Explanation🔥|| 🔥Daily Challenges🔥 | beginner-friendly-solution-with-detail-e-qwae | Intuition\n\n\n# Complexity\n- Time complexity:O(2nm)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity:O(1)\n Add your space complexity here, e | Shree_Govind_Jee | NORMAL | 2023-11-26T03:46:54.680703+00:00 | 2023-11-26T03:46:54.680725+00:00 | 1,214 | false | # Intuition\n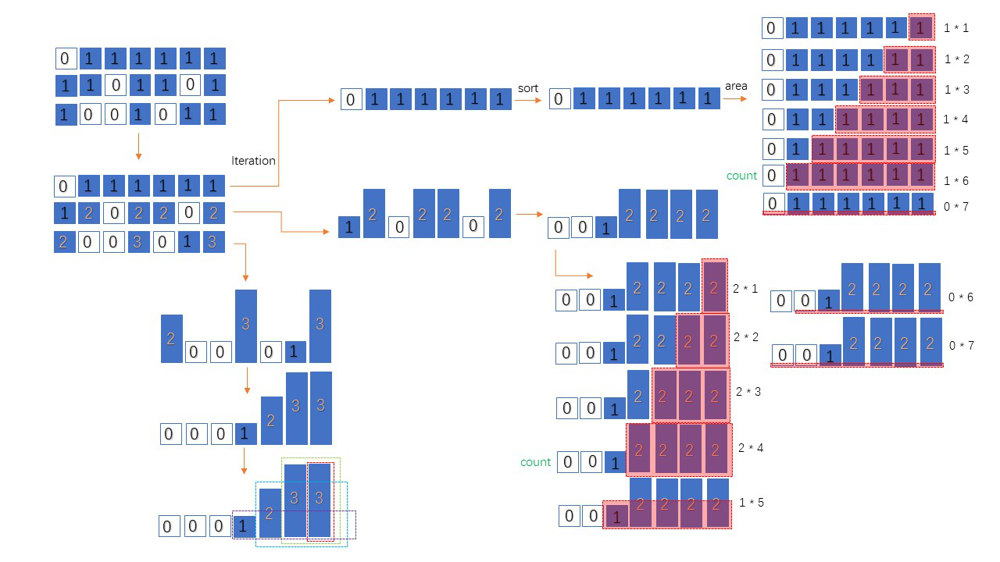\n\n# Complexity\n- Time complexity:$$O(2*n*m)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int largestSubmatrix(int[][] matrix) {\n for(int i=1; i<matrix.length; i++){\n for(int j=0; j<matrix[0].length; j++){\n if(matrix[i][j] == 1) matrix[i][j] = matrix[i-1][j] + 1;\n }\n }\n\n int maxi=0;\n for(int i=0; i<matrix.length; i++){\n Arrays.sort(matrix[i]);\n for(int j=1; j<=matrix[0].length; j++){\n maxi = Math.max(maxi, j*matrix[i][matrix[0].length-j]);\n }\n }\n return maxi;\n }\n}\n``` | 19 | 1 | ['Array', 'Greedy', 'Sorting', 'Matrix', 'Java'] | 5 |
largest-submatrix-with-rearrangements | Javascript | Simple Solution w/ Explanation & Visuals | beats 100% / 100% | javascript-simple-solution-w-explanation-f57b | Idea:\n\nSince the elements in each column can\'t move, we can think of each consecutive group of 1s in each column as a solid pillar within that column.\n\nmat | sgallivan | NORMAL | 2021-01-18T07:31:21.992871+00:00 | 2021-01-18T07:31:41.047778+00:00 | 608 | false | ***Idea:***\n\nSince the elements in each column can\'t move, we can think of each consecutive group of **1**s in each column as a solid pillar within that column.\n```\nmatrix: [ [ 0, 1, 0, 1, 0 ],\n [ 1, 1, 0, 1, 1 ],\n [ 1, 1, 1, 0, 1 ],\n [ 1, 0, 1, 1, 0 ],\n [ 1, 1, 1, 1, 1 ],\n [ 0, 1, 0, 1, 1 ] ]\n```\n\n\nWe can iterate through the matrix once and convert each cell into a running total of the number of consecutive **1**s that stretch up from each cell in the row. That number represents the height of the pillar that would exist upward from this row.\n```\nmatrix: [ [ 0, 1, 0, 1, 0 ],\n [ 1, 2, 0, 2, 1 ],\n [ 2, 3, 1, 0, 2 ],\n [ 3, 0, 2, 1, 0 ],\n [ 4, 1, 3, 2, 1 ],\n [ 0, 2, 0, 3, 2 ] ]\n```\nWe can then iterate down the rows and on each row sort the pillar heights together in order to evaluate the maximum value found ending on that row.\n```\nmatrix[4]: [ 4, 1, 3, 2, 1 ]\n [ 4, 3, 2, 1, 1 ] // The row after it\'s sorted in descending order\n```\n\n```\n col. 0: cols. 0-1: cols. 0-2: cols. 0-3: cols. 0-4:\n 4 * 1 = 4 3 * 2 = 6 2 * 3 = 6 1 * 4 = 4 1 * 5 = 5\n```\nAfter we iterate through, we can return the best result.\n\nThe best result for the code below is **144ms / 55.3MB**.\n\n` `\n***Implementation:***\n\nFirst, we need to iterate through the matrix **M** and update each cell\'s value. If the cell is a **1**, then replace it with the value from the cell above, incremented.\n\nSince each row will now "remember" the height above it, we\'re free to sort each row when we iterate through again. After sorting, run through the pillar height values and multiply them by the submatrix width and check if they\'re better than the current best answer. If so, update **ans**.\n\nThen just **return ans.**\n\n` `\n***Code:***\n```\nvar largestSubmatrix = function(M) {\n let y = M.length, x = M[0].length, ans = 0\n for (let i = 1; i < y; i++)\n for (let j = 0; j < x; j++)\n if (M[i][j]) M[i][j] += M[i-1][j]\n for (let i = 0; i < y; i++) {\n let row = M[i].sort((a,b) => b - a)\n for (let j = 0; j < x; j++)\n ans = Math.max(ans, (j + 1) * row[j])\n }\n return ans\n};\n``` | 17 | 0 | ['JavaScript'] | 3 |
largest-submatrix-with-rearrangements | Simple Python3 | 9 Lines | Beats 100% | Detailed Explanation | simple-python3-9-lines-beats-100-detaile-a0iz | Logic: Prefix sum from top to the bottom row for every column, by doing this we have number of continuous 1st stacked on top so far at matrix[i][j] . So for exa | sushanthsamala | NORMAL | 2021-01-17T04:01:17.262825+00:00 | 2021-01-17T14:15:46.860527+00:00 | 2,169 | false | Logic: Prefix sum from top to the bottom row for every column, by doing this we have number of continuous 1st stacked on top so far at matrix[i][j] . So for example if the matrix is \n[0,0,1]\n[1,1,1]\n[1,0,1]\nWe have the prefix summed matrix:\n[0, 0, 1]\n[1, 1, 2]\n[2, 0, 3]\nNow the we could just go row by row and check the maximum possible area till that row. In row one the maximum area can only be 1, in row two the max area can be 2 == matrix[1][2] or we could use matrix[1][1] and matrix[1][2] now we have a 1x1 matrix = area => 2 i.e, min(matrix[1][1], matrix[1][2]) * (numbers of elements involved == 2 here). You observe that by sorting each row in descending order we get the following matrix.\n\n[1, 0, 0]\n[2, 1, 1]\n[3, 2, 0]\n\nNow since the row is sorted in descending order we can directly assume that matrix[i][j] is the minimum value so far and we can directly say that the area is (number of elements involved == j+1) * (minimum element so far in the row == matrix[i][j]).\n```\nclass Solution:\n def largestSubmatrix(self, matrix: List[List[int]]) -> int:\n m, n, ans = len(matrix), len(matrix[0]), 0\n \n for j in range(n):\n for i in range(1, m):\n matrix[i][j] += matrix[i-1][j] if matrix[i][j] else 0\n \n for i in range(m): \n matrix[i].sort(reverse=1)\n for j in range(n):\n ans = max(ans, (j+1)*matrix[i][j])\n return ans\n``` | 17 | 2 | ['Python3'] | 3 |
largest-submatrix-with-rearrangements | Beat 100%! O(m*n*logn ) easy solution | beat-100-omnlogn-easy-solution-by-lawren-47rr | Example 1\n\n[0,0,1],\n[1,1,1],\n[1,0,1] \n\nFor every column, we count the the number of continuous 1 by the current position. the result matrix will be\n\n[0 | lawrenceflag | NORMAL | 2021-01-17T04:01:22.574114+00:00 | 2021-01-17T04:30:14.089900+00:00 | 1,120 | false | Example 1\n\n[0,0,1],\n[1,1,1],\n[1,0,1] \n\nFor every column, we count the the number of continuous 1 by the current position. the result matrix will be\n\n[0,0,1],\n[1,1,2],\n[2,0,3] \n\nNow let\u2019s consider every row. \nFor the first row, we reversely sort the row\nWe got [1,0,0]. It\'s very easy to get the largest matrix for this row. For other rows, we do the same thing.\n\nFor example, for the second row, We reversely sort the row,\n[2,1,1]\nFor the third row, We reversely sort the row,\n[3,2,0]\n\n```\n public int largestSubmatrix(int[][] A) {\n \n int m = A.length;\n int n = A[0].length;\n \n int[][] sum = new int[m][n];\n \n for(int j = 0; j < n; j++){\n int cnt = 0;\n for(int i = 0; i < m; i++){ \n if(A[i][j] == 0){\n cnt = 0;\n sum[i][j] = 0;\n }else{\n cnt++;\n sum[i][j] = cnt;\n }\n }\n }\n \n int max = 0;\n for(int i = 0; i < m; i++){\n Arrays.sort(sum[i]);\n for(int j = 0; j < n; j++){\n int a = (n - j)*sum[i][j];\n max = Math.max(a, max);\n }\n }\n return max;\n } | 16 | 8 | [] | 4 |
largest-submatrix-with-rearrangements | C++ sort row vs Freq count||124 ms Beats 98.30% | c-sort-row-vs-freq-count124-ms-beats-983-4n3q | Intuition\n Describe your first thoughts on how to solve this problem. \nUse the matrix to store the height for each column.\n\nLater try other approach!\n# App | anwendeng | NORMAL | 2023-11-26T03:10:57.628557+00:00 | 2023-11-26T08:34:09.690840+00:00 | 2,575 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUse the `matrix` to store the height for each column.\n\nLater try other approach!\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUse sort!\n\nThe approach using counting sort leads to TLE & fails , for the testcase `100000*[[1]]`. After some trials( one using hash table(unordered_map), other using array), it is finally accepted!\n\nThe revised code using counting sort with special dealing n=1 & m=1 cases (thanks to the idea of @Sergei ) becomes a fast code which runs in 124 ms & beats 98.30%!\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(nm \\log n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$ \n# Code 136 ms Beats 93.75%\n```\n#pragma GCC optimize("O3")\nclass Solution {\npublic:\n int largestSubmatrix(vector<vector<int>>& matrix) {\n int m=matrix.size(), n=matrix[0].size();\n int area=count(matrix[0].begin(), matrix[0].end(), 1);\n for(int i=1; i<m; i++){\n #pragma unroll\n for(int j=0; j<n; j++){\n if (matrix[i][j]!=0)\n matrix[i][j]+=matrix[i-1][j];\n }\n auto row=matrix[i];\n sort(row.begin(), row.end());\n #pragma unroll\n for(int i=0; i<n; i++)\n area=max(area, row[i]*(n-1-i+1));\n }\n return area;\n }\n};\nauto init = []()\n{ \n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n```\n# revised Code using Frequency Count 124 ms Beats 98.30%\n```\n#pragma GCC optimize("O3")\nclass Solution {\npublic: \n int largestSubmatrix(vector<vector<int>>& matrix) {\n int m=matrix.size(), n=matrix[0].size();\n int area=count(matrix[0].begin(), matrix[0].end(), 1);\n if (m==1) return area;\n if (n==1){\n #pragma unroll\n for(int i=1; i<m; i++){\n if (matrix[i][0]!=0)\n matrix[i][0]+=matrix[i-1][0];\n area=max(area, matrix[i][0]);\n }\n return area;\n }\n \n #pragma unroll\n for(int i=1; i<m; i++){\n #pragma unroll\n for(int j=0; j<n; j++){\n if (matrix[i][j]!=0)\n matrix[i][j]+=matrix[i-1][j];\n }\n \n auto row=matrix[i];\n int minH=i+1, maxH=0;\n #pragma unroll\n for(int x: row){\n minH=min(minH, x);\n maxH=max(maxH, x);\n }\n vector<int> freq(maxH-minH+1, 0);\n #pragma unroll\n for(int x: row){\n freq[x-minH]++;\n }\n int acc=0;\n #pragma unroll\n for(int x=maxH-minH; acc<n; x--){\n if (freq[x]>0){\n acc+=freq[x];\n area=max(area, acc*(x+minH));\n }\n } \n }\n return area;\n }\n};\n\n```\n# Code using Frequency Count & Hash table\n```\n#pragma GCC optimize("O3")\nclass Solution {\npublic: \n int largestSubmatrix(vector<vector<int>>& matrix) {\n int m=matrix.size(), n=matrix[0].size();\n int area=count(matrix[0].begin(), matrix[0].end(), 1);\n #pragma unroll\n for(int j=0; j<n; j++){\n #pragma unroll\n for(int i=1; i<m; i++){\n if (matrix[i][j]!=0)\n matrix[i][j]+=matrix[i-1][j];\n }\n }\n unordered_map<int, int> freq;\n #pragma unroll\n for(int i=0; i<m; i++){\n auto row=matrix[i];\n freq.clear();\n int maxH=0;\n #pragma unroll\n for(int x: row){\n maxH=max(maxH, x);\n freq[x]++;\n }\n int acc=0;\n #pragma unroll\n for(int x=maxH; acc<n; x--){\n if (freq.count(x)>0){\n acc+=freq[x];\n area=max(area, acc*x);\n }\n } \n }\n return area;\n }\n};\n```\n | 11 | 1 | ['Array', 'Hash Table', 'Sorting', 'Counting Sort', 'C++'] | 3 |
largest-submatrix-with-rearrangements | 【Video】Sorting solution | video-sorting-solution-by-niits-ylte | Intuition\nUsing sort for width.\n\n---\n\n# Solution Video\n\nhttps://youtu.be/odAv92zWKqs\n\nThese days, many people watch my video more than 70% of whole tim | niits | NORMAL | 2024-04-23T16:38:01.350989+00:00 | 2024-04-23T16:38:01.351018+00:00 | 129 | false | # Intuition\nUsing sort for width.\n\n---\n\n# Solution Video\n\nhttps://youtu.be/odAv92zWKqs\n\nThese days, many people watch my video more than 70% of whole time, which is good to my channel reputation. Thank you!\n\nI\'m creating this video or post with the goal of ensuring that viewers, whether they read the post or watch the video, won\'t waste their time. I\'m confident that if you spend 10 minutes watching the video, you\'ll grasp the understanding of this problem.\n\n\u25A0 Timeline of the video\n\n`0:05` How we can move columns\n`1:09` Calculate height\n`2:48` Calculate width\n`4:10` Let\'s make sure it works\n`5:40` Demonstrate how it works\n`7:44` Coding\n`9:59` Time Complexity and Space Complexity\n`10:35` Summary of the algorithm with my solution code\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 4,543\nMy first goal is 10,000 (It\'s far from done \uD83D\uDE05)\nThank you for your support!\n\n**My channel reached 3,000 subscribers these days. Thank you so much for your support!**\n\n---\n\n# Approach\n## How we think about a solution\n\nWe should return the largest square in the metrix. Simply formula is\n\n```\nheight * width\n```\nLet\'s think about this.\n```\nInput: matrix = [[0,0,1],[1,1,1],[1,0,1]]\n```\nSince we can rearrange the matrix by entire columns, we can consider entire columns as a height.\n\n### How can we rearrange the matrix?\n\nFor example, we can move entire columns at index 2 to left.\n```\n \u2193 \u2193\n[0,0,1] [0,1,0]\n[1,1,1] \u2192 [1,1,1]\n[1,0,1] [1,1,0]\n```\nWe can\'t move part of columns like this.\n```\n[0,0,1] [0,0,1]\n[1,1,1] \u2192 [1,1,1]\n[1,0,1] [1,1,0]\u2190\n```\n### Calculate height at each column.\n```\nAt column index 0\n\n[0,0,1] [0,0,1]\n[1,1,1] \u2192 [1,1,1]\n[1,0,1] [2,0,1]\n\nmatrix[0][0] is 0 height.\nmatrix[1][0] is 1 height.\nmatrix[2][0] is 2 height.(= from matrix[1][0] to matrix[2][0])\n```\n```\nAt column index 1\n\n[0,0,1] [0,0,1]\n[1,1,1] \u2192 [1,1,1] \n[2,0,1] [2,0,1]\n\nmatrix[0][1] is 0 height.\nmatrix[1][1] is 1 height.\nmatrix[2][1] is 0 height.\n```\n```\nAt column index 2\n\n[0,0,1] [0,0,1]\n[1,1,1] \u2192 [1,1,2] \n[2,0,1] [2,0,3]\n\nmatrix[0][2] is 1 height.\nmatrix[1][2] is 2 height. (= from matrix[0][2] to matrix[1][2])\nmatrix[2][2] is 3 height. (= from matrix[0][2] to matrix[2][2])\n```\nIn the end\n```\nOriginal\n[0,0,1] [0,0,1]\n[1,1,1] \u2192 [1,1,2]\n[1,0,1]. [2,0,3]\n```\nIn my solution code, we iterate through each row one by one, then calculate heights. It\'s not difficult. When current number is `1`, add height from above row to current place. You can check it later in my solution code.\n\n### Calculate width at each row.\n\nNext, we need to think about width. We know that if each number is greater than `0`, it means that there is at least `1` in each position, so we can consider non zero position as `1` length for width.\n\nSince we can rearrange the matrix by entire columns, we can sort each row to move zero position to small index(left side).\n\nIn the solution code, we sort each row one by one but image of entire matrix after sorting is like this.\n```\n[0,0,1] [0,0,1]\n[1,1,2] \u2192 [1,1,2]\n[2,0,3] [0,2,3]\n```\nAfter sorting, all zeros in each row move to left side, that means we have some numbers on the right side, so we can consider right side as part of width.\n\nCalculation of each postion\nHeight is each number.\nWidth is length of row - current column index\n```\n[0,0,1]\n[1,1,2]\n[0,2,3]\n\n h w a\nmatrix[0][0]: 0 3 0\nmatrix[0][1]: 0 2 0\nmatrix[0][2]: 1 1 1\nmatrix[1][0]: 1 3 3\nmatrix[1][1]: 1 2 3\nmatrix[1][2]: 2 1 3\nmatrix[2][0]: 0 3 3\nmatrix[2][1]: 2 2 4\nmatrix[2][2]: 3 1 4\n\nh: height\nw: width\na: max area so far\n```\n```\nOutput: 4\n```\n### Are you sure sorting works?\n \nSomebody is wondering "Are you sure sorting works?"\n\nLet\'s focus on `[0,2,3]`. This means at `column index 1`, there is `2` heights and at `column index 2`(different column index from `column index 1`), there are `3` heights.\n\nSo we are sure that we can create this matrix.\n```\n[0,0,1] \n[1,1,1]\n[0,1,1]\n \u2191 \u2191\n 2 3\n```\nThat\'s why at `matrix[2][1]`, we calculate `2`(= height from `matrix[1][1]` to `matrix[2][1]`) * `2`(= width from `matrix[2][1]` to `matrix[2][2]`).\n\nSorting enables the creation of heights from right to left in descending order. In other words, we are sure after `column index 1`, we have `at least 2 height or more`(in this case, we have `3 heights`), so definitely we can calculate size of the square(in this case, `2 * 2`).\n\nThank you sorting algorithm!\nLet\'s wrap up the coding part quickly and grab a beer! lol\n\n---\n\n\n\n### Algorithm Overview:\n\n1. Calculate Heights:\n2. Calculate Maximum Area:\n\n### Detailed Explanation:\n\n1. **Calculate Heights:**\n```python\nclass Solution:\n def largestSubmatrix(self, matrix: List[List[int]]) -> int:\n row, col = len(matrix), len(matrix[0])\n\n # Calculate Heights for Each Column\n for i in range(1, row):\n for j in range(col):\n if matrix[i][j] == 1:\n matrix[i][j] += matrix[i - 1][j]\n```\n\n**Explanation:**\n- This part iterates through each row (starting from the second row) and each column.\n- If the current element is 1 (`matrix[i][j] == 1`), it adds the value from the previous row to the current element.\n- This creates a cumulative sum of heights for each column, forming a "height matrix."\n\n\n2. **Calculate Maximum Area:**\n\n```python\n res = 0\n\n # Calculate Maximum Area\n for i in range(row):\n # Sort the heights in ascending order\n matrix[i].sort()\n\n # Iterate through the sorted heights\n for j in range(col):\n height = matrix[i][j]\n width = col - j\n\n # Calculate the area using the current height and remaining width\n res = max(res, height * width)\n```\n\n**Explanation:**\n- This part initializes `res` to 0, which will store the maximum area.\n- It then iterates through each row of the matrix.\n- For each row, it sorts the heights in ascending order. This is crucial for calculating the maximum area.\n- It iterates through the sorted heights and calculates the area for each height and its corresponding width.\n- The maximum area is updated in the variable `res` if a larger area is found.\n\n\n---\n\n\n\n# Complexity\n- Time complexity: $$O(row * col * log(col))$$\nSort each row and each row has length of col.\n\n- Space complexity: $$O(log col)$$ or $$O(col)$$\nExcept matrix. The sort() operation on the heights array utilizes a temporary working space, which can be estimated as $$O(log col)$$ or $$O(col)$$ in the worst case.\n\n```python []\nclass Solution:\n def largestSubmatrix(self, matrix: List[List[int]]) -> int:\n row, col = len(matrix), len(matrix[0])\n\n # Calculate heights for each column\n for i in range(1, row):\n for j in range(col):\n if matrix[i][j] == 1:\n matrix[i][j] += matrix[i - 1][j]\n\n res = 0\n for i in range(row):\n # Sort the heights in ascending order\n matrix[i].sort()\n\n # Iterate through the sorted heights\n for j in range(col):\n height = matrix[i][j]\n width = col - j\n res = max(res, height * width)\n\n return res\n```\n```javascript []\nvar largestSubmatrix = function(matrix) {\n const row = matrix.length;\n const col = matrix[0].length;\n\n // Calculate heights for each column\n for (let i = 1; i < row; i++) {\n for (let j = 0; j < col; j++) {\n if (matrix[i][j] === 1) {\n matrix[i][j] += matrix[i - 1][j];\n }\n }\n }\n\n let res = 0;\n for (let i = 0; i < row; i++) {\n // Sort the heights in ascending order\n matrix[i].sort((a, b) => a - b);\n\n // Iterate through the sorted heights\n for (let j = 0; j < col; j++) {\n const height = matrix[i][j];\n const width = col - j;\n res = Math.max(res, height * width);\n }\n }\n\n return res; \n};\n```\n```java []\nclass Solution {\n public int largestSubmatrix(int[][] matrix) {\n int row = matrix.length;\n int col = matrix[0].length;\n\n // Calculate heights for each column\n for (int i = 1; i < row; i++) {\n for (int j = 0; j < col; j++) {\n if (matrix[i][j] == 1) {\n matrix[i][j] += matrix[i - 1][j];\n }\n }\n }\n\n int res = 0;\n for (int i = 0; i < row; i++) {\n // Sort the heights in ascending order\n Arrays.sort(matrix[i]);\n\n // Iterate through the sorted heights\n for (int j = 0; j < col; j++) {\n int height = matrix[i][j];\n int width = col - j;\n res = Math.max(res, height * width);\n }\n }\n\n return res; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int largestSubmatrix(vector<vector<int>>& matrix) {\n int row = matrix.size();\n int col = matrix[0].size();\n\n // Calculate heights for each column\n for (int i = 1; i < row; i++) {\n for (int j = 0; j < col; j++) {\n if (matrix[i][j] == 1) {\n matrix[i][j] += matrix[i - 1][j];\n }\n }\n }\n\n int res = 0;\n for (int i = 0; i < row; i++) {\n // Sort the heights in ascending order\n sort(matrix[i].begin(), matrix[i].end());\n\n // Iterate through the sorted heights\n for (int j = 0; j < col; j++) {\n int height = matrix[i][j];\n int width = col - j;\n res = max(res, height * width);\n }\n }\n\n return res; \n }\n};\n```\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n\u25A0 Twitter\nhttps://twitter.com/CodingNinjaAZ\n\n### My next daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/number-of-ways-to-divide-a-long-corridor/solutions/4340183/video-give-me-7-minutes-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/DF9NXNW0G6E\n\n\u25A0 Timeline of the video\n\n`0:05` Return 0\n`0:38` Think about a case where we can put dividers\n`4:44` Coding\n`7:18` Time Complexity and Space Complexity\n`7:33` Summary of the algorithm with my solution code\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/sum-of-absolute-differences-in-a-sorted-array/solutions/4329227/video-give-me-10-minutes-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/bwQh44GWME8\n\n\u25A0 Timeline of the video\n\n`0:05` How we can solve this question\n`1:56` Calculate left total\n`6:32` Calculate right total\n`11:12` Create answers\n`11:51` Coding\n`14:14` Time Complexity and Space Complexity\n`14:39` Summary of the algorithm with my solution code\n\n | 8 | 0 | ['C++', 'Java', 'Python3', 'JavaScript'] | 0 |
largest-submatrix-with-rearrangements | Beat 100% - Easy solution with explanation similar problem - maximal-rectangle | beat-100-easy-solution-with-explanation-j9phz | intuition\n matrix[i][j] is sum of continous 1\'s\n sort the each row to keep largest matrix because we can swap the columns\n\nadd the continous 1\'s from top | aravind_dev | NORMAL | 2021-01-17T04:03:08.636047+00:00 | 2021-01-17T15:36:20.754502+00:00 | 617 | false | **intuition**\n* matrix[i][j] is sum of continous 1\'s\n* sort the each row to keep largest matrix because we can swap the columns\n\nadd the continous 1\'s from top to bottom.\nsort the each row to find the largest matrix\n\nEx:\n```\nmatrix= [[1,0,0],\n\t\t[1,0,1],\n\t\t[1,1,1]];\n```\n\nafter counting continous 1\'s, we get\n\n```\nmatrix=[[1,0,0],\n\t\t[2,0,1],\n\t\t[3,1,2]];\n```\n\n* sort each row since we can rearrange the columns \n* for each element a[i] in row, find the length of array k such that **k=i-j** where `a[i]<=a[i+1]<=a[i+2]....<=a[j]`\n* find the largest matrix by `a[i] * n-i`, n is length of array. \n\n\n in 3rd row, after sorting we get a[] = [1,2,3], n=3\n* \tfor a[0], res = a[0]*3-0 =>3\n* \tfor a[1], res = a[1]*3-1 =>4\n* \tfor a[2], res = a[2]*3-2 =>3\n\n so, the largest matrix is 4\n\nIts similar to \nhttps://leetcode.com/problems/maximal-rectangle/\n```\nclass Solution {\n public int largestSubmatrix(int[][] matrix) {\n\t\tfor (int i = 1; i < matrix.length; i++) {\n\t\t\tfor (int j = 0; j < matrix[i].length; j++) {\n\t\t\t\tif (matrix[i][j] != 0) {\n\t\t\t\t\tmatrix[i][j] += matrix[i - 1][j];\n\t\t\t\t}\n\t\t\t}\n\t\t}\n\t\tint res = 0;\n\t\tfor (int i = 0; i < matrix.length; i++) {\n\t\t\tArrays.sort(matrix[i]);\n\t\t\tfor (int j = 0; j < matrix[i].length; j++) {\n\t\t\t\tres = Math.max(res, matrix[i][j] * (matrix[i].length - j ));\n\t\t\t}\n\t\t}\n\t\treturn res;\n }\n}\n``` | 7 | 0 | [] | 5 |
largest-submatrix-with-rearrangements | [C++] count 1s and then sort | c-count-1s-and-then-sort-by-ddddyliu-7cbf | \nclass Solution {\npublic:\n int largestSubmatrix(vector<vector<int>>& matrix) {\n int m = matrix.size(), n = matrix[0].size();\n vector<vecto | ddddyliu | NORMAL | 2021-01-17T04:01:56.924656+00:00 | 2021-01-17T04:30:09.288373+00:00 | 804 | false | ```\nclass Solution {\npublic:\n int largestSubmatrix(vector<vector<int>>& matrix) {\n int m = matrix.size(), n = matrix[0].size();\n vector<vector<int>> cntOne(m, vector<int>(n, 0));\n for (int j = 0; j < n; j++) {\n if (matrix[0][j] == 1) {cntOne[0][j] = 1;}\n }\n for (int i = 1; i < m; i++) {\n for (int j = 0; j < n; j++) {\n if (matrix[i][j] == 0) {cntOne[i][j] = 0;}\n else {cntOne[i][j] = cntOne[i - 1][j] + 1;}\n }\n }\n \n int ans = 0;\n for (int i = 0; i < m; i++) {\n vector<int> curr = cntOne[i];\n sort(curr.begin(), curr.end(), greater());\n for (int j = 0; j < n; j++) {\n ans = max(ans, curr[j] * (j + 1));\n }\n }\n return ans;\n }\n};\n``` | 7 | 1 | ['C', 'Sorting'] | 1 |
largest-submatrix-with-rearrangements | 😀 Fully Explained Solution With Example and Dry Run 💡 | fully-explained-solution-with-example-an-nna4 | Problem \nFinding the maximum area of submatrix which has 1 in its each cell.\n\n# How do we calculate area?\nArea = Length * breadth\nIn this problem, we will | mohd-usman | NORMAL | 2023-11-26T15:43:56.004730+00:00 | 2023-11-26T15:43:56.004755+00:00 | 297 | false | # Problem \nFinding the maximum area of submatrix which has 1 in its each cell.\n\n# How do we calculate area?\n**$$Area = Length * breadth$$**\nIn this problem, we will calculate through **width** and **height**.\n\n**But wait, how to find the height \uD83E\uDD14?**\nWell, we have to find the height of those cells that have 1.\n\nIt can be understood through an example.\nFor example \n```\n 0 0 1\nmatrix = 1 1 1\n 1 0 1\n```\nIn first column, start from top to down -\n\n1. height of 0 = 0\n2. height of 1 = 1\n3. height of 1 = 2 (why 2? since there is already one element with value 1 above the 1 of third row).\n\nso the matrix becomes - \n```\n 0 0 1\nmatrix = 1 1 1\n 2 0 1\n```\nIn second column, start from top to down -\n\n1. height of 0 = 0\n2. height of 1 = 1\n3. height of 0 = 0 (since we don\'t want the submatrix with 0, so we will not calculate its height or its height will beome 0).\n\nso the matrix becomes - \n```\n 0 0 1\nmatrix = 1 1 1\n 2 0 1\n```\nIn third column, start from top to down -\n\n1. height of 1 = 1\n2. height of 1 = 2\n3. height of 1 = 3 (since we don\'t want the submatrix with 0, so we will not calculate its height or its height will beome 0).\n\nso the matrix becomes - \n```\n 0 0 1\nmatrix = 1 1 2\n 2 0 3\n```\n\nIf we **sort** the matrix in **ascending order** then all the cells with highest height will shift towards right.\n\nso the final becomes - \n```\n 0 0 1\nmatrix = 1 1 2\n 0 2 3\n```\n\nNow observe , that the cell with maximum height will be from bottom down corner. while move from the last cell towards first, we observe that the height is getting decreased.\n\n**Maximum height and maximum width = maximum area**\n\nIf we start iterating the last element (3), width is 1 and height is 3, so the area becomes = 3.\n\nBut wait, can we get more area than this? May be!\n\nSo we move to last second element (2) and take the width as 2.\nBut why the height is 2.\n\nSince every cell right to the current element (2) has the height greater than the current (2). So the right columns automatically involve in the area while calculating.\n\nSo the area becomes 2*2 = 4.\n\nSince it is getting complexed, so lets\'s name the cells as 1st, 2nd, 3rd, 4th, ... 9th. Remember that the naming is done by left to right.\n\n```\n 0 0 1\nmatrix = 1 1 2\n 0 2 3\n```\n\n1st cell = 0\n2nd cell = 0\n3rd cell = 1\n4th cell = 1\n5th cell = 1\n6th cell = 2\n7th cell = 0\n8th cell = 2\n9th cell = 3\n\nStart from the last cell\n**1st Iteration :-**\n**$$cell = 9th$$**\n**$$width = 1$$**\n**$$height = 3$$**\n**$$area = width*height = 1 * 3 = 3$$**\n\n**2nd Iteration :-**\n**$$cell = 8th$$**\n**$$width = 2$$**\n**$$height = 2$$**\n**$$area = width*height = 2 * 2 = 4$$**\n\n\n**4th Iteration :-**\n**$$cell = 6th$$**\nSince we are again at the last column, so the width is resetted to 1.\n**$$width = 1$$**\n**$$height = 2$$**\n**$$area = width*height = 1 * 2 = 2$$**\n\n**5th Iteration :-**\n**$$cell = 5th$$**\n**$$width = 2$$**\n**$$height = 1$$**\n**$$area = width*height = 2 * 1 = 2$$**\n\n**6th Iteration :-**\n**$$cell = 4th$$**\n**$$width = 3$$**\n**$$height = 1$$**\n**$$area = width*height = 3 * 1 = 3$$**\n\n**7th Iteration :-**\n**$$cell = 3th$$**\nSince we are again at the last column, so the width is resetted to 1.\n**$$width = 1$$**\n**$$height = 1$$**\n**$$area = width*height = 1 * 1 = 1$$**\n\n**8th Iteration :-**\n**$$cell = 2th$$**\n**$$width = 2$$**\n**$$height = 0$$**\n**$$area = width*height = 2*0 = 0$$**\n\n**9th Iteration :-**\n**$$cell = 1th$$**\n**$$width = 3$$**\n**$$height = 0$$**\n**$$area = width*height = 3*0 = 0$$**\n\nMaximum area is obtained is 4th in second iteration. So this is the answer.\n\n# Complexity\n- Time complexity: $$O(m*nlogn)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int largestSubmatrix(vector<vector<int>>& matrix) {\n int m = matrix.size();\n int n = matrix[0].size();\n int area = 0;\n\n for(int i=1; i<m; i++){\n for(int j=0; j<n; j++){\n if(matrix[i][j]==1){\n matrix[i][j] += matrix[i-1][j];\n }\n }\n }\n\n for(int i=m-1; i>=0; i--){\n sort(matrix[i].begin(), matrix[i].end());\n int k = 1;\n for(int j=n-1; j>=0; j--){\n area = max(area, matrix[i][j]*k);\n k++;\n }\n }\n\n return area;\n \n\n return area;\n }\n};\n``` | 6 | 2 | ['C++'] | 2 |
largest-submatrix-with-rearrangements | [C++] ✅ Histogram Max Area Finding Problem || Count ones and sort | c-histogram-max-area-finding-problem-cou-zfrs | Approach:\n\nImagine each column in the matrix as a vertical bar, where its height represents the count of consecutive ones above it, including itself.\n\nIt is | anupam8nith | NORMAL | 2023-11-26T09:22:31.151474+00:00 | 2023-11-27T15:16:02.418735+00:00 | 220 | false | **Approach:**\n\nImagine each column in the matrix as a vertical bar, where its height represents the count of consecutive ones above it, including itself.\n\nIt is similar to **Histogram Area Finding Problem:** `Calculating the maximum area of a histogram for each row: This helps in determining the maximum rectangle that can be formed considering the consecutive 1s in each column.`\n\nFor example, the given matrix:\n```\n[[0,0,1],\n [1,1,1],\n [1,0,1]]\n```\nTransforming it into a \'height\' array gives us `[2, 0, 3]`. Sorting this array becomes `[3, 2, 0]`. \n\n**We can also sort it in ascending and use** `ans = max(ans,height[i] * (n-i));` **or for descending sort of heights we will assign** `ans = max(ans,height[i] * (i+1));` \n\nNow, after sorting \'height\' array, let\'s find the largest submatrix:\n- At column 0 with a height of 3, there\'s only one column, so the area is 3x1=3.\n- Moving to column 1 with a height of 2, we have two columns that can form a base of height 2, resulting in an area of 2x2.\n- Finally, at column 2 with a base height of 0, there\'s only one column that fulfills this, resulting in an area of 0.\n\nTherefore, the maximum area achievable with rearranged columns to create a submatrix of consecutive 1s is 4."\n\n**Code : [C++]**\n```\nclass Solution \n{\npublic:\n int largestSubmatrix(vector<vector<int>>& matrix) \n {\n ios::sync_with_stdio(0);cout.tie(0);cin.tie(0);\n \n int m = matrix.size(), n = matrix[0].size();int ans = 0;\n \n for (int x = 0; x<m; x++)\n {\n for(int y = 0; y<n; y++)\n if(matrix[x][y] != 0 && x > 0)\n matrix[x][y] += matrix[x-1][y];\n \n vector<int> height = matrix[x]; sort(height.begin(), height.end());\n \n for(int i=0; i<n;i++) ans = max(ans, height[i] * (n-i));\n }\n return ans;\n }\n};\n\n//Please Upvote\n```\n\n\n\n\n | 6 | 0 | ['C', 'Sorting'] | 2 |
largest-submatrix-with-rearrangements | C++||Largest Submatrix With Rearrangements to Largest Rectangle in Histogram||logic explained | clargest-submatrix-with-rearrangements-t-4wda | Simple conversion from Largest Submatrix With Rearrangements to Largest Rectangle in Histogram\nIdea:\n\n1.for each a[i][j] cell count number of continuos 1\'s | tejpratapp468 | NORMAL | 2021-01-17T04:06:47.385130+00:00 | 2021-01-20T07:20:56.835425+00:00 | 387 | false | **Simple conversion from Largest Submatrix With Rearrangements to Largest Rectangle in Histogram\nIdea:**\n\n1.for each a[i][j] cell count number of continuos 1\'s in its column,so we have column height of a[i][j];\n2.for each row we will sort the row in descending order of column heights since you are allowed to rearrange the columns of the matrix in any order and for each row apply largest area of histogram concept to find largest area possible by row of column heights.\n \nA Dry run of above approach \ne.g. [[0,0,1],\n [1,1,1],\n [1,0,1]]\nstep 1:calculating column hegiht for each cell as:\n [[0,0,1],\n [1,1,2],\n [2,0,3]]\n \nstep 2:for each row sort it in descending order of column heights and apply gest area of histogram concept\nfor row 1 we have [1,0,0] largest area=1;\nfor row 2 we have [2,1,1] largest area=3;\nfor row 3 we have [3,2,0] largest area=4;\nhence our answer is 4;\n\nHope this help :)\n Please upvote if this help;\n\n```\n\n\n\nclass Solution {\npublic:\n int hist(int h[],int n){\n stack<int> s;\n //cout<<Jai Shree Ram\n int i=0,ans=0;\n while(i<n)\n {\n if(s.empty() || h[s.top()]<=h[i])\n {\n s.push(i++);\n }\n else\n {\n int tp=s.top();s.pop();\n int res=h[tp]*(s.empty()?i:i-s.top()-1);\n ans=max(ans,res);\n }\n }\n while(!s.empty())\n {\n int tp=s.top();s.pop();\n int res=h[tp]*(s.empty()?i:i-s.top()-1);\n ans=max(ans,res);\n }\n return ans;\n }\n int largestSubmatrix(vector<vector<int>>& a) {\n int n=a.size(),m=a[0].size();\n int v[n][m];memset(v,0,sizeof(v));\n for(int i=0;i<m;i++)\n {\n int cnt=0;int start,end;\n for(int j=0;j<n;j++)\n {\n if(a[j][i]) cnt++;\n else cnt=0;\n v[j][i]=cnt;\n }\n }\n int ans=0;\n for(int i=0;i<n;i++)\n sort(v[i],v[i]+m,greater<int>());\n for(int i=0;i<n;i++)\n {\n ans=max(ans,hist(v[i],m));\n }\n return ans;\n }\n};\n``` | 6 | 0 | [] | 2 |
largest-submatrix-with-rearrangements | Simple C++ solution || TC: O(nmlog(m)) || SC:O(1) | simple-c-solution-tc-onmlogm-sco1-by-zee-6k7k | Intuition\nThis code finds the largest submatrix with all 1s in a binary matrix. It first transforms the matrix to represent the height of \'buildings\' of 1s. | Zeeshan_2512 | NORMAL | 2023-11-26T02:31:25.136786+00:00 | 2023-11-26T02:31:25.136807+00:00 | 936 | false | # Intuition\nThis code finds the largest submatrix with all 1s in a binary matrix. It first transforms the matrix to represent the height of \'buildings\' of 1s. Then, for each row, it calculates the maximum area of the rectangle that can be formed using the \'building\' at each cell as the shortest \'building\'. The maximum of these areas is the result.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nThis code is a solution to a problem where we need to find the largest submatrix with all 1s in a given binary matrix. The approach used in this code is dynamic programming and sorting.\n\nHere\'s a step-by-step breakdown of the approach:\n\n1. **Preprocessing**: For each cell in the matrix, if the cell value is not `0`, add the value of the cell just above it to the current cell. This step transforms the matrix such that each cell now contains the height of the \'building\' at that cell, i.e., the number of consecutive `1`s above that cell including itself.\n\n2. **Finding Maximum Area**: For each row in the matrix, sort the elements in non-increasing order. Then, for each cell in the row, calculate the area of the rectangle that can be formed using the \'building\' at that cell as the shortest \'building\'. The area is calculated as the product of the height of the shortest \'building\' and the number of \'buildings\'. Update the maximum area if the calculated area is greater.\n\n3. **Final Result**: If the maximum area remains as `INT_MIN`, it means there are no `1`s in the matrix, so return `0`. Otherwise, return the maximum area.\n\nThis approach ensures that we consider all possible submatrices of `1`s and choose the one with the maximum area. The use of dynamic programming helps to avoid redundant calculations and improves the efficiency of the solution. \n\n# Complexity\n- Time complexity: O(nmlog(m))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int largestSubmatrix(vector<vector<int>>& matrix) {\n int n=matrix.size();\n int m=matrix[0].size();\n for(int i=1; i<n; i++){\n for(int j=0; j<m; j++){\n if(matrix[i][j]!=0)matrix[i][j]+=matrix[i-1][j];\n }\n }\n int maxarea=INT_MIN;\n for(int i=0; i<n; i++){\n sort(matrix[i].begin(), matrix[i].end(),greater<int>());\n int temp=INT_MAX;\n for(int j=0; j<m; j++){\n if(matrix[i][j]==0)continue;\n temp=min(temp,matrix[i][j]);\n int area=(j+1)*temp;\n maxarea=max(maxarea,area);\n }\n }\n if(maxarea==INT_MIN)return 0;\n return maxarea;\n }\n};\n``` | 5 | 0 | ['C++'] | 1 |
largest-submatrix-with-rearrangements | Python solution easy-understanding with comments | python-solution-easy-understanding-with-p2x9c | class Solution:\n\n def largestSubmatrix(self, matrix: List[List[int]]) -> int:\n row, col = len(matrix), len(matrix[0])\n for j in range(col): | flyingspa | NORMAL | 2021-04-12T09:29:09.989971+00:00 | 2021-04-12T09:29:09.990002+00:00 | 608 | false | class Solution:\n\n def largestSubmatrix(self, matrix: List[List[int]]) -> int:\n row, col = len(matrix), len(matrix[0])\n for j in range(col): # calculate the prefix consecutive one for each column \n for i in range(1,row):\n if matrix[i][j]:\n matrix[i][j]+=matrix[i-1][j]\n ans = 0\n for i in range(row): # for every row we sort the list in ascending order\n matrix[i].sort()\n for j in range(col-1,-1,-1): \n if matrix[i][j]==0:\n break\n ans = max(ans, (col-j)*matrix[i][j]) # record the largest submatrix\n return ans | 5 | 0 | ['Python'] | 0 |
largest-submatrix-with-rearrangements | Python solution: Largest Rectangular Area in a Rearrangable Histogram | python-solution-largest-rectangular-area-ib1f | \n def largestSubmatrix(self, matrix: List[List[int]]) -> int:\n def largestRectangleArea(heights):\n heights.sort(reverse=True)\n | otoc | NORMAL | 2021-01-17T04:06:22.620016+00:00 | 2021-01-17T04:07:56.980001+00:00 | 402 | false | ```\n def largestSubmatrix(self, matrix: List[List[int]]) -> int:\n def largestRectangleArea(heights):\n heights.sort(reverse=True)\n res = heights[0]\n for i in range(1, len(heights)):\n res = max(res, heights[i] * (i + 1))\n return res\n \n m, n = len(matrix), len(matrix[0])\n max_area = 0\n for i in range(m):\n if i >= 1:\n for j in range(n):\n if matrix[i][j] == 1:\n matrix[i][j] += matrix[i-1][j]\n max_area = max(max_area, largestRectangleArea([x for x in matrix[i]]))\n return max_area\n``` | 5 | 0 | [] | 0 |
largest-submatrix-with-rearrangements | Easy explained with best approach|| C++||greedy | easy-explained-with-best-approach-cgreed-ng4b | Intuition\nIntution is the precomputation of cells find the height for every column in the subsequent array.Then sorting of row according in non decreasing orde | dev_ved | NORMAL | 2023-11-26T06:11:44.526081+00:00 | 2023-11-26T06:11:44.526112+00:00 | 770 | false | # Intuition\nIntution is the precomputation of cells find the height for every column in the subsequent array.Then sorting of row according in non decreasing order and calculating the area since the cell number would provide the height and take width for subsequent column.\n\n# Approach\n1.precomputation\n2. for any row ith (for every jth column) matrix[i][j]=matrix[i-1][j]+1 only if matrix[i][j]=1.\n3. Traverse through each row sort it using sort(itr.begin(),itr.end())\n and traverse the whole row (from last since to find max)\n output the maximum ans by computing area as itr[k]*w where\n itr[k] defines the height and w width which increases by 1 at \n subsequent steps.\n \n# Complexity\n- Time complexity:\nO(m*n*log(n)) is the time complexity.\n\n- Space complexity\n- O(1) constant space is used.\n\n# Code\n```\nclass Solution {\npublic:\n int largestSubmatrix(vector<vector<int>>& matrix) {\n int m=matrix.size();\n int n=matrix[0].size();\n for(int i=1;i<m;i++)\n {\n for(int j=0;j<n;j++)\n {\n if(matrix[i][j]==1)\n {\n matrix[i][j]=matrix[i-1][j]+1;\n }\n }\n }\n int ans=0;\n for(auto itr:matrix)\n {\n sort(itr.begin(),itr.end());\n \n for(int k=n-1,w=1;k>=0 && itr[k]>0;k--,w++)\n { \n int area=itr[k]*w;\n ans=max(ans,area);\n }\n }\n return ans;\n // 0 0 1\n // 1 1 2\n // 2 0 3\n\n // 0 0 1\n // 1 1 2\n // 0 2 3\n }\n};\n``` | 4 | 0 | ['Math', 'Greedy', 'Sorting', 'Matrix', 'C++'] | 0 |
largest-submatrix-with-rearrangements | ✅ Beats 96.02% 🚀 c++ code 🔥 | beats-9602-c-code-by-omar_walied_ismail-gqz8 | Intuition\n- I need all indexes in result matrix with only ones.\n\n# Approach\n- Save for everyone in the matrix, the number of consecutive ones before it.\n- | omar_walied_ismail | NORMAL | 2023-11-26T05:26:19.032101+00:00 | 2023-11-26T05:26:19.032131+00:00 | 305 | false | # Intuition\n- I need all indexes in result matrix with only ones.\n\n# Approach\n- Save for everyone in the matrix, the number of consecutive ones before it.\n- Take these numbers and sort it in ascending order. \n- Iterate on these numbers from back to front to get the greater high every time.\n- Take the minimum every time for this numbers to get the lowest high.\n- The take maximum multiplication with man and the current number.\n\n# Complexity\n- Time complexity:\n- $$O(m*nlog(n))$$\n\n- Space complexity:\n- $$O(m*n)$$\n\n# Code\n```\nclass Solution {\npublic:\n int largestSubmatrix(vector<vector<int>>& matrix) {\n ios_base::sync_with_stdio(0), cout.tie(0), cin.tie(0);\n int ans=0,n=matrix.size(),m=matrix[0].size(),i,j,mn,cnt=0;\n vector<vector<int>>use(n,vector<int>(m));\n for(i=0;i<m;i++)\n if(matrix[0][i]==1)\n use[0][i]=1,cnt++;\n ans=max(ans,cnt);\n int help[100000];\n for(i=1;i<n;i++){\n cnt=0;\n for(j=0;j<m;j++)\n if(matrix[i][j]==1)\n use[i][j]=use[i-1][j]+1,help[cnt++]=use[i][j];\n sort(help,help+cnt);\n mn=1e9;\n for(j=cnt-1;j>=0;j--)\n mn=min(mn,help[j]),ans=max(ans,(cnt-j)*mn);\n }\n return ans;\n }\n};\n``` | 4 | 0 | ['Math', 'Dynamic Programming', 'Sorting', 'Matrix', 'C++'] | 3 |
largest-submatrix-with-rearrangements | 🚀😎 BEATS 100% | MOST EASY APPROACH🔥🔥| C++ | JAVA | PYTHON | JS | beats-100-most-easy-approach-c-java-pyth-bn2s | Intuition\nUPVOTE IF YOU FOUND THIS HELPFUL !!\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n\n\n Describe your approach to solvi | The_Eternal_Soul | NORMAL | 2023-11-26T02:48:04.202426+00:00 | 2023-11-26T02:48:04.202459+00:00 | 995 | false | # Intuition\nUPVOTE IF YOU FOUND THIS HELPFUL !!\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n\n\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(N*M)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int largestSubmatrix(vector<vector<int>>& matrix) {\n ios_base::sync_with_stdio(false);\n cin.tie(0);\n cout.tie(0);\n \n // Code\n int n = matrix.size(); // Row Size\n int m = matrix[0].size(); // Col Size\n\n int ans = INT_MIN;\n for(int j = 0; j < m; j++) // Col\n {\n for(int i = 1; i < n; i++) // Row\n {\n if(matrix[i][j] == 1)\n matrix[i][j] += matrix[i-1][j];\n }\n }\n\n for(int i = 0; i < n; i++) // Row\n {\n // Arrange the row in sorted and decreasing order\n sort(matrix[i].begin(),matrix[i].end(),greater<int>());\n for(int j = 0; j < m; j++) // Col\n {\n int length = matrix[i][j];\n int breadth = j + 1;\n ans = max( ans, length * breadth);\n }\n }\n return ans;\n }\n};\n``` | 4 | 0 | ['Array', 'Greedy', 'C', 'Sorting', 'Matrix', 'Python', 'C++', 'Java', 'JavaScript'] | 2 |
largest-submatrix-with-rearrangements | Walkthrough of the general algorithm | walkthrough-of-the-general-algorithm-by-bluh5 | Just my notes of a walkthrough of the general algorithm people used to solve this question, hope this helps\n\n\n\t/\n * 1. Precalculate the # of consecutiv | qmscorp | NORMAL | 2021-07-14T01:35:33.985759+00:00 | 2021-07-14T01:35:33.985792+00:00 | 283 | false | Just my notes of a walkthrough of the general algorithm people used to solve this question, hope this helps\n\n\n\t/**\n * 1. Precalculate the # of consecutive ones (vertically) in the matrix,\n * --> which we are actually calculating the height of each column/histogram\n *\n * [0,0,1] [0,0,1]\n * [1,1,1] --> [1,1,2]\n * [1,0,1] [2,0,3]\n *\n * 2. Sort each row in decreasing order (Theoretically)\n * We need to do this, so that we are ensuring the taller\n * histograms are always before the shorter ones, which\n * allows us to calculate the area later as (current height) * (current width)\n * Row 0: Row 1: Row 2:\n * [0,0,1] [0,0,1] [1,0,0] [0,0,1] [1,0,0]\n * [1,1,1] --> [1,1,2] --> [2,1,1] [1,1,2] [2,1,1]\n * [1,0,1] [2,0,3] [3,0,2] [2,0,3] [3,2,0]\n *\n * And actually, we don\'t need to sort the entire matrix everytime when we\n * sort a single row. We can just sort the single row to get the largest submatrix\n * as if the entire matrix is sorted, because we are able to calculate the largest matrix\n * with the information from that singly sorted row.\n *\n * For example, if we only sort row 2 (last row):\n * Row 2:\n * [0,0,1] [0,0,1] [0,0,1]\n * [1,1,1] --> [1,1,2] [1,1,2]\n * [1,0,1] [2,0,3] --> [3,2,0]\n *\n * At row=2, col=0,\n * --> we know there are 3 consecutive \'1\'s vertically from the top\n * --> there is a submatrix/rectangle of (height=3) * (width=1)=3\n * At row=2, col=1,\n * --> we know there are 2 consecutive \'1\'s vertically from the top\n * --> there is a submatrix/rectangle of (height=2) * (width=2)=4\n * --> which you may notice, width=(col+1)\n * At row=2, col=2\n * --> we know there are 0 consecutive \'1\'s vertically from the top\n * --> there is a submatrix/rectangle of (height=0) * (width=3)=0\n *\n * Let\'s go back and sort just row 0, and row 1\n * Row 0:\n * [0,0,1] [0,0,1] --> [1,0,0]\n * [1,1,1] --> [1,1,2] [1,1,2]\n * [1,0,1] [2,0,3] [2,0,3]\n * - At row=0, col=0,\n * --> we know there is only 1 consecutive \'1\'s vertically from the top\n * --> there is a submatrix/rectangle of (height=1)*(width=1)=1\n * - At row=0, col=1 & col=2\n * --> we know there are 0 consecutive \'1\' vertically from the top\n * --> there are submatrix/rectangle of (height=0)*(width=2,3)=0 for both\n *\n * Row 1:\n * [0,0,1] [0,0,1] [0,0,1]\n * [1,1,1] --> [1,1,2] --> [2,1,1]\n * [1,0,1] [2,0,3] [2,0,3]\n * - At row=1, col=0\n * --> we know there are 2 consecutive \'1\'s vertically from the top\n * --> there is a submatrix/rectangle of (height=2)*(width=1)=2\n * - At row=1, col=0\n * --> we know there is only 1 consecutive \'1\'s vertically from the top\n * --> there is a submatrix/rectangle of (height=1)*(width=2)=2\n * - At row=1, col=1,\n * --> we know there is only 1 consecutive \'1\'s vertically from the top\n * --> there is a submatrix/rectangle of (height=1)*(width=3)=3\n *\n */ | 4 | 0 | [] | 1 |
largest-submatrix-with-rearrangements | [Python3] Faster than 100% - Easy [Explanation + Comments] | python3-faster-than-100-easy-explanation-1sqc | The core logic of my program is :\nFor any cell (i,j) for all cells in the same row store the number of ones starting from that row.\nFor example, matrix = [[0, | mihirrane | NORMAL | 2021-01-17T04:36:26.540213+00:00 | 2021-01-17T19:07:51.760750+00:00 | 485 | false | The core logic of my program is :\nFor any cell (i,j) for all cells in the same row store the number of ones starting from that row.\nFor example, matrix = [[0,0,1],[1,1,1],[1,0,1]]\nCorresponding map (d) = {1: [2,1,2], 2: [1,1], 0: [3]}\nExplanation of map: \nKey corresponds to the row number. \nLet\'s look at row number 0, \n* for column 2 - 3 ones\n\nLet\'s look at row number 1, \n* for column 0 - 2 ones\n* for column 1 - 2 ones\n* for column 2 - 1 one\n\nLet\'s look at row number 2, \n* for column 0 - 1 one\n* for column 1 - 1 one\n \nNow that we have the map constructed, we will use this map to find the maximum size submatrix.\n\nTo find the maximum size submatrix, we will sort list for each key in the descending order and find the maximum height possible (minimum of the list till that index) for the particular width.\nMaximum size = Area = height x width\nLet look at row number 1:\n[2,1,2]\nSorted list = [2,2,1]\n* for width = 1\n\theight = min([2])\n\tArea = min([2])x1 = 2\n\t\n* for width = 2\n\theight = min([2,2])\n\tArea = min([2,2]) x 2 = 4\n\n* for width = 3\n\theight = min([2,2,1]) = 1\n\tArea = min([2,2,1]) x 2 = 2\n\t\n\tSimilarly, area will be calculated for row number 0 and 2. Maximum area = 4\n\t\nRunning time : O(mn<sup>2</sup>log<sub>2</sub>(n))\n\n```\nclass Solution:\n def largestSubmatrix(self, matrix: List[List[int]]) -> int:\n d = {} # dictionary storing row number and corresponding list of the number of ones\n m, n = len(matrix), len(matrix[0])\n \n for col in range(n): # for each column\n start = -1 # start is initialized to -1, when we will encounter streak ones it will be initialized\n \n for row in range(m):\n if matrix[row][col]: # when the cell contains 1\n if start == -1: # when the first one is encountered\n start = row # set start to the row number \n else: # when the cell contains a 0\n if start!=-1: # if there was a streak ones encountered before\n end = row\n for row_index in range(start, end): \n # iterate over the beginning of the streak till the end\n\t\t\t\t\t\t# for each row index in the streak assign the key to be row index and the corresponding length of streak starting from that point.\n \n if row_index not in d: # if the row index is not present in the dictionary\n d[row_index] = [] # create an empty list for the row index\n \n d[row_index].append(end - row_index) # append the length of the streak from the row index\n \n start = -1 # re-initialize start to -1 as the streak is over\n \n if start!=-1: # if the column has ended but the streak was present uptil the end\n\t\t\t# repeat the same process we did above with an exception, end = m\n end = m\n for row_index in range(start, end):\n if row_index not in d:\n d[row_index] = []\n d[row_index].append(end - row_index)\n \n\t\t## finding the max area\n area = 0 # initialize area to be 0\n for key in d: # for each key -> row index\n l = sorted(d[key], reverse = True) # sort the list of streak lengths\n ht = l[0] # initialize height with the max height\n for i in range(len(l)): # iterate over the list \n ht = min(ht, l[i]) # maximum height possible\n width = i + 1 # width = i + 1\n area = max(area, ht*width) # area = height x width\n return area\n```\nEdit:\nAn alternate solution would be to calculate the number of ones till current cell. This avoids the iteration over the row indexes to assign streak length. \n```\nclass Solution:\n def largestSubmatrix(self, matrix: List[List[int]]) -> int:\n m,n = len(matrix), len(matrix[0])\n res = 0\n dp = [0]*n\n \n for i in range(m):\n for j in range(n):\n dp[j] = matrix[i][j]*(dp[j] + 1)\n \n cnt = 1\n for x in sorted(dp, reverse = True):\n res = max(x*cnt, res)\n cnt += 1\n \n return res\n``` | 4 | 0 | ['Python', 'Python3'] | 1 |
largest-submatrix-with-rearrangements | 🚀✅🚀 Beats 101% -1727. Largest Submatrix With Rearrangements | beats-101-1727-largest-submatrix-with-re-dxqz | Example Explanation\nLet\'s break down the process step by step using an example matrix:\n\nExample Matrix:\n\n[\n [0, 0, 1],\n [1, 1, 1],\n [1, 0, 1]\n]\n\nSte | arshbhatia1551 | NORMAL | 2023-11-26T10:28:13.772766+00:00 | 2023-11-26T10:28:13.772799+00:00 | 158 | false | **Example Explanation**\nLet\'s break down the process step by step using an example matrix:\n\n**Example Matrix:**\n```\n[\n [0, 0, 1],\n [1, 1, 1],\n [1, 0, 1]\n]\n```\n**Step 1: Preprocessing**\n```\n[\n [0, 0, 1],\n [1, 1, 2],\n [2, 0, 3]\n]\n```\nFor each cell matrix[i][j] = 1, update it with the height of consecutive 1s ending at this cell (matrix[i][j] += matrix[i-1][j]).\n\n**Step 2: Sorting Rows**\nSort each row in non-decreasing order.\n```\n[\n [0, 0, 1],\n [1, 1, 2],\n [0, 2, 3]\n]\n```\n\n**Step 3: Calculate Area**\nIterate through each row and calculate the area for each cell.\n```\n[\n [0, 0, 1], Area: row[j]*k = 1*1\n [1, 1, 2], Area: Max(row[j]*k) = Max(2x1,1x2,1x3)\n [0, 2, 3] Area: Max(row[j]*k) = Max(3x1,2x2)\n]\n```\n\n* For each cell, the area is the height * width.\n* For example in the last row, we are moving from backwards to forward, so j starts with n-1 and k=1.\n* In the first iteration row[j]= 3 but k = 1, so area becomes 3 but in the next iteration, row[j]=2 and k=2 so the area becomes 4, which is the maximum of all the areas of submatrix.\n\n**Step 4: Maximum Area**\nThe maximum area among all cells is 4.\n\n**Explanation:**\nThe maximum area of the submatrix containing only 1s after rearranging the columns optimally is 4, achieved at matrix[2][2].\n\n#### Intuition\nThe problem asks for the area of the largest submatrix containing only 1s after rearranging the columns optimally. The solution involves preprocessing the matrix to store the height of consecutive 1s ending at each cell. Then, for each row, we sort the heights in non-decreasing order and calculate the area for each possible submatrix.\n\nThe problem asks for the area of the largest submatrix containing only 1s after rearranging the columns optimally. The solution involves preprocessing the matrix to store the height of consecutive 1s ending at each cell. Then, for each row, we sort the heights in non-decreasing order and calculate the area for each possible submatrix.\n\n### Approach\n1. Iterate through the matrix starting from the second row (i = 1).\n2. For each cell matrix[i][j]:\n3. If matrix[i][j] is 1, update it to store the height of consecutive 1s ending at this cell by adding the height of the previous row\'s corresponding cell (matrix[i - 1][j]).\n4. After preprocessing, for each row, sort the row in non-decreasing order.\n5. For each cell in the sorted row, calculate the area of the submatrix that ends at this cell, considering the consecutive 1s.\n6. The area is given by height * width, where height is the height of consecutive 1s ending at this cell, and width is the position of the cell in the sorted row.\n7. Update the maximum area accordingly.\n8. Return the maximum area as the result.\n\n### Complexity\n* Time Complexity: O(m * n * log(n)) - Sorting is done for each row.\n* Space Complexity: O(1) - No additional space is used except for variables.\n\n# CODE\n\n### Java\n```\nclass Solution {\n public int largestSubmatrix(int[][] matrix) {\n int m = matrix.length, n = matrix[0].length;\n for (int i = 1; i < m; ++i) {\n for (int j = 0; j < n; ++j) {\n if (matrix[i][j] == 1) {\n matrix[i][j] = matrix[i - 1][j] + 1;\n }\n }\n }\n int ans = 0;\n for (var row : matrix) {\n Arrays.sort(row);\n for (int j = n - 1, k = 1; j >= 0 && row[j] > 0; --j, ++k) {\n int s = row[j] * k;\n ans = Math.max(ans, s);\n }\n }\n return ans;\n }\n}\n```\n\n### C++\n\n```\nclass Solution\n{\npublic:\n int largestSubmatrix(vector<vector<int>>& matrix)\n {\n int m = matrix.size(), n = matrix[0].size();\n int ans = 0;\n for(int j = 0; j < n; j++)\n for(int i = 1; i < m; i++)\n if(matrix[i][j] == 1)\n matrix[i][j] += matrix[i-1][j];\n for(int i = 0; i < m; i++)\n {\n sort(matrix[i].begin(), matrix[i].end());\n reverse(matrix[i].begin(), matrix[i].end());\n for(int j = 0; j < n; j++)\n ans = max(ans, matrix[i][j]*(j+1));\n }\n return ans;\n }\n};\n```\n\nPython\n```\nclass Solution(object):\n def largestSubmatrix(self, matrix):\n m, n = len(matrix), len(matrix[0])\n \n for i in range(1, m):\n for j in range(n):\n if matrix[i][j] == 1:\n matrix[i][j] += matrix[i - 1][j]\n \n ans = 0\n \n for row in matrix:\n row.sort(reverse=True)\n for j in range(n):\n ans = max(ans, row[j] * (j + 1))\n \n return ans\n```\n\n\n\n | 3 | 0 | ['Array', 'Greedy', 'C', 'Sorting', 'Matrix', 'Python', 'Java', 'JavaScript'] | 0 |
largest-submatrix-with-rearrangements | O(N*M*LogM) | onmlogm-by-3s_akb-3w04 | \n# Code\n\npublic class Solution {\n public int LargestSubmatrix(int[][] matrix) {\n int Y = matrix.Length; //rows count\n int X = matrix[0 | 3S_AKB | NORMAL | 2023-07-31T20:23:12.380373+00:00 | 2023-07-31T20:23:12.380392+00:00 | 47 | false | \n# Code\n```\npublic class Solution {\n public int LargestSubmatrix(int[][] matrix) {\n int Y = matrix.Length; //rows count\n int X = matrix[0].Length; //columns count\n\n //transform matrix to (matrix[y][x] = count of 1s upper (<y))\n for (int x = 0; x < X; x++) \n for (int y = 1; y < Y; y++)\n matrix[y][x] = matrix[y][x] == 0 ? 0 : matrix[y - 1][x] + 1;\n\n int res = 0; \n for (int y = 0; y < Y; y++)\n {\n //get y-th row and sort it descending\n Array.Sort(matrix[y], (a, b) => b.CompareTo(a)); \n for (int x = 0; x < X; x++)\n res = Math.Max(res, (x + 1) * matrix[y][x]);\n }\n return res;\n }\n}\n``` | 3 | 0 | ['C#'] | 1 |
largest-submatrix-with-rearrangements | C++ | Variation of Leetcode 85.Maximal Rectangle | c-variation-of-leetcode-85maximal-rectan-7l5z | \nclass Solution {\npublic:\n int largestSubmatrix(vector<vector<int>>& v) {\n int n=v.size();\n int m=v[0].size();\n int res;\n | GeekyBits | NORMAL | 2022-10-10T12:55:49.812259+00:00 | 2022-10-10T12:55:49.812363+00:00 | 469 | false | ```\nclass Solution {\npublic:\n int largestSubmatrix(vector<vector<int>>& v) {\n int n=v.size();\n int m=v[0].size();\n int res;\n vector<int> vv(m,0);\n for(int i=0;i<n;i++){\n for(int j=0;j<m;j++){\n if(v[i][j]==1){\n vv[j]+=1;\n }\n else{\n vv[j]=0;\n }\n }\n auto b=vv;//this is the step actually which might be missed\n sort(b.begin(),b.end());\n res=max(res,helper(b));\n }\n return res;\n }\n int helper(vector<int>& heights){\n int n=heights.size();\n stack<int> st;\n vector<int> prevsmaller(n,-1),nextsmaller(n,n);\n for(int i=0;i<n;i++){\n while(st.empty()==false and heights[st.top()]>heights[i]){\n nextsmaller[st.top()]=i;\n st.pop();\n }\n st.push(i);\n }\n for(int i=n-1;i>=0;i--){\n while(st.empty()==false and heights[st.top()]>heights[i]){\n prevsmaller[st.top()]=i;\n st.pop();\n }\n st.push(i);\n }\n \n int area=0;\n for(int i=0;i<=n-1;i++){\n int l=prevsmaller[i];\n int r=nextsmaller[i];\n //cout<<l<<" "<<r<<" "<<heights[i]<<endl;\n //in between l and r we can make a histogram of atleast height: heights[i]\n area=max(area,(r-l-1)*(heights[i]));\n }\n return area;\n }\n};\n``` | 3 | 0 | [] | 0 |
largest-submatrix-with-rearrangements | C++ Solution | O(m * n * logn) | c-solution-om-n-logn-by-horcrux903-mzvd | \nclass Solution {\npublic:\n\n\tint largestSubmatrix(vector<vector<int>>& a)\n\t{\n\t\tint ans = 0;\n\t\tint n = a.size(), m = a[0].size();\n\n\t\tint tmp[m];\ | horcrux903 | NORMAL | 2022-01-04T19:01:27.881769+00:00 | 2022-01-04T19:01:27.881814+00:00 | 150 | false | ```\nclass Solution {\npublic:\n\n\tint largestSubmatrix(vector<vector<int>>& a)\n\t{\n\t\tint ans = 0;\n\t\tint n = a.size(), m = a[0].size();\n\n\t\tint tmp[m];\n\t\tmemset(tmp, 0, sizeof(tmp));\n\n\t\tfor (int i = 0; i < n; i++)\n\t\t{\n\t\t\tvector<int> v;\n\n\t\t\tfor (int j = 0; j < m; j++)\n\t\t\t{\n\t\t\t\tif (a[i][j] == 1)\n\t\t\t\t{\n\t\t\t\t\ttmp[j] += a[i][j];\n\t\t\t\t}\n\t\t\t\telse\n\t\t\t\t{\n\t\t\t\t\ttmp[j] = 0;\n\t\t\t\t}\n\t\t\t\tv.push_back(tmp[j]);\n\t\t\t}\n\n\t\t\tsort(v.begin(), v.end());\n\n\t\t\tfor (int j = 0; j < v.size(); j++)\n\t\t\t{\n\t\t\t\tans = max(ans, v[j] * (m - j));\n\t\t\t}\n\t\t}\n\n\t\treturn ans;\n\t}\n};\n``` | 3 | 0 | ['Sorting'] | 0 |
largest-submatrix-with-rearrangements | Easy C++ solution || commented | easy-c-solution-commented-by-saiteja_bal-j505 | \nclass Solution {\npublic:\n int largestSubmatrix(vector<vector<int>>& matrix) {\n \n //for every column keep a track of number of consecutive | saiteja_balla0413 | NORMAL | 2021-07-05T16:32:23.619671+00:00 | 2021-07-05T16:32:23.619704+00:00 | 349 | false | ```\nclass Solution {\npublic:\n int largestSubmatrix(vector<vector<int>>& matrix) {\n \n //for every column keep a track of number of consecutive ones upto the index\n int m=matrix.size();\n int n=matrix[0].size();\n for(int j=0;j<n;j++)\n {\n for(int i=0;i<m;i++)\n {\n if(matrix[i][j]==1)\n {\n matrix[i][j]+=(i > 0 ) ? matrix[i-1][j] : 0;\n }\n }\n }\n \n //now for every row sort the values in reverse order(non increasing order)\n int res=INT_MIN;\n for(int i=0;i<m;i++)\n {\n sort(matrix[i].rbegin(),matrix[i].rend());\n \n //the problem can be now assumed as to find the maximum rectangle area from the histogram\n int currRes=INT_MIN;\n for(int j=0;j<n;j++)\n {\n currRes=max(currRes,matrix[i][j] * (j+1));\n }\n res=max(res,currRes);\n \n }\n return res;\n }\n};\n```\n**Upvote if this helps you:)** | 3 | 0 | ['C'] | 0 |
largest-submatrix-with-rearrangements | Java Priority Queue Solution | java-priority-queue-solution-by-mayank_p-op8i | https://achievementguru.com/leetcode-1727-largest-submatrix-with-rearrangements-java-solution/\n\nclass Solution {\n public int largestSubmatrix(int[][] matr | mayank_pratap | NORMAL | 2021-01-18T08:24:18.300532+00:00 | 2021-01-18T08:25:20.941304+00:00 | 538 | false | https://achievementguru.com/leetcode-1727-largest-submatrix-with-rearrangements-java-solution/\n```\nclass Solution {\n public int largestSubmatrix(int[][] matrix) {\n //Store matrix[i][j]= total number of consecutive 1s along column j ending at index (i,j).\n for(int i=1;i<matrix.length;i++) //Start from row 1 because row 0 will be unaffected as no row above it.\n {\n for(int j=0;j<matrix[i].length;j++)\n {\n if(matrix[i][j]==0) continue;\n else matrix[i][j]=matrix[i-1][j]+1;\n }\n }\n \n int maxSize=0;\n for(int i=0;i<matrix.length;i++)\n {\n \n PriorityQueue<Integer> pq = new PriorityQueue<Integer>();// minheap\n for(int j=0;j<matrix[i].length;j++)\n {\n if(matrix[i][j]>0) pq.add(matrix[i][j]); // Add all the entries from row i in minheap\n }\n int size=0,curr=0;\n /*\n In current row, total entries with value k or greater than k will contribute the squares of\n\t\t\t\tsize=k*(number of squares of size k or greater than k).Largest square ending at current\n\t\t\t\trow= k * (all entries greater than or equal to k in current row) for all ks in current row\n */\n while(!pq.isEmpty()) \n {\n curr=pq.peek(); \n \n size=curr*pq.size();\n maxSize=Math.max(maxSize,size);\n \n pq.poll();\n }\n }\n return maxSize;\n \n \n \n }\n}\n``` | 3 | 0 | ['Heap (Priority Queue)', 'Java'] | 0 |
largest-submatrix-with-rearrangements | My Java Solution with small explanation 1) Count the 1's in column 2) Sort the rows and count | my-java-solution-with-small-explanation-iy26l | \nclass Solution {\n public int largestSubmatrix(int[][] matrix) {\n // count number of 1 in each column and update it\n int row = matrix.lengt | vrohith | NORMAL | 2021-01-18T05:06:40.617611+00:00 | 2021-01-18T05:06:40.617696+00:00 | 380 | false | ```\nclass Solution {\n public int largestSubmatrix(int[][] matrix) {\n // count number of 1 in each column and update it\n int row = matrix.length;\n int col = matrix[0].length;\n int count = 0;\n for (int i=1; i<row; i++) {\n for (int j=0; j<col; j++) {\n if (matrix[i][j] == 1)\n matrix[i][j] = matrix[i-1][j] + 1;\n }\n }\n /*\n 0 0 1 0 0 1\n 1 1 1 -> changes to -> 1 1 2\n 1 0 1 2 1 3\n */\n for (int i=0; i<row; i++) {\n // sort it\n Arrays.sort(matrix[i]);\n for (int j=1; j<=col; j++) {\n count = Math.max(count, j * matrix[i][col - j]);\n }\n }\n /*\n 0 0 1 0 0 1\n 1 1 2 -> Sorting -> 1 1 2\n 2 1 3 1 2 3\n \n */\n return count;\n }\n}\n``` | 3 | 0 | ['Sorting', 'Matrix', 'Java'] | 1 |
largest-submatrix-with-rearrangements | C# - Sorting by heights to get max area | c-sorting-by-heights-to-get-max-area-by-0mzex | csharp\npublic int LargestSubmatrix(int[][] matrix)\n{\n\tint[] heights = new int[matrix[0].Length];\n\tint result = 0;\n\n\tfor (int row = 0; row < matrix.Leng | christris | NORMAL | 2021-01-18T02:39:14.126668+00:00 | 2021-01-18T02:39:14.126695+00:00 | 94 | false | ```csharp\npublic int LargestSubmatrix(int[][] matrix)\n{\n\tint[] heights = new int[matrix[0].Length];\n\tint result = 0;\n\n\tfor (int row = 0; row < matrix.Length; row++)\n\t{\n\t\tfor (int column = 0; column < matrix[0].Length; column++)\n\t\t{\n\t\t\tif (matrix[row][column] == 0)\n\t\t\t{\n\t\t\t\theights[column] = 0;\n\t\t\t}\n\n\t\t\telse\n\t\t\t{\n\t\t\t\theights[column]++;\n\t\t\t}\n\t\t}\n\n\t\tint[] sortedHeights = heights.OrderByDescending(x => x).ToArray();\n\t\tfor (int column = 0; column < sortedHeights.Length; column++)\n\t\t{\n\t\t\tresult = Math.Max(result, sortedHeights[column] * (column + 1));\n\t\t}\n\t}\n\n\treturn result;\n}\n``` | 3 | 0 | [] | 0 |
largest-submatrix-with-rearrangements | 16 line Python solution (998ms) | 16-line-python-solution-998ms-by-15sawye-psck | Intuition\n Describe your first thoughts on how to solve this problem. \nIterate over rows while keeping track of the height of columns of 1\'s above the row. S | 15sawyer | NORMAL | 2023-11-26T20:04:44.982906+00:00 | 2023-11-26T20:46:36.465858+00:00 | 425 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIterate over rows while keeping track of the height of columns of 1\'s above the row. Sort the heights after each iteration and check the area of all possible rectangles that would fit into the graph of heights.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n \\cdot log(n)\\cdot m)$$ with `n = matrix[i].length` and `m = matrix.length`\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$ with `n = matrix[i].length`\n# Code\n```python\nclass Solution:\n def largestSubmatrix(self, matrix: List[List[int]]) -> int:\n m = len(matrix) # num rows\n n = len(matrix[0]) # num cols\n # The height of a column of 1\'s at a specific index\n heights = matrix[0].copy()\n maxArea = heights.count(1)\n for ri in range(1, m):\n # Increase or reset height of the column\n for ci in range(n):\n if matrix[ri][ci] == 1:\n heights[ci] += 1\n else:\n heights[ci] = 0\n # Bring columns into a "triangle" form, with descending values\n sortedHeights = sorted(heights.copy(), reverse=True)\n # Check the area of all possible rectangles inside the imagined triangle\n for i in range(n):\n area = sortedHeights[i] * (i+1)\n if area > maxArea:\n maxArea = area\n return maxArea\n\n``` | 2 | 0 | ['Python3'] | 1 |
largest-submatrix-with-rearrangements | ✅☑[C++/Java/Python/JavaScript] || 3 Approaches || EXPLAINED🔥 | cjavapythonjavascript-3-approaches-expla-szh1 | PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n(Also explained in the code)\n\n#### Approach 1(Sort By Height On Each Baseline Row)\n1. Matrix traversal:\ | MarkSPhilip31 | NORMAL | 2023-11-26T19:40:48.424908+00:00 | 2023-11-26T19:40:48.424930+00:00 | 231 | false | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n#### ***Approach 1(Sort By Height On Each Baseline Row)***\n1. **Matrix traversal:**\n - The code iterates through each row of the matrix.\n1. **Accumulating consecutive ones:**\n - For each non-zero element in the matrix (except in the first row), the code accumulates its value with the element directly above it. This accumulation happens vertically, tracking consecutive ones.\n\n - For example, if we start with the first row, the elements with 1s in the second row get incremented by the value in the first row if the element in the first row at the same column is also 1. It accumulates the count of consecutive ones vertically.\n\n1. **Finding the largest submatrix:**\n - After accumulating the consecutive ones, it creates a copy of the current row and sorts it in descending order.\n\n - By sorting, the largest consecutive blocks of ones are moved to the front of the row.\n\n - The code then calculates the area of the largest submatrix by multiplying the height (number of consecutive ones) with the width (position in the sorted row). It updates and keeps track of the maximum area found.\n\n*In the example matrix:*\n\n- **For the first row:** `[0, 1, 1, 0, 1]`, the consecutive ones count would be `[0, 1, 1, 0, 2]`.\n- **For the second row:** `[1, 2, 1, 2, 0]`, the consecutive ones count would be `[1, 2, 1, 2, 0]`.\n- **For the third row:** `[1, 2, 3, 4, 0]`, the consecutive ones count would be `[1, 2, 3, 4, 0]`.\n- **For the fourth row:** `[2, 3, 4, 5, 1]`, the consecutive ones count would be `[2, 3, 4, 5, 1]`.\n\n# Complexity\n- *Time complexity:*\n $$O(m.n.logn)$$\n \n\n- *Space complexity:*\n $$O(m.n)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int largestSubmatrix(vector<vector<int>>& matrix) {\n int m = matrix.size(); // Number of rows in the matrix\n int n = matrix[0].size(); // Number of columns in the matrix\n int ans = 0; // Initialize the maximum area of the largest submatrix\n \n // Traverse through each row in the matrix\n for (int row = 0; row < m; row++) {\n // For each non-zero element in the matrix (except the first row),\n // accumulate its value with the element directly above it\n for (int col = 0; col < n; col++) {\n if (matrix[row][col] != 0 && row > 0) {\n matrix[row][col] += matrix[row - 1][col];\n }\n }\n \n // Create a copy of the current row to work with\n vector<int> currRow = matrix[row];\n \n // Sort the elements in the current row in descending order\n sort(currRow.begin(), currRow.end(), greater<int>());\n \n // Calculate the maximum area of the largest submatrix with consecutive ones\n for (int i = 0; i < n; i++) {\n ans = max(ans, currRow[i] * (i + 1));\n }\n }\n \n return ans; // Return the maximum area of the largest submatrix\n }\n};\n\n\n\n```\n```C []\n\n#include <stdio.h>\n#include <stdlib.h>\n\n// Function to calculate the maximum area of the largest submatrix with consecutive ones\nint largestSubmatrix(int** matrix, int m, int n) {\n int ans = 0; // Initialize the maximum area of the largest submatrix\n\n // Traverse through each row in the matrix\n for (int row = 0; row < m; row++) {\n // For each non-zero element in the matrix (except the first row),\n // accumulate its value with the element directly above it\n for (int col = 0; col < n; col++) {\n if (matrix[row][col] != 0 && row > 0) {\n matrix[row][col] += matrix[row - 1][col];\n }\n }\n\n // Create a copy of the current row to work with\n int* currRow = malloc(n * sizeof(int));\n for (int i = 0; i < n; i++) {\n currRow[i] = matrix[row][i];\n }\n\n // Sort the elements in the current row in descending order\n for (int i = 0; i < n - 1; i++) {\n for (int j = 0; j < n - i - 1; j++) {\n if (currRow[j] < currRow[j + 1]) {\n int temp = currRow[j];\n currRow[j] = currRow[j + 1];\n currRow[j + 1] = temp;\n }\n }\n }\n\n // Calculate the maximum area of the largest submatrix with consecutive ones\n for (int i = 0; i < n; i++) {\n ans = ans > currRow[i] * (i + 1) ? ans : currRow[i] * (i + 1);\n }\n\n free(currRow);\n }\n\n return ans; // Return the maximum area of the largest submatrix\n}\n\n\n```\n```Java []\nclass Solution {\n public int largestSubmatrix(int[][] matrix) {\n int m = matrix.length;\n int n = matrix[0].length;\n int ans = 0;\n \n for (int row = 0; row < m; row++) {\n for (int col = 0; col < n; col++) {\n if (matrix[row][col] != 0 && row > 0) {\n matrix[row][col] += matrix[row - 1][col];\n }\n }\n \n int[] currRow = matrix[row].clone();\n Arrays.sort(currRow);\n for (int i = 0; i < n; i++) {\n ans = Math.max(ans, currRow[i] * (n - i));\n }\n }\n \n return ans;\n }\n}\n\n\n```\n```python3 []\nclass Solution:\n def largestSubmatrix(self, matrix: List[List[int]]) -> int:\n m = len(matrix)\n n = len(matrix[0])\n ans = 0\n\n for row in range(m):\n for col in range(n):\n if matrix[row][col] != 0 and row > 0:\n matrix[row][col] += matrix[row - 1][col]\n\n curr_row = sorted(matrix[row], reverse=True)\n for i in range(n):\n ans = max(ans, curr_row[i] * (i + 1))\n\n return ans\n\n```\n\n```javascript []\nfunction largestSubmatrix(matrix) {\n let m = matrix.length; // Number of rows\n let n = matrix[0].length; // Number of columns\n let ans = 0; // Initialize the maximum area of the largest submatrix\n\n // Traverse through each row in the matrix\n for (let row = 0; row < m; row++) {\n // For each non-zero element in the matrix (except the first row),\n // accumulate its value with the element directly above it\n for (let col = 0; col < n; col++) {\n if (matrix[row][col] !== 0 && row > 0) {\n matrix[row][col] += matrix[row - 1][col];\n }\n }\n\n // Create a copy of the current row to work with\n let currRow = matrix[row].slice();\n \n // Sort the elements in the current row in descending order\n currRow.sort((a, b) => b - a);\n\n // Calculate the maximum area of the largest submatrix with consecutive ones\n for (let i = 0; i < n; i++) {\n ans = Math.max(ans, currRow[i] * (i + 1));\n }\n }\n\n return ans; // Return the maximum area of the largest submatrix\n}\n\n\n\n```\n\n---\n\n#### ***Approach 2(Without Modifying Input)***\n1. **Initialization:** Define the matrix\'s size, initialize the `prevRow` vector, and initialize ans to store the maximum area.\n1. **Iteration through Rows:** Traverse through each row of the matrix.\n1. **Cumulative Sum:** Calculate the cumulative sum for each element in the current row by adding the element with its corresponding element in the `prevRow`.\n1. **Sorting:** Sort the elements of the current row in descending order.\n1. **Calculate Maximum Area:** For each index `i`, calculate the area considering the sorted row and update `ans` if a larger area is found.\n1. **Update Previous Row:** Update the `prevRow` for the next iteration with the current row.\n1. **Return Result:** Return the maximum area found.\n\n\n\n# Complexity\n- *Time complexity:*\n $$O(m\u22C5n\u22C5logn)$$\n \n\n- *Space complexity:*\n $$O(n)$$\n \n\n\n# Code\n```C++ []\n\n\nclass Solution {\npublic:\n int largestSubmatrix(vector<vector<int>>& matrix) {\n int m = matrix.size(); // Number of rows in the matrix\n int n = matrix[0].size(); // Number of columns in the matrix\n vector<int> prevRow = vector<int>(n, 0); // Vector to store the previous row\n int ans = 0; // Initialize the maximum area of the largest submatrix\n \n for (int row = 0; row < m; row++) {\n vector<int> currRow = matrix[row]; // Copy the current row of the matrix\n \n // Calculate the cumulative sum for each element in the current row\n for (int col = 0; col < n; col++) {\n if (currRow[col] != 0) {\n currRow[col] += prevRow[col]; // Add the element with its corresponding element in the previous row\n }\n }\n \n // Sort the elements in the current row in descending order\n vector<int> sortedRow = currRow;\n sort(sortedRow.begin(), sortedRow.end(), greater<int>());\n \n // Calculate the maximum area of the largest submatrix with consecutive ones\n for (int i = 0; i < n; i++) {\n ans = max(ans, sortedRow[i] * (i + 1)); // Update the maximum area\n }\n \n prevRow = currRow; // Update the previous row for the next iteration\n }\n\n return ans; // Return the maximum area of the largest submatrix\n }\n};\n\n\n\n```\n```C []\n\n#include <stdio.h>\n#include <stdlib.h>\n\n// Function to calculate the largest submatrix\nint largestSubmatrix(int** matrix, int m, int n) {\n int ans = 0;\n int* prevRow = (int*)malloc(n * sizeof(int));\n for (int i = 0; i < n; i++) {\n prevRow[i] = 0;\n }\n\n for (int row = 0; row < m; row++) {\n int* currRow = matrix[row];\n\n for (int col = 0; col < n; col++) {\n if (currRow[col] != 0) {\n currRow[col] += prevRow[col];\n }\n }\n\n int sortedRow[n];\n for (int i = 0; i < n; i++) {\n sortedRow[i] = currRow[i];\n }\n // Sort the row in descending order\n for (int i = 0; i < n - 1; i++) {\n for (int j = 0; j < n - i - 1; j++) {\n if (sortedRow[j] < sortedRow[j + 1]) {\n int temp = sortedRow[j];\n sortedRow[j] = sortedRow[j + 1];\n sortedRow[j + 1] = temp;\n }\n }\n }\n\n for (int i = 0; i < n; i++) {\n ans = ans > sortedRow[i] * (i + 1) ? ans : sortedRow[i] * (i + 1);\n }\n\n for (int i = 0; i < n; i++) {\n prevRow[i] = currRow[i];\n }\n }\n\n free(prevRow);\n return ans;\n}\n\n\n```\n```Java []\n\nclass Solution {\n public int largestSubmatrix(int[][] matrix) {\n int m = matrix.length;\n int n = matrix[0].length;\n int[] prevRow = new int[n];\n int ans = 0;\n \n for (int row = 0; row < m; row++) {\n int[] currRow = matrix[row].clone();\n for (int col = 0; col < n; col++) {\n if (currRow[col] != 0) {\n currRow[col] += prevRow[col];\n }\n }\n \n int[] sortedRow = currRow.clone();\n Arrays.sort(sortedRow);\n for (int i = 0; i < n; i++) {\n ans = Math.max(ans, sortedRow[i] * (n - i));\n }\n \n prevRow = currRow;\n }\n \n return ans;\n }\n}\n\n\n```\n```python3 []\nclass Solution:\n def largestSubmatrix(self, matrix: List[List[int]]) -> int:\n m = len(matrix)\n n = len(matrix[0])\n prev_row = [0] * n\n ans = 0\n \n for row in range(m):\n curr_row = matrix[row][:]\n for col in range(n):\n if curr_row[col] != 0:\n curr_row[col] += prev_row[col]\n\n sorted_row = sorted(curr_row, reverse=True)\n for i in range(n):\n ans = max(ans, sorted_row[i] * (i + 1))\n\n prev_row = curr_row\n\n return ans\n\n```\n\n```javascript []\nfunction largestSubmatrix(matrix) {\n let m = matrix.length;\n let n = matrix[0].length;\n let prevRow = Array(n).fill(0);\n let ans = 0;\n\n for (let row = 0; row < m; row++) {\n let currRow = [...matrix[row]];\n\n for (let col = 0; col < n; col++) {\n if (currRow[col] !== 0) {\n currRow[col] += prevRow[col];\n }\n }\n\n let sortedRow = [...currRow].sort((a, b) => b - a);\n\n for (let i = 0; i < n; i++) {\n ans = Math.max(ans, sortedRow[i] * (i + 1));\n }\n\n prevRow = [...currRow];\n }\n\n return ans;\n}\n\n```\n\n---\n#### ***Approach 3(No Sort)***\n\n1. **largestSubmatrix Function:**\n - Finds the largest submatrix of consecutive ones in the given matrix.\n \n1. **Variables Used:**\n - **`m` and `n`:** Number of rows and columns in the matrix, respectively.\n - **prevHeights:** Stores heights of 1s from the previous row.\n - **ans:** Tracks the maximum submatrix area.\n1. **Iterating Through Each Row:**\n - The outer loop iterates through each row of the matrix.\n1. **Finding Heights of Ones in Each Row:**\n - For each row, it tracks the heights of consecutive 1s and columns seen in the previous row.\n - **heights:** Vector that stores pairs of heights and corresponding columns for the current row.\n - **seen:** Tracks the columns that have already been seen in the previous row.\n1. **Calculating Heights:**\n - It iterates through the previous heights and increments the height for each 1 encountered in the current row.\n - For new 1s in the current row (not seen in the previous row), it sets a new height.\n1. **Calculating Maximum Submatrix Area:**\n - For each height, it calculates the area by multiplying the height by the width (i + 1) and updates `ans` if a larger area is found.\n1. **Updating Heights for the Next Row:**\n - Updates `prevHeights` with the heights from the current row to prepare for the next row iteration.\n1. **Returns:**\n - Returns the maximum submatrix area found.\n\n# Complexity\n- *Time complexity:*\n $$O(m.n)$$\n \n\n- *Space complexity:*\n $$O(n)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int largestSubmatrix(vector<vector<int>>& matrix) {\n int m = matrix.size(); // Number of rows in the matrix\n int n = matrix[0].size(); // Number of columns in the matrix\n vector<pair<int,int>> prevHeights; // To store heights of 1s from the previous row\n int ans = 0; // Initialize the maximum submatrix area\n \n for (int row = 0; row < m; row++) {\n vector<pair<int,int>> heights; // Heights of 1s for the current row\n vector<bool> seen = vector(n, false); // To track the columns already seen\n \n // Process the heights from the previous row\n for (auto [height, col] : prevHeights) {\n if (matrix[row][col] == 1) {\n heights.push_back({height + 1, col}); // Increase the height if the current element is 1\n seen[col] = true; // Mark the column as seen\n }\n }\n \n // Process the new heights in the current row\n for (int col = 0; col < n; col++) {\n if (seen[col] == false && matrix[row][col] == 1) {\n heights.push_back({1, col}); // New height for a new column\n }\n }\n \n // Calculate the area for each height and update the maximum area\n for (int i = 0; i < heights.size(); i++) {\n ans = max(ans, heights[i].first * (i + 1));\n }\n \n prevHeights = heights; // Update the heights for the next row\n }\n\n return ans; // Return the maximum submatrix area\n }\n};\n\n\n\n```\n```C []\n\n#include <stdio.h>\n#include <stdlib.h>\n\nstruct Pair {\n int first;\n int second;\n};\n\nint max(int a, int b) {\n return (a > b) ? a : b;\n}\n\nint largestSubmatrix(int** matrix, int m, int n) {\n struct Pair* prevHeights = malloc(sizeof(struct Pair) * n);\n int ans = 0;\n \n for (int row = 0; row < m; row++) {\n struct Pair* heights = malloc(sizeof(struct Pair) * n);\n int* seen = calloc(n, sizeof(int));\n \n for (int i = 0; i < n; i++) {\n heights[i].first = 0;\n heights[i].second = 0;\n }\n \n for (int i = 0; i < n; i++) {\n heights[i].first = prevHeights[i].first;\n heights[i].second = prevHeights[i].second;\n }\n \n for (int col = 0; col < n; col++) {\n if (matrix[row][col] == 1) {\n if (row > 0 && matrix[row - 1][col] == 1) {\n heights[col].first++;\n }\n else {\n heights[col].first = 1;\n heights[col].second = col;\n }\n seen[col] = 1;\n }\n }\n \n for (int col = 0; col < n; col++) {\n if (seen[col] == 0 && matrix[row][col] == 1) {\n heights[col].first = 1;\n heights[col].second = col;\n }\n }\n \n for (int i = 0; i < n; i++) {\n ans = max(ans, heights[i].first * (i + 1));\n }\n \n for (int i = 0; i < n; i++) {\n prevHeights[i].first = heights[i].first;\n prevHeights[i].second = heights[i].second;\n }\n \n free(heights);\n free(seen);\n }\n\n free(prevHeights);\n return ans;\n}\n\n\n```\n```Java []\nclass Solution {\n public int largestSubmatrix(int[][] matrix) {\n int m = matrix.length;\n int n = matrix[0].length;\n List<Pair<Integer,Integer>> prevHeights = new ArrayList();\n int ans = 0;\n \n for (int row = 0; row < m; row++) {\n List<Pair<Integer,Integer>> heights = new ArrayList();\n boolean[] seen = new boolean[n];\n \n for (Pair<Integer, Integer> pair : prevHeights) {\n int height = pair.getKey();\n int col = pair.getValue();\n if (matrix[row][col] == 1) {\n heights.add(new Pair(height + 1, col));\n seen[col] = true;\n }\n }\n \n for (int col = 0; col < n; col++) {\n if (seen[col] == false && matrix[row][col] == 1) {\n heights.add(new Pair(1, col));\n }\n }\n \n for (int i = 0; i < heights.size(); i++) {\n ans = Math.max(ans, heights.get(i).getKey() * (i + 1));\n }\n\n prevHeights = heights;\n }\n \n return ans;\n }\n}\n\n\n\n\n```\n```python3 []\nclass Solution:\n def largestSubmatrix(self, matrix: List[List[int]]) -> int:\n m = len(matrix)\n n = len(matrix[0])\n prev_heights = []\n ans = 0\n\n for row in range(m):\n heights = []\n seen = [False] * n\n \n for height, col in prev_heights:\n if matrix[row][col] == 1:\n heights.append((height + 1, col))\n seen[col] = True\n\n for col in range(n):\n if seen[col] == False and matrix[row][col] == 1:\n heights.append((1, col))\n \n for i in range(len(heights)):\n ans = max(ans, heights[i][0] * (i + 1))\n \n prev_heights = heights\n\n return ans\n\n```\n\n```javascript []\nfunction largestSubmatrix(matrix) {\n let m = matrix.length;\n let n = matrix[0].length;\n let prevHeights = new Array(n).fill({ first: 0, second: 0 });\n let ans = 0;\n\n for (let row = 0; row < m; row++) {\n let heights = new Array(n).fill({ first: 0, second: 0 });\n let seen = new Array(n).fill(0);\n\n for (let i = 0; i < n; i++) {\n heights[i].first = prevHeights[i].first;\n heights[i].second = prevHeights[i].second;\n }\n\n for (let col = 0; col < n; col++) {\n if (matrix[row][col] === 1) {\n if (row > 0 && matrix[row - 1][col] === 1) {\n heights[col].first++;\n } else {\n heights[col].first = 1;\n heights[col].second = col;\n }\n seen[col] = 1;\n }\n }\n\n for (let col = 0; col < n; col++) {\n if (seen[col] === 0 && matrix[row][col] === 1) {\n heights[col].first = 1;\n heights[col].second = col;\n }\n }\n\n for (let i = 0; i < n; i++) {\n ans = Math.max(ans, heights[i].first * (i + 1));\n }\n\n prevHeights = heights;\n }\n\n return ans;\n}\n\n```\n\n---\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 2 | 0 | ['Array', 'Greedy', 'C', 'Sorting', 'Matrix', 'C++', 'Java', 'Python3', 'JavaScript'] | 1 |
largest-submatrix-with-rearrangements | One line solution. Runtime 100%!!! | one-line-solution-runtime-100-by-xxxxkav-7cnp | \n\nclass Solution:\n def largestSubmatrix(self, matrix: List[List[int]]) -> int:\n return max(max(map(mul, sorted(row, reverse = True), count(1))) fo | xxxxkav | NORMAL | 2023-11-26T13:56:13.945467+00:00 | 2023-11-26T13:56:13.945501+00:00 | 98 | false | \n```\nclass Solution:\n def largestSubmatrix(self, matrix: List[List[int]]) -> int:\n return max(max(map(mul, sorted(row, reverse = True), count(1))) for row in accumulate(matrix, lambda row_s, row: list(map(lambda s, n: (s+n)*n, row_s, row))))\n```\n> More readable\n```\nclass Solution:\n def largestSubmatrix(self, matrix: List[List[int]]) -> int:\n def prefix_sum(row_s, row):\n return list(map(lambda s, n: (s+n)*n, row_s, row))\n return max(max(map(mul, sorted(row, reverse = True), count(1))) for row in accumulate(matrix, prefix_sum))\n``` | 2 | 0 | ['Python3'] | 0 |
largest-submatrix-with-rearrangements | C# Solution for Largest Submatrix With Rearrangements Problem | c-solution-for-largest-submatrix-with-re-qveu | Intuition\n Describe your first thoughts on how to solve this problem. \nThis solution maintains a count of consecutive 1s vertically in the input matrix and th | Aman_Raj_Sinha | NORMAL | 2023-11-26T11:32:19.495160+00:00 | 2023-11-26T11:32:19.495189+00:00 | 46 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis solution maintains a count of consecutive 1s vertically in the input matrix and then sorts each row to find the maximum area of the submatrix containing only 1s after rearranging the columns optimally.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1.\tIterate through the matrix starting from the second row.\n2.\tFor each cell containing \u20181\u2019, add the value of the cell above it. This operation accumulates the count of consecutive 1s vertically.\n3.\tSort each row of the matrix.\n4.\tTraverse each row and calculate the maximum area by considering the maximum consecutive 1s in a row, multiplied by its width.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\u2022\tThe iteration through the matrix to update the counts of consecutive 1s vertically takes O(m * n) time.\n\u2022\tSorting each row takes O(n * log n) time, and since it\u2019s performed for each of the \u2018m\u2019 rows, the overall sorting takes O(m * n * log n) time.\n\u2022\tFinding the maximum area by traversing the sorted rows takes O(m * n) time.\nHence, the overall time complexity is O(m * n * log n), dominated by the sorting step.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\u2022\tThe space complexity is O(1) because the operations are performed in place on the input matrix.\n\u2022\tAdditionally, there\u2019s some extra space used for variables and temporary storage, but they don\u2019t significantly impact the overall space complexity.\n\n# Code\n```\npublic class Solution {\n public int LargestSubmatrix(int[][] matrix) {\n int m = matrix.Length;\n int n = matrix[0].Length;\n\n // Update the matrix to maintain the count of consecutive 1s vertically\n for (int i = 1; i < m; i++) {\n for (int j = 0; j < n; j++) {\n if (matrix[i][j] == 1) {\n matrix[i][j] += matrix[i - 1][j];\n }\n }\n }\n\n // Sort each row to find the maximum area\n int maxArea = 0;\n for (int i = 0; i < m; i++) {\n Array.Sort(matrix[i]);\n for (int j = n - 1; j >= 0; j--) {\n maxArea = Math.Max(maxArea, matrix[i][j] * (n - j));\n }\n }\n\n return maxArea;\n }\n}\n``` | 2 | 0 | ['C#'] | 0 |
largest-submatrix-with-rearrangements | C++ | Simple Code | Beats 85.23% of users with C++ | c-simple-code-beats-8523-of-users-with-c-hw63 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Ankita2905 | NORMAL | 2023-11-26T11:11:14.344781+00:00 | 2023-11-26T11:11:14.344808+00:00 | 26 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int largestSubmatrix(vector<vector<int>>& matrix) {\n int m=matrix.size(), n=matrix[0].size();\n int area=count(matrix[0].begin(), matrix[0].end(), 1);\n for(int i=1; i<m; i++){\n #pragma unroll\n for(int j=0; j<n; j++){\n if (matrix[i][j]!=0)\n matrix[i][j]+=matrix[i-1][j];\n }\n auto row=matrix[i];\n sort(row.begin(), row.end());\n #pragma unroll\n for(int i=0; i<n; i++)\n area=max(area, row[i]*(n-1-i+1));\n }\n return area;\n }\n};\nauto init = []()\n{ \n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n``` | 2 | 0 | ['C++'] | 0 |
largest-submatrix-with-rearrangements | Easy C++ || O(m*n) solution | easy-c-omn-solution-by-jpank1983-b1vk | Intuition\n Describe your first thoughts on how to solve this problem. \nThis is similar problem to Largest Rectangle in Histogram. We just need to find height | jPank1983 | NORMAL | 2023-11-26T10:59:16.385405+00:00 | 2023-11-26T16:00:44.627777+00:00 | 25 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis is similar problem to Largest Rectangle in Histogram. We just need to find height of every column through every row taking every row as base.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe hight of every column in $$0th$$ row is same as given. Iterating through row 1 to m-1 if at matrix[row][column] is not zero then the height of the column is just 1 + height of same column at $$row - 1$$.\nNow after counting every height we can move on finding the maximum area. We iterate through $$row$$ m - 1 to 0 and sorting every row in descending order therefore the area can be found by just doing $$area$$ = (matrix[row][column] * (column+1)). The max Area is area is stored in $$maxArea$$ and it can be found out by taking maximum of $$maxArea$$ and $$area$$\n# Complexity\n- Time complexity: $$O(m*n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int largestSubmatrix(vector<vector<int>>& matrix) {\n int m = matrix.size();\n int n = matrix[0].size();\n\n for(int i = 1; i < m; i++){\n for(int j = 0; j < n; j++){\n if(matrix[i][j] != 0){\n matrix[i][j] = matrix[i-1][j] + 1;\n }\n else{\n matrix[i][j] = 0;\n }\n }\n }\n int maxArea = 0;\n for(int i = m-1; i >= 0; i--){\n sort(matrix[i].begin(), matrix[i].end(), greater<int>());\n int area = 0;\n for(int j = 0; j < n; j++){\n area = (matrix[i][j] * (j+1));\n maxArea = max(maxArea, area);\n }\n }\n\n return maxArea;\n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
largest-submatrix-with-rearrangements | Beats 95% simple prefix sum like solution | beats-95-simple-prefix-sum-like-solution-l9k3 | Intuition\n Describe your first thoughts on how to solve this problem. \ncount the continuous ones on each column for each row and sort them in descending order | rk_ninjaa__404 | NORMAL | 2023-11-26T10:28:17.733239+00:00 | 2023-11-26T10:28:17.733256+00:00 | 259 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\ncount the continuous ones on each column for each row and sort them in descending order so that the first column contains the most number of continuous ones. Sorting so that we can align the ones continuously to make it a submatrix. \n\n**this line may confuse you: ans=max(ans,temp[j]*(j+1)); use a note and pen to make it clear**\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nFor each row find the number of continuos ones by adding the previous rows ones , then sort them so that the ones are aligned continuously\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(M*N*log(N))\n M->number of rows\n N->number of columns \n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(M*N)\n# Code\n```\nclass Solution {\npublic:\n int largestSubmatrix(vector<vector<int>>& mat) {\n ios::sync_with_stdio(0);cout.tie(0);cin.tie(0);\n int r=mat.size(),c=mat[0].size();\n int ans=0;\n for(int i=0;i<r;i++){\n for(int j=0;j<c;j++){\n if(mat[i][j]!=0 and i!=0)\n mat[i][j]+=mat[i-1][j];\n }\n vector<int>temp=mat[i];\n sort(temp.begin(),temp.end(),greater());\n for(int j=0;j<c;j++){\n ans=max(ans,temp[j]*(j+1));\n }\n }\n return ans;\n }\n};\n``` | 2 | 0 | ['Greedy', 'Sorting', 'Prefix Sum', 'C++'] | 2 |
largest-submatrix-with-rearrangements | Java Beginner Friendly Code | java-beginner-friendly-code-by-ritikranj-dx2g | Explanation\n Describe your first thoughts on how to solve this problem. \nStep 1: Preprocessing (as given is Hint 1)\nStep 2: Sorting Rows (as given in Hint 2) | ritikranjan12 | NORMAL | 2023-11-26T09:16:00.444249+00:00 | 2023-11-26T09:16:00.444272+00:00 | 156 | false | # Explanation\n<!-- Describe your first thoughts on how to solve this problem. -->\nStep 1: Preprocessing (as given is Hint 1)\nStep 2: Sorting Rows (as given in Hint 2)\nStep 3: Calculate Area\nIterate through each row and calculate the area for each cell.\n\n# Complexity\n- Time complexity: O(matrix.length * matrix[0].length * log(matrix[0].length))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int largestSubmatrix(int[][] matrix) {\n // Preprocessing each column to find the number of consecutive ones\n for(int i=1;i<matrix.length;i++){\n for(int j=0;j<matrix[0].length;j++){\n if(matrix[i][j] == 1) {\n matrix[i][j] = matrix[i-1][j] + 1;\n }\n }\n }\n // System.out.println(Arrays.toString(matrix));\n int maxArea = 0;\n // Now performing operations on each row to find the answer\n for(int[] arr : matrix){\n // Sort the current row\n Arrays.sort(arr);\n int k=1;\n // Find the area\n for(int i=arr.length-1;i>=0;i--){\n // Exclude the area where 0 is present\n if(arr[i] != 0) {\n maxArea = Math.max(maxArea, (arr[i] * k));\n k++;\n }\n }\n }\n return maxArea;\n }\n}\n``` | 2 | 0 | ['Array', 'Math', 'Sorting', 'Java'] | 1 |
largest-submatrix-with-rearrangements | [C] Sorting | c-sorting-by-leetcodebug-653t | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | leetcodebug | NORMAL | 2023-11-26T05:30:14.013214+00:00 | 2023-11-26T05:30:14.014825+00:00 | 101 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(m * nlogn)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(m * n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/*\n * 1727. Largest Submatrix With Rearrangements\n *\n * You are given a binary matrix matrix of size m x n, and \n * you are allowed to rearrange the columns of the matrix in \n * any order.\n * \n * Return the area of the largest submatrix within matrix where \n * every element of the submatrix is 1 after reordering the columns \n * optimally.\n *\n * m == matrix.length\n * n == matrix[i].length\n * 1 <= m * n <= 10^5\n * matrix[i][j] is either 0 or 1.\n */\n\n#define MAX(a, b) ((a) > (b) ? (a) : (b))\n#define MIN(a, b) ((a) < (b) ? (a) : (b))\n\nint cmp(const void *a, const void *b)\n{\n return *((int *)b) - *((int *)a);\n}\n\nint largestSubmatrix(int** matrix, int matrixSize, int* matrixColSize) {\n\n /*\n * Input:\n * **matrix\n * matrixSize\n * *matrixColSize\n */\n\n int **ones = (int **)malloc(sizeof(int *) * matrixSize), ans = 0;\n\n for (int i = 0; i < matrixSize; i++) {\n ones[i] = (int *)malloc(sizeof(int) * matrixColSize[i]);\n }\n\n for (int i = 0; i < matrixColSize[0]; i++) {\n\n /* Find number of consecutive ones ending at each position */\n for (int j = matrixSize - 1, cnt = 0; j >=0; j--) {\n if (matrix[j][i] == 1) {\n cnt++;\n }\n else {\n cnt = 0;\n }\n\n ones[j][i] = cnt;\n }\n }\n\n for (int i = 0; i < matrixSize; i++) {\n\n /* Sort by consecutive ones value in descending order */\n qsort(ones[i], matrixColSize[i], sizeof(int), cmp);\n\n /* Compare the height and area */\n for (int j = 0, height = INT_MAX; j < matrixColSize[i]; j++) {\n height = MIN(height, ones[i][j]);\n ans = MAX(ans, height * (j + 1));\n }\n\n free(ones[i]);\n }\n\n free(ones);\n\n /*\n * Output:\n * Return the area of the largest submatrix within matrix where \n * every element of the submatrix is 1 after reordering the columns \n * optimally.\n */\n\n return ans;\n}\n``` | 2 | 0 | ['Array', 'Greedy', 'C', 'Sorting', 'Matrix'] | 1 |
largest-submatrix-with-rearrangements | Python3 Solution | python3-solution-by-motaharozzaman1996-63xv | \n\nclass Solution:\n def largestSubmatrix(self, matrix: List[List[int]]) -> int:\n row=len(matrix)\n col=len(matrix[0])\n ans=0\n | Motaharozzaman1996 | NORMAL | 2023-11-26T03:00:50.325226+00:00 | 2023-11-26T03:00:50.325247+00:00 | 904 | false | \n```\nclass Solution:\n def largestSubmatrix(self, matrix: List[List[int]]) -> int:\n row=len(matrix)\n col=len(matrix[0])\n ans=0\n for r in range(1,row):\n for c in range(col):\n matrix[r][c]+=matrix[r-1][c] if matrix[r][c] else 0\n\n for r in range(row):\n matrix[r].sort(reverse=True)\n for c in range(col):\n ans=max(ans,(c+1)*matrix[r][c])\n return ans \n``` | 2 | 0 | ['Python', 'Python3'] | 0 |
largest-submatrix-with-rearrangements | ✅ Swift: Easy to Understand and Simple Solution | swift-easy-to-understand-and-simple-solu-o52v | Complexity\n- Time complexity: O(mn.log.n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(n)\n Add your space complexity here, e.g. O(n) \ | sohagkumarbiswas | NORMAL | 2023-11-26T02:58:08.454603+00:00 | 2023-11-26T02:58:08.454620+00:00 | 26 | false | # Complexity\n- Time complexity: $$O(mn.log.n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n func largestSubmatrix(_ matrix: [[Int]]) -> Int {\n var ans = 0\n var hist = Array(repeating: 0, count: matrix[0].count)\n \n for row in matrix {\n for i in 0..<row.count {\n hist[i] = row[i] == 0 ? 0 : hist[i] + 1\n }\n \n let sortedHist = hist.sorted()\n \n for i in 0..<sortedHist.count {\n let h = sortedHist[i]\n ans = max(ans, h * (row.count - i))\n }\n }\n \n return ans\n }\n}\n``` | 2 | 0 | ['Array', 'Greedy', 'Swift', 'Sorting', 'Matrix'] | 0 |
largest-submatrix-with-rearrangements | O(m*n*log(n)) Solution || | omnlogn-solution-by-yashmenaria-asju | Complexity\n- Time complexity:O(mnlog(n))\n Add your time complexity here, e.g. O(n) \n\n- Space complexity:O(1)\n Add your space complexity here, e.g. O(n) \n# | yashmenaria | NORMAL | 2023-11-26T02:55:51.379392+00:00 | 2023-11-26T02:55:51.379411+00:00 | 16 | false | # Complexity\n- Time complexity:O(m*n*log(n))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n# Code\n# C++\n```\nclass Solution {\npublic:\n int largestSubmatrix(vector<vector<int>>& matrix) {\n for (int i = 0; i < matrix[0].size(); i++){\n for (int j = 1; j < matrix.size(); j++) \n if (matrix[j][i]) matrix[j][i] += matrix[j - 1][i];\n\t\t}\n int ans = 0;\n for (auto& v : matrix){\n sort(v.begin(), v.end(), greater <>()); \n for (int i = 0; i < v.size(); i++) \n ans = max(ans, v[i] * (i + 1));\n\t\t}\n return ans;\n }\n};\n```\n# Java\n```\nclass Solution {\n public int largestSubmatrix(int[][] matrix) {\n for(int i = 0; i < matrix[0].length; i++){\n\t\t\tfor(int j = 1; j < matrix.length; j++)\n\t\t\t if(matrix[j][i] != 0) matrix[j][i] += matrix[j - 1][i];\n\t\t}\n \n\t\tint ans = 0;\n\t\tfor(int [] v : matrix){\n\t\t\tArrays.sort(v); \n\t\t\tint left = 0, right = v.length - 1;\n while (left < right) {\n int temp = v[left];\n v[left] = v[right];\n v[right] = temp;\n left++;\n right--;\n }\n\t\t\tfor(int i = 0; i < v.length; i++)\n\t\t\t ans = Math.max(ans, v[i] * (i + 1));\n\t\t}\n\t\treturn ans;\n }\n}\n``` | 2 | 0 | ['Array', 'Greedy', 'Sorting', 'Matrix', 'C++', 'Java'] | 0 |
largest-submatrix-with-rearrangements | C# || Solution with LINQ | c-solution-with-linq-by-vdmhunter-k3a3 | Code\n\npublic class Solution\n{\n public int LargestSubmatrix(int[][] matrix)\n {\n for (var i = 1; i < matrix.Length; i++)\n for (var | vdmhunter | NORMAL | 2023-11-26T00:15:51.511349+00:00 | 2023-11-26T00:15:51.511375+00:00 | 83 | false | # Code\n```\npublic class Solution\n{\n public int LargestSubmatrix(int[][] matrix)\n {\n for (var i = 1; i < matrix.Length; i++)\n for (var j = 0; j < matrix[0].Length; j++)\n if (matrix[i][j] == 1)\n matrix[i][j] = matrix[i - 1][j] + 1;\n\n return matrix.Max(row =>\n {\n Array.Sort(row);\n\n return Enumerable.Range(1, row.Length).Max(j => j * row[^j]);\n });\n }\n}\n\n``` | 2 | 1 | ['C#'] | 0 |
largest-submatrix-with-rearrangements | Simple greedy approach || Not a medium level question probably hard one 🤨 | simple-greedy-approach-not-a-medium-leve-3s21 | \nclass Solution\n{\n public:\n int largestSubmatrix(vector<vector < int>> &mat)\n {\n int m = mat.size();\n int n = mat[ | Tan_B | NORMAL | 2023-04-19T06:34:01.517736+00:00 | 2023-04-19T06:34:01.517779+00:00 | 121 | false | ```\nclass Solution\n{\n public:\n int largestSubmatrix(vector<vector < int>> &mat)\n {\n int m = mat.size();\n int n = mat[0].size();\n vector<int> h(n, 0);//array for counting height at each level.\n vector<int> x;\n int ans = 0;\n for (int i = 0; i < m; i++)//iterating at every level.\n {\n for (int j = 0; j < n; j++)\n {\n if (mat[i][j] == 0)// if cuurent height is 0 then discard the previously stored .height.\n h[j] = 0;\n else\n h[j] += 1;// increment the height if it is continuous.\n }\n x = h;\n sort(x.begin(), x.end(), greater<int> ());//sort and calculate max area.\n int curr = 0;\n int height = INT_MAX;\n for (int j = 0; j < n; j++)\n {\n height = min(height, x[j]);\n curr = max(curr, height *(j + 1));\n }\n ans = max(ans, curr);\n }\n return ans;\n }\n};\n``` | 2 | 0 | ['Math', 'Greedy', 'C', 'Sorting'] | 0 |
largest-submatrix-with-rearrangements | C++ using 2 traversals by Sorting | c-using-2-traversals-by-sorting-by-divya-axhg | \nclass Solution {\npublic:\n int largestSubmatrix(vector<vector<int>>& mat) {\n int m= mat.size();\n int n= mat[0].size();\n for(int i= | divyanshugupta5901 | NORMAL | 2022-07-16T15:18:10.110353+00:00 | 2022-07-16T15:18:10.110396+00:00 | 373 | false | ```\nclass Solution {\npublic:\n int largestSubmatrix(vector<vector<int>>& mat) {\n int m= mat.size();\n int n= mat[0].size();\n for(int i=1; i<m ; i++){\n for(int j=0; j<n; j++){\n if(mat[i][j]!=0)\n mat[i][j]+= mat[i-1][j];\n }\n }\n int ans=0;\n for(int i=0; i<m; i++){\n sort(mat[i].begin(), mat[i].end(), greater<int>());\n for(int j=0; j<n; j++){\n ans= max(ans, mat[i][j]*(j+1));\n }\n }\n return ans;\n }\n};\n``` | 2 | 0 | ['C'] | 0 |
largest-submatrix-with-rearrangements | Java solution with approach | java-solution-with-approach-by-soumya00-ad17 | Approach:\n\n1. Traverse the matrix column wise\n2. For every column, calculate the continuous running sum and update the array itself. If any cell value is 0, | soumya00 | NORMAL | 2022-07-16T04:57:22.723395+00:00 | 2022-07-16T04:57:22.723452+00:00 | 186 | false | **Approach:**\n\n1. Traverse the matrix column wise\n2. For every column, calculate the continuous running sum and update the array itself. If any cell value is 0, reset the continuous sum to 0\n3. Next traverse the matrix row wise, and sort every row in decsending order\n4. Calculate the maximum area greedily and store the maxArea\n\n**Java solution:**\n\n```\nclass Solution {\n public int largestSubmatrix(int[][] matrix) {\n \n int rows = matrix.length, cols = matrix[0].length, maxArea = 0;\n \n for(int j=0, contsum = 0; j<cols; ++j, contsum=0) \n for(int i=0; i<rows; ++i) {\n if(matrix[i][j] == 0) {\n contsum=0;\n continue;\n }\n \n ++contsum;\n matrix[i][j] = contsum;\n }\n \n for(int i=0; i<rows; ++i) {\n \n List<Integer> tempList = new ArrayList<>(cols);\n \n for(int j=0; j<cols; ++j)\n tempList.add(matrix[i][j]);\n \n Collections.sort(tempList, (a, b) -> b-a);\n \n for(int j=0; j<cols; ++j) \n maxArea = Math.max(maxArea, (j+1)*tempList.get(j));\n \n }\n \n return maxArea;\n }\n}\n```\n\n**Time Complexity:** O(rows * columns * log (columns))\n**Space Complexity:** O(columns) for the temporary list for sorting\n\nThank you\n\nDo upvote the solution if you have liked it!\n\n | 2 | 0 | ['Greedy', 'Sorting', 'Simulation'] | 0 |
largest-submatrix-with-rearrangements | ✅✅Faster || Easy To Understand || C++ Code | faster-easy-to-understand-c-code-by-__kr-vkrf | This Problem is like Maximum Rectangle In Histogram\n\n Using Sorting\n\n Time Complexity :- O(N * M * logM)\n\n Space Complexity :- O(M)*\n\n\nclass Solution { | __KR_SHANU_IITG | NORMAL | 2022-07-15T05:59:26.285714+00:00 | 2022-07-15T05:59:26.285778+00:00 | 301 | false | * ***This Problem is like Maximum Rectangle In Histogram***\n\n* ***Using Sorting***\n\n* ***Time Complexity :- O(N * M * logM)***\n\n* ***Space Complexity :- O(M)***\n\n```\nclass Solution {\npublic:\n int largestSubmatrix(vector<vector<int>>& matrix) {\n \n int n = matrix.size();\n \n int m = matrix[0].size();\n \n vector<int> height(m, 0);\n \n int max_area = 0;\n \n for(int i = 0; i < n; i++)\n {\n // update the height array\n \n for(int j = 0; j < m; j++)\n {\n if(matrix[i][j] == 1)\n {\n height[j]++;\n }\n else\n {\n height[j] = 0;\n }\n }\n \n // sort the height array, because we can rearrange the column\n \n vector<int> sorted_height = height;\n \n sort(sorted_height.begin(), sorted_height.end());\n \n // find the max_area\n \n for(int j = 0; j < m; j++)\n {\n int curr_area = sorted_height[j] * (m - j);\n \n max_area = max(max_area, curr_area);\n }\n }\n \n return max_area;\n }\n};\n``` | 2 | 0 | ['C', 'Sorting', 'C++'] | 0 |
largest-submatrix-with-rearrangements | Java | Basic Math + Intuitive | java-basic-math-intuitive-by-dz_adman-83wf | Approach:\nJust use basic math for AreaOfRectangle = height * width\nNow all we need is height and width for each cell while calculating area (that cell being t | dz_adman | NORMAL | 2022-06-27T11:10:47.002769+00:00 | 2022-06-27T11:10:47.002832+00:00 | 169 | false | **Approach**:\nJust use basic math for **AreaOfRectangle = height * width**\nNow all we need is **height and width for each cell while calculating area** (that cell being the bottom right end of the rectangle being considered)\n\nThis can be done in following 2 major steps:\n1. Modify matrix values to keep track of max height for each cell (height increases with continuous sequence of ```1```\'s)\n1.1. Sort row values in non-decreasing order (as columns can be moved)\n\t\t[Here, sorting retains the column values of respective columns i.e. whole columns are moved. (Try dry-run to understand \'how?/why?\')]\n2. Calculate width on the fly while calculating area till each cell (traversing row wise).\n```\nclass Solution {\n public int largestSubmatrix(int[][] matrix) {\n // modify matrix values in-place to keep track of max heights\n\t\tfor(int i = 1; i < matrix.length; ++i)\n\t\t\tfor(int j = 0; j < matrix[i].length; ++j)\n\t\t\t\tif(matrix[i][j] != 0) matrix[i][j] += matrix[i - 1][j];\n \n\t\tint maxArea = 0;\n\t\tfor(int i = 0; i < matrix.length; ++i) {\n\t\t\t// sort rows in non-decreasing order \n\t\t\tArrays.sort(matrix[i]);\n\t\t\tfor(int j = 0; j < matrix[i].length; ++j)\n\t\t\t\t// height = matrix[i][j]; width = matrix[i] - j\n\t\t\t\t// areaOfRectangle = height * width\n\t\t\t\tmaxArea = Math.max(maxArea, matrix[i][j] * (matrix[i].length - j));\n\t\t}\n\t\treturn maxArea;\n }\n}\n``` | 2 | 0 | ['Math'] | 0 |
largest-submatrix-with-rearrangements | Python O(MN log N) with comments | python-omn-log-n-with-comments-by-vsavki-ais3 | \nfrom collections import Counter\n\nclass Solution:\n def largestSubmatrix(self, matrix: List[List[int]]) -> int:\n M = len(matrix)\n N = len( | vsavkin | NORMAL | 2021-06-06T11:37:43.750437+00:00 | 2021-06-06T11:37:43.750483+00:00 | 290 | false | ```\nfrom collections import Counter\n\nclass Solution:\n def largestSubmatrix(self, matrix: List[List[int]]) -> int:\n M = len(matrix)\n N = len(matrix[0])\n \n colcons = [] # preprocess columns\n for c in range(N):\n cons = []\n s = 0\n for r in range(M):\n if not matrix[r][c]:\n s = 0\n else:\n s += 1\n cons.append(s)\n colcons.append(cons)\n # colcons[c][r] is how much 1\'s we\'ll get if we start from column c at row r and go up\n \n best = 0\n for r in range(M):\n # try r as the lowest row\n C = Counter(colcons[c][r] for c in range(N))\n vs = sorted(C.keys(), reverse=True)\n cs = accumulate(C[v] for v in vs)\n for v,c in zip(vs,cs):\n best = max(best,v*c)\n return best\n``` | 2 | 0 | ['Sorting', 'Python'] | 0 |
largest-submatrix-with-rearrangements | SIMPLE SOLUTION 6MS FASTER THAN 100% | simple-solution-6ms-faster-than-100-by-s-n4us | JAVA CODE IS:\n# \n\nclass Solution {\n int find(int arr[]){\n Arrays.sort(arr);\n int res=0;\n for(int i=0;i<arr.length;i++)\n | shivam_gupta_ | NORMAL | 2021-03-18T06:51:03.900907+00:00 | 2021-03-18T06:51:03.900938+00:00 | 143 | false | JAVA CODE IS:\n# \n```\nclass Solution {\n int find(int arr[]){\n Arrays.sort(arr);\n int res=0;\n for(int i=0;i<arr.length;i++)\n res=Math.max(res,arr[i]*(arr.length-i));\n return res;\n }\n public int largestSubmatrix(int[][] matrix) {\n //size of matrix is n*m\n int n=matrix.length;\n if(n==0) return 0;\n int m=matrix[0].length;\n for(int j=0;j<m;j++){\n for(int i=1;i<n;i++)\n matrix[i][j]=matrix[i][j]==0 ? 0 : 1+matrix[i-1][j];\n }\n int res=0;\n for(int arr[] : matrix){\n res=Math.max(res,find(arr));\n }\n return res;\n }\n}\n```\n***PLEASE,UPVOTE IF THIS IS HELPFUL*** | 2 | 0 | [] | 1 |
largest-submatrix-with-rearrangements | [Python] prefix sum, sort rows, compute areas - O(m*nlogn) runtime - with explanation | python-prefix-sum-sort-rows-compute-area-ugi4 | \nApproach: O(m\*nlogn) runtime O(1) space - 1116ms (97.79%), 40.7MB (47.17%)\nCompute prefix from top to bottom. Reset everytime we reach a 0.\nNow go to each | vikktour | NORMAL | 2021-01-23T17:41:24.036855+00:00 | 2024-09-27T23:03:53.442573+00:00 | 444 | false | \nApproach: O(m\\*nlogn) runtime O(1) space - 1116ms (97.79%), 40.7MB (47.17%)\nCompute prefix from top to bottom. Reset everytime we reach a 0.\nNow go to each row and compute area for each value (starting from right to left). For each value, we will use all values to the right of it (including itself) to compute area.\nSo basically we are getting the area for each given value in the row.\nDiagram example: https://drive.google.com/file/d/1W0LWFdMwXqstlwySBERkJ_I11QWIq-0V/view?usp=sharing\nNote that the sorting of the previous row would not ruin the answer obtained from calculating area in the next row because we\'re using prefix sum.\n```\nfrom typing import List\nimport numpy as np #for printing\nclass Solution:\n def largestSubmatrix(self, matrix: List[List[int]]) -> int:\n \n m = len(matrix)\n n = len(matrix[0])\n\n #get prefix sum of rows (reset upon hitting 0)\n for j in range(n):\n for i in range(m):\n #for each column iterate down the rows and calculate prefix sum\n if i > 0:\n if matrix[i][j] != 0:\n #0 means reset\n matrix[i][j] += matrix[i-1][j]\n \n #print(np.array(matrix))\n\n #iterate through each row, sort, and compute max area\n maxArea = 0\n for row in matrix:\n row.sort()\n #iterate from right to left and compute area for each set of number\n index = len(row) - 1\n while index >= 0:\n #get value\n value = row[index]\n #keep going left if it\'s still the same value\n while index-1 >= 0 and row[index-1] == value:\n index -= 1\n #compute area (we multiply value by the number of items to the right including itself)\n area = value * (len(row)-index)\n if area > maxArea:\n maxArea = area\n index -= 1\n return maxArea\n``` | 2 | 0 | ['Sorting', 'Prefix Sum', 'Python', 'Python3'] | 1 |
largest-submatrix-with-rearrangements | Java Solution | O(m * n * logn) time complexity | java-solution-om-n-logn-time-complexity-glk55 | \nclass Solution {\n public int largestSubmatrix(int[][] matrix) {\n \n int m = matrix.length;\n int n = matrix[0].length;\n \n | vishal_sherawat | NORMAL | 2021-01-21T08:08:08.959956+00:00 | 2023-11-26T07:02:40.747236+00:00 | 337 | false | ```\nclass Solution {\n public int largestSubmatrix(int[][] matrix) {\n \n int m = matrix.length;\n int n = matrix[0].length;\n \n for(int i = 1; i < m; i++){\n \n for(int j = 0; j < n; j++){\n \n if(matrix[i][j] == 1){\n matrix[i][j] = matrix[i - 1][j] + 1;\n }\n }\n }\n \n int res = 0;\n \n for(int i = 0; i < m; i++){\n \n Arrays.sort(matrix[i]);\n \n for(int j = 0; j < n; j++){\n \n res = Math.max(res, matrix[i][j] * (n - j));\n }\n }\n \n return res;\n }\n}\n``` | 2 | 0 | ['Java'] | 0 |
largest-submatrix-with-rearrangements | O(n^2log(n)) 100% better time complexity[C++} | on2logn-100-better-time-complexityc-by-a-tcy3 | Detail Description Is In Code Itself\nIf You like My Code Then Please Upvot\n\nclass Solution {\npublic:\n int largestSubmatrix(vector<vector<int>>& matrix) | anil111 | NORMAL | 2021-01-18T04:46:23.777348+00:00 | 2021-01-18T04:54:08.598538+00:00 | 81 | false | **Detail Description Is In Code Itself**\nIf You like My Code Then Please Upvot\n```\nclass Solution {\npublic:\n int largestSubmatrix(vector<vector<int>>& matrix) \n {\n int row=matrix.size(),col=matrix[0].size();\n int sum[row][col];\n // calculate no of 1\'s continue in the column\n for(int i=0;i<col;i++)\n {\n int h=0;\n for(int j=0;j<row;j++)\n {\n if(matrix[j][i]==0)\n {\n h=0;\n sum[j][i]=0;\n }\n else\n {\n h+=1;\n sum[j][i]=h;\n }\n }\n }\n int ans=0;\n for(int i=0;i<row;i++)\n {\n // sort the arry in row wise\n sort(sum[i],sum[i]+col);\n for(int j=0;j<col;j++)\n {\n ans=max(ans,(col-j)*sum[i][j]);\n //why?\n //because if we think this arry\n //1 1 1 1\n //1 0 1 0\n //0 0 0 0\n //0 0 1 0\n //1 1 1 1\n //1 1 1 1\n //0 0 0 0\n //0 1 0 1\n //then after counting no of continue\'s 1\'s in the arry \n /*1 1 1 1\n 2 0 2 0\n 0 0 0 0\n 0 0 1 0\n 1 1 2 1\n 2 2 3 2\n 0 0 0 0\n 0 1 0 1\n and after sorting arry in row wise we get this arry\n 1 1 1 1\n 0 0 2 2\n 0 0 0 0\n 0 0 0 1\n 1 1 1 2\n 2 2 2 3\n 0 0 0 0\n 0 0 1 1\n now from doing this \n if we think for first row and first element then we ansure\n that after [0,0] we get gretaer then or equal 1 element\n so we multiply 1 with (4-0) and we get 4 as local max element\n now if we think about 5\'th row(0 based) then in first element we \n got 2 and now from 2 we can think that after [5,0] element other element are \n grater then or equal to 2 so definetly after [5,0] we have more 1\'s(means greter then 2) so directly\n multiply 2 with 4 and get ans as 8\n */\n \n }\n \n }\n return ans;\n \n }\n};\n``` | 2 | 0 | [] | 0 |
largest-submatrix-with-rearrangements | [Python] Clear Solution with Video Explanation | python-clear-solution-with-video-explana-wu53 | Video with clear visualization and explanation:\nhttps://youtu.be/-YVsiCrbeRE\n\n\n\nIntuition: Largest rectangle in histogram with reversed sort\n\n\nCode\n\nc | iverson52000 | NORMAL | 2021-01-17T22:30:15.723926+00:00 | 2021-01-17T22:30:15.723955+00:00 | 237 | false | Video with clear visualization and explanation:\nhttps://youtu.be/-YVsiCrbeRE\n\n\n\nIntuition: Largest rectangle in histogram with reversed sort\n\n\n**Code**\n```\nclass Solution:\n def largestSubmatrix(self, matrix: List[List[int]]) -> int:\n n_r, n_c, res = len(matrix), len(matrix[0]), 0\n\n for r in range(1, n_r):\n for c in range(n_c):\n matrix[r][c] += matrix[r-1][c] if matrix[r][c] else 0\n\n for r in range(n_r): \n matrix[r].sort(reverse = True)\n for c in range(n_c):\n res = max(res, (c+1)*matrix[r][c])\n \n return res\n```\n\n\nTime: O(m*n *logn) / Space: O(1)\n\n\nFeel free to subscribe to my channel. More LeetCoding videos coming up! | 2 | 0 | ['Python'] | 0 |
largest-submatrix-with-rearrangements | C++|| Implementation || DP used | c-implementation-dp-used-by-wargraver-cj0a | \nclass Solution {\npublic:\n int largestSubmatrix(vector<vector<int>>& matrix) {\n int i,j,k,n,m,ct=0,ans=0;\n n=matrix.size();m=matrix[0].siz | wargraver | NORMAL | 2021-01-17T05:34:02.737627+00:00 | 2021-01-17T05:34:02.737683+00:00 | 66 | false | ```\nclass Solution {\npublic:\n int largestSubmatrix(vector<vector<int>>& matrix) {\n int i,j,k,n,m,ct=0,ans=0;\n n=matrix.size();m=matrix[0].size();\n int dp[n+5][m+5];\n for(j=0;j<m;j++){\n int flag=0,ct=0;\n for(i=n-1;i>=0;i--){\n if(matrix[i][j]==0) {\n dp[i][j]=0;\n ct=0;\n flag=0;\n }\n else{\n ct++;\n dp[i][j]=ct;\n flag=1;\n }\n }\n }\n for(i=0;i<n;i++){\n multiset<int> dict;\n for(j=0;j<m;j++) dict.insert(dp[i][j]);\n auto it=dict.end();\n it--;int flag=1;ct=0;int val=1e9;\n while(flag==1){\n ct++;\n val=*it;\n ans=max(ans,ct*val);\n if(it==dict.begin()) flag=0;\n else it--;\n }\n }\n return ans;\n }\n};\n``` | 2 | 0 | [] | 0 |
largest-submatrix-with-rearrangements | SIMPLE SORT, beats 100% easy sorting solution | simple-sort-beats-100-easy-sorting-solut-qabw | `\nclass Solution {\npublic:\n int maxArea(vector<vector<int>> mat,int R,int C) \n{ \n \n vector<vector<int>> hist(R,vector<int> (C,0));\n \n for (i | rdas18246 | NORMAL | 2021-01-17T04:32:07.999880+00:00 | 2021-01-17T04:32:07.999917+00:00 | 61 | false | ````\nclass Solution {\npublic:\n int maxArea(vector<vector<int>> mat,int R,int C) \n{ \n \n vector<vector<int>> hist(R,vector<int> (C,0));\n \n for (int i = 0; i < C; i++) { \n \n hist[0][i] = mat[0][i]; \n \n \n for (int j = 1; j < R; j++) \n hist[j][i] = (mat[j][i] == 0) ? 0 : hist[j - 1][i] + 1; \n } \n \n for(int i=0;i<R;i++)\n {\n sort(hist[i].rbegin(),hist[i].rend());\n }\n \n\n \n\n int curr_area, max_area = 0; \n for (int i = 0; i < R; i++) { \n for (int j = 0; j < C; j++) { \n \n curr_area = (j + 1) * hist[i][j]; \n if (curr_area > max_area) \n max_area = curr_area; \n } \n } \n return max_area; \n} \n int largestSubmatrix(vector<vector<int>>& matrix) {\n int n=matrix.size();\n int m=matrix[0].size();\n \n return maxArea(matrix,n,m);\n \n \n \n }\n};\n``` | 2 | 0 | [] | 0 |
largest-submatrix-with-rearrangements | [Python] scanning row strategy | python-scanning-row-strategy-by-21eleven-6kb8 | Make a scanning row (r) that you will compare with each row in the matrix. This scanning row tracks the "streak" for each column (how many previous rows had the | 21eleven | NORMAL | 2021-01-17T04:26:54.849160+00:00 | 2021-01-17T15:50:30.484596+00:00 | 148 | false | Make a scanning row (`r`) that you will compare with each row in the matrix. This scanning row tracks the "streak" for each column (how many previous rows had the bit set in that column). If a row does has a zero for a column the scanning row at that column position gets reset to zero, otherwise the streak count at that column on the scanning row is incremented. \n\nAfter the scanning row is compared with a row, a copy of the scanning row is made and sorted so large values come first (this is equvialent to reordering the columns). Then the value at each row is multiplied by its index plus one. This operation sizes the submatrix and we greedily store the submatrix with the largest size.\n\n```\nclass Solution:\n def largestSubmatrix(self, matrix: List[List[int]]) -> int:\n cols = len(matrix[0])\n r = [0]*cols # scanning row\n big = 0\n for row in matrix:\n for c in range(cols):\n if 0 == row[c]:\n r[c] = 0\n else:\n r[c] += 1\n count = sorted(r, reverse=True)\n for idx, v in enumerate(count): # v = streak size aka height of submatrix, idx+1 = width of submatrix\n big = max((idx+1)*v, big)\n return big\n``` | 2 | 0 | [] | 1 |
largest-submatrix-with-rearrangements | Vertical Profiling with const input | vertical-profiling-with-const-input-by-m-unhm | Still a O(RC) but will less operations than required if modifying the matrix.Code | michelusa | NORMAL | 2025-03-21T00:09:21.042536+00:00 | 2025-03-21T00:09:21.042536+00:00 | 4 | false |
Still a O(RC) but will less operations than required if modifying the matrix.
# Code
```cpp []
class Solution {
public:
int largestSubmatrix(const std::vector<std::vector<int>>& matrix) {
const size_t R = matrix.size();
const size_t C = matrix[0].size();
int max_area = 0;
std::vector<int> heights(C, 0);
std::vector<int> sorted_height;
sorted_height.reserve(C);
for (size_t r = 0; r < R; ++r) {
for (size_t c = 0; c < C; ++c) {
if (matrix[r][c]) {
++heights[c];
} else {
// Reset cumulative count.
heights[c] = 0;
}
}
sorted_height = heights;
std::sort(sorted_height.begin(), sorted_height.end(), std::greater<int>());
for (size_t c = 0; c < C; ++c) {
if (sorted_height[c]) {
const int area = (c + 1) * sorted_height[c];
max_area = std::max(max_area, area);
} else {
break;
}
}
}
return max_area;
}
};
``` | 1 | 0 | ['C++'] | 0 |
largest-submatrix-with-rearrangements | Best Solution | C++ | best-solution-c-by-nssvaishnavi-pyq1 | IntuitionTo solve this problem optimally, we need to make the best use of the column rearrangement to maximize the area of a submatrix consisting entirely of 1s | nssvaishnavi | NORMAL | 2025-02-06T18:10:23.611413+00:00 | 2025-02-06T18:10:23.611413+00:00 | 21 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
To solve this problem optimally, we need to make the best use of the column rearrangement to maximize the area of a submatrix consisting entirely of 1s
# Approach
<!-- Describe your approach to solving the problem. -->
We can treat each row of the matrix as a histogram of heights, where each element represents the number of consecutive 1s in the matrix up to that row. The idea is to calculate the maximum area of 1s you can get from the histogram by sorting the heights in non-decreasing order.
Step 1: Calculate Heights: Convert each row into a histogram of heights. For each column in the matrix, calculate the consecutive number of 1s from the current row upwards. If the element is 0, reset the height to 0.
Step 2: Sort Heights: After calculating the histogram of heights for each row, sort the heights in descending order for the maximum area calculation. Sorting ensures that we can maximize the rectangle area by using the largest heights first.
Step 3: Calculate Maximum Area: For each row, after sorting the heights, compute the area by multiplying the height by its column index (since the heights are sorted). Track the maximum area found.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
Height computation:
O(m×n), as we iterate through every element once.
Sorting each row:
O(nlogn), as we sort each row individually.
Total:
O(m×nlogn).
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(m×n)
# Code
```cpp []
#include <vector>
#include <algorithm>
class Solution {
public:
int largestSubmatrix(std::vector<std::vector<int>>& matrix) {
int m = matrix.size(), n = matrix[0].size();
// Convert matrix to height representation
for (int i = 1; i < m; ++i) {
for (int j = 0; j < n; ++j) {
if (matrix[i][j] == 1) {
matrix[i][j] += matrix[i - 1][j]; // Accumulate heights
}
}
}
int maxArea = 0;
// Process each row independently
for (int i = 0; i < m; ++i) {
// Sort the row in descending order
std::vector<int> heights = matrix[i];
std::sort(heights.rbegin(), heights.rend()); // Sort in decreasing order
// Compute max area using sorted heights
for (int j = 0; j < n; ++j) {
maxArea = std::max(maxArea, heights[j] * (j + 1));
}
}
return maxArea;
}
};
``` | 1 | 0 | ['C++'] | 0 |
largest-submatrix-with-rearrangements | In-place solutions, Beats >90% | in-place-solutions-beats-90-by-simolekc-sszb | Code | simolekc | NORMAL | 2025-01-28T12:28:26.513215+00:00 | 2025-01-28T12:28:26.513215+00:00 | 6 | false |
# Code
```javascript []
/**
* @param {number[][]} matrix
* @return {number}
*/
var largestSubmatrix = function (matrix) {
let n = matrix.length;
let m = matrix[0].length;
for (let i = 1; i < n; i++) {
for (let j = 0; j < m; j++) {
if (matrix[i][j]) matrix[i][j] += matrix[i - 1][j];
}
}
let maxArea = 0;
for (let i = 0; i < n; i++) {
matrix[i].sort((a, b) => b - a);
for (let j = 0; j < m; j++) {
maxArea = Math.max(maxArea, matrix[i][j] * (j + 1));
}
}
return maxArea;
};
``` | 1 | 0 | ['JavaScript'] | 0 |
largest-submatrix-with-rearrangements | Brute force solution | brute-force-solution-by-execrox-08cu | Code\n\nclass Solution:\n def largestSubmatrix(self, matrix: List[List[int]]) -> int:\n m, n, ans = len(matrix), len(matrix[0]), 0\n \n | execrox | NORMAL | 2024-04-26T19:10:16.666172+00:00 | 2024-04-26T19:10:57.843303+00:00 | 4 | false | # Code\n```\nclass Solution:\n def largestSubmatrix(self, matrix: List[List[int]]) -> int:\n m, n, ans = len(matrix), len(matrix[0]), 0\n \n for j in range(n):\n for i in range(1, m):\n matrix[i][j] += matrix[i-1][j] if matrix[i][j] else 0\n \n for i in range(m): \n matrix[i].sort(reverse=1)\n for j in range(n):\n ans = max(ans, (j + 1) * matrix[i][j])\n\n return ans\n```\n# Complexity\n- Time complexity: $$O(n^2m^2)$$\n- Space complexity: $$O(1)$$\n | 1 | 0 | ['Matrix', 'Python3'] | 1 |
largest-submatrix-with-rearrangements | Easyest way to Largest Submatrix With Rearrangements. | easyest-way-to-largest-submatrix-with-re-7bkb | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | saslo0165 | NORMAL | 2023-11-27T13:42:13.188207+00:00 | 2023-11-27T13:42:13.188243+00:00 | 21 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n int customMax(int a, int b) => a > b ? a : b;\n\n int largestSubmatrix(List<List<int>> matrix) {\n int m = matrix.length;\n int n = matrix[0].length;\n\n for (int i = 1; i < m; i++) {\n for (int j = 0; j < n; j++) {\n if (matrix[i][j] == 1) {\n matrix[i][j] += matrix[i - 1][j];\n }\n }\n }\n\n for (List<int> row in matrix) {\n row.sort((a, b) => b - a);\n }\n\n int maxArea = 0;\n for (List<int> row in matrix) {\n for (int j = 0; j < n; j++) {\n maxArea = customMax(maxArea, row[j] * (j + 1));\n }\n }\n\n return maxArea;\n }\n}\n\n``` | 1 | 0 | ['Dart'] | 0 |
largest-submatrix-with-rearrangements | [JS] DP (w/Explanation) | Beats 90.91% & 72.73% | js-dp-wexplanation-beats-9091-7273-by-ja-hxuh | Intuition\nUpon encountering this problem, the first idea is to maximize the area of 1s in a binary matrix by rearranging the columns. A key realization is that | jamesBaxtuh | NORMAL | 2023-11-26T22:30:30.563077+00:00 | 2023-11-28T00:59:25.049087+00:00 | 5 | false | # Intuition\nUpon encountering this problem, the first idea is to maximize the area of 1s in a binary matrix by rearranging the columns. A key realization is that we can count the number of 1s in each column and then sort these counts row by row. This sorting effectively simulates rearranging the columns so that rows with more 1s are aligned together, thereby potentially forming larger rectangles of 1s. The challenge lies in figuring out the best way to calculate the maximum area of the submatrix after this rearrangement.\n\n# Approach\n1.) **Column-wise 1s Counting:** Iterate through the matrix. For each cell that is a 1, add to its value the value of the cell directly above it. This process transforms each cell to represent the height of a \'tower\' of 1s in that column up to the current row, effectively creating a histogram in each row.\n\n**2.) Row-wise Sorting:** Sort the counts in each row in non-increasing order. This step is crucial as it simulates the rearrangement of columns such that those with more 1s are moved to the left, thereby maximizing the potential area of rectangles formed by consecutive 1s.\n\n**3.) Area Calculation:** Iterate over each row. For each cell, calculate the area of the rectangle that could be formed with the cell\'s value as the height. This is done by multiplying the value (height of the rectangle) by the column index plus one (as the width). Keep track of and update the maximum area found.\n\n# Complexity\n- Time complexity: O($$m$$\xD7$$n$$log$$n$$) (Runtime: 119ms, beats 90.91%)\n - Step 1, counting 1s in each column, requires O($$m$$\xD7$$n$$) as it involves a single pass through all elements. \n - Step 2, the sorting step, has a complexity of O($$n$$log$$n$$) for each row, and since there are $$m$$ rows, the total complexity for sorting is O($$m$$\xD7$$n$$log$$\u2061n$$).\n - Step 3, the final area calculation, requires a pass through all elements, adding another O($$m$$\xD7$$n$$), which does not dominate the sorting complexity.\n\n- Space complexity: O(1) (Runtime: 70.2mb, beats 72.73%)\n - The space complexity is O(1) if we disregard the input space, as the transformation is done in-place and no additional significant space is used. If we consider the input space, then the space complexity is O($$m$$\xD7$$n$$), which is the size of the input matrix.\n - Runtime: \n\n# Code\n```\n/**\n * @param {number[][]} matrix\n * @return {number}\n */\n\nfunction largestSubmatrix(matrix) {\n const m = matrix.length, n = matrix[0].length;\n let maxArea = 0;\n\n // Step 1: Count 1s in each column\n for (let i = 1; i < m; i++) {\n for (let j = 0; j < n; j++) {\n if (matrix[i][j] === 1) {\n matrix[i][j] += matrix[i - 1][j];\n }\n }\n }\n\n // Step 2: Sort counts in each row\n for (let i = 0; i < m; i++) {\n matrix[i].sort((a, b) => b - a);\n }\n\n // Step 3: Calculate maximum area\n for (let i = 0; i < m; i++) {\n for (let j = 0; j < n; j++) {\n maxArea = Math.max(maxArea, matrix[i][j] * (j + 1));\n }\n }\n\n return maxArea;\n}\n\n``` | 1 | 0 | ['Dynamic Programming', 'Greedy', 'Sorting', 'Matrix', 'JavaScript'] | 0 |
largest-submatrix-with-rearrangements | Easy Solution - Ashutosh Kumar | easy-solution-ashutosh-kumar-by-ak180920-zq2v | Intuition\nThe basic intuition to solve this question is first see that we can only swap columns. This means the vertical order of the 1s doesn\'t change. \n\n# | ak18092000 | NORMAL | 2023-11-26T20:57:44.076189+00:00 | 2023-11-26T20:57:44.076230+00:00 | 45 | false | # Intuition\nThe basic intuition to solve this question is first see that we can only swap columns. This means the vertical order of the 1s doesn\'t change. \n\n# Approach\nWe calculate the no. of consecutive 1s vertically in each row and update the elements according to that. The count resets to 0 whenever we encounter 0. Now we have calculated various base values which means how much 1s are above the base. And the base can contribute its width i.e 1 * height i.e the base value. Now we will sort the rows in non increasing order. Now start count from 1 and traverse left to right in all the rows.\n\nRequired value => ans = max(ans, count*basevalue)\n# Complexity\n- Time complexity:\nAdd your time complexity here, e.g. $$O(m*n)$$\n\n# Space complexity:\nAdd your space complexity here, e.g. $$O(1)$$\n\n# Code\n```\nclass Solution {\npublic:\n int largestSubmatrix(vector<vector<int>>& arr) {\n int m = arr.size();\n int n = arr[0].size();\n for(int j=0;j<n;j++)\n {\n for(int i=1;i<m;i++)\n {\n if(arr[i][j] == 1)\n {\n arr[i][j] = arr[i-1][j]+1;\n }\n }\n }\n for(int i=0;i<m;i++)\n {\n sort(arr[i].begin(), arr[i].end(), greater<int>());\n }\n\n int ans = 0;\n \n for(int i=0;i<m;i++)\n {\n for(int j=0;j<n;j++)\n {\n ans = max(ans, arr[i][j]*(j+1));\n }\n }\n\n return ans;\n\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
largest-submatrix-with-rearrangements | Sorting + expand consecutive 1s || Faster than 96% || O(n*m*m) || Clean Java Code | sorting-expand-consecutive-1s-faster-tha-hgds | Complexity\n- Time complexity: O(nmm)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(1)\n Add your space complexity here, e.g. O(n) \n\n# | youssef1998 | NORMAL | 2023-11-26T18:38:58.045329+00:00 | 2023-11-26T18:38:58.045353+00:00 | 132 | false | # Complexity\n- Time complexity: $$O(n*m*m)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int largestSubmatrix(int[][] matrix) {\n int maxArea = 0, n = matrix.length, m = matrix[0].length;\n for (int i = n - 1; i >= 0; i--) {\n for (int j = 0; j < m; j++) {\n if (matrix[i][j] == 1) {\n matrix[i][j] += i + 1 >= n ? 0: matrix[i + 1][j];\n }\n }\n }\n for (int[] row : matrix) Arrays.sort(row);\n for (int[] row : matrix) {\n for (int j = 0; j < m; j++) {\n if (row[j] > 0) {\n maxArea = Math.max(maxArea, row[j] * (m - j));\n }\n }\n }\n return maxArea;\n }\n}\n``` | 1 | 0 | ['Sorting', 'Java'] | 0 |
largest-submatrix-with-rearrangements | Beats 100.00% of users with Python in runtime and memory | beats-10000-of-users-with-python-in-runt-hfmp | Approach\nUsing dynamic programming to calculate the height of each column, representing the number of consecutive ones ending at that column.\nThen sorting the | anushkaTonk | NORMAL | 2023-11-26T17:58:21.400679+00:00 | 2023-11-26T17:58:21.400701+00:00 | 17 | false | # Approach\nUsing dynamic programming to calculate the height of each column, representing the number of consecutive ones ending at that column.\nThen sorting the columns based on their height.\nThen, calculating the maximum area of the submatrix containing only ones.\n\n# Complexity\n- Time complexity:\nO(m * n * log(n))\n\n- Space complexity:\nO(n) <--array storing the heights\n\n# Code\n```\nclass Solution(object):\n def largestSubmatrix(self, matrix):\n """\n :type matrix: List[List[int]]\n :rtype: int\n """\n if not matrix or not matrix[0]:\n return 0\n\n m, n = len(matrix), len(matrix[0])\n height = [0] * n\n max_area = 0\n\n for i in range(m):\n for j in range(n):\n height[j] = height[j] + 1 if matrix[i][j] == 1 else 0\n\n sorted_height = sorted(height)\n for j in range(n):\n max_area = max(max_area, sorted_height[j] * (n - j))\n\n return max_area\n\n``` | 1 | 0 | ['Python'] | 0 |
largest-submatrix-with-rearrangements | Unique solution || bests 100% || Well Expalined and easy to understand | unique-solution-bests-100-well-expalined-pm6s | \n# Approach\n\n\n1. Iterate through the matrix, updating each element to represent the height of consecutive 1s above it.\n2. Sort the heights of each row in a | DeepakVrma | NORMAL | 2023-11-26T17:46:53.528418+00:00 | 2023-11-26T17:46:53.528447+00:00 | 160 | false | \n# Approach\n\n\n1. Iterate through the matrix, updating each element to represent the height of consecutive 1s above it.\n2. Sort the heights of each row in ascending order.\n3. Iterate through each row, calculating the area for each height and width combination, updating the maximum area encountered.\n4. Return the maximum area found during the iteration, representing the largest submatrix of consecutive 1s.\n# Code\n```\nclass Solution {\npublic:\n int largestSubmatrix(vector<vector<int>>& matrix) {\n int n = matrix.size();\n int m = matrix[0].size();\n for(int i = 1;i<n; i++){\n for(int j=0;j<m;j++){\n if(matrix[i][j] == 1){\n matrix[i][j]+=matrix[i-1][j];\n }\n }\n }\n int ans = 0;\n for(int i = 0;i<n;i++){\n sort(matrix[i].begin(), matrix[i].end());\n\n for(int j=0;j<m;j++){\n int h = matrix[i][j];\n int w = m-j;\n ans = max(ans, h*w);\n }\n }\n return ans;\n }\n};\n``` | 1 | 0 | ['Sorting', 'C++'] | 2 |
largest-submatrix-with-rearrangements | Java Easiest Solution | java-easiest-solution-by-shivansu_7-mstk | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Shivansu_7 | NORMAL | 2023-11-26T17:30:40.895917+00:00 | 2023-11-26T17:30:40.895948+00:00 | 10 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int largestSubmatrix(int[][] matrix) {\n \n// [0,0,1]\n// [1,1,1]\n// [1,0,1]\n \n int m = matrix.length;\n int n = matrix[0].length;\n \n int[] colRes = new int[n];\n \n for(int i=1;i<m;i++){\n for(int j=0;j<n;j++){\n if(matrix[i][j]==1)\n matrix[i][j] += matrix[i-1][j]; \n }\n }\n \n // [0,0,1] => [1,0,0] \n // [1,1,2] => [2,1,1]\n // [2,0,3] => [3,2,0] \n \n // for i=0\n // __ \n // |1|__|__| => [1,0,0] => hieght*base = 1*(i+1) => 1*1 for 1st ele \n // => hieght*base = 0*(i+1) => 0*2 for 2nd ele \n // => hieght*base = 0*(i+1) => 0*3 for 3rd ele\n \n // for i=1\n // ___ \n // |1|___\n // |1|1|1| => [2,1,1] => hieght*base = 2*(i+1) => 2*1 for 1st ele = 2 \n // => hieght*base = 1*(i+1) => 1*2 for 2nd ele = 2 \n // => hieght*base = 1*(i+1) => 1*3 for 3rd ele = 3\n \n \n // for i=2\n //___\n // |1|__ \n // |1|1|\n // |1|1|__| => [3,2,0] => hieght*base = 3*(i+1) => 3*1 for 1st ele = 3 \n // => hieght*base = 2*(i+1) => 2*2 for 2nd ele = 4 \n // => hieght*base = 0*(i+1) => 0*3 for 3rd ele = 0\n \n \n // in all the above areas 4 is largest , hence the answer\n \n int maxArea = 0;\n \n for(int[] row:matrix){\n int[] heights = row;\n revSort(heights);\n for(int i=0;i<heights.length;i++){\n int myheight = heights[i];\n int mybase = i+1; //since max area should be covered \n maxArea = Math.max(maxArea,myheight*mybase);\n }\n }\n \n return maxArea;\n \n }\n public int[] revSort(int[] arr){\n Arrays.sort(arr);\n int left = 0;\n int right = arr.length-1;\n while(left<=right){\n int temp = arr[left];\n arr[left] = arr[right];\n arr[right] = temp;\n left++;\n right--;\n }\n return arr;\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
largest-submatrix-with-rearrangements | Java 100% Efficient code || comment line by line understable | java-100-efficient-code-comment-line-by-d3aux | \n\n# Code\n```\nclass Solution\n {\n \n // Function to find the size of the largest submatrix containing only 1s\n \n public int largestSubmatrix(int[][] m | Dheerajkumar9631r | NORMAL | 2023-11-26T16:36:24.904666+00:00 | 2023-11-26T16:37:41.659803+00:00 | 12 | false | \n\n# Code\n```\nclass Solution\n {\n \n // Function to find the size of the largest submatrix containing only 1s\n \n public int largestSubmatrix(int[][] matrix) {\n // Get the number of rows and columns in the matrix\n \n int m = matrix.length;\n int n = matrix[0].length;\n \n // Initialize the variable to store the result\n int ans = 0;\n \n // Iterate through each row of the matrix\n \n for (int row = 0; row < m; row++) {\n // Iterate through each column of the current row\n for (int col = 0; col < n; col++) {\n // If the current element is not zero and the row is greater than 0\n \n if (matrix[row][col] != 0 && row > 0) {\n // Update the current element by adding the value of the element above it\n matrix[row][col] += matrix[row - 1][col];\n }\n }\n \n // Create a copy of the current row and sort it in ascending order\n \n int[] currRow = matrix[row].clone();\n Arrays.sort(currRow);\n \n // Iterate through the sorted row in reverse order\n for (int i = 0; i < n; i++) {\n // Update the result by taking the maximum of the current result and\n // the product of the current element in the sorted row and the width of the submatrix\n ans = Math.max(ans, currRow[i] * (n - i));\n }\n }\n \n // Return the final result\n return ans;\n }\n}\n\n | 1 | 0 | ['Java'] | 0 |
largest-submatrix-with-rearrangements | Easy Python Solution - Beats 100% | easy-python-solution-beats-100-by-u_day-aclb | Intuition\nThe problem requires finding the largest submatrix within the given matrix, where every element of the submatrix is 1, after reordering the columns o | U_day | NORMAL | 2023-11-26T16:35:16.210907+00:00 | 2023-11-26T16:35:16.210932+00:00 | 22 | false | # Intuition\nThe problem requires finding the largest submatrix within the given matrix, where every element of the submatrix is 1, after reordering the columns optimally.\n# Approach\n- Initialize variables m and n to store the number of rows and columns in the matrix, respectively.\n- Iterate over the matrix from the second row onwards (index i from 1 to m-1):\n - For each row, iterate over all columns (index j from 0 to n-1):\n - If the current cell value is 1, add the value of the corresponding cell in the previous row to the current cell. This step accumulates the number of consecutive 1s vertically.\n- Initialize a variable ans to store the maximum area of the submatrix initialized to 0.\n- Iterate over each row in the matrix:\n - Sort the row in reverse order. This step rearranges the elements in descending order based on the accumulated consecutive 1s. By doing this, the largest submatrix will consist of consecutive 1s from left to right.\n - Iterate over each column (index j from 0 to n-1):\n - Update ans by calculating the maximum of the current value of ans and the product of the current element in the sorted row and the column index j + 1. This step calculates the area of the submatrix composed of consecutive 1s.\n- Return the value of ans, which represents the area of the largest submatrix with all 1s after reordering the columns optimally.\n# Complexity\n- Time complexity: The code consists of two nested loops iterating over the rows and columns of the matrix. Hence, the time complexity is O(m * n), where m is the number of rows and n is the number of columns in the matrix.\n- Space complexity: The code utilizes a constant amount of extra space to store the variables. Therefore, the space complexity is O(1).\n\n\n\n\n# Code\n```\nclass Solution(object):\n def largestSubmatrix(self, matrix):\n m, n = len(matrix), len(matrix[0])\n for i in range(1, m):\n for j in range(n):\n if matrix[i][j] == 1:\n matrix[i][j] += matrix[i - 1][j]\n ans = 0\n for r in matrix:\n r.sort(reverse=True)\n for j in range(n):\n ans = max(ans, r[j] * (j + 1))\n \n return ans \n``` | 1 | 0 | ['Python'] | 0 |
largest-submatrix-with-rearrangements | Dynamic programming approach | dynamic-programming-approach-by-tanmaybh-60b3 | \n# Approach\n Describe your approach to solving the problem. \nThe current approach iterates over each row and column, updating the matrix values and then sort | tanmaybhujade | NORMAL | 2023-11-26T16:08:43.137775+00:00 | 2023-11-26T16:08:43.137803+00:00 | 7 | false | \n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe current approach iterates over each row and column, updating the matrix values and then sorting for each row. To make it more efficient, we can keep track of the height of consecutive ones for each cell in a separate array. This eliminates the need to sort for each row, improving the time complexity.\n\nThe updated approach calculates the heights for each column, maintains an array of heights, and sorts it once. Then, it iterates over the rows, updating the heights array and computing the maximum submatrix sum. This avoids redundant sorting and should result in a slight improvement in efficiency.\n\n# Complexity\n- Time complexity: \n O(m*nlog n)\n \n\n- Space complexity:\n O(n)\n\n# Code\n```\nclass Solution {\n public int largestSubmatrix(int[][] matrix) {\n int m = matrix.length;\n int n = matrix[0].length;\n int ans = 0;\n int[] heights = new int[n];\n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n if (matrix[i][j] == 0) {\n heights[j] = 0;\n } else {\n heights[j] += matrix[i][j];\n }\n }\n int[] sortedHeights = Arrays.copyOf(heights, n);\n Arrays.sort(sortedHeights);\n for (int k = 0; k < n; k++) {\n ans = Math.max(ans, sortedHeights[k] * (n - k));\n }\n }\n return ans;\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
largest-submatrix-with-rearrangements | 213ms Beats 100.00%of users with C | 213ms-beats-10000of-users-with-c-by-salm-05zi | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \nHistogram Calculation:\ | SalmaHisham | NORMAL | 2023-11-26T14:26:53.376547+00:00 | 2023-11-26T14:26:53.376569+00:00 | 14 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n**Histogram Calculation:**\nFor each element in the matrix, the algorithm computes the height of the column up to that element by accumulating the consecutive occurrences of 1s in the column. This operation results in a histogram representation for each column in every row.\n**Sorting:**\nAfter obtaining the histograms, the algorithm sorts each row\'s histogram in non-decreasing order. This sorting step is crucial for identifying the maximum area efficiently.\n**Maximum Area Computation:**\nThe algorithm then iterates through each row and calculates the maximum rectangular area achievable by considering different column orders. The maximum area is determined by multiplying the minimum histogram height within a row by the corresponding width, which is the remaining number of columns after sorting.\n\n\n# Complexity\n- Time complexity: **O(m * n * log(n))**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n**Histogram Calculation:**\nIn the worst case, for each element in the matrix, we perform a constant amount of work to calculate the histogram.\nThis step takes **O(m * n)** time, where m is the number of rows, and n is the number of columns.\n**Sorting:**\nFor each row, we sort the histogram array.\nSorting a single row takes **O(n * log(n))** time.\nSince we do this for m rows, the total time complexity for sorting is **O(m * n * log(n))**.\nThe dominant factor is the sorting step, so the overall time complexity is **O(m * n * log(n)).**\n\n\n- Space complexity:**O(m * n)**\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n**Histogram Array:**\nWe allocate a 2D histogram array to store the heights for each column in each row. The space required for this array is **O(m * n).**\n**Sorting:**\nThe space complexity for sorting is usually considered as **O(1)** since it\'s an in-place sort (qsort in C).\nso the overall space complexity is **O(m * n)**.\n\n# Code\n```\nint compare(const void* a, const void* b) \n{\n return (*(int*)a - *(int*)b);\n}\n\nint largestSubmatrix(int** matrix, int matrixSize, int* matrixColSize) \n{\n if (matrix == NULL || matrixSize == 0 || matrixColSize == NULL || *matrixColSize == 0)\n return 0;\n\n int m = matrixSize;\n int n = *matrixColSize;\n\n // Calculate the histogram for each column\n int** histogram = (int**)malloc(m * sizeof(int*));\n for (int i = 0; i < m; ++i) \n {\n histogram[i] = (int*)malloc(n * sizeof(int));\n for (int j = 0; j < n; ++j) \n {\n if (i == 0) \n histogram[i][j] = matrix[i][j];\n else \n histogram[i][j] = (matrix[i][j] == 0) ? 0 : histogram[i - 1][j] + 1;\n }\n }\n // Calculate the maximum area for each row\n int result = 0;\n for (int i = 0; i < m; ++i) \n {\n qsort(histogram[i], n, sizeof(int), compare);\n for (int j = 0; j < n; ++j)\n result = fmax(result, histogram[i][j] * (n - j));\n }\n\n // Free allocated memory\n for (int i = 0; i < m; ++i)\n free(histogram[i]);\n free(histogram);\n\n return result;\n}\n``` | 1 | 0 | ['C'] | 0 |
largest-submatrix-with-rearrangements | Runtime 100% | Intuitive aproach | runtime-100-intuitive-aproach-by-user876-70no | Approach\n Describe your approach to solving the problem. \nFor each cell in column we count how long streak of 1 is above them.\n\nThen we are checking row by | user8764IR | NORMAL | 2023-11-26T13:01:33.486547+00:00 | 2023-11-26T13:01:33.486572+00:00 | 86 | false | # Approach\n<!-- Describe your approach to solving the problem. -->\nFor each cell in column we count how long streak of `1` is above them.\n\nThen we are checking row by row, how we can replace columns so they will form the best submatrix of `1` -> we can acomplish it by sorting the row. \nNow we need to check which combination will give us max result, so it becomes easy task when row is sorted -> `int newSubMatrix = row[j] * (rowLen - j);`, where in `row[j]` we have height of submatrix and multiplying it by number of remaining cells on the right of `j` in the row. We are chcecking there which rectangle will have max num of `1`.\n\nYou might doubt why we can just sort row, omitting all ones and zeros above in colums. This is coz we are checking combinations from the top row to the bottom and in each cell now we have the streak from the top.\n\nYou may also optimise code by skipping zeros in the second for loop.\nHave a great day!\n# Code\n```\nclass Solution {\n public int largestSubmatrix(int[][] matrix) {\n int rowLen = matrix[0].length;\n for (int i = 1; i < matrix.length; ++i) {\n for (int j = 0; j < rowLen; ++j) {\n if (matrix[i][j] == 1) {\n matrix[i][j] += matrix[i - 1][j];\n }\n }\n }\n int result = 0;\n for (int [] row : matrix) {\n Arrays.sort(row);\n for (int j = 0; j < rowLen; ++j) {\n int newSubMatrix = row[j] * (rowLen - j);\n if (result < newSubMatrix) {\n result = newSubMatrix;\n }\n }\n }\n return result;\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
largest-submatrix-with-rearrangements | Ruby || O(m*n*log(n))/O(1) | ruby-omnlogno1-by-alecn2002-k3az | \n# Complexity\n- Time complexity:\nO(mnlog(n))\n\n- Space complexity:\nO(1)\n\n# Code\nruby\nclass Numeric\n def max(v) = (self < v ? v : self)\nend\n\ndef | alecn2002 | NORMAL | 2023-11-26T12:00:35.236982+00:00 | 2023-11-26T12:00:35.237015+00:00 | 7 | false | \n# Complexity\n- Time complexity:\n$$O(m*n*log(n))$$\n\n- Space complexity:\n$$O(1)$$\n\n# Code\n```ruby\nclass Numeric\n def max(v) = (self < v ? v : self)\nend\n\ndef largest_submatrix(matrix)\n h, w = matrix.size, matrix.first.size\n matrix.each_cons(2).inject(matrix.first.filter(&:positive?).size) {|res, (row1, row2)|\n row1.each_with_index {|v, cidx| row2[cidx] += v if row2[cidx].positive? }\n row2.sort.each_with_index.inject(res) {|res1, (v, i)| res1.max(v * (w - i))}\n }\nend\n\n``` | 1 | 0 | ['Ruby'] | 0 |
largest-submatrix-with-rearrangements | accumulate the height | accumulate-the-height-by-mr_stark-uvd6 | \nclass Solution {\npublic:\n int largestSubmatrix(vector<vector<int>>& mt) {\n \n int n = mt.size();\n int m = mt[0].size();\n int r | mr_stark | NORMAL | 2023-11-26T11:52:07.968869+00:00 | 2023-11-26T11:52:38.401563+00:00 | 23 | false | ```\nclass Solution {\npublic:\n int largestSubmatrix(vector<vector<int>>& mt) {\n \n int n = mt.size();\n int m = mt[0].size();\n int res = 0;\n for(int i = 0;i<n;i++)\n {\n for(int j=0;j<m;j++)\n {\n if(mt[i][j] == 1 && i>0)\n {\n mt[i][j] += mt[i-1][j];\n }\n }\n \n vector<int> temp = mt[i];\n sort(temp.begin(),temp.end(),greater<int>());\n \n for(int k = 0;k<m;k++)\n {\n int b = k+1;\n int h = temp[k];\n res = max(res, b*h);\n }\n \n }\n \n return res;\n \n \n }\n};\n``` | 1 | 0 | ['C'] | 0 |
largest-submatrix-with-rearrangements | Swift solution | swift-solution-by-azm819-jufu | Complexity\n- Time complexity: O(m * n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(n)\n Add your space complexity here, e.g. O(n) \n\n | azm819 | NORMAL | 2023-11-26T11:47:03.219979+00:00 | 2023-11-26T11:47:03.220010+00:00 | 16 | false | # Complexity\n- Time complexity: $$O(m * n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n func largestSubmatrix(_ matrix: [[Int]]) -> Int {\n var result = 0\n\n var prevHeights = [(col: Int, height: Int)]()\n for i in 0 ..< matrix.count {\n var newHeights = [(col: Int, height: Int)]()\n var visited = Set<Int>()\n for prev in prevHeights where matrix[i][prev.col] == 1 {\n visited.insert(prev.col)\n newHeights.append((prev.col, prev.height + 1))\n }\n for j in 0 ..< matrix[0].count where matrix[i][j] == 1 && !visited.contains(j) {\n newHeights.append((j, 1))\n }\n\n for j in 0 ..< newHeights.count {\n result = max(result, newHeights[j].height * (j + 1))\n }\n\n prevHeights = newHeights\n }\n\n return result\n }\n}\n``` | 1 | 0 | ['Array', 'Greedy', 'Swift', 'Sorting', 'Matrix'] | 0 |
largest-submatrix-with-rearrangements | Java Solution for Largest Submatrix With Rearrangements Problem | java-solution-for-largest-submatrix-with-co1q | Intuition\n Describe your first thoughts on how to solve this problem. \nThe approach aims to find the largest submatrix containing only 1s after rearranging th | Aman_Raj_Sinha | NORMAL | 2023-11-26T11:28:24.118896+00:00 | 2023-11-26T11:28:24.118923+00:00 | 106 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe approach aims to find the largest submatrix containing only 1s after rearranging the columns optimally. It works by first computing the height of each column by counting the consecutive 1s from the top. Then, it sorts each row\u2019s heights to determine the maximum area by considering the maximum consecutive 1s in a row, multiplied by its width.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1.\tCompute the height of consecutive 1s in each column by iterating through the matrix.\n2.\tStore these heights in a separate 2D array.\n3.\tSort each row\u2019s heights array to find the maximum consecutive 1s for each column.\n4.\tCalculate the maximum area by multiplying the maximum height in a row by its width (the number of columns).\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\u2022\tComputing the heights for each cell in the matrix takes O(m * n) time.\n\u2022\tSorting each row\u2019s heights takes O(m * n * log n) time.\n\u2022\tFinding the maximum area involves traversing the sorted heights, which takes O(m * n) time.\nOverall, the time complexity is O(m * n * log n) due to the sorting step dominating the computation.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\u2022\tThe space complexity is O(m * n) because we create a 2D heights array to store the heights of consecutive 1s for each cell in the matrix.\n\u2022\tAdditionally, there\u2019s some extra space used for variables and temporary storage, but they don\u2019t significantly impact the overall space complexity.\n\n# Code\n```\nclass Solution {\n public int largestSubmatrix(int[][] matrix) {\n int m = matrix.length;\n int n = matrix[0].length;\n\n // Calculate heights for each column\n int[][] heights = new int[m][n];\n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n if (matrix[i][j] == 1) {\n heights[i][j] = i == 0 ? 1 : heights[i - 1][j] + 1;\n }\n }\n }\n\n // Sort rows to find the maximum area\n int maxArea = 0;\n for (int i = 0; i < m; i++) {\n Arrays.sort(heights[i]);\n for (int j = 0; j < n; j++) {\n maxArea = Math.max(maxArea, heights[i][j] * (n - j));\n }\n }\n\n return maxArea;\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
largest-submatrix-with-rearrangements | Typescript: sort and without sort solutions (Runtime beats 100%) | typescript-sort-and-without-sort-solutio-jhcg | Complexity\n- Time complexity:\nO(n * m)\n\n- Space complexity:\nO(n)\n\n# Code\n\n// TC (m * n), SC: (n)\nfunction largestSubmatrix(matrix: number[][]): number | alexgavrilov | NORMAL | 2023-11-26T09:57:21.787438+00:00 | 2023-11-26T09:57:21.787464+00:00 | 50 | false | # Complexity\n- Time complexity:\nO(n * m)\n\n- Space complexity:\nO(n)\n\n# Code\n```\n// TC (m * n), SC: (n)\nfunction largestSubmatrix(matrix: number[][]): number {\n const m: number = matrix.length;\n const n: number = matrix[0].length;\n let maxArea: number = 0;\n let prevHeights: [number, number][] = [];\n\n for (let row = 0; row < m; row++) {\n const heights: [number, number][] = [];\n const seen: boolean[] = new Array(n).fill(false);\n\n for (const [height, col] of prevHeights) {\n if (matrix[row][col] == 1) {\n heights.push([height + 1, col]);\n seen[col] = true;\n }\n }\n\n for (let col = 0; col < n; col++) {\n if (!seen[col] && matrix[row][col] == 1) {\n heights.push([1, col]);\n }\n }\n\n for (let i = 0; i < heights.length; i++) {\n maxArea = Math.max(maxArea, heights[i][0] * (i + 1));\n }\n\n prevHeights = heights;\n }\n\n return maxArea;\n}\n\n// TC: O(m * n * logn), SC: O(m * n)\nfunction largestSubmatrixSort(matrix: number[][]): number {\n const m: number = matrix.length;\n const n: number = matrix[0].length;\n let maxArea: number = 0;\n\n for (let row = 0; row < m; row++) {\n for (let col = 0; col < n; col++) {\n if (matrix[row][col] != 0 && row > 0) {\n matrix[row][col] += matrix[row - 1][col];\n }\n }\n\n const currentRow = [...matrix[row]].sort((a, b) => b - a);\n\n for (let i = 0; i < n; i++) {\n maxArea = Math.max(maxArea, currentRow[i] * (i + 1));\n }\n }\n\n return maxArea;\n};\n``` | 1 | 0 | ['Array', 'Greedy', 'Sorting', 'Matrix', 'TypeScript', 'JavaScript'] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.