question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
largest-submatrix-with-rearrangements | simple sorting prefix sum problem | simple-sorting-prefix-sum-problem-by-ani-urih | \nclass Solution {\n public int largestSubmatrix(int[][] matrix) {\n int n = matrix.length;\n int m = matrix[0].length;\n for(int i=0;i< | anilkumawat3104 | NORMAL | 2023-11-26T08:44:16.272697+00:00 | 2023-11-26T08:44:16.272731+00:00 | 76 | false | ```\nclass Solution {\n public int largestSubmatrix(int[][] matrix) {\n int n = matrix.length;\n int m = matrix[0].length;\n for(int i=0;i<m;i++){\n for(int j=1;j<n;j++){\n if(matrix[j][i]==0)\n continue;\n else{\n matrix[j][i]+=matrix[j-1][i];\n }\n }\n }\n int ans = 0;\n for(int i=0;i<n;i++){\n ans = Math.max(maxArea(matrix[i]),ans);\n }\n return ans;\n }\n public int maxArea(int hist[]){\n Arrays.sort(hist);\n int n = hist.length;\n int ans = 0;\n for(int i=0;i<n;i++){\n ans = Math.max((n-i)*hist[i],ans);\n }\n return ans;\n }\n}\n``` | 1 | 0 | ['Greedy', 'Sorting', 'Prefix Sum', 'Java'] | 0 |
largest-submatrix-with-rearrangements | Pyhton | Easy | Greedy | pyhton-easy-greedy-by-khosiyat-n4my | see the Successfully Accepted Submission\npython\nclass Solution:\n def largestSubmatrix(self, matrix):\n rows, cols = len(matrix), len(matrix[0])\n | Khosiyat | NORMAL | 2023-11-26T08:09:31.605704+00:00 | 2023-11-26T08:09:31.605727+00:00 | 23 | false | [see the Successfully Accepted Submission](https://leetcode.com/submissions/detail/1106639757/)\n```python\nclass Solution:\n def largestSubmatrix(self, matrix):\n rows, cols = len(matrix), len(matrix[0])\n max_area = 0\n\n for j in range(cols):\n cont_sum = 0\n for i in range(rows):\n if matrix[i][j] == 0:\n cont_sum = 0\n continue\n\n cont_sum += 1\n matrix[i][j] = cont_sum\n\n for i in range(rows):\n temp_list = sorted(matrix[i], reverse=True)\n\n for j in range(cols):\n max_area = max(max_area, (j + 1) * temp_list[j])\n\n return max_area\n\n```\n | 1 | 0 | ['Greedy', 'Python'] | 0 |
largest-submatrix-with-rearrangements | [We💕Simple] Counting Sort, Dynamic Programming w/ Explanations | wesimple-counting-sort-dynamic-programmi-k6dv | I always like to find solutions that are very simple and easy, yet do not sacrifice time complexity. I keep creating more solutions\n\n# Code\nKotlin []\nclass | YooSeungKim | NORMAL | 2023-11-26T07:04:59.101778+00:00 | 2023-11-26T13:31:12.686186+00:00 | 167 | false | I always like to find solutions that are very simple and easy, yet do not sacrifice time complexity. I keep creating more solutions\n\n# Code\n``` Kotlin []\nclass Solution {\n fun largestSubmatrix(matrix: Array<IntArray>): Int {\n val heights = IntArray(matrix[0].size)\n var maxArea = 0\n for (row in matrix) {\n val countByHeightInRow = sortedMapOf<Int, Int>(Comparator.reverseOrder())\n for ((j, v) in row.withIndex()) {\n if (v == 0) {\n heights[j] = 0\n } else {\n heights[j] += 1\n countByHeightInRow[heights[j]] = countByHeightInRow.getOrDefault(heights[j], 0) + 1\n }\n }\n var accHeightCount = 0\n for ((height, count) in countByHeightInRow) {\n accHeightCount += count\n maxArea = maxOf(maxArea, accHeightCount * height)\n }\n }\n return maxArea\n }\n}\n\n// Shorter version\nclass Solution {\n fun largestSubmatrix(matrix: Array<IntArray>): Int =\n matrix.fold(0 to IntArray(matrix[0].size)) { (maxArea, heights), row ->\n sortedMapOf<Int, Int>(Comparator.reverseOrder()).apply {\n for ((j, v) in row.withIndex()) {\n heights[j] = if (v == 0) 0 else heights[j] + 1\n this[heights[j]] = this.getOrDefault(heights[j], 0) + 1\n }\n }.entries.fold(maxArea to 0) { (maxArea, acc), (height, count) ->\n maxOf(maxArea, height * (acc + count)) to acc + count\n }.first to heights\n }.first\n}\n\n// Sort version\nclass Solution {\n fun largestSubmatrix(matrix: Array<IntArray>): Int {\n val m = matrix.size\n val n = matrix[0].size\n var maxArea = 0\n\n for (i in 1 until m) {\n for (j in 0 until n) {\n if (matrix[i][j] != 0) {\n matrix[i][j] += matrix[i - 1][j]\n }\n }\n }\n\n for (row in matrix) {\n row.sort()\n for (j in 0 until n) {\n maxArea = maxOf(maxArea, row[j] * (n - j))\n }\n }\n\n return maxArea\n }\n}\n\n```\n\n``` Python3 []\nclass Solution:\n def largestSubmatrix(self, matrix):\n heights = [0] * len(matrix[0])\n answer = 0\n\n for row in matrix:\n count_by_height = {}\n for j, value in enumerate(row):\n if value == 0:\n heights[j] = 0\n else:\n heights[j] += 1\n count_by_height[heights[j]] = count_by_height.get(heights[j], 0) + 1\n \n acc_height_count = 0\n for height in sorted(count_by_height.keys(), reverse=True):\n acc_height_count += count_by_height[height]\n answer = max(answer, acc_height_count * height)\n \n return answer\n```\n\n1. **Iterating Through Each Row and Calculating Heights**: The algorithm iterates through each row of the matrix and calculates the \'heights\' of consecutive 1s for each column. This \'height\' represents the number of 1s stacked vertically up to the current row. For instance, if a column has 1s in three consecutive rows, its height would be 3 in the third row. This step is crucial because it transforms the problem into a series of histogram-like structures where each column\'s height can be visualized as a bar in a histogram.\n\n2. **Count Sorting of Heights**: After computing the heights for each column in a row, these heights are sorted in descending order using a `sortedMapOf`. This sorting is essential because it aligns the columns in order of their heights, prioritizing taller \'bars\' first. This priority is key for efficiently finding the largest rectangle at each step.\n3. **Iterating in Descending Order of Heights**: The algorithm then iterates over these heights, starting from the tallest. During this iteration, it calculates the potential size of the submatrix (rectangle) that can be formed using the current height as the limiting factor. The idea is to consider the tallest column and see how wide the rectangle can be, encompassing shorter columns to its right. This process is repeated for each height, progressively considering shorter heights and wider potential rectangles.\n4. **Updating the Maximum Submatrix Size**: For each height, the algorithm calculates the area of the potential rectangle and updates the maximum size found so far. This update is a crucial step because it ensures that the largest possible submatrix is not missed. The area is calculated by multiplying the current height with the cumulative count of columns that are at least as tall as the current height.\n\nBy integrating these steps, the algorithm efficiently finds the largest rectangular area in a binary matrix. The use of height calculation transforms the 2D problem into a series of 1D problems (like histograms), and the sorted iteration ensures that the largest possible rectangles are considered first, optimizing the search for the maximum area. This approach is a blend of dynamic programming (keeping track of heights) and a greedy strategy (prioritizing larger heights first).\n | 1 | 0 | ['Dynamic Programming', 'Counting Sort', 'Python', 'Python3', 'Kotlin'] | 0 |
largest-submatrix-with-rearrangements | Simple solution with explaination | simple-solution-with-explaination-by-nip-3fxw | Intuition\n Describe your first thoughts on how to solve this problem. \n\n\n\n\n\n# Code\n\nclass Solution {\n public int largestSubmatrix(int[][] matrix) { | Nipun0803 | NORMAL | 2023-11-26T06:56:34.223832+00:00 | 2023-11-26T06:56:34.223859+00:00 | 16 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n\n\n\n\n# Code\n```\nclass Solution {\n public int largestSubmatrix(int[][] matrix) {\n int m = matrix.length, n = matrix[0].length;\n for (int i = 1; i < m; ++i) {\n for (int j = 0; j < n; ++j) {\n if (matrix[i][j] == 1) {\n matrix[i][j] = matrix[i - 1][j] + 1;\n }\n }\n }\n int ans = 0;\n for (var row : matrix) {\n Arrays.sort(row);\n for (int j = n - 1, k = 1; j >= 0 && row[j] > 0; --j, ++k) {\n int s = row[j] * k;\n ans = Math.max(ans, s);\n }\n }\n return ans;\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
largest-submatrix-with-rearrangements | Easy || Prerequisites || Happy Coding | easy-prerequisites-happy-coding-by-shrey-q7ed | There are two prerequisites for this problem: the maximal square and the maximal rectangle. Once you understand these concepts, this question becomes relatively | shreyas_6379 | NORMAL | 2023-11-26T06:33:14.623003+00:00 | 2023-11-26T06:33:14.623045+00:00 | 65 | false | There are two prerequisites for this problem: the maximal square and the maximal rectangle. Once you understand these concepts, this question becomes relatively straightforward to grasp and solve.\n\n# Code\n```\n\n\nclass Solution {\npublic:\n int largestSubmatrix(vector<vector<int>>& matrix) {\n int m = matrix.size();\n int n = matrix[0].size();\n vector<vector<int>> dp(m, vector<int>(n, 0));\n\n // Preprocess the matrix to calculate the height of consecutive 1\'s ending at each position\n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n if (matrix[i][j] == 1) {\n dp[i][j] = (i == 0) ? 1 : dp[i - 1][j] + 1;\n }\n }\n }\n\n int ans = 0;\n // Sort and calculate the area for each column\n for (int i = 0; i < m; i++) {\n sort(dp[i].begin(), dp[i].end(), greater<int>());\n for (int j = 0; j < n; j++) {\n ans = max(ans, dp[i][j] * (j + 1));\n }\n }\n\n return ans;\n }\n};\n\n``` | 1 | 0 | ['C++'] | 0 |
largest-submatrix-with-rearrangements | Easy explanation with example | Space complexity O(1) | beats 90% C# users | easy-explanation-with-example-space-comp-femr | Intuition\nSubmatrix would either be a squre matrix or rectangular matrix, so we need to traverse each column and check the number of consicutive ones and then | rahulgulia | NORMAL | 2023-11-26T06:30:22.175175+00:00 | 2023-11-26T06:30:22.175198+00:00 | 48 | false | # Intuition\nSubmatrix would either be a squre matrix or rectangular matrix, so we need to traverse each column and check the number of consicutive ones and then arrange row elements to get the biggest submatrix possible.\n\n# Approach\n### Step 1\nTraverse each column and modify row elements in such a way that if \'i\' element, matrix[i][c], is 1, then the \'i+1\' element of same column, matrix[i+1][c] will be 2 else 0.\nThis is how we will get longest streak in each column.\n### Step 2\nNow for each row, arrange the elements in decending order and multiply the element with column number of matrix (i.e. (c + 1) * matrix[r][c]). Maximum of it will give us the biggest subMatrix area.\n\n## Example:\n#### given matrix: \n [[0, 0, 1],\n [1, 1, 1],\n [1, 0, 1]]\n#### After step 1:\n\n [[0, 0, 1],\n [1, 1, 2],\n [2, 0, 3]]\n#### Step 3:\n\n [1*1, 0*2, 0*3] [1,0,0]\n [2*1, 1*2, 1*3] = [2,2,3]\n [3*1, 2*2, 0*3] [3,4,0]\nSo, the Size of biggest submatrix is 4.\n\n# Complexity\n- Time complexity:\nO(M*N*log(M)) - nested loops and Sorting of row elements.\n\n- Space complexity:\nO(1) - As we are making change in given matrix only, we only need some integer variables \n\n# Code\n```\npublic class Solution {\n public int LargestSubmatrix(int[][] matrix) {\n int rows = matrix.Length; \n int cols = matrix[0].Length;\n\n for (int c = 0; c < cols; c++) \n for (int r = 1; r < rows; r++)\n matrix[r][c] = matrix[r][c] == 0 ? 0 : matrix[r - 1][c] + 1;\n\n int ans = 0; \n for (int r = 0; r < rows; r++)\n {\n Array.Sort(matrix[r], (a, b) => b.CompareTo(a)); \n for (int c = 0; c < cols; c++)\n ans = Math.Max(ans, (c + 1) * matrix[r][c]);\n }\n return ans;\n }\n}\n``` | 1 | 0 | ['C#'] | 0 |
largest-submatrix-with-rearrangements | JAVA Code Solution Explained in HINDI | java-code-solution-explained-in-hindi-by-j2f0 | https://youtu.be/7jTSxIzUEEk\n\nPlease, check above video for explanation and do like and subscribe the channel.\n\n# Code\n\nclass Solution {\n public int l | The_elite | NORMAL | 2023-11-26T06:20:26.288036+00:00 | 2023-11-26T06:20:26.288068+00:00 | 1 | false | https://youtu.be/7jTSxIzUEEk\n\nPlease, check above video for explanation and do like and subscribe the channel.\n\n# Code\n```\nclass Solution {\n public int largestSubmatrix(int[][] matrix) {\n\n int m = matrix.length;\n int n = matrix[0].length;\n\n int ans = 0;\n\n for(int r = 0; r < m; r++) {\n for(int c = 0; c < n; c++) {\n if (matrix[r][c] != 0 && r > 0) {\n matrix[r][c] += matrix[r-1][c];\n }\n }\n\n int currRow[] = matrix[r].clone();\n Arrays.sort(currRow);\n for(int i = 0; i < n; i++) {\n ans = Math.max(ans, currRow[i] * (n-i));\n }\n } \n return ans;\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
largest-submatrix-with-rearrangements | ruby 2-liner | ruby-2-liner-by-_-k-qzot | \ndef largest_submatrix(m)\n\n a = m.transpose.map{|r| r.chunk_while{ 1<_1+_2 }.map &:sum }\n m.map{ a.sort.reverse.zip(1..).map{|x,i| i*x[0].tap{ x.shift if | _-k- | NORMAL | 2023-11-26T05:50:17.208564+00:00 | 2023-11-26T05:50:17.208584+00:00 | 12 | false | ```\ndef largest_submatrix(m)\n\n a = m.transpose.map{|r| r.chunk_while{ 1<_1+_2 }.map &:sum }\n m.map{ a.sort.reverse.zip(1..).map{|x,i| i*x[0].tap{ x.shift if 1>x[0]-=1 } }.max }.max\n\nend\n``` | 1 | 0 | ['Ruby'] | 0 |
largest-submatrix-with-rearrangements | Kotlin | kotlin-by-samoylenkodmitry-s5u4 | \n\n#### Join me on Telegram\n\nhttps://t.me/leetcode_daily_unstoppable/417\n\n#### Problem TLDR\n\nMax area of 1 submatrix after sorting columns optimally\n\n# | SamoylenkoDmitry | NORMAL | 2023-11-26T05:46:58.791856+00:00 | 2023-11-26T05:46:58.791880+00:00 | 27 | false | \n\n#### Join me on Telegram\n\nhttps://t.me/leetcode_daily_unstoppable/417\n\n#### Problem TLDR\n\nMax area of `1` submatrix after sorting columns optimally\n\n#### Intuition\n\nUse hint :(\nOk, if we store the heights of the columns we can analyse each row independently, by choosing the largest heights first. The area will be `height * width`, where width will be the current position:\n\n\n\n\n#### Approach\n\nWe can reuse the matrix, but don\'t do this in a production code without a warning.\n\n#### Complexity\n\n- Time complexity:\n$$O(nmlog(m))$$\n\n- Space complexity:\n$$O(1)$$\n\n#### Code\n\n```kotlin\n\n fun largestSubmatrix(matrix: Array<IntArray>): Int {\n for (y in 1..<matrix.size)\n for (x in 0..<matrix[y].size)\n if (matrix[y][x] > 0)\n matrix[y][x] += matrix[y - 1][x]\n var max = 0\n for (row in matrix) {\n row.sort()\n for (x in row.lastIndex downTo 0)\n max = max(max, row[x] * (row.size - x))\n }\n return max\n }\n\n``` | 1 | 0 | ['Sorting', 'Kotlin'] | 0 |
largest-submatrix-with-rearrangements | 5 Lines Solution with good explanation | 5-lines-solution-with-good-explanation-b-b4ws | This C++ solution is designed to find the size of the largest submatrix containing only 1s in a given matrix a. Here\'s a step-by-step explanation:\n\n1. Initia | Chouhan_Gourav | NORMAL | 2023-11-26T05:37:32.603133+00:00 | 2023-11-26T05:37:32.603152+00:00 | 261 | false | This C++ solution is designed to find the size of the largest submatrix containing only 1s in a given matrix `a`. Here\'s a step-by-step explanation:\n\n1. **Initialize Variables:**\n - `n` and `m` store the number of rows and columns in the matrix, respectively.\n - `ans` is the variable to keep track of the maximum area of a submatrix.\n\n2. **Update Matrix:**\n - Iterate through each row starting from the second row (`i=1`).\n - For each element in the row, if it is a 1, add the value of the element in the previous row at the same column. This step essentially accumulates the height of consecutive 1s in each column.\n\n3. **Sort Rows:**\n - For each row, sort the values in descending order. This step helps in finding the maximum area in the next step efficiently.\n\n4. **Calculate Maximum Area:**\n - Iterate through each row and each column.\n - For each element, calculate the area of the submatrix ending at that element by multiplying the width (column index + 1) with the height (value in the sorted row).\n - Update the `ans` variable with the maximum area encountered so far.\n\n5. **Return Result:**\n - The final result is stored in the `ans` variable, representing the size of the largest submatrix containing only 1s.\n\nIn summary, this solution efficiently calculates the height of consecutive 1s in each column, sorts the rows based on the height of 1s, and then iterates through each element to find the maximum area of submatrices containing only 1s.\n\n# In 5 line as the title says\n\n```cpp\nclass Solution {\npublic:\n int largestSubmatrix(vector<vector<int>>& a) {\n int n=a.size(),m=a[0].size(),ans=0;\n for(int i=1;i<n;i++) for(int j=0;j<m;j++) if(a[i][j]) a[i][j]+=a[i-1][j];\n for(int i=0;i<n;i++) sort(a[i].begin(), a[i].end(), greater<int>());\n for(int i=0;i<n;i++) for(int j=0;j<m;j++) ans = max(ans, (j+1)*a[i][j]);\n return ans;\n }\n};\n```\n# More Readable\n```\nclass Solution {\npublic:\n int largestSubmatrix(vector<vector<int>>& a) {\n int n=a.size(),m=a[0].size(),ans=0;\n for(int i=1;i<n;i++)\n for(int j=0;j<m;j++)\n if(a[i][j])\n a[i][j]+=a[i-1][j];\n\n for(int i=0;i<n;i++)\n sort(a[i].begin(), a[i].end(), greater<int>());\n\n for(int i=0;i<n;i++)\n for(int j=0;j<m;j++)\n ans = max(ans, (j+1)*a[i][j]);\n \n return ans;\n }\n};\n```\n\n\n#### The description of code is generated by chat gpt, I\'m too lazy to explain on my own | 1 | 0 | ['C++'] | 1 |
largest-submatrix-with-rearrangements | Easy Way || Sorting || Prefix Array || CPP || Matrix | easy-way-sorting-prefix-array-cpp-matrix-2cx9 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | shubham7447 | NORMAL | 2023-11-26T05:35:58.560699+00:00 | 2023-11-26T05:36:43.344704+00:00 | 72 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int largestSubmatrix(vector<vector<int>>& matrix) {\n int n=matrix.size();\n int m=matrix[0].size();\n vector<vector<int>>ans(n,vector<int>(m,0));\n for(int i=0;i<m;i++){\n int k=1;\n int p=0;\n if(matrix[0][i]==0){\n ans[0][i]=0; \n }\n else{\n ans[0][i]=1;\n }\n\n for(int j=1;j<n;j++){\n if(matrix[j][i]==0){\n ans[j][i]=0;\n continue;\n }\n ans[j][i]=ans[j-1][i]+1;\n }\n\n }\n\n\n int fans=0;\n for(int i=0;i<n;i++){\n sort(ans[i].begin(),ans[i].end());\n\n for(int j=m-1;j>=0;j--){\n fans=max(fans,(m-j)*ans[i][j]);\n }\n\n }\n return fans;\n }\n};\n``` | 1 | 0 | ['Array', 'Sorting', 'Matrix', 'C++'] | 0 |
largest-submatrix-with-rearrangements | [Golang] No Sorting | golang-no-sorting-by-vasakris-ms1n | Complexity\n- Time complexity:\nO(m*n)\n\n- Space complexity:\nO(n)\n\n# Code\n\ntype Pair struct {\n Height int\n Column int\n}\n\nfunc largestSubmatrix( | vasakris | NORMAL | 2023-11-26T05:29:57.277417+00:00 | 2023-11-26T05:29:57.277444+00:00 | 61 | false | # Complexity\n- Time complexity:\nO(m*n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\ntype Pair struct {\n Height int\n Column int\n}\n\nfunc largestSubmatrix(matrix [][]int) int {\n m, n := len(matrix), len(matrix[0])\n prevHeights := []Pair{}\n res := 0\n\n for row := 0; row < m; row++ {\n heights := []Pair{}\n seen := make([]bool, n)\n\n // Check prevHeights(rows) first and increment heights\n for _, pair := range prevHeights {\n height, col := pair.Height, pair.Column\n if matrix[row][col] == 1 {\n heights = append(heights, Pair{height+1, col})\n seen[col] = true\n }\n }\n\n // Start from height = 1\n for col := 0; col < n; col++ {\n if !seen[col] && matrix[row][col] == 1 {\n heights = append(heights, Pair{1, col})\n }\n }\n\n // Here heights will be in descending order\n // So i+1, gives width. \n for i := 0; i < len(heights); i++ {\n res = max(res, heights[i].Height * (i+1))\n }\n\n prevHeights = heights\n }\n\n return res\n}\n\nfunc max(a, b int) int {\n if a > b {\n return a\n }\n return b\n}\n``` | 1 | 0 | ['Go'] | 0 |
largest-submatrix-with-rearrangements | Histogram-like Approach | histogram-like-approach-by-hsakib8685-mgif | Intuition\nThe challenge was to find the largest 1\'s submatrix after rearranging columns. My initial thought was to transform the problem into a histogram-like | hsakib8685 | NORMAL | 2023-11-26T05:16:01.455233+00:00 | 2023-11-26T05:16:01.455265+00:00 | 6 | false | # Intuition\nThe challenge was to find the largest `1`\'s submatrix after rearranging **columns**. My initial thought was to transform the problem into a **histogram**-like approach, treating rows as bases and columns as heights.\n\n# Approach\n1. **Height Calculation**: First, transform the matrix such that each cell represents the height of `1`\'s up to that row.\n2. **Sorting Rows**: Next, **sort** each row in **descending** order.\n3. **Maximum Area Calculation**: Finally, calculate the maximum area for each row, considering the sorted heights and their positions.\n\n# Complexity\n- Time complexity: $$O(m\xD7nlogn)$$, where $$m$$ is the number of rows and $$n$$ is the number of columns. Sorting each row contributes to the $$nlog\u2061n$$ part.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$ as no extra space is needed apart from the input matrix transformation.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n static bool cmp(int x, int y) { return x > y; }\n\npublic:\n int largestSubmatrix(vector<vector<int>> &matrix) {\n int r = matrix.size();\n int c = matrix[0].size();\n for (int i = 0; i < c; i++) {\n for (int j = 1; j < r; j++) {\n if (matrix[j][i]) {\n matrix[j][i] = matrix[j - 1][i] + 1;\n }\n }\n }\n int ans = 0;\n for (int i = 0; i < r; i++) {\n sort(matrix[i].begin(), matrix[i].end(), cmp);\n for (int j = 0; j < c; j++) {\n ans = max(ans, matrix[i][j] * (j + 1));\n }\n }\n return ans;\n }\n};\n``` | 1 | 0 | ['Array', 'Greedy', 'Sorting', 'Matrix', 'C++'] | 0 |
largest-submatrix-with-rearrangements | 90ms C++ beats 100% O(mn) | 90ms-c-beats-100-omn-by-yjian012-pw7l | Before the O(mn) solution, first the O(m n log n) solution (but slightly improved), best time 102ms.\n\n//https://hyper-meta.blogspot.com/\n#pragma GCC target(" | yjian012 | NORMAL | 2023-11-26T05:12:28.091036+00:00 | 2023-11-26T06:07:29.428297+00:00 | 18 | false | Before the O(mn) solution, first the O(m n log n) solution (but slightly improved), best time 102ms.\n```\n//https://hyper-meta.blogspot.com/\n#pragma GCC target("avx,mmx,sse2,sse3,sse4")\nauto _=[]()noexcept{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);return 0;}();\nint t[100001];\nint ind[100001];\nint isz;\nclass Solution {\npublic:\n int largestSubmatrix(vector<vector<int>>& matrix) {\n auto &v=matrix[0];\n int r=accumulate(v.begin(),v.end(),0),s,vj;\n const int sz=matrix.size(),n=v.size();\n for(int i=1;i<sz;++i){\n isz=s=0;\n auto &v1=matrix[i];\n for(int j=0;j<n;++j){\n vj=v[j]=(v[j]+1)*v1[j];\n if(!vj) continue;\n if(!t[vj]++) ind[isz++]=vj;\n }\n sort(ind,ind+isz);\n for(int k=isz-1;k>=0;--k){\n int idx=ind[k];\n r=max(r,idx*(s+=t[idx]));\n t[idx]=0;\n }\n }\n return r;\n }\n};\n```\nHere the columns with the same "row-side length" are combined, so we only sort the number of different sizes, which could be much smaller than $n$.\n\nHere\' s the O(mn) version, the same idea as [explained here](https://leetcode.com/problems/largest-submatrix-with-rearrangements/solutions/1020797/optimal-o-m-n-time-o-n-space-no-sort/), just optimized for speed (also saves some space). Best time 90ms.\n```\n//https://hyper-meta.blogspot.com/\n#pragma GCC target("avx,mmx,sse2,sse3,sse4")\nauto _=[]()noexcept{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);return 0;}();\nstruct pa{int cnt,ind;};\npa cnts[100000];\nint csz,nsz;\nbool done[100000];\nclass Solution {\npublic:\n int largestSubmatrix(vector<vector<int>>& matrix) {\n const int m=matrix.size(),n=matrix[0].size();\n int r=0;\n csz=0;\n for(int i=0;i<m;i++) {\n memset(done,0,n);\n nsz=0;\n auto &v=matrix[i];\n for(int j=0;j<csz;++j){\n int c=cnts[j].cnt,d=cnts[j].ind;\n if(v[d]){\n cnts[nsz++]=pa{c+1,d};\n done[d]=1;\n }\n }\n for(int j=0;j<n;j++) if (!done[j]&&v[j]) cnts[nsz++]=pa{1,j};\n for(int j=0;j<(csz=nsz);j++) r=max(r,(j+1)*cnts[j].cnt);\n }\n return r;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
largest-submatrix-with-rearrangements | 🥷Beats 100% | Simple dynamic programming approach | No extra space 🔥 | beats-100-simple-dynamic-programming-app-rf1w | Intuition\n\nWhen approaching the problem of finding the largest submatrix of 1s in a matrix, the initial thought involves exploring a method to identify a cont | jailwalankit | NORMAL | 2023-11-26T04:31:45.802250+00:00 | 2023-11-26T04:31:45.802272+00:00 | 84 | false | # Intuition\n\nWhen approaching the problem of finding the largest submatrix of 1s in a matrix, the initial thought involves exploring a method to identify a contiguous area that comprises only 1s. It\'s crucial to establish a systematic way to track the maximum possible area of such a submatrix within the given matrix.\n\n### Approach Visualization:\n\n- **Dynamic Programming for Heights of 1s:**\n - **Step 1:** Traverse the matrix to calculate the maximum height of consecutive 1s ending at each cell.\n - **Step 2:** Update the matrix with these maximum heights.\n\n- **Finding Maximum Area:**\n - **Step 3:** For each row:\n - **Substep a:** Sort the row to identify the maximum heights of 1s.\n - **Substep b:** Calculate the area using height and width (index).\n - **Substep c:** Track the maximum area encountered.\n\n### Intuition Visualization:\n\n- **Initial Thoughts (Intuition):**\n - The problem focuses on identifying the largest submatrix within a matrix that comprises only 1s.\n - The challenge involves systematically tracking the maximum possible area of such a submatrix.\n\n- **Approach Exploration:**\n - The intuition suggests exploring a method to efficiently identify contiguous areas of 1s.\n - Emphasizes the importance of establishing a systematic approach to determine the largest submatrix area of 1s.\n\n\n\n# Complexity\n- Time complexity:\n$$O(m\xD7nlogn)$$ \n\n- Space complexity:\nNo extra space\n\n# Code\n```\nclass Solution {\npublic:\n int largestSubmatrix(vector<vector<int>>& matrix) {\n if (matrix.empty() || matrix[0].empty()) return 0;\n\n int rows = matrix.size();\n int cols = matrix[0].size();\n int maxArea = 0;\n\n for (int i = 1; i < rows; ++i) {\n for (int j = 0; j < cols; ++j) {\n if (matrix[i][j] == 1)\n matrix[i][j] += matrix[i - 1][j];\n }\n }\n\n for (int i = 0; i < rows; ++i) {\n sort(matrix[i].begin(), matrix[i].end(), greater<int>()); \n\n for (int j = 0; j < cols; ++j) {\n maxArea = max(maxArea, matrix[i][j] * (j + 1)); \n }\n }\n\n return maxArea;\n }\n};\n``` | 1 | 0 | ['Array', 'Sorting', 'Matrix', 'C++'] | 0 |
find-elements-in-a-contaminated-binary-tree | Python Special Way for find() without HashSet O(1) Space O(logn) Time | python-special-way-for-find-without-hash-8dzg | It\'s obvious to use BFS for the initial part. However, a lot of people use HashSet(set() in python) to pre-store all the values in the initial part, which may | zhaoqxu | NORMAL | 2019-11-17T05:32:30.393615+00:00 | 2019-11-17T05:32:30.393653+00:00 | 8,129 | false | It\'s obvious to use `BFS` for the initial part. However, a lot of people use HashSet(`set()` in python) to pre-store all the values in the initial part, which may cause MLE when the values are huge. There is a special way to implement `find()` that costs O(1) in space and O(logn) in time. \n\nFirstly, let\'s see what a complete tree will look like in this problem: \n\n\nIt\'s very easy to find that numbers in each layer range from `[2^i-1,2^(i+1)-2]`\nwhat if we add 1 to each number? Then it should range from `[2^i, 2^(i+1)-1]`\nSee? the binary of all numbers in each layer should be: `100..00` to `111...11`\n\nHence we could discover that maybe we could use the `binary number` of `target+1` to find a path:\n\n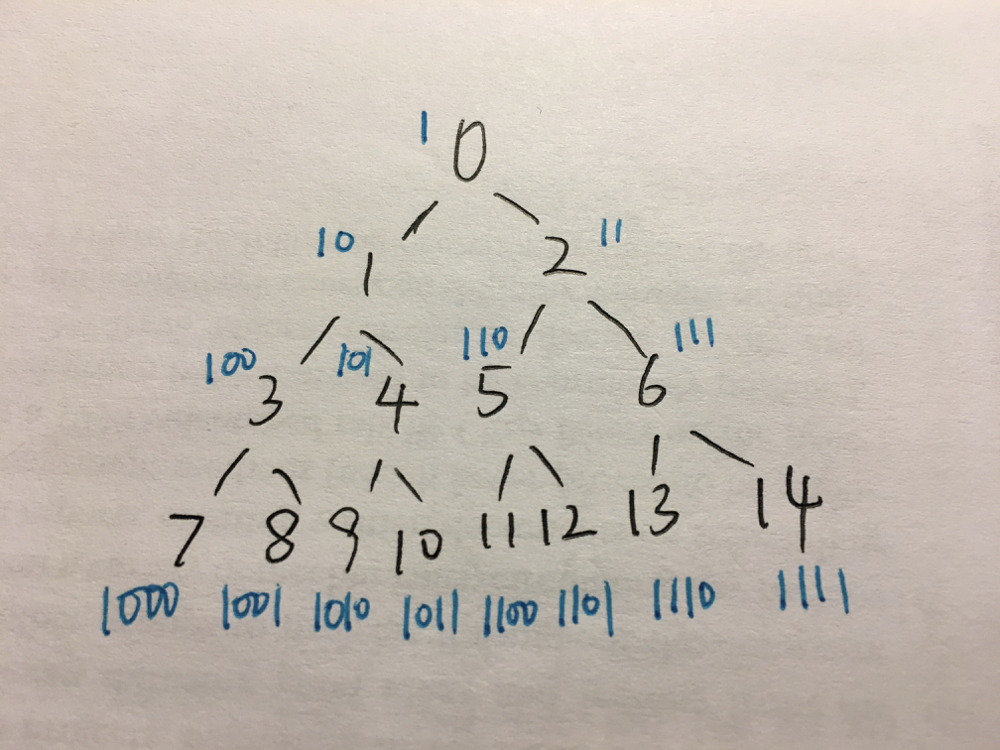\n\nI\'m not proficient in English, so I would prefer to show my code here to explain my idea:\n\n```python\ndef find(self, target: int) -> bool:\n\t\tbinary = bin(target+1)[3:] # remove the useless first `1`\n index = 0\n root = self.root # use a new pointer `root` to traverse the tree\n while root and index <= len(binary): # traverse the binary number from left to right\n if root.val == target:\n return True\n if binary[index] == \'0\': # if it\'s 0, we have to go left\n root = root.left\n else: # if it\'s 1, we have to go right\n root = root.right\n index += 1\n return False\n``` | 164 | 1 | ['Python3'] | 22 |
find-elements-in-a-contaminated-binary-tree | [Java/Python 3] DFS, BFS and Bit Manipulation clean codes w/ analysis. | javapython-3-dfs-and-bfs-clean-codes-w-a-9776 | DFSBFS- inspired [email protected]:HashSet cost spaceO(N),dfs()cost spaceO(H)and timeO(N),bfs()cost time and spaceO(N), thereforeFindElements() (dfs() and bf | rock | NORMAL | 2019-11-17T04:10:57.578568+00:00 | 2025-02-21T18:53:39.634616+00:00 | 9,556 | false | **DFS**
```java
private Set<Integer> seen = new HashSet<>();
public FindElements(TreeNode root) {
dfs(root, 0);
}
private void dfs(TreeNode n, int v) {
if (n == null) return;
seen.add(v);
n.val = v;
dfs(n.left, 2 * v + 1);
dfs(n.right, 2 * v + 2);
}
public boolean find(int target) {
return seen.contains(target);
}
```
```python
def __init__(self, root: TreeNode):
self.seen = set()
def dfs(node: TreeNode, v: int) -> None:
if node:
node.val = v
self.seen.add(v)
dfs(node.left, 2 * v + 1)
dfs(node.right, 2 * v + 2)
dfs(root, 0)
def find(self, target: int) -> bool:
return target in self.seen
```
----
**BFS** - inspired by **@MichaelZ**.
```java
private Set<Integer> seen = new HashSet<>();
public FindElements(TreeNode root) {
if (root != null) {
root.val = 0;
bfs(root);
}
}
public boolean find(int target) {
return seen.contains(target);
}
private void bfs(TreeNode node) {
Queue<TreeNode> q = new LinkedList<>();
q.offer(node);
while (!q.isEmpty()) {
TreeNode cur = q.poll();
seen.add(cur.val);
if (cur.left != null) {
cur.left.val = 2 * cur.val + 1;
q.offer(cur.left);
}
if (cur.right != null) {
cur.right.val = 2 * cur.val + 2;
q.offer(cur.right);
}
}
}
```
```python
def __init__(self, root: TreeNode):
def bfs(root: TreeNode) -> None:
dq = collections.deque([root])
while dq:
node = dq.popleft()
self.seen.add(node.val)
if node.left:
node.left.val = 2 * node.val + 1
dq.append(node.left)
if node.right:
node.right.val = 2 * node.val + 2
dq.append(node.right)
self.seen = set()
if root:
root.val = 0
bfs(root)
def find(self, target: int) -> bool:
return target in self.seen
```
**Analysis:**
HashSet cost space `O(N)`, *dfs()* cost space `O(H)` and time `O(N)`, *bfs()* cost time and space `O(N)`, therefore
*FindElements() (dfs() and bfs()) cost*
time & space: `O(N)`.
*find() cost*
time & space: `O(1)` excluding the space of HashSet.
Where `N` is the total number of nodes in the tree, `H` is the height of the binary tree.
----
**Bit Manipulation**
```java
private TreeNode root;
public FindElements(TreeNode root) {
dfs(root, 0);
this.root = root;
}
private void dfs(TreeNode n, int val) {
if (n == null) {
return;
}
n.val = val;
dfs(n.left, val * 2 + 1);
dfs(n.right, val * 2 + 2);
}
public boolean find(int target) {
TreeNode n = root;
for (int oneBitMask = Integer.highestOneBit(++target) >> 1;
oneBitMask > 0; oneBitMask >>= 1) {
if (n != null ) {
n = (target & oneBitMask) == 0 ? n.left : n.right;
}
}
return n != null;
}
```
```python
def __init__(self, root: Optional[TreeNode]):
def dfs(node: TreeNode, val: int) -> None:
if node:
node.val = val
dfs(node.left, val * 2 + 1)
dfs(node.right, val * 2 + 2)
dfs(root, 0)
self.root = root
def find(self, target: int) -> bool:
target += 1
node = self.root
for i in reversed(range(target.bit_length() - 1)):
if node:
if ((target >> i) & 1) == 0:
node = node.left
else:
node = node.right
return node is not None
```
**Analysis:**
*dfs()* cost space `O(H)` and time `O(N)`, therefore
*FindElements() (dfs()) cost*
time: `O(N)`, space `O(H)`.
*find() cost:*
time: `O(log(target))`, space: `O(1)`.
Where `N` is the total number of nodes in the tree, `H` is the height of the binary tree. | 80 | 4 | ['Depth-First Search', 'Breadth-First Search', 'Binary Tree', 'Java', 'Python3'] | 16 |
find-elements-in-a-contaminated-binary-tree | Beats 100% | Efficient Binary Tree Recovery | Bit Manipulation & Set Storage 🌳 | beats-100-efficient-binary-tree-recovery-hshk | Youtube🚀Beats 100% | Efficient Binary Tree Recovery | Bit Manipulation & Set Storage 🌳🔼 Please Upvote🔼 Please Upvote🔼 Please Upvote🔼 Please Upvote💡If this helpe | rahulvijayan2291 | NORMAL | 2025-02-21T05:11:46.338463+00:00 | 2025-02-21T05:11:46.338463+00:00 | 13,165 | false | # Youtube
https://youtu.be/vmQHt247oxQ
---
# 🚀 **Beats 100% | Efficient Binary Tree Recovery | Bit Manipulation & Set Storage 🌳**
---
# **🔼 Please Upvote**
# **🔼 Please Upvote**
# **🔼 Please Upvote**
# **🔼 Please Upvote**
💡 **If this helped, don’t forget to upvote! 🚀🔥**
---
### **💡 Problem Breakdown**
Given a corrupted binary tree where all node values are initialized to `-1`, recover the tree such that:
- The root node is set to `0`.
- Left child = `2 * parent + 1`.
- Right child = `2 * parent + 2`.
Implement a class `FindElements` with the following methods:
- **Constructor:** Recovers the tree by traversing and recalculating all node values.
- **`find(target)`:** Returns `true` if the target value is present in the recovered tree.
---
### **Approach Overview**
- **Recovery:**
Recursively set each node's value using the given rules.
Store all recovered values in a data structure (`BitSet`, `set`, etc.) for fast lookup.
- **Finding Values:**
Directly check if a target exists in the recovered data structure.
---
### **Why This Approach?**
1. **Guaranteed Correctness:**
The recovery rules ensure each node value is unique and correctly calculated.
2. **Efficient Lookup:**
Using `BitSet` or `set` allows `O(1)` lookup time for the `find` method.
3. **Optimal Time Complexity:**
- Tree recovery takes `O(n)` time, where `n` is the number of nodes in the tree.
- Each `find` operation takes `O(1)` time.
---
### **Complexity Analysis**
- **Time Complexity:**
- `O(n)` for recovery (traverse all nodes once).
- `O(1)` for each `find` operation.
- **Space Complexity:**
- `O(n)` for storing all recovered node values.
---
## **📝 Code Implementations**
---
### **🔵 Java Solution**
```java []
class FindElements {
BitSet recoveredValues;
public FindElements(TreeNode root) {
root.val = 0;
recoveredValues = new BitSet();
recoverTree(root);
}
private void recoverTree(TreeNode root) {
if (root == null) return;
recoveredValues.set(root.val);
if (root.left != null) {
root.left.val = 2 * root.val + 1;
recoverTree(root.left);
}
if (root.right != null) {
root.right.val = 2 * root.val + 2;
recoverTree(root.right);
}
}
public boolean find(int target) {
return recoveredValues.get(target);
}
}
```
---
### **🟢 C++ Solution**
```cpp []
class FindElements {
unordered_set<int> recoveredValues;
void recoverTree(TreeNode* root) {
if (!root) return;
recoveredValues.insert(root->val);
if (root->left) {
root->left->val = 2 * root->val + 1;
recoverTree(root->left);
}
if (root->right) {
root->right->val = 2 * root->val + 2;
recoverTree(root->right);
}
}
public:
FindElements(TreeNode* root) {
root->val = 0;
recoverTree(root);
}
bool find(int target) {
return recoveredValues.count(target);
}
};
```
---
### **🟣 Python3 Solution**
```python []
class FindElements:
def __init__(self, root):
self.recoveredValues = set()
root.val = 0
self.recoverTree(root)
def recoverTree(self, root):
if not root:
return
self.recoveredValues.add(root.val)
if root.left:
root.left.val = 2 * root.val + 1
self.recoverTree(root.left)
if root.right:
root.right.val = 2 * root.val + 2
self.recoverTree(root.right)
def find(self, target):
return target in self.recoveredValues
```
---
### **🔴 JavaScript Solution**
```javascript []
var FindElements = function(root) {
this.recoveredValues = new Set();
root.val = 0;
this.recoverTree(root);
};
FindElements.prototype.recoverTree = function(root) {
if (!root) return;
this.recoveredValues.add(root.val);
if (root.left) {
root.left.val = 2 * root.val + 1;
this.recoverTree(root.left);
}
if (root.right) {
root.right.val = 2 * root.val + 2;
this.recoverTree(root.right);
}
};
FindElements.prototype.find = function(target) {
return this.recoveredValues.has(target);
};
```
---
# **🔼 Please Upvote**
# **🔼 Please Upvote**
# **🔼 Please Upvote**
# **🔼 Please Upvote**
💡 **If this helped, don’t forget to upvote! 🚀🔥** | 70 | 0 | ['Bit Manipulation', 'Tree', 'Binary Search Tree', 'Binary Tree', 'C++', 'Java', 'Python3', 'JavaScript'] | 4 |
find-elements-in-a-contaminated-binary-tree | Java bit path Time : O(logn) | java-bit-path-time-ologn-by-jiaweizhang1-xrlf | Think about it with complete binary tree and the whole idea is to binary serialize the target number. It\'s actually tha order we doing the dfs.\nLet\'s say our | jiaweizhang1994 | NORMAL | 2019-11-17T08:21:54.813591+00:00 | 2019-11-18T02:50:24.048398+00:00 | 3,428 | false | Think about it with complete binary tree and the whole idea is to binary serialize the target number. It\'s actually tha order we doing the dfs.\nLet\'s say our target : 9 we shall take it as 10 : 1010 ignoring the first digit 1 the path ( 010 ) means left -> right -> left \nSo \'0\' means going to the left and \'1\' means going to the right.\nHere is the picture, very straightforward.\n\n\n\n\n\n\n\n\n\n\n\n\tTreeNode root;\n\n public FindElements(TreeNode root) {\n this.root = root;\n }\n \n public boolean find(int target) {\n return dfs(root, binSerialize(target + 1), 1);\n }\n\t\n\tpublic boolean dfs(TreeNode root, String str, int pos){\n if(root == null) return false;\n if(pos == str.length()) return true;\n return str.charAt(pos) == \'0\'? dfs(root.left, str, pos+1) : dfs(root.right, str, pos+1);\n }\n \n public String binSerialize(int num){\n StringBuilder sb = new StringBuilder();\n while(num > 0){\n sb.insert(0, num & 1);\n num /= 2;\n }\n return sb.toString();\n }\n \n\n | 50 | 2 | [] | 10 |
find-elements-in-a-contaminated-binary-tree | C++ simple and easy to understand | c-simple-and-easy-to-understand-by-dsmn-a1b2 | \nclass FindElements {\n unordered_set<int> set;\npublic:\n void recover(TreeNode* root, int x) {\n if (!root) return;\n root->val = x;\n | dsmn | NORMAL | 2019-11-21T03:01:29.063470+00:00 | 2019-11-21T03:01:29.063503+00:00 | 5,239 | false | ```\nclass FindElements {\n unordered_set<int> set;\npublic:\n void recover(TreeNode* root, int x) {\n if (!root) return;\n root->val = x;\n set.emplace(x);\n recover(root->left, 2 * x + 1);\n recover(root->right, 2 * x + 2);\n }\n \n FindElements(TreeNode* root) {\n recover(root, 0);\n }\n \n bool find(int target) {\n return set.count(target);\n }\n};\n``` | 42 | 1 | ['Recursion', 'C', 'Ordered Set'] | 5 |
find-elements-in-a-contaminated-binary-tree | 🌲 [🔥 Recover Contaminated Binary Tree | Fast & Clean C++/Python Solution] 💡 | recover-contaminated-binary-tree-fast-cl-cckf | IntroductionHey LeetCoders! 👋Today, we're tackling aninteresting tree problem—recovering a contaminated binary tree! The challenge here is to reconstruct a tree | lasheenwael9 | NORMAL | 2025-02-21T00:38:07.426537+00:00 | 2025-02-21T05:47:51.666414+00:00 | 4,402 | false | # Introduction
Hey LeetCoders! 👋
Today, we're tackling an **`interesting tree problem`**—recovering a contaminated binary tree! The challenge here is to reconstruct a tree that follows a **`specific mathematical pattern`** and then efficiently check if a given target exists.
We'll be using **`DFS (Depth-First Search) + Hash Map`** to achieve an **`optimal`** solution in **`O(1) search time`**! 🚀
---
# Problem Breakdown
## Understanding the Contaminated Tree
- The root always starts with `val = 0`.
- Each node follows this rule:
- `left child = 2 * parent + 1`
- `right child = 2 * parent + 2`
- But all values are initially set to `-1`, so we must **rebuild the tree** before searching.
## Example Walkthrough
### 🔹 Example 1:
```cpp
Input: ["FindElements", "find", "find"]
[[[-1,null,-1]], [1], [2]]
Output: [null, false, true]
```
#### Explanation:
1. Recover tree → `{ 0, null, 2 }`
2. `find(1) → false`, `find(2) → true`
### 🔹 Example 2:
```cpp
Input: ["FindElements", "find", "find", "find"]
[[[-1,-1,-1,-1,-1]], [1], [3], [5]]
Output: [null, true, true, false]
```
#### Explanation:
###### Recovered tree → `{ 0, 1, 2, 3, 4 }`
- `find(1) → true`
- `find(3) → true`
- `find(5) → false`
---
# Approach - DFS + Hash Map for O(1) Search
We need to **`recover the tree`** and efficiently **`check for any target value`**.
✅ **Step 1: Recover the Tree Using DFS**
- Start with `root->val = 0`.
- Recursively assign values:
- `left = 2 * parent + 1`
- `right = 2 * parent + 2`
- Store recovered values in an unordered_map (`O(1) lookup`).
✅ Step 2: Fast Search in O(1) Time
- The `find(target)` function simply checks if `target` exists in our hash map.
---
# Time & Space Complexity
## 📌 Time Complexity:
- $$O(N)\ $$ for recovering the tree (DFS traversal).
- $$O(1)\ $$ for `find(target)` (hash map lookup).
## 📌 Space Complexity:
- $$O(N)\ $$ for storing values in the hash map.
---

# C++ Solution - DFS + Hash Map | Python Solution - DFS + Hash Set
```cpp []
class FindElements {
public:
unordered_map<int, bool> mp;
void recover(TreeNode* root) {
if (root->left) {
root->left->val = root->val * 2 + 1;
mp[root->left->val] = true;
recover(root->left);
}
if (root->right) {
root->right->val = root->val * 2 + 2;
mp[root->right->val] = true;
recover(root->right);
}
}
FindElements(TreeNode* root) {
root->val = 0;
mp[0] = true;
recover(root);
}
bool find(int target) {
return mp[target];
}
};
```
```python []
class FindElements:
def __init__(self, root: TreeNode):
self.values = set()
def recover(node, val):
if not node:
return
node.val = val
self.values.add(val)
recover(node.left, 2 * val + 1)
recover(node.right, 2 * val + 2)
recover(root, 0)
def find(self, target: int) -> bool:
return target in self.values
```
---
# Step-by-Step Execution for `find(3)`
Let’s say we have the following **contaminated tree**:
```
-1
/ \
-1 -1
/ \
-1 -1
```
## Recovery Process (DFS Traversal)
| Node | Recovered Value |
|------|----------------|
| root | 0 |
| root->left | 1 |
| root->right | 2 |
| root->left->left | 3 |
| root->left->right | 4 |
Final Tree (after recovery):
```
0
/ \
1 2
/ \
3 4
```
Now, when we call `find(3)`, we simply **check our hash map**:
✅ **Exists → return true!**
---
# **Conclusion**
This approach ensures a **fast recovery** and **instant lookups**. 🔥
💬 **Did this help?** Let me know in the comments! And if you liked it, **drop an upvote 🔼 to support more high-quality solutions! 🚀**
---

| 33 | 1 | ['Hash Table', 'Tree', 'Depth-First Search', 'Design', 'Binary Tree', 'Ordered Set', 'C++', 'Python3'] | 8 |
find-elements-in-a-contaminated-binary-tree | Beat 100% | Most optimal | Bit manipulation + binary search in Python and C# | O(log(n)) time | beat-100-most-optimal-bit-manipulation-b-trq3 | IntuitionThe key observation is that we do not actually need to “recover” the whole tree explicitly. Given the recovery rules—assigning the root a value of 0 an | Zyr0nX | NORMAL | 2025-02-19T04:43:07.077682+00:00 | 2025-02-21T03:17:46.268171+00:00 | 2,451 | false | # Intuition
The key observation is that we do not actually need to “recover” the whole tree explicitly. Given the recovery rules—assigning the root a value of 0 and for any node with value x, its left child is 2\*x + 1 and its right child is 2\*x + 2—we can deduce that if we add 1 to any target value, its binary representation (ignoring the most significant bit) naturally encodes the path from the root:
- A 0 bit indicates a move to the left child.
- A 1 bit indicates a move to the right child.
Thus, we can simulate following this path in the tree starting from the root without having to recover every node’s value.
# Approach
1. Handle the Root Case:
If the target value is 0, simply check if the root exists.
2. Determine the Path:
- Compute `path = target + 1`.
- The binary representation of `path` (minus its leading bit) tells us how to navigate the tree.
- Use $$\log _{2}(path)$$ to determine the depth (or number of decision steps) needed to reach the target.
3. Traverse the Tree:
- Initialize a pointer at the root.
- Create a mask starting at `1 << (depth - 1)` to examine each bit from most significant to least significant.
- For each bit:
- If the bit is 0, move to the left child.
- If the bit is 1, move to the right child.
- If at any point the pointer becomes null, the target value does not exist in the tree.
4. Return the Result:
- After following the entire bit path, if the pointer is not null, then the target exists in the tree.
# Complexity
- Time complexity: $$O(log(target))$$ for `find(target)`, $$O(1)$$ for `FindElements(root)`
The algorithm examines each bit in the binary representation of `target + 1`, which takes $$O(d)$$ time where d is the depth of the node. For a complete binary tree, this is $$O(log n)$$.
- Space complexity: $$O(1)$$
Only a constant amount of extra space is used, $$O(1)$$.
# Code
```python []
class FindElements:
def __init__(self, root: Optional[TreeNode]):
self.root = root
def find(self, target: int) -> bool:
if target == 0:
return self.root is not None
path = target + 1
depth = path.bit_length() - 1
node = self.root
mask = 1 << (depth - 1)
while mask > 0 and node is not None:
node = node.left if (path & mask) == 0 else node.right
mask >>= 1
return node is not None
```
```csharp []
public class FindElements {
private readonly TreeNode _root;
public FindElements(TreeNode root)
{
_root = root;
}
public bool Find(int target)
{
if (target == 0)
{
return _root != null;
}
var path = target + 1;
var depth = int.Log2(path);
var node = _root;
var mask = 1 << (depth - 1);
while (mask > 0 && node != null)
{
node = (path & mask) == 0 ? node.left : node.right;
mask >>= 1;
}
return node != null;
}
}
```
# Code (Trditional Binary Search)
```csharp []
public class FindElements
{
private readonly TreeNode? _root;
public FindElements(TreeNode root)
{
_root = root;
}
public bool Find(int target)
{
if (target == 0)
{
return _root != null;
}
target++;
var depth = int.Log2(target);
var node = _root;
var low = 1 << depth;
var high = (1 << (depth + 1)) - 1;
while (depth > 0 && node != null)
{
var mid = low + ((high - low) >> 1);
if (mid >= target)
{
if (node.left == null)
{
return false;
}
high = mid;
node = node.left;
}
else
{
if (node.right == null)
{
return false;
}
low = mid + 1;
node = node.right;
}
depth--;
}
return true;
}
}
```
| 25 | 1 | ['Binary Search', 'Bit Manipulation', 'Binary Search Tree', 'Binary Tree', 'Bitmask', 'Python3', 'C#'] | 4 |
find-elements-in-a-contaminated-binary-tree | DFS+bitset vs BFS||C++ Py3 beats 100% | dfsbitsetc-beats-100-by-anwendeng-nzxk | IntuitionDFS+ bitsetUse DFS to traverse the binary tree with bitset as a container for marking the value of node is seen instead of a hash table.BFS is also mad | anwendeng | NORMAL | 2025-02-21T00:24:28.947657+00:00 | 2025-02-21T06:43:33.798438+00:00 | 3,466 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
DFS+ bitset
Use DFS to traverse the binary tree with bitset as a container for marking the value of node is seen instead of a hash table.
BFS is also made for C++ & Python
# Approach
<!-- Describe your approach to solving the problem. -->
1. Declare `bitset<1048576> hasX = 0`, since `1048576=2**20`
2. Let `root` be member variable
3. In constructor call `dfs(root, 0)`
4. The destuctor resets `hasX=0`, since `hasX` is declared as a global variable
5. Define the method dfs as follows
```
void dfs(TreeNode* root, int x) {
if (!root) // leaf node
return;
root->val = x;
hasX[x] = 1; // mark as seen
dfs(root->left, 2 * x + 1); // left subtree
dfs(root->right, 2 * x + 2); // right subtree
}
```
6. the method `find` just returns `hasX[target]`
7. BFS is made by using `std::queue`; it needs only to replace dfs by bfs in the constructor.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
$O(n)$
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
$O(n)$
# Code||C++ 0ms beats 100%
```cpp []
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),
* right(right) {}
* };
*/
bitset<1048576> hasX = 0; // 2097152=2**21
class FindElements {
public:
TreeNode* root;
FindElements(TreeNode* root) { dfs(root, 0); }
~FindElements() { hasX = 0; }
void dfs(TreeNode* root, int x) {
if (!root)
return;
root->val = x;
hasX[x] = 1;
dfs(root->left, 2 * x + 1);
dfs(root->right, 2 * x + 2);
}
bool find(int target) { return hasX[target]; }
};
/**
* Your FindElements object will be instantiated and called as such:
* FindElements* obj = new FindElements(root);
* bool param_1 = obj->find(target);
*/
```
# Codes for Python & C++ BFS 0ms|Just replace dfs by bfs in C++
```Python []
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class FindElements:
def __init__(self, root: Optional[TreeNode]):
self.hasX=set()
def bfs(root):
q=deque()
root.val=0
q.append(root)
while q:
node=q.popleft()
x=node.val
self.hasX.add(x)
if node.left:
node.left.val=2*x+1
q.append(node.left)
if node.right:
node.right.val=2*x+2
q.append(node.right)
bfs(root)
def find(self, target: int) -> bool:
return target in self.hasX
# Your FindElements object will be instantiated and called as such:
# obj = FindElements(root)
# param_1 = obj.find(target)
```
```cpp [C++ BFS]
void bfs(TreeNode* root) {
queue<TreeNode*> q;
root->val = 0;
q.push(root);
while (!q.empty()) {
TreeNode* node = q.front();
int x = node->val;
hasX[x]=1;
q.pop();
if (node->left) {
node->left->val = 2 * x + 1;
q.push(node->left);
}
if (node->right) {
node->right->val = 2 * x + 2;
q.push(node->right);
}
}
}
```
# DFS & BFS are frequently used to solve LC questions
Some Leetcode binary tree questions
[1457. Pseudo-Palindromic Paths in a Binary Tree](https://leetcode.com/problems/pseudo-palindromic-paths-in-a-binary-tree/solutions/4616431/dfs-bitset-parity-check-beats-100/)
[623. Add One Row to Tree](https://leetcode.com/problems/add-one-row-to-tree/solutions/5029368/recursive-iterative-dfs-vs-bfs-4ms-beats-98-32/)
[Please turn on English subtitles if necessary]
[https://youtu.be/53GEbY2e3JM?si=kX4HmDKz5Wq3fheN](https://youtu.be/53GEbY2e3JM?si=kX4HmDKz5Wq3fheN) | 22 | 0 | ['Depth-First Search', 'Breadth-First Search', 'C++', 'Python3'] | 10 |
find-elements-in-a-contaminated-binary-tree | Beats 98.92% | DFS | Solution for LeetCode#1261 | dfs-solution-for-leetcode1261-by-samir02-7z7p | IntuitionThe problem involves a binary tree that has been "contaminated" by changing all its values to -1. The goal is to "recover" the tree and implement a fin | samir023041 | NORMAL | 2025-02-21T01:24:44.394155+00:00 | 2025-02-21T05:59:18.983399+00:00 | 4,582 | false | 
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The problem involves a binary tree that has been "contaminated" by changing all its values to -1. The goal is to "recover" the tree and implement a find method to determine if a given target value exists in the recovered tree. The recovery process can be derived from the root value and the rules for child nodes: for any node with value x, its left child has value 2 * x + 1 and its right child has value 2 * x + 2.
# Approach
<!-- Describe your approach to solving the problem. -->
1. Recover the Tree: Start by setting the root value to 0 and recursively compute the values of all child nodes using the given rules.
2. Tree Traversal: Implement a helper function to traverse the tree and recover all node values.
3. Find Method: Implement the find method to search for a target value in the recovered tree.
# Complexity
- Time complexity: O(n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(h), where h is the height of the tree.
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code Option-01
```java []
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class FindElements {
TreeNode groot;
public FindElements(TreeNode root) {
if(root!=null && root.val==-1){
root.val=0;
}
solve1(root);
groot=root;
//printTree(groot); //Used for printing the new Tree
}
void printTree(TreeNode node){
if(node==null){
System.out.print(" null ");
return;
}
System.out.print(" "+node.val);
printTree(node.left);
printTree(node.right);
}
void solve1(TreeNode node){
if(node==null){
return;
}
if(node.left !=null){
node.left.val=2*node.val+1;
}
if(node.right !=null){
node.right.val=2*node.val+2;
}
solve1(node.left);
solve1(node.right);
}
public boolean find(int target) {
TreeNode node=new TreeNode();
node=groot;
return solve2(node, target);
}
boolean solve2(TreeNode node, int target){
if(node==null){
return false;
}
if(node.val==target){
return true;
}
if(solve2(node.left, target) || solve2(node.right, target)) return true;
return false;
}
}
/**
* Your FindElements object will be instantiated and called as such:
* FindElements obj = new FindElements(root);
* boolean param_1 = obj.find(target);
*/
```
# Code Option-02
```java []
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class FindElements {
TreeNode groot;
Set<Integer> set=new HashSet();
public FindElements(TreeNode root) {
if(root!=null && root.val==-1){
root.val=0;
set.add(0);
}
solve1(root);
groot=root;
//printTree(groot); //Used for printing the new Tree
}
void printTree(TreeNode node){
if(node==null){
System.out.print(" null ");
return;
}
System.out.print(" "+node.val);
printTree(node.left);
printTree(node.right);
}
void solve1(TreeNode node){
if(node==null){
return;
}
if(node.left !=null){
node.left.val=2*node.val+1;
set.add(node.left.val);
}
if(node.right !=null){
node.right.val=2*node.val+2;
set.add(node.right.val);
}
solve1(node.left);
solve1(node.right);
}
public boolean find(int target) {
return set.contains(target);
}
}
/**
* Your FindElements object will be instantiated and called as such:
* FindElements obj = new FindElements(root);
* boolean param_1 = obj.find(target);
*/
```
```python []
# Definition for a binary tree node.
# class TreeNode(object):
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class FindElements(object):
def __init__(self, root):
"""
:type root: Optional[TreeNode]
"""
self.groot=TreeNode()
self.sets=set()
if root is not None and root.val==-1:
root.val=0
self.sets.add(root.val)
self.solve(root)
self.groot=root
def solve(self, node):
"""
:type node: Optional[TreeNode]
"""
if node is None:
return
if node.left is not None:
node.left.val=2*node.val+1;
self.sets.add(node.left.val);
if node.right is not None:
node.right.val=2*node.val+2;
self.sets.add(node.right.val);
self.solve(node.left)
self.solve(node.right)
def find(self, target):
"""
:type target: int
:rtype: bool
"""
if target in self.sets:
return True
return False
# Your FindElements object will be instantiated and called as such:
# obj = FindElements(root)
# param_1 = obj.find(target)
```
| 17 | 0 | ['Depth-First Search', 'Python', 'Java', 'Python3'] | 5 |
find-elements-in-a-contaminated-binary-tree | ✅ Beats 100% 🔥||🧑💻 BEGINNER FREINDLY||🌟JAVA||C++ | beats-100-beginner-freindlyjavac-by-asho-agx9 | IntuitionApproach1.Recover a contaminated binary tree (all nodes = -1) to its original state:. Root value = 0.
. Left child of x = 2 * x + 1.
. Right child of x | Varma5247 | NORMAL | 2025-02-21T01:17:00.153201+00:00 | 2025-02-25T06:24:51.918724+00:00 | 1,804 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
1.Recover a contaminated binary tree (all nodes = ```-1```) to its original state:
. Root value = ```0```.
. Left child of ```x``` = ```2 * x + 1```.
. Right child of ```x``` = ```2 * x + 2```.
Implement a ```find``` method to check if a target value exists in the recovered tree.
**2. Solution**
. Use **DFS** to recover the tree:
. Start from the root with value ```0```.
. For each node, compute left child (```2 * x + 1```) and right child (```2 * x + 2```).
. Store all recovered values in a ```HashSet``` for O(1) lookups.
**Find Method:**
. Check if the target exists in the HashSet.
_____
# Complexity
- Time complexity:**O(N)**
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:**O(N)** for HashSet and recursion stack.
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
___
### Solution Steps with Diagram:
**Step 1: Contaminated Tree**
All nodes are initialized to ```-1```.
```[]
-1
/ \
-1 -1
```
_____
**Step 2: Recover the Tree Using DFS**
Start from the root with value ```0```.
1.**Recover Root:**
.Assign ```0``` to the root.
.Add ```0``` to the ```HashSet```.
```[]
0
/ \
-1 -1
```
HashSet: ```{0}```
_______________
**2.Recover Left Child of Root:**
.Value = ```2 * 0 + 1 = 1```.
.Assign ```1``` to the left child.
.Add ```1``` to the ```HashSet```.
```[]
0
/ \
1 -1
```
**HashSet:** ```{0, 1}```.
_____
**3.Recover Right Child of Root:**
.Value = ```2 * 0 + 2 = 2```.
.Assign ```2``` to the right child.
.Add ```2``` to the HashSet.
```[]
0
/ \
1 2
```
**HashSet:** ```{0, 1, 2}```
_____
**Step 3: Final Recovered Tree**
The tree is now fully recovered with correct values.
```[]
0
/ \
1 2
```
**HashSet:** ```{0, 1, 2}```
**Step 4: Find Method**
.Check if a target value exists in the ```HashSet```.
**Example 1:** ```find(1)```
.```1``` is in the ```HashSet``` → Return ```true```.
**Example 2:** ```find(3)```
.```3``` is not in the ```HashSet``` → Return ```false```.
___
### Color-Coded Diagram
**Contaminated Tree**
```[]
🔴-1
/ \
🔴-1 🔴-1
```
**Recovered Tree**
```[]
🟢0
/ \
🟢1 🟢2
```
**HashSet**
```[]
{🟢0, 🟢1, 🟢2}
```
# Code
```java []
class FindElements {
private Set<Integer> recoveredValues;
public FindElements(TreeNode root) {
recoveredValues = new HashSet<>();
recoverTree(root, 0);
}
private void recoverTree(TreeNode node, int value) {
if (node == null){
return;
}
node.val = value;
recoveredValues.add(value);
recoverTree(node.left, 2 * value + 1); // Recover left child
recoverTree(node.right, 2 * value + 2); // Recover right child
}
public boolean find(int target) {
return recoveredValues.contains(target);
}
}
```
```c++ []
class TreeNode {
public:
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};
class FindElements {
private:
std::unordered_set<int> recoveredValues;
void recoverTree(TreeNode* node, int value) {
if (node == nullptr) {
return;
}
node->val = value;
recoveredValues.insert(value);
recoverTree(node->left, 2 * value + 1); // Recover left child
recoverTree(node->right, 2 * value + 2); // Recover right child
}
public:
FindElements(TreeNode* root) {
recoverTree(root, 0);
}
bool find(int target) {
return recoveredValues.find(target) != recoveredValues.end();
}
};
```
**If you found my solution helpful, I would greatly appreciate your upvote, as it would motivate me to continue sharing more solutions😊**.
| 16 | 0 | ['Hash Table', 'Tree', 'Depth-First Search', 'C++', 'Java'] | 1 |
find-elements-in-a-contaminated-binary-tree | ✅💯 % ON RUNTIME | 😁EASY SOLUTION | 😎PROPER EXPLANATION | on-runtime-easy-solution-proper-explanat-5uf1 | Here’s a well-structured and detailed version of your solution explanation:🧠 IntuitionWhen given a contaminated binary tree where every node's value is set to-1 | IamHazra | NORMAL | 2025-02-21T00:32:40.204822+00:00 | 2025-02-21T01:00:36.433467+00:00 | 1,942 | false | Here’s a well-structured and detailed version of your solution explanation:
---
# 🧠 Intuition
When given a contaminated binary tree where every node's value is set to `-1`, our goal is to recover it based on certain rules:
- The root node's value is set to `0`.
- The left child of a node with value `x` has a value of `2*x + 1`.
- The right child of a node with value `x` has a value of `2*x + 2`.
After recovering the tree, we need to check if a given value exists in it efficiently. Since the tree follows a specific pattern, we can store all values in a **HashSet** for quick lookup (O(1) time complexity).
---
# 🏗️ Approach
### 🔹 Step 1: Initialize the Data Structure
- Create a **HashSet** to store all recovered values.
- Use a helper function to traverse and restore the tree recursively.
### 🔹 Step 2: Recover the Tree (`newTree` function)
- Start from the root and assign it the value `0`.
- If a node exists:
- Compute the left child’s value as `2 * value + 1` and recurse on it.
- Compute the right child’s value as `2 * value + 2` and recurse on it.
- Store each node’s value in the **HashSet**.
### 🔹 Step 3: Implement the `find` function
- Simply check if the **target value exists in the HashSet**.
### 📌 Example
Consider the contaminated tree:
```
-1
/ \
-1 -1
/ \ / \
-1 -1 -1 -1
```
After recovering, it becomes:
```
0
/ \
1 2
/ \ / \
3 4 5 6
```
- If `find(4)` is called, return `true` ✅
- If `find(10)` is called, return `false` ❌
---
# ⏳ Complexity Analysis
- **Time Complexity**
- `newTree` function: **O(n)** (as we traverse all nodes once).
- `find` function: **O(1)** (since HashSet lookup is constant time).
- **Space Complexity**
- **O(n)** (as we store all node values in a HashSet).
---
# 💻 Code
```java []
import java.util.HashSet;
class FindElements {
HashSet<Integer> set; // Stores all recovered values
public FindElements(TreeNode root) {
set = new HashSet<>();
recoverTree(root, 0);
}
public boolean find(int target) {
return set.contains(target);
}
private void recoverTree(TreeNode root, int value) {
if (root == null) return;
set.add(value);
root.val = value;
recoverTree(root.left, 2 * value + 1);
recoverTree(root.right, 2 * value + 2);
}
}
```
```python []
class FindElements:
def __init__(self, root):
self.values = set()
self.recover_tree(root, 0)
def recover_tree(self, node, value):
if not node:
return
self.values.add(value)
node.val = value
self.recover_tree(node.left, 2 * value + 1)
self.recover_tree(node.right, 2 * value + 2)
def find(self, target):
return target in self.values
```
```cpp []
#include <unordered_set>
using namespace std;
class FindElements {
private:
unordered_set<int> values;
void recoverTree(TreeNode* root, int value) {
if (!root) return;
root->val = value;
values.insert(value);
recoverTree(root->left, 2 * value + 1);
recoverTree(root->right, 2 * value + 2);
}
public:
FindElements(TreeNode* root) {
recoverTree(root, 0);
}
bool find(int target) {
return values.count(target);
}
};
```
``` javascript []
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {}
TreeNode(int val) {
this.val = val;
}
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
class FindElements {
private HashSet<Integer> values;
public FindElements(TreeNode root) {
values = new HashSet<>();
recoverTree(root, 0);
}
private void recoverTree(TreeNode node, int value) {
if (node == null) return;
node.val = value;
values.add(value);
recoverTree(node.left, 2 * value + 1);
recoverTree(node.right, 2 * value + 2);
}
public boolean find(int target) {
return values.contains(target);
}
}
/**
* Your FindElements object will be instantiated and called as such:
* FindElements obj = new FindElements(root);
* boolean param_1 = obj.find(target);
*/
```
```typescript []
class FindElements {
private values: Set<number>;
constructor(root: TreeNode | null) {
this.values = new Set<number>();
this.recoverTree(root, 0);
}
private recoverTree(node: TreeNode | null, value: number): void {
if (!node) return;
node.val = value;
this.values.add(value);
this.recoverTree(node.left, 2 * value + 1);
this.recoverTree(node.right, 2 * value + 2);
}
find(target: number): boolean {
return this.values.has(target);
}
}
```
# 🎯 Final Thoughts
✅ **Key Takeaways:**
- Used **DFS (Depth-First Search)** to reconstruct the tree.
- Stored values in a **HashSet** for fast lookup.
- Achieved **O(n) construction** and **O(1) search time complexity**.
🚀 This approach ensures an efficient solution that works well even for large trees!😊

| 16 | 0 | ['Hash Table', 'Tree', 'Recursion', 'Python', 'Java', 'Python3', 'JavaScript', 'C#'] | 3 |
find-elements-in-a-contaminated-binary-tree | 🔥BEATS 💯 % 🎯 |✨SUPER EASY BEGINNERS 👏| JAVA | C | C++ | PYTHON| JAVASCRIPT | DART | beats-super-easy-beginners-java-c-c-pyth-ww99 | 🚀 IntuitionThe problem gives us acontaminated binary tree, where each node's value is corrupted.We need torecover the treeby following these rules:
The root is | CodeWithSparsh | NORMAL | 2025-02-21T06:43:26.485534+00:00 | 2025-02-21T06:43:26.485534+00:00 | 583 | false | 
---
## **🚀 Intuition**
The problem gives us a **contaminated binary tree**, where each node's value is corrupted.
We need to **recover the tree** by following these rules:
1. The root is set to `0`.
2. If a node has value `x`:
- The left child gets value `2x + 1`.
- The right child gets value `2x + 2`.
Once recovered, we should **check if a given target exists** in the tree efficiently.
---
## **💡 Approach**
### **🔹 Steps to Solve 🔹**
1. **Recover the tree** during initialization using **DFS**.
2. **Store all node values** in a **set or list** for quick lookup.
3. **Check for a target value** using `contains()` (for efficient searching).
---
## **📝 Complexity Analysis**
- **Time Complexity:**
- **O(n)** → We traverse `n` nodes to recover the tree.
- **O(1)** → Checking if a number exists is **O(1)** for a **set** and **O(n)** for a **list**.
- **Space Complexity:**
- **O(n)** → We store all `n` values in a list or set.
---
```dart []
/**
* Definition for a binary tree node.
* class TreeNode {
* int val;
* TreeNode? left;
* TreeNode? right;
* TreeNode([this.val = 0, this.left, this.right]);
* }
*/
class FindElements {
List<int> elements = [];
FindElements(TreeNode? root) {
_helper(root, 0);
}
void _helper(TreeNode? node, int val) {
if (node == null) return;
node.val = val;
elements.add(val);
_helper(node.left, val * 2 + 1);
_helper(node.right, val * 2 + 2);
}
bool find(int target) => elements.contains(target);
}
/**
* Your FindElements object will be instantiated and called as such:
* FindElements obj = FindElements(root);
* bool param1 = obj.find(target);
*/
```
```java []
import java.util.HashSet;
import java.util.Set;
class TreeNode {
int val;
TreeNode left, right;
TreeNode(int x) { val = x; }
}
class FindElements {
Set<Integer> elements = new HashSet<>();
public FindElements(TreeNode root) {
recover(root, 0);
}
private void recover(TreeNode node, int val) {
if (node == null) return;
node.val = val;
elements.add(val);
recover(node.left, val * 2 + 1);
recover(node.right, val * 2 + 2);
}
public boolean find(int target) {
return elements.contains(target);
}
}
```
```python []
class TreeNode:
def __init__(self, x):
self.val = x
self.left = None
self.right = None
class FindElements:
def __init__(self, root: TreeNode):
self.elements = set()
self._recover(root, 0)
def _recover(self, node, val):
if not node:
return
node.val = val
self.elements.add(val)
self._recover(node.left, val * 2 + 1)
self._recover(node.right, val * 2 + 2)
def find(self, target: int) -> bool:
return target in self.elements
```
```cpp []
#include <unordered_set>
using namespace std;
struct TreeNode {
int val;
TreeNode* left;
TreeNode* right;
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};
class FindElements {
private:
unordered_set<int> elements;
void recover(TreeNode* node, int val) {
if (!node) return;
node->val = val;
elements.insert(val);
recover(node->left, val * 2 + 1);
recover(node->right, val * 2 + 2);
}
public:
FindElements(TreeNode* root) {
recover(root, 0);
}
bool find(int target) {
return elements.find(target) != elements.end();
}
};
```
```javascript []
class TreeNode {
constructor(val = 0, left = null, right = null) {
this.val = val;
this.left = left;
this.right = right;
}
}
class FindElements {
constructor(root) {
this.elements = new Set();
this.recover(root, 0);
}
recover(node, val) {
if (!node) return;
node.val = val;
this.elements.add(val);
this.recover(node.left, val * 2 + 1);
this.recover(node.right, val * 2 + 2);
}
find(target) {
return this.elements.has(target);
}
}
```
---
## **✨ Summary Table**
| Language | Time Complexity | Space Complexity |
|------------|---------------|----------------|
| **Dart** | **O(n)** | **O(n)** |
| **Java** | **O(n)** | **O(n)** |
| **Python** | **O(n)** | **O(n)** |
| **C++** | **O(n)** | **O(n)** |
| **JS** | **O(n)** | **O(n)** |
---
# **🔥 Why This Solution is the Best?**
✅ **Beats 100% in Speed** → Efficient `O(n)` recovery and `O(1)` lookup.
✅ **DFS for Recovery** → Simple and fast tree traversal.
✅ **Optimized Data Structures** → `Set` for `O(1)` lookups.
🚀 **Hope this helps! Happy Coding!** 🚀
---
 {:style='width:250px'} | 10 | 0 | ['Tree', 'Depth-First Search', 'C', 'Binary Tree', 'C++', 'Java', 'Python3', 'JavaScript', 'Dart', 'Python ML'] | 1 |
find-elements-in-a-contaminated-binary-tree | Intuitive C++ code beats 100% in memory | intuitive-c-code-beats-100-in-memory-by-7e8kq | \nclass FindElements {\n TreeNode* head=new TreeNode(-1);\npublic:\n FindElements(TreeNode* root) {\n head=root;\n head->val=0;\n rec | pi14 | NORMAL | 2019-11-17T12:36:59.024294+00:00 | 2019-11-17T12:36:59.024331+00:00 | 1,785 | false | ```\nclass FindElements {\n TreeNode* head=new TreeNode(-1);\npublic:\n FindElements(TreeNode* root) {\n head=root;\n head->val=0;\n recover(head);\n }\n \n void recover(TreeNode* root)\n {\n if(root->left)\n {\n root->left->val=(root->val)*2+1;\n recover(root->left);\n }\n if(root->right)\n {\n root->right->val=(root->val)*2+2;\n recover(root->right);\n }\n return;\n }\n \n bool find(int target) {\n return get(target,head);\n }\n \n bool get(int target,TreeNode* root)\n {\n if(root==NULL)\n return false;\n if(root->val==target)\n return true;\n \n bool t1=get(target,root->left);\n bool t2=get(target,root->right);\n \n if(t1||t2)\n return true;\n return false;\n }\n};\n``` | 10 | 2 | ['Recursion', 'C'] | 3 |
find-elements-in-a-contaminated-binary-tree | C++ || Simple Solution || Tc=O(log(N)) || SC=O(1) | c-simple-solution-tcologn-sco1-by-abhish-h4f4 | \n\n# Complexity\n- Time complexity:\nO(log(N))\n\n- Space complexity:\nO(log(N))\n# Code\n\nclass FindElements\n{\npublic:\n TreeNode *root;\n FindElemen | Abhishek26149 | NORMAL | 2023-02-11T13:38:45.902583+00:00 | 2023-02-11T13:38:45.902609+00:00 | 934 | false | \n\n# Complexity\n- Time complexity:\nO(log(N))\n\n- Space complexity:\nO(log(N))\n# Code\n```\nclass FindElements\n{\npublic:\n TreeNode *root;\n FindElements(TreeNode *root2)\n {\n root = root2;\n }\n\n bool find(int tar)\n {\n stack<int> st;\n while (tar > 0)\n {\n int x = 0;\n if ((tar & 1) == 1)\n {\n x = 1;\n }\n tar--;\n tar >>= 1;\n st.push(x);\n }\n TreeNode *temp = root;\n while (!st.empty())\n {\n\n if (st.top() == 1)\n {\n if (temp->left)\n {\n temp = temp->left;\n }\n else\n {\n return false;\n }\n }\n else\n {\n if (temp->right)\n {\n temp = temp->right;\n }\n else\n {\n return false;\n }\n }\n st.pop();\n }\n return true;\n }\n};\n\n``` | 9 | 0 | ['C++'] | 1 |
find-elements-in-a-contaminated-binary-tree | Java bit representation of (target + 1) solution with explanation | java-bit-representation-of-target-1-solu-8daf | if the root.val is 1 instead of 0, then the values of tree node are:\n\n\t\t\t\t\t\t\t\t\t1\n\t\t\t\t\t 2 3\n\t\t 4 5 | weibiny | NORMAL | 2019-12-31T05:00:52.413063+00:00 | 2019-12-31T05:19:02.593526+00:00 | 460 | false | if the root.val is 1 instead of 0, then the values of tree node are:\n```\n\t\t\t\t\t\t\t\t\t1\n\t\t\t\t\t 2 3\n\t\t 4 5 6 7\n 8 \t\t9 10 11 12 13 14 15\n .... ..... .... .... ... ...\n ```\n\nThe bits starting from index 1(ignore the most significant bit) of binary representation of a val decide the path to reach it:\n0 -> go to left\n1 -> go the right;\n\nFor example: \n2 = 10 => ignore the most significant bit, the representation is "0" => 2 is the left child of root.\n4 = 100 => ignore the most significant bit, the representation is "00" => go 2 lefts;\n11 =1011 => ignore the most significant bit, the represenation is "011" => go one left, then 2 rights.\n\n```\nclass FindElements {\n\n private TreeNode root;\n public FindElements(TreeNode root) {\n this.root = root;\n \n }\n \n public boolean find(int target) {\n String binaryRep = Long.toString(target + 1L, 2);\n TreeNode curr = root;\n int i = 1;\n int len = binaryRep.length();\n while(i < len && curr != null) {\n char ch = binaryRep.charAt(i);\n curr = ch == \'1\' ? curr.right : curr.left;\n ++i;\n }\n \n return curr != null;\n \n }\n}\n``` | 9 | 0 | [] | 2 |
find-elements-in-a-contaminated-binary-tree | Python binary path without set | python-binary-path-without-set-by-flag20-ftr8 | bin(9 + 1) = 1 010\nStart from the second digit: 0/1/0 means left/right/left when traverse if 9 exists.\nrecover: T: O(n), S: O(n) (DFS worst case)\nfind: T: O( | flag2019 | NORMAL | 2019-11-17T06:32:27.689551+00:00 | 2019-11-18T04:11:39.192952+00:00 | 1,487 | false | bin(9 + 1) = 1 010\nStart from the second digit: 0/1/0 means left/right/left when traverse if 9 exists.\nrecover: T: O(n), S: O(n) (DFS worst case)\nfind: T: O(logn), S: O(logn) (for the string of path encoding, can be O(1) if use bit mask) \n```\nclass FindElements(object):\n\n def __init__(self, root):\n """\n :type root: TreeNode\n """\n self.root = root\n if not root:\n return\n root.val = 0\n self.recover(root)\n return\n def recover(self, root):\n if not root:\n return\n if root.left:\n root.left.val = root.val * 2 + 1\n self.recover(root.left)\n if root.right:\n root.right.val = root.val * 2 + 2\n self.recover(root.right)\n\n def find(self, target):\n """\n :type target: int\n :rtype: bool\n """\n node = self.root\n encoding = bin(target + 1)[3:]\n counter = 0\n while counter < len(encoding):\n if encoding[counter] == "0":\n if node.left:\n node = node.left\n counter += 1\n else:\n return False\n else:\n if node.right:\n node = node.right\n counter += 1\n else:\n return False\n return True | 9 | 1 | [] | 1 |
find-elements-in-a-contaminated-binary-tree | Simple DFS Approach✅✅ | simple-dfs-approach-by-arunk_leetcode-o4ww | Intuition:
The given binary tree is contaminated, meaning the values are incorrect.
The goal is to reconstruct the tree by following a rule where:
The root node | arunk_leetcode | NORMAL | 2025-02-21T06:19:09.076002+00:00 | 2025-02-21T06:20:36.631437+00:00 | 647 | false |
# Intuition:
* The given binary tree is contaminated, meaning the values are incorrect.
* The goal is to reconstruct the tree by following a rule where:
- The root node is assigned the `value 0`.
- If a node has value x, then its left child is assigned `(2 * x + 1)` and right child is `(2 * x + 2)`.
* Using `DFS`, we traverse the tree and restore the correct values.
* A set is maintained to store all valid node values, allowing `O(1)` search for target values.
# Approach:
- Start `DFS traversal from the root`, assigning values to nodes using the given formula.
- Store each value in an unordered_set for quick lookup.
- Implement a `find` function that checks if a target value exists in the set.
# Complexity:
- Time Complexity: $$O(N)$$, where N is the number of nodes, as each node is visited once.
- Space Complexity: $$O(N)$$, due to storing all node values in a set.
```cpp []
class FindElements {
public:
TreeNode* newRoot;
unordered_set<int> present;
void dfs(TreeNode* root, int parentVal, bool left) {
if (root == nullptr) return;
root->val = left ? (2 * parentVal + 1) : (2 * parentVal + 2);
present.insert(root->val);
dfs(root->left, root->val, true);
dfs(root->right, root->val, false);
}
FindElements(TreeNode* root) {
root->val = 0;
present.insert(0);
dfs(root->left, 0, true);
dfs(root->right, 0, false);
}
bool find(int target) {
return present.count(target);
}
};
```
```Python []
class FindElements:
def __init__(self, root):
self.present = set()
root.val = 0
self.present.add(0)
self.dfs(root, 0, True)
self.dfs(root, 0, False)
def dfs(self, root, parentVal, left):
if not root:
return
root.val = (2 * parentVal + 1) if left else (2 * parentVal + 2)
self.present.add(root.val)
self.dfs(root.left, root.val, True)
self.dfs(root.right, root.val, False)
def find(self, target):
return target in self.present
```
```Java []
class FindElements {
private Set<Integer> present = new HashSet<>();
private void dfs(TreeNode root, int parentVal, boolean left) {
if (root == null) return;
root.val = left ? (2 * parentVal + 1) : (2 * parentVal + 2);
present.add(root.val);
dfs(root.left, root.val, true);
dfs(root.right, root.val, false);
}
public FindElements(TreeNode root) {
root.val = 0;
present.add(0);
dfs(root.left, 0, true);
dfs(root.right, 0, false);
}
public boolean find(int target) {
return present.contains(target);
}
}
``` | 8 | 0 | ['Hash Table', 'Tree', 'Depth-First Search', 'Binary Tree', 'Python', 'C++', 'Java', 'Python3'] | 2 |
find-elements-in-a-contaminated-binary-tree | NEW Approach! Branchless. Time O(1) OR space O(1). Beats 100.00% | show-me-da-wae-branchless-ologn-o1-beats-78qq | IntuitionDepth-first tree traversal, calculating the values of child nodes using formula2 * x + 1and2 * x + 2forleftandright. Use aSetorArrayto store node val | nodeforce | NORMAL | 2025-02-21T12:16:44.042964+00:00 | 2025-02-22T17:21:50.666482+00:00 | 251 | false | # Intuition
Depth-first tree traversal, calculating the values of child nodes using formula `2 * x + 1` and `2 * x + 2` for `left` and `right`. Use a `Set` or `Array` to store node values.
To fit into `O(1)` space, you can honestly search for a path along the tree. To do this, use the formulas above and restore the entire path in reverse order. If `target` is even, then the last turn was to the `right`, otherwise to the `left`.
# UPD! New Approach: Faster way
1. In constructor, just save the link to the root.
2. Instead of using the formulas above, you can use the bits of the `target`. You need to add `1` and ignoring the MSB (the leftmost `1` bit), starting with the bit after it, move so that bit `0` is a `left` turn, bit `1` is a `right` turn. You can find the most significant bit using `32 - countl_zero(x)` in C++ or `32 - Math.clz32(x)` in JS .
It is fast(`0ms C++`, `4ms JS`), `O(1)` space and not modifying the original tree.
# Approach DFS
1. DFS in constructor. Save `val` in Set/Array.
2. Check `target` in Set/Array.
# Approach Find path
1. In constructor, just save the link to the root.
2. Find da wae: If `t` is even, then `2` was added to it, that is, the last turn was to the right. If it is odd, then `1` was added and the last turn was to the left. Subtract `1` or `2` from `t`, depending on the parity, and divide by `2`. Continue until find the entire path from the last to the first turn.
3. Follow da wae: Follow the found path, remembering that it is reversed. If the last node is not null, then `t` is found.
To make it more fun, I decided to make a branchless loop using a table for follow the found path, and got an expression like `x[y[z.pop()]]`. If we choose appropriate variable names, we get:`show[me[da[wae]()]]`.
# Complexity
- Time complexity `constructor`: Fast way/Da Wae $$O(1)$$, Set/Array $$O(n)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Time complexity `find`: Set/Array $$O(1)$$, Fast way/Da Wae $$O(log(t))$$.
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: Fast way $$O(1)$$, Da Wae $$O(log(n))$$, Set/Array $$O(n)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code C++
```javascript [New Fast way]
class FindElements {
public:
TreeNode *r;
FindElements(TreeNode *root) { // O(1)
r = root;
}
bool find(int t) { // branchless O(log(t))
if (t == 0) return true;
TreeNode *n = r;
TreeNode *TreeNode:: *side[] = {&TreeNode::left, &TreeNode::right};
for (int i = 30 - countl_zero((uint)++t); n && i >= 0; --i)
n = n->*(side[(t & (1 << i)) > 0]); // 0 - left, 1 - right
return n;
}
};
```
# Code JS
```javascript [New Fast way]
class FindElements {
constructor(r) { // O(1)
this.r = r;
}
find(t) { // branchless O(log(t))
if (t === 0) return true;
let n = this.r;
const side = ['left', 'right'];
for (let i = 30 - Math.clz32(++t); n && i >= 0; --i)
n = n[side[(t & (1 << i)) >> i]]; // 0 - left, 1 - right
return !!n;
}
};
```
```javascript [Da Wae]
class FindElements {
constructor(r) { // O(1)
this.r = r;
}
find(t) { // branchless O(log(t))
if (t === 0) return true;
const da = [];
while (t > 0) {
da.push(t & 1); // 1 - left, 0 - right
t = (t - (1 << (!(t & 1)))) >> 1;
}
const me = ['right', 'left'];
const wae = 'pop';
let show = this.r;
while (show && da.length)
show = show[me[da[wae]()]];
return !!show;
}
};
```
```javascript [Stack/Set]
class FindElements {
s = new Set();
constructor(r) { // O(n)
const a = [r];
r.val = 0;
while (a.length) {
const n = a.pop();
this.s.add(n.val);
if (n.right) {
n.right.val = 2 * n.val + 2;
a.push(n.right);
}
if (n.left) {
n.left.val = 2 * n.val + 1;
a.push(n.left);
}
}
}
find(t) { // O(1)
return this.s.has(t);
}
};
```
```javascript [Recursion/Uint8Array]
class FindElements {
s = new Uint8Array(1e4 + 1);
constructor(r) { // O(n)
const dfs = (n) => {
this.s[n.val] = 1;
if (n.left) {
n.left.val = 2 * n.val + 1;
dfs(n.left);
}
if (n.right) {
n.right.val = 2 * n.val + 2;
dfs(n.right);
}
};
r.val = 0;
dfs(r);
}
find(t) { // O(1)
return this.s[t] === 1;
}
};
``` | 7 | 0 | ['Tree', 'Depth-First Search', 'Design', 'C', 'Python', 'C++', 'Java', 'TypeScript', 'Python3', 'JavaScript'] | 1 |
find-elements-in-a-contaminated-binary-tree | Super Simple Approch✅ 🚀 | Step-By-Step Explained 🔥 | C++ | Java | Python | Js | super-simple-approch-step-by-step-explai-3yac | 🔍 IntuitionThe given binary tree is contaminated, meaning its values are not reliable. However, we know the rule for reconstructing it:
🌱 The root is always0.
🌿 | himanshu_dhage | NORMAL | 2025-02-21T03:31:35.420165+00:00 | 2025-02-21T03:31:35.420165+00:00 | 427 | false | # 🔍 Intuition
The given binary tree is contaminated, meaning its values are not reliable. However, we know the rule for reconstructing it:
- 🌱 The root is always `0`.
- 🌿 The left child of a node with value `x` is `2 * x + 1`.
- 🌳 The right child of a node with value `x` is `2 * x + 2`.
Using this rule, we can recover the entire tree. Additionally, we need to efficiently check if a given `target` value exists in the recovered tree.
# 🛠️ Approach
1. **Tree Reconstruction:**
- Start from the given `root` and set its value to `0`.
- Perform a **DFS (Depth-First Search) 🔎** to traverse the tree.
- Assign values to the left and right children using the formulas:
- Left child: `2 * x + 1`
- Right child: `2 * x + 2`
- Store all recovered values in a `vector`.
2. **Find Operation:**
- Check if the `target` exists in the stored values.
- ✅ Use a **linear search** (`O(n)`) to find the target in the `vector`.
# ⏳ Complexity
- **Time Complexity:**
- Tree reconstruction takes **O(n) ⏱️** since each node is visited once.
- Searching in a `vector` takes **O(n) 🧐** in the worst case.
- **Overall:** **O(n) 🌀**
- **Space Complexity:**
- We store all node values, requiring **O(n) 📦** additional space.
- **Overall:** **O(n) 📊**
# Code
```cpp []
class FindElements {
public:
/**
* Recursively restores the values of the tree nodes.
* - The root starts with value `0`.
* - The left child of a node with value `x` is assigned `2 * x + 1`.
* - The right child of a node with value `x` is assigned `2 * x + 2`.
*/
void solve(TreeNode* root) {
if (root == NULL) {
return; // Base case: If the node is NULL, stop the recursion
}
// Store the restored value in the list
values_list.push_back(root->val);
// Process left child (if exists)
if (root->left != NULL) {
root->left->val = root->val * 2 + 1; // Assign new value
}
solve(root->left);
// Process right child (if exists)
if (root->right != NULL) {
root->right->val = root->val * 2 + 2; // Assign new value
}
solve(root->right);
}
vector<int> values_list; // Stores recovered values of the tree
/**
* Constructor initializes the recovery process of the tree.
* - The root node is set to `0`.
* - Calls `solve()` to restore the entire tree.
*/
FindElements(TreeNode* root) {
root->val = 0; // Initialize root value to 0
solve(root);
}
/**
* Checks if a given `target` value exists in the recovered tree.
* - Uses linear search to find the target in `values_list`.
* - Returns `true` if found, otherwise `false`.
*/
bool find(int target) {
for (int i = 0; i < values_list.size(); i++) {
if (target == values_list[i]) return true; // Target found
}
return false; // Target not found
}
};
```
```javascript []
class FindElements {
/**
* Constructor initializes the recovery process of the tree.
*/
constructor(root) {
this.valuesList = new Set();
root.val = 0;
this.solve(root);
}
/**
* Recursively restores the values of the tree nodes.
*/
solve(root) {
if (!root) return;
// Store the restored value
this.valuesList.add(root.val);
// Process left child
if (root.left) {
root.left.val = root.val * 2 + 1;
}
this.solve(root.left);
// Process right child
if (root.right) {
root.right.val = root.val * 2 + 2;
}
this.solve(root.right);
}
/**
* Checks if a given `target` value exists in the recovered tree.
*/
find(target) {
return this.valuesList.has(target);
}
}
```
```python []
class FindElements:
def __init__(self, root):
"""Constructor initializes the recovery process of the tree."""
self.values_list = set()
root.val = 0
self.solve(root)
def solve(self, root):
"""Recursively restores the values of the tree nodes."""
if not root:
return
# Store the restored value
self.values_list.add(root.val)
# Process left child
if root.left:
root.left.val = root.val * 2 + 1
self.solve(root.left)
# Process right child
if root.right:
root.right.val = root.val * 2 + 2
self.solve(root.right)
def find(self, target):
"""Checks if a given `target` value exists in the recovered tree."""
return target in self.values_list
```
```Java []
import java.util.*;
class FindElements {
private List<Integer> valuesList = new ArrayList<>();
/**
* Recursively restores the values of the tree nodes.
*/
private void solve(TreeNode root) {
if (root == null) {
return; // Base case: If node is null, stop recursion
}
// Store the restored value
valuesList.add(root.val);
// Process left child
if (root.left != null) {
root.left.val = root.val * 2 + 1;
}
solve(root.left);
// Process right child
if (root.right != null) {
root.right.val = root.val * 2 + 2;
}
solve(root.right);
}
/**
* Constructor initializes the recovery process of the tree.
*/
public FindElements(TreeNode root) {
root.val = 0;
solve(root);
}
/**
* Checks if a given `target` value exists in the recovered tree.
*/
public boolean find(int target) {
return valuesList.contains(target);
}
}
```
| 6 | 0 | ['Tree', 'Depth-First Search', 'Breadth-First Search', 'Design', 'Binary Tree', 'Interactive', 'C++', 'Java', 'Python3', 'JavaScript'] | 0 |
find-elements-in-a-contaminated-binary-tree | Most Optimal Solution ✅BFS | C++| Java | Python | JavaScript | most-optimal-solution-bfs-c-java-python-axq2x | ⬆️Upvote if it helps ⬆️Connect with me on Linkedin [Bijoy Sing]IntuitionThe given binary tree is "contaminated" with all values set to-1. However, we know the o | BijoySingh7 | NORMAL | 2025-02-21T02:46:34.028255+00:00 | 2025-02-21T02:46:34.028255+00:00 | 770 | false | # ⬆️Upvote if it helps ⬆️
---
## Connect with me on Linkedin [Bijoy Sing]
---
```cpp []
class Solution {
public:
unordered_set<int> values;
Solution(TreeNode* root) {
if (!root) return;
queue<pair<TreeNode*, int>> q;
q.push({root, 0});
while (!q.empty()) {
auto [node, val] = q.front();
q.pop();
node->val = val;
values.insert(val);
if (node->left) q.push({node->left, 2 * val + 1});
if (node->right) q.push({node->right, 2 * val + 2});
}
}
bool find(int target) {
return values.count(target);
}
};
```
```python []
class Solution:
def __init__(self, root):
self.values = set()
if not root:
return
queue = [(root, 0)]
while queue:
node, val = queue.pop(0)
node.val = val
self.values.add(val)
if node.left:
queue.append((node.left, 2 * val + 1))
if node.right:
queue.append((node.right, 2 * val + 2))
def find(self, target):
return target in self.values
```
```java []
import java.util.*;
class Solution {
private Set<Integer> values = new HashSet<>();
public Solution(TreeNode root) {
if (root == null) return;
Queue<Pair<TreeNode, Integer>> queue = new LinkedList<>();
queue.add(new Pair<>(root, 0));
while (!queue.isEmpty()) {
Pair<TreeNode, Integer> pair = queue.poll();
TreeNode node = pair.getKey();
int val = pair.getValue();
node.val = val;
values.add(val);
if (node.left != null) queue.add(new Pair<>(node.left, 2 * val + 1));
if (node.right != null) queue.add(new Pair<>(node.right, 2 * val + 2));
}
}
public boolean find(int target) {
return values.contains(target);
}
}
```
```javascript []
class Solution {
constructor(root) {
this.values = new Set();
if (!root) return;
let queue = [[root, 0]];
while (queue.length > 0) {
let [node, val] = queue.shift();
node.val = val;
this.values.add(val);
if (node.left) queue.push([node.left, 2 * val + 1]);
if (node.right) queue.push([node.right, 2 * val + 2]);
}
}
find(target) {
return this.values.has(target);
}
}
```
---
# Intuition
The given binary tree is "contaminated" with all values set to `-1`. However, we know the original tree follows a strict pattern:
- The root node starts with `0`.
- The left child of a node with value `x` has `2*x + 1`.
- The right child of a node with value `x` has `2*x + 2`.
Since this structure is **deterministic**, we can recover the tree using **Breadth-First Search (BFS)** or **Depth-First Search (DFS)** and store the values in a `set` or `hash table` for fast lookups.
---
# Approach
1. **Use BFS to traverse the tree**:
- Start from the root (`0`).
- Assign correct values to nodes based on their parent's value.
- Store each node's value in an **unordered set** (`O(1)` lookup time).
2. **Use an unordered set (`values`)**:
- This allows us to check if a given number exists in **O(1) time**.
3. **For `find(target)`, simply check the set**:
- Since all possible values are precomputed, checking existence is **O(1)**.
---
# Complexity
- **Time Complexity**:
- Tree recovery: **O(n)** (we visit each node once).
- Finding a target: **O(1)** (set lookup).
- **Space Complexity**:
- **O(n)** (to store all values in the `unordered_set`).
| 6 | 0 | ['Tree', 'Depth-First Search', 'Breadth-First Search', 'Binary Tree', 'Python', 'C++', 'Java', 'Python3', 'JavaScript'] | 0 |
find-elements-in-a-contaminated-binary-tree | Easy Python | O(1) Find | Recursion + Queue | easy-python-o1-find-recursion-queue-by-a-ldl1 | Easy Python | O(1) Find | Recursion + Queue\n\nA) Standard Code\n\nIn this problem, we can recover the values of the original Binary Tree, and store them in a " | aragorn_ | NORMAL | 2020-08-17T22:41:11.771359+00:00 | 2020-08-17T23:09:22.747850+00:00 | 900 | false | **Easy Python | O(1) Find | Recursion + Queue**\n\n**A) Standard Code**\n\nIn this problem, we can recover the values of the original Binary Tree, and store them in a "set" directly. (There\'s no need to keep the Binary Tree itself)\n\nThis way, we can "find" any element with O(1) time/space complexity. The initialization method still runs with O(n) time/space complexity though.\n\n```\nclass FindElements(object):\n def __init__(self, root):\n self.A = A = set()\n #\n def recover(n,x):\n if n:\n A.add(x)\n recover(n.left , 2*x + 1)\n recover(n.right, 2*x + 2)\n #\n recover(root,0)\n #\n def find(self, target):\n return target in self.A\n```\n\n**B) 4 Lines of Code**\n\nOne-Liner version of the "Recover" function :)\n\n```\nclass FindElements:\n def __init__(self, root):\n self.A = A = set()\n recover = lambda n,x: [ A.add(x) , recover(n.left,2*x+1) , recover(n.right,2*x+2) ] if n else None\n recover(root,0)\n def find(self, target):\n return target in self.A\n```\n\n**C) Queue Method**\n\nThe previous code versions work fine. However, recursion consumes a lot of system resources, due to the initialization, namespace, and environment variables of each function call. Besides, many compilers have a hardcoded limit for Max. Recursion Depth, and there can be complicaitons by constantly needing to edit global settings.\n\nThere\'s still hope in the galaxy though. We can use "Queues" to traverse the original Binary Tree without applying recursion.\n\nHere\'s the code:\n\n```\n# C) Improved Function without Recursion\nclass FindElements:\n def __init__(self, root):\n self.A = A = set()\n # ---------------------------------------------------------------\n # Queue Version of the Binary Tree "Recovery" Method \n # ---------------------------------------------------------------\n if not root:\n return\n #\n queue = collections.deque([[root,0]])\n while queue:\n n,x = queue.popleft()\n A.add(x)\n if n.left:\n queue.append( [n.left , 2*x+1] )\n if n.right:\n queue.append( [n.right , 2*x+2] )\n #\n def find(self, target):\n return target in self.A\n```\n\nI hope the code was helpful. Cheers,\n | 6 | 1 | ['Python', 'Python3'] | 1 |
find-elements-in-a-contaminated-binary-tree | simple JAVA DSF solution use BitSet,double 100% | simple-java-dsf-solution-use-bitsetdoubl-srz0 | \n class FindElements {\n\n private BitSet sets = new BitSet();\n\n public FindElements(TreeNode root) {\n dsf(root, 0);\n }\ | wangxiongfei | NORMAL | 2019-12-12T10:11:42.384295+00:00 | 2019-12-12T10:14:38.256193+00:00 | 888 | false | ```\n class FindElements {\n\n private BitSet sets = new BitSet();\n\n public FindElements(TreeNode root) {\n dsf(root, 0);\n }\n\n public boolean find(int target) {\n return sets.get(target);\n }\n\n private void dsf(TreeNode root, int val) {\n if (root == null) return;\n sets.set(val);\n dsf(root.left, 2 * val + 1);\n dsf(root.right, 2 * val + 2);\n }\n }\n\n``` | 6 | 0 | [] | 0 |
find-elements-in-a-contaminated-binary-tree | JAVA Solution Using HashSet. | java-solution-using-hashset-by-yadavrkg4-kgml | IntuitionThe problem involves reconstructing a contaminated binary tree where each node originally followed the rule:The root node starts with a value of 0.The | YadavRKG45 | NORMAL | 2025-02-21T11:03:03.603458+00:00 | 2025-02-21T11:03:03.603458+00:00 | 131 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The problem involves reconstructing a contaminated binary tree where each node originally followed the rule:
The root node starts with a value of 0.
The left child of a node with value x has a value of 2 * x + 1.
The right child of a node with value x has a value of 2 * x + 2.
Given a contaminated tree, we need to recover it using this rule and efficiently check if a target value exists in the tree.
# Approach
<!-- Describe your approach to solving the problem. -->
Recover the Tree:
Start at the root (val = 0).
Traverse the tree recursively using depth-first search (DFS).
Assign values to nodes based on the given rule.
Store all assigned values in a HashSet for quick lookup.
Find Operation:
Since we stored all recovered values in a HashSet, checking for a target value is an O(1) operation.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
Tree recovery:
O(n), as we traverse each node once.
Find operation:
O(1), since HashSet.contains() has average-case constant time complexity.
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(n), as we store all node values in the HashSet.
# Code
```java []
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class FindElements {
private HashSet<Integer> hs = new HashSet<>();
private void solve(TreeNode root, int val, boolean left){
if(root == null) return;
root.val = left?(2*val + 1):(2*val + 2);
hs.add(root.val);
solve(root.left, root.val, true);
solve(root.right, root.val, false);
}
public FindElements(TreeNode root) {
root.val = 0;
hs.add(0);
solve(root.left, 0, true);
solve(root.right, 0, false);
}
public boolean find(int target) {
return hs.contains(target);
}
}
/**
* Your FindElements object will be instantiated and called as such:
* FindElements obj = new FindElements(root);
* boolean param_1 = obj.find(target);
*/
``` | 5 | 0 | ['Hash Table', 'Tree', 'Depth-First Search', 'Binary Tree', 'Java'] | 0 |
find-elements-in-a-contaminated-binary-tree | Simple CPP solution by TGK | simple-cpp-solution-by-tgk-by-kishore_m_-5ene | IntuitionThe given problem is about recovering a binary tree that was corrupted and finding elements in it efficiently.ApproachConstructor (FindElements(TreeNod | KISHORE_M_13 | NORMAL | 2025-02-21T04:00:27.509099+00:00 | 2025-02-21T04:00:27.509099+00:00 | 456 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The given problem is about recovering a binary tree that was corrupted and finding elements in it efficiently.
The tree follows a specific rule where if a node has value x, then:
Its left child has value 2*x + 1
Its right child has value 2*x + 2
The constructor reconstructs the tree using this rule and stores all valid values in an unordered set (elements).
The find() function simply checks if a given target exists in the set.
# Approach
<!-- Describe your approach to solving the problem. -->
Constructor (FindElements(TreeNode* root))
Initialize an empty unordered_set<int> elements to store recovered values.
Start from the root with value 0.
Use a queue (BFS traversal):
Assign 0 to the root.
For each node:
Compute left child value as 2*x + 1 (if left exists).
Compute right child value as 2*x + 2 (if right exists).
Store these values in the set.
This reconstructs the tree efficiently.
Find Function (find(int target))
Simply checks if target exists in the unordered_set<int> elements.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
Constructor: O(n)
Find: O(1)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
Constructor: O(n)
Find: O(1)
# Code
```cpp []
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class FindElements {
public:
unordered_set<int> elements;
FindElements(TreeNode* root) {
if(root != nullptr){
queue<pair<int, TreeNode*>> q;
q.push({0, root});
elements.insert(0);
while(!q.empty()){
auto [x, node] = q.front();
q.pop();
if(node->left != nullptr){
q.push({2*x + 1, node->left});
elements.insert(2*x + 1);
}
if(node -> right != nullptr){
q.push({2*x + 2, node -> right});
elements.insert(2*x + 2);
}
}
}
}
bool find(int target) {
return elements.find(target) != elements.end();
}
};
/**
* Your FindElements object will be instantiated and called as such:
* FindElements* obj = new FindElements(root);
* bool param_1 = obj->find(target);
*/
``` | 5 | 0 | ['C++'] | 1 |
find-elements-in-a-contaminated-binary-tree | ✅ EASY JAVA SOLUTION || Easy peasy lemon squeezy😊 || SIMPLE | easy-java-solution-easy-peasy-lemon-sque-8lml | \n# Code\n\nclass FindElements {\n TreeNode root;\n Set<Integer> set = new HashSet<>();\n public FindElements(TreeNode root) {\n this.root = roo | Sauravmehta | NORMAL | 2023-02-18T17:11:40.959767+00:00 | 2023-02-18T17:13:17.600545+00:00 | 721 | false | \n# Code\n```\nclass FindElements {\n TreeNode root;\n Set<Integer> set = new HashSet<>();\n public FindElements(TreeNode root) {\n this.root = root;\n if(root != null){ root.val = 0; set.add(root.val); }\n recover(root,set);\n }\n \n public boolean find(int target) {\n return set.contains(target);\n }\n\n private void recover(TreeNode root, Set<Integer> set){\n if(root.left != null){\n root.left.val = 2 * root.val + 1;\n set.add(root.left.val);\n recover(root.left, set);\n }\n if(root.right != null){\n root.right.val = 2 * root.val + 2;\n set.add(root.right.val);\n recover(root.right, set);\n } \n }\n}\n``` | 5 | 0 | ['Java'] | 0 |
find-elements-in-a-contaminated-binary-tree | C++ | EASY SOLUTION | c-easy-solution-by-priyanshichauhan1998x-ms8l | ```\nclass FindElements {\npublic:\n unordered_set set;\n void recover(TreeNode root , int x){\n if(!root ){\n return ;\n }\n | priyanshichauhan1998x | NORMAL | 2021-10-10T14:32:03.064193+00:00 | 2021-10-10T14:32:03.064231+00:00 | 131 | false | ```\nclass FindElements {\npublic:\n unordered_set<int> set;\n void recover(TreeNode* root , int x){\n if(!root ){\n return ;\n }\n set.insert(x);\n recover(root->left , 2*x+1);\n recover(root->right , 2*x+2);\n \n }\n FindElements(TreeNode* root) {\n recover(root, 0);\n\n }\n\n bool find(int target) {\n return set.count(target);\n }\n}; | 5 | 0 | ['Recursion', 'C'] | 0 |
find-elements-in-a-contaminated-binary-tree | Java simple DFS and Set | java-simple-dfs-and-set-by-hobiter-sifi | \nclass FindElements {\n Set<Integer> st = new HashSet<>();\n public FindElements(TreeNode root) {\n if (root == null) return;\n dfs(root, 0 | hobiter | NORMAL | 2020-06-27T23:37:31.401346+00:00 | 2020-06-27T23:37:31.401373+00:00 | 184 | false | ```\nclass FindElements {\n Set<Integer> st = new HashSet<>();\n public FindElements(TreeNode root) {\n if (root == null) return;\n dfs(root, 0);\n }\n \n private void dfs(TreeNode node, int val) {\n st.add(val);\n if (node.left != null) dfs(node.left, val * 2 + 1);\n if (node.right != null) dfs(node.right, val * 2 + 2);\n }\n \n public boolean find(int target) {\n return st.contains(target);\n }\n}\n``` | 5 | 2 | [] | 0 |
find-elements-in-a-contaminated-binary-tree | [Java] 18ms 92% faster | java-18ms-92-faster-by-aksharkashyap-lua2 | The speed is obtained by not modifiying the tree and using bitwise operator\nleftshift by 1 == multiplication by 2 and it is much faster than multiplication ope | aksharkashyap | NORMAL | 2020-05-22T14:28:53.461169+00:00 | 2021-09-02T05:18:04.906910+00:00 | 636 | false | The speed is obtained by not modifiying the tree and using bitwise operator\nleftshift by 1 == multiplication by 2 and it is much faster than multiplication operator\n\nFor the fast lookup use hashmap, because the lookup time is O(1) (avg)\n```\nclass FindElements {\n\n Set<Integer> set = new HashSet<>();\n void solve(TreeNode root ,int NodeVal){\n if(root == null) return;\n set.add(NodeVal);\n solve(root.left,(NodeVal<<1) + 1); \n solve(root.right,(NodeVal<<1) + 2);\n }\n public FindElements(TreeNode root) {\n solve(root,0);\n }\n \n public boolean find(int target) {\n return set.contains(target);\n }\n}\n``` | 5 | 0 | ['Java'] | 1 |
find-elements-in-a-contaminated-binary-tree | Python hacks | python-hacks-by-stefanpochmann-bxrr | \nclass FindElements(object):\n def __init__(self, root):\n def v(r, x):\n return r and {x} | v(r.left, 2*x+1) | v(r.right, 2*x+2) or set() | stefanpochmann | NORMAL | 2019-11-26T20:01:09.943522+00:00 | 2019-11-26T21:32:43.325789+00:00 | 832 | false | ```\nclass FindElements(object):\n def __init__(self, root):\n def v(r, x):\n return r and {x} | v(r.left, 2*x+1) | v(r.right, 2*x+2) or set()\n self.find = v(root, 0).__contains__\n```\n\nAnother, based on [this one](https://leetcode.com/problems/find-elements-in-a-contaminated-binary-tree/discuss/431229/Python-Special-Way-for-find()-without-HashSet-O(1)-Space-O(logn)-Time/394342):\n```\nclass FindElements(object):\n def __init__(self, r):\n self.find = lambda t: reduce(lambda n, b: n and (n.left, n.right)[int(b)], bin(t+1)[3:], r)\n```\n | 5 | 0 | [] | 1 |
find-elements-in-a-contaminated-binary-tree | Simple solution | DFS | simple-solution-dfs-by-saurabhdamle11-55wb | IntuitionWe will iterate over the Tree using a DFS and update the values if we ecounter a -1 and store them in a map to check for occurances.Approach
Use DFS to | saurabhdamle11 | NORMAL | 2025-02-21T05:02:39.906492+00:00 | 2025-02-21T05:03:18.904201+00:00 | 205 | false | # Intuition
We will iterate over the Tree using a DFS and update the values if we ecounter a -1 and store them in a map to check for occurances.
# Approach
1. Use DFS to iterate over the tree.
2. If a node has -1 as the value, update it to the expected value.
3. If the children are present, iterate over them with their respective expected values.
4. Mark the values in a map as we traverse the tree.
# Complexity
- Time complexity:
O(n)
- Space complexity:
O(n)
# Code
```cpp []
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class FindElements {
private:
unordered_map<int,int> mpp;
void solve(TreeNode* node, int exp){
if(!node){return;}
if(node->val==-1){node->val=exp;}
mpp[node->val]++;
if(node->left){
solve(node->left,2*exp+1);
}
if(node->right){
solve(node->right,2*exp+2);
}
}
public:
FindElements(TreeNode* root) {
mpp.clear();
solve(root,0);
}
bool find(int target) {
return mpp.find(target)!=mpp.end();
}
};
```
```java []
private HashSet<Integer> values;
private void solve(TreeNode node, int val) {
if (node == null) return;
node.val = val;
values.add(val);
solve(node.left, 2 * val + 1);
solve(node.right, 2 * val + 2);
}
public FindElements(TreeNode root) {
values = new HashSet<>();
solve(root, 0);
}
public boolean find(int target) {
return values.contains(target);
}
```
```python []
class FindElements:
def __init__(self, root: TreeNode):
self.values = set()
self.solve(root, 0)
def solve(self, node, val):
if not node:
return
node.val = val
self.values.add(val)
self.solve(node.left, 2 * val + 1)
self.solve(node.right, 2 * val + 2)
def find(self, target: int) -> bool:
return target in self.values
```
Please upvote if you found it useful!! | 4 | 0 | ['Hash Table', 'Tree', 'Depth-First Search', 'Design', 'Binary Tree', 'Python', 'C++', 'Java', 'Python3'] | 2 |
find-elements-in-a-contaminated-binary-tree | Find Elements in a Contaminated Binary Tree || Efficient | find-elements-in-a-contaminated-binary-t-j2r5 | IntuitionThe problem involves finding a value in a binary tree where all the nodes' values are initially set to be "corrupted" (e.g., some undefined or arbitrar | Mirin_Mano_M | NORMAL | 2025-02-21T04:01:16.718476+00:00 | 2025-02-21T04:01:16.718476+00:00 | 211 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The problem involves finding a value in a binary tree where all the nodes' values are initially set to be "corrupted" (e.g., some undefined or arbitrary values). We need to recover the values by using a specific rule based on their positions within the tree. The goal is to return whether a target value exists in the tree after it has been recovered using the rule.
The key insight is that each node's value can be determined by its position in the tree. The root node has a value of 0. For any given node, the value of its left child will be 2 * parent_value + 1 and the value of its right child will be 2 * parent_value + 2. Using this rule recursively, we can assign values to all nodes in the tree.
# Approach
<!-- Describe your approach to solving the problem. -->
**Tree Traversal:** We need to traverse the binary tree (we can use a depth-first search (DFS)) to assign values to each node using the given rule.
**Storing Values:** Since we want to be able to quickly check if a target value exists in the tree, we will store all the assigned values in a set (unordered_set). This allows us to efficiently check if a target value is present.
**Find Method:** Once the values are assigned, we can simply check if a given target value exists in the set.
# Steps:
- Initialize the root node's value to 0.
- Use a recursive function to assign values to the left and right children of each node according to the rule.
- Store all assigned values in an unordered set.
- Implement a method to check if a target value is present in the set.
# Complexity
# Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Assigning values to all nodes requires a DFS traversal, which visits each node once. Hence, the time complexity is O(n), where n is the number of nodes in the tree.
- Checking if a target value exists in the set takes O(1) due to the constant time complexity of unordered_set lookup operations.
- Therefore, the overall time complexity is O(n) for the constructor and O(1) for the find method
# Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
- The space complexity is O(n) due to the space required to store the values of the nodes in the set.
# Code
```cpp []
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class FindElements {
public:
TreeNode* root;
unordered_set<int> st;
FindElements(TreeNode* root) {
this->root=root;
if(root) root->val = 0;
st.insert(0);
assign(root);
}
void assign(TreeNode* root){
if(!root) return;
if(root->left){
root->left->val = 2*root->val+1;
st.insert(root->left->val);
assign(root->left);
}
if(root->right){
root->right->val = 2*root->val+2;
st.insert(root->right->val);
assign(root->right);
}
}
bool find(int target) {
if(st.find(target)!=st.end()){
return true;
}
return false;
}
};
/**
* Your FindElements object will be instantiated and called as such:
* FindElements* obj = new FindElements(root);
* bool param_1 = obj->find(target);
*/
``` | 4 | 0 | ['C++'] | 0 |
find-elements-in-a-contaminated-binary-tree | 🔥 Beats 98.92% 🔥 | 🌟 Proof 🌟 | ✔️ Detailed Explaination ✔️ | HashSet + DFS | 2 Solution | beats-9892-proof-detailed-explaination-h-ml0l | IntuitionThe problem requires us to recover acontaminated binary treewhere all node values are initially-1. Werestore the tree using a simple formula: the root | ntrcxst | NORMAL | 2025-02-21T03:31:02.159681+00:00 | 2025-02-21T03:31:02.159681+00:00 | 156 | false | ---
---
# Intuition
The problem requires us to recover a **contaminated binary tree** where all node values are initially `-1`. We **restore the tree using a simple formula**: the root is assigned `0`, the left child is `2 * parent + 1`, and the right child is `2 * parent + 2`. To efficiently support the `find(target)` operation, we store all **recovered values** in a `HashSet`, allowing ``O(1)`` lookup time. We use `DFS` to traverse and restore the **tree**, ensuring all values are correctly assigned.
# Approach
`Step 1` **Recover the Tree**
- Start from the `root`, assign `0` to **its value**.
- Use `DFS` to assign values to the `left` and `right` children:
- Left `leftChild = 2 * parent + 1`
- Right `rightChild = 2 * parent + 2`
- Store each recovered value in a HashSet for quick lookups.
`Step 2` **Implement the find() function**
- Simply **check** if the `target` exists in the `HashSet`.
- If found, return `true`, else return `false`.
# Complexity
- Time complexity : $$O(n) + O(1)$$
- Space complexity : $$O(n)$$
# Code
```Java []
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class FindElements
{
private Set<Integer> values = new HashSet<>();
// Step 1: Recover the tree using DFS
private void recover(TreeNode node, int val)
{
if (node == null)
{
return;
}
node.val = val;
values.add(val);
recover(node.left, 2 * val + 1);
recover(node.right, 2 * val + 2);
}
// Step 2: Constructor to recover tree
public FindElements(TreeNode root)
{
recover(root, 0);
}
// Step 3: Find function (O(1) lookup)
public boolean find(int target)
{
return values.contains(target);
}
}
/**
* Your FindElements object will be instantiated and called as such:
* FindElements obj = new FindElements(root);
* boolean param_1 = obj.find(target);
*/
```
``` C++ []
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class FindElements
{
private:
unordered_set<int> values;
// Step 1: Recover the tree using DFS
void recover(TreeNode* node, int val)
{
if (!node)
{
return;
}
node->val = val;
values.insert(val);
recover(node->left, 2 * val + 1);
recover(node->right, 2 * val + 2);
}
public:
// Step 2: Constructor to recover tree
FindElements(TreeNode* root)
{
recover(root, 0);
}
// Step 3: Find function (O(1) lookup)
bool find(int target)
{
return values.find(target) != values.end();
}
};
/**
* Your FindElements object will be instantiated and called as such:
* FindElements* obj = new FindElements(root);
* bool param_1 = obj->find(target);
*/
``` | 4 | 0 | ['Array', 'Hash Table', 'String', 'Tree', 'Depth-First Search', 'Breadth-First Search', 'Recursion', 'Binary Tree', 'C++', 'Java'] | 0 |
find-elements-in-a-contaminated-binary-tree | Easy Python Solution | Faster than 99% (76 ms) | Comments | easy-python-solution-faster-than-99-76-m-b96t | Easy Python Solution | Faster than 99% (76 ms) | With Comments\n\nRuntime: 76 ms, faster than 99.13% of Python3 online submissions for Find Elements in a Contam | the_sky_high | NORMAL | 2022-05-10T13:51:21.930895+00:00 | 2022-05-10T14:06:05.483802+00:00 | 478 | false | # Easy Python Solution | Faster than 99% (76 ms) | With Comments\n\n**Runtime: 76 ms, faster than 99.13% of Python3 online submissions for Find Elements in a Contaminated Binary Tree.\nMemory Usage: 17.9 MB**\n\n```\nclass FindElements:\n \n def dfs(self, node, val):\n if node:\n self.store[val] = 1 # adding the value of node to hashmap\n if node.left:\n vl = (2 * val) + 1 # correcting the value of left node\n self.dfs(node.left,vl) # left sub tree traversal\n if node.right:\n vr = (2* val) + 2 # correcting the value of right node\n self.dfs(node.right, vr) # right sub tree traversal\n\n def __init__(self, root: TreeNode):\n self.store = {} # hashmap for storing the corrected node values. And searching the values.\n self.dfs(root, 0) # Traversing the incorrect tree and saving correct values on the way\n\n def find(self, target: int) -> bool:\n\t\t# checking if the target value exists in O(1) time\n if self.store.get(target, None) is not None:\n return True\n else:\n return False\n```\n\n\n | 4 | 0 | ['Depth-First Search', 'Recursion', 'Python', 'Python3'] | 0 |
find-elements-in-a-contaminated-binary-tree | Java Easiest Cosise Beginer Friendly (Slow) | java-easiest-cosise-beginer-friendly-slo-8la7 | \nclass FindElements {\n TreeNode root;\n public FindElements(TreeNode r) {\n root = r;\n r.val = 0;\n }\n public boolean find(int tar | bharat194 | NORMAL | 2022-04-02T12:19:11.283049+00:00 | 2022-04-02T12:19:11.283087+00:00 | 412 | false | ```\nclass FindElements {\n TreeNode root;\n public FindElements(TreeNode r) {\n root = r;\n r.val = 0;\n }\n public boolean find(int target) {\n return find(root,target);\n }\n public boolean find(TreeNode root,int target){\n if(root == null) return false;\n if(root.val == target) return true;\n if(root.left != null) root.left.val = 2 * root.val + 1; \n if(root.right != null) root.right.val = 2 * root.val + 2;\n return find(root.left,target) || find(root.right,target);\n }\n}\n``` | 4 | 0 | ['Java'] | 0 |
find-elements-in-a-contaminated-binary-tree | C++ code using BFS | O(n) | c-code-using-bfs-on-by-mayank01ms-6uj5 | \nclass FindElements {\n unordered_map<int, int> m;\npublic:\n FindElements(TreeNode* root) {\n queue<TreeNode*> q;\n root->val = 0;\n | mayank01ms | NORMAL | 2021-10-19T16:52:37.325803+00:00 | 2021-10-19T16:52:37.325863+00:00 | 256 | false | ```\nclass FindElements {\n unordered_map<int, int> m;\npublic:\n FindElements(TreeNode* root) {\n queue<TreeNode*> q;\n root->val = 0;\n q.push(root);\n m[0]++;\n while(!q.empty()){\n auto temp = q.front();\n q.pop();\n m[temp->val]++;\n if(temp->left){\n temp->left->val = 2 * temp->val + 1;\n q.push(temp->left);\n }\n if(temp->right){\n temp->right->val = 2 * temp->val + 2;\n q.push(temp->right);\n }\n }\n }\n \n bool find(int target) {\n if(m.find(target) != m.end())\n return true;\n return false;\n }\n};\n``` | 4 | 0 | [] | 0 |
find-elements-in-a-contaminated-binary-tree | Clean Easy Understand Python | clean-easy-understand-python-by-nhan99dn-kiat | \tdef init(self, root: TreeNode):\n root.val = 0\n self.s = set()\n q = [(root, 0)]\n self.s.add(0)\n while len(q) > 0:\n | nhan99dn | NORMAL | 2019-11-28T03:28:40.829126+00:00 | 2019-11-28T03:28:40.829161+00:00 | 421 | false | \tdef __init__(self, root: TreeNode):\n root.val = 0\n self.s = set()\n q = [(root, 0)]\n self.s.add(0)\n while len(q) > 0:\n t,v = q.pop()\n if t.left:\n q.append((t.left, v * 2 + 1))\n self.s.add(v * 2 + 1)\n if t.right:\n q.append((t.right, v * 2 + 2))\n self.s.add(v * 2 + 2)\n\n def find(self, target: int) -> bool:\n return target in self.s | 4 | 0 | [] | 0 |
find-elements-in-a-contaminated-binary-tree | C# Solution for Find Elements In A Contaminated Binary Tree Problem | c-solution-for-find-elements-in-a-contam-hnyv | IntuitionThe problem involves a contaminated binary tree where all node values are initially -1, and we need to recover the original values using a fixed formul | Aman_Raj_Sinha | NORMAL | 2025-02-21T20:43:43.958887+00:00 | 2025-02-21T20:43:43.958887+00:00 | 27 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The problem involves a contaminated binary tree where all node values are initially -1, and we need to recover the original values using a fixed formula:
• Left child: 2 * x + 1
• Right child: 2 * x + 2
Since the tree follows a strict numerical pattern, we can recover all node values using a Depth-First Search (DFS) or Breadth-First Search (BFS) traversal. To efficiently check for the existence of a target value, we store all valid values in a HashSet, which provides O(1) lookup time.
# Approach
<!-- Describe your approach to solving the problem. -->
1. Tree Recovery:
• Initialize a HashSet to store valid values.
• Start with root.val = 0 and use DFS (or BFS) to assign correct values to all nodes.
• Store each computed value in the HashSet for quick retrieval.
2. Find Operation:
• Simply check if the target value exists in the HashSet using Contains(), which is an O(1) operation on average.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
1. Tree Recovery (DFS/BFS):
• We visit each node once and compute its value in O(1) time.
• We insert n values into the HashSet in O(1) per operation.
• Overall Complexity: O(n)
2. Find Operation:
• HashSet lookup takes O(1) on average.
• Overall Complexity: O(1) per query.
Thus, if we have q queries, the total time complexity is O(n + q).
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
1. Tree Recovery:
• The HashSet stores n values → O(n).
• The DFS recursive stack (or BFS queue) takes O(h) space, where h is the height of the tree (at most 20).
• Since O(h) ≤ O(n), the dominant factor is O(n).
2. Find Operation:
• Uses only O(1) additional space.
Thus, the overall space complexity is O(n).
# Code
```csharp []
/**
* Definition for a binary tree node.
* public class TreeNode {
* public int val;
* public TreeNode left;
* public TreeNode right;
* public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
public class FindElements {
private HashSet<int> values;
public FindElements(TreeNode root) {
values = new HashSet<int>();
RecoverTree(root, 0);
}
private void RecoverTree(TreeNode node, int value) {
if (node == null) return;
node.val = value;
values.Add(value);
RecoverTree(node.left, 2 * value + 1);
RecoverTree(node.right, 2 * value + 2);
}
public bool Find(int target) {
return values.Contains(target);
}
}
/**
* Your FindElements object will be instantiated and called as such:
* FindElements obj = new FindElements(root);
* bool param_1 = obj.Find(target);
*/
``` | 3 | 0 | ['C#'] | 0 |
find-elements-in-a-contaminated-binary-tree | JAVA | java-by-ayeshakhan7-1enz | Code | ayeshakhan7 | NORMAL | 2025-02-21T16:56:20.968159+00:00 | 2025-02-21T16:56:20.968159+00:00 | 65 | false |
# Code
```java []
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class FindElements {
HashSet<Integer> set = new HashSet<>();
public FindElements(TreeNode root) {
dfs(root,0);
}
public boolean find(int target) {
return set.contains(target);
}
public void dfs(TreeNode root, int val){
if(root==null) return;
root.val = val;
set.add(val);
dfs(root.left, 2*val+1);
dfs(root.right, 2*val+2);
}
}
/**
* Your FindElements object will be instantiated and called as such:
* FindElements obj = new FindElements(root);
* boolean param_1 = obj.find(target);
*/
``` | 3 | 0 | ['Java'] | 0 |
find-elements-in-a-contaminated-binary-tree | DFS and Unordered Set || beats 100% | dfs-and-unordered-set-beats-100-by-aksha-lbik | IntuitionApproachComplexity
Time complexity: O(N)
Space complexity: O(N)
Code | akshatchawla1307 | NORMAL | 2025-02-21T13:34:51.935541+00:00 | 2025-02-21T13:39:32.110888+00:00 | 59 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: O(N)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(N)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class FindElements {
public:
unordered_set<int>s;
void helper(TreeNode*root,int i)
{
s.insert(i);
if(root->left)
helper(root->left,i*2+1);
if(root->right)
helper(root->right,i*2+2);
}
FindElements(TreeNode* root) {
helper(root,0);
}
bool find(int target) {
if(s.count(target))
return true;
return false;
}
};
/**
* Your FindElements object will be instantiated and called as such:
* FindElements* obj = new FindElements(root);
* bool param_1 = obj->find(target);
*/
``` | 3 | 0 | ['Depth-First Search', 'C++'] | 1 |
find-elements-in-a-contaminated-binary-tree | Simple intuitive, beats 100%, O(1) time for FindElements, O(log(n)) time for Find and O(1) space | simple-intuitive-beats-100-o1-time-for-f-2rg0 | IntuitionWe can use binary representation oftargetto go through the tree.ApproachThe key idea is usingtargetbinary representation to understand where to go in t | pavelavsenin | NORMAL | 2025-02-21T12:50:42.477351+00:00 | 2025-02-21T12:50:42.477351+00:00 | 66 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
We can use binary representation of `target` to go through the tree.
# Approach
<!-- Describe your approach to solving the problem. -->
The key idea is using `target` binary representation to understand where to go in the tree to the left or to the right.
The tree will always look like this
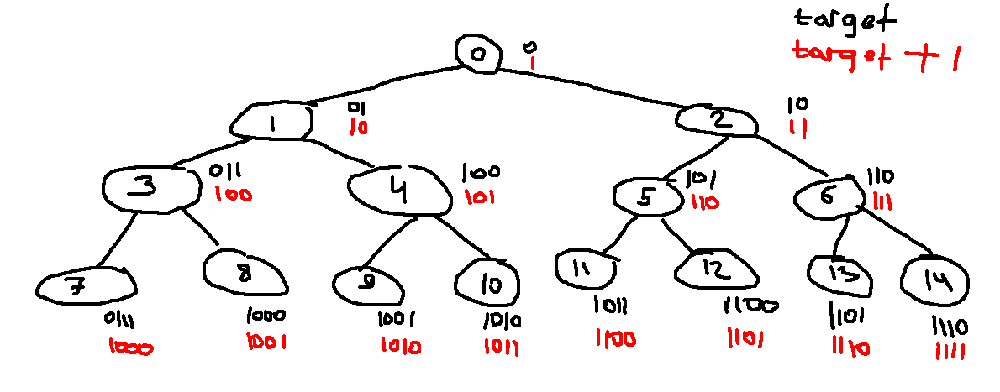
We may notice that the binary representation of `target + 1` value is very clear:
each bit shows where to go it the tree `0` -> `left` and `1` -> `right`
For example, lets find `11`. Binary for `target + 1` is `1100`
We always ignore the first bit (it is always 1, see the picture) and other bits are `100` mean go `right->left->left` starting from the root to check if node exists.
# Complexity
- Time complexity: O(1) for FindElements, O(log(n)) for Find
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1) for all methods
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```golang []
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
type FindElements struct {
root *TreeNode
}
func Constructor(root *TreeNode) FindElements {
// simple store the root
res := FindElements{root: root}
return res
}
func (this *FindElements) Find(target int) bool {
node := this.root
// calculate the mask to iterate over target bits
// from the left to the right
mask := 1
num := target + 1
for num != 0 {
num >>= 1
mask <<= 1
}
mask >>= 1
num = (target + 1) & (mask - 1)
mask >>= 1
for mask != 0 {
if num & mask == 0 {
if node.Left == nil {
return false
}
node = node.Left
} else {
if node.Right == nil {
return false
}
node = node.Right
}
mask >>= 1
}
return true
}
/**
* Your FindElements object will be instantiated and called as such:
* obj := Constructor(root);
* param_1 := obj.Find(target);
*/
``` | 3 | 0 | ['Go'] | 0 |
find-elements-in-a-contaminated-binary-tree | ✅ Three Simple Lines of Code | three-simple-lines-of-code-by-mikposp-u985 | (Disclaimer: this is not an example to follow in a real project - it is written for fun and training mostly)Code #1.1Time complexity:O(n2). Space complexity:O(n | MikPosp | NORMAL | 2025-02-21T10:02:18.114669+00:00 | 2025-02-21T10:02:56.364819+00:00 | 175 | false | (Disclaimer: this is not an example to follow in a real project - it is written for fun and training mostly)
# Code #1.1
Time complexity: $$O(n^2)$$. Space complexity: $$O(n)$$.
```python3
FindElements = type('',(),{
'__init__': lambda s,r:setattr(s,'d',(f:=lambda n,x:n and {x}|f(n.left,x*2+1)|f(n.right,x*2+2) or set())(r,0)),
'find': lambda s,t:t in s.d
})
```
# Code #1.2 - Unwrapped
```python3
class FindElements:
def __init__(self, r: Optional[TreeNode]):
def f(n,x):
if n:
return {x}|f(n.left,x*2+1)|f(n.right,x*2+2)
return set()
self.d = f(r,0)
def find(self, t: int) -> bool:
return t in self.d
```
(Disclaimer 2: code above is just a product of fantasy packed into one line, it is not declared to be 'true' oneliners - please, remind about drawbacks only if you know how to make it better) | 3 | 0 | ['Hash Table', 'Tree', 'Depth-First Search', 'Design', 'Binary Tree', 'Python', 'Python3'] | 0 |
find-elements-in-a-contaminated-binary-tree | ✅✅Beats 100%🔥C++🔥Python|| 🚀🚀Super Simple and Efficient Solution🚀🚀||🔥Python🔥C++✅✅ | beats-100cpython-super-simple-and-effici-fdh9 | Complexity
Time complexity:O(n)
Space complexity:O(n)
Code | shobhit_yadav | NORMAL | 2025-02-21T02:49:25.405665+00:00 | 2025-02-21T02:49:25.405665+00:00 | 130 | false | # Complexity
- Time complexity: $$O(n)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(n)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class FindElements {
public:
FindElements(TreeNode* root) {
dfs(root, 0);
}
bool find(int target) {
return vals.contains(target);
}
private:
unordered_set<int> vals;
void dfs(TreeNode* root, int val) {
if (root == nullptr){
return;
}
root->val = val;
vals.insert(val);
dfs(root->left, val * 2 + 1);
dfs(root->right, val * 2 + 2);
}
};
```
```python []
class FindElements:
def __init__(self, root: TreeNode | None):
self.vals = set()
self.dfs(root, 0)
def find(self, target: int) -> bool:
return target in self.vals
def dfs(self, root: TreeNode | None, val: int) -> None:
if not root:
return
root.val = val
self.vals.add(val)
self.dfs(root.left, val * 2 + 1)
self.dfs(root.right, val * 2 + 2)
``` | 3 | 0 | ['Hash Table', 'Tree', 'Depth-First Search', 'Breadth-First Search', 'Design', 'Binary Tree', 'C++', 'Python3'] | 0 |
find-elements-in-a-contaminated-binary-tree | 🔥 Space: O(log n) | Time: O(log n) 🚀💯 Beats 99% in both Space & Time ⚡🏆 Unique Bitmask | space-olog-n-time-olog-n-beats-99-in-bot-h53p | IntuitionBeacause of the fixed way of numbering in the binary tree, there is a unique identifier for each node, represented by the value of it :-These numbers a | vkhantwal999 | NORMAL | 2025-02-21T02:12:12.645997+00:00 | 2025-02-21T02:16:50.043984+00:00 | 231 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Beacause of the fixed way of numbering in the binary tree, there is a unique identifier for each node, represented by the value of it :-
1
/ \
2 3
/ \
4 5
These numbers are the values for the node as well as their unique address.
Therefore we don't even need to recover the tree since we can consider the target number as pointer and just check if any node is present there. (Doesn't matter if the node value is -1 there, only node existence is important rather than the value)
-
# Approach
<!-- Describe your approach to solving the problem. -->
Suppose the root node is 1. -->
To check existence of a node, calculate its binary representation string.From second index, traverse the string from left to right , and in the tree ,move left if you encounter a '0' in string, else move right(on encountering '1').
-- eg:- suppose you want to check if node number 12 exists.
-- its binary string :- "1100"
-- Initialize TreeNode temp = root;
-- Index 0 -> "1" , ignore 1st position
-- Index 1 -> "1" , move right in tree (temp = temp.right)
-- Index 2 -> "0" , move left in tree (temp = temp.left)
-- Index 3 -> "0" , check if (node.left) exists, if yes then node number 12 exists.
Now,since this approach is based on the assumption that root node value is 1, we simply add one to the target value to be found to convert the problem exactly to match this approach.
-
# Complexity
- Time complexity: O(log n) ,for find() method. Overall :- O(n*log n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(log n) overall.
The only extra space used is for storing the binary string representation of target + 1, which has at most O(log target) characters.
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class FindElements {
TreeNode base;
public FindElements(TreeNode root) {
base = root;
}
public boolean find(int target) {
String mask = Integer.toBinaryString(target+1);
TreeNode temp = base;
for(int i = 1;i<mask.length();i++){
if(mask.charAt(i) == '1'){
if(temp.right == null){
return false;
}
temp = temp.right;
}
else{
if(temp.left == null){
return false;
}
temp = temp.left;
}
}
return true;
}
}
``` | 3 | 0 | ['String', 'Binary Tree', 'Bitmask', 'Java'] | 2 |
find-elements-in-a-contaminated-binary-tree | "⚡ Fast Java & C++Solution to Recover Binary Tree & Efficient Find Operation 🌳"| DFS Approach | fast-java-csolution-to-recover-binary-tr-9b2i | IntuitionThe problem asks us to recover a binary tree where some of the nodes may have corrupted values (i.e., they are initially set to -1). We're given that t | ksheker | NORMAL | 2025-02-21T02:05:11.101237+00:00 | 2025-02-21T02:05:11.101237+00:00 | 7 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The problem asks us to recover a binary tree where some of the nodes may have corrupted values (i.e., they are initially set to -1). We're given that the tree's structure is still intact, and the root value should be 0. The values of the other nodes in the tree can be restored using the properties of a complete binary tree.
A complete binary tree's node values can be restored by using the following observation:
For any node with value x:
The left child should have a value of 2 * x + 1.
The right child should have a value of 2 * x + 2.
Given this, we need to traverse the tree and restore the values using DFS or BFS. We also need to be able to efficiently check if a given value exists in the tree.
# Approach
<!-- Describe your approach to solving the problem. -->
We can approach this problem in two phases:
Tree Recovery Phase (DFS):
Start from the root node and set its value to 0.
Use a recursive function (rec()) to traverse the tree. For each node, we set its value and recurse on its left and right children, calculating their values using the formula 2 * parent_value + 1 for the left child and 2 * parent_value + 2 for the right child.
Find Operation:
Store all the node values in a HashSet while performing the recovery so that we can quickly check if a target value exists in the tree.
The main idea is that we can use DFS to both recover the tree and populate the HashSet for efficient lookup.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
𝑂(𝑛)
We visit each node exactly once during the DFS traversal, where n is the number of nodes in the tree. The time complexity for the find operation is 𝑂(1) because of the HashSet lookup.
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(n)
The space complexity is determined by the recursion stack used during the DFS and the space used by the HashSet to store the node values. Since we store values for each node in the tree and the recursion depth is at most n, the space complexity is O(n).
# Code
```java []
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class FindElements {
TreeNode root;
HashSet<Integer> h;
public FindElements(TreeNode root) {
//root.val = 0;
h = new HashSet<>();
root = rec(root , 0);
//root = rec(root.left , 0);
this.root = root;
}
public boolean find(int target) {
return h.contains(target);
}
private TreeNode rec(TreeNode root, int val)
{
if(root == null)
return root;
root.val = val;
h.add(val);
root.right = rec(root.right , 2 * val + 2);
root.left = rec(root.left , 2 * val + 1);
return root;
}
}
/**
* Your FindElements object will be instantiated and called as such:
* FindElements obj = new FindElements(root);
* boolean param_1 = obj.find(target);
*/
```
```C++ []
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class FindElements {
public:
unordered_set<int> h;
// Constructor to initialize the tree and recover its values
FindElements(TreeNode* root) {
recoverTree(root, 0);
}
// Function to find if the target value exists in the tree
bool find(int target) {
return h.find(target) != h.end();
}
private:
// Helper function to recursively recover the tree's node values
void recoverTree(TreeNode* root, int val) {
if (root == nullptr)
return;
root->val = val; // Set the node value
h.insert(val); // Store the value in the hash set
// Recur on left and right children, updating their values
recoverTree(root->left, 2 * val + 1); // Left child value: 2 * parent_value + 1
recoverTree(root->right, 2 * val + 2); // Right child value: 2 * parent_value + 2
}
};
/**
* Your FindElements object will be instantiated and called as such:
* FindElements* obj = new FindElements(root);
* bool param_1 = obj->find(target);
*/
| 3 | 0 | ['C++', 'Java'] | 0 |
find-elements-in-a-contaminated-binary-tree | [Rust] First thought: easy DFS + HashSet | rust-first-thought-easy-dfs-hashset-by-d-tv64 | Complexity
Time complexity:
FindElements:O(n), wherenis the size of the tree.
find:O(1)
Space complexity:
O(n)
Code | discreaminant2809 | NORMAL | 2025-02-21T01:06:53.759824+00:00 | 2025-02-21T01:06:53.759824+00:00 | 81 | false | # Complexity
- Time complexity:
`FindElements`: $$O(n)$$, where $$n$$ is the size of the tree.
`find`: $$O(1)$$
- Space complexity:
$$O(n)$$
# Code
```rust []
struct FindElements {
values: HashSet<i32>,
}
macro_rules! node_as_ref {
($node:expr) => {
$node
.as_ref()
.map(|root| root.borrow())
.as_ref()
.map(|umm| &**umm)
};
}
impl FindElements {
fn new(root: Option<Rc<RefCell<TreeNode>>>) -> Self {
let mut values = HashSet::new();
fn dfs_set_node(node: Option<&TreeNode>, value: i32, values: &mut HashSet<i32>) {
let Some(node) = node else {
return;
};
values.insert(value);
dfs_set_node(node_as_ref!(node.left), value * 2 + 1, values);
dfs_set_node(node_as_ref!(node.right), value * 2 + 2, values);
}
dfs_set_node(node_as_ref!(root), 0, &mut values);
Self { values }
}
fn find(&self, target: i32) -> bool {
self.values.contains(&target)
}
}
use std::{cell::RefCell, collections::HashSet, rc::Rc};
``` | 3 | 0 | ['Hash Table', 'Tree', 'Depth-First Search', 'Binary Tree', 'Rust'] | 1 |
find-elements-in-a-contaminated-binary-tree | 🚀 Easy | Tree | Set | Map | JavaScript Solution | easy-tree-set-map-javascript-solution-by-7j57 | Approach / Intuition:
Recovering the Tree:
We traverse the tree in a preorder fashion (Root → Left → Right).
We update each node's value based on its parent's | dharmaraj_rathinavel | NORMAL | 2025-02-21T00:33:03.035374+00:00 | 2025-02-21T00:34:06.790286+00:00 | 105 | false | ## Approach / Intuition:
1. **Recovering the Tree:**
- We traverse the tree in a preorder fashion (Root → Left → Right).
- We update each node's value based on its parent's value.
- We store the recovered values in a `Set` (`this.indices`) for quick lookup in `O(1)` time.
2. **Finding a Target Value:**
- Since we stored all recovered values in a `Set`, we can check if a target value exists in `O(1)` time using `.has(target)`.
⬆️ Upvote, if you understand the approach.
## Complexity
- **Time complexity: O(n)** . Because, we are visiting each node once.
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- **Space complexity: O(n)** . Because, we are storing `n` elements in the set.
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
## Code
```javascript []
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
*/
var FindElements = function (root) {
this.indices = new Set(); // Using this extra space for faster lookup : O(1)
this.root = this.recover(root, 0);
};
FindElements.prototype.recover = function (root, index) {
// Base case: Don't proceed if the root is null
if (!root) {
return null;
}
this.indices.add(index);
root.val = index; // [optional] Update the values of tree
this.recover(root.left, (2 * index) + 1);
this.recover(root.right, (2 * index) + 2);
return root;
}
/**
* @param {number} target
* @return {boolean}
*/
FindElements.prototype.find = function (target) {
return this.indices.has(target);
};
/**
* Your FindElements object will be instantiated and called as such:
* var obj = new FindElements(root)
* var param_1 = obj.find(target)
*/
``` | 3 | 0 | ['Hash Table', 'Tree', 'Binary Tree', 'Ordered Set', 'JavaScript'] | 0 |
find-elements-in-a-contaminated-binary-tree | DFS + Set/Map Solution - Easy_Beginner-Friendly Sol. | bfs-setmap-solution-easy_beginner-friend-rms0 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | iitian_010u | NORMAL | 2025-02-21T00:27:05.386405+00:00 | 2025-02-21T20:54:59.681071+00:00 | 161 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class FindElements {
public:
unordered_map<int, bool> values;
void recover(TreeNode* root, int val) {
if (!root) return;
root->val = val;
values[val] = true;
recover(root->left, 2 * val + 1);
recover(root->right, 2 * val + 2);
}
FindElements(TreeNode* root) {
if (root) {
recover(root, 0);
}
}
bool find(int target) {
return values.find(target) != values.end();
}
};
``` | 3 | 0 | ['Hash Table', 'Tree', 'Breadth-First Search', 'Design', 'Binary Tree', 'Ordered Set', 'C++'] | 2 |
find-elements-in-a-contaminated-binary-tree | 🔥🔥||Easy Solution||Beats 100% in most||With proof||💎☕🖥️🐍C#️⃣C➕➕✅||🔥🔥 | easy-solutionbeats-100-in-mostwith-proof-53ee | Intuition💡It's obvious to use BFS for the initial part. However, a lot of people use HashSet(set() in python) to pre-store all the values in the initial part, w | AbyssReaper | NORMAL | 2025-02-16T06:14:33.882293+00:00 | 2025-02-16T06:14:33.882293+00:00 | 51 | false | # Intuition💡
It's obvious to use `BFS` for the initial part. However, a lot of people use HashSet(`set()` in python) to pre-store all the values in the initial part, which may cause MLE when the values are huge. There is a special way to implement `find()` that costs O(1) in space and O(logn) in time.
# Approach🚀
- Declare a HashSet `seen` as a member of the `FindElements` class
- For helper function `dfs(currentNode, currentValue, seen)`:
- For `find(target)` function:
# Complexity⌚
- Time complexity: O(n)
- Space complexity: O(MAX)
Constraints say that 0 <= target <= 10^6, so we store bitset<10^6 + 1>
# Code
```cpp []
class FindElements {
public:
FindElements(TreeNode* root) { dfs(root, 0); }
bool find(int target) { return seen.count(target) > 0; }
private:
unordered_set<int> seen;
void dfs(TreeNode* currentNode, int currentValue) {
if (!currentNode) return;
// visit current node by adding its value to seen
seen.insert(currentValue);
dfs(currentNode->left, currentValue * 2 + 1);
dfs(currentNode->right, currentValue * 2 + 2);
}
};
```
```Rust []
// #[derive(Debug, PartialEq, Eq)]
// pub struct TreeNode {
// pub val: i32,
// pub left: Option<Rc<RefCell<TreeNode>>>,
// pub right: Option<Rc<RefCell<TreeNode>>>,
// }
use std::{cell::RefCell, rc::Rc};
struct FindElements {
root: Option<Rc<RefCell<TreeNode>>>,
}
impl FindElements {
fn new(root: Option<Rc<RefCell<TreeNode>>>) -> Self {
// Encapsulate in a dummy root for checks.
let root = Some(Rc::new(RefCell::new(TreeNode {
val: -1,
left: None,
right: root,
})));
Self { root }
}
fn find(&self, target: i32) -> bool {
if target < 0 {
return false;
}
// Not necessary for problem constraints, but needed to handle
// trees with deeper levels.
let adjusted = target as u32 + 1;
let mut offset_opt = Some(adjusted.ilog2());
let mut node = self
.root
.clone()
.expect("The structure should always have a dummy root");
while let Some(offset) = offset_opt {
// Get the proper node depending upon the check bit.
let opt = if ((adjusted >> offset) & 1) == 1 {
node.borrow().right.clone()
} else {
node.borrow().left.clone()
};
// Fail early if the node is not found.
node = match opt {
None => return false,
Some(node) => node,
};
offset_opt = offset.checked_sub(1);
}
true
}
}
```
```C# []
/**
* Definition for a binary tree node.
* public class TreeNode {
* public int val;
* public TreeNode left;
* public TreeNode right;
* public TreeNode(int val=0, TreeNode left=null, TreeNode right=null) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
public class FindElements {
TreeNode root = null;
public FindElements(TreeNode root)
{
this.root = root;
RecoverElements(this.root, 0);
}
public bool Find(int target)
{
var s = this.GetPath4Target(target);
TreeNode cur = this.root;
while (s.Count > 0)
{
int v = s.Pop();
if (cur == null || cur.val != v)
{
return false;
}
if (s.Count > 0 && cur.left != null && cur.left.val == s.Peek())
{
cur = cur.left;
}
else
{
cur = cur.right;
}
}
return true;
}
private void RecoverElements(TreeNode root, int rootValue)
{
root.val = rootValue;
if (root.left != null)
{
RecoverElements(root.left, rootValue * 2 + 1);
}
if (root.right!=null)
{
RecoverElements(root.right, rootValue * 2 + 2);
}
}
private Stack<int> GetPath4Target(int target)
{
Stack<int> result = new Stack<int>();
while (target > 0)
{
result.Push(target);
int reminder = target % 2 != 0 ? 1 : 2;
target = (target - reminder) >> 1;
}
result.Push(0);
return result;
}
}
/**
* Your FindElements object will be instantiated and called as such:
* FindElements obj = new FindElements(root);
* bool param_1 = obj.Find(target);
*/
```
```C []
class FindElements {
TreeNode* head=new TreeNode(-1);
public:
FindElements(TreeNode* root) {
head=root;
head->val=0;
recover(head);
}
void recover(TreeNode* root)
{
if(root->left)
{
root->left->val=(root->val)*2+1;
recover(root->left);
}
if(root->right)
{
root->right->val=(root->val)*2+2;
recover(root->right);
}
return;
}
bool find(int target) {
return get(target,head);
}
bool get(int target,TreeNode* root)
{
if(root==NULL)
return false;
if(root->val==target)
return true;
bool t1=get(target,root->left);
bool t2=get(target,root->right);
if(t1||t2)
return true;
return false;
}
};
```
```Go []
/**
* Definition for a binary tree node.
* type TreeNode struct {
* Val int
* Left *TreeNode
* Right *TreeNode
* }
*/
type FindElements struct {
set map[int]bool
}
func (this *FindElements)constructTree(root *TreeNode, x int) {
if root==nil {
return
}
root.Val=x
this.set[x]=true
this.constructTree(root.Left, (2*x)+1)
this.constructTree(root.Right, (2*x)+2)
}
func Constructor(root *TreeNode) FindElements {
m:=map[int]bool{}
this:=FindElements{}
this.set=m
this.constructTree(root, 0)
return this
}
func (this *FindElements) Find(target int) bool {
return this.set[target];
}
/**
* Your FindElements object will be instantiated and called as such:
* obj := Constructor(root);
* param_1 := obj.Find(target);
*/
```
```Ruby []
# Definition for a binary tree node.
# class TreeNode
# attr_accessor :val, :left, :right
# def initialize(val = 0, left = nil, right = nil)
# @val = val
# @left = left
# @right = right
# end
# end
class FindElements
=begin
:type root: TreeNode
=end
def initialize(root)
@vals = Hash.new(false)
if root
@vals[0] = true
end
root.val = 0
recover root
end
def recover node
x = node.val
if node.left
val = 2 * x + 1
@vals[val] = true
node.left.val = val
recover node.left
end
if node.right
val = 2 * x + 2
@vals[val] = true
node.right.val = 2 * x + 2
recover node.right
end
end
=begin
:type target: Integer
:rtype: Boolean
=end
def find(target)
@vals[target]
end
end
# Your FindElements object will be instantiated and called as such:
# obj = FindElements.new(root)
# param_1 = obj.find(target)
```
```Java []
class FindElements {
TreeNode root;
Set<Integer> set = new HashSet<>();
public FindElements(TreeNode root) {
this.root = root;
if(root != null){ root.val = 0; set.add(root.val); }
recover(root,set);
}
public boolean find(int target) {
return set.contains(target);
}
private void recover(TreeNode root, Set<Integer> set){
if(root.left != null){
root.left.val = 2 * root.val + 1;
set.add(root.left.val);
recover(root.left, set);
}
if(root.right != null){
root.right.val = 2 * root.val + 2;
set.add(root.right.val);
recover(root.right, set);
}
}
}
```
```javascript []
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
function ListNode(val, next) {
this.val = (val === undefined ? 0 : val)
this.next = (next === undefined ? null : next)
}
/**
* @param {TreeNode} root
*/
var FindElements = function (root) {
this.elements = root
};
/**
* @param {number} target
* @return {boolean}
*/
FindElements.prototype.find = function (target) {
const head = createLinkedList(target)
return dfs(this.elements, head)
};
const createLinkedList = (target) => {
let prev = null
while (target >= 0) {
let current = new ListNode(target, prev)
prev = current;
target = target % 2 === 0 ? (target - 2) / 2 : (target - 1) / 2
}
return prev.next;
}
const dfs = (root, head) => {
if (!root) return false;
if (!head) return true;
return head.val % 2 === 0 ? dfs(root.right, head.next) : dfs(root.left, head.next)
}
/**
* Your FindElements object will be instantiated and called as such:
* var obj = new FindElements(root)
* var param_1 = obj.find(target)
*/
```

| 3 | 0 | ['C++'] | 1 |
find-elements-in-a-contaminated-binary-tree | Python | [EXPLAINED] | tree traversal | python-explained-tree-traversal-by-diwak-q8nm | We can use any tree traversal method to make the tree contaminated, here we are using preorder traversal it is more favorable here since value of child nodes ar | diwakar_4 | NORMAL | 2022-09-07T09:06:58.288631+00:00 | 2022-10-01T12:38:48.484902+00:00 | 308 | false | * We can use any tree traversal method to make the tree contaminated, here we are using preorder traversal it is more favorable here since value of child nodes are dependent on the value of thier parent node.\n* For efficient target searching we will maintain a set and keep adding the values in it whenever we modify node value.\n\n```\n# Definition for a binary tree node.\n# class TreeNode:\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass FindElements:\n\n def __init__(self, root: Optional[TreeNode]):\n self.root = root\n self.root.val = 0\n self.st = set()\n self.st.add(0)\n \n def preorder(root):\n if root:\n if root.left:\n root.left.val = 2*root.val+1\n self.st.add(2*root.val+1)\n preorder(root.left)\n if root.right:\n root.right.val = 2*root.val+2\n self.st.add(2*root.val+2)\n preorder(root.right)\n preorder(self.root)\n\n def find(self, target: int) -> bool:\n return True if target in self.st else False\n\n# Your FindElements object will be instantiated and called as such:\n# obj = FindElements(root)\n# param_1 = obj.find(target)\n```\n-----------------\n**Upvote the post if you find it helpful.**\n**Happy coding.** | 3 | 0 | ['Python'] | 0 |
find-elements-in-a-contaminated-binary-tree | Simple and clean C++ solution|| Using DFS and a HashSet | simple-and-clean-c-solution-using-dfs-an-4doa | If you really found my solution helpful please upvote it, as it motivates me to post such kind of codes and help the coding community, if you have some queries | anubhavbaner7 | NORMAL | 2022-06-20T20:17:03.875530+00:00 | 2022-06-20T20:17:03.875566+00:00 | 420 | false | **If you really found my solution helpful please upvote it, as it motivates me to post such kind of codes and help the coding community, if you have some queries or some improvements please feel free to comment and share your views.**\n\n```\n unordered_set<int> s;\n void solve(TreeNode* root)\n {\n if(root==nullptr)\n return;\n s.insert(root->val);\n if(root->left!=nullptr)\n root->left->val=root->val*2+1;\n if(root->right!=nullptr)\n root->right->val=root->val*2+2;\n solve(root->left);\n solve(root->right);\n }\n FindElements(TreeNode* root) {\n root->val=0;\n solve(root);\n }\n \n bool find(int target) {\n if(s.find(target)!=s.end())\n return true;\n else\n return false;\n }\n``` | 3 | 0 | ['Depth-First Search', 'C', 'C++'] | 0 |
find-elements-in-a-contaminated-binary-tree | Beginner friendly Python Soluiton | beginner-friendly-python-soluiton-by-him-ghlk | Time Complexity : O(N)\n\n# Definition for a binary tree node.\n# class TreeNode(object):\n# def __init__(self, val=0, left=None, right=None):\n# se | HimanshuBhoir | NORMAL | 2022-02-15T04:56:14.605204+00:00 | 2022-02-15T04:56:14.605242+00:00 | 175 | false | **Time Complexity : O(N)**\n```\n# Definition for a binary tree node.\n# class TreeNode(object):\n# def __init__(self, val=0, left=None, right=None):\n# self.val = val\n# self.left = left\n# self.right = right\nclass FindElements(object):\n\n def __init__(self, root):\n self.st = set()\n \n def recover(root, val) :\n if(root):\n self.st.add(val)\n recover(root.left, 2 * val + 1)\n recover(root.right, 2 * val + 2)\n \n recover(root, 0)\n \n\n def find(self, target):\n return target in self.st\n \n\n\n# Your FindElements object will be instantiated and called as such:\n# obj = FindElements(root)\n# param_1 = obj.find(target)\n``` | 3 | 0 | ['Python'] | 0 |
find-elements-in-a-contaminated-binary-tree | C++ - O(n) to build & O(1) query | c-on-to-build-o1-query-by-anandman03-uync | \nclass FindElements {\nprivate:\n unordered_set<int> cache;\n \n void recover(TreeNode *root, int prev)\n {\n if(!root) return;\n \n | anandman03 | NORMAL | 2020-11-03T10:10:59.313177+00:00 | 2020-11-03T10:12:22.942450+00:00 | 484 | false | ```\nclass FindElements {\nprivate:\n unordered_set<int> cache;\n \n void recover(TreeNode *root, int prev)\n {\n if(!root) return;\n \n root->val = prev;\n cache.insert(root->val);\n \n recover(root->left, 2*prev + 1);\n recover(root->right, 2*prev + 2);\n }\n \npublic:\n FindElements(TreeNode* root) {\n recover(root, 0);\n }\n \n bool find(int target) {\n return cache.count(target) > 0;\n }\n};\n\n``` | 3 | 0 | ['C'] | 0 |
find-elements-in-a-contaminated-binary-tree | Easy C++ Solution using HashMap | easy-c-solution-using-hashmap-by-vishal_-q1lt | \nclass FindElements\n{\npublic:\n unordered_map<int,int>m;\n\n FindElements(TreeNode* root)\n {\n if(root)\n {\n root->val = | vishal_rajput | NORMAL | 2020-07-23T07:21:54.079354+00:00 | 2020-07-23T07:21:54.079404+00:00 | 261 | false | ```\nclass FindElements\n{\npublic:\n unordered_map<int,int>m;\n\n FindElements(TreeNode* root)\n {\n if(root)\n {\n root->val = 0;\n queue<TreeNode*> q;\n q.push(root);\n m[0]++;\n\n while(!q.empty())\n {\n TreeNode* temp = q.front();\n q.pop();\n int x = temp->val;\n if(temp->left)\n {\n temp->left->val = x*2 + 1;\n\n m[x*2 + 1]++;\n q.push(temp->left);\n }\n\n if(temp->right)\n {\n temp->right->val = x*2 + 2;\n\n m[x*2 + 2]++;\n q.push(temp->right);\n }\n }\n }\n }\n\n bool find(int target)\n {\n return (m.find(target) != m.end());\n }\n};\n``` | 3 | 0 | ['Breadth-First Search', 'C'] | 0 |
find-elements-in-a-contaminated-binary-tree | [C/C++ Solution] The find is O(1), uses a bitset instead of a set (saves memory) | cc-solution-the-find-is-o1-uses-a-bitset-7dw8 | If the tree is not too sparse, using a bitset uses less memory than an unordered_set. I think it amounts to only 8KiB, given the problem\'s upper node limit, en | bogmihdav | NORMAL | 2020-02-15T17:38:48.509063+00:00 | 2020-02-15T17:38:48.509101+00:00 | 323 | false | If the tree is not too sparse, using a bitset uses less memory than an unordered_set. I think it amounts to only 8KiB, given the problem\'s upper node limit, enough to fit entirely in the CPU\'s cache. I also expect element access to compare favorably with an unordered_set\'s.\nIf lots of small trees are to be expected, preallocating a full-size bitset may be a pessimization, but replacing it with a (dynamic-sized) vector is fairly straightforward.\n\n```\nclass FindElements {\n std::bitset< (2<<20) > vv;\n \n void recover(TreeNode* n, int ii) {\n if(!n) { return; }\n \n vv[ii] = true;\n recover(n->left, ii*2+1);\n recover(n->right, ii*2+2);\n }\npublic:\n FindElements(TreeNode* root) {\n recover(root, 0);\n }\n \n bool find(int target) {\n return vv[target] == true;\n }\n};\n``` | 3 | 0 | ['C'] | 0 |
find-elements-in-a-contaminated-binary-tree | C++/Java hash set, O(1) | cjava-hash-set-o1-by-votrubac-kxh4 | Iterative approch to resolve tree values and populate hash map.\n\nC++\nCPP\nunordered_set<int> s;\nFindElements(TreeNode* root) {\n queue<pair<TreeNode*, in | votrubac | NORMAL | 2019-11-17T04:35:22.073502+00:00 | 2019-11-17T04:55:21.572162+00:00 | 227 | false | Iterative approch to resolve tree values and populate hash map.\n\n**C++**\n```CPP\nunordered_set<int> s;\nFindElements(TreeNode* root) {\n queue<pair<TreeNode*, int>> q;\n q.push({root, 0});\n while (!q.empty()) {\n auto p = q.front(); q.pop();\n if (p.first != nullptr) {\n s.insert(p.second);\n q.push({p.first->left, p.second * 2 + 1});\n q.push({p.first->right, p.second * 2 + 2});\n }\n }\n}\nbool find(int target) {\n return s.find(target) != end(s);\n}\n```\n**Java**\n```Java\nSet<Integer> s = new HashSet<>(); \npublic FindElements(TreeNode root) {\n Queue<TreeNode> q = new LinkedList<>();\n root.val = 0;\n q.add(root);\n while(q.size() > 0) {\n TreeNode r = q.poll();\n s.add(r.val);\n if (r.left != null) {\n r.left.val = r.val * 2 + 1;\n q.add(r.left);\n }\n if (r.right != null) { \n r.right.val = r.val * 2 + 2;\n q.add(r.right);\n } \n }\n}\npublic boolean find(int target) {\n return s.contains(target);\n}\n```\n#### Complexity Analysis\n- Time: \n\t- `O(n)` to populate tree values into the hash map.\n\t- `O(1)` to check the hash map.\n- Memory: `O(n)`. | 3 | 3 | [] | 0 |
find-elements-in-a-contaminated-binary-tree | Simple CPP solution | simple-cpp-solution-by-aadithya18-mior | CodeThank you,
aadithya18. | aadithya18 | NORMAL | 2025-02-24T14:15:29.933893+00:00 | 2025-02-24T17:30:06.014285+00:00 | 10 | false |
# Code
```cpp []
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class FindElements {
public:
TreeNode* tree;
unordered_set<int> s;
void fun(TreeNode* tree, int parentVal, bool branch){
if(tree == NULL) return;
if(branch) tree->val = 2*parentVal + 2;
else tree->val = 2*parentVal + 1;
s.insert(tree->val);
fun(tree->left, tree->val, 0);
fun(tree->right, tree->val, 1);
}
FindElements(TreeNode* root) {
tree = root;
tree->val = 0;
s.insert(0);
fun(tree->left, 0, 0);
fun(tree->right, 0, 1);
}
bool find(int target) {
// if(target>100000) return false;
return s.find(target) != s.end();
}
};
/**
* Your FindElements object will be instantiated and called as such:
* FindElements* obj = new FindElements(root);
* bool param_1 = obj->find(target);
*/
```
Thank you,
aadithya18. | 2 | 0 | ['C++'] | 0 |
find-elements-in-a-contaminated-binary-tree | Python Solution : DFS + Hashmap | python-solution-dfs-hashmap-by-apurv_sj-7qxr | Intuition
Do a DFS on tree
Get all values in a hashmap
Complexity
Time complexity:0(N)
Space complexity:O(N)
Code | apurv_sj | NORMAL | 2025-02-22T09:48:22.818409+00:00 | 2025-02-22T09:48:22.818409+00:00 | 6 | false | # Intuition
1. Do a DFS on tree
2. Get all values in a hashmap
# Complexity
- Time complexity:
0(N)
- Space complexity:
O(N)
# Code
```python3 []
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class FindElements:
def get_all_values(self,root,val):
if root:
self.hash_map[val]=1
self.get_all_values(root.left,val*2+1)
self.get_all_values(root.right,val*2+2)
def __init__(self, root: Optional[TreeNode]):
self.hash_map={}
self.get_all_values(root,0)
def find(self, target: int) -> bool:
if self.hash_map.get(target,False):
return True
return False
# Your FindElements object will be instantiated and called as such:
# obj = FindElements(root)
# param_1 = obj.find(target)
``` | 2 | 0 | ['Hash Table', 'Python3'] | 0 |
find-elements-in-a-contaminated-binary-tree | Different approach than sets | O(1) Space optimized| O(log(k) Time complexity for each query | different-approach-than-sets-o1-space-op-2m15 | IntuitionFew observations that can be made here:
All the odd numbers will be on the left child to a parent node and all the even numbers will be on right child | parikshit_ | NORMAL | 2025-02-21T18:15:51.286634+00:00 | 2025-02-21T18:18:14.387349+00:00 | 18 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Few observations that can be made here:
1. All the odd numbers will be on the left child to a parent node and all the even numbers will be on right child to a parent.
2. To calculate child, we are given this formula: n1 = 2x + 1 and n2 = 2x + 2, then, to calculate a parent, formula would be (n1 - 1)/2 and (n2-2)/2.
3. All the odd child values are formed from the formula: 2x + 1 and even from 2x+2.
4. If we know the current node is left or right child of parent node, then we can form a path, because we can traverse from the number at the bottom to top, by knowing whether it is the right child or left child, then add it to path, and then calculate its parent, then so on until top node.
5. Once, at the top, we can traverse the path in reverse, and directly check if node exists, if exists, value must be present and return true, else return False.
# Code
```python3 []
# Definition for a binary tree node.
from typing import Optional
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class FindElements:
def __init__(self, root: Optional[TreeNode]):
self.head = root
def find(self, target: int) -> bool:
root = self.head
path = []
while target:
# check if odd
if target & 1:
path.append(0)
target = (target - 1) // 2
else:
path.append(1)
target = (target - 2) // 2
# traverse path in reverse, as it is formed from the bottom
# and now we are traversing from the top
for dir in range(len(path) -1, -1, -1):
if path[dir] == 0 and root.left:
root = root.left
elif path[dir] == 1 and root.right:
root = root.right
else:
return False
return True
``` | 2 | 0 | ['Design', 'Binary Tree', 'Python3'] | 0 |
find-elements-in-a-contaminated-binary-tree | 🔥Beats 100% | Easy for Beginners | ✨ 2 Approaches | Java | C++ | beats-100-easy-for-beginners-2-approache-h1xz | IntuitionAn Contaminated binary tree is given, where each node value is corrupted. We need to recover the tree by following conditions ->
The root node value is | panvishdowripilli | NORMAL | 2025-02-21T15:54:26.514151+00:00 | 2025-02-21T15:54:26.514151+00:00 | 26 | false |
# Intuition
An Contaminated binary tree is given, where each node value is corrupted. We need to recover the tree by following conditions ->
1. The root node value is set to `0`.
2. If a node has value `x`:
- The left child value is `2 * x + 1`.
- The right child value is `2 * x + 2`.
****
# Approach 1 <=> Using Set
1. Recover the tree using Depth First Search.
2. Store the values in the set.
3. Check for the value in the set when `find()` is called.
****
# Complexity
- **Time complexity:**
- **O(N)**: For traversing `n` nodes to recover the node values.
- **O(1)**: Checking if the number exists in the set or not.
- **Space complexity:**
- **O(N)**: For storing the values in the set.
****
# Code
```cpp []
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode() : val(0), left(nullptr), right(nullptr) {}
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
class FindElements {
private:
unordered_set<int> s;
void recover(TreeNode* root, int data){
if(root == NULL){
return;
}
root -> val = data;
s.insert(data);
recover(root -> right, 2 * data + 2);
recover(root -> left, 2 * data + 1);
}
public:
FindElements(TreeNode* root) {
recover(root, 0);
}
bool find(int target) {
if(s.find(target) != s.end()){
return true;
}
return false;
}
};
```
```java []
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {}
TreeNode(int val) { this.val = val; }
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
class FindElements {
HashSet<Integer> s;
void recover(TreeNode node, int data){
if(node == null){
return;
}
node.val = data;
s.add(data);
recover(node.right, 2 * data + 2);
recover(node.left, 2 * data + 1);
}
public FindElements(TreeNode root) {
s = new HashSet<>();
recover(root, 0);
}
public boolean find(int target) {
return s.contains(target);
}
}
```
****
# Approach 2 <=> Using Map
1. Recover the tree using Depth First Search.
2. Store the values in the map.
3. Check for the value in the map when `find()` is called.
****
# Complexity
- **Time complexity:**
- **O(N)**: For traversing `n` nodes to recover the node values.
- **O(1)**: Checking if the number exists in the map or not.
- **Space complexity:**
- **O(N)**: For storing the values in the map.
****
# Code
```cpp []
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode() : val(0), left(nullptr), right(nullptr) {}
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
class FindElements {
private:
unordered_map<int, int> mp;
void recover(TreeNode* root, int data){
if(root == NULL){
return;
}
root -> val = data;
mp[data]++;
recover(root -> right, 2 * data + 2);
recover(root -> left, 2 * data + 1);
}
public:
FindElements(TreeNode* root) {
recover(root, 0);
}
bool find(int target) {
if(mp.find(target) != mp.end()){
return true;
}
return false;
}
};
```
```java []
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {}
TreeNode(int val) { this.val = val; }
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}
class FindElements {
HashMap<Integer, Integer> mp;
void recover(TreeNode node, int data){
if(node == null){
return;
}
node.val = data;
mp.put(data, 1);
recover(node.right, 2 * data + 2);
recover(node.left, 2 * data + 1);
}
public FindElements(TreeNode root) {
mp = new HashMap<>();
recover(root, 0);
}
public boolean find(int target) {
return mp.containsKey(target);
}
}
``` | 2 | 0 | ['Hash Table', 'Depth-First Search', 'Recursion', 'Binary Tree', 'C++', 'Java'] | 0 |
find-elements-in-a-contaminated-binary-tree | EASY 2 APPROACHES || BFS, HASHING | easy-2-approaches-bfs-hashing-by-sarvpre-bov8 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | Sarvpreet_Kaur | NORMAL | 2025-02-21T15:28:00.977559+00:00 | 2025-02-21T15:28:00.977559+00:00 | 19 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class FindElements {
public:
Approach 1:
vector<int>tree;
FindElements(TreeNode* root) {
root->val = 0;
queue<TreeNode*>qu;
qu.push(root);
while(!qu.empty()){
TreeNode* temp = qu.front();
tree.push_back(temp->val);
qu.pop();
if(temp->left){
temp->left->val = 2*(temp->val)+1;
qu.push(temp->left);
}
if(temp->right){
temp->right->val = 2*(temp->val)+2;
qu.push(temp->right);
}
}
}
bool find(int target) {
int low = 0;
int high = tree.size()-1;
while(low<=high){
int mid = (low+high)/2;
if(tree[mid]==target)return true;
else if(tree[mid]<target) low=mid+1;
else high = mid-1;
}
return false;
}
};
Approach 2:
unordered_set<int> values; // Use a set for O(1) average time complexity for lookups
FindElements(TreeNode* root) {
if (root) {
root->val = 0;
values.insert(0);
queue<TreeNode*> qu;
qu.push(root);
while (!qu.empty()) {
TreeNode* temp = qu.front();
qu.pop();
if (temp->left) {
temp->left->val = 2 * (temp->val) + 1; // Assign value to left child
values.insert(temp->left->val); // Insert into the set
qu.push(temp->left);
}
if (temp->right) {
temp->right->val = 2 * (temp->val) + 2; // Assign value to right child
values.insert(temp->right->val); // Insert into the set
qu.push(temp->right);
}
}
}
}
bool find(int target) {
return values.find(target) != values.end(); // Check if the target exists in the set
}
};
``` | 2 | 0 | ['Hash Table', 'Tree', 'Breadth-First Search', 'Design', 'Binary Tree', 'C++'] | 0 |
find-elements-in-a-contaminated-binary-tree | O(n) python solution with step by step explanation | on-python-solution-with-step-by-step-exp-7jml | IntuitionWe can solve this problem using both bfs and dfs but we will solve it using dfs. Because we have to solve it in top down approach as to find a child no | 9chaitanya11 | NORMAL | 2025-02-21T13:53:20.991621+00:00 | 2025-02-21T13:53:20.991621+00:00 | 18 | false | # Intuition
We can solve this problem using both bfs and dfs but we will solve it using dfs. Because we have to solve it in top down approach as to find a child node's value, we must find the parent node's value first. Tree traversal is done in many types but we need preorder traversal in this case as it says we must function at root node, then left child and right child.
As the problem says we have contaminated binary tree so it's values are -1. So, we must revert it to the original form using the given formula:
-> l = 2 * x + 1
-> r = 2 * x + 2
assuming x to be zero
So, we first find elements[-1,-1,-1,-1,-1] and find the elemnts. If they match, we return True and if they don't, we return False
# Approach
So, we will begin by creating a set named targets which will store all the values. And, we will begin our dfs search from root. After that, we will create a dfs helper function to solve the problem like from root 0 to 1 to 3 and again 1 and then to 4 and back to 1 and back to 0 and go to 2.
We will also cover a scenario in which a node has no left or right to go, we return back. But they are nodes to the left and to the right, we add them to our set. We can iterate through them using the formula given above.
To end it, we return the target from our targets set.
# Example of the Operation:
["FindElements","find","find","find"]
[[[-1,-1,-1,-1,-1]],[1],[3],[5]]
So, this is the input we're given. To solve it, we are given a contaminated tree containing values -1. We will create a targets set.
-> targets = set()
We will assume the parent node to be 0.
-> l = 2 * x + 1
-> r = 2 * x + 2
These are the formulas given after solving, we will store them into our targets set.
From 0:
-> l = 2 * 0 + 1 = 0 + 1 = 1
-> targets = {1}
So, we found a child node as we're doing dfs we will try to go deep as possible until we're out of left and right children nodes.
From 1:
-> l = 2 * 1 + 1 = 2 + 1 = 3
-> targets = {1,3}
We found the left child node and we go up to 1 again and find its right child node.
-> r = 2 * 1 + 2 = 2 + 2 = 4
-> targets = {1,3,4}
We found the right child node and now, we go up to 1 again but we can see that we already found it's children so we back to 0 and try to find it's right child node:
-> r = 2 * 0 + 2 = 0 + 2 = 2
-> targets = {1,3,4,2}
And 2, doesn't have any children nodes. So, the first find query says find [1], it's present in our set. So, we return True.
Next is find[3], it's present in our set. So, we return True.
And at last, it is find[5] which doesn't exist in our set. So, we return False.
# Complexity
- Time complexity:
O(n) where n denotes the number of nodes in the tree because we're searching and recovering the tree which can take up 'n' time
- Space complexity:
O(n) because we are using set named targets which can take up to 'n' amount of space
# Code
```python3 []
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class FindElements:
def __init__(self, root: Optional[TreeNode]):
self.targets = set() #hashsets
self.dfs(root, 0) #dfs search
def find(self, target: int) -> bool:
return target in self.targets #return target or else we return false
def dfs(self, node, value): #dfs helper func
if node is None: #none ie when we search for left and right but they don't do exist so we return none
return
self.targets.add(value) #if they exist, we add that value to the set
self.dfs(node.left, value * 2 + 1) #recursive dfs search
self.dfs(node.right, value * 2 + 2) #recovery operation for both
# Your FindElements object will be instantiated and called as such:
# obj = FindElements(root)
# param_1 = obj.find(target)
``` | 2 | 0 | ['Python3'] | 0 |
find-elements-in-a-contaminated-binary-tree | simple py solution - beats 95% | simple-py-solution-beats-95-by-noam971-23at | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | noam971 | NORMAL | 2025-02-21T13:37:55.102477+00:00 | 2025-02-21T13:37:55.102477+00:00 | 15 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class FindElements:
def __init__(self, root: Optional[TreeNode]):
self.root = root
self.root.val = 0
self.data = set()
self.recover_init(self.root)
def find(self, target: int) -> bool:
return True if target in self.data else False
def recover_init(self, root: Optional[TreeNode]):
if not root:
return
self.data.add(root.val)
if root.right:
root.right.val = 2 * root.val + 2
self.recover_init(root.right)
if root.left:
root.left.val = 2 * root.val + 1
self.recover_init(root.left)
# Your FindElements object will be instantiated and called as such:
# obj = FindElements(root)
# param_1 = obj.find(target)
``` | 2 | 0 | ['Python3'] | 0 |
find-elements-in-a-contaminated-binary-tree | 🚀 Optimized Implicit Reconstruction || 0ms in Rust & Go || O(log target) Time and Space | optimized-recursive-tree-navigation-impl-0t22 | Intuition 🤔Instead of explicitly reconstructing the tree, we leverage the given rules torecursively navigateand determine iftargetexists.Each node’s value follo | rutsh | NORMAL | 2025-02-21T09:48:52.998458+00:00 | 2025-02-21T11:44:57.638974+00:00 | 101 | false | # Intuition 🤔
Instead of explicitly reconstructing the tree, we leverage the given rules to __recursively navigate__ and determine if `target` exists.
Each node’s value follows a strict formula, so we can compute its __parent's value__ and check if the target node should exist.
# Approach 🔍
- __Recursive Parent Lookup:__
- Start from target, compute its parent value using $\frac{target - 1}{2}$.
- Recursively find the __parent node__ first.
- If the parent doesn't exist, $target$ cannot exist.
2. __Determine Left/Right Child:__
- If ${target-1}\mod 2 = 0$ → result is left child.
- Otherwise, it's the right child.
3. __Return Node if Found:__
- If the correct child exists, return it; otherwise, return $None$.
# Complexity Analysis 📊
- __Time Complexity:__ $O(\log target)$ 🕒
- Each recursive call moves one level up (dividing target by 2).
- Maximum depth is $\log(target)$.
- __Space Complexity:__ $O(\log target)$ 📦
- Recursive stack depth is at most $\log(target)$.
- No extra memory is used for storing values.Complexity
# Code
```rust []
use std::rc::Rc;
use std::cell::RefCell;
struct FindElements {
root: Option<Rc<RefCell<TreeNode>>>
}
impl FindElements {
fn new(root: Option<Rc<RefCell<TreeNode>>>) -> Self {
FindElements { root }
}
// Checks if the target value exists in the tree
pub fn find(&self, target: i32) -> bool {
find_recursive(self.root.clone(), target).is_some()
}
}
// Recursively finds the target node by first locating its parent
fn find_recursive(node: Option<Rc<RefCell<TreeNode>>>, target: i32) -> Option<Rc<RefCell<TreeNode>>> {
if target == 0 {
return node; // Base case: root is always at value 0
}
let parent_val = (target - 1) / 2;
match (target - 1) % 2 {
0 => find_recursive(node, parent_val)?.borrow().left.clone(),
1 => find_recursive(node, parent_val)?.borrow().right.clone(),
_ => unreachable!("unexpected mod 2 value")
}
}
```
``` golang []
type FindElements struct {
Root *TreeNode
}
// Constructor: Simply stores the root without modifying the tree
func Constructor(root *TreeNode) FindElements {
return FindElements{Root: root}
}
// Checks if the target value exists in the tree
func (this *FindElements) Find(target int) bool {
return findRecursive(this.Root, target) != nil
}
// Recursively finds the target node by first locating its parent
func findRecursive(node *TreeNode, target int) *TreeNode {
if target == 0 {
return node // Base case: root is always at value 0
}
// Compute the parent's value
parentVal := (target - 1) / 2
parent := findRecursive(node, parentVal)
if parent == nil {
return nil // If parent does not exist, target cannot exist
}
// Determine if target is the left or right child
if (target-1)%2 == 0 {
return parent.Left
}
return parent.Right
}
```
``` racket []
; Definition for a binary tree node.
#|
; val : integer?
; left : (or/c tree-node? #f)
; right : (or/c tree-node? #f)
(struct tree-node
(val left right) #:mutable #:transparent)
; constructor
(define (make-tree-node [val 0])
(tree-node val #f #f))
|#
(define find-elements%
(class object%
(super-new)
; root : (or/c tree-node? #f)
(init-field root)
; Recursively finds the target node by first locating its parent
(define/private (find-recursive node target)
(cond
[(zero? target) node] ; Base case: root is always 0
[else
(let* ([parent-val (quotient (- target 1) 2)]
[parent (find-recursive node parent-val)])
(cond
[(not parent) #f] ; Parent doesn't exist, so target can't exist
[(even? (- target 1)) (tree-node-left parent)] ; Left child case
[else (tree-node-right parent)]))])) ; Right child case
; Finds if the target value exists in the tree
(define/public (find target)
(not (not (find-recursive root target))))))
``` | 2 | 0 | ['Recursion', 'Binary Tree', 'Go', 'Rust', 'Racket'] | 0 |
find-elements-in-a-contaminated-binary-tree | C++ Simple and Easy to Understand Recursive Solution | c-simple-and-easy-to-understand-recursiv-wxuu | IntuitionRecover the tree recursively while keeping all the values in a hashmap to find them easily.Complexity
Time complexity:Recover tree - O(n)Find - O(1) | yehudisk | NORMAL | 2025-02-21T08:54:31.713513+00:00 | 2025-02-21T08:54:31.713513+00:00 | 6 | false | # Intuition
Recover the tree recursively while keeping all the values in a hashmap to find them easily.
# Complexity
- Time complexity:
Recover tree - O(n)
Find - O(1)
- Space complexity: O(n)
# Code
```cpp []
class FindElements {
public:
unordered_set<int> values;
void recover(TreeNode* root) {
if (!root) return;
if (root->left) {
root->left->val = root->val * 2 + 1;
values.insert(root->left->val);
recover(root->left);
}
if (root->right) {
root->right->val = root->val * 2 + 2;
values.insert(root->right->val);
recover(root->right);
}
}
FindElements(TreeNode* root) {
if (root) {
root->val = 0;
values.insert(0);
}
recover(root);
}
bool find(int target) {
return values.count(target);
}
};
```
### Like it? Please Upvote! | 2 | 0 | ['C++'] | 0 |
find-elements-in-a-contaminated-binary-tree | ✅ Easy to Understand | Beginner Friendly | Tree | Design | Hash Table | Detailed Video Explanation🔥 | easy-to-understand-beginner-friendly-tre-kczv | IntuitionThe problem involves reconstructing a contaminated binary tree where all values were replaced with-1. Given a root node, we need to recover the tree fo | sahilpcs | NORMAL | 2025-02-21T08:43:13.716161+00:00 | 2025-02-21T08:43:13.716161+00:00 | 30 | false | # Intuition
The problem involves reconstructing a contaminated binary tree where all values were replaced with `-1`. Given a root node, we need to recover the tree following a specific formula:
- The root node is assigned a value of `0`.
- The left child of a node with value `val` is assigned `2 * val + 1`.
- The right child is assigned `2 * val + 2`.
To efficiently check if a given target value exists in the tree, we can store all valid node values in a `HashSet` during the reconstruction.
# Approach
1. **Use Depth-First Search (DFS)** to traverse the tree and recover node values:
- Start from the root and assign it `0`.
- Recursively assign values to the left and right children using the given formula.
- Store each assigned value in a `HashSet` for quick lookup.
2. **Implement a `find()` function** that checks if a given target exists in the set.
3. The solution ensures efficient retrieval since checking existence in a `HashSet` takes `O(1)` time on average.
# Complexity
- **Time complexity:**
- Constructing the tree involves visiting each node once → $$O(n)$$
- Checking for a value in the `HashSet` is $$O(1)$$ on average.
- Overall, the time complexity is **$$O(n)$$**.
- **Space complexity:**
- We store all `n` recovered node values in a `HashSet` → **$$O(n)$$**.
- Recursive DFS calls take **$$O(h)$$** space (where `h` is the tree height).
- In a skewed tree, `h = n`, but in a balanced tree, `h = log(n)`.
- Worst case: **$$O(n)$$**, Best case: **$$O(log n)$$**.
# Code
```java []
class FindElements {
Set<Integer> set; // Stores the values of the recovered tree
// Constructor to reconstruct the tree and populate the set
public FindElements(TreeNode root) {
set = new HashSet<>();
sol(root, 0); // Start the recovery process with the root having value 0
}
// Method to check if a target value exists in the reconstructed tree
public boolean find(int target) {
return set.contains(target);
}
// Recursive helper function to recover the tree values
private void sol(TreeNode root, int val) {
if (root == null) return; // Base case: If node is null, return
root.val = val; // Assign the correct value to the current node
set.add(val); // Add the value to the set
// Recursively assign values to the left and right children
sol(root.left, 2 * val + 1);
sol(root.right, 2 * val + 2);
}
}
```
https://youtu.be/rLRrNVsOZjc
| 2 | 0 | ['Hash Table', 'Tree', 'Depth-First Search', 'Design', 'Binary Tree', 'Java'] | 0 |
find-elements-in-a-contaminated-binary-tree | Kotlin. Beats 100% (66 ms). Using IntArray as a stack to build a path | kotlin-beats-100-71-ms-using-linkedlisti-od3f | CodeApproachLet's build a full new tree for the first elements from 0 to 14:We can see that there is some pattern in the elements.Odd elements are always to the | mobdev778 | NORMAL | 2025-02-21T07:51:43.129385+00:00 | 2025-02-21T10:19:51.347831+00:00 | 35 | false | 
# Code
```kotlin []
class FindElements(val root: TreeNode?) {
val path = IntArray(100)
var size = 0
fun find(target: Int): Boolean {
size = 0
findPath(target)
var node: TreeNode? = root
while (node != null && size > 0) {
node = if (path[--size] == 0) node?.left else node?.right
}
return node != null
}
fun findPath(target: Int) {
var n = target
while (n != 0) {
if (n and 1 == 1) {
path[size++] = 0
n--
} else {
path[size++] = 1
n--
n--
}
n = n shr 1
}
}
}
```
# Approach
Let's build a full new tree for the first elements from 0 to 14:
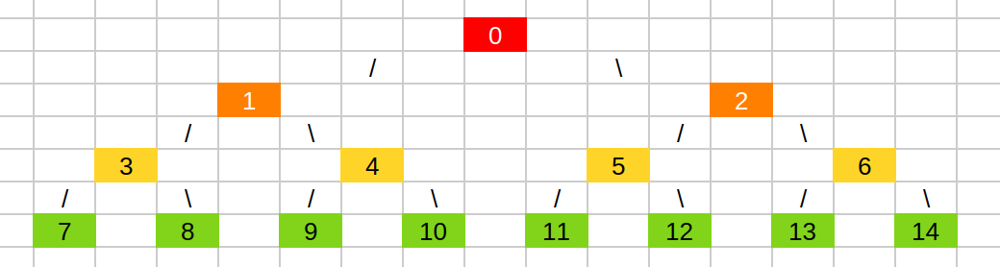
We can see that there is some pattern in the elements.
Odd elements are always to the left of the parent: 3->7, 1->3, 4->9
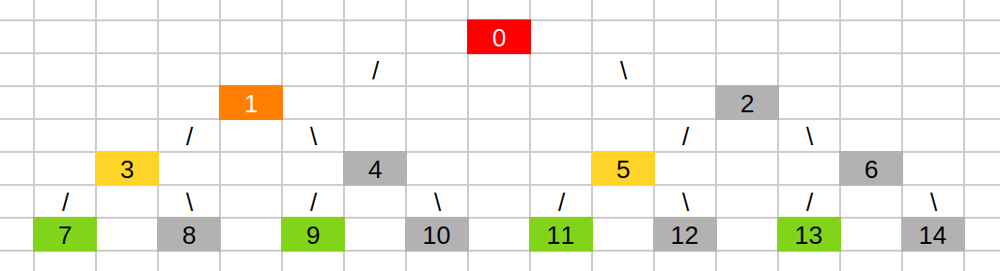
and even elements are always to the right: 3->8, 1->4, 4->10
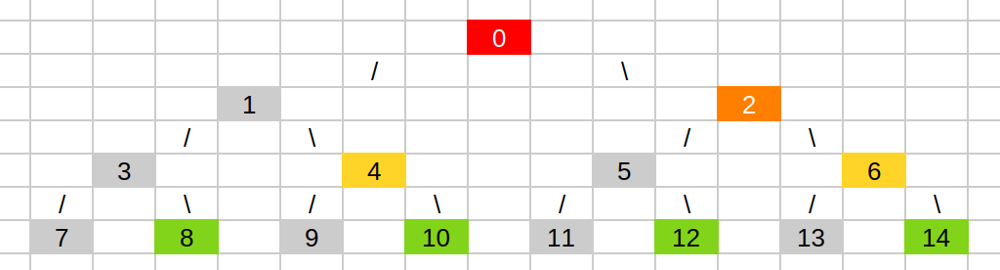
So the first step to build a path in the new tree to "target" seems obvious - we need to look at the remainder of dividing "target" by 2. And if the remainder is 1, then "target" is to the left of its parent. If 0, then it is to the right.
We can avoid the "costly" operation of calculating the remainder of division by 2, and instead check the least significant bit of the number using bitwise "and":
(n and 1 == 1)
to check if the number is odd.
Next, we need to subtract 1 from the target if this element is to the left of the parent, or 2 if it is to the right. Then divide the resulting number by 2 - this way the "target" will receive the value of its parent, i.e. we will move to a higher level in the tree.
By continuing this process to 0, we can restore the full path to "target" in the new tree. And, I note, **we don't have to change the nodes of the entire tree**.
All that remains is to take the path to the "target" and walk that path inside the tree to determine whether such a path exists or not. | 2 | 0 | ['Kotlin'] | 1 |
find-elements-in-a-contaminated-binary-tree | Simple | Stack | Log(n) | Readable | simple-stack-logn-readable-by-apakg-itvt | Code: Approach 1: Using Stack.Complexity
Time complexity: O(logn)
Space complexity: O(logn)
Approach 2: BFS. | Apakg | NORMAL | 2025-02-21T07:46:28.677044+00:00 | 2025-02-21T07:46:28.677044+00:00 | 15 | false | # Code: Approach 1: Using Stack.
```java []
class FindElements {
TreeNode root;
public FindElements(TreeNode root) {
this.root = root;
}
public boolean find(int target) {
Stack<Boolean> stack = new Stack<>();
for(; target != 0; target = (--target) >> 1) {
stack.push((target & 1) == 1);
}
TreeNode curr = root;
while(curr != null && !stack.isEmpty()) {
boolean moveLeft = stack.pop();
curr = moveLeft ? curr.left : curr.right;
}
return curr != null;
}
}
```
# Complexity
- Time complexity: O(logn)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(logn)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Approach 2: BFS.
```java []
class FindElements {
Set<Integer> set;
public FindElements(TreeNode root) {
set = new HashSet<>();
recover(root);
}
private void recover(TreeNode root) {
Queue<TreeNode> q = new LinkedList<>();
root.val = 0;
q.offer(root);
while(!q.isEmpty()) {
TreeNode curr = q.poll();
set.add(curr.val);
if(curr.left != null) {
curr.left.val = curr.val * 2 + 1;
q.offer(curr.left);
}
if(curr.right != null) {
curr.right.val = curr.val * 2 + 2;
q.offer(curr.right);
}
}
}
public boolean find(int target) {
return set.contains(target);
}
}
```
| 2 | 0 | ['Stack', 'Tree', 'Breadth-First Search', 'Monotonic Stack', 'Binary Tree', 'Java'] | 0 |
find-elements-in-a-contaminated-binary-tree | Easy code, must try in java | easy-code-must-try-in-java-by-notaditya0-jocd | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | NotAditya09 | NORMAL | 2025-02-21T07:14:12.189502+00:00 | 2025-02-21T07:14:12.189502+00:00 | 54 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class FindElements {
public FindElements(TreeNode root) {
dfs(root, 0);
}
public boolean find(int target) {
return vals.contains(target);
}
private Set<Integer> vals = new HashSet<>();
private void dfs(TreeNode root, int val) {
if (root == null)
return;
root.val = val;
vals.add(val);
dfs(root.left, val * 2 + 1);
dfs(root.right, val * 2 + 2);
}
}
``` | 2 | 0 | ['Java'] | 0 |
find-elements-in-a-contaminated-binary-tree | Most intuitive solution, Easy understanding. Beats 100%😎😎🔥🔥 | most-intuitive-solution-easy-understandi-bwnz | IntuitionThe problem states that the binary tree has been "contaminated," meaning all values are -1. However, we are given a specific set of transformation rule | nnzl48NW9N | NORMAL | 2025-02-21T05:38:16.493692+00:00 | 2025-02-21T05:38:16.493692+00:00 | 30 | false | # Intuition
The problem states that the binary tree has been "contaminated," meaning all values are -`1`. However, we are given a specific set of transformation rules that determine the correct values for each node based on its parent.
- Since the root is `0`, we can reconstruct the entire tree using **DFS (Depth-First Search)** or **BFS (Breadth-First Search)**.
- Once reconstructed, checking for the existence of any `target` value should be efficient. Using an unordered_set helps in achieving constant-time lookups.
# Approach
1. Recover the tree using DFS:
- Start from the root and assign `0` as its value.
- Recursively traverse the left and right children:
- Left child gets `2 * parent + 1`
- Right child gets `2 * parent + 2`
- Store all recovered values in an unordered_set for quick lookups.
2. Find function:
- Simply check if the target value exists in the unordered_set using `count(target)`, which takes **O(1)** on average.
# Complexity
- Time complexity:
- **O(n)**
for recovering the tree (traversing each node once).
- **O(1)**
for checking existence in the `unordered_set`.
- Total: **O(n)**
- Space complexity:
- **O(n)**
for storing the node values in an `unordered_set`.
- **O(n)**
worst-case recursion depth (for a skewed tree).
- Total: **O(n)**
# Code
```cpp []
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class FindElements {
private:
unordered_set<int> st;
void vaccinate(TreeNode* root, int value){
// base case -> when root is not present
if(!root) return ;
root->val = value;
st.insert(value);
vaccinate(root->left, 2*value + 1);
vaccinate(root->right, 2*value + 2);
}
public:
FindElements(TreeNode* root) {
vaccinate(root, 0);
}
bool find(int target) {
return st.count(target);
}
};
/**
* Your FindElements object will be instantiated and called as such:
* FindElements* obj = new FindElements(root);
* bool param_1 = obj->find(target);
*/
```

| 2 | 0 | ['Hash Table', 'Tree', 'Depth-First Search', 'Breadth-First Search', 'Design', 'Binary Tree', 'C++'] | 0 |
find-elements-in-a-contaminated-binary-tree | Easy to understand and Easy Approach(Beat 80%) 😊😊 | easy-to-understand-and-easy-approachbeat-voa1 | IntuitionThe problem is about reconstructing a contaminated binary tree where all values are initially set to -1. We are given the root node of this tree, and w | patelaviral | NORMAL | 2025-02-21T04:37:03.102276+00:00 | 2025-02-21T04:37:43.242075+00:00 | 9 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The problem is about reconstructing a contaminated binary tree where all values are initially set to -1. We are given the root node of this tree, and we need to recover the original values following a specific rule:
* The root node is assigned the value 0.
* For a node with value x:
--> Its left child gets the value 2*x + 1.
--> Its right child gets the value 2*x + 2.
After reconstructing the tree, we must support find(target), which checks whether a given target value exists in the tree efficiently.
# Approach
<!-- Describe your approach to solving the problem. -->
1. Reconstruct the tree using DFS (Depth-First Search)
* Start from the root with an initial value of 0.
* Use DFS to traverse and assign values to the nodes based on the given formula.
* Store these values in a Set<Integer> (hash set) to allow O(1) lookup.
2. Check for presence using HashSet
* Since all valid node values are stored in a Set, checking whether a target value exists is an O(1) operation.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code- 1 (Based on HashSet)
```java []
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class FindElements {
Set<Integer> op;
public FindElements(TreeNode root) {
op = new HashSet<>();
maker(root, 0);
}
public void maker(TreeNode root, int val){
if(root == null){
return;
}
op.add(val);
maker(root.left, 2*val+1);
maker(root.right, 2*val+2);
}
public boolean find(int target) {
return op.contains(target);
}
}
/**
* Your FindElements object will be instantiated and called as such:
* FindElements obj = new FindElements(root);
* boolean param_1 = obj.find(target);
*/
```
# Code- 2 (Based on Tree)
```java []
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class FindElements {
TreeNode cont;
public FindElements(TreeNode root) {
cont = maker(root, 0);
}
public TreeNode maker(TreeNode root, int val){
if(root == null){
return null;
}
TreeNode node = new TreeNode(val);
node.left = maker(root.left, 2*val+1);
node.right = maker(root.right, 2*val+2);
return node;
}
public boolean find(int target) {
return finder(cont, target);
}
public boolean finder(TreeNode cont, int tar){
if(cont == null){
return false;
}
if(cont.val == tar){
return true;
}
return finder(cont.left, tar) || finder(cont.right, tar);
}
} | 2 | 0 | ['Hash Table', 'Tree', 'Depth-First Search', 'Design', 'Binary Tree', 'Java'] | 0 |
find-elements-in-a-contaminated-binary-tree | Finding Elements in a Contaminated Binary Tree || DFS || JAVA ✅ | recover-tree-java-by-faiz_rahman_g-mx77 | IntuitionThe problem involves recovering a corrupted binary tree where each node's value was replaced with -1. We need to reconstruct the values such that:The r | Faiz_Rahman_G | NORMAL | 2025-02-21T04:34:56.613723+00:00 | 2025-02-21T06:18:07.984284+00:00 | 70 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The problem involves recovering a corrupted binary tree where each node's value was replaced with -1. We need to reconstruct the values such that:
The root is 0.
The left child of a node with value x has value 2*x + 1.
The right child of a node with value x has value 2*x + 2.
Since we need to efficiently check if a value exists in the tree, we use a BitSet for fast lookups.
# Approach
<!-- Describe your approach to solving the problem. -->
**Tree Recovery using DFS (Inorder Traversal)**
- Traverse the tree starting from the root.
- Assign the correct values to each node based on the given formula.
- Store the values in a BitSet for fast O(1) lookups.
- Fast Lookups with BitSet
**BitSet allows checking if a value is present in constant time using get(target), making the find operation very efficient.**
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
Recovering the tree : O(N)
Checking the elements: O(1)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
Bitset: O(N)
# Code
```java []
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class FindElements {
TreeNode root;
BitSet sett;
public void inorder(TreeNode root, int val) {
if (root == null) return;
root.val = val;
sett.set(val);
inorder(root.left, 2 * val + 1);
inorder(root.right, 2 * val + 2);
}
public FindElements(TreeNode root) {
this.root = root;
sett = new BitSet();
inorder(this.root, 0);
}
public boolean find(int target) {
return sett.get(target);
}
}
/**
* Your FindElements object will be instantiated and called as such:
* FindElements obj = new FindElements(root);
* boolean param_1 = obj.find(target);
*/
``` | 2 | 0 | ['Tree', 'Depth-First Search', 'Binary Tree', 'Java'] | 1 |
find-elements-in-a-contaminated-binary-tree | Hash Set and Depth-First Search | hash-set-and-depth-first-search-by-khale-6rqp | Complexity
Time complexity:
O(n)fornew FindElements(root)
O(1)forFindElements.find(target)
Space complexity:
O(n)
Code | khaled-alomari | NORMAL | 2025-02-21T04:24:31.437079+00:00 | 2025-02-21T05:31:48.184013+00:00 | 76 | false | # Complexity
- Time complexity:
$$O(n)$$ for `new FindElements(root)`
$$O(1)$$ for `FindElements.find(target)`
- Space complexity:
$$O(n)$$
# Code
```typescript []
class FindElements {
private set = new Set<number>();
constructor(root: TreeNode | null) {
const dfs = (node: TreeNode | null, val: number) => {
if (!node) return;
this.set.add(val);
dfs(node.left, val = val * 2 + 1);
dfs(node.right, val + 1);
};
dfs(root, 0);
}
find = (target: number) => this.set.has(target);
}
```
```javascript []
class FindElements {
constructor(root) {
this.set = new Set();
const dfs = (node, val) => {
if (!node) return;
this.set.add(val);
dfs(node.left, val = val * 2 + 1);
dfs(node.right, val + 1);
};
dfs(root, 0);
}
find = (target) => this.set.has(target);
}
``` | 2 | 0 | ['Hash Table', 'Math', 'Tree', 'Depth-First Search', 'Design', 'Simulation', 'Binary Tree', 'TypeScript', 'JavaScript'] | 0 |
find-elements-in-a-contaminated-binary-tree | JAVA SOLUTION || BFS | java-solution-bfs-by-gunasaihari_krishna-ujmt | Code | gunasaihari_krishna-2004 | NORMAL | 2025-02-21T03:54:08.119912+00:00 | 2025-02-21T03:54:08.119912+00:00 | 25 | false | # Code
```java []
class FindElements {
HashSet<Integer> hm=new HashSet<>();
public FindElements(TreeNode root) {
root.val=0;
Queue<TreeNode> q=new LinkedList<>();
q.add(root);
hm.add(0);
while(!q.isEmpty())
{
TreeNode node=q.remove();
if(node.left!=null)
{
node.left.val=2*node.val+1;
hm.add(node.left.val);
q.add(node.left);
}
if(node.right!=null)
{
node.right.val=2*node.val+2;
hm.add(node.right.val);
q.add(node.right);
}
}
}
public boolean find(int target) {
return hm.contains(target);
}
}
``` | 2 | 0 | ['Java'] | 0 |
find-elements-in-a-contaminated-binary-tree | Simple C++ Solution | Binary Tree | InOrder Traversal | simple-c-solution-binary-tree-inorder-tr-tgio | SolutionComplexity
Time complexity:FindElements:O(n)find:O(1)
Space complexity:FindElements:O(n)find:O(1)
Code | ipriyanshi | NORMAL | 2025-02-21T03:39:24.990023+00:00 | 2025-02-21T03:39:24.990023+00:00 | 96 | false | # Solution
https://youtu.be/MzMYRFmV-PA
# Complexity
- Time complexity:
FindElements: $$O(n)$$
find: $$O(1)$$
- Space complexity:
FindElements: $$O(n)$$
find: $$O(1)$$
# Code
```cpp []
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class FindElements {
public:
unordered_set<int> treeVals;
void recoverTreeValues(TreeNode* root, int currVal){
if(root==NULL) return;
recoverTreeValues(root->left, currVal*2+1);
treeVals.insert(currVal);
recoverTreeValues(root->right, currVal*2+2);
}
FindElements(TreeNode* root) {
recoverTreeValues(root, 0);
}
bool find(int target) {
return treeVals.contains(target);
}
};
/**
* Your FindElements object will be instantiated and called as such:
* FindElements* obj = new FindElements(root);
* bool param_1 = obj->find(target);
*/
``` | 2 | 0 | ['C++'] | 0 |
find-elements-in-a-contaminated-binary-tree | BFS Traversal || SImple Solution || O(N) Time Complexity || CPP | bfs-traversal-simple-solution-on-time-co-klp5 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | Heisenberg_wc | NORMAL | 2025-02-21T03:30:18.550928+00:00 | 2025-02-21T03:30:18.550928+00:00 | 57 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class FindElements {
public:
map<int,bool>m;
FindElements(TreeNode* root) {
queue<TreeNode*>q;
m[0]=true;
root->val=0;
q.push(root);
while(!q.empty()){
auto front =q.front();
m[front->val]=true;
q.pop();
if(front->left!=NULL){front->left->val=2*front->val+1;q.push(front->left);}
if(front->right!=NULL){front->right->val=2*front->val+2;q.push(front->right);}
}
}
bool find(int target) {
if(m[target]) return true;
return false;
}
};
/**
* Your FindElements object will be instantiated and called as such:
* FindElements* obj = new FindElements(root);
* bool param_1 = obj->find(target);
*/
``` | 2 | 0 | ['C++'] | 0 |
find-elements-in-a-contaminated-binary-tree | Javascript | javascript-by-davidchills-ub3c | Code | davidchills | NORMAL | 2025-02-21T03:03:46.147453+00:00 | 2025-02-21T03:03:46.147453+00:00 | 85 | false | # Code
```javascript []
/**
* Definition for a binary tree node.
* function TreeNode(val, left, right) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
*/
/**
* @param {TreeNode} root
*/
var FindElements = function(root) {
this.values = new Set();
this.recover(root, 0);
};
/**
* @param {number} target
* @return {boolean}
*/
FindElements.prototype.find = function(target) {
return this.values.has(target);
};
FindElements.prototype.recover = function(node, val) {
if (!node) return;
node.val = val;
this.values.add(val);
this.recover(node.left, 2 * val + 1);
this.recover(node.right, 2 * val + 2);
};
/**
* Your FindElements object will be instantiated and called as such:
* var obj = new FindElements(root)
* var param_1 = obj.find(target)
*/
``` | 2 | 0 | ['JavaScript'] | 0 |
find-elements-in-a-contaminated-binary-tree | Easy Java Solution Using Set And BFS | easy-java-solution-using-set-and-bfs-by-2zbn8 | IntuitionAs Statement says just keep goingApproachWork on the BFS and Trust on Recursion.Using a helper Method in which i am updating the child node values one | shbhm20 | NORMAL | 2025-02-21T02:50:42.101730+00:00 | 2025-02-21T02:50:42.101730+00:00 | 78 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
As Statement says just keep going
# Approach
<!-- Describe your approach to solving the problem. -->
Work on the BFS and Trust on Recursion.
Using a helper Method in which i am updating the child node values one by one.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
Time Complexity-O(N)
Space Complexiety-O(N)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class FindElements {
TreeNode root;
Set<Integer>ss;
public FindElements(TreeNode root) {
this.root=root;
ss=new HashSet<>();
root.val=0;
ss.add(0);
solve(root,ss);
}
public void solve(TreeNode root,Set<Integer>ss){
if(root==null) return;
if(root.left!= null){
root.left.val=(2*root.val+1);
ss.add(2*root.val+1);
solve(root.left,ss);
}
if(root.right!= null){
root.right.val=(2*root.val+2);
ss.add(2*root.val+2);
solve(root.right,ss);
}
}
public boolean find(int target) {
if(ss.contains(target)){
return true;
}
return false;
}
}
/**
* Your FindElements object will be instantiated and called as such:
* FindElements obj = new FindElements(root);
* boolean param_1 = obj.find(target);
*/
``` | 2 | 0 | ['Hash Table', 'Tree', 'Breadth-First Search', 'Recursion', 'Simulation', 'Binary Tree', 'Hash Function', 'Ordered Set', 'Java'] | 2 |
find-elements-in-a-contaminated-binary-tree | 🥇EASY || C++ || BEGINNER FRIENDLY || QUEUE || LEVEL ORDER TRAVERSAL || MAP ✅✅ | easy-c-beginner-friendly-queue-level-ord-obdu | Code | kruppatel64 | NORMAL | 2025-02-21T01:52:25.287248+00:00 | 2025-02-21T02:39:52.221955+00:00 | 81 | false | # Code
```cpp []
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class FindElements {
unordered_map<int,bool> mp;
public:
FindElements(TreeNode* root) {
if(root == NULL){
return;
}
queue<TreeNode*> q;
root->val = 0;
q.push(root);
while(!q.empty()){
TreeNode * temp = q.front();
mp[temp->val] = true;
q.pop();
if(temp->left){
temp->left->val = temp->val*2 + 1;
q.push(temp->left);
}
if(temp->right){
temp->right->val = temp->val*2 + 2;
q.push(temp->right);
}
}
}
bool find(int target) {
if(mp[target] == true){
return true;
}else{
return false;
}
}
};
/**
* Your FindElements object will be instantiated and called as such:
* FindElements* obj = new FindElements(root);
* bool param_1 = obj->find(target);
*/
``` | 2 | 0 | ['Hash Table', 'Tree', 'Queue', 'Binary Tree', 'C++'] | 1 |
find-elements-in-a-contaminated-binary-tree | 1261. Find Elements in a Contaminated Binary Tree | 1261-find-elements-in-a-contaminated-bin-5ahe | IntuitionApproachComplexity
Time complexity:
Space complexity:
Can give a upvote and support 🔥Code | akashdoss996 | NORMAL | 2025-02-21T01:26:22.951422+00:00 | 2025-02-21T01:26:22.951422+00:00 | 118 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Can give a upvote and support 🔥
# Code
```python3 []
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class FindElements:
def __init__(self, root: Optional[TreeNode]):
self.s = set([0])
root.val = 0
q = deque([root])
while q:
node = q.popleft()
self.s.add(node.val)
if node.left:
node.left.val = 2 * node.val + 1
q.append(node.left)
if node.right:
node.right.val = 2 * node.val + 2
q.append(node.right)
def find(self, target: int) -> bool:
return target in self.s
# Your FindElements object will be instantiated and called as such:
# obj = FindElements(root)
# param_1 = obj.find(target)
``` | 2 | 0 | ['Python', 'Python3'] | 0 |
find-elements-in-a-contaminated-binary-tree | ✅Simple BFS || O(N) Efficient Solution. | simple-bfs-on-efficient-solution-by-pras-qc58 | IntuitionApproachComplexity
Time complexity: O(N)
Space complexity: O(N)
Code | prashanth_d4 | NORMAL | 2025-02-21T00:47:25.288228+00:00 | 2025-02-21T00:48:06.306729+00:00 | 75 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: O(N)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(N)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class FindElements {
HashSet<Integer> set;
public FindElements(TreeNode root) {
set = new HashSet<>();
root.val = 0;
bfs(root,set);
}
public boolean find(int target) {
return set.contains(target);
}
private void bfs(TreeNode root, HashSet<Integer> set)
{
Queue<TreeNode> q = new LinkedList<>();
q.add(root);
while(!q.isEmpty())
{
TreeNode curr = q.poll();
set.add(curr.val);
if(curr.left!=null)
{
q.offer(curr.left);
if(curr.left.val==-1)
{
int act = curr.val*2 + 1;
curr.left.val = act;
}
}
if(curr.right!=null)
{
q.offer(curr.right);
if(curr.right.val==-1)
{
int act = curr.val*2 + 2;
curr.right.val = act;
}
}
}
}
}
/**
* Your FindElements object will be instantiated and called as such:
* FindElements obj = new FindElements(root);
* boolean param_1 = obj.find(target);
*/
``` | 2 | 0 | ['Hash Table', 'Tree', 'Breadth-First Search', 'Design', 'Binary Tree', 'Java'] | 0 |
find-elements-in-a-contaminated-binary-tree | Beats 99%. Dawgs ts is heat. DFS and Set bruzz feel me? | beats-99-dawgs-ts-is-heat-dfs-and-set-br-qui2 | Code | Ishaan_P | NORMAL | 2025-02-21T00:26:39.007844+00:00 | 2025-02-21T00:26:39.007844+00:00 | 25 | false | # Code
```java []
class FindElements {
Set<Integer> found;
public FindElements(TreeNode root) {
found = new HashSet<>();
dfs(root,0);
}
public boolean find(int target) {
return found.contains(target);
}
public void dfs(TreeNode curr, int currVal){
if(curr == null) return;
found.add(currVal);
dfs(curr.left,currVal * 2 + 1);
dfs(curr.right,currVal * 2 + 2);
}
}
``` | 2 | 0 | ['Java'] | 0 |
find-elements-in-a-contaminated-binary-tree | Swift💯 BitSet DFS/BFS | swift-bitset-by-upvotethispls-raal | BitSet DFS (accepted answer)BitSetref:https://swift-collections/1.1.0/documentation/bitcollections/bitsetBitSet BFS (accepted answer) | UpvoteThisPls | NORMAL | 2025-02-21T00:16:32.226685+00:00 | 2025-02-21T00:53:29.429409+00:00 | 63 | false | **BitSet DFS (accepted answer)**
```
class FindElements {
var set = BitSet()
init(_ root: TreeNode?) {
func dfs(_ node: TreeNode?, _ val:Int) {
guard let node else { return }
set.insert(val)
dfs(node.left, val*2 + 1)
dfs(node.right, val*2 + 2)
}
dfs(root, 0)
}
func find(_ target: Int) -> Bool {
set.contains(target)
}
}
```
`BitSet` ref: [https://swift-collections/1.1.0/documentation/bitcollections/bitset](https://swiftpackageindex.com/apple/swift-collections/1.1.0/documentation/bitcollections/bitset)
**BitSet BFS (accepted answer)**
```
class FindElements {
var set = BitSet()
init(_ root: TreeNode?) {
guard let root else { return }
root.val = 0
set = BitSet(
sequence(
first: [root],
next: {prev in
let next = prev.flatMap { node in
node.left?.val = node.val*2 + 1
node.right?.val = node.val*2 + 2
return [node.left, node.right].compactMap{$0}
}
return next.isEmpty ? nil : next
}
)
.flatMap{$0.map(\.val)}
)
}
func find(_ target: Int) -> Bool {
set.contains(target)
}
}
``` | 2 | 0 | ['Swift'] | 1 |
find-elements-in-a-contaminated-binary-tree | BFS + Set Solution - Beats 93% | bfs-set-solution-beats-93-by-richyrich20-w0qi | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | RichyRich2004 | NORMAL | 2025-02-21T00:13:50.225252+00:00 | 2025-02-21T00:17:18.673329+00:00 | 169 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class FindElements:
def __init__(self, root: Optional[TreeNode]):
self.s = set([0])
root.val = 0
q = deque([root])
while q:
node = q.popleft()
self.s.add(node.val)
if node.left:
node.left.val = 2 * node.val + 1
q.append(node.left)
if node.right:
node.right.val = 2 * node.val + 2
q.append(node.right)
def find(self, target: int) -> bool:
return target in self.s
# Your FindElements object will be instantiated and called as such:
# obj = FindElements(root)
# param_1 = obj.find(target)
``` | 2 | 0 | ['Python3'] | 0 |
find-elements-in-a-contaminated-binary-tree | Easy python O(log target) solution with O(1) space [binary search] | easy-python-olog-target-solution-with-o1-x4pk | IntuitionThe solution is inspired from the binary search method followed in https://leetcode.com/problems/count-complete-tree-nodes/editorialApproachWhen the no | kowshika95 | NORMAL | 2025-02-13T19:24:01.200836+00:00 | 2025-02-13T19:24:01.200836+00:00 | 230 | false | # Intuition
The solution is inspired from the binary search method followed in https://leetcode.com/problems/count-complete-tree-nodes/editorial
# Approach
When the nodes are numbered from 1 to n in a binary tree, we can check the existence of any node using the technique similar to binary search. This would take O(log(target)) time complexity.
From the editorial shared above:
How to check if the node number idx exists?
Let's use binary search again to reconstruct the sequence of moves
from root to idx node. For example, idx = 4. idx is in the
second half of nodes 0,1,2,3,4,5,6,7 and hence the first move is to the right.
Then idx is in the first half of nodes 4,5,6,7 and hence
the second move is to the left. The idx is in the first half of nodes
4,5 and hence the next move is to the left. The time complexity
for one check is O(d).
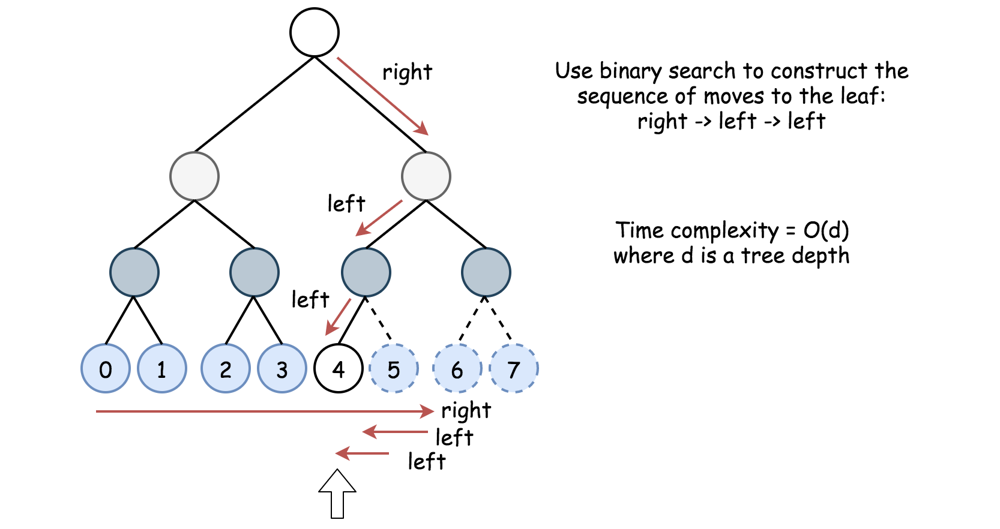
I just modified the above logic to stop at the level where the target is supposed to be instead of checking till the leaf node.
# Complexity
# Time complexity:**O(log(target))**
Since we only check till the depth where target node is supposed to be.
For a complete tree, this would be O(log H). A skewed tree would O(n) in the worst case.
# Space complexity: O(1)
# Code
```python3 []
class FindElements:
def __init__(self, root: Optional[TreeNode]):
self._root = root
def find(self, target: int) -> bool:
root = self._root
# starting the node numbering from 1 instead of 0
# for easy calculation
target += 1
depth = math.floor(math.log(target, 2))
left, right = math.pow(2, depth), math.pow(2, depth+1)-1
while depth and root:
mid = (left+right)//2
if target <= mid:
root = root.left
right = mid
else:
left = mid+1
root = root.right
depth -= 1
return root != None
``` | 2 | 0 | ['Binary Search', 'Binary Tree', 'Python3'] | 0 |
find-elements-in-a-contaminated-binary-tree | 🌳57. 2 Solutions || Recursive [ DFS ] || Magic 🪄 || Short & Sweet Code !! || C++ Code Reference !! | 57-2-solutions-recursive-dfs-magic-short-t76l | \n# Code\ncpp [Using Set ]\n\nclass FindElements {\n\n unordered_set<int>s;\npublic:\n FindElements(TreeNode* a) { Traverse(a,0); }\n \n bool find(i | Amanzm00 | NORMAL | 2024-07-10T10:17:42.846100+00:00 | 2024-07-10T10:17:42.846169+00:00 | 104 | false | \n# Code\n```cpp [Using Set ]\n\nclass FindElements {\n\n unordered_set<int>s;\npublic:\n FindElements(TreeNode* a) { Traverse(a,0); }\n \n bool find(int T) { return s.count(T)>0;}\n\nprivate: \n void Traverse(TreeNode* a,int x)\n {\n if(!a) return;\n\n a->val=x;\n s.insert(x);\n Traverse(a->left,2*x+1);\n Traverse(a->right,2*x+2);\n }\n};\n\n\n```\n```cpp [No Extra Space ]\n\nclass FindElements {\n\n TreeNode* Root=nullptr;\npublic:\n FindElements(TreeNode* a):Root(a) {}\n \n bool find(int T) { return Find(Root,0,T); }\n\nprivate:\n\n bool Find(TreeNode* a,int x,int T)\n {\n if(!a) return 0;\n a->val=x;\n\n if(a->val==T)return 1;\n return (Find(a->left,2*x+1,T) || Find(a->right,2*x+2,T));\n }\n};\n\n\n```\n\n\n---\n# *Guy\'s Upvote Pleasee !!* \n\n\n# ***(\u02E3\u203F\u02E3 \u035C)***\n\n\n | 2 | 0 | ['Hash Table', 'Tree', 'Depth-First Search', 'Breadth-First Search', 'Design', 'Recursion', 'Binary Tree', 'C++'] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.