question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
max-chunks-to-make-sorted-ii | O(n) beats 100% precomputing. | on-beats-100-precomputing-by-luudanhhieu-g9n6 | Intuition
Array arr can seperate to 2 chunks arr1, arr2 only if data in arr1 < any data in arr2
Approach
Precomputing calculate maxLeft and minRight of arr
Com | luudanhhieu | NORMAL | 2025-03-06T07:19:32.787943+00:00 | 2025-03-06T07:19:32.787943+00:00 | 66 | false | # Intuition
- Array `arr` can seperate to 2 chunks `arr1, arr2 only if data in arr1 < any data in arr2 `
# Approach
- Precomputing calculate `maxLeft` and `minRight` of `arr`
- Compare and choose the right index to seperate
- `i == len(arr)-1` or `maxLeft[i] == minRight[i]` or `maxLeft[i] <= minRight[i+1] `
# Complexity
- Time complexity: O(n)
- Space complexity: O(n)
# Code
```golang []
func maxChunksToSorted(arr []int) int {
maxLeft := make([]int, len(arr))
maxLeft[0] = arr[0]
for i := 1; i < len(arr); i++ {
maxLeft[i] = max(maxLeft[i-1], arr[i])
}
minRight := make([]int, len(arr))
minRight[len(arr)-1] = arr[len(arr)-1]
for i := len(arr) - 2; i >= 0; i-- {
minRight[i] = min(minRight[i+1], arr[i])
}
rs := 0
for i := range maxLeft {
if i == len(arr)-1 || maxLeft[i] == minRight[i] || maxLeft[i] <= minRight[i+1] {
rs++
}
}
return rs
}
``` | 1 | 0 | ['Go'] | 0 |
max-chunks-to-make-sorted-ii | Beats 100.00% || Used PrefixMax And SuffixMin Array || Very Easy Solution || C++ | beats-10000-used-prefixmax-and-suffixmin-q3e8 | Complexity -:
Time complexity -: O(n)
Space complexity -: O(n)
Code -: | ShivamShrivastav | NORMAL | 2024-12-30T06:04:57.545525+00:00 | 2024-12-30T06:04:57.545525+00:00 | 12 | false |
# Complexity -:
- Time complexity -: O(n)
- Space complexity -: O(n)
# Code -:
```cpp []
class Solution { // prefixMax, suffixMin -:
public:
int maxChunksToSorted(vector<int>& arr) {
int n=arr.size();
// find the prefix Max array
vector<int>pre(n);
pre[0]=arr[0];
for(int i=1; i<n; i++){
pre[i]=max(arr[i], pre[i-1]);
}
// find the suffix min array
vector<int>suf(n);
suf[n-1]=arr[n-1];
for(int i=n-2; i>=0; i--){
suf[i]=min(arr[i], suf[i+1]);
}
// apply condition -:
int count=1;
for(int i=1; i<n; i++){
if(suf[i]>=pre[i-1]){
count++;
}
}
return count;
}
};
``` | 1 | 0 | ['Array', 'Greedy', 'Sorting', 'C++'] | 0 |
max-chunks-to-make-sorted-ii | Easy way to solve this problem, easy to understand for beginner | easy-way-to-solve-this-problem-easy-to-u-wj4n | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | Beshoy25 | NORMAL | 2024-12-19T22:59:16.468644+00:00 | 2024-12-19T22:59:16.468644+00:00 | 61 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Easy solution to solve this problem and easy to understand
# Approach
<!-- Describe your approach to solving the problem. -->
I used another array as a index.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(n)+function sort = o(nlogn)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(n)
# Code
```cpp []
class Solution {
public:
int maxChunksToSorted(vector<int>& arr) {
int cont=0;
long long current = 0;
vector<int> arr1;
for(int i = 0 ; i < arr.size();i++)
{
arr1.push_back(arr[i]);
}
sort(arr1.begin(),arr1.end());
for(int i = 0 ; i < arr.size();i++)
{
current+= arr[i]-arr1[i];
cont+=(current==0);
}
return cont;
}
};
``` | 1 | 0 | ['C++'] | 1 |
max-chunks-to-make-sorted-ii | Java Monotonic Stack O(n) Solution with Simple Explanation | java-monotonic-stack-on-solution-with-si-opym | IntuitionKeep the max number of each chunk in the stack in ascending order.If the current number is less than previous chunk's max number, then we should merge | _BugMaker_ | NORMAL | 2024-12-19T20:51:38.528490+00:00 | 2024-12-19T20:52:02.250660+00:00 | 145 | false | # Intuition
Keep the max number of each chunk in the stack in ascending order.
If the current number is less than previous chunk's max number, then we should merge current number into the previous chunk. Here ‘previous chunk’ means the chunk currently at the top of the stack, they are represented by their max numbers.
# Complexity
- Time complexity: O(n)
- Space complexity: O(n)
# Code
```java []
class Solution {
public int maxChunksToSorted(int[] arr) {
Stack<Integer> stack = new Stack<>();
for (int i : arr) {
int max = i;
while (!stack.isEmpty() && stack.peek() > i) {
max = Math.max(max, stack.pop());
}
stack.push(max);
}
return stack.size();
}
}
``` | 1 | 0 | ['Monotonic Stack', 'Java'] | 0 |
max-chunks-to-make-sorted-ii | O(n) -->TIME COMPLEXITY, PREFIX_MAXIMUM AND SUFFIX_MINIMUM | on-time-complexity-prefix_maximum-and-su-fjlt | IntuitionTo split the array into the maximum number of chunks such that each chunk, when sorted individually and concatenated, results in a fully sorted array, | Star5courage1436 | NORMAL | 2024-12-19T19:28:56.153051+00:00 | 2024-12-19T19:28:56.153051+00:00 | 60 | false | # Intuition
To split the array into the maximum number of chunks such that each chunk, when sorted individually and concatenated, results in a fully sorted array, we need to identify partition points. The key insight is that the maximum element on the left of a partition must be less than or equal to the minimum element on the right of the partition.
# Approach
1. **Prefix Maximum Array**: Create an array pfxMax where each element represents the maximum value from the start of the array to the current index.
2. **Suffix Minimum Array**: Create an array sfxMin where each element represents the minimum value from the current index to the end of the array.
3. **Partition Check**: For every possible partition point, check if the maximum value in the left partition (pfxMax[i-1]) is less than or equal to the minimum value in the right partition (sfxMin[i]). If true, increment the chunk count.
# Complexity
- Time complexity: **O(n)**
Calculating the prefix maximum and suffix minimum arrays takes O(n), and iterating over the array to count chunks also takes O(n).
- Space complexity: **O(n)**
Two additional arrays (pfxMax and sfxMin) are used, each of size 𝑛.
# Code
```cpp []
class Solution {
public:
int maxChunksToSorted(vector<int>& arr) {
int n = arr.size();
vector<long long> pfxMax(n), sfxMin(n);
pfxMax[0] = arr[0];
for (int i = 1; i < n; ++i) {
pfxMax[i] = max(pfxMax[i - 1], 1LL * arr[i]);
}
sfxMin[n - 1] = arr[n - 1];
for (int i = n - 2; i >= 0; --i) {
sfxMin[i] = min(sfxMin[i + 1], 1LL * arr[i]);
}
int chunk = 0;
for (int i = 0; i < n; ++i) {
long long pfxMx = (i > 0 ? pfxMax[i - 1] : -1);
long long sfxMn = sfxMin[i];
if (pfxMx <= sfxMn) {
chunk += 1;
}
}
return chunk;
}
};
``` | 1 | 0 | ['Greedy', 'C++'] | 0 |
max-chunks-to-make-sorted-ii | Simple C++ code | O(N) | Monotonic Stack solution | | simple-c-code-on-monotonic-stack-solutio-f7eq | Approach -> Monotonic StackComplexity
Time complexity : O(N)
Space complexity : O(N)
Code | Akt_00 | NORMAL | 2024-12-19T14:03:14.791154+00:00 | 2024-12-19T14:03:14.791154+00:00 | 113 | false | # Approach -> Monotonic Stack
# Complexity
- Time complexity : O(N)
- Space complexity : O(N)
# Code
```cpp []
class Solution {
public:
int maxChunksToSorted(vector<int>& arr) {
int n = arr.size();
stack<int> st;
for(int i=0; i<n; i++){
int ele = arr[i];
while(!st.empty() && arr[i] < st.top()){
ele = max(st.top(), ele);
st.pop();
}
st.push(ele);
}
return st.size();
}
};
``` | 1 | 0 | ['Array', 'Stack', 'Monotonic Stack', 'C++'] | 0 |
max-chunks-to-make-sorted-ii | Easy Solution here. using the concept of leftMax and RightMin to check | easy-solution-here-using-the-concept-of-xlb8n | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | HYDRO2070 | NORMAL | 2024-12-19T11:36:18.985912+00:00 | 2024-12-19T11:36:18.985912+00:00 | 148 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int maxChunksToSorted(vector<int>& arr) {
int n = arr.size();
int ans = 1;
vector<int> left(n,0);
vector<int> right(n,0);
left[0] = arr[0];
right[n-1] = arr[n-1];
for(int i = 1;i < n;i++){
left[i] = max(left[i-1],arr[i]);
right[n-i-1] = min(right[n-i],arr[n-i-1]);
}
for(int i = 0;i < n-1;i++){
if(left[i] <= right[i+1]){
ans++;
}
}
return ans;
}
};
``` | 1 | 0 | ['C++'] | 1 |
max-chunks-to-make-sorted-ii | beats 100% fastest solution monotonic stack | beats-100-fastest-solution-monotonic-sta-f96b | IntuitionApproachmonotonic stack approach, code is commented for explanation, this is very similar to maxChunksToSorted medium questionComplexity
Time complexit | neilpant | NORMAL | 2024-12-19T11:19:08.749633+00:00 | 2024-12-19T11:19:08.749633+00:00 | 11 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
monotonic stack approach, code is commented for explanation, this is very similar to maxChunksToSorted medium question
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: N
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: N
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def maxChunksToSorted(self, arr: List[int]) -> int:
mono=[]
for i in range(len(arr)):
if not mono or mono[-1]<=arr[i]: # if the curr is greater than or equal to the top of the chunk we add it. ie. create a new chunk
mono.append(arr[i])
else:
top=mono[-1]
while mono and mono[-1]>arr[i]:# if the curr element is less than the top of the chunk we consume it in the chunk
mono.pop()
mono.append(top)
return len(mono)
``` | 1 | 0 | ['Python3'] | 0 |
max-chunks-to-make-sorted-ii | beats 100% fastest solution monotonic stack | beats-100-fastest-solution-monotonic-sta-1z5l | IntuitionApproachmonotonic stack approach, code is commented for explanation, this is very similar to maxChunksToSorted medium questionComplexity
Time complexit | neilpant | NORMAL | 2024-12-19T11:19:02.480250+00:00 | 2024-12-19T11:19:02.480250+00:00 | 13 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
monotonic stack approach, code is commented for explanation, this is very similar to maxChunksToSorted medium question
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: N
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: N
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def maxChunksToSorted(self, arr: List[int]) -> int:
mono=[]
for i in range(len(arr)):
if not mono or mono[-1]<=arr[i]: # if the curr is greater than or equal to the top of the chunk we add it. ie. create a new chunk
mono.append(arr[i])
else:
top=mono[-1]
while mono and mono[-1]>arr[i]:# if the curr element is less than the top of the chunk we consume it in the chunk
mono.pop()
mono.append(top)
return len(mono)
``` | 1 | 0 | ['Python3'] | 0 |
max-chunks-to-make-sorted-ii | Simple 10 line C++ O(N) Solution! | simple-10-line-c-on-solution-by-knightfu-zsgy | IntuitionJust sort the array and compare the prefix sums at each index!Complexity
Time complexity: O(N)
Space complexity: O(1)
Code | knightfury24 | NORMAL | 2024-12-19T06:41:24.762423+00:00 | 2024-12-19T06:41:24.762423+00:00 | 29 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Just sort the array and compare the prefix sums at each index!
# Complexity
- Time complexity: O(N)
- Space complexity: O(1)
# Code
```cpp []
class Solution {
public:
int maxChunksToSorted(vector<int>& arr) {
vector<int> nums = arr;
sort(nums.begin(),nums.end());
int n = arr.size();
long long int s = 0,s2 = 0,ans = 0;
for(int i=0;i<n;i++){
s+=nums[i];
s2+=arr[i];
if(s==s2)ans++;
}
return ans;
}
};
``` | 1 | 1 | ['C++'] | 0 |
max-chunks-to-make-sorted-ii | Beats 100%🔥|| easy JAVA Solution✅ | beats-100-easy-java-solution-by-priyansh-mx31 | Code\n\nclass Solution {\n public int maxChunksToSorted(int[] arr) {\n int n=arr.length;\n int min[]=new int[n];\n min[n-1]=arr[n-1];\n | priyanshu1078 | NORMAL | 2023-12-05T10:03:41.074858+00:00 | 2023-12-05T10:03:41.074888+00:00 | 107 | false | # Code\n```\nclass Solution {\n public int maxChunksToSorted(int[] arr) {\n int n=arr.length;\n int min[]=new int[n];\n min[n-1]=arr[n-1];\n for(int i=n-2;i>=0;i--){\n min[i]=Math.min(min[i+1],arr[i]);\n }\n int ans=0,max=Integer.MIN_VALUE;\n for(int i=0;i<n-1;i++){\n max=Math.max(max,arr[i]);\n if(max<=min[i+1]) ans++;\n }\n return ans+1;\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
max-chunks-to-make-sorted-ii | Solution by using two pointers approach | solution-by-using-two-pointers-approach-kco3s | Intuition\n Describe your first thoughts on how to solve this problem. \nTwo pointers\n\n# Approach\nTwo Pointers Approach\n\n# Complexity\n- Time complexity:\n | naman05022002 | NORMAL | 2023-09-07T12:30:18.011047+00:00 | 2023-09-07T12:30:18.011071+00:00 | 17 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTwo pointers\n\n# Approach\nTwo Pointers Approach\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n# Code\n```\nclass Solution {\npublic:\n int maxChunksToSorted(vector<int>& arr) {\n int n=arr.size();\n vector<int> v=arr;\n sort(v.begin(),v.end());\n map<int,set<int>> m;\n for(int i=0;i<n;i++)\n {\n m[v[i]].insert(i);\n }\n for(int i=0;i<n;i++)\n { auto it=m[arr[i]].begin();\n int k=(*it);\n m[arr[i]].erase(it);\n arr[i]=k;\n \n }\n int curr=0,maxi=-1;\n int ans=0;\n while(maxi<n-1&&curr<n)\n {\n maxi=max(maxi,arr[curr]);\n if(maxi==n-1){ans++; break;}\n if(arr[curr]<=curr&&maxi==curr){ans++;}\n curr++;\n \n }\n return ans;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
max-chunks-to-make-sorted-ii | C++ Easy Sorting | c-easy-sorting-by-xenox_grix-2n67 | Intuition\nThe last number that belongs to the chunk should be present at that index or before that index.\n\nbefore sorting [array, index] :{{2,0},{1,1},{3,2}, | xenox_grix | NORMAL | 2023-04-01T09:19:37.710474+00:00 | 2023-04-01T10:02:46.962297+00:00 | 27 | false | # Intuition\nThe last number that belongs to the chunk should be present at that index or before that index.\n\nbefore sorting [array, index] :{{2,0},{1,1},{3,2},{4,3},{4,4}}\nafter sorting.... [array, index] :{{1,1},{2,0},{3,2},{4,3},{4,4}}\n\nNow, while traversing the sorted array arr[n][2], we know that we need to include elements upto arr[i][1](the index in the original array) in the chunk for it to come at the right place after sorting chunk wise. \n\n# Complexity\n- Time complexity:\nO(nlogn)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution {\npublic:\n int maxChunksToSorted(vector<int>& nums) {\n int n = nums.size(), max_index = 0, ans = 0; \n vector<vector<int>> v; \n for(int i=0; i<n; i++){\n v.push_back({nums[i], i}); \n }\n sort(v.begin(), v.end());\n for(int i=0; i<n; i++){\n max_index = max(max_index, v[i][1]); \n if(i==max_index) ans++;\n }\n return ans;\n }\n};\n``` | 1 | 0 | ['Sorting', 'C++'] | 0 |
max-chunks-to-make-sorted-ii | Python || Sorting+Hashmap || O(n logn) | python-sortinghashmap-on-logn-by-in_sidi-mo3h | We have 2 arrays. One sorted and one unsorted.Now traverse over both.For one array increment by one for every value and for other decrement.We delete an element | iN_siDious | NORMAL | 2023-01-13T16:32:01.606711+00:00 | 2023-01-13T16:38:01.798799+00:00 | 313 | false | We have 2 arrays. One sorted and one unsorted.Now traverse over both.For one array increment by one for every value and for other decrement.We delete an element from map when its count is reached 0, it means when one element who was in excess in one array has been compensated by the same value in other array.(basically its +1-1=0 or +2-2=0 .....)Finally we will have a chunk when we have common elements in both subarrays i.e. when length of map will be 0.\n```\nclass Solution:\n def maxChunksToSorted(self, arr: List[int]) -> int:\n arr2=sorted(arr)\n n=len(arr)\n cnt={}\n ans=0\n for i in range(n):\n if arr[i] not in cnt:\n cnt[arr[i]]=1\n else:\n cnt[arr[i]]+=1\n if cnt[arr[i]]==0:\n del cnt[arr[i]]\n if arr2[i] not in cnt:\n cnt[arr2[i]]=-1\n else:\n cnt[arr2[i]]-=1\n if cnt[arr2[i]]==0:\n del cnt[arr2[i]]\n ans+=(1 if len(cnt)==0 else 0)\n return ans\n \n``` | 1 | 0 | ['Sorting', 'Python3'] | 0 |
max-chunks-to-make-sorted-ii | Easy and Fast Java Solution || Beats 100% | easy-and-fast-java-solution-beats-100-by-xu6v | \n\n# Code\n\nclass Solution {\n public int maxChunksToSorted(int[] arr) {\n int rightMin[]=new int[arr.length+1];\n rightMin[arr.length]=Integ | 20_Saurabh-kumar | NORMAL | 2023-01-12T20:33:37.289420+00:00 | 2023-01-12T20:33:37.289451+00:00 | 138 | false | \n\n# Code\n```\nclass Solution {\n public int maxChunksToSorted(int[] arr) {\n int rightMin[]=new int[arr.length+1];\n rightMin[arr.length]=Integer.MAX_VALUE;\n for(int i=arr.length-1; i>=0; i--){\n rightMin[i]=Math.min(rightMin[i+1], arr[i]);\n }\n int count=0;\n int leftMax=Integer.MIN_VALUE;\n for(int i=0; i<arr.length; i++){\n leftMax=Math.max(leftMax, arr[i]);\n if(leftMax <= rightMin[i+1]){\n count++;\n }\n }\n return count;\n }\n}\n``` | 1 | 0 | ['Array', 'Stack', 'Greedy', 'Monotonic Stack', 'Java'] | 0 |
max-chunks-to-make-sorted-ii | Advance Sorting Technique | advance-sorting-technique-by-shrey0811-c3d2 | class Solution {\npublic:\n int maxChunksToSorted(vector& arr)\n {\n vector right_min(arr.size()+1,INT_MAX);\n int count = 0;\n int l | shrey0811 | NORMAL | 2022-11-16T18:19:05.230808+00:00 | 2022-11-16T18:19:05.230844+00:00 | 1,121 | false | class Solution {\npublic:\n int maxChunksToSorted(vector<int>& arr)\n {\n vector<int> right_min(arr.size()+1,INT_MAX);\n int count = 0;\n int left_max = INT_MIN;\n for(int i=arr.size()-1;i>=0;i--)\n {\n right_min[i] = min(right_min[i+1],arr[i]);\n }\n \n for(int i =0; i<arr.size();i++)\n {\n left_max = max(left_max,arr[i]);\n if(left_max <= right_min[i+1])\n count +=1;\n }\n return count; \n }\n}; | 1 | 0 | [] | 1 |
max-chunks-to-make-sorted-ii | C++ || DP || TLE (128 Passed out of 136) || O(n^2) || Partition based | c-dp-tle-128-passed-out-of-136-on2-parti-thm8 | \n bool check(vector<int> &nums , int l , int r , vector<int> &sorted_arr)\n {\n unordered_map< int , int > mp;\n \n for(int i=l;i<=r;i+ | KR_SK_01_In | NORMAL | 2022-10-08T14:04:31.429715+00:00 | 2022-10-08T14:04:31.429742+00:00 | 34 | false | ```\n bool check(vector<int> &nums , int l , int r , vector<int> &sorted_arr)\n {\n unordered_map< int , int > mp;\n \n for(int i=l;i<=r;i++)\n {\n mp[sorted_arr[i]]++;\n }\n \n for(int i=l;i<=r;i++)\n {\n if(mp.find(nums[i])==mp.end())\n {\n return false;\n }\n else\n {\n mp[nums[i]]--;\n \n if(mp[nums[i]]==0)\n {\n mp.erase(nums[i]);\n }\n }\n }\n \n return true;\n }\n \n int dp[2005];\n \n int func(vector<int> &nums , int l , int r , vector<int> &sorted_arr)\n {\n if(l>r)\n {\n return 0 ;\n }\n \n if(dp[l]!=-1)\n {\n return dp[l];\n }\n \n int ans=0;\n \n int val=0;\n \n for(int k=l;k<=r;k++)\n {\n // partition \n \n if(check(nums , l , k , sorted_arr))\n {\n val = 1 + func(nums , k+1 , r , sorted_arr);\n ans=max(ans , val);\n }\n \n \n }\n \n return dp[l]=ans;\n }\n \n int maxChunksToSorted(vector<int>& nums) {\n \n vector<int> arr=nums;\n \n sort(arr.begin() , arr.end());\n \n memset(dp , -1 , sizeof(dp));\n \n \n return func(nums , 0 , nums.size()-1 , arr);\n \n \n \n }\n``` | 1 | 0 | ['Array', 'Dynamic Programming', 'C', 'C++'] | 0 |
number-of-ways-to-split-array | Prefix Sum with O(1) space||C++beats 100% | prefix-sum-with-o1-spacebeats-100-by-anw-q7hw | IntuitionFind the number of ways splitting the array nums such that sum(nums[0...i])>=sum(nums[i+1...]).
How?
compute sum=sum(nums)
Use a loop to find whether i | anwendeng | NORMAL | 2025-01-03T00:15:05.380090+00:00 | 2025-01-03T11:20:33.931162+00:00 | 14,683 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Find the number of ways splitting the array `nums` such that `sum(nums[0...i])>=sum(nums[i+1...])`.
How?
1. compute `sum=sum(nums)`
2. Use a loop to find whether i satisfying `sum(nums[0..i])>=sum(nums[i+1..])=sum-sum(nums[0..i])`
2 pass solution. Python is also made
Using inequality $$\sum_{k=0}^i nums[k]\geq \sum_{k=i+1 }^{n-1}nums[k] \iff 2 \sum_{k=0}^i nums[k]\geq sum$$ can simplify the code.
# Approach
<!-- Describe your approach to solving the problem. -->
[Please Turn on English subtitles if necessary]
[https://youtu.be/WQLBMjpeal4?si=_-2AouMRypgCpRGi](https://youtu.be/WQLBMjpeal4?si=_-2AouMRypgCpRGi)
1. Compute `sum=sum(nums)` by using `std::accumulate`
2. Set `acc=0` as the variable for prefix sum (Note using long long to avoid of overflowing)
3. Initialize `cnt=0`
4. Procced a loop as follow
```
for(int i=0; i<n-1; i++){
acc+=nums[i];// prefix sum
cnt+=(2*acc>=sum);// acc>=sum/2.0<=>acc>=sum-acc
}
```
5. `cnt` is the answer
6. Python code is made with the same logic.
7. A slight variant of C++ is made by using `std::count_if` with lambda instead of the for-loop in the 1st C++.
8. 2nd Python using accumulate( for Python prefix sum). A 2-line code is made. In contrary to Python, C++ `std::partial_sum` may have problem with int overflowing for using the similar method.
9. Python 1-liner is done modified from the 2-line code. More 1-liner codes can be ref the comments by @maria_q ref. https://leetcode.com/problems/number-of-ways-to-split-array/solutions/6223222/one-line-solution/
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O( n)$$-->
$O(n)$
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
$O(1)$
# Code||C++ 0ms beats 100%
```cpp []
class Solution {
public:
static int waysToSplitArray(vector<int>& nums) {
const int n=nums.size();
long long sum=accumulate(nums.begin(), nums.end(), 0LL);
long long acc=0LL;
int cnt=0;
for(int i=0; i<n-1; i++){
acc+=nums[i];
cnt+=(2*acc>=sum);
}
return cnt;
}
};
```
```Python []
class Solution:
def waysToSplitArray(self, nums: List[int]) -> int:
n=len(nums)
Sum=sum(nums)
acc, cnt=0, 0
for i in range(n-1):
acc+=nums[i]
cnt+=(2*acc>=Sum)
return cnt
```
# 2nd C++ using count_if instead of the for-loop
```
class Solution {
public:
static int waysToSplitArray(vector<int>& nums) {
long long sum=accumulate(nums.begin(), nums.end(), 0LL);
return count_if(nums.begin(), nums.end()-1, [acc=0LL, sum](int x) mutable{
acc+=x;
return 2*acc>=sum;
});
}
};
```
# 2nd Python 2-line TC: O(n) SC: O(n)
```
class Solution:
def waysToSplitArray(self, nums: List[int]) -> int:
nums=list(accumulate(nums))
return sum(1 if 2*x>=nums[-1] else 0 for x in nums[0:len(nums)-1])
```
# Python 1-liner
```
class Solution:
def waysToSplitArray(self, nums: List[int]) -> int:
return (nums:=list(accumulate(nums))) and sum(2*x>=nums[-1] for x in nums[0:-1])
``` | 56 | 2 | ['Math', 'Prefix Sum', 'C++', 'Python3'] | 14 |
number-of-ways-to-split-array | Detailed Explanation Total Sum | Prefix Sum 100%Beats | detailed-explanation-without-prefix-100b-ab3z | 🌟 IntuitionThe task requires finding the number of ways to split the array such that the sum of the left part is greater than or equal to the sum of the right p | Sumeet_Sharma-1 | NORMAL | 2025-01-03T00:34:59.684174+00:00 | 2025-01-03T09:25:53.931433+00:00 | 12,156 | false | # 🌟 **Intuition**
The task requires finding the number of ways to split the array such that the **sum of the left part is greater than or equal to the sum of the right part**.
To solve this, consider:
- **Brute force approach**: For every possible split, calculate the sum of the left and right parts. This is inefficient as it involves recalculating sums repeatedly for each split, leading to $$O(n^2)$$ time complexity.
- **Optimized approach**: Use a **running sum** technique where:
1. Precompute the total sum of the array.
2. Dynamically update the left and right sums as you traverse the array.
This reduces redundant calculations and ensures a linear $$O(n)$$ solution.
**Subscribe For Video Solution Startind today : https://shorturl.at/zM3iG**
---
# 🛠️ **Approach**
### 1️⃣ **Precompute the Total Sum**
- Calculate the **total sum** of the array (`rightSideSum`). This represents the initial sum of the "right side" before any split.
### 2️⃣ **Simulate Splits Efficiently**
- Use two variables:
- `leftSideSum` initialized to 0.
- `rightSideSum` initialized to the total sum of the array.
- Traverse the array:
- For each split at index `i`, update:
- Add `nums[i]` to `leftSideSum` (growing the left part).
- Subtract `nums[i]` from `rightSideSum` (shrinking the right part).
- Check the condition: **`leftSideSum >= rightSideSum`**.
### 3️⃣ **Count Valid Splits**
- For every valid split (where the condition is satisfied), increment the count.
---
# 📊 **Complexity**
- **Time Complexity**:
$$O(n)$$ — Two passes: one for the total sum and one for simulating splits.
- **Space Complexity**:
$$O(1)$$ — Only a few variables are used for computations.
---
# 📋 **Example Walkthrough**
Consider the input:
`nums = [10, 4, 1, 3, 5]`
### **Step 1: Compute Total Sum**
- `rightSideSum = 10 + 4 + 1 + 3 + 5 = 23`
### **Step 2: Simulate Splits**
- Initialize `leftSideSum = 0` and `rightSideSum = 23`.
| **Index** | **Left Side Sum** | **Right Side Sum** | **Condition (`>=`)?** | **Valid Split?** |
|-----------|--------------------|--------------------|------------------------|------------------|
| 0 | 10 | 13 | ❌ No | No |
| 1 | 14 | 9 | ✅ Yes | Yes |
| 2 | 15 | 8 | ✅ Yes | Yes |
| 3 | 18 | 5 | ✅ Yes | Yes |
- **Result**: 3 valid splits.
---
# 🌈 **Detailed Steps**
### **Step 1: Precompute the Total Sum**
- Sum up all the elements in `nums` to get `rightSideSum`.
- This value represents the entire array sum before any split.
---
### **Step 2: Traverse and Simulate Splits**
- Use a loop to iterate through each index except the last one (splits are made between elements).
- For each index:
1. Add the current element to `leftSideSum`.
2. Subtract the current element from `rightSideSum`.
3. Check the condition: **`leftSideSum >= rightSideSum`**. If true, increment the count of valid splits.
---
### **Step 3: Return the Count**
- After the loop, return the total count of valid splits.
### First Video Solution Show Some Support I Am Nervous ###
https://www.youtube.com/watch?v=43qs6v4Wtzo&ab_channel=Mr.Destroy
---
# 💻 **Code**
#**Prefix Sume Method**
```C++ []
class Solution {
public:
int waysToSplitArray(vector<int>& nums) {
int N = nums.size();
vector<long long> Prefix(N + 1, 0);
for (int i = 0; i < N; i++) {
Prefix[i + 1] = Prefix[i] + nums[i];
}
int ANS = 0;
for (int i = 1; i < N; i++) {
if (Prefix[i] >= Prefix[N] - Prefix[i]) {
ANS++;
}
}
return ANS;
}
};
```
**Runing Sum Method**
```cpp []
class Solution {
public:
int waysToSplitArray(vector<int>& nums) {
long long leftSideSum = 0, rightSideSum = 0;
for (int num : nums) {
rightSideSum += num;
}
int validSplits = 0;
for (int i = 0; i < nums.size() - 1; i++) {
leftSideSum += nums[i];
rightSideSum -= nums[i];
if (leftSideSum >= rightSideSum) {
validSplits++;
}
}
return validSplits;
}
};
```
```Java []
class Solution {
public int waysToSplitArray(int[] nums) {
long leftSum = 0, rightSum = 0;
for (int num : nums) {
rightSum += num;
}
int validSplits = 0;
for (int i = 0; i < nums.length - 1; i++) {
leftSum += nums[i];
rightSum -= nums[i];
if (leftSum >= rightSum) {
validSplits++;
}
}
return validSplits;
}
}
```
```Python3 []
class Solution:
def waysToSplitArray(self, nums: List[int]) -> int:
leftSideSum = 0
rightSideSum = sum(nums)
validSplits = 0
for i in range(len(nums) - 1):
leftSideSum += nums[i]
rightSideSum -= nums[i]
if leftSideSum >= rightSideSum:
validSplits += 1
return validSplits
```
```C []
int waysToSplitArray(int* nums, int numsSize) {
long long leftSum = 0, rightSum = 0;
for (int i = 0; i < numsSize; i++) {
rightSum += nums[i];
}
int validSplits = 0;
for (int i = 0; i < numsSize - 1; i++) {
leftSum += nums[i];
rightSum -= nums[i];
if (leftSum >= rightSum) {
validSplits++;
}
}
return validSplits;
}
```
```C# []
public class Solution {
public int WaysToSplitArray(int[] nums) {
long leftSideSum = 0, rightSideSum = 0;
foreach (int num in nums) {
rightSideSum += num;
}
int validSplits = 0;
for (int i = 0; i < nums.Length - 1; i++) {
leftSideSum += nums[i];
rightSideSum -= nums[i];
if (leftSideSum >= rightSideSum) {
validSplits++;
}
}
return validSplits;
}
}
```
```java_script []
var waysToSplitArray = function(nums) {
let leftSideSum = 0, rightSideSum = nums.reduce((acc, num) => acc + num, 0);
let validSplits = 0;
for (let i = 0; i < nums.length - 1; i++) {
leftSideSum += nums[i];
rightSideSum -= nums[i];
if (leftSideSum >= rightSideSum) {
validSplits++;
}
}
return validSplits;
};
```
```Ruby []
def ways_to_split_array(nums)
leftSideSum = 0
rightSideSum = nums.sum
validSplits = 0
(0...nums.length - 1).each do |i|
leftSideSum += nums[i]
rightSideSum -= nums[i]
validSplits += 1 if leftSideSum >= rightSideSum
end
return validSplits
end
```
| 37 | 0 | ['Array', 'C', 'C++', 'Java', 'Python3', 'Ruby', 'JavaScript', 'C#'] | 12 |
number-of-ways-to-split-array | Prefix Sum | O(1) Space | prefix-sum-o1-space-by-kamisamaaaa-u22i | \nclass Solution {\npublic:\n int waysToSplitArray(vector<int>& nums) {\n \n long long sumFromBack(0), sumFromFront(0);\n for (auto& i : nu | kamisamaaaa | NORMAL | 2022-05-14T16:01:28.805268+00:00 | 2022-05-14T16:27:16.862806+00:00 | 4,706 | false | ```\nclass Solution {\npublic:\n int waysToSplitArray(vector<int>& nums) {\n \n long long sumFromBack(0), sumFromFront(0);\n for (auto& i : nums) sumFromBack += i;\n \n int n(size(nums)), res(0);\n for (auto i=0; i<n-1; i++) {\n \n sumFromFront += nums[i]; // sum of the first i + 1 elements\n sumFromBack -= nums[i]; // sum of the last n - i - 1 elements.\n if (sumFromFront >= sumFromBack) res++;\n }\n return res;\n }\n};\n``` | 35 | 1 | ['C', 'Prefix Sum'] | 15 |
number-of-ways-to-split-array | Python: Easily explained brute force to optimized | python-easily-explained-brute-force-to-o-1av8 | Here, they are asking to count such events/occurances where:\n the array can be splitted into two non-empty parts, such that \n the sum of elements in first par | meaditya70 | NORMAL | 2022-05-14T17:08:25.894911+00:00 | 2022-05-15T00:41:05.355797+00:00 | 1,496 | false | Here, they are asking to **count such events**/occurances where:\n* the array can be splitted into **two non-empty parts**, such that \n* the sum of elements in first part **>=** sum of elements in second parts.\n\nA prefix sum array is an array that stores at ith index, the sum of all elements encountered from 0th index upto the ith index (inclusive). How can this help?\n* The prefix sum has a property that it `avoids recomputation of sum`. \n* The sum upto element i can be obtained by `prefix_sum[i]`.\n* The sum from i + 1 to last element of array can be obtained by `prefix_sum[n-1] - prefix_sum[i]`\n\nThe full code (***written during contest***) is given below:\n```\nclass Solution:\n def waysToSplitArray(self, nums: List[int]) -> int:\n prefix_sum = [nums[0]]\n n = len(nums)\n for i in range(1, n):\n prefix_sum.append(nums[i] + prefix_sum[-1]) \n \n count = 0\n for i in range(n-1):\n if prefix_sum[i] >= prefix_sum[n-1] - prefix_sum[i]:\n count += 1\n return count\n```\n\n**Time and Space Complexity Analysis:**\nWe iterate through each element of the array in a linear fashion. Hence, **time complexity = O(n)**.\nAlso, we maintain a extra space of size \'n\' for prefix_sum array. Hence, **space complexity = O(n)**.\n\n***Can we do any better?***\n* In terms of time: **NO**. We will need to traverse the array atleast once (at any cost, in any situation).\n* In terms of space: **YES**. We actually do not need a complete prefix array.\n\nLet\'s see how!\n\nWe just need to have two sum variables storing the sum of left part and right part.\nInitially, the left part will contain the `first element` and right part will contain `sum of array - the first element`.\nAs we increment the index, we take the current nums[i] value and add it to the left part and remove it from the right part.\n\nHence ***reducing the space complexity to O(1).***\n\nSimple and Sweet.\n\nThe full code (***space optimized***) is given below:\n```\nclass Solution:\n def waysToSplitArray(self, nums: List[int]) -> int:\n count = 0\n left_sum, right_sum = 0, sum(nums)\n for i in range(len(nums) - 1):\n left_sum += nums[i]\n right_sum -= nums[i]\n if left_sum >= right_sum:\n count += 1\n return count\n```\n\nUpvote, if helpful. | 26 | 0 | ['Python'] | 4 |
number-of-ways-to-split-array | Beats 100% | Prefix Sum | Solution for LeetCode#2270 | beats-100-prefix-sum-solution-for-leetco-u70n | IntuitionThe problem asks us to split an array into two non-empty parts such that the sum of the left part is greater than or equal to the sum of the right part | samir023041 | NORMAL | 2025-01-03T01:12:00.074297+00:00 | 2025-01-03T01:12:00.074297+00:00 | 3,258 | false | 
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The problem asks us to split an array into two non-empty parts such that the sum of the left part is greater than or equal to the sum of the right part. To solve this efficiently, we can calculate the total sum of the array once and then iterate through the array while maintaining a running sum for the left part.
# Approach
<!-- Describe your approach to solving the problem. -->
1. Calculate Total Sum:
- Compute the total sum of the array (sumTotal) in a single pass.
2. Iterate Through the Array:
- Maintain a running sum (sumCurr) for the left part of the array as you iterate.
- For each index i (except the last one, since both parts must be non-empty), check if sumCurr >= sumTotal - sumCurr. If true, increment a counter (cnt).
3. Return Result:
- After iterating through the array, return cnt, which represents the number of valid splits.
# Complexity
- Time complexity: O(n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code Option-01
```java []
class Solution {
public int waysToSplitArray(int[] nums) {
int n=nums.length;
long sumTotal=0;
long sumCurr=0;
int cnt=0;
// Calculate total sum
for(int i=0; i<n; i++){
sumTotal+=nums[i];
}
// Check valid splits condition
for(int i=0; i<n-1; i++){
sumCurr+=nums[i];
if(sumCurr >= sumTotal-sumCurr){
cnt++;
}
}
return cnt;
}
}
```
# Code Option-02 : Used Prefix Sum
- Time complexity: O(n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(n)
```java []
class Solution {
public int waysToSplitArray(int[] nums) {
int n=nums.length;
int m=n+1;
long[] arr=new long[m];
int cnt=0;
//Doing the Prefix sum
arr[0]=0;
for(int i=1; i<m; i++){
arr[i]=arr[i-1]+nums[i-1];
}
//Checking a valid split
for(int i=1; i<m-1; i++){
if(arr[i] >= arr[m-1]-arr[i]){
cnt++;
}
}
return cnt;
}
}
``` | 19 | 1 | ['Prefix Sum', 'Java'] | 6 |
number-of-ways-to-split-array | Prefix Sum | prefix-sum-by-votrubac-qh6v | Python 3\npython\nclass Solution:\n def waysToSplitArray(self, n: List[int]) -> int:\n n = list(accumulate(n))\n return sum(n[i] >= n[-1] - n[i | votrubac | NORMAL | 2022-05-14T17:16:29.055856+00:00 | 2022-05-14T18:13:37.894102+00:00 | 2,781 | false | **Python 3**\n```python\nclass Solution:\n def waysToSplitArray(self, n: List[int]) -> int:\n n = list(accumulate(n))\n return sum(n[i] >= n[-1] - n[i] for i in range(len(n) - 1))\n```\n\n**C++**\nWe could use a prefix sum, but in C++ we would need to store it in another `long long` vector (because of overflow). So, we are using a running sum here for efficiency.\n```cpp\nint waysToSplitArray(vector<int>& n) {\n long long right = accumulate(begin(n), end(n), 0LL), left = 0, res = 0;\n for (int i = 0; i < n.size() - 1; ++i) {\n left += n[i];\n right -= n[i];\n res += left >= right;\n }\n return res;\n}\n``` | 18 | 1 | ['C', 'Python3'] | 6 |
number-of-ways-to-split-array | ✅C++ || Easy to Understand || Simple Sum || O(N) | c-easy-to-understand-simple-sum-on-by-ma-9xiq | Please Upvote If It Helps\n\n store total sum of nums in right_sum and iterate over nums\n\n add nums[i] in left sum and subtract nums[i] from right sum\n* when | mayanksamadhiya12345 | NORMAL | 2022-05-14T16:44:30.701173+00:00 | 2022-05-14T16:44:30.701204+00:00 | 1,119 | false | **Please Upvote If It Helps**\n\n* store total sum of nums in right_sum and iterate over nums\n\n* add nums[i] in left sum and subtract nums[i] from right sum\n* when condition (left_sum>=right_sum) match increase valid_split by 1.\n\n```\nclass Solution {\npublic:\n int waysToSplitArray(vector<int>& nums) \n {\n int valid_split=0;\n long long right_sum=0;\n long long left_sum =0;\n \n //counting the total sum and store it into the right sum\n for(int i=0; i<nums.size(); i++) \n right_sum += nums[i];\n \n for(int i=0; i<nums.size()-1; i++)\n {\n // add nums[i] in left sum \n // subtract nums[i] from right sum\n left_sum += nums[i]; \n right_sum -= nums[i]; \n \n //check whether left_sum is greater than or equal to right_sum\n //if it is , then increase split by 1\n if(left_sum >= right_sum) \n valid_split++; \n }\n return valid_split; \n }\n};\n``` | 13 | 0 | [] | 1 |
number-of-ways-to-split-array | 🚀💻Efficient Solution for Counting Valid Array Splits Using Prefix Sums | JAVA | PYTHON🐍🚀 | efficient-solution-for-counting-valid-ar-xbur | IntuitionThe problem requires splitting an array into two non-empty parts such that the sum of the left part greater than or 🟰 sum of the right part. To solve t | manoj55802 | NORMAL | 2025-01-03T04:48:32.155985+00:00 | 2025-01-03T08:05:30.939595+00:00 | 1,081 | false | # Intuition
The problem requires splitting an array into two non-empty parts such that the sum of the left part greater than or 🟰 sum of the right part. To solve this efficiently, we can use a prefix sum 🤷♂️ to calculate the sums for both parts in constant time during each iteration.
# Approach
1. Prefix Sum Calculation:
1. Compute the prefix sum array pref where pref[i] stores the sum of the first i+1 elements.
2. The sum of the left part for index i is pref[i].
3. The sum of the right part can be calculated as the total sum of the array minus pref[i].
2. Iterate Through Splits:
1. For each possible split index i (from 0 to n−2):
2. Check if the left sum (pref[i]) is greater than or equal to the right sum (total_sum - pref[i]).
3. If true, increment the count.
3. Return the Count:The count of valid splits is returned as the result.
# Complexity
- Time complexity:
Calculating the prefix sum: O(n).
Iterating through the splits: O(n).
Total: O(n).
- Space complexity:
Prefix sum array pref: O(n).
Total: O(n).
# Code
```java []
class Solution {
public int waysToSplitArray(int[] nums) {
long[] pref=new long[nums.length];
pref[0]=nums[0];
for(int i=1;i<nums.length;i++){
pref[i]=pref[i-1]+nums[i];
}
int count=0;
for(int i=0;i<nums.length-1;i++){
if(pref[i]>=pref[nums.length-1]-pref[i]) count++;
}
return count;
}
}
```
```Python3 []
class Solution:
def waysToSplitArray(self, nums: List[int]) -> int:
pref=[nums[0]]
for i in range(1, len(nums)):
pref.append(pref[i-1]+nums[i])
res=0
for i in range(len(pref)-1):
if pref[i]>=pref[-1]-pref[i]:
res+=1
return res
```
**** | 11 | 0 | ['Array', 'Prefix Sum', 'Python', 'Java', 'Python3'] | 6 |
number-of-ways-to-split-array | Easy Optimal Solution Beats💯|| with explanation||Java||JavaScript||Go||C++||C||Python✅✅ | java-easy-solution-with-explanation-by-j-m2o8 | Here’s the revised content including Java, Python, Python3, C, C++, JavaScript, and Go implementations:IntuitionThe problem is to determine how many ways an arr | jeril-johnson | NORMAL | 2025-01-03T04:27:39.060151+00:00 | 2025-01-03T04:54:00.587280+00:00 | 653 | false | Here’s the revised content including Java, Python, Python3, C, C++, JavaScript, and Go implementations:
---
### Intuition
The problem is to determine how many ways an array can be split such that the sum of elements in the left part is greater than or equal to the sum of elements in the right part. The main insight is to compute the total sum of the array once, then track the running sum while iterating to evaluate conditions at each potential split point.
---
### Approach
1. **Initial Setup**: Compute the total sum of the array.
2. **Iterate Through the Array**:
- Maintain a running sum (`curSum`) of the left part.
- At each split point \( i \), check if `curSum` is greater than or equal to the sum of the right part (`sum - curSum`).
- If the condition holds, increment the count (`count`).
3. **Return Result**: After processing all valid split points, return the count.
---
### Complexity
- **Time Complexity**:
- The loop iterating through the array runs in \( O(n) \), where \( n \) is the size of the array.
- Computing the total sum initially also takes \( O(n) \).
- Hence, the overall time complexity is \( O(n) \).
- **Space Complexity**:
- The algorithm uses \( O(1) \) additional space since the computation only requires a few variables.
---
To make the code for Java, Python, Go, and other languages appear in different tabs of a single code box, you can use Markdown with tabbed code syntax supported by tools like GitHub or other Markdown renderers that support tabbed views. Below is an example of how to format it:
### Tabbed Code Example
### Implementation
Here’s the updated tabbed code snippet including implementations in C, C++, Python3, and the original languages:
```java [Java]
class Solution {
public int waysToSplitArray(int[] nums) {
if (nums.length < 2) return 0;
long totalSum = 0, leftSum = 0;
for (int num : nums) {
totalSum += num;
}
int count = 0;
for (int i = 0; i < nums.length - 1; i++) {
leftSum += nums[i];
if (leftSum >= (totalSum - leftSum)) {
count++;
}
}
return count;
}
}
```
```python [Python3]
class Solution:
def waysToSplitArray(self, nums: List[int]) -> int:
total_sum = sum(nums)
left_sum = 0
count = 0
for i in range(len(nums) - 1):
left_sum += nums[i]
if left_sum >= (total_sum - left_sum):
count += 1
return count
```
```cpp [C++]
class Solution {
public:
int waysToSplitArray(vector<int>& nums) {
long long totalSum = 0, leftSum = 0;
int count = 0;
for (int num : nums) {
totalSum += num;
}
for (int i = 0; i < nums.size() - 1; i++) {
leftSum += nums[i];
if (leftSum >= (totalSum - leftSum)) {
count++;
}
}
return count;
}
};
```
```c [C]
#include <stdio.h>
int waysToSplitArray(int* nums, int numsSize) {
long long totalSum = 0, leftSum = 0;
int count = 0;
// Calculate total sum
for (int i = 0; i < numsSize; i++) {
totalSum += nums[i];
}
// Iterate to find valid splits
for (int i = 0; i < numsSize - 1; i++) {
leftSum += nums[i];
if (leftSum >= (totalSum - leftSum)) {
count++;
}
}
return count;
}
```
```javascript [JavaScript]
/**
* @param {number[]} nums
* @return {number}
*/
var waysToSplitArray = function(nums) {
let totalSum = nums.reduce((sum, num) => sum + num, 0);
let leftSum = 0;
let count = 0;
for (let i = 0; i < nums.length - 1; i++) {
leftSum += nums[i];
if (leftSum >= (totalSum - leftSum)) {
count++;
}
}
return count;
};
```
```go [Go]
func waysToSplitArray(nums []int) int {
totalSum := 0
leftSum := 0
count := 0
for _, num := range nums {
totalSum += num
}
for i := 0; i < len(nums)-1; i++ {
leftSum += nums[i]
if leftSum >= (totalSum - leftSum) {
count++
}
}
return count
}
```
 | 10 | 0 | ['Prefix Sum', 'Python', 'Java', 'Go', 'Python3', 'JavaScript'] | 2 |
number-of-ways-to-split-array | ✅C++ | ✅Prefix Sum | ✅Easy O(N) solution | c-prefix-sum-easy-on-solution-by-yash2ar-s7t8 | Please upvote if you find this solution helpful :)\n\nTC- O(N), SC- O(1)\n\nclass Solution {\npublic:\n \n //store total sum of nums in right_sum and iter | Yash2arma | NORMAL | 2022-05-14T16:10:36.742463+00:00 | 2022-05-14T16:12:06.426825+00:00 | 1,066 | false | **Please upvote if you find this solution helpful :)**\n\n**TC- O(N), SC- O(1)**\n```\nclass Solution {\npublic:\n \n //store total sum of nums in right_sum and iterate over nums\n //add nums[i] in left sum and subtract nums[i] from right sum\n //when condition match increase valid_split by 1.\n int waysToSplitArray(vector<int>& nums) \n {\n int valid_split=0;\n long long right_sum=0, left_sum=0;\n \n //store total sum of nums in right_sum\n for(int i=0; i<nums.size(); i++) right_sum += nums[i];\n \n for(int i=0; i<nums.size()-1; i++)\n {\n left_sum += nums[i]; //add nums[i] in left sum \n right_sum -= nums[i]; // and subtract nums[i] from right sum\n \n //check whether left_sum is greater than or equal to right_sum\n //and increase the valid_split by 1\n if(left_sum >= right_sum) \n valid_split++; \n }\n return valid_split;\n \n }\n};\n``` | 10 | 0 | ['C', 'Prefix Sum', 'C++'] | 2 |
number-of-ways-to-split-array | Simple and Easy Solution | ✅Beats 100% | C++| Java | Python3 | simple-and-easy-solution-beats-100-c-jav-ql8h | 🛠️ ApproachThe problem is to find the number of ways to split an array into two non-empty parts such that the sum of the left part is greater than or equal to t | adhamsafir | NORMAL | 2025-01-03T04:56:07.425956+00:00 | 2025-01-03T04:56:07.425956+00:00 | 1,380 | false | # **🛠️ Approach**
The problem is to find the number of ways to split an array into two non-empty parts such that the sum of the left part is greater than or equal to the sum of the right part. The approach involves:
1. **Prefix Sum Calculation:**
Compute the prefix sum for the array. This allows efficient calculation of the sum of the left and right parts of the array during iteration.
2. **Condition Checking:**
Iterate through the array and for each valid split point (except the last index), check if the sum of the left part is greater than or equal to the sum of the right part.
3. **Count Valid Splits:**
Maintain a counter for valid splits and return the count after processing the entire array.
# Complexity
**Time Complexity:**
- Prefix sum calculation takes 𝑂(𝑛)
- Iterating through the array to count valid splits takes 𝑂(𝑛)
- Overall time complexity is 𝑂(𝑛)
**Space Complexity:**
- The prefix sum array requires 𝑂(𝑛)
- Total space complexity is 𝑂(𝑛)
# 🔄 Detailed Steps
1. Initialize an empty list l for prefix sums, and variables cur (current sum) and res (result counter).
2. Traverse the nums array:
- Add each number to cur.
- Append cur to l.
3. Iterate through the prefix sum list l (excluding the last index):
- Check if l[i] (left sum) is greater than or equal to l[-1] - l[i] (right sum).
- If true, increment res.
4. Return res as the final count of valid splits.
# Code
```python []
class Solution:
def waysToSplitArray(self, nums: List[int]) -> int:
l = []
cur,res = 0,0
for i in nums:
cur+=i
l.append(cur)
for i in range(len(l)-1):
if l[i]>=(l[-1]-l[i]):
res+=1
return res
```
```c++ []
class Solution {
public:
int waysToSplitArray(vector<int>& nums) {
long long totalSum = 0, leftSum = 0;
int res = 0;
for (int num : nums) {
totalSum += num;
}
for (int i = 0; i < nums.size() - 1; ++i) {
leftSum += nums[i];
if (leftSum >= totalSum - leftSum) {
res++;
}
}
return res;
}
};
```
``` java []
class Solution {
public int waysToSplitArray(int[] nums) {
long totalSum = 0, leftSum = 0;
int res = 0;
for (int num : nums) {
totalSum += num;
}
for (int i = 0; i < nums.length - 1; i++) {
leftSum += nums[i];
if (leftSum >= totalSum - leftSum) {
res++;
}
}
return res;
}
}
```
| 9 | 0 | ['Array', 'Prefix Sum', 'Python', 'C++', 'Java', 'Python3'] | 1 |
number-of-ways-to-split-array | ✅ One Line Solution | one-line-solution-by-mikposp-u8r5 | (Disclaimer: this is not an example to follow in a real project - it is written for fun and training mostly)Code #1 - ShortTime complexity: O(n). Space complexi | MikPosp | NORMAL | 2025-01-03T09:54:58.176449+00:00 | 2025-01-03T10:09:46.234392+00:00 | 328 | false | (Disclaimer: this is not an example to follow in a real project - it is written for fun and training mostly)
# Code #1 - Short
Time complexity: $$O(n)$$. Space complexity: $$O(n)$$.
```python3
class Solution:
def waysToSplitArray(self, a: List[int]) -> int:
return sum(map(ge,accumulate(a),[*accumulate(a[:0:-1])][::-1]))
```
# Code #2
Time complexity: $$O(n)$$. Space complexity: $$O(n)$$.
```
class Solution:
def waysToSplitArray(self, a: List[int]) -> int:
return (p:=[*accumulate(a)]) and sum(2*q>=p[-1] for q in p[:-1])
```
# Code #3 - Memory Saving
Time complexity: $$O(n)$$. Space complexity: $$O(1)$$.
```python3
class Solution:
def waysToSplitArray(self, a: List[int]) -> int:
return sum(map(ge,accumulate(a),accumulate(a[1:-1],sub,initial=sum(a[1:]))))
```
(Disclaimer 2: code above is just a product of fantasy packed into one line, it is not claimed to be 'true' oneliners - please, remind about drawbacks only if you know how to make it better) | 8 | 0 | ['Array', 'Prefix Sum', 'Python', 'Python3'] | 1 |
number-of-ways-to-split-array | python beginner friendly code must check it for simply code and neat explaination . | python-beginner-friendly-code-must-check-nk3t | Intuitionsoo basically what we want in this problem is that to find the number of pairs that can be formed with splitting the nums ( array) given through.thats | RAHULMOST | NORMAL | 2025-01-03T05:18:29.591618+00:00 | 2025-01-03T05:18:29.591618+00:00 | 204 | false | # Intuition
soo basically what we want in this problem is that to find the number of pairs that can be formed with splitting the nums ( array) given through.thats the basic idea of this problem except under few critereas for those who are new to solve python u totally need not to understand the whole logic of the code instead the basic criteria of the question and what to do except whats given in the question.
# Approach
<!-- Describe your approach to solving the problem. -->
i have mentioned the approach in comments within the solution code
1) from the question : i+ 1 >= n-i-1 (left >= right) im taking the
(i + 1 ) as left and (n- i-1 ) as right ,
2)Declare "c" to increment the count by one .
3)find the total sum of the array
4)declare left = 0 we can increment the array later
5)for i in range(len(nums) - 1) : ------> what this does is that simply take the array ie the nums in the loop and store it in i
6)add the nums[i] into the left section .
7)then use the formula given in the question that is right = total - left(n-i-1).
8)compare the left and right if left >= right
9) increment c by 1
10)return c
GUYS CODING AINT THAT HARD AS U THINK ITS HARD CUS YOU GUYS DONT THINK THANK YOU AND HAVE A NICE DAY AHEAD
# Code
```python3 []
class Solution:
def waysToSplitArray(self, nums: List[int]) -> int:
#i+ 1 >= n-i-1 (left >= right)
#total = sum(nums)
# one element to the right ( i (right) = total - left )
total = sum(nums)
c = 0
left = 0
for i in range( len(nums) - 1 ) :
left += nums[i]
right = total - left
if left >= right :
c += 1
return c
``` | 8 | 0 | ['Python3'] | 1 |
number-of-ways-to-split-array | Java Easy Solutions | 3ms | java-easy-solutions-3ms-by-swaythak-kpff | IntuitionThe problem involves finding the number of ways to split an array into two non-empty parts such that the sum of the left subarray is greater than or eq | SwaythaK | NORMAL | 2025-01-03T04:42:11.442521+00:00 | 2025-01-03T04:42:11.442521+00:00 | 179 | false | # Intuition
The problem involves finding the number of ways to split an array into two non-empty parts such that the sum of the left subarray is greater than or equal to the sum of the right subarray. This can be achieved efficiently by maintaining cumulative sums for both parts and updating them as we iterate through the array.
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
Calculate the Total Sum:
Start by computing the total sum of the array (totalSum). This represents the sum of the entire array before any split.
Iterate Through the Array:
Use a variable currentSum to maintain the sum of the left subarray as elements are added to it.
During each iteration:
Add the current element to currentSum (representing the left subarray).
Subtract the current element from totalSum (updating it to represent the sum of the right subarray).
Check if currentSum is greater than or equal to totalSum. If true, increment the validSplit counter.
Ensure Non-Empty Subarrays:
Stop the loop at nums.length - 1 to ensure the right subarray is always non-empty.
Return the Result:
After completing the loop, return the validSplit counter.
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: 𝑂(𝑛)
O(𝑛) to compute the total sum initially.
O(𝑛) to iterate through the array and calculate the number of valid splits.
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: 𝑂(1)
Uses a few variables (totalSum, currentSum, validSplit) for computation.
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int waysToSplitArray(int[] nums) {
long totalSum = 0;
for(int i = 0; i < nums.length; i++){
totalSum += nums[i];
}
long currentSum = 0;
int validSplit = 0;
for(int i = 0; i < nums.length - 1; i++){
currentSum += nums[i];
totalSum -= nums[i];
if(currentSum >= totalSum){
validSplit++;
}
}
return validSplit;
}
}
``` | 7 | 0 | ['Java'] | 1 |
number-of-ways-to-split-array | Simple Prefix Sum Approach✅✅ | simple-prefix-sum-approach-by-arunk_leet-8sft | IntuitionThe problem involves splitting the array into two non-empty parts such that the sum of the left part is greater than or equal to the sum of the right p | arunk_leetcode | NORMAL | 2025-01-03T03:57:33.310744+00:00 | 2025-01-03T03:57:33.310744+00:00 | 764 | false | # Intuition
The problem involves splitting the array into two non-empty parts such that the sum of the left part is greater than or equal to the sum of the right part. To solve this, we need to efficiently calculate the prefix sum and compare the left and right sums for every possible split point.
# Approach
1. Compute the prefix sum array `pref`, where `pref[i]` represents the sum of the first `i + 1` elements.
2. The total sum of the array is stored in `pref[n-1]` (where `n` is the size of the array).
3. Iterate through the array up to the second-to-last element. For each split point `i`:
- The sum of the left part is `pref[i]`.
- The sum of the right part is `pref[n-1] - pref[i]`.
- If the left sum is greater than or equal to the right sum, increment the counter `ans`.
4. Return the final count of valid split points stored in `ans`.
# Complexity
- Time complexity: $$O(n)$$
Constructing the prefix sum and iterating over the array both take linear time.
- Space complexity: $$O(n)$$
Space is used for the prefix sum array.
# Code
```cpp []
class Solution {
public:
#define ll long long
int waysToSplitArray(vector<int>& nums) {
int n = nums.size();
ll ans = 0;
// Step 1: Calculate prefix sum
vector<ll> pref(n, 0);
pref[0] = nums[0];
for (int i = 1; i < n; i++) {
pref[i] = nums[i] + pref[i - 1];
}
// Step 2: Calculate total sum
ll totalSum = pref[n - 1];
// Step 3: Iterate through split points and check conditions
for (int i = 0; i < n - 1; i++) {
if (pref[i] >= (totalSum - pref[i])) {
ans++;
}
}
return ans;
}
};
```
``` Java []
class Solution {
public int waysToSplitArray(int[] nums) {
int n = nums.length;
long ans = 0;
// Step 1: Calculate prefix sum
long[] pref = new long[n];
pref[0] = nums[0];
for (int i = 1; i < n; i++) {
pref[i] = nums[i] + pref[i - 1];
}
// Step 2: Calculate total sum
long totalSum = pref[n - 1];
// Step 3: Iterate through split points and check conditions
for (int i = 0; i < n - 1; i++) {
if (pref[i] >= (totalSum - pref[i])) {
ans++;
}
}
return (int) ans;
}
}
```
```Python []
class Solution:
def waysToSplitArray(self, nums: List[int]) -> int:
n = len(nums)
ans = 0
# Step 1: Calculate prefix sum
pref = [0] * n
pref[0] = nums[0]
for i in range(1, n):
pref[i] = nums[i] + pref[i - 1]
# Step 2: Calculate total sum
total_sum = pref[-1]
# Step 3: Iterate through split points and check conditions
for i in range(n - 1):
if pref[i] >= (total_sum - pref[i]):
ans += 1
return ans
``` | 7 | 0 | ['Array', 'Prefix Sum', 'Python', 'C++', 'Java'] | 4 |
number-of-ways-to-split-array | ✅💯🔥Simple Code🚀📌|| 🔥✔️Easy to understand🎯 || 🎓🧠Beats 100%🔥|| Beginner friendly💀💯 | simple-code-easy-to-understand-beats-100-zsbj | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | atishayj4in | NORMAL | 2024-07-31T20:17:41.686081+00:00 | 2024-08-01T19:23:27.533032+00:00 | 326 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int waysToSplitArray(int[] nums) {\n int n=nums.length;\n long maxi=0;\n int ans=0;\n long submaxi=0;\n for(int i=0; i<n; i++){\n maxi+=nums[i];\n }\n for(int i=0; i<n-1; i++){\n submaxi+=nums[i];\n long sum = maxi-submaxi;\n if(submaxi>=sum){\n ans++;\n }\n }\n return ans;\n }\n}\n```\n | 7 | 1 | ['Array', 'C', 'Prefix Sum', 'Python', 'C++', 'Java'] | 0 |
number-of-ways-to-split-array | JAVA | O(N) Time and O(1) Space | Easy | java-on-time-and-o1-space-easy-by-sambar-jmeo | \nclass Solution {\n public int waysToSplitArray(int[] nums) {\n long sum = 0;\n for(int num : nums) {\n sum += num;\n }\n | sambarannnn | NORMAL | 2022-05-14T16:26:00.778985+00:00 | 2022-05-14T16:36:44.972844+00:00 | 1,036 | false | ```\nclass Solution {\n public int waysToSplitArray(int[] nums) {\n long sum = 0;\n for(int num : nums) {\n sum += num;\n }\n \n long leftSum = 0;\n int res = 0;\n for(int i = 0; i < nums.length-1; i++) {\n leftSum += nums[i];\n long rightSum = sum - leftSum;\n if(leftSum >= rightSum) {\n res++;\n }\n }\n return res;\n }\n}\n``` | 7 | 0 | ['Prefix Sum'] | 6 |
number-of-ways-to-split-array | JAVA || 2ms || 100% Beat || Easy to Understand for Beginners🙌 | java-2ms-100-beat-easy-to-understand-for-fyho | IntuitionApproachComplexity
Time complexity:o(n)
Space complexity:o(1)
Code | sathish-77 | NORMAL | 2025-01-03T04:45:55.145274+00:00 | 2025-01-03T04:45:55.145274+00:00 | 213 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
prefix sum, suffix sum
# Complexity
- Time complexity:o(n)
- Space complexity:o(1)
# Code
```java []
class Solution {
public int waysToSplitArray(int[] nums) {
long total_sum=0;
for(int i=0;i<nums.length;++i){
total_sum+=nums[i];
}
long sum_order=0;
int result=0;
for(int i=0;i<nums.length-1;++i){
sum_order+=nums[i];
if(sum_order>=(total_sum-sum_order))result++;
}
return result;
}
}
``` | 6 | 0 | ['Array', 'Prefix Sum', 'Java'] | 2 |
number-of-ways-to-split-array | 0ms || Beats 100% || Efficient & Easy C++ Solution || Full Explained | 0ms-beats-100-efficient-easy-c-solution-kfqyb | IntuitionThe goal is to find the number of ways to split the array into two non-empty parts such that the sum of the left part is greater than or equal to the s | HarshitSinha | NORMAL | 2025-01-03T01:27:54.058682+00:00 | 2025-01-03T01:27:54.058682+00:00 | 233 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The goal is to find the number of ways to split the array into two non-empty parts such that the sum of the left part is greater than or equal to the sum of the right part.
If we know the total sum of the array, we can calculate the sum of the right part dynamically as we iterate through the array, by subtracting the running sum of the left part from the total sum.This approach avoids recalculating the sums for each split, making it efficient.
# Approach
<!-- Describe your approach to solving the problem. -->
**Step 1: Compute the Total Sum**
Calculate the total sum of the array. This will help compute the right part's sum efficiently during the split-checking phase.
**Step 2: Iterate Through the Array**
As we iterate through the array:
Maintain a running sum (leftSum) for the left part.
Calculate the right part's sum dynamically as
rightSum = totalSum - leftSum.
**Step 3: Check the Split Condition**
For each index i: Check if
leftSum >= rightSum.
If the condition holds, increment the count of valid splits.
Return the Result: After processing all indices, return the count of valid splits.
# Complexity
- Time complexity:O(n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int waysToSplitArray(vector<int>& nums) {
long long leftSideSum = 0, rightSideSum = 0;
for (int num : nums) {
rightSideSum += num;
}
int validSplits = 0;
for (int i = 0; i < nums.size() - 1; i++) {
leftSideSum += nums[i];
rightSideSum -= nums[i];
if (leftSideSum >= rightSideSum) {
validSplits++;
}
}
return validSplits;
}
};
``` | 6 | 0 | ['Array', 'Prefix Sum', 'C++'] | 2 |
number-of-ways-to-split-array | Simple O(n) Time and O(1) Space Solution || Python | simple-on-time-and-o1-space-solution-pyt-ycvx | If you have any doubts or suggestion, put in comments.\n\nclass Solution(object):\n def waysToSplitArray(self, nums):\n lSum, rSum = 0, sum(nums)\n | krush_r_sonwane | NORMAL | 2022-11-05T12:08:40.262047+00:00 | 2022-11-05T12:08:40.262082+00:00 | 545 | false | If you have any ***doubts*** or ***suggestion***, put in comments.\n```\nclass Solution(object):\n def waysToSplitArray(self, nums):\n lSum, rSum = 0, sum(nums)\n ans = 0\n for i in range(len(nums) - 1):\n lSum += nums[i]\n rSum -= nums[i]\n if lSum >= rSum: ans += 1\n return ans\n```\n**UpVote**, if you like it **:)** | 6 | 0 | ['Python', 'Python3'] | 1 |
number-of-ways-to-split-array | 🌟🧩 One Loop, Many Splits:💡 The Optimized Prefix Sum Trick!⚡🚀 | one-loop-many-splits-the-optimized-prefi-5jt2 | Intuition 🤔We split the array into two 🧩 parts: left and right. The goal is to count how many splits make the left sum ≥ right sum. Easy, right? 🚀Approach 🛠️
To | mansimittal935 | NORMAL | 2025-01-03T06:07:40.779519+00:00 | 2025-01-03T06:07:40.779519+00:00 | 196 | false | # Intuition 🤔
We split the array into two 🧩 parts: left and right. The goal is to count how many splits make the left sum ≥ right sum. Easy, right? 🚀
---
# Approach 🛠️
1. Total Sum ➕: Compute the sum of all elements.
2. Iterate 🔄:
- Start with leftSum = 0.
- For each index i, add the current element to leftSum.
- Calculate rightSum = totalSum - leftSum.
3. Check ✅: If leftSum >= rightSum, count it! 📊
4. Return: Boom! Output the count! 🎯
---
# Complexity ⚡
- Time ⏰:
O(n), since we loop once to compute the sums.
- Space 🪶:
O(1), using only variables.
---
# Code
```cpp []
class Solution {
public:
int waysToSplitArray(vector<int>& nums) {
/*
// better approach..
int n = nums.size();
vector<long long> left (n, 0), right (n, 0);
long long sum = 0;
for(int i = 0; i < n; i++) {
sum += nums[i];
left[i] = sum;
}
sum = 0;
for(int i = n-1; i >= 0; i--) {
sum += nums[i];
right[i] = sum;
}
int ans = 0;
for(int i = 0; i < n-1; i++) {
if(left[i] >= right[i+1]) ans++;
}
return ans;
*/
// optimal approach..
int n = nums.size();
long long leftSum = 0, totalSum = 0;
for(int val: nums) {
totalSum += val;
}
int ans = 0;
for(int i = 0; i < n-1; i++) {
leftSum += nums[i];
long long rightSum = totalSum - leftSum;
if(leftSum >= rightSum) ans++;
}
return ans;
}
};
```
```java []
class Solution {
public int waysToSplitArray(int[] nums) {
int n = nums.length;
long totalSum = 0, leftSum = 0;
for (int val : nums) {
totalSum += val;
}
int ans = 0;
for (int i = 0; i < n - 1; i++) {
leftSum += nums[i];
long rightSum = totalSum - leftSum;
if (leftSum >= rightSum) {
ans++;
}
}
return ans;
}
}
```
```python []
class Solution:
def waysToSplitArray(self, nums):
totalSum = sum(nums)
leftSum = 0
ans = 0
for i in range(len(nums) - 1):
leftSum += nums[i]
rightSum = totalSum - leftSum
if leftSum >= rightSum:
ans += 1
return ans
```
```javascript []
class Solution {
waysToSplitArray(nums) {
let totalSum = nums.reduce((a, b) => a + b, 0);
let leftSum = 0, ans = 0;
for (let i = 0; i < nums.length - 1; i++) {
leftSum += nums[i];
let rightSum = totalSum - leftSum;
if (leftSum >= rightSum) {
ans++;
}
}
return ans;
}
}
```
```ruby []
class Solution
def ways_to_split_array(nums)
total_sum = nums.sum
left_sum = 0
ans = 0
(0...nums.length - 1).each do |i|
left_sum += nums[i]
right_sum = total_sum - left_sum
ans += 1 if left_sum >= right_sum
end
ans
end
end
```
```rust []
impl Solution {
pub fn ways_to_split_array(nums: Vec<i32>) -> i32 {
let total_sum: i64 = nums.iter().map(|&x| x as i64).sum();
let mut left_sum: i64 = 0;
let mut ans = 0;
for i in 0..nums.len() - 1 {
left_sum += nums[i] as i64;
let right_sum = total_sum - left_sum;
if left_sum >= right_sum {
ans += 1;
}
}
ans
}
}
```
```go []
func waysToSplitArray(nums []int) int {
totalSum := 0
for _, val := range nums {
totalSum += val
}
leftSum, ans := 0, 0
for i := 0; i < len(nums)-1; i++ {
leftSum += nums[i]
rightSum := totalSum - leftSum
if leftSum >= rightSum {
ans++
}
}
return ans
}
```
```c# []
public class Solution {
public int WaysToSplitArray(int[] nums) {
long totalSum = 0, leftSum = 0;
foreach (int val in nums) {
totalSum += val;
}
int ans = 0;
for (int i = 0; i < nums.Length - 1; i++) {
leftSum += nums[i];
long rightSum = totalSum - leftSum;
if (leftSum >= rightSum) {
ans++;
}
}
return ans;
}
}
```
```typescript []
class Solution {
waysToSplitArray(nums: number[]): number {
let totalSum = nums.reduce((a, b) => a + b, 0);
let leftSum = 0, ans = 0;
for (let i = 0; i < nums.length - 1; i++) {
leftSum += nums[i];
let rightSum = totalSum - leftSum;
if (leftSum >= rightSum) {
ans++;
}
}
return ans;
}
}
```
```dart []
class Solution {
int waysToSplitArray(List<int> nums) {
int totalSum = nums.reduce((a, b) => a + b);
int leftSum = 0, ans = 0;
for (int i = 0; i < nums.length - 1; i++) {
leftSum += nums[i];
int rightSum = totalSum - leftSum;
if (leftSum >= rightSum) {
ans++;
}
}
return ans;
}
}
```
```swift []
class Solution {
func waysToSplitArray(_ nums: [Int]) -> Int {
let totalSum = nums.reduce(0, +)
var leftSum = 0
var ans = 0
for i in 0..<nums.count - 1 {
leftSum += nums[i]
let rightSum = totalSum - leftSum
if leftSum >= rightSum {
ans += 1
}
}
return ans
}
}
``` | 5 | 0 | ['Swift', 'Prefix Sum', 'Python', 'C++', 'Java', 'Go', 'Rust', 'Ruby', 'JavaScript', 'Dart'] | 1 |
number-of-ways-to-split-array | Explanation with Diagram 💨 | Prefix Sum | O(N) Approach | Beats 100% Users | Python | explanation-with-diagram-prefix-sum-on-a-13q2 | IntuitionThe task is to split the array into two parts such that the sum of the left subarray is greater than or equal to the sum of the right subarray. To achi | i_god_d_sanjai | NORMAL | 2025-01-03T04:45:09.032758+00:00 | 2025-01-03T04:47:21.475634+00:00 | 83 | false | # Intuition
The task is to split the array into two parts such that the sum of the left subarray is greater than or equal to the sum of the right subarray. To achieve this efficiently, we can use a prefix sum approach to compute the cumulative sums of the array and compare the left and right sums for potential splits.
# Approach
### Compute Prefix Sums:
- Use a prefix array where ``prefix[i]`` represents the sum of the elements of the array from index 0 to `i`.
- This allows us to compute the left and right sums efficiently for any split.
### Iterate and Check Splits:
- For each index `i` from 0 to `n−2` (as the array must be split into two non-empty parts), calculate:
- Left Sum: `prefix[i]` (sum of the first i+1i+1 elements).
- Right Sum: `prefix[-1]` - `prefix[i]` (total sum of the array minus the left sum).
- Check if the left sum is greater than or equal to the right sum. If true, increment the count.
### Return the Count:
- The total number of valid splits is stored in count.
# Explanation:
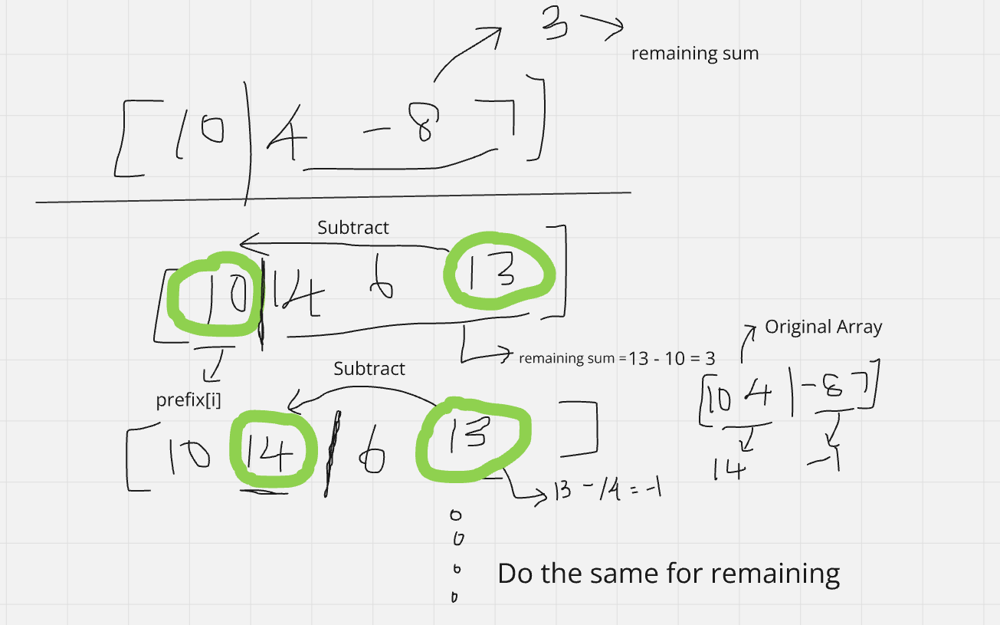
# Complexity
- Time complexity:
$$O(n)$$
- Space complexity:
$$O(n)$$
# Code
```python3 []
class Solution:
def waysToSplitArray(self, nums: List[int]) -> int:
#சூரியா அய்யா துணை | நிர்மல் ஸ்காரியா துணை
prefix = [0]*(len(nums))
prefix[0] = nums[0]
for i in range(1,len(nums)):
prefix[i] = nums[i] + prefix[i-1]
count = 0
for i in range(len(nums)-1): # comparing with last element
if prefix[i] >= prefix[-1] - prefix[i]:
count += 1
return count
``` | 5 | 0 | ['Array', 'Prefix Sum', 'Python3'] | 1 |
number-of-ways-to-split-array | C++ | Prefix Sum | Number of Ways to Split Array | O(n) Time, O(1) Space | c-prefix-sum-number-of-ways-to-split-arr-1l1h | IntuitionThe problem involves finding the number of valid splits in an array where the sum of the left part is greater than or equal to the sum of the right par | AureliusPyron | NORMAL | 2025-01-03T02:53:26.565763+00:00 | 2025-01-03T02:53:26.565763+00:00 | 206 | false | # Intuition
The problem involves finding the number of valid splits in an array where the sum of the left part is greater than or equal to the sum of the right part. A brute-force approach would involve calculating sums for every split, which is inefficient. Instead, we use the **prefix sum** technique to optimize the solution.
# Approach
### Normal Prefix Sum Approach:
1. Compute a `prefixSum` array where `prefixSum[i]` represents the sum of the first \(i+1\) elements of `nums`.
2. The total sum of the array is stored in `prefixSum[n-1]`.
3. For each index \(i\) from 0 to \(n-2\), check if the sum of the left part (`prefixSum[i]`) is greater than or equal to the sum of the right part (`prefixSum[n-1] - prefixSum[i]`).
4. Count the indices where the condition is satisfied.
### Space-Optimized Approach:
1. Instead of maintaining a `prefixSum` array, use a variable `prefixSum` to calculate the left sum on the fly.
2. Compute the total sum of the array (`totalSum`).
3. For each index \(i\), dynamically update `prefixSum` and check the same condition as in the normal approach.
# Complexity
- **Time complexity**:
- Computing prefix sums takes $$O(n)$$.
- Checking valid splits also takes $$O(n)$$.
- Overall: $$O(n)$$.
- **Space complexity**:
- **Normal Prefix Sum Approach**: $$O(n)$$ due to the `prefixSum` array.
- **Space-Optimized Approach**: $$O(1)$$ since it uses only variables for calculations.
# Code
### Normal Prefix Sum Approach
```cpp
class Solution {
public:
int waysToSplitArray(vector<int>& nums) {
int n = nums.size();
vector<long long> prefixSum(n, 0); // Use long long for prefixSum to avoid overflow
// Compute prefix sums
prefixSum[0] = nums[0];
for (int i = 1; i < n; i++) {
prefixSum[i] = prefixSum[i - 1] + nums[i];
}
int cnt = 0;
// Check valid splits
for (int i = 0; i < n - 1; i++) {
if (prefixSum[i] >= (prefixSum[n - 1] - prefixSum[i])) {
cnt++;
}
}
return cnt;
}
};
```
### Space-Optimized Approach
```cpp
class Solution {
public:
int waysToSplitArray(vector<int>& nums) {
int n = nums.size();
long long totalSum = 0, prefixSum = 0;
// Compute total sum of the array
for (int num : nums) {
totalSum += num;
}
int cnt = 0;
// Dynamically compute prefix sum and check valid splits
for (int i = 0; i < n - 1; i++) {
prefixSum += nums[i];
if (prefixSum >= (totalSum - prefixSum)) {
cnt++;
}
}
return cnt;
}
};
| 5 | 0 | ['Array', 'Prefix Sum', 'C++'] | 1 |
number-of-ways-to-split-array | Easy Java Solution using Arrays - O(n) | easy-java-solution-using-arrays-on-by-de-sf3y | This is one of the easiest question, where we need to compare leftsum and rightsum\n\nNote that we have to take leftSum and rightSum as long type and not of int | devesh096 | NORMAL | 2022-12-04T09:54:24.597220+00:00 | 2022-12-04T09:54:24.597264+00:00 | 1,085 | false | This is one of the easiest question, where we need to compare leftsum and rightsum\n\nNote that we have to take leftSum and rightSum as long type and not of int type looking at the constraints given in the problem.\n\nSteps: \n1.First Calculate the sum of all elements present in the array.\n2.Then Calculate left sum and rightSum for every index.\n3.Compare leftSum and rightSum and if leftSum>rightSum, then increment the value of count.\n4.return the count.\n\n```\n\nclass Solution {\n public int waysToSplitArray(int[] nums) {\n int n = nums.length;\n int count = 0;\n long sum = 0;\n long leftSum = 0;\n long rightSum = 0;\n \n for(int i=0;i<n;i++){\n \n sum += nums[i];\n }\n \n for(int j = 0;j<n-1;j++){\n leftSum += nums[j];\n rightSum = sum-leftSum;\n \n if(leftSum>=rightSum){\n count++;\n }\n }\n \n return count;\n }\n}\n```\n\n## Please upvote if it helped. | 5 | 0 | ['Array', 'Java'] | 2 |
number-of-ways-to-split-array | Python || Easy || Faster Than 99 % | python-easy-faster-than-99-by-workingpay-y3cn | \nclass Solution:\n def waysToSplitArray(self, nums: List[int]) -> int:\n sumtot= sum(nums)-nums[0]\n leftsum = nums[0]\n res = 0\n | workingpayload | NORMAL | 2022-09-02T19:50:03.954332+00:00 | 2022-09-02T19:50:03.954375+00:00 | 444 | false | ```\nclass Solution:\n def waysToSplitArray(self, nums: List[int]) -> int:\n sumtot= sum(nums)-nums[0]\n leftsum = nums[0]\n res = 0\n \n \n for i in range(1,len(nums)):\n if leftsum>=sumto:\n res+=1\n sumtot-=nums[i]\n leftsum+=nums[i]\n \n return res\n \n``` | 5 | 0 | ['Python'] | 1 |
number-of-ways-to-split-array | ✅Detailed Explanation | 100% Beats | O(N) Solution | Java | C++ | Python | detailed-explanation-100-beats-on-soluti-nyla | IntuitionTo split the array into two non-empty parts such that the left sum is greater than or equal to the right sum, we can efficiently calculate prefix and s | prashanth_d4 | NORMAL | 2025-03-11T01:45:01.401807+00:00 | 2025-03-11T01:45:01.401807+00:00 | 53 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
To split the array into two non-empty parts such that the left sum is greater than or equal to the right sum, we can efficiently calculate prefix and suffix sums while iterating through the array.
# Approach
<!-- Describe your approach to solving the problem. -->
1. Compute Total Sum: Start with the total sum of the array as the initial "right" sum.
2. Iterate Through the Array:
- Maintain dummy as the left sum and fullSum as the right sum.
- For each split, update dummy and fullSum by adding/removing the current element.
- Check if dummy >= fullSum and increment the count if true.
3. Edge Case: Check the split after the first element separately before the loop starts.
# Complexity
- Time complexity: O(N)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int waysToSplitArray(int[] nums) {
long fullSum = 0;
for (int i = 1; i < nums.length; i++) {
fullSum += nums[i];
}
int cnt = 0;
long dummy = nums[0];
if (dummy >= fullSum) {
cnt = 1;
}
for (int i = 1; i < nums.length - 1; i++) {
dummy += nums[i];
fullSum -= nums[i];
if (dummy >= fullSum) {
cnt++;
}
}
return cnt;
}
}
```
```C++ []
class Solution {
public:
int waysToSplitArray(vector<int>& nums) {
long long fullSum = 0;
for (int i = 1; i < nums.size(); i++) {
fullSum += nums[i];
}
int cnt = 0;
long long dummy = nums[0];
if (dummy >= fullSum) {
cnt = 1;
}
for (int i = 1; i < nums.size() - 1; i++) {
dummy += nums[i];
fullSum -= nums[i];
if (dummy >= fullSum) {
cnt++;
}
}
return cnt;
}
};
```
```python []
class Solution:
def waysToSplitArray(self, nums):
full_sum = sum(nums[1:])
cnt = 0
dummy = nums[0]
if dummy >= full_sum:
cnt = 1
for i in range(1, len(nums) - 1):
dummy += nums[i]
full_sum -= nums[i]
if dummy >= full_sum:
cnt += 1
return cnt
```
| 4 | 0 | ['Array', 'Prefix Sum', 'Python', 'C++', 'Java', 'Python3'] | 0 |
number-of-ways-to-split-array | Best Solution for Arrays, Prefix Sum 🚀 in C++, Python and Java || 100% working | best-solution-for-arrays-prefix-sum-in-c-9kn8 | Intuition😊 First, calculate the total sum of the array. We will split the array at each index and compare the sum of the left and right parts.Approach👉 Use a pr | BladeRunner150 | NORMAL | 2025-01-04T08:49:53.718849+00:00 | 2025-01-04T08:49:53.718849+00:00 | 22 | false | # Intuition
😊 First, calculate the total sum of the array. We will split the array at each index and compare the sum of the left and right parts.
# Approach
👉 Use a prefix sum to calculate the left part's sum at each index. Subtract it from the total sum to get the right part's sum.
✨ Check if the left sum is greater than or equal to the right sum and count such splits.
# Complexity
- Time complexity: $$O(n)$$
We traverse the array once to compute the prefix sums and compare them.
- Space complexity: $$O(1)$$
Only a few variables are used.
# Code
```cpp []
#define ll long long
class Solution {
public:
int waysToSplitArray(vector<int>& nums) {
ll tot = accumulate(nums.begin(),nums.end(),0LL);
ll left_sum = 0;
ll ans = 0;
for(int i=0;i<nums.size()-1;i++){
left_sum += nums[i];
ll right_sum = tot - left_sum;
if(left_sum >= right_sum){
ans++;
}
}
return ans;
}
};
```
```python []
class Solution:
def waysToSplitArray(self, nums: List[int]) -> int:
tot = sum(nums)
left_sum = 0
ans = 0
for i in range(len(nums) - 1):
left_sum += nums[i]
right_sum = tot - left_sum
if left_sum >= right_sum:
ans += 1
return ans
```
```java []
class Solution {
public int waysToSplitArray(int[] nums) {
long tot = 0;
for (int num : nums) tot += num;
long left_sum = 0;
int ans = 0;
for (int i = 0; i < nums.length - 1; i++) {
left_sum += nums[i];
long right_sum = tot - left_sum;
if (left_sum >= right_sum) {
ans++;
}
}
return ans;
}
}
```
<img src="https://assets.leetcode.com/users/images/7b864aef-f8a2-4d0b-a376-37cdcc64e38c_1735298989.3319144.jpeg" alt="upvote" width="150px">
# Connect with me on LinkedIn for more insights! 🌟 Link in bio | 4 | 0 | ['Array', 'Prefix Sum', 'Python', 'C++', 'Java', 'Python3'] | 0 |
number-of-ways-to-split-array | Simple py,JAVA code expalined!! Prefixsum || arrays !! | simple-pyjava-code-expalined-prefixsum-a-4dr2 | Approach:Prefix sumIntuition
read the question twice and understand what they are asking!
Since we need to find the sum of all the previous prefixes and sum of | arjunprabhakar1910 | NORMAL | 2025-01-03T19:02:04.834289+00:00 | 2025-01-03T19:02:04.834289+00:00 | 24 | false |
# Approach:Prefix sum
<!-- Describe your approach to solving the problem. -->
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
> read the question twice and understand what they are asking!
- Since we need to find the sum of all the previous *prefixes* and sum of all values for *suffixes* for the interval **0 to n-1** we will use `prefixSum` and `suffixSum` array to calulate those sums.
- Then we check for `prefixSum[i]>=suffixSum[i]` where `i` is the is the split interval.
- `count` is used to track the valid split.
# Complexity
- Time complexity:$$O(N)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:$$O(N)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def waysToSplitArray(self, nums: List[int]) -> int:
prefixSum=[0]*len(nums)
suffixSum=[0]*len(nums)
prefix=suffix=0
for i in range(len(nums)):
prefix+=nums[i]
prefixSum[i]=prefix
for i in range(len(nums)-1,-1,-1):
suffix+=nums[i]
suffixSum[i]=suffix
#print(prefixSum,suffixSum)
count=0
for i in range(len(nums)-1):
if prefixSum[i]>=suffixSum[i+1]:
count+=1
return count
```
```JAVA []
class Solution {
public int waysToSplitArray(int[] nums) {
int l=nums.length;
long[] prefixSum=new long[l];
long[] suffixSum=new long[l];
long prefix=0,suffix=0;
for(int i=0;i<l;i++){
prefix+=nums[i];
prefixSum[i]=prefix;
}
for(int i=l-1;i>-1;i--){
suffix+=nums[i];
suffixSum[i]=suffix;
}
int count=0;
for(int i=0;i<l-1;i++){
if(prefixSum[i]>=suffixSum[i+1]){
count++;
}
}
return count;
}
}
```` | 4 | 0 | ['Array', 'Prefix Sum', 'Java', 'Python3'] | 0 |
number-of-ways-to-split-array | Beats 100% || O(1) space || C++ || Prefix Sum | beats-100-o1-space-c-prefix-sum-by-akash-jyg3 | Complexity
Time complexity: O(n)
Space complexity: O(1)
Code | akash92 | NORMAL | 2025-01-03T10:50:54.582963+00:00 | 2025-01-03T10:50:54.582963+00:00 | 79 | false | # Complexity
- Time complexity: $$O(n)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(1)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
#define ll long long
class Solution {
public:
int waysToSplitArray(vector<int>& nums) {
int n = nums.size();
if(n == 1) return 0;
ll rsum = accumulate(nums.begin(), nums.end(), 0LL), lsum = 0LL;
int cnt = 0;
for(int i=0; i<n-1; i++){
lsum += nums[i];
rsum -= nums[i];
if(lsum >= rsum) cnt++;
}
return cnt;
}
};
``` | 4 | 0 | ['Array', 'Prefix Sum', 'C++'] | 0 |
number-of-ways-to-split-array | Easy to understand Prefix Sum with O(1) space || C++ beats 100% Time Complexity. | easy-to-understand-prefix-sum-with-o1-sp-veyb | IntuitionThe problem requires splitting an array into two parts such that the sum of the left part is greater than or equal to the sum of the right part. This c | RishubhChahar2001 | NORMAL | 2025-01-03T09:08:33.040274+00:00 | 2025-01-03T09:14:31.200970+00:00 | 128 | false | # Intuition
The problem requires splitting an array into two parts such that the sum of the left part is greater than or equal to the sum of the right part. This can be solved by maintaining a running sum or using a prefix sum array for efficient computation of sums.
# Approach 1: Using Running Sums
1. **Calculate Total Sum**: Start by calculating the total sum of the array to compute the right sum dynamically.
2. **Iterate Through the Array**: Use a loop to evaluate all possible split points up to the second-to-last element.
3. **Track Left and Right Sums**: Maintain a running sum for the left part. Compute the right part as `rightSum = totalSum - leftSum`.
4. **Check Valid Splits**: For each split point, check if `leftSum >= rightSum`. If true, increment the result counter.
5. **Return Result**: Return the total count of valid splits.
# Approach 2: Using Prefix Sum
1. **Calculate Prefix Sums**: Build a prefix sum array, where `prefix[i]` stores the sum of the array elements from the start up to index `i`.
2. **Iterate Through the Array**: Iterate through the array up to the second-to-last index.
3. **Compare Sums**: For each index, check if the left sum (`prefix[idx]`) is greater than or equal to the right sum (`prefix[n-1] - prefix[idx]`).
4. **Update Result**: Increment the counter if the condition is met.
5. **Return Result**: Return the count of valid splits.
# Complexity for Both Approaches
### Approach 1
- **Time Complexity**:
$$O(n)$$ — One pass to calculate the total sum and another pass to check valid splits.
- **Space Complexity**:
$$O(1)$$ — Only variables for tracking sums and the result are used.
### Approach 2
- **Time Complexity**:
$$O(n)$$ — One pass to calculate the prefix sum array and another pass to evaluate splits.
- **Space Complexity**:
$$O(n)$$ — The prefix sum array requires additional space proportional to the input size.
# Code
### Approach 1: Using Running Sums
```cpp
class Solution {
public:
int waysToSplitArray(vector<int>& nums) {
int n = nums.size();
int res = 0;
long totalSum = 0, leftSum = 0;
// Calculate the total sum of the array
for (int num : nums) {
totalSum += num;
}
// Iterate through the array and check valid splits
for (int i = 0; i < n - 1; i++) {
leftSum += nums[i];
long rightSum = totalSum - leftSum;
if (leftSum >= rightSum) {
res++;
}
}
return res;
}
};
```
### Approach 2: Using Prefix Sum
```cpp
class Solution {
public:
int waysToSplitArray(vector<int>& nums) {
int n = nums.size(), res = 0;
vector<long> prefix(n, 0);
// Build the prefix sum array
for (int i = 0; i < n; i++) {
prefix[i] = i > 0 ? prefix[i - 1] + nums[i] : nums[i];
}
// Check valid splits using prefix sums
for (int idx = 0; idx < n - 1; idx++) {
if (prefix[idx] >= prefix[n - 1] - prefix[idx]) {
res++;
}
}
return res;
}
};
```
| 4 | 0 | ['C++'] | 2 |
number-of-ways-to-split-array | 💢Faster✅💯 Lesser C++✅Python3🐍✅Java✅C✅Python🐍✅C#✅💥🔥💫Explained☠💥🔥 Beats 💯 | faster-lesser-cpython3javacpythoncexplai-rk0w | IntuitionApproach
JavaScript Code --> https://leetcode.com/problems/number-of-ways-to-split-array/submissions/1495859295
C++ Code --> https://leetcode.com/probl | Edwards310 | NORMAL | 2025-01-03T05:26:31.211944+00:00 | 2025-01-03T16:23:26.718819+00:00 | 96 | false | 
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your first thoughts on how to solve this problem. -->
- ***JavaScript Code -->*** https://leetcode.com/problems/number-of-ways-to-split-array/submissions/1495859295
- ***C++ Code -->*** https://leetcode.com/problems/number-of-ways-to-split-array/submissions/1495839879
- ***Python3 Code -->*** https://leetcode.com/problems/number-of-ways-to-split-array/submissions/1495851145
- ***Java Code -->*** https://leetcode.com/problems/number-of-ways-to-split-array/submissions/1495849175
- ***C Code -->*** https://leetcode.com/problems/number-of-ways-to-split-array/submissions/1495853666
- ***Python Code -->*** https://leetcode.com/problems/number-of-ways-to-split-array/submissions/1495850767
- ***C# Code -->*** https://leetcode.com/problems/number-of-ways-to-split-array/submissions/1495856422
- ***Go Code -->*** https://leetcode.com/problems/number-of-ways-to-split-array/submissions/1495862942
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(N)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(1)
# Code

| 4 | 0 | ['Array', 'C', 'Prefix Sum', 'Python', 'C++', 'Java', 'Go', 'Python3', 'JavaScript', 'C#'] | 0 |
number-of-ways-to-split-array | 💡 C++ | O(N) | Very Easy Sol | Simple Logic | With Full Explanation ✏ | c-on-very-easy-sol-simple-logic-with-ful-u40e | IntuitionWe have to find the count of the left subarrays having sum >= the right subarraysApproach
We will store the sum of the whole array in the rs
Then we wi | Tusharr2004 | NORMAL | 2025-01-03T05:11:32.762909+00:00 | 2025-01-03T05:11:32.762909+00:00 | 26 | false | # Intuition
We have to find the count of the left subarrays having sum >= the right subarrays
# Approach
- We will store the sum of the whole array in the `rs`
- Then we will traverse the array and use sliding window concept and store the element sum in the `ls` and subtract it from the `rs`
- Run the check if the `ls` >= `rs`. If yes then we will increment the ans
# Complexity
- Time complexity:
```O(n)```
- Space complexity:
```O(1)```
# Code
```cpp []
class Solution {
public:
int waysToSplitArray(vector<int>& nums) {
int ans=0;
long long ls=0;
long long rs=0;
for(int i:nums)rs+=i;
for(int j=0;j<nums.size()-1;j++){
ls+=nums.at(j);
rs-=nums.at(j);
if(ls>=rs) ans++;
}
return ans;
}
};
```

# Ask any doubt !!!
Reach out to me 😊👇
🔗 https://tushar-bhardwaj.vercel.app/ | 4 | 0 | ['Array', 'Math', 'Sliding Window', 'Prefix Sum', 'C++'] | 0 |
number-of-ways-to-split-array | 📌100% || C++ || Python || Prefix Sum ||🌟Beginner-Friendly | 100-c-python-prefix-sum-beginner-friendl-m0gp | IntuitionTo solve this problem, we need to find the valid split points in the array where the sum of the first part is greater than or equal to the sum of the s | Rohithaaishu16 | NORMAL | 2025-01-03T04:41:28.174535+00:00 | 2025-01-03T04:41:28.174535+00:00 | 71 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
To solve this problem, we need to find the valid split points in the array where the sum of the first part is greater than or equal to the sum of the second part. By iterating through the array and maintaining a running total for both parts, we can efficiently check each split point.
# Approach
<!-- Describe your approach to solving the problem. -->
1. Calculate Total Sum: First, we calculate the total sum of the array, which we will use to initialize the sum of the second part (b).
2. Iterate through the Array: As we iterate through the array, we maintain two running sums: a for the first part and b for the second part.
3. Update Sums: At each index i, update a by adding nums[i] and b by subtracting nums[i].
4. Check Condition: If at any point a >= b, it means we have a valid split. We increment our count of valid splits.
5. Return Result: Finally, return the count of valid splits
# Complexity
- Time complexity: $$𝑂(𝑛)$$ We iterate through the array twice: once for calculating the total sum and once for checking the valid splits. This results in linear time complexity.
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$𝑂(1)$$ We use a fixed amount of extra space for the variables a, b, and cou, making the space complexity constant.
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int waysToSplitArray(vector<int>& nums) {
long long a=0,b=0;
for(auto& i:nums) b=b+i;
int n=nums.size(),cou=0;
for(auto i=0;i<n-1;i++){
a+=nums[i];
b-=nums[i];
if(a>=b) cou++;
}
return cou;
}
};
```
``` python []
class Solution:
def waysToSplitArray(self, nums: List[int]) -> int:
a = 0
b = sum(nums)
n = len(nums)
cou = 0
for i in range(n - 1):
a += nums[i]
b -= nums[i]
if a >= b:
cou += 1
return cou
``` | 4 | 0 | ['Array', 'Prefix Sum', 'C++', 'Python3'] | 0 |
number-of-ways-to-split-array | C# Solution for Number of Ways To Split Array Problem | c-solution-for-number-of-ways-to-split-a-zgrn | IntuitionThe goal is to determine how many valid splits exist in the array, where the sum of the left subarray is greater than or equal to the sum of the right | Aman_Raj_Sinha | NORMAL | 2025-01-03T04:30:09.846776+00:00 | 2025-01-03T04:30:09.846776+00:00 | 56 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The goal is to determine how many valid splits exist in the array, where the sum of the left subarray is greater than or equal to the sum of the right subarray. The intuition is to avoid recalculating subarray sums repeatedly by leveraging cumulative sums:
• Use a running total (leftSum) for the left subarray.
• Derive the right subarray sum dynamically as rightSum = totalSum - leftSum.
# Approach
<!-- Describe your approach to solving the problem. -->
1. Calculate Total Sum:
• Compute the total sum of the array in a single pass. This allows us to derive the sum of the right subarray dynamically.
2. Iterate Over Splits:
• Iterate through the array from index 0 to n-2 to ensure the right subarray always contains at least one element.
3. Track Left and Right Sums:
• Maintain a leftSum variable to track the cumulative sum of elements in the left subarray.
• Use the formula rightSum = totalSum - leftSum to compute the right subarray sum dynamically.
4. Check Valid Splits:
• For each split index, check if leftSum >= rightSum. If true, increment the count of valid splits.
5. Return Result:
• After the loop, return the count of valid splits.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
1. Total Sum Calculation:
• Calculating the total sum of the array takes O(n).
2. Split Iteration:
• Iterating through the array to check splits also takes O(n).
Overall Time Complexity: O(n) + O(n) = O(n)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
1. Auxiliary Space:
• The solution uses a constant amount of additional space, including variables like totalSum, leftSum, and validSplits.
Overall Space Complexity: O(1)
# Code
```csharp []
public class Solution {
public int WaysToSplitArray(int[] nums) {
int n = nums.Length;
long totalSum = 0;
foreach (int num in nums) {
totalSum += num;
}
long leftSum = 0;
int validSplits = 0;
for (int i = 0; i < n - 1; i++) {
leftSum += nums[i];
long rightSum = totalSum - leftSum;
if (leftSum >= rightSum) {
validSplits++;
}
}
return validSplits;
}
}
``` | 4 | 0 | ['C#'] | 0 |
number-of-ways-to-split-array | Easy Approach in O(n) | Python | easy-approach-in-on-python-by-omtejaswin-jcll | IntuitionWe are given a list nums of integers. The goal is to determine how many ways we can split the array nums into two non-empty subarrays such that the sum | OmTejaswini2802 | NORMAL | 2025-01-03T03:39:34.284559+00:00 | 2025-01-03T03:39:34.284559+00:00 | 111 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
We are given a list nums of integers. The goal is to determine how many ways we can split the array nums into two non-empty subarrays such that the sum of the elements in the left subarray is greater than or equal to the sum of the elements in the right subarray.
# Approach
<!-- Describe your approach to solving the problem. -->
1. **Prefix Sum Calculation:**
We start by calculating the prefix sums of the array. The prefix sum at index i is the sum of all elements in the array from the beginning up to index i.
This allows us to quickly calculate the sum of any subarray by using the relation:
Sum of elements from index 0 to i-1: prefix_sum[i-1]
Sum of elements from index i to n-1: total_sum - prefix_sum[i-1] where total_sum is the sum of all elements in the array.
2. **Iterate Over Possible Splits:**
We then iterate through the array and consider each possible position i where we can split the array into two subarrays:
The left subarray contains elements from index 0 to i-1.
The right subarray contains elements from index i to n-1.
For each split, we check whether the sum of the left subarray (prefix_sum[i-1]) is greater than or equal to the sum of the right subarray (total_sum - prefix_sum[i-1]). If this condition is satisfied, we increment the result counter.
3. **Return the Count:**
The final result is the number of valid splits where the left subarray sum is greater than or equal to the right subarray sum.
# Complexity
### **Time complexity:**
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
**Prefix Sum Calculation:** The loop for computing the prefix sum runs in O(n) time.
**Iterating Through Array:** After that, we loop through the array from index 1 to n-1 to check the condition. This loop also runs in O(n) time.
**Overall Time Complexity:** O(n)
### Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
We store the prefix_sum array, which requires O(n) space.
# Code
```python3 []
class Solution:
def waysToSplitArray(self, nums: List[int]) -> int:
n = len(nums)
s = sum(nums)
prefix_sum = [0]*n
for i in range(n):
prefix_sum[i] = prefix_sum[i-1] + nums[i]
res = 0
for i in range(1, n):
x = prefix_sum[i-1]
if x >= s - x:
res += 1
return res
``` | 4 | 0 | ['Prefix Sum', 'Python3'] | 0 |
number-of-ways-to-split-array | [Rust / Elixir] 2 passes | rust-2-passes-by-minamikaze392-7ktt | Let the sum of the first i + 1 elements be left, and the sum of the others be right. Then left + right = total where total is the total sum.
If a cut is valid, | Minamikaze392 | NORMAL | 2025-01-03T02:19:50.184622+00:00 | 2025-01-03T02:51:03.341636+00:00 | 74 | false | Let the sum of the first `i + 1` elements be `left`, and the sum of the others be `right`. Then `left + right = total` where `total` is the total sum.
If a cut is valid, then:
```text
left >= right
left >= total - left
total - 2 * left <= 0
```
# Complexity
- Time complexity: $$O(n)$$
- Space complexity: $$O(1)$$
# Code
```Rust []
impl Solution {
pub fn ways_to_split_array(nums: Vec<i32>) -> i32 {
let mut acc = nums.iter().map(|&x| x as i64).sum::<i64>();
let mut ans = 0;
let mut iter = nums.iter();
iter.next_back(); // skip the last element.
for &x in iter {
acc -= x as i64 * 2;
if acc <= 0 {
ans += 1;
}
}
ans
}
}
```
```Elixir []
defmodule Solution do
@spec ways_to_split_array(nums :: [integer]) :: integer
def ways_to_split_array(nums) do
Enum.sum(nums)
|> solve(nums, 0)
end
defp solve(_, [_], ans), do: ans
defp solve(acc, [x | tail], ans) do
acc2 = acc - x * 2
if acc2 <= 0 do
solve(acc2, tail, ans + 1)
else
solve(acc2, tail, ans)
end
end
end
``` | 4 | 0 | ['Rust', 'Elixir'] | 1 |
number-of-ways-to-split-array | Easiest C++ solution || Beginner-friendly approach || O(N) time complexity | easiest-c-solution-beginner-friendly-app-5gze | Code\n\nclass Solution {\npublic:\n int waysToSplitArray(vector<int>& nums) {\n long long int sumLeft = 0, sumRight = 0, ans = 0;\n for(int i=0 | prathams29 | NORMAL | 2023-07-03T11:18:35.976422+00:00 | 2023-07-03T11:18:35.976457+00:00 | 216 | false | # Code\n```\nclass Solution {\npublic:\n int waysToSplitArray(vector<int>& nums) {\n long long int sumLeft = 0, sumRight = 0, ans = 0;\n for(int i=0; i<nums.size(); i++)\n sumRight += nums[i];\n for(int i=0; i<nums.size()-1; i++){\n sumLeft += nums[i];\n sumRight -= nums[i];\n if(sumLeft >= sumRight)\n ans++;\n }\n return ans;\n }\n};\n``` | 4 | 0 | ['C++'] | 0 |
number-of-ways-to-split-array | Python3 || beats 99% || simple solution | python3-beats-99-simple-solution-by-salt-xio0 | \nclass Solution:\n\tdef waysToSplitArray(self, nums: List[int]) -> int:\n s0 = sum(nums)\n s1, d = 0, 0\n for i in nums[:-1]:\n | Saltkroka | NORMAL | 2022-12-04T20:21:22.605776+00:00 | 2022-12-04T20:32:03.342748+00:00 | 375 | false | ```\nclass Solution:\n\tdef waysToSplitArray(self, nums: List[int]) -> int:\n s0 = sum(nums)\n s1, d = 0, 0\n for i in nums[:-1]:\n s1 += i\n if s1 >= (s0-s1):\n d += 1\n return d\n``` | 4 | 0 | ['Array', 'Prefix Sum', 'Python3'] | 0 |
number-of-ways-to-split-array | [C++/Python3] Very Concise Prefix Sum O(1) | cpython3-very-concise-prefix-sum-o1-by-s-z466 | Python\n\nclass Solution:\n def waysToSplitArray(self, nums: List[int]) -> int:\n lsum, rsum, ans = 0, sum(nums), 0\n for i in range(len(nums) | Suraj1199 | NORMAL | 2022-05-14T16:11:39.252074+00:00 | 2022-05-14T16:15:52.618272+00:00 | 377 | false | **Python**\n```\nclass Solution:\n def waysToSplitArray(self, nums: List[int]) -> int:\n lsum, rsum, ans = 0, sum(nums), 0\n for i in range(len(nums) - 1):\n lsum += nums[i]\n rsum -= nums[i]\n ans += (lsum >= rsum)\n return ans\n\t\t\n```\n\n**C++**\n```\nclass Solution {\npublic:\n int waysToSplitArray(vector<int>& nums) {\n long long lsum = 0, rsum = 0, ans = 0;\n for (int& num: nums) rsum += num;\n for (int i = 0; i < nums.size() - 1; ++i) {\n lsum += nums[i];\n rsum -= nums[i];\n ans += (lsum >= rsum);\n }\n return ans;\n }\n};\n``` | 4 | 0 | ['Prefix Sum', 'Python3'] | 1 |
number-of-ways-to-split-array | Short and easy python solution using a queue. O(n) | short-and-easy-python-solution-using-a-q-skke | \nAlgorithm.\nInitialize 2 sums, Left and Right. where left = nums[0] and right will sum of the rest of the elements from 1 to n.\nNow create a queue with nums[ | vineeth_moturu | NORMAL | 2022-05-14T16:00:52.236751+00:00 | 2022-05-14T16:18:34.823612+00:00 | 447 | false | \n**Algorithm.**\nInitialize 2 sums, Left and Right. where `left = nums[0]` and right will sum of the rest of the elements from 1 to n.\nNow create a queue with `nums[1:]`\nPop elements from the queue one by one until none are left.\nFor each element\n\t - add this to left sum\n\t - subtract this from right sum\n\t - if our condition is satisfied, add 1 to our count.\n\n```\ndef waysToSplitArray(self, nums: List[int]) -> int:\n\n left_sum = nums[0]\n right_sum = sum(nums[1: ])\n count = 0\n queue = deque(nums[1:])\n\n while queue:\n if left_sum >= right_sum:\n count += 1\n\n ele = queue.popleft()\n\n # add to left_sum\n left_sum += ele\n # remove from right\n right_sum -= ele\n\n return count\n``` | 4 | 0 | ['Python'] | 2 |
number-of-ways-to-split-array | Easy Aproach O(N) - Time complexity only | easy-aproach-on-time-complexity-only-by-0dref | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | muhammednihas2218 | NORMAL | 2025-01-03T19:24:52.729383+00:00 | 2025-01-03T19:24:52.729383+00:00 | 12 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def waysToSplitArray(self, nums: List[int]) -> int:
result=0
n=len(nums)
l_sum,r_sum=0,sum(nums)
for i in range(n-1):
l_sum+=nums[i]
r_sum-=nums[i]
if l_sum>=r_sum:
result+=1
return result
``` | 3 | 0 | ['Array', 'Python3'] | 0 |
number-of-ways-to-split-array | Beginner Friendly Solution - Core Logic Building approach. Java | Python | C++ | beginner-friendly-solution-core-logic-bu-idmz | IntuitionThe problem involves splitting the array into two non-empty parts and comparing their sums. Instead of recalculating sums repeatedly for every split, w | v-athithyaramaa | NORMAL | 2025-01-03T18:44:21.219489+00:00 | 2025-01-03T18:44:21.219489+00:00 | 9 | false | # Intuition
The problem involves splitting the array into two non-empty parts and comparing their sums. Instead of recalculating sums repeatedly for every split, we can use a prefix sum array to efficiently compute the left and right sums for each split.
# Approach
1. Compute the prefix sum array, where `prefixSum[i]` stores the sum of elements from the start of the array to index `i`. This allows us to calculate the sum of any subarray in constant time.
2. Calculate the total sum of the array using the last value of the prefix sum array.
3. Iterate through the array, checking for all valid splits:
- The left sum is `prefixSum[i]`.
- The right sum is `total_sum - prefixSum[i]`.
- Increment the count if the left sum is greater than or equal to the right sum.
4. Return the count of valid splits.
# Complexity
- Time complexity:
The prefix sum calculation and the iteration through the array are both \(O(n)\), so the total time complexity is **$$O(n)$$**.
- Space complexity:
We use an additional array of size \(n\) for storing the prefix sums, so the space complexity is **$$O(n)$$**.
# Code
```python3 []
class Solution:
def waysToSplitArray(self, nums: List[int]) -> int:
n = len(nums)
cnt = 0
pSum = [0]*n
pSum[0] = nums[0]
for i in range(1, n):
pSum[i] = pSum[i - 1] + nums[i]
full = pSum[-1]
for i in range(n - 1):
l = pSum[i]
r = full - l
if l >= r:
cnt += 1
return cnt
```
```java []
class Solution {
public int waysToSplitArray(int[] nums) {
int n = nums.length;
long[] prefixSum = new long[n];
prefixSum[0] = nums[0];
for (int i = 1; i < n; i++) {
prefixSum[i] = prefixSum[i - 1] + nums[i];
}
long totalSum = prefixSum[n - 1];
int count = 0;
for (int i = 0; i < n - 1; i++) {
long left = prefixSum[i];
long right = totalSum - left;
if (left >= right) {
count++;
}
}
return count;
}
}
```
``` C++ []
class Solution {
public:
int waysToSplitArray(vector<int>& nums) {
int n = nums.size();
vector<long long> prefixSum(n);
prefixSum[0] = nums[0];
for (int i = 1; i < n; i++) {
prefixSum[i] = prefixSum[i - 1] + nums[i];
}
long long totalSum = prefixSum[n - 1];
int count = 0;
for (int i = 0; i < n - 1; i++) {
long long left = prefixSum[i];
long long right = totalSum - left;
if (left >= right) {
count++;
}
}
return count;
}
};
``` | 3 | 0 | ['Python3'] | 0 |
number-of-ways-to-split-array | ✨ Explained in Hindi!! 🤩 Prefix Ka Jaadu🔮 | explained-in-hindi-prefix-ka-jaadu-by-an-9v53 | Intuition"Yaar, problem yeh hai ki array ko do parts mein todna hai—ek left aur ek right. Aur left ka sum right se bada ya at least barabar hona chahiye. Matlab | ANJ_07 | NORMAL | 2025-01-03T09:15:49.326346+00:00 | 2025-01-03T09:15:49.326346+00:00 | 16 | false | # Intuition
<img src="https://assets.leetcode.com/users/images/e6e437b6-a4c0-4c91-beaf-540d635534d9_1735895579.0807717.png" width="200" height="30">
"Yaar, problem yeh hai ki array ko do parts mein todna hai—ek left aur ek right. Aur left ka sum right se bada ya at least barabar hona chahiye. Matlab, socho ek jagah cut lagao aur check karo, 'Left ka paisa zyada hai kya?' Bas wahi karna hai efficiently!"
---
# Approach
### 1. **Prefix Sum ka Jaadu**
"Sabse pehle hum ek prefix sum array banate hain—samjho yeh ek jaadu hai jo cumulative sum ko store karta hai. Iska fayda yeh hai ki kisi bhi subarray ka sum fatafat nikal lenge, bina baar-baar calculate kiye."
### 2. **Extreme Values Ka Scene**
"Ab yeh array na kabhi kabhi overdramatic hoti hai, jaise `-100000` ya `100000`. So, hum inko thoda adjust karte hain: `-100000` ko `-1` aur `100000` ko `1` banake simple kar diya. Matlab zyada emotional hone ka nahi!"
### 3. **Split Check Karna**
"Har index pe (0 se leke n-2 tak) hum yeh dekhte hain ki:
- Left ka sum kya hai: `pre[i]`
- Right ka sum kya hai: `pre[n-1] - pre[i]`
Aur agar left ka paisa right se zyada ya barabar hai, toh valid counter ko 'Ek aur add kar de bhai!'"
### 4. **Finally, Answer De Do**
"Ab jitne valid splits mile, unka total return kar denge. Simple hai na?"
---
<img src="https://assets.leetcode.com/users/images/0c30b11f-1261-400c-be69-df125c0dc601_1735895328.2966905.png" width="200" height="30">
# Code Walkthrough
"Yeh dekho, code kaise kaam kar raha hai. Thoda focus maar lo! 👇
# Code
```cpp []
class Solution {
public:
int waysToSplitArray(vector<int>& nums) {
int n = nums.size();
vector<long long> pre(n, 0); // Prefix sum ka jugad
long long sum = 0;
// Prefix sum banate hue edge cases sambhalo
for (int i = 0; i < n; i++) {
if (nums[i] == -100000) nums[i] = -1; // Emotional values ko handle karo
else if (nums[i] == 100000) nums[i] = 1;
sum += (nums[i] % 100000); // Sum mein contribution
pre[i] = sum;
}
int valid = 0;
// Har split ko check karo
for (int i = 0; i < n - 1; i++) {
if (pre[i] >= pre[n - 1] - pre[i]) {
valid++; // Ek aur valid split mila!
}
}
return valid; // Answer dedo yaar
}
};
```
```java []
// Java Solution
class Solution {
public int waysToSplitArray(int[] nums) {
int n = nums.length;
long[] prefix = new long[n]; // Prefix sum ka jugad
long sum = 0;
// Prefix sum banate hue edge cases sambhalo
for (int i = 0; i < n; i++) {
if (nums[i] == -100000) nums[i] = -1; // Emotional values ko handle karo
else if (nums[i] == 100000) nums[i] = 1;
sum += nums[i] % 100000; // Sum mein contribution
prefix[i] = sum;
}
int valid = 0;
// Har split ko check karo
for (int i = 0; i < n - 1; i++) {
if (prefix[i] >= prefix[n - 1] - prefix[i]) {
valid++; // Ek aur valid split mila!
}
}
return valid; // Answer dedo yaar
}
}
```
```python []
# Python Solution
class Solution:
def waysToSplitArray(self, nums: List[int]) -> int:
n = len(nums)
prefix = [0] * n # Prefix sum ka jugad
total_sum = 0
# Prefix sum banate hue edge cases sambhalo
for i in range(n):
if nums[i] == -100000:
nums[i] = -1 # Emotional values ko handle karo
elif nums[i] == 100000:
nums[i] = 1
total_sum += nums[i] % 100000 # Sum mein contribution
prefix[i] = total_sum
valid = 0
# Har split ko check karo
for i in range(n - 1):
if prefix[i] >= prefix[-1] - prefix[i]:
valid += 1 # Ek aur valid split mila!
return valid # Answer dedo yaar
```
# Complexity
## Time Complexity
- Prefix sum banane mein lagega $$O(n)$$.
- Split check karne mein bhi $$O(n)$$.
- Toh total: **$$O(n)$$**.
"Matlab fast hai, chill karo!"
## Space Complexity
- Prefix sum array ko store karne ke liye $$O(n)$$ space.
- Aur koi bada space nahi use ho raha. Bas itna hi.
---
# Key Notes
Samjho, prefix sum toh yaar ultimate hack hai yaha. Aur extreme values ka drama handle karke kaafi efficient solution ban gaya. Mazedaar baat yeh hai ki code bada smartly kaam kar raha hai!
---
Kya samjh aa gaya? Aur nahi toh puch lo, bina jhijhak! 😄

| 3 | 0 | ['C++'] | 1 |
number-of-ways-to-split-array | 🧩 Ways to Split Array (⏱ Runtime: 0ms, 🚀 Beats 100%) | ways-to-split-array-runtime-0ms-beats-10-5woc | ✨ IntuitionWhen splitting an array, the goal is to count splits where the sum of the left part is greater than or equal to the sum of the right part. By leverag | rishisahu193 | NORMAL | 2025-01-03T06:15:46.544924+00:00 | 2025-01-03T06:15:46.544924+00:00 | 43 | false |
### ✨ Intuition
When splitting an array, the goal is to count splits where the sum of the left part is greater than or equal to the sum of the right part. By leveraging prefix sums, we can efficiently calculate the left and right segment sums during a single pass.
### 🔍 Approach
1️⃣ Compute the total sum of the array (`sum`) to help calculate the right segment sum as (`rightsum = sum - leftsum`).
2️⃣ Traverse the array up to the second-to-last element, maintaining a running sum (`leftsum`) for the left segment.
3️⃣ For each split point, check if (`leftsum >= rightsum`). If true, increment the counter.
4️⃣ Return the counter after evaluating all split points.
### 📊 Complexity
- **Time complexity:** \( O(n) \)
- The array is traversed twice: once to calculate the total sum and once to determine valid splits.
- **Space complexity:** \( O(1) \)
- Only a few variables are used for computation, regardless of input size.
### 💡 Runtime
⏱ **0ms** – 🚀 Beats **100.00%** of submissions! 🎉
# Code
```cpp []
class Solution {
public:
int waysToSplitArray(vector<int>& nums) {
const int n = nums.size();
long long sum = 0;
long long cnt = 0;
for (int i = 0; i < n; i++) {
sum += nums[i];
}
long long leftsum = 0;
long long rightsum = 0;
for (int i = 0; i < n - 1; i++) {
leftsum += nums[i];
rightsum = sum - leftsum;
if (leftsum >= rightsum) {
cnt += 1;
}
}
return cnt;
}
};
``` | 3 | 0 | ['Array', 'Prefix Sum', 'C++'] | 1 |
number-of-ways-to-split-array | Simple Python Solution || Prefix Sum || O(n) | simple-python-solution-prefix-sum-on-by-zjs6l | if it's help, please up ⬆ vote! ❤️Complexity
Time complexity: O(n)
Space complexity: O(n)
Code | shishirRsiam | NORMAL | 2025-01-03T06:04:47.292107+00:00 | 2025-01-03T06:04:47.292107+00:00 | 35 | false | # if it's help, please up ⬆ vote! ❤️
# Complexity
- Time complexity: O(n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(n)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def waysToSplitArray(self, nums: List[int]) -> int:
pref = [0]
for val in nums:
pref.append(pref[-1] + val)
ans, n = 0, len(nums)
for i in range(1, n):
if pref[i] >= pref[-1] - pref[i]:
ans += 1
return ans
``` | 3 | 0 | ['Array', 'Hash Table', 'Math', 'Prefix Sum', 'Python', 'Python3'] | 1 |
number-of-ways-to-split-array | Simple C++ Solution || Prefix Sum || O(n) | simple-c-solution-by-shishirrsiam-kf7v | if it's help, please up ⬆ vote! ❤️Complexity
Time complexity: O(n)
Space complexity: O(n)
Code | shishirRsiam | NORMAL | 2025-01-03T05:57:55.780760+00:00 | 2025-01-03T06:06:34.710163+00:00 | 85 | false | # if it's help, please up ⬆ vote! ❤️
# Complexity
- Time complexity: O(n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(n)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int waysToSplitArray(vector<int>& nums)
{
vector<long> pref;
pref.push_back(0);
for(auto val : nums) pref.push_back(pref.back() + val);
int ans = 0, n = nums.size();
for(int i = 1; i < n; i++)
if(pref[i] >= pref.back() - pref[i]) ans++;
return ans;
}
};
``` | 3 | 0 | ['Array', 'Hash Table', 'Math', 'Prefix Sum', 'C++'] | 4 |
number-of-ways-to-split-array | ✅ Beginner Friendly | Easy to Understand | 100% Faster | Prefix Sum | Java | Video Explanation 🔥 | beginner-friendly-easy-to-understand-100-nkim | IntuitionTo solve this problem, the key observation is that for any split of the array into two non-empty parts, the left part's sum (psum) must be greater than | sahilpcs | NORMAL | 2025-01-03T05:03:40.955133+00:00 | 2025-01-03T05:03:55.985726+00:00 | 53 | false | # Intuition
To solve this problem, the key observation is that for any split of the array into two non-empty parts, the left part's sum (`psum`) must be greater than or equal to the right part's sum (`sum - psum`). By iterating through the array and maintaining a running prefix sum, we can efficiently check this condition for every potential split.
# Approach
1. **Calculate the Total Sum:** First, compute the total sum of the array, as it will help determine the sum of the right part for any split.
2. **Iterate Through the Array:** Use a loop to traverse the array up to the second last element. For each iteration:
- Update the prefix sum (`psum`) by adding the current element.
- Compare the prefix sum with the right part's sum (`sum - psum`). If `psum` is greater than or equal, count it as a valid split.
3. **Return the Result:** Finally, return the count of valid splits.
This approach ensures that we check each possible split in a single pass of the array.
# Complexity
- **Time complexity:**
$$O(n)$$
The algorithm involves a single traversal of the array to calculate the total sum, followed by another traversal to check the condition for valid splits. Thus, it is linear in time complexity.
- **Space complexity:**
$$O(1)$$
The solution uses a constant amount of extra space, as we only maintain variables for the total sum, prefix sum, and the count of valid splits.
# Code
```java []
class Solution {
public int waysToSplitArray(int[] nums) {
// Calculate the total sum of the array
long sum = 0;
for(int num : nums) {
sum += num;
}
// Initialize prefix sum (psum) and answer (ans)
long psum = 0;
int ans = 0;
// Iterate through the array up to the second last element
for(int i = 0; i < nums.length - 1; i++) {
// Add the current element to the prefix sum
psum += nums[i];
// Check if the prefix sum is greater than or equal to the remaining sum
if(psum >= (sum - psum)) {
// Increment the count of valid splits
ans++;
}
}
// Return the total number of valid splits
return ans;
}
}
```
LeetCode 2270 Number of Ways to Split Array | Prefix Sum | Asked in Amazon
https://youtu.be/icKP3DC9Gq8 | 3 | 0 | ['Array', 'Prefix Sum', 'Java'] | 1 |
number-of-ways-to-split-array | Easy approach for beginner || Prefix Sum Algorithm | easy-approach-for-beginner-prefix-sum-al-ats5 | IntuitionTo determine the number of valid splits, we need to divide the array into two non-empty parts at each possible index and compare their sums. The key in | minhle106cse | NORMAL | 2025-01-03T04:29:34.568311+00:00 | 2025-01-03T04:29:34.568311+00:00 | 91 | false | # Intuition
To determine the number of valid splits, we need to divide the array into two non-empty parts at each possible index and compare their sums. The key insight is to precompute the prefix sums of the array, allowing efficient calculation of the sum for any subarray.
# Approach
1. **Prefix Sum Calculation**:
- Compute a `prefix` array where `prefix[i]` represents the sum of the first `i` elements of the array `nums`.
- This allows us to compute the sum of any subarray efficiently using the formula:
$$\text{sum of subarray from index } i \text{ to } j = \text{prefix}[j+1] - \text{prefix}[i]$$
2. **Iterating Over Split Indices**:
- Iterate through all possible split indices `i` from `0` to `n-2` (inclusive), since the last element must belong to the right part to satisfy the condition.
- For each index `i`:
- Compute the sum of the left part as $\text{prefix}[i+1] - \text{prefix}[0]$.
- Compute the sum of the right part as $\text{prefix}[n] - \text{prefix}[i+1]$.
- Check if the left part's sum is greater than or equal to the right part's sum.
3. **Count Valid Splits**:
- If the condition is satisfied for an index, increment the count of valid splits.
4. **Return the Count**:
- Return the total count of valid splits.
# Complexity
- **Time complexity**:
$$O(n)$$
- Computing the `prefix` array requires $O(n)$.
- Iterating over the array to check split indices also requires $O(n)$.
- **Space complexity**:
$$O(n)$$
- The `prefix` array stores $n+1$ elements.
# Code
```javascript
/**
* @param {number[]} nums
* @return {number}
*/
var waysToSplitArray = function(nums) {
let count = 0
const prefix = Array(nums.length + 1).fill(0)
for(let i=0; i<nums.length; i++){
prefix[i+1] = prefix[i] + nums[i]
}
for(let i=0; i<nums.length-1; i++){
const slpit_index = i + 1
const left_sum = prefix[slpit_index] - prefix[0]
const right_sum = prefix[prefix.length-1] - prefix[slpit_index]
if(left_sum >= right_sum) count++
}
return count
};
``` | 3 | 0 | ['Prefix Sum', 'JavaScript'] | 1 |
number-of-ways-to-split-array | Simple Approach with Efficient time and space complexity :- | simple-approach-with-efficient-time-and-i2y4l | IntuitionThe problem involves splitting an array such that the left sum is greater than or equal to the right sum.
By precomputing the total sum (rSum) and dyna | Ayush_ranjan00 | NORMAL | 2025-01-03T04:29:16.539481+00:00 | 2025-01-03T04:29:16.539481+00:00 | 45 | false | # Intuition
The problem involves splitting an array such that the left sum is greater than or equal to the right sum.
By precomputing the total sum (rSum) and dynamically adjusting it during iteration, we avoid recomputation, making the solution efficient.
## At every step, the split condition
lSum≥rSum ensures only valid splits are counted.
# Approach
1. Calculate Total Sum (Right Sum):
Compute the total sum of the array nums, which will serve as the initial right sum (rSum).
2.Iterate Through the Array:
For each element (except the last one):
Add the current element to the left sum (lSum).
Subtract the current element from the right sum (rSum).
Check if lSum >= rSum. If true, increment the count.
3.Return Count:
After iterating, the final count represents the number of valid splits
# Complexity
- Time complexity: O(n) + O(n) = O(n)
- Space complexity: O(1) (constant space)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int waysToSplitArray(int[] nums) {
long rSum = 0;
for(int i=0 ; i<nums.length ; i++){
rSum += nums[i];
}
long lSum = 0;
int count = 0;
for(int i=0 ; i<nums.length-1 ; i++){
lSum += nums[i];
rSum -= nums[i];
if(lSum >= rSum) count++;
}
return count;
}
}
``` | 3 | 0 | ['Array', 'Java'] | 1 |
number-of-ways-to-split-array | Simple and Easy Solution | ✅Beats 100% | C++| Java | Python | JavaScript | simple-and-easy-solution-beats-100-c-jav-90p0 | ⬆️Upvote if it helps ⬆️Connect with me on Linkedin [Bijoy Sing]Solution in C++, Python, Java, and JavaScriptIntuitionThe goal is to split the array such that th | BijoySingh7 | NORMAL | 2025-01-03T04:04:20.841743+00:00 | 2025-01-03T04:04:20.841743+00:00 | 231 | false | # ⬆️Upvote if it helps ⬆️
---
## Connect with me on Linkedin [Bijoy Sing]
---
### Solution in C++, Python, Java, and JavaScript
```cpp []
class Solution {
public:
int waysToSplitArray(vector<int>& nums) {
long long tot = 0, left = 0;
int ans = 0;
for (int num : nums) {
tot += num;
}
for (int i = 0; i < nums.size() - 1; ++i) {
left += nums[i];
if (left >= tot - left) {
++ans;
}
}
return ans;
}
};
```
```python []
class Solution:
def waysToSplitArray(self, nums):
tot = 0
left = 0
ans = 0
for num in nums:
tot += num
for i in range(len(nums) - 1):
left += nums[i]
if left >= tot - left:
ans += 1
return ans
```
```java []
class Solution {
public int waysToSplitArray(int[] nums) {
long tot = 0, left = 0;
int ans = 0;
for (int num : nums) {
tot += num;
}
for (int i = 0; i < nums.length - 1; i++) {
left += nums[i];
if (left >= tot - left) {
ans++;
}
}
return ans;
}
}
```
```javascript []
class Solution {
waysToSplitArray(nums) {
let tot = 0, left = 0;
let ans = 0;
for (let num of nums) {
tot += num;
}
for (let i = 0; i < nums.length - 1; i++) {
left += nums[i];
if (left >= tot - left) {
ans++;
}
}
return ans;
}
}
```
---
# Intuition
The goal is to split the array such that the sum of the left part is greater than or equal to the sum of the right part. We iterate through the array, calculating the total sum and then comparing the running sum (left side) to the remaining sum (right side).
# Approach
1. Calculate the total sum of the array.
2. Traverse the array, maintaining a running sum of the left part.
3. For each split, check if the left sum is greater than or equal to the right sum.
4. Count the number of valid splits.
# Complexity
- Time complexity: \(O(n)\)
- We iterate over the array twice, once to calculate the total sum and once to check each possible split.
- Space complexity: \(O(1)\)
- Only a few variables are used to store sums and the result.
### *If you have any questions or need further clarification, feel free to drop a comment! 😊* | 3 | 2 | ['Array', 'C', 'Prefix Sum', 'Python', 'C++', 'Java', 'Python3', 'JavaScript'] | 9 |
number-of-ways-to-split-array | Java🍵|Prefix Sum✅|Easy🔥 | javaprefix-sumeasy-by-mani-26-t5nt | Complexity
Time complexity: O(n)
Space complexity: O(1)
Code | mani-26 | NORMAL | 2025-01-03T03:27:23.053176+00:00 | 2025-01-03T03:27:23.053176+00:00 | 19 | false | # Complexity
- Time complexity: **O(n)**
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: **O(1)**
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int waysToSplitArray(int[] nums) {
long right = 0;
long left = 0;
for (int i : nums) {
right += i;
}
int count = 0;
for (int i = 0; i < nums.length - 1; i++) {
right -= nums[i];
left += nums[i];
if (left >= right) {
count++;
}
}
return count;
}
}
``` | 3 | 0 | ['Array', 'Prefix Sum', 'Java'] | 0 |
number-of-ways-to-split-array | beats 100% || very easy solution! | beats-100-very-easy-solution-by-ishwarya-v1lt | IntuitionThe intuition is to find the number of ways the array can be splitted such the left subarray is always maximum then the right subarray.Note: The array | Ishwaryaice | NORMAL | 2025-01-03T03:25:01.266799+00:00 | 2025-01-03T03:25:01.266799+00:00 | 11 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The intuition is to find the number of ways the array can be splitted such the left subarray is always maximum then the right subarray.
**Note:** The array also consists of negative integers and should be split such that atleast one element should lies in the left and right!
# Approach
<!-- Describe your approach to solving the problem. -->
The approach is simple, we need to keep track of the count of the ways the array can be splitted so there is no need to actually include the array, just the count is enough. So we can keep track of the three variables here **adding** , which is used to add the upcoming elements, **tot**, helps to calculate the total sum of the array and finally **res**, used to return the total possible ways the array can be splitted.
# Complexity
- Time complexity: O(N)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int waysToSplitArray(int[] nums) {
long adding=0;
long tot=0;
for(int i=0;i<nums.length;i++){
tot+=nums[i];
}
int res=0;
for(int i=0;i<nums.length-1;i++){
adding+=nums[i];
tot-=nums[i];
if (adding>=tot){
res++;
}
}
return res;
}
}
```
```python []
class Solution:
def waysToSplitArray(self, nums: List[int]) -> int:
adding=0
tot=sum(nums)
res=0
for i in range(len(nums)-1):
adding+=nums[i]
tot-=nums[i]
if adding>=tot:
res+=1
return res
```
```C++ []
class Solution {
public:
int waysToSplitArray(vector<int>& nums) {
long adding=0;
long tot=0;
for(int i=0;i<nums.size();i++){
tot+=nums[i];
}
int res=0;
for(int i=0;i<nums.size()-1;i++){
adding+=nums[i];
tot-=nums[i];
if (adding>=tot){
res++;
}
}
return res;
}
};
```

# Happy Leetcoding~
| 3 | 0 | ['Java'] | 0 |
number-of-ways-to-split-array | Beats 100% of users with C++ | beats-100-of-users-with-c-by-sahilsaw-cb63 | IntuitionTo solve the problem, I first considered the idea of iterating through the array and trying to split it into two non-empty parts. The challenge is to f | SahilSaw | NORMAL | 2025-01-03T00:07:22.897358+00:00 | 2025-01-03T00:07:22.897358+00:00 | 168 | false |
# Intuition
To solve the problem, I first considered the idea of iterating through the array and trying to split it into two non-empty parts. The challenge is to find a point where the sum of the left part is greater than or equal to the sum of the right part. This is where the comparison between the left and right sums comes into play.
# Approach
1. Calculate the total sum of the array to have a reference for comparisons.
2. Iterate through the array, maintaining the sum of the left part (`left_sum`).
3. For each index, calculate the right part sum by subtracting `left_sum` from the `total_sum`.
4. If the sum of the left part is greater than or equal to the right part, increment the count of valid splits.
5. Return the total count of valid splits.
# Complexity
- Time complexity: $$O(n)$$
- The total sum is calculated in a single pass over the array, and the left sum is updated in each iteration. Hence, the time complexity is linear in terms of the number of elements.
- Space complexity: $$O(1)$$
- The space complexity is constant because only a few extra variables are used for storing sums and the result.
# Code
```cpp
class Solution {
public:
int waysToSplitArray(vector<int>& nums) {
int n = nums.size();
long total_sum = 0;
for (int num : nums) {
total_sum += num; // Calculate total sum of the array
}
long left_sum = 0;
int count = 0;
for (int i = 0; i < n - 1; ++i) { // We need at least one element in the right part
left_sum += nums[i];
if (left_sum >= total_sum - left_sum) {
count++;
}
}
return count;
}
};
```
| 3 | 0 | ['C++'] | 1 |
number-of-ways-to-split-array | Beats 100% of users with C++|| Using Presum and Postsum || Faster Solution || Easy to Understand || | beats-100-of-users-with-c-using-presum-a-j6mg | Intuition\n Describe your first thoughts on how to solve this problem. \n\nif you like the approach please upvote it\n\n\n\n\n\n\nif you like the approach pleas | abhirajpratapsingh | NORMAL | 2023-12-21T10:53:27.863465+00:00 | 2023-12-21T10:53:27.863504+00:00 | 80 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nif you like the approach please upvote it\n\n\n\n\n\n\nif you like the approach please upvote it\n\n\n\n\n\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->O ( N )\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int waysToSplitArray(vector<int>& nums) \n {\n long long int total=0;\n long long int leftsum=0;\n long long int rightsum=0;\n int count=0;\n for(int i=0;i<nums.size();i++)\n total=nums[i]+total;\n for(int i=0;i<nums.size()-1;i++)\n {\n leftsum=leftsum+nums[i];\n rightsum=total-leftsum;\n if(leftsum>=rightsum)\n count++;\n }\n return count;\n }\n};\n``` | 3 | 0 | ['Array', 'Prefix Sum', 'C++'] | 0 |
number-of-ways-to-split-array | 7 Lines Python Code || Beats 82 % | 7-lines-python-code-beats-82-by-jigglyyp-wght | Intuition\nso you have to count the number of ways we can split array basically in two parts such that sum of left Part >= right Part\nso first find the total | JigglyyPuff | NORMAL | 2023-07-12T06:56:47.543697+00:00 | 2023-07-12T06:56:47.543724+00:00 | 127 | false | # Intuition\nso you have to count the number of ways we can split array basically in two parts such that `sum of left Part >= right Part`\nso first find the total sum of the array\nand loop through your given array and add each element to left Part and subtract it from your totalSum (which is now your right Part)\nif the condition satisfies increase count\nreturn count of subarray as your ans\n\n# Code\n```\nclass Solution:\n def waysToSplitArray(self, nums: List[int]) -> int:\n summ = sum(nums)\n leftSum, count = 0, 0\n for i in range(len(nums) - 1):\n leftSum += nums[i]\n summ -= nums[i]\n if leftSum >= summ:\n count += 1\n return count\n \n``` | 3 | 0 | ['Python3'] | 0 |
number-of-ways-to-split-array | Simple JAVA Solution | simple-java-solution-by-kumarabhinav88-8alh | ```\nclass Solution {\n public int waysToSplitArray(int[] nums) {\n long sum = 0;\n for(int i : nums){\n sum+=i;\n }\n | kumarabhinav88 | NORMAL | 2022-05-14T16:31:50.529683+00:00 | 2022-05-14T16:31:50.529723+00:00 | 941 | false | ```\nclass Solution {\n public int waysToSplitArray(int[] nums) {\n long sum = 0;\n for(int i : nums){\n sum+=i;\n }\n int sol = 0;\n long localSum = 0;\n for(int i=0; i<nums.length-1;i++){\n localSum += nums[i];\n if(localSum >= sum-localSum){\n sol++;\n }\n }\n return sol;\n }\n} | 3 | 0 | ['Java'] | 0 |
number-of-ways-to-split-array | javascript 112ms | javascript-112ms-by-growthfromnewbie-fvv5 | \n/**\n * @param {number[]} nums\n * @return {number}\n */\nvar waysToSplitArray = function(nums) {\n let result = 0;\n let letsum = 0;\n let rightsum | growthfromnewbie | NORMAL | 2022-05-14T16:22:04.276737+00:00 | 2022-07-17T11:18:52.635200+00:00 | 185 | false | ```\n/**\n * @param {number[]} nums\n * @return {number}\n */\nvar waysToSplitArray = function(nums) {\n let result = 0;\n let letsum = 0;\n let rightsum = nums.reduce((a,b)=> a+b);\n let end = nums.length-1;\n for (let i = 0;i<end;i++) {\n letsum+=nums[i];\n rightsum-=nums[i];\n if (letsum>=rightsum) {\n result++;\n }\n }\n return result;\n};\n``` | 3 | 1 | ['JavaScript'] | 0 |
number-of-ways-to-split-array | C++ || O(n) solution || With comments | c-on-solution-with-comments-by-hrishilam-knz3 | \nclass Solution {\npublic:\n int waysToSplitArray(vector<int>& nums) {\n \n long long sum=0, lsum=0,rsum=0;\n \n //calculate sum | hrishilamdade | NORMAL | 2022-05-14T16:21:52.858185+00:00 | 2022-05-14T16:21:52.858212+00:00 | 258 | false | ```\nclass Solution {\npublic:\n int waysToSplitArray(vector<int>& nums) {\n \n long long sum=0, lsum=0,rsum=0;\n \n //calculate sum of all values in nums\n for(auto i:nums){\n sum+=i;\n }\n \n int n=nums.size(),res=0;\n \n for(int i=0;i<n;i++){\n lsum+=nums[i];//calculate left sum\n \n rsum=sum-lsum;//calculate right sum\n \n if(i<n-1 && lsum>=rsum){\n // increment result if there is atleast \n //one element after i and left sum is \n //greater than equal to right sum\n res++; \n }\n }\n return res;\n }\n};\n``` | 3 | 0 | ['C', 'Prefix Sum'] | 1 |
number-of-ways-to-split-array | CPP | Short and Simple | Prefix Sum | cpp-short-and-simple-prefix-sum-by-amirk-2cvz | \nclass Solution {\npublic:\n typedef long ll;\n int waysToSplitArray(vector<int>& v,ll ss=0,ll ans=0) {\n ll s=accumulate(v.begin(),v.end(),0LL);\ | amirkpatna | NORMAL | 2022-05-14T16:01:33.739303+00:00 | 2022-05-14T16:03:30.366534+00:00 | 260 | false | ```\nclass Solution {\npublic:\n typedef long ll;\n int waysToSplitArray(vector<int>& v,ll ss=0,ll ans=0) {\n ll s=accumulate(v.begin(),v.end(),0LL);\n for(int i=0;i<v.size()-1;i++){\n ss+=v[i];\n ans+=ss>=s-ss;\n }\n return ans;\n }\n};\n``` | 3 | 0 | ['Prefix Sum', 'C++'] | 0 |
number-of-ways-to-split-array | beginner friendly solution beats 99.9% user in JAVA | beginner-friendly-solution-beats-999-use-5oek | IntuitionApproachComplexity
Time complexity: O(n)
Space complexity: O(1)
Code | soumya_kumar_gupta | NORMAL | 2025-01-21T06:38:26.246389+00:00 | 2025-01-21T06:38:26.246389+00:00 | 10 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: O(n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int waysToSplitArray(int[] nums) {
long left=0;
long right=0;
for(int num: nums){
right= right+num;
}
int count=0;
for(int i=0;i<nums.length-1;i++){
left= left + nums[i];
right= right - nums[i];
if(left>=right)count++;
}
return count;
}
}
``` | 2 | 0 | ['Java'] | 0 |
number-of-ways-to-split-array | Count Valid Array Splits Based on Prefix and Suffix Sums | count-valid-array-splits-based-on-prefix-l22z | IntuitionThe problem seems to involve checking if the prefix sum of an array up to a certain index is greater than or equal to the sum of the remaining elements | abhivatsa1185 | NORMAL | 2025-01-04T14:08:45.208267+00:00 | 2025-01-04T14:08:45.208267+00:00 | 11 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The problem seems to involve checking if the prefix sum of an array up to a certain index is greater than or equal to the sum of the remaining elements of the array. This makes the problem a good fit for a prefix sum approach.
# Approach
<!-- Describe your approach to solving the problem. -->
- Calculate the Total Sum: First, compute the total sum of the array.
- Iterate Through the Array: Use a loop to calculate the prefix sum (left) and derive the suffix sum (right) by subtracting left from the total sum.
- Check Condition: For each index i, check if the prefix sum (left) is greater than or equal to the suffix sum (right). If true, increment the count.
- Return Count: Return the total count of valid splits.
# Complexity
- Time complexity: O(n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int waysToSplitArray(int[] nums) {
int n = nums.length;
long left = 0, right = 0; // Variables to store prefix and suffix sums
int count = 0; // Variable to count valid splits
long sum = 0; // Variable to store total sum of the array
// Calculate the total sum of the array
for (int num : nums) {
sum += num;
}
// Iterate through the array to check conditions
for (int i = 0; i < n - 1; i++) {
left += nums[i]; // Update prefix sum
right = sum - left; // Derive suffix sum
if (left >= right) { // Check if prefix sum is >= suffix sum
count++;
}
}
return count; // Return the number of valid splits
}
}
``` | 2 | 0 | ['Java'] | 1 |
number-of-ways-to-split-array | ✅ Java ✅ Beats 100% ✅ Simple ✅ | java-beats-100-simple-by-abdullohmaraimo-8lby | Complexity
Time complexity: O(n)
Space complexity: O(1)
Code | AbdullohMaraimov | NORMAL | 2025-01-03T17:54:40.711325+00:00 | 2025-01-03T17:55:49.459419+00:00 | 21 | false |
# Complexity
- Time complexity: O(n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int waysToSplitArray(int[] nums) {
long leftSum = 0;
int res = 0;
long rightSum = 0;
for(int i = 0; i < nums.length; i++) {
rightSum += nums[i];
}
for(int i = 0; i < nums.length - 1; i++) {
leftSum += nums[i];
rightSum -= nums[i];
if(leftSum >= rightSum) {
res++;
}
}
return res;
}
}
``` | 2 | 0 | ['Java'] | 2 |
number-of-ways-to-split-array | Beats 100% ✨ | beats-100-by-hriii11-hq3f | IntuitionApproachComplexity
Time complexity:
O(n)
Space complexity:
O(1)
Code | Hriii11 | NORMAL | 2025-01-03T16:56:39.858133+00:00 | 2025-01-03T16:56:39.858133+00:00 | 10 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
$$O(n)$$
- Space complexity:
$$O(1)$$
# Code
```cpp []
class Solution {
public:
int waysToSplitArray(vector<int>& nums) {
long long sum=0;
for(int i=0; i<nums.size();i++){
sum+=nums[i];
}
long long psum=0;
int ans=0;
for(int i=0; i<nums.size()-1;i++){
psum+=nums[i];
sum-=nums[i];
if(psum>=sum){
ans++;
}
}
return ans;
}
};
``` | 2 | 0 | ['Prefix Sum', 'C++'] | 0 |
number-of-ways-to-split-array | Simple Java Solution with O(n) tc | Beats 100%. | simple-java-solution-with-on-tc-beats-10-ipse | IntuitionApproachTo solve this problem, first calculate the total sum of the array. Then, iterate through the array while keeping a running sum for the left par | AnaghaBharadwaj | NORMAL | 2025-01-03T15:42:29.304744+00:00 | 2025-01-03T15:42:29.304744+00:00 | 8 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
To solve this problem, first calculate the total sum of the array. Then, iterate through the array while keeping a running sum for the left part (leftsum). At each step, check if leftsum is greater than or equal to the remaining right part (sum - leftsum). If true, increment the count. Finally, return the count.
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:O(n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int waysToSplitArray(int[] nums) {
int count=0;
long sum=0;
long leftsum=0;
for(int n:nums){
sum+=n;
}
for(int i=0;i<nums.length-1;++i){
leftsum+=nums[i];
if(leftsum>=sum-leftsum) count++;
}
return count;
}
}
``` | 2 | 0 | ['Prefix Sum', 'Java'] | 0 |
number-of-ways-to-split-array | 6 lines logic || very simple | 6-lines-logic-very-simple-by-shashwat191-g3m6 | Code | shashwat1915 | NORMAL | 2025-01-03T14:37:06.323869+00:00 | 2025-01-03T14:37:06.323869+00:00 | 12 | false | # Code
```cpp []
class Solution {
public:
int waysToSplitArray(vector<int>& nums) {
int ans=0;
long long total_sum=accumulate(nums.begin(),nums.end(),0L),last_sum=0;
for(int i=0;i<nums.size()-1;i++){
total_sum-=nums[i];
last_sum+=nums[i];
if(total_sum<=last_sum) ans++;
}
// cout<<total_sum;
return ans;
}
};
``` | 2 | 0 | ['Array', 'Prefix Sum', 'C++'] | 0 |
number-of-ways-to-split-array | C++ || Prefix Sum || Number of Ways to Split Array - Solution Explanation || O(n) Time | c-prefix-sum-number-of-ways-to-split-arr-7dor | IntuitionTo determine the number of valid splits in the array, we need to check whether the sum of elements in the left part (up to index i) is greater than or | lokeshsingh07 | NORMAL | 2025-01-03T14:11:05.549350+00:00 | 2025-01-03T14:11:05.549350+00:00 | 4 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
To determine the number of valid splits in the array, we need to check whether the sum of elements in the left part (up to index i) is greater than or equal to the sum of elements in the right part (from index i+1 onward). Using prefix sums allows us to compute these sums efficiently.
# Approach
<!-- Describe your approach to solving the problem. -->
1. **Prefix Sum Calculation**:
- First, calculate the prefix sum of the array. This array stores the cumulative sum up to each index.
- For example, for nums = [10, 4, -8, 7], the prefix sum would be [10, 14, 6, 13].
2. **Iterate Through Possible Splits**:
- Loop through the array up to `n-1` (to ensure there is at least one element in the right part).
- For each index `i`:
- The sum of the left part is the prefix sum at index `i` (`prefixSum[i]`).
- The sum of the right part is the total sum of the array (`prefixSum[n-1]`) minus the prefix sum at index `i` (`prefixSum[i]`).
- Check if the left sum is greater than or equal to the right sum. If so, increment the count of valid splits.
3. **Return the Count**:
- After iterating through all possible splits, return the count of valid splits.
# Complexity
- **Time Complexity**:
- Calculating the prefix sum takes $$O(n)$$ time.
- Iterating through the array to count valid splits also takes $$O(n)$$ time.
- Overall, the time complexity is $$O(n)$$.
- **Space Complexity**:
- The prefix sum array requires $$O(n)$$ space.
- Thus, the space complexity is $$O(n)$$.
# Code
```cpp []
class Solution {
public:
int waysToSplitArray(vector<int>& nums) {
int n = nums.size();
vector<long long> prefixSum(n);
int count = 0;
// calculate prefix sum
prefixSum[0] = nums[0];
for(int i=1; i<n; i++){
prefixSum[i] = prefixSum[i-1] + nums[i];
}
for(int i=0; i<n-1; i++){
long long leftSum = prefixSum[i];
long long rightSum = prefixSum[n-1] - prefixSum[i];
if(leftSum >= rightSum) count++;
}
return count;
}
};
``` | 2 | 0 | ['C++'] | 0 |
number-of-ways-to-split-array | O(n) Solution using Prefix Sum with explaination! | 96.04% \ 87.64% | on-solution-using-prefix-sum-with-explai-ghgd | Intuition
The problem involves finding the number of ways to split an array such that the sum of the left part is greater than or equal to the sum of the right | Delta7Actual | NORMAL | 2025-01-03T13:00:04.378276+00:00 | 2025-01-03T13:00:04.378276+00:00 | 9 | false | # Intuition
- The problem involves finding the number of ways to split an array such that the sum of the left part is greater than or equal to the sum of the right part.
- Initially, it may seem like calculating the sums of both parts for every split is necessary, but this can be optimized by using cumulative sums.
---
# Approach
1. Compute the total sum of the array.
2. Initialize a variable `left_sum` to track the cumulative sum of elements on the left part of the split.
3. Iterate through the array (excluding the last element since we cannot split there).
- Add the current element to `left_sum`.
- Calculate the sum of the right part as `total - left_sum`.
- Check if `left_sum >= right_sum`. If true, increment the counter `ways`.
4. Return the counter `ways` after completing the iteration.
#### This approach ensures that we calculate the sums efficiently without recomputing them repeatedly for each split.
---
# Complexity
- ### Time complexity: $$O(n)$$
- The algorithm iterates through the array once and performs constant-time operations in each iteration.
- ### Space complexity: $$O(1)$$
- Only a few variables are used for calculations, and no additional space is required proportional to the input size.
---
# Code
```python3 []
class Solution:
def waysToSplitArray(self, nums: List[int]) -> int:
ways = 0
total = sum(nums)
left_sum = 0
for i in range(len(nums)-1):
left_sum += nums[i]
if left_sum >= (total - left_sum):
ways += 1
return ways
```
--- | 2 | 0 | ['Array', 'Prefix Sum', 'Python3'] | 0 |
number-of-ways-to-split-array | Easy JavaScript Solution ❤️⭐ | easy-javascript-solution-by-priyanshuson-8f0k | IntuitionSo Here We need to observe one things which is that , at every index we need to verify if sum of left side is** >=** sum of right side , that's why i w | priyanshusoniii | NORMAL | 2025-01-03T12:42:42.805621+00:00 | 2025-01-03T12:42:42.805621+00:00 | 20 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
So Here We need to observe one things which is that , at every index we need to verify if sum of left side is** >=** sum of right side , that's why i will always point to last index-1 (at max.) to satisfy given question constraint , Hence **Second **Condition**** can be easily achieved by just running a loop through i =0 to i< nums.length-1
Now we need to observe that at every index we need to determine sum of left elements >= sum of right elements , so for that we can use prefixSum array approach instead of brute force , we will create a prefixSum array which will store sum of elements till that particular index , such that
prefix[i] = sum of elements till index i (inclusive)
now we will run a loop again to nums array and at every index we will check if the sum of the elements till that index from prefixSum array is greater than sum of the elements from i+1 to nums.length-1 elements
for that we can use this condition
if(prefixSum[i] >= (prefixSum[nums.length-1]- prefixSum[i])){
noOfSplittingWays++;
}
# Approach
<!-- Describe your approach to solving the problem. -->
To solve this problem, we need to determine if, at each index i (from 0 to n-2), the sum of elements on the left side (from the start to i) is greater than or equal to the sum of elements on the right side (from i+1 to the end).
**Key Observations:**
We can achieve this by iterating up to nums.length - 1 because there must be at least one element on the right side for a valid split.
Instead of recalculating sums for the left and right parts repeatedly (as in a brute force approach), we can use a prefix sum array:
prefix[i] will store the sum of elements from the start of the array up to index i.
Using this array, we can compute the sum of the left and right sides efficiently at each index.
**Prefix Sum Calculation:**
The prefix sum array helps us calculate the required sums in constant time:
**$$Left sum$$**: prefix[i]
**$$Right sum$$**: prefix[nums.length - 1] - prefix[i]
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(N)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(N)
# Code
```javascript []
/**
* @param {number[]} nums
* @return {number}
*/
var waysToSplitArray = function(nums) {
//Problem can be Solved USing Prefix Sum
// Nums = [10 , 4 , -8 , 7 ]
let noOfways =0;
let prefixSum = [];
let temp=0;
for(let i=0;i<nums.length;i++){
temp+=nums[i];
prefixSum[i] = temp;
}
//PrefixSum = [ 10, 14, 6, 13 ]
for(let i=0;i<nums.length-1;i++){
if(prefixSum[i] >= (prefixSum[nums.length-1]- prefixSum[i])){
noOfways++;
}
}
return noOfways;
};
``` | 2 | 0 | ['JavaScript'] | 0 |
number-of-ways-to-split-array | ✅✅Beats 100%🔥C++🔥Python|| 🚀🚀Super Simple and Efficient Solution🚀🚀||🔥Python🔥C++✅✅ | beats-100cpython-super-simple-and-effici-jf2r | Complexity
Time complexity: O(n)
Space complexity: O(1)
Code | shobhit_yadav | NORMAL | 2025-01-03T12:41:29.094735+00:00 | 2025-01-03T12:41:29.094735+00:00 | 9 | false | # Complexity
- Time complexity: $$O(n)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(1)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int waysToSplitArray(vector<int>& nums) {
int ans = 0;
long prefix = 0;
long suffix = accumulate(nums.begin(), nums.end(), 0L);
for (int i = 0; i < nums.size() - 1; ++i) {
prefix += nums[i];
suffix -= nums[i];
if (prefix >= suffix)
++ans;
}
return ans;
}
};
```
```python []
class Solution:
def waysToSplitArray(self, nums: list[int]) -> int:
ans = 0
prefix = 0
suffix = sum(nums)
for i in range(len(nums) - 1):
prefix += nums[i]
suffix -= nums[i]
if prefix >= suffix:
ans += 1
return ans
``` | 2 | 0 | ['Array', 'Prefix Sum', 'C++', 'Python3'] | 0 |
number-of-ways-to-split-array | 🔥BEATS 💯 % 🎯 |✨SUPER EASY BEGINNERS 👏 | beats-super-easy-beginners-by-codewithsp-m5ka | IntuitionTo split an array into two non-empty parts such that the sum of the left part is greater than or equal to the sum of the right part, we can leverage pr | CodeWithSparsh | NORMAL | 2025-01-03T12:35:50.831541+00:00 | 2025-01-03T12:35:50.831541+00:00 | 51 | false | 
---
### Intuition
To split an array into two non-empty parts such that the sum of the left part is greater than or equal to the sum of the right part, we can leverage prefix and suffix sums. We maintain a running total for the left and right sums as we iterate through the array.
---
### Approach
1. Calculate the total sum of the array, which will initially represent the right sum.
2. Iterate through the array up to the second-to-last element.
- Update the left sum by adding the current element.
- Update the right sum by subtracting the current element.
- Check if the left sum is greater than or equal to the right sum.
3. Increment the result counter if the condition is satisfied.
4. Return the final result.
---
### Complexity
- **Time Complexity**: $$O(n)$$, where $$n$$ is the length of the array, as we traverse the array once.
- **Space Complexity**: $$O(1)$$, as we use constant extra space.
---
```dart []
class Solution {
int waysToSplitArray(List<int> nums) {
int res = 0;
int leftSum = 0;
int rightSum = nums.reduce((a, b) => a + b); // Total sum
int n = nums.length;
for (int i = 0; i < n - 1; i++) {
leftSum += nums[i];
rightSum -= nums[i];
if (leftSum >= rightSum) res++;
}
return res;
}
}
```
```python []
class Solution:
def waysToSplitArray(self, nums: List[int]) -> int:
res = 0
left_sum = 0
right_sum = sum(nums) # Total sum
for i in range(len(nums) - 1):
left_sum += nums[i]
right_sum -= nums[i]
if left_sum >= right_sum:
res += 1
return res
```
```java []
class Solution {
public int waysToSplitArray(int[] nums) {
long leftSum = 0, rightSum = 0;
int res = 0;
// Calculate total sum
for (int num : nums) {
rightSum += num;
}
// Iterate through the array
for (int i = 0; i < nums.length - 1; i++) {
leftSum += nums[i];
rightSum -= nums[i];
if (leftSum >= rightSum) {
res++;
}
}
return res;
}
}
```
```cpp []
class Solution {
public:
int waysToSplitArray(vector<int>& nums) {
long long leftSum = 0, rightSum = accumulate(nums.begin(), nums.end(), 0LL);
int res = 0;
for (int i = 0; i < nums.size() - 1; i++) {
leftSum += nums[i];
rightSum -= nums[i];
if (leftSum >= rightSum) {
res++;
}
}
return res;
}
};
```
```javascript []
var waysToSplitArray = function(nums) {
let leftSum = 0;
let rightSum = nums.reduce((a, b) => a + b, 0); // Total sum
let res = 0;
for (let i = 0; i < nums.length - 1; i++) {
leftSum += nums[i];
rightSum -= nums[i];
if (leftSum >= rightSum) {
res++;
}
}
return res;
};
```
```go []
func waysToSplitArray(nums []int) int {
leftSum, rightSum := 0, 0
for _, num := range nums {
rightSum += num
}
res := 0
for i := 0; i < len(nums)-1; i++ {
leftSum += nums[i]
rightSum -= nums[i]
if leftSum >= rightSum {
res++
}
}
return res
}
```
---
 {:style='width:250px'}
| 2 | 0 | ['Array', 'C', 'Prefix Sum', 'C++', 'Java', 'Go', 'Python3', 'JavaScript', 'Dart'] | 2 |
number-of-ways-to-split-array | Easy C++ solution || Beats 100% | easy-c-solution-beats-100-by-prashant_71-ozs6 | IntuitionWhen splitting an array into two non-empty subarrays, the sum of elements in the left subarray and the right subarray determines whether the split is v | prashant_71200 | NORMAL | 2025-01-03T11:54:33.840576+00:00 | 2025-01-03T11:54:33.840576+00:00 | 20 | false | # Intuition
When splitting an array into two non-empty subarrays, the sum of elements in the left subarray and the right subarray determines whether the split is valid. A split is valid if the left subarray's sum is greater than or equal to the right subarray's sum. The challenge is to efficiently compute these sums for every possible split.
# Approach
1) Calculate Total Sum:
* Compute the total sum of the array elements once before processing splits.
* This allows us to calculate the sum of the right subarray dynamically by subtracting the left sum from the total sum.
2) Calculate Total Sum:
* Compute the total sum of the array elements once before processing splits.
* This allows us to calculate the sum of the right subarray dynamically by subtracting the left sum from the total sum.
3) Return the Count:
* After iterating through the array, return the count of valid splits.
# Complexity
- Time complexity:
O(n)
# Code
```cpp []
class Solution {
public:
int waysToSplitArray(vector<int>& nums) {
long long totalSum = 0;
long long leftSum = 0;
int ans = 0;
for (int num : nums) {
totalSum += num;
}
for (int i = 0; i < nums.size() - 1; i++) {
leftSum += nums[i];
long long rightSum = totalSum - leftSum;
if (leftSum >= rightSum) {
ans++;
}
}
return ans;
}
};
``` | 2 | 0 | ['C++'] | 0 |
number-of-ways-to-split-array | easy solution prefix sum | easy-solution-prefix-sum-by-harshulgarg-7xf9 | IntuitionThe problem involves splitting the array into two non-empty parts such that the sum of the left part is greater than or equal to the sum of the right p | harshulgarg | NORMAL | 2025-01-03T11:32:03.723342+00:00 | 2025-01-03T11:32:03.723342+00:00 | 10 | false | # Intuition
The problem involves splitting the array into two non-empty parts such that the sum of the left part is greater than or equal to the sum of the right part. To solve this, we need a way to calculate the sums of both parts efficiently at each potential split point.
# Approach
Suffix Sums: Precompute an array p with suffix sums for quick right-part calculations.
Left Sum Calculation: Use a running sum s for the left part while iterating through the array.
Count Splits: For each split point, if s >= p[i+1], increment the count.
Result: Return the count of valid splits.
# Complexity
- Time complexity:
O(n)
- Space complexity:
O(n)
# Code
```python3 []
class Solution:
def waysToSplitArray(self, nums: List[int]) -> int:
n=len(nums)
p=[0]*n
p[-1]=nums[-1]
for i in range(n-2,-1,-1):
p[i]=p[i+1]+nums[i]
c=0
s=0
for i in range(n-1):
s+=nums[i]
if s>=p[i+1]:
c+=1
return c
``` | 2 | 0 | ['Python3'] | 0 |
number-of-ways-to-split-array | JAVA CODE | java-code-by-ayeshakhan7-d6qv | ApproachUsing cummulativeSum array/Prefix Sum ArrayComplexity
Time complexity: O(N)
Space complexity: O(1)
Code | ayeshakhan7 | NORMAL | 2025-01-03T11:19:35.984418+00:00 | 2025-01-03T11:19:35.984418+00:00 | 13 | false |
# Approach
<!-- Describe your approach to solving the problem. -->
Using cummulativeSum array/Prefix Sum Array
# Complexity
- Time complexity: O(N)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int waysToSplitArray(int[] nums) {
int n = nums.length;
// Calculate the total sum of the array
long sum = 0;
for (int num : nums) {
sum += num;
}
long leftSum = 0;
long rightSum = 0;
int split = 0;
// Iterate through the array to calculate leftSum and rightSum
for (int i = 0; i < n - 1; i++) {
leftSum += nums[i];
rightSum = sum - leftSum;
if (leftSum >= rightSum) {
split++;
}
}
return split;
}
}
``` | 2 | 0 | ['Java'] | 0 |
number-of-ways-to-split-array | 🎉BEATS 100%🏆| O(n)🕒 O(1)🚀 Shortest most easiest optimal code Explained💻 | Running Sum 📈 PHP🌟 | beats-100-on-o1-shortest-most-easiest-op-86im | CodeIntuition:The function waysToSplitArray calculates the number of ways to split an array of integers nums into two non-empty parts such that the sum of the e | webdevanjali | NORMAL | 2025-01-03T11:08:05.458178+00:00 | 2025-01-03T11:38:35.554574+00:00 | 12 | false |
# Code
```php []
class Solution {
/**
* @param Integer[] $nums
* @return Integer
*/
function waysToSplitArray($nums) {
$total = array_sum($nums);
$len = count($nums);
$count = $leftSum = 0;
for ($i = 0; $i < $len - 1; $i++) {
$leftSum += $nums[$i];
if ($leftSum >= $total - $leftSum) $count++;
}
return $count;
}
}
```
# Intuition:
The function `waysToSplitArray` calculates the number of ways to split an array of integers `nums` into two non-empty parts such that the sum of the elements on the left is greater than or equal to the sum of the elements on the right. Let's break down the intuition:
- **Total Sum Calculation**: The total sum of the array elements is calculated first using `array_sum($nums)`. This will be used to keep track of the sum of elements on the right side as we iterate through the array.
- **Iterate and Maintain Sums**: We iterate through the array from the first element to the second-to-last element. For each iteration, we calculate the running sum of elements from the left (`$leftSum`), and compare it with the sum of elements from the right (`$total - $leftSum`).
- **Count Valid Splits**: Each time the condition `if ($leftSum >= $total - $leftSum)` is satisfied, it means that splitting the array at this point (after the current element) results in a valid partition where the left part has a sum greater than or equal to the right part. We increment the counter `$count` each time this condition is met.
- **Return the Result**: Finally, the function returns the value of `count`, which represents the number of valid ways to split the array.
---
# Approach:
1. **Initialization**:
- First, we calculate the total sum of all elements in the array. This will help us calculate the sum of the right part of the array dynamically as we update the left sum.
- We also initialize a variable `$leftSum` to track the sum of elements from the left part, and a variable `$count` to keep track of the number of valid splits.
2. **Loop through the Array**:
- We loop through the array from index 0 to `len - 2` (since we need at least one element on both sides of the split).
- In each iteration, we add the current element to the left sum (`leftSum`), and then check if the left sum is greater than or equal to the right sum (`total - leftSum`).
- If the condition is satisfied, we increment the count of valid splits.
-----
# Complexity:
### Time Complexity: **O(n)**
- **Calculating the Total Sum**: `array_sum($nums)` takes **O(n)** time, where `n` is the length of the array.
- **Iterating Over the Array**: The `for` loop iterates through `n-1` elements, and for each iteration, constant-time operations (addition, subtraction, comparison) are performed. Therefore, the loop runs in **O(n)** time.
Thus, the **total time complexity** is **O(n)**, where `n` is the number of elements in the array.
### Space Complexity: **O(1)**
- The space complexity is **O(1)** because the solution only uses a constant amount of extra space: `total`, `leftSum`, and `count` (all variables are scalar values).
| 2 | 0 | ['Array', 'PHP'] | 0 |
number-of-ways-to-split-array | ✅✅ easy prefix sum approch 🔥🔥 || o(n) Space Complexity || o(n) Time Complexity | easy-prefix-sum-approch-on-space-complex-b3fd | IntuitionThe problem requires dividing the array into two non-overlapping parts such that the sum of the left part is greater than or equal to the sum of the ri | ishanbagra | NORMAL | 2025-01-03T11:07:19.034599+00:00 | 2025-01-03T11:07:19.034599+00:00 | 8 | false | Intuition
The problem requires dividing the array into two non-overlapping parts such that the sum of the left part is greater than or equal to the sum of the right part.
To efficiently solve this, we use prefix sums to compute the total sum of any part of the array in constant time.
Approach
Calculate Prefix Sums from Front:
Create a prefixfront array where each element at index i contains the sum of elements from the beginning of the array up to index i.
Calculate Prefix Sums from Back:
Create a prefixback array where each element at index i contains the sum of elements from index i to the end of the array.
Iterate and Compare:
For each index i (up to n - 2), check if the sum of the left part (prefixfront[i]) is greater than or equal to the sum of the right part (prefixback[i + 1]).
If the condition is satisfied, increment the count.
Return the Result:
Return the total count of valid splits.
Complexity
Time Complexity:
Calculating prefix sums takes O(n).Iterating through the array to count valid splits also takes O(n).Overall time complexity: O(n).
Space Complexity:
Space used for prefixfront and prefixback arrays: O(n).
Overall space complexity: O(n).
# Code
```cpp []
class Solution {
public:
int waysToSplitArray(vector<int>& nums) {
int n=nums.size();
vector<long long>prefixfront(n);
vector<long long>prefixback(n);
for(int i=0;i<n;i++)
{
if(i==0)
{
prefixfront[i]=nums[i];
}
else
{
prefixfront[i]=prefixfront[i-1]+nums[i];
}
}
for(int i=n-1;i>=0;i--)
{
if(i==n-1)
{
prefixback[i]=nums[i];
}
else
{
prefixback[i]=prefixback[i+1]+nums[i];
}
}
int count=0;
for(int i=0;i<n-1;i++)
{
if(prefixfront[i]>=prefixback[i+1])
{
count++;
}
}
return count;
}
};
``` | 2 | 0 | ['Prefix Sum', 'C++'] | 2 |
number-of-ways-to-split-array | Kotlin | Rust | kotlin-rust-by-samoylenkodmitry-rpz3 | Join me on Telegramhttps://t.me/leetcode_daily_unstoppable/853Problem TLDRCount splits left_sum >= right_sum #medium #prefix_sumIntuitionPrefix sum can help sol | SamoylenkoDmitry | NORMAL | 2025-01-03T11:05:48.140308+00:00 | 2025-01-03T11:06:12.961092+00:00 | 28 | false | 
https://youtu.be/MjsYNhMxHnM
#### Join me on Telegram
https://t.me/leetcode_daily_unstoppable/853
#### Problem TLDR
Count splits left_sum >= right_sum #medium #prefix_sum
#### Intuition
Prefix sum can help solve this.
#### Approach
* careful with an `int` overflow
* this is not about the balance and con't be done in a single pass, as adding negative number decreases the sum, we should hold `left` and `right` part separately
#### Complexity
- Time complexity:
$$O(n)$$
- Space complexity:
$$O(1)$$
#### Code
```kotlin []
fun waysToSplitArray(nums: IntArray): Int {
var r = nums.sumOf { it.toLong() }; var l = 0L
return (0..<nums.lastIndex).count {
l += nums[it]; r -= nums[it]; l >= r
}
}
```
```rust []
pub fn ways_to_split_array(nums: Vec<i32>) -> i32 {
let (mut l, mut r) = (0, nums.iter().map(|&x| x as i64).sum());
(0..nums.len() - 1).filter(|&i| {
l += nums[i] as i64; r -= nums[i] as i64; l >= r
}).count() as _
}
```
```c++ []
int waysToSplitArray(vector<int>& nums) {
int res = 0; long long r = reduce(begin(nums), end(nums), 0LL), l = 0;
for (int i = 0; i < nums.size() - 1; ++i)
res += (l += nums[i]) >= (r -= nums[i]);
return res;
}
``` | 2 | 0 | ['Prefix Sum', 'C++', 'Rust', 'Kotlin'] | 0 |
number-of-ways-to-split-array | Easy approach ✅✅✅ || Prefix Sum || Simple Explanation 💯 💯 | easy-approach-prefix-sum-simple-explanat-va5s | IntuitionThe Problem aims to count the number of "valid split points" in an array nums, where the prefix sum of the left subarray (from index 0 to i) is greater | prabhas_rakurthi | NORMAL | 2025-01-03T08:49:47.134218+00:00 | 2025-01-03T08:49:47.134218+00:00 | 15 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The Problem aims to count the number of **"valid split points"** in an array nums, where the prefix sum of the left subarray (from index 0 to i) is greater than or equal to the sum of the right subarray (from index i+1 to the end of the array).
A valid split point satisfies the condition:
- Prefix sum of left subarray >= prefix sum of right subarray
- ` pre[i] >= total-pre[i]`
# Approach
<!-- Describe your approach to solving the problem. -->
- Calculate the Total Sum and Prefix Sum Array
- Count Valid Split Points
- Return the Count
# Complexity
- Time complexity: $$O(n)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(n)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int waysToSplitArray(int[] nums) {
int n=nums.length;
long[] pre=new long[n];
long sum=0;
long total=0;
for(int i=0;i<n;i++){
total+=nums[i];
sum+=nums[i];
pre[i]=sum;
}
int res=0;
for(int i=0;i<n-1;i++){
if(pre[i]>=total-pre[i]){
res++;
}
}
return res;
}
}
``` | 2 | 0 | ['Java'] | 0 |
number-of-ways-to-split-array | 0ms(100.00%) 10.12 MB(95.00%) | Go solution | 0ms10000-1012-mb9500-go-solution-by-kita-79qy | null | kitanoyoru_ | NORMAL | 2025-01-03T08:47:10.647176+00:00 | 2025-01-03T08:47:10.647176+00:00 | 17 | false | ```golang
func waysToSplitArray(nums []int) int {
var result, prefixSum, arraySum int
for _, num := range nums {
arraySum += num
}
for i := 0; i < len(nums)-1; i++ {
prefixSum += nums[i]
if prefixSum >= arraySum-prefixSum {
result++
}
}
return result
}
``` | 2 | 0 | ['Go'] | 1 |
number-of-ways-to-split-array | EASIEST SOLUTION | C/C++ | JavaScript | Python | easiest-solution-cc-javascript-python-by-cg7h | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | Nurliaidin | NORMAL | 2025-01-03T08:05:23.894554+00:00 | 2025-01-03T08:05:23.894554+00:00 | 34 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int waysToSplitArray(vector<int>& nums) {
long long end = 0, start = 0;
for(int i=0; i<nums.size(); i++)
end += nums[i];
int res = 0;
for(int i=0; i<nums.size()-1; i++) {
start += nums[i];
end -= nums[i];
if (start >= end) res++;
}
return res;
}
};
```
```c []
int waysToSplitArray(int* nums, int numsSize) {
long long end = 0, start = 0;
for(int i=0; i<numsSize; i++)
end += nums[i];
int res = 0;
for(int i=0; i<numsSize-1; i++) {
start += nums[i];
end -= nums[i];
if (start >= end) res++;
}
return res;
}
```
```javascript []
/**
* @param {number[]} nums
* @return {number}
*/
var waysToSplitArray = function(nums) {
let end = 0, start = 0;
for(let i=0; i<nums.length; i++)
end += nums[i];
let res = 0;
for(let i=0; i<nums.length-1; i++) {
start += nums[i];
end -= nums[i];
if (start >= end) res++;
}
return res;
};
```
```python []
class Solution:
def waysToSplitArray(self, nums: List[int]) -> int:
end, start = 0, 0
for i in range(0, len(nums)):
end += nums[i]
res = 0
for i in range(0, len(nums)-1):
start += nums[i]
end -= nums[i]
if start >= end: res += 1
return res
``` | 2 | 0 | ['Array', 'C', 'Prefix Sum', 'C++', 'Python3', 'JavaScript'] | 1 |
number-of-ways-to-split-array | BEATS 100% EASY TO UNDERSTAND | beats-100-easy-to-understand-by-shubhtro-ixcs | IntuitionWe have to split the array in such a way that left hand side is equal to right hand side and atmost 1 element each side
OK
then we make left hand side | ShubhTron | NORMAL | 2025-01-03T08:00:42.208078+00:00 | 2025-01-03T08:00:42.208078+00:00 | 5 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
We have to split the array in such a way that left hand side is equal to right hand side and atmost 1 element each side
OK
then we make left hand side and right hand side total whenever lhs sum is greater than rhs sum we increment the answer by 1
# Approach
<!-- Describe your approach to solving the problem. -->
Find totalSum
Then make LHS sum here i took it as curr were we start from the beggining and keep adding up
Make RHS sum here totalSum - each element from beggining
# Complexity
- Time complexity: O(n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int waysToSplitArray(int[] nums) {
long totalSum = 0;
for(int n : nums){
totalSum += n;
}
long curr = 0;
int ans = 0;
for(int i = 0;i<nums.length-1;i++){
curr += nums[i];
totalSum -= nums[i];
if(curr >= totalSum){
ans++;
}
}
return ans;
}
}
``` | 2 | 0 | ['Prefix Sum', 'Java'] | 0 |
number-of-ways-to-split-array | Easy Solution || Explained | easy-solution-explained-by-namandas918-bl14 | IntuitionThe idea is to iterate through the array while keeping track of the sum of the elements to the left and right of the current split. If the sum of the l | Hexagon_6_ | NORMAL | 2025-01-03T07:55:54.867785+00:00 | 2025-01-03T07:55:54.867785+00:00 | 13 | false | # Intuition
The idea is to iterate through the array while keeping track of the sum of the elements to the left and right of the current split. If the sum of the left part is greater than or equal to the sum of the right part, it counts as a valid split.
# Approach
1. **Calculate Total Sum:** First, compute the total sum of the array.
2. **Iterate through the Array:** Iterate through the array, keeping a running sum of the left side (`s`).
3. **Check Condition:** For each split (except the last element), check if the left sum (`s`) is greater than or equal to the remaining sum (`sum`).
4. **Update Count:** If the condition holds, increment the count of valid splits.
5. **Return the Count:** Return the total number of valid splits.
# Complexity
- **Time complexity:** \(O(n)\) – The algorithm traverses the array once.
- **Space complexity:** \(O(1)\) – Only a few variables are used for summing, so the space usage is constant.
# Code
```cpp
class Solution {
public:
int waysToSplitArray(vector<int>& nums) {
long long sum = 0;
for(auto i: nums) sum += i; // Calculate the total sum
long long s = 0, ans = 0;
for(int i = 0; i < nums.size() - 1; ++i) {
s += nums[i]; // Update left sum
sum -= nums[i]; // Update right sum
if (s >= sum) ans++; // Check condition and update count
}
return ans;
}
};
| 2 | 0 | ['Array', 'Math', 'C++'] | 0 |
number-of-ways-to-split-array | BEATS 100%❤️🔥DRY-RUM❤️🔥SLIGHTLY AROUSING🤤 | beats-100dry-rumslightly-arousing-by-int-l7xy | IntuitionThe problem requires splitting the array into two non-empty parts such that the sum of the left part is greater than or equal to the sum of the right p | intbliss | NORMAL | 2025-01-03T07:40:16.366782+00:00 | 2025-01-03T07:40:16.366782+00:00 | 56 | false |
#### **Intuition**
The problem requires splitting the array into two non-empty parts such that the sum of the left part is greater than or equal to the sum of the right part. To achieve this, we can use prefix sums to efficiently calculate the sum of the left and right parts as we iterate through the array.
- As we traverse the array, we maintain a running sum (`currSum`) for the left part.
- The right part's sum can be calculated as the difference between the total sum of the array (`totalSum`) and the current running sum (`currSum`).
- By comparing `currSum` with `remainingSum` at each split point, we count valid splits.
---
#### **Approach**
1. **Calculate the Total Sum:**
Compute the total sum of the array to allow efficient computation of the right part's sum.
2. **Iterate Through the Array:**
For each index `i` (excluding the last index to ensure both parts are non-empty):
- Add the current element to the running sum (`currSum`).
- Calculate the right part's sum as `totalSum - currSum`.
- If `currSum >= remainingSum`, increment the result count.
3. **Return the Count:**
After traversing the array, return the total count of valid splits.
---
#### **Dry Run**
Example Input: `nums = [10, 4, -8, 7]`
| Step | `currSum` | `remainingSum` | Comparison `currSum >= remainingSum` | Result Count |
|------|-----------|----------------|---------------------------------------|--------------|
| Start| `0` | `13` | N/A | `0` |
| `i=0`| `10` | `3` | `10 >= 3` (True) | `1` |
| `i=1`| `14` | `-1` | `14 >= -1` (True) | `2` |
| `i=2`| `6` | `7` | `6 >= 7` (False) | `2` |
**Output:** `2`
---
#### **Code**
```java
class Solution {
public int waysToSplitArray(int[] nums) {
// Calculate the total sum of the array
long totalSum = 0;
for (int num : nums) {
totalSum += num;
}
// Initialize variables to track the count of valid splits and the running sum
int res = 0;
long currSum = 0;
// Iterate through the array up to the second last index
for (int i = 0; i < nums.length - 1; i++) {
currSum += nums[i]; // Update the running sum for the left part
long remainingSum = totalSum - currSum; // Calculate the right part's sum
// Check if the left sum is greater than or equal to the right sum
if (currSum >= remainingSum) {
res++; // Increment the count of valid splits
}
}
return res; // Return the total count of valid splits
}
}
```
---
#### **Complexity Analysis**
1. **Time Complexity:**
- Computing the total sum: O(n).
- Iterating through the array: O(n).
- Overall: **O(n)**.
2. **Space Complexity:**
- No additional data structures are used apart from a few variables: **O(1)**.
---
| 2 | 1 | ['Array', 'Suffix Array', 'Prefix Sum', 'Java'] | 2 |
number-of-ways-to-split-array | 🔥Space optimized Solution for Beginners! Beats 100%!🔥 | space-optimized-solution-for-beginners-b-szjr | ApproachComplexity
Time complexity:O(N)
Space complexity:O(1)
Code | Ansh_Ghawri | NORMAL | 2025-01-03T07:38:57.983172+00:00 | 2025-01-03T07:38:57.983172+00:00 | 4 | false | # Approach
<!-- Describe your approach to solving the problem. -->
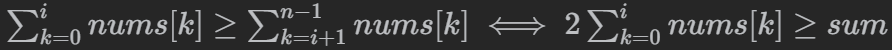
# Complexity
- Time complexity:O(N)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
using ll=long long int;
int waysToSplitArray(vector<int>& nums) {
int n=nums.size();
ll totalSum=accumulate(nums.begin(),nums.end(),0LL);
ll leftSum=0;
int validSplits=0;
for(int i=0;i<n-1;i++){
leftSum+=nums[i];
//ll rightSum=totalSum-leftSum;
if(2*leftSum>=totalSum)validSplits++;
}
return validSplits;
}
};
``` | 2 | 0 | ['C++'] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.