question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
find-the-k-sum-of-an-array | C++ solution | c-solution-by-hujinxin0607-i3hz | \nclass Solution {\npublic:\n long long kSum(vector<int>& nums, int k) {\n long sum = 0;\n vector<int> q;\n \n for (auto x: nums) | hujinxin0607 | NORMAL | 2022-08-21T05:04:12.882543+00:00 | 2022-08-21T05:04:33.652348+00:00 | 110 | false | ```\nclass Solution {\npublic:\n long long kSum(vector<int>& nums, int k) {\n long sum = 0;\n vector<int> q;\n \n for (auto x: nums) {\n if (x >= 0){\n sum += x;\n q.push_back(-x);\n } else q.push_back(x);\n }\n \n sort(q.begin(), q.end(), greater<int>());\n \n if (q.size() > k) q.erase(q.begin() + k, q.end());\n vector<long> a(1, sum), b;\n int t = 1;\n \n for (auto x: q) {\n b.clear();\n int i = 0, j = 0;\n t = min(t * 2, k);\n while (i < a.size() && j < a.size() && b.size() < t)\n if (a[i] > a[j] + x) b.push_back(a[i++]);\n else b.push_back(a[j++] + x);\n while (i < a.size() && b.size() < t) b.push_back(a[i++]);\n while (j < a.size() && b.size() < t) b.push_back(a[j++] + x);\n a = b;\n }\n return a[k - 1];\n }\n};\n``` | 0 | 1 | [] | 0 |
find-the-k-sum-of-an-array | Python solution | python-solution-by-andrewpeng-185v | ```\nimport heapq\n\n\nclass Solution:\n def kSum(self, nums: List[int], k: int) -> int:\n heap = []\n \n # get maximal subsequence sum\ | andrewpeng | NORMAL | 2022-08-21T04:51:23.357962+00:00 | 2022-08-21T04:51:36.444787+00:00 | 222 | false | ```\nimport heapq\n\n\nclass Solution:\n def kSum(self, nums: List[int], k: int) -> int:\n heap = []\n \n # get maximal subsequence sum\n max_subset = sum(n for n in nums if n > 0)\n removal_candidates = list(sorted(nums, key=lambda x: abs(x)))\n \n # keep max_heap of next largest subset sum\n heap.append((-max_subset, -1))\n ans = max_subset\n\n # pop k times\n for _ in range(k):\n candidate, idx = heapq.heappop(heap)\n ans = min(ans, -candidate)\n \n # while we still have items to remove, create new candidate subseq sum\n if idx + 1 < len(removal_candidates):\n # remove candidate element and keep track of last index\n heapq.heappush(heap, (candidate + abs(removal_candidates[idx + 1]), idx + 1))\n # if we need to readd elements previously removed\n if idx >= 0:\n heapq.heappush(heap, (candidate - abs(removal_candidates[idx]) + abs(removal_candidates[idx + 1]), idx + 1))\n\n return ans | 0 | 0 | [] | 0 |
find-the-k-sum-of-an-array | O(n * klogk) solution + clever tricks | on-klogk-solution-clever-tricks-by-chuan-glao | Starting point: given a multiset of subsequence sums sl, adding an element x in nums results in a new multiset of subsequence sums sl.extend([n + x for n in sl] | chuan-chih | NORMAL | 2022-08-21T04:26:13.469954+00:00 | 2022-08-21T04:36:04.200966+00:00 | 335 | false | Starting point: given a multiset of subsequence sums `sl`, adding an element `x` in `nums` results in a new multiset of subsequence sums `sl.extend([n + x for n in sl])`. We want to keep the top `k` of them. However, straight implementation of this is too slow.\n\nIntuition: if `x` is negative, we probably don\'t have to change `sl` much. More precisely, if `len(sl) == k` already, we only have to consider the new sums from the current max down to the smallest possible sum `sl[index]` such that `sl[index] + x` is at least as big as the current k-sum. If `len(sl) < k`, adjust the index downward by at most `k - len(sl)` accordingly. We can do this inplace with a bit of index traversal trick. This trick helps more than it sounds because the `abs(x)` is bounded (`-10 ** 9 <= x <= 10 ** 9`), so the top `k` subsequence sums quickly grow to such magnitude relative to `x` that few changes will be made.\n\nWhat about `x >= 0`? All top `k` subsequence sums shift upward by `x`, and then interleave with the original sums that are big enough. So, we keep track of the accumulative upward shifts. Then after the shift, it looks as if `x` is subtracted from the original sums: `x = -x`. The solution is then finally fast enough.\n\n...I can\'t believe all these tricks are required to solve this \uD83D\uDE26\n```\nfrom sortedcontainers import SortedList\n\nclass Solution:\n def kSum(self, nums: List[int], k: int) -> int:\n sl = SortedList([0])\n base = 0\n for x in nums:\n if x >= 0:\n base += x\n x = -x\n index = sl.bisect_left(sl[0] - x)\n if len(sl) < k:\n index -= k - len(sl)\n index = max(0, index)\n while index < len(sl):\n sl.add(sl[index] + x)\n index += 2\n if len(sl) > k:\n sl.pop(0)\n index -= 1\n return sl[0] + base\n``` | 0 | 0 | ['Python'] | 0 |
find-the-k-sum-of-an-array | [Java] Priority Queue | java-priority-queue-by-xuanzhang98-6pfa | \n\nclass Solution {\n public long kSum(int[] nums, int k) {\n long sum = 0;\n for(int i=0;i<nums.length;i++){\n if(nums[i] > 0) sum | Xuanzhang98 | NORMAL | 2022-08-21T04:26:00.489438+00:00 | 2022-08-21T04:26:00.489468+00:00 | 267 | false | \n```\nclass Solution {\n public long kSum(int[] nums, int k) {\n long sum = 0;\n for(int i=0;i<nums.length;i++){\n if(nums[i] > 0) sum += nums[i];\n else nums[i] = -nums[i];\n }\n PriorityQueue<long[]> pq = new PriorityQueue(new Comparator<long[]>(){\n @Override\n public int compare(long[] a, long[] b){\n return a[0] - b[0] > 0 ? -1 : 1; \n }\n });\n Arrays.sort(nums);\n pq.add(new long[]{sum - nums[0], 0});\n long res = sum;\n k--;\n while(k > 0){\n long[] cur = pq.poll();\n res = cur[0];\n if(cur[1] < (long)nums.length - 1) {\n pq.add(new long[]{cur[0] + nums[(int)cur[1]]- nums[(int)cur[1]+1], cur[1]+1});\n pq.add(new long[]{cur[0] - nums[(int)cur[1] + 1], cur[1]+1});\n }\n k--;\n }\n return res;\n }\n}\n``` | 0 | 0 | ['Heap (Priority Queue)', 'Java'] | 0 |
find-the-k-sum-of-an-array | Java Solution with explanation O(N log(N) + k log(k)) | java-solution-with-explanation-on-logn-k-srh4 | from: https://stackoverflow.com/questions/72114300/how-to-generate-k-largest-subset-sums-for-a-given-array-contains-positive-and-n/72117947#72117947\n\nFirst, i | binglelove | NORMAL | 2022-08-21T04:19:52.838736+00:00 | 2022-08-21T04:26:06.624956+00:00 | 307 | false | **from:** https://stackoverflow.com/questions/72114300/how-to-generate-k-largest-subset-sums-for-a-given-array-contains-positive-and-n/72117947#72117947\n\nFirst, in a single pass, we find the sum of the positive numbers. This is the maximum sum. We initialize our answer array with [maximum_sum].\n\nNext, we create an array av of the absolute values, sorted from smallest to largest.\n\nNext, we create a priority queue upcoming. It will start with one pair in it. That pair will be (maximum_sum - av[0], 0). The pairs are compared lexicographically with largest sum first.\n\nUntil we have enough elements in answer we will:\n\nget (next_sum, i) from upcoming\nadd next_sum to answer\nif i < N:\n add (next_sum + av[i] - av[i+1], i+1) to upcoming\n add (next_sum - av[i+1], i+1) to upcoming\nThis algorithm will take O(N+k) memory and O(N log(N) + k log(k)) work to generate the top k answers. It depends on both N and k but is exponential in neither.\n\n```\nclass Solution {\n public long kSum(int[] nums, int k) {\n int n = nums.length;\n \n int[] absArray=Arrays.stream(nums).map(i->Math.abs(i)).toArray();\n Arrays.sort(absArray);\n \n long maxSum = Arrays.stream(nums).filter(i -> i > 0).summaryStatistics().getSum();\n \n\t\tPriorityQueue<long[]> pq=new PriorityQueue<>((a,b)->Long.compare(b[0], a[0]));\n pq.add(new long[]{maxSum-absArray[0],0});\n \n long res = maxSum;\n\t\t\n while(--k > 0) {\n long cur[]=pq.poll();\n long curSum=cur[0];\n int i=(int)cur[1];\n res = curSum;\n \n if(i + 1 < n) {\n pq.add(new long[]{curSum+absArray[i]-absArray[i+1],i+1});\n pq.add(new long[]{curSum-absArray[i+1],i+1});\n }\n \n }\n \n return res;\n }\n}\n``` | 0 | 0 | [] | 0 |
find-the-k-sum-of-an-array | [Java] greedy : sort + max heap | java-greedy-sort-max-heap-by-caoxz0815-5o14 | ```\n public long kSum(int[] nums, int k) {\n int len = nums.length;\n long maxSum = 0;\n for (int temp : nums) {\n if (temp > 0 | caoxz0815 | NORMAL | 2022-08-21T04:09:56.136075+00:00 | 2022-08-21T04:09:56.136112+00:00 | 357 | false | ```\n public long kSum(int[] nums, int k) {\n int len = nums.length;\n long maxSum = 0;\n for (int temp : nums) {\n if (temp > 0) maxSum += temp;\n }\n if (k==1) return maxSum;\n\n int[] absArray = IntStream.of(nums).map(Math::abs).sorted().toArray();\n\n PriorityQueue<long[]> pq = new PriorityQueue<>(Comparator.comparingLong(e -> -e[0]));\n List<Long> ans = new ArrayList<>();\n ans.add((long) maxSum);\n\n pq.add(new long[]{maxSum - absArray[0], 0});\n\n while (ans.size() < k-1) {\n long cur[] = pq.poll();\n long curSum = cur[0];\n long i = cur[1];\n ans.add(curSum);\n\n if (i + 1 < len) {\n pq.add(new long[]{curSum + absArray[(int) i] - absArray[(int) i + 1], (int) i + 1});\n pq.add(new long[]{curSum - absArray[(int) i + 1], i + 1});\n }\n\n }\n long res = 0;\n if (!pq.isEmpty()) res = pq.poll()[0];\n return res;\n\n\n } | 0 | 0 | ['Java'] | 0 |
random-point-in-non-overlapping-rectangles | Trying to explain why the intuitive solution wont work | trying-to-explain-why-the-intuitive-solu-i3vv | Problem\nThe intuitive solution is randomly pick one rectangle from the rects and then create a random point within it. But this approach wont work. It took me | murushierago | NORMAL | 2019-06-22T03:06:54.272642+00:00 | 2021-05-12T03:21:51.208418+00:00 | 7,705 | false | ### Problem\nThe intuitive solution is randomly pick one rectangle from the `rects` and then create a random point within it. But this approach wont work. It took me a while to understand, I am trying to explain it:\n\n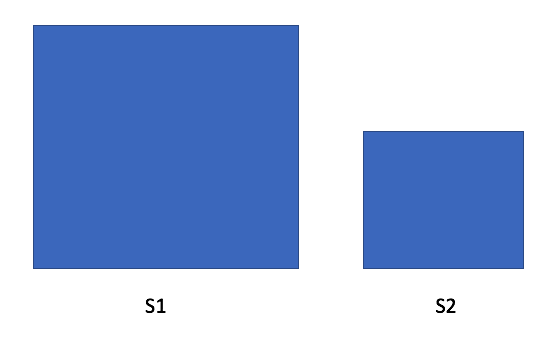\n\nAs shown in the picture above, you have two rectangles. Lets declare `S1` to be the set of points within rectanle 1, and `S2` to be point set within rectable 2. So, mathematically we have:\n```\nS1 = {p11, p12, p13, ........................, p1n}\nS2 = {p21, p22, p23, ......, p2m}\nn > m\n```\nObviously, you can see that `rectangle 1` is larger than `rectangle 2` and therefore `S1` has bigger size `(n > m)`. \nAccording to the problem, `"randomly and uniformily picks an integer point in the space covered by the rectangles"`. It is very difficult to understand, lets translated it into another way of expression. \n\nIt is saying that, now I am providing you a new set `S = S1 + S2`, where `S = {p11, p12, ............, p1n, p21, p22, ........., p2m}` , **within this new set of points** that are merged together, randomly pick a point from it. What do you think of the probability of getting `p1i` and `p2j` right now ? They are exactly the same, which is `1 / (n + m)`.\n\nNow, we can answer why the intuitive solution wont work. If you first randomy pick a rectangle, you have 50% to get either `S1` or `S2`, how ever, once you select on rectangle, you have selected `S1` as your candidate point set, no matter how many time you try to pick you will never get the points in the second set `S2`. If size of S1 and S2 are the same, that would be ok, but if `S1` is bigger than `S2`, you will run into a problem. \n\nFor example, the chance of getting `S1` and `S2` are both `1 / 2`, so far so good. How ever, within `S1` and `S2`, the chance of getting point `p1i` and `p2j` are `1 / n` and `1 / m`. So the final chance of getting `p1i` and `p2j` are:\n```\nprobability_of_getting_p1i = 1 / (2 * n)\nprobability_of_getting_p2j = 1 / (2 * m)\n\nWhere n is the size of S1, and m is size of S2\n```\nThe probability depends on the size of two rectangle.\n\n### Solution\nSo how can we solve the problem that descibed in previous section ? One way is to really merge all the point set of every rectangle and radnomly pick one from them, but this may not be a good idea since it requires very hight space somplexity. What if we make the chance of getting reactangle`S1` higher than rectangle `S2` (from rects) base on the size of each of them.\nfor example, for simplification, lets assume:\n```\nn = size_of_s1 = 70\nm = size_of_s2 = 30\n\nn + m = 100\n```\n\nif we can have the chance of getting `S1` to be `70 %` and chance of getting `S2` to be `30 %`, the chance of getting `p1i` from `S1` is `1 / 70`, and chance of getting `p2j` from `S2` is `1 / 30`, we have:\n```\nprobality_of_getting_p1i = (70 / 100) * (1 / 70) = 1 / 100\n\nprobability_of_getting_p2j = (30 / 100) * (1 / 30) = 1 / 100\n```\n\nproblem sovled !\n\nSo, our mission **is to implement an algorithm that allows us to have higher chance to pick the larger rectangle**, and then generate a random point with it. Lets use code pseudo to make a rough design, still base on the previous example, imagine you have a map:\n\n```\n\nmap = \n{\n\t30: S1,\n\t30 + 70: S2\n}\n\nor \n\nmap = \n{\n 30: S1,\n 100: S2\n}\n\n\nrandomNumer = random(0, 100)\n\nif 30 < randomNumber <= 100:\n\treturn S2\nelse\n\treturn S1\n\n```\n\nIf we can design an algorithm like that, we will have 70% chance gitting S2, and 30% chance hitting S1. With number of intervals already known, we can simply use `if .. else` block or `switch` to implement this, but the problem did not specify how many rects, so the popular solution uses `TreeMap` .\n\n\n | 192 | 1 | [] | 13 |
random-point-in-non-overlapping-rectangles | [Python] Short solution with binary search, explained | python-short-solution-with-binary-search-hjnb | Basically, this problem is extention of problem 528. Random Pick with Weight, let me explain why. Here we have several rectangles and we need to choose point fr | dbabichev | NORMAL | 2020-08-22T08:31:13.442681+00:00 | 2020-08-22T08:31:13.442711+00:00 | 5,382 | false | Basically, this problem is extention of problem **528. Random Pick with Weight**, let me explain why. Here we have several rectangles and we need to choose point from these rectangles. We can do in in two steps:\n\n1. Choose rectangle. Note, that the bigger number of points in these rectangle the more should be our changes. Imagine, we have two rectangles with 10 and 6 points. Then we need to choose first rectangle with probability `10/16` and second with probability `6/16`.\n2. Choose point inside this rectangle. We need to choose coordinate `x` and coordinate `y` uniformly.\n\nWhen we `initailze` we count weights as `(x2-x1+1)*(y2-y1+1)` because we also need to use boundary. Then we evaluate cumulative sums and normalize.\n\nFor `pick` function, we use **binary search** to find the right place, using uniform distribution from `[0,1]` and then we use uniform discrete distribution to choose coordinates `x` and `y`. \n\n**Complexity**: Time and space complexity of `__init__` is `O(n)`, where `n` is number of rectangles. Time complexity of `pick` is `O(log n)`, because we use binary search. Space complexity of `pick` is `O(1)`.\n\n**Remark**: Note, that there is solution with `O(1)` time/space complexity for `pick`, using smart mathematical trick, see my solution of problem **528**: https://leetcode.com/problems/random-pick-with-weight/discuss/671439/Python-Smart-O(1)-solution-with-detailed-explanation\n\n\n```\nclass Solution:\n def __init__(self, rects):\n w = [(x2-x1+1)*(y2-y1+1) for x1,y1,x2,y2 in rects]\n self.weights = [i/sum(w) for i in accumulate(w)]\n self.rects = rects\n\n def pick(self):\n n_rect = bisect.bisect(self.weights, random.random())\n x1, y1, x2, y2 = self.rects[n_rect] \n return [random.randint(x1, x2),random.randint(y1, y2)]\n```\n\nIf you have any questions, feel free to ask. If you like solution and explanations, please **Upvote!** | 100 | 5 | ['Binary Tree'] | 12 |
random-point-in-non-overlapping-rectangles | Java Solution. Randomly pick a rectangle then pick a point inside. | java-solution-randomly-pick-a-rectangle-1s3l2 | \nclass Solution {\n TreeMap<Integer, Integer> map;\n int[][] arrays;\n int sum;\n Random rnd= new Random();\n \n public Solution(int[][] rect | uynait | NORMAL | 2018-07-27T10:16:53.570404+00:00 | 2018-10-25T06:31:10.024100+00:00 | 12,704 | false | ```\nclass Solution {\n TreeMap<Integer, Integer> map;\n int[][] arrays;\n int sum;\n Random rnd= new Random();\n \n public Solution(int[][] rects) {\n arrays = rects;\n map = new TreeMap<>();\n sum = 0;\n \n for(int i = 0; i < rects.length; i++) {\n int[] rect = rects[i];\n\t\t\t\t\t\t\n // the right part means the number of points can be picked in this rectangle\n sum += (rect[2] - rect[0] + 1) * (rect[3] - rect[1] + 1);\n\t\t\t\n map.put(sum, i);\n }\n }\n \n public int[] pick() {\n // nextInt(sum) returns a num in [0, sum -1]. After added by 1, it becomes [1, sum]\n int c = map.ceilingKey( rnd.nextInt(sum) + 1);\n \n return pickInRect(arrays[map.get(c)]);\n }\n \n private int[] pickInRect(int[] rect) {\n int left = rect[0], right = rect[2], bot = rect[1], top = rect[3];\n \n return new int[]{left + rnd.nextInt(right - left + 1), bot + rnd.nextInt(top - bot + 1) };\n }\n}\n``` | 69 | 2 | [] | 14 |
random-point-in-non-overlapping-rectangles | Java TreeMap solution only one random per pick | java-treemap-solution-only-one-random-pe-jzhj | \nclass Solution {\n private int[][] rects;\n private Random r;\n private TreeMap<Integer, Integer> map;\n private int area;\n\n public Solution( | wangzi6147 | NORMAL | 2018-07-31T19:20:10.623383+00:00 | 2018-09-09T03:34:23.268190+00:00 | 4,533 | false | ```\nclass Solution {\n private int[][] rects;\n private Random r;\n private TreeMap<Integer, Integer> map;\n private int area;\n\n public Solution(int[][] rects) {\n this.rects = rects;\n r = new Random();\n map = new TreeMap<>();\n area = 0;\n for (int i = 0; i < rects.length; i++) {\n area += (rects[i][2] - rects[i][0] + 1) * (rects[i][3] - rects[i][1] + 1);\n map.put(area, i);\n }\n }\n \n public int[] pick() {\n int randInt = r.nextInt(area);\n int key = map.higherKey(randInt);\n int[] rect = rects[map.get(key)];\n int x = rect[0] + (key - randInt - 1) % (rect[2] - rect[0] + 1);\n int y = rect[1] + (key - randInt - 1) / (rect[2] - rect[0] + 1);\n return new int[]{x, y};\n }\n}\n``` | 50 | 2 | [] | 8 |
random-point-in-non-overlapping-rectangles | C++ concise solution using binary search (pick with a weight) | c-concise-solution-using-binary-search-p-umf1 | First pick a random rectangle with a weight of their areas.\nThen pick a random point inside the rectangle.\n\n\nclass Solution {\npublic:\n vector<int> v;\n | zhoubowei | NORMAL | 2018-07-29T15:30:40.220539+00:00 | 2018-09-09T03:36:48.337001+00:00 | 2,767 | false | First pick a random rectangle with a weight of their areas.\nThen pick a random point inside the rectangle.\n\n```\nclass Solution {\npublic:\n vector<int> v;\n vector<vector<int>> rects;\n \n int area(vector<int>& r) {\n return (r[2] - r[0] + 1) * (r[3] - r[1] + 1);\n }\n \n Solution(vector<vector<int>> _) {\n rects = _;\n for (auto& r : rects) {\n v.push_back(area(r) + (v.empty() ? 0 : v.back()));\n }\n }\n \n vector<int> pick() {\n // https://leetcode.com/problems/random-pick-with-weight/description/\n int rnd = rand() % v.back();\n auto it = upper_bound(v.begin(), v.end(), rnd);\n int idx = it - v.begin();\n \n // pick a random point in rect[idx]\n auto r = rects[idx];\n return {\n rand() % (r[2] - r[0] + 1) + r[0],\n rand() % (r[3] - r[1] + 1) + r[1]\n };\n }\n};\n``` | 37 | 2 | [] | 6 |
random-point-in-non-overlapping-rectangles | Python weighted probability solution | python-weighted-probability-solution-by-smx1b | \nclass Solution:\n\n def __init__(self, rects):\n self.rects, self.ranges, sm = rects, [], 0\n for x1, y1, x2, y2 in rects:\n sm += | cenkay | NORMAL | 2018-07-27T11:32:06.048473+00:00 | 2018-10-25T06:31:05.731286+00:00 | 5,374 | false | ```\nclass Solution:\n\n def __init__(self, rects):\n self.rects, self.ranges, sm = rects, [], 0\n for x1, y1, x2, y2 in rects:\n sm += (x2 - x1 + 1) * (y2 - y1 + 1)\n self.ranges.append(sm)\n\n def pick(self):\n x1, y1, x2, y2 = self.rects[bisect.bisect_left(self.ranges, random.randint(1, self.ranges[-1]))]\n return [random.randint(x1, x2), random.randint(y1, y2)]\n``` | 36 | 3 | [] | 7 |
random-point-in-non-overlapping-rectangles | C++ solution using reservoir sampling with explanation - concise and easy to understand | c-solution-using-reservoir-sampling-with-f285 | I found no other guys solved this problem using reservoir sampling method. Take a look at my solution.\n\n\nclass Solution {\npublic:\n vector<vector<int>> r | heesub | NORMAL | 2018-09-15T14:11:20.093182+00:00 | 2018-09-15T14:11:20.093227+00:00 | 3,407 | false | I found no other guys solved this problem using reservoir sampling method. Take a look at my solution.\n\n```\nclass Solution {\npublic:\n vector<vector<int>> rects;\n \n Solution(vector<vector<int>> rects) : rects(rects) {\n }\n \n vector<int> pick() {\n int sum_area = 0;\n vector<int> selected;\n \n /* Step 1 - select a random rectangle considering the area of it. */\n for (auto r : rects) {\n /*\n * What we need to be aware of here is that the input may contain\n * lines that are not rectangles. For example, [1, 2, 1, 5], [3, 2, 3, -2].\n * \n * So, we work around it by adding +1 here. It does not affect\n * the final result of reservoir sampling.\n */\n int area = (r[2] - r[0] + 1) * (r[3] - r[1] + 1);\n sum_area += area;\n \n if (rand() % sum_area < area)\n selected = r;\n }\n \n /* Step 2 - select a random (x, y) coordinate within the selected rectangle. */\n int x = rand() % (selected[2] - selected[0] + 1) + selected[0];\n int y = rand() % (selected[3] - selected[1] + 1) + selected[1];\n \n return { x, y };\n }\n};\n```\n\nThis problem is VERY BAD in the sense that the input actually contains something that is not a rectangle at all. It is different from what the title claims.\n\nIn the code above, reservoir sampling technique was used when we select a random rectangle in proportional to their area. Following resources will help you understand it:\n* https://en.wikipedia.org/wiki/Reservoir_sampling\n* https://www.youtube.com/watch?v=A1iwzSew5QY\n\n**However, using reservoir sampling may not be an optimal solution.** It is because of that picking a random rectangle by using reservoir sampling consumes high costs of O(n) time complexity each time, where n is the number of rectangles. So, overall time complexity goes up to O(nm), where m is the number of calls to pick(). On the other hand, its space complexity is O(1), because additional spaces are not required.\n\nAs other guys did, if we use binary search on the prefix sum of the weights, time complexity reduces to O(m log n), where m is the number of calls to pick() and n is the number of rectangles. However, its space complexity is O(n), requiring additional spaces for prefix sum of weight. | 28 | 1 | [] | 3 |
random-point-in-non-overlapping-rectangles | java Accepted. Clean and Concise. !! Commented ! | java-accepted-clean-and-concise-commente-7o67 | Please upvote if helpful\n\n\nclass Solution {\n \n Random random;\n TreeMap<Integer,int[]> map;\n int areaSum = 0;\n \n public Solution(int[] | kunal3322 | NORMAL | 2020-08-22T13:37:51.346533+00:00 | 2020-08-22T14:30:18.660345+00:00 | 2,131 | false | * **Please upvote if helpful**\n\n```\nclass Solution {\n \n Random random;\n TreeMap<Integer,int[]> map;\n int areaSum = 0;\n \n public Solution(int[][] rects) {\n this.random = new Random();\n this.map = new TreeMap<>();\n \n for(int i = 0; i < rects.length; i++){\n int [] rectangeCoordinates = rects[i];\n int length = rectangeCoordinates[2] - rectangeCoordinates[0] + 1 ; // +1 as we need to consider edges also.\n int breadth = rectangeCoordinates[3] - rectangeCoordinates[1] + 1 ;\n \n areaSum += length * breadth;\n \n map.put(areaSum,rectangeCoordinates);\n \n }\n \n }\n \n public int[] pick() {\n int key = map.ceilingKey(random.nextInt(areaSum) + 1); //Don\'t forget to +1 here, because we need [1,area] while nextInt generates [0,area-1]\n \n int [] rectangle = map.get(key);\n \n int length = rectangle[2] - rectangle[0] + 1 ; // +1 as we need to consider edges also.\n int breadth = rectangle[3] - rectangle[1] + 1 ;\n \n int x = rectangle[0] + random.nextInt(length); //return random length from starting position of x\n int y = rectangle[1] + random.nextInt(breadth); // return random breadth from starting position of y\n \n return new int[]{x,y};\n \n }\n}\n\n``` | 25 | 2 | ['Java'] | 1 |
random-point-in-non-overlapping-rectangles | [C++] Simple Solution | c-simple-solution-by-sahilgoyals-47du | \nclass Solution {\npublic:\n vector<int> v;\n vector<vector<int>> rects;\n // I add the +1 here because in some inputs they contain lines also like \n | sahilgoyals | NORMAL | 2020-08-22T08:04:07.891938+00:00 | 2020-08-22T18:48:25.203047+00:00 | 3,361 | false | ```\nclass Solution {\npublic:\n vector<int> v;\n vector<vector<int>> rects;\n // I add the +1 here because in some inputs they contain lines also like \n\t// [ 1,2,1,3 ] ( rectangle with height 0 or width 0 but this also contains 2 points )\n\t// to also add these points I add +1.\n int area(vector<int>& r) {\n return (r[2] - r[0] + 1) * (r[3] - r[1] + 1);\n }\n \n Solution(vector<vector<int>> rect) {\n rects = rect;\n int totalArea=0;\n for (auto r: rects) {\n totalArea+=area(r);\n v.push_back(totalArea);\n }\n }\n \n vector<int> pick() {\n // pick a random reactangle in rects\n int rnd = rand() % v.back();\n int idx = upper_bound(v.begin(), v.end(), rnd) - v.begin();\n \n // pick a random point in rects[idx]\n auto r = rects[idx];\n int x = rand() % (r[2] - r[0] + 1) + r[0];\n int y = rand() % (r[3] - r[1] + 1) + r[1];\n return { x, y };\n }\n};\n``` | 25 | 1 | ['C', 'C++'] | 5 |
random-point-in-non-overlapping-rectangles | Python [Probability/Monte Carlo] | python-probabilitymonte-carlo-by-gsan-kcb8 | This is a straightforward idea from probability theory. Say you have two rectangles, the first one contains 7 points inside and the second one contains 3. A ran | gsan | NORMAL | 2020-08-22T07:41:15.250544+00:00 | 2020-08-22T09:51:03.537977+00:00 | 1,372 | false | This is a straightforward idea from probability theory. Say you have two rectangles, the first one contains 7 points inside and the second one contains 3. A randomly drawn point has a probability of coming from the first rectangle equal to 0.7. So you calculate the number of points in each rectangle, and then use the inverse CDF* rule to simulate a random draw of rectangles based on the number of points they contain. (So you select the first rectangle with probability 0.7 in the example above.) Once you pick the rectangle, choose any point uniformly at random.\n\nCDF rule is at the core of simulations, Monte Carlo methods, and many machine learning algorithms.\n\nTime: `O(K)` where `K` is the number of rectangles. This is where we calculate the weights in the constructor.\nSpace: `O(K)` as we store the rectangle coordinates.\n\n*CDF: Cumulative distribution function\n\n```\nimport random\nimport bisect\nclass Solution:\n def __init__(self, rects: List[List[int]]):\n self.rects = rects\n #\n weig, c = [], 0\n for rect in rects:\n x1, y1, x2, y2 = rect\n c += (x2-x1+1)*(y2-y1+1)\n weig.append(c)\n self.weigc = [e/c for e in weig]\n \n \n def pick(self) -> List[int]:\n u = random.random()\n ix = bisect.bisect_left(self.weigc, u)\n x1, y1, x2, y2 = self.rects[ix]\n x = random.randint(x1,x2)\n y = random.randint(y1,y2)\n return [x,y]\n``` | 13 | 0 | [] | 2 |
random-point-in-non-overlapping-rectangles | [C++] Easy solution with explanation | c-easy-solution-with-explanation-by-_ris-rlro | If you are unable to solve this question, I would highly suggest you try this one first:\nhttps://leetcode.com/problems/random-pick-with-weight/\n\nIf you had s | _rishabharora | NORMAL | 2020-08-22T12:11:18.330334+00:00 | 2020-08-22T12:11:18.330371+00:00 | 707 | false | If you are unable to solve this question, I would highly suggest you try this one first:\nhttps://leetcode.com/problems/random-pick-with-weight/\n\nIf you had solved the above question, you would understand that here the probablity of picking up a random rectangle is proportional to the number if points enclosed in the rectangle (Area). In short the number of points enclosed by the rectangle is its weight (area). \n\nNow let\'s break this problem into 2 subproblems:\n1. Pick a random rectangle based on weight (area).\n2. Pick a random point in the rectangle obtained in the first step.\n\n\n```\nclass Solution {\npublic:\n vector<int> np;\n vector<vector<int>> Rects;\n Solution(vector<vector<int>>& rects) {\n Rects = rects;\n for(auto rect : rects){\n int l1 = rect[2] - rect[0] + 1;\n int l2 = rect[3] - rect[1] + 1;\n int val = np.size() ? np.back() + (l1*l2) : l1*l2; \n np.push_back(val);\n }\n }\n \n vector<int> pick() {\n int m = np.back();\n int r = rand() % m;\n auto it = upper_bound(np.begin(), np.end(), r);\n int rect = it - np.begin(); //end of step 1\n\t\t//step 2 begins\n vector<int> R = Rects[rect];\n int x = rand() % (R[2]-R[0]+1) + R[0];\n int y = rand() % (R[3]-R[1]+1) + R[1];\n return {x, y};\n }\n};\n``` | 9 | 0 | [] | 2 |
random-point-in-non-overlapping-rectangles | C++, easy and slow, beats 100% | c-easy-and-slow-beats-100-by-chrisys-ey9i | ```\nclass Solution {\npublic:\n vector> rect;\n vector r_area;\n int total_area;\n Solution(vector> rects) {\n rect = rects;\n int to | chrisys | NORMAL | 2019-01-29T16:01:45.291709+00:00 | 2019-01-29T16:01:45.291777+00:00 | 1,483 | false | ```\nclass Solution {\npublic:\n vector<vector<int>> rect;\n vector<int> r_area;\n int total_area;\n Solution(vector<vector<int>> rects) {\n rect = rects;\n int total = 0;\n for (int i = 0; i < rects.size(); i++) {\n total += (rects[i][2] - rects[i][0]+1)*(rects[i][3] - rects[i][1]+1);\n r_area.push_back(total);\n }\n total_area = total;\n }\n \n vector<int> pick() {\n int random_area = rand()%total_area+1;\n int i = 0;\n for (; i < r_area.size(); i++) {\n if (random_area <= r_area[i]) break;\n }\n int dis_x = rand()%(rect[i][2] - rect[i][0]+1);\n int dis_y = rand()%(rect[i][3] - rect[i][1]+1);\n return {rect[i][0] + dis_x, rect[i][1] + dis_y};\n }\n};\n\n/**\n * Your Solution object will be instantiated and called as such:\n * Solution obj = new Solution(rects);\n * vector<int> param_1 = obj.pick();\n */ | 9 | 0 | [] | 4 |
random-point-in-non-overlapping-rectangles | Random Point testcase 32/35 fault | random-point-testcase-3235-fault-by-user-6onp | I cannot understand why the testcase 32 fails.\nAll points inside rectangles. Whats wrong ?\n\n\nclass Solution {\n int[][] rects;\n\n public Solution(int | user0181c | NORMAL | 2020-08-22T11:36:44.291315+00:00 | 2020-08-22T11:39:01.261361+00:00 | 815 | false | I cannot understand why the testcase 32 fails.\nAll points inside rectangles. Whats wrong ?\n\n```\nclass Solution {\n int[][] rects;\n\n public Solution(int[][] rects) {\n this.rects = rects;\n }\n\n public int[] pick() {\n int [] res = new int[2];\n Random random = new Random();\n\n int maxWidth = 0;\n for (int i = 0 ; i < rects.length; i++) {\n maxWidth = maxWidth + Math.abs(rects[i][2] - rects[i][0]);\n }\n\n int x = random.nextInt(maxWidth);\n\n int rectWidth = 0;\n int rectNum = 0;\n for (int i = 0 ; i < rects.length; i++) {\n rectWidth = Math.abs(rects[i][2] - rects[i][0]);\n x = x - rectWidth;\n if (x <= 0) {\n res[0] = rects[i][2] - Math.abs(x);\n rectNum = i;\n break;\n }\n }\n\n int y = 0;\n int rectHeight = Math.abs(rects[rectNum][3] - rects[rectNum][1]);\n if ( rectHeight > 0 ) y = random.nextInt(Math.abs(rects[rectNum][3] - rects[rectNum][1]));\n\n res[1] = rects[rectNum][1] + y;\n\n return res;\n }\n}\n``` | 8 | 0 | ['Java'] | 10 |
random-point-in-non-overlapping-rectangles | JAVA 10+ lines TreeMap Sorted With Area | java-10-lines-treemap-sorted-with-area-b-2qcb | I borrow the idea from 880. Random Pick with Weight\nBut this time we use area as key.\n\nclass Solution {\n TreeMap<Integer, int[]> map= new TreeMap<>();\n | caraxin | NORMAL | 2018-07-27T05:24:06.059570+00:00 | 2018-09-09T03:36:24.263796+00:00 | 1,588 | false | I borrow the idea from [880. Random Pick with Weight\n](https://leetcode.com/problems/random-pick-with-weight/discuss/154024/JAVA-8-lines-TreeMap)But this time we use area as key.\n```\nclass Solution {\n TreeMap<Integer, int[]> map= new TreeMap<>();\n Random rnd= new Random();\n int area= 0;\n public Solution(int[][] rects) {\n for (int[] r: rects){\n int x1=r[0], y1=r[1], x2=r[2], y2=r[3];\n area+=(x2-x1+1)*(y2-y1+1); \\\\Don\'t forget to +1 here, because e.g 1~5 has 5 valid numbers\n map.put(area, r);\n }\n }\n \n public int[] pick() {\n int key= map.ceilingKey(rnd.nextInt(area)+1); \\\\Don\'t forget to +1 here, because we need [1,area] while nextInt generates [0,area-1]\n int[] curRec= map.get(key);\n int x1=curRec[0], y1=curRec[1], x2=curRec[2], y2=curRec[3], length=x2-x1, width=y2-y1;\n int x=x1+rnd.nextInt(length+1), y=y1+rnd.nextInt(width+1);\n return new int[]{x, y};\n }\n}\n```\nHappy Coding! | 8 | 1 | [] | 1 |
random-point-in-non-overlapping-rectangles | Java solution with just call one Random() for each Pick()!!!666 | java-solution-with-just-call-one-random-xubm4 | So for the first Random, we can get a Point which is already random and uniform, then We just need to represent it based on its Index in the corresponding Rect. | yunwei_qiu | NORMAL | 2018-07-31T19:53:46.278549+00:00 | 2018-10-25T06:31:18.712561+00:00 | 1,123 | false | So for the first Random, we can get a Point which is already random and uniform, then We just need to represent it based on its Index in the corresponding Rect. \n```\n int[][] rects;\n TreeMap<Integer, Integer> map;\n Random random;\n int sum = 0;\n public Solution(int[][] rects) {\n this.rects = rects;\n map = new TreeMap<>();\n random = new Random();\n for (int i = 0; i < rects.length; i++) {\n int[] rect = rects[i];\n sum += (rect[2] - rect[0] + 1) * (rect[3] - rect[1] + 1);\n map.put(sum, i);\n }\n }\n \n public int[] pick() {\n int randInt = random.nextInt(sum) + 1;\n int key = map.ceilingKey(randInt);\n int index = key - randInt; if randInt is 5 and the key is 6, so the index = 1 means its second point in that Rect. \n int[] rect = rects[map.get(key)];\n int left = rect[0], bottom = rect[1], right = rect[2], top = rect[3];\n int x = left + index % (right - left + 1);\n int y = bottom + index / (right - left + 1);\n return new int[]{x, y};\n }\n\t``` | 7 | 2 | [] | 3 |
random-point-in-non-overlapping-rectangles | Python O(n) with approach | python-on-with-approach-by-obose-20dk | Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem is asking us to pick a random point within a given list of rectangles. The | Obose | NORMAL | 2023-01-13T15:27:05.107948+00:00 | 2023-01-13T15:27:05.108003+00:00 | 714 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem is asking us to pick a random point within a given list of rectangles. The key to solving this problem is to understand the concept of weighting. We can assign a weight to each rectangle based on the number of points it contains, and then use a random number generator to pick a rectangle based on its weight.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Create an instance variable weights that will store the weights of each rectangle.\n- For each rectangle in the input list, calculate the number of points it contains and store it in weights.\n- Calculate the total number of points in all rectangles and store it in the total variable.\n- Create a prefix sum of weights to make it easier to pick a rectangle based on its weight.\n- In the pick() method, use a bisect function to find the index of the rectangle that the random number falls within.\n- Use a random number generator to pick a point within the selected rectangle.\n# Complexity\n- Time complexity: O(n) \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nwhere n is the number of rectangles. We need to iterate through the rectangles once to calculate their weights and create the prefix sum.\n- Space complexity: O(n) \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nwhere n is the number of rectangles. We need to store the weights of each rectangle in an array.\n# Code\n```\nclass Solution:\n\n def __init__(self, rects: List[List[int]]):\n self.rects = rects\n self.weights = []\n for rect in rects:\n self.weights.append((rect[2] - rect[0] + 1) * (rect[3] - rect[1] + 1))\n self.total = sum(self.weights)\n for i in range(1, len(self.weights)):\n self.weights[i] += self.weights[i - 1]\n self.weights = [0] + self.weights\n \n\n def pick(self) -> List[int]:\n index = bisect.bisect_left(self.weights, random.randint(1, self.total))\n rect = self.rects[index - 1]\n return [random.randint(rect[0], rect[2]), random.randint(rect[1], rect[3])]\n\n# Your Solution object will be instantiated and called as such:\n# obj = Solution(rects)\n# param_1 = obj.pick()\n``` | 6 | 0 | ['Python3'] | 1 |
random-point-in-non-overlapping-rectangles | C++ solutions | c-solutions-by-infox_92-2467 | \nclass Solution {\npublic:\n vector<vector<int>> rects;\n \n Solution(vector<vector<int>> rects) : rects(rects) {\n }\n \n vector<int> pick() | Infox_92 | NORMAL | 2022-12-01T15:28:12.381860+00:00 | 2022-12-01T15:28:12.381898+00:00 | 1,275 | false | ```\nclass Solution {\npublic:\n vector<vector<int>> rects;\n \n Solution(vector<vector<int>> rects) : rects(rects) {\n }\n \n vector<int> pick() {\n int sum_area = 0;\n vector<int> selected;\n \n /* Step 1 - select a random rectangle considering the area of it. */\n for (auto r : rects) {\n /*\n * What we need to be aware of here is that the input may contain\n * lines that are not rectangles. For example, [1, 2, 1, 5], [3, 2, 3, -2].\n * \n * So, we work around it by adding +1 here. It does not affect\n * the final result of reservoir sampling.\n */\n int area = (r[2] - r[0] + 1) * (r[3] - r[1] + 1);\n sum_area += area;\n \n if (rand() % sum_area < area)\n selected = r;\n }\n \n /* Step 2 - select a random (x, y) coordinate within the selected rectangle. */\n int x = rand() % (selected[2] - selected[0] + 1) + selected[0];\n int y = rand() % (selected[3] - selected[1] + 1) + selected[1];\n \n return { x, y };\n }\n};\n``` | 6 | 0 | ['C', 'C++'] | 1 |
random-point-in-non-overlapping-rectangles | Python readable, commented solution, without using bisect | python-readable-commented-solution-witho-ra58 | The idea is simple;\n\n1. Choose a rect, then choose a point inside it.\n2. The bigger the rectangle, the higher the probability of it getting chosen\n\n\nimpor | rainsaremighty | NORMAL | 2020-08-22T10:00:34.415946+00:00 | 2020-08-22T11:59:20.202749+00:00 | 426 | false | The idea is simple;\n\n1. Choose a rect, then choose a point inside it.\n2. The bigger the rectangle, the higher the probability of it getting chosen\n\n```\nimport random\n\nclass Solution:\n\n def __init__(self, rects: List[List[int]]):\n self.rects = rects\n\n \n # I am more of a list comprehensions guy, but if you prefer to\n # put more effort with the keyboard, here\'s an unrolled version.\n \n # self.weights = []\n # for rect in rects:\n # x1, y1, x2, y2 = rect\n # area = (x2-x1+1)*(y2-y1+1)\n # self.weights.append(area)\n \n self.weights = [(x2-x1+1)*(y2-y1+1) for x1, y1, x2, y2 in rects]\n \n \n # library functions are always faster\n # it beats the runtime of using an extra variable \n # to calculate sum_of_weights in the loop above\n # even if that means, we have to iterate once more.\n # Such is the world of python :D\n sum_of_weights = sum(self.weights)\n \n self.weights = [x/sum_of_weights for x in self.weights]\n \n\n def pick(self) -> List[int]:\n rect = random.choices(\n population=self.rects,\n weights=self.weights,\n k=1\n )[0] # random.choices returns a list, we extract the first (and only) element.\n\n x1, y1, x2, y2 = rect # tuple unpacking\n \n rnd_x = random.randint(x1, x2)\n rnd_y = random.randint(y1, y2)\n return [rnd_x, rnd_y]\n \n\n\n# Your Solution object will be instantiated and called as such:\n# obj = Solution(rects)\n# param_1 = obj.pick()\n```\n | 6 | 0 | ['Python'] | 2 |
random-point-in-non-overlapping-rectangles | Python O(n) by pool sampling. [w/ Visualization] | python-on-by-pool-sampling-w-visualizati-9ldd | Hint:\n\nThink of pool sampling.\n\nTotal n pools, and total P points\n\n\n\nEach rectangle acts as pool_i with points p_i by itself,\nwhere p_i = ( x_i_2 - x_ | brianchiang_tw | NORMAL | 2020-08-22T09:44:40.997786+00:00 | 2020-08-22T09:45:09.812317+00:00 | 1,171 | false | **Hint**:\n\nThink of **pool sampling**.\n\nTotal **n** pools, and total **P** points\n\n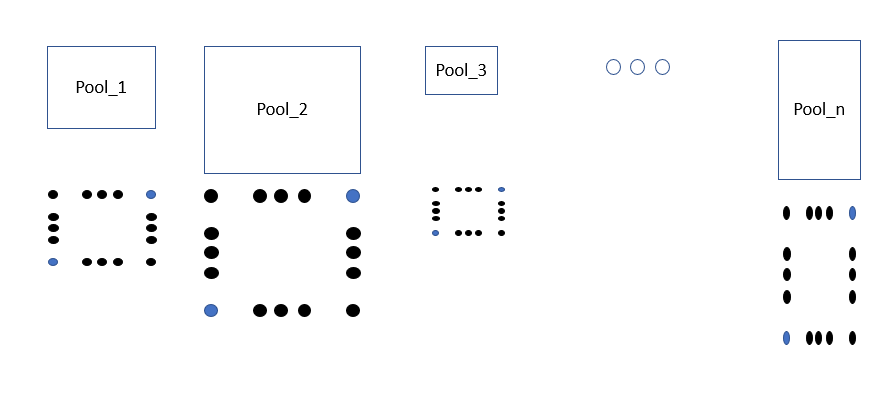\n\nEach **rectangle** acts as **pool_i** with points **p_i** by itself,\nwhere p_i = ( x_i_2 - x_i_1 + 1) * ( y_i_2 - y_i_1 + 1 )\n\n\n\n\nSo, p_1 + p_2 + ... + p_n = P, and\neach pool_i has a **weight** of **p_i / P** during **pool sampling**.\n\nThen, generate a random number **r** from 1 to P\n\nCompute the **pool index** (i.e., **rectangle index**) from r by bisection\n\nThen compute the **corresponding x, y coordinate** in that pool from r by modulo and division.\n\n---\n\n```\nfrom random import randint\nfrom bisect import bisect_left\n\nclass Solution:\n\n def __init__(self, rects: List[List[int]]):\n \n self.rectangles = rects\n \n # record prefix sum of points number (i.e., acts like the CDF)\n self.prefix_points_sum = []\n \n for x1, y1, x2, y2 in rects:\n \n # compute current number of points\n cur_points = ( x2 - x1 + 1 ) * ( y2 - y1 + 1)\n \n # update to prefix table\n if self.prefix_points_sum:\n self.prefix_points_sum.append( self.prefix_points_sum[-1] + cur_points )\n \n else:\n self.prefix_points_sum.append( cur_points )\n \n \n\n def pick(self) -> List[int]:\n \n total_num_of_points = self.prefix_points_sum[-1]\n \n # get a random point serial, sampling from 1 ~ total number of points\n random_point_serial = randint(1, total_num_of_points)\n \n # get the rectangle index by looking up prefix table with bisection\n idx_of_rectangle = bisect_left(self.prefix_points_sum, random_point_serial)\n \n # get the point range of that rectangle by index\n x1, y1, x2, y2 = self.rectangles[idx_of_rectangle]\n \n # compute the offset value between prefix sum and random point serial\n offset = self.prefix_points_sum[idx_of_rectangle] - random_point_serial\n \n # compute corresponding x, y points coordination in that rectangle\n x = offset % ( x2 - x1 + 1) + x1\n y = offset // ( x2 - x1 + 1) + y1\n \n return [x, y]\n``` | 6 | 0 | ['Math', 'Python', 'Python3'] | 1 |
random-point-in-non-overlapping-rectangles | No TreeMap, Use Reservoir Sampling Java Solution, One Pass | no-treemap-use-reservoir-sampling-java-s-2is4 | \nclass Solution {\n Random random;\n int[][] rects;\n public Solution(int[][] rects) {\n random = new Random();\n this.rects = rects;\n | jkone | NORMAL | 2019-07-25T06:16:48.057001+00:00 | 2019-07-25T06:16:48.057035+00:00 | 330 | false | ```\nclass Solution {\n Random random;\n int[][] rects;\n public Solution(int[][] rects) {\n random = new Random();\n this.rects = rects;\n }\n \n public int[] pick() {\n int sum = 0;\n // the idx of rect that will be selected\n int idx = 0;\n for (int i = 0; i < rects.length; i++) {\n int[] r = rects[i];\n int w = r[2] - r[0] + 1;\n int l = r[3] - r[1] + 1;\n // count of points\n int count = w * l;\n sum += count;\n if (random.nextInt(sum) < count) idx = i;\n }\n \n int x = rects[idx][0] + random.nextInt(rects[idx][2] - rects[idx][0] + 1);\n int y = rects[idx][1] + random.nextInt(rects[idx][3] - rects[idx][1] + 1);\n \n return new int[] {x, y};\n }\n}\n```\n | 6 | 0 | [] | 2 |
random-point-in-non-overlapping-rectangles | Is [1,0,3,0] a valid rectangle? | is-1030-a-valid-rectangle-by-branzhang-kpde | From Description:\n\nExample 2:\n\nInput: \n["Solution","pick","pick","pick","pick","pick"]\n[[[[-2,-2,-1,-1],[1,0,3,0]]],[],[],[],[],[]]\nOutput: \n[null,[-1,- | branzhang | NORMAL | 2018-08-29T09:38:32.156629+00:00 | 2018-08-29T09:38:32.156675+00:00 | 717 | false | From Description:\n\nExample 2:\n```\nInput: \n["Solution","pick","pick","pick","pick","pick"]\n[[[[-2,-2,-1,-1],[1,0,3,0]]],[],[],[],[],[]]\nOutput: \n[null,[-1,-2],[2,0],[-2,-1],[3,0],[-2,-2]]\n```\n\nIs [1,0,3,0] a valid rectangle? | 6 | 0 | [] | 1 |
random-point-in-non-overlapping-rectangles | Easy Code, Intuition😇 & Explanation 🎯 | easy-code-intuition-explanation-by-iamor-bwcc | IntuitionRead comments inside the code, easy to understandApproachBinary search on points of rectangle, rand() will always bring unique valueComplexity
Time co | Iamorphouz | NORMAL | 2025-01-05T06:30:16.989610+00:00 | 2025-01-05T06:30:16.989610+00:00 | 384 | false | # Intuition
Read comments inside the code, easy to understand
# Approach
Binary search on points of rectangle, rand() will always bring unique value
# Complexity
- Time complexity:
$$O(log(N))$$ : for each pick(binary Search)
- Space complexity:
$$O(N)$$ : store points count
# Code
```cpp []
class Solution {
public:
vector<int> v;
vector<vector<int>> rects;
// [ 4,5,4,6 ] ( rectangle with height 0 or width 0 but this also contains 2 points )
int cntPoints(vector<int>& r) {
return (r[2] - r[0] + 1) * (r[3] - r[1] + 1);
}
Solution(vector<vector<int>> rect) {
rects = rect;
int totalPts=0;
for (auto r: rects) {
totalPts+=cntPoints(r);
v.push_back(totalPts);
}
}
vector<int> pick() {
// picking a random reactangle in rects
int pt = rand() % v.back(); // v.back is totalPts
// pt is one of that Total points
int idx = upper_bound(v.begin(), v.end(), pt) - v.begin();
// idx is index of rectangle in which that pt exist
// picking a random point in rects[idx]
vector<int> r = rects[idx];
int x = rand() % (r[2] - r[0] + 1) + r[0]; // pick x cords for pt from rect
int y = rand() % (r[3] - r[1] + 1) + r[1]; // pick y cords for pt from rect
return { x, y };
}
};
/**
* Your Solution object will be instantiated and called as such:
* Solution* obj = new Solution(rects);
* vector<int> param_1 = obj->pick();
*/
``` | 5 | 0 | ['Array', 'Math', 'Binary Search', 'Prefix Sum', 'C++'] | 0 |
random-point-in-non-overlapping-rectangles | 497: Space 95.52%, Solution with step by step explanation | 497-space-9552-solution-with-step-by-ste-xyrw | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n1. Initialize the Solution class with a list of non-overlapping axis-alig | Marlen09 | NORMAL | 2023-03-11T18:09:52.458547+00:00 | 2023-03-11T18:09:52.458589+00:00 | 815 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Initialize the Solution class with a list of non-overlapping axis-aligned rectangles rects.\n\n2. Inside the init function, calculate the total area covered by all the rectangles and store it in a variable called total_area.\n\n3. Create a list called areas to store the area of each rectangle cumulatively, starting from the first rectangle to the last.\n\n4. Loop through each rectangle in the input list rects and calculate the area of the rectangle using the formula: (xi - ai + 1) * (yi - bi + 1), where xi, yi are the top-right corner points of the ith rectangle and ai, bi are the bottom-left corner points of the ith rectangle.\n\n5. Add the area of each rectangle to the previous cumulative area, starting from the first rectangle, and append the result to the list areas.\n\n6. Inside the pick function, generate a random integer r between 1 and the total area covered by all the rectangles.\n\n7. Loop through each rectangle in the input list rects and compare the value of r with the cumulative area stored in the list areas for that rectangle. If r is less than or equal to the cumulative area, then the random point should be generated inside that rectangle.\n\n8. Generate two random integers x and y using the randint function from the random module, such that ai <= x <= xi and bi <= y <= yi, where ai, bi, xi, yi are the corner points of the current rectangle.\n\n9. Return the random point [x, y] as the output of the pick function.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def __init__(self, rects: List[List[int]]):\n self.rects = rects\n self.areas = []\n self.total_area = 0\n \n # Calculate the total area covered by all the rectangles\n for rect in rects:\n area = (rect[2] - rect[0] + 1) * (rect[3] - rect[1] + 1)\n self.total_area += area\n self.areas.append(self.total_area)\n \n def pick(self) -> List[int]:\n # Generate a random integer between 0 and the total area covered by all the rectangles\n r = random.randint(1, self.total_area)\n \n # Loop through each rectangle, subtracting its area from r\n for i in range(len(self.rects)):\n if r <= self.areas[i]:\n # Once we find the rectangle, generate a random point inside it\n rect = self.rects[i]\n x = random.randint(rect[0], rect[2])\n y = random.randint(rect[1], rect[3])\n return [x, y]\n\n``` | 4 | 0 | ['Array', 'Math', 'Binary Search', 'Python', 'Python3'] | 1 |
random-point-in-non-overlapping-rectangles | [Javascript] AREA is NOT an Appropriate Weight! | javascript-area-is-not-an-appropriate-we-a98c | Here\'s an intuitive thought:\n\n> If rect A is bigger than rect B, it should have a larger weight to get selected.\n> While its # of points are also more, each | lynn19950915 | NORMAL | 2022-05-25T06:15:48.601547+00:00 | 2023-05-27T05:02:05.613938+00:00 | 292 | false | Here\'s an intuitive thought:\n\n> If `rect A` is bigger than `rect B`, it should have a larger weight to get selected.\n> While its `# of points` are also more, **each point** within it has a smaller chance for picked then.\n\nSounds fair, but that\'s not completely right.\n.\n\nTaking `rect A`=2x1, `rect B`=1x1 for example:\n\nThough A\'s area is twice as B, there are **6 points in A** while **4 in B**.\nSo the correct ratio should be `(2+1)*(1+1):(1+1)*(1+1)=6:4`\nWhich can then distribute to all points uniformly.\n.\n.\n**Conclusion**\n\nWe should take **\\# OF POINTS** within a rectangle (instead of area) as weight.\n```\nFor size=m*n, there are (m+1)*(n+1) points\nwhich stands for possible choices in X&Y direction.\n```\n\nThanks for your reading and **up-voting** :)\n\n**\u2B50 Check [HERE](https://github.com/Lynn19950915/LeetCode_King) for my full Leetcode Notes ~**\n\n\n\n | 4 | 0 | ['JavaScript'] | 1 |
random-point-in-non-overlapping-rectangles | Minimum Cost For Tickets Solution | C++ | Easy | minimum-cost-for-tickets-solution-c-easy-14rm | Cost[i] -> total amount spent till day i to travell at all the days before it.\n\n\nclass Solution {\npublic:\n int mincostTickets(vector<int>& days, vector< | prisonmike | NORMAL | 2020-08-25T07:34:17.862620+00:00 | 2020-08-25T07:34:56.428859+00:00 | 413 | false | Cost[i] -> total amount spent till day i to travell at all the days before it.\n\n```\nclass Solution {\npublic:\n int mincostTickets(vector<int>& days, vector<int>& costs) {\n set<int> dd(days.begin(),days.end());\n int cost[366];\n memset(cost,0,sizeof(cost));\n int one=costs[0],seven=costs[1],thirty=costs[2];\n for(int i=1;i<=365;i++)\n {\n cost[i]=cost[i-1];\n if(dd.find(i)!=dd.end())\n {\n cost[i] = min(cost[i-1>=0?i-1:0]+one,min(seven+cost[i-7>=0?i-7:0],thirty+cost[i-30>=0?i-30:0]));\n }\n }\n \n return cost[365];\n }\n};\n``` | 4 | 2 | ['Dynamic Programming', 'C'] | 1 |
random-point-in-non-overlapping-rectangles | C# easy solution | c-easy-solution-by-quico14-jni3 | \npublic class Solution {\n public int[][] SolutionPoints { get; set; }\n public SortedDictionary<int, int> RectangleByArea = new SortedDictionary<int, in | quico14 | NORMAL | 2020-08-22T10:23:05.556632+00:00 | 2020-08-22T10:23:05.556664+00:00 | 241 | false | ```\npublic class Solution {\n public int[][] SolutionPoints { get; set; }\n public SortedDictionary<int, int> RectangleByArea = new SortedDictionary<int, int>();\n public int NumberOfSolutions { get; set; }\n public Random Random = new Random();\n \n public Solution(int[][] rects)\n {\n SolutionPoints = rects;\n for (var i = 0 ; i < rects.Length ; i++)\n {\n var rect = rects[i];\n NumberOfSolutions += (rect[2] - rect[0] + 1) * (rect[3] - rect[1] + 1);\n RectangleByArea.Add(NumberOfSolutions, i);\n }\n }\n\n public int[] Pick()\n {\n var randomNumber = Random.Next(NumberOfSolutions) + 1;\n var rectangleIndex = RectangleByArea.First(x => x.Key >= randomNumber).Value;\n\n return Pick(SolutionPoints[rectangleIndex]);\n }\n public int[] Pick(int[] rectangle)\n {\n var x = Random.Next(rectangle[0], rectangle[2] + 1);\n var y = Random.Next(rectangle[1], rectangle[3] + 1);\n return new[] { x, y };\n }\n}\n``` | 4 | 0 | [] | 0 |
random-point-in-non-overlapping-rectangles | C++ solution using std::discrete_distribution | c-solution-using-stddiscrete_distributio-e9gd | discrete_distribution can be used to select a random rectangle with weighted probabilities.\n- uniform_int_distribution can be used to select random coordinates | yessenamanov | NORMAL | 2019-12-08T18:19:08.986973+00:00 | 2020-02-12T17:43:06.082238+00:00 | 254 | false | - [discrete_distribution](https://en.cppreference.com/w/cpp/numeric/random/discrete_distribution) can be used to select a random rectangle with weighted probabilities.\n- [uniform_int_distribution](https://en.cppreference.com/w/cpp/numeric/random/uniform_int_distribution) can be used to select random coordinates of a point inside the selected rectangle.\n\n```c++\nclass Solution {\n vector<vector<int>> rects;\n mt19937 rng;\n discrete_distribution<int> dist;\n \npublic:\n Solution(vector<vector<int>>& rects_): \n rects(rects_),\n rng(random_device()())\n {\n vector<int> weights(rects.size());\n for (int i = 0; i < rects.size(); ++i) {\n weights[i] = (rects[i][2]-rects[i][0]+1)*(rects[i][3]-rects[i][1]+1);\n }\n dist = discrete_distribution<int>(weights.begin(), weights.end());\n }\n \n vector<int> pick() {\n auto &r = rects[dist(rng)];\n int x = uniform_int_distribution<int>(r[0], r[2])(rng);\n int y = uniform_int_distribution<int>(r[1], r[3])(rng);\n return {x, y};\n }\n};\n``` | 4 | 0 | [] | 0 |
random-point-in-non-overlapping-rectangles | Python 3 Weighting by area | python-3-weighting-by-area-by-thaeliosra-nd87 | I am a bit baffled by this problem in particular and how leetcode judges problems involving randomness in general. The code below selects a rectangle at random | thaeliosraedkin1 | NORMAL | 2020-08-22T17:52:22.892116+00:00 | 2020-08-22T17:52:55.166030+00:00 | 169 | false | I am a bit baffled by this problem in particular and how leetcode judges problems involving randomness in general. The code below selects a rectangle at random weighted by its area. This is necessary because to select some point with uniform probability means the selected point is more likely to land in a rectangle with a larger area. \n\nThe following code contains an error.\n```\nimport random\nclass Solution:\n\n def __init__(self, rects: List[List[int]]):\n self.rects = rects\n self.areas = [abs(r[0]-r[2])*abs(r[1]-r[3]) for r in rects]\n\n def pick(self) -> List[int]:\n rect = random.choices(self.rects, weights=self.areas)[0]\n return [random.randint(rect[0], rect[2]), random.randint(rect[1], rect[3])]\n```\n\nBut when I make the subtle correction `self.areas = [(abs(r[0]-r[2])+1)*(abs(r[1]-r[3])+1) for r in rects]`, the code passes all test cases. :-/ It\'s horrendously slow in comparison to binary search, but it works. | 3 | 0 | [] | 0 |
random-point-in-non-overlapping-rectangles | Explained Javascript Solution, Using binary search | explained-javascript-solution-using-bina-2v8m | \n/**\n /**\n * @param {number[][]} rects\n */\nvar Solution = function(rects) {\n this.rects = rects;\n this.map = {};\n this.sum = 0;\n // we put | thebigbadwolf | NORMAL | 2020-08-22T10:00:18.052349+00:00 | 2020-08-22T10:02:44.735583+00:00 | 498 | false | ```\n/**\n /**\n * @param {number[][]} rects\n */\nvar Solution = function(rects) {\n this.rects = rects;\n this.map = {};\n this.sum = 0;\n // we put in the map the number of points that belong to each rect\n for(let i in rects) {\n const rect = rects[i];\n // the number of points can be picked in this rectangle\n this.sum += (rect[2] - rect[0] + 1) * (rect[3] - rect[1] + 1);\n this.map[this.sum] = i;\n }\n this.keys = Object.keys(this.map);\n};\n\n/**\n * @return {number[]}\n */\nSolution.prototype.pick = function() {\n // random point pick between [1, this.sum]\n const randomPointPick = Math.floor(Math.random() * this.sum) + 1;\n \n // we look for the randomPointPick in the keys of the map\n let pointInMap;\n // the keys exists in map\n if(this.map[randomPointPick]) pointInMap = randomPointPick;\n // the key is the first in the map (we do this check before doing binary search because its out of boundery)\n else if(randomPointPick < this.keys[0]) pointInMap = this.keys[0];\n let high = this.keys.length;\n let low = 1;\n // binary search to find the closest key that bigger than randomPointPick\n while(low <= high && !pointInMap) {\n const mid = Math.floor((low + (high-low)/2));\n if(randomPointPick > this.keys[mid-1] && randomPointPick < this.keys[mid]) {\n pointInMap = this.keys[mid];\n break;\n } else if (randomPointPick > this.keys[mid]){\n low = mid+1;\n } else {\n high = mid-1;\n }\n }\n \n // we have the point, now we can get which rect belong to that point\n const pointInRects = this.map[pointInMap];\n const chosen = this.rects[pointInRects];\n const rightX = chosen[2];\n const leftX = chosen[0];\n const topY = chosen[3];\n const bottomY = chosen[1];\n const pickX = Math.floor(Math.random() * (rightX-leftX+1)) + leftX;\n const pickY = Math.floor(Math.random() * (topY-bottomY+1)) + bottomY;\n return [pickX, pickY]\n};\n\n/** \n * Your Solution object will be instantiated and called as such:\n * var obj = new Solution(rects)\n * var param_1 = obj.pick()\n */\n``` | 3 | 0 | ['Binary Tree', 'JavaScript'] | 1 |
random-point-in-non-overlapping-rectangles | Python 1-liner | python-1-liner-by-ekovalyov-c2ye | The solution uses library function choice from package random.\n\nFinal version after refactoring:\n\nclass Solution:\n def __init__(self, rects: List[List[i | ekovalyov | NORMAL | 2020-08-22T09:38:55.852633+00:00 | 2020-08-22T11:17:35.803998+00:00 | 234 | false | The solution uses library function choice from package random.\n\nFinal version after refactoring:\n```\nclass Solution:\n def __init__(self, rects: List[List[int]]):\n self.r=[*zip(*[[r,(r[2]-r[0]+1)*(r[3]-r[1]+1)]for r in rects])]\n def pick(self) -> List[int]:\n return [[randint(r[0],r[2]), randint(r[1],r[3])] for r in choices(*self.r)][0]\n``` \n\nPrevious version:\n```\nclass Solution:\n def __init__(self, rects: List[List[int]]):\n self.r=[*zip(*reduce(lambda a,r:a+[[[(r[0],r[2]),(r[1],r[3])],(r[2]-r[0]+1)*(r[3]-r[1]+1)]],rects,[]))]\n def pick(self) -> List[int]:\n return [[randint(*x), randint(*y)] for x,y in choices(*self.r)][0]\n```\n\nVersion before previous with 2 variables for rectangles and weights:\n```\nclass Solution:\n def __init__(self, rects: List[List[int]]):\n self.r,self.w=zip(*reduce(lambda a,r:a+[[[(r[0],r[2]),(r[1],r[3])],(r[2]-r[0]+1)*(r[3]-r[1]+1)]],rects,[]))\n \n def pick(self) -> List[int]:\n return [[randint(*x), randint(*y)] for x,y in choices(self.r, self.w)][0]\n```\n | 3 | 0 | [] | 0 |
random-point-in-non-overlapping-rectangles | Python Random choices with weights | python-random-choices-with-weights-by-fo-asq1 | \n(x2-x1+1)*(y2-y1+1) stands for the number of points in rectangle [x1,y1,x2,y2]. So with the weights, we can ensure for every point the chance of being picked | formatmemory | NORMAL | 2019-02-09T01:16:17.490317+00:00 | 2019-02-09T01:16:17.490360+00:00 | 426 | false | \n(x2-x1+1)*(y2-y1+1) stands for the number of points in rectangle [x1,y1,x2,y2]. So with the weights, we can ensure for every point the chance of being picked is evenly.\n\n```\nclass Solution:\n\n def __init__(self, rects: \'List[List[int]]\'):\n self.rects_weight = []\n self.rects = rects\n for [x1,y1,x2,y2] in rects:\n self.rects_weight.append((x2-x1+1)*(y2-y1+1))\n \n def pick(self) -> \'List[int]\':\n [x1,y1,x2,y2] = random.choices(self.rects, weights = self.rects_weight)[0]\n x = random.randrange(x1,x2+1)\n y = random.randrange(y1,y2+1)\n return [x,y]\n``` | 3 | 0 | [] | 1 |
random-point-in-non-overlapping-rectangles | Microsoft⭐ || Easy Solution🔥 | microsoft-easy-solution-by-priyanshi_gan-e9mt | #ReviseWithArsh #6Companies30Days challenge 2k24\nCompany 2 :- Microsoft\n\n\n# Code\n\nclass Solution {\npublic:\n Solution(std::vector<std::vector<int>>& r | Priyanshi_gangrade | NORMAL | 2024-01-09T11:18:07.917758+00:00 | 2024-01-09T11:18:07.917786+00:00 | 632 | false | ***#ReviseWithArsh #6Companies30Days challenge 2k24\nCompany 2 :- Microsoft***\n\n\n# Code\n```\nclass Solution {\npublic:\n Solution(std::vector<std::vector<int>>& rects)\n : rects(rects), x(rects[0][0] - 1), y(rects[0][1]), i(0) {}\n\n std::vector<int> pick() {\n // Increment x until reaching the right boundary of the current rectangle\n if (x != rects[i][2]) {\n ++x;\n }\n // If x reaches the right boundary, reset x to the left boundary and increment y\n else if (x == rects[i][2] && y != rects[i][3]) {\n x = rects[i][0];\n ++y;\n }\n // If both x and y reach the boundaries, move to the next rectangle\n else if (x == rects[i][2] && y == rects[i][3]) {\n i = (i < rects.size() - 1) ? i + 1 : 0;\n x = rects[i][0];\n y = rects[i][1];\n }\n return {x, y};\n }\n\nprivate:\n std::vector<std::vector<int>> rects;\n int x, y, i; // x, y represent the current point, i represents the current rectangle index\n};\n\n``` | 2 | 0 | ['C++'] | 1 |
random-point-in-non-overlapping-rectangles | Simple Solution using binary search and math || C++ | simple-solution-using-binary-search-and-obwql | Intuition\n Describe your first thoughts on how to solve this problem. \nCount number of points in every rectangle and push till number points in su vector to s | rkkumar421 | NORMAL | 2022-11-12T12:19:40.271031+00:00 | 2022-11-12T12:19:40.271063+00:00 | 526 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nCount number of points in every rectangle and push till number points in su vector to search in which rectangle random point will lie .\n# Approach\n<!-- Describe your approach to solving the problem. -->\nBinary Search\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int N;\n long int ar;\n vector<vector<int>> rec;\n vector<long int> su;\n Solution(vector<vector<int>>& rects) {\n N = rects.size();\n ar = 0;\n for(auto x: rects){\n ar += (x[2]-x[0]+1)*(x[3]-x[1]+1);\n su.push_back(ar);\n }\n rec = rects;\n }\n \n vector<int> pick() {\n int rval = (rand()%ar);\n int ithrec = upper_bound(su.begin(), su.end() , rval) - su.begin();\n long int x = rec[ithrec][2] - rec[ithrec][0] + 1; // number of x points \n long int y = rec[ithrec][3] - rec[ithrec][1] + 1; // number of y points\n // Now according to area\n // rval = su[ithrec] - rval;\n int fx = rec[ithrec][0] + (rand()%(x));\n int fy = rec[ithrec][1] + (rand()%(y));\n return {fx,fy};\n }\n};\n``` | 2 | 0 | ['Math', 'Binary Search', 'C++'] | 1 |
random-point-in-non-overlapping-rectangles | Python3 Solution Explained | Easy to understand | python3-solution-explained-easy-to-under-mmeo | Solution:\n1. First find the sum of the area of all the given rectangles\n2. Create a probability list to determine which rectangle should be selected. A rectan | abrahamshimekt | NORMAL | 2022-10-27T19:56:27.633975+00:00 | 2022-10-27T19:56:27.634013+00:00 | 397 | false | **Solution:**\n1. First find the sum of the area of all the given rectangles\n2. Create a probability list to determine which rectangle should be selected. A rectangle with higher probability will be selected. The ith element of the probability list is the area of the ith rectangle devided by the sum of the area of all rectangles.\n3. Find the index of the highest probability rectangle which has the highest area by definition based on the probability list.\n4. Finaly find the 4 points of the rectangle which are x1,x2, y1,y2 and take random integer between [x1,x2] and [y1,y2] .\n```\ndef __init__(self, rects: List[List[int]]):\n\tw = 0\n\tself.rects = rects\n\tself.probability =[]\n\tself.indexes = []\n\tfor i in range(len(self.rects)):\n\t\tself.indexes.append(i)\n\t\tw += (self.rects[i][2]-self.rects[i][0] +1)*(self.rects[i][3]-self.rects[i][1] +1)\n\tfor i in range(len(self.rects)):\n\t\tself.probability.append((self.rects[i][2]-self.rects[i][0] +1)*(self.rects[i][3]-self.rects[i][1] +1)/w)\ndef pick(self) -> List[int]:\n\tindex = random.choices(self.indexes,weights = self.probability,k=1)[-1]\n\tx1,y1,x2,y2 = self.rects[index]\n\treturn [random.randint(x1,x2),random.randint(y1,y2)] | 2 | 0 | ['Prefix Sum', 'Probability and Statistics', 'Python', 'Python3'] | 0 |
random-point-in-non-overlapping-rectangles | C++ beat 99% | c-beat-99-by-huimingzhou-2kf4 | cpp\nclass Solution {\npublic:\n vector<vector<int>> data;\n int area = 0;\n \n Solution(vector<vector<int>>& rects) {\n for (auto& x : rects | huimingzhou | NORMAL | 2020-10-07T23:25:17.965052+00:00 | 2020-10-07T23:25:17.965087+00:00 | 204 | false | ```cpp\nclass Solution {\npublic:\n vector<vector<int>> data;\n int area = 0;\n \n Solution(vector<vector<int>>& rects) {\n for (auto& x : rects) {\n area += (x[2] - x[0] + 1) * (x[3] - x[1] + 1);\n data.push_back({area, x[0], x[2] - x[0] + 1, x[1], x[3] - x[1] + 1});\n }\n }\n \n vector<int> pick() {\n int num = rand() % area;\n int l = 0, r = data.size() - 1;\n while (l < r) {\n int m = l + (r - l) / 2;\n if (data[m][0] < num) l = m + 1;\n else r = m;\n }\n \n if (data[l][0] == num && l != data.size() - 1) ++l;\n \n vector<int>& y = data[l];\n \n return {rand() % y[2] + y[1], rand() % y[4] + y[3]};\n }\n};\n``` | 2 | 0 | [] | 0 |
random-point-in-non-overlapping-rectangles | [C++] Random Points | Simple | c-random-points-simple-by-jmbryan10-ewuh | Build a weighted list of rectangles where the weight is equal to each rectangle\'s area. When picking a random point, first pick a rect from the weighted list a | jmbryan10 | NORMAL | 2020-08-22T18:14:51.853886+00:00 | 2020-08-22T18:15:29.629980+00:00 | 219 | false | Build a weighted list of rectangles where the weight is equal to each rectangle\'s area. When picking a random point, first pick a rect from the weighted list and then pick a random point from within that rect.\n```\nclass Solution {\npublic:\n vector<pair<int, vector<int>>> weightedRects;\n long long totalWeight = 0;\n \n Solution(vector<vector<int>>& rects) {\n for (auto& rect : rects) {\n int area = (rect[2] - rect[0] + 1) * (rect[3] - rect[1] + 1);\n totalWeight += area;\n weightedRects.push_back(make_pair(area, rect));\n }\n }\n \n vector<int> pick() {\n int weight = rand() % (totalWeight + 1);\n for (auto& entry : weightedRects) {\n if (weight <= entry.first) {\n auto& rect = entry.second;\n int px = rect[0] + rand() % (rect[2] - rect[0] + 1);\n int py = rect[1] + rand() % (rect[3] - rect[1] + 1);\n return {px, py};\n }\n weight -= entry.first;\n }\n return {};\n }\n};\n``` | 2 | 0 | [] | 0 |
random-point-in-non-overlapping-rectangles | Short and easy solution but something's wrong! Cannot pass 3 testcases - used random.choice() | short-and-easy-solution-but-somethings-w-2dm7 | Hi, I tried solving it using random.choice(). Firstly, I made an array that had X and Y ranges in a list for each rectangle. Later, I simply used random.choice | sanya638 | NORMAL | 2020-08-22T09:58:52.996713+00:00 | 2020-08-22T09:58:52.996765+00:00 | 257 | false | Hi, I tried solving it using random.choice(). Firstly, I made an array that had X and Y ranges in a list for each rectangle. Later, I simply used random.choice in selecting the rectangle and later on points by applying choice on selecting x_coordinate and y_coordinate.\n\nI don\'t know how to explain the approach exactly, but you can see the working code here. 32/35 cases passed and logic seems somewhat correct to me. Can anyone help me find out what the issue is?\n\n```\nclass Solution:\n\n def __init__(self, rects: List[List[int]]):\n \n self.another_array_with_limits = []\n for rec in rects:\n X_and_Y_range = [[rec[0],rec[2]], [rec[1],rec[3]]] # [[x-range], [y_range]]\n self.another_array_with_limits.append(X_and_Y_range)\n \n def pick(self) -> List[int]:\n \n get_random_array = random.choice(self.another_array_with_limits)\n random_x = random.choice(range(get_random_array[0][0], get_random_array[0][1] + 1))\n random_y = random.choice(range(get_random_array[1][0], get_random_array[1][1] + 1))\n \n return [random_x, random_y]\n\n\n``` | 2 | 0 | [] | 4 |
random-point-in-non-overlapping-rectangles | [Java] Distribute The Points via TreeMap | java-distribute-the-points-via-treemap-b-2x83 | \nclass Solution {\n private TreeMap<Integer, Integer> map;\n private int[][] minmax;\n private int len;\n private int sum;\n \n public Soluti | blackspinner | NORMAL | 2020-08-22T05:12:21.318425+00:00 | 2020-08-22T05:12:21.318577+00:00 | 271 | false | ```\nclass Solution {\n private TreeMap<Integer, Integer> map;\n private int[][] minmax;\n private int len;\n private int sum;\n \n public Solution(int[][] rects) {\n map = new TreeMap<>();\n len = rects.length;\n minmax = new int[len][4];\n sum = 0;\n for (int i = 0; i < len; i++) {\n minmax[i][0] = Math.min(rects[i][0], rects[i][2]);\n minmax[i][1] = Math.max(rects[i][0], rects[i][2]);\n minmax[i][2] = Math.min(rects[i][1], rects[i][3]);\n minmax[i][3] = Math.max(rects[i][1], rects[i][3]);\n sum += (rects[i][3] - rects[i][1] + 1) * (rects[i][2] - rects[i][0] + 1);\n map.put(sum, i);\n }\n }\n \n public int[] pick() {\n int rand = 1 + (int)(Math.random() * sum);\n int index = map.get(map.ceilingKey(rand));\n int[] rect = minmax[index];\n int xrange = rect[1] - rect[0] + 1;\n int yrange = rect[3] - rect[2] + 1;\n return new int[]{rect[0] + (int)(Math.random() * xrange), rect[2] + (int)(Math.random() * yrange)};\n }\n}\n``` | 2 | 1 | [] | 0 |
random-point-in-non-overlapping-rectangles | C# Solution | c-solution-by-leonhard_euler-4ab7 | \npublic class Solution \n{\n private int[][] rects;\n private int[] sums;\n private Random random;\n\n public Solution(int[][] rects) \n {\n | Leonhard_Euler | NORMAL | 2019-07-27T04:20:07.983033+00:00 | 2019-07-27T04:20:07.983063+00:00 | 178 | false | ```\npublic class Solution \n{\n private int[][] rects;\n private int[] sums;\n private Random random;\n\n public Solution(int[][] rects) \n {\n this.rects = rects;\n sums = new int[rects.Length];\n for(int i = 0; i <rects.Length; i++)\n {\n var area = RectAreaPoints(rects[i]);\n sums[i] = i == 0 ? area : sums[i - 1] + area;\n }\n\n random = new Random();\n }\n \n public int[] Pick() \n {\n int index = random.Next(sums[sums.Length - 1]) + 1;\n int left = Array.BinarySearch(sums, index);\n if(left < 0) left = ~left;\n int rect_index = sums[left] - index;\n int rect_long = rects[left][2] - rects[left][0] + 1;\n return new int[]{rects[left][0] + rect_index % rect_long, rects[left][1] + rect_index / rect_long};\n }\n \n private int RectAreaPoints(int[] p)\n {\n return (p[2] - p[0] + 1) * (p[3] - p[1] + 1); \n }\n}\n``` | 2 | 0 | [] | 1 |
random-point-in-non-overlapping-rectangles | Python 3 Solution (using random.randint and bisect.bisect_left) | python-3-solution-using-randomrandint-an-b35d | \nimport bisect\nimport random\n\n\nclass Solution:\n\n def __init__(self, rects: List[List[int]]):\n self.rects = rects\n # number of points i | jinjiren | NORMAL | 2019-02-28T11:30:40.036695+00:00 | 2019-02-28T11:30:40.036740+00:00 | 514 | false | ```\nimport bisect\nimport random\n\n\nclass Solution:\n\n def __init__(self, rects: List[List[int]]):\n self.rects = rects\n # number of points in each rectangle\n self.counts = [(x2 - x1 + 1) * (y2 - y1 + 1) \n for x1, y1, x2, y2 in rects]\n self.total = sum(self.counts)\n # accumulated (prefix) count of points\n self.accumulate_counts = []\n accumulated = 0\n for count in self.counts:\n accumulated += count\n self.accumulate_counts.append(accumulated)\n\n def pick(self) -> List[int]:\n # rand is in [1, n], including both ends\n rand = random.randint(1, self.total)\n # find rightmost index with value <= rand\n # e.g., for accumulate_count of [2, 5, 8], with rand inputs range [1, 8]\n # there are 3 groups {1,2 | 3,4,5 | 6,7,8}, corresponding to index [0, 1, 2] respectively\n rect_index = bisect.bisect_left(self.accumulate_counts, rand)\n # use rand to find point_index, too\n point_index = rand - self.accumulate_counts[rect_index] + self.counts[rect_index] - 1\n x1, y1, x2, y2 = self.rects[rect_index]\n i, j = divmod(point_index, y2 - y1 + 1)\n return [x1 + i, y1 + j]\n``` | 2 | 0 | [] | 0 |
random-point-in-non-overlapping-rectangles | [Rust] Solution using BTreeMap | rust-solution-using-btreemap-by-talalsha-a7rl | Check @remember8964 for explanation\n\n# Code\nrust []\nuse rand::Rng;\nuse std::collections::BTreeMap;\n\nstruct Solution {\n total_sum: i32,\n mp: BTree | talalshafei | NORMAL | 2024-11-27T20:01:05.299227+00:00 | 2024-11-27T20:01:05.299260+00:00 | 20 | false | Check @[remember8964](https://leetcode.com/problems/random-point-in-non-overlapping-rectangles/solutions/316890/trying-to-explain-why-the-intuitive-solution-wont-work) for explanation\n\n# Code\n```rust []\nuse rand::Rng;\nuse std::collections::BTreeMap;\n\nstruct Solution {\n total_sum: i32,\n mp: BTreeMap<i32, Vec<i32>>,\n}\n\nimpl Solution {\n\n fn new(rects: Vec<Vec<i32>>) -> Self {\n let (mut total_sum, mut mp) = (0, BTreeMap::new());\n \n for rec in rects {\n let (x1, y1, x2, y2) = (rec[0], rec[1], rec[2], rec[3]);\n total_sum += (x2-x1+1)*(y2-y1+1);\n mp.insert(total_sum, rec);\n }\n\n Self {total_sum, mp}\n }\n \n fn pick(&self) -> Vec<i32> {\n let mut rng = rand::thread_rng();\n let area = rng.gen_range(0..=self.total_sum);\n let rec = self.mp.range(area..).next().unwrap().1;\n\n let (x1, y1, x2, y2) = (rec[0], rec[1], rec[2], rec[3]);\n\n let x = rng.gen_range(x1..=x2);\n let y = rng.gen_range(y1..=y2);\n\n vec![x,y]\n }\n}\n``` | 1 | 0 | ['Binary Search', 'Rust'] | 0 |
random-point-in-non-overlapping-rectangles | Based on the area | based-on-the-area-by-gorums-n9jy | Intuition\nUsing copilot\n\n# Approach\n1.\tInitialization (Solution constructor): The algorithm starts by calculating the area of each rectangle. The area is c | gorums | NORMAL | 2024-03-05T16:47:17.501673+00:00 | 2024-03-05T16:47:17.501701+00:00 | 80 | false | # Intuition\nUsing copilot\n\n# Approach\n1.\tInitialization (Solution constructor): The algorithm starts by calculating the area of each rectangle. The area is calculated as (x2 - x1 + 1) * (y2 - y1 + 1), where (x1, y1) are the coordinates of the bottom-left corner and (x2, y2) are the coordinates of the top-right corner. The "+1" is because the points on the rectangle\'s perimeter are included. The areas are accumulated in the areas array. This array will be used to pick a rectangle with a probability proportional to its area.\n2.\tPick a rectangle: When the Pick method is called, the algorithm first needs to decide which rectangle to pick a point from. This is done by generating a random number between 1 and the total area of all rectangles (which is the last element in the areas array). Then, it uses a binary search (Array.BinarySearch) to find the index of the rectangle that this random number falls into. The binary search returns the index of the first rectangle in areas where the cumulative area is greater than or equal to the random number. This way, rectangles with larger areas (and thus larger ranges in the areas array) are more likely to be chosen.\n3.\tPick a point within the rectangle: Once a rectangle is chosen, the algorithm generates two more random numbers: one for the x-coordinate and one for the y-coordinate. These numbers are between the minimum and maximum x and y values of the rectangle, respectively. The point with these x and y coordinates is the point that the Pick method returns.\n\n# Complexity\n- Time complexity:\n$$O(log n)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\nusing System;\nusing System.Linq;\n\npublic class Solution {\n\n private int[][] rects;\n private int[] areas;\n private Random rand = new Random();\n\n public Solution(int[][] rects) {\n this.rects = rects;\n this.areas = new int[rects.Length];\n int totalArea = 0;\n for (int i = 0; i < rects.Length; i++)\n {\n // calculate the area of the rectangle\n int area = (rects[i][2] - rects[i][0] + 1) * (rects[i][3] - rects[i][1] + 1);\n totalArea += area;\n this.areas[i] = totalArea;\n }\n }\n \n public int[] Pick() {\n // pick a rectangle\n int randArea = rand.Next(areas.Last()) + 1;\n int index = Array.BinarySearch(areas, randArea);\n if (index < 0)\n index = ~index;\n\n // pick a point within the rectangle\n int[] rect = rects[index];\n int x = rand.Next(rect[0], rect[2] + 1);\n int y = rand.Next(rect[1], rect[3] + 1);\n return new int[] { x, y };\n }\n}\n\n/**\n * Your Solution object will be instantiated and called as such:\n * Solution obj = new Solution(rects);\n * int[] param_1 = obj.Pick();\n */\n``` | 1 | 0 | ['Randomized', 'C#'] | 0 |
random-point-in-non-overlapping-rectangles | Try to Explain with pen ,paper... | try-to-explain-with-pen-paper-by-ankit14-a0wu | Similar Question - https://leetcode.com/problems/random-pick-with-weight/description/\n# Approach\n Describe your approach to solving the problem. \n### Look c | ankit1478 | NORMAL | 2024-01-09T13:06:12.200036+00:00 | 2024-01-09T13:24:27.104526+00:00 | 287 | false | Similar Question - https://leetcode.com/problems/random-pick-with-weight/description/\n# Approach\n<!-- Describe your approach to solving the problem. -->\n### Look code after each step of Explanation \n\n\n\n\n\n\n\n# Code\n```\nclass Solution {\n Random rand;\n TreeMap<Integer, Integer> map;\n int area;\n int rect[][];\n\n public Solution(int[][] rects) {\n this.rect = rects;\n rand = new Random();\n area =0;\n map = new TreeMap<>();\n\n for(int i =0;i<rect.length;i++){\n area += (rect[i][2] - rect[i][0]+1) * (rect[i][3] - rect[i][1]+1);\n map.put(area,i);\n }\n }\n\n public int[] pick() {\n int randVal = rand.nextInt(area);\n int key = map.higherKey(randVal);\n int rects[] = rect[map.get(key)];\n\n int offset = key - randVal - 1;\n int width = rects[2] - rects[0] + 1; \n\n // The modulo operation ensures that the result is within the range [0, width-1].\n int x = offset % (width) + rects[0];\n \n // The divide operation ensures that the result is within the range [0, width-1].\n int y = offset / (width) + rects[1];\n\n return new int[] { x, y};\n }\n}\n``` | 1 | 0 | ['Ordered Map', 'Java'] | 1 |
random-point-in-non-overlapping-rectangles | EAZY || 90% || 30DAYS 6COMPAINES | eazy-90-30days-6compaines-by-bhav1729-oajo | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | bhav1729 | NORMAL | 2024-01-06T19:40:28.060781+00:00 | 2024-01-06T19:40:28.060815+00:00 | 20 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic: \n vector<vector<int>> rects;\n int i=0;\n int x,y;\n Solution(vector<vector<int>>& rects) {\n this->rects=rects;\n x=rects[i][0];\n y=rects[i][1];\n }\n \n vector<int> pick() {\n vector<int>ans={x,y};\n x++;\n if(x>rects[i][2]){\n x=rects[i][0];\n y++;\n }\n if(y>rects[i][3]){\n if(i+1<rects.size()){\n i++;\n }\n else{\n i=0;\n }\n x=rects[i][0];\n y=rects[i][1];\n }\n return ans;\n }\n};\n\n/**\n * Your Solution object will be instantiated and called as such:\n * Solution* obj = new Solution(rects);\n * vector<int> param_1 = obj->pick();\n */\n```\n# JOIN\n-Let\'s collaborate! Join me on GitHub to work on this challenge together :-\n-[https://github.com/MITTALBHAVYA/6companies30dayschallange]()\n# UPVOTE PLEASE\n\n | 1 | 0 | ['Array', 'Math', 'Binary Search', 'Reservoir Sampling', 'Prefix Sum', 'Ordered Set', 'Randomized', 'C++'] | 0 |
random-point-in-non-overlapping-rectangles | Java solution with comment explanation | java-solution-with-comment-explanation-b-l190 | \n\n# Code\n\nclass Solution {\n \n int[][] rects;\n TreeMap<Integer, Integer> weightedRectIndex = new TreeMap<>();\n int nPoints = 0;\n \n Ra | safo-samson | NORMAL | 2023-05-12T09:54:10.140279+00:00 | 2023-05-12T09:54:10.140305+00:00 | 788 | false | \n\n# Code\n```\nclass Solution {\n \n int[][] rects;\n TreeMap<Integer, Integer> weightedRectIndex = new TreeMap<>();\n int nPoints = 0;\n \n Random rng = new Random();\n\n public Solution(int[][] rects) {\n this.rects = rects;\n int index = 0;\n for (int[] rect : rects) {\n\t\t // inserts cumulative weight key pointing to rectangle index\n weightedRectIndex.put(nPoints, index++);\n nPoints += width(rect) * height(rect);\n }\n }\n \n public int[] pick() {\n\t // generates random point within total weight\n int point = rng.nextInt(nPoints);\n\t\t// finds appropriate rectangle\n var entry = weightedRectIndex.floorEntry(point);\n\t\t// find point within the current rectangle\n int rectPoint = point - entry.getKey();\n int[] rect = rects[entry.getValue()];\n return new int[]{\n rect[0] + rectPoint % width(rect), \n rect[1] + rectPoint / width(rect)};\n }\n \n private int width(int[] rect) {\n return rect[2] - rect[0] + 1;\n }\n \n private int height(int[] rect) {\n return rect[3] - rect[1] + 1;\n }\n}\n``` | 1 | 0 | ['Array', 'Math', 'Binary Search', 'Reservoir Sampling', 'Java'] | 0 |
random-point-in-non-overlapping-rectangles | Solution | solution-by-deleted_user-pgif | C++ []\nclass Solution {\npublic:\n vector<vector<int>> r;\n vector<int> acc;\n Solution(vector<vector<int>>& rects){\n\n std::ios_base::sync_wi | deleted_user | NORMAL | 2023-05-10T08:10:26.165510+00:00 | 2023-05-10T08:58:05.372264+00:00 | 340 | false | ```C++ []\nclass Solution {\npublic:\n vector<vector<int>> r;\n vector<int> acc;\n Solution(vector<vector<int>>& rects){\n\n std::ios_base::sync_with_stdio(false);\n cin.tie(0);\n\n r = rects;\n int len = rects.size();\n acc = vector<int>(len, 0);\n\n for(int i = 0; i < len; i++){\n const vector<int> &v = rects[i];\n acc[i] = ( i==0 ? 0: acc[i-1]) + (v[2] - v[0] + 1)*(v[3]-v[1]+1);\n }\n srand((unsigned)time(NULL));\n }\n vector<int> pick() {\n int target = rand()%acc.back();\n\n int start = 0;\n int end = acc.size();\n while (start < end){\n int mid = (start+end)/2;\n int mval = acc[mid];\n if (target == mval){\n start = mid + 1;\n break;\n }\n else if (target > mval){\n start = mid + 1;\n }\n else{\n end = mid;\n }\n }\n const vector<int> &v = r[start];\n int dx = v[2] - v[0] + 1;\n int x = v[0] + rand()%dx;\n int dy = v[3] - v[1] + 1;\n int y = v[1] + rand()%dy;\n return {x,y};\n }\n};\n```\n\n```Python3 []\nfrom typing import Generator\n\nclass Solution:\n def __init__(self, rects: List[List[int]]):\n self._rects = rects\n self._pg = self._pick_generator()\n \n def _pick_generator(self) -> Generator[List[int], None, None]:\n for a, b, x, y in self._rects:\n for i in range (a, x+1):\n for j in range (b, y+1):\n yield [i, j]\n\n def pick(self) -> List[int]:\n try:\n return next(self._pg)\n except StopIteration:\n self._pg = self._pick_generator()\n return next(self._pg)\n```\n\n```Java []\nclass Solution {\n public Solution(int[][] rects) {\n this.rects = rects;\n areas = new int[rects.length];\n for (int i = 0; i < rects.length; ++i)\n areas[i] = getArea(rects[i]) + (i > 0 ? areas[i - 1] : 0);\n }\n public int[] pick() {\n final int target = rand.nextInt(areas[areas.length - 1]);\n final int index = firstGreater(areas, target);\n final int[] r = rects[index];\n return new int[] {\n rand.nextInt(r[2] - r[0] + 1) + r[0],\n rand.nextInt(r[3] - r[1] + 1) + r[1],\n };\n }\n private int[][] rects;\n private int[] areas;\n private Random rand = new Random();\n\n private int getArea(int[] r) {\n return (r[2] - r[0] + 1) * (r[3] - r[1] + 1);\n }\n private int firstGreater(int[] areas, int target) {\n int l = 0;\n int r = areas.length;\n while (l < r) {\n final int m = (l + r) / 2;\n if (areas[m] > target)\n r = m;\n else\n l = m + 1;\n }\n return l;\n }\n}\n```\n | 1 | 0 | ['C++', 'Java', 'Python3'] | 1 |
random-point-in-non-overlapping-rectangles | Python | Binary Search | O(logn) per Pick | python-binary-search-ologn-per-pick-by-a-13fw | ```\nfrom itertools import accumulate\nfrom random import randint\nfrom bisect import bisect_left\nclass Solution:\n\n def init(self, rects: List[List[int]]) | aryonbe | NORMAL | 2022-08-25T03:02:59.296710+00:00 | 2022-08-25T03:02:59.296746+00:00 | 122 | false | ```\nfrom itertools import accumulate\nfrom random import randint\nfrom bisect import bisect_left\nclass Solution:\n\n def __init__(self, rects: List[List[int]]):\n self.rects = rects\n self.acc = list(accumulate([ (x2-x1+1)*(y2-y1+1) for x1, y1, x2, y2 in rects ], initial = 0))\n\n def pick(self) -> List[int]:\n r = randint(1, self.acc[-1])\n i = bisect_left(self.acc, r)\n delta = r - self.acc[i-1] - 1\n x1, y1, x2, y2 = self.rects[i-1]\n dx, dy = delta % (x2-x1+1), delta // (x2-x1+1) \n return (x1 + dx, y1 + dy) | 1 | 0 | ['Python'] | 0 |
random-point-in-non-overlapping-rectangles | Help! Why no working for the last 3 case? (Resolved: count the total pts inside each rec not area) | help-why-no-working-for-the-last-3-case-7kz1v | Now I understand. In order to solve this problem, we assume that the proportion is on the number of total points each rectangle not the area.\nThe difference is | vonnan | NORMAL | 2022-08-13T05:22:07.909102+00:00 | 2023-04-14T17:09:43.539008+00:00 | 336 | false | Now I understand. In order to solve this problem, we assume that the proportion is on the number of total points each rectangle not the area.\nThe difference is as follows\nAssume the rectangle is [x1, y1, x2, y2] where (x1,y1) the bottom left corner and (x2,y2) the top right corner\nThe area of the rectangle is (x2 - x1) * (y2 - y1) while the total points are (x2 - x1 + 1) * (y2 - y1 + 1)\n\n\n```\nfrom bisect import bisect_left\nfrom random import randint\n\nclass Solution:\n\n def __init__(self, rects: List[List[int]]):\n self.res = []\n self.tot = 0\n self.dic = {}\n for a, b, c, d in rects:\n area = (c - a + 1) * (d - b + 1)\n self.tot += area\n self.res.append(self.tot)\n self.dic[self.tot] = [a, b, c, d]\n\n def pick(self) -> List[int]:\n random = randint(1, self.tot)\n idx = bisect_left(self.res, random)\n a, b, c, d = self.dic[self.res[idx]]\n return [randint(a, c), randint(b, d)]\n\n\n```\n------------------------------------------------------------------------\n\nI did the picking proportionally to the area. I tried several ways. One way is by randint, oneway is using choices with weight function of individual weight. None is working...Please help!\n\n"""\nfrom bisect import bisect\nfrom random import randint\n\nclass Solution:\n\n def __init__(self, rects: List[List[int]]):\n self.x = [[a, c] for a,b,c,d in rects]\n self.y = [[b, d] for a,b,c,d in rects]\n sa, self.area = 0, []\n for a,b,c,d in rects:\n sa += (d -b) * (c - a)\n self.area.append(sa)\n \n\n def pick(self) -> List[int]:\n idx = bisect(self.area, randint(1, self.area[-1])) - 1\n x1,x2 = self.x[idx]\n y1,y2 = self.y[idx]\n return randint(x1, x2), randint(y1,y2)\n"""\n | 1 | 0 | ['Python3'] | 1 |
random-point-in-non-overlapping-rectangles | [Java] 100% Solution | java-100-solution-by-a_love_r-ycfl | ~~~java\n\nclass Solution {\n // 1. pick a rect\n // 2. pick a point inside this rect\n int[][] rects;\n int[] prefixWeights;\n Random rd;\n\n | a_love_r | NORMAL | 2022-01-30T19:32:23.921130+00:00 | 2022-01-30T19:32:23.921173+00:00 | 136 | false | ~~~java\n\nclass Solution {\n // 1. pick a rect\n // 2. pick a point inside this rect\n int[][] rects;\n int[] prefixWeights;\n Random rd;\n\n public Solution(int[][] rects) {\n this.rects = rects;\n this.prefixWeights = new int[rects.length];\n this.rd = new Random();\n \n for (int i = 0; i < rects.length; i++) {\n int[] rect = rects[i];\n int width = rect[2] - rect[0] + 1;\n int height = rect[3] - rect[1] + 1;\n prefixWeights[i] = (i == 0 ? 0 : prefixWeights[i - 1]) + width * height;\n }\n }\n \n public int[] pick() {\n int rdWeight = rd.nextInt(prefixWeights[prefixWeights.length - 1]);\n int rectIdx = findFirstGreater(rdWeight);\n int[] rect = rects[rectIdx];\n \n int width = rect[2] - rect[0] + 1;\n int height = rect[3] - rect[1] + 1;\n int total = width * height;\n int rdPoint = rd.nextInt(total);\n return new int[]{\n rect[0] + rdPoint % width,\n rect[1] + rdPoint / width\n };\n }\n \n private int findFirstGreater(int target) {\n int l = 0, r = prefixWeights.length - 1;\n while (l < r - 1) {\n int mid = l + (r - l) / 2;\n if (prefixWeights[mid] <= target) {\n l = mid + 1;\n } else {\n r = mid;\n }\n }\n return prefixWeights[l] > target ? l : r;\n }\n}\n\n\n~~~ | 1 | 0 | [] | 0 |
random-point-in-non-overlapping-rectangles | Why using one Rand() failed 3 out of 35 test cases, while using 3 Rand() passed all? | why-using-one-rand-failed-3-out-of-35-te-hsx5 | Following is the version of using one rand() per pick, and it failed 3 test cases.\n\nclass Solution {\npublic:\n vector<int> prefix_sum;\n vector<vector< | Peak_2250_MID_in_King-of-Glory | NORMAL | 2022-01-08T01:21:20.631226+00:00 | 2022-01-08T01:21:20.631273+00:00 | 153 | false | Following is the version of using one rand() per pick, and it failed 3 test cases.\n```\nclass Solution {\npublic:\n vector<int> prefix_sum;\n vector<vector<int>> rects_vec;\n int total = 0;\n \n Solution(vector<vector<int>>& rects) {\n int cur = 0;\n for (int i = 0; i < rects.size(); ++i) {\n cur += (rects[i][2] - rects[i][0] + 1) * (rects[i][3] - rects[i][1] + 1);\n prefix_sum.push_back(cur);\n }\n rects_vec = rects;\n total = cur;\n }\n \n vector<int> pick() {\n int l = 0, r = prefix_sum.size() - 1, mid = 0;\n int rand_num = rand();\n int target = (rand_num % total) + 1;\n\t\t\n while (l <= r) {\n mid = l + (r - l) / 2;\n if (prefix_sum[mid] < target) l = mid + 1;\n else r = mid - 1;\n }\n \n return {rand_num % (rects_vec[l][2] - rects_vec[l][0] + 1) + rects_vec[l][0],\n rand_num % (rects_vec[l][3] - rects_vec[l][1] + 1) + rects_vec[l][1]};\n }\n};\n```\n\nThen I changed rand_num to rand(), it passes all the test cases, what could be the reason??? Really confused\n```\nclass Solution {\npublic:\n vector<int> prefix_sum;\n vector<vector<int>> rects_vec;\n int total = 0;\n \n Solution(vector<vector<int>>& rects) {\n int cur = 0;\n for (int i = 0; i < rects.size(); ++i) {\n cur += (rects[i][2] - rects[i][0] + 1) * (rects[i][3] - rects[i][1] + 1);\n prefix_sum.push_back(cur);\n }\n rects_vec = rects;\n total = cur;\n }\n \n vector<int> pick() {\n int l = 0, r = prefix_sum.size() - 1, mid = 0;\n int rand_num = rand();\n int target = (rand_num % total) + 1;\n \n while (l <= r) {\n mid = l + (r - l) / 2;\n if (prefix_sum[mid] < target) l = mid + 1;\n else r = mid - 1;\n }\n \n return {rand() % (rects_vec[l][2] - rects_vec[l][0] + 1) + rects_vec[l][0],\n rand() % (rects_vec[l][3] - rects_vec[l][1] + 1) + rects_vec[l][1]};\n }\n};\n``` | 1 | 0 | ['C'] | 0 |
random-point-in-non-overlapping-rectangles | Python Binary Search | python-binary-search-by-ypatel38-iy4v | \nclass Solution:\n def __init__(self, rects: List[List[int]]):\n self.rects = rects\n self.search_space = []\n\n for i, rect in enumera | ypatel38 | NORMAL | 2021-09-09T02:06:02.911312+00:00 | 2021-09-09T02:07:05.961048+00:00 | 310 | false | ```\nclass Solution:\n def __init__(self, rects: List[List[int]]):\n self.rects = rects\n self.search_space = []\n\n for i, rect in enumerate(rects):\n a, b, c, d = rect\n self.search_space.append((d - b + 1) * (c - a + 1))\n if i != 0:\n self.search_space[i] += self.search_space[i - 1]\n \n\n def pick(self) -> List[int]:\n randval = random.randint(0, self.search_space[-1] - 1)\n\n low = 0\n high = len(self.search_space) - 1\n\n while low < high:\n midpt = low + (high - low) // 2\n\n if self.search_space[midpt] <= randval:\n low = midpt + 1\n else:\n high = midpt\n\n\n rect = self.rects[low]\n rect_range = randval\n\n if low > 0:\n rect_range -= self.search_space[low - 1] \n\n\n a, b, c, d = rect\n\n return [(rect_range % (c - a + 1)) + a, (rect_range // (c - a + 1)) + b]\n``` | 1 | 0 | ['Binary Tree', 'Python', 'Python3'] | 0 |
random-point-in-non-overlapping-rectangles | Python using choices with weight | python-using-choices-with-weight-by-iori-t9uf | \nimport random\nclass Solution:\n def __init__(self, rects: List[List[int]]):\n self.rects = rects\n self.weights = []\n for i, r in en | iorilan | NORMAL | 2021-06-30T13:28:56.733917+00:00 | 2021-06-30T13:28:56.733964+00:00 | 128 | false | ```\nimport random\nclass Solution:\n def __init__(self, rects: List[List[int]]):\n self.rects = rects\n self.weights = []\n for i, r in enumerate(self.rects):\n x1, y1, x2, y2 = r\n self.weights.append((x2-x1+1)*(y2-y1+1))\n def pick(self) -> List[int]:\n points = []\n for i, r in enumerate(self.rects):\n x1, y1, x2, y2 = r\n x, y = random.randint(x1, x2), random.randint(y1, y2)\n points.append((x,y))\n # using weights is the weight the possibility based on area of each rect\n # bigger area will get higher chance\n return random.choices(points, weights=self.weights, cum_weights=None, k=1)[0]\n``` | 1 | 0 | [] | 0 |
random-point-in-non-overlapping-rectangles | C++ Solution using Binary search with explanation | c-solution-using-binary-search-with-expl-ab92 | \nclass Solution {\n //concept is simple\n //we need to pick the coordinates from the rectangle space\n //for that we will use rand() function to find | jyotsnamunjal9 | NORMAL | 2021-01-02T06:09:12.772212+00:00 | 2021-01-02T06:09:12.772256+00:00 | 249 | false | ```\nclass Solution {\n //concept is simple\n //we need to pick the coordinates from the rectangle space\n //for that we will use rand() function to find out randomly any rectangle\n //but to which we will apply rand()\n //that should be cumulative sum of areas why?? because we can\'t use area of any rect that\'s not unique but cumulative sum is unique\n //area of any rectangle can be given by (x[2]-x[0]+1) * (x[3]-x[1]+1)\n //we will store this inside a rectangle to store the cumulative sum for each rectange\nprivate:\n vector<vector<int>> rects;\n vector<pair<int,int>> sums;\n int sum = 0;\n \n //returns index of random sum if found returns that index else returns lowerBound(index with value not lesser than randomSum)\n int findIndexOfRandomSum(int randomSum) {\n int lowerBound = 0, upperBound = sums.size() - 1;\n while(lowerBound <= upperBound) {\n int middle = lowerBound + (upperBound - lowerBound)/2;\n int sumValue = sums[middle].first;\n if(sumValue > randomSum) {\n upperBound = middle - 1;\n } else if(sumValue < randomSum) {\n lowerBound = middle + 1; \n } else {\n return middle;\n } \n }\n return lowerBound; \n }\n \npublic:\n Solution(vector<vector<int>>& rects) {\n int size = rects.size();\n this->rects = rects;\n for(int i = 0; i < size; i++) {\n int x1 = rects[i][0], x2 = rects[i][2], y1 = rects[i][1], y2 = rects[i][3];\n sum += ((x2-x1+1)*(y2-y1+1));\n sums.push_back(make_pair(sum, i));\n } \n }\n \n vector<int> pick() {\n int randomSum = rand()%(sum) + 1; //gives random value from 0 to sum inclusive all\n int index = findIndexOfRandomSum(randomSum);\n int x1 = rects[index][0], x2 = rects[index][2], y1 = rects[index][1], y2 = rects[index][3];\n vector<int> result;\n result.push_back(x1 + rand()%(x2-x1+1));\n result.push_back(y1+rand()%(y2-y1+1));\n return result; \n }\n};\n\n/**\n * Your Solution object will be instantiated and called as such:\n * Solution* obj = new Solution(rects);\n * vector<int> param_1 = obj->pick();\n */\n``` | 1 | 0 | [] | 0 |
random-point-in-non-overlapping-rectangles | Java solution explained using array | java-solution-explained-using-array-by-r-a9ms | class Solution {\n\n int arr[];\n Random rand;\n int cumulativeSum;\n int rectangles[][];\n public Solution(int[][] rects) {\n rectangles | rocx96 | NORMAL | 2020-09-25T05:03:30.826380+00:00 | 2020-09-25T05:11:14.659029+00:00 | 230 | false | class Solution {\n\n int arr[];\n Random rand;\n int cumulativeSum;\n int rectangles[][];\n public Solution(int[][] rects) {\n rectangles = rects;\n rand = new Random();\n int n = rects.length;\n arr = new int[n];\n cumulativeSum = 0;\n for(int i=0;i<n;i++) {\n int each[] = rects[i];\n\t\t\t// finding the number of points within this rectangle \n int curPoints = (each[2] - each[0] + 1) * (each[3] - each[1] + 1);\n\t\t\t\n\t\t\t// It will be easier to select index if we maintain cumulative probabilities.\n\t\t\t// Because binary search works on sorted array. \n\t\t\t// If we maintain only curPoints, then we need to sort that array. Then it takes a lot of time.\n\t\t\t// If we maintain cumulative curPoints then it will always be in sorted manner and then difference between two adjacent curPoints is more, then then there are more chances to get that index.\n cumulativeSum += curPoints;\n arr[i] = cumulativeSum;\n }\n }\n \n public int[] pick() {\n\t\n\t\t// Finding random integer between [1, cumulativeSum]\n int randSum = rand.nextInt(cumulativeSum + 1);\n \n int l = 0;\n int r = arr.length;\n \n\t\t// Picking the upper bound\n while(l < r) {\n int m = l + (r-l)/2;\n \n if(arr[m] > randSum)\n r = m;\n else\n l = m+1;\n }\n \n int pickedRect[] = l < arr.length ? rectangles[l]: rectangles[l-1];\n \n int bl = pickedRect[0];\n int br = pickedRect[1];\n int tl = pickedRect[2];\n int tr = pickedRect[3];\n \n\t\t// Picking the random point within the chosen rectangle\n\t\t// We need to choose a point , let it be (x, y)\n\t\t// x can run from pickedRect[0] to pickedRect[2]\n\t\t// y can run from pickedRect[1] to pickedRect[3]\n return new int[]{bl + rand.nextInt(tl-bl+1), br + rand.nextInt(tr-br+1)};\n \n }\n}\n\n/**\n * Your Solution object will be instantiated and called as such:\n * Solution obj = new Solution(rects);\n * int[] param_1 = obj.pick();\n */ | 1 | 0 | ['Binary Tree'] | 0 |
random-point-in-non-overlapping-rectangles | Go | go-by-dynasty919-na6b | \ntype Solution struct {\n list []rec\n sum int\n}\n\ntype rec struct {\n bottomleft [2]int\n l int\n w int\n prefixPoints int\n}\n\nfunc Cons | dynasty919 | NORMAL | 2020-09-20T08:12:10.018763+00:00 | 2020-09-20T08:12:10.018806+00:00 | 58 | false | ```\ntype Solution struct {\n list []rec\n sum int\n}\n\ntype rec struct {\n bottomleft [2]int\n l int\n w int\n prefixPoints int\n}\n\nfunc Constructor(rects [][]int) Solution {\n list := make([]rec, len(rects))\n sum := 0\n for i, v := range rects {\n a, b := v[2] - v[0] + 1, v[3] - v[1] + 1\n list[i] = rec{bottomleft: [2]int{v[0], v[1]},\n l: a,\n w: b,\n prefixPoints: sum + a * b}\n sum += a * b\n }\n return Solution{list: list,\n sum: sum}\n}\n\n\nfunc (this *Solution) Pick() []int {\n tar := rand.Intn(this.sum + 1)\n index := sort.Search(len(this.list), func(i int) bool {\n return this.list[i].prefixPoints >= tar\n })\n l := this.list[index].l\n w := this.list[index].w\n return []int{rand.Intn(l) + this.list[index].bottomleft[0], \n rand.Intn(w) + this.list[index].bottomleft[1],\n }\n}\n``` | 1 | 0 | [] | 0 |
random-point-in-non-overlapping-rectangles | Python 3 + Prefix Sum & Binary Search Explanation | python-3-prefix-sum-binary-search-explan-3hqs | Since the question asks us to sample a random point in the available space marked out by the rectangles with a uniform probability, we need to weight our choice | amronagdy | NORMAL | 2020-09-13T18:53:05.582712+00:00 | 2020-09-13T18:53:05.582757+00:00 | 116 | false | * Since the question asks us to sample a random point in the available space marked out by the rectangles **with a uniform probability**, we need to weight our choice of which rectangle to pick a random point from by its area.\n\t* Therefore this question can be reduced to a weighted probability selection question.\n\t* I.e. A bigger rectangle (in terms of area) should be proportionately more likely to be selected than a smaller one.\n* For readability you can delegate methods to do with rectangles into a `Rectangle` class.\n* We use a `prefixAreaSum` array that is just a prefix sum array of all rectangles\' areas.\n\t* We will use this `prefixAreaSum` array as a way of choosing a specific rectangle to sample a random point from.\n* We can weight our selection of rectangles by area by:\n\t1. Selecting a random number between 0 and the `totalAreaSum`.\n\t2. Searching for the nearest index that has that random number (using binary search, `bisect` in Python).\n\t3. Getting the rectangle corresponding to the index in the `prefixAreaSum` array and getting a random point from it.\n```\nfrom typing import Tuple\nfrom random import randint\nfrom bisect import bisect\n\nclass Rectangle:\n \n def __init__(self, x1: int, y1: int, x2: int, y2: int):\n self.x1 = x1\n self.y1 = y1\n self.x2 = x2\n self.y2 = y2\n\n def getRandomPoint(self) -> Tuple[int, int]:\n return (randint(self.x1, self.x2), randint(self.y1, self.y2))\n \n def getArea(self) -> int:\n return (self.x2 - self.x1 + 1) * (self.y2 - self.y1 + 1)\n\nclass Solution:\n\n def __init__(self, rects: List[List[int]]):\n self.rectangles = [Rectangle(x1, y1, x2, y2) for x1, y1, x2, y2 in rects]\n\n currentAreaSum = 0\n self.prefixAreaSum = []\n for rectangle in self.rectangles:\n currentAreaSum += rectangle.getArea()\n self.prefixAreaSum.append(currentAreaSum)\n \n self.totalAreaSum = self.prefixAreaSum[-1]\n \n \n def pick(self) -> List[int]:\n index = bisect(self.prefixAreaSum, randint(0, self.totalAreaSum))\n return self.rectangles[min(index, len(self.prefixAreaSum) - 1)].getRandomPoint()\n``` | 1 | 0 | [] | 0 |
random-point-in-non-overlapping-rectangles | Largest Component Size by Common Factor in C++ | largest-component-size-by-common-factor-rfj2f | An understandable approach using C++ : map all the elements with its factors, so mapping process would take o(n*sqrt(n)) for all the elements. Then iterate thro | chandms | NORMAL | 2020-08-30T13:38:51.628988+00:00 | 2020-08-30T13:38:51.629025+00:00 | 497 | false | An understandable approach using C++ : map all the elements with its factors, so mapping process would take o(n*sqrt(n)) for all the elements. Then iterate through map and connect consecutive elements under a key, except key=1.Then apply dfs for rest of the process.\n```\nclass Solution {\n void fac(map <int,vector<int> > &mp,int a,int p){\n for(int i=1;i<=sqrt(a);i++){\n if(a%i==0){\n if(a/i==i)\n mp[i].push_back(p);\n else \n {\n mp[i].push_back(p);\n mp[a/i].push_back(p);\n }\n }\n }\n }\n void print(vector < vector<int> > &v){\n \n for(int i=0;i<v.size();i++){\n cout<<i<<" : ";\n for(int k=0;k<v[i].size();k++)\n cout<<v[i][k]<<" ";\n cout<<endl;\n }\n }\n void dfs(vector <vector<int> > &g, vector<bool>&b,int s,int &t){\n stack <int> st;\n st.push(s);\n \n while(!st.empty()){\n int x=st.top();\n st.pop();\n if(b[x]==0){\n b[x]=1;\n t++;\n for(int j=0;j<g[x].size();j++){\n if(b[g[x][j]]==0)\n st.push(g[x][j]);\n \n }\n }\n }\n \n }\npublic:\n int largestComponentSize(vector<int>& A) {\n \n map<int, vector<int> > mp;\n for(int i=0;i<A.size();i++){\n fac(mp,A[i],i);\n }\n \n vector < vector<int> > g(A.size());\n for(auto u : mp){\n if(u.second.size()>1 && u.first!=1){\n for(int i=0;i<u.second.size()-1;i++){\n g[u.second[i]].push_back(u.second[i+1]);\n g[u.second[i+1]].push_back(u.second[i]);\n }\n }\n }\n \n //print(g);\n \n int mc=1;\n vector <bool> b(A.size(),0);\n for(int j=0;j<b.size();j++){\n if(b[j]==0){\n int t=0;\n dfs(g,b,j,t);\n mc=max(mc,t);\n \n }\n }\n return mc;\n \n \n \n }\n};\n``` | 1 | 1 | [] | 0 |
random-point-in-non-overlapping-rectangles | simplest pancake C++ soution using vector , reverse function | simplest-pancake-c-soution-using-vector-i70l0 | \nclass Solution {\npublic:\n void flip(vector<int> &v , int k){\n reverse(v.begin() , v.begin() + k+1);\n }\n vector<int> pancakeSort(vector<in | holmes_36 | NORMAL | 2020-08-29T15:27:44.641504+00:00 | 2020-08-29T15:29:36.333655+00:00 | 120 | false | ```\nclass Solution {\npublic:\n void flip(vector<int> &v , int k){\n reverse(v.begin() , v.begin() + k+1);\n }\n vector<int> pancakeSort(vector<int>& A) {\n vector<int>ans;\n int n = A.size();\n //int mx = INT_MIN , imx ;\n for(int sz = n;sz>1;sz--){\n int mx = INT_MIN , imx ; // mx = max element within sz and imx = index of max element\n for(int i =0;i<sz;i++){\n if(mx < A[i]){\n imx = i;\n mx = A[i];\n }\n }\n \n ans.push_back(imx + 1);\n flip(A , imx);\n ans.push_back(sz);\n flip(A , sz -1);\n \n }\n \n return ans;\n }\n};\n```\n\n\n | 1 | 1 | [] | 0 |
random-point-in-non-overlapping-rectangles | Minimum Cost For Tickets | minimum-cost-for-tickets-by-shin_crayon-ikw8 | Let OPT(i, j) is the minimum cost you need to spend to travel from day i-th to day j-th.\nWe have 3 options to buy ticket at a day:\n Buy 1-day pass with the pr | shin_crayon | NORMAL | 2020-08-27T10:24:37.713789+00:00 | 2020-08-27T10:24:37.713834+00:00 | 127 | false | Let OPT(i, j) is the minimum cost you need to spend to travel from day i-th to day j-th.\nWe have 3 options to buy ticket at a day:\n* Buy 1-day pass with the price costs[0]\n* Buy 7-day pass with the price costs[1]\n* Buy 30-day pass with the price costs[2]\n\nTherefore, we can set a target function as follow:\n```\nOPT(i, j) = min(costs[0] + OPT(i+1, j), \n costs[1] + OPT(i+7, j), \n costs[2] + OPT(i+30, j))\n```\n\nFrom this target function, we can easily to write python code as\n\n```\nimport bisect\nimport functools\nclass Solution:\n def mincostTickets(self, days: List[int], costs: List[int]) -> int:\n def find_next_day(start: int, no_of_days: int) -> int:\n next_idx = bisect.bisect_left(days, days[start] + no_of_days)\n \n # print (f\'{next_idx} {days}\')\n \n if next_idx < len(days):\n while next_idx - 1 >= 0 and days[next_idx] == days[next_idx - 1]:\n next_idx -= 1\n \n next_days = next_idx if next_idx < len(days) else -1\n \n return next_days\n \n @functools.lru_cache(maxsize=None)\n def solve(start: int) -> int:\n if start < 0 or start >= len(days):\n return 0\n \n one_day = costs[0] + solve(start + 1 if start + 1 < len(days) else -1)\n \n next_days = find_next_day(start, 7)\n \n seven_days = costs[1] + solve(next_days) \n \n next_days = find_next_day(start, 30)\n \n thiry_days = costs[2] + solve(next_days) \n \n return min(one_day, seven_days, thiry_days)\n \n return solve(0)\n``` | 1 | 0 | ['Dynamic Programming', 'Python3'] | 1 |
random-point-in-non-overlapping-rectangles | Minimum Cost For Tickets : Dynamic Programming: C++ | minimum-cost-for-tickets-dynamic-program-1nse | \nclass Solution {\npublic:\n int mincostTickets(vector<int>& days, vector<int>& costs) {\n set<int> dd(days.begin(),days.end());\n int cost[36 | isimran18 | NORMAL | 2020-08-25T10:43:00.870537+00:00 | 2020-08-25T10:43:00.870596+00:00 | 107 | false | ```\nclass Solution {\npublic:\n int mincostTickets(vector<int>& days, vector<int>& costs) {\n set<int> dd(days.begin(),days.end());\n int cost[366];\n memset(cost,0,sizeof(cost));\n int one=costs[0], seven=costs[1], thirty=costs[2];\n for(int i=1;i<=365;i++){\n cost[i] = cost[i-1];\n if(dd.find(i)!= dd.end()){\n cost[i] = min(cost[max(0,i-1)]+one, min(cost[max(0,i-7)]+seven, cost[max(0,i-30)]+thirty));\n }\n }\n return cost[365];\n }\n};\n``` | 1 | 0 | [] | 0 |
random-point-in-non-overlapping-rectangles | Java Solution with Explanation | java-solution-with-explanation-by-uddant-5d8x | \nclass Solution {\n Random random;\n TreeMap<Integer,int[]> map;\n int areaSum = 0;\n public Solution(int[][] rects) {\n random = new Random | uddantisaketh2001 | NORMAL | 2020-08-23T07:33:04.310148+00:00 | 2020-08-23T07:33:54.424650+00:00 | 103 | false | ```\nclass Solution {\n Random random;\n TreeMap<Integer,int[]> map;\n int areaSum = 0;\n public Solution(int[][] rects) {\n random = new Random();\n map = new TreeMap<>();\n \n for(int i = 0; i < rects.length; i++){\n int[] rectangleCoordinates = rects[i];\n int length = rectangleCoordinates[2] - rectangleCoordinates[0] + 1;\n int breadth = rectangleCoordinates[3] - rectangleCoordinates[1] + 1;\n \n areaSum += length * breadth;\n \n map.put(areaSum,rectangleCoordinates);\n }\n }\n \n public int[] pick() {\n //random.nextInt gives a int in the range of 0 to areaSum and ceilingKey returns a key greater than or equal to the argument passed\n //to it.\n int key = map.ceilingKey(random.nextInt(areaSum) + 1);\n int[] rectangle = map.get(key);\n \n int length = rectangle[2] - rectangle[0] + 1;\n int breadth = rectangle[3] - rectangle[1] + 1;\n \n //length denotes the no of x coordinates we can have.\n //breadth denotes the no of y coordinates we can have\n \n //random.nextInt gives a random value from x1 - x2-1 which we can add to the current x and we can have a valid x .\n //random.nextInt gives a random value from y1 - y2-1 which we can add to the current y and we can have a valid y .\n \n int x = rectangle[0] + random.nextInt(length);\n int y = rectangle[1] + random.nextInt(breadth);\n \n return new int[]{x,y};\n }\n}\n\n/**\n * Your Solution object will be instantiated and called as such:\n * Solution obj = new Solution(rects);\n * int[] param_1 = obj.pick();\n */\n``` | 1 | 0 | [] | 0 |
random-point-in-non-overlapping-rectangles | C# solution (prefixSum + binary search) | c-solution-prefixsum-binary-search-by-ne-0eeb | ```\npublic class Solution {\n\n public Random random;\n public int[][] rects;\n \n public int[] areasPrefixSum;\n public int areaSum;\n \n | newbiecoder1 | NORMAL | 2020-08-23T06:14:36.100470+00:00 | 2020-08-23T06:14:36.100508+00:00 | 51 | false | ```\npublic class Solution {\n\n public Random random;\n public int[][] rects;\n \n public int[] areasPrefixSum;\n public int areaSum;\n \n public Solution(int[][] rects) {\n \n random = new Random();\n this.rects = rects; \n areasPrefixSum = new int[rects.Length];\n \n for(int i = 0; i < rects.Length; i++)\n { \n // area: total points can be picked from current rectangle\n int area= (rects[i][2] - rects[i][0] + 1) * (rects[i][3] - rects[i][1] + 1);\n \n // areasPrefixSum[i]: total number of points can be picked from 0-th retangle to i-th retangle\n areasPrefixSum[i] = i == 0 ? area: areasPrefixSum[i - 1] + area;\n } \n \n areaSum = areasPrefixSum[rects.Length - 1]; \n }\n \n public int[] Pick() {\n \n int target = random.Next(0, areaSum) + 1; \n int rectIndex = BinarySearch(areasPrefixSum, target);\n\n int x = random.Next(rects[rectIndex][0], rects[rectIndex][2] + 1);\n int y = random.Next(rects[rectIndex][1], rects[rectIndex][3] + 1);\n \n return new int[]{x, y};\n }\n \n public int BinarySearch(int[] arr, int target)\n {\n int left = 0, right = arr.Length - 1;\n \n while(left <= right)\n {\n int mid = (right - left) + left / 2;\n if(arr[mid] == target)\n return mid;\n if(arr[mid] > target)\n right = mid - 1;\n else\n left = mid + 1;\n }\n \n return left;\n }\n} | 1 | 0 | [] | 0 |
random-point-in-non-overlapping-rectangles | Swift Explanation | swift-explanation-by-jtbergman-bzrp | A First Approach\nAn initial idea may be to select a rectangle at random then select a random point in that rectangle. However, we want to select a point unifor | jtbergman | NORMAL | 2020-08-23T02:37:45.019523+00:00 | 2020-08-23T02:37:45.019582+00:00 | 59 | false | **A First Approach**\nAn initial idea may be to select a rectangle at random then select a random point in that rectangle. However, we want to select a point uniformly at random from the entire space. Selecting a rectangle first, then selecting a point from that rectangle would give rectangles with small areas the same probability as rectangles with larger areas. Instead we need to find a method that gives rectangles with larger areas a higher probability. \n\n**A Correct Approach: Initialization**\nInitialization\n* We will store the total `area` of all the rectangles \n* To handle rectangles with `0` width or height we will add `1` to each dimension \n* We map the cumulative sum of the rectangles to the corresponding rectangle \n\nFor example, suppose we have rectangles `A, B, C` with area `2, 4, 8`. Then we would have `area = 14` and we would have \n``` \nareas = [2, 6, 14]\nmap = [\n 2: A, \n 6: B, \n 14: \n]\n```\n\n**A Correct Approach: Picking a Rectangle**\n1. Select any point in `0 ... area` and call it `rand`\n2. Select the first index in `areas` larger than or equal to `rand` \n3. Select the corresponding rectangle using `map[areas[idx]]`\n4. Select a random point from that rectangle\n\n**Solution**\n```swift\nclass Solution {\n \n // MARK: Properties \n \n var area = 0 \n var areas = [Int]()\n var map = [Int: [Int]]() \n \n\n // MARK: Initializer \n \n init(_ rects: [[Int]]) {\n for idx in 0 ..< rects.count {\n let rect = rects[idx]\n area += (rect[2] - rect[0] + 1) * (rect[3] - rect[1] + 1)\n areas.append(area)\n map[area] = rect\n }\n }\n \n func pick() -> [Int] {\n let rand = Int.random(in: 0 ... area)\n \n for idx in 0 ..< areas.count {\n if rand <= areas[idx] {\n let rect = map[areas[idx]]!\n return [\n Int.random(in: rect[0] ... rect[2]),\n Int.random(in: rect[1] ... rect[3])\n ]\n }\n }\n \n return [] \n }\n}\n``` | 1 | 0 | [] | 0 |
random-point-in-non-overlapping-rectangles | Python Simple Solution Explained (video + code) | python-simple-solution-explained-video-c-pyu5 | https://www.youtube.com/watch?v=mED_K_EaZIo\n\n\nimport random\nclass Solution:\n\n def __init__(self, rects: List[List[int]]):\n self.rects = rects\n | spec_he123 | NORMAL | 2020-08-22T22:07:12.938148+00:00 | 2020-08-22T22:07:12.938181+00:00 | 206 | false | https://www.youtube.com/watch?v=mED_K_EaZIo\n[](https://www.youtube.com/watch?v=mED_K_EaZIo)\n```\nimport random\nclass Solution:\n\n def __init__(self, rects: List[List[int]]):\n self.rects = rects\n self.weights = []\n self.sum_ = 0\n \n for x1, y1, x2, y2 in rects:\n num_points = (x2 - x1 + 1) * (y2 - y1 + 1)\n self.weights.append(num_points)\n self.sum_ += num_points\n \n self.weights = [x / self.sum_ for x in self.weights]\n\n def pick(self) -> List[int]:\n rectangle = random.choices(population = self.rects, weights = self.weights, k=1)[0]\n x1, y1, x2, y2 = rectangle\n return [random.randint(x1,x2), random.randint(y1,y2)]\n\n\n# Your Solution object will be instantiated and called as such:\n# obj = Solution(rects)\n# param_1 = obj.pick()\n``` | 1 | 0 | ['Python', 'Python3'] | 0 |
random-point-in-non-overlapping-rectangles | Most unreadable 1-Liner - just for fun! | most-unreadable-1-liner-just-for-fun-by-fvgei | class Solution:\n\n def __init__(self, rects: List[List[int]]):\n self.W = list(itertools.accumulate((x[2]-x[0]+1)*(x[3]-x[1]+1) for x in rects))\n | user0571rf | NORMAL | 2020-08-22T20:51:21.816974+00:00 | 2020-08-22T20:51:21.817023+00:00 | 171 | false | ```class Solution:\n\n def __init__(self, rects: List[List[int]]):\n self.W = list(itertools.accumulate((x[2]-x[0]+1)*(x[3]-x[1]+1) for x in rects))\n self.rects = rects\n\n def pick(self) -> List[int]:\n return [(xr:=random.randint)((c := self.rects[(ans := bisect.bisect_left(self.W,xr(0,self.W[-1]) ))])[0],c[2]),xr(c[1],c[3])]\n``` | 1 | 0 | ['Python3'] | 0 |
random-point-in-non-overlapping-rectangles | Clean, straight forward Java solution with step-wise explanation | clean-straight-forward-java-solution-wit-m3gi | Process the input co-ordinates and transform into rectangle objects. Calculate the area of the rectangle and keep a total sum of areas. Use TreeMap to simulate | shivkumar | NORMAL | 2020-08-22T20:42:35.114259+00:00 | 2020-08-22T20:42:35.114308+00:00 | 134 | false | 1. Process the input co-ordinates and transform into rectangle objects. Calculate the area of the rectangle and keep a total sum of areas. Use TreeMap to simulate a ranged map where the rectangle occupies a range block proportional to its area. \n2. The pick would only be uniform if the solution ensures weighted bias based on the rectange area. In other words, a larger rectangle has more points to pick from compared to a rectangle with smaller area. \n3. Use random to pick a number between 1 and total sum of areas. The choice of TreeMap as the map implementation is intentional since it offers the *ceilingKey* function to round up to an end of the range / existent entry in the map. \n4. Once a range and its appropriate rectangle is picked, the pick function in the rectangle object returns one valid x,y co-ordinates within the area of the rectangle, including on its perimeter. \n\nPlease **up-vote** if you like the solution and the explanation. \n\n```\n\tprivate Random random = new Random();\n\tprivate TreeMap<Integer, Rectangle> rectangles;\n\tprivate int areaSum = 0;\n \n public Solution(int[][] rects) \n {\n areaSum = 0;\n\t\trectangles = new TreeMap<Integer, Rectangle>();\n\t\tfor (int[] rect : rects)\n {\n \tRectangle rectangle = new Rectangle(rect);\n \tareaSum = areaSum + rectangle.area;\n \trectangles.put(areaSum, rectangle);\n }\n }\n \n public int[] pick() \n {\n Integer key = random.nextInt(areaSum) + 1;\n return rectangles.get(rectangles.ceilingKey(key)).pick();\n }\n \n private class Rectangle\n {\n \tpublic Rectangle(int[] coordinates)\n \t{\n \t\tleft = coordinates[0];\n \t\tbottom = coordinates[1];\n \t\tright = coordinates[2];\n \t\ttop = coordinates[3];\n \t\tarea = (right - left + 1) * (top - bottom + 1); \t\t\n \t}\n \t\n \tpublic int left, right; \n \tpublic int top, bottom;\n \tpublic int area;\n \t\n \tpublic int[] pick()\n \t{\n \t\tint x = left + random.nextInt(right - left + 1);\n \t\tint y = bottom + random.nextInt(top - bottom + 1);\n \t\treturn new int[]{x, y};\n \t}\n }\n``` | 1 | 0 | [] | 0 |
random-point-in-non-overlapping-rectangles | [Python] Readable & Clean Solution with Binary Search | python-readable-clean-solution-with-bina-s0eg | \nimport random\nclass Solution:\n\n def numberOfPoints(self, rect):\n x1, y1, x2, y2 = rect\n return ((abs(x1-x2)+1) * (abs(y1-y2)+1)) \n \ | dschradick | NORMAL | 2020-08-22T19:21:04.711487+00:00 | 2020-08-22T19:26:36.315126+00:00 | 110 | false | ```\nimport random\nclass Solution:\n\n def numberOfPoints(self, rect):\n x1, y1, x2, y2 = rect\n return ((abs(x1-x2)+1) * (abs(y1-y2)+1)) \n \n def sampleFromRect(self, rect):\n x1, y1, x2, y2 = rect\n x = random.randint(x1, x2) \n y = random.randint(y1, y2) \n return [x, y]\n \n def chooseRect(self):\n x = random.randint(0,self.n_points)\n left = 0\n right = len(self.rects) - 1\n while left < right:\n mid = (left + right) // 2\n if x < self.prefix_sum[mid] :\n right = mid\n else:\n left = left +1\n return self.rects[left]\n \n def generatePrefixSum(self):\n self.prefix_sum = [0] * len(self.rects)\n self.prefix_sum[0] = self.numberOfPoints(self.rects[0]) \n for i in range(1,len(self.rects)):\n self.prefix_sum[i] = self.prefix_sum[i-1] + self.numberOfPoints(self.rects[i]) \n self.n_points = self.prefix_sum[-1]\n print(self.prefix_sum )\n \n \n def __init__(self, rects: List[List[int]]):\n self.rects = rects\n self.generatePrefixSum()\n\n def pick(self) -> List[int]:\n rect = self.chooseRect()\n return self.sampleFromRect(rect)\n\n``` | 1 | 0 | [] | 0 |
random-point-in-non-overlapping-rectangles | C++ Beats 100% on space and time. O(1), a simple goto , to represent a for | c-beats-100-on-space-and-time-o1-a-simpl-k0zn | \nclass Solution {\n int x1, y1, x2, y2;\n int RectPos;\n int Reset;\n vector<vector<int>> *R;\npublic:\n Solution(vector<vector<int>>& rects) {\ | riou23 | NORMAL | 2020-08-22T18:46:27.398231+00:00 | 2020-08-22T18:46:27.398287+00:00 | 81 | false | ```\nclass Solution {\n int x1, y1, x2, y2;\n int RectPos;\n int Reset;\n vector<vector<int>> *R;\npublic:\n Solution(vector<vector<int>>& rects) {\n RectPos = 0;\n Reset = rects[0][2];\n x1 = rects[0][0];\n y1 = rects[0][1];\n x2 = rects[0][2];\n y2 = rects[0][3];\n R = &rects;\n }\n \n vector<int> pick() {\n vector<int> ans(2);\n \n label:\n if(y1 <= y2)\n {\n if(x1 <= x2)\n ans[0] = x2, ans[1] = y1, x2--;\n else\n {\n x2 = Reset;\n y1++;\n goto label;\n }\n }\n else\n {\n RectPos++;\n if(RectPos == R->size())\n RectPos = 0;\n Reset = (*R)[RectPos][2];\n x1 = (*R)[RectPos][0];\n y1 = (*R)[RectPos][1];\n x2 = (*R)[RectPos][2];\n y2 = (*R)[RectPos][3];\n goto label;\n }\n \n return ans;\n }\n};\n\n/**\n * Your Solution object will be instantiated and called as such:\n * Solution* obj = new Solution(rects);\n * vector<int> param_1 = obj->pick();\n */\n``` | 1 | 1 | [] | 2 |
random-point-in-non-overlapping-rectangles | Someone explain why the simple approach fails here. Thanks...!!! | someone-explain-why-the-simple-approach-xwtmw | Can anyone explain why the below approach is failing...\nI am trying to pick a random rectangle first, then within that rect. , trying to generate x and y coord | shubhamu68 | NORMAL | 2020-08-22T17:18:33.791148+00:00 | 2020-08-22T17:19:32.387770+00:00 | 56 | false | Can anyone explain why the below approach is failing...\nI am trying to pick a random rectangle first, then within that rect. , trying to generate x and y coordinates within range.\nFails for a very large TC->32.\n\n```\nint rects[][];\n\tint len = 0;\n public Solution(int[][] rects) {\n \tthis.rects = rects;\n \tlen = rects.length;\n }\n \n public int[] pick() {\n \t\n \tint p = generateRandomWithinRange(0, len);\n \t\n \tint x_str = rects[p][0];\n \tint x_end = rects[p][2];\n \tint y_str = rects[p][1];\n \tint y_end = rects[p][3];\n \t\n \treturn new int[]{generateRandomWithinRange(x_str, x_end),generateRandomWithinRange(y_str, y_end)};\n }\n \n public int generateRandomWithinRange(int str, int end) {\n \t\n \tif(str == 0 && end == 0)\n \t\treturn 0;\n \t\n \tRandom r = new Random();\n \tint res = r.nextInt(end-str+1) + str;\n \treturn res;\n }\n \n``` | 1 | 1 | [] | 1 |
random-point-in-non-overlapping-rectangles | What's wrong with my solution of using random numbers | whats-wrong-with-my-solution-of-using-ra-l59z | I am saving all the rectagles and then picking one rectangle from among them and then I am picking a x that is between the min and max x of that rectangle and t | in10se | NORMAL | 2020-08-22T14:39:57.542125+00:00 | 2020-08-22T17:38:12.097485+00:00 | 98 | false | I am saving all the rectagles and then picking one rectangle from among them and then I am picking a x that is between the min and max x of that rectangle and then picking a y that is between the min and max of that rectangle. Could anyone point out to me what I am doing wrong here?\n\n```\nclass Solution {\n int recta[][];\n Random r = new Random();\n public Solution(int[][] rects) {\n this.recta = new int[rects.length][5];\n for(int i = 0; i < rects.length; i++){\n this.recta[i][0] = rects[i][0];\n this.recta[i][1] = rects[i][1];\n this.recta[i][2] = rects[i][2];\n this.recta[i][3] = rects[i][3];\n int dist = (int)Math.pow(Math.abs(rects[i][0] - rects[i][2]), 2) + (int)Math.pow(Math.abs(rects[i][1] - rects[i][3]), 2);\n this.recta[i][4] = dist;\n }\n }\n \n public int[] pick() {\n int tot = 0;\n for(int[] r : this.recta){\n tot += r[4];\n }\n // Now choose a random item\n int recNum = -1;\n double random = Math.random() * tot;\n for (int i = 0; i < this.recta.length; ++i)\n {\n random -= this.recta[i][4];\n if (random <= 0.0d)\n {\n recNum = i;\n break;\n }\n }\n \n int xMax = this.recta[recNum][0] > this.recta[recNum][2] ? this.recta[recNum][0] : this.recta[recNum][2] ;\n int xMin = this.recta[recNum][0] < this.recta[recNum][2] ? this.recta[recNum][0] : this.recta[recNum][2] ;\n int yMax = this.recta[recNum][1] > this.recta[recNum][1] ? this.recta[recNum][1] : this.recta[recNum][3] ;\n int yMin = this.recta[recNum][1] < this.recta[recNum][3] ? this.recta[recNum][1] : this.recta[recNum][3] ;\n \n \n \n int xR = Integer.MIN_VALUE;\n int yR = Integer.MIN_VALUE;\n if(xMax == xMin)\n xR = xMax;\n else\n xR = xMin + r.nextInt(xMax-xMin);\n if(yMax == yMin)\n yR = yMax;\n else\n yR = yMin + r.nextInt(yMax-yMin);\n int[] coor = new int[2];\n coor[0] = xR;\n coor[1] = yR;\n return coor;\n }\n}\n\n/**\n * Your Solution object will be instantiated and called as such:\n * Solution obj = new Solution(rects);\n * int[] param_1 = obj.pick();\n */\n``` | 1 | 0 | [] | 1 |
random-point-in-non-overlapping-rectangles | JavaScript HashMap + Binary Search. ES6, approach included with time and space. comments welcome. | javascript-hashmap-binary-search-es6-app-m2y1 | \n/*\neach rectangle will have to have a number in a map {cumulative area : [Xrange, yrange]}\nfind the range of x and y per rectangle\nuse random number * leng | alexanderywang | NORMAL | 2020-08-22T14:19:14.230707+00:00 | 2020-08-22T15:58:30.351963+00:00 | 133 | false | ```\n/*\neach rectangle will have to have a number in a map {cumulative area : [Xrange, yrange]}\nfind the range of x and y per rectangle\nuse random number * length of range + low of range\n\n** need to pick randomly from sum of all areas. picking random rect and then random point inside rect won\'t do that. if one area is disproportionately bigger, it should get chosen more often.\n\nwhat if we set rect number to it\'s cumulative area -> cumulative to avoid collisions of same area rects. find random number that but <= key. in order to efficiently find the key, binary search through this.map.keys()\n*/\nclass Solution{\n constructor(rects){\n this.map = new Map(); // {cumulative area : [[xLo,xHi], [yLo,yHi]]}\n this.area = 0;\n this.getRange(rects);\n }\n pick(){ \n // O(log N) for binary search through N rectangles for random key\n let random = Math.ceil(this.area * Math.random());\n let randomRectKey = this.getKey(random);\n let [xRange, yRange] = this.map.get(randomRectKey)\n let xLength = xRange[1]-xRange[0]+1\n let yLength = yRange[1]-yRange[0]+1\n let xRandom = Math.floor(Math.random() * xLength) + xRange[0];\n let yRandom = Math.floor(Math.random() * yLength) + yRange[0];\n return [xRandom, yRandom];\n }\n getRange(rects){\n // O(N) for N rectangles, construction of this.map\n for (const rect of rects){\n let x = rect[2] - rect[0] + 1\n let y = rect[3] - rect[1] + 1\n this.area += x*y\n this.map.set(this.area, []);\n this.map.get(this.area).push([rect[0],rect[2]]);\n this.map.get(this.area).push([rect[1],rect[3]]);\n }\n // console.log(this.map)\n }\n getKey(num){ \n // binary search for arr[left] just greater than num\n // O(log N) for N rectangles\n let arr = [...this.map.keys()];\n let left = 0\n let right = arr.length-1\n while (left < right){\n let mid = left + Math.floor((right-left)/2);\n if (arr[mid] === num) return arr[mid];\n if (arr[mid] < num){\n left = mid + 1\n } else {\n right = mid\n }\n }\n return arr[left];\n }\n}\n``` | 1 | 0 | [] | 0 |
random-point-in-non-overlapping-rectangles | Solution without binary search | solution-without-binary-search-by-bhadr3-rfx2 | \nclass Solution {\n int[][] rects;\n int[] range;\n int totArea = 0;\n Random r = new Random();\n\n public Solution(int[][] rects) {\n th | bhadr3 | NORMAL | 2020-08-22T13:35:10.004522+00:00 | 2020-08-22T14:40:49.102543+00:00 | 194 | false | ```\nclass Solution {\n int[][] rects;\n int[] range;\n int totArea = 0;\n Random r = new Random();\n\n public Solution(int[][] rects) {\n this.rects = rects;\n range = new int[rects.length];\n int id = 0; \n for(int[] rect : rects){\n int area = Math.abs((rect[2]-rect[0]+1) * (rect[3]-rect[1]+1));\n this.totArea = this.totArea + area;\n range[id++] = totArea;\n }\n }\n \n public int[] pick() {\n \n int[] res = new int[2];\n int area = r.nextInt(totArea+1);\n int index = 0;\n \n while(index < range.length && range[index] < area){\n index++;\n }\n \n int[] rect = rects[index];\n \n res[0] = rect[0] + (r.nextInt(rect[2]-rect[0]+1));\n res[1] = rect[1] + (r.nextInt(rect[3]-rect[1]+1));\n\n return res;\n \n }\n}\n\n\n====================Binary Search Approch========================\n\n\nclass Solution {\n int[][] rects;\n int[] range;\n int totArea = 0;\n Random r = new Random();\n\n public Solution(int[][] rects) {\n this.rects = rects;\n range = new int[rects.length];\n int id = 0; \n for(int[] rect : rects){\n int area = Math.abs((rect[2]-rect[0]+1) * (rect[3]-rect[1]+1));\n this.totArea = this.totArea + area;\n range[id++] = totArea;\n }\n }\n \n public int[] pick() {\n \n int[] res = new int[2];\n int area = r.nextInt(totArea+1);\n \n /*\n \n Solution without binary search\n \n int index = 0;\n while(index < range.length && range[index] < area){\n index++;\n }\n \n */\n \n int index = bs(area, 0, range.length-1);\n \n int[] rect = rects[index];\n \n res[0] = rect[0] + (r.nextInt(rect[2]-rect[0]+1));\n res[1] = rect[1] + (r.nextInt(rect[3]-rect[1]+1));\n\n return res;\n \n }\n \n public int bs(int area, int start , int end){\n \n int mid = 0;\n while(start != end){\n mid = ((end+start)/2);\n if(area >= range[mid]){\n start = mid+1; \n }else{\n end = mid;\n }\n }\n return start;\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
random-point-in-non-overlapping-rectangles | Javascript O(n) initiation O(1) picking using Alias Method | javascript-on-initiation-o1-picking-usin-ecd7 | \nvar Solution = function(rects) {\n // Imagine we put the boxes into a 2D pool and pick one. Then the bigger box will more likely to be seen and picked\n // | hillisanoob | NORMAL | 2020-08-22T11:57:28.573938+00:00 | 2020-08-22T11:57:42.269003+00:00 | 263 | false | ```\nvar Solution = function(rects) {\n // Imagine we put the boxes into a 2D pool and pick one. Then the bigger box will more likely to be seen and picked\n // So first we initialize the pool with the area of the boxes\n let totalArea = 0;\n this.boxes = rects.map(([x1, y1, x2, y2], index, area) => (\n totalArea += area = (x2 - x1 + 1) * (y2 - y1 + 1),\n { area, index, x1, y1, x2, y2 }\n ));\n // Alias method says that, for example you have n boxes, and n rooms with can contain exactly the average area of the boxes,\n // you can distribute the content of the boxes into the rooms such that each room contains only content of 2 type of boxes.\n // So the idea is putting each box into each room. Then some box will be larger than the room, and some will be smaller\n // You can then split the larger box and put into the room which contains the smaller box\n // So now let\'s classify the boxes base on if it\'s larger or smaller than the room size\n const avgArea = this.avg = totalArea / rects.length;\n const smallers = this.boxes.filter(box => box.area < avgArea);\n const largers = this.boxes.filter(box => box.area > avgArea);\n while (smallers.length !== 0 && largers.length !== 0) {\n const smaller = smallers.shift();\n const larger = largers[0];\n smaller.added = larger.index;\n larger.area -= avgArea - smaller.area;\n\t// After splitting the larger box, calling A for example, and put into the room of the smaller box, that room is now full, and we no longer care about it\n\t// About the box A, if it is now still bigger than the room capacity, keep it in the "largers" stack to work with later\n\t// If it is now fit into its room, forget about it\n\t// If it becomes smaller for a typical room, we put it into the "smallers" stack to find it a new "larger boxie"\n larger.area <= avgArea && (\n largers.shift(),\n larger.area < avgArea && (smallers[smallers.length] = larger)\n );\n }\n this.pick = function() {\n // Now we just need to pick a random room\n const box = this.boxes[Math.random() * this.boxes.length | 0];\n\t// And then pick 1 of the 2 boxes in that room, based on their area as above\n const { x1, y1, x2, y2 } = Math.random() * this.avg > box.area ? this.boxes[box.added] : box;\n\t// Finally return a point inside that box\n return [\n Math.floor(x1 + Math.random() * (x2 - x1 + 1)),\n Math.floor(y1 + Math.random() * (y2 - y1 + 1))\n ];\n }\n};\n```\n | 1 | 1 | ['JavaScript'] | 0 |
random-point-in-non-overlapping-rectangles | Python O(n) time/space solution w/ explanation | python-on-timespace-solution-w-explanati-rjoe | Thought process:\nThis problem asks us to find a way to generate a point inside n rectangles with uniform probability, we have a few options:\nOption 1: a trivi | algorithm_cat | NORMAL | 2020-08-22T10:25:22.733139+00:00 | 2020-08-22T10:45:49.975852+00:00 | 112 | false | **Thought process:**\nThis problem asks us to find a way to generate a point inside n rectangles with uniform probability, we have a few options:\nOption 1: a trivial solution is to keep track of all the valid integer points, when `pick()` is called just generate a random index and return the integer point at that index. space is `O(nm)` where n is max x coordinate and m is max y coordinate, not space-efficient!\nOption2: instead of tracking all valid integer points, can we track a way to recreate valid integer points? What minimal information do we need to determine whether a integer point is valid?\n* we need all of the rectangles\' x and y borders at least, so space efficiency is lower bounded at `Omega(N)` where `N` is the number of rectangles.\n\nWith information on the rectangles boundaries, we can now pick a rectangle first. The probability of rectangle `i` getting chosen should be `numPoints(rectangle i)/numPoints(total)`--with the rectangle boundaries we have enough information to determine this! If there is a built-in weighted random number generator in your language, you can just use that, I am using Python3 so I have to write this logic manually. There is a couple implementations for this:\n1. we can use a list with each rectangle index appearing n times to mock weight, but this would use `O(nm)` space like option 1. Not efficient!\n2. we can map each rectangle to a range of ints, when a random number is generated we go through each range to identify the rectangle, this would be O(n) time/space where n is the number of rectangles. If you optimize this using binary search the time would be O(logN).\n\nOnce we pick a rectangle, it should be trivial to generate a random point in that rectangle.\n\n**Generalized algorithm:**\n*On initialization:*\n - build a list of integer point index range for each rectangle, (for example, a rectangle containing 4 valid points would occupy the range(x, x+4)). This is for picking the triangle\n \n*On `pick()`:*\n * pick the rectangle using weighted random number, using the range map built during initialization\n * pick a point from the rectangle by randomly generating x and y within rectangle boundaries\n\n**Code:**\n```\nfrom random import randint\nclass Solution:\n def __init__(self, rects: List[List[int]]):\n self.rect_rngs = []\n range_start = 0\n for x1,y1,x2,y2 in rects:\n num_points_in_rect = (x2-x1+1) * (y2-y1+1)\n self.rect_rngs.append([[range_start,range_start+num_points_in_rect], [x1,y1,x2,y2]])\n range_start = range_start+num_points_in_rect\n self.total_points = range_start\n def pick(self) -> List[int]:\n def pick_rectangle():\n rnd_int = randint(0,self.total_points-1)\n for rng, rect in self.rect_rngs:\n if rng[0]<=rnd_int<rng[1]:\n return rect\n raise ValueError("No matching rectangle found!")\n x1,y1,x2,y2 = pick_rectangle()\n pick_x = randint(x1,x2) # randint(a,b) is inclusive!\n pick_y = randint(y1,y2)\n return [pick_x, pick_y]\n```\n\nBinary search implementation of `pick`:\n```\n def pick(self) -> List[int]:\n def pick_rectangle_binary(l,r, target):\n if l > r:\n raise ValueError("No matching rectangle found!")\n middle = l + (r-l)//2 \n start = self.rect_rngs[middle][0][0]\n end = self.rect_rngs[middle][0][1]\n if start <= target < end:\n return self.rect_rngs[middle][1]\n if target < start:\n return pick_rectangle_binary(l,middle-1,target)\n else:\n return pick_rectangle_binary(middle+1,r,target)\n x1,y1,x2,y2 = pick_rectangle_binary(0,len(self.rect_rngs)-1,randint(0,self.total_points-1))\n pick_x = randint(x1,x2) # randint(a,b) is inclusive!\n pick_y = randint(y1,y2)\n return [pick_x, pick_y]\n```\n\n**Space/time efficiency:**\n`initialization`: Linear time/linear space\n`pick`: Logarithmic time/constant extra space | 1 | 0 | [] | 0 |
random-point-in-non-overlapping-rectangles | C++ Easy Implementation | c-easy-implementation-by-alpha98-abzi | \nclass Solution {\npublic:\n vector<int> v;\n vector<vector<int>> rect;\n Solution(vector<vector<int>>& rects) \n {\n rect=rects;\n i | alpha98 | NORMAL | 2020-08-22T09:08:23.825800+00:00 | 2020-08-22T09:08:23.825854+00:00 | 104 | false | ```\nclass Solution {\npublic:\n vector<int> v;\n vector<vector<int>> rect;\n Solution(vector<vector<int>>& rects) \n {\n rect=rects;\n int area=0;\n for(auto rec:rect)\n {\n int a= (rec[2]- rec[0]+1)*(rec[3]-rec[1]+1);\n area+=a;\n v.push_back(area);\n }\n }\n \n vector<int> pick() \n {\n int rnd= rand()%v.back();\n int idx= upper_bound(v.begin(),v.end(),rnd) - v.begin();\n \n auto l=rect[idx];\n int x= rand() % (l[2]-l[0]+1) + l[0];\n int y= rand() % (l[3]-l[1]+1) + l[1];\n return {x,y};\n }\n};\n``` | 1 | 1 | [] | 1 |
random-point-in-non-overlapping-rectangles | Represent points using offsets - FULL explanation with example | represent-points-using-offsets-full-expl-v1kk | Idea:\n\n\n\n Consider above mentioned 3 rectangles. As you can see, rectangles contains 12, 9, 15 integer coordinates respectively.\n So, in total, we have 36 | parin2 | NORMAL | 2020-08-22T08:27:20.034650+00:00 | 2020-08-22T08:28:09.542459+00:00 | 93 | false | **Idea:**\n\n\n\n* Consider above mentioned 3 rectangles. As you can see, rectangles contains `12, 9, 15` integer coordinates respectively.\n* So, in total, we have 36 points to represent. We can represent them using indices `[0 ... 35]`. Let\'s call them `pointId`\n* Let\'s make an array `offset` which mentions the starting of `pointIdx` that a particular rectangle contains. For example,\n\t* Rectangle 1 will contain pointId `0 to 11 (12 points in total),`, so `offset[0] = 0` (starting value of pointId for rectangle-1)\n\t* Rectangle 2 will contain pointId `12 to 20 (9 points in total)`, so `offset[1] = 12` (starting value of pointId for rectangle-2)\n\t* Rectangle 3 will contains pointId `21 to 35 (36 points in total)`, so `offset[2] = 21` (starting value of pointId for rectangle-3)\n\t* Hence, the `offset = [0, 12, 21]`\n* Now, you can randomly select a pointId from `0` (inclusive) to `36` (exclusive).\n* As you can see, `offset` is in increasing order, so we can perform binary search to find the right position of random pointId, which is basically the rectangle it belongs to.\n* For example, let\'s say random pointId is `20`, we can determine using binary search on `offset`, that it belongs to rectangle-2 (which has pointIds of range `12` to `20`)\n* Now, take the start coordinates of rectangle-2 (using given grid), and determine the `8`th coordinate in that rectangle-2 (because 20 - 12 = 8).\n\n```\nclass Solution {\n\n int[][] rects;\n int[] offsets;\n int range;\n Random r;\n public Solution(int[][] rects) {\n this.rects = rects;\n this.offsets = new int[rects.length];\n this.range = 0;\n r = new Random();\n \n for (int i = 0; i < rects.length; i++) {\n int[] rect = rects[i];\n \n int x1 = rect[0],\n y1 = rect[1],\n x2 = rect[2],\n y2 = rect[3];\n \n offsets[i] = range;\n range += (x2 - x1 + 1) * (y2 - y1 + 1);\n }\n \n }\n \n public int[] pick() {\n int randIdx = r.nextInt(range), \n rectIdx = Arrays.binarySearch(offsets, randIdx); \n \n if (rectIdx < 0) {\n rectIdx = Math.abs(rectIdx + 2);\n }\n \n int[] rect = rects[rectIdx];\n \n int idx = randIdx - offsets[rectIdx], \n x = rect[0], \n y = rect[1],\n width = rect[2] - rect[0] + 1, \n height = rect[3] - rect[1] + 1, \n row = idx / width, \n col = idx % width; \n \n return new int[]{x + col, y + row}; \n }\n}\n```\n | 1 | 0 | [] | 0 |
random-point-in-non-overlapping-rectangles | simple, short and clean java solution | simple-short-and-clean-java-solution-by-71j46 | we are using tree map to increase the chance of selecting a rectangle with larger area, then selecting a point in its area randomly.\n\nclass Solution {\n in | frustrated_employee | NORMAL | 2020-08-22T08:18:59.445995+00:00 | 2020-08-22T08:20:11.371259+00:00 | 216 | false | we are using tree map to increase the chance of selecting a rectangle with larger area, then selecting a point in its area randomly.\n```\nclass Solution {\n int[][] rect;\n TreeMap<Integer,Integer> tm=new TreeMap<>();\n int sum=0;\n Random ran=new Random();\n public Solution(int[][] rects) {\n rect=rects;\n for(int k=0;k<rects.length;k++){\n sum+=(rect[k][2]-rect[k][0]+1)*(rect[k][3]-rect[k][1]+1);\n tm.put(sum,k);\n }\n }\n public int[] pick() {\n int k=tm.get(tm.ceilingKey(ran.nextInt(sum+1))); // sum can also be picked\n int x=ran.nextInt(rect[k][2]-rect[k][0]+1)+rect[k][0];\n int y=ran.nextInt(rect[k][3]-rect[k][1]+1)+rect[k][1];\n return new int[]{x,y};\n }\n}\n``` | 1 | 0 | [] | 1 |
random-point-in-non-overlapping-rectangles | Java TreeMap | java-treemap-by-hobiter-hz2v | \nclass Solution {\n TreeMap<Integer, Integer> map;\n int[][] rs;\n int sum = 0;\n Random rand = new Random();\n public Solution(int[][] rects) { | hobiter | NORMAL | 2020-07-28T02:34:10.949996+00:00 | 2020-07-28T02:34:10.950041+00:00 | 166 | false | ```\nclass Solution {\n TreeMap<Integer, Integer> map;\n int[][] rs;\n int sum = 0;\n Random rand = new Random();\n public Solution(int[][] rects) {\n map = new TreeMap<>();\n rs = rects;\n for (int i = 0; i < rs.length; i++) {\n map.put(sum, i);\n sum += (rs[i][2] - rs[i][0] + 1) * (rs[i][3] - rs[i][1] + 1);\n }\n }\n \n public int[] pick() {\n int rd = rand.nextInt(sum), k = map.floorKey(rd), r[] = rs[map.get(k)], diff = rd - k, w = r[2] - r[0] + 1;\n return new int[]{r[0] + diff % w, r[1] + diff / w};\n }\n}\n``` | 1 | 0 | [] | 0 |
random-point-in-non-overlapping-rectangles | Easy to understand Python 3 Solution | easy-to-understand-python-3-solution-by-ne413 | The crux of the problem is understanding that the solution is also evaluated on the kind of random distribution your solution offers. A random distribution, uni | subwayharearmy | NORMAL | 2020-07-26T08:42:39.952623+00:00 | 2020-07-26T08:42:39.952666+00:00 | 122 | false | The crux of the problem is understanding that the solution is also evaluated on the kind of random distribution your solution offers. A random distribution, uniform over the areas of the rectangles is expected. \n\nUses Python3\'s random.choices() function that allows weighted sampling from a specified population. The important thing to note here is that while calculaating the areas, we compute area as: (x2 - x1 + 1) x (y2 - y1 +1) instead of the (x2 - x1) x (y2 - y1 ). \nThis is because a rectaangle of area 1 corresponds to 4 integer points, not just one integer point.\n\n```\nclass Solution:\n\n def __init__(self, rects):\n """\n :type rects: List[List[int]]\n """\n self.rects = rects\n \n self.areas = []\n for _ in range(len(rects)):\n self.areas.append((rects[_][2] - rects[_][0] + 1)*(rects[_][3] - rects[_][1] + 1))\n \n def pick(self):\n """\n :rtype: List[int]\n """\n temp = [i for i in range(len(self.rects))]\n rect = random.choices(population = temp, weights = self.areas)[0]\n \n x_min = self.rects[rect][0]\n x_max = self.rects[rect][2]\n \n y_min = self.rects[rect][1]\n y_max = self.rects[rect][3]\n \n p_x = random.randint(x_min, x_max)\n p_y = random.randint(y_min, y_max)\n \n return[p_x, p_y]\n```\n\n\nSame solution but shortened (minor improvements)\n\n```\nclass Solution:\n\n def __init__(self, rects):\n """\n :type rects: List[List[int]]\n """\n self.rects = rects\n self.areas = [(rects[_][2] - rects[_][0] + 1)*(rects[_][3] - rects[_][1] + 1) for _ in range(len(rects))]\n \n \n def pick(self):\n """\n :rtype: List[int]\n """\n rect = random.choices(population = range(len(self.rects)), weights = self.areas)[0]\n return[random.randint(self.rects[rect][0], self.rects[rect][2]), random.randint(self.rects[rect][1], self.rects[rect][3])]\n\n```\n | 1 | 0 | [] | 0 |
random-point-in-non-overlapping-rectangles | C++: Sweet&Simple solution with explanation | c-sweetsimple-solution-with-explanation-raj2v | It\'s similar to question#528. My Explanation is here:\n\nhttps://leetcode.com/problems/random-pick-with-weight/discuss/672072/C%2B%2B%3A-Sweet-and-simple-solut | bingabid | NORMAL | 2020-06-06T12:56:17.553676+00:00 | 2020-06-06T12:58:56.255477+00:00 | 156 | false | It\'s similar to question#528. My Explanation is here:\n```\nhttps://leetcode.com/problems/random-pick-with-weight/discuss/672072/C%2B%2B%3A-Sweet-and-simple-solution\n```\nHere is my implementation. For any doubt feel free to comment. \n```\nclass Solution {\n vector<vector<int>> rect;\n vector<int> area;\n int n,tarea;\npublic:\n Solution(vector<vector<int>>& rects) {\n n = rects.size();\n this->rect = rects;\n for(int i=0;i<n;i++){\n \n int x1 = rects[i][0], x2 = rects[i][2];\n int y1 = rects[i][1], y2 = rects[i][3];\n int dx = x2-x1+1, dy = y2-y1+1;\n int a = abs(dx*dy);\n i==0?area.push_back(a):area.push_back(a+area[i-1]);\n }\n tarea = area[n-1];\n }\n \n vector<int> pick(){\n int randArea = rand()%tarea;\n int idx = upper_bound(area.begin(),area.end(),randArea) - area.begin();\n int x1 = rect[idx][0], x2 = rect[idx][2];\n int y1 = rect[idx][1], y2 = rect[idx][3];\n int dx = x2-x1+1, dy = y2-y1+1;\n int X = x1 + rand()%dx;\n int Y = y1 + rand()%dy;\n return {X,Y};\n \n }\n};\n``` | 1 | 0 | [] | 0 |
random-point-in-non-overlapping-rectangles | Python, readable, simple and short. | python-readable-simple-and-short-by-g2co-k2lh | python\nfrom random import randint\n\nclass Solution:\n\n def __init__(self, rects: List[List[int]]):\n self.rects = rects\n self.cellSum = [0] | g2codes | NORMAL | 2020-03-19T05:24:35.497394+00:00 | 2020-03-19T05:24:35.497427+00:00 | 214 | false | ```python\nfrom random import randint\n\nclass Solution:\n\n def __init__(self, rects: List[List[int]]):\n self.rects = rects\n self.cellSum = [0]\n \n # Count the number of cells in each rectangle and add to cellSum as a\n # cumulative sum.\n # cellSum is initialized to 0, the reason for this will become evident\n # later in the code.\n for rect in self.rects:\n # The +1 here exists to add one to the width and height.\n # Because we think of each point as a cell. This allows\n # us to return a random point in and on the rectange easily.\n height = abs(abs(rect[3]) - abs(rect[1])) + 1\n width = abs(abs(rect[0]) - abs(rect[2])) + 1\n self.cellSum.append(self.cellSum[-1] + (height * width))\n\n def pick(self) -> List[int]:\n # Generate a random that falls in the cellSum.\n # The -1 here makes it so that the following\n # binary search does not go out of bounds.\n randomCell = randint(0, self.cellSum[-1] - 1)\n # Find the cell sum that prior to the random number.\n idx = self.closestSmaller(self.cellSum, randomCell)\n # Remove the cell sum so that we can find the point\n # in the rectangle at idx.\n randomCell -= self.cellSum[idx]\n # We are going to return a point in this rectangle.\n rect = self.rects[idx]\n # Compute the width of the rectangle so that\n # we may remove the number of rows that are full.\n width = abs(abs(rect[0]) - abs(rect[2])) + 1\n # Remove full rows and returnt the rowId\n rowId = rect[1] + randomCell // width\n # Identify the col by wrapping the width around.\n colId = rect[0] + randomCell % width\n \n return [colId, rowId]\n \n def closestSmaller(self, nums, target):\n low = 0\n high = len(nums) - 1\n idx = -1\n while low <= high:\n mid = low + (high - low) // 2\n if target >= nums[mid]:\n idx = mid\n low = mid + 1\n else:\n high = mid - 1\n return idx\n \n# Your Solution object will be instantiated and called as such:\n# obj = Solution(rects)\n# param_1 = obj.pick()\n``` | 1 | 0 | [] | 1 |
random-point-in-non-overlapping-rectangles | c++ simple solution by transfering all 2D rectangles to a 1D line | c-simple-solution-by-transfering-all-2d-5aean | My idea is to transfer all rectangles to a 1D line, then random pick up one point from the line. Finally convert the point in the line back to its\' real positi | hanzhoutang | NORMAL | 2019-09-19T04:44:55.367146+00:00 | 2019-09-20T02:50:45.968027+00:00 | 247 | false | My idea is to transfer all rectangles to a 1D line, then random pick up one point from the line. Finally convert the point in the line back to its\' real position. \n```\nclass Solution {\npublic:\n map<int,int> toRect;\n vector<vector<int>> rs;\n int total = 0;\n Solution(vector<vector<int>>& rects) : rs(rects){\n toRect[0] = 0;\n for(int i = 0;i<rs.size();i++){\n auto& x = rs[i];\n int area = (x[2] - x[0] + 1) * (x[3] - x[1] + 1);\n total += area;\n toRect[total] = i+1;\n }\n }\n \n vector<int> f(const vector<int>& r, int i){\n int width = r[2] - r[0] + 1;\n int _x = i % width;\n int _y = i / width; \n return {r[0] + _x, r[1] + _y};\n }\n \n vector<int> pick() {\n int r = rand() % total;\n auto ptr = toRect.upper_bound(r);\n ptr = next(ptr,-1);\n return f(rs[ptr->second],r - ptr->first);\n }\n};\n``` | 1 | 0 | [] | 0 |
random-point-in-non-overlapping-rectangles | Python intuitive solution | python-intuitive-solution-by-mikeyliu-ft71 | i\'m sure this can be optimized in some ways.\n\nfrom random import randint,choices\nclass Solution:\n\n def __init__(self, R: List[List[int]]):\n sel | mikeyliu | NORMAL | 2019-08-28T06:47:40.736856+00:00 | 2019-08-28T06:47:40.736890+00:00 | 145 | false | i\'m sure this can be optimized in some ways.\n```\nfrom random import randint,choices\nclass Solution:\n\n def __init__(self, R: List[List[int]]):\n self.R=R\n self.A=[(c-a+1)*(d-b+1) for a,b,c,d in R]\n\n def pick(self) -> List[int]:\n a,b,c,d=choices(population=self.R,weights=self.A,k=1)[0]\n return [randint(a,c),randint(b,d)]\n\n\n# Your Solution object will be instantiated and called as such:\n# obj = Solution(rects)\n# param_1 = obj.pick()\n``` | 1 | 1 | [] | 0 |
random-point-in-non-overlapping-rectangles | Anyone Know what it wrong with this? (C# Easy) | anyone-know-what-it-wrong-with-this-c-ea-tjsj | Failing 3 testcases from 35. I did not know what is wrong here.\n\n private static int[][] arrs;\n private static int arrsIndex = 0;\n priv | daviti | NORMAL | 2019-06-05T07:39:36.412937+00:00 | 2019-06-05T07:39:36.412975+00:00 | 127 | false | Failing 3 testcases from 35. I did not know what is wrong here.\n```\n private static int[][] arrs;\n private static int arrsIndex = 0;\n private static Random rnd = new Random();\n\n public static void Solution(int[][] rects)\n {\n arrs = rects.Where(r => r.Length != 0).ToArray();\n }\n\n public static int[] pick()\n { \n\t\t\tarrsIndex = ++arrsIndex >= arrs.Length ? 0 : arrsIndex;\n \n int x = rnd.Next(arrs[arrsIndex][0], arrs[arrsIndex][2] + 1);\n int y = rnd.Next(arrs[arrsIndex][1], arrs[arrsIndex][3] + 1);\n\n return new int[] {x, y};\n }\n``` | 1 | 0 | [] | 1 |
random-point-in-non-overlapping-rectangles | For help ! I don't know why I was wrong | for-help-i-dont-know-why-i-was-wrong-by-s1qhv | here is my answer. \nit pass 32/35 testcase,\nbut when use \n[[[82918473, -57180867, 82918476, -57180863],\n[83793579, 18088559, 83793580, 18088560],\n[66574245 | leeqh | NORMAL | 2018-09-04T06:17:39.075962+00:00 | 2018-09-04T06:17:39.076005+00:00 | 331 | false | here is my answer. \nit pass 32/35 testcase,\nbut when use \n**[[[82918473, -57180867, 82918476, -57180863],\n[83793579, 18088559, 83793580, 18088560],\n[66574245, 26243152, 66574246, 26243153],\n[72983930, 11921716, 72983934, 11921720]]]**\nit wiil be wrong.\n\n```\nfrom random import *\nclass Solution(object):\n \n def __init__(self, rects):\n """\n :type rects: List[List[int]]\n """\n areas = rects\n self.maps = list()\n for index,area in enumerate(areas):\n minX = area[0]\n maxX = area[2]\n minY = area[1]\n maxY = area[3]\n self.maps.append(dict({"minX": minX,"maxX":maxX,"minY":minY,"maxY":maxY}))\n\n def pick(self):\n """\n :rtype: List[int]\n """\n select_area = randint(0,len(self.maps) - 1)\n x = randint(self.maps[select_area].get("minX"),self.maps[select_area].get("maxX"))\n y = randint(self.maps[select_area].get("minY"),self.maps[select_area].get("maxY"))\n return [x,y]\n\n\n# Your Solution object will be instantiated and called as such:\n# obj = Solution(rects)\n# param_1 = obj.pick()\n```\nThank you very much. | 1 | 0 | [] | 1 |
random-point-in-non-overlapping-rectangles | Easy Java with a List | easy-java-with-a-list-by-bianhit-cotx | \nclass Solution {\n int area = 0;\n List<Integer> list = new ArrayList<>();\n int[][] rects;\n public Solution(int[][] rects) {\n this.rects | bianhit | NORMAL | 2018-08-01T14:53:16.691975+00:00 | 2018-09-09T03:36:33.319374+00:00 | 177 | false | ```\nclass Solution {\n int area = 0;\n List<Integer> list = new ArrayList<>();\n int[][] rects;\n public Solution(int[][] rects) {\n this.rects = rects;\n for (int[] rect : rects) {\n area += (rect[2]-rect[0] + 1)*(rect[3] - rect[1] + 1);\n list.add(area);\n }\n }\n \n public int[] pick() {\n Random r = new Random();\n int rand = r.nextInt(area) + 1, i = 0;\n while (list.get(i) < rand) i++;\n int[] cord = rects[i];\n int num = list.get(i) - rand, width = cord[2] - cord[0] + 1;\n return new int[]{cord[0] + num%width, cord[1] + num/width};\n }\n}\n``` | 1 | 1 | [] | 0 |
random-point-in-non-overlapping-rectangles | Python3 O(log(n)) solution using statistical ideas | python3-ologn-solution-using-statistical-nldu | I am currently studying statistics, so thought it would be a nice practice to apply a bit of that here.\n\nWhat we want here, per requirement, is that every int | de_mexico | NORMAL | 2018-07-30T21:10:40.983817+00:00 | 2018-07-30T21:10:40.983817+00:00 | 281 | false | I am currently studying statistics, so thought it would be a nice practice to apply a bit of that here.\n\nWhat we want here, per requirement, is that every integer point has the same probability of being picked. Now, since points are distributed among rectangles we could use a sampling technique where we pick first a rectangle based on its "weight" (size), and then we use simple random sampling within such rectangle. I actually made the exercise of proving this implicit claim with two rectangles.\n\nSay we have 10 points, where 6 live in first rectangle and 4 live in the other one. We could think of a decision tree where first branching is done by picking the rectangle and second branching is done by picking the actual point within each rectangle (so first branch has 6 leaves and second branch has 4).\n\nSince we know that we want to use simple random sampling (SRS) within each rectangle, we know that:\n\nP(x_i | R_1) = 1/6 for i in {1,2,3,4,5,6}\nP(x_i | R_2) = 1/4 for i in {7, 8, 9, 10}\n\nwhere x_i is the event of picking element x_i, and R_j is the event of picking rectangle 1 or 2.\n\nNow, using definition of conditional probability (used backwards) we know that the probability of reaching every leaf in decision tree is given by:\n\nP(R_j and x_i) = P(R_j) P(x_i | R_j)\n\nand we would like the following equality to hold, if every leaf in the decision tree is to be equally likely to be picked (as each leaf represents one of the integer points from our total set):\n\nP(R_1) P(x_i | R_1) = P(R_2) P(x_i | R_2)\n\nReplacing the constants we setup for our example, equality becomes:\n\nP(R_1) (1/6) = P(R_2) (1/4)\n\nSince we just have two rectangles P(R_2) = 1 - P(R_1), hence\n\nP(R_1) (1/6) = (1 - P(R_1)) (1/4)\n\nSolving that linear equation for P(R_1) will give us 0.6, hence leaving P(R_2) = 0.4. And that is precisely the intuitive "weight" we could think of assigning, if wanting to make probability proportional to the size of each rectangle. I did not do it, but suspect this proof-template could we extended to any probabilities and number of rectangles. So, let us buy for now that such sampling technique is valid.\n\nNow, one way of implementing it is to to compute the percentages out of the total that each rectangle contributes with, and think that as the desired probability to pick such rectangle. Then we could use an enumerative sampling algorithm like the one mentioned at page 27 of this presentation:\n\nhttp://www.eustat.eus/productosServicios/52.1_Unequal_prob_sampling.pdf\n\nIn such algorithm we compute the the cumulative sum of probabilities for each rectangle, using the order they have already in input param. Such cumulative probability could be thought as the high end of a probabilities range. Then the algorithm generates a uniformly random number in [0,1] and searches for the rectangle whose probability range contains such random number. We can do such search efficiently with a binary search.\n\nOnce we picked the rectangle, we proceed to generate a random number from there by using another result from Probability: in order to select a random point within a rectangle, we can think of two independent random variables for each axis. Hence, generating one tuple where first element is uniform random number for axis-X range, and second element is uniform random number for axis-Y range; should be equivalent to picking one point randomly from rectangle formed by cartesian product of those two ranges. See proof/comment from this discussion (The one starting with "That statement is incorrect, direct product of two independent uniform measures is a uniform measure. This can be shown as follows ...")\n\nhttps://stackoverflow.com/questions/6884003/generate-a-random-point-within-a-rectangle-uniformly\n\nAnd voil\xE0, putting all that together gives following snippet. At the time of this writing, it beats all the Python3 solutions.\n\n```\nfrom bisect import bisect_left\nfrom random import random, randint\n\nclass Solution:\n\n def __init__(self, rects):\n self.rects = rects\n self.cump = []\n total = 0\n for x1,y1,x2,y2 in rects:\n w, h = x2 - x1 + 1, y2 - y1 + 1\n total += w * h\n self.cump.append(total)\n for i in range(len(self.cump)):\n self.cump[i] /= total\n\n def pick(self):\n i = bisect_left(self.cump, random())\n x1,y1,x2,y2 = self.rects[i]\n x = randint(x1, x2)\n y = randint(y1, y2)\n return (x,y)\n``` | 1 | 0 | [] | 0 |
random-point-in-non-overlapping-rectangles | C++ single rand() call | c-single-rand-call-by-stkoso-gms8 | Revised from Random Pick with weight, use area as weight\n\nclass Solution {\n random_device rd;\n vector<int> areas;\n vector<vector<int>> rects;\npub | stkoso | NORMAL | 2018-07-30T06:37:39.730564+00:00 | 2018-09-09T19:54:59.327901+00:00 | 567 | false | Revised from [Random Pick with weight](https://leetcode.com/problems/random-pick-with-weight), use area as weight\n```\nclass Solution {\n random_device rd;\n vector<int> areas;\n vector<vector<int>> rects;\npublic:\n Solution(vector<vector<int>> input_rects) {\n int total = 0;\n rects = move(input_rects);\n for (auto& rect : rects)\n areas.push_back(total += (rect[2]-rect[0] + 1)*(rect[3]-rect[1] + 1));\n }\n \n vector<int> pick() {\n int p = rd() % areas.back(); // -1 for picking left-bottom point\n int i = lower_bound(areas.begin(), areas.end(), p + 1) - areas.begin();\n if (i > 0) p -= areas[i-1]; // get area of picked rectangle\n int x = rects[i][2]-rects[i][0] + 1;\n return {rects[i][0] + p%x, rects[i][1] + p/x};\n }\n};\n```\n | 1 | 1 | [] | 1 |
random-point-in-non-overlapping-rectangles | c++ wighted random, O(logn) for pick() | c-wighted-random-ologn-for-pick-by-gemhu-7a5j | \nclass Solution {\npublic:\n Solution(vector<vector<int>> rects):rects(rects) {\n\n sum = 0;\n \n for(auto& e : rects){\n \n | gemhung | NORMAL | 2018-07-29T07:14:23.421569+00:00 | 2018-10-25T06:31:43.025849+00:00 | 255 | false | ```\nclass Solution {\npublic:\n Solution(vector<vector<int>> rects):rects(rects) {\n\n sum = 0;\n \n for(auto& e : rects){\n \n const auto row = e[2]-e[0]+1;\n const auto col = e[3]-e[1]+1;\n \n sum += row*col;\n \n dp.push_back(sum);\n }\n }\n \n vector<int> pick() {\n \n const auto r = rand() % sum;\n \n const auto it = std::upper_bound(begin(dp), end(dp), r);\n\n const auto index = std::distance(dp.begin(), it);\n \n const auto row = (rects[index][3]-rects[index][1]) +1;\n const auto col = (rects[index][2]-rects[index][0]) +1;\n \n const auto x = rects[index][0] + rand()%col;\n const auto y = rects[index][1] + rand()%row;\n \n return {x, y};\n }\n \nprivate: \n vector<vector<int>> rects;\n int sum;\n std::vector<int> dp;\n};\n``` | 1 | 1 | [] | 0 |
random-point-in-non-overlapping-rectangles | Python Easy Solution | python-easy-solution-by-crazyphotonzz-fo66 | This is simply a Python implementation of the solution at: https://leetcode.com/problems/random-point-in-non-overlapping-rectangles/discuss/154130/Java-randomly | crazyphotonzz | NORMAL | 2018-07-27T20:51:01.029244+00:00 | 2018-07-27T20:51:01.029244+00:00 | 442 | false | This is simply a Python implementation of the solution at: https://leetcode.com/problems/random-point-in-non-overlapping-rectangles/discuss/154130/Java-randomly-pick-a-rectangle-then-pick-a-point-inside\n\nThe idea is simply to pick a rectangle and pick points in it randomly. \nA dictionary is created to store the sum (total sum) and the corresponding rectangle index. A random sum is chosen and the corresponding key is chosen from the dictionary and random coordinates are generated.\n\n```\nimport random\nclass Solution:\n\n def __init__(self, rects):\n """\n :type rects: List[List[int]]\n """\n self.rects = rects\n self.d = {}\n self.sum = 0\n for i in range(len(rects)):\n self.sum += (rects[i][2] - rects[i][0]+1)*(rects[i][3]-rects[i][1]+1)\n self.d[self.sum] = i\n \n def pick(self):\n """\n :rtype: List[int]\n """\n area = random.randint(1, self.sum)\n rect = self.getRect(area)\n \n # get a random point from this rectangle\n coordinates = self.rects[rect]\n rand_x = random.randint(coordinates[0], coordinates[2])\n rand_y = random.randint(coordinates[1], coordinates[3])\n return ([rand_x, rand_y])\n\n def getRect(self, area):\n if area in self.d:\n return self.d[area]\n \n mini = []\n for key in self.d:\n if key > area:\n mini.append(key)\n return self.d[min(mini)]\n# can be simply done as return self.d[min(key for key in self.d if key > area)] \n``` | 1 | 0 | [] | 0 |
random-point-in-non-overlapping-rectangles | Easy Solution with math | easy-solution-with-math-by-skh37744-bh8x | Code | skh37744 | NORMAL | 2025-03-16T04:18:43.885704+00:00 | 2025-03-16T04:18:43.885704+00:00 | 5 | false | # Code
```python3 []
import random
class Solution:
def __init__(self, rects: List[List[int]]):
self.tot = 0
self.S, self.X, self.Y = [], [], []
self.rects = []
# For each rectangle, there are (x_i - a_i + 1) * (y_i - b_i + 1) integer points
for rect in rects:
a,b,x,y = rect[0], rect[1], rect[2], rect[3]
self.tot += (x-a+1) * (y-b+1)
self.S.append(self.tot)
self.X.append([x,a])
self.Y.append([y,b])
def pick(self) -> List[int]:
rand = random.randint(0, self.tot-1)
i = 0
while rand >= self.S[i]:
i += 1
if i > 0:
rand -= self.S[i-1]
a,b,x,y = self.X[i][1], self.Y[i][1], self.X[i][0], self.Y[i][0]
du, dv = rand % (x-a+1), rand // (x-a+1)
return [a+du, b+dv]
``` | 0 | 0 | ['Python3'] | 0 |
random-point-in-non-overlapping-rectangles | Help me figure out why do 3 test cases get WA | help-me-figure-out-why-do-3-test-cases-g-ij15 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | harry331 | NORMAL | 2025-03-14T11:59:50.039214+00:00 | 2025-03-14T11:59:50.039214+00:00 | 2 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
vector<int> v;
vector<vector<int>> rects;
// I add the +1 here because in some inputs they contain lines also like
// [ 1,2,1,3 ] ( rectangle with height 0 or width 0 but this also contains 2 points )
// to also add these points I add +1.
int area(vector<int>& r) {
return (r[2] - r[0] + 1) * (r[3] - r[1] + 1);
}
Solution(vector<vector<int>> rect) {
rects = rect;
int totalArea=0;
for (auto r: rects) {
totalArea+=area(r);
v.push_back(totalArea);
}
}
vector<int> pick() {
// pick a random reactangle in rects
int rnd = rand() % v.back();
int idx = upper_bound(v.begin(), v.end(), rnd) - v.begin();
// pick a random point in rects[idx]
auto r = rects[idx];
int x = rand() % (r[2] - r[0] + 1) + r[0];
int y = rand() % (r[3] - r[1] + 1) + r[1];
return { x, y };
}
};
``` | 0 | 0 | ['C++'] | 0 |
random-point-in-non-overlapping-rectangles | Point in non-overlapping rectangles [C] (Not recommended in C) | point-in-non-overlapping-rectangles-c-no-l0ix | IntuitionMy first idea was to parse all the points from each rectangle and put them in the Solution struct such that each "pick" call is effectively just O(1) w | isjoltz | NORMAL | 2025-03-13T22:18:25.411557+00:00 | 2025-03-13T22:18:25.411557+00:00 | 4 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
My first idea was to parse all the points from each rectangle and put them in the Solution struct such that each "pick" call is effectively just O(1) with the random number selection on size; the problem with that is the worst case could make my Solution struct balloon to $$2*(10pow10) * sizeof(int)$$:
One rectangle of -MAX_INT to +MAX_INT would be about... 2(x,y point values) * 32(int bits) * 2^30(all points)... for memory.
I didn't want to do that, so I looked around for other ideas. One way is to select a rectangle based of of its area as a proportion of the total area of all rectangles together. Example like this:
rectangle1 [0,3] -> [2,5]: area = $$((2-0)+1) * ((5-3)+1) = 9$$
rectangle2 [-4,-3] -> [0,1]: area = $$((0-(-4))+1) * ((1-(-3))+1) = 5 * 4 = 20$$
The total area is 29 (29 points to choose from); if I randomly select a number 0 to 28, I can select a point within one of those by checking "is the number i chose greater than the current rectangle area?": if yes, move to the next one and subtract so I don't go out of the bound of "indexes".
# Approach
<!-- Describe your approach to solving the problem. -->
Copy over the rectangles and calculate their area into the solution struct. This should contain the size for "how many rectangles", and each rectangle array should have the points that define it and the area.
As I calculate the area of rectangles, I add to a "total area" field on Solution to index out of.
Pick will run through the rectangles checking for the area to select from and use a random index in the appropriate range (lowest to highest on x/y ranges).
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(r) for the initial rectangle parsing,
O(r) for the picking.
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(r), I have ints on Solution for capacity of rectangles, size, and total area (O(1)), pointers to arrays of rectangles (O(128) defined capacity with O(r) non-null pointers initialized), and the array of rectangles have 5 ints (a,b,x,y,area);
# Code
```c []
#include <stdlib.h>
#define RECTANGLES_CAP 128
typedef struct {
int** rects;
int size;
long int totalArea;
int capacity; //count of pointers to rectangles
} Solution;
Solution* solutionCreate(int** rects, int rectsSize, int* rectsColSize) {
//rectangle pointers for storing on Solution
int** rectPoints = malloc(RECTANGLES_CAP * sizeof(int*));
for (int c = 0; c < RECTANGLES_CAP; c++) {
rectPoints[c] = NULL;
}
//init memory for it
Solution* sol = malloc(sizeof(Solution));
sol->rects = rectPoints;
sol->capacity = RECTANGLES_CAP;
sol->size = 0;
sol->totalArea = 0;
//pass first time is to parse the rectangle for their points and create a growing vector of space...
for (int i = 0; i < rectsSize; i++) {
//allocate the array of rectangles:
//I will allocate the rectangle with its area (int size X rectangles);
int *rect = calloc(5, sizeof(int));
//calculate the area
int *thisRect = rects[i];
if (rectsColSize[i] >= 4) {
memcpy(rect, thisRect, 4 * sizeof(int));
//last index will be area:
//length/width is end to end, inclusive (+1)
int len = thisRect[2] - thisRect[0] + 1;
int wid = thisRect[3] - thisRect[1] + 1;
int area = len * wid;
rect[4] = area;
sol->totalArea += area;
//could use i for index since it should basically match as I increase size, but this is also fine
sol->rects[sol->size] = rect;
sol->size++;
printf("Rectangle Added: area=%ld; points=[%d,%d]->[%d,%d]\n",
rect[4], rect[0], rect[1], rect[2], rect[3]);
}
}
printf("Solution created: totArea=%ld\n", sol->totalArea);
//random number generator: I don't need to...
return sol;
}
int* solutionPick(Solution* obj, int* retSize) {
//return array
int* pick = NULL;
//I have rectangles, not wasting memory space on (10^10 x 2)int points
//how do I select space? do by area of rectangles (first rectangle a1, )
//get a random int between 0 and total area; when I reach 0, that's the rectangle I use.
long int areaSelect = rand() % obj->totalArea;
printf("areaSelect = %ld\n", areaSelect);
//loop through rectangle pointers checking if the area is less, then select a point within the rectangle
int* rectangle = NULL;
for (int i = 0; i < obj->size; i++) {
rectangle = obj->rects[i];
//do i have a proper pointer?
if (rectangle) {
//I'm making an assumption on the length because I created the array:
//array size should be in idx=4
int area = rectangle[4];
//not in this rectangle if we have more area to traverse
if (areaSelect >= area) {
areaSelect -= area;
continue;
}
//this rectangle, just break and do the "point finding" outside
break;
} else {
//if I have a null rectangle, i shouldn't bother continuing;
break;
}
}
if (!rectangle) {
return NULL;
}
//I have successful pick, can use the remaining part of area select to choose a point within the rectangle area
int len = rectangle[2] - rectangle[0] + 1;
int wid = rectangle[3] - rectangle[1] + 1;
pick = calloc(2, sizeof(int));
//index the length first:
pick[0] = rectangle[0] + (rand() % len);
pick[1] = rectangle[1] + (rand() % wid);
*retSize = 2;
return pick;
}
void solutionFree(Solution* obj) {
for (int i = 0; i < obj->size; i++) {
int *rect = obj->rects[i];
if (rect) {
free(rect);
}
}
//freed the individual rectangles, now the pointers to rects and solution container
free(obj->rects);
free(obj);
}
void reallocRects(Solution* solution) {
int** rects = realloc(solution->rects, solution->capacity << 2);
if (!rects) {
//something went wrong
printf("couldn't reallocate\n");
free(rects);
solutionFree(solution);
exit(1);
}
solution->rects = rects;
}
/**
* Your Solution struct will be instantiated and called as such:
* Solution* obj = solutionCreate(rects, rectsSize, rectsColSize);
* int* param_1 = solutionPick(obj, retSize);
* solutionFree(obj);
*/
``` | 0 | 0 | ['C'] | 0 |
random-point-in-non-overlapping-rectangles | C++ 100% beat | c-100-beat-by-aviadblumen-91qd | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | aviadblumen | NORMAL | 2025-02-26T18:22:52.845137+00:00 | 2025-02-26T18:22:52.845137+00:00 | 4 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
vector<vector<int>>& rects;
int total_area;
vector<int> range_by_rect;
mt19937 rng;
public:
Solution(vector<vector<int>>& rects) : rng(random_device{}()),rects(rects){
range_by_rect.resize(size(rects));
range_by_rect[0] = 0;
total_area = 0;
for(int i=0;i<size(rects);i++){
int curr_area = (rects[i][3] - rects[i][1] +1)*(rects[i][2] - rects[i][0]+1);
total_area += curr_area;
if (i < size(rects)-1)
range_by_rect[i+1] = range_by_rect[i] + curr_area;
}
}
int get_rand(int n){
uniform_int_distribution<int> dist(0, n-1);
return dist(rng);
}
vector<int> pick() {
int rand_rect_indx = (upper_bound(range_by_rect.begin(),range_by_rect.end(),get_rand(total_area))-1)
-range_by_rect.begin();
auto& random_rect = rects[rand_rect_indx];
int w= random_rect[2] - random_rect[0] +1;
int h= random_rect[3] - random_rect[1] + 1;
int x = random_rect[0] + get_rand(w);
int y = random_rect[1] + get_rand(h);
return {x,y};
}
};
/**
* Your Solution object will be instantiated and called as such:
* Solution* obj = new Solution(rects);
* vector<int> param_1 = obj->pick();
*/
``` | 0 | 0 | ['C++'] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.