question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
single-element-in-a-sorted-array | easy c++ solution using binary search || self explanatory code | easy-c-solution-using-binary-search-self-6hib | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Rhythm_1383 | NORMAL | 2023-08-15T10:17:07.694251+00:00 | 2023-08-15T10:17:07.694270+00:00 | 326 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n int left=0;\n int right=nums.size()-1;\n while(left<right) \n {\n int mid=(left+right)/2;\n if(mid%2==1)\n {\n mid--;\n }\n if(nums[mid]!=nums[mid+1])\n {\n right=mid;\n }\n else{\n left=mid+2;\n }\n }\n return nums[left];\n }\n};\n``` | 4 | 0 | ['C++'] | 0 |
single-element-in-a-sorted-array | Very Simple (Easy to Understand) 0ms , c++ soln | very-simple-easy-to-understand-0ms-c-sol-0ywv | \n\n# Approach\n\n Let There be 2 arrays .\n a1 = [1,1,2,2,3,3,4,4]; -> point 1\n a2 = [1,1,2,2,3,3]; -> point 2\n\n here , let start = 0 , end = a | gowrijaswanth3 | NORMAL | 2023-05-13T00:07:18.143856+00:00 | 2023-05-14T08:25:08.867404+00:00 | 206 | false | \n\n# Approach\n\n Let There be 2 arrays .\n a1 = [1,1,2,2,3,3,4,4]; -> point 1\n a2 = [1,1,2,2,3,3]; -> point 2\n\n here , let start = 0 , end = arr.size() -1;\n\n a1 has even no of pairs = 4 , s = 0 , e = 7;\n a2 has odd no of pairs = 3 , s = 0, e = 5;\n\n Let us assume 1 element added to the 2 arrays .\n now,\n for a1 -> s = 0, e = 8; pairs = (s-e)/2 = 4;\n for a2 -> s = 0 , e = 6; pairs = (s-e)/2 = 3;\n\n now when you find mid for both the arrays ;\n m = (s+e)/2;\n for a1; \n m = (0+8)/2 = 4;\n from point 1 you can see that nums[m] = 3 and nums[m+1] also 3;\n This means , \n if we get nums[m]=nums[m+1] then element to be found will be on right\n if not this means the a1 in point1 is shifted by 1 space which is present on left of m;\n \n\n for a2; \n m = (0+6)/2 = 3;\n from point 1 you can see that nums[m] = 2 and nums[m-1] also 2;\n This means , \n if we get nums[m]=nums[m-1] then element to be found will be on right\n if not this means the a1 in point1 is shifted by 1 space which is present on left of m;\n\n PLEASE UPVOTE;\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n int n = nums.size() ,s = 0, e = n-1;// x = number of pairs excluding single element\n if(n==1 || nums[0]!=nums[1]) // if nums have single element or first element is the answer\n return nums[0];\n if(nums[n-2]!=nums[n-1]) // if last element is the answer\n return nums[n-1];\n while(s<=e){\n int m = (s+e)/2 , x = (s-e)/2;\n if(nums[m]!=nums[m+1] && nums[m]!=nums[m-1])\n return nums[m];\n if(x%2==0) // even number of pairs\n {\n if(nums[m-1]==nums[m]) // move left\n e=m-2;\n else // move right\n s=m+2;\n }\n else // odd number of pairs \n {\n if(nums[m-1]==nums[m]) // move right\n s=m+1;\n else // move left\n e=m-1;\n }\n }\n return -1; // PLEASE UPVOTE \uD83E\uDD7A\n }\n};\n``` | 4 | 0 | ['C++'] | 1 |
single-element-in-a-sorted-array | Easy 5 line Solution JAVA 100 % beats 0ms | easy-5-line-solution-java-100-beats-0ms-7kpjg | Intuition\nonly odd number of elements will contain 1 non duplicate elment\n# Approach\nmove towards the segment which has odd number of elements \n\n//checking | rajAbhinav | NORMAL | 2023-04-12T08:37:00.095914+00:00 | 2023-04-12T08:37:00.095955+00:00 | 520 | false | # Intuition\nonly odd number of elements will contain 1 non duplicate elment\n# Approach\nmove towards the segment which has odd number of elements \n```\n//checking for odd sequence\n if((high+1-mid)%2!=0) return solve(low,mid,nums);\n//checking for odd sequence\n if((high+1-mid+1)%2!=0) return solve(mid+1,high,nums);\n```\nand try to check if true then increamment mid so that we end up having non duplicate on the left segment.\n``` if(nums[mid]==nums[mid+1]) mid++;```\n\n# Complexity\n- Time complexity:\n0ms 100% beats\n\n# Code\n```\nclass Solution {\n int solve(int low,int high,int[] nums)\n {\n int mid=(low+high)/2; \n// special condition sometimes occurs while serching for duplicate\n //and it contains non duplicate value thus returning it as well\n if(high==low)return nums[low];\n if(nums[mid]==nums[mid+1]) mid++;\n//stoppping the recursion at 3 elements and it is obvious that \n // 1 element will be non duplicate among 3 elemnts thus returning it\n if(high-low==2) return(nums[high]^nums[mid]^nums[low]);\n//checking for odd sequence\n if((high+1-mid)%2!=0) return solve(low,mid,nums);\n//checking for odd sequence\n if((high+1-mid+1)%2!=0) return solve(mid+1,high,nums);\n return -1;\n }\n public int singleNonDuplicate(int[] nums) {\n return solve(0,nums.length-1,nums);\n }\n}\n``` | 4 | 0 | ['Binary Search', 'Java'] | 0 |
single-element-in-a-sorted-array | 540: Time 93.53%, Solution with step by step explanation | 540-time-9353-solution-with-step-by-step-a13z | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n- Initialize two pointers left and right to point to the first and last e | Marlen09 | NORMAL | 2023-03-14T05:00:53.868321+00:00 | 2023-03-14T05:00:53.868357+00:00 | 234 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n- Initialize two pointers left and right to point to the first and last element of the array respectively.\n- Implement binary search until left and right point to the same element.\n- Compute the mid index as the average of left and right.\n- Check if the element at the mid index is the single element.\n- If the element at the mid index is not equal to the elements adjacent to it, return it as the single element.\n- Check if the single element is on the left side of the array.\n- If the element at mid is equal to the element at mid-1, then the single element is on the left side.\n- Compute the distance between left and mid and check if it is even or odd.\n- If it is even, then the single element is to the left of mid. Update right to mid-2.1\n- If it is odd, then the single element is to the right of mid. Update left to mid+1.\n- Check if the single element is on the right side of the array.\n- If the element at mid is equal to the element at mid+1, then the single element is on the right side.\n- Compute the distance between mid and right and check if it is even or odd.\n- If it is even, then the single element is to the right of mid. Update left to mid+2.\n- If it is odd, then the single element is to the left of mid. Update right to mid-1.\n- If we reach here, the single element is at the left index. Return it.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def singleNonDuplicate(self, nums: List[int]) -> int:\n # Initialize pointers\n left, right = 0, len(nums) - 1\n \n # Binary search\n while left < right:\n mid = (left + right) // 2\n \n # Check if mid is the single element\n if nums[mid] != nums[mid-1] and nums[mid] != nums[mid+1]:\n return nums[mid]\n \n # Check if the single element is on the left side\n if nums[mid] == nums[mid-1]:\n if (mid - left) % 2 == 0:\n right = mid - 2\n else:\n left = mid + 1\n \n # Check if the single element is on the right side\n elif nums[mid] == nums[mid+1]:\n if (right - mid) % 2 == 0:\n left = mid + 2\n else:\n right = mid - 1\n \n # If we reach here, the single element is at the last index\n return nums[left]\n\n``` | 4 | 0 | ['Array', 'Binary Search', 'Python', 'Python3'] | 0 |
single-element-in-a-sorted-array | Beats 91.47%||C++||Binary Search||Easy | beats-9147cbinary-searcheasy-by-heisenbe-wmnb | Complexity\n- Time complexity:\nO(logn)\n\n- Space complexity:\nO(1)\n\n# Code\n\nclass Solution {\npublic:\n//index of form:(even,odd) before pivot and of form | Heisenberg2003 | NORMAL | 2023-02-21T12:16:22.807614+00:00 | 2023-02-21T12:16:22.807647+00:00 | 358 | false | # Complexity\n- Time complexity:\nO(logn)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution {\npublic:\n//index of form:(even,odd) before pivot and of form (odd,even) after pivot for equal elements\n int singleNonDuplicate(vector<int>&nums) \n {\n int left=0,right=nums.size()-1;\n while(left<=right)\n {\n int mid=(left+right)/2;\n if(left==right)\n {\n return nums[mid];\n }\n if(mid==0 && nums[mid+1]!=nums[mid])\n {\n return nums[mid];\n }\n if(nums[mid+1]!=nums[mid] && nums[mid-1]!=nums[mid])\n {\n return nums[mid];\n }\n else if((nums[mid+1]==nums[mid] && mid%2==1)||(nums[mid-1]==nums[mid] && mid%2==0))\n {\n right=mid-1;\n }\n else if((nums[mid+1]==nums[mid] && mid%2==0)||(nums[mid-1]==nums[mid] && mid%2==1))\n {\n left=mid+1;\n }\n }\n return -1;\n }\n};\n``` | 4 | 0 | ['C++'] | 0 |
single-element-in-a-sorted-array | Best C++✅Solution💥||Beats 87%🔥||Intuition Explained✅||O(logn)TC||O(1) SC | best-csolutionbeats-87intuition-explaine-5gx7 | Follow Daily Dose of DSA Blog where I post important DSA Questions and different approaches for solving it!!!\nhttps://legolas12.hashnode.dev/\n\n\n# Intuition | legolas12 | NORMAL | 2023-02-21T10:59:39.188083+00:00 | 2023-02-21T12:01:40.075069+00:00 | 799 | false | Follow Daily Dose of DSA Blog where I post important DSA Questions and different approaches for solving it!!!\nhttps://legolas12.hashnode.dev/\n\n\n# Intuition \nAs we all know the element can be found by binary search. But to decide the region we have to write the check function .Lets assume the required element is in the right region. Then we have two cases \n1) mid is 1st element in the pair\n2) mid is 2nd element in the pair\n\n1st case: if mid is 1st element in the pair and required singleton element is in right region. Then left of mid has even number of elements (present in pairs) \n2nd case: if mid is 2nd element in the pair and required singleton element is in the right region . Then left of mid has odd number of elements (elements in pair + pair of mid)\nwhile checking mid is even or odd be aware of the 0 based indexing which will reverse the meaning of even and odd. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nMade two check functions . Check 1 for checking mid has dissimilar elements to the right and left , if present return mid.\nI have written Check 2 if the element is present in the right region.\nand remaining all cases are covered in else statement.\n\n\nBasic Intuition for writing this check function is written above\nThen finally wrote BS code with this two check functions . Corner cases are handled seperately.\n```\nbool check(vector<int> &nums , int x )\n {\n if(nums[x]!=nums[x+1] && nums[x]!=nums[x-1])\n {\n return true;\n }\n else return false;\n } \n\nbool check2(vector<int> &nums , int x)\n {\n if((nums[x]==nums[x+1] && x%2==0) || (nums[x]==nums[x-1] && x%2!=0))\n {\n return true;\n }\n else return false;\n }\n```\n\n# Complexity\n- Time complexity: O(logn)\n\n\n- Space complexity:O(1)\n\n\n# Code\n```\nclass Solution {\npublic:\n\n bool check(vector<int> &nums , int x )\n {\n if(nums[x]!=nums[x+1] && nums[x]!=nums[x-1])\n {\n return true;\n }\n else return false;\n } \n\n bool check2(vector<int> &nums , int x)\n {\n if((nums[x]==nums[x+1] && x%2==0) || (nums[x]==nums[x-1] && x%2!=0))\n {\n return true;\n }\n else return false;\n }\n int singleNonDuplicate(vector<int>& nums) \n {\n int n =(int)nums.size();\n \n int ans;\n int low = 0 , high= n-1;\n if(n==1) return nums[0];\n if(nums[0]!=nums[1]) return nums[0];\n\n if(nums[high]!=nums[high-1]) return nums[high];\n while(low<high)\n {\n int mid = (low+high)/2;\n if(check(nums,mid))\n {\n return nums[mid];\n }\n else if(check2(nums,mid))\n {\n low = mid+1;\n }\n\n else high=mid-1;\n }\n \n return nums[low];\n}\n};\n``` | 4 | 0 | ['Binary Search', 'C++'] | 0 |
single-element-in-a-sorted-array | [Runtime 0 ms] clear and easy solution | runtime-0-ms-clear-and-easy-solution-by-kgm6d | Intuition\nIf the number in the current index is not equal to one of the numbers on either side, then the number we are looking for is that\n\n# Approach\n Desc | jasurbekaktamov080 | NORMAL | 2023-02-21T10:13:13.788590+00:00 | 2023-02-21T10:14:40.697571+00:00 | 45 | false | # Intuition\nIf the number in the current index is not equal to one of the numbers on either side, then the number we are looking for is that\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nRuntime : 0 ms Beats : 100%\nMemory :48 MB Beats :72.85%\n\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int singleNonDuplicate(int[] nums) {\n if(nums.length == 1 ) return nums[0];\n\n if(nums[0] != nums[1]) return nums[0]; // first index\n if(nums[nums.length-1] != nums[nums.length-2]) return nums[nums.length-1]; // last index \n\n for (int i = 1; i < nums.length-1; i++) {\n if(!isD(nums,i)){\n return nums[i];\n }\n }\n \n return -1;\n\n }\n private static boolean isD(int[] nums, int index){\n return nums[index - 1] == nums[index] || nums[index] == nums[index + 1];\n }\n}\n``` | 4 | 0 | ['Array', 'Binary Search', 'Java'] | 0 |
single-element-in-a-sorted-array | [C#] Simple binary search | c-simple-binary-search-by-busigor-xh4e | Approach\nPosition of the searched element is always even. We can find the position by using binary search.\n\nTime complexity: O(log(n)) Space complexity: O(1) | busigor | NORMAL | 2023-02-21T05:21:06.426251+00:00 | 2023-02-21T05:21:06.426302+00:00 | 1,535 | false | # Approach\nPosition of the searched element is always even. We can find the position by using binary search.\n\nTime complexity: $$O(log(n))$$ Space complexity: $$O(1)$$\n\n# Code\n```\npublic class Solution {\n public int SingleNonDuplicate(int[] nums) {\n int l = 0, r = nums.Length / 2;\n while (l < r)\n {\n var mid = (l + r) / 2;\n if (nums[mid * 2] == nums[mid * 2 + 1])\n l = mid + 1;\n else\n r = mid;\n }\n\n return nums[l * 2];\n }\n}\n``` | 4 | 0 | ['C#'] | 3 |
single-element-in-a-sorted-array | Binary Search Easy Left and Right Half Approach | binary-search-easy-left-and-right-half-a-obcl | Intuition\ncheck for left half and right half\n\n# Approach\nobservation->in left half odd index->2nd occurance of some no\neven index->1st occurance of no\nin | sumitpadadune1689 | NORMAL | 2023-02-21T04:43:27.027159+00:00 | 2023-02-21T04:45:20.067828+00:00 | 698 | false | # Intuition\ncheck for left half and right half\n\n# Approach\nobservation->in left half odd index->2nd occurance of some no\neven index->1st occurance of no\nin right half\nodd index ->first occurance of no\neven index->second occurance\naccording reduce search space by applying mid+1 or mid-1 for \nperticular conditions\nIF (YOU UNDERSTOOD THIS SOLUTION){UPVOTE}\nELSE {CHECK CODE AND THEN UPVOTE}\n\n# Complexity\n- Time complexity:\no(log(n))\n\n- Space complexity:\no(1)\n\n# Code\n```\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n int s=0;\n int e=nums.size()-2;\n int mid=s+(e-s)/2;\n while(s<=e)\n {\n\n if((mid&1)==0)\n {if(nums[mid]==nums[mid+1])\n {\n s=mid+1;\n }\n else{\n e=mid-1;\n }\n }\n else{\n if(nums[mid]==nums[mid+1])\n {\n e=mid-1;\n }\n else\n {\n s=mid+1;\n }\n }\n mid=s+(e-s)/2;\n\n }\n return nums[mid];\n }\n};\n``` | 4 | 0 | ['C++'] | 0 |
single-element-in-a-sorted-array | C# Binary Search Explained | c-binary-search-explained-by-lavinamall-lxbn | Approach\n1. if there\'s only one element return it\n2. check if the unique element is the first or last element of the array\n\nCASE 1: element at mid and mid | lavinamall | NORMAL | 2023-02-21T03:33:47.264498+00:00 | 2023-02-21T03:33:47.264546+00:00 | 288 | false | # Approach\n1. if there\'s only one element return it\n2. check if the unique element is the first or last element of the array\n\n**CASE 1**: element at mid and mid - 1 are equal; \n - get count of left array and check if it is even or odd\n - in case it is even, discard and search **right**\n - in case of odd, continue search on the **left** side\n\n**CASE 2**: element at mid and mid + 1 are equal; get right count\n\nto decide the direction of search check which part of the array has odd number of elements.\n\nif number of element from start to mid is odd then unique element will be present on this left side of the array else search on the right side.\n\n# Complexity\n- Time complexity: ```O(log n)```\n\n- Space complexity: ```O(1)```\n\n# Code\n```\npublic class Solution {\n public int SingleNonDuplicate(int[] nums) {\n int start = 0, end = nums.Length - 1; \n if(nums.Length == 1) return nums[end];\n\n // if the unique element is the first or last element of the array\n if(nums[0] != nums[1]) return nums[0];\n\n // if the unique element is the last element of the array\n if(nums[end] != nums[end - 1]) return nums[end];\n\n while(start <= end) { \n int mid = start + (end - start) /2;\n if(nums[mid] != nums[mid - 1] && nums[mid] != nums[mid + 1])\n return nums[mid];\n\n if(nums[mid] == nums[mid - 1]) {\n int leftCount = mid - start + 1;\n if(leftCount % 2 == 0) start = mid + 1;\n else end = mid - 2; \n }\n else if(nums[mid] == nums[mid + 1]) {\n int rightCount = end + mid - 1;\n if(rightCount % 2 == 0) end = mid - 1;\n else start = mid + 2;\n }\n }\n return -1;\n }\n}\n``` | 4 | 0 | ['Binary Search', 'C#'] | 1 |
single-element-in-a-sorted-array | Python short and clean. Binary Search. | python-short-and-clean-binary-search-by-r64hw | Approach\n1. Since nums is sorted and it is guaranteed that all but one number occurs exactly twice. We can binary search for the number with no pair.\n\n2. Say | darshan-as | NORMAL | 2023-02-21T03:26:12.690876+00:00 | 2023-02-21T18:09:18.941018+00:00 | 118 | false | # Approach\n1. Since `nums` is sorted and it is guaranteed that all but one number occurs exactly twice. We can binary search for the number with no pair.\n\n2. Say `m` is the mid point in the search and if all numbers had pairs,\n If `m` is even index, the repeating pair should be at `m + 1`.\n If `m` is odd index, the repeating pair should be at `m - 1`.\n Let\'s call them `i, j = (m - 1, m) if m % 2 else (m, m + 1)`\n\n3. Now, if `nums[i] == nums[j]` we know all numbers to the left of `j` has a pair. Hence Binary Search on the right sub array.\n If `nums[i] != nums[j]` we know the additional number is to the left of `j`. Hence Binary Search on the left sub array.\n\n4. Return when `i == j`.\n\n# Complexity\n- Time complexity: $$O(log(n))$$\n\n- Space complexity: $$O(1)$$\n\nwhere, `n is the length of nums`.\n\n# Code\n```\nclass Solution:\n def singleNonDuplicate(self, nums: list[int]) -> int:\n l, r = 0, len(nums) - 1\n while l < r:\n m = (l + r) // 2\n i, j = (m - 1, m) if m % 2 else (m, m + 1)\n l, r = (j + 1, r) if nums[i] == nums[j] else (l, i)\n return nums[r]\n\n\n``` | 4 | 0 | ['Array', 'Math', 'Python', 'Python3'] | 0 |
single-element-in-a-sorted-array | ✅Python || 💥C++ ||✔ Clean and Concise Solution💥||🚀 O(logN) Binary Search | python-c-clean-and-concise-solution-olog-aij3 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | santhosh1608 | NORMAL | 2023-02-21T02:23:47.779811+00:00 | 2023-02-21T02:23:47.779848+00:00 | 395 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(log n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code Upvote please\uD83D\uDE4C\uD83D\uDE09\n```\nclass Solution(object):\n def singleNonDuplicate(self, nums):\n """\n :type nums: List[int]\n :rtype: int\n """\n start , end = 0 , len(nums) -1\n while start < end :\n mid = (start + end) // 2\n if(nums[mid]==nums[mid+1]):\n mid = mid-1\n \n if((mid-start+1)%2!=0):\n end = mid\n \n else:\n start = mid+1\n return nums[start]\n \n```\n\n# UPVOTE ME \uD83D\uDE09\uD83E\uDD1E\uD83D\uDE22 | 4 | 0 | ['Array', 'Binary Search', 'Python'] | 0 |
single-element-in-a-sorted-array | Swift | Binary Search | 6 SLOC | swift-binary-search-6-sloc-by-upvotethis-znws | \u26A0\uFE0F - Solution is supposed to be O(log n)/O(1). Seeing many Swift posted solutions that are O(n)/O(n).\n\n---\nBinary Search (accepted answer)\n\nclass | UpvoteThisPls | NORMAL | 2023-02-21T00:23:05.417067+00:00 | 2023-02-21T02:54:43.272461+00:00 | 985 | false | \u26A0\uFE0F - Solution is supposed to be O(log n)/O(1). Seeing many Swift posted solutions that are O(n)/O(n).\n\n---\n**Binary Search (accepted answer)**\n```\nclass Solution {\n func singleNonDuplicate(_ nums: [Int]) -> Int {\n var (left, right) = (0, nums.count-1)\n while left < right {\n let mid = (left+right)/2\n (left, right) = nums[mid & ~1] == nums[mid & ~1+1] ? (mid+1, right) : (left, mid)\n }\n return nums[left]\n }\n}\n```\n\n---\n\n**SEE ALSO:** [A One-Liner Solution](https://leetcode.com/problems/single-element-in-a-sorted-array/discuss/3212093/Swift-or-One-Liner) | 4 | 0 | ['Swift'] | 0 |
single-element-in-a-sorted-array | 🗓️ Daily LeetCoding Challenge February, Day 21 | daily-leetcoding-challenge-february-day-w19rn | This problem is the Daily LeetCoding Challenge for February, Day 21. Feel free to share anything related to this problem here! You can ask questions, discuss wh | leetcode | OFFICIAL | 2023-02-21T00:00:16.174853+00:00 | 2023-02-21T00:00:16.174921+00:00 | 11,315 | false | This problem is the Daily LeetCoding Challenge for February, Day 21.
Feel free to share anything related to this problem here!
You can ask questions, discuss what you've learned from this problem, or show off how many days of streak you've made!
---
If you'd like to share a detailed solution to the problem, please create a new post in the discuss section and provide
- **Detailed Explanations**: Describe the algorithm you used to solve this problem. Include any insights you used to solve this problem.
- **Images** that help explain the algorithm.
- **Language and Code** you used to pass the problem.
- **Time and Space complexity analysis**.
---
**📌 Do you want to learn the problem thoroughly?**
Read [**⭐ LeetCode Official Solution⭐**](https://leetcode.com/problems/single-element-in-a-sorted-array/solution) to learn the 3 approaches to the problem with detailed explanations to the algorithms, codes, and complexity analysis.
<details>
<summary> Spoiler Alert! We'll explain these 3 approaches in the official solution</summary>
**Approach 1:** Brute Force
**Approach 2:** Binary Search
**Approach 3:** Binary Search on Evens Indexes Only
</details>
If you're new to Daily LeetCoding Challenge, [**check out this post**](https://leetcode.com/discuss/general-discussion/655704/)!
---
<br>
<p align="center">
<a href="https://leetcode.com/subscribe/?ref=ex_dc" target="_blank">
<img src="https://assets.leetcode.com/static_assets/marketing/daily_leetcoding_banner.png" width="560px" />
</a>
</p>
<br> | 4 | 0 | [] | 36 |
single-element-in-a-sorted-array | Simple C++ code in log(n) complexity | simple-c-code-in-logn-complexity-by-vish-4d06 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | vishu_0123 | NORMAL | 2023-02-11T13:24:17.327520+00:00 | 2023-02-11T13:24:17.327552+00:00 | 864 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n int n=nums.size(),l=0,r=n-1,m;\n while(l<r){\n m=l+(r-l)/2;\n if(m%2==0){\n if(nums[m]==nums[m+1]) l=m+1;\n else {r=m;} }\n else{\n if(nums[m]!=nums[m+1]) l=m+1;\n else {r=m;}\n }\n }\n return nums[l];\n }\n};\n``` | 4 | 0 | ['C++'] | 0 |
single-element-in-a-sorted-array | Best O(LogN) Solution | best-ologn-solution-by-kumar21ayush03-xupt | Approach 1\nXOR\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n\nclass Solution {\npublic:\n int singleNonDuplicate(vector | kumar21ayush03 | NORMAL | 2023-01-26T15:04:50.837749+00:00 | 2023-01-26T15:04:50.837795+00:00 | 353 | false | # Approach 1\nXOR\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(1)$$\n\n# Code\n```\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n int ans = 0;\n for (int i = 0; i < nums.size(); i++)\n ans = ans ^ nums[i];\n return ans; \n }\n};\n```\n# Approach 2\nLinear Search\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(1)$$\n\n# Code\n```\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n int n = nums.size();\n if (n == 1)\n return nums[0];\n for (int i = 1; i < n; i = i + 2)\n if (nums[i - 1] != nums[i])\n return nums[i - 1];\n return nums[n - 1]; \n }\n};\n```\n\n# Approach 3\nBinary Search\n\n# Complexity\n- Time complexity:\n$$O(logn)$$\n\n- Space complexity:\n$$O(1)$$\n\n# Code\n```\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n int n = nums.size();\n if (n == 1)\n return nums[0];\n if (nums[0] != nums[1])\n return nums[0]; \n int low = 0, high = n - 1;\n while (low <= high) {\n int mid = (low + high) / 2;\n if ((nums[mid] != nums[mid - 1] || mid == 0) &&\n (nums[mid] != nums[mid + 1] || mid == n - 1))\n return nums[mid];\n else if ((mid % 2 == 0 && nums[mid] == nums[mid - 1]) || \n (mid % 2 == 1 && nums[mid] == nums[mid + 1])) \n high = mid - 1;\n else\n low = mid + 1; \n }\n return -1;\n }\n};\n``` | 4 | 0 | ['C++'] | 0 |
number-of-subarrays-with-bounded-maximum | Python , standard DP solution with explanation | python-standard-dp-solution-with-explana-nddk | Suppose dp[i] denotes the max number of valid sub-array ending with A[i]. We use following example to illustrate the idea: A = [2, 1, 4, 2, 3], L = 2, R = 3 if | charleszhou327 | NORMAL | 2018-03-04T17:49:28.590992+00:00 | 2018-10-18T05:29:20.324187+00:00 | 15,306 | false | Suppose __dp[i]__ denotes the max number of valid sub-array ending with __A[i]__. We use following example to illustrate the idea:
_A = [2, 1, 4, 2, 3], L = 2, R = 3_
1. if A[i] < L
For example, i = 1. We can only append A[i] to a valid sub-array ending with A[i-1] to create new sub-array. So we have __dp[i] = dp[i-1] (for i > 0)__
2. if A[i] > R:
For example, i = 2. No valid sub-array ending with A[i] exist. So we have __dp[i] = 0__.
We also record the position of the invalid number 4 here as __prev__.
3. if L <= A[i] <= R
For example, i = 4. In this case any sub-array starts after the previous invalid number to A[i] (A[prev+1..i], A[prev+2..i]) is a new valid sub-array. So __dp[i] += i - prev__
Finally the sum of the dp array is the solution. Meanwhile, notice dp[i] only relies on dp[i-1] (and also __prev__), we can reduce the space complexity to O(1)
```python
class Solution(object):
def numSubarrayBoundedMax(self, A, L, R):
"""
:type A: List[int]
:type L: int
:type R: int
:rtype: int
"""
res, dp = 0, 0
prev = -1
for i in range(len(A)):
if A[i] < L and i > 0:
res += dp
if A[i] > R:
dp = 0
prev = i
if L <= A[i] <= R:
dp = i - prev
res += dp
return res
``` | 314 | 1 | [] | 24 |
number-of-subarrays-with-bounded-maximum | C++, O(n), <10 lines | c-on-10-lines-by-johnsontau-khxn | class Solution { public: int numSubarrayBoundedMax(vector<int>& A, int L, int R) { int result=0, left=-1, right=-1; for (int i=0; i<A.size() | johnsontau | NORMAL | 2018-03-04T04:46:14.582871+00:00 | 2018-10-24T20:15:35.083669+00:00 | 12,037 | false | ```
class Solution {
public:
int numSubarrayBoundedMax(vector<int>& A, int L, int R) {
int result=0, left=-1, right=-1;
for (int i=0; i<A.size(); i++) {
if (A[i]>R) left=i;
if (A[i]>=L) right=i;
result+=right-left;
}
return result;
}
};
``` | 241 | 4 | [] | 18 |
number-of-subarrays-with-bounded-maximum | [C++/Java/Python] Easy to understand solution - Clean & Concise - O(N) | cjavapython-easy-to-understand-solution-twkq3 | Idea\n- Let count(bound) is the number of subarrays which have all elements less than or equal to bound.\n- Finally, count(right) - count(left-1) is our result. | hiepit | NORMAL | 2021-06-17T10:58:05.384125+00:00 | 2021-06-17T17:10:01.087574+00:00 | 9,268 | false | **Idea**\n- Let `count(bound)` is the number of subarrays which have all elements less than or equal to `bound`.\n- Finally, `count(right) - count(left-1)` is our result.\n- How to compute `count(bound)`?\n\t- Let `ans` is our answer\n\t- Let `cnt` is the number of consecutive elements less than or equal to `bound` so far\n\t- For index `i` in `0..n-1`:\n\t\t- If `nums[i] <= bound` then `cnt = cnt + 1`\n\t\t- Else `cnt = 0`\n\t\t- `ans += cnt` // We have total `cnt` subarrays which end at index `i_th` and have all elements are less than or equal to `bound`\n\n**Complexity**\n- Time: `O(N)`\n- Space: `O(1)`\n\n**Python 3**\n```python\nclass Solution:\n def numSubarrayBoundedMax(self, nums: List[int], left: int, right: int) -> int:\n def count(bound):\n ans = cnt = 0\n for x in nums:\n cnt = cnt + 1 if x <= bound else 0\n ans += cnt\n return ans\n\n return count(right) - count(left - 1)\n```\n\n**C++**\n```c++\nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& nums, int left, int right) {\n return count(nums, right) - count(nums, left - 1);\n }\n int count(const vector<int>& nums, int bound) {\n int ans = 0, cnt = 0;\n for (int x : nums) {\n cnt = x <= bound ? cnt + 1 : 0;\n ans += cnt;\n }\n return ans;\n }\n};\n```\n\n**Java**\n```java\nclass Solution {\n public int numSubarrayBoundedMax(int[] nums, int left, int right) {\n return count(nums, right) - count(nums, left - 1);\n }\n int count(int[] nums, int bound) {\n int ans = 0, cnt = 0;\n for (int x : nums) {\n cnt = x <= bound ? cnt + 1 : 0;\n ans += cnt;\n }\n return ans;\n }\n}\n```\n\n | 207 | 16 | [] | 16 |
number-of-subarrays-with-bounded-maximum | JS, Python, Java, C++ | Easy Triangular Number Solution w/ Explanation | js-python-java-c-easy-triangular-number-sciyf | (Note: This is part of a series of Leetcode solution explanations. If you like this solution or find it useful, please upvote this post.)\n\n---\n\n#### Idea:\n | sgallivan | NORMAL | 2021-06-17T08:06:32.751788+00:00 | 2021-06-17T09:24:43.005862+00:00 | 5,027 | false | *(Note: This is part of a series of Leetcode solution explanations. If you like this solution or find it useful,* ***please upvote*** *this post.)*\n\n---\n\n#### ***Idea:***\n\nThe key to this problem is realizing that we\'re dealing with overlapping **triangular number** issues. Importantly, the total number of possible subarrays that are contained within any larger subarray is the **N**th triangular number, where **N** is the length of that larger subarray. \n\nSo the **nums** array starts with the (**nums.length**)th triangular number total subarrays. We want to exclude any subarray that includes a number larger than **right**, however. The easiest way to do this is to consider numbers larger than **right** to be dividers, splitting **nums** into many subarrays. We can add the triangular number for each of these resulting subarrays together to be the total number of subarrays that exclude numbers higher than **right**.\n\nTo do this, we can iterate through **nums** and keep track of how many contiguous numbers are less than **right** (**mid**) and each point that **mid** increments, we can add **mid** to **ans**, representing the increase to the next triangular number. The value for **mid** will then reset whenever we see a number higher than **right**.\n\nBut this only does half of the problem, because we still have to also exclude any subarray that does not have any number at least **left** high. To do this, we can use a similar method as for **mid**. We can keep track of how many contiguous numbers are lower than **left** (**low**) and _decrease_ **ans** by that amount every time it increments, representing the next triangular number. Similar to **mid**, **low** will reset whenever we see a number at least **left** high.\n\nOnce we\'re done iterating, we can **return ans**.\n\nVisual example:\n\n\n\n - _**Time Complexity: O(N)** where **N** is the length of **nums**_\n - _**Space Complexity: O(1)**_\n\n---\n\n#### ***Javascript Code:***\n\nThe best result for the code below is **72ms / 42.2MB** (beats 100% / 84%).\n```javascript\nvar numSubarrayBoundedMax = function(nums, left, right) {\n let ans = 0, low = 0, mid = 0\n for (let i = 0; i < nums.length; i++) {\n let num = nums[i]\n if (num > right) mid = 0\n else ans += ++mid\n if (num >= left) low = 0\n else ans -= ++low\n }\n return ans\n};\n```\n\n---\n\n#### ***Python Code:***\n\nThe best result for the code below is **316ms / 15.5MB** (beats 98% / 97%).\n```python\nclass Solution:\n def numSubarrayBoundedMax(self, nums: List[int], left: int, right: int) -> int:\n ans, low, mid = 0, 0, 0\n for num in nums:\n if num > right: mid = 0\n else:\n mid += 1\n ans += mid\n if num >= left: low = 0\n else:\n low += 1\n ans -= low\n return ans\n```\n\n---\n\n#### ***Java Code:***\n\nThe best result for the code below is **2ms / 46.8MB** (beats 100% / 75%).\n```java\nclass Solution {\n public int numSubarrayBoundedMax(int[] nums, int left, int right) {\n int ans = 0, low = 0, mid = 0;\n for (int num : nums) {\n if (num > right) mid = 0;\n else ans += ++mid;\n if (num >= left) low = 0;\n else ans -= ++low;\n }\n return ans;\n }\n}\n```\n\n---\n\n#### ***C++ Code:***\n\nThe best result for the code below is **24ms / 32.4MB** (beats 99% / 86%).\n```c++\nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& nums, int left, int right) {\n int ans = 0, low = 0, mid = 0;\n for (auto num : nums) {\n if (num > right) mid = 0;\n else ans += ++mid;\n if (num >= left) low = 0;\n else ans -= ++low;\n }\n return ans;\n }\n};\n``` | 144 | 36 | ['C', 'Python', 'Java', 'JavaScript'] | 10 |
number-of-subarrays-with-bounded-maximum | Short Java O(n) Solution | short-java-on-solution-by-kay_deep-fmfi | ``` class Solution { public int numSubarrayBoundedMax(int[] A, int L, int R) { int j=0,count=0,res=0; for(int i=0;i<A.length;i++){ if(A[ | kay_deep | NORMAL | 2018-03-04T04:11:25.036176+00:00 | 2018-10-20T22:21:12.328395+00:00 | 14,099 | false | ```
class Solution {
public int numSubarrayBoundedMax(int[] A, int L, int R) {
int j=0,count=0,res=0;
for(int i=0;i<A.length;i++){
if(A[i]>=L && A[i]<=R){
res+=i-j+1;count=i-j+1;
}
else if(A[i]<L){
res+=count;
}
else{
j=i+1;
count=0;
}
}
return res;
}
}
``` | 106 | 4 | [] | 15 |
number-of-subarrays-with-bounded-maximum | Number of Subarrays with Bounded Maximum | JS, Python, Java, C++ | Easy Triang. Number Sol. w/ Expl. | number-of-subarrays-with-bounded-maximum-42m1 | (Note: This is part of a series of Leetcode solution explanations. If you like this solution or find it useful, please upvote this post.)\n\n---\n\n#### Idea:\n | sgallivan | NORMAL | 2021-06-17T08:07:32.730295+00:00 | 2021-06-17T09:24:49.879118+00:00 | 2,572 | false | *(Note: This is part of a series of Leetcode solution explanations. If you like this solution or find it useful,* ***please upvote*** *this post.)*\n\n---\n\n#### ***Idea:***\n\nThe key to this problem is realizing that we\'re dealing with overlapping **triangular number** issues. Importantly, the total number of possible subarrays that are contained within any larger subarray is the **N**th triangular number, where **N** is the length of that larger subarray. \n\nSo the **nums** array starts with the (**nums.length**)th triangular number total subarrays. We want to exclude any subarray that includes a number larger than **right**, however. The easiest way to do this is to consider numbers larger than **right** to be dividers, splitting **nums** into many subarrays. We can add the triangular number for each of these resulting subarrays together to be the total number of subarrays that exclude numbers higher than **right**.\n\nTo do this, we can iterate through **nums** and keep track of how many contiguous numbers are less than **right** (**mid**) and each point that **mid** increments, we can add **mid** to **ans**, representing the increase to the next triangular number. The value for **mid** will then reset whenever we see a number higher than **right**.\n\nBut this only does half of the problem, because we still have to also exclude any subarray that does not have any number at least **left** high. To do this, we can use a similar method as for **mid**. We can keep track of how many contiguous numbers are lower than **left** (**low**) and _decrease_ **ans** by that amount every time it increments, representing the next triangular number. Similar to **mid**, **low** will reset whenever we see a number at least **left** high.\n\nOnce we\'re done iterating, we can **return ans**.\n\nVisual example:\n\n\n\n - _**Time Complexity: O(N)** where **N** is the length of **nums**_\n - _**Space Complexity: O(1)**_\n\n---\n\n#### ***Javascript Code:***\n\nThe best result for the code below is **72ms / 42.2MB** (beats 100% / 84%).\n```javascript\nvar numSubarrayBoundedMax = function(nums, left, right) {\n let ans = 0, low = 0, mid = 0\n for (let i = 0; i < nums.length; i++) {\n let num = nums[i]\n if (num > right) mid = 0\n else ans += ++mid\n if (num >= left) low = 0\n else ans -= ++low\n }\n return ans\n};\n```\n\n---\n\n#### ***Python Code:***\n\nThe best result for the code below is **316ms / 15.5MB** (beats 98% / 97%).\n```python\nclass Solution:\n def numSubarrayBoundedMax(self, nums: List[int], left: int, right: int) -> int:\n ans, low, mid = 0, 0, 0\n for num in nums:\n if num > right: mid = 0\n else:\n mid += 1\n ans += mid\n if num >= left: low = 0\n else:\n low += 1\n ans -= low\n return ans\n```\n\n---\n\n#### ***Java Code:***\n\nThe best result for the code below is **2ms / 46.8MB** (beats 100% / 75%).\n```java\nclass Solution {\n public int numSubarrayBoundedMax(int[] nums, int left, int right) {\n int ans = 0, low = 0, mid = 0;\n for (int num : nums) {\n if (num > right) mid = 0;\n else ans += ++mid;\n if (num >= left) low = 0;\n else ans -= ++low;\n }\n return ans;\n }\n}\n```\n\n---\n\n#### ***C++ Code:***\n\nThe best result for the code below is **24ms / 32.4MB** (beats 99% / 86%).\n```c++\nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& nums, int left, int right) {\n int ans = 0, low = 0, mid = 0;\n for (auto num : nums) {\n if (num > right) mid = 0;\n else ans += ++mid;\n if (num >= left) low = 0;\n else ans -= ++low;\n }\n return ans;\n }\n};\n``` | 73 | 8 | [] | 4 |
number-of-subarrays-with-bounded-maximum | Java Explained Solution || O(1) Space || 2 Pointers || Similar Question | java-explained-solution-o1-space-2-point-yuzd | There are 3 Possible Cases :\n1. A[i] is between L and R (inclusive)\n2. A[i] is less than L\n3. A[i] is greater than R\n\nCASE 1: L<=A[i]<=R\nIt means that I( | himanshuchhikara | NORMAL | 2021-03-19T13:34:40.514198+00:00 | 2021-03-19T13:34:40.514227+00:00 | 3,283 | false | There are 3 Possible Cases :\n1. A[i] is between L and R (inclusive)\n2. A[i] is less than L\n3. A[i] is greater than R\n\n**CASE 1: L<=A[i]<=R**\n*It means that I(current element) can be part of previous subarrays (i-j) and also Can start a subarray from me (+1)\nSo add (i-j+1) in total Subarrays*\n\n**CASE 2: A[i]<L**\n*It means that I(current element) can be part of previous subarrays(contigous) but cannot start subarray from me.\nSo add (i-j) in total subarrays(ans)*\n\n**CASE3: A[i]>R**\n*It means that I cannot be part of previous subarrays and also cannot start subarray from me.\nAs its subarray so put j=i+1 . now valid subarrays are going to start from next to me.* \n\n```\npublic int numSubarrayBoundedMax(int[] A, int L, int R) {\n int i=0;\n int j=0;\n int ans=0;\n int smaller=0;\n \n while(i!=A.length){\n \n if(A[i]>=L && A[i]<=R){\n smaller=i-j+1;\n ans+=smaller;\n }else if(A[i]<L){\n ans+=smaller;\n }else{\n j=i+1;\n smaller=0;\n }\n i++;\n }\n return ans;\n }\n```\n**Time:O(n) and Space:O(1)**\nPlease **upvote** if found it helpful :)\nSimilar Question : [Subarray product less than k](https://leetcode.com/problems/subarray-product-less-than-k/) | 61 | 0 | ['Two Pointers', 'Java'] | 6 |
number-of-subarrays-with-bounded-maximum | Clean & simple O(n) Java | clean-simple-on-java-by-octavila-7ss2 | \n public int numSubarrayBoundedMax(int[] A, int L, int R) {\n int start = -1, last = -1, res = 0;\n for(int i = 0; i < A.length; i++) {\n | octavila | NORMAL | 2018-03-14T03:18:15.666427+00:00 | 2018-10-24T06:47:28.404868+00:00 | 3,958 | false | ```\n public int numSubarrayBoundedMax(int[] A, int L, int R) {\n int start = -1, last = -1, res = 0;\n for(int i = 0; i < A.length; i++) {\n if(A[i] > R) {\n start = last = i;\n continue;\n }\n \n if(A[i] >= L)\n last = i;\n\n res += last - start;\n }\n \n return res;\n }\n``` | 58 | 1 | [] | 5 |
number-of-subarrays-with-bounded-maximum | C++ O(n) solution with explanations | c-on-solution-with-explanations-by-nicky-q8xu | The idea is to keep track of 3 things while iterating: the number of valid subarrays (res), the number of valid subarray starting points (heads), and the number | nickyh | NORMAL | 2018-03-04T04:39:55.519776+00:00 | 2018-10-13T11:00:39.408351+00:00 | 5,152 | false | The idea is to keep track of 3 things while iterating: the number of valid subarrays (`res`), the number of valid subarray starting points (`heads`), and the number of not-yet valid starting points (`tails`).
* Values between `L` and `R` are heads. Every contiguous value afterwards that is less than R afterwards can extend them, creating new subarrays.
* Values less than `L` are tails. If they connect to a head later in the array, they become a head for valid subarrays.
* Values greater than `R` are combo breakers. They stop all heads and tails from forming from subarrays.
Therefore, we keep a rolling count of valid subarrays as we iterate through `A`, the main array.
* If a `head` is encountered, it joins the existing heads to form subarrays at each iteration. All `tails` are promoted to heads. All existing heads create a new valid subarray.
* The new head creates subarray of a single element ([head])
* Each promoted head creates subarrays from its tail index to current index (e.g. [tail1, tail2, head, ...], encountering head promotes tail1 and tail2 to heads and creates [tail1, tail2, head] and [tail2, head])
* If a tail is encountered, all existing heads can create another subarray with it. The tail remains useless until it encounters a head (see above).
* If a combo breaker is met, all existing heads and tails become useless, and are reset to 0.
Counts of new subarrays (i.e. head count) are added to `res` at each iteration, if valid.
```
class Solution {
public:
int numSubarrayBoundedMax(vector<int>& A, int L, int R) {
int res = 0, heads = 0, tails = 0;
for (int val : A) {
if (L <= val && val <= R) {
// val is a head. All tails promoted to heads
heads+= tails + 1;
tails = 0;
res += heads;
}
else if (val < L) {
// val is a tail, can extend existing subarrays
tails++;
res += heads;
}
else {
// combo breaker
heads = 0;
tails = 0;
}
}
return res;
}
};
``` | 50 | 2 | [] | 6 |
number-of-subarrays-with-bounded-maximum | a few solutions | a-few-solutions-by-claytonjwong-8f88 | There are 3 buckets which numbers in can be placed into:\n\n1) less than L\n2) less than or equal to R\n3) greater than R\n\nBucket 1 is a subset of Bucket 2. | claytonjwong | NORMAL | 2018-03-05T00:02:04.721767+00:00 | 2021-06-18T03:15:34.341432+00:00 | 2,129 | false | There are 3 buckets which numbers in can be placed into:\n\n1) less than `L`\n2) less than or equal to `R`\n3) greater than `R`\n\nBucket 1 is a subset of Bucket 2. Return the ongoing count of bucket 2 numbers minus the ongoing count of bucket 1 numbers. Completely ignore bucket 3. The ongoing count of bucket 1 and 2 is reset back to 0 when a number no longer meets the ongoing count criteria ( "less than L" for bucket 1 and "less than or equal to R" for bucket 2 ).\n\n---\n\n**Solutions from June 17<sup>th</sup> 2021\'s daily challenge:**\n\nConsider the question: "what is the limiting factor for creating a contiguous sub-array?" The limiting factor can be thought of as the "bare minimum necessity", ie. for each contiguous sub-array the limiting factor is: "the sub-array must include an arbitrary value `x` such that `x` is clamped by `L..R` inclusive." Let `c` be the count of such sub-arrays. So let\'s find and return `c`...\n\nLet `a` and `b` be ongoing the count of bucket 1 and 2 correspondingly for values `x` seen during a linear scan of the input array `A`. Then return the ongoing count `c` of sub-arrays as the accumulated absolute difference between `a` and `b` for each `x` under consideration, ie. since bucket 1 is a subset of bucket 2, we subtract `a` from `b` to accumulate the ongoing count `c` of subarrays with limiting factor `x` as a maximal value between `L..R` inclusive. Note: `a` is non-inclusive of `L` so when we subtract `a` from `b`, `b` is inclusive of `L`, and thus `b` satisfies count of the property `x` clamped by `L..R` inclusive, ie. `a` is the ongoing count for the contiguous sub-array under considersation\'s `0, 1, 2, ..., L - 3, L - 2, L - 1` inclusive values and `b` is the ongoing count for the contiguous sub-array under consideration\'s `0, 1, 2, ..., L - 3, L - 2, L - 1, L, L + 1, L + 2, ... , R - 2, R - 1, R` inclusive values, this is why we erase the count of the first `0..L-1` inclusive to only include the count of `L..R` inclusive to be accumulated in `c`.\n\n**Procedural Solutions:**\n\n*Kotlin*\n```\nclass Solution {\n fun numSubarrayBoundedMax(A: IntArray, L: Int, R: Int): Int {\n var (a, b, c) = listOf(0, 0, 0)\n for (x in A) {\n a = if (x < L) 1 + a else 0\n b = if (x <= R) 1 + b else 0\n c += b - a\n }\n return c\n }\n}\n```\n\n*Javascript*\n```\nlet numSubarrayBoundedMax = (A, L, R) => {\n let [a, b, c] = [0, 0, 0];\n for (let x of A) {\n a = x < L ? 1 + a : 0;\n b = x <= R ? 1 + b : 0;\n c += b - a;\n }\n return c;\n};\n```\n\n*Python3*\n```\nclass Solution:\n def numSubarrayBoundedMax(self, A: List[int], L: int, R: int) -> int:\n a, b, c = 0, 0, 0\n for x in A:\n a = 1 + a if x < L else 0\n b = 1 + b if x <= R else 0\n c += b - a\n return c\n```\n\n*C++*\n```\nclass Solution {\npublic:\n using VI = vector<int>;\n int numSubarrayBoundedMax(VI& A, int L, int R) {\n auto [a, b, c] = make_tuple(0, 0, 0);\n for (auto x: A) {\n a = x < L ? 1 + a : 0;\n b = x <= R ? 1 + b : 0;\n c += b - a;\n }\n return c;\n }\n};\n```\n\n---\n\n**Legacy Solutions (March 4, 2018 5:02 PM):**\n\n**Verbose Solution #1:**\n```\nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& A, int L, int R) {\n int cnt=0,lessThanLeft=0,lessThanOrEqToRight=0;\n for (auto n: A){\n \n if (n<L)\n ++lessThanLeft;\n else\n lessThanLeft=0;\n \n if (n<=R)\n ++lessThanOrEqToRight;\n else\n lessThanOrEqToRight=0;\n \n cnt+=lessThanOrEqToRight-lessThanLeft;\n }\n return cnt;\n }\n};\n```\n\n**Concise Solution #2:**\n* Let ```i``` represent the ongoing count of bucket 1 numbers ( less than L ).\n* Let ```j``` represent the ongoing count of bucker 2 numbers ( less than or equal to R )\n```\nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& A, int L, int R) {\n int cnt=0,i=0,j=0;\n for (auto n: A){\n i=(n<L) ? i+1 : 0;\n j=(n<=R) ? j+1 : 0;\n cnt+=j-i;\n }\n return cnt;\n }\n};\n```\n\n**More Concise Solution #3:**\n* Let ```i``` represent the ongoing count of bucket 1 numbers ( less than L ).\n* Let ```j``` represent the ongoing count of bucket 2 numbers ( less than or equal to R )\n```\nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& A, int L, int R) {\n int cnt=0,i=0,j=0;\n for (auto n: A) cnt+=( ++j*=(n<=R) ) - ( ++i*=(n<L) );\n return cnt;\n }\n};\n``` | 39 | 0 | [] | 1 |
number-of-subarrays-with-bounded-maximum | [Python] simple O(n) solution, explained | python-simple-on-solution-explained-by-d-lgfq | Let us iterate through numbers and keep index of last number which is >= L and index of last number, which is > R. Then, we can quickly calculate number of suba | dbabichev | NORMAL | 2021-06-17T10:11:03.722452+00:00 | 2021-06-17T11:06:24.673783+00:00 | 1,664 | false | Let us iterate through numbers and keep index of last number which is `>= L` and index of last number, which is `> R`. Then, we can quickly calculate number of subarrays with bounded maximum which ends on symbol with index `i`: in our window at least one number `>= L`, no numbers `> R`, so we calculate`L_ind - R_ind`. Note, that this number can never be negative, because if `num > R` then `num >= L` since L <= R.\n\n#### Complexity\nTime complexity is `O(n)`, space is `O(1)`.\n\n#### Code\n\n```python\nclass Solution:\n def numSubarrayBoundedMax(self, A, L, R):\n L_ind, R_ind, ans = -1, -1, 0\n for i, num in enumerate(A):\n if num >= L: L_ind = i\n if num > R: R_ind = i\n ans += L_ind - R_ind\n return ans\n```\n\nIf you have any question, feel free to ask. If you like the explanations, please **Upvote!** | 38 | 3 | [] | 4 |
number-of-subarrays-with-bounded-maximum | C++ Simple and Easy Explained Solution | c-simple-and-easy-explained-solution-by-dodmi | Brief Explanation:\nThere are three cases:\n1. The current number is greater than right - there are no new subarrays to add to res. We just update prev_bigger_t | yehudisk | NORMAL | 2021-06-17T08:38:18.359458+00:00 | 2021-06-17T09:02:35.832478+00:00 | 2,394 | false | **Brief Explanation:**\nThere are three cases:\n1. The current number is greater than right - there are no new subarrays to add to res. We just update prev_bigger_than_r = current index.\n2. The current number is smaller than left - we can add the new number to all valid previous subarrays which end here so far. But the current number can\'t form it\'s own valid subarray.\n3. The current number is between right and left. In this case we add the new number to all valid previous subarrays which end here so far and the number itself can form a valid subarray too.\n```\nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& nums, int left, int right) {\n int res = 0;\n int prev_bigger_than_r = -1;\n int count_prev = 0;\n \n for (int i = 0; i < nums.size(); i++) {\n if (nums[i] > right) {\n prev_bigger_than_r = i;\n count_prev = 0;\n }\n \n else if (nums[i] < left) {\n res += count_prev;\n }\n \n else {\n count_prev = i - prev_bigger_than_r;\n res += count_prev;\n \n }\n }\n return res;\n }\n};\n``` | 32 | 1 | ['C'] | 3 |
number-of-subarrays-with-bounded-maximum | Python Easy and Concise, one-pass O(N) time O(1) space, with Detailed Explanation | python-easy-and-concise-one-pass-on-time-eobv | py\nclass Solution(object):\n\tdef numSubarrayBoundedMax(self, A, L, R):\n\t\t"""\n\t\t:type A: List[int]\n\t\t:type L: int\n\t\t:type R: int\n\t\t:rtype: int\n | jianhaoz | NORMAL | 2019-01-25T03:24:11.493846+00:00 | 2019-01-25T03:24:11.493965+00:00 | 1,475 | false | ```py\nclass Solution(object):\n\tdef numSubarrayBoundedMax(self, A, L, R):\n\t\t"""\n\t\t:type A: List[int]\n\t\t:type L: int\n\t\t:type R: int\n\t\t:rtype: int\n\t\t"""\n\t\t# spec:\n\t\t# Return the number of (contiguous, non-empty) subarrays\n\t\t# such that the value of the maximum array element in that\n\t\t# subarray is at least L and at most R.\n\t\t# \n\t\t# which means: at least one number >= L, no number > R\n\n\t\t# lastIn: last index of an element >= L (must be included)\n\t\t# lastEx: last index of an element > R (must not be included)\n\t\t# at each step i, count valid subarrays ending at index i\n\t\t# the starting index should be lastEx < start <= lastIn\n\t\t# lastIn - lastEx is the number of valid starting indices\n\t\t# if it\'s non-positive, then there are no valid starting indices\n\n\t\t# example:\n\t\t# L: last number >= L, R: last number > R\n\t\t# _____R___L___i___\n\t\t# for valid subarrays ending at i, it\n\t\t# must start between (R, L]\n\t\tans = 0\n\t\tlastIn, lastEx = -1, -1\n\t\tfor i in xrange(len(A)):\n\t\t\tif A[i] >= L:\n\t\t\t\tlastIn = i\n\t\t\tif A[i] > R:\n\t\t\t\tlastEx = i\n\t\t\tans += max(lastIn - lastEx, 0)\n\t\treturn ans\n``` | 24 | 0 | [] | 2 |
number-of-subarrays-with-bounded-maximum | [Cpp] Concept , explanation and dry run | cpp-concept-explanation-and-dry-run-by-s-utn4 | For the element at each index we check below\n- If the current element is greater than R (A[i]>R) than we can not have any subarray ending with current element | spjparmar | NORMAL | 2020-07-04T12:13:39.911200+00:00 | 2020-07-04T12:14:06.645165+00:00 | 954 | false | For the element at each index we check below\n- If the current element is greater than R (A[i]>R) than we can not have any subarray ending with current element and we keep track of the current index for the future.\n- If current element is withing the range of L<=A[i]<=R than all possible subarrays ending with current element is the difference of i and previous out of range element\n- If current element is smaller than L A[i]<L , then all posisble subarrays ending with this element must include previous valid element(Dry run will clear this further).\n\nDry Run.\n```\nEg: 1,2,5,3,4,1,2\nL=3\nR=4\n```\n\n```\nfor i=0 , 1 < L so doesn\'t matter\n```\n```\nfor i=1, 2 < L so doesnt matter\n```\n```\nfor i=2, 5>R so we save this index for future.we still could not get any subarray\n```\n```\nfor i=3, 3>=L and 3<=R so all possible subarray ending with 3 is all possible elements between previous invalid index and i\nsubarrays= (3)\nres=1\n```\n\n```\nfor i=4, 4>=L and 4<=R so all possible subarray ending with 4 is all possible elements between previous invalid index and i\nsubarrays: (3,4),(4)\nres=3\n```\n```\nfor i=5, 1<L so all possible subarrays ending with 1 must have atleast one valid element so it will be all possible elements between previous valid element(4 in this case) and invalid element(5 in this case).\nsubarrays: (4,1), (3,4,1)\nres=5 so far\n```\n\n```\nfor i=6, 2<L this is similar to above case so all possible subarray here are these\nsubarrays: (4,1,2),(3,4,1,2)\nres=7 so far.\n```\n\nSo the intuition is at each index , all possible subarrays is the count of elements between previous valid element and invalid element.\n\n```\nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& A, int L, int R) {\n int res=0;\n int n = A.size(); \n int ind=-1,valid=-1; \n for(int i=0;i<n;i++){ \n \n if(A[i]>R){\n ind=i;\n valid=i;\n }\n else if(A[i]>=L && A[i]<=R)\n valid = i;\n \n res+= valid-ind; \n }\n return res;\n }\n};\n```\ntime: O(N)\nspace: O(1) | 22 | 0 | [] | 3 |
number-of-subarrays-with-bounded-maximum | Java O(n) concise solution with explanations | java-on-concise-solution-with-explanatio-nx0v | The idea is to consider the subarrays ending at each index i in the input array A. With i fixed, the subarray will be uniquely determined by its start index j, | fun4leetcode | NORMAL | 2018-03-04T16:14:29.383089+00:00 | 2018-03-04T16:14:29.383089+00:00 | 1,371 | false | The idea is to consider the subarrays ending at each index `i` in the input array `A`. With `i` fixed, the subarray will be uniquely determined by its start index `j`, and the subarray itself will be denoted as `A[j, i]` (left inclusive, right inclusive). If there are no additional constraints, `j` can take any integer value in the range `[0, i]`. But now we do want the maximum element of the subarray to lie in the range `[L, R]`, which has two implications:
1. There is **at least one** element in the subarray that is `>= L`.
2. There is **no** element in the subarray that is `> R`.
To meet the first condition, we need to scan `j` from `i` down to `0` until we find the first element that is `>= L`; we denote the index of this element as `r` (if no such element exists, `r = -1`). To guarantee the second condition, we need to continue the scanning until we find the first element that is `> R`; we denote the index of this element as `l` (again `l = -1` if no such element exists). Note that we always have `l <= r` as long as `L <= R`. Then we conclude `j` can only take integer value in the range `(l, r]` (left exclusive, right inclusive). Since each `j` value corresponds to a unique subarray, this further implies the total number of subarrays ending at index `i` with their maximum element lying in the range `[L, R]` is given by `r - l`.
Now the key is to find the indices `l` and `r` for each `i`. Of course we cannot afford to do the actual scanning of `j` as described above. The observation here is that `l` is essentially the largest index such that `l <= i && A[l] > R`, while `r` is the largest index such that `r <= i && A[r] >= L`. Therefore, as we are scanning the input array from left to right, `l` will be updated only if `A[i] > R` and `r` will be updated only if `A[r] >= L`. So here is the `O(n)` time, `O(1)` space Java solution:
<br>
```
public int numSubarrayBoundedMax(int[] A, int L, int R) {
int res = 0;
for (int i = 0, l = -1, r = -1; i < A.length; i++) {
if (A[i] > R) l = i;
if (A[i] >= L) r = i;
res += r - l;
}
return res;
}
``` | 20 | 0 | [] | 2 |
number-of-subarrays-with-bounded-maximum | ✅ Number of Subarrays with Bounded Maximum | Easy Divide elements into Buckets w/Explanation | number-of-subarrays-with-bounded-maximum-5mqf | Thought Process:\n\n1) There can be three cases for every element in the array.\n* element < left (Case 1)\n* element <= right (Case 2)\n* element > right (Case | shivaye | NORMAL | 2021-06-17T07:26:14.430925+00:00 | 2021-06-17T09:46:08.805486+00:00 | 296 | false | **Thought Process:**\n```\n1) There can be three cases for every element in the array.\n* element < left (Case 1)\n* element <= right (Case 2)\n* element > right (Case 3)\n\n2) Case 1 and Case 2 are overlapping.\n* But we need to consider only that subarrays whose maximum element lies between [left,right].\n* This can be done by calculating all the possible candidaties with Case 1 and Case 2 seperately,\nand then Our required answer can be calculated as (Case2 - Case1).\n\n3) We will consider all the elements < left into bucket1,\n4) And all the elements <= right into bucket2,\n\n# NOTE: We need not consider Case 3.\n\n5) All the elements between range [left,right] can be calculated by taking difference of bucket2 and bucket1.\n\nOne Possible candidate = bucket2-bucket1.\n\nAs we need to find all the possible candidates.\nSo we can sum up all the possible candidates answer\n```\n**Time Complexity**\n```\nO(N)\nwhere N = Number of elements in the array.\n```\n\n**Space Complexity:**\n```\nO(1) (Excluding the input array)\n```\n\n**C++:**\n```\nclass Solution {\n public:\n int numSubarrayBoundedMax(vector < int > & nums, int left, int right) {\n int bucket1 = 0, bucket2 = 0;\n int cnt = 0;\n for (int ele: nums) {\n bucket1 = (ele < left) ? bucket1 + 1 : 0;\n bucket2 = (ele <= right) ? bucket2 + 1 : 0;\n cnt += bucket2 - bucket1;\n }\n return cnt;\n }\n};\n```\n\n**Python:**\n```\nclass Solution:\n def numSubarrayBoundedMax(self, nums: List[int], left: int, right: int) -> int:\n bucket1 = 0\n bucket2 = 0\n cnt = 0\n for ele in nums:\n if ele < left:\n bucket1 += 1\n else:\n bucket1 = 0\n if ele <= right:\n bucket2 += 1\n else:\n bucket2 = 0\n cnt += bucket2 - bucket1\n return cnt \n```\n\n**JavaScript:**\n```\n/**\n * @param {number[]} nums\n * @param {number} left\n * @param {number} right\n * @return {number}\n */\nvar numSubarrayBoundedMax = function(nums, left, right) {\n bucket1 = 0;\n bucket2 = 0;\n cnt = 0;\n nums.forEach(assignBuckets);\n function assignBuckets(item, index)\n {\n if(item<left)\n bucket1++;\n else\n bucket1=0;\n if(item<=right)\n bucket2++;\n else\n bucket2=0;\n cnt += bucket2-bucket1;\n }\n return cnt;\n};\n```\n\n**JAVA:**\n```\nclass Solution {\n public int numSubarrayBoundedMax(int[] nums, int left, int right) {\n int bucket1 = 0;\n int bucket2 = 0;\n int cnt = 0;\n for(int ele:nums)\n {\n bucket1 = (ele<left)?bucket1+1:0;\n bucket2 = (ele<=right)?bucket2+1:0;\n cnt += bucket2-bucket1;\n }\n return cnt;\n }\n}\n```\n\n**Swift:**\n```\nclass Solution {\n func numSubarrayBoundedMax(_ nums: [Int], _ left: Int, _ right: Int) -> Int {\n var bucket1 = 0;\n var bucket2 = 0;\n var cnt = 0;\n for ele in nums{\n bucket1 = (ele<left) ? (bucket1+1) : 0;\n bucket2 = (ele<=right) ? (bucket2+1) : 0;\n cnt += bucket2-bucket1;\n }\n return cnt;\n }\n}\n```\n\n**GO:**\n```\nfunc numSubarrayBoundedMax(nums []int, left int, right int) int {\n var bucket1 int = 0\n var bucket2 int = 0\n var cnt int = 0\n for _,ele := range nums{\n if ele<left{\n bucket1++\n }else{\n bucket1 = 0\n }\n \n if ele<=right{\n bucket2++\n }else{\n bucket2 = 0\n }\n cnt += bucket2 - bucket1\n }\n return cnt\n}\n```\n**Kotlin:**\n```\nclass Solution {\n fun numSubarrayBoundedMax(nums: IntArray, left: Int, right: Int): Int {\n var bucket1 = 0\n var bucket2 = 0\n var cnt = 0\n for(ele in nums)\n {\n bucket1 = if(ele<left) (bucket1+1) else 0\n bucket2 = if(ele<=right) (bucket2+1) else 0\n cnt += bucket2-bucket1\n }\n return cnt\n }\n}\n```\n\n```\nPlease Upvote the solution if you find it useful thanks.\n``` | 19 | 17 | [] | 2 |
number-of-subarrays-with-bounded-maximum | Python Sliding Window | python-sliding-window-by-aayuskh-g1hr | \nclass Solution(object):\n def numSubarrayBoundedMax(self, A, L, R):\n """\n :type A: List[int]\n :type L: int\n :type R: int\n | aayuskh | NORMAL | 2020-12-31T23:05:06.231606+00:00 | 2020-12-31T23:05:06.231649+00:00 | 903 | false | ```\nclass Solution(object):\n def numSubarrayBoundedMax(self, A, L, R):\n """\n :type A: List[int]\n :type L: int\n :type R: int\n :rtype: int\n """\n # using Sliding window\n windowStart = count = curr = 0\n \n for windowEnd, num in enumerate(A):\n \n if L <= num <= R:\n curr = windowEnd - windowStart + 1\n elif num > R:\n curr = 0\n windowStart = windowEnd + 1\n \n count += curr\n \n return count\n \n``` | 18 | 1 | ['Sliding Window', 'Python'] | 3 |
number-of-subarrays-with-bounded-maximum | Python: Easy Explained, Linear time and constant space solution: Sliding Window Approach. | python-easy-explained-linear-time-and-co-qbu2 | Idea: Keep increasing the size of the window, till any element \'x\' is nums is not found such that x > right.\nOnce x is greater than right, shift the start of | meaditya70 | NORMAL | 2021-06-17T08:24:30.051120+00:00 | 2021-06-17T08:33:47.320512+00:00 | 1,170 | false | Idea: Keep increasing the size of the window, till any element \'x\' is nums is not found such that **x > right**.\nOnce x is greater than right, shift the start of the window to the element that occurs next after \'x\'.\n\nThere will be 3 possible cases:\n1. If a number is in the bound [left, right], we simply increment the count of the prefectly bound elements(count) and increment the answer because that element can stand-alone as a subarray.\n2. If a number is less than the left boundary, then it cannot stand alone but can stand with each of the prevoius #count elements in the subarray, so, increment the answer by adding count.\n3. If the number is greater then the right bound, then its time to create a fresh subarray for the next element onwards, so shrink the window and move the start of the window i = the current index(j) + 1 and make the count of perfectly bounded elements between [left, right] to 0.\n\nDry Run:\n\n\nThe Full Code:\n```\nclass Solution:\n def numSubarrayBoundedMax(self, nums: List[int], left: int, right: int) -> int:\n i = 0\n j = 0\n n = len(nums)\n \n count = 0\n ans = 0\n \n while i<=j and j<n:\n if left <= nums[j] and nums[j] <= right:\n ans += (j - i + 1)\n count = (j - i + 1)\n elif right < nums[j]:\n i = j + 1\n count = 0\n else:\n ans += count\n j += 1\n return ans\n ```\n Time = O(n) and Space = O(1).\n Here, i = start of window.\n j = end of window.\n count = number of element in the perfectly bounded subarray.\n ans = number of subarray satisfying the required condition.\n \n**Perfectly Bounded Subarray** means that the elements are in range [left,right] and present in the current window [i,j]. | 17 | 1 | ['Sliding Window', 'Python'] | 2 |
number-of-subarrays-with-bounded-maximum | How to think when you meet the question?(thinking process) | how-to-think-when-you-meet-the-questiont-p346 | Considered straightly counting all the subarrays that have maximum value between (L, R).\nIt costs O(n^2) time and O(n^2) space.\n\n\nint numSubarrayBoundedMax( | txy3000 | NORMAL | 2018-09-22T19:37:42.014655+00:00 | 2018-10-25T04:33:49.895363+00:00 | 1,607 | false | Considered straightly counting all the subarrays that have maximum value between (L, R).\nIt costs O(n^2) time and O(n^2) space.\n\n```\nint numSubarrayBoundedMax(vector<int>& A, int L, int R) {\n int l = A.size();\n int dp[l][l] = {0};\n\n for(int i = 0; i < l; ++i)\n for(int j = i + 1; j < l; ++j)\n dp[i][j] = max(dp[i][j - 1], A[j]);\n \n int ans = 0;\n for(int i = 0; i < l; ++i)\n {\n for(int j = i; j < l; ++j)\n if (dp[i][j] >= L && dp[i][j] <= R) ans++;\n }\n return ans;\n }\n```\n\t\nNo need to store every substring. To get the maxium of (i, j) (dp[i, j] denotes the maxium of (i, j)), according to dp[i, j] = max(dp[i,j-1],A[j]) \n\n ```\n int numSubarrayBoundedMax(vector<int>& A, int L, int R) {\n int l = A.size();\n int cur = 0, pre = 0, ans = 0;\n for(int i = 0; i < l; ++i)\n {\n pre = A[i];\n if (pre >= L && pre <= R) ans++;\n for(int j = i + 1; j < l; ++j)\n {\n cur = max(pre, A[j]);\n if (cur >= L && cur <= R) ans++;\n pre = cur;\n }\n }\n return ans;\n }\n```\npre means dp[i, j-1], cur means dp[i, j], remember **dp[i, j] denotes the maxium of (i, j)**\nspace down to O(1), then to think about how to reduce time cost.\nIn fact, when maxium(i, j -1) > R, all maxium(i, j + k) larger than R holds, then no need to compute them.\n```\n\nint numSubarrayBoundedMax(vector<int>& A, int L, int R) {\n int l = A.size();\n int cur = 0, pre = 0, ans = 0;\n for(int i = 0; i < l; ++i)\n {\n pre = A[i];\n if (pre >= L && pre <= R) ans++;\n if (pre > R) continue; //here\n for(int j = i + 1; j < l; ++j)\n {\n cur = max(pre, A[j]);\n if (cur >= L && cur <= R) ans++;\n if (cur > R) break; //here\n pre = cur;\n }\n }\n return ans;\n }\n```\nThis is my thinking process. | 16 | 1 | [] | 1 |
number-of-subarrays-with-bounded-maximum | O(n) with easy readable comments | 100% faster | Java | on-with-easy-readable-comments-100-faste-r8jc | Please upvote if you find this simple to understand\n\npublic int numSubarrayBoundedMax(int[] nums, int left, int right) {\n \n // Initialize star | ankit03jangra | NORMAL | 2021-06-17T08:06:43.282712+00:00 | 2021-06-17T08:06:43.282746+00:00 | 894 | false | Please upvote if you find this simple to understand\n\npublic int numSubarrayBoundedMax(int[] nums, int left, int right) {\n \n // Initialize start and end with -1 \n int start = -1, end = -1, count = 0;\n for(int i=0; i<nums.length; i++){\n \n // If number less than left then only prefix count will be added again\n if(nums[i] < left)\n count += end - start;\n \n // If number is greater than right then we reset values and start building prefix again\n else if(nums[i] > right){\n start = i;\n end = i;\n }\n \n // else if number is valid then we can update end at current position and get add the new prefix\n else{\n end = i;\n count += end - start;\n }\n }\n return count;\n } | 14 | 3 | ['Java'] | 1 |
number-of-subarrays-with-bounded-maximum | Java 9 liner | java-9-liner-by-shawngao-fyyn | class Solution { public int numSubarrayBoundedMax(int[] A, int L, int R) { int res = 0; for (int i = 0; i < A.length; i++) { if | shawngao | NORMAL | 2018-03-04T04:04:59.415404+00:00 | 2018-10-24T06:37:43.662707+00:00 | 1,824 | false | ```
class Solution {
public int numSubarrayBoundedMax(int[] A, int L, int R) {
int res = 0;
for (int i = 0; i < A.length; i++) {
if (A[i] > R) continue;
int max = Integer.MIN_VALUE;
for (int j = i; j < A.length; j++) {
max = Math.max(max, A[j]);
if (max > R) break;
if (max >= L) res++;
}
}
return res;
}
}
``` | 13 | 2 | [] | 1 |
number-of-subarrays-with-bounded-maximum | C++ Solution | Monotonic Stack modification | c-solution-monotonic-stack-modification-ryg64 | This appraoach is a modification Of monotonic stack to store the Previous Greater Element(pge) - (stored in vector named left) and Next Greater Element (nge) fo | its_gupta_ananya | NORMAL | 2021-05-10T07:00:44.729549+00:00 | 2021-06-17T14:04:32.387192+00:00 | 1,210 | false | This appraoach is a modification Of monotonic stack to store the Previous Greater Element(pge) - (stored in vector named left) and Next Greater Element (nge) for every element(stored in vector named right).\nFor any element i, it forms a part of valid subarrays till it encounters it\'s next greater elements from the left as well as the right side, that is, we count the number of subarrays for a particular i for which that element would be the maximum element. The size of the subarray is calculated as ```(i-left[i])*(right[i]-i)``` \nFor example, in the example [2,1,4,3]:-\n1. 2 lies in the given raneg [L,R) and The previous greater element for 2 does not exist i.e. left = -1 and the next greater element is at index 3. Hence number of subarrays **including 2 as the maximum element** become (0-(-1))*(3-0) = 3.\n2. Similarly we calculate number of subarrays for every index i (if nums[i] lies in the range).\nYou can read more about Monotonic Stacks on this great discuss post [https://leetcode.com/problems/sum-of-subarray-minimums/discuss/178876/stack-solution-with-very-detailed-explanation-step-by-step] \n\nCode implementing the same is:-\n```\nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& A, int L, int R) {\n \n int n = A.size();\n\n stack<int> pge,nge; //Previous greater element(pge) and Next Greater element(nge)\n vector<int> left(n,-1);//Stores PGE for index i\n vector<int> right(n,n);//Stores NGE for index i\n int ans= 0;\n for(int i=0;i<n;++i)\n {\n while(!pge.empty() && A[pge.top()] < A[i])\n pge.pop();\n if(!pge.empty()) left[i] = pge.top();\n pge.push(i);\n \n while(!nge.empty() && A[nge.top()] < A[i]){\n right[nge.top()] = i;\n nge.pop();\n }\n nge.push(i);\n }\n\n for(int i=0;i<n;++i){\n if(A[i] >=L && A[i]<=R){\n ans+=(right[i]-i)*(i-left[i]);//Adds contribution of particular index into the ans value\n }\n }\n return ans; \n }\n};\n \n \n```\nHope this helps!\nStay Safe! | 12 | 0 | ['C', 'Monotonic Stack', 'C++'] | 2 |
number-of-subarrays-with-bounded-maximum | Java O(n) Sliding Window | java-on-sliding-window-by-aswinsureshk-6g7b | For each window if the new element is in range (L,R), we add window size m=(j-i+1) to the count. This remains same until we get a new element in range (then we | aswinsureshk | NORMAL | 2019-07-30T04:34:43.268031+00:00 | 2019-09-12T15:27:07.210936+00:00 | 969 | false | For each window if the new element is in range (L,R), we add window size m=(j-i+1) to the count. This remains same until we get a new element in range (then we recompute window size m=j-i+1. If new element is greater than R, we update i to j and we set m=0;\n```\nclass Solution {\n public int numSubarrayBoundedMax(int[] A, int L, int R) {\n int i=0,j=0,cnt=0,m=0; //m is the number of subarrays that will be added when this element got added\n while(j<A.length){\n if(A[j]>=L && A[j]<=R)\n m=j-i+1;\n else if(A[j]>R){ \n m=0;\n i=j+1;\n }\n cnt+=m;\n j++;\n }\n return cnt;\n }\n}\n``` | 10 | 0 | [] | 3 |
number-of-subarrays-with-bounded-maximum | Java: Sliding Window , O(n) , passes 100% runtime | java-sliding-window-on-passes-100-runtim-vazp | \nclass Solution {\n public int numSubarrayBoundedMax(int[] nums, int left, int right) {\n int leftPointer = 0, rightPointer = 0;\n int n = num | BlackHam33r | NORMAL | 2021-06-17T15:32:48.403237+00:00 | 2021-06-18T16:48:20.332950+00:00 | 752 | false | ```\nclass Solution {\n public int numSubarrayBoundedMax(int[] nums, int left, int right) {\n int leftPointer = 0, rightPointer = 0;\n int n = nums.length;\n int count = 0;\n int number = 0;\n while(leftPointer<n && rightPointer<n) {\n if(nums[rightPointer]>=left && nums[rightPointer]<=right) {\n\t\t\t\t\t/* variable "number" signifies the last element greater satisfying this condition. \n\t\t\t\t\tWhy we are keeping this count is if a number less than left is there, then this number can be a part of that array.\n\t\t\t\t\tExample: \n\t\t\t\t\t[79,69,33,52,68,5,78] , left = 32, right = 80\n\t\t\t\t\t for number 5 present in 5th index of the array, the possible combinations will include \n\t\t\t\t\t [79,69,33,52,68,5],\n\t\t\t\t\t [69,33,52,68,5],\n\t\t\t\t\t [33,52,68,5],\n\t\t\t\t\t [52,68,5]\n\t\t\t\t\t [68,5]\n\t\t\t\t\t \n\t\t\t\t\t if you see clearly here, the number of combinations that include 5 are the same as the number \n\t\t\t\t\t of combinations that are possible with 68( the last element till 5 which is greater than 32 and less than 80).\n\t\t\t\t\t To keep track of this count we have stored this in variable "number".\n\t\t\t\t\t*/\n\t\t\t\t\n count+=(rightPointer-leftPointer+1);\n number = (rightPointer-leftPointer+1); \n } else if(nums[rightPointer]<left) {count+=number;}\n else {\n if(nums[rightPointer]>right) { \n\t\t\t\t\t// reset everything if the array element is greater than right.\n rightPointer++; \n leftPointer = rightPointer;\n number = 0;\n continue;\n }\n }\n rightPointer++;\n }\n return count;\n }\n```\n\nHope this solution helps you. Please comment down if you have any doubts. | 9 | 0 | ['Sliding Window', 'Java'] | 2 |
number-of-subarrays-with-bounded-maximum | [CPP] O(N) time and O(1) space with explanation | cpp-on-time-and-o1-space-with-explanatio-1d7k | \nstatic auto fast=[]{ios_base::sync_with_stdio(false);cin.tie(nullptr);return 0;}();\n#define mod 1000000007\nclass Solution \n{\npublic:\n int numSubarrayB | himanshu__nsut | NORMAL | 2020-03-10T11:05:15.576197+00:00 | 2020-03-10T11:05:15.576229+00:00 | 440 | false | ```\nstatic auto fast=[]{ios_base::sync_with_stdio(false);cin.tie(nullptr);return 0;}();\n#define mod 1000000007\nclass Solution \n{\npublic:\n int numSubarrayBoundedMax(vector<int>& A, int L, int R) \n {\n //for an element there are 3 cases possible:\n //case 1 :element is greater than R. In this case,there will be no valid subarrays ending with this element\n // because all the subarrays ending with this element will have a maximum value >=current element \n // hence will not be valid.\n //case 2: element is less than L. In this case element itself will not form a valid subarray but can append\n // to all the valid subarrays ending with previous element.hence number of valid subarrays ending \n // with current element will be equal to the number of valid subarrays ending with previous element.\n // this is possible because a valid subarray will have maximum value at least L and at most R and since\n // current element\'s value is less than L,max value of the subarray will not be changed when this element\n // is appended to the end.\n //case 3: element at least L and at most R.In this case element itself will form a valid subarray plus it will\n // also form other valid subarrays as follows: we\'ll look for recent/latest element having value >R.all\n // the elements between this element and current element(including current element) will form valid sub-\n // -arrays ending with current element.\n \n int ans=0;\n int index=-1; //index of recent element having >R\n int prev=0; //number of valid subarrays ending with previous element\n for(int i=0;i<A.size();i++)\n {\n if(A[i]>R) //case 1\n {\n prev=0;\n index=i; \n }\n else if(A[i]<L) //case 2\n {\n ans+=prev;\n //prev=prev; \n }\n else //if(A[i]>=L&&A[i]<=R) //case 3\n {\n ans+=i-index;\n prev=i-index; \n }\n }\n return ans;\n }\n};\n``` | 9 | 0 | [] | 1 |
number-of-subarrays-with-bounded-maximum | C++ solution | O(N) - Time complexity | c-solution-on-time-complexity-by-kritika-ewcs | \nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& nums, int left, int right) {\n int n = nums.size();\n int si =0;//startin | kritika_12 | NORMAL | 2021-07-04T07:39:57.686949+00:00 | 2021-07-04T07:48:01.182200+00:00 | 893 | false | ```\nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& nums, int left, int right) {\n int n = nums.size();\n int si =0;//starting index\n int ei = 0; //ending index\n int result =0, prev_count =0;\n while(ei < n){\n if(left <= nums[ei] && nums[ei]<= right){\n prev_count = ei- si +1;\n result += prev_count;\n }else if ( nums[ei] < left){\n result += prev_count;\n }else{\n //right < nums[ei]\n si = ei +1;\n prev_count =0;\n }\n ei++;\n }\n return result;\n }\n};\n``` | 8 | 1 | ['C', 'C++'] | 0 |
number-of-subarrays-with-bounded-maximum | Number of Subarrays with Bounded Maximum || Simple Python Sliding Window | number-of-subarrays-with-bounded-maximum-oeu4 | \nclass Solution:\n def numSubarrayBoundedMax(self, nums: List[int], left: int, right: int) -> int:\n windowStart=0\n count=0\n curr=0\n | techie_sis | NORMAL | 2021-06-17T07:17:19.515590+00:00 | 2021-06-17T07:17:58.195136+00:00 | 644 | false | ```\nclass Solution:\n def numSubarrayBoundedMax(self, nums: List[int], left: int, right: int) -> int:\n windowStart=0\n count=0\n curr=0\n \n for windowEnd, num in enumerate(nums):\n if left <= num <= right:\n curr = windowEnd - windowStart + 1\n elif num > right:\n curr = 0\n windowStart = windowEnd + 1\n \n count += curr\n return count\n``` | 8 | 2 | ['Sliding Window', 'Python', 'Python3'] | 1 |
number-of-subarrays-with-bounded-maximum | Python | Two pointer technique | Easy solution | python-two-pointer-technique-easy-soluti-06ij | Do hit like button if helpful!!!!\n\nclass Solution:\n def numSubarrayBoundedMax(self, nums: List[int], left: int, right: int) -> int:\n start,end = - | __Asrar | NORMAL | 2022-07-19T12:38:07.409751+00:00 | 2022-07-19T12:38:07.409791+00:00 | 1,071 | false | ***Do hit like button if helpful!!!!***\n```\nclass Solution:\n def numSubarrayBoundedMax(self, nums: List[int], left: int, right: int) -> int:\n start,end = -1, -1\n res = 0\n for i in range(len(nums)):\n if nums[i] > right:\n start = end = i\n continue\n \n if nums[i] >= left:\n end = i\n \n res += end - start\n return res\n``` | 7 | 0 | ['Two Pointers', 'Python', 'Python3'] | 3 |
number-of-subarrays-with-bounded-maximum | Easy C++ solution || Simple approach with dry-run of example || O(N) time complexity | easy-c-solution-simple-approach-with-dry-bym6 | Intuition\nWe simply store the position of the current invalid number, i.e. the number with value greater than R and then subtract its position with the positio | prathams29 | NORMAL | 2023-06-30T10:08:50.188096+00:00 | 2023-06-30T10:09:41.881905+00:00 | 799 | false | # Intuition\nWe simply store the position of the current invalid number, i.e. the number with value greater than R and then subtract its position with the position of the current valid number and sum it over the array. \n`Example: nums = [1,2,5,3,4,1,2], L=3, R=4`\nInitially, ans = 0, left = -1 and right = -1\n`For i=0, 1 < L so no change`\n`For i=1, 2 < L so no change`\n`For i=2, 5>R so we save this index for future. We still could not get any subarray`\n```\nFor i=3, 3>=L and 3<=R so all possible subarray ending with 3 is all possible elements between previous invalid index and i\nsubarrays= (3)\nans=1\n```\n```\nFor i=4, 4>=L and 4<=R so all possible subarray ending with 4 is all possible elements between previous invalid index and i\nsubarrays: (3,4),(4)\nans=3\n```\n```\nFor i=5, 1<L so all possible subarrays ending with 1 must have atleast one valid element so it will be all possible elements between previous valid element(4 in this case) and invalid element(5 in this case).\nsubarrays: (4,1), (3,4,1)\nans=5 so far\n```\n```\nFor i=6, 2<L this is similar to above case so all possible subarray here are these\nsubarrays: (4,1,2),(3,4,1,2)\nans=7 so far.\n```\n\n# Code\n```\nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& nums, int L, int R) {\n int ans = 0, left = -1, right = -1;\n for (int i = 0; i < nums.size(); i++) \n {\n if(nums[i] > R) \n left = i;\n if(nums[i] >= L) \n right = i;\n ans += right-left;\n }\n return ans;\n }\n};\n``` | 6 | 0 | ['Two Pointers', 'C++'] | 0 |
number-of-subarrays-with-bounded-maximum | Very simple Python3 and C++ with explanation | very-simple-python3-and-c-with-explanati-etkt | Whenever we come accross any counting subarray type of questions, the approach is to use two pointer and maintain a counter "num_subarrays" to keep the count of | geekcoder1989 | NORMAL | 2019-11-21T04:54:05.827473+00:00 | 2019-11-21T04:54:05.827540+00:00 | 405 | false | Whenever we come accross any counting subarray type of questions, the approach is to use two pointer and maintain a counter "num_subarrays" to keep the count of number of subarrays.\nLet i, j be the two pointers, then total number of subarrays from i:j is `num_subarrays += (j-i+1)`. see below for eg.\n[1 2 3]\ni | j | num_subarrays\n0 | 0 | 0 + (0-0+1) = 1\n0 | 1 | 1 + (1-0+1) = 3\n0 | 2 | 3 + (2-0+1) = 6\n\ntotal subarrays is 6!\n\nWe have to use the same strategy here whenever the currently element is between [L,R].\nIf the element is below L, then we add the previous count the subarray.\nIf the element is above R, then we change the i = j + 1 and reset the prev value.\n\n\nPython\n```\nclass Solution:\n def numSubarrayBoundedMax(self, A: List[int], L: int, R: int) -> int:\n i = j = count = prev = 0\n while(j < len(A)):\n if (L <= A[j] <= R):\n prev = j - i + 1\n count += prev\n elif (A[j] < L):\n count += prev\n else:\n i = j+1\n prev = 0\n j += 1\n return count\n```\nC++\n```\nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& A, int L, int R) {\n if(A.empty()) return 0;\n int i = 0, j = 0;\n int count = 0;\n int prev = 0;\n while(j < A.size()){\n \n if ((L <= A[j]) && (A[j]<= R)){\n prev = j - i + 1;\n count += prev;\n \n }\n else if (A[j] < L){\n count += prev;\n }\n else{\n i = j + 1;\n prev = 0;\n }\n j++;\n }\n return count;\n }\n};\n```\n | 6 | 0 | [] | 1 |
number-of-subarrays-with-bounded-maximum | Sliding window Approach, Very easy to understand, faster than 97% | sliding-window-approach-very-easy-to-und-1wjy | Using the sliding window technique we first find the number of subarrays which have maximum value smaller than L and then we find the number of subarrays whose | 2020201089_janme | NORMAL | 2020-12-03T15:52:58.772125+00:00 | 2020-12-03T15:52:58.772172+00:00 | 255 | false | Using the sliding window technique we first find the number of subarrays which have maximum value smaller than L and then we find the number of subarrays whose maximum value is smaller than R+1. We subtract these two numbers to find the number of subarrays which have max value in [L,R]\n```\nint numSubarrayBoundedMax(vector<int>& A, int L, int R) {\n\tint n = A.size();\n\tlong long i = 0, j = 0;\n\tlong long smaller_than_L = 0, smaller_than_R_plus_one = 0;\n\twhile(j < n){\n\t\tif(A[j] >= L){\n\t\t\ti = j+1;\n\t\t}\n\t\telse{\n\t\t\tsmaller_than_L += j-i+1;\n\t\t}\n\t\tj++;\n\t}\n\ti = 0, j = 0;\n\twhile(j < n){\n\t\tif(A[j] >= R+1){\n\t\t\ti = j+1;\n\t\t}\n\t\telse{\n\t\t\tsmaller_than_R_plus_one += j-i+1;\n\t\t}\n\t\tj++;\n\t}\n\t//cout << smaller_than_L << "," << smaller_than_R_plus_one;\n\treturn (int)(smaller_than_R_plus_one - smaller_than_L);\n} | 5 | 0 | [] | 0 |
number-of-subarrays-with-bounded-maximum | java solution || easy to understand | java-solution-easy-to-understand-by-gau5-0bgt | Please UPVOTE if you like my solution!\n\nclass Solution {\n public int numSubarrayBoundedMax(int[] nums, int left, int right) {\n int count = 0,ans = | gau5tam | NORMAL | 2023-03-25T12:41:53.680441+00:00 | 2023-03-25T12:41:53.680483+00:00 | 591 | false | Please **UPVOTE** if you like my solution!\n```\nclass Solution {\n public int numSubarrayBoundedMax(int[] nums, int left, int right) {\n int count = 0,ans = 0,i = 0,j = 0;\n \n while(j<nums.length){\n if(nums[j]>right){\n count = 0;\n i = j+1;\n }\n else if(nums[j]>=left && nums[j]<=right){\n count = j-i+1;\n }\n ans += count;\n j++;\n }\n \n return ans;\n }\n}\n``` | 4 | 0 | ['Java'] | 0 |
number-of-subarrays-with-bounded-maximum | ✅ CPP || Explained with Comments || Easy Understanding || Sliding Window is everywhere | cpp-explained-with-comments-easy-underst-be6g | \n// super smart intuition\n // basic idea is to calculate how many subarrays possible such that\n // we include an element which satisfies >=left | ajinkyakamble332 | NORMAL | 2022-08-17T15:14:19.337853+00:00 | 2022-08-17T15:14:19.337885+00:00 | 482 | false | ```\n// super smart intuition\n // basic idea is to calculate how many subarrays possible such that\n // we include an element which satisfies >=left and <=right\n // i.e all subarrays with satisfying that element to be the maximum\n // suppose we start from 0th index\n \n\t\t//Case1 // we encounter an element which is less than the lower bound\n // i.e the "left" ==> it alone cant be a part of the answer\n // but there can be some element which fits in the range\n // so we increment j in search of that element\n // if we find any such element ==> all subarrays including that element should be calculated\n // which will be j-i\n \n //Case2 // if we dont encounter any such element j will finally go to n and we wont find any such answer\n // what if there is an element greater than right in the array\n // smart to exclude that element, right?\n // so just jump both i and j to the next value of that element;\n // without adding any of it to result\n \n //Case3 // suppose we calculate answer for all subarrays between i to j \n // after that we move j and encounter an element x which is smaller than x;\n // now it can be a part of all the subarrays generated earlier\n // so we store it in some temporary variable to use it again\n // similarly if we get some greater element the temporary variable\n // needs to be reinitialized to 0 since the greater element wont produce any subarrays\n\t\n```\n\t\t\t\t\n```\nint numSubarrayBoundedMax(vector<int>& nums, int left, int right) {\n \n int n=nums.size();\n int i=-1,j=0;\n int ans=0;\n int prev=0;\n \n \n while(j<n){\n if(nums[j]>=left and nums[j]<=right){\n ans+=j-i;\n prev=j-i;\n j++;\n }\n else if(nums[j]<=left){\n ans+=prev;\n j++;\n }\n else{\n prev=0;\n i=j;\n j++;\n }\n }\n \n return ans;\n \n \n } | 4 | 0 | ['Sliding Window', 'C++'] | 0 |
number-of-subarrays-with-bounded-maximum | [JAVA] 100% FAST SOLUTION WITH COMMENTS || TWO POINTERS | java-100-fast-solution-with-comments-two-ljoa | class Solution {\n\n public int numSubarrayBoundedMax(int[] nums, int left, int right) {\n int ans = 0; \n int i = 0; \n int j = 0;\n | avneetsingh2001 | NORMAL | 2022-07-19T19:01:16.833553+00:00 | 2022-07-19T19:01:16.833585+00:00 | 632 | false | class Solution {\n\n public int numSubarrayBoundedMax(int[] nums, int left, int right) {\n int ans = 0; \n int i = 0; \n int j = 0;\n int prev = 0;\n while(j<nums.length){\n if(nums[j]>=left && nums[j]<=right){\n prev = j-i+1; //if in range adding all subarrays including the curr element\n ans += prev;\n }else if(nums[j]<left){\n ans += prev; // if curr ele less than left then add all the subarrays except the subarray with only one elemnt with curr ele val.\n }else{\n i = j+1;\n prev = 0; // if greater than range then reset prev subarrays counter and shift starting point to next elemnt.\n }\n j++;\n }\n return ans;\n }\n} | 4 | 0 | ['Two Pointers', 'Java'] | 3 |
number-of-subarrays-with-bounded-maximum | Easy to understand Java Solution (Beats 99%) [Java] | easy-to-understand-java-solution-beats-9-3lnm | The question asks us to count the subarrays where max element for that subarray lies in a particular range. It clearly means if there is say a single element in | innovatoronspree | NORMAL | 2021-06-21T16:32:00.941752+00:00 | 2021-06-21T16:34:42.427805+00:00 | 159 | false | The question asks us to count the subarrays where max element for that subarray lies in a particular range. It clearly means if there is say a single element in the subarray and we encounter another element in the array which is smaller than left, then without any hassle we can increment answer by 1, if it is out of range we need to end this subarray, and other case could be the element is within range of left and right, we can increase answer by 2 if previous element is also included, because we will include this new element also as a seperate subarray.\n\t\nConsider this example [1,2,4,3] and left = 1, right = 3.\nWe encounter 1, ans += 1 => [1]\nWe encounter 2 ans += 2 => [2],[1,2]\nWe encounter 4 ans += 0 (Out of range)\nWe encounter 3 ans += 1 => [3]\n\t\nFirst off, let us consider a brute force solution using a sliding window approach, we start from i=0 and move untill i=nums.length - 1. For each j we move from i to nums.length - 1\nand if the local maximum is within range, we increment answer by 1.\n\nBut this approach has a Time Complexity of O(N^2) and it will lead to Time Limit Exceeded.\n\nThe code for this is as follows: \n\n```\nclass Solution {\n public int numSubarrayBoundedMax(int[] nums, int left, int right) {\n if(nums.length == 0)\n return 0;\n int ans = 0;\n for(int i=0;i<nums.length;i++)\n {\n int local_maxima = 0;\n for(int j=i;j<nums.length;j++)\n {\n local_maxima = Math.max(local_maxima,nums[j]);\n if(local_maxima >= left && local_maxima <= right)\n ans++;\n }\n }\n return ans;\n }\n}\n```\n\nThere is also some kind of optimization possible to make the solution of linear order. How?\n\nBy considering a window, whenever we reach element nums[i] such that nums[i] >= right, \nwe set low = i and whenever we see a element that is within range we set high = i\nand keep increment answer by high-low.\nThe code for this is as follows:\n\n```\nclass Solution {\n public int numSubarrayBoundedMax(int[] nums, int left, int right) {\n int high = -1;\n int low = -1;\n int ans = 0;\n for(int i=0;i<nums.length;i++)\n {\n if(nums[i] > right)\n low = i;\n if(nums[i] >= left)\n high = i;\n ans += high - low;\n }\n return ans;\n }\n}\n```\nLet us consider an example for this:\n\n[2,1,4,3], left = 2, right = 3.\n\nInitially, low = -1, high = -1\ni = 0, nums[0] = 2\nHere, nums[i] >= left\nhigh = 0 , low = -1\nans += (0-1) = 1\n\ni=1, low = -1, high = 0\nHere nums[1] = 1\nLow and high remains same, low = -1, high = 0\nans += (0-(-1) = 2\n\ni=2, low = -1, high = 0\nHere nums[i] > right\nhigh = 2, \nAlso nums[i] >= left\nhigh = 2, low = 2\nans += (2-2) = 2\n\ni=3, low = 2, high = 2\nnums[i] >= 3\nhigh = 3, low = 2\nans += (3-2) = 3\n\nSo finally we return 3.\n\nTime Complexity: O(N)\nSpace Complexity: O(1)\n\nIf you find the solution useful, please upvote it. It motivates me to write even better articles. | 4 | 0 | [] | 1 |
number-of-subarrays-with-bounded-maximum | ✅ Number of Subarrays with Bounded Maximum| W/Explanation | Linear time,Logic+Maths | number-of-subarrays-with-bounded-maximum-spj3 | Consider following test case: \n\n\n\t\t[3,4,1,2,1,3]\n\t\tleft=3\n\t\tright=5\n Here, we can see that any element which is between left & right are always incl | Projan_179 | NORMAL | 2021-06-17T19:36:34.996907+00:00 | 2021-06-17T19:36:34.996953+00:00 | 137 | false | Consider following test case: \n\n\n\t\t[3,4,1,2,1,3]\n\t\tleft=3\n\t\tright=5\n* Here, we can see that any element which is between `left` & `right` are always included for counting in the answer without watching which element is maximum.\n* Now we can also notice that if any element which is less than `left` occurs than it will affect the successive elements which are also less than `left`. Here the element is `1 & 2 & then 1`. Thus `[1],[1,2],[1,2,1],[2],[2,1],[1]` are `subtracted` from the answer. This count is nothing but `(z*(z+1))/2` where `z` is number of consecutive elements less than left (In this case z=3 therefore count=6).\n\n\n\nNow Follow the steps for coding part:\n1.Increase the count of variable **tp** till we encounter an element which is greater than `right`. The moment we encounter it, update the value of **tp** to 0 and add `(tp*(tp+1))/2` to the **ans**.\n2.If we encounter an element which is less than `left` than we have to iterate through the next indices until we get an element>=`left` count such iteration as **z**. Now we have to subtrat the `(z*(z+1))/2 `elements as they will not have any maximum element between `left` & `right`.\n\n```\nTime Complexity: O(N)\nSpace Complexity: O(1),excluding the Input array\n```\n\n```\nint numSubarrayBoundedMax(vector<int>& nums, int left, int right) {\n int n=nums.size();\n int ans=0;\n int tp=0;\n for(int i=0;i<n;i++){\n if(nums[i]>=left&&nums[i]<=right) tp++;\n else if(nums[i]>right){\n ans+=(tp*(tp+1))/2;\n tp=0;\n \n }\n else{\n int z=1;\n tp++;\n while(i+1<n && nums[i+1]<left){\n z++;\n tp++;\n i++;\n }\n ans-=(z*(z+1))/2;\n }\n }\n if(tp>0)ans+=(tp*(tp+1))/2;\n return ans;\n}\n```\n | 4 | 1 | ['Math', 'C'] | 1 |
number-of-subarrays-with-bounded-maximum | Easy C++ stack solution || commented | easy-c-stack-solution-commented-by-saite-3b5j | \nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& nums, int left, int right) {\n \n //get the number of elements that are small | saiteja_balla0413 | NORMAL | 2021-06-17T08:51:36.718209+00:00 | 2021-06-17T13:13:34.532623+00:00 | 196 | false | ```\nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& nums, int left, int right) {\n \n //get the number of elements that are smaller to the left and right of every element in nums\n\t\t/by calculating this we can get number of subarrays that can be formed with the ele as a maximum and in range of [left,right]\n \n stack<int> s;\n //stack stores the indices\n int n=nums.size();\n //calculate the number of elements that are smaller or equal to right for every ele in nums\n vector<int> smallToRight(n);\n for(int i=n-1;i>=0;i-- )\n {\n while(!s.empty() && nums[s.top()]<=nums[i])\n s.pop();\n if(s.empty())\n smallToRight[i]=n-i-1;\n else\n smallToRight[i]=s.top()-i-1;\n s.push(i);\n }\n \n //calculate the number of elements that are strictly less than it for every element in nums\n \n stack<int> s2;\n \n vector<int> smallToLeft(n);\n for(int i=0;i<n;i++)\n {\n while(!s2.empty() && nums[s2.top()]<nums[i] )\n s2.pop();\n if(s2.empty()) //all the elements to left of i are small\n smallToLeft[i]=i;\n else\n smallToLeft[i]=i-s2.top()-1;\n s2.push(i);\n }\n \n int res=0;\n //now calculate the number of subarrays that would possible if we consider the ele as max and it is in range of [left,right]\n for(int i=0;i<n;i++)\n {\n if(nums[i]>=left && nums[i]<=right)\n {\n //get the number of subarrays possible\n int possible=smallToLeft[i]+smallToRight[i] + smallToLeft[i]*smallToRight[i] + 1; \n res+=possible;\n }\n }\n return res;\n \n }\n};\n```\nFor those who are being confused by why we are considering only number which are strictly less than the element in smallToLeft[I] is \xA0not to calculate the duplicate subarrays if a ele is present twice. \n\nex- [1,1,2,1,2,1]\nwe should not consider the subarray [2, 1,2] two times if left=2 and right =3! \n**Please upvote if this helps you :)** | 4 | 1 | [] | 0 |
number-of-subarrays-with-bounded-maximum | SIMPLE TWO-POINTER COMMENTED C++ SOLUTION | simple-two-pointer-commented-c-solution-xanzv | IntuitionApproachComplexity
Time complexity:o(n)
Space complexity:O(1)
Code | Jeffrin2005 | NORMAL | 2024-07-23T12:49:28.818443+00:00 | 2025-02-18T16:45:41.260444+00:00 | 464 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:o(n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```
class Solution {
public:
int numSubarrayBoundedMax(vector<int>& nums, int left, int right){
int count = 0, leftIndex = -1, lastValidIndex = -1;
// lastvalidexIndex means the end
int n = nums.size();
for (int i = 0; i <n;i++){
if (nums[i] > right){
leftIndex = i;
}
if(nums[i] >= left && nums[i] <= right){
lastValidIndex = i;
}
if(lastValidIndex > leftIndex){
count += (lastValidIndex - leftIndex);
}
}
return count;
/*
Dry Run with Example [2, 9, 2, 5, 6]:
Initialization: count = 0, leftIndex = -1, lastValidIndex = -1.
i = 0 (nums[0] = 2)
nums[0] is within [left, right] → lastValidIndex = 0.
count += (lastValidIndex - leftIndex) = 0 + (0 - (-1)) = 1.
i = 1 (nums[1] = 9)
nums[1] is greater than right → leftIndex = 1.
lastValidIndex is not updated as nums[1] is out of range.
i = 2 (nums[2] = 2)
nums[2] is within [left, right] → lastValidIndex = 2.
count += (lastValidIndex - leftIndex) = 1 + (2 - 1) = 2.
i = 3 (nums[3] = 5)
nums[3] is within [left, right] → lastValidIndex = 3.
count += (lastValidIndex - leftIndex) = 2 + (3 - 1) = 4.
i = 4 (nums[4] = 6)
nums[4] is within [left, right] → lastValidIndex = 4.
count += (lastValidIndex - leftIndex) = 4 + (4 - 1) = 7.
*/
}
};
``` | 3 | 0 | ['C++'] | 0 |
number-of-subarrays-with-bounded-maximum | Sliding Window Solution | Python | 0(N) 0(1) clean code | 98 % memory efficent | 95 % faster | sliding-window-solution-python-0n-01-cle-894k | count of subarrays having maximum element between left and right will be difference of count of subarrays having maximum element as right and count of subarrays | abhisheksanwal745 | NORMAL | 2024-06-15T09:30:43.173360+00:00 | 2024-06-15T09:31:39.844941+00:00 | 395 | false | count of subarrays having maximum element between left and right will be difference of count of subarrays having maximum element as right and count of subarrays having maximum elements less than left. Rest solution is trivial.\n\n\n```\nclass Solution:\n def numSubarrayBoundedMax(self, nums: List[int], left: int, right: int) -> int:\n \n def count_subarrays_with_max_atmost_x(x):\n \n front = count = 0\n\n for rear in range(len(nums)):\n\n if nums[rear] > x:\n\n front = rear + 1\n continue\n\n count += rear - front +1\n \n return count\n \n return count_subarrays_with_max_atmost_x(right) - count_subarrays_with_max_atmost_x(left-1)\n\t\t``` | 3 | 1 | ['Sliding Window', 'Python3'] | 0 |
number-of-subarrays-with-bounded-maximum | C++ solution in O(N) | c-solution-in-on-by-sachin_kumar_sharma-weo1 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Sachin_Kumar_Sharma | NORMAL | 2024-04-14T02:07:14.553740+00:00 | 2024-04-14T02:07:14.553757+00:00 | 27 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\nint solve(vector<int> &nums,int x){\n int i,n=nums.size(),cnt=0,ans=0;\n\n for(i=0;i<n;i++){\n if(nums[i]<=x){\n cnt++;\n ans+=cnt;\n }\n else{\n cnt=0;\n }\n }\n return ans;\n}\n int numSubarrayBoundedMax(vector<int>& nums, int left, int right) {\n int a=solve(nums,right);\n int b=solve(nums,left-1);\n\n return a-b;\n }\n};\n``` | 3 | 0 | ['C++'] | 0 |
number-of-subarrays-with-bounded-maximum | Java || Beats 100% || Two Pointers O(N) time, O(1) space. | java-beats-100-two-pointers-on-time-o1-s-wtxk | Intuition\nTwo pointers\n Describe your first thoughts on how to solve this problem. \n\n# Approach\nThe main points in this problem are :\n- If we pick a subar | abhinayd | NORMAL | 2023-07-05T07:11:15.079189+00:00 | 2023-07-09T10:40:48.010452+00:00 | 546 | false | # Intuition\n**Two pointers**\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n**The main points in this problem are :**\n- If we pick a subarray it should contain a element within left and right .\n- The subarray should not contain a element greater than right due to which we can break the array and solve the left and right sub-arrays independently.\n- The pointer i represents the index of the last split.\n- We should also maintain the index of last occurence of the desired element(>=left && <= right).\n- The count of subarrays for this split ending with this element (j) would be (lastoccurence - i +1).\n- Eg: Imagine left as 2 and right as 3\n\n---\n\n\nFor the elements,\n0 1 2 3 4 5 => index\n1 2 3 1 1 1 => values\nThe subarrays ending with the last index are : \n1 2 3 1 1 1\n2 3 1 1 1\n3 1 1 1\nlastoccurence = 2\ni = 0\nCount of subarrays ending with index 5 would be (2 - 0 + 1) = 3\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity : $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity : $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int numSubarrayBoundedMax(int[] nums, int left, int right) {\n int i = 0, j = 0, res = 0, maxind = -1;\n while(j < nums.length){\n if(nums[j] >= left && nums[j] <= right){\n maxind = j;\n }\n if(nums[j] > right){\n j++;\n i = j;\n maxind = -1;\n continue;\n }\n if(maxind != -1){\n res += maxind - i + 1;\n }\n j++;\n }\n return res;\n }\n}\n``` | 3 | 0 | ['Two Pointers', 'Greedy', 'Sliding Window', 'Java'] | 3 |
number-of-subarrays-with-bounded-maximum | With Explanation Comments: Time: 82 ms (86.62%), Space: 52.2 MB (94.04%) | with-explanation-comments-time-82-ms-866-zq2j | Like it? ->Upvote please! \u30C4\n\nSolution 1: Two-Pointers Approach\n\nTC: O(n) //iterate the array\nSC: O(1)\nTime: 174 ms (11.26%), Space: 52.2 MB (68.61% | deleted_user | NORMAL | 2022-09-20T16:51:21.402425+00:00 | 2022-09-20T16:51:21.402465+00:00 | 603 | false | **Like it? ->Upvote please!** \u30C4\n\n**Solution 1: Two-Pointers Approach**\n\nTC: O(n) //iterate the array\nSC: O(1)\nTime: 174 ms (11.26%), Space: 52.2 MB (68.61%)\n\n\'\'\'\nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& nums, int left, int right) {\n \n //initialize a counter & two pointers for the boundaries\n int counter=0, start=-1, end=-1;\n \n for(int i=0;i<nums.size();i++){\n \n //move the end pointer to the position of the next invalid number\n if(nums[i]>right)\n end=i;\n //move the start pointer to the position of the first valid number\n if(nums[i]>=left)\n start=i;\n \n //subtract the two ones to get the distance, number of valid values, between the two poiters & add it to the counter\n counter+=start-end;\n }\n \n //return the final counter value\n return counter;\n }\n};\n\'\'\'\n\n**Solution 2: Three-Pointers Approach**\n\nTC: O(n) //iterate the array\nSC: O(1)\nTime: 82 ms (86.62%), Space: 52.2 MB (94.04%)\n\n\n\'\'\'\nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& nums, int left, int right) {\n \n //initialize a counter & two pointers\n int counter=0, j=0, k=0;\n \n for(int i=0;i<nums.size();i++){\n \n //case 1: if the current value is smaller than the bound\n if(nums[i]<left){\n //add the third pointer value to the counter\n counter+=k;\n }\n //case 2: if the current value is bigger than the bound\n else if(nums[i]>right){\n //return the third pointer to its initial position again\n k=0;\n //move the second pointer in the next position of the first one\n j=i+1;\n }\n //case 3: if the current value is in the bound\n else{\n //move the third position in the middle position\n k=(i-j+1);\n //add the third pointer value to the counter\n counter+=k;\n }\n \n }\n \n //return the final value of the counter\n return counter;\n }\n};\n\'\'\'\n\n**Like it? ->Upvote please!** \u30C4\n**If still not understood, feel free to comment. I will help you out**\n**Happy Coding :)** | 3 | 0 | ['Array', 'Two Pointers', 'C', 'C++'] | 1 |
number-of-subarrays-with-bounded-maximum | 📌JAVA || Easy || Sliding window || O(n)✅ | java-easy-sliding-window-on-by-soyebsark-44bt | If it helps, do an Upvote \u2B06\uFE0F\uD83C\uDD99 So others can also find it helpful\n\nclass Solution {\n public int numSubarrayBoundedMax(int[] nums, int | soyebsarkar563 | NORMAL | 2022-07-06T05:31:56.698736+00:00 | 2022-07-06T05:33:06.338688+00:00 | 253 | false | **If it helps, do an Upvote \u2B06\uFE0F\uD83C\uDD99 So others can also find it helpful**\n```\nclass Solution {\n public int numSubarrayBoundedMax(int[] nums, int left, int right) {\n \n int i=0;\n int j=0;\n int m=0;\n int count=0;\n \n while(j<nums.length){\n \n if(nums[j] > right){\n m=0;\n i=j+1;\n }\n \n if(nums[j]>=left && nums[j] <=right){\n m = j-i+1;\n }\n count+=m;\n j++;\n \n \n }\n \n return count;\n \n }\n}\n``` | 3 | 0 | ['Sliding Window', 'Java'] | 0 |
number-of-subarrays-with-bounded-maximum | JAVA| Time - o(n) | Space - o(1) | Two Pointer | java-time-on-space-o1-two-pointer-by-shi-glyg | ```\n // time:- o(n)\n // space:- o(1)\n \n int i=0;\n int j=0;\n int count=0;\n int prev_count=0;\n \n | shivangijain | NORMAL | 2021-09-17T14:03:37.636676+00:00 | 2021-09-17T14:03:37.636705+00:00 | 216 | false | ```\n // time:- o(n)\n // space:- o(1)\n \n int i=0;\n int j=0;\n int count=0;\n int prev_count=0;\n \n // only i varies\n while(i<nums.length){\n if(left <= nums[i] && nums[i]<=right){\n // it is in range\n count += i-j+1;\n prev_count=i-j+1;\n }else if( nums[i] < left){\n // left se chote h value\n count += prev_count;\n }else{\n // right se bade h value\n prev_count=0;\n j=i+1;\n }\n i++;\n }\n return count; | 3 | 0 | [] | 0 |
number-of-subarrays-with-bounded-maximum | Java | O(N^2) to O(N) optimization | Intuition | java-on2-to-on-optimization-intuition-by-f9tl | Bruteforce solution is straightforward, we consider every possibility (all subarrays), maintain a maximum and as long as there is valid maximum within range we | apooos3 | NORMAL | 2021-06-17T15:43:46.070473+00:00 | 2021-06-17T15:46:00.799003+00:00 | 259 | false | Bruteforce solution is straightforward, we consider every possibility (all subarrays), maintain a maximum and as long as there is valid maximum within range we increment the count. But this results in **O(n<sup>2</sup>)**\n\nObservations:\n\t1. \tOnce we encounter an element, *j* which is greater than the maximum range, we don\'t need to consider further any more subarrays for element at *i* (we are reseting our count).\n\t2. \tIf we encounter an element *j* which is within the range, it contributes equal to the length of valid subarray so far + 1 (+1 for it\'s count as an individual element).\n\t3. \tIf we counter an element *j* which is less the minimum range, it contributes equal amount to the length of valid subarray - the length of elments that are smaller than the minimum range. For e.g., in an array of [2,2,1,1] for left = 2 and right = 3, \nwe will have counts like \n```\n[1, \n(1(previous value) + 1(length) + 1(individual)) = 3, \n3(previous value) + 2(valid length) + 0(individual) = 5, \n5(previous value) + 2(valid length = distance till last maximum value) + 0(individual) = 7] = 7.\n```\n\nHere goes the implementation,\n\n**O(n<sup>2</sup>)** **[TLE]**\n```\nclass Solution {\n public int numSubarrayBoundedMax(int[] nums, int left, int right) {\n int count = 0;\n \n for(int i=0; i<nums.length; i++) {\n int max = 0;\n for(int j=i; j<nums.length; j++) {\n max = Math.max(max, nums[j]);\n if(max <= right && max >= left) {\n count++;\n }\n }\n }\n \n return count;\n }\n}\n```\n\n**O(n)**\n```\nclass Solution {\n public int numSubarrayBoundedMax(int[] nums, int left, int right) { \n int res = 0, start = 0, end = 0, curr = 0, lastGoodIndex = -1;\n for(int i=0; i<nums.length; i++) {\n if(nums[i] >= left && nums[i] <= right) {\n curr += end - start + 1;\n lastGoodIndex = i;\n end++;\n }else if(nums[i] < left) {\n if(lastGoodIndex != -1) {\n curr += ((end - start) - (i - 1 - lastGoodIndex));\n }\n end++;\n }else{\n start = i+1;\n end = i+1;\n res += curr;\n curr = 0;\n lastGoodIndex = -1;\n } \n }\n \n res += curr;\n \n return res;\n }\n}\n``` | 3 | 0 | ['Array', 'Dynamic Programming', 'Java'] | 0 |
number-of-subarrays-with-bounded-maximum | [C++] trick of number of subarray | c-trick-of-number-of-subarray-by-codeday-vqc7 | Approach 1: trick of number of subarray [1]\nTime/Space Complexity: O(N); O(1)\n\nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& A, int L, | codedayday | NORMAL | 2021-06-17T15:04:04.164800+00:00 | 2021-06-17T15:04:04.164849+00:00 | 203 | false | Approach 1: trick of number of subarray [1]\nTime/Space Complexity: O(N); O(1)\n```\nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& A, int L, int R) {\n return count(A, R) - count(A, L - 1);\n }\nprivate:\n // Count # of sub arrays whose max element is <= N\n int count(const vector<int>& A, int N) {\n int ans = 0;\n int cur = 0;\n for (int a: A) {\n if (a <= N) // continue grow sub arrays\n ans += ++cur; // small trick, refer [1]\n else // reset the starting of sub array\n cur = 0;\n }\n return ans;\n }\n};\n```\n\nApproach 2: compact version of Approach 1\n```\nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& A, int L, int R) {\n return count(A, R) - count(A, L - 1);\n }\n\nprivate:\n // Count # of sub arrays whose max element is <= N\n int count(const vector<int>& A, int N) {\n int ans = 0;\n int cur = 0;\n for (int a: A) \n a <= N ? ans += ++cur : cur = 0;\n return ans;\n }\n};\n```\n\nReference:\n[1] https://leetcode.com/problems/count-substrings-with-only-one-distinct-letter/discuss/1268334/c-sum-equation-of-arithmetic-sequence\n[2] https://leetcode.com/problems/number-of-subarrays-with-bounded-maximum/solution/ | 3 | 1 | ['C'] | 1 |
number-of-subarrays-with-bounded-maximum | Java: Sliding Window | java-sliding-window-by-shreyas_kadiri-05a7 | ```\nclass Solution {\n public int numSubarrayBoundedMax(int[] nums, int left, int right) {\n int count = 0;\n int i = 0;\n int j = 0;\n | shreyas_kadiri | NORMAL | 2021-06-17T12:53:55.707303+00:00 | 2021-06-17T12:53:55.707351+00:00 | 175 | false | ```\nclass Solution {\n public int numSubarrayBoundedMax(int[] nums, int left, int right) {\n int count = 0;\n int i = 0;\n int j = 0;\n int windowSize = 0; \n \n while(j < nums.length){\n if(nums[j]>=left && nums[j]<=right){\n windowSize = j - i + 1; \n }else if(nums[j] > right){\n windowSize = 0;\n i = j + 1;\n }\n count+= windowSize;\n j++;\n }\n return count;\n }\n} | 3 | 0 | [] | 0 |
number-of-subarrays-with-bounded-maximum | Python standard solution | python-standard-solution-by-adityachauha-97ch | \nclass Solution:\n def numSubarrayBoundedMax(self, nums: List[int], left: int, right: int) -> int:\n end,start=-1,-1\n result=0\n for i | adityachauhan343 | NORMAL | 2021-06-17T10:26:40.453466+00:00 | 2021-06-17T10:26:40.453510+00:00 | 161 | false | ```\nclass Solution:\n def numSubarrayBoundedMax(self, nums: List[int], left: int, right: int) -> int:\n end,start=-1,-1\n result=0\n for i in range(len(nums)): \n if nums[i]>=left and nums[i]<=right:\n end=i\n result+=end-start\n elif nums[i]>right:\n start,end=i,i\n else:\n result+=end-start\n \n return result\n``` \nref video:Youtube channel(code_report)\nIf found helpful **PLEASE UPVOTE.** | 3 | 1 | ['Python'] | 0 |
number-of-subarrays-with-bounded-maximum | Java || Sliding Window + DP || 2ms || beats 100% || T.C - O(N) S.C - O(1) | java-sliding-window-dp-2ms-beats-100-tc-0s4w6 | \n // O(A.length) O(1)\n\tpublic int numSubarrayBoundedMax(int[] A, int L, int R) {\n\n\t\tint len = A.length, sum = 0, count = 0, j = -1;\n\t\tfor (int i = | LegendaryCoder | NORMAL | 2021-05-01T12:22:10.148664+00:00 | 2021-05-01T12:22:10.148695+00:00 | 136 | false | \n // O(A.length) O(1)\n\tpublic int numSubarrayBoundedMax(int[] A, int L, int R) {\n\n\t\tint len = A.length, sum = 0, count = 0, j = -1;\n\t\tfor (int i = 0; i < len; i++) {\n\n\t\t\tif (A[i] >= L && A[i] <= R) {\n\t\t\t\tcount = i - j;\n\t\t\t\tsum += count;\n\t\t\t} else if (A[i] < L) {\n\t\t\t\tsum += count;\n\t\t\t} else{\n\t\t\t\tj = i;\n count = 0;\n }\n\t\t}\n\n\t\treturn sum;\n\t} | 3 | 0 | [] | 0 |
number-of-subarrays-with-bounded-maximum | c++ solution | c-solution-by-dilipsuthar60-39d4 | \nclass Solution {\npublic:\n int find(vector<int>&nums,int k)\n {\n int j=0;\n int ans=0;\n for(int i=0;i<nums.size();i++)\n | dilipsuthar17 | NORMAL | 2021-04-13T08:15:01.953499+00:00 | 2021-04-13T08:15:01.953540+00:00 | 311 | false | ```\nclass Solution {\npublic:\n int find(vector<int>&nums,int k)\n {\n int j=0;\n int ans=0;\n for(int i=0;i<nums.size();i++)\n {\n if(nums[i]>k)\n {\n j=i+1;\n }\n ans+=i-j+1;\n }\n return ans;\n }\n int numSubarrayBoundedMax(vector<int>& A, int L, int R) {\n return find(A,R)-find(A,L-1);\n }\n};\n``` | 3 | 0 | ['C', 'C++'] | 0 |
number-of-subarrays-with-bounded-maximum | C++| Very simple code | c-very-simple-code-by-arpitsingh53-c5h9 | \n int atmost(vector<int>& A,int t)\n {\n int mx=INT_MIN;\n int res=0;\n int l=0;\n for(int i=0;i<A.size();i++)\n {\n | arpitsingh53 | NORMAL | 2020-08-05T11:16:54.276550+00:00 | 2020-08-05T11:16:54.276590+00:00 | 241 | false | ```\n int atmost(vector<int>& A,int t)\n {\n int mx=INT_MIN;\n int res=0;\n int l=0;\n for(int i=0;i<A.size();i++)\n {\n mx=max(mx,A[i]);\n \n if(mx>t)\n {\n while(l<=i)\n {\n l=l+1;\n\n }\n mx=INT_MIN;\n }\n res+=i-l+1;\n }\n return res;\n \n }\n int numSubarrayBoundedMax(vector<int>& A, int L, int R) {\n \n if(A.size()==0)\n {\n return 0;\n }\n \n \n return atmost(A,R)-atmost(A,L-1);\n \n \n }\n};\n``` | 3 | 0 | [] | 3 |
number-of-subarrays-with-bounded-maximum | C++ | Check within valid window | c-check-within-valid-window-by-wh0ami-0ewg | \nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& A, int L, int R) {\n \n int n = A.size();\n int res = 0, left = -1, | wh0ami | NORMAL | 2020-06-20T11:06:58.843909+00:00 | 2020-06-20T11:06:58.843943+00:00 | 164 | false | ```\nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& A, int L, int R) {\n \n int n = A.size();\n int res = 0, left = -1, right = -1;\n \n for (int i = 0; i < n; i++) {\n if (A[i] >= L && A[i] <= R)\n right = i;\n else if (A[i] > R) {\n left = right = i;\n }\n res += right-left;\n }\n \n return res;\n }\n};\n``` | 3 | 0 | [] | 0 |
number-of-subarrays-with-bounded-maximum | Python O(n) | python-on-by-prosun-8ei1 | \n def numSubarrayBoundedMax(self, A, L, R):\n """\n :type A: List[int]\n :type L: int\n :type R: int\n :rtype: int\n | prosun | NORMAL | 2018-04-21T19:38:43.656135+00:00 | 2018-08-23T21:08:28.702369+00:00 | 630 | false | ```\n def numSubarrayBoundedMax(self, A, L, R):\n """\n :type A: List[int]\n :type L: int\n :type R: int\n :rtype: int\n """\n start = 0\n lastMatch = None\n count = 0\n for idx in range(0, len(A)):\n num = A[idx]\n if num >= L and num <= R:\n count += (idx - start) + 1\n lastMatch = idx\n elif num < L:\n if lastMatch != None:\n count += (lastMatch - start) + 1\n elif num > R:\n start = idx + 1\n lastMatch = None\n return count\n``` | 3 | 0 | [] | 0 |
number-of-subarrays-with-bounded-maximum | Java easy to understand | java-easy-to-understand-by-wangxlsb-yxqt | \nclass Solution {\n public int numSubarrayBoundedMax(int[] A, int L, int R) {\n int prevHigh = -1, sum = 0, prev = 0;\n for(int i = 0; i < A.l | wangxlsb | NORMAL | 2018-03-09T03:59:17.595544+00:00 | 2018-03-09T03:59:17.595544+00:00 | 335 | false | ```\nclass Solution {\n public int numSubarrayBoundedMax(int[] A, int L, int R) {\n int prevHigh = -1, sum = 0, prev = 0;\n for(int i = 0; i < A.length; i++) {\n if(A[i] >= L && A[i] <= R) {\n prev = i - prevHigh;\n }\n else if(A[i] > R){\n prev = 0;\n prevHigh = i;\n }\n sum += prev;\n }\n return sum;\n }\n}\n```\nExplanation: for each i, we count the number of subarrays ending with i (denoted as f(i)), and the result is the sum of f(i) over i. prevHigh is the previous position with respect to i where A[prevHigh] > R, and prev is the number of subarrays ending with i-1. So if A[i] > R, we reset prevHigh = i and prev = 0; if A[i] < L, then f(i) = f(i-1), because the subarray ending with i is basically extension of the previous subarray; if A[i] in [L, R], f(i) = i - prevHigh. | 3 | 0 | [] | 0 |
number-of-subarrays-with-bounded-maximum | 4 lines C++ | 4-lines-c-by-kellybundy-tif6 | int numSubarrayBoundedMax(vector<int>& A, int L, int R) { int x = 0, y = 0, z = 0; for (int a : A) z += (++x *= a <= R) - (++y *= a < L); re | KellyBundy | NORMAL | 2018-03-04T09:11:35.301735+00:00 | 2018-03-04T09:11:35.301735+00:00 | 398 | false | int numSubarrayBoundedMax(vector<int>& A, int L, int R) {
int x = 0, y = 0, z = 0;
for (int a : A)
z += (++x *= a <= R) - (++y *= a < L);
return z;
}
`x` counts the subarrays whose maximum is low enough.
`y` counts the subarrays whose maximum is too low.
`z` counts the subarrays whose maximum is just right, low enough but not too low. | 3 | 0 | [] | 1 |
number-of-subarrays-with-bounded-maximum | Ridiculously Simple O(n)/O(1) Java Solution based on State Machine | ridiculously-simple-ono1-java-solution-b-oir9 | I literally submitted this in the last 10 seconds left in the contest and I'm surprised I didn't miss any corner cases, lol... Imagine you have a state machine. | wannacry89 | NORMAL | 2018-03-04T04:15:26.426915+00:00 | 2018-03-04T04:15:26.426915+00:00 | 701 | false | I literally submitted this in the last 10 seconds left in the contest and I'm surprised I didn't miss any corner cases, lol...
Imagine you have a state machine. You really only have the following two states:
1 - Since seeing the last >R element, you have not yet seen an [L,R]-element. (call "haveYet = false")
2 - Since seeing the last >R element, you have seen at least one or more [L,R]-element. (call "haveYet = true")
We initialize like this: we pretend A has a >R element at index -1 (imaginary index) and we are walking first at index 0, and we are in state (1).
If we see a new >R element, we transition to state (1) no matter whether we are currently in state (1) or state (2). Save the position of this as 'LastGR' (stands for last index greater than R).
If we see a new [L,R]-element, we transition from (1)-->(2) and mark this as the 'lastViable'.
Now, when we are on index i, we want to see if we can use this as an end index for ALL subarrays that could possibly end at this position. We are only able to do this if we are in state (2) AND the subarray encapsulates at least the last [L,R]-element we have seen. So, for a start index, everything since the position lastGR+1 up to and including the lastViable (last [L,R]-element we saw) is a possible starting position. We add those to our global running sum.
```
class Solution {
public int numSubarrayBoundedMax(int[] A, int L, int R) {
int lastGR = -1;
int sum = 0;
boolean haveYet = false;
int lastViable = -1;
for (int i = 0; i < A.length; i++) {
if (A[i] > R) { lastGR = i; haveYet = false; continue; }
if (A[i] >= L && A[i] <= R) { lastViable = i; haveYet = true; }
if (haveYet) {
sum += lastViable - lastGR;
}
}
return sum;
}
}
``` | 3 | 0 | [] | 0 |
number-of-subarrays-with-bounded-maximum | Simplest approach conceptually? - n Choose 2 | simplest-approach-conceptually-n-choose-cnohi | Intuition\n\nNumbers above the maximum bound (right) will never be included in any subarray, so just skip those. \n\nA number below the minimum (left) can be in | MoggleToggles | NORMAL | 2023-12-27T21:10:56.836938+00:00 | 2023-12-29T21:49:49.597506+00:00 | 17 | false | # Intuition\n\nNumbers above the maximum bound (right) will never be included in any subarray, so just skip those. \n\nA number below the minimum (left) can be included in a subarray, but it can\'t stand by itself, so just compute the total number of subarrays where all values are below the maximum, then subtract the number of subarrays formed exclusively by elements less than the minimum\n\n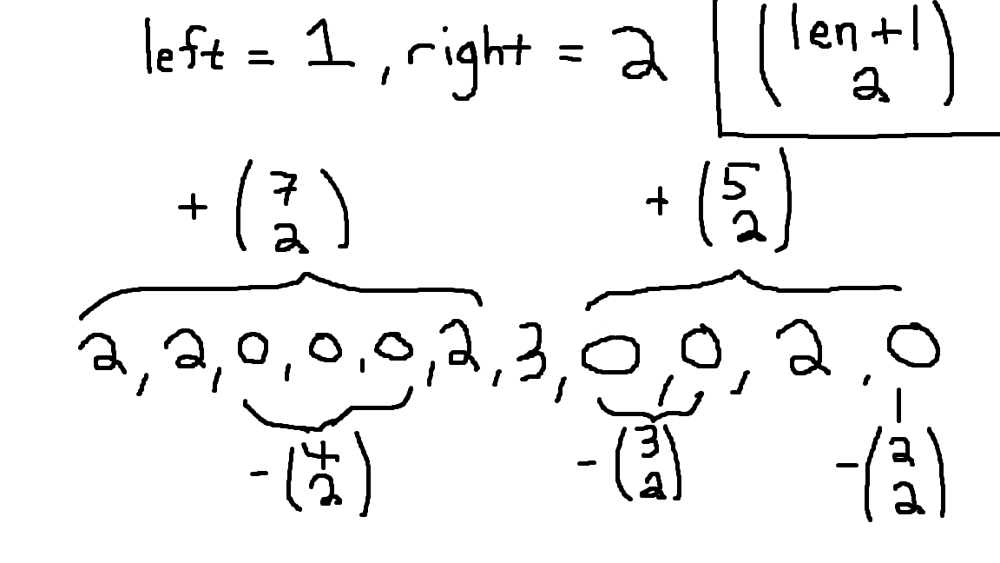\n\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\n O(1)\n\n# Code\n```\nclass Solution {\n fun numSubarrayBoundedMax(nums: IntArray, left: Int, right: Int): Int {\n var subarrayCount = 0L\n var j = 0\n var countBelowMin = 0L\n var countBelowMax = 0L\n while (j <= nums.size) {\n if (j == nums.size || nums[j] > right) {\n subarrayCount += countBelowMax.numberOfSubarrays()\n subarrayCount -= countBelowMin.numberOfSubarrays()\n countBelowMax = 0L\n countBelowMin = 0L\n } else if (nums[j] < left) {\n countBelowMax += 1\n countBelowMin += 1\n } else {\n subarrayCount -= countBelowMin.numberOfSubarrays()\n countBelowMin = 0L\n countBelowMax += 1\n }\n j++\n }\n\n return subarrayCount.toInt()\n }\n\n private fun Long.numberOfSubarrays(): Long {\n return (this + 1) * this / 2\n }\n}\n``` | 2 | 0 | ['Kotlin'] | 0 |
number-of-subarrays-with-bounded-maximum | c++ | easy | fast | c-easy-fast-by-venomhighs7-19z7 | \n\n# Code\n\n\n class Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& nums, int left, int right) {\n return count(nums, right) - count( | venomhighs7 | NORMAL | 2022-11-20T12:09:11.083901+00:00 | 2022-11-20T12:09:11.083944+00:00 | 1,588 | false | \n\n# Code\n```\n\n class Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& nums, int left, int right) {\n return count(nums, right) - count(nums, left - 1);\n }\n int count(const vector<int>& nums, int bound) {\n int ans = 0, cnt = 0;\n for (int x : nums) {\n cnt = x <= bound ? cnt + 1 : 0;\n ans += cnt;\n }\n return ans;\n }\n\n};\n``` | 2 | 0 | ['C++'] | 0 |
number-of-subarrays-with-bounded-maximum | C++||Two Pointers||Easy to Understand | ctwo-pointerseasy-to-understand-by-retur-mn52 | ```\nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector& nums, int left, int right) \n {\n int res=0,l=-1,r=-1;\n for(int i=0;irigh | return_7 | NORMAL | 2022-09-03T09:54:03.349187+00:00 | 2022-09-03T09:54:03.349230+00:00 | 314 | false | ```\nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& nums, int left, int right) \n {\n int res=0,l=-1,r=-1;\n for(int i=0;i<nums.size();i++)\n {\n if(nums[i]>right)\n l=i;\n if(nums[i]>=left)\n r=i;\n res+=r-l;\n }\n return res;\n }\n};\n//if you like the solution plz upvote. | 2 | 0 | ['Two Pointers', 'C'] | 1 |
number-of-subarrays-with-bounded-maximum | Easy C++ Solution | easy-c-solution-by-subhanshu_babbar-57p4 | \nclass Solution {\npublic:\n int Requirement(vector<int>& nums,int right,int left){\n int cnt=0,j=0;\n \n for(int i=0;i<nums.size();i++ | Subhanshu_Babbar | NORMAL | 2022-05-23T19:29:13.696484+00:00 | 2022-05-23T19:29:13.696523+00:00 | 242 | false | ```\nclass Solution {\npublic:\n int Requirement(vector<int>& nums,int right,int left){\n int cnt=0,j=0;\n \n for(int i=0;i<nums.size();i++){\n if(nums[i]>right) j=0;\n else j++;\n cnt+=j;\n }\n return cnt;\n }\n int numSubarrayBoundedMax(vector<int>& nums, int left, int right) {\n return Requirement(nums,right,0)-Requirement(nums,left-1,0);\n }\n};\n``` | 2 | 0 | ['C'] | 0 |
number-of-subarrays-with-bounded-maximum | Best Explanation <10 lines || 2 pointer approach, No DP || Easy-Understanding | best-explanation-10-lines-2-pointer-appr-z820 | //FOR 1ST TEST CASE GIVEN IN QUESTUON-> FIND NUMBER OF SUBARRAYS WITH MAX ELEMENT GREATER THAN 1 AND SUBTRACT ALL THE SUBARRAYS WITH MAX ELEMENT GREATER THAN 3 | lavishmalik | NORMAL | 2022-05-01T20:43:10.887156+00:00 | 2022-05-01T20:45:17.522138+00:00 | 363 | false | //FOR 1ST TEST CASE GIVEN IN QUESTUON-> FIND NUMBER OF SUBARRAYS WITH MAX ELEMENT GREATER THAN 1 AND SUBTRACT ALL THE SUBARRAYS WITH MAX ELEMENT GREATER THAN 3 FROM IT\n//THIS WILL GIVE YOU ALL SUBARRAYS WITH MAX ELEMENT IN RANGE [2,3]\n//FOR [2,1,4,3] THERE WILL BE 9 SUBARRAYS I.E 2, 21 , 214 , 2143 , 14 , 4 , 143 , 43 , 3 FOR MAX ELEMENT GREATER THAN 1 AND 6 SUBARRAYS FOR GREATER THAN 3 I.E 214 , 14 , 4 ,2143 ,143 , 43\n\n\nclass Solution {\npublic:\n \n int countSubarray(vector<int>& nums,int x){\n \n long long ans=0;\n int idx=-1;\n \n for(int i=0;i<nums.size();i++){\n \n if(nums[i]>x){\n idx=i;\n }\n \n ans+=idx+1;\n }\n return ans;\n }\n \n int numSubarrayBoundedMax(vector<int>& nums, int left, int right) {\nlong long ans=countSubarray(nums,left-1)-countSubarray(nums,right);\n return int(ans);\n }\n};\n\n//Pls upvote if you like my solution\n//Happy Coding : ) | 2 | 0 | ['C', 'C++'] | 0 |
number-of-subarrays-with-bounded-maximum | Hints | Approach | Explanation | C++ | hints-approach-explanation-c-by-dangebvi-yuwl | Approach\n\nIn this question, we have to find max. no. of subaarays whose maximum number is in the range [L,R] both inclusive.\n\nHere the idea is we keep to po | dangebvishal | NORMAL | 2022-03-21T08:16:22.128681+00:00 | 2022-03-21T08:16:22.128724+00:00 | 143 | false | **Approach**\n\nIn this question, we have to find max. no. of subaarays whose maximum number is in the range [L,R] both inclusive.\n\nHere the idea is we keep to pointers to maintain a window (subarray) which is satisfying the condition.\nIf we see our window no longer satisfying the condition( i.e.max. of subarray is not in the range) then we change left and right accordingly.\n\n*When to change left and why ?*\n\n If we see our max. element is greater than rightmost boundary means We can\'t continue with the subarray anymore , so we update `left = i,` start i onwards\n \n *When to change right and why ?*\n \n If we see our current element is less than leftmost boundary means we can form a subarray with curr element but not just with curr elem because currr elem < L.\n So,we will not update` right = i`, \n Ex . (2 1 4 3 )\n here , when right is at 1,the no. of subarray with max in range = no. of subarrays with max in range when right is at 0\n \n \n So, if curr elem >= leftmost boundary ,then only we change right =i,\n and calulate no. of subarrays at every iteration.\n i.e `result += right-left; `\n\n**CODE**\n\n```\n int numSubarrayBoundedMax(vector<int>& A, int L, int R) {\n int result=0, left=-1, right=-1;\n for (int i=0; i<A.size(); i++) {\n if (A[i]>R) left=i;\n if (A[i]>=L) right=i;\n result+=right-left;\n }\n return result;\n``` | 2 | 0 | ['C', 'C++'] | 0 |
number-of-subarrays-with-bounded-maximum | C++ two pointer | c-two-pointer-by-abhishek23a-pdwi | \nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& nums, int left, int right) {\n int first=0,sec=0,len=nums.size(),ans=0,cons=0;\n | abhishek23a | NORMAL | 2022-01-20T19:37:10.083502+00:00 | 2022-01-20T19:37:10.083536+00:00 | 177 | false | ```\nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& nums, int left, int right) {\n int first=0,sec=0,len=nums.size(),ans=0,cons=0;\n bool check=true;\n while(sec<len){\n if(first==sec){\n if(nums[sec]>=left && nums[sec]<=right)\n ans++;\n else if(nums[sec]>right){\n first=sec+1;\n }\n else if(nums[sec]<left){\n check=false;\n }\n sec++;\n }\n else{\n if(nums[sec]>right){\n cons=0;\n first=sec+1;\n check=true;\n }\n else if(nums[sec]<left && check==true){\n ans+=sec-first-cons;\n cons++;\n }\n else if(nums[sec]>=left && nums[sec]<=right){\n cons=0;\n check=true;\n ans+=sec-first+1;\n }\n sec++;\n }\n }\n return ans;\n }\n};\n``` | 2 | 0 | ['Two Pointers'] | 0 |
number-of-subarrays-with-bounded-maximum | [Java] solution with explanation beating 100% - O(N) | java-solution-with-explanation-beating-1-yhy9 | We will go through the nums once from left to right and count the valid subarrays ending at the current index. Summing up all the results will give us the final | heijinganghuasheng | NORMAL | 2021-11-27T20:50:15.854235+00:00 | 2021-11-27T20:51:12.951219+00:00 | 222 | false | We will go through the `nums` once from left to right and count `the valid subarrays ending at the current index`. Summing up all the results will give us the final result.\n\nFor each num, we can categorize them into three types:\n1. nums in between of [left, right]. We could construct valid subarrays ending with the current num all the way till the last index that\'s larger than `right`. For example, left = 2, right = 5, nums = [6,5,4,`3`,2,1,0]. At position 4, we have num as `3`, we can construct subarrays ending with `3` till position 0(exclusive), which is the index with the last num larger than the right: [3], [4,3], [5,4,3]. Based on this, we know that we need to note the latest index of the num that\'s larger than the right;\n2. nums less than left. This num itself cannot construct the valid subarray; but if we have some other nums in between of [left, right] before that, we can still construct valid subarrys ending with the current num together with those nums in between of [left, right]. However, we cannot go too far; we can only construct valid subarrys till the num that\'s larger than the right. For example, left = 2, right = 5, nums = [6,5,4,3,2,1,`0`]. At position 6, we have num as `0`, which is smaller than the left, but we can construct subarrays with previous nums till `6`. [1,0] is still not valid because both of them are smaller than the left, so this tell us that we need to start with the num that\'s in between of [left, right], which is `2` in this case, and till the num that\'s larger than right, which is `6`. Based on this, we realize that we need a running counter to tell us the distance between the last number in between of [left, right] and the last number larger than right. This running count will be updated whenever we hit the num in case 1 and case 3.\n3. nums larger than right. There will be no valid subarrays ending with this number and when we hit this number, it will reset our running counter to 0 and we will also update the index of the last number larger than right to the current index.\n\nThe final code looks like below:\n```\nclass Solution {\n public int numSubarrayBoundedMax(int[] nums, int left, int right) {\n int result = 0;\n \n int lastTooLarge = -1; // the index of last num that\'s larger than the right; we initialize it as -1\n int count = 0;\n int index = 0;\n while (index < nums.length) {\n if (nums[index] <= right && nums[index] >= left) {\n count = index - lastTooLarge; // update the running counter: distance between the last valid number to the last num larger than the right\n result += count; // construct with nums between [last number larger than the right, last valid number in between of left and right]\n } else if (nums[index] < left) {\n result += count; // construct with nums between [last number larger than the right, last valid number in between of left and right]\n } else {\n lastTooLarge = index; // update the index of the last num that\'s larger than the right\n count = 0; // reseet the running counter to 0\n }\n index++;\n }\n \n return result;\n }\n}\n``` | 2 | 0 | ['Java'] | 1 |
number-of-subarrays-with-bounded-maximum | Java | Sliding Window | java-sliding-window-by-aakashhsingla-510b | It would be little tricky to find subarrays with maximum value b/w a specific range. But, finding subarrays with maximum value till a max specified value would | aakashhsingla | NORMAL | 2021-11-23T18:19:27.302976+00:00 | 2021-11-23T18:19:27.303008+00:00 | 191 | false | It would be little tricky to find subarrays with maximum value b/w a specific range. But, finding subarrays with maximum value till a max specified value would be easy. So, what we could do is find number of subarrays with maximum value less than equal to **right** and find number of subarrays with maximum value less than equal to **left - 1**. Then by subtracting the second one from first one would be our answer. \nTime Complexity -> **O(n)** \nSpace Complexity -> **O(1)**\n\n```\nclass Solution {\n public int numSubarrayBoundedMax(int[] nums, int left, int right) {\n return subarraysWithMax(nums, right) - subarraysWithMax(nums, left - 1);\n }\n \n private int subarraysWithMax(int[] nums, int max) {\n int n = nums.length;\n int i = 0, j = 0, count = 0, maxTillNow = Integer.MIN_VALUE;\n \n while(j < n) {\n maxTillNow = Math.max(maxTillNow, nums[j]);\n \n if(maxTillNow <= max) {\n count += (j - i + 1);\n } else {\n i = j + 1;\n maxTillNow = Integer.MIN_VALUE;\n }\n j++;\n }\n \n return count;\n }\n} \n``` | 2 | 0 | ['Sliding Window', 'Java'] | 1 |
number-of-subarrays-with-bounded-maximum | java easy to understand solution 2 pointers O(n) | java-easy-to-understand-solution-2-point-kk2k | \nclass Solution {\n public int numSubarrayBoundedMax(int[] nums, int left, int right) {\n int ans =0;\n int prevValueCount=0;\n int n = n | sinhaneha455 | NORMAL | 2021-07-16T05:37:44.603403+00:00 | 2021-07-16T05:37:44.603451+00:00 | 182 | false | ```\nclass Solution {\n public int numSubarrayBoundedMax(int[] nums, int left, int right) {\n int ans =0;\n int prevValueCount=0;\n int n = nums.length;\n int i=0;\n for(int j=0;j<n;j++){\n if(nums[j]>=left && nums[j]<=right){\n ans+=j-i+1;\n prevValueCount=j-i+1;\n }\n else if(nums[j]<left){\n ans+=prevValueCount;\n }\n else{ // nums[j]>Right\n prevValueCount=0;\n i=j+1;\n }\n }\n \n return ans;\n }\n}\n\n```\n\n\n\n\n\n\n\n\n**Please upvote it if you find this solution helpful** | 2 | 1 | ['Java'] | 0 |
number-of-subarrays-with-bounded-maximum | JAVA || Clean & Concise & Optimal Code || O(N) Time || Easy to Understand || 100% Faster Solution | java-clean-concise-optimal-code-on-time-5emhs | \nclass Solution {\n \n public int countSubarray (int[] nums, int bound) {\n \n int answer = 0, count = 0;\n \n for (int num : | anii_agrawal | NORMAL | 2021-06-20T00:10:10.700129+00:00 | 2021-06-20T00:10:10.700168+00:00 | 129 | false | ```\nclass Solution {\n \n public int countSubarray (int[] nums, int bound) {\n \n int answer = 0, count = 0;\n \n for (int num : nums) {\n count = num <= bound ? count + 1 : 0;\n answer += count;\n }\n \n return answer;\n }\n \n public int numSubarrayBoundedMax(int[] nums, int left, int right) {\n \n return countSubarray (nums, right) - countSubarray (nums, left - 1);\n }\n}\n```\n\nPlease help to **UPVOTE** if this post is useful for you.\nIf you have any questions, feel free to comment below.\n\n**LOVE CODING :)\nHAPPY CODING :)\nHAPPY LEARNING :)** | 2 | 1 | ['Java'] | 1 |
number-of-subarrays-with-bounded-maximum | Sliding Window | sliding-window-by-randomnumber7-oylg | They key is to keep on capturing the sliding window size whenever we get a number at end of sliding window that is in valid range.\n\nWhy does it work?\n1. If t | randomNumber7 | NORMAL | 2021-06-18T06:05:15.642231+00:00 | 2021-06-18T06:06:09.849663+00:00 | 138 | false | They key is to keep on capturing the sliding window size whenever we get a number at end of sliding window that is in valid range.\n\nWhy does it work?\n1. If the last element is found to be such a large number that it crosses the valid range (maxWindow > right) - In this case we reset our window. So the window with this state where max element in the subarray is greater than the RIGHT will always have a size of 1 because of reset.\n2. If the last element is found to be in range, then state of sliding window will be one of these - \n(a) The last element is in range and it is the max element\n(b) The last element is in range and it is not the max element\nFor case (a) we calculate the size of the sliding window and keep it in PREFIX so that future items who are smaller than the range keep on making subarray that passes through this END element => total count of the subarray would be PREFIX for this specific future item.\nFor case (b) we still calculate the size of the sliding window again and keep it in PREFIX because any future smaller item needs to just have this END item in its subarray to make the subarray valid.\n\nThe structure of the code is very similar to - \nhttps://leetcode.com/problems/count-number-of-nice-subarrays/\n\n\n```\n public int NumSubarrayBoundedMax(int[] nums, int left, int right) \n {\n int start = 0;\n int end = 0;\n int subArrayCount = 0;\n int maxWindow = Int32.MinValue;\n int prefix = 0;\n \n while(end < nums.Length)\n {\n if(nums[end] > maxWindow)\n {\n maxWindow = nums[end];\n }\n \n if(maxWindow < left)\n {\n prefix = 0;\n }\n else if(maxWindow > right)\n {\n //reset window\n start = end+1;\n prefix = 0;\n maxWindow = Int32.MinValue;\n }\n \n //If last element is in the range then the window\'s max is not greater than right\n if(nums[end] >= left && nums[end] <= right)\n {\n prefix = (end-start+1);\n }\n \n //If the window is valid add the prefix to it as item at end will be a part of prefix number of subArrays\n if(maxWindow >= left && maxWindow <= right)\n {\n subArrayCount += prefix;\n }\n\n end++;\n }\n \n return subArrayCount;\n }\n``` | 2 | 0 | [] | 0 |
number-of-subarrays-with-bounded-maximum | Number of Subarrays with Bounded Maximum DYNAMIC PROGRAMMING Solution | number-of-subarrays-with-bounded-maximum-izp6 | INTUITION :-\nThere are three cases :-\n1. nums[i] > right\n2. nums[i] < left \n3. nums[i] >= left && nums[i] >= right\n\ndp[i] represents number of | grasper1 | NORMAL | 2021-06-18T04:27:54.308879+00:00 | 2021-06-18T06:31:18.335327+00:00 | 137 | false | INTUITION :-\nThere are three cases :-\n1. nums[i] > right\n2. nums[i] < left \n3. nums[i] >= left && nums[i] >= right\n\ndp[i] represents number of subarrays \n1. satisfying condition (3) above , and\n2. ending at nums[i] \n(nums[i] may or may not be maximum)\n\nCode :-\n```\nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& nums, int l, int r) {\n int n=nums.size();\n int dp[n];\n int ct=0,ind=-1;\n (nums[0]>=l && nums[0]<=r)?dp[0]=1:dp[0]=0;\n if(nums[0]>r)ind=0;\n for(int i=1;i<n;i++){\n if(nums[i]>r){\n ind=i;\n dp[i]=0;\n }\n else if(nums[i]<l)\n dp[i]=dp[i-1];\n else if(nums[i]>=l && nums[i]<=r)\n dp[i]=i-ind;\n \n ct=ct+dp[i]; //ct is count of all subarrays \n // cout<<dp[i];\n }\n return ct+dp[0]; \n }\n};\n```\nHope it helps.\n | 2 | 0 | ['Dynamic Programming', 'C'] | 0 |
number-of-subarrays-with-bounded-maximum | Two Pointer Approach C++ | two-pointer-approach-c-by-alamin-tokee-jfks | \nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& nums, int left, int right) {\n int i=0, j=0;\n int count = 0;\n int | alamin-tokee | NORMAL | 2021-06-17T15:07:50.849153+00:00 | 2021-06-17T15:07:50.849195+00:00 | 202 | false | ```\nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& nums, int left, int right) {\n int i=0, j=0;\n int count = 0;\n int prevCount=0;\n int n=nums.size();\n \n while(j < n){\n if(nums[j] >= left && nums[j] <= right){\n prevCount= j-i+1;\n count+=prevCount;\n }else if(nums[j] < left){\n count+=prevCount;\n }else{\n i=j+1;\n prevCount=0;\n }\n j++;\n }\n \n return count;\n }\n};\n``` | 2 | 0 | ['C'] | 0 |
number-of-subarrays-with-bounded-maximum | Easy solution in O(N) in cpp | easy-solution-in-on-in-cpp-by-iamhkr-f942 | \nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& nums, int left, int right) {\n int estart=0,send=0,elong=0,ans=0;\n for(in | iamhkr | NORMAL | 2021-05-30T06:49:59.585374+00:00 | 2021-05-30T06:49:59.585405+00:00 | 100 | false | ```\nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& nums, int left, int right) {\n int estart=0,send=0,elong=0,ans=0;\n for(int i=0;i<nums.size();i++)\n {\n if(nums[i]>=left and nums[i]<=right)\n {\n elong=i-estart+1;// 2 1 4 3 3 4\n }\n else if(nums[i]>right)\n {\n elong=0;\n estart=i+1;\n }\n ans=ans+elong;\n }\n return ans;\n }\n};\n``` | 2 | 0 | [] | 0 |
number-of-subarrays-with-bounded-maximum | Simple Java Solution | O(n) | simple-java-solution-on-by-sagarguptay2j-xioo | \nclass Solution {\n public int numSubarrayBoundedMax(int[] nums, int left, int right) {\n int res = 0,n = nums.length,count = 0,dist = 0;\n bo | sagarguptay2j | NORMAL | 2021-05-18T07:52:11.682242+00:00 | 2021-05-18T07:52:11.682288+00:00 | 77 | false | ```\nclass Solution {\n public int numSubarrayBoundedMax(int[] nums, int left, int right) {\n int res = 0,n = nums.length,count = 0,dist = 0;\n boolean flag = false;\n for(int i = 0;i<n;i++){\n if(nums[i] <= right)\n count++;\n else{ \n count = 0;\n flag = false;\n dist = 0;\n }\n if(nums[i] < left && flag == true){\n dist++;\n res += count-dist;\n }\n else if(nums[i] >= left && nums[i]<= right){\n res += count;\n flag = true;\n dist = 0;\n }\n }\n return res;\n }\n}\n``` | 2 | 0 | [] | 0 |
number-of-subarrays-with-bounded-maximum | Python 3 - counting | python-3-counting-by-yunqu-kmd5 | Use 2 counters: count1 keeps track of the length of subarrays that do not exceed R. count2 keeps the length of the subarrays that also do not go below L. While | yunqu | NORMAL | 2021-04-01T13:22:12.707502+00:00 | 2021-04-01T13:22:26.800226+00:00 | 141 | false | Use 2 counters: `count1` keeps track of the length of subarrays that do not exceed R. `count2` keeps the length of the subarrays that also do not go below L. While if we have an element falling below L, we update the answer only based on the old value of `count2`, but we still keep `count1` incrementing.\n\n```python\nclass Solution:\n def numSubarrayBoundedMax(self, A: List[int], L: int, R: int) -> int:\n ans = count1 = count2 = 0\n size = len(A)\n for j in range(size):\n if A[j] > R:\n count1 = count2 = 0\n elif L <= A[j] <= R:\n count2 = count1 = count1 + 1\n ans += count1\n else:\n count1 += 1\n ans += count2\n return ans\n``` | 2 | 0 | [] | 0 |
number-of-subarrays-with-bounded-maximum | DP Solution + Explanation | dp-solution-explanation-by-halfpolygon-hvh8 | \nA = [2,1,4,3]\nL = 2 ; R = 3\n\nSubarrays which sum to range[L,R]\n\n[2] O, [2,1] O , [1,4] X, [4,3] X, [2,3] X, [2,4] X\n\nWe use permutation\n\n dp[ , , , , | halfpolygon | NORMAL | 2021-03-16T13:18:33.461846+00:00 | 2021-03-16T13:18:33.461884+00:00 | 232 | false | \nA = [2,1,4,3]\nL = 2 ; R = 3\n\nSubarrays which sum to range[L,R]\n\n[2] O, [2,1] O , [1,4] X, [4,3] X, [2,3] X, [2,4] X\n\nWe use permutation\n\n* dp[ , , , , , i, ]\n* dp[i] : denotes max no of valid subarr ending with A[i]\n\n* Case 1: A[i] < L\nWe can only append A[i] with a valid subarr ending with A[i-1] hence cnt of valid is same dp[i] = dp[i-1]\n* Case 2: A[i] > R\nAs the value itself greater than the limit hence not possibe with this element dp[i]=0\n\n* Case 3: In b/w\nAny subarr starts after the previous invalid\ndp[i] = dp[i] + i - prev\n\n\n```\n res, dp = 0,0\n prev = -1\n for i in range(len(A)):\n if A[i] < L and i > 0:\n res += dp\n elif A[i] > R: # Reset\n dp = 0\n prev = i\n elif L <= A[i] <= R:\n dp = i - prev\n res += dp\n return res | 2 | 1 | ['Dynamic Programming', 'Python'] | 0 |
number-of-subarrays-with-bounded-maximum | C++ + Well explained + Easy + Linear time | c-well-explained-easy-linear-time-by-i_a-9qx5 | \nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& A, int L, int R) {\n\t\t// Sum will store the total number of subarrays\n int sum | i_am_pringle | NORMAL | 2020-09-15T17:05:38.404924+00:00 | 2020-09-15T17:06:26.120049+00:00 | 209 | false | ```\nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& A, int L, int R) {\n\t\t// Sum will store the total number of subarrays\n int sum = 0;\n\t\t// Count will store count of all the elements with value <= R\n int count = 0;\n\t\t// X will store count of all the subarrays which has maximum array element at least L and at most R\n int x = 0;\n for( int i = 0 ; i < A.size() ; i++ ){\n if( A[i] > R ){\n count = 0;\n x = 0;\n continue;\n }\n count++;\n if( A[i] >= L && A[i] <= R ){\n sum += count;\n x = count;\n continue;\n }\n\t\t\t// This is main why i am incrementing sum by x\n\t\t\t// Ex -> 1 , 2 , 1\n\t\t\t// This is to handle condition when my index is at 2, and i have to count subarray containing index 2.\n\t\t\t// At index 1, i have subrrays with indices (1) (0,1) which has maximum array element at least L and at most R\n\t\t\t// and x = 2.\n\t\t\t// At index 2, my subarray includes with indices (1,2), (0,1,2) which has maximum array element at least L and at most R.\n\t\t\t// So i need to includes all the subarray when i encountered condition A[i] >= L && A[i] <= R.\n sum += x;\n }\n return sum;\n }\n}; \n``` | 2 | 0 | [] | 0 |
number-of-subarrays-with-bounded-maximum | [Java] O(N) with Monotonic Stack | java-on-with-monotonic-stack-by-yuhwu-6uto | \n public int numSubarrayBoundedMax(int[] A, int L, int R) {\n int n = A.length;\n int[] prevL = new int[n];\n int[] nextL = new int[n]; | yuhwu | NORMAL | 2020-09-12T21:20:49.601182+00:00 | 2020-09-12T21:20:49.601223+00:00 | 135 | false | ```\n public int numSubarrayBoundedMax(int[] A, int L, int R) {\n int n = A.length;\n int[] prevL = new int[n];\n int[] nextL = new int[n];\n Arrays.fill(nextL, n);\n Stack<Integer> decS = new Stack();\n for(int i=0; i<n; i++){\n while(!decS.isEmpty() && A[decS.peek()]<A[i]){\n nextL[decS.pop()] = i;\n }\n prevL[i] = decS.isEmpty() ? -1 : decS.peek();\n decS.push(i);\n }\n int res = 0;\n for(int i=0; i<n; i++){\n if(A[i]>=L && A[i]<=R){\n res += (nextL[i]-i)*(i-prevL[i]);\n }\n }\n return res;\n }\n``` | 2 | 0 | [] | 0 |
number-of-subarrays-with-bounded-maximum | 795-Number of Subarrays with Bounded Maximum-Py All-in-One by Talse | 795-number-of-subarrays-with-bounded-max-3xgy | Get it Done, Make it Better, Share the Best -- Talse\nI). Slide Window\n| O(T): O(n) | O(S): O(1) | Rt: 340ms | \npython\n def numSubarrayBoundedMax(self, A: | talse | NORMAL | 2020-03-11T22:32:44.823031+00:00 | 2020-03-11T22:32:44.823067+00:00 | 85 | false | **Get it Done, Make it Better, Share the Best -- Talse**\n**I). Slide Window**\n| O(T): O(n) | O(S): O(1) | Rt: 340ms | \n```python\n def numSubarrayBoundedMax(self, A: List[int], L: int, R: int) -> int:\n rst = count = st = 0; \n for i in range(len(A)):\n if L <= A[i] <= R: \n count = i - st + 1\n rst += count\n elif A[i] < L: rst += count\n else: count, st = 0, i+1\n return rst\n```\nReferrence: https://leetcode.com/problems/number-of-subarrays-with-bounded-maximum/discuss/117595/Short-Java-O(n)-Solution\n\n | 2 | 0 | [] | 0 |
number-of-subarrays-with-bounded-maximum | C++ O(n) simple solution | c-on-simple-solution-by-gwqi-l6e7 | \nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& A, int L, int R) {\n int count = 0, maxCurrent=-1, maxCurrentIndex = -1;\n | gwqi | NORMAL | 2018-08-19T09:24:01.290821+00:00 | 2018-09-05T09:40:56.566350+00:00 | 316 | false | ```\nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& A, int L, int R) {\n int count = 0, maxCurrent=-1, maxCurrentIndex = -1;\n for (int i = 0, j = 0; i < A.size(); ++i)\n {\n if (A[i] <= R)\n {\n if (A[i] >= L)\n maxCurrentIndex = i;\n count += maxCurrentIndex - j + 1;\n }\n else\n {\n j = i + 1;;\n maxCurrent = -1;\n maxCurrentIndex = i;\n }\n }\n return count;\n }\n};\n``` | 2 | 0 | [] | 0 |
number-of-subarrays-with-bounded-maximum | [JAVA] 2 O(n) solutions | java-2-on-solutions-by-tyuan73-44sn | public int numSubarrayBoundedMax(int[] A, int L, int R) { int s = 0, ans = 0, c = 0; for(int i = 0; i < A.length; i++) { if (A[i] > R) { | tyuan73 | NORMAL | 2018-03-04T04:09:34.534153+00:00 | 2018-03-04T04:09:34.534153+00:00 | 325 | false | public int numSubarrayBoundedMax(int[] A, int L, int R) {
int s = 0, ans = 0, c = 0;
for(int i = 0; i < A.length; i++) {
if (A[i] > R) {
c = 0;
s = i+1;
} else if (A[i] >= L) {
c = i - s + 1;
ans += i - s + 1;
} else {
ans += c;
}
}
return ans;
}
Another solution, the idea is very simple: if we can answer this question: how many subarrays that have max elements no greater than a given value? Suppose the answer is numMax(A, V), then the answer to the original question is the difference between numMax(A, R) - numMax(A, L-1).
```
public int numSubarrayBoundedMax(int[] A, int L, int R) {
return numMax(A, R) - numMax(A, L-1);
}
private int numMax(int[] A, int b) {
int ans = 0, pre = 0, n = A.length;
for(int i = 0; i < n; i++) {
if (A[i] > b)
pre = i+1;
else
ans += i-pre+1;
}
return ans;
}
``` | 2 | 1 | [] | 0 |
number-of-subarrays-with-bounded-maximum | Linear Time complexity , well explained | linear-time-complexity-well-explained-by-mkqs | Intuition 1For 1Number of possibilities are1
Total cases: 1
adding 1 more number 1,212
2Total cases: previous + size of current sub array -> 1 + 2 -> 3adding 1 | dev2411 | NORMAL | 2025-01-28T10:43:45.032560+00:00 | 2025-01-28T10:43:45.032560+00:00 | 71 | false | # Intuition 1
For **1**
Number of possibilities are
1
**Total cases: 1**
adding 1 more number **1,2**
12
2
**Total cases: previous + size of current sub array -> 1 + 2 -> 3**
adding 1 more number **1,2,3**
123
23
3
**Total cases: previous + size of current sub array -> 3 + 3 -> 6**
adding 1 more number **1,2,3,4**
1234
234
34
4
**Total cases: previous + size of current sub array -> 6 + 4 -> 10**
*So for each new number added we have to add size to previous possibilities.*
Now comes the intresting part.
We have to consider the constraint that the max number in the sub arry should be in range [left,right]
# Intuition 2
So let consider this array
1,2,3,1,1,1,2
left = 2;
right = 3;
**Iteration 1:**
sub array : 1
possiblities will be
1
but 1 is less that left so dont add to sum.
**Iteration 2:**
sub array 1,2
previous sum = 0
as we have seen in intuition
Total cases: previous + size of current sub array -> 0 + 2 -> 2
**Iteration 3:**
sub array 1,2,3
previous sum = 2
Total cases: previous + size of current sub array -> 2 + 3 -> 5
**Iteration 4:**
sub array 1,2,3,1
previous sum = 5
Let dive in new cases added
1231
231
31
1
**Wait here we should not consider the last case**
Total cases: previous + size of current sub array - excluded case -> 5 + 4 -1 -> 8
**Iteration 5:**
sub array 1,2,3,1,1
previous sum = 8
Let dive in new cases added
12311
2311
311
11
1
Wait here we should not consider the last two cases case
Total cases: previous + size of current sub array - excluded case -> 8 + 5 - 2 -> 11
Hmm we have to subtract previously excluded cases + 1
**Iteration 6:**
sub array 1,2,3,1,1,1
previous sum = 11
Let dive in new cases added
123111
23111
3111
111
11
1
**Wait here we should not consider the last two cases case**
Total cases: previous + size of current sub array - excluded case -> 11 + 6 - 3 -> 14
**Final iteration**
sub array 1,2,3,1,1,1
previous sum = 14
Let dive in new cases added
1231112
231112
31112
1112
112
12
2
Oh here we dont have to exclude any cases when nums[i] > left
Total cases: previous + size of current sub array - excluded case -> 14 + 7 -> 21
# Intuition 3
Consider 2,3,5,2
**Iteration 1**
Sub array 2
Ans: 1
**Iteration 2**
Sub array 2,3
Ans: 1 + 2 = 3
**Iteration 3**
Sub array 2,3,5
Now element is 5 > right.
So 5 cannot be included in any aaray to move on
Iteration
New Sub array 2
Ans: 3 + 1 = 4
So here is the conclusion
1) For each new element added, no of possibilities increase by sub array size
2) For element less that left we need to keep track of them
3) For Element greater that right we need to start a new sub array
# Code
```java []
class Solution {
public int numSubarrayBoundedMax(int[] nums, int left, int right) {
int len = nums.length;
if(len == 0) {
return 0;
}
int ans = 0;
int n = 0;
int i = 0 ;
int s = 0 ;
while(i<len) {
if(nums[i] > right) {
n=0;
s=0;
} else if(nums[i] < left) {
s++;
n++;
} else {
s = 0;
n++;
}
ans = ans + n - s;
i++;
}
return ans;
}
}
```
# Complexity
- Time complexity:
O(n)
| 1 | 0 | ['Array', 'Java'] | 0 |
number-of-subarrays-with-bounded-maximum | ✅Simple | Best Explanation | O(n) | simple-best-explanation-on-by-mridul__si-kd28 | Intuition\n Describe your first thoughts on how to solve this problem. \nTo count the number of subarrays where the maximum element lies between given bounds le | Mridul__Singh__ | NORMAL | 2024-07-21T18:40:51.913177+00:00 | 2024-07-21T18:40:51.913229+00:00 | 67 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo count the number of subarrays where the maximum element lies between given bounds left and right, we can leverage a sliding window approach. The idea is to keep track of valid subarrays as we iterate through the array and reset counters when we encounter elements outside the bounds.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n**Sliding Window:** Use two pointers, i and j, to create a sliding window. The pointer j iterates through the array, while i marks the start of a valid subarray.\n**Reset on Exceeding Bound:** If an element exceeds the upper bound right, reset i to j + 1 and reset preCount (which tracks the count of valid subarrays ending at the previous position).\n**Count Valid Subarrays:** If an element falls within the bounds [left, right], update preCount to the number of valid subarrays ending at j.\nAccumulate Counts: Add preCount to the total count for every element within the bounds.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& nums, int left, int right) {\n int i=0,j=0;\n int count=0,preCount=0;\n while(j<nums.size()){\n if(nums[j]>right){\n preCount=0;\n i=j+1;\n }\n else if(left<=nums[j] && nums[j]<=right){\n preCount=j-i+1;\n }\n count=count+preCount;\n j++;\n }\n return count;\n }\n};\n```\nPlease Upvote \uD83D\uDC4A\uD83D\uDC47\n\n | 1 | 0 | ['Array', 'Two Pointers', 'C', 'C++', 'Java'] | 0 |
number-of-subarrays-with-bounded-maximum | MONTONIC STACK OPPP | montonic-stack-oppp-by-adityaarora12-7xs5 | **Bold**# Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexit | adi_arr | NORMAL | 2024-06-13T19:34:37.391500+00:00 | 2024-06-13T19:34:37.391576+00:00 | 23 | false | ****************Bold****************# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def numSubarrayBoundedMax(self, nums: List[int], left: int, right: int) -> int:\n inf = 2**32\n nums = [inf]+nums+[inf]\n stack=[]\n count=0 \n\n \n for i,x in enumerate(nums):\n\n while stack and nums[stack[-1]] < x:\n \n j =stack.pop()\n k= stack[-1]\n\n if left<=nums[j]<=right:\n count+=(i-j)*(j-k)\n stack.append(i)\n return count\n\n\n \n``` | 1 | 0 | ['Python3'] | 0 |
number-of-subarrays-with-bounded-maximum | [C++] Scan with Prefix Sum, O(n), Explained with Simple Visualization | c-scan-with-prefix-sum-on-explained-with-47yi | Intuition\n### We can classify each element x into three categories:\n P: Good/Pivot i.e. left <= x <= right: it can form a Pivot\n L: Low/Aux i.e. x < left : i | fzh | NORMAL | 2024-06-07T21:08:06.071252+00:00 | 2024-06-07T21:08:06.071279+00:00 | 33 | false | # Intuition\n### We can classify each element x into three categories:\n* P: Good/Pivot i.e. left <= x <= right: it can form a Pivot\n* L: Low/Aux i.e. x < left : it can contribute to a nearby pivot if reachable.\n* H: High/Barrier i.e. right < x: it is a barrier that split the array into subarrays,\n and each subarray becomes an independent subproblem, which is great for problem solving.\n It\'s a place to reset the internal accumulators in our code.\n\n### Visualization:\nIf we use P to represent a Pivot, and `-` for a low/aux element, and `|` for a High element, then the input array can be visualized as:\n \n\n Left: 6\n Right: 8\n Array: 128123612 9 612368 9\n Visualization: --P---P-- | P---PP | \nWith proper visualization, it\'s easier to come up with algorithms.\n\n# Approach\nLet\'s scan the array from left to right.\n* If the current element is a Pivot, then itself is a good subarray,\nand it can form (psum+aux) subarrays with the Pivots and Aux elements before it. \n* If the current element is an Aux, then it can form (psum) subarrays with the privots and the aux elements before its nearest pivot. \n* If the current element is a Barrier/High, then it splits the input array into subproblems, and the array elements to its rightside forms an independent subproblem. Thus we clear the accumulators. \n\n`psum` is the count of elements since the first reachable pivot or aux, until the last pivot before current element.\n`aux` is the count of aux elements since the last pivot before current element.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution {\npublic:\n // Idea: O(n) fast algorithm: Scan with prefix sum\n int numSubarrayBoundedMax(vector<int>& v, int left, int right) {\n // Idea: scan for pivots, and accumulate the result.\n // we can classify each element x into three categories:\n // P: Good/Pivot i.e. left <= x <= right: it can form a Pivot\n // L: Low/Aux i.e. x < left : it can contribute to a nearby pivot if reachable.\n // H: High i.e. right < x: it is a barrier that split the array into subarrays,\n // and each subarray is an independent subproblem.\n // It\'s a place to reset the internal accumulators in the code.\n // Scan:\n // --P---P--|P---PP| ==>\n // distilled representation: <PivotPos, CountOfPrecedingAuxElements>:\n // <2, 2>, <5,2>, <6,2>\n // but we actually don\'t need to store the Pivot Pos\n int res = 0;\n int aux = 0; // count of the auxilliary elements in the current span.\n int psum = 0;\n for (int a : v) {\n if (a > right) {\n // High: it is a barrier that split the array into subarrays,\n // and each subarray is an independent subproblem.\n aux = 0;\n psum = 0;\n } else if (a < left) {\n // Low/Aux: it can contribute to a nearby pivot if reachable.\n ++aux;\n res += psum;\n } else {\n // Good/Pivot i.e. left <= x <= right: it can form a Pivot\n psum += aux + 1;\n res += psum;\n aux = 0;\n }\n }\n return res;\n }\n\n int numSubarrayBoundedMax_O_NSqaured(vector<int>& v, int left, int right) {\n // Idea: scan for pivots, and accumulate the result.\n // we can classify each element x into three categories:\n // P: Good/Pivot i.e. left <= x <= right: it can form a Pivot\n // L: Low/Aux i.e. x < left : it can contribute to a nearby pivot if reachable.\n // H: High i.e. right < x: it is a barrier that split the array into subarrays,\n // and each subarray is an independent subproblem.\n // Scan:\n // --P---P--|P---PP| ==>\n // distilled representation: <PivotPos, CountOfPrecedingAuxElements>:\n // <2, 2>, <5,2>, <6,2>\n // but we actually don\'t need to store the Pivot Pos\n int res = 0;\n vector<int> spans;\n int aux = 0; // count of the auxilliary elements in the current span.\n for (int a : v) {\n if (a > right) {\n // High: it is a barrier that split the array into subarrays,\n // and each subarray is an independent subproblem.\n spans.clear(); // reset, for the next subproblem.\n aux = 0;\n } else if (a < left) {\n // Low/Aux: it can contribute to a nearby pivot if reachable.\n ++aux;\n // todo: optimization: we can have a prefix sum here\n for (const int span : spans) {\n res += span + 1;\n }\n } else {\n // Good/Pivot i.e. left <= x <= right: it can form a Pivot\n res += aux + 1;\n for (const int span : spans) {\n res += span + 1;\n }\n spans.emplace_back(aux);\n aux = 0;\n }\n }\n return res;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
number-of-subarrays-with-bounded-maximum | Python sliding window w/ explanation. | python-sliding-window-w-explanation-by-r-h920 | Intuition\n Describe your first thoughts on how to solve this problem. \nUsing a sliding window, we can check for subarrays that have a maximum value that lies | rkv_086 | NORMAL | 2024-03-19T01:41:22.607410+00:00 | 2024-03-19T01:41:22.607432+00:00 | 131 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUsing a **sliding window**, we can check for subarrays that have a maximum value that lies within a range [left, right].\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe initialize **two pointers** that are used to represent the start and end of the window, respectively. The window slides through the \'nums\' list, and for each position, checks if the **maximum** value within the window falls within the range [left, right]. The length of the sliding window calculated allows us to determine how many subsequences there are. \n\nCases:\ni) The new element is within the range **[left, right]**. This means the whole subsequence preceding it is valid, so we set the length of the current sliding window. If the sequence so far is [a,b,c,d] (sliding window size is 4), and \'d\' lies in the range [left, right], there are 4 valid subsequences which are: [a, b, c, d], [b, c, d], [c, d] and [d]. This is why we add the **length of the sliding window directly to the count**.\n\nii) The new element is greater than **right**. This means the subsequence is **no longer valid**, so we reset the current sliding window length and move the left pointer to one after the end of the current window - as the current element will never be a part of a valid sliding window.\n\niii) The new element is **less than left**. This doesn\'t affect the validity of the subsequence - and so we don\'t change anything.\n\nAt the end of all these cases, we increment the count of subarrays by the current length of the sliding window.\n\nThanks @techie_sis for demonstrating that it\'s possible to do this using a sliding window! My intention with this solution is to hopefully go one step further into explaining how these sliding window approaches work.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe right pointer iterates through the length of the provided array once, so this is an O(n) operation. \n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThere are 4 ints used, so the space complexity is O(1).\n# Code\n```\nclass Solution:\n def numSubarrayBoundedMax(self, nums: List[int], left: int, right: int) -> int:\n # Maximum of subarray lies in range [left, right]\n left_ptr: int = 0\n curr_arr_len: int = 0\n count_of_subarr: int = 0\n right_ptr: int = 0\n for right_ptr in range(len(nums)):\n # Traversing the provided array with the right pointer\n if left <= nums[right_ptr] <= right:\n curr_arr_len = right_ptr - left_ptr + 1\n elif nums[right_ptr] > right:\n # Maximum of subarray is past the upper bound\n curr_arr_len = 0\n left_ptr = right_ptr + 1 \n # Set new sliding window\'s left to one after end.\n count_of_subarr += curr_arr_len\n # Add \n return count_of_subarr\n``` | 1 | 0 | ['Sliding Window', 'Python3'] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.