question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
word-search | Java DFS with Explanations | java-dfs-with-explanations-by-gracemeng-mb8v | For each cell in board, if it matches the first character of word, we implement DFS starting at it to see if we could find word. \nThe bottleneck of it is to ma | gracemeng | NORMAL | 2018-09-09T05:59:30.904545+00:00 | 2018-09-15T15:33:38.272333+00:00 | 2,640 | false | For each cell in board, if it matches the first character of word, we implement DFS starting at it to see if we could find word. \nThe bottleneck of it is to mark cell visited for we cannot visit a cell multiple times. The fastest way is to modify the original cell rather than to use external storage.\n****\n```\n private static int m, n;\n private static final int[][] dirs = {{0, -1}, {0, 1}, {-1, 0}, {1, 0}};\n \n public boolean exist(char[][] board, String word) {\n if (word == null || word.length() == 0)\n return true;\n \n m = board.length; \n n = board[0].length;\n char firstChar = word.charAt(0);\n \n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n if (board[i][j] == firstChar) {\n // Mark as visited.\n board[i][j] = \'-\';\n if (searchFrom(i, j, board, word, 1))\n return true;\n // Restore to unvisited.\n board[i][j] = firstChar;\n }\n }\n }\n \n return false;\n }\n \n private static boolean searchFrom(int x, int y, char[][] board, String word, int wi) { \n // Acception case, leaf.\n if (wi == word.length()) \n return true;\n \n for (int[] dir : dirs) {\n int nx = x + dir[0];\n int ny = y + dir[1];\n \n if (nx < 0 || nx >= m || ny < 0 || ny >= n || word.charAt(wi) != board[nx][ny])\n continue;\n // Mark as visited.\n board[nx][ny] = \'-\';\n if (searchFrom(nx, ny, board, word, wi + 1))\n return true;\n // Restore to unvisited.\n board[nx][ny] = word.charAt(wi);\n }\n \n return false;\n }\n```\n**(\uFF89>\u03C9<)\uFF89 Vote up, please!** | 25 | 1 | [] | 4 |
word-search | C++ & Python Solution || DFS Traversal || Backtracking (Easiest Solution)🔥✅ | c-python-solution-dfs-traversal-backtrac-vaxo | C++ Solution\n\n// If it helps plz upvote :)\n\nclass Solution {\nprivate:\n bool dfs(vector<vector<char>> &board,vector<vector<int>> &visited,string &word,i | chamoli2k2 | NORMAL | 2022-08-29T12:47:43.250699+00:00 | 2024-07-08T06:13:40.578613+00:00 | 1,793 | false | **C++ Solution**\n```\n// If it helps plz upvote :)\n\nclass Solution {\nprivate:\n bool dfs(vector<vector<char>> &board,vector<vector<int>> &visited,string &word,int i,int j,int idx){\n // base case\n if(idx == word.size()) return true;\n\n if(i < 0 || i >= board.size() || j < 0 || j >= board[0].size() || visited[i][j] == 1 || board[i][j] != word[idx]){\n return false;\n }\n\n // Marking visited\n visited[i][j] = 1;\n\n // traversing all side\n bool ls = dfs(board,visited,word,i,j-1,idx+1); // left\n bool rs = dfs(board,visited,word,i,j+1,idx+1); // right\n bool ds = dfs(board,visited,word,i+1,j,idx+1); // down\n bool us = dfs(board,visited,word,i-1,j,idx+1); // up\n\n // Backtracking (If no one is found suitable match)\n visited[i][j] = 0;\n\n return ls | rs | ds | us;\n }\npublic:\n bool exist(vector<vector<char>>& board, string word) {\n int n = board.size();\n int m = board[0].size();\n vector<vector<int>> visited(n,vector<int>(m,0));\n\n for(int i=0;i<n;i++){\n for(int j=0;j<m;j++){\n if(visited[i][j] == 0 && word[0] == board[i][j]){\n if(dfs(board,visited,word,i,j,0)){\n return true;\n }\n }\n }\n }\n\n return false;\n }\n};\n\n// If it helps plz upvote :)\n```\n\n\n---\n\n**Python Solution**\n```\nclass Solution:\n def __init__(self):\n self.visited = []\n\n def solve(self, board, word, i, j, idx):\n n, m, sz = len(board), len(board[0]), len(word)\n\n # Base case\n if idx == sz:\n return True\n\n # Checking if index is out of bound or current word not not matching with the word at current position at board or it is already visited or not\n if i == n or j == m or i < 0 or j < 0 or self.visited[i][j] == 1 or board[i][j] != word[idx]:\n return False\n\n self.visited[i][j] = 1\n\n # Traversing all sides and checking each possibility\n c1 = self.solve(board, word, i+1, j, idx+1)\n c2 = self.solve(board, word, i-1, j, idx+1)\n c3 = self.solve(board, word, i, j+1, idx+1)\n c4 = self.solve(board, word, i, j-1, idx+1)\n\n self.visited[i][j] = 0\n\n # Returning true if we get true from any possibility\n return c1 or c2 or c3 or c4\n \n def exist(self, board: List[List[str]], word: str) -> bool:\n n, m = len(board), len(board[0])\n self.visited = [[0 for _ in range(m)] for _ in range(n)] \n\n for i in range(0, n):\n for j in range(0, m):\n if board[i][j] == word[0]:\n if self.solve(board, word, i, j, 0) == True:\n return True\n \n\n return False\n``` | 22 | 0 | ['Backtracking', 'Depth-First Search', 'C', 'C++'] | 5 |
word-search | Python sol by DFS [w/ Comment ] | python-sol-by-dfs-w-comment-by-brianchia-bfqh | Python sol by DFS with 4-connected path\n\n---\n\nImplementation by DFS:\n\n\nclass Solution:\n def exist(self, board: List[List[str]], word: str) -> bool:\n | brianchiang_tw | NORMAL | 2020-07-21T09:37:10.763030+00:00 | 2020-07-21T09:37:10.763073+00:00 | 4,657 | false | Python sol by DFS with 4-connected path\n\n---\n\n**Implementation** by DFS:\n\n```\nclass Solution:\n def exist(self, board: List[List[str]], word: str) -> bool:\n \n if not board: \n \n # Quick response for empty board\n return False\n \n h, w = len(board), len(board[0])\n \n # ------------------------------------------------------\n \n def dfs_search(idx: int, x: int, y: int) -> bool:\n \n if x < 0 or x == w or y < 0 or y == h or word[idx] != board[y][x]:\n # Reject if out of boundary, or current grid cannot match the character word[idx]\n return False\n\n if idx == len(word) - 1: \n # Accept when we match all characters of word during DFS\n return True\n\n cur = board[y][x]\n \n # mark as \'#\' to avoid repeated traversal\n board[y][x] = \'#\'\n \n # visit next four neighbor grids\n found = dfs_search(idx + 1, x + 1, y) or dfs_search(idx + 1, x - 1, y) or dfs_search(idx + 1, x, y + 1) or dfs_search(idx + 1, x, y - 1)\n \n # recover original grid character after DFS is completed\n board[y][x] = cur\n \n return found\n\n # ------------------------------------------------------\n \n return any(dfs_search(0, x, y) for y in range(h) for x in range(w)) \n``` | 20 | 0 | ['Depth-First Search', 'Recursion', 'Python', 'Python3'] | 3 |
word-search | Java || 0ms || Fast || Explanation of optimizations | java-0ms-fast-explanation-of-optimizatio-sijb | The Java code below runs at 0ms in April 2024. \n\n---\nFast solutions previously on the runtime graph with coding errors\nUpdate: As of November 2022, the ru | dudeandcat | NORMAL | 2021-10-08T04:46:16.814460+00:00 | 2024-04-03T05:12:24.814604+00:00 | 1,323 | false | The Java code below runs at 0ms in April 2024. \n\n---\n**Fast solutions** previously **on the runtime graph with coding errors**\nUpdate: As of November 2022, the runtime graph has been reset. The code from the runtime graph that is discussed in this section, no longer appears on the runtime graph but may still appear in some discussion/solution entries.\n\n(Outdated) On the graph of execution times for this leetcode problem, there are multiple bars on the graph with fast execution times in the range 0ms to 5ms, but the example code for those bars have a flaw that can produce a wrong answer with some test cases. By clicking on those faster bars of the graph, I have found the example code for that bar. Many of these code examples from the graph have special handling for the following test case from this leetcode problem:\n```\n [["A","B","C","E"],["S","F","E","S"],["A","D","E","E"]]\n "ABCESEEEFS"\n```\nWithout the special checks for this test case, some of those code examples would get the wrong answer. In example code for 0ms on the execution-time graph, if the passed word is the word from the above test case, then the code immediately returns `true`, because without this check the code would give the wrong result. Some other examples from the fastest bars of the graph look at surrounding board squares in an order which allows this test case to be accepted, because they look in the valid direction first. For the fastest code examples from the execution-time graph that correctly handle the above case, most will get the wrong answer for a test case:\n```\n [["A","B","C","E"],["S","F","E","S"],["A","D","E","E"],["A","D","E","E"]]\n "ABCESEEEEEFS"\n```\nThe flaw in these fastest code examples is that they keep a flag for each board square, which indicates if that square has been searched with a specific index into the word and that search failed. This optimization flag is used to stop extra searches at a board square with the same index into the word. But this optimization is flawed because it doesn\'t handle a board square being searched at the same index into the word, but where the search path through the board may approach the same square at the same word index from **different directions** of approach to that square. In the above test cases, the many "E"s on the board and many "E"s in the word can cause many paths through the board\'s "E"s to be searched. Not all of these paths lead to a valid solution. The optimization flags for the squares do not contain any information as to which direction that board square was approached from. \n\nAn example from the above test cases showing how this optimization fails, is that an "E" on the board may be searched with, for example, the 3rd "E" of the word and that path through the board eventually doesn\'t match the word. Then that "E" on the board is flagged as already having been tried with the 3rd letter of the word and that search failed. But a later search path through the board approaches that same "E" on the board but from a different direction and wants to use that "E" from the board for the 3rd "E" of the word. But that board square already has that "E"\'s square flagged as having failed when trying to use it for the 3rd "E" of the word. So that optimization flag causes that search to be terminated early as a failure, when that "E" could actually have been used to match the 3rd "E" of the word as part of a valid match for the entire word. In this case, these optimization flags prevent a valid word match from being found. In most test cases, this optimization works to produce the correct answer, but for some situations such as the above test cases, this optimization can fail.\n\n---------\n**Explaining the code below.**\n\nThe Java code example below uses a Depth First Search (DFS) to recursively try many paths on the board to try to match the passed word. The DFS recursively looks for the next letter in the word in the surrounding squares (up, down, left, right) of the board. If the DFS successfully searches to the end of the word, then the DFS returns `true` unwinding back through the recursive calls, and the search is terminated with a success in finding the word on the board.\n\nSeveral optimizations to try to decide the answer before starting the DFS are used to make the code faster. These optimizations are described in paragraphs below.\n\n**Optimization - Check if word can fit on the board:** If the word has more letters than the board has squares, then return false because the word is too long to fit on the board. Within the documented constraints of this leetcode problem, the worst case that this optimization prevents is a 3x4 `board` of all the same letter, with a 13-letter `word` of all that same letter. If the DFS searching was done on this worst case example, it would waste a lot of time searching many many paths but never finding a solution. In fact, this is an actual leetcode test case:\n```\n [["a","a","a","a"],["a","a","a","a"],["a","a","a","a"]]\n "aaaaaaaaaaaaa"\n```\n**Optimization - Put the word String into a char array:** The code below could have been written to access the String `word` using `word.charAt(i)`, and the code would still work correctly. But instead the Stringf `word` is copied into a `char` array named `wordc`. There is some overhead time to allocate the char array, then to copy the String. But with many repeated access to the characters in the word, it is faster to access a char array than to access the String.\n\nAnother faster method of accessing the letters of the word, would be to copy the word to a `byte` array, which is possible because the word only uses ASCII characters, which all fit into the low 7-bits of a byte. Therefore the code:\n```\n byte[] wordc = new byte[word.length()];\n\t\tword.getBytes(0, word.length(), wordc, 0);\n```\nwill use a `byte` array that can be faster than a `char` array. But this method is not the best programming practices because it does not correctly handle Unicode characters. However, if working on a project that has strict timing requirements, and Unicode is not used, then using this form of `getBytes` may be needed to meet the timing requirements. \n\n**Optimization - Check if all word letters are on the board:** The biggest improvement in speed came from checking if all the letters in the word exist somewhere on the board. If the word contains a letter not found on the board, then return `false` and don\'t waste time doing the DFS. To do this check, scan the word, building a count of the number of occurrences of each letter in the word. Then scan the entire board building a count of the number of occurrences of each letter on the board. Compare the counts of the letters in the word and the letters on the board. If a letter in the word does not have enough of that letter on the board, then return false because the word cannot exist on the board. The advantage of this optimization is best shown with the leetcode problem\'s actual test case:\n```\n [["A","A","A","A","A","A"],["A","A","A","A","A","A"],\n ["A","A","A","A","A","A"],["A","A","A","A","A","A"],\n ["A","A","A","A","A","A"],["A","A","A","A","A","A"]]\n "AAAAAAAAAAAAAAB"\n```\nWithout this optimization and the following optimization, the recursive Depth First Search would waste time searching through all of the "A"s. This optimization would detect that the "B" in the word does not exist on the board, and would quickly return a false.\n\n**Optimization - Reverse word if word\'s last letter appears less frequently on the board:** There is no difference in the final answer if the word is found on the board by scanning forward through the word, or by scanning backward through the word. But a speed improvement can be gained by starting the Depth First Search (DFS) from the word\'s first letter or last letter, whichever occurs least on the board. Using the letter counts from the previous optimization, if the last letter in `word` occurs less that the first letter of `word`, then simply reverse the letters in the word. Reversing the word, allows the DFS to be simpler and faster code that always processes the letters in the word in a forward direction. For example, if the `word` being searched for is "AAAAAB" and the board has many "A"s but has only a few "B"s, then it reverses the word to "BAAAAA" before searching the board.\n\n**Optimization - Scan `board` for first letter of the `word`:** With nested row and column loops, scan the board, looking for only the first letter of the word, before starting a recursive DFS search at a board square that contains the word\'s first letter. Using a simple `if` to look for the first letter of the word, is faster than doing a DFS at each square of the board.\n\n**If useful, please upvote.**\n\n**--- Clean code ---**\n(Commented code further below)\n```\npublic class Solution {\n public boolean exist(final char[][] board, final String word) {\n if (word.length() > board.length * board[0].length) \n return false;\n \n final int[] freqForBoard = new int[128]; \n final int[] freqForWord = new int[128]; \n char[] wordc = word.toCharArray();\n for (int cc : wordc) \n freqForWord[cc]++; \n for (int r = board.length - 1; r >= 0; r--) \n for (int c = board[0].length - 1; c >= 0; c--) \n freqForBoard[board[r][c]]++; \n for (int cc : wordc) \n if (freqForBoard[cc] < freqForWord[cc]) \n return false; \n\n if (freqForBoard[wordc[0]] > freqForWord[wordc[wordc.length - 1]]) {\n for (int left = wordc.length / 2 - 1, right = (wordc.length + 1) / 2; \n left >= 0; ) {\n final char temp = wordc[left];\n wordc[left--] = wordc[right];\n wordc[right++] = temp;\n }\n }\n\n final boolean[][] visited = new boolean[board.length][board[0].length];\n final char firstChar = wordc[0];\n for (int r = 0; r < board.length; r++) \n for (int c = 0; c < board[0].length; c++) \n if ((firstChar == board[r][c]) && search(board, wordc, r, c, 0, visited)) \n return true;\n \n return false;\n }\n \n private boolean search(char[][] board, char[] wordc, int r, int c, \n int index, boolean[][] visited) {\n if (board[r][c] != wordc[index] || visited[r][c]) \n return false;\n if (index == wordc.length - 1) \n return true;\n \n visited[r][c] = true;\n if ((r > 0 && search(board, wordc, r-1, c, index+1, visited)) || \n (r < board.length - 1 && search(board, wordc, r+1, c, index+1, visited)) ||\n (c > 0 && search(board, wordc, r, c-1, index+1, visited)) || \n (c < board[0].length - 1 && search(board, wordc, r, c+1, index+1, visited)))\n return true;\n visited[r][c] = false;\n return false;\n }\n}\n```\n**--- Commented code ---**\n```\npublic class Solution {\n public boolean exist(final char[][] board, final String word) {\n // If word is longer than the board has letters, then \n // word cannot be on the board.\n if (word.length() > board.length * board[0].length) \n return false;\n \n // Make sure the board contains all the letters in the word, \n // while not checking the positions of those letters. \n // Just check the count of each unique letter on the board \n // and in the word.\n final int[] freqForBoard = new int[128]; \n final int[] freqForWord = new int[128]; \n char[] wordc = word.toCharArray();\n for (int cc : wordc) // Count letters in word.\n freqForWord[cc]++; \n for (int r = board.length - 1; r >= 0; r--) // Count letters on board.\n for (int c = board[0].length - 1; c >= 0; c--) \n freqForBoard[board[r][c]]++; \n for (int cc : wordc) // Test for enough letters.\n if (freqForBoard[cc] < freqForWord[cc]) \n return false; \n\n // If first letter in word has a higher count on the board \n // then the last letter in word, then reverse the letters \n // in word so we start the search with the least used letter \n // from either end of the word.\n if (freqForBoard[wordc[0]] > freqForWord[wordc[wordc.length - 1]]) {\n for (int left = wordc.length / 2 - 1, right = (wordc.length + 1) / 2; \n left >= 0; ) {\n final char temp = wordc[left];\n wordc[left--] = wordc[right];\n wordc[right++] = temp;\n }\n }\n\n // Scan the board for the first letter of the word. (Remember \n // that the word may have been reversed.) If first letter found, \n // then call recursive routine to search for the rest of the word.\n final boolean[][] visited = new boolean[board.length][board[0].length];\n final char firstChar = wordc[0];\n for (int r = 0; r < board.length; r++) \n for (int c = 0; c < board[0].length; c++) \n if ((firstChar == board[r][c]) && search(board, wordc, r, c, 0, visited)) \n return true;\n \n return false;\n }\n \n \n // Recursively look for the next letter of the word, until \n // the end of the word, or next letter not found.\n private boolean search(char[][] board, char[] wordc, int r, int c, \n int index, boolean[][] visited) {\n if (board[r][c] != wordc[index] || visited[r][c]) \n return false;\n if (index == wordc.length - 1) \n return true;\n \n visited[r][c] = true;\n if ((r > 0 && search(board, wordc, r-1, c, index+1, visited)) || \n (r < board.length - 1 && search(board, wordc, r+1, c, index+1, visited)) ||\n (c > 0 && search(board, wordc, r, c-1, index+1, visited)) || \n (c < board[0].length - 1 && search(board, wordc, r, c+1, index+1, visited)))\n return true;\n visited[r][c] = false;\n return false;\n }\n}\n``` | 19 | 0 | ['Java'] | 2 |
word-search | Swift Solution -- Clean & Easy Understand | swift-solution-clean-easy-understand-by-bi4oc | \nclass Solution {\n func exist(_ board: [[Character]], _ word: String) -> Bool {\n guard board.count != 0, board[0].count != 0, word.count != 0 else | qilio | NORMAL | 2019-07-30T03:06:33.195019+00:00 | 2019-08-18T01:58:46.987788+00:00 | 1,303 | false | ```\nclass Solution {\n func exist(_ board: [[Character]], _ word: String) -> Bool {\n guard board.count != 0, board[0].count != 0, word.count != 0 else { return false }\n \n let word = Array(word)\n let rows = board.count, cols = board[0].count\n var isVisited = Array(repeating: Array(repeating: false, count: cols), count: rows)\n \n for row in 0..<rows {\n for col in 0..<cols where board[row][col] == word.first {\n if check(board, word, row, col, 0, &isVisited) {\n return true\n }\n }\n }\n return false\n }\n \n func check(_ board: [[Character]], _ word: [Character], _ row: Int, _ col: Int, _ index: Int, _ isVisited: inout [[Bool]]) -> Bool {\n // check if reached the end\n guard index < word.count else { return true }\n \n // check if it match requirements\n guard row >= 0, \n row < board.count, \n col >= 0, \n col < board[0].count,\n !isVisited[row][col],\n board[row][col] == word[index]\n else { return false }\n \n // once we found matched case, we mark isVisited as true\n isVisited[row][col] = true\n \n // try each way, to find if there any valid path\n let hasValidPath = check(board, word, row-1, col, index+1, &isVisited) || // go up\n check(board, word, row+1, col, index+1, &isVisited) || // go down\n check(board, word, row, col-1, index+1, &isVisited) || // go left\n check(board, word, row, col+1, index+1, &isVisited) // go right\n \n // reset isVisited after each DFS search, for re use\n isVisited[row][col] = false\n \n return hasValidPath\n }\n}\n``` | 19 | 0 | ['Backtracking', 'Swift'] | 2 |
word-search | AC in 84ms, by using DFS. | ac-in-84ms-by-using-dfs-by-hongzhi-tloa | I used DFS, and got AC in 84ms, any improvement?\n\n class Solution {\n private:\n vector > board;\n string word;\n bool used;\n | hongzhi | NORMAL | 2014-06-25T02:39:18+00:00 | 2014-06-25T02:39:18+00:00 | 11,042 | false | I used DFS, and got AC in 84ms, any improvement?\n\n class Solution {\n private:\n vector<vector<char> > *board;\n string *word;\n bool **used;\n private:\n bool isInboard(int i, int j)\n {\n if(i < 0)return false;\n if(i >= board->size())return false;\n if(j < 0)return false;\n if(j >= (*board)[i].size())return false;\n return true;\n }\n \n bool DFS(int si, int sj, int n)\n {\n if(n == word->size())return true;\n if(isInboard(si, sj))\n {\n if(!used[si][sj] && (*board)[si][sj] == (*word)[n])\n {\n used[si][sj] = true;\n bool ret = false;\n if(DFS(si+1, sj, n+1))\n ret = true;\n else if(DFS(si-1, sj, n+1))\n ret = true;\n else if(DFS(si, sj+1, n+1))\n ret = true;\n else if(DFS(si, sj-1, n+1))\n ret = true;\n used[si][sj] = false;\n return ret;\n }\n }\n return false;\n }\n \n public:\n bool exist(vector<vector<char> > &board, string word) {\n if(board.size() == 0)return false;\n this->board = &board;\n this->word = &word;\n used = new bool*[board.size()];\n for(int i = 0; i < board.size(); i ++)\n {\n used[i] = new bool[board[i].size()];\n for(int j = 0; j < board[i].size(); j ++)\n used[i][j] = false;\n }\n for(int i = 0; i < board.size(); i ++)\n for(int j = 0; j < board[i].size(); j ++)\n if(DFS(i, j, 0))return true;\n return false;\n }\n }; | 19 | 3 | [] | 9 |
word-search | Using DFS and Backtracking to Search for Word in Grid | using-dfs-and-backtracking-to-search-for-axmw | Intuition\nTo solve this problem, we can utilize a depth-first search (DFS) approach to explore all possible paths in the grid starting from each cell. We will | CS_MONKS | NORMAL | 2024-04-03T00:28:48.786486+00:00 | 2024-04-03T09:10:12.921055+00:00 | 4,218 | false | # Intuition\nTo solve this problem, we can utilize a depth-first search (DFS) approach to explore all possible paths in the grid starting from each cell. We will recursively search for the word by traversing horizontally and vertically neighboring cells while ensuring that each letter is used only once.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Implement a DFS function that takes the grid, current cell position, current index in the word, and the word itself as parameters.\n2. Within the DFS function, check if the current index equals the length of the word minus 1. If so, and the current cell contains the corresponding letter, return true as we have found the word.\n3. Explore all four neighboring cells (up, down, left, right) from the current cell. If a neighboring cell matches the next character in the word and is not already visited, mark it as visited and recursively call the DFS function with the updated parameters.\n4. Backtrack by unmarking the cell after exploring its neighbors.\n5. Iterate over each cell in the grid and start DFS from each cell, checking if the word can be found.\n# Complexity\n- Time complexity: O(m * n * 4^k), m=rows, n=cols , k=length of word\n \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(k), \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```c++ []\nclass Solution {\n int dr1[4]={1,-1,0,0};\n int dr2[4]={0,0,1,-1};\npublic:\n bool solve(vector<vector<char>>& board,int& row,int& col,int i,int j,string& word,int ind,int n){\n if(ind==n-1 && word[ind]==board[i][j])return true;\n for(int d=0;d<4;d++){\n int x=i+dr1[d],y=j+dr2[d];\n if(x>=0&&x<row&&y>=0&&y<col && board[x][y]!=\'.\' && board[x][y]==word[ind]){\n char ch=board[x][y];\n board[x][y]=\'.\';\n if(ind==n-1)return true;\n if(solve(board,row,col,x,y,word,ind+1,n)==true)return true;\n board[x][y]=ch; \n }\n }\n return false;\n }\n bool exist(vector<vector<char>>& board, string word) {\n int row=board.size(),col=board[0].size(),n=word.size();\n for(int i=0;i<row;i++){\n for(int j=0;j<col;j++){\n if(solve(board,row,col,i,j,word,0,n)==true)return true;\n }\n }\n return false;\n }\n};\n```\n```java []\nclass Solution {\n int[] dr1 = {1, -1, 0, 0};\n int[] dr2 = {0, 0, 1, -1};\n\n public boolean solve(char[][] board, int row, int col, int i, int j, String word, int ind, int n) {\n if (ind == n - 1 && word.charAt(ind) == board[i][j]) return true;\n for (int d = 0; d < 4; d++) {\n int x = i + dr1[d], y = j + dr2[d];\n if (x >= 0 && x < row && y >= 0 && y < col && board[x][y] != \'.\' && board[x][y] == word.charAt(ind)) {\n char ch = board[x][y];\n board[x][y] = \'.\';\n if (ind == n - 1) return true;\n if (solve(board, row, col, x, y, word, ind + 1, n)) return true;\n board[x][y] = ch;\n }\n }\n return false;\n }\n\n public boolean exist(char[][] board, String word) {\n int row = board.length, col = board[0].length, n = word.length();\n for (int i = 0; i < row; i++) {\n for (int j = 0; j < col; j++) {\n if (solve(board, row, col, i, j, word, 0, n)) return true;\n }\n }\n return false;\n }\n}\n\n```\n```python3 []\nfrom typing import List\n\nclass Solution:\n def exist(self, board: List[List[str]], word: str) -> bool:\n def solve(i, j, ind):\n if ind == len(word):\n return True\n if i < 0 or i >= row or j < 0 or j >= col or visited[i][j] or board[i][j] != word[ind]:\n return False\n visited[i][j] = True\n if (solve(i+1, j, ind+1) or\n solve(i-1, j, ind+1) or\n solve(i, j+1, ind+1) or\n solve(i, j-1, ind+1)):\n return True\n visited[i][j] = False\n return False\n \n row, col = len(board), len(board[0])\n visited = [[False] * col for _ in range(row)]\n \n for i in range(row):\n for j in range(col):\n if solve(i, j, 0):\n return True\n return False\n\n```\n\n\n\n | 18 | 0 | ['Backtracking', 'Depth-First Search', 'Python', 'C++', 'Java', 'Python3'] | 7 |
word-search | ✅C++ solution using backtracking with explanations! | c-solution-using-backtracking-with-expla-ekbg | If you\u2019re interested in coding you can join my Discord Server, link in the comment section. Also if you find any mistake please let me know. Thank you!\u27 | dhruba-datta | NORMAL | 2022-01-15T12:30:52.663573+00:00 | 2022-01-22T17:40:37.313538+00:00 | 2,595 | false | > **If you\u2019re interested in coding you can join my Discord Server, link in the comment section. Also if you find any mistake please let me know. Thank you!\u2764\uFE0F**\n> \n\n---\n\n## Explanation:\n\n### Solution 01\n\n- We are given a matrix of (m x n) and we are required to check whether the given word exists in the matrix or not!!!\n- We can solve this by Backtracking. Match character-by-character, go ahead and check if the adjacent cells match the next character, and go back if it does not match.\n- For each cell, traverse the entire matrix.\n- Check if\xA0`matrix[i][j] == word[index]`. (we are using\xA0the `index`\xA0to keep track of the characters that we have already checked in the\xA0`word`\xA0during backtracking.)\n - If it is true, then check to repeat the same process for the adjacent cells and for the next index in the word.\n - If it is false, then return to the previous state where we received a\xA0`true`\xA0value and then further check any remaining and unvisited cells.\n- **Time complexity:** O(n) | *actually it\u2019s O(4n) because we traverse 4 neighbours*.\n\n---\n\n## Code:\n\n```cpp\n//Solution 01:\nclass Solution {\npublic:\n bool exist(vector<vector<char>> &board, string word) {\n int row=board.size(), col=board[0].size();\n for(int i = 0 ; i < row ; ++i)\n for(int j = 0 ; j < col ; ++j)\n if(search(0 , i , j , board , word))\n return true;\n return false;\n }\n bool search(int index , int x , int y , vector<vector<char>> &board , string &word)\n {\n if(index == word.size())\n return true;\n \n if(x < 0 || y < 0 || x >= board.size() || y >= board[0].size() || board[x][y] == \'.\') \n return false;\n \n if(board[x][y] != word[index])\n return false;\n \n char temp = board[x][y];\n board[x][y] = \'.\'; \n if(search(index + 1 , x - 1 , y , board , word) || search(index + 1 , x + 1 , y , board , word) || search(index + 1 , x , y - 1 , board , word) || search(index + 1 , x , y + 1 , board , word))\n return true;\n \n board[x][y] = temp;\n return false;\n \n }\n \n};\n```\n\n---\n\n> **Please upvote this solution**\n> | 18 | 0 | ['Backtracking', 'Depth-First Search', 'C++'] | 5 |
word-search | Java | TC: O(RC*(3^L)) | SC: O(L) | Optimal DFS solution without visited matrix | java-tc-orc3l-sc-ol-optimal-dfs-solution-h0qg | java\n/**\n * For each char, perform Depth-First Search in all four directions.\n *\n * Time Complexity:\n * 1. If L > R*C ==> TC = O(1)\n * 2. If L <= R*C ==> | NarutoBaryonMode | NORMAL | 2021-10-14T08:36:59.150880+00:00 | 2021-10-14T09:26:32.782731+00:00 | 1,790 | false | ```java\n/**\n * For each char, perform Depth-First Search in all four directions.\n *\n * Time Complexity:\n * 1. If L > R*C ==> TC = O(1)\n * 2. If L <= R*C ==> TC = O(R*C * 4*(3^L))\n * 3^L ==> For the dfsHelper function, first time we have at most 4 directions\n * to explore, but the choices are reduced to 3 (since no need to go back to the\n * cell from where we came). Therefore, in the worst case, the total number of\n * calls to dfsHelper will be 3^L\n *\n * Space Complexity:\n * 1. If L > R*C ==> SC = O(1)\n * 2. If L <= R*C ==> SC = O(L)\n *\n * R = Number of rows. C = Number of columns. L = Length of word.\n */\nclass Solution {\n private static final int[][] DIRS = new int[][] { { 0, 1 }, { 1, 0 }, { -1, 0 }, { 0, -1 } };\n\n public boolean exist(char[][] board, String word) {\n if (board == null || board.length == 0 || board[0].length == 0 || word == null || word.length() == 0) {\n return false;\n }\n\n int rows = board.length;\n int cols = board[0].length;\n if (rows * cols < word.length()) {\n return false;\n }\n\n for (int i = 0; i < rows; i++) {\n for (int j = 0; j < cols; j++) {\n if (board[i][j] == word.charAt(0) && dfsHelper(board, word, i, j, 0)) {\n return true;\n }\n }\n }\n return false;\n }\n\n private boolean dfsHelper(char[][] board, String word, int x, int y, int wIdx) {\n if (wIdx == word.length()) {\n return true;\n }\n if (x < 0 || x >= board.length || y < 0 || y >= board[0].length || board[x][y] != word.charAt(wIdx)) {\n return false;\n }\n\n board[x][y] = \'#\';\n for (int[] d : DIRS) {\n if (dfsHelper(board, word, x + d[0], y + d[1], wIdx + 1)) {\n board[x][y] = word.charAt(wIdx);\n return true;\n }\n }\n board[x][y] = word.charAt(wIdx);\n return false;\n }\n}\n```\n\n---\n\nSolutions to other parts of Word Search question on LeetCode:\n- [212. Word Search II](https://leetcode.com/problems/word-search-ii/discuss/1520723/Java-or-TC%3A-O(RC*(3L))-or-SC%3A-O(N%2BL)-or-Optimal-Trie%2BDFS-solution) | 17 | 0 | ['Array', 'Backtracking', 'Depth-First Search', 'Recursion', 'Matrix', 'Java'] | 1 |
word-search | JAVA | Clean and Simple ✅ | java-clean-and-simple-by-sourin_bruh-va4m | Please Upvote :D\n##### 1. Using a visited boolean array:\nWe use a visited boolean array to mark if we have already visited a certain position or not.\nWhile l | sourin_bruh | NORMAL | 2022-11-05T14:45:36.212423+00:00 | 2022-11-24T10:24:54.392319+00:00 | 1,932 | false | ### **Please Upvote** :D\n##### 1. Using a visited boolean array:\nWe use a visited boolean array to mark if we have already visited a certain position or not.\nWhile looking for the next letter, we set the current position to `true`, then we call our DFS then set the position back to `false` because if we don\'t find the word, we might have to visit that position again during future iterations and DFS calls.\n```\nclass Solution {\n private boolean[][] visited;\n \n public boolean exist(char[][] board, String word) {\n\t int m = board.length, n = board[0].length;\n visited = new boolean[m][n];\n \n for (int i = 0; i < m; i++) {\n for (int j = 0; j < n; j++) {\n if (board[i][j] == word.charAt(0) && \n dfs(board, i, j, 0, word)) return true;\n }\n }\n \n return false;\n }\n \n public boolean dfs(char[][] board, int i, int j, int index, String word) {\n if (index == word.length()) return true;\n \n if (i < 0 || j < 0 || i >= board.length || j >= board[0].length || board[i][j] != word.charAt(index) || visited[i][j]) {\n return false;\n }\n \n visited[i][j] = true;\n \n boolean found = \n dfs(board, i + 1, j, index + 1, word) ||\n dfs(board, i - 1, j, index + 1, word) ||\n dfs(board, i, j + 1, index + 1, word) ||\n dfs(board, i, j - 1, index + 1, word);\n \n visited[i][j] = false;\n\t\t\n return found;\n }\n}\n\n// TC: O(m * n), SC: O(m * n)\n```\n##### 2. Marking if visited in place:\nWe mark a certain position as visited by changing the value to some character, say whitespace (`\' \'`), after our calls are done, we set it back to the original character.\n```\nclass Solution {\n public boolean exist(char[][] board, String word) {\n for (int i = 0; i < board.length; i++) {\n for (int j = 0; j < board[0].length; j++) {\n if (board[i][j] == word.charAt(0) && \n dfs(board, i, j, 0, word)) return true;\n }\n }\n \n return false;\n }\n \n public boolean dfs(char[][] board, int i, int j, int index, String word) {\n if (index == word.length()) return true;\n \n if (i < 0 || j < 0 || i >= board.length || j >= board[0].length || board[i][j] != word.charAt(index)) {\n return false;\n }\n \n char temp = board[i][j];\n board[i][j] = \' \';\n \n boolean found = \n dfs(board, i + 1, j, index + 1, word) ||\n dfs(board, i - 1, j, index + 1, word) ||\n dfs(board, i, j + 1, index + 1, word) ||\n dfs(board, i, j - 1, index + 1, word);\n \n board[i][j] = temp;\n \n return found;\n }\n}\n\n// TC: O(m * n), SC: O(m * n)\n``` | 16 | 0 | ['Backtracking', 'Depth-First Search', 'Recursion', 'Java'] | 1 |
word-search | C++ backtracking solution without extra data structure | c-backtracking-solution-without-extra-da-1ip1 | Use board itself to mark whether we have visited it before.\n\n class Solution {\n public:\n bool exist(vector>& board, string word) {\n | froxie | NORMAL | 2015-10-24T23:59:50+00:00 | 2015-10-24T23:59:50+00:00 | 2,806 | false | Use board itself to mark whether we have visited it before.\n\n class Solution {\n public:\n bool exist(vector<vector<char>>& board, string word) {\n if (board.size() == 0) return false;\n for (int i=0; i<board.size(); ++i) {\n for (int j=0; j<board[i].size(); ++j) {\n if (search(board, word, i, j, 0)) return true;\n }\n }\n return false;\n }\n \n bool search(vector<vector<char>>& board, string word, int i, int j, int pos) {\n \n if (pos == word.size()) return true;\n if ((i<0) || (i >= board.size()) || (j <0) || (j >= board[i].size())) return false;\n char c = board[i][j];\n if (c == word[pos]) {\n board[i][j] = '#';\n if (search(board, word, i - 1, j, pos + 1)) return true;\n if (search(board, word, i+1, j, pos+1)) return true;\n if (search(board, word, i, j-1, pos+1)) return true;\n if (search(board, word, i, j+1, pos+1)) return true;\n board[i][j] = c;\n }\n return false;\n \n }\n }; | 16 | 0 | ['C++'] | 3 |
word-search | DFS+ Backtracking|Trie| Frequency Count||27ms Beats 98.55% | dfs-backtrackingtrie-frequency-count27ms-g9la | Intuition\n Describe your first thoughts on how to solve this problem. \nDFS+ Backtracking\n\nLater try other better approach.\n2nd approach is Trie+DFS+Backtra | anwendeng | NORMAL | 2024-04-03T01:03:09.314148+00:00 | 2024-04-03T05:54:53.434151+00:00 | 2,159 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nDFS+ Backtracking\n\nLater try other better approach.\n2nd approach is Trie+DFS+Backtracking; with some improvement, there is no need extra handeling for edge cases. Good for pratice for implementing Trie! Almost the same speed like 1st one.\n\n3rd approach is the 1st one with checking on frequency counting before performing DFS function which can exclude some impossible cases & becomes much faster with a speed-up x 180/27 ~6.66666666667\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUse DFS in 4 directions to solve.\nThe implementation uses marking with `@` for the visited grid & backtracking.\n\n# C++ DFS+backtracking||180ms Beats 95.61%\n```\n#pragma GCC optimize("O3", "unroll-loops")\nclass Solution {\npublic:\n int n, m, s;\n bool dfs (int i, int j, int k, vector<vector<char>>& board, string& word)\n {\n if (i < 0 || i >= n || j < 0 || j >= m ||board[i][j] != word[k])\n return 0;\n if (k == s-1)\n return 1;\n char recover=board[i][j];\n board[i][j] = \'@\';\n bool a1 = dfs(i+1, j, k+1, board, word);\n bool a2 = dfs(i, j+1, k+1, board, word);\n bool a3 = dfs(i-1, j, k+1, board, word);\n bool a4 = dfs(i, j-1, k+1, board, word);\n board[i][j] = recover; // backtracking\n return a1 || a2 || a3 || a4;\n }\n\n bool exist(vector<vector<char>>& board, string& word) {\n n = board.size();\n m = board[0].size();\n s = word.size();\n \n for (int i = 0; i < n; i++) {\n for (int j = 0; j < m; j++) {\n if (dfs(i, j, 0, board, word)) return 1;\n }\n }\n return 0;\n }\n};\n\nauto init = []()\n{ \n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n\n```\n# C++ using Trie+DFS+Backtracking||176ms Beats 95.98%\nTrie struct with constructor, destructor & insert. What\'s to do is the searching, which uses DFS+backtracking!\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nNode->insert(word): $O(|word|)$\nDFS: $O(nm4^k)$ where $k$=average searching, $k$ might be very small, or near $|word|$.\nIn total: $O(|word|+nm4^k)$\n\n# revised C++ Code no need for handeling edge case\n```\n#pragma GCC optimize("O3", "unroll-loops")\nconst int N=58;// \'z\'-\'A\'+1=122-65+1=58\nstruct Trie {\n Trie* next[N];\n bool isEnd = 0;\n\n Trie() {\n fill(next, next+N, (Trie*)NULL);\n }\n\n ~Trie() {\n // cout<<"Destructor\\n";\n for (int i=0; i<N; ++i) {\n if (next[i] !=NULL) {\n delete next[i];\n }\n }\n }\n\n void insert(string& word) {\n Trie* Node=this;\n for(char c: word){\n int i=c-\'A\';\n if(Node->next[i]==NULL)\n Node->next[i]=new Trie();\n Node=Node->next[i];\n }\n Node->isEnd=1;\n }\n};\n\nclass Solution {\npublic:\n int n, m, s;\n Trie trie;\n bool dfs (int i, int j, vector<vector<char>>& board, Trie* Node)\n {\n if (i < 0 || i >= n || j < 0 || j >= m )\n return 0;\n // if (Node->isEnd)\n // return 1;\n int index=board[i][j]-\'A\';\n Node=Node->next[index];\n if (!Node) return 0;\n board[i][j]=\'_\';// ascii code 95 for \'_\' is between \'Z\' & \'a\'\n if (Node->isEnd) return 1;\n bool a1 = dfs(i+1, j, board, Node);\n bool a2 = dfs(i, j+1, board, Node);\n bool a3 = dfs(i-1, j, board, Node);\n bool a4 = dfs(i, j-1, board, Node);\n board[i][j]=\'A\'+index; // Backtracking\n return a1 || a2 || a3 || a4;\n }\n\n bool exist(vector<vector<char>>& board, string& word) {\n n = board.size();\n m = board[0].size();\n s = word.size();\n // if (n==1 && m==1 && s==1)//edge case \n // return board[0][0]==word[0];\n Trie* Node=new Trie();\n Node->insert(word);\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < m; j++) {\n if (dfs(i, j, board, Node)) return 1; \n }\n }\n return 0;\n }\n};\n\n\n\nauto init = []()\n{ \n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n\n \n```\n# C++ DFS+backtracking+Frequency Count||27ms Beats 98.55%\n```\n#pragma GCC optimize("O3", "unroll-loops")\nclass Solution {\npublic:\n int n, m, s;\n bool dfs (int i, int j, int k, vector<vector<char>>& board, string& word)\n {\n if (i < 0 || i >= n || j < 0 || j >= m ||board[i][j] != word[k])\n return 0;\n if (k == s-1)\n return 1;\n char recover=board[i][j];\n board[i][j] = \'@\';\n bool a1 = dfs(i+1, j, k+1, board, word);\n bool a2 = dfs(i, j+1, k+1, board, word);\n bool a3 = dfs(i-1, j, k+1, board, word);\n bool a4 = dfs(i, j-1, k+1, board, word);\n board[i][j] = recover; // backtracking\n return a1 || a2 || a3 || a4;\n }\n\n bool exist(vector<vector<char>>& board, string& word) {\n n = board.size();\n m = board[0].size();\n s = word.size();\n int freq[58]={0};\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < m; j++)\n freq[board[i][j]-\'A\']++;\n }\n for (char c: word) //Exclude the impossible cases\n if(--freq[c-\'A\']<0) return 0;\n \n for (int i = 0; i < n; i++) {\n for (int j = 0; j < m; j++) {\n if (dfs(i, j, 0, board, word)) return 1;\n }\n }\n return 0;\n }\n};\n\nauto init = []()\n{ \n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n``` | 15 | 0 | ['String', 'Backtracking', 'Depth-First Search', 'Trie', 'C++'] | 5 |
word-search | TLE->8000ms->3500ms | Finally Python with NO "TLE"!! | Pro optimization | Hushh | tle-8000ms-3500ms-finally-python-with-no-zkpk | Optimization number 1\n Using if -elif instead of for loop helped me resolve TLE:\nAs if will return as soon as it gets TRUE, for will keep checking next condit | dhanrajbhosale7797 | NORMAL | 2022-10-31T19:20:42.138662+00:00 | 2022-10-31T19:28:11.741804+00:00 | 774 | false | **Optimization number 1**\n* Using if -elif instead of for loop helped me resolve TLE:\nAs if will return as soon as it gets TRUE, for will keep checking next conditions.\n(Even multiple "or" did\'nt work for me)\n\n**"PLEASE UPVOTE FOR MY AN HOUR SPENT"**\n\n```\nclass Solution:\n def exist(self, board: List[List[str]], word: str) -> bool: \n\t\t# as start is not restricted to 0,0 we can start from anywhere, will loop\n for i in range(len(board)):\n for j in range(len(board[0])):\n if self.dfs(i,j,word, board, 0):\n return True\n return False\n \n def dfs(self, x, y, word, board, c):\n\t\t# return True if can make word starting from x, y\n if len(word)==c:\n return True \n\t\t# Exit if out of board or char is not required\n if x<0 or y<0 or x>=len(board) or y>=len(board[0]) or board[x][y]!=word[c]:\n return False \n\t\t# move ahead by marking board in path just not to visit again\n board[x][y] = "#"\n if self.dfs(x+1, y, word, board, c+1):\n return True\n elif self.dfs(x, y+1, word, board, c+1):\n return True\n elif self.dfs(x-1, y, word, board, c+1):\n return True\n elif self.dfs(x, y-1, word, board, c+1):\n return True \n\t\t# if from x,y no one making True, we need to restore x, y as it is not in path\n\t\t# so it is open to use by other paths\n board[x][y] = word[c]\n return False\n```\n\n**Optimization Pro Max number 2**\n* Check char in starting only\n```\nclass Solution:\n def exist(self, board: List[List[str]], word: str) -> bool: \n # Count number of letters in board and store it in a dictionary\n boardDic = collections.defaultdict(int)\n for i in range(len(board)):\n for j in range(len(board[0])):\n boardDic[board[i][j]] += 1\n\n # Count number of letters in word\n # Check if board has all the letters in the word and they are atleast same count from word\n wordDic = collections.Counter(word)\n for c in wordDic:\n if c not in boardDic or boardDic[c] < wordDic[c]:\n return False\n \n for i in range(len(board)):\n for j in range(len(board[0])):\n if self.dfs(i,j,word, board, 0):\n return True\n return False\n \n def dfs(self, x, y, word, board, c):\n if len(word)==c:\n return True \n if x<0 or y<0 or x>=len(board) or y>=len(board[0]) or board[x][y]!=word[c]:\n return False \n board[x][y] = "#"\n if self.dfs(x+1, y, word, board, c+1):\n return True\n elif self.dfs(x, y+1, word, board, c+1):\n return True\n elif self.dfs(x-1, y, word, board, c+1):\n return True\n elif self.dfs(x, y-1, word, board, c+1):\n return True \n board[x][y] = word[c]\n return False\n```\n\n | 15 | 1 | ['Depth-First Search', 'Python'] | 3 |
word-search | C++ Simple and Clean DFS Solution | c-simple-and-clean-dfs-solution-by-yehud-qtl4 | \nclass Solution {\npublic:\n bool startsHere(vector<vector<char>>& board, int x, int y, string& word, int idx) {\n if (idx == word.size()) return tru | yehudisk | NORMAL | 2021-08-07T23:19:20.346782+00:00 | 2021-09-24T14:09:58.996884+00:00 | 1,693 | false | ```\nclass Solution {\npublic:\n bool startsHere(vector<vector<char>>& board, int x, int y, string& word, int idx) {\n if (idx == word.size()) return true;\n if (x < 0 || x >= board.size() || y < 0 || y >= board[0].size() || \n board[x][y] == \'.\' || board[x][y] != word[idx]) return false;\n \n char c = board[x][y];\n board[x][y] = \'.\';\n bool res = startsHere(board, x+1, y, word, idx+1) ||\n startsHere(board, x-1, y, word, idx+1) ||\n startsHere(board, x, y+1, word, idx+1) ||\n startsHere(board, x, y-1, word, idx+1);\n board[x][y] = c;\n return res;\n }\n \n bool exist(vector<vector<char>>& board, string word) {\n for (int i = 0; i < board.size(); i++) {\n for (int j = 0; j < board[0].size(); j++) {\n if (startsHere(board, i, j, word, 0)) return true;\n }\n }\n return false;\n }\n};\n```\n**Like it? please upvote!** | 15 | 0 | ['C'] | 4 |
word-search | CPP Solution; 20 ms runtime; better than 100% memory usage; | cpp-solution-20-ms-runtime-better-than-1-zumy | Implements a simple DFS; Code is commented where I thought necessary, hope this helps. Comment if you have any queries!\n\n\tclass Solution {\n\tpulic:\n boo | sidthakur1 | NORMAL | 2019-08-18T21:51:04.071259+00:00 | 2019-08-18T21:51:04.071294+00:00 | 2,023 | false | Implements a simple DFS; Code is commented where I thought necessary, hope this helps. Comment if you have any queries!\n\n\tclass Solution {\n\tpulic:\n bool exist(vector<vector<char>>& board, string word) \n {\n\t\t\tif(board.empty())\n\t\t\t\treturn false;\n \n\t\t\tfor(int i=0; i<board.size(); i++)\n\t\t\t{\n\t\t\t\tfor(int j=0; j<board[0].size(); j++)\n\t\t\t\t{\n\t\t\t\t\tif(dfs(board, 0, i, j, word))\n\t\t\t\t\t\treturn true;\n\t\t\t\t}\n\t\t\t}\n \n return false;\n }\n \n bool dfs(vector<vector<char>>&board, int count, int i, int j, string& word)\n {\n if(word.size() == count) //Signifies that we have reached the end of search\n return true;\n \n if(i<0 || j<0 || i>=board.size() || j>=board[0].size() || board[i][j]!=word[count])\n\t\treturn false;\n //We check if element is within bounds and then check if the character at that is the same as the corresponding character in string word\n \n \n char temp = board[i][j];\n board[i][j] = \' \'; //To show that we have visited this node\n \n bool res = dfs(board, count+1, i+1, j, word) || dfs(board, count+1, i-1, j, word) || dfs(board, count+1, i, j+1, word) ||dfs(board, count+1, i, j-1, word); //DFS in all 4 directions\n \n board[i][j] = temp; //Restore the element after checking\n \n return res;\n }\n\t}; | 15 | 1 | ['Depth-First Search', 'C++'] | 2 |
word-search | Python 3 || dfs with a little bit of pruning || T/S: 99% / 99% | python-3-dfs-with-a-little-bit-of-prunin-84er | \nclass Solution:\n def exist(self, board: List[List[str]], word: str) -> bool:\n\n row, col = len(board), len(board[0])\n R, C, seen = range(r | Spaulding_ | NORMAL | 2022-11-24T02:56:29.233651+00:00 | 2024-05-26T19:00:59.011023+00:00 | 1,866 | false | ```\nclass Solution:\n def exist(self, board: List[List[str]], word: str) -> bool:\n\n row, col = len(board), len(board[0])\n R, C, seen = range(row), range(col), set()\n\n def dfs(coord, i=0):\n \n if len(word) == i: return True\n \n r,c = coord\n\n if (r not in R or c not in C or \n coord in seen or \n board[r][c] != word[i]): return False\n \n seen.add(coord)\n\n res = (dfs((r+1,c), i+1) or dfs((r,c+1), i+1) or\n dfs((r-1,c), i+1) or dfs((r,c-1), i+1))\n \n seen.remove(coord)\n\n return res\n\n boardCt, wrdCt = Counter(chain(*board)), Counter(word)\n if any (boardCt[ch] < wrdCt[ch] for ch in wrdCt): return False\n\n if boardCt[word[0]] > boardCt[word[-1]]: word = word[::-1]\n \n return any(dfs((r, c)) for c in C for r in R)\n```\n[https://leetcode.com/problems/word-search/submissions/848874764/](https://leetcode.com/problems/word-search/submissions/848874764/)\n\nI could be wrong, but I think that time complexity is *O*(*MN* * 4^*L*) and space complexity is *O*(*L*), in which *M*, *N* ~ `row`, `col` and *L* ~ `len(word)`. | 14 | 0 | ['Python', 'Python3'] | 2 |
word-search | 0ms TLE_explained 100%faster | 0ms-tle_explained-100faster-by-gkeshav_1-1wzr | Do upvote\n# Sol #1. DFS (800ms)\n\nclass Solution {\npublic:\n bool dfs(vector<vector<char>> &arr, string word, int k, int r, int c)//pass arr by reference\ | gkeshav_1 | NORMAL | 2022-05-31T09:49:10.229268+00:00 | 2022-06-01T07:09:39.360030+00:00 | 782 | false | Do upvote\n# Sol #1. DFS (800ms)\n```\nclass Solution {\npublic:\n bool dfs(vector<vector<char>> &arr, string word, int k, int r, int c)//pass arr by reference\n {\n \n if(r>=arr.size()||r<0||c>=arr[0].size()||c<0||arr[r][c] != word[k])\n return false;\n\n k++;\n if(k==word.size())\n return true;\n \n\t\t\tarr[r][c]=\'*\'; // changed in orignal arr to avoid taking same occurence of alphabet in arr for different occurences in word\n \n\t\t\tbool res = dfs(arr,word,k,r+1,c) || \n\t\t\t\t\t\tdfs(arr,word,k,r-1,c) || \n\t\t\t\t\t\tdfs(arr,word,k,r,c+1) ||\n\t\t\t\t\t\tdfs(arr,word,k,r,c-1);\n \n arr[r][c]=word[k-1]; //as arr is passed by reference all changes must be reversed before next iteration\n return res;\n \n\n\n }\n \n bool exist(vector<vector<char>>& arr, string word) \n {\n for(int i=0;i<arr.size();i++)\n for(int j=0;j<arr[0].size();++j)\n if(dfs(arr,word,0,i,j))\n return true;\n return false;\n \n }\n};\n```\n* This solution will take around 800ms\n* you will get **TLE** if *arr* is passed by value like this in *dfs* function ```bool dfs(vector<vector<char>> arr, string word, int k, int r, int c) ```\n\n\n# Sol #2. DFS with Pruning 0ms sol\n```\nclass Solution \n{\n bool dfs(vector<vector<char>> &arr, string word, int k, int r, int c)\n {\n \n if(r>=arr.size()||r<0||c>=arr[0].size()||c<0||arr[r][c] != word[k])\n return false;\n\n k++;\n if(k==word.size())\n return true;\n arr[r][c]=\'.\';\n bool res = dfs(arr,word,k,r+1,c) || \n\t\t\t\t\t\tdfs(arr,word,k,r-1,c) || \n\t\t\t\t\t\tdfs(arr,word,k,r,c+1) ||\n\t\t\t\t\t\tdfs(arr,word,k,r,c-1);\n \n arr[r][c]=word[k-1];\n return res;\n }\n \npublic:\n bool exist(vector<vector<char>>& arr, string& word) {\n int R = arr.size(), C = arr[0].size(), N = word.size();\n\n // Prune #1: the arr cannot contain the word.\n if (N > R * C) return false;\n\n // Prune #2: the arr does not contain all occurrences of the chars in the word.\n unordered_map<char, int> occ;\n for (auto& row : arr) for (auto& c : row) ++occ[c];\n for (auto& c : word) if(--occ[c] < 0) return false;\n\n // Prune #3: Find the longest prefix/suffix of the same character. If the longest\n // suffix is longer than the longest prefix, swap the strigns (so we are less\n // likely to have a long prefix with a lot of the same character).\n int left = word.find_first_not_of(word[0]);\n int right = N - word.find_last_not_of(word[N - 1]);\n if (left > right) reverse(begin(word), end(word));\n\n for(int i=0;i<arr.size();i++)\n for(int j=0;j<arr[0].size();++j)\n if(dfs(arr,word,0,i,j))\n return true;\n return false;\n }\n};\n```\n* **We use the same DFS with some prior analysis.**\n* **Prune 3 is for such cases**\n[["A","A","A","A","A","A"],["A","A","A","A","A","A"],["A","A","A","A","A","A"],["A","A","A","A","A","A"],["A","A","A","A","A","A"],["A","A","A","A","A","A"]]\n"AAAAAAAAAAAAAAB"\nit changes word to "BAAAAAAAAAAAAAA"\n\n | 14 | 0 | ['C', 'C++'] | 2 |
word-search | C++ | DFS with explanation | c-dfs-with-explanation-by-ashwinfury1-0xs2 | Approach\n1. Search the board for the first letter in the word.\n2. When we encouter that letter set index to 0 perform DFS. (index - 0 = first letter of word)\ | ashwinfury1 | NORMAL | 2020-07-21T07:46:53.315401+00:00 | 2020-07-21T07:46:53.315445+00:00 | 1,467 | false | ### Approach\n1. Search the board for the first letter in the word.\n2. When we encouter that letter set index to 0 perform DFS. (index - 0 = first letter of word)\n\t1. Use a visited array to mark the letters we visited to avoid duplicates\n\t2. increment the index to look for the next letter in the word.\n\t3. If we have reached the end of the word return true.\n\t4. Go to the adjacent 4 cells and see if the next letter is true.\n\t5. Each of the adjacent elements will also perform the same process\n\t5. If any of the adjacent cell returns true return true.\n\t6. If none of the neighbours returned true. mark this node as unvisited and return false\n3. If any of the starting letter DFS searches return true the return true\n4. If word was not found return false\n\nNOTE: \n1. Checkbounds function\nThis function checks if the given indices are valid\n2. To iterate adjacent cells we use vector - dirs {0,1},{0,-1},{1,0},{-1,0}\nThese four values will be added to the current index to get new indices.\n```\nclass Solution {\npublic:\n \n bool checkBounds(int i,int j,int r,int c){\n return i>=0 && i<r && j>=0 && j<c;\n }\n \n bool dfs(vector<vector<char>>& board,vector<vector<int>>& visited,string& word,int i,int j,int p,int r,int c){\n if(visited[i][j]) return false;\n visited[i][j] = 1;\n p++;\n if(p == word.length()) return true;\n vector<pair<int,int>>dirs = {{0,1},{0,-1},{1,0},{-1,0}};\n for(auto dir : dirs){\n int ii = i+dir.first, jj=j+dir.second;\n if(checkBounds(ii,jj,r,c) && board[ii][jj] == word[p] && dfs(board,visited,word,ii,jj,p,r,c)){\n return true;\n }\n }\n visited[i][j] = 0;\n return false;\n }\n \n bool exist(vector<vector<char>>& board, string word) {\n int r = board.size();\n int c = board[0].size();\n char s = word[0];\n vector<vector<int>>visited(r,vector<int>(c));\n for(int i=0;i<r;i++){\n for(int j=0;j<c;j++){\n if(board[i][j] == s && dfs(board,visited,word,i,j,0,r,c)) return true;\n }\n }\n return false;\n }\n};\n``` | 14 | 2 | [] | 3 |
word-search | JavaScript Clean DFS Solution | javascript-clean-dfs-solution-by-control-9110 | javascript\nvar exist = function(board, word) {\n const ROW_NUM = board.length, COL_NUM = board[0].length;\n \n function callDFS(r, c, idx) {\n | control_the_narrative | NORMAL | 2020-06-17T15:24:13.013166+00:00 | 2020-06-30T19:24:38.098487+00:00 | 2,014 | false | ```javascript\nvar exist = function(board, word) {\n const ROW_NUM = board.length, COL_NUM = board[0].length;\n \n function callDFS(r, c, idx) {\n if(word.length === idx) return true;\n if(r >= ROW_NUM || r < 0 || board[r][c] !== word[idx]) return false; \n \n board[r][c] = \'#\'; // mark as visited\n \n if (callDFS(r+1, c, idx+1)||\n callDFS(r-1, c, idx+1)||\n callDFS(r, c+1, idx+1)||\n callDFS(r, c-1, idx+1)) return true;\n \n board[r][c] = word[idx]; // reset the board\n }\n \n for(let r = 0; r < ROW_NUM; r++) {\n for(let c = 0; c < COL_NUM; c++) {\n if(board[r][c] === word[0] && callDFS(r, c, 0)) return true;\n }\n }\n return false; \n};\n``` | 14 | 0 | ['Depth-First Search', 'JavaScript'] | 5 |
word-search | 99.77% Python Solution with Precheck | 9977-python-solution-with-precheck-by-bb-aw1i | class Solution(object):\n def exist(self, board, word):\n """\n :type board: List[List[str]]\n :type word: str\n :rtype: bool\n | bby880201 | NORMAL | 2016-03-14T18:59:02+00:00 | 2018-09-02T01:12:02.412855+00:00 | 4,521 | false | class Solution(object):\n def exist(self, board, word):\n """\n :type board: List[List[str]]\n :type word: str\n :rtype: bool\n """\n def preCheck():\n preDict = {}\n\n for i in word:\n if i in preDict: preDict[i]+=1\n else: preDict[i] = 1\n \n for i in board:\n for j in i:\n if j in preDict and preDict[j]>0: preDict[j]-=1\n for i in preDict.values():\n if i>0: return False\n return True\n \n def helper(wordIdx, x, y):\n if board[x][y] != word[wordIdx]: return False\n elif wordIdx == l-1: return True\n else:\n wordIdx += 1\n tempChar = board[x][y]\n board[x][y] = None\n for d in [(0,1),(0,-1),(1,0),(-1,0)]:\n xNext = x+d[0]\n yNext = y+d[1]\n if -1<xNext<m and -1<yNext<n and board[xNext][yNext]: \n if helper(wordIdx, xNext, yNext): return True\n board[x][y] = tempChar\n return False\n \n if not board: return False\n if not word: return True\n\n if not preCheck(): return False\n \n m = len(board)\n n = len(board[0])\n l = len(word)\n for i in xrange(m):\n for j in xrange(n):\n if helper(0,i,j): return True\n\n return False | 14 | 1 | ['Python'] | 6 |
word-search | Java solutions || easy to solve | java-solutions-easy-to-solve-by-infox_92-77ta | \npublic class Solution {\n static boolean[][] visited;\n public boolean exist(char[][] board, String word) {\n visited = new boolean[board.length] | Infox_92 | NORMAL | 2022-11-04T14:26:45.502976+00:00 | 2022-11-04T14:26:45.503017+00:00 | 3,196 | false | ```\npublic class Solution {\n static boolean[][] visited;\n public boolean exist(char[][] board, String word) {\n visited = new boolean[board.length][board[0].length];\n \n for(int i = 0; i < board.length; i++){\n for(int j = 0; j < board[i].length; j++){\n if((word.charAt(0) == board[i][j]) && search(board, word, i, j, 0)){\n return true;\n }\n }\n }\n \n return false;\n }\n \n private boolean search(char[][]board, String word, int i, int j, int index){\n if(index == word.length()){\n return true;\n }\n \n if(i >= board.length || i < 0 || j >= board[i].length || j < 0 || board[i][j] != word.charAt(index) || visited[i][j]){\n return false;\n }\n \n visited[i][j] = true;\n if(search(board, word, i-1, j, index+1) || \n search(board, word, i+1, j, index+1) ||\n search(board, word, i, j-1, index+1) || \n search(board, word, i, j+1, index+1)){\n return true;\n }\n \n visited[i][j] = false;\n return false;\n }\n}\n``` | 13 | 0 | ['Bit Manipulation', 'Java', 'JavaScript'] | 1 |
word-search | Without using Visited Array | 6ms Simple Easy to Understand | without-using-visited-array-6ms-simple-e-a3fj | \nclass Solution {\n public boolean exist(char[][] board, String word) {\n for(int i = 0; i < board.length; i++)\n for(int j = 0; j < board | fordbellman1 | NORMAL | 2020-07-21T13:01:50.550753+00:00 | 2020-07-21T13:01:50.550886+00:00 | 682 | false | ```\nclass Solution {\n public boolean exist(char[][] board, String word) {\n for(int i = 0; i < board.length; i++)\n for(int j = 0; j < board[0].length; j++)\n if(board[i][j] == word.charAt(0) && isFound(board, i, j, word, 0))\n return true;\n \n return false;\n }\n \n private boolean isFound(char[][] board, int i, int j, String word, int index) {\n if(index == word.length()) return true;\n if(i < 0 || j < 0 || i >= board.length || j >= board[0].length) return false;\n if(word.charAt(index) != board[i][j]) return false;\n char temp = board[i][j];\n board[i][j] = \'*\';\n if(isFound(board, i + 1, j, word, index + 1) ||\n isFound(board, i - 1, j, word, index + 1) ||\n isFound(board, i, j + 1, word, index + 1) ||\n isFound(board, i, j - 1, word, index + 1))\n return true;\n board[i][j] = temp;\n return false;\n }\n}\n``` | 13 | 1 | [] | 1 |
word-search | Java clean DFS (Backtracking) solution, with explanation | java-clean-dfs-backtracking-solution-wit-o4qf | \nclass Solution {\n boolean[][] visited;\n public boolean exist(char[][] board, String word) {\n visited = new boolean[board.length][board[0].leng | allenchan09 | NORMAL | 2019-09-10T01:07:02.776300+00:00 | 2019-09-10T01:13:44.275187+00:00 | 2,758 | false | ```\nclass Solution {\n boolean[][] visited;\n public boolean exist(char[][] board, String word) {\n visited = new boolean[board.length][board[0].length];\n /* ensure all the nodes will be searched as the beginning point */\n for (int i = 0; i < board.length; i++) {\n for (int j = 0; j < board[0].length; j++) {\n if (dfs(i, j, 0, board, word)) {\n return true;\n }\n }\n }\n return false;\n }\n \n private boolean dfs(int row, int col, int index, char[][] board, String word) {\n /* 1. out of bound \n 2. already visited\n 3. not match */\n if (checkBound(row, col, board) == -1 || \n visited[row][col] || \n word.charAt(index) != board[row][col]) {\n return false;\n }\n \n /* find one matched character, mark the current node as visited */\n visited[row][col] = true;\n \n /* find the whole word! */\n if (index == word.length() - 1) {\n return true;\n }\n \n /* continue searching the next char by extending the index of string,\n note that the current char may not belong to the word in the final.\n even though it matches until now */\n index++;\n \n /* down, right, up, left search */\n if (dfs(row + 1, col, index, board, word) ||\n dfs(row, col + 1, index, board, word) ||\n dfs(row - 1, col, index, board, word) ||\n dfs(row, col - 1, index, board, word)) {\n return true;\n }\n \n /* current position is wrong, backtracking */\n visited[row][col] = false;\n return false;\n }\n \n private int checkBound(int row, int col, char[][] board) {\n if (row == -1 || row == board.length || col == -1 || col == board[0].length) {\n return -1;\n }\n return 0;\n }\n}\n``` | 13 | 0 | ['Backtracking', 'Depth-First Search', 'Java'] | 8 |
word-search | C++ Solution using Backtracking | c-solution-using-backtracking-by-chaseth-mud5 | class Solution {\n public:\n bool exist(vector<vector<char>>& board, string word) {\n if(board.size()==0 || board[0].size()==0 )\n | chasethebug | NORMAL | 2016-01-11T03:23:06+00:00 | 2018-09-10T14:40:05.638156+00:00 | 2,651 | false | class Solution {\n public:\n bool exist(vector<vector<char>>& board, string word) {\n if(board.size()==0 || board[0].size()==0 )\n return true;\n \n for(int i=0; i<board.size(); i++){\n for(int j=0; j<board[0].size(); j++){\n if(check(board, word, i, j))\n return true;\n }\n }\n return false;\n }\n \n bool check(vector<vector<char>>& board, string word, int i, int j){\n if(word.length()==0)\n return true;\n if(i<0 || j<0 ||i>=board.size() ||j>=board[0].size())\n return false;\n if(word[0]==board[i][j]){\n char c = word[0];\n board[i][j]='\\0';\n if(check(board,word.substr(1), i+1, j)||\n check(board,word.substr(1), i-1, j)||\n check(board,word.substr(1), i, j+1)||\n check(board,word.substr(1), i, j-1))\n return true;\n board[i][j]=c;\n }\n return false;\n }\n }; | 13 | 0 | [] | 2 |
word-search | Easy Python Solution : 90.29 beats% || With Comments | easy-python-solution-9029-beats-with-com-p8sa | Code\n\nclass Solution:\n def exist(self, board: List[List[str]], word: str) -> bool:\n ROWS, COLS = len(board), len(board[0])\n visited = set( | ypranav | NORMAL | 2023-08-10T14:39:15.162557+00:00 | 2023-08-10T19:18:37.042507+00:00 | 1,768 | false | # Code\n```\nclass Solution:\n def exist(self, board: List[List[str]], word: str) -> bool:\n ROWS, COLS = len(board), len(board[0])\n visited = set()\n\n def dfs(r,c,idx):\n # if idx == len(word), then word has been found\n if idx == len(word):\n return True\n\n # out of bounds\n # OR current letter does not match letter on board\n # OR letter already visited\n if ( \n r<0 or r>=ROWS \n or c<0 or c>=COLS\n or word[idx] != board[r][c]\n or (r,c) in visited\n ):\n return False\n \n # to keep track of the letter already visited, add it\'s position to the set\n # after DFS we can remove it from the set.\n visited.add((r,c))\n\n # performing DFS \n res = (\n dfs(r+1,c,idx+1) \n or dfs(r-1,c,idx+1) \n or dfs(r,c+1,idx+1) \n or dfs(r,c-1,idx+1)\n )\n \n visited.remove((r,c))\n return res\n \n for i in range(ROWS):\n for j in range(COLS):\n if dfs(i,j,0):\n return True\n return False\n\n``` | 12 | 0 | ['Backtracking', 'Depth-First Search', 'Recursion', 'Python3'] | 1 |
word-search | JAVA solution || DFS || Backtracking || full explanation | java-solution-dfs-backtracking-full-expl-fxg3 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | kadamyogesh7218 | NORMAL | 2022-11-24T07:47:23.738317+00:00 | 2022-11-24T07:47:23.738359+00:00 | 2,382 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n boolean [][] visited;\n int n,m;\n public boolean exist(char[][] board, String word) {\n n=board.length;\n m=board[0].length;\n visited=new boolean[n][m];\n\n for(int i=0;i<n;i++){\n for(int j=0;j<m;j++){\n if(board[i][j]==word.charAt(0)){\n if(valid(i,j,0,board,word)){\n return true;\n }\n }\n }\n }\n return false;\n }\n\n public boolean valid(int i,int j,int count,char [][] board,String word){\n /*-------------base conditions-------------*/\n //out of bound\n if(i<0 || i>=n || j<0 || j>=m ){\n return false;\n }\n\n //if already visited\n if(visited[i][j]){\n return false;\n }\n\n //mismatch\n if(word.charAt(count)!=board[i][j]){\n return false;\n }\n\n //if word is found\n if(count==word.length()-1){\n return true;\n }\n\n /*----------------calculation and recursive calls----------*/\n\n //mark current visited\n visited[i][j]=true;\n\n //inc count\n count++;\n\n //down,right,up,left search\n if(valid(i+1,j,count,board,word) ||\n valid(i,j+1,count,board,word) ||\n valid(i-1,j,count,board,word) ||\n valid(i,j-1,count,board,word) ){\n return true;\n }\n \n //mark current cell unvisited\n visited[i][j]=false;\n \n return false;\n\n }\n\n}\n``` | 12 | 0 | ['Array', 'Backtracking', 'Matrix', 'Java'] | 2 |
word-search | Some Thoughts about the Follow Up: Pruning | some-thoughts-about-the-follow-up-prunin-aapw | Since there are already many excellent posts discussing the solution, I\'ll ignore the discussion of the solution and go directly with the follow up. My solutio | hywrynn | NORMAL | 2021-12-28T19:39:07.930258+00:00 | 2022-01-16T20:45:14.983964+00:00 | 1,501 | false | Since there are already many excellent posts discussing the solution, I\'ll ignore the discussion of the solution and go directly with the follow up. My solution used backtracking.\n\nA very common way for pruning is memoization, in which, we keep record of the "state" and the corresponding "answer". And once we encounter the same "state" again, we can return the "answer" directly instead of stepping into the recursion and calculate the answer again. Next, I\'ll explain how this is implemented and why **memoization doesn\'t work in this problem**.\n\nIn this backtracking, there are three states: the integer i and j represent our current position in the board and an integer d represents the number of digit in the word. Therefore, we can construct the state key as at position 1 in the backtrack method by combining the three states as a String key. Once we encounter the same state again, we return the previously calculated result directly. And at position 2, once we know that the current state works, we record true and false at position 3.\n\nHowever, this doesn\'t work in this situation. Let\'s say we started at B(i1, j1, 0) and currently we are at state A(i0, j0, d0) and we calculated that state A(i0, j0, d0) is false. Does that mean if we start with state A(i0, j0, d0), we can\'t find a match for the remaining words? No. Remeber that we can\'t visit the positions in the board that was visited in the current path. Therefore if we start from B(i1, j1, 0) and reach A(i0, j0, d0), and then we start from A(i0, j0, d0), there are some positions that we can\'t visit. But if we start from a different position say C(i2, j2, 0) and reach A(i0, j0, d0), and then start from A(i0, j0, d0), we may be able visit some positions which we can\'t in the (B->A) path. In short, even if the state A is a "false" in the (B->A) path, it still may be a "true" in the (C->A) path where C != B. Therefore, memoization doesn\'t work in this problem.\n\nAn **example** here to illustrate:\n\nword: "AABCCA", board(with index):\n\n(x, 0, 1, 2, 3, 4)\n(0, A, A, B, A, A)\n(1, D, C, C, D, D)\n\nWe start from A(0, 0) -> A(0, 1) -> B(0, 2) -> C(1, 2) -> C(1, 1), and we can\'t go any further and we record the corresponding states as false. Is this logically correct? No. If later we start from A(0, 4) -> A(0, 3) -> B(0, 2) -> C(1, 2) -> C(1, 1) -> A(0, 1), we can find a valid match. But if we have recorded those states as false, we won\'t be able to reach this valid match.\n\nBut still, there are some ways that we can improve the performance:\n\n- Check if the word has more characters than the board does and check if the board contains enough characters of the word. Thanks for @JulianZheng\'s post [here](https://leetcode.com/problems/word-search/discuss/1225276/Java-99-backtracking-%2B-pruning).\n- While triggering the backtracking, return true once we find a valid match with a certain start point. Also in the backtrack method, return true once we find a valid match. (Imagine we have a board and a word with all same letters, this can save a lot)\n\n**The code is a demo of incorrectly using memo, so it can\'t pass.**\n```\nclass Solution {\n int[][] dirs;\n Map<String, Boolean> memo;\n \n public boolean exist(char[][] board, String word) {\n dirs = new int[][]{{1, 0}, {0, 1}, {-1, 0}, {0, -1}};\n memo = new HashMap<>();\n int m = board.length;\n int n = board[0].length;\n \n // if the word has more chars than the board does\n if (word.length() > m * n) {\n return false;\n }\n \n // if the board doesn\'t contain enough chars of the word\n Map<Character, Integer> count = new HashMap<>();\n for (int i = 0; i < m; i += 1) {\n for (int j = 0; j < n; j += 1) {\n char c = board[i][j];\n count.put(c, count.getOrDefault(c, 0) + 1);\n }\n }\n for (int i = 0; i < word.length(); i += 1) {\n char c = word.charAt(i);\n if (!count.containsKey(c)) {\n return false;\n } else {\n int charCount = count.get(c);\n if (charCount == 1) {\n count.remove(c);\n } else {\n count.put(c, charCount - 1);\n }\n }\n }\n \n // backtracking\n for (int i = 0; i < m; i += 1) {\n for (int j = 0; j < n; j += 1) {\n boolean exists = backtrack(board, i, j, word, 0);\n if (exists) {\n return true;\n }\n }\n }\n return false;\n }\n \n private boolean backtrack(char[][] board, int i, int j, String word, int d) {\n\t\t// position 1\n\t\tString key = i + "," + j + "," + d;\n if (memo.containsKey(key)) {\n return memo.get(key);\n }\n if (d == word.length()) {\n return true;\n }\n int m = board.length;\n int n = board[0].length;\n if (i < 0 || i >= m || j < 0 || j >= n) {\n return false;\n }\n if (board[i][j] == \'#\' || board[i][j] != word.charAt(d)) {\n return false;\n }\n \n char c = board[i][j];\n board[i][j] = \'#\';\n for (int[] dir : dirs) {\n boolean exists = backtrack(board, i + dir[0], j + dir[1], word, d + 1);\n if (exists) {\n\t\t\t\t// position 2\n\t\t\t\tmemo.put(key, true);\n return true;\n }\n }\n board[i][j] = c;\n\t\t// position 3\n\t\tmemo.put(key, false);\n return false;\n }\n}\n``` | 12 | 1 | ['Memoization'] | 3 |
word-search | simple c++ solution | Backtracking | DFS | simple-c-solution-backtracking-dfs-by-xo-t75n | \nclass Solution {\npublic:\n bool issafe(vector<vector<char>>& board,int i, int j,string word, int k){\n if(board[i][j]==word[k]){\n retur | xor09 | NORMAL | 2021-02-02T03:32:01.757643+00:00 | 2021-02-02T03:32:01.757679+00:00 | 1,540 | false | ```\nclass Solution {\npublic:\n bool issafe(vector<vector<char>>& board,int i, int j,string word, int k){\n if(board[i][j]==word[k]){\n return true;\n }\n return false;\n }\n \n bool solve(vector<vector<char>>& board,int i, int j,int m,int n,string word, int k){\n if(k==word.size()){\n return true;\n }\n if(i < 0 || i == m || j < 0 || j == n){\n return false;\n }\n if(issafe(board,i,j,word,k)){\n char temp=board[i][j];\n board[i][j]=\'0\';\n if((solve(board,i+1,j,m,n,word,k+1) || solve(board,i-1,j,m,n,word,k+1) || solve(board,i,j+1,m,n,word,k+1) || solve(board,i,j-1,m,n,word,k+1))){\n return true;\n }\n //backtracking\n board[i][j]=temp;\n }\n \n return false;\n }\n bool exist(vector<vector<char>>& board, string word) {\n int m=board.size();\n int n=board[0].size();\n int k=0;\n for(int i=0;i<m;i++){\n for(int j=0;j<n;j++){\n if(solve(board,i,j,m,n,word,k)){\n return true;\n }\n }\n }\n return false;\n }\n};\n```\nPlease **UPVOTE** | 12 | 0 | ['Backtracking', 'Depth-First Search', 'C'] | 4 |
word-search | EASY CODE WITH COMMENTS || Simple backtracking || dfs based approach | easy-code-with-comments-simple-backtrack-qw7p | Intuition\nThe idea is to use backtracking and dfs keeping track of the visited cells.\n\n# Approach\n\n- Traverse through each cell \n- check if the current le | vebzb | NORMAL | 2024-04-03T07:15:55.844710+00:00 | 2024-04-03T07:15:55.844767+00:00 | 1,034 | false | # Intuition\nThe idea is to use backtracking and dfs keeping track of the visited cells.\n\n# Approach\n\n- Traverse through each cell \n- check if the current letter matches or not\n- If the current cell matches with the current letter:\n 1. mark the cell visited(\'#\')\n 2. Recursively explore each of the adjacent cells (Reiterate to the first step in the Approach colon)\n 3. If the last letter of the word matches, return 1(*true*)\n\n# Complexity\n- Time complexity:\n **O**(*m* * *n* * *4^l*)\n\n- Space complexity:\nO(*l*) \n// For recursion\n\n# Code\n```\nclass Solution {\npublic:\n vector<pair<int,int>> v={{0,1},{0,-1},{1,0},{-1,0}};\n string word;\n int dfs(int x,int y,vector<vector<char>>& board,int pos)\n {\n if(pos==word.length()-1)\n return 1;\n char temp=board[x][y];\n //mark the current cell visited\n board[x][y]=\'#\';\n //For each of the adjacent cell, call the function recursively\n for(auto u:v)\n if(x+u.first>=0&&x+u.first<board.size()&&y+u.second>=0&&y+u.second<board[0].size())\n {\n int res=0;\n if(board[x+u.first][y+u.second]==word[pos+1])\n res=dfs(x+u.first,y+u.second,board,pos+1);\n //return true if a word match is found in one of the neighbours\n if(res==1)\n return 1;\n }\n //mark the current cell unvisited\n board[x][y]=temp;\n return 0;\n }\n\n bool exist(vector<vector<char>>& board, string word1) {\n word=word1;\n vector<int> v(board[0].size(),0);\n for(int i=0;i<board.size();i++)\n {\n for(int j=0;j<board[0].size();j++)\n {\n if(board[i][j]==word[0]&&dfs(i,j,board,0))\n return 1;\n }\n }\n return 0;\n }\n};\n```\n**PLEASE UPVOTE IF YOU FIND IT USEFUL**\uD83E\uDD7A\uD83E\uDD7A\uD83E\uDD7A\n\n---\n | 11 | 0 | ['Backtracking', 'Depth-First Search', 'C++'] | 0 |
word-search | ✔️ 100% Fastest Swift Solution | 100-fastest-swift-solution-by-sergeylesc-q6mn | \nclass Solution {\n func exist(_ board: [[Character]], _ word: String) -> Bool {\n let chs = reverseIfNeeded(Array(word))\n if isValid(board, | sergeyleschev | NORMAL | 2022-04-06T05:49:17.241452+00:00 | 2022-04-06T05:49:17.241496+00:00 | 1,060 | false | ```\nclass Solution {\n func exist(_ board: [[Character]], _ word: String) -> Bool {\n let chs = reverseIfNeeded(Array(word))\n if isValid(board, chs) == false { return false }\n var res = false\n \n func backtrack(_ path: [[Int]], _ position: [Int], _ target: Int) {\n if res || path.count == target { res = true; return }\n \n let char = chs[path.count]\n let positions = next(board, position, char)\n var path = path\n \n for position in positions {\n if path.contains(position) { continue }\n \n path.append(position)\n backtrack(path, position, target)\n path.remove(at: path.count - 1)\n }\n }\n \n backtrack([], [-1, -1], chs.count)\n return res\n }\n\n \n func isValid(_ board: [[Character]], _ chars: [Character]) -> Bool {\n var res = true\n \n loop1: for c in chars {\n var tmp = false\n \n loop2: for i in 0..<board.count {\n for j in 0..<board[0].count {\n if board[i][j] == c { tmp = true; break loop2 }\n }\n }\n \n if tmp == false { res = false; break loop1 }\n }\n \n return res\n }\n\n \n func reverseIfNeeded(_ chars: [Character]) -> [Character] {\n var headCount = 0\n var tailCount = 0\n \n for c in chars {\n if c == chars[0] {\n headCount += 1\n }\n if c == chars[chars.count - 1] {\n tailCount += 1\n }\n }\n \n if tailCount < headCount {\n return chars.reversed()\n \n } else {\n return chars\n }\n }\n\n \n func next(_ board: [[Character]], _ position: [Int], _ char: Character) -> [[Int]] {\n var res: [[Int]] = []\n \n if position[0] == -1 {\n for i in 0..<board.count {\n for j in 0..<board[0].count {\n if board[i][j] == char {\n res.append([i, j])\n }\n }\n }\n } else {\n var c: Character = " "\n \n if position[0] > 0 {\n let i = position[0] - 1\n let j = position[1]\n c = board[i][j]\n c == char ? res.append([i, j]) : ()\n }\n \n if position[0] < board.count - 1 {\n let i = position[0] + 1\n let j = position[1]\n c = board[i][j]\n c == char ? res.append([i, j]) : ()\n }\n \n if position[1] > 0 {\n let i = position[0]\n let j = position[1] - 1\n c = board[i][j]\n c == char ? res.append([i, j]) : ()\n }\n \n if position[1] < board[0].count - 1 {\n let i = position[0]\n let j = position[1] + 1\n c = board[i][j]\n c == char ? res.append([i, j]) : ()\n }\n }\n \n return res\n }\n\n}\n```\n\nLet me know in comments if you have any doubts. I will be happy to answer.\n\nPlease upvote if you found the solution useful. | 11 | 0 | ['Swift'] | 1 |
word-search | JS | DFS + Backtracking | Beats 88% | Clean Code | js-dfs-backtracking-beats-88-clean-code-q3r7j | DFS + Backtracking will take you far\n\n\nconst exist = function(board, word) {\n const n = board.length, m = board[0].length;\n if (word.length < 1) retu | adt | NORMAL | 2021-10-07T18:20:36.131722+00:00 | 2021-10-11T17:39:07.261400+00:00 | 1,412 | false | DFS + Backtracking will take you far\n\n```\nconst exist = function(board, word) {\n const n = board.length, m = board[0].length;\n if (word.length < 1) return false;\n\n const dfs = (i, j, pos) => {\n if (i === n || i < 0 || j === m || j < 0 || board[i][j] !== word[pos]) return false;\n if (pos === word.length-1) return true;\n board[i][j] = "."; // choose this elem so we don\'t find it again\n const found = \n dfs(i+1,j, pos+1) || // check every direction and see if any of them return a match\n dfs(i-1,j, pos+1) ||\n dfs(i,j+1, pos+1) ||\n dfs(i,j-1, pos+1);\n\n board[i][j] = word[pos]; // unchoose element\n return found;\n };\n \n for (let i=0;i<n;i++) {\n for (let j=0;j<m;j++) {\n if (board[i][j] === word[0]) {\n const match = dfs(i,j, 0);\n if (match) return true;\n }\n }\n }\n\n return false;\xA0\n};\n``` | 11 | 0 | ['Backtracking', 'Depth-First Search', 'Recursion', 'JavaScript'] | 1 |
word-search | In Detail Explanation 💯 || [Java/C++/JavaScript/Python3/C#/Go] | in-detail-explanation-javacjavascriptpyt-vzs3 | Approach\n\n#### Main Method (exist):\n1. Iterate through each cell of the board using nested loops.\n2. For each cell, if the character matches the first chara | Shivansu_7 | NORMAL | 2024-04-03T07:56:00.548231+00:00 | 2024-04-03T07:56:00.548265+00:00 | 861 | false | # Approach\n\n#### Main Method (`exist`):\n1. Iterate through each cell of the board using nested loops.\n2. For each cell, if the character matches the first character of the word:\n - Initiate a DFS from that cell to search for the entire word.\n - If the DFS returns true (indicating the word is found), return true.\n3. If no match is found after iterating through all cells, return false.\n\n#### DFS Method (`dfs`):\n1. Base Case:\n - If the count of characters processed equals the length of the word, return true (indicating the entire word is found).\n - If the current cell is out of bounds or does not match the next character of the word, return false.\n2. Store the current character of the board in a temporary variable and mark the current cell as visited.\n3. Recursively explore neighboring cells in all four directions (up, down, left, right) to find the remaining characters of the word.\n4. If any of the recursive calls return true, indicating the word is found, set `found` to true.\n5. Restore the original character at the current cell and return `found`.\n\n# Complexity\n- Time complexity: $$O(m \\cdot n \\cdot 4^{L})$$\n - *In the given scenario, `m` and `n` denote the dimensions of a grid, while `l` signifies the length of word. The expression `4^l` denotes the potential maximum number of recursive iterations required for each starting cell.*\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(L)$$\n - *where l is the length of the word. The space complexity is primarily due to the recursive stack depth during the DFS traversal.* \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```Java []\nclass Solution {\n public boolean exist(char[][] board, String word) {\n for(int i=0; i<board.length; i++) {\n for(int j=0; j<board[0].length; j++) {\n if(board[i][j] == word.charAt(0) && dfs(board, i, j, 0, word)) {\n return true;\n }\n }\n }\n return false;\n }\n\n private boolean dfs(char[][] board, int i, int j, int count, String word) {\n if(count == word.length()) {\n return true;\n }\n\n if(i==-1 || i==board.length || j==-1 || j==board[0].length || board[i][j]!=word.charAt(count)) {\n return false;\n }\n\n char temp = board[i][j];\n board[i][j] = \'*\';\n boolean found = dfs(board, i+1, j, count+1, word) ||\n dfs(board, i-1, j, count+1, word) ||\n dfs(board, i, j+1, count+1, word) ||\n dfs(board, i, j-1, count+1, word);\n board[i][j] = temp;\n return found;\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n bool exist(vector<vector<char>>& board, string word) {\n for (int i = 0; i < board.size(); ++i) {\n for (int j = 0; j < board[0].size(); ++j) {\n if (board[i][j] == word[0] && dfs(board, i, j, 0, word)) {\n return true;\n }\n }\n }\n return false;\n }\n\nprivate:\n bool dfs(vector<vector<char>>& board, int i, int j, int count, string word) {\n if (count == word.length()) {\n return true;\n }\n\n if (i == -1 || i == board.size() || j == -1 || j == board[0].size() || board[i][j] != word[count]) {\n return false;\n }\n\n char temp = board[i][j];\n board[i][j] = \'*\';\n bool found = dfs(board, i + 1, j, count + 1, word) ||\n dfs(board, i - 1, j, count + 1, word) ||\n dfs(board, i, j + 1, count + 1, word) ||\n dfs(board, i, j - 1, count + 1, word);\n board[i][j] = temp;\n return found;\n }\n```\n```Python3 []\nclass Solution:\n def exist(self, board: List[List[str]], word: str) -> bool:\n for i in range(len(board)):\n for j in range(len(board[0])):\n if board[i][j] == word[0] and self.dfs(board, i, j, 0, word):\n return True\n return False\n\n def dfs(self, board: List[List[str]], i: int, j: int, count: int, word: str) -> bool:\n if count == len(word):\n return True\n\n if i < 0 or i >= len(board) or j < 0 or j >= len(board[0]) or board[i][j] != word[count]:\n return False\n\n temp = board[i][j]\n board[i][j] = \'*\'\n found = self.dfs(board, i + 1, j, count + 1, word) or \\\n self.dfs(board, i - 1, j, count + 1, word) or \\\n self.dfs(board, i, j + 1, count + 1, word) or \\\n self.dfs(board, i, j - 1, count + 1, word)\n board[i][j] = temp\n return found\n```\n```Go []\nfunc exist(board [][]byte, word string) bool {\n for i := 0; i < len(board); i++ {\n for j := 0; j < len(board[0]); j++ {\n if board[i][j] == word[0] && dfs(board, i, j, 0, word) {\n return true\n }\n }\n }\n return false\n}\n\nfunc dfs(board [][]byte, i, j, count int, word string) bool {\n if count == len(word) {\n return true\n }\n\n if i < 0 || i >= len(board) || j < 0 || j >= len(board[0]) || board[i][j] != word[count] {\n return false\n }\n\n temp := board[i][j]\n board[i][j] = \'*\'\n found := dfs(board, i+1, j, count+1, word) ||\n dfs(board, i-1, j, count+1, word) ||\n dfs(board, i, j+1, count+1, word) ||\n dfs(board, i, j-1, count+1, word)\n board[i][j] = temp\n return found\n}\n```\n```C# []\npublic class Solution {\n public bool Exist(char[][] board, string word) {\n for (int i = 0; i < board.Length; i++) {\n for (int j = 0; j < board[0].Length; j++) {\n if (board[i][j] == word[0] && Dfs(board, i, j, 0, word)) {\n return true;\n }\n }\n }\n return false;\n }\n\n private bool Dfs(char[][] board, int i, int j, int count, string word) {\n if (count == word.Length) {\n return true;\n }\n\n if (i < 0 || i >= board.Length || j < 0 || j >= board[0].Length || board[i][j] != word[count]) {\n return false;\n }\n\n char temp = board[i][j];\n board[i][j] = \'*\';\n bool found = Dfs(board, i + 1, j, count + 1, word) ||\n Dfs(board, i - 1, j, count + 1, word) ||\n Dfs(board, i, j + 1, count + 1, word) ||\n Dfs(board, i, j - 1, count + 1, word);\n board[i][j] = temp;\n return found;\n }\n}\n```\n```JavaScript []\n/**\n * @param {character[][]} board\n * @param {string} word\n * @return {boolean}\n */\nvar exist = function(board, word) {\n for (let i = 0; i < board.length; i++) {\n for (let j = 0; j < board[0].length; j++) {\n if (board[i][j] === word[0] && dfs(board, i, j, 0, word)) {\n return true;\n }\n }\n }\n return false;\n};\n\nfunction dfs(board, i, j, count, word) {\n if (count === word.length) {\n return true;\n }\n\n if (i < 0 || i >= board.length || j < 0 || j >= board[0].length || board[i][j] !== word[count]) {\n return false;\n }\n\n let temp = board[i][j];\n board[i][j] = \'*\';\n let found = dfs(board, i + 1, j, count + 1, word) ||\n dfs(board, i - 1, j, count + 1, word) ||\n dfs(board, i, j + 1, count + 1, word) ||\n dfs(board, i, j - 1, count + 1, word);\n board[i][j] = temp;\n return found;\n}\n```\n\n---\n\n\n---\n\n\n\n | 10 | 0 | ['Backtracking', 'Python', 'C++', 'Java', 'Go', 'Python3', 'C#'] | 3 |
word-search | C++ || DFS || Backtracking || easy Solution | c-dfs-backtracking-easy-solution-by-indr-6msk | \nclass Solution {\npublic:\n bool search(int index,int i,int j,vector<vector<char>> &board, string word){\n if(index == word.size()){\n re | indresh149 | NORMAL | 2022-11-24T07:24:45.726800+00:00 | 2022-11-24T07:24:45.726832+00:00 | 1,090 | false | ```\nclass Solution {\npublic:\n bool search(int index,int i,int j,vector<vector<char>> &board, string word){\n if(index == word.size()){\n return true;\n }\n if(i<0 || j<0 || i >= board.size() || j >= board[0].size()){\n return false;\n }\n bool ans = false;\n if(word[index] == board[i][j]){\n board[i][j] = \'*\';\n \n ans = search(index+1,i+1,j,board,word) || search(index+1,i,j+1,board,word) || \n search(index+1,i-1,j,board,word) ||search(index+1,i,j-1,board,word);\n \n board[i][j] = word[index];\n }\n return ans;\n }\n \n bool exist(vector<vector<char>>& board, string word) {\n int m = board[0].size();\n int n = board.size();\n int index = 0;\n \n bool ans = false;\n \n for(int i=0;i<n;i++){\n for(int j=0;j<m;j++){\n if(word[index] == board[i][j]){\n if(search(index,i,j,board,word)){\n return true;\n }\n }\n }\n }\n return ans;\n }\n};\n```\n**Please upvote if it was helpful for you, thank you!** | 10 | 0 | ['Depth-First Search', 'Recursion', 'C'] | 1 |
word-search | C++ solution||easy understanding||recursion||dfs | c-solutioneasy-understandingrecursiondfs-1xjm | \nclass Solution {\npublic:\n bool search(int i,int j,int n,int m,vector<vector<char>>& board, string word,int k){\n if(k==word.size()) return true;\n | Shankhadeep2000 | NORMAL | 2022-10-12T12:07:16.820463+00:00 | 2022-10-12T12:07:16.820502+00:00 | 1,932 | false | ```\nclass Solution {\npublic:\n bool search(int i,int j,int n,int m,vector<vector<char>>& board, string word,int k){\n if(k==word.size()) return true;\n if(i<0||j<0||i==n||j==m||board[i][j]!=word[k]) return false;\n char ch = board[i][j];\n board[i][j]=\'#\';\n bool opt1= search(i+1,j,n,m,board,word,k+1);\n bool opt2= search(i,j+1,n,m,board,word,k+1);\n bool opt3= search(i-1,j,n,m,board,word,k+1);\n bool opt4= search(i,j-1,n,m,board,word,k+1);\n board[i][j]=ch;\n return opt1||opt2||opt3||opt4;\n }\n bool exist(vector<vector<char>>& board, string word) {\n int n =board.size();\n int m = board[0].size();\n for(int i =0;i<n;i++){\n for(int j = 0;j<m;j++){\n if(search(i,j,n,m,board,word,0)) return true;\n }\n }\n return false;\n \n }\n};\n``` | 10 | 0 | ['Depth-First Search', 'Recursion', 'C'] | 3 |
word-search | Rust | Backtracking | Nice and Concise with Functional Style | rust-backtracking-nice-and-concise-with-o53lp | I like the fact that a significant part of this already short (in comparison) solution is just assigning some variables for convenience and legibility (first 4 | wallicent | NORMAL | 2022-06-12T17:25:09.981262+00:00 | 2022-06-12T17:33:54.214723+00:00 | 365 | false | I like the fact that a significant part of this already short (in comparison) solution is just assigning some variables for convenience and legibility (first 4 lines of `exist(...)`. Using iterators, `any()` and the `windows(2)` trick shortens down the solution quite a bit compared to a more imperative. Note that `dfs` is in essence a single expression.\n\n```\nimpl Solution {\n fn dfs(board: &[Vec<char>], word: &[char], visited: &mut [Vec<bool>], m: usize, n: usize, len: usize, i: usize, j: usize, depth: usize) -> bool {\n depth == len || (i < m && j < n && !visited[i][j] && word[depth] == board[i][j] && {\n visited[i][j] = true;\n let rez = [0, 1, 0, !0, 0]\n .windows(2)\n .any(|w| Self::dfs(board, word, visited, m, n, len, i.wrapping_add(w[0]), j.wrapping_add(w[1]), depth + 1));\n visited[i][j] = false;\n rez\n })\n }\n\n pub fn exist(board: Vec<Vec<char>>, word: String) -> bool {\n let m = board.len();\n let n = board[0].len();\n let word = word.chars().collect::<Vec<_>>();\n let len = word.len();\n let mut visited = vec![vec![false; n]; m];\n\n (0..m).any(|i| (0..n).any(|j| Self::dfs(&board, &word, &mut visited, m, n, len, i, j, 0)))\n }\n}\n``` | 10 | 0 | ['Rust'] | 0 |
word-search | ✔️ C# - Simple to understand using DFS, With Comments | c-simple-to-understand-using-dfs-with-co-tdub | Thumbs up if you find this helpful \uD83D\uDC4D\n\n\npublic class Solution {\n public bool Exist(char[][] board, string word) {\n \n // Create | keperkjr | NORMAL | 2021-10-07T03:52:22.444082+00:00 | 2021-10-07T03:54:34.313556+00:00 | 401 | false | **Thumbs up if you find this helpful** \uD83D\uDC4D\n\n```\npublic class Solution {\n public bool Exist(char[][] board, string word) {\n \n // Create a \'visitied\' node matrix to keep track of the\n // items we\'ve already seen\n var rowsVisited = new bool[board.Length][];\n for (int rowIndex = 0; rowIndex < board.Length; ++rowIndex) {\n rowsVisited[rowIndex] = new bool[board[rowIndex].Length];\n }\n \n // Start at the root node and explore as far as possible along each branch\n for (int rowIndex = 0; rowIndex < board.Length; ++rowIndex) {\n for (int colIndex = 0; colIndex < board[rowIndex].Length; ++colIndex) {\n if (DFS(board, rowIndex, colIndex, 0, word, rowsVisited)) {\n return true; \n }\n }\n }\n return false;\n }\n \n bool DFS(char[][] board, int row, int col, int searchIndex, string word, bool[][] rowsVisited) {\n // Make sure the search paramaters are in bounds\n if (searchIndex >= word.Length) {\n return true; \n }\n if (row < 0 || row >= board.Length || col < 0 || col >= board[row].Length) {\n return false; \n } \n if (rowsVisited[row][col]) {\n return false; \n } \n if (board[row][col] != word[searchIndex]) {\n return false; \n } \n \n // Mark that this row has been visited\n rowsVisited[row][col] = true;\n \n var searchResult = \n // Search left\n DFS(board, row, col - 1, searchIndex + 1, word, rowsVisited) ||\n \n // Search right\n DFS(board, row, col + 1, searchIndex + 1, word, rowsVisited) ||\n \n // Search top\n DFS(board, row - 1, col, searchIndex + 1, word, rowsVisited) ||\n \n // Search bottom\n DFS(board, row + 1, col, searchIndex + 1, word, rowsVisited);\n \n // Unmark that this row has been visited\n rowsVisited[row][col] = false;\n \n return searchResult;\n }\n}\n``` | 10 | 0 | ['Depth-First Search'] | 0 |
word-search | C++ || Concise DFS | c-concise-dfs-by-suniti0804-4ej3 | \nbool dfs(vector<vector<char>>& board, int i, int j, string& word)\n {\n if(word.size() == 0) \n return true;\n if(i < 0 || i >= bo | suniti0804 | NORMAL | 2021-07-11T04:29:59.930535+00:00 | 2021-07-11T04:29:59.930563+00:00 | 1,272 | false | ```\nbool dfs(vector<vector<char>>& board, int i, int j, string& word)\n {\n if(word.size() == 0) \n return true;\n if(i < 0 || i >= board.size() || j < 0 || j >= board[0].size() || board[i][j] != word[0])\n return false;\n \n char ch = board[i][j];\n board[i][j] = \'*\';\n string s = word.substr(1);\n bool res = dfs(board, i-1, j, s) || dfs(board, i+1, j, s) || dfs(board, i, j-1, s) || dfs(board, i, j+1, s);\n \n board[i][j] = ch;\n return res;\n }\n \n bool exist(vector<vector<char>>& board, string word) \n {\n int m = board.size();\n int n = board[0].size();\n \n for(int i = 0; i < m; i++)\n {\n for(int j = 0; j < n; j++)\n {\n if(dfs(board, i, j, word))\n return true;\n }\n }\n \n return false;\n }\n``` | 10 | 0 | ['Depth-First Search', 'C', 'C++'] | 2 |
word-search | python 3 || DFS || Backtracking | python-3-dfs-backtracking-by-adarshbirad-5o8q | ```\n\nclass Solution:\n def exist(self, board: List[List[str]], word: str) -> bool:\n def dfs(board,i,j,count,word):\n if(count == len(wor | adarshbiradar | NORMAL | 2020-07-22T06:38:21.944237+00:00 | 2020-07-22T06:38:21.944287+00:00 | 1,845 | false | ```\n\nclass Solution:\n def exist(self, board: List[List[str]], word: str) -> bool:\n def dfs(board,i,j,count,word):\n if(count == len(word)):\n return True\n if i<0 or j<0 or i>=len(board) or j>=len(board[0]) or word[count]!=board[i][j]:\n return False\n temp = board[i][j]\n board[i][j] = ""\n found = dfs(board,i+1,j,count+1,word) or dfs(board,i-1,j,count+1,word) or dfs(board,i,j+1,count+1,word) or dfs(board,i,j-1,count+1,word)\n board[i][j] = temp\n return found\n \n for i in range(len(board)):\n for j in range(len(board[0])):\n if board[i][j] == word[0] and dfs(board,i,j,0,word):\n return True\n return False | 10 | 0 | ['Backtracking', 'Depth-First Search', 'Python3'] | 2 |
word-search | JAVA DFS Simple solution | java-dfs-simple-solution-by-anjali100btc-zkc4 | If you found the solution helpful, kindly upvote or like. :)\n\n\nclass Solution {\n boolean visited[][];\n public boolean exist(char[][] board, String wo | anjali100btcse17 | NORMAL | 2020-07-21T07:54:59.729883+00:00 | 2020-07-21T07:54:59.729916+00:00 | 893 | false | If you found the solution helpful, kindly upvote or like. :)\n\n```\nclass Solution {\n boolean visited[][];\n public boolean exist(char[][] board, String word) {\n \tvisited= new boolean[board.length][board[0].length];\n\t\tfor(int i=0; i<board.length; i++)\n\t\t\tfor(int j=0; j<board[0].length; j++)\n\t\t\t\tif(board[i][j]==word.charAt(0) && search(i,j,0,board,word))\n\t\t\t\t\treturn true;\n\t\treturn false;\n\t}\n\tprivate boolean search(int i, int j, int index, char[][] board, String word) {\n\t\tif(index==word.length())\n\t\t\treturn true;\n\t\tif(i>=board.length|| i<0 || j<0 || j>= board[0].length \n\t\t\t\t|| visited[i][j] || word.charAt(index)!=board[i][j])\n\t\t\treturn false;\n\t\t\n\t\tvisited[i][j]=true;\n\t\tif(search(i+1, j, index+1, board, word)||\n\t\t\tsearch(i-1, j, index+1, board, word)||\n\t\t\tsearch(i, j+1, index+1, board, word)||\n\t\t\tsearch(i, j-1, index+1, board, word))\n\t\t\treturn true;\n\t\t\n\t\tvisited[i][j]=false;\n\t\treturn false;\n }\n}\n``` | 10 | 1 | [] | 1 |
word-search | Word search - Python3 Solution with a Detailed Explanation | word-search-python3-solution-with-a-deta-zzp3 | This solution comes from here. The idea is that you loop over every element of a matrix one by one (lines #1 and #2), and check whether you can find the word. T | peyman_np | NORMAL | 2020-07-20T05:10:01.481015+00:00 | 2020-08-25T22:11:59.856726+00:00 | 2,161 | false | This solution comes from [here](https://leetcode.com/problems/word-search/discuss/27665/Python-simple-dfs-solution). The idea is that you loop over every element of a matrix one by one (lines `#1` and `#2`), and check whether you can find the word. The main part is the `dfs` function that for each value (`board[i][j]`) check whether it\'s the first letter of the `word`. If it\'s not it returns `False` (line `#5`). Otherwise, it moves forward (line `#4`). After satisfying line `#4` (meaning first letter is found), we replace that cell in `board` with space so that we now we\'ve visited it (line `#6`). Then, we try four different scenarios in the neighborhood of `[i][j]` and see whether we can find the second letter of `word` (line `#7, 8, 9, 10`). This is done recursively. After we find the first letter in line `#4`, we focus on the rest of the `word`, meaning `word[1:]`. If the second letter is one of the right, left, top, or bottom cells of `board[i][j]`, we focus of `word[2:]` in the next cycle. We keep doing this until we find all the letters. Now say, we find the first letter, but the second letter is not in the neighborhood, we go to a new `board[i][j]` by checking a new cell in lines `#1, 2, 3` and start the process from scratch for the whole `word`. \n\n\nNote that the conditions of lines `#7` ( `i>0`), `#8` (` i < len(board) - 1 `), etc. takes care of matrix edges. If it wasn\'t there, and you\'re on the first column of matrix (`j=0`), then `j - 1` would give you `-1` which is corresponding to the right side. \n\n\n\n\nDoes this make sense? \n\n\n```\nclass Solution:\n def exist(self, board: List[List[str]], word: str) -> bool:\n if not board:\n return False\n if not word:\n return True\n \n for i in range(len(board)): # 1\n for j in range(len(board[0])): # 2\n if self.dfs(board, word, i, j): #3\n return True\n return False \n \n \n def dfs(self, board, word, i, j):\n if board[i][j] == word[0]: #4\n if not word[1:]:\n return True\n \n board[i][j] = " " #6\n \n if i > 0 and self.dfs(board, word[1:], i - 1, j): #7\n return True\n if i < len(board) - 1 and self.dfs(board, word[1:], i + 1, j): #8\n return True\n if j > 0 and self.dfs(board, word[1:], i, j - 1): #9\n return True\n if j < len(board[0]) - 1 and self.dfs(board, word[1:], i, j + 1): #10\n return True\n \n board[i][j] = word[0]\n return False\n else: #5\n return False\n```\n\n========================================================================\nFinal note: Please let me know if you found any typo/error/etc. I\'ll try to fix it. \n\nFinal note 2: Explaning things in a simple language is instructive for me. Thanks for reading. | 10 | 0 | ['Python', 'Python3'] | 2 |
word-search | DFS + Backtracking Solution without extra space (visited map) | dfs-backtracking-solution-without-extra-f81al | \nfunc exist(board [][]byte, word string) bool {\n\tfor i := 0; i < len(board); i++ {\n\t\tfor j := 0; j < len(board[0]); j++ {\n\t\t\tif board[i][j] == word[0] | humoyun | NORMAL | 2020-07-02T04:21:19.307175+00:00 | 2020-07-02T04:24:17.031334+00:00 | 894 | false | ```\nfunc exist(board [][]byte, word string) bool {\n\tfor i := 0; i < len(board); i++ {\n\t\tfor j := 0; j < len(board[0]); j++ {\n\t\t\tif board[i][j] == word[0] {\n\t\t\t\trs := dfs(board, i, j, 0, word)\n\n\t\t\t\tif rs {\n\t\t\t\t\treturn true\n\t\t\t\t}\n\t\t\t}\n\t\t}\n\t}\n\n\treturn false\n}\n\nfunc dfs(board [][]byte, i, j, pos int, word string) bool {\n\tif i < 0 || j < 0 || i >= len(board) || j >= len(board[0]) || board[i][j] == \'*\' {\n\t\treturn false\n\t}\n\n\tif word[pos] != board[i][j] {\n\t\treturn false\n\t}\n \n\tif len(word)-1 == pos {\n\t\treturn true\n\t}\n\n\tpos++\n tmp := board[i][j]\n\tboard[i][j] = \'*\'\n\n\tdfsResult :=\n\t\tdfs(board, i-1, j, pos, word) ||\n\t\t\tdfs(board, i+1, j, pos, word) ||\n\t\t\tdfs(board, i, j+1, pos, word) ||\n\t\t\tdfs(board, i, j-1, pos, word)\n board[i][j] = tmp\n \n\treturn dfsResult\n```\n | 10 | 0 | ['Backtracking', 'Depth-First Search', 'Go'] | 2 |
word-search | Java | Brute force to Search Pruning | Fully Explained | java-brute-force-to-search-pruning-fully-sk49 | Intuition\nWe need to construct the given word from the characters in the board. This is a trial-and-error algorithm which we will solve using backtracking.\n\n | nadaralp | NORMAL | 2022-11-24T07:26:15.348718+00:00 | 2022-11-24T07:33:06.161410+00:00 | 3,532 | false | # Intuition\nWe need to construct the given word from the characters in the board. This is a trial-and-error algorithm which we will solve using `backtracking`.\n\nNote: While meeting this question for the first time a few years ago, I thought of doing it with DP. The reason why DP doesn\'t work here is that you cannot form smaller sub-problems because the path with which you arrive at some cell `(r, c)` changes with every move. Hence, you have conditional state that cannot be memoized (calculated for other problems).\n\nThe naive approach is to construct all the possible words of `length = given_word.length` and check for equality.\n\nThe code will look like this\n\n```\nclass Solution {\n public boolean exist(char[][] board, String word) {\n int m = board.length;\n int n = board[0].length;\n StringBuilder s = new StringBuilder();\n boolean[][] vis = new boolean[m][n];\n\n for (int r = 0; r < m; r++) {\n for (int c = 0; c < n; c++) {\n if (dfs(board, vis, word, r, c, s)) return true;\n }\n }\n return false;\n }\n\n private boolean dfs(char[][] board, boolean[][] vis, String word, int row, int col, StringBuilder s) {\n // The reason I mutate the state here, and not before calling dfs() is because there are 2 places calling the function. And I don\'t want to duplicate the logic\n s.append(board[row][col]);\n vis[row][col] = true;\n\n if (s.length() == word.length()) {\n boolean hasFound = s.toString().equals(word);\n s.deleteCharAt(s.length() - 1);\n vis[row][col] = false;\n return hasFound;\n }\n\n int m = board.length;\n int n = board[0].length;\n\n int[][] dirs = new int[][]{{1, 0}, {-1, 0}, {0, 1}, {0, -1}};\n for (int[] dir : dirs) {\n int newRow = row + dir[0];\n int newCol = col + dir[1];\n \n if (newRow >= 0 && newRow < m && newCol >= 0 && newCol < n && !vis[newRow][newCol]) {\n if (dfs(board, vis, word, newRow, newCol, s)) {\n return true;\n }\n }\n }\n\n s.deleteCharAt(s.length() - 1);\n vis[row][col] = false;\n return false;\n }\n}\n```\n\nThis is inefficient because if we are looking for the word "hello" there is no point matching it with "abcdef". We can prune the searching on the first index, i.e. "h" != "a", therefore we don\'t have to continue searching on that path.\n\nSo to optimize our algorithm we will keep track of the index we located at, and compare the letter on each index. If we reach the last index it means we built the whole string.\n\n# Code\n```\nclass Solution {\n public boolean exist(char[][] board, String word) {\n int m = board.length;\n int n = board[0].length;\n StringBuilder s = new StringBuilder();\n boolean[][] vis = new boolean[m][n];\n\n for (int r = 0; r < m; r++) {\n for (int c = 0; c < n; c++) {\n if (dfs(board, vis, word, r, c, 0)) return true;\n }\n }\n return false;\n }\n\n private boolean dfs(char[][] board, boolean[][] vis, String word, int row, int col, int i) {\n if(board[row][col] != word.charAt(i)) return false;\n\n if (i == word.length() -1) return true;\n\n vis[row][col] = true;\n\n int m = board.length;\n int n = board[0].length;\n\n int[][] dirs = new int[][]{{1, 0}, {-1, 0}, {0, 1}, {0, -1}};\n for (int[] dir : dirs) {\n int newRow = row + dir[0];\n int newCol = col + dir[1];\n\n if (newRow >= 0 && newRow < m && newCol >= 0 && newCol < n && !vis[newRow][newCol]) {\n if (dfs(board, vis, word, newRow, newCol, i + 1)) {\n return true;\n }\n }\n }\n\n vis[row][col] = false;\n return false;\n }\n}\n```\n\nNote 2: you can optimize the algorithm by doing the checks before calling dfs(). I omitted that here for brevity. | 9 | 0 | ['Java'] | 1 |
word-search | JS | Backtrack(DFS) | js-backtrackdfs-by-dynamicrecursion-sw4k | \n//approach: backtracking(dfs)\n//basic template of backtracking would be to loop, choose, explore and unchoose\n//loop: you want to iterate over all the numbe | dynamicRecursion | NORMAL | 2021-08-25T19:43:14.401920+00:00 | 2021-08-25T19:43:14.401964+00:00 | 921 | false | ```\n//approach: backtracking(dfs)\n//basic template of backtracking would be to loop, choose, explore and unchoose\n//loop: you want to iterate over all the numbers so that you can find it\'s possible values\n//choose: you start with the index value(the 0th index number), so that you can find the next combined possible values for the 0th value\n//explore: basically recursion to add all the next values to the 0th value\n//unchoose: you pop the value (Oth value), so then you can now start with other value to make that other value 0th value\n//in this case: \n//since its a 2D array, instead of looping once, we will loop twice, over the row and column of the board\n//then to choose, we will just mark the visited index with \'*\'\n//to explore, we will be exploring left, right, up, down of the board from the current spot/box\n//then to unchoose, we will just replace the \'*\' with the letter we had replaced\n//\n//so basically, \n//we will start from the [0][0] of the board, and start checking if the letter in that spot is equal to the letter in the given word\n//if it is equal, we recurse to find possible matching letter from the board\n//we increment the wordIndex by 1, we also replace the spot with \'*\' \n//and then backtrack check to see if the neighbors(left, right, up, down) have the new letter from the given word\n//if somehow the boundary check fails or the letter check fails, we return false, \n//if all of the check fails while backtracking we start replacing the \'*\' with the actual letters we stored in our temp variable\n//then return the result back.\nvar exist = function(board, word) {\n if(board == null || word == null || board.length == 0) //edge case\n return false;\n \n \n for(let row = 0; row < board.length; row++){\n for(let col = 0; col < board[0].length; col++){\n if(helper(board, word, row, col, 0)) //recursive check\n return true;\n }\n }\n \n \n function helper(board, word, row, col, wordIndex){\n \n if(wordIndex == word.length) \n return true;\n \n //out of bounds check\n if(row < 0 || row >= board.length || col < 0 || col >= board[0].length)\n return false;\n \n //letter check in the box (if the letter at the board is not equal to the letter of the given word return false)\n if(board[row][col] != word[wordIndex])\n return false;\n \n //choose\n let temp = board[row][col];\n board[row][col] = \'*\'; //marking the visited box\n \n //explore\n let bool = helper(board, word, row-1, col, wordIndex+1) ||\n helper(board, word, row+1, col, wordIndex+1) ||\n helper(board, word, row, col-1, wordIndex+1) ||\n helper(board, word, row, col+1, wordIndex+1);\n \n //unchoose\n board[row][col] = temp; //setting back the value from \'*\' to the letter\n \n return bool;\n }\n \n \n return false;\n};\n``` | 9 | 0 | ['Backtracking', 'Recursion', 'JavaScript'] | 0 |
word-search | Java Solution 4 ms, faster than 99.10% using backtracking | java-solution-4-ms-faster-than-9910-usin-5bgq | PLEASE UPVOTE THIS SOLUTION IF YOU LIKE THIS \u270C\uFE0F\n\nIntiuition: \n- To search a word in grid, we can start from a index (x, y) and then try every dire | satyaDcoder | NORMAL | 2021-02-16T08:40:16.380412+00:00 | 2021-03-05T08:03:21.979434+00:00 | 1,045 | false | **PLEASE UPVOTE THIS SOLUTION IF YOU LIKE THIS** \u270C\uFE0F\n\nIntiuition: \n- To search a word in grid, we can start from a index (x, y) and then try every direction using dfs.\n- If word char is match with the cell than Increment the wordIndex and try that cell neighbour.\n- if word doesn\'t match then replace the char with original cell char\n\n\n```\nclass Solution {\n public boolean exist(char[][] board, String word) {\n \n for(int x = 0; x < board.length; x++){\n\t\t for(int y = 0; y < board[0].length; y++){\n\t\t\t\t//start from every cell, \n\t\t\t\t//if any of found the word in the grid, return true\n if(exist(board, x, y, word, 0)) return true;\n }\n }\n \n\t\t//if not found\n return false;\n }\n \n public boolean exist(char[][] board, int x, int y, String word, int wordIndex){\n\n if(wordIndex == word.length()) return true;\n \n\t\t//check boundary of grid\n if( x < 0 || x >= board.length || y < 0 || y >= board[0].length) return false;\n\t\t\n\t\tchar currCellChar = board[x][y];\n\t\t\n\t\t//check currently, this cell is being used for dfs\n\t\tif(currCellChar == \'$\') return false;\n\t\t \n\t\t //check cell char is equal to current char of word\n\t\tif(currCellChar != word.charAt(wordIndex)) return false;\n \n\t\t//mark this cell as used\n board[x][y] = \'$\';\n \n boolean isExist = exist(board, x + 1, y, word, wordIndex + 1) || // direction UP \n\t\t\t\t\t\t\t\t\t exist(board, x - 1, y, word, wordIndex + 1) || // direction DOWN\n\t\t\t\t\t\t\t\t\t exist(board, x, y + 1, word, wordIndex + 1) || // direction RIGHT\n\t\t\t\t\t\t\t\t\t exist(board, x, y - 1, word, wordIndex + 1); // direction LEFT\n \n\t\t//for the backtracking, try different possibilty, now unmark this cell as free, \t\n board[x][y] = currCellChar;\n \n return isExist;\n }\n \n}\n``` | 9 | 0 | ['Backtracking', 'Java'] | 3 |
word-search | ✅Easy✨||C++|| Beats 100% || With Explanation || | easyc-beats-100-with-explanation-by-olak-id6l | \n# Approach\n Describe your approach to solving the problem. \n1. Search function:\n\n. The recursive search function explores the board to find a match for th | olakade33 | NORMAL | 2024-04-03T07:31:13.090001+00:00 | 2024-04-03T07:31:13.090036+00:00 | 929 | false | \n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Search function:\n\n. The recursive search function explores the board to find a match for the given word starting from the current position (i, j).\n. It returns true if the entire word is found, and false otherwise.\nThe function explores neighbors in all four directions (up, down, left, right) if the current cell matches the current character of the word.\n2. Exist function:\n\nThe exist function iterates over each cell in the board and checks if the word can be formed starting from that cell using the search function.\nIt returns true if any match is found, indicating that the word exists on the board. Otherwise, it returns false.\n3. Marking Visited Cells:\n\n. The function marks visited cells with the character \'#\' to avoid revisiting the same cell in the recursive exploration.\n\n4. Backtracking:\n\n. Before returning from the search function, the original character of the current cell is restored, allowing backtracking.\n\nOverall, the code uses a backtracking approach to explore all possible paths on the board to find a match for the given word. The time complexity depends on the number of cells in the board and the length of the word. In the worst case, it is O(N * M * 4^k), where N and M are the dimensions of the board, and k is the length of the word.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n0(N * M * 4^k)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\nclass Solution {\npublic:\n bool search(int i, int j, int n, int m, vector<vector<char>>& board, int k, string word) {\n if (k == word.size()) return true; // If we have matched all characters in the word, return true\n if (i == n || i < 0 || j < 0 || j == m || board[i][j] != word[k]) {\n return false; // If current cell is out of bounds or does not match the current character in word, return false\n }\n \n char ch = board[i][j]; // Store the current character before exploring neighbors\n board[i][j] = \'#\'; // Mark the current cell as visited to avoid revisiting it\n \n // Explore neighbors in all four directions\n bool op1 = search(i + 1, j, n, m, board, k + 1, word); // Down\n bool op2 = search(i - 1, j, n, m, board, k + 1, word); // Up\n bool op3 = search(i, j + 1, n, m, board, k + 1, word); // Right\n bool op4 = search(i, j - 1, n, m, board, k + 1, word); // Left\n \n board[i][j] = ch; // Restore the original character in the board\n \n return op1 || op2 || op3 || op4; // Return true if any of the recursive calls return true\n }\n\n bool exist(vector<vector<char>>& board, string word) {\n int n = board.size(); // Number of rows in the board\n int m = board[0].size(); // Number of columns in the board\n int k = word.size(); // Length of the target word\n\n // Iterate over each cell in the board\n for (int i = 0; i < n; i++) {\n for (int j = 0; j < m; j++) {\n // Check if the word can be formed starting from the current cell\n if (search(i, j, n, m, board, 0, word)) {\n return true; // If found, return true\n }\n }\n }\n\n return false; // If no match is found, return false\n }\n};\n``` | 8 | 0 | ['C++'] | 0 |
word-search | Backtracking || Simple Explanation with comments | backtracking-simple-explanation-with-com-oiv0 | Intuition\nThis problem seems to be a classic application of Depth First Search (DFS) in addition with Backtracking. We traverse the board starting from each ce | tourism | NORMAL | 2024-04-03T05:27:29.422558+00:00 | 2024-04-03T07:14:06.578769+00:00 | 737 | false | # Intuition\nThis problem seems to be a classic application of Depth First Search (DFS) in addition with Backtracking. We traverse the board starting from each cell, and at each step, we check if the current cell matches the current character of the word. If it does, we explore its neighbors recursively to find the next character of the word. If we find the entire word, we return true; otherwise, we backtrack and try other paths.\n\n# Approach\n- We iterate through each cell of the board.\n- For each cell, we start DFS from that cell to search for the given word.\n- During DFS, we check if the current cell matches the current character of the word. If it does, we proceed to explore its neighbors.\n- We mark the visited cells to avoid revisiting them.\n- If at any point during the DFS, we find the entire word, we return true.\n- If DFS cannot find the word starting from the current cell, we backtrack and explore other paths.\n- If no path leads to finding the word, we return false.\n\n# Complexity\n **Time complexity:** O(N*M*4^Len of word)\n **Space complexity:** O(1)\n\n# Code\n```\nclass Solution {\npublic:\n // Helper function for DFS traversal\n bool dfs(vector<vector<char>>& board, string word, int i, int j, int k) {\n // If we have found all characters of the word, return true\n if (k == word.size())\n return true;\n \n // Boundary check and character mismatch check\n if (i < 0 || i >= board.size() || j < 0 || j >= board[0].size() || word[k] != board[i][j])\n return false;\n \n // Temporarily mark the current cell as visited\n char ch = board[i][j];\n board[i][j] = \'/\';\n \n // Explore the neighbors recursively\n if (dfs(board, word, i + 1, j, k + 1) ||\n dfs(board, word, i, j + 1, k + 1) ||\n dfs(board, word, i - 1, j, k + 1) ||\n dfs(board, word, i, j - 1, k + 1))\n return true; // If any neighbor leads to finding the word, return true\n \n // Backtrack: Restore the original character in the current cell\n board[i][j] = ch;\n return false;\n }\n \n // Main function to check if the word exists on the board\n bool exist(vector<vector<char>>& board, string word) {\n int n = board.size(), m = board[0].size();\n // Iterate through each cell of the board\n for (int i = 0; i < n; ++i) {\n for (int j = 0; j < m; ++j) {\n // If the current cell matches the first character of the word, start DFS from here\n if (board[i][j] == word[0]) {\n if (dfs(board, word, i, j, 0)) // If DFS finds the word, return true\n return true;\n }\n }\n }\n // If no cell leads to finding the word, return false\n return false;\n }\n};\n\n``` | 8 | 0 | ['Array', 'String', 'Backtracking', 'Depth-First Search', 'Matrix', 'C++'] | 3 |
word-search | DFS / Backtracking in C++, Js & Python | dfs-backtracking-in-c-js-python-by-nuoxo-uudv | C++\ncpp\nclass Solution\n{\n public:\n\n bool exist(vector<vector<char>>& board, string word)\n {\n int rows, cols;\n\n | nuoxoxo | NORMAL | 2022-11-24T00:02:54.426183+00:00 | 2022-11-24T00:05:31.558832+00:00 | 2,127 | false | # C++\n```cpp\nclass Solution\n{\n public:\n\n bool exist(vector<vector<char>>& board, string word)\n {\n int rows, cols;\n\n if (!board.size())\n\t\t return (false);\n rows = (int) board.size();\n cols = (int) board[0].size();\n for (int i = 0; i < rows; i++)\n for (int j = 0; j < cols; j++)\n if (dfs(board, word, 0, i, j))\n\t\t\t return (true);\n return (false);\n }\n\n bool dfs(vector<vector<char>> &board, string &word, int i, int x, int y)\n {\n int rows, cols;\n bool found;\n char c;\n\n if (!board.size())\n\t\t return (false);\n rows = (int) board.size();\n cols = (int) board[0].size();\n if (x < 0 || x == rows || y < 0 || y == cols || word[i] != board[x][y])\n return (false);\n if (i == (int) word.length() - 1)\n return (true);\n c = board[x][y];\n board[x][y] = 0;\n found = dfs(board, word, i + 1, x + 1, y) ||\n dfs(board, word, i + 1, x - 1, y) ||\n dfs(board, word, i + 1, x, y + 1) ||\n dfs(board, word, i + 1, x, y - 1);\n board[x][y] = c;\n return (found);\n }\n};\n```\n# Js\n```js\nvar exist = function(board, word) {\n let i = -1\n while (++i < board.length) {\n let j = -1\n while (++j < board[0].length) {\n if (dfs(board, word, 0, i, j))\n return true\n }\n }\n return false\n};\n\nvar dfs = function(board, word, index, x, y) {\n if (index == word.length)\n return true\n let c = board[0].length\n let r = board.length\n if (x < 0 || y < 0 || x > r - 1 || y > c - 1 || board[x][y] != word[index])\n return false\n board[x][y] = \'#\'\n let isFound = (\n dfs(board, word, index + 1, x + 1, y) ||\n dfs(board, word, index + 1, x - 1, y) ||\n dfs(board, word, index + 1, x, y + 1) ||\n dfs(board, word, index + 1, x, y - 1)\n )\n board[x][y] = word[index]\n return isFound\n}\n```\n# Python\n```py\nclass Solution:\n def exist(self, board: List[List[str]], word: str) -> bool:\n for x in range(len(board)):\n for y in range(len(board[0])):\n if self.DFS(board, word, 0, x, y):\n return True\n return False\n\n def DFS(self, board: List[List[str]], word:str, index: int, x: int, y: int) -> bool:\n if index == len(word):\n return True\n c = len(board[0])\n r = len(board)\n if x < 0 or y < 0 or x > r - 1 or y > c - 1 or word[index] != board[x][y] :\n return False\n board[x][y] = chr(0)\n found = (\n self.DFS(board, word, index + 1, x + 1, y) or\n self.DFS(board, word, index + 1, x - 1, y) or\n self.DFS(board, word, index + 1, x, y + 1) or\n self.DFS(board, word, index + 1, x, y - 1))\n board[x][y] = word[index]\n return found\n```\n# C\n```c\nbool solve(char **board, char *word, int i, int x, int y, int r, int c);\n\nbool exist(char** board, int boardSize, int* boardColSize, char * word)\n{\n if (!board || !boardSize || !boardColSize) return (false);\n if (!word) return (true);\n for (int i = 0; i < boardSize; i++)\n for (int j = 0; j < boardColSize[0]; j++)\n if (solve(board, word, 0, i, j, boardSize, boardColSize[0]))\n return (true);\n return (false);\n}\n\nbool solve(char **board, char *word, int i, int x, int y, int r, int c)\n{\n bool found;\n char temp;\n\n if (x < 0 || x == r || y < 0 || y == c || word[i] != board[x][y])\n\t\t return (false);\n if (i == strlen(word) - 1)\n\t\t return (true);\n temp = board[x][y];\n board[x][y] = 0;\n found = solve(board, word, i + 1, x + 1, y, r, c) ||\n solve(board, word, i + 1, x - 1, y, r, c) ||\n solve(board, word, i + 1, x, y + 1, r, c) ||\n solve(board, word, i + 1, x, y - 1, r, c);\n board[x][y] = temp;\n return (found);\n}\n``` | 8 | 1 | ['C', 'Python', 'C++', 'JavaScript'] | 2 |
word-search | ✅ Python Simple and Clean || Backtracking Solution | python-simple-and-clean-backtracking-sol-4egq | If you like Pls Upvote :-)\n\n\nclass Solution:\n def exist(self, board: List[List[str]], word: str) -> bool:\n rows=len(board)\n cols=len(boar | gyanesh09 | NORMAL | 2022-08-01T03:42:08.974698+00:00 | 2022-08-01T03:42:41.287216+00:00 | 884 | false | **If you like Pls Upvote :-)**\n\n```\nclass Solution:\n def exist(self, board: List[List[str]], word: str) -> bool:\n rows=len(board)\n cols=len(board[0])\n visited=set()\n def dfs(i,j,curr):\n if curr==len(word):\n return True\n \n if i<0 or j>=cols or j<0 or i>=rows or board[i][j]!=word[curr] or (i,j) in visited:\n return False\n \n visited.add((i,j))\n res=dfs(i+1,j,curr+1) or dfs(i-1,j,curr+1) or dfs(i,j+1,curr+1) or dfs(i,j-1,curr+1)\n visited.remove((i,j))\n return res\n \n for i in range(rows):\n for j in range(cols):\n if dfs(i,j,0): return True\n return False\n``` | 8 | 0 | ['Backtracking', 'Python'] | 1 |
word-search | 0ms TLE_EXPLAINED EASY || 100%FAST | 0ms-tle_explained-easy-100fast-by-gkesha-f4d1 | \t Do upvote\u2764\uFE0F\n# Sol #1. DFS (800ms)\n\nclass Solution {\npublic:\n bool dfs(vector<vector<char>> &arr, string word, int k, int r, int c)//pass ar | gkeshav_1 | NORMAL | 2022-06-07T20:04:48.411309+00:00 | 2022-11-24T12:58:13.861608+00:00 | 659 | false | \t Do upvote\u2764\uFE0F\n# Sol #1. DFS (800ms)\n```\nclass Solution {\npublic:\n bool dfs(vector<vector<char>> &arr, string word, int k, int r, int c)//pass arr by reference\n {\n \n if(r>=arr.size()||r<0||c>=arr[0].size()||c<0||arr[r][c] != word[k])\n return false;\n\n k++;\n if(k==word.size())\n return true;\n \n\t\t\tarr[r][c]=\'*\'; // changed in orignal arr to avoid taking same occurence of alphabet in arr for different occurences in word\n \n\t\t\tbool res = dfs(arr,word,k,r+1,c) || \n\t\t\t\t\t\tdfs(arr,word,k,r-1,c) || \n\t\t\t\t\t\tdfs(arr,word,k,r,c+1) ||\n\t\t\t\t\t\tdfs(arr,word,k,r,c-1);\n \n arr[r][c]=word[k-1]; //as arr is passed by reference all changes must be reversed before next iteration\n return res;\n \n\n\n }\n \n bool exist(vector<vector<char>>& arr, string word) \n {\n for(int i=0;i<arr.size();i++)\n for(int j=0;j<arr[0].size();++j)\n if(dfs(arr,word,0,i,j))\n return true;\n return false;\n \n }\n};\n```\n* This solution will take around 800ms\n* you will get **TLE** if *arr* is passed by value like this in *dfs* function ```bool dfs(vector<vector<char>> arr, string word, int k, int r, int c) ```\n\n\n# Sol #2. DFS with Pruning 0ms sol\n```\nclass Solution \n{\n bool dfs(vector<vector<char>> &arr, string word, int k, int r, int c)\n {\n \n if(r>=arr.size()||r<0||c>=arr[0].size()||c<0||arr[r][c] != word[k])\n return false;\n\n k++;\n if(k==word.size())\n return true;\n arr[r][c]=\'.\';\n bool res = dfs(arr,word,k,r+1,c) || \n\t\t\t\t\t\tdfs(arr,word,k,r-1,c) || \n\t\t\t\t\t\tdfs(arr,word,k,r,c+1) ||\n\t\t\t\t\t\tdfs(arr,word,k,r,c-1);\n \n arr[r][c]=word[k-1];\n return res;\n }\n \npublic:\n bool exist(vector<vector<char>>& arr, string& word) {\n int R = arr.size(), C = arr[0].size(), N = word.size();\n\n // Prune #1: the arr cannot contain the word.\n if (N > R * C) return false;\n\n // Prune #2: the arr does not contain all occurrences of the chars in the word.\n unordered_map<char, int> occ;\n for (auto& row : arr) for (auto& c : row) ++occ[c];\n for (auto& c : word) if(--occ[c] < 0) return false;\n\n // Prune #3: Find the longest prefix/suffix of the same character. If the longest\n // suffix is longer than the longest prefix, swap the strigns (so we are less\n // likely to have a long prefix with a lot of the same character).\n int left = word.find_first_not_of(word[0]);\n int right = N - word.find_last_not_of(word[N - 1]);\n if (left > right) reverse(begin(word), end(word));\n\n for(int i=0;i<arr.size();i++)\n for(int j=0;j<arr[0].size();++j)\n if(dfs(arr,word,0,i,j))\n return true;\n return false;\n }\n};\n```\n* **We use the same DFS with some prior analysis.**\n* **Prune 3 is for such cases**\n[["A","A","A","A","A","A"],["A","A","A","A","A","A"],["A","A","A","A","A","A"],["A","A","A","A","A","A"],["A","A","A","A","A","A"],["A","A","A","A","A","A"]]\n"AAAAAAAAAAAAAAB"\nit changes word to "BAAAAAAAAAAAAAA"\n\n | 8 | 0 | ['Backtracking', 'Depth-First Search', 'C', 'C++'] | 3 |
word-search | JS | Backtracking | Read this if you are having problems using a Set | js-backtracking-read-this-if-you-are-hav-q6l4 | I spent some time confused as to why my solution, which was seamingly very similar to other\'s in Java and Python was not working. There are two main ways to so | dadavivid | NORMAL | 2022-04-11T13:20:21.935282+00:00 | 2022-04-11T13:22:18.927491+00:00 | 548 | false | I spent some time confused as to why my solution, which was seamingly very similar to other\'s in Java and Python was not working. There are two main ways to solve this problem with backtracking: changing the value of the board when visiting a position, or keeping a record of your visited positions and check against it. \n\nA Set is a great data structure for that record of visited positions. There is a caveat, however. In JavaScript, values put into the Set are stored by reference, so when looking them up, if you pass anything else other than the same reference, your item wont be found.\n\nWhy is this relevant?\n\n```\nconst set = new Set();\n//.....\nconst arr = [1,4]\nset.add(arr);\n\nset.has(arr) // true\nset.has([1,4]) // false!\n\n```\nAs you can see, looking up an array (or object) by values does not work, since when we pass the `[1,4]` array, we are essentially creating a new array, so the references are different.\n\nTo solve this, you have to convert your array to a unique value. I converted the coordinate array to a string with an "r|c" format. \n\nKeep in mind that the way in which you convert your array to a unique value has a runtime impact. Avoid `array.join()` or other iterartive approaches if possible.\n\nI hope this is helpful to anyone trying to implement this with a Set.\n\n```\n/**\n * @param {character[][]} board\n * @param {string} word\n * @return {boolean}\n */\nvar exist = function(board, word) {\n \n const M = board.length;\n const N = board[0].length;\n \n const path = new Set();\n \n function backtrack(r,c,idx){\n \n if(idx === word.length) return true;\n if(r < 0 || c < 0 || r >= M || c >= N) return false;\n if(board[r][c] !== word.charAt(idx)) return false;\n \n const arrStr = `${r}|${c}`;\n if(path.has(arrStr)) return false;\n \n path.add(arrStr);\n const found = \n backtrack(r+1, c, idx+1) ||\n backtrack(r-1,c,idx+1) || \n backtrack(r,c+1, idx+1) || \n backtrack(r,c-1, idx+1);\n path.delete(arrStr); \n return found;\n \n }\n \n \n for(let i = 0; i<M; i++){\n for(let j = 0; j<N; j++){\n if(board[i][j] === word.charAt(0))\n if(backtrack(i,j,0)) return true; \n }\n }\n\t\n return false;\n} | 8 | 0 | ['Backtracking', 'Ordered Set', 'JavaScript'] | 2 |
word-search | Easy C++ dfs solution | easy-c-dfs-solution-by-ab1533489-epdq | \nclass Solution {\nprivate:\n bool dfs(vector<vector<char>>& board,int i, int j , int count, string word){\n if(count == word.length())\n | ab1533489 | NORMAL | 2022-03-11T13:54:28.396455+00:00 | 2022-03-11T13:54:28.396478+00:00 | 301 | false | ```\nclass Solution {\nprivate:\n bool dfs(vector<vector<char>>& board,int i, int j , int count, string word){\n if(count == word.length())\n return true;\n if(i<0 || i>=board.size()||j<0 || j>=board[i].size() || board[i][j]!=word[count])\n return false;\n char temp = board[i][j];\n board[i][j]= \' \';\n bool found = dfs(board,i+1,j,count+1,word)||dfs(board,i-1,j,count+1,word)||dfs(board,i,j+1,count+1,word)||dfs(board,i,j-1,count+1,word);\n board[i][j]= temp;\n return found;\n }\npublic:\n bool exist(vector<vector<char>>& board, string word) {\n for(int i=0;i<board.size();i++){\n for(int j=0;j<board[i].size();j++){\n if(board[i][j]==word[0] and dfs(board,i,j,0,word))\n return true;\n }\n }\n return false;\n }\n\n};\n``` | 8 | 0 | ['Depth-First Search', 'Recursion', 'C'] | 0 |
word-search | Python solution using backtracking with explanation | python-solution-using-backtracking-with-a5wxd | \n######################################################\n\n# Runtime: 1412ms - 94.74%\n# Memory: 14.2MB - 71.98%\n\n################################ | saisasank25 | NORMAL | 2021-10-24T13:14:03.306650+00:00 | 2021-10-24T13:14:03.306675+00:00 | 755 | false | ```\n######################################################\n\n# Runtime: 1412ms - 94.74%\n# Memory: 14.2MB - 71.98%\n\n######################################################\n\nclass Solution:\n def exist(self, board: List[List[str]], word: str) -> bool:\n \n # Below code will help in reducing time complexity significantly.\n # What below code does is, it creates a set with all chars present in board\n # and then it will check whether all chars in word are present in board\n # If a char in word is not present in the board, we can\'t find the word in \n # board. So we return False\n # Without these lines of code, I got a Time Complexity of 8000+ ms\n # After adding these lines of code, my TC reduced to just 1400+ ms\n # Why this drastic change is, since we are checking all possible strings\n # using a backtracking paradigm, there will be some cases where we go to so\n # much deep just to find the required char is not even present in the board\n # So we are eliminating it before hand.\n characters = set()\n for i in range(len(board)):\n for j in range(len(board[0])):\n if board[i][j] not in characters: characters.add(board[i][j])\n \n for s in word: \n if s not in characters: return False\n \n def dfs(row, col, index, visited):\n # index represents current index of word string\n # Checking for out of bounds indices and returning False\n if row < 0 or row > len(board) - 1 or col < 0 or col > len(board[0]) - 1: return False\n # If we already visited current cell, return False\n if (row, col) in visited: return False\n # If char at cell (row, col) matches with word[index] we go next char\n # in all the 4 directions\n if board[row][col] == word[index]:\n visited.add((row, col))\n # If we reach end of word return Trur\n if index == len(word) - 1: return True\n isExist = (\n dfs(row, col - 1, index + 1, visited) or \n dfs(row, col + 1, index + 1, visited) or\n dfs(row - 1, col, index + 1, visited) or \n dfs(row + 1, col, index + 1, visited)\n ) \n # Why we are removing at the end is, we might encounter this cell\n # again in some other path if this path didn\'t give us required \n # word. In that path, we haven\'t yet visited the cell right. So, we\n # are removing it.\n visited.remove((row, col))\n return isExist\n \n return False\n \n # Running DFS when the char in the cell (i,j) matches with word[0] i.e; \n # starting of the word\n for i in range(len(board)):\n for j in range(len(board[0])):\n if board[i][j] == word[0]:\n visited = set()\n if dfs(i, j, 0, visited): return True\n \n return False\n``` | 8 | 0 | ['Backtracking', 'Depth-First Search', 'Python'] | 3 |
word-search | [Python] Simple Solution | DFS | python-simple-solution-dfs-by-ianliuy-bn7j | python\nclass Solution(object):\n def exist(self, board, word):\n for i in xrange(len(board)):\n for j in xrange(len(board[0])):\n | ianliuy | NORMAL | 2021-01-06T07:21:18.709636+00:00 | 2021-01-09T05:43:02.396582+00:00 | 1,991 | false | ```python\nclass Solution(object):\n def exist(self, board, word):\n for i in xrange(len(board)):\n for j in xrange(len(board[0])):\n if self.dfs(board, word, i, j): return True\n return False\n \n def dfs(self, board, word, i, j):\n if i <= -1 or i >= len(board) or j <= -1 or j >= len(board[0]): return False\n if board[i][j] == -1 or board[i][j] != word[0]: return False\n if len(word) == 1: return True\n \n temp, board[i][j] = board[i][j], -1\n if self.dfs(board, word[1:], i-1, j): return True\n if self.dfs(board, word[1:], i+1, j): return True\n if self.dfs(board, word[1:], i, j-1): return True\n if self.dfs(board, word[1:], i, j+1): return True\n board[i][j] = temp\n return False\n``` | 8 | 0 | ['Depth-First Search', 'Python', 'Python3'] | 0 |
word-search | C++ [Simplest Solution possible] (Beats 85% Solution) | c-simplest-solution-possible-beats-85-so-vdd3 | \n// Using DFS + Backtracking\nclass Solution {\npublic:\n\t// Check the boundary cases of the board.\n bool isSafe(int N, int M, int i, int j){\n ret | not_a_cp_coder | NORMAL | 2020-07-21T08:39:30.147149+00:00 | 2020-07-22T05:34:56.913815+00:00 | 1,515 | false | ```\n// Using DFS + Backtracking\nclass Solution {\npublic:\n\t// Check the boundary cases of the board.\n bool isSafe(int N, int M, int i, int j){\n return (i<N) && (i>=0) && (j>=0) && (j<M);\n }\n bool backtrack(vector<vector<char>>& board, string& word, int pos, int i, int j){\n if(word[pos]!=board[i][j]){\n return false;\n }\n if(pos==word.length()-1){\n return true;\n }\n\t\t// to avoid using of this character again in the backtracking\n board[i][j] = \'#\';\n if(isSafe(board.size(), board[0].size(), i+1, j)){\n if(backtrack(board, word, pos+1, i+1, j))\n return true;\n }\n if(isSafe(board.size(), board[0].size(), i-1, j)){\n if(backtrack(board, word, pos+1, i-1, j))\n return true;\n }\n if(isSafe(board.size(), board[0].size(), i, j+1)){\n if(backtrack(board, word, pos+1, i, j+1))\n return true;\n }\n if(isSafe(board.size(), board[0].size(), i, j-1)){\n if(backtrack(board, word, pos+1, i, j-1))\n return true;\n }\n\t\t// Reassigning the character as backtracking is complete.\n board[i][j] = word[pos];\n return false;\n }\n bool exist(vector<vector<char>>& board, string word) {\n for(int i=0;i<board.size();i++){\n for(int j=0;j<board[i].size();j++){\n if(board[i][j]==word[0]) // This condition is not necessary as it will also be checked in the backtracking function.\n if(backtrack(board, word, 0, i, j))\n return true;\n }\n }\n return false;\n }\n};\n```\nFeel free to ask any doubts in the **comment** section. \nHappy Coding :) | 8 | 1 | ['Backtracking', 'Depth-First Search', 'Recursion', 'C++'] | 4 |
word-search | [Java] Trie based Approach | Google asked | java-trie-based-approach-google-asked-by-ishk | \nclass Solution {\n TrieNode root;\n int row, col;\n public boolean exist(char[][] board, String word) {\n //Approach - Trie Approach\n | akshaybahadur21 | NORMAL | 2020-03-29T22:27:39.734440+00:00 | 2020-03-29T22:27:39.734497+00:00 | 1,511 | false | ```\nclass Solution {\n TrieNode root;\n int row, col;\n public boolean exist(char[][] board, String word) {\n //Approach - Trie Approach\n root = new TrieNode();\n insertInTrie(word);\n TrieNode curr = root;\n row = board.length;\n col = board[0].length;\n for (int i = 0; i < row; i++){\n for (int j = 0; j < col; j++){\n char ch = board[i][j];\n if(curr.children.containsKey(ch) && dfs(curr, board, i, j))\n return true;\n }\n }\n return false;\n\n }\n private boolean dfs(TrieNode curr, char[][] board, int i, int j){\n\n if (curr.isEnd) return curr.isEnd;\n if(i < 0 || j <0 || i>= row || j >= col || !curr.children.containsKey(board[i][j])) return false;\n char ch = board[i][j];\n char temp = board[i][j];\n board[i][j] = \' \';\n\n if (dfs(curr.children.get(ch), board, i+1, j) || dfs(curr.children.get(ch), board, i-1, j)\n || dfs(curr.children.get(ch), board, i, j+1) || dfs(curr.children.get(ch), board, i, j-1))\n return true;\n\n board[i][j] = temp;\n return false;\n\n }\n private void insertInTrie(String word){\n TrieNode curr = root;\n for (int i = 0; i<word.length(); i++){\n char c = word.charAt(i);\n if (curr.children.containsKey(c)) {\n curr = curr.children.get(c);\n continue;\n }\n curr.children.put(c,new TrieNode());\n curr = curr.children.get(c);\n }\n curr.isEnd = true;\n }\n}\n \nclass TrieNode{\n Map<Character, TrieNode> children;\n boolean isEnd;\n TrieNode(){\n children = new HashMap<>();\n isEnd = false;\n }\n}\n``` | 8 | 0 | ['Trie', 'Java'] | 3 |
word-search | Python Easy to understand- 95% Faster | python-easy-to-understand-95-faster-by-l-dyf3 | Please let me know if explanation is needed.\n\nclass Solution:\n def exist(self, board: List[List[str]], word: str) -> bool:\n m = len(board)\n | logan_kd | NORMAL | 2020-01-18T21:10:21.263540+00:00 | 2020-06-16T14:13:15.745875+00:00 | 2,142 | false | Please let me know if explanation is needed.\n```\nclass Solution:\n def exist(self, board: List[List[str]], word: str) -> bool:\n m = len(board)\n n = len(board[0])\n for i in range(m):\n for j in range(n):\n if board[i][j] == word[0]:\n res = self.backtrack(board,m,n,i,j,word[1:])\n if res:\n return True\n return False\n \n \n def backtrack(self, board,m,n, i, j, target):\n temp = board[i][j]\n if len(target) == 0:\n return True\n board[i][j] = \'#\'\n for x,y in (i+1,j),(i-1,j),(i,j+1),(i,j-1):\n if 0<=x<m and 0<=y<n and target[0] == board[x][y]:\n dec = self.backtrack(board,m,n,x,y,target[1:])\n if dec:\n return True\n board[i][j] = temp\n return False\n``` | 8 | 1 | ['Python', 'Python3'] | 4 |
word-search | Beats100%|| simple backtracking approach ||easy solution||explained code | beats100-simple-backtracking-approach-ea-9e05 | Intuition\njust like rat in maze problem.\n\n# Approach\njust using backtracking.\n\n# Complexity\n- Time complexity:\nO(m n word.length() back)\n\n- Space comp | twaritagrawal | NORMAL | 2024-04-03T07:40:47.509565+00:00 | 2024-04-03T07:40:47.509597+00:00 | 560 | false | # Intuition\njust like rat in maze problem.\n\n# Approach\njust using backtracking.\n\n# Complexity\n- Time complexity:\nO(m* n* word.length() back)\n\n- Space complexity:\nO(m * n)\n\n\n# Code\n```\nclass Solution {\npublic:\n bool backtrack(vector<vector<char>>& board,string &word,int i,int j,int &m,int &n,int &index, vector<vector<int>>&v){\n if(index==word.length()){\n return true;\n }\n\n //down\n if(i+1<m) {\n if(board[i+1][j]==word[index] && v[i+1][j]==0){\n v[i+1][j]=1;\n index++;\n i=i+1;\n bool ans=backtrack(board,word,i,j,m,n,index,v);\n if(ans){\n return true;\n }else{\n v[i][j]=0;\n index--;\n i--;\n }\n }\n }\n //right\n if(j+1<n) {\n if(board[i][j+1]==word[index] && v[i][j+1]==0){\n v[i][j+1]=1;\n index++;\n j=j+1;\n bool ans=backtrack(board,word,i,j,m,n,index,v);\n if(ans){\n return true;\n }else{\n v[i][j]=0;\n index--;\n j--;\n }\n }\n }\n\n //up\n if(i-1>=0){\n if(board[i-1][j]==word[index] && v[i-1][j]==0){\n v[i-1][j]=1;\n index++;\n i=i-1;\n bool ans=backtrack(board,word,i,j,m,n,index,v);\n if(ans){\n return true;\n }else{\n v[i][j]=0;\n index--;\n i++;\n }\n }\n }\n //left\n if(j-1>=0){\n if(board[i][j-1]==word[index] && v[i][j-1]==0){\n v[i][j-1]=1;\n index++;\n j=j-1;\n bool ans=backtrack(board,word,i,j,m,n,index,v);\n if(ans){\n return true;\n }else{\n v[i][j]=0;\n index--;\n j++;\n }\n }\n}\nreturn false;\n }\n bool exist(vector<vector<char>>& board, string word) {\n int m=board.size();\n int n=board[0].size();\n int index=0;\n \n vector<vector<int>> v(m,vector<int>(n,0)); \n for(int i=0;i<m;i++){\n for(int j=0;j<n;j++){\n if(board[i][j]==word[index]){\n index++;\n v[i][j]=1;\n //function backtrack if true then return true else move until last element\n bool answer=backtrack(board,word,i,j,m,n,index,v);\n if(answer){\n \n return true;\n }\n index--;\n v[i][j]=0;\n }\n }\n }\nreturn false;\n }\n};\n``` | 7 | 0 | ['Array', 'String', 'Backtracking', 'Recursion', 'Matrix', 'C++'] | 4 |
word-search | [C++, Java, Kotlin] Simple Explained Solution ✅ | c-java-kotlin-simple-explained-solution-evu5k | Approach\nSo, the idea is to go through all the positions, and if a position in the matrix contains the first character of the word, I start a depth-first searc | Z3ROsum | NORMAL | 2024-04-03T01:15:11.869457+00:00 | 2024-04-03T01:15:11.869496+00:00 | 318 | false | # Approach\nSo, the idea is to go through all the positions, and if a position in the matrix contains the first character of the word, I start a depth-first search starting from that position.\nAt each step, I check if I can go left, right, up, or down (if those positions\u2019 characters match the next character in the word) and continue. If I get to the end of the word, then it exists.\n\n# Complexity\n- Time complexity:\n$$O((mn)^2)$$\n\n- Space complexity:\n$$O(2mn)$$\n\n# Code\n```kotlin []\nclass Solution {\n var dirs = listOf(1 to 0, -1 to 0, 0 to 1, 0 to -1)\n var board = arrayOf<CharArray>()\n var word = ""\n fun exist(board: Array<CharArray>, word: String): Boolean {\n this.board = board\n this.word = word\n \n var visited = Array(board.size) { BooleanArray(board[0].size) }\n for (i in board.indices)\n for (j in board[0].indices)\n if (board[i][j] == word[0] && check(i, j, 0, visited))\n return true\n return false\n }\n fun check(i: Int, j: Int, strIdx: Int, visited: Array<BooleanArray>): Boolean {\n if (strIdx == word.length - 1) return true\n visited[i][j] = true\n var next = word[strIdx + 1]\n for ((x, y) in dirs) {\n if (i + x !in board.indices || j + y !in board[0].indices) continue\n if (board[i + x][j + y] != next || visited[i + x][j + y]) continue\n \n if (check(i + x, j + y, strIdx + 1, visited)) return true\n }\n visited[i][j] = false\n return false\n }\n}\n```\n```Java []\npublic class Solution {\n private int[][] dirs = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};\n private char[][] board;\n private String word;\n\n public boolean exist(char[][] board, String word) {\n this.board = board;\n this.word = word;\n\n boolean[][] visited = new boolean[board.length][board[0].length];\n for (int i = 0; i < board.length; i++) {\n for (int j = 0; j < board[0].length; j++) {\n if (board[i][j] == word.charAt(0) && check(i, j, 0, visited)) {\n return true;\n }\n }\n }\n return false;\n }\n\n private boolean check(int i, int j, int strIdx, boolean[][] visited) {\n if (strIdx == word.length() - 1) {\n return true;\n }\n visited[i][j] = true;\n char next = word.charAt(strIdx + 1);\n for (int[] dir : dirs) {\n int x = i + dir[0];\n int y = j + dir[1];\n if (x >= 0 && x < board.length && y >= 0 && y < board[0].length\n && board[x][y] == next && !visited[x][y]) {\n if (check(x, y, strIdx + 1, visited)) {\n return true;\n }\n }\n }\n visited[i][j] = false;\n return false;\n }\n}\n\n```\n```C++ []\nclass Solution {\nprivate:\n vector<pair<int, int>> dirs = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};\n vector<vector<char>> board;\n string word;\n\npublic:\n bool exist(vector<vector<char>>& board, string word) {\n this->board = board;\n this->word = word;\n\n vector<vector<bool>> visited(board.size(), vector<bool>(board[0].size(), false));\n for (int i = 0; i < board.size(); i++) {\n for (int j = 0; j < board[0].size(); j++) {\n if (board[i][j] == word[0] && check(i, j, 0, visited)) {\n return true;\n }\n }\n }\n return false;\n }\n\nprivate:\n bool check(int i, int j, int strIdx, vector<vector<bool>>& visited) {\n if (strIdx == word.length() - 1) {\n return true;\n }\n visited[i][j] = true;\n char next = word[strIdx + 1];\n for (const auto& dir : dirs) {\n int x = i + dir.first;\n int y = j + dir.second;\n if (x >= 0 && x < board.size() && y >= 0 && y < board[0].size()\n && board[x][y] == next && !visited[x][y]) {\n if (check(x, y, strIdx + 1, visited)) {\n return true;\n }\n }\n }\n visited[i][j] = false;\n return false;\n }\n};\n```\n | 7 | 0 | ['Kotlin'] | 1 |
word-search | Word Search Java Solution || Easy Recursive Approach || T.C :- O(m * n) | word-search-java-solution-easy-recursive-lqk3 | \nclass Solution {\n public boolean exist(char[][] board, String word) {\n\t\n\t//finding first character of given word in given matrix \n for(int i=0 | palpradeep | NORMAL | 2022-11-07T02:17:21.928069+00:00 | 2022-11-07T02:17:21.928116+00:00 | 1,485 | false | ```\nclass Solution {\n public boolean exist(char[][] board, String word) {\n\t\n\t//finding first character of given word in given matrix \n for(int i=0; i<board.length; i++)\n {\n for(int j=0; j<board[0].length; j++)\n {\n\t\t\t//if first character found then we call recursion for remaining task else return false\n if(board[i][j]==word.charAt(0)){\n if(helper(board,word,0,i,j,board.length,board[0].length))\n return true;\n }\n }\n }\n return false;\n }\n boolean helper(char[][] board, String word,int index,int i,int j, int rowLen,int colLen)\n {\n \n if(index==word.length())\n return true;\n \n if(i<0 || j<0 || i == rowLen || j == colLen || board[i][j] != word.charAt(index))\n return false;\n \n\t\t// mark that character cell so that we can\'t revisit that cell to avoid infinity calls\n char temp = board[i][j];\n board[i][j] = \'#\';\n boolean ans1 = helper(board,word,index+1,i,j+1,rowLen,colLen);\n boolean ans2 = helper(board,word,index+1,i+1,j,rowLen,colLen);\n boolean ans3 = helper(board,word,index+1,i-1,j,rowLen,colLen);\n boolean ans4 = helper(board,word,index+1,i,j-1,rowLen,colLen);\n board[i][j] = temp;\n return ans1 || ans2 || ans3 || ans4;\n \n \n }\n}\nT.C :- O(m * n), m and n are the numbe rof row and column , at max for finding word we have to traverse whole matrix cell\n``` | 7 | 0 | ['Java'] | 0 |
word-search | C++ | DFS | 2 Methods 0(n) & O(1) | Backtracking | c-dfs-2-methods-0n-o1-backtracking-by-va-47z3 | \n\nMethod - 1:\nO(n * word size)\nn = rowscol\n\nclass Solution {\npublic:\n \n bool search(vector<vector<char>>& board, int i, int j, string& word, int | vaibhav4859 | NORMAL | 2021-10-09T16:14:41.176161+00:00 | 2021-10-09T16:14:41.176194+00:00 | 1,141 | false | 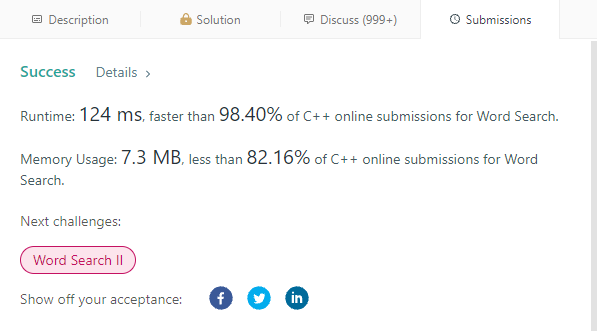\n\n***Method - 1:***\nO(n * word size)\nn = rows*col\n```\nclass Solution {\npublic:\n \n bool search(vector<vector<char>>& board, int i, int j, string& word, int pos, vector<vector<bool>>& visited){\n if(pos == word.length() - 1)\n return true;\n \n visited[i][j] = true;\n \n if(i > 0 && !visited[i-1][j] && board[i-1][j] == word[pos+1] &&search(board ,i-1 ,j ,word, pos+1, visited))\n return true;\n if(j > 0 && !visited[i][j-1] && board[i][j-1] == word[pos+1] &&search(board ,i ,j-1 ,word, pos+1, visited))\n return true;\n if(i < board.size()-1 && !visited[i+1][j] && board[i+1][j] == word[pos+1] &&search(board ,i+1 ,j ,word, pos+1, visited))\n return true;\n if(j < board[0].size()-1 && !visited[i][j+1] && board[i][j+1] == word[pos+1] &&search(board ,i ,j+1 ,word, pos+1, visited))\n return true;\n \n visited[i][j] = false;\n return false;\n }\n \n bool exist(vector<vector<char>>& board, string word) {\n \n vector<vector<bool>> visited(board.size(), vector<bool>(board[0].size(), false));\n for(int i = 0; i < board.size(); i++)\n for(int j = 0; j < board[0].size(); j++)\n if(board[i][j] == word[0] && search(board,i,j,word,0,visited))\n return true;\n \n return false;\n }\n};\n```\n\n***Method - 2:***\n0(1)\n```\nclass Solution {\npublic:\n \n bool search(vector<vector<char>>& board, int i, int j, string& word, int pos){\n if(pos == word.length() - 1)\n return true;\n \n /* ASCII value of A-Z : 65-90 && a-z : 97-122\n That\'s why i took 65, i.e ASCII value of A so that when i subtract it goes out of range of a-z & A-Z \n U can take any other no. also but after subtracting it should go out of range of words\n It works similar as visited just having less space now*/\n board[i][j] -= 65;\n \n if(i > 0 && board[i-1][j] == word[pos+1] && search(board ,i-1 ,j ,word, pos+1))\n return true;\n if(j > 0 && board[i][j-1] == word[pos+1] && search(board ,i ,j-1 ,word, pos+1))\n return true;\n if(i < board.size()-1 && board[i+1][j] == word[pos+1] &&search(board ,i+1 ,j ,word, pos+1))\n return true;\n if(j < board[0].size()-1 && board[i][j+1] == word[pos+1] &&search(board ,i ,j+1 ,word, pos+1))\n return true;\n \n board[i][j] += 65;\n return false;\n }\n \n bool exist(vector<vector<char>>& board, string word) {\n \n for(int i = 0; i < board.size(); i++)\n for(int j = 0; j < board[0].size(); j++)\n if(board[i][j] == word[0] && search(board,i,j,word,0))\n return true;\n \n return false;\n }\n};\n```\nHope you liked it , kindly upvote !!\n\nHappy Coding \uD83E\uDD17\n\n\n | 7 | 0 | ['Backtracking', 'Depth-First Search', 'Recursion', 'C', 'C++'] | 1 |
word-search | C++ solution || Easy Understand | c-solution-easy-understand-by-kannu_priy-mc7t | \nclass Solution {\npublic:\n bool backtrack(vector<vector<char>>& board, string& word, int pos, int i, int j, int r, int c){\n if(i >= r || j >= c || | kannu_priya | NORMAL | 2021-04-20T12:46:33.237922+00:00 | 2021-04-20T12:47:00.471946+00:00 | 832 | false | ```\nclass Solution {\npublic:\n bool backtrack(vector<vector<char>>& board, string& word, int pos, int i, int j, int r, int c){\n if(i >= r || j >= c || i < 0 || j < 0 || word[pos] != board[i][j])\n return false;\n \n if(pos == word.length()-1)\n return true;\n \n board[i][j] = \'#\'; // to avoid using of this character again in the backtracking\n if(backtrack(board, word, pos+1, i+1, j, r, c) || backtrack(board, word, pos+1, i-1, j, r, c) || backtrack(board, word, pos+1, i, j+1, r, c) || backtrack(board, word, pos+1, i, j-1, r, c))\n return true;\n\t\n board[i][j] = word[pos]; // Reassigning the character as backtracking is complete.\n return false;\n }\n bool exist(vector<vector<char>>& board, string word) {\n for(int i=0;i<board.size();i++)\n for(int j=0;j<board[i].size();j++)\n if(backtrack(board, word, 0, i, j, board.size(), board[0].size()))\n return true;\n return false;\n }\n};\n``` | 7 | 1 | ['Backtracking', 'C', 'C++'] | 2 |
count-of-sub-multisets-with-bounded-sum | [C++/Python] Knapsack DP | cpython-knapsack-dp-by-lee215-gl6q | Intuition\nKnapsack DP problem, where we can have multiple same item.\n\n\n# Explanation\nIn this Knapsack DP problem,\ndp[i] is the ways to sum up i.\ndp[0] = | lee215 | NORMAL | 2023-10-14T16:04:31.171670+00:00 | 2023-10-15T03:30:14.030040+00:00 | 4,351 | false | # **Intuition**\nKnapsack DP problem, where we can have multiple same item.\n<br>\n\n# **Explanation**\nIn this Knapsack DP problem,\n`dp[i]` is the ways to sum up `i`.\n`dp[0] = 1` for empty set,\nand we want to find `sum(dp[l] + ... + dp[r])`.\n\nIterate all items,\nassume we have `c` item of size `a`,\niterate `i` from `r` to `1`,\nupdate `dp[i] += dp[i - a] + dp[i - a * 2] + ...+ dp[i - a * c]`.\n\nImprove the process of calculation,\nwith idea of sliding window by keep the sum of\n`dp[i - a] + ... + dp[i - a * c]`\n<br>\n\n# **Complexity**\nTime `O(rm)`\nSpace `O(r)`\nwhere `m` is the number of different `A[i]`,\n`(1 + m) * m / 2 <= sum`,\nso `O(m) = O(sqrt(sum))`\n<br>\n\n**C++**\n```cpp\n int countSubMultisets(vector<int>& A, int l, int r) {\n vector<int> dp(20010);\n dp[0] = 1;\n int mod = 1e9 + 7;\n unordered_map<int, int> count;\n for (int a : A)\n count[a]++;\n for (auto it = count.begin(); it != count.end(); ++it) {\n int a = it->first, c = it->second;\n for (int i = r; i > max(0, r - a); --i) {\n long v = 0;\n for (int k = 0; k < c && i - a * k >= 0; ++k) {\n v += dp[i - a * k];\n }\n for (int j = i; j > 0; j -= a) {\n if (j - a * c >= 0)\n v = (v + dp[j - a * c]) % mod;\n v = (v - dp[j] + mod) % mod;\n dp[j] = (dp[j] + v) % mod;\n }\n }\n }\n long res = 0;\n for (int i = l; i <= r; ++i)\n res = (res + dp[i]) % mod;\n return res * (count[0] + 1) % mod;\n }\n```\n\n**Python**\n```py\n def countSubMultisets(self, A: List[int], l: int, r: int) -> int:\n dp = [1] + [0] * 50000\n mod = 10 ** 9 + 7\n count = Counter(A)\n for a,c in count.items():\n for i in range(r, max(r - a, 0), -1):\n v = sum(dp[i - a * k] for k in range(c))\n for j in range(i, 0, -a):\n v -= dp[j] - dp[j - a * c]\n dp[j] = (dp[j] + v) % mod\n return (count[0] + 1) * sum(dp[l:r + 1]) % mod\n```\n | 54 | 1 | [] | 19 |
count-of-sub-multisets-with-bounded-sum | Optimized Dynamic Programming | optimized-dynamic-programming-by-jeffrey-b9eu | Intuition\nThis problem is similar to knapsack, so DP seems like a good approach.\n\n# Approach\nWe can try to approach this like a modified knapsack problem, w | jeffreyhu8 | NORMAL | 2023-10-14T16:01:00.712811+00:00 | 2023-10-14T16:07:58.818378+00:00 | 2,448 | false | # Intuition\nThis problem is similar to knapsack, so DP seems like a good approach.\n\n# Approach\nWe can try to approach this like a modified knapsack problem, where we take special care to account for duplicate elements. We can take care of duplicate elements by keeping a map from elements to their frequencies, then accounting for this while updating our cache.\n\nHowever, this will TLE.\n\nA key observation is to notice how the bounds state that $$\\mathrm{sum(nums)}\\le 2\\cdot 10^4$$. This means the number of distinct elements in $$\\mathrm{nums}$$ is limited. At best, we can have $1+2+\\dots+x\\le \\mathrm{sum(nums)}\\implies x\\le O(\\sqrt{\\mathrm{sum(nums)}})$ distinct elements. We can use this to our advantage.\n\nConsider adding or not adding some element `num`, and let `cache[i]` be the number of ways to obtain a sum of `i`. One downside of our DP is that it is slow to update `cache[i] = cache[i] + cache[i - num] + cache[i - 2 * num] + ... + cache[i - freq * num]`, especially if `freq` is large (i.e. when the number of distinct elements is small).\n\nHowever, we can speed this up by preprocessing with a prefix sum. This speeds up cases where the number of distinct elements is small, which is precisely what we want.\n\n# Complexity\n- Time complexity: $$O(r\\cdot \\min(n, \\sqrt{\\mathrm{sum(nums)}}))$$, where $$n=\\mathrm{len(nums)}$$\n\n- Space complexity: $$O(r + \\min(n, \\sqrt{\\mathrm{sum(nums)}}))$$\n\n# Code\n```java\nclass Solution {\n static final int MOD = 1_000_000_007;\n\n public int countSubMultisets(List<Integer> nums, int l, int r) {\n TreeMap<Integer, Integer> numsMap = new TreeMap<>();\n for (int num : nums) {\n numsMap.put(num, numsMap.getOrDefault(num, 0) + 1);\n }\n\n long[] cache = new long[r + 1];\n cache[0] = 1;\n\n for (Map.Entry<Integer, Integer> entry : numsMap.entrySet()) {\n int num = entry.getKey();\n int freq = entry.getValue();\n\n // preprocessing\n long[] pSum = Arrays.copyOf(cache, r + 1);\n for (int i = 0; i <= r; ++i) {\n if (i >= num) {\n pSum[i] += pSum[i - num];\n pSum[i] %= MOD;\n }\n }\n\n // update dp cache\n for (int i = r; i >= 0; --i) {\n if (num > 0) {\n int j = i - (freq + 1) * num;\n cache[i] = pSum[i] - (j >= 0 ? pSum[j] : 0);\n cache[i] = Math.floorMod(cache[i], MOD);\n } else {\n cache[i] *= freq + 1;\n cache[i] %= MOD;\n }\n }\n }\n\n long res = 0;\n for (int i = l; i <= r; ++i) {\n res += cache[i];\n res %= MOD;\n }\n return (int) res;\n }\n}\n``` | 38 | 0 | ['Dynamic Programming', 'Java'] | 6 |
count-of-sub-multisets-with-bounded-sum | Simple Explanation for Optimized Knapsack | simple-explanation-for-optimized-knapsac-pl9k | PLEASE UPVOTE!\n\n\n# Intuition\n\nKnapsack DP - Count all the multisets with sum k (dp[k]) for all k <= r, then the answer is just sum(dp[l:r+1]). The challeng | dayoadeyemi | NORMAL | 2023-10-14T18:06:59.956306+00:00 | 2023-10-14T18:06:59.956338+00:00 | 1,008 | false | PLEASE UPVOTE!\n\n\n# Intuition\n\nKnapsack DP - Count all the multisets with sum `k` (`dp[k]`) for all `k <= r`, then the answer is just `sum(dp[l:r+1])`. The challenge is in optimizing the knapsack so that it can be solved without TLE.\n\n# Approach\nThe code for the "Unoptimized" Knapsack DP is:\n```\nclass Solution:\n def countSubMultisets(self, nums: List[int], l: int, r: int) -> int:\n dp = [1] + [0] * r\n counts = collections.Counter(nums)\n for a, c in collections.Counter(nums).items():\n for k in range(r, -1, -1):\n dp[k] = sum(dp[k - a*m] for m in range(c+1) if k >= a*m)\n return sum(dp[l:r+1]) % (10 ** 9 + 7)\n```\n\nWe note that we can optimize out the lowest level loop by precomputing the "strided" sums.\n```\n ...\n strided_sums = dp[:]\n for i in range(a, r + 1):\n strided_sums[i] += stride_sums[i - a]\n ...\n```\nThen we can replace the sums with the precomputed values:\n\ni.e replace\n```python3\nsum(dp[k - a*m] for m in range(c+1) if k >= a*m)\n```\n\nwith\n```python3\nif k >= a * c + a:\n stride_sums[k] - stride_sums[k - a * c - a]\nelse:\n stride_sums[k]\n```\n\nNote that we also have to be careful here to handle `0` correctly, we just remove all zeros from the counts and multiply the final answer by `counts[0] + 1`.\n\n# Complexity\n- Time complexity:\n$$O(n \\sqrt n)$$ as the number of unique elements is a most $$O(\\sqrt n)$$ - as the sum of k unique elements is $$O(\\sum_k k ) = O(k (k + 1) /2) = O(k ^2)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\nclass Solution:\n def countSubMultisets(self, nums: List[int], l: int, r: int) -> int:\n dp = [1] + [0] * r\n counts = collections.Counter(nums)\n zeros = counts.pop(0, 0) + 1\n for a, c in counts.items():\n stride_sums = dp[:]\n for i in range(a, r + 1):\n stride_sums[i] += stride_sums[i - a]\n for k in range(r, 0, -1):\n dp[k] = stride_sums[k] - stride_sums[k - a * c - a] if k >= a * c + a else stride_sums[k]\n\n return zeros * sum(dp[l:r+1]) % (10 ** 9 + 7)\n``` | 35 | 0 | ['Dynamic Programming', 'Python3'] | 5 |
count-of-sub-multisets-with-bounded-sum | EASY DP! 3D -> 2D and explaining WHY we use sliding window | easy-dp-3d-2d-and-explaining-why-we-use-90dlc | Intuition\nClearly, there can only be $\sqrt{r}$ distinct numbers. The way to see this is to notice the smallest possible sum of $n$ distinct numbers is\n\large | gtsmarmy | NORMAL | 2023-10-14T22:37:25.473792+00:00 | 2023-10-20T17:14:53.607684+00:00 | 892 | false | # Intuition\nClearly, there can only be $\\sqrt{r}$ distinct numbers. The way to see this is to notice the smallest possible sum of $n$ distinct numbers is\n$$\\large 1+2+3+\\dotsc+m = \\frac{m(m+1)}{2}$$, therefore if $\\frac{m(m+1)}{2} \\leqslant r$ then $m \\leqslant O(\\sqrt{r})$\n\nWith this in mind, let\'s represent the array as distinct numbers coupled with their frequencies.\n\nExample:\n$[1,2,2,3] \\to [1_1,2_2,3_1]$\n\nAnyway, a naive DP idea is \n$\\large \\text{dp}[i][L][R]$ represents the number of multisums between $L$ and $R$ considering only $[i:]$ onwards. (from index $i$ to the end)\n\nThe transitions for this are:\n\n$\\large \\text{dp}[i][L][R] = \\sum\\limits_{h=0}^{\\text{freq}[a_i]} \\text{dp}[i+1][\\text{max}(0,L-h \\cdot a_i)][R-h \\cdot a_i]$\nwhere $h$ basically counts how MUCH of element $i$ we take.\n\nand if $R-h \\cdot a_i < 0$ then return $0$ as it\'s not possible to make a sum fit within $L \\leqslant S \\leqslant R$ (we\'re only dealing with positive numbers here!)\n\nAnyway, this is horribly slow. At least it\'s polynomial time. The TC of this is $O(n \\cdot r^2)$, despite the loop, because it runs once for every element in the original array (including dupes).\n\n\n## Optimization #1\n\nWe don\'t need to track both $L$ and $R$. Just one. Let\'s track $R$ and say $\\text{dp}[i][R]$ epresents the number of multisums $\\leqslant R$ considering only $[i:]$ onwards. (from index $i$ to the end)\n\nThen, our answer is $\\text{dp}[0][R] - \\text{dp}[0][L-1]$\n\n$\\Large \\text{dp}[i][R] = \\sum\\limits_{h=0}^{\\text{freq}[a_i]} \\text{dp}[i+1][R-h \\cdot a_i]$\n\nNow we are in business. However, evaluating this is $O(nr)$. It ain\'t gonna pass. We need $O(mr)$. That sum is the annoying part. There\'s guaranteed to be dupes, so we need to make use of that.\n\n## Optimization #2\n\nOkay this one is weird, I\'ll show then explain.\n\nSuppose we are at index $3$ with current sum $9$, and $a[3] = 3$, $\\text{freq}[a_3] = 2$\nThen our sum looks like \n\n$\\Large \\color{white} \\text{dp}[3][9] = \\sum\\limits_{h=0}^{2} \\text{dp}[4][9-h \\cdot 3] = \\boxed{\\text{dp}[4][9] + \\text{dp}[4][6] + \\text{dp}[4][3]}$\n\nOkay, nothing special here. NOW! Let\'s look at the EXACT same scenario but this time $R = 12$. Just watch what happens.\n$\\large \\text{dp}[3][12] = \\sum\\limits_{h=0}^{2} \\text{dp}[4][12-h \\cdot 3] = \\text{dp}[4][12] + \\text{dp}[4][9] + \\text{dp}[4][6]$\n\nThis is exactly the same as \n$\\large \\color{white} \\text{dp}[4][12] + \\text{dp}[4][9] + \\text{dp}[4][6] = \\color{red} \\text{dp}[4][12] \\color{white} + \\boxed{\\text{dp}[4][9] + \\text{dp}[4][6] + \\text{dp}[4][3]} \\color{red} - \\text{dp}[4][3]$\n\nIn other words,\n$\\Large \\color{white} \\text{dp}[3][12] = \\color{red} \\text{dp}[4][12] \\color{white} + \\text{dp}[3][9] \\color{red} - \\text{dp}[4][3]$\n\nOur sum is gone. Just like that. Now, to encapsulate what we have learned, we can write it in this equation.\n\n$\\large \\color{white} \\text{dp}[i][R] = \\color{red} \\text{dp}[i+1][R] \\color{white} + \\text{dp}[i][R-a_i] \\color{red} - \\text{dp}[i+1][R-(\\text{freq}[a_i] + 1)a_i)]$\n\nNice!\n\nOur base case is quite simple, $\\large \\text{dp}[n][x] = 1$ for $x \\leqslant r$\nYou can think of it as a reward for reaching the finish line while being less than $r$.\n\n## Complication\n\nIf you have 0\'s. It breaks (LOL). It shouldn\'t be too hard to see why, the DP golden equation we derived just breaks. So the way to deal with it is to realise what the presence of a 0 really means. Let\'s say the answer to the question WITHOUT any 0\'s is $x$. Then, adding one zero will double that answer. Why? Because we can add a 0 to each of those subsets that works, and we can leave it alone. So we get the original PLUS the original with a 0 appended to it. \n\nIf we have two 0\'s, you might think it\'s quadruple. But, we can\'t have the **same** multiset (i.e. you can only append nothing, one zero, or both zeroes.). So really it\'s just the same situation but we add $x$ again. \n\nBasically, it\'s $\\huge (1+\\text{number of 0\'s}) \\cdot \\text{ans}$ \n\n\n# Complexity\n- Time complexity: $$\\large \\color{pink} O\\left(r \\cdot \\text{min}(n,\\sqrt{r})\\right)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$\\large \\color{pink} O\\left(r \\cdot \\text{min}(n,\\sqrt{r})\\right)$$\n\n# Code\n\nIgnore the Mint stuff, that\'s just to make the actual CODE cleaner (no need to fill the screen with nasty % MOD\'s).\n```\ntypedef long long ll;\ntypedef unsigned long long ull;\ntypedef vector<int> vi;\nconst int MOD = (int) 1e9 + 7;\n\ntemplate<ll mod = MOD>\nstruct mint {\n ll x;\n\n mint() : x(0) {}\n\n mint(ll _x) {\n _x %= mod;\n if (_x < 0) _x += mod;\n x = _x;\n }\n\n mint &operator+=(const mint &a) {\n x += a.x;\n if (x >= mod) x -= mod;\n return *this;\n }\n\n mint &operator-=(const mint &a) {\n x += mod - a.x;\n if (x >= mod) x -= mod;\n return *this;\n }\n\n mint &operator*=(const mint &a) {\n x = (ull) x * a.x % mod;\n return *this;\n }\n\n mint pow(ll pw) const {\n mint res = 1;\n mint cur = *this;\n while (pw) {\n if (pw & 1) res *= cur;\n cur *= cur;\n pw >>= 1;\n }\n return res;\n }\n\n mint inv() const {\n assert(x != 0);\n ll t = x;\n ll res = 1;\n while (t != 1) {\n ll z = mod / t;\n res = (ull) res * (mod - z) % mod;\n t = mod - t * z;\n }\n return res;\n }\n\n mint &operator/=(const mint &a) {\n return *this *= a.inv();\n }\n\n mint operator+(const mint &a) const {\n return mint(*this) += a;\n }\n\n mint operator-(const mint &a) const {\n return mint(*this) -= a;\n }\n\n mint operator*(const mint &a) const {\n return mint(*this) *= a;\n }\n\n mint operator/(const mint &a) const {\n return mint(*this) /= a;\n }\n\n bool operator==(const mint &a) const {\n return x == a.x;\n }\n\n bool operator!=(const mint &a) const {\n return x != a.x;\n }\n\n bool operator<(const mint &a) const {\n return x < a.x;\n }\n\n friend ostream &operator<<(ostream &out, const mint &m) {\n out << m.x;\n return out;\n }\n};\n\nusing Mint = mint<MOD>;\n\n\nclass Solution {\npublic:\n\n Mint dp[201][(int) 2e4 + 3];\n int freq[(int) 2e4 + 3];\n int countSubMultisets(vector<int>& a, int l, int r) {\n vi b;\n for (auto x: a) {\n if (freq[x] == 0 && x != 0)\n b.emplace_back(x);\n freq[x]++;\n\n }\n\n int n = b.size();\n for (int j = 0; j <= r; ++j) \n dp[n][j] = 1;\n \n\n for (int i = n-1; i >= 0; --i){\n for (int j = 0; j <= r; ++j){\n dp[i][j] = dp[i+1][j];\n if (j-b[i] >= 0) {\n dp[i][j] += dp[i][j - b[i]];\n if (j-(freq[b[i]]+1)*b[i] >= 0)\n dp[i][j] -= dp[i+1][j-(freq[b[i]]+1)*b[i]];\n }\n }\n }\n\n\n return ((dp[0][r] - (l-1 >= 0 ? dp[0][l-1] : 0))*(1+freq[0])).x;\n }\n};\n``` | 16 | 0 | ['Math', 'Dynamic Programming', 'Sliding Window', 'C++'] | 4 |
count-of-sub-multisets-with-bounded-sum | Video Explanation (Intuition with proof of Amorized Time complexity) | video-explanation-intuition-with-proof-o-9e3a | Explanation\n\nClick here for the video\n\n# Code\n\nclass Solution {\npublic:\n static const int N = 2e4;\n int mod= 1e9+7;\n int cnt[N+1];\n int c | codingmohan | NORMAL | 2023-10-15T08:13:45.423612+00:00 | 2023-10-15T08:13:45.423628+00:00 | 527 | false | # Explanation\n\n[Click here for the video](https://youtu.be/V6AoVVxt18Y)\n\n# Code\n```\nclass Solution {\npublic:\n static const int N = 2e4;\n int mod= 1e9+7;\n int cnt[N+1];\n int countSubMultisets(vector<int>& a, int l, int r) {\n int dp[N+1];\n memset(cnt,0,sizeof(cnt));\n memset(dp,0,sizeof(dp));\n \n int n=a.size();\n for(int x:a)cnt[x]++;\n dp[0]=cnt[0]+1;\n for(int i=1;i<=N;i++)\n {\n if(!cnt[i])continue;\n for(int j=N-i;j>=0;j--)\n {\n if(!dp[j])continue;\n for(int k=1;k<=cnt[i];k++)\n {\n int pos=k*i+j;\n if(pos>N)break;\n (dp[pos]+=dp[j]);\n if(dp[pos]>=mod)dp[pos]-=mod;\n }\n }\n }\n int ans=0;\n for(int i=l;i<=r;i++)\n {\n ans+=dp[i];\n if(ans>=mod)ans-=mod;\n }\n return ans;\n }\n};\n``` | 12 | 1 | ['C++'] | 2 |
count-of-sub-multisets-with-bounded-sum | ✅☑[C++/C/Java/Python/JavaScript] || DP || EXPLAINED🔥 | ccjavapythonjavascript-dp-explained-by-m-rrg6 | PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n(Also explained in the code)\n\n1. Problem Context: The code aims to calculate the number of multisets with | MarkSPhilip31 | NORMAL | 2023-10-14T16:12:44.917909+00:00 | 2023-10-14T16:12:44.917929+00:00 | 1,510 | false | # *PLEASE UPVOTE IF IT HELPED*\n\n---\n\n\n# Approaches\n***(Also explained in the code)***\n\n1. **Problem Context:** The code aims to calculate the number of multisets with sums within a specified range [l, r] for a given set of integers.\n\n1. **Initialization:**\n\n - The code defines constants for modulo arithmetic (MOD) and the maximum number of elements (MAXN).\n - It initializes an array `dp` to store dynamic programming values.\n\n1. **Dynamic Programming:**\n\n - The code employs dynamic programming to compute the number of multisets efficiently.\n - It initializes the `dp` array with zeros and sets `dp[0] = 1` as the base case for an empty set.\n1. **Sorting and Processing:**\n\n - It sorts the input numbers in ascending order to handle duplicates more efficiently.\n - The sorted array is reversed so that processing begins with the largest numbers.\n1. **Handling Leading Zeros:**\n\n - The code checks and handles leading zeros in the sorted array.\n - It increments dp[0] for each leading zero and removes these zeros from the array.\n1. **Iterating Through Unique Numbers:**\n\n- The code iterates through the sorted array and identifies unique numbers.\n- It counts the occurrences of each unique number and calculates a variable `chg` based on the sum of elements processed so far.\n1. **Counting Multisets:**\n\n - It uses nested loops to count the number of multisets that contribute to each sum in the range [l, r].\n - The inner loops handle various combinations of elements to achieve the target sum.\n - The dynamic programming values are updated as the code progresses.\n1. **Final Result:**\n\n - The code calculates the final result for the given range [l, r].\n - It returns the result after applying modulo operation (MOD) to avoid integer overflow.\n\n\n\n\n# Complexity\n- **Time complexity:**\n $$O(r * n^2)$$\n (where \'r\' is the range and \'n\' is the number of unique elements.)\n\n- **Space complexity:**\n $$O(MAXN)$$ \n(The space complexity is constant since the \'dp\' array has a fixed size)\n \n\n\n# Code\n```C++ []\nclass Solution {\n const int MOD = 1000000007; // Define a constant for modulo arithmetic.\n const int MAXN = 20000; // Define a constant for the maximum number of elements in the array.\n\n int dp[20005]; // Initialize an array to store dynamic programming values.\n\npublic:\n int countSubMultisets(vector<int>& nums, int l, int r) {\n for (int i = 0; i <= r; i++) {\n dp[i] = 0; // Initialize the DP array with zeros.\n }\n dp[0] = 1; // The base case for an empty set is 1.\n\n sort(nums.begin(), nums.end()); // Sort the input numbers in ascending order.\n reverse(nums.begin(), nums.end()); // Reverse the sorted array to start with the largest numbers.\n int sf = 0; // Initialize a variable to keep track of the sum of elements.\n\n // Handle leading zeros in the sorted array.\n while (nums.size() && nums.back() == 0) {\n dp[0]++;\n nums.pop_back(); // Remove leading zeros.\n }\n\n // Process the sorted array.\n while (nums.size()) {\n int tt = nums.back(); // Get the next unique number.\n int cn = 0; // Initialize a counter for this number.\n while (nums.size() && nums.back() == tt) {\n nums.pop_back();\n cn++; // Count the occurrences of the current number.\n }\n\n int chg = min(sf + tt * cn, r); // Calculate the change variable based on the sum so far.\n for (int i = chg; i >= tt; i--) {\n for (int j = 1; j <= cn && i - (j * tt) >= 0; j++) {\n dp[i] += dp[i - j * tt]; // Calculate the number of subsets for the current sum.\n if (dp[i] >= MOD) dp[i] -= MOD; // Apply modulo operation.\n }\n }\n\n sf += tt * cn; // Update the sum so far.\n }\n\n int ans = 0;\n for (int i = l; i <= r; i++) {\n ans += dp[i]; // Calculate the answer by summing the DP values within the given range.\n ans %= MOD; // Apply modulo operation to the final answer.\n }\n\n return ans;\n }\n};\n\n\n```\n```C []\n#include <stdio.h>\n#include <stdlib.h>\n\nconst int MOD = 1000000007;\nconst int MAXN = 20000;\n\nint dp[20005];\n\nvoid reverseArray(int arr[], int n) {\n int start = 0;\n int end = n - 1;\n while (start < end) {\n int temp = arr[start];\n arr[start] = arr[end];\n arr[end] = temp;\n start++;\n end--;\n }\n}\n\nvoid removeLastElement(int arr[], int *n) {\n if (*n > 0) {\n int *newArr = (int *)malloc((*n - 1) * sizeof(int));\n for (int i = 0; i < *n - 1; i++) {\n newArr[i] = arr[i];\n }\n free(arr);\n arr = newArr;\n (*n)--;\n }\n}\n\nint countSubMultisets(int nums[], int n, int l, int r) {\n for (int i = 0; i <= r; i++) {\n dp[i] = 0;\n }\n dp[0] = 1;\n\n reverseArray(nums, n);\n\n int sf = 0;\n\n while (n > 0 && nums[n - 1] == 0) {\n dp[0]++;\n removeLastElement(nums, &n);\n }\n\n while (n > 0) {\n int tt = nums[n - 1];\n int cn = 0;\n while (n > 0 && nums[n - 1] == tt) {\n removeLastElement(nums, &n);\n cn++;\n }\n\n int chg = (sf + tt * cn) < r ? (sf + tt * cn) : r;\n for (int i = chg; i >= tt; i--) {\n for (int j = 1; j <= cn && (i - (j * tt)) >= 0; j++) {\n dp[i] += dp[i - j * tt];\n if (dp[i] >= MOD) dp[i] -= MOD;\n }\n }\n\n sf += tt * cn;\n }\n\n int ans = 0;\n for (int i = l; i <= r; i++) {\n ans += dp[i];\n ans %= MOD;\n }\n\n return ans;\n}\n\n```\n```Java []\npublic class Solution {\n private final int MOD = 1000000007;\n private final int MAXN = 20000;\n private int[] dp = new int[20005];\n\n public int countSubMultisets(int[] nums, int l, int r) {\n for (int i = 0; i <= r; i++) {\n dp[i] = 0;\n }\n dp[0] = 1;\n\n Arrays.sort(nums);\n reverseArray(nums);\n int sf = 0;\n\n while (nums.length > 0 && nums[nums.length - 1] == 0) {\n dp[0]++;\n removeLastElement(nums);\n }\n\n while (nums.length > 0) {\n int tt = nums[nums.length - 1];\n int cn = 0;\n while (nums.length > 0 && nums[nums.length - 1] == tt) {\n removeLastElement(nums);\n cn++;\n }\n\n int chg = Math.min(sf + tt * cn, r);\n for (int i = chg; i >= tt; i--) {\n for (int j = 1; j <= cn && i - (j * tt) >= 0; j++) {\n dp[i] += dp[i - j * tt];\n if (dp[i] >= MOD) {\n dp[i] -= MOD;\n }\n }\n }\n\n sf += tt * cn;\n }\n\n int ans = 0;\n for (int i = l; i <= r; i++) {\n ans += dp[i];\n ans %= MOD;\n }\n\n return ans;\n }\n\n private void reverseArray(int[] arr) {\n int start = 0;\n int end = arr.length - 1;\n while (start < end) {\n int temp = arr[start];\n arr[start] = arr[end];\n arr[end] = temp;\n start++;\n end--;\n }\n }\n\n private void removeLastElement(int[] arr) {\n if (arr.length > 0) {\n int[] newArr = new int[arr.length - 1];\n for (int i = 0; i < newArr.length; i++) {\n newArr[i] = arr[i];\n }\n arr = newArr;\n }\n }\n}\n\n```\n```python3 []\n\nclass Solution:\n MOD = 1000000007\n MAXN = 20000\n\n def __init__(self):\n self.dp = [0] * 20005\n\n def countSubMultisets(self, nums, l, r):\n for i in range(r + 1):\n self.dp[i] = 0\n self.dp[0] = 1\n\n nums.sort()\n nums.reverse()\n sf = 0\n\n while nums and nums[-1] == 0:\n self.dp[0] += 1\n nums.pop()\n\n while nums:\n tt = nums[-1]\n cn = 0\n while nums and nums[-1] == tt:\n nums.pop()\n cn += 1\n\n chg = min(sf + tt * cn, r)\n for i in range(chg, tt - 1, -1):\n for j in range(1, cn + 1):\n if i - (j * tt) >= 0:\n self.dp[i] += self.dp[i - j * tt]\n if self.dp[i] >= self.MOD:\n self.dp[i] -= self.MOD\n\n sf += tt * cn\n\n ans = 0\n for i in range(l, r + 1):\n ans += self.dp[i]\n ans %= self.MOD\n\n return ans\n\n\n```\n```javascript []\n\nclass Solution {\n constructor() {\n this.MOD = 1000000007;\n this.MAXN = 20000;\n this.dp = new Array(20005).fill(0);\n }\n\n countSubMultisets(nums, l, r) {\n for (let i = 0; i <= r; i++) {\n this.dp[i] = 0;\n }\n this.dp[0] = 1;\n\n nums.sort((a, b) => a - b);\n nums.reverse();\n let sf = 0;\n\n while (nums.length > 0 && nums[nums.length - 1] === 0) {\n this.dp[0]++;\n nums.pop();\n }\n\n while (nums.length > 0) {\n const tt = nums[nums.length - 1];\n let cn = 0;\n while (nums.length > 0 && nums[nums.length - 1] === tt) {\n nums.pop();\n cn++;\n }\n\n const chg = Math.min(sf + tt * cn, r);\n for (let i = chg; i >= tt; i--) {\n for (let j = 1; j <= cn; j++) {\n if (i - j * tt >= 0) {\n this.dp[i] += this.dp[i - j * tt];\n if (this.dp[i] >= this.MOD) {\n this.dp[i] -= this.MOD;\n }\n }\n }\n }\n\n sf += tt * cn;\n }\n\n let ans = 0;\n for (let i = l; i <= r; i++) {\n ans += this.dp[i];\n ans %= this.MOD;\n }\n\n return ans;\n }\n}\n\n\n\n```\n---\n\n\n# *PLEASE UPVOTE IF IT HELPED*\n\n---\n---\n\n\n---\n\n | 8 | 1 | ['Dynamic Programming', 'C', 'Sorting', 'C++', 'Java', 'Python3', 'JavaScript'] | 4 |
count-of-sub-multisets-with-bounded-sum | C++ recursive dp solution O(sqrt(r) * r) | c-recursive-dp-solution-osqrtr-r-by-dmit-6hew | We have at most 200 distinct elements so let\'s compress our array to array of pairs (a, c), where a - value, c - number of times it repeats in array\nLet\'s de | dmitrii_bokovikov | NORMAL | 2023-10-15T17:23:28.184441+00:00 | 2023-10-15T17:41:04.043828+00:00 | 391 | false | We have at most 200 distinct elements so let\'s compress our array to array of pairs (a, c), where a - value, c - number of times it repeats in array\nLet\'s define function get(i, s) - number of subsequences with sum less or equal than s starting from index i and tricky part of this problem is simplifying complexity of this function to constant, and it can be done using the equations below\n```\nget(i, s) = get(i + 1, s) + get(i + 1, s - a) + ... + get(i + 1, s - c * a)\nget(i, s + a) = get(i + 1, s + a) + get(i + 1, s) + ... + get(i + 1, s - (c - 1) * a) = get(i, s) + get(i + 1, s + a) - get(i + 1, s - c * a)\nlet x = s + a => get(i, x) = get(i, x - a) + get(i + 1, x) - get(i + 1, x - (c + 1) * a)\n```\nso now solution for the problem is straight-forward\n```\n int countSubMultisets(vector<int>& nums, int l, int r) {\n using ll = long long;\n constexpr int MOD = 1\'000\'000\'007;\n unordered_map<int, int> m;\n for (const auto v: nums) {\n ++m[v];\n }\n vector<pair<int, int>> v;\n const ll zeroesCount = m[0];\n m.erase(0);\n for (const auto& p : m) {\n v.push_back(p);\n } \n const int n = size(v);\n vector<vector<int>> dp(n, vector<int>(r + 1, -1));\n function<ll(int, int)> getOrCompute;\n getOrCompute = [&](int i, int sum) -> ll {\n if (sum < 0) {\n return 0;\n }\n if (i == n) {\n return 1;\n }\n if (dp[i][sum] != -1) {\n return dp[i][sum];\n }\n const auto[x, c] = v[i];\n return dp[i][sum] = (getOrCompute(i + 1, sum) + getOrCompute(i, sum - x) - getOrCompute(i + 1, sum - (c + 1) * x) + MOD) % MOD;\n };\n return (getOrCompute(0, r) - getOrCompute(0, l - 1) + MOD) * (zeroesCount + 1) % MOD;\n }\n```\nAdditional note: we have to treat zeroes separately because \n```\nget(i, x) = get(i, x - a) + ...\n```\nwill lead to endless recursion | 6 | 0 | ['C++'] | 0 |
count-of-sub-multisets-with-bounded-sum | 🔥🔥🔥 C++ Solution 🔥🔥🔥 | c-solution-by-07dishwasherbob8-1j60 | Intuition\n Describe your first thoughts on how to solve this problem. \nThe number of unique elements can be at most 200. We can optimize our dp using that use | 07dishwasherbob8 | NORMAL | 2023-10-14T21:00:00.178392+00:00 | 2023-10-14T21:00:00.178433+00:00 | 655 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe number of unique elements can be at most 200. We can optimize our dp using that use sliding window. We get this number by approximating sqrt(n). \n# Approach\ndp[i] is the number of unique sorted multisets of sum i lets say that we use a new number, a that occurs c times within the array we can add a 1 to c times to every multiset to create new ones, so the dp transition will look like dp[i] += dp[i - a] + dp[i - a * 2] + ... + dp[i - a * c] \n\nSince the sum of c across all a is n, doing dp like this will result in n^2 time complexity. We can speed up the update for each pair of a, c by using sliding window. We do this by\nwe want to add to dp[i] dp[i - a] + dp[i - a * 2] + ... + dp[i - a * c]. \n\nNote that the stuff we add to dp[i - a] is very similar: dp[i - a * 2] + dp[i - a * 3] + ... + dp[i - a * (c + 1)] dp[i - a] got removed, and dp[i - a * (c + 1)] got added once you know the amount to add for dp[i], it takes constant time to compute the amount to add for dp[i - a]. \n\nI claim that when sped up, each pair will only take O(n) time to process and since the number of unique a is at most 200.\n\n# Complexity\n- Time complexity: $$O(200n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(200n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\ntypedef long long ll;\nconst ll MOD = 1e9 + 7;\n\nclass Solution {\npublic:\n int countSubMultisets(vector<int>& nums, int l, int r) {\n const ll N = 2e4;\n vector<ll> dp(N + 1);\n map<ll,ll> m;\n dp[0] = 1;\n m[0] = 1;\n for(auto x : nums) {\n m[x]++;\n }\n ll mult = m[0]; m.erase(0);\n for(auto x : m) {\n //{a, c}\n ll a = x.first;\n ll c = x.second;\n vector<ll> help(N + 1);\n for(int i = 1; i <= N; i++) {\n ll sum = 0;\n if(i - a >= 0) {\n sum += dp[i-a];\n sum += help[i-a];\n }\n if(i - a * (c + 1) >= 0) {\n sum -= dp[i - a * (c + 1)];\n }\n help[i] = (sum + MOD) % MOD;\n }\n for(int i = 0; i <= N; i++) {\n dp[i] += help[i];\n if(dp[i] >= MOD) dp[i] -= MOD;\n }\n }\n ll sum = 0;\n for(int i = l; i <= r; i++) {\n sum += dp[i];\n if(sum >= MOD) sum -= MOD;\n }\n return sum * mult % MOD;\n }\n};\n```\n\n# Upvote if you found this helpful :) | 6 | 0 | ['Dynamic Programming', 'C++'] | 0 |
count-of-sub-multisets-with-bounded-sum | Nice optimisation trick on Coin Change Problem ( using 2 dp) | nice-optimisation-trick-on-coin-change-p-4oyh | Intuition\nFirst Observation one need to make is that # of distint element in array cannot exceed 200.\nUsing this observation we will make our dp (similar to c | i_m_karank | NORMAL | 2023-10-14T18:27:46.010314+00:00 | 2023-10-14T19:47:50.401308+00:00 | 338 | false | # Intuition\nFirst Observation one need to make is that # of distint element in array cannot exceed 200.\nUsing this observation we will make our dp (similar to coin change)\nlet dp[i][sumleft]=no of ways make Sumleft using index (i---n-1)\n# Approach\n Let\'s move to transitions\n dp[i][sumleft]=dp[i+1][sumleft] // don\'t include current element \n dp[i][sumleft]=dp[i+1][sumleft-j*(nums[i])] // where j varies from 1 to occ(nums[i])\nNote: having above transition and states will avoid overcounting as dp will consider each group of same nums[i] as an single unit , so contribution from each nums[i] will only depend on different occurance of it taken in dp \n\nNow coming to optimising the transition ( without it it will tle because worst case complexity is O(200*n*r)), so lets make another dp array named dp2, which will store the sum of values of transitions i.e dp2[i][sleft]=(dp1[i+1][sleft-nums[i]]+dp2[i+1][sleft-nums[i]*2]+.....+dp[i+1][sleft%nums[i]])\nUsing this dp2 array we can now write transitions for original dp as \ndp[i][sleft]=(dp[i][sleft]+dp2[i+1][sleft]-dp2[i+1][(sleft-(occ(nums[i]))*nums[i])])\n\nYou can try implementing it, or refer to the code. \n\n# Complexity\n- Time complexity:\n O(no_of_distinct(nums[i])*r)\n- Space complexity:\n O(200*sum)\n\n# Code\n```\nconst int mod=1e9+7;\nvector<pair<int,int>>v;\nint dp1[201][20010];\nint dp2[201][20010];\nint n;\n int rec(int level,int sleft);\n int go(int level,int sleft){\n if(sleft<0) return 0;\n if(dp2[level][sleft]!=-1) return dp2[level][sleft];\n int ans=(go(level,sleft-v[level-1].first)+rec(level,sleft-v[level-1].first))%mod;\n return dp2[level][sleft]=ans;\n }\n int rec(int level,int sleft){\n if(sleft<0) return 0;\n if(level==n){\n if(sleft) return 0;\n return 1;\n }\n auto &ans=dp1[level][sleft];\n if(ans!=-1) return ans;\n if(v[level].first){\n ans=(rec(level+1,sleft)+go(level+1,sleft))%mod;\n ans-=(go(level+1,sleft-(v[level].first*(v[level].second))));\n ans%=mod;\n if(ans<0) ans+=mod;\n }\n else ans=(1ll*rec(level+1,sleft)*(v[level].second+1))%mod; // handle case for 0 o/w infinite recursion (go )\n return ans;\n }\nclass Solution {\npublic:\n \n int countSubMultisets(vector<int>& nums, int l, int r) {\n int sum=0;\n map<int,int>mp;\n for(auto i:nums) sum+=i,mp[i]++;\n n=mp.size();\n v.clear();\n for(auto i:mp) v.push_back({i.first,i.second});\n r=min(r,sum);\n for(int i=0;i<=n;i++){\n for(int j=0;j<=r;j++) dp1[i][j]=dp2[i][j]=-1;\n }\n int ans=0;\n for(int i=l;i<=r;i++){\n ans=(ans*1ll+rec(0,i))%mod;\n }\n return ans;\n }\n};\n``` | 4 | 1 | ['C++'] | 1 |
count-of-sub-multisets-with-bounded-sum | [Python3] Optimised knapsack DP with sliding window, <1s (faster than 100% at time of writing) | python3-optimised-knapsack-dp-with-slidi-s2pu | Note that this is intended to explain additional optimisations to the knapsack DP with sliding window solution method given in other solutions (e.g. lee215), wh | sveng101 | NORMAL | 2023-10-15T00:41:51.827096+00:00 | 2023-10-15T00:41:51.827122+00:00 | 169 | false | Note that this is intended to explain additional optimisations to the knapsack DP with sliding window solution method given in other solutions (e.g. lee215), which is not itself explained in detail here (although the code is commented with rationale behind individual steps). I would therefore recommend looking at other solutions first and then returning if you do not follow the general solution method.\n\nPlease comment below if you do not find this satisfactory and you would like me to include a more in-depth explanation of the general method.\n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThis was an interesting problem that needed to be tackled in a specific way (i.e. using sliding window with DP) in order to achieve the requisite execution speed. However, even after solving in a way that passed all the required time, there were still further optimisations which, although not influencing the time or space complexity, could eliminate unnecessary calculations and so speed up the evaluation time. The main 2 were:\n\n- For a given index i strictly less than l, stopping the calculation of the DP array once the value at this index no longer influences the DP array values of interest (i.e. from l to r inclusive).\nFor example, say $$l = 100$$ and we are on the penultimate iteration and the final iteration will address the number $$6$$ with a frequency of $$2$$. Consider an index $$i < 100 - 2 * 6 = 88$$. In the final iteration, the largest index of the final DP array this can influence is $$i + 2 * 6 < l$$, so it does not influence the final result. Therefore, for the current iteration, the result will remain unchanged if the DP array values with indices less than $$88$$ are not updated. This can cut down a lot of unnecessary calculation, at least for later iterations and large $$l$$.\nThis appears to contribute a reduction in time of a factor of approximately 1.5\n- Instead of for every step of the process updating all indices up to r, not iterating beyond the largest index that can be changed.\nFor example, say we have a situation where $$r = 1000$$, and we are in the first iteration (so all elements of the DP array are $$0$$ except for at index $$0$$, which is $$1$$) and number addressed in this iteration $$2$$ which has a frequency of $$3$$. Given that the largest index in the DP array with non-zero value is $$0$$ and the largest contribution that can be made by $$2$$s in terms of the multiset sum is $$2 * 3 = 6$$, the largest index of the DP array whose value can (and indeed will) be changed during this itereration is $$0 + 6 = 6$$. It is therefore unnecessary to perform the calculations for indices between $$7$$ and $$r = 1000$$. This can also cut down a lot of unnecessary calculation, at least for early iterations.\nThis appears to contribute a reduction in time of a factor of approximately 2.\n\nAdditionally, by iterating over the numbers in ascending order of size turned out to be marginally faster than from descending order of size, though this is empirical and I do not at present have an intuitive explanation as to why that should be the case.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe general approach is similar to most other solutions (e.g. lee215- see these and the comments in the code below for a more detailed explanation), incorporating the above optimisations which collectively contributed a reduction in execution time of approximately 3.\n\n# Complexity\nWith $$n = len(nums)$$ and $$m$$ as the number of distinct elements of $$nums$$ (which itself is $$O(\\sqrt{n})$$):\n\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(nm)$$ or, in terms of just the explicitly restricted parameters, $$O(n^{3 / 2})$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(r + m)$$ or, in terms of just the explicitly restricted parameters, $$O(r + \\sqrt{n})$$\n\n# Code\n```\nclass Solution:\n def countSubMultisets(self, nums: List[int], l: int, r: int) -> int:\n md = 10 ** 9 + 7\n dp = [0] * (r + 1)\n dp[0] = 1\n mx_nonzero = 0\n f_dict = Counter(nums)\n nums2 = sorted(f_dict.keys(), reverse=True)\n if not nums2[-1]: nums2.pop()\n n = len(nums2)\n cumu_rev = sum(x * f_dict[x] for x in nums2)\n for idx in reversed(range(n)):\n num = nums2[idx]\n # The largest possible collective contribution from the\n # iterations after this one to any multiset sum\n cumu_rev -= num * f_dict[num]\n # The smallest index in the DP array that can influence\n # the final result (and so the smallest index that needs\n # to be updated)\n mn = max(0, l - cumu_rev)\n # The largest index in the DP that can be non-zero after\n # the current iteration\n mx_nonzero = min(r, mx_nonzero + num * f_dict[num])\n # Iterating over different congruences modulo num of the\n # endpoints of the sliding windows (which themselves slide\n # by increments of num to the left, thus requiring up to\n # num sliding windows for complete coverage)\n for i1 in reversed(range(max(mx_nonzero - num + 1, mn), mx_nonzero + 1)):\n # The largest frequency of num that can appear in a\n # multiset with sum i1\n f0 = min(f_dict[num], i1 // num)\n # The initial sum over the sliding window\n curr = sum(dp[i1 - num * j] for j in range(1, f0 + 1)) % md\n # The (possibly empty) range of indices (in increments of num)\n # for which the left end of the sliding window is no less than\n # num, and so when shifting the sliding window to the left by a\n # displacement of num, updating the sliding window value requires\n # adding a new value on the left end\n i_rng1 = (i1, min(i1, max((i1 % num) + (f0 * num), max(mn, num) - 1)))\n # The (possibly empty) range of indices (in increments of num)\n # for which the left end of the sliding window is strictly less than\n # num, and so when shifting the sliding window to the left by a\n # displacement of num, updating the sliding window value does not\n # require adding a new value on the left end\n i_rng2 = (i_rng1[1], min(i_rng1[1], max(mn, num) - 1))\n for i in range(*i_rng1, -num):\n dp[i] = (dp[i] + curr) % md\n curr = (curr - dp[i - num] + dp[i - (f0 + 1) * num]) % md\n for i in range(*i_rng2, -num):\n dp[i] = (dp[i] + curr) % md\n curr = (curr - dp[i - num]) % md\n # As adding any number of 0s to a multiset does not affect\n # its sum, the zero count\'s net effect is to multiply the\n # result when ignoring the zeros by the zero count plus 1\n return ((sum(dp[l:]) % md) * (f_dict.get(0, 0) + 1)) % md\n``` | 3 | 0 | ['Python3'] | 1 |
count-of-sub-multisets-with-bounded-sum | Bottom-Up DP & Sliding Window to avoid TLE | bottom-up-dp-sliding-window-to-avoid-tle-6i1u | Intuition\n Describe your first thoughts on how to solve this problem. \nThe number of distinct elements (let it be m) the array can have is at most 200. It can | CelonyMire | NORMAL | 2023-10-14T20:03:51.927819+00:00 | 2023-10-16T19:16:08.057257+00:00 | 373 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe number of **distinct** elements (let it be `m`) the array can have is at most `200`. It can be verified by the sum of first `199` positive elements (`199*(199+1)/2=19900`, and then `0`). With this, we can develop a `O(sum*m)` solution.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nLet `dp[i]` be the number of ways we can make the sum `i`. We go through each distinct element and update our DP that way. Our goal is to traverse every sum once for each unique number.\n\nIn order to traverse every sum only once, we can treat every sum as `sum % current_number`, which means we try every modulo (which is `0 <= k < current_number`) and work with sums only with that modulo.\n\nFor example, if our number is `5`, and our modulo is `2`, we traverse `2,7,12,17,...`\n\nThe code doesn\'t actually use the modulo of the sum, but rather it starts from some offset from `sum`.\n\n**Since every offset covers an unique set of sums, trying every offset will cover all the sums!**\n\nIn order to update the DP, we take into account of the occurences of each number we try (`cnt[current_number]`). For example, if `current_number` is 5, and `cnt[5] = 4`, and we are updating the DP for sum `k`:\n`dp[k] += dp[k - 5] + dp[k - 10] + dp[k - 15] + dp[k - 20]`\n\nTo avoid TLE of going through occurences of the number and adding up all the DP values we can get, we use a sliding window. For the above example, when we move the window, if `dp[k - 5] + dp[k - 10] + dp[k - 15] + dp[k - 20]` is `cur`, we do `cur + dp[k - 25] - dp[k - 5]`\n\n**IMPORTANT: We must go from right to left, because that eliminates the possibility of using the updated dp values for the current number. We want to use the dp values from the previous number**\n\n\n# Complexity\n- Time complexity: $$O(sum(nums)*m)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(sum(nums))$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution\n{\npublic:\n int countSubMultisets(vector<int> &nums, int l, int r)\n {\n const int M = 1e9 + 7;\n int ma = ranges::max(nums); // maximum element\n int sum = accumulate(nums.begin(), nums.end(), 0);\n nums.push_back(0); // clever handle case of nums having no 0\n vector<int> cnt(ma + 1);\n for (int v : nums)\n cnt[v]++;\n ranges::sort(nums);\n nums.erase(unique(nums.begin(), nums.end()), nums.end());\n vector<int> dp(sum + 1);\n dp[0] = cnt[0];\n for (int v : nums)\n {\n for (int j = 0; j < v; j++) // every modulo j\n {\n int cur = 0; // sum of all the appropriate DP values for the window\n int p = sum - j; // points to left index of sliding window when the window is shifted\n for (; p >= 0 && (sum - j - p) / v <= cnt[v]; p -= v)\n cur = (cur + dp[p]) % M;\n for (int k = sum - j; k >= 0; k -= v)\n {\n cur = (cur - dp[k] + M) % M; // take away, because dp[k] means we didn\'t use any occurence of the number\n dp[k] = (dp[k] + cur) % M;\n if (p >= 0)\n { // include the next DP in the sliding window\n cur = (cur + dp[p]) % M;\n p -= v;\n }\n }\n }\n }\n int ans = 0;\n for (int i = l; i <= min(r, sum); i++)\n ans = (ans + dp[i]) % M;\n return ans;\n }\n};\n``` | 3 | 1 | ['Dynamic Programming', 'Sliding Window', 'C++'] | 0 |
count-of-sub-multisets-with-bounded-sum | DP + Sliding window [EXPLAINED] | dp-sliding-window-explained-by-r9n-w9vp | IntuitionWe need to count the number of subsets of a given list of integers that can sum to values between l and r. We also have to handle duplicates in the lis | r9n | NORMAL | 2025-01-15T22:40:06.475116+00:00 | 2025-01-15T22:40:06.475116+00:00 | 17 | false | # Intuition
We need to count the number of subsets of a given list of integers that can sum to values between l and r. We also have to handle duplicates in the list and perform efficient calculations using DP.
# Approach
I used DP where I maintain an array (dp) to keep track of the possible sums, and for each unique value in the list, I update possible sums by sliding a window to efficiently calculate how each number contributes to the total subsets that match the sum condition.
# Complexity
- Time complexity:
O(n * sum), where n is the number of unique elements in the list and sum is the total sum of all numbers. This is because we loop through the list of numbers and for each value, we update possible sums.
- Space complexity:
O(sum), where sum is the total sum of all numbers because the dp array stores sums up to that total. The space is used to store the count of all subset sums up to sum.
# Code
```python3 []
class Solution:
def countSubMultisets(self, nums, l, r):
M = 1_000_000_007
ma = max(nums) # maximum element
total_sum = sum(nums)
nums.append(0) # clever handle case of nums having no 0
# Create the count array
cnt = [0] * (ma + 1)
for v in nums:
cnt[v] += 1
# Sort and remove duplicates
nums = sorted(set(nums))
# Initialize the dp array
dp = [0] * (total_sum + 1)
dp[0] = cnt[0]
for v in nums:
for j in range(v): # every modulo j
cur = 0 # sum of all the appropriate DP values for the window
p = total_sum - j # points to left index of sliding window when the window is shifted
while p >= 0 and (total_sum - j - p) // v <= cnt[v]:
cur = (cur + dp[p]) % M
p -= v
for k in range(total_sum - j, -1, -v):
cur = (cur - dp[k] + M) % M # take away, because dp[k] means we didn't use any occurrence of the number
dp[k] = (dp[k] + cur) % M
if p >= 0:
# Include the next DP in the sliding window
cur = (cur + dp[p]) % M
p -= v
ans = 0
for i in range(l, min(r, total_sum) + 1):
ans = (ans + dp[i]) % M
return ans
``` | 2 | 0 | ['Math', 'Dynamic Programming', 'Memoization', 'Sliding Window', 'Python3'] | 0 |
count-of-sub-multisets-with-bounded-sum | C++ solution | c-solution-by-pejmantheory-omal | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | pejmantheory | NORMAL | 2023-10-18T11:08:23.849303+00:00 | 2023-10-18T11:08:23.849332+00:00 | 178 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public:\n int countSubMultisets(vector<int>& nums, int l, int r) {\n constexpr int kMod = 1\'000\'000\'007;\n // dp[i] := # of submultisets of nums with sum i\n vector<long> dp(r + 1);\n dp[0] = 1;\n unordered_map<int, int> count;\n\n for (const int num : nums)\n ++count[num];\n\n const int zeros = count[0];\n count.erase(0);\n\n for (const auto& [num, freq] : count) {\n // stride[i] := dp[i] + dp[i - num] + dp[i - 2 * num] + ...\n vector<long> stride = dp;\n for (int i = num; i <= r; ++i)\n stride[i] += stride[i - num];\n for (int i = r; i > 0; --i)\n if (i >= num * (freq + 1))\n // dp[i] + dp[i - num] + dp[i - freq * num]\n dp[i] = (stride[i] - stride[i - num * (freq + 1)]) % kMod;\n else\n dp[i] = stride[i] % kMod;\n }\n\n long ans = 0;\n for (int i = l; i <= r; ++i)\n ans = (ans + dp[i]) % kMod;\n return ((zeros + 1) * ans) % kMod;\n }\n};\n\n``` | 2 | 0 | ['C++'] | 0 |
count-of-sub-multisets-with-bounded-sum | Read this if you couldn't understand from any other solution. Comment if you still have a doubt. | read-this-if-you-couldnt-understand-from-48oa | Intuition\n Describe your first thoughts on how to solve this problem. \nI am assuming that you can solve question the simpler version of the problem where all | Adarsh-Roy | NORMAL | 2023-10-16T14:15:11.773895+00:00 | 2023-10-16T14:15:11.773913+00:00 | 227 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nI am assuming that you can solve question the simpler version of the problem where all elements of the array are unique via dynamic programming considering the cases of picking or not picking the elements as we traverse the array, if not then first go and solve coin change II on leetcode. Now in this problem the change is that instead of considering whether to pick or not pick some number, we need to consider how many of that number should we pick. Also, we will handle zeroes separately as the logic we will use in the DP transitions will be inefficient with zeroes. If by ignoring the zeroes you get the answer $$ans$$, then the answer with zeroes is just $$ans*(1 + occ[0])$$, as in every set we can have either no zeroes, one zero, two zero, ... or $occ[0]$ zeroes.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSince our recursion logic requires us to decide how many of a number to pick, we should make that decision for every number for which we need to have a count of all the unique elements ready to be traversed for populating the table. We store this in an `unordered_map<int,int> count`. Now we can traverse this map with the following transition:\n```\nfor(int j = 0;j<=r;j++){\n for(int k=0;k<=freq and j>=k*num;k++){\n dp[idx][j] = (dp[idx][j] + dp[idx-1][j-k*num])%mod; \n }\n}\n```\nHere `dp[idx][j]` stores the number of sub-multisets with sum `j` while considering only the first `1+idx` elements of the `count` map. In this transition we are computing number of ways to sum upto `j` till index `idx` by summing up the number of ways when we are picking the current element `k` times, where `k` varies from `0` to the count of the element or the maximum number of times we can pick the element, whichever is smaller. This solutio is correct, but it will give TLE.\n\nNow we consider three cases (`num` is the current element and `freq` it\'s frequency)\n1. `(1+freq)*num <= j`:\nNotice here that, \n```\ndp[idx][j] = dp[idx-1][j] + dp[idx-1][j-num] + dp[idx-1][j-2*num] ... dp[idx-1][j - freq*num]\n\nand\n\ndp[idx][j-num] = dp[idx-1][j-num] + dp[idx-1][j-2*num] ... dp[idx-1][j - freq*num] + dp[idx-1][j - (1+freq)*num]\n\nso\n\ndp[idx][j] = dp[idx-1][j] + dp[idx][j-num] - dp[idx-1][j - (1+freq)*num]\n```\n\n2. Not 1. but `num <= j`:\nIn this case, since 1. is not true, let `p` be the maximum natural number such that `p*num <= j`, then:\n```\ndp[idx][j] = p[idx-1][j] + dp[idx-1][j-num] + dp[idx-1][j-2*num] ... dp[idx-1][j - p*num]\n\nand\n\ndp[idx][j-num] = dp[idx-1][j-num] + dp[idx-1][j-2*num] ... + dp[idx-1][j - p*num]\n\nso\n\ndp[idx][j] = dp[idx-1][j] + dp[idx][j-num]\n``` \n\n3. None of 2 and 3 :\nIn this case we just simple do:\n```\ndp[idx][j-num] = dp[idx-1][j-num] + dp[idx-1][j-2*num] ... + dp[idx-1][j - p*num]\n```\n\nNow instead of adding up from `k = 0` till `k = p` (`p` maybe same as `freq`), we can see if the current element falls among the first two categeries and just use the precalculated entries to speed up the process significantly.\nNow our transition will look like:\n```\nfor(int j = 0;j<=r;j++){\n if(((freq+1)*num <= j)){\n dp[idx][j] = \n (dp[idx-1][j] + dp[idx][j-num] - \n dp[idx-1][j-(freq+1)*num] + mod)%mod;\n }\n else if(num<=j){\n dp[idx][j] =\n (dp[idx-1][j] + dp[idx][j-num])%mod;\n }\n else{\n for(int k=0;k<=freq and j>=k*num;k++){\n dp[idx][j] = \n (dp[idx][j] + dp[idx-1][j-k*num])%mod; \n }\n }\n}\n```\n\nThis does get accepted but we can further improve the space complexity as anytime we are updating the `idx` row of the table, we only need `idx-1` row of the table, so essentially we can just store two 1D vectors and keep updating them.\nYou can include zero too in the transition itself but I prefer to keep it simpler/faster and handle zero separately.\n\n# Complexity\n- Time complexity:\n$$O(rd)$$, where $d$ is number of distinct elements.\n\n- Space complexity:\n$$O(r)$$\n\n# Code\n```\n#define mod 1000000007\nclass Solution {\npublic:\n int countSubMultisets(vector<int>& nums, int l, int r) {\n unordered_map<int,int> count;\n for(auto num:nums) count[num]++;\n //handle zero separately\n int zeroFreq = 0;\n if(count.find(0)!=count.end()){\n zeroFreq = count[0];\n count.erase(0);\n if(count.empty()) return zeroFreq + 1;\n }\n int n = count.size();\n vector<long long> cur(r+1,0);\n vector<long long> prev(r+1,0);\n\n //base case\n auto it = count.begin();\n int base_num = it->first;\n int base_freq = it->second;\n for(int i=0;i<=r;i++){\n if(i%base_num == 0 and i/base_num<=base_freq){\n prev[i] = 1; \n//for zero it wouldn\'t have been simply 1, zero is the only number\n//that can give the sum of 0 in more than one ways, but it has been \n//dealt with already so base_num will surely not be zero.\n }\n }\n it++;\n while(it!=count.end()){\n int num = it->first;\n int freq = it->second;\n for(int j = 0;j<=r;j++){\n if(((freq+1)*num <= j)){\n cur[j] = \n (prev[j] + cur[j-num] - \n prev[j-(freq+1)*num] + mod)%mod;\n }\n else if(num<=j){\n cur[j] =\n (prev[j] + cur[j-num])%mod;\n }\n else{\n for(int k=0;k<=freq and j>=k*num;k++){\n cur[j] = \n (cur[j] + prev[j-k*num])%mod; \n }\n }\n }\n it++;\n prev = cur;\n cur.assign(r+1,0);\n }\n long ans = 0;\n for(int i = l;i<=r;i++){\n ans = (ans + prev[i]) % mod;\n }\n return (ans*(zeroFreq + 1))%mod;\n }\n}; \n\n\n``` | 2 | 0 | ['Dynamic Programming', 'C++'] | 0 |
count-of-sub-multisets-with-bounded-sum | Easy DP Solution | easy-dp-solution-by-ming_91-ootr | Approach\n Describe your approach to solving the problem. \nCount occurrences of each distinct number in countArr.\n\ndp[i][sum] = dp[i+1][sum + k * countArr[i] | Ming_91 | NORMAL | 2023-10-14T16:30:17.674103+00:00 | 2023-10-14T16:30:17.674129+00:00 | 396 | false | # Approach\n<!-- Describe your approach to solving the problem. -->\nCount occurrences of each distinct number in `countArr`.\n\n`dp[i][sum] = dp[i+1][sum + k * countArr[i].number]`, where k is in range `[0, countArr[i].count]`.\n\nIf `sum > r` we can early stop since all number are non-negative.\nIf `i == countArr.length` return `1` if `sum` in range `[l, r]` or `0` otherwise.\n\n\n# Complexity\n- Time complexity: $$O(n * r)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n * r)$$ but can reduced to $$O(r)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n static final int MOD = 1_000_000_007;\n int l, r, n;\n int calc(Integer[][] dp, int[][] countArr, int idx, int sum) {\n if (sum > r) {\n return 0;\n }\n if (idx == n) {\n if (sum >= l && sum <= r) {\n return 1; \n }\n return 0;\n }\n if (dp[idx][sum] != null) {\n return dp[idx][sum];\n }\n int res = 0;\n int currNum = countArr[idx][0];\n int currCount = countArr[idx][1];\n int currSum = sum;\n for (int i = 0; i <= currCount; i++) {\n res = (res + calc(dp, countArr, idx + 1, currSum)) % MOD;\n currSum += currNum;\n }\n dp[idx][sum] = res;\n return res;\n }\n public int countSubMultisets(List<Integer> nums, int l, int r) {\n this.l = l;\n this.r = r;\n Map<Integer, Integer> count = new HashMap<>();\n for (int num : nums) {\n if (num <= r) {\n count.put(num, count.getOrDefault(num, 0) + 1);\n }\n }\n n = count.size();\n int i = 0;\n int[][] countArr = new int[n][2];\n for (Map.Entry<Integer, Integer> e : count.entrySet()) {\n countArr[i][0] = e.getKey();\n countArr[i][1] = e.getValue();\n i++;\n }\n Integer[][] dp = new Integer[n + 1][r + 1];\n return calc(dp, countArr, 0, 0);\n }\n}\n``` | 2 | 0 | ['Java'] | 2 |
count-of-sub-multisets-with-bounded-sum | K-Knapsack Problem || Detailed Explanation || Different Way to Think ||O(N*r) | k-knapsack-problem-detailed-explanation-84wnx | Intuition\n Describe your first thoughts on how to solve this problem. \n\nThis is a standard knapsack problem and a variation of 2585.\n\nIn general, knapsack | orekihoutarou | NORMAL | 2023-10-19T19:51:24.539934+00:00 | 2023-10-19T19:51:24.539961+00:00 | 73 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nThis is a standard knapsack problem and a variation of [2585](https://leetcode.com/problems/number-of-ways-to-earn-points/description/).\n\nIn general, knapsack DP problem is categorized into two sets: (1) 1-knapsack, with only 1 count per item; (2) infinite-knapsack, with infinitely many items. (1) requires us to iterate backwards in order not to double count while (2) requires us to iterate forwards in order to count all possibilities.\n\nFor k-knapsack question, with a specific count per item, there is also two ways starting from either (1) and (2) to think about it. (1) is the most intuitive and the most common way where you only need to add a few more items per iteration compared to 1-knapsack code. I learned(2) earlier and this approach doesn\'t seem very intuitive.\n\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n`dp[i]` represents the number of ways to get a sum of `i`.\n\nWe get the count of each item first then iterate over the item and the count.\n\nIn each iteration, we first assume that we have infinitely many items and iterate forward. Now the meaning of `dp[i]` has slightly changed: we count the ways to `i` using infinitely many current item **plus** we also count the previous items for multiple times. So, next step is to remove the effect of multiple counts. Luckily, you can do this in one line and this should be done backwards.\n\nOther detail like count of 0 is omitted in the discussion.\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N*r)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(r)\n\n# Code\n```\nclass Solution:\n def countSubMultisets(self, nums: List[int], l: int, r: int) -> int:\n\n MOD = 10**9+7\n\n count = Counter(nums)\n\n dp = [0 for i in range(r+1)]\n dp[0] = 1\n\n for key,val in count.items():\n if key == 0:\n continue\n for i in range(key,r+1):\n dp[i] = (dp[i] + dp[i-key]) % MOD\n for i in range(r,(val+1)*key-1,-1):\n dp[i] = (dp[i] - dp[i-(val+1)*key]) % MOD\n \n return sum(dp[l:r+1]) * (count[0]+1) % MOD\n \n``` | 1 | 0 | ['Python3'] | 0 |
count-of-sub-multisets-with-bounded-sum | The secret: faster than 100% | the-secret-faster-than-100-by-mbeceanu-szhr | Intuition\n Describe your first thoughts on how to solve this problem. \nThe dirty secret of this problem is that the distinct values in the array cannot be ver | mbeceanu | NORMAL | 2023-10-15T00:13:59.615903+00:00 | 2023-10-15T22:08:40.831528+00:00 | 107 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe dirty secret of this problem is that the distinct values in the array cannot be very many.\nIndeed, the sum of the first $n$ natural numbers is $\\frac {n(n+1)} 2$. It is given in the problem that the sum of all values is no more than $20,000$. Thus, there cannot be more than $200$ distinct values in the array.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe need an algorithm that deals well with values of high multiplicity.\nSuch an algorithm is given in a simplified and straightforward form below.\nLet $c_0, \\ldots, c_r$ be the list of the counts, that is the number of ways each value $0, \\ldots, r$ can be obtained as a sum. In the beginning, $c_0=1$ and all the other counts are $0$.\nFor a number $n$ in the array with multiplicity $m$, the list gets updated as follows:\n$c_k$ gets replaced by $c_k + c_{k-n} + \\ldots + c_{k-mn}$, where the terms with negative indices are $0$.\nWe can do this summation in just two passes through the list of length $r$, so this only takes $O(r)$ time. In the first pass, we compute the partial sums and replace $c_k$ by\n$c_k + c_{k-n} + c_{k-2n} + \\ldots + c_{k-jn} + \\ldots$,\ndisregarding $m$. In the second pass we take the differences of these partial sums in order to truncate at $k-mn$.\n\nWe can go through the distinct values in the array in any order, but it is useful to consider $0$ separately. Having $0$ in the array with multiplicity $m$ just means that every count $c_k$ in the list gets multiplied by $m+1$.\n\nThe final answer is the sum of the counts in the desired range.\n\n# Complexity\n- Time complexity: $O(\\min(s, r) n)$, where $n$ is the number of distinct values in the array, $s$ is the sum of all values, and $r$ is the right endpoint of the interval.\n\nDoing this naively, without taking advantage of multiplicity, as I tried during the contest, results in a factor that is the total number of values in the array, not just the number of distinct values. Such a solution will potentially be up to $100$ times slower than the above and will exceed the time limit.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(\\min(s, r))$.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countSubMultisets(self, nums: List[int], l: int, r: int) -> int:\n s=sum(nums)\n if l>s:\n return 0\n r=min(r, s)\n d=defaultdict(int)\n for n in nums:\n d[n]+=1\n lst=list(d.items())\n lst.sort(key=lambda x:-x[0])\n mult=1\n if lst[-1][0]==0:\n mult+=lst.pop()[1]\n p=10**9+7\n dct=[0]*(r+1)\n dct[0]=1\n for k, (n, m) in enumerate(lst):\n for cur in range(r-n+1):\n dct[cur+n]+=dct[cur]\n m=n*(m+1)\n for cur in range(r, m-1, -1):\n dct[cur]-=dct[cur-m]\n if k%20==0:\n for val in range(r+1):\n dct[val]%=p\n return sum(dct[val] for val in range(l, r+1))*mult%p\n``` | 1 | 0 | ['Python3'] | 0 |
count-of-sub-multisets-with-bounded-sum | Counting Sub-Multisets with a Given Sum Range | counting-sub-multisets-with-a-given-sum-ascdg | IntuitionThe problem involves counting the number of multisets (subsets with repetitions allowed) that sum up within a given range [𝑙,𝑟].We need to efficiently | kuldeepchaudhary123 | NORMAL | 2025-03-19T12:41:39.606696+00:00 | 2025-03-19T12:41:39.606696+00:00 | 4 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
The problem involves counting the number of multisets (subsets with repetitions allowed) that sum up within a given range [𝑙,𝑟].
We need to efficiently compute how many valid multisets exist that sum up to each value in this range.
Since the input can have duplicate elements, we need to ensure that each element is selected within its frequency limits.
A dynamic programming (DP) approach is suitable to efficiently compute the answer.
# Approach
<!-- Describe your approach to solving the problem. -->
1. Preprocessing:
Count frequencies of all numbers in a using freq[x].
Filter unique elements into array b, skipping zeros initially.
Let n = b.size() (number of unique nonzero elements).
2. DP Definition:
Let dp[i][j] represent the number of ways to form sum j using elements from index i onward in b.
Base Case: If j = 0, there's always one way (empty set).
Initialize dp[n][j] = 1 for all j since an empty set can form any j.
3. DP Transition:
Iterate from last element to first (i from n-1 to 0).
4. At each step:
Inherit previous state: dp[i][j] = dp[i+1][j].
Include element b[i] up to its frequency using the standard DP approach for bounded knapsack.
Use inclusion-exclusion to ensure elements are counted within limits.
5. Final Computation:
Compute dp[0][r] - dp[0][l-1] to count multisets within the range.
Multiply by (1 + freq[0]) to account for zero values (which can be included in any subset).
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
Preprocessing (frequency count & unique filtering): 𝑂(𝑛)
DP Table Computation:
Iterates over n elements and sums up to r, leading to 𝑂(𝑛⋅𝑟).
Final Computation: 𝑂(1).
Total Complexity: 𝑂(𝑛⋅𝑟), which is efficient for moderate constraints.
# Code
```cpp []
typedef long long ll;
typedef unsigned long long ull;
typedef vector<int> vi;
const int MOD = (int) 1e9 + 7;
template<ll mod = MOD>
struct mint {
ll x;
mint() : x(0) {}
mint(ll _x) {
_x %= mod;
if (_x < 0) _x += mod;
x = _x;
}
mint &operator+=(const mint &a) {
x += a.x;
if (x >= mod) x -= mod;
return *this;
}
mint &operator-=(const mint &a) {
x += mod - a.x;
if (x >= mod) x -= mod;
return *this;
}
mint &operator*=(const mint &a) {
x = (ull) x * a.x % mod;
return *this;
}
mint pow(ll pw) const {
mint res = 1;
mint cur = *this;
while (pw) {
if (pw & 1) res *= cur;
cur *= cur;
pw >>= 1;
}
return res;
}
mint inv() const {
assert(x != 0);
ll t = x;
ll res = 1;
while (t != 1) {
ll z = mod / t;
res = (ull) res * (mod - z) % mod;
t = mod - t * z;
}
return res;
}
mint &operator/=(const mint &a) {
return *this *= a.inv();
}
mint operator+(const mint &a) const {
return mint(*this) += a;
}
mint operator-(const mint &a) const {
return mint(*this) -= a;
}
mint operator*(const mint &a) const {
return mint(*this) *= a;
}
mint operator/(const mint &a) const {
return mint(*this) /= a;
}
bool operator==(const mint &a) const {
return x == a.x;
}
bool operator!=(const mint &a) const {
return x != a.x;
}
bool operator<(const mint &a) const {
return x < a.x;
}
friend ostream &operator<<(ostream &out, const mint &m) {
out << m.x;
return out;
}
};
using Mint = mint<MOD>;
class Solution {
public:
Mint dp[201][(int) 2e4 + 3];
int freq[(int) 2e4 + 3];
int countSubMultisets(vector<int>& a, int l, int r) {
vi b;
for (auto x: a) {
if (freq[x] == 0 && x != 0)
b.emplace_back(x);
freq[x]++;
}
int n = b.size();
for (int j = 0; j <= r; ++j)
dp[n][j] = 1;
for (int i = n-1; i >= 0; --i){
for (int j = 0; j <= r; ++j){
dp[i][j] = dp[i+1][j];
if (j-b[i] >= 0) {
dp[i][j] += dp[i][j - b[i]];
if (j-(freq[b[i]]+1)*b[i] >= 0)
dp[i][j] -= dp[i+1][j-(freq[b[i]]+1)*b[i]];
}
}
}
return ((dp[0][r] - (l-1 >= 0 ? dp[0][l-1] : 0))*(1+freq[0])).x;
}
};
``` | 0 | 0 | ['Dynamic Programming', 'Sliding Window', 'C++'] | 0 |
count-of-sub-multisets-with-bounded-sum | 2902. Count of Sub-Multisets With Bounded Sum | 2902-count-of-sub-multisets-with-bounded-vtfh | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | G8xd0QPqTy | NORMAL | 2025-01-21T16:27:30.990927+00:00 | 2025-01-21T16:27:30.990927+00:00 | 5 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def countSubMultisets(self, A: List[int], l: int, r: int) -> int:
MODULO = 10 ** 9 + 7
max_sum = 50000
ways = [1] + [0] * max_sum
element_counts = Counter(A)
for value, frequency in element_counts.items():
for target in range(r, max(r - value, 0), -1):
current_sum = sum(ways[target - value * multiplier] for multiplier in range(frequency))
for step in range(target, 0, -value):
current_sum -= ways[step] - ways[step - value * frequency]
ways[step] = (ways[step] + current_sum) % MODULO
total_count = (element_counts[0] + 1) * sum(ways[l:r + 1]) % MODULO
return total_count
``` | 0 | 0 | ['Python3'] | 0 |
count-of-sub-multisets-with-bounded-sum | ☕ Java solution | java-solution-by-barakamon-atr6 | null | Barakamon | NORMAL | 2025-01-11T09:54:11.782829+00:00 | 2025-01-11T09:54:11.782829+00:00 | 7 | false | 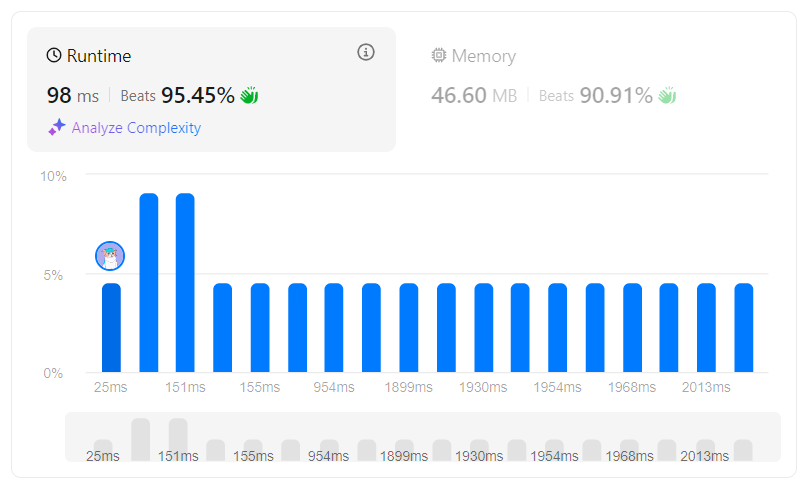
```java []
class Solution {
private static final int MOD = (int) 1e9 + 7;
public int countSubMultisets(List<Integer> nums, int l, int r) {
int[] numsArray = nums.stream().mapToInt(Integer::intValue).toArray();
return countSubMultisets(numsArray, l, r);
}
private int countSubMultisets(int[] nums, int l, int r) {
Map<Integer, Integer> freqMap = new HashMap<>();
for (int num : nums) {
freqMap.put(num, freqMap.getOrDefault(num, 0) + 1);
}
long[] dp = new long[r + 1];
dp[0] = 1;
for (Map.Entry<Integer, Integer> entry : freqMap.entrySet()) {
int num = entry.getKey();
int count = entry.getValue();
if (num == 0) {
dp[0] = (dp[0] + count) % MOD;
continue;
}
long[] prefix = Arrays.copyOf(dp, dp.length);
for (int i = num; i <= r; i++) {
prefix[i] = (prefix[i] + prefix[i - num]) % MOD;
}
for (int j = r; j >= 1; j--) {
int k = j - num * (count + 1);
if (k < 0) {
dp[j] = prefix[j];
} else {
dp[j] = (prefix[j] - prefix[k] + MOD) % MOD;
}
}
}
long result = 0;
for (int i = l; i <= r; i++) {
result = (result + dp[i]) % MOD;
}
return (int) result;
}
}
``` | 0 | 0 | ['Java'] | 0 |
count-of-sub-multisets-with-bounded-sum | Explained 38ms, beat 100% ; avoid tmp DP array for optimization | explained-38ms-beat-100-avoid-tmp-dp-arr-025q | IntuitionGroup identical numbers. Process each distinct number separately since total distinct numbers ≤ sqrt(sum). For each number, process all possible counts | ivangnilomedov | NORMAL | 2024-12-25T16:12:29.631802+00:00 | 2024-12-25T16:12:29.631802+00:00 | 7 | false | # Intuition
Group identical numbers. Process each distinct number separately since total distinct numbers ≤ sqrt(sum). For each number, process all possible counts (0 to max_count) using sliding window technique to group positions with same remainder efficiently.
# Approach
1. Group identical numbers and count occurrences
2. Handle zeros separately - multiply existing combinations by (count+1)
3. For each non-zero number:
- Process each remainder sequence using sliding window
- Window size = count+1 (all possible quantities of current number)
- Update dp array sum2count[i] = ways to make sum i
4. Return sum of combinations in range [l,r]
# Complexity
- Time complexity: $$O(N\sqrt{S} + R)$$ where N = nums.size(), S = sum(nums), R = r
- Sorting: O(N log N)
- Per distinct number: O(num * r/num) = O(r) for window operations
- Total distinct numbers ≤ sqrt(S)
- Space complexity: $$O(R)$$ for dp array sum2count
# Code
```cpp []
class Solution {
public:
int countSubMultisets(vector<int>& nums, int l, int r) {
vector<pair<int, int>> num_counts;
sort(nums.begin(), nums.end());
for (int i = 1, beg = 0; i <= nums.size(); ++i) {
if (i == nums.size() || nums[i] != nums[beg]) {
num_counts.emplace_back(nums[beg], i - beg);
beg = i;
}
}
vector<long long> sum2count(r + 1); // [i] number of ways to make sum i
sum2count[0] = 1;
int sum_lim = 0; // maximum possible sum achieved so far
for (const auto [num, count] : num_counts) {
if (num == 0) { // zero - handle separately, multoply count+1
for (long long& c : sum2count)
c *= count + 1;
continue;
}
// process each remainder mod num using sliding window
sum_lim = min(r, sum_lim + num * count);
for (int num_rem_offset = 0; num_rem_offset < num; ++num_rem_offset) {
long long window_sum = 0;
int q = sum_lim - num_rem_offset + num;
for (int i = 0; i <= count && q >= 0; ++i) { // initial window of size count+1
q -= num;
if (q < 0) break;
window_sum += sum2count[q];
}
for (int p = sum_lim - num_rem_offset; p >= 0 ; p -= num) { // slide window
long long up_count = window_sum % kMod; // allows to avoid tmp update_sum2count
window_sum -= sum2count[p]; // remove leftmost
sum2count[p] = up_count; // update current
q -= num;
if (q >= 0)
window_sum += sum2count[q]; // add rightmost
}
}
}
// sum range [l,r]
return (accumulate(sum2count.begin() + l, sum2count.end(), 0LL) % kMod + kMod) % kMod;
}
private:
static constexpr long long kMod = 1e9 + 7;
};
``` | 0 | 0 | ['C++'] | 0 |
count-of-sub-multisets-with-bounded-sum | Python, knapsack dp solution with explanation | python-knapsack-dp-solution-with-explana-vs3n | knapsack dp\nThe problem ask that how many ways to fill up [l, r]size of knapsacks,\nand if numbers are the same, there are the same items.\ndp[i][j] is number | shun6096tw | NORMAL | 2024-11-25T07:48:49.122317+00:00 | 2024-11-25T07:48:49.122348+00:00 | 7 | false | ### knapsack dp\nThe problem ask that how many ways to fill up ```[l, r]```size of knapsacks,\nand if numbers are the same, there are the same items.\ndp[i][j] is number of ways to fill up size j of knapsack.\nwe have ```y``` of number ```x```,\ndp[i][j] = dp[i-1][j] + dp[i-1][j-x] + dp[i-1][j-2x] + ... + dp[i-1][j-y*x].\n\nand j = j-x (mod x)= j-2x (mod x) = ... = j-y* x(mod x),\nwe can use prefix sum to get dp[i-1][j] + dp[i-1][j-x] + dp[i-1][j-2x] + ... + dp[i-1][j-y*x],\nFirst, calculate prefix sum of same remainder of x,\ndp[j] += dp[j-x],\nand we only have ```y``` of number ```x```,\nso, dp[j] - dp[j - (y + 1) * x].\n\ntc is O(r * number of distinct item in nums), sc is O(r).\n```python\nMOD = int(1e9+7)\nclass Solution:\n def countSubMultisets(self, nums: List[int], l: int, r: int) -> int:\n cnt = defaultdict(int)\n dp = [0] * (1 + r)\n dp[0] = 1\n for x in nums:\n if x == 0:\n dp[0] += 1\n elif x <= r:\n cnt[x] += 1\n for x, y in cnt.items():\n for j in range(x, 1 + r):\n dp[j] = (dp[j] + dp[j - x]) % MOD\n for j in range(r, (1 + y) * x - 1, -1):\n dp[j] = (dp[j] - dp[j - (y + 1) * x] + MOD) % MOD\n return reduce(lambda acc, x: (acc + dp[x]) % MOD, range(l, r+1), 0)\n```\n\n### optimization\n1. if sum of nums < l, return 0\n2. maximum size of knapsack is max(r, sum of nums) \n```python\nclass Solution:\n def countSubMultisets(self, nums: List[int], l: int, r: int) -> int:\n sum_ = 0\n cnt = defaultdict(int)\n for x in nums:\n if x <= r:\n cnt[x] += 1\n sum_ += x\n if l > sum_:\n return 0\n r = min(r, sum_)\n dp = [0] * (1 + r)\n dp[0] = 1 + cnt[0]\n del cnt[0]\n for x, y in cnt.items():\n for j in range(x, 1 + r):\n dp[j] = (dp[j] + dp[j - x]) % MOD\n for j in range(r, (1 + y) * x - 1, -1):\n dp[j] = (dp[j] - dp[j - (y + 1) * x] + MOD) % MOD\n return reduce(lambda acc, x: (acc + dp[x]) % MOD, range(l, r+1), 0)\n``` | 0 | 0 | ['Prefix Sum', 'Python'] | 0 |
count-of-sub-multisets-with-bounded-sum | easy implementation | easy-implementation-by-ani_vishwakarma-vo0m | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Ani_vishwakarma | NORMAL | 2024-10-24T09:48:27.136442+00:00 | 2024-10-24T09:48:27.136477+00:00 | 8 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\n#define ll long long\nconst int mod = 1e9 + 7;\n\nclass Solution {\npublic:\n \n int countSubMultisets(vector<int>& a, int l, int r) {\n vector<ll> dp(r + 1 , 0);\n \n unordered_map<int,int> mp;\n for(auto i : a) mp[i]++;\n dp[0] = ++mp[0];\n for(auto i : mp){\n if(i.first == 0) continue;\n for(int j = r; j >= 0; j--){\n if(dp[j]){\n for(int k = 1; k<= i.second; k++){\n if(j + k * i.first <= r) dp[j + k * i.first] = (dp[j] + dp[j + k * i.first]) % mod;\n }\n }\n }\n }\n ll ans = 0;\n for(int i = l; i<=r; i++) ans = (ans + dp[i]) % mod;\n return ans;\n }\n};\n``` | 0 | 0 | ['Dynamic Programming', 'C++'] | 0 |
count-of-sub-multisets-with-bounded-sum | Beginner Friendly Beats 90% | beginner-friendly-beats-90-by-l_u_c_a_s-h4ws | \n\n# Code\npython3 []\nfrom collections import Counter\nimport numpy as np\n\nclass Solution:\n def countSubMultisets(self, nums: List[int], l: int, r: int) | L_U_C_A_S | NORMAL | 2024-10-02T06:26:43.364384+00:00 | 2024-10-02T06:26:43.364409+00:00 | 9 | false | \n\n# Code\n```python3 []\nfrom collections import Counter\nimport numpy as np\n\nclass Solution:\n def countSubMultisets(self, nums: List[int], l: int, r: int) -> int:\n # Step 1: Define the modulo value for large numbers\n MOD = 10**9 + 7\n \n # Step 2: Count the frequency of each number in the nums list\n count = Counter(nums)\n \n # Step 3: Create a dynamic programming (dp) array to store intermediate results\n # We need an array with a size of \'r + 1\' to store the sum of different combinations\n dp = np.zeros(r + 1, dtype=np.int64)\n dp[0] = 1 # There\'s one way to make sum 0 (by choosing no elements)\n \n # Step 4: Iterate over each unique number in the count dictionary\n for num in count:\n if num == 0:\n continue # Skip the number 0 because it doesn\'t change the sum\n \n # Create a new dp array to store updated results after adding current number\n new_dp = np.array(dp)\n \n # Step 5: For each frequency of the current number, update the new dp array\n for i in range(1, count[num] + 1):\n # Update the new dp array for sums that can be made by adding the number \'num\' multiple times\n new_dp[num * i:] += dp[:-num * i]\n \n # Update the original dp array with the new values and apply the modulo to keep numbers manageable\n dp = new_dp % MOD\n \n # Step 6: Calculate the final result by summing up the valid combinations\n # We need to sum the dp values between \'l\' and \'r\' and account for how many times \'0\' appears in nums\n return (count[0] + 1) * sum(dp[l:r + 1]) % MOD\n\n``` | 0 | 0 | ['Python3'] | 0 |
count-of-sub-multisets-with-bounded-sum | Knapsack DP + Pack Update Trick (Sliding Window) | knapsack-dp-pack-update-trick-sliding-wi-n6co | Intuition\nKnapsack DP. See also lee215\'s solution.\n\n \u274C(Low to High) One approach is given a dp[j] > 0, update dp[j+i], dp[j+2i], ... dp[j+ci]. But this | outerridgesavage | NORMAL | 2024-08-20T05:18:31.956685+00:00 | 2024-08-20T05:20:46.499342+00:00 | 20 | false | # Intuition\nKnapsack DP. See also [lee215\'s solution](https://leetcode.com/problems/count-of-sub-multisets-with-bounded-sum/solutions/4168129/c-python-knapsack-dp/).\n\n* \u274C(Low to High) One approach is given a `dp[j] > 0`, update `dp[j+i]`, `dp[j+2i]`, ... `dp[j+ci]`. But this leads to $$O(nr\\mathrm{max}(c))$$ time where $n$ is the num of different numbers.\n* \u2705(High to Low) The other approach is to a "Pack Update Trick":\n $$\\mathrm{dp}_j+=\\mathrm{dp}_{j-i}+\\mathrm{dp}_{j-2i}+\\cdots+\\mathrm{dp}_{j-ci}$$\n $$\\mathrm{dp}_{j-i}+=\\mathrm{dp}_{j-2i}+\\cdots+\\mathrm{dp}_{j-ci}+\\mathrm{dp}_{j-(c+1)i}$$\n The "pack update" is a sliding window. This leads to $$O(n\\mathrm{max}(i)\\mathrm{max}(c))$$ time.\n\n\n# Approach\nConsider this sequence and update them from hi to lo:\n$$r-(c+1)i$$, $$r-ci$$, ..., $$r-2i$$, $$r-i$$, $$r$$.\n\nThen do the same for\n$$r-1-(c+1)i$$, $$r-1-ci$$, ..., $$r-1-2i$$, $$r-1-i$$, $$r-1$$.\n\nand so on.\n\n\n\n# Complexity\n- Time complexity: $$O(n\\mathrm{max}(i)\\mathrm{max}(c))$$\n- Space complexity: $$O(n+r)$$\n\n# Code\n```cpp []\nclass Solution {\npublic:\n using ll = long long;\n static constexpr ll M = 1\'000\'000\'007;\n static void Add(ll& x, ll y) { x = (x + y) % M; }\n int countSubMultisets(vector<int>& a, int l, int r) {\n vector<ll> dp(r + 1, 0);\n dp[0] = 1;\n unordered_map<int, int> s;\n for (int i : a) s[i]++;\n for (const auto [i, c] : s) {\n if (i == 0) continue;\n for (int j = r; j >= r-i+1; --j) {\n ll pack = 0;\n for (int k = 1; k <= c && j-k*i >= 0; ++k) {\n Add(pack, dp[j-k*i]);\n }\n for (int l = j; l-i >= 0; l -= i) {\n Add(dp[l], pack);\n for (pack -= dp[l-i]; pack < 0; pack += M);\n if (l-(c+1)*i >= 0) Add(pack, dp[l-(c+1)*i]);\n }\n }\n }\n ll ans = 0;\n for (int i = l; i <= r; ++i) {\n Add(ans, dp[i]);\n }\n return ans * (s[0] + 1) % M;\n }\n};\n```\n\n# Similar Problems\nTODO | 0 | 0 | ['Dynamic Programming', 'Sliding Window', 'C++'] | 0 |
count-of-sub-multisets-with-bounded-sum | [Python] Numpy-powered O(NR) code (Beats 90%) | python-numpy-powered-onr-code-beats-90-b-mmay | Approach\n Describe your approach to solving the problem. \nThanks to numpy that is optimized for vector computation, you can get AC with $O(NR)$ code. Actually | nakanolab | NORMAL | 2024-07-07T08:09:37.042470+00:00 | 2024-07-07T08:14:38.654296+00:00 | 13 | false | # Approach\n<!-- Describe your approach to solving the problem. -->\nThanks to numpy that is optimized for vector computation, you can get AC with $O(NR)$ code. Actually, it is pretty fast!\nAs an illustration, for `nums = [1, 3, 3]`, the code works as follows:\n- For `num = 1`, add a vector shifted right by 1 into `dp`.\n```\n+---------+-----+-----+-----+-----+-----+-----+-----+-----+-----+\n| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |\n+=========+=====+=====+=====+=====+=====+=====+=====+=====+=====+\n| dp | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |\n+---------+-----+-----+-----+-----+-----+-----+-----+-----+-----+\n| dp >> 1 | | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |\n+=========+=====+=====+=====+=====+=====+=====+=====+=====+=====+\n| result | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |\n+---------+-----+-----+-----+-----+-----+-----+-----+-----+-----+\n```\n- For 2 occurrences of `num = 3`, add vectors shifted right by 3 and 6 into `dp`.\n```\n+---------+-----+-----+-----+-----+-----+-----+-----+-----+-----+\n| index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |\n+=========+=====+=====+=====+=====+=====+=====+=====+=====+=====+\n| dp | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |\n+---------+-----+-----+-----+-----+-----+-----+-----+-----+-----+\n| dp >> 3 | | | | 1 | 1 | 0 | 0 | 0 | 0 |\n+---------+-----+-----+-----+-----+-----+-----+-----+-----+-----+\n| dp >> 6 | | | | | | | 1 | 1 | 0 |\n+=========+=====+=====+=====+=====+=====+=====+=====+=====+=====+\n| result | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 |\n+---------+-----+-----+-----+-----+-----+-----+-----+-----+-----+\n```\n\n# Complexity\n- Time complexity: $O(NR)$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(N + R)$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfrom collections import Counter\nimport numpy as np\n\nclass Solution:\n def countSubMultisets(self, nums: List[int], l: int, r: int) -> int:\n mod = 10**9 + 7\n count = Counter(nums)\n dp = np.zeros(r + 1, dtype=np.int64)\n dp[0] = 1\n for num in count:\n if num == 0:\n continue\n dpnew = np.array(dp)\n for i in range(1, count[num] + 1):\n dpnew[num*i:] += dp[:-num*i]\n dp = dpnew % mod\n return (count[0] + 1) * sum(dp[l:r+1]) % mod\n``` | 0 | 0 | ['Python3'] | 0 |
count-of-sub-multisets-with-bounded-sum | JAVA SOLUTION | java-solution-by-danish_jamil-xmgr | Intuition\n\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Tim | Danish_Jamil | NORMAL | 2024-06-29T06:11:30.109778+00:00 | 2024-06-29T06:11:30.109810+00:00 | 9 | false | # Intuition\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n static final int MOD = 1_000_000_007;\n int l, r, n;\n int calc(Integer[][] dp, int[][] countArr, int idx, int sum) {\n if (sum > r) {\n return 0;\n }\n if (idx == n) {\n if (sum >= l && sum <= r) {\n return 1; \n }\n return 0;\n }\n if (dp[idx][sum] != null) {\n return dp[idx][sum];\n }\n int res = 0;\n int currNum = countArr[idx][0];\n int currCount = countArr[idx][1];\n int currSum = sum;\n for (int i = 0; i <= currCount; i++) {\n res = (res + calc(dp, countArr, idx + 1, currSum)) % MOD;\n currSum += currNum;\n }\n dp[idx][sum] = res;\n return res;\n }\n public int countSubMultisets(List<Integer> nums, int l, int r) {\n this.l = l;\n this.r = r;\n Map<Integer, Integer> count = new HashMap<>();\n for (int num : nums) {\n if (num <= r) {\n count.put(num, count.getOrDefault(num, 0) + 1);\n }\n }\n n = count.size();\n int i = 0;\n int[][] countArr = new int[n][2];\n for (Map.Entry<Integer, Integer> e : count.entrySet()) {\n countArr[i][0] = e.getKey();\n countArr[i][1] = e.getValue();\n i++;\n }\n Integer[][] dp = new Integer[n + 1][r + 1];\n return calc(dp, countArr, 0, 0);\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
count-of-sub-multisets-with-bounded-sum | Thought process explained for interview. (C++) | thought-process-explained-for-interview-2j7c4 | Observations:\n- Order of number matter here, because 1,2,1 is same as 1,1,2. So we don\'t want duplicates.\n- For a particular number num, we can either take 1 | aaditya-pal | NORMAL | 2024-06-18T06:39:44.595834+00:00 | 2024-06-18T06:39:44.595865+00:00 | 40 | false | Observations:\n- Order of number matter here, because 1,2,1 is same as 1,1,2. So we don\'t want duplicates.\n- For a particular number num, we can either take 1 times, 2 times... frequency[num] times.\n- What if the required problem was to get ans for a particular sum.\n- It would be coin change problem, where order matters.\n- Let dp[i] = Answer for sum i\n- Since order of number matter here, the transition would be, we want to calculate all possible sum that we can make from a particular number *num* (including multple times). So for that we would need the frequencey of that number too.\n- The transition would be like this\n```\nfor(auto &c : coins){\n int num = c.first;\n int freq = c.second;\n //Calculate all possibile sum that we could make from a particular number num\n\n //Iterate over the sum\n for(int sum = r;sum>=0;sum--){\n\n //Iterate over all the numbers that we can make from num.\n for(int f = 1;f<=k;f++){\n if(sum - f*num>=0)\n dp[sum]+=dp[sum - f*num];\n }\n }\n}\n```\nWhy are traversing from r to 0 and not from 0 to r?\nNo one would tell you that! But the intuition behind is that, we have limited supply of each number. So we want to calculate all the sum that we have made without the use of the number num. When we are calculating from 0 to r, what happens let me explain with an example.\n\nLets suppose num = 3 with a frequencey of 1\nAnd we update dp[6] += dp[6-3]\nif dp[3] = 2, then dp[6] would be 2 (assumption) and we have used the number 3 here.\n\nNow when we calculate dp[9], we would do dp[9-3] which is dp[6]. But in dp[6] contains the answer to make 6 including the number 3(our num). But we have already used that number 3 in making 6. So, how are we calculating to do that for 9?\n\nBut we we first calculate for 9\ndp[9] += dp[6]. Now dp[6] contains the answer without using 3.\nThen we calculate dp[6].\nand so on.\nGot the point?\n\n***Now,what is the time complexity of this?\nO(c*r*f)***\nc can be upto 200 because sum of n is 40000. If we take each element unique,then we have 1 + 2 + 3 ... last = 40000. last(last+1)/2 = 40000.\nLast is approxamitely 200.\n\nBut f could be large. So we need to reduce f right?\n\n### How are we doing to do that?\n\nI initially got confused about this. Here is a beautiful implementation of prefix sum.\nSee in this loop what we are doning?\n```\n for(int sum = r;sum>=0;sum--){\n\n //Iterate over all the numbers that we can make from num.\n for(int f = 1;f<=k;f++){\n if(sum - f*num>=0)\n dp[sum]+=dp[sum - f*num];\n }\n }\n```\n\nIf we write for each sum \ndp[sum] = dp[sum - num] + dp[sum - 2*num] + dp[sum - 3*num]....\nLets see example, assume num = 3\nThen what would be dp[10]? It will be dp[7] + dp[4] + dp[1]...\nWhat would be dp[15]? It would be dp[12] + dp[9] + dp[6]..\nSee the intervals? 1 4 7 10 13...\nNext is 2 5 8 11 14 17\nNext is 3 6 9 12 15....\n\nLets create the prefix for interval 3 6 9 12 15\nNow lets assume the frequency of element 3 is 2\nWhat would be my ans?\ndp[15] = dp[12] + dp[9]\nCan we say that it is prefix[12] - prefix[6]?\nOr prefix[15] - prefix[15 - (3 * 3)]\n\n*Or prefix[sum] - prefix[sum - (freq + 1) * num];*\n\nNext how do we create the prefix array?\nSimple\n```\nprefix = dp;\nfor(int i = 0;i<=r;i++){\n prefix[i]+=prefix[i-num];\n}\n```\n\nNow our code becomes\n```\n for(auto &i : m){\n if(i.first==0){\n dp[0]+=i.second;\n continue;\n }\n long long ele = i.first,c = i.second;\n vector<long long>prefix = dp;\n for(int i = 0;i<=r;i++){\n if(i-ele>=0){\n prefix[i]+=prefix[i-ele];\n }\n }\n for(int j = r;j>=1;j--){\n int k = j - ele * (c+1);\n if(k<0) dp[j] = prefix[j];\n else dp[j] = prefix[j] - prefix[k];\n }\n\n }\n\n```\nJust add the mod.\n\nOur final answer becomes dp[l] + dp[l+1]..dp[r].\nWe successfully removed the f factor from the code. \n\n\n# Code\n```\nclass Solution {\npublic:\n const int mod = 1e9 + 7;\n //For all the sum\n int countSubMultisets(vector<int>& nums, int l, int r) {\n map<int,int>m;\n for(auto &i : nums) m[i]++;\n vector<long long>dp(r+1,0);\n dp[0] = 1;\n for(auto &i : m){\n if(i.first==0){\n dp[0]+=i.second%mod;\n continue;\n }\n long long ele = i.first,c = i.second;\n vector<long long>prefix = dp;\n for(int i = 0;i<=r;i++){\n if(i-ele>=0){\n prefix[i]+=prefix[i-ele]%mod;\n prefix[i]%=mod;\n }\n }\n for(int j = r;j>=1;j--){\n int k = j - ele * (c+1);\n if(k<0) dp[j] = prefix[j];\n else dp[j] = prefix[j] - prefix[k];\n dp[j]+=mod;\n dp[j]%=mod;\n }\n\n }\n long int ans = 0;\n for(int i = l;i<=r;i++){\n ans+=dp[i];\n ans%=mod;\n }\n return ans;\n }\n \n};\n``` | 0 | 0 | ['C++'] | 0 |
count-of-sub-multisets-with-bounded-sum | Alternative Fast Fourier Transform solution | alternative-fast-fourier-transform-solut-3937 | Intuition\nWe can use the Fast Fourier Transform (FFT) to determine the number of multisets having sum $k$ for all $k$ simultaneously by encoding the Knapsack p | mishai | NORMAL | 2024-06-13T18:24:45.261616+00:00 | 2024-06-13T18:24:45.261647+00:00 | 2 | false | # Intuition\nWe can use the [Fast Fourier Transform (FFT)](https://en.wikipedia.org/wiki/Fast_Fourier_transform) to determine the number of multisets having sum $k$ for all $k$ simultaneously by encoding the Knapsack problem as one of polynomial multiplication.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSuppose the (deduped) entries of `nums` are $k_1, k_2, \\ldots, k_s$ with occurrences $v_1, v_2, \\ldots, v_s$. Then, consider the polynomial $$f(x) = \\prod_{i=1}^{s}\\left(\\sum_{j=0}^{v_i} x^{k_i\\cdot j}\\right)$$. We claim that the coefficient of $x^i$ in this polynomial is exactly the number of ways to form a multiset summing to $i$: indeed, this comes from expanding the polynomial.\n\nTo actually compute this polynomial, we use the Fast Fourier Transform, which when applied to two polynomials of degree $a$ and $b$ takes time $O((a + b)\\log(a + b))$ to compute their product. To make sure we don\'t accidentally multiply the highest degree polynomial over and over, we use the [Huffman Coding](https://en.wikipedia.org/wiki/Huffman_coding#Compression) priority queue idea to multiply the two polynomials of smallest degree at each iteration. Since the total degree of the final polynomial $f(x)$ is $m$, this takes time $O(m\\log^2 m)$ (it\'s possible this bound is too loose). To simulate the priority queue, we need $O(n\\log n)$ time giving the full bound.\n\n# Complexity\n- Time complexity:\nLet $m$ be the sum of all entries. Then, the runtime is $O(n\\log n + m\\log^2 m)$.\n\n- Space complexity:\nThe space complexity is $O(m + n)$.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nusing ll = long long;\nusing ld = long double;\nusing pii = pair<int, int>;\nusing vi = vector<int>;\n#define rep(i, a, b) for(int i = a; i < (b); ++i)\n#define all(x) begin(x), end(x)\n#define sz(x) (int)(x).size()\n#define smx(a, b) a = max(a, b);\n#define smn(a, b) a = min(a, b);\n#define pb push_back\n#define endl \'\\n\'\n\nconst ll MOD = 1e9 + 7;\n\ntypedef complex<double> C;\ntypedef vector<double> vd;\nvoid fft(vector<C>& a) {\n\tint n = sz(a), L = 31 - __builtin_clz(n);\n\tstatic vector<complex<long double>> R(2, 1);\n\tstatic vector<C> rt(2, 1); // (^ 10% faster if double)\n\tfor (static int k = 2; k < n; k *= 2) {\n\t\tR.resize(n); rt.resize(n);\n\t\tauto x = polar(1.0L, acos(-1.0L) / k);\n\t\trep(i,k,2*k) rt[i] = R[i] = i&1 ? R[i/2] * x : R[i/2];\n\t}\n\tvi rev(n);\n\trep(i,0,n) rev[i] = (rev[i / 2] | (i & 1) << L) / 2;\n\trep(i,0,n) if (i < rev[i]) swap(a[i], a[rev[i]]);\n\tfor (int k = 1; k < n; k *= 2)\n\t\tfor (int i = 0; i < n; i += 2 * k) rep(j,0,k) {\n\t\t\t// C z = rt[j+k] * a[i+j+k]; // (25% faster if hand-rolled) /// include-line\n\t\t\tauto x = (double *)&rt[j+k], y = (double *)&a[i+j+k]; /// exclude-line\n\t\t\tC z(x[0]*y[0] - x[1]*y[1], x[0]*y[1] + x[1]*y[0]); /// exclude-line\n\t\t\ta[i + j + k] = a[i + j] - z;\n\t\t\ta[i + j] += z;\n\t\t}\n}\n\ntypedef vector<ll> vl;\ntemplate<int M> vl convMod(const vl &a, const vl &b) {\n\tif (a.empty() || b.empty()) return {};\n\tvl res(sz(a) + sz(b) - 1);\n\tint B=32-__builtin_clz(sz(res)), n=1<<B, cut=int(sqrt(M));\n\tvector<C> L(n), R(n), outs(n), outl(n);\n\trep(i,0,sz(a)) L[i] = C((int)a[i] / cut, (int)a[i] % cut);\n\trep(i,0,sz(b)) R[i] = C((int)b[i] / cut, (int)b[i] % cut);\n\tfft(L), fft(R);\n\trep(i,0,n) {\n\t\tint j = -i & (n - 1);\n\t\toutl[j] = (L[i] + conj(L[j])) * R[i] / (2.0 * n);\n\t\touts[j] = (L[i] - conj(L[j])) * R[i] / (2.0 * n) / 1i;\n\t}\n\tfft(outl), fft(outs);\n\trep(i,0,sz(res)) {\n\t\tll av = ll(real(outl[i])+.5), cv = ll(imag(outs[i])+.5);\n\t\tll bv = ll(imag(outl[i])+.5) + ll(real(outs[i])+.5);\n\t\tres[i] = ((av % M * cut + bv) % M * cut + cv) % M;\n\t}\n\treturn res;\n}\n\nclass Solution {\npublic:\n int countSubMultisets(vector<int>& nums, int l, int r) {\n map<int, int> occ;\n for (auto x : nums) {\n occ[x]++;\n }\n vector<vector<ll>> polys;\n for (auto [k, v] : occ) {\n vector<ll> poly(k * v + 1);\n for (int r = 0; r <= v; r++) {\n poly[k * r]++;\n }\n polys.push_back(poly);\n }\n\n priority_queue<pii, vector<pii>, greater<>> pq;\n for (int i = 0; i < polys.size(); i++) {\n pq.push({polys[i].size(), i});\n }\n while (pq.size() > 1) {\n auto [d1, i1] = pq.top(); pq.pop();\n auto [d2, i2] = pq.top(); pq.pop();\n pq.push({d1 + d2 - 1, polys.size()});\n polys.push_back(convMod<MOD>(polys[i1], polys[i2]));\n }\n\n ll ans = 0;\n\n for (int i = l; i <= min(r, sz(polys.back()) - 1); i++) {\n ans = (ans + polys.back()[i]) % MOD;\n }\n\n return ans;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
count-of-sub-multisets-with-bounded-sum | Beasts 100% users || JS || Fully explained | beasts-100-users-js-fully-explained-by-a-sqvf | \n# Code\n\nlet MOD = 1000000007; // Define the modulo value\nlet sumsMapPre = Array(20001).fill(0); // Initialize an array to store the prefix sum counts\nlet | aastha_b | NORMAL | 2024-04-19T20:08:04.400481+00:00 | 2024-04-19T20:10:09.051495+00:00 | 6 | false | \n# Code\n```\nlet MOD = 1000000007; // Define the modulo value\nlet sumsMapPre = Array(20001).fill(0); // Initialize an array to store the prefix sum counts\nlet sumsMapCur = Array(20001).fill(0); // Initialize an array to store the current sum counts\nlet sumsArr = Array(20001).fill(0); // Initialize an array to store the sums\n\n/**\n * Function to count the number of sub-multisets in a given range.\n * @param {number[]} nums - The array of numbers.\n * @param {number} l - The left bound of the range.\n * @param {number} r - The right bound of the range.\n * @return {number} - The count of sub-multisets in the specified range.\n */\nvar countSubMultisets = function(nums, l, r) {\n let n = nums.length; // Get the length of the input array\n nums.sort(); // Sort the input array\n \n // Initialize the prefix sum arrays and variables\n sumsMapCur.fill(0);\n sumsMapPre.fill(0);\n sumsMapCur[0] = 1;\n let t = 0;\n let tt = 0;\n\n let acc = 0; // Initialize an accumulator variable\n \n // Iterate through the numbers in the input array\n for (let i = 0; i < n; i++) {\n if (nums[i] == nums[i - 1]) acc += nums[i]; // Accumulate the sum if the current number is the same as the previous one\n else {\n tt = t; // Update the temporary variable tt\n acc = nums[i]; // Update the accumulator variable\n\t \n // Update the sumsMapPre and sumsMapCur arrays\n for (let j = t; j >= 0; j--) {\n sumsMapPre[sumsArr[j]] = (sumsMapCur[sumsArr[j]] + sumsMapPre[sumsArr[j]]) % MOD;\n sumsMapCur[sumsArr[j]] = 0;\n }\n }\n\n // Calculate the counts of sub-multisets for each sum\n for (let j = tt; j >= 0; j--) {\n let newSum = sumsArr[j] + acc; // Calculate the new sum\n if (newSum <= r) {\n if (!sumsMapCur[newSum] && !sumsMapPre[newSum]) {\n sumsArr[++t] = newSum; // Store the new sum in the sumsArr array\n }\n\n // Update the counts in sumsMapCur\n let cnt = (sumsMapPre[sumsArr[j]] + sumsMapCur[newSum]) % MOD;\n sumsMapCur[newSum] = cnt;\n }\n }\n }\n\n let res = 0; // Initialize the result variable\n // Calculate the final result by summing the counts within the specified range\n for (let i = l; i <= r; i++) {\n res = (res + sumsMapPre[i] + sumsMapCur[i] ?? 0) % MOD;\n }\n\n return res; // Return the final result\n};\n\n``` | 0 | 0 | ['JavaScript'] | 0 |
count-of-sub-multisets-with-bounded-sum | Recursion->Memo->DP, not best solution, no explanation. | recursion-memo-dp-not-best-solution-no-e-q7m3 | Intuition\nIn order to understand DP better for DP newbie :)\n\n# Recursion (TLE)\n\nclass Solution {\n int mod = 1_0000_0000_7;\n public int countSubMult | jon371449 | NORMAL | 2024-04-11T17:04:14.076066+00:00 | 2024-04-11T17:04:14.076101+00:00 | 43 | false | # Intuition\nIn order to understand DP better for DP newbie :)\n\n# Recursion (TLE)\n```\nclass Solution {\n int mod = 1_0000_0000_7;\n public int countSubMultisets(List<Integer> nums, int l, int r) {\n Map<Integer, Integer> map = new HashMap<>();\n for (int num : nums) {\n map.put(num, map.getOrDefault(num, 0) + 1);\n }\n List<Pair<Integer, Integer>> list = new ArrayList<>();\n for (int key : map.keySet()) {\n list.add(new Pair<>(key, map.get(key)));\n }\n \n return helper(l, r, 0, list, 0);\n }\n\n int helper(int l, int r, int sum, List<Pair<Integer, Integer>> list, int index) {\n if (index >= list.size()) return l <= sum && sum <= r ? 1 : 0;\n Pair<Integer, Integer> pair = list.get(index);\n int key = pair.getKey(), val = pair.getValue();\n int res = 0;\n for (int j = 0; j <= val; j++) {\n res = (res + helper(l, r, sum + j*key, list, index+1)) % mod;\n }\n return res;\n }\n}\n```\n\n# Memo (Pass)\n```\nclass Solution {\n int mod = 1_0000_0000_7;\n public int countSubMultisets(List<Integer> nums, int l, int r) {\n Map<Integer, Integer> map = new HashMap<>();\n int sum = 0;\n for (int num : nums) {\n map.put(num, map.getOrDefault(num, 0) + 1);\n sum += num;\n }\n List<Pair<Integer, Integer>> list = new ArrayList<>();\n for (int key : map.keySet()) {\n list.add(new Pair<>(key, map.get(key)));\n }\n \n Integer[][] memo = new Integer[list.size()][sum+1];\n return helper(l, r, 0, list, 0, memo);\n }\n\n int helper(int l, int r, int sum, List<Pair<Integer, Integer>> list, int index, Integer[][]memo) {\n if (sum > r) return 0;\n if (index >= list.size()) return sum >= l && sum <= r ? 1 : 0;\n if(memo[index][sum] != null) return memo[index][sum];\n Pair<Integer, Integer> pair = list.get(index);\n int key = pair.getKey(), val = pair.getValue();\n int res = 0;\n for (int j = 0; j <= val; j++) {\n res = (res + helper(l, r, sum + j * key, list, index + 1, memo)) % mod;\n }\n return memo[index][sum] = res;\n }\n}\n```\n\n# DP, knapsack (TLE)\n```\nclass Solution {\n public int countSubMultisets(List<Integer> nums, int l, int r) {\n int mod = 1_0000_0000_7;\n Map<Integer, Integer> map = new HashMap<>();\n for (int num : nums) {\n map.put(num, map.getOrDefault(num, 0) + 1);\n }\n List<Pair<Integer, Integer>> list = new ArrayList<>();\n for (int key : map.keySet()) {\n list.add(new Pair<>(key, map.get(key)));\n }\n \n int[][] dp = new int[list.size()+1][r+1];\n dp[0][0] = 1;\n for(int i = 1; i <= list.size(); i++){\n Pair<Integer, Integer> pair = list.get(i-1);\n int key = pair.getKey(), val = pair.getValue();\n for(int j = 0; j <= r; j++){\n for(int k = 0; k <= val; k++){\n if(j - k*key >= 0) dp[i][j] = (dp[i][j] + dp[i-1][j-k*key]) % mod;\n }\n }\n }\n int res = 0;\n for(int i = l; i <= r; i++){\n res = (res + dp[list.size()][i]) % mod;\n }\n return res;\n }\n}\n``` | 0 | 0 | ['Dynamic Programming', 'Recursion', 'Memoization', 'Java'] | 0 |
count-of-sub-multisets-with-bounded-sum | Solution Like Never Before | solution-like-never-before-by-gp_777-gguc | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | GP_777 | NORMAL | 2024-04-07T14:29:11.964543+00:00 | 2024-04-07T14:29:11.964568+00:00 | 14 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n static final int MOD = 1_000_000_007;\n\n public int countSubMultisets(List<Integer> nums, int l, int r) {\n TreeMap<Integer, Integer> numsMap = new TreeMap<>();\n for (int num : nums) {\n numsMap.put(num, numsMap.getOrDefault(num, 0) + 1);\n }\n\n long[] cache = new long[r + 1];\n cache[0] = 1;\n\n for (Map.Entry<Integer, Integer> entry : numsMap.entrySet()) {\n int num = entry.getKey();\n int freq = entry.getValue();\n\n // preprocessing\n long[] pSum = Arrays.copyOf(cache, r + 1);\n for (int i = 0; i <= r; ++i) {\n if (i >= num) {\n pSum[i] += pSum[i - num];\n pSum[i] %= MOD;\n }\n }\n\n // update dp cache\n for (int i = r; i >= 0; --i) {\n if (num > 0) {\n int j = i - (freq + 1) * num;\n cache[i] = pSum[i] - (j >= 0 ? pSum[j] : 0);\n cache[i] = Math.floorMod(cache[i], MOD);\n } else {\n cache[i] *= freq + 1;\n cache[i] %= MOD;\n }\n }\n }\n\n long res = 0;\n for (int i = l; i <= r; ++i) {\n res += cache[i];\n res %= MOD;\n }\n return (int) res;\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
count-of-sub-multisets-with-bounded-sum | Python numpy solution. Simple logic without tricks | python-numpy-solution-simple-logic-witho-aimo | Intuition\nIdea is knapsack using dynamic programming. In normal knapsack we need to iterate through each number and either add it to the set, or not. Here, mul | omikad | NORMAL | 2024-03-29T20:43:43.997109+00:00 | 2024-03-29T20:51:23.277509+00:00 | 12 | false | # Intuition\nIdea is knapsack using dynamic programming. In normal knapsack we need to iterate through each number and either add it to the set, or not. Here, multiset definition makes us to use Counter first, to compress numbers with their frequences.\n\n\n# Approach\n\n`DP[i, sm]` is a number of ways to get a sum `sm` using first `(i+1)` items from the counter.\n\nEach `DP[i, :]` depends only on `DP[i - 1, :]` - so we need to have only two of those at the same time in memory. I called them `DP` for the previous `i` and `NewDP` for the new `i`\n\n# Complexity\n- Time complexity: $$O(n*m)$$\n\n- Space complexity: $$O(n + m)$$\n\n# Code\n```\nfrom collections import Counter\nimport numpy as np\n\nMOD = int(1e9 + 7)\n\nclass Solution:\n def countSubMultisets(self, nums: List[int], l: int, r: int) -> int:\n\n # Replace nums to distinct values and their frequences\n C = Counter(nums)\n\n # DP[x] is a number of valid multisets to get sum of x\n DP = np.zeros(r + 1, np.int64)\n DP[0] = 1\n\n for x, cnt in C.items():\n if x == 0:\n # Easy case, we can take any number of x from 0 to cnt, without changing the sum\n DP = DP * (cnt + 1) % MOD\n\n else:\n # We could ignore x completely\n NewDP = np.copy(DP)\n\n # Or add x few times: from 1 to cnt\n # Then new sum will be old sum + i*x\n for shift in range(x, min(r, x * cnt) + 1, x):\n NewDP[shift:] += DP[:-shift]\n\n # Replace old DP array with the new\n DP = NewDP % MOD\n\n # Need to return only for the l..r range sums\n return DP[l:].sum() % MOD\n``` | 0 | 0 | ['Python3'] | 0 |
count-of-sub-multisets-with-bounded-sum | Python AC | python-ac-by-anonymous_k-s7ky | Intuition\n Describe your first thoughts on how to solve this problem. \nWhat are the options for an element \'a\', it can be selected from [0, c[a]] times.\nSi | anonymous_k | NORMAL | 2024-03-02T11:41:16.294668+00:00 | 2024-03-02T11:41:16.294699+00:00 | 20 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWhat are the options for an element \'a\', it can be selected from [0, c[a]] times.\nSimple DP is giving TLE, others have mentioned a logic to turn internal linear time options logic to constant time.\nWrite down f(i, s) and f(i, s+a), get f(i, s+a) in terms of f(i, s), substitute s+a with s.\nf(i, s) = f(i+1, s) + f(i, s-nums[i]) + f(i+1, s-(c[nums[i]]+1)*nums[i]) \nConsider zero cases separately otherwise inf recursion cause of f(i, s-nums[i]). zeros can be added to any subset, you can add [0, c[0]] to all the subsets.\n\n# Code\n```\nclass Solution:\n def countSubMultisets(self, nums: List[int], l: int, r: int) -> int:\n numsCount = {}\n zeroCount = 0\n\n for num in nums:\n if num == 0:\n zeroCount += 1\n else:\n if num not in numsCount:\n numsCount[num] = 1\n else:\n numsCount[num] += 1\n numsList = list(numsCount.keys())\n dp = [[-1 for j in range(20001)] for i in range(len(numsList))]\n m = 1000000007\n \n def countSubMultisetsRec(idx: int, s: int) -> int:\n if s < 0:\n return 0\n if idx == len(numsList):\n return 1\n if dp[idx][s] != -1:\n return dp[idx][s]\n \n ans = 0\n nextIdx = idx + 1\n maxCount = numsCount[numsList[idx]]\n ans = (countSubMultisetsRec(nextIdx, s) + countSubMultisetsRec(idx, s - numsList[idx]) - countSubMultisetsRec(nextIdx, s - (maxCount + 1) * numsList[idx]) + m) % m\n dp[idx][s] = ans\n return ans\n \n ans = 0\n ans = (countSubMultisetsRec(0, r) - countSubMultisetsRec(0, l - 1) + m) % m\n return (ans * (zeroCount + 1)) % m\n``` | 0 | 0 | ['Python3'] | 1 |
count-of-sub-multisets-with-bounded-sum | C++ DP solution, I think pretty standard one. | c-dp-solution-i-think-pretty-standard-on-zbq9 | Intuition\nI first thought of too brute method.\n\n# Approach\nWith sort of brute-force method I passed all but ~15 samples.\nWhen I realized I don\'t know how | ohennel667 | NORMAL | 2024-02-01T08:07:11.532489+00:00 | 2024-02-01T08:07:11.532520+00:00 | 19 | false | # Intuition\nI first thought of too brute method.\n\n# Approach\nWith sort of brute-force method I passed all but ~15 samples.\nWhen I realized I don\'t know how to improve it further, I tried to think of completely different approach (DP).\n\n# Complexity\n- Time complexity: did not evaluate.\n\n- Space complexity: O(n).\n\n# Code\n```\n#include <algorithm>\n#include <vector>\n#include <array>\n#include <set>\nusing namespace std;\n\n// 643/643 testcases passed, 1570ms, 42MB\n\n#define MAXNUM 20000\n#define MODULUS 1000000007\n\nstruct ValueAndCount\n{\n int value;\n int count;\n int product;\n\n ValueAndCount(int a_value, int a_count, int a_product) : value(a_value), count(a_count), product(a_product)\n {\n }\n\n bool operator<(const ValueAndCount& o) const\n {\n int dproduct = product - o.product;\n if (dproduct) return dproduct < 0; // azeby si\u0119 jak najwolniej rozje\u017Cd\u017Ca\u0142o\n return value < o.value;\n }\n};\n\nlong long sums[2][1 + MAXNUM];\nset<ValueAndCount> nextValueAndCount;\n\nclass Solution\n{\npublic:\n static int countSubMultisets(vector<int>& a_nums, int a_lowSum, int a_highSum);\n};\n\nint Solution::countSubMultisets(vector<int>& a_nums, int a_lowSum, int a_highSum)\n{\n std::sort(a_nums.begin(), a_nums.end(), [](int a, int b) {return a > b; });\n\n nextValueAndCount.clear();\n int thisValue = a_nums[0];\n int thisIndex = 0;\n int howManyLeft = 0;\n int c, vc;\n for (int curIndex = 1; curIndex < a_nums.size(); curIndex++)\n {\n if (a_nums[curIndex] != thisValue)\n {\n c = curIndex - thisIndex;\n vc = thisValue * c;\n nextValueAndCount.emplace(thisValue,c,vc);\n howManyLeft += vc;\n thisValue = a_nums[curIndex];\n thisIndex = curIndex;\n }\n }\n c = (int)a_nums.size() - thisIndex;\n vc = thisValue * c;\n nextValueAndCount.emplace(thisValue, c, vc);\n howManyLeft += vc;\n\n int currIdx = 0;\n int prevIdx = 1;\n\n sums[prevIdx][0] = 1;\n int highSumAvail = 0;\n\n for (const auto& valueAndCount : nextValueAndCount)\n {\n // warto\u015B\u0107 howManyLeft m\xF3wi o tym, ile jeszcze sumy maksymalnie mog\u0105 si\u0119 zwiekszy\u0107\n // poniewa\u017C jeste\u015Bmy zainteresowani zakresem od a_lowSum, to w prevIdx jest sens siega\u0107 nie od 0 a od a_lowSum-howManyLeft\n int minOldValue = max(0, a_lowSum - howManyLeft);\n if (minOldValue > highSumAvail)\n {\n currIdx = 1 - currIdx;\n prevIdx = 1 - prevIdx;\n break;\n }\n\n const auto& v = valueAndCount.value;\n const auto& c = valueAndCount.count;\n const auto& vc = valueAndCount.product;\n\n if (v == 0)\n {\n for (int oldValue = minOldValue; oldValue <= highSumAvail; oldValue++)\n {\n sums[currIdx][oldValue] = sums[prevIdx][oldValue] ? ((1 + c) * sums[prevIdx][oldValue]) % MODULUS : 0;\n }\n }\n else\n {\n int oldValue;\n if (highSumAvail < a_highSum)\n {\n oldValue = 1 + highSumAvail;\n highSumAvail = min(highSumAvail + vc, a_highSum);\n while (oldValue <= highSumAvail)\n {\n sums[prevIdx][oldValue] = 0;\n oldValue++;\n }\n }\n\n int m, newValue;\n long long temp;\n for (newValue = 0; newValue <= highSumAvail; newValue++)\n {\n temp = 0;\n for (m = c, oldValue = newValue; oldValue >= minOldValue && m >= 0; m--, oldValue -= v)\n {\n temp += sums[prevIdx][oldValue];\n }\n sums[currIdx][newValue] = temp ? (temp % MODULUS) : 0;\n }\n }\n\n howManyLeft -= vc;\n currIdx = 1 - currIdx;\n prevIdx = 1 - prevIdx;\n }\n\n long long answ = 0;\n for (int sum = a_lowSum; sum <= highSumAvail; sum++)\n {\n answ += sums[prevIdx][sum];\n }\n answ %= MODULUS;\n\n return (int)answ;\n}\n\n``` | 0 | 0 | ['C++'] | 0 |
count-of-sub-multisets-with-bounded-sum | 13-Line Solution with DP in Python | 13-line-solution-with-dp-in-python-by-me-lv9o | Intuition\n Describe your first thoughts on how to solve this problem. \nNaive $O(NM)$ DP is too slow for the test size. However, the size of distinct numbers i | metaphysicalist | NORMAL | 2024-01-27T18:21:09.221822+00:00 | 2024-01-27T18:21:09.221849+00:00 | 49 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nNaive $O(NM)$ DP is too slow for the test size. However, the size of distinct numbers is up to $O(\\sqrt{N})$ only, so we try to find a DP solution that adds each distinct number in $O(N)$. As a result, the overall complexity is $O(N\\sqrt{N}) = O(N^{1.5})$, which is fast enough for passing the test cases. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nLet $S(i, j)$ is the ways to make a summation of $j$ with the distinct elements $v_1, v_2, ..., v_i$.\nFor the distinct number $v_i$, which appears $k_i$ times, \n$S(i, j) = S(i-1, j) + S(i-1, j-v_i) + S(i-1, j-2v_i) + ... + S(i-1, j-k_i v_i) $\nSo we can maintain $v_i$ sliding windows to keep $S(i-1, j-v_i) + S(i-1, j-2v_i) + ... + S(i-1, j-k_i v_i)$. \nIn this way, each distinct number can be processed in $O(N)$ only.\nThe number of distinct number is $O(\\sqrt{N})$, so the overall complexity is $O(N^{1.5})$.\n\n# Complexity\n- Time complexity: $O(N^{1.5})$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(N)$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countSubMultisets(self, nums: List[int], l: int, r: int) -> int:\n cnt = Counter(nums)\n prev = [1 + cnt[0]] + [0] * r\n for v, k in cnt.items():\n if v > 0:\n current = [0] * (r+1)\n table = [0] * v\n for j in range(v, r+1):\n table[j % v] += prev[j - v]\n current[j] += table[j % v]\n if j - v * k >= 0:\n table[j % v] -= prev[j - v * k]\n prev = [(a + b) % 1000000007 for a, b in zip(prev, current)]\n return sum(prev[l:r+1]) % 1000000007\n``` | 0 | 0 | ['Dynamic Programming', 'Sliding Window', 'Python3'] | 0 |
count-of-sub-multisets-with-bounded-sum | C++ | c-by-tinachien-t6io | \nusing LL = long long;\nLL M = 1e9+7;\nclass Solution {\n int count0 = 0;\n vector<pair<int, int>>arr;\npublic:\n int countSubMultisets(vector<int>& n | TinaChien | NORMAL | 2023-12-06T13:38:37.598755+00:00 | 2023-12-06T13:38:37.598783+00:00 | 6 | false | ```\nusing LL = long long;\nLL M = 1e9+7;\nclass Solution {\n int count0 = 0;\n vector<pair<int, int>>arr;\npublic:\n int countSubMultisets(vector<int>& nums, int l, int r) {\n unordered_map<int, int>Map;\n for(auto x : nums){\n if(x == 0)\n count0++;\n else\n Map[x]++;\n }\n\n for(auto& [key, count] : Map)\n arr.push_back({key, count}) ;\n arr.insert(arr.begin(), {0, 0});\n return (helper(r) - helper(l-1) + M) % M ;\n }\n \n LL helper(int capability){\n if(capability < 0 )\n return 0 ;\n int m = arr.size() ;\n if(m == 1)\n return count0 + 1;\n vector<vector<LL>>dp(m, vector<LL>(capability+1, 0));\n dp[0][0] = 1 ;\n for(int i = 1; i < m; i++){\n auto [v, c] = arr[i]; \n for (int j=0; j<=capability; j++)\n { \n dp[i][j] = (j<v?0:dp[i][j-v]) + dp[i-1][j] - (j<v*(c+1)?0:dp[i-1][j-v*(c+1)]);\n dp[i][j] = (dp[i][j]+M) % M;\n }\n }\n LL ret = 0;\n for(int i = 0; i<= capability; i++)\n ret = (ret + dp[m-1][i]) % M;\n return ret * (count0 + 1) % M;\n }\n};\n``` | 0 | 0 | [] | 0 |
count-of-sub-multisets-with-bounded-sum | Go - Dynamic Programming Knapsack + Prefix Sum Solution | go-dynamic-programming-knapsack-prefix-s-c5mx | Intuition\nThe problem equals to slightly modified Knapsack. It can be solved using the Dynamic Programming approach, very similar to Coin Change problem(s).\n\ | erni27 | NORMAL | 2023-11-04T14:36:43.042288+00:00 | 2023-11-04T14:36:43.042308+00:00 | 26 | false | # Intuition\nThe problem equals to slightly modified *Knapsack*. It can be solved using the *Dynamic Programming* approach, very similar to *Coin Change* problem(s).\n```\nfunc countSubMultisets(nums []int, l int, r int) int {\n\tmultiset := make(map[int]int)\n\tfor _, num := range nums {\n\t\tmultiset[num]++\n\t}\n\tmem := make([]int, r+1)\n\tmem[0] = 1\n\tfor num, occ := range multiset {\n\t\tfor sum := r; sum >= 0; sum-- {\n\t\t\tvar ways int\n\t\t\tfor c := 0; c <= occ && sum-num*c >= 0; c++ {\n\t\t\t\tways = (ways + mem[sum-num*c]) % mod\n\t\t\t}\n\t\t\tmem[sum] = ways\n\t\t}\n\t}\n\tvar result int\n\tfor sum := l; sum <= r; sum++ {\n\t\tresult = (result + mem[sum]) % mod\n\t}\n\treturn result\n}\n\nvar mod int = 1e9 + 7\n```\nThe above solution yields pseudo-polynomial time complexity $$O(r \\cdot n)$$, where $$n$$ is the length of the input array. It results in TLE though for last test case(s).\nOne can improve the running time by relying on the problem constraint saying: $$sum(nums) \\le 2\\cdot 10^4$$. Since the nums consists of non-negative integers, we expect the limited number of unique elements, hence a lot of duplicates.\n\n# Approach\n1. Store all unique elements and their frequency in the *HashMap*.\n2. Initialize the cache $$mem$$, where $$mem[sum]$$ equals to the number of sub-multisets summing up to the $$sum$$.\n3. Base Case: $$mem[0]=1$$ (there is at least 1 sub-multisets summing up to 0, empty one).\n4. Iterate through all unique elements.\n4.1. Calculate the *Prefix Sum* based on the current cache state.\n4.2. Calculate the number of sub-multisets summing up to each $$sum \\in <0, r>$$ based on the *Prefix Sum*. Be careful with 0 element(s)!\n\n# Complexity\n- Time complexity:\n$$O(r\\cdot u)$$, where $$u$$ is the number of unique elements in the input array.\n\n- Space complexity:\n$$O(r+u)$$.\n\n# Code\n```\nfunc countSubMultisets(nums []int, l int, r int) int {\n\tmultiset := make(map[int]int)\n\tfor _, num := range nums {\n\t\tmultiset[num]++\n\t}\n\tmem := make([]int, r+1)\n\tmem[0] = 1\n\tprefix := make([]int, len(mem))\n\tfor num, occ := range multiset {\n\t\tcopy(prefix, mem)\n\t\tfor sum := num; sum <= r; sum++ {\n\t\t\tprefix[sum] = (prefix[sum] + prefix[sum-num]) % mod\n\t\t}\n\t\tfor sum := r; sum >= 0; sum-- {\n\t\t\tif num > 0 {\n\t\t\t\tmem[sum] = prefix[sum]\n\t\t\t\tif sum >= num*(occ+1) {\n\t\t\t\t\tmem[sum] = (mem[sum] - prefix[sum-num*(occ+1)] + mod) % mod\n\t\t\t\t}\n\t\t\t} else {\n\t\t\t\tmem[sum] = (mem[sum] * (occ + 1)) % mod\n\t\t\t}\n\t\t}\n\t}\n\tvar result int\n\tfor sum := l; sum <= r; sum++ {\n\t\tresult = (result + mem[sum]) % mod\n\t}\n\treturn result\n}\n\nvar mod int = 1e9 + 7\n``` | 0 | 0 | ['Dynamic Programming', 'Prefix Sum', 'Go'] | 0 |
count-of-sub-multisets-with-bounded-sum | C++ - Bottom up DP | c-bottom-up-dp-by-mumrocks-od2i | Intuition\nI first came up with top down DP but got OOM. Then looked into https://leetcode.com/problems/count-of-sub-multisets-with-bounded-sum/solutions/416806 | MumRocks | NORMAL | 2023-10-25T16:50:23.738805+00:00 | 2023-10-25T16:50:48.509734+00:00 | 43 | false | # Intuition\nI first came up with top down DP but got OOM. Then looked into https://leetcode.com/problems/count-of-sub-multisets-with-bounded-sum/solutions/4168064/optimized-dynamic-programming/ to implement bottom up DP solution. \n\n# Code\n```\nclass Solution {\n int MOD = 1000000007;\n \npublic:\n int countSubMultisets(vector<int>& nums, int l, int r) {\n unordered_map<int,int> m;\n \n for (auto n: nums) m[n]++;\n\n vector<int> dp(r+1,0);\n dp[0]=1;\n for (auto [k,v]: m){\n vector<int> cp(dp.begin(),dp.end());\n for (int i=0;i<=r;i++){\n if (i>=k) cp[i] = (1LL*(cp[i] + cp[i-k]))%MOD;\n }\n for (int i=r;i>=0;i--){\n if (k>0){\n dp[i] = (cp[i] - (i-k*(v+1)>=0?cp[i-k*(v+1)]:0)+MOD)%MOD;\n }\n else{\n long t= (1LL*dp[i]*(v+1))%MOD;\n dp[i]=t;\n }\n }\n }\n\n int ans=0;\n for (int i=l;i<=r;i++) ans = (ans + dp[i])%MOD;\n return ans;\n \n }\n};\n``` | 0 | 0 | ['Dynamic Programming', 'C++'] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.