question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
count-of-sub-multisets-with-bounded-sum | TypeScript Solution | typescript-solution-by-soraya1725-itai | Intuition\n\n\n# Approach\nThis function works by leveraging dynamic programming. The core idea is to maintain a list (dp) that keeps track of all possible sums | soraya1725 | NORMAL | 2023-10-25T16:09:08.365138+00:00 | 2023-10-25T16:09:08.365160+00:00 | 4 | false | # Intuition\n\n\n# Approach\nThis function works by leveraging dynamic programming. The core idea is to maintain a list (dp) that keeps track of all possible sums that can be obtained using the numbers from the input array nums.\n\nInitially, the function sorts the numbers in descending order. It first handles any zeros in the nums because zeros don\'t affect the sum but increase the count of combinations.\n\nThen, the function processes each unique number in the array and computes possible sums that can be formed using this number. It does this by iterating through the current sums in dp and updating them with combinations of the current number.\n\nOnce all numbers are processed, it computes the final answer by summing up the counts of valid sums in the range [l, r].\n\nThe usage of MOD is to ensure that the results do not overflow the given limit, which is a common technique in competitive programming problems.\n\n# Complexity\n- Time complexity:\nitialization and Sorting:\n\nInitializing the dp array is O(r) where r is the upper bound of the range.\nSorting the nums array is log O(nlogn), where n is the length of the nums array.\n\nProcessing zeros:\n\nIn the worst case, the loop for processing zeros will run n times, thus O(n).\nMain Loop:\n\nThe outer loop runs for each unique element of the nums array. In the worst case, it will run n times.\n\nInside the loop, we have another loop that can iterate at most up to r, the range\'s upper bound.\n\nNested inside is another loop which runs at most n times (in the case where all numbers in nums are the same).\n\nThis gives a worst-case complexity of O(n\xD7r\xD7n) for this portion. But in practical scenarios, it\'s likely to be much less since not all numbers in nums will be the same.\n\nFinal Loop:\n\nIterates in the range [l, r], so it is O(r). Combining all parts, the worst-case time complexity can be approximated as O(nlogn+n\xD7r\xD7n). If n is significantly smaller than r, you can simplify it further to(n^2\xD7r). However, in typical scenarios where the array doesn\'t consist of all identical numbers, the time complexity will be much better than this worst-case estimation.\n\n- Space complexity:\nThe space complexity is dominated by the dp array, which is O(r).\n\n# Code\n```\nfunction countSubMultisets(nums: number[], l: number, r: number): number {\n const MOD: number = 1000000007;\n const MAXN: number = 20000;\n let dp: number[] = new Array(20005).fill(0);\n \n for (let i = 0; i <= r; i++) {\n dp[i] = 0;\n }\n dp[0] = 1;\n\n nums.sort((a, b) => a - b);\n nums.reverse();\n let sf = 0;\n\n while (nums.length > 0 && nums[nums.length - 1] === 0) {\n dp[0]++;\n nums.pop();\n }\n\n while (nums.length > 0) {\n const tt = nums[nums.length - 1];\n let cn = 0;\n while (nums.length > 0 && nums[nums.length - 1] === tt) {\n nums.pop();\n cn++;\n }\n\n const chg = Math.min(sf + tt * cn, r);\n for (let i = chg; i >= tt; i--) {\n for (let j = 1; j <= cn; j++) {\n if (i - j * tt >= 0) {\n dp[i] += dp[i - j * tt];\n if (dp[i] >= MOD) {\n dp[i] -= MOD;\n }\n }\n }\n }\n\n sf += tt * cn;\n }\n\n let ans = 0;\n for (let i = l; i <= r; i++) {\n ans += dp[i];\n ans %= MOD;\n }\n\n return ans;\n}\n``` | 0 | 0 | ['TypeScript'] | 0 |
count-of-sub-multisets-with-bounded-sum | knapsack multiset | knapsack-multiset-by-dongts-5fap | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | dongts | NORMAL | 2023-10-18T15:27:16.907039+00:00 | 2023-10-18T15:27:16.907065+00:00 | 51 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int countSubMultisets(vector<int>& a, int l, int r) {\n const int mod = 1e9 + 7;\n const int n = a.size();\n // \n map<int,int> mp; // val - cnt\n for(auto&x:a) mp[x]++;\n // knapsack\n vector<int> dp(r+1);\n dp[0] = 1;\n // Ex val, cnt = 2 3\n // dp = 1 2 3 4 5 6 7 8 9 10\n // 1 2 3 4 5 6 7 8\n // 1 2 3 4 5 6\n // 1 2 3 4\n for(auto&[val, cnt]:mp) {\n if(val == 0) continue;\n for(int i = r; i >= max(0,r-val+1); i--) { // 10, 9\n int sum = 0;\n for(int j=0; j<cnt; j++) { // (10), (8), (6)\n if(i-j*val >= 0) sum = (sum + dp[i-j*val])%mod;\n }\n for(int j=i; j>=0; j-=val) { // 10, 8, 6, 4, 2, 0\n sum = (sum - dp[j] + mod)%mod;\n if(j-val*cnt >= 0) sum = (sum + dp[j-val*cnt])%mod;\n dp[j] = (dp[j] + sum)%mod;\n }\n }\n }\n // res\n int64_t res = 0;\n for(int i=l; i<=r; i++) {\n res = (res + dp[i])%mod;\n }\n return (res*(mp[0]+1))%mod;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
count-of-sub-multisets-with-bounded-sum | [Python3] numpy dp | python3-numpy-dp-by-nottheswimmer-96of | A lot of the complicated looking parts are just small optimizations. There\'s also a lot of crud in here from attempted optimizations that didn\'t end up matter | nottheswimmer | NORMAL | 2023-10-18T04:57:32.439530+00:00 | 2023-10-18T04:59:02.216385+00:00 | 11 | false | A lot of the complicated looking parts are just small optimizations. There\'s also a lot of crud in here from attempted optimizations that didn\'t end up mattering, so feel free to learn by cleaning this up.\n\n```python\nimport numpy as np\n\nclass Solution:\n def countSubMultisets(self, nums: List[int], l: int, r: int, mod: int = 10 ** 9 + 7) -> int:\n nums = np.array(nums)\n nonzero = nums[nums != 0]\n multiplier = (len(nums) - len(nonzero) + 1)\n unique_nums, counts = np.unique(nonzero, return_counts=True)\n counts = np.minimum(counts, r // unique_nums)\n product = unique_nums * counts\n dp = np.zeros(min(r, np.sum(product)) + 1, dtype=np.int64)\n dp[0] = 1\n for x, upper in zip(unique_nums, product + unique_nums):\n pd = np.zeros_like(dp)\n for m in np.arange(x, upper, x):\n pd[m:] += dp[:-m]\n dp[x:].__iadd__(pd[x:]).__imod__(mod)\n return dp[l:].sum() * multiplier % mod\n``` | 0 | 0 | [] | 0 |
count-of-sub-multisets-with-bounded-sum | scala | scala-by-len_master-9rqv | scala\nimport scala.collection.mutable\n\nobject Solution {\n def countSubMultisets(nums: List[Int], l: Int, r: Int): Int = {\n val M = 1000000007\n var | len_master | NORMAL | 2023-10-16T10:14:08.118709+00:00 | 2023-10-16T10:14:08.118734+00:00 | 10 | false | ```scala\nimport scala.collection.mutable\n\nobject Solution {\n def countSubMultisets(nums: List[Int], l: Int, r: Int): Int = {\n val M = 1000000007\n var total = 0\n val cnt = mutable.HashMap.empty[Int, Int].withDefaultValue(0)\n nums.foreach(x => {\n total += x\n cnt(x) += 1\n })\n if (l > total) return 0\n\n val r1 = r.min(total)\n val f = Array.fill[Int](r1 + 1)(0)\n f(0) = cnt.getOrElse(0, 0) + 1\n cnt.remove(0)\n\n var sum = 0\n cnt.foreach { case (x, c) =>\n val newF = f.clone()\n sum = math.min(sum + x * c, r1)\n (x to sum).foreach(j => {\n newF(j) = (newF(j) + newF(j - x)) % M\n if (j >= (c + 1) * x) newF(j) = (newF(j) - f(j - (c + 1) * x) + M) % M\n })\n Array.copy(newF, 0, f, 0, newF.length)\n }\n\n var res = 0\n (l to r1).foreach(i => res = (res + f(i)) % M)\n res\n }\n}\n``` | 0 | 0 | ['Scala'] | 0 |
count-of-sub-multisets-with-bounded-sum | 90% (149ms) C++ solution following Google C++ Style Guide with Parallelization | 90-149ms-c-solution-following-google-c-s-iemn | Motivation\n\nLets implement fast C++ solution based on DP sticking to the Google C++ Style Guide. We will have a look at rules which make our code readable and | ldimat | NORMAL | 2023-10-16T00:37:27.907072+00:00 | 2023-10-16T11:26:52.346228+00:00 | 58 | false | # Motivation\n\nLets implement fast C++ solution based on DP sticking to the [Google C++ Style Guide](https://google.github.io/styleguide/cppguide.html). We will have a look at rules which make our code readable and robust. Also, we will try to use modern C++ constructions. In the end we will look into a parallelization opportunity in our code and how to leverage modern C++ Extention for Parallelizm.\n\n# Intuition\n\nFor each number `value` we would like to know how many occurancies `count` it has in the input array.\n\nIf we maintain an array `reached` in which `reached[summ]` is the number of ways to construct `summ` using previous numbers, then we can say that the new amount of ways in the `new_reached[summ]` will be a summ of the ways using none of the new values, one, two, ... `count`.\n\nTo generate the output - we will have to find a summ of values in the `reached` array from `left` to `right`.\n\n# Approach\n\nWe will introduce a constant to keep our modulo value. According to the [Constant Names](https://google.github.io/styleguide/cppguide.html#Constant_Names) rules it should be named something like `kModulo`.\n\n[Function names](https://google.github.io/styleguide/cppguide.html#Function_Names) requires to have first capital letter in the names of functions. Due to the platform requirements we will have to ignore this rule. But to stay concistent - we will name other functions using camelCase with the first lower letter.\n\nFrom the [General Naming Rules](https://google.github.io/styleguide/cppguide.html#Function_Names) we can see that the names of the variables (and other names) should be optimized for readability. We can rename input parameters of our function to match this rule better.\n\n[Write Short Functions](https://google.github.io/styleguide/cppguide.html#Write_Short_Functions) forces us to break our future code into smaller pieces. This also lets us design our main algorithm in the main function and add details in the functions.\n\nWe will break out two functions:\n\n1. Calculating `frequences` of the values in the input array\n2. Propagating some `value` with the given `offset` in the `new_reached` array.\n\nAccording to the [Inputs and Outputs](https://google.github.io/styleguide/cppguide.html#Inputs_and_Outputs) rule first function will const reference to the input numbers and return an `std::map<int, int>` ([Namespaces](https://google.github.io/styleguide/cppguide.html#Namespaces) rule does not allow us to skip `std::` prefix). According to the new C++ rules this will not introduce copy in the place where we will use it.\n\nThe `propagateNumber` function will have multiple parameters and one output parameter `new_reached`. It should be last and passed by reference, because it is not optional.\n\n[Looping and branching statements](https://google.github.io/styleguide/cppguide.html#Formatting_Looping_Branching) forces us to put a space after the statement keyword (`if`, `for`). Usually we should wrap the body of the loop or a branch into braces, but there is also an exception for smaller pieces of code, which we are going to use in our solution.\n\n# Code\n```\nconstexpr int kModulo = 1000000007;\n\nstd::map<int, int> buildFrequences(const std::vector<int>& nums) {\n std::map<int, int> frequences;\n for (int value : nums) ++frequences[value];\n return frequences;\n}\n\nvoid propagateNum(\n int value, int count, int offset, int right,\n const std::vector<int> &reached,\n std::vector<int> &new_reached) {\n new_reached[offset] = reached[offset];\n long long summ = reached[offset];\n int front = offset + value;\n int current_count = 1;\n while (front <= right) {\n summ += reached[front];\n if (summ >= kModulo) summ -= kModulo;\n new_reached[front] = summ;\n ++current_count;\n if (current_count > count) {\n summ -= reached[front - count * value];\n if (summ < 0) summ += kModulo;\n }\n front += value;\n }\n}\n\nclass Solution {\npublic:\n int countSubMultisets(std::vector<int>& nums, int left, int right) {\n // Check Input data for correctness.\n if (nums.size() == 0) return 0;\n if (left > right) return 0;\n if (left < 0) return 0;\n\n std::map<int, int> frequences = buildFrequences(nums);\n std::vector<int> reached(right + 1);\n std::vector<int> new_reached(right + 1);\n reached[0] = frequences[0] + 1;\n for (const auto &[value, count] : frequences) {\n if (value == 0) continue;\n if (value > right) continue;\n for (int offset = 0; offset < value; ++offset) {\n propagateNum(value, count, offset, right, reached, new_reached);\n }\n std::swap(reached, new_reached);\n }\n int res = 0;\n for (int ind = left; ind <= right; ++ind) {\n res = (res + reached[ind]) % kModulo;\n }\n return res;\n }\n};\n```\n\n# Parallelizing the solution\n\nIn the main body we have an opportunity for the paralellization. just replace the the loop which wraps the `propagateNum` function call with this code:\n\n```\n#include <execution>\n// ...\nstd::vector<int> steps(value);\nfor (int step = 0; step < value; ++step) steps[step] = step;\nstd::for_each(\n std::execution::par_unseq, steps.begin(), steps.end(), \n [this, value, count, right, &reached, &new_reached](int step) {\n this->propagateNum(value, count, step, right, reached, &new_reached);\n });\n```\n\nThis propagations do not intersect and can be run in parallel using up to `value` cores.\n\nI am using g++ on WSL:\n\n```\ng++ -O3 --std=c++17 main.cc -pthread -ltbb\n```\n\nI had to install `libtbb` to be able to use C++ paralellization.\n\nWith the big enough input and the `-O3` optimizations parallel solution was almost 4 times faster than the simple one. | 0 | 0 | ['Dynamic Programming', 'C++'] | 0 |
count-of-sub-multisets-with-bounded-sum | My Solution | my-solution-by-hope_ma-zec5 | \nclass Solution {\n public:\n int countSubMultisets(const vector<int> &nums, const int l, const int r) {\n constexpr int range = 2;\n constexpr int mod | hope_ma | NORMAL | 2023-10-15T11:19:48.145296+00:00 | 2023-10-15T11:19:48.145319+00:00 | 22 | false | ```\nclass Solution {\n public:\n int countSubMultisets(const vector<int> &nums, const int l, const int r) {\n constexpr int range = 2;\n constexpr int mod = 1000000007;\n unordered_map<int, int> num_to_count;\n for (const int num : nums) {\n ++num_to_count[num];\n }\n \n auto itr_zero = num_to_count.find(0);\n const int zero_count = itr_zero == num_to_count.end() ? 0 : itr_zero->second;\n if (itr_zero != num_to_count.end()) {\n num_to_count.erase(itr_zero);\n }\n\n const int n = static_cast<int>(num_to_count.size());\n /**\n * dp[i][j] stands for the count of sub-multisets within the first `i` numbers\n * in the unordered_map<int, int> `num_to_count`\n * where the sum of elements in each subset is equal to `j`\n * please note for each number `num` of `num_to_count`, there exist `num_to_count[num]` `num`s\n *\n * initial:\n * dp[0][0] = 1 + `zero_count`\n *\n * induction:\n * for a number `num` in `num_to_count`, let `count` = `num_to_count[num]`\n * dp[i][j] = dp[i - 1][j] + dp[i - 1][j - 1 * num] + dp[i - 1][j - 2 * num] + ... + dp[i - 1][j - count * num]\n * dp[i][j - num] = dp[i - 1][j - 1 * num] + dp[i - 1][j - 2 * num] + ... + dp[i - 1][j - (count + 1) * num]\n * the following induction can be got\n * dp[i][j] = dp[i - 1][j] + dp[i][j - num] - dp[i - 1][j - (count + 1) * num]\n *\n * target:\n * accumulate(dp[num_to_count.size()] + l, dp[num_to_count.size()] + r + 1, 0)\n */\n int dp[range][r + 1];\n memset(dp, 0, sizeof(dp));\n int previous = 0;\n int current = 1;\n dp[previous][0] = 1 + zero_count;\n for (const auto [num, count] : num_to_count) {\n for (int sum = 0; sum < r + 1; ++sum) {\n dp[current][sum] = dp[previous][sum];\n if (sum >= num) {\n dp[current][sum] = (dp[current][sum] + dp[current][sum - num]) % mod;\n }\n if (sum >= static_cast<long long>(count + 1) * num) {\n dp[current][sum] = (mod + dp[current][sum] - dp[previous][sum - (count + 1) * num]) % mod;\n }\n }\n \n previous ^= 1;\n current ^= 1;\n memset(dp[current], 0, sizeof(dp[current]));\n }\n \n int ret = 0;\n for (int i = l; i < r + 1; ++i) {\n ret = (ret + dp[previous][i]) % mod;\n }\n return ret;\n }\n};\n``` | 0 | 0 | [] | 0 |
count-of-sub-multisets-with-bounded-sum | [c++] 100% [100ms] | c-100-100ms-by-lyronly-mwqi | \ntypedef long long ll;\nclass Solution {\npublic:\n const static int mod = (int)(1e9 +7);\n int countSubMultisets(vector<int>& nums, int l, int r) {\n | lyronly | NORMAL | 2023-10-14T20:07:06.438649+00:00 | 2023-10-14T20:07:06.438668+00:00 | 67 | false | ```\ntypedef long long ll;\nclass Solution {\npublic:\n const static int mod = (int)(1e9 +7);\n int countSubMultisets(vector<int>& nums, int l, int r) {\n int n = nums.size();\n sort(nums.begin(), nums.end()); \n int m = nums.back();\n \n vector<int> cnt(m + 1, 0);\n int sum = 0;\n for (auto v : nums) { \n cnt[v]++;\n sum += v;\n }\n if (l > sum) return 0;\n \n vector<pair<int, int>> vp;\n for (int i = 1; i <= m; i++) {\n if (cnt[i] == 0) continue;\n vp.push_back({i, cnt[i]});\n }\n \n vector<ll> dp(sum + 1, 0);\n dp[0] =1 + cnt[0];\n int cur = 0;\n for (auto[x, y] : vp) {\n cur = cur + x * y; \n for (int i = cur; i > cur - x; i--) {\n int cs = 0;\n int a = i - x;\n for (int b = a; b >= max(0,i - x * y); b -= x) cs = (cs + dp[b]) % mod;\n dp[i] = (cs + dp[i]) % mod;\n for (int j = i - x; j > 0; j -= x) {\n int b = j - x * y;\n if (a >= 0) cs = (cs + mod - dp[a]) % mod;\n if (b >= 0) cs = (cs + dp[b]) % mod;\n dp[j] = (cs + dp[j]) % mod;\n a = j - x;\n }\n }\n }\n \n long long ans = 0;\n for (int i = l; i <= min(sum, r); i++) {\n ans = (ans + dp[i]) % mod;\n }\n return ans;\n }\n};\n``` | 0 | 0 | [] | 0 |
count-of-sub-multisets-with-bounded-sum | Rust/C++ DP with Optimized Double Loop | rustc-dp-with-optimized-double-loop-by-x-r45k | Intuition\n Describe your first thoughts on how to solve this problem. \nNoticed that the sum of all numbers is no more 20000. When we add the numbers in sunseq | xiaoping3418 | NORMAL | 2023-10-14T18:54:17.135828+00:00 | 2023-10-14T18:54:17.135855+00:00 | 53 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nNoticed that the sum of all numbers is no more 20000. When we add the numbers in sunsequences, their sums are slowly growing to the up bound, which is no more than 20000.\nWe will use an array int dp[20001] to track the frequencies of the sums. We set dp[0] = 1 (empty sub-sequence) and everything else to 0 initially.\nWe then different count, uo to its frequency, of the same number for making different subsequences. Instead of tracking the nubers of different sequences, we track the frequences of their sums.\nIf upBound is the total sum of the numbers processed so far, then dp[k] == 0 for k > upBound. Therefore, we only need to loop to upBound.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n//Rust\nuse std::collections::BTreeMap;\nimpl Solution {\n pub fn count_sub_multisets(nums: Vec<i32>, l: i32, r: i32) -> i32 {\n let mut mp = BTreeMap::<i32, i32>::new();\n let mut count0 = 0i64;\n for a in nums { \n if a == 0 { count0 += 1; }\n else { *mp.entry(a).or_insert(0) += 1; }\n }\n \n let mut dp = vec![0; 20001];\n let mut sum = 0;\n let MOD = 1_000_000_007;\n\n dp[0] = 1;\n for (val, cnt) in &mp {\n for j in (0..= sum).rev() {\n for k in 1 ..= (*cnt) as usize {\n let it = j + k * (*val) as usize;\n dp[it] = (dp[it] + dp[j]) % MOD;\n }\n }\n sum += (*val) as usize * (*cnt) as usize;\n }\n\n let mut ret = 0;\n for i in l as usize ..= r as usize {\n ret = (ret + dp[i]) % MOD;\n }\n\n (ret as i64 * (count0 + 1) % MOD as i64) as _ \n }\n}\n```\n~~~\n//C++\nlong long dp[20001];\nclass Solution {\npublic:\n int countSubMultisets(vector<int>& nums, int l, int r) {\n map<int, int> mp;\n \n for (auto &a: nums) ++mp[a];\n memset(dp, 0, sizeof(dp));\n dp[0] = 1;\n \n int sum = 0, mod = 1000000007;\n for (auto &it: mp) {\n if (it.first == 0) continue;\n \n for (int j = sum; j >= 0; --j) {\n for (int k = 1; k <= it.second; ++k) {\n dp[j + k * it.first] = (dp[j + k * it.first] + dp[j]) % mod;\n }\n }\n sum += it.second * it.first;\n }\n \n int ret = 0;\n for (int i = l; i <= r; ++i) {\n ret = (ret + dp[i]) % mod; \n }\n \n return 1LL * ret * (mp[0] + 1) % mod;\n }\n};\n~~~ | 0 | 0 | ['Rust'] | 0 |
count-of-sub-multisets-with-bounded-sum | Javascript multi knapsack | javascript-multi-knapsack-by-henrychen22-wspb | \nconst counter = (a_or_s) => { let m = new Map(); for (const x of a_or_s) m.set(x, m.get(x) + 1 || 1); return m; };\n\nconst mod = 1e9 + 7;\nconst countSubMult | henrychen222 | NORMAL | 2023-10-14T17:53:04.773984+00:00 | 2023-10-14T17:53:04.774012+00:00 | 44 | false | ```\nconst counter = (a_or_s) => { let m = new Map(); for (const x of a_or_s) m.set(x, m.get(x) + 1 || 1); return m; };\n\nconst mod = 1e9 + 7;\nconst countSubMultisets = (a, l, r) => {\n let f = Array(r + 1).fill(0), m = counter(a), res = 0;\n f[0] = 1;\n for (const [x, occ] of m) {\n if (x == 0) {\n f = f.map(e => e * (occ + 1));\n } else {\n for (let i = x; i <= r; i++) {\n f[i] += f[i - x];\n f[i] %= mod;\n }\n for (let i = r; i >= (occ + 1) * x; i--) {\n f[i] -= f[i - (occ + 1) * x];\n f[i] %= mod;\n }\n }\n }\n for (let i = l; i <= r; i++) {\n res += f[i];\n res %= mod;\n }\n return (res + mod) % mod;\n};\n``` | 0 | 0 | ['Dynamic Programming', 'JavaScript'] | 0 |
count-of-sub-multisets-with-bounded-sum | DP (Knapsack) | dp-knapsack-by-dnitin28-258c | \n\n# Code\n\nclass Solution {\npublic:\n const int mod = 1e9 + 7;\n int countSubMultisets(vector<int>& nums, int l, int r) {\n int n = nums.size() | gyrFalcon__ | NORMAL | 2023-10-14T17:35:47.277703+00:00 | 2023-10-14T17:35:47.277731+00:00 | 181 | false | \n\n# Code\n```\nclass Solution {\npublic:\n const int mod = 1e9 + 7;\n int countSubMultisets(vector<int>& nums, int l, int r) {\n int n = nums.size();\n int sum = 0, mx = 0;\n vector<int> freq(2e4 + 1);\n set<int> s;\n for(int i=0;i<n;i++){\n freq[nums[i]] ++;\n mx = max(mx, nums[i]);\n sum += nums[i];\n s.insert(nums[i]);\n }\n vector<int> v;\n for(auto j : s){\n v.push_back(j);\n }\n sort(v.begin(), v.end());\n n = v.size();\n vector<vector<int>> dp(n, vector<int>(sum + 1));\n for(int i=0;i<=freq[v[0]];i++){\n dp[0][i * v[0]] += 1;\n }\n vector<int> ndp(sum + 1);\n if(n > 1){\n for(int i=0;i<=sum;i++){\n if(i - v[1] >= 0){\n ndp[i] = (ndp[i - v[1]] + dp[0][i])%mod;\n if(i - ((freq[v[1]] + 1) * v[1]) >= 0){\n ndp[i] = (ndp[i] - dp[0][i - ((freq[v[1]] + 1) * v[1])] + mod)%mod;\n }\n }\n else{\n ndp[i] = dp[0][i];\n }\n }\n }\n for(int i=1;i<n;i++){\n for(int j=0;j<=sum;j++){\n dp[i][j] = (dp[i][j] + ndp[j])%mod;\n }\n if(i + 1 < n){\n ndp = vector<int> (sum + 1);\n for(int j=0;j<=sum;j++){\n if(j - v[i+1] >= 0){\n ndp[j] = (ndp[j - v[i+1]] + dp[i][j])%mod;\n if(j - ((freq[v[i+1]] + 1) * v[i+1]) >= 0){\n ndp[j] = (ndp[j] - dp[i][j - ((freq[v[i+1]] + 1) * v[i+1])] + mod)%mod;\n }\n }\n else{\n ndp[j] = dp[i][j];\n }\n }\n }\n }\n int ans = 0;\n if(l > sum){\n return 0;\n }\n for(int i=l;i<=min(sum, r);i++){\n ans = (ans + dp[n-1][i])%mod;\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
count-of-sub-multisets-with-bounded-sum | 🔥🔥🔥 Python Simple Solution 🔥🔥🔥 | python-simple-solution-by-hululu0405-0dof | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | hululu0405 | NORMAL | 2023-10-14T17:09:47.003754+00:00 | 2023-10-14T17:09:47.003777+00:00 | 75 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(nr)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(r)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countSubMultisets(self, nums: List[int], l: int, r: int) -> int:\n dp = defaultdict(int)\n dp[0] = 1\n counter = Counter(nums)\n for num, count in counter.items():\n for i in range(num):\n total = sum(dp[r-i-num*c] for c in range(1, count+1))\n for n in range(r-i, 0, -num):\n dp[n] += total\n total = total - dp[n-num] + dp[n-num*(count+1)]\n\n res = 0\n for i in range(l, r+1):\n res = (res + dp[i]) % (10**9 + 7)\n return res * (counter[0] + 1) % (10**9 + 7)\n\n``` | 0 | 0 | ['Python3'] | 0 |
count-of-sub-multisets-with-bounded-sum | 🔥🔥🔥 Python Simple Solution 🔥🔥🔥 | python-simple-solution-by-hululu0405-qcz2 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | hululu0405 | NORMAL | 2023-10-14T17:09:46.153107+00:00 | 2023-10-14T17:09:46.153123+00:00 | 35 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(nr)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(r)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def countSubMultisets(self, nums: List[int], l: int, r: int) -> int:\n dp = defaultdict(int)\n dp[0] = 1\n counter = Counter(nums)\n for num, count in counter.items():\n for i in range(num):\n total = sum(dp[r-i-num*c] for c in range(1, count+1))\n for n in range(r-i, 0, -num):\n dp[n] += total\n total = total - dp[n-num] + dp[n-num*(count+1)]\n\n res = 0\n for i in range(l, r+1):\n res = (res + dp[i]) % (10**9 + 7)\n return res * (counter[0] + 1) % (10**9 + 7)\n\n``` | 0 | 0 | ['Python3'] | 0 |
count-of-sub-multisets-with-bounded-sum | dp knackbag | dp-knackbag-by-alkut-pnm0 | Intuition\ncount of unique positive numbers <= sqrt(nums[i]) \n\n# Complexity\n- Time complexity: O(r * sqrt(sum(nums[i])))\n\n- Space complexity: O(r)\n\n# Co | alkut | NORMAL | 2023-10-14T16:47:50.965479+00:00 | 2023-10-14T16:47:50.965503+00:00 | 133 | false | # Intuition\ncount of unique positive numbers <= $$ sqrt(nums[i]) $$\n\n# Complexity\n- Time complexity: $$O(r * sqrt(sum(nums[i])))$$\n\n- Space complexity: $$O(r)$$\n\n# Code\n```\nclass Solution {\npublic:\n int countSubMultisets(const vector<int> &nums, int l, int r) {\n map<int, int> m;\n long long zeroes = 0;\n for (const auto it : nums)\n if (it != 0) ++m[it];\n else ++zeroes;\n const vector<pair<const int, int>> v(m.cbegin(), m.cend());\n int n = v.size();\n vector<vector<int>> dp(2, vector<int>(r + 1, 0));\n dp[0][0] = 1;\n const int mod = 1e9 + 7;\n for (int i = 0; i < n; ++i) {\n vector<int> sums(v[i].first, 0);\n for (int su = 0; su <= r; ++su) {\n sums[su % v[i].first] = (sums[su % v[i].first] + dp[0][su]) % mod;\n if (su - v[i].first * (v[i].second + 1) >= 0) {\n sums[su % v[i].first] = (mod + sums[su % v[i].first] - dp[0][su - v[i].first * (v[i].second + 1)]) % mod;\n }\n dp[1][su] = sums[su % v[i].first];\n }\n swap(dp[0], dp[1]);\n }\n long long ans = 0;\n for (int i = l; i <= r; ++i) {\n ans = (ans + dp[0][i]) % mod;\n }\n ans = (ans * (zeroes + 1)) % mod;\n return ans;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
count-of-sub-multisets-with-bounded-sum | 2D DP accepted solution Java | 2d-dp-accepted-solution-java-by-kartikey-x1me | \n# Code\n\nclass Solution {\n\n int MOD = (int) 1e9 + 7;\n\n HashMap<Integer, Integer> map;\n\n int dp[][];\n\n int solve(ArrayList<Integer> al, in | kartikeysemwal | NORMAL | 2023-10-14T16:40:38.351920+00:00 | 2023-10-14T16:40:38.351941+00:00 | 92 | false | \n# Code\n```\nclass Solution {\n\n int MOD = (int) 1e9 + 7;\n\n HashMap<Integer, Integer> map;\n\n int dp[][];\n\n int solve(ArrayList<Integer> al, int l, int r, int index, int sum) {\n if (sum > r) {\n return 0;\n }\n\n long ans = 0;\n\n // if (sum >= l && sum <= r) {\n // ans = ans + 1;\n // }\n\n if (index >= al.size()) {\n return (int) ans;\n }\n\n if (dp[index][sum] != -1) {\n return dp[index][sum];\n }\n\n int cur = al.get(index);\n int count = map.get(cur);\n\n for (int i = 0; i <= count; i++) {\n int curSum = sum + cur * i;\n\n if (curSum > r) {\n break;\n }\n\n ans = ans + solve(al, l, r, index + 1, curSum);\n\n if (i != 0 && curSum >= l && curSum <= r) {\n ans = ans + 1;\n }\n\n ans = ans % MOD;\n }\n\n dp[index][sum] = (int) ans;\n\n return (int) ans;\n }\n\n public int countSubMultisets(List<Integer> nums, int l, int r) {\n map = new HashMap<>();\n\n ArrayList<Integer> al = new ArrayList<>();\n\n for (int i = 0; i < nums.size(); i++) {\n int cur = nums.get(i);\n\n int count = map.getOrDefault(cur, 0) + 1;\n map.put(cur, count);\n\n if (count == 1) {\n al.add(cur);\n }\n }\n\n int n = al.size();\n\n dp = new int[n][r + 1];\n\n for (int i = 0; i < dp.length; i++) {\n for (int j = 0; j < dp[0].length; j++) {\n dp[i][j] = -1;\n }\n }\n\n Collections.sort(al);\n\n int ans = solve(al, l, r, 0, 0);\n\n if (l == 0) {\n ans = ans + 1;\n }\n\n ans = ans % MOD;\n\n return ans;\n }\n}\n``` | 0 | 0 | ['Dynamic Programming', 'Java'] | 0 |
count-of-sub-multisets-with-bounded-sum | Java dfs(r) - dfs(l-1) = ans | java-dfsr-dfsl-1-ans-by-scsonic-4woh | Intuition\n1. reorder the nums into: uniqueNums and cnt, resolv the multi-set problem\n2. make dfs(at, target) means index at i, remain sum = target, return how | scsonic | NORMAL | 2023-10-14T16:37:26.888372+00:00 | 2023-10-14T17:03:20.773706+00:00 | 244 | false | # Intuition\n1. reorder the nums into: uniqueNums and cnt, resolv the multi-set problem\n2. make dfs(at, target) means index at i, remain sum = target, return how many ans in it\n3. return dfs(r) - dfs(l-1) = ans\n\n# Approach\ntwo key point in dfs:\n\n def dfs(at, target)\n # 1. do not select nums[at]\n total += dfs(at+1, target)\n\n # 2. how many count nums[at], use it in 1 ~ count times\n # for example, [1,2,2,3] there are 2 and count of 2\n total += dfs(at+1, target - (2*1)) # use 1 of nums[at]\n total += dfs(at+1, target - (2*2)) # use 2 of nums[at]\n ... for ...\n\n return total\n\n\n# Complexity\n- Time complexity:\nn = len(nums)\nm = max(l, r, sum(nums))\nO(n*m)\n\nthere a super ticky input that is r > sum(nums)\nmake array of 20001 x 20001 will OOM\n\n- Space complexity:\nO(n*m)\n\n# Code\n```\nclass Solution {\n long MOD00 = 100000000700L;\n long dp[][] = null ;\n \n public int countSubMultisets(List<Integer> nums, int l, int r) {\n long MOD = 1000000007;\n \n int sum = 0;\n Map<Integer, Integer> cnt = new HashMap<>();\n for (int num : nums) {\n cnt.put(num, cnt.getOrDefault(num, 0) + 1);\n sum += num;\n }\n \n int[] uniqueNums = new int[cnt.size()];\n int index = 0;\n for (int key : cnt.keySet()) {\n uniqueNums[index] = key;\n index++;\n }\n \n Arrays.sort(uniqueNums);\n int n = uniqueNums.length;\n\n sum = Math.max(sum, r);\n dp = new long[uniqueNums.length][sum+1] ;\n \n long rr = dfs(0, r, uniqueNums, cnt, n);\n long ll = dfs(0, l - 1, uniqueNums, cnt, n);\n System.out.println("lr = " + rr + " " + ll);\n return (int) ((MOD00 + rr - ll) % MOD);\n }\n\n private long dfs(int at, int target, int[] uniqueNums, Map<Integer, Integer> cnt, int n) {\n if (target < 0) {\n return 0;\n }\n\n if (at >= n) {\n return 1;\n }\n \n if (dp[at][target] != 0) {\n return dp[at][target] ;\n }\n\n long total = 0;\n // not choose at\n total += dfs(at + 1, target, uniqueNums, cnt, n);\n // choose at\n int count = cnt.get(uniqueNums[at]);\n for (int i = 1; i <= count; i++) {\n total += dfs(at + 1, target - uniqueNums[at] * i, uniqueNums, cnt, n);\n }\n\n dp[at][target] = total % MOD00 ;\n return dp[at][target] ;\n }\n \n}\n``` | 0 | 0 | ['Memoization', 'Java'] | 0 |
count-of-sub-multisets-with-bounded-sum | JS Solution - Knapsack - It somehow got accepted LOL | js-solution-knapsack-it-somehow-got-acce-3rm5 | I solved it as a variant of snapsack, which may not be efficient, but it somehow got accepted.\nAt first, I used Maps for sumsMapPre and sumsMapCur, and it hit | CuteTN | NORMAL | 2023-10-14T16:08:52.473053+00:00 | 2023-10-14T16:37:03.627370+00:00 | 182 | false | I solved it as a variant of **snapsack**, which may not be efficient, but it somehow got accepted.\nAt first, I used **Maps** for `sumsMapPre` and `sumsMapCur`, and it hit me with a TLE. So I switch to arrays, I\'m a little surprised that this small optimization can beat the judge.\n\n# Complexity\n- let `n = nums.length`\n- Time complexity: $$O(nr)$$\n- Space complexity: $$O(r)$$\n\n# Code\n```js\nlet MOD = 1000000007;\nlet sumsMapPre = Array(20001).fill(0);\nlet sumsMapCur = Array(20001).fill(0);\nlet sumsArr = Array(20001).fill(0);\n\n/**\n * @param {number[]} nums\n * @param {number} l\n * @param {number} r\n * @return {number}\n */\nvar countSubMultisets = function (nums, l, r) {\n let n = nums.length;\n nums.sort();\n sumsMapCur.fill(0);\n sumsMapPre.fill(0);\n sumsMapCur[0] = 1;\n let t = 0;\n let tt = 0;\n\n let acc = 0;\n for (let i = 0; i < n; i++) {\n if (nums[i] == nums[i - 1]) acc += nums[i];\n else {\n tt = t;\n acc = nums[i];\n\n for (let j = t; j >= 0; j--) {\n sumsMapPre[sumsArr[j]] =\n (sumsMapCur[sumsArr[j]] + sumsMapPre[sumsArr[j]]) % MOD;\n sumsMapCur[sumsArr[j]] = 0;\n }\n }\n\n for (let j = tt; j >= 0; j--) {\n let newSum = sumsArr[j] + acc;\n if (newSum <= r) {\n if (!sumsMapCur[newSum] && !sumsMapPre[newSum]) {\n sumsArr[++t] = newSum;\n }\n\n let cnt = (sumsMapPre[sumsArr[j]] + sumsMapCur[newSum]) % MOD;\n sumsMapCur[newSum] = cnt;\n }\n }\n }\n\n let res = 0;\n for (let i = l; i <= r; i++)\n res = (res + sumsMapPre[i] + sumsMapCur[i] ?? 0) % MOD;\n\n return res;\n};\n``` | 0 | 0 | ['Dynamic Programming', 'JavaScript'] | 0 |
count-of-sub-multisets-with-bounded-sum | Hard DP | python | hard-dp-python-by-betoscl-jymv | Approach\nThe number of different numbers is at most $\sqrt n$ so we can iterate over all the different numbers and make a DP , the problem here is that even th | BetoSCL | NORMAL | 2023-10-14T16:06:19.861465+00:00 | 2023-10-14T16:32:33.016184+00:00 | 514 | false | # Approach\nThe number of different numbers is at most $\\sqrt n$ so we can iterate over all the different numbers and make a DP , the problem here is that even the different numbers are relatively small, we still have to update the DP in a clever way in order to reduce the complexity.\n\nThe $DP$ transitions are:\n\n$DP[start +w \\times i]+= \\sum OldDP[start + w \\times i]$.\n\n$OldDP$ is just the state of the $DP$ one step before, i.e in the last $w$ ,we do it to save memory.\n\nWe have to iterate over all possible $start$ and then update the multiples of $w$ for each unique number while the multiple not pass the maximum sum called $N$.\n\n\nwith $DP[0] = freq[0]+1$.\n\nI can explain it better later if supported but for now I leave the code.\n\nI also have to say that in c++ I could not solve it because of the overflow.\n\n# Complexity\n- $O(n \\times \\sqrt(n))$\n# Code\n```\nclass Solution:\n def countSubMultisets(self, nums: List[int], l: int, r: int) -> int:\n N = 0\n for c in nums:\n N+=c\n \n freq = [0]*(N+1)\n for c in nums:\n freq[c]+=1\n\n \n compressed =[]\n \n for i in range(1,N+1):\n if freq[i] > 0 :\n compressed.append((i, freq[i]))\n\n \n dp = [0]*(N+1)\n dp[0] = freq[0]+1\n mod = 10**9 + 7\n \n for w,k in compressed:\n ndp = dp.copy()\n \n for p in range(w):\n sum = 0\n \n multiple = p\n count = 0\n while multiple <=N:\n if (count > k):\n sum -= dp[multiple - (w * count)]\n count-=1\n\n ndp[multiple] += sum\n sum += dp[multiple]\n multiple+=w\n count+=1\n\n dp,ndp = (ndp,dp)\n \n ans = 0\n for i in range(l,min(N+1,r+1)):\n ans+=dp[i]\n ans%=mod\n \n return ans\n \n \n``` | 0 | 0 | ['Python3'] | 1 |
single-element-in-a-sorted-array | Java | C++ | Python3 | Easy explanation | O(logn) | O(1) | java-c-python3-easy-explanation-ologn-o1-71nt | \nEXPLANATION:-\nSuppose array is [1, 1, 2, 2, 3, 3, 4, 5, 5]\nwe can observe that for each pair, \nfirst element takes even position and second element takes o | logan138 | NORMAL | 2020-05-12T08:18:59.747723+00:00 | 2024-09-26T10:32:52.786027+00:00 | 57,755 | false | ```\nEXPLANATION:-\nSuppose array is [1, 1, 2, 2, 3, 3, 4, 5, 5]\nwe can observe that for each pair, \nfirst element takes even position and second element takes odd position\nfor example, 1 is appeared as a pair,\nso it takes 0 and 1 positions. similarly for all the pairs also.\n\nthis pattern will be missed when single element is appeared in the array.\n\nFrom these points, we can implement algorithm.\n1. Take left and right pointers . \n left points to start of list. right points to end of the list.\n2. find mid.\n if mid is even, then it\'s duplicate should be in next index.\n\tor if mid is odd, then it\'s duplicate should be in previous index.\n\tcheck these two conditions, \n\tif any of the conditions is satisfied,\n\tthen pattern is not missed, \n\tso check in next half of the array. i.e, left = mid + 1\n\tif condition is not satisfied, then the pattern is missed.\n\tso, single number must be before mid.\n\tso, update end to mid.\n3. At last return the nums[left]\n\nTime: - O(logN)\nspace:- O(1)\n\n\nIF YOU HAVE ANY DOUBTS, FEEL FREE TO ASK\nIF YOU UNDERSTAND, DON\'T FORGET TO UPVOTE.\n```\n```\nJava:-\nclass Solution {\n public int singleNonDuplicate(int[] nums) {\n int left = 0, right = nums.length-1;\n while(left < right){\n int mid = (left + right)/2;\n if( (mid % 2 == 0 && nums[mid] == nums[mid +1]) || (mid %2 == 1 && nums[mid] == nums[mid - 1]) )\n left = mid + 1;\n else\n right = mid;\n }\n return nums[left];\n } \n}\n\nPython3:-\nclass Solution:\n def singleNonDuplicate(self, nums: List[int]) -> int:\n left, right = 0, len(nums)-1\n while left < right:\n mid = int((left + right)/2)\n if (mid % 2 == 1 and nums[mid - 1] == nums[mid]) or (mid%2 == 0 and nums[mid] == nums[mid + 1]):\n left = mid + 1\n else:\n right = mid\n return nums[left]\n\t\t\nC++:-\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n int left = 0, right = nums.size() - 1;\n while(left < right){\n int mid = (left + right)/2;\n if((mid % 2 == 0 && nums[mid] == nums[mid + 1]) || (mid % 2 == 1 && nums[mid] == nums[mid - 1]))\n left = mid + 1;\n else\n right = mid;\n }\n \n return nums[left];\n }\n};\n```\n\n\nI have started a series on solid principles and design patterns. If anyone is interested, please check [it](https://medium.com/@bhanu150138/mastering-solid-principles-and-design-patterns-a-blog-series-for-writing-clean-scalable-code-aae3809310db) out. | 1,222 | 7 | ['C++', 'Java', 'Python3'] | 72 |
single-element-in-a-sorted-array | Day 52 || Binary Search || Easiest Beginner Friendly Sol | day-52-binary-search-easiest-beginner-fr-sqyl | Intuition of this Problem:\nSince every element in the sorted array appears exactly twice except for the single element, we know that if we take any element at | singhabhinash | NORMAL | 2023-02-21T01:15:03.395992+00:00 | 2023-04-01T10:19:49.048468+00:00 | 68,024 | false | # Intuition of this Problem:\nSince every element in the sorted array appears exactly twice except for the single element, we know that if we take any element at an even index (0-indexed), the next element should be the same. Similarly, if we take any element at an odd index, the previous element should be the same. Therefore, we can use binary search to compare the middle element with its adjacent elements to determine which side of the array the single element is on.\n\nIf the middle element is at an even index, then the single element must be on the right side of the array, since all the elements on the left side should come in pairs. Similarly, if the middle element is at an odd index, then the single element must be on the left side of the array.\n\nWe can continue this process by dividing the search range in half each time, until we find the single element.\n\n ***Another interesting observation you might have made is that this algorithm will still work even if the array isn\'t fully sorted. As long as pairs are always grouped together in the array (for example, [10, 10, 4, 4, 7, 11, 11, 12, 12, 2, 2]), it doesn\'t matter what order they\'re in. Binary search worked for this problem because we knew the subarray with the single number is always odd-lengthed, not because the array was fully sorted numerically***\n<!-- Describe your first thoughts on how to solve this problem. -->\n**NOTE - PLEASE READ APPROACH FIRST THEN SEE THE CODE. YOU WILL DEFINITELY UNDERSTAND THE CODE LINE BY LINE AFTER SEEING THE APPROACH.**\n\n# Approach for this Problem:\n1. Initialize two pointers, left and right, to the first and last indices of the input array, respectively.\n2. While the left pointer is less than the right pointer:\n - a. Compute the index of the middle element by adding left and right and dividing by 2.\n - b. If the index of the middle element is odd, subtract 1 to make it even.\n - c. Compare the middle element with its adjacent element on the right:\n - i. If the middle element is not equal to its right neighbor, the single element must be on the left side of the array, so update the right pointer to be the current middle index.\n - ii. Otherwise, the single element must be on the right side of the array, so update the left pointer to be the middle index plus 2.\n1. When the left and right pointers converge to a single element, return that element.\n<!-- Describe your approach to solving the problem. -->\n\n# Code:\n```C++ []\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n int left = 0, right = nums.size() - 1;\n while (left < right) {\n int mid = (left + right) / 2;\n if (mid % 2 == 1) {\n mid--;\n }\n if (nums[mid] != nums[mid + 1]) {\n right = mid;\n } else {\n left = mid + 2;\n }\n }\n return nums[left];\n }\n};\n```\n```Java []\nclass Solution {\n public int singleNonDuplicate(int[] nums) {\n int left = 0, right = nums.length - 1;\n while (left < right) {\n int mid = (left + right) / 2;\n if (mid % 2 == 1) {\n mid--;\n }\n if (nums[mid] != nums[mid + 1]) {\n right = mid;\n } else {\n left = mid + 2;\n }\n }\n return nums[left];\n }\n}\n\n```\n```Python []\nclass Solution:\n def singleNonDuplicate(self, nums: List[int]) -> int:\n left, right = 0, len(nums) - 1\n while left < right:\n mid = (left + right) // 2\n if mid % 2 == 1:\n mid -= 1\n if nums[mid] != nums[mid + 1]:\n right = mid\n else:\n left = mid + 2\n return nums[left]\n\n```\n\n# Time Complexity and Space Complexity:\n- Time complexity: **O(logn)**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: **O(1)**\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> | 577 | 5 | ['Array', 'Binary Search', 'C++', 'Java', 'Python3'] | 26 |
single-element-in-a-sorted-array | Java Binary Search, short (7l), O(log(n)) w/ explanations | java-binary-search-short-7l-ologn-w-expl-iwqg | All credits go to @Penghuan who thought of using the pairs wisely.\n\nThis method seems to be a bit simpler to understand, since it doesn't start with the left | baguette | NORMAL | 2017-04-24T18:10:27.569000+00:00 | 2018-10-23T19:06:48.740691+00:00 | 49,506 | false | All credits go to [@Penghuan](/post/175763) who thought of using the pairs wisely.\n\nThis method seems to be a bit simpler to understand, since it doesn't start with the left half and stays a little bit closer to the conventional solutions.\n\n```\n public static int singleNonDuplicate(int[] nums) {\n int start = 0, end = nums.length - 1;\n\n while (start < end) {\n // We want the first element of the middle pair,\n // which should be at an even index if the left part is sorted.\n // Example:\n // Index: 0 1 2 3 4 5 6\n // Array: 1 1 3 3 4 8 8\n // ^\n int mid = (start + end) / 2;\n if (mid % 2 == 1) mid--;\n\n // We didn't find a pair. The single element must be on the left.\n // (pipes mean start & end)\n // Example: |0 1 1 3 3 6 6|\n // ^ ^\n // Next: |0 1 1|3 3 6 6\n if (nums[mid] != nums[mid + 1]) end = mid;\n\n // We found a pair. The single element must be on the right.\n // Example: |1 1 3 3 5 6 6|\n // ^ ^\n // Next: 1 1 3 3|5 6 6|\n else start = mid + 2;\n }\n\n // 'start' should always be at the beginning of a pair.\n // When 'start > end', start must be the single element.\n return nums[start];\n }\n``` | 393 | 15 | [] | 54 |
single-element-in-a-sorted-array | Short, compare nums[i] with nums[i^1] | short-compare-numsi-with-numsi1-by-stefa-5wdy | Simply find the first index whose "partner index" (the index xor 1) holds a different value.\n\nRuby:\n\ndef single_non_duplicate(nums)\n nums[(0..nums.size).b | stefanpochmann | NORMAL | 2017-03-17T19:54:16.158000+00:00 | 2018-10-20T03:00:09.308060+00:00 | 19,105 | false | Simply find the first index whose "partner index" (the index xor 1) holds a different value.\n\n**Ruby:**\n```\ndef single_non_duplicate(nums)\n nums[(0..nums.size).bsearch { |i| nums[i] != nums[i^1] }]\nend\n```\n**Python**\n\n def singleNonDuplicate(self, nums):\n lo, hi = 0, len(nums) - 1\n while lo < hi:\n mid = (lo + hi) / 2\n if nums[mid] == nums[mid ^ 1]:\n lo = mid + 1\n else:\n hi = mid\n return nums[lo]\n\n**Java:**\n\n public int singleNonDuplicate(int[] nums) {\n int lo = 0, hi = nums.length - 1;\n while (lo < hi) {\n int mid = (lo + hi) >>> 1;\n if (nums[mid] == nums[mid ^ 1])\n lo = mid + 1;\n else\n hi = mid;\n }\n return nums[lo];\n } | 292 | 5 | [] | 34 |
single-element-in-a-sorted-array | ✅ [C++/Python] 7 Simple Solutions w/ Explanation | Brute + Hashmap + XOR + Linear +2 Binary Search | cpython-7-simple-solutions-w-explanation-h5yo | We are given a sorted array nums consisting of elements each of which occurs twice except one. We need to return that element which occurs once.\n\n\nTable of C | archit91 | NORMAL | 2021-11-20T02:18:49.178042+00:00 | 2021-11-20T19:43:08.872935+00:00 | 10,441 | false | We are given a sorted array `nums` consisting of elements each of which occurs twice except one. We need to return that element which occurs once.\n\n<details>\n<summary><i>Table of Contents</i></summary>\n<p align=middle>\n<table>\n <tr>\n <th>No.</th>\n <th>Approach</th>\n <th>Time</th>\n <th>Space</th>\n </tr>\n <tr>\n <td>1</td>\n <td>\u26A0\uFE0F\u2714\uFE0F <b>Brute-Force</b></td>\n <td><code>O(N<sup>2</sup>)</code></td>\n <td><code>O(1)</code></td>\n </tr>\n <tr>\n <td>2</td>\n <td>\u2714\uFE0F <b>Hashmap</b></td>\n <td><code>O(N)</code></td>\n <td><code>O(N)</code></td>\n </tr>\n <tr>\n <td>3</td>\n <td>\u2714\uFE0F <b> Hashset</b></td>\n <td><code>O(N)</code></td>\n <td><code>O(N)</code></td>\n </tr>\n <tr>\n <td>4</td>\n <td>\u2714\uFE0F <b>XOR</b></td>\n <td><code>O(N)</code></td>\n <td><code>O(1)</code></td>\n </tr>\n <tr>\n <td>5</td>\n <td>\u2714\uFE0F <b>Linear-Search</b></td>\n <td><code>O(N)</code></td>\n <td><code>O(1)</code></td>\n </tr>\n <tr>\n <td>6</td>\n <td>\u2714\uFE0F <b>Binary Search</b></td>\n <td><code>O(logN)</code></td>\n <td><code>O(1)</code></td>\n </tr> \n <tr>\n <td>7</td>\n <td>\u2714\uFE0F <b>Binary Search - 2nd Approach</b></td>\n <td><code>O(logN)</code></td>\n <td><code>O(1)</code></td>\n </tr> \n</table>\n</p>\n</details>\n\n---\n\n\n\n\u26A0\uFE0F \u2714\uFE0F <em><b>Solution - I (Brute-Force)</b></em>\n\nThe most naive, brute-force way of solving this problem would be to consider each element in `nums` and check how many times it occurs. If it occurs just once, we can return that element as answer.\n\n**C++**\n```cpp\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n for(auto c : nums) {\n int occurence = 0;\n for(auto c2 : nums)\n occurence += c == c2;\n if(occurence == 1) return c;\n }\n return -1;\n }\n};\n```\n\n**Python**\n```python\nclass Solution:\n def singleNonDuplicate(self, nums):\n for c in nums:\n if nums.count(c) == 1: \n\t\t\t\treturn c\n```\n\n***Time Complexity :*** **<code>O(N<sup>2</sup>)</code>**, where `N` is the number of elements in the `nums` array. We take `O(N)` time to check occurences of an element in `nums`. In the worst case, there are `N` elements for which this operation is performed giving a total time complexity of <code>O(N<sup>2</sup>)</code>\n***Space Complexity :*** **`O(1)`**\n\n**Note :** The above solution passes for now but that\'s due to weak test cases.\n\n---\n\n\u2714\uFE0F ***Solution - II (Hashmap)***\n\nWe can use a hashmap to iterate over the `nums` array and count the number of times each element occurs. Finally, the element that has frequency of 1 will be returned.\n\n**C++**\n```cpp\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n unordered_map<int, int> mp;\n for(auto c : nums) mp[c]++; // counting frequency of elements\n for(auto [c, freq] : mp)\n if(freq == 1) return c; // return element occuring once\n return -1; // wont be reached\n }\n};\n```\n\n**Python**\n```python\nclass Solution:\n def singleNonDuplicate(self, nums):\n mp = Counter(nums)\n for c, freq in mp.items():\n if freq == 1: \n return c\n```\n\n\n***Time Complexity :*** **`O(N)`**, where `N` is the number of elements in the `nums` array. We required `O(N)` time to iterate over `nums` and populate hashmap and another `O(N)` to iterate over the hashmap.\n***Space Complexity :*** **`O(N)`**, required to maintain the hashmap.\n\n---\n\n\u2714\uFE0F ***Solution - III (Hashset)***\n\nWe can do slightly better on average space complexity by using a hashset. Since every element occurs twice except one, we can insert into set when we find 1st occurence and remove from set when its found again. Finally the set will consist of only 1 element which will be the required answer.\n\n**C++**\n```cpp\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n unordered_set<int> s;\n for(auto c : nums) \n if(s.count(c)) s.erase(c); // erase on 2nd occurence\n else s.insert(c); // insert on 1st occurence\n return *begin(s); // only element at end is the element occuring once\n }\n};\n```\n\n**Python**\n```python\nclass Solution:\n def singleNonDuplicate(self, nums):\n s = set()\n for c in nums:\n if c in s: s.remove(c)\n else: s.add(c)\n return s.pop()\n```\n\n***Time Complexity :*** **`O(N)`**\n***Space Complexity :*** **`O(N)`**, required to maintain the hashset. Here the average case complexity is `O(N/2)`, slight improvement from `O(N)` in case of hashmap.\n\n---\n\n\u2714\uFE0F ***Solution - IV (XOR)***\n\nWe can use the property of xor operation in this problem. We know that `a \u2295 a = 0`, i.e, two same numbers when xor-ed, cancels each other out. In our case, every element occurs twice except the one. Thus, if we xor all the elements from `nums`, every element will cancel each other out except the required answer.\n\n**C++**\n```cpp\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n int ans = 0;\n for(auto c : nums) ans ^= c; // xor-ing all elements of array\n return ans;\n }\n};\n```\n\n**Python**\n```python\nclass Solution:\n def singleNonDuplicate(self, nums):\n return reduce(xor, nums)\n```\n\n***Time Complexity :*** **`O(N)`**\n***Space Complexity :*** **`O(1)`** only constant extra space is being used.\n\n\n---\n\n\u2714\uFE0F ***Solution - V (Linear Search)***\n\nWe know that the given array is sorted and so duplicates occur adjacently. So, we can just iterate over the array and starting from the 1st element of array, we compare each one with its next adjacent element. If the next element is not equal, we know that current element has occured only once and thus return it as answer.\n\n**C++**\n```cpp\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n for(int i = 0; i < size(nums)-1; i+=2) \n\t\t\tif(nums[i] != nums[i+1])\n return nums[i];\n return nums.back();\n }\n};\n```\n\n**Python**\n```python\nclass Solution:\n def singleNonDuplicate(self, nums):\n for i in range(0, len(nums)-1, 2):\n if nums[i] != nums[i+1]:\n return nums[i]\n return nums[-1]\n```\n\n***Time Complexity :*** **`O(N)`**, for iterating array once.\n***Space Complexity :*** **`O(1)`** only constant extra space is being used.\n\n---\n\n\u2714\uFE0F ***Solution - VI (Binary Search)***\n\nThis approach uses the fact that since the array is sorted, every duplicate element occur adjacently. We can also see that the length of given array must be odd (Why? All element occur twice while only 1 element occurs once). \n\nLet the search range be `[L, R]`. Now, when we consider the mid element, the array is split into two equal halves on the left and right sides. Then we have following cases -\n1. `nums[mid] == nums[mid+1]`:\n\t* **Left Half Length = Right Half Length = Even :** In this case, we can be sure that our answer lies in the right half. How? One element of right half: `nums[mid+1]` matches with `nums[mid]`. So, leaving `nums[mid+1]` aside, we only have odd number of elements to pair up with each other in the right half. This means one element must be such that it cannot be paired with anyone and this is our required answer that occurs only once. So do **`L = mid+2`** (`+2` to skip `nums[mid]` and `nums[mid+1]` & keep search space odd for next iteration)\n\t* **Left Half Length = Right Half Length = Odd :** In this case, we can be sure that our answer lies in the left half. Again, how? Following same reasoning, one element of left half: `nums[mid+1]` matches with `nums[mid]`. So, leaving `nums[mid+1]` aside, the right half consists of even number of elements which can pair up with each other completely. However, left half only consists odd elements and thus one element which cannot be paired with anyone is our required answer. So do **`R = mid-1`** (`-1` to skip `nums[mid]` & keep search space odd for next iteration)\n\n2. `nums[mid] == nums[mid-1]`: We can follow similar reasoning based on array lengths as above -\n\t* **Left Half Length = Right Half Length = Even :** The answer lies in the left half. How? One element of left half: `nums[mid-1]` matches with `nums[mid]`. This leaves left half with odd number of elements to pair up with each other and one element that cant be paired with anyone is the required answer. So do **`R = mid-2`**\n\t* **Left Half Length = Right Half Length = Odd :** The answer lies in right half. How? One element of left half: `nums[mid-1]` matches with `nums[mid]`. This leaves left half with even number of elements which can pair up with each other completely. However, right half only consists odd elements and thus one element which cannot be paired with any other is the required answer. So do **`L = mid+1`**.\n\n3. If neither of above condition are satisfied, then we can be sure that `nums[mid]` itself is the required element occuring once (since it doesnt match with its neighbours). So we can just return it.\n\n```python\nnums = [1,2,2,3,3,4,4,8,8]\n\n1. [L = 0, R = 8] => mid = 4 and nums[mid] == nums[mid-1]\n The left half length is even and 1 element is equal to nums[mid].\n This tells us that left half is left with odd elements to pair up with each other\n One element will be left out which is our answer. So search in left half - [0, 2]\n We decremented R by 2 to keep remaining search space of odd length so we can repeat same process\n \n2. [L = 0, R = 2] => mid = 1 and nums[mid] == nums[mid+1]\n The left half is of odd length and one element cant be paired with another.\n So our answer exist in left half. So search in left half - [0, 0]\n \n3. [L = 0, R = 0] => mid = 1 and nums[mid] != nums[mid-1] and nums[mid] != nums[mid+1]\n This means nums[mid] is our final answer since it is not equal to either of its neighbours\n```\n\nThe below code is a direct translation of above logic -\n\n**C++**\n```cpp\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n int n = size(nums), L = 0, R = n-1, mid;\n while(L <= R) {\n mid = (L + R) >> 1;\n bool isHalfEven = (mid-L) % 2 == 0; // check length of each half is odd or even\n\t\t\t\n if(mid+1 < n && nums[mid] == nums[mid+1]) // case: 1\n if(isHalfEven) L = mid+2;\n else R = mid-1;\n\t\t\t\t\n else if(mid && nums[mid] == nums[mid-1]) // case: 2\n if(isHalfEven) R = mid-2;\n else L = mid+1;\n\t\t\t\t\n else return nums[mid]; // case: 3\n }\n return -1; // wont be reached since we will always find required element inside loop\n }\n};\n```\n\n**Python**\n```python\nclass Solution:\n def singleNonDuplicate(self, nums):\n L, R, mid = 0, len(nums)-1, 0\n while L <= R:\n mid = (L + R) >> 1\n isHalfEven = (mid-L) % 2 == 0\n \n if mid+1 < len(nums) and nums[mid] == nums[mid+1]:\n if isHalfEven: L = mid + 2\n else: R = mid - 1\n elif mid and nums[mid] == nums[mid-1]:\n if isHalfEven: R = mid - 2\n else: L = mid + 1\n else: \n return nums[mid]\n```\n\n***Time Complexity :*** **`O(logN)`**, each time we are eliminating half of search space using binary search\n***Space Complexity :*** **`O(1)`** only constant extra space is being used.\n\n---\n\n\u2714\uFE0F ***Solution VII (Binary Search - 2nd Approach)***\n\nWe can apply binary search using slightly different logic as well. \n\nSuppose you are given a sorted array with all elements occur twice. For eg. `[1,1,2,2,5,5,7,7,8,8]`. So, here we can see that the elements follow the condition - **`nums[0] == nums[1], nums[2] == nums[3],..., nums[2*k] == nums[2*k+1]`**. Now, if we insert an element somewhere in the array, the above relation wont be satisfied from that point of insertion. Eg. `[1,1,2,2,4,5,5,7,7,8,8]` the condition starts to fail from element `4`, that is from point where single-occurence element is present.\n\nThus, we can use this observation to apply binary-search to find the starting point from where the above condition starts to fail. This start point is the index of element occuring once. The binary search will be applied as follows -\n\n1. Initialize the search space as `[L, R] = [0, n-1]` and repeat the following step till `L <= R`.\n2. Find the `mid` position and check if the above condition **`nums[2*k] == nums[2*k+1]`** is satisifed or not. \nFor this, firstly we must ensure that `mid` is even. If `mid` is odd, decrease it by 1 to make it even. \nThen, we need to check if the condition is satisfied or not - \n\t* **`nums[mid] == nums[mid+1]` :** The condition is correctly satisfied till index `mid+1`. So, the required element must occur somewhere on the right of `mid+1`. So do `L = mid+2`.\n\t* **`nums[mid] != nums[mid+1]` :** The condition is not satisfied at this point. So, the required element must either be `nums[mid]` or occur somewhere on the left of `mid` due to which the relation is not satisfied. Mark `nums[mid]` as a potential answer and search if condition is satisfied to the left of `mid` by doing `R = mid-1`\n\nFinally, we return the `ans` which was marked as potential answer during the binary search. \n\n```python\nnums = [1,1,2,2,3,3,4,4,5,5,6]\n\n1. [L = 0, R = 10] => mid = 5\n Since mid is odd. We subtract 1 and mid becomes 4. Now, nums[mid] == nums[mid+1]\n So condition is satisfied upto this point.\n So the answer exists in right half in the [mid+2, R] = [6, 10] range\n \n2. [L = 6, R = 10] => mid = 8 and nums[mid] == nums[mid+1]\n Again, condition is satisfied upto this point\n So, answer must exist in the right half in [mid+2, R] = [10, 10]\n \n3. [L = 10, R = 10] => mid = 10\n Now, mid+1 >= n and so we get nums[mid] != nums[mid+1]\n So the condtion fails here. So mid is a potential answer. \n We mark nums[mid] as ans and search in [L, mid-1] = [10, 9] range\n \n But since L > R, we break out of loop,\n We finally return the marked answer which is nums[10] = 6\n```\n\n\n\n\n**C++**\n```cpp\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n int n = size(nums), L = 0, R = n-1, mid, ans;\n while(L <= R) {\n mid = (L + R) >> 1;\n if(mid & 1) mid--; // make mid even to check for required condition\n if(mid+1 < n && nums[mid] == nums[mid+1]) // condition satisfied upto mid+1:\n L = mid+2; // so search in [mid+2, R] to find point where condition starts to fail\n else // condition not satisfied:\n R = mid-1, ans = nums[mid]; // nums[mid] is potential answer. search [L, mid-1] to see if condition started to fail somewhere before\n }\n return ans;\n }\n};\n```\n\n**Python**\n```python\nclass Solution:\n def singleNonDuplicate(self, nums):\n L, R, mid, ans = 0, len(nums)-1, 0, 0\n while L <= R:\n mid = ((L + R) >> 2) << 1 # Does the same thing as above, i.e, ensuring mid is even\n if mid+1 < len(nums) and nums[mid] == nums[mid+1]:\n L = mid + 2\n else: \n R, ans = mid - 1, nums[mid]\n return ans\n```\n\nOr instead of the usual way of declaring `[L,R]` as extremes of binary search space and searching within it, we can make a slight change to make the code a bit more concise (and also directly apply condition of `nums[2*k]==nums[2*k+1]`):\n\n**C++**\n\n```cpp\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {;\n int L = 0, R = size(nums) / 2, mid;\n while(L < R){\n mid = (L + R) >> 1;\n if(nums[2*mid] == nums[2*mid + 1])\n L = mid + 1;\n else\n R = mid;\n }\n return nums[2 * R];\n }\n};\n```\n\n***Time Complexity :*** **`O(logN)`**, each time we are eliminating half of search space using binary search\n***Space Complexity :*** **`O(1)`**\n\n---\n\n\uD83D\uDCA1 **Note :**\n* If you observe both binary search approaches carefully, you can see that it wouldn\'t have mattered if the array was unsorted. The only thing we required to apply binary search is that the duplicate elements occur adjacent to each other. \n\tSo the above **Binary-Search approach works for both sorted & un-sorted arrays given that duplicates occur adjacently.**\n\n---\n---\n\n\uD83D\uDCBBIf there are any suggestions / questions / mistakes in my post, comment below \uD83D\uDC47 \n\n---\n--- | 238 | 11 | [] | 20 |
single-element-in-a-sorted-array | Java Binary Search O(log(n)) Shorter Than Others | java-binary-search-ologn-shorter-than-ot-5e0x | My solution using binary search. lo and hi are not regular index, but the pair index here. Basically you want to find the first even-index number not followed b | less_is_more_duluth | NORMAL | 2017-03-10T00:08:14.302000+00:00 | 2018-10-07T18:34:34.798352+00:00 | 32,596 | false | My solution using binary search. lo and hi are not regular index, but the pair index here. Basically you want to find the first even-index number not followed by the same number.\n```\npublic class Solution {\n public int singleNonDuplicate(int[] nums) {\n // binary search\n int n=nums.length, lo=0, hi=n/2;\n while (lo < hi) {\n int m = (lo + hi) / 2;\n if (nums[2*m]!=nums[2*m+1]) hi = m;\n else lo = m+1;\n }\n return nums[2*lo];\n }\n}\n``` | 196 | 5 | [] | 24 |
single-element-in-a-sorted-array | ✅ [C++] EASY Intuitive Solution|| 2 approaches || Binary Search || TC:O(log(N)), SC:O(1) | c-easy-intuitive-solution-2-approaches-b-eda5 | Hello everyone, I hope you all are doing great!\n\nNOTE: If you found this post helpful, then please do upvote it!\n\nBrute Force Approach: (XOR) Since we know | riemeltm | NORMAL | 2021-11-20T02:05:06.160607+00:00 | 2021-11-20T05:11:40.747025+00:00 | 7,112 | false | Hello everyone, I hope you all are doing great!\n\n***NOTE: If you found this post helpful, then please do upvote it!***\n\n**Brute Force Approach: (XOR)** Since we know every element occurs exactly twice, where as our target element occurs once, then we can simple take xor of all the elements of the array. In the end we will be left with our target element that appeared once (Because A^A = 0).\n\n**Code:**\n```\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n int n = nums.size();\n int xr{};\n \n for(auto num: nums)\n xr = xr^num;\n \n return xr;\n }\n};\n```\n\n**Time Complexity:** ***O(N)***\n**Space Complexity:** ***O(1)***\n\n<hr></hr>\n\n**Optimal Approach: (Binary Search)**\n1. We will use the fact that the vector is sorted.\n2. **Observation:** If you divide the array in two parts, `PART A`: where elements are before target element and `PART B`: where elements are after target element then:\n\n\ta. In `PART A`, the first instance of element occurs at even index and the second instance of the element occurs at odd index.\n\t\n\tb. In `PART B`, the first instance of element occurs at odd index and the second instance of the element occurs at even index.\n\t\n\tc. You can visualize using following example: \n\t```\n\tindex: 0 1 2 3 4 5 6 7 8\n\tvector: [1,1,2,3,3,4,4,8,8]\n\t \uD83D\uDC46 (Target element is 2 since it appears once)\n\t```\n\tIn this example, before `2` every first instance of element occurs at even index and second instance at odd index (see element `1`) and after `2` every first instance of element occurs at odd index and second instance at even index (see element `3`, `4` and `8`).\n\t\n\t3. So from the above observation we will apply binary search on our array, and if we are on the `PART - B` side of array, we go to left, otherwise we go right.\n\n**Code:**\n```\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n int low = 0, high = nums.size()-2; \n \n while(low <= high){\n \n int mid = low + (high-low)/2;\n \n\t\t\t// If we are on left side, move right\n if(nums[mid] == nums[mid^1]) low = mid+1;\n\t\t\t// if we are on right side, move left\n else high = mid-1;\n }\n \n return nums[low];\n }\n};\n\n// mid^1 explanation:\n// If mid is odd then (mid^1) will always be the even number before mid\n// If mid is even then (mid^1) will always be the odd number after mid\n\n// And hence I am able to check whether mid is in left half or right half as:\n\n// Suppose mid is odd: then mid^1 will give even number before it, \n// then if nums[mid] == nums[mid^1] \n// then 1st instance at even (mid^1) and 2nd instance at odd (mid), \n// hence we are on left side otherwise we are on right side.\n\n// Suppose mid is even: then mid^1 will give odd number after it, \n// then if nums[mid] == nums[mid^1]\n// then 1st instance at even (mid) and 2nd instance at odd (mid^1), \n// hence we are on left side otherwise we are on right side\n```\n\n**Time Complexity:** ***O(Log(N))***\n**Space Complexity:** ***O(1)***\n\n**NOTE: Please \uD83D\uDD3C Upvote if you found this post helpful** | 163 | 20 | [] | 13 |
single-element-in-a-sorted-array | ✔️ [C++] Easy and Concise O(logn) Solution (W/ Explanation) | c-easy-and-concise-ologn-solution-w-expl-t6oq | Hello everyone, firstly thanks for refering to my solution in advance :)\n\nAPPROACH : \n So, the array has all the elements repeating twice except for one elem | Mythri_Kaulwar | NORMAL | 2021-11-20T02:01:08.507263+00:00 | 2021-11-20T02:17:48.287243+00:00 | 6,312 | false | Hello everyone, firstly thanks for refering to my solution in advance :)\n\n**APPROACH :** \n* So, the array has all the elements repeating twice except for one element which appears only once and the array is sorted. \n* This means that in every number that\'s repeated, the first number is at an even index (index%2==0) and the 2nd number is at an odd index. \n* The idea is to peform a binary search over the entire array and find out if this pattern follows. If somewhere this pattern is broken, then we\'re going to know in which half of the array there is an element that appears only once. \n* We reduce the search space to that half an search again, until we\'re left with a single element, which is the final answer.\n\nLet us look at the first example : \n \n```\n 0 1 2 3 4 5 6 7 8\nnums = [1, 1, 2, 3, 3, 4, 4, 8, 8]\n\nWe start with left = 0, right = 8 => mid = 0+(8-0)/2 = 4\nNow, 4 is an even index which means the first repeating number should be at 4 and the next at 5. \nBut nums[4] != nums[5]. So on the left half the pattern\'s broken. \n\nNow, left = 0, right = 4 => mid = 0+(4-0)/2 = 2\nNow again 2 is an even number so nums[2] should be equal to nums[3], but it is not. \n\nSo again, left = 0, right = 2 => mid = 0+(2-0)/2 = 1\n1 is an odd number and nums[1] == nums[0]. So, we do l = mid+1 (Since the left half has the pattern). \n\nNow l = r = 2. \nHence stop the search and return nums[l] = 2.\n```\nLet us look at another example : \n \n```\n 0 1 2 3 4 5 6 \nnums = [3, 3, 7, 7, 10, 11, 11]\n\nWe start with left = 0, right = 6 => mid = 0+(6-0)/2 = 3\nNow, 3 is an odd index and nums[3] == nums[2]. So on the left half the pattern is followed. We move to the right half. \n\nNow, left = 4, right = 6 => mid = 4+(6-4)/2 = 5\nNow 5 is an odd number so nums[5] should be equal to nums[4], but it is not. \n\nSo now, left = 4, right = 5 => mid = 4+(5-4)/2 = 4\n4 is an even number but nums[4] != nums[5]. So, the pattern is not followed on the left side.\n\nNow l = r = 4. \nHence stop the search and return nums[l] = 10.\n```\n\n**Time Complexity :** O(logn); where n=length of the array\n**Space Complexity :** O(1) ; no extra space is required. \n\n**Code :**\n```\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n if(nums.size()==1) return nums[0];\n int l=0, r=nums.size()-1, mid, num;\n \n while(l < r){\n mid = l+(r-l)/2;\n num = (mid%2 == 0) ? mid+1 : mid-1;\n if(nums[mid]==nums[num]) l = mid+1;\n else r = mid;\n }\n return nums[l];\n }\n\n};\n``` \n\nIf the question was to solve the problem in O(n) time complexity; we could use bit-manipulation.\n\n**Code :**\n```\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n int xOR=0; //a^a = 0. So all the elements repeating twice become \'0\' and we return the non-repeating element.\n for(int i=0;i<nums.size();i++) xOr ^= nums[i];\n \n return xOR;\n }\n\n};\n```\nIf you like my solution and explanation, **please UPVOTE!** | 125 | 0 | ['C', 'Binary Tree', 'C++'] | 11 |
single-element-in-a-sorted-array | Java Binary Search | Beats 100% | Most Intutive | Explanation Using Image | java-binary-search-beats-100-most-intuti-igno | Intution: keep dividing your array in two halves and check in which half there are odd number of elements...that will be your required part.\n\n\n\n\n\n\n\n\ncl | Chaitanya1706 | NORMAL | 2021-11-20T03:00:23.225069+00:00 | 2022-06-01T07:27:01.322285+00:00 | 5,990 | false | **Intution:** keep dividing your array in two halves and check in which half there are odd number of elements...that will be your required part.\n\n\n\n\n\n\n\n```\nclass Solution {\n public int singleNonDuplicate(int[] nums) {\n if(nums.length==1) return nums[0];\n int l = 0;\n int h = nums.length-1;\n \n while(l<h){\n int mid = l+(h-l)/2; // divide the array\n \n if(nums[mid]==nums[mid+1]) mid = mid-1; //two same elements should be in same half\n \n if((mid-l+1)%2!=0) h = mid; // checking the length of left half. If its is odd then update ur right pointer to mid\n \n else l = mid+1; // else your right half will be odd then update your left pointer to mid+1\n }\n \n return nums[l]; //left pointer will have the answer at last\n }\n}\n```\n | 113 | 2 | ['Binary Tree', 'Java'] | 9 |
single-element-in-a-sorted-array | Python Binary Search O(logn) - explained | python-binary-search-ologn-explained-by-43ag7 | If every element in the sorted array were to appear exactly twice, they would occur in pairs at indices i, i+1 for all even i. \n\nEquivalently, nums[i] = nums[ | cjporteo | NORMAL | 2020-05-12T09:42:14.719822+00:00 | 2020-05-12T10:56:29.376280+00:00 | 7,446 | false | If every element in the sorted array were to appear exactly twice, they would occur in pairs at indices `i`, `i+1` for all **even** `i`. \n\nEquivalently, `nums[i] = nums[i+1]` and `nums[i+1] != nums[i+2]` for all **even** `i`.\n\nWhen we insert the unique element into this list, the indices of all the pairs following it will be shifted by one, negating the above relationship. \n\nSo, for any **even** index `i`, we can compare `nums[i]` to `nums[i+1]`. \n* If they are equal, the unique element must occur somewhere **after** index `i+1`\n* If they aren\'t equal, the unique element must occur somewhere **before** index `i+1`\n\nUsing this knowledge, we can use binary search to find the unique element.\n\nWe just have to make sure that our pivot index is always even, so we can use `mid = 2 * ((lo + hi) // 4)` instead of the usual `mid = (lo + hi) // 2`.\n<hr>\n\n**Solution:**\n\nTime: `O(logn)`\nSpace: `O(1)`\n\n```\ndef singleNonDuplicate(self, nums: List[int]) -> int:\n\tlo, hi = 0, len(nums) - 1\n\twhile lo < hi:\n\t\tmid = 2 * ((lo + hi) // 4)\n\t\tif nums[mid] == nums[mid+1]:\n\t\t\tlo = mid+2\n\t\telse:\n\t\t\thi = mid\n\treturn nums[lo]\n``` | 113 | 0 | ['Binary Search', 'Python'] | 12 |
single-element-in-a-sorted-array | [C++] O(log n) time O(1) space | Simple and clean | Use xor to keep track of odd even pair | c-olog-n-time-o1-space-simple-and-clean-hjyqf | nums[mid] == nums[mid ^ 1] for odd position compares with the previous number; for even position compares with the next number. The unique number must be at eve | sonugiri | NORMAL | 2020-05-12T07:07:48.788912+00:00 | 2020-05-12T09:37:47.774537+00:00 | 8,025 | false | **nums[mid] == nums[mid ^ 1]** for odd position compares with the previous number; for even position compares with the next number. The unique number must be at even position.\n \n```\nint singleNonDuplicate(vector<int>& nums) {\n\tint start=0, end = nums.size()-1, mid;\n\twhile( start < end ) {\n\t\tmid = start + (end-start)/2;\n\t\tif( nums[mid] == nums[mid ^ 1] )\n\t\t\tstart = mid + 1;\n\t\telse\n\t\t\tend = mid;\n\t}\n\treturn nums[start];\n}\n```\n\nIn case above one looks more complicated to you:\n\n```\nint singleNonDuplicate(vector<int>& nums) {\n\tint left = 0, right = nums.size() - 1;\n\twhile(left < right){\n\t\tint mid = (left + right)/2;\n\t\tif((mid % 2 == 0 && nums[mid] == nums[mid + 1]) || (mid % 2 == 1 && nums[mid] == nums[mid - 1]))\n\t\t\tleft = mid + 1;\n\t\telse\n\t\t\tright = mid;\n\t}\n\treturn nums[left];\n}\n``` | 107 | 2 | [] | 16 |
single-element-in-a-sorted-array | C++ Solution O(logn) with detailed explanation | c-solution-ologn-with-detailed-explanati-gcx6 | \nWe use binary search to solve this.\n\nThe problem of using binary search is how to determine the conditions inside the while loop?\n\nWell this logic maynot | leodicap99 | NORMAL | 2020-05-12T10:41:41.312989+00:00 | 2020-05-12T10:41:41.313046+00:00 | 4,364 | false | ```\nWe use binary search to solve this.\n\nThe problem of using binary search is how to determine the conditions inside the while loop?\n\nWell this logic maynot come that intuitively but if u observe a few examples u will quickly get the idea.\n\nLet num=[1,1,2,3,3,4,4,8,8]\n 0,1,2,3,4,5,6,7,8 <----indices\n\nLet us do our traditional binary search start and see what happens:-\nl=0,r=nums.size()-1=8\nm=4\n\n[1,1,2,3,3,4,4,8,8]\n ^\n |\n mid\nNotice that once we hit the mid and remove its duplicate(if it doesnt have any that would be the answer)-> the answer will lie in the subarray \nconstaining odd length (cuz everything will be paired up except for 1 thus odd length)\n\n[1,1,2, ,4,4,8,8]\n\\_____/ \\______/\n | |\n odd even \n length length\n\n Thus our answer is present in the odd length of the array.\n\n But one problem here is how to find after the split whether its odd and even by making sure we stick to the complexity of o(logn).\n\n U initialize a bool variable and check if the r-mid is even or not.\n[1,1,2,3,3,4,4,8,8]\nFor this example 8-4=4 is even that mean ur answer cant lie in the right side of the array.\nSo we can test our solution like this\n\nbool even_length=(r-m)%2==0\nif(nums[m]==nums[m-1])\n{\n\tif(even_length)\n\t\tr=m-2;\n\telse \n\t\tl=m+1;\n}\n\ndid u understand? ->I am writing the code to suit for the above example \n\nNow what if nums[m]==nums[m+1]\nnums=[1,1,4,4,5,5,6,7,7]\n ^\n |\n mid \nHere r-m=even but wait...\nm+1 has to be removed too \nthus eventhough the right side show even due to the above property it has to odd cuz we subtract 1 element\nThen just follow the same procedure\n\nif(nums[m]==nums[m+1])\n{\n\tif(even_length)\n\t\tl=m+2;\n\telse\n\t\tr=m-1;\n}\n\n\nCode:-\n\n int singleNonDuplicate(vector<int>& nums) {\n int l=0,r=nums.size()-1;\n while(l<r)\n {\n int m=l+(r-l)/2;\n bool even_length=(r-m)%2==0;\n if(nums[m]==nums[m+1])\n {\n if(even_length)\n l=m+2;\n else\n r=m-1;\n }\n else if(nums[m]==nums[m-1])\n {\n if(even_length)\n r=m-2;\n else\n l=m+1;\n }\n else\n return nums[m];\n }\n return nums[l];\n }\n\n\n\n``` | 69 | 2 | ['C', 'C++'] | 4 |
single-element-in-a-sorted-array | Java Binary Search with Detailed Explanation | java-binary-search-with-detailed-explana-2vmn | Let's start with two simple observations.\n\nExample 1: An array with length 2*4 + 1\nleft = 0, right = 8, mid = 4.\nIf the single element X is on the left hand | coshchen | NORMAL | 2017-12-13T16:24:11.479000+00:00 | 2018-10-19T04:38:06.097890+00:00 | 5,055 | false | Let's start with two simple observations.\n\n**Example 1**: An array with length ```2*4 + 1```\n```left = 0```, ```right = 8```, ```mid = 4```.\nIf the single element ```X``` is on the left hand side, ```nums[mid] == nums[mid-1]```: \n```[1, 1, X, 2, 2(mid), 3, 3, 4, 4]```\nIf the single element ```X``` is on the right hand side, ```nums[mid] == nums[mid+1]```: \n```[1, 1, 2, 2, 3(mid), 3, X, 4, 4]```\n\n**Example 2**: An array with length ```2*3 + 1```\n```left = 0```, ```right = 6```, ```mid = 3```.\nIf the single element ```X``` is on the left hand side, ```nums[mid] == nums[mid+1]```: \n```[1, 1, X, 2(mid), 2, 3, 3]```\nIf the single element ```X``` is on the right hand side, ```nums[mid] == nums[mid-1]```: \n```[1, 1, 2, 2(mid), 3, 3, X]```\n\nIn general, for an array with length ```2*n + 1```, if ```n``` is even, the behavior of ```mid``` will be the same as that in Example 1. Otherwise, it will be as in Example 2.\n\nBelow is the solution.\n```\nclass Solution {\n public int singleNonDuplicate(int[] nums) {\n if(nums.length == 1) return nums[0];\n \n int len = nums.length;\n int left = 0;\n int right = len - 1;\n \n while(left <= right && left < len && right >= 0){\n int mid = left + (right - left)/2;\n \n if((mid-1 >= 0 && nums[mid-1] == nums[mid]) || (mid + 1 < len && nums[mid+1] == nums[mid])){ // nums[mid] is not single\n int currLen = right - left; // actual length - 1 \n if((currLen/2) % 2 == 0){\n if(nums[mid-1] == nums[mid]){\n // The element is on the left hand side\n right = mid - 2; // Skip mid-1 and mid as we know they are not single\n }\n else{\n // The element is on the right hand side\n left = mid + 2;\n }\n }\n else{\n if(nums[mid-1] == nums[mid]){\n // The element is on the right hand side\n left = mid + 1; // Skip mid\n }\n else{\n // The element is on the left hand side\n right = mid - 1;\n }\n }\n }\n else return nums[mid];\n }\n \n return nums[left];\n }\n}\n``` | 69 | 1 | [] | 6 |
single-element-in-a-sorted-array | [Python] 3 Simple Approaches with Explanation | python-3-simple-approaches-with-explanat-dduw | Approach 1: (Optimised) Brute Force\n\nThere are a few ways to brute force a solution. One way is to count the number of times each element appears in the array | zayne-siew | NORMAL | 2021-11-20T02:41:07.779475+00:00 | 2021-11-20T07:35:19.765310+00:00 | 4,849 | false | ### Approach 1: (Optimised) Brute Force\n\nThere are a few ways to brute force a solution. One way is to count the number of times each element appears in the array, and then return the value with a counter of 1.\n\n```python\nclass Solution:\n def singleNonDuplicate(self, nums: List[int]) -> int:\n counts = defaultdict(int)\n for num in nums:\n counts[num] += 1\n for num, count in counts.items():\n if count == 1:\n return num\n return -1 # this will never be reached\n\t\t# return Counter(nums).most_common()[-1][0] # one-liner, but TC O(nlogn)\n```\n\n**TC: O(2n) ~ O(n)**, since we loop through the array twice.\n**SC: O(n)**, since we used a dictionary / Counter object.\n\nAnother way is to check if each element has been seen before in the array. This method is intrinsically highly optimised since we know that duplicate elements are adjacent to each other.\n\n```python\nclass Solution:\n def singleNonDuplicate(self, nums: List[int]) -> int:\n val, seen = -1, True\n for num in nums:\n if val == num:\n seen = True\n elif seen:\n val = num\n seen = False\n else:\n return val\n return -1 # this will never be reached\n```\n\n**TC: O(n)**, since we only loop through the array once.\n**SC: O(1)**, since no additional data structures are used.\n\nWe can further optimise this method by abusing the adjacency of the duplicate elements: checking elements pairwise for equality.\n\n```python\nclass Solution:\n def singleNonDuplicate(self, nums: List[int]) -> int:\n for i in range(0, len(nums)-1, 2): # pairwise comparison\n if nums[i] != nums[i+1]: # found the single element\n return nums[i]\n return nums[-1] # the last element is the single element\n```\n\n**TC: O(<img src="http://latex.codecogs.com/png.image?\\dpi{110}&space;\\frac{n}{2}" title="\\frac{n}{2}" />) ~ O(n)**, since we loop through the array two-by-two.\n**SC: O(1)**; no additional data structures used.\n\n---\n\n### Approach 2: (One-liner) Reducing Operations\n\nSince we know that every element repeats twice except for the single element, we can try to apply a function where all duplicate elements cancel each other out, leaving only the single element.\n\nOne such operation is to take the summation of all elements, but have each element alternate between positive and negative absolute values. This guarantees that each pair of duplicate elements has one positive and one neagtive absolute value, thereby cancelling each other out when added together.\n\n```python\nclass Solution:\n def singleNonDuplicate(self, nums: List[int]) -> int:\n result = 0\n for i in range(len(nums)):\n if i%2: # alternate between +ve and -ve\n result -= nums[i]\n else:\n result += nums[i]\n return result\n\t\t# return sum((-1)**i*v for i,v in enumerate(nums)) # one-liner\n```\n\nAnother such operation: bitwise-XOR. Bitwise-XOR works because `a XOR 0 = a` and `a XOR a = 0` for all real numbers `a`, therefore, chaining bitwise-XORs on `nums` will cancel out all duplicates and leave us with the single element.\n\n```python\nclass Solution:\n def singleNonDuplicate(self, nums: List[int]) -> int:\n result = 0\n for num in nums:\n result ^= num\n return result\n # return reduce(xor, nums) # one-liner\n```\n\n**TC: O(n)**, since we loop through all elements in the array.\n**SC: O(1)**, as discussed previously.\n\nWe can further optimise these approaches by looping through the array pairwise as per Approach 1.\n\n```python\nclass Solution:\n def singleNonDuplicate(self, nums: List[int]) -> int:\n result = nums[0]\n for i in range(1, len(nums), 2):\n result += nums[i+1]-nums[i]\n return result\n\t\t# return nums[0] + sum(nums[i+1]-nums[i] for i in range(1, len(nums), 2)) # one-liner\n```\n\n```python\nclass Solution:\n def singleNonDuplicate(self, nums: List[int]) -> int:\n result = nums[0]\n for i in range(1, len(nums), 2):\n result ^= nums[i]^nums[i+1]\n return result\n # return reduce(lambda x,i: x^nums[i]^nums[i+1], range(1, len(nums), 2), nums[0]) # one-liner\n```\n\n**TC: O(<img src="http://latex.codecogs.com/png.image?\\dpi{110}&space;\\frac{n}{2}" title="\\frac{n}{2}" />) ~ O(n)**, as discussed previously.\n**SC: O(1)**, as discussed previously.\n\n---\n\n### Approach 3: Binary Search\n\nSince the array is sorted and the requirement is for the TC to be O(<img src="http://latex.codecogs.com/svg.image?log(n)" title="log(n)" />), it should be clear that binary search is to be used. But what exactly is the condition to check for? Consider the following example:\n\n```text\nnums = [ 1, 1, 2, 2, 3, 3, 4, 5, 5, 6, 6, 7, 7, 8, 8 ]\nfirst: ^ ^ ^ ^ ^ ^ ^ ^\nindex: 0 2 4 6 7 9 11 13\n```\n\nIt becomes clear that the index of the first of each duplicate element shows us where the single element is: **if the index is even, the single element lies in the upper end of the search space; but if the index is odd, the single element lies in the lower end of the search space**.\n\n```python\nclass Solution:\n def singleNonDuplicate(self, nums: List[int]) -> int:\n lo, hi = 0, len(nums)-1\n while lo < hi:\n mid = lo+(hi-lo)//2\n if nums[mid] == nums[mid-1]: # duplicate found\n if mid%2: # target > mid\n lo = mid+1 # exclude second index mid; mid+1\n else: # target < mid\n hi = mid-2 # exclude first index mid-1; mid-1-1\n elif nums[mid] == nums[mid+1]: # duplicate found\n if mid%2: # target < mid\n hi = mid-1 # exclude first index mid; mid-1\n else: # target > mid\n lo = mid+2 # exclude second index mid+1; mid+1+1\n else: # no duplicate found, target == mid\n return nums[mid]\n return nums[lo]\n```\n\nA shorter but more unintuitive way: checking pairwise at `mid` via `mid^1`. `mid^1` returns the next odd number if `mid` is even, and returns the previous even number if `mid` is odd (you can try it for yourself). By checking pairwise, if the numbers are the same, it is equivalent to the first index being even. Likewise, the numbers not being equal is equivalent to the first index being odd.\n\n```python\nclass Solution:\n def singleNonDuplicate(self, nums: List[int]) -> int:\n lo, hi = 0, len(nums)-2 # hi starts from an even index so that hi^1 gives the next odd number\n while lo <= hi:\n mid = lo+(hi-lo)//2\n if nums[mid] == nums[mid^1]:\n lo = mid+1\n else:\n hi = mid-1\n return nums[lo]\n```\n\n**TC: O(<img src="http://latex.codecogs.com/svg.image?log(n)" title="log(n)" />)**, classic binary search time complexity.\n**SC: O(1)**, as discussed previously.\n\n---\n\nPlease upvote if this has helped you! Appreciate any comments as well :) | 65 | 2 | ['Binary Tree', 'Python', 'Python3'] | 11 |
single-element-in-a-sorted-array | 🗓️ Daily LeetCoding Challenge November, Day 20 | daily-leetcoding-challenge-november-day-h65t1 | This problem is the Daily LeetCoding Challenge for November, Day 20. Feel free to share anything related to this problem here! You can ask questions, discuss wh | leetcode | OFFICIAL | 2021-11-20T00:00:24.945182+00:00 | 2021-11-20T00:00:24.945231+00:00 | 5,615 | false | This problem is the Daily LeetCoding Challenge for November, Day 20.
Feel free to share anything related to this problem here!
You can ask questions, discuss what you've learned from this problem, or show off how many days of streak you've made!
---
If you'd like to share a detailed solution to the problem, please create a new post in the discuss section and provide
- **Detailed Explanations**: Describe the algorithm you used to solve this problem. Include any insights you used to solve this problem.
- **Images** that help explain the algorithm.
- **Language and Code** you used to pass the problem.
- **Time and Space complexity analysis**.
---
**📌 Do you want to learn the problem thoroughly?**
Read [**⭐ LeetCode Official Solution⭐**](https://leetcode.com/problems/single-element-in-a-sorted-array/solution) to learn the 3 approaches to the problem with detailed explanations to the algorithms, codes, and complexity analysis.
<details>
<summary> Spoiler Alert! We'll explain these 3 approaches in the official solution</summary>
**Approach 1:** Brute Force
**Approach 2:** Binary Search
**Approach 3:** Binary Search on Evens Indexes Only
</details>
If you're new to Daily LeetCoding Challenge, [**check out this post**](https://leetcode.com/discuss/general-discussion/655704/)!
---
<br>
<p align="center">
<a href="https://leetcode.com/subscribe/?ref=ex_dc" target="_blank">
<img src="https://assets.leetcode.com/static_assets/marketing/daily_leetcoding_banner.png" width="560px" />
</a>
</p>
<br> | 39 | 3 | [] | 34 |
single-element-in-a-sorted-array | Easy Binary Search Explanation | O(logn) | O(1) | easy-binary-search-explanation-ologn-o1-s9x8z | Intuition\nLet\'s look at an example array [3,3,4,4,5,6,6,7,7]. We look at indicies 0, 2, 4, 6, 8 and check if the number is equal to the number on its right.\n | fromdihpout | NORMAL | 2023-02-21T00:53:21.372228+00:00 | 2023-02-21T00:53:21.372270+00:00 | 8,524 | false | # Intuition\nLet\'s look at an example array `[3,3,4,4,5,6,6,7,7]`. We look at indicies `0, 2, 4, 6, 8` and check if the number is equal to the number on its right.\n```\n index: 0 1 2 3 4 5 6 7 8\n nums: 3 3 4 4 5 6 6 7 7\nmatches: T T F F F\n```\nAt the singleton number, the numbers stop matching with the number to its right. We can do binary serach to find this position where the numbers stop matching.\n\n# Complexity\n- Time complexity: Binary search on an array of size `n` takes O(logn).\n\n- Space complexity: Constant space is needed for binary search, so O(1).\n\n# Code\n```\nclass Solution:\n def singleNonDuplicate(self, nums: List[int]) -> int:\n l, r = 0, len(nums) // 2\n ans = -1\n while l <= r:\n mid = (l + r) // 2\n idx = mid * 2\n if idx + 1 >= len(nums) or nums[idx] != nums[idx + 1]:\n r = mid - 1\n ans = nums[idx]\n else:\n l = mid + 1\n return ans\n``` | 35 | 3 | ['Python3'] | 10 |
single-element-in-a-sorted-array | ✅☑️ Best C++ 5 Solution || Binary Search || XOR || Hash Table || Brute Force->Optimize. | best-c-5-solution-binary-search-xor-hash-32a7 | Intuition\n Describe your first thoughts on how to solve this problem. \nWe can solve this question using Multiple Approaches. (Here I have explained all the po | its_vishal_7575 | NORMAL | 2023-02-15T16:04:33.469570+00:00 | 2023-02-15T16:04:33.469617+00:00 | 1,772 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe can solve this question using Multiple Approaches. (Here I have explained all the possible solutions of this problem).\n\n1. Solved using Array(Two Nested Loop). Brute Force Approach.\n2. Solved using Array + Hash Table(Unordered map).\n3. Solved using Linear Search.\n4. Solved using Bit Manipulation(xor).\n5. Solved using Binary Search. Optimized Approach.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe can easily understand the All the approaches by seeing the code which is easy to understand with comments.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nTime complexity is given in code comment.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nSpace complexity is given in code comment.\n\n# Code\n```\n/*\n\n Time Complexity : O(N^2), Here Two nested loop creates the time complexity. Where N is the size of the\n Array(nums).\n\n Space Complexity : O(1), Constant space.\n\n Solved using Array(Two Nested Loop). Brute Force Approach.\n\n Note : this will give TLE.\n\n*/\n\n\n/***************************************** Approach 1 *****************************************/\n\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n int n = nums.size();\n for(int i=0; i<n; i++){\n int count = 0;\n for(int j=0; j<n; j++){\n if(nums[i] == nums[j]) count++;\n }\n if(count == 1) return nums[i];\n }\n return -1;\n }\n};\n\n\n\n\n\n\n/*\n\n Time Complexity : O(N), Here we are doing N iteration which creates the time complexity. Where N is the size\n of the array(nums).\n\n Space Complexity : O(N), Hash Table(unordered map) space.\n\n Solved using Array + Hash Table(unordered map).\n\n*/\n\n\n/***************************************** Approach 2 *****************************************/\n\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n unordered_map<int, int> map;\n for(auto num : nums){\n map[num]++;\n }\n for(auto num : map){\n if(num.second == 1) return num.first;\n }\n return -1;\n }\n};\n\n\n\n\n\n\n/*\n\n Time Complexity : O(N), because in the worst case we traverse the <= N element. Where N is the size of the\n Array(nums).\n \n Space Complexity : O(1), the space complexity is constant.\n\n Solved using Linear Search.\n\n*/\n\n\n/***************************************** Approach 3 *****************************************/\n\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n int n = nums.size();\n for(int i=0; i<n-1; i+=2){\n if(nums[i] != nums[i+1]){\n return nums[i];\n }\n }\n return nums[n-1];\n }\n};\n\n\n\n\n\n\n/*\n\n Time Complexity : O(N), because in the worst case we traverse the <= N element. Where N is the size of the\n Array(nums).\n \n Space Complexity : O(1), the space complexity is constant.\n\n Solved using Bit manupulation(xor).\n\n*/\n\n\n/***************************************** Approach 4 *****************************************/\n\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n int Xor = 0;\n for(auto num : nums){\n Xor ^= num;\n }\n return Xor;\n }\n};\n\n\n\n\n\n\n/*\n\n Time Complexity : O(log N), since we have used binary search to find the target element. The time complexity\n is logarithmic.\n\n Space Complexity : O(1), since we stored only some constant number of elements, the space complexity is\n constant.\n\n Solved using Binary Search.\n\n*/\n\n\n/***************************************** Approach 5 *****************************************/\n\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n int low = 0, high = nums.size()-1;\n while(low < high){\n int mid = (low + high) >> 1;\n int num = (mid%2==0) ? mid+1 : mid-1;\n if(nums[mid] == nums[num]) low = mid+1;\n else high = mid;\n }\n return nums[low];\n }\n};\n\n```\n\n***IF YOU LIKE THE SOLUTION THEN PLEASE UPVOTE MY SOLUTION BECAUSE IT GIVES ME MOTIVATION TO REGULARLY POST THE SOLUTION.***\n\n | 32 | 0 | ['Array', 'Hash Table', 'Binary Search', 'Bit Manipulation', 'C++'] | 1 |
single-element-in-a-sorted-array | Java Code by using binary search O(log(n)) | java-code-by-using-binary-search-ologn-b-chui | public int singleNonDuplicate(int[] nums) {\n int low = 0;\n int high = nums.length-1;\n \n while(low < high) {\n int mid | dhawal9035 | NORMAL | 2017-03-09T03:05:40.569000+00:00 | 2018-09-22T06:54:08.147224+00:00 | 10,667 | false | public int singleNonDuplicate(int[] nums) {\n int low = 0;\n int high = nums.length-1;\n \n while(low < high) {\n int mid = low + (high - low)/2;\n if(nums[mid] != nums[mid+1] && nums[mid] != nums[mid-1])\n return nums[mid];\n else if(nums[mid] == nums[mid+1] && mid % 2 == 0)\n low = mid+1;\n else if(nums[mid] == nums[mid-1] && mid % 2 == 1)\n low = mid+1;\n else\n high = mid-1;\n }\n return nums[low];\n } | 30 | 1 | [] | 5 |
single-element-in-a-sorted-array | C++ Solution with step by step explanation. | c-solution-with-step-by-step-explanation-qaev | Attacking the problem\nYou start with B.S. as the question is tagged as B.S. and then think that the array is sorted so B.S. it is.\nStuck!! How do I know if I | tars2412 | NORMAL | 2021-06-01T06:55:43.148090+00:00 | 2021-08-24T06:38:00.228913+00:00 | 1,384 | false | **Attacking the problem**\nYou start with B.S. as the question is tagged as B.S. and then think that the array is sorted so B.S. it is.\n**Stuck!! How do I know if I go left or right from the middle :(**\nOkay jokes apart this is a really good problem on B.S. and let us carefully analyse what we are given.\nThe array is sorted and as only one unique element and other elements exist as pairs. \nDIY take few example arrays and write the indices above all the elements. \n**Observe** \nGot something?\nNo?\n**Observe again and look at the indices of pairs on the left of the unique element and on the right of the unique element**\n\nWe see that for every case on the left of the unique element the pairs exist as (even,odd), (even,odd),......(even)\nwhere singular (even) is the index of the unique element. \n(It can be easily concluded that the index of the unique element will always be even.)\nAfter the unique element the pairs on the right exist as (odd,even),(odd,even),........\nSo are we still stuck on where to go, left or right? \nBy seeing this pattern we have found two distinct search spaces and we can move towards the unique element by checking in which search space we are in.\nIf we are in the left search space we go right.\nIf we are in the right search space we go left.\nI leave the code for your reference below. \n\n```\nint singleNonDuplicate(vector<int>& nums) {\n if(nums.size()==1)\n return nums[0];\n int l = 0,r=nums.size()-1;\n while(l<=r){\n int m = l + (r-l)/2;\n if(m%2){\n\t\t\t\t// (even odd) i.e. we are on the left side of unique element--> go right\n if(nums[m-1]==nums[m])\n l = m+1;\n\t\t\t\t// (even odd) pair violated, happens on the right side of unique element--> go left\n else{\n r = m-1;\n }\n }else{\n\t\t\t\t// (even odd) i.e. we are on the left side of unique element--> go right\n if(nums[m]==nums[m+1]){\n l = m+1;\n\t\t\t\t// (even odd) pair violated, happens on the right side of unique element--> go left\n }else{\n r = m-1;\n }\n }\n }\n return nums[l];\n }\n``` | 26 | 0 | ['C', 'Binary Tree'] | 4 |
single-element-in-a-sorted-array | Java Binary Search O(lgN) : clear, easy, explained, no tricks | java-binary-search-olgn-clear-easy-expla-bt39 | First, the code:\njava\npublic class Solution {\n public int singleNonDuplicate(int[] nums) {\n int n = nums.length;\n int lo = 0, hi = n;\n | vegito2002 | NORMAL | 2017-07-26T00:45:11.535000+00:00 | 2018-09-26T07:27:46.454322+00:00 | 2,963 | false | First, the code:\n```java\npublic class Solution {\n public int singleNonDuplicate(int[] nums) {\n int n = nums.length;\n int lo = 0, hi = n;\n while (lo < hi) {\n int mid = lo + (hi - lo) / 2;\n if ((mid % 2 == 0 && mid + 1 < n && nums[mid] == nums[mid + 1]) ||\n (mid % 2 == 1 && mid - 1 >= 0 && nums[mid] == nums[mid - 1]))\n lo = mid + 1;\n else\n hi = mid;\n }\n return nums[lo];\n }\n}\n```\nThe logic behind this is very easy: for each `mid`, we try to find understand whether the single number is on the **left** half. The `if` header tests that *`nums[mid]` is not single and neither is anything on its left*.\n* if `mid` is even, then there are `2m` numbers on the left of `mid`. For the statement of *`nums[mid]` is not single and neither is anything on its left* to hold, we need the `2m` numbers to the left of `mid` to be `m` pairs, and also `nums[mid]` be in a pair with `nums[mid + 1]`. Indeed, we only have to make sure in this case that `nums[mid], nums[mid + 1]` is a pair. You can prove by contradiction that as long as this holds, the sole single number can\'t be on the left of `mid`. Now that the statement of *`nums[mid]` is not single and neither is anything on its left* is proven, we can just go to the right half.\n* if `mid` is odd, then to prove *`nums[mid]` is not single and neither is anything on its left*, we only need to prove that `nums[mid - 1], nums[mid]` is a pair. `mid - 1` is even, and as long as `nums[mid - 1], nums[mid - 1 + 1]` forms a pair, we can actually use the argument of previous paragraph to prove that no entry to the left of `mid` is single. And neither is `mid` itself obviously. With *`nums[mid]` is not single and neither is anything on its left* proven, we can again to the right half.\n* If *`nums[mid]` is not single and neither is anything on its left* not provable, then go to left half since the single number is there.\n\nI am not entirely sure the above explanation suffices, but I do hope it helps. | 25 | 0 | [] | 3 |
single-element-in-a-sorted-array | Multiple_Approaches.py | multiple_approachespy-by-jyot_150-hgqp | UPVOTE IF YOU LIKE SOLN \n\n# Approach\n Brute Force -> Optimization\n\n# Complexity\n- Time complexity:\nO(n) --> O(log n)\n# Codes\n```\n//Brute Force OP\ncla | jyot_150 | NORMAL | 2023-02-21T03:15:46.558698+00:00 | 2023-02-21T14:46:05.178413+00:00 | 1,235 | false | <h3>UPVOTE IF YOU LIKE SOLN</h3>\n\n# Approach\n<h4>Brute Force -> Optimization\n\n# Complexity\n- Time complexity:\n$$O(n)$$ --> $$O(log n)$$\n# Codes\n```\n//Brute Force OP\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n for(int p=0;p<nums.size()-1;p+=2){\n if(nums[p]!=nums[p+1]){\n return nums[p];\n }\n }\n return nums[nums.size()-1];\n }\n};\n```\n```\n#Using XOR\nclass Solution:\n def singleNonDuplicate(self, nums: List[int]) -> int:\n x=0\n for i in nums:\n x=x^i\n return x\n```\n```\n#One-Liner Using Set\nclass Solution:\n def singleNonDuplicate(self, nums: List[int]) -> int:\n return ((2*sum(set(nums)))-sum(nums))\n\n```\n```\n#One_liner Xor\nclass Solution:\n def singleNonDuplicate(self, nums: List[int]) -> int:\n return reduce(lambda m,n:m^n,nums)\n```\n```\n//Another One\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n map<int,int>mp;\n int n=nums.size();\n for(int p=0;p<n;p++) mp[nums[p]]++;\n for(auto i:mp){\n if(i.second==1) return i.first;\n }\n return 0;\n }\n};\n```\n```\n//Final One\n//Binary Search Optimised\nclass Solution:\n def singleNonDuplicate(self, nums: List[int]) -> int:\n l,r=0,len(nums)//2\n ans=-1\n while l<=r:\n mid=(l+r)//2\n i=mid*2\n if i+1>=len(nums) or nums[i]!=nums[i+1]:\n r=mid-1\n ans=nums[i]\n else:\n l=mid+1\n return ans\n```\n\n | 24 | 1 | ['Python3'] | 3 |
single-element-in-a-sorted-array | Java Super Elegent solution (log(n) Runtime O(1) extra space, bit trick). [Detailed explanation] | java-super-elegent-solution-logn-runtime-ol9e | Idea behind the solution:\n\n1. If the current index in the binary search is I (0 index based), the we can decide the next search space based on:\n\ta. If I is | cool_rohan | NORMAL | 2020-05-12T08:34:51.576742+00:00 | 2020-05-12T12:51:43.806502+00:00 | 1,933 | false | Idea behind the solution:\n\n1. If the current index in the binary search is `I` (0 index based), the we can decide the next search space based on:\n\ta. If `I` is even, and `nums[I] == nums[I + 1]`, then size of subarray `[0...I-1]` (left side) is even (since the element count is `I`), so left side does not contain the single occurance element. Hence we need to check in `[I + 1, ..., N]` subarray (right side of `I`)\n\tb. If `I` is odd, and `nums[I] == nums[I - 1]`, then size of subarray `[0...I-2]` (left side) is even (since the element count is `I - 1`, and `I-1` is even since `I` is odd), so left side does not contain the single occurance element. Hence we need to check in `[I + 1, ..., N]` subarray (right side of `I`) </br>\n\tNote: How can you implement the check operation. Remember the xor operation, and if you xor any number with 1, then it flips the LSB (Least significant bit)\nEx. 1) `100^1=101` [i.e `4^1=5`, flips the first bit from right side] </br> 2) `101^1=100` [i.e `5^1=4`, again flips the first bit from right side]\nSo, if `I` is even, to find the next element we do `I^1`\n\tand if `I` is odd, to find the previous element we do `I^1`\n```\nclass Solution {\n public int singleNonDuplicate(int[] nums) {\n int l = 0;\n int h = nums.length - 1;\n while (l < h) {\n int m = (l + h) / 2;\n if (nums[m] == nums[m ^ 1]) {\n l = m + 1;\n } else {\n h = m;\n }\n }\n return nums[h];\n }\n}\n``` | 23 | 4 | ['Binary Search', 'Java'] | 4 |
single-element-in-a-sorted-array | 🚀Simplest Solution🚀||🔥Binary Search||🔥C++🔥|| Python3 | simplest-solutionbinary-searchc-python3-pj7k7 | Consider\uD83D\uDC4D\n\n Please Upvote If You Find It Helpful\n\n# Intuition \nIntitution is very simple we have to find the which appears on | naman_ag | NORMAL | 2023-02-21T03:42:23.924018+00:00 | 2023-02-21T03:42:23.924061+00:00 | 2,259 | false | # Consider\uD83D\uDC4D\n```\n Please Upvote If You Find It Helpful\n```\n# Intuition \nIntitution is very simple we have to find the which appears once.\nWe can see in array it follows a pattern all the duplicate pairs are at **Even and Odd positions** this pattern is not satisfied when there is a single element in the array.\nFor example : [1,1,2,3,3,4,4,8,8]\nIn this array `1` is at 0 and 1 index. This pattern follows for all pairs.\n\n How we can implement Binary Search here.\n 1. Take left and right pointers . \n `start` points to start of list. `end` points to end of the list.\n 2. Find `mid`.\n If mid is `even`, then it\'s duplicate should be in next index.\n or if `mid` is `odd`, then it\'s duplicate should be in previous index.\n For checking `mid` I am using Bit manipulation `mid^1` it means if `mid` is `even` it check at `odd` position and if it is `odd` it will check at `even` position.\n check these two conditions, \n if any of the conditions is satisfied,\n then pattern is not missed, \n so check in next half of the array. i.e, `start` = mid + 1\n if condition is not satisfied, then the pattern is missed.\n so, single number must be before mid.\n so, update `end` to mid-1.\n 3. At last return the nums[start]\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach : Binary Search\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(logn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n int start=0, end=nums.size()-2;\n while(end>=start){\n int mid = (end+start)/2;\n if(nums[mid] == nums[mid^1])\n start = mid+1;\n else\n end = mid-1;\n }\n return nums[start];\n }\n};\n\n```\n```python []\nclass Solution:\n def singleNonDuplicate(self, nums: List[int]) -> int:\n start = 0\n end = len(nums)-2\n while end>=start:\n mid = (end+start)//2\n if nums[mid] == nums[mid^1]:\n start = mid+1\n else:\n end = mid-1\n return nums[start]\n```\n```\n Give a \uD83D\uDC4D. It motivates me alot\n```\nLet\'s Connect On [Linkedin](https://www.linkedin.com/in/naman-agarwal-0551aa1aa/) | 20 | 0 | ['Array', 'Binary Search', 'Python', 'C++', 'Python3'] | 1 |
single-element-in-a-sorted-array | ✅ [Java] EASY Intuitive Sol | Full Explanation | 100% Faster | Bit Manipulation | Binary Search | java-easy-intuitive-sol-full-explanation-mqsq | Hello everyone, I hope you all are doing great.\nNote: If you found this post helpful then please do upvote!\n\nIn this post i\'ll explain 4 approach from worst | kumarav1nash | NORMAL | 2021-11-20T08:47:41.954454+00:00 | 2021-11-20T14:39:27.409205+00:00 | 1,156 | false | Hello everyone, I hope you all are doing great.\n**Note: If you found this post helpful then please do upvote!**\n\nIn this post i\'ll explain 4 approach from worst to best time complexity, and i\'ll also i\'ll try to explain the intution behind this.\nBefore we proceed to various approaches let\'s keep this thing in mind.\nAs You can see in the image below all the second element in the pair before the target or ans index is at odd index and after the target they shifted to one index and are at even indexes.\n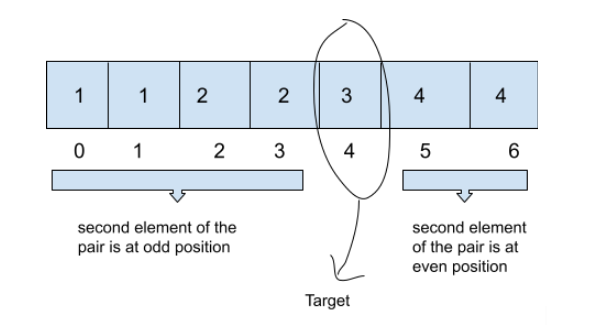\n\n___\n**Approach 1 : Linear Search - TC O(n) - SC O(1)**\n\nIn this approach we simply traverse through every pair from the nums array and keep checking if the current element is equal to the prev one, if not we will simply return the prev element. \n\n```\nclass Solution {\n public int singleNonDuplicate(int[] nums) {\n\t//traverse through arrau and check if prev is equal to curr ,if not return prev\n for(int i=1;i<nums.length;i+=2){\n if(nums[i]!=nums[i-1]){\n return nums[i-1];\n } \n }\n\t\t//if didn\'t find means last element is single, here\'s the example [1,1,2,2,3]\n return nums[nums.length-1];\n }\n}\n```\n**Time Complexity: O(n)\nSpace Complexity : O(1)**\n___\n\n**Approach 2 : Bit manupulation - TC O(n) - SC (1)**\nHere we use the fact that performing **XOR** with two same numbers give us **zero** and doing XOR with zero and other number will give us that number itself.\nhere\'s the example \n2 - 0010\n2 - 0010\n3 - 0011\n\nSo 2^2^3 = 3\n\nSo we simply iterate through the loop and do XOR and the final ans will be the required ans\n```\nclass Solution {\n\tpublic int singleNonDuplicate(int[] nums) {\n\t\tint ans = 0;\n for(int num:nums){\n ans^=num;\n }\n return ans;\n\t}\n}\n```\n**Time Complexity: O(n)\nSpace Complexity : O(1)**\n___\n**Approach 3 : Bit Manupulation Improved - TC O(n) - SC O(1)**\n\nSince we already know that every odd index represent second element of the pair which means at every odd index the **XOR** value will be **zero**, and if we found a situation where XOR is not zero at odd index which means last element was single element and that is the ans.\nwith this approach we will not iterate every time till last index and we can return when we find odd one.\n\n```\nclass Solution {\n\tpublic int singleNonDuplicate(int[] nums) {\n\t\tint ans = 0;\n int prev = 0;\n for(int i=0;i<nums.length;i++){\n prev=ans;\n ans^=nums[i];\n if((i&1)==1 && ans!=0){ //here we are checking if the index is odd and ans is not zero\n return prev;\n }\n }\n return ans;\n\t}\n}\n```\n**Time Complexity: O(n)\nSpace Complexity : O(1)**\n___\n\n**Approach 4 : Binary Search - TC O(logn) - SC O(1)**\nSince the array is already sorted we can apply binary search to find the single element.\nBefore proceeding to this solution recall the above rule that i\'ve explained with the image.\n\n```\nclass Solution {\n public int singleNonDuplicate(int[] nums) {\n //the idea is to find mid element and if mid is single return it\n //else mid is first element of the pair and \n //is at even pos means ans will be to it\'s right\n //else ans will be it\'s left\n //else mid is second element and \n //is at odd pos means ans will be towards right\n //else ans will be towards left\n \n if(nums.length==1){\n return nums[0];\n }\n \n int lo = 0,hi = nums.length-1;\n while(lo<=hi){\n int mid = lo +(hi-lo)/2;\n \n \n //means mid is second element of the pair\n if(mid-1>=0 &&(nums[mid]==nums[mid-1])){ \n //check if mid is at odd pos\n if((mid&1)==1){\n lo = mid+1;\n }else{\n hi = mid;\n }\n \n }else if(mid+1<nums.length &&(nums[mid]==nums[mid+1])){ //means mid is first element of the pair\n //check if mid is at even pos\n if((mid&1)==0){\n lo = mid+2;\n }else{\n hi = mid;\n }\n \n }else{ //means mid is single\n return nums[mid];\n }\n }\n return -1;\n }\n}\n```\n\n**Time Complexity: O(logn)\nSpace Complexity : O(1)**\n\n\uD83D\uDCCC **Please Upvote \u2705 if you found this post useful for you!** | 20 | 0 | ['Bit Manipulation', 'Binary Tree', 'Java'] | 3 |
single-element-in-a-sorted-array | Python beats 100% | python-beats-100-by-ethuoaiesec-xwkw | Use binary search. It mid is even, then check nums[mid] and nums[mid + 1]. If they are equal, then the target must be on the right half. Similarly for mid is od | ethuoaiesec | NORMAL | 2020-12-04T05:27:31.360357+00:00 | 2020-12-04T05:27:59.717507+00:00 | 1,616 | false | Use binary search. It mid is even, then check nums[mid] and nums[mid + 1]. If they are equal, then the target must be on the right half. Similarly for mid is odd, check nums[mid] and nums[mid - 1].\n```\nclass Solution(object):\n def singleNonDuplicate(self, nums):\n """\n :type nums: List[int]\n :rtype: int\n """\n left, right = 0, len(nums) - 1\n while left + 1 < right:\n mid = (left + right) // 2\n if mid % 2 == 1:\n if nums[mid] == nums[mid - 1]:\n left = mid\n else:\n right = mid\n else:\n if nums[mid] == nums[mid + 1]:\n left = mid\n else:\n right = mid\n #print(left, right)\n if left % 2 == 0:\n return nums[left]\n return nums[right]\n```\nPlease upvote if you find it helpful\uFF01 | 18 | 0 | ['Binary Tree', 'Python', 'Python3'] | 5 |
single-element-in-a-sorted-array | ✅JAVA || C++ || PYTHON || 🚀log n || 💯Beginners can Understand ||🔥Easy & Intuitive | java-c-python-log-n-beginners-can-unders-kae6 | Upvote if you like the Soltution and Explanation :)\n\n# Intuition \n- Element in pairs, even index, odd index, so find mid and check if it\'s at correct positi | AshLuvCode | NORMAL | 2023-02-21T00:51:08.933377+00:00 | 2023-02-21T13:37:18.935934+00:00 | 3,236 | false | **Upvote if you like the Soltution and Explanation :)**\n\n# Intuition \n- Element in pairs, even index, odd index, so find mid and check if it\'s at correct position or not.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n- I already handled the corner cases separately.\n\n- if nums[mid] is same as previous and it is at odd position then it\'s at correct position and if nums[mid] is same as it\'s next and it is at even position then it\'s at correct position so there must be our answer is in right of the mid otherwise it must be in left.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(log n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code JAVA\n```\nclass Solution {\n public int singleNonDuplicate(int[] nums) {\n int n = nums.length;\n int l = 0;\n int r = n-1;\n \n if(n==1)\n return nums[0];\n if(nums[0] != nums[1])\n return nums[0];\n if(nums[n-1] != nums[n-2])\n return nums[n-1];\n \n while(l<=r){\n int mid = l+(r-l)/2;\n \n if(mid>0 && mid < n-1){\n if(nums[mid] > nums[mid-1] && nums[mid] < nums[mid+1])\n return nums[mid];\n else if((nums[mid] == nums[mid-1] && mid%2==1) || (nums[mid] == nums[mid+1] && mid%2==0))\n l = mid+1;\n else \n r = mid -1;\n }\n }\n return 0;\n }\n}\n```\n\n\n# Code PYHTON 3\n```\nclass Solution:\n def singleNonDuplicate(self, nums: List[int]) -> int:\n n = len(nums)\n l = 0\n r = n - 1\n \n if n == 1:\n return nums[0]\n if nums[0] != nums[1]:\n return nums[0]\n if nums[n - 1] != nums[n - 2]:\n return nums[n - 1]\n \n while l <= r:\n mid = l + (r - l) // 2\n \n if mid > 0 and mid < n - 1:\n if nums[mid] > nums[mid - 1] and nums[mid] < nums[mid + 1]:\n return nums[mid]\n elif (nums[mid] == nums[mid - 1] and mid % 2 == 1) or (nums[mid] == nums[mid + 1] and mid % 2 == 0):\n l = mid + 1\n else:\n r = mid - 1\n \n return 0\n\n```\n\n# Code C++\n```\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n int n = nums.size();\n int l = 0;\n int r = n - 1;\n \n if (n == 1)\n return nums[0];\n if (nums[0] != nums[1])\n return nums[0];\n if (nums[n - 1] != nums[n - 2])\n return nums[n - 1];\n \n while (l <= r) {\n int mid = l + (r - l) / 2;\n \n if (mid > 0 && mid < n - 1) {\n if (nums[mid] > nums[mid - 1] && nums[mid] < nums[mid + 1])\n return nums[mid];\n else if ((nums[mid] == nums[mid - 1] && mid % 2 == 1) || (nums[mid] == nums[mid + 1] && mid % 2 == 0))\n l = mid + 1;\n else\n r = mid - 1;\n }\n }\n \n return 0;\n }\n};\n```\n | 17 | 0 | ['Binary Search', 'C', 'Binary Tree', 'Python', 'Java'] | 3 |
single-element-in-a-sorted-array | [Python] short binary search, explained | python-short-binary-search-explained-by-67scc | Straightforward way is to just iterate over all elements in O(n). There is smarter binary search solution. For example we have aa bb cc dd ee ff gg h ii jj kk. | dbabichev | NORMAL | 2021-11-20T06:44:24.664253+00:00 | 2021-11-20T06:44:24.664287+00:00 | 391 | false | Straightforward way is to just iterate over all elements in `O(n)`. There is smarter binary search solution. For example we have `aa bb cc dd ee ff gg h ii jj kk`. Let us find middle element, but shift it by one if number of element in the left part is odd: we always consider even number of elements in the left part. Then if `nums[mid] == nums[mid-1]` it means, that in the left part all elements are paired and we need to look in the right part. In the opposite case it means, that we need to look into the left half.\n\n#### Complexity\nTime complexity is `O(log n)`, space complexity is `O(1)`.\n\n#### Code\n```python\nclass Solution:\n def singleNonDuplicate(self, nums):\n beg, end = 0, len(nums) - 1\n\n while end > beg + 1:\n mid = (beg + end)//2\n if (mid - beg) % 2 == 0: mid += 1 \n if nums[mid] == nums[mid - 1]: \n beg = mid + 1\n else:\n end = mid \n\n return nums[beg]\n```\n\nIf you have any questoins, feel free to ask. If you like the solution and explanation, please **upvote!** | 16 | 1 | ['Binary Search'] | 2 |
single-element-in-a-sorted-array | Java - Binary Search O(log N) time and O(1) memory | java-binary-search-olog-n-time-and-o1-me-1jsm | \nclass Solution {\n public int singleNonDuplicate(int[] nums) {\n int N = nums.length;\n if(N == 1)\n return nums[0];\n \n | cpp_to_java | NORMAL | 2020-05-12T07:08:21.668852+00:00 | 2020-05-14T08:57:13.953741+00:00 | 1,169 | false | ```\nclass Solution {\n public int singleNonDuplicate(int[] nums) {\n int N = nums.length;\n if(N == 1)\n return nums[0];\n \n int left = 0;\n int right = N - 1;\n int mid;\n \n while(left < right){\n mid = left + ((right - left) >> 1);\n if(nums[mid] == nums[mid + 1]){\n // from index mid to (N - 1) - if even then check left interval\n if(((N - mid) & 1) == 0)\n right = mid - 1;\n else\n left = mid + 2;\n }else if(nums[mid] == nums[mid - 1]){\n // from index (mid - 1) to (N - 1) - if even then check left interval\n if(((N - mid + 1) & 1) == 0)\n right = mid - 2;\n else\n left = mid + 1;\n }else\n return nums[mid];\n }\n \n return nums[left];\n }\n}\n``` | 14 | 1 | [] | 3 |
single-element-in-a-sorted-array | C++ binary search | c-binary-search-by-hellotest-5rzj | \nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n int n = nums.size(), left = 0, right = n - 1;\n while (left < right | hellotest | NORMAL | 2017-03-09T03:28:23.724000+00:00 | 2018-08-09T00:15:03.397146+00:00 | 7,850 | false | ```\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n int n = nums.size(), left = 0, right = n - 1;\n while (left < right) {\n int mid = left + (right - left) / 2;\n if (mid % 2 == 0) {\n if (nums[mid] == nums[mid-1]) right = mid - 2;\n else if (nums[mid] == nums[mid+1]) left = mid + 2;\n else return nums[mid];\n }\n else {\n if (nums[mid] == nums[mid-1]) left = mid + 1;\n else if (nums[mid] == nums[mid+1]) right = mid - 1;\n }\n }\n return nums[left];\n }\n};\n``` | 14 | 0 | [] | 8 |
single-element-in-a-sorted-array | Python | Binary Search | O(logn) time & O(1) space | Simple Solution With Explanation | python-binary-search-ologn-time-o1-space-gj7f | Logic\n1. Since we don\'t have any target element to search for so we can\'t directly decide which part of array we need to look for single element.\n2. Since w | akash3anup | NORMAL | 2021-11-20T05:33:42.150073+00:00 | 2022-03-11T07:24:13.312797+00:00 | 700 | false | # Logic\n1. Since we don\'t have any target element to search for so we can\'t directly decide which part of array we need to look for single element.\n2. Since we know that every element has a duplicate except one so we can commit that the length of array will always be odd.\n3. Now, based on the above logic we can decide which part of array to look for. We can simply check which part of array([start:mid+1] OR [mid+1:end]) has odd number of elements.\n\n**NOTE:** In this solution, I\'m always updating the mid to be on the second index of every duplicate and then I count. You may do the vice-versa also by keeping the mid on first index of every duplicate and update start and end accordingly.\n\n```\nclass Solution:\n def singleNonDuplicate(self, nums: List[int]) -> int:\n if len(nums) == 1:\n return nums[0]\n start = 0\n end = len(nums) - 1\n while start <= end:\n mid = start + ((end - start) // 2)\n # Check if mid is the single number\n if start < mid < end and nums[mid-1] < nums[mid] < nums[mid+1]:\n return nums[mid]\n else:\n # Else goto the second index of nums[mid](duplicate) if already not there.\n if mid < end and nums[mid] == nums[mid+1]:\n mid += 1\n \n if (mid - start + 1) % 2:\n end = mid - 2\n else:\n start = mid + 1\n return nums[start]\n```\n\n***If you liked the above solution then please upvote!*** | 12 | 1 | ['Binary Search', 'Binary Tree', 'Python'] | 2 |
single-element-in-a-sorted-array | Visually Explained, Binary Search Solution. | visually-explained-binary-search-solutio-3kot | \u200B\nMain points from Question :\n It\'s been stated that elements appear exactly twice except for one element which is to be found.\n Solution must run in | Devansh2907 | NORMAL | 2024-02-25T12:32:53.866150+00:00 | 2024-02-25T12:32:53.866180+00:00 | 458 | false | \u200B\n**Main points from Question :**\n* It\'s been stated that elements appear exactly twice except for one element which is to be found.\n* Solution must run in O(log n) time and O(1) space.\n\u200B\n**Intuition developed :**\n* So from what we can discern from the given inputs that the inputs will be same for every two elements from start and increasing after as array is sorted.\n* As it\'s sorted, binary search should be the first go to logic.\n\u200B\n**Main Solution :**\n\n* The approach is simple. We take middle element and compare it to it\'s adjacent elements. \n* How we compare the middle element can be divided into two ways based on the following intuition:\n1. The elements will be in pair so every two elements will be common among value ideally.\n2. So, using that logic the 0\'th and 1\'th index will be same ideally if they aren\'t the element to be found.\n3. So, we can form a pair of two elements having common values.\n\n* Now, how we can use this in our approach? We take the middle element and check if it is even or not. \n1. If it\'s even, then we compare it to next element and check if they are equal or not.\n2. If they are equal that would mean in the array before that there is no single elemenet becaue if there was then the indexes wouldn\'t be in pairs from start and our even index wouldn\'t be equal to odd index (0 and 1 taken into context). So we increment start by mid+2 because till mid+1 there can\'t be surely any element single.\n3. In the case of mid and mid+1 not being equal then we decrement end to mid as single element would surely lie in before or at mid.\n4. In the case of middle element not being even, then it would mean that mid and mid+1 would be equal. So, in case they are, then we just increase start by mid+1 because of the earlier even and odd index logic explained in point 2.\n5. If the elements aren\'t equal for odd middle element then we decrement end to mid.\n* At the end, we return starting element with the breaking condition of the loop being end greater than start.\n\n* **Visual Explanation**\n\n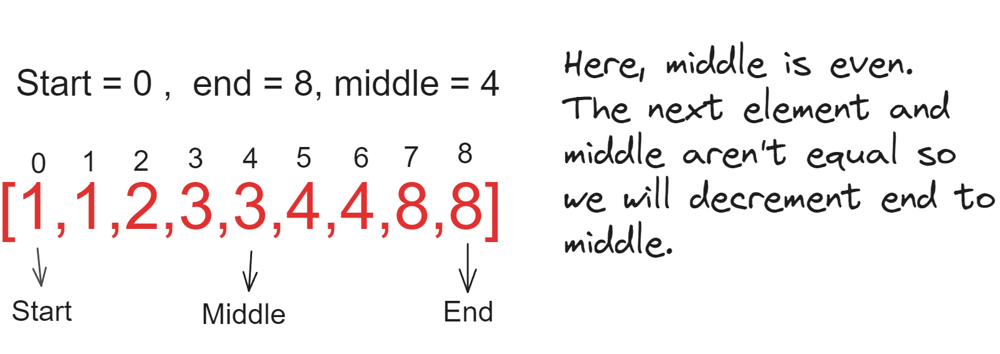\n\n\n\n\n```\n public int singleNonDuplicate(int[] nums) {\n int start = 0;\n int end = nums.length-1;\n while(start <end){\n int mid = start + (end - start)/2;\n boolean isEven = mid%2==0;\n \n if(isEven){\n if(nums[mid] == nums[mid+1]){\n start = mid+2;\n }else{\n end = mid;\n }\n } else {\n if(nums[mid] == nums[mid-1]){\n start = mid+1;\n } else {\n end = mid-1;\n }\n }\n }\n return nums[start];\n }\n```\n\n | 11 | 0 | ['Binary Tree', 'Java'] | 2 |
single-element-in-a-sorted-array | ⭐ Binary Search - Time Complexity + Space Complexity + Explanation ⭐ | binary-search-time-complexity-space-comp-mh9d | Time Complexity - Binary search takes O(logN base 2) time.\nSpace Complexity - Space taken is O(1).\nExplanation - To solve this problem, we use a modified vers | psy_0 | NORMAL | 2022-10-27T05:47:33.107504+00:00 | 2022-10-27T05:49:19.565899+00:00 | 1,499 | false | Time Complexity - Binary search takes O(logN base 2) time.\nSpace Complexity - Space taken is O(1).\nExplanation - To solve this problem, we use a modified version of binary search.\nWe know that mid is our target element, if the element is not equal to either its next or previous element (since array is sorted array).\nIf our mid isn\'t the target element, we need to search the left/right part of the array.\n\nIn an array where every element appears twice (1, 1, 2, 2) will always have an even number of elements.\nIn such an array, any element at an odd index is equal to the element at its previous index.\nHowever, an array with 1 non-repeated element will always have an odd number of elements.\nIn such an array, we can easily identify where the non-repeated element lies based upon whether our mid element satisfies this property.\n\nSatisfying either (mid is odd and nums[mid] == nums[prev]) or (mid is even and nums[mid] == nums[next]) means that all elements to the left of mid are in pairs - so we should search to its right.\n*Example:*\n[1, 1, 2, 2, 3, 4, 4]\n 0 1 2 3 4 5 6\n \nmid = 3, nums[mid] = 2\nmid doesn\'t hold our target element since arr[mid] = arr[prev], thus we need to move left/right.\nWe know mid is an odd index, and this is a result of having only elements which are in pairs to the left of mid.\nHence we should search to the right of mid for our target element.\n \n[1, 1, 2, 2, 3]\n 0 1 2 3 4 \n \n mid = 2, nums[mid] = 2\n mid doesn\'t hold our target element since arr[mid] = arr[next], thus we need to move left/right.\n We know mid is an even index, and this is a result of having only elements which are in pairs to the left of arr[next].\n Hence we should search to the right of mid for our target element.\n \n ```\n class Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums){\n int n = nums.size(), start = 0, end = n - 1, mid, next, prev;\n if(n == 1) return nums[0];\n while(start <= end){\n mid = start + (end - start) / 2;\n next = (mid + 1) % n;\n prev = (mid + n - 1) % n;\n if(nums[mid] != nums[prev] && nums[mid] != nums[next]) return nums[mid];\n else if((mid % 2 && nums[mid] == nums[prev]) || (!(mid % 2) && nums[mid] == nums[next])) start = mid + 1;\n else end = mid - 1;\n }\n return -1;\n }\n};\n```\n\nKindly upvote if you found the solution helpful :)\n**For more such explanations of LeetCode problems along with their C++ solutions:**\nhttps://github.com/Arya-Gupta/LeetCode | 11 | 0 | ['Array', 'C', 'Binary Tree', 'C++'] | 3 |
single-element-in-a-sorted-array | Python O(lg n) by binary search 85%+ [w/ Visualization] | python-olg-n-by-binary-search-85-w-visua-et3v | Python O(lg n) by binary search\n\n---\n\nHint:\n\nGroup each numbers in pairs, and launch binary search to locate the first index of mis-matched pair.\n\n---\n | brianchiang_tw | NORMAL | 2020-05-12T09:09:32.877342+00:00 | 2020-05-12T09:53:58.486989+00:00 | 1,025 | false | Python O(lg n) by binary search\n\n---\n\nHint:\n\nGroup each numbers in pairs, and launch binary search to locate the first index of mis-matched pair.\n\n---\n\n**Illustration and Visualization**:\n\n\n\n---\n\n**Implementation** by binary search:\n\n```\nclass Solution:\n def singleNonDuplicate(self, nums: List[int]) -> int:\n \n size = len(nums)\n \n left, right = 0, size // 2\n \n while left < right:\n \n pair_index = left + ( right - left ) // 2\n \n if nums[2*pair_index] != nums[2*pair_index+1]:\n # If current pair is mis-matched\n # then go left-half to find the first pair of mis-match\n right = pair_index\n \n else:\n # If current pair is with the same number appeared twice\n # then go right-half to find the first pair of mis-match\n left = pair_index + 1\n \n # when the while loop terminates, left = right = the first pair index of mis-match\n return nums[2*left]\n``` | 11 | 0 | ['Binary Search', 'Python', 'Python3'] | 1 |
single-element-in-a-sorted-array | Very easy solution in C++ || Basic approach (beats 100%) | very-easy-solution-in-c-basic-approach-b-0cqw | iam explained indetail in my website and youtube vedio if you have more clearity on this problem and approachs visite the below website and youtube channel:\nWE | vinaykumar333j | NORMAL | 2024-11-26T17:31:40.919621+00:00 | 2024-11-26T17:31:40.919646+00:00 | 386 | false | iam explained indetail in my website and youtube vedio if you have more clearity on this problem and approachs visite the below website and youtube channel:\nWEBSITE:\nhttps://vinayhac.blogspot.com/2023/06/540.%20Single%20Element%20in%20a%20Sorted%20Array.html\nYOUTUBE VEDIO:\nhttps://youtu.be/vGtAZA62xC8\n\nin this problem we solve this using 3 approachs \n1. bitwise operations\n2. unodered_map algorithm\n3. general basic concepts \n**APPROACH- 1:**\nlets start with the first bitwise opertaion this problem we solve applying the xor to all elements then it find the single element in the entire array\n**CODE:**\n```\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n // bit \n // unordered map \n // generally basics \n \n /* \n xor operation (^)\n 1-> 8421= 0001\n 3-> 8421= 0011\n --------------\n output:\n 0010 (2)\n \n 1-> 8421= 0001 3-> 8421 =0011\n 1-> 8421= 0001 3-> 8421 =0011\n \n 0000(0)*/\n int s=0;\n int i;//index\n for(i=0;i<nums.size();i++){\n s=s^nums[i]; \n }\n return s;\n \n }\n};\n```\n**APPROACH-2:**\nin this we use the unodered map algorithm here finding the each element frequency the unordered_map help alot to solve this problems and based on the problem the use will be changed\n**CODE:**\n```\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n // bit \n // unordered map \n // generally basics \n \n /* \n unordered_map<int,int>mp;\n key value*/\n unordered_map<int,int>map;\n int i;//index\n int n=nums.size();//size\n for(i=0;i<n;i++){\n map[nums[i]]++;\n }\n for(auto l:map){\n if(l.second==1){\n return l.first;\n }\n }\n return 0; \n \n }\n};\n```\n**APPROACH-3:**\nin this method in problem statement only given the array is the sorted array and each integer appers twice but on e integer appers only once we travelling in even index format to find the single apper integer\n**CODE:**\n```\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n // bit \n // unordered map \n // generally basics \n \n /* \n even index \n 0 1 2 3 4 5 6\n 1 1 2 3 3 4 4\n \n \n */\n if(nums.size()==1){\n return nums[0];\n }\n int i;//index\n for(i=0;i<nums.size();i+=2){\n if(nums[i]!=nums[i+1]){\n return nums[i];\n }\n }\n return 0;\n \n }\n};\n```\n | 10 | 0 | ['Math'] | 0 |
single-element-in-a-sorted-array | ✅ Multiple Javascript Solutions || Brute Force O(n) O(1) || Binary Search O(logn) O(1) || XOR | multiple-javascript-solutions-brute-forc-xiu4 | Feel free to ask Q\'s...\n#happytohelpu\n\nDo upvote if you find this solution useful. Happy Coding!\n\nSolution 1 : Brute Force (with XOR)\nTime Complexity : O | lakshmikant4u | NORMAL | 2023-02-21T06:56:56.025455+00:00 | 2023-04-10T19:31:46.996057+00:00 | 1,175 | false | **Feel free to ask Q\'s...**\n*#happytohelpu*\n\n***Do upvote if you find this solution useful. Happy Coding!***\n\n**Solution 1 : Brute Force (with XOR)**\nTime Complexity : O(n)\nSpace Complexity : O(1)\n\n```\n\nconst singleNonDuplicate = nums => nums.reduce((a, b) => a ^ b); // XOR to get the single value\n\n```\n\n\n**Solution 2 : Brute Force**\nTime Complexity : O(n)\nSpace Complexity : O(1) \n\n```\n\nconst singleNonDuplicate = nums => {\n //Compare consecutive numbers and increment by 2 in each iteration\n for (let i = 0; i < nums.length - 1; i += 2) {\n if (nums[i] != nums[i + 1]) {\n return nums[i];\n }\n }\n return nums[nums.length - 1]; // The last element is the only single element.\n}\n\n```\n\n**Solution 3 : Binary Search**\nTime Complexity : O(log(n))\nSpace Complexity : O(1) \n\n```\n\nconst singleNonDuplicate = (nums, left = 0, right = nums.length - 1) => {\n\n while (left < right) {\n let mid = left + (right - left) / 2;\n if (nums[mid] == nums[mid + 1]) mid = mid - 1;\n if ((mid - left + 1) % 2 != 0) right = mid;\n else left = mid + 1;\n }\n return nums[left];\n};\n\n```\n\n\n | 10 | 0 | ['Binary Search', 'Bit Manipulation', 'Binary Tree', 'Iterator', 'JavaScript'] | 0 |
single-element-in-a-sorted-array | C++✅✅ | Faster🧭 than 85%🔥| Hashing🆗 | Very Easy Code | Clean code | | c-faster-than-85-hashingok-very-easy-cod-2c1y | \n\n# Code\n# PLEASE DO UPVOTE!!!!!\n\n\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n\n unordered_map<int,int>mpp;\n f | mr_kamran | NORMAL | 2023-02-21T01:44:31.243367+00:00 | 2023-02-21T01:44:31.243414+00:00 | 2,265 | false | \n\n# Code\n# PLEASE DO UPVOTE!!!!!\n```\n\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n\n unordered_map<int,int>mpp;\n for(auto i:nums) mpp[i]++;\n \n for(auto it:mpp)\n if(it.second==1) return it.first;\n \n return -1;\n }\n};\n\n\n``` | 10 | 1 | ['C++'] | 3 |
single-element-in-a-sorted-array | C++ | Clean Code (5 Lines) | Easy to understand | XOR Method | Well explained | c-clean-code-5-lines-easy-to-understand-4n293 | Pls upvote the thread if you found it helpful.\n\n# Intuition\n Describe your first thoughts on how to solve this problem. \n We know :-\n - XOR(x,x) | forkadarshp | NORMAL | 2023-02-21T01:07:08.009778+00:00 | 2023-02-21T10:14:55.092105+00:00 | 2,337 | false | **Pls upvote the thread if you found it helpful.**\n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n We know :-\n - XOR(x,x) = 0\n - XOR(x,0) = x\nUsing this the **repeating elements** will become 0 and the element that is **present once** will be left.\nIterate over the given sorted array and maintain a curr_xor which will store XOR of the elements.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n 1. Initialize variables. \n curr_xor = 0 and n (size of the given sorted array)\n 2. Iterate over the given array \n 3. XOR elements.\n curr_xor ^= nums[i]\n 4. Return curr_xor\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(N) \n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(1)\n# Code\n```\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n int n = nums.size();\n int curr_xor=0; //variable will store XOR\n for(int i =0;i<n;i++){\n curr_xor ^= nums[i]; // XOR\n }\n return curr_xor;\n }\n};\n``` | 10 | 4 | ['Array', 'Math', 'Binary Search', 'Bit Manipulation', 'C++'] | 4 |
single-element-in-a-sorted-array | C++ Simple and Clean Solutions, O(logn), With Explanation | c-simple-and-clean-solutions-ologn-with-6g66q | O(logn) Binary Search Solution:\nExplanation:\nFor a regular sorted array where each element is double, be have the first in an even index and the second in an | yehudisk | NORMAL | 2021-08-03T10:13:53.434614+00:00 | 2021-08-03T10:15:11.107899+00:00 | 624 | false | **O(logn) Binary Search Solution:**\nExplanation:\nFor a regular sorted array where each element is double, be have the first in an even index and the second in an odd index.\nIf somewhere in the middle we have an element that appears only once, this pattern will be broken, and from there on the first element will be in an odd index and the second one in an even index.\nSo, we makr a regular binary search. If the pattern is still holding in "mid", then we continue searching in the right side.\nIf it\'s already broken, we continue the search on the left side.\n```\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n int lo = 0, hi = nums.size()-1, mid;\n while (lo < hi) {\n mid = (lo + hi) / 2;\n if ((mid % 2 && nums[mid - 1] == nums[mid]) || (!(mid % 2) && nums[mid] == nums[mid + 1])) lo = mid + 1;\n else hi = mid;\n }\n return nums[lo];\n }\n};\n```\n**O(n) Bitwise Solution:**\nA number XOR itself is always 0.\nA number XOR 0 always stays the number.\nSo if we just XOR the entire array, we will be left with the element that appears only once.\n```\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n int res = nums[0];\n for (int i=1; i<nums.size(); i++)\n res ^= nums[i];\n return res;\n }\n};\n```\n**Like it? please upvote!** | 10 | 0 | ['C'] | 1 |
single-element-in-a-sorted-array | Find the Single Element in a Sorted Array (Binary Search) #EfficientAlgorithms | find-the-single-element-in-a-sorted-arra-uuzi | Intuition
The array is sorted, and every element appears exactly twice — except one.
In such arrays, duplicates always occupy even-odd index pairs: (0-1), (2-3) | anill056 | NORMAL | 2025-03-26T19:51:06.194740+00:00 | 2025-03-26T19:51:06.194740+00:00 | 542 | false | # Intuition
- The array is sorted, and every element appears exactly twice — except one.
- In such arrays, **duplicates always occupy even-odd index pairs**: (0-1), (2-3), etc.
- When a single non-duplicate disrupts this structure, **the pattern breaks**.
- So we can use binary search to find **where this break happens** by examining indices.
# Approach
1. Apply binary search on index pairs (not values).
2. Always ensure mid is even — so it aligns with pair starts.
3. Compare nums[mid] with nums[mid + 1] to detect broken pairing.
4. Narrow down the search until only the single element remains.
# Complexity
- Time complexity:
O(Log n)
- Each iteration eliminates half of the remaining elements.
- Space complexity:
O(1)
- No extra memory is used; purely in-place logic.
# Code
```cpp []
class Solution {
public:
int singleNonDuplicate(vector<int>& nums) {
int left = 0;
int right = nums.size() - 1;
while (left < right) {
int middle = left + (right - left) / 2;
// Force middle to be even to compare with its pair
if(middle % 2 == 1) {
middle--;
}
// If the pair is valid, move right
if(nums[middle] == nums[middle + 1]) {
left = middle + 2;
}
// Pair is broken, single element must be on the left side
else right = middle;
}
// Left points to the single element
return nums[left];
}
};
``` | 9 | 0 | ['Array', 'Binary Search', 'Bit Manipulation', 'C++'] | 1 |
single-element-in-a-sorted-array | Easy in C++😎 ||Binary Search|| (21st Feb 2023) | easy-in-c-binary-search-21st-feb-2023-by-utch | A good solution here would work even if the elements were not sorted, but just kept in pairs and that is because the searching criterium we will use is not rel | spyder_master | NORMAL | 2023-02-21T04:02:14.609140+00:00 | 2023-02-21T04:02:14.609187+00:00 | 1,280 | false | *A good solution here would work even if the elements were not sorted, but just kept in pairs and that is because the searching criterium we will use is not related to their own ordering, but to the fact that numbers to the left of the unique element will have the format nums[k] == nums[k + 1] with k being an even index and the ones to the right of it will have the same with k being an odd index.*\n\n*First of all, we will declare a couple of support variables:*\n\n*lmt as the name implies will be the upper limit of our search, set to be the very last index (nums.size() - 1);\nmid, the middle element of our binary search.\nWe will then proceeed to loop with a few more variables:*\n\n*l and r are the two pointers to the left and right interval we will be binary searching - initially set to be 0 and lmt, respectively;\nprev and nxt will be the values we will consider for the elements around the one pointed by mid.\nIn our loop, running as long as l <= r, we will then:*\n\n*compute mid, as the average between l and r;\ncompute prev so that is equal to the previous element if mid is not on the first element or nums[mid] - 1 otherwise;\ncompute nxt so that is equal to the previous element if mid is not on the first element or nums[mid] + 1 otherwise - and, yes: I found delight in the elegance of having an expression moving the - 1 / + 1 part inside or outside the square brackets;\ntime to go for the actual binary search and we will deal with 3 cases:\nif nums[mid] is different from both prev and nxt, we know we have a match, so we can just return nums[mid];\nif nums[mid] is different from the previous element with an odd value of mid or from the next one with an even value of mid, it means we were looking too much to the right, so we will lower r to be mid - 1 in the next iteration (we might also have written the condition here as nums[mid] != nums[mid + (mid & 1 ? -1 : 1)], which was my first version, before storing prev and nxt for convenience);\notherwise, it means we were looking too much to the left, so we will adjust l to be mid + 1.\nI am not sure we will ever hit exit the loop and execute what is next, but just to make the compiler happy about the signature of our function, we will then just in case return nums[mid] and be done with it :)*\n\n**The code:**\n\n```\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n // support variables\n int lmt = nums.size() - 1, mid;\n // binary search\n for (int l = 0, r = lmt, prev, nxt; l <= r;) {\n // updating loop variables\n mid = (l + r) >> 1;\n prev = mid ? nums[mid - 1] : nums[mid] - 1;\n nxt = mid != lmt ? nums[mid + 1] : nums[mid] + 1;\n // checking the element pointed by mid:\n // match\n if (nums[mid] != prev && nums[mid] != nxt) return nums[mid];\n // too high\n else if (nums[mid] != (mid & 1 ? prev : nxt)) r = mid - 1;\n // too low\n else l = mid + 1;\n }\n return nums[mid];\n }\n};\n```\n\n\n\n | 9 | 0 | ['C', 'Binary Tree', 'C++'] | 1 |
single-element-in-a-sorted-array | Easy C++ O(log n) & O(1) soln. | easy-c-olog-n-o1-soln-by-hirakmondal2000-vzfx | for (mid % 2 == 0) cases \n 0 1 2 3 4 5 6 7 8 -> index \n 1 1 2 2 3 5 5 7 7 - ON MID \n\t1 1 3 5 5 7 7 9 9 - ON LEFT | hirakmondal2000 | NORMAL | 2022-02-15T20:26:35.617260+00:00 | 2022-02-15T20:30:26.454661+00:00 | 180 | false | for (mid % 2 == 0) cases \n 0 1 2 3 4 5 6 7 8 -> index \n 1 1 2 2 **3** 5 5 7 7 - ON MID \n\t1 1 **3** 5 5 7 7 9 9 - ON LEFT \n\t1 1 2 2 3 3 **5** 7 7 - ON RIGHT \n\t\nFor (mid % 2 != 0) cases \n0 1 2 3 4 5 6 -> index\n1 1 2 2 **3** 5 5 - ON RIGHT\n1 1 **3** 5 5 7 7 - ON LEFT\n\n\n```\nint singleNonDuplicate(vector<int>& v) \n {\n if(v.size() == 1)// if only one element is present\n return v[0];\n int low = 0;\n int high = v.size() - 1;\n while(low <= high)\n {\n int mid = low + (high - low) / 2;\n if(mid % 2 == 0)\n {\n if(low == high) //if element is on the left most side , in that case, v[mid - 1] is not possible\n { \n return v[mid];\n }\n else if(v[mid] == v[mid - 1])\n {\n high = mid - 2;\n }\n else if(v[mid] == v[mid + 1])\n {\n low = mid + 2;\n }\n else\n {\n return v[mid];\n }\n }\n else\n {\n if(v[mid] == v[mid - 1])\n {\n low = mid + 1;\n }\n else if(v[mid] == v[mid + 1])\n {\n high = mid - 1;\n }\n }\n }\n return 0;\n }\n``` | 9 | 0 | [] | 1 |
single-element-in-a-sorted-array | 🔥 [LeetCode The Hard Way] 🔥 Explained Line By Line | leetcode-the-hard-way-explained-line-by-0n5uy | \uD83D\uDD34 Check out LeetCode The Hard Way for more solution explanations and tutorials. \n\uD83D\uDFE0 Check out our Discord Study Group for live discussion. | __wkw__ | NORMAL | 2023-02-21T02:48:08.309133+00:00 | 2023-02-21T07:09:53.531577+00:00 | 1,258 | false | \uD83D\uDD34 Check out [LeetCode The Hard Way](https://wingkwong.github.io/leetcode-the-hard-way/) for more solution explanations and tutorials. \n\uD83D\uDFE0 Check out our [Discord Study Group](https://discord.gg/Nqm4jJcyBf) for live discussion.\n\uD83D\uDFE2 Give a star on [Github Repository](https://github.com/wingkwong/leetcode-the-hard-way) and upvote this post if you like it.\n\uD83D\uDD35 Check out [Screencast](https://www.youtube.com/watch?v=UayPePcTQIY&list=PLBu4Bche1aEU-8z7xl3-B9lfw_DJtT_xs&index=21) if you are interested.\n\n---\n\n**Suggested Problems**\n\n- https://leetcode.com/problems/binary-search/\n- https://leetcode.com/problems/find-minimum-in-rotated-sorted-array/\n- https://leetcode.com/problems/find-peak-element/\n- https://leetcode.com/problems/find-minimum-in-rotated-sorted-array-ii/\n\n**Approach: Binary Search**\n\nSee [Binary Search](https://leetcodethehardway.com/tutorials/basic-topics/binary-search) for the tutorial.\n\n```cpp\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n // init possible boundary\n int n = nums.size(), l = 0, r = n - 1;\n while (l < r) {\n // get the middle one\n // for even number of elements, take the lower one\n int m = l + (r - l) / 2;\n // handle case like [3,3,7,7,10,11,11]\n m -= m & 1;\n // exclude m\n if (nums[m] == nums[m + 1]) l = m + 2;\n // include m\n else r = m;\n }\n return nums[l];\n }\n};\n```\n\n```py\nclass Solution:\n def singleNonDuplicate(self, nums: List[int]) -> int:\n n = len(nums)\n l, r = 0, n - 1\n while l < r:\n m = (l + r) // 2\n if m & 1:\n m -= 1\n if nums[m] == nums[m + 1]:\n l = m + 2\n else:\n r = m\n return nums[l]\n``` | 8 | 0 | ['Binary Search', 'Python'] | 4 |
single-element-in-a-sorted-array | Deep Explanation | Leetcode Official Solution | Visual | [Python] | deep-explanation-leetcode-official-solut-vbdn | Overview \n\nWe must find the only unique element in a sorted array where all two copies of all other elements exist (or duplicate) \n \nfirst let us make some | gtshepard | NORMAL | 2021-01-15T04:20:01.445192+00:00 | 2021-01-18T02:02:16.246563+00:00 | 288 | false | ### Overview \n\nWe must find the ***only unique*** element in a ***sorted array*** where all **two copies*** of all other elements exist (or duplicate) \n \nfirst let us make some key observtions about the problem \n\nassuming the constraints of the problem hold true, if there is a match for an element it always exists to the ***adajcent left*** or the ***adjacent right*** of that number; otherwise the number is ***unique***.\n\nObserve key observation 1 in ***Figure 1***\n\n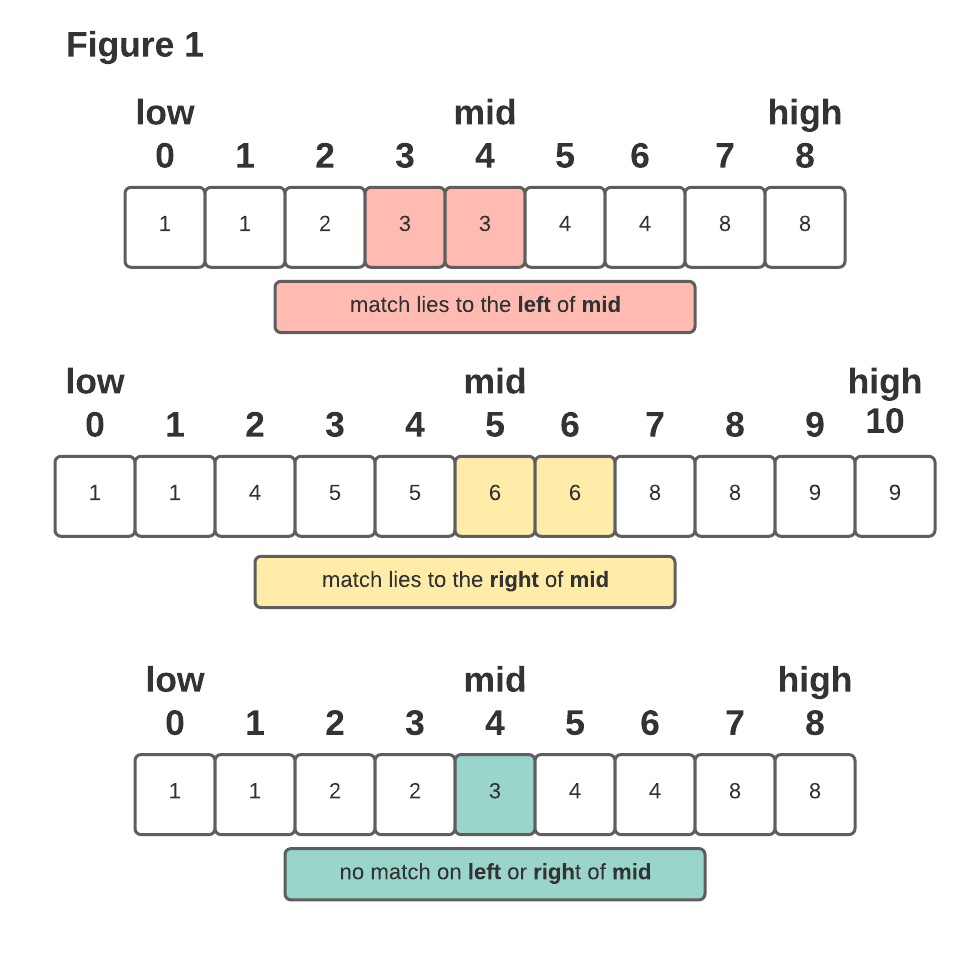\n\n* * * \n\n\nRecall there are ***two copies*** of all elements ***except*** the unique value.\n\ninother words there are ***p*** pairs of ***duplicates*** where each pair is distinct. There is one value that cannot form a pair, this value is ***unique***. This means the length of the input array is ***2p + 1***\n\n***Observe key observation 2 in Figure 2***\n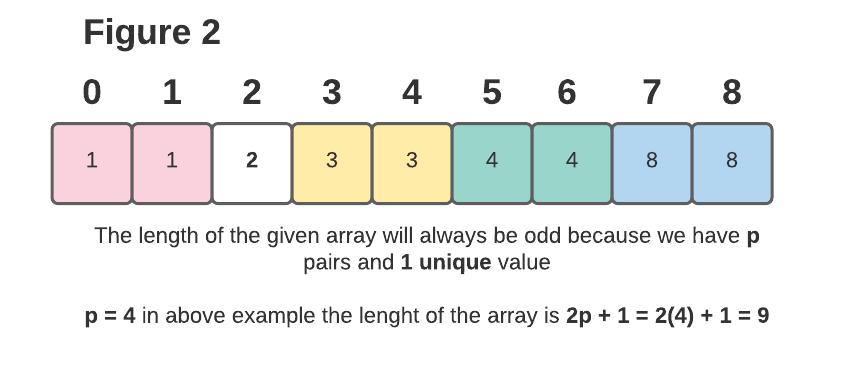\n\n* * * \n\n***we know that a unique value can only exist if the array is of odd length***. We can use this ***principle to search*** the array for the ***unique value***. \n\nsince this array is sorted a binary search like approach may prove useful. if we repeatedly divide the array in half and leverage our search principle mentioned above, we can always find the unique value in ```O(log N)``` time and ```O(1)``` space.\n\nWe always look for the unique value in the half that is odd length. because the half that is odd length, has some number of pairs ***k***, and ***1 unique value***. the other half would contain only pairs \n\n* * * \n***The question now becomes, how do we do this?***\n* * * \n\nyou may have already noticed that if we section an array of odd length into two parts by a mid point, ***both halves will contain the same number of elements.***\n\n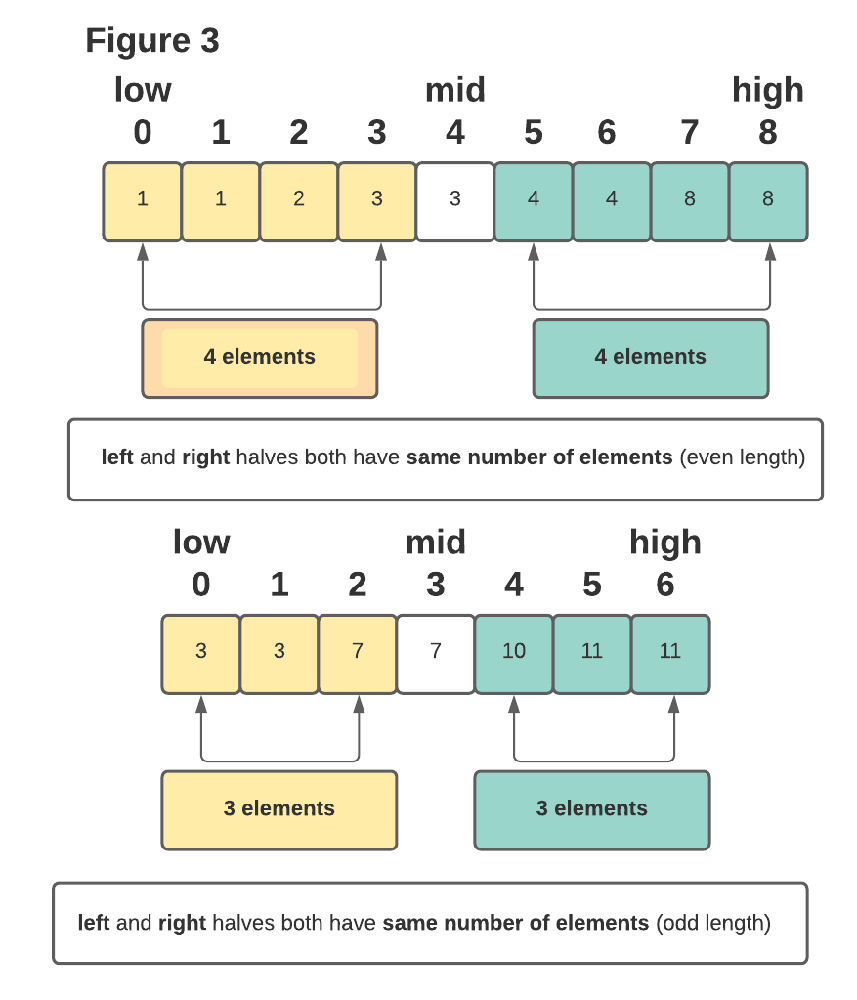\n\nRecall that we said our search criteria was to always visit the half that is of ***odd length*** until we find our unique value, but from what we just saw in ***Figure 3*** it seems like this is going to be problem.\n\n* in the first example in ***Figure 3*** there is ***neither*** the ***left*** or ***right half*** is of ***odd length***, both halves are ***even length***. \n\n* in the second example in ***Figure 3*** both the ***left*** and the ***right*** halves are of ***odd length***, so it is unclear which half should be searched next. \n\nif we combine our key observations from above with our search principle, a solution is possible. \n\n***we always check to see if the mid point is the unique value*** \n\n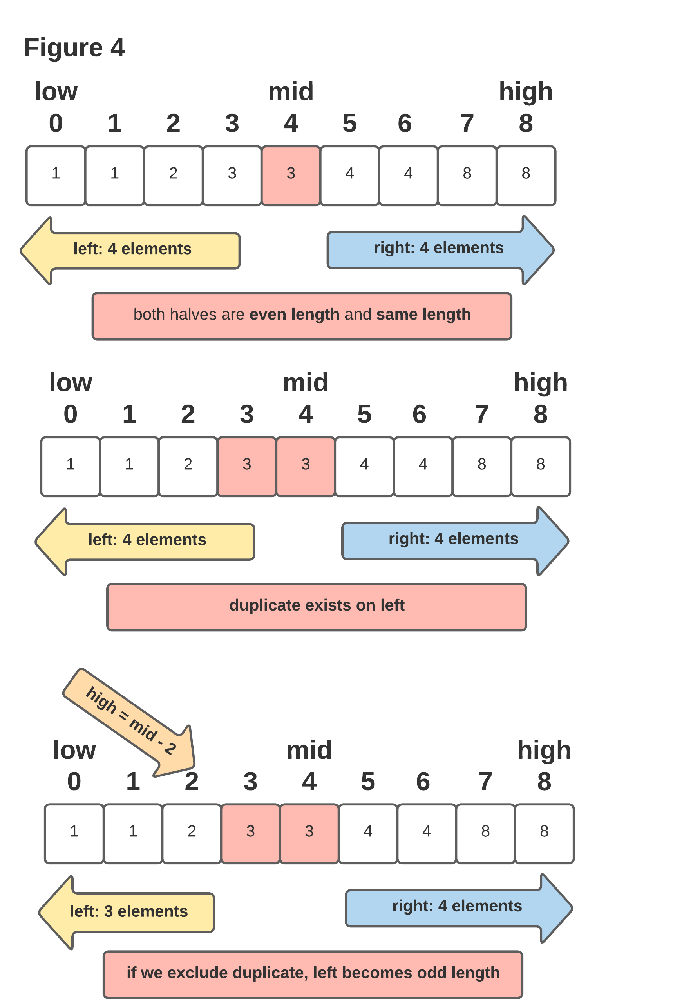\n\nwe can see the unique value lies in the left half. what happens next?\n\n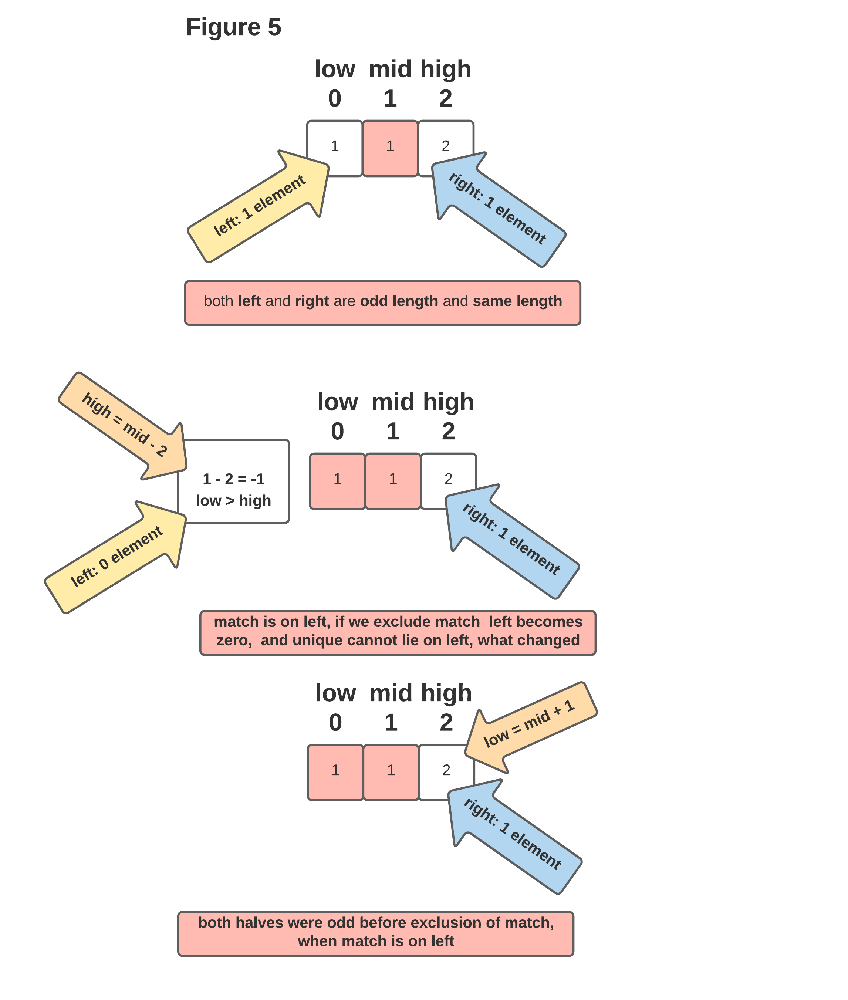\n\n\n\n\n\nfrom here we can see that the 4 cases mentioned in the leetcode official solution arise\n\n\n1. match is on ***left of mid point*** and both ****left and right halves*** are of ***even length***\n\t* exclude match and mid point and go left, that is ```high = mid - 2``` \t\n\n2. match is on ***left of mid point*** and both ***left and right halves*** are of ***odd length***\n\t\t* exclude match mid point and go right, that is ```low = mid + 1``` \t\n\n3. match is on ***right of mid point*** and both ****left and right halves*** are of ***even length***\n\t * exclude match and mid point and go right, that is ```low = mid + 2``` \n4. match is on ***right of mid point*** and both ***left and right halves*** are of ***odd length***\n\t * exclude match mid point and go left, that is ```high = mid - 1``` \n\n\n ```python\n def singleNonDuplicate(self, nums: List[int]) -> int:\n lo = 0\n hi = len(nums) - 1 \n while lo < hi:\n mid = (lo + hi) // 2\n\t\t\t# look to right for pair \n if nums[mid + 1] == nums[mid]:\n\t\t\t\t# both halves are even length,\n if (hi - mid) % 2 == 0:\n lo = mid + 2\n else:\n hi = mid - 1\n\t\t\t # look to left for pair \n elif nums[mid - 1] == nums[mid]:\n\t\t\t\t# both halves are even length\n if (hi - mid) % 2 == 0:\n hi = mid - 2\n else:\n lo = mid + 1\n else:\n\t\t\t\t# no pair on either side, must be unique \n return nums[mid]\n return nums[lo]\n``` \n\ncode courtesy of leetcode official solution \n\n\n\n\n\n\n \n | 8 | 1 | ['Binary Tree'] | 0 |
single-element-in-a-sorted-array | Simple Solution with Diagrams in Video - JavaScript, C++, Java, Python | simple-solution-with-diagrams-in-video-j-nrg2 | Video\nPlease upvote here so others save time too!\n\nLike the video on YouTube if you found it useful\n\nClick here to subscribe on YouTube:\nhttps://www.youtu | danieloi | NORMAL | 2024-11-11T11:52:15.802768+00:00 | 2024-11-11T11:52:15.802805+00:00 | 625 | false | # Video\nPlease upvote here so others save time too!\n\nLike the video on YouTube if you found it useful\n\nClick here to subscribe on YouTube:\nhttps://www.youtube.com/@mayowadan?sub_confirmation=1\n\nThanks!\n\nhttps://youtu.be/WHC5muNp2NQ?si=VHyNJgx7J1kZXjD_\n\n\n```Javascript []\n/**\n * @param {number[]} nums\n * @return {number}\n */\nvar singleNonDuplicate = function (nums) {\n // initilaize the left and right pointer\n let l = 0,\n r = nums.length - 1;\n\n while (l != r) {\n\n // set the value of mid\n let mid = l + Math.floor((r - l) / 2);\n\n // if mid is odd, decrement it to make it even\n if (mid % 2 == 1) {\n mid--;\n }\n // if the elements at mid and mid + 1 are the same, then the single element must appear after the midpoint\n if (nums[mid] == nums[mid + 1]) {\n l = mid + 2;\n }\n\n else {\n // otherwise, we must search for the single element before the midpoint\n r = mid;\n }\n }\n return nums[l];\n};\n```\n```Python []\nclass Solution:\n def singleNonDuplicate(self, nums: List[int]) -> int:\n # Initialize the left and right pointers\n l, r = 0, len(nums) - 1\n\n while l != r:\n # Set the value of mid\n mid = l + (r - l) // 2\n\n # If mid is odd, decrement it to make it even\n if mid % 2 == 1:\n mid -= 1\n\n # If the elements at mid and mid + 1 are the same,\n # then the single element must appear after the midpoint\n if nums[mid] == nums[mid + 1]:\n l = mid + 2\n # Otherwise, we must search for the single element\n # before the midpoint\n else:\n r = mid\n\n return nums[l]\n\n```\n```Java []\nclass Solution {\n public int singleNonDuplicate(int[] nums) {\n // initilaize the left and right pointer\n int l = 0;\n int r = nums.length - 1;\n\n while (l < r) {\n\n // if mid is odd, decrement it to make it even\n int mid = l + (r - l) / 2;\n if (mid % 2 == 1)\n mid--;\n\n // if the elements at mid and mid + 1 are the same, \n // then the single element must\n // appear after the midpoint\n if (nums[mid] == nums[mid + 1]) {\n l = mid + 2;\n }\n // otherwise, we must search for the \n // single element before the midpoint\n else {\n r = mid;\n }\n }\n return nums[l];\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n // Initialize the left and right pointers\n int l = 0;\n int r = nums.size() - 1;\n\n while (l < r) {\n // Set the value of mid\n int mid = l + (r - l) / 2;\n\n // If mid is odd, decrement it to make it even\n if (mid % 2 == 1) {\n mid--;\n }\n\n // If the elements at mid and mid + 1 are the same,\n // then the single element must appear after the midpoint\n if (nums[mid] == nums[mid + 1]) {\n l = mid + 2;\n }\n // Otherwise, we must search for the single element before the\n // midpoint\n else {\n r = mid;\n }\n }\n\n return nums[l];\n }\n};\n\n```\n | 7 | 0 | ['Python', 'C++', 'Java', 'Python3', 'JavaScript'] | 0 |
single-element-in-a-sorted-array | Simple Binary Search Approach | simple-binary-search-approach-by-hemants-4838 | Basic Idea: Find the number of element to the right of nums[m], and reduce search space according to it.\n\nclass Solution {\npublic:\n int singleNonDuplicat | hemantsingh_here | NORMAL | 2024-07-22T18:29:48.553887+00:00 | 2024-07-22T18:29:48.553920+00:00 | 1,881 | false | **Basic Idea:** Find the number of element to the right of nums[m], and reduce search space according to it.\n```\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n \n int l = 0;\n int h = nums.size() - 1;\n \n \n while(l<h){\n int m = l + (h-l)/2;\n bool isEven = false;\n \n if((h-m)%2 == 0){\n isEven = true; // there are even number of elements present in right side of nums[m]\n }\n else if((h-m)%2 == 1){\n isEven = false; // there are odd number of elements present in right side of nums[m]\n }\n \n if(nums[m] == nums[m+1]){\n if(isEven){\n l = m + 2;\n }else{\n h = m - 1;\n }\n }else{\n if(isEven){\n h = m;\n }else{\n l = m + 1;\n }\n }\n }\n return nums[l];\n }\n};\n``` | 7 | 0 | ['Math', 'Binary Tree'] | 0 |
single-element-in-a-sorted-array | Beats 100% Java Solutions | beats-100-java-solutions-by-atharvakote8-wkix | Code Explanation\n\njava\npublic int singleNonDuplicate(int[] nums) {\n int low = 0;\n int high = nums.length - 1;\n\n while (low < high) {\n in | AtharvaKote81 | NORMAL | 2024-06-17T08:51:06.337549+00:00 | 2024-06-17T08:51:06.337580+00:00 | 191 | false | ## Code Explanation\n\n```java\npublic int singleNonDuplicate(int[] nums) {\n int low = 0;\n int high = nums.length - 1;\n\n while (low < high) {\n int mid = low + (high - low) / 2;\n if (mid % 2 == 1) {\n mid--;\n }\n\n if (nums[mid] == nums[mid + 1]) {\n low = mid + 2;\n } else {\n high = mid;\n }\n }\n return nums[low];\n}\n```\n\n#### Detailed Breakdown:\n\n1. **Initialization**:\n ```java\n int low = 0;\n int high = nums.length - 1;\n ```\n - `low` and `high` are initialized to the start and end of the array, respectively.\n\n2. **Binary Search Loop**:\n ```java\n while (low < high) {\n ```\n - This loop continues until `low` is equal to `high`.\n\n3. **Finding the Middle Element**:\n ```java\n int mid = low + (high - low) / 2;\n if (mid % 2 == 1) {\n mid--;\n }\n ```\n - `mid` is calculated to be the middle index between `low` and `high`.\n - If `mid` is odd, it is decremented by 1 to make it even. This ensures that we are always comparing pairs starting with an even index.\n\n4. **Comparison**:\n ```java\n if (nums[mid] == nums[mid + 1]) {\n low = mid + 2;\n } else {\n high = mid;\n }\n ```\n - If the element at `mid` is equal to the element at `mid + 1`, it means that the single non-duplicate element is in the right half of the array. So, `low` is updated to `mid + 2`.\n - If `nums[mid]` is not equal to `nums[mid + 1]`, it means the single non-duplicate element is in the left half of the array, including the current `mid`. Hence, `high` is updated to `mid`.\n\n5. **Return Statement**:\n ```java\n return nums[low];\n ```\n - When `low` equals `high`, the loop exits and the single non-duplicate element is at the index `low`.\n\n### Example Walkthrough:\n\nConsider the array `[1, 1, 2, 3, 3, 4, 4, 5, 5]`:\n- Initial state: `low = 0`, `high = 8`\n- First iteration:\n - `mid = 4` (even)\n - `nums[mid]` (3) == `nums[mid + 1]` (3)\n - Update `low = mid + 2 = 6`\n- Second iteration:\n - `mid = 7`\n - `mid` is odd, so adjust to `mid = 6` (even)\n - `nums[mid]` (4) != `nums[mid + 1]` (5)\n - Update `high = mid = 6`\n- Third iteration:\n - `low = 6`, `high = 6`\n - Exit loop and return `nums[low] = 2`\n\nThis approach ensures O(log n) time complexity due to the binary search mechanism, making it efficient for large arrays. | 7 | 0 | [] | 0 |
single-element-in-a-sorted-array | HashMap || Bitwise XOR ||Easy to understand || Java 2 Solutions | hashmap-bitwise-xor-easy-to-understand-j-pq00 | Approach\n Describe your approach to solving the problem. \nApproach 1: Bit manupulation - TC O(n) - SC (1)\nHere we use the fact that performing XOR with two s | SidSai | NORMAL | 2023-02-21T05:25:37.796896+00:00 | 2023-02-21T05:25:37.796936+00:00 | 92 | false | # Approach\n<!-- Describe your approach to solving the problem. -->\n**Approach 1**: Bit manupulation - TC O(n) - SC (1)\nHere we use the fact that performing XOR with two same numbers give us zero and doing XOR with zero and other number will give us that number itself.\nhere\'s the example\n2 - 0010\n2 - 0010\n3 - 0011\n\nSo 2^2^3 = 3\n\nSo we simply iterate through the loop and do XOR and the final ans will be the required ans\n**Approach 2**:HashMap\nWe use an HashMap to make a frequency table to note number of occurrences of the elements.\nThen we use an Entry Set to iterate and return the element with the single occurrence.\n\n\n# Code\n```\nclass Solution {\n public int singleNonDuplicate(int[] nums) {\n int ans=0;\n for(int i=0;i<nums.length;i++){\n ans^=nums[i];\n }\n return ans;\n }\n}\n```\n```\nclass Solution {\n public int singleNonDuplicate(int[] nums) {\n HashMap<Integer,Integer> hs= new HashMap<>();\n for(int i:nums)\n {\n hs.put(i,hs.getOrDefault(i,0)+1);\n }\n System.out.println(hs);\n for(Map.Entry<Integer,Integer> mp:hs.entrySet())\n {\n if(mp.getValue()==1)\n return mp.getKey();\n }\n return -1;\n }\n}\n``` | 7 | 0 | ['Java'] | 1 |
single-element-in-a-sorted-array | 🅰️ Java | easy explained | two approach | a-java-easy-explained-two-approach-by-ha-og9u | \n# Approach 1\n Describe your approach to solving the problem. \nSo, Here we go what about the problem think carefully The first solution for this problem that | harshitisback | NORMAL | 2023-02-21T05:14:06.820920+00:00 | 2023-02-21T05:14:38.912859+00:00 | 379 | false | \n# Approach 1\n<!-- Describe your approach to solving the problem. -->\nSo, Here we go what about the problem think carefully The first solution for this problem that get accepted. what i did i just run a for loop with starting index of 1 and check for its previous one and with incremental value is +2 here we go. \n1. if it get match then we move ahead other wise it is our element that is single. \n2. consider one of the edge case that is last index what if its last index is that element that nothing to worry about if we did no found any element during this loop that simple mean it is last element and we will return the last element. \n\n# Code in Java \n```\nclass Solution {\n public int singleNonDuplicate(int[] nums) {\n \n for(int i=1; i<nums.length; i+=2){\n if(nums[i]!=nums[i-1]){\n return nums[i-1];\n }\n }\n return nums[nums.length-1];\n }\n}\n```\nso if you can see in this code that exactly what it did. \n\n# About it complexity :- sorry to say but it is not required complexity even if it get accepted so what? \n- Time complexity: $$O(n)$$\n\n# Approach 2\n Here All we need to modify the solution and as given in question it is sorted array and what it mean the simple strike that comes in mind is ```binary search``` all we need to apply binary search so lets discuss the another problem with like how I can apply ? \nyus exactly that the way like in normal binary search for deciding the left and right pointer we have condition to check what here there is nothing like that. \uD83D\uDE12\n\nAlright after thinking and analyzing some of the patterns here simple look. \n1. there are some basic pattern like first number of pair is present in even index and the another its partner present on the right mean odd index so \n2. suppose if there is no single element thsi pattern will always follow till the end. \n3. but here is a catch this pattern will get disturbed when single element comes into the picture. \n4. so at that exact time we will get to know that yeah there is pattern mismatch and rather then setting left we will set right to mid. \n\n# More Explain \n- Alright here we go for little more explanation \n- Here is input nums = ``[1,1,2,3,3,4,4,8,8]``\n- look closely every first element is on even index and another one is on odd position \n\n\n\n- So here is approach if any how we will encounter an element of mid and if it is and even index then it have next same in odd mean next place (mid+1) odd side\n- and if we encounter any odd mid element its partner will present on mid-1;(even side)\n- and if in any case these conditions are not matching what it mean simply that mean pattern get disturbed in between and then we have to set the right to middle \n\n# Code\n```\nclass Solution {\n public int singleNonDuplicate(int[] nums) {\n \n int l = 0; int r=nums.length-1;\n\n while(l<r){\n // simple check for the condition\n int mid = (r+l)/2;\n\n if(mid%2==0 && nums[mid+1]==nums[mid]|| mid%2!=0 && nums[mid-1]==nums[mid]){\n l = mid+1;\n }else{\n r = mid;\n }\n\n }\n\n return nums[l];\n\n }\n}\n```\n\n# Complexity\n- Time complexity:$$O(logn)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# :> Thanks for visiting my Solution. \n | 7 | 0 | ['Java'] | 2 |
single-element-in-a-sorted-array | ✅Python3 two approaches 🔥🔥 | python3-two-approaches-by-shivam_1110-eki3 | Intuition\n Describe your first thoughts on how to solve this problem. \nUsing xor approach and binary search we can solve this.\n\n# Approach 1: XOR 170ms\n De | shivam_1110 | NORMAL | 2023-02-21T04:28:43.272560+00:00 | 2023-02-21T04:37:08.037420+00:00 | 913 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n**Using xor approach and binary search we can solve this.**\n\n# Approach 1: XOR 170ms\n<!-- Describe your approach to solving the problem. -->\n- traverse in array linearly and xor every element.\n- which ever element is not repeted it\'s xor will not be canclled out.\n- return found xor.\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def singleNonDuplicate(self, nums: List[int]) -> int:\n def helper():\n xor = 0\n for i in nums:\n xor ^= i\n return xor\n return helper()\n```\n---\n\n# Approach 2: Binary search 180ms\n<!-- Describe your approach to solving the problem. -->\n- here if we explore problem then we can see if we have even length of array then no element will be singlton and every even index will have next element same as it.\n- but if we insert any simgleton element between repeted element(not in between pair) then we can see that if even index element is not having same element as next then singleton must be in left side.\n- if that\'s not the case then singleton is not inserted in left side because we\'re having behavior like even length array and no singleton is present in it, so to search in left side is not in our favour.\n- so singleton must be in right side.\n- where we find right < left there, we stop.\n- return nums[left].\n\n# Complexity\n- Time complexity: O(logN)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def singleNonDuplicate(self, nums: List[int]) -> int:\n def helper():\n left, right = 0, len(nums) - 1\n while left < right:\n middle = (left + right) // 2\n if middle % 2 == 1:\n middle -= 1\n if nums[middle] != nums[middle+1]:\n right = middle - 1\n else:\n left = middle + 2\n return nums[left]\n return helper()\n```\n---\n# Please like and comment below.\n# (\uD83D\uDC4D\u2256\u203F\u203F\u2256)\uD83D\uDC4D \uD83D\uDC4D(\u2256\u203F\u203F\u2256\uD83D\uDC4D) | 7 | 0 | ['Array', 'Binary Search', 'Python3'] | 0 |
single-element-in-a-sorted-array | Simple C++ code || Approach discussed || TC : O(logN) & SC : O(1) || Binary search | simple-c-code-approach-discussed-tc-olog-tbhq | \n\n\n\n\n// Please upvote if it helps :)\n\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n int e = nums.size();\n / | chamoli2k2 | NORMAL | 2022-07-22T23:31:17.705296+00:00 | 2022-07-23T15:49:35.142167+00:00 | 447 | false | \n\n\n```\n\n// Please upvote if it helps :)\n\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n int e = nums.size();\n // Checking the boundary first\n if(e == 1){\n return nums[0];\n }\n \n if(nums[0] != nums[1]){\n return nums[0];\n }\n \n if(nums[e-1] != nums[e-2]){\n return nums[e-1];\n }\n \n int s = 0;\n int mid = s + (e - s) / 2;\n int ans = -1;\n \n while(s <= e){\n if(nums[mid] != nums[mid-1] && nums[mid] != nums[mid+1]){\n ans = nums[mid];\n break;\n }\n // check if it is left half or right half\n else if((nums[mid] == nums[mid+1] && mid % 2 == 0) || (mid % 2 == 1 && nums[mid] == nums[mid-1])){\n s = mid + 1;\n }\n else{\n e = mid - 1;\n }\n \n mid = s + (e - s) / 2;\n }\n \n return ans;\n }\n};\n\n// Please upvote if it helps :)\n\n``` | 7 | 0 | ['Binary Search', 'C', 'Python', 'C++'] | 0 |
single-element-in-a-sorted-array | O(logN) time , O(1) space , easy to understand. | ologn-time-o1-space-easy-to-understand-b-esan | \nclass Solution {\n public int singleNonDuplicate(int[] nums) {\n int low=0;\n int high=nums.length;\n while(low<=high){\n i | nandini29110 | NORMAL | 2022-01-17T07:56:08.681092+00:00 | 2022-01-25T18:20:59.961266+00:00 | 258 | false | ```\nclass Solution {\n public int singleNonDuplicate(int[] nums) {\n int low=0;\n int high=nums.length;\n while(low<=high){\n int mid=low+(high-low)/2;\n if(mid-1>=0 && nums[mid]==nums[mid-1]){\n // this is second occurance\n if(mid%2==1){\n // it must be odd if all numbers are paired in left, then unpaired element must found in right\n low=mid+1;\n }else{\n // if it is not odd then element in in left\n high=mid-1;\n }\n }else if(mid+1< nums.length && nums[mid]==nums[mid+1]){\n // this is first occurance\n if(mid%2==0){\n low=mid+1;\n }else{\n high=mid-1;\n }\n }else{\n return nums[mid];\n }\n }\n return -1;\n }\n}\n``` | 7 | 0 | [] | 0 |
single-element-in-a-sorted-array | C++ Two Simple and Clean Solutions, O(logn) / O(n), With Explanation | c-two-simple-and-clean-solutions-ologn-o-tso3 | O(logn) Binary Search Solution:\nExplanation:\nFor a regular sorted array where each element is double, be have the first in an even index and the second in an | yehudisk | NORMAL | 2021-11-20T17:10:46.495838+00:00 | 2021-11-20T17:10:46.495870+00:00 | 270 | false | **O(logn) Binary Search Solution:**\nExplanation:\nFor a regular sorted array where each element is double, be have the first in an even index and the second in an odd index.\nIf somewhere in the middle we have an element that appears only once, this pattern will be broken, and from there on the first element will be in an odd index and the second one in an even index.\nSo, we makr a regular binary search. If the pattern is still holding in "mid", then we continue searching in the right side.\nIf it\'s already broken, we continue the search on the left side.\n```\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n int lo = 0, hi = nums.size()-1, mid;\n while (lo < hi) {\n mid = (lo + hi) / 2;\n if ((mid % 2 && nums[mid - 1] == nums[mid]) || (!(mid % 2) && nums[mid] == nums[mid + 1])) lo = mid + 1;\n else hi = mid;\n }\n return nums[lo];\n }\n};\n```\n**O(n) Bitwise Solution:**\nA number XOR itself is always 0.\nA number XOR 0 always stays the number.\nSo if we just XOR the entire array, we will be left with the element that appears only once.\n```\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n int res = nums[0];\n for (int i=1; i<nums.size(); i++)\n res ^= nums[i];\n return res;\n }\n};\n```\n**Like it? please upvote!** | 7 | 0 | ['C'] | 0 |
single-element-in-a-sorted-array | You Will Never Forget this Approach || Handwritten Dry Run | you-will-never-forget-this-approach-hand-fz6b | Please Upvote,it helps a lot to write Such Posts\n\n\n////////////////////////////////////////////////////////////////////////////////////////////////////////// | ayushdevrani | NORMAL | 2021-11-20T14:02:15.423049+00:00 | 2021-11-20T14:12:13.678208+00:00 | 568 | false | **Please Upvote,it helps a lot to write Such Posts**\n\n\n/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////\n\n\n```\n/*Time Complexity : O(log n)\nSpace complexity : O(1)\n\nExplanation: We know that log n time Complexity can be Achieved by B.Search\nonly and sorted array is given so definitely we can try B.Search. But only one\nissue is there how to determine where to move from mid, so only solution is to\ncheck the number of elements from 0 to mid, so that we can determine on \nwhich side violation is there, then only we can move when we find on which\nside violation is there and it can be found out only using the odd/even number of elements and comparing the\nmid with mid -1 and mid + 1 to \ndetermince which side we have to go */\n\nclass Solution {\n public int singleNonDuplicate(int[] nums) {\n \n int low = 0,high = nums.length - 1, mid = 0;\n \n while(low <= high){\n mid = (low + high )/2;\n \n int num = mid + 1; //to find total number of elements from 0 to mid\n \n if(num % 2 == 0){ //even number of elements between low and high\n if(mid > 0 && nums[mid] == nums[mid - 1]) low = mid + 1;\n else if(mid < nums.length - 1 && nums[mid] == nums[mid + 1]) high = mid - 1;\n else return nums[mid]; \n }else{\n if(mid > 0 && nums[mid] == nums[mid - 1]) high = mid - 1;\n else if(mid < nums.length - 1 && nums [mid] == nums[mid + 1]) low = mid + 1;\n else return nums[mid];\n }\n }\n return nums[mid];\n }\n}\n``` | 7 | 0 | ['Binary Search', 'Binary Tree', 'Java'] | 0 |
single-element-in-a-sorted-array | C++ Binary Search Solution O(LogN) | c-binary-search-solution-ologn-by-ahsan8-terw | Runtime: 4 ms, faster than 97.93% of C++ online submissions for Single Element in a Sorted Array.\nMemory Usage: 11.1 MB, less than 39.06% of C++ online submiss | ahsan83 | NORMAL | 2021-07-17T18:17:51.571437+00:00 | 2021-07-17T18:48:36.735035+00:00 | 609 | false | Runtime: 4 ms, faster than 97.93% of C++ online submissions for Single Element in a Sorted Array.\nMemory Usage: 11.1 MB, less than 39.06% of C++ online submissions for Single Element in a Sorted Array.\n\n```\nWe can do binary search over the sorted array to find the single element. But on which condition we should\nmove to left half or right half ? During binary search we always make move decision based on mid value,\nhere we do the same too but we consider both mid value and index and there are 4 possible cases:\n\n1. Mid Index Odd: \nMeans the length of array from start till mid value (included) is even. As the length of subarray [0, mid] is even\nthe single element can be in [0, mid] or [mid+1, n-1]. Subarray [0, mid] length is even and if all elements in\nsubarray are twice means no single element, then nums[mid] and nums[mid-1] will be same and single\nelement will be in the right half [mid+1, n-1], so we move to right half. Otherwise nums[mid]!=nums[mid-1]\nand there is a single element in the left half [0, mid] and so we move to left half.\n\nExample:\n[1,1,2,3,3,5,5] => mid = 3 => nums[mid]!=nums[mid-1] => nums[3]!=nums[2] =>move to left half\n[1,1,2,2,3,5,5] => mid = 3 => nums[mid]==nums[mid-1] => nums[3]==nums[2] => move to right half\n\n2. Mid Index Even:\nMeans the length of array from start till mid value (included) is odd. As the length of subarray [0, mid] is\nodd the single element can be in [0, mid] or [mid+1, n-1]. Subarray [0, mid] length is odd and if nums[mid]\nand nums[mid+1] are same then the single element is in the right half, otherwise it is in the left half.\n\nExample:\n[1,1,3,2,2,4,4,5,5] => mid = 3 => nums[mid]!=nums[mid+1] => nums[3]!=nums[4] =>move to left half\n[1,1,2,2,4,4,5,6,6] => mid = 3 => nums[mid]==nums[mid+1] => nums[3]==nums[4] =>move to right half\n```\n\n\n```\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n \n int n = nums.size();\n // base cases\n if(n==1)return nums[0];\n if(nums[n-1]!=nums[n-2])return nums[n-1];\n if(nums[0]!=nums[1]) return nums[0];\n \n // iterative binary search\n int left = 0;\n int right = n-1;\n int mid;\n while(left<right)\n {\n int mid = left + (right-left)/2;\n \n // mid is odd means subarray [0,mid] length is even\n // single element in the right half if nums[mid]==nums[mid-1], otherwise left half\n if(mid % 2 ==1)\n {\n if(nums[mid]!=nums[mid-1])right = mid;\n else left = mid + 1; \n }\n // mid is even means subarray [0,mid] length is odd\n // single element in the right half if nums[mid]==nums[mid+1], otherwise left half\n else\n {\n if(nums[mid]!=nums[mid+1])right = mid;\n else left = mid + 1;\n } \n }\n \n // after binary search the left element will contain the single element\n return nums[left];\n }\n};\n``` | 7 | 2 | ['Array', 'C', 'Binary Tree'] | 2 |
single-element-in-a-sorted-array | Short Javascript Binary Search Solution | short-javascript-binary-search-solution-3re9i | \nvar singleNonDuplicate = function(nums) {\n if (nums.length == 1) return nums[0];\n return bsa(0, nums.length - 1);\n function bsa(start, end) {\n | zaq258123 | NORMAL | 2020-05-12T09:25:58.750829+00:00 | 2020-05-19T02:36:24.844747+00:00 | 1,529 | false | ```\nvar singleNonDuplicate = function(nums) {\n if (nums.length == 1) return nums[0];\n return bsa(0, nums.length - 1);\n function bsa(start, end) {\n let mid = Math.floor((start + end) / 2);\n if (nums[mid] == nums[mid - 1]) return mid % 2 ? bsa(mid + 1, end) : bsa(start, mid);\n if (nums[mid] == nums[mid + 1]) return mid % 2 ? bsa(start, mid - 1) : bsa(mid, end);\n return nums[mid];\n }\n};\n```\n | 7 | 0 | ['Binary Tree', 'JavaScript'] | 1 |
single-element-in-a-sorted-array | C++ 100% Beats. | c-100-beats-by-ramudarsingh46-bpsi | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | ramudarsingh46 | NORMAL | 2024-08-16T09:55:37.733718+00:00 | 2024-08-16T09:55:37.733762+00:00 | 31 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n // Initialize the left and right pointers\n int l = 0;\n int r = nums.size() - 1;\n\n while (l < r) {\n // Set the value of mid\n int mid = l + (r - l) / 2;\n\n // If mid is odd, decrement it to make it even\n if (mid % 2 == 1) {\n mid--;\n }\n\n // If the elements at mid and mid + 1 are the same,\n // then the single element must appear after the midpoint\n if (nums[mid] == nums[mid + 1]) {\n l = mid + 2;\n }\n // Otherwise, we must search for the single element before the\n \n else {\n r = mid;\n }\n }\n\n return nums[l];\n }\n};\n``` | 6 | 0 | ['C++'] | 0 |
single-element-in-a-sorted-array | Java beats 100% | java-beats-100-by-deleted_user-3yaz | Java beats 100%\n\n\n\n# Code\n\nclass Solution {\n public int singleNonDuplicate(int[] nums) {\n int left = 0, right = nums.length - 1;\n whil | deleted_user | NORMAL | 2024-05-11T06:22:18.351645+00:00 | 2024-05-11T06:22:18.351677+00:00 | 50 | false | Java beats 100%\n\n\n\n# Code\n```\nclass Solution {\n public int singleNonDuplicate(int[] nums) {\n int left = 0, right = nums.length - 1;\n while (left < right) {\n int mid = (left + right) / 2;\n if (mid % 2 == 1) {\n mid--;\n }\n if (nums[mid] != nums[mid + 1]) {\n right = mid;\n } else {\n left = mid + 2;\n }\n }\n return nums[left];\n }\n}\n``` | 6 | 0 | ['Java'] | 0 |
single-element-in-a-sorted-array | PuTtA EaSY Solution C++ ✅ | Beats 96% 🔥🔥 Binary Search | | putta-easy-solution-c-beats-96-binary-se-jvx8 | Intuition\n Describe your first thoughts on how to solve this problem. \nBinary Search\n\n\n# Complexity\n- Time complexity:O(logn)\n Add your time complexity h | Saisreeramputta | NORMAL | 2023-02-21T07:44:02.959868+00:00 | 2023-02-21T07:44:02.959915+00:00 | 3,503 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nBinary Search\n\n\n# Complexity\n- Time complexity:$$O(logn)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n int left = 0;\n int n = nums.size()-1;\n int right = n;\n while(left<=right){\n int mid = left+(right-left)/2;\n //edge case, if mid is single element\n if((mid == 0 || nums[mid] != nums[mid-1]) &&( mid == n || nums[mid] != nums[mid+1] )) return nums[mid];\n //as size of nums is odd logic to find which side to move\n int leftpart;\n if(nums[mid] == nums[mid-1])\n leftpart = mid-1;\n else leftpart = mid;\n \n if(leftpart%2 == 1) right = mid-1;\n else left = mid+1;\n\n }\n return 0;\n }\n};\n``` | 6 | 0 | ['Binary Search', 'C++'] | 1 |
single-element-in-a-sorted-array | 📌📌Python3 || ⚡166 ms, faster than 95.30% of Python3 | python3-166-ms-faster-than-9530-of-pytho-tv18 | \n\n\nclass Solution:\n def singleNonDuplicate(self, nums: List[int]) -> int:\n n = len(nums)\n start = 0\n end = n - 1\n \n | harshithdshetty | NORMAL | 2023-02-21T00:07:38.854761+00:00 | 2023-02-21T00:08:51.833300+00:00 | 1,412 | false | \n\n```\nclass Solution:\n def singleNonDuplicate(self, nums: List[int]) -> int:\n n = len(nums)\n start = 0\n end = n - 1\n \n while start <= end:\n mid = start + (end - start) // 2\n a = mid % 2 == 0 and nums[mid] == nums[mid - 1]\n b = mid % 2 != 0 and nums[mid] == nums[mid + 1]\n if a or b:\n end = mid - 1\n else: \n start = mid + 1\n return nums[start - 1]\n```\n\nThe code is implementing the binary search algorithm to find the single element in a sorted array which appears only once. Here\'s a step by step explanation of the code:\n1. First, the length of the input array is stored in the variable \'n\'.\n1. Then, the start and end indices of the array are set to 0 and n - 1 respectively.\n1. A while loop is initiated that continues while the start index is less than or equal to the end index.\n1. Inside the while loop, the mid index is calculated using the formula "start + (end - start) // 2". This is equivalent to (start + end) // 2 but avoids potential integer overflow issues.\n1. Two boolean variables \'a\' and \'b\' are created to check if the mid index is pointing to the single element. \'a\' is True if the mid index is even and the element at mid is equal to the element at mid - 1. \'b\' is True if the mid index is odd and the element at mid is equal to the element at mid + 1.\n1. If either \'a\' or \'b\' is True, then it means that the single element is in the left half of the array. Therefore, the end index is updated to mid - 1.\n1. If \'a\' and \'b\' are both False, then the single element is in the right half of the array. Therefore, the start index is updated to mid + 1.\n1. After the while loop completes, the function returns the element at index start - 1. This is because the start index will always point to the first occurrence of the single element, and decrementing it by 1 gives the index of the single element. | 6 | 0 | ['Binary Search', 'Binary Tree', 'Python', 'Python3'] | 1 |
single-element-in-a-sorted-array | ✔️ Straightforward Approach Using Binary Search, With Comments | straightforward-approach-using-binary-se-1ci4 | Thumbs up if you find this helpful \uD83D\uDC4D\n\nThe idea of this solution is the following:\n\nSuppose we have the following array: [1,1,2,2,3,3,4,4,6,8,8]\n | keperkjr | NORMAL | 2021-11-20T05:16:22.202533+00:00 | 2022-04-27T05:05:20.824487+00:00 | 135 | false | **Thumbs up if you find this helpful** \uD83D\uDC4D\n\nThe idea of this solution is the following:\n\nSuppose we have the following array: ```[1,1,2,2,3,3,4,4,6,8,8]```\n\nWe can observe that for each pair: \n\n* The first pair element takes the even array index position \n* The second pair element takes the odd array index position\n\nFor example, when examining the number 1 as a pair, we see it takes the array index positions ```0``` and ```1```. \n\nSimilarly for all other pairs, the first pair element takes the even array index position, and the second pair element takes the odd array index position.\n\nUsing this idea, we can see that this pattern for pairs will break when a single element appears in the array.\n\nIn this solution, we use binary search to look for the point in the array where the pattern mentioned above for the pairs first breaks.\n\n```\npublic class Solution {\n public int SingleNonDuplicate(int[] nums) { \n var lo = 0;\n var hi = nums.Length - 1;\n \n while (lo < hi) {\n // Get the mipoint\n var mid = lo + (hi - lo) / 2;\n \n // Check to see if mid is even\n var isEven = mid % 2 == 0;\n \n // If mid is even, its duplicate should be the next index\n // If mid is odd, its duplicate should be the previous index\n if ((isEven && nums[mid] == nums[mid + 1]) || (!isEven && nums[mid] == nums[mid - 1])) {\n // Duplicate found, advance to next index. Single element is > mid\n lo = mid + 1;\n } else {\n // Pattern is broken. Single element is <= mid\n hi = mid;\n } \n } \n return nums[lo];\n }\n}\n``` | 6 | 0 | [] | 0 |
single-element-in-a-sorted-array | one line python | one-line-python-by-fjp666-gd81 | \nreturn sum(set(nums)) * 2 - sum(nums)\n | fjp666 | NORMAL | 2019-07-08T07:48:33.381574+00:00 | 2019-07-08T07:49:46.389698+00:00 | 670 | false | ```\nreturn sum(set(nums)) * 2 - sum(nums)\n``` | 6 | 2 | ['Python3'] | 4 |
single-element-in-a-sorted-array | Binary Search based approach in Python | binary-search-based-approach-in-python-b-i6z1 | \nclass Solution(object):\n def singleNonDuplicate(self, list):\n low, high = 0 , len(list)-1\n while (low<high):\n mid = low + (hig | rudra_pratap | NORMAL | 2017-04-20T20:12:25.953000+00:00 | 2018-08-24T08:14:27.975538+00:00 | 1,458 | false | ```\nclass Solution(object):\n def singleNonDuplicate(self, list):\n low, high = 0 , len(list)-1\n while (low<high):\n mid = low + (high-low)/2\n if (list[mid]!=list[mid+1] and list[mid]!=list[mid-1]):\n return list[mid]\n elif (mid%2 ==1 and list[mid]==list[mid-1]):\n low = mid+1\n elif (mid%2 ==0 and list[mid]==list[mid+1]):\n low = mid+1\n else:\n high = mid-1\n return list[low]\n``` | 6 | 0 | [] | 0 |
single-element-in-a-sorted-array | Fundamental Binary Search Pattern | fundamental-binary-search-pattern-by-dix-jllp | \n# Code\njava []\nclass Solution {\n public int singleNonDuplicate(int[] nums) {\n\n int n = nums.length;\n\n if (n==1) return nums[0];\n | Dixon_N | NORMAL | 2024-07-14T12:59:46.316724+00:00 | 2024-07-14T12:59:46.316748+00:00 | 1,318 | false | \n# Code\n```java []\nclass Solution {\n public int singleNonDuplicate(int[] nums) {\n\n int n = nums.length;\n\n if (n==1) return nums[0];\n if(nums[0]!=nums[1]) return nums[0];\n if(nums[n-1]!=nums[n-2]) return nums[n-1];\n\n int low =1;\n int high = n-2;\n while (low<=high){\n\n int mid = (low+high)/2;\n\n if(nums[mid]!=nums[mid-1] && nums[mid]!=nums[mid+1]) return nums[mid];\n\n else if (\n (mid%2==1 && nums[mid]== nums[mid-1]) ||\n (mid%2==0 && nums[mid]== nums[mid+1])\n )\n {\n low = mid+1;\n }\n else {\n high = mid-1;\n }\n }\n return -1;\n \n }\n}\n``` | 5 | 0 | ['Java'] | 4 |
single-element-in-a-sorted-array | ✅ 0 ms | simple java solution | 🚀100% faster | 0-ms-simple-java-solution-100-faster-by-ctsfw | \n\n# Code\n\nclass Solution {\n public int singleNonDuplicate(int[] nums) {\n if(nums.length == 1) return nums[0];\n //create the search space | Sauravmehta | NORMAL | 2023-02-21T16:19:55.317556+00:00 | 2023-02-21T16:19:55.317606+00:00 | 74 | false | \n\n# Code\n```\nclass Solution {\n public int singleNonDuplicate(int[] nums) {\n if(nums.length == 1) return nums[0];\n //create the search space\n int low = 0;\n int high = nums.length-1;\n while(low <= high){\n //find the middle index;\n int mid = low+(high - low)/2;\n if(mid-1 >=0 && nums[mid] == nums[mid-1]){\n mid--;\n int left_space = mid - low;\n int right_space = high - (mid - 1);\n if(left_space%2 != 0){\n high = mid - 1;\n }\n else if(right_space%2 != 0){\n low = mid + 2;\n }\n }\n else if(mid+1 <= nums.length-1 && nums[mid] == nums[mid+1]){\n mid++;\n int left_space = (mid-1) - low;\n int right_space = high - mid;\n if(left_space%2 != 0){\n high = mid - 2;\n }\n else if(right_space%2 != 0){\n low = mid + 1;\n }\n }\n else\n return nums[mid];\n }\n return -1;\n }\n}\n``` | 5 | 0 | ['Java'] | 0 |
single-element-in-a-sorted-array | JavaScript | 96% | O(log n) time | O(1) space | Binary Search | javascript-96-olog-n-time-o1-space-binar-wtxu | \n\n# Approach\n\n### Linear search\n\nA \bigoplus A = 0 (XOR-ing a number with itself always equals zero)\nA \bigoplus 0 = A (XOR-ing a number with zero always | costa73 | NORMAL | 2023-02-21T10:44:44.872535+00:00 | 2023-02-21T11:55:17.194864+00:00 | 911 | false | \n\n# Approach\n\n### Linear search\n\n$$A \\bigoplus A = 0$$ ($$XOR$$-ing a number with itself always equals zero)\n$$A \\bigoplus 0 = A$$ ($$XOR$$-ing a number with zero always equals original number)\n\nIf we had an array where each element is present exactly twice, $$XOR$$-ing all elements together would equal zero (as per first rule).\nSince we have one element with no duplicate, $$XOR$$-ing it with the rest of the array would equal this element (as per second rule).\n\n```\nvar singleNonDuplicate = function(nums) {\n let sum = 0;\n \n for (const num of nums) sum ^= num;\n \n return sum;\n};\n```\n\nOr, as a one-liner:\n\n```\nvar singleNonDuplicate = function(nums) {\n return nums.reduce((acc, num) => acc ^ num, 0);\n};\n```\n\n### Binary search\n\nAssuming we already know how binary search works, the main question to answer is - **how to know when to move the pointer to the left or to the right**?\n\nLook at the array below, where each element has a duplicate.\n\n<table>\n <tr>\n <td style="background-color:#555;color:red">0</td>\n <td style="color:red">0</td>\n <td style="background-color:#555;color:orange">1</td>\n <td style="color:orange">1</td>\n <td style="background-color:#555;color:yellow">2</td>\n <td style="color:yellow">2</td>\n <td style="background-color:#555;color:green">3</td>\n <td style="color:green">3</td>\n <td style="background-color:#555;color:cyan">4</td>\n <td style="color:cyan">4</td>\n </tr>\n</table>\n\nYou can notice that every element at an odd index (grey background) is equal to the next element, and every element at an even index is equal to the previous element.\n\nIf we remove a single element from the left (such that there will be one element in the array with no duplicate), 0 in this case, the condition above would switch. Now, every element at an odd index (grey background) is equal to the previous element, and every element at an even index is equal to the next element.\n\n<table>\n <tr>\n <td style="background-color:#555;color:red">0</td>\n <td style="color:orange">1</td>\n <td style="background-color:#555;color:orange">1</td>\n <td style="color:yellow">2</td>\n <td style="background-color:#555;color:yellow">2</td>\n <td style="color:green">3</td>\n <td style="background-color:#555;color:green">3</td>\n <td style="color:cyan">4</td>\n <td style="background-color:#555;color:cyan">4</td>\n </tr>\n</table>\n\nThis won\'t happen if we remove an element from the right, 4 in this case.\n\n<table>\n <tr>\n <td style="background-color:#555;color:red">0</td>\n <td style="color:red">0</td>\n <td style="background-color:#555;color:orange">1</td>\n <td style="color:orange">1</td>\n <td style="background-color:#555;color:yellow">2</td>\n <td style="color:yellow">2</td>\n <td style="background-color:#555;color:green">3</td>\n <td style="color:green">3</td>\n <td style="background-color:#555;color:cyan">4</td>\n </tr>\n</table>\n\nWhat this means is, if we pick an arbitrary index in the array, and it matches the first condition, the single element must be on the right, otherwise, it\'s on the left, with one exception.\n\nIf the element does not equal the element on it\'s right, and neither the element on the left, we have found the element with no duplicate.\n\n```\nfunction singleNonDuplicate(nums) {\n let left = 0;\n let right = nums.length;\n \n while (left < right) {\n let mid = (left + right) >>> 1;\n if (mid % 2 !== 0) mid--;\n\n const value = nums[mid];\n \n if (value !== nums[mid + 1] && \n value !== nums[mid - 1]) {\n return value;\n }\n \n if (value === nums[mid - 1]) {\n right = mid;\n } else {\n left = mid + 1;\n }\n }\n}\n```\n\n# Complexity\n- Time complexity: $$O(log n)$$\n\n- Space complexity: $$O(1)$$ | 5 | 0 | ['Math', 'Binary Search', 'JavaScript'] | 0 |
single-element-in-a-sorted-array | ✅C++✅3 Lines✅XOR Solution | c3-linesxor-solution-by-bhushan_mahajan-sj8n | \n# Approach\n- XOR of a number with itself results 0\n- XOR of a number with 0 results a number only\n- XOR of a number with itself, odd number of times result | Bhushan_Mahajan | NORMAL | 2023-02-21T07:20:13.793953+00:00 | 2023-02-21T07:20:13.794012+00:00 | 293 | false | \n# Approach\n- XOR of a number with itself results 0\n- XOR of a number with 0 results a number only\n- XOR of a number with itself, odd number of times results a number only\n- XOR of a number with itself, even number of times reuslts 0 \n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n\n int sum = 0;\n\n for( auto &it : nums ) \n sum ^= it;\n\n return sum ;\n }\n};\n``` | 5 | 0 | ['C++'] | 0 |
single-element-in-a-sorted-array | ✅ JAVA fastest solution | java-fastest-solution-by-coding_menance-yzqm | 0ms runtime\n# JAVA Code\nJAVA []\nclass Solution {\n public int singleNonDuplicate(int[] nums) {\n int left = 0, right = nums.length-1;\n whil | coding_menance | NORMAL | 2023-02-21T06:32:46.994083+00:00 | 2023-02-21T06:32:46.994124+00:00 | 909 | false | 0ms runtime\n# JAVA Code\n``` JAVA []\nclass Solution {\n public int singleNonDuplicate(int[] nums) {\n int left = 0, right = nums.length-1;\n while(left < right){\n int mid = (left + right)/2;\n if( (mid % 2 == 0 && nums[mid] == nums[mid +1]) || (mid %2 == 1 && nums[mid] == nums[mid - 1]) )\n left = mid + 1;\n else\n right = mid;\n }\n return nums[left];\n } \n}\n```\n\n | 5 | 0 | ['Java'] | 0 |
single-element-in-a-sorted-array | Using advantage of sorted array, Java o(n) | using-advantage-of-sorted-array-java-on-aapo6 | \n# Approach\n Describe your approach to solving the problem. \nAs the given array is sorted, if the element is present twice,we can simply check by checking th | Kiruthick_Nvp | NORMAL | 2023-02-21T02:58:25.680880+00:00 | 2023-03-07T01:49:47.207380+00:00 | 89 | false | \n# Approach\n<!-- Describe your approach to solving the problem. -->\nAs the given array is sorted, if the element is present twice,we can simply check by checking the element with i+1 element, if twice the element found we can skip the next element, until the elements appearing twice we can search with i+=2, then if the element is not equal to i+1, then we return the element.\nWe have to make sure the i wont reach the out of index.\n# Complexity\n- Time complexity:\n- o(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n# Code\n```\nclass Solution {\n public int singleNonDuplicate(int[] nums) {\n for(int i=0;i<nums.length;i++)\n {\n if(i == nums.length-1)\n {\n return nums[i];\n }\n else\n {\n if(nums[i] == nums[i+1])\n {\n if((i+1) != nums.length-1)\n {\n i++;\n }\n }\n else\n {\n return nums[i];\n }\n }\n }\n return 0;\n }\n}\n``` | 5 | 0 | ['Java'] | 1 |
single-element-in-a-sorted-array | JAVA || 2 LINE CODE || HASHMAP | java-2-line-code-hashmap-by-sharforaz_ra-u180 | PLEASE UPVOTE, IF YOU LIKE IT\n# Code\n\nclass Solution {\n public int singleNonDuplicate(int[] arr) {\n HashMap<Integer, Integer> map = new HashMap<> | sharforaz_rahman | NORMAL | 2022-12-31T14:39:52.088134+00:00 | 2023-04-29T09:08:26.417214+00:00 | 486 | false | **PLEASE** **UPVOTE**, **IF YOU LIKE IT**\n# Code\n```\nclass Solution {\n public int singleNonDuplicate(int[] arr) {\n HashMap<Integer, Integer> map = new HashMap<>();\n for (int i : arr) map.put(i, map.getOrDefault(i, 0) + 1);\n for (int i : arr) if (map.get(i) == 1) return i;\n return 0;\n }\n}\n``` | 5 | 0 | ['Hash Table', 'Hash Function', 'Java'] | 1 |
single-element-in-a-sorted-array | C++ | O(Log n) | O(1) | c-olog-n-o1-by-aastha30-o4w1 | \n int singleNonDuplicate(vector<int>& nums) {\n int start = 0 , end = nums.size()-1;\n \n if(nums.size() == 1) return nums[0]; \n | Aastha30 | NORMAL | 2022-05-07T08:59:47.137465+00:00 | 2022-05-07T08:59:47.137493+00:00 | 185 | false | ```\n int singleNonDuplicate(vector<int>& nums) {\n int start = 0 , end = nums.size()-1;\n \n if(nums.size() == 1) return nums[0]; \n if(nums[0] != nums[1]) return nums[0];\n if(nums[end] != nums[end-1]) return nums[end];\n \n while(start<=end)\n {\n int mid = (start+end)/2;\n if(mid%2 == 0)\n {\n if(nums[mid] == nums[mid+1])\n start = mid+1;\n else\n end = mid-1;\n }\n else if(mid%2 != 0)\n {\n if(nums[mid] == nums[mid+1])\n end = mid-1;\n else\n start = mid+1;\n }\n if(nums[mid] != nums[mid+1] && nums[mid] != nums[mid-1])\n return nums[mid];\n }\n \n return 0;\n }\n\t``` | 5 | 0 | ['C', 'Binary Tree'] | 1 |
single-element-in-a-sorted-array | Easy java binary solution 100% faster | easy-java-binary-solution-100-faster-by-8ld7y | Please upvote if you find it helpful\n\nclass Solution {\n public int singleNonDuplicate(int[] nums) {\n if(nums.length==1){\n return nums[ | debanamika | NORMAL | 2022-02-14T07:35:12.445550+00:00 | 2022-02-14T07:35:12.445591+00:00 | 420 | false | Please upvote if you find it helpful\n```\nclass Solution {\n public int singleNonDuplicate(int[] nums) {\n if(nums.length==1){\n return nums[0];\n }\n int l=0, h=nums.length-1;\n while(l<h){\n int mid = l + (h-l)/2;\n if(mid-1>=0 && nums[mid] == nums[mid-1]){ \n if(mid%2 == 1){ \n l = mid+1;\n }\n else h = mid-1;\n }\n else if(mid+1<nums.length && nums[mid] == nums[mid+1]){\n if(mid%2 == 1){\n h = mid-1;\n }\n else l = mid+1;\n }\n else return nums[mid];\n }\n return nums[h];\n }\n}\n\n``` | 5 | 0 | ['Binary Search', 'Binary Tree', 'Java'] | 1 |
single-element-in-a-sorted-array | [JAVA] Binary Search || 100% fast || Each step explained with comments | java-binary-search-100-fast-each-step-ex-s49s | \'\'\'\nclass Solution {\n public int singleNonDuplicate(int[] nums) {\n \n // As we are given a sorted array + it says that our solution must | Shourya112001 | NORMAL | 2021-11-21T14:57:14.692601+00:00 | 2021-11-21T14:57:58.863980+00:00 | 309 | false | \'\'\'\nclass Solution {\n public int singleNonDuplicate(int[] nums) {\n \n // As we are given a sorted array + it says that our solution must be of 0(log n) time\n // We, get the idea that we have to do BINARY SEARCH\n \n //BOUNDARY CONDITIONS:\n \n //1. Check if the length of nums is only 1 \n \n if(nums.length == 1)\n {\n return nums[0];\n }\n \n //2. Check if the first element is our answer?\n \n else if(nums[0] != nums[1])\n {\n return nums[0];\n }\n \n //3. Check if the last element of the array is our answer?\n \n else if(nums[nums.length-1] != nums[nums.length-2])\n {\n return nums[nums.length-1];\n }\n \n int start = 0;\n int end = nums.length-1;\n \n while(start <= end)\n {\n int mid = start + (end - start)/2;\n \n\t\t\t// Here, we are checking that if the value at mid is not equal to any of its adjacent then that is our answer\n \n if((nums[mid] != nums[mid+1]) && (nums[mid] != nums[mid-1]))\n {\n return nums[mid];\n } \n \n\t\t\t//Here for odd positions, we are checking the condition with mid-1, as the pair would definitely be on its left\n\t\t\t//And for the even position we have mid+1 as the pair would be on the right\n \n else if(((mid % 2 == 0) && (nums[mid] == nums[mid+1])) || ((mid % 2 == 1) && (nums[mid] == nums[mid-1])))\n {\n start = mid + 1;\n }\n else\n {\n end = mid - 1;\n } \n }\n \n return -1;\n }\n}\n\'\'\' | 5 | 0 | ['Binary Search', 'Binary Tree', 'Java'] | 0 |
single-element-in-a-sorted-array | Easy Java Solution | Faster than 100% | O(logN) | easy-java-solution-faster-than-100-ologn-bt1d | \npublic int singleNonDuplicate(int[] nums) {\n\tif(nums.length <= 2){\n\t\treturn nums[0];\n\t}\n\tint low = 0;\n\tint high = nums.length - 1;\n\tint mid;\n\tw | codelife148 | NORMAL | 2021-09-23T21:27:03.132416+00:00 | 2021-09-23T21:27:03.132446+00:00 | 444 | false | ```\npublic int singleNonDuplicate(int[] nums) {\n\tif(nums.length <= 2){\n\t\treturn nums[0];\n\t}\n\tint low = 0;\n\tint high = nums.length - 1;\n\tint mid;\n\twhile(low <= high){\n\t\tmid = low + (high - low) /2;\n\t\t\n\t\t//Check to see if element is in the middle\n\t\tif(mid > 0 && mid < nums.length - 1 && nums[mid] != nums[mid - 1] && nums[mid] != nums[mid + 1]){\n\t\t\treturn nums[mid];\n\t\t}\n\t\t//This check\'s if the array on then left part, till the mid has first occurence of the pair in even index position\n\t\t//Because once the single element comes the first occurrence of the pair will always be in odd index position\n\t\t//In that case we have to search for the element on the right part of the array\n\t\telse if((mid > 0 && nums[mid] == nums[mid - 1] && (mid - 1) % 2 == 0) || ( mid < nums.length - 1 && nums[mid] == nums[mid + 1] && (mid + 1) % 2 != 0)){\n\t\t\tlow = mid + 1;\n\t\t}\n\t\telse{\n\t\t\thigh = mid - 1;\n\t\t}\n\t}\n\n\treturn nums[low];\n}\n``` | 5 | 0 | ['Binary Tree', 'Java'] | 1 |
single-element-in-a-sorted-array | Java Binary Search, O(log n) solution | java-binary-search-olog-n-solution-by-ra-wfwk | \nclass Solution {\n public int singleNonDuplicate(int[] nums) {\n int start = 0;\n int end = nums.length-1;\n \n if(nums.length | raj02 | NORMAL | 2021-08-31T15:07:49.144771+00:00 | 2021-08-31T15:07:49.144823+00:00 | 470 | false | ```\nclass Solution {\n public int singleNonDuplicate(int[] nums) {\n int start = 0;\n int end = nums.length-1;\n \n if(nums.length == 0) return 0;\n else if(nums.length ==1) return nums[0];\n else if(nums[0] != nums[1]) return nums[0];\n else if(nums[end] != nums[end-1]) return nums[end];\n \n while(start <= end) {\n int mid = start + (end - start) / 2;\n \n if(nums[mid] != nums[mid-1] && nums[mid] != nums[mid+1]) return nums[mid];\n \n else if(mid % 2 == 0) {\n if(nums[mid] == nums[mid+1]) start = mid + 1;\n else end = mid - 1;\n }\n else if(mid % 2 != 0) {\n if(nums[mid] == nums[mid-1]) start = mid +1;\n else end = mid - 1;\n } \n }return -1;\n }\n}\n``` | 5 | 0 | ['Binary Search', 'Java'] | 0 |
single-element-in-a-sorted-array | 0 ms sol using java (bit manipulation & binary search) | 0-ms-sol-using-java-bit-manipulation-bin-kuwy | Bit manipulation\n\nclass Solution {\n public int singleNonDuplicate(int[] nums) {\n int res = 0;\n for(int i=0;i<nums.length;i++)\n {\n | rmanish0308 | NORMAL | 2021-07-11T08:32:58.860820+00:00 | 2021-07-11T08:45:24.098783+00:00 | 220 | false | Bit manipulation\n```\nclass Solution {\n public int singleNonDuplicate(int[] nums) {\n int res = 0;\n for(int i=0;i<nums.length;i++)\n {\n res = res^nums[i];\n }\n return res;\n }\n}\n```\nbinary search\n```\nclass Solution {\n public int singleNonDuplicate(int[] nums) {\n int start = 0,end = nums.length-1;\n while(start < end)\n {\n int mid = start + (end-start)/2;\n if(mid % 2 == 1)\n mid--;\n \n if(nums[mid] != nums[mid+1])\n end = mid;\n else start = mid+2;\n }\n return nums[start];\n }\n}\n```\n\nPlease upvote if u find my code easy to understand | 5 | 0 | ['Bit Manipulation', 'Binary Tree', 'Java'] | 0 |
single-element-in-a-sorted-array | [Figure] Use example as your guide: generalization | figure-use-example-as-your-guide-general-c766 | \nIntuition:\nSorted array!\nThat suggests we can use binary search.\nThen I will use classical binary search template: [low_index, high_index)\nThe middle valu | codedayday | NORMAL | 2020-05-12T16:41:49.101230+00:00 | 2020-05-12T22:37:21.257456+00:00 | 132 | false | \n**Intuition:**\nSorted array!\nThat suggests we can use binary search.\nThen I will use classical binary search template: [low_index, high_index)\nThe middle value are highlighted in red color.\n\nThere is some observation about potential place for the unique item: it must be in an even-indexed position\n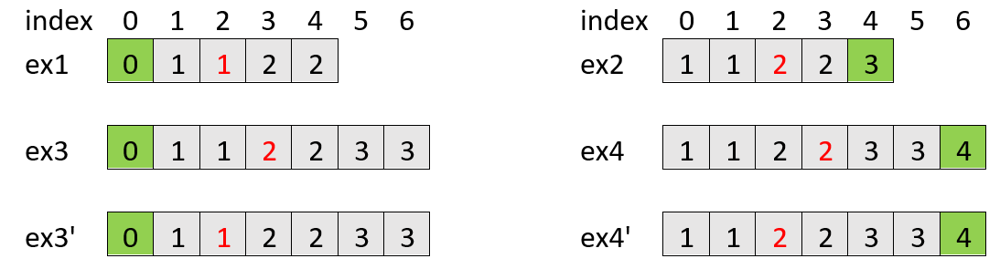\n\nNote, for original middle value of ex3 and ex4, the middle indices need to be decreased by 1 and converted in ex3\u2019, and ex4\u2019 respectively. The unique number, highlighted in green, must occupied an even-index position.\n\nOne more fun knowledge about i-th index in zero-index space is that i means there are i items have smaller indices then current i-th item:\nFor example,\nnums[i]\nmeans there are i items are in the left of nums[i].\nWhat does it mean to this question?\nOkay, if some index, say, mid, is even, then it means there are even number of items in the left of the mid.\n\n```\nclass Solution {//BEST: binary search\npublic://Time/Space: O(logN); O(1)\n int singleNonDuplicate(vector<int>& nums) {\n const int n = nums.size();\n int lo = 0, hi = n;\n if(n==1) return nums[0];\n while(lo<hi){\n int mid = lo + (hi - lo) / 2;\n if(mid%2 == 1) mid--; // if mid%2 == 1; then at least two items are there.\n if(nums[mid] == nums[mid+1]) // left and current duet are all alright\n lo = mid +2; // then move right by two positions.\n else hi = mid; // note, mid is even index, a potential home for unique number\n }\n return nums[lo];\n }\n};\n\n\n``` | 5 | 1 | [] | 0 |
single-element-in-a-sorted-array | Python 3, today's one-liner | python-3-todays-one-liner-by-l1ne-qsfr | Method 1 - xor\n\nJust xor all the numbers together. You\'ll get the unique number. \n\nUse functools.reduce and operator.xor to do it one line.\n\nTime: O(n)\n | l1ne | NORMAL | 2020-05-12T07:19:09.773636+00:00 | 2020-05-12T21:55:52.146543+00:00 | 272 | false | # Method 1 - xor\n\nJust xor all the numbers together. You\'ll get the unique number. \n\nUse [functools.reduce](https://docs.python.org/3/library/functools.html#functools.reduce) and [operator.xor](https://docs.python.org/3/library/operator.html#operator.xor) to do it one line.\n\nTime: `O(n)`\nSpace: `O(1)`\n\n## One line\n\n```python\nclass Solution:\n def singleNonDuplicate(self, A: List[int]) -> int:\n return reduce(xor, A)\n```\n\n## True one-liner\n\n```python\nclass Solution: singleNonDuplicate = lambda A: reduce(xor, A)\n```\n\n-----\n# Method 2 - bisect\n\nIt\'s a sorted list, so we should be able to use binary search. Which means we should be able to use [bisect](https://docs.python.org/3/library/bisect.html) somehow. But how?\n\nLet\'s take the numbers and pair every two...\n```\n[1,1,3,3,4,4,7,8,8,9,9]\n...\n[(1,1), (3,3), (4,4), (7,8), (8,9), (9)]\n...\n[ match, match, match, no-match, no-match, single]\n```\nSo let\'s assigning `match` and `no-match` values and chop off the single at the end. If we have `match` be `0` and `no-match` be `1`, the array is sorted and we\'re looking for where the `0`\'s become `1\'s`. If they\'re all 0\'s, then our number is the single one at the end.\n\nWe can use [bisect_left](https://docs.python.org/3/library/bisect.html#bisect.bisect_left) to find the first 1, or [bisect_right](https://docs.python.org/3/library/bisect.html#bisect.bisect_right) to find the last 0. Either works, but you need an extra +1 if you use the position of the last 0.\n\nThen we take the position returned by bisect_left and double it, and that is the index of our answer.\n\nNote that to actually perform this version of the binary search, we have to create a class wrapper to override the [`A[i]` operation](https://docs.python.org/3/reference/datamodel.html#object.__getitem__).\n\nTime: `O(log n)`\nSpace: `O(1)`\n\n## Four lines\n\n```python\nclass Solution:\n def singleNonDuplicate(self, A: List[int]) -> int:\n class Wrapper:\n def __getitem__(self, i):\n return A[2*i] != A[2*i+1]\n return A[2*bisect_left(Wrapper(), 1, 0, len(A)//2)]\n```\n\n## True one-liner\n\nUse the [type function](https://docs.python.org/3/library/functions.html#type) instead of defining a `class`.\n\n```python\nclass Solution: singleNonDuplicate = lambda _,A: A[2*bisect_left(type(\'\', (), {\'__getitem__\': lambda _,i: A[2*i] != A[2*i+1]})(), 1, 0, len(A)//2)]\n``` | 5 | 0 | [] | 4 |
single-element-in-a-sorted-array | [C++] Binary Search O(log N) | Use xor to maintain n and n+1 even, odd pair | c-binary-search-olog-n-use-xor-to-mainta-p3nt | \nint singleNonDuplicate(vector<int>& nums) {\n\tint start=0, end = nums.size()-1, mid;\n\twhile( start < end ) {\n\t\tmid = start + (end-start)/2;\n\t\tif( num | sonugiri | NORMAL | 2020-05-03T21:21:13.775537+00:00 | 2020-05-05T05:17:48.026648+00:00 | 366 | false | ```\nint singleNonDuplicate(vector<int>& nums) {\n\tint start=0, end = nums.size()-1, mid;\n\twhile( start < end ) {\n\t\tmid = start + (end-start)/2;\n\t\tif( nums[mid] == nums[mid ^ 1] )\n\t\t\tstart = mid + 1;\n\t\telse\n\t\t\tend = mid;\n\t}\n\treturn nums[start];\n}\n``` | 5 | 0 | ['Binary Tree'] | 1 |
single-element-in-a-sorted-array | easy peasy python with lot of comments | easy-peasy-python-with-lot-of-comments-b-1mwr | \tdef singleNonDuplicate(self, nums: List[int]) -> int:\n ln = len(nums)\n if ln == 1:\n return nums[0]\n \n s, e = 0, ln | lostworld21 | NORMAL | 2019-09-02T00:50:08.096786+00:00 | 2019-09-02T00:50:08.096831+00:00 | 1,234 | false | \tdef singleNonDuplicate(self, nums: List[int]) -> int:\n ln = len(nums)\n if ln == 1:\n return nums[0]\n \n s, e = 0, ln-1\n while s <= e:\n mid = (e-s)//2 + s\n # print(s, e, mid)\n if (mid == 0 or nums[mid-1] != nums[mid]) and (mid == ln-1 or nums[mid+1] != nums[mid]):\n return nums[mid]\n # total elements on left of mid including mid is (mid+1)\n # case 1: mid-1 == mid and elements on left including mid are even\n # case 2: mid+1 == mid and elements on left excluding mid are even\n # for case 1 and case 2: s = mid + 1 or s = mid + 2 (for case 2, mid == mid+1)\n # so can move to mid + 2\n if(mid == 0 or nums[mid-1] == nums[mid]) and (mid+1) % 2 == 0:\n s = mid + 1\n elif (mid == ln-1 or nums[mid+1] == nums[mid]) and (mid) % 2 == 0:\n s = mid + 2\n else:\n e = mid - 1\n \n return -1 | 5 | 0 | ['Binary Search', 'Binary Tree', 'Python', 'Python3'] | 0 |
single-element-in-a-sorted-array | Python binary search O(logn) | python-binary-search-ologn-by-doqin-8xdo | \nclass Solution(object):\n def singleNonDuplicate(self, nums):\n """\n :type nums: List[int]\n :rtype: int\n """\n if len | doqin | NORMAL | 2018-10-30T02:14:32.144404+00:00 | 2018-10-30T02:14:32.144444+00:00 | 1,808 | false | ```\nclass Solution(object):\n def singleNonDuplicate(self, nums):\n """\n :type nums: List[int]\n :rtype: int\n """\n if len(nums) < 1:\n return None\n l, r = 0, len(nums)-1\n while l < r:\n m = l + (r - l)/2\n if m - 1 < l or m + 1 > r:\n break\n if m % 2 == 0:\n if nums[m] == nums[m+1]:\n l = m + 2\n else:\n r = m\n else:\n if nums[m] == nums[m-1]:\n l = m + 1\n else:\n r = m\n return nums[l]\n``` | 5 | 0 | [] | 2 |
single-element-in-a-sorted-array | Beats 100% || Binary Search || O(log n) | beats-100-binary-search-olog-n-by-aditya-13ot | Explanation:
We perform a binary search to find the single non-duplicate element.
If mid is even:
If nums[mid] == nums[mid + 1], the unique element must be on t | Aditya_4444 | NORMAL | 2025-01-29T06:24:32.927763+00:00 | 2025-01-29T06:24:32.927763+00:00 | 437 | false | Explanation:
We perform a binary search to find the single non-duplicate element.
If mid is even:
If nums[mid] == nums[mid + 1], the unique element must be on the right, so we move l = mid + 2.
Otherwise, we move r = mid.
If mid is odd:
If nums[mid] == nums[mid - 1], the unique element must be on the right, so we move l = mid + 1.
Otherwise, we move r = mid.
The loop terminates when l == r, and nums[l] is the unique element.
This solution runs in O(log n) time complexity, leveraging binary search.
# Code
```python3 []
from typing import List
class Solution:
def singleNonDuplicate(self, nums: List[int]) -> int:
l, r = 0, len(nums) - 1
while l < r:
mid = (l + r) // 2
if mid % 2 == 0:
if nums[mid] == nums[mid + 1]:
l = mid + 2
else:
r = mid
else:
if nums[mid] == nums[mid - 1]:
l = mid + 1
else:
r = mid
return nums[l]
``` | 4 | 0 | ['Python3'] | 1 |
single-element-in-a-sorted-array | EASY TO C++ SOLUTION || 540. Single Element in a Sorted Array Solved Medium Topics | easy-to-c-solution-540-single-element-in-5xfh | IntuitionThe problem is based on the observation that in a sorted array where every element appears twice except for one, the position of elements can help us d | shivambit | NORMAL | 2024-12-15T15:18:32.232826+00:00 | 2024-12-15T15:18:32.232826+00:00 | 358 | false | # Intuition\n\nThe problem is based on the observation that in a sorted array where every element appears twice except for one, the position of elements can help us determine which half of the array to search. The key insight is that pairs of identical elements will always be positioned in such a way that their indices will either both be even or both be odd. When you encounter an index that does not conform to this pattern, it indicates that the single non-duplicate element lies in that half of the array.\n\n\n# Approach\n\n1. Initial Checks:\n - If the array size is 0 or 1, return the only element (if present).\n - Check if the first or last elements are the unique element (if they do not match their adjacent elements).\n2. Binary Search:\n - Use a binary search approach to efficiently locate the single non-duplicate element.\n - Initialize low to 1 and high to n-2 to avoid boundary issues while checking adjacent elements.\n - Calculate mid as the average of low and high.\n - Check if nums[mid] is different from both its neighbors (nums[mid - 1] and nums[mid + 1]). If so, return nums[mid].\n - Determine which half of the array to search next:\n - If mid is odd and nums[mid] matches nums[mid - 1], it indicates that the unique element must be in the right half. Thus, set low = mid + 1.\n - If mid is even and nums[mid] matches nums[mid + 1], it also indicates that the unique element must be in the right half. Again, set low = mid + 1.\n - Otherwise, search in the left half by setting high = mid - 1.\n3. End Condition:\n - The loop continues until low exceeds high, ensuring all possibilities are covered.\n\n# Complexity\n- Time complexity:O(logn), The algorithm uses binary search which divides the search space in half at each step, leading to logarithmic time complexity.\n\n- Space complexity: O(1), The algorithm uses a constant amount of extra space for variables (low, high, and mid), regardless of the input size.\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int singleNonDuplicate(vector<int>& nums) {\n int n = nums.size(), low = 1,high = n-2;\n\n if(n == 0 || n == 1) return nums[0]; //singe element array\n if(nums[0] != nums[1]) return nums[0]; //last element in array\n if(nums[n-1] != nums[n-2]) return nums[n-1];\n\n while(low <= high){\n int mid = (low + high)/2;\n\n if(nums[mid] != nums[mid - 1] && nums[mid] != nums[mid + 1]) return nums[mid];\n\n //chcek for left half\n if(((mid % 2 == 1) && (nums[mid] == nums[mid - 1])) || ((mid % 2 == 0) && (nums[mid] == nums[mid + 1]))){\n low = mid + 1; //eliminate the left half\n }\n //we are in the right half\n else high = mid - 1; //eliminate the right half\n }\n return -1;\n }\n};\n``` | 4 | 0 | ['Array', 'Binary Search', 'C++'] | 0 |
single-element-in-a-sorted-array | ✅💯🔥Simple Code🚀📌|| 🔥✔️Easy to understand🎯 || 🎓🧠Beats 100%🔥|| Beginner friendly💀💯 | simple-code-easy-to-understand-beats-100-sxy1 | Solution tuntun mosi ki photo ke baad hai. Scroll Down\n\n# Code\njava []\nclass Solution {\n public int singleNonDuplicate(int[] nums) {\n int i=0; i | atishayj4in | NORMAL | 2024-08-20T21:02:16.112997+00:00 | 2024-08-20T21:02:16.113029+00:00 | 361 | false | Solution tuntun mosi ki photo ke baad hai. Scroll Down\n\n# Code\n```java []\nclass Solution {\n public int singleNonDuplicate(int[] nums) {\n int i=0; int j=nums.length-1;\n while(i<j){\n int mid=i+(j-i)/2;\n if(mid%2==1){\n mid--;\n }\n if(nums[mid]==nums[mid+1]){\n i=mid+2;\n }else{\n j=mid;\n }\n }\n return nums[i];\n }\n}\n```\n | 4 | 1 | ['Array', 'Binary Search', 'C', 'Python', 'C++', 'Java', 'JavaScript'] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.