question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
number-of-subarrays-with-bounded-maximum | King and its Empire !! T.C : O(N) & S.C : O(!) | king-and-its-empire-tc-on-sc-o-by-anurag-1onq | Intuition\n Describe your first thoughts on how to solve this problem. \nKing and his Empire\na[i] > R -> villan\na[i] < L -> am janta\na[e]>=L and a[e]<=R -> K | anuragino | NORMAL | 2023-12-07T07:29:10.854438+00:00 | 2023-12-07T07:29:10.854474+00:00 | 33 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nKing and his Empire\na[i] > R -> villan\na[i] < L -> am janta\na[e]>=L and a[e]<=R -> King \n \n*Alone King and King + am janta can built the empire\nif Villan comes , he destory the empire .*\n\n# Approach\n1. declare start ,end , ans and empire.\n2. traverse the end 0->N\n3. if ***King*** encounter set the empire \n4. if **villan** encounter reset the empire .\n5. ans + = empire.\n6. return ans;\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& a, int left, int right) {\n int n = a.size();\n int s = 0, e =0, ans = 0;\n int empire = 0;\n for( ; e<n;e++){\n if(a[e]>=left and a[e]<=right){\n // king built the empire with or without am janta\n empire = e - s + 1;\n }\n else if(a[e]>right){\n // villan aa gya empire tut jyga;\n empire = 0;\n s = e+1;\n }\n \n ans += empire;\n }\n \n return ans;\n }\n};\n``` | 1 | 1 | ['Array', 'Two Pointers', 'Sliding Window', 'C++'] | 0 |
number-of-subarrays-with-bounded-maximum | Sliding Window O(N) TC | sliding-window-on-tc-by-venomancer-6lg4 | Approach\n Describe your approach to solving the problem. \napply sliding window approach to solve the problem, maintain a prevcount for test cases to avoid sub | Venomancer | NORMAL | 2023-10-26T04:24:58.803676+00:00 | 2023-10-26T04:24:58.803711+00:00 | 140 | false | # Approach\n<!-- Describe your approach to solving the problem. -->\napply sliding window approach to solve the problem, maintain a prevcount for test cases to avoid subarrays with all elements below the range\n\n# Code\n```\nclass Solution {\n public int numSubarrayBoundedMax(int[] nums, int left, int right) {\n int p1=0;\n int p2=0;\n int count=0;\n int prevcount=0;\n while(p2!=nums.length){\n if(nums[p2]>=left && nums[p2]<=right){\n count+=p2-p1+1;\n p2++;\n prevcount=0;\n }\n else if(nums[p2]<left){\n count+=p2-p1-prevcount;\n p2++;\n prevcount++;\n }\n else{\n p2++;\n p1=p2;\n prevcount=0;\n }\n }\n return count;\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
number-of-subarrays-with-bounded-maximum | Best Java Solution || Beats 98% | best-java-solution-beats-98-by-ravikumar-5j8b | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | ravikumar50 | NORMAL | 2023-09-09T15:34:40.888342+00:00 | 2023-09-09T15:34:40.888374+00:00 | 224 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n\n // Taken Help\n public int numSubarrayBoundedMax(int[] nums, int left, int right) {\n int i = 0, j = 0, res = 0, maxind = -1;\n while(j < nums.length){\n if(nums[j] >= left && nums[j] <= right){\n maxind = j;\n }\n if(nums[j] > right){\n j++;\n i = j;\n maxind = -1;\n continue;\n }\n if(maxind != -1){\n res += maxind - i + 1;\n }\n j++;\n }\n return res;\n }\n}\n``` | 1 | 0 | ['Java'] | 1 |
number-of-subarrays-with-bounded-maximum | ✅✔️Easy implementation using NGL and NGR concepts of stack || C++ Solution✈️✈️✈️✈️✈️ | easy-implementation-using-ngl-and-ngr-co-9haf | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | ajay_1134 | NORMAL | 2023-07-05T10:54:52.741737+00:00 | 2023-07-05T10:54:52.741758+00:00 | 696 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& arr, int left, int right) {\n int n = arr.size(), mod = 1e9+7;\n vector<int>maxLeft(n,-1), maxRight(n,n);\n stack<pair<int,int>>st1, st2;\n\n for(int i=0; i<n; i++){\n while(!st1.empty() && st1.top().first <= arr[i]) st1.pop();\n if(!st1.empty()) maxLeft[i] = st1.top().second;\n st1.push({arr[i],i});\n }\n\n for(int i=n-1; i>=0; i--){\n while(!st2.empty() && st2.top().first < arr[i]) st2.pop();\n if(!st2.empty()) maxRight[i] = st2.top().second;\n st2.push({arr[i],i});\n }\n\n int ans = 0;\n for(int i=0; i<n; i++){\n if(arr[i] >= left && arr[i] <= right){\n ans += ((i - maxLeft[i]) * (maxRight[i]-i) );\n }\n }\n\n return ans;\n }\n};\n``` | 1 | 0 | ['Array', 'Stack', 'Monotonic Stack', 'C++'] | 0 |
number-of-subarrays-with-bounded-maximum | Solution | solution-by-deleted_user-x8h0 | C++ []\n#pragma GCC optimize("Ofast","inline","-ffast-math")\n#pragma GCC target("avx,mmx,sse2,sse3,sse4")\n\nclass Solution {\npublic:\n int numSubarrayBoun | deleted_user | NORMAL | 2023-04-30T03:42:32.925909+00:00 | 2023-04-30T04:03:03.088032+00:00 | 470 | false | ```C++ []\n#pragma GCC optimize("Ofast","inline","-ffast-math")\n#pragma GCC target("avx,mmx,sse2,sse3,sse4")\n\nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& nums, int left, int right) {\n ios::sync_with_stdio(false);\n cin.tie(0);\n cout.tie(0);\n \n int i = 0, t1 = -1, t0 = -1, res = 0;\n for(int &x : nums) {\n if(x > right) t1 = i;\n if(x >= left) t0 = i;\n \n res += t0 - t1;\n ++i;\n }\n return res;\n }\n};\n```\n\n```Python3 []\nclass Solution:\n def numSubarrayBoundedMax(self, A: List[int], left: int, right: int) -> int:\n dp = 0\n res = 0\n prev = -1\n for i,n in enumerate(A):\n if n > right:\n dp = 0\n prev = i\n elif left <= n <= right:\n dp = i - prev\n res += dp\n else:\n res += dp\n return res\n```\n\n```Java []\nclass Solution {\n public int numSubarrayBoundedMax(int[] nums, int left, int right)\n {\n int lb = -1, rb = -1;\n int max = Integer.MIN_VALUE;\n int total = 0;\n int count = 0;\n while(rb < nums.length - 1)\n {\n rb++;\n int num = nums[rb];\n\n if(num >= left && num <= right)\n count = rb - lb; \n else if(num > right)\n {\n count = 0;\n lb = rb;\n }\n total += count;\n }\n return total;\n }\n}\n```\n | 1 | 0 | ['C++', 'Java', 'Python3'] | 0 |
number-of-subarrays-with-bounded-maximum | 📌📌 C++ || Two Pointers || Faster || Easy To Understand || C++ Code | c-two-pointers-faster-easy-to-understand-hafx | Using Two Pointer\n\n Time Complexity :- O(N)\n\n Space Complexity :- O(1)\n\n\nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& nums, int | __KR_SHANU_IITG | NORMAL | 2022-10-16T14:33:49.926901+00:00 | 2022-10-16T14:33:49.926933+00:00 | 95 | false | * ***Using Two Pointer***\n\n* ***Time Complexity :- O(N)***\n\n* ***Space Complexity :- O(1)***\n\n```\nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& nums, int left, int right) {\n\n int n = nums.size();\n\n long long ans = 0;\n\n // first of all count the total no. of subarrays which has maximum <= right\n\n int i = 0;\n\n while(i < n)\n {\n long long j = i;\n\n while(j < n && nums[j] <= right)\n {\n j++;\n }\n\n // count will store the no. of elements in the subarray\n\n long long count = j - i;\n\n // total subarrays of size n will be (n * (n + 1)) / 2\n\n ans += (count * (count + 1)) / 2;\n\n // move pointer\n\n i = j + 1;\n }\n\n // now decrement all the subarrays which has maximum < left\n\n // follow the same process as above\n\n i = 0;\n\n while(i < n)\n {\n long long j = i;\n\n while(j < n && nums[j] < left)\n {\n j++;\n }\n\n // count will store the no. of elements in the subarray\n\n long long count = j - i;\n\n // total subarrays of size n will be (n * (n + 1)) / 2\n\n ans -= (count * (count + 1)) / 2;\n\n // move pointer\n\n i = j + 1;\n }\n\n return ans;\n }\n};\n``` | 1 | 0 | ['Two Pointers', 'C', 'C++'] | 0 |
number-of-subarrays-with-bounded-maximum | Java O(n) Faster than 100%, Memory consumption less than 96% | java-on-faster-than-100-memory-consumpti-vu4r | Here,\nsum = the total number of subarray which fit the condition\nc = the streak of numbers which are less than the right value\nav = avoid = the streak of num | Raunak49 | NORMAL | 2022-09-08T10:02:41.959349+00:00 | 2022-09-08T10:02:41.959388+00:00 | 52 | false | Here,\n**sum** = the total number of subarray which fit the condition\n**c** = the streak of numbers which are less than the right value\n**av** = **avoid** = the streak of numbers which are less than the left value\n- - - ------------\nBecause the av can be more than one for eg [2,1,1,3,4] left=2, right=5. here av will be 2 at index 2. so we need to subtract the av from sum\n- - ----\n```\nclass Solution {\n public int numSubarrayBoundedMax(int[] arr, int l, int r) {\n long sum=0, c=0, av=0;\n for(int i=0; i<arr.length; i++){\n if(arr[i]>=l && arr[i]<=r){\n c++;\n sum += c;\n av=0;\n }\n else{\n if(arr[i]>r){\n c=0;\n av=0;\n }\n else{\n av++;\n c++;\n sum += c-av;\n }\n }\n }\n return (int)sum;\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
number-of-subarrays-with-bounded-maximum | Python - 2 Pointers Approach | python-2-pointers-approach-by-beingab329-fgu0 | ```\nclass Solution:\n def numSubarrayBoundedMax(self, nums: List[int], left: int, right: int) -> int:\n \n start=count=cur=0\n | beingab329 | NORMAL | 2022-08-22T07:12:40.742715+00:00 | 2022-08-22T07:13:52.551534+00:00 | 189 | false | ```\nclass Solution:\n def numSubarrayBoundedMax(self, nums: List[int], left: int, right: int) -> int:\n \n start=count=cur=0\n \n for i in range(len(nums)):\n \n if left <= nums[i] <= right:\n cur=i-start+1\n \n elif nums[i] > right:\n cur=0\n start=i+1\n \n count+=cur\n \n return count | 1 | 0 | ['Python'] | 0 |
number-of-subarrays-with-bounded-maximum | O(n) solution beats 90% in C | on-solution-beats-90-in-c-by-vgagrani-laf1 | \nint numSubarrayBoundedMax(int* nums, int numsSize, int left, int right){\n \n int l=0,r=0;\n int count=0;\n int prev=0;\n while (r < numsSize)\ | vgagrani | NORMAL | 2022-08-18T17:20:46.498148+00:00 | 2022-08-18T17:30:41.206470+00:00 | 115 | false | ```\nint numSubarrayBoundedMax(int* nums, int numsSize, int left, int right){\n \n int l=0,r=0;\n int count=0;\n int prev=0;\n while (r < numsSize)\n {\n if (nums[r] >= left && nums[r] <= right)\n {\n prev = r-l;\n count = 1 + count + prev;\n }\n else\n {\n if (nums[r] > right) \n {\n r++;\n l=r;\n prev=0;\n continue;\n }\n else \n {\n if (l!=r)\n {\n if (nums[r-1] >= left && nums[r-1] <= right) \n {\n prev = r-l;\n\t\t\t\t\t}\n count = count + prev;\n }\n }\n }\n r++;\n }\n return count;\n}\n``` | 1 | 0 | ['C'] | 0 |
number-of-subarrays-with-bounded-maximum | C++ || Self explanable | c-self-explanable-by-get_the_guns-ykr7 | \nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& nums, int left, int right) {\n int s=0;\n int n=nums.size();\n int e=0; | Get_the_Guns | NORMAL | 2022-07-26T20:02:54.940727+00:00 | 2022-07-26T20:02:54.940764+00:00 | 103 | false | ```\nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& nums, int left, int right) {\n int s=0;\n int n=nums.size();\n int e=0;\n int prev=0;\n int ans=0;\n while(e<n){\n if(left<=nums[e]&&nums[e]<=right){\n prev=e-s+1;\n ans+=prev;\n }\n else if(left>nums[e]){\n ans+=prev;\n \n }\n else{\n prev=0;\n s=e+1;\n \n }\n e++;\n }\n return ans;\n }\n};\n``` | 1 | 0 | [] | 0 |
number-of-subarrays-with-bounded-maximum | C++ || TC : O(N) SC : O(1) || Optimized ✅ | c-tc-on-sc-o1-optimized-by-ajayyadavcste-4sxe | \nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& nums, int left, int right) {\n int ans = 0; // store ans\n int j=-1; // st | ajayyadavcstech | NORMAL | 2022-07-24T15:32:10.580281+00:00 | 2022-07-24T15:33:20.341275+00:00 | 132 | false | ```\nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& nums, int left, int right) {\n int ans = 0; // store ans\n int j=-1; // starting window\n int sub = 0; // if current element is less than left bound then count how may element before current element which is less than left and must be continues(it means any element which is greater than left bound reset the count to 0 )\n for(int i=0;i<nums.size();i++){\n if(nums[i]>right){\n j = i;\n sub = 0;\n }\n else if(nums[i]<left){\n sub++;\n }\n else sub = 0;\n ans = ans + i - j - sub;\n }\n return ans;\n }\n};\n```\nIf You Like Solution Please Upvote :)\nHappy Coding :) | 1 | 0 | ['C'] | 0 |
number-of-subarrays-with-bounded-maximum | Short and easy JAVA solution !! | short-and-easy-java-solution-by-utkarshb-v3o4 | \npublic int numSubarrayBoundedMax(int[] nums, int left, int right) {\n \n int ans = 0;\n \n int s = -1;\n int e = -1;\n | utkarshbisht116 | NORMAL | 2022-07-19T20:32:11.168938+00:00 | 2022-07-19T20:32:11.168969+00:00 | 152 | false | ```\npublic int numSubarrayBoundedMax(int[] nums, int left, int right) {\n \n int ans = 0;\n \n int s = -1;\n int e = -1;\n \n for(int i = 0; i < nums.length; i++){\n\n if(nums[i] >= left && nums[i] <= right){ // in range\n e = i;\n }else if(nums[i] > right){ // max\n s = e = i;\n }else{ // minimum\n // do nothing\n }\n \n ans += (e - s);\n }\n \n return ans;\n }\n``` | 1 | 0 | ['Java'] | 0 |
number-of-subarrays-with-bounded-maximum | TC: O(N) | Easy and clean solution using two-pointers | tc-on-easy-and-clean-solution-using-two-am4vm | \nclass Solution {\n public int numSubarrayBoundedMax(int[] nums, int left, int right) {\n int start = -1, end = -1, res = 0;\n for(int i=0; i< | __Asrar | NORMAL | 2022-07-19T12:45:02.766186+00:00 | 2022-07-19T12:45:02.766228+00:00 | 180 | false | ```\nclass Solution {\n public int numSubarrayBoundedMax(int[] nums, int left, int right) {\n int start = -1, end = -1, res = 0;\n for(int i=0; i<nums.length; i++){\n if(nums[i] > right){\n start = end = i;\n continue;\n }\n if(nums[i] >=left){\n end = i;\n }\n res += end - start;\n }\n return res;\n }\n}\n``` | 1 | 0 | ['Two Pointers', 'Java'] | 0 |
number-of-subarrays-with-bounded-maximum | 1D dp | 1d-dp-by-aniketash57-45c5 | in this solution we are storing ans for every element in the dp array \nwe are breaking the array where the number which is bigger than r \nand for number sma | aniketash57 | NORMAL | 2022-05-09T11:07:32.227280+00:00 | 2022-05-09T11:09:27.847442+00:00 | 172 | false | in this solution we are storing ans for every element in the dp array \nwe are breaking the array where the number which is bigger than r \nand for number smaller than l ans will be of previous valid sequence \nand for the valid sequence ans will be the length from where last bigger than r element came \n\nand the total ans for solution will be the sum of all those answeres\n```\nclass Solution {\npublic:\n int l , r;\n bool check(int x ) \n { \n return (x>=l && x<=r);\n }\n bool isbig(int x) \n { \n return (x>r);\n }\n int numSubarrayBoundedMax(vector<int>& nums, int left, int right) {\n int valid_id = 0 , invalid_bigid=0;\n l = left,r=right;\n int n = nums.size();\n vector<int> dp(n+1);\n //dp(i)->gives total number of ways to form substring such that ith char is the last one \n for(int i =1;i<=n;i++)\n { \n if(check(nums[i-1]))\n { \n valid_id=i;\n dp[i]=valid_id-invalid_bigid;\n }\n else \n { \n if(isbig(nums[i-1]))\n { \n invalid_bigid=i;\n }\n if(invalid_bigid<valid_id)\n { \n dp[i]=dp[valid_id];\n }\n }\n }\n int sum = 0 ;\n for(int i = 0 ;i<=n;i++)\n { \n sum+=dp[i];\n }\n return sum;\n \n }\n};\n``` | 1 | 0 | ['Two Pointers', 'Dynamic Programming', 'C'] | 0 |
number-of-subarrays-with-bounded-maximum | Faster || Easy To Understand || C++ Code | faster-easy-to-understand-c-code-by-__kr-jae1 | Using Two Pointer\n\n Time Complexity : O(N)\n\n Space Complexity : O(1)\n\n\nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& nums, int le | __KR_SHANU_IITG | NORMAL | 2022-04-21T10:00:52.220457+00:00 | 2022-04-21T10:00:52.220504+00:00 | 152 | false | * ***Using Two Pointer***\n\n* ***Time Complexity : O(N)***\n\n* ***Space Complexity : O(1)***\n\n```\nclass Solution {\npublic:\n int numSubarrayBoundedMax(vector<int>& nums, int left, int right) {\n \n int n = nums.size();\n \n int start = 0;\n \n int end = 0;\n \n int prev_count = 0;\n \n int ans = 0;\n \n while(end < n)\n {\n if(nums[end] >= left && nums[end] <= right)\n {\n prev_count = end - start + 1;\n \n ans += prev_count;\n }\n \n else if(nums[end] < left)\n {\n ans += prev_count;\n }\n \n else if(nums[end] > right)\n {\n start = end + 1;\n \n prev_count = 0;\n }\n \n end++;\n }\n \n return ans;\n }\n};\n``` | 1 | 0 | ['C'] | 0 |
find-the-k-sum-of-an-array | Priority Queue || C++ | priority-queue-c-by-kbp12-hg94 | Intuition: First find the maximum sum possible. We will get maximum possible sum after adding all the elements greater than 0. Next, if we want to find 2nd | kbp12 | NORMAL | 2022-08-21T06:06:07.522001+00:00 | 2022-09-29T04:47:26.951650+00:00 | 9,702 | false | **Intuition**: First find the maximum sum possible. We will get maximum possible sum after adding all the elements greater than 0. Next, if we want to find 2nd maximum sum what we can do?\nWe can either subtract a smallest positive number from this sum or add largest (minimum(abs(num)) negative number in the sum to get 2nd maximum number.\nSimilarly, we have to add or subtract numbers from current sum to get next largest sum.\n**Key**: We can convert all the negative numbers to positive and then simply can subtract them instead of adding.\nSo to get the maximum sum we will store the least values that needs to be subtracted from maxsum in priority queue (minheap).\nTime O(nlogn + KlogK)\nSpace O(K)\n```\nclass Solution {\npublic:\n long long kSum(vector<int>& nums, int k) {\n int n = nums.size();\n long long maxsum = 0;\n\t //subtract stores the sum which needs to be subtracted from the maximum sum\n vector<long long> subtract;\n //find the maxsum and update nums so that all elements are positive\n for(int i=0;i<n;i++){\n if(nums[i]>=0){\n maxsum+=nums[i];\n }else{\n nums[i] = abs(nums[i]);\n }\n }\n //sorting nums as per absolute values\n sort(nums.begin(), nums.end());\n \n //Initialize priority queue (minheap) to store current least value which needs to be\n //subtracted from maxsum and the index of nums we are currently at.\n priority_queue<pair<long long,int>, vector<pair<long long,int>>, greater<pair<long long,int>>> pq;\n //start from index 0 with minimum value as nums[0]\n pq.push({nums[0], 0});\n while(!pq.empty() && subtract.size()<k-1){\n pair<long long,int> topp = pq.top(); \n pq.pop();\n long long subt = topp.first;\n int idx = topp.second;\n //push this value to subtract array\n subtract.push_back(subt);\n //if we are not at last idx then we can add further values to pq\n if(idx<n-1){\n pq.push({subt+nums[idx+1] , idx+1});\n pq.push({nums[idx+1] + (subt-nums[idx]) , idx+1});\n }\n }\n \n //ans stores all the largest sum in decreasing order\n vector<long long>ans;\n ans.push_back(maxsum);\n for(long long subt:subtract) {\n ans.push_back(maxsum - subt);\n }\n //return Kth largest sum \n return ans[k-1];\n }\n};\n```\n**Similar Problem** which helps to implement priority queue : 373. Find K Pairs with Smallest Sums\n\nUpvote if it helps!!! | 118 | 0 | ['C', 'Heap (Priority Queue)'] | 13 |
find-the-k-sum-of-an-array | [Python3] Heap/Priority Queue, O(NlogN + klogk) | python3-heappriority-queue-onlogn-klogk-1dxwy | Initial Observation\n1. Given n can be as large as 10^5, the time complexity of this problem has to be no worse than log-linear.\n2. This problem is dealing wit | xil899 | NORMAL | 2022-08-21T04:05:17.945238+00:00 | 2022-08-23T14:41:14.043021+00:00 | 9,114 | false | **Initial Observation**\n1. Given `n` can be as large as `10^5`, the time complexity of this problem has to be no worse than log-linear.\n2. This problem is dealing with *subsequences* but not *subarrays*, indicating we can shuffle the order of the original array, e.g. by sorting it.\n3. Given `-10^9 <= nums[i] <= 10^9`, indicating we need to be *clever* when dealing with positive and negative numbers.\n4. Given we need to return the `k`-th largest subsequence sum, indicating we can use a min-heap to store the possible results.\n\n**Implementation**\n1. We find the sum of all positive numbers. This is the maximum possible sum among all subsequence sums. We initialize our min-heap `ans` to be `[maxSum]`.\n2. We create an array `absNums` of the absolute values, sorted from smallest to largest.\n3. We create a max-heap `maxHeap`. It will start with one pair in it. That pair will be `(maxSum - absNums[0], 0)`. The pairs are compared each time with largest sum first.\n4. Before we have `k` elements in `ans`, we will:\n```\npop (nextSum, i) from maxHeap\npush nextSum to ans\nif i + 1 < N:\n\tpush (nextSum + absNums[i] - absNums[i + 1], i + 1) to maxHeap\n\tpush (nextSum - absNums[i + 1], i + 1) to maxHeap\n```\n\n**Why we need two pushs following each pop from the max-heap?** (by @gonpachiro)\nIn this [post](https://stackoverflow.com/a/33220735), [David Eisenstat](https://stackoverflow.com/users/2144669/david-eisenstat) shared an intuitive explanation. Basically, we maintain a tree-structure via a min-heap to record the subsequence sums. Each time we delete a node, we insert its children. This way, we don\'t need to calculate every subsequence sum explicitly (i.e. by adding and subtracting rather than summing from scratch).\n\n**Complexity**\nTime Complexity: `O(NlogN + klogk)` for sorting and heap operations\nSpace Complexity: `O(N + k)`, for using `absNums`, `ans` and `maxHeap`\n \n **Solution**\n```\nclass Solution:\n def kSum(self, nums: List[int], k: int) -> int:\n maxSum = sum([max(0, num) for num in nums])\n absNums = sorted([abs(num) for num in nums])\n maxHeap = [(-maxSum + absNums[0], 0)]\n ans = [maxSum]\n while len(ans) < k:\n nextSum, i = heapq.heappop(maxHeap)\n heapq.heappush(ans, -nextSum)\n if i + 1 < len(absNums):\n heapq.heappush(maxHeap, (nextSum - absNums[i] + absNums[i + 1], i + 1))\n heapq.heappush(maxHeap, (nextSum + absNums[i + 1], i + 1))\n return ans[0]\n```\n\nPlease upvote if you find the solution helpful. Kudos to [btilly](https://stackoverflow.com/users/585411/btilly)\'s [post](https://stackoverflow.com/questions/72114300) for inspiration.\n\n**Cleaner Solution Using One Heap** (by @celestez)\n```\nclass Solution:\n def kSum(self, nums: List[int], k: int) -> int:\n maxSum = sum([max(0, num) for num in nums])\n absNums = sorted([abs(num) for num in nums])\n maxHeap, nextSum = [(-maxSum + absNums[0], 0)], -maxSum\n for _ in range(k - 1):\n nextSum, i = heapq.heappop(maxHeap)\n if i + 1 < len(absNums):\n heapq.heappush(maxHeap, (nextSum - absNums[i] + absNums[i + 1], i + 1))\n heapq.heappush(maxHeap, (nextSum + absNums[i + 1], i + 1))\n return -nextSum\n``` | 97 | 1 | ['Heap (Priority Queue)', 'Python', 'Python3'] | 16 |
find-the-k-sum-of-an-array | Decreasing Subsequence Sums | decreasing-subsequence-sums-by-votrubac-9lg6 | This problem needs some serious unpacking.\n\n#### 1. Sort the Array\nEven though the description says:\n\n> A subsequence is an array that can be derived from | votrubac | NORMAL | 2022-08-22T22:28:52.438709+00:00 | 2022-08-25T05:54:09.482241+00:00 | 5,505 | false | This problem needs some serious unpacking.\n\n#### 1. Sort the Array\nEven though the description says:\n\n> A **subsequence** is an array that can be derived from another array by deleting some or no elements without changing the order of the remaining elements.\n\n...sum is a commutative operation, and we can rearrange elements as we please. Thus, we will sort elements, as it is essential for the next step.\n\n#### 2. K-th Smallest Subsequence Sum\nThere is a similar problem - [1918. Kth Smallest Subarray Sum](https://leetcode.com/problems/kth-smallest-subarray-sum/), but it\'s for subarrays (not subsequences).\n\nOn some other platforms, I found a heap-based solution, which generates next sums as we go, which is more appropriate for this problem.\n\nGenerating all possible subarrays is extremely time-consuming. Note that `k` is small, and it gives us a hint that we should generate increasing sum subarrays as we go.\n\nThis algorithm is very cool, and it requires the array to be sorted. We use a min heap, where we store the current sum **and** the index of the last element in the subsequence.\n\nWe start with one element with the index 0 (which gives us the smallest sum). For each step:\n1. We pop `sum`, and index `i` from the min heap (smallest sum so far).\n2. We push two new sums to the heap (and increase index `i`):\n\t- `sum + nums[i + 1]`\n\t- `sum + nums[i + 1] - nums[i]`.\n\nFor the `[1, 2, 3, 4]` example, we have the following subarrays (and their representation in the heap).\n- `[1]`: `{1, 0}`\n\t- `[1, 2]`: `{3, 1}`\n\t\t- `[1, 2, 3]`: `{6, 2}`\n\t\t\t- `[1, 2, 3, 4]`: `{10, 3}`\n\t\t\t- `[1, 2, 4]`: `{7, 3}`\n\t\t- `[1, 3]`: `{4, 2}`\n\t\t\t- `[1, 3, 4]`: `{8, 3}`\n\t\t\t- `[1, 4]`: `{5, 3}`\n\t- `[2]`: `{2, 1}`\n\t\t- `[2, 3]`: `{5, 2}`\n\t\t\t- `[2, 3, 4]`: `{9, 3}`\n\t\t\t- `[2, 4]`: `{6, 3}`\n\t\t- `[3]`: `{3,2}`\n\t\t\t- `[3, 4]`: `{7, 3}`\n\t\t\t- `[4]`: `{4, 3}`\n\nWe get these increasing sums as we pop elements from the heap: `1, 2, 3, 3, 4, 5, 5, 6, 6, 7, 7, 8, 9, 10`.\n\n#### 3. K-th Largest Sum\nFor this problem, we will start with the sum of all elements, and then subtract increasing subsequence sums (generated using the above approach).\n\nFor the above example, the initial sum is 10 (`[1, 2, 3, 4]`). The next sum is 9 (`[2, 3, 4]`), then 8 (`[1, 3, 4]`), and so on.\n\nOf course, we need to use max heap instead of min heap.\n\n#### 4. Handling Negatives\nThe initial maximum sum should include all positive elements. \n\nExcluding a positive element from the subsequence is not much different than including a negative element - both operations decrease the sum.\n\nTherefore, we sort the array by absolute values, and also decrease the sum by `abs(nums[i + 1])`.\n\n**C++**\n```cpp\nlong long kSum(vector<int>& nums, int k) {\n sort(begin(nums), end(nums), [](int a, int b){ return abs(a) < abs(b); });\n long long res = accumulate(begin(nums), end(nums), 0LL, [](long long sum, int n){ return sum + max(0, n); });\n priority_queue<pair<long long, int>> pq;\n pq.push({res - abs(nums[0]), 0});\n while(--k) {\n auto [sum, i] = pq.top(); pq.pop();\n if (i + 1 < nums.size()) {\n pq.push({sum - abs(nums[i + 1]), i + 1});\n pq.push({sum + abs(nums[i]) - abs(nums[i + 1]), i + 1});\n }\n res = sum;\n }\n return res;\n}\n``` | 84 | 1 | ['C'] | 8 |
find-the-k-sum-of-an-array | [Python3] priority queue | python3-priority-queue-by-ye15-n8q7 | Please pull this commit for solutions of weekly 307. \n\nIntuition\nHere, I will discuss a strategy to find the kth largest subsequence sum. \n We start from th | ye15 | NORMAL | 2022-08-21T04:03:09.382320+00:00 | 2022-08-22T15:21:38.097548+00:00 | 3,353 | false | Please pull this [commit](https://github.com/gaosanyong/leetcode/commit/b7391a11acc4e9dbe563ebef84f8d78f7943a0f7) for solutions of weekly 307. \n\n**Intuition**\nHere, I will discuss a strategy to find the kth largest subsequence sum. \n* We start from the sum of all positive numbers in `nums` which is the largest one (say `m`); \n* To proceed, we subtract absolute values from `m`; \n\t* If the number is positive, this is equivalent to removing the number from the subsequence sum; \n\t* If the number is negative, this is equivalent to adding the number to the subsequence sum; \n* To enumerate all possitibilites, we generate a tree-ish path to cover different combinations;\n\t* This can be done by repeatedly generating two branches at each point with one always include a value at a given index `i` and the other always exclude the value. \n\nHere, I use a priority queue to control for the size so that the runtime won\'t explode. \n\n**Analysis**\nTime complexity O(NlogN + KlogK)\nSpace complexity O(N + K)\n\n```\nclass Solution:\n def kSum(self, nums: List[int], k: int) -> int:\n m = sum(x for x in nums if x > 0)\n pq = [(-m, 0)] \n vals = sorted(abs(x) for x in nums)\n for _ in range(k): \n x, i = heappop(pq)\n if i < len(vals): \n heappush(pq, (x+vals[i], i+1))\n if i: heappush(pq, (x-vals[i-1]+vals[i], i+1))\n return -x\n``` | 45 | 0 | ['Python3'] | 8 |
find-the-k-sum-of-an-array | Heap | Java | Find "Smallest" | heap-java-find-smallest-by-student2091-djy9 | A pretty difficult problem I think. Here is how I solved it during the contest: \n\nFirst, I consider only the case where the array contains positive integers o | Student2091 | NORMAL | 2022-08-21T04:12:28.696578+00:00 | 2022-08-21T21:00:21.110212+00:00 | 3,068 | false | A pretty difficult problem I think. Here is how I solved it during the contest: \n\nFirst, I consider only the case where the array contains positive integers only. It is obviously that we can find the `k`th smallest subsequence and subtract it from sum of all (positive) elements. Second, I consider the case when negative elements mixed in. We have 2 options to decrease the max sum. Either include a biggest negative number or exclud the smallest positive number. In either cases, the sum will be reduced by its absolute value. \n\nSo, I add up all positive values. Sort it, and make all negative elements positive. But I think here is the difficult part.\nHow do we find the `k`th smallest subsequence? I consider heap, and we just need a way such that we iterate through all the subsequence somehow. \nso, consider the smallest element `{0}`, we can split it like so\n\n`{0} -> {0, 1} and {1}`\n`{1} -> {1, 2} and {2}`\n`{0, 1} -> {0, 1, 2} and {0, 2}`\n`{a, a+1, a+2, ..., a+k} -> {a, a+1, a+2, ..., a+k, a+k+1} and {a, a+1, a+2, ..., a+k+1}`\nIn short, heap item ending in `a_k` spliting into 2 subsequences, both ending in `a_(k+1)` but one with `a_k` and the other without. \nIt\'s a tree where 2 children are at least as large as its parent.\n\n`Time O(nlogn + KlogK)`\n`Space O(K)`\n```Java\nclass Solution {\n public long kSum(int[] nums, int k) {\n long minus = 0, all = 0;\n for (int i = 0; i < nums.length; i++){\n all += Math.max(nums[i], 0); // take all positive values \n nums[i] = Math.abs(nums[i]); // make all non-negative\n }\n Arrays.sort(nums); // sort it\n var minheap = new PriorityQueue<long[]>(Comparator.comparingLong(o -> o[0]));\n minheap.offer(new long[]{nums[0], 0});\n while(--k>0){ // construct the smallest subsequence value in a smart way\n long[] top = minheap.poll();\n int i = (int)top[1]++;\n long val = top[0];\n minus = val;\n if (i < nums.length-1){ // each item (node) branches out into 2 (children)\n top[0] += nums[i+1];\n minheap.offer(new long[]{val - nums[i] + nums[i+1], i+1});\n minheap.offer(top);\n }\n }\n return all - minus;\n }\n}\n``` | 33 | 0 | ['Heap (Priority Queue)', 'Java'] | 4 |
find-the-k-sum-of-an-array | Java Solution | java-solution-by-solved-2xyv | \nclass Solution {\n public long kSum(int[] nums, int k) {\n long sum = 0;\n Queue<Pair<Long, Integer>> pq = new PriorityQueue<>((a, b) -> Long | solved | NORMAL | 2022-08-21T04:03:12.603898+00:00 | 2022-08-21T04:03:12.603927+00:00 | 2,702 | false | ```\nclass Solution {\n public long kSum(int[] nums, int k) {\n long sum = 0;\n Queue<Pair<Long, Integer>> pq = new PriorityQueue<>((a, b) -> Long.compare(b.getKey(), a.getKey()));\n for (int i = 0; i < nums.length; i++) {\n sum = sum + Math.max(0, nums[i]);\n }\n for (int i = 0; i < nums.length; i++) {\n nums[i] = Math.abs(nums[i]);\n }\n Arrays.sort(nums);\n long result = sum;\n pq.offer(new Pair<>(sum - nums[0], 0));\n while (--k > 0) {\n Pair<Long, Integer> pair = pq.poll();\n result = pair.getKey();\n int index = pair.getValue();\n if (index < nums.length - 1) {\n pq.offer(new Pair<>(result + nums[index] - nums[index + 1], index + 1));\n pq.offer(new Pair<>(result - nums[index + 1], index + 1));\n }\n } \n return result;\n }\n}\n``` | 23 | 1 | ['Heap (Priority Queue)', 'Java'] | 5 |
find-the-k-sum-of-an-array | c++ solution | c-solution-by-dilipsuthar60-4gp0 | \nclass Solution {\npublic:\n long long kSum(vector<int>& nums, int k) {\n int n=nums.size();\n vector<long long>ans;\n priority_queue<p | dilipsuthar17 | NORMAL | 2022-08-21T04:29:46.440359+00:00 | 2022-08-21T04:29:46.440399+00:00 | 2,338 | false | ```\nclass Solution {\npublic:\n long long kSum(vector<int>& nums, int k) {\n int n=nums.size();\n vector<long long>ans;\n priority_queue<pair<long long,long long>>pq;\n long long sum=0;\n for(int i=0;i<n;i++)\n {\n if(nums[i]>0)\n {\n sum+=nums[i];\n }\n nums[i]=abs(nums[i]);\n }\n sort(nums.begin(),nums.end());\n pq.push({sum-nums[0],0});\n ans.push_back(sum);\n while(ans.size()<k)\n {\n auto [val,index]=pq.top();\n pq.pop();\n ans.push_back(val);\n if(index+1<n)\n {\n pq.push({val+nums[index]-nums[index+1],index+1});\n pq.push({val-nums[index+1],index+1});\n }\n }\n return ans[k-1];\n }\n};\n``` | 20 | 4 | ['C', 'Heap (Priority Queue)', 'C++'] | 2 |
find-the-k-sum-of-an-array | C++ || Priority Queue || Explained | c-priority-queue-explained-by-anis23-hxqb | Approach:\n\n we need to find the kth largest subsequence sum\n the array consist of both +ve and -ve numbers\n the subsequence with maxsum will be the one with | anis23 | NORMAL | 2022-08-22T08:47:59.146067+00:00 | 2022-08-22T08:47:59.146108+00:00 | 1,335 | false | **Approach:**\n\n* we need to find the kth largest subsequence sum\n* the array consist of both +ve and -ve numbers\n* the subsequence with maxsum will be the one with all the non-neg values\n* now, the 2nd maxsum subsequence will either be\n\t* ``` maxsum- min_pos_value```\n\t* ```maxsum + max_neg_value``` (remember that -2>-10) or we can say ```maxsum- min_abs_neg_value```\n* so we find the maxsum first\n* then update all the neg values to their abs values and sort the array\n* now, we make a maxheap to store the {current max sum, index}\n* we run the loop till the size of our ans array is <k\n* now let\'s say we have the currSum as curr and the index as i\n* now the next maxSum can be\n\t* subtract the next min element from the sorted_nums\n\t\t* ```pq.push({curr - nums[i + 1], i + 1});```\n\t* get back to the previous maxSum and instead of subtracting the ith element subtract the (i+1)th element\n\t\t* ```pq.push({curr - nums[i + 1] + nums[i], i + 1});```\n* example:\n\t\t* sorted nums = {1,2,3,4,10,12}\n\t\t* maxsum = 12+4+3+1 = 20\n\t\t* push {20-1,0}\n\t\t* now,\n\t\t\t* curr=19, i=0\n\t\t\t* store 19 in the ans\n\t\t\t* next possible max sum can be:\n\t\t\t\t* 19-2 i.e ```curr-nums[i+1]```\n\t\t\t\t* or \n\t\t\t\t* 20-2 i.e ```curr+nums[i]-nums[i+1]```\n* return the kth subsequence sum i.e ans[k-1]\n\n**Code:**\n\n```\nclass Solution\n{\npublic:\n typedef pair<long long, long long> pi;\n long long kSum(vector<int> &nums, int k)\n {\n int n = nums.size();\n priority_queue<pi> pq; //{sum,index}\n long long maxsum = 0;\n for (auto &x : nums)\n (x >= 0) ? maxsum += x : x *= -1;\n\n sort(nums.begin(), nums.end());\n pq.push({maxsum - nums[0], 0});\n vector<long long> ans;\n ans.push_back(maxsum);\n\n while (ans.size() < k)\n {\n auto [curr, i] = pq.top();\n pq.pop();\n ans.push_back(curr);\n if (i + 1 < n)\n {\n pq.push({curr - nums[i + 1], i + 1});\n pq.push({curr - nums[i + 1] + nums[i], i + 1});\n }\n }\n return ans[k - 1];\n }\n};\n``` | 18 | 0 | ['C', 'Heap (Priority Queue)', 'C++'] | 3 |
find-the-k-sum-of-an-array | Detailed, Clean Code Explained with Comments! C++ 🔥 Easy to understand | detailed-clean-code-explained-with-comme-08sm | Upvote if it helped! :)\n\n\nApproach-\n\nTake the sum of all positive values in nums, it will be maximum sum of any subsequence possible.\nMake all the element | ishaankulkarnii | NORMAL | 2022-08-21T08:58:01.188430+00:00 | 2022-08-23T08:11:16.381343+00:00 | 1,600 | false | Upvote if it helped! :)\n\n\n**Approach-**\n\nTake the sum of all positive values in nums, it will be maximum sum of any subsequence possible.\nMake all the elements of nums positive (Reason- Later we will include or exclude the nums[i] in sum,\n\n-> Case1- If nums[i] was negative, if we subtract it from sum, it will be same as including it into subsequence and if we add/consider it to sum, it will be same as excluding it from subsequence.\n\n-> Case2 - If nums[i] was positive, if we subtract it from sum, it will be same as excluding it from subsequence and if we add/consider it to sum, it will be same as including it into subsequence.\n\nSort the nums vector and create a priority_queue of type pair (to insert current sum and index).\nInsert the {sum-nums[0],0} into the priority_queue.\nNow while we didn\'t get kth highest sum of subsequence, do the following-\ntake the top of priority queue, if the ind+1 < n , then either include the ind+1 and ind value or exclude ind+1 value ( ind value is already excluded).\nIt will same as taking subsequences.\n\n```\n\n#define ll long long\nclass Solution {\npublic:\n long long kSum(vector<int>& nums, int k) {\n \n\t\tll sum=0,n=nums.size();\n vector<ll> ans; // vector to store first k maximum subsequence sum\n for(ll i=0;i<nums.size();i++)\n {\n if(nums[i]>0)\n sum+=nums[i]; // find the maximum possible sum\n nums[i]=abs(nums[i]); // make all values of nums >=0\n\t\t\t\n }\n ans.push_back(sum); // push the highest possible sum\n priority_queue<pair<ll,ll>> pq; // priority queue to store the pair of sum and index, which denotes maximum sum if the current index value is excluded.\n sort(nums.begin(),nums.end()); // sort the nums so that we include and exclude minimum value first to get highest subsequence values \n pq.push({sum-nums[0],0}); // push sum-nums[0], 0 ....which denotes max subsequence sum when index 0 is excluded.\n\t\t// while we don\'t get the kth highest subsequence sum do the operation\n while(ans.size()<k)\n {\n auto [sum,ind]=pq.top();\n pq.pop();\n if(ind+1<n)\n {\n\t\t\t\n pq.push({sum+nums[ind]-nums[ind+1],ind+1}); // if next index is possible, this case considers if we take the previous index and exclude the latest one i.e. ind+1\n pq.push({sum-nums[ind+1],ind+1}); // if next is possible, this case considers, if we exclude both previous index as well as latest possible index i.e. ind+1\n }\n ans.push_back(sum);\t\t\t//push the next highest subsequence sum\n }\n return ans.back(); \n }\n\t\n\t\n\t\n\t\n};\n\n\n\n\n```\n\nUpvote if it helpded! :) | 18 | 0 | [] | 3 |
find-the-k-sum-of-an-array | [Java] Priority Queue with Thought Process and Explanation | java-priority-queue-with-thought-process-qzfy | Thought Process\nWe can start by considering what the first few largest subsequence sums are by going through an example. Let\'s take the array [-4, -3, -2, -1, | austincheng | NORMAL | 2022-08-21T13:10:39.439758+00:00 | 2022-08-21T13:11:11.433765+00:00 | 796 | false | **Thought Process**\nWe can start by considering what the first few largest subsequence sums are by going through an example. Let\'s take the array `[-4, -3, -2, -1, 2, 5]` as our example.\n\nFor `k == 1`, i.e. the largest subsequence sum, we should be able to see fairly quickly that in general this is just the sum of all the positive integers. For our example, this is `5 + 2 = 7`. Let\'s call this number `maxSubsequenceSum`.\n\nFor `k == 2`, the next largest subsequence sum will come from applying the smallest "change" we can make from our previous subsequence sum. We should be able to see that a "change" means that we either need to add a negative number or remove a positive number. Clearly, the smallest change we can make is choosing either the smallest positive number or the smallest (in absolute value) negative number. For our example, let\'s find the smallest "change" we can make. Two of the candidates are adding -1 or removing 2, but clearly adding -1 is smaller, so the next largest subsequence sum is `5 + 2 - 1 = 6`. Notice that removing the smallest positive number or adding the smallest (in absolute value) negative number are essentially doing the same thing, which is just substracting the smallest absolute value from the previous subsequence sum. So, the easiest way to find the smallest "change" is to sort the absolute values of the array and choose the smallest value. If the smallest absolute value is positive, the "change" would be to remove the positive number. If the smallest absolute value is negative, the "change" would be to add the negative number. Therefore, once we have a sorted absolute value array of `nums`, let\'s call this `abs`, the next largest subsequence sum just amounts to doing `maxSubsequenceSum - abs[0]`. \n\nFor `k == 3`, we have more choices to consider. We could potentially do the same process as the previous largest subsequence sum in which we find the smallest "change" we can make and apply it. However, notice that this actually isn\'t the next largest subsequence sum, as instead of applying the next smallest "change", we can just replace the last "change" we made with the next smallest "change". For our example, this would be adding the -2 or removing the 2, so replacing our previous "change" of adding -1 would either be adding -2 to get `5 + 2 - 2 = 5` or removing 2 to just get `5`. As we saw before, these are the exact same in code, which amount to doing `maxSubsequenceSum - abs[1]`.\n\nFor `k == 4`, we could potentially use what we tried for `k == 3`, which is to combine the smallest two "changes", however there is another possibility here as well. The third smallest "change" could be smaller than the combination of the two smallest "changes". For our example, the third smallest change is actually removing the 2 (or adding -2, since one of these was done for `k == 3` we can use the other here), giving us just `5`. This amounts to doing `maxSubsequenceSum - abs[2]`. However, in general we aren\'t sure if this is larger or if `maxSubsequenceSum - abs[0] - abs[1]` is larger.\n\nFrom `k == 4` onward, we see that the formula for the subsequence sum isn\'t as simple, since we aren\'t sure which combination of "changes" would be larger. However, we can see that in general, if we cannot use "changes" from lower indices, the next largest subsequence sum would be would be to replace the current "change" with the next smallest "change". For example, the next largest subsequence sum from `maxSubsequenceSum - abs[1]` would be `maxSubsequenceSum - abs[2]` if we disallow using the "change" at index 0. If we didn\'t disallow using the "change" at index 0, we saw before that we aren\'t sure in general if `maxSubsequenceSum - abs[0] - abs[1]` is larger. But we are guaranteed that one of these is the value for `k == 4` since using `abs[3]` is guaranteed to be a larger (or equal) "change" since the array is sorted.\n\nSo, when considering the next largest subsequence sums, we need to consider both possibilities: either keep the last "change" and continue it or replace the last "change" with the next smallest "change". For example, from `maxSubsequenceSum - abs[0]`, we can either continue it with `maxSubsequenceSum - abs[0] - abs[1]` or replace it with `maxSubsequenceSum - abs[1]`. In the continuation possibility, we continue using the "change" at index 0, but in the replacement possibility, we disallow using the "change" at index 1. So `maxSubsequenceSum - abs[1]` would branch out with `maxSubsequenceSum - abs[1] - abs[2]` and `maxSubsequenceSum - abs[2]`. This way, we ensure that we cover all possibilities for the next few largest subsequence sums.\n\nWe also want to explore next largest subsequence sums in order, which motivates us to use a max heap / priority queue structure. From a certain subsequence sum, we will put both possibilities into the heap and keep track of the last "change" that we applied. By using a heap, we can ensure that the top of the heap is the next largest subsequence sum, so we can then pop from the heap in order and continue to explore possibilities.\n\n**Code**\n```\nclass Solution {\n public long kSum(int[] nums, int k) {\n // Calculate maxSubsequenceSum and abs.\n long maxSubsequenceSum = 0;\n int[] abs = new int[nums.length];\n for (int i = 0; i < nums.length; ++i) {\n int num = nums[i];\n if (num > 0) {\n maxSubsequenceSum += num;\n }\n abs[i] = Math.abs(num);\n }\n Arrays.sort(abs);\n \n // Max heap to maintain the largest subsequence sums. \n\t\t// The first number in the pair is the subsequence sum. \n\t\t// The second number is the index of the last "change" we made to obtain this subsequence sum.\n PriorityQueue<Pair<Long, Integer>> pq = new PriorityQueue<>((p1, p2) -> {\n return Long.compare(p2.getKey(), p1.getKey()); \n });\n \n // List of subsequence sums in order.\n ArrayList<Long> subsequenceSums = new ArrayList<>();\n subsequenceSums.add(maxSubsequenceSum);\n \n // Start with the smallest "change" we can make.\n pq.add(new Pair(maxSubsequenceSum - abs[0], 0));\n while (subsequenceSums.size() < k) {\n // Get previous largest subsequence sum and add it to list.\n Pair<Long, Integer> subsequenceSum = pq.poll();\n long lastSubsequenceSum = subsequenceSum.getKey();\n int lastChange = subsequenceSum.getValue();\n subsequenceSums.add(lastSubsequenceSum);\n \n if (lastChange < nums.length - 1) {\n // Continue with the last "change"\n pq.add(new Pair(lastSubsequenceSum - abs[lastChange + 1], lastChange + 1));\n // Replace the last "change"\n pq.add(new Pair(lastSubsequenceSum + abs[lastChange] - abs[lastChange + 1], lastChange + 1));\n }\n }\n \n return subsequenceSums.get(k - 1);\n }\n}\n``` | 16 | 0 | ['Heap (Priority Queue)', 'Java'] | 5 |
find-the-k-sum-of-an-array | [Detailed Explanation & Cpp Code] Greedy Counting + Time O(N*log(N)+K*log(K)) + Space O(K) | detailed-explanation-cpp-code-greedy-cou-55wj | \n//Document History\n//2022/08/21 Created\n//2022/08/22 Updated: Fix Typos, Edit Typeset\n//2022/08/23. Updated: Add Figure to show the | mkyang | NORMAL | 2022-08-21T08:39:07.539081+00:00 | 2022-08-23T12:13:28.875682+00:00 | 860 | false | ```\n//Document History\n//2022/08/21 Created\n//2022/08/22 Updated: Fix Typos, Edit Typeset\n//2022/08/23. Updated: Add Figure to show the greedy approach of exploring \n```\n\n**The Problem**\nThe "**subsequence**" in the description is misleading. Actually, the order should be ignored. The problem can be described as: ***Given N numbers, we want to find the Kth-Largest Sum of any subset of the numbers (empty set included).***\n\n**The Algorithm**\n**Step 1: Preprocess & 1st-Largetest Sum**\nWe do the following things at the very beginning.\n* **Calculate Sum of Positive Numbers**\n We pick all positive numbers and calculate the **SUM**. As you all know, this is the 1-Sum or 1st-largest sum.\n* **Multiple -1 for Negative Numbers**\nTo make the discussion simple, we multiple every negative number by -1.\n* **Sort the Numbers**\nWe sort the numbers and prepare for our **greedy strategy.**\n\nThe new problem becomes:***Given N non-negative numbers, we want to find the Kth-Smallest Sum of any subset of the numbers (empty set included).***\n\n**Step 2: Repeatly find the subset of the numbers with smallest sum**\nWe maintain a buffer of subsets. Repeatly, we pick the subset whose sum is smallest from the buffer and explore **at most two** new subsets. For your information, we cannot afford to store the subset. We store the sum of the subset instead, as you can guess. Besides, we store information about the next element to visit. Finally, we employ a greedy strategy as following: \n* We keep tracking **(running sum, next element to visit)** \n* Given a subset, we explore two more subset\n\t* the size of the subset is keep unchanged but replace the largest element with the **next element**.\n\t* increase the size of subset by 1 to include the **next element**.\n\nAccording to the request of @xiaominglu, we show the greedy strategy with **Example 1: [1,2,3,4]**. We show all subset as nodes. Beginning with **[1]**, we explore at most two new subsets. At any time, every un-explored subset will bigger than one subset in the buffer (w.r.t. the sum of elements). In other words, the buffer is the **greedy frontier**. Furthermore, we guarantee that there will be **one and only one path** from the root (a.k.. empty set) to any node. As a result, we don\'t need to track nodes visited.\n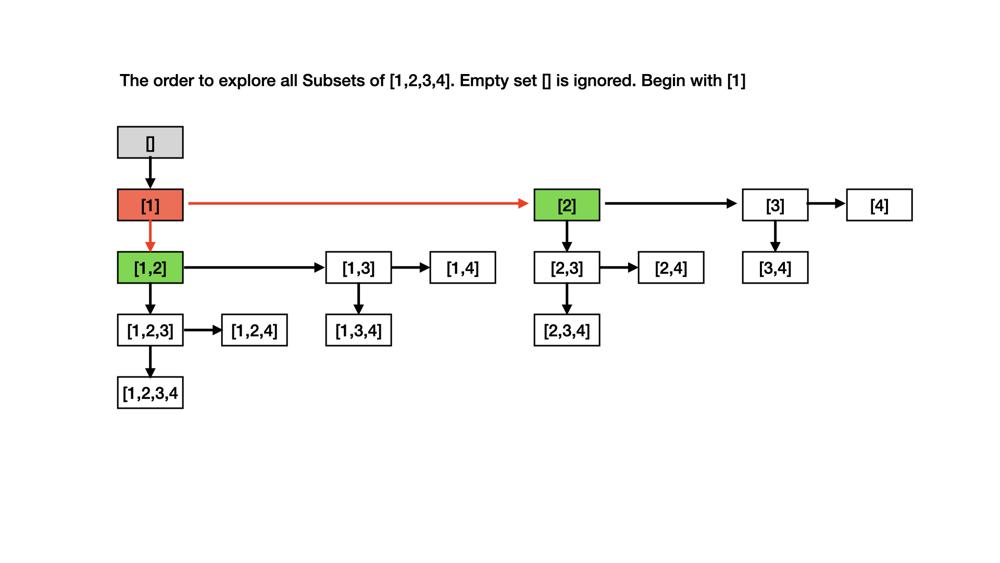\n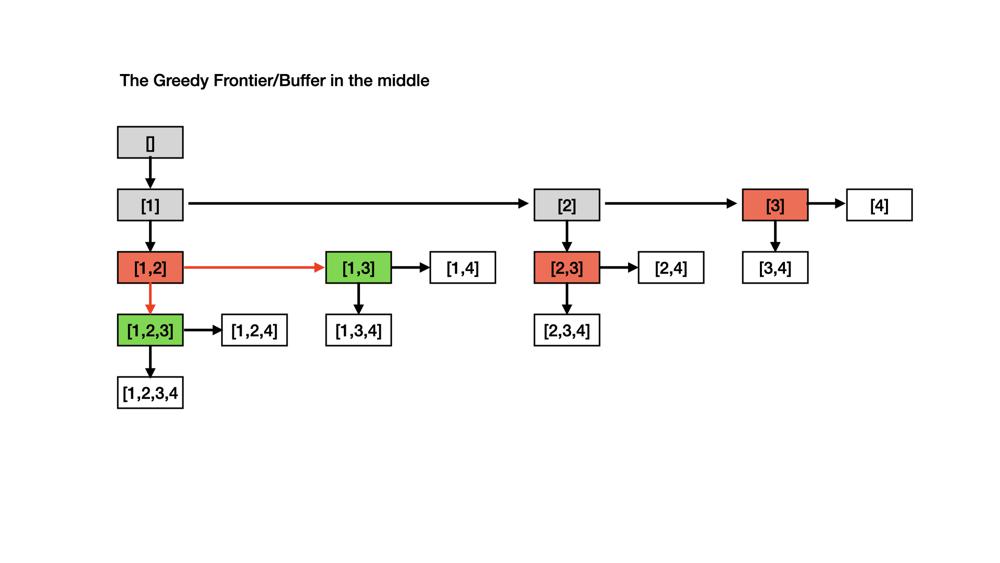\n\n\n\nWe use a MIN-heap to buffer the subset. Let\'s show what we can do with the aforementioned exmaple. For clarity, we show the candidate subset as well as the note. Please remember that we just keep record of limited information, a.k.a. **notes**, in the code.\n\nIn the following, we show our algorithm with **Example 2: [1,-2,3,4,-10,12]**\nNow, we have **SUM**=20, and the numbers are sorted **[1,2,3,4,10,12]**. For clarity, let **S** be a subset of the numbers, and **Sum(S)** be the sum of the subset. **SUM-Sum(S)** will be the sum of a corresponding subset of the original numbers. \n\n\n\n* **Step 2.1 | 1-Sum=20-0**\nInital the buffer w.r.t. **[1,2,3,4,10,12]**\nBuffer Subset: **[1]**\nSubset Notes: **(1,1),** \n* **Step 2.2 | 2-Sum=20-1**\nSubset Removed: **[1]**\nSubset Explored: **[2], [1,2]** \nBuffer Subset: **[2], [1,2]**\nSubset Notes: **(2,2), (3,2)**\n* **Step 2.3 | 3-Sum=20-2**\nSubset Removed: **[2]**\nSubset Explored: **[3], [2,3]** \nBuffer Subset: **[1,2], [3], [2,3]**\nSubset Notes: **(3,2), (3,3), (5,3)**\n* **Step 2.4 | 4-Sum=20-3**\nSubset Removed: **[1,2]**\nSubset Explored: **[1,3], [1,2,3]** \nBuffer Subset: **[3], [2,3], [1,3], [1,2,3]**\nSubset Notes: **(3,3), (5,3), (4,3), (6,3)**\n* **Step 2.5 | 5-Sum=20-3**\nSubset Removed: **[3]**\nSubset Explored: **[4], [3,4]** \nBuffer Subset: **[2,3], [1,3], [1,2,3],[4], [3,4]**\nSubsetNotes: **(5,3), (4,3), (6,3), (4,4),(7,4)**\n* **Step 2.6 | 6-Sum=20-4**\nSubset Removed: **[1,3]**\nSubset Explored: **[1,4], [1,3,4]** \nBuffer Subset: **[2,3], [1,2,3], [4], [3,4], [1,4], [1,3,4]**\nSubset Notes: **(5,3),(6,3), (4,4), (7,4),(5,4), (8,4)**\n* **Step 2.7 | 7-Sum=20-4**\nSubset Removed: **[4]**\nSubset Explored: **[10], [4,10]** \nBuffer Subset: **[2,3], [1,2,3], [3,4], [1,4], [1,3,4], [10], [4,10]**\nSubset Notes: **(5,3),(6,3), (7,4), [5,4], (8,4), (10,5),(14,5)**\n* **Step 2.8 | 8-Sum=20-5**\nSubset Removed: **[2,3]**\nSubset Explored: **[2,4], [2,3,4]** \nBuffer Subset: **[1,2,3], [3,4], [1,4], [1,3,4],[10], [4,10], [2,4], [2,3,4]**\nSubset Notes: **(6,3), (7,4), [5,4], (8,4), (10,5), (14,5),(6,4),(9,4)**\n* **Step 2.9 | 9-Sum=20-5**\nSubset Removed: **[1,4]**\nSubset Explored: **[1,10], [1,4,10]** \nBuffer Subset: **[1,2,3], [3,4], [1,3,4],[10], [4,10], [2,4], [2,3,4],[1,10], [1,4,10]**\nSubset Notes: **(6,3), (7,4), (8,4), (10,5),(14,5), (6,4), (9,4), (11,5), (15,5)**\n* **Step 2.10 | 10-Sum=20-6**\nSubset Removed: **[1,2,3]**\nSubset Explored: **[1,2,4], [1,2,3,4]** \nBuffer Subset: **[3,4], [1,3,4],[10], [4,10], [2,4], [2,3,4],[1,10], [1,4,10], [1,2,4], [1,2,3,4]**\nSubset Notes: **(7,4), (8,4), (10,5),(14,5), (6,4), (9,4), (11,5), (15,5) (7,4), (10,4)**\n* **Step 2.11 | 11-Sum=20-6**\nSubset Removed: **[2,4]**\nSubset Explored: **[2,10], [2,4,10]** \nBuffer Subset: **[3,4], [1,3,4],[10], [4,10], [2,3,4],[1,10], [1,4,10],[1,2,4], [1,2,3,4],[2,10], [2,4,10]**\nSubset Notes: **(7,4),(8,4), (10,5),(14,5),(9,4), (11,5),(15,5), (7,4), (10,4), (12,5),(16,5)**\n* **Step 2.12 | 12-Sum=20-7**\nSubset Removed: **[3,4]**\nSubset Explored: **[3,10], [3,4,10]** \nBuffer Subset: **[1,3,4],[10], [4,10], [2,3,4],[1,10], [1,4,10],[1,2,4], [1,2,3,4],[2,10], [2,4,10],[3,10], [3,4,10]**\nSubset Notes: **(8,4), (10,5),(14,5),(9,4), (11,5),(15,5), (7,4), (10,4), (12,5),(16,5),(13,5),(17,5)**\n* **Step 2.13 | 13-Sum=20-7**\nSubset Removed: **[1,2,4]**\nSubset Explored: **[1,2,10], [1,2,4,10]** \nBuffer Subset: **[1,3,4],[10], [4,10], [2,3,4],[1,10], [1,4,10], [1,2,3,4],[2,10], [2,4,10],[3,10], [3,4,10],[1,2,10], [1,2,4,10]**\nSubset Notes: **(8,4), (10,5),(14,5),(9,4), (11,5),(15,5), (10,4), (12,5), (16,5), (13,5),(17,5), (13,5), (17,5)**\n* **Step 2.14 | 14-Sum=20-8**\nSubset Removed: **[1,3,4]**\nSubset Explored: **[1,3,10], [1,3,4,10]** \nBuffer Subset: **[10], [4,10], [2,3,4],[1,10], [1,4,10], [1,2,3,4],[2,10], [2,4,10],[3,10], [3,4,10],[1,2,10], [1,2,4,10],[1,3,10], [1,3,4,10]**\nSubset Notes: **(10,5),(14,5),(9,4), (11,5),(15,5), (10,4), (12,5), (16,5), (13,5),(17,5),(13,5), (17,5), (14,5), (18,5)**\n* **Step 2.15 | 15-Sum=20-9**\nSubset Removed: **[2,3,4]**\nSubset Explored: **[2,3,10], [2,3,4,10]** \nBuffer Subset: **[10], [4,10], [1,10], [1,4,10], [1,2,3,4],[2,10], [2,4,10],[3,10], [3,4,10],[1,2,10], [1,2,4,10],[1,3,10], [1,3,4,10],[2,3,10], [2,3,4,10]**\nSubset Notes: **(10,5),(14,5),(11,5),(15,5),(10,4),(12,5),(16,5),(13,5),(17,5),(13,5),(17,5),(14,5),(18,5),(15,5),(19,5)**\n* **Step 2.16 | 15-Sum=20-10**\nSubset Removed: **[1,2,3,4]**\nSubset Explored: **[1,2,3,10], [1,2,3,4,10]** \nBuffer Subset: **[10], [4,10], [1,10], [1,4,10],[2,10], [2,4,10],[3,10], [3,4,10],[1,2,10], [1,2,4,10],[1,3,10], [1,3,4,10],[2,3,10], [2,3,4,10],[1,2,3,10], [1,2,3,4,10]**\nSubset Notes: **(10,5),(14,5),(11,5),(15,5),(12,5),(16,5),(13,5),(17,5),(13,5),(17,5),(14,5),(18,5),(15,5),(19,5),(16,5),(20,5)**\n\nWow. Solve it Manually. I Made It !! **In case my guide helps you. Please upvote to support.** \n\n**Performance:**\n```\nRuntime: 181 ms, faster than 100.00% of C++ online submissions for Find the K-Sum of an Array.\nMemory Usage: 59.4 MB, less than 66.67% of C++ online submissions for Find the K-Sum of an Array.\n```\n\n**C++ Code Example**\n```\nclass Solution {\npublic:\n long long kSum(vector<int>& nums, int k) {\n ios::sync_with_stdio(false);\n cin.tie(nullptr);\n long long sum=0, val, next, n=nums.size();\n typedef pair<long long, long long> Data;\n priority_queue<Data, vector<Data>, greater<Data>> buf;\n for(long long i=0; i<n; ++i) {\n if(nums[i]>=0) {\n sum+=nums[i];\n } else if(nums[i]<0){\n nums[i]=-nums[i];\n }\n }\n if(!--k)\n return sum;\n sort(nums.begin(), nums.end());\n buf.push({nums[0], 1});\n for(--k; k; --k) {\n val=buf.top().first;\n next=buf.top().second;\n buf.pop();\n if(next<n) {\n buf.push({val+nums[next]-nums[next-1], next+1});\n buf.push({val+nums[next], next+1});\n }\n }\n return sum-buf.top().first;\n }\n};\n``` | 16 | 0 | ['Greedy', 'Heap (Priority Queue)'] | 6 |
find-the-k-sum-of-an-array | Simple solution with a detailed proof | Heap | NlogN + klogK | simple-solution-with-a-detailed-proof-he-fxk3 | I got very frustrated when I failed to tackle this problem and people are sharing their code w/o any proof like "I just know it". Inspired by ye15, finally I co | harttle | NORMAL | 2022-08-21T07:24:18.738537+00:00 | 2022-08-21T07:30:28.839825+00:00 | 607 | false | I got very frustrated when I failed to tackle this problem and people are sharing their code w/o any proof like "I just know it". Inspired by [ye15](https://leetcode.com/problems/find-the-k-sum-of-an-array/discuss/2456675/Python3-priority-queue), finally I come up with a proof for this problem.\n\n## The idea\n\nObviously, the largest sum (`posSum`) is the sum of all positive numbers. Using `posSum` as a baseline, we now substract numbers from it. Note that "adding a negative number" and "removing a positive number" are the same in effect, all we care about is a subset of absolute values of `nums`. For k-th largest sum, we need get the k-th smallest (in terms of sum of items) of such subsets.\n\nFor k-th largest, we\'ll need to consider all combinations. The problem is *how to do this while controlling the size of candidates*.\n\n- Use heap to track all candidates, so we can extract the minimum in `log` time.\n- Enumerate the combinations in a treeish way, so we only need to check the root before go into deeper leafs.\n\nOnce we get the k-th smallest subset, we know the k-th largest sum is `posSum - sum(<k-th smallest subset>)`.\n\n## The proof\nThe most important problem is **how to define this tree**. It\'s defined as:\n\n- Let `nums` be the absolute values of `nums`, and sorted increasingly.\n- The value of root node is the smallest `num`\n- On level `i+1`, each node has two children.\n\t- The value of left child is its `parent + nums[i+1]`\n\t- The value of right child is its `parent + nums[i+1] - nums[i]`\n\nNote that all subsets on level `i` contain the element `nums[i]`, that meas nodes on level `i` are the subsets which ends with `nums[i]`.\n\nAnd this tree has two important features:\n\n1. **Each path starting from root defines a subset**: when we go left, we keep `nums[i]`; when we go right, we remove `nums[i]`.\n2. **Both left/right child >= parent**:\n\t- Left: `parent + nums[i+1] >= parent`\n\t- Right: `parent + nums[i+1] - nums[i] >= parent`, that\'s because we already sorted nums, so `nums[i+1] >= nums[i]`.\n\nFrom (1) we know this tree covers all possible `2**n` subsets, the tree is a variant of [decision tree](https://en.wikipedia.org/wiki/Decision_tree), in which path from node to internal node is also a valid decision path.\nFrom (2) we know children is always larger than parent, so we need use parent first. This indicates that only after parent is used and removed, then we need add children as candidates.\n\n## The code\n\n```javascript\nvar kSum = function(nums, k) {\n let posSum = nums.reduce((prev, curr) => curr > 0 ? prev + curr : prev, 0)\n nums = nums.map(x => Math.abs(x)).sort((l, r) => l - r)\n let heap = new Heap([{sum: nums[0], i: 0}], (l, r) => l.sum - r.sum)\n let ans = posSum\n for (let i = 1; i < k; i++) {\n let {sum, i} = heap.pop()\n ans = posSum - sum\n if (i + 1 >= nums.length) continue\n heap.push({sum: sum + nums[i + 1], i: i + 1})\n heap.push({sum: sum - nums[i] + nums[i + 1], i: i + 1})\n }\n return ans\n};\n```\n\nNote that the `Heap` class is from [harttle/contest.js](https://github.com/harttle/contest.js/blob/master/src/heap.mjs), here\'s my submission: https://leetcode.com/submissions/detail/779204351/\n | 10 | 0 | ['Heap (Priority Queue)', 'JavaScript'] | 3 |
find-the-k-sum-of-an-array | Heap soultion [EXPLAINED] | heap-soultion-explained-by-r9n-7rin | IntuitionWe want the k-th largest sum from all possible subsequences of an array. To do this efficiently, we focus on maintaining the largest sums dynamically u | r9n | NORMAL | 2024-12-23T22:00:49.393895+00:00 | 2024-12-23T22:00:49.393895+00:00 | 295 | false | # Intuition
We want the k-th largest sum from all possible subsequences of an array. To do this efficiently, we focus on maintaining the largest sums dynamically using a priority queue, avoiding the need to generate all subsequences explicitly.
# Approach
Sort the array by absolute values, calculate the maximum sum using positives, and use a priority queue to simulate extracting the k largest sums efficiently.
This solution uses a heap (priority queue) to efficiently manage and extract the k largest subsequence sums. In Python, this is implemented using the heapq module, which provides a min-heap by default. By pushing negative values into the heap, we simulate a max-heap behavior.
# Complexity
- Time complexity:
O(k log k + n log n) due to sorting and managing the priority queue.
- Space complexity:
O(k) for the priority queue.
# Code
```python3 []
class Solution:
def kSum(self, nums: list[int], k: int) -> int:
# Calculate the maximum sum using all positive numbers
max_sum = sum(x for x in nums if x > 0)
# Convert all numbers to their absolute values for easier processing
nums = sorted(abs(x) for x in nums)
# Priority queue to track the largest sums (negative for max-heap simulation)
pq = [(-max_sum, 0)]
# Variable to store the current kth largest sum
result = max_sum
# Extract the kth largest sum
for _ in range(k):
# Pop the largest sum from the priority queue
result, index = heappop(pq)
result = -result # Convert back to positive
# If possible, add the next subsequence sums to the priority queue
if index < len(nums):
heappush(pq, (-(result - nums[index]), index + 1))
if index > 0:
heappush(pq, (-(result - nums[index] + nums[index - 1]), index + 1))
return result
``` | 9 | 0 | ['Sorting', 'Heap (Priority Queue)', 'Python3'] | 0 |
find-the-k-sum-of-an-array | [c++] priority queue with explanation on the required knowledge | c-priority-queue-with-explanation-on-the-v6gu | The biggest hurdle is the knowledge of generating a complete set of subsequences of an array. Using [1, 2, 4] as an example, we start with the first element and | coolwenwen | NORMAL | 2022-08-21T07:31:43.578808+00:00 | 2022-08-21T07:42:35.483260+00:00 | 600 | false | The biggest hurdle is the knowledge of generating a complete set of subsequences of an array. Using [1, 2, 4] as an example, we start with the first element and get only one subsequence **[1]** to start filling the subseq set **{[1]}**. Next we take **[1]** out and add two new subsequences back into the set:\n\na). by adding the element next to 1 and we will get **[1, 2]**;\nb). by replace 1 by the element next to 1 and we will get **[2]**.\n\nIf we repeat this process we get:\n\n**{[1]} => {[1, 2], [2]} => {[1, 2, 4], [1, 4], [2, 4], [4]}** <= Note in each step the number of subsequences that is generated is doubled.\n\nEventually the complete set of subsequences is:\n\n**{[1], [1, 2], [2], [1, 2, 4], [1, 4], [2, 4], [4] plus []}**\n\nWith this if we sort the absolute value of elements, and pre-calculate the max sum among all subsequences which is the sum of all positive elements, and add the "-elements" back to the max sum. We use priority_queue to always start with the larger max sum. We also sort the array to ensure that we first deduct from the max sum smaller elements. Once we obtain the k-max sum, we have our answer.\n\nPlease upvote if you think this explanation helps.\n\n```\nclass Solution {\npublic:\n long long kSum(vector<int>& nums, int k) {\n vector<long long> res;\n priority_queue<pair<long long, int>> pq{};\n long long maxSum = 0;\n for (auto& n : nums) {\n if (n > 0) maxSum += n;\n else n = -n;\n }\n res.push_back(maxSum);\n sort(nums.begin(), nums.end());\n pq.push(make_pair(maxSum - nums[0], 0));\n while (res.size() <= k) {\n auto cur = pq.top();\n pq.pop();\n res.push_back(cur.first);\n if (cur.second + 1 < nums.size()) {\n pq.push(make_pair(cur.first - nums[cur.second + 1], cur.second + 1));\n pq.push(make_pair(cur.first + nums[cur.second] - nums[cur.second + 1], cur.second + 1));\n }\n }\n return res[k - 1];\n }\n};\n | 9 | 0 | ['C', 'Heap (Priority Queue)'] | 0 |
find-the-k-sum-of-an-array | [c++]Priority queue | cpriority-queue-by-karthik1600-jj2l | cpp\n#define ll long long \nclass Solution {\npublic: \n long long kSum(vector<int>& nums, int k) {\n ll maxsum=0;\n for(auto &num : nums){\n | karthik1600 | NORMAL | 2022-08-21T08:15:17.972728+00:00 | 2022-08-21T08:16:14.496005+00:00 | 575 | false | ```cpp\n#define ll long long \nclass Solution {\npublic: \n long long kSum(vector<int>& nums, int k) {\n ll maxsum=0;\n for(auto &num : nums){\n maxsum+=max(0,num);// adding all pos numbers\n num = abs(num); // we take abs because for pos numbers we remove from maxsum and negitive numbers decrease maxsum on adding with maxsum so by taking abs we just need to dec num\n }\n sort(nums.begin(),nums.end());\n priority_queue<pair<ll,int>> pq;\n ll res = maxsum;\n int curr_k = 1; //maxsum is first largest\n pq.push({maxsum-nums[0],0});\n while(curr_k<k){ \n auto [curr_sum,ind] = pq.top();pq.pop();\n curr_k++; \n res = curr_sum; // res contains the curr_k th greatest number\n if(ind+1<nums.size()){ // gonna remove the next smallest from currsum i.e nums[ind+1]\n ll include_curr = curr_sum - nums[ind+1]; // we dont remove current ind from maxsum\n ll exclude_curr = curr_sum + nums[ind] -nums[ind+1]; // we undo the previous removal by adding curr_ind and then remove the next smallest part from maxsum\n pq.push({include_curr,ind+1});\n pq.push({exclude_curr,ind+1});\n }\n \n }\n return res;\n }\n};\n``` | 7 | 0 | ['C', 'Heap (Priority Queue)'] | 0 |
find-the-k-sum-of-an-array | C++ Solution || Priority Queue || Easy to Understand | c-solution-priority-queue-easy-to-unders-hu91 | \nclass Solution {\npublic:\n long long kSum(vector<int>& nums, int k) {\n long long sum = 0;\n for(int i=0; i<nums.size(); ++i) {\n | aksharma071 | NORMAL | 2022-08-26T17:17:35.444940+00:00 | 2022-08-26T17:17:35.444982+00:00 | 903 | false | ```\nclass Solution {\npublic:\n long long kSum(vector<int>& nums, int k) {\n long long sum = 0;\n for(int i=0; i<nums.size(); ++i) {\n if(nums[i]>=0) sum+=nums[i];\n else nums[i]*=-1;\n }\n sort(nums.begin(), nums.end());\n typedef pair<long long, int> p;\n priority_queue<p> pq;\n pq.push({sum-nums[0], 0});\n long long ans = sum;\n while(!pq.empty() && k>1) {\n p curr = pq.top();\n pq.pop();\n sum = curr.first;\n int i = curr.second;\n if(i<nums.size()-1) {\n pq.push({sum+nums[i]-nums[i+1], i+1});\n pq.push({sum-nums[i+1], i+1});\n }\n k--;\n ans = sum;\n }\n return ans;\n }\n};\n/**\nif(find helpful) {\ndo upvote();\n}\n*/\n``` | 5 | 0 | ['C', 'Sorting', 'Heap (Priority Queue)'] | 0 |
find-the-k-sum-of-an-array | Java | max Heap | 100% faster | with explanation | java-max-heap-100-faster-with-explanatio-ktlh | \n### Intuitively thinking\n1. The largest sum of the array is the sum of all positive numbers.\n2. The sum of any subsequences is equivalent to the substractin | Rinka006 | NORMAL | 2022-08-21T19:18:40.545925+00:00 | 2022-08-21T19:18:40.545967+00:00 | 694 | false | \n### Intuitively thinking\n1. The largest ***sum*** of the array is the sum of all positive numbers.\n2. The sum of any subsequences is **equivalent** to the **substracting** some positive numbers and **adding** some negative numbers from the sum.\n3. The second largest sum of the array is the **[sum - the minimum number in the absolute values array]**\n\n### Implementation\n1. We traversal this array. For one number in the array, we sum it if it\'s a positive number; we change it into positive if it\'s negative. We get the sum of all positive numbers and an array with absolute values\n2. Sort the array.\n3. Use max heap to maintain the max sum of subsequences.\n\n```\nclass Solution {\n public long kSum(int[] nums, int k) {\n long sum=0L;\n for (int i = 0; i < nums.length; i++) {\n if (nums[i]>0) sum+=nums[i];\n else nums[i]=-nums[i];\n }\n Arrays.sort(nums);\n PriorityQueue<Pair<Long,Integer>> pq=new PriorityQueue<>((a,b)->Long.compare(b.getKey(),a.getKey()));\n pq.offer(new Pair<>(sum,0));\n while(k-->1){\n Pair<Long, Integer> top = pq.poll();\n long s=top.getKey();\n int i=top.getValue();\n if(i<nums.length){\n pq.offer(new Pair<>(s-nums[i],i+1));\n if(i>0) pq.offer(new Pair<>(s-nums[i]+nums[i-1],i+1));\n }\n }\n return pq.peek().getKey();\n }\n}\n``` | 4 | 0 | ['Heap (Priority Queue)', 'Java'] | 1 |
find-the-k-sum-of-an-array | C++ Solution using Priority_Queue || With Comments | c-solution-using-priority_queue-with-com-jt92 | \nclass Solution {\npublic:\n long long kSum(vector<int>& nums, int k) {\n \n long long totSum = 0;\n \n // calculate sum of all | manoj-22 | NORMAL | 2022-08-21T04:30:19.087661+00:00 | 2022-08-21T08:07:17.545073+00:00 | 755 | false | ```\nclass Solution {\npublic:\n long long kSum(vector<int>& nums, int k) {\n \n long long totSum = 0;\n \n // calculate sum of all positive numbers, i.e maxSubseqSum (2^nth sum)\n for(auto &num : nums)\n {\n if(num > 0)\n totSum += num;\n \n num = abs(num);\n }\n \n // sort ascending order\n sort(nums.begin(), nums.end());\n \n // maintain {subseqSum, index which we taken to reduce the sum}\n priority_queue<pair<long long, int>> pq;\n \n // push totSum - first num, num pos is 0\n pq.push({totSum - nums[0], 0});\n \n long long res = totSum, n = nums.size();\n \n while(--k)\n {\n auto cur = pq.top(); pq.pop();\n \n res = cur.first;\n \n int idx = cur.second;\n \n if(idx < n - 1)\n {\n // generate next possible sum\n \n // pick curIdx and try with the next idx\n pq.push({res + nums[idx] - nums[idx + 1], idx + 1});\n \n // notPick curIdx and try with the next idx\n pq.push({res - nums[idx + 1], idx + 1});\n }\n }\n \n return res;\n }\n};\n```\n\nLogic from this Post: https://leetcode.com/problems/find-the-k-sum-of-an-array/discuss/2456676/Java-Solution | 4 | 1 | ['C', 'Heap (Priority Queue)'] | 0 |
find-the-k-sum-of-an-array | C++ O(K^2) solution (solved the question 3 minutes after contest : ( ) | c-ok2-solution-solved-the-question-3-min-f4e2 | cpp\ntypedef long long ll;\n\n\nconst ll MAXK = 2e3 + 5;\n\n\nll dp[MAXK];\nll lst[MAXK];\n\nclass Solution {\npublic:\n \n long long kSum(vector<int>& nu | xktz | NORMAL | 2022-08-21T04:07:57.155221+00:00 | 2022-08-21T04:08:19.684566+00:00 | 1,148 | false | ```cpp\ntypedef long long ll;\n\n\nconst ll MAXK = 2e3 + 5;\n\n\nll dp[MAXK];\nll lst[MAXK];\n\nclass Solution {\npublic:\n \n long long kSum(vector<int>& nums, int k) {\n ll N = nums.size();\n memset(dp, 0, sizeof(dp));\n memset(lst, 0, sizeof(lst));\n for (auto &i: nums) {\n dp[1] += max(i, 0);\n i = abs(i);\n }\n sort(nums.begin(), nums.end());\n \n for (ll i = 2; i <= k; i ++) {\n ll chosen = 0, chosenval = -0x3f3f3f3f3f3f3f3f;\n for (ll j = 1; j < i; j ++) {\n if (lst[j] < N && chosenval < dp[j] - nums[lst[j]]) {\n chosenval = dp[j] - nums[lst[j]];\n chosen = j;\n }\n }\n dp[i] = chosenval;\n lst[chosen] ++;\n lst[i] = lst[chosen];\n }\n \n return dp[k];\n }\n};\n```\n\nThe idea is, the x\'s answer could only be the answer by removing an element from all x-1s answer\'s sequence. We maintain a lst[i] to save which element index we are on to remove.\n\nFor the negative value we only add them into removing but not getting dp[1].\n\np.s. I got how to solve on the last 3 minutes of contest, after I written solution, I forgot to add the lst[i] = lst[chosen] row. So I did not pass. \uD83D\uDE2D | 4 | 0 | ['Dynamic Programming'] | 1 |
find-the-k-sum-of-an-array | ✅ Beat 100% | ✨ O(N + k log k) | 🏆 Fastest Solution | 👍 Detailed Explanation | beat-100-on-k-log-k-fastest-solution-det-jt2a | Intuition\n Describe your first thoughts on how to solve this problem. \n\n## Preprocessing\nWe have both positive numbers and negative numbers in the input. Th | hero080 | NORMAL | 2023-04-29T06:00:54.839453+00:00 | 2023-05-26T15:52:28.239111+00:00 | 266 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n## Preprocessing\nWe have both positive numbers and negative numbers in the input. They are actually very different. The **largest sum** is obviously the sum of **all** positive numbers, while the negative numbers will only enter the "picture" one by one.\nWe first choose all positive number to form our `offset` which is the largest sum, then we can convert all positive numbers to their negative part. For example, 3 becomes -3 and it is as if we have a -3 in the `nums`. For this -3, by "choose it" we actually mean "do not choose the original 3" and "do not choose this -3" means "choose the original 3". The final result of the new `nums` just need to add the `offset`.\n\n## Picking the first k elements and sort (decreasingly).\nOnce we have all numbers as negative, we get the nice *greedy property* of "sum of some numbers is worse than the individuals". Therefore we can concluded that we will never want to use an element in nums other than the first k elements (decreasing order).\n\n## Use a Priority Queue\nAgain we apply the *greedy property* and have the following conclustion: a combinations of some numbers `... + nums[i]` is always *worse* than `...` alone, assuming i is the largest index there. Hence, we can add the numbers into the queue one by one.\n\n 1. we put `{nums[0], 0}` in.\n 2. We pop the top element of the priority queue and if its index is not at the end, we push two new sums in `old_sum + nums[index + 1]` and `old_sum - nums[index] + nums[index + 1]`.\n 3. We record the poped element into an array.\n 4. We return the kth element of the array plus the `offset`.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe intuition above described the approach.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$\\Theta(N + k \\log k)$$\nThis is better than most other solutions as we used selection algorithm to pick the first `k` elements from `n` nums and only sort the first `k` elements, so we avoided the $N \\log N$ part.\n\n*Caveat*: The C++ standard does not require `std::nth_element()` to be implemented with worse case linear time algorithm and STL usually implements it with a version that has very good average linear time but worse case $\\Theta(N \\log N)$ time. It can be fixed by switching `std::nth_element()` with other libraries. Nevertheless it is practically good enough (and much faster than a full array sort).\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$\\Theta(k)$$ extra space.\n\nAs I finished the solution, I noticed that I can actually omit the array and only record the count and last element. It would save an array but the space complexity is still the same as the priority queue could use k space\n\n# Code\n```\nclass Solution {\npublic:\n long long kSum(vector<int>& nums, int k) {\n int64_t offset = 0;\n for (int& num : nums) {\n if (num > 0) {\n offset += num;\n num = -num;\n }\n }\n if (nums.size() > k) {\n std::nth_element(nums.begin(), nums.begin() + k - 1, nums.end(),\n std::greater());\n nums.resize(k);\n }\n sort(nums.begin(), nums.end(), std::greater());\n vector<int64_t> sums = {0};\n sums.reserve(k);\n priority_queue<pair<int64_t, int>> q;\n q.push({nums.front(), 0});\n // Omitted q.empty() check since we are guaranteed with enough nums.\n while (sums.size() < k) {\n auto [sum, index] = q.top();\n // cout << sums.size() << ": ";\n sums.push_back(sum);\n // cout << sum << endl;\n q.pop();\n if (index + 1 >= nums.size()) {\n continue;\n }\n int64_t new_sum = sum + nums[index + 1];\n q.push({new_sum, index + 1});\n q.push({new_sum - nums[index], index + 1});\n }\n\n return sums[k - 1] + offset;\n }\n};\n``` | 3 | 0 | ['C++'] | 1 |
find-the-k-sum-of-an-array | Share My Solution | Explanation with Logic in code | C++ | share-my-solution-explanation-with-logic-esqg | Preriquisites:\nMerge Sorted Array\nPriority Queue (Heap)\nSubsets\n\nTime Complexity: O( nlog(n) + k + klog(k) )\n\nSpace Complexity: O( n + k )\n\n/*\n Log | shantanu_joshi21 | NORMAL | 2022-08-22T19:02:47.727421+00:00 | 2022-08-22T19:02:47.727468+00:00 | 263 | false | **Preriquisites:**\n[Merge Sorted Array](https://leetcode.com/problems/merge-sorted-array/)\nPriority Queue (Heap)\n[Subsets](https://leetcode.com/problems/subsets/)\n\n**Time Complexity:** O( n*log(n) + k + k*log(k) )\n\n**Space Complexity:** O( n + k )\n```\n/*\n Logic:\n \n The largest sum possible is the sum of all positive elements.\n \n Now we have to consequently decrease some amount from this largest sum.\n \n We have to do this k times.\n \n Like num= [-1,1,2,3]\n sum=6\n \n All possible seq in decreasing order =[6,5,5,4,4,3..]\n \n It is same as: [6-0,6-1,6-1,6-2,6-2,6-3,...]\n \n Here every time, we are subtracting some elements from largest sum. \n \n Example 2 = {1+2+3} - {2,1} + {-1}\n \n {Largest Sum} - {sum of some Positive elements} + {sum of some negative elements}\n \n Here any number is derived by removing some positive elements from largest sum and adding some negative elements to sum.\n \n How to decide which positive numbers to be removed and which negative numbers to be added?\n \n There will be so many subsets of positive as well as negative elements.\n \n We will generate k+1 smallest subset sums of positive and negative numbers separately. (k non-empty and 1 empty subset)\n \n Now there might be (k+1)*(k+1) ways to choose positive and negative subsets.\n \n \n \n But note that:\n \n Let us denote (i,j) as the sum of i\'th smallest positive subset and j\'th smallest negative subset \n Then (i,j) < (i,j+1). Since both positive and negative subset sums are sorted.\n \n Using above fact we can reduce the time complexity from O(k*k) to O(k*log(k))\n \n We will use one priority queue.\n Initially push all pairs (0,0) (1,0) (2,0) ... (k,0) in priority queue.\n \n Priority queue will give us the pair which is having smallest sum.\n Let us consider, it as (i,j) then now we will push (i,j+1) to the priority queue.\n \n We will repeat this process k times, since we want k\'th smallest number\n \n*/\n\nclass Solution {\npublic:\n \n /*\n For a given array of lenth n, there are 2^n possible subsets.\n Since we have 2 options for every element to take or not.\n \n How subset sum works?\n \n example: nums=[1,2,3,4]\n Keep previous records as it is and add all records with sum of new element\n \n Initially ans={0}\n \n Added 1: {0,(0+1)}={0,1}\n Added 2: {0,1,(0+2),(1+2)}={0,1,2,3}\n Added 3: {0,1,2,3,(0+3),(1+3),(2+3),(3+3)}={0,1,2,3,3,4,5,6}\n \n It appears that subset sums calculated in this way will always be sorted. Right?\n \n Added 4: {0,1,2,3,3,4,5,6,{0+4},{1+4},{2+4}...} ={0,1,2,3,3,4,5,6,4,5,6,...}\n \n It is not sorted, as we can see in the last step.\n \n But we want k smallest subset sums.\n \n How to do that?\n \n Take new vector/array called newRecords. Keep ans as it is. ans is sorted already. \n Calculate newRecords.\n \n In the given example: \n ans ={0,1,2,3,3,4,5,6}\n newRecords={4,5,6,7,7,8,9,10} Added 4\n \n Merge ans and newRecords into new vector called newAns.\n Here both ans and newRecords both are sorted. So we will use.\n \n newAns= {0,1,2,3,3,4,4,5,5,6,6,7,7,8,9,10}\n Use this newAns as ans for next iterations\n */\n \n void makeSubsetSum(vector<int>&nums,int k,vector<long long>&ans){\n //function which calculates k smallest subset sums of nums\n\n ans.push_back(0ll);//0 for the empty subset\n \n for(int i=0;i<nums.size();i++){\n \n //We are trying to add nums[i] to previously added records\n vector<long long int>newRecords;\n \n //There are two scenarios \n //1. ans is having records less than k\n //2. ans is having records exactly equal to k\n \n //In the second scenario, \n //if the (nums[i]+ans[j]) is greater than greatest element in the ans, \n //then it will not be the part of the final ans (kind of pruning)\n for(int j=0;j<ans.size()&&(ans.size()<=k||(nums[i]+ans[j])<ans.back());j++){\n newRecords.push_back(nums[i]+ans[j]);\n }\n \n \n if(newRecords.size()==0){\n //No new records added, so we can break\n break;\n }\n \n vector<long long int>newAns;\n \n //merging starts\n int ii=0,jj=0;\n while(ii<ans.size() && jj<newRecords.size() && newAns.size()<=k){\n if(ans[ii]<newRecords[jj]){\n newAns.push_back(ans[ii]);\n ii++;\n }else{\n newAns.push_back(newRecords[jj]);\n jj++;\n }\n }\n \n while(ii<ans.size() && newAns.size()<=k ){\n newAns.push_back(ans[ii]);\n ii++;\n }\n \n while(jj<newRecords.size() && newAns.size()<=k ){\n newAns.push_back(newRecords[jj]);\n jj++;\n }\n //mering ends\n \n swap(ans,newAns);\n }\n \n }\n \n \n long long kSum(vector<int>& nums, int k) {\n \n vector<int>pos,neg;\n long long int sum=0;\n \n //separate out the positive and negative elements\n for(int num:nums){\n if(num>=0){\n sum+=num;\n pos.push_back(num);\n }else{\n neg.push_back(-num);\n }\n }\n \n //sort them\n sort(pos.begin(),pos.end());\n sort(neg.begin(),neg.end());\n \n vector<long long>subsetPos,subsetNeg;\n \n // Calculate first smallest k subset sums for positive and negative elements\n makeSubsetSum(pos,k,subsetPos);\n makeSubsetSum(neg,k,subsetNeg);\n //Now we have k smallest subset sums\n \n //Comaparator for priority queue\n auto comp=[&](pair<int,int>&a,pair<int,int>&b){\n \n long long int first=subsetPos[a.first]+subsetNeg[a.second];\n long long int second=subsetPos[b.first]+subsetNeg[b.second];\n \n //refer stack overflow\n \n return first>second;\n };\n \n //https://stackoverflow.com/questions/5807735/c-priority-queue-with-lambda-comparator-error\n priority_queue<pair<int,int>,vector<pair<int,int>>,decltype(comp)>pq(comp);\n \n for(int i=0;i<subsetPos.size();i++){\n pq.push(make_pair(i,0));\n }\n \n long long int ans=sum;\n \n for(int i=0;i<k;i++){\n \n pair<int,int>p=pq.top();\n pq.pop();\n \n long long int fromPos=p.first,fromNeg=p.second;\n \n ans=sum-subsetPos[fromPos]-subsetNeg[fromNeg];\n \n if(fromNeg+1<subsetNeg.size()){\n pq.push(make_pair(fromPos,fromNeg+1));\n }\n \n }\n \n return ans;\n }\n};\n``` | 3 | 0 | ['C', 'Heap (Priority Queue)', 'C++'] | 0 |
find-the-k-sum-of-an-array | [JAVA] Simplest explanation and Intuition [ Priority Queue ] | java-simplest-explanation-and-intuition-jkhog | I was having trouble understanding answers from ye15 (link to answer)) and xil899 (link to answer)\n\nSimplest Explanation:\n\nIntuition:\n1. we need Kth large | vivekgpt107 | NORMAL | 2022-08-21T11:19:57.199104+00:00 | 2022-08-21T11:19:57.199152+00:00 | 342 | false | I was having trouble understanding answers from ye15 ([link to answer](https://leetcode.com/problems/find-the-k-sum-of-an-array/discuss/2456675/Python3-priority-queue))) and xil899 ([link to answer](https://leetcode.com/problems/find-the-k-sum-of-an-array/discuss/2456716/Python3-HeapPriority-Queue-O(NlogN-%2B-klogk)))\n\nSimplest Explanation:\n\nIntuition:\n1. we need Kth largest number -> due to time constraints we cannot check all the possible subsequence sum resulting in O(2 ^ n)\n2. so we need some iterative way that we can run k times to get the answer\n3. generally DP works for these problems but can\'t plug it here\n4. one thing is clear that the maximum and minimum sum can be found by summing all positive numbers or negative numbers respectively. But for this problem we are focusing on maximum sum (**msum**).\n5. once we have the *maximum number* we need the *next maximum number* => this is found by either removing some positive number from the **msum** or adding some negative numbers to the **msum**\n6. we already know that **msum** is only consisting of all of positive numbers but **not** containing negative numbers.\n7. we can achieve the [*either removing some positive number from the msum or adding some negative numbers to the msum*] step by following simple technique:\n\t* create a new array by taking absolute values of numbers in **nums** call it array **A**\n\t* we sort array **A** it by ascending order\n\t* now subtracting the value **A[i]** from **msum** means two things:\n\t\t* if **A[i]** was positive in **nums**, subtracting **A[i]** from **msum** means removing a number from **msum**\n\t\t* if **A[i]** was negative in **nums**, subtracting **A[i]** from **msum** means adding a negative number to **msum**, eg. if nu**ms[i] == -2** then **A[i] == 2** (now positive), so since msum was not having **-2** value in it(as it only holds positive numbers) thus if we subtract the **A[i]** from msum means : **msum - A[i]** or **msum + nums[i]**\n8. hence if we subtract the **A[0]** value from msum we will get the **next sum** which is <= **msum**\n9. Now to find the subsequent smaller sums, we make use of max heap\n\t* we store the **msum** value and the **index** of element to remove in A into the max heap: **maxH**. Initially this should be **( msum, 0 )** . 0 here is the index of array A that we need to remove from the **msum**.\n\t* if we pop the heap then we should get the next highest sum.\n\n\n```\nclass Solution {\n public long kSum(int[] A, int k) {\n PriorityQueue<long[]> maxH = new PriorityQueue<>((a,b) -> (b[0]-a[0])>0?1: (b[0]-a[0]) < 0 ?-1: 0 );\n \n // finding the maximum sum -> sum of positive numbers\n // also making all the numbers in original array as positive\n long msum = 0;\n for(int i = 0; i < A.length; i++){\n msum += A[i]>0?A[i]:0;\n A[i] = A[i]<0?-A[i]: A[i];\n }\n \n long ans = msum; // this holds the Kth largest number\n \n // sorting all the positive numbers in the array A\n Arrays.sort(A);\n // System.out.println(Arrays.toString(A));\n \n maxH.add(new long[]{msum,0});\n \n for(int i = 0; i < k; i++){\n // get the next maximum sum (cur_sum) and the indexes covered for A array (idx_to_include) for that sum\n long[] poll = maxH.poll();\n long cur_sum = poll[0];\n ans = cur_sum;\n \n int idx_to_include = (int)poll[1];\n \n // System.out.println(cur_sum+", "+ idx);\n \n // remove idx\n if(idx_to_include < A.length)\n maxH.add(new long[]{ cur_sum - A[idx_to_include] , idx_to_include+1 });\n \n // remove idx and add prev idx\n if(idx_to_include > 0 && idx_to_include < A.length)\n maxH.add(new long[]{ cur_sum + A[idx_to_include-1] - A[idx_to_include] , idx_to_include+1 });\n }\n\n return ans;\n\n }\n}\n```\n | 3 | 0 | ['Heap (Priority Queue)', 'Java'] | 1 |
find-the-k-sum-of-an-array | [Javascript] | explanation | Code commented | PriorityQueue | O(NlogN + klogk) | javascript-explanation-code-commented-pr-quuz | Explanation in comment,\nhope it makes sense\n\n```\n/*\n * @param {number[]} nums\n * @param {number} k\n * @return {number}\n /\nvar kSum = function(nums, k) | Atikur-Rahman-Sabuj | NORMAL | 2022-08-21T08:20:31.380449+00:00 | 2022-08-25T05:26:50.848006+00:00 | 287 | false | Explanation in comment,\nhope it makes sense\n\n```\n/**\n * @param {number[]} nums\n * @param {number} k\n * @return {number}\n */\nvar kSum = function(nums, k) {\n let pq = new MaxPriorityQueue(), sum = 0, n = nums.length;\n \n //sort numbers in ascending order with absolute value\n nums.sort((a,b) => Math.abs(a) - Math.abs(b));\n \n //calculate sum of positive integers\n for(let i = 0 ; i < n ; i++){\n if(nums[i] > 0) sum += nums[i];\n }\n \n //we have the biggest possible sum , now we just substract abs values of nums to get smaller ones\n //this satisfies because\n //for positive numbers we are removing them from subsequence and getting smaller sum\n //for negetive numbers we are adding them to subsequence and getting smaller sum\n\n //to get all possible combinations in decreasing order we will start from zero index,\n //for current index we will subtract abs(nums[index]) from the current sum\n //and we will subtract abs(nums[index]) and add(nums[index-1]) from the current sum \n //because we know the previous number was not in the current sum \n //as we subtracting the current sum every time we increasing index\n \n //we go like this untill we get the kth sum\n \n pq.enqueue(0, sum);\n let q;\n while(k--){\n q = pq.dequeue();\n if(q.element < n){\n pq.enqueue(q.element+1, q.priority - Math.abs(nums[q.element]));\n if(q.element>0) pq.enqueue(q.element+1, q.priority + Math.abs(nums[q.element-1]) - Math.abs(nums[q.element]));\n }\n }\n return q.priority;\n}; | 3 | 0 | ['JavaScript'] | 0 |
find-the-k-sum-of-an-array | ✅ C++ Must know Min/Max Heap Algo Intuition | Explained in Hindi | c-must-know-minmax-heap-algo-intuition-e-fgjb | It was an interesting challenge, The same concept has been used in multiple Leetcode medium/hard challenges.\nThe min/max heap algo to find top k sums.\n\nMy th | Leetcode_Hindi | NORMAL | 2022-08-24T14:35:47.186296+00:00 | 2022-08-29T16:41:33.923574+00:00 | 298 | false | It was an interesting challenge, The same concept has been used in multiple Leetcode medium/hard challenges.\nThe min/max heap algo to find top k sums.\n\nMy thought process with code below:\n\n 1. Naive solution: Number of subsequences that can be created by N sized array are\n 2^N (each element can be considered/not considered 2 choices for N elements)\n Now if we create these 2^N elements and find sum of each of them and then sort\n them to get the kth largest subsequence sum. O(N*2^N)\n \n 2. N constraint is 10^5 so we definitely need a better solution.\n Hold on folks, we are going deep :) \n One **IMPT point is that input can have -ive numbers also.\n \n 3. Another **IMPT point is that from k constraints can be max 2000, which means\n that we can store the top k elements in a heap/multiset structure.\n \n 4.So the maximum sum that we can have is sum of all +ive values. that is 1 sum.\n we have to find k sum.\n \n 5. Another way of seeing this is that once we have max sum = all positive integers\n sum the total sum can only decrease after that. So if we take absolute value of\n elements and find kth smallest sum of that array we can subtract that from total\n to get kth maximum sum of array.\n \n 6. Question boils down to finding kth minimum subsequence sum. we sort the absolute \n array, start by considering 1st element and moving forward we have 2 options: take minimum\n value from priority queue(sum, cur_index), and consider 2 combinations:\n a. take index+1 value along with current sum\n b. remove index value and consider index+1\n now we can pop top of queue and insert value in our min vector. Do this until we reach size of\n min set = k. Now we can find the kth minimal sum from this array.\n \n Also store current index, which we need to consider to remove the current element.\n ex. nums = [2, 4, -2]\n max sum = 6 = k = 1 sum\n sorted(abs(nums)) = [2, 2, 4] 5th smallest subsequence sum\n queue = (2, 0) min_sum_values = [0]\n queue = (2 + 2, 1) (2+2-2, 1) = (4, 1), (2, 1) min_sum_values = [0, 2]\n queue = (2+4, 2) (2+4-2, 2) (2, 1) = (4, 1) (4, 2) (6, 2) min_sum_values = [0, 2, 2]\n queue = (8, 3) (4+4-4, 3) (4, 2) (6, 2) = min_sum_values = [0, 2, 2, 4]\n queue = (4, 2) (4, 3) (6, 2) (8,3)= min_sum_values = [0, 2, 2, 4, 4]\n min_sum_values[k-1] = 4\n ans = 6-4 = 2\n\n yay finally solved.\n time complexity = NlogN(sorting the nums) + KlogK(addition and removal from priority queue)\n space = O(K)\n\t\n\t\n\tIf you prefer video explanation: Please refer https://youtu.be/Jv_Oe3GjfzQ\n\n | 2 | 0 | [] | 0 |
find-the-k-sum-of-an-array | very easy to understand, | very-easy-to-understand-by-pratyushaggar-0smx | IntuitionThe problem requires finding the k-th largest subsequence sum in an array.Key observations:
The maximum possible sum is obtained by summing all positiv | pratyushaggarwal1281 | NORMAL | 2025-02-11T13:51:47.028365+00:00 | 2025-02-11T13:51:47.028365+00:00 | 40 | false | # Intuition
The problem requires finding the k-th largest subsequence sum in an array.
**Key observations:**
The maximum possible sum is obtained by summing all positive numbers in the array.
Each subset sum can be derived by selectively subtracting elements from this maximum sum.
We can efficiently generate the largest subset sums using a priority queue (min-heap), which tracks the smallest reductions from the maximum sum.
# Approach
**Compute the Maximum Possible Sum:**
Sum all positive numbers in nums to get maxSum, which is the largest subset sum.
Convert all elements in nums to their absolute values to simplify calculations.
Sort nums in increasing order of absolute values to process smaller reductions first.
**Use a Min-Heap to Track the k-th Largest Subset Sum:**
Start with the smallest possible reduction (nums[0]), stored in a min-heap.
Pop the smallest reduction, compute the new subset sum (maxSum - currSum), and push new possible reductions:
Include the next element in the sequence.
Replace the last element of the current sequence with the next one.
Repeat until we extract the k-th largest sum.
**Return the k-th Largest Subset Sum.**
# Complexity
- Time complexity:
O(nlogn+klogk).
- Space complexity:
O(k).
# Code
```cpp []
class Solution {
public:
long long kSum(vector<int>& nums, int k) {
long long maxSum = 0;
for (int &num : nums) {
if (num > 0) maxSum += num; // Compute the max possible sum
num = abs(num); // Convert numbers to absolute values
}
// Sort in increasing order of absolute value
sort(nums.begin(), nums.end());
// Min-heap to track the k smallest sum reductions
priority_queue<pair<long long, int>, vector<pair<long long, int>>, greater<>> pq;
pq.push({nums[0], 0}); // Smallest subset sum starts from the first element
long long res = maxSum;
// Extract (k-1) elements since maxSum is the 1st largest subset sum
for (int i = 1; i < k; ++i) {
auto [currSum, idx] = pq.top();
pq.pop();
res = maxSum - currSum; // The k-th largest sum
// Push next possible sums into the min-heap
if (idx + 1 < nums.size()) {
pq.push({currSum + nums[idx + 1], idx + 1});
pq.push({currSum - nums[idx] + nums[idx + 1], idx + 1});
}
}
return res;
}
};
``` | 1 | 0 | ['C++'] | 0 |
find-the-k-sum-of-an-array | Beats 100% time, Solution with Explanation | beats-100-time-solution-with-explanation-e3pq | Intuition\n\n- For an example let\'s take an array [-5, -3,-2, 1, 7], the largest sum that can be formed from a subsequence is 8. when k = 1, the answer is obvi | Hariprasath_N | NORMAL | 2023-01-05T14:55:19.201714+00:00 | 2023-01-05T14:55:19.201761+00:00 | 118 | false | # Intuition\n\n- For an example let\'s take an array [-5, -3,-2, 1, 7], the largest sum that can be formed from a subsequence is 8. when k = 1, the answer is obviously 10.\n- If k = 2, the second largest subsequence sum is supposed to be returned. In this case we can add(if negative) or subtract(if positive) the lowest number of array. So the second largest subsequence sum will be 7 - 1 = 6.\n- If k = 3, the third largest subsequence sum is supposed to be returned. In this case 6 +(-2) = 4, which is not correct because adding -2 with the largest subsequence(8) sum gives 6. and further for k = 4, adding -3 with 8 gives 5.\n- This shows that the previous subsequence sums are supposed to be considered before adding or subtracting the minimum number.\n- So the code should have two cases for every number as (sum-Currnumber) and (sum-currNumber+prevNumber) which means (6-2) and (6-2+1).\n\n# Explanation:\n\n- Find the maximum sum subsequence of the input array and store it in variable max(simply the sum of all positive numbers).\n- Adding a negative number and subtracting the positive number, both means the same, that is subtracting from the max. So negative numbers are unsigned.\n- In the function a min heap is declared and initialized with the first number for sum and its index for tarcking the previous number.\n- A variable curr is declared and used for returning(if curr == k) the sum that needs to be deducted from max.\n- Both the cases as explained in intuition are added to the heap.\n- The returned value is deducted from max to kth min is found.\n\n\n\n\n\n# Code\n```\nclass Solution {\n class Pair {\n long sum;\n int tail;\n Pair(long sum, int tail) {\n this.sum = sum;\n this.tail = tail;\n }\n }\n public long kSum(int[] nums, int k) {\n int n = nums.length;\n long max = 0L;\n for (int i = 0; i < n; i++) {\n if (nums[i] < 0) nums[i] = -nums[i];\n else max += nums[i];\n }\n Arrays.sort(nums);\n long kmin = getKthSubset(nums, k);\n return max - kmin;\n }\n private long getKthSubset(int[] nums, int k) {\n int n = nums.length;\n PriorityQueue<Pair> minHeap = new PriorityQueue<>((a, b) -> Long.compare(a.sum, b.sum));\n int cur = 1;\n minHeap.add(new Pair(nums[0], 0));\n while (cur < k) {\n Pair min = minHeap.poll();\n long sum = min.sum;\n int next = min.tail + 1;\n cur++;\n if (cur == k) return sum;\n if (next < n) {\n minHeap.add(new Pair(sum + nums[next], next));\n minHeap.add(new Pair(sum + nums[next]- nums[min.tail], next));\n } \n }\n return 0L;\n }\n}\n``` | 1 | 0 | ['Heap (Priority Queue)', 'Java'] | 0 |
find-the-k-sum-of-an-array | c++ | priority queue | 85% faster than all | c-priority-queue-85-faster-than-all-by-v-dg56 | ```\nclass Solution {\npublic:\n long long kSum(vector& nums, int k) {\n long long sum = 0;\n for(int i=0; i=0) sum+=nums[i];\n else | venomhighs7 | NORMAL | 2022-09-17T11:44:55.026081+00:00 | 2022-09-17T11:44:55.026125+00:00 | 230 | false | ```\nclass Solution {\npublic:\n long long kSum(vector<int>& nums, int k) {\n long long sum = 0;\n for(int i=0; i<nums.size(); ++i) {\n if(nums[i]>=0) sum+=nums[i];\n else nums[i]*=-1;\n }\n sort(nums.begin(), nums.end());\n typedef pair<long long, int> p;\n priority_queue<p> pq;\n pq.push({sum-nums[0], 0});\n long long ans = sum;\n while(!pq.empty() && k>1) {\n p curr = pq.top();\n pq.pop();\n sum = curr.first;\n int i = curr.second;\n if(i<nums.size()-1) {\n pq.push({sum+nums[i]-nums[i+1], i+1});\n pq.push({sum-nums[i+1], i+1});\n }\n k--;\n ans = sum;\n }\n return ans;\n }\n}; | 1 | 0 | [] | 0 |
find-the-k-sum-of-an-array | Priority Queue | C++ | priority-queue-c-by-shubhamdoke-1ifb | \ntypedef long long ll;\n\nclass Solution {\npublic:\n long long kSum(vector<int>& nums, int k) {\n\n int n = nums.size();\n ll tot = 0;\n | ShubhamDoke | NORMAL | 2022-09-06T19:24:30.516931+00:00 | 2022-09-06T19:32:40.102107+00:00 | 289 | false | ```\ntypedef long long ll;\n\nclass Solution {\npublic:\n long long kSum(vector<int>& nums, int k) {\n\n int n = nums.size();\n ll tot = 0;\n for(int i=0;i<n;i++){\n if(nums[i]>0)\n tot += nums[i];\n if(nums[i]<0)\n nums[i] *= -1;\n }\n \n if(k==1)\n return tot;\n\n k--;\n sort(nums.begin(),nums.end());\n \n priority_queue<pair<ll,int>,vector<pair<long long,int>>, greater<pair<long long,int>>>pq;\n \n int cur = 0;\n \n ll ans = nums[0];\n \n pq.push({(ll)nums[0],1});\n \n while(cur<=k){\n cur++;\n auto a = pq.top();\n pq.pop();\n \n if(cur==k)\n return tot- a.first;\n \n if(a.second != n){\n \n ll x = a.first;\n int y = a.second;\n x -= nums[y-1];\n pq.push({x+nums[y],y+1});\n \n x += nums[y-1];\n pq.push({x+nums[y],y+1});\n }\n }\n return 1;\n }\n};\n``` | 1 | 0 | ['C', 'Heap (Priority Queue)'] | 0 |
find-the-k-sum-of-an-array | [Python / Go / C++] heap vs BST on sorted array O(NlogN+KlogK) | python-go-c-heap-vs-bst-on-sorted-array-jwsbe | Python w/ ascending min heap\n\npython\ndef kSum(self, nums, k):\n res, nums = -sum(max(num, 0) for num in nums), sorted(map(abs, nums))\n q = [(res + num | lotceedoo | NORMAL | 2022-08-31T06:49:33.312222+00:00 | 2022-09-03T05:00:32.440286+00:00 | 247 | false | *Python* w/ ascending min heap\n\n```python\ndef kSum(self, nums, k):\n res, nums = -sum(max(num, 0) for num in nums), sorted(map(abs, nums))\n q = [(res + nums[0], 0)]\n for _ in range(k - 1):\n res, i = heapq.heappop(q)\n if (j := i + 1) < len(nums):\n heapq.heappush(q, (res + nums[j], j))\n heapq.heappush(q, (res + nums[j] - nums[i], j))\n return -res\n```\n\n*Go* w/ descending max heap in 169ms\n\n```go\ntype Node struct {\n\tsum int64\n\ti int\n}\n\ntype queue []*Node\n\nfunc (q queue) Len() int { return len(q) }\nfunc (q queue) Less(i, j int) bool { return q[i].sum > q[j].sum }\nfunc (q queue) Swap(i, j int) { q[i], q[j] = q[j], q[i] }\nfunc (q *queue) Push(x interface{}) { *q = append(*q, x.(*Node)) }\nfunc (q *queue) Pop() interface{} {\n\ti := len(*q) - 1\n\tx := (*q)[i]\n\t*q = (*q)[:i]\n\treturn x\n}\n\nfunc kSum(nums []int, k int) int64 {\n\tvar (\n\t\tres int64\n\t\tq queue\n\t)\n\tfor i, num := range nums {\n\t\tif num > 0 {\n\t\t\tres += int64(num)\n\t\t} else {\n\t\t\tnums[i] = -num\n\t\t}\n\t}\n\tsort.Ints(nums)\n\theap.Push(&q, &Node{res - int64(nums[0]), 0})\n\tfor ; k > 1; k-- {\n\t\tx := heap.Pop(&q).(*Node)\n\t\tif j := x.i + 1; j < len(nums) {\n\t\t\theap.Push(&q, &Node{x.sum - int64(nums[j]), j})\n\t\t\theap.Push(&q, &Node{x.sum - int64(nums[j]) + int64(nums[x.i]), j})\n\t\t}\n\t\tres = x.sum\n\t}\n\treturn res\n}\n```\n\n*C++* w/ ascending max priority queue\n\n```c++\nlong long kSum(vector<int> &nums, int k) {\n long long res = 0;\n priority_queue<pair<long long, int>> q;\n for (int i = 0; i < nums.size(); ++i) {\n if (nums[i] > 0) res += nums[i];\n else nums[i] = -nums[i];\n }\n sort(begin(nums), end(nums));\n q.push({res - nums[0], 0});\n while (--k) {\n auto[sum, i] = q.top(); q.pop();\n if (int j = i + 1; j < nums.size()) {\n q.push({sum - nums[j], j});\n q.push({sum - nums[j] + nums[i], j});\n }\n res = sum;\n }\n return res;\n}\n```\n\n*C++* w/ ascending min multimap\n\n```c++\nlong long kSum(vector<int> &nums, int k) {\n long long res = 0;\n for (int i = 0; i < nums.size(); ++i) {\n if (nums[i] > 0) res -= nums[i];\n else nums[i] = -nums[i];\n }\n sort(begin(nums), end(nums));\n multimap<long long, int> m({{res + nums[0], 0}});\n for (auto it = begin(m); --k; ++it) {\n auto[sum, i] = *it;\n if (int j = i + 1; j < nums.size()) {\n m.insert({sum + nums[j], j});\n m.insert({sum + nums[j] - nums[i], j});\n }\n res = sum;\n }\n return -res;\n}\n``` | 1 | 0 | [] | 0 |
find-the-k-sum-of-an-array | Priority Queue||C++||Simple Solution||Loaded with comments for better understanding | priority-queuecsimple-solutionloaded-wit-knlc | \nclass Solution {\npublic:\n // Here the approach is that we want K max right ? so the max value is equal to the sum of the positive integers and after that | gargshivam2001 | NORMAL | 2022-08-25T11:45:59.701201+00:00 | 2022-08-25T11:46:23.917881+00:00 | 305 | false | ```\nclass Solution {\npublic:\n // Here the approach is that we want K max right ? so the max value is equal to the sum of the positive integers and after that it will \n // decrease. So, for decreasing the numbers, we have to add -ve numbers and minus +ve numbers.\n // Since we have taken abs of the numbers, so we have to subtract only.\n long long kSum(vector<int>& nums, int k) {\n long long sum=0,n=nums.size();\n vector<long long> ans;\n for(int i=0;i<n;i++){\n if(nums[i]>=0)\n sum+=nums[i]; // Max possible sum obtained from numbers\n nums[i]=abs(nums[i]);\n }\n sort(nums.begin(),nums.end());\n ans.push_back(sum); //pushing max val i.e. sum of positive integers\n priority_queue<pair<long long,int>> pq;\n pq.push({sum-nums[0],0});\n while(ans.size()<k){\n auto p=pq.top();\n pq.pop();\n if((p.second+1)<n){\n pq.push({p.first-nums[p.second+1],p.second+1});//Subtract nextIndex\n pq.push({p.first+nums[p.second]-nums[p.second+1],p.second+1});// Subtract nextIndex and add current Index\n }\n ans.push_back(p.first); // add max val\n }\n return ans.back();\n }\n};\n```\nHappy Coding ;-) | 1 | 0 | ['C', 'Heap (Priority Queue)'] | 0 |
find-the-k-sum-of-an-array | Java | heap | java-heap-by-darling_of_02-6699 | java\nclass Solution {\n public long kSum(int[] nums, int k) {\n //1. the max value will be the sum of all the positives\n //2. sums of every s | darling_of_02 | NORMAL | 2022-08-23T17:10:06.883075+00:00 | 2022-08-23T17:10:06.883114+00:00 | 258 | false | ```java\nclass Solution {\n public long kSum(int[] nums, int k) {\n //1. the max value will be the sum of all the positives\n //2. sums of every subsequence can be derived by removing positives from or adding negetives to the max value\n //3. we can turn every negetive into its absolute value, \n // so "max - abs(neg)" means we add negetives to the max-value subsequence.\n // "max - pos" means we remove positives from the max-value subsequence.\n //4. we transform original question into "finding the (k-1)th smallest sum of subsequence"\n // eg: the 1th largest subsequnce will be "max - 0"\n // the 2th largest subsequnce will be "max - 1th smallest sum of subsequence"\n //5. to get the kth smallest sum of subsequence in nlogn, \n // we will try to iterate sum of subsequnce in increasing order,\n // then use a heap to store them\n //6. for an increasing array [a, b, c], we can choose draw a tree to interate it\n // a\n // / \\\n // b a+b\n // / \\ / \\\n // c b+c a+c a+b+c\n //7. interate in this way and find the (k-1)th smallest sum of subsequnce using heap\n // answer will be max - (k-1)th smallest sum of subsequence\n \n \n long max = 0;\n for (int i = 0; i < nums.length; i ++) {\n if (nums[i] > 0)\n max += nums[i];\n else\n nums[i] = -nums[i];\n }\n Arrays.sort(nums);\n PriorityQueue<long[]> que = new PriorityQueue<>((n1, n2) -> (Long.compare(n1[0], n2[0])));\n que.offer(new long[]{nums[0], 0});\n\n long kmin = 0;\n for (int i = 1; i < k; i ++) {\n long[] node = que.poll();\n kmin = node[0];\n if (node[1] == nums.length - 1)\n continue;\n que.offer(new long[] {kmin + nums[(int)node[1]+1], node[1]+1});\n que.offer(new long[] {kmin - nums[(int)node[1]] + nums[(int)node[1]+1], node[1]+1});\n }\n \n return max - kmin;\n }\n}\n``` | 1 | 0 | ['Heap (Priority Queue)'] | 0 |
find-the-k-sum-of-an-array | [Python3] Finding next bigger sum from an all-positive sorted nums | python3-finding-next-bigger-sum-from-an-ah4cz | Max k = 2000. The best strategy is finding next smaller sum one by one for 2000 times.\nHow to find next smaller sum?\nBiggest sum is the sum of all positive nu | yuanzhi247012 | NORMAL | 2022-08-22T03:27:04.335224+00:00 | 2022-08-22T03:35:56.674847+00:00 | 97 | false | Max k = 2000. The best strategy is finding next smaller sum one by one for 2000 times.\nHow to find next smaller sum?\nBiggest sum is the sum of all positive numbers. We start from there and finding the next smaller sum.\nTricky part:\nDon\'t "add" or "remove" numbers to or from subsequence. Instead, we introduce the concept of "use".\n"Use" a negative number means: **add** negative number to subsequence\n"Use" a positive number means: **remove** positive number from subsequence\nEither way "use" a number means reduce sum by abs(nums[i]) no matter positive or negative.\n"Un-use" a number does the reverse, it adds sum by abs(nums[i]) no matter positive or negative.\nA number in "use" cannot be used again. You must "un-use" it first.\nBy doing so, we can now make all numbers positive, and controlling the subsequence sum by choosing which number to "use" or "un-use".\n\nFirst we add all positive numbers to the sequence, making the biggest sum. In this subsequence, all numbers are in "not-in-use" state. Because for positive number, being picked means not in use, for negative number **not** being picked means not in use.\n\nWe make all numbers positive and sort them. Then one by one check which one to use or unuse from small to big.\nThe question becomes finding next bigger subsequence in this new all-positive sorted nums.\nThis can be achieved using heap.\n\n```\n def kSum(self, nums: List[int], k: int) -> int:\n maxSum = sum(v for v in nums if v>0)\n if k==1: \n return maxSum\n absNums = sorted(abs(v) for v in nums)\n que = [(absNums[0],0)]\n for _ in range(k-1):\n v,i = heapq.heappop(que) # subsequence with absNums[i] in use\n if i+1<len(absNums):\n heapq.heappush(que,(v-absNums[i]+absNums[i+1],i+1))\n heapq.heappush(que,(v+absNums[i+1],i+1))\n return maxSum-v\n``` | 1 | 0 | [] | 1 |
find-the-k-sum-of-an-array | Java solution using min heap | java-solution-using-min-heap-by-legit_12-9zpw | Derived from : https://leetcode.com/problems/find-the-k-sum-of-an-array/discuss/2457384/Priority-Queue-oror-C%2B%2B\n\n\n/*\n\n-> Find max sum possible, we get | legit_123 | NORMAL | 2022-08-21T14:32:08.234108+00:00 | 2022-08-21T14:32:08.234150+00:00 | 477 | false | Derived from : https://leetcode.com/problems/find-the-k-sum-of-an-array/discuss/2457384/Priority-Queue-oror-C%2B%2B\n\n```\n/*\n\n-> Find max sum possible, we get max sum after adding all elements greater than or equal to zero\n-> For finding second max sum we can either subtract smallest positive number from sum or add largest negative number to sum\n-> Add or subtract numbers from current sum to get next largest sum\n-> Hack : We can convert all negative numbers to positive and then simply subtract them instead of adding\n-> Apply include/exclude method to generate subsequences\n\nTC : O(len*log(len) + klogk)\nSC : O(k)\n\n*/\n\nclass Solution {\n public long kSum(int[] nums, int k) {\n int len = nums.length;\n int absNums[] = new int[len];\n long maxSum = 0;\n \n for(int idx=0;idx<len;idx++){\n int num = nums[idx];\n if(num>=0) maxSum+=num;\n absNums[idx] = Math.abs(num);\n }\n \n Arrays.sort(absNums);\n PriorityQueue<Pair> minHeap = new PriorityQueue();\n List<Long> sumsList = new ArrayList();\n \n minHeap.add(new Pair(absNums[0],0));\n sumsList.add(maxSum);\n \n while(minHeap.size()>0&&sumsList.size()<k){\n Pair pair = minHeap.remove();\n long sumSoFar = pair.sumSoFar;\n int idx = pair.idx;\n \n sumsList.add(maxSum-sumSoFar);\n \n if(idx+1<len){\n minHeap.add(new Pair(sumSoFar+absNums[idx+1],idx+1));\n minHeap.add(new Pair(sumSoFar+absNums[idx+1]-absNums[idx],idx+1));\n }\n }\n \n return sumsList.get(k-1);\n }\n \n private class Pair implements Comparable<Pair>{\n private long sumSoFar;\n private int idx;\n \n Pair(long sumSoFar,int idx){\n this.sumSoFar = sumSoFar;\n this.idx = idx;\n }\n \n public int compareTo(Pair other){\n if(this.sumSoFar>=other.sumSoFar) return 1;\n return -1;\n }\n }\n}\n```\n\nUpvote if you like my codes ! | 1 | 0 | ['Greedy', 'Heap (Priority Queue)', 'Java'] | 1 |
find-the-k-sum-of-an-array | Java | Merge Sort | O(n) + O(k^2) | java-merge-sort-on-ok2-by-l9s-lutk | \n public long kSum(int[] nums, int k) {\n //get sum \n long sum = 0;\n for(int i = 0; i < nums.length; i ++ ){\n if(nums[i] | l9s | NORMAL | 2022-08-21T10:10:31.946668+00:00 | 2022-08-21T10:10:31.946711+00:00 | 93 | false | \n public long kSum(int[] nums, int k) {\n //get sum \n long sum = 0;\n for(int i = 0; i < nums.length; i ++ ){\n if(nums[i] > 0){\n sum += nums[i];\n }else{\n nums[i] *= -1;\n }\n }\n \n //sort increasing.\n\t\t//=> sum - 0, sum - a0, .., sum - an, => find an, which is the kth smallest sum in nums.\n Arrays.sort(nums);\n\n \n ArrayList<Long> a = new ArrayList<>();\n ArrayList<Long> b = new ArrayList<>();\n a.add(0L);\n //merge sort. merge a and a + nums[i]\n //let b always <= k, stop at i == k\n // a1: [0,n], a2: [0,n+1], aka, a1 + x\n for(int i = 0; i < nums.length && i < k; i ++ ){\n int x = nums[i];\n int p1 = 0, p2 = 0;\n b.clear();\n \n while(p1 < a.size() && p2 < a.size() && b.size() < k){\n if(a.get(p1) < a.get(p2) + x){\n b.add(a.get(p1));\n p1++;\n }else{\n b.add(a.get(p2) + x);\n p2++;\n }\n }\n \n while(p1 < a.size() && b.size() < k){\n b.add(a.get(p1));\n p1++;\n }\n \n while(p2 < a.size() && b.size() < k ){\n b.add(a.get(p2) + x);\n p2++;\n }\n \n ArrayList<Long> tmp = a;\n a = b;\n b = tmp;\n }\n \n \n return sum - a.get(k - 1);\n } | 1 | 0 | [] | 0 |
find-the-k-sum-of-an-array | C++ solution || Priority Queue || With Explanation || Beats 100% runtime and space complexity | c-solution-priority-queue-with-explanati-b5ok | The plan is to find the biggest possible sum first, and then go through the array and find the sums of all possible subsequences, from biggest to smallest, unti | manavdoda7 | NORMAL | 2022-08-21T09:40:03.590452+00:00 | 2022-08-21T09:49:03.354517+00:00 | 99 | false | The plan is to find the biggest possible sum first, and then go through the array and find the sums of all possible subsequences, from biggest to smallest, until we find the kth sum.\nHere, we start by putting the largest sum in the priority queue and making all of the array\'s elements positive.\nThen, we use this line to find the next sums by taking away the lowest number from the current sum:\n```\npq.push({it.first-nums[it.second], it.second+1});\n```\nAnd at the same time, we use this method to see if we can make a sum by adding back the element\xA0we left out while calculating the current sum:\n```\nif(it.second>0) pq.push({it.first-nums[it.second]+nums[it.second-1], it.second+1});\n```\nThe last thing we do is find the kth largest sum and return it.\xA0Here is how the given logic is implemented effectively:\n```\nclass Solution {\npublic:\n long long kSum(vector<int>& nums, int k) {\n priority_queue<pair<long long, int>> pq;\n long long sum=0;\n for(int i=0;i<nums.size();i++) {\n if(nums[i]>0) sum+=nums[i];\n else nums[i]*=-1;\n }\n sort(nums.begin(), nums.end());\n pq.push({sum, 0});\n while(k--) {\n auto it = pq.top();\n pq.pop();\n if(it.second<nums.size()) {\n pq.push({it.first-nums[it.second], it.second+1});\n if(it.second>0) pq.push({it.first-nums[it.second]+nums[it.second-1], it.second+1});\n }\n if(k==0) return it.first;\n }\n return -1;\n }\n};\n``` | 1 | 1 | ['C', 'Heap (Priority Queue)'] | 0 |
find-the-k-sum-of-an-array | C++ || EXPLAINATION|| with Comments|| | c-explaination-with-comments-by-prabhjot-hhqe | Approach-\n\nTake the sum of all positive values in nums, it will be maximum sum of any subsequence possible.\nMake all the elements of nums positive (Reason- L | prabhjot_2 | NORMAL | 2022-08-21T07:04:25.140168+00:00 | 2022-08-21T07:04:25.140201+00:00 | 171 | false | **Approach**-\n\nTake the sum of all positive values in nums, it will be maximum sum of any subsequence possible.\nMake all the elements of nums positive (Reason- Later we will include or exclude the nums[i] in sum,\n**Case1**- If nums[i] was negative, if we subtract it from sum, it will be same as including it into subsequence and if we add/consider it to sum, it will be same as excluding it from subsequence.\n**Case2** - If nums[i] was positive, if we subtract it from sum, it will be same as excluding it from subsequence and if we add/consider it to sum, it will be same as including it into subsequence.\n\n\nSort the nums vector and create a priority_queue of type pair (to insert current sum and index).\nInsert the {sum-nums[0],0} into the priority_queue.\nNow while we didn\'t get kth highest sum of subsequence, do the following-\ntake the top of priority queue, if the ind+1 < n , then either include the ind+1 and ind value or exclude ind+1 value ( ind value is already excluded) .....\nIt will same as taking subsequences.\n```\n#define ll long long\nclass Solution {\npublic:\n long long kSum(vector<int>& nums, int k) {\n \n\t\tll sum=0,n=nums.size();\n vector<ll> ans; // vector to store first k maximum subsequence sum\n for(ll i=0;i<nums.size();i++)\n {\n if(nums[i]>0)\n sum+=nums[i]; // find the maximum possible sum\n nums[i]=abs(nums[i]); // make all values of nums >=0\n\t\t\t\n }\n ans.push_back(sum); // push the highest possible sum\n priority_queue<pair<ll,ll>> pq; // priority queue to store the pair of sum and index, which denotes maximum sum if the current index value is excluded.\n sort(nums.begin(),nums.end()); // sort the nums so that we include and exclude minimum value first to get highest subsequence values \n pq.push({sum-nums[0],0}); // push sum-nums[0], 0 ....which denotes max subsequence sum when index 0 is excluded.\n\t\t// while we don\'t get the kth highest subsequence sum do the operation\n while(ans.size()<k)\n {\n auto [sum,ind]=pq.top();\n pq.pop();\n if(ind+1<n)\n {\n\t\t\t\n pq.push({sum+nums[ind]-nums[ind+1],ind+1}); // if next index is possible, this case considers if we take the previous index and exclude the latest one i.e. ind+1\n pq.push({sum-nums[ind+1],ind+1}); // if next is possible, this case considers, if we exclude both previous index as well as latest possible index i.e. ind+1\n }\n ans.push_back(sum);\t\t\t//push the next highest subsequence sum\n }\n return ans.back(); \n }\n};\n``` | 1 | 0 | [] | 0 |
find-the-k-sum-of-an-array | C++ Solution with explaination | c-solution-with-explaination-by-cybergho-3d9d | Approach-\n1. Take the sum of all positive values in nums, it will be maximum sum of any subsequence possible.\n2. Make all the elements of nums positive (Reaso | cyberghost2023 | NORMAL | 2022-08-21T06:36:34.271650+00:00 | 2022-08-21T06:36:34.271692+00:00 | 160 | false | Approach-\n1. Take the sum of all positive values in nums, it will be maximum sum of any subsequence possible.\n2. Make all the elements of nums positive (Reason- Later we will include or exclude the nums[i] in sum, \n\t* Case1- If nums[i] was negative, if we subtract it from sum, it will be same as including it into subsequence and if we add/consider it to sum, it will be same as excluding it from subsequence.\n\t* Case2 - If nums[i] was positive, if we subtract it from sum, it will be same as excluding it from subsequence and if we add/consider it to sum, it will be same as including it into subsequence.\n3. Sort the nums vector and create a priority_queue of type pair (to insert current sum and index).\n4. Insert the {sum-nums[0],0} into the priority_queue.\n5. Now while we didn\'t get kth highest sum of subsequence, do the following-\n\t\ttake the top of priority queue, if the ind+1 < n , then either include the ind+1 and ind value or exclude ind+1 value ( ind value is already excluded) .....It will same as taking subsequences.\n\t \t\t\n\t\n\n```\n#define ll long long\nclass Solution {\npublic:\n long long kSum(vector<int>& nums, int k) {\n \n\t\tll sum=0,n=nums.size();\n vector<ll> ans; // vector to store first k maximum subsequence sum\n for(ll i=0;i<nums.size();i++)\n {\n if(nums[i]>0)\n sum+=nums[i]; // find the maximum possible sum\n nums[i]=abs(nums[i]); // make all values of nums >=0\n\t\t\t\n }\n ans.push_back(sum); // push the highest possible sum\n priority_queue<pair<ll,ll>> pq; // priority queue to store the pair of sum and index, which denotes maximum sum if the current index value is excluded.\n sort(nums.begin(),nums.end()); // sort the nums so that we include and exclude minimum value first to get highest subsequence values \n pq.push({sum-nums[0],0}); // push sum-nums[0], 0 ....which denotes max subsequence sum when index 0 is excluded.\n\t\t// while we don\'t get the kth highest subsequence sum do the operation\n while(ans.size()<k)\n {\n auto [sum,ind]=pq.top();\n pq.pop();\n if(ind+1<n)\n {\n\t\t\t\n pq.push({sum+nums[ind]-nums[ind+1],ind+1}); // if next index is possible, this case considers if we take the previous index and exclude the latest one i.e. ind+1\n pq.push({sum-nums[ind+1],ind+1}); // if next is possible, this case considers, if we exclude both previous index as well as latest possible index i.e. ind+1\n }\n ans.push_back(sum);\t\t\t//push the next highest subsequence sum\n }\n return ans.back(); \n }\n};\n```\n\nI tried my best to explain the given solution, any suggestions to improve it will be appreciated! | 1 | 0 | ['C', 'Heap (Priority Queue)'] | 0 |
find-the-k-sum-of-an-array | O(nk) brute force solution | onk-brute-force-solution-by-panyan7-w2rl | First of all, I didn\'t pass (TLE), but I saw someone passed using same brute-force approach with many tricks to optimize the constant https://leetcode.com/prob | panyan7 | NORMAL | 2022-08-21T04:53:10.222061+00:00 | 2022-08-21T05:00:01.462565+00:00 | 228 | false | First of all, I didn\'t pass (TLE), but I saw someone passed using same brute-force approach with many tricks to optimize the constant https://leetcode.com/problems/find-the-k-sum-of-an-array/discuss/2456909/O(n-*-klogk)-solution-%2B-clever-tricks, so I guess my solution is worth mentioning.\nThe idea is to keep only the top k sums as you iterate through the array, since if a sum is not in the top k at some moment, it will never be in top k in the end, so we can safely discard it.\n\nHere, I\'ll just show how to optimize the O(nk log k) solution to O(nk). Instead of using a set or sorted list, notice that if the maintained list is sorted, then nums[i] + the list is also sorted. Now, we can just merge the two different lists into one sorted list (like what we do in merge sort). I used `std::inplace_merge` in C++ to do this, but I guess it is still not fast enough.\n\n```cpp\nclass Solution {\npublic:\n long long kSum(vector<int>& nums, int k) {\n vector<long long> st;\n st.push_back(0);\n int n = nums.size();\n for (int i = 0; i < n; i++) {\n int m = st.size();\n for (int j = 0; j < min(k, m); j++)\n st.push_back(st[j] + (long long)nums[i]);\n auto it = st.begin() + m;\n inplace_merge(st.begin(), it, st.end(), greater<long long>());\n if (st.size() > k)\n st.resize(k);\n }\n return st[k-1];\n }\n};\n``` | 1 | 0 | [] | 0 |
find-the-k-sum-of-an-array | Walk Through of my Understanding || Detailed Explaination 💡. | walk-through-of-my-understanding-detaile-xqso | Understanding optimised take or leave :
-> i like to define it as , you should take atleast one element at any point
-> how can we maintain this and get all uni | naveen_gunnam | NORMAL | 2025-03-06T00:51:46.116230+00:00 | 2025-03-06T00:51:46.116230+00:00 | 9 | false | Understanding optimised take or leave :
-> i like to define it as , you should take atleast one element at any point
-> how can we maintain this and get all unique combinations?
instead of starting with a case of not taking any element, we start with "take" case. 1 -take , 0 - leave .
1
01 11
001 011 101 111
0001 0011 0101 0111 1001 1011 1101 1111
it is like expanding by taking last element each time and leave/take second last element, this will reduce the search space signiificantly as we considering only unique sates at any point.
in this way we can generate all the unique combinations, where we take atleast one element.
example :
0 1 2 (index)
2 2 4
(2) 1 a
(2-2+2) 01 b (2+2) 11 c
(2-2+4) 001 d (2+4) 011 (4-2+4) 101 (4+2) 111
2 4 -2
largest sum = 6
sort by abs vals (i will explain why at last)
0 1 2
2 2 4
first we have 6 which is 1st largest sum
* we remove smallest combination sum from that to get second smallest. *
we use that above tree traversel in greedy way to get next smallest combination sum.
add the visited states with current sum to min priority queue
we greedily visit the branches that giving the smallest current sum.
1st 6
2nd 6-2 (a)
3rd 6-2 (b)
4th 6-4 (c)
5th 6-4 (d) => ans = 2
we stop after d as we got k largests sums
we are getting abs values of nums because adding a negative to val will be same as
removing positive value from largest sum.
so instead of dealing with -ve nums , we just make them as +ve.
and this nums has to sorted in asc order , as we are greedily visting them first.
# Complexity
- Time complexity: N * log(N) (for sorting) + K *log(K) (for k pq operations )
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(k) , at most k values in pq.
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public long kSum(int[] nums, int k) {
long lsum = 0;
int n = nums.length;
for(int i =0 ; i<n ; i++){
if(nums[i]>0) lsum+=nums[i];
nums[i] = Math.abs(nums[i]);
}
Arrays.sort(nums);
PriorityQueue<long[]> pq = new PriorityQueue<>((a,b)->Long.compare(a[0],b[0])); //(sum,lastIndex)
long ans = lsum;
pq.add(new long[]{nums[0],0});
while(--k>0 && !pq.isEmpty()){
int lastInd = (int)pq.peek()[1];
long prevSum = pq.poll()[0];
ans = lsum - prevSum;
if(lastInd<n-1){
pq.add(new long[]{prevSum-nums[lastInd]+nums[lastInd+1],lastInd+1});
pq.add(new long[]{prevSum+nums[lastInd+1],lastInd+1});
}
}
return ans;
}
}
/*
4
0
6
4
2
0
4
2
0
-2
merge
-10 -2 1 3 4 12
considering 12
12 take
0 not take
considering 4
not take 4
12 16
0 12
merge 4
take 4 0
16
4
considering 3
not take 3
16
12 19
4 15
0 12
merge 7
not take 3 4
19 3
15 0
7
3
considering 1
not take 1
19
15
12
7
4
3
0
20
16
13
8
5
4
1
20 18
19 17
16 14
15 13
13 11
12 10
8 6
7 5
5 3
4 2
3 1
1 -1
0 -2
-10 -2 1 3 4 12
20
19
18
18
17
this gonna be never ending shit
*/
``` | 0 | 0 | ['Array', 'Sorting', 'Heap (Priority Queue)', 'Java'] | 0 |
find-the-k-sum-of-an-array | Beats 100.00% | beats-10000-by-rhyd3dxa6x-yu01 | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | rhyD3DxA6x | NORMAL | 2025-02-01T18:04:18.141246+00:00 | 2025-02-01T18:04:18.141246+00:00 | 16 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
int cnt;
public long kSum(int[] nums, int k) {
long right = 0, sum = 0;
cnt = k - 1;
for (int i = 0; i < nums.length; i++) {
if (nums[i] >= 0) {
sum += nums[i];
} else {
nums[i] = -nums[i];
}
right += nums[i];
}
Arrays.sort(nums);
long left = -1;
while (left + 1 < right) {
long mid = left + (right - left) / 2;
cnt = k - 1;
dfs(nums, mid, 0);
if (cnt == 0) {
right = mid;
} else {
left = mid;
}
}
return sum - right;
}
private void dfs(int[] nums, long mid, int index) {
if (index == nums.length || cnt == 0 || mid < nums[index]) {
return;
}
cnt--;
dfs(nums, mid, index + 1);
dfs(nums, mid - nums[index], index + 1);
}
}
``` | 0 | 0 | ['Java'] | 0 |
find-the-k-sum-of-an-array | quickselect + bruteforce | quickselect-bruteforce-by-kotomord-8beh | \n# Complexity\n- Time complexity: O(N + K^2)\n\n- Space complexity: O(N)\n\n# Code\n\nclass Solution {\npublic:\n long long kSum(vector<int>& nums, int k) { | kotomord | NORMAL | 2024-07-25T12:07:43.956376+00:00 | 2024-07-25T12:07:43.956410+00:00 | 8 | false | \n# Complexity\n- Time complexity: O(N + K^2)\n\n- Space complexity: O(N)\n\n# Code\n```\nclass Solution {\npublic:\n long long kSum(vector<int>& nums, int k) {\n vector<int> nonneg;\n vector<int> neg;\n vector<int> effect;\n for(auto i: nums) {\n if(i>=0) nonneg.push_back(i);\n else neg.push_back(-i);\n }\n if(neg.size()>2*k) {\n nth_element(neg.begin(), neg.begin()+2*k, neg.end());\n for(int i = 0; i<2*k; ++i) effect.push_back(-neg[i]);\n }else{\n for (auto i: neg) effect.push_back(-i); \n }\n\n long ans = 0;\n if(nonneg.size()>2*k) {\n nth_element(nonneg.begin(), nonneg.begin()+2*k, nonneg.end());\n for(int i = 0; i<2*k; ++i) effect.push_back(nonneg[i]);\n for(int i = 2*k; i<nonneg.size(); ++i) ans+= nonneg[i];\n \n }else{\n for (auto i: nonneg) effect.push_back(i);\n }\n\n\n long long* state = new long long[2*k];\n state[0] = 0;\n int count = 1;\n for(auto v: effect) {\n for(int i = 0; i<count; ++i) \n state[i+count] = state[i] - v;\n count*=2;\n if(count > k) {\n std::nth_element(state, state + k - 1, state + count);\n count = k;\n } \n }\n std::nth_element(state, state+k-1, state+count);\n return ans - state[k-1];\n\n }\n};\n``` | 0 | 0 | ['Quickselect', 'C++'] | 0 |
find-the-k-sum-of-an-array | C++ | Binary search + Brute-force solution | c-binary-search-brute-force-solution-by-h13zp | \n# Approach\nUse binary-search to search for the possible sum value, which can generate >= k subsets, so that we can find the kth largest sum from that value.\ | bietdoikiem | NORMAL | 2024-07-20T17:00:54.403626+00:00 | 2024-07-20T17:04:45.184376+00:00 | 41 | false | \n# Approach\nUse binary-search to search for the possible sum value, which can generate >= k subsets, so that we can find the **kth largest sum** from that value.\n\n# Complexity\n- Time complexity: O(NlogN + Klog(|MaxSum| + |MinSum|))\n\n# Code\n```\nclass Solution {\npublic:\n long long INF = 1e18;\n void countSubset(vector<int>& nums, int& k, long long& targetSum, int idx, long long curSum, int& cnt) {\n if (cnt >= k) return;\n if (idx >= nums.size()) return;\n if (curSum - nums[idx] >= targetSum) {\n cnt++;\n countSubset(nums, k, targetSum, idx+1, curSum - nums[idx], cnt);\n } else {\n return;\n }\n countSubset(nums, k, targetSum, idx+1, curSum, cnt);\n }\n\n long long kSum(vector<int>& nums, int k) {\n int n = nums.size();\n long long maxSum = 0;\n long long minSum = 0;\n for (int i = 0; i < n; i++) {\n if (nums[i] >= 0) {\n maxSum += nums[i];\n } else {\n minSum += nums[i];\n nums[i] = abs(nums[i]);\n }\n }\n sort(nums.begin(), nums.end());\n\n long long l = minSum;\n long long r = maxSum;\n long long ans = -INF;\n while (l <= r) {\n long long mid = (l + r) >> 1;\n int cnt = 1;\n countSubset(nums, k, mid, 0, maxSum, cnt);\n if (cnt >= k) {\n ans = max(ans, mid);\n l = mid + 1;\n } else {\n r = mid - 1; // lower right to generate more subsets \n }\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['Binary Search', 'Recursion', 'C++'] | 0 |
find-the-k-sum-of-an-array | Heap with candidate values | heap-with-candidate-values-by-vilmos_pro-8eys | Intuition\n\nThe largest sum is obviously the sum of all positive elements of the array. For the $k$-th largest sum we have to remove some of the positive terms | vilmos_prokaj | NORMAL | 2024-07-04T11:33:52.374258+00:00 | 2024-07-04T11:35:00.165462+00:00 | 25 | false | # Intuition\n\nThe largest sum is obviously the sum of all positive elements of the array. For the $k$-th largest sum we have to remove some of the positive terms from this maximal sum and probably add some negative terms. So it has the form:\n\n$$\n \\sum_{i: a_i>0} a_i - \\sum_{j \\in S} |a_j|\n$$\nNow the problem is actually find the $k$-th smallest sum for the the array of absolute values. For a subset of indices $S$ denote $a_S=\\sum_{i\\in S} a_i$ the corresponding sum.\n\nSuppose now that the numbers in the array are sorted in **non-decreasing** order. Introduce a partial order on the subset of indices. The ``key\'\' function is $S\\mapsto (a_S, \\max S)$. That is $S\'< S\'\'$ if $a_{S\'}< a_{S\'\'}$ or $a_{S\'}= a_{S\'\'}$ and $\\max S\' < \\max S\'\'$.\n\nWe want to enumerate the subsets of indices according to this ordering. The first element of the sequence is $S_0=\\emptyset$.\n\nSuppose that we already have $S_0\\leq \\cdots\\leq S_k$. $S_{k+1}$ is one of the smallest element not in $\\{S_0, \\dots, S_k\\}$.\n\nLet $x+1=\\max S_{k+1}$ and $S\' = (S_{k+1}\\setminus\\{x+1\\})\\cup\\{x\\}$. That is we replace the largest element $x+1$ of $S_{k+1}$ with $x$.\n\n$S\'< S_{k+1}$ so it is one of $S_0, S_1, \\dots, S_k$. If it is $S_j$ then the largest element of $S_j$ is $x$ and $S_{k+1}$ is either $(S_j\\setminus\\{x\\})\\cup \\{x+1\\}$ or $S_j\\cup\\{x+1\\}$.\n\nIn order to generate the first $k$ element of $(S_j)$ we can keep the possible values in a heap and when $S_k$ is obtained update the set of possible values. Of course $S_k$ is not interesting at the end only $a_{S_k}$. \n\nIn the implementation, $(a_S, 1+\\max S)$ is stored in the heap.\n\n\n# Complexity\n- Time complexity: $$O(n(\\log k))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(k)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\ndef kth_smallest_sum(k, nums):\n \n values = [(0, 0)]\n k -= 1\n nums = heapq.nsmallest(k, nums)\n while k > 0:\n k -= 1\n s, i = heapq.heappop(values)\n if i < len(nums):\n heapq.heappush(values, (s+nums[i], i+1))\n if i > 0:\n heapq.heappush(values, (s+nums[i]-nums[i-1], i+1))\n \n return values[0][0]\n\nclass Solution:\n def kSum(self, nums: List[int], k: int) -> int:\n max_sum = sum(num for num in nums if num >0)\n return max_sum - kth_smallest_sum(k, (num if num >= 0 else -num for num in nums))\n\n``` | 0 | 0 | ['Python3'] | 0 |
find-the-k-sum-of-an-array | Rudimentary explanation for any language / code in go | rudimentary-explanation-for-any-language-agpg | Code\n\ntype Item struct {\n Sum int64\n Index int\n}\n\nfunc kSum(nums []int, k int) int64 {\n\n // ================================================= | no3371 | NORMAL | 2024-04-29T18:45:47.352228+00:00 | 2024-04-29T18:45:47.352259+00:00 | 10 | false | # Code\n```\ntype Item struct {\n Sum int64\n Index int\n}\n\nfunc kSum(nums []int, k int) int64 {\n\n // ===========================================================================================\n\n // I have never really worked on LeetCode before, yet somehow stumbled on this problem and I decided to figure this out\n // I got pretty close, but failed to find a algo that works for all testcase (my primitive solution got up to 12)\n // After severals days I decided to look at people\'s solutions and they are mostly consonant with my findings\n // ...Except they are extremyly clean! There is clearly some knowledge gap here\n // I\'m the type of people that when learning stuff I can not move on if I don\'t understand how things works\n // So I digged in more and eventually sorted it out\n // And I decided to write a explanation that can be understand by anyone with rudimentary knowledege\n \n // Given [1,-2,3,4,-10,12]\n // The sum of this consequense is 8, but if we ignore negative numbers, it would be 20, which is 8 -(-2) -(-10), which means we are excluding -2 and -10\n // So we know that the max possible sum is always the sum of all positive numbers\n // What could be the next largest sum, apparently, if we exclude the smallest positive number (1), we get 19\n // Then... what could be the next?\n // A) Excluding 3 we get 17\n // B) Re-including the excluded -2, we get 18\n // C) Excluding 1 and Re-including the excluded -2, we get 17\n // It turns out, because our max sum comes from excluding negative numbers and including positive ones\n // Picking a positive number means removing it from our max sum, and pick a negative number means adding it to our max sum\n // In other words, picking a number means subtracting its absolute value from our max sum\n // [1,-2,3,4,-10,12] is not much differnt from [1,2,3,4,10,12] in this case\n\n // We are looking for Kth largest sum\n // This means we are repeating K times the process of finding the next number combination that gives the smallest sum to exclude\n \n // How do we find the next combination which gives the smallest sum?\n // If we sort the absolute numbers consequence from smallest to largest\n // Say [1, 2, 3, 4, 10, 12]\n // It\'s easy to notice that, the fewer numbers to the right included, the sum will be smaller\n // For example: [1, 2] is smaller than [1, 2, 3]\n // For example: [2, 3] is smaller than [3, 4]\n \n // But because the numbers can be anything as long as they are bigger than their left neighbours\n // Combinations of more amount of numbers are not guaranteed to sum bigger than combinations of fewer amount of numbers\n // Say [1, 2, 3, 4], [1, 2] >= [3] but not [4], [1, 2, 3] >= [2,4] but < [3, 4]\n\n // Before we continue, we need to know how do we iterate through all possible combinations\n // To iterate all subconsequences of a given consequence of N numbers, Say [1, 2, 3] (N=3)\n // We can break it down to iterations of all N=1, N=2 and N=3 subconsequences\n // How do we iterate through all subconsequences of a given N?\n // We swap the tail!\n // In the subconsequences of single number: [1], [2], [3], the numbers are tails, and the head is []-- yes, an empty head.\n // In the subconsequences of 2 number: [1, 2] [1, 3], Here 2 and 3 are the tails, [1,] is the head.\n\n // So we iterate through all subconsequences of 1 numbers\n // then 2 numbers, then 3... all the way to the final combination of absolute of all given numbers (ex: [1,2,3] of [1,2,3])\n // This way we can iterate through all possible combinations\n\n // However, it\'s not practical to simply iterate through all possible combinations and sort the sums\n // For any given consequence, every number is either included or not included\n // This means there would be 2^N possible consequences, it\'s unacceptable both cpu and memory wise\n\n // Therefore, we\'ll need a way to step through combinations while always picking the next one that gives the smallest sum\n // This is NOT possible without keeping track of all combinations we\'ve iterated through\n\n // Luckily, we\'ve got everything we need to get this solved.\n\n // Because the absolute numbers consequence from smallest to largest\n // The next combination of smallest sum TO THE CURRENT COMBINATION ALWAYs comes from either:\n // A) Swapping the tail of current combination to the next larger number\n // B) Increase N (the numbers of combinations) and include the next larger number to current combination \n\n // Any other combination would be definitely bigger than these 2 possibilities\n\n // Say we\'re given a 6-nums consequence\n // Say [1, 2, 3, 4, 10, 12] (Which is sorted absolute of [1,-2,3,4,-10,12])\n // We already know that the max sum if [1,-2,3,4,-10,12] is 20\n // Which is the sum of only positive numbers\n // Which actually means we are excluding an empty combination []\n\n // Now, we are looking for the next combination of smallest sum\n // Because we got an empty combination [] and got not tail to swap\n // We\'ll try B: Increase N (the numbers of combinations) and include the next larger number\n // This will give us [1]\n // We can now go A or B for the next possibility\n // Route A gives us [2] (which is the result of 1 getting swapped out)\n // Route B gives us [1,2]\n \n // Of course we pick [2] because it sums smaller than [1,2] (1+2=3)\n\n // What now? We got [2] as our current combination\n // Route A gives us [3] (which is the result of 2 getting swapped out)\n // Route B gives us [2,3]\n\n // We should just pick [3] because it sums smaller than [2,3] (2+3=5), right?\n // NO, because while [3] sums smaller than [2,3]\n // It sums equal to [1,2], which is left in previous comparison\n\n // That\'s where priority queue or min/max heap comes in\n // They are just a storage of all combinations we\'ve iterated through and it\'s eaasy to access the max or min\n\n // In this case it\'s a equal, so we can pick either one, but this would not always be true\n\n // Let\'s pick [1,2] this time\n // Route A gives us [1,3] (which is the result of 2 getting swapped out)\n // Route B gives us [1,2,3]\n\n // We\'ll going to pick [1,3] because it sums smaller than [1,2,3] and [2,3]\n // And then we continue...\n\n // But we\'ll not continue the simulation here\n // The above is enough to demonstrate the idea and explain people\'s solutions\n\n // ===========================================================================================\n\n maxSum := int64(0) // The biggest sum of subsequences (all positive)\n for i := 0; i < len(nums); i++ { // sort by absolute values\n if (nums[i] > 0) {\n maxSum += int64(nums[i])\n }\n if (nums[i] < 0) {\n nums[i] *= -1\n }\n }\n\n // Inefficient sorting will results in exceeding time limit\n mergeSort(nums, 0, len(nums))\n\n // Dumb array storage and operation also causes timeout\n dumbHeap := make([]Item, 0, k)\n dumbHeap = minHeapInsert(dumbHeap, Item{Sum: int64(nums[0]), Index: 0})\n k -= 1 // We\'ve got 0th sum (max sum)\n\n var taking Item\n\n for x := 0; x < k; x++ {\n dumbHeap, taking = minHeapTake(dumbHeap)\n\n if taking.Index < len(nums) - 1 {\n a := Item { Sum: taking.Sum + int64(-nums[taking.Index] + nums[taking.Index + 1]), Index: taking.Index + 1 } // Route A (Swapping the tail)\n b := Item { Sum: taking.Sum + int64(nums[taking.Index + 1]), Index: taking.Index + 1 } // Route B (Include more number)\n\n dumbHeap = minHeapInsert(dumbHeap, a)\n dumbHeap = minHeapInsert(dumbHeap, b)\n\n if len(dumbHeap) > k*2+1 {\n dumbHeap = dumbHeap[:k*2+1]\n }\n }\n }\n\n return maxSum - taking.Sum\n}\n\nfunc mergeSort(array []int, left, right int) {\n\tif left >= right-1 {\n\t\treturn\n\t}\n\n\tif right-left == 2 {\n\t\tif array[left] > array[right-1] {\n\t\t\tarray[left], array[right-1] = array[right-1], array[left]\n\t\t\treturn\n\t\t}\n\t}\n\n\tmid := (right + left) / 2\n\tmergeSort(array, left, mid)\n\tmergeSort(array, mid, right)\n\n\tcache := make([]int, right-left)\n\tcopy(cache, array[left:])\n\tleftSub := cache[:mid-left]\n\trightSub := cache[mid-left : right-left]\n\n\tmerged := left\n\tidLeft, idRight := 0, 0\n\tfor idLeft < len(leftSub) && idRight < len(rightSub) {\n\t\tif leftSub[idLeft] <= rightSub[idRight] {\n\t\t\tarray[merged] = leftSub[idLeft]\n\t\t\tidLeft++\n\t\t} else {\n\t\t\tarray[merged] = rightSub[idRight]\n\t\t\tidRight++\n\t\t}\n\t\tmerged++\n\t}\n\n\tfor idLeft < len(leftSub) {\n\t\tarray[merged] = leftSub[idLeft]\n\t\tidLeft++\n\t\tmerged++\n\t}\n\n\tfor idLeft < len(leftSub) {\n\t\tarray[merged] = leftSub[idLeft]\n\t\tidLeft++\n\t\tmerged++\n\t}\n}\n\n\nfunc minHeapInsert (heap []Item, item Item) []Item {\n // In complete binary trees stored as an array\n // For any element at index N, its parent is at index (N-1)/2 and its children are at index 2N+1 and 2N+2\n\n heap = append(heap, item)\n\n for cursor := len(heap) -1;cursor > 0;{\n parentId := (cursor-1)/2\n if heap[parentId].Sum > heap[cursor].Sum {\n heap[parentId], heap[cursor] = heap[cursor], heap[parentId]\n } else {\n break\n }\n cursor = parentId\n }\n\n return heap\n}\n\nfunc minHeapTake (heap []Item) ([]Item, Item) {\n taking := heap[0]\n heap[0], heap[len(heap)-1] = heap[len(heap)-1], heap[0]\n heap = heap[:len(heap)-1]\n for cursor := 0;; {\n leftChildId := cursor*2+1\n rightChildId := cursor*2+2\n swapping := leftChildId\n if rightChildId < len(heap) && heap[rightChildId].Sum < heap[leftChildId].Sum {\n swapping = rightChildId\n }\n if swapping >= len(heap) {\n break\n }\n if heap[swapping].Sum < heap[cursor].Sum {\n heap[swapping], heap[cursor] = heap[cursor], heap[swapping]\n cursor = swapping\n } else {\n break\n }\n }\n return heap, taking\n}\n``` | 0 | 0 | ['Go'] | 0 |
find-the-k-sum-of-an-array | Python (Simple Heap) | python-simple-heap-by-rnotappl-tws4 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | rnotappl | NORMAL | 2024-04-29T16:53:50.145858+00:00 | 2024-04-29T16:53:50.145894+00:00 | 62 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def kSum(self, nums, k):\n m = sum([i for i in nums if i > 0])\n ans = [(-m,0)]\n vals = sorted([abs(i) for i in nums])\n\n for _ in range(k):\n x,i = heapq.heappop(ans)\n if i < len(vals):\n heapq.heappush(ans,(x+vals[i],i+1))\n if i: heapq.heappush(ans,(x-vals[i-1]+vals[i],i+1))\n\n return -x\n``` | 0 | 0 | ['Python3'] | 0 |
find-the-k-sum-of-an-array | list| sorting | list-sorting-by-11srj11-xfo3 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | 11srj11 | NORMAL | 2024-03-25T10:00:35.191824+00:00 | 2024-03-25T10:00:35.191860+00:00 | 26 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def kSum(self, nums: List[int], k: int) -> int:\n lis=[]\n sumi=0\n t=[]\n for i in nums:\n if i>=0:\n sumi+=i\n t.append(-i)\n else:\n t.append(i)\n t.sort(reverse=True)\n t=t[:k+2]\n lis.append(sumi)\n for i in t:\n n=len(lis)\n for j in range(n):\n lis.append(i+lis[j])\n lis.sort(reverse=True) \n if len(lis)>k:\n lis=lis[:k]\n return lis[k-1] \n``` | 0 | 0 | ['Python3'] | 0 |
find-the-k-sum-of-an-array | Easy Java Solution || Priority Queue || Beats 80% | easy-java-solution-priority-queue-beats-xxu5s | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | ravikumar50 | NORMAL | 2023-08-19T15:16:32.762936+00:00 | 2023-08-19T15:16:32.762960+00:00 | 33 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n\n\n // TLE\n\n // Brute force Approach by finding all the sum ans then sortin\n\n // static void kSumInArary(int arr[], int x, int idx, ArrayList<Long> curr, PriorityQueue<Long> pq, int k){\n // if(idx==arr.length) return;\n // if(x==1){\n // for(int i=idx; i<arr.length; i++){\n // long a = curr.get(0)+(long)arr[i];\n // if(pq.size()<k) pq.add(a);\n // else{\n // if(a>pq.peek()){\n // pq.remove();\n // pq.add(a);\n // }\n // }\n // }\n // return;\n // }\n\n // for(int i=idx; i<=arr.length-x; i++){\n // curr.set(0,curr.get(0)+(long)arr[i]);\n // kSumInArary(arr,x-1,i+1,curr,pq,k);\n // curr.set(0,curr.get(0)-(long)arr[i]);\n // }\n // }\n\n // static int helper(int arr[], int k){\n // PriorityQueue<Long> pq = new PriorityQueue<>();\n // pq.add((long)0);\n\n // int n = arr.length;\n\n\n // for(int i=1; i<=n; i++){\n // ArrayList<Long> sum = new ArrayList<>();\n // sum.add((long)0);\n // kSumInArary(arr,i,0,sum,pq,k);\n // }\n\n // return pq.peek();\n // }\n\n public long kSum(int[] nums, int k) {\n long sum=0L;\n for (int i = 0; i < nums.length; i++) {\n if (nums[i]>0) sum+=nums[i];\n else nums[i]=-nums[i];\n }\n Arrays.sort(nums);\n PriorityQueue<Pair<Long,Integer>> pq=new PriorityQueue<>((a,b)->Long.compare(b.getKey(),a.getKey()));\n pq.offer(new Pair<>(sum,0));\n while(k-->1){\n Pair<Long, Integer> top = pq.poll();\n long s=top.getKey();\n int i=top.getValue();\n if(i<nums.length){\n pq.offer(new Pair<>(s-nums[i],i+1));\n if(i>0) pq.offer(new Pair<>(s-nums[i]+nums[i-1],i+1));\n }\n }\n return pq.peek().getKey();\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
find-the-k-sum-of-an-array | Understand the approch to solve this problem | understand-the-approch-to-solve-this-pro-4vtr | Intuition\n Describe your first making a good problem solving skills to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \nap | D9261 | NORMAL | 2023-08-04T07:02:53.542889+00:00 | 2023-08-04T07:02:53.542915+00:00 | 57 | false | # Intuition\n<!-- Describe your first making a good problem solving skills to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\napproach-> our answer store to max_sum and aprove to abs value and compare the vector ele, of kth ele to add the index add adn push the our queue get answer and lkast subtract to ans which store the queue and return max_sum value\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nbecouse subtract the kth ele in a loop and find the top and insert the queue\nN(logN) + k(log)N\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(k);\n# Code\n```\nclass Solution {\npublic:\n long long kSum(vector<int>& nums, int k) {\n // traverse the whole array and get the max and abs value\n int n = nums.size();\n long long max_sum = 0;\n for(int i=0;i<n;i++){\n max_sum += (long long)max(0,nums[i]);\n nums[i] = abs(nums[i]);\n }\n // sort nums array element\n sort(nums.begin(),nums.end());\n vector<long long>value_to_sub = {0};\n // making queue to store the max value and index of the array\n priority_queue<pair<long long, int>,vector<pair<long long, int>>,\n greater<pair<long long, int>>> minCheck;\n minCheck.push({nums[0] , 0});\n// using loop we travers the nums and get the top ele ans second ele and push to our value \n while(value_to_sub.size() < k){\n auto top = minCheck.top();\n long long value = top.first;\n int index = top.second;\n\n minCheck.pop();\n value_to_sub.push_back(value);\n \n if(index < n-1){\n minCheck.push({value + nums[index+1],index+1});\n minCheck.push({value + nums[index+1] - nums[index],index+1});\n }\n }\n// return to get the value and subtract of the maxSum \n return max_sum - value_to_sub[k-1]; \n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
find-the-k-sum-of-an-array | Golang by Priority Queue | golang-by-priority-queue-by-alexchangtw-6cmo | Intuition\n Describe your first thoughts on how to solve this problem. \nUsing same method from https://leetcode.com/problems/find-the-k-sum-of-an-array/solutio | alexchangtw | NORMAL | 2023-02-10T05:10:01.146815+00:00 | 2023-02-10T08:06:01.334348+00:00 | 53 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nUsing same method from https://leetcode.com/problems/find-the-k-sum-of-an-array/solutions/2456716/python3-heap-priority-queue-o-nlogn-klogk/\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nUse Priority Queue to solve this problem.\n\n# Complexity\n- Time complexity: O(NlogN + klogk)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N + k)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\ntype KSumItem struct {\n\tSum int64\n\tIndex int\n}\n\ntype PQ []KSumItem\n\nfunc (m PQ) Len() int { return len(m) }\nfunc (m PQ) Less(i, j int) bool {\n\treturn m[i].Sum > m[j].Sum\n}\nfunc (m PQ) Swap(i, j int) { m[i], m[j] = m[j], m[i] }\nfunc (m *PQ) Push(x interface{}) { *m = append(*m, x.(KSumItem)) }\nfunc (m *PQ) Pop() interface{} {\n\told := *m\n\tn := len(old)\n\tx := old[n-1]\n\t*m = old[0 : n-1]\n\treturn x\n}\n\nfunc kSum(nums []int, k int) int64 {\n\tmaxSum := int64(0)\n\tfor i := range nums {\n\t\tif nums[i] >= 0 {\n\t\t\tmaxSum += int64(nums[i])\n\t\t} else {\n\t\t\tnums[i] = -nums[i]\n\t\t}\n\t}\n\tsort.Ints(nums)\n\n\tmaxHeap := make(PQ, 0)\n\tvar nextSum int64\n\theap.Push(&maxHeap, KSumItem{maxSum - int64(nums[0]), 0})\n\tnextSum = maxSum\n\tfor ; k > 1; k-- {\n\t\tnum := heap.Pop(&maxHeap).(KSumItem)\n\t\tnextSum = num.Sum\n\t\ti := num.Index\n\t\tif i+1 < len(nums) {\n\t\t\theap.Push(&maxHeap, KSumItem{nextSum + int64(nums[i]) - int64(nums[i+1]), i + 1})\n\t\t\theap.Push(&maxHeap, KSumItem{nextSum - int64(nums[i+1]), i + 1})\n\t\t}\n\t}\n\treturn nextSum\n}\n\n``` | 0 | 0 | ['Go'] | 0 |
find-the-k-sum-of-an-array | explaining so that anybody can understand easily| priority queue | beats 100% time | nlogn +klogk | explaining-so-that-anybody-can-understan-oodw | This is one of the hardest problems that I solved myself!\nPlease upvote if the post helps!\n# Intuition\nlet\'s first start assuming that the given array has a | TheBuddhist | NORMAL | 2023-01-27T05:09:30.554517+00:00 | 2023-01-27T13:47:35.072312+00:00 | 38 | false | This is one of the hardest problems that I solved myself!\nPlease upvote if the post helps!\n# Intuition\nlet\'s first start assuming that the given array has all positive numbers, that will make the question easy to understand.\nlook at the subsequence lengthwise of the sorted array\n```\n[]\n\n[1],[2],[3],[4],[5]\n\n[1,2],[1,3],[1,4],[1,5],[2,3],[2,4],[2,5],[3,4],[3,5],[4,5]\n\n[1,2,3],[1,2,4],[1,2,5],[1,3,4],[1,3,5],[1,4,5],[2,3,4],[2,3,5],[2,4,5],[3,4,5]\n\n[1,2,3,4],[1,2,3,5],[1,2,4,5],[1,3,4,5],[2,3,4,5]\n\n[1,2,3,4,5]\n\n```\nNow applying round braces to denote the subsequences that are extension by just one element to the subsequence of length one less. \n```\n[]\n\n([1]),([2]),([3]),([4]),([5])\n\n([1,2],[1,3],[1,4],[1,5]),([2,3],[2,4],[2,5]),([3,4],[3,5]),([4,5])\n\n([1,2,3],[1,2,4],[1,2,5]),([1,3,4],[1,3,5]),([1,4,5]),([2,3,4],[2,3,5]),([2,4,5]),([3,4,5])\n\n([1,2,3,4],[1,2,3,5]),([1,2,4,5]),([1,3,4,5]),([2,3,4,5])\n\n([1,2,3,4,5])\n\n\n\n```\nIf you analyse both the "diagrams", you will realize that all subsequences can be written as prevSubsequence+oneExtraElement.\n\nTwo points that will help you solve the problem now:\n1)adding one element just increases the sum,we go down in such process in the diagram.ALL OF THE DOWN SUBSEQUENCES MUST COME AFTER THE UP SUBSEQUENCES IN THE SUM WEIGHT. \n2)continuing with the same length and going right just increases the sum.ALL OF THE RIGHT SUBSEQUENCES MUST COME AFTER THE LEFT SUBSEQUENCES IN THE SUM WEIGHT.\n\nso for each time we just consider the least sum of the subsequence that is to the right or to the down side!...Why?...technically we should consider all the down and all the right elements but what is the point considering them when only two of them will always come before them in sum. \n\nSo the last thing to do is to handle negative values, so the maximum sum that we can get is sum of all the positives,now we can just remove positive elements and add the negative elements to get smaller sums ,which is equivalent of removing the smallest sums, so we can use the positive number analysis that we did.\n \n# Approach\n\nWe maintain a priority queue and get the smallest sum, now the next sum has two more candidates, the right and the down,for next priority_queue pop,we consider these candidates too.\n \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(nlogn +klogk)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(k)$$\n\n# Code\n```\nclass Solution {\npublic:\n long long kSum(vector<int>&a, int k) \n {\n\n long long totalPositive=0;\n for(auto &x:a)\n {\n if(x<0)x=-x;\n else totalPositive+=x;\n }\n //returning the highest sum possible minus the smallest positive sum \n return totalPositive-kPositives(a,k);\n \n }\n long long kPositives(vector<int>&a,int k)\n {\n //sorting the array\n sort(a.begin(),a.end());\n priority_queue<tuple<long long,int,int>,vector<tuple<long long,int,int>>,greater<>>pq;\n pq.push({0LL,-1,0});\n while(--k)\n {\n auto [sum,lastIndex,length]=pq.top();\n pq.pop();\n //going right\n if(lastIndex!=-1&&lastIndex+1<a.size())\n pq.push({sum-a[lastIndex]+a[lastIndex+1],lastIndex+1,length});\n //going down\n if(lastIndex+1<a.size())\n pq.push({sum+a[lastIndex+1],lastIndex+1,length+1});\n \n }\n return get<0>(pq.top());\n }\n};\n\n``` | 0 | 0 | ['Sorting', 'Heap (Priority Queue)'] | 0 |
find-the-k-sum-of-an-array | Clear Py3 solution | clear-py3-solution-by-seraph1212-ftiz | Code\n\nfrom sortedcontainers import SortedList\n\nclass Solution:\n def kSum(self, nums: List[int], k: int) -> int:\n ps = sum([x for x in nums if x | seraph1212 | NORMAL | 2023-01-10T02:04:59.336609+00:00 | 2023-01-10T02:04:59.336647+00:00 | 172 | false | # Code\n```\nfrom sortedcontainers import SortedList\n\nclass Solution:\n def kSum(self, nums: List[int], k: int) -> int:\n ps = sum([x for x in nums if x >= 0])\n al = sorted([x if x >= 0 else -x for x in nums])\n # print(al)\n q = SortedList()\n q.add((ps, 0))\n \n for i in range(k):\n # print(q, q[-1])\n s, idx = q.pop()\n # print(s)\n for j in range(idx, min(len(al), idx + k)):\n if len(q) > k and s - al[j] < q[-k][0]:\n break\n q.add((s - al[j], j + 1))\n return s\n \n``` | 0 | 0 | ['Python3'] | 0 |
find-the-k-sum-of-an-array | FSM + full binary tree + SortedList | fsm-full-binary-tree-sortedlist-by-matho-f9na | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | mathorlee | NORMAL | 2022-12-06T15:38:25.626800+00:00 | 2022-12-06T15:38:25.626843+00:00 | 204 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def kSum(self, nums: List[int], k: int) -> int:\n \n\n """\n 1: delete abs(nums[_]), 0: do not delete abs[nums[_]] from max_value\n FSM(\u6709\u9650\u72B6\u6001\u673A) is a full binary tree\n 1\n 11\n 111\n 101\n 01\n 011\n 001\n binary tree must satisfy:\n 1. child != father + "0"\n 2. each node at least one digit is "1"\n """\n from sortedcontainers import SortedList\n\n max_value = sum(_ for _ in nums if _ > 0)\n nums = sorted(abs(_) for _ in nums)\n sl = SortedList([(max_value, 0)]) # sub first element\n\n for _ in range(k):\n v, index = sl.pop(-1)\n if index < len(nums):\n sl.add((v - nums[index], index + 1))\n if index > 0:\n sl.add((v + nums[index - 1] - nums[index], index + 1))\n return v\n \n``` | 0 | 0 | ['Python3'] | 0 |
find-the-k-sum-of-an-array | [Python] min heap + max heap | python-min-heap-max-heap-by-wdhiuq-4wif | \nclass Solution:\n def kSum(self, nums: List[int], k: int) -> int:\n \n sum1 = sum(num for num in nums if num > 0)\n min_q, max_q, q = | wdhiuq | NORMAL | 2022-11-18T14:22:12.543782+00:00 | 2022-11-18T14:34:22.569927+00:00 | 38 | false | ```\nclass Solution:\n def kSum(self, nums: List[int], k: int) -> int:\n \n sum1 = sum(num for num in nums if num > 0)\n min_q, max_q, q = [0], [0], []\n\n for num in islice(sorted(map(abs, nums)), k-1):\n v = min_q[0]\n if len(max_q) == k and v > - max_q[0]:\n break \n \n while min_q:\n v = heappop(min_q)\n q.append(v)\n w = v + num\n if len(max_q) == k and w > - max_q[0]:\n break\n heappush(max_q, -w)\n if len(max_q) > k:\n heappop(max_q)\n q.append(w)\n \n while q:\n heappush(min_q, q.pop())\n\n return sum1 + max_q[0] \n``` | 0 | 0 | [] | 0 |
find-the-k-sum-of-an-array | C# max heap and sorting | c-max-heap-and-sorting-by-clewby-9fvz | \npublic class Solution {\n public long KSum(int[] nums, int k) {\n long sum = 0;\n foreach(int n in nums)\n if(n > 0) sum += n;\n | clewby | NORMAL | 2022-11-13T01:19:24.129556+00:00 | 2022-11-13T01:19:24.129588+00:00 | 81 | false | ```\npublic class Solution {\n public long KSum(int[] nums, int k) {\n long sum = 0;\n foreach(int n in nums)\n if(n > 0) sum += n;\n Array.Sort(nums, (a,b) => { return Math.Abs(a)-Math.Abs(b); } );\n PriorityQueue<(long, long), long> pq = new();\n pq.Enqueue((sum-Math.Abs(nums[0]),0), sum-Math.Abs(nums[0]*-1));\n while(--k > 0){\n (long Sum, long Idx) c = pq.Dequeue();\n if(c.Idx+1 <= nums.Length-1){\n long nextIdx = c.Idx+1, nextSum = c.Sum-Math.Abs(nums[nextIdx]);\n pq.Enqueue((nextSum, nextIdx), nextSum*-1);\n pq.Enqueue((nextSum+Math.Abs(nums[c.Idx]), nextIdx), (nextSum+Math.Abs(nums[c.Idx]))*-1);\n }\n sum = c.Sum;\n }\n return sum;\n }\n}\n``` | 0 | 0 | ['Heap (Priority Queue)', 'C#'] | 0 |
find-the-k-sum-of-an-array | C++ | priority queue | c-priority-queue-by-ajaythakran1998-2fmt | \ntypedef long long ll;\ntypedef pair<ll, ll> IntPr;\n\nclass Solution {\npublic:\n\n long long kSum(vector<int>& nums, int k) {\n ll sum = 0;\n | ajaythakran1998 | NORMAL | 2022-10-22T14:23:31.804176+00:00 | 2022-10-22T14:23:31.804205+00:00 | 59 | false | ```\ntypedef long long ll;\ntypedef pair<ll, ll> IntPr;\n\nclass Solution {\npublic:\n\n long long kSum(vector<int>& nums, int k) {\n ll sum = 0;\n for(auto& val : nums){\n if(val > 0) sum += val;\n else val = -val;\n }\n if(k == 1) return sum;\n priority_queue<IntPr> pq;\n sort(nums.begin(), nums.end());\n int cnt = 1;\n pq.push({sum-(ll)nums[0], 0});\n int n = nums.size();\n \n while(pq.empty() == false){\n ll currVal = pq.top().first, idx = pq.top().second;\n pq.pop();\n cnt++;\n if(cnt == k)\n return currVal;\n if(idx < n-1){\n pq.push({currVal-(ll)nums[idx+1], idx+1});\n pq.push({currVal+(ll)(nums[idx]-nums[idx+1]), idx+1});\n }\n }\n return 0;\n }\n};\n``` | 0 | 0 | ['C', 'Heap (Priority Queue)'] | 0 |
find-the-k-sum-of-an-array | Python Min-Heap solution, O(NlogN + KlogK), commented | python-min-heap-solution-onlogn-klogk-co-pggg | \nclass Solution:\n def kSum(self, nums: List[int], k: int) -> int:\n # subtract stores the sum which needs to be subtracted from the maximum sum\n | hemantdhamija | NORMAL | 2022-10-16T06:58:45.780415+00:00 | 2022-10-16T06:58:45.780458+00:00 | 220 | false | ```\nclass Solution:\n def kSum(self, nums: List[int], k: int) -> int:\n # subtract stores the sum which needs to be subtracted from the maximum sum\n # ans stores all the largest sum in decreasing order\n # Initialize heap (minheap) to store current least value which needs to be\n # subtracted from maxsum and the index of nums we are currently at.\n sz, maxSum, subtract, heap, ans = len(nums), 0, [], [], []\n # find the maxsum and update nums so that all elements are positive\n for i in range(sz):\n if nums[i] >= 0:\n maxSum += nums[i]\n else:\n nums[i] = abs(nums[i])\n # sorting nums as per absolute values\n nums.sort()\n # start from index 0 with minimum value as nums[0]\n heappush(heap, (nums[0], 0))\n while heap and len(subtract) < k - 1:\n # pop the value to be subtracted and the current index from the heap\n valToSubtract, idx = heappop(heap)\n # push this value to subtract array\n subtract.append(valToSubtract)\n if idx < sz - 1:\n # considering nums[i] in the subsequence\n heappush(heap, (valToSubtract + nums[idx + 1], idx + 1))\n # not considering nums[i] in the subsequence\n heappush(heap, (nums[idx + 1] + (valToSubtract - nums[idx]) , idx + 1))\n ans.append(maxSum)\n for valToSubtract in subtract:\n ans.append(maxSum - valToSubtract)\n # return Kth largest sum \n return ans[k - 1]\n``` | 0 | 0 | ['Heap (Priority Queue)', 'Python'] | 0 |
find-the-k-sum-of-an-array | Python minheap | python-minheap-by-jzhanggg-sbta | ```\ndef kSum(self, nums: List[int], k: int) -> int:\n n=len(nums)\n mxs=sum(a for a in nums if a>0)\n if k==1:\n return mxs\n | jzhanggg | NORMAL | 2022-09-28T16:08:22.613569+00:00 | 2022-09-28T16:08:22.613599+00:00 | 57 | false | ```\ndef kSum(self, nums: List[int], k: int) -> int:\n n=len(nums)\n mxs=sum(a for a in nums if a>0)\n if k==1:\n return mxs\n k-=1\n q=[]\n heapq.heapify(q)\n nums=[abs(a) for a in nums]\n nums.sort()\n heappush(q,[nums[0],0])\n while k>0:\n s,i=heappop(q)\n k-=1\n if k==0:\n return mxs-s\n if i+1<n:\n heappush(q,[s-nums[i]+nums[i+1],i+1])\n heappush(q,[s+nums[i+1],i+1])\n | 0 | 0 | [] | 0 |
find-the-k-sum-of-an-array | Java time O(n log n + k log k) space O(k), detailed comments. | java-time-on-log-n-k-log-k-space-ok-deta-10ek | Java\nclass Solution {\n /*\n\t Thanks for Huifeng Guan \'s explanation. ref : https://www.youtube.com/watch?v=pquoywwK0_w \n 1. the largest Sum is | gavinzhan | NORMAL | 2022-09-10T06:53:29.500307+00:00 | 2022-09-10T17:22:31.206403+00:00 | 241 | false | ```Java\nclass Solution {\n /*\n\t Thanks for Huifeng Guan \'s explanation. ref : https://www.youtube.com/watch?v=pquoywwK0_w \n 1. the largest Sum is the sum of all no negative numbers.\n 2. to get the next largest sum we can remove a no negative number (- nogegative) \n or add a negative number (- abs(negative)).\n 3. the problem turn to (the largest sum) - (the k-th smallest sum of sequence of a nonegative array)\n 4. to get the K smallest sum\n eg. \n index: 0, 1, 2, 3\n arr: [1, 2, 3, 4]\n the smallest is 1 then 2, 1+2 could be the second smallest.\n to get the k smallest sum, please see the following binary tree, \n\t\t a. the value of the node is the sum of elements in this node.\n b. we use the 0-th element as the root. \n c. the left child: remove the parent last number + the next number\n d. the right child: keep the parent + the next number\n e. the children are always greater than or equal to (if there are duplicates) its parent. \n\t\t because the left child use a greater number (the next number) take the place of the \n\t\t last number in the parent. and the right child add an extra number (the next number)\n 1 \n 2 1+2\n 3 2+3 1+3 1+2+3\n 4 3+4 2+4 2+3+4 1+4 1+3+4 1+2+4 1+2+3+4\n */\n public long kSum(int[] nums, int k) {\n long maxSum = 0;\n int n = nums.length;\n \n // O(n)\n for (int i = 0; i < n; i++) {\n if (nums[i] > 0) maxSum += (long)nums[i];\n if (nums[i] < 0) nums[i] = -nums[i]; // nums[i] = abs(nums[i]);\n }\n \n // O(n log n)\n Arrays.sort(nums);\n // pq long[]{sum, the index of Last Element}, eg 2+3+4 -> {9, 4};\n PriorityQueue<long[]> pq = new PriorityQueue<>((a, b) -> Long.compare(a[0], b[0]));\n pq.add(new long[]{nums[0], 0});\n if (k == 1) return maxSum;\n \n // O(k log 2k)\n while (k-- > 1) {\n long[] s = pq.poll();\n long sum = s[0];\n int lastIndex = (int)s[1];\n long res = maxSum - sum;\n \n if (k == 1) return res;\n \n if (lastIndex + 1 < n) {\n pq.add(new long[]{sum - nums[lastIndex] + nums[lastIndex + 1], lastIndex + 1});\n pq.add(new long[]{sum + nums[lastIndex + 1], lastIndex + 1});\n }\n }\n \n return Long.MAX_VALUE; // should never be here.\n }\n}\n``` | 0 | 0 | [] | 0 |
find-the-k-sum-of-an-array | Set a limitation and other tips (812 ms in Python3) | set-a-limitation-and-other-tips-812-ms-i-3fej | \nThe fastest solution till now seem like a priority queue(PQ)\nwhile there is still a little step to optimize.\n\nOne of that could be find a approximate downb | yjyjyj | NORMAL | 2022-08-26T05:05:48.184348+00:00 | 2022-08-26T13:55:58.169809+00:00 | 104 | false | \nThe fastest solution till now seem like a priority queue(PQ)\nwhile there is still a little step to optimize.\n\nOne of that could be find a approximate downbound value.\nWith that value, some of the sum will be filtered out, so it maintain a smaller priority queue, in this way, it will cost less to maitain the PQ.\n\nWhile the important thing is how to find that value with less effort.\n\nFirst lets pick x biggest numbers, these numbers could give 2 ** x count of sums , in the other words, \nthere is 2**x sums are large enough to tell how the downbound value could be.\nThat will be the sum of the x nums.\n\n```\nx = ceil(log(k) / log(2))\n```\n\nAnd hereby, the final code include three optimizes based on a python PQ solution.\n\n\n```\nclass Solution:\n def kSum(self, nums: List[int], k: int) -> int: \n m = sum(x for x in nums if x > 0)\n vals = sorted(abs(x) for x in nums if x)\n k = (k - 1) // (2 ** (len(nums) - len(vals))) + 1\n k1 = 2 ** len(vals) + 1 - k\n reverse = k > k1\n if reverse:\n k = k1\n m = sum(vals) - m\n pq = [(-m, 0)] # priority queue \n lim = -m + sum(vals[: ceil(log(k) / log(2))])\n for _ in range(k): \n x, i = heappop(pq)\n if i < len(vals): \n if x+vals[i] <= lim:\n heappush(pq, (x+vals[i], i+1))\n if i : heappush(pq, (x-vals[i-1]+vals[i], i+1))\n return x if reverse else -x\n \n ```\n\n\nReference from my submissions:\noptimize a little bit more\n08/26/2022 09:42\tAccepted\t812 ms\t28.3 MB\tpython3\n\noptimize by less check approximate bound based on the submitted fastest solution\n08/26/2022 00:53\tAccepted\t1034 ms\t29.8 MB\tpython3\n\noptimize by check approximate bound based on the submitted fastest solution\n08/26/2022 00:53\tAccepted\t1548 ms\t28.4 MB\tpython3\n\noptimize by remove zeros based on the submitted fastest solution\n08/26/2022 00:34\tAccepted\t1187 ms\t28.1 MB\tpython3\n\ncopy of submitted fastest solution\n08/26/2022 00:27\tAccepted\t1437 ms\t29 MB\tpython3\n\nMy silly solution\n08/26/2022 00:24\tAccepted\t9533 ms\t479.1 MB\tpython3\n\n\n\n\n | 0 | 0 | [] | 0 |
find-the-k-sum-of-an-array | Process from smallest end | process-from-smallest-end-by-yjyjyj-d1no | \nWhen the k is big enough, it could be nearer to the smallest end.\nIn this kind of situation, convert to a problem that find a (2**n + 1 - k) smallest value | yjyjyj | NORMAL | 2022-08-26T04:47:52.020635+00:00 | 2022-08-26T04:47:52.020673+00:00 | 83 | false | \nWhen the k is big enough, it could be nearer to the smallest end.\nIn this kind of situation, convert to a problem that find a (2**n + 1 - k) smallest values\nin the mean time turn all nums to their opposite number\nThen the same logic for the rest of code | 0 | 0 | [] | 0 |
find-the-k-sum-of-an-array | Handle the zeros. | handle-the-zeros-by-yjyjyj-7di0 | \n zeros are so special in this case,\n zeros could make duplicated sum.\n that means all values could repeat at least 2 **(count(0 in nums))\n \n \nremove zero | yjyjyj | NORMAL | 2022-08-26T04:42:19.061754+00:00 | 2022-08-26T04:42:19.061786+00:00 | 55 | false | \n zeros are so special in this case,\n zeros could make duplicated sum.\n that means all values could repeat at least 2 **(count(0 in nums))\n \n \nremove zeros from the array will make it fast when any zero present in the array. while it cost very few if there is no zero\n\nk = (k - 1) // (2 ** iCountOfZeros) + 1\n\n | 0 | 0 | [] | 0 |
find-the-k-sum-of-an-array | well commented easy to understand C++ solution with dummy example | well-commented-easy-to-understand-c-solu-p532 | \nclass Solution {\npublic:\n long long kSum(vector<int>& nums, int k) {\n long long sum = 0;\n for (auto &n : nums) {\n if (n >= 0) | vishalrathi02 | NORMAL | 2022-08-24T05:08:08.108712+00:00 | 2022-08-24T05:08:08.108753+00:00 | 105 | false | ```\nclass Solution {\npublic:\n long long kSum(vector<int>& nums, int k) {\n long long sum = 0;\n for (auto &n : nums) {\n if (n >= 0)\n sum += n;\n else\n n = abs(n);\n }\n // get sum of all possitive integers in variable sum\n // later reverse all negative numbers to possitive as removing them can help \n \n // sort helps all the smaller numbers to be tried first so as to reduce total sum\n // as small as possible\n sort(nums.begin(),nums.end()); \n priority_queue<pair<long long, int>> pq;\n \n pq.push({sum-nums[0],0});\n vector<long long> result;\n result.push_back(sum); // first largest sum we can enter\n // if no possitive integer then inserting 0 is also fine as \n // empty sequence is also a subsequence\n \n int n = nums.size();\n while(result.size() < k) {\n auto [sum,index] = pq.top();\n result.push_back(sum);\n pq.pop();\n // there are 2 possiblitity for current index\n // extend the sequence with current index\n // or all the sequence which earlier ended with index \n // remove than element and insert this index\n // this cummunlative relation so it will have all cases\n // for e.g combination of {a,b} with all sequence ending with b will\n // be {b},{a,b}\n // so now c will extenend sequence first so it will {b,c},{a,b,c}\n // by remvoing b and extending sequence from it will be {c}, {a,c} \n // thus covering all sequences which ends with c\n // i.e {b,c},{a,b,c},{c}, {a,c} \n if (index+1 < n) {\n pq.push({sum-nums[index+1],index+1}); // extending the sequence\n pq.push({sum+nums[index]-nums[index+1], index+1}); // removing the earlier number and adding the current number\n }\n }\n return result[k-1];\n }\n};\n``` | 0 | 0 | [] | 0 |
find-the-k-sum-of-an-array | Rust Sort & BinaryHeap | rust-sort-binaryheap-by-xiaoping3418-od14 | ~~~\nuse std::collections::BinaryHeap;\n\nimpl Solution {\n pub fn k_sum(nums: Vec, k: i32) -> i64 {\n let mut sum = 0i64;\n let n = nums.len() | xiaoping3418 | NORMAL | 2022-08-22T12:04:39.135165+00:00 | 2022-08-22T12:04:39.135202+00:00 | 80 | false | ~~~\nuse std::collections::BinaryHeap;\n\nimpl Solution {\n pub fn k_sum(nums: Vec<i32>, k: i32) -> i64 {\n let mut sum = 0i64;\n let n = nums.len();\n let mut data = vec![];\n \n for a in nums { \n if a > 0 { sum += a as i64; }\n data.push(i64::abs(a as i64));\n }\n data.sort();\n \n let mut pq = BinaryHeap::<(i64, usize)>::new();\n let mut ret = sum;\n \n pq.push((-data[0], 0));\n for _ in 2..=k {\n let (val, i) = pq.pop().unwrap(); \n ret = sum + val;\n if i == n - 1 { continue; }\n pq.push((val - data[i + 1], i + 1));\n pq.push((val + data[i] - data[i + 1], i + 1));\n }\n \n ret\n }\n}\n~~~ | 0 | 0 | ['Sorting', 'Rust'] | 0 |
find-the-k-sum-of-an-array | [Python]Fast and Easy solution.(Runtime:87.5%,Memory:87.5%) | pythonfast-and-easy-solutionruntime875me-cdr0 | **Solution\n\n\tclass Solution:\n\t\tdef kSum(self, nums: List[int], k: int) -> int:\n\t\t\tle = len(nums)\n\n\t\t\tnums = [0] + sorted(nums,key = abs)\n\n\t\t\ | p147896325p | NORMAL | 2022-08-22T09:31:38.840677+00:00 | 2022-08-22T09:31:38.840703+00:00 | 288 | false | **Solution\n\n\tclass Solution:\n\t\tdef kSum(self, nums: List[int], k: int) -> int:\n\t\t\tle = len(nums)\n\n\t\t\tnums = [0] + sorted(nums,key = abs)\n\n\t\t\theap = [(-sum(num for num in nums if num > 0), 0)]\n\t\t\tfor _ in range(k):\n\t\t\t\ttmp = heappop(heap)\n\t\t\t\ti_sum = -tmp[0]\n\t\t\t\tpos = tmp[1]\n\n\t\t\t\tif pos < le:\n\t\t\t\t\t# remove next\n\t\t\t\t\tval = i_sum - abs(nums[pos + 1])\n\t\t\t\t\theappush(heap, (-val, pos + 1))\n\t\t\t\t\tif pos:\n\t\t\t\t\t\tval = i_sum + abs(nums[pos]) - abs(nums[pos + 1])\n\t\t\t\t\t\theappush(heap, (-val, pos + 1))\n\n\t\t\treturn i_sum\n | 0 | 0 | ['Python'] | 0 |
find-the-k-sum-of-an-array | Python, 3 lines for fun! | python-3-lines-for-fun-by-404akhan-ydgs | Just for fun, condensed solution in 3 lines! It sometimes TLs, should run several times.\n\nBasically, solution is similar as everyone\'s priority queue observa | 404akhan | NORMAL | 2022-08-22T08:49:05.431771+00:00 | 2022-08-22T08:49:05.431802+00:00 | 107 | false | Just for fun, condensed solution in 3 lines! It sometimes TLs, should run several times.\n\nBasically, solution is similar as everyone\'s priority queue observation, Dijkstra logic. Except since you keep track of only 2000 nodes, you can manually append new possibilities to the `pq` list and sort it again.\n\nTime complexity: N * log N + K ^ 2 * log K\n\n```\nclass Solution:\n def kSum(self, nums, k):\n pos_sum, pos, pq = sum(t for t in nums if t > 0), sorted(abs(t) for t in nums), [(0, -1)]\n for ct in range(k - 1): pq = sorted(pq[1:] + [(pq[0][0] + pos[i], i) for i in range(pq[0][1] + 1, min(pq[0][1] + k - ct, len(nums)))])[:k - ct]\n return pos_sum - pq[0][0]\n``` | 0 | 0 | [] | 0 |
find-the-k-sum-of-an-array | Rust idiomatic solution | binary heap | rust-idiomatic-solution-binary-heap-by-p-uuhp | \nuse std::collections::BinaryHeap;\nuse std::cmp::Reverse;\nimpl Solution {\n pub fn k_sum(mut nums: Vec<i32>, mut k: i32) -> i64 {\n let mut sum = n | pierrewang | NORMAL | 2022-08-22T08:20:21.267449+00:00 | 2022-08-22T08:20:21.267479+00:00 | 58 | false | ```\nuse std::collections::BinaryHeap;\nuse std::cmp::Reverse;\nimpl Solution {\n pub fn k_sum(mut nums: Vec<i32>, mut k: i32) -> i64 {\n let mut sum = nums.iter().filter(|&&v| v > 0).map(|&v| v as i64).sum::<i64>();\n let mut nums: Vec<_> = nums.into_iter().map(|v| v.abs()).collect();\n nums.sort_unstable();\n \n let mut curr = 0;\n let mut min_heap = BinaryHeap::new();\n min_heap.push(Reverse((nums[0] as i64, 0)));\n k -= 1;\n while !min_heap.is_empty() && k > 0 {\n let Reverse((val, idx)) = min_heap.pop().unwrap();\n curr = val;\n if idx + 1 < nums.len() {\n min_heap.push(Reverse((val + nums[idx + 1] as i64, idx + 1)));\n min_heap.push(Reverse((val - nums[idx] as i64 + nums[idx + 1] as i64, idx + 1)));\n }\n k -= 1;\n }\n sum - curr\n }\n}\n``` | 0 | 0 | ['Rust'] | 0 |
find-the-k-sum-of-an-array | [C++] Explained heuristic DFS 296ms faster than 77% | c-explained-heuristic-dfs-296ms-faster-t-xbv0 | Firstly, sum up all positive number as base, sort numbers as abs value and try to search a combination of numbers to subtract from base.\nObserver that 2^11 = 2 | mopriestt | NORMAL | 2022-08-22T07:47:26.170274+00:00 | 2022-08-22T07:52:11.074718+00:00 | 60 | false | Firstly, sum up all positive number as **base**, sort numbers as abs value and try to search a combination of numbers to subtract from **base**.\nObserver that 2^11 = 2048 >= 2000 so we will never pick more than 11 elements\n\nThen, loop through how many numbers we will pick, use a stack to maintain the combinations. Whenever the stack size is greater than k, pop until the size becomes k.\n\nA very important pruning:\nIf we have **x** numbers left to pick, and number in currenct index is **v**, when stack already has k elements, then **x * v < pq.top()** must be satisified, otherwise it\'s not possible to get a better solution in this branch.\n\n```\nclass Solution {\npublic:\n priority_queue<long long> candidates;\n int _k;\n \n void dfs(vector<int> &a, int index, int pick, long long val) {\n if (pick == 0) {\n candidates.push(val);\n while (candidates.size() > _k) candidates.pop();\n return;\n }\n if (index >= a.size()) return;\n // Important prune!!\n if (candidates.size() == _k && (long long) pick * a[index] + val >= candidates.top()) return;\n \n dfs(a, index + 1, pick - 1, val + a[index]);\n dfs(a, index + 1, pick, val);\n }\n \n long long kSum(vector<int>& a, int k) {\n long long base = 0;\n _k = k;\n for (int i = 0; i < a.size(); i ++) {\n if (a[i] > 0) base += a[i];\n else a[i] = -a[i];\n }\n sort(a.begin(), a.end());\n \n candidates.push(0);\n // Only select one\n for (int i = 0; i < k && i < a.size(); i ++) candidates.push(a[i]);\n \n for (int pick = 2; pick <= 10; pick ++) {\n dfs(a, 0, pick, 0LL);\n }\n \n return base - candidates.top();\n }\n};\n```\n\nAn even greedier pruning strategy is to use the interval sum instead of **x * v**. | 0 | 0 | [] | 0 |
find-the-k-sum-of-an-array | Two way Merge || C ++ || O(max(nlogn, k^2)) | two-way-merge-c-omaxnlogn-k2-by-rebe1li0-4zv2 | \nclass Solution {\npublic:\n typedef long long LL;\n long long kSum(vector<int>& nums, int k) {\n LL sum = 0;\n vector<int> pos;\n f | rebe1li0n | NORMAL | 2022-08-22T07:23:39.763908+00:00 | 2022-08-22T07:24:15.886679+00:00 | 57 | false | ```\nclass Solution {\npublic:\n typedef long long LL;\n long long kSum(vector<int>& nums, int k) {\n LL sum = 0;\n vector<int> pos;\n for(auto x : nums){\n if(x > 0){\n sum += x;\n pos.push_back(-x);\n }else{\n pos.push_back(x);\n }\n }\n sort(pos.begin(), pos.end(), greater<int>());\n if(pos.size() > k) pos.erase(pos.begin() + k, pos.end()); //accelerate 1;\n vector<LL> a(1, sum), b;\n \n for(auto x : pos){\n b.clear();\n int i = 0, j = 0, n = a.size(), m = min(k, n * 2), cnt = 0;\n while(i < n && j < n && cnt < m){ //accelerate 2;\n if(a[i] > a[j] + x) b.push_back(a[i ++]), cnt ++;\n else b.push_back(a[j ++] + x), cnt ++;\n } \n while(i < n && cnt < m) b.push_back(a[i ++]), cnt ++;\n while(j < n && cnt < m) b.push_back(a[j ++] + x), cnt ++;\n a = b; \n }\n\n return a[k - 1];\n }\n};\n``` | 0 | 0 | [] | 0 |
find-the-k-sum-of-an-array | python heap | python-heap-by-sh1v2m-53hc | ```\nclass Solution:\n def kSum(self, nums: List[int], k: int) -> int:\n max_sum = sum([n for n in nums if n > 0])\n ns = sorted([abs(n) for n | sh1v2m | NORMAL | 2022-08-22T06:18:42.884699+00:00 | 2022-08-22T06:18:42.884740+00:00 | 191 | false | ```\nclass Solution:\n def kSum(self, nums: List[int], k: int) -> int:\n max_sum = sum([n for n in nums if n > 0])\n ns = sorted([abs(n) for n in nums])\n \n h = [(ns[0], 0)]\n val = 0\n for _ in range(k - 1):\n val, i = heapq.heappop(h)\n if i < len(ns) - 1:\n heapq.heappush(h, (val + ns[i + 1], i + 1))\n heapq.heappush(h, (val + ns[i + 1] - ns[i], i + 1))\n return max_sum - val | 0 | 0 | ['Greedy', 'Heap (Priority Queue)', 'Python'] | 0 |
find-the-k-sum-of-an-array | C++ | Build a maxHeap storing the subset sums as a tree (with clear explanations) | c-build-a-maxheap-storing-the-subset-sum-j32c | After the contest I came here looking for some insights. This is the same method as suggested by other top posts. I had difficulty understanding how the min hea | baihuaxie | NORMAL | 2022-08-22T03:50:55.702299+00:00 | 2022-08-22T03:53:19.549142+00:00 | 53 | false | After the contest I came here looking for some insights. This is the same method as suggested by other top posts. I had difficulty understanding how the min heap method was constructed after reading other posts, in particular why there were two pushes for each node; so I added some explanations here. Two references: [1](https://leetcode.com/problems/find-the-k-sum-of-an-array/discuss/2457783/c%2B%2B-priority-queue-with-explanation-on-the-required-knowledge), [2](https://stackoverflow.com/questions/33219712/find-k-th-minimum-sum-of-every-possible-subset/33220735#33220735).\n\nThe intuition behind the solution is a systematic method to search through all of the `2^n` possible subsequences i.e. all subsets in a binary tree structure. Take the example of `[2, 4, -2]`, we can do it in the following way: we pick the first element as the first node, then we add two child nodes by the following two choices:\n1. replace it by the 2nd node;\n2. add the 2nd node;\n\nWith the above procedure, we get the following binary tree for all the subsets:\n```\n// tree 1\n2_____\n| \\\n4 __ 2,4________\n| \\ | \\\n-2 4,-2 2,-2 2,4,-2\n```\nFor the `i`-th node, its left child is always to replace the `i`-th element by the `i+1`-th element, and its right child is always to just add the `i+1`-th element. In this way the binary tree would contain all `2^n-1` possible subsets as its nodes, with one more subset being the empty set. As a reference, below is the same tree as above, but storing the corresponding subset\' element indices instead of the elements themselves:\n```\n// tree 2\n0_____\n| \\\n1 __ 0,1________\n| \\ | \\\n2 1,2 0,2 0,1,2\n```\n\nThe above trees are keyed by the index of the corresponding elements in the original array; this is not useful for the problem. Another problem is that the complexity of building the full tree is still exponential, and we need at most log-linear complexity to solve the problem. So one way is to make sure that the nodes with the larger sum values should be added first, in this way we only need to add `k` nodes into the tree and the tree would in fact beome a `maxHeap`. Since a heap insert costs `O(log k)` where `k` is the number of nodes, the time complexity will be `O(k log k)`.\n\nHere we repeat the previous procedure to buid the binary tree but this time keyed by subset sums and in descending order:\n1) the largest sum value `maxSum` will be equal to the sum of all non-negative elements in the original array; this value can be pre-computed;\n2) the 2nd largest sum value will be `max(maxSum - a, maxSum + x)`, where `a` is the smallest positive value and `x` is the largest negative value (largest in the sense that it has the smallest absolute value) in the original array, respectively; if we first convert the array `nums` to include all absolute values, then the expression can simply be `maxSum - a`; this will be the first node in the tree;\n3) with the previous construction procedure, we now add two child nodes; for the left child node, we replace `a` with the next smallest element in `nums` e.g. `b` (note: `b>a`), so we insert `maxSum - b`; for the right child node, we subtract both `a` and `b` so we insert `maxSum - (a+b)`;\n4) next we need to subtracct the next smallest element, say `c`; a problem arises: we have no idea if `c` is larger or smaller than `a+b`, so we won\'t know which node comes first in the final order; this is why we need to maintain the tree as a max heap so that all the inserted nodes will be ordered properly;\n\nIn the previous example, the `maxSum` is 6=2+4. The original `nums` will need to store all absolute values and sorted in ascending order, so `[2,4,-2]` should become `[2,2,4]`. With the above procedure, the max heap for the previous example, storing subset sums, will be as follows:\n```\n// tree 3\n4_____\n| \\\n4 __ 2_______\n| \\ | \\\n2 0 0 -2\n```\nNote that the corresponding tree storing element indices will be exactly the same as tree 2. For instance the first node `4=maxSum-nums[0]=6-2=4`, etc.. Here already we can get the subset sums ordered as `6,4,4,2,2,0,0,-2`. All that remains is to limit the number of nodes inserted to the maxHeap to be the first `k-1` nodes (the first node is implicitly `maxSum` so not inserted into the heap), this can be done by using a simple counter.\n\nBelow is the accepted code in C++:\n```\nclass Solution {\npublic:\n long long kSum(vector<int>& nums, int k) {\n \n int n = nums.size();\n \n // compute the maxSum = sum of all positive values in `nums`\n // if nums[i] is negative convert it to absolute value\n long long maxSum = 0;\n for (int i = 0; i < n; ++i) {\n if (nums[i] >= 0)\n maxSum += nums[i];\n else\n nums[i] = abs(nums[i]);\n }\n \n // sort `nums` by ascending order\n // takes O(n log n)\n sort(nums.begin(), nums.end());\n \n // the maxHeap or max priority queue implements the binary tree keyed by\n // the sum value of the subset\n // each node has two possible children\n // 1) replaces nums[i] with nums[i+1], so childnode.val = node.val + nums[i] - nums[i+1]\n // 2) add nums[i+1] to be subtracted too, so childnode.val = node.val - nums[i+1]\n // obviously the index `i` would also need to be stored in the maxHeap along w/t the sum\n // values, so the elements in the heap is {sum, index}\n // only first k nodes are needed, for each node the heapify operation takes log k\n // so it takes O(k log k) time complexity\n priority_queue<pair<long long, int>> pq;\n pq.push({maxSum - nums[0], 0});\n\n // note that first node is always to subtract zero i.e. the sum is maxSum itself\n // so only need to insert/pop k-1 nodes\n int count = 0;\n long long ans;\n while (!pq.empty() && count < k-1) {\n auto u = pq.top();\n pq.pop();\n long long sub = u.first;\n int idx = u.second;\n count++;\n ans = sub;\n\t\t\t// make sure no overflow\n if (idx < n-1) {\n // 1. replace nums[idx] and subtract nums[idx+1]\n pq.push({sub + nums[idx] - nums[idx+1], idx+1});\n // 2. keep nums[idx] and further subtract nums[idx+1]\n pq.push({sub - nums[idx+1], idx+1});\n }\n }\n \n // if k==1 then return maxSum directly, no subtraction\n // else return the (k-1)-th subtracted value which is just ans from the while-loop\n return k == 1 ? maxSum : ans;\n }\n};\n```\n\nTime complexity: 1) the heap operations take `O(k log k)` for there are `k` nodes in the heap and each heapify i.e. `push` operation takes log time; 2) the array needs to be sorted, which usually takes `O(n log n)` where `n` is the array size. So the total time complexity is `O(n log n + k log k)`.\nSpace complexity: needs to store the `k` nodes in the heap, so takes up `O(k)` additional space.\n\n\n\n\n\n\n\n\n\n\n | 0 | 0 | [] | 0 |
find-the-k-sum-of-an-array | C++ | priority_queue | c-priority_queue-by-joey-q0sl | Got TLEs for enumerating all cases.\nUse this case generator instead:\n1. branch one: including element in index i\n2. branch two: excluding element in index i\ | joey___ | NORMAL | 2022-08-22T02:28:00.350411+00:00 | 2022-08-22T02:28:00.350453+00:00 | 43 | false | Got TLEs for enumerating all cases.\nUse this case generator instead:\n1. branch one: including element in index i\n2. branch two: excluding element in index i\nwith those two branches, we are able to generate all cases.\n\n```\n#define pls pair<long long, int>\n\nclass Solution {\npublic:\n long long kSum(vector<int>& nums, int k) {\n long long sum = 0;\n int len = nums.size();\n for (int i = 0; i < len; ++i) {\n if (nums[i] > 0) {\n sum += nums[i];\n }\n nums[i] = (int)(abs(nums[i]));\n }\n auto cmp = [](const pls &lhs, const pls &rhs) {\n return lhs.first > rhs.first;\n };\n sort(nums.begin(), nums.end());\n priority_queue<pls, vector<pls>, greater<>> que;\n que.push({nums[0], 0});\n long long minus = 0;\n while (--k > 0) {\n auto front = que.top();\n que.pop();\n minus = front.first;\n if (front.second < len - 1) {\n que.push({front.first - nums[front.second] + nums[front.second + 1], front.second + 1});\n que.push({front.first + nums[front.second + 1], front.second + 1});\n }\n }\n return sum - minus;\n }\n};\n``` | 0 | 0 | [] | 0 |
find-the-k-sum-of-an-array | [CPP]: solution with explanation | cpp-solution-with-explanation-by-a1exreb-nj6v | Based on others suggestions. Check the explanation here: https://math.stackexchange.com/questions/89419/algorithm-wanted-enumerate-all-subsets-of-a-set-in-order | a1exrebys | NORMAL | 2022-08-21T22:08:44.452755+00:00 | 2022-08-21T22:25:13.540914+00:00 | 126 | false | Based on others suggestions. Check the explanation here: https://math.stackexchange.com/questions/89419/algorithm-wanted-enumerate-all-subsets-of-a-set-in-order-of-increasing-sums\n```\nlong long kSum(vector<int>& nums, int k) {\n\tlong long maxsum = 0;\n\tfor (auto& n : nums) {\n\t\tif (n >= 0) maxsum += n;\n\t\telse n = -n;\n\t}\n\tif (k == 1) return maxsum;\n\tsort(nums.begin(), nums.end());\n\tvector<long long> candidates;\n\tusing ip = std::pair<long long, int>;\n\tpriority_queue<ip, vector<ip>, greater<ip>> pq;\n\tpq.push({nums[0], 0});\n\twhile (!pq.empty() && candidates.size() < k - 1) { \n\t\tauto [el, ind] = pq.top(); pq.pop();\n\t\tcandidates.push_back(el);\n\t\tif (ind < nums.size() - 1) {\n\t\t\tpq.push({el + nums[ind + 1], ind + 1});\n\t\t\tpq.push({nums[ind + 1] + (el - nums[ind]), ind + 1});\n\t\t}\n\t}\n\treturn maxsum - candidates[k - 2];\n}\n``` | 0 | 0 | ['C++'] | 0 |
find-the-k-sum-of-an-array | [C++] Priority queue | c-priority-queue-by-phi9t-f7y6 | We know the max sum is the sum of all positive values.\nWith the max sum as the starting point, the problem (to find any subsequence sum) becomes to remove any | phi9t | NORMAL | 2022-08-21T16:30:59.556220+00:00 | 2022-08-21T16:32:14.769178+00:00 | 71 | false | We know the max sum is the sum of all positive values.\nWith the max sum as the starting point, the problem (to find any subsequence sum) becomes to remove any subset `|val| : nums`. \nFor any particular sum, we shall proceed by the absolute values in ascending order. \n\nReference\nhttps://leetcode.com/problems/find-the-k-sum-of-an-array/discuss/2456716/Python3-HeapPriority-Queue-O(NlogN-%2B-klogk)\n\n```\nclass Solution {\n using integer = long long;\n static constexpr integer kZero = 0;\n\n enum Indexing : int {\n VALUE = 0, INDEX \n };\n \npublic:\n long long kSum(vector<int>& nums, int k) { \n std::vector<integer> vals_abs;\n vals_abs.reserve(nums.size());\n integer total = kZero;\n for (const integer val : nums) {\n vals_abs.push_back(std::abs(val));\n total += std::max(kZero, val);\n }\n std::sort(vals_abs.begin(), vals_abs.end());\n std::priority_queue<\n integer, \n std::vector<integer>, \n std::greater<integer>> vals_ord;\n vals_ord.push(total);\n std::priority_queue<std::pair<integer, int>> records_ord;\n records_ord.push({\n total - vals_abs[0],\n 0\n });\n \n while (vals_ord.size() < k) {\n assert(!records_ord.empty());\n const auto record = records_ord.top();\n records_ord.pop();\n const integer val = std::get<Indexing::VALUE>(record);\n vals_ord.push(val);\n const int idx = std::get<Indexing::INDEX>(record);\n if (idx + 1 < vals_abs.size()) {\n records_ord.push({\n val - vals_abs[idx + 1],\n idx + 1\n });\n records_ord.push({\n val + vals_abs[idx] - vals_abs[idx + 1],\n idx + 1\n });\n }\n }\n \n return vals_ord.top();\n }\n};\n``` | 0 | 0 | [] | 0 |
find-the-k-sum-of-an-array | [Java] PriorityQueue || MaxSum ➖ Kth Smallest Comb Sum | java-priorityqueue-maxsum-kth-smallest-c-66nu | \nclass Solution {\n public long kSum(int[] nums, int k) {\n long maxSum = 0L;\n int n = nums.length;\n for(int i = 0; i < n; i++){\n | cooper-- | NORMAL | 2022-08-21T15:33:43.732415+00:00 | 2022-08-21T15:34:09.401463+00:00 | 118 | false | ```\nclass Solution {\n public long kSum(int[] nums, int k) {\n long maxSum = 0L;\n int n = nums.length;\n for(int i = 0; i < n; i++){\n if(nums[i] < 0){\n nums[i] = -nums[i];\n }else{\n maxSum += nums[i];\n }\n }\n \n Arrays.sort(nums);\n\n // smallest comb to remove\n PriorityQueue<long[]> pq = new PriorityQueue<long[]>((a, b) -> (a[0] > b[0] ? 1 : a[0] == b[0] ? 0 : -1));\n pq.offer(new long[]{nums[0], 0});\n List<Long> removedCombo = new ArrayList<>();\n \n if(k == 1) return maxSum;\n \n while(!pq.isEmpty() && k > 1){\n long[] curr = pq.poll();\n long value = curr[0];\n long idx = curr[1];\n removedCombo.add(value);\n \n if(idx + 1 < n){\n pq.offer(new long[]{value + nums[(int)idx + 1], idx + 1});\n pq.offer(new long[]{value - nums[(int)idx] + nums[(int)idx + 1], idx + 1});\n }\n k--;\n }\n \n return maxSum - removedCombo.get(removedCombo.size() - 1);\n \n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
find-the-k-sum-of-an-array | C++ Easy solution | c-easy-solution-by-kunj_m-nrug | class Solution {\npublic:\n \n #define ll long long\n #define pp pair\n \n long long kSum(vector& A, int k) {\n \n | kunj_m | NORMAL | 2022-08-21T12:56:16.212677+00:00 | 2022-08-21T12:56:16.212732+00:00 | 84 | false | **class Solution {\npublic:\n \n #define ll long long\n #define pp pair<long long, int>\n \n long long kSum(vector<int>& A, int k) {\n \n int n = A.size();\n \n vector<ll> sub;\n \n ll mx = 0;\n \n \n for(int i =0; i<n; i++){\n \n if(A[i]>=0){\n mx+=A[i];\n } else{\n \n A[i] = abs(A[i]);\n }\n }\n \n sort(A.begin(), A.end());\n \n priority_queue<pp ,vector<pp>, greater<pp>> q;\n \n q.push({A[0], 0});\n \n while(q.size()){\n \n auto it = q.top(); q.pop();\n \n ll val = it.first;\n int ind = it.second;\n \n sub.push_back(val);\n \n if(sub.size()>=k-1) break;\n \n if(ind<n-1){\n \n q.push({val+(ll)A[ind+1], ind+1});\n q.push({(ll)A[ind+1]+(val-(ll)A[ind]), ind+1});\n }\n }\n \n vector<ll> ans;\n ans.push_back(mx);\n \n for(int i =0; i<sub.size(); i++){\n ans.push_back(mx-sub[i]);\n }\n \n return ans[k-1];\n }\n};**\n\nExplantion\n\nwe need find max sum (that is greatest) from array so 1st we add all positive number. Then whatt will be the next greatest Number so for this I need to subtract abs(-ve Num) or smallest positive number. | 0 | 0 | ['C', 'Heap (Priority Queue)'] | 0 |
find-the-k-sum-of-an-array | Video Explanation (with Intuition of every step) | video-explanation-with-intuition-of-ever-cfxx | https://www.youtube.com/watch?v=VknH84HSeNM | codingmohan | NORMAL | 2022-08-21T11:12:50.423282+00:00 | 2022-08-21T16:26:42.444862+00:00 | 54 | false | https://www.youtube.com/watch?v=VknH84HSeNM | 0 | 0 | ['Breadth-First Search', 'Heap (Priority Queue)'] | 0 |
find-the-k-sum-of-an-array | [C++] Max Heap (Explained 🙂) | c-max-heap-explained-by-mjustboring-r841 | \n\u2022 Find sum of +ve numbers. (Max Sum)\n\u2022 Prepare a sorted array of absolute values of the given array\n\u2022 push(sum - a[0], 0) to a max heap.\n\u2 | mjustboring | NORMAL | 2022-08-21T10:24:11.484437+00:00 | 2022-08-21T17:12:25.527378+00:00 | 86 | false | \n\u2022 Find sum of +ve numbers. (Max Sum)\n\u2022 Prepare a sorted array of absolute values of the given array\n\u2022 push(sum - a[0], 0) to a max heap.\n\u2022 for k-1 iterations do\n pop the top from heap (say {sum, i})\n push(sum - a[i+1] + a[i], i+1)\n push(sum - a[i+1], i+1)\n \n> Basically we are simulating the knapsack procedure iteratively.\n\n##### Example\n\n```\nQ: a[] = {2, -2, 4}, k = 5\n\nMAX_SUM = 6 {2, 4}\nABS_ARR = {2, 2, 4} \n\n(6-2,0)\n(4,0) | (4,1) (2,1)\n(4,1) | (2,2) (2,1) (0,2)\n(2,2) | (2,1) (0,2)\n(2,1) | (0,2) (0,2) (-2,2)\n\nANS = 2\n```\n</br>\n\n##### C++ Solution\n```\nstruct Solution {\n \n int n, i;\n long long ans = 0;\n priority_queue<pair<long long, int>> q;\n \n long long kSum(vector<int> &a, int k) {\n \n n = a.size();\n \n for (auto &x : a) {\n if (x >= 0) ans += x;\n else x = -x;\n }\n \n sort(a.begin(), a.end());\n q.emplace(ans - a[0], 0);\n \n while (--k) {\n tie(ans, i) = q.top();\n q.pop();\n \n if (i+1 < n) {\n q.emplace(ans - a[i+1] + a[i], i+1);\n q.emplace(ans - a[i+1], i+1);\n }\n }\n \n return ans;\n }\n};\n```\nTC: O(N\u2022Log(N) + K\u2022Log(K))\nSC: O(K) | 0 | 0 | ['C', 'Heap (Priority Queue)'] | 0 |
find-the-k-sum-of-an-array | [C++] Priority Queue Solution with Explanation | c-priority-queue-solution-with-explanati-98bi | Idea:\n1. Find the largest summation of this array, which is sum of all positive numbers.\n2. There are two types of operation to get next number:\n\ta. Remove | acebenson0704 | NORMAL | 2022-08-21T09:50:47.744687+00:00 | 2022-08-21T09:51:43.572156+00:00 | 59 | false | Idea:\n1. Find the largest summation of this array, which is sum of all positive numbers.\n2. There are two types of operation to get next number:\n\ta. Remove one positive number from largest number.\n\tb. Add a new negtive number\n3. Repeat step2 k times.\n```c++\n/*\nTake [2, 4, -3] as example\nmax: 6 (2 + 4)\na. Remove one positive number from largest number: 6 - 2 = 4\nb. Add a new negtive number: 6 + (-3) = 3\n*/\n```\nIf we convert all positive number in nums to negative, and sort it.\nStep 2.a and 2.b can be consider to the same operation.\n```c++\n/*\noriginal array: [2, 4, -3]\nconverted and sorted array: [-2, -3, -4]\nThe following list all combinations.\n6 = 6 // 2 + 4\n6 + (-2) = 4 // 4\n6 + (-3) = 3 // 2 + 4 + (-3)\n6 + (-4) = 2 // 2\n6 + (-2) + (-3) = 1 // 4 + (-3)\n6 + (-2) + (-4) = 0 // x\n6 + (-3) + (-4) = -1 // 2 + (-3)\n6 + (-2) + (-3) + (-4) = -3 // -3\n*/\n```\nWe can see there are 2^3 = 8 conditions. (all subsets of the sorted array)\nBut we don\'t need to list all subset and sort it to get kth item.\n\nWe can use priority queue instead.\nIn each time we pop from priority queue\nWe add two new elements:\n1. Add next number\n2. Remove current number and add next number\n\n```c++\n/*\n0.\npush {4, 0} // 6 + nums[0]\n1. \n* pop {4, 0} // 6 + nums[0]\n* push {1, 1} // 6 + nums[0] + nums[1]\n* push {3, 1} // 6 + nums[1]\n2. \n* pop {3, 1}\n3. ...\n*/\n```\n\n\n```c++\ntypedef pair<long long, int> pli;\nclass Solution {\npublic:\n long long kSum(vector<int>& nums, int k) {\n int n = nums.size();\n long long maxSum = 0;\n for (long long i=0; i<n; ++i) {\n if (nums[i] > 0) {\n maxSum += nums[i];\n nums[i] *= -1;\n }\n }\n \n long long res = maxSum;\n sort(nums.begin(), nums.end(), greater<int>());\n \n priority_queue<pli> pq;\n pq.push({maxSum + nums[0], 0});\n \n for (int i=0; i<k-1; ++i) {\n auto [val, idx] = pq.top(); pq.pop();\n res = val;\n if (idx+1 < n) {\n pq.push({val - nums[idx] + nums[idx+1], idx+1});\n pq.push({val + nums[idx+1], idx+1});\n }\n }\n \n return res;\n }\n};\n``` | 0 | 0 | ['C'] | 0 |
find-the-k-sum-of-an-array | Please guide me on how to optimize recursive solution | please-guide-me-on-how-to-optimize-recur-aaiz | Can we optimise a recursive solution. I am getting TLE as this has huge time complexity.\n\ncpp\nclass Solution {\npublic:\n\tvoid solve(int ind, long long sum, | iamshubhamj | NORMAL | 2022-08-21T08:07:50.003413+00:00 | 2022-08-21T08:07:50.003452+00:00 | 189 | false | Can we optimise a recursive solution. I am getting TLE as this has huge time complexity.\n\n```cpp\nclass Solution {\npublic:\n\tvoid solve(int ind, long long sum, vector<int> &nums, vector<long long> &ans, int n, int k) {\n\t\tif(ind < 0) {\n\t\t\tans.push_back(sum);\n\t\t\treturn;\n\t\t}\n\n\t\tsolve(ind-1, sum + nums[ind], nums, ans, n, k); // take\n\t\tsolve(ind-1, sum, nums, ans, n, k); // notake\n\t}\n\n long long kSum(vector<int>& nums, int k) {\n\t\tint n = nums.size();\n\t\tvector<long long> ans;\n\n\t\tsolve(n-1, 0, nums, ans, n, k);\n\t\tsort(ans.rbegin(), ans.rend());\n\n\t\treturn ans[k-1];\n }\n};\n```\n\nLet me know how can we optimise it. Thanks in advance. | 0 | 0 | ['Dynamic Programming', 'Recursion'] | 1 |
find-the-k-sum-of-an-array | easy short efficient clean code | easy-short-efficient-clean-code-by-maver-xvji | \nclass Solution {\n typedef long long ll;\n typedef pair<ll, ll> pi;\npublic:\n long long kSum(vector<int>& v, int k) {\n ll sz = v.size(), ans | maverick09 | NORMAL | 2022-08-21T07:55:45.340941+00:00 | 2022-08-21T07:55:45.340981+00:00 | 77 | false | ```\nclass Solution {\n typedef long long ll;\n typedef pair<ll, ll> pi;\npublic:\n long long kSum(vector<int>& v, int k) {\n ll sz = v.size(), ans = 0;\n for (auto& it : v) {\n if (it > -1) {\n ans += it;\n }\n it = abs(it);\n }\n sort(v.begin(), v.end());\n priority_queue<pi>pq;\n pq.push({ ans - v[0],0 });\n while (--k) {\n pi p = pq.top();\n pq.pop();\n ans = p.first;\n if (p.second < sz - 1) {\n pq.push({ p.first - v[p.second + 1],p.second + 1 });\n pq.push({ p.first - v[p.second + 1] + v[p.second],p.second + 1 });\n }\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['C', 'Sorting', 'Heap (Priority Queue)'] | 0 |
find-the-k-sum-of-an-array | Merge sorted lists | merge-sorted-lists-by-wddd-n349 | This problem is more or less similar to the "Merge sorted lists" problem. https://leetcode.com/problems/merge-k-sorted-lists/\n\nSay the nums array is [1,2,3,4, | wddd | NORMAL | 2022-08-21T07:36:13.815021+00:00 | 2022-08-21T07:36:13.815072+00:00 | 60 | false | This problem is more or less similar to the "Merge sorted lists" problem. https://leetcode.com/problems/merge-k-sorted-lists/\n\nSay the `nums` array is `[1,2,3,4,5]`, then we have 5 sorted lists (desending order) for the subsequence sums:\n\n```\nsum-1, sum-1-2, sum-1-2-3, sum-1-2-3-4, sum-1-2-3-4-5\nsum-2, sum-2-3, sum-2-3-4, sum-2-3-4-5\nsum-3, sum-3-4, sum-3-4-5\nsum-4, sum-4-5\nsum-5\n```\n\nNow, in order to find the kth largest subsequence sum, we just need to use a heap to merge the sorted lists.\n\nFor me, the tricky part of this problem is that the input array contains both positive and negative numbers, and we need to combine them using abs.\n\nThe code is simpler because we don\'t really need to initialize the heap with 5 numbers.\n\n```\n /*\n Runtime: 95 ms, faster than 100.00% of Java online submissions for Find the K-Sum of an Array.\n Memory Usage: 87.6 MB, less than 33.33% of Java online submissions for Find the K-Sum of an Array.\n */\n public long kSum(int[] nums, int k) {\n int[] abs = new int[nums.length];\n long max = 0;\n\n for (int i = 0; i < nums.length; i++) {\n if (nums[i] >= 0) {\n abs[i] = nums[i];\n max += nums[i];\n } else {\n abs[i] = -nums[i];\n }\n }\n\n if (k == 1) {\n return max;\n }\n\n Arrays.sort(abs);\n\n Queue<long[]> queue = new PriorityQueue<>(Comparator.comparingLong(l -> -l[0]));\n queue.add(new long[] {max - abs[0], 0});\n\n while (k > 2) {\n long[] curr = queue.poll();\n\n if (curr[1] + 1 < abs.length) {\n queue.add(new long[] {curr[0] + abs[(int) curr[1]] - abs[(int) (curr[1] + 1)], curr[1] + 1});\n queue.add(new long[] {curr[0] - abs[(int) (curr[1] + 1)], curr[1] + 1});\n }\n\n k--;\n }\n\n return queue.poll()[0];\n }\n``` | 0 | 0 | [] | 0 |
find-the-k-sum-of-an-array | My Solution | my-solution-by-hope_ma-qb3r | \n/**\n * Time Complexity: O(n_nums * log(n_nums) + k * log(k)), where `n_nums` is the length of the vector `nums`\n * Space Complexity: O(k)\n */\nclass Soluti | hope_ma | NORMAL | 2022-08-21T07:30:21.401503+00:00 | 2022-08-21T07:30:21.401542+00:00 | 51 | false | ```\n/**\n * Time Complexity: O(n_nums * log(n_nums) + k * log(k)), where `n_nums` is the length of the vector `nums`\n * Space Complexity: O(k)\n */\nclass Solution {\n public:\n long long kSum(vector<int> &nums, const int k) {\n long long sum = 0LL;\n for (int &num : nums) {\n if (num > 0) {\n sum += num;\n }\n if (num < 0) {\n num *= -1;\n }\n }\n sort(nums.begin(), nums.end());\n \n const int n = static_cast<int>(nums.size());\n auto compare = [](const pair<long long, int> &lhs, const pair<long long, int> &rhs) -> bool {\n return !(lhs.first > rhs.first || (lhs.first == rhs.first && lhs.second < rhs.second));\n };\n priority_queue<pair<long long, int>, vector<pair<long long, int>>, decltype(compare)> pq(compare);\n pq.emplace(sum, 0);\n for (int i = 0; i < k - 1; ++i) {\n const auto [max_sum, index] = pq.top();\n pq.pop();\n if (index >= n) {\n continue;\n }\n pq.emplace(max_sum - nums[index], index + 1);\n if (index > 0) {\n pq.emplace(max_sum - nums[index] + nums[index - 1], index + 1);\n }\n }\n return pq.top().first;\n }\n};\n``` | 0 | 0 | [] | 0 |
find-the-k-sum-of-an-array | Why DP sol getting TLE O( N * min(1<<N,2000)) ?? | why-dp-sol-getting-tle-o-n-min1n2000-by-k7yt0 | \n#define ll long long\nclass Solution {\npublic:\n long long kSum(vector<int>& nums, int k) {\n int n = nums.size();\n vector<ll> dp(1);\n\n | cyborg_05 | NORMAL | 2022-08-21T06:06:11.862510+00:00 | 2022-08-21T06:06:11.862572+00:00 | 241 | false | ```\n#define ll long long\nclass Solution {\npublic:\n long long kSum(vector<int>& nums, int k) {\n int n = nums.size();\n vector<ll> dp(1);\n\n for (int i = 1; i <= n; i++) {\n int size = (int)dp.size();\n for (int j = 0; j < size; j++) {\n dp.push_back(dp[j] + nums[i - 1]);\n }\n sort(dp.begin(), dp.end(), greater<ll>());\n dp.resize(min((int)dp.size(),2000));\n }\n return dp[k-1];\n }\n};\n``` | 0 | 0 | ['Dynamic Programming'] | 2 |
find-the-k-sum-of-an-array | javascript max heap/pq 453ms | javascript-max-heappq-453ms-by-henrychen-364q | \nconst kSum = (a, k) => {\n let sum = 0, n = a.length, pq = new MaxPriorityQueue({ compare: (x, y) => y[0] - x[0] });\n for (let i = 0; i < n; i++) {\n | henrychen222 | NORMAL | 2022-08-21T05:59:57.294783+00:00 | 2022-08-21T05:59:57.294816+00:00 | 204 | false | ```\nconst kSum = (a, k) => {\n let sum = 0, n = a.length, pq = new MaxPriorityQueue({ compare: (x, y) => y[0] - x[0] });\n for (let i = 0; i < n; i++) {\n if (a[i] < 0) {\n a[i] *= -1;\n } else {\n sum += a[i];\n }\n }\n if (k == 1) return sum;\n a.sort((x, y) => x - y);\n pq.enqueue([sum - a[0], 0]);\n for (let i = 2; i < k; i++) {\n let [x, idx] = pq.dequeue();\n if (idx + 1 < n) {\n pq.enqueue([x + a[idx] - a[idx + 1], idx + 1]);\n pq.enqueue([x - a[idx + 1], idx + 1]);\n }\n }\n return pq.front()[0];\n};\n``` | 0 | 0 | ['Heap (Priority Queue)', 'JavaScript'] | 0 |
find-the-k-sum-of-an-array | Python Solution - we don't need a heap queue! | python-solution-we-dont-need-a-heap-queu-2ndp | Solving for k== 0 is obvious: simply calculate the sum of the positive numbers.\n\nFor each case of k > 0 you need a less optimum answer. You get a lower answer | shepherd_a | NORMAL | 2022-08-21T05:48:34.428991+00:00 | 2022-08-22T05:56:19.493727+00:00 | 223 | false | Solving for k== 0 is obvious: simply calculate the sum of the positive numbers.\n\nFor each case of *k > 0* you need a less optimum answer. You get a lower answer by \n\n- Subtracting one or more of the positive items you added\n- Adding one of more of the negative items you didn\'t add originally\n\nThere are *n* possible actions to choose from. You can choose to make each change independentally of every other changes, which means there are *2^n* **combinations** of actions to choose from. Each action doubles the number of possible results.\n\nYou obviously cannot calculate every possible combination of actions for a non-minimal size of n.\n\nSo just continually pare down the result set. With each action you double the possible number of combinations, then reduce it down to the top *k* combinations. \n\n````\nclass Solution:\n def kSum(self, nums, k: int) -> int:\n sumPositives = sum(n for n in nums if n > 0)\n diffs = sorted([abs(n) for n in nums])\n subtractValues = [0]\n for n in diffs:\n newValues = []\n for p in subtractValues:\n newValue = p+n\n if len(subtractValues) == k and subtractValues[-1] < newValue:\n break\n newValues.append(newValue)\n if not newValues:\n break\n subtractValues.extend(newValues)\n subtractValues.sort()\n del subtractValues[k:]\n \n return sumPositives - subtractValues[-1]\n```` | 0 | 0 | ['Python'] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.