question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
recover-the-original-array | [Python]||Set||Binary-search | pythonsetbinary-search-by-u_knw_who-7kd6 | Create a set with all possible values of K and iterate over the list for each element to find corresponding high one \n\n\ndef recoverArray(self, nums):\n\n | u_knw_who | NORMAL | 2022-05-17T02:41:33.729641+00:00 | 2022-05-17T02:41:33.729669+00:00 | 130 | false | Create a set with all possible values of K and iterate over the list for each element to find corresponding high one \n\n```\ndef recoverArray(self, nums):\n```\n \n def bsearch(x,nums):\n n = len(nums)\n low = 0\n end = n-1\n \n while low<=end:\n mid = (low+end)//2\n if nums[mid] == x:\n return (True,mid)\n elif nums[mid]>x:\n end = mid-1\n else:\n low = mid+1\n \n return (False,-1) \n \n \n nums.sort()\n \n k_lis = set([(nums[i]-nums[0])//2 for i in range(1,len(nums)) if (nums[i]-nums[0])%2==0])\n if 0 in k_lis:\n k_lis.remove(0)\n \n \n for i in k_lis:\n temp = [j for j in nums]\n k_arr = []\n while temp:\n x = temp.pop(0)\n a,b = bsearch(x+ 2*i,temp)\n if not a:\n break\n k_arr.append(x+i) \n temp.pop(b)\n if not temp:\n return k_arr\n | 0 | 0 | ['Binary Tree', 'Ordered Set'] | 0 |
recover-the-original-array | [C++] try out the candidates of K. | c-try-out-the-candidates-of-k-by-fzh-4ej3 | \n\n\n// 2122. Recover the Original Array\nclass Solution {\n static inline bool isEven(int n) {\n return (n & 1) == 0;\n }\n\n static tuple<boo | fzh | NORMAL | 2022-04-26T23:37:02.671144+00:00 | 2022-04-26T23:37:02.671175+00:00 | 138 | false | \n\n```\n// 2122. Recover the Original Array\nclass Solution {\n static inline bool isEven(int n) {\n return (n & 1) == 0;\n }\n\n static tuple<bool, vector<int>> isGoodK(const int k, const vector<int>& A) {\n unordered_multiset nset(A.begin(), A.end());\n vector<int> originals;\n originals.reserve(A.size() / 2);\n // time complexity: O(n).\n // space is also O(n).\n for (int i = 0; i < A.size() && nset.size() > 0; ++i) {\n const int upper = A[i] + 2 * k;\n if (auto iter1 = nset.find(A[i]), iter2 = nset.find(upper);\n iter1 != nset.end() && iter2 != nset.end()) {\n // successfully paired up A[i] with another number.\n originals.emplace_back(A[i] + k);\n nset.erase(iter1);\n nset.erase(iter2);\n } else if (iter1 != nset.end()) {\n // A[i] is available for pairing, but cannot find another number to pair it up.\n // so, return earlier to indicate the failure.\n return {false, {}};\n }\n }\n return {true, originals};\n }\n\npublic:\n vector<int> recoverArray(vector<int>& nums) {\n if (!isEven(nums.size())) {\n return {}; // no valid answer.\n }\n\n sort(nums.begin(), nums.end());\n const int smallest = nums.front();\n // possible values for k\n for (size_t i = 1; i < nums.size(); ++i) {\n int diff = nums[i] - smallest;\n if (isEven(diff) && diff >= 2) { // it should be 2*k, which is an even number\n // this step is O(n)\n auto [isGood, originalVec] = isGoodK(diff / 2, nums);\n if (isGood) {\n return originalVec;\n }\n }\n }\n // Overall it\'s O(n ** 2).\n return {}; // no valid answer\n }\n};\n\n\n``` | 0 | 0 | ['C'] | 0 |
recover-the-original-array | Ruby Solution | ruby-solution-by-rosssg-p5pb | ```\n# @param {Integer[]} nums\n# @return {Integer[]}\ndef recover_array(nums)\n nums.sort!\n uniques = nums.uniq\n start = uniques.shift\n tests = | rosssg | NORMAL | 2022-04-09T01:45:23.229495+00:00 | 2022-04-09T01:45:23.229521+00:00 | 30 | false | ```\n# @param {Integer[]} nums\n# @return {Integer[]}\ndef recover_array(nums)\n nums.sort!\n uniques = nums.uniq\n start = uniques.shift\n tests = []\n n = nums.length / 2\n for i in 0...uniques.length\n tests << (uniques[i] - start) / 2 if (uniques[i] - start) % 2 == 0 \n end\n \n \n puts "start=#{start} tests=#{tests}"\n \n while true\n test_nums = nums.dup\n test_offset = tests.shift\n result = []\n n.times do\n # look for offset match for leftmost value of test_nums. If not found, fail; if found, delete it and leftmost value\n test_number = test_nums.shift\n found = test_nums.index(test_number + test_offset * 2)\n break if found == nil\n test_nums.delete_at(found)\n result << test_number + test_offset\n end\n return result if test_nums == []\n end\n \n \n [3,7,11]\n \n \nend\n | 0 | 0 | [] | 0 |
recover-the-original-array | O(n^2) | on2-by-sammos-6j3y | If we have the lowest value of the lower array and the lowest value of the higher array we can recunstruct it in linear time. We just keep adding the next lowes | sammos | NORMAL | 2022-02-01T17:36:37.446291+00:00 | 2022-02-01T17:41:40.380420+00:00 | 98 | false | If we have the lowest value of the lower array and the lowest value of the higher array we can recunstruct it in linear time. We just keep adding the next lowest from the set + k to the result and remove the lowest and the lowest + 2 * k from the set.\nWe already know the lowest value of the lower array, because it must be the lowest value in nums. So we sort the array and use the first element as the lowest of the lower array, and then we try all possible values in nums as the lowest of the higher array and try to recunstruct it.\n\nI used recursion to recunstruct the array. It should also be possile to do it iteratively, but I found it easier doing it backtracking. The recursive function runs in linear time.\n\n```\nclass Solution {\npublic:\n bool recunstruct(int i, int diff, vector<int>& nums, unordered_map<int, int>& freq, vector<int>& res) {\n if (i == nums.size()) return true;\n if (!freq[nums[i]]) return recunstruct(i + 1, diff, nums, freq, res);\n if (!freq[nums[i] + diff]) return false;\n\t\t\n\t// remove it from map so we don\'t use it again\n freq[nums[i]]--;\n freq[nums[i] + diff]--;\n res.push_back(nums[i] + diff / 2);\n if (recunstruct(i + 1, diff, nums, freq, res)) return true;\n res.pop_back();\n\t\t\n\t// add it back to map\n freq[nums[i] + diff]++;\n freq[nums[i]]++;\n return false;\n }\n vector<int> recoverArray(vector<int>& nums) {\n sort(nums.begin(), nums.end());\n\t\t\n\t// map to store the values that are not used yet\n unordered_map<int, int>freq;\n for (int n : nums) freq[n]++;\n vector<int>res;\n for (int i = 1; i < nums.size(); i++) {\n\t\t\n\t\t// if we\'ve already tried this value we can skip it\n if (nums[i] == nums[i - 1]) continue;\n int diff = nums[i] - nums[0];\n\t\t\t\n\t\t// if diff is odd or equals zero we can skip it\n if (diff & 1 || diff == 0) continue;\n if (recunstruct(0, diff, nums, freq, res)) return res;\n }\n return {};\n }\n};\n``` | 0 | 0 | [] | 0 |
recover-the-original-array | C# AC - check if number and number+2*k exists | c-ac-check-if-number-and-number2k-exists-urbb | checking if the array is valid for K logic is similar to these 2 problems. so solve these first\nhttps://leetcode.com/problems/find-original-array-from-doubled- | rajanikanthr | NORMAL | 2022-02-01T00:27:22.974136+00:00 | 2022-02-01T01:58:55.516785+00:00 | 84 | false | checking if the array is valid for K logic is similar to these 2 problems. so **solve these first**\nhttps://leetcode.com/problems/find-original-array-from-doubled-array/discuss/1735246/c-ac-check-frequencies\nhttps://leetcode.com/problems/array-of-doubled-pairs/discuss/1735322/C-AC-check-frequencies\n\n\nIf we check every value of k it will time out. As we know there is a valid output, for nums[0] there should be a value exist in the array for which \n```\nnum[i] = nums[0] + 2* k\nk = (nums[i]-nums[0])/2;\n```\n\n\n\n```\npublic int[] RecoverArray(int[] nums)\n{\n\tint n = nums.Length;\n\tif(n%2 != 0) return new int[0];\n\tArray.Sort(nums);\n\tint[] result = new int[n/2];\n\n\tDictionary<int, int> counts = new Dictionary<int, int>();\n\tforeach (var num in nums)\n\t{\n\t\tif (counts.ContainsKey(num)) counts[num]++;\n\t\telse counts.Add(num, 1);\n\t}\n\n\tfor (int i = 1; i < n; i++)\n\t{\n\t\tint k = nums[i] - nums[0];\n\t\tif(k== 0 || k%2 != 0) continue; \n\t\tk = k/2;\n\t\tif(IsKValid(nums, k, new Dictionary<int, int>(counts), result ))\n\t\t{\n\t\t\treturn result;\n\t\t}\n\t}\n\treturn result;\n}\n\nprivate bool IsKValid(int[] nums, int k, Dictionary<int, int> counts, int[] result)\n{\t\n\tint carry = 2*k;\n\tint index=0;\n\tforeach (var num in nums)\n\t{\n\t\tif(counts[num]==0) continue;\n\t\t\n\t\t// lower(num) = value-k so value = num+k\n\t\t// higher = num+k+k = 2*k + num\n\t\tint target = carry+num;\n\t\tif(!counts.ContainsKey(target) || counts[target] == 0)\n\t\treturn false;\n\t\t\n\t\tresult[index++] = num+k;\n\t\tcounts[num]--;\n\t\tcounts[target]--;\n\t}\t\n\treturn true;\t\n}\n\n``` | 0 | 0 | [] | 0 |
find-the-maximum-sum-of-node-values | Greedy Sacrifice | greedy-sacrifice-by-votrubac-neo2 | \nIn a tree, we can freely change any even number of nodes.\n\n> I got this intuitioin by drawing a few trees and trying to change some nodes without changing t | votrubac | NORMAL | 2024-03-02T16:01:04.812227+00:00 | 2024-03-02T17:45:00.872504+00:00 | 6,195 | false | \nIn a tree, we can freely change any even number of nodes.\n\n> I got this intuitioin by drawing a few trees and trying to change some nodes without changing the others.\n \nSo, we count nodes that we want to change (where n ^ k > n).\n \nIf the count is even, we just return the best `sum`.\n \nIf the count is odd, we need to `sacrifice` one node:\n- Do not change a node we want to change, or\n- Change a node that we do not want to change.\n \nWe track the smallest sacrifice `min(abs(n - (n ^ k))`, and subtract it from the best `sum`.\n\n**Python 3**\n```python\nclass Solution:\n def maximumValueSum(self, nums: List[int], k: int, edges: List[List[int]]) -> int:\n best_sum = sum(max(n, k ^ n) for n in nums)\n cnt = sum((n ^ k) > n for n in nums) \n return best_sum - (min(abs(n - (n ^ k)) for n in nums) if cnt % 2 else 0)\n```\n**C++** \n```cpp\nlong long maximumValueSum(vector<int>& nums, int k, vector<vector<int>>& edges) {\n long long sum = 0, cnt = 0, sacrifice = INT_MAX;\n for (long long n : nums) {\n sum += max(n ^ k, n);\n cnt += (n ^ k) > n;\n sacrifice = min(sacrifice, abs(n - (n ^ k)));\n }\n return sum - (cnt % 2 ? sacrifice : 0);\n}\n```\n\n\n | 181 | 0 | ['C', 'Python3'] | 22 |
find-the-maximum-sum-of-node-values | Extreme detailed Explanation, that could ever exists | extreme-detailed-explanation-that-could-62lfv | So, the first thing you should notice that, this problem doesn\'t have any big examples. So, whenever you see something like this, you should have your examples | hi-malik | NORMAL | 2024-05-19T01:41:33.631994+00:00 | 2024-05-19T20:37:23.204299+00:00 | 15,114 | false | So, the first thing you should notice that, this problem doesn\'t have any big examples. So, whenever you see something like this, you should have your examples, because working on a example, will give you some hints. Because the Questioner doesn\'t wanted you to get the hint\'s easily just via there examples!\n\nLet\'s take our on example. But will take one with letters for now,\n\nNow, the first question you should be asking yourself is,\nWhat will happen if I want to work on path between **a** & **d**\n```\n->a will become, because first we have choose the edge between a and b\n\na----b----c----d\na ^ k\n```\n->b will become, \n```\na------b------c------d\na ^ k b ^ k\n```\n-> The next edge we will choose between b and c\n```\na------b------c------d\na ^ k b ^ k\n b ^ k ^ k\n```\nas `b ^ k ^ k` will become `b`\n```\na------b------c------d\na ^ k b ^ k\n b \n```\n```\na------b------c------d\na ^ k b ^ k c ^ k\n b \n```\n-> The next edge we will choose between c and d\n```\na------b------c------d\na ^ k b ^ k c ^ k\n b c ^ k ^ k\n```\nas `c ^ k ^ k` will become `c`\n```\na------b------c------d\na ^ k b ^ k c ^ k\n b c \n```\nand finally\n```\na------b------c------d\na ^ k b ^ k c ^ k d ^ k\n b c \n```\n\nNow from this, we can see that. If we choose any two numbers and apply the operarion over them. \n\nThe next question, you should have is! \n> Okay so, I can pick any two numbers, I have for example :\n```\na, b, c, d\n```\nand now you can look at the input as a list, because the tree structure is **irrelevant** and what will happen is that for each number, you should pick that number **at most once**\nBecause if you pick it twice, it will become\n```\na, b, c, d\na^k^k\n```\nas ~~a^k^k~~ is a, basically it\'s not going to change.\n\nSo, this is the set that the other observation of the property of the **XOR** you should think about this, that I should pick any number **at most once**\n> Next you should think, which number should I pick?\nLet\'s say you are picking **a** and **b**\n* a will become `a^k`\n* b will become `b^k`\n\nBut there\'s some property, that :\n* Greater than a `a^k` > `a` or Smaller than a `a^k` < `a`\nAs, it\'s either becoming bigger or becoming smaller. Because **k** is not **0**, only **`a ^ 0 = a`** and **k** is greater than **0**\n\nSo, now we should think of the input as **two sets**, if we pick them :\n* We have a set of **A**, the numbers becoming **bigger**\n* And a set of **B**, the numbers becoming **smaller**\n\n\nLet\'s now think about this difference,\n**`a^k` > `a`**\nlet\'s called it \n```\ndiff = a^k-a\n```\nSo, here\'s all the diff going to be **+ve** one like:\n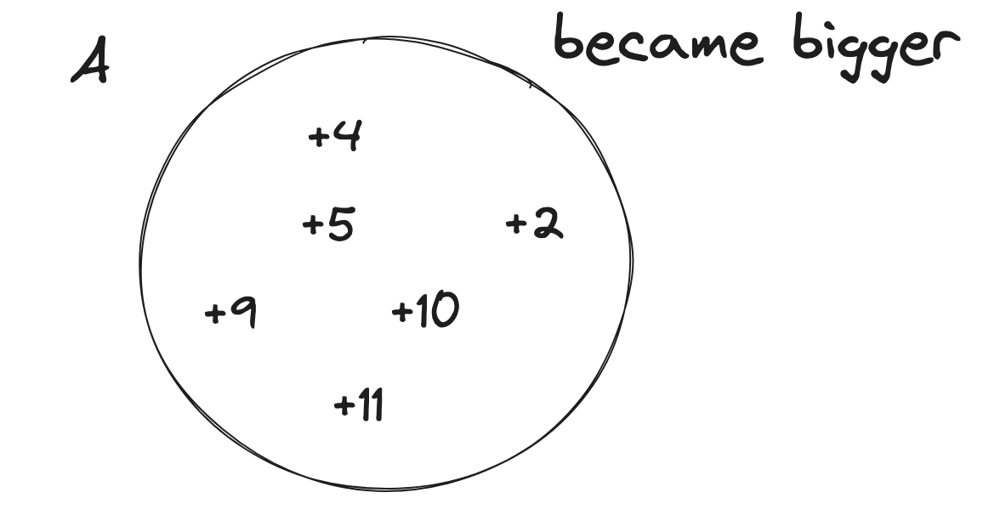\nAnd in the B, we going to have **-ve** one like:\n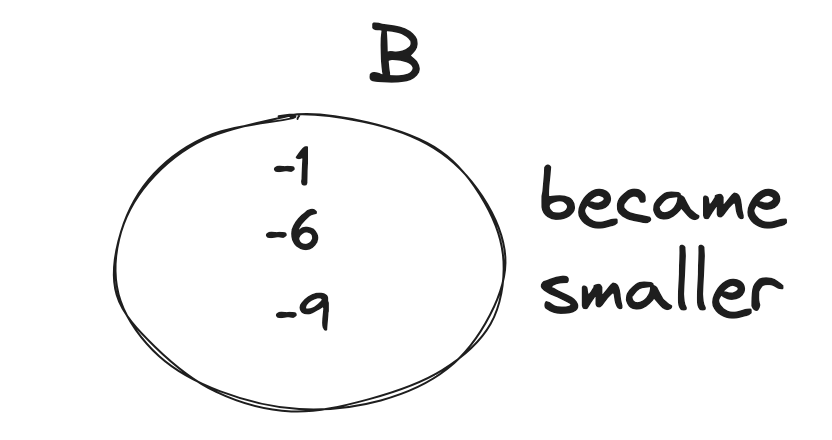\nThese numbers may not be correct, but I just wanna make an example, so what happens is that because we have even number of them those that are becoming bigger, we just going to pair them together. As our operation\'s says we should pick 2 numbers\n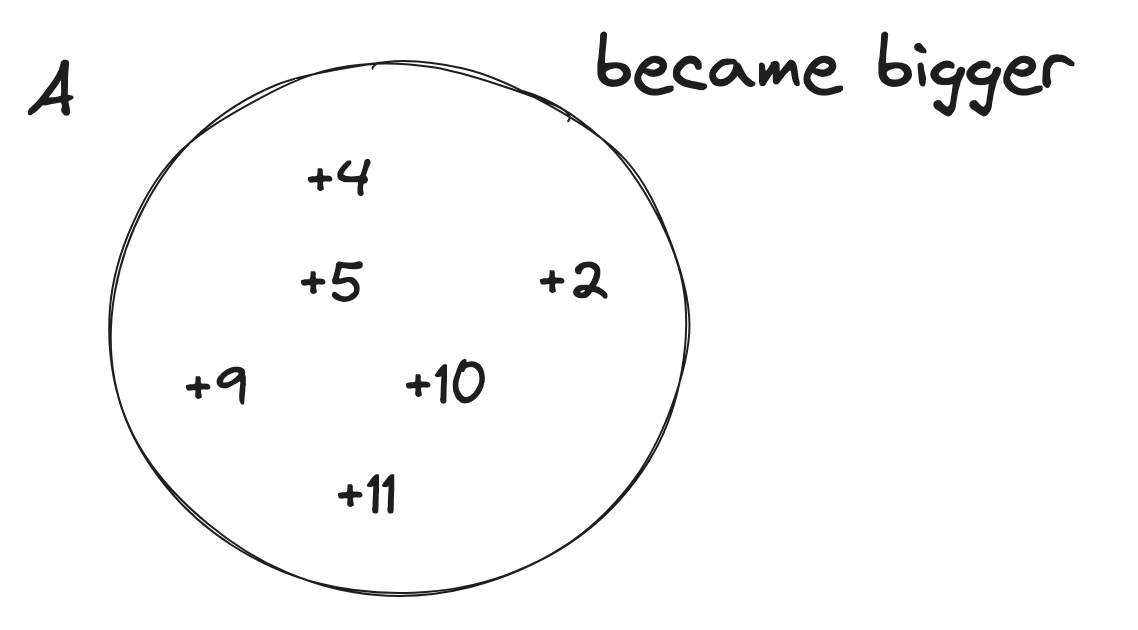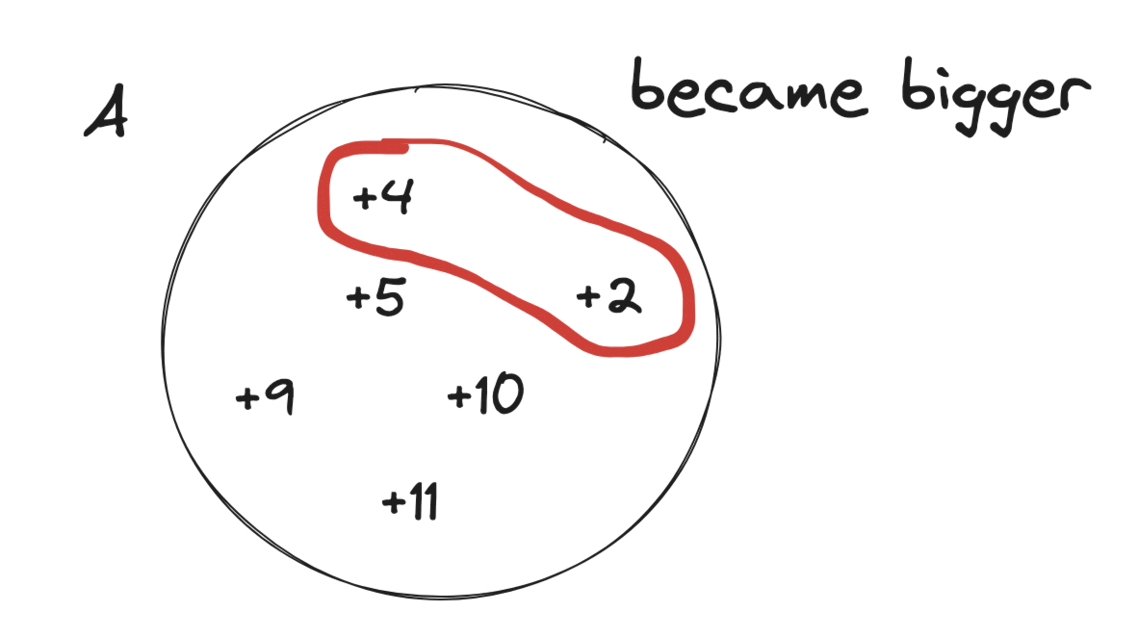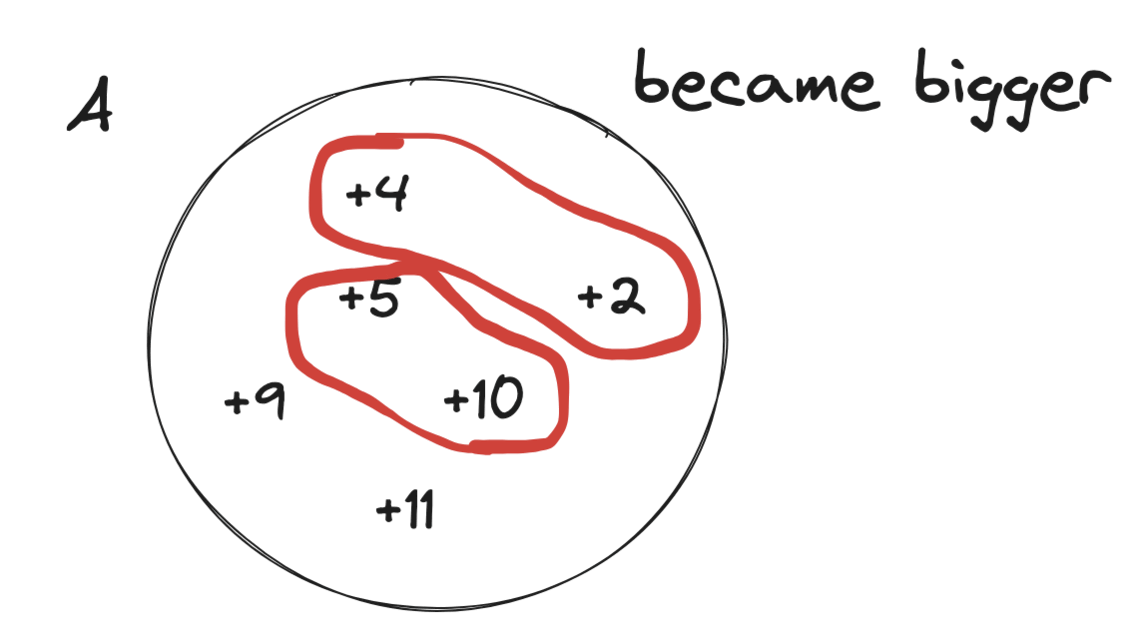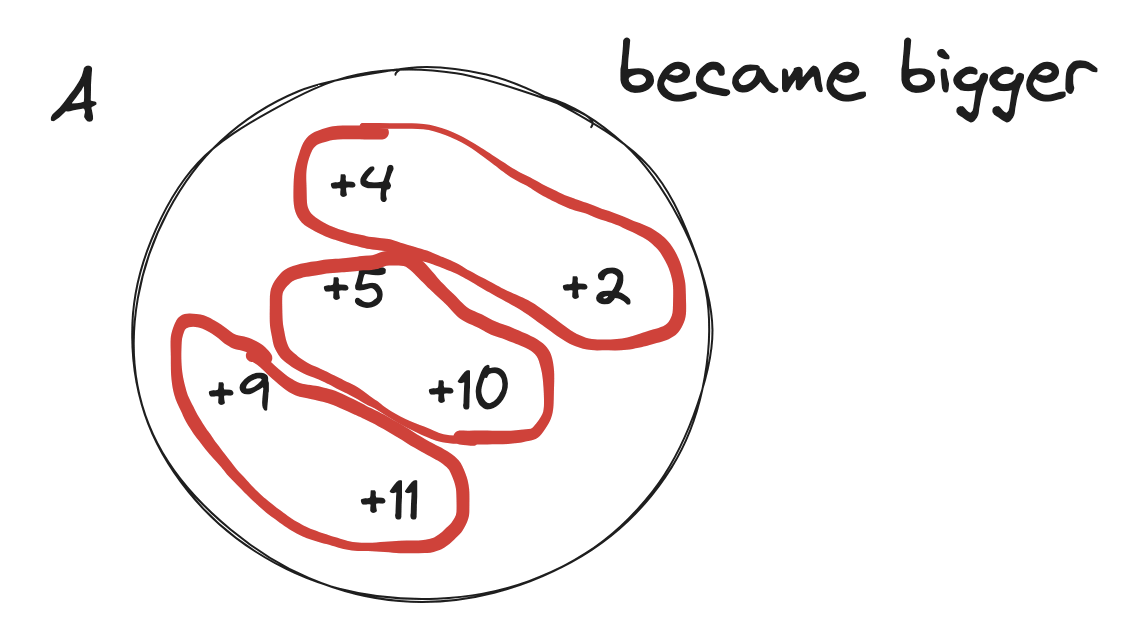\nSo, basically our answer would be sum of all of the numbers, because that is going to be the answer, plus these numbers like **`4 2 5 10 9 11`**. \nSo it\'s going to **sum of X, X is input + sum of ai** \ni.e. **`\u2211x + \u2211ai`**\nbut right now, we don\'t care about **bi**, but we added the numbers that are becoming a smaller but we just ignored the difference as for the numbers that are becoming bigger, we added them but also added the difference.\n> So, this was a one example\n> > Let\'s have another example\n\nIn this example, we going to have **set A** and **set B**. In them we going to have :\n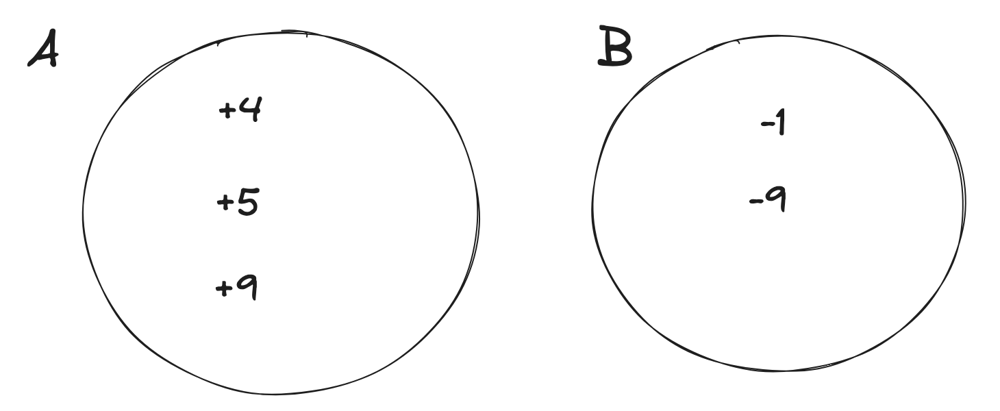\n\nIn **set A** we can pair\n```\n A\n|-----------|\n| +5 +9 |\n|-----------|\n```\nand add the difference to the answer, also in this case we can pair\n```\n A B\n|-----------|---------|-----------|\n| +4 -1 |\n|-----------|---------|-----------|\n```\nAs **`+4 -1` > `0`**, as it\'s good to pair these two. This is the one case\n\n**The other case could be**\n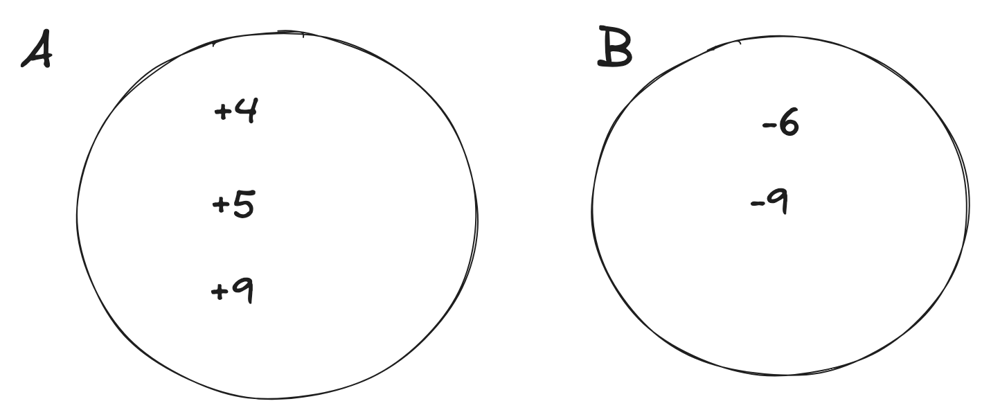\n\nIn **set A** we can pair\n```\n A\n|-----------|\n| +5 +9 |\n|-----------|\n```\n\nbut we can\'t pair **`+4` and `-6`**, as it is less than **0** **`+4 -6` < `0`**, this won\'t be beneficial for us to Peak these two.\n\n---\n\n\nWhen the number of positiveCount is odd, we have two choices, either to remove one of the positiveCount occurrence from set of performed XORs or we can include one of the numbers from not performed XORs to be included in the set to make the XOR operation count to even. Basically we need the XOR op count to be even.\n\nNow lets see how we achieve this using absolute diff -\nLet XOR of a number n be n\'. All the positive (n\'-n) diffs are already included in total diff.\n\nHow will you remove one of these n\'s to maximize the sum? Simple - you will not perform xor when the difference is minimal. And subtract that minimum diff.\n\nBut, it might be more beneficial to include a negative diff i.e which was not already included - the decision to choose to that extra n which reduces the total sum would be to choose the diff which reduces the sum the least. You can find that by including the least negative diff or by maximizing (n-n\').\n\nThe implementation does both these things in one shot by using Absolute diff.\n**This part explaination by :-** [@kharashubham](https://leetcode.com/u/kharashubham/)\n\n---\n\nNow, you will ask, how do we write the code? The code is super simple, we just add all of the number as I said, **`\u2211xi + \u2211ai`**\nLet me try to explain in code!\n\n### Explanation:\n\n1. **Initialization**:\n - Calculate the initial total sum of the `nums` array.\n - Initialize `total_diff` to store the cumulative positive differences.\n - Initialize `positive_count` to count how many positive differences exist.\n - Initialize `min_abs_diff` to store the smallest absolute difference encountered.\n\n2. **Loop through each element in `nums`**:\n - Calculate the difference `diff` when XORing the current element with `k`.\n - If `diff` is positive, add it to `total_diff` and increment `positive_count`.\n - Track the minimum absolute difference encountered using `min_abs_diff`.\n\n3. **Adjust for Odd Positive Count**:\n - If `positive_count` is odd, subtract the smallest absolute difference (`min_abs_diff`) from `total_diff` to maximize the total sum.\n\n4. **Return the Final Sum**:\n - Return the sum of `total` and `total_diff`.\n\nLet\'s code it UP\n\n**`C++`**\n```\nclass Solution {\npublic:\n long long maximumValueSum(vector<int>& v, int k, vector<vector<int>>& edges) {\n long long total = accumulate(v.begin(), v.end(), 0ll);\n \n long long total_diff = 0;\n long long diff;\n int positive_count = 0;\n long long min_abs_diff = numeric_limits<int>::max();\n for(auto p : v){\n diff = (p^k) - p;\n \n if(diff > 0){\n total_diff += diff;\n positive_count++;\n }\n min_abs_diff = min(min_abs_diff, abs(diff));\n }\n if(positive_count % 2 == 1){\n total_diff = total_diff - min_abs_diff;\n }\n return total + total_diff;\n }\n};\n```\n**`JAVA`**\n```\nclass Solution {\n public long maximumValueSum(int[] nums, int k, int[][] edges) {\n long total = 0;\n for (int num : nums) {\n total += num;\n }\n\n long totalDiff = 0;\n long diff;\n int positiveCount = 0;\n long minAbsDiff = Long.MAX_VALUE;\n for (int num : nums) {\n diff = (num ^ k) - num;\n\n if (diff > 0) {\n totalDiff += diff;\n positiveCount++;\n }\n minAbsDiff = Math.min(minAbsDiff, Math.abs(diff));\n }\n if (positiveCount % 2 == 1) {\n totalDiff -= minAbsDiff;\n }\n return total + totalDiff;\n }\n}\n```\n**`PYTHON`**\n```\nclass Solution:\n def maximumValueSum(self, nums: List[int], k: int, edges: List[List[int]]) -> int:\n total = sum(nums)\n \n total_diff = 0\n positive_count = 0\n min_abs_diff = float(\'inf\')\n \n for num in nums:\n diff = (num ^ k) - num\n \n if diff > 0:\n total_diff += diff\n positive_count += 1\n min_abs_diff = min(min_abs_diff, abs(diff))\n \n if positive_count % 2 == 1:\n total_diff -= min_abs_diff\n \n return total + total_diff\n```\n\n---\nComplexity Analysis\n\n---\n\n* **Time Complexity :-** BigO(N)\n\n\n* **Space Complexity :-** BigO(N)\n\n\n\n | 169 | 1 | ['C', 'Python', 'Java'] | 33 |
find-the-maximum-sum-of-node-values | [Java/C++/Python] Edges are Useless | javacpython-edges-are-useless-by-lee215-4onw | TLDR\nToo long don\'t read:\n\nThe shape of tree doesn\'t matter.\nedges are useless.\nEach operation, change two nodes,\nso in the end, we change whichever eve | lee215 | NORMAL | 2024-03-02T16:07:32.003459+00:00 | 2024-03-02T16:35:15.662443+00:00 | 4,965 | false | # **TLDR**\nToo long don\'t read:\n\nThe shape of tree doesn\'t matter.\nedges are useless.\nEach operation, change two nodes,\nso in the end, we change whichever even nodes.\n<br>\n\n# **Intuition**\nAfter the previous excercise on the tree,\nI was confident to handle dfs on the tree.\n\nNow each node can XOR or stay the same.\nEasy, we can do dp on the tree with DFS.\n<br>\n\n\n# **Intuition 2**\nWait,\nactually each node can xor with its parent.\n\nAnd we can choose the bigger one in `max(a, a ^ k)`,\nand leave the problem to its parent.\nFinally the root will be `a` or `a ^ k`.\n<br>\n\n# **Intuition 3**\nWait wait,\nwill the root in a good status (changed to bigger)?\n\nEach time, we will change on one of `edges`,\nand this will flip two nodes.\nSo the changes nodes count will always be even.\n\nSo just need to know the number of nodes to change.\nIf it\'s even, we are even, great.\nIf it\'s odd, this is odd:\nwe need keep one from bigger or make one smaller.\n<br>\n\n\n# **Intuition 3**\nWait wait wait,\ntalking about the `edges`\nwe used `a` of nodes\' value for sure.\nwe used `k` to change the value, good.\nIt seems we don\'t need the `edges` at all,\nand any node can be the one (root).\n<br>\n\n# **Explanation**\nFor each node value `a`,\nwe can change it to `b = a ^ k`,\nso we add `max(a, b)` to result `res`.\n\nAlso we count the if it\'s `a < b`, if so `c ^= 1`,\nAlso we update minimum diff `d` between `a - b`.\n\n\nIn the end, we check if we make the change for even time.\nIf so, we return `res`,\nOtherwise we return `res - d`.\n<br>\n\n# **Complexity**\nTime `O(n)`\nSpace `O(1)`\n<br>\n\n**Java**\n```java\n public long maximumValueSum(int[] A, int k, int[][] edges) {\n long res = 0;\n int d = 1 << 30, c = 0;\n for (int a : A) {\n int b = a ^ k;\n res += Math.max(a, b);\n c ^= a < b ? 1 : 0;\n d = Math.min(d, Math.abs(a - b));\n }\n return res - d * c;\n }\n```\n\n**C++**\n```cpp\n long long maximumValueSum(vector<int>& A, int k, vector<vector<int>>& edges) {\n long long res = 0;\n int d = 1 << 30, c = 0;\n for (int a : A) {\n int b = a ^ k;\n res += max(a, b);\n c ^= a < b;\n d = min(d, abs(a - b));\n }\n return res - d * c;\n }\n```\n\n**Python**\n```py\n def maximumValueSum(self, A: List[int], k: int, edges: List[List[int]]) -> int:\n res = c = 0\n d = 1 << 30\n for a in A:\n res += max(a, b:= a ^ k)\n c ^= a < b\n d = min(d, abs(a - b))\n return res - d * c\n```\n | 82 | 1 | ['C', 'Python', 'Java'] | 15 |
find-the-maximum-sum-of-node-values | ✅Detailed Explanation🔥2 Approaches🔥🔥Extremely Simple and effective🔥🔥🔥 | detailed-explanation2-approachesextremel-7lof | \uD83C\uDFAFProblem Explanation:\nYou are given an undirected tree with n nodes numbered from 0 to n - 1 where each node has some value (see nums) and array nod | heir-of-god | NORMAL | 2024-05-19T06:06:44.731931+00:00 | 2024-05-19T10:10:56.771402+00:00 | 9,324 | false | # \uD83C\uDFAFProblem Explanation:\nYou are given an undirected tree with ```n``` nodes numbered from **0 to n - 1** where each node has some value (see ```nums```) and array ```nodes``` which represents edges beetwen nodes. You can perform XOR operation with number ```k``` any number of times on any two nodes which have edge between them in ```edges```. After perfoming them you want to achieve and return maximum possible sum of the tree.\n\n# \uD83D\uDCE5Input:\n- Integer array ```nums``` which represents values for every node.\n- Array ```edges``` which contain list with two values - ```node from``` and ```node to``` (In fact, just forget about this parameter, it\'s just confusing and useless)\n- Integer ```k``` - number with which you will perform XOR operation on connected nodes.\n\n# \uD83D\uDCE4Output:\nThe maximum possible sum of all nodes after perfoming any number of operations.\n\n# \uD83E\uDD14 Intuition\n- The main point in this question is specific of XOR operation. **SO first of all, if you don\'t know what XOR means read this explanation**:\n - *The XOR (exclusive OR) (frequently indicated as "^") operator compares corresponding bits of two operands and returns 1 if the bits are different and 0 if they are the same. For instance, in binary **1010 ^ 1100 = 0110** indicating that the second and third bits differ while the first and fourth bits are the same.*\n- Now you know about XOR let\'s talk a little about its feature. Let\'s get number from explanation **0110** and then perform on it XOR with **1100**, we will get **0110 ^ 1100 = 1010** -> something familiar, isn\'t it? If you look closer you can see that this is the first operand from example from the explanation. Do you know what it means? That means that for two number **a** and **b** will be true that ```(a ^ b) ^ b = a```. **This is one of main point for the solutions so I strongly recommend you to reread this if you haven\'t understanded, consider your own examples or ask questions in comment secion.**\n- Another very important point that, considering last point, you can choose not just any conected nodes to perform XOR but any two from the tree because in the tree you always have a path from one node to another (this is why array ```edges``` is useless). Of course I need to explain this. Imagine you have 3 nodes 0, 1, 2 and edges (0, 1) and (0, 2) (the same tree as in the description section) and look on picture.\n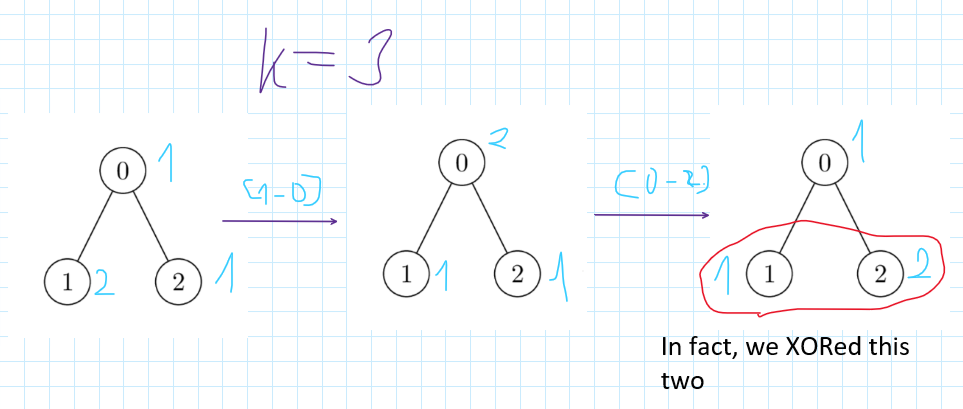\n\n- So, we are managed to XOR two nodes which haven\'t edge beetwen them, in such way I can XOR some node after the second node and so on. Considering that in the tree all nodes have some path between them we can XOR any pair of nodes we want. Now, let\'s move on to the approaches which based on this observations.\n\n\n# \uD83E\uDDE0 Approach 1: Recursion with memoization\nFirst of all - don\'t give up if you don\'t understand this approach. It\'s quite hard to come up with or understand so just move on to the next approach if you don\'t like this.\n- We will do something like Fibonacci numbers - we will go from top to the bottom, calculating all possible states of the problem using recursion and memoization\n- We want to apply this steps to write code for recursion solution:\n - Initialize memoization array ```temp```\n - We want to choose "root" of our tree so we can be sure that we traverse it all so let\'s just start with 0. In recursion we want to know on which node we currently are and parity of number of nodes we have XORed all the way to this node.\n - If we\'ve gone through last node and now we are on the non-existing node then we want to return ```-inf``` if number of nodes we XORed is odd (because we can XOR only pair of them) or 0 if it\'s even (non-existing node mustn\'t affect the sum).\n - If we already encountered this state then return its maximum result from ```temp```.\n - Call recursion for both occasions - we are XORing this node and we aren\'t.\n - Find maximum from two values, write it to the memoization array and return it.\n- Just return result from our recursion function using node 0 as root and is_even to true (we have XORed 0 nodes which is even)\n\n# \uD83D\uDCD2 Complexity\n- \u23F0 Time complexity: O(n), there can be at most 2 * n subproblems (check the size for ```temp``` array)\n- \uD83E\uDDFA Space complexity: O(n) we use O(n) for recursion stack and O(2 * n) for memoization so O(3n) in total or just O(n)\n\n# \uD83E\uDDD1\u200D\uD83D\uDCBB Code\n``` python []\nclass Solution:\n def maximumValueSum(self, nums: list[int], k: int, edges: list[list[int]]) -> int:\n n: int = len(nums)\n temp: list[list[int]] = [[-1 for _ in range(2)] for _ in range(n)] # temp[current_index(node)][is_even]\n\n def calculate_max(cur_ind, is_even) -> int: # cur_ind -> cur_index of the tree and is_even represents whether we have already changed (XOR) even or odd number of nodes \n if cur_ind == n: # if we go to node which doesn\'t exist\n return 0 if is_even else -float("inf")\n if temp[cur_ind][is_even] != -1: # if we\'ve already encountered this state\n return temp[cur_ind][is_even]\n\n # checking all possible variants (no XOR or XOR)\n no_xor = nums[cur_ind] + calculate_max(cur_ind + 1, is_even) # we don\'t change the number of XOR nodes\n with_xor = (nums[cur_ind] ^ k) + calculate_max(cur_ind + 1, not is_even) # we added 1 XORed node\n\n mx_possible = max(no_xor, with_xor)\n temp[cur_ind][is_even] = mx_possible\n return mx_possible\n\n return calculate_max(0, 1) # is_even == 1 because we have XORed 0 nodes which is even\n```\n``` C++ []\nclass Solution {\npublic:\n long long maximumValueSum(vector<int>& nums, int k, vector<vector<int>>& edges) {\n int n = nums.size();\n vector<vector<long long>> temp(n, vector<long long>(2, -1)); // temp[current_index(node)][is_even]\n \n return calculateMax(nums, n, k, 0, 1, temp);\n }\n\nprivate:\n // calculate_max -> cur_ind -> cur_index of the tree and is_even represents whether we have already changed (XOR) even or odd number of nodes \n long long calculateMax(vector<int>& nums, int n, int k, int curInd, int isEven, vector<vector<long long>>& temp) {\n if (curInd == n) { // if we go to node which doesn\'t exist\n return isEven == 1 ? 0 : LLONG_MIN;\n }\n if (temp[curInd][isEven] != -1) { // if we\'ve already encountered this state\n return temp[curInd][isEven];\n }\n\n // checking all possible variants (no XOR or XOR)\n long long noXor = nums[curInd] + calculateMax(nums, n, k, curInd + 1, isEven, temp); // we don\'t change the number of XOR nodes\n long long withXor = (nums[curInd] ^ k) + calculateMax(nums, n, k, curInd + 1, !isEven, temp); // we added 1 XORed node\n\n long long mxPossible = max(noXor, withXor);\n temp[curInd][isEven] = mxPossible;\n return mxPossible;\n }\n};\n```\n``` JavaScript []\nvar maximumValueSum = function(nums, k, edges) {\n const n = nums.length;\n const temp = Array.from({ length: n }, () => [-1, -1]);\n\n // calculate_max -> cur_ind -> cur_index of the tree and is_even represents whether we have already changed (XOR) even or odd number of nodes \n function calculateMax(curInd, isEven) {\n if (curInd === n) { // if we go to node which doesn\'t exist\n return isEven === 1 ? 0 : -Infinity;\n }\n if (temp[curInd][isEven] !== -1) { // if we\'ve already encountered this state\n return temp[curInd][isEven];\n }\n\n // checking all possible variants (no XOR or XOR)\n const noXor = nums[curInd] + calculateMax(curInd + 1, isEven); // we don\'t change the number of XOR nodes\n const withXor = (nums[curInd] ^ k) + calculateMax(curInd + 1, 1 - isEven); // we added 1 XORed node\n\n const mxPossible = Math.max(noXor, withXor);\n temp[curInd][isEven] = mxPossible;\n return mxPossible;\n }\n\n return calculateMax(0, 1); // is_even == 1 because we have XORed 0 nodes which is even\n};\n```\n``` Java []\nclass Solution {\n public long maximumValueSum(int[] nums, int k, int[][] edges) {\n int n = nums.length;\n long[][] temp = new long[n][2]; // temp[current_index(node)][is_even]\n for (int i = 0; i < n; i++) {\n temp[i][0] = -1;\n temp[i][1] = -1;\n }\n\n return calculateMax(nums, n, k, 0, 1, temp); // is_even == 1 because we have XORed 0 nodes which is even\n }\n\n // calculate_max -> cur_ind -> cur_index of the tree and is_even represents whether we have already changed (XOR) even or odd number of nodes \n private long calculateMax(int[] nums, int n, int k, int curInd, int isEven, long[][] temp) {\n if (curInd == n) { // if we go to node which doesn\'t exist\n return isEven == 1 ? 0 : Long.MIN_VALUE;\n }\n if (temp[curInd][isEven] != -1) { // if we\'ve already encountered this state\n return temp[curInd][isEven];\n }\n\n // checking all possible variants (no XOR or XOR)\n long noXor = nums[curInd] + calculateMax(nums, n, k, curInd + 1, isEven, temp); // we don\'t change the number of XOR nodes\n long withXor = (nums[curInd] ^ k) + calculateMax(nums, n, k, curInd + 1, 1 - isEven, temp); // we added 1 XORed node\n\n long mxPossible = Math.max(noXor, withXor);\n temp[curInd][isEven] = mxPossible;\n return mxPossible;\n }\n}\n```\n``` C []\nlong long calculateMax(int* nums, int n, int k, int curInd, int isEven, long long** temp) {\n if (curInd == n) { // if we go to a node that doesn\'t exist\n return isEven == 1 ? 0 : LLONG_MIN;\n }\n if (temp[curInd][isEven] != -1) { // if we\'ve already encountered this state\n return temp[curInd][isEven];\n }\n\n // checking all possible variants (no XOR or XOR)\n long long noXor = nums[curInd] + calculateMax(nums, n, k, curInd + 1, isEven, temp); // we don\'t change the number of XOR nodes\n long long withXor = (nums[curInd] ^ k) + calculateMax(nums, n, k, curInd + 1, !isEven, temp); // we added 1 XORed node\n\n long long mxPossible = noXor > withXor ? noXor : withXor;\n temp[curInd][isEven] = mxPossible;\n return mxPossible;\n}\n\nlong long maximumValueSum(int* nums, int numsSize, int k, int** edges, int edgesSize, int* edgesColSize) {\n int n = numsSize;\n long long** temp = (long long**)malloc(n * sizeof(long long*)); // temp[current_index(node)][is_even]\n for (int i = 0; i < n; i++) {\n temp[i] = (long long*)malloc(2 * sizeof(long long));\n temp[i][0] = -1;\n temp[i][1] = -1;\n }\n\n long long result = calculateMax(nums, n, k, 0, 1, temp); // is_even == 1 because we have XORed 0 nodes which is even\n\n for (int i = 0; i < n; i++) {\n free(temp[i]);\n }\n free(temp);\n\n return result;\n}\n```\n\n\n# \uD83E\uDDE0 Approach 2: Calculating deltas and sorting\nThis approach is quite easier both to write and understand but have worse time complexity.\n- For every number we want to XOR it with ```k``` and check how we\'ll benefit from this, obviously we always want to increase our sum.\n- Sort the array ```deltas``` which contain XORed values (as we can XOR any pair of nodes as described above we will first XOR those, which will give us better change in sum)\n- Now we want to go through this array by pairs of elements and perform this logic:\n - If sum of this pair is > 0 then our sum will increase after XORing this two elements, we do so and add this sum to res.\n - If sum is < 0 then this pair and all pairs after will decrease our sum so we will just go out of loop \n- Return maximum result we have reached\n\n# \uD83D\uDCD2 Complexity\n- \u23F0 Time complexity: O(n logn), we use sorting which is use nlogn time in most languages\n- \uD83E\uDDFA Space complexity: O(n) since we creating array ```deltas``` of size n\n\n# \uD83E\uDDD1\u200D\uD83D\uDCBB Code\n``` python []\nclass Solution:\n def maximumValueSum(self, nums: list[int], k: int, edges: list[list[int]]) -> int:\n n: int = len(nums)\n deltas: list[int] = [(nums[i] ^ k) - nums[i] for i in range(n)] # represents how will change number after XOR\n deltas.sort(reverse=True)\n res: int = sum(nums)\n\n for start_ind in range(0, n - 1, 2):\n changing_delta: int = deltas[start_ind] + deltas[start_ind + 1] # showing whether if would be beneficial if we XOR this two nodes \n if changing_delta > 0:\n res += changing_delta\n else:\n break\n\n return res\n```\n``` Java []\nclass Solution {\n public long maximumValueSum(int[] nums, int k, int[][] edges) {\n int n = nums.length;\n long[] deltas = new long[n]; // represents how will change number after XOR\n for (int i = 0; i < n; i++) {\n deltas[i] = (nums[i] ^ k) - nums[i];\n }\n Arrays.sort(deltas);\n for (int i = 0; i < n / 2; i++) {\n long temp = deltas[i];\n deltas[i] = deltas[n - i - 1];\n deltas[n - i - 1] = temp;\n }\n\n long res = 0;\n for (int num : nums) {\n res += num;\n }\n\n for (int startInd = 0; startInd < n - 1; startInd += 2) {\n long changingDelta = deltas[startInd] + deltas[startInd + 1]; // showing whether if would be beneficial if we XOR this two nodes \n if (changingDelta > 0) {\n res += changingDelta;\n } else {\n break;\n }\n }\n\n return res;\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n long long maximumValueSum(vector<int>& nums, int k, vector<vector<int>>& edges) {\n int n = nums.size();\n vector<long long> deltas(n); // represents how will change number after XOR\n for (int i = 0; i < n; i++) {\n deltas[i] = (nums[i] ^ k) - nums[i];\n }\n sort(deltas.rbegin(), deltas.rend());\n\n long long res = 0;\n for (int num : nums) {\n res += num;\n }\n\n for (int startInd = 0; startInd < n - 1; startInd += 2) {\n long long changingDelta = deltas[startInd] + deltas[startInd + 1]; // showing whether if would be beneficial if we XOR this two nodes \n if (changingDelta > 0) {\n res += changingDelta;\n } else {\n break;\n }\n }\n\n return res;\n }\n};\n```\n``` JavaScript []\nvar maximumValueSum = function(nums, k, edges) {\n let n = nums.length;\n let deltas = new Array(n).fill(0).map((_, i) => (nums[i] ^ k) - nums[i]); // represents how will change number after XOR\n deltas.sort((a, b) => b - a);\n\n let res = nums.reduce((acc, num) => acc + num, 0);\n\n for (let startInd = 0; startInd < n - 1; startInd += 2) {\n let changingDelta = deltas[startInd] + deltas[startInd + 1]; // showing whether if would be beneficial if we XOR this two nodes \n if (changingDelta > 0) {\n res += changingDelta;\n } else {\n break;\n }\n }\n\n return res;\n};\n```\n``` C []\n// Comparator function for qsort to sort in descending order\nint cmpfunc(const void *a, const void *b) {\n return (*(long long *)b - *(long long *)a);\n}\n\nlong long maximumValueSum(int* nums, int numsSize, int k, int** edges, int edgesSize, int* edgesColSize) {\n int n = numsSize;\n long long* deltas = (long long*)malloc(n * sizeof(long long)); // represents how will change number after XOR\n\n for (int i = 0; i < n; i++) {\n deltas[i] = (nums[i] ^ k) - nums[i];\n }\n qsort(deltas, n, sizeof(long long), cmpfunc);\n\n long long res = 0;\n for (int i = 0; i < n; i++) {\n res += nums[i];\n }\n\n for (int startInd = 0; startInd < n - 1; startInd += 2) {\n long long changingDelta = deltas[startInd] + deltas[startInd + 1]; // showing whether if would be beneficial if we XOR this two nodes \n if (changingDelta > 0) {\n res += changingDelta;\n } else {\n break;\n }\n }\n\n free(deltas);\n return res;\n}\n```\n\n## \uD83D\uDCA1I encourage you to check out [my profile](https://leetcode.com/heir-of-god/) and [Project-S](https://github.com/Heir-of-God/Project-S) project for detailed explanations and code for different problems (not only Leetcode). Happy coding and learning! \uD83D\uDCDA\n\n### Please consider *upvote* because I try really hard not just to put here my code and rewrite testcase to show that it works but explain you WHY it works and HOW. Thank you\u2764\uFE0F\n\n## If you have any doubts or questions feel free to ask them in comments. I will be glad to help you with understanding\u2764\uFE0F\u2764\uFE0F\u2764\uFE0F\n\n\n | 70 | 0 | ['Dynamic Programming', 'Greedy', 'Bit Manipulation', 'Tree', 'C', 'Python', 'C++', 'Java', 'Python3', 'JavaScript'] | 17 |
find-the-maximum-sum-of-node-values | C++ || Greedy Solution || Visualized || Comprehensive explanation | c-greedy-solution-visualized-comprehensi-1p0w | Welcome to a comprehensive solution which will leave all your doubts cleared. \n\n# Intuition\n\nThere are two things we need to keep in mind in this problem\n- | akramshafeek | NORMAL | 2024-03-02T18:44:51.480830+00:00 | 2024-03-03T02:15:04.661831+00:00 | 2,273 | false | Welcome to a comprehensive solution which will leave all your doubts cleared. \n\n# Intuition\n\nThere are two things we need to keep in mind in this problem\n- `XOR` and `Tree`\n- The tree is connected, which means we can reach any node from any other node freely. There always exists a path between any two nodes.\n- ` a ^ b ^ b = a ` --> The important property of `XOR`.\n\nLet us consider two examples to figure out how can we use the above two properties to maximise our results.\n\n\n# Example 1:\n\n The node is in the form : (nodeName, nodeValue)\n Let k = 4 -> 100 in binary\n\n (e,4) \n |\n (a,3)___(b,2)\n | |\n (c,6) (d,4)\n\n The optimal nodes which can be applied xor with k are a and b as\n other nodes will give a lesser value when applied xor with k.\n a and b when xorred with k will give a greater value, thereby \n increasing the total sum of the tree nodes\n \n Hence pick the edge a-b and apply xor with k to both a and b to \n increase the value of a and b to maximise the sum.\n\n# Example 2:\n\n The node is in the form : (nodeName, nodeValue)\n Let k = 4 -> 100 in binary\n\n (e,4) \n |\n (a,3)___(b,4)\n | |\n (c,6) (d,6)___(e,2)\n\n Here the optimal nodes are a and e. There is no direct edge\n between them to apply the xor operation on them. \n\n But consider the following path where we apply xor operation to \n every edge in the path:\n\n a -> b -> d -> e\n \n The resulting xor operations are: (a^k, b^k), (b^k, d^k), (d^k, e^k)\n If you look carefully b and d has been xored twice which leaves us \n b and d with it\'s initial value.\n \n- Hence we can conclude that in any path between two nodes `x` and `y`, all the intermediate nodes will be xorred twice and have no effect in their values at the end except for `x` and `y` which will be xorred only once with `k`.\n- The above conclusion is the most important part of the solution, so if you have not understood it please read it again.\n\n# Now we can start building up our solution\n\n- If there are any two nodes, whose values can be increased by applying the xor operation with `k`, no matter where the two nodes are present in the tree, we can exactly apply the xor operations to only these two nodes as per the conclusion we got from the previous examples.\n- Hence if the number of nodes whose values can be increased by applying xor operation with `k` are `even` in number, then we can apply the xor operation to every pair of nodes using the above approach.\n- If the number of such nodes are `odd` in number, then we won\'t be able to apply the operation to one of the nodes whose value can be increased by xor with `k`.\n- In such case we must either include another node among the nodes whose values on applying xor with `k` decreases to pair it with the remaining one node whose value can be increased by xor with `k`. \n- An alternative option would be to let go of the remaining one node by without trying to apply the xor operation on it.\n\n# Consider the following examples for better understanding\n\n ---------(X)------\n / | \\\n / | \\\n (O) (O) (O)\n / \\ | \\\n / \\ | \\ \n (X) (O) (O) (X)\n / /\n / / \n (X) (O)\n\n Nodes marked "X" are the ones whose values can be increased by \n applying the xor operation with k, where "O" are the nodes whose \n values cannot be increased by the given operation. \n\n We can see that the number of "X" nodes above is even in number\n hence we can pair each of them into groups of 2 and apply the xor\n operation along their paths to increase their values.\n\n Note again that by applying the xor operation accross all the edges\n in a path between two nodes, only the end two nodes would be\n affected as all intermediate nodes would be xorred twice and the\n xor operation would cancel out.\n\n ____________________________________________________________________\n\n ---------(X)------\n / | \\\n / | \\\n (O) (O) (O)\n / \\ | \\\n / \\ | \\ \n (X,*) (O) (O) (O,*)\n / /\n / / \n (X) (O)\n\n Here the "X" nodes are odd in number, due to which we won\'t be able\n to apply the xor operation to every pair of nodes as one node would\n be left out.\n\n We can either pair that left out node with another "O" node though \n xor operation on "O" will reduce its value, but if the "X" node can \n increase the sum substantially, then it would be a good tradeoff.\n\n Alternatively we can let go of the left out "X" node without \n applying the xor operation, which may give us the optimal answer\n\n In the above tree, the "X" and "O" nodes marked with a "*" are\n the arbitary nodes which we have to include in the xor operation or\n exclude from the xor operation.\n\n Now the task is to find those nodes and try including and excluding.\n Which can be pretty easily done in O(N)\n \n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n\n# Code\n```\nclass Solution {\npublic:\n long long maximumValueSum(vector<int>& nums, int k, vector<vector<int>>& edges) {\n\n long long sum1 = 0;\n long long sum2 = 0;\n int count = 0;\n \n for(auto i: nums) {\n // if the value of node can be increased with xor operation\n // then add it to sum1 and increase the count\n if((i ^ k) > i) {\n sum1 += (i ^ k);\n count++;\n }\n // else add it to sum2\n else\n sum2 += i; \n }\n \n // if the count is even, we can pair each of the nodes\n // along their paths and increase the overall sum\n if(count % 2 == 0)\n return sum1 + sum2;\n \n // else we need to check a suitable inclusion from sum2 into sum1\n // or a suitable exclusion from sum1 into sum2\n long long maxi1 = 0;\n long long maxi2 = 0; \n for(auto i: nums) {\n // if value of the node can be increased with xor\n // try removing the value from sum1 and add it to sum2\n if((i ^ k) > i) \n maxi1 = max(maxi1, sum1 - (i ^ k) + sum2 + i); \n // else try removing the value from sum2 and add it to sum1\n else\n maxi2 = max(maxi2, sum1 + (i ^ k) + sum2 - i); \n }\n\n return max(maxi1, maxi2);\n }\n};\n```\n | 53 | 0 | ['Greedy', 'Bit Manipulation', 'Tree', 'C++'] | 9 |
find-the-maximum-sum-of-node-values | 🔥 🔥 🔥 Fastest (100%) || Video Explanation || Easy to understand 🔥 🔥 🔥 | fastest-100-video-explanation-easy-to-un-hu6o | Detailed Approach Explained in Video Here\n\n\n\n\n# Intuition\n- The intuition behind this approach is that XOR operations on elements in the list can either i | bhanu_bhakta | NORMAL | 2024-05-19T00:18:38.257845+00:00 | 2024-05-19T05:32:54.660449+00:00 | 7,634 | false | # [Detailed Approach Explained in Video Here](https://www.youtube.com/watch?v=bmwQtId0Z2Q)\n\n\n\n\n# Intuition\n- The intuition behind this approach is that XOR operations on elements in the list can either increase or decrease their values. The goal is to maximize the overall sum after these operations. By tracking the minimum positive change and the maximum negative change, the solution ensures that if the count of beneficial operations (positive changes) is odd, we can adjust the sum to ensure it remains maximized.\n\n# Approach\n# [Detailed Approach Explained in Video Here](https://www.youtube.com/watch?v=bmwQtId0Z2Q)\n\n**Initialization:**\n\n- totalSum keeps track of the total sum of elements after potential XOR operations.\n- count tracks the number of elements that were increased by the XOR operation.\n- positiveMin is initialized to infinity and will store the minimum positive net change from the XOR operation.\n- negativeMax is initialized to negative infinity and will store the maximum negative net change from the XOR operation.\n\n**Iterating Through Elements:**\n\n- For each element in nums, compute the result of XOR-ing the element with k (i.e., nodeValAfterOperation = nodeValue ^ k).\n- Calculate the netChange which is the difference between the XOR-ed value and the original value (netChange = nodeValAfterOperation - nodeValue).\n\n**Updating totalSum:**\n\n- Add the original value of the element to totalSum.\n- If the netChange is positive (i.e., the XOR operation results in a higher value), update positiveMin if this change is the smallest positive change encountered and add this net change to totalSum.\n- If the netChange is negative, update negativeMax if this change is the largest negative change encountered.\n\n**Counting Operations:**\n\n- Increment the count for each positive net change since we are tracking how many elements were beneficially changed by the XOR operation.\nBalancing the Count of Changes:\n\n- If the count (number of beneficial changes) is even, return totalSum directly since an even count of positive changes ensures the sum is maximized.\n\n- If the count is odd, we face a dilemma since adding or subtracting an odd number of beneficial changes can be suboptimal. Hence, we need to decide whether to:\n - Remove the smallest positive change to make the count even (maximizing totalSum - positiveMin).\n - Add the largest negative change (potentially minimizing the loss) to balance out the sum (maximizing totalSum + negativeMax).\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(1)\n\n# Code\n```Python []\nclass Solution:\n def maximumValueSum(self, nums: List[int], k: int, edges: List[List[int]]) -> int:\n totalSum = 0\n count = 0\n positiveMin = float("inf")\n negativeMax = float("-inf")\n\n for nodeValue in nums:\n nodeValAfterOperation = nodeValue ^ k\n\n totalSum += nodeValue\n netChange = nodeValAfterOperation - nodeValue\n\n if netChange > 0:\n positiveMin = min(positiveMin, netChange)\n totalSum += netChange\n count += 1\n else:\n negativeMax = max(negativeMax, netChange)\n\n if count % 2 == 0:\n return totalSum\n return max(totalSum - positiveMin, totalSum + negativeMax)\n\n```\n```C++ []\nclass Solution {\npublic:\n long long maximumValueSum(vector<int>& nums, int k,\n vector<vector<int>>& edges) {\n long long totalSum = 0;\n int count = 0;\n int positiveMin = INT_MAX;\n int negativeMax = INT_MIN;\n\n for (int nodeValue : nums) {\n int nodeValAfterOperation = nodeValue ^ k;\n totalSum += nodeValue;\n int netChange = nodeValAfterOperation - nodeValue;\n\n if (netChange > 0) {\n positiveMin = min(positiveMin, netChange);\n totalSum += netChange;\n count += 1;\n } else {\n negativeMax = max(negativeMax, netChange);\n }\n }\n\n if (count % 2 == 0) {\n return totalSum;\n }\n return max(totalSum - positiveMin, totalSum + negativeMax);\n }\n};\n```\n```Java []\nclass Solution {\n public long maximumValueSum(int[] nums, int k, int[][] edges) {\n long totalSum = 0;\n int count = 0;\n int positiveMin = Integer.MAX_VALUE;\n int negativeMax = Integer.MIN_VALUE;\n\n for (int nodeValue : nums) {\n int nodeValAfterOperation = nodeValue ^ k;\n totalSum += nodeValue;\n int netChange = nodeValAfterOperation - nodeValue;\n\n if (netChange > 0) {\n positiveMin = Math.min(positiveMin, netChange);\n totalSum += netChange;\n count += 1;\n } else {\n negativeMax = Math.max(negativeMax, netChange);\n }\n }\n\n if (count % 2 == 0) {\n return totalSum;\n }\n return Math.max(totalSum - positiveMin, totalSum + negativeMax);\n }\n}\n```\n```Javascript []\n/**\n * @param {number[]} nums\n * @param {number} k\n * @param {number[][]} edges\n * @return {number}\n */\nvar maximumValueSum = function (nums, k, edges) {\n let totalSum = 0;\n let count = 0;\n let positiveMin = Infinity;\n let negativeMax = -Infinity;\n\n for (let nodeValue of nums) {\n let nodeValAfterOperation = nodeValue ^ k;\n totalSum += nodeValue;\n let netChange = nodeValAfterOperation - nodeValue;\n\n if (netChange > 0) {\n positiveMin = Math.min(positiveMin, netChange);\n totalSum += netChange;\n count += 1;\n } else {\n negativeMax = Math.max(negativeMax, netChange);\n }\n }\n\n if (count % 2 === 0) {\n return totalSum;\n }\n return Math.max(totalSum - positiveMin, totalSum + negativeMax);\n};\n```\n```Go []\nfunc maximumValueSum(nums []int, k int, edges [][]int) int64 {\n\tvar totalSum int64\n\tcount := 0\n\tpositiveMin := math.MaxInt64\n\tnegativeMax := math.MinInt64\n\n\tfor _, nodeValue := range nums {\n\t\tnodeValAfterOperation := nodeValue ^ k\n\t\ttotalSum += int64(nodeValue)\n\t\tnetChange := nodeValAfterOperation - nodeValue\n\n\t\tif netChange > 0 {\n\t\t\tif netChange < positiveMin {\n\t\t\t\tpositiveMin = netChange\n\t\t\t}\n\t\t\ttotalSum += int64(netChange)\n\t\t\tcount++\n\t\t} else {\n\t\t\tif netChange > negativeMax {\n\t\t\t\tnegativeMax = netChange\n\t\t\t}\n\t\t}\n\t}\n\n\tif count%2 == 0 {\n\t\treturn totalSum\n\t}\n\treturn int64(math.Max(float64(totalSum-int64(positiveMin)), float64(totalSum+int64(negativeMax))))\n}\n```\n```Kotlin []\nclass Solution {\n fun maximumValueSum(nums: IntArray, k: Int, edges: Array<IntArray>): Long {\n var totalSum: Long = 0\n var count = 0\n var positiveMin = Int.MAX_VALUE\n var negativeMax = Int.MIN_VALUE\n\n for (nodeValue in nums) {\n val nodeValAfterOperation = nodeValue xor k\n totalSum += nodeValue\n val netChange = nodeValAfterOperation - nodeValue\n\n if (netChange > 0) {\n positiveMin = minOf(positiveMin, netChange)\n totalSum += netChange\n count += 1\n } else {\n negativeMax = maxOf(negativeMax, netChange)\n }\n }\n\n return if (count % 2 == 0) {\n totalSum\n } else {\n maxOf(totalSum - positiveMin, totalSum + negativeMax)\n }\n }\n}\n```\n\n# **Please Upvote if you like the solution** | 32 | 2 | ['C++', 'Java', 'Go', 'Python3', 'JavaScript'] | 10 |
find-the-maximum-sum-of-node-values | DP recurion+memo->tabular->space O(1)||119ms Beats 100% | dp-recurionmemo-tabular-space-o1119ms-be-8kfj | Intuition\n Describe your first thoughts on how to solve this problem. \nQuestion is hard. Use DP to solve. edges is ignored!\nDP recurion+memo->tabular->optimi | anwendeng | NORMAL | 2024-05-19T02:53:34.119038+00:00 | 2024-05-19T13:30:49.677710+00:00 | 1,910 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nQuestion is hard. Use DP to solve. `edges` is ignored!\nDP recurion+memo->tabular->optimized space\n# Approach\n<!-- Describe your approach to solving the problem. -->\nLet `0` be the root.\nLet `f(i, c)=dp[i][c]` denote the max sum from the root to i where `c` is the number (modulo 2) of XORing operations applied.\n\nThe hardest part is to find the recursive relation between vertices `i` & `i+1`. Since LC says that this undirected graph is a tree, there exists always a path between `i` & `i+1`. An operation is applied, then 2 operations for XORing with `k` are done.\n```\n# Let x=nums[i], consider not taking x^k , taking x^k\nf(i, c)= max(x+f(i+1, c),(x^k)+f(i+1,1-c)) \n```\nXoring is performing in pair, for base case, let `n=len(nums)`,\n```\nif i==n:\n# invalid path, any negative integer with large enough absolute value\n if c==1: return -(1<<31) \nreturn 0 # base case\n```\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n $$O(n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n $$O(n)\\to O(1)$$\n# Codes: Recursion+Memo||C++ 149ms Beats 96.44%\n```Python []\nclass Solution:\n def maximumValueSum(self, nums: List[int], k: int, edges: List[List[int]]) -> int:\n n=len(nums)\n @cache\n def f(i, c):\n if i==n:\n if c==1: return -(1<<31)\n return 0\n x=nums[i]\n return max(x+f(i+1, c),(x^k)+f(i+1,1-c))\n return f(0, 0)\n \n```\n```C++ []\nclass Solution {\npublic:\n int n, k;\n long long dp[20000][2];\n long long f(int i, bool c, vector<int>& nums ){\n if (i==n) return (c)?INT_MIN:0;\n if (dp[i][c]!=-1) return dp[i][c];\n long long x=nums[i]; \n return dp[i][c]=max(x+f(i+1,c, nums), (x^k)+f(i+1,!c, nums));\n }\n \n long long maximumValueSum(vector<int>& nums, int k, vector<vector<int>>& edges) {\n n=nums.size();\n this->k=k;\n fill(&dp[0][0], &dp[0][0]+20000*2, -1);\n return f(0, 0, nums);\n }\n};\n\n```\n# C++ iterative DP||139ms Beats 98.89%\nRewrite the top-down design to bottom-up solution\n```\n#pragma GCC optimize("O3", "unroll-loops")\nclass Solution {\npublic:\n long long maximumValueSum(vector<int>& nums, int k, vector<vector<int>>& edges) {\n int n=nums.size();\n long long dp[20001][2]={0};\n dp[n][0]=0, dp[n][1]=INT_MIN;\n for(int i=n-1; i>=0; i--){\n long long x=nums[i];\n for ( int c=0; c<=1; c++)\n dp[i][c]=max(x+dp[i+1][c], (x^k)+dp[i+1][!c]);\n }\n\n return dp[0][0];\n }\n};\n\nauto init = []() {\n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n```\n# Code with optimized space||153ms Beats 96.44%\n\nUsing the trick `&1` same as `%2`\n```\n#pragma GCC optimize("O3", "unroll-loops")\nclass Solution {\npublic:\n long long maximumValueSum(vector<int>& nums, int k, vector<vector<int>>& edges) {\n int n=nums.size();\n long long dp[2][2]={0};\n dp[n&1][0]=0, dp[n&1][1]=INT_MIN;\n for(int i=n-1; i>=0; i--){\n long long x=nums[i];\n for (int c=0; c<=1; c++)\n dp[i&1][c]=max(x+dp[(i+1)&1][c], (x^k)+dp[(i+1)&1][!c]);\n }\n return dp[0][0];\n }\n};\n\n```\n# C++ dual version\nbase case: `dp[0][0]=0, dp[0][1]=INT_MIN`\nrecursion: `x=nums[i-1]` ,`dp[i&1][c]=max(x+dp[(i-1)&1][c], (x^k)+dp[(i-1)&1][!c]);`\n```\n#pragma GCC optimize("O3", "unroll-loops")\nclass Solution {\npublic:\n static long long maximumValueSum(vector<int>& nums, int k, vector<vector<int>>& edges) \n {\n const int n=nums.size();\n long long dp[2][2]={0};\n dp[0][0]=0, dp[0][1]=INT_MIN;\n for(int i=1; i<=n; i++){\n long long x=nums[i-1];\n for (int c=0; c<=1; c++)\n dp[i&1][c]=max(x+dp[(i-1)&1][c], (x^k)+dp[(i-1)&1][!c]);\n }\n return dp[n&1][0];\n }\n};\n```\n# C++ optimpized version||119ms beats 100%\n\nThanks to @Sergei99, an optimized version using just variables is done.\n```\n#pragma GCC optimize("O3", "unroll-loops")\nclass Solution {\npublic:\n static long long maximumValueSum(vector<int>& nums, const int k, vector<vector<int>>& edges) \n {\n const int n=nums.size();\n long long dp0=0, dp1=INT_MIN;\n for(int i=1; i<=n; i++){\n const long long x=nums[i-1], xk=x^k;\n const long long dp_0=max(x+dp0, xk+dp1);\n dp1=max(x+dp1, xk+dp0);\n dp0=dp_0;\n }\n return dp0;\n }\n};\n\nauto init = []() {\n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n``` | 23 | 0 | ['Dynamic Programming', 'C++', 'Python3'] | 8 |
find-the-maximum-sum-of-node-values | Beats 99% ️🔥Python3 || Greedy solution with intuition and explanation ✅ | beats-99-python3-greedy-solution-with-in-7k7c | Intuition\nAt first, the problem seems to constrain us to picking nodes from the given edges and consider them pairwise. We need a few key observations to appro | reas0ner | NORMAL | 2024-05-19T00:54:39.359576+00:00 | 2024-05-19T01:24:04.725598+00:00 | 1,409 | false | # Intuition\nAt first, the problem seems to constrain us to picking nodes from the given edges and consider them pairwise. We need a few key observations to approach this problem:\n\n1. **XOR with k is like a toggle:** Either the node value will increase, or it will decrease. Observe that (x ^ a) ^ a = x. We want the maximum value from these two.\n2. **XORing a bunch of nodes connected by a path is the same as toggling the first and last nodes**: \n\n Consider a path a->b->c->d->e where we want to XOR each of the edges.\n\n If we XOR each edge in a->b, b->c, c->d, d->e, what happens? **a is toggled once, b to d are flipped twice, d is toggled once.**\n\n This means, we can **effectively pick any pair of nodes in the tree and treat them as connected via a single edge,** regardless of whether this edge is part of the edges list or not. The length of this path, how far they are does not matter either, as **we are only concerned about the maximum sum and do not care about the number of toggles.**\n\n3. **Even number of nodes in the final selection:** As we see above, even though we have simplified the edge requirement, we at least one edge, ie, **at least need a pair of nodes** to choose at each turn. We need to find the best possible even number of such nodes.\n4. One way to do this is by greedily picking either each node\'s value, or value ^ k - whichever is higher. And then, if we have an odd number of node toggles having a higher value, remove, or rather, **sacrifice the smallest (toggled) value out of them to get the maximum possible XOR sum.**\n\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def maximumValueSum(self, nums: List[int], k: int, edges: List[List[int]]) -> int:\n changes = 0\n min_sacrifice = inf\n final = 0\n\n for val in nums:\n tmp = val ^ k\n if tmp > val:\n changes += 1\n final += tmp\n # cost of not changing this node\n min_sacrifice = min(min_sacrifice, tmp - val)\n else:\n final += val\n # cost of changing this node\n min_sacrifice = min(min_sacrifice, val - tmp)\n\n # if the number of changes is odd, smallest sacrifice from the sum to make it even\n if changes % 2:\n final -= min_sacrifice\n\n return final\n\n``` | 23 | 0 | ['Python3'] | 11 |
find-the-maximum-sum-of-node-values | Java O(n) time and O(1) extra memory DP simple solution | java-on-time-and-o1-extra-memory-dp-simp-mbgb | Intuition\nNote that you can actually pick any two nodes and apply the xor operation on them. \n\nYou can do this by applying the given operation consecutively | skinnysnakelimb | NORMAL | 2024-03-02T16:03:38.230173+00:00 | 2024-03-02T19:23:01.810403+00:00 | 789 | false | # Intuition\nNote that **you can actually pick any two nodes and apply the xor operation on them**. \n\nYou can do this by applying the given operation consecutively on the chosen nodes and their parents, and then their parents and their parents\' parents and so on until the lowest common ancestor (lca), which would leave the value of the lca unchanged, as `num xor k xor k == num` holds for any numbers num and k.\n\n# Approach\nWe can now reduce this problem to the following problem:\n\n\n>Given two arrays, `options1` and `options2`, both of size n, where **options1[i] = nums[i]** and **options2[i] = nums[i] xor k**, choose an **even** amount of elements from the second array, such that the sum of those elements and the sum of the remaining elements from the first array (the ones with different indices than the selected numbers in the second array) is **maximized**.\n\nWe can solve this with dynamic programming, where at each step we keep track of the best sum if we have an odd amount of numbers from the second array and the best sum if we have an even amount of numbers from the second array.\n\nThe recursions are\n> bestSumOdd<sub>i</sub> = max(bestSumOdd<sub>i - 1</sub> + options1[i], bestSumEven<sub>i - 1</sub> + options2[i])\n> bestSumEven<sub>i</sub> = max(bestSumEven<sub>i - 1</sub> + options1[i], bestSumOdd<sub>i - 1</sub> + options2[i])\n\n> by choosing at step i an element from options1 we do not add an extra element from the second array (so if we had an odd amount of elements from the second array before, we still do at this step)\n\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(n)$$ in the code, but could easily be reduced to $$O(1)$$ extra memory by generating options1[i] and options2[i] when needed. \n\n# Code\n```\nclass Solution {\n public long maximumValueSum(int[] nums, int k, int[][] edges) {\n int n = nums.length;\n\n if (n == 1) {\n return nums[0];\n }\n \n int[] options1 = new int[n];\n int[] options2 = new int[n];\n \n for (int i = 0; i < n; i++) {\n options1[i] = nums[i];\n options2[i] = nums[i] ^ k;\n }\n \n long bestOdd = options2[0];\n long bestEven = options1[0];\n \n for (int i = 1; i < n; i++) {\n long newOdd = Math.max(bestOdd + options1[i], \n bestEven + options2[i]);\n long newEven = Math.max(bestEven + options1[i], \n bestOdd + options2[i]);\n \n bestOdd = newOdd;\n bestEven = newEven;\n }\n \n return bestEven;\n }\n}\n``` | 18 | 0 | ['Java'] | 6 |
find-the-maximum-sum-of-node-values | Beats 100% Video Solution | Java C++ Python | beats-100-video-solution-java-c-python-b-slrw | \n\nPython Beats 100%\n\n\n\nclass Solution {\n public long maximumValueSum(int[] nums, int k, int[][] edges) {\n \n int n = nums.length;\n | jeevankumar159 | NORMAL | 2024-05-19T02:13:40.822559+00:00 | 2024-05-19T02:13:40.822577+00:00 | 1,267 | false | <iframe width="560" height="315" src="https://www.youtube.com/embed/Wo-MsfKNoq4?si=EZxKeHwSqgw4VtTY" title="YouTube video player" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture; web-share" referrerpolicy="strict-origin-when-cross-origin" allowfullscreen></iframe>\n\nPython Beats 100%\n\n\n```\nclass Solution {\n public long maximumValueSum(int[] nums, int k, int[][] edges) {\n \n int n = nums.length;\n Integer [] diff = new Integer[n];\n long sum = 0;\n for(int i = 0;i<n;i++){\n diff[i] = (nums[i]^k)-nums[i];\n sum+=nums[i];\n }\n \n Arrays.sort(diff, Collections.reverseOrder());\n \n for(int i = 0;i<n;i+=2){\n if(i+1 == n) return sum;\n int pair = diff[i]+diff[i+1];\n if(pair>0)sum+=pair;\n }\n return sum;\n }\n}\n```\n\n```\nclass Solution {\npublic:\n long maximumValueSum(std::vector<int>& nums, int k, std::vector<std::vector<int>>& edges) {\n int n = nums.size();\n std::vector<int> diff(n);\n long sum = 0;\n\n for (int i = 0; i < n; ++i) {\n diff[i] = (nums[i] ^ k) - nums[i];\n sum += nums[i];\n }\n\n std::sort(diff.begin(), diff.end(), std::greater<int>());\n\n for (int i = 0; i < n; i += 2) {\n if (i + 1 == n) return sum;\n int pair = diff[i] + diff[i + 1];\n if (pair > 0) sum += pair;\n }\n\n return sum;\n }\n};\n```\n```\nclass Solution:\n def maximumValueSum(self, nums, k, edges):\n n = len(nums)\n diff = [0] * n\n total_sum = sum(nums)\n \n for i in range(n):\n diff[i] = (nums[i] ^ k) - nums[i]\n \n diff.sort(reverse=True)\n \n for i in range(0, n, 2):\n if i + 1 == n:\n return total_sum\n pair_sum = diff[i] + diff[i + 1]\n if pair_sum > 0:\n total_sum += pair_sum\n \n return total_sum\n\n``` | 15 | 0 | ['C', 'Python', 'Java'] | 5 |
find-the-maximum-sum-of-node-values | ✅ Beat 100% | ✨ O(n) O(1) | 🏆 Most Efficient Solution | 💯 One pass with Easy to Read code. | beat-100-on-o1-most-efficient-solution-o-dcq4 | Intuition\n Describe your first thoughts on how to solve this problem. \n * Each node is like a toggle button, when we push it, its value becomes x XOR k; when | hero080 | NORMAL | 2024-03-04T05:14:04.514450+00:00 | 2024-03-04T05:14:46.549072+00:00 | 322 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n * Each node is like a toggle button, when we push it, its value becomes `x XOR k`; when we push it again, it\'s value becomes `x XOR k XOR k = x`. Yes it recovers its original value!\n * We are allowed to push two buttons that are adjacent in the graph. However, we can choose any path $a_1 \\rightarrow a_2 \\rightarrow a_3$ and apply the operations on both $a_1 \\leftrightarrow a_2$ and $a_2 \\leftrightarrow a_3$, and end result is that $a_2$ recovers while $a_1$ and $a_3$ is pushed. We can extend the path to any length to connect **any** two nodes and push them at the same time. This means we can choose push **any** group of even number of nodes.\n * When we push a button, we *gain* some value to the total sum, which is `(x XOR k) - x`. If this *gain* is positive, we consider it a `gain`. Otherwise, we consider it a `lost` (negative of the *gain*)\n * The optimal solution, at this point, is intuitively to:\n * pick *all* the `gain`s if the count of `gain`s is even, or if it\'s odd, we pick the best of the following two:\n * pick all the `gain`s except the smallest `gain`\n * pick all the `gain`s *and* the smallest `lost`\n * Edges are not needed. As long as the graph is connected we can always reach the optimal solution.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWe run through the `nums` array once to gather the necessary stats:\n * `sum`: sum of `nums` + all `gain`\n * `smallest_gain`: the smallest `gain` (positive *gain*)\n * `smallest_lost`: the smallest `-gain` (negative *gain*)\n * `gain_count`: the number of `gain`\n\nAnd then we apply the optimal solution.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$\\Theta(n)$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$\\Theta(1)$\n\n# Code\n```\nclass Solution {\npublic:\n long long maximumValueSum(vector<int>& nums, int k, vector<vector<int>>& edges) {\n int64_t sum = 0;\n int smallest_gain = 2 * k + 1;\n int smallest_lost = 2 * k + 1;\n int gain_count = 0;\n for (int num : nums) {\n int gain = (num ^ k) - num;\n if (gain > 0) {\n smallest_gain = min(smallest_gain, gain);\n sum += num + gain;\n ++gain_count;\n } else {\n smallest_lost = min(smallest_lost, -gain);\n sum += num;\n }\n }\n if (gain_count % 2 == 1) {\n sum -= min(smallest_gain, smallest_lost);\n }\n return sum;\n }\n};\n``` | 11 | 0 | ['Math', 'C++'] | 4 |
find-the-maximum-sum-of-node-values | 🔥 All 4 DP Solutions 🔥 Easiest Hard Problem | all-4-dp-solutions-easiest-hard-problem-7r7xv | Intuition\nAny node say A can be paired with any other node say B by pairing all the nodes from A to B path resulting in double xor of in between elements which | bhavik_11 | NORMAL | 2024-05-19T05:32:14.500066+00:00 | 2024-05-19T05:32:14.500102+00:00 | 562 | false | # Intuition\nAny node say A can be paired with any other node say B by pairing all the nodes from A to B path resulting in double xor of in between elements which doesn\'t change it, So the edges are useless here\n\n# Approach\nWe just need to keep sure that the nodes that are changed are even, as they were paired \nThat\'s it, now its a simple DP problem with just a node and a (even counter or flag) states\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity:$$O(n)$$ to $$O(1)$$\n\n# Code\n# Memoization\n```\nclass Solution {\nprivate:\n long long dp[20001][2];\n long long f(int idx,int even,vector<int> &nums,int k) {\n // base cases\n if(idx >= nums.size()) return even? 0 : -1e9;\n if(dp[idx][even] != -1) return dp[idx][even];\n\n long long take = (nums[idx]^k) + f(idx+1,even^1,nums,k); \n long long notTake = nums[idx] + f(idx+1,even,nums,k);\n\n return dp[idx][even] = max(take,notTake);\n }\npublic:\n long long maximumValueSum(vector<int>& nums, int k, vector<vector<int>>& edges) {\n memset(dp,-1,sizeof(dp));\n return f(0,1,nums,k);\n }\n};\n```\n\n# Tabulation\n```\nclass Solution {\nprivate:\n long long dp[20002][2];\npublic:\n long long maximumValueSum(vector<int>& nums, int k, vector<vector<int>>& edges) {\n int n = nums.size();\n memset(dp,0,sizeof(dp));\n // base cases\n dp[n][0] = -1e9;\n dp[n][1] = 0;\n for(int idx=n-1;idx>=0;--idx) {\n for(int even=0;even<2;++even) {\n long long take = (nums[idx]^k) + dp[idx+1][even^1]; \n long long notTake = nums[idx] + dp[idx+1][even];\n\n dp[idx][even] = max(take,notTake);\n }\n }\n return dp[0][1]; \n }\n};\n```\n\n# Space-Optimized Tabulation (2 dp array)\n```\nclass Solution {\npublic:\n long long maximumValueSum(vector<int>& nums, int k, vector<vector<int>>& edges) {\n int n = nums.size();\n vector<long long> curr(2,0),next(2,0);\n // base cases\n next[0] = -1e9;\n next[1] = 0;\n for(int idx=n-1;idx>=0;--idx) {\n for(int even=0;even<2;++even) {\n long long take = (nums[idx]^k) + next[even^1]; \n long long notTake = nums[idx] + next[even];\n\n curr[even] = max(take,notTake);\n }\n next = curr;\n }\n return curr[1]; \n }\n};\n```\n\n# Space Optimized Tabulation (1 dp array)\n```\nclass Solution {\npublic:\n long long maximumValueSum(vector<int>& nums, int k, vector<vector<int>>& edges) {\n int n = nums.size();\n vector<long long> curr(2,0);\n // base cases\n curr[0] = -1e9;\n curr[1] = 0;\n for(int idx=n-1;idx>=0;--idx) {\n long long take1 = (nums[idx]^k) + curr[1]; \n long long notTake1 = nums[idx] + curr[0];\n\n long long take2 = (nums[idx]^k) + curr[0]; \n long long notTake2 = nums[idx] + curr[1];\n\n curr[0] = max(take1,notTake1);\n curr[1] = max(take2,notTake2);\n }\n return curr[1]; \n }\n};\n```\n\n\nHope you found this helpful\nIf so please do Upvote it\nHappy Coding!!\n\n\n\n | 10 | 0 | ['Dynamic Programming', 'Tree', 'C++'] | 1 |
find-the-maximum-sum-of-node-values | 🔥 BEATS 100% |✅ [ Java / C++ / Py / C / C# / JS / GO ] | beats-100-java-c-py-c-c-js-go-by-neoni_7-nb4f | Intuition\nTo maximize the sum of values of tree nodes, we need to carefully choose which edges to update and which to leave unchanged. Since updating an edge a | Neoni_77 | NORMAL | 2024-05-19T05:27:32.805038+00:00 | 2024-08-08T17:46:37.259319+00:00 | 890 | false | # Intuition\nTo maximize the sum of values of tree nodes, we need to carefully choose which edges to update and which to leave unchanged. Since updating an edge affects the values of both nodes connected by that edge, we need to consider the effect of each update on the overall sum of values.\n\n# Approach\n1. Initialize variables `sum` to store the current sum of values, `minExtra` to track the minimum extra value gained from performing operations, and `count` to count the number of nodes whose values are updated by operations.\n2. Iterate through each node\'s value in the `nums` array.\n3. For each node\'s value `val`, if `(val ^ k) > val`, it means updating this node and its connected node with XOR operation will increase the sum. Update `sum` by adding `(val ^ k)` to it and update `minExtra` by taking the minimum of its current value and `(val ^ k) - val`. Increment `count`.\n4. If `(val ^ k) <= val`, it means updating this node and its connected node won\'t increase the sum. Update `sum` by adding `val` to it and update `minExtra` by taking the minimum of its current value and `val - (val ^ k)`.\n5. After iterating through all nodes, if `count` is even, return the current `sum`, else return `sum - minExtra`.\n\n# Complexity\n- Time complexity: $$O(n)$$, where $$n$$ is the number of nodes in the tree.\n- Space complexity: $$O(1)$$\n\n```Java []\nclass Solution {\n public long maximumValueSum(int[] nums, int k, int[][] edges) { \n long sum = 0;\n long minExtra = 1000000;\n int count = 0;\n\n for( int val : nums) {\n if ((val ^ k) > val ) {\n sum += val ^ k;\n minExtra = Math.min(minExtra, (val ^ k)- val);\n count++;\n } else {\n sum += val;\n minExtra = Math.min(minExtra, val - (val ^ k));\n }\n }\n\n if ( count %2 ==0 ) {\n return sum;\n } else {\n return sum - minExtra;\n }\n\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n long long maximumValueSum(std::vector<int>& nums, int k, std::vector<std::vector<int>>& edges) {\n long long sum = 0;\n long long minExtra = 1000000;\n int count = 0;\n\n for (int val : nums) {\n if ((val ^ k) > val) {\n sum += (val ^ k);\n minExtra = std::min(minExtra, static_cast<long long>((val ^ k) - val));\n count++;\n } else {\n sum += val;\n minExtra = std::min(minExtra, static_cast<long long>(val - (val ^ k)));\n }\n }\n\n if (count % 2 == 0) {\n return sum;\n } else {\n return sum - minExtra;\n }\n }\n};\n\n```\n```python []\nclass Solution:\n def maximumValueSum(self, nums: List[int], k: int, edges: List[List[int]]) -> int:\n sum_ = 0\n min_extra = 1000000\n count = 0\n\n for val in nums:\n if (val ^ k) > val:\n sum_ += val ^ k\n min_extra = min(min_extra, (val ^ k) - val)\n count += 1\n else:\n sum_ += val\n min_extra = min(min_extra, val - (val ^ k))\n\n if count % 2 == 0:\n return sum_\n else:\n return sum_ - min_extra\n\n```\n```C []\nlong long maximumValueSum(int* nums, int numsSize, int k, int** edges, int edgesSize, int* edgesColSize) {\n long long sum = 0;\n long long minExtra = 1000000; // Large initial value for minExtra\n int count = 0;\n\n for (int i = 0; i < numsSize; i++) {\n if ((nums[i] ^ k) > nums[i]) {\n sum += nums[i] ^ k;\n minExtra = (minExtra < ((nums[i] ^ k) - nums[i])) ? minExtra : ((nums[i] ^ k) - nums[i]);\n count++;\n } else {\n sum += nums[i];\n minExtra = (minExtra < (nums[i] - (nums[i] ^ k))) ? minExtra : (nums[i] - (nums[i] ^ k));\n }\n }\n\n if (count % 2 == 0) {\n return sum;\n } else {\n return sum - minExtra;\n }\n}\n\n```\n```C# []\npublic class Solution {\n public long MaximumValueSum(int[] nums, int k, int[][] edges) {\n long sum = 0;\n long minExtra = 1000000; \n int count = 0;\n\n foreach (int val in nums) {\n if ((val ^ k) > val) {\n sum += val ^ k;\n minExtra = Math.Min(minExtra, (val ^ k) - val);\n count++;\n } else {\n sum += val;\n minExtra = Math.Min(minExtra, val - (val ^ k));\n }\n }\n\n return (count % 2 == 0) ? sum : sum - minExtra;\n }\n}\n\n```\n```javascript []\nvar maximumValueSum = function(nums, k, edges) {\n let sum = 0;\n let minExtra = 1000000; \n let count = 0;\n\n for (const val of nums) {\n if ((val ^ k) > val) {\n sum += val ^ k;\n minExtra = Math.min(minExtra, (val ^ k) - val);\n count++;\n } else {\n sum += val;\n minExtra = Math.min(minExtra, val - (val ^ k));\n }\n }\n\n return count % 2 === 0 ? sum : sum - minExtra;\n};\n\n```\n```Go []\nfunc maximumValueSum(nums []int, k int, edges [][]int) int64 {\n var sum int64 = 0\n var minExtra int64 = 1000000 \n count := 0\n\n for _, val := range nums {\n if (val ^ k) > val {\n sum += int64(val ^ k)\n minExtra = min(minExtra, int64((val ^ k) - val))\n count++\n } else {\n sum += int64(val)\n minExtra = min(minExtra, int64(val - (val ^ k)))\n }\n }\n\n if count % 2 == 0 {\n return sum\n } else {\n return sum - minExtra\n }\n}\n\nfunc min(a, b int64) int64 {\n if a < b {\n return a\n }\n return b\n}\n\n```\n**NOTE: THE FOLLOWING IMPLEMENTATION BEATS 100% IN JAVA .. DON\'T KNOW ABOUT OTHER CODES** \n```\nUPVOTE\u2B06\uFE0F IF IT HELPED\uD83D\uDE0A\n```\n | 8 | 1 | ['C', 'Python', 'C++', 'Java', 'Go', 'Python3', 'JavaScript', 'C#'] | 3 |
find-the-maximum-sum-of-node-values | Python 3 || 2 lines, maps, lambdas, and a filter || T/S: 91% / 77% | python-3-2-lines-maps-lambdas-and-a-filt-1s6q | You likely can get the spirit of this solution from others\' great explications that have already been posted.\n\nclass Solution:\n def maximumValueSum(self, | Spaulding_ | NORMAL | 2024-03-04T03:53:06.777276+00:00 | 2024-05-25T01:26:38.163885+00:00 | 207 | false | You likely can get the spirit of this solution from others\' great explications that have already been posted.\n```\nclass Solution:\n def maximumValueSum(self, nums: List[int], k: int, \n edges: List[List[int]]) -> int:\n\n dif = sorted(map(lambda x: x - (x^k), nums)) \n \n return sum(nums) - sum(filter(lambda x: x < 0, \n map(sum, zip(dif[::2],dif[1::2]))))\n```\n[https://leetcode.com/problems/find-the-maximum-sum-of-node-values/submissions/1193152707/](https://leetcode.com/problems/find-the-maximum-sum-of-node-values/submissions/1193152707/)\n\n\n\nI could be wrong, but I think that time complexity is *O*(*N*log*N*) and space complexity is *O*(*N*), in which *N* ~ `len(nums)`. | 8 | 0 | ['Python3'] | 2 |
find-the-maximum-sum-of-node-values | O(n) || Greedy || Very easy to understand | on-greedy-very-easy-to-understand-by-ay7-5s8o | Intuition\n Describe your first thoughts on how to solve this problem. \nThe main intuition lies in the fact there is nothing to do with edges because it is com | AY73 | NORMAL | 2024-05-19T06:52:41.370751+00:00 | 2024-05-19T06:52:41.370779+00:00 | 506 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe main intuition lies in the fact there is nothing to do with edges because it is completely connected graph we can take any 2 nodes to do xor operation for suppose my tree is \na->b->c then for doing xor between a and c we have to do with (a , b) and then (b,c) since b was involved twice b^k^k = b \n \n# Approach\n<!-- Describe your approach to solving the problem. -->\nIf we are performing xor operation for 2 nodes at a time then time complexity will be o(n^2) so somehow we have to come up with a approach where we don\'t care about second node and can do xor operation for each node , Take an example of tree a->b->c->d \nall the possible trees after doing xor operations are\n\n1) a\'->b\'->c->d (Note :- a\' = a^k)\n2) a\'->b->c\'->d\n3) a\'->b->c->d\'\n4) a->b\'->c\'->d\n5) a->b\'->c->d\'\n6) a->b->c\'->d\'\n7) a\'->b\'>c\'->d\'\n\nWe can observe that in all the possible outcomes number of nodes where xor operation is performed is always even .\n\nSo traverse all the nodes store sum of max(a , a\')\n\nIf we perform an XOR operation on an odd number of nodes, we have two choices: either we skip the XOR operation on one of the nodes where we would normally perform it, or we perform the XOR operation on a node where we wouldn\'t normally do so. Either way, this adjustment will result in the number of nodes where XOR is performed being even.\n\nSo store min difference\'s of a\'-a where we performed XOR and a-a\' where we didn\'t perform XOR subract the minumum of those if the count is odd \n\n\nNote :- If it is not fully connected graph then we can\'t follow this approach .\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: o(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n long long maximumValueSum(vector<int>& nums, int k, vector<vector<int>>& edges) {\n int n = nums.size() ; \n long long ans = 0 ; \n int xor_d = 1e9 ; // The min difference we have to sacrifice without doing xor operation\n int nxor_d = 1e9 ; // The min difference we have to sacrifice by doing xor .\n int cnt = 0 ; // No of elements where xor val is greater than node val\n for(int i = 0 ; i < n ; i++){\n int xor_val = nums[i]^k ;\n if(xor_val > nums[i]){\n cnt++;\n ans += xor_val ; \n xor_d = min(xor_d , xor_val - nums[i]);\n }else{\n ans += nums[i] ;\n nxor_d = min(nxor_d , nums[i]-xor_val) ; \n }\n }\n if(cnt%2 == 0){\n return ans ;\n }\n return ans - min(xor_d , nxor_d) ;\n }\n};\n``` | 7 | 0 | ['Greedy', 'Bit Manipulation', 'C++'] | 4 |
find-the-maximum-sum-of-node-values | Video Explanation (Both DP & Greedy approach with Intuition) | video-explanation-both-dp-greedy-approac-sbh5 | Explanation\n\nClick here for the video\n\n# Code\n\ntypedef long long int ll;\n\nconst int N = 2e4+1;\n\nll dp[2][N];\nint par[N];\n\nclass Solution {\n \n | codingmohan | NORMAL | 2024-03-03T11:48:29.358983+00:00 | 2024-03-03T11:48:29.359038+00:00 | 292 | false | # Explanation\n\n[Click here for the video](https://youtu.be/BYF3vGQ49Zw)\n\n# Code\n```\ntypedef long long int ll;\n\nconst int N = 2e4+1;\n\nll dp[2][N];\nint par[N];\n\nclass Solution {\n \n ll K;\n vector<vector<int>> g;\n vector<ll> val;\n \n void CalculateParent(int root, int p) {\n par[root] = p;\n \n for (auto i : g[root]) \n if (i != p) CalculateParent(i, root);\n }\n \n ll dfs (int src, bool taken) {\n ll &ans = dp[taken][src];\n if (ans != -1) return ans;\n \n ans = 0;\n ll min_diff = 1e18;\n ll best = 0, taken_in_best = 0;\n \n min_diff = min (min_diff, abs(val[src] - (val[src]^K)));\n best += max(val[src], val[src]^K);\n if (val[src] < (val[src]^K)) taken_in_best ++;\n \n for (auto i: g[src]) {\n if (i == par[src]) continue;\n \n ll with = dfs(i, true);\n ll without = dfs(i, false);\n \n min_diff = min(min_diff, abs(with-without));\n \n best += max(with, without);\n if (with > without) taken_in_best ++;\n }\n \n taken_in_best %= 2;\n \n if (taken_in_best == taken) return (ans = best);\n return (ans = best-min_diff);\n }\n \npublic:\n long long maximumValueSum(vector<int>& nums, int k, vector<vector<int>>& edges) {\n memset(dp, -1, sizeof(dp));\n memset(par, -1, sizeof(par));\n g.clear(), g.resize(nums.size());\n val.clear();\n \n for (auto i : nums) val.push_back(i);\n K = k;\n for (auto e : edges) {\n g[e[0]].push_back(e[1]);\n g[e[1]].push_back(e[0]);\n }\n \n CalculateParent(0, -1);\n return dfs (0, false);\n }\n};\n``` | 7 | 0 | ['C++'] | 1 |
find-the-maximum-sum-of-node-values | O(N) approach | Easy | Tricky | C++ | Beat 100% | on-approach-easy-tricky-c-beat-100-by-al-yiki | Intuition\nwe firstly check from the given nodes which gives me profit. \nwe store nodes which gave us profit in x vector.\nand rest all to nx vector.\n\n# App | allrounderankit | NORMAL | 2024-03-02T16:16:39.332805+00:00 | 2024-03-02T17:45:15.662810+00:00 | 621 | false | # Intuition\nwe firstly check from the given nodes which gives me profit. \nwe store nodes which gave us profit in x vector.\nand rest all to nx vector.\n\n# Approach\n if size of x vector is EVEN than we can take XOR with all nodes because there will always exist 1 way to XOR them.\n\n\nbut if size is ODD than we have two options.\n 1. neglect node from x vector which have least PROFIT.\n 2. take node from nx vector which have lowest LOSS if exist.\n\n# Complexity\n- Time complexity:\n n(logn) but can we optimised to O(n) by not sorting x and nx array rather finding minimum of both array by ittrating it.\n\n- Space complexity:\nO(n)\n\n# NO Use of Edges (:\n\n# Code\n```\n#define ll long long int\nclass Solution {\npublic:\n \n long long maximumValueSum(vector<int>& nums, int k, vector<vector<int>>& e) {\n \n int n = nums.size();\n ll ans = 0;\n ll sum1 = 0;\n ll sum2 = 0;\n vector<ll> x,nx;\n \n for(int i=0;i<n;i++){\n int diff = ( nums[i]^k ) - nums[i];\n \n if( diff >= 0 ){\n x.push_back( diff );\n sum1 += ( nums[i]^k );\n }\n else{\n nx.push_back( abs(diff) );\n sum2 += nums[i];\n }\n }\n \n sort( x.begin() , x.end() );\n sort( nx.begin(), nx.end() );\n \n if( x.size()%2 == 0 ){\n ans = max( ans, sum1+sum2); \n }\n else{\n \n if( nx.size() )\n ans = max( sum1 + sum2 - x[0] , sum1 + sum2 - nx[0] );\n else\n ans = sum1 + sum2 - x[0]; \n }\n \n return ans;\n }\n};\n``` | 7 | 0 | ['Bit Manipulation', 'C++'] | 2 |
find-the-maximum-sum-of-node-values | Python | XOR | python-xor-by-khosiyat-2iwx | see the Successfully Accepted Submission\n\n# Code\n\nclass Solution:\n def maximumValueSum(self, nums: list[int], k: int, edges: list[list[int]]) -> int:\n | Khosiyat | NORMAL | 2024-05-19T04:46:48.718957+00:00 | 2024-05-19T04:46:48.718975+00:00 | 269 | false | [see the Successfully Accepted Submission](https://leetcode.com/problems/find-the-maximum-sum-of-node-values/submissions/1261915101/?envType=daily-question&envId=2024-05-19)\n\n# Code\n```\nclass Solution:\n def maximumValueSum(self, nums: list[int], k: int, edges: list[list[int]]) -> int:\n import sys\n n = len(nums)\n cnt = 0\n sac = sys.maxsize # Use sys.maxsize to represent INT_MAX\n total_sum = 0\n \n for num in nums:\n x = num\n y = num ^ k\n if x > y:\n total_sum += x\n else:\n total_sum += y\n cnt += 1\n sac = min(sac, abs(x - y))\n \n if cnt % 2 == 1:\n total_sum -= sac\n \n return total_sum\n```\n | 6 | 0 | ['Python3'] | 2 |
find-the-maximum-sum-of-node-values | Ignore edge Greedy approach with explanation | clean code | [c++/java/python/go] | ignore-edge-greedy-approach-with-explana-gpoc | Intuition\n- This solution is based on we can xor operation on any pair of nodes irrespective of any direct edge between them. How??\n - For a parent node we | anupsingh556 | NORMAL | 2024-05-19T07:53:12.244963+00:00 | 2024-05-19T07:53:12.244995+00:00 | 243 | false | # Intuition\n- This solution is based on we can xor operation on any pair of nodes irrespective of any direct edge between them. How??\n - **For a parent node we can xor of it with any of its direct child or indirect child node.**\n - Suppose we have a parent node a with direct child b which has child c like a--->b--->c. Now we can take xor for edge b->c as mentioned in problem statement. We can again take xor on a->b.\n - Since we did xor twice on b so its value wont change effectively we did xor between a & c. hence proving our first statement.\n - **We can take xor between two nodes present in left and right subtree.**\n - For two nodes a, b having common parent c. We can take xor of a^c then b^c since we did xor twice on c its value wont change so effectively its xor on a&b proving our original statement.\n- Now we can greedily pick pairs whose xored value will give us maximum sum result.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n- Create a difference array which stores difference in values if we take original value vs xored value\n- sort this on descending order and pick pairs such that net sum is positive\n- Add this with net sum of all initial nodes and we get our result.\n- We can also use discard approach where we keep track of mim difference and discard it to make pairs\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(nlogn) for sorting difference array. We can make it O(n) if we use discard approach\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n) for storing diff array. We can make it constant space if we use discard based approach\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```c++ []\nclass Solution {\npublic:\n long long maximumValueSum(vector<int>& nodes, int k, vector<vector<int>>& e) {\n int n = nodes.size();\n vector<int> diff(n, 0);\n long long sum = 0l;\n for(int i=0;i<n;i++) {\n diff[i] = (nodes[i]^k )- nodes[i];\n sum+=nodes[i]*1l;\n } \n sort(diff.begin(), diff.end(), greater<int>());\n for(int i=0;i<n-1;i+=2) {\n if((diff[i] + diff[i+1])>0) {\n sum+=(diff[i] + diff[i+1])*1l;\n }\n }\n return sum;\n }\n};\n```\n```python []\nclass Solution(object):\n def maximumValueSum(self, nums, k, edges):\n n = len(nums)\n diff = [0] * n\n total_sum = 0\n\n for i in range(n):\n diff[i] = (nums[i] ^ k) - nums[i]\n total_sum += nums[i]\n\n diff.sort(reverse=True)\n\n for i in range(0, n-1, 2):\n if diff[i] + diff[i+1] > 0:\n total_sum += diff[i] + diff[i+1]\n\n return total_sum\n\n```\n```go []\n\nfunc maximumValueSum(nodes []int, k int, e [][]int) int64 {\n\tn := len(nodes)\n\tdiff := make([]int, n)\n\tvar sum int64\n\n\tfor i := 0; i < n; i++ {\n\t\tdiff[i] = (nodes[i] ^ k) - nodes[i]\n\t\tsum += int64(nodes[i])\n\t}\n\n\tsort.Slice(diff, func(i, j int) bool {\n\t\treturn diff[i] > diff[j]\n\t})\n\n\tfor i := 0; i < n-1; i += 2 {\n\t\tif diff[i]+diff[i+1] > 0 {\n\t\t\tsum += int64(diff[i] + diff[i+1])\n\t\t}\n\t}\n\n\treturn sum\n}\n```\n``` Java []\nclass Solution {\n public long maximumValueSum(int[] nums, int k, int[][] edges) {\n int n = nums.length;\n int[] diff = new int[n];\n long totalSum = 0;\n\n for (int i = 0; i < n; i++) {\n diff[i] = (nums[i] ^ k) - nums[i];\n totalSum += nums[i];\n }\n\n Arrays.sort(diff);\n \n for (int i = n - 1; i > 0; i -= 2) {\n if ((diff[i] + diff[i - 1]) > 0) {\n totalSum += (diff[i] + diff[i - 1]);\n }\n }\n\n return totalSum;\n }\n}\n\n```\n | 5 | 0 | ['C++'] | 3 |
find-the-maximum-sum-of-node-values | Surprisingly easy solution | surprisingly-easy-solution-by-winston_wo-zjtx | Code\n\npublic class Solution \n{\n public long MaximumValueSum(int[] nums, int k, int[][] edges) \n {\n long result = 0;\n\n foreach (long | winston_wolfe | NORMAL | 2024-03-02T19:27:59.728314+00:00 | 2024-03-02T19:27:59.728338+00:00 | 117 | false | # Code\n```\npublic class Solution \n{\n public long MaximumValueSum(int[] nums, int k, int[][] edges) \n {\n long result = 0;\n\n foreach (long num in nums)\n result += num;\n \n var queue = new PriorityQueue<int, int>();\n \n foreach (var num in nums)\n {\n var xor = num ^ k;\n var diff = xor - num;\n \n queue.Enqueue(diff, -diff);\n }\n \n while (queue.Count >= 2)\n {\n var value = queue.Dequeue() + queue.Dequeue();\n \n if (value > 0)\n result += value;\n }\n \n return result;\n }\n}\n``` | 5 | 0 | ['C#'] | 2 |
find-the-maximum-sum-of-node-values | take, Not take || Easy✅ || Beats 100%🎯|| C++ | take-not-take-easy-beats-100-c-by-ajay_g-zmnq | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Ajay_Gupta_01 | NORMAL | 2024-03-02T18:33:34.190349+00:00 | 2024-03-02T18:33:34.190380+00:00 | 446 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n*2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n*2)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int n;\n vector<vector<long long>>dp;\n\n long long solve(int i,int j,vector<int>&nums,int k)\n {\n if(i==n)\n return j==0 ? 0 : -INT_MAX;\n\n if(dp[i][j]!=-1)\n return dp[i][j];\n\n long long notake = nums[i] + solve(i+1,j,nums,k);\n long long take = (nums[i]^k) + solve(i+1,(j+1)%2,nums,k);\n \n return dp[i][j]= max(take,notake);\n }\n long long maximumValueSum(vector<int>& nums, int k, vector<vector<int>>& edges) {\n\n n=nums.size();\n dp.resize(n,vector<long long>(2,-1));\n return solve(0,0,nums,k);\n }\n};\n``` | 5 | 0 | ['Dynamic Programming', 'Recursion', 'C++'] | 3 |
find-the-maximum-sum-of-node-values | [C++] XOR Again If Needed (Greedy) | c-xor-again-if-needed-greedy-by-awesome-dsinj | Intuition\n Describe your first thoughts on how to solve this problem. \n- Apply max(nums[i], nums[i] ^ k) for each element in the array\n- We can always change | pepe-the-frog | NORMAL | 2024-03-02T16:02:01.268776+00:00 | 2024-03-02T16:14:11.174581+00:00 | 481 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- Apply `max(nums[i], nums[i] ^ k)` for each element in the array\n- We can always change the even number of times because this is a tree\n- If we changed the odd number of times, we need to XOR an integer again\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- find the number of changes and the maximum sum\n- if the number of changes is even, we can submit the sum directly\n- if the number of changes is odd, we need to pick one of the integers in the array to XOR it again\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n // time/space: O(n)/O(1)\n long long maximumValueSum(vector<int>& nums, int k, vector<vector<int>>& edges) {\n // find the number of changes and the maximum sum\n int change = 0;\n long long sum = 0LL;\n for (auto& num : nums) {\n if ((num ^ k) > num) {\n change++;\n sum += (num ^ k);\n }\n else {\n sum += num;\n }\n }\n \n // if the number of changes is even, we can submit the sum directly\n if ((change & 1) == 0) return sum;\n \n // if the number of changes is odd, we need to pick one of the integers in the array to XOR it again\n long long maxSum = 0LL;\n for (int i = 0; i < nums.size(); i++) {\n maxSum = max(maxSum, sum - abs(nums[i] - (nums[i] ^ k)));\n }\n return maxSum;\n }\n};\n``` | 5 | 0 | ['Greedy', 'Bit Manipulation', 'Tree', 'C++'] | 3 |
find-the-maximum-sum-of-node-values | ✅ One Line Solution | one-line-solution-by-mikposp-fdux | (Disclaimer: this is not an example to follow in a real project - it is written for fun and training mostly)\n\n# Code #1.1 - One Line\nTime complexity: O(n). S | MikPosp | NORMAL | 2024-05-19T11:24:22.962885+00:00 | 2024-05-19T11:24:22.962910+00:00 | 537 | false | (Disclaimer: this is not an example to follow in a real project - it is written for fun and training mostly)\n\n# Code #1.1 - One Line\nTime complexity: $$O(n)$$. Space complexity: $$O(1)$$.\n```\nclass Solution:\n def maximumValueSum(self, a: List[int], k: int, e: List[List[int]]) -> int:\n return (r:=reduce(lambda q,v:(q[0]+max(v,x:=v^k),min(q[1],abs(x-v)),q[2]+(x>v)),a,(0,inf,0)))[0]-r[2]%2*r[1]\n```\n\n# Code #1.2 - Unwrapped\n```\nclass Solution:\n def maximumValueSum(self, a: List[int], k: int, e: List[List[int]]) -> int:\n summ, minDiff, cnt = 0, inf, 0\n for v in a:\n x = v^k\n summ += max(v, x)\n minDiff = min(minDiff, abs(x-v))\n cnt += x > v\n \n return summ - cnt%2*minDiff\n```\n\n(Disclaimer 2: all code above is just a product of fantasy, it is not claimed to be perfect oneliners - please, remind about drawbacks only if you know how to make it better) | 4 | 1 | ['Array', 'Greedy', 'Bit Manipulation', 'Tree', 'Python', 'Python3'] | 4 |
find-the-maximum-sum-of-node-values | Python3 || O(n) and O(1) TIME AND SPACE || May 19 2024 Daily | python3-on-and-o1-time-and-space-may-19-cqi1m | Intuition\nTo maximize the sum of the values of tree nodes, we need to carefully apply the XOR operation using the given integer \nk. The XOR operation can pote | praneelpa | NORMAL | 2024-05-19T00:23:03.091435+00:00 | 2024-05-19T00:23:03.091460+00:00 | 444 | false | # Intuition\nTo maximize the sum of the values of tree nodes, we need to carefully apply the XOR operation using the given integer \nk. The XOR operation can potentially increase the value of a node, but we must consider how to maximize the overall sum by selectively applying this operation to the tree\'s edges. The goal is to determine when performing the XOR operation yields a higher sum and handle the parity (odd or even nature) of the total number of value changes optimally.\n\n# Approach\nInitial Calculation: For each node, calculate the maximum value it can achieve by comparing its current value with its value after applying the XOR operation. This can be expressed as max(num, num ^ k).\nCount Changes: Count how many nodes would change if the XOR operation was applied to all nodes.\nHandle Even and Odd Changes:\nIf the number of changes is even, simply return the maximum sum because we can always pair changes to maintain an optimal sum.\nIf the number of changes is odd, find the smallest possible change difference to make the total sum of changes even, thereby maximizing the sum.\nCompute the Result: Return the computed maximum possible sum with the necessary adjustments based on the parity of changes.\n\n# Complexity\n- Time complexity:\n$$O(n)$$ because we iterate through the list of nodes to compute the sums and determine the minimal change difference.\n\n- Space complexity:\n$$O(1)$$ as we use a fixed amount of extra space regardless of the input size.\n\n# Code\n```\nclass Solution:\n def maximumValueSum(self, nums: List[int], k: int, edges: List[List[int]]) -> int:\n maxSum = sum(max(num, num ^ k) for num in nums)\n changedCount = sum((num ^ k) > num for num in nums)\n if changedCount % 2 == 0:\n return maxSum\n minChangeDiff = min(abs(num - (num ^ k)) for num in nums)\n return maxSum - minChangeDiff\n``` | 4 | 0 | ['Array', 'Dynamic Programming', 'Greedy', 'Bit Manipulation', 'Tree', 'Sorting', 'Python3'] | 4 |
find-the-maximum-sum-of-node-values | ✅ O(n) DP + Greedy Solution in C++ | on-dp-greedy-solution-in-c-by-mayank_mot-l1s4 | Intuition\nTo find the maxSum for a subtree corresponding to a node curr, we need to find the maxSum for each children of curr in two cases:\nThe operation is p | Mayank_Motwani | NORMAL | 2024-03-03T12:37:11.665502+00:00 | 2024-03-03T12:38:28.553574+00:00 | 222 | false | # Intuition\nTo find the maxSum for a subtree corresponding to a node `curr`, we need to find the maxSum for each children of `curr` in two cases:\nThe operation is performed on the edge between them - `withOp`\nThe operation is not performed on the edge between them - `withoutOp`\n\nThe number of nodes whose values can be changed should be even since we are operating on an edge which involves two nodes. If the number of nodes is not even, we have two options:\nEither take the least possible loss i.e. change the value of a node despite a decrease.\nOr leave the least gain i.e. undo a change which resulted in an increase.\n\n# Approach\nTo find `maxSum`, we will accumulate the maximum of two possible values for each node (parent and children) in `sum` and will count the number of favourable changes in `numChanges`. At the end, if `numChanges` is odd, we can simply subtract the least absolute difference of `withOp` and `withoutOp` (stored in `minChange`) from `sum` which will result in subtraction of either the least loss or the least gain.\n\nThe initial value of `curr` depends on whether the operation was performed on the edge to its parent. A boolean argument `c` indicates whether the operation was performed or not.\n\nTo optimize the solution, we will store the `maxSum` values for each node in a `dp` array to avoid repeated calculations.\n\nAlso, it should be noted that we can take any of the nodes as the root of the tree, it won\'t make any difference.\n\n# Complexity\n- Time complexity: `O(N)`\nwhere `N` is the number of nodes in the tree.\nSince, we traverse the whole tree and visit each edge. The number of edges is `N - 1`.\n\n\n- Space complexity: `O(N * E\')`\nwhere `E\'` is the average number of edges for each node.\n\n# Code\n```\nclass Solution {\n vector<vector<long long>> dp;\n long long maxSum (int curr, bool c, int parent, vector<int> & nums, int k, vector<vector<int>> & adjList) {\n if (dp[curr][c] != -1)\n return dp[curr][c];\n int val = (c ? nums[curr] ^ k : nums[curr]);\n long long sum = max(val ^ k, val);\n int numChanges = (val ^ k) > val, minChange = abs((val ^ k) - val);\n for (int nbr : adjList[curr]) {\n if (nbr == parent)\n continue;\n long long withOp = maxSum(nbr, true, curr, nums, k, adjList);\n long long withoutOp = maxSum(nbr, false, curr, nums, k, adjList);\n sum += max(withOp, withoutOp);\n // cout << nbr << ": " << sum << endl;\n numChanges += (withOp > withoutOp);\n minChange = min(minChange, (int)abs(withOp - withoutOp));\n }\n dp[curr][c] = (sum - (numChanges % 2 ? minChange : 0));\n // cout << "dp[" << curr << "," << c << "] = " << dp[curr][c] << endl;\n return dp[curr][c];\n }\npublic:\n long long maximumValueSum(vector<int> & nums, int k, vector<vector<int>> & edges) {\n int n = nums.size();\n vector adjList(n, vector<int>());\n for (auto & e : edges) {\n adjList[e[0]].push_back(e[1]);\n adjList[e[1]].push_back(e[0]);\n }\n dp.resize(n, vector<long long>(2, -1));\n // cout << "Ok\\n";\n return maxSum(0, false, -1, nums, k, adjList);\n }\n};\n```\n\nA better solution has been given by [votrubac](https://leetcode.com/votrubac/) which does not requires the use of `dp` or even the given `edges`! You can check it out [here](https://leetcode.com/problems/find-the-maximum-sum-of-node-values/solutions/4811460/greedy-sacrifice).\n | 4 | 0 | ['C++'] | 1 |
find-the-maximum-sum-of-node-values | C++ O(N) time, O(1) space | c-on-time-o1-space-by-user8383x-87uh | Intuition\n1. First idea is that we can xor any pair of nodes in the tree, not only directly connected ones. Explanation: the tree is connected (as per descript | user8383x | NORMAL | 2024-03-02T16:07:19.622723+00:00 | 2024-03-02T16:24:24.326310+00:00 | 265 | false | # Intuition\n1. First idea is that we can xor any pair of nodes in the tree, not only directly connected ones. Explanation: the tree is connected (as per description), thus, there always exists a path between nodes `a` and `b`: `a -> ... -> b`. Short reminder: `x^k^k = x`.By xor\'ing every pair on the path, we have:\n 1. `a^k -> x1^k -> x2 -> ... -> xn -> b`\n 2. `a^k -> x1 -> x2^k -> ... -> xn -> b`\n 3. `...`\n 4. `a^k -> x1 -> x2 -> ... -> xn^k -> b`\n 5. `a^k -> x1 -> x2 -> ... -> xn -> b^k`\n2. Second idea: total number of xor operations should be even, as we always change nodes in pairs. I.e. we are allowed to xor only 0 (do not touch tree at all), 2, 4, ..., 2*m nodes. So, we traverse all node values in `nums`, and keep two results: `result` (current best result achieved with even count of xor operations) and `alt_result` (current best result achieved with odd count of xor operations). For every `n` from `nums` we update both `result` and `alt_result`:\n 1. `result` = `max` of { `result + n` (still even number of xors), `alt_result + n^k` (odd number of xors + 1 more xor = even number of xors) }\n 2. `alt_result` = `max` of { `alt_result + n` (still odd number of xors), `result + n^k` (even number of xors + 1 more xor = odd number of xors) }\n\n\n# Complexity\n- Time complexity: O(N)\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution {\npublic:\n long long maximumValueSum(vector<int>& nums, int k, vector<vector<int>>& edges) {\n long long result = 0, alt_result = -1e9;\n for (auto n : nums) {\n int alt_n = n ^ k;\n long long tmp = result;\n result = max(result + n, alt_result + alt_n);\n alt_result = max(alt_result + n, tmp + alt_n);\n //cout << result << "," << alt_result << endl;\n }\n return result;\n }\n};\n``` | 4 | 0 | ['C++'] | 1 |
find-the-maximum-sum-of-node-values | 💥 Memory beats 100% [EXPLAINED] | memory-beats-100-explained-by-r9n-bv2i | IntuitionThe problem asks for finding the maximum value sum based on a sequence of numbers where you can either choose the number as is or apply a bitwise XOR o | r9n | NORMAL | 2025-01-30T02:43:08.351728+00:00 | 2025-01-30T02:43:08.351728+00:00 | 5 | false | # Intuition
The problem asks for finding the maximum value sum based on a sequence of numbers where you can either choose the number as is or apply a bitwise XOR operation with a given constant k. The XOR operation flips the bits of the number and may change its value, so we need to decide whether to include the number as is or apply XOR based on the current state (even or odd index).
# Approach
We use dynamic programming to solve this problem, where dp[index][isEven] stores the maximum value obtainable from the index position onward, given whether the current state is even or odd. Starting from the first index, we can either take the number as is or apply XOR with k, and for each decision, we recursively calculate the result for the next index, updating the DP table to avoid redundant calculations. At the base case, if we've processed all numbers, we return 0 for the even state or a very small value for the odd state.
# Complexity
- Time complexity:
O(n) where n is the number of elements in the array nums. Each index is processed once, and for each, we only do constant-time operations (max calculation and recursion).
- Space complexity:
O(n) for storing the DP table, where n is the length of nums. The space is used to memoize the results for each state at each index.
# Code
```kotlin []
class Solution {
fun maximumValueSum(nums: IntArray, k: Int, edges: Array<IntArray>): Long {
val dp = Array(nums.size) { LongArray(2) { -1L } }
return dfs(nums, k, edges, 0, 1, dp)
}
private fun dfs(nums: IntArray, k: Int, edges: Array<IntArray>, index: Int, isEven: Int, dp: Array<LongArray>): Long {
if (index == nums.size) {
return if (isEven == 1) 0 else Long.MIN_VALUE
}
if (dp[index][isEven] != -1L) {
return dp[index][isEven]
}
val val1 = nums[index] + dfs(nums, k, edges, index + 1, isEven, dp)
val val2 = (nums[index] xor k) + dfs(nums, k, edges, index + 1, isEven xor 1, dp)
dp[index][isEven] = maxOf(val1, val2)
return dp[index][isEven]
}
}
``` | 3 | 0 | ['Math', 'Dynamic Programming', 'Backtracking', 'Greedy', 'Bit Manipulation', 'Depth-First Search', 'Graph', 'Binary Search Tree', 'Sorting', 'Kotlin'] | 0 |
find-the-maximum-sum-of-node-values | 👏💯PYTHON 🎉|| JS 🎉|| JAVA 🎉|| 🔥🔥 Best Visualization ||✅ New Question || 🫰Only Sorting | python-js-java-best-visualization-new-qu-w4xs | Screenshot \uD83C\uDF89\n\n\n\n\n---\n\n\n# Intuition \uD83E\uDD14\n Describe your first thoughts on how to solve this problem. \n maximum possible sum of th | Prakhar-002 | NORMAL | 2024-05-19T11:09:51.569021+00:00 | 2024-05-19T12:07:33.425167+00:00 | 119 | false | # Screenshot \uD83C\uDF89\n\n\n\n\n---\n\n\n# Intuition \uD83E\uDD14\n<!-- Describe your first thoughts on how to solve this problem. -->\n maximum possible sum of the values \n\n Let\'s understand the problem first and make it easy\n\n1. `Given` \n `A.` An `undirected tree` with `n Node` whose value are `0 to n - 1`\n\n `B.` Value of tree can be our `index value`\n\n `C.` `Array (nums)` which actually tells us the `exact value of node`\n\n `D.` A number `k` by which `we have to take XOR` with `tree value`\n\n2. `Work to do`\n\n `A.` we\'ve to `select any edge` from tree\n\n `B.` Then `take XOR` with `both the connected node` with that edge\n\n `C.` and then `sum all actual values` of node from `given nums array`\n\n3. `Return the sum` of all value `after taking after xor`\n\n ### We have to maximize this sum ---------\n---\n\n\n# Approach \uD83E\uDD73\n<!-- Describe your approach to solving the problem. -->\n Break this in a very simple problem ...\n\n1. Let\'s `understand the XOR` first\n \n `A.` `1 time XOR` --> It give s`one value either greater or lower or 0`\n 10 ^ 2 = 8 \n\n `B.` `2 time XOR` --> It give the `same value`\n 10 ^ 2 ^ 2 = 10\n\n2. Solve `by understanding problem` --> `K = 3`\n \n \n 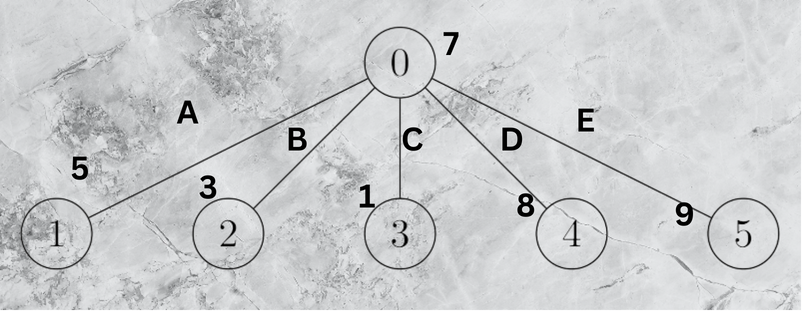\n\n `A.` First we\'ll select `( A C D E edge)` \n\n `B.` Take the `xor of value` with **`k = 3`**\n\n `C.` only `Take XOR or that value which give a large value`\n\n `D.`We did not take XOR of 3 because `it\'ll give 0` (Lower value)\n \n \n 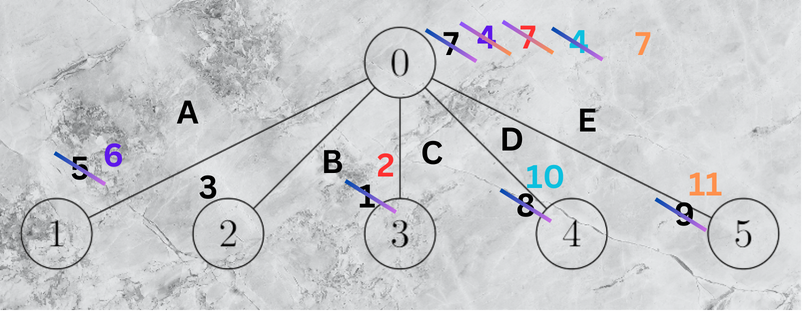\n\n\n `E.` `sum will be 39`\n\n---\n\n3. `As we see node 0 does not mean anything to us`\n\n ```\n // Best appoach\n\n 1. Either take one edge or just take 2 node\n 2. Take one node and do not touch it\n 3. Or take any 2 node and take \n\n --> We can\'t just take every node and take xor of that\n ```\n 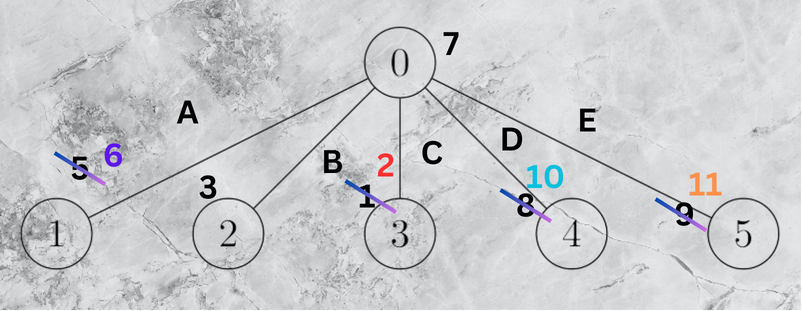\n\n Take 1st and 3th at a time\n and\n Take 4th and 5th at a time\n and\n Do not touch any node\n\n4. Now `problem is that how to choose our node`\n\n Simple -> take XOR if value inc take it otherwise leave it \n\n---\n\n# Understand with code \uD83E\uDD73\n\n We will use best Approach method\n\n - In which we have 5 works to do\n \n 1. Make one diff array give us values if inc or dec after XOR.\n 2. Sort this array because we need only increased values\n 3. take sum of previous values\n 4. Add the positive that comes after the xor from our XOR array\n 5. add 2 values at a time as we guessed that and return the some\n---\n\n`Step 1` **Make a xorArray** \n\n Which will store if value inc or dec either +ve or -ve\n\n Take XOR of value and given K and subtract with itself \n\n So It will give the diffrence only either +Ve or -ve or 0\n\n```python []\n xor_arr = [(n ^ k) - n for n in nums]\n```\n```JAVASCRIPT []\n let xorArr = nums.map(n => (n ^ k) - n)\n\n``` \n```JAVA []\n public Integer[] xorArrCreator(int arr[], int k) {\n Integer xorArr[] = new Integer[arr.length];\n\n for (int i = 0; i < arr.length; i++) {\n xorArr[i] = (arr[i] ^ k) - arr[i];\n }\n\n return xorArr;\n }\n\n // function will return our require array\n Integer xorArr[] = xorArrCreator(nums, k);\n```\n\n---\n\n`Step 2 - 3` **Sort in reverse order and take the sum of nums array** \n\n because we just need only +ve values\n\n```python []\n xor_arr.sort(reverse=True)\n res = sum(nums)\n\n```\n```JAVASCRIPT []\n xorArr.sort((a, b) => b - a);\n let sum = nums.reduce((a, b) => a + b);\n``` \n```JAVA []\n // Give our sum of array\n public long numArrSum(int arr[]) {\n long sum = 0;\n\n for (int i = 0; i < arr.length; i++) {\n sum += arr[i];\n }\n\n return sum;\n }\n\n // Sort in reverse order\n Arrays.sort(xorArr, Collections.reverseOrder());\n\n // taking sum of all values in nums array\n long sum = numArrSum(nums);\n```\n---\n\n`Step 4` **Apply loop and add values 2 at a time** \n\n allthough we are adding 2 values at a time \n\n In case of odd it will leave one value \n\n But It will not gonna add because if we add that node \n \n it will dec other node connected with same edge\n\n```python []\n for i in range(0, len(nums), 2):\n if i == len(nums) - 1:\n break\n\n path_sum = xor_arr[i] + xor_arr[i + 1]\n\n if path_sum <= 0:\n break\n\n res += path_sum\n```\n```JAVASCRIPT []\n for (let i = 0; i < nums.length; i += 2) {\n if (i == nums.length - 1) {\n break;\n }\n\n let pathSum = xorArr[i] + xorArr[i + 1]\n\n if (pathSum <= 0) {\n break;\n }\n\n sum += pathSum;\n }\n``` \n```JAVA []\n for (int i = 0; i < xorArr.length; i += 2) {\n if (i == xorArr.length - 1) {\n break;\n }\n long pathSum = xorArr[i] + xorArr[i + 1];\n if (pathSum <= 0) {\n break;\n }\n sum += pathSum;\n }\n```\n---\n\n`Step 5` **Make a xorArray** \n\n return sum\n\n```python []\n return res\n\n```\n```JAVASCRIPT []\n return sum\n\n``` \n```JAVA []\n return sum;\n```\n\n---\n\n# Complexity \uD83D\uDD25\n- Time complexity: $$O(nlogn)$$ `For sorting`\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$ `For Array `\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n---\n\n\n# Code\n\n```PYTHON []\nclass Solution:\n def maximumValueSum(self, nums: List[int], k: int, edges: List[List[int]]) -> int:\n xor_arr = [(n ^ k) - n for n in nums]\n xor_arr.sort(reverse=True)\n res = sum(nums)\n\n for i in range(0, len(nums), 2):\n if i == len(nums) - 1:\n break\n\n path_sum = xor_arr[i] + xor_arr[i + 1]\n\n if path_sum <= 0:\n break\n\n res += path_sum\n\n return res\n\n```\n```JAVASCRIPT []\nvar maximumValueSum = function (nums, k, edges) {\n let xorArr = nums.map(n => (n ^ k) - n)\n xorArr.sort((a, b) => b - a);\n let sum = nums.reduce((a, b) => a + b);\n\n for (let i = 0; i < nums.length; i += 2) {\n if (i == nums.length - 1) {\n break;\n }\n\n let pathSum = xorArr[i] + xorArr[i + 1]\n\n if (pathSum <= 0) {\n break;\n }\n\n sum += pathSum;\n }\n\n return sum\n};\n```\n```JAVA []\nclass Solution {\n\n public Integer[] xorArrCreator(int arr[], int k) {\n Integer xorArr[] = new Integer[arr.length];\n\n for (int i = 0; i < arr.length; i++) {\n xorArr[i] = (arr[i] ^ k) - arr[i];\n }\n\n return xorArr;\n }\n\n public long numArrSum(int arr[]) {\n long sum = 0;\n\n for (int i = 0; i < arr.length; i++) {\n sum += arr[i];\n }\n\n return sum;\n }\n\n // Main problem solver fun\n public long maximumValueSum(int[] nums, int k, int[][] edges) {\n // Making xorArr\n Integer xorArr[] = xorArrCreator(nums, k);\n\n // Sort in reverse order\n Arrays.sort(xorArr, Collections.reverseOrder());\n\n // taking sum of all values in nums array\n long sum = numArrSum(nums);\n\n for (int i = 0; i < xorArr.length; i += 2) {\n if (i == xorArr.length - 1) {\n break;\n }\n long pathSum = xorArr[i] + xorArr[i + 1];\n if (pathSum <= 0) {\n break;\n }\n sum += pathSum;\n }\n\n return sum;\n }\n}\n```\n\n | 3 | 0 | ['Array', 'Dynamic Programming', 'Greedy', 'Bit Manipulation', 'Tree', 'Sorting', 'Python', 'Java', 'JavaScript'] | 1 |
find-the-maximum-sum-of-node-values | Easy C++ Solution | Beats 100 💯✅ | easy-c-solution-beats-100-by-shobhitkush-msn4 | Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem involves maximizing the sum of a vector v of integers by performing a bitwi | shobhitkushwaha1406 | NORMAL | 2024-05-19T05:00:05.470385+00:00 | 2024-05-19T05:00:05.470407+00:00 | 421 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem involves maximizing the sum of a vector v of integers by performing a bitwise XOR operation with an integer k on some or all of the elements. The aim is to determine the optimal approach to achieve the maximum possible sum of the modified vector.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initial Total Sum: Calculate the initial sum of all elements in the vector v.\n2. Difference Calculation: For each element p in the vector, compute the difference diff between the XOR result (p ^ k) and the original value p.\n3. Positive Differences: Focus on differences that are positive (diff > 0) as they represent an increase in the sum when the XOR operation is applied.\n4. Total Difference: Accumulate the total positive differences to determine the potential increase in the sum.\n5. Handling Odd Positive Count: If the number of positive differences is odd, adjust by subtracting the smallest absolute difference to ensure the result is maximized.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n long long maximumValueSum(vector<int>& v, int k, vector<vector<int>>& edges) {\n long long total = accumulate(v.begin(), v.end(), 0ll);\n \n long long totalDiff = 0;\n long long diff;\n int positiveCount = 0;\n long long minDiff = numeric_limits<int>::max();\n for(auto p : v)\n {\n diff = (p^k) - p;\n \n if(diff > 0)\n {\n totalDiff += diff;\n positiveCount++;\n }\n minDiff = min(minDiff, abs(diff));\n }\n if(positiveCount % 2 == 1)\n {\n totalDiff = totalDiff - minDiff;\n }\n return total + totalDiff;\n }\n};\n``` | 3 | 0 | ['Bit Manipulation', 'Tree', 'C++'] | 1 |
find-the-maximum-sum-of-node-values | DFS from any vertex | dfs-from-any-vertex-by-avulanov-aqu9 | Intuition\nEven number of XOR is the same as no XOR, odd number of XOR is the same as 1 XOR. We can do DFS on the graph and try to find max between two cases. I | avulanov | NORMAL | 2024-05-19T03:09:02.664579+00:00 | 2024-05-19T03:09:02.664619+00:00 | 230 | false | # Intuition\nEven number of XOR is the same as no XOR, odd number of XOR is the same as 1 XOR. We can do DFS on the graph and try to find max between two cases. It does not matter which node to start with. This one is hard to prove, but its easy to see empyrically once code is ready.\n\n# Approach\nDFS on the graph with keeping track of two cases: with even and odd number of XORs applied at a given Vertice. Return max result with even and odd number of XORs.\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(N)\n\n# Code\n```\nclass Solution:\n def maximumValueSum(self, nums: List[int], k: int, edges: List[List[int]]) -> int:\n # returns max result without xor and with xor applied\n # on the value of the vertice at index "index"\n def dfs(graph, index, visited):\n visited[index] = True\n no_xor, xor = nums[index], nums[index] ^ k\n # maximum sum, number xors used, minimal diff\n max_sum, num_xors, min_diff = 0, 0, abs(no_xor - xor)\n if xor > no_xor:\n max_sum = xor\n num_xors = 1\n else:\n max_sum = no_xor\n for neigh in graph[index]:\n if not visited[neigh]:\n no_xor, xor = dfs(graph, neigh, visited)\n min_diff = min(min_diff, abs(no_xor - xor))\n # add to max_sum and increment xor number\n # if the bigger value comes from xor of child\n if xor > no_xor:\n max_sum += xor\n num_xors += 1\n else:\n max_sum += no_xor\n # if we have even number of xors, we can use max_sum as result w/o xor\n # and max_sum - min_diff a result with xor (with even number of xors)\n if num_xors % 2 == 0:\n return max_sum, max_sum - min_diff\n # inverse case\n else:\n return max_sum - min_diff, max_sum\n # build graph\n graph = defaultdict(list)\n n = len(nums)\n for fr, to in edges:\n graph[fr].append(to)\n graph[to].append(fr)\n # return case with even number of xors\n return dfs(graph, 0, [False] * n)[0]\n``` | 3 | 0 | ['Python3'] | 1 |
find-the-maximum-sum-of-node-values | [C++ / Go] Greedily from Leaves and Sacrifice Chosen Root - O(n) time + O(1) space | c-go-greedily-from-leaves-and-sacrifice-z51bk | Intuition\n## Optimize Greedily from Leaves and Sacrifice Chosen Root\n- Greedily optimize from leaves:\n - Each node can either be num or num ^ k. To maximi | mikazuki4712 | NORMAL | 2024-05-19T02:03:30.001130+00:00 | 2024-05-19T02:28:27.294422+00:00 | 301 | false | # Intuition\n## Optimize Greedily from Leaves and Sacrifice Chosen Root\n- Greedily optimize from leaves:\n - Each node can either be `num` or `num ^ k`. To maximize the sum, we choose the more optimal value between `num` and `num ^ k`.\n - Start the optimization process from the leaves, and move towards the parent nodes, continuously optimizing each node using its parent.\n - This iterative optimization ensures that by the time we reach the root, all other nodes have been optimized, just the root remained unsure to be optimize.\n- Sacrifice chosen root:\n - The root node is not fixed initially so we can choose any node to be the root. \n - The optimal root is the node where the difference between its value and the value after applying the XOR operation is minimal. \n - This root node can then be sacrificed to achieve the best overall optimization.\n## Optimize calculating process\n- Each node is used to optimize their children, and then its parent will optimize it\n=> Each node can be optimize independely to calculate optimize value and add to the total result.\n- For each operation, two nodes will be changed so the total number of changed nodes always is even number.\n - After optimize independely all nodes, if the numbers of change nodes is even then the root is also optimized.\n - Else the root is not optimized and we have to sacrifice it.\n\n# Approach\n- For each nodes with value `num`:\n - If `num < num ^ k`:\n - This node will be changed.\n - Total result is added by `num ^ k`\n - Else\n - This node is optimized already\n - Total result is added by `num`\n - Keep track of minimum difference of `num` and `num ^ k` for sacrificing if needed.\n- After optimize independely all nodes:\n - If the numbers of change nodes is even then the root is also optimized, return current total result.\n - Else return current total result - minimum difference node.\n\n# Complexity\n- Time complexity: $O(n)$\n- Space complexity: $O(1)$\n\n# Code\n```C++ []\nclass Solution {\npublic:\n long long maximumValueSum(vector<int>& nums, int k, vector<vector<int>>& edges) {\n long long res = 0;\n int changes = 0;\n int minDiff = INT_MAX;\n \n for (int num : nums) {\n int xorNum = num ^ k;\n\n if (num < xorNum) {\n changes++;\n res += xorNum;\n } else {\n res += num;\n }\n\n minDiff = min(minDiff, abs(num - xorNum));\n }\n\n if (changes % 2 == 1)\n return res - minDiff;\n else\n return res;\n }\n};\n```\n```Go []\nfunc maximumValueSum(nums []int, k int, edges [][]int) int64 {\n var res int64\n changes := 0\n minDiff := math.MaxInt32\n\n for _, num := range nums {\n xorNum := num ^ k\n\n if num < xorNum {\n changes++\n res += int64(xorNum)\n } else {\n res += int64(num)\n }\n\n diff := abs(num - xorNum)\n if diff < minDiff {\n minDiff = diff\n }\n }\n\n if changes % 2 == 1 {\n return res - int64(minDiff)\n } else {\n return res\n }\n}\n\nfunc abs(a int) int {\n if a < 0 {\n return -a\n }\n return a\n}\n``` | 3 | 0 | ['Greedy', 'C++', 'Go'] | 1 |
find-the-maximum-sum-of-node-values | Fastest execution || Beats 100% users with java & typescript || python3 || C++ || Greedy | fastest-execution-beats-100-users-with-j-o7tp | Approach\nGreedy\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(1)\n\n# Explanation\n1. Class Definition:\n\n- We define a class Solution whi | SanketSawant18 | NORMAL | 2024-05-19T00:31:52.349323+00:00 | 2024-05-19T00:31:52.349352+00:00 | 256 | false | # Approach\nGreedy\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(1)\n\n# Explanation\n1. **Class Definition:**\n\n- We define a class Solution which contains the method maximumValueSum.\n2. **Method Signature:**\n\n- **The method maximumValueSum takes three parameters:**\n - int[] nums: An array of integers representing the values of the nodes.\n - int k: An integer to be used for XOR operations.\n - int[][] edges: A 2D array representing the edges of the tree (though it\'s not actually used in the computation).\n3. **Variables Initialization:**\n\n- bestSum (of type long): This will store the best possible sum we can achieve.\n- cnt (of type int): This will count how many times the value of a node increases when XORed with k.\n4. **Loop through nums:**\n\n- **For each num in nums:**\n - Calculate the maximum of the original value num and the value after XORing with k (num ^ k). Add this maximum value to bestSum.\n - Check if XORing num with k results in a larger value than num. If it does, increment the cnt counter.\n5. **Adjusting the Sum for Odd cnt:**\n\n- If cnt is odd, it means that we have an imbalance in the number of nodes that benefit from XORing with k.\n- To balance it, we need to subtract the smallest possible difference between a node\'s original value and its XORed value from bestSum.\n- We initialize minDifference to the maximum possible integer value (Integer.MAX_VALUE).\n- Loop through each num in nums to find the minimum difference Math.abs(num - (num ^ k)).\n- Subtract this minDifference from bestSum.\n6. **Return the Result:**\n\n- Finally, return the calculated bestSum.\n\n---\n\n```java []\nclass Solution {\n public long maximumValueSum(int[] nums, int k, int[][] edges) {\n long bestSum = 0;\n int cnt = 0;\n \n // Compute the best possible sum and count the number of nodes where XORing increases the value\n for (int num : nums) {\n bestSum += Math.max(num, num ^ k);\n if ((num ^ k) > num) {\n cnt++;\n }\n }\n \n // If cnt is odd, we need to adjust the sum\n if (cnt % 2 != 0) {\n int minDifference = Integer.MAX_VALUE;\n for (int num : nums) {\n minDifference = Math.min(minDifference, Math.abs(num - (num ^ k)));\n }\n bestSum -= minDifference;\n }\n \n return bestSum;\n }\n}\n\n```\n```python3 []\nclass Solution:\n def maximumValueSum(self, nums: List[int], k: int, edges: List[List[int]]) -> int:\n best_sum = sum(max(n, k ^ n) for n in nums)\n cnt = sum((n ^ k) > n for n in nums) \n return best_sum - (min(abs(n - (n ^ k)) for n in nums) if cnt % 2 else 0)\n```\n```C++ []\n#include <vector>\n#include <algorithm>\n#include <cmath>\n#include <numeric>\nusing namespace std;\n\nclass Solution {\npublic:\n long long maximumValueSum(vector<int>& nums, int k, vector<vector<int>>& edges) {\n long long bestSum = 0;\n int cnt = 0;\n\n // Compute the best possible sum and count the number of nodes where XORing increases the value\n for (int num : nums) {\n bestSum += max(num, num ^ k);\n if ((num ^ k) > num) {\n cnt++;\n }\n }\n\n // If cnt is odd, we need to adjust the sum\n if (cnt % 2 != 0) {\n int minDifference = INT_MAX;\n for (int num : nums) {\n minDifference = min(minDifference, abs(num - (num ^ k)));\n }\n bestSum -= minDifference;\n }\n\n return bestSum;\n }\n};\n\n```\n```Typescript []\nfunction maximumValueSum(nums: number[], k: number, edges: number[][]): number {\n let bestSum: number = 0;\n let cnt: number = 0;\n\n // Compute the best possible sum and count the number of nodes where XORing increases the value\n for (let num of nums) {\n bestSum += Math.max(num, num ^ k);\n if ((num ^ k) > num) {\n cnt++;\n }\n }\n\n // If cnt is odd, we need to adjust the sum\n if (cnt % 2 !== 0) {\n let minDifference: number = Number.MAX_SAFE_INTEGER;\n for (let num of nums) {\n minDifference = Math.min(minDifference, Math.abs(num - (num ^ k)));\n }\n bestSum -= minDifference;\n }\n\n return bestSum;\n}\n```\n | 3 | 0 | ['Array', 'Dynamic Programming', 'Greedy', 'Tree', 'C++', 'Java', 'TypeScript', 'Python3'] | 1 |
find-the-maximum-sum-of-node-values | 🏆💢💯 Faster✅💯 Lesser🧠 🎯 C++✅Python3🐍✅Java✅C✅Python🐍✅💥🔥💫Explained☠💥🔥 Beats 💯 | faster-lesser-cpython3javacpythonexplain-j9kd | Intuition\n\n\n\njava []\nclass Solution {\n public long maximumValueSum(int[] A, int k, int[][] edges) {\n long res = 0;\n int d = 1 << 30, c | Edwards310 | NORMAL | 2024-03-02T16:35:55.355491+00:00 | 2024-05-19T00:10:00.275520+00:00 | 111 | false | # Intuition\n\n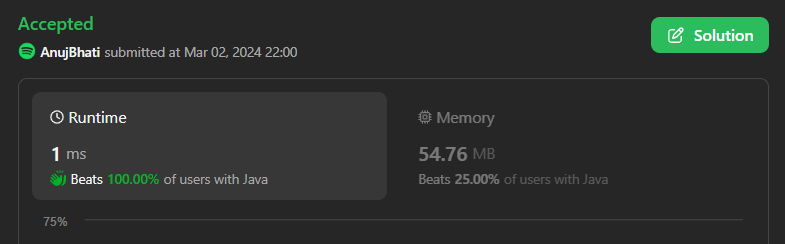\n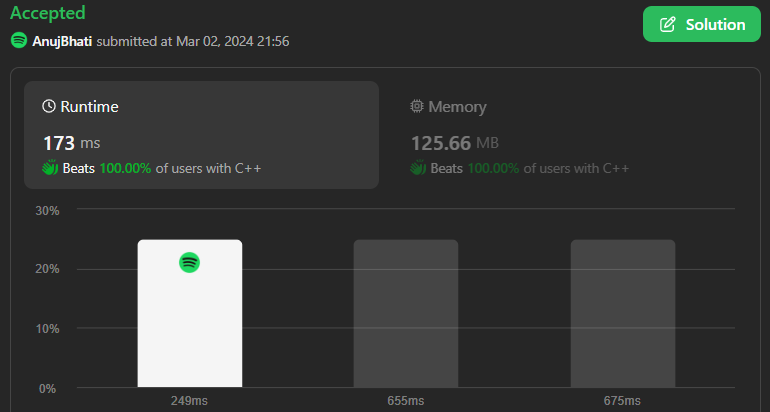\n```java []\nclass Solution {\n public long maximumValueSum(int[] A, int k, int[][] edges) {\n long res = 0;\n int d = 1 << 30, c = 0;\n for (int a : A) {\n int b = a ^ k;\n res += Math.max(a, b);\n c ^= a < b ? 1 : 0;\n d = Math.min(d, Math.abs(a - b));\n }\n return res - d * c;\n }\n}\n```\n```python3 []\nclass Solution:\n def maximumValueSum(self, A: List[int], k: int, edges: List[List[int]]) -> int:\n res = c = 0\n d = 1 << 30\n for a in A:\n res += max(a, b := a ^ k)\n c ^= a < b\n d = min(d, abs(a - b))\n return res - d * c\n```\n```C++ []\nclass Solution {\npublic:\n long long maximumValueSum(vector<int>& nums, int k, vector<vector<int>>& edges) {\n int cnt = 0, Min = 2e9;\n long long ans = 0;\n for (auto it : nums) {\n int x = it;\n int y = it ^ k;\n if (x > y)\n ans += x;\n else\n ans += y, cnt++;\n Min = min(Min, abs(x - y));\n }\n if (cnt % 2 == 1)\n ans -= Min;\n return ans;\n }\n};\n```\n```python []\nclass Solution(object):\n def maximumValueSum(self, nums, k, edges):\n """\n :type nums: List[int]\n :type k: int\n :type edges: List[List[int]]\n :rtype: int\n """\n n, cnt, min_diff = len(nums), 0, float(\'inf\')\n for i, v in enumerate(nums):\n if v ^ k > v:\n nums[i] ^= k\n cnt += 1\n min_diff = min(min_diff, nums[i] - (nums[i] ^ k))\n return sum(nums) - (min_diff if cnt & 1 else 0)\n```\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(1)\n# Code\n```\nclass Solution:\n def maximumValueSum(self, A: List[int], k: int, edges: List[List[int]]) -> int:\n res = c = 0\n d = 1 << 30\n for a in A:\n res += max(a, b := a ^ k)\n c ^= a < b\n d = min(d, abs(a - b))\n return res - d * c\n\n```\n\n | 3 | 0 | ['Array', 'Dynamic Programming', 'Greedy', 'Bit Manipulation', 'Tree', 'C', 'Python', 'C++', 'Java', 'Python3'] | 3 |
find-the-maximum-sum-of-node-values | Greedy Approach O(N) Solution || C++ 🔥💯 | greedy-approach-on-solution-c-by-_rishab-7tm2 | Maximum Value Sum\n\n## Problem Statement\n\nGiven a tree represented by nums and edges, and an integer k, we need to maximize the sum of the values in nums aft | _Rishabh_96 | NORMAL | 2024-05-19T13:16:07.496844+00:00 | 2024-05-19T13:16:07.496874+00:00 | 220 | false | # Maximum Value Sum\n\n## Problem Statement\n\nGiven a tree represented by `nums` and `edges`, and an integer `k`, we need to maximize the sum of the values in `nums` after potentially transforming each value using the bitwise XOR operation with `k`. Specifically, for each value `num` in `nums`, we can either leave it as is or transform it to `num ^ k`.\n\n## Approach\n\n### Initial Calculation\n- Iterate through the given `nums` array to compute the initial sum. For each number in `nums`, calculate the maximum value between the number itself and its bitwise XOR with `k` (`num ^ k`). Add this maximum value to the sum.\n- Simultaneously, keep track of the count of numbers where `num ^ k` is greater than `num`.\n\n### Count and Sacrifice Calculation\n- If the count of numbers where `num ^ k` is greater than `num` is odd, find the minimum difference between any number in `nums` and its `num ^ k`. This minimum difference is called `sacrifice`.\n- The `sacrifice` is needed to adjust the final sum to be maximal when the count is odd. By subtracting this `sacrifice`, we ensure that the resulting sum is optimal.\n\n### Final Adjustment\n- If the count is odd, subtract the smallest `sacrifice` from the sum.\n- If the count is even, the initial sum is already optimal.\n\n## Complexity\n\n- **Time Complexity**: \\(O(n)\\)\n - We iterate through the `nums` array once to compute the initial sum and count, which takes \\(O(n)\\).\n - Finding the minimum `sacrifice` also takes \\(O(n)\\).\n \n- **Space Complexity**: \\(O(1)\\)\n - We use a constant amount of extra space regardless of the input size.\n\n## Solution\n\n```cpp\nclass Solution {\npublic:\n long long maximumValueSum(vector<int>& nums, int k, vector<vector<int>>& edges) {\n long long sum = 0, cnt = 0;\n int sacrifice = INT_MAX;\n \n for (int n : nums) {\n int xorValue = n ^ k;\n if (xorValue > n) {\n sum += xorValue;\n cnt++;\n sacrifice = min(sacrifice, xorValue - n);\n } else {\n sum += n;\n sacrifice = min(sacrifice, n - xorValue);\n }\n }\n \n if (cnt % 2 != 0) {\n sum -= sacrifice;\n }\n \n return sum;\n }\n};\n | 2 | 0 | ['Array', 'Greedy', 'C++'] | 0 |
find-the-maximum-sum-of-node-values | Swift solution | swift-solution-by-azm819-6gs7 | Complexity\n- Time complexity: O(n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(1)\n Add your space complexity here, e.g. O(n) \n\n# Co | azm819 | NORMAL | 2024-05-19T10:47:19.921568+00:00 | 2024-05-19T10:47:19.921600+00:00 | 27 | false | # Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n func maximumValueSum(_ nums: [Int], _ k: Int, _: [[Int]]) -> Int {\n var minPositiveDiff: Int = .max\n var maxNegativeDiff: Int = .min\n var changedSum: Int = .zero\n var increasedNumCount: Int = .zero\n for num in nums {\n let changedNum = num ^ k\n let diff = changedNum - num\n\n if diff > .zero {\n increasedNumCount += 1\n minPositiveDiff = min(minPositiveDiff, diff)\n changedSum += changedNum\n } else {\n maxNegativeDiff = max(maxNegativeDiff, diff)\n changedSum += num\n }\n }\n\n if increasedNumCount % 2 == .zero {\n return changedSum\n } else {\n return max(changedSum - minPositiveDiff, changedSum + maxNegativeDiff)\n }\n }\n}\n``` | 2 | 0 | ['Array', 'Greedy', 'Bit Manipulation', 'Tree', 'Swift'] | 0 |
find-the-maximum-sum-of-node-values | Beginner friendly || Nice approach || i take help | beginner-friendly-nice-approach-i-take-h-kfee | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Saksham_chaudhary_2002 | NORMAL | 2024-05-19T06:23:07.100364+00:00 | 2024-05-19T06:23:07.100402+00:00 | 148 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maximumValueSum(self, nums: List[int], k: int, edges: List[List[int]]) -> int:\n totalSum = 0\n count = 0\n positiveMin = float("inf")\n negativeMax = float("-inf")\n\n for nodeValue in nums:\n nodeValAfterOperation = nodeValue ^ k\n\n totalSum += nodeValue\n netChange = nodeValAfterOperation - nodeValue\n\n if netChange > 0:\n positiveMin = min(positiveMin, netChange)\n totalSum += netChange\n count += 1\n else:\n negativeMax = max(negativeMax, netChange)\n\n if count % 2 == 0:\n return totalSum\n return max(totalSum - positiveMin, totalSum + negativeMax)\n``` | 2 | 0 | ['Array', 'Dynamic Programming', 'Greedy', 'Bit Manipulation', 'Tree', 'Sorting', 'Python3'] | 1 |
find-the-maximum-sum-of-node-values | Easy To Understand | easy-to-understand-by-heerkshah434-l9kn | Intuition\n Describe your first thoughts on how to solve this problem. \n- I will try to XOR every element such that the sum increases.\n- XORing an element twi | heerkshah434 | NORMAL | 2024-05-19T06:20:04.933726+00:00 | 2024-05-19T06:20:04.933757+00:00 | 90 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- I will try to XOR every element such that the sum increases.\n- XORing an element twice will not affect the sum.\n- I can choose any two nodes to apply XOR regardless of whether there is an edge between them or not, as reaching that node will result in every intermediate node being XORed twice, which will not affect the intermediate nodes.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Iterate over all nodes in nums, and if XORing an element increases its value, include that node in sum1 and increase the counter of operations.\n- Otherwise, include it in sum2, meaning no operation is done on it.\n- If the count is even, meaning we have chosen 2 nodes in every operation, we can directly return sum1 + sum2.\n- If the count is odd, meaning we have an extra node to remove from our operation or an extra node to add to our operation.\n- As mentioned above, we will do that for every node and store values in ans1 and ans2.\n- Finally, we will return the maximum of both.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n long long maximumValueSum(vector<int>& nums, int k, vector<vector<int>>& edges) {\n long sum1=0,sum2=0;\n int cnt=0;\n for(long long it:nums){\n if((it^k)>it){\n sum1+=(it^k);\n cnt++;\n }\n else{\n sum2+=it;\n }\n }\n if(cnt%2==0){\n return sum1+sum2;\n }\n long long ans1=0,ans2=0;\n for(long long it:nums){\n if((it^k)>it) ans1=max(ans1,sum1+sum2-(it^k)+it);\n else ans2=max(ans2,sum1+sum2+(it^k)-it);\n }\n return max(ans1,ans2);\n }\n};\n``` | 2 | 0 | ['Dynamic Programming', 'Greedy', 'Bit Manipulation', 'Tree', 'C++'] | 1 |
find-the-maximum-sum-of-node-values | javascript Six Lines Only Method with explanation | javascript-six-lines-only-method-with-ex-v6hs | Intuition\n##### we do not need list of agdes at all\nIt is easy to demonstrate that we can perform an operation between any nums[u] and nums[v] with multiple o | charnavoki | NORMAL | 2024-05-19T05:44:45.921134+00:00 | 2024-05-19T05:59:11.242498+00:00 | 55 | false | # Intuition\n##### we do not need list of `agdes` at all\nIt is easy to demonstrate that we can perform an operation between any `nums[u]` and `nums[v]` with multiple operations, even if there is no direct edge between them.\n##### calculate `(nums[u] ^ k) - nums[u]` for each number\nAfter calculations, we received an array with differences between numbers after operations. From this array we have to keep only an even number, only one (or none) of them can be negative for maximization or summing.\n\n\n\n# Code\n```\nvar maximumValueSum = (nums, k) =>\n nums.reduce((x, y) => x + y) +\n nums.map(v => (v ^ k) - v)\n .sort((x, y) => y - x)\n .map((v, i, a) => a[2 * i] + a[2 * i + 1])\n .filter(v => v > 0)\n .reduce((x, y) => x + y, 0);\n\n```\n\n##### please upvote, you motivate me to solve problems in original ways | 2 | 0 | ['JavaScript'] | 1 |
find-the-maximum-sum-of-node-values | AB | ab-by-anil-budamakuntla-1fae | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | ANIL-BUDAMAKUNTLA | NORMAL | 2024-05-19T05:13:34.490221+00:00 | 2024-05-19T05:13:34.490249+00:00 | 3 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n long long maximumValueSum(vector<int>& nums, int k,\n vector<vector<int>>& e) {\n int i, j = 0, m = INT_MAX, n = nums.size(), p = m;\n long s = 0;\n\n for (i = 0; i < n; i++) {\n if ((nums[i] ^ k) > nums[i]) {\n s += nums[i] ^ k;\n m = min(m, (nums[i] ^ k) - nums[i]);\n\n j++;\n } else {\n if ((nums[i] - (nums[i] ^ k)) < p) {\n p = nums[i] - (nums[i] ^ k);\n }\n s += nums[i];\n }\n }\n\n if (j % 2 == 0)\n return s;\n\n return max(s - m, s - p);\n }\n};\n``` | 2 | 0 | ['C++'] | 2 |
find-the-maximum-sum-of-node-values | Greedy Delta | Sorting | Python | greedy-delta-sorting-python-by-pragya_23-za9p | Complexity\n- Time complexity: O(nlogn)\n\n- Space complexity: O(n)\n\n# Code\n\nclass Solution:\n def maximumValueSum(self, nums: List[int], k: int, edges: | pragya_2305 | NORMAL | 2024-05-19T04:56:41.995787+00:00 | 2024-05-19T04:56:41.995818+00:00 | 146 | false | # Complexity\n- Time complexity: O(nlogn)\n\n- Space complexity: O(n)\n\n# Code\n```\nclass Solution:\n def maximumValueSum(self, nums: List[int], k: int, edges: List[List[int]]) -> int:\n delta = [(num^k)-num for num in nums]\n delta.sort(reverse=True)\n ans = sum(nums)\n\n for i in range(0,len(nums)-1,2):\n path = delta[i]+delta[i+1]\n if path<=0:\n break\n ans+=path\n\n return ans\n``` | 2 | 0 | ['Array', 'Greedy', 'Bit Manipulation', 'Tree', 'Sorting', 'Python', 'Python3'] | 2 |
find-the-maximum-sum-of-node-values | Dart solution | dart-solution-by-dartist-lzhv | Code\n\nclass Solution {\n int maximumValueSum(List<int> nums, int k, List<List<int>> edges) {\n int d = 1 << 30, cnt = 0, sum = 0;\n for (int num in num | Dartist | NORMAL | 2024-05-19T00:55:55.818116+00:00 | 2024-05-19T00:55:55.818136+00:00 | 19 | false | # Code\n```\nclass Solution {\n int maximumValueSum(List<int> nums, int k, List<List<int>> edges) {\n int d = 1 << 30, cnt = 0, sum = 0;\n for (int num in nums) {\n final b = num ^ k;\n sum += max(num, b);\n cnt ^= num < b ? 1 : 0;\n d = min(d, (num - b).abs());\n }\n return sum - d * cnt;\n }\n}\n``` | 2 | 0 | ['Dart'] | 0 |
find-the-maximum-sum-of-node-values | :: Kotlin :: Don't be distracted from the tree! | kotlin-dont-be-distracted-from-the-tree-6qnue | \'edges\' is just a macguffin.\n\nAll information needed from the tree structure is\nThis means that an even number of xor operations can be performed.\n\n# Cod | znxkznxk1030 | NORMAL | 2024-05-03T05:03:39.372867+00:00 | 2024-05-03T05:03:39.372896+00:00 | 50 | false | # \'edges\' is just a macguffin.\n\nAll information needed from the tree structure is\nThis means that an even number of xor operations can be performed.\n\n# Code\n```\nclass Solution {\n fun maximumValueSum(nums: IntArray, k: Int, edges: Array<IntArray>): Long {\n var result = nums.map{it.toLong()}.sum()!!\n val n = nums.size\n var xors = Array(n){ intArrayOf(nums[it], nums[it] xor k) }\n\n val list = xors.sortedWith(compareBy({ it[0] - it[1] }))\n\n for (i in 1 until n step 2) {\n val temp = result - list[i][0] - list[i - 1][0] + list[i][1] + list[i - 1][1]\n if (temp < result) break\n result = temp\n }\n\n return result\n }\n}\n``` | 2 | 0 | ['Kotlin'] | 2 |
find-the-maximum-sum-of-node-values | One liner Solution || Python3 | one-liner-solution-python3-by-yangzen09-tn0g | One Liner--Best Solution \n\nApproach/Logic:-\n\n1- performing bitwise XOR operations on the input numbers and then applying some transformations to calculate t | YangZen09 | NORMAL | 2024-03-06T21:10:05.498582+00:00 | 2024-03-06T21:10:36.764799+00:00 | 77 | false | **One Liner--Best Solution** \n\n**Approach/Logic:-**\n\n1- performing bitwise XOR operations on the input numbers and then applying some transformations to calculate the maximum sum.\n\n2- calculates the XOR of each number with the given integer \'k\', sorts the resulting list, and then groups the elements in pairs.\n\n3- For each pair, calculates the sum of the XOR results and filters out negative values.\n\n4- Finally, the function subtracts the sum of negative values from the total sum of the input list to get the maximum value.\n\n**Code->**\n```\nclass Solution:\n def maximumValueSum(self, nums: List[int], k: int, edges: List[List[int]]) -> int:\n return sum(nums) - sum(filter(lambda x: x < 0, map(sum, zip(sorted(map(lambda x: x - (x^k), nums))[::2], sorted(map(lambda x: x - (x^k), nums))[1::2]))))\n```\n**Time Complexity:-** **O(N)**\n**Space Complexity:-** **O(N)**\n\n**Code BreakDown->**\n\n=> sorted(map(lambda x: x - (x^k), nums)): Calculates the XOR of each element with k, sorts the results.\n\n=> [::2] and [1::2]: Slices the sorted list into even and odd indexed elements.\n\n=> map(sum, zip(...)): Calculates the sum of each pair of elements.\n\n=> filter(lambda x: x < 0, ...): Filters out negative values.\n\n=> sum(...): Calculates the sum of negative values.\n\n=> sum(nums) - sum(...): Calculates the maximum value sum.\n\n**Code Explaination->**\n\n=> The maximumValueSum function takes three arguments: nums (list of integers), k (integer), and edges (list of lists).\n\n=> The code calculates the maximum value sum using the following steps:-\n > XOR each element of nums with k using (x^k) where x is each element of nums.\n > Sort the resulting list of XOR results.\n > Split the sorted list into two parts using slicing: even-indexed elements and odd-indexed elements.\n > Calculate the sum of each pair of elements in the two lists.\n > Filter out the negative sums using the filter function with a lambda function that checks if the value is less than 0.\n > Subtract the sum of negative values from the total sum of nums using sum(nums) - sum(...).\n > Return the final result, which is the maximum value sum.\n\n\nIf this explaination is impressive please give a like/vote...\n\n**JAI SHREE RAM**\n\n\n | 2 | 1 | ['Python3'] | 1 |
find-the-maximum-sum-of-node-values | Easy C++ Solution || Using DP (Beats 100%) ✅✅ | easy-c-solution-using-dp-beats-100-by-ab-3gnr | Code\n\nclass Solution {\npublic:\n long long helper(int i,vector<int>& values,vector<vector<long long>> &dp,int n,int count,int k){\n if(i==n){\n | Abhi242 | NORMAL | 2024-03-04T17:18:01.502296+00:00 | 2024-03-04T17:18:01.502328+00:00 | 308 | false | # Code\n```\nclass Solution {\npublic:\n long long helper(int i,vector<int>& values,vector<vector<long long>> &dp,int n,int count,int k){\n if(i==n){\n if(count==0){\n return 0;\n }else{\n return INT_MIN;\n }\n }\n if(dp[i][count]!=-1){\n return dp[i][count];\n }\n long long x=(values[i]^k) + helper(i+1,values,dp,n,!count,k);\n long long y=values[i] + helper(i+1,values,dp,n,count,k);\n return dp[i][count]=max(x,y);\n }\n long long maximumValueSum(vector<int>& nums, int k, vector<vector<int>>& edges) {\n int n=nums.size();\n vector<vector<long long>> dp(n,vector<long long>(2,-1));\n return helper(0,nums,dp,n,0,k);\n }\n};\n``` | 2 | 0 | ['Dynamic Programming', 'Tree', 'Recursion', 'C++'] | 1 |
find-the-maximum-sum-of-node-values | GREEDY APPROACH (C++) BEATS 100 % | greedy-approach-c-beats-100-by-binarywiz-9r4k | Intuition\n Describe your first thoughts on how to solve this problem. \n\nFIRST INTUITION : The Moment One Reads XOR, These Properties Should Strike One\'s Bra | BinaryWizard_8 | NORMAL | 2024-03-03T05:47:43.973603+00:00 | 2024-03-03T16:03:32.732789+00:00 | 21 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n**FIRST INTUITION** : The Moment One Reads XOR, These Properties Should Strike One\'s Brain Immediately.\n\n1. a ^ a = 0.\n2. a ^ 0 = a.\n3. a ^ b = b ^ a. (Would Be Our Master-Stroke For XOR On Edges)\n\nIn This Entire Question, We Will Play With These Properties.\n\n**SECOND INTUITION** : Now, Second Part Demands For Maximum Sum. Reading This Brings Two Algorithm Paradigm Mainly To Any Coder\'s Mind :- DP And Greedy Approach.\n\nCan Be Solved Using DP As Well, But I Would Like To Be Greedy Here XD !!\n\n# Approach\n<!-- Describe your approach to solving the problem. --> \n1. Keep Count Of Nodes Whose Values Can Be Increased By XOR.\n\n2. If They Are Even, We Can Pair Them Up. (XOR IS COMMUTATIVE, Hence We Can Again XOR On Adjacent Edge To Neutralise The Decreament Of Other Node\'s Value) :- **PROPAGATION OF XOR IN TREE/GRAPH.**\n\n3. In Case Count Is Odd -> *MOYE MOYE* (One Individual Node Is Remaining). Now, It\'s Time To Be Greedy And Greed Leads To Sacrifice. Find The Sacrificial Lamb (Whose Loss Won\'t Hurt Our Maximum Sum As Compared To Others) In The Entire Tree.\n\n4. In Case We Can Pair, No Need To Sarifice :- Return The Sum.\n\n5. In Case We Can\'t, Return (Sum - Sacrifice).\n\nPLEASE UPVOTE IF HELPED.. FEEL FREE TO ASK IN COMMENT SECTION.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ --> \n$$O(N)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> \n$$O(1)$$\n# Code\n```\n#define ll long long\n\nclass Solution {\npublic:\n long long maximumValueSum(vector<int> &nums, int k, vector<vector<int>> &edges) {\n \n // Count The Node Values To Be Increased.\n ll sum = 0, count = 0, sacrifice = INT_MAX;\n\n for (auto x : nums) {\n\n // XOR Increases The Value.\n if ((x ^ k) > x) {\n\n sum += x ^ k;\n count++;\n\n // Some Node Value Would Be Decreased, And We Need To Minimise It.\n sacrifice = min (sacrifice, (ll) (x ^ k) - x);\n }\n\n else {\n\n sum += x;\n sacrifice = min (sacrifice, (ll) x - (x ^ k));\n }\n }\n\n // Even Counts Of Node Values (Pair Nodes) -> XOR Operation On Edges May Propagate In Tree.\n // Simply, Return The Sum.\n\n if (count % 2 == 0)\n return sum;\n \n // Odd Count Of Node Values (One Individual Node) -> One Node Has To Sacrifice.\n // Sacrifice :- Either Remain Same Or Decrease Its Value After XOR.\n // Return :- Greedy / Most Optimal Sum We Wish To Obtain - Sacrifice.\n\n return sum - sacrifice;\n } \n};\n``` | 2 | 0 | ['C++'] | 0 |
find-the-maximum-sum-of-node-values | Easy To Understand: Java Solution | easy-to-understand-java-solution-by-maya-kkbk | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Mayank1733 | NORMAL | 2024-03-02T16:18:47.151861+00:00 | 2024-03-02T16:18:47.151884+00:00 | 265 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public long maximumValueSum(int[] nums, int k, int[][] edges) {\n int n = nums.length;\n long[] getXORDiff = new long[n];\n for (int i = 0; i < n; ++i)\n getXORDiff[i] = (nums[i]^k)-nums[i];\n Arrays.sort(getXORDiff);\n long maxSum = 0;\n for (int x : nums)\n maxSum+=x;\n for (int i = n-1; i >= 1; i-=2) {\n if (getXORDiff[i]+getXORDiff[i-1]<0)\n return maxSum;\n maxSum += getXORDiff[i]+getXORDiff[i-1];\n }\n return maxSum;\n }\n}\n``` | 2 | 0 | ['Java'] | 2 |
find-the-maximum-sum-of-node-values | C++ SOLUTION BEATS 100% DETAILED COMMENTS | c-solution-beats-100-detailed-comments-b-gjk4 | \n# Code\n\nclass Solution {\npublic:\n // Function to find the maximum value sum\n long long maximumValueSum(vector<int>& values, int k, vector<vector<in | Quinos2003 | NORMAL | 2024-03-02T16:04:13.146526+00:00 | 2024-03-02T16:04:13.146566+00:00 | 170 | false | \n# Code\n```\nclass Solution {\npublic:\n // Function to find the maximum value sum\n long long maximumValueSum(vector<int>& values, int k, vector<vector<int>>& edges) {\n int n = values.size(); // Number of nodes\n // Creating an adjacency list to represent the graph\n vector<int> adjacencyList[n];\n\n // Building the adjacency list\n for(int i = 0; i < n - 1; i++) {\n adjacencyList[edges[i][0]].push_back(edges[i][1]);\n adjacencyList[edges[i][1]].push_back(edges[i][0]);\n }\n\n vector<int> nodesWithIncreasedValue; // Store the nodes whose value can be increased\n // Loop through each node\'s value and determine if it can be increased by XOR operation with k\n for(int i = 0; i < n; i++) {\n long long newValue = (long long)values[i] ^ k; // Calculate the new value using XOR\n if(newValue > values[i]) // If the new value is greater than the current value\n nodesWithIncreasedValue.push_back(i); // Store the index of the node\n }\n\n int increasedNodesCount = nodesWithIncreasedValue.size(); // Count of nodes with increased value\n\n if(increasedNodesCount % 2 == 0) { // If the count of increased nodes is even\n long long totalSum = 0; // Initialize the total sum of values\n for(int i = 0; i < n; i++) {\n totalSum += values[i]; // Calculate the total sum of values\n }\n // Adjust the total sum by adding the increased values and subtracting the original values\n for(int i = 0; i < increasedNodesCount; i++) {\n totalSum -= values[nodesWithIncreasedValue[i]]; // Subtract the original value\n long long newValue = (long long)values[nodesWithIncreasedValue[i]] ^ k; // Calculate the new value\n totalSum += newValue; // Add the new value\n }\n return totalSum; // Return the final total sum\n } else { // If the count of increased nodes is odd\n long long totalSum = 0; // Initialize the total sum of values\n for(int i = 0; i < n; i++) {\n totalSum += (long long)values[i]; // Calculate the total sum of values\n }\n long long finalTotalSum = totalSum; // Initialize the final total sum with the original total sum\n\n // Adjust the total sum by adding the increased values and subtracting the original values\n for(int i = 0; i < increasedNodesCount; i++) {\n totalSum -= values[nodesWithIncreasedValue[i]]; // Subtract the original value\n long long newValue = (long long)values[nodesWithIncreasedValue[i]] ^ k; // Calculate the new value\n totalSum += newValue; // Add the new value\n }\n\n // Try different combinations of nodes to maximize the total sum\n for(int i = 0; i < increasedNodesCount; i++) {\n long long newValue = (long long)values[nodesWithIncreasedValue[i]] ^ k; // Calculate the new value\n long long currentTotalSum = totalSum - newValue + values[nodesWithIncreasedValue[i]]; // Adjust the total sum\n finalTotalSum = max(finalTotalSum, currentTotalSum); // Update the final total sum if necessary\n }\n\n // Explore other nodes to maximize the total sum\n vector<int> visitedNodes(n, 0); // Initialize visited nodes\n for(int i = 0; i < increasedNodesCount; i++) {\n visitedNodes[nodesWithIncreasedValue[i]] = 1; // Mark the increased nodes as visited\n }\n\n // Iterate through all nodes to find optimal combinations\n for(int i = 0; i < n; i++) {\n if(visitedNodes[i] == 0) { // If the node is not visited\n long long newValue = (long long)values[i] ^ k; // Calculate the new value\n long long currentTotalSum = totalSum - values[i] + newValue; // Adjust the total sum\n finalTotalSum = max(finalTotalSum, currentTotalSum); // Update the final total sum if necessary\n }\n }\n return finalTotalSum; // Return the final total sum\n }\n }\n};\n\n\n\n``` | 2 | 0 | ['C++'] | 1 |
find-the-maximum-sum-of-node-values | Insight into XOR | Full explaination with comments | insight-into-xor-full-explaination-with-ve5i6 | Intuition\n- XOR is associative and commutative, meaning we can shift around the order it\'s applied and still get the same result.\n- If a single node has the | awesson | NORMAL | 2024-03-02T16:03:53.793454+00:00 | 2024-03-03T00:03:40.299416+00:00 | 134 | false | # Intuition\n- XOR is associative and commutative, meaning we can shift around the order it\'s applied and still get the same result.\n- If a single node has the operation applied to it multiple times, (x XOR k) XOR k... each k XOR k pair will cancel to 0, and 0 XOR x is just x.\n - In other words, if we apply the operation to the same node an even number of times, it will stay unchanged. If we apply it an odd number of times, then it will be the same as applying it once.\n- Each node in a tree is always connected to every other node in a tree.\n- Consider applying the operations to every edge along a path between two nodes. For every node which isn\'t the starting and ending node, the operation is applied for both the incoming and outgoing edge of the path. Since this is applying the operation an even number of times, it will leave those nodes unchanged.\n- Therefore we can pick any pair of nodes and decide to apply the XOR to just those two nodes.\n- This implies the best we can do is to pair all the nodes which will increase after the XOR is applied with each other. If there is one leftover, we can decide to pair it with the node which is decreased by the XOR the least if that\'s a net gain.\n\n# Approach\n- Sum the current node\'s values\n- Check the delta change when XOR is applied for each node and sort them based on this delta\n- Consider each positive delta as being paired and add them all to the total sum\n- If there are an odd number of positive gains, then check the last and smallest positive gain to see if it\'s worth pairing it with the smallest negative delta\n\n# Complexity\n- Time complexity: $$O(n*log(n))$$\n- Space complexity: $$O(n)$$\n\n# Code\n```\nclass Solution\n{\npublic:\n\tlong long maximumValueSum(vector<int>& nums, int k, vector<vector<int>>& edges)\n\t{\n\t\t// In the first pass through the numbers we calculat the current total\n\t\t// and keep track of the deltas if the xor is applied to each node\n\t\tvector<int> negativeDeltas;\n\t\tvector<int> positiveDeltas;\n\t\tlong long ans = 0;\n\t\tfor (int n : nums)\n\t\t{\n\t\t\tans += n;\n\n\t\t\tint after = n ^ k;\n\t\t\tif (after > n)\n\t\t\t\tpositiveDeltas.push_back(after - n);\n\t\t\telse\n\t\t\t\tnegativeDeltas.push_back(n - after);\n\t\t}\n\n\t\t// We then sort the deltas to know which are the smallest\n\t\t// (could have used a heap as well, but in retrospect I realize a simple min could be tracked as well)\n\t\tsort(negativeDeltas.begin(), negativeDeltas.end());\n\t\tsort(positiveDeltas.begin(), positiveDeltas.end());\n\n\t\tbool evenNumPositives = positiveDeltas.size() % 2 == 0;\n\t\t// If there is a node which can be made greater, but can\'t be paired \n\t\t// (because there are an odd number of positive nodes)\n\t\t// then we can either not pair the smallest one, or\n\t\t// pair it with the smallest negative if the positive delta\n\t\t// outwieghs the negative delta.\n\t\tif (!evenNumPositives && !negativeDeltas.empty())\n\t\t{\n\t\t\tif (positiveDeltas[0] > negativeDeltas[0])\n\t\t\t\tans += positiveDeltas[0] - negativeDeltas[0];\n\t\t}\n\n\t\t// We always pair as many positives as we can, adding their deltas to the total\n\t\tfor (int i = evenNumPositives ? 0 : 1; i < positiveDeltas.size(); ++i)\n\t\t\tans += positiveDeltas[i];\n\n\t\treturn ans;\n\t}\n};\n``` | 2 | 0 | ['Math', 'Tree', 'C++'] | 1 |
find-the-maximum-sum-of-node-values | C# | c-by-adchoudhary-m3fl | Code | adchoudhary | NORMAL | 2025-02-26T04:12:51.422003+00:00 | 2025-02-26T04:12:51.422003+00:00 | 5 | false | # Code
```csharp []
public class Solution {
public long MaximumValueSum(int[] nums, int k, int[][] edges)
{
long[][] memo = new long[nums.Length][];
for (int i = 0; i < nums.Length; i++)
{
memo[i] = new long[] {-1, -1, -1};
// Array.Fill(memo[i], -1);
}
return MaxSumOfNodes(0, 1, nums, k, memo);
}
private long MaxSumOfNodes(int index, int isEven, int[] nums, int k,
long[][] memo)
{
if (index == nums.Length)
{
// If the operation is performed on an odd number of elements, return
// int.MinValue
return isEven == 1 ? 0 : int.MinValue;
}
if (memo[index][isEven] != -1)
{
return memo[index][isEven];
}
// No operation performed on the element
long noXorDone = nums[index] + MaxSumOfNodes(index + 1, isEven, nums, k, memo);
// XOR operation is performed on the element
long xorDone = (nums[index] ^ k) +
MaxSumOfNodes(index + 1, isEven ^ 1, nums, k, memo);
// Memoize and return the result
return memo[index][isEven] = Math.Max(xorDone, noXorDone);
}
}
``` | 1 | 0 | ['C#'] | 0 |
find-the-maximum-sum-of-node-values | Easiest c++ solution (Beats 100% users) | easiest-c-solution-beats-100-users-by-co-h0yu | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | cookie_33 | NORMAL | 2024-05-20T06:07:12.543773+00:00 | 2024-05-20T06:32:06.732386+00:00 | 10 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n typedef long long ll;\n long long maximumValueSum(vector<int>& nums, int k, vector<vector<int>>& edges) {\n \n ll sum =0 ;\n int count =0;\n ll minLoss = INT_MAX;\n\n for( ll num : nums){\n if((num^k) > num){\n count++;\n sum += (num^k);\n }\n else{\n sum += num;\n }\n\n minLoss = min(minLoss,abs(num - (num^k)));\n }\n\n if(count % 2 == 0){\n return sum;\n }\n\n return sum - minLoss; \n }\n};\n``` | 1 | 0 | ['Greedy', 'C++'] | 0 |
find-the-maximum-sum-of-node-values | Racket Solution | racket-solution-by-nerasnow-i0yt | Code\nracket\n(define (vector-sum vec count)\n (for/sum ([i vec][j (in-range count)]) i))\n\n(define/contract (maximum-value-sum nums k edges)\n (-> (listof | nerasnow | NORMAL | 2024-05-19T20:28:34.425279+00:00 | 2024-05-19T20:28:34.425304+00:00 | 4 | false | # Code\n```racket\n(define (vector-sum vec count)\n (for/sum ([i vec][j (in-range count)]) i))\n\n(define/contract (maximum-value-sum nums k edges)\n (-> (listof exact-integer?) exact-integer? (listof (listof exact-integer?)) exact-integer?)\n (define change (vector-sort (list->vector (map (\u03BB (i) (- (bitwise-xor k i) i)) nums)) >))\n (define count (for/sum ([i change] #:when (positive? i)) 1))\n (define s (+ (apply + nums) (vector-sum change count)))\n (cond\n [(even? count) s]\n [(odd? count)\n (let ([tmp (- s (vector-ref change (sub1 count)))]) \n (if (< (add1 count) (vector-length change)) \n (max tmp (+ s (vector-ref change count))) \n tmp))]))\n``` | 1 | 0 | ['Racket'] | 1 |
find-the-maximum-sum-of-node-values | ✅All 4 approach explained || Detailed explanation ever available on internet || Must watch Sol✨ | all-4-approach-explained-detailed-explan-atx2 | \n# Overview\n\nWe aim to maximize the sum of values of all nodes in an undirected tree by performing a specific operation. \nThe operation allows us to replac | prakhar_arya | NORMAL | 2024-05-19T19:33:11.846443+00:00 | 2024-05-19T19:33:11.846471+00:00 | 22 | false | \n# Overview\n\nWe aim to maximize the sum of values of all nodes in an undirected tree by performing a specific operation. \nThe operation allows us to replace the values of any two **adjacent** nodes with their XOR values, with a given integer `k`.\n\n**Key Observations:**\n\n1. Alice can perform an operation on any edge `[u, v]` by XOR-ing the values of nodes `u` and `v` with a positive integer `k`.\n2. Alice wants to maximize the sum of the values of the tree nodes. This means she aims to maximize the total value represented by the sum of individual node values after performing the specified operations.\n3. Alice can perform the operation any number of times (including zero) on the tree. This implies she can selectively choose edges and perform the XOR operation to maximize the sum of node values.\n\n> **Note:** The XOR (exclusive OR) operator compares corresponding bits of two operands and returns 1 if the bits are different and 0 if they are the same. For instance, in binary 1010XOR1100=01101010 XOR 1100 = 01101010XOR1100\\=0110 indicating that the second and third bits differ while the first and fourth bits are the same. \n> Bitwise XOR operation is commutative and associative. That means aXORbXORb=aa XOR b XOR b = aaXORbXORb\\=a, and aXORb=bXORaa XOR b = b XOR aaXORb\\=bXORa. Hence, the order of applying XOR operations doesn\'t matter. \n> XORing a number with itself (aXORaa XOR aaXORa) results in 000. Therefore, performing the XOR operation twice on the same number yields the original number.\n\n---\n\n### Approach 1: Top-Down Dynamic Programming - Memoization\n\n#### Intuition\n\nLet\'s assume we want to replace the values of any two arbitrary nodes `U` and `V` with their XOR values, where `U` and `V` are not adjacent. Since, the tree is connected, undirected, and acyclic, there always exists a path between `U` and `V`. Let\'s assume the length of this path is `L` and P={P1,P2,P3...PL\u22121}P =\\\\{P\\_1, P\\_2, P\\_3...P\\_{L-1}\\\\}P\\={P1\u200B,P2\u200B,P3\u200B...PL\u22121\u200B} denotes the set of nodes on this path, following the order in which they appear on the path from `U` to `V`. Below is a diagram for better understanding:\n\n\n\nNow, let\'s operate on every edge from `U` to `V`. Since, there are exactly `L` edges between both the nodes, we will be performing `L` operations in total.\n\nThe value of each node after these `L` operations will change as shown below:\n\n\n\nSince the XOR operation obeys the properties of commutativity and identity, A\u2005\u200AXOR\u2005\u200AB\u2005\u200AXOR\u2005\u200AB=AA\\\\; XOR\\\\; B\\\\; XOR\\\\; B = AAXORBXORB\\=A for any two integers `A` and `B`. Therefore, the values of all nodes in the set `P` will remain unchanged. However, for the nodes `U` and `V`, their value will be replaced with the XOR value with `k`.\n\nSo, for any two non-adjacent nodes `U` and `V` in the tree we can replace their values with the XOR values as if they were connected by an edge. Let\'s call this operation as "effective operation" for simplicity.\n\nAfter performing a sequence of effective operations on some pairs of nodes, exactly `m` nodes in the tree have their value replaced with the XOR value (where `m <= n` and `n` denotes the number of nodes in the tree). It can be observed that the value of `m` will always be `even` because "effective operation" is performed on a pair of nodes.\n\nNow, the brute force approach is based on recursion. During recursion, it\'s crucial to incorporate both: the node\'s value with XOR operation (XORing with `k`) and without XOR operation while traversing the tree. We try to maximize the total sum of the values, where the operation is performed on an **even** number of nodes.\n\nLet\'s adapt our recursive solution based on these insights:\n\n- The base case occurs when we have traversed through all the nodes of the tree. If the number of nodes on which we have performed the operation is even, we return 0. Otherwise, we return `INT_MIN` (minimum integer value).\n \n- We also need to include the parity of the number of elements on which the operation has been performed as a parameter in the recursive solution. If the number of operated elements is even, it is a valid assignment.\n \n\n> Parity of a number refers to whether it contains an odd or even number of 1-bits.\n\n- The two choices that we have here for every node are to perform an operation on it or not. The recursive calls for each case can be explained as:\n \n - If we perform the operation on the node at the position `index`, then the value of this node would be modified to `nums[index] XOR k`. Since we are operating on a node, the parity of the total number of elements on which the XOR operation has been performed will be flipped. Therefore, even parity flips to odd, and vice versa. To obtain the answer for this case, we will store the sum of `nums[index] XOR k` and the subsequent recursive function call for the next node at `index+1` and the flipped parity (denoted by `isEven XOR 1`).\n \n - If we do not perform the operation on the node at the position `index`, then the value of this node would remain the same. The parity of the total number of elements on which the operation is performed will remain the same. To obtain the answer for this case, we will store the sum of `nums[index]` and the subsequent recursive function call for the next node at `index+1` and the given parity.\n \n- Since we want to maximize the sum of all nodes, we will return the maximum value of both the cases discussed above.\n \n\nThe recursive approach will result in Time Limit Exceeded (TLE) issues due to the exponential nature of possibilities.\n\nTo tackle this issue, we\'ll use dynamic programming (DP) with a two-dimensional table.\n\nThe DP table caches the results of subproblems, with rows representing different indices of the nodes given by `index` and columns representing the parity of the number of operated nodes denoted by `isEven`(`0` indicates `odd`, `1` indicates `even` parity). Each cell stores an integer denoting the maximum possible sum of all the nodes up to `index` and where the parity of the number of operated nodes is `isEven`.\n\nBy caching the calculated states in the dp table, we can avoid recalculating the result for the same combination of index and parity. When encountering a state that has already been computed and stored in the dp table, instead of recursively exploring further, we can directly retrieve the cached result, significantly reducing the time complexity of the algorithm.\n\n#### Algorithm\n\n##### Main Function: `maximumValueSum(nums, k, edges)`\n\n1. Initialize a 2D memoization array `memo` with all values set to `-1`.\n2. Call the helper function `maxSumOfNodes` with the initial parameters:\n - `index = 0`\n - `isEven = 1` (start with an odd number of elements)\n - `nums = the input array`\n - `k = the given XOR value`\n - `memo = the initialized memoization array`\n3. Return the result from the `maxSumOfNodes` function.\n\n##### Recursive Function: `maxSumOfNodes(index, isEven, nums, k, memo)`\n\n1. If the `index` is equal to the size of the `nums` array, return:\n - If `isEven` is 1, return 0 (no operation performed on an odd number of elements).\n - Else, return `INT_MIN`.\n2. If the result for the current `index` and `isEven` is already memoized, return the memoized value.\n3. Calculate the maximum sum of nodes in two cases:\n - `noXorDone`: No XOR operation is performed on the current element.\n - The sum is the current element value `nums[index]` plus the maximum sum of the remaining elements.\n - `xorDone`: The XOR operation is performed on the current element.\n - The sum is the current element value `nums[index] ^ k` plus the maximum sum of the remaining elements with `isEven` flipped.\n4. Memoize the maximum of `noXorDone` and `xorDone`, and return the result.\n\n#### Implementation\n```java []\nclass Solution {\n\n public long maximumValueSum(int[] nums, int k, int[][] edges) {\n long[][] memo = new long[nums.length][2];\n for (long[] row : memo) {\n Arrays.fill(row, -1);\n }\n return maxSumOfNodes(0, 1, nums, k, memo);\n }\n\n private long maxSumOfNodes(int index, int isEven, int[] nums, int k,\n long[][] memo) {\n if (index == nums.length) {\n // If the operation is performed on an odd number of elements return\n // INT_MIN\n return isEven == 1 ? 0 : Integer.MIN_VALUE;\n }\n if (memo[index][isEven] != -1) {\n return memo[index][isEven];\n }\n // No operation performed on the element\n long noXorDone = nums[index] + maxSumOfNodes(index + 1, isEven, nums, k, memo);\n // XOR operation is performed on the element\n long xorDone = (nums[index] ^ k) +\n maxSumOfNodes(index + 1, isEven ^ 1, nums, k, memo);\n\n // Memoize and return the result\n return memo[index][isEven] = Math.max(xorDone, noXorDone);\n }\n }\n```\n```python []\nclass Solution:\n def maxSumOfNodes(self, index, isEven, nums, k, memo):\n if index == len(nums):\n # If the operation is performed on an odd number of elements return INT_MIN\n return 0 if isEven == 1 else -float("inf")\n if memo[index][isEven] != -1:\n return memo[index][isEven]\n\n # No operation performed on the element\n noXorDone = nums[index] + self.maxSumOfNodes(index + 1, isEven, nums, k, memo)\n # XOR operation is performed on the element\n xorDone = (nums[index] ^ k) + self.maxSumOfNodes(\n index + 1, isEven ^ 1, nums, k, memo\n )\n\n # Memoize and return the result\n memo[index][isEven] = max(xorDone, noXorDone)\n return memo[index][isEven]\n\n def maximumValueSum(self, nums: List[int], k: int, edges: List[List[int]]) -> int:\n memo = [[-1] * 2 for _ in range(len(nums))]\n return self.maxSumOfNodes(0, 1, nums, k, memo)\n```\n```c++ []\nclass Solution {\npublic:\n long long maximumValueSum(vector<int>& nums, int k,\n vector<vector<int>>& edges) {\n vector<vector<long long>> memo(nums.size(), vector<long long>(2, -1));\n return maxSumOfNodes(0, 1, nums, k, memo);\n }\n\nprivate:\n long long maxSumOfNodes(int index, int isEven, vector<int>& nums, int k,\n vector<vector<long long>>& memo) {\n if (index == nums.size()) {\n // If the operation is performed on an odd number of elements return\n // INT_MIN\n return isEven == 1 ? 0 : INT_MIN;\n }\n if (memo[index][isEven] != -1) {\n return memo[index][isEven];\n }\n // No operation performed on the element\n long long noXorDone =\n nums[index] + maxSumOfNodes(index + 1, isEven, nums, k, memo);\n // XOR operation is performed on the element\n long long xorDone = (nums[index] ^ k) +\n maxSumOfNodes(index + 1, isEven ^ 1, nums, k, memo);\n\n // Memoize and return the result\n return memo[index][isEven] = max(xorDone, noXorDone);\n }\n};\n```\n\n\n \n\n#### Complexity Analysis\n\nLet nnn be the number of nodes in the tree.\n\n- Time complexity: $$O(n)$$\n \n The time complexity of the `maxSumOfNodes` function can be analyzed by considering the number of unique subproblems that need to be solved. There are at most n\u22C52n \\\\cdot 2n\u22C52 unique subproblems, indexed by `index` and `isEven` values, because the number of possible values for `index` is `n` and `isEven` is `2` (parity).\n \n Here, each subproblem is computed only once (due to memoization). So, the time complexity is bounded by the number of unique subproblems.\n \n Therefore, the time complexity can be stated as $$O(n)$$.\n \n- Space complexity: $$O(n)$$\n \n The space complexity of the algorithm is primarily determined by two factors: the auxiliary space used for memoization and the recursion stack space. The memoization table, denoted as `memo`, consumes O(n) space due to its size being proportional to the length of the input node list.\n \n Additionally, the recursion stack space can grow up to O(n) in the worst case, constrained by the length of the input node list, as each recursive call may add a frame to the stack.\n \n Therefore, the overall space complexity is the sum of these two components, resulting in O(n)+O(n) + O(n), which simplifies to $$O(n)$$.\n \n\n---\n\n### Approach 2: Bottom-up Dynamic Programming (Tabulation)\n\n#### Intuition\n\nTabulation is a dynamic programming technique that involves systematically iterating through all possible combinations of changing parameters. Since tabulation operates iteratively, rather than recursively, it does not require overhead for the recursive stack space, making it more efficient than memoization. We have two variables that change as we progress through the node values: the current index we\'re considering and the parity of even elements. To thoroughly explore the combinations, we use two nested loops to iterate through these variables.\n\nFirst, let\'s establish the base case:\n\n```cpp\nif (index == nums.size()) { \n return isEven == 1 ? 0 : INT_MIN;\n} \n```\n\nWe represent this base case in our tabulation matrix as `dp[nums.size()][1] = 0` and `dp[nums.size()][0] = INT_MIN`. This indicates that if the parity of the number of operations after iterating the array is odd, then it is an invalid assignment.\n\nOur ultimate goal is to determine the maximum sum of all node values after performing the operation on an even number of nodes, and this information will be stored in `dp[0][1]`. To accomplish this, we traverse through every combination of index and parity using the two nested loops. The outer loop iterates over the index, while the inner loop makes the choice of parity (1 for even and 0 for odd).\n\nThroughout this traversal, we evaluate each state and update our tabulation matrix accordingly. Upon completing the traversal of the entire array, the value of `dp[0][1]` represents the maximum node value sum possible after performing all operations.\n\n#### Algorithm\n\n1. Initialize a 2D dynamic programming array `dp` with dimensions `(n + 1) x 2`, where `n` is the size of the `nums` array.\n2. Initialize the base case values:\n - `dp[n][1] = 0` (no operation performed on an odd number of elements)\n - `dp[n][0] = INT_MIN`\n3. Iterate through the `nums` array in reverse order (from `n - 1` to `0`):\n - For each index `index` and each parity state `isEven` (0 or 1):\n - Calculate the maximum value sum in two cases:\n - `performOperation`: Perform the XOR operation on the current element.\n - The sum is `dp[index + 1][isEven ^ 1] + (nums[index] ^ k)`.\n - `dontPerformOperation`: Don\'t perform the XOR operation on the current element.\n - The sum is `dp[index + 1][isEven] + nums[index]`.\n - Update `dp[index][isEven]` with the maximum of `performOperation` and `dontPerformOperation`.\n4. Return the value stored in `dp[0][1]`, which represents the maximum value sum when starting with an odd number of elements.\n\n#### Implementation\n\n```java []\nclass Solution {\n public long maximumValueSum(int[] nums, int k, int[][] edges) {\n int n = nums.length;\n long[][] dp = new long[n + 1][2];\n dp[n][1] = 0;\n dp[n][0] = Integer.MIN_VALUE;\n \n for (int index = n - 1; index >= 0; index--) {\n for (int isEven = 0; isEven <= 1; isEven++) {\n // Case 1: we perform the operation on this element.\n long performOperation = dp[index + 1][isEven ^ 1] + (nums[index] ^ k);\n // Case 2: we don\'t perform operation on this element.\n long dontPerformOperation = dp[index + 1][isEven] + nums[index];\n\n dp[index][isEven] = Math.max(performOperation, dontPerformOperation);\n }\n }\n \n return dp[0][1];\n }\n}\n```\n```python []\nclass Solution:\n def maximumValueSum(self, nums: List[int], k: int, edges: List[List[int]]) -> int:\n n = len(nums)\n dp = [[0] * 2 for _ in range(n + 1)]\n dp[n][1] = 0\n dp[n][0] = -float(\'inf\')\n \n for index in range(n - 1, -1, -1):\n for isEven in range(2):\n # Case 1: we perform an operation on this element.\n performOperation = dp[index + 1][isEven ^ 1] + (nums[index] ^ k)\n # Case 2: we don\'t perform operation on this element.\n dontPerformOperation = dp[index + 1][isEven] + nums[index]\n\n dp[index][isEven] = max(performOperation, dontPerformOperation)\n \n return dp[0][1]\n```\n```c++ []\nclass Solution {\npublic:\n long long maximumValueSum(vector<int>& nums, int k,\n vector<vector<int>>& edges) {\n int n = nums.size();\n vector<vector<long long>> dp(n + 1, vector<long long>(2, 0));\n dp[n][1] = 0;\n dp[n][0] = INT_MIN;\n \n for (int index = n - 1; index >= 0; index--) {\n for (int isEven = 0; isEven <= 1; isEven++) {\n // Case 1: we perform the operation on this element.\n long long performOperation =\n dp[index + 1][isEven ^ 1] + (nums[index] ^ k);\n // Case 2: we don\'t perform operation on this element.\n long long dontPerformOperation =\n dp[index + 1][isEven] + nums[index];\n\n dp[index][isEven] = max(performOperation, dontPerformOperation);\n }\n }\n return dp[0][1];\n }\n};\n```\n\n#### Complexity Analysis\n\nLet nnn be the number of elements in the node value list.\n\n- Time complexity: $$O(n)$$\n \n We iterate through a nested loop where the total number of iterations is given by n\u22C52n \\\\cdot 2n\u22C52. Inside the nested loops, we perform constant time operations. Therefore, time complexity is given by O(n).\n \n- Space complexity: $$O(n)$$\n \n Since we create a new `dp` matrix of size n\u22C52n \\\\cdot 2n\u22C52, the total additional space becomes n\u22C52n \\\\cdot 2n\u22C52. So, the net space complexity is O(n).\n \n\n---\n\n### Approach 3: Greedy (Sorting based approach)\n\n#### Intuition\n\nIf the operation is performed on a node indexed at `U`, the new value of the node would become `nums[U] XOR k`. For every node, the net change in its value after performing the operation is given by `netChange[U] = nums[U] XOR k - nums[U]`.\n\nIf this net change is greater than zero, it will increase the total sum of all node values. Otherwise, it would decrease it.\n\nLet\'s assume we want to perform the "effective operation" on a pair of nodes that would provide the greatest increment to the node sum. Observe that choosing the nodes with the greatest positive `netChange` values will provide the greatest increment to node sum.\n\nFor all nodes, we can calculate their net change values using the formula discussed above. On sorting these values in **decreasing** order, we can pick the values in pairs from the start of the sorted `netChange` array with a positive sum.\n\nIf the sum of a pair is positive, then it will increase the value of the total node sum when the operation is performed on this pair.\n\n#### Algorithm\n\n1. Initialise the `netChange` array of size `n` and an integer `nodeSum` that stores the current sum of `nums`. Here, `n` is the size of the `nums` array.\n2. Iterate through the `nums` array (from `0` to `n-1`):\n - For each index, store the value of `netChange` using the idea discussed in intuition.\n3. Sort the array `netChange` in decreasing order.\n4. Iterate through the `netChange` array (from `0` to `n-1`, stepsize = `2`):\n - If we can not create a pair of adjacent elements, break the iteration.\n - If the sum of a pair of adjacent elements is positive then add this sum to `nodeSum`.\n5. After iterating through all `netChange` elements, return `nodeSum` as the maximum possible sum of nodes after performing the operations.\n\n\n#### Implementation\n\n```java []\nclass Solution {\n public long maximumValueSum(int[] nums, int k, int[][] edges) {\n int n = nums.length;\n int[] netChange = new int[n];\n long nodeSum = 0;\n\n for (int i = 0; i < n; i++) {\n netChange[i] = (nums[i] ^ k) - nums[i];\n nodeSum += nums[i];\n }\n\n Arrays.sort(netChange);\n // Reverse the sorted array\n for (int i = 0; i < n / 2; i++) {\n int temp = netChange[i];\n netChange[i] = netChange[n - 1 - i];\n netChange[n - 1 - i] = temp;\n }\n\n for (int i = 0; i < n; i += 2) {\n // If netChange contains odd number of elements break the loop\n if (i + 1 == n) {\n break;\n }\n long pairSum = netChange[i] + netChange[i + 1];\n // Include in nodeSum if pairSum is positive\n if (pairSum > 0) {\n nodeSum += pairSum;\n }\n }\n return nodeSum;\n }\n}\n```\n```python []\nclass Solution:\n def maximumValueSum(self, nums: List[int], k: int, edges: List[List[int]]) -> int:\n n = len(nums)\n netChange = [(nums[i] ^ k) - nums[i] for i in range(n)]\n nodeSum = sum(nums)\n\n netChange.sort(reverse=True)\n\n for i in range(0, n, 2):\n # If netChange contains odd number of elements break the loop\n if i + 1 == n:\n break\n pairSum = netChange[i] + netChange[i + 1]\n # Include in nodeSum if pairSum is positive\n if pairSum > 0:\n nodeSum += pairSum\n\n return nodeSum\n```\n```c++ []\nclass Solution {\npublic:\n long long maximumValueSum(vector<int>& nums, int k,\n vector<vector<int>>& edges) {\n vector<int> netChange;\n long long nodeSum = 0;\n \n for (int i = 0; i < nums.size(); i++) {\n netChange.push_back((nums[i] ^ k) - nums[i]);\n nodeSum += 1ll * nums[i];\n }\n \n // Sort netChange in decreasing order\n sort(netChange.begin(), netChange.end(), greater<int>());\n \n for (int i = 0; i < netChange.size(); i += 2) {\n // If netChange contains odd number of elements break the loop\n if (i + 1 == netChange.size()) {\n break;\n }\n long long pairSum = netChange[i] + netChange[i + 1];\n \n // Include in nodeSum if pairSum is positive\n if (pairSum > 0) {\n nodeSum += pairSum;\n }\n }\n return nodeSum;\n }\n};\n```\n\n\n\n\n#### Complexity Analysis\n\nLet nnn be the number of elements in the node value list.\n\n- Time complexity:O(n\u22C5logn)\n \n Other than the `sort` invocation, we perform simple linear operations on the list, so the runtime is dominated by the O(n\u22C5logn) complexity of sorting.\n \n- Space complexity: O(n)\n \n Since we create a new `netChange` array of size `n` and sort it, the additional space becomes O(n) for `netChange` array and O(logn) or O(n) for sorting it (depending on the sorting algorithm used). So, the net space complexity is O(n).\n \n\n---\n\n### Approach 4: Greedy (Finding local maxima and minima)\n\n#### Intuition\n\nRecall that "effective operation" allows us to pick any two nodes and perform an operation on it. Let\'s assume for two nodes, the `netChange` values are positive. If we pick both these nodes as a pair to perform "effective operation", the node sum value will be increased. So, we can observe that if the number of elements with positive `netChange` values is even, then all of them can be included in the final sum to maximize it.\n\nIf the number of elements with positive `netChange` values is **odd**, then let\'s assume that `positiveMinimum` denotes the **minimum positive** value and `negativeMaximum` denotes the **maximum non-positive** value in the `netChange` array. It is clear that both these values will occur as a pair in the `netChange` array.\n\nNow, there can be two cases for the same:-\n\n1. If the sum of `positiveMinimum` and `negativeMaximum` is greater than zero, then the node value sum will be increased by including this pair. So, we include both elements.\n \n2. If the sum of `positiveMinimum` and `negativeMaximum` is less than or equal to zero, then the node value sum will be decreased or have no change on including this pair. So, we exclude this pair.\n \n\nTherefore, we don\'t need the `netChange` array from the previous approach. We calculate `positiveMinimum` and `negativeMaximum` values which is enough to calculate the maximum node value sum possible for the array.\n\n#### Algorithm\n\n1. Initialize integers `positiveMinimum` and `negativeMaximum` with `INT_MAX` and `INT_MIN` respectively. Also, initialize `count` and `sum` with `0`.\n2. Iterate through the `nums` array (from `0` to `n - 1`):\n - Add the unchanged node values to `sum`.\n - Calculate the value of `netChange` for the current node.\n - If `netChange` is positive, assign the minimum of `netChange` and `positiveMinimum` to `positiveMinimum`. Add `netChange` to the `sum` and increment the `count` by 1.\n - If `netChange` is non-positive, assign the maximum of `netChange` and `negativeMaximum` to `negativeMaximum`.\n3. If the `count` of number values with positive `netChange` is even, we return the current `sum` as the maximum node value sum possible.\n4. If the `count` is odd, we can either subtract `positiveMinimum` or add `negativeMaximum` to make the `count` even. The maximum of both these cases is returned as the maximum node value sum.\n\n\n\n#### Implementation\n```java []\nclass Solution {\n public long maximumValueSum(int[] nums, int k, int[][] edges) {\n long sum = 0;\n int count = 0, positiveMinimum = (1 << 30), negativeMaximum = -1 * (1 << 30);\n\n for (int nodeValue : nums) {\n int operatedNodeValue = nodeValue ^ k;\n sum += nodeValue;\n int netChange = operatedNodeValue - nodeValue;\n if (netChange > 0) {\n positiveMinimum = Math.min(positiveMinimum, netChange);\n sum += netChange;\n count++;\n } else {\n negativeMaximum = Math.max(negativeMaximum, netChange);\n }\n }\n\n // If the number of positive netChange values is even, return the sum.\n if (count % 2 == 0) {\n return sum;\n }\n\n // Otherwise return the maximum of both discussed cases.\n return Math.max(sum - positiveMinimum, sum + negativeMaximum);\n }\n}\n```\n```python []\nclass Solution:\n def maximumValueSum(self, nums: List[int], k: int, edges: List[List[int]]) -> int:\n sumVal = 0\n count = 0\n positiveMinimum = 1 << 30\n negativeMaximum = -1 * (1 << 30)\n\n for nodeValue in nums:\n operatedNodeValue = nodeValue ^ k\n sumVal += nodeValue\n netChange = operatedNodeValue - nodeValue\n if netChange > 0:\n positiveMinimum = min(positiveMinimum, netChange)\n sumVal += netChange\n count += 1\n else:\n negativeMaximum = max(negativeMaximum, netChange)\n\n # If the number of positive netChange values is even, return the sum.\n if count % 2 == 0:\n return sumVal\n\n # Otherwise return the maximum of both discussed cases.\n return max(sumVal - positiveMinimum, sumVal + negativeMaximum)\n```\n```c++ []\nclass Solution {\npublic:\n long long maximumValueSum(vector<int>& nums, int k,\n vector<vector<int>>& edges) {\n long long sum = 0;\n int count = 0, positiveMinimum = (1 << 30),\n negativeMaximum = -1 * (1 << 30);\n \n for (int nodeValue : nums) {\n int operatedNodeValue = nodeValue ^ k;\n sum += nodeValue;\n int netChange = operatedNodeValue - nodeValue;\n \n if (netChange > 0) {\n positiveMinimum = min(positiveMinimum, netChange);\n sum += netChange;\n count++;\n } else {\n negativeMaximum = max(negativeMaximum, netChange);\n }\n }\n \n // If the number of positive netChange values is even return the sum.\n if (count % 2 == 0) {\n return sum;\n }\n \n // Otherwise return the maximum of both discussed cases.\n return max(sum - positiveMinimum, sum + negativeMaximum);\n }\n};\n```\n\n```\n\n```\n\n#### Complexity Analysis\n\nLet nnn be the number of elements in the node value list.\n\n- Time complexity: O(n)\n \n We perform a single pass linear scan on the list which takes O(n) time. All other operations are performed in constant time. This makes the net time complexity as O(n).\n \n- Space complexity: O(1)\n \n We do not allocate any additional auxiliary memory proportional to the size of the given node list. Therefore, overall space complexity is given by O(1).\n\n\n# Code\n```\nclass Solution {\n public long maximumValueSum(int[] nums, int k, int[][] edges) {\n long sum = 0;\n int count = 0, positiveMinimum = (1 << 30), negativeMaximum = -1 * (1 << 30);\n\n for (int nodeValue : nums) {\n int operatedNodeValue = nodeValue ^ k;\n sum += nodeValue;\n int netChange = operatedNodeValue - nodeValue;\n if (netChange > 0) {\n positiveMinimum = Math.min(positiveMinimum, netChange);\n sum += netChange;\n count++;\n } else {\n negativeMaximum = Math.max(negativeMaximum, netChange);\n }\n }\n\n // If the number of positive netChange values is even, return the sum.\n if (count % 2 == 0) {\n return sum;\n }\n\n // Otherwise return the maximum of both discussed cases.\n return Math.max(sum - positiveMinimum, sum + negativeMaximum);\n }\n}\n``` | 1 | 0 | ['Python', 'C++', 'Java', 'Python3'] | 0 |
find-the-maximum-sum-of-node-values | C++ Easy Solution | c-easy-solution-by-skill_improve-u6ol | Intuition\n Describe your first thoughts on how to solve this problem. \n\nJust calculate the xor of elements and check store the max of both element or xor of | skill_improve | NORMAL | 2024-05-19T18:59:13.359601+00:00 | 2024-05-19T18:59:13.359642+00:00 | 17 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\nJust calculate the xor of elements and check store the max of both element or xor of it with k ....and check how many of the elements get the xor greater than the element ..if the count of element xored with k are odd then we can\'t pair or can\'t maker edge of 1 element so we will subtract the min differnce of the element and the element xored with k ... if xored with k is less than the element .\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n\n# Code\n```\n#define ll long long \nclass Solution {\npublic:\n long long maximumValueSum(vector<int>& nums, int k, vector<vector<int>>& edges) {\n ll ans=0,cnt=0,mn=INT_MAX;\n for(ll i:nums){\n if((i ^ k) > i){\n cnt++;\n ans+=(i ^ k);\n }\n else{\n ans+=i;\n }\n mn=min(mn,abs(i-(i ^ k)));\n }\n return (cnt & 1)?ans-mn:ans;\n }\n};\n```\nHappy Coding\uD83D\uDE0A\uD83D\uDE0A | 1 | 0 | ['Array', 'Dynamic Programming', 'Greedy', 'Bit Manipulation', 'Tree', 'Sorting', 'C++'] | 0 |
find-the-maximum-sum-of-node-values | 100% beats, C, O(n), Gready, one additional variable to find best change to sacrifize. | 100-beats-c-on-gready-one-additional-var-zhdd | Intuition\nWe actually can change any pair of nodes. Let\'s find the best value (xored or not) for all nodes, then sum them up. If the number of changed values | stivsh | NORMAL | 2024-05-19T18:35:39.604418+00:00 | 2024-05-19T18:55:09.181191+00:00 | 12 | false | # Intuition\nWe actually can change any pair of nodes. Let\'s find the best value (xored or not) for all nodes, then sum them up. If the number of changed values is odd (indicating we have a redundant change), we will sacrifice the smallest non-optimal change.\n\n\n# Code\n```\nlong long maximumValueSum(int* nums, int numsSize, int k, int** edges, int edgesSize, int* edgesColSize) {\n long long best_solution = 0;\n char is_changes_count_odd = 0;\n // the smallest possible value to be subtructed if is_changes_count_odd\n int best_to_sacrifize = abs((nums[0] ^ k) - nums[0]); // init with any(first)\n\n for (size_t i = 0; i != numsSize; ++i) {\n int n = nums[i];\n // what is better? value or xored with k value?\n if ((n ^ k) > n) {\n is_changes_count_odd ^= 1;\n best_solution += n ^ k;\n\n } else {\n best_solution += n;\n }\n\n // find min of all possible best_to_sacrifize\n if ( best_to_sacrifize > abs((n ^ k) - n) ) {\n best_to_sacrifize = abs((n ^ k) - n);\n }\n }\n\n // we have one redundunt change, lets pair it one with the min sacrifize\n // (or get rid of the less important one)\n if (is_changes_count_odd){\n best_solution -= best_to_sacrifize;\n }\n return best_solution;\n\n}\n``` | 1 | 0 | ['C'] | 0 |
find-the-maximum-sum-of-node-values | # Optimizing Array Values with Bitwise XOR | optimizing-array-values-with-bitwise-xor-f4kh | \n## Intuition\nWhen I first looked at this problem, my goal was to maximize the sum of the array after performing a bitwise XOR operation on its elements with | kazakie96 | NORMAL | 2024-05-19T18:14:33.669355+00:00 | 2024-05-19T18:14:33.669391+00:00 | 10 | false | \n## Intuition\nWhen I first looked at this problem, my goal was to maximize the sum of the array after performing a bitwise XOR operation on its elements with a given integer `k`. The key observation is that the XOR operation can sometimes increase the value of a number and sometimes decrease it. Therefore, we need to find a way to leverage this operation to get the maximum possible sum of the array.\n\n## Approach\nHere\'s a step-by-step breakdown of my approach:\n\n1. **Calculate the Initial Total Sum**: First, I calculate the total sum of the array elements as a baseline.\n\n2. **Analyze the XOR Differences**: For each element in the array, I compute the difference between the result of the XOR operation and the original value. This difference helps to determine whether the XOR operation is beneficial (i.e., it results in a higher value).\n\n3. **Summing Positive Differences**: I maintain a running total of all positive differences (cases where the XOR operation increases the value). This helps in identifying the potential maximum gain.\n\n4. **Handling Odd Count of Positive Differences**: If the number of positive differences is odd, subtract the smallest absolute difference. This step ensures that the final total remains as high as possible because an odd number of changes might end up decreasing the overall sum when summed together.\n\n5. **Calculate the Final Total**: Add the total positive differences (adjusted for odd count if necessary) to the initial total sum to get the final result.\n\nBy following this method, the solution efficiently determines the maximum possible sum after the XOR operations.\n\n## Complexity\n- **Time complexity**: The solution involves iterating through the array twice: once for calculating the initial sum and once for computing differences and making adjustments. Therefore, the time complexity is $$O(n)$$, where `n` is the number of elements in the array.\n\n- **Space complexity**: The space complexity is $$O(1)$$ because we only use a few extra variables for storing intermediate results, and no additional data structures are required.\n\n\n\n# Code\n```\nclass Solution {\n public long maximumValueSum(int[] nums, int k, int[][] edges) {\n long total = 0;\n for (int num : nums) {\n total += num;\n }\n\n long totalDiff = 0;\n long diff;\n int positiveCount = 0;\n long minAbsDiff = Long.MAX_VALUE;\n for (int num : nums) {\n diff = (num ^ k) - num;\n\n if (diff > 0) {\n totalDiff += diff;\n positiveCount++;\n }\n minAbsDiff = Math.min(minAbsDiff, Math.abs(diff));\n }\n if (positiveCount % 2 == 1) {\n totalDiff -= minAbsDiff;\n }\n return total + totalDiff;\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
find-the-maximum-sum-of-node-values | C# Solution for Find the Maximum Sum of Node Values Problem | c-solution-for-find-the-maximum-sum-of-n-dq45 | Intuition\n Describe your first thoughts on how to solve this problem. \nThe key intuition behind this solution is to leverage dynamic programming to maximize t | Aman_Raj_Sinha | NORMAL | 2024-05-19T17:36:21.721535+00:00 | 2024-05-19T17:36:21.721561+00:00 | 45 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe key intuition behind this solution is to leverage dynamic programming to maximize the sum of node values after potentially performing XOR operations on the tree edges. We use a 2D dynamic programming array (dp) to track the maximum sums for different states: whether the number of XOR operations performed so far is even or odd.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1.\tInitialization:\n\t\u2022\tCreate a dp array of size (n + 1) x 2, where n is the length of the nums array.\n\t\u2022\tInitialize the base cases: dp[n, 1] to 0 (no operations performed on an odd number of elements), and dp[n, 0] to long.MinValue.\n2.\tDynamic Programming Transition:\n\t\u2022\tIterate through the nums array in reverse order, from n-1 to 0.\n\t\u2022\tFor each index and each parity state (isEven), calculate the maximum value sum by considering:\n\t\u2022\tNo XOR Operation: The sum if no XOR operation is performed on the current element.\n\t\u2022\tXOR Operation: The sum if an XOR operation is performed on the current element.\n\t\u2022\tUpdate the dp array with the maximum of these two sums.\n3.\tResult Extraction:\n\t\u2022\tThe desired result is stored in dp[0, 1], representing the maximum possible sum when starting from the first element with an even number of XOR operations.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\u2022\tTraversal: We iterate over each element in the nums array once.\n\u2022\tDP Transition: For each element, we consider two states (isEven being 0 or 1).\n\u2022\tThus, the time complexity is O(n), where n is the length of the nums array.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\u2022\tDP Array: We use a 2D array of size (n + 1) x 2.\n\u2022\tThus, the space complexity is O(n), which accounts for the dp array.\n\n# Code\n```\npublic class Solution {\n public long MaximumValueSum(int[] nums, int k, int[][] edges) {\n int n = nums.Length;\n long[,] dp = new long[n + 1, 2];\n \n // Base case initialization\n dp[n, 1] = 0;\n dp[n, 0] = long.MinValue;\n \n // Iterate through the nums array in reverse order\n for (int index = n - 1; index >= 0; index--) {\n for (int isEven = 0; isEven <= 1; isEven++) {\n long dontPerformOperation = dp[index + 1, isEven] + nums[index];\n long performOperation = dp[index + 1, isEven ^ 1] + (nums[index] ^ k);\n \n dp[index, isEven] = Math.Max(dontPerformOperation, performOperation);\n }\n }\n \n // The result is the maximum sum starting with an even number of operations\n return dp[0, 1];\n }\n}\n``` | 1 | 0 | ['C#'] | 0 |
find-the-maximum-sum-of-node-values | C++ || Thinking Process And Explanation | c-thinking-process-and-explanation-by-br-8sul | Intuition\n1. Consider the property of the xor operation, where any number do xor twice remains unchanged, so considering how can we apply this property to get | brm | NORMAL | 2024-05-19T17:34:19.734886+00:00 | 2024-05-20T02:38:04.263022+00:00 | 29 | false | # Intuition\n1. Consider the property of the `xor` operation, where any number do `xor` twice remains unchanged, so considering how can we apply this property to get the result.\n2. Given the `edges`, we can perform the `xor` operation on two adjacent nodes. However, it seems not using the property, we think beyond adjacent nodes and consider applying the `xor` operation to any two nodes in the tree.\n3. Since the input is a tree, any two nodes are connected by a path. When performing `xor` on the values of two nodes, all intermediate nodes on the path (excluding the start and end nodes) will undergo the `xor` operation twice, remaining unchanged. Thus, we can perform the `xor` operation on any two nodes.\n4. As a result, The problem reduces to selecting any two nodes at a time, performing the `xor` operation, and maximizing the sum of the resulting values.\n5. Calculate the potential change in value (delta) for each node if `xor` with `k`, and store these deltas in a vector. Sort this delta vector in descending order.\n6. Traverse the delta vector, select two delta, and add them to the final result in each round if the sum of them contributes positively to the final answer.\n\n# Approach\n1. Calculate the potential delta for each node value if `xor` with `k`.\n2. Sort the delta values in descending order.\n3. Traverse the delta vector and add 2 delta values to final result at a time in each round if they contribute the final answer.\n\n# Complexity\n- Time complexity: $$O(n*log(n))$$\n- Space complexity: $$O(n)$$\n\n# Code\n```\nclass Solution {\npublic:\n long long maximumValueSum(vector<int>& nums, int k, vector<vector<int>>& edges) {\n int n = nums.size();\n vector<int> delta;\n for (int i = 0; i < n; i++) {\n int value = nums[i];\n delta.push_back((value^k)-value);\n }\n sort(delta.rbegin(), delta.rend());\n\n long long res = accumulate(begin(nums), end(nums), 0LL);\n for (int i = 0; i+1 < n; i+= 2) {\n int delta_1 = delta[i];\n int delta_2 = delta[i+1];\n if (delta_1+delta_2 > 0) {\n res += delta_1+delta_2;\n }\n }\n return res;\n }\n};\n\n``` | 1 | 0 | ['C++'] | 0 |
find-the-maximum-sum-of-node-values | Java Solution for Find the Maximum Sum of Node Values Problem | java-solution-for-find-the-maximum-sum-o-n7gz | Intuition\n Describe your first thoughts on how to solve this problem. \nThe key idea is to maximize the sum of node values by strategically deciding whether to | Aman_Raj_Sinha | NORMAL | 2024-05-19T17:32:00.370768+00:00 | 2024-05-19T17:32:00.370801+00:00 | 35 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe key idea is to maximize the sum of node values by strategically deciding whether to perform XOR operations on connected nodes. In a linear structure (like an array), this would involve deciding for each element whether to XOR it with a given value k.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1.\tInitialization:\n\t\u2022\tMemoization Array: memo is used to store results for subproblems to avoid redundant calculations.\n\t\u2022\tDFS Traversal: The function dfs traverses the nodes starting from node 0 and considers both the scenarios: applying XOR and not applying XOR.\n2.\tRecursive Function dfs:\n\t\u2022\tBase Case: If node equals the length of nums, it returns 0 if isEven is 1 (indicating an even number of operations) or Integer.MIN_VALUE if isEven is 0.\n\t\u2022\tMemoization Check: If the result for the current node and state (even/odd) is already computed, return the stored result.\n\t\u2022\tCompute No XOR Case: Calculate the sum if no XOR operation is performed on the current node.\n\t\u2022\tCompute XOR Case: Calculate the sum if XOR operation is performed on the current node.\n\t\u2022\tMemoize and Return: Store the maximum of the above two sums in the memoization array and return it.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\u2022\tDFS Traversal: Each node is visited once, and for each node, we make decisions based on its children.\n\u2022\tMemoization: The memo array stores results for each node with two possible states (even/odd).\n\u2022\tTotal time complexity is O(n) because we visit each node once and perform constant-time operations.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\u2022\tMemoization Array: The memoization array has a size of O(n \\times 2) = O(n).\n\u2022\tCall Stack: The recursive DFS call stack can go as deep as the number of nodes in the tree, which is O(n) in the worst case.\n\u2022\tTotal space complexity is O(n).\n\n# Code\n```\nclass Solution {\n public long maximumValueSum(int[] nums, int k, int[][] edges) {\n // Build the adjacency list for the tree\n int n = nums.length;\n \n // Initialize memoization array\n long[][] memo = new long[n][2];\n for (long[] row : memo) {\n Arrays.fill(row, -1);\n }\n \n // Call the helper function to calculate the max sum starting from node 0\n return dfs(0, 1, nums, k, memo);\n }\n\n private long dfs(int node, int isEven, int[] nums, int k, long[][] memo) {\n if (node == nums.length) {\n return isEven == 1 ? 0 : Integer.MIN_VALUE;\n }\n\n if (memo[node][isEven] != -1) {\n return memo[node][isEven];\n }\n\n long noXorDone = nums[node] + dfs (node + 1, isEven, nums, k, memo);\n\n long xorDone = (nums[node] ^ k) + dfs (node + 1, isEven ^ 1, nums, k, memo); \n \n \n return memo[node][isEven] = Math.max(xorDone, noXorDone);\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
find-the-maximum-sum-of-node-values | Simple python3 solution | DFS + Greedy | simple-python3-solution-dfs-greedy-by-ti-adt1 | Complexity\n- Time complexity: O(n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(n)\n Add your space complexity here, e.g. O(n) \n\n# Co | tigprog | NORMAL | 2024-05-19T17:28:36.975213+00:00 | 2024-05-19T17:29:10.878863+00:00 | 33 | false | # Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` python3 []\nclass Solution:\n def maximumValueSum(self, nums: List[int], k: int, edges: List[List[int]]) -> int:\n vs = defaultdict(list)\n for u, v in edges:\n vs[u].append(v)\n vs[v].append(u)\n \n def dfs(u, prev):\n not_swap, swap = 0, -float(\'inf\')\n for v in vs[u]:\n if v == prev:\n continue\n child_not_swap, child_swap = dfs(v, u)\n not_swap, swap = (\n max(not_swap + child_not_swap, swap + child_swap),\n max(swap + child_not_swap, not_swap + child_swap),\n )\n \n value = nums[u]\n value_xor = nums[u] ^ k\n return (\n max(not_swap + value, swap + value_xor),\n max(swap + value, not_swap + value_xor),\n )\n \n return dfs(0, -1)[0]\n``` | 1 | 0 | ['Greedy', 'Depth-First Search', 'Recursion', 'Binary Tree', 'Python3'] | 1 |
find-the-maximum-sum-of-node-values | Easy JAVA Solution using Greedy Approach with intuition beats 100% | easy-java-solution-using-greedy-approach-jnmn | Intuition\n Describe your first thoughts on how to solve this problem. \nKey Observations:-\n- xor only those node\'s value with k which gives a result>node val | aRko_ | NORMAL | 2024-05-19T17:18:17.631512+00:00 | 2024-05-19T17:18:17.631564+00:00 | 32 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nKey Observations:-\n- xor only those node\'s value with k which gives a result>node val(nums[i]^k>nums[i])\n- we can choose any pair of nodes and xor them beacuase all are connected(indirectly & no. of edges=n-1).\n- we need to count for how many nodes we have performed the xor value,if the count is odd, then we have to perform xor on one more node which gives the minLoss(Math.abs(nums[i]-nums[i]^k)).\n- If the count is even, we add all the xor values with the original values of those node which we didn\'t perform xor.\n- If the count is odd, we return the sum subtracted by the minLoss.\n\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public long maximumValueSum(int[] nums, int k, int[][] edges) {\n long sum=0;\n int cnt=0;\n int min_Loss=Integer.MAX_VALUE;\n for(int it:nums){\n if((it^k)>it){\n cnt++;\n sum+=it^k;\n }\n else\n sum+=it;\n min_Loss=Math.min(min_Loss,Math.abs(it-(it^k)));\n } \n if(cnt%2==1){\n return sum-min_Loss;\n }\n else\n return sum;\n }\n}\n``` | 1 | 0 | ['Greedy', 'Tree', 'Graph', 'Java'] | 0 |
find-the-maximum-sum-of-node-values | Find the Maximum Sum of Node Values | find-the-maximum-sum-of-node-values-by-k-bjxy | Intuition\n Describe your first thoughts on how to solve this problem. \nTo solve the problem of finding the maximum sum of values in the nums array after perfo | kalpanahepzi_2k2 | NORMAL | 2024-05-19T15:29:38.541692+00:00 | 2024-05-19T15:29:38.541719+00:00 | 13 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo solve the problem of finding the maximum sum of values in the nums array after performing at most one XOR operation per element with a given integer k, we can break down the solution into a few key steps:\n1. XOR Operation: Understand how the XOR operation affects the numbers. XORing a number with k can either increase or decrease the value depending on the bits.\n2. Maximizing Sum: For each number in the array, decide whether to apply the XOR operation to maximize the overall sum.\n3. Handling Odd Changes: If the number of changes (XOR operations that increase the value) is odd, we might need to adjust the sum by potentially removing the smallest beneficial change to make it even, thereby ensuring the sum is optimal.1\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Iterate Over Array: Loop through each element in the nums array and calculate the potential new value after applying the XOR operation with k.\n2. Track Changes: Maintain a count of how many changes (XOR operations) actually increase the value.\n3. Track Minimum Change Difference: Keep track of the smallest difference between the original and XORed value for potential adjustment if the number of beneficial changes is odd.\n4. Adjust Final Sum: If the number of beneficial changes is odd, subtract the smallest difference from the total sum to ensure the final sum is maximized.\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public:\n long long maximumValueSum(vector<int>& nums, int k,\n vector<vector<int>>& edges) {\n long long maxSum = 0;\n int changedCount = 0;\n int minChangeDiff = INT_MAX;\n\n for (const int num : nums) {\n maxSum += max(num, num ^ k);\n changedCount += ((num ^ k) > num) ? 1 : 0;\n minChangeDiff = min(minChangeDiff, abs(num - (num ^ k)));\n }\n\n if (changedCount % 2 == 0)\n return maxSum;\n return maxSum - minChangeDiff;\n }\n};\n``` | 1 | 0 | ['Array', 'Dynamic Programming', 'Greedy', 'Bit Manipulation', 'Tree', 'Sorting'] | 0 |
find-the-maximum-sum-of-node-values | Just practice | just-practice-by-rshakthi443-0niq | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | rshakthi443 | NORMAL | 2024-05-19T15:25:52.176213+00:00 | 2024-05-19T15:25:52.176232+00:00 | 10 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution(object):\n def maximumValueSum(self, nums, k, edges):\n """\n :type nums: List[int]\n :type k: int\n :type edges: List[List[int]]\n :rtype: int\n """\n l1 = list(map(lambda x, k=k: (x ^ k, 1) if (x ^ k) > x else (x, 0), nums))\n\n sum_ = sum(list(map(lambda x: x[0], l1)))\n\n val_cnt = len(list(filter(lambda x: x[1], l1)))\n\n l3 = list(map(lambda x, k=k: (x ^ k) -x if (x ^ k) > x else x -(x^k) , nums))\n\n return sum_ if val_cnt % 2== 0 else sum_ - min(l3)\n \n``` | 1 | 0 | ['Python'] | 0 |
find-the-maximum-sum-of-node-values | Python3 Solution | python3-solution-by-motaharozzaman1996-83cw | \n\nclass Solution:\n def maximumValueSum(self, nums: List[int], k: int, edges: List[List[int]]) -> int:\n ans=0\n c=0\n d=1<<30\n | Motaharozzaman1996 | NORMAL | 2024-05-19T14:25:30.403903+00:00 | 2024-05-19T14:25:30.403936+00:00 | 22 | false | \n```\nclass Solution:\n def maximumValueSum(self, nums: List[int], k: int, edges: List[List[int]]) -> int:\n ans=0\n c=0\n d=1<<30\n for num in nums:\n ans+=max(num, num1:=num^k)\n c^=num<num1\n d=min(d,abs(num-num1))\n return ans-d*c \n``` | 1 | 0 | ['Python', 'Python3'] | 0 |
find-the-maximum-sum-of-node-values | Simple Solution | simple-solution-by-varunsh5687-t9t0 | Intuition\n Describe your first thoughts on how to solve this problem. \nThe intuition behind this approach is that XOR operations on elements in the list can e | varunsh5687 | NORMAL | 2024-05-19T10:41:46.249929+00:00 | 2024-05-19T10:41:46.249964+00:00 | 17 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition behind this approach is that XOR operations on elements in the list can either increase or decrease their values. The goal is to maximize the overall sum after these operations. By tracking the minimum positive change and the maximum negative change, the solution ensures that if the count of beneficial operations (positive changes) is odd, we can adjust the sum to ensure it remains maximized.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n<b>Initialization:</b>\n\n1. totalSum keeps track of the total sum of elements after potential XOR operations.\n2. count tracks the number of elements that were increased by the XOR operation.\n3. positiveMin is initialized to infinity and will store the minimum positive net change from the XOR operation.\n4. negativeMax is initialized to negative infinity and will store the maximum negative net change from the XOR operation.\n<b>\nIterating Through Elements:</b>\n\n1. For each element in nums, compute the result of XOR-ing the element with k (i.e., nodeValAfterOperation = nodeValue ^ k).\n2. Calculate the netChange which is the difference between the XOR-ed value and the original value (netChange = nodeValAfterOperation - nodeValue).\n<b>\nUpdating totalSum:</b>\n\n1. Add the original value of the element to totalSum.\n2. If the netChange is positive (i.e., the XOR operation results in a higher value), update positiveMin if this change is the smallest positive change encountered and add this net change to totalSum.\n3. If the netChange is negative, update negativeMax if this change is the largest negative change encountered.\n<b>\nCounting Operations:</b>\n\n1. Increment the count for each positive net change since we are tracking how many elements were beneficially changed by the XOR operation.\nBalancing the Count of Changes:\n\n2. If the count (number of beneficial changes) is even, return totalSum directly since an even count of positive changes ensures the sum is maximized.\n\n3. If the count is odd, we face a dilemma since adding or subtracting an odd number of beneficial changes can be suboptimal. Hence, we need to decide whether to:\n\n4. Remove the smallest positive change to make the count even (maximizing totalSum - positiveMin).\n5. Add the largest negative change (potentially minimizing the loss) to balance out the sum (maximizing totalSum + negativeMax).\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\n/**\n * @param {number[]} nums\n * @param {number} k\n * @param {number[][]} edges\n * @return {number}\n */\nvar maximumValueSum = function (nums, k, edges) {\n let totalSum = 0;\n let count = 0;\n let positiveMin = Infinity;\n let negativeMax = -Infinity;\n\n for (let nodeValue of nums) {\n let nodeValAfterOperation = nodeValue ^ k;\n totalSum += nodeValue;\n let netChange = nodeValAfterOperation - nodeValue;\n\n if (netChange > 0) {\n positiveMin = Math.min(positiveMin, netChange);\n totalSum += netChange;\n count += 1;\n } else {\n negativeMax = Math.max(negativeMax, netChange);\n }\n }\n\n if (count % 2 === 0) {\n return totalSum;\n }\n return Math.max(totalSum - positiveMin, totalSum + negativeMax);\n};\n``` | 1 | 0 | ['JavaScript'] | 0 |
find-the-maximum-sum-of-node-values | Python solution with n in time and 1 in space | python-solution-with-n-in-time-and-1-in-frbd2 | Complexity\n- Time complexity:\nO(n) \n\n- Space complexity:\nO(1)\n\n# Code\n\nclass Solution:\n def maximumValueSum(self, nums, k, edges):\n maxSum = sum( | Rimkomatic | NORMAL | 2024-05-19T10:26:35.223000+00:00 | 2024-05-19T10:26:35.223025+00:00 | 8 | false | # Complexity\n- Time complexity:\n$$O(n)$$ \n\n- Space complexity:\n$$O(1)$$\n\n# Code\n```\nclass Solution:\n def maximumValueSum(self, nums, k, edges):\n maxSum = sum(max(num, num ^ k) for num in nums)\n changedCount = sum((num ^ k) > num for num in nums)\n if changedCount % 2 == 0:\n return maxSum\n minChangeDiff = min(abs(num - (num ^ k)) for num in nums)\n return maxSum - minChangeDiff\n``` | 1 | 0 | ['Python'] | 0 |
find-the-maximum-sum-of-node-values | 💯🔥✅ Simple JS/TS solution | simple-jsts-solution-by-serge15-jnxf | \n\n# Code\n\nfunction maximumValueSum(nums: number[], k: number, edges: number[][]): number {\n const delta = nums.map((n) => (n ^ k) - n).sort((a, b) => b | zavacode | NORMAL | 2024-05-19T10:22:17.041183+00:00 | 2024-05-19T10:22:17.041219+00:00 | 35 | false | \n\n# Code\n```\nfunction maximumValueSum(nums: number[], k: number, edges: number[][]): number {\n const delta = nums.map((n) => (n ^ k) - n).sort((a, b) => b - a)\n\tlet res = nums.reduce((acc, curr) => acc + curr, 0)\n\n\tfor (let i = 0; i < nums.length; i += 2) {\n\t\tif (i === nums.length - 1) break\n\t\t\n const sum = delta[i] + delta[i + 1]\n\n\t\tif (sum > 0) res += sum\n\t}\n\n\treturn res\n};\n``` | 1 | 0 | ['Array', 'Greedy', 'Bit Manipulation', 'Tree', 'Sorting', 'TypeScript', 'JavaScript'] | 0 |
find-the-maximum-sum-of-node-values | Find the Maximum Sum of Node Values | find-the-maximum-sum-of-node-values-by-a-gacn | Intuition\n \n# Approach\n\n# Complexity\n- Time complexity:\n\n- Space complexity:\n\n\n# Code\n\nclass Solution {\npublic:\n long long maximumValueSum(vect | Ayushivts | NORMAL | 2024-05-19T10:07:10.969276+00:00 | 2024-05-19T10:07:10.969299+00:00 | 2 | false | # Intuition\n \n# Approach\n\n# Complexity\n- Time complexity:\n\n- Space complexity:\n\n\n# Code\n```\nclass Solution {\npublic:\n long long maximumValueSum(vector<int>& nums, int k, vector<vector<int>>& edges) {\n long long totalSum = 0;\n int count = 0;\n int positiveMin = INT_MAX;\n int negativeMax = INT_MIN;\n\n for (int nodeValue : nums) {\n int nodeValAfterOperation = nodeValue ^ k;\n totalSum += nodeValue;\n int netChange = nodeValAfterOperation - nodeValue;\n\n if (netChange > 0) {\n positiveMin = min(positiveMin, netChange);\n totalSum += netChange;\n count += 1;\n } else {\n negativeMax = max(negativeMax, netChange);\n }\n }\n\n if (count % 2 == 0) {\n return totalSum;\n }\n return max(totalSum - positiveMin, totalSum + negativeMax); \n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
find-the-maximum-sum-of-node-values | Python easy and best O(N) solution | python-easy-and-best-on-solution-by-mas5-m95k | Intuition\n Describe your first thoughts on how to solve this problem. \nplaying with maximum and minimum\n# Approach\n Describe your approach to solving the pr | MAS5236 | NORMAL | 2024-05-19T09:42:30.816478+00:00 | 2024-05-19T09:42:30.816507+00:00 | 7 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nplaying with maximum and minimum\n# Approach\n<!-- Describe your approach to solving the problem. -->\niterating\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N)\n# Code\n```\nclass Solution:\n \n def maximumValueSum(self, nums: List[int], k: int, edges: List[List[int]]) -> int:\n total = sum(nums)\n \n total_diff = 0\n positive_count = 0\n min_abs_diff = float(\'inf\')\n \n for num in nums:\n diff = (num ^ k) - num\n \n if diff > 0:\n total_diff += diff\n positive_count += 1\n min_abs_diff = min(min_abs_diff, abs(diff))\n \n if positive_count % 2 == 1:\n total_diff -= min_abs_diff\n \n return total + total_diff\n``` | 1 | 0 | ['Python3'] | 0 |
find-the-maximum-sum-of-node-values | C# Simple - THE QUESTION IS MISLEADING, first i got confused we can choose only nodes from edges | c-simple-the-question-is-misleading-firs-m2zm | Seems we can select any pair of nodes\n\n# Code\n\npublic class Solution {\n public long MaximumValueSum(int[] nums, int k, int[][] edges) {\n int len | expected_error | NORMAL | 2024-05-19T08:58:29.359154+00:00 | 2024-05-19T08:58:29.359181+00:00 | 11 | false | Seems we can select any pair of nodes\n\n# Code\n```\npublic class Solution {\n public long MaximumValueSum(int[] nums, int k, int[][] edges) {\n int len=nums.Length;\n int[] delta=new int[len];\n long sum=0;\n for(int i=0;i<len;i++)\n {\n delta[i]=(nums[i]^k)-nums[i];\n sum+=nums[i];\n }\n\n Array.Sort(delta);\n\n for(int i=len-1;i>0;i-=2)\n {\n long s=delta[i]+delta[i-1];\n if(s<=0)\n break;\n \n sum+=s;\n }\n\n return sum;\n }\n}\n``` | 1 | 0 | ['C#'] | 0 |
find-the-maximum-sum-of-node-values | EASIEST PYTHON3 CODE!!! | easiest-python3-code-by-amanshukla07-fhid | Intuition\n Describe your first thoughts on how to solve this problem. \nThe operation Alice performs essentially flips the bits of nums[u] and nums[v] at corre | AmanShukla07 | NORMAL | 2024-05-19T08:56:34.834475+00:00 | 2024-05-19T08:56:34.834503+00:00 | 4 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe operation Alice performs essentially flips the bits of nums[u] and nums[v] at corresponding positions using the XOR (^) operator. This operation has some key properties that help us find the maximum sum:\n\nXOR with itself is zero: a ^ a = 0 for any value a. This means performing the operation on a node twice brings its value back to the original.\nCommutative: a ^ b = b ^ a. The order of nodes chosen for the operation doesn\'t matter.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nIdentify independent groups: Since the tree has no cycles, we can analyze each connected component (subtree) independently. Nodes within a subtree are connected by edges, and the operation can influence each other\'s values.\n\nMaximize value within a group: We want to maximize the sum within each subtree. This can be achieved by ensuring all nodes in a subtree have the same bit value at a specific position (either 0 or 1) through XOR operations.\n\nMultiple bits, independent decisions: Each position in the binary representation of k represents an independent decision. We can analyze each bit of k separately.\n\nCounting nodes with desired bit: For each bit position in k, we need to find the number of nodes in a subtree that would contribute the most to the sum if their bit at that position is set to 0 or 1.\n\nMaximize sum based on bit counts: By comparing the count of nodes with 0 or 1 at a specific bit position, we can determine which configuration (all 0s or all 1s) maximizes the sum within the subtree for that bit position.\n\nCombine maximums for all bits: Finally, we add the maximum contribution from each bit position in k to get the overall maximum sum achievable for the entire tree.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n**O(n)**\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n**O(1)**\n# Code\n```\nclass Solution:\n def maximumValueSum(self, nums: List[int], k: int, edges: List[List[int]]) -> int:\n maxSum = sum(max(num, num ^ k) for num in nums)\n changedCount = sum((num ^ k) > num for num in nums)\n if changedCount % 2 == 0:\n return maxSum\n minChangeDiff = min(abs(num - (num ^ k)) for num in nums)\n return maxSum - minChangeDiff\n \n``` | 1 | 0 | ['Python3'] | 0 |
find-the-maximum-sum-of-node-values | Scala FP: sorting (actually even unnecessary), not using edges | scala-fp-sorting-actually-even-unnecessa-v7d9 | Code\n\nobject Solution {\n def maximumValueSum(nums: Array[Int], k: Int, edges: Array[Array[Int]]): Long = {\n val nProfit = nums.map(n => n -> ((n ^ k) - | SerhiyShaman | NORMAL | 2024-05-19T08:39:20.190437+00:00 | 2024-05-19T08:39:20.190474+00:00 | 8 | false | # Code\n```\nobject Solution {\n def maximumValueSum(nums: Array[Int], k: Int, edges: Array[Array[Int]]): Long = {\n val nProfit = nums.map(n => n -> ((n ^ k) - n)).sortBy(-_._2)\n val evenCount = nProfit.count(_._2 > 0) / 2 * 2\n val xorCount = if (evenCount + 2 <= nums.length && nProfit(evenCount)._2 + nProfit(evenCount + 1)._2 > 0) evenCount + 2 else evenCount\n\n nProfit.indices.foldLeft(0L)((sum, i) => sum + (if (i < xorCount) nProfit(i)._1 ^ k else nProfit(i)._1))\n }\n}\n``` | 1 | 0 | ['Scala'] | 0 |
find-the-maximum-sum-of-node-values | cpp solution | cpp-solution-by-sinchanar2000-lsot | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | sinchanar2000 | NORMAL | 2024-05-19T08:30:38.800023+00:00 | 2024-05-19T08:30:38.800052+00:00 | 29 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n long long maximumValueSum(vector<int>& nums, int k, vector<vector<int>>& edges) {\n long long sum = 0;\n bool odd = false;\n int min_diff = INT_MAX;\n for(int num: nums) {\n int flip = num^k;\n if(flip>num) {\n odd = !odd;\n sum += (num^k);\n min_diff = min(min_diff, flip-num);\n } else {\n sum+=num;\n min_diff = min(min_diff, num-flip);\n }\n }\n if(!odd) return sum;\n else return sum-min_diff;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
find-the-maximum-sum-of-node-values | EASY PYTHON SOLUTION || | easy-python-solution-by-gagansharmadev-am9q | TIME COMPLEXITY - O(nlogn)\nSPACE COMPLEXITY - O(n)\n\nPERFORMING THE XOR OPERATION ON ANY 2 NODES AND FINDING DELTA THE DIFFERENCE BETWEEN ORIGINAL AND NEW NOD | gagansharmadev | NORMAL | 2024-05-19T07:51:17.332056+00:00 | 2024-05-19T07:51:17.332088+00:00 | 30 | false | TIME COMPLEXITY - O(nlogn)\nSPACE COMPLEXITY - O(n)\n\nPERFORMING THE XOR OPERATION ON ANY 2 NODES AND FINDING DELTA THE DIFFERENCE BETWEEN ORIGINAL AND NEW NODE VALUES .\nIF THE DIFFERENCE IS POSITIVE WE ADD IT TO THE TOTAL DEALTA OTHERWISE BREAK IT .\n\n# Code PYTHON\n```\nclass Solution:\n def maximumValueSum(self, nums: List[int], k: int, edges: List[List[int]]) -> int:\n delta = [(n^k)- n for n in nums]\n delta.sort(reverse=True)\n res=sum(nums)\n\n for i in range(0,len(nums),2):\n if i == len(nums)-1:\n break\n total_delta = delta[i]+delta[i+1]\n if total_delta <= 0:\n break\n\n res+=total_delta\n\n return res\n``` | 1 | 0 | ['Python3'] | 0 |
find-the-maximum-sum-of-node-values | Can XOR any two nodes | can-xor-any-two-nodes-by-shynggys-asnx | Intuition\nCan XOR any two nodes\n\n# Approach\nXOR elements in the path = XOR only first and last element in the path. So we don\'t even need edges, and we can | shynggys | NORMAL | 2024-05-19T07:32:39.091743+00:00 | 2024-05-19T07:32:39.091780+00:00 | 8 | false | # Intuition\nCan XOR any two nodes\n\n# Approach\nXOR elements in the path = XOR only first and last element in the path. So we don\'t even need edges, and we can XOR any two nodes in the tree. \n\n\n# Complexity\n- Time complexity: O(n * log(n)), n = number of nodes\n\n- Space complexity: O(n) -> storing XOR values\n\n# Code\n```\nclass Solution:\n def maximumValueSum(self, nums: List[int], k: int, edges: List[List[int]]) -> int:\n for i in range(len(nums)):\n nums[i] = [nums[i], nums[i] ^ k]\n \n nums.sort(key = lambda x: x[1] - x[0], reverse = True)\n\n s = 0\n j = 0\n for i in range(1, len(nums), 2):\n x = nums[i][1] + nums[i - 1][1]\n y = nums[i][0] + nums[i - 1][0]\n s += max(x, y)\n j = i + 1\n\n for i in range(j, len(nums)):\n s += nums[i][0]\n\n return s\n``` | 1 | 0 | ['Python3'] | 1 |
find-the-maximum-sum-of-node-values | Edges Not Required || Greedy Maximise XOR || C++ | edges-not-required-greedy-maximise-xor-c-qmuh | Intuition\n Describe your first thoughts on how to solve this problem. \nAs we can join whichever edges we like, the edges given are not required, as we can jus | traveler1 | NORMAL | 2024-05-19T06:44:51.292346+00:00 | 2024-05-19T06:44:51.292373+00:00 | 86 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nAs we can join whichever edges we like, the edges given are not required, as we can just greedily choose the best values to increase the overall sum.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. The min value of answer can be the sum of the given array, so we store that in the ans variable.\n2. Now we store the xor values of the elements with k in a vector of pairs. Although the 2nd entry (the element iteself) is not necessary, I did that during implementation. We also store the minimum positive difference for further usage.\n3. Then we sort the vector based on the first entry (the difference). For simple implementation, I have sorted the negative differences in the reverse order so that we can extract the least diference (i.e with the max negative value) easily.\n4. We maintain the count of the positive and negative differences.\n5. Since the positive differences are always beneficial, we add them to the ans.\n\n6. In case the count of positive differences is odd:- \n We took one extra and has to remove it\n Case1 : If no negative difference exist - Remove the positive difference with the least value.\n Case2 : Negative difference exists\n SubCase1 : If the least neg diff (in terms of absolute value) is smaller than the min pos diff - Then we include all the pos differences and the least neg diff, as overall it results in a positive value\n SubCase2 : If the least neg diff is larger than the min pos diff, then we cant include the min pos diff value.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n) - n is the size of values array\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n) - For storing the differences\n# Code\n```\nclass Solution {\npublic:\n static bool cmp(pair<int, int>& p1, pair<int, int>& p2) {\n if (p1.first < 0 and p2.first < 0) return p2.first > p1.first;\n return p1 > p2;\n }\n long long maximumValueSum(vector<int>& v, int k,\n vector<vector<int>>& edges) {\n vector<pair<int, int>> xors;\n int mn = INT_MAX;\n for (auto& i : v) {\n xors.push_back({(i ^ k) - i, (i ^ k)});\n if ((i ^ k) - i > 0) mn = min(mn, (i ^ k) - i);\n }\n sort(xors.begin(), xors.end(), cmp);\n long long ans = accumulate(v.begin(), v.end(), 0ll);\n int ct1 = 0, ct2 = 0;\n for (int i = 0; i < v.size(); i++) {\n if ((v[i] ^ k) > v[i])\n ct1++;\n else\n ct2++;\n }\n for (int i = 0; i < xors.size() and xors[i].first > 0; i++)\n ans += xors[i].first;\n if (ct1 & 1) {\n if (ct2 == 0) {\n ans -= mn;\n } \n else {\n if (mn - abs(xors.back().first) >= 0) {\n ans -= (-1 * xors.back().first);\n } \n else {\n ans -= mn;\n }\n }\n }\n return ans;\n }\n \n};\n``` | 1 | 0 | ['Greedy', 'C++'] | 2 |
find-the-maximum-sum-of-node-values | 🔥✅ | 99.78% beats ✅ | ✅ Easy Code | ✅🔥 | 9978-beats-easy-code-by-b_i_t-7cwc | \n# Intuition and Approach\nThe goal of this solution is to maximize the sum of values of nodes in a tree after possibly performing XOR operations with a given | B_I_T | NORMAL | 2024-05-19T06:06:38.810759+00:00 | 2024-05-19T06:07:39.075616+00:00 | 33 | false | 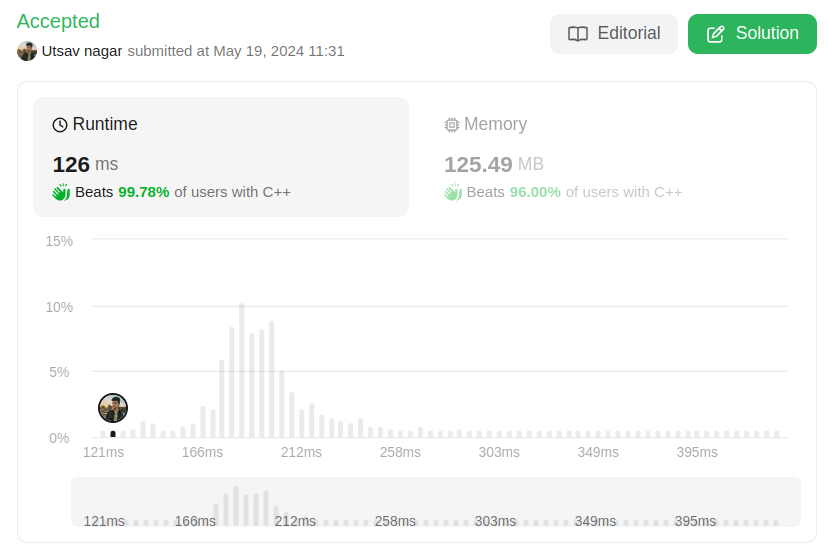\n# Intuition and Approach\nThe goal of this solution is to maximize the sum of values of nodes in a tree after possibly performing XOR operations with a given integer k on the nodes any number of times. Here\'s the intuition and approach behind the code:\n\n# Initial Sum Calculation:\n\n- Iterate through the list of node values (nums).\n- For each node value, calculate its XOR with k (X = num ^ k).\n- If the XOR-ed value (X) is greater than the original value (num), include X in the sum and increase a counter (cnt) to keep track of how many times the XOR operation was beneficial.\n- If the XOR-ed value is not greater, include the original value in the sum.\n# Adjust for Even Count:\n\n- If the number of beneficial XOR operations (cnt) is even, the result is directly the computed sum.\n- If the number of beneficial XOR operations is odd, subtract the smallest difference between the XOR-ed value and the original value (minDiff). This adjustment ensures that the sum is maximized while keeping the beneficial operations count even, which is essential because each XOR operation can be reversed by applying it again.\n# Complexity:\n\n- Time Complexity: O(n), where n is the number of nodes. This is because we iterate through the node values once to compute the sum and the beneficial XOR operations.\n- Space Complexity: O(1), as we use a few additional variables but no extra space that scales with input size.\n# Code\n```C++ []\nclass Solution {\npublic:\n long long maximumValueSum(vector<int>& nums, int k, vector<vector<int>>& edges) {\n ios::sync_with_stdio(false);\n cin.tie(NULL);\n cout.tie(NULL);\n\n long long sum = 0;\n int cnt=0,minDiff = INT_MAX;\n for(const auto & num : nums){\n int X = (num^k);\n if(X > num)\n {\n sum += X;\n cnt++;\n }\n else\n {\n sum += num;\n }\n minDiff = min(minDiff,abs(X-num));\n }\n if(cnt&1){\n return (sum - minDiff);\n }\n return sum;\n }\n};\n```\n```Java []\n\npublic class Solution {\n public long maximumValueSum(int[] nums, int k, List<int[]> edges) {\n long sum = 0;\n int cnt = 0;\n int minDiff = Integer.MAX_VALUE;\n\n for (int num : nums) {\n int X = num ^ k;\n if (X > num) {\n sum += X;\n cnt++;\n } else {\n sum += num;\n }\n minDiff = Math.min(minDiff, Math.abs(X - num));\n }\n\n if ((cnt & 1) == 1) {\n return sum - minDiff;\n }\n return sum;\n }\n}\n\n```\n```Python []\nclass Solution:\n def maximumValueSum(self, nums, k, edges):\n sum = 0\n cnt = 0\n minDiff = float(\'inf\')\n\n for num in nums:\n X = num ^ k\n if X > num:\n sum += X\n cnt += 1\n else:\n sum += num\n minDiff = min(minDiff, abs(X - num))\n\n if cnt % 2 == 1:\n return sum - minDiff\n return sum\n```\n```Javascript []\nclass Solution {\n maximumValueSum(nums, k, edges) {\n let sum = 0;\n let cnt = 0;\n let minDiff = Infinity;\n\n for (const num of nums) {\n const X = num ^ k;\n if (X > num) {\n sum += X;\n cnt++;\n } else {\n sum += num;\n }\n minDiff = Math.min(minDiff, Math.abs(X - num));\n }\n\n if (cnt % 2 === 1) {\n return sum - minDiff;\n }\n return sum;\n }\n}\n```\n\n\n | 1 | 0 | ['Array', 'Greedy', 'Bit Manipulation', 'Tree', 'Python', 'C++', 'Java', 'JavaScript'] | 0 |
find-the-maximum-sum-of-node-values | [Kotlin] Easy solution, time O(n), space O(1) | kotlin-easy-solution-time-on-space-o1-by-otno | Approach\n- Step 1: For any two non-adjacent nodes U and V in the tree we can replace their values with the XOR values\n- Step 2: If the number of netChange is | namanh11611 | NORMAL | 2024-05-19T05:33:12.246861+00:00 | 2024-05-19T05:33:12.246881+00:00 | 8 | false | # Approach\n- Step 1: For any two non-adjacent nodes U and V in the tree we can replace their values with the XOR values\n- Step 2: If the number of netChange is positive is even, we can return current sum\n- Step 3: If the number of netChange is positive is odd, we have to reduce minChange\n\n# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution {\n fun maximumValueSum(nums: IntArray, k: Int, edges: Array<IntArray>): Long {\n var sum = 0L\n var minChange = Int.MAX_VALUE\n var count = 0\n for (num in nums) {\n val xorValue = num xor k\n sum += maxOf(num, xorValue)\n if (xorValue >= num) count++\n minChange = minOf(minChange, abs(xorValue - num))\n }\n return if (count and 1 == 0) sum else sum - minChange\n }\n}\n``` | 1 | 0 | ['Kotlin'] | 1 |
find-the-maximum-sum-of-node-values | Faster⏰||Simpler🧠||Efficient✅ | fastersimplerefficient-by-rexton_george_-05ax | \n# Code\npython3 []\nclass Solution:\n def maximumValueSum(self, nums: List[int], k: int, edges: List[List[int]]) -> int:\n totalSum = 0\n cou | Rexton_George_R | NORMAL | 2024-05-19T05:17:46.808850+00:00 | 2024-05-19T05:17:46.808898+00:00 | 109 | false | \n# Code\n```python3 []\nclass Solution:\n def maximumValueSum(self, nums: List[int], k: int, edges: List[List[int]]) -> int:\n totalSum = 0\n count = 0\n positiveMin = float("inf")\n negativeMax = float("-inf")\n\n for nodeValue in nums:\n nodeValAfterOperation = nodeValue ^ k\n\n totalSum += nodeValue\n netChange = nodeValAfterOperation - nodeValue\n\n if netChange > 0:\n positiveMin = min(positiveMin, netChange)\n totalSum += netChange\n count += 1\n else:\n negativeMax = max(negativeMax, netChange)\n\n if count % 2 == 0:\n return totalSum\n return max(totalSum - positiveMin, totalSum + negativeMax)\n```\n```C++ []\nclass Solution {\npublic:\n long long maximumValueSum(vector<int>& nums, int k,\n vector<vector<int>>& edges) {\n long long totalSum = 0;\n int count = 0;\n int positiveMin = INT_MAX;\n int negativeMax = INT_MIN;\n\n for (int nodeValue : nums) {\n int nodeValAfterOperation = nodeValue ^ k;\n totalSum += nodeValue;\n int netChange = nodeValAfterOperation - nodeValue;\n\n if (netChange > 0) {\n positiveMin = min(positiveMin, netChange);\n totalSum += netChange;\n count += 1;\n } else {\n negativeMax = max(negativeMax, netChange);\n }\n }\n\n if (count % 2 == 0) {\n return totalSum;\n }\n return max(totalSum - positiveMin, totalSum + negativeMax);\n }\n};\n```\n```Java []\nclass Solution {\n public long maximumValueSum(int[] nums, int k, int[][] edges) {\n long totalSum = 0;\n int count = 0;\n int positiveMin = Integer.MAX_VALUE;\n int negativeMax = Integer.MIN_VALUE;\n\n for (int nodeValue : nums) {\n int nodeValAfterOperation = nodeValue ^ k;\n totalSum += nodeValue;\n int netChange = nodeValAfterOperation - nodeValue;\n\n if (netChange > 0) {\n positiveMin = Math.min(positiveMin, netChange);\n totalSum += netChange;\n count += 1;\n } else {\n negativeMax = Math.max(negativeMax, netChange);\n }\n }\n\n if (count % 2 == 0) {\n return totalSum;\n }\n return Math.max(totalSum - positiveMin, totalSum + negativeMax);\n }\n}\n```\n``` JavaScript []\n/**\n * @param {number[]} nums\n * @param {number} k\n * @param {number[][]} edges\n * @return {number}\n */\nvar maximumValueSum = function (nums, k, edges) {\n let totalSum = 0;\n let count = 0;\n let positiveMin = Infinity;\n let negativeMax = -Infinity;\n\n for (let nodeValue of nums) {\n let nodeValAfterOperation = nodeValue ^ k;\n totalSum += nodeValue;\n let netChange = nodeValAfterOperation - nodeValue;\n\n if (netChange > 0) {\n positiveMin = Math.min(positiveMin, netChange);\n totalSum += netChange;\n count += 1;\n } else {\n negativeMax = Math.max(negativeMax, netChange);\n }\n }\n\n if (count % 2 === 0) {\n return totalSum;\n }\n return Math.max(totalSum - positiveMin, totalSum + negativeMax);\n};\n``` | 1 | 0 | ['C++', 'Java', 'Python3', 'JavaScript'] | 1 |
find-the-maximum-sum-of-node-values | ✅ [Beats 100%] Swift. Accepted solution | beats-100-swift-accepted-solution-by-pro-s53o | \n\n# Complexity\n- Time complexity:\nO(nlogn)\n\n- Space complexity:\nO(n)\n\n# Code\n\nclass Solution {\n func maximumValueSum(_ nums: [Int], _ k: Int, _ e | protodimbo | NORMAL | 2024-05-19T05:09:58.898121+00:00 | 2024-05-19T05:09:58.898139+00:00 | 21 | false | ![CleanShot 2024-05-19 at [email protected]](https://assets.leetcode.com/users/images/1dca5358-8508-4cd0-a71e-aec2fa6d7e8d_1716095250.4755497.png)\n\n# Complexity\n- Time complexity:\n$$O(nlogn)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\nclass Solution {\n func maximumValueSum(_ nums: [Int], _ k: Int, _ edges: [[Int]]) -> Int {\n var delta = nums.map { ($0 ^ k) - $0 }\n delta.sort(by: >)\n var res = nums.reduce(0, +)\n for i in stride(from: 0, to: nums.count, by: 2) {\n if i == nums.count - 1 {\n break\n }\n var totalDelta = delta[i] + delta[i + 1]\n if totalDelta <= 0 {\n break\n }\n res += totalDelta\n }\n return res\n }\n}\n``` | 1 | 0 | ['Swift'] | 0 |
find-the-maximum-sum-of-node-values | Can Somebody find Error in Above Code | can-somebody-find-error-in-above-code-by-19zg | Code\n\n// class Solution {\n// public long maximumValueSum(int[] nums, int k, int[][] edges) {\n// int n = nums.length;\n// int[] vis = new | Shree_Govind_Jee | NORMAL | 2024-05-19T04:12:10.351586+00:00 | 2024-05-19T04:12:10.351612+00:00 | 70 | false | # Code\n```\n// class Solution {\n// public long maximumValueSum(int[] nums, int k, int[][] edges) {\n// int n = nums.length;\n// int[] vis = new int[n];\n// for (int i = 0; i < n - 1; i++) {\n// vis[edges[i][0]] = edges[i][0];\n// vis[edges[i][0]] = edges[i][0];\n// }\n\n// List<Integer> list = new ArrayList<>();\n// for (int i = 0; i < n; i++) {\n// long val = (long) Math.pow(nums[i], k);\n// if (val > nums[i]) {\n// list.add(i);\n// }\n// }\n\n// int size = list.size();\n// if (size % 2 == 0) {\n// long ans = 0;\n// for (int i = 0; i < n; i++) {\n// ans += nums[i];\n// }\n// for (int i = 0; i < list.size(); i++) {\n// ans -= nums[list.get(i)];\n// long add = (long) Math.pow(nums[list.get(i)], k);\n// ans += add;\n// }\n// return ans;\n// } else {\n// long ans = 0;\n// for (int i = 0; i < n; i++) {\n// ans += nums[i];\n// }\n\n// long res = ans;\n// for (int i = 0; i < list.size(); i++) {\n// ans -= nums[list.get(i)];\n// long add = (long) (Math.pow(nums[list.get(i)], k));\n// ans += add;\n// }\n// for (int i = 0; i < size; i++) {\n// long add = (long) Math.pow(nums[list.get(i)], k);\n// long cur = ans - add + nums[list.get(i)];\n// res = Math.max(res, cur);\n// }\n\n// int[] temp = new int[n];\n// Arrays.fill(temp, 0);\n// long sum = 0;\n// for (int i = 0; i < size; i++) {\n// temp[list.get(i)] = 1;\n// }\n// for (int i = 0; i < n; i++) {\n// if (temp[i] == 0) {\n// long add = (long) (Math.pow(nums[i], k));\n// long cur = ans - nums[i] + add;\n// res = Math.max(res, cur);\n// }\n// }\n// return res;\n// }\n// }\n// }\n\nclass Solution {\n public long maximumValueSum(int[] nums, int k, int[][] edges) {\n long res = 0;\n int diff = 1 << 30, c = 0;\n for (int num : nums) {\n int b = num ^ k;\n res += Math.max(num, b);\n c ^= num < b ? 1 : 0;\n diff = Math.min(diff, Math.abs(num - b));\n }\n return res - diff * c;\n }\n}\n``` | 1 | 0 | ['Array', 'Dynamic Programming', 'Greedy', 'Bit Manipulation', 'Tree', 'Java'] | 1 |
find-the-maximum-sum-of-node-values | ✅✅understandable solution in java | understandable-solution-in-java-by-manto-d5gn | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | mantosh_kumar04 | NORMAL | 2024-05-19T04:00:44.195781+00:00 | 2024-05-19T04:00:44.195812+00:00 | 6 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public long maximumValueSum(int[] nums, int k, int[][] edges) {\n long[][] memo = new long[nums.length][2];\n for (long[] row : memo) {\n Arrays.fill(row, -1);\n }\n return maxSumOfNodes(0, 1, nums, k, memo);\n }\n\n private long maxSumOfNodes(int index, int isEven, int[] nums, int k,\n long[][] memo) {\n if (index == nums.length) {\n // If the operation is performed on an odd number of elements return\n // INT_MIN\n return isEven == 1 ? 0 : Integer.MIN_VALUE;\n }\n if (memo[index][isEven] != -1) {\n return memo[index][isEven];\n }\n // No operation performed on the element\n long noXorDone = nums[index] + maxSumOfNodes(index + 1, isEven, nums, k, memo);\n // XOR operation is performed on the element\n long xorDone = (nums[index] ^ k) +\n maxSumOfNodes(index + 1, isEven ^ 1, nums, k, memo);\n\n // Memoize and return the result\n return memo[index][isEven] = Math.max(xorDone, noXorDone);\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
find-the-maximum-sum-of-node-values | python, ruby 1-liners | python-ruby-1-liners-by-_-k-03k1 | ruby\n\ndef maximum_value_sum(a, k, edges) =\n\n a.sum{ [k^_1,_1].max } - a.count{ k^_1>_1 }%2 * a.map{ (_1.-_1^k).abs }.min\n\n\npython\n\nclass Solution:\n | _-k- | NORMAL | 2024-05-19T03:49:04.623162+00:00 | 2024-05-19T05:03:01.534712+00:00 | 52 | false | ruby\n```\ndef maximum_value_sum(a, k, edges) =\n\n a.sum{ [k^_1,_1].max } - a.count{ k^_1>_1 }%2 * a.map{ (_1.-_1^k).abs }.min\n```\n\npython\n```\nclass Solution:\n def maximumValueSum(self, a, k, edges):\n\n return sum( max(x,x^k) for x in a ) - sum( x^k>x for x in a )%2 * min( abs(x-(x^k)) for x in a )\n``` | 1 | 0 | ['Python', 'Python3', 'Ruby'] | 1 |
find-the-maximum-sum-of-node-values | ✅ Easy C++ Solution | easy-c-solution-by-moheat-5m6q | Code\n\nclass Solution {\npublic:\n long long maximumValueSum(vector<int>& v, int k, vector<vector<int>>& edges) {\n long long total = accumulate(v.be | moheat | NORMAL | 2024-05-19T03:47:32.775376+00:00 | 2024-05-19T03:47:32.775400+00:00 | 198 | false | # Code\n```\nclass Solution {\npublic:\n long long maximumValueSum(vector<int>& v, int k, vector<vector<int>>& edges) {\n long long total = accumulate(v.begin(), v.end(), 0ll);\n \n long long totalDiff = 0;\n long long diff;\n int positiveCount = 0;\n long long minDiff = numeric_limits<int>::max();\n for(auto p : v)\n {\n diff = (p^k) - p;\n \n if(diff > 0)\n {\n totalDiff += diff;\n positiveCount++;\n }\n minDiff = min(minDiff, abs(diff));\n }\n if(positiveCount % 2 == 1)\n {\n totalDiff = totalDiff - minDiff;\n }\n return total + totalDiff;\n }\n};\n``` | 1 | 0 | ['C++'] | 1 |
find-the-maximum-sum-of-node-values | Simple C Solution | simple-c-solution-by-anshadk-v50j | Complexity\n- Time complexity: O(n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(n)\n Add your space complexity here, e.g. O(n) \n\n# Co | anshadk | NORMAL | 2024-05-19T03:10:52.645994+00:00 | 2024-05-19T03:10:52.646016+00:00 | 32 | false | # Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\ntypedef struct {\n long long first;\n long long second;\n} pair;\n\nlong long maximumValueSum(int* nums, int n, int k, int** edges, int edgesSize, int* edgesColSize) {\n pair *dp = calloc(n + 1, sizeof(pair));\n dp[n].first = 0;\n dp[n].second = INT_MIN;\n for(int i = n - 1; i >= 0; i--) {\n dp[i].first = fmax(\n dp[i + 1].second + (nums[i] ^ k),\n dp[i + 1].first + nums[i]\n );\n dp[i].second = fmax(\n dp[i + 1].first + (nums[i] ^ k),\n dp[i + 1].second + nums[i]\n );\n }\n return dp[0].first;\n}\n``` | 1 | 0 | ['C'] | 0 |
find-the-maximum-sum-of-node-values | Pick (or) Not-Pick || Damn Easy Solution | pick-or-not-pick-damn-easy-solution-by-j-kj96 | Approach\n\n- DFS\n- flag_index is the state of the current node.\n- If the current_index is picked then the flag_index is flipped to indicate the change of sta | Jagadish_Shankar | NORMAL | 2024-05-19T02:43:03.382869+00:00 | 2024-05-19T02:43:55.128237+00:00 | 131 | false | # Approach\n\n- DFS\n- ```flag_index``` is the state of the current node.\n- If the ```current_index``` is picked then the ```flag_index``` is flipped to indicate the change of state of the node.\n\n# Complexity\n\n- Time complexity : $$O(N)$$\n\n- Space complexity : $$O(H)$$\n\n# Code\n\n```\nclass Solution {\n\n public long depth_first_search(int K , int flag_index , int current_index , int N , int[] array , Long[][] dp_matrix){\n\n if(current_index >= N){\n return ((flag_index == 0) ? (0) : (Integer.MIN_VALUE));\n }\n\n if(dp_matrix[current_index][flag_index] != null){\n return dp_matrix[current_index][flag_index];\n }\n\n long pick = ((array[current_index] ^ K) + depth_first_search(K , ((flag_index + 1) % 2) , (current_index + 1) , N , array , dp_matrix));\n\n long not_pick = (array[current_index] + depth_first_search(K , flag_index , (current_index + 1) , N , array , dp_matrix));\n\n dp_matrix[current_index][flag_index] = Math.max(pick , not_pick);\n\n return dp_matrix[current_index][flag_index];\n }\n\n public long maximumValueSum(int[] array , int K , int[][] edges_details_matrix){\n \n int N = array.length;\n\n return depth_first_search(K , 0 , 0 , N , array , (new Long[N][2]));\n }\n}\n``` | 1 | 0 | ['Dynamic Programming', 'Depth-First Search', 'Recursion', 'Memoization', 'Java'] | 1 |
find-the-maximum-sum-of-node-values | rust simplest solution with explain | rust-simplest-solution-with-explain-by-s-zf44 | Intuition\nWhy I need edges? If you want to flip a and b, you can always find a path from a to b, and file all the path twice.\n\nSo you can filp as many time y | sovlynn | NORMAL | 2024-05-19T02:21:43.481069+00:00 | 2024-05-19T02:21:43.481121+00:00 | 82 | false | # Intuition\nWhy I need edges? If you want to flip a and b, you can always find a path from a to b, and file all the path twice.\n\nSo you can filp as many time you want, just make sure the total flip time is even.\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(1)$$\n\n# Code\n```\nimpl Solution {\n pub fn maximum_value_sum(nums: Vec<i32>, k: i32, edges: Vec<Vec<i32>>) -> i64 {\n let k = k as i64;\n let mut res=0;\n let mut sac=std::i64::MAX;\n let mut count=0;\n for &i in &nums{\n let i = i as i64;\n let fi=i^k;\n if fi>i{\n res+=fi;\n count+=1;\n sac=std::cmp::min(sac, fi-i);\n }else{\n res+=i;\n sac=std::cmp::min(sac, i-fi);\n }\n }\n if count%2==1{\n res-sac\n }else{\n res\n }\n }\n}\n``` | 1 | 0 | ['Rust'] | 0 |
find-the-maximum-sum-of-node-values | JS | Clean Code (RunTime Beats 100% | Memory Beats 100%) | js-clean-code-runtime-beats-100-memory-b-f5xj | \n\n# Code\n\n/**\n * @param {number[]} nums\n * @param {number} k\n * @param {number[][]} edges\n * @return {number}\n */\nvar maximumValueSum = function (nums | nanlyn | NORMAL | 2024-05-19T01:48:12.484104+00:00 | 2024-05-19T01:48:12.484170+00:00 | 21 | false | 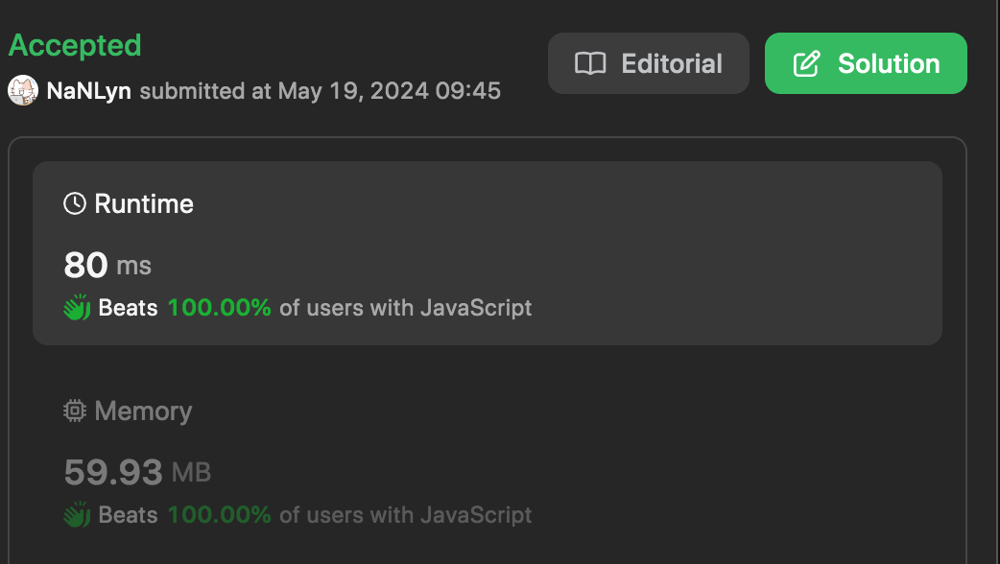\n\n# Code\n```\n/**\n * @param {number[]} nums\n * @param {number} k\n * @param {number[][]} edges\n * @return {number}\n */\nvar maximumValueSum = function (nums, k, edges) {\n let count = 0;\n let sum = 0;\n let minDiff = Infinity;\n for (let num of nums) {\n let xorNum = (num ^ k);\n if (xorNum > num) {\n count++;\n }\n sum += Math.max(xorNum, num);\n minDiff = Math.min(Math.abs(xorNum - num), minDiff);\n }\n\n if (count % 2 === 1) sum -= minDiff;\n\n return sum;\n};\n``` | 1 | 0 | ['JavaScript'] | 0 |
find-the-maximum-sum-of-node-values | 🔥 Go Beat 100% || O(n) / O(1) || With explanation 🔥 | go-beat-100-on-o1-with-explanation-by-co-tiev | Intuition\n1. XORing a number twice with k leaves it unchanged.\uFF08a XOR k XOR k = a\uFF09\n2. For a path from node a to node b in a tree, if each edge on the | ConstantineJin | NORMAL | 2024-05-19T01:43:11.172831+00:00 | 2024-05-19T01:43:11.172859+00:00 | 30 | false | # Intuition\n1. XORing a number twice with `k` leaves it unchanged.\uFF08a XOR k XOR k = a\uFF09\n2. For a path from node `a` to node `b` in a tree, if each edge on the path is XORed, then all nodes on the path except `a` and `b` undergo an even number of XOR operations, keeping their values unchanged. Hence, the problem is equivalent to XORing `k` simultaneously to any two nodes, eliminating the need for constructing a tree.\n3. There are always an even number of elements XORed with k.\nTherefore, the problem transforms into: select an even number of elements from nums to XOR with k, maximizing the sum of all elements in nums.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nDefine `f[i][0]` as the maximum sum of elements obtained by XORing `k` with an even number of elements chosen from the first `i` numbers in `nums`, while `f[i][1]` as the maximum sum of elements obtained by XORing `k` with an odd number of elements chosen from the first `i` numbers in `nums`.\nTherefore, we have the following transition equations: \n$$f[i][0] = \\max(f[i-1][0]+nums[i-1], f[i-1][1] + nums[i-1] \u2295 k) $$\n$$f[i][1] = \\max(f[i-1][0]+nums[i-1], f[i-1][0] + nums[i-1] \u2295 k) $$\nAlso we can optimize the space complexity from $O(n)$ to $O(1)$ by using only two variables to store the maximum sum of elements.\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfunc maximumValueSum(nums []int, k int, edges [][]int) int64 {\n\tf0, f1 := 0, math.MinInt\n\tfor _, num := range nums {\n\t\tf0, f1 = max(f0+num, f1+(num^k)), max(f1+num, f0+(num^k))\n\t}\n\treturn int64(f0)\n}\n``` | 1 | 0 | ['Dynamic Programming', 'Go'] | 0 |
find-the-maximum-sum-of-node-values | Fastest Solution | fastest-solution-by-deleted_user-dhan | Code\n\n// sample 116 ms submission\nstatic auto speedup = []() { std::ios_base::sync_with_stdio(false); std::cout.tie(nullptr); std::cin.tie(nullptr); return N | deleted_user | NORMAL | 2024-05-19T01:35:27.149139+00:00 | 2024-05-19T01:35:27.149156+00:00 | 17 | false | # Code\n```\n// sample 116 ms submission\nstatic auto speedup = []() { std::ios_base::sync_with_stdio(false); std::cout.tie(nullptr); std::cin.tie(nullptr); return NULL; }();\nclass Solution\n{\npublic:\n long long maximumValueSum(vector<int> &nums, int k, vector<vector<int>> &edges)\n {\n long long cnt = 0;\n long long res = 0;\n long long minn = INT_MAX;\n long long maxx = INT_MAX;\n\n for(long long i : nums)\n {\n long long x = i;\n long long y = i ^ k;\n\n if(x > y)\n {\n res += x;\n maxx = min(maxx, x);\n }\n else\n {\n res += y;\n ++cnt;\n }\n\n minn = min(minn, abs(x - y));\n }\n\n if(cnt & 1)\n {\n res -= minn;\n }\n\n return res;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
find-the-maximum-sum-of-node-values | 💯Beats💯Python✅Java✅C++✅Step-By-Step🔥Clean code w/ Explanation⚡️ | beatspythonjavacstep-by-stepclean-code-w-u534 | Step 1: Possibilities For Each Node \uD83D\uDE2E\n\n- Each node can either be nums[i] or nums[i]^k\n- This is because nums[i]^k^k = nums[i] \uD83D\uDCDD\n\n# St | CutSandstone | NORMAL | 2024-05-19T01:31:24.876260+00:00 | 2024-05-19T01:31:24.876286+00:00 | 15 | false | # Step 1: Possibilities For Each Node \uD83D\uDE2E\n\n- Each node can either be ```nums[i]``` or ```nums[i]^k```\n- This is because ```nums[i]^k^k = nums[i]``` \uD83D\uDCDD\n\n# Step 2: Removing The Tree \uD83C\uDF32\n\n- By definition of a tree, there exists a path \uD83C\uDFDE between any 2 nodes\n- If we apply the operation on every edge on a path between 2 nodes, only the start and end nodes will be changed \uD83D\uDD00 (Write some examples)\n- This means that we can take any 2 nodes ```nums[i]``` and ```nums[j]``` and set them both to ```nums[i]^k``` and ```nums[j]^k```, regardless of the edges \u274C\n\n# Step 3: Picking pairs \u26CF\uFE0F\n\n- If we can xor any 2 nodes by ```k``` multiple times, we can xor any even number of nodes by ```k``` \uD83E\uDD14\n- Lets try to pick every node where ```nums[i]^k > nums[i]```, meaning that our sum increases by picking that node \uD83E\uDDE0\n- If there are an even number of nodes like that, we just pick all of them \uD83E\uDD2F\n- Otherwise, we have to choose between not picking a node that we have picked, or picking another node\n\n# Step 4: Code explanation\n\n- Let ```sum``` be the sum of all ```nums[i]``` \u2795\n- Let ```add[i]``` be ```nums[i]^k - nums[i]```\n- If ```add[i]``` is positive, ```nums[i]^k > nums[i]```\n- Let ```sum``` be our baseline answer, and lets try to take as many positive ```add[i]``` as we can\n- Let\'s also keep track of the minimum positive number in ```add```, and the maximum negative number \u261D\uFE0F\n- These numbers are useful when we are deciding whether to remove a node or add the node if the number of nodes we pick is odd\n\n# Complexity\n- Time complexity: $$O(n)$$\u26A1\uFE0F\u26A1\uFE0F\n- Space complexity: $$O(n)$$\u26A1\uFE0F\u26A1\uFE0F\n\n# \uD83E\uDDD1\u200D\uD83D\uDCBB\uFE0F\n``` Python []\nclass Solution:\n def maximumValueSum(self, nums: List[int], k: int, edges: List[List[int]]) -> int:\n sum = 0\n add = [0]*len(nums)\n for i in range(len(nums)):\n sum+=nums[i]\n xor = nums[i]^k\n add[i] = xor-nums[i]\n minPos = 1e20\n maxNeg = -1e20\n posCount = 0\n posSum = 0\n for i in add:\n if i>0:\n minPos = min(minPos,i)\n posSum+=i\n posCount+=1\n else:\n maxNeg = max(maxNeg,i)\n if posCount%2 == 0:\n return posSum+sum\n else:\n removePos = posSum-minPos+sum\n addNeg = posSum+maxNeg+sum\n return max(removePos,addNeg)\n```\n``` C++ []\nclass Solution {\npublic:\n long long maximumValueSum(vector<int>& nums, int k, vector<vector<int>>& edges) {\n long long sum = 0;\n vector<int> add(nums.size());\n for(int i = 0; i<nums.size(); i++){\n sum+=nums[i];\n int xorVal = nums[i]^k;\n add[i] = xorVal-nums[i];\n }\n int minPos = INT_MAX, maxNeg = INT_MIN;\n int posCount = 0;\n long long posSum = 0;\n for(int i: add){\n if(i>0){\n minPos = min(minPos,i);\n posSum+=i;\n posCount++;\n }else{\n maxNeg = max(maxNeg,i);\n }\n }\n if(posCount%2 == 0){\n return posSum+sum;\n }else{\n long long removePos = posSum-minPos+sum;\n long long addNeg = posSum+maxNeg+sum;\n return max(removePos,addNeg);\n }\n }\n};\n```\n``` Java []\nclass Solution {\n public long maximumValueSum(int[] nums, int k, int[][] edges) {\n long sum = 0;\n int[] add = new int[nums.length];\n for(int i = 0; i<nums.length; i++){\n sum+=nums[i];\n int xor = nums[i]^k;\n add[i] = xor-nums[i];\n }\n int minPos = Integer.MAX_VALUE, maxNeg = Integer.MIN_VALUE;\n int posCount = 0;\n long posSum = 0;\n for(int i: add){\n if(i>0){\n minPos = Math.min(minPos,i);\n posSum+=i;\n posCount++;\n }else{\n maxNeg = Math.max(maxNeg,i);\n }\n }\n if(posCount%2 == 0){\n return posSum+sum;\n }else{\n long removePos = posSum-minPos+sum;\n long addNeg = posSum+maxNeg+sum;\n return Math.max(removePos,addNeg);\n }\n }\n}\n``` | 1 | 0 | ['Bit Manipulation', 'C++', 'Java', 'Python3'] | 0 |
find-the-maximum-sum-of-node-values | scala solution | scala-solution-by-lyk4411-2oid | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | lyk4411 | NORMAL | 2024-05-19T01:06:43.149418+00:00 | 2024-05-19T01:06:43.149446+00:00 | 20 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nobject Solution {\n def maximumValueSum(nums: Array[Int], k: Int, edges: Array[Array[Int]]): Long = {\n val res = nums.foldLeft(0L, Integer.MAX_VALUE, 0)((acc, num) => {\n val temp = num ^ k\n (acc._1 + Math.max(num, temp), acc._2.min(Math.abs(num - temp)), acc._3 ^ (if((num < temp)) 1 else 0))\n })\n res._1 - res._2 * res._3\n }\n}\n``` | 1 | 0 | ['Scala'] | 0 |
find-the-maximum-sum-of-node-values | Count Number of Changed Nodes || C++, C, Python, Java | count-number-of-changed-nodes-c-c-python-fzjh | Approach\n Describe your approach to solving the problem. \nSince the graph we\'re given is connected, undirected and acyclic, there is a path between any two n | not_yl3 | NORMAL | 2024-05-19T00:37:02.932890+00:00 | 2024-05-19T02:25:42.826096+00:00 | 222 | false | # Approach\n<!-- Describe your approach to solving the problem. -->\nSince the graph we\'re given is connected, undirected and acyclic, there is a path between any two nodes in the graph. Moreover, because of the properties of the XOR operation, any nodes in the path between node `u` and node `v` will remain the same since `x XOR x = x`. Thus we can treat each node independently and disregard the `edges`. \n\nTherefore, we can solve this by maintaining a `sum` where we would add the `max(nums[i] ^ k, nums[i])` in each iteration of a loop. However, another since in each operation we need to change an even number of nodes, we need to make sure that the number of nodes we change (to its higher XOR value) is even. We can do this by using `count` to sum the number of times we do an operation. Lastly, we will also use `minDiff` to keep track of the minimum absolute change between a node and its XOR value so that if we need to change a node in the end because of `count` being odd, then we can make the minimum change necessary.\n\nIn the end return `sum` and subtract `minDiff` from it if `count` is odd, which will represent changing a node back to its original value to balance out the number of operations.\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```C++ []\nclass Solution {\npublic:\n long long maximumValueSum(vector<int>& nums, int k, vector<vector<int>>& edges) {\n long long sum = 0, count = 0, minDiff = INT_MAX;\n for (long long num : nums){\n sum += max(num ^ k, num);\n count += (num ^ k) > num;\n minDiff = min(minDiff, abs(num - (num ^ k)));\n }\n return sum - (count % 2 ? minDiff : 0);\n }\n};\n```\n```C []\nlong long maximumValueSum(int* nums, int numsSize, int k, int** edges, int edgesSize, int* edgesColSize) {\n long long res = 0, count = 0, minDiff = 1 << 30;\n for (int i = 0; i < numsSize; i++){\n int curr = nums[i] ^ k;\n res += (curr > nums[i]) ? curr : nums[i];\n count += (curr > nums[i]);\n minDiff = (minDiff < abs(nums[i] - curr)) ? minDiff : abs(nums[i] - curr);\n }\n return res - (count % 2 ? minDiff : 0);\n}\n```\n```python3 []\nclass Solution:\n def maximumValueSum(self, nums: List[int], k: int, edges: List[List[int]]) -> int:\n sum, count, minDiff = 0, 0, float(\'inf\')\n for num in nums:\n sum += max(num ^ k, num)\n count += (num ^ k > num)\n minDiff = min(minDiff, abs(num - (num ^ k)))\n return sum - (minDiff if count % 2 else 0)\n```\n```Java []\nclass Solution {\n public long maximumValueSum(int[] nums, int k, int[][] edges) {\n long sum = 0, count = 0, minDiff = Integer.MAX_VALUE;\n for (long num : nums){\n sum += Math.max(num ^ k, num);\n count += ((num ^ k) > num) ? 1 : 0;\n minDiff = Math.min(minDiff, Math.abs(num - (num ^ k)));\n }\n return sum - (count % 2 == 1 ? minDiff : 0);\n }\n}\n```\n | 1 | 0 | ['Array', 'Dynamic Programming', 'Greedy', 'Tree', 'C', 'Sorting', 'Python', 'C++', 'Java', 'Python3'] | 1 |
find-the-maximum-sum-of-node-values | Java Solution NO DFS | java-solution-no-dfs-by-shaurya_malhan-zwm4 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Shaurya_Malhan | NORMAL | 2024-03-07T06:56:19.193713+00:00 | 2024-03-07T06:56:19.193745+00:00 | 75 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public long maximumValueSum(int[] nums, int k, int[][] edges) {\n int n = nums.length;\n int count = 0;\n int max = Integer.MAX_VALUE;\n int min = Integer.MAX_VALUE;\n long ans = 0;\n for(int i = 0; i < n; i++){\n if((nums[i] ^ k) > nums[i]){\n max = Math.min(max, (nums[i] ^ k) - nums[i]);\n ans += (nums[i] ^ k);\n count++;\n }else{\n min = Math.min(min, nums[i] - (nums[i] ^ k));\n ans += nums[i];\n }\n }\n if(count % 2 != 0){\n ans -= Math.min(max, min);\n }\n return ans;\n }\n}\n``` | 1 | 0 | ['Java'] | 1 |
find-the-maximum-sum-of-node-values | Just a runnable solution | just-a-runnable-solution-by-ssrlive-7p5f | \n\nimpl Solution {\n pub fn maximum_value_sum(nums: Vec<i32>, k: i32, _edges: Vec<Vec<i32>>) -> i64 {\n let nums: Vec<i64> = nums.iter().map(|&x| x a | ssrlive | NORMAL | 2024-03-05T10:20:39.471518+00:00 | 2024-05-20T00:53:46.842548+00:00 | 51 | false | \n```\nimpl Solution {\n pub fn maximum_value_sum(nums: Vec<i32>, k: i32, _edges: Vec<Vec<i32>>) -> i64 {\n let nums: Vec<i64> = nums.iter().map(|&x| x as i64).collect();\n let k = k as i64;\n let mut sum = 0;\n let mut cnt = 0;\n let mut sacrifice = i64::MAX;\n for &n in nums.iter() {\n let tmp = n ^ k;\n sum += tmp.max(n);\n cnt += if tmp > n { 1 } else { 0 };\n sacrifice = sacrifice.min((n - tmp).abs());\n }\n sum - if cnt % 2 == 1 { sacrifice } else { 0 }\n }\n}\n\n``` | 1 | 0 | ['Rust'] | 1 |
find-the-maximum-sum-of-node-values | Best c++ solution || Beats 100%🎯 | best-c-solution-beats-100-by-lovy4200-v1nf | Intuition\n Describe your first thoughts on how to solve this problem. XORing an even number of times by the same element results in the original number. \na ^ | lovy4200 | NORMAL | 2024-03-04T05:51:51.004219+00:00 | 2024-03-04T09:18:45.103416+00:00 | 104 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->XORing an even number of times by the same element results in the original number. \na ^ b ^ b = a --> The important property of XOR.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. For each element in the given array, store both the original value and the XOR-ed value with k in variables x and y respectively.\n\n2. Determine which value between x and y is greater and add it to the sum.\n\n3. If the XOR-ed value is greater, increment the counter cnt, which keeps track of the number of changes made.\n\n4. Calculate the sacrifice element, sac, by taking the minimum of the absolute difference between x and y.\n\n5. If the number of changes (cnt) is odd, remove the sacrifice (sac) from the sum and return the result.\n\n\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->O(N)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->O(1)\n\n# Code\n```\n#include<bits/stdc++.h>\n#include <algorithm>\nusing namespace std;\n\nclass Solution {\npublic:\n long long maximumValueSum(vector<int>& nums, int k, vector<vector<int>>& edges) {\n int n = nums.size();\n int cnt=0;\n long long sac=INT_MAX,sum=0;\n for(auto it:nums)\n {\n int x= it;\n int y=it^k;\n if(x>y)\n {\n sum+=x;\n }\n else\n {\n sum+=y;\n cnt++;\n }\n sac=min(sac,static_cast<long long> (abs(x-y)));\n \n }if(cnt%2==1)\n sum-=sac;\n return sum;\n }\n};\n\n``` | 1 | 0 | ['C++'] | 3 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.