question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
find-the-maximum-sum-of-node-values | Simple solution with linear time complexity and constant extra space complexity | simple-solution-with-linear-time-complex-zwgf | Intuition\n\nFirst of, let\'s think about situation when the operation was applied two time for the same edge, or in particular, to the same vertex. As of verte | pioneer10 | NORMAL | 2024-03-02T21:48:06.546809+00:00 | 2024-03-02T21:48:06.546830+00:00 | 79 | false | # Intuition\n\nFirst of, let\'s think about situation when the operation was applied two time for the same edge, or in particular, to the same vertex. As of vertex, the second operation reverts the first one since `(nums[u] XOR k) XOR k == nums[u]`. Two conclusions out of this:\n\n1. we may consider at most one operation on particular edge without losing commonality\n2. the order of operations doesn\'t matter, and the value of specific vertex is determined by parity of the number of edges from that vertex for which we applied operation.\n\nIn other words, each number in `nums` would either stay the same, or be `XOR`ed.\n\nThen, let\'s figure out which subsets of `nums` could be `XOR`ed. Obviously, subset should contain even number of elements.\n\nCan any pair of elements be `XOR`ed (while the rest are the same)?\nYes, for any pair `(u, v)` there is path `u -> u_1 -> ... -> u_m -> v`. After applying operations to every edge on this path the value of `u` and `v` would be `XOR`ed, while the value of every `u_i` would be the same (formally, for every `u_i` there is exactly two operations, so the value would be the same).\n\nOk, any pair could be `XOR`ed. Can any subset consisting of even number of elements be `XOR`ed (while the rest are the same)? Well, yes. We just split such subset into pairs (we can do it since subset contains even number of elements) and then do the steps described above. NB: it doesn\'t matter whether these paths are crossing, share some edges, or even if one path is subpath of another. this is because for every intermediate vertex the operation is applied two times, so it doesn\'t change its value.\n\n# Approach\n\nAs explained above, we need to consider all subsets consisting of even elements, apply `XOR k` to every element, and find maximum sum of elements.\n\nLet\'s use dynamic programming for such purposes.\n\nSo, we need to remember just two numbers:\n\n1. `a` \u2014 maximum sum of elements if even number of elements were `XOR`ed\n2. `b` \u2014 maximum sum of elements if odd number of elements were `XOR`ed\n\nInitially, `a = nums[0]` and `b = nums[0] XOR k`. Then, we add `nums[1]`, `nums[2]`, etc.\n\nEvery step the new number is either stays the same, or is `XOR`ed.\n\n- `new_a = max(a + num, b + num XOR k)`\n- `new_b = max(a + num XOR k, b + num)`\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(1)$$\n\n# Code\n```\nfunc maximumValueSum(nums []int, k int, edges [][]int) int64 {\n a, b := int64(nums[0]), int64(nums[0] ^ k)\n for _, num := range nums[1:] {\n a, b = max(a + int64(num), b + int64(num ^ k)), max(a + int64(num ^ k), b + int64(num))\n }\n return a\n}\n\nfunc max(a, b int64) int64 {\n if b > a {\n return b\n }\n return a\n}\n``` | 1 | 0 | ['Dynamic Programming', 'Go'] | 2 |
find-the-maximum-sum-of-node-values | Easiest logical implementation | without DP or Tree | easiest-logical-implementation-without-d-g1a1 | Intuition\nWe have to find the max sum we can achieve by doing xor of element and k.\n# Approach\n- Lets update each element whose value increases after xor wit | DikshaMakkar | NORMAL | 2024-03-02T19:14:51.224130+00:00 | 2024-03-02T19:14:51.224155+00:00 | 40 | false | # Intuition\nWe have to find the max sum we can achieve by doing xor of element and k.\n# Approach\n- Lets update each element whose value increases after xor with k.\n- Also track the count of number of elements updated with xor -- cnt variable.\n- The problem says that we have to take two nodes which are connected(elements given in nums) and then xor them. \n- So, for the case where xor is not done in pair means if cnt is odd(cnt&1) -- check the parity bit, we have to go through the updated nums array and find the element which was update by least value and then subract it from the sum.\n\nProblem Solved!\n\n# Complexity\n- Time complexity: O(N)\n\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution {\npublic:\n #define ll long long\n long long maximumValueSum(vector<int>& nums, int k, vector<vector<int>>& edges) {\n ll sum=0,cnt=0;\n for(auto &i:nums){\n if((i^k)>i) cnt++,i^=k;\n sum+=i;\n }\n if(cnt&1){\n int mn=1e9;\n for(auto i:nums) mn=min(mn,i-(i^k));\n sum-=mn;\n }\n return sum;\n }\n};\n``` | 1 | 0 | ['C++'] | 1 |
find-the-maximum-sum-of-node-values | Greedy approach | greedy-approach-by-aman_g011-q44n | \n\n# Code\n\n#define ll long long\nclass Solution {\npublic:\n long long maximumValueSum(vector<int>& nums, int k, vector<vector<int>>& edges) {\n ll | Aman_G011 | NORMAL | 2024-03-02T18:53:51.956612+00:00 | 2024-03-02T18:53:51.956640+00:00 | 18 | false | \n\n# Code\n```\n#define ll long long\nclass Solution {\npublic:\n long long maximumValueSum(vector<int>& nums, int k, vector<vector<int>>& edges) {\n ll n = nums.size();\n vector<int> g, l;\n for(int i = 0 ; i < n ; i++){\n int x = (nums[i] ^ k);\n if(x > nums[i]){\n g.push_back(x-nums[i]);\n }\n else{\n l.push_back(nums[i]-x);\n }\n }\n if(g.size() % 2 == 0){\n ll ans = 0;\n for(auto it : nums) ans += it;\n for(auto it : g) ans += it;\n return ans;\n }\n sort(g.begin(), g.end());\n sort(l.begin(), l.end());\n ll ans = 0;\n for(auto it : nums) ans += it;\n for(auto it : g) ans += it;\n ans -= g[0];\n ll ans2 = ans;\n if(l.size() > 0){\n ans2 = ans + g[0] - l[0];\n }\n return max(ans, ans2);\n }\n};\n``` | 1 | 0 | ['C++'] | 1 |
find-the-maximum-sum-of-node-values | Python, O(n), no edges needed, with intuition | python-on-no-edges-needed-with-intuition-rga1 | Intuition\nWe could think of our problem in next way: for each node we can take either nums[i] or nums[i]^k into the sum. We can think of node as being in even | raggzy | NORMAL | 2024-03-02T18:38:41.731036+00:00 | 2024-03-02T19:00:22.059403+00:00 | 194 | false | # Intuition\nWe could think of our problem in next way: for each node we can take either `nums[i]` or `nums[i]^k` into the sum. We can think of node as being in `even` and `odd` (modified) states. That is some `2**n` combinations. However some combinations are invalid. \n\nWe can prove, that required and sufficient condition for a combination to be valid is next:\nAmout of `nums[i]^k` is *even*. \nMore formally - combination will be valid iff amount of `odd` nodes is *even*. \n\nRequired part: is obvious by nature of operation. Since we always change one edge (2 nodes), we always flip the state of two nodes, so \nparity of `odd` nodes is invariant (and intially it\'s even). \n\nSufficient part: since we have a tree, by definition there is always a path between *ANY* `i` and `j` nodes. So we can always revert *ANY* `i` and `j` (not only neighbors) by just applying operation along each edge of a path `i->n1->n2->...->nk->j`. All nodes in between (`n1,...,nk`) will be get touched twice (left in the same state since `(x^k)^k==x`), and `i` and `j` will get touched once (both flip it\'s states). So as long as amount of `odd` nodes is even (we could form pairs) - we can flip them and reach initial state. Which proves any such state can be reached from initial state.\n\n**That drives us to conclusion - we don\'t care about the edges structure at all.**\n\nSo, we just need to find `max sum` over all `even` combinations (subsets). `Odd` subset is a subset that has odd amount of odd nodes, `even` subset - even amount of `odd` nodes (or odd amount of `1`s in it\'s binary representation if thinking `1==odd`, `0==even`).\n\nThat is kind of classical DP problem.\n\n\n# Approach\nDriven by intuition, instead of DP array we just use two variables (`so`,`se`) which hold maximum sums at current step for `odd` and `even` subsets.\n- at each step we take `odd` and `even` element (`o`, `e`) and update sums accordingly, picking best option.\n- we can get `odd` sum by adding `odd` elemen to `even` sum or adding `even` element to `odd` sum.\n- we can get `even` sum by adding `even` element to `even` sum or adding `odd` element to `odd` sum.\n- initially we can\'t have `odd` sum, and `even` sum is `0`.\n\n# Complexity\n- Time complexity: `O(n)`\n- Space complexity: `O(1)`\n\n# Code\n```\nclass Solution:\n def maximumValueSum(self, nums: List[int], k: int, edges: List[List[int]]) -> int:\n so,se=float(\'-inf\'),0\n for n in nums:\n o,e=n^k,n\n so,se=max(so+e,se+o),max(so+o,se+e)\n return se\n```\n1-liner\n```\nclass Solution:\n def maximumValueSum(self, nums: List[int], k: int, edges: List[List[int]]) -> int:\n return reduce(lambda acc,n:(max(acc[0]+n,acc[1]+(n^k)),max(acc[0]+(n^k),acc[1]+n)), nums, (float(\'-inf\'), 0))[1]\n\n``` | 1 | 0 | ['Dynamic Programming', 'Python3'] | 2 |
maximum-product-of-two-elements-in-an-array | C++ Biggest and Second Biggest | c-biggest-and-second-biggest-by-votrubac-ui88 | Just one linear scan to find the biggest m1, and the second biggest m2 numbers.\n\ncpp\nint maxProduct(vector<int>& nums) {\n\tauto m1 = 0, m2 = 0;\n\tfor (auto | votrubac | NORMAL | 2020-05-31T04:07:36.197286+00:00 | 2020-05-31T04:23:21.938363+00:00 | 15,429 | false | Just one linear scan to find the biggest `m1`, and the second biggest `m2` numbers.\n\n```cpp\nint maxProduct(vector<int>& nums) {\n\tauto m1 = 0, m2 = 0;\n\tfor (auto n: nums) {\n\t\tif (n > m1)\n m2 = exchange(m1, n);\n\t\telse\n\t\t\tm2 = max(m2, n);\n\t}\n\treturn (m1 - 1) * (m2 - 1);\n}\n``` | 141 | 3 | [] | 22 |
maximum-product-of-two-elements-in-an-array | [Java/Python 3] Find the max 2 numbers. | javapython-3-find-the-max-2-numbers-by-r-akgo | \n\njava\n public int maxProduct(int[] nums) {\n int mx1 = Integer.MIN_VALUE, mx2 = mx1;\n for (int n : nums) {\n if (n > mx1) {\n | rock | NORMAL | 2020-05-31T04:02:24.814215+00:00 | 2022-04-01T05:27:44.282474+00:00 | 13,554 | false | \n\n```java\n public int maxProduct(int[] nums) {\n int mx1 = Integer.MIN_VALUE, mx2 = mx1;\n for (int n : nums) {\n if (n > mx1) {\n mx2 = mx1;\n mx1 = n;\n }else if (n > mx2) {\n mx2 = n;\n }\n }\n return (mx1 - 1) * (mx2 - 1);\n }\n```\n\n```python\n def maxProduct(self, nums: List[int]) -> int:\n mx1 = mx2 = -math.inf\n for n in nums:\n if n > mx1:\n mx2 = mx1\n mx1 = n\n elif n > mx2:\n mx2 = n\n return (mx1 - 1) * (mx2 - 1)\n``` | 82 | 8 | [] | 11 |
maximum-product-of-two-elements-in-an-array | ✅ Beats 100% - Explained with [ Video ] - Without Sorting- C++/Java/Python/JS - Visualized | beats-100-explained-with-video-without-s-r8rm | \n\n# YouTube Video Explanation:\n\n\nhttps://youtu.be/5QFTlws__p8\n **If you want a video for this question please write in the comments** \n\n\uD83D\uDD25 Ple | lancertech6 | NORMAL | 2023-12-12T01:13:43.515981+00:00 | 2023-12-12T01:51:15.316167+00:00 | 14,477 | false | \n\n# YouTube Video Explanation:\n\n\n[https://youtu.be/5QFTlws__p8](https://youtu.be/5QFTlws__p8)\n<!-- **If you want a video for this question please write in the comments** -->\n\n**\uD83D\uDD25 Please like, share, and subscribe to support our channel\'s mission of making complex concepts easy to understand.**\n\nSubscribe Link: https://www.youtube.com/@leetlogics/?sub_confirmation=1\n\n*Subscribe Goal: 800 Subscribers*\n*Current Subscribers: 738*\n\n---\n\n# Example Explanation\nLet\'s create a step-by-step explanation using a table:\n\n| **Iteration** | **Array Element** | **max1** | **max2** |\n|---------------|-------------------|----------|----------|\n| 1 | 3 | 3 | -\u221E |\n| 2 | 4 | 4 | 3 |\n| 3 | 5 | 5 | 4 |\n| 4 | 2 | 5 | 4 |\n\nNow, we have the two maximum elements, `max1` and `max2`. The result is calculated as `(max1 - 1) * (max2 - 1)`:\n\n**Result = (5 - 1) x (4 - 1) = 4 x 3 = 12**\n\nSo, for the input array \\([3, 4, 5, 2]\\), the maximum product is \\(12\\).\n\n---\n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo maximize the product `(nums[i]-1) * (nums[j]-1)`, we need to find the two maximum elements in the array. Subtracting 1 from each of these maximum elements will result in the maximum possible product.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialize two variables, `max1` and `max2`, to store the two maximum elements. Set them to `Integer.MIN_VALUE`.\n2. Iterate through the array, updating `max1` and `max2` accordingly.\n3. Calculate and return the maximum product using the formula `(max1 - 1) * (max2 - 1)`.\n\n# Complexity\n- Time Complexity: `O(N)`, where N is the length of the array. We iterate through the array once.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space Complexity: `O(1)`, as we use a constant amount of extra space.\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public int maxProduct(int[] nums) {\n int max1 = Integer.MIN_VALUE;\n int max2 = Integer.MIN_VALUE;\n\n for (int num : nums) {\n if (num >= max1) {\n max2 = max1;\n max1 = num;\n } else if (num > max2) {\n max2 = num;\n }\n }\n\n return (max1 - 1) * (max2 - 1);\n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n int max1 = INT_MIN;\n int max2 = INT_MIN;\n\n for (int num : nums) {\n if (num >= max1) {\n max2 = max1;\n max1 = num;\n } else if (num > max2) {\n max2 = num;\n }\n }\n\n return (max1 - 1) * (max2 - 1);\n }\n};\n```\n```Python []\nclass Solution(object):\n def maxProduct(self, nums):\n max1 = float(\'-inf\')\n max2 = float(\'-inf\')\n\n for num in nums:\n if num >= max1:\n max2 = max1\n max1 = num\n elif num > max2:\n max2 = num\n\n return (max1 - 1) * (max2 - 1)\n \n```\n```JavaScript []\nvar maxProduct = function(nums) {\n let max1 = Number.MIN_SAFE_INTEGER;\n let max2 = Number.MIN_SAFE_INTEGER;\n\n for (const num of nums) {\n if (num >= max1) {\n max2 = max1;\n max1 = num;\n } else if (num > max2) {\n max2 = num;\n }\n }\n\n return (max1 - 1) * (max2 - 1);\n};\n```\n\n | 81 | 0 | ['Array', 'Two Pointers', 'Python', 'C++', 'Java', 'JavaScript'] | 7 |
maximum-product-of-two-elements-in-an-array | Python/JS/Go/C++ O(n) by linear scan. [w/ Comment] 有中文解題文章 | pythonjsgoc-on-by-linear-scan-w-comment-nvyrq | \u4E2D\u6587\u89E3\u984C\u6587\u7AE0\n\nO(n) by linear scan.\n\n---\n\nHint:\n\nMaintain a record of first largest number as well as second largest\n\n---\n\nIm | brianchiang_tw | NORMAL | 2020-06-22T06:23:27.001872+00:00 | 2023-12-12T07:30:28.270252+00:00 | 6,790 | false | [\u4E2D\u6587\u89E3\u984C\u6587\u7AE0](https://vocus.cc/article/65780468fd897800013c9ad1)\n\nO(n) by linear scan.\n\n---\n\n**Hint**:\n\nMaintain a record of first largest number as well as second largest\n\n---\n\n**Implementation**:\n\nPython:\n\n```\nclass Solution(object):\n def maxProduct(self, nums):\n\n first, second = 0, 0\n \n for number in nums:\n \n if number > first:\n # update first largest and second largest\n first, second = number, first\n \n elif number > second:\n # update second largest\n second = number\n \n return (first - 1) * (second - 1)\n```\n\n---\n\nJavascript:\n\n```\nvar maxProduct = function(nums) {\n \n let [first, second] = [0, 0];\n \n for( const number of nums){\n \n if( number > first ){\n [first, second] = [number, first];\n \n }else if( number > second ){\n second = number;\n }\n } \n \n return ( first - 1 ) * ( second - 1 );\n \n};\n```\n\n---\n\nGo:\n\n```\nfunc maxProduct(nums []int) int {\n \n first, second := 0, 0\n \n for _, number := range nums{\n \n if number > first{\n first, second = number, first\n \n }else if number > second {\n second = number\n }\n }\n \n return ( first - 1 )*( second - 1 )\n}\n```\n\n---\n\nC++\n\n```\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n \n int first = 0, second = 0;\n \n for( const int& number: nums){\n \n if( number > first ){\n second = first;\n first = number;\n \n }else if( number > second ){\n second = number;\n }\n \n }\n \n return ( first - 1 ) * ( second - 1 );\n }\n};\n``` | 48 | 0 | ['Math', 'C', 'Iterator', 'Python', 'C++', 'Go', 'Python3', 'JavaScript'] | 9 |
maximum-product-of-two-elements-in-an-array | Accepted Java O(N), O(1) (beats 100%) | accepted-java-on-o1-beats-100-by-pd93-nbk2 | \nTime : O(N)\nSpace : O(1)\nIterate array\n 1.) if cur val is more than max1, put curr val in max1 and max1 val in max2\n 2.) else if curr val is more th | pd93 | NORMAL | 2020-05-31T04:02:34.657969+00:00 | 2020-10-08T03:45:20.666647+00:00 | 7,912 | false | \nTime : O(N)\nSpace : O(1)\nIterate array\n 1.) if cur val is more than max1, put curr val in max1 and max1 val in max2\n 2.) else if curr val is more than max2, put curr val in max2\n\n```\nclass Solution {\n public int maxProduct(int[] nums) {\n int max1 = 0;\n int max2 = 0;\n for(int i:nums){\n if(i>max1){\n max2 = max1;\n max1 = i;\n }\n else if(i>max2){\n max2 = i;\n }\n }\n return (max1-1)*(max2-1);\n }\n}\n``` | 48 | 5 | ['Java'] | 6 |
maximum-product-of-two-elements-in-an-array | [JavaScript] Easy to understand - 3 solutions | javascript-easy-to-understand-3-solution-jhci | Since the integers in nums are in range [1, 10^3], the key to this problem is to find out the biggest and the second biggest number in nums.\n\n## SOLUTION 1\n\ | poppinlp | NORMAL | 2020-06-01T15:54:38.490669+00:00 | 2020-06-01T15:54:38.490746+00:00 | 2,654 | false | Since the integers in `nums` are in range `[1, 10^3]`, the key to this problem is to find out the biggest and the second biggest number in `nums`.\n\n## SOLUTION 1\n\nWe use 2 variables to maintain our targets during the traversal of `nums`. It\'s pretty straight forward.\n\n```js\nconst maxProduct = nums => {\n let m1 = 0, m2 = 0;\n for (const val of nums) {\n m2 = Math.max(m2, Math.min(m1, val));\n m1 = Math.max(m1, val);\n }\n return (m1 - 1) * (m2 - 1);\n};\n```\n\n## SOLUTION 2\n\nWe use 2 pointers - one starts from 0 and the other one starts from `nums.length - 1` - to traversal to the middle.\n\nDuring the traversal, we maintain current biggest number in `i` or `j`. If `i` is smaller, we do `++i`. If `j` is smaller, we do `--j`.\n\nSo, when the traversal finished, we must have met this situation - the biggest number and the second biggest number have been in `i` and `j`.\n\n```js\nconst maxProduct = nums => {\n let max = 0;\n for (let i = 0, j = nums.length - 1; i < j;) {\n max = Math.max(max, (nums[i] - 1) * (nums[j] - 1));\n nums[i] < nums[j] ? ++i : --j;\n }\n return max;\n};\n```\n\n## SOLUTION 3\n\nWe use the `Array.prototype.reduce` to make solution 1 to an 1-line version.\n\n```js\nconst maxProduct = (nums, max = nums.reduce((prev, val) => [Math.max(prev[1], Math.min(prev[0], val)), Math.max(prev[0], val)], [0, 0])) => (max[0] - 1) * (max[1] - 1);\n```\n | 36 | 3 | ['JavaScript'] | 4 |
maximum-product-of-two-elements-in-an-array | 【Video】Give me 5 minutes - 2 solutions - How we think about a solution | video-give-me-5-minutes-2-solutions-how-x7zey | Intuition\nKeep the largest number so far\n\n---\n\n# Solution Video\n\nhttps://youtu.be/JV5Kuinx-m0\n\n\u25A0 Timeline of the video\n\n0:05 Explain algorithm o | niits | NORMAL | 2023-12-12T00:44:00.111309+00:00 | 2023-12-13T06:13:29.667803+00:00 | 4,668 | false | # Intuition\nKeep the largest number so far\n\n---\n\n# Solution Video\n\nhttps://youtu.be/JV5Kuinx-m0\n\n\u25A0 Timeline of the video\n\n`0:05` Explain algorithm of Solution 1\n`3:18` Coding of solution 1\n`4:18` Time Complexity and Space Complexity of solution 1\n`4:29` Step by step algorithm of solution 1\n`4:36` Explain key points of Solution 2\n`5:25` Coding of Solution 2\n`6:50` Time Complexity and Space Complexity of Solution 2\n`7:03` Step by step algorithm with my stack solution code\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 3,424\nMy first goal is 10,000 (It\'s far from done \uD83D\uDE05)\nThank you for your support!\n\n---\n\n# Approach\n\n## How we think about a solution\n\nSeems like all numbers are positive, so simply all we have to do is to find the two largest numbers in input array.\n\nThe key point of my first solution is\n\n---\n\n\u2B50\uFE0F Points\n\nKeep the largest number(= `cur_max` in the solution code) so far and compare \n\n```\nres vs (cur_max - 1) * (nums[i] - 1)\n```\n\n`res` is current max result so far\n`nums[i]` is current number\n\n---\n\nLet\'s see one by one.\n\n```\nInput: nums = [1,5,4,5]\n```\nWe keep the number at index 0 as a current max number.\n```\nres = 0\ncur_max = 1 (= nums[0])\n```\nStart iteration from index 1. \n```\nAt index 1, Compare\n\nmax(res, (cur_max - 1) * (nums[i] - 1))\n\u2192 max(0, (1 - 1) * (5 - 1))\n= 0\n\nres = 0\n```\n`res` is still `0` and we need to update `cur_max` if current number is greater than `cur_max`.\n```\ncur_max = max(cur_max, nums[i])\n= 1 vs 5\n\ncur_max = 5\n``` \nI\'ll speed up.\n```\nAt index 2, Compare\n\nmax(res, (cur_max - 1) * (nums[i] - 1))\n\u2192 max(0, (5 - 1) * (4 - 1))\n= 12\n\nres = 12\ncur_max = 5 (= max(5, 4))\n```\n\n```\nAt index 3, Compare\n\nmax(res, (cur_max - 1) * (nums[i] - 1))\n\u2192 max(12, (5 - 1) * (5 - 1))\n= 16\n\nres = 16\ncur_max = 5 (= max(5, 5))\n```\n```\nOutput: 16\n```\n\nEasy \uD83D\uDE06!\nLet\'s see a real algorithm!\n\n\n---\n\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n```python []\nclass Solution:\n def maxProduct(self, nums: List[int]) -> int:\n res = 0\n cur_max = nums[0]\n\n for i in range(1, len(nums)):\n res = max(res, (cur_max - 1) * (nums[i] - 1))\n cur_max = max(cur_max, nums[i])\n\n return res \n```\n```javascript []\n/**\n * @param {number[]} nums\n * @return {number}\n */\nvar maxProduct = function(nums) {\n let res = 0;\n let curMax = nums[0];\n\n for (let i = 1; i < nums.length; i++) {\n res = Math.max(res, (curMax - 1) * (nums[i] - 1));\n curMax = Math.max(curMax, nums[i]);\n }\n\n return res; \n};\n```\n```java []\nclass Solution {\n public int maxProduct(int[] nums) {\n int res = 0;\n int curMax = nums[0];\n\n for (int i = 1; i < nums.length; i++) {\n res = Math.max(res, (curMax - 1) * (nums[i] - 1));\n curMax = Math.max(curMax, nums[i]);\n }\n\n return res; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n int res = 0;\n int curMax = nums[0];\n\n for (int i = 1; i < nums.size(); i++) {\n res = max(res, (curMax - 1) * (nums[i] - 1));\n curMax = max(curMax, nums[i]);\n }\n\n return res; \n }\n};\n```\n\n## Step by step algorithm\n\n**Initialization:**\n```python\nres = 0\ncur_max = nums[0]\n```\nIn this section, `res` is initialized to 0, and `cur_max` is initialized to the first element of the `nums` list. These variables will be used to keep track of the maximum product and the maximum value encountered during the iterations, respectively.\n\n**Iteration through the List:**\n```python\nfor i in range(1, len(nums)):\n res = max(res, (cur_max - 1) * (nums[i] - 1))\n cur_max = max(cur_max, nums[i])\n```\nIn this section, the code iterates through the list starting from the second element (index 1). For each element at index `i`:\n- `res` is updated to the maximum of its current value and the product of `(cur_max - 1) * (nums[i] - 1)`. This ensures that `res` always holds the maximum product found so far.\n- `cur_max` is updated to the maximum of its current value and the current element `nums[i]`. This ensures that `cur_max` always holds the maximum value encountered in the list up to the current index.\n\n**Return Result:**\n```python\nreturn res\n```\nAfter the loop completes, the final value of `res` represents the maximum product of two distinct elements in the list. The function returns this maximum product.\n\n\n---\n\n# Solution 2\n\nBasically, we try to find the first max and second max numbers.\n\n---\n\n\u2B50\uFE0F Points\n\nIf current number is greater than the first max number so far, then \n\n```\ncurrent number will be the first max number\ncurrent first max number will be second max number\n```\nIf current number is less than the first max number so far, then compare \n```\nsecond max number = max(second max number, current number)\n```\n\nBecause there is still possibility that current number will be the second max number.\n\n---\n\nAt last, we multiply the first and second max numbers.\n\nEasy!\uD83D\uDE04\nLet\'s see a real algorithm\n\n\n---\n\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n```python []\nclass Solution:\n def maxProduct(self, nums: List[int]) -> int:\n first_max, second_max = 0, 0\n for num in nums:\n if num > first_max:\n second_max, first_max = first_max, num\n else:\n second_max = max(second_max, num)\n\n return (first_max - 1) * (second_max - 1)\n```\n```javascript []\nvar maxProduct = function(nums) {\n let firstMax = 0;\n let secondMax = 0;\n\n for (let num of nums) {\n if (num > firstMax) {\n [secondMax, firstMax] = [firstMax, num];\n } else {\n secondMax = Math.max(secondMax, num);\n }\n }\n\n return (firstMax - 1) * (secondMax - 1); \n};\n```\n```java []\nclass Solution {\n public int maxProduct(int[] nums) {\n int firstMax = 0;\n int secondMax = 0;\n\n for (int num : nums) {\n if (num > firstMax) {\n secondMax = firstMax;\n firstMax = num;\n } else {\n secondMax = Math.max(secondMax, num);\n }\n }\n\n return (firstMax - 1) * (secondMax - 1); \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n int firstMax = 0;\n int secondMax = 0;\n\n for (int num : nums) {\n if (num > firstMax) {\n swap(secondMax, firstMax);\n firstMax = num;\n } else {\n secondMax = max(secondMax, num);\n }\n }\n\n return (firstMax - 1) * (secondMax - 1); \n }\n};\n```\n\n## Step by step algorithm\n\n1. **Initialization:**\n\n```\nfirst_max, second_max = 0, 0\n```\n - `first_max` and `second_max` are initialized to 0. These variables will be used to keep track of the two largest elements in the list.\n\n2. **Iteration through the List:**\n\n```\nfor num in nums:\n if num > first_max:\n second_max, first_max = first_max, num\n else:\n second_max = max(second_max, num)\n```\n\n - The code iterates through each element `num` in the `nums` list.\n - For each `num`:\n - If `num` is greater than `first_max`, it means `num` is the new maximum. Therefore, the values of `second_max` and `first_max` are updated accordingly. This is done using the simultaneous assignment technique in Python: `second_max, first_max = first_max, num`.\n - If `num` is not greater than `first_max` but is greater than `second_max`, it means `num` is the new second maximum. Therefore, `second_max` is updated using `second_max = max(second_max, num)`.\n\n3. **Return Result:**\n\n```\nreturn (first_max - 1) * (second_max - 1)\n```\n\n - After the loop completes, the function returns the product of `(first_max - 1)` and `(second_max - 1)`. This is because the task is to find the maximum product of two distinct elements, so we subtract 1 from each of the largest elements before multiplying.\n\nThe algorithm efficiently finds the two largest elements in the list and returns their product minus 1.\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n\u25A0 Twitter\nhttps://twitter.com/CodingNinjaAZ\n\n\n### My next daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/special-positions-in-a-binary-matrix/solutions/4397604/video-give-me-5-minutes-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/qTAh4HGfUHk\n\n\u25A0 Timeline of the video\n\n`0:05` Explain algorithm of the first step\n`1:06` Explain algorithm of the second step\n`2:36` Coding\n`4:17` Time Complexity and Space Complexity\n`4:55` Step by step algorithm of my solution code\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/element-appearing-more-than-25-in-sorted-array/solutions/4388310/video-give-me-5-minutes-2-solutions-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/bTm-6y7Ob0A\n\n\u25A0 Timeline of the video\n\n`0:07` Explain algorithm of Solution 1\n`2:46` Coding of solution 1\n`3:49` Time Complexity and Space Complexity of solution 1\n`4:02` Step by step algorithm of solution 1\n`4:09` Explain key points of Solution 2\n`4:47` Explain the first key point\n`6:06` Explain the second key point\n`7:40` Explain the third key point\n`9:33` Coding of Solution 2\n`14:20` Time Complexity and Space Complexity of Solution 2\n`14:48` Step by step algorithm with my stack solution code\n\n | 30 | 0 | ['C++', 'Java', 'Python3', 'JavaScript'] | 4 |
maximum-product-of-two-elements-in-an-array | ✅☑[C++/Java/Python/JavaScript] || 3 Approaches || Beats 100% || EXPLAINED🔥 | cjavapythonjavascript-3-approaches-beats-1vys | PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n(Also explained in the code)\n\n#### Approach 1(Brute Force)\n1. The function iterates through the elements | MarkSPhilip31 | NORMAL | 2023-12-12T00:21:52.167242+00:00 | 2023-12-12T00:21:52.167266+00:00 | 4,148 | false | # PLEASE UPVOTE IF IT HELPED\n\n---\n\n\n# Approaches\n**(Also explained in the code)**\n\n#### ***Approach 1(Brute Force)***\n1. The function iterates through the elements in the `nums` array using two nested loops (`i` and `j`) to consider all possible pairs of elements.\n1. For each pair of elements (`nums[i], nums[j]`), it calculates the product of `(nums[i] - 1) * (nums[j] - 1)`.\n1. It updates the `ans` variable to hold the maximum product found among all pairs considered.\n1. Finally, it returns the maximum product of two distinct elements in the array.\n\n# Complexity\n- *Time complexity:*\n $$O(n^2)$$\n \n\n- *Space complexity:*\n $$O(1)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n // Function to find the maximum product of two distinct elements in the \'nums\' array\n int maxProduct(vector<int>& nums) {\n int ans = 0; // Initializing the variable \'ans\' to store the maximum product\n \n // Nested loops to iterate through pairs of elements in the \'nums\' array\n for (int i = 0; i < nums.size(); i++) {\n for (int j = i + 1; j < nums.size(); j++) {\n // Calculating the product of (nums[i] - 1) and (nums[j] - 1)\n // and updating \'ans\' to hold the maximum product found so far\n ans = max(ans, (nums[i] - 1) * (nums[j] - 1));\n }\n }\n \n return ans; // Returning the maximum product of two distinct elements\n }\n};\n\n\n\n```\n```C []\nint maxProduct(int nums[], int numsSize) {\n int ans = 0;\n \n for (int i = 0; i < numsSize; i++) {\n for (int j = i + 1; j < numsSize; j++) {\n ans = (ans > (nums[i] - 1) * (nums[j] - 1)) ? ans : (nums[i] - 1) * (nums[j] - 1);\n }\n }\n \n return ans;\n}\n\n\n\n```\n```Java []\n\nclass Solution {\n public int maxProduct(int[] nums) {\n int ans = 0;\n for (int i = 0; i < nums.length; i++) {\n for (int j = i + 1; j < nums.length; j++) {\n ans = Math.max(ans, (nums[i] - 1) * (nums[j] - 1));\n }\n }\n \n return ans;\n }\n}\n\n```\n```python3 []\nclass Solution:\n def maxProduct(self, nums: List[int]) -> int:\n ans = 0\n for i in range(len(nums)):\n for j in range(i + 1, len(nums)):\n ans = max(ans, (nums[i] - 1) * (nums[j] - 1))\n \n return ans\n\n```\n\n```javascript []\nfunction maxProduct(nums) {\n let ans = 0;\n\n for (let i = 0; i < nums.length; i++) {\n for (let j = i + 1; j < nums.length; j++) {\n ans = Math.max(ans, (nums[i] - 1) * (nums[j] - 1));\n }\n }\n\n return ans;\n}\n\n```\n\n---\n\n#### ***Approach 2(Sorting)***\n1. The function sorts the input array `nums` in ascending order using `sort(nums.begin(), nums.end())`.\n1. It then retrieves the largest element (`x`) and the second largest element (`y`) from the sorted array.\n1. The function returns the product of `(x - 1) * (y - 1)`, which is the maximum possible product of two distinct elements in the array after subtracting 1 from each of the two largest elements.\n\n# Complexity\n- *Time complexity:*\n $$O(nlogn)$$\n \n\n- *Space complexity:*\n $$O(logn)$$ or $$O(n)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n // Function to find the maximum product of two distinct elements in the \'nums\' array\n int maxProduct(vector<int>& nums) {\n sort(nums.begin(), nums.end()); // Sorting the \'nums\' array in ascending order\n \n int x = nums[nums.size() - 1]; // Getting the largest element\n int y = nums[nums.size() - 2]; // Getting the second largest element\n \n return (x - 1) * (y - 1); // Returning the product of (largest - 1) * (second largest - 1)\n }\n};\n\n\n\n```\n```C []\n\nint compare(const void *a, const void *b) {\n return (*(int*)a - *(int*)b);\n}\n\nint maxProduct(int* nums, int numsSize) {\n qsort(nums, numsSize, sizeof(int), compare);\n\n int x = nums[numsSize - 1];\n int y = nums[numsSize - 2];\n\n return (x - 1) * (y - 1);\n}\n\n\n```\n```Java []\nclass Solution {\n public int maxProduct(int[] nums) {\n Arrays.sort(nums);\n int x = nums[nums.length - 1];\n int y = nums[nums.length - 2];\n return (x - 1) * (y - 1);\n }\n}\n\n\n```\n```python3 []\nclass Solution:\n def maxProduct(self, nums: List[int]) -> int:\n nums.sort()\n x = nums[-1]\n y = nums[-2]\n return (x - 1) * (y - 1)\n\n```\n\n```javascript []\nfunction maxProduct(nums) {\n nums.sort((a, b) => a - b);\n\n const x = nums[nums.length - 1];\n const y = nums[nums.length - 2];\n\n return (x - 1) * (y - 1);\n}\n\n```\n\n---\n#### ***Approach 3(Second Biggest)***\n1. The function `maxProduct` iterates through each element (`num`) in the `nums` array.\n1. It maintains two variables, `biggest` and `secondBiggest`, to keep track of the largest and second largest numbers encountered in the array.\n1. If the current `num` is greater than the current `biggest`, it updates `secondBiggest` to the previous value of `biggest` and updates `biggest` to the current `num`.\n1. If the current `num` is not greater than `biggest`, it updates `secondBiggest` if necessary (keeping track of the second largest number encountered).\n1. Finally, it returns the product of `(biggest - 1) * (secondBiggest - 1)`, which is the maximum product of two distinct elements in the array after subtracting 1 from each of the two largest elements.\n\n# Complexity\n- *Time complexity:*\n $$O(n)$$\n \n\n- *Space complexity:*\n $$O(1)$$\n \n\n\n# Code\n```C++ []\nclass Solution {\npublic:\n // Function to find the maximum product of two distinct elements in the \'nums\' array\n int maxProduct(vector<int>& nums) {\n int biggest = 0; // Variable to store the largest number in \'nums\'\n int secondBiggest = 0; // Variable to store the second largest number in \'nums\'\n \n for (int num : nums) { // Iterating through each number in \'nums\'\n if (num > biggest) {\n // If the current number is greater than \'biggest\',\n // update \'secondBiggest\' and \'biggest\'\n secondBiggest = biggest;\n biggest = num;\n } else {\n // If the current number is not greater than \'biggest\',\n // update \'secondBiggest\' if necessary (keeping track of the second largest)\n secondBiggest = max(secondBiggest, num);\n }\n }\n \n return (biggest - 1) * (secondBiggest - 1); // Return the product of (biggest - 1) and (secondBiggest - 1)\n }\n};\n\n\n\n```\n```C []\nint maxProduct(int* nums, int numsSize) {\n int biggest = INT_MIN; // Variable to store the largest number in \'nums\'\n int secondBiggest = INT_MIN; // Variable to store the second largest number in \'nums\'\n\n for (int i = 0; i < numsSize; i++) { // Iterating through each number in \'nums\'\n if (nums[i] > biggest) {\n // If the current number is greater than \'biggest\',\n // update \'secondBiggest\' and \'biggest\'\n secondBiggest = biggest;\n biggest = nums[i];\n } else {\n // If the current number is not greater than \'biggest\',\n // update \'secondBiggest\' if necessary (keeping track of the second largest)\n secondBiggest = max(secondBiggest, nums[i]);\n }\n }\n\n return (biggest - 1) * (secondBiggest - 1); // Return the product of (biggest - 1) and (secondBiggest - 1)\n}\n\n\n\n```\n```Java []\nclass Solution {\n public int maxProduct(int[] nums) {\n int biggest = 0;\n int secondBiggest = 0;\n for (int num : nums) {\n if (num > biggest) {\n secondBiggest = biggest;\n biggest = num;\n } else {\n secondBiggest = Math.max(secondBiggest, num);\n }\n }\n \n return (biggest - 1) * (secondBiggest - 1);\n }\n}\n\n\n```\n```python3 []\nclass Solution:\n def maxProduct(self, nums: List[int]) -> int:\n biggest = 0\n second_biggest = 0\n for num in nums:\n if num > biggest:\n second_biggest = biggest\n biggest = num\n else:\n second_biggest = max(second_biggest, num)\n \n return (biggest - 1) * (second_biggest - 1)\n\n```\n\n```javascript []\nfunction maxProduct(nums) {\n let biggest = Number.MIN_SAFE_INTEGER; // Variable to store the largest number in \'nums\'\n let secondBiggest = Number.MIN_SAFE_INTEGER; // Variable to store the second largest number in \'nums\'\n\n for (let i = 0; i < nums.length; i++) { // Iterating through each number in \'nums\'\n if (nums[i] > biggest) {\n // If the current number is greater than \'biggest\',\n // update \'secondBiggest\' and \'biggest\'\n secondBiggest = biggest;\n biggest = nums[i];\n } else {\n // If the current number is not greater than \'biggest\',\n // update \'secondBiggest\' if necessary (keeping track of the second largest)\n secondBiggest = Math.max(secondBiggest, nums[i]);\n }\n }\n\n return (biggest - 1) * (secondBiggest - 1); // Return the product of (biggest - 1) and (secondBiggest - 1)\n}\n\n```\n\n---\n\n\n\n# PLEASE UPVOTE IF IT HELPED\n\n---\n---\n\n\n--- | 27 | 0 | ['Array', 'C', 'Sorting', 'Heap (Priority Queue)', 'C++', 'Java', 'Python3', 'JavaScript'] | 4 |
maximum-product-of-two-elements-in-an-array | C++ || 7 different approaches || lots of STL and the optimal solution || clean code | c-7-different-approaches-lots-of-stl-and-e18m | If you are looking for the best solution to the problem skip to approach 7. That said the other approach outline some different ideas that could be useful in si | heder | NORMAL | 2022-10-21T17:58:11.246140+00:00 | 2025-01-02T16:49:19.521579+00:00 | 1,562 | false | If you are looking for the best solution to the problem skip to approach 7. That said the other approach outline some different ideas that could be useful in similar situations.
Please let me know if you have more ideas or suggestions for one of the approaches below.
**Please upvote if you learned something new. :)**
# Approach 1: brute force
The length of the input is small enough that we can just use brute force.
```cpp
static int maxProduct(const vector<int>& nums) {
int ans = 0;
for (int i = 0; i < size(nums); ++i)
for (int j = i + 1; j < size(nums); ++j)
ans = max(ans, (nums[i] - 1) * (nums[j] - 1));
return ans;
}
```
**Complexity Analysis**
* Time complexity: $$O(n^2)$$
* Space complexity: $$O(1)$$
# Approach 2: std::sort
If we sort descending the answer is based on the first two elements.
```cpp
static int maxProduct(vector<int>& nums) {
sort(begin(nums), end(nums), greater<int>());
return (nums[0] - 1) * (nums[1] - 1);
}
```
**Complexity Analysis**
* Time complexity: $$O(n \log n)$$
* Space complexity: $$O(1)$$
# Approach 3: std::partial_sort
We don't need to sort all of ```nums```, we only care about the first two elements, hence a ```std::partial_sort``` does the trick.
```cpp
static int maxProduct(vector<int>& nums) {
partial_sort(begin(nums), next(begin(nums), 2), end(nums), greater<int>());
return (nums[0] - 1) * (nums[1] - 1);
}
```
**Complexity Analysis**
* Time complexity: $$O(n \log 2)$$ see details for std::partial_sort
* Space complexity: $$O(1)$$
# Approach 4: std::nth_element
Multiplication is commutative, therefore we don't care about the order of the two largest elements and can use quick select to find them.
```cpp
static int maxProduct(vector<int>& nums) {
nth_element(begin(nums), next(begin(nums), 2), end(nums), greater<int>());
return (nums[0] - 1) * (nums[1] - 1);
}
```
**Complexity Analysis**
* Time complexity: $$O(n)$$ for quick select
* Space complexity: $$O(1)$$
# Approach 5: std::priority_queue (min heap)
That that this approach of using a min heap is keeping the min heap at a boundest size, i.e. there is no need to push all of ```nums``` onto the heap just to pull the largest two from a max heap.
```cpp
static int maxProduct(const vector<int>& nums) {
priority_queue<int, vector<int>, greater<int>> pq;
for (int num : nums) {
if (size(pq) < 2 || num >= pq.top()) {
pq.push(num);
if (size(pq) == 3) pq.pop();
}
}
const int max1 = pq.top(); pq.pop();
return (max1 - 1) * (pq.top() - 1);
}
```
**Complexity Analysis**
* Time complexity: $$O(n \log 2)$$ so basically $$O(n)$$
* Space complexity: $$O(1)$$ since the size of the min heap is bounded
# Approach 6: std::make_heap / std::pop_heap
Instead of creating an extra heap (```std::priority_queue```) we can create a max heap in place of ```nums``` and modify this heap.
```cpp
static int maxProduct(vector<int>& nums) {
make_heap(begin(nums), end(nums));
const int max1 = nums.front();
pop_heap(begin(nums), end(nums));
return (max1 - 1) * (nums.front() - 1);
}
```
@fusu06ck610 pointet out that this could also look like this, as ```pop_heap``` moves the largest element to the back of ```nums```. Thanks!
```cpp
static int maxProduct(vector<int>& nums) {
make_heap(begin(nums), end(nums));
pop_heap(begin(nums), end(nums));
return (nums.back() - 1) * (nums.front() - 1);
}
```
**Complexity Analysis**
* Time complexity: $$O(n)$$ for make_heap and $$O(\log n)$$ for pop_heap.
* Space complexity: $$O(1)$$
# Approach 7: biggest and second biggest
This is the obvious solution for the problem, and the solution you should probably reach for.
```cpp
static int maxProduct(const vector<int>& nums) {
int m1 = 0;
int m2 = 0;
for (int num : nums) {
if (num >= m1) {
m2 = m1;
m1 = num;
} else if (num > m2) {
m2 = num;
}
}
return (m1 - 1) * (m2 - 1);
}
```
FWIW I learned something from @votrubac's post on this topic, which is a nice of use ```std::exchange``` and instead of
```cpp
if (num >= m1) {
m2 = m1;
m1 = num;
}
```
@votrubac does the following, which I find really neat:
```cpp
if (num >= m1) {
m2 = exchange(m1, num);
}
```
**Complexity Analsysis**
* Time complexity: $$O(n)$$
* Space complexity: $$O(1)$$
_As always: Feedback, questions, and comments are welcome. Leaving an upvote sparks joy! :)_
**p.s. Join us on the [LeetCode The Hard Way Discord Server](https://discord.gg/hFUyVyWy2E)!** | 17 | 0 | ['C'] | 2 |
maximum-product-of-two-elements-in-an-array | C++ || O(n) solution || Easy Approach | c-on-solution-easy-approach-by-himanshut-o8fs | ```\nclass Solution {\npublic:\n int maxProduct(vector& nums) {\n int max1 = INT_MIN;\n int flag = 0;\n for(int i = 0;i<nums.size();i++) | himanshutiwariji | NORMAL | 2022-01-08T21:11:33.586681+00:00 | 2022-01-08T21:11:33.586721+00:00 | 1,545 | false | ```\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n int max1 = INT_MIN;\n int flag = 0;\n for(int i = 0;i<nums.size();i++){\n if(max1 < nums[i]){\n max1 = nums[i];\n flag = i;\n }\n }\n int max2= INT_MIN;\n for(int i = 0;i< nums.size();i++){\n if(nums[i] > max2 && i != flag) max2 = nums[i];\n }\n \n return (max2 - 1) * (max1 - 1);\n }\n}; | 14 | 0 | ['C'] | 0 |
maximum-product-of-two-elements-in-an-array | ✅✅|| EASY PEASY || C#, Java, Python || 🔥🔥🔥 | easy-peasy-c-java-python-by-ilxamovic-41tl | Intuition\nThe problem involves finding the maximum product of two elements in an array. The provided code suggests an approach of iteratively updating the two | ilxamovic | NORMAL | 2023-12-12T04:19:43.605609+00:00 | 2023-12-12T04:19:43.605640+00:00 | 1,169 | false | # Intuition\nThe problem involves finding the maximum product of two elements in an array. The provided code suggests an approach of iteratively updating the two largest elements in the array as we traverse through it.\n\n# Approach\n1. Initialize two variables, `max1` and `max2`, to store the two largest elements in the array.\n2. Iterate through the array, updating `max1` and `max2` as needed.\n3. Calculate and return the product of `(max1 - 1) * (max2 - 1)`.\n\n# Complexity\n- **Time complexity:** O(n), where n is the length of the array. The algorithm makes a single pass through the array.\n- **Space complexity:** O(1), as the algorithm uses a constant amount of extra space to store `max1` and `max2`.\n\n```csharp []\npublic class Solution {\n public int MaxProduct(int[] nums) {\n int max1 = 0, max2 = 0;\n\n foreach (var num in nums) {\n if (num > max1) {\n max2 = max1;\n max1 = num;\n } else if (num > max2) {\n max2 = num;\n }\n }\n\n return (max1 - 1) * (max2 - 1);\n }\n}\n```\n```python []\nclass Solution:\n def maxProduct(self, nums):\n max1, max2 = 0, 0\n\n for num in nums:\n if num > max1:\n max2 = max1\n max1 = num\n elif num > max2:\n max2 = num\n\n return (max1 - 1) * (max2 - 1)\n\n```\n``` Java []\nimport java.util.Arrays;\n\npublic class Solution {\n public int maxProduct(int[] nums) {\n int max1 = 0, max2 = 0;\n\n for (int num : nums) {\n if (num > max1) {\n max2 = max1;\n max1 = num;\n } else if (num > max2) {\n max2 = num;\n }\n }\n\n return (max1 - 1) * (max2 - 1);\n }\n}\n```\n\n\n\n- Please upvote me !!! | 13 | 0 | ['Java', 'Python3', 'C#'] | 1 |
maximum-product-of-two-elements-in-an-array | C++ O(n) | c-on-by-ayushme007-sroz | \nclass Solution {\npublic:\n int maxProduct(vector<int>& a) {\n \n int i,max1,max2;\n max1=max2=INT_MIN;\n for(int i=0;i<a.size( | ayushme007 | NORMAL | 2020-06-04T12:03:59.822843+00:00 | 2022-03-05T09:16:29.389654+00:00 | 2,117 | false | ```\nclass Solution {\npublic:\n int maxProduct(vector<int>& a) {\n \n int i,max1,max2;\n max1=max2=INT_MIN;\n for(int i=0;i<a.size();i++){\n if(a[i]>max1){\n max2 = max1;\n max1 = a[i];\n }\n else if(a[i]>max2){\n max2 = a[i];\n }\n }\n int ans = (max1-1) * (max2-1);\n return ans;\n }\n};\n``` | 13 | 0 | [] | 5 |
maximum-product-of-two-elements-in-an-array | 【Video】Give me 5 minutes - 2 solutions - How we think about a solution | video-give-me-5-minutes-2-solutions-how-ock3g | Intuition\nKeep the largest number so far\n\n---\n\n# Solution Video\n\nhttps://youtu.be/JV5Kuinx-m0\n\n\u25A0 Timeline of the video\n\n0:05 Explain algorithm o | niits | NORMAL | 2024-05-19T13:47:36.902899+00:00 | 2024-05-19T13:47:36.902931+00:00 | 463 | false | # Intuition\nKeep the largest number so far\n\n---\n\n# Solution Video\n\nhttps://youtu.be/JV5Kuinx-m0\n\n\u25A0 Timeline of the video\n\n`0:05` Explain algorithm of Solution 1\n`3:18` Coding of solution 1\n`4:18` Time Complexity and Space Complexity of solution 1\n`4:29` Step by step algorithm of solution 1\n`4:36` Explain key points of Solution 2\n`5:25` Coding of Solution 2\n`6:50` Time Complexity and Space Complexity of Solution 2\n`7:03` Step by step algorithm with my stack solution code\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 3,424\nMy first goal is 10,000 (It\'s far from done \uD83D\uDE05)\nThank you for your support!\n\n---\n\n# Approach\n\n## How we think about a solution\n\nSeems like all numbers are positive, so simply all we have to do is to find the two largest numbers in input array.\n\nThe key point of my first solution is\n\n---\n\n\u2B50\uFE0F Points\n\nKeep the largest number(= `cur_max` in the solution code) so far and compare \n\n```\nres vs (cur_max - 1) * (nums[i] - 1)\n```\n\n`res` is current max result so far\n`nums[i]` is current number\n\n---\n\nLet\'s see one by one.\n\n```\nInput: nums = [1,5,4,5]\n```\nWe keep the number at index 0 as a current max number.\n```\nres = 0\ncur_max = 1 (= nums[0])\n```\nStart iteration from index 1. \n```\nAt index 1, Compare\n\nmax(res, (cur_max - 1) * (nums[i] - 1))\n\u2192 max(0, (1 - 1) * (5 - 1))\n= 0\n\nres = 0\n```\n`res` is still `0` and we need to update `cur_max` if current number is greater than `cur_max`.\n```\ncur_max = max(cur_max, nums[i])\n= 1 vs 5\n\ncur_max = 5\n``` \nI\'ll speed up.\n```\nAt index 2, Compare\n\nmax(res, (cur_max - 1) * (nums[i] - 1))\n\u2192 max(0, (5 - 1) * (4 - 1))\n= 12\n\nres = 12\ncur_max = 5 (= max(5, 4))\n```\n\n```\nAt index 3, Compare\n\nmax(res, (cur_max - 1) * (nums[i] - 1))\n\u2192 max(12, (5 - 1) * (5 - 1))\n= 16\n\nres = 16\ncur_max = 5 (= max(5, 5))\n```\n```\nOutput: 16\n```\n\nEasy \uD83D\uDE06!\nLet\'s see a real algorithm!\n\n\n---\n\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n```python []\nclass Solution:\n def maxProduct(self, nums: List[int]) -> int:\n res = 0\n cur_max = nums[0]\n\n for i in range(1, len(nums)):\n res = max(res, (cur_max - 1) * (nums[i] - 1))\n cur_max = max(cur_max, nums[i])\n\n return res \n```\n```javascript []\n/**\n * @param {number[]} nums\n * @return {number}\n */\nvar maxProduct = function(nums) {\n let res = 0;\n let curMax = nums[0];\n\n for (let i = 1; i < nums.length; i++) {\n res = Math.max(res, (curMax - 1) * (nums[i] - 1));\n curMax = Math.max(curMax, nums[i]);\n }\n\n return res; \n};\n```\n```java []\nclass Solution {\n public int maxProduct(int[] nums) {\n int res = 0;\n int curMax = nums[0];\n\n for (int i = 1; i < nums.length; i++) {\n res = Math.max(res, (curMax - 1) * (nums[i] - 1));\n curMax = Math.max(curMax, nums[i]);\n }\n\n return res; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n int res = 0;\n int curMax = nums[0];\n\n for (int i = 1; i < nums.size(); i++) {\n res = max(res, (curMax - 1) * (nums[i] - 1));\n curMax = max(curMax, nums[i]);\n }\n\n return res; \n }\n};\n```\n\n## Step by step algorithm\n\n**Initialization:**\n```python\nres = 0\ncur_max = nums[0]\n```\nIn this section, `res` is initialized to 0, and `cur_max` is initialized to the first element of the `nums` list. These variables will be used to keep track of the maximum product and the maximum value encountered during the iterations, respectively.\n\n**Iteration through the List:**\n```python\nfor i in range(1, len(nums)):\n res = max(res, (cur_max - 1) * (nums[i] - 1))\n cur_max = max(cur_max, nums[i])\n```\nIn this section, the code iterates through the list starting from the second element (index 1). For each element at index `i`:\n- `res` is updated to the maximum of its current value and the product of `(cur_max - 1) * (nums[i] - 1)`. This ensures that `res` always holds the maximum product found so far.\n- `cur_max` is updated to the maximum of its current value and the current element `nums[i]`. This ensures that `cur_max` always holds the maximum value encountered in the list up to the current index.\n\n**Return Result:**\n```python\nreturn res\n```\nAfter the loop completes, the final value of `res` represents the maximum product of two distinct elements in the list. The function returns this maximum product.\n\n\n---\n\n# Solution 2\n\nBasically, we try to find the first max and second max numbers.\n\n---\n\n\u2B50\uFE0F Points\n\nIf current number is greater than the first max number so far, then \n\n```\ncurrent number will be the first max number\ncurrent first max number will be second max number\n```\nIf current number is less than the first max number so far, then compare \n```\nsecond max number = max(second max number, current number)\n```\n\nBecause there is still possibility that current number will be the second max number.\n\n---\n\nAt last, we multiply the first and second max numbers.\n\nEasy!\uD83D\uDE04\nLet\'s see a real algorithm\n\n\n---\n\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n```python []\nclass Solution:\n def maxProduct(self, nums: List[int]) -> int:\n first_max, second_max = 0, 0\n for num in nums:\n if num > first_max:\n second_max, first_max = first_max, num\n else:\n second_max = max(second_max, num)\n\n return (first_max - 1) * (second_max - 1)\n```\n```javascript []\nvar maxProduct = function(nums) {\n let firstMax = 0;\n let secondMax = 0;\n\n for (let num of nums) {\n if (num > firstMax) {\n [secondMax, firstMax] = [firstMax, num];\n } else {\n secondMax = Math.max(secondMax, num);\n }\n }\n\n return (firstMax - 1) * (secondMax - 1); \n};\n```\n```java []\nclass Solution {\n public int maxProduct(int[] nums) {\n int firstMax = 0;\n int secondMax = 0;\n\n for (int num : nums) {\n if (num > firstMax) {\n secondMax = firstMax;\n firstMax = num;\n } else {\n secondMax = Math.max(secondMax, num);\n }\n }\n\n return (firstMax - 1) * (secondMax - 1); \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n int firstMax = 0;\n int secondMax = 0;\n\n for (int num : nums) {\n if (num > firstMax) {\n swap(secondMax, firstMax);\n firstMax = num;\n } else {\n secondMax = max(secondMax, num);\n }\n }\n\n return (firstMax - 1) * (secondMax - 1); \n }\n};\n```\n\n## Step by step algorithm\n\n1. **Initialization:**\n\n```\nfirst_max, second_max = 0, 0\n```\n - `first_max` and `second_max` are initialized to 0. These variables will be used to keep track of the two largest elements in the list.\n\n2. **Iteration through the List:**\n\n```\nfor num in nums:\n if num > first_max:\n second_max, first_max = first_max, num\n else:\n second_max = max(second_max, num)\n```\n\n - The code iterates through each element `num` in the `nums` list.\n - For each `num`:\n - If `num` is greater than `first_max`, it means `num` is the new maximum. Therefore, the values of `second_max` and `first_max` are updated accordingly. This is done using the simultaneous assignment technique in Python: `second_max, first_max = first_max, num`.\n - If `num` is not greater than `first_max` but is greater than `second_max`, it means `num` is the new second maximum. Therefore, `second_max` is updated using `second_max = max(second_max, num)`.\n\n3. **Return Result:**\n\n```\nreturn (first_max - 1) * (second_max - 1)\n```\n\n - After the loop completes, the function returns the product of `(first_max - 1)` and `(second_max - 1)`. This is because the task is to find the maximum product of two distinct elements, so we subtract 1 from each of the largest elements before multiplying.\n\nThe algorithm efficiently finds the two largest elements in the list and returns their product minus 1.\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n\u25A0 Twitter\nhttps://twitter.com/CodingNinjaAZ\n\n\n### My next daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/special-positions-in-a-binary-matrix/solutions/4397604/video-give-me-5-minutes-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/qTAh4HGfUHk\n\n\u25A0 Timeline of the video\n\n`0:05` Explain algorithm of the first step\n`1:06` Explain algorithm of the second step\n`2:36` Coding\n`4:17` Time Complexity and Space Complexity\n`4:55` Step by step algorithm of my solution code\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/element-appearing-more-than-25-in-sorted-array/solutions/4388310/video-give-me-5-minutes-2-solutions-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/bTm-6y7Ob0A\n\n\u25A0 Timeline of the video\n\n`0:07` Explain algorithm of Solution 1\n`2:46` Coding of solution 1\n`3:49` Time Complexity and Space Complexity of solution 1\n`4:02` Step by step algorithm of solution 1\n`4:09` Explain key points of Solution 2\n`4:47` Explain the first key point\n`6:06` Explain the second key point\n`7:40` Explain the third key point\n`9:33` Coding of Solution 2\n`14:20` Time Complexity and Space Complexity of Solution 2\n`14:48` Step by step algorithm with my stack solution code\n\n | 12 | 0 | ['C++', 'Java', 'Python3', 'JavaScript'] | 0 |
maximum-product-of-two-elements-in-an-array | [Python] Simple & Faster than 99.27% of submissions | python-simple-faster-than-9927-of-submis-zwpv | \nclass Solution(object):\n def maxProduct(self, nums):\n """\n :type nums: List[int]\n :rtype: int\n """\n max_1 = max(nu | parkershamblin | NORMAL | 2020-06-25T09:21:40.653333+00:00 | 2020-06-25T09:22:53.006348+00:00 | 2,320 | false | ```\nclass Solution(object):\n def maxProduct(self, nums):\n """\n :type nums: List[int]\n :rtype: int\n """\n max_1 = max(nums)\n nums.remove(max_1)\n max_2 = max(nums)\n return (max_1-1)*(max_2-1)\n\t\n``` | 12 | 1 | ['Python', 'Python3'] | 1 |
maximum-product-of-two-elements-in-an-array | 3 Approach to solve using C++ STL | 3-approach-to-solve-using-c-stl-by-akb7-n1me | Before getting into the problem this is somewhat easy problem and introduction to concept called as Heap.\n\nHere we need to get the maximum product so sort the | akb7 | NORMAL | 2021-07-09T06:02:50.735513+00:00 | 2021-07-09T06:02:50.735559+00:00 | 1,506 | false | *Before getting into the problem this is somewhat easy problem and introduction to concept called as **Heap**.*\n\nHere we need to get the maximum product so sort the array and multiply last-1 and penultimate number - 1 will give us the answer.\n\nTime Complexity: O(nlogn).\n```\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n sort(nums.begin(),nums.end());\n int n=nums.size();\n return (nums[n-1]-1)*(nums[n-2]-1);\n }\n};\n```\n**Introduction to Heap:**\n* \t**Using min Heap:**\n\t\tMin heap can be easily implemented using priority_queue and this solution provide a time Complexity of O(nlog(n-2))\n```\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n // here we can use min heap \n // using c++ stl priority queue\n priority_queue<int,vector<int>,greater<int>> minh;\n for(auto curr:nums) minh.push(curr);\n while(minh.size()!=2) minh.pop();\n int a = minh.top();\n minh.pop();;\n int b = minh.top();\n return (a-1)*(b-1);\n }\n};\n```\n* **Using max Heap:**\n\t\tMax heap is somewhat better approach as we need to just pop() first two elements. And Time Complexity is O(nlog(2))\n```\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n // here we can use max heap \n // using c++ stl priority queue\n priority_queue<int> maxh;\n for(auto curr:nums) maxh.push(curr);\n int a = maxh.top();\n maxh.pop();;\n int b = maxh.top();\n return (a-1)*(b-1);\n }\n};\n```\n\nHere is the final Result:\n\n | 11 | 0 | ['C', 'Heap (Priority Queue)', 'C++'] | 2 |
maximum-product-of-two-elements-in-an-array | simple python solution | simple-python-solution-by-kedaar_kalyan-sg4i | ```\n def maxProduct(self, nums: List[int]) -> int:\n nums.sort()\n return (nums[-1]-1)*(nums[-2]-1) | Kedaar_Kalyan | NORMAL | 2020-12-02T12:22:29.583649+00:00 | 2020-12-02T12:22:29.583675+00:00 | 1,055 | false | ```\n def maxProduct(self, nums: List[int]) -> int:\n nums.sort()\n return (nums[-1]-1)*(nums[-2]-1) | 10 | 1 | [] | 2 |
maximum-product-of-two-elements-in-an-array | 2 C++ 1 pass, priority_queue O(1) vs 3 Python 1-line codes|| 0ms beats 100% | 2-c-1-pass-priority_queue-o1-vs-3-python-gkxk | Intuition\n Describe your first thoughts on how to solve this problem. \nIterate the nums to find the max & 2nd max.\n\n2nd O(1) C++ solution uses priority_queu | anwendeng | NORMAL | 2023-12-12T04:54:57.307053+00:00 | 2023-12-12T10:58:38.247155+00:00 | 1,633 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIterate the `nums` to find the max & 2nd max.\n\n2nd O(1) C++ solution uses priority_queue of size at most 3 which is also fast & beats 100%.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nPython codes are provided with 1-line codes.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$ vs $$O(n\\log n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n# Code 0ms beats 100%\n```\n#pragma GCC optimize("O3", "unroll-loops")\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n int n=nums.size();\n if (n<3) return (nums[0]-1)*(nums.back()-1);\n int m0=nums[0],m1=nums[1];\n if(m0<m1) swap(m0,m1);\n for (int i=2;i<n;i++){\n int x=nums[i];\n if(x>m0){\n m1=m0, m0=x;\n }\n else if(x>m1) m1=x;\n }\n return (m0-1)*(m1-1);\n }\n};\nauto init = []()\n{ \n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n```\n# C++ using priority_queue|| 0ms beats 100%\n```\n#pragma GCC optimize("O3", "unroll-loops")\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n priority_queue<int, vector<int>, greater<int>> pq;\n for (int x: nums){\n pq.push(x);\n if (pq.size()>2) pq.pop(); \n }\n int product=pq.top()-1;\n pq.pop();\n product*=(pq.top()-1);\n return product;\n }\n};\n\n```\n# Python 1 line using sorted\n\n```\nclass Solution:\n def maxProduct(self, nums: List[int]) -> int:\n return ((x:=sorted(nums))[-1]-1)*(x[-2]-1) \n```\n# Python 1 line 49ms beats 92.92%\n```\nclass Solution:\n def maxProduct(self, nums: List[int]) -> int:\n return ((x:=sorted(nums)[-2:])[-1]-1)*(x[-2]-1) \n```\n# Python 1 line using heap.nlargest\n```\nclass Solution:\n def maxProduct(self, nums: List[int]) -> int:\n return ((x:=heapq.nlargest(2, nums))[0]-1)*(x[1]-1)\n``` | 9 | 0 | ['Array', 'Sorting', 'Heap (Priority Queue)', 'C++', 'Python3'] | 2 |
maximum-product-of-two-elements-in-an-array | Python 3 -> Using heap | python-3-using-heap-by-mybuddy29-0k3i | Suggestions to make it better are always welcomed.\n\n\nclass Solution:\n def maxProduct(self, nums: List[int]) -> int:\n # approach 1: find 2 max num | mybuddy29 | NORMAL | 2022-04-23T17:11:35.306319+00:00 | 2022-04-23T17:12:34.964770+00:00 | 1,522 | false | **Suggestions to make it better are always welcomed.**\n\n```\nclass Solution:\n def maxProduct(self, nums: List[int]) -> int:\n # approach 1: find 2 max numbers in 2 loops. T = O(n). S = O(1)\n\t\t# approach 2: sort and then get the last 2 max elements. T = O(n lg n). S = O(1)\n\t\t# approach 3: build min heap of size 2. T = O(n lg n). S = O(1)\n\t\t# python gives only min heap feature. heaq.heappush(list, item). heapq.heappop(list)\n \n heap = [-1]\n for num in nums:\n if num > heap[0]:\n if len(heap) == 2:\n heapq.heappop(heap)\n heapq.heappush(heap, num)\n \n return (heap[0]-1) * (heap[1]-1)\n```\n**I hope that you\'ve found this useful.\nIn that case, please upvote. It only motivates me to write more such posts\uD83D\uDE03** | 9 | 0 | ['Heap (Priority Queue)', 'Python3'] | 4 |
maximum-product-of-two-elements-in-an-array | Max and Second Max number in Array | max-and-second-max-number-in-array-by-hi-5fzq | public int maxProduct(int[] nums) {\n \n int max = Integer.MIN_VALUE;\n int secondMax = Integer.MIN_VALUE;\n \n for(int i = | hitler069 | NORMAL | 2020-07-04T16:31:13.089192+00:00 | 2020-07-04T16:31:13.089222+00:00 | 14,115 | false | public int maxProduct(int[] nums) {\n \n int max = Integer.MIN_VALUE;\n int secondMax = Integer.MIN_VALUE;\n \n for(int i = 0;i< nums.length;i++){\n \n if(nums[i] > max){ \n secondMax = max;\n max = nums[i];\n }else if(nums[i] > secondMax){\n secondMax = nums[i];\n }\n }\n \n return (max-1)*(secondMax-1);\n \n } | 9 | 1 | [] | 1 |
maximum-product-of-two-elements-in-an-array | ✅Beats 100 % Easy Clean Code✅✅✅ | beats-100-easy-clean-code-by-sourav_n06-k4l2 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Tim | sourav_n06 | NORMAL | 2023-12-12T02:26:18.086093+00:00 | 2023-12-12T02:26:18.086130+00:00 | 1,132 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: o(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n**C++**\n```\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n int n = nums.size();\n sort(nums.begin(), nums.end());\n return (nums[n-2] - 1) * (nums[n-1] - 1);\n }\n};\n```\n**Java**\n```\nclass Solution {\n public int maxProduct(int[] nums) {\n int n = nums.length;\n Arrays.sort(nums);\n return (nums[n - 2] - 1) * (nums[n - 1] - 1);\n }\n}\n```\n**JavaScript**\n```\nvar maxProduct = function(nums) {\n const n = nums.length;\n nums.sort((a, b) => a - b);\n return (nums[n - 2] - 1) * (nums[n - 1] - 1);\n};\n```\n\n | 8 | 1 | ['Array', 'Sorting', 'Heap (Priority Queue)', 'C++', 'Java', 'JavaScript'] | 2 |
maximum-product-of-two-elements-in-an-array | ✅ 2 line solution || ✅ simple || ✅ python | 2-line-solution-simple-python-by-naveen_-kutf | Intuition\nThe problem asks for the maximum product of two distinct elements in the given list. Sorting the list in ascending order allows us to access the two | naveen_kumar_g | NORMAL | 2023-12-12T01:41:01.472626+00:00 | 2023-12-12T01:41:01.472663+00:00 | 1,224 | false | # Intuition\nThe problem asks for the maximum product of two distinct elements in the given list. Sorting the list in ascending order allows us to access the two largest elements at the end of the sorted list.\n\n\n# Approach\nThe approach involves sorting the input list in ascending order. After sorting, the two largest elements will be at the end of the list, and we can simply return the product of these two elements minus one.\n\n\n# Complexity\n- Time complexity:\nO(nlogn) - The dominant factor is the sorting operation, which has a time complexity of O(nlogn) for the average case.\n- Space complexity:\nO(1) - The space complexity is constant because the sorting is done in-place, and no additional space is used other than the input list.\n# Code\n```\nclass Solution:\n def maxProduct(self, nums: List[int]) -> int:\n nums=sorted(nums)\n return (nums[-1]-1) * (nums[-2]-1)\n\n\n\n \n``` | 8 | 0 | ['Python3'] | 5 |
maximum-product-of-two-elements-in-an-array | ✅Java Simple Solution || ✅Runtime 0ms || ✅ Beats100% | java-simple-solution-runtime-0ms-beats10-4qn8 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | ahmedna126 | NORMAL | 2023-08-01T14:02:12.458979+00:00 | 2023-11-07T11:44:23.208589+00:00 | 453 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int maxProduct(int[] nums) {\n int max1 = nums[0];\n int max2 = nums[1];\n\n for (int i = 2 ; i < nums.length ; i++) {\n if (nums[i] > max1){\n max2 = (max1 > max2) ? max1 : max2;\n max1 = nums[i];\n }else if (nums[i] > max2){\n max1 = (max2 > max1) ? max2 : max1;\n max2 = nums[i];\n }\n }\n return (max1 - 1 ) * (max2 - 1);\n }\n}\n```\n\n\n## For additional problem-solving solutions, you can explore my repository on GitHub: [GitHub Repository](https://github.com/ahmedna126/java_leetcode_challenges)\n\n\n\n | 8 | 0 | ['Java'] | 0 |
maximum-product-of-two-elements-in-an-array | [JavaScript] Elegant one line solution using sort and reduce (with explanation) | javascript-elegant-one-line-solution-usi-d18z | Unfortunately, due use of .sort() method time complexity is \u0398(n^2) at best\n\njavascript\nconst maxProduct = (nums) => nums.sort((a, b) => a - b).splice(-2 | mrhyde | NORMAL | 2020-10-30T07:09:31.130636+00:00 | 2020-10-30T07:16:53.330023+00:00 | 608 | false | Unfortunately, due use of `.sort()` method time complexity is \u0398(n^2) at best\n\n```javascript\nconst maxProduct = (nums) => nums.sort((a, b) => a - b).splice(-2).reduce((i, j) => (i-1)*(j-1))\n```\n\nExplanation:\n1. `.sort((a, b) => a - b)` - sort array elements in ascending order (by default it sorts elements alphabetically)\n2. `.splice(-2)` - take two last elements\n3. `.reduce((i, j) => (i-1)*(j-1))` - since there are only two elements we are not accumulating anything and simply calculating the result using both numbers from the array | 8 | 1 | ['JavaScript'] | 0 |
maximum-product-of-two-elements-in-an-array | Python O(n) | python-on-by-minionjosh-u4z0 | \n def maxProduct(self, nums: List[int]) -> int:\n \n max1, max2 = -1, -1\n for n in nums:\n if n >= max1:\n m | minionjosh | NORMAL | 2020-07-31T18:45:01.799839+00:00 | 2020-07-31T18:45:01.799872+00:00 | 694 | false | ```\n def maxProduct(self, nums: List[int]) -> int:\n \n max1, max2 = -1, -1\n for n in nums:\n if n >= max1:\n max1, max2 = n, max1\n elif n > max2:\n max2 = n\n \n \n return (max1-1) * (max2-1)\n``` | 8 | 0 | ['Python'] | 0 |
maximum-product-of-two-elements-in-an-array | 2 methods || sorting || priority queue || Brute force to optimized | 2-methods-sorting-priority-queue-brute-f-g2uo | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n 1. sort and access | ankitraj15 | NORMAL | 2023-06-16T05:47:20.701664+00:00 | 2023-06-16T05:47:20.701695+00:00 | 727 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n 1. sort and access last 2 elements\n 2. use max heap i.e. priority queue and acess top 2 elements. \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n sorting: O(nlogn)\n priority queue: O(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n sorting: O(1)\n priority queue: O(n)\n\n# Code\n```\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n sort(nums.begin(),nums.end());\n return (nums[nums.size()-1]-1)*(nums[nums.size()-2]-1);\n }\n};\n\n```\n```\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n priority_queue<int>pq;\n for(int i:nums) pq.push(i);\n int x=pq.top();\n pq.pop();\n int y=pq.top();\n return (x-1)*(y-1);\n }\n};\n``` | 7 | 0 | ['Array', 'Sorting', 'Heap (Priority Queue)', 'C++'] | 2 |
maximum-product-of-two-elements-in-an-array | C++ ONE PASS 100% time 99.9% space (with explanation) | c-one-pass-100-time-999-space-with-expla-81pj | Here variable a will store max value of array nums, while b will store 2nd max value\n\n\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n | joshuako | NORMAL | 2021-03-27T09:00:55.264572+00:00 | 2021-03-27T09:00:55.264600+00:00 | 637 | false | Here variable `a` will store max value of array `nums`, while `b` will store 2nd max value\n\n```\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n int a = 0, b = 0;\n for (int i = 0;i < nums.size();i++) {\n if (nums[i] > a) {\n b = a; // delegate previous max value to 2nd max value\n a = nums[i]; // set new max value\n } else if (nums[i] > b) {\n b = nums[i];\n }\n }\n return (a-1)*(b-1);\n }\n};\n``` | 7 | 0 | [] | 0 |
maximum-product-of-two-elements-in-an-array | 1 liner - Python 3 | 1-liner-python-3-by-mb557x-nn1h | Approach:\nThe list is first sorted. After sorting, 1 is subtracted from the last and the second last elements and their product is returned.\n\nclass Solution: | mb557x | NORMAL | 2020-07-15T05:47:28.645441+00:00 | 2020-07-15T05:47:28.645474+00:00 | 856 | false | Approach:\nThe list is first sorted. After sorting, ```1``` is subtracted from the last and the second last elements and their **product** is returned.\n```\nclass Solution:\n def maxProduct(self, nums: List[int]) -> int:\n return ((sorted(nums)[-1]) - 1) * ((sorted(nums)[-2] - 1))\n```\n```\n#Runtime: 56ms\n#80%\n``` | 7 | 3 | ['Python3'] | 3 |
maximum-product-of-two-elements-in-an-array | Best 3 Approaches [0ms , 7ms , 9ms] [Java] | best-3-approaches-0ms-7ms-9ms-java-by-cr-w92c | \n1. Most optimal solution T.C- O(n) , S.C -O(1)\n\nclass Solution {\n\n public int maxProduct(int[] nums) {\n int max1 = Integer.MIN_VALUE; // Integ | crusifixx | NORMAL | 2022-11-24T08:37:21.133152+00:00 | 2023-01-08T14:06:32.538074+00:00 | 1,235 | false | \n**1. Most optimal solution T.C- O(n) , S.C -O(1)**\n\nclass Solution {\n\n public int maxProduct(int[] nums) {\n int max1 = Integer.MIN_VALUE; // Integer.MIN_VALUE -> To handel negative numbers in array\n int max2 = Integer.MIN_VALUE; // Integer.MIN_VALUE -> To handel negative numbers in array\n for(int n:nums){\n if(n>max1){\n max2 = max1;\n max1 = n; //first max element in array\n }\n else if(n>max2){\n max2 = n; //second max element in array\n }\n }\n return (max1-1)*(max2-1);\n }\n}\n\n\n**2. Time-space tradeoff using priority queue T.C-O(n log n),S.C-O(n)**\n\nclass Solution {\n\n public int maxProduct(int[] nums) {\n PriorityQueue<Integer> pq=new PriorityQueue<>(Collections.reverseOrder()); //max-heap\n \n \n for(int n:nums) pq.offer(n);\n \n int max1=pq.poll(); //first max element in array\n int max2=pq.poll(); //second max element in array\n \n return (max1-1)*(max2-1);\n }\n}\n\n**3. Bruteforce solution T.C- O(n^2) , S.C -O(1)**\n\nclass Solution {\n\n public int maxProduct(int[] nums) {\n \n int max=0;\n for(int i=0;i<nums.length;i++){\n for(int j=i+1;j<nums.length;j++){\n int temp=(nums[i]-1)*(nums[j]-1);\n max=Math.max(max,temp);\n }\n }\n return max;\n }\n}\n | 6 | 0 | ['Heap (Priority Queue)', 'Java'] | 1 |
maximum-product-of-two-elements-in-an-array | Simple Java Solution, 100% Faster (Easy to Understand) | simple-java-solution-100-faster-easy-to-fbld7 | Time Complexity : O(N)\n\nclass Solution {\n public int maxProduct(int[] nums) {\n \n int max = Integer.MIN_VALUE;\n int sec_max = Integ | Shiv_Mishra | NORMAL | 2021-10-08T10:14:23.609154+00:00 | 2021-10-08T10:14:23.609199+00:00 | 1,039 | false | Time Complexity : O(N)\n```\nclass Solution {\n public int maxProduct(int[] nums) {\n \n int max = Integer.MIN_VALUE;\n int sec_max = Integer.MIN_VALUE;\n \n for(int i=0;i<nums.length;i++){\n if(nums[i] > max){\n sec_max = max;\n max = nums[i];\n }\n else if(nums[i] >= sec_max){\n sec_max = nums[i];\n }\n }\n \n return ((max-1)*(sec_max-1));\n }\n}\n```\n\nComment down if you don\'t understand anything.\n\nThank you! | 6 | 0 | ['Array', 'Java'] | 2 |
maximum-product-of-two-elements-in-an-array | JavaScript solution: 86% faster, 100% less memory | javascript-solution-86-faster-100-less-m-k9l4 | \nvar maxProduct = function(nums) {\n nums.sort((a,b)=>b-a);\n return (nums[0]-1)*(nums[1]-1);\n};\n | cyberain | NORMAL | 2020-06-04T07:40:47.275872+00:00 | 2020-06-04T07:40:47.275920+00:00 | 616 | false | ```\nvar maxProduct = function(nums) {\n nums.sort((a,b)=>b-a);\n return (nums[0]-1)*(nums[1]-1);\n};\n``` | 6 | 1 | ['JavaScript'] | 2 |
maximum-product-of-two-elements-in-an-array | [Python] Built-in sort method (100 % speed, 100 % mem) | python-built-in-sort-method-100-speed-10-lhtl | Built-in sort method \n\nWhy write efficient code when it\'s been written for you? \n\n\nclass Solution(object):\n def maxProduct(self, nums):\n nums. | drblessing | NORMAL | 2020-05-31T12:49:53.104970+00:00 | 2020-05-31T12:50:42.755790+00:00 | 767 | false | # Built-in sort method \n\nWhy write efficient code when it\'s been written for you? \n\n```\nclass Solution(object):\n def maxProduct(self, nums):\n nums.sort()\n return (nums[-1] -1) * (nums[-2]-1)\n """\n :type nums: List[int]\n :rtype: int\n """\n \n```\n\n## **100 % on both memory and speed! (28 ms, 12.6 MB)**\n | 6 | 4 | ['Python', 'Python3'] | 3 |
maximum-product-of-two-elements-in-an-array | 2 Different Approach using Sorting and Priority Queue (Heaps) | 2-different-approach-using-sorting-and-p-tzvb | First Approach Using Sorting \n# Intuition\nTo maximize the product (nums[i]\u22121)\xD7(nums[j]\u22121), you need to find the two largest numbers in the array | _sxrthakk | NORMAL | 2024-07-20T04:55:50.295934+00:00 | 2024-07-20T04:55:50.295966+00:00 | 849 | false | # First Approach Using Sorting \n# Intuition\nTo maximize the product (nums[i]\u22121)\xD7(nums[j]\u22121), you need to find the two largest numbers in the array since subtracting 1 from a larger number will still result in a relatively large value. Sorting the array helps to easily identify the two largest numbers, and thus the desired product can be calculated using these two numbers.\n\n# Approach\n1. **Sort the Array :** Begin by sorting the array nums in ascending order. This will arrange the numbers such that the largest numbers are at the end of the array. \n2. **Identify the Two Largest Numbers :** After sorting, the two largest numbers in the array will be at the last two indices. Specifically, the largest number will be at nums[nums.size() - 1] and the second largest will be at nums[nums.size() - 2].\n3. **Calculate the Product :** Subtract 1 from each of these two largest numbers and then calculate their product.\n4. # Complexity\n- **Time complexity :** O(n*log(n))\nThe time complexity of this solution is O(n log n) due to the sorting operation, where n is the number of elements in the input vector.\n- **Space complexity :** O(1)\n# Code\n```\nint maxProduct(vector<int>& nums) {\n sort(nums.begin(),nums.end());\n return (nums[nums.size()-1]-1)*(nums[nums.size()-2]-1);\n }\n```\n---\n---\n---\n# Second Approach using Max Heap (Priority Queue)\n# Intuition\nThe maximum value of (nums[i]\u22121)\u2217(nums[j]\u22121) is achieved when nums[i] and nums[j] are the two largest numbers in the array. By using a max-heap (priority queue), we can efficiently extract these two largest numbers. The code pushes all elements into the heap, extracts the largest, then the second largest, and computes the product of their decrements.\n\n# Approach\n1. **Initialize a Max-Heap :** Use a max-heap (priority queue) to store all the elements of the array. This allows efficient retrieval of the largest elements. \n2. **Insert Elements :** Iterate over the array and push each element into the max-heap.\n3. **Extract the Largest Element :** Extract the largest element from the max-heap, which represents the maximum value in the array. Let\'s call this value x.\n4. **Remove the Largest Element :**Pop the largest element from the max-heap to access the second largest element.\n5. **Extract the Second Largest Element :** Extract the next largest element from the max-heap (that is pq.top()).\n6. **Compute the Result :** Calculate the product (x\u22121)\xD7(secondlargest\u22121) and return this value as the result.\n\n# Complexity\n- **Time complexity :** O(n*log(n))\nThe time complexity of this solution is O(n log n) where n is the number of elements in the input vector. This is because we are iterating through each element in the vector to insert it into the priority queue, which has a time complexity of O(log n) for each insertion. Additionally, we are performing two pop operations on the priority queue, each with a time complexity of O(log n).\n- **Space complexity :** O(n)\n\n# Code\n```\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n priority_queue<int> pq;\n for(int i : nums) pq.push(i);\n int x=pq.top();\n pq.pop();\n return (x-1)*(pq.top()-1);\n }\n};\n``` | 5 | 0 | ['Array', 'Sorting', 'Heap (Priority Queue)', 'C++'] | 0 |
maximum-product-of-two-elements-in-an-array | 【Video】Give me 5 minutes - 2 solutions - How we think about a solution | video-give-me-5-minutes-2-solutions-how-2rd1w | Intuition\nKeep the largest number so far\n\n---\n\n# Solution Video\n\nhttps://youtu.be/JV5Kuinx-m0\n\n\u25A0 Timeline of the video\n\n0:05 Explain algorithm o | niits | NORMAL | 2024-04-24T16:34:39.436356+00:00 | 2024-04-24T16:34:39.436386+00:00 | 367 | false | # Intuition\nKeep the largest number so far\n\n---\n\n# Solution Video\n\nhttps://youtu.be/JV5Kuinx-m0\n\n\u25A0 Timeline of the video\n\n`0:05` Explain algorithm of Solution 1\n`3:18` Coding of solution 1\n`4:18` Time Complexity and Space Complexity of solution 1\n`4:29` Step by step algorithm of solution 1\n`4:36` Explain key points of Solution 2\n`5:25` Coding of Solution 2\n`6:50` Time Complexity and Space Complexity of Solution 2\n`7:03` Step by step algorithm with my stack solution code\n\n### \u2B50\uFE0F\u2B50\uFE0F Don\'t forget to subscribe to my channel! \u2B50\uFE0F\u2B50\uFE0F\n\n**\u25A0 Subscribe URL**\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\nSubscribers: 3,424\nMy first goal is 10,000 (It\'s far from done \uD83D\uDE05)\nThank you for your support!\n\n---\n\n# Approach\n\n## How we think about a solution\n\nSeems like all numbers are positive, so simply all we have to do is to find the two largest numbers in input array.\n\nThe key point of my first solution is\n\n---\n\n\u2B50\uFE0F Points\n\nKeep the largest number(= `cur_max` in the solution code) so far and compare \n\n```\nres vs (cur_max - 1) * (nums[i] - 1)\n```\n\n`res` is current max result so far\n`nums[i]` is current number\n\n---\n\nLet\'s see one by one.\n\n```\nInput: nums = [1,5,4,5]\n```\nWe keep the number at index 0 as a current max number.\n```\nres = 0\ncur_max = 1 (= nums[0])\n```\nStart iteration from index 1. \n```\nAt index 1, Compare\n\nmax(res, (cur_max - 1) * (nums[i] - 1))\n\u2192 max(0, (1 - 1) * (5 - 1))\n= 0\n\nres = 0\n```\n`res` is still `0` and we need to update `cur_max` if current number is greater than `cur_max`.\n```\ncur_max = max(cur_max, nums[i])\n= 1 vs 5\n\ncur_max = 5\n``` \nI\'ll speed up.\n```\nAt index 2, Compare\n\nmax(res, (cur_max - 1) * (nums[i] - 1))\n\u2192 max(0, (5 - 1) * (4 - 1))\n= 12\n\nres = 12\ncur_max = 5 (= max(5, 4))\n```\n\n```\nAt index 3, Compare\n\nmax(res, (cur_max - 1) * (nums[i] - 1))\n\u2192 max(12, (5 - 1) * (5 - 1))\n= 16\n\nres = 16\ncur_max = 5 (= max(5, 5))\n```\n```\nOutput: 16\n```\n\nEasy \uD83D\uDE06!\nLet\'s see a real algorithm!\n\n\n---\n\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n```python []\nclass Solution:\n def maxProduct(self, nums: List[int]) -> int:\n res = 0\n cur_max = nums[0]\n\n for i in range(1, len(nums)):\n res = max(res, (cur_max - 1) * (nums[i] - 1))\n cur_max = max(cur_max, nums[i])\n\n return res \n```\n```javascript []\n/**\n * @param {number[]} nums\n * @return {number}\n */\nvar maxProduct = function(nums) {\n let res = 0;\n let curMax = nums[0];\n\n for (let i = 1; i < nums.length; i++) {\n res = Math.max(res, (curMax - 1) * (nums[i] - 1));\n curMax = Math.max(curMax, nums[i]);\n }\n\n return res; \n};\n```\n```java []\nclass Solution {\n public int maxProduct(int[] nums) {\n int res = 0;\n int curMax = nums[0];\n\n for (int i = 1; i < nums.length; i++) {\n res = Math.max(res, (curMax - 1) * (nums[i] - 1));\n curMax = Math.max(curMax, nums[i]);\n }\n\n return res; \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n int res = 0;\n int curMax = nums[0];\n\n for (int i = 1; i < nums.size(); i++) {\n res = max(res, (curMax - 1) * (nums[i] - 1));\n curMax = max(curMax, nums[i]);\n }\n\n return res; \n }\n};\n```\n\n## Step by step algorithm\n\n**Initialization:**\n```python\nres = 0\ncur_max = nums[0]\n```\nIn this section, `res` is initialized to 0, and `cur_max` is initialized to the first element of the `nums` list. These variables will be used to keep track of the maximum product and the maximum value encountered during the iterations, respectively.\n\n**Iteration through the List:**\n```python\nfor i in range(1, len(nums)):\n res = max(res, (cur_max - 1) * (nums[i] - 1))\n cur_max = max(cur_max, nums[i])\n```\nIn this section, the code iterates through the list starting from the second element (index 1). For each element at index `i`:\n- `res` is updated to the maximum of its current value and the product of `(cur_max - 1) * (nums[i] - 1)`. This ensures that `res` always holds the maximum product found so far.\n- `cur_max` is updated to the maximum of its current value and the current element `nums[i]`. This ensures that `cur_max` always holds the maximum value encountered in the list up to the current index.\n\n**Return Result:**\n```python\nreturn res\n```\nAfter the loop completes, the final value of `res` represents the maximum product of two distinct elements in the list. The function returns this maximum product.\n\n\n---\n\n# Solution 2\n\nBasically, we try to find the first max and second max numbers.\n\n---\n\n\u2B50\uFE0F Points\n\nIf current number is greater than the first max number so far, then \n\n```\ncurrent number will be the first max number\ncurrent first max number will be second max number\n```\nIf current number is less than the first max number so far, then compare \n```\nsecond max number = max(second max number, current number)\n```\n\nBecause there is still possibility that current number will be the second max number.\n\n---\n\nAt last, we multiply the first and second max numbers.\n\nEasy!\uD83D\uDE04\nLet\'s see a real algorithm\n\n\n---\n\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n```python []\nclass Solution:\n def maxProduct(self, nums: List[int]) -> int:\n first_max, second_max = 0, 0\n for num in nums:\n if num > first_max:\n second_max, first_max = first_max, num\n else:\n second_max = max(second_max, num)\n\n return (first_max - 1) * (second_max - 1)\n```\n```javascript []\nvar maxProduct = function(nums) {\n let firstMax = 0;\n let secondMax = 0;\n\n for (let num of nums) {\n if (num > firstMax) {\n [secondMax, firstMax] = [firstMax, num];\n } else {\n secondMax = Math.max(secondMax, num);\n }\n }\n\n return (firstMax - 1) * (secondMax - 1); \n};\n```\n```java []\nclass Solution {\n public int maxProduct(int[] nums) {\n int firstMax = 0;\n int secondMax = 0;\n\n for (int num : nums) {\n if (num > firstMax) {\n secondMax = firstMax;\n firstMax = num;\n } else {\n secondMax = Math.max(secondMax, num);\n }\n }\n\n return (firstMax - 1) * (secondMax - 1); \n }\n}\n```\n```C++ []\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n int firstMax = 0;\n int secondMax = 0;\n\n for (int num : nums) {\n if (num > firstMax) {\n swap(secondMax, firstMax);\n firstMax = num;\n } else {\n secondMax = max(secondMax, num);\n }\n }\n\n return (firstMax - 1) * (secondMax - 1); \n }\n};\n```\n\n## Step by step algorithm\n\n1. **Initialization:**\n\n```\nfirst_max, second_max = 0, 0\n```\n - `first_max` and `second_max` are initialized to 0. These variables will be used to keep track of the two largest elements in the list.\n\n2. **Iteration through the List:**\n\n```\nfor num in nums:\n if num > first_max:\n second_max, first_max = first_max, num\n else:\n second_max = max(second_max, num)\n```\n\n - The code iterates through each element `num` in the `nums` list.\n - For each `num`:\n - If `num` is greater than `first_max`, it means `num` is the new maximum. Therefore, the values of `second_max` and `first_max` are updated accordingly. This is done using the simultaneous assignment technique in Python: `second_max, first_max = first_max, num`.\n - If `num` is not greater than `first_max` but is greater than `second_max`, it means `num` is the new second maximum. Therefore, `second_max` is updated using `second_max = max(second_max, num)`.\n\n3. **Return Result:**\n\n```\nreturn (first_max - 1) * (second_max - 1)\n```\n\n - After the loop completes, the function returns the product of `(first_max - 1)` and `(second_max - 1)`. This is because the task is to find the maximum product of two distinct elements, so we subtract 1 from each of the largest elements before multiplying.\n\nThe algorithm efficiently finds the two largest elements in the list and returns their product minus 1.\n\n---\n\nThank you for reading my post.\n\u2B50\uFE0F Please upvote it and don\'t forget to subscribe to my channel!\n\n\u25A0 Subscribe URL\nhttp://www.youtube.com/channel/UC9RMNwYTL3SXCP6ShLWVFww?sub_confirmation=1\n\n\u25A0 Twitter\nhttps://twitter.com/CodingNinjaAZ\n\n\n### My next daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/special-positions-in-a-binary-matrix/solutions/4397604/video-give-me-5-minutes-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/qTAh4HGfUHk\n\n\u25A0 Timeline of the video\n\n`0:05` Explain algorithm of the first step\n`1:06` Explain algorithm of the second step\n`2:36` Coding\n`4:17` Time Complexity and Space Complexity\n`4:55` Step by step algorithm of my solution code\n\n### My previous daily coding challenge post and video.\n\npost\nhttps://leetcode.com/problems/element-appearing-more-than-25-in-sorted-array/solutions/4388310/video-give-me-5-minutes-2-solutions-how-we-think-about-a-solution/\n\nvideo\nhttps://youtu.be/bTm-6y7Ob0A\n\n\u25A0 Timeline of the video\n\n`0:07` Explain algorithm of Solution 1\n`2:46` Coding of solution 1\n`3:49` Time Complexity and Space Complexity of solution 1\n`4:02` Step by step algorithm of solution 1\n`4:09` Explain key points of Solution 2\n`4:47` Explain the first key point\n`6:06` Explain the second key point\n`7:40` Explain the third key point\n`9:33` Coding of Solution 2\n`14:20` Time Complexity and Space Complexity of Solution 2\n`14:48` Step by step algorithm with my stack solution code\n\n | 5 | 0 | ['C++', 'Java', 'Python3', 'JavaScript'] | 0 |
maximum-product-of-two-elements-in-an-array | 🚀🚀 Beats 100% | 0ms 🔥🔥 | beats-100-0ms-by-sanket_deshmukh_07-nkbn | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | The_Eternal_Soul | NORMAL | 2023-12-12T03:37:01.203847+00:00 | 2023-12-12T03:37:01.203869+00:00 | 434 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n ios_base::sync_with_stdio(false);\n cin.tie(0);\n cout.tie(0);\n \n auto maxi1 = max_element(nums.begin(),nums.end());\n int index1 = maxi1 - nums.begin();\n int num1 = (nums[index1]);\n num1 = num1 - 1;\n cout << num1 << endl;\n nums.erase(nums.begin()+index1);\n int maxi2 = *max_element(nums.begin(),nums.end());\n maxi2 = maxi2 - 1;\n cout << maxi2 << endl;\n return (num1 * maxi2);\n }\n};\n``` | 5 | 0 | ['Array', 'C', 'Sorting', 'Heap (Priority Queue)', 'Python', 'C++', 'Java', 'Python3', 'JavaScript'] | 1 |
maximum-product-of-two-elements-in-an-array | 💥|| EXPLAINED IN HINGLISH || OPTIMAL || BEGINNER FRIENDLY || 💥 | explained-in-hinglish-optimal-beginner-f-5vrb | Intuition\n1)START:\nBanayein ek max heap priority_queue ko istemal karke.\n\n2)Data Insertion:\nHar element nums array mein traverse karein.\nHar ek element ko | Sautramani | NORMAL | 2023-12-12T03:22:43.133607+00:00 | 2023-12-12T03:27:37.957017+00:00 | 279 | false | # Intuition\n1)**START**:\nBanayein ek max heap priority_queue ko istemal karke.\n\n2)**Data Insertion:**\nHar element nums array mein traverse karein.\nHar ek element ko max heap mein daalein (maxheap.push(i)).\n\n3)**Do Sabse Bade Elements**:\ni)Top method se max heap se sabse bada element (a) nikalein.\nUsse hatayein (maxheap.pop()).\nii)Fir se top method se doosra sabse bada element (b) nikalein.\nUsse bhi hatayein (maxheap.pop()).\n\n4)**Result Calculation**:\nIn dono bade elements se ek chhota karke ((a - 1) * (b - 1)) result nikalein.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n1)inserting elements into the max heap: O(N * log(N))\n\nHere, \'N\' is the number of elements in the \'nums\' array.\nFor each element, inserting into the max heap takes logarithmic time.\n\n2)Extracting two largest elements: O(2 * log(N)) \u2248 O(log(N))\n\nExtracting the top element from the max heap is a logarithmic operation.\nSince we do it twice, we consider it as O(log(N)).\n\n3)Overall Time Complexity: O(N * log(N))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n1)Priority Queue (max heap): O(N)\n\nIn the worst case, the priority queue can store all \'N\' elements of the \'nums\' array.\n\n2)integer Variables (a and b): O(1)\n\nConstant space is used for storing two variables.\n\n3)Overall Space Complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```C++ []\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n// Create a max heap (priority queue)\n priority_queue<int>maxheap;\n// Insert elements into the max heap\n for(auto i : nums)\n {\n maxheap.push({i});\n }\n // Extract two largest elements\n int a = maxheap.top();\n maxheap.pop();\n int b= maxheap.top();\n maxheap.pop();\n// Calculate and return the result\n return ((a-1)*(b-1));\n \n }\n};\n```\n```java []\n\nclass Solution {\n public int maxProduct(int[] nums) {\n // Create a max heap (priority queue)\n PriorityQueue<Integer> maxHeap = new PriorityQueue<>((a, b) -> b - a);\n\n // Insert elements into the max heap\n for (int num : nums) {\n maxHeap.offer(num);\n }\n\n // Extract two largest elements\n int a = maxHeap.poll();\n int b = maxHeap.poll();\n\n // Calculate and return the result\n return (a - 1) * (b - 1);\n }\n}\n\n```\n```python []\n def maxProduct(self, nums):\n # Create a max heap (priority queue)\n max_heap = [-num for num in nums]\n heapq.heapify(max_heap)\n\n # Extract two largest elements\n a = -heapq.heappop(max_heap)\n b = -heapq.heappop(max_heap)\n\n # Calculate and return the result\n return (a - 1) * (b - 1)\n```\n\n\n | 5 | 0 | ['Array', 'Sorting', 'Heap (Priority Queue)', 'Python', 'C++', 'Java'] | 3 |
maximum-product-of-two-elements-in-an-array | Java One Liner Solution | java-one-liner-solution-by-janhvi__28-qwpt | \nclass Solution {\n public int maxProduct(int[] nums) {\n Arrays.sort(nums);\n return (nums[nums.length-1]-1)*(nums[nums.length-2]-1);\n }\ | Janhvi__28 | NORMAL | 2022-10-23T18:23:18.030333+00:00 | 2022-10-23T18:23:18.030388+00:00 | 620 | false | ```\nclass Solution {\n public int maxProduct(int[] nums) {\n Arrays.sort(nums);\n return (nums[nums.length-1]-1)*(nums[nums.length-2]-1);\n }\n}\n``` | 5 | 0 | ['Java'] | 1 |
maximum-product-of-two-elements-in-an-array | [C++] 2 solns | c-2-solns-by-turbotorquetiger-t810 | \n// Sorting Soln\n// Time: O(N.logN)\n// Space: O(1)\n\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) \n {\n sort(nums.begin(), nu | ihavehiddenmyid | NORMAL | 2021-07-08T11:45:56.469347+00:00 | 2021-07-08T11:45:56.469389+00:00 | 469 | false | ```\n// Sorting Soln\n// Time: O(N.logN)\n// Space: O(1)\n\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) \n {\n sort(nums.begin(), nums.end());\n return (nums[nums.size() - 1] - 1) * (nums[nums.size() - 2] - 1);\n }\n};\n```\n```\n// Heaps Soln\n// Time: O(N.logK)\n// Space: O(N)\n\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) \n {\n priority_queue<int> maxheap;\n for (int n : nums) {\n maxheap.push(n);\n }\n \n int a = maxheap.top();\n maxheap.pop();\n int b = maxheap.top();\n \n return (a - 1) * (b - 1);\n }\n};\n``` | 5 | 0 | ['C', 'Sorting', 'Heap (Priority Queue)', 'C++'] | 3 |
maximum-product-of-two-elements-in-an-array | Very EASY java solution | very-easy-java-solution-by-gauravtaparia-ey0f | class Solution {\n public int maxProduct(int[] nums) {\n Arrays.sort(nums);\n return ((nums[nums.length-1]-1)*(nums[nums.length-2]-1));\n }\ | GauravTaparia | NORMAL | 2021-06-25T18:18:00.357075+00:00 | 2021-06-25T18:18:00.357120+00:00 | 580 | false | class Solution {\n public int maxProduct(int[] nums) {\n Arrays.sort(nums);\n return ((nums[nums.length-1]-1)*(nums[nums.length-2]-1));\n }\n} | 5 | 1 | ['Java'] | 1 |
maximum-product-of-two-elements-in-an-array | 2 lines java | 2-lines-java-by-logesh056-7fdl | {Arrays.sort(nums);\n int l=nums.length-1;\n return nums.length>1?((nums[l-1]-1)*(nums[l]-1)):0;\n } | logesh056 | NORMAL | 2020-07-10T10:25:38.678414+00:00 | 2020-07-10T10:25:38.678446+00:00 | 614 | false | {Arrays.sort(nums);\n int l=nums.length-1;\n return nums.length>1?((nums[l-1]-1)*(nums[l]-1)):0;\n } | 5 | 1 | ['Java'] | 0 |
maximum-product-of-two-elements-in-an-array | Python Solution - 90% Speed - O(n) Time, O(1) Space Complexity | python-solution-90-speed-on-time-o1-spac-76s7 | Python Solution - 90% Speed - O(n) Time, O(1) Space Complexity\n\nThe code below tracks two variables (a,b) representing the two highest values found in the arr | aragorn_ | NORMAL | 2020-07-02T16:23:01.936987+00:00 | 2021-05-19T23:31:19.154437+00:00 | 1,190 | false | **Python Solution - 90% Speed - O(n) Time, O(1) Space Complexity**\n\nThe code below tracks two variables (a,b) representing the two highest values found in the array. After one linear pass, we can use these values to return the answer.\nCheers,\n```\nclass Solution:\n def maxProduct(self, nums):\n a = b = float(\'-inf\')\n for x in nums:\n if x>a:\n a, b = x, a\n elif x>b:\n b = x\n return (a-1)*(b-1)\n``` | 5 | 0 | ['Python', 'Python3'] | 3 |
maximum-product-of-two-elements-in-an-array | For Absolute Beginner !!! Must See Solution | for-absolute-beginner-must-see-solution-mqwv5 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n- First we sort the whole array\n- with the help of for loop we will take | RamHD | NORMAL | 2024-06-12T15:45:47.470042+00:00 | 2024-06-12T15:45:47.470085+00:00 | 7 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n- First we sort the whole array\n- with the help of for loop we will take last and second last number present in sorted array\n- simply do the needful in the end\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n sort(nums.begin(),nums.end());\n int n=nums.size();\n int p=0;\n int q=0;\n for(int i=0;i<n;i++)\n {\n p=nums[n-2];\n q=nums[n-1];\n }\n return (p-1)*(q-1);\n }\n};\n``` | 4 | 0 | ['C++'] | 0 |
maximum-product-of-two-elements-in-an-array | 🔥🔥 Explicación y Resolución Del Ejercicio En Español Java | Python | PHP | JavaScript | C++ 🔥🔥 | explicacion-y-resolucion-del-ejercicio-e-opiu | Lectura\nProducto m\xE1ximo de dos elementos en un array(Java, Python, PHP, C++, Javascript)\n\nDado un array nums, obtenga los 2 valores mayores y devuelva el | hermescoder02 | NORMAL | 2023-12-15T04:33:14.189568+00:00 | 2024-03-22T19:08:09.868964+00:00 | 32 | false | # Lectura\n*Producto m\xE1ximo de dos elementos en un array(Java, Python, PHP, C++, Javascript)*\n\nDado un array nums, obtenga los 2 valores mayores y devuelva el siguiente resultado :\n\n (mayor - 1) * (segundo_mayor - 1)\n\n\n\n# Video\n\nhttps://youtu.be/J8qwWF67x-E\n\nSi te gust\xF3 el contenido \xA1te invito a suscribirte!:\n\u2705https://www.youtube.com/@hermescoder?sub_confirmation=1\n\n# Pasos para realizar el algoritmo:\n\n**1.-** Se inicializan dos variables, **mayor** y **segundo_mayor**, a 0. \n\nEstas variables se utilizar\xE1n para almacenar los dos n\xFAmeros m\xE1s grandes del arreglo nums.\n \n**2.**- Se recorre el arreglo nums y se compara el n\xFAmero actual con la variable mayor.\n\nSi el n\xFAmero actual tiene un valor superior, se establece la variable mayor con el n\xFAmero actual y segundo_mayor en el valor anterior de mayor.\n\nDe lo contrario, se establece segundo_mayor con el n\xFAmero m\xE1s grande entre la variable mayor y el n\xFAmero evaluado.\n\n**3.-** Se devuelve la multiplicaci\xF3n de mayor y segundo_mayor. Este es el resultado de los dos m\xE1ximos n\xFAmeros en el arreglo nums.\n# C\xF3digo \n\n```Java []\nclass Solution {\n public int maxProduct(int[] nums) {\n \n //paso#1\n int mayor = 0;\n int segundo_mayor = 0;\n \n for (int num : nums) {\n //paso#2\n if (num > mayor) {\n segundo_mayor = mayor ;\n mayor = num;\n continue;\n } \n else segundo_mayor = Math.max(segundo_mayor , num);\n }\n \n //paso#3\n return (mayor - 1) * (segundo_mayor - 1);\n }\n}\n```\n```Python []\nclass Solution(object):\n def maxProduct(self, nums):\n # Paso #1\n mayor = 0\n segundo_mayor = 0\n \n for num in nums:\n # Paso #2\n if num > mayor:\n segundo_mayor = mayor\n mayor = num\n continue\n else:\n segundo_mayor = max(segundo_mayor, num)\n \n # Paso #3\n return (mayor - 1) * (segundo_mayor - 1)\n```\n```PHP []\nclass Solution {\n \n /**\n * @param Integer[] $nums\n * @return Integer\n */\n function maxProduct(array $nums): int {\n // Paso #1\n $mayor = 0;\n $segundo_mayor = 0;\n \n foreach ($nums as $num) {\n // Paso #2\n if ($num > $mayor) {\n $segundo_mayor = $mayor;\n $mayor = $num;\n continue;\n } else {\n $segundo_mayor = max($segundo_mayor, $num);\n }\n }\n \n // Paso #3\n return ($mayor - 1) * ($segundo_mayor - 1);\n }\n }\n```\n```JavaScript []\nfunction maxProduct(nums) {\n // Paso #1\n let mayor = 0;\n let segundoMayor = 0;\n \n for (let num of nums) {\n // Paso #2\n if (num > mayor) {\n segundoMayor = mayor;\n mayor = num;\n continue;\n } else {\n segundoMayor = Math.max(segundoMayor, num);\n }\n }\n \n // Paso #3\n return (mayor - 1) * (segundoMayor - 1);\n}\n```\n```C++ []\nclass Solution {\n public:\n int maxProduct(vector<int>& nums) {\n // Paso #1\n int mayor = 0;\n int segundoMayor = 0;\n \n for (int num : nums) {\n // Paso #2\n if (num > mayor) {\n segundoMayor = mayor;\n mayor = num;\n continue;\n } else {\n segundoMayor = max(segundoMayor, num);\n }\n }\n \n // Paso #3\n return (mayor - 1) * (segundoMayor - 1);\n }\n };\n```\n\n\n\n# Imagenes de la Explicaci\xF3n\n\n\n\n\n\n\n\n\n\n\n\n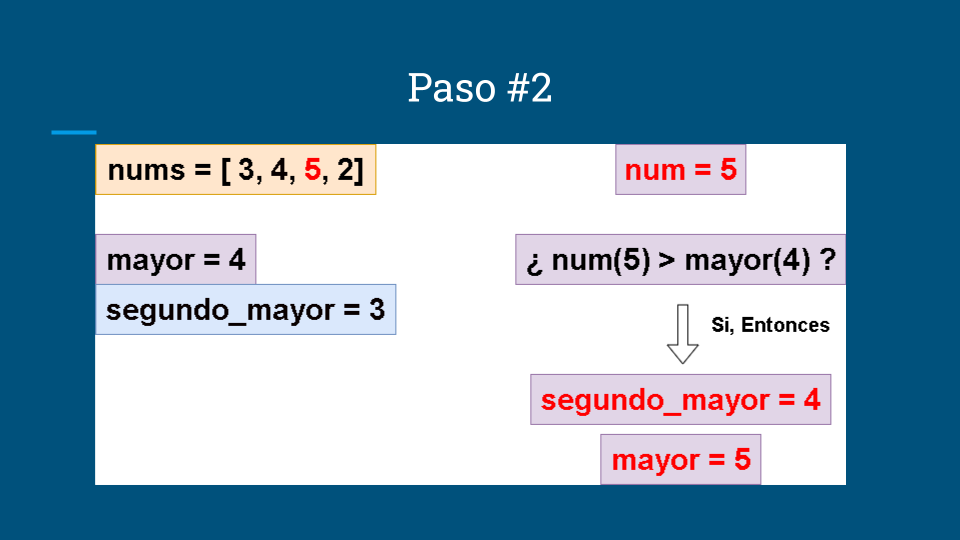\n\n\n\n\n | 4 | 0 | ['Array', 'PHP', 'Python', 'C++', 'Java', 'JavaScript'] | 0 |
maximum-product-of-two-elements-in-an-array | ✅ One Line Solution | one-line-solution-by-mikposp-a1cf | Code #1 - The Fastest\nTime complexity: O(n). Space complexity: O(1).\n\nclass Solution:\n def maxProduct(self, nums: List[int]) -> int:\n return prod | MikPosp | NORMAL | 2023-12-12T12:09:04.539270+00:00 | 2023-12-12T12:50:57.057959+00:00 | 273 | false | # Code #1 - The Fastest\nTime complexity: $$O(n)$$. Space complexity: $$O(1)$$.\n```\nclass Solution:\n def maxProduct(self, nums: List[int]) -> int:\n return prod(x-1 for x in nlargest(2,nums)) \n```\n\n# Code #2 - The Least Efficient\nTime complexity: $$O(n*log(n))$$. Space complexity: $$O(n)$$.\n```\nclass Solution:\n def maxProduct(self, nums: List[int]) -> int:\n return prod(x-1 for x in sorted(nums)[-2:])\n```\n\n# Code #3 - Using Max() Twice\nTime complexity: $$O(n)$$. Space complexity: $$O(1)$$.\n```\nclass Solution:\n def maxProduct(self, nums: List[int]) -> int:\n return (max(chain(nums[:(i:=nums.index(max(nums)))], nums[i+1:]))-1)*(nums[i]-1)\n```\n\n# Code #4 - Using Argmax()\nTime complexity: $$O(n)$$. Space complexity: $$O(1)$$.\n```\nfrom numpy import argmax\nclass Solution:\n def maxProduct(self, nums: List[int]) -> int:\n return (max(chain(nums[:(i:=argmax(nums))], nums[i+1:]))-1)*(nums[i]-1)\n``` | 4 | 0 | ['Array', 'Sorting', 'Heap (Priority Queue)', 'Python', 'Python3'] | 0 |
maximum-product-of-two-elements-in-an-array | C++ || Easy Solution || O(N) Solution | c-easy-solution-on-solution-by-deepak140-gdag | Intuition\nLet us say the pair is nums[i] and nums[j] (where nums[i]>=nums[j]) where i!=j and 0<=i,j=mx we found an element greater than mx so our mx is nums[i] | deepak1408 | NORMAL | 2023-12-12T07:29:26.141000+00:00 | 2023-12-12T07:29:26.141027+00:00 | 570 | false | # Intuition\nLet us say the pair is nums[i] and nums[j] (where nums[i]>=nums[j]) where i!=j and 0<=i,j<n.\n(nums[i]-1)*(nums[j]-1) will be maximum if nums[i] and nums[j] are the first and second maximum elements in the array respectively.\n\n# Approach\n- **Sorting:**\nLet us sort the array last two elements will be our target elements so return (nums[n-1]-1)*(nums[n-2]-1).\n\n- **Two Variable Approach:**\nLet us consider two variables mx and smx. Now initialise mx with maximum of nums[0] & nums[1] and smx with minimum of nums[0] & nums[1] so till 2 elements these are the first and second maximum elements in the array. \n\nLet us traverse the array from index 2. If nums[i]>=mx we found an element greater than mx so our mx is nums[i] but smx is also changed smx will be our previous mx.\n\nThere is a catch here. There might be a case where nums[i]<mx but nums[i]>smx then we need to change smx to nums[i] because that would be our second maximum element.\n\n\n# Complexity\n- Time complexity:\nSorting: \nO(NLogN)\nTwo Variable Approach\nO(N)\n\n- Space complexity:\nSorting: \nO(1)\nTwo Variable Approach\nO(1)\n\n# Code\n```\n// TC: O(NLOGN)\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n int n = nums.size();\n sort(nums.begin(),nums.end());\n return (nums[n-1]-1)*(nums[n-2]-1);\n }\n};\n```\n```\n// TC: O(N)\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n int n = nums.size();\n int mx = max(nums[0],nums[1]);\n int smx = min(nums[0],nums[1]);\n for(int i = 2;i<n;i++){\n if(mx <= nums[i]){\n smx = mx;\n mx = nums[i];\n }else if(mx>nums[i] && smx<nums[i]){\n smx = nums[i];\n }\n }\n mx--;\n smx--;\n int ans = mx*smx;\n return ans;\n }\n};\n``` | 4 | 0 | ['C++'] | 0 |
maximum-product-of-two-elements-in-an-array | Java | Find 2 max nums | Simple | Clean code | java-find-2-max-nums-simple-clean-code-b-bcmm | Complexity\n- Time complexity: O(n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(1)\n Add your space complexity here, e.g. O(n) \n\n# Co | judgementdey | NORMAL | 2023-12-12T06:32:28.845380+00:00 | 2023-12-12T06:32:28.845413+00:00 | 345 | false | # Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int maxProduct(int[] nums) {\n int max1 = 0, max2 = 0;\n\n for (var n : nums) {\n if (n > max1) {\n max2 = max1;\n max1 = n;\n } else if (n > max2) {\n max2 = n;\n }\n }\n return (max1 - 1) * (max2 - 1);\n }\n}\n```\nIf you like my solution, please upvote it! | 4 | 0 | ['Array', 'Java'] | 0 |
maximum-product-of-two-elements-in-an-array | Python3 Solution | python3-solution-by-motaharozzaman1996-9evf | \n\nclass Solution:\n def maxProduct(self, nums: List[int]) -> int:\n nums.sort()\n return (nums[-1]-1)*(nums[-2]-1)\n | Motaharozzaman1996 | NORMAL | 2023-12-12T03:03:34.519922+00:00 | 2023-12-12T03:03:34.519950+00:00 | 273 | false | \n```\nclass Solution:\n def maxProduct(self, nums: List[int]) -> int:\n nums.sort()\n return (nums[-1]-1)*(nums[-2]-1)\n``` | 4 | 0 | ['Python', 'Python3'] | 1 |
maximum-product-of-two-elements-in-an-array | 0ms||beats 100%users||beginner friendly||easy approach | 0msbeats-100usersbeginner-friendlyeasy-a-seey | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Hitheash | NORMAL | 2023-12-12T01:53:08.460590+00:00 | 2023-12-12T01:53:08.460625+00:00 | 441 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n int max1=INT_MIN,max2=INT_MIN;\n for(auto &it:nums){\n if(it>max1){\n max2=max1;\n max1=it;\n }\n else if(it>max2&&max2!=max1){\n max2=it;\n }\n }\n //cout<<max1<<" "<<max2;\n return (max1-1)*(max2-1);\n }\n};\n``` | 4 | 0 | ['C++'] | 3 |
maximum-product-of-two-elements-in-an-array | Java | 2 liner | Easy to Understand | for Beginners | 0 ms | fast💡 | java-2-liner-easy-to-understand-for-begi-l397 | Approach\n- using quicksort to sort nums\n- returning [last element - 1] * [second last element - 1]\n\n# Complexity\n- Time complexity: O(n log n)\n\n- Space c | AbirDey | NORMAL | 2023-04-22T05:12:53.823285+00:00 | 2023-04-22T05:12:53.823306+00:00 | 379 | false | # Approach\n- using quicksort to sort nums\n- returning [last element - 1] * [second last element - 1]\n\n# Complexity\n- Time complexity: O(n log n)\n\n- Space complexity: O(log n)\n\n# Code\n```\nclass Solution {\n public int maxProduct(int[] nums) {\n Arrays.sort(nums);\n return (nums[nums.length-1]-1)*(nums[nums.length-2]-1);\n }\n}\n```\n\n\n | 4 | 0 | ['Array', 'Sorting', 'Java'] | 0 |
maximum-product-of-two-elements-in-an-array | ☕ Java Solution | O(n) approach | Runtime 0 ms | Beats 100% 📕 | java-solution-on-approach-runtime-0-ms-b-ohqf | Intuition\nIn order to solve this problem we need to find max1 and max2. \n\nA naive approach to this task will be to sort the array, but we do not want to do i | B10nicle | NORMAL | 2023-02-25T16:20:27.054839+00:00 | 2023-02-26T18:22:21.303538+00:00 | 552 | false | # Intuition\nIn order to solve this problem we need to find max1 and max2. \n\nA naive approach to this task will be to sort the array, but we do not want to do it because we will get O(n log n) due to sorting. All we need to do is to find max1 and max2 and multiply them. How will we do it?\n\n# Approach\n1. Initialize max1 and max2 and minimum possible values.\n2. Iterate over the array and find max1 and max2 with the following logic:\n\n ```\n if (max1 <= nums[i]) {\n max2 = max1;\n max1 = nums[i];\n }\n if (nums[i] < max1 && nums[i] > max2) {\n max2 = nums[i];\n }\n ```\n3. Do math and return the result.\n\n# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n```\nclass Solution {\n public int maxProduct(int[] nums) {\n int max1 = Integer.MIN_VALUE;\n int max2 = Integer.MIN_VALUE;\n for (int i = 0; i < nums.length; i++) {\n if (max1 <= nums[i]) {\n max2 = max1;\n max1 = nums[i];\n }\n if (nums[i] < max1 && nums[i] > max2) {\n max2 = nums[i];\n }\n }\n return (max1 - 1) * (max2 - 1);\n }\n}\n```\n\n | 4 | 0 | ['Java'] | 1 |
maximum-product-of-two-elements-in-an-array | EASY AND NAIVE SOLUTION USING C++ | easy-and-naive-solution-using-c-by-king_-1dax | Intuition\n Describe your first thoughts on how to solve this problem. \nNO NEED OF SORTING\n# Approach\n Describe your approach to solving the problem. \nTwo V | King_of_Kings101 | NORMAL | 2022-12-27T14:02:56.162692+00:00 | 2022-12-27T14:04:54.808495+00:00 | 520 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nNO NEED OF SORTING\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTwo Variable and one time traversal to array.\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ --> O(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n int a = INT_MIN;\n int b = INT_MIN;\n\n for(int i = 0 ; i < nums.size() ; i++)\n {\n if(b<nums[i])\n {\n if(a<nums[i])\n {\n b = a ;\n a = nums[i];\n }\n else\n b = nums[i];\n }\n }\n return (a-1)*(b-1);\n }\n};\n``` | 4 | 0 | ['Array', 'C++'] | 0 |
maximum-product-of-two-elements-in-an-array | Java solution with 0ms runtime | Beats 100% | No Sorting | java-solution-with-0ms-runtime-beats-100-v2de | If you found it easy to understand, Please do upvote :)\nThankyou!!\n------------------------------------------------------------------------------------------- | JavithSadhamHussain | NORMAL | 2022-12-03T11:27:22.842788+00:00 | 2022-12-03T11:27:22.842838+00:00 | 563 | false | **If you found it easy to understand, Please do upvote :)\nThankyou!!**\n**---------------------------------------------------------------------------------------------------------------**\n\n\n**---------------------------------------------------------------------------------------------------------------**\n```\nTime Complexity = O(n)\nSpace Complexity = O(1)\n```\n**---------------------------------------------------------------------------------------------------------------**\n```\npublic int maxProduct(int[] nums) \n {\n //Declare 2 values & assign them to 0\n //Its ok to assign zero\n //Since range of elemnts is given as, 1 <= nums[i] <= 10^3,\n int winner=0, runner=0;\n \n\t\t//Now, our task to find the maximum 2 values.\n\t\tfor(int i=0; i<nums.length; i++)\n {\n if(nums[i] > winner)\n {\n runner = winner;\n winner = nums[i];\n }\n else if(nums[i] > runner)\n {\n runner = nums[i];\n }\n }\n \n\t\t//Finally returning the result.\n return (winner-1) * (runner-1);\n }\n``` | 4 | 0 | ['Java'] | 0 |
maximum-product-of-two-elements-in-an-array | Java Solution | Two Approaches - Heap based and find the 2 max numbers. | java-solution-two-approaches-heap-based-wanee | Heap Based Solution : Time complexity : O(n)\n\n\nclass Solution {\n\n public int maxProduct(int[] nums) {\n PriorityQueue<Integer> pq = new PriorityQ | 1605448777 | NORMAL | 2022-08-20T18:03:04.442995+00:00 | 2022-08-20T18:03:04.443044+00:00 | 684 | false | **Heap Based Solution :** Time complexity : O(n)\n\n```\nclass Solution {\n\n public int maxProduct(int[] nums) {\n PriorityQueue<Integer> pq = new PriorityQueue<>();\n for (int i = 0; i < 2; i++) pq.add(nums[i]);\n for (int i = 2; i < nums.length; i++) {\n if (pq.peek() < nums[i]) {\n pq.poll();\n pq.add(nums[i]);\n }\n }\n return (pq.poll() - 1) * (pq.poll() - 1);\n }\n}\n```\n\n**Finding biggest and second biggest nos :** Time complexity : O(n)\n\n```\nclass Solution {\n\n public int maxProduct(int[] arr) {\n int first = Integer.MIN_VALUE, second = Integer.MIN_VALUE;\n for (int i = 0; i < arr.length; i++) {\n if (arr[i] > first) {\n second = first;\n first = arr[i];\n } else if (arr[i] > second) second = arr[i];\n }\n return (first - 1) * (second - 1);\n }\n}\n``` | 4 | 0 | ['Heap (Priority Queue)', 'Java'] | 0 |
maximum-product-of-two-elements-in-an-array | Heap Java Solution | heap-java-solution-by-codertuhin094-07nk | \nclass Solution {\n public int maxProduct(int[] nums) {\n PriorityQueue<Integer> pq = new PriorityQueue<>(Collections.reverseOrder());\n for ( | codertuhin094 | NORMAL | 2021-08-25T08:28:29.012399+00:00 | 2021-08-25T08:28:29.012439+00:00 | 237 | false | ```\nclass Solution {\n public int maxProduct(int[] nums) {\n PriorityQueue<Integer> pq = new PriorityQueue<>(Collections.reverseOrder());\n for (int i =0;i<nums.length;i++){\n pq.add(nums[i]);\n }\n\n int n1 = pq.poll();\n int n2 = pq.poll();\n\n return (n1-1)*(n2-1);\n }\n}\n``` | 4 | 0 | [] | 0 |
maximum-product-of-two-elements-in-an-array | Java beats 100% without sorting | java-beats-100-without-sorting-by-red_hu-a28l | \nclass Solution {\n public int maxProduct(int[] nums) {\n int max1 = nums[0]>nums[1]?nums[0]:nums[1];\n int max2 = nums[0]<nums[1]?nums[0]:num | red_hue | NORMAL | 2021-08-20T09:16:09.337783+00:00 | 2021-08-20T09:16:09.337811+00:00 | 220 | false | ```\nclass Solution {\n public int maxProduct(int[] nums) {\n int max1 = nums[0]>nums[1]?nums[0]:nums[1];\n int max2 = nums[0]<nums[1]?nums[0]:nums[1];\n for(int i=2;i<nums.length;i++){\n if(nums[i]>max1){\n max2=max1;\n max1=nums[i]; \n }\n else if(nums[i]>max2)\n max2=nums[i];\n }\n return (max1-1)*(max2-1);\n }\n}\n``` | 4 | 0 | [] | 0 |
maximum-product-of-two-elements-in-an-array | [C++]| 0 ms| Faster than 100% | Speedy solution | c-0-ms-faster-than-100-speedy-solution-b-b04n | ```\nint maxProduct(vector& nums) {\n int max1=-1,max2=-1;\n for(auto i: nums){\n auto temp = max(i , min(max1,max2));\n max2 = max( | dexter_2000 | NORMAL | 2021-06-06T07:11:50.339946+00:00 | 2021-06-06T07:11:50.339993+00:00 | 436 | false | ```\nint maxProduct(vector<int>& nums) {\n int max1=-1,max2=-1;\n for(auto i: nums){\n auto temp = max(i , min(max1,max2));\n max2 = max(max1,max2);\n max1=temp;\n }\n return (max1-1)*(max2-1);\n } | 4 | 1 | ['C', 'C++'] | 1 |
maximum-product-of-two-elements-in-an-array | Java O(n) solution, 100% faster | java-on-solution-100-faster-by-backend_e-1i0x | ```\n public int maxProduct(int[] nums) {\n int len = nums.length;\n if(len == 1){\n return nums[0];\n }\n int first = I | Backend_engineer123 | NORMAL | 2021-03-24T17:45:08.910284+00:00 | 2021-03-24T17:46:12.735679+00:00 | 314 | false | ```\n public int maxProduct(int[] nums) {\n int len = nums.length;\n if(len == 1){\n return nums[0];\n }\n int first = Integer.MIN_VALUE;\n int second = Integer.MIN_VALUE;\n\n if(len == 2){\n return (nums[0]-1) * (nums[1]-1);\n }\n for(int i = 0 ; i < len; i++){\n if(nums[i] >= second){\n if(nums[i] >= first){\n second = first;\n first = nums[i];\n }\n else {\n second = nums[i];\n }\n }\n }\n return (first-1) * (second-1);\n } | 4 | 0 | ['Java'] | 0 |
maximum-product-of-two-elements-in-an-array | C++ Short and Simple O(n) Solution | c-short-and-simple-on-solution-by-yehudi-aawq | \nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n // Find first max\n int m1_ind = max_element(nums.begin(), nums.end()) - nu | yehudisk | NORMAL | 2020-12-17T15:13:22.697089+00:00 | 2020-12-17T15:13:22.697131+00:00 | 272 | false | ```\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n // Find first max\n int m1_ind = max_element(nums.begin(), nums.end()) - nums.begin();\n int m1 = nums[m1_ind]-1;\n nums[m1_ind] = 0;\n // Find second max\n int m2_ind = max_element(nums.begin(), nums.end()) - nums.begin();\n \n return m1 * (nums[m2_ind]-1);\n }\n};\n```\n**Like it? please upvote...** | 4 | 3 | ['C'] | 1 |
maximum-product-of-two-elements-in-an-array | JAVA | 2-line Solution | java-2-line-solution-by-onefineday01-cfi2 | \nclass Solution {\n public int maxProduct(int[] nums) {\n Arrays.sort(nums);\n return Math.max(((nums[0]-1)*(nums[1]-1)), ((nums[nums.length-2 | onefineday01 | NORMAL | 2020-06-07T10:36:39.866574+00:00 | 2020-06-07T10:37:43.864775+00:00 | 489 | false | ```\nclass Solution {\n public int maxProduct(int[] nums) {\n Arrays.sort(nums);\n return Math.max(((nums[0]-1)*(nums[1]-1)), ((nums[nums.length-2]-1)*(nums[nums.length-1]-1)));\n }\n}\n```\n**do upvote if you like the solution** | 4 | 1 | ['Java'] | 1 |
maximum-product-of-two-elements-in-an-array | C++ | Largest and second Largest | Commented with explanation | c-largest-and-second-largest-commented-w-fj67 | Find the largest and second largest from the array, by traversing the array once\n It is possible that the largest number = second largest number, eg. [1,5,4,5] | ayzastark | NORMAL | 2020-06-03T08:55:35.796090+00:00 | 2020-06-03T08:55:35.796135+00:00 | 489 | false | * Find the largest and second largest from the array, by traversing the array *once*\n* It is possible that the largest number = second largest number, eg. ```[1,5,4,5]``` \n\n```\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) \n {\n int max1 = INT_MIN; //largest number\n int max2 = INT_MIN; //second largest number\n \n for(int i=0; i<nums.size(); i++)\n {\n int val = nums[i];\n \n if(val > max1) //value greater than max1, update second largest with largest so far \n {\n max2 = max1;\n max1 = val;\n }\n \n else if(val <= max1 && val > max2) //equality holds as max1 = max2 can be possible\n {\n max2 = val;\n }\n }\n \n return (max1-1)*(max2-1);\n }\n};\n```\n\n**Upvote if this helped!** | 4 | 0 | ['C', 'C++'] | 0 |
maximum-product-of-two-elements-in-an-array | Java all positive or negative | java-all-positive-or-negative-by-hobiter-0i66 | \npublic int maxProduct(int[] nums) {\n Arrays.sort(nums);\n return Math.max((nums[0] - 1) * (nums[1] - 1), (nums[nums.length - 1] - 1) * (nums[nu | hobiter | NORMAL | 2020-05-31T04:01:05.048202+00:00 | 2020-05-31T04:01:05.048387+00:00 | 480 | false | ```\npublic int maxProduct(int[] nums) {\n Arrays.sort(nums);\n return Math.max((nums[0] - 1) * (nums[1] - 1), (nums[nums.length - 1] - 1) * (nums[nums.length - 2] - 1));\n }\n``` | 4 | 2 | [] | 0 |
maximum-product-of-two-elements-in-an-array | SIMPLE MAX-HEAP C++ SOLUTION | simple-max-heap-c-solution-by-jeffrin200-7lb2 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Jeffrin2005 | NORMAL | 2024-08-01T16:57:27.692441+00:00 | 2024-08-01T16:57:27.692477+00:00 | 18 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:o(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:o(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n // Max-heap to store larger elements in the top \n priority_queue<int> pq(nums.begin(),nums.end());\n int max1 = pq.top();\n pq.pop();\n int max2 = pq.top();\n pq.pop();\n return (max1 - 1) * (max2 - 1);\n }\n};\n``` | 3 | 0 | ['C++'] | 0 |
maximum-product-of-two-elements-in-an-array | Beats 100% in Runtime | beats-100-in-runtime-by-nurliaidin-xhzz | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Nurliaidin | NORMAL | 2023-12-20T12:19:22.013721+00:00 | 2023-12-20T12:19:22.013782+00:00 | 190 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```javascript []\n/**\n * @param {number[]} nums\n * @return {number}\n */\nvar maxProduct = function(nums) {\n nums.sort((a, b) => (b - a));\n return (nums[0]-1)*(nums[1]-1);\n};\n```\n```cpp []\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n sort(nums.begin(), nums.end());\n reverse(nums.begin(), nums.end());\n return (nums[0]-1)*(nums[1]-1);\n }\n};\n```\n\n | 3 | 0 | ['C++', 'JavaScript'] | 0 |
maximum-product-of-two-elements-in-an-array | Maximum Product Of Two Elements In Array||Beats 100%💯|| Full commented code with explanation✅✅ | maximum-product-of-two-elements-in-array-wld5 | Approach\n Describe your approach to solving the problem. \n- largest and secondLargest are initialized to the minimum integer value. \n- The code iterates thro | Vishu6403 | NORMAL | 2023-12-20T09:55:27.302508+00:00 | 2023-12-20T09:56:33.469479+00:00 | 1,114 | false | # Approach\n<!-- Describe your approach to solving the problem. -->\n- `largest` and `secondLargest` are initialized to the minimum integer value. \n- The code iterates through the input array nums. For each element `nums[i]`, it compares with the current largest and secondLargest.\n- If `nums[i]` is greater than the current largest, it becomes the new largest, and the previous largest becomes the new secondLargest.\n- If `nums[i]` is not greater than largest but is greater than the current secondLargest, it becomes the new secondLargest.\n- After iterating through the array and finding the two largest elements, the code calculates the maximum product of two largest elements. `(largest-1) * (secondLargest-1)`\n- ALSO NOTE WE HAVE NOT CHECKED FOR `nums[i]<largest` IN ELSE IF LOOP BECAUSE WE ARE NOT GIVEN THAT THE TWO NUMBERS SHOULD BE UNIQUE.\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int maxProduct(int[] nums) {\n // Initialize\n int largest = Integer.MIN_VALUE;\n int secondLargest = Integer.MIN_VALUE;\n\n // Iterate through the array to find the two largest elements.\n for (int i = 0; i < nums.length; i++) {\n if (nums[i] > largest) {\n // If the current element is greater than the largest, update both largest and secondLargest.\n secondLargest = largest;\n largest = nums[i];\n } else if (nums[i] > secondLargest) {\n // If the current element is greater than the second largest, update only secondLargest.\n secondLargest = nums[i];\n }\n }\n\n // Calculate the maximum product of two largest elements minus 1.\n int ans = (largest - 1) * (secondLargest - 1);\n return ans;\n }\n}\n\n``` | 3 | 0 | ['Array', 'Sorting', 'Java'] | 0 |
maximum-product-of-two-elements-in-an-array | ✅ EASY C++ SOLUTION ☑️ | easy-c-solution-by-2005115-x988 | PLEASE UPVOTE MY SOLUTION IF YOU LIKE IT\n# CONNECT WITH ME\n### https://www.linkedin.com/in/pratay-nandy-9ba57b229/\n#### https://www.instagram.com/pratay_nand | 2005115 | NORMAL | 2023-12-12T14:57:54.329467+00:00 | 2023-12-12T14:57:54.329501+00:00 | 638 | false | # **PLEASE UPVOTE MY SOLUTION IF YOU LIKE IT**\n# **CONNECT WITH ME**\n### **[https://www.linkedin.com/in/pratay-nandy-9ba57b229/]()**\n#### **[https://www.instagram.com/pratay_nandy/]()**\n\n# Approach\nThe provided C++ code is aiming to find the maximum product of two distinct elements in the given vector `nums`. It uses two variables, `num1` and `num2`, to keep track of the two largest elements encountered while iterating through the vector. The final result is the product of these two largest elements minus one.\n\nHere\'s a step-by-step explanation of the approach:\n\n1. Initialize two variables, `num1` and `num2`, to store the two largest elements. Initialize them with the minimum possible integer value (`INT_MIN`) to ensure that any element in the array will be greater.\n\n2. Iterate through each element `num` in the vector `nums`.\n\n3. Check if the current element `num` is greater than or equal to the current largest element `num1`. If true:\n - Update `num2` with the value of `num1`.\n - Update `num1` with the current element `num`.\n\n4. If the current element `num` is not greater than or equal to `num1` but is greater than `num2`, update `num2` with the value of the current element `num`.\n\n5. After the loop, `num1` and `num2` will contain the two largest elements in the vector.\n\n6. Return the product of the two largest elements minus one: `(num2 - 1) * (num1 - 1)`.\n\n\n# Complexity\n- Time complexity:**0(N)**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:**0(1)**\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n int n = nums.size();\n int num1 = INT_MIN;\n int num2 = INT_MIN;\n for(int num : nums)\n {\n if(num >= num1){\n num2 = num1;\n num1 = num; \n }\n else if(num > num2)\n {\n num2 = num;\n }\n }\n return (num2-1)*(num1-1);\n }\n};\n``` | 3 | 0 | ['Array', 'C++'] | 1 |
maximum-product-of-two-elements-in-an-array | Beats 100% of users with C++ , Brute Force Approach ( Constant Space ) | beats-100-of-users-with-c-brute-force-ap-si8o | Intuition\n Describe your first thoughts on how to solve this problem. \n\n\n\n\n\n\n\nif you like the approach please upvote it\n\n\n\n\n\n\nif you like the ap | abhirajpratapsingh | NORMAL | 2023-12-12T10:45:21.630186+00:00 | 2023-12-12T10:45:21.630206+00:00 | 7 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n\n\n\n\n\n\nif you like the approach please upvote it\n\n\n\n\n\n\nif you like the approach please upvote it\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ --> O ( N )\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ --> O ( 1 )\n\n# Code\n```\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) \n {\n int max;\n int second_max;\n int ans=0;\n if(nums[0]>nums[1])\n { max=nums[0];\n second_max=nums[1];\n }\n else\n {\n second_max=nums[0];\n max=nums[1];\n }\n for(int i=2;i<nums.size();i++)\n {\n if(nums[i]>max)\n {\n second_max=max;\n max=nums[i];\n }\n else\n {\n if(nums[i]>second_max)\n second_max=nums[i];\n }\n }\n max--;\n second_max--;\n ans=max*second_max;\n return ans;\n }\n};\n``` | 3 | 0 | ['Math', 'C++'] | 0 |
maximum-product-of-two-elements-in-an-array | JAVA Solution Explained in HINDI | java-solution-explained-in-hindi-by-the_-kdax | https://youtu.be/4BXBsrpglNk\n\nFor explanation, watch the above video and do like, share and subscribe the channel. \u2764\uFE0F\n# Code\n\nclass Solution {\n | The_elite | NORMAL | 2023-12-12T04:34:22.801502+00:00 | 2023-12-12T04:34:22.801527+00:00 | 455 | false | https://youtu.be/4BXBsrpglNk\n\nFor explanation, watch the above video and do like, share and subscribe the channel. \u2764\uFE0F\n# Code\n```\nclass Solution {\n public int maxProduct(int[] nums) {\n \n Arrays.sort(nums);\n int x = nums[nums.length - 1];\n int y = nums[nums.length - 2];\n\n return (x - 1) * ( y - 1);\n }\n}\n``` | 3 | 0 | ['Java'] | 0 |
maximum-product-of-two-elements-in-an-array | Try with Heap | Simple Solution | try-with-heap-simple-solution-by-saim75-3wdy | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | saim75 | NORMAL | 2023-12-12T03:10:31.128062+00:00 | 2023-12-12T03:10:31.128085+00:00 | 42 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxProduct(self, nums: List[int]) -> int:\n heap = []\n for num in nums:\n heapq.heappush(heap, -num)\n max_val = -heapq.heappop(heap)\n second_max_val = -heapq.heappop(heap)\n return (max_val-1) * (second_max_val-1)\n``` | 3 | 0 | ['Python3'] | 0 |
maximum-product-of-two-elements-in-an-array | C# Solution for Maximum Product of Two Elements In An Array Problem | c-solution-for-maximum-product-of-two-el-g143 | Intuition\n Describe your first thoughts on how to solve this problem. \nThe intuition behind the provided solution: find the two largest elements in the array | Aman_Raj_Sinha | NORMAL | 2023-12-12T03:00:09.079690+00:00 | 2023-12-12T03:00:09.079719+00:00 | 453 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe intuition behind the provided solution: find the two largest elements in the array and then calculate their product after subtracting 1 from each, giving the maximum possible value of (nums[i]-1)*(nums[j]-1).\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1.\tInitialize max1 and max2 as the two minimum integer values.\n2.\tIterate through the array.\n3.\tUpdate max1 and max2 accordingly if a larger value is found.\n4.\tReturn the product of (max1 - 1) and (max2 - 1).\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nThe time complexity of this solution is O(n), where \u2018n\u2019 is the length of the input array nums. This is because it iterates through the array only once to find the two maximum elements.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nThe space complexity is O(1), as the solution uses only a constant amount of extra space to store max1 and max2, irrespective of the input array\u2019s size.\n\n# Code\n```\npublic class Solution {\n public int MaxProduct(int[] nums) {\n int max1 = int.MinValue;\n int max2 = int.MinValue;\n \n foreach (int num in nums) {\n if (num >= max1) {\n max2 = max1;\n max1 = num;\n } else if (num > max2) {\n max2 = num;\n }\n }\n \n return (max1 - 1) * (max2 - 1);\n }\n}\n``` | 3 | 0 | ['C#'] | 0 |
maximum-product-of-two-elements-in-an-array | Rust/Python 2 lines sort. Also can do linear | rustpython-2-lines-sort-also-can-do-line-2ots | Intuition\nOf course you can just check each pair and it will pass, but you do not need to. If the values are all positive, the maximum will be attained with ma | salvadordali | NORMAL | 2023-12-12T02:33:03.839603+00:00 | 2023-12-12T02:33:03.839624+00:00 | 142 | false | # Intuition\nOf course you can just check each pair and it will pass, but you do not need to. If the values are all positive, the maximum will be attained with maximum values of two elements in the product.\n\nSo all you need is to get two maximum values in this list. You can do this in linear time (find one maximum and its position and then find next maximum which is not in that position). But this is a lot of work (more than 2 lines).\n\nInstead you can just sort and then check last two elements.\n\n# Complexity\n- Time complexity: $O(n \\log n)$\n- Space complexity: $O(1)$\n\n# Code\n```Python []\nclass Solution:\n def maxProduct(self, nums: List[int]) -> int:\n nums.sort()\n return (nums[-1] - 1) * (nums[-2] - 1)\n```\n```Rust []\nimpl Solution {\n pub fn max_product(mut nums: Vec<i32>) -> i32 {\n nums.sort_unstable();\n return (nums[nums.len() - 1] - 1) * (nums[nums.len() - 2] - 1);\n }\n}\n``` | 3 | 0 | ['Python', 'Rust'] | 0 |
maximum-product-of-two-elements-in-an-array | C++ || No Sorting || O(N) || O(1) | c-no-sorting-on-o1-by-n_i_v_a_s-t11z | Code\n\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n // Intuition\n // The idea in here is pretty simple. We will find the | __SAI__NIVAS__ | NORMAL | 2023-12-12T01:41:51.997462+00:00 | 2023-12-12T01:41:51.997488+00:00 | 486 | false | # Code\n```\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n // Intuition\n // The idea in here is pretty simple. We will find the maximum two elemens of the nums vector and then return the required answer.\n int firstMax = -1;\n int secondMax = -1;\n for(auto &ele : nums){\n if(ele > firstMax) {\n secondMax = firstMax;\n firstMax = ele;\n }\n else if(ele > secondMax) secondMax = ele;\n }\n return (firstMax - 1) * (secondMax - 1);\n }\n};\n``` | 3 | 0 | ['C++'] | 3 |
maximum-product-of-two-elements-in-an-array | Java || 100% || 0(N) | java-100-0n-by-saurabh_kumar1-a2bo | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | saurabh_kumar1 | NORMAL | 2023-08-06T17:23:47.421780+00:00 | 2023-08-06T17:23:47.421815+00:00 | 3 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:0(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:0(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int maxProduct(int[] nums) {\n int max1 = 0 , max2 = 0;\n for(int i=0; i<nums.length; i++){\n if(nums[i]>=max1 || nums[i]>=max2){\n max2 = Math.max(max1,max2);\n max1 = nums[i];\n } \n }\n return (max1-1)*(max2-1);\n }\n}\n``` | 3 | 0 | ['Java'] | 0 |
maximum-product-of-two-elements-in-an-array | Simple Solution || Beats 100% || 0(n) time ||0(1) space | simple-solution-beats-100-0n-time-01-spa-gb9q | you can also use sorting method but that takes o(nlogn) time\n# Below code take o(n) time\n# Please upvote if you feel it easy\n# Code\n\nclass Solution {\n | ProfessionalMonk | NORMAL | 2023-07-09T05:23:42.207588+00:00 | 2023-07-09T05:23:42.207608+00:00 | 177 | false | # you can also use sorting method but that takes o(nlogn) time\n# Below code take o(n) time\n# Please upvote if you feel it easy\n# Code\n```\nclass Solution {\n public int maxProduct(int[] nums) {\n int first=0;\n int second=0;\n for(int i=0;i<nums.length;i++) {\n if(nums[i]>first) {\n second = first;\n first = nums[i];\n }\n else if(nums[i]>second) {\n second = nums[i];\n }\n }\n return (first-1)*(second-1);\n\n }\n}\n``` | 3 | 0 | ['Java'] | 0 |
maximum-product-of-two-elements-in-an-array | Brute Better Good Optimal <---> Interview Prep. | brute-better-good-optimal-interview-prep-6y7r | Approach 1\nUsing Heap Sort (Priority queue)\n\n# Complexity\n- Time complexity: O(n log(n))\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: | lokesh1911e | NORMAL | 2023-04-09T16:40:13.786533+00:00 | 2023-04-09T16:45:32.160448+00:00 | 68 | false | # Approach 1\nUsing Heap Sort (Priority queue)\n\n# Complexity\n- Time complexity: **O(n log(n))**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: **O(n)**\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n priority_queue<int> pq;\n for(auto x: nums){\n pq.push(x);\n }\n int n = pq.top();\n pq.pop();\n int m = pq.top();\n\n return ((n-1)*(m-1)); \n }\n};\n```\n# Approach 2\n<!-- Describe your approach to solving the problem. -->\nSort using STL function\n# Complexity\n- Time complexity: **O(n log(n))**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: **O(1)**\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n sort(nums.begin(),nums.end());\n return (nums[nums.size()-1]-1)*(nums[nums.size()-2]-1);\n }\n};\n```\n# Approach 3\n<!-- Describe your approach to solving the problem. -->\nDifferent Loops to find Max and Second Max element;\n# Complexity\n- Time complexity: **O(2n)**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: **O(1)**\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) { \n int first = *max_element(nums.begin(),nums.end());\n int count = 0;\n int second=0;\n for(auto x: nums){\n if(count == 1 && first == x){\n second = x;\n break;\n };\n if(count == 0 && first == x){\n count++;\n continue;\n };\n second = max(second,x);\n }\n return (maxi-1)*(second-1);\n }\n};\n```\n# Approach 4\n<!-- Describe your approach to solving the problem. -->\nUsing Single loop to find Max and second element;\n# Complexity\n- Time complexity: **O(n)**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: **O(1)**\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n int first=0,second=0;\n \n for(auto x: nums){\n if(x > first){\n second = first;\n first = x;\n }\n else if(x > second){\n second = x;\n }}\n return (first-1)*(second-1);\n }\n};\n```\n\n\n\n\n\n | 3 | 0 | ['Two Pointers', 'Sorting', 'Heap (Priority Queue)', 'C++'] | 0 |
maximum-product-of-two-elements-in-an-array | Java | Beats 100% | O(n) | java-beats-100-on-by-vasujhawar2001-cv6t | Complexity\n- Time complexity: O(N)\n\n- Space complexity: O(1)\n\n# Code\n\nclass Solution {\n public int maxProduct(int[] nums) {\n int max1 = 0;\n | vasujhawar2001 | NORMAL | 2023-04-03T08:34:43.204918+00:00 | 2023-04-03T08:34:43.204949+00:00 | 429 | false | # Complexity\n- Time complexity: O(N)\n\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution {\n public int maxProduct(int[] nums) {\n int max1 = 0;\n int max2 = 0;\n int result = 0;\n for(int i=0; i<nums.length;i++){\n if(nums[i]>max1){\n max2 = max1;\n max1 = nums[i];\n }\n else if(nums[i]>max2){\n max2 = nums[i];\n }\n result = (max1-1)*(max2-1);\n }\n return result;\n }\n}\n``` | 3 | 0 | ['Java'] | 0 |
maximum-product-of-two-elements-in-an-array | Simple Java Solution || T.C = O(n), S.C. = O(1) | simple-java-solution-tc-on-sc-o1-by-jaya-egac | Complexity\n- Time complexity: O(n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(1)\n Add your space complexity here, e.g. O(n) \n\n# Co | Jayant334 | NORMAL | 2023-03-27T09:30:56.696103+00:00 | 2023-03-27T09:30:56.696143+00:00 | 912 | false | # Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int maxProduct(int[] nums) {\n int max1=0 , max2=0;\n for(int i=0;i<nums.length;i++){\n if(nums[i] >= max1){\n max2 = max1;\n max1 = nums[i];\n }\n else max2 = Math.max(max2, nums[i]);\n } \n return (max1-1)*(max2-1);\n }\n}\n``` | 3 | 0 | ['Java'] | 0 |
maximum-product-of-two-elements-in-an-array | only in one loop java | only-in-one-loop-java-by-bhupendra082002-92dw | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | bhupendra082002 | NORMAL | 2023-03-19T15:44:12.801910+00:00 | 2023-03-19T15:44:12.801942+00:00 | 724 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int maxProduct(int[] nums) {\n int ans =0;\n Arrays.sort(nums);\n //return(nums[nums.length-1]-1 * nums[nums.length-2]-1);\n for(int i =0; i<nums.length; i++){\n ans = (nums[nums.length-1]-1) * (nums[nums.length-2]-1);\n\n }\n return ans;\n \n }\n}\n``` | 3 | 0 | ['Java'] | 2 |
maximum-product-of-two-elements-in-an-array | C++ Solution | c-solution-by-asad_sarwar-3ht4 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Asad_Sarwar | NORMAL | 2023-02-06T19:48:51.048642+00:00 | 2023-02-26T04:36:38.569522+00:00 | 1,087 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n\n int n=nums.size();\n int ans = INT16_MIN;\n for (int i = 0; i < n - 1; i++)\n {\n for (int j = i + 1; j < n; j++)\n {\n\n ans = max(ans, ((nums[i] - 1) * (nums[j] - 1)));\n }\n }\nreturn ans;\n\n\n }\n};\n``` | 3 | 0 | ['C++'] | 0 |
maximum-product-of-two-elements-in-an-array | C++ 0ms Solution using priority queue | c-0ms-solution-using-priority-queue-by-p-5ku7 | \n# Code\n\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n priority_queue<pair<int,int>> pq;\n for(int i=0;i<nums.size();i++ | Paras027 | NORMAL | 2023-01-06T21:23:50.640659+00:00 | 2023-01-06T21:23:50.640691+00:00 | 651 | false | \n# Code\n```\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n priority_queue<pair<int,int>> pq;\n for(int i=0;i<nums.size();i++)\n {\n pq.push({nums[i],i});\n }\n int a = pq.top().first;\n pq.pop();\n int b =pq.top().first;\n int ans = (a-1)*(b-1);\n return ans;\n }\n};\n``` | 3 | 0 | ['Array', 'Sorting', 'Heap (Priority Queue)', 'C++'] | 1 |
maximum-product-of-two-elements-in-an-array | C++ | 2 liner | 0ms | c-2-liner-0ms-by-lraml-bpa5 | Sort nums\n2. multiply the last two nums \n (since they\'re the max and second max)\n\nc++\n int maxProduct(vector<int>& nums) {\n sort(nums.begin(),n | lRaml | NORMAL | 2022-12-28T16:57:26.832570+00:00 | 2022-12-28T16:59:45.269260+00:00 | 487 | false | 1. Sort nums\n2. multiply the last two nums \n (since they\'re the max and second max)\n\n```c++\n int maxProduct(vector<int>& nums) {\n sort(nums.begin(),nums.end());\n return (nums[nums.size()-1]-1)*(nums[nums.size()-2]-1);\n```\n\n## Another Method\n```c++\nint maxProduct(vector<int>& nums) {\n int max1 = 0;\n int max2 = 0;\n\n for(int n : nums)\n if(n > max1){\n max2 = max1;\n max1 = n;\n }else if(n > max2)\n max2 = n;\n\n return (max1-1)*(max2-1);\n``` | 3 | 0 | ['C++'] | 0 |
maximum-product-of-two-elements-in-an-array | c# Beats 89.56% | c-beats-8956-by-abettertomorrow-jcty | \n\npublic class Solution {\n public int MaxProduct(int[] nums) {\n int first = 0;\n int second = 0;\n List<int> list = nums.ToL | abettertomorrow | NORMAL | 2022-12-19T11:27:25.953586+00:00 | 2022-12-19T11:27:25.953622+00:00 | 380 | false | \n```\npublic class Solution {\n public int MaxProduct(int[] nums) {\n int first = 0;\n int second = 0;\n List<int> list = nums.ToList<int>();\n\n first = list.Max();\n list.Remove(first);\n second = list.Max();\n\n\n return (first-1)*(second-1);\n }\n}\n``` | 3 | 0 | ['C#'] | 0 |
maximum-product-of-two-elements-in-an-array | Java | java-by-niyazjava-rroo | Upvote if u like it\n\npublic int maxProduct(int[] nums) {\n int firstMax = 0;\n int secondMax = 0;\n\n for (int num : nums) {\n if (num > first | NiyazJava | NORMAL | 2022-11-22T08:08:59.130730+00:00 | 2022-11-22T08:08:59.130769+00:00 | 243 | false | Upvote if u like it\n```\npublic int maxProduct(int[] nums) {\n int firstMax = 0;\n int secondMax = 0;\n\n for (int num : nums) {\n if (num > firstMax) {\n secondMax = firstMax;\n firstMax = num;\n } else if (secondMax < num) {\n secondMax = num;\n }\n }\n\n return (firstMax - 1) * (secondMax - 1);\n}\n``` | 3 | 0 | ['Java'] | 0 |
maximum-product-of-two-elements-in-an-array | c++ one liner simple approach | c-one-liner-simple-approach-by-sailakshm-4w5j | PLEASE UPVOTE IF U FIND HELPFUL\n\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n sort(nums.rbegin(),nums.rend()); return (nums[0]- | sailakshmi1 | NORMAL | 2022-06-01T10:21:24.601274+00:00 | 2022-06-01T10:21:24.601300+00:00 | 158 | false | **PLEASE UPVOTE IF U FIND HELPFUL**\n```\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n sort(nums.rbegin(),nums.rend()); return (nums[0]-1)*(nums[1]-1);\n }\n};\n``` | 3 | 0 | ['C', 'Sorting'] | 1 |
maximum-product-of-two-elements-in-an-array | [swift] || Using Heap Sort || Easy explanation | swift-using-heap-sort-easy-explanation-b-qwea | The solution follows the idea of using a maxHeap, wherein the root object is the object with the highest value. \n\nA maxHeap also has a property that every chi | sadyojat | NORMAL | 2021-08-04T05:01:33.769750+00:00 | 2021-08-04T05:01:33.769810+00:00 | 271 | false | The solution follows the idea of using a maxHeap, wherein the root object is the object with the highest value. \n\nA maxHeap also has a property that every child of a node will have a lower weight than its parent, so while it does not deliver ordered sorting, the elements are in a semi sorted order. \n\nThe simplest fix here is to pass the incoming array thru a heapify construct, which transforms the input array into a maxHeap, and then extract the top 2 heaviest elements from the heap. \n\n`Time Complexity :: worst case :: O(n lg(n))`\n\n```\nclass Solution { \n func maxProduct(_ nums: [Int]) -> Int {\n let heap = heapify(nums) \n if heap.count > 2 {\n let first = heap[0]\n let second = heap[1] > heap[2] ? heap[1] : heap[2]\n return (first - 1) * (second - 1)\n } else {\n return (heap[0] - 1) * (heap[1] - 1)\n }\n \n }\n \n func heapify(_ nums: [Int]) -> [Int] {\n var nums = nums\n var newNums = [Int]()\n let maxCount = nums.count\n for i in 0..<maxCount { \n newNums.append(nums[i])\n var j = i\n var parentIdx = (j-1)/2\n while parentIdx >= 0, newNums[parentIdx] < newNums[j] { \n let temp = newNums[j]\n newNums[j] = newNums[parentIdx]\n newNums[parentIdx] = temp\n j = parentIdx\n parentIdx = (j-1)/2 \n }\n }\n return newNums\n }\n}\n``` | 3 | 0 | ['Swift', 'Heap (Priority Queue)'] | 2 |
maximum-product-of-two-elements-in-an-array | Rust O(N) solution | rust-on-solution-by-bigmih-twly | Sorting is unnecessary in such a task. \nWe only need to keep track of the 2 maximum values while traversing the vector.\n\nimpl Solution {\n pub fn max_prod | BigMih | NORMAL | 2021-06-05T21:08:50.005163+00:00 | 2021-06-05T21:28:12.872292+00:00 | 90 | false | Sorting is unnecessary in such a task. \nWe only need to keep track of the 2 maximum values while traversing the vector.\n```\nimpl Solution {\n pub fn max_product(nums: Vec<i32>) -> i32 {\n let (mut max1, mut max2) = (0, 0);\n nums.iter().for_each(|&n| {\n if n > max2 {\n max1 = std::mem::replace(&mut max2, n);\n } else if n > max1 {\n max1 = n;\n }\n });\n (max1 - 1) * (max2 - 1)\n }\n}\n``` | 3 | 0 | ['Rust'] | 0 |
maximum-product-of-two-elements-in-an-array | C++ 3 Solutions: Max_Heap, Linear Scan, Sort | c-3-solutions-max_heap-linear-scan-sort-9nmrt | FIRST\n\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n priority_queue<int, vector<int>, greater<int>> que;\n \n for( | paulariri | NORMAL | 2020-06-22T06:58:20.584584+00:00 | 2020-06-22T06:58:20.584615+00:00 | 225 | false | FIRST\n```\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n priority_queue<int, vector<int>, greater<int>> que;\n \n for(int i = 0; i < (int)nums.size(); ++i){\n if(que.size() < 2) { que.push(nums[i]); continue; }\n \n if(que.top() < nums[i]){\n que.pop();\n que.push(nums[i]);\n }\n }\n \n int temp = que.top() - 1; que.pop();\n \n return ((que.top() - 1) * temp);\n }\n};\n```\n\nSECOND\n```\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n sort(nums.begin(), nums.end());\n \n return (nums[nums.size() - 1] - 1) * (nums[nums.size() - 2] - 1);\n }\n};\n```\n\nTHIRD\n```\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n int highest = 0, highest_two = 0, max_index = 0;\n \n for(int i = 0; i < (int)nums.size(); ++i){\n if(nums[i] > highest) { highest = nums[i]; max_index = i; }\n }\n \n for(int i = 0; i < (int)nums.size(); ++i){\n if(nums[i] > highest_two && max_index != i ) highest_two = nums[i];\n }\n \n return (highest - 1) * (highest_two - 1);\n }\n};\n``` | 3 | 2 | ['C', 'Sorting', 'Heap (Priority Queue)', 'C++'] | 0 |
maximum-product-of-two-elements-in-an-array | [Rust] O(N) 1 pass 0ms simple solution | rust-on-1-pass-0ms-simple-solution-by-ru-icer | A naive way will be: \n1. sort the vector \n2. multiply (max - 1) * (second_max - 1)\n\nrust\nimpl Solution {\n pub fn max_product(ref mut nums: Vec<i32>) -> | rudy__ | NORMAL | 2020-06-01T01:56:54.289688+00:00 | 2020-06-01T02:19:21.485973+00:00 | 69 | false | A naive way will be: \n1. sort the vector \n2. multiply `(max - 1) * (second_max - 1)`\n\n```rust\nimpl Solution {\n pub fn max_product(ref mut nums: Vec<i32>) -> i32 {\n nums.sort();\n (nums.last().unwrap() - 1) * (nums[nums.len() - 2] - 1)\n }\n}\n```\n\nBut I guess the interviewer will not like it since time complexity of sort is `O(n log n)`. For weekly contests, it does not matter what algorithm you choose as long as it does not cause `LTE`. But when you talk with others on this problem, I recommend the following`O(n)` method. \n\n\n```rust\nimpl Solution {\n pub fn max_product(nums: Vec<i32>) -> i32 {\n let (mut ma, mut mb) = (0, 0);\n for n in nums.iter() {\n if *n > ma {\n mb = ma; \n ma = *n; \n } else {\n mb = max(mb, *n);\n }\n }\n (mb - 1) * (ma - 1)\n }\n}\n```\n\n | 3 | 0 | [] | 1 |
maximum-product-of-two-elements-in-an-array | Javascript sorting solution | javascript-sorting-solution-by-seriously-en0a | \nvar maxProduct = function(nums) {\n nums.sort(function(a,b){return b-a});\n return (nums[0]-1)*(nums[1]-1)\n};\n | seriously_ridhi | NORMAL | 2020-05-31T15:18:54.412522+00:00 | 2020-05-31T15:18:54.412569+00:00 | 214 | false | ```\nvar maxProduct = function(nums) {\n nums.sort(function(a,b){return b-a});\n return (nums[0]-1)*(nums[1]-1)\n};\n``` | 3 | 1 | [] | 1 |
maximum-product-of-two-elements-in-an-array | C++ simple solution | c-simple-solution-by-oleksam-f2s7 | \nint maxProduct(vector<int>& nums) {\n\tpriority_queue<int> pq(nums.begin(), nums.end());\n\tint first = pq.top();\n\tpq.pop();\n\tint second = pq.top();\n\tre | oleksam | NORMAL | 2020-05-31T10:25:12.547489+00:00 | 2020-05-31T10:25:12.547536+00:00 | 446 | false | ```\nint maxProduct(vector<int>& nums) {\n\tpriority_queue<int> pq(nums.begin(), nums.end());\n\tint first = pq.top();\n\tpq.pop();\n\tint second = pq.top();\n\treturn (first - 1) * (second - 1);\n}\n```\n | 3 | 0 | ['C', 'C++'] | 1 |
maximum-product-of-two-elements-in-an-array | Python 3 beats 100% | python-3-beats-100-by-alankrit_03-kpje | \nclass Solution:\n def maxProduct(self, nums: List[int]) -> int:\n max_val = nums[0]\n second_max = 0\n \n for i in range(1,len( | alankrit_03 | NORMAL | 2020-05-31T08:25:04.443290+00:00 | 2020-05-31T08:25:04.443325+00:00 | 378 | false | ```\nclass Solution:\n def maxProduct(self, nums: List[int]) -> int:\n max_val = nums[0]\n second_max = 0\n \n for i in range(1,len(nums)):\n if nums[i]>=max_val:\n second_max = max_val\n max_val = nums[i]\n elif nums[i]>second_max:\n second_max = nums[i]\n \n return (max_val-1)*(second_max-1)\n``` | 3 | 1 | ['Python3'] | 1 |
maximum-product-of-two-elements-in-an-array | simple cpp solution | simple-cpp-solution-by-_mrbing-du4q | Runtime: 24 ms, faster than 50.00% of C++ online submissions for Maximum Product of Two Elements in an Array.\nMemory Usage: 10 MB, less than 100.00% of C++ onl | _mrbing | NORMAL | 2020-05-31T04:13:11.798619+00:00 | 2020-05-31T04:13:11.798665+00:00 | 231 | false | Runtime: 24 ms, faster than 50.00% of C++ online submissions for Maximum Product of Two Elements in an Array.\nMemory Usage: 10 MB, less than 100.00% of C++ online submissions for Maximum Product of Two Elements in an Array.\n```\n class Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n sort(nums.begin(),nums.end());\n int n = nums.size();\n return (nums[n-1] -1) * (nums[n-2] - 1);\n }\n}; | 3 | 2 | ['C++'] | 0 |
maximum-product-of-two-elements-in-an-array | [Java] One Iteration Solution | java-one-iteration-solution-by-adityarew-lf4e | \n int m1 = 1; // second largest num\n int m2 = 1; // largest num\n for (int i=0; i<nums.length; i++){\n if (nums[i] >= m2) {\n m1 = m2;\n | adityarewari | NORMAL | 2020-05-31T04:01:46.219381+00:00 | 2020-05-31T04:03:19.267361+00:00 | 271 | false | ```\n int m1 = 1; // second largest num\n int m2 = 1; // largest num\n for (int i=0; i<nums.length; i++){\n if (nums[i] >= m2) {\n m1 = m2;\n m2 = nums[i];\n continue;\n } else if(nums[i] > m1) {\n m1 = nums[i];\n continue;\n }\n }\n return (m2-1)*(m1-1);\n\t``` | 3 | 1 | [] | 0 |
maximum-product-of-two-elements-in-an-array | BEST SOLUTION FOR BEGINERS IN JAVA | best-solution-for-beginers-in-java-by-an-5rbo | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | antonypraveen004 | NORMAL | 2025-03-07T16:12:30.197793+00:00 | 2025-03-07T16:12:30.197793+00:00 | 143 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int maxProduct(int[] nums) {
int firstMax=0;
int secondMax=0;
for(int i=0;i<nums.length;i++){
if(nums[i]>=firstMax){
secondMax=firstMax;
firstMax=nums[i];
}else if(nums[i]>=secondMax && nums[i]<=firstMax){ //[6,5,4,3,2,1] then the secondMax will be zero but thats wrong
secondMax=nums[i];
}
}
return (firstMax-1)*(secondMax-1);
//If there exist negative Value too in the input Use this Method.
// int firstMax=0;
// int secondMax=0;
// int firstMin=Integer.MAX_VALUE;
// int secondMin=Integer.MAX_VALUE;
// for(int i=0;i<nums.length;i++){
// if(nums[i]>=firstMax){
// secondMax=firstMax;
// firstMax=nums[i];
// }else if(nums[i]>=secondMax && nums[i]<=firstMax){
// secondMax=nums[i];
// }
// //Finding the Minimum for the same/
// if(nums[i]<=firstMin){
// secondMin=firstMin;
// firstMin=nums[i];
// }else if(nums[i]<=secondMin && nums[i]>=firstMin){
// secondMin=nums[i];
// }
// }
// // System.out.println("firstMax "+firstMax);
// // System.out.println("SecondMax "+secondMax);
// // System.out.println("firstMin "+firstMin);
// // System.out.println("SecondMin "+secondMin);
// // System.out.println("The maximum product value in the array is "+Math.max((firstMin*secondMin),(firstMax*secondMax)));
// return Math.max(((firstMin-1)*(secondMin-1)),((firstMax-1)*(secondMax-1)));
}
}
``` | 2 | 0 | ['Java'] | 0 |
maximum-product-of-two-elements-in-an-array | C++ Optimized Solution | 4 line Code | beginner level | BEATS 100% | c-optimized-solution-4-line-code-beginne-zsup | IntuitionThe problem requires finding the two largest numbers in the array and computing their modified product (max1−1)×(max2−1).Instead of sorting, we can eff | Harisharen | NORMAL | 2025-01-31T16:31:41.880899+00:00 | 2025-01-31T16:31:41.880899+00:00 | 114 | false | # Intuition
The problem requires finding the two largest numbers in the array and computing their modified product ***(max1−1)×(max2−1)***.
Instead of sorting, we can efficiently track the two largest numbers while iterating through the array.
# Approach
1. Initialize max1 and max2 to the smallest possible integer values.
2. Traverse the array:
- If the current element is greater than max1, update max2 to store the previous max1, and assign max1 to the current element.
- Else if the current element is greater than max2, update max2 with the current element.
3. Compute the result using (max1−1)×(max2−1).
This approach ensures we find the two largest numbers in a single pass.
# Complexity
- Time complexity:
O(n) — We iterate through the array once
- Space complexity:
O(1) — We use only a few integer variables, regardless of input size.
# Code
```cpp []
class Solution {
public:
int maxProduct(vector<int>& nums) {
int max1 = INT_MIN;
int max2 = INT_MIN;
for(int i=0 ; i<nums.size() ; i++){
if(nums[i]>max1){
max2 = max1;
max1 = nums[i];
}
else if(nums[i]>max2 ){
max2 = nums[i];
}
}
int ans = (max1-1)*(max2-1) ;
return ans;
}
};
``` | 2 | 0 | ['Array', 'Sorting', 'C++'] | 0 |
maximum-product-of-two-elements-in-an-array | Three different approaches || Beats 100% | three-different-approaches-beats-100-by-g4mw9 | Intuition\nThe problem requires finding the maximum product of two distinct elements in an array after reducing each by 1. The first thought is to find the two | mayanknayal5306069 | NORMAL | 2024-11-09T21:42:36.781443+00:00 | 2024-11-09T21:42:36.781482+00:00 | 46 | false | # Intuition\nThe problem requires finding the maximum product of two distinct elements in an array after reducing each by 1. The first thought is to find the two largest elements in the array, as they will maximize the product.\n\n# Approach\nFirst Approach (Bubble Sort):\n\nSort the array in non-decreasing order using a custom bubble sort and return the product of the two largest elements, reduced by 1 each.\nThis approach works but is inefficient for large arrays due to its \nO(n^2)complexity.\n\nSecond Approach (Built-in Sort):\n\nSort the array using Arrays.sort(), which has O(nlogn) complexity, and then return the product of the two largest elements (last two elements in the sorted array) minus 1 each.\nThis is more efficient than the bubble sort but still involves sorting.\n\nOptimized Approach (Single Pass):\n\nUse a single pass through the array to find the two largest elements, max1 and max2, by updating them as we traverse the array.\nReturn (max1\u22121)\xD7(max2\u22121).\nThis approach is the most efficient, with a time complexity of \nO(n), as it only requires a single traversal.\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```java []\nclass Solution {\n public int maxProduct(int[] nums) {\n\n // first way:- \n\n\n // boolean isSorted;\n // for (int i = 0; i<nums.length;i++) {\n // isSorted = false;\n // for (int j = 1; j < nums.length-i;j++) {\n // if (nums[j] < nums[j-1]) {\n // int temp = nums[j];\n // nums[j] = nums[j-1];\n // nums[j-1] = temp;\n\n // isSorted = true;\n // }\n // }\n // if (isSorted == false) {\n // return ((nums[nums.length-1]-1)*(nums[nums.length-2]-1));\n // }\n // }\n // return ((nums[nums.length-1]-1)*(nums[nums.length-2]-1));\n\n\n // second way:-\n\n\n // Arrays.sort(nums);\n // return ((nums[nums.length-1]-1)*(nums[nums.length-2]-1));\n\n\n // third way:-\n\n int max1 = Integer.MIN_VALUE;\n int max2 = Integer.MIN_VALUE;\n\n for (int num : nums) {\n if(num >= max1) {\n max2 = max1;\n max1 = num;\n } else if (num > max2) {\n max2 = num;\n }\n }\n return ((max1-1)*(max2-1));\n }\n}\n``` | 2 | 0 | ['Java'] | 0 |
maximum-product-of-two-elements-in-an-array | A simple two-line solution with a step-by-step process. | a-simple-two-line-solution-with-a-step-b-4z8s | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n1. Sort the array from larger to small\n2. Took 0,1 index values from tha | shamnad_skr | NORMAL | 2024-10-11T12:05:22.783674+00:00 | 2024-10-11T12:05:22.783703+00:00 | 77 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Sort the array from larger to small\n2. Took 0,1 index values from that array ( since after sort they are the largest or same)\n3. calculate the anser and return ind\n\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```typescript []\nfunction maxProduct(nums: number[]): number {\n\n //sort values from larger to small\n nums.sort((a,b) => b-a);\n //Calculating and returning the first two values.\n return ( (nums[0]-1)* (nums[1]-1) );\n \n};\n``` | 2 | 0 | ['TypeScript', 'JavaScript'] | 0 |
maximum-product-of-two-elements-in-an-array | Q.1463 | ☑️One line Python3 solution | EZ💯 | q1463-one-line-python3-solution-ez-by-ch-8dbq | \uD83D\uDCA1Intuition\nGrab the two biggest numbers using inbuilt functions, knock them down by one, and bring out the product.\n\n# \uD83E\uDDE0 Approach\n Des | charan1kh | NORMAL | 2024-09-18T18:12:54.473766+00:00 | 2024-09-18T18:12:54.473797+00:00 | 20 | false | # \uD83D\uDCA1Intuition\nGrab the two biggest numbers using inbuilt functions, knock them down by one, and bring out the product.\n\n# \uD83E\uDDE0 Approach\n<!-- Describe your approach to solving the problem. -->\nIn this solution, the input list nums is first sorted in descending order, and then the top two largest numbers are used to compute the maximum product after subtracting 1 from each.\n\n# \uD83E\uDD72Complexity\n- Time complexity: \uD835\uDC42(\uD835\uDC5Blog\uD835\uDC5B)\n\uD835\uDC42(\uD835\uDC5Blog\uD835\uDC5B) due to the sorting operation. While this solution achieves the correct result in one line, sorting the list hampers the performance compared to an \uD835\uDC42(\uD835\uDC5B).\n\n\n\n- Space complexity: \uD835\uDC42(\uD835\uDC5B)\nAs the sorting operation creates a new list.\n\n# \uD83D\uDCDCCode\n```python3 []\nclass Solution:\n def maxProduct(self, nums: List[int]) -> int:\n return ((sorted(nums)[::-1])[0]-1) * ((sorted(nums)[::-1])[1]-1)\n``` | 2 | 0 | ['Python3'] | 1 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.