question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
movement-of-robots | C++ video | c-video-by-mwca2024-vw8h | \nusing ll = long long;\nclass Solution {\npublic:\n int sumDistance(vector& nums, string s, int d) {\n int mod = 1e9+7;\n vector pos;\n | mwca2024 | NORMAL | 2023-06-11T09:38:26.348024+00:00 | 2023-06-11T09:38:26.348072+00:00 | 13 | false | \nusing ll = long long;\nclass Solution {\npublic:\n int sumDistance(vector<int>& nums, string s, int d) {\n int mod = 1e9+7;\n vector<int> pos;\n \n int n = nums.size();\n for(int i = 0; i < n; ++i) {\n if(s[i] == \'L\') pos.push_back(nums[i] - d);\n else pos.push_back(nums[i] + d);\n }\n \n std::sort(begin(pos), end(pos));\n\n \n ll pref_sum = 0;\n\n ll ans = 0;\n for(int i = 1; i <n; ++i) {\n \n pref_sum += i*((ll)pos[i] - pos[i-1]);\n ans = (ans + pref_sum) % mod;\n }\n \n return ans;\n }\n };\nhttps://youtu.be/vZ2A6cdyFyg\n | 0 | 0 | ['C++'] | 0 |
movement-of-robots | EASY C++ solution using sorting and prefix sum | easy-c-solution-using-sorting-and-prefix-i84t | \n\n# Complexity\n- Time complexity:\nO(nlogn)\n\n- Space complexity:\nO(1sorting)\n\n# Code\n\nclass Solution {\npublic:\n int sumDistance(vector<int>& nums | levii_31 | NORMAL | 2023-06-11T09:26:12.606816+00:00 | 2023-06-11T09:28:03.527587+00:00 | 50 | false | \n\n# Complexity\n- Time complexity:\nO(nlogn)\n\n- Space complexity:\nO(1sorting)\n\n# Code\n```\nclass Solution {\npublic:\n int sumDistance(vector<int>& nums, string s, int d) {\n int n=nums.size();\n long long ans=0,sum=0;\n int mod=1e9+7;\n //as we need only final position of robots irrespective of which robot;\n for(int i=0;i<n;i++){\n if(s[i]==\'L\')\n nums[i]-=d;\n else\n nums[i]+=d;\n }\n //to calculate distance in nlogn time\n sort(nums.begin(),nums.end());\n \n //effect of adding a new point xi will contribute as xi *i - (previous distance sum)\n for(long long i=0;i<n;i++){\n ans+=(nums[i]*i -sum)%mod;\n ans%=mod;\n \n sum+=nums[i];\n sum%=mod;\n }\n\n return ans;\n\n }\n};\n``` | 0 | 0 | ['Math', 'Sorting', 'Prefix Sum', 'C++'] | 0 |
movement-of-robots | 🦅 Python3 🎃 Clear Code with Intuition and Brainstorm Procedure | python3-clear-code-with-intuition-and-br-18hr | Intuition\nI can\'t solve this problem until realize the first difficulty, changing direction, it is a honey pot to decrease our focus.\nAnd second difficulty i | liuliugit | NORMAL | 2023-06-11T08:48:17.071825+00:00 | 2023-06-11T08:48:17.071871+00:00 | 25 | false | # Intuition\nI can\'t solve this problem until realize the first difficulty, changing direction, it is a honey pot to decrease our focus.\nAnd second difficulty is how to get distances sum in sufficient time complexity.\n\n# Approach\nHow to Solve Second Difficulty:\n> When nums is unordered list, we need to use abs() to get positive distances.\n If ordered nums to increasing order, we can calculate distance by simply substract each items.\n\n> eg:\n> unordered nums = [3, -1, 2], then distances need to use abs() like this:\n> result = abs(-1 - 3) + abs(2 - 3) + abs(2 - (-1)) \n> ordered nums = [-1, 2, 3], then distances like this:\n result = (2 - (-1)) + (3 - (-1)) + (3 - 2) = (2 * 1 - (-1)) + (3 * 2 - (-1 + 2))\n\n# Complexity\n\n- Time complexity:\n$$O(NLogN)$$\n\n- Space complexity:\n$$O(N)$$\n\n# Code\n## 1. Change Moving Direction, ERROR: "Time Limit Exceeded"\n```python []\nclass Solution:\n def sumDistance(self, nums: List[int], s: str, d: int) -> int:\n MOD = 10**9+7\n for _ in range(d):\n mapping = defaultdict(list)\n for index in range(len(nums)):\n target = nums[index] + 1 if s[index] == \'R\' else nums[index] - 1\n mapping[target].append(index)\n nums[index] = target\n for k, item in mapping.items():\n if len(item) > 1:\n for i in item:\n s = list(s)\n s[i] = \'R\' if s[i] == \'L\' else \'L\'\n s = \'\'.join(s)\n result = 0\n for i in range(len(nums)):\n for j in range(i+1, len(nums)):\n result = (result + (abs(nums[i] - nums[j]) % MOD)) % MOD\n return result\n```\n\n## 2. Force Sum, ERROR: "Time Limit Exceeded"\n```python []\nclass Solution:\n def sumDistance(self, nums: List[int], s: str, d: int) -> int:\n MOD = 10**9+7\n for index in range(len(nums)):\n nums[index] += d if s[index] == \'R\' else -d\n result = 0\n for i in range(len(nums)):\n for j in range(i+1, len(nums)):\n result = (result + (abs(nums[i] - nums[j]) % MOD)) % MOD\n return result\n```\n\n## 3. Order Positions from smallest to largest\n```python []\nclass Solution:\n def sumDistance(self, nums: List[int], s: str, d: int) -> int:\n for index in range(len(nums)):\n nums[index] += d if s[index] == \'R\' else -d\n\n MOD = 10**9+7\n nums.sort()\n result = 0\n substract = nums[0]\n for index in range(1, len(nums)):\n result = (result + nums[index] * index % MOD - substract) % MOD\n substract = (substract + nums[index]) % MOD\n return result\n``` | 0 | 0 | ['Python3'] | 0 |
flatten-a-multilevel-doubly-linked-list | Easy Understanding Java beat 95.7% with Explanation | easy-understanding-java-beat-957-with-ex-d34s | Basic idea is straight forward: \n1. Start form the head , move one step each time to the next node\n2. When meet with a node with child, say node p, follow its | kyleluchina | NORMAL | 2018-07-16T04:09:47.449252+00:00 | 2018-10-23T21:52:38.704662+00:00 | 50,425 | false | Basic idea is straight forward: \n1. Start form the `head` , move one step each time to the next node\n2. When meet with a node with child, say node `p`, follow its `child chain` to the end and connect the tail node with `p.next`, by doing this we merged the `child chain` back to the `main thread`\n3. Return to `p` and proceed until find next node with child.\n4. Repeat until reach `null`\n\n```\nclass Solution {\n public Node flatten(Node head) {\n if( head == null) return head;\n\t// Pointer\n Node p = head; \n while( p!= null) {\n /* CASE 1: if no child, proceed */\n if( p.child == null ) {\n p = p.next;\n continue;\n }\n /* CASE 2: got child, find the tail of the child and link it to p.next */\n Node temp = p.child;\n // Find the tail of the child\n while( temp.next != null ) \n temp = temp.next;\n // Connect tail with p.next, if it is not null\n temp.next = p.next; \n if( p.next != null ) p.next.prev = temp;\n // Connect p with p.child, and remove p.child\n p.next = p.child; \n p.child.prev = p;\n p.child = null;\n }\n return head;\n }\n}\n``` | 554 | 8 | [] | 65 |
flatten-a-multilevel-doubly-linked-list | c++, about 10 lines solution | c-about-10-lines-solution-by-zjzh-sxls | \nNode* flatten(Node* head) {\n\tfor (Node* h = head; h; h = h->next)\n\t{\n\t\tif (h->child)\n\t\t{\n\t\t\tNode* next = h->next;\n\t\t\th->next = h->child;\n\t | zjzh | NORMAL | 2018-07-21T12:31:55.366483+00:00 | 2018-10-23T05:29:12.651725+00:00 | 19,832 | false | ```\nNode* flatten(Node* head) {\n\tfor (Node* h = head; h; h = h->next)\n\t{\n\t\tif (h->child)\n\t\t{\n\t\t\tNode* next = h->next;\n\t\t\th->next = h->child;\n\t\t\th->next->prev = h;\n\t\t\th->child = NULL;\n\t\t\tNode* p = h->next;\n\t\t\twhile (p->next) p = p->next;\n\t\t\tp->next = next;\n\t\t\tif (next) next->prev = p;\n\t\t}\n\t}\n\treturn head;\n}\n``` | 329 | 3 | [] | 30 |
flatten-a-multilevel-doubly-linked-list | [C++] Simple 5 line recursive solution (with diagram) | c-simple-5-line-recursive-solution-with-cd75q | C++\nNode* flatten(Node* head, Node* rest = nullptr) {\n if (!head) return rest;\n head->next = flatten(head->child, flatten(head->next, rest));\n if (head-> | mhelvens | NORMAL | 2019-05-20T13:12:38.135853+00:00 | 2019-07-21T15:17:06.257832+00:00 | 11,372 | false | ```C++\nNode* flatten(Node* head, Node* rest = nullptr) {\n if (!head) return rest;\n head->next = flatten(head->child, flatten(head->next, rest));\n if (head->next) head->next->prev = head;\n head->child = nullptr;\n return head;\n}\n```\n\nThis function modifies the structure in place. It\'s not the fastest implementation out there, but I love short recursive algorithms, and I thought this was rather nice.\n\nThe trick to make this work is to add a second parameter to the function signature. A call to `flatten(head, rest)` will flatten `head` _and_ concatenate `rest` to the end of it. That allows our recursive definition:\n\n```C++\nhead->next = flatten(head->child, flatten(head->next, rest));\n```\n\n\n\n(The first line of code is a simple base-case. The third and fourth lines are just pointer-cleanup.)\n\nWhat we\'re passing to `rest` is an already flattened `head->next`, in order to concatenate it to the end of a flattened `head->child`. | 226 | 1 | ['Recursion', 'C'] | 20 |
flatten-a-multilevel-doubly-linked-list | Python easy solution using stack | python-easy-solution-using-stack-by-shri-91ld | \nclass Solution(object):\n def flatten(self, head):\n if not head:\n return\n \n dummy = Node(0,None,head,None) \n | shrivilb | NORMAL | 2018-07-29T23:29:31.063338+00:00 | 2018-09-18T19:03:55.605316+00:00 | 16,423 | false | ```\nclass Solution(object):\n def flatten(self, head):\n if not head:\n return\n \n dummy = Node(0,None,head,None) \n stack = []\n stack.append(head)\n prev = dummy\n \n while stack:\n root = stack.pop()\n\n root.prev = prev\n prev.next = root\n \n if root.next:\n stack.append(root.next)\n root.next = None\n if root.child:\n stack.append(root.child)\n root.child = None\n prev = root \n \n \n dummy.next.prev = None\n return dummy.next\n``` | 154 | 0 | [] | 23 |
flatten-a-multilevel-doubly-linked-list | Java Recursive Solution | java-recursive-solution-by-zhiying_qian-3l1z | \n public Node flatten(Node head) {\n \tflattentail(head);\n \treturn head;\n }\n\n // flattentail: flatten the node "head" and return the tail i | zhiying_qian | NORMAL | 2018-08-07T14:56:56.990428+00:00 | 2018-10-23T15:43:38.044318+00:00 | 17,169 | false | ```\n public Node flatten(Node head) {\n \tflattentail(head);\n \treturn head;\n }\n\n // flattentail: flatten the node "head" and return the tail in its child (if exists)\n // the tail means the last node after flattening "head"\n\n // Five situations:\n // 1. null - no need to flatten, just return it\n // 2. no child, no next - no need to flatten, it is the last element, just return it\n // 3. no child, next - no need to flatten, go next\n // 4. child, no next - flatten the child and done\n // 5. child, next - flatten the child, connect it with the next, go next\n\n private Node flattentail(Node head) {\n \tif (head == null) return head; // CASE 1\n \tif (head.child == null) {\n \t\tif (head.next == null) return head; // CASE 2\n \t\treturn flattentail(head.next); // CASE 3\n \t}\n \telse {\n \t\tNode child = head.child; \n \t\thead.child = null;\n \t\tNode next = head.next;\n \t\tNode childtail = flattentail(child);\n \t\thead.next = child;\n \t\tchild.prev = head; \n\t\t\tif (next != null) { // CASE 5\n\t\t\t\tchildtail.next = next;\n\t\t\t\tnext.prev = childtail;\n\t\t\t\treturn flattentail(next);\n\t\t\t}\n return childtail; // CASE 4\n \t}\t \t\n }\n``` | 124 | 1 | [] | 15 |
flatten-a-multilevel-doubly-linked-list | [Python] DFS with stack, 2 solutions, exaplained | python-dfs-with-stack-2-solutions-exapla-lyrr | In this problem we need to traverse our multilevel doubly linked list in some special order and rebuild some connections. We can consider our list as graph, whi | dbabichev | NORMAL | 2020-07-10T07:35:41.807325+00:00 | 2020-07-10T08:58:38.218844+00:00 | 6,049 | false | In this problem we need to traverse our multilevel doubly linked list in some special order and rebuild some connections. We can consider our list as graph, which we now need to traverse. What graph traversal algorighms do we know? We should think about dfs and bfs. Why I choose dfs? Because we need to traverse as deep as possible, before we traverse neibhour nodes, and that is what dfs do exactly! When you realise this, problem becomes much more easier. So, algorighm look like:\n\n1. Put `head` of our list to stack and start to traverse it: `pop` element from it and add two two elements instead: its `next` and its `child`. The order is **important**: we first want to visit `child` and then `next`, that is why we put `child` to the top of our stack.\n2. Each time we `pop` last element from stack, I write it to auxilary `order` list.\n3. Last step is to rebuild from our `order` list flattened doubly linked list.\n\n**Complexity**: time complexity is `O(n)`, where `n` is number of nodes in our list. In this approach we also use `O(n)` additional space, because I keep `order` list. This can be avoid, if we make connections on the fly, but it is a bit less intuitive in my opinion, but ofcourse more optimal in space complexity.\n\n```\nclass Solution:\n def flatten(self, head):\n if not head: return head\n stack, order = [head], []\n\n while stack:\n last = stack.pop()\n order.append(last)\n if last.next:\n stack.append(last.next)\n if last.child:\n stack.append(last.child)\n \n for i in range(len(order) - 1):\n order[i+1].prev = order[i]\n order[i].next = order[i+1]\n order[i].child = None\n \n return order[0]\n```\n\n**Solution without extra array**: the same idea, where we reconnect our nodes directly, without `order` array. It is `O(h)` in memory, where `h` is number of levels (in the worst case it will be `O(n)`).\n\n```\nclass Solution(object):\n def flatten(self, head):\n if not head: return head\n \n dummy = Node(0)\n curr, stack = dummy, [head]\n while stack:\n last = stack.pop() \n if last.next:\n stack.append(last.next)\n if last.child:\n stack.append(last.child)\n curr.next = last\n last.prev = curr \n last.child = None\n curr = last\n \n res = dummy.next\n res.prev = None\n return res\n```\n\nIf you have any questions, feel free to ask. If you like solution and explanations, please **Upvote!** | 105 | 6 | ['Depth-First Search'] | 8 |
flatten-a-multilevel-doubly-linked-list | C++ Super Simple, Short and Clean Iterative Solution, 4ms O(n) TC O(1) SC | c-super-simple-short-and-clean-iterative-z1ml | \nclass Solution {\npublic:\n Node* flatten(Node* head) {\n Node *ptr = head, *tmp_next, *runner;\n \n while (ptr) {\n if (pt | yehudisk | NORMAL | 2021-10-31T08:41:51.842736+00:00 | 2021-10-31T08:41:51.842767+00:00 | 4,296 | false | ```\nclass Solution {\npublic:\n Node* flatten(Node* head) {\n Node *ptr = head, *tmp_next, *runner;\n \n while (ptr) {\n if (ptr->child) {\n \n // Save the current next and connect the child to next\n tmp_next = ptr->next;\n ptr->next = ptr->child;\n ptr->next->prev = ptr;\n ptr->child = NULL;\n \n // Run till the end of the current list and connect last node to saved next\n runner = ptr->next;\n while (runner->next) runner = runner->next;\n runner->next = tmp_next;\n if (runner->next) runner->next->prev = runner;\n }\n \n ptr = ptr->next;\n }\n \n return head;\n }\n};\n```\n**Like it? please upvote!** | 82 | 1 | ['C'] | 7 |
flatten-a-multilevel-doubly-linked-list | Python solution with explanation | python-solution-with-explanation-by-snit-x3jb | The Idea\n\t\nWe will process the list "depth first" (i.e. to the lowest child), redirecting parent nodes next pointers to their children, and saving the previo | snitkovskiy | NORMAL | 2018-07-23T01:15:41.905869+00:00 | 2018-10-17T03:03:13.313645+00:00 | 6,878 | false | ## The Idea\n\t\nWe will process the list "depth first" (i.e. to the lowest child), redirecting parent nodes next pointers to their children, and saving the previous values of their next pointers in a Stack to be reattached once the bottom-most non-parent node has no siblings. \n\n## The algorithm\n### Pseudocode\n1. Initialize a current reference to the head of the list and an empty stack\n2. If our current reference is a Node, then see if it has a child. \n\t* (case 1) If it does have a child, then push its next reference (if it has one) to the top of the Stack. Then, reset the next reference of the current reference and the current\'s child reference appropriately. After this operation, the current reference should have lost a child reference, but have their next reference pointing to the former child. \n\t* (case 2) If it does not have a child, then, if it lacks a next reference and there are references left in the Stack, then reassign its next reference and the current top of the Stack appropriately. After this operation, the next reference of the current reference should be the top of the Stack, and the top of the Stack\'s previous reference should be the current reference. \n3. Advance the current reference forward to its next reference. \n4. Repeat 2 and 3 until the current reference is None. \n\n### Example\nSay we have the following list:\n```\n(head)\n [1] --> [2] --> [5] \n \\--> [3]\n```\t\t\t\t\t\n\n1 current = [1]; stack = []\n2a. N/A\n3a. Since current has lacks a child and has a next pointer, simply advance it (i.e. current = [2])\n2b. Since current has a child, save [5] to the top of the stack, and set the list to be the following:\n```\n[1] --> [2] --> [3]\n```\n3b. Advance current to its next pointer (i.e. current = [3])\n2c. Since current lacks a next pointer, and the stack is non-empty (i.e. it contains [5]), then set the list to be the following:\n```\n[1] --> [2] --> [3] --> [5]\n```\n3c. Advance the current to its next pointer (i.e. current = [5]). \n2d. N/A\n3d. Advance the current to its next pointer (i.e. None). \n4. Since current is None, stop. \n\n## The Code\n\n```\nclass Solution(object):\n def flatten(self, head):\n # Initialize the current reference and stack of saved next pointers\n curr, tempStack = head, [];\n while curr:\n if curr.child:\n # If the current node is a parent\n if curr.next:\n # Save the current node\'s old next pointer for future reattachment\n tempStack.append(curr.next);\n # Current <-> Current.child\n # \\-> None\n curr.next, curr.child.prev, curr.child = curr.child, curr, None;\n if not curr.next and len(tempStack):\n # If the current node is a child without a next pointer\n temp = tempStack.pop();\n # Current <-> Temp\n temp.prev, curr.next = curr, temp;\n curr = curr.next;\n return head; | 56 | 0 | [] | 10 |
flatten-a-multilevel-doubly-linked-list | Easy Understand Java Recursive solution beat 100% with Explanation | easy-understand-java-recursive-solution-8aupc | The idea is simple. We always keep a pre global variable to keep track of the last node we visited and connect current node head with this pre node. So for each | jiangjennifer | NORMAL | 2018-10-21T17:17:42.623204+00:00 | 2018-10-24T23:15:04.765672+00:00 | 4,113 | false | The idea is simple. We always keep a `pre` global variable to keep track of the last node we visited and connect current node `head` with this `pre` node. So for each recursive call, we do \n- Connect last visited node with current node by letting `pre.next` point to current node `head` and current node\'s `prev` point to `pre`\n- Mark current node as pre. `pre = head`\n- If there is `head.child`, we recursively visit and flatten its child node \n- Recursively visit and flatten its next node \n```java\nclass Solution {\n/*Global variable pre to track the last node we visited */\n Node pre = null;\n public Node flatten(Node head) {\n if (head == null) {\n return null; \n }\n/*Connect last visted node with current node */\n if (pre != null) {\n pre.next = head; \n head.prev = pre;\n }\n\n pre = head; \n/*Store head.next in a next pointer in case recursive call to flatten head.child overrides head.next*/\n Node next = head.next; \n\n flatten(head.child);\n head.child = null;\n\n flatten(next); \n return head; \n }\n}\n``` | 44 | 0 | [] | 7 |
flatten-a-multilevel-doubly-linked-list | Java solution using stack. readable | java-solution-using-stack-readable-by-co-cyr8 | \nclass Solution {\n public Node flatten(Node head) {\n Stack<Node> stack = new Stack<>();\n Node travel = head;\n while(travel != null | CoachIWantToLeetcode | NORMAL | 2018-08-01T04:27:59.334505+00:00 | 2018-09-20T21:27:25.975733+00:00 | 2,400 | false | ```\nclass Solution {\n public Node flatten(Node head) {\n Stack<Node> stack = new Stack<>();\n Node travel = head;\n while(travel != null || !stack.isEmpty()) {\n if(travel.child != null) {\n if(travel.next != null) stack.push(travel.next);\n travel.next = travel.child;\n travel.next.prev = travel;\n travel.child = null;\n }else {\n if(travel.next == null && !stack.isEmpty()) {\n travel.next = stack.pop();\n travel.next.prev = travel;\n }\n }\n travel = travel.next;\n }\n return head;\n }\n}\n``` | 32 | 1 | [] | 4 |
flatten-a-multilevel-doubly-linked-list | Python O(n), O(1) easy solution with explanation | python-on-o1-easy-solution-with-explanat-pztm | Easy iterative approach without using extra memory.\nO(n) time complexity\nO(1) space complexity\n\n\n"""\n# Definition for a Node.\nclass Node(object):\n de | jiriVFX | NORMAL | 2021-05-09T14:51:42.999144+00:00 | 2021-05-09T15:00:23.219452+00:00 | 3,742 | false | Easy iterative approach without using extra memory.\nO(n) time complexity\nO(1) space complexity\n\n```\n"""\n# Definition for a Node.\nclass Node(object):\n def __init__(self, val, prev, next, child):\n self.val = val\n self.prev = prev\n self.next = next\n self.child = child\n"""\n\nclass Solution(object):\n def flatten(self, head):\n """\n :type head: Node\n :rtype: Node\n """\n # traverse the list and look for nodes, where self.child is not None\n # keep the pointer to the previous node and to the original next node\n # merge a child list to the parent list - connect prev and next pointers\n # continue traversing until encountering another node where self.child is not None, \n # or reaching the end of the main list\n \n current = head\n \n while current is not None:\n # check for child node\n if current.child is not None:\n # merge child list into the parent list\n self.merge(current)\n \n # move to the next node\n current = current.next\n \n return head\n \n \n def merge(self, current):\n child = current.child\n \n # traverse child list until we get the last node\n while child.next is not None:\n child = child.next\n \n # child is now pointing at the last node of the child list\n # we need to connect child.next to current.next, if there is any\n if current.next is not None:\n child.next = current.next\n current.next.prev = child\n \n # now, we have to connect current to the child list\n # child is currently pointing at the last node of the child list, \n # so we need to use pointer (current.child) to get to the first node of the child list\n current.next = current.child\n current.child.prev = current\n \n # at the end remove self.child pointer\n current.child = None\n \n``` | 31 | 0 | ['Iterator', 'Python', 'Python3'] | 8 |
flatten-a-multilevel-doubly-linked-list | Simple Java solution without recursion faster than 100% and memory less than 99% | simple-java-solution-without-recursion-f-atli | \nclass Solution {\n public Node flatten(Node head) {\n Node curr=head;\n while(curr!=null){\n if(curr.child != null){\n | neutrino10 | NORMAL | 2021-03-04T04:20:55.502110+00:00 | 2021-03-06T10:08:16.055083+00:00 | 2,338 | false | ```\nclass Solution {\n public Node flatten(Node head) {\n Node curr=head;\n while(curr!=null){\n if(curr.child != null){\n Node tail = findTail(curr.child);\n if(curr.next != null){\n curr.next.prev=tail;\n }\n \n tail.next = curr.next;\n curr.next =curr.child;\n curr.child.prev = curr;\n curr.child =null;\n }\n curr = curr.next;\n }\n return head;\n }\n \n public Node findTail(Node child){\n while(child.next != null){\n child=child.next;\n }\n return child;\n }\n}\n``` | 30 | 0 | ['Java'] | 6 |
flatten-a-multilevel-doubly-linked-list | python recursive and iterative | python-recursive-and-iterative-by-maxwel-ofu1 | Recursive:\n\nclass Solution:\n def flatten(self, head: \'Node\') -> \'Node\':\n if not head: return None\n def travel(node):\n whil | maxwellnorah | NORMAL | 2019-04-06T20:47:09.119661+00:00 | 2019-04-06T20:47:09.119729+00:00 | 5,074 | false | Recursive:\n```\nclass Solution:\n def flatten(self, head: \'Node\') -> \'Node\':\n if not head: return None\n def travel(node):\n while node:\n q = node.next\n if not q: tail = node\n if node.child:\n node.next = node.child\n node.child.prev = node\n t = travel(node.child)\n if q:\n q.prev = t\n t.next= q\n node.child = None\n node = node.next\n return tail\n travel(head)\n return head\n```\n\nDFS with stack:\n```\nclass Solution:\n def flatten(self, head: \'Node\') -> \'Node\':\n if not head: return None\n stack = [head]; p = None\n while stack:\n r = stack.pop()\n if p:\n p.next,r.prev = r,p\n p = r\n if r.next:\n stack.append(r.next)\n if r.child:\n stack.append(r.child)\n r.child = None\n return head\n``` | 30 | 0 | ['Recursion', 'Iterator', 'Python'] | 4 |
flatten-a-multilevel-doubly-linked-list | 💡JavaScript Solution | javascript-solution-by-aminick-d0dt | The idea\n1. Use a stack to keep track of different levels of child nodes\n2. For each node, link back to the prev node. This way it\'s easier to link the end o | aminick | NORMAL | 2019-12-20T02:42:28.230962+00:00 | 2019-12-20T02:42:28.231011+00:00 | 2,050 | false | ### The idea\n1. Use a stack to keep track of different levels of child nodes\n2. For each node, link back to the `prev` node. This way it\'s easier to link the end of a child list to the parent list.\n``` javascript\nvar flatten = function(head) {\n if (!head) return null;\n let dummyHead = new Node(0, null, head, null);\n\n let stack = [head];\n let current = dummyHead;\n let prev = null;\n\n while(stack.length!=0) { \n current = stack.pop();\n \n if (prev) {\n current.prev = prev;\n prev.next = current;\n } \n\n if (current.next!=null) stack.push(current.next);\n if (current.child!=null) { // has a child\n stack.push(current.child);\n current.child = null; // remove child reference\n }\n \n prev = current; \n }\n \n return dummyHead.next;\n};\n``` | 27 | 0 | ['JavaScript'] | 0 |
flatten-a-multilevel-doubly-linked-list | [C++] Easy & Intuitive Recursive Solution | With Whiteboard Diagrams | No extra space | c-easy-intuitive-recursive-solution-with-530r | Explanation:\n\n\n\n\n/*\n// Definition for a Node.\nclass Node {\npublic:\n int val;\n Node* prev;\n Node* next;\n Node* child;\n};\n*/\n\nclass So | abhisharma404 | NORMAL | 2020-08-15T07:04:53.122730+00:00 | 2020-08-15T07:06:06.887947+00:00 | 2,416 | false | **Explanation:**\n\n\n\n```\n/*\n// Definition for a Node.\nclass Node {\npublic:\n int val;\n Node* prev;\n Node* next;\n Node* child;\n};\n*/\n\nclass Solution {\npublic:\n Node* flatten(Node* head) {\n if (!head) return nullptr;\n Node* tail = head;\n \n Node* next1 = flatten(head->child);\n Node* next2 = flatten(head->next);\n\n if (next1) {\n tail->next = next1;\n while (tail->next) {\n tail->next->prev = tail;\n tail->child = nullptr;\n tail = tail->next;\n }\n }\n \n tail->next = next2;\n if (next2) {\n next2->prev = tail;\n }\n \n return head;\n }\n};\n``` | 24 | 1 | ['Recursion', 'C', 'C++'] | 1 |
flatten-a-multilevel-doubly-linked-list | C++ | Two Solutions | c-two-solutions-by-ashwinfury1-fibc | Solution 1 - using array\n1. Iterate through nodes\n2. Add current node to array\n3. If the node has a child traverse the child\n4. At the end we will have an a | ashwinfury1 | NORMAL | 2020-07-10T08:37:29.602703+00:00 | 2020-07-10T08:48:47.980476+00:00 | 2,874 | false | ## Solution 1 - using array\n1. Iterate through nodes\n2. Add current node to array\n3. If the node has a child traverse the child\n4. At the end we will have an array in the order we want.\n5. Iterate through array and set next and prev pointer correctly also remove child nodes\n\nLet\'s take an example\n``` \n1---2---3---4---5---6--NULL\n |\n 7---8---9---10--NULL\n |\n 11--12--NULL\n```\nFor the above example our array will be\n{1} , {1,2}, {1,2,3}. Now three has a child go to child\n{1,2,3,7}, {1,2,3,7,8}. 8 has a child.\n{1,2,3,7,8,11}, {1,2,3,7,8,11,12}. Now the next element is NULL return and we will be at 9\n{1,2,3,7,8,11,12,9,10} again NULL return we will be at 4\n{1,2,3,7,8,11,12,9,10,4,5,6}\nThis is the order we want.\nIterate over the array and set prev and next pointers.\n\nCODE: \n\n```\n// Helper method to insert node in array - iteration\n void TravNodes(Node* head, vector<Node*>& ans){\n ans.push_back(head); // Insert the current node\n\t\t // if node has a child recursive call to the child\n if(head->child) TravNodes(head->child,ans); \n if(!head->next) return; // if next node is NULL return\n TravNodes(head->next,ans); // Traverse the next node\n }\n \n Node* flatten(Node* head) {\n if(!head) return head; // If there is node head return\n vector<Node*>ans; // ans array to store nodes in order\n ans.push_back(NULL); // Let the first element be NULL as head->prev = NULL;\n TravNodes(head,ans); // Helper function call\n\t\t// Iterate from the second element till second last element (1st ele is NULL)\n for(int i = 1;i<ans.size()-1;i++){ \n ans[i]->prev = ans[i-1]; // set prev ele\n ans[i]->next = ans[i+1]; // set next ele\n ans[i]->child = nullptr; // remove child ptr\n }\n\t\t// Set next and prev for last element\n ans[ans.size()-1]->prev = ans[ans.size()-2]; \n ans[ans.size()-1]->next = NULL;\n ans[ans.size()-1]->child = NULL;\n return ans[1]; // Return the head stored in ans[1]\n }\n```\n\n## Solution 2 - Recursion without array\n1. Iterate through the nodes\n2. If node has child save the next node to a variable; call recursive function call on child (Will return child as head)\n3. Set next of current node to child\n4. Remove child ptr from current node\n5. Iterate through the child node sequence to get last node\n6. Set next of last child sequence node to the variable we saved in step 2\n7. Set next of this node to the next we saved on step 2\n8. If that next was not NULL then set its previous to this last node\n9. Return head\n```\n Node* flatten(Node* head) {\n if(!head) return NULL;\n Node* trav = head;\n while(trav){\n if(trav->child){\n Node* next = trav->next;\n Node* child = flatten(trav->child);\n trav->child = NULL;\n trav->next = child;\n child->prev = trav;\n Node* lastNode = child;\n while(lastNode->next) lastNode = lastNode->next;\n lastNode->next = next;\n if(next) next->prev = lastNode;\n }\n trav = trav->next;\n }\n return head;\n }\n```\nHope this helps! Happy Coding :) | 23 | 2 | [] | 4 |
flatten-a-multilevel-doubly-linked-list | Java 1ms Recursion beats 100% with explaination | java-1ms-recursion-beats-100-with-explai-p88i | Go through the linked list;\nIf \n1. Node cur.child == null, skip, don\'t go into recursion.\n2. Node cur.child != null, recurse and get child\'s tail node. Nod | 351221254 | NORMAL | 2018-08-14T03:49:03.960524+00:00 | 2018-09-08T18:06:34.670198+00:00 | 2,471 | false | Go through the linked list;\nIf \n1. Node cur.child == null, skip, don\'t go into recursion.\n2. Node cur.child != null, recurse and get child\'s tail node. Node tmp = cur.next, (1)connect cur <-> child, (2)connect child\'s tail <->tmp.\n\nThe helper function returns the tail node of current level.\n\n```\npublic Node flatten(Node head) {\n helper(head);\n return head;\n}\n\nprivate Node helper(Node head) {\n Node cur = head, pre = head;\n while(cur != null) {\n if(cur.child == null) {\n pre = cur;\n cur = cur.next;\n } else {\n Node tmp = cur.next;\n Node child = helper(cur.child);\n cur.next = cur.child;\n cur.child.prev = cur;\n cur.child = null;\n child.next = tmp;\n if(tmp != null) tmp.prev = child;\n pre = child;\n cur = tmp;\n }\n }\n return pre;\n}\n``` | 23 | 0 | [] | 1 |
flatten-a-multilevel-doubly-linked-list | 😎Brute Force to Efficient Method 100% beat🤩 | Java | C++ | brute-force-to-efficient-method-100-beat-grar | 1st Method :- Brute force\n>The brute-force approach involves using recursion to traverse the nested doubly linked list and flatten it. Here\'s how you can do i | Akhilesh21 | NORMAL | 2023-10-03T15:16:46.747722+00:00 | 2023-10-03T15:22:06.733628+00:00 | 2,044 | false | # 1st Method :- Brute force\n>The brute-force approach involves using recursion to traverse the nested doubly linked list and flatten it. Here\'s how you can do it step by step:\n\n1. Start at the head of the doubly linked list.\n2. Initialize a helper recursive function that takes a node as an argument.\n3. In the helper function:\n - Check if the current node has a child (sub-list).\n - If it does, recursively call the helper function on the child node to flatten it.\n - After flattening the child list, connect the current node\'s `next` pointer to the flattened child\'s head.\n - Update the child\'s `prev` pointer to point back to the current node.\n - Set the current node\'s `child` pointer to null to remove the child link\n4. Continue this process for each node in the doubly linked list\n\n\n# Code\n``` Java []\nclass Solution {\n\n public Node flatten(Node head) {\n if (head == null) {\n return null;\n }\n \n // Helper function to flatten a node and its children\n flattenNode(head);\n \n return head;\n }\n\n private Node flattenNode(Node node) {\n Node current = node;\n Node tail = node; // To keep track of the tail of the flattened list\n \n while (current != null) {\n if (current.child != null) {\n Node child = current.child;\n current.child = null;\n \n // Flatten the child list and get the child list\'s tail\n Node childTail = flattenNode(child);\n \n // Connect the current node to the flattened child\n childTail.next = current.next;\n if (current.next != null) {\n current.next.prev = childTail;\n }\n current.next = child;\n child.prev = current;\n \n // Update the tail to be the tail of the merged list\n tail = childTail;\n }\n \n // Move to the next node in the original list\n current = current.next;\n if (current != null) {\n tail = current; // Update the tail for non-null current nodes\n }\n }\n \n return tail; // Return the tail of the merged list\n }\n}\n```\n``` C++ []\n\nclass Solution {\npublic:\n Node* flatten(Node* head) {\n if (head == nullptr) {\n return nullptr;\n }\n\n // Helper function to flatten a node and its children\n flattenNode(head);\n\n return head;\n }\n\nprivate:\n Node* flattenNode(Node* node) {\n Node* current = node;\n Node* tail = node; // To keep track of the tail of the flattened list\n\n while (current != nullptr) {\n if (current->child != nullptr) {\n Node* child = current->child;\n current->child = nullptr;\n\n // Flatten the child list and get the child list\'s tail\n Node* childTail = flattenNode(child);\n\n // Connect the current node to the flattened child\n childTail->next = current->next;\n if (current->next != nullptr) {\n current->next->prev = childTail;\n }\n current->next = child;\n child->prev = current;\n\n // Update the tail to be the tail of the merged list\n tail = childTail;\n }\n\n // Move to the next node in the original list\n current = current->next;\n if (current != nullptr) {\n tail = current; // Update the tail for non-null current nodes\n }\n }\n\n return tail; // Return the tail of the merged list\n }\n};\n```\n\n\n\n\n\n# Complexity\n#### Time complexity: O(N) ;\n- The time complexity of the brute-force approach is O(N), where N is the total number of nodes in the doubly linked list. This is because we visit each node exactly once while flattening the list.\n#### Space complexity: O(n) ; \n- The space complexity of the brute-force approach is O(H), where H is the maximum depth of the nested structure. This is because the recursion depth is bounded by the depth of the nested lists. In the worst case, when the list is completely nested, H can be equal to N (the total number of nodes), leading to a space complexity of O(N).\n\n> This brute-force approach recursively flattens the nested doubly linked list. However, it can be inefficient for large input lists with deep nesting because of the recursion overhead.\n\n# 2nd Method :- Efficient Method\n>To optimize the solution, we can use an iterative approach without recursion. Here\'s the step-by-step explanation:\n\n1. Start at the head of the doubly linked list.\n2. Use a stack to keep track of nodes with potential child lists.\n3. While traversing the list:\n - If the current node has a child (sub-list):\n - Save the next node in the main list.\n - Connect the current node to the child list.\n - Push the next node onto the stack for later processing.\n - Update the current node to be the child list\'s last node.\n - If the current node does not have a child and there are nodes in the stack, pop a node from the stack and connect it to the current node.\n4. Continue this process until you have processed all nodes in the list.\n\n``` Java []\nclass Solution {\n\n public Node flatten(Node head) {\n if (head == null) {\n return null;\n }\n \n Node current = head;\n Stack<Node> stack = new Stack<>();\n \n while (current != null) {\n if (current.child != null) {\n Node nextNode = current.next;\n \n // Connect current node to the child list\n current.next = current.child;\n current.child.prev = current;\n current.child = null;\n \n // Push the next node onto the stack for later processing\n if (nextNode != null) {\n stack.push(nextNode);\n }\n } else if (current.next == null && !stack.isEmpty()) {\n // If there are no more nodes in the current level,\n // pop a node from the stack and connect it to the current node\n Node nextNode = stack.pop();\n current.next = nextNode;\n nextNode.prev = current;\n }\n \n current = current.next;\n }\n \n return head;\n }\n}\n```\n``` C++ []\nclass Solution {\npublic:\n Node* flatten(Node* head) {\n if (head == nullptr) {\n return nullptr;\n }\n\n Node* current = head;\n stack<Node*> nodeStack;\n\n while (current != nullptr) {\n if (current->child != nullptr) {\n Node* nextNode = current->next;\n\n // Connect current node to the child list\n current->next = current->child;\n current->child->prev = current;\n current->child = nullptr;\n\n // Push the next node onto the stack for later processing\n if (nextNode != nullptr) {\n nodeStack.push(nextNode);\n }\n } else if (current->next == nullptr && !nodeStack.empty()) {\n // If there are no more nodes in the current level,\n // pop a node from the stack and connect it to the current node\n Node* nextNode = nodeStack.top();\n nodeStack.pop();\n current->next = nextNode;\n nextNode->prev = current;\n }\n\n current = current->next;\n }\n\n return head;\n }\n};\n```\n\nThis efficient approach uses an iterative process with a stack to flatten the nested doubly linked list, avoiding the overhead of recursion and making it more suitable for large input lists.\n\n\n# Complexity\n#### Time complexity: O(N) ;\n- The time complexity of the efficient approach is also O(N), where N is the total number of nodes in the doubly linked list. This is because we traverse each node in the list exactly once.\n#### Space complexity: O(1) ;\n- The space complexity of the efficient approach is O(1) because we use a constant amount of extra space, mainly for variables like current, stack, and temporary pointers. The space used is independent of the input size and does not depend on the depth of nesting. Therefore, it is a constant space algorithm.\n | 22 | 1 | ['Stack', 'C++', 'Java'] | 4 |
flatten-a-multilevel-doubly-linked-list | javascript stack | javascript-stack-by-dolphinfight-6xz9 | \nvar flatten = function(head) {\n if (!head) return head;\n let stack = []; //store all rest part of linkedlist nodes when has child\n let cur = head; | dolphinfight | NORMAL | 2020-07-10T21:41:23.763102+00:00 | 2020-07-10T21:41:49.168113+00:00 | 991 | false | ```\nvar flatten = function(head) {\n if (!head) return head;\n let stack = []; //store all rest part of linkedlist nodes when has child\n let cur = head;\n while (cur){\n if (cur.child){\n if (cur.next) stack.push(cur.next); //must check cur.next is null or not before added to stack\n cur.next = cur.child;\n cur.next.prev = cur; //because it is doubly linkedlist\n cur.child = null; //already assigned to next so now no child anymore. set null\n }\n else if (!cur.next && stack.length!= 0){ //now reach tail of linkedlist \n cur.next = stack.pop();\n cur.next.prev = cur; // because it is doubly linkedlist\n }\n cur = cur.next;\n }\n return head; //return reference of head\n};\n``` | 16 | 0 | ['JavaScript'] | 3 |
flatten-a-multilevel-doubly-linked-list | TC: O(n), SC: O(1) No stack, No recursion Simple One Pass Python Solution | tc-on-sc-o1-no-stack-no-recursion-simple-hdp0 | \ndef flatten(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n if not head: return\n curr = head\n while curr:\n if curr | azaansherani | NORMAL | 2022-04-14T20:42:21.711687+00:00 | 2022-06-12T13:03:35.663514+00:00 | 1,016 | false | ```\ndef flatten(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n if not head: return\n curr = head\n while curr:\n if curr.child:\n childNode = curr.child\n childNode.prev = curr #setting previous pointer\n \n while childNode.next:\n childNode = childNode.next\n \n childNode.next = curr.next\n \n if childNode.next: childNode.next.prev = childNode\n \n curr.next = curr.child\n curr.child = None\n \n curr = curr.next\n \n return head\n```\nThe traversal technique used here is known as Morris Traversal.\nMorris traversal is generally used to traverse binary trees, but if you give it some thought, the doubly linked list given in this problem is just like a Binary Tree with previous pointers.\nChild pointer and next pointer can be thought of as left pointer and right pointer of a tree respectively.\nOnce we look at the problem like this it becomes similar to flattening a binary tree to a linked list, just with two extra steps to set the previous pointers.\n\n\nIf you remove the two extra steps where you set the previous pointers, you get a solution to this problem: https://leetcode.com/problems/flatten-binary-tree-to-linked-list/\n```\ndef flatten(self, root: Optional[TreeNode]) -> None:\n if root == None: return\n curr = root\n while curr:\n if curr.left:\n childNode = curr.left\n while childNode.right:\n childNode = childNode.right\n childNode.right = curr.right\n curr.right = curr.left\n curr.left = None\n curr = curr.right\n```\n\n | 15 | 0 | ['Python', 'Python3'] | 4 |
flatten-a-multilevel-doubly-linked-list | Simple Java Pre-Order Solution | simple-java-pre-order-solution-by-wecanc-8rdj | \nclass Solution {\n public Node flatten(Node h) {\n if (h == null) return h;\n \n Stack<Node> st = new Stack<>();\n Node prev = | wecancode | NORMAL | 2018-12-28T06:59:04.596322+00:00 | 2018-12-28T06:59:04.596381+00:00 | 926 | false | ```\nclass Solution {\n public Node flatten(Node h) {\n if (h == null) return h;\n \n Stack<Node> st = new Stack<>();\n Node prev = null;\n st.push(h);\n while (!st.isEmpty()){\n Node cur = st.pop();\n if (prev != null) {\n prev.next = cur;\n cur.prev = prev;\n prev.child = null;\n }\n if (cur.next != null) st.push(cur.next);\n if (cur.child != null) st.push(cur.child);\n prev = cur;\n }\n \n return h;\n }\n}\n``` | 14 | 0 | [] | 1 |
flatten-a-multilevel-doubly-linked-list | Java pre-order and post-order solution same idea with 114. Flatten Binary Tree to Linked List | java-pre-order-and-post-order-solution-s-7pqu | The idea is same as 114. Just imagine the attrs "child" and "next" in the Node as "left" and "right" in the TreeNode. You will find actually, this multi-level l | yunwei_qiu | NORMAL | 2019-05-30T23:27:42.764633+00:00 | 2019-05-30T23:28:29.431244+00:00 | 582 | false | The idea is same as 114. Just imagine the attrs "child" and "next" in the Node as "left" and "right" in the TreeNode. You will find actually, this multi-level linkedList is a tree but just add parent node as "prev". (Note: I met this problem when I was onsite interview with Bloomberg last year, that time I cannot solve it, wish I have done it before interview. lol )\nPre-Order\n```\n Node pre = null;\n public Node flatten(Node head) {\n if (head == null) return head;\n Node child = head.child;\n Node next = head.next;\n if (pre == null) {\n pre = head;\n } else {\n pre.next = head;\n head.prev = pre;\n pre.child = null;\n }\n pre = head;\n flatten(child);\n flatten(next);\n return head;\n }\n```\nPost-Order\n```\n\tNode pre = null;\n public Node flatten(Node head) {\n if (head == null) return head;\n \n flatten(head.next);\n flatten(head.child);\n \n head.next = pre;\n \n if (pre != null) {\n pre.prev = head;\n }\n\n head.child = null;\n pre = head;\n return head;\n \n }\n | 13 | 0 | [] | 4 |
flatten-a-multilevel-doubly-linked-list | [Python] Easy to read 1 pass iterative, while loop + stack + 3 if statements | python-easy-to-read-1-pass-iterative-whi-4ti7 | O(n) time and space complexity\n \n\n def flatten(self, head: \'Node\') -> \'Node\':\n if head:\n n_stack = [] \n curr_no | briantsui2018 | NORMAL | 2020-01-15T03:49:14.495374+00:00 | 2020-01-15T03:49:14.495417+00:00 | 725 | false | O(n) time and space complexity\n \n```\n def flatten(self, head: \'Node\') -> \'Node\':\n if head:\n n_stack = [] \n curr_node = head\n while curr_node:\n if curr_node.next:\t\t\t\t\t\t# Push the "next" (if there\'s a "next") first.\n n_stack.append(curr_node.next)\n if curr_node.child:\t\t\t\t\t\t# Then push the "child" (if there\'s a child), \n n_stack.append(curr_node.child)\t\t# so that the "stack" would pop the immediate "child" \n curr_node.child = None \t\t\t\t# before any previous encountered "next".\n if n_stack:\t\t\t\t\t\t\t\t# It will "recurse" down and bubble back up eventually.\n next_node = n_stack.pop()\t\t\t# Unless it has traversed through all the nodes,\n curr_node.next = next_node # there\'s always some node left in the stack to pop. \n next_node.prev = curr_node \t\t\t# Simply link up with whatever comes from the stack.\n curr_node = curr_node.next \t\t\t\t# To the next node, or None if there\'s no more\n return head\n``` | 11 | 0 | ['Iterator', 'Python'] | 0 |
flatten-a-multilevel-doubly-linked-list | Simple Java Iteration solution beats 100% with explanation | simple-java-iteration-solution-beats-100-8t2q | We can use a stack to store the next node when the current node has a child, so we can go back to it when we reach to the end of the current list. \n\n\n pub | jay_fyi | NORMAL | 2019-04-26T22:35:01.230311+00:00 | 2019-04-26T22:35:01.230376+00:00 | 1,663 | false | We can use a stack to store the next node when the current node has a child, so we can go back to it when we reach to the end of the current list. \n\n\n public Node flatten(Node head) {\n //We can use a stack to store the next node when the current node has a child, so we can go back to it when we reach to the end of the current list.\n Stack<Node> stack = new Stack<>();\n \n\t\t// Keep the head pointer and traverse the list using current node (curNode)\n Node curNode = head;\n \n\t\t\n while(curNode != null){\n \n if(curNode.child != null){\n\t\t\t // if the current node has a child, then add the next node to the stack\n stack.add(curNode.next);\n\t\t\t\t// point the next node to the child\n curNode.next = curNode.child;\n\t\t\t\t// remove the child\'s pointer\n curNode.child = null;\n }\n\t\t\t\n // Determine which is the next node, if reached to the end of the current list and the stack is NOT empty, then pop the lastest node to be the next. \n Node next = (curNode.next == null && !stack.isEmpty()) ? stack.pop() : curNode.next;\n \n if(next != null){\n\t\t\t // make sure all the pointers are correct\n next.prev = curNode; \n curNode.next = next;\n }\n \n curNode = next;\n }\n return head;\n }\n | 11 | 0 | ['Stack', 'Doubly-Linked List', 'Iterator', 'Java'] | 4 |
flatten-a-multilevel-doubly-linked-list | Easy Java Solution, 100% faster and takes 0ms and O(1) space | easy-java-solution-100-faster-and-takes-s09ko | \npublic Node flatten(Node head) {\n if(head==null) return head;\n Node curr = head;\n \n while(curr!=null){\n if(curr.ch | harshadan03 | NORMAL | 2020-07-10T12:05:47.326902+00:00 | 2020-07-10T12:05:47.326949+00:00 | 512 | false | ```\npublic Node flatten(Node head) {\n if(head==null) return head;\n Node curr = head;\n \n while(curr!=null){\n if(curr.child!=null){\n Node down = curr.child;\n while(down.next!=null) down = down.next;\n Node temp = curr.next;\n curr.next = curr.child;\n curr.child.prev = curr;\n curr.child= null;\n down.next = temp;\n if(temp!=null) temp.prev = down;\n }\n curr = curr.next;\n }\n return head;\n }\n\n``` | 10 | 1 | [] | 3 |
flatten-a-multilevel-doubly-linked-list | The linked list [x,y,z] is not a valid doubly linked list error?? | the-linked-list-xyz-is-not-a-valid-doubl-f7gj | \n\n public Node flatten(Node head) {\n Node curr = head;\n while(curr!=null){\n if(curr.child!=null){\n Node next = | faanged | NORMAL | 2020-02-12T07:05:00.374122+00:00 | 2020-02-12T07:05:41.092809+00:00 | 1,805 | false | ```\n\n public Node flatten(Node head) {\n Node curr = head;\n while(curr!=null){\n if(curr.child!=null){\n Node next = flatten(curr.child);\n curr.child = null;\n Node dummyNext = next;\n next.prev = curr;\n while(next.next!=null){\n next = next.next;\n }\n next.next = curr.next;\n if(curr.next!=null)curr.next.prev = next.next;\n curr.next = dummyNext;\n curr = next.next;\n }else{\n curr = curr.next;\n }\n \n }\n return head;\n }\n\t```\n\t\n\tI made sure all children are null. The output is the following:\n\t\n\t```\n\tOutput: The linked list [1,2,3,7,8,11,12,9,10,4,5,6] is not a valid doubly linked list.\n\tExpected: [1,2,3,7,8,11,12,9,10,4,5,6]\n\t```\n\t | 10 | 5 | [] | 7 |
flatten-a-multilevel-doubly-linked-list | Non recursive Simple C++ solution | non-recursive-simple-c-solution-by-aadit-u7d6 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | aadityajawanjal34 | NORMAL | 2023-02-24T07:18:49.218957+00:00 | 2023-02-24T07:18:49.218998+00:00 | 695 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/*\n// Definition for a Node.\nclass Node {\npublic:\n int val;\n Node* prev;\n Node* next;\n Node* child;\n};\n*/\n\nclass Solution {\npublic:\n Node* flatten(Node* head) {\n Node*temp=head;\n while(temp!=NULL){\n if(temp->child!=NULL){\n Node*temp2=temp->child;\n Node*front=temp->next;\n temp->next=temp2;\n temp->child=NULL;\n temp2->prev=temp;\n while(temp2->next!=NULL){\n temp2=temp2->next;\n }\n if(front!=NULL){\n front->prev=temp2;\n temp2->next=front;\n }\n\n temp=temp->next;\n\n }\n else{\n temp=temp->next;\n }\n }\n return head;\n }\n};\n``` | 9 | 0 | ['C++'] | 1 |
flatten-a-multilevel-doubly-linked-list | Python Recursion: Easy-to-understand with Explanation | python-recursion-easy-to-understand-with-b31f | Intuition\n\nSince we are working with a doubly-linked list, for every node.child that we handle, we need to obtain the end node of the list at that particular | zayne-siew | NORMAL | 2021-10-31T06:47:50.253361+00:00 | 2021-10-31T06:47:50.253408+00:00 | 1,356 | false | ### Intuition\n\nSince we are working with a doubly-linked list, for every `node.child` that we handle, we need to obtain the end `node` of the list at that particular level, so that we can assign its `node.next` appropriately. We can thus write a recursive function that does the following:\n\n- Loop through each `node` in the list (at that particular level).\n- Upon encountering a `node` with a `child`, call the function again starting with `node.child`.\n- Once we reach the end of the list (at that particular level), return the end `node` so we can handle it accordingly on the previous level.\n\n---\n\n### Code\n\n```python\nclass Solution:\n def flatten(self, head: \'Node\') -> \'Node\':\n def getTail(node):\n prev = None\n while node:\n _next = node.next\n if node.child:\n\t\t\t\t\t# ... <-> node <-> node.child <-> ...\n node.next = node.child\n node.child = None\n node.next.prev = node\n\t\t\t\t\t# get the end node of the node.child list\n prev = getTail(node.next)\n if _next:\n\t\t\t\t\t\t# ... <-> prev (end node) <-> _next (originally node.next) <-> ...\n _next.prev = prev\n prev.next = _next\n else:\n prev = node\n node = _next # loop through the list of nodes\n return prev # return end node\n \n getTail(head)\n return head\n```\n\n---\n\n### Final Result\n\n\n\nPlease upvote if this has helped you! Appreciate any comments as well ;) | 9 | 0 | ['Recursion', 'Python', 'Python3'] | 1 |
flatten-a-multilevel-doubly-linked-list | [a,b,c]is not a valid doubly linked list. | abcis-not-a-valid-doubly-linked-list-by-fzoc6 | [a,b,c]is not a valid doubly linked list.\nIf you are getting the following error it is probably because you have not set the child of "flattened" node to NULL | vijayshank | NORMAL | 2021-04-10T19:45:39.279901+00:00 | 2021-04-10T19:45:39.279946+00:00 | 267 | false | `[a,b,c]is not a valid doubly linked list.`\nIf you are getting the following error it is probably because you have not set the child of "flattened" node to `NULL` | 9 | 0 | [] | 1 |
flatten-a-multilevel-doubly-linked-list | Javascript recursive and array | javascript-recursive-and-array-by-bloddy-2tpt | Walk recursively by the order of child and next\n2. Store path sequentially into an array\n3. Untangle the pointers (prev points to previous node next points to | bloddybear | NORMAL | 2019-10-22T17:44:26.163629+00:00 | 2019-10-22T17:44:26.163665+00:00 | 818 | false | 1. Walk recursively by the order of `child` and `next`\n2. Store path sequentially into an array\n3. Untangle the pointers (`prev` points to previous node `next` points to next node)\n```\n/**\n * @param {Node} head\n * @return {Node}\n */\nvar flatten = function(head) {\n const arr = [];\n const helper = (node) => {\n if(!node) return;\n arr.push(node);\n helper(node.child);\n helper(node.next);\n };\n helper(head);\n for(let i = 0; i < arr.length; i++) {\n arr[i].prev = arr[i-1] || null;\n arr[i].next = arr[i+1] || null;\n arr[i].child = null;\n }\n return arr[0] || null;\n};\n``` | 9 | 0 | ['Recursion', 'JavaScript'] | 1 |
flatten-a-multilevel-doubly-linked-list | Java Recursive Solution 6 lines 0 ms | java-recursive-solution-6-lines-0-ms-by-jc6wq | \nclass Solution {\n Node end = null;\n public Node flatten(Node head) {\n if(head == null) return end;\n\t\t// 0. head -> flatten(head.child) -> f | echo999 | NORMAL | 2019-08-20T04:43:36.528330+00:00 | 2019-08-20T04:45:47.202368+00:00 | 780 | false | ```\nclass Solution {\n Node end = null;\n public Node flatten(Node head) {\n if(head == null) return end;\n\t\t// 0. head -> flatten(head.child) -> flatten(head.next) -> end \n\t\t// 1. flatten(head.next) -> end \n end = flatten(head.next);\n\t\t// 2. head -> flatten(head.child) \n head.next = flatten(head.child);\n\t\t// 3. flatten(head.child) -> flatten(head.next)\n if(head.next != null) head.next.prev = head;\n head.child = null;\n return head;\n }\n``` | 9 | 0 | ['Recursion', 'Java'] | 1 |
flatten-a-multilevel-doubly-linked-list | Different python solutions | different-python-solutions-by-otoc-tc2i | Solution 1: recursive solution\n\n def flatten(self, head: \'Node\') -> \'Node\':\n def recursive(h):\n p_prev, p = None, h\n wh | otoc | NORMAL | 2019-07-16T05:07:40.058607+00:00 | 2019-07-16T05:21:21.470490+00:00 | 710 | false | Solution 1: recursive solution\n```\n def flatten(self, head: \'Node\') -> \'Node\':\n def recursive(h):\n p_prev, p = None, h\n while p and not p.child:\n p_prev, p = p, p.next\n if not p:\n return h, p_prev\n else:\n p_head, p_tail = recursive(p.child)\n p_nxt = p.next\n p.child = None\n p.next = p_head\n p_head.prev = p\n p_tail.next = p_nxt\n if not p_nxt:\n return h, p_tail\n else:\n p_nxt.prev = p_tail\n return h, recursive(p_nxt)[1]\n \n if not head:\n return head\n else:\n return recursive(head)[0]\n```\n\nSolution 2:\n```\n def flatten(self, head: \'Node\') -> \'Node\':\n if not head:\n return None\n p = head\n while p:\n if not p.child:\n p = p.next\n else:\n q = p.child\n while q.next:\n q = q.next\n q.next = p.next\n if p.next:\n p.next.prev = q\n p.next = p.child\n p.child.prev = p\n p.child = None\n return head\n``` | 9 | 0 | [] | 3 |
flatten-a-multilevel-doubly-linked-list | [Python 3] Using recursion || beats 98% || 36ms 🥷🏼 | python-3-using-recursion-beats-98-36ms-b-clez | \npython3 []\nclass Solution:\n def flatten(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n def unpack(head):\n cur = tail = head\ | yourick | NORMAL | 2023-08-03T17:37:18.018783+00:00 | 2023-08-14T13:54:52.849544+00:00 | 1,010 | false | \n```python3 []\nclass Solution:\n def flatten(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n def unpack(head):\n cur = tail = head\n while cur:\n if cur.child:\n start, end = unpack(cur.child)\n if cur.next: cur.next.prev = end\n cur.next, start.prev, end.next, cur.child = start, cur, cur.next, None\n cur = end\n tail = cur\n cur = cur.next\n return (head, tail)\n\n return unpack(head)[0]\n```\n\n | 8 | 0 | ['Linked List', 'Recursion', 'Python', 'Python3'] | 0 |
flatten-a-multilevel-doubly-linked-list | 430: Solution with step by step explanation | 430-solution-with-step-by-step-explanati-ojwj | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n1. Define the function flattenDFS which takes a Node object as input and | Marlen09 | NORMAL | 2023-03-07T18:23:18.024248+00:00 | 2023-03-07T18:23:18.024294+00:00 | 1,667 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Define the function flattenDFS which takes a Node object as input and returns a Node object.\n2. Check if the node object is None. If it is, return None.\n3. Check if node object has no child and no next pointers. If it does not, return the node object.\n4. Check if the node object has no child pointer. If it does not, call flattenDFS with the next node and return its result.\n5. Call flattenDFS with the child node and store its result in childTail.\n6. Get the next node of node and store it in nextNode.\n7. If nextNode is not None, set childTail.next to nextNode and set nextNode.prev to childTail.\n8. Set node.next to node.child and set node.child.prev to node.\n9. Set node.child to None.\n10. Call flattenDFS with nextNode if it is not None, otherwise call it with childTail. Store the result in a variable.\n11. Return the head of the flattened linked list after calling flattenDFS with the input head and completing the process.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def flatten(self, head: \'Node\') -> \'Node\':\n def flattenDFS(node):\n if not node:\n return None\n if not node.child and not node.next:\n return node\n if not node.child:\n return flattenDFS(node.next)\n childTail = flattenDFS(node.child)\n nextNode = node.next\n if nextNode:\n childTail.next = nextNode\n nextNode.prev = childTail\n node.next = node.child\n node.child.prev = node\n node.child = None\n return flattenDFS(nextNode) if nextNode else childTail\n flattenDFS(head)\n return head\n\n``` | 8 | 0 | ['Linked List', 'Depth-First Search', 'Doubly-Linked List', 'Python', 'Python3'] | 0 |
flatten-a-multilevel-doubly-linked-list | Easy Preorder Traversal of Binary Tree Approach (with diagram) | easy-preorder-traversal-of-binary-tree-a-ct3z | Consider the following Multilevel Linked List, with N denotes next pointer, P denotes previous pointer and C denotes Child Pointer!\n\n\n\nIn this example, the | kashish098 | NORMAL | 2022-09-01T19:10:06.276517+00:00 | 2022-09-01T19:12:03.976179+00:00 | 623 | false | Consider the following Multilevel Linked List, with N denotes next pointer, P denotes previous pointer and C denotes Child Pointer!\n\n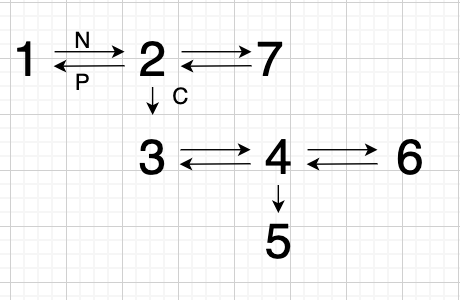\n\nIn this example, the answer will be [1,2,3,4,5,6,7]\n\nThis given multilevel linked list can be think of binary tree with left Child as Child pointer and right pointer as next pointer.\n\n\n\nPreorder traversal of this tree gives us the same result as of multilevel linked list. [1,2,3,4,5,6,7], hence applying preorder traversal.\n```\npublic Node flatten(Node head) {\n if(head == null) return null;\n\t\t\n Node left = flatten(head.child);\n Node right = flatten(head.next);\n \n Node temp = head;\n head.next = left;\n \n if(left != null) {\n left.prev = head;\n head.child = null;\n }\n \n while(temp.next != null) {\n temp = temp.next;\n }\n \n temp.next = right;\n \n if(right != null) {\n right.prev = temp;\n }\n \n return head;\n }\n```\n\n## Explanation\n- In given solution, we are recursively building linked list from left and right subtree. \n- Flatten function returns the head of linked list created. When we apply recursion, we consider what needs to be done at a given node, considering left and right subtree call will provide the required solution.\n- Now we have left and right linked list and a node.\n- We have added `head.next` to head of linked list returned from left subtree and if left linked list exists, we have added `left.prev = head`\n- After left linked list is attached to head, we traverse the linked list and reach to end, from there we are linking the right linked list from end of first linked list\n- `head.child = null` deletes the child pointer | 8 | 0 | ['Depth-First Search', 'Recursion', 'C', 'Binary Tree', 'Java'] | 0 |
flatten-a-multilevel-doubly-linked-list | JavaScript Iterative Solution| Easy- with example walkthrough | javascript-iterative-solution-easy-with-d4z48 | \n /*\n Time: O(n) || Space: O(n)\n Please upvote if you find implementation with example useful, \n i\'ll try to implement examples in my future posts as well | Gift369 | NORMAL | 2021-03-10T14:45:35.139773+00:00 | 2021-03-10T14:59:54.002356+00:00 | 517 | false | ```\n /*\n Time: O(n) || Space: O(n)\n Please upvote if you find implementation with example useful, \n i\'ll try to implement examples in my future posts as well :) \n*/\nvar flatten = function(head) {\n let temp = head;\n let stack = [];\n \n while (head) {\n if (head.child) {\n if (head.next) {\n stack.push(head.next);\n }\n head.next = head.child;\n head.next.prev = head;\n head.child = null;\n } else if (!head.next && stack.length > 0) { //if head.next is null but there are still nodes in stack\n head.next = stack.pop(); //head.next will point to the popped value from stack\n head.next.prev = head;\n }\n head = head.next; //so the iteration continues to the next node and then next node\n }\n return temp;\n};\n\n/*\n\n 1---2---3---4---5---6--NULL\n |\n 7---8---9---10--NULL\n |\n 11--12--NULL\n\nStep1:\nhead is 3\nstack = [---4---5---6--NULL]\n \n 1---2---3\n |\n 7---8---9---10--NULL\n |\n 11--12--NULL\n \n\nStep2:\nstack = [---4---5---6--NULL]\n \n 1---2---3--7---8---9---10--NULL\n |\n 11--12--NULL\n \n\nStep3:\nstack = [---4---5---6--NULL, ---9---10--NULL]\n \n 1---2---3--7---8---11--12--NULL \n \nStep4:\nstack.pop() and append it to the next of last node in linked list, it will look like this\nstack = [---4---5---6--NULL]\n \n 1---2---3--7---8---11--12---9---10--NULL \n \n\nStep5:\nstack.pop() and append it to the next of last node in linked list, it will look like this\nstack = []\n \n 1---2---3--7---8---11--12---9---10----4---5---6--NULL\n \n \n Step6:\n return the result = 1---2---3--7---8---11--12---9---10----4---5---6--NULL\n \n */\n```\n | 8 | 0 | ['Stack', 'Depth-First Search', 'Iterator', 'JavaScript'] | 0 |
flatten-a-multilevel-doubly-linked-list | C++ Easy Recursive Solution | c-easy-recursive-solution-by-nivedit-l4kz | ```\nclass Solution {\npublic:\n Node flatten(Node head) {\n if(!head) return head;\n Node curr=head;\n while(curr)\n {\n | nivedit | NORMAL | 2020-07-10T07:29:22.920864+00:00 | 2020-07-10T07:29:22.920914+00:00 | 795 | false | ```\nclass Solution {\npublic:\n Node* flatten(Node* head) {\n if(!head) return head;\n Node* curr=head;\n while(curr)\n {\n if(curr->child)\n {\n Node* temp = curr->next;\n Node* x = flatten(curr->child);\n x->prev= curr;\n curr->next = x;\n Node* end = x;\n while(end->next)\n end=end->next;\n end->next = temp;\n if(temp)\n temp->prev = end;\n curr->child = NULL;\n }\n curr=curr->next;\n }\n return head;\n }\n}; | 8 | 0 | [] | 0 |
flatten-a-multilevel-doubly-linked-list | Python sol by recursion. 80%+ [w/ Visualization ] | python-sol-by-recursion-80-w-visualizati-upgr | Python sol by recursion\n\n---\n\nIllustration and Visualization:\n\n\n\n---\n\nImplemetation by recursion\n\n\nclass Solution:\n def flatten(self, head: \'N | brianchiang_tw | NORMAL | 2020-05-22T12:58:31.845088+00:00 | 2020-05-22T12:58:31.845138+00:00 | 1,081 | false | Python sol by recursion\n\n---\n\n**Illustration and Visualization**:\n\n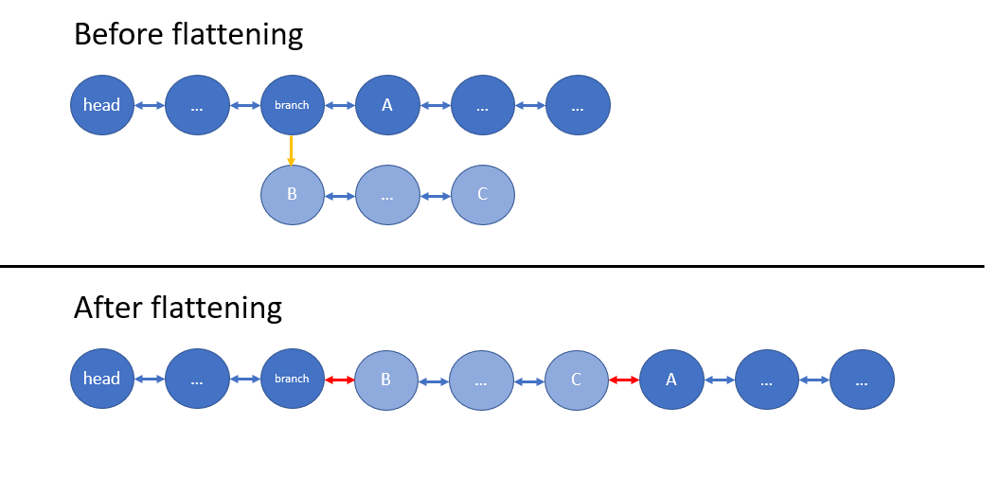\n\n---\n\n**Implemetation** by recursion\n\n```\nclass Solution:\n def flatten(self, head: \'Node\') -> \'Node\':\n \n def helper(head) -> \'None\':\n \n prev, current_node = None, head\n \n while current_node:\n \n if current_node.child:\n \n # flatten child linked list\n current_child, current_tail = current_node.child, helper(current_node.child)\n \n # After next level flattening is completed\n # Handle for the concatenation between current linked list and child linked list\n \n # current node\'s child points to None after flattening\n current_node.child = None\n \n ## Update the linkage between original next and current tail \n original_next = current_node.next\n \n if original_next: \n original_next.prev = current_tail \n \n current_tail.next = original_next\n \n ## Update the linkage between current node and current child\n current_node.next, current_child.prev = current_child, current_node\n \n # update prev and cur, move to next position\n prev, current_node = current_tail, original_next\n \n \n else:\n \n # update prev and cur, move to next position\n prev, current_node = current_node, current_node.next\n \n \n # return tail node\n return prev\n \n\t# ------------------------------------------------------------------------------\n\n helper(head)\n \n return head\n``` | 8 | 1 | ['Recursion', 'Python', 'Python3'] | 0 |
flatten-a-multilevel-doubly-linked-list | Python Recursive Solution + Analysis | python-recursive-solution-analysis-by-ha-a2kq | The key idea is to recursively flatten sublists, given the head. Flattening a child sublist and flattening a tail (contents of head.next) sublist is the same pr | hai_dee | NORMAL | 2018-08-12T06:25:06.512060+00:00 | 2018-08-12T06:25:06.512130+00:00 | 523 | false | The key idea is to recursively flatten sublists, given the head. Flattening a child sublist and flattening a tail (contents of head.next) sublist is the same procedure. Once we\'ve made the recursive calls, we need to assemble the list so that it\'s of the form head->[result of child flattening]->[result of tail flattening].\n\n## Analysis\n\nIf n is the number of nodes...\n\nThe algorithm only requires ***```O(1)```*** extra space on the heap, ***BUT*** in the worst case, it requires ***```O(n)```*** extra space on the stack, as we could need to put the entire list on. \n\nThe amount of space required is dependent on:\n1) The length of the longest stretch of nodes that only have child or next pointers.\n2) The percentage of nodes which have both a child and a next pointer on them (the higher the percentage, the better the performance, because we have nearer to a balanced tree structure).\n\nDue to this structure being equivalent to a (rather stringy in a lot of cases I suspect) binary tree, I\'m pretty sure it\'s impossible to write an iterative algorithm that uses ***```O(1)```*** space. The stack/ queue you use to keep track of the work still to do could potentially grow to ***```O(n)```*** in the worst case, and like I said, this worst case is probably common.\n\nThe time complexity is ***```O(n)```*** . We handle each node once. It is impossible to do better than ***```O(n)```*** time, because we need to actually check the child and next pointers of every node, otherwise we could miss some parts of the structure out!\n\n## Algorithm\n\n```py\nclass Solution(object):\n def flatten(self, head):\n """\n :type head: Node\n :rtype: Node\n """\n self.recursively_flatten(head)\n return head\n \n # Takes the head of the list to be flattened, and returns the tail of the flattened list.\n def recursively_flatten(self, head):\n \n # Could happen if outer caller passes in an empty list.\n if head == None:\n return None\n \n # Base case - there is nothing left to flatten.\n if head.next == None and head.child == None:\n return head\n \n # Recursive case - we need to flatten the child and the tail.\n tail = head.next # We need to store this as doing child first.\n current_end = head # Where will we be attaching next?\n \n if head.child != None:\n child_end = self.recursively_flatten(head.child)\n self.link(current_end, head.child)\n current_end = child_end\n head.child = None\n \n if tail != None:\n tail_end = self.recursively_flatten(tail)\n self.link(current_end, tail)\n current_end = tail_end\n \n return current_end\n \n def link(self, node_1, node_2):\n node_1.next = node_2\n node_2.prev = node_1\n```\n\n## Another way of looking at it...\nAnother interesting observation one could make is that this linked list structure is actually a binary tree!\n Instead of having left/ right nodes to "child" through, we have child/next. \n \n If we pretend that "child" means the left node, and "next" means the right node, then the order of nodes in the linked list the pre-order traversal of the "tree". \n \n We first included the node itself, and then the result of going over left (tail), and finallly the result of going over right (next). | 8 | 0 | [] | 2 |
flatten-a-multilevel-doubly-linked-list | simple java and python solution | simple-java-and-python-solution-by-keert-1hc6 | Java solution\n\nclass Solution {\n public Node flatten(Node head) \n {\n Node curr=head;\n while(curr!=null)\n {\n if(cur | keerthy0212 | NORMAL | 2021-10-31T14:30:00.744910+00:00 | 2021-11-01T03:43:02.539386+00:00 | 727 | false | **Java solution**\n```\nclass Solution {\n public Node flatten(Node head) \n {\n Node curr=head;\n while(curr!=null)\n {\n if(curr.child==null)//if the current node doesnt have a child then lets just move to the next node\n {\n curr=curr.next;\n continue;\n }\n //if incase a node has child\n Node temp=curr.child;\n while(temp.next!=null)\n {\n temp=temp.next;//transverse till the tail of that child node\n }\n \n temp.next=curr.next;//again coming back to parent node and transversing thro next nodes\n if(curr.next!=null)\n {\n curr.next.prev=temp;\n }\n //merging all nodes\n curr.next=curr.child;\n curr.child.prev=curr;\n curr.child=null;\n }\n \n return head;\n }\n}\n```\n\n**Python solution**\n```\nclass Solution(object):\n def flatten(self, head):\n """\n :type head: Node\n :rtype: Node\n """\n curr=head\n while curr!=None:\n if curr.child==None:\n curr=curr.next\n continue\n \n temp=curr.child\n while temp.next!=None:\n temp=temp.next\n \n temp.next=curr.next\n if curr.next!=None:\n curr.next.prev=temp\n \n curr.next=curr.child\n curr.child.prev=curr\n curr.child=None\n \n return head\n \n \n \n``` | 7 | 0 | ['Python', 'Java'] | 1 |
flatten-a-multilevel-doubly-linked-list | C++ Super Simple, Short and Clean Iterative Solution, 4ms O(n) TC O(1) SC | c-super-simple-short-and-clean-iterative-djwh | \nclass Solution {\npublic:\n Node* flatten(Node* head) {\n Node *ptr = head, *tmp_next, *runner;\n \n while (ptr) {\n if (pt | yehudisk | NORMAL | 2021-07-31T21:34:11.561974+00:00 | 2021-07-31T21:34:11.562014+00:00 | 413 | false | ```\nclass Solution {\npublic:\n Node* flatten(Node* head) {\n Node *ptr = head, *tmp_next, *runner;\n \n while (ptr) {\n if (ptr->child) {\n \n // Save the current next and connect the child to next\n tmp_next = ptr->next;\n ptr->next = ptr->child;\n ptr->next->prev = ptr;\n ptr->child = NULL;\n \n // Run till the end of the current list and connect last node to saved next\n runner = ptr->next;\n while (runner->next) runner = runner->next;\n runner->next = tmp_next;\n if (runner->next) runner->next->prev = runner;\n }\n \n ptr = ptr->next;\n }\n \n return head;\n }\n};\n```\n**Like it? please upvote!** | 7 | 0 | ['C'] | 0 |
flatten-a-multilevel-doubly-linked-list | 430. Flatten a Multilevel Doubly Linked List most easiest sol c++ | 430-flatten-a-multilevel-doubly-linked-l-931c | \nNode* flatten(Node* head) {\n if(!head) return head;\n if(!head->next and !head->child)\n return head;\n Node *p=head;\n | LakshyaVijh | NORMAL | 2020-07-10T07:14:02.739806+00:00 | 2020-07-10T07:16:37.891869+00:00 | 305 | false | ```\nNode* flatten(Node* head) {\n if(!head) return head;\n if(!head->next and !head->child)\n return head;\n Node *p=head;\n while(p)\n {\n if(p->child)\n {\n Node *r=p->child,*q=p->next;\n p->next=r;\n r->prev=p;\n while(r->next)\n r=r->next;\n if(q) q->prev=r;\n r->next=q;\n p->child=NULL;\n p=p->next;\n }\n else\n p=p->next;\n }\n return head;\n }\n\t```\n\t\n\tPlease Give an upvote if you like it | 7 | 1 | [] | 0 |
flatten-a-multilevel-doubly-linked-list | 💯 Beats 100% || ✅ Easy to understand & Best solution ⬆️🆙 || O(n)💥👏🔥 | beats-100-easy-to-understand-best-soluti-z5o9 | Please upvote if my solution and efforts helped you.\n***\n\n\n\n# Code\n\nclass Solution {\n public Node flatten(Node head) {\n Node curr=head;\n | SumitMittal | NORMAL | 2024-06-17T17:14:35.909144+00:00 | 2024-06-17T17:14:35.909177+00:00 | 416 | false | # Please upvote if my solution and efforts helped you.\n***\n\n\n\n# Code\n```\nclass Solution {\n public Node flatten(Node head) {\n Node curr=head;\n while(curr!=null){\n if(curr.child != null){\n Node tail = findTail(curr.child);\n if(curr.next != null){\n curr.next.prev=tail;\n }\n tail.next = curr.next;\n curr.next =curr.child;\n curr.child.prev = curr;\n curr.child =null;\n }\n curr = curr.next;\n }\n return head;\n }\n public Node findTail(Node child){\n while(child.next != null){\n child=child.next;\n }\n return child;\n }\n}\n```\n\n | 6 | 0 | ['Linked List', 'Doubly-Linked List', 'Java'] | 2 |
flatten-a-multilevel-doubly-linked-list | Java | 0ms | easy to understand | java-0ms-easy-to-understand-by-venkat089-b1kr | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Venkat089 | NORMAL | 2023-01-09T15:58:32.074604+00:00 | 2023-01-09T15:58:32.074638+00:00 | 1,004 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/*\n// Definition for a Node.\nclass Node {\n public int val;\n public Node prev;\n public Node next;\n public Node child;\n};\n*/\n\nclass Solution {\n public Node flatten(Node head) {\n Node temp=head;\n while(temp!=null)\n {\n if(temp.child==null)temp=temp.next;\n else{\n if(temp.next!=null)\n link(temp.child,temp.next);\n temp.next=temp.child;\n temp.child.prev=temp;\n temp.child=null;\n }\n }\n return head;\n \n }\n public void link(Node n1,Node n2)\n {\n while(n1.next!=null)n1=n1.next;\n n1.next=n2;\n n2.prev=n1;\n }\n}\n``` | 6 | 0 | ['Java'] | 0 |
flatten-a-multilevel-doubly-linked-list | python || O(1) space || iterative || detailed explanation || very fast | python-o1-space-iterative-detailed-expla-k2cj | \n"""\n# Definition for a Node.\nclass Node:\n def __init__(self, val, prev, next, child):\n self.val = val\n self.prev = prev\n self.ne | Yared_betsega | NORMAL | 2022-07-27T11:51:24.773145+00:00 | 2022-07-27T11:51:24.773192+00:00 | 481 | false | ```\n"""\n# Definition for a Node.\nclass Node:\n def __init__(self, val, prev, next, child):\n self.val = val\n self.prev = prev\n self.next = next\n self.child = child\n"""\n\nclass Solution:\n def flatten(self, head: \'Optional[Node]\') -> \'Optional[Node]\': \n node = head\n while node:\n if node.child: # If there is a child travel to last node of the child\n child = node.child\n while child.next:\n child = child.next\n child.next = node.next # Update the next of child to the the next of the current node\n if node.next: # update the prev of the next node to chile to make it valid doubly linked list\n node.next.prev = child\n node.next = node.child # Update the child to become the next of the current\n node.next.prev = node # update the prev of the next node to chile to make it valid doubly linked list\n node.child = None # Make the child of the current node None to fulfill the requirements\n node = node.next\n return head\n\n# time and space complexity\n# time: O(n)\n# space: O(1)\n``` | 6 | 0 | ['Iterator', 'Python'] | 0 |
flatten-a-multilevel-doubly-linked-list | 2 Different Ways, Iterative & Recursive, With Comments | 2-different-ways-iterative-recursive-wit-hjda | 1. Iterative using Stack\n\n\npublic class Solution { \n public Node Flatten(Node head) { \n var current = head;\n var stack = new Stack<Nod | keperkjr | NORMAL | 2021-10-31T04:36:12.477618+00:00 | 2021-10-31T05:40:25.152255+00:00 | 112 | false | **1. Iterative using Stack**\n\n```\npublic class Solution { \n public Node Flatten(Node head) { \n var current = head;\n var stack = new Stack<Node>();\n \n // Loop through nodes\n while (current != null) {\n \n // Check to see if node has child\n if (current.child != null) {\n // If current node has a next node, save to stack \n // so we can reconnect it to the tail \n // of the child node later\n if (current.next != null) {\n stack.Push(current.next);\n }\n \n // Set the next node as the child,\n // we will now iterate down this path\n current.next = current.child; \n \n // Set the previous node as the current\n current.next.prev = current;\n \n // Set child to null\n current.child = null; \n \n } else if (current.next == null) {\n // Reconnect node at the top of the \n // stack to the tail child node\n if (stack.Count > 0) {\n // Set the next node as the reconnected node,\n // we will now iterate down this path\n current.next = stack.Pop();\n current.next.prev = current; \n }\n }\n current = current.next;\n }\n \n return head;\n }\n}\n```\n\n\n**2. Recursive**\n\n```\npublic class Solution { \n public Node Flatten(Node head) { \n Flatten(head, null); \n return head;\n }\n \n private Node Flatten(Node current, Node previous) {\n if (current == null) {\n return previous;\n }\n \n // If previous node exists, set the next and previous values\n if (previous != null) {\n previous.next = current;\n current.prev = previous;\n }\n \n // Save the next node so we can reconnect it to the tail \n // of the child node later\n var next = current.next;\n \n // Traverse down child path. \n // If children exist, this returns the last child for the current node\n var tail = Flatten(current.child, current);\n \n // Child path has been explored, set to null\n current.child = null;\n \n // Reconnect next node to the tail child node\n return Flatten(next, tail); \n }\n}\n``` | 6 | 1 | [] | 1 |
flatten-a-multilevel-doubly-linked-list | C++ Simple list traversal without using stack/queue/DFS | c-simple-list-traversal-without-using-st-fxou | \nclass Solution {\npublic:\n Node* flatten(Node* head) {\n Node* lead=head;\n Node* ptr=NULL; \n Node* beta=NULL; // beta is chi | blue_jerry | NORMAL | 2020-09-14T18:24:00.863134+00:00 | 2020-09-14T18:24:00.863189+00:00 | 341 | false | ```\nclass Solution {\npublic:\n Node* flatten(Node* head) {\n Node* lead=head;\n Node* ptr=NULL; \n Node* beta=NULL; // beta is child node\n while(head){\n if(head->child){\n ptr=head->next;\n beta=head->child;\n head->child=NULL;\n head->next=beta;\n beta->prev=head;\n while(beta->next){\n beta=beta->next;\n }\n if(ptr)\n ptr->prev=beta;\n beta->next=ptr;\n }\n head=head->next;\n }\n return lead;\n }\n};\n``` | 6 | 0 | ['C'] | 1 |
flatten-a-multilevel-doubly-linked-list | Java short and concise with stack | java-short-and-concise-with-stack-by-vij-puy2 | \npublic Node flatten(Node head) {\n if(head == null){\n return head;\n }\n \n Stack<Node> stack = new Stack<>();\n | vijai_a | NORMAL | 2020-07-10T14:31:33.480318+00:00 | 2020-07-10T14:33:26.647154+00:00 | 535 | false | ```\npublic Node flatten(Node head) {\n if(head == null){\n return head;\n }\n \n Stack<Node> stack = new Stack<>();\n stack.push(head);\n Node prev = null;\n \n while(!stack.empty()){\n Node node = stack.pop();\n if(node.next != null){\n stack.push(node.next);\n }\n if(node.child != null){\n stack.push(node.child);\n node.child = null;\n }\n node.next = stack.empty() ? null : stack.peek();\n node.prev = prev;\n prev = node;\n }\n \n return head;\n }\n``` | 6 | 0 | ['Java'] | 1 |
flatten-a-multilevel-doubly-linked-list | C# DFS | c-dfs-by-bacon-lj9i | \npublic class Solution {\n public Node Flatten(Node head) {\n if (head == null) return null;\n DFS(head);\n return head;\n }\n\n | bacon | NORMAL | 2019-07-14T18:11:00.615457+00:00 | 2019-07-14T18:11:00.615520+00:00 | 333 | false | ```\npublic class Solution {\n public Node Flatten(Node head) {\n if (head == null) return null;\n DFS(head);\n return head;\n }\n\n private Node DFS(Node head) {\n var cur = head;\n\n while (cur != null && cur.child == null) {\n cur = cur.next;\n }\n\n if (cur != null) {\n var next = cur.next;\n var childHead = DFS(cur.child);\n cur.child = null;\n cur.next = childHead;\n childHead.prev = cur;\n // go down to the child end\n var curChild = childHead;\n while (curChild.next != null) {\n curChild = curChild.next;\n }\n\n // connect with the next\n curChild.next = next;\n if (next != null) next.prev = curChild;\n DFS(next);\n }\n\n return head;\n }\n}\n``` | 6 | 0 | [] | 1 |
flatten-a-multilevel-doubly-linked-list | 0ms solution || beats 100% || easy to understand || O(n) time complexity || O(1) space complexity | 0ms-solution-beats-100-easy-to-understan-5l0d | Intuition\n Describe your first thoughts on how to solve this problem. Intuition is to insert all child nodes between parent node and parent->next node and the | coder_adi_ | NORMAL | 2024-07-09T03:16:15.280987+00:00 | 2024-07-11T04:31:34.670733+00:00 | 386 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->Intuition is to insert all child nodes between parent node and parent->next node and the again check for child nodes from parent node\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n\n\n# Code\n```\n/*\n// Definition for a Node.\nclass Node {\npublic:\n int val;\n Node* prev;\n Node* next;\n Node* child;\n};\n*/\n\nclass Solution {\npublic:\n Node* flatten(Node* head) {\n Node* temp=head;\n\n while(temp!=NULL){\n if(temp->child!=NULL){\n Node* forward=temp->next;\n Node* temp_child=temp;\n temp=temp->child;\n temp_child->child=NULL;\n temp_child->next=temp;\n temp->prev=temp_child;\n\n while(temp->next!=NULL){\n temp=temp->next;\n }\n\n temp->next=forward;\n if(forward!=NULL) forward->prev=temp;\n temp=temp_child;\n }\n temp=temp->next;\n }\n\n return head;\n }\n};\n```\n\n | 5 | 0 | ['Linked List', 'C++'] | 1 |
flatten-a-multilevel-doubly-linked-list | 0ms simple 100% faster using recursion in java | 0ms-simple-100-faster-using-recursion-in-ry2l | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | bhargavsuhagiya99 | NORMAL | 2023-04-23T05:38:36.862530+00:00 | 2023-04-23T05:39:15.250146+00:00 | 758 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/*\n// Definition for a Node.\nclass Node {\n public int val;\n public Node prev;\n public Node next;\n public Node child;\n};\n*/\nclass Solution {\n public Node flatten(Node head) {\n Node curr=head;\n while(curr!=null){\n if(curr.child != null){\n Node tail = findTail(curr.child);\n if(curr.next != null){\n curr.next.prev=tail;\n }\n \n tail.next = curr.next;\n curr.next =curr.child;\n curr.child.prev = curr;\n curr.child =null;\n }\n curr = curr.next;\n }\n return head;\n }\n \n public Node findTail(Node child){\n while(child.next != null){\n child=child.next;\n }\n return child;\n }\n}\n``` | 5 | 0 | ['Recursion', 'Java'] | 1 |
flatten-a-multilevel-doubly-linked-list | ✅ [C++] | Beginner Friendly | Two Solutions DFS & Iterative | O(1) | c-beginner-friendly-two-solutions-dfs-it-ab9c | Complexity\n- Time complexity: O(n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(n)\n Add your space complexity here, e.g. O(n) \n\n## D | psycho_programer | NORMAL | 2023-01-11T11:53:46.486585+00:00 | 2023-01-11T11:53:46.486635+00:00 | 703 | false | ## Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n## DFS\n```\nclass Solution {\npublic:\n vector<Node*> nodes;\n void dfs(Node* head) {\n if(!head) return;\n nodes.push_back(head);\n if(head->child) dfs(head->child);\n dfs(head->next);\n }\n\n Node* flatten(Node* head) {\n dfs(head);\n for(auto x : nodes) cout << x -> val << " ";\n\n int n = nodes.size();\n if(n == 0) return nullptr;\n\n for(int i = 0; i < n - 1; i++) {nodes[i]->next = nodes[i+1]; nodes[i] -> child = nullptr;}\n for(int i = n -1 ; i > 0; i--) {nodes[i]->prev = nodes[i-1]; nodes[i] -> child = nullptr;}\n nodes[0] -> prev = nullptr;\n nodes[n - 1] -> next = nullptr;\n\n return nodes[0];\n }\n};\n\n```\n## Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n## Iterative Method\n```\n/*\nclass Solution {\npublic:\n Node* flatten(Node* head) {\n for(Node* h = head; h != nullptr; h = h -> next) {\n if(h -> child) {\n Node* next = h -> next;\n h->next = h->child;\n h->child->prev = h;\n h->child = nullptr;\n\n Node* p = h -> next;\n while(p -> next) p = p -> next;\n p -> next = next;\n if(next) next -> prev = p; \n }\n }\n\n return head;\n }\n};\n``` | 5 | 0 | ['C++'] | 0 |
flatten-a-multilevel-doubly-linked-list | very simple java beats 100% , beginner friendly | very-simple-java-beats-100-beginner-frie-00bz | \npublic Node flatten(Node head) {\n Node temp = head ;\n Node prev = null ;\n Node next = null ;\n Node child = null ;\n Sta | rinshu2510 | NORMAL | 2021-10-31T09:20:10.399288+00:00 | 2021-10-31T09:20:10.399335+00:00 | 290 | false | ```\npublic Node flatten(Node head) {\n Node temp = head ;\n Node prev = null ;\n Node next = null ;\n Node child = null ;\n Stack<Node> s = new Stack<Node>();\n while( temp != null || !s.isEmpty()){\n if(temp == null){\n next = s.pop();\n next.prev = prev ;\n prev.next = next ;\n temp = next ;\n \n }\n if(temp.child != null){\n child = temp.child ;\n temp.child = null ;\n prev = temp;\n if(temp.next !=null){\n temp.next.prev = null; \n s.push(temp.next);\n }\n temp.next = child ;\n child.prev = temp ;\n temp = child ;\n }\n else if(temp.child == null){\n prev = temp ;\n temp = temp.next ;\n }\n }\n return head ;\n }\n``` | 5 | 1 | [] | 2 |
flatten-a-multilevel-doubly-linked-list | Flatten a Multilevel Doubly Linked List || Java O(N) Solution using Recursion | flatten-a-multilevel-doubly-linked-list-htg43 | \npublic Node flatten(Node head) {\n helper(head);\n return head;\n }\n public Node helper(Node node){\n while(node != null){\n | ridhamsheel | NORMAL | 2021-09-01T08:24:50.220017+00:00 | 2021-09-01T08:24:50.220058+00:00 | 119 | false | ```\npublic Node flatten(Node head) {\n helper(head);\n return head;\n }\n public Node helper(Node node){\n while(node != null){\n if(node.child != null){ // If the current node has a child\n Node stored = node.next; // we store its old next node\n Node childLast = helper(node.child); //and make a recursive call to find the last child in the multilevel list\n \n node.next = node.child; // Make the child of the current node its next node\n node.child.prev = node; // And similarly link the prev of the new next to the current node \n \n if(stored != null){\n childLast.next = stored; // Make the stored node the last node by making it the next node of the childlast node\n stored.prev = childLast;\n }\n node.child = null; // Important: Setting the child to null to avoid errors\n node = childLast; // To avoid reiterating over the entire list again, we directly jump to the childlast node and continue\n }else{\n if(node.next == null){\n break;\n }\n node = node.next; // if the current node doesn\'t have a child, keep iterating until you find a node with a child\n }\n }\n return node;\n }\n``` | 5 | 0 | [] | 1 |
flatten-a-multilevel-doubly-linked-list | C++ solution using stack (easy to understand) well commented + explanation | c-solution-using-stack-easy-to-understan-fj0t | main idea:: a stack is kept for the puspose of storing the the next value of a particular node which has a child node\n\n \n1---2---3---4---5---6--NULL\n | gunjan10 | NORMAL | 2020-07-10T11:21:17.777784+00:00 | 2020-07-10T11:21:17.777818+00:00 | 261 | false | main idea:: a stack is kept for the puspose of storing the the next value of a particular node which has a child node\n\n ```\n1---2---3---4---5---6--NULL\n |\n 7---8---9---10--NULL\n |\n 11--12--NULL\n```\n\nlet me explain with this example :: \nstep 1) when 1 is encountered we simply move to the next value since it has so child node.\nstep 2) similar operation is done in case of node 2\nstep 3) in this step we use the stack datastructure for storing the next value of 3 .....so 4 gets inserted in the stack\n\t\t\t\tand we store 7 to the next of 3 so the link list looks like this \n* \t\t\t\t\t\t1--2--3--7\n* \t\t\t\t\t\tstack has : 4\n\t\t\t\t\t\t\nstep 4)\t we do the same operation in node 7 as in step 1\nstep 5) same oeration of node 8 as in node \n\t\t\t\tso now the link list looks like :: 1--2--3--7--8--11\n* \t\t\t\tstack contains :: 9 (11 is present at stack.top() )\n \t\t\t\t 4\nstep 6) lets come to the end nodes ...... in case of node 12 ::\n\t\t\t link list would look like \n* \t\t\t 1--2--3--7--8--11--12\n* \t\t\t stack has : 9\n\t\t\t\t\t* \t 4 \n\t\t\t\tso now we have to bring the stack.top() in the game and add the address of the stack.top() at the next position of the node 12 and we pop 9 from the stack\n\t\t\t\tso after that operation list looks like this :\n* \t\t\t\t`\t1--2--3--7--8--11--12--9`\nwe do this steps untill we reach a position in which we have stack empty and its a end node( child node and next node **null**) \n\n# HAPPY CODING \n\n/*\n```\n 1---2---3---4---5---6--NULL\n |\n 7---8---9---10--NULL\n |\n 11--12--NULL\n```\n\n*/\n\n\n\n/*\n// Definition for a Node.\nclass Node {\npublic:\n int val;\n Node* prev;\n Node* next;\n Node* child;\n};\n*/\n\nclass Solution {\npublic:\n Node* flatten(Node* head) \n {\n if(!head)\n return head;\n Node* original_head = head;\n stack< Node* > paser_mal;\n \n //paser_mal.push(head->next);\n \n while(!paser_mal.empty() or head) //joto khun na bondho korbo cholbe\n {\n //idea : jodi head null hoi tahole stack check hobe ota o khali hole kaaj sesh\n \n if(!head and paser_mal.empty())\n break;\n if(!head->next and !head->child) // last er element\n {\n if(paser_mal.empty()) //in the example node 6;\n break;\n else \n {\n head->next = paser_mal.top(); // in case of node 10,12 :: 12-> tahole 12->next will be 9\n paser_mal.pop();\n auto temp = head;\n //head->next->prev = head;\n if(!head->next) break; \n head= head->next ; \n head->prev = temp;``\n head->child = NULL;\n }\n } //last elements cases\n \n else if(head->child) //cases with childs\n {\n \n paser_mal.push(head->next); //stack e next er mal store holo \n head->next = head->child;\n head->next->prev = head;\n head->child = NULL;\n head = head->next;\n \n \n }\n \n else if(!head->child and head->next) //child nei stack empty and next element ache\n {\n //head->next->prev = head;\n auto temp = head;\n head->child = NULL;\n head= head->next ; // no child and no element in stack so porer element e jacchi\n head->prev = temp;\n \n }\n \n cout<< head->val<<" ";\n }\n //head->next = NULL;\n original_head->prev = NULL;\n return original_head ;\n }\n};****\n | 5 | 0 | ['Linked List', 'Doubly-Linked List'] | 1 |
flatten-a-multilevel-doubly-linked-list | Python DFS | python-dfs-by-liketheflower-6pba | DFS traverse the node and put everything into a list. The list will contain the correct order of the visited nodes.\nThen from the list rebuild a single level l | liketheflower | NORMAL | 2020-04-11T17:27:10.588748+00:00 | 2020-05-11T17:59:04.815406+00:00 | 329 | false | DFS traverse the node and put everything into a list. The list will contain the correct order of the visited nodes.\nThen from the list rebuild a single level linked list.\nThis algorithm has time complexity of O(n), however, the space complexity is also O(n). It is easy to understand.\n```python\nclass Solution:\n def flatten(self, head: \'Node\') -> \'Node\':\n if not head:return None\n nodes = []\n def dfs(node):\n if node is None:return\n nodes.append(node)\n if node.child:dfs(node.child)\n if node.next:dfs(node.next)\n dfs(head)\n head = nodes[0]\n head.child=None\n for i in range(1, len(nodes)):\n node = nodes[i]\n prev = nodes[i-1]\n node.child=None\n node.prev=prev\n prev.next = node\n return head\n```\n | 5 | 0 | [] | 1 |
flatten-a-multilevel-doubly-linked-list | Javascript 90% faster, 100% less memory. Recursive. | javascript-90-faster-100-less-memory-rec-oayr | The idea is the following: \n If a node has a child:\n1. Keep a reference of node.next as nextNode;\n1. Find the tail of node\'s child (implement a findTail fun | javgc | NORMAL | 2020-03-19T23:31:15.520587+00:00 | 2020-03-19T23:31:15.520639+00:00 | 518 | false | The idea is the following: \n* If a node has a child:\n1. Keep a reference of node.next as nextNode;\n1. Find the tail of node\'s child (implement a findTail function)\n1. The tail of node\'s child will have nextNode as its next.\n1. Change node.next to the child and set node.child = null;\n* Recursively do this over the child (which at this point should be node.next)\n* Keep a reference to the original head and return it.\n\n \n```JS\nvar flatten = function(head) {\n \n if(head===null){\n return null;\n }\n \n let current = head;\n \n if(current.child){\n let tail = findTail(current.child);\n let nextNode = current.next;\n current.next = current.child;\n current.child.prev = current;\n if(nextNode) nextNode.prev = tail;\n tail.next = nextNode;\n current.child = null;\n }\n \n flatten(current.next)\n \n return head;\n};\n\n\nfunction findTail(node){\n \n while(node.next){\n node = node.next;\n }\n return node; \n\t\n}\n``` | 5 | 0 | ['Linked List', 'Recursion', 'JavaScript'] | 3 |
flatten-a-multilevel-doubly-linked-list | C++, Concise solution | Beats 98.6% | c-concise-solution-beats-986-by-naman_nm-kgwg | void func(Node head, Node q) {\n \n if(!head) return;\n \n func(head->next, q);\n if(q && !head->next)\n {\n | naman_nm | NORMAL | 2019-05-30T17:12:19.050736+00:00 | 2019-06-20T05:48:00.420319+00:00 | 1,158 | false | void func(Node* head, Node* q) {\n \n if(!head) return;\n \n func(head->next, q);\n if(q && !head->next)\n {\n head->next=q;\n q->prev = head;\n }\n \n \n if(head->child)\n {\n Node* temp = head->next;\n func(head->child, temp);\n head->next = head->child;\n head->child->prev = head;\n head->child=NULL;\n }\n \n return;\n }\n \n Node* flatten(Node* head) {\n \n if(head)\n func(head, NULL);\n \n return head;\n } | 5 | 0 | ['C++'] | 1 |
flatten-a-multilevel-doubly-linked-list | C++ Recursive and Iterative | c-recursive-and-iterative-by-jianchao-li-j7t0 | The recursive idea is simple: each time when we reach a node with child, recursively flatten the child and insert it between the current node and its next node. | jianchao-li | NORMAL | 2019-02-03T13:46:24.528720+00:00 | 2019-02-03T13:46:24.528765+00:00 | 550 | false | The recursive idea is simple: each time when we reach a node with `child`, recursively flatten the child and insert it between the current node and its next node. Remember to take care of the `prev` pointers.\n\n```cpp\nclass Solution {\npublic:\n Node* flatten(Node* head) {\n Node* cur = head;\n while (cur) {\n if (cur -> child) {\n Node* next = cur -> next;\n Node* child = flatten(cur -> child);\n cur -> child = NULL;\n cur -> next = child;\n child -> prev = cur;\n while (cur -> next) {\n cur = cur -> next;\n }\n cur -> next = next;\n if (next) {\n next -> prev = cur;\n }\n }\n cur = cur -> next;\n }\n return head;\n }\n};\n```\n\nThe iterative one is: each time when we see a node with `child`, find the tail node in the `child` level and connect it with the `next` node of the current node. Then make the `child` node the `next` node and move on.\n\n```cpp\nclass Solution {\npublic:\n Node* flatten(Node* head) {\n Node* cur = head;\n while (cur) {\n if (cur -> child) {\n Node* next = cur -> next;\n cur -> next = cur -> child;\n cur -> next -> prev = cur;\n cur -> child = NULL;\n Node* tail = cur -> next;\n while (tail -> next) {\n tail = tail -> next;\n }\n tail -> next = next;\n if (next) {\n next -> prev = tail;\n }\n }\n cur = cur -> next;\n }\n return head;\n }\n};\n``` | 5 | 0 | [] | 1 |
flatten-a-multilevel-doubly-linked-list | composite recursion method | composite-recursion-method-by-cissyyao-plp4 | Inspired by 114. Flatten Binary Tree to Linked List, using head and tail as parameters in recursive method. \n\nclass Solution {\n public Node flatten(Node h | cissyyao | NORMAL | 2018-07-23T19:47:31.331607+00:00 | 2018-08-21T20:52:47.297132+00:00 | 549 | false | Inspired by 114. Flatten Binary Tree to Linked List, using head and tail as parameters in recursive method. \n\nclass Solution {\n public Node flatten(Node head) { \n return flatten(head, null);\n }\n \n private Node flatten(Node head, Node tail){\n if (head == null) return tail;\n if (head.child == null) { //no child, just convert head.next\n Node next = flatten(head.next, tail);\n head.next = next;\n if (next != null) next.prev = head; \n } else { //child is flattened and inserted between head and head.next\n Node child = flatten(head.child, flatten(head.next, tail));\n head.next = child;\n if (child !=null) child.prev = head;\n head.child = null;\n }\n return head;\n }\n} | 5 | 0 | [] | 2 |
flatten-a-multilevel-doubly-linked-list | Java Easy to Understand Solution with Explanation || 100% beats | java-easy-to-understand-solution-with-ex-seua | Intuition\n> We can solve this easily using an iterative approach. When there is a child node, we need to point that child as the next node. For the end of that | leo_messi10 | NORMAL | 2024-05-30T08:16:32.250502+00:00 | 2024-05-30T08:16:32.250526+00:00 | 257 | false | # Intuition\n> We can solve this easily using an iterative approach. When there is a child node, we need to point that child as the next node. For the end of that child\'s sublist, we need to connect it to the next node of the main list.\n\n# Approach\n\n\n### Function Signature\n```java\npublic Node flatten(Node head) {\n```\nThe function `flatten` takes the head node of a multilevel doubly linked list and returns the head of the flattened list.\n\n### Initialization\n```java\nfor (Node curr = head; curr != null; curr = curr.next)\n```\n- We use a `for` loop to iterate through the nodes of the list using a pointer `curr`.\n- The loop continues until `curr` becomes `null`, indicating the end of the list.\n\n### Checking for Child Nodes\n```java\nif (curr.child != null) {\n```\n- Within the loop, we check if the current node (`curr`) has a `child` node.\n- If it does, we proceed to flatten the `child` list into the main list.\n\n### Storing the Next Node\n```java\nNode cachedNext = curr.next;\n```\n- We store the next node (`curr.next`) in a temporary variable `cachedNext` because we will temporarily disrupt this link to insert the child list.\n\n### Linking Child to the Main List\n```java\ncurr.next = curr.child;\ncurr.child.prev = curr;\ncurr.child = null;\n```\n- We make the `child` node the next node of the current node (`curr.next = curr.child`).\n- We set the `prev` pointer of the `child` node to the current node (`curr.child.prev = curr`).\n- We nullify the `child` pointer of the current node (`curr.child = null`).\n\n### Finding the Tail of the Child List\n```java\nNode tail = curr.next;\n\nwhile (tail.next != null) {\n tail = tail.next;\n}\n```\n- We initialize a pointer `tail` to the start of the child list (`curr.next`).\n- We then traverse to the end of the child list to find its tail.\n\n### Linking the Tail of the Child List to the Cached Next Node\n```java\ntail.next = cachedNext;\n\nif (cachedNext != null)\n cachedNext.prev = tail;\n```\n- We connect the tail of the child list to the `cachedNext` node.\n- If `cachedNext` is not `null`, we set its `prev` pointer to the tail of the child list.\n\n### Return the Flattened List\n```java\nreturn head;\n```\n- Finally, we return the head of the modified list, which is now flattened.\n\n### Example Walkthrough\n\nConsider a multilevel doubly linked list like this:\n\n```\n1 - 2 - 3\n |\n 4 - 5\n```\n\n1. We start with `curr` at node 1.\n2. Move to node 2 (since node 1 has no child).\n3. Node 2 has a child (node 4). We:\n - Cache `curr.next` (node 3).\n - Set `curr.next` to `curr.child` (node 4).\n - Nullify `curr.child`.\n4. Traverse the child list to its tail (node 5).\n5. Connect the tail (node 5) to the cached next node (node 3).\n6. Move `curr` to the next node and continue until the end of the list.\n\nThe final flattened list:\n\n```\n1 - 2 - 4 - 5 - 3\n```\n\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public Node flatten(Node head) {\n for (Node curr = head; curr != null; curr = curr.next)\n if (curr.child != null) {\n\n Node cachedNext = curr.next;\n curr.next = curr.child;\n curr.child.prev = curr;\n curr.child = null;\n Node tail = curr.next;\n\n while (tail.next != null) {\n tail = tail.next;\n }\n\n tail.next = cachedNext;\n\n if (cachedNext != null)\n cachedNext.prev = tail;\n }\n\n return head;\n }\n}\n```\n\n\n\n | 4 | 0 | ['Linked List', 'Doubly-Linked List', 'Java'] | 3 |
flatten-a-multilevel-doubly-linked-list | 0 ms | 100% beat Solution | C++ | Very Easy Approach | 0-ms-100-beat-solution-c-very-easy-appro-z4w0 | Approach\n Describe your approach to solving the problem. \n1. Traverse the list while handling child pointers:\n - Iterate through the list nodes.\n - If | yshivhare163 | NORMAL | 2023-08-02T09:49:59.813283+00:00 | 2023-08-06T10:19:26.895441+00:00 | 397 | false | # Approach\n<!-- Describe your approach to solving the problem. -->\n1. Traverse the list while handling child pointers:\n - Iterate through the list nodes.\n - If a node has a `child`, update the `next` and `child` pointers accordingly.\n - Collect the next node after the current level in a vector `nodes` (stack can also be used) for later connection.\n\n1. Reverse Process Child Nodes:\n - Reverse the `nodes` vector to traverse child nodes in the correct order.\n - `next` pointer always indicate last node at end of each iteration. So that you can attach the next list\'s head to previous one\'s end\n - Connect each child node to its parent node.\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n Node* flatten(Node* head) {\n Node* curr = head; // Initialize the current node to the head of the list\n Node* next;\n vector<Node*> nodes; // To keep track of nodes with child lists or you could use stack\n\n // Traverse through the list\n while (curr) {\n Node* it = curr;\n\n // Traverse to the end of the current level without a child\n while (it->child == NULL && it->next != NULL) {\n it = it->next;\n }\n\n Node* forward = it->next; // Store the next node at this level\n nodes.push_back(forward); // Store it for future processing\n\n Node* ch = it->child; // Get the child node if it exists\n it->next = ch; // Connect the child as the next node at this level\n it->child = NULL; // Set child pointer to NULL\n\n if (ch)\n ch->prev = it; // Update the previous pointer of the child\n\n next = it; // Update the \'next\' pointer to the last node at this level\n curr = ch; // Move the current pointer to the start of the child list\n }\n\n reverse(nodes.begin(), nodes.end()); // Reverse the vector to process nodes in reverse order (see the examples)\n\n // Connect child nodes after their parent node\n for (auto node : nodes) {\n Node* temp = node;\n\n if (temp) {\n next->next = node; // Connect the parent node to the child node\n node->prev = next; // Update the previous pointer of the child node\n\n // Traverse to the end of the child list\n while (temp->next != NULL) {\n temp = temp->next;\n }\n next = temp; // Update \'next\' pointer to the last node in the child list\n }\n }\n\n return head; // Return the head of the flattened list\n }\n};\n\n```\nPlease upvote if you liked the solution :) | 4 | 0 | ['Linked List', 'Stack', 'Depth-First Search', 'Doubly-Linked List', 'C++'] | 1 |
flatten-a-multilevel-doubly-linked-list | [Java] Easy 100% solution | java-easy-100-solution-by-ytchouar-nszi | java\n/*\n// Definition for a Node.\nclass Node {\n public int val;\n public Node prev;\n public Node next;\n public Node child;\n};\n*/\n\nclass So | YTchouar | NORMAL | 2023-07-10T04:20:51.125405+00:00 | 2023-07-10T04:20:51.125434+00:00 | 543 | false | ```java\n/*\n// Definition for a Node.\nclass Node {\n public int val;\n public Node prev;\n public Node next;\n public Node child;\n};\n*/\n\nclass Solution {\n public Node flatten(Node head) {\n Node curr = head;\n\n while(curr != null) {\n if(curr.child != null) {\n Node tail = helper(curr.child);\n\n if(curr.next != null)\n curr.next.prev = tail;\n\n tail.next = curr.next;\n curr.next = curr.child;\n curr.child.prev = curr;\n curr.child = null;\n }\n \n curr = curr.next;\n }\n\n return head;\n }\n\n private Node helper(Node head) {\n while(head.next != null)\n head = head.next;\n\n return head;\n }\n}\n``` | 4 | 0 | ['Java'] | 0 |
flatten-a-multilevel-doubly-linked-list | Without recurssion c++ easy peasy solution | without-recurssion-c-easy-peasy-solution-ard5 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | underdogsourav | NORMAL | 2023-03-20T07:38:52.278646+00:00 | 2023-03-20T07:38:52.278700+00:00 | 633 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/*\n// Definition for a Node.\nclass Node {\npublic:\n int val;\n Node* prev;\n Node* next;\n Node* child;\n};\n*/\n\nclass Solution {\npublic:\nNode* a=new Node(0);\n\n Node* flatten(Node* head) {\n Node* temp= head;\n stack<Node*> st;\n while(head){\n if(head->child){\n if(head->next)st.push(head->next);\n head->next=head->child;\n head->next->prev=head;\n head->child=NULL;\n }else if(head->next==NULL&& !st.empty()){\n head->next=st.top();\n st.pop();\n head->next->prev=head;\n }\n head=head->next;\n }\n return temp;\n }\n};\n``` | 4 | 0 | ['C++'] | 0 |
flatten-a-multilevel-doubly-linked-list | Simple solution using stack || C++ | simple-solution-using-stack-c-by-rkkumar-db0i | Please upvote if you like my solution .\n\nclass Solution {\npublic:\n Node* flatten(Node* head) {\n stack<Node*> st;\n if(head == NULL) retur | rkkumar421 | NORMAL | 2022-07-17T05:39:12.222578+00:00 | 2022-07-17T05:39:12.222625+00:00 | 211 | false | Please upvote if you like my solution .\n```\nclass Solution {\npublic:\n Node* flatten(Node* head) {\n stack<Node*> st;\n if(head == NULL) return head;\n Node* ptr = head;\n \n while(ptr->next != NULL || ptr->child != NULL){\n if(ptr->child != NULL){\n st.push(ptr->next);\n ptr->next = ptr->child;\n ptr->child->prev = ptr;\n ptr->child = NULL;\n }\n ptr = ptr->next;\n }\n while(!st.empty()){\n Node* t = st.top(); st.pop();\n if(t != NULL){\n ptr->next = t;\n t->prev = ptr;\n while(t->next != NULL) t = t->next;\n ptr = t;\n }\n }\n return head;\n }\n};\n``` | 4 | 0 | ['Stack', 'C', 'Iterator'] | 1 |
flatten-a-multilevel-doubly-linked-list | Flatten a Multilevel Doubly Linked List | c++ recursive/recursion SOLUTION | 8ms | flatten-a-multilevel-doubly-linked-list-jieos | \nclass Solution {\npublic:\n // THINK OF THE PROBLEM AS NODES AS ROOMS PRESENT IN DIFFERENT DEPTHS/LEVELS OF AN\n // HIGH RISE BUILDING\n // Naturally | looneyd_noob | NORMAL | 2022-07-12T12:39:25.155039+00:00 | 2022-07-12T12:39:25.155094+00:00 | 204 | false | ```\nclass Solution {\npublic:\n // THINK OF THE PROBLEM AS NODES AS ROOMS PRESENT IN DIFFERENT DEPTHS/LEVELS OF AN\n // HIGH RISE BUILDING\n // Naturally we need to traverse the list, and hence we do that\n // Whenever we encounter any child node, we recursively go to the depth and make\n // changes to required links, and then call the function for the upcoming nodes\n // present in that level.\n \n // Below is the step by step breakdown of the problem in my intuition\n Node* solve(Node* head){\n // base case\n // first checking if either list is empty or we have reached a dead end\n // dead end = child and next both point to NULL\n if( head==NULL || (head->child==NULL && head->next==NULL)) return head;\n \n \n // storing the next, for the time being because if we go deeper into the child nodes\n // next may get lost\n Node* t = head->next;\n Node* n = NULL;\n \n // if child exists we go deeper into the list, and alongside change the links\n // as required\n if(head->child!=NULL){\n \n // connecting head\'s child to the next position and vice versa\n // and making head\'s child NULL\n Node* temp = head->child;\n head->next = temp;\n temp->prev = head;\n head->child = NULL;\n \n // this returns a value where we have either got NULL or reached a dead end\n n = solve(temp);\n \n // if we have reached a dead end for a particular level and above that level the\n // list still has its nodes then we link them.\n if(t!=NULL && n!=NULL){\n n->next = t;\n t->prev = n;\n }\n }\n \n // after making required connections on the previous node\'s child branches, we\n // call it for the next nodes in that level\n if(t!=NULL)\n return solve(t);\n \n // if no next nodes are present on that level, that means we need the last node\n // of the last level of our succeeding levels, and hence we return it.\n return n;\n \n }\n Node* flatten(Node* head) {\n solve(head);\n return head;\n }\n};\n``` | 4 | 0 | ['Linked List', 'Recursion'] | 2 |
flatten-a-multilevel-doubly-linked-list | Easy Recursive and Iterative solutions | easy-recursive-and-iterative-solutions-b-krwc | Iterative:\n\n\nvar flatten = function(head) {\n const stack = [];\n let ptr = head;\n \n while(ptr || stack.length) {\n if(ptr.child) {\n | dollysingh | NORMAL | 2022-05-14T10:35:18.771316+00:00 | 2022-05-14T10:35:18.771356+00:00 | 447 | false | **Iterative**:\n\n```\nvar flatten = function(head) {\n const stack = [];\n let ptr = head;\n \n while(ptr || stack.length) {\n if(ptr.child) {\n if(ptr.next)\n stack.push(ptr.next);\n let child = ptr.child;\n ptr.child = null;\n ptr.next = child;\n child.prev = ptr;\n ptr = child;\n } else if(ptr.next === null && stack.length) {\n let next = stack[stack.length - 1];\n ptr.next = next;\n next.prev = ptr;\n stack.pop();\n } else {\n ptr = ptr.next;\n }\n } \n \n return head;\n};\n```\n\n**Recursive:**\n\n```\nvar flatten = function(head) {\n const dfs = (ptr) => {\n let last = null;\n while(ptr) {\n if(ptr.child) {\n\t\t\t //go deep and return to previous caller\n let node = dfs(ptr.child);\n \n let next = ptr.next;\n let newHead = ptr.child;\n ptr.child = null;\n ptr.next = newHead;\n newHead.prev = ptr;\n node.next = next;\n \n if(next)\n next.prev = node;\n }\n last = ptr;\n ptr = ptr.next;\n }\n return last;\n }\n \n dfs(head);\n}\n``` | 4 | 0 | ['Recursion', 'Iterator', 'JavaScript'] | 1 |
flatten-a-multilevel-doubly-linked-list | Java recursive, beat 100%, similar to flatten tree | java-recursive-beat-100-similar-to-flatt-3ajk | Think of structure as being a binary tree structure. Then you can solve it similarly to the flatten tree problem: https://leetcode.com/problems/flatten-binary-t | jbuns | NORMAL | 2022-05-09T21:56:33.078718+00:00 | 2022-05-09T21:56:33.078747+00:00 | 394 | false | Think of structure as being a binary tree structure. Then you can solve it similarly to the flatten tree problem: https://leetcode.com/problems/flatten-binary-tree-to-linked-list/\n\n\n```\nclass Solution {\n \n Node prev = null;\n \n public Node flatten(Node head) {\n dfsHelper(head);\n return head;\n }\n \n public void dfsHelper(Node current) {\n if (current == null) return;\n // postorder traversal, going right first or next in this case\n dfsHelper(current.next);\n dfsHelper(current.child);\n\t\t// don\'t forget to set prev.prev pointer \n if (prev != null) prev.prev = current;\n\t\t// see explanation below\n current.next = prev;\n current.child = null;\n prev = current;\n }\n}\n```\n\nWhat\'s happening with pointer assignments\n\n```\n * 1\n * / \\\n * 2 5\n * / \\ \\\n * 3 4 6\n * -----------\n * pre = 5\n * cur = 4\n *\n * 1\n * /\n * 2\n * / \\\n * 3 4\n * \\\n * 5\n * \\\n * 6\n * -----------\n * pre = 4\n * cur = 3\n *\n * 1\n * /\n * 2\n * /\n * 3\n * \\\n * 4\n * \\\n * 5\n * \\\n * 6\n * -----------\n * cur = 2\n * pre = 3\n *\n * 1\n * /\n * 2\n * \\\n * 3\n * \\\n * 4\n * \\\n * 5\n * \\\n * 6\n * -----------\n * cur = 1\n * pre = 2\n *\n * 1\n * \\\n * 2\n * \\\n * 3\n * \\\n * 4\n * \\\n * 5\n * \\\n * 6\n``` | 4 | 0 | ['Depth-First Search', 'Recursion', 'Java'] | 0 |
flatten-a-multilevel-doubly-linked-list | JAVA Recursion Code or DFS 100% faster with Explaination | java-recursion-code-or-dfs-100-faster-wi-8yjo | use of simple dfs firstOrder\n\n\n/*\n// Definition for a Node.\nclass Node {\n public int val;\n public Node prev;\n public Node next;\n public Nod | VIVEK_8877 | NORMAL | 2021-10-31T02:13:03.968484+00:00 | 2022-03-17T04:12:43.293929+00:00 | 333 | false | use of simple dfs firstOrder\n\n```\n/*\n// Definition for a Node.\nclass Node {\n public int val;\n public Node prev;\n public Node next;\n public Node child;\n};\n*/\n\nclass Solution {\n public static Node ans;\n public static Node help; // used to keep at top of node\n public static void DFS(Node n) {\n if(n==null) {\n return;\n }\n if(ans.val==0) { // if call is 1st time\n ans.val=n.val;\n help=ans;\n } else {\n Node currentNode = new Node();\n currentNode.val=n.val;\n help.next=currentNode;\n currentNode.prev=help;\n help=currentNode; // put help at top\n }\n DFS(n.child); // 1st call child as we have to putchild 1st\n DFS(n.next);\n }\n public Node flatten(Node head) {\n if(head==null) { // if Node is Empty return\n return head;\n }\n ans=new Node(); // make new\n help=new Node(); // make new\n DFS(head); // call DFS function\n return ans;\n }\n}\n``` | 4 | 1 | [] | 0 |
flatten-a-multilevel-doubly-linked-list | Easy to understand 4ms code | easy-to-understand-4ms-code-by-ladyengg-qliy | \nNode *flatten(Node *head)\n {\n\n Node *temp = head;\n\n while (temp != NULL)\n {\n if (temp->child)\n {\n | ladyengg | NORMAL | 2021-06-08T18:59:56.475300+00:00 | 2021-06-08T18:59:56.475351+00:00 | 273 | false | ```\nNode *flatten(Node *head)\n {\n\n Node *temp = head;\n\n while (temp != NULL)\n {\n if (temp->child)\n {\n Node *node_child = temp->child;\n if (temp->next == NULL)\n {\n temp->next = node_child;\n node_child->prev = temp;\n temp->child = NULL;\n continue;\n }\n Node *next_node= temp->next; // this next node pointer is required to remove infinte loop\n \n\n temp->next = node_child;\n node_child->prev = temp;\n temp->child = NULL;\n while (node_child->next != NULL)\n {\n node_child = node_child->next;\n }\n node_child->next = next_node;\n next_node->prev = node_child;\n }\n\n temp = temp->next;\n }\n return head;\n }\n\t``` | 4 | 0 | ['C'] | 0 |
flatten-a-multilevel-doubly-linked-list | Elegant Iterative Solution | elegant-iterative-solution-by-ysingla-fsbq | \nclass Solution:\n def traverseChild(self, head):\n tail = head\n while tail and tail.next:\n tail = tail.next\n return tail | ysingla | NORMAL | 2020-11-25T04:35:28.692203+00:00 | 2020-11-25T04:36:58.614717+00:00 | 293 | false | ```\nclass Solution:\n def traverseChild(self, head):\n tail = head\n while tail and tail.next:\n tail = tail.next\n return tail\n \n def flatten(self, head: \'Node\') -> \'Node\':\n curr = head\n while curr:\n if curr.child:\n tail = self.traverseChild(curr.child)\n tail.next = curr.next\n if tail.next:\n tail.next.prev = tail\n curr.next = curr.child\n curr.child.prev = curr\n curr.child = None \n curr = curr.next\n return head\n\t\t\n```\n\n# Explanation\n1. Flatten function traverses linked list to find any nodes with a child node.\n2. Once it finds a node with a child node it calls traverseChild on the child node\n3. TraverseChild returns tail of the child LinkedList\n4. Now it is a simple linked list insertion in a doubly linked list\n\t* \tprevious of curr node\'s next (`curr.next.prev`) becomes tail node and\n\t* \tchild node becomes curr node\'s next | 4 | 0 | ['Iterator', 'Python', 'Python3'] | 0 |
flatten-a-multilevel-doubly-linked-list | Easy solution 99% fast [C++] | easy-solution-99-fast-c-by-meyrlan-7g73 | \nclass Solution {\npublic:\n \n vector < Node > v;\n \n void dfs(Node head){\n v.push_back(head);\n if(head -> child != nullptr){\n df | meyrlan | NORMAL | 2020-08-14T08:52:31.022014+00:00 | 2020-08-14T08:52:31.022046+00:00 | 117 | false | \nclass Solution {\npublic:\n \n vector < Node* > v;\n \n void dfs(Node* head){\n v.push_back(head);\n if(head -> child != nullptr){\n dfs(head -> child);\n }\n if(head -> next != nullptr){\n dfs(head -> next);\n }\n }\n \n Node* flatten(Node* head) {\n \n if(head == nullptr){\n return head;\n }\n \n dfs(head);\n \n if(v.size() == 1){\n v[0] -> prev = NULL;\n v[0] -> child = NULL;\n v[0] -> next = NULL;\n return head;\n }\n \n for(int i = 0; i < v.size(); i++){\n if(i == 0){\n v[i] -> prev = NULL;\n v[i] -> child = NULL;\n v[i] -> next = v[i + 1];\n }\n else if(i == v.size() - 1){\n v[i] -> prev = v[i - 1];\n v[i] -> child = NULL;\n v[i] -> next = NULL;\n }\n else{\n v[i] -> prev = v[i - 1];\n v[i] -> child = NULL;\n v[i] -> next = v[i + 1];\n }\n }\n \n return head;\n }\n}; | 4 | 0 | [] | 1 |
flatten-a-multilevel-doubly-linked-list | Java Solution using a Stack | java-solution-using-a-stack-by-pirty6-z7aq | We can just use a stack to pile the next nodes when there is a child node. For it to be valid remember to set the child node to null and change the prev pointer | pirty6 | NORMAL | 2020-07-11T01:23:05.488613+00:00 | 2020-07-11T01:23:05.488654+00:00 | 256 | false | We can just use a stack to pile the next nodes when there is a child node. For it to be valid remember to set the child node to null and change the prev pointers (while validating that they are not null)\n\n```\n public Node flatten(Node head) {\n Stack<Node> prevs = new Stack();\n Node cur = head;\n while(cur != null) {\n if(cur.child != null) {\n prevs.add(cur.next);\n cur.next = cur.child;\n cur.child.prev = cur;\n cur.child = null;\n }\n if (cur.next == null && !prevs.isEmpty()){\n cur.next = prevs.pop();\n if (cur.next != null) cur.next.prev = cur;\n }\n cur = cur.next;\n }\n return head;\n }\n``` | 4 | 1 | [] | 0 |
flatten-a-multilevel-doubly-linked-list | Java - Two Pointers - 0 ms | java-two-pointers-0-ms-by-mt-xtina-mwjw | O(n) time, O(1) space (where n is the total number of nodes in the linked list).\n\nWe traverse until we find a node with a child - let\'s call it parent. From | mt-xtina | NORMAL | 2020-07-10T15:41:19.161166+00:00 | 2020-07-10T15:43:47.529854+00:00 | 260 | false | O(n) time, O(1) space (where n is the total number of nodes in the linked list).\n\nWe traverse until we find a node with a child - let\'s call it parent. From here, we set up a few variables: the parent\'s original next node, and the parent\'s child. Additionally, we traverse the child list to find its last node. First, we clear the parent\'s child pointer. Now it\'s just a matter of joining three lists, with the second spliced in-between the first and the third. We take care to check that our third list is not null. And finally, we repeat this process until we\'re at the end of the list.\n\n```\npublic Node flatten(Node head) {\n Node curr = head;\n \n while (curr != null) {\n if (curr.child == null) {\n curr = curr.next;\n } else {\n Node parent = curr;\n Node parentNext = parent.next;\n Node child = curr.child;\n Node childLast = child;\n parent.child = null;\n while (childLast != null && childLast.next != null) {\n childLast = childLast.next;\n }\n parent.next = child;\n child.prev = parent;\n childLast.next = parentNext;\n if (parentNext != null) {\n parentNext.prev = childLast;\n }\n }\n }\n \n return head;\n }\n```\n\nI think we could optimize this solution in the case where the child list has its own child list and splice that list in before continuing with the original. | 4 | 0 | ['Two Pointers', 'Java'] | 1 |
flatten-a-multilevel-doubly-linked-list | recursive java solution, beats 100% | recursive-java-solution-beats-100-by-vsa-yn0u | \nclass Solution {\n public Node flatten(Node head) {\n if(head == null) return null;\n recursiveHelper(head);\n return head;\n }\n | vsavko | NORMAL | 2020-07-10T08:22:58.726616+00:00 | 2020-07-10T08:22:58.726663+00:00 | 213 | false | ```\nclass Solution {\n public Node flatten(Node head) {\n if(head == null) return null;\n recursiveHelper(head);\n return head;\n }\n \n private Node recursiveHelper(Node head){\n Node tmp = head.next;\n if(head.child != null){\n head.next = head.child;\n head.child.prev = head;\n Node last = recursiveHelper(head.child);\n head.child = null;\n if(tmp == null) return last;\n last.next = tmp;\n tmp.prev = last;\n }\n if(tmp == null)\n return head; \n return recursiveHelper(tmp); \n }\n}\n``` | 4 | 2 | [] | 0 |
flatten-a-multilevel-doubly-linked-list | [c++] Stack solution with explanation | c-stack-solution-with-explanation-by-sli-um9s | simple explanation: as we go along our list, if we reach a node where its child is not a null pointer then we push the next node on to our stack and set the nex | slicedkiwis | NORMAL | 2020-07-10T07:22:43.456419+00:00 | 2020-07-11T05:54:28.527649+00:00 | 288 | false | simple explanation: as we go along our list, if we reach a node where its child is not a null pointer then we push the next node on to our stack and set the next node to the child node. Of course we also have to set the child to a null pointer, and set our next nodes previous node to the current node.\n\nWe repeat this process untill we eventually reach an end.\nfrom there we start unloading the stack, this cycle repeats eventually flattening out the list.\n\n\n```\nclass Solution {\npublic:\n Node* flatten(Node* head) {\n Node * dummyHead = head; \n stack <Node*> stack; \n while(head || !stack.empty())\n {\n if(head && head -> child)\n { \n if(head -> next) stack.push(head -> next); \n \n head -> next = head -> child; \n head -> next -> prev = head; \n head -> child = nullptr; \n }\n else if(!head -> next && !stack.empty())\n { \n head -> next= stack.top(); \n head -> next -> prev = head; \n stack.pop();\n\t }\n if(head) head = head -> next; \n } \n return dummyHead;\n }\n};\n``` | 4 | 2 | ['Stack', 'C', 'C++'] | 1 |
flatten-a-multilevel-doubly-linked-list | Easy to understand C++ Solution, 88ms, beats 95% | easy-to-understand-c-solution-88ms-beats-lc2c | Runtime: 88 ms, faster than 95.78% of C++ online submissions for Flatten a Multilevel Doubly Linked List.\nMemory Usage: 31.1 MB, less than 62.50% of C++ online | pooja0406 | NORMAL | 2019-10-22T20:58:38.690818+00:00 | 2019-10-22T20:58:38.690869+00:00 | 426 | false | Runtime: 88 ms, faster than 95.78% of C++ online submissions for Flatten a Multilevel Doubly Linked List.\nMemory Usage: 31.1 MB, less than 62.50% of C++ online submissions for Flatten a Multilevel Doubly Linked List.\n\n```\n/*\n// Definition for a Node.\nclass Node {\npublic:\n int val;\n Node* prev;\n Node* next;\n Node* child;\n\n Node() {}\n\n Node(int _val, Node* _prev, Node* _next, Node* _child) {\n val = _val;\n prev = _prev;\n next = _next;\n child = _child;\n }\n};\n*/\nclass Solution {\npublic:\n Node* flatten(Node* head) {\n \n flattenHelper(head);\n return head;\n }\n \n Node* flattenHelper(Node* head)\n {\n if(head == nullptr)\n return head;\n \n while(head->next)\n {\n if(head->child)\n {\n Node* nextNode = head->next;\n Node* end = flattenHelper(head->child);\n head->next = head->child;\n head->child->prev = head;\n end->next = nextNode;\n nextNode->prev = end;\n head->child = nullptr;\n head = nextNode;\n }\n else\n head = head->next;\n }\n \n if(head->child)\n {\n Node* end = flattenHelper(head->child);\n head->next = head->child;\n head->child->prev = head;\n head->child = nullptr;\n }\n \n return head;\n }\n}; | 4 | 0 | ['Recursion'] | 0 |
flatten-a-multilevel-doubly-linked-list | Java solution | java-solution-by-lliu97d-j7ys | \nclass Solution {\n public Node flatten(Node head) {\n Node p = head;\n while(p != null){\n if(p.child != null){\n N | lliu97d | NORMAL | 2019-07-09T02:36:46.315749+00:00 | 2019-07-09T02:36:46.315778+00:00 | 333 | false | ```\nclass Solution {\n public Node flatten(Node head) {\n Node p = head;\n while(p != null){\n if(p.child != null){\n Node tmp = p.child;\n while(tmp.next != null)\n tmp = tmp.next;\n tmp.next = p.next;\n if(p.next != null)\n p.next.prev = tmp;\n p.next = p.child;\n p.child.prev = p;\n p.child = null;\n }\n p = p.next;\n }\n return head;\n }\n}\n```\n\nRuntime: 0 ms, faster than 100.00% of Java online submissions for Flatten a Multilevel Doubly Linked List.\nMemory Usage: 37.2 MB, less than 96.89% of Java online submissions for Flatten a Multilevel Doubly Linked List. | 4 | 0 | ['Java'] | 0 |
flatten-a-multilevel-doubly-linked-list | Simple Java Solution | simple-java-solution-by-waiyip-16d9 | with global variable\n\nclass Solution {\n Node prev;\n public Node flatten(Node head) {\n Node cur = head;\n while (cur != null) {\n | waiyip | NORMAL | 2018-06-09T02:31:43.554688+00:00 | 2018-06-09T02:31:43.554688+00:00 | 1,935 | false | with global variable\n```\nclass Solution {\n Node prev;\n public Node flatten(Node head) {\n Node cur = head;\n while (cur != null) {\n if (cur.child != null) {\n Node next = cur.next;\n cur.child.prev = cur;\n cur.next = flatten(cur.child);\n cur.child = null;\n\t\t\t\t\t\t\n if (next != null) {\n prev.next = next;\n next.prev = prev;\n }\n }\n\n prev = cur;\n cur = cur.next;\n }\n\n return head;\n } \n}\n \n```\n\n\n<br><br>\n\nwithout using global variable\n```\n public Node flatten(Node head) {\n return helper(head, new Node());\n }\n \n public Node helper(Node head, Node prevDummy) {\n Node cur = head;\n while (cur != null) {\n if (cur.child != null) {\n Node next = cur.next;\n cur.child.prev = cur;\n cur.next = helper(cur.child, prevDummy);\n cur.child = null;\n if (next != null) {\n Node prev = prevDummy.next;\n prev.next = next;\n next.prev = prev;\n }\n }\n\n prevDummy.next = cur;\n cur = cur.next;\n }\n\n return head;\n }\n``` | 4 | 1 | [] | 2 |
flatten-a-multilevel-doubly-linked-list | ✅EASY JAVA SOLUTION | easy-java-solution-by-swayam28-dohs | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | swayam28 | NORMAL | 2024-08-21T03:21:35.506676+00:00 | 2024-08-21T03:21:35.506713+00:00 | 293 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n\n\n```java []\n/*\n// Definition for a Node.\nclass Node {\n public int val;\n public Node prev;\n public Node next;\n public Node child;\n};\n*/\n\nclass Solution {\n private Queue<Node> store = new LinkedList<>();\n\npublic void helper(Node head)\n{\n Node temp;\n while (head != null)\n {\n temp = head.next;\n head.next = null;\n head.prev = null;\n store.offer(head);\n if (head.child != null)\n helper(head.child);\n head.child = null;\n head = temp;\n }\n}\n\npublic Node flatten(Node head) {\n helper(head);\n if (store.peek() == null)\n return head;\n Node retval = store.poll();\n Node first = retval;\n while (store.peek() != null)\n {\n Node second = store.poll();\n first.next = second;\n second.prev = first;\n first = second;\n }\n first.next = null;\n return retval;\n}\n}\n``` | 3 | 0 | ['Queue', 'Java'] | 0 |
flatten-a-multilevel-doubly-linked-list | ⬆️🆙✅ Easy to understand & Best solution 💥👏🔥 | up-easy-to-understand-best-solution-by-s-us3d | Please upvote if my solution and efforts helped you.\n***\n\n# Code\n\nclass Solution {\n public Node flatten(Node head) {\n Node temp = head;\n | SumitMittal | NORMAL | 2024-06-17T17:03:48.876414+00:00 | 2024-06-17T17:03:48.876442+00:00 | 366 | false | # Please upvote if my solution and efforts helped you.\n***\n\n# Code\n```\nclass Solution {\n public Node flatten(Node head) {\n Node temp = head;\n while(temp != null){\n Node list1Tail = temp;\n Node list3Head = temp.next;\n // if the node has child node then append all its node in between\n\n if(temp.child != null){\n // we are assuming that recursion will give us flatten output, so we just need to adjust the pointers\n Node list2Head = flatten(temp.child);\n \n // find list2 tail\n Node list2Tail = list2Head;\n while(list2Tail.next != null){\n list2Tail = list2Tail.next;\n }\n\n // attach the lists\n list1Tail.next = list2Head;\n list2Head.prev = list1Tail;\n list2Tail.next = list3Head;\n if(list3Head != null)\n list3Head.prev = list2Tail;\n temp.child = null;\n }\n temp = temp.next;\n }\n return head;\n }\n}\n```\n\n | 3 | 0 | ['Linked List', 'Doubly-Linked List', 'Java'] | 0 |
flatten-a-multilevel-doubly-linked-list | Best code || easy to understand || must see | best-code-easy-to-understand-must-see-by-egwh | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Shubhadip_009 | NORMAL | 2024-06-10T10:57:06.239781+00:00 | 2024-06-10T10:57:06.239832+00:00 | 337 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n Node* flatten(Node* head) {\n Node*temp=head;\n while(temp){\n Node*a=temp->next;\n if(temp->child!=NULL){\n Node*c=temp->child;\n temp->child=NULL;\n c=flatten(c); // recursion\n temp->next=c;\n c->prev=temp;\n while(c->next!=NULL) c=c->next;\n c->next=a;\n if(a!=NULL) a->prev=c;\n }\n temp=a;\n }\n \n return head;\n }\n};\n``` | 3 | 0 | ['C++'] | 0 |
flatten-a-multilevel-doubly-linked-list | Java | Recursion | 0 ms | Time: O(n) | Space: O(1) | java-recursion-0-ms-time-on-space-o1-by-dzx89 | Intuition\nWe iterate the list untill we reach a node which has child node, when we reach it, we will call the function again to flatten the child too.\nAnd the | leetcodeally | NORMAL | 2024-01-03T17:11:42.342796+00:00 | 2024-01-03T17:11:42.342822+00:00 | 558 | false | # Intuition\nWe iterate the list untill we reach a node which has child node, when we reach it, we will call the function again to flatten the child too.\nAnd the function will return the last node of the child as we need to connnect it with next node of curent node. The process continues untill we reach end of the list.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n1. Create a recursive function that flattens linkedlist and returns the last node of linkedList\n2. Inside function iterate over the curr node, when you reach a node which has child, call the function again\n3. Called function returns child node\'s last node, put it before current node\'s next node and after curr node.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/*\n// Definition for a Node.\nclass Node {\n public int val;\n public Node prev;\n public Node next;\n public Node child;\n};\n*/\n\nclass Solution {\n public Node flatten(Node head) {\n flat(head);\n return head;\n }\n \n public Node flat(Node head){\n Node curr = head;\n Node last = head;\n while(curr!=null){\n if(curr.child!=null){\n //if we encounter child we will try to flatten that child and return its tail\n Node midTail = flat(curr.child);\n\n //if current node next is not null we need to connect it with curr next\n Node next = curr.next;\n if(next!=null){\n midTail.next = next;\n next.prev = midTail; \n }\n\n //there we are connecting mid node\'s first node with curr node next pointer\n curr.next = curr.child;\n curr.child.prev = curr;\n\n //we make sure all child nodes should be null;\n curr.child = null;\n\n //there, we are giving curr pointer to midTail which is the end of child linked list\n curr = midTail;\n }\n //we used last pointer to get the last node of child\n last = curr;\n curr = curr.next;\n }\n return last;\n }\n}\n```\n# **Please, upvote if you liked it** | 3 | 0 | ['Java'] | 2 |
flatten-a-multilevel-doubly-linked-list | Implementation using stack and dummy pointer [99% Space Complexity] | implementation-using-stack-and-dummy-poi-tt3d | Intuition\n Describe your first thoughts on how to solve this problem. \nMy First thoughts upon viewing the questions is to some how save the head.next nodes wh | bhanuprabhath123 | NORMAL | 2023-11-06T09:34:23.026597+00:00 | 2023-11-06T09:34:23.026625+00:00 | 121 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nMy First thoughts upon viewing the questions is to some how save the `head.next` nodes when encountering the nodes with the `head.child` nodes. As saving the `head.next` once we continue moving forward in the child node and reach the end I can pop the stack, make curent node.next to the pop and pop.prev to current and can finish the problem.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n1. The `end` list is used to keep track of nodes next to the nodes with children that need to be reconnected after flattening. `res` is used to store the original head of the linked list, and it will be returned as the result.\n\n2. The solution enters a while loop that iterates through the linked list, starting with the `head`.\n\n3. Inside the loop, it checks if the current node has a child (the `child` attribute is not None). If it does have a child, it performs the following steps:\n - If the current node also has a next node (`head.next` is not None), it pushes the next node onto the `end` stack for later reconnection.\n - It updates the `head.next` to point to the child node and sets the child node\'s `prev` pointer to the current `head`.\n - Finally, it sets the current node\'s `child` attribute to None, effectively detaching the child.\n\n4. The solution then checks if the current node has reached the end of the list (`head.next` is None) and if there are nodes in the `end` stack waiting to be reconnected. If both conditions are met, it pops a node (`no`) from the `end` stack, and if `no` is not None, it reconnects it to the current node as the next node, and updates the `prev` pointer accordingly.\n\n5. The `head` pointer is then moved to the next node in the original list, and the loop continues until it reaches the end of the list.\n\n6. Finally, the `res` (original head) is returned as the flattened doubly linked list.\n\nThis approach effectively flattens a multilevel doubly linked list while maintaining the original order of nodes. It uses a stack (`end`) to keep track of nodes next to the nodes with children, and it modifies the pointers accordingly to achieve the desired result.\n\n\n\n# Complexity\n- Time complexity:$$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(n)$$\n<small>In only the wort case scenario it will be $$O(n)$$, which is the case where every node has a child. Excluding that every other case will have much better time complexity.</small>\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n"""\n# Definition for a Node.\nclass Node:\n def __init__(self, val, prev, next, child):\n self.val = val\n self.prev = prev\n self.next = next\n self.child = child\n"""\n\nclass Solution:\n def flatten(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n if not head:\n return None\n\n end = []\n res = head\n while head:\n if head.child:\n if head.next:\n end.append(head.next)\n head.next = head.child\n head.next.prev = head\n head.child=None\n if not head.next and end:\n no = end.pop() if end else None\n if no :\n head.next = no\n no.prev = head\n head = head.next\n\n return res\n``` | 3 | 0 | ['Two Pointers', 'Stack', 'Python3'] | 0 |
flatten-a-multilevel-doubly-linked-list | O(n) Solution in one function. TypeScript/JavaScript | on-solution-in-one-function-typescriptja-csvl | Intuition\nSolution in one function\n Describe your first thoughts on how to solve this problem. \n\n# Approach\nflatten function that recursively flattens a li | evlbon | NORMAL | 2023-10-29T11:44:41.439847+00:00 | 2023-10-29T11:44:41.439871+00:00 | 33 | false | # Intuition\nSolution in one function\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n`flatten` function that recursively flattens a linked list. Has a `next` parameter to link the flattened child list to the next node of the parent list, null if the parent list is missing.\n\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfunction flatten(head: Node | null, next: Node = null): Node | null {\n if(!head) return head\n \n let current = head\n while(current){\n if(current.child){\n current.next = flatten(current.child, current.next)\n current.next.prev = current\n current.child = null\n }\n \n if(!current.next && next){\n current.next = next\n next.prev = current\n break\n }\n else\n current = current.next\n }\n \n \n return head\n};\n``` | 3 | 0 | ['TypeScript'] | 1 |
flatten-a-multilevel-doubly-linked-list | Unlocking the Mysteries of the Squiggly List: A Tale of Flattening Multilevel Doubly Linked Lists | unlocking-the-mysteries-of-the-squiggly-tbecz | Intuition\nWhen reading the question to flatten a multilevel doubly linked list, a first intuition would be to use recursion or iteration to traverse the list a | ajayramani | NORMAL | 2023-06-24T17:54:17.198764+00:00 | 2023-06-24T17:57:47.673089+00:00 | 872 | false | # Intuition\nWhen reading the question to flatten a multilevel doubly linked list, a first intuition would be to use recursion or iteration to traverse the list and handle the child nodes.\n\n# Approach\nThe approach used in this code is a recursive traversal of the multilevel doubly linked list to flatten it.\nThe flatten function takes the head of the multilevel doubly linked list as input and returns the flattened version of the list.\n\n- Check if the head is None. If it is, return None.\n- Initialize an empty list T to store the values of the nodes in the desired order.\n- Invoke the traverse function with the head node and the T list as arguments.\n- The traverse function recursively traverses the multilevel doubly linked list and appends the values of the nodes to the result list.\n-- If the current node is None, return.\n-- Append the value of the current node to the result list.\n-- Recursively traverse the child node by calling the traverse function with the child node and result.\n-- Recursively traverse the next node by calling the traverse function with the next node and result.\n- After the traverse function completes, the T list contains the values of the nodes in the desired order.\n- Create a new node ret_head using the first value from the T list.\n- Initialize curr as the ret_head node.\n- Set the child pointer of ret_head to None.\n- Iterate over the remaining values in the T list from index 1.\n -- Create a new node new_node with the current value.\n -- Set the prev pointer of new_node to curr.\n -- Set the child pointer of new_node to None.\n -- Set the next pointer of curr to new_node.\n -- Update curr to the newly created new_node.\n- Return ret_head, which is the head of the flattened linked list.\n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n $$O(n)$$ \n\n# Code\n```\n"""\n# Definition for a Node.\nclass Node:\n def __init__(self, val, prev, next, child):\n self.val = val\n self.prev = prev\n self.next = next\n self.child = child\n"""\n\nclass Solution:\n def flatten(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n if head is None:\n return \n T = self.traverse(head,[])\n ret_head = Node(T[0])\n curr = ret_head\n ret_head.child = None\n for i in range(1,len(T)):\n new_node = Node(T[i])\n new_node.prev = curr\n new_node.child = None\n curr.next = new_node\n curr = curr.next\n return ret_head\n def traverse(self,head,result):\n if head is None:\n return\n result.append(head.val)\n self.traverse(head.child,result)\n self.traverse(head.next,result)\n return result\n``` | 3 | 0 | ['Linked List', 'Python', 'Python3'] | 0 |
flatten-a-multilevel-doubly-linked-list | using stack simple approch | using-stack-simple-approch-by-deviltrek-mn1t | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | deviltrek | NORMAL | 2023-05-08T14:29:31.882420+00:00 | 2023-05-08T14:29:31.882462+00:00 | 257 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/*\n// Definition for a Node.\nclass Node {\npublic:\n int val;\n Node* prev;\n Node* next;\n Node* child;\n};\n*/\n\nclass Solution {\npublic:\n Node* flatten(Node* head) {\n stack<Node*>st;\n Node *p = head;\n Node *f = NULL;\n while(p!=NULL or !st.empty()){\n if(p==NULL){\n f->next = st.top();\n st.top()->prev = f;\n st.pop();\n p = f->next;\n continue;\n }\n if(p->child!=NULL){\n f = p;\n if(p->next)st.push(p->next);\n p->next = p->child;\n p->child->prev = p;\n p->child = NULL;\n p = p->next;\n }else{\n f = p;\n p = p->next;\n }\n }\n return head;\n }\n};\n``` | 3 | 0 | ['C++'] | 0 |
flatten-a-multilevel-doubly-linked-list | Simple Clean & Clear | simple-clean-clear-by-abhishek1210aka-rtah | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Abhishek1210AkA | NORMAL | 2023-04-13T14:12:29.547171+00:00 | 2023-04-13T14:12:29.547215+00:00 | 375 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/*\n// Definition for a Node.\nclass Node {\npublic:\n int val;\n Node* prev;\n Node* next;\n Node* child;\n};\n*/\n\nclass Solution {\npublic:\n Node* flatten(Node* head) {\n Node* temp=head;\n while(temp){\n if(temp->child){\n Node* fake=temp->child;\n while(fake->next){\n fake=fake->next;\n }\n fake->next=temp->next;\n if(temp->next){\n temp->next->prev=fake;\n }\n temp->child->prev=temp;\n temp->next=temp->child;\n temp->child=NULL;\n }\n else{\n temp=temp->next;\n }\n }\n return head;\n }\n};\n``` | 3 | 0 | ['C++'] | 0 |
flatten-a-multilevel-doubly-linked-list | Python simple solution beats 100% || Explained | python-simple-solution-beats-100-explain-qjkq | \n# Code\n\n\nclass Solution(object):\n def flatten(self, head):\n if not head:\n return head\n current_node = head\n while c | TomSavage | NORMAL | 2023-01-22T08:06:29.288704+00:00 | 2023-01-22T08:06:29.288736+00:00 | 1,099 | false | \n# Code\n```\n\nclass Solution(object):\n def flatten(self, head):\n if not head:\n return head\n current_node = head\n while current_node != None:\n if current_node.child == None:\n current_node = current_node.next\n else:\n tail_child = current_node.child\n while tail_child.next != None:\n tail_child = tail_child.next\n tail_child.next = current_node.next\n if tail_child.next != None:\n tail_child.next.prev = tail_child\n current_node.next = current_node.child\n current_node.next.prev = current_node\n current_node.child = None\n return head\n```\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n | 3 | 0 | ['Linked List', 'Doubly-Linked List', 'Python'] | 0 |
flatten-a-multilevel-doubly-linked-list | C++ | Simple Recursion | c-simple-recursion-by-ravi_raj_k-b4hp | Intuition\n Describe your first thoughts on how to solve this problem. \nWe can iterate through our linked list while adding Child Lists in between after flatte | Ravi_Raj_K | NORMAL | 2022-12-08T17:58:46.955424+00:00 | 2022-12-08T18:01:06.835223+00:00 | 937 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe can iterate through our linked list while adding **Child Lists** in between after flattening them using simple Recursion.\n\n# Approach\nWhenever in our list, if we found a node with child list:\n1) Save the **next** node\n2) Flatten the child list using **recursion**\n3) Patch the list in between **current** and **next** node.\n\n# Complexity\n- Time complexity: O(n) (Each node visited once)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1) (Constant extra space used)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n Node* flatten(Node* head) {\n Node* itr1 = head;\n while(itr1){\n if(itr1->child){\n Node* itr2 = flatten(itr1->child);\n Node* next = itr1->next;\n // Add child-list next to current node\n patch(itr1, itr2); \n while(itr2->next) itr2 = itr2->next;\n // Add \'next\' node after last element of child list\n patch(itr2, next);\n itr1->child = NULL;\n itr1 = next;\n }\n else itr1 = itr1->next;\n }\n return head;\n }\n\n void patch(Node* node1, Node* node2){\n if(node1) node1->next = node2;\n if(node2) node2->prev = node1;\n }\n};\n```\nHope you will find it helpful...\n``` | 3 | 0 | ['Recursion', 'C++'] | 0 |
flatten-a-multilevel-doubly-linked-list | ✅ Java | 2 Solutions - Iterative, Recursive | java-2-solutions-iterative-recursive-by-x2bwy | Approach 1: Recursive\n\n\n// Time complexity: O(n)\n// Space complexity: O(n)\n\nclass Solution {\n public Node flatten(Node head) {\n\t\thelper(head, null) | prashantkachare | NORMAL | 2022-09-30T16:03:10.237937+00:00 | 2022-09-30T16:03:10.237976+00:00 | 414 | false | **Approach 1: Recursive**\n\n```\n// Time complexity: O(n)\n// Space complexity: O(n)\n\nclass Solution {\n public Node flatten(Node head) {\n\t\thelper(head, null);\n return head;\n }\n\n public Node helper(Node curr, Node prev) {\n if (curr == null)\n return prev;\n \n if (curr.child == null)\n return helper(curr.next, curr);\n \n Node next = curr.next;\n curr.next = curr.child;\n\t\t\n curr.child.prev = curr;\n curr.child = null;\n\t\t\n Node tail = helper(curr.next, curr);\n tail.next = next;\n\t\t\n if (next != null)\n next.prev = tail;\n \n return helper(next, tail);\n }\n}\n```\n\n**Approach 2: Iterative**\n\n```\n// Time complexity: O(n)\n// Space complexity: O(1)\n\npublic Node flatten(Node head) {\n\tNode curr = head;\n\n\twhile (curr != null) {\n\t\tif (curr.child != null) {\n\t\t\tNode tail = curr.child;\n\n\t\t\twhile (tail.next != null)\n\t\t\t\ttail = tail.next;\n\n\t\t\ttail.next = curr.next;\n\t\t\tif (curr.next != null)\n\t\t\t\tcurr.next.prev = tail;\n\n\t\t\tcurr.next = curr.child;\n\t\t\tcurr.child.prev = curr;\n\t\t\t\n\t\t\tcurr.child = null;\n\t\t}\n\n\t\tcurr = curr.next;\n\t}\n\n\treturn head;\n}\n```\n\n**Please upvote if you find this post useful. Happy Coding!** | 3 | 0 | [] | 0 |
flatten-a-multilevel-doubly-linked-list | C++ solution with explanation | c-solution-with-explanation-by-maitreya4-562t | Original solution: https://leetcode.com/problems/flatten-a-multilevel-doubly-linked-list/discuss/152066/c%2B%2B-about-10-lines-solution\nI will try to explain t | maitreya47 | NORMAL | 2022-09-27T22:50:50.395290+00:00 | 2022-09-27T22:50:50.395328+00:00 | 565 | false | Original solution: https://leetcode.com/problems/flatten-a-multilevel-doubly-linked-list/discuss/152066/c%2B%2B-about-10-lines-solution\nI will try to explain the logic behind the code. Here we are iterating though our doubly linked list, if the current node does not have a child, go on. If it does, we first store the next node in a temporary variable next, as we will change the next pointer of the current node to its child. Then do the same, change next pointer of current node to child, prev pointer of child (now next) node to current node and child pointer of current node to NULL. Now store the next pointer of current node in another temporary variable tmp. We need a temporary variable, as we will be iterating through it and we already have a loop going on for h, and hence, cant iterate through it. Iterate until we have next pointer to a tmp node. Once tmp reach the last node in that level, assign its next pointer to previosuly stored next pointer and if next does exist, assign its prev pointer to tmp. \nLogic is simple, as we try to flatten 1 layer at a time, kinda like BFS. Note that we have a inner while loop that accomodates all the nodes in the child level of the current node and assigns next pointer of the last node in child level to the current nodes next --> that\'s what we wanted. But what if some node in child level has a child? That will be handled in our for loop as now the next pointer to curent node is child itself, so every node in the child level will be checked for this condition further in the for loop. Same case for their child and same their child of child and so on.\n\n```\n/*\n// Definition for a Node.\nclass Node {\npublic:\n int val;\n Node* prev;\n Node* next;\n Node* child;\n};\n*/\n\nclass Solution {\npublic:\n Node* flatten(Node* head) {\n for(Node* h = head; h!=NULL; h = h->next)\n {\n if(h->child)\n {\n Node* next = h->next;\n h->next = h->child;\n h->next->prev = h;\n h->child= NULL;\n Node* tmp = h->next;\n while(tmp->next)\n tmp=tmp->next;\n tmp->next = next;\n if(next)\n next->prev = tmp;\n }\n }\n return head;\n }\n};\n```\nTime complexity: O(N)\nSpace complexity: O(1) | 3 | 0 | ['C', 'Iterator', 'C++'] | 0 |
flatten-a-multilevel-doubly-linked-list | Java recursive solution : Similar to flatten a binary tree | java-recursive-solution-similar-to-flatt-4r64 | Notice that if we perform a preorder traversal of the linked list, we would have the nodes in the desired order. In other words, if we perform a \'reverse posto | akil003 | NORMAL | 2022-08-31T15:10:11.310881+00:00 | 2022-08-31T15:10:11.310922+00:00 | 160 | false | Notice that if we perform a preorder traversal of the linked list, we would have the nodes in the desired order. In other words, if we perform a \'reverse postorder\', we would get the nodes in reverse order. We would keep track of those nodes using \'prev\' and append them to the next node we get from the call stack. Similarly, we would also set the prev of \'prev\' to that node and child of that node to null.\n\n```\nclass Solution {\n Node prev = null;\n \n public Node flatten(Node head) {\n if (head == null) return head;\n \n flatten(head.next);\n flatten(head.child);\n \n if (prev != null){\n head.next = prev;\n prev.prev = head;\n head.child = null;\n }\n \n prev = head;\n \n return head;\n }\n}\n```\n\n | 3 | 0 | ['Recursion'] | 0 |
flatten-a-multilevel-doubly-linked-list | Where is C? | where-is-c-by-bezlant-81j5 | Could we add C to the list of languages we can submit this problem, please? | bezlant | NORMAL | 2022-07-27T04:21:39.592631+00:00 | 2022-07-27T04:21:39.592669+00:00 | 102 | false | Could we add C to the list of languages we can submit this problem, please? | 3 | 0 | ['C'] | 0 |
flatten-a-multilevel-doubly-linked-list | JAVA Solution || 100% faster | java-solution-100-faster-by-gavadiya-i8b3 | \nclass Solution {\n public Node flatten(Node head) {\n \n if(head == null ){\n return head;\n }\n Stack<Node> stk = n | Gavadiya | NORMAL | 2022-07-01T17:02:11.121539+00:00 | 2022-07-01T17:02:11.121590+00:00 | 213 | false | ```\nclass Solution {\n public Node flatten(Node head) {\n \n if(head == null ){\n return head;\n }\n Stack<Node> stk = new Stack<>();\n Node temp = head;\n \n while(temp.next != null || temp.child != null ){\n \n if(temp.child != null ){\n if(temp.next != null) stk.push(temp.next);\n \n temp.next = temp.child;\n temp.child.prev = temp;\n temp.child=null;\n \n }\n temp = temp.next;\n }\n while(!stk.empty()){\n Node x = stk.pop();\n temp.next = x;\n x.prev = temp;\n while(temp.next!= null){\n temp = temp.next;\n }\n }\n \n return head;\n \n }\n}\n``` | 3 | 0 | ['Stack', 'Java'] | 1 |
flatten-a-multilevel-doubly-linked-list | EASY CPP CODE || 0 ms, faster than 100.00% | easy-cpp-code-0-ms-faster-than-10000-by-7xh3v | \n/*\n// Definition for a Node.\nclass Node {\npublic:\n int val;\n Node* prev;\n Node* next;\n Node* child;\n};\n*/\n\nclass Solution {\npublic:\n | user8782zV | NORMAL | 2022-06-27T18:28:30.628521+00:00 | 2022-06-27T18:28:30.628568+00:00 | 71 | false | ```\n/*\n// Definition for a Node.\nclass Node {\npublic:\n int val;\n Node* prev;\n Node* next;\n Node* child;\n};\n*/\n\nclass Solution {\npublic:\n \n Node* flatten(Node* head , Node* tail = NULL) {\n // to solve this question we will introduce tail to the list \n if ( !head ) return tail; \n \n head -> next = flatten ( head -> child , flatten ( head -> next , tail));\n \n if ( head -> next ) head -> next -> prev = head ;\n \n head -> child = NULL;\n \n return head;\n }\n};\n``` | 3 | 0 | [] | 0 |
flatten-a-multilevel-doubly-linked-list | ✅ Python - Simple - Recursion | python-simple-recursion-by-fractal393-b3mx | Concept: Recursion - insert the node in the list not the val, then create a new linked list and return the head of the linked list.\n\n def flatten(self, hea | Fractal393 | NORMAL | 2022-04-10T19:34:08.088910+00:00 | 2022-04-10T19:35:45.513105+00:00 | 165 | false | Concept: Recursion - insert the node in the list not the val, then create a new linked list and return the head of the linked list.\n\n def flatten(self, head: \'Optional[Node]\') -> \'Optional[Node]\':\n \n ans = []\n if not head:\n return head\n \n def traverse(node):\n if not node:\n return \n ans.append(node)\n if node.child:\n traverse(node.child)\n if node.next:\n traverse(node.next)\n \n traverse(head)\n \n head = Node(ans[0].val)\n curr = t = head\n for i in range(1,len(ans)):\n head = Node(ans[i].val)\n curr.next = head\n head.prev = curr\n curr = head\n return t\n\t\t\n**Upvote if you found it useful**\n | 3 | 0 | ['Linked List', 'Recursion', 'Python'] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.