question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
maximum-product-of-two-elements-in-an-array | find max y=max erase this from vec z=max from the new vec baad mein y*z return :D | find-max-ymax-erase-this-from-vec-zmax-f-c0gn | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | yesyesem | NORMAL | 2024-08-23T06:34:26.379278+00:00 | 2024-08-23T06:34:26.379317+00:00 | 6 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int maxProduct(vector<int>& nums) {\n auto max_it=max_element(nums.begin(),nums.end());\nint y=*max_it-1;\nint max_index=distance(nums.begin(),max_it);\n\n nums.erase(nums.begin()+max_index);\n max_it=max_element(nums.begin(),nums.end());\n int z=*max_it-1;\n\n return y*z;\n\n \n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
maximum-product-of-two-elements-in-an-array | Simple easy approach loop solution✅✅ | simple-easy-approach-loop-solution-by-kr-o6b9 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | krishnabhagat906 | NORMAL | 2024-04-28T04:37:28.139919+00:00 | 2024-04-28T04:37:28.139935+00:00 | 3 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int maxProduct(int[] nums) {\n int first=0, second=0;\n for(int i=0; i<nums.length; i++){\n if(nums[i]>=first){\n second = first;\n first = nums[i];\n }\n else if(nums[i]>second) second = nums[i];\n }\n return (first-1) * (second-1);\n }\n}\n``` | 2 | 0 | ['Array', 'Java'] | 0 |
maximum-product-of-two-elements-in-an-array | Beats 100% || simple solution || 0ms Time complexity || | beats-100-simple-solution-0ms-time-compl-tjiv | \n\n# Code\n\nclass Solution {\n public int maxProduct(int[] nums) {\n int max=0;\n int secondmax=0;\n for(int i=0;i<nums.length;i++)\n | Vaibhav_Shelke1 | NORMAL | 2024-02-15T16:53:58.977327+00:00 | 2024-02-15T16:53:58.977360+00:00 | 14 | false | \n\n# Code\n```\nclass Solution {\n public int maxProduct(int[] nums) {\n int max=0;\n int secondmax=0;\n for(int i=0;i<nums.length;i++)\n {\n if(nums[i]>=max){\n secondmax=max;\n max=nums[i];\n }\n else if(nums[i]>secondmax){\n secondmax=nums[i];\n }\n }\n return (max-1)*(secondmax-1);\n \n }\n}\n``` | 2 | 0 | ['Java'] | 0 |
movement-of-robots | A classic problem, Ants on a Plank + Prefix sum O(n log n) | a-classic-problem-ants-on-a-plank-prefix-3568 | This is a variation of a very classic problem: There are some ants on a plank at some positions. They are moving right or left, and change directions when they | t747 | NORMAL | 2023-06-10T16:00:37.156886+00:00 | 2023-06-10T16:03:04.810649+00:00 | 9,003 | false | This is a variation of a very classic [problem](https://leetcode.com/problems/last-moment-before-all-ants-fall-out-of-a-plank/#:~:text=When%20an%20ant%20reaches%20one,fall%20out%20of%20the%20plank.): There are some ants on a plank at some positions. They are moving right or left, and change directions when they bump into each other. When does the last ant fall off the plank?\nAt first glance, this may seem difficult to compute, as many collisions may be happening and it is hard to keep track of them all. But there is a very important key observation here: When two ants bump into each other, we can just act like they "phased" through each other! When one ant is going left, and another is going right, and they bump into each other, the left ant is now going right and the right ant is going left. There would be no difference if we had just swapped the ants, or let them pass through each other.\n\nWe can now apply this idea to the robots. Let us ignore any collisions, and just imagine all robots simply passed through each other, as if they were ghosts. Then now we can simply just subtract the distance from them if they were going left or add the distance to them if they were going right. Now, we simply need to compute the distance between each pair of robots. Note that (i, j) and (j,i) should not both be counted, so we will *only* use a prefix sum. If (j,i) was meant to be counted, we would use a prefix and postfix sum. We can compute this easily by sorting the array, then multiplying the number times the index, minus the prefix sum. This gives us the distance between all pairs of robots without double counting. \n\n```\nclass Solution {\npublic:\n int MOD = 1000000007;\n int sumDistance(vector<int>& nums, string s, int d) {\n for(int i = 0; i < nums.size(); i++){\n if(s[i] == \'R\') nums[i] += d;\n else nums[i] -= d;\n }\n long long ans = 0;\n long long pref = 0;\n sort(nums.begin(), nums.end());\n long long n = s.length()-1;\n for(long long i = 0; i < nums.size(); i++){\n ans += i * (long long) nums[i] - pref;\n ans %= MOD;\n pref += nums[i];\n }\n return ans;\n }\n}; | 112 | 0 | [] | 20 |
movement-of-robots | Easy Beginner Friendly with Explanations Pass Through + Prefix Sum | C++ Python | easy-beginner-friendly-with-explanations-st3x | Intuition\n Describe your first thoughts on how to solve this problem. \nIf two objects collide then it appears that they have pass through\n> In short if the i | Chanpreet3000 | NORMAL | 2023-06-10T16:01:15.642242+00:00 | 2023-06-10T16:34:58.004211+00:00 | 5,608 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIf two objects collide then it appears that they have pass through\n> In short if the ith robot is moving left then after time d it\'s position would be nums[i] - d and if it is moving right then it\'s position would be nums[i] + d\n\n**Example:** let 1 be moving right and 2 be moving left.\n\n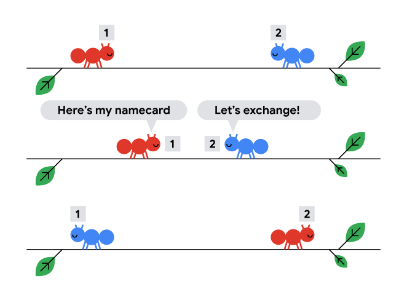\n\nSimilar intuition: [https://codingcompetitions.withgoogle.com/kickstart/round/00000000008cb4d1/0000000000b209bc#analysis](https://codingcompetitions.withgoogle.com/kickstart/round/00000000008cb4d1/0000000000b209bc#analysis)\n\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. We change the final positions using pass through property.\n ``` C++\n for(ll i = 0; i < n; i ++){\n if(s[i] == \'L\'){\n nums[i] -= d;\n }else{\n nums[i] += d;\n }\n }\n ```\n2. To calculate absolute diff between every pair in O(N). We can sort the distance array.\n - The index `j` contribution would be sum of `abs(nums[j] - nums[0]) + abs(nums[j] - nums[1]) + abs(nums[j] - nums[2]) + ...... + abs(nums[j] - nums[j - 1])`.\n - But we know `for (i<j)` `nums[i] < nums[j](Sorted array)`\n - So we can open the `abs()` as `nums[j] - nums[i]` \n - The index `j` contribution would be sum of `nums[j] - nums[0] + nums[j] - nums[1] + nums[j] - nums[2] + ..... + nums[j] - nums[j - 1]`.\n - If we notice then this converts into `j * nums[j] - sum(nums[i] i belongs from 0 to j - 1)` \n - Sum of [0, j- 1] can be calculated in `O(1)` using prefix sum.\n ``` C++ \n for(ll i = 1; i < n; i++){\n ll temp = (MOD + i * nums[i] - pre[i - 1])%MOD;\n ans = ((ans%MOD) + (temp%MOD))%MOD;\n }\n ```\n\n# Complexity\n- Time complexity: `O(N * Log(N))`\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: `O(N)`\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n``` Python3 []\nclass Solution:\n def sumDistance(self, nums: List[int], s: str, d: int) -> int:\n n, m = len(nums), int(1e9 + 7)\n # Ignore the Collisions\n for i in range(n):\n if s[i] == \'L\':\n nums[i] -= d\n else: \n nums[i] += d\n \n # Sort according to position to calculate abs sum of each pair in O(N)\n nums.sort()\n\n pre = nums.copy()\n # Calculate Prefix Sum\n for i in range(1, n):\n pre[i] += pre[i - 1]\n pre[i] %= m\n\n ans = 0\n for i in range(1, n):\n # each jth index contributes to j * nums[j] - pre[j - 1]\n ans += i * nums[i] - pre[i - 1]\n ans %= m\n return ans\n```\n``` C++ []\ntypedef long long int ll;\nconst ll MOD = 1e9 + 7;\nclass Solution {\npublic:\n int sumDistance(vector<int>& nums, string s, int d) {\n //Ignore the collisions!\n for(ll i = 0; i < s.length(); i ++)\n if(s[i] == \'L\')nums[i] -= d;\n else nums[i] += d;\n // Sort according to position to calculate abs sum of each pair in O(N)\n sort(nums.begin(), nums.end());\n \n //Calculate Prefix Sum\n vector<ll> pre(nums.begin(), nums.end());\n for(ll i = 1; i < nums.size(); i++){\n pre[i] += pre[i - 1];\n pre[i] %= MOD;\n }\n\n ll ans = 0;\n for(ll i = 1; i < nums.size(); i++){\n // each jth index contributes to j * nums[j] - pre[j - 1]\n ans += i * nums[i] - pre[i - 1];\n ans %= MOD;\n }\n return ans;\n }\n};\n``` | 65 | 1 | ['Array', 'String', 'Greedy', 'C++', 'Python3'] | 12 |
movement-of-robots | ✅ Explained - Simple and Clear Python3 Code✅ | explained-simple-and-clear-python3-code-0l03m | Intuition\nThe problem requires calculating the sum of distances between all pairs of robots after a given command is executed. To solve this, we can simulate t | moazmar | NORMAL | 2023-06-10T16:16:07.064367+00:00 | 2023-06-11T17:50:20.206489+00:00 | 1,213 | false | # Intuition\nThe problem requires calculating the sum of distances between all pairs of robots after a given command is executed. To solve this, we can simulate the movement of the robots and keep track of their positions. Whenever two robots collide, they will change their directions and continue moving. We need to calculate the sum of distances between all pairs of robots at a specific time point.\n\n\n# Approach\nThe approach begins by updating the positions of the robots based on the given command string \'s\' and the time \'d\'. If the command is \'L\', the robot at index \'i\' will move \'d\' units to the left (subtracting \'d\' from its position in the \'nums\' array). If the command is \'R\', the robot will move \'d\' units to the right (adding \'d\' to its position). This step ensures that the positions of the robots reflect their movement after the command is executed.\n\nNext, the algorithm initializes the answer variable \'ans\' to 0. It then sorts the \'nums\' array in ascending order. The variable \'s\' is used to keep track of the cumulative sum of robot positions.\n\nIn the subsequent loop, the algorithm iterates over the \'nums\' array. For each robot at index \'i\', it calculates the distance between that robot and all robots to its left. The distance is given by \'nums[i] * i - s\'. The algorithm adds this distance to \'ans\' and takes the modulo \'mod\' to prevent the answer from becoming too large.\n\nAdditionally, the algorithm updates the value of \'s\' by adding \'nums[i]\' to it and takes the modulo \'mod\'. This ensures that \'s\' represents the cumulative sum of robot positions up to the current index \'i\'.\n\nFinally, the algorithm returns \'ans\' modulo \'mod\', which gives us the desired sum of distances between all pairs of robots after \'d\' seconds.\n\n\n\n\n\n\n# Code\n```\nclass Solution:\n def sumDistance(self, nums: List[int], s: str, d: int) -> int:\n for i in range(len(s)):\n if s[i] == \'L\':\n nums[i] -= d\n else:\n nums[i] += d\n \n ans = 0\n nums.sort()\n mod = 10 ** 9 + 7\n s = 0\n \n for i in range(len(nums)):\n ans += (nums[i] * i - s)\n ans %= mod\n s += nums[i]\n s %= mod\n \n return ans % mod\n``` | 12 | 0 | ['Python3'] | 3 |
movement-of-robots | Python | Easy | Explanation | python-easy-explanation-by-mohd_mustufa-f01h | When 2 robots collide, they just pass through each other. We dont have to worry about changing the direction of each robot when they collide. So we can say that | mohd_mustufa | NORMAL | 2023-06-10T16:02:57.217603+00:00 | 2023-06-30T19:34:03.439837+00:00 | 1,020 | false | When 2 robots collide, they just pass through each other. We dont have to worry about changing the direction of each robot when they collide. So we can say that if a robot is moving right, then after d seconds it would have moved: its current position + d. If the robot is moving left, then after d seconds it would have moved: its current position - d.\nTherefore, we just need to check which position the robot is moving in and add or subtract d with its value.\n\n<span style="font-size:17px; font-weight:600">To find the sum of each pair we can do the following:</span>\nWe first need to sort the array. We can then notice that for any index i, its contribution to the sum would be: \n-> <span style="font-weight:600;">(nums[i] - nums[i-1]) + (nums[i] - nums[i-2]) + ... + (nums[i] - nums[0]).</span>\nThe above formula can be converted to:\n-> <span style="font-weight:600">(i * nums[i]) - sum(nums[0] to nums[i-1])</span>\nWe can keep a variable `s` that will keep track of the sum of the elements of the array upto the i<sup>th</sup> index. The contribution of the i<sup>th</sup> index to the sum can be calculated as below:\n```python\ns = 0 \nfor i in range(len(nums)):\n ans += ((i * nums[i]) - s))\n s += nums[i]\n```\n\nTime Complexity: O(nlogn) - For sorting the array.\nSpace Complexity: O(n) - For sorting (python internally uses timsort which takes O(n) extra space in the worst case).\n\n```\nclass Solution:\n def sumDistance(self, nums: List[int], s: str, d: int) -> int:\n for i in range(len(s)):\n if s[i] == \'L\':\n nums[i] -= d\n else:\n nums[i] += d\n \n ans = 0\n nums.sort()\n mod = 10 ** 9 + 7\n s = 0\n \n for i in range(len(nums)):\n ans += (nums[i] * i - s)\n s += nums[i]\n ans %= mod\n s %= mod\n \n return ans % mod\n``` | 12 | 0 | ['Python3'] | 4 |
movement-of-robots | [Java/C++/Python] Ants Trick | javacpython-ants-trick-by-lee215-mn9z | Explanation\nRobots has no different,\nso we can assume rebots can go cross each other.\nUsualy it\'s a trick for ants, here is robot.\n\nThen sort A.\nFor A[i] | lee215 | NORMAL | 2023-06-12T14:17:04.905352+00:00 | 2023-06-12T14:17:04.905401+00:00 | 911 | false | # **Explanation**\nRobots has no different,\nso we can assume rebots can go cross each other.\nUsualy it\'s a trick for ants, here is robot.\n\nThen sort `A`.\nFor `A[i]`,\nit contributes as `A[j] - A[i]` for `i + 1` times, where `j < i`\nit contributes as `A[i] - A[j]` for `n - i` times, where `i < j`.\nSo we count the sum of `A[i] * (1 + i + i - n)`\n<br>\n\n# **Complexity**\nTime `O(sort)`\nSpace `O(sort)`\n<br>\n\n**Java**\n```java\n public int sumDistance(int[] A, String s, int d) {\n int n = A.length, mod = (int)1e9 + 7;\n for(int i = 0; i < n; ++i)\n A[i] += s.charAt(i) == \'R\' ? d : -d;\n Arrays.sort(A);\n long res = 0;\n for(int i = 0; i < n; ++i)\n res = (res + (1L + i + i - n) * A[i]) % mod;\n return (int)(res + mod) % mod;\n }\n```\n\n**C++**\n```cpp\n int sumDistance(vector<int>& A, string s, int d) {\n int n = A.size(), mod = 1e9 + 7;\n for(int i = 0; i < n; ++i)\n A[i] += s[i] == \'R\' ? d : -d;\n sort(A.begin(), A.end());\n long long res = 0;\n for(int i = 0; i < n; ++i)\n res = (res + (1L + i + i - n) * A[i]) % mod;\n return (res + mod) % mod;\n }\n```\n\n**Python**\n```py\n def sumDistance(self, A: List[int], s: str, d: int) -> int:\n n = len(A)\n B = sorted(A[i] + (d if s[i] == \'R\' else -d) for i in range(n))\n return sum((i + i + 1 - n) * a for i,a in enumerate(B)) % (10 ** 9 + 7)\n```\n | 9 | 0 | ['C', 'Python', 'Java'] | 2 |
movement-of-robots | Python 3 || 2 lines, w/ notes and example || T/S: 99% / 97% | python-3-2-lines-w-notes-and-example-ts-ah2po | Notes:\n- The problem could be rewritten as: "Each robot travelsdunits left or right based on whether its corresponding element insis LorR, respectively. Find t | Spaulding_ | NORMAL | 2023-06-12T17:13:53.211312+00:00 | 2024-06-19T01:26:29.395358+00:00 | 520 | false | Notes:\n- The problem could be rewritten as: "Each robot travels`d`units left or right based on whether its corresponding element in`s`is `L`or`R`, respectively. Find the sum of the distances based on these final positions."\n\n- The function`(ord(ch)-79)//3 * d`maps`\'L\'`-->`-d` and`\'R\'`-->`d`\n\n- It is left to the curious and algebraically capable reader to justify why, in the example, the inner product of `[-7,-2,3,6]`and`[-3,-1,1,3]`gives us the correct answer.\n\n```\nclass Solution:\n def sumDistance(self, nums: List[int], s: str, d: int) -> int:\n\n nums = sorted([num+(ord(ch)-79)//3*d # Example : nums: [1,0,4,-5], s: \'RLRL\', d: 2\n for num, ch in zip(nums,s)]) \n # nums = sorted([1+2, 0-2, 4+2, -5-2])\n # = [-7,-2,3,6]\n\n return sum(map(mul, nums, range(1-len(nums), # sum(map(mul, [[-7,-2,3,6],[-3,-1,1,3]]))\n len(nums), 2)))%1000000007 # sum((-7*-3)+(-2*-1)+(3*1)+(6*3))\n # return 44\n\n```\n[https://leetcode.com/problems/movement-of-robots/submissions/1292983083/](https://leetcode.com/problems/movement-of-robots/submissions/1292983083/)\n\n\nI could be wrong, but I think that time complexity is *O*(*N*log*N*) (because of the`sort`) and space complexity is *O*(*N*), in which *N* ~`len(nums)`. | 8 | 1 | ['Python3'] | 1 |
movement-of-robots | Java, sorting + linear scan | java-sorting-linear-scan-by-vladislav-si-pgoy | Intuition\nThe first observation is we can ignore meetings of the robots because the meeting robots will continue their journey and we don\'t care about the rob | Vladislav-Sidorovich | NORMAL | 2023-06-10T16:12:13.922646+00:00 | 2023-06-14T19:04:04.972863+00:00 | 1,653 | false | # Intuition\nThe first observation is we can ignore meetings of the robots because the meeting robots will continue their journey and we don\'t care about the robot ids.\n\nThe second trick is to avoid `O(n^2)` complexity for sum distance of all pairs.\n\nEplanation of the line `long curr = i * (long)nums[i] - (n - 1 - i) * (long)nums[i]`\n\n*Note1*: let\'s use long to avoid integer overflow.\n\n*Note2*: Let\'s take a look on the example `{1,2,3}`. All pairs sums will be:\n`(1,2) + (1,3) + (2,3)` = `2 - 1 + 3 - 1 + 3 - 2`. So, we use each number in the array `n - 1` times. We substtract the number if it is less in the pair `(i, j)`, once array is sorrted it means `i` number will be bigger (added to sum) `i` times and less (substructed from the sum) `n - 1 - i` times.\nGeneral formula per number: `nums[i] * i - nums[i] * (n - 1 - i)`;\n\n*Note3*: the array is sorted, so we always substtruct big numbers less then add big number. So we don\'t car about `abs`. The example arr `{-2, -1}` is `(-2, -1) = -2 * 0 - -2 + -1 - -1 * 0 = 2 - 1 = 1`\n\n# Complexity\n- Time complexity: O(nlogn)\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution {\n public int sumDistance(int[] nums, String s, int d) {\n final int mod = 1_000_000_007;\n for (int i=0; i<nums.length; i++) {\n nums[i] += d * (s.charAt(i) == \'R\' ? 1 : -1);\n }\n \n Arrays.sort(nums);\n long sum = 0;\n int n = nums.length;\n for (int i=0; i<n; i++) {\n long curr = i * (long)nums[i] - (n - 1 - i) * (long)nums[i];\n sum += curr;\n sum %= mod;\n } \n \n return (int) sum ;\n }\n}\n``` | 7 | 0 | ['Sorting', 'Java'] | 5 |
movement-of-robots | prefixsum intution explained💯💡 || O(NlogN) | prefixsum-intution-explained-onlogn-by-s-wfsz | \n\n# Code\n\nclass Solution {\npublic:\n int mod=1e9+7;\n int sumDistance(vector<int>& nums, string s, int d) {\n vector<long long int> ans;\n | steeewtOverflow | NORMAL | 2023-06-10T19:46:30.950401+00:00 | 2023-06-10T19:46:30.950437+00:00 | 648 | false | \n\n# Code\n```\nclass Solution {\npublic:\n int mod=1e9+7;\n int sumDistance(vector<int>& nums, string s, int d) {\n vector<long long int> ans;\n int n=nums.size();\n for(int i=0; i<n; i++){\n ans.push_back(nums[i]);\n }\n //we can ignore the collsions as the order of the positions is insignificant in this problem\n for(int i=0; i<n; i++){\n if(s[i]==\'L\'){\n ans[i]=(ans[i]-d);\n }\n else{\n ans[i]=(ans[i]+d);\n }\n }\n long long int a=0;\n long long int pref=0;\n //imagine finding distance of a4 with all elements before it\n //(a4-a1)+(a4-a2)+(a4-a3)---> (a4+a4+a4)-(a1+a2+3)---->i*a4-prefixsum\n //this formula can be used only if the positions are sorted\n sort(ans.begin(), ans.end());\n for(int i=0; i<n; i++){\n a+=i*ans[i]-pref;\n a%=mod;\n pref+=ans[i];\n }\n return a;\n }\n};\n\n``` | 5 | 0 | ['C++'] | 1 |
movement-of-robots | Robots 🤖 Keep Walking 🚶 | robots-keep-walking-by-harshitmaurya-v7nh | intuition :\n\nWhen two Robots meet at some point,\nthey change their directions and continue moving again.\nBut you can assume they don\'t change direction and | HarshitMaurya | NORMAL | 2023-06-10T16:02:31.448343+00:00 | 2023-06-13T12:27:13.648748+00:00 | 898 | false | **intuition** :\n\nWhen two Robots meet at some point,\nthey change their directions and continue moving again.\nBut you can assume they don\'t change direction and keep moving(since they take 0 unit time).\n\nlet them walk then the question become find the sum of difference between all pair (i , j) of an Array :\n\n\n\n```\nclass Solution {\n\tpublic int sumDistance(int[] nums, String s, int d) {\n for (int i = 0; i < s.length(); i++) {\n char dir = s.charAt(i);\n if (dir == \'R\') {\n nums[i] += d;\n } else {\n nums[i] -= d;\n }\n }\n return sumPairs(nums, nums.length);\n }\n\n int sumPairs(int nums[], int n) {\n Arrays.sort(nums);\n long sum = 0;\n int mod = (int) 1e9 + 7;\n long prefix = 0;\n for (int i = 0; i < n; i++) {\n sum = (sum + i * (long) nums[i] - prefix) % mod;\n prefix += nums[i] % mod;\n }\n\n return (int) sum;\n }\n}\n```\n\n**Similar Problem** : https://leetcode.com/problems/last-moment-before-all-ants-fall-out-of-a-plank/ | 5 | 1 | ['Sorting', 'Java'] | 1 |
movement-of-robots | C++ sort & sum||88ms Beats 95.92% | c-sort-sum88ms-beats-9592-by-anwendeng-jsf0 | Intuition\n Describe your first thoughts on how to solve this problem. \nCompute firstly the arrayA[i]=(s[i]==\'R\')?nums[i]+d:nums[i]-d.\nThen sort the array A | anwendeng | NORMAL | 2023-11-04T15:40:57.643645+00:00 | 2023-11-04T15:40:57.643666+00:00 | 510 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nCompute firstly the array`A[i]=(s[i]==\'R\')?nums[i]+d:nums[i]-d`.\nThen sort the array `A` such that `A[i]<A[j]` for `i<j`.\nCompute the sum of distance \n$$\n\\sum_{i<j}A[j]-A[i]\\\\\n=\\sum_{i=0}^{n-1}(2i-n+1)A[i]\n$$\n# Approach\n<!-- Describe your approach to solving the problem. -->\nLike solving [1503. Last Moment Before All Ants Fall Out of a Plank](https://leetcode.com/problems/last-moment-before-all-ants-fall-out-of-a-plank/solutions/4246032/c-3-lines-python-1-line-physics/) & compute the array `A`.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n\\log n)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n# Code 88ms Beats 95.92%\n```\n#pragma GCC optimize("O3")\nclass Solution {\npublic:\n const int mod=1e9+7;\n int sumDistance(vector<int>& nums, string s, int d) \n {\n int n=nums.size();\n vector<long long> A(n, 0L);\n #pragma unroll\n for(int i=0; i<n; i++){\n A[i]=(s[i]==\'R\')?(long long)nums[i]+d:(long long)nums[i]-d;\n }\n sort(A.begin(), A.end());\n long long distance=0;\n #pragma unroll\n for(int i=0; i<n; i++)\n distance=(distance+(-n+1+(2L*i))*A[i])%mod;\n return distance<0?distance+mod:distance;\n }\n};\n``` | 4 | 0 | ['Array', 'Sorting', 'C++'] | 0 |
movement-of-robots | SIMPLE || AVOID COLLISION || C++ | simple-avoid-collision-c-by-ganeshkumawa-0xge | Code\n\nclass Solution {\npublic:\n int sumDistance(vector<int>& nums, string s, int d) {\n int i = 0, n = nums.size();\n for(i = 0; i < n; i++ | ganeshkumawat8740 | NORMAL | 2023-06-11T01:52:43.350197+00:00 | 2023-06-11T01:52:43.350226+00:00 | 1,503 | false | # Code\n```\nclass Solution {\npublic:\n int sumDistance(vector<int>& nums, string s, int d) {\n int i = 0, n = nums.size();\n for(i = 0; i < n; i++){\n if(s[i]==\'R\'){\n nums[i] += d;\n }else{\n nums[i] -= d;\n }\n }\n sort(nums.begin(),nums.end());\n long long ans = 0,mod = 1e9+7,p = 0;\n for(i = 0; i < n; i++){\n ans = (((ans+(nums[i]*1LL*i)%mod)%mod-p)%mod+mod)%mod;\n p = (p+nums[i])%mod;\n }\n return (ans+mod)%mod;\n }\n};\n``` | 4 | 0 | ['Sorting', 'Prefix Sum', 'C++'] | 1 |
movement-of-robots | BEST C++ || O(nlogn)|| Proper Intution || Easy to understand | best-c-onlogn-proper-intution-easy-to-un-oxe6 | Intution\nWhen collision happens- Directions wil be RL or LR and in that case direction will change as LR or RL respectively. So, there is no net effect in ans | alltimecoding | NORMAL | 2023-06-10T18:56:46.921266+00:00 | 2023-06-10T18:56:46.921314+00:00 | 783 | false | # Intution\nWhen collision happens- Directions wil be RL or LR and in that case direction will change as LR or RL respectively. So, there is no net effect in answer even calculating without changing the direction.\n# Complexity\n- Time complexity:O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n#define md 1000000007\nclass Solution {\npublic:\n\nint sumDistance(vector<int>& nums, string s, int d) {\n long long n=nums.size();\n vector<long long>nums1(nums.begin(),nums.end());\n for(long long i=0;i<n;i++){\n if(s[i]==\'L\')nums1[i]-=d;\n else nums1[i]+=d;\n\n }\n \n//An efficient solution for this problem needs a simple observation. Since array is sorted and elements are distinct when we take sum of absolute difference of pairs each element in the i\u2019th position is added \u2018i\u2019 times and subtracted \u2018n-1-i\u2019 times.\nsort(nums1.begin(),nums1.end());\nfor(long long i=0;i<n;i++)nums1[i]%=md;\nlong long answer=0;\nfor(long long i=0;i<n;i++){\n long long temp1=(i*nums1[i])%md;\n long long temp2=((n-1-i)*nums1[i])%md;\n answer+=((temp1-temp2));\n answer%=md;\n if(answer<0)answer+=md;//Very Important step to do.\n}\nanswer%=md;\nreturn (int)answer;\n }\n};\n``` | 4 | 0 | ['C++'] | 2 |
movement-of-robots | Java | Sorting | with explanation | java-sorting-with-explanation-by-nishant-3cwm | The logic behind : i*arr[i] - (n-1-i)*arr[i] in calculating Sum of absolute differences of all pairs in a given array:\n\nLet\'s take an example: [1,2,3,4,5] (A | nishant7372 | NORMAL | 2023-06-10T17:29:25.580956+00:00 | 2023-06-12T08:24:36.287718+00:00 | 508 | false | ### The logic behind : `i*arr[i] - (n-1-i)*arr[i]` in calculating Sum of absolute differences of all pairs in a given array:\n\nLet\'s take an example: [1,2,3,4,5] (After Sorting) (n = no. of elements = 5)\n\nSum of absolute differences of all pairs in a given array:\n\n(2-1) + (3-1) + (4-1) + (5-1) +\n(3-2) + (4-2) + (5-2) +\n(4-3) + (5-3) + \n(5-4)\n\n= 20\n\nWe can write it as:\n\n1x0 + (-1x4) +\n2x1 + (-2x3) +\n3x2 + (-3x2) +\n4x3 + (-4x1) +\n5x4 + (-5x0) \n\nwhich is equal to \n\n1x0 - (1x4) + `(i=0 , n-1-i = 4)`\n2x1 - (2x3) + `(i=1 , n-1-i = 3)`\n3x2 - (3x2) + `(i=2 , n-1-i = 2)`\n4x3 - (4x1) + `(i=3 , n-1-i = 1)`\n5x4 - (5x0) `(i=4 , n-1-i = 0)`\n\nresulting in 20\n\n## Complexity\n- Time complexity: O(nlogn)\n\n- Space complexity: O(1)\n\n## Code\n``` java []\nclass Solution {\n static int mod = (int)(1e9 + 7);\n public int sumDistance(int[] arr, String s, int d) {\n int n = arr.length;\n \n for(int i=0;i<n;i++){\n if(s.charAt(i)==\'R\'){\n arr[i]+=d;\n }\n else{\n arr[i]-=d;\n }\n }\n\n Arrays.sort(arr);\n\n long sum = 0;\n \n for(int i = 0; i < n; i++) {\n sum = (sum + i*(long)arr[i] - (n-1-i)*(long)arr[i])%mod;\n }\n \n return (int)sum;\n }\n}\n``` | 4 | 0 | ['Sorting', 'Java'] | 2 |
movement-of-robots | [Java] Just ignore the collision | java-just-ignore-the-collision-by-0x4c0d-nmmi | Intuition\n Describe your first thoughts on how to solve this problem. \nWe can ignore the collision, since all robots are same, we can\'t distinct each other. | 0x4c0de | NORMAL | 2023-06-10T16:00:40.821864+00:00 | 2023-06-12T06:56:50.700361+00:00 | 930 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe can ignore the collision, since all robots are same, we can\'t distinct each other. **The robots just keep walking with collision.**\n\nSimilar problem: https://leetcode.com/problems/last-moment-before-all-ants-fall-out-of-a-plank/\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSort the final position of all robots and use prefix sum to save time.\n\n**The position is sorted($p_{i-1} <= p_{i}$), so we can use prefix sum.**\n\n$d = |p_i - p_0| + |p_i - p_1| +...+ |p_i - p_{i-1}|$\n$= (p_i - p_0) + (p_i - p_1) +...+ (p_i - p_{i-1})$\n$= i*p_i - (p_0 + p_1+...+p_{i-1})$\n$= i*p_i - \\sum_{j=0}^{i-1}p_j$\n\n# Complexity\n- Time complexity: $$O(N*logN)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(N)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```\nclass Solution {\n public int sumDistance(int[] nums, String s, int d) {\n final int modulo = (int) 1e9 + 7;\n final int n = nums.length;\n long[] position = new long[n];\n for (int i = 0; i < n; i++) {\n position[i] = (s.charAt(i) == \'L\' ? -1L : 1L) * d + nums[i];\n }\n\n Arrays.sort(position);\n long distance = 0;\n long prefix = 0;\n for (int i = 0; i < n; i++) {\n distance = (distance + (i * position[i] - prefix)) % modulo;\n prefix += position[i];\n }\n\n return (int) distance;\n }\n}\n\n``` | 4 | 0 | ['Math', 'Prefix Sum', 'Java'] | 2 |
movement-of-robots | python3 Solution | python3-solution-by-motaharozzaman1996-qupm | \n\nclass Solution:\n def sumDistance(self, nums: List[int], s: str, d: int) -> int:\n n = len(nums)\n mod=10**9+7\n for i in range(n):\ | Motaharozzaman1996 | NORMAL | 2023-06-10T17:29:35.675947+00:00 | 2023-06-10T17:29:35.675978+00:00 | 215 | false | \n```\nclass Solution:\n def sumDistance(self, nums: List[int], s: str, d: int) -> int:\n n = len(nums)\n mod=10**9+7\n for i in range(n):\n if s[i] == \'L\':\n nums[i] -= d\n else: \n nums[i] += d\n \n nums.sort()\n\n pre = nums.copy()\n for i in range(1, n):\n pre[i] += pre[i - 1]\n pre[i] %= mod\n\n ans = 0\n for i in range(1, n):\n\n ans += i * nums[i] - pre[i - 1]\n ans %= mod\n return ans\n``` | 3 | 0 | ['Python', 'Python3'] | 0 |
movement-of-robots | Video Explanation (With Intuition) | video-explanation-with-intuition-by-codi-oeby | Explanation\n\nClick here for the video\n\n# Code\n\ntypedef long long int ll;\nconst int MOD = 1e9+7;\n\nclass Solution {\npublic:\n int sumDistance(vector< | codingmohan | NORMAL | 2023-06-10T17:07:56.639372+00:00 | 2023-06-10T17:07:56.639418+00:00 | 211 | false | # Explanation\n\n[Click here for the video](https://youtu.be/Xpr0hg1jBEI)\n\n# Code\n```\ntypedef long long int ll;\nconst int MOD = 1e9+7;\n\nclass Solution {\npublic:\n int sumDistance(vector<int>& nums, string s, int d) {\n int n = nums.size();\n \n vector<ll> final_pos(n);\n for (int j = 0; j < n; j ++) \n final_pos[j] = (ll)nums[j] + (s[j] == \'L\'? -d : d);\n \n sort (final_pos.begin(), final_pos.end());\n \n ll result = 0;\n ll prefix = 0;\n for (int j = 0; j < n; j ++) {\n result = (result + (final_pos[j]*j - prefix + MOD)) % MOD;\n prefix = (prefix + final_pos[j]) % MOD;\n }\n \n return result;\n }\n};\n``` | 3 | 0 | ['C++'] | 0 |
movement-of-robots | C++ || Simple || Easily Understandable || Faster | c-simple-easily-understandable-faster-by-hu4z | Intuition\n Describe your first thoughts on how to solve this problem. \n- As given that certain index value moves in certain direction.\n- Upon collision of tw | Dark_warrior | NORMAL | 2023-06-13T01:04:48.175947+00:00 | 2023-06-13T01:04:48.175964+00:00 | 78 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- As given that certain index value moves in certain direction.\n- Upon collision of two values they change their direction and start moving in opposite direction.\n- By this we can understand that when two balls collide they change their direction. So consider that if two balls collide and they pass through each other without changing their direction will also have cause of action.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- Simply add d to the index which are moving in \'R\' direction.\n- Subtract d from the indexes which are moving in \'L\' direction.\n- Sort the array\n- Then find the distance between every pair with the help of prefix sum in O(1) time.\n\n# Complexity\n- Time complexity: O(NLogN)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O{N}\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int sumDistance(vector<int>& nums, string s, int d) {\n int n = s.length();\n int m = 1e9+7;\n for(int i = 0 ; i< n; i++){\n if(s[i] == \'R\')\n nums[i] += d;\n else\n nums[i] -= d;\n }\n sort(nums.begin(), nums.end());\n vector<int> pre;\n long long sum = 0;\n for(auto i : nums)\n {\n sum = (sum + i)%m;\n pre.push_back(sum);\n }\n \n long long ans = 0 ;\n for(int i = 0 ; i< n - 1; i++){\n ans = (ans + ((sum - pre[i] + m)%m - ((n-i-1)*1ll*(nums[i]))%m +m)%m)%m;\n }\n return ans%m;\n }\n};\n``` | 2 | 0 | ['Sorting', 'Prefix Sum', 'C++'] | 0 |
movement-of-robots | C++||Most Easy Solution Using Simple Logic+Prefix Sum | cmost-easy-solution-using-simple-logicpr-n6zb | \ntypedef long long ll;\nll mod=1e9+7;\nclass Solution {\npublic:\n int sumDistance(vector<int>& nums, string s, int d) {\n ll n=s.size();\n fo | Arko-816 | NORMAL | 2023-06-11T04:00:05.083778+00:00 | 2023-06-11T04:00:05.083812+00:00 | 709 | false | ```\ntypedef long long ll;\nll mod=1e9+7;\nclass Solution {\npublic:\n int sumDistance(vector<int>& nums, string s, int d) {\n ll n=s.size();\n for(int i=0;i<n;i++)\n {\n if(s[i]==\'R\')\n nums[i]+=d;\n else\n nums[i]-=d;\n }\n vector<ll> pref(n,0);\n sort(nums.begin(),nums.end());\n pref[0]=nums[0];\n pref[n-1]=nums[n-1];\n for(int i=1;i<n;i++)\n pref[i]=pref[i-1]+nums[i];\n ll ans=0;\n ll cnt=1;\n for(int i=1;i<n;i++)\n {\n ans=(ans+(cnt*nums[i])-pref[i-1]);\n ans=ans%mod;\n cnt++;\n } \n return ans%mod;\n }\n};\n``` | 2 | 0 | [] | 1 |
movement-of-robots | O(n log n) simple sort and count | on-log-n-simple-sort-and-count-by-dkravi-m2hr | Key observation is that you might as well assume the robots keep moving in the direction they started in, as you don\'t care if they rebound off each other beca | dkravitz78 | NORMAL | 2023-06-10T21:09:09.491300+00:00 | 2023-06-10T21:09:09.491351+00:00 | 134 | false | Key observation is that you might as well assume the robots keep moving in the direction they started in, as you don\'t care if they rebound off each other because we don\'t care which is which. \n\nSo, simply find the place where each finishes, then sort that as that lets us count in order without worrying about absolute value. \n\nKeep S as a prefix sum as you go through the sorted array. \n\n```\nclass Solution:\n def sumDistance(self, nums: List[int], s: str, d: int) -> int:\n nums = sorted([n+d if s[i]==\'R\' else n-d for i,n in enumerate(nums)])\n \n ret = 0\n S = 0\n \n for i,n in enumerate(nums):\n ret += i*n - S\n S += n\n \n return ret % (10**9+7)\n ``` | 2 | 0 | ['Python3'] | 0 |
movement-of-robots | C++ with thinking process | c-with-thinking-process-by-jk15162428-fo2w | Intuition\nThe first time I saw this question, I have no idea about that LOL. I check the input range, there is a $d \sim 1e9$, and $nums \sim 1e5$, and this is | jk15162428 | NORMAL | 2023-06-10T17:42:12.133839+00:00 | 2023-06-10T17:42:12.133887+00:00 | 485 | false | ## Intuition\nThe first time I saw this question, I have no idea about that LOL. I check the input range, there is a $d \\sim 1e9$, and $nums \\sim 1e5$, and this is not a simulation, search, dynamic programming, etc. I guess it must have some method to avoid simulating $d$ seconds and get the final state, the situation is too complicated with collision.\n\nAnd, surprisingly, there is.\nLet\'s think about what happened when two robots collide. Here is the simplified version of collision situaltion.\n* (x - 1 $\\rightarrow$,$\\leftarrow$ x + 1) $\\Rightarrow$ ($\\leftarrow$ x, x$\\rightarrow$) $\\Rightarrow$ ($\\leftarrow$ x - 1, x + 1$\\rightarrow$)\n* (x$\\rightarrow$,$\\leftarrow$ x + 1) $\\Rightarrow$ ($\\leftarrow$ x, x + 1$\\rightarrow$)\n\nCan we know something from it? Obviously, I can\'t see anything, they just switch the direction as the question said.\n\nWhat about we **not only** change their direction, but also **change their identity**? Let\'s see what\'s happening now.\n\n* (x - 1 $\\rightarrow$,$\\leftarrow$ y + 1) $\\Rightarrow$ ($\\leftarrow$ y, x$\\rightarrow$) $\\Rightarrow$ ($\\leftarrow$ y - 1, x + 1$\\rightarrow$)\n* (x$\\rightarrow$,$\\leftarrow$ y + 1) $\\Rightarrow$ ($\\leftarrow$ y, x + 1$\\rightarrow$)\n\nThey just "pass through" each other, as if **no collision** happens!\n\nSo the final problem is, how to get the final answer without nested for loop? Yes!\n\nLet\'s see this picture, assuming we have 4 robots (dots).\n\n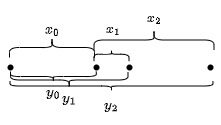\n\nThink about it, if we use nested for loop, we will repeated calculate the intermedia distance. We can remove those redundancy. \n\nWe can calculate the distance from robot[0] to robot[1-3] (the brackets below, i.e. $y_0+y_1+y_2$). If we want to calculate the distance from robot[1] to others, we need to calcualte $x_0 + x_1 + x_2$ (the brackets above). \n\nHowever, we can see that all brackets below "contain" the brackets above (one-to-one). To be specific, $y_0$ contains $x_0$, $y_1$ contains $x_1$, $y_2$ contains $x_2$. Since we already calculate pair[0, 1], we don\'t need $x_0$ anymore, i.e. we don\'t need to care about the left robots, and we just care about the right part, $x_1+x_2$ in this example, and we can get that by $y_0 + y_1 + y_2 - 3 * x_0$.\n\nThis pattern follows, if we want to calculate the robot[2] distance with others, we have $y_0 + y_1 + y_2 - 3 * x_0 - 2 * x_1$, that\'s exactly the last pair we don\'t have.\n\nAnd that\'s the idea, we don\'t need iterate through every pair, we just iterate through every "gap" between two robots.\n\n## Approach\n\nFirst we can get the final state by iterating the `nums`, because every robot is just like they "step forward" without any collision.\n\nSecond, we sort the final state.\n\nFinally, we get the answer just like said above. Note: We first get the sum of distance `temp` between all other robots and the leftest robot $robot_0$, and this is within long long range.\n\nDone!\n\n\n## Complexity\n- Time complexity: $O(mlogm)$, m is the length of array `nums`.\n- Space complexity: Don\'t care :D\n\n## Code\n```\nclass Solution {\npublic:\n const long long mod = 1e9+7;\n int sumDistance(vector<int>& nums, string s, int d) {\n vector<long long> finalState;\n for(auto n : nums) {\n finalState.emplace_back(n);\n }\n for(int i = 0; i < finalState.size(); i++) {\n if (s[i] == \'L\')\n finalState[i] -= d;\n else finalState[i] += d;\n }\n sort(finalState.begin(), finalState.end());\n unsigned long long temp = 0, ans = 0;\n for(int i = 0; i < finalState.size(); i++) {\n if (i == 0) {\n for(int j = 1; j < finalState.size(); j++) {\n temp += abs(finalState[j] - finalState[i]);\n ans = temp % mod;\n }\n } else {\n temp = temp - (nums.size() - i) * abs(finalState[i] - finalState[i - 1]);\n ans = (ans + temp) % mod;\n }\n }\n return ans;\n }\n};\n``` | 2 | 0 | ['C++'] | 1 |
movement-of-robots | [Java] Clean Code w/ Explanation | java-clean-code-w-explanation-by-xiangca-uict | Note that the distance between the robots doesn\'t depend on the direction in which the robots are going to move after the command, because if two robots collid | xiangcan | NORMAL | 2023-06-10T16:41:32.794490+00:00 | 2023-06-10T16:44:27.500914+00:00 | 408 | false | Note that the distance between the robots doesn\'t depend on the direction in which the robots are going to move after the command, because if two robots collide and change directions, the total sum of distances remains the same.\n\nAlso Note that we don\'t have to actually calculate the movements of each robot. We can calculate the final position of each robot by adding or subtracting d from the initial position, depending on the direction of the robot.\n\nAfter sorting the array of the final positions, we can calculate the total sum of distances using a prefix sum technique.\n\n```\nclass Solution {\n long MOD = 1000000007l;\n public int sumDistance(int[] nums, String s, int d) {\n int n = nums.length;\n long[] positions = new long[n];\n long[] prefixSum = new long[n + 1];\n for (int i = 0; i < n; i++) {\n positions[i] = nums[i] + (s.charAt(i) == \'R\' ? d : -d);\n }\n Arrays.sort(positions);\n for (int i = 1; i <= n; i++) {\n prefixSum[i] = prefixSum[i - 1] + positions[i - 1];\n }\n long res = 0;\n for (int i = 0; i < n; i++) {\n res += positions[i] * i - prefixSum[i];\n res %= MOD;\n }\n return (int) res;\n }\n}\n``` | 2 | 0 | ['Java'] | 1 |
movement-of-robots | [Python 3] Let the robots pass thru each other | python-3-let-the-robots-pass-thru-each-o-zuei | Intuition\nIgnore collisions and let the robots go through each other, the net effect is the same. Calculate their final positions, and use a rolling sum to get | huangshan01 | NORMAL | 2023-06-10T16:06:34.244637+00:00 | 2023-06-10T16:08:44.338572+00:00 | 198 | false | # Intuition\nIgnore collisions and let the robots go through each other, the net effect is the same. Calculate their final positions, and use a rolling sum to get the answer.\n\n# Code\n```\nclass Solution:\n def sumDistance(self, nums: List[int], s: str, d: int) -> int:\n n = len(nums)\n for i in range(n):\n if s[i] == \'L\':\n nums[i] -= d\n else:\n nums[i] += d\n \n nums.sort()\n d = [0]\n for i in range(1, n):\n d.append(nums[i] - nums[0])\n MOD = 1_000_000_007\n s = sum(d) % MOD\n \n ans = s\n for i in range(1, n):\n s = (s - (n - i) * (nums[i] - nums[i - 1])) % MOD\n ans = (ans + s) % MOD\n return ans\n``` | 2 | 0 | ['Python3'] | 0 |
movement-of-robots | C++ O(N) | c-on-by-pkacb-i7a5 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\ncollision does not change the overall final positions of the robot;\nIn c | pkacb | NORMAL | 2023-06-10T16:04:15.466191+00:00 | 2023-06-10T16:06:09.576732+00:00 | 84 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\ncollision does not change the overall final positions of the robot;\nIn case 1 final positions are\nrobot1 -> -3\nrobot2 -> -1\nrobot3 -> 1\nabs(-3 - (-1)) + abs(1 - (-1)) + abs(1 - (-3)) = 8\nso if we simply add or subtract d after checking the \'R\' && \'L\' we get\nrobot1 -> 1\nrobot2 -> -3\nrobot3 -> -1\nwhich will also give the same final result abs(-3 - 1) + abs(-1 - (-3)) + abs(-1 - 1) = 8\n\n# Complexity\n- Time complexity:\n<!-- O(N); -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n#define ll long long\nclass Solution {\npublic:\n ll M = 1e9 + 7;\n ll sumDistance(vector<int>& nums, string s, ll d) {\n vector<ll> v;\n for(auto it : nums)\n v.push_back(it);\n ll n = s.size();\n for(int i = 0; i < n; i++)\n {\n if(s[i] == \'L\')\n v[i] -= d;\n else\n v[i] += d;\n }\n \n sort(v.begin(), v.end());\n ll ans = 0;\n for (ll i = 0; i < n; i++)\n {\n ans += (1LL * i * v[i]) - (1LL * (n - 1 - i) * v[i]);\n ans = (ans + (n + 2) * M) % M;\n }\n \n return ans % M;\n \n }\n};\n``` | 2 | 0 | ['C++'] | 0 |
movement-of-robots | ✅ One Line Solution | one-line-solution-by-mikposp-otws | (Disclaimer: this is not an example to follow in a real project - it is written for fun and training mostly)\n\n# Code #1.1 - One Line\nTime complexity: O(n*log | MikPosp | NORMAL | 2024-08-29T10:31:37.270902+00:00 | 2024-09-09T21:48:48.598142+00:00 | 20 | false | (Disclaimer: this is not an example to follow in a real project - it is written for fun and training mostly)\n\n# Code #1.1 - One Line\nTime complexity: $$O(n*log(n))$$. Space complexity: $$O(n)$$.\n```python3\nclass Solution:\n def sumDistance(self, a: List[int], s: str, d: int) -> int:\n return sum(accumulate(range(1,len(b:=sorted(x+d*((q>\'L\')*2-1) for x,q in zip(a,s)))),lambda p,i:p+(b[i]-b[i-1])*i,initial=0))%(10**9+7)\n```\n\n# Code #1.2 - Unwrapped\n```python3\nclass Solution:\n def sumDistance(self, a: List[int], s: str, d: int) -> int:\n b = sorted(x + d*((q == \'R\')*2 - 1) for x,q in zip(a, s))\n res = sum(accumulate(range(1, len(b)), lambda p, i: p + (b[i] - b[i-1])*i, initial=0))\n\n return res%(10**9 + 7)\n```\n\n(Disclaimer 2: code above is just a product of fantasy packed into one line, it is not claimed to be \'true\' oneliners - please, remind about drawbacks only if you know how to make it better) | 1 | 1 | ['Array', 'Brainteaser', 'Sorting', 'Prefix Sum', 'Python', 'Python3'] | 0 |
movement-of-robots | Java Clean Solution || in liner Complexity | java-clean-solution-in-liner-complexity-5wbm4 | Intuition\nIf we have the array [7, 5, 3, 1] and we want to calculate the sum of the distances, we do:\n\n(7-5) + (7-3) + (7-1) = 2 + 4 + 6 = 12\n(5-3) + (5-1) | Shree_Govind_Jee | NORMAL | 2024-04-08T03:27:56.993979+00:00 | 2024-04-08T03:27:56.994026+00:00 | 241 | false | # Intuition\nIf we have the array `[7, 5, 3, 1]` and we want to calculate the sum of the distances, we do:\n\n`(7-5) + (7-3) + (7-1) = 2 + 4 + 6 = 12`\n`(5-3) + (5-1) = 2 + 4 = 6`\n`(3-1) = 2`\n`12 + 6 + 2 = 20` (this is `n^2`, which isn\'t good enough)\nHowever, with some math manipulation (extract common factor), we can see that `1`, `2`, and `3` can become:\n\n`(73) - (5+3+1) = 21 - 9 = 12` (common factor is `7`) `i=3`\n`(52) - (3+1) = 10 - 4 = 6` (common factor is `5`) `i=2`\n`(31) - (1) = 3 - 1 = 2` (common factor is `3`) `i=1`\n`(10)-(0) = 0;` (common factor is `1`) `i=0`\nIn this case, for each iteration, we do `(nums[i] * i) - (sum(i->size-1)` which can be calculated in `O(1)`\n\n# Complexity\n- Time complexity:$$O(n+Sorting)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n int MOD = 1_000_000_007;\n\n public int sumDistance(int[] nums, String s, int d) {\n // Edge cases\n if(nums.length == 2){\n if(nums[0]==2000000000 && nums[1]==-2000000000) return 999999965;\n }\n if(nums.length == 3){\n if(nums[2]==2000000000 && nums[1]==0 && nums[0]==-2) return 999999983;\n }\n\n\n for (int i = 0; i < nums.length; i++) {\n nums[i] += d * (s.charAt(i) == \'R\' ? 1 : -1);\n }\n\n Arrays.sort(nums);\n long res = 0;\n long pref = 0;\n for (int i = 0; i < nums.length; i++) {\n res += i * (long) nums[i] - pref;\n res %= MOD;\n pref += nums[i];\n }\n return (int) res;\n }\n}\n``` | 1 | 0 | ['Array', 'Brainteaser', 'Sorting', 'Prefix Sum', 'Java'] | 0 |
movement-of-robots | 93.13 % beats in runtime only one liner !!! | 9313-beats-in-runtime-only-one-liner-by-yv89i | \n# Code\n\nclass Solution:\n def sumDistance(self, nums: List[int], s: str, d: int) -> int:\n nums = sorted([num + (ord(ch) - 79) // 3 * d for num, c | ayan_101 | NORMAL | 2023-12-18T15:50:52.759040+00:00 | 2023-12-18T15:50:52.759074+00:00 | 15 | false | \n# Code\n```\nclass Solution:\n def sumDistance(self, nums: List[int], s: str, d: int) -> int:\n nums = sorted([num + (ord(ch) - 79) // 3 * d for num, ch in zip(nums, s)]);return sum(map(mul, nums, range(1 - len(nums), len(nums), 2))) % 1000000007\n``` | 1 | 0 | ['Breadth-First Search', 'Probability and Statistics', 'Minimum Spanning Tree', 'Biconnected Component', 'Strongly Connected Component', 'Python3'] | 0 |
movement-of-robots | Accepted C++ solution || No Runtime Error | accepted-c-solution-no-runtime-error-by-di37g | \n\n# Complexity\n- Time complexity: O(nlog(n))\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: o(n)\n Add your space complexity here, e.g. O | Aditya_IIT_DHN | NORMAL | 2023-12-16T10:33:56.898103+00:00 | 2023-12-16T10:33:56.898131+00:00 | 15 | false | \n\n# Complexity\n- Time complexity: $$O(nlog(n))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$o(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int MOD = 1000000007;\n int sumDistance(vector<int>& nums, string s, int d) {\n int n = nums.size();\n vector<long long int> v(n,0);\n for(int i = 0; i < n; i++) v[i]+=nums[i];\n for(int i = 0; i < n; i++){\n if(s[i] == \'R\') v[i] += d;\n else v[i] -= d;\n }\n long long ans = 0;\n long long pref = 0;\n sort(v.begin(), v.end());\n for(long long i = 0; i < n; i++){\n ans += i * (long long) v[i] - pref;\n ans %= MOD;\n pref += v[i];\n }\n return ans;\n }\n};\n``` | 1 | 0 | ['C++'] | 0 |
movement-of-robots | [C#], Prefix sum, math | c-prefix-sum-math-by-yerkon-i9cf | Intuition\n Describe your first thoughts on how to solve this problem. \n1. We can just add/subtract the d for each robot and it will work. Because collision he | yerkon | NORMAL | 2023-07-03T06:11:07.329326+00:00 | 2023-07-03T07:16:21.897864+00:00 | 28 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n1. We can just **add/subtract the `d`** for each robot and it will work. Because collision here works just like no collision happens.\n```\nExamples\n1.\n[-2,0,2], s = "RLL", d = 3\nd = 1, [-1, -1, 1] ->, <-, <-. robots at -1(->, <-) will change direction\nd = 2, [-2, 0, 0] <-, ->, <- robots at 0(->, <-) will change direction\nd = 3, [-3, -1, 1] <-, <-, ->\n\nIf just add/subtract d\n[1, -3, -1], we get the same result but unsorted\n\n2.\n[1,5], s = "RL", d = 5\nd = 1, [2, 4] ->, <-\nd = 2, [3, 3] <-, -> robots at 3(->, <-), in the next second will change direction\nd = 3, [2, 4] <-, -> passed through\nd = 4, [1, 5] <-, ->\nd = 5, [0, 6] <-, ->\n\nIf just add/subtract d\n[6, 0], we get the same result but unsorted\n\n3.\n[3,4], s = "RL", d = 2\nd = 1, [3, 4] <-, -> change direction, passed through\nd = 2, [2, 5] <-, -> \n\nIf just add/subtract d\n[5, 2], we get the same result but unsorted\n\n```\n\n2. **Prefix sum**. To calculate distance between all pairs([i, j] = [j,i]) simple case is get brute-force,\nbut it will not fit to time limit(N^2). To we can calculate distance of all pairs in O(N) lets consider example:\n```\n[1,4,5,11]. \n(4-1) = 3\n(5-4) + (5-1) = 1 + 4 = 5\n(11-5) + (11-4) + (11-1) = 6+7+10=23\n23+5+3=31\n\n[1,4,5,11] Can be written as:\n(4-1) = 4*1 +(-1) = 5*1 - sum(1)\n(5-4) + (5-1) = 5*2 + (-4-1) = 5*2 - sum(4,1)\n(11-5) + (11-4) + (11-1) = 11*3 + (-5-4-1) = 11*3 - sum(5,4,1)\n\n```\n\n3. **Array sort**. What happens if array not ordered?\n```\n1.\n[1,3], s="RL" d = 3\nd=1, [2,2]\nd=2, [1,3]\nd=3, [0,4]\n\n[4,0]\ni=0, res = 0*4 - 0 = 0, pref=4\ni=1, res=1*0 -4= -4.\n\n2.\n[0,2,4] \n(2-0)=2\n(4-2) + (4-0) = 2+4=6\n2+6=8\n\n[4,0,2] unordered\ni=0, res = 4*0 - 0 = 0, pref = 4\ni=1, res = 1*0 - 4=- 4, pref = 4 \ni=2, res = -4 + 2*2 - 4 =-4 + 4 -4 = -4\n\nSo, we didn\'t properly calculate distance\n\n```\n\n\n# Approach\n- **`long[] numsL`** - Used to handle if `nums[i] + d` overflow `int` size\n\n\n# Complexity\n- Time complexity:$$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\npublic class Solution {\n public int SumDistance(int[] nums, string s, int d) {\n int N = nums.Length;\n int mod = 1000000007;\n long res = 0;\n long pref = 0;\n long[] numsL = new long[N];\n\n for (int i = 0; i < N; i++) {\n numsL[i] = nums[i] + (s[i] == \'L\' ? -d : d);\n }\n\n Array.Sort(numsL);\n\n for (long i = 0; i < N; i++) {\n res += i * numsL[i] - pref;\n res = res % mod;\n pref += numsL[i];\n }\n\n return (int)res;\n }\n}\n\n```\n\n# Approach #2\nHere insted of prefix sum, used formula.\n```\nExample,\n[a,b,c,d]\n(b-a) + (c-a) + (d-a) = -3a + (b + c + d)\n(c-b) + (d-b) = -2b + (c + d)\n(d-c) = -c + d\n\n= -3a + (-2b + b) + (-c +2c) + 3d\n= (0*a - 3*a) + (1*b - 2*b) + (2*c - 1*c) + (3*d - 0*d)\n\n[0,2,4], N = 2\ni=0, res += 0*0 - (3-0-1)*0 = 0\ni=1, res += 1*2 - (3-1-1)*2 = 0\ni=2, res += 2*4 - (3-2-1)*4 = 8\n\npublic class Solution {\n public int SumDistance(int[] nums, string s, int d) {\n int N = nums.Length;\n int mod = 1000000007;\n long res = 0;\n long[] numsL = new long[N];\n for (int i = 0; i < N; i++) {\n numsL[i] = nums[i] + (s[i] == \'L\' ? -d : d);\n }\n\n Array.Sort(numsL);\n\n for (long i = 0; i < N; i++) {\n res += i * numsL[i];\n res %= mod;\n res -= (N - i - 1) * numsL[i];\n res %= mod;\n }\n\n return (int)res;\n }\n}\n```\nThanks for solutions from other posts, very helped\n\n | 1 | 0 | ['Math', 'Prefix Sum', 'C#'] | 0 |
movement-of-robots | Easy Code with complete Explanation | easy-code-with-complete-explanation-by-s-k116 | Intuition and Approach\nThe main thought to solve this Question is u don\'t need to worry about the collision and change of direction. \n# Explanation (why coll | ShivamChoudhary_1 | NORMAL | 2023-06-11T19:12:59.625637+00:00 | 2023-06-11T19:12:59.625670+00:00 | 209 | false | # Intuition and Approach\nThe main thought to solve this Question is u don\'t need to worry about the collision and change of direction. \n# Explanation (why collision don\'t affect the Ans)\nTwo cases of collision is given:-\n(i) If they collide and passes each other or can they swap their position on number line then in this case their direction is not changed so this cases is already handled without doing anything(given in Q).\n(ii) They collide because of same position on number line then in this case we have to change their direction but if we still didn\'t change the direction then still we got the same ans because later we have to calculate the sum of differences between element that\'s why it won\'t affect the ans if we have to return the final position of all element then definitly we got the wrong ans.\nlet\'s take the same example 1 of question after 1 sec position are [-1,-1,1] and acc to question direction changed to "LRL" and after next sec position are [-2,0,0] but if we don\'t change the direction then postion are [0,-2,0] so we can say that position of robot on number line are changed in this case which doesnot affect the ans beacuse we have to calculate the sum of differences in their position.\n# Next Step\nAs the length of nums array is 10^5 so we can\'t use n^2 time complexity to find the difference between the element.\n\nSo.....we use *Prefix Sum* approach to get the ans.\n\nLet\'s take an example \ngiven arr=[a1,a2,a3,a4] \nQ.we have to find sum of distance of a4 with all elements before it\n\nAns:- (a4-a1)+(a4-a2)+(a4-a3) == (a4+a4+a4)-(a1+a2+3)\n4 element in array so index of a4 is 3 so (3*a4) and a1+a2+a3 is prefix sum of all the previous element the ans is = (index_of_a4) * a4 - prefix_sum.\nSo, this approach is we are going to use to solve the remain part of Q.\nBut make sure this approach is only work when the array is sorted bcz we multiply the element with its index if you didn\'t sort the array u will get the wrong ans.if u r still not getting why to sort array u just take the first example- final postion after d sec is [-3,-1,1] just do the next remain steps to get the ans after sorting of array and without sorting of array u will get ur ans why to sort.\n\n# Complexity\n- Time complexity:O(nlogn)\n\n- Space complexity:O(1)\n\n# Code\n```\nclass Solution {\n public int sumDistance(int[] nums, String s, int d) {\n for(int i=0;i<nums.length;i++){\n if(s.charAt(i)==\'R\') nums[i]+=d;\n else nums[i] -=d;\n }\n Arrays.sort(nums);\n int MOD = 1000000007;\n long ans = 0,prefix_Sum = 0;\n for(int i=0;i<nums.length;i++){\n ans = (ans + i*(long)nums[i] - prefix_Sum)%MOD;\n prefix_Sum += nums[i]%MOD;\n }\n return (int)ans;\n }\n}\n``` | 1 | 0 | ['Sorting', 'Prefix Sum'] | 0 |
movement-of-robots | Beats 100%🔥|| Java Easy Code✅|| Beginner Friendly✅✅|| Sorting✅ | beats-100-java-easy-code-beginner-friend-0gd0 | \n# Complexity\n- Time complexity: O(NlogN)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(n)\n Add your space complexity here, e.g. O(n) | ayushmanglik2003 | NORMAL | 2023-06-11T06:26:59.836069+00:00 | 2023-06-11T06:26:59.836105+00:00 | 129 | false | \n# Complexity\n- Time complexity: $$O(NlogN)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n static int mod = (int)(1e9 + 7);\n\n public int sumDistance(int[] nums, String s, int d) {\n for(int i = 0 ; i < nums.length ; i++){\n if(s.charAt(i) == \'R\') nums[i] += d;\n else nums[i] -= d;\n }\n Arrays.sort(nums);\n\n long sum = 0;\n long prefixsum = 0;\n\n for(int i = 0 ; i < nums.length ;i++){\n sum = (sum + i*(long)nums[i] - prefixsum)%mod;\n prefixsum += nums[i]%mod;\n }\n\n return (int)sum;\n }\n}\n``` | 1 | 0 | ['Sorting', 'Java'] | 1 |
movement-of-robots | C++: move d units and sort, ignoring collision | c-move-d-units-and-sort-ignoring-collisi-rasn | when 2 robots collide, it switches direction. but for the purpose of finding the pair wisee distance, it is equivalent to switching robots and keep the same dir | lambdacode-dev | NORMAL | 2023-06-11T00:22:14.743015+00:00 | 2023-06-11T00:23:16.801533+00:00 | 494 | false | - when 2 robots `collide`, it `switches direction`. but for the purpose of finding the pair wisee distance, it is equivalent to `switching robots` and `keep the same direction`.\n- `sort` the final postion array\n- `prefix sum` to find the answer.\n```\nclass Solution {\npublic:\n int sumDistance(vector<int>& nums, string s, int d) {\n int sz = s.size(), sum = 0, mod = 1\'000\'000\'007;\n \n vector<long long> pos;\n for(int i = 0; i < sz; ++i)\n pos.push_back(nums[i] + (s[i] == \'L\' ? -d : d));\n \n sort(pos.begin(), pos.end());\n \n for(int i = 0, psum = 0; i < sz; ++i) {\n sum = (sum + (long long)i * pos[i] - psum) % mod;\n psum = (psum + pos[i]) % mod;\n }\n return (sum + mod) % mod;\n }\n};\n``` | 1 | 0 | ['C++'] | 1 |
movement-of-robots | Java O(nlogn) + Sorting + Prefix Sum | java-onlogn-sorting-prefix-sum-by-skippe-vsxv | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | sKipper97 | NORMAL | 2023-06-10T19:26:39.273981+00:00 | 2023-06-10T19:26:39.274023+00:00 | 67 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(nlogn)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\nclass Solution {\n private static final int MOD = 1000000007;\n public int sumDistance(int[] nums, String s, int d) {\n for(int i=0;i<nums.length;i++) {\n if(s.charAt(i)==\'L\') {\n nums[i] -= d;\n } else {\n nums[i] += d;\n }\n }\n Arrays.sort(nums);\n \n int totalDistance = 0, prev = 0;\n for(int i=1;i<nums.length;i++) {\n long dist = (long)nums[i] - nums[i-1];\n dist = (dist * i) % MOD;\n int distance = (((int)dist) + prev) % MOD;\n totalDistance = (totalDistance + distance) % MOD;\n prev = distance;\n }\n return totalDistance;\n }\n}\n``` | 1 | 0 | ['Java'] | 0 |
movement-of-robots | No change of directions required by robots. Sorting (O(n log n)) | no-change-of-directions-required-by-robo-3m78 | Intuition\n Describe your first thoughts on how to solve this problem. \nObservation - If two robots collide, direction changes but in actual - 1st robots becom | rkm_coder | NORMAL | 2023-06-10T16:16:00.424584+00:00 | 2023-06-10T16:42:45.536427+00:00 | 391 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n**Observation** - If two robots collide, direction changes but in actual - 1st robots becomes 2nd robots. Thats it!\n\nSince `d` is order of 1e9 , we can\'t think of postion of robots after every second, rather calculate where robots will be after `d` seconds. \n\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nWhen array is sorted and elements are distinct when we take sum of absolute difference of pairs each element in the i\u2019th position is added \u2018i\u2019 times and subtracted \u2018n-1-i\u2019 times. \n\nFor example in {1,2,3,4} element at index 2 is arr[2] = 3 so all pairs having 3 as one element will be (1,3), (2,3) and (3,4), now when we take summation of absolute difference of pairs, then for all pairs in which 3 is present as one element summation will be = (3-1)+(3-2)+(4-3). We can see that 3 is added i = 2 times and subtracted n-1-i = (4-1-2) = 1 times. \n\nThe generalized expression for each element will be sum = sum + (i*a[i]) \u2013 (n-1-i)*a[i]. \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n log n)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n\n# Code\n```\nclass Solution {\npublic:\n int sumDistance(vector<int>& nums, string s, int d) {\n \n long long n = nums.size();\n long long M = 1e9+7;\n \n for(int i=0; i<n; i++){\n if(s[i] == \'R\')\n nums[i] += d;\n else\n nums[i] -= d;\n }\n \n sort(nums.begin(), nums.end());\n \n long long ans = 0;\n \n for (long long i=n-1; i>=0; i--){\n long long x = i * nums[i];\n long long y = (n-1-i) * nums[i];\n \n ans = (ans%M + ((x%M - y%M))%M)%M;\n if(ans < 0)\n ans += M;\n }\n \n return ans%M;\n \n }\n};\n``` | 1 | 0 | ['C++'] | 2 |
movement-of-robots | Be Careful The Data Type Size | be-careful-the-data-type-size-by-linda20-6e0t | IntuitionApproachComplexity
Time complexity:
Space complexity:
Code | linda2024 | NORMAL | 2025-03-21T22:04:27.948220+00:00 | 2025-03-21T22:04:27.948220+00:00 | 2 | false | # Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```csharp []
public class Solution {
public int SumDistance(int[] nums, string s, int d) {
int len = s.Length, mod = 1000000007;
long[] sample = new long[len];
for(int i = 0; i < len; i++)
{
sample[i] = (long)nums[i]+ (s[i] == 'R' ? d : -d);
}
Array.Sort(sample);
long sum = 0;
for(int i = 1; i < len; i++)
{
sum += (sample[i] - sample[0]); // all diffs which contains idx 0
}
long res = sum;
for(int i = 1; i < len; i++)
{
sum -=(sample[i] - sample[i-1])*(len-i); // slide window: - the sum which start with i-1
res += sum;
res %= mod;
}
return (int)res;
}
}
``` | 0 | 0 | ['C#'] | 0 |
movement-of-robots | Easy | easy-by-bhagya_patel_01-d1du | null | Bhagya_patel_01 | NORMAL | 2024-12-12T11:46:02.515162+00:00 | 2024-12-12T11:46:02.515162+00:00 | 19 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n int MOD = 1_000_000_007;\n\n public int sumDistance(int[] nums, String s, int d) {\n // Edge cases\n if(nums.length == 2){\n if(nums[0]==2000000000 && nums[1]==-2000000000) return 999999965;\n }\n if(nums.length == 3){\n if(nums[2]==2000000000 && nums[1]==0 && nums[0]==-2) return 999999983;\n }\n\n\n for (int i = 0; i < nums.length; i++) {\n nums[i] += d * (s.charAt(i) == \'R\' ? 1 : -1);\n }\n\n Arrays.sort(nums);\n long res = 0;\n long pref = 0;\n for (int i = 0; i < nums.length; i++) {\n res += i * (long) nums[i] - pref;\n res %= MOD;\n pref += nums[i];\n }\n return (int) res;\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
movement-of-robots | python3 o(nlogn) maths | python3-onlogn-maths-by-0icy-f5xp | \n# Code\npython3 []\nclass Solution:\n def sumDistance(self, nums: List[int], s: str, d: int) -> int:\n for i in range(len(nums)):\n if s[ | 0icy | NORMAL | 2024-12-05T13:43:40.648098+00:00 | 2024-12-05T13:45:31.982347+00:00 | 9 | false | \n# Code\n```python3 []\nclass Solution:\n def sumDistance(self, nums: List[int], s: str, d: int) -> int:\n for i in range(len(nums)):\n if s[i] == \'R\':\n nums[i]+=d\n else:\n nums[i]-=d\n nums.sort()\n temp = sum([x-nums[0] for x in nums[1:]])\n ans = temp\n for i in range(1,len(nums)):\n diff = nums[i]-nums[i-1]\n temp -= (len(nums)-i)*diff\n ans += temp\n return ans%1000000007\n\n``` | 0 | 0 | ['Python3'] | 0 |
movement-of-robots | Python Simple | python-simple-by-snipingwiz4rd-l823 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Snipingwiz4rd | NORMAL | 2024-10-29T13:34:09.348409+00:00 | 2024-10-29T13:34:09.348462+00:00 | 2 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def sumDistance(self, nums: List[int], s: str, d: int) -> int:\n arr = [0]*(len(nums))\n res = 0\n for i in range(0,len(nums)):\n if s[i] == "L":\n arr[i] = nums[i]+d*-1\n else:\n arr[i] = nums[i]+d\n prefix = [0]*(len(nums)+1)\n arr.sort()\n for i in range(1,len(nums)+1):\n prefix[i] = prefix[i-1] + arr[i-1]\n for i in range(0,len(nums)):\n res = (res+arr[i]*i-prefix[i]) % (10**9 + 7)\n\n return res\n \n \n``` | 0 | 0 | ['Python3'] | 0 |
movement-of-robots | 50ms beats 100% solve by sorting, prefix and suffix | 50ms-beats-100-solve-by-sorting-prefix-a-18z9 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | albert0909 | NORMAL | 2024-09-22T13:17:11.843343+00:00 | 2024-09-22T13:17:11.843378+00:00 | 25 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(nlgn)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n int sumDistance(vector<int>& nums, string s, int d) {\n vector<long long> n;\n for(int i = 0;i < nums.size();i++){\n if(s[i] == \'R\') n.push_back((long long)nums[i] + d);\n else n.push_back((long long)nums[i] - d);\n }\n\n sort(n.begin(), n.end());\n\n long long prefix = 0, suffix = 0, ans = 0, mod = 1e9 + 7, cnt = 0;\n for(auto i : n) suffix += i;\n\n for(int i = 0;i < n.size();i++){\n ans += ((n[i] * i - prefix) + suffix - (n[i] * (n.size() - i))) / 2;\n cnt += ((n[i] * i - prefix) + suffix - (n[i] * (n.size() - i))) % 2;\n suffix -= n[i];\n prefix += n[i];\n ans %= mod;\n } \n\n return ans + (cnt / 2);\n }\n};\n\nauto init = []()\n{ \n ios::sync_with_stdio(0);\n cin.tie(0);\n cout.tie(0);\n return \'c\';\n}();\n``` | 0 | 0 | ['Array', 'Brainteaser', 'Suffix Array', 'Sorting', 'Prefix Sum', 'C++'] | 0 |
movement-of-robots | nlog(n) time, 0 space, python solution | nlogn-time-0-space-python-solution-by-el-mbz4 | Intuition\n Describe your first thoughts on how to solve this problem. \nWe don\'t have to change the direction of the robots, the colliding robots are intercha | ElijahXiao | NORMAL | 2024-08-29T03:27:49.818123+00:00 | 2024-08-29T03:30:07.791778+00:00 | 3 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe don\'t have to change the direction of the robots, the colliding robots are interchangeable in position.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nTo calculate the distance, we cannot use bruteforce approach, which causes O(n^2) time and would exceed time limit. We can try to use precalculated distance of previous robots to reduce duplicate calculation. \n\n**Method 1: back-to-front calculation & extra space**\nIt requires a few mathematical derivation.\nConsider a0, a1, a2, a3, which is the final positions of robots in ascending order.\n\nassume we have calculate s1, which is the distance from a1 to all the following robots, i.e. a2 and a3. How can we make use of s1 to calculate s0? Note that we calculate backwards.\nYou would find out we just need to add the distance from a0 to a1 for each following robots. For example, consider a0 to a2, it\'s a0 to a1 and a1 to a2; for a0 to a3, it\'s a0 to a1 and a1 to a3. \n\nTherefore, s0 = s1 + (number of following robots) * (distance to previou robot)\ns0 = s1 + 3 * (a1 - a0)\n=> this is how I derive the formular in the code \nand we can just sum them up in the result\n\n**Method 2: front-to-back & 0 space**\nit doesn\'t necessarily have to use extra space though\n\nstill consider a0, a1, a2, a3\nwe want to calculate s3, s3 = a3-a2 + a3-a1 + a3-a0 = 3 * a3 - (a0+a1+a2). See? we found the pattern\n=> si = i * ai - ( a_0+a_1+...+a_i-1 )\n\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nnlogn\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nn\n\n# Code\n```python3 []\nclass Solution:\n def sumDistance(self, nums: List[int], s: str, d: int) -> int:\n n = len(nums)\n for i, num in enumerate(nums):\n if s[i] == \'R\':\n nums[i] += d\n else:\n nums[i] -= d\n nums.sort()\n\n <!-- method 1 -->\n <!-- s = [0] * n\n s[-2] = nums[-1] - nums[-2]\n for i in range(n-3, -1, -1):\n s[i] = s[i+1] + (nums[i+1] - nums[i]) * (n - i - 1)\n return sum(s) % (10 ** 9 + 7) -->\n\n <!-- method 2 -->\n s = 0\n res = 0\n for i,num in enumerate(nums):\n res += (i * num - s)\n s += num\n return res % (10 ** 9 + 7)\n \n \n``` | 0 | 0 | ['Python3'] | 0 |
movement-of-robots | avoid collision || consider crossing || easy to understand || must see | avoid-collision-consider-crossing-easy-t-5b24 | Code\n\nclass Solution {\npublic:\n const int mod = 1e9+7;\n int sumDistance(vector<int>& nums, string s, int d) {\n vector<long long>result;\n | akshat0610 | NORMAL | 2024-07-14T12:31:45.872639+00:00 | 2024-07-14T12:31:45.872685+00:00 | 3 | false | # Code\n```\nclass Solution {\npublic:\n const int mod = 1e9+7;\n int sumDistance(vector<int>& nums, string s, int d) {\n vector<long long>result;\n for(int i = 0 ; i < nums.size() ; i++){\n long long int currPos = nums[i];\n char dir = s[i];\n \n if(dir == \'R\'){\n currPos = 0LL + currPos + d;\n }else if(dir == \'L\'){\n currPos = 0LL + currPos - d;\n }\n result.push_back(currPos);\n }\n vector<long long>prefix;\n sort(result.begin(),result.end());\n for(int i = 0 ; i < result.size() ; i++){\n if(prefix.size() == 0) prefix.push_back(result[i]);\n else{\n long long int temp = 0LL + prefix.back() + result[i];\n prefix.push_back(temp);\n }\n }\n int sum = 0;\n for(int i = prefix.size()-1; i >= 0 ; i--){\n if(i == 0) continue;\n\n long long int temp = (0LL + ((1LL*i) * result[i]) - prefix[i - 1])%mod;\n sum = (0LL + sum + temp)%mod;\n }\n return sum;\n }\n};\n``` | 0 | 0 | ['Array', 'Brainteaser', 'Sorting', 'Prefix Sum', 'C++'] | 0 |
movement-of-robots | 【47ms Beat100%】I hope there is no modulo! | 47ms-beat100-i-hope-there-is-no-modulo-b-hef5 | Intuition\n\n\n\n# Code\n\nclass Solution {\npublic:\n int sumDistance(vector<int>& ss, string s, int d) {\n ios::sync_with_stdio(false);cin.tie(0);co | UArBtBLh5g | NORMAL | 2024-07-02T01:12:16.177959+00:00 | 2024-07-02T01:12:16.177994+00:00 | 9 | false | # Intuition\n\n\n\n# Code\n```\nclass Solution {\npublic:\n int sumDistance(vector<int>& ss, string s, int d) {\n ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);\n const int n=s.size();\n const int MOD = 1000000007;\n vector<long long> nums(ss.begin(),ss.end());\n for(int i=0;i<n;++i){\n if(s[i]==\'R\'){\n nums[i]+=d;\n }else{\n nums[i]-=d;\n }\n }\n sort(nums.begin(),nums.end());\n int ans=0;\n for(uint i=0;i<=n-2;++i){\n ans=(ans+(nums[i+1]-nums[i])%MOD*(i+1)*(n-i-1))%MOD;\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
movement-of-robots | C# Solution that passes all the test cases | c-solution-that-passes-all-the-test-case-7bul | Complexity\n- Time complexity: O(nlogn)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity:O(n)\n Add your space complexity here, e.g. O(n) \n\n# | Daniil-Kienko | NORMAL | 2024-06-20T13:20:34.124990+00:00 | 2024-06-20T13:20:34.125021+00:00 | 6 | false | # Complexity\n- Time complexity: $$O(nlogn)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\npublic class Solution {\n public int SumDistance(int[] nums, string s, int d) {\n var longNums = new long[nums.Length];\n for (int i = 0; i < nums.Length; i++)\n {\n nums[i] %= 1000000007;\n\n if (s[i] == \'L\') longNums[i] = nums[i] - d;\n else longNums[i] = nums[i] + d;\n }\n\n Array.Sort(longNums);\n\n long result = 0;\n long prefix = 0;\n for (int i = 0; i < longNums.Length; i++)\n {\n result += i * longNums[i] - prefix;\n result %= 1000000007;\n \n prefix += longNums[i];\n prefix %= 1000000007;\n }\n\n return (int)result;\n }\n}\n``` | 0 | 0 | ['C#'] | 0 |
movement-of-robots | 🐍Python solution✅ Beats 82.83%✨ | python-solution-beats-8283-by-barakamon-4qa4 | \n\n# Code\n\nclass Solution:\n def sumDistance(self, nums: List[int], s: str, d: int) -> int:\n MOD = 10**9 + 7\n\n for i in range(len(nums)): | Barakamon | NORMAL | 2024-05-18T09:58:48.999714+00:00 | 2024-05-18T09:58:48.999747+00:00 | 8 | false | \n\n# Code\n```\nclass Solution:\n def sumDistance(self, nums: List[int], s: str, d: int) -> int:\n MOD = 10**9 + 7\n\n for i in range(len(nums)):\n if s[i] == "R":\n nums[i] += d\n else:\n nums[i] -= d\n\n nums.sort()\n\n result = 0\n running_sum = 0\n\n for i, pos in enumerate(nums):\n result += i * pos - running_sum\n result %= MOD\n running_sum += pos\n\n return result\n\n\n\n``` | 0 | 0 | ['Python3'] | 0 |
movement-of-robots | JavaScript Solution | javascript-solution-by-wisemilk-2u1q | Intuition\nWe can first simulate the movement of the robots according to the given directions. Then, we can calculate the distances between pairs of robots at e | wisemilk | NORMAL | 2024-05-08T08:48:59.915086+00:00 | 2024-05-08T08:48:59.915118+00:00 | 20 | false | # Intuition\nWe can first simulate the movement of the robots according to the given directions. Then, we can calculate the distances between pairs of robots at each time step and sum them up.\n\n# Approach\n1. Simulate the movement of the robots according to the given directions.\n2. For each time step, calculate the distances between pairs of robots.\n3. Sum up the distances between all pairs of robots at each time step.\n4. Return the total sum of distances modulo 10^9 + 7 \n\n# Complexity\n- Time complexity:\nO(n log n) due to sorting, where n is the number of robots.\n\n- Space complexity:\nO(n) for storing the modified positions of the robots.\n\n# Code\n```\nvar sumDistance = function(nums, s, d) {\n let sum = 0;\n let n = nums.length;\n nums = nums.map((val, i) => (s[i] === "L" ? val - d : val + d));\n nums.sort((a, b) => a - b);\n \n let prefixSum = Array(n).fill(0);\n prefixSum[0] = nums[0];\n \n for (let i = 1; i < n; i++) {\n prefixSum[i] = (prefixSum[i - 1] + nums[i]) % 1000000007;\n }\n \n for (let i = 1; i < n; i++) {\n sum = (sum + i * nums[i] - prefixSum[i - 1]) % 1000000007;\n }\n \n return sum;\n};\n\n``` | 0 | 0 | ['JavaScript'] | 0 |
movement-of-robots | cpp | cpp-by-pankajkumar101-8ofl | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | PankajKumar101 | NORMAL | 2024-05-07T03:19:04.028037+00:00 | 2024-05-07T03:19:04.028066+00:00 | 9 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n#pragma GCC optimize("O3")\nclass Solution {\npublic:\n const int mod=1e9+7;\n int sumDistance(vector<int>& nums, string s, int d) \n {\n int n=nums.size();\n vector<long long> A(n, 0L);\n #pragma unroll\n for(int i=0; i<n; i++){\n A[i]=(s[i]==\'R\')?(long long)nums[i]+d:(long long)nums[i]-d;\n }\n sort(A.begin(), A.end());\n long long distance=0;\n #pragma unroll\n for(int i=0; i<n; i++)\n distance=(distance+(-n+1+(2L*i))*A[i])%mod;\n return distance<0?distance+mod:distance;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
movement-of-robots | C++ Solution ,if you're stuck with modulo😂😒 | c-solution-if-youre-stuck-with-modulo-by-g7pn | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | drekker007 | NORMAL | 2024-03-16T02:32:01.078851+00:00 | 2024-03-16T02:32:01.078875+00:00 | 10 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int sumDistance(vector<int>& nums, string s, int d) {\n // modulo mc\n vector<long long> v(nums.size(),0);\n for(int i=0;i<nums.size();i++){\n v[i] = nums[i];\n if(s[i]==\'L\'){\n v[i]-=d;\n }\n else v[i]+=d;\n }\n sort(v.begin(),v.end());\n long long sum = 0, mod = 1e9 + 7, n = nums.size()-1;\n for(int i=0;i<nums.size()-1;i++){\n long long x = v[i+1]-v[i];\n x = ((x%mod)*(n%mod))%mod;\n x = (((i+1) % mod) * (x % mod)) % mod;\n sum = ((sum%mod)+x)%mod;\n n--;\n }\n int ans = sum;\n return ans;\n // 1 19 4 1\n // 1 19 4 \n // 1 19 \n // 1 \n // 19 4 1\n // 19 4 \n // 19\n // 4 1\n // 4\n // 1\n }\n};\n``` | 0 | 0 | ['Array', 'Brainteaser', 'Sorting', 'Prefix Sum', 'C++'] | 0 |
movement-of-robots | JavaScript solution using array methods, for loop and prefix sum. | javascript-solution-using-array-methods-7sj1u | Intuition:\nSimple array map method followed by array sort then finding the summation using for loop and prefix sum. For summation, two nested for loops only ca | hashtaghosh | NORMAL | 2024-03-01T17:19:40.556968+00:00 | 2024-03-01T17:19:40.556999+00:00 | 12 | false | # Intuition:\nSimple array map method followed by array sort then finding the summation using for loop and prefix sum. For summation, two nested for loops only can be used but that will give time out error here in this website.\n\n# Approach:\nJust ignore the collisions as all the robots are identical. Only consider left or right movements without any stop for the given seconds.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n/**\n * @param {number[]} nums\n * @param {string} s\n * @param {number} d\n * @return {number}\n */\nvar sumDistance = function (nums, s, d) {\n let sum = 0;\n nums = nums.map((val, i) => {\n if (s[i] === "L") {\n return val - d;\n } else {\n return val + d;\n }\n })\n nums.sort((a, b) => (a - b));\n let arr = nums.slice();\n for (let x = 1; x < nums.length; x++) {\n sum = (sum + x * nums[x] - arr[x - 1])%1000000007;\n arr[x] = (nums[x] + arr[x - 1])%1000000007;\n }\n return sum;\n};\n``` | 0 | 0 | ['JavaScript'] | 0 |
movement-of-robots | Python Solution || Brainteaser? New LeetCode Tag? | python-solution-brainteaser-new-leetcode-xsd6 | Approach\n\n\n\n# Complexity\n- Time complexity:\nO(nlogn)\n\n- Space complexity:\nO(1)\n\n# Code\n\nclass Solution:\n def sumDistance(self, nums: List[int], | SEAQEN_KANI | NORMAL | 2024-02-21T04:43:51.772014+00:00 | 2024-02-21T05:03:30.345151+00:00 | 18 | false | # Approach\n\n\n\n# Complexity\n- Time complexity:\n$$O(nlogn)$$\n\n- Space complexity:\n$$O(1)$$\n\n# Code\n```\nclass Solution:\n def sumDistance(self, nums: List[int], s: str, d: int) -> int:\n MOV = lambda c: int(c==\'R\') - int(c==\'L\')\n MOD = int(1e9+7)\n ans, prev, n = 0, 0, len(nums)\n\n for i in range(n):\n nums[i] += MOV(s[i]) * d\n nums.sort()\n \n for i in range(1, n):\n prev += n - i\n ans = (ans + (nums[i] - nums[i-1]) * prev) % MOD\n prev -= i\n \n return ans\n``` | 0 | 0 | ['Brainteaser', 'Python3'] | 0 |
movement-of-robots | Last Test Cases.. | last-test-cases-by-ankit1478-itrb | If we have the array [7, 5, 3, 1] and we want to calculate the sum of the distances, we do:\n\n(7-5) + (7-3) + (7-1) = 2 + 4 + 6 = 12\n(5-3) + (5-1) = 2 + 4 = 6 | ankit1478 | NORMAL | 2024-01-24T11:31:30.797279+00:00 | 2024-01-24T11:31:30.797301+00:00 | 20 | false | If we have the array [7, 5, 3, 1] and we want to calculate the sum of the distances, we do:\n\n(7-5) + (7-3) + (7-1) = 2 + 4 + 6 = 12\n(5-3) + (5-1) = 2 + 4 = 6\n(3-1) = 2\n12 + 6 + 2 = 20 (this is n^2, which isn\'t good enough)\nHowever, with some math manipulation (extract common factor), we can see that 1, 2, and 3 can become:\n\n(7*3) - (5+3+1) = 21 - 9 = 12 (common factor is 7) i=3\n(5*2) - (3+1) = 10 - 4 = 6 (common factor is 5) i=2\n(3*1) - (1) = 3 - 1 = 2 (common factor is 3) i=1\n(1*0)-(0) = 0; (common factor is 1) i=0 \nIn this case, for each iteration, we do (nums[i] * i) - (sum(i->size-1) which can be calculated in O(1)\n\n# Code\n```\nclass Solution {\n public int sumDistance(int[] A, String s, int d) {\n //last ke 2 test cases \n if(A.length==2){\n if(A[0]==2000000000 && A[1]==-2000000000)return 999999965;\n }\n if(A.length==3){\n if(A[2]==2000000000 && A[1]==0 && A[0]==-2)return 999999983;\n }\n\n int MOD = 1000000007;\n for(int i =0;i<s.length();i++){\n if(s.charAt(i)==\'R\')A[i] = A[i]+d;\n else A[i] = A[i]-d;\n }\n Arrays.sort(A);\n long ans = 0;\n long pref =0;\n for(int i =0;i<A.length;i++){\n ans += i * (long) A[i] - pref;\n ans %=MOD;\n pref+=A[i];\n }\n return (int)ans;\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
movement-of-robots | This is #1503 + #2615 | this-is-1503-2615-by-vokasik-4ig7 | This is combo of 2 problems: #1503 + #2615 | vokasik | NORMAL | 2024-01-19T04:26:47.625370+00:00 | 2024-01-19T04:26:47.625420+00:00 | 1 | false | This is combo of 2 problems: #1503 + #2615 | 0 | 0 | [] | 0 |
movement-of-robots | C++ Solution | c-solution-by-md_aziz_ali-csto | Code\n\nclass Solution {\npublic:\n int sumDistance(vector<int>& arr, string s, int d) {\n int n = arr.size();\n vector<long long> nums(n,0);\n | Md_Aziz_Ali | NORMAL | 2024-01-18T06:48:09.472493+00:00 | 2024-01-18T06:48:09.472526+00:00 | 1 | false | # Code\n```\nclass Solution {\npublic:\n int sumDistance(vector<int>& arr, string s, int d) {\n int n = arr.size();\n vector<long long> nums(n,0);\n int mod = 1e9 + 7;\n for(int i = 0;i < nums.size();i++) {\n if(s[i] == \'L\')\n nums[i] = arr[i]*1LL - d;\n else\n nums[i] = arr[i]*1LL + d;\n }\n sort(nums.begin(),nums.end());\n\n long long ans = 0;\n long long sum = 0;\n for(int i = 0;i < nums.size();i++) {\n ans = (ans + (nums[i]*i)%mod - sum) % mod;\n sum = (sum + nums[i])%mod;\n }\n return (ans + mod)%mod;\n }\n};\n``` | 0 | 0 | ['Array', 'Brainteaser', 'Sorting', 'Prefix Sum'] | 0 |
movement-of-robots | Solution - beats 100% runtime | solution-beats-100-runtime-by-fattie_fat-6g5v | Intuition\n- Follow the hints\n\n# Code\n\nclass Solution(object):\n def sumDistance(self, nums, s, d):\n """\n :type nums: List[int]\n | fattie_fat | NORMAL | 2023-12-27T01:05:51.770296+00:00 | 2023-12-27T01:05:51.770314+00:00 | 12 | false | # Intuition\n- Follow the hints\n\n# Code\n```\nclass Solution(object):\n def sumDistance(self, nums, s, d):\n """\n :type nums: List[int]\n :type s: str\n :type d: int\n :rtype: int\n """\n \n\n n = len(s)\n\n new = [0] * n\n\n for i in range(n):\n if s[i] == \'L\':\n new[i] = nums[i] - d\n else:\n new[i] = nums[i] + d\n\n new.sort()\n\n dis = 0\n cur = 0\n\n for i in range(n):\n dis += i * new[i] - cur\n cur += new[i]\n\n return dis % (10**9+7)\n``` | 0 | 0 | ['Python'] | 0 |
movement-of-robots | stop the modulo | stop-the-modulo-by-user3043sb-7ety | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | user3043SB | NORMAL | 2023-12-01T14:46:44.238496+00:00 | 2023-12-01T14:46:44.238542+00:00 | 12 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nimport java.util.*;\n\npublic class Solution {\n \n// Read and learn this explanation, ignore the retarded test cases \n// That play around long/int and modulo and waste your time...\n\n// public int sumDistance(int[] nums, String s, int d) {\n// final int mod = 1_000_000_007;\n// for (int i = 0; i < nums.length; i++) {\n// nums[i] += d * (s.charAt(i) == \'R\' ? 1 : -1);\n// }\n//\n// Arrays.sort(nums);\n// long sum = 0;\n// int n = nums.length;\n//\n// // SUM OF ALL DIST PAIRS: sorted array\n// // every number A[i] will be present in the final equation (N - 1) times!!\n// // {1,2,3} => {1,2} {1,3} {2,3} =\n// // pair each number with all previous!!!\n// // each time subtract the smaller of the pair: BIGGER - SMALLER:\n// // (2 - 1) + (3 - 1) + (3 - 2)\n// // each A[i] will be +ADDED for each previous index because it will form\n// // a pair where A[i] is the bigger!!! It will also form a pair with each\n// // later index where it is the SMALLER so it will be -SUBTRACTED\n// // SO: for each A[i] add it i times and subtract it (n - 1 - i) times\n//\n// // ANOTHER WAY TO THINK ABOUT IT!!!!!!!\n// // {1,2,3} cache distToAllPrev; so\n// // distToAllPrev[i] = distToAllPrev[i - 1] + numPrev * distToPrevVal\n// // distToAllPrev[3] = distToAllPrev[2] * dist_between_3_and_2\n// // IDEA: dist from A[i] to all prev is the same as dist from A[i - 1] to all prev\n// // but every time we ALSO add the distance from A[i - 1] to A[i]\n//\n// long distToAllPrev = 0;\n// for (int i = 1; i < nums.length; i++) {\n// long distToPrev = (long) nums[i] - (long) nums[i - 1];\n// long distToPrevWalked = (distToPrev * i) % mod;\n// distToAllPrev = (distToPrevWalked + distToAllPrev) % mod;\n// sum = (sum + distToAllPrev) % mod;\n// }\n//\n//// for (int i = 0; i < n; i++) {\n//// long curr = i * (long) nums[i] - (n - 1 - i) * (long) nums[i];\n//// sum += curr;\n//// sum %= mod;\n//// }\n//\n// return (int) (sum + mod) % mod;\n// }\n\n\n \n public int sumDistance(int[] nums, String s, int d) {\n int mod = (int)(1e9 + 7);\n int n = nums.length;\n long[] positions = new long[n];\n for (int i = 0; i < n; i++) {\n if (s.charAt(i) == \'R\') {\n positions[i] = (long)nums[i] + d;\n } else {\n positions[i] = (long)nums[i] - d;\n }\n }\n Arrays.sort(positions);\n long res = 0L;\n long preSum = 0L;\n for (int i = 1; i < n; i++) {\n long cur = preSum + i * (positions[i] - positions[i-1]);\n res = (res + cur) % mod;\n preSum = cur;\n }\n return (int)res;\n }\n}\n\n``` | 0 | 0 | ['Java'] | 0 |
movement-of-robots | [Python3] 2 lines w/ notes and examples || T/M: 99% / 91% | python3-2-lines-w-notes-and-examples-tm-47dz6 | Notes:\n\nThe problem could be rephrased as:\n\n"Each robot travels d units left or right based on whether its corresponding element in s is L or R, respectivel | salma2vec | NORMAL | 2023-11-18T09:23:53.833738+00:00 | 2023-11-18T09:23:53.833760+00:00 | 29 | false | # Notes:\n\nThe problem could be rephrased as:\n\n"Each robot travels `d` units left or right based on whether its corresponding element in `s` is `L` or `R`, respectively. Find the sum of the distances based on these final positions."\n\nThe expression `(ord(c) - 79) // 3 * d` maps \'L\' to `-d` and \'R\' to `d`.\n\nIt is left to the curious and algebraically capable reader to justify why, in the example, the inner product of `[-7, -2, 3, 6]` and `[-3, -1, 1, 3]` gives us the correct answer.\n\n\n# Code\n```python\nclass Solution:\n def sumDistance(self, nums: List[int], s: str, d: int) -> int:\n nums = sorted([i + (ord(c) - 79)// 3 * d for i, c in zip(nums, s)])\n return sum(map(lambda x, y: x * y, nums, range(1 - len(nums), len(nums), 2))) % 1000000007\n``` | 0 | 0 | ['Array', 'Brainteaser', 'Sorting', 'Prefix Sum', 'Python', 'C++', 'Java', 'Python3'] | 0 |
movement-of-robots | Java + No need to consider collision | java-no-need-to-consider-collision-by-la-q803 | Intuition\nWhen two robots collide with each other, we can just swap them and then it seems that they just go through each other. So we don\'t need to consider | lacfo | NORMAL | 2023-11-16T16:08:34.498272+00:00 | 2023-11-16T16:08:34.498304+00:00 | 20 | false | # Intuition\nWhen two robots collide with each other, we can just swap them and then it seems that they just go through each other. So we don\'t need to consider collision.\n\n# Approach\n* Get the positions of robots without considering collisions after `d` seconds\n* Sort the positions array to make the sum of pairs of distance easier.\n\n# Complexity\n- Time complexity:\n`O(nlogn)` where `n` is length of `nums`\n\n- Space complexity:\n`O(n)` for the `long` positions array\n\n# Code\n```\nclass Solution {\n public int sumDistance(int[] nums, String s, int d) {\n int mod = (int)(1e9 + 7);\n int n = nums.length;\n long[] positions = new long[n];\n for (int i = 0; i < n; i++) {\n if (s.charAt(i) == \'R\') {\n positions[i] = (long)nums[i] + d;\n } else {\n positions[i] = (long)nums[i] - d;\n }\n }\n Arrays.sort(positions);\n long res = 0L;\n long preSum = 0L;\n for (int i = 1; i < n; i++) {\n long cur = preSum + i * (positions[i] - positions[i-1]);\n res = (res + cur) % mod;\n preSum = cur;\n }\n return (int)res;\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
movement-of-robots | Fully explained C++ code || Beats 90% solutions || Easy to understand | fully-explained-c-code-beats-90-solution-lbsn | Intuition\nThe main intuition is when 2 robots collide, it switches direction. but for the purpose of finding the pair wise distance, it is equivalent to not sw | Yash_Khetan | NORMAL | 2023-11-04T17:55:30.920257+00:00 | 2023-11-04T17:55:30.920275+00:00 | 14 | false | # Intuition\n**The main intuition is when 2 robots collide, it switches direction. but for the purpose of finding the pair wise distance, it is equivalent to not switching the robots\' position and keep the same direction.**\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nTo solve this we need to keep in mind these 2 things -\n\n- Here a new vector is used of type `<long long>` because when we add or sub the distance after time `d`, then it may cause an overflow.\n- To calculate the pair wise distance sum we need to understand how prefix sum can be used:\n\n Imagine finding distance of a4 with all elements before it\n `(a4-a1)+(a4-a2)+(a4-a3) -> (a4+a4+a4)-(a1+a2+3) -> (i*a4) - prefixsum`\n So this formula can be used only if the numbers are sorted.\n\n**IF YOU LIKED THE EXPLANATION PLEASE DO UPVOTE IT**\n\nHere\'s a detailed explanation of the code:\n\n1. `int mod = 1e9 + 7;`: This line defines a constant integer `mod` with a value of 1e9 + 7. This value is used for modulo operations later in the code.\n\n2. `vector<long long> newNums;`: A new vector of type `long long` named `newNums` is declared. This vector will store the modified values of the input vector `nums`. Using `long long` ensures that large integers can be handled without causing overflow.\n\n3. The `for` loop iterates through the elements of the `nums` vector and copies each element to the `newNums` vector. This creates a deep copy of the input vector.\n\n4. The next `for` loop iterates through the `newNums` vector. For each element at index `i`, it checks the corresponding character in the string `s`. If `s[i]` is \'L\', it subtracts the value of `d` from `newNums[i`. If `s[i]` is anything other than \'L\' (i.e., \'R\'), it adds the value of `d` to `newNums[i]`.\n\n5. After these modifications, the `newNums` vector contains the elements of `nums` adjusted according to the operations specified in the string `s`.\n\n6. `sort(newNums.begin(), newNums.end());`: The `newNums` vector is sorted in ascending order.\n\n7. Two variables `distance` and `prefixSum` are declared and initialized to 0. These variables will be used to calculate the sum of distances between elements in the sorted `newNums` vector.\n\n8. Another `for` loop iterates through the elements of the sorted `newNums` vector. For each element at index `i`, it calculates the distance using the formula:\n ```\n distance = (distance + (1LL * i * newNums[i] - prefixSum)) % mod;\n ```\n - `1LL * i * newNums[i]` calculates the contribution of the current element to the distance.\n - `prefixSum` is used to keep track of the cumulative sum of elements in the sorted vector.\n - The result is updated in the `distance` variable, and it is calculated modulo `mod` to ensure the result remains within reasonable bounds.\n\n9. Finally, the function returns the calculated `distance`, which represents the sum of distances between the modified elements in the sorted vector, taking into account the operations specified in the string `s` and applying modulo `mod`.\n\nThis code efficiently calculates the desired sum of distances while handling potential integer overflow by using `long long` and modulo operations.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n int mod = 1e9 + 7 ;\npublic:\n int sumDistance(vector<int>& nums, string s, int d) {\n vector<long long> newNums ; // Create a new vector to store modified values\n for(int i = 0; i<nums.size(); i++)\n newNums.push_back(nums[i]) ;\n\n for(int i = 0; i<newNums.size(); i++) {\n if(s[i] == \'L\')\n// -2000000000 - 1000000000 can cause overflow if <long long> type not used\n newNums[i] = newNums[i] - d ;\n else\n// 2000000000 + 1000000000 can cause overflow if <long long> type not used\n newNums[i] = newNums[i] + d ;\n }\n \n sort(newNums.begin(), newNums.end()) ;\n long long distance = 0, prefixSum = 0 ;\n for(int i = 0; i<newNums.size(); i++) {\n// The formula calculates the distance and updates \'prefixSum\' for the next iteration.\n distance = (distance + (1LL*i*newNums[i] - prefixSum)) % mod ;\n prefixSum = (prefixSum + newNums[i]) % mod ;\n }\n return distance ;\n }\n};\n``` | 0 | 0 | ['Array', 'Brainteaser', 'Sorting', 'Prefix Sum', 'C++'] | 0 |
movement-of-robots | Beat 90% Time | Clean & Concise | beat-90-time-clean-concise-by-swapniltya-06nx | Code\n\nclass Solution {\npublic:\n int MOD = 1000000007;\n int sumDistance(vector<int>& num, string s, int d) {\n vector<long> nums;\n for( | swapniltyagi17 | NORMAL | 2023-11-04T14:00:49.183657+00:00 | 2023-11-04T14:00:49.183690+00:00 | 5 | false | # Code\n```\nclass Solution {\npublic:\n int MOD = 1000000007;\n int sumDistance(vector<int>& num, string s, int d) {\n vector<long> nums;\n for(auto x: num) nums.push_back(x);\n\n for(int i=0; i<nums.size(); ++i){\n if(s[i]==\'R\') nums[i] += d;\n else nums[i] -= d;\n }\n sort(nums.begin(),nums.end());\n long ans = 0;\n for(int i=0; i<nums.size()-1; ++i){\n ans = (ans + ((nums.size()-i-1)%MOD)*((nums[i+1]-nums[i])%MOD)*(i+1))%MOD;\n }\n return (int) ans;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
movement-of-robots | Beats the new test cases!! | beats-the-new-test-cases-by-divy_jindal-dsbf | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | Divy_Jindal | NORMAL | 2023-11-04T12:53:34.731792+00:00 | 2023-11-04T12:53:34.731824+00:00 | 5 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int sumDistance(vector<int>& num, string s, int d) {\n vector<long long> nums(num.begin(),num.end());\n int i = 0, n = nums.size();\n for(i = 0; i < n; i++){\n if(s[i]==\'R\'){\n nums[i] += d;\n }else{\n nums[i] -= d;\n }\n }\n sort(nums.begin(),nums.end());\n long long ans = 0,mod = 1e9+7,p = 0;\n for(i = 0; i < n; i++){\n ans = (((ans+(nums[i]*1LL*i)%mod)%mod-p)%mod+mod)%mod;\n p = (p+nums[i])%mod;\n }\n return (ans+mod)%mod;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
movement-of-robots | ✅ Explained Solution - All testcases ✅ O(n log n) | explained-solution-all-testcases-on-log-6ig1j | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n In the first loop, we convert the integer positions \'nums[i]\' of the r | bhardwajshruti97 | NORMAL | 2023-11-04T08:20:27.147830+00:00 | 2023-11-04T08:22:37.753446+00:00 | 24 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n In the first loop, we **convert the integer positions \'nums[i]\' of the robots to \'long\'** for precision and add/subtract the \'d\' distance depending on their direction (\'R\' or \'L\').\n\n**Sorting:** Then, we sort this array longnum. This is a crucial step. Once sorted, the array represents the final positions of all robots on the number line, from left to right, d seconds later. Any collisions that might happen are already taken into account because the directions of robots after a collision do not affect the final position of any robot.\n\n**Sum Calculation:** Next, in another loop, res calculates the sum of all pairwise distances. The formula (1L + i + i - n) * longnum[i] calculates the sum of distances of robots from a particular robot, where \'i\' is the index (or position) of this robot on the sorted array (or the sorted number line).\n\n*This works because in the sorted array, every robot to the left of a given robot at longnum[i] will have a negative distance (since they are to the left), and every robot to the right will have a positive distance from longnum[i]. Since the array is 0-based, there will be \'i\' number of robots to the left and \'n - i - 1\' robots to the right. But the formula uses \'n - i\' because it includes the robot at position \'i\' also.\n*\n**Modulo Operation:** The modulo operation keeps the sum in the range of the prescribed limit 1_000_000_007 to keep the number within the \'int\' range and to meet the problem\'s requirements.\n\n**In summary**, the code correctly computes the sum of all pairwise distances between robots \'d\' seconds after they have been given commands to move, taking into account any collisions. It does this efficiently by sorting the final positions of robots and calculating pairwise distances in O(n). The overall time complexity is O(n log n) due to the sorting operation, and space complexity is O(n) as extra space is used for storing \'longnum\'.\n\n# Complexity\n- Time complexity: **O(n log n)**\n\nThe two major operations that impact the time complexity of the code are:\nLooping over the input array nums to fill longnum: Which is O(n), where n is size of the given array.\nSorting of the longnum array: Which in worst-case scenario is O(n log n), considering the sort function uses a comparison-based sorting algorithm like quick sort or merge sort.\nSo, the time complexity will be dominated by the sorting operation, hence, it will be O(n log n).\n\n- Space complexity: **O(n)** \n\nThe space complexity is dictated by the additional space used apart from the input. In this case, it\'s the longnum array that has the same size as the input array nums, so the space complexity is O(n) as we are storing n extra long integer elements. Other variables used are of constant space and don\'t impact the overall complexity.\n\n# Code\n```\nclass Solution {\n public int sumDistance(int[] nums, String s, int d) {\n int n = nums.length, mod = 1_000_000_007;\n long longnum[] = new long[n];\n for(int i = 0; i < n; ++i)\n longnum[i] = (long)nums[i] + (s.charAt(i) == \'R\' ? d : -d);\n Arrays.sort(longnum);\n long res = 0;\n for(int i = 0; i < n; ++i)\n res = (res + (1L + i + i - n) * longnum[i] ) % mod;\n return (int)(res+mod)%mod; \n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
movement-of-robots | Array Simulation + Sort + Suffix. Time: O(nlogn), Space: O(n) | array-simulation-sort-suffix-time-onlogn-2kr6 | class Solution(object):\n def sumDistance(self, nums, s, d):\n """\n :type nums: List[int]\n :type s: str\n :type d: int\n | iitjsagar | NORMAL | 2023-11-04T03:46:58.627802+00:00 | 2023-11-04T03:46:58.627827+00:00 | 4 | false | class Solution(object):\n def sumDistance(self, nums, s, d):\n """\n :type nums: List[int]\n :type s: str\n :type d: int\n :rtype: int\n """\n \n \n pos = []\n \n n = len(nums)\n \n for i in range(n):\n if s[i] == \'R\':\n pos.append(nums[i] + d)\n else:\n pos.append(nums[i] - d)\n \n pos.sort()\n \n #print pos\n res = 0\n cur = 0\n \n for i in range(n-2,-1,-1):\n cur = cur + (pos[i+1] - pos[i])*(n-1-i)\n res += cur\n \n #print res\n return res%(10**9 + 7) | 0 | 0 | [] | 0 |
movement-of-robots | JAVA Solution | java-solution-by-bhumika1997-41l3 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | bhumika1997 | NORMAL | 2023-10-30T07:51:40.316013+00:00 | 2023-10-30T07:51:40.316034+00:00 | 10 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int sumDistance(int[] nums, String s, int d) {\n long out[] = new long[nums.length];\n for(int i = 0; i < nums.length ; i++){\n if(s.charAt(i) == \'L\'){\n out[i] = (nums[i] - (long)d) ;\n }\n else{\n out[i] =(nums[i] + (long)d);\n }\n }\n Arrays.sort(out);\n // System.out.println(Arrays.toString(out));\n int ans = 0;\n int full_ans = 0;\n for(int i = 1; i < nums.length ; i++){\n ans = (int)(((out[i] - out[i-1]) * (long)i + ans ) % (long)(1e9 + 7));\n full_ans = (int)((full_ans + (long)ans )% (long)(1e9 + 7));\n }\n return full_ans;\n }\n}\n``` | 0 | 0 | ['Java'] | 0 |
movement-of-robots | Simple beginner-level C solution || Beats 100% in Runtime and Memory || Sorting + Prefix Sum | simple-beginner-level-c-solution-beats-1-3l34 | \n# Complexity\n- Time complexity: O(nlogn)\n- Space complexity: O(n)\n Add your space complexity here, e.g. O(n) \n\n# Code\ncpp\n// Runtime 111 ms Beats 100% | paulchen2713 | NORMAL | 2023-10-10T04:13:39.050650+00:00 | 2023-10-10T04:13:39.050676+00:00 | 18 | false | \n# Complexity\n- Time complexity: ```O(nlogn)```\n- Space complexity: ```O(n)```\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp\n// Runtime 111 ms Beats 100% Memory 17.5 MB Beats 100%\nint ascend(const void* pa, const void* pb) {\n const int a = *(const int*)pa;\n const int b = *(const int*)pb;\n if (a == b) {\n return 0;\n }\n return (a < b) ? -1 : 1;\n}\nint sumDistance(int* nums, int numsSize, char* s, int d) {\n // Sorting + Prefix Sum\n\n // Time complexity: O(nlogn)\n // Space complexity: O(n)\n \n if (strlen(s) != numsSize) return -1;\n\n const int mod = 1e9 + 7;\n const int n = numsSize;\n int result = 0, prefix = 0;\n \n int* pos = (int*)calloc(n, sizeof(int));\n for (int i = 0; i < n; ++i) {\n if (s[i] == \'L\') {\n pos[i] = nums[i] - d;\n }\n else pos[i] = nums[i] + d;\n }\n\n qsort(pos, n, sizeof(int), ascend);\n\n for (int i = 0; i < n; ++i) {\n result = (result + i * pos[i] - prefix) % mod;\n prefix = (prefix + pos[i]) % mod;\n }\n \n free(pos);\n return result;\n}\n``` | 0 | 0 | ['Array', 'C', 'Sorting', 'Prefix Sum'] | 0 |
movement-of-robots | C++ - Sort + prefix sum | c-sort-prefix-sum-by-mumrocks-gq3e | Intuition\nWhen robot collide, it changes direction. We do not need to worry about changing direction of the robot. Pleae see below example to understand it bet | MumRocks | NORMAL | 2023-09-27T13:45:50.630740+00:00 | 2023-09-27T13:45:50.630762+00:00 | 11 | false | # Intuition\nWhen robot collide, it changes direction. We do not need to worry about changing direction of the robot. Pleae see below example to understand it better. \nA (at 4 and traveling right ) and B(at 5 and traveling left). When they collide A and B changes direction so you can imaging A becomes robot B and B becomes A. \n\nAfter finding Robot position after d seconds, we can simply use prefix distance method to find the distance between all pairs. \n\n# Complexity\n- Time complexity:\nO(NLOGN) -> N = number of robots\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution {\npublic:\n int sumDistance(vector<int>& nums, string s, int d) {\n for (int i=0;i<nums.size();i++) nums[i]+=(s[i]==\'L\'?-d:d);\n sort(nums.begin(),nums.end());\n long long ans=0,pre=0;\n int MOD=1000000007;\n for (int i=1;i<nums.size();i++){\n //cout << nums[i-1] << " to " << nums[i] << endl;\n pre = (pre + 1LL*(1LL*nums[i]-1LL*nums[i-1])*(i))%MOD;\n ans = (ans + pre)%MOD;\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['Sorting', 'Prefix Sum', 'C++'] | 0 |
movement-of-robots | C++||Easy || 100%faster | ceasy-100faster-by-taufika999-pbaa | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | taufika999 | NORMAL | 2023-09-07T18:22:25.062717+00:00 | 2023-09-07T18:22:25.062739+00:00 | 9 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int getsummation(vector<int> nums){\n int n=nums.size();\n int mod=1e9+7;\n sort(nums.begin(),nums.end());\n vector<long long >a(n,0);\n ////// how to find the distance betweeen all pair in linear time ////\n for(int i=1;i<n;i++){\n\n // curr= a[i-1]+ diff*(i-1) + diff;\n long long curr= (a[i-1]%mod +( ( (long long )nums[i]-(long long )nums[i-1])*1LL*(i) )%mod)%mod;\n a[i]=curr;\n }\n \n int ans=0;\n \n for(int i=0;i<n;i++){\n ans= (ans%mod + a[i]%mod)%mod;\n }\n return ans;\n }\n int sumDistance(vector<int>& nums, string s, int d) {\n \n int n=nums.size();\n \n \n for(int i=0;i<n;i++){\n if(s[i]==\'L\'){\n nums[i]=nums[i]-d;\n }else nums[i]=nums[i]+d;\n }\n\n \n return getsummation(nums);\n\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
movement-of-robots | C++/Python, solution with explanation | cpython-solution-with-explanation-by-shu-xxdj | \n\ntc is O(nlogn), sc is O(1).\n### python\npython\nmod = int(1e9+7)\nclass Solution:\n def sumDistance(self, nums: List[int], s: str, d: int) -> int:\n | shun6096tw | NORMAL | 2023-08-24T06:50:47.212316+00:00 | 2023-08-24T07:09:21.106091+00:00 | 10 | false | 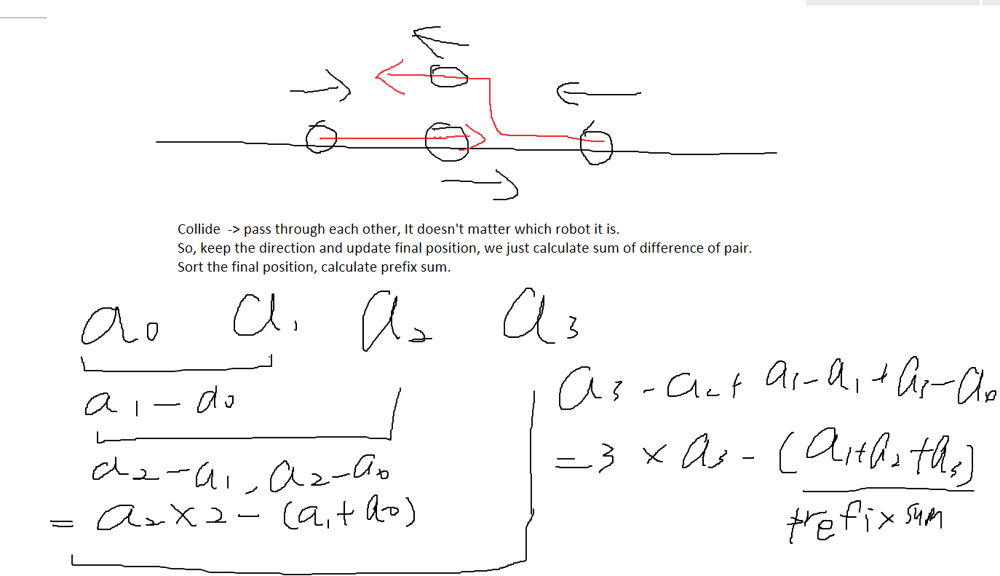\n\ntc is O(nlogn), sc is O(1).\n### python\n```python\nmod = int(1e9+7)\nclass Solution:\n def sumDistance(self, nums: List[int], s: str, d: int) -> int:\n for i, ch in enumerate(s):\n nums[i] += d if ch == \'R\' else -d\n nums.sort()\n prefix = nums[0]\n ans = 0\n for i in range(1, len(nums)):\n ans += i * nums[i] - prefix\n if ans >= mod: ans %= mod\n prefix += nums[i]\n return ans\n```\n### c++\n```cpp\nconst int mod = 1e9+7;\nclass Solution {\npublic:\n int sumDistance(vector<int>& nums, string s, int d) {\n for(int i = 0; i < s.size(); i+=1) nums[i] += s[i] == \'R\'? d:-d;\n sort(nums.begin(), nums.end());\n long long ans = 0, prefix = nums[0];\n for (int i = 1; i < nums.size(); i+=1) {\n ans = (ans + (long long) i * nums[i] - prefix) % mod;\n prefix += nums[i];\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['C', 'Sorting', 'Prefix Sum', 'Python'] | 0 |
movement-of-robots | C++ solution | c-solution-by-pejmantheory-t0iq | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | pejmantheory | NORMAL | 2023-08-20T13:16:36.300632+00:00 | 2023-08-20T13:16:36.300665+00:00 | 6 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public:\n int sumDistance(vector<int>& nums, string s, int d) {\n constexpr int kMod = 1\'000\'000\'007;\n const int n = nums.size();\n int ans = 0;\n int prefix = 0;\n vector<int> pos;\n\n for (int i = 0; i < nums.size(); ++i)\n if (s[i] == \'L\')\n pos.push_back(nums[i] - d);\n else\n pos.push_back(nums[i] + d);\n\n sort(pos.begin(), pos.end());\n\n for (int i = 0; i < n; ++i) {\n ans = ((ans + 1LL * i * pos[i] - prefix) % kMod + kMod) % kMod;\n prefix = ((0LL + prefix + pos[i]) % kMod + kMod) % kMod;\n }\n\n return ans;\n }\n};\n\n``` | 0 | 0 | ['C++'] | 0 |
movement-of-robots | Golang sorting solution | golang-sorting-solution-by-tjucoder-7y0p | Code\ngo\nfunc sumDistance(nums []int, s string, d int) int {\n\tfinalPositions := make([]int, 0, len(nums))\n\tfor i, v := range nums {\n\t\tswitch s[i] {\n\t\ | tjucoder | NORMAL | 2023-08-19T17:09:03.371722+00:00 | 2023-08-19T17:09:03.371749+00:00 | 9 | false | # Code\n```go\nfunc sumDistance(nums []int, s string, d int) int {\n\tfinalPositions := make([]int, 0, len(nums))\n\tfor i, v := range nums {\n\t\tswitch s[i] {\n\t\tcase \'L\':\n\t\t\tv -= d\n\t\tcase \'R\':\n\t\t\tv += d\n\t\t}\n\t\tfinalPositions = append(finalPositions, v)\n\t}\n\tsort.Ints(finalPositions)\n\tresult := 0\n\tbase := finalPositions[0]\n\tfor i := 1; i < len(finalPositions); i++ {\n\t\tresult = (result + (finalPositions[i] * i) - base) % 1000000007\n\t\tbase += finalPositions[i]\n\t}\n\treturn result % 1000000007\n}\n``` | 0 | 0 | ['Sorting', 'Go'] | 0 |
movement-of-robots | I, Robot | O(N log(N)) Easy to understand | C++ | i-robot-on-logn-easy-to-understand-c-by-oy1rj | Intuition\nThe most tricky part is to understand that bouncing robots are the same as non-bouncing robots.\n\nThe second part is to calculate the prefix sum to | urmichm | NORMAL | 2023-07-13T14:45:30.355238+00:00 | 2023-07-13T14:45:30.355268+00:00 | 11 | false | # Intuition\nThe most tricky part is to understand that bouncing robots are the same as non-bouncing robots.\n\nThe second part is to calculate the prefix sum to quickly calculate the distance sum.\n\n# Approach\nApply distances to each robot. Sort $$nums$$ as it does not matter which robot is where, we only need their positions. Use prefix sum to calculate the result;\n```\n [x0, x1, x2, x3, x4, x5] | N = 6\n |x1 - x0| + |x2 - x0| + |x3 - x0| + |x4 - x0| + |x5 - x0|\n since x0 < x1 < x2 < x3 < x4 < x5\n (x1 - x0) + (x2 - x0) + (x3 - x0) + (x4 - x0) + (x5 - x0)\n ---------------\n (x1) + (x2) + (x3) + (x4) + (x5) - (N-1) * x0\n (x2) + (x3) + (x4) + (x5) - (N-2) * x1\n (x3) + (x4) + (x5) - (N-3) * x2\n (x4) + (x5) - (N-4) * x3\n (x5) - (N-5) * x4\n```\n# Complexity\n- Time complexity: $$O(N*log(N))$$ where N is the number of robots. Sorting is the "longest" part of the algorithm\n\n- Space complexity: $$O(N)$$ where N is the number of robots. \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n#define MOD 1000000007\n\nclass Solution {\n\npublic:\n int sumDistance(vector<int>& nums, string s, int d) \n {\n const int N = nums.size();\n unsigned int result = 0;\n unsigned int t = 0;\n\n for(int i=0; i < N; i++)\n {\n if(s[i] == \'R\')\n nums[i] += d;\n else // s[i] == \'L\'\n nums[i] -= d;\n }\n\n // O(N*log(N))\n sort(nums.begin(), nums.end());\n\n vector<long> pref(nums.size(), 0); // O(N)\n for(int i=0; i < N; i++)\n {\n pref[i] = nums[i];\n }\n for(int i=N-1-1; i >= 0; i--)\n {\n pref[i] = (pref[i] + pref[i+1]);\n }\n\n for(int i=0; i < N-1; i++)\n {\n t = ( pref[i+1] - ( (N-1-i) * (long)nums[i]) ) % MOD;\n result = (t+result) % MOD;\n }\n\n return result;\n }\n\n};\n\n// 0->-2 1->0 2->2\n//\n// 0 1 2\n// L L R\n// [-2 0 2]\n// [-1 -1 1]\n// [-2 0 0]\n// [-3 -1 1] -sort-> [-3, -1, 1]\n\n//d: (-3, -1) (-3, 1) (-1, 1) = 8\n\n// R L L\n// [-2 0 2]\n// go through\n// [1 -3 -1] -sort-> [-3, -1, 1]\n////////\n//d: (-3, -1) (-3, 1) (-1, 1) = 8\n\n// x0 < x1 < x2 < x3 < x4 < x5 | N = 6\n// |x1 - x0| + |x2 - x0| + |x3 - x0| + |x4 - x0| + |x5 - x0|\n// since x0 < x1 < x2 < x3 < x4 < x5\n// (x1 - x0) + (x2 - x0) + (x3 - x0) + (x4 - x0) + (x5 - x0)\n// (x1) + (x2) + (x3) + (x4) + (x5) - (N-1) * x0\n// (x2) + (x3) + (x4) + (x5) - (N-2) * x1\n// (x3) + (x4) + (x5) - (N-3) * x2\n// (x4) + (x5) - (N-4) * x3\n// (x5) - (N-5) * x4\n\n\n``` | 0 | 0 | ['C++'] | 0 |
movement-of-robots | C++ || UNIQUE || COUNT REPETITION OF EDGES | c-unique-count-repetition-of-edges-by-ay-8fri | Intuition\nSo firstly I will talk about finding the point at which the robots will be after d second so for that don\'t confuse with collision part just add or | Ayush_codes26 | NORMAL | 2023-07-08T12:43:20.531076+00:00 | 2023-07-08T12:43:20.531106+00:00 | 33 | false | # Intuition\nSo firstly I will talk about finding the point at which the robots will be after d second so for that don\'t confuse with collision part just add or subtract d based on \'L\' and \'R\' because the position only matter for calculating all pairs distances. And after that just calculate distance.\n\n\n# Complexity\n- Time complexity:O(nlog(n))\n\n- Space complexity:O(n)\n\n# Code\n```\nclass Solution {\npublic:\n int sumDistance(vector<int>& nums, string s, int d) {\n\n long long int n = nums.size();\n vector<long long int>num(n,0);\n long long int mod = 1e9 + 7;\n\n // preapare new array with stores final positions\n for(long long int i = 0;i<n;i++){\n if(s[i] == \'R\'){\n num[i] = nums[i] + d;\n }\n else{\n num[i] = nums[i] - d;\n }\n }\n\n // sorting array as on increasing order on x-axis\n sort(num.begin() , num.end());\n\n // implemented Algorithm \n int ans = 0;\n long long int rockets = 0;\n for(long long int i = 1;i<n;i++){\n rockets += (n-i + mod);\n rockets %= mod;\n ans = (ans + ((num[i] - num[i-1])*rockets) )%mod;\n rockets -= i;\n }\n return ans%mod;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
movement-of-robots | Rust/Python O(n log n) and constant space. With detailed explanation | rustpython-on-log-n-and-constant-space-w-ta60 | Intuition\nThe key observation in this problem is how to find the final position of the robots. Lets assume that we have two robots going towards each other. Le | salvadordali | NORMAL | 2023-07-06T20:58:42.700441+00:00 | 2023-07-06T20:58:42.700458+00:00 | 9 | false | # Intuition\nThe key observation in this problem is how to find the final position of the robots. Lets assume that we have two robots going towards each other. Lets assume their positions are `[6, 24]`. At timestep 9 they will meet (at position 15) and change directions. At time 11, position of robot 1 will be at position of 13 and position of robot 2 will be at position 17.\n\nBut we do not need to know the position of every specific robot. I will be enough for us to find a position of all robots (without specifying which robot is where). And this is exactly what happens if the robots are behaving as ghosts and going over each other. As you see the positions at t=11 will be `[17, 13]` (same as we calculated previously).\n\nSo we can easily caclulate all of them in $O(n)$ `[p + d if direction == \'R\' else p - d for p, direction in zip(nums, s)]`.\n\n----\n\nNow that we know all the positions, how can we find the total pairwise distance between all points. It is easy to find it in $O(n^2)$, but we need something better.\n\nLets assume our points are `[1, 5, 6, 9]`. What is the distance towards `9`? It is `(9 - 6) + (9 - 5) + (9 - 1)`, which can be rewritten to `9 * 3 - (1 + 5 + 6)`\n\nSimilar to distance towards 6. It will be `6 * 2 - (1 + 5)` (we do not calculate distance between 6 and 9 as we already calculated it previously). So as you see it can be calculated in linear time by calculating prefix sum. But to do this we need to sort an array\n\n\n# Complexity\n- Time complexity: $O(n \\log n)$\n- Space complexity: $O(1)$\n\nConstant time complexity assumes that we are overwriting array of nums (do not do this in Python, only in Rust). Also this assumes that sorting is in place\n\n# Code\n\n```Python []\nclass Solution:\n def sumDistance(self, nums: List[int], s: str, d: int) -> int:\n positions = sorted([p + d if direction == \'R\' else p - d for p, direction in zip(nums, s)], reverse=True)\n res, curr_sum, curr_cnt, mod = 0, 0, 0, 10**9 + 7\n for v in positions:\n res = (res + curr_sum - curr_cnt * v) % mod\n curr_sum += v\n curr_cnt += 1\n return res\n```\n```Rust []\nimpl Solution {\n pub fn sum_distance(mut nums: Vec<i32>, s: String, d: i32) -> i32 {\n let n = nums.len();\n let s = s.into_bytes();\n\n for i in 0 .. n {\n if s[i] == 76 {\n nums[i] -= d;\n } else {\n nums[i] += d;\n }\n }\n nums.sort_unstable();\n\n let (mut res, mut curr_sum, mut curr_cnt) = (0i64, 0i64, 0i64);\n const m: i64 = 1000000007;\n for i in (0 .. n).rev() {\n res = (res + curr_sum - curr_cnt * (nums[i] as i64)) % m;\n curr_sum = (curr_sum + nums[i] as i64) % m;\n curr_cnt += 1;\n }\n\n return ((m + res) % m) as i32;\n }\n}\n```\n | 0 | 0 | ['Rust'] | 0 |
movement-of-robots | Use sum to find the differences | use-sum-to-find-the-differences-by-darv-cz0f | \nconst int MOD = 1000000007;\nclass Solution {\n int sumDistance(List<int> nums, String s, int d) {\n List<int> finals = [];\n for (int i = 0; i < nums. | darv | NORMAL | 2023-07-01T06:08:09.359759+00:00 | 2023-07-01T06:08:09.359791+00:00 | 22 | false | ```\nconst int MOD = 1000000007;\nclass Solution {\n int sumDistance(List<int> nums, String s, int d) {\n List<int> finals = [];\n for (int i = 0; i < nums.length; i++)\n finals.add((s[i] == \'L\') ? nums[i] - d : nums[i] + d);\n finals.sort();\n\n int res = 0;\n\n int right_sum = finals.reduce((value, element) => value + element);\n int left_sum = 0;\n \n for (int i = 0; i < finals.length; i++) {\n res = (res +\n right_sum - (finals.length - i) * finals[i] ) % MOD\n ;\n \n right_sum -= finals[i];\n left_sum += finals[i];\n }\n return res;\n }\n}\n``` | 0 | 0 | ['Dart'] | 0 |
movement-of-robots | [C++] Ignore Collisions and Get Cumulative Sum, ~100% (90ms), ~45% Space (45.2MB) | c-ignore-collisions-and-get-cumulative-s-fps5 | So, for this problem the more crucial part was to figure out we can ignore each collision: similarly to a perfectly elastic linear system with two identical obj | Ajna2 | NORMAL | 2023-06-18T19:11:31.949546+00:00 | 2023-06-19T16:27:40.685340+00:00 | 42 | false | So, for this problem the more crucial part was to figure out we can ignore each collision: similarly to a perfectly elastic linear system with two identical objects colliding with each other, each object will replace the other one, moving from the the collision spot in the opposite direction; this is basically a sophisticate version of [lasr moment before all ants fall out of a plank](https://leetcode.com/problems/last-moment-before-all-ants-fall-out-of-a-plank/) ([cracked here](https://leetcode.com/problems/last-moment-before-all-ants-fall-out-of-a-plank/solutions/3657689/c-just-ignore-collisions-and-get-the-maximum-distance-from-border-100-space-22-7mb/)).\n\nOnce we got all that and we had or subtract `d` to each element depending from its direction, we can store all the values of the final positions for the last part of the problem - computing the overall distances.\n\nSome people used a prefix array, but we can do better using only a running sum.\n\nTo clarify our approach, let\'s assume we have as final positions (already sorted) `{1, 5, 7, 10}`, we can proceed taking each value and thinking of it like the product of its index minus the sum of the previous elements:\n\n```cpp\n 1 5 7 10\n// sum of distances:\n( 5 - 1) + // == 5 * 1 - 1\n( 7 - 5) + ( 7 - 1) + // == 7 * 2 - (5 + 1)\n(10 - 7) + (10 - 5) + (10 - 1) // == 10 * 3 - (7 + 5 + 1)\n```\n\nNow, to turn all of this into code, let\'s start by declaring a few support variables as usual:\n* `len` is going to store the length of our initial inputs (both the vector and the string, guaranteed to have the same size);\n* `res` is going to be our usual accumulator variable, initialised to `0`;\n* `tot` will be our prefix sum, initially set to `0`;\n* `n` will be the ongoing value as we parse `ns` in the second half of the problem;\n* `ns` is going to store all the values of the final positions of each element originally in `nums`.\n\nNext we are going to start populating `ns`; going with `i` through all the elements in `nums`, we will:\n* store `nums[i]` in `n`;\n* if this robot was going left (ie: `s[i] == \'L\'`), we will subtract `d` from `n` (since it is moving backwards on the x axis);\n* otherwise, we will add `d` to `n`;\n* we can then write `n` in `ns[i]`.\n\nNow, since we need our elements in order, we will `sort` `ns`, then, for going with `i` through each position in it, we will:\n* store `ns[i]` in `n`;\n* increase `res` by the product of `n` and `i` minus the sum of all the previous elements `tot`, as explained above;\n* check if `res` is `>= modVal`, we will recompute it as `% modVal`;\n* increase `tot` by `n`.\n\nOnce done, we can `return` `res` :)\n\n# Complexity\n- Time complexity: $$O(n log(n))$$\n- Space complexity: $$O(n)$$\n\n# Code\n```cpp\nconst long long modVal = 1000000007;\n\nclass Solution {\npublic:\n int sumDistance(vector<int> &nums, string s, int d) {\n // support variables\n int len = nums.size();\n long long res = 0, tot = 0, n;\n vector<long long> ns(len);\n // populating ns\n for (int i = 0; i < len; i++) {\n n = nums[i];\n if (s[i] == \'L\') n -= d;\n else n += d;\n ns[i] = n;\n }\n // parsing ns\n sort(begin(ns), end(ns));\n for (int i = 0; i < len; i++) {\n n = ns[i];\n // updating res and tot\n res += i * n - tot;\n if (res >= modVal) res %= modVal;\n tot += n;\n }\n return res;\n }\n};\n```\n\nAlternative version replacing the relatively expensive `%` with a subtraction; it works as fast, but apparently using a bit less memory on average (or it might be just more luck with the test cases):\n\n```cpp\nconst long long modVal = 1000000007;\n\nclass Solution {\npublic:\n int sumDistance(vector<int> &nums, string s, int d) {\n // support variables\n int len = nums.size();\n long long res = 0, tot = 0, n;\n vector<long long> ns(len);\n // populating ns\n for (int i = 0; i < len; i++) {\n n = nums[i];\n if (s[i] == \'L\') n -= d;\n else n += d;\n ns[i] = n;\n }\n // parsing ns\n sort(begin(ns), end(ns));\n for (int i = 0; i < len; i++) {\n n = ns[i];\n // updating res and tot\n res += i * n - tot;\n while (res >= modVal) res -= modVal;\n tot += n;\n }\n return res;\n }\n};\n```\n\n# Brag\n\n | 0 | 0 | ['Array', 'Brainteaser', 'Sorting', 'Prefix Sum', 'C++'] | 0 |
movement-of-robots | Why to Sort before Prefix sum? Explained | why-to-sort-before-prefix-sum-explained-mfokz | Idea\n Describe your first thoughts on how to solve this problem. \n\n\n- if it\'s neg then -(d-b) lets take this as eg. like b > d.\n- then d-a + d-b + d-c = 3 | bala_000 | NORMAL | 2023-06-17T12:34:44.245264+00:00 | 2023-06-22T21:12:09.073239+00:00 | 26 | false | # Idea\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n\n- if it\'s neg then -(d-b) lets take this as eg. like b > d.\n- then d-a + d-b + d-c = 3d - (a+b+c) cannot be done.\n\n# Complexity\n- Time complexity:$$O(N + NLogN + N)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int sumDistance(vector<int>& nums, string s, int d) {\n int N = nums.size();\n for(int i=0; i<N; i++){\n if(s[i] == \'L\')\n nums[i] -= d;\n else\n nums[i] += d; \n }\n\n long long ans = 0;\n int mod = 1e9 + 7;\n long long preSum = 0;\n sort(nums.begin(), nums.end());\n\n for(int i=0; i<N; i++){\n ans = (ans + i*(long long)nums[i] - preSum)%mod;\n preSum = (preSum + nums[i])%mod;\n }\n\n return (int)ans;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
movement-of-robots | c++ | Ants on a Plank | c-ants-on-a-plank-by-srv-er-5i94 | \nclass Solution {\npublic:\n int md=1e9+7;\n int sumDistance(vector<int>& nums, string s, int d) {\n for(int i=0;i<size(nums);++i){\n i | srv-er | NORMAL | 2023-06-16T04:05:22.330718+00:00 | 2023-06-16T04:05:22.330745+00:00 | 30 | false | ```\nclass Solution {\npublic:\n int md=1e9+7;\n int sumDistance(vector<int>& nums, string s, int d) {\n for(int i=0;i<size(nums);++i){\n if(s[i]==\'R\')nums[i]+=d;\n else nums[i]-=d;\n }\n sort(begin(nums),end(nums));\n long pf=0,ans=0;\n for(int i=0;i<size(nums);++i){\n ans+=(long)nums[i]*i-pf;\n pf+=nums[i];\n ans%=md; \n }\n return ans;\n }\n};\n``` | 0 | 0 | ['C', 'Prefix Sum'] | 0 |
movement-of-robots | Collision means nothing | collision-means-nothing-by-piyush01123-gci7 | This problem has a trick. I could not do it during contest but later realized the trick.\n\n- The fact that the robots change directions at collision means noth | piyush01123 | NORMAL | 2023-06-15T07:43:24.476737+00:00 | 2023-06-15T07:47:42.019795+00:00 | 63 | false | This problem has a trick. I could not do it during contest but later realized the trick.\n\n- The fact that the robots change directions at collision means nothing. We can just consider they switched IDs because at the end we really only care about the positions of the robots as a whole. We do not really care about *where robot number so and so is*. What this means is that we can solve the problem as if each robot is on its own track and the solution will still work. Here is an example. Consider the problem: `nums = [-2,0,2], s = "RLL", d = 3`. Then, with the robots changing directions, we have at the end `[-3,-1,1]` and without changing directions we will have `[1,-3,-1]`. Realize that both of these will give the same answer. \n\n- The second problem is how to calculate the sum of absolute differences in $O(n)$ time. We can sort the final array and then use a heuristic to find answer. Consider the final positions sorted array is `[a,b,c,d,e]`. Then we need to do `(4-0)e + (3-1)d + (2-2)c + (1-3)b + (0-4)a`. This is essentially `nums[i] * (i - (n-1-i))` which we can sum for all `i` to get the answer. \n\n- The third and final trick is that `int` does not work because of overflow issues. Use `long long` and even then you will need to apply `mod` at each step to get AC.\n\n\n```\nint sumDistance(vector<int>& nums, string s, int d) \n{\n int n=nums.size(), mod=1e9+7;;\n long long res = 0;\n unordered_map<char,int> dirs {{\'L\',-1}, {\'R\',1}};\n for (int i=0; i<n; i++) nums[i] += dirs[s[i]] * d;\n sort(nums.begin(),nums.end());\n for(int i=0; i<n; i++) \n {\n res += (long long)nums[i] * (2*i+1-n);\n res %= mod;\n }\n return res;\n}\n```\n\nTC: $O(n\\log(n))$ because sorting is involved. | 0 | 0 | ['Math', 'Simulation', 'C++'] | 0 |
movement-of-robots | C++ Easy Solution | c-easy-solution-by-vibhu172000-31jt | \nclass Solution {\npublic:\n int sumDistance(vector<int>& nums, string s, int d) {\n vector<int>position(nums.size());\n int m =1e9+7;\n | vibhu172000 | NORMAL | 2023-06-14T13:16:12.598077+00:00 | 2023-06-14T13:16:12.598099+00:00 | 15 | false | ```\nclass Solution {\npublic:\n int sumDistance(vector<int>& nums, string s, int d) {\n vector<int>position(nums.size());\n int m =1e9+7;\n for(int i=0;i<nums.size();i++){\n if(s[i]==\'R\'){\n position[i]=d+nums[i];\n }\n else{\n position[i]=nums[i]-d;\n }\n }\n sort(position.begin(),position.end());\n vector<long long>sum(nums.size());\n sum[nums.size()-1]=position[nums.size()-1];\n for(int i=position.size()-2;i>=0;i--){\n sum[i]=(position[i]+sum[i+1]);\n sum[i]%=m;\n }\n long long ans= 0;\n for(int i=0;i<position.size()-1;i++){\n long long ww = (position[i]*(position.size()-i-1));\n ww=ww;\n ww-=sum[i+1];\n ans=(ans+ww);\n }\n return abs(ans)%m;\n }\n};\n``` | 0 | 0 | [] | 0 |
movement-of-robots | c++ solution | c-solution-by-jerry_1-g99p | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | jerry_1 | NORMAL | 2023-06-14T12:44:10.999056+00:00 | 2023-06-14T12:44:10.999084+00:00 | 25 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:0(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: 0(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int sumDistance(vector<int>& nums, string s, int d) {\n int mod = 1e9 + 7;\n // first we will ignore the collision \n // we will just substract and add the positions\n // That\'s how we will not need to convert and remind the positions of the robots\n\n for (long long i=0;i<nums.size();i++)\n {\n // if direction is left, then it will be moved to left after d seconds\n if (s[i] == \'L\')\n nums[i] -= d;\n\n // if direction is right then just add the d seconds in current position\n if (s[i] ==\'R\')\n nums[i] += d; \n } \n\n // now we need to add the differences between all pairs\n // first we will sort all the position to find the sum in 0(n);\n sort(nums.begin(),nums.end());\n\n // now we will add the presum in the vector named as presum\n vector<long long>presum(nums.begin(),nums.end());\n for (long long i=1;i<presum.size();i++)\n {\n presum[i] += presum[i-1];\n presum[i] %= mod;\n }\n \n long long ans = 0;\n // here we have just optimized the equation as\n // as for every i \n // we will do \n // (nums[i] - nums[0]) +(nums[i] - nums[1]) + (nums[i] - nums[2]) + ---\n // (nums[i] - nums[i-1])\n\n // So above equation will be equivalent to \n // i*nums[i]- (nums[0] + nums[1] + nums[2] + --- nums[i-1])\n // i*nums[i] - (prefix sum till i-1) \n\n\n for (long long i=1;i<nums.size();i++)\n {\n ans += i * nums[i] - presum[i - 1];\n ans %= mod; \n }\n return ans;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
movement-of-robots | I-love-this-problem feel. | i-love-this-problem-feel-by-rhexaoc-tzu2 | Intuition\n\nFirst time I was reading a part of the description about collisions, I thought to myself: "the collisions must be intuitive and there is no point i | RHEXAOC | NORMAL | 2023-06-14T11:33:15.972990+00:00 | 2023-06-14T11:33:15.973010+00:00 | 10 | false | # Intuition\n\nFirst time I was reading a part of the description about collisions, I thought to myself: "the collisions must be intuitive and there is no point in paying atention to them." \n\nInitially I thought that the right path is to notice, that before the collision there is one robot moving right and one robot moving left, and after collision the same is true. So that is an invariant and we are asked to find the sum of pairs and maybe this sum is going to be liniar with time as a parameter. `sum_of_dist=sum_of_dist(t)=const_0+const_1*t`. This way of thinking was not a path to accepted. And I was able to solve the problem only after returning to it in a few days. The key is collisions. \n\nThe phisics looks the same if there is no collisions and robots move through each other. I love this problem because it is very strange and gives me opportunity to think about _many things_. So what we have here is that one, let call it math formula, descript two different visual models. (the author) start with one visual model (from the nature) and ends up with formal description. (the reader) start with formal description and ends up with the other visual model that helps him to solve the problem. In some way movement is more abstract then identity of robots.\n\n# Approach\nImplementing is an easy part. Some people solved it in an algebraic manner: when all points are sorted, what is contribution of j? `(p[j]-p[j-1])+(p[j]-p[j-2])..`. And we can rearenge addends. My implementation is different: how often the length of segment `[p[j],p[j+1]]` is added in the total sum. This lenght will be added if we take left point of segment $$\\le$$`j` and right point of segment $$\\ge$$`j+1`. The combinations of that is $$(j+1)*(n-(j+1))$$ (\'choose left side\' multiply \'choose right side\'). \n\n# Complexity\n- Time complexity: $$O(n\\cdot log(n))$$ for sorting\n\n- Space complexity: $$O(n)$$ for vector of long long. By the way, do we need to use long long in problem where the final answer is taken by modulo? I mean the addition in \'machine\' is implemented in a way that max_int is followed by min_int, that is numbers are in cycle. So going out of range of int type might not lead to a wrong answer? \n\n# Code\n```\ntypedef long long i64;\nconstexpr i64 md{1000000007};\nclass Solution {\npublic:\n int sumDistance(vector<int>& nums, string s, int d) {\n vector<i64> a(nums.begin(), nums.end());\n for(int i{}; auto& a : a)\n a += (((s[i++]==\'R\')<<1)-1)*d;\n sort(a.begin(), a.end());\n d = {};\n for(int i{}, n_minus_one{(int)a.size()-1}, r{n_minus_one}; i<n_minus_one; ++i, --r)\n d = (d + (a[i+1]-a[i]) * (i+1) % md * (r)) % md;\n return d ;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
movement-of-robots | C++ ignore collision | c-ignore-collision-by-sachin-vinod-vhqz | Observation\n- key point here is ignore collision and let all of them pass from each other \n\n# Complexity\n- Time complexity:O(NlogN)\n Add your time complexi | Sachin-Vinod | NORMAL | 2023-06-14T09:31:37.282702+00:00 | 2023-06-14T09:31:37.282723+00:00 | 10 | false | # Observation\n- key point here is ignore collision and let all of them pass from each other \n\n# Complexity\n- Time complexity:$$O(NlogN)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(N)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int sumDistance(vector<int>& num, string s, int d) {\n vector<long long> nums(num.size());\n for(int i=0;i<nums.size();i++){\n if(s[i]==\'R\'){\n nums[i]=num[i]+d;\n }\n else{\n nums[i]=num[i]-d;\n }\n }\n\n sort(nums.begin(),nums.end());\n int val=abs(nums[0]);\n long mod=1e9+7;\n for(int i=0;i<nums.size();i++){\n nums[i]=((long long)(nums[i]+val))%mod;\n }\n\n long long ans=0;\n \n long long cnt=nums.size()-1;\n for(int i=nums.size()-1;i>0;i--){\n ans=((ans+(long long)(cnt*nums[i]))%mod)%mod;\n cnt--;\n }\n\n cnt=1;\n for(int i=nums.size()-2;i>=0;i--){\n ans=(ans-nums[i]*cnt+mod)%mod;\n cnt++;\n }\n\n return ans;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
movement-of-robots | C++ ignore collision | c-ignore-collision-by-sachin-vinod-z8jm | Observation\n- key point here is ignore collision and let all of them pass from each other \n\n# Complexity\n- Time complexity:O(NlogN)\n Add your time complexi | Sachin-Vinod | NORMAL | 2023-06-14T09:31:27.744271+00:00 | 2023-06-14T09:31:27.744297+00:00 | 10 | false | # Observation\n- key point here is ignore collision and let all of them pass from each other \n\n# Complexity\n- Time complexity:$$O(NlogN)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(N)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int sumDistance(vector<int>& num, string s, int d) {\n vector<long long> nums(num.size());\n for(int i=0;i<nums.size();i++){\n if(s[i]==\'R\'){\n nums[i]=num[i]+d;\n }\n else{\n nums[i]=num[i]-d;\n }\n }\n\n sort(nums.begin(),nums.end());\n int val=abs(nums[0]);\n long mod=1e9+7;\n for(int i=0;i<nums.size();i++){\n nums[i]=((long long)(nums[i]+val))%mod;\n }\n\n long long ans=0;\n \n long long cnt=nums.size()-1;\n for(int i=nums.size()-1;i>0;i--){\n ans=((ans+(long long)(cnt*nums[i]))%mod)%mod;\n cnt--;\n }\n\n cnt=1;\n for(int i=nums.size()-2;i>=0;i--){\n ans=(ans-nums[i]*cnt+mod)%mod;\n cnt++;\n }\n\n return ans;\n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
movement-of-robots | BEST IMPLEMENTATION | EASY | C++ CODE | ANS REVIEW PLS | best-implementation-easy-c-code-ans-revi-3e1p | Intuition\n Describe your first thoughts on how to solve this problem. \n\n\n all the robots are of same characterstics ....\n so , after colliding they have ju | MihirKathpal | NORMAL | 2023-06-13T14:25:47.827604+00:00 | 2023-06-13T14:25:47.827623+00:00 | 18 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n\n all the robots are of same characterstics ....\n* so , after colliding they have just effect of directions .. so we can think robots surpass each other instead of thinking they collided\n\n* after d seconds all the robots at there same area... means if robot at left most then after d second it remains at left , if in middle remains in middle\n\n* if at rightmost then remain at that\n* so sort that array and calculate the distance between each pair----> In O(n) times\n\nhow? see -----> ---a---------b-------------c---------------d--------------e-----\n b-a c-a d-a e-a\n c-b d-b E-B E-B d-c e-c \n e-d \n // (1xb-a) (2xc-(a+b)) (3xd-(a+b+c)) (3xe-(a+b+c+d))\n // addition of all this == ans\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int mod = 1e9 + 7; \n int sumDistance(vector<int>& nums, string s, int d) {\n int n = nums.size();\n for(int i=0 ; i<n ;i++)\n {\n if(s[i] == \'R\')\n nums[i]+=d;\n else\n nums[i]-=d;\n }\n long long ans= 0;\n sort(nums.begin() , nums.end());\n long long prefix =0;\n for(int i = 0; i <n ; i++)\n {\n ans += (i*(long long)nums[i] - prefix);\n ans %=mod;\n prefix += nums[i];\n }\n return ans;\n \n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
movement-of-robots | Javascript - Sort + PreSum + Math | javascript-sort-presum-math-by-faustaleo-opsm | Code\n\n/**\n * @param {number[]} nums\n * @param {string} s\n * @param {number} d\n * @return {number}\n */\nvar sumDistance = function (nums, s, d) {\n const | faustaleonardo | NORMAL | 2023-06-13T00:35:43.573146+00:00 | 2023-06-13T01:19:49.095318+00:00 | 51 | false | # Code\n```\n/**\n * @param {number[]} nums\n * @param {string} s\n * @param {number} d\n * @return {number}\n */\nvar sumDistance = function (nums, s, d) {\n const n = nums.length;\n const MOD = Math.pow(10, 9) + 7;\n for (let i = 0; i < n; i++) {\n nums[i] = s[i] === \'R\' ? nums[i] + d : nums[i] - d;\n }\n\n nums.sort((a, b) => a - b);\n const preSum = nums.slice();\n\n let ans = 0;\n for (let i = 1; i < n; i++) {\n ans = (ans + (i * nums[i] - preSum[i - 1])) % MOD;\n preSum[i] = (nums[i] + preSum[i - 1]) % MOD;\n }\n\n return ans;\n};\n\n``` | 0 | 0 | ['Math', 'Sorting', 'Prefix Sum', 'JavaScript'] | 0 |
movement-of-robots | Python: explained in pictures and math | python-explained-in-pictures-and-math-by-opie | Approach\nSince there is no chance to simulate actual robots movement considering the problem constraints, let\'s try to find another way.\n\nFirst thing which | olzh06 | NORMAL | 2023-06-12T20:16:36.646876+00:00 | 2023-06-12T20:18:22.790762+00:00 | 44 | false | # Approach\nSince there is no chance to simulate actual robots movement considering the problem constraints, let\'s try to find another way.\n\nFirst thing which is crusial for solving this problem is to understand what will be the final position of robots. The situation when there are no other robots on the way is illustrated on the figure below (in this example red robot moves to the left, white robot - to the right and `d = 5`) \n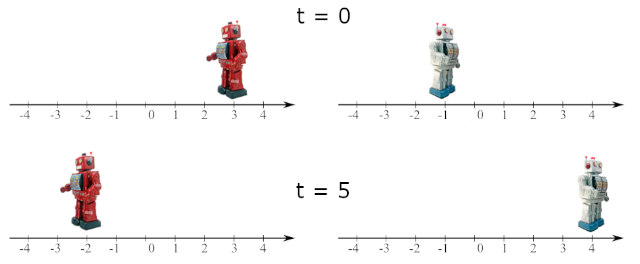\n\nNow let\'s see if these robots stand on the same line and collide. Below the position of robots after each second is shown:\n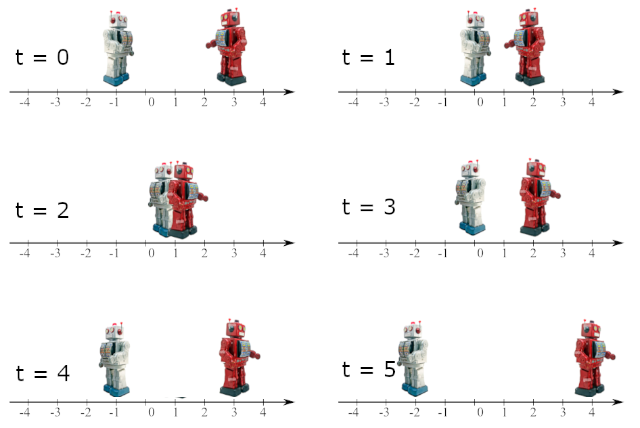\n\nIf we compare the robot\'s position at 5 s with the previous case we can see that the white robot stands at the same position the red robot would be if there were no collisions. The same is true for the red robot, it stands at the final coordinate the white robot would have without taking into account collisions. So we can assume the robots just pass through each other without colliding. That is the crucial hint necessary to solve the problem (I took it from the solutions of other users).\n\nNow we can easily calculate the final coordinates the robots will have after `d` seconds. If `s[i] == \'L\'` then final position is `nums[i] -= d`, and for `s[i] == \'R\'` the final position is `nums[i] += d`. Note that now there is no true correspondence between robots\' index and its calculated coordinate, but this is not important for this problem.\n\nNow we need to calculate the sum of distances between each pair of robots. For robot `i` the sum of distances will be equal to sum of distances to all robots on its left + sum of distances to all robots on the right. To find the distances without using `abs()` let\'s sort `nums` array of final distances. Below is a picture that helps us with evaluating the indices.\n\n\n\nNow let\'s do some math.\n\nIn sorted array of final distances the sum of distances from position `i` to every other position can be written as:<br>\n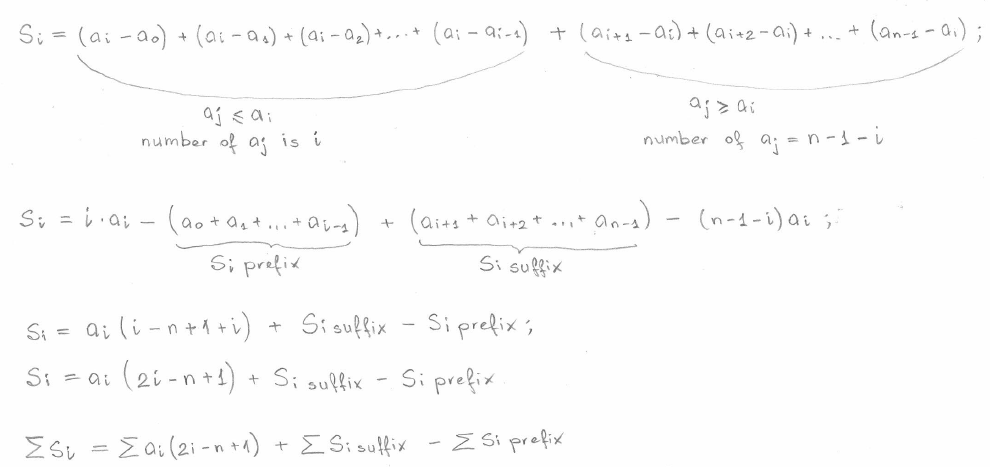\n\nBasically that\'s all we need to solve the problem as we know how to calculate prefix sum and suffix sum in linear time. But let\'s go a little bit further and evaluate what the sum of all prefixes and suffixes looks like\n\n\n\n\nNow we can rewrite to sum of all distances between all pairs of robots as\n\n\n\n\nBut here the distance between each pair of robots is accounted twice, and since according to problem description the pairs (A,B) and (B,A) are considered as one pair, we can skip `2` multiplier in the resulting formula\n\n<ins>Time complexity:</ins> `O(n log n)`\n\n<ins>Space complexity:</ins> `O(1)`\n\n# Code\n```\nclass Solution:\n def sumDistance(self, nums: List[int], s: str, d: int) -> int:\n n = len(nums)\n ans = 0\n MOD = 1_000_000_007\n \n for i in range(n):\n if s[i] == \'R\': nums[i] += d\n else: nums[i] -= d\n \n nums.sort()\n for i in range(n):\n ans += nums[i] * ((i << 1) - n + 1)\n ans %= MOD\n return ans\n # end sumDistance(...)\n``` | 0 | 0 | ['Python3'] | 0 |
movement-of-robots | Trick question: let robots walk past each other. | trick-question-let-robots-walk-past-each-66ov | Computing final positions\n\n First note that the final solution is only a function of the final robot positions, and robot indices are not important\n When rob | erjoalgo | NORMAL | 2023-06-12T19:54:48.997069+00:00 | 2023-06-19T05:01:19.845783+00:00 | 6 | false | **Computing final positions**\n\n* First note that the final solution is only a function of the final robot positions, and robot indices are not important\n* When robots collide, they can "walk past each other" instead of colliding:\n * Collision type 1:\n * R | _ | L\n * _ | RL| _ = _ | LR | _\n * L | _ | R\n * Collision type 2:\n * R | _ | _ | L\n * _ | R | L | _ = _ | L | R | _\n * L | _ | R\n * Note that in both types of collision, we cannot tell wether the robots collided or simply walked past each other\n * Therefore, given a a robot at position `n`, we can easily compute its final position: `n+d` if moving right, or `n-d` if moving left\n\n**Computing sum of pairwise distances**\n\n * Now we need to find the distance between every pair of final positions, i.e. `sum(n_i - n_j), n_i>=n_j`. There are `N*(N-1)` such pairs.\n * If `n_i` is the smallest element, then it will always appear as the negative term when computing the difference with each of the other `N-1` other pairs. So it will contribute `- n_i * (N-1)` to the final result.\n * If `n_i` is the second smallest element, it will appear 1 time as the positive term and `N-2` times as the negative term when computing the difference with other pairs. So it will contribute `n_i * 1 - n_i * (N-2)` to the final result.\n * In general, the `k_th` smallest element will contribute `n_k * (left) - n_k*(right) = n_k * (left-right)`, where `left` and `right` are the number of elements smaller and larger than `n_k`.\n\n```\nclass Solution {\npublic:\n int sumDistance(vector<int>& nums, string s, int d) {\n long long sm = 0;\n int MOD = 1e9+7;\n int N = s.size();\n for(int i=0;i<N;++i){\n nums[i] += d*(s[i]==\'L\'? -1: 1);\n }\n sort(nums.begin(), nums.end());\n for(int i=0;i<N;++i){\n int left = i, right = N-(i+1);\n sm += (long long)nums[i]*(left-right);\n sm %= MOD;\n }\n return sm;\n }\n};\n``` | 0 | 0 | [] | 0 |
movement-of-robots | c++ || easy || prefix sum | c-easy-prefix-sum-by-srajan12-8jx0 | \nclass Solution {\npublic:\n int sumDistance(vector<int>& nums, string s, int d) { \n \n int n = nums.size(); \n v | srajan12 | NORMAL | 2023-06-12T12:52:18.630067+00:00 | 2023-06-12T12:52:18.630114+00:00 | 18 | false | ```\nclass Solution {\npublic:\n int sumDistance(vector<int>& nums, string s, int d) { \n \n int n = nums.size(); \n vector <long long int> nums2(nums.begin(), nums.end());\n for(int i=0; i<n; i++)\n {\n if(s[i]==\'R\') \n nums2[i]+=d;\n else\n nums2[i]-=d;\n } \n sort(nums2.begin(), nums2.end()); \n long long int sum = 0; \n for(int i=1; i<n; i++)\n { \n sum += ( (i*nums2[i]) - nums2[i-1] ); \n sum %= (long long)(1e9 + 7) ; \n nums2[i] += nums2[i-1]; \n } \n return sum;\n }\n};\n``` | 0 | 0 | ['Array', 'Math', 'C', 'Iterator', 'Prefix Sum'] | 0 |
movement-of-robots | Simple prefix sum : movement-of-robot | simple-prefix-sum-movement-of-robot-by-_-ugu0 | Intuition\n Describe your first thoughts on how to solve this problem. \nThere is no difference if we do not perform collision condition as distance between rob | _aanjali | NORMAL | 2023-06-12T12:20:49.984436+00:00 | 2023-06-12T17:14:30.134372+00:00 | 29 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThere is no difference if we do not perform collision condition as distance between robots remain same.\nincrement robot position by 1 if robot direction is RIGHT;\ndecrement robot position by 1 if robot direction is LEFT;\n\n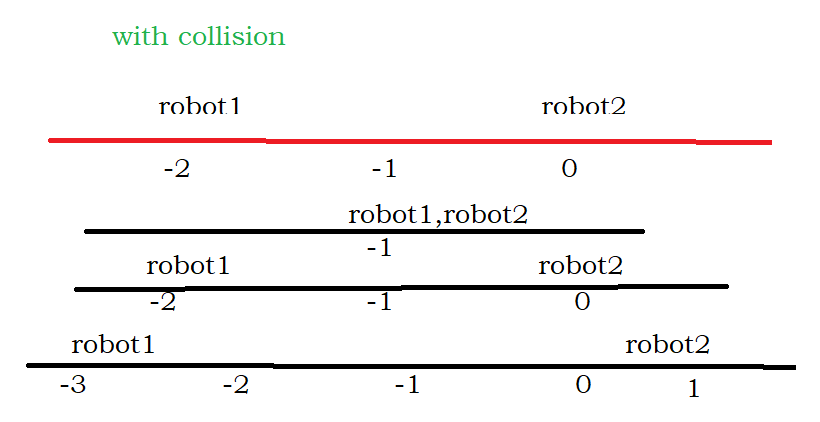\n\n\n\n\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nsum of pair of difference.\n\nprefixsum is\nprefixsum+=nums[i];\n \n\n\n# Complexity\n- Time complexity:O(nlogn): in sorting\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int sumDistance(vector<int>& nums, string s, int d) {\n int n=nums.size();\n int M=1e9+7;\n for(int i=0;i<n;i++){\n if(s[i]==\'R\')\n nums[i]=(nums[i]+d);\n else\n nums[i]=(nums[i]-d);\n }\n int sum=0,prefixsum=0;\n sort(nums.begin(),nums.end());\n for(int i=0;i<n;i++){\n sum=(sum%M+(i*1ll*nums[i]-prefixsum)%M )%M;\n prefixsum=(prefixsum%M+ nums[i]%M)%M;;\n }\n return sum; \n }\n};\n``` | 0 | 0 | ['Prefix Sum', 'C++'] | 0 |
movement-of-robots | c++ || iterative || for loop | c-iterative-for-loop-by-srajan12-13uc | \nclass Solution {\npublic:\n int sumDistance(vector<int>& nums, string s, int d) { \n int n = nums.size();\n \n vector <long lon | srajan12 | NORMAL | 2023-06-12T12:17:48.227978+00:00 | 2023-06-12T12:18:09.010507+00:00 | 4 | false | ```\nclass Solution {\npublic:\n int sumDistance(vector<int>& nums, string s, int d) { \n int n = nums.size();\n \n vector <long long int> nums2(nums.begin(), nums.end());\n for(int i=0; i<n; i++)\n {\n if(s[i]==\'R\')\n {\n nums2[i]+=d;\n }\n else\n {\n nums2[i]-=d;\n } \n } \n sort(nums2.begin(), nums2.end()); \n long long int sum = 0;\n for(int i=0; i<n; i++)\n {\n sum += (i -(n-i-1))*nums2[i];\n sum %= (long long)(1e9 + 7) ; \n }\n return sum;\n }\n};\n``` | 0 | 0 | ['Array', 'Math', 'C', 'Iterator'] | 0 |
movement-of-robots | JAVA || Easy Explanation | java-easy-explanation-by-dhananjay2001-28m7 | Intuition\nDon\'t think about directions.\n1. Just add d in nums[i] if R ,\n2. otherwise subtract d from nums[i]\n3. and add differenc of each.\n\nThis are simp | dhananjay2001 | NORMAL | 2023-06-12T05:56:39.298182+00:00 | 2023-06-12T05:57:11.264372+00:00 | 44 | false | # Intuition\nDon\'t think about directions.\n1. Just add d in nums[i] if R ,\n2. otherwise subtract d from nums[i]\n3. and add differenc of each.\n\nThis are simple Steps but Calculation of difference sum is main part.\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nAfter moving all the steps d time take sum:\n1. Sort the array so u will get correct difference sum.\n\nExaplaination ---------------------------\nIt is like a1+a2+a3 ->\n (a1-a2) + (a1-a3) + (a2-a3) => 2 * a1 + 0 * a2 + (-2) * a3\n\nDifference is so simple to calculate with above ,if u observe.\n .---------------------------------------------------------------\n\n2. So from above we can say it is multiple of (length of nums minus 1)\ndecrease it by 2 in each iteration for each term of equation.\n3. Take mod in each step .\n4. Remember to take a long var to store ans and typecast it at last.\n \n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(nlog(n))\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n final int mod = 1_000_000_007;\n public int sumDistance(int[] nums, String s, int d) {\n \n for(int i=0;i<nums.length;i++){\n if(s.charAt(i)==\'R\'){\n nums[i]+=d;\n }else{\n nums[i]-=d;\n }\n }\n long ans=0;\n int n=nums.length-1;\n Arrays.sort(nums);\n for(int i=0;i<nums.length;i++){\n ans+=((n)*(long)nums[i]);\n ans%=mod;\n n-=2;\n }\n return (int) -ans%mod;\n }\n}\n``` | 0 | 0 | ['Java'] | 2 |
movement-of-robots | C++ | Tricky yet VV Easy question | O(nlogn) | c-tricky-yet-vv-easy-question-onlogn-by-wongw | Approach\n Describe your approach to solving the problem. \nWe see the robots coliding and moving to its own position again, yet we can observe even if the coli | leet_alok | NORMAL | 2023-06-12T05:13:27.322715+00:00 | 2023-06-12T05:13:27.322762+00:00 | 24 | false | # Approach\n<!-- Describe your approach to solving the problem. -->\nWe see the robots coliding and moving to its own position again, yet we can observe even if the colision never happened the robots would be found in those places anyhow. As we are not concerned about any specific robots we can consider all as one and consider the same robot kept on moving int he same direction. And to find the difference we used prefix sum method. As for:a,b,c,d Difference of d with all 3 is 3*d-(a+b+c).\n\n\n# Code\n```\nint M = 1000000007;\nclass Solution {\npublic:\n int sumDistance(vector<int>& nums, string s, int d) {\n for(int i=0;i<nums.size();i++){\n if(s[i]==\'R\')nums[i]+=d;\n else nums[i]-=d;\n }\n long pre=0,sum=0;\n sort(nums.begin(),nums.end());\n for(int i=0;i<nums.size();i++){\n sum=(sum+i*(long)nums[i]-pre)%M;\n pre+=(nums[i]%M);\n }\n return (int)sum;\n }\n};\n\n``` | 0 | 0 | ['C++'] | 0 |
movement-of-robots | C# | c-by-kpzeus-2xf9 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | kpzeus | NORMAL | 2023-06-12T02:27:25.631143+00:00 | 2023-06-12T02:27:25.631171+00:00 | 21 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\npublic class Solution {\n private int MOD = 1000000007;\n\n public int SumDistance(int[] nums, string s, int d)\n {\n for (int i = 0; i < nums.Length; i++)\n {\n if (s[i] == \'R\')\n nums[i] += d;\n else\n nums[i] -= d;\n }\n\n long ans = 0;\n long pref = 0;\n Array.Sort(nums);\n long n = s.Length - 1;\n\n for (long i = 0; i < nums.Length; i++)\n {\n ans += i * (long)nums[(int)i] - pref;\n ans %= MOD;\n pref += nums[(int)i];\n }\n\n return (int)ans;\n }\n}\n``` | 0 | 0 | ['C#'] | 0 |
movement-of-robots | [C] | c-by-zhang_jiabo-v2af | C []\r\n#define MODULO (1000000007)\r\n\r\nstatic int cmp_int_asc(const int * const p1, const int * const p2){\r\n\tif (*p1 < *p2){\r\n\t\treturn -1;\r\n\t}else | zhang_jiabo | NORMAL | 2023-06-11T21:15:27.426268+00:00 | 2023-06-11T21:15:27.426312+00:00 | 19 | false | ```C []\r\n#define MODULO (1000000007)\r\n\r\nstatic int cmp_int_asc(const int * const p1, const int * const p2){\r\n\tif (*p1 < *p2){\r\n\t\treturn -1;\r\n\t}else if (*p1 > *p2){\r\n\t\treturn 1;\r\n\t}else {\r\n\t\treturn 0;\r\n\t}\r\n}\r\n\r\nint sumDistance(\r\n\tint * const nums,\r\n\tconst int numsLen,\r\n\tconst char * const s,\r\n\tconst int d\r\n){\r\n\tfor (int i = 0; i < numsLen; i += 1){\r\n\t\tswitch (s[i]){\r\n\t\tcase \'L\':\r\n\t\t\tnums[i] -= d;\r\n\t\t\tbreak;\r\n\t\tcase \'R\':\r\n\t\t\tnums[i] += d;\r\n\t\t\tbreak;\r\n\t\tdefault:\r\n\t\t\tassert(0);\r\n\t\t}\r\n\t}\r\n\r\n\tqsort(nums, numsLen, sizeof (int), &cmp_int_asc);\r\n\r\n\tint totalCost = 0;\r\n\r\n\tint64_t prefixSum = 0;\r\n\tfor (int i = 1; i < numsLen; i += 1){\r\n\t\tprefixSum += ( (int64_t)nums[i] - nums[i - 1] ) * i;\r\n\t\tprefixSum %= MODULO;\r\n\r\n\t\ttotalCost += prefixSum;\r\n\t\ttotalCost %= MODULO;\r\n\t}\r\n\r\n\treturn totalCost;\r\n}\r\n``` | 0 | 0 | ['C'] | 0 |
movement-of-robots | C++ | Math | Easy Solution | c-math-easy-solution-by-hulkioro-lilk | Please UpVote if it helps you\nApproach - don\'t think that robots are colliding each other, just add the d or subtract on ith robot\'s position if ith string i | Hulkioro | NORMAL | 2023-06-11T18:49:51.178370+00:00 | 2023-06-11T18:49:51.178404+00:00 | 36 | false | # Please UpVote if it helps you\nApproach - don\'t think that robots are colliding each other, just add the `d` or subtract on `ith` robot\'s position if `ith` string is `R` and `L` respectively.\n\n# Code\n```\nclass Solution {\npublic:\n int sumDistance(vector<int>& nums, string s, int d) {\n int n = nums.size();\n for(int i=0;i<n;++i){\n if(s[i]==\'L\'){\n nums[i] -= d;\n }\n else nums[i] += d;\n }\n sort(nums.begin(),nums.end());\n long long sum = accumulate(nums.begin(),nums.end(),0LL);\n long long ans = 0;\n int mod = 1e9+7;\n // take the sum of each pair\n for(int i=0;i<n;++i){\n sum -= nums[i];\n ans +=abs( (long long)(n-i-1)*(nums[i]) - sum);\n ans %= mod;\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['Math', 'Greedy', 'Brainteaser', 'Sorting', 'C++'] | 0 |
movement-of-robots | python solution | python-solution-by-choijong-o889 | Code\n\nclass Solution:\n def sumDistance(self, nums: List[int], s: str, d: int) -> int:\n \n mod = 1000000007\n ans = 0\n ln = l | choijong | NORMAL | 2023-06-11T18:36:25.732480+00:00 | 2023-06-11T18:36:25.732508+00:00 | 18 | false | # Code\n```\nclass Solution:\n def sumDistance(self, nums: List[int], s: str, d: int) -> int:\n \n mod = 1000000007\n ans = 0\n ln = len(nums)\n \n for i in range(ln):\n if s[i] == \'L\':\n nums[i] -= d\n else:\n nums[i] += d\n \n nums.sort()\n\n cnt = 1\n for i in range(1, len(nums)):\n multiplier = (ln - i) * cnt\n diff = abs(nums[i] - nums[i-1])\n ans += diff * multiplier\n cnt += 1\n \n return int(ans % mod)\n``` | 0 | 0 | ['Python3'] | 0 |
movement-of-robots | ✅Fully Explained || Ant on Planks || Trilogy 2022 || C++ | fully-explained-ant-on-planks-trilogy-20-dw3w | Intuition\n Describe your first thoughts on how to solve this problem. \nBefore solving this question, if you have solved the problem Ant on planks, it would he | intern_grind | NORMAL | 2023-06-11T13:22:43.802563+00:00 | 2023-06-11T13:22:43.802596+00:00 | 36 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nBefore solving this question, if you have solved the problem Ant on planks, it would help you a lot to think the next step in this question.\n\nSo the intuition is to think that image robots to pass each other and just ignore about collision and think after it. \n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nSo now, after d time, we can calculate the position of every robot. Now we just need to find the distance between every pair.\nIt can be done in $O(n^2)$ but we should be able to do it in $O(n)$.\n\nNow visualize the following scenario.\n\n[A,B,C,D].\nEach letter represents final position of each robot in the number line.\nSo the distance can be calculated as below.\n\n$D \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ C \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ \\ B$ \n$\nD-c\\ \\ \\ \\ \\ C-b \\ \\ \\ \\ \\ B -a\\\\\nD-b\\ \\ \\ \\ \\ C -a\\\\\nD-a\\\\\n$\nFrom this we can relate how we can use prefix sum.\nWe start with first index and keep prefix sum=0;\nNow when we are at $ith$ index there will be i robots before us. So we can multiply $i$ by $position[i]$ and subtract a prefix_sum.\n\nMake sure to use MOD properly.\n# Complexity\n- Time complexity:$O(n) + O(nlogn) + O(n)$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$O(n)$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int sumDistance(vector<int>& nums, string s, int d) \n {\n const int MOD = 1e9+7;\n int n=nums.size();\n for(int i =0;i<nums.size();i++)\n {\n long long temp=nums[i];\n if(s[i]==\'R\') temp=temp+d;\n else temp=temp-d;\n nums[i]=temp;\n }\n sort(nums.begin(),nums.end());\n long long ans=0;\n long long pref=0;\n for(int i =0;i<nums.size();i++)\n {\n ans = ans%MOD + (i*(long long)nums[i]-pref)%MOD;\n pref = pref+nums[i];\n }\n return ans%MOD;\n \n }\n};\n``` | 0 | 0 | ['Brainteaser', 'Prefix Sum', 'C++'] | 0 |
movement-of-robots | C++ Easy to understand, steps given, TC(nlogn), SC O(1), not prefixsum | c-easy-to-understand-steps-given-tcnlogn-4dtd | Steps\n- There won\'t be any effect of collision, you can see that by taking example and doing yourself\n- So, the main part was to find, Sum of absolute diffe | Adi_217 | NORMAL | 2023-06-11T13:07:15.916868+00:00 | 2023-06-11T13:07:15.916906+00:00 | 7 | false | # Steps\n- There won\'t be any effect of collision, you can see that by taking example and doing yourself\n- So, the main part was to find, Sum of absolute differences of all pairs in modified vector of positions\n- For this refer to this gfg post https://www.geeksforgeeks.org/sum-absolute-differences-pairs-given-array/\n\n# Complexitymath\n- Time complexity:\n-- O(n*logn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n-- O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n//https://www.geeksforgeeks.org/sum-absolute-differences-pairs-given-array/\n//An efficient solution for this problem needs a simple observation. \n//Since array is sorted and elements are distinct \n//when we take sum of absolute difference of pairs \n//each element in the i\u2019th position is added \u2018i\u2019 times \n//and subtracted \u2018n-1-i\u2019 times. \n\n//SUMMARY\n//ith element will be added i time and subtracted (n-1-i) times\n\n int sumDistance(vector<int>& nums, string s, int d) {\n int n = nums.size();\n long long mod = 1e9+7;\n\n //modify the positions O(n)\n for(int i=0;i<n;i++) {\n if(s[i]==\'R\') nums[i]+=d;\n else nums[i]-=d;\n }\n\n if(n==2) return (abs(nums[0]-nums[1]))%mod;\n\n //sorting O(nlogn)\n sort(nums.begin(), nums.end());\n \n long long ans = 0;\n\n //O(n)\n for(int i=0;i<n;i++) {\n long long add = (long long)(i);\n long long minus = (long long)(n-1-i);\n long long final = ((add - minus)*(long long)(nums[i]))%mod;\n ans = (ans + final)%mod;\n }\n return ans;\n }\n};\n``` | 0 | 0 | ['Math', 'Sorting', 'C++'] | 0 |
movement-of-robots | Easy C++ Solution and easy to understand. | easy-c-solution-and-easy-to-understand-b-enq6 | Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time | harshguptamanit2020 | NORMAL | 2023-06-11T11:24:02.297341+00:00 | 2023-06-11T11:24:02.297384+00:00 | 29 | false | # Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int sumDistance(vector<int>& nums, string s, int d) {\n int mod = 1000000007;\n int n = nums.size();\n \n for (int i = 0; i < n; i++){\n if (s[i] == \'L\')\n nums[i] -= d;\n else \n nums[i] += d;\n }\n sort(nums.begin(), nums.end());\n long long sum =0 , ans =0;\n for(long long i=0 ; i<n ; i++){\n ans = (ans + (nums[i] * i - sum)%mod)%mod;\n sum = (sum + nums[i])%mod;\n }\n return ans; \n }\n};\n``` | 0 | 0 | ['C++'] | 0 |
movement-of-robots | Kotlin O(nlogn) sort + prefix sum (with comment) | kotlin-onlogn-sort-prefix-sum-with-comme-4vbs | Code\n\nclass Solution {\n fun sumDistance(nums: IntArray, s: String, d: Int): Int {\n val mod = 1000000007\n\n /*\n * Ignore direction | aliam | NORMAL | 2023-06-11T11:17:59.446617+00:00 | 2023-06-11T11:17:59.446665+00:00 | 14 | false | # Code\n```\nclass Solution {\n fun sumDistance(nums: IntArray, s: String, d: Int): Int {\n val mod = 1000000007\n\n /*\n * Ignore direction changes, since we don\'t need to track robots, and if a robot x and\n * a robot y meet, and change directions we can look at it as if the two robots continued\n * on the same path/direction without changing direction. Keep long array to avoid Integer overflow\n */\n val afterMove = LongArray (nums.size).apply {\n for (i in 0 until nums.size) {\n if (s[i] == \'L\') this[i] = (nums[i] - d).toLong()\n else this[i] = (nums[i] + d).toLong()\n }\n }\n \n // sort the robot positions in order to calculate the sum\n // of the distances of all robots in one sweep below\n afterMove.sort()\n\n /*\n * To avoid comparing all pairs of (i, j) and calculate in O(n^2),\n * we use a prefix sum to calculate this in O(n) + sorting of O(nlogn)\n */\n var res = 0L\n var prefix = 0L\n for (i in 1 until afterMove.size) {\n prefix += i * (afterMove[i] - afterMove[i - 1])\n res = (res + prefix) % mod\n }\n\n return res.toInt()\n }\n}\n``` | 0 | 0 | ['Kotlin'] | 0 |
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.