question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
maximum-value-of-k-coins-from-piles
|
Python 3 || 9 lines, recursion || T/S: 78% / 91%
|
python-3-9-lines-recursion-ts-78-91-by-s-yqw4
|
\nclass Solution:\n def maxValueOfCoins(self, piles: List[List[int]], k: int) -> int:\n \n @lru_cache(None)\n def dfs(coins, moves):\n
|
Spaulding_
|
NORMAL
|
2023-04-15T16:53:34.275882+00:00
|
2024-06-13T02:07:17.653179+00:00
| 238
| false
|
```\nclass Solution:\n def maxValueOfCoins(self, piles: List[List[int]], k: int) -> int:\n \n @lru_cache(None)\n def dfs(coins, moves):\n if len(piles) == coins: return 0\n\n ans, curr, pile = dfs(coins+1, moves), 0, piles[coins]\n\n for j in range(min(len(pile), moves)):\n curr += pile[j]\n ans = max(ans, curr + dfs(coins+1, moves-j-1))\n\n return ans\n \n return dfs(0,k)\n```\n[https://leetcode.com/problems/maximum-value-of-k-coins-from-piles/submissions/1286535343/\n](https://leetcode.com/problems/maximum-value-of-k-coins-from-piles/submissions/1286535343/\n)\nI could be wrong, but I think that time complexity is *O*(*N* * *K*) and space complexity is *O*(*N* * *K*).
| 8
| 0
|
['Python3']
| 0
|
maximum-value-of-k-coins-from-piles
|
[GoLang] Recursive -> Mem Optimised DP
|
golang-recursive-mem-optimised-dp-by-dko-wi0d
|
Intuition\nWe need to find a Min/Max of something in an array/matrix => It\'s a Dynamic Programming problem (rarely a Greedy problem).\n\n# Approach - Simple re
|
dkochetov
|
NORMAL
|
2023-04-15T11:06:30.517421+00:00
|
2023-04-15T16:27:29.415061+00:00
| 159
| false
|
# Intuition\nWe need to find a Min/Max of something in an array/matrix => It\'s a Dynamic Programming problem (rarely a Greedy problem).\n\n# Approach - Simple recursive function\nDon\'t try to write a final optimized code from the start, it will break your mind. Always start with defining a recursive function:\n\n`rec(pile_idx, used) = max_over_j(sum_of_j_coins_from_this_pile + rec(pile_idx + 1, used - j)`\nAnd the answer can be found with `rec(0, k)`\n\nThe following code works fine with small test cases but will hit the TimeLimit if you submit it. Check out the next approach.\n\n\n# Code - Simple recursive function\n```\nfunc maxValueOfCoins(piles [][]int, k int) int {\n n := len(piles)\n\n var rec func(int, int) int\n rec = func(i int, used int) int {\n if i == n { return 0 }\n accum := 0\n res := rec(i+1, used)\n for j:=0; j<min(len(piles[i]), used); j++ {\n accum += piles[i][j]\n res = max(res, accum + rec(i+1, used-j-1))\n }\n return res\n }\n return rec(0, k)\n}\n\nfunc min(a, b int) int {\n if a < b { return a }\n return b\n}\nfunc max(a, b int) int {\n if a > b { return a }\n return b\n}\n```\n\n---\n\n# Approach - Recursive function with Memo\nCreate a memo matrix with size of `len(piles)\u22C5k` and use it for caching `rec()` results. It will pass all test cases.\n\n\n\n# Code - Recursive function with Memo\n\n```\nfunc maxValueOfCoins(piles [][]int, k int) int {\n n := len(piles)\n memo := make([][]int, n)\n for i := range memo {\n memo[i] = make([]int, k+1)\n }\n\n var rec func(int, int) int\n rec = func(i int, used int) int {\n if i == n { return 0 }\n if memo[i][used] > 0 { return memo[i][used] }\n accum := 0\n res := rec(i+1, used)\n for j:=0; j<min(len(piles[i]), used); j++ {\n accum += piles[i][j]\n res = max(res, accum + rec(i+1, used-j-1))\n }\n memo[i][used] = res\n return res\n }\n return rec(0, k)\n}\n\nfunc min(a, b int) int {\n if a < b { return a }\n return b\n}\nfunc max(a, b int) int {\n if a > b { return a }\n return b\n}\n```\n\n---\n\n# Approach - Bottom-up DP\nWe understand how our memo matrix must look like and how we can fill it in recursively. Now we need to do the same using loops.\n\nTraverse all `piles` and `used` in a nested loop and change `rec(i+1, used)` into `memo[i+1][used]`. Almost all the code remains the same (that\'s the neat part of this process).\n\n\n\n# Code - Bottom-up DP\n\n```\nfunc maxValueOfCoins(piles [][]int, k int) int {\n n := len(piles)\n memo := make([][]int, n+1)\n for i := range memo {\n memo[i] = make([]int, k+1)\n }\n\n for i:=n-1; i>=0; i-- {\n for used:=0; used<=k; used++ {\n accum := 0\n res := memo[i+1][used]\n for j:=0; j<min(len(piles[i]), used); j++ {\n accum += piles[i][j]\n res = max(res, accum + memo[i+1][used-j-1])\n }\n memo[i][used] = res\n }\n }\n return memo[0][k]\n}\n\nfunc min(a, b int) int {\n if a < b { return a }\n return b\n}\nfunc max(a, b int) int {\n if a > b { return a }\n return b\n}\n```\n\n---\n\n# Approach - Bottom-up Mem Optimised DP\nNotice that we need only the values from `memo[i]` and `memo[i+1]`, so no need to keep the whole matrix in the memory. Just create a one dimensional list `dp` of size `k`.\n\n\n\n# Code - Bottom-up Mem Optimised DP\n\n```\nfunc maxValueOfCoins(piles [][]int, k int) int {\n n := len(piles)\n dp := make([]int, k+1)\n\n for i:=n-1; i>=0; i-- {\n for used:=k; used>=0; used-- {\n accum := 0\n res := dp[used]\n for j:=0; j<min(len(piles[i]), used); j++ {\n accum += piles[i][j]\n res = max(res, accum + dp[used-j-1])\n }\n dp[used] = res\n }\n }\n return dp[k]\n}\n\nfunc min(a, b int) int {\n if a < b { return a }\n return b\n}\nfunc max(a, b int) int {\n if a > b { return a }\n return b\n}\n```\n\n### Do some code optimisations\n\n```\nfunc maxValueOfCoins(piles [][]int, k int) int {\n dp := make([]int, k+1)\n\n for i := range piles {\n for used:=k; used>=0; used-- {\n accum := 0\n for j:=0; j<min(len(piles[i]), used); j++ {\n accum += piles[i][j]\n dp[used] = max(dp[used], accum + dp[used-j-1])\n }\n }\n }\n return dp[k]\n}\n\nfunc min(a, b int) int {\n if a < b { return a }\n return b\n}\nfunc max(a, b int) int {\n if a > b { return a }\n return b\n}\n```\n\n\n# Complexity\n- Time complexity: $$O(totalCoinsNum\u22C5k)$$\n\n- Space complexity: $$O(k)$$
| 8
| 0
|
['Array', 'Dynamic Programming', 'Recursion', 'Matrix', 'Go']
| 0
|
maximum-value-of-k-coins-from-piles
|
✅C++ || EASY DP (Recursive + Memoization)
|
c-easy-dp-recursive-memoization-by-chiik-61ht
|
Code\n\nclass Solution {\n #define ll long long\npublic:\n int c(vector<vector<int>>& p,int i,int k,vector<vector<int>>&dp){\n if(k==0)return 0;\n
|
CHIIKUU
|
NORMAL
|
2023-04-15T08:08:52.057511+00:00
|
2023-04-15T08:08:52.057542+00:00
| 1,021
| false
|
# Code\n```\nclass Solution {\n #define ll long long\npublic:\n int c(vector<vector<int>>& p,int i,int k,vector<vector<int>>&dp){\n if(k==0)return 0;\n if(i>=p.size())return 0;\n if(dp[i][k]!=-1)return dp[i][k];\n int ans=0;\n int mx=c(p,i+1,k,dp);\n for(int j=0;j<p[i].size();j++){\n ans += p[i][j];\n if(k>=j+1)\n mx = max(mx,ans+c(p,i+1,k-j-1,dp));\n else break;\n }\n dp[i][k]=mx;\n return mx;\n }\n int maxValueOfCoins(vector<vector<int>>& p, int k) {\n int n=p.size();\n vector<vector<int>>dp(n,vector<int>(k+1,-1));\n return c(p,0,k,dp);\n }\n};\n```\n\n
| 7
| 1
|
['Dynamic Programming', 'Prefix Sum', 'C++']
| 6
|
maximum-value-of-k-coins-from-piles
|
C++ | Memoization
|
c-memoization-by-vaibhavshekhawat-hxxi
|
```\nvector> dp;\n int func(vector>& p,int i,int k){\n if(i==p.size()) return 0;\n if(dp[i][k]!=-1) return dp[i][k];\n int ans=func(p,i+
|
vaibhavshekhawat
|
NORMAL
|
2022-03-27T04:02:48.906995+00:00
|
2022-03-27T04:04:22.675569+00:00
| 620
| false
|
```\nvector<vector<int>> dp;\n int func(vector<vector<int>>& p,int i,int k){\n if(i==p.size()) return 0;\n if(dp[i][k]!=-1) return dp[i][k];\n int ans=func(p,i+1,k);\n int a=0;\n for(int j=0;j<p[i].size()&&j<k;j++){\n a+=p[i][j];\n ans=max(ans,a+func(p,i+1,k-j-1));\n }\n return dp[i][k]=ans;\n }\n int maxValueOfCoins(vector<vector<int>>& p, int k) {\n dp=vector<vector<int>>(p.size(),vector<int>(k+1,-1));\n return func(p,0,k);\n }
| 7
| 0
|
['Dynamic Programming', 'Memoization', 'C']
| 0
|
maximum-value-of-k-coins-from-piles
|
[Java] Bottom Up DP
|
java-bottom-up-dp-by-nihalanim9-ei1k
|
\nclass Solution {\n public int maxValueOfCoins(List<List<Integer>> piles, int k) {\n int n = piles.size();\n int[][] ans = new int[n+1][2001];
|
nihalanim9
|
NORMAL
|
2022-03-27T04:01:09.007094+00:00
|
2022-03-27T04:01:09.007139+00:00
| 972
| false
|
```\nclass Solution {\n public int maxValueOfCoins(List<List<Integer>> piles, int k) {\n int n = piles.size();\n int[][] ans = new int[n+1][2001];\n Collections.sort(piles, (List<Integer> a, List<Integer> b) -> b.size() - a.size());\n for(int i = 1; i <= k; i++) {\n for(int j = 1; j <= n; j++) {\n int sizeOfPile = piles.get(j-1).size();\n List<Integer> pile = piles.get(j-1);\n int sum = 0;\n ans[j][i] = ans[j-1][i];\n for(int l = 1; l <= Math.min(i, sizeOfPile); l++) {\n // Take K from this pile + remaining from previous piles\n sum += pile.get(l-1);\n int rem = i - l;\n ans[j][i] = Math.max(ans[j][i], sum + ans[j-1][rem]);\n }\n }\n }\n \n return ans[n][k];\n }\n}\n```
| 7
| 0
|
['Dynamic Programming', 'Java']
| 1
|
maximum-value-of-k-coins-from-piles
|
🏆SPACE OPTIMISED - 💯TABULATION - ✅MEMOIZATION - ❗️RECURSION
|
space-optimised-tabulation-memoization-r-e16j
|
Intuition\nThe problem is to maximize the sum of k coins collected from n piles of coins, where each pile has a different number of coins. The constraint is tha
|
bose_aritra2003
|
NORMAL
|
2023-04-15T05:25:28.359962+00:00
|
2023-04-15T05:42:23.106219+00:00
| 369
| false
|
# Intuition\nThe problem is to maximize the sum of k coins collected from n piles of coins, where each pile has a different number of coins. The constraint is that you can only take coins from the top of each pile. The given solution uses a depth-first search (DFS) approach to explore all possible choices of taking coins from different piles and computes the maximum sum of coins that can be collected.\n\n<hr>\n\n# Approach\nThe solution is implemented using a recursive function `helper()` which takes three parameters: `idx` (the current pile index), `coins` (the number of coins left to collect), and `piles` (the 2D vector of piles with coins).\n\nThe base case for the recursion is when the current pile index `idx` reaches the total number of `piles`. In this case, the function `returns 0`, as no more coins can be collected.\n\nThe main logic is divided into two cases:\n1. Not taking any coins from the current pile, in which case we move to the next pile by calling the `helper()` function with `idx + 1` and the same number of coins left to collect.\n2. Taking some coins from the current pile. In this case, we iterate through the coins in the current pile, taking at most `min(n, coins)` coins, where n is the total number of coins in the current pile. For each coin taken, we add its value to the `curr_total`, and then call the `helper()` function for the next pile with `idx + 1` and the updated number of coins left to collect `(coins - i - 1)`. We keep track of the maximum total coins collected in `max_total`.\n\nIn the end, the helper function returns `max_total` which is the maximum sum of coins that can be collected by considering all possible choices of taking coins from the current pile and subsequent piles.\n\nThe main function `maxValueOfCoins()` initiates the recursion by calling the `helper()` function with `idx = 0` (starting pile) and `coins = k` (the total number of coins to collect).\n<hr>\n\n# Implementations\n\n## Recursion - _Time Limit Exceeded_ \u203C\uFE0F\n```\nclass Solution {\nprivate:\n int helper(int idx, int coins, vector<vector<int>>& piles) {\n //Base case\n if(idx == piles.size()) {\n return 0;\n }\n\n //Explore all paths\n int n = piles[idx].size();\n\n //Path 1 - Not take any coin from the current pile\n int max_total = helper(idx + 1, coins, piles);\n\n //Path 2 - Take (i + 1) number of coins from the current pile\n int curr_total = 0;\n for(int i = 0; i < min(n, coins); i++) {\n curr_total += piles[idx][i];\n int next_total = helper(idx + 1, coins - i - 1, piles);\n max_total = max(max_total, curr_total + next_total);\n }\n return max_total;\n }\npublic:\n int maxValueOfCoins(vector<vector<int>>& piles, int k) {\n return helper(0, k, piles);\n }\n};\n```\n\nIf `k` is the number of coins to collect, `m` is the number of piles and `n` is the total number of coins in all piles then:\n- **Time complexity:** $$O(k^n)$$\n\n- **Space complexity:** $$O(k * m)$$\n<hr>\n\n## Memoization (Top-Down) - _Accepted_ \u2705\nIt can be clearly seen from the recursive approcah that we are doing a lot of repeated work and there are overlapping sub-problems hence we can use dynamic programming to optimise out recursive approach. So let us memoize our recursion.\n```\nclass Solution {\nprivate:\n int helper(int idx, int coins, vector<vector<int>>& piles, vector<vector<int>>& dp) {\n //Base case\n if(idx == piles.size()) {\n return 0;\n }\n if(dp[idx][coins] != -1) {\n return dp[idx][coins];\n }\n\n //Explore all paths\n int n = piles[idx].size();\n\n //Path 1 - Not take any coin from the current pile\n int max_total = helper(idx + 1, coins, piles, dp);\n\n //Path 2 - Take (i + 1) number of coins from the current pile\n int curr_total = 0;\n for(int i = 0; i < min(n, coins); i++) {\n curr_total += piles[idx][i];\n int next_total = helper(idx + 1, coins - i - 1, piles, dp);\n max_total = max(max_total, curr_total + next_total);\n }\n return dp[idx][coins] = max_total;\n }\npublic:\n int maxValueOfCoins(vector<vector<int>>& piles, int k) {\n int n = piles.size();\n vector<vector<int>> dp(n + 1, vector<int>(k + 1, -1));\n return helper(0, k, piles, dp);\n }\n};\n```\n\nIf `k` is the number of coins to collect, `m` is the number of piles and `n` is the total number of coins in all piles then:\n- **Time complexity:** $$O(k * n)$$\n\n- **Space complexity:** $$O(k * m)$$\n<hr>\n\n## Tabulation (Bottom-Up) - _Accepted_ \u2705\u2705\nLet us now tabulise the memoization solution that we did above.\n```\nclass Solution {\npublic:\n int maxValueOfCoins(vector<vector<int>>& piles, int k) {\n int m = piles.size();\n vector<vector<int>> dp(m + 1, vector<int>(k + 1, 0));\n for(int idx = m - 1; idx >= 0; idx--) {\n for(int coins = 1; coins <= k; coins++) {\n //Explore all paths\n int n = piles[idx].size();\n\n //Path 1 - Not take any coin from the current pile\n int max_total = dp[idx + 1][coins];\n\n //Path 2 - Take (i + 1) number of coins from the current pile\n int curr_total = 0;\n for(int i = 0; i < min(n, coins); i++) {\n curr_total += piles[idx][i];\n int next_total = dp[idx + 1][coins - i - 1];\n max_total = max(max_total, curr_total + next_total);\n }\n dp[idx][coins] = max_total; \n }\n }\n return dp[0][k];\n }\n};\n```\n\nIf `k` is the number of coins to collect, `m` is the number of piles and `n` is the total number of coins in all piles then:\n- **Time complexity:** $$O(k * n)$$\n\n- **Space complexity:** $$O(k * m)$$\n<hr>\n\n## Space Optimised Tabulation - _Accepted_ \u2705\u2705\u2705\nFrom the above tabulation code we can observe that the current pile `(dp[idx])` is always dependant on the next pile `(dp[idx + 1])`. So why not just keep 2 vectors of size `k + 1` each, one for `dp[idx]` and one for `dp[idx + 1]`. In this way we can save a lot of space by just computing two rows of the dp table at any instant instead of the entire `k x n` grid.\n```\nclass Solution {\npublic:\n int maxValueOfCoins(vector<vector<int>>& piles, int k) {\n int m = piles.size();\n vector<int> curr(k + 1), next(k + 1, 0);\n for(int idx = m - 1; idx >= 0; idx--) {\n for(int coins = 1; coins <= k; coins++) {\n //Explore all paths\n int n = piles[idx].size();\n\n //Path 1 - Not take any coin from the current pile\n int max_total = next[coins];\n\n //Path 2 - Take (i + 1) number of coins from the current pile\n int curr_total = 0;\n for(int i = 0; i < min(n, coins); i++) {\n curr_total += piles[idx][i];\n int next_total = next[coins - i - 1];\n max_total = max(max_total, curr_total + next_total);\n }\n curr[coins] = max_total; \n }\n next = curr; //Make next = current for the next iteration\n }\n return next[k];\n }\n};\n```\n\nIf `k` is the number of coins to collect, `m` is the number of piles and `n` is the total number of coins in all piles then:\n- **Time complexity:** $$O(k * n)$$\n\n- **Space complexity:** $$O(k)$$\n<hr>\n\n\uD83D\uDE4F **_If you like the entire explanation and all the implementations I showed, please do take a moment to upvote this post._** \uD83D\uDE4F
| 6
| 0
|
['Dynamic Programming', 'Recursion', 'Memoization', 'C++']
| 1
|
maximum-value-of-k-coins-from-piles
|
Easy || C++ || DP
|
easy-c-dp-by-amankatiyar783597-yr6s
|
Intuition\nSome point that are directly hit to mind.\nif we take piles[i][j] coin we need to take all the coins above index j in that i pile.\n\nfrom above we c
|
amankatiyar783597
|
NORMAL
|
2023-04-15T04:13:23.046312+00:00
|
2023-04-15T04:13:23.046340+00:00
| 1,469
| false
|
# Intuition\nSome point that are directly hit to mind.\n`if we take piles[i][j] coin we need to take all the coins above index j in that i pile.`\n\n`from above we can conlude that instead of taking one by one coin from a given row we take in bunch`\n\n# Approach\n\n`TRY ALL POSSIBLE WAYS`\n\n`To take bunch of coins we used presum of all indivisual piles of coins`\n```\nfor(int i=0;i<n;i++){\n int su=0;\n for( int a : pp[i]){\n pre[i].push_back(su);\n su+=a;\n }\n pre[i].push_back(su);\n}\n```\nZero index means we are not taking any coin from that pile.\n\nNow we can take connect whole problem to 0/1 knapsack\n\nNeed to select a index from every presum of piles of coins and add to aur answer , and eqaully dicreasing count of k.\n\n`NOW USE DP`\n\nHere we can easily see only current number of pile and count remaning to add (k) is changing in our recursive code.\n\nso lets make 2D DP vector to store. \n\n# Complexity\n- Time complexity:\nO(N2) {mota mota}\n\n- Space complexity:\nO(N*K)\n\n# Code\n```\nclass Solution {\npublic:\n\n int fun(vector<vector<int>> &pp , int cu , int k, vector<vector<int>> &dp ){\n if(cu>=pp.size()) return 0;\n if(dp[cu][k] != -1 ) return dp[cu][k];\n int mx=0;\n for(int i=0;i<pp[cu].size();i++){\n if(k-i>=0) mx = max(mx , pp[cu][i]+fun(pp,cu+1,k-i,dp));\n }\n return dp[cu][k] = mx;\n }\n\n int maxValueOfCoins(vector<vector<int>>& pp, int k) {\n int n = pp.size();\n vector<vector<int>> pre(n);\n vector<vector<int>> dp(n+2,vector<int>(k+2,-1));\n for(int i=0;i<n;i++){\n int su=0;\n for( int a : pp[i]){\n pre[i].push_back(su);\n su+=a;\n }\n pre[i].push_back(su);\n }\n return fun(pre,0,k,dp);\n }\n};\n```
| 6
| 2
|
['C++']
| 1
|
maximum-value-of-k-coins-from-piles
|
C++ RECURSION + TOP-DOWN
|
c-recursion-top-down-by-abhishek26149-s57u
|
// recursion \n\nint solve(vector<vector<int>>& arr,int i,int k,int n){\n if (k==0 || i==n)\n {\n return 0;\n }\n int ans=0;\n for (int j
|
Abhishek26149
|
NORMAL
|
2022-10-24T08:22:32.359178+00:00
|
2022-10-24T08:30:01.670916+00:00
| 651
| false
|
// recursion \n```\nint solve(vector<vector<int>>& arr,int i,int k,int n){\n if (k==0 || i==n)\n {\n return 0;\n }\n int ans=0;\n for (int j = 0; j <=k; j++)\n {\n if (arr[i].size()>=j)\n {\n if(j==0){\n ans=max(ans,solve(arr,i+1,k,n)) ;\n }\n else{\n ans=max(ans,arr[i][j-1]+solve(arr,i+1,k-j,n));\n }\n }\n else{\n return ans;\n }\n }\n return ans;\n}\n int maxValueOfCoins(vector<vector<int>>& arr, int k) {\n int n=arr.size();\n for (int i = 0; i < n; i++)\n {\n for (int j = 1; j < arr[i].size(); j++)\n {\n arr[i][j]+=arr[i][j-1];\n }\n \n }\n return solve(arr,0,k,n);\n }\n\t\n\t\n\t\n\t\n```\n\t// Top-Down\n\n```\nint solve(vector<vector<int>>& arr,int k2,int n){\n vector<vector<int>>dp(n+1,vector<int>(k2+1,0));\n for (int i = n-1; i >=0; i--)\n {\n for (int k = 0; k<=k2; k++)\n {\n \n for (int j = 0; j <=k; j++)\n {\n if (arr[i].size()>=j)\n {\n if(j==0){\n dp[i][k]=max(dp[i][k],dp[i+1][k]) ;\n }\n else{\n dp[i][k]=max(dp[i][k],arr[i][j-1]+dp[i+1][k-j]);\n }\n }\n else{\n break;\n }\n }\n \n\n\n }\n \n }\n return dp[0][k2];\n \n\n\n\n }\n\n int maxValueOfCoins(vector<vector<int>>& arr, int k) {\n int n=arr.size();\n for (int i = 0; i < n; i++)\n {\n for (int j = 1; j < arr[i].size(); j++)\n {\n arr[i][j]+=arr[i][j-1];\n }\n \n }\n return solve(arr,k,n);\n }\n```
| 6
| 0
|
['Recursion', 'C++']
| 0
|
maximum-value-of-k-coins-from-piles
|
Prefix-Sum + Bottom-up dp. DETAILED EXPLANATION. [C++/Python]
|
prefix-sum-bottom-up-dp-detailed-explana-89bx
|
\n\n# Code\n\nclass Solution {\npublic:\n int maxValueOfCoins(vector<vector<int>>& piles, int k) {\n int n = piles.size();\n // total n piles a
|
tryingall
|
NORMAL
|
2023-04-15T00:39:12.486349+00:00
|
2023-04-15T00:45:10.211104+00:00
| 1,676
| false
|
\n\n# Code\n```\nclass Solution {\npublic:\n int maxValueOfCoins(vector<vector<int>>& piles, int k) {\n int n = piles.size();\n // total n piles and k coins we can choose.\n // so for any dp[i][j] it will store the max coins we\n // get using i piles and j coins used.\n vector<vector<int>> dp(n + 1, vector<int>(k + 1, 0));\n // Since we want to be dealing with the sums of coins,\n // it would be real convenient, if our piles just stored\n // the prefix sum instead. This can be done on the piles\n // matrix directly, however, it is a good practice to not\n // to change anything provided in the problem. Make pref\n vector<vector<int>> pref(n, vector<int>()); // prefix-sum\n for (int i = 0; i < n; i++) {\n pref[i].resize(piles[i].size()); // uneven matrix so resize()\n pref[i][0] = piles[i][0]; // initialize for pref_sum\n for (int j = 1; j < piles[i].size(); j++) {\n // calculating prefix sum\n pref[i][j] = pref[i][j - 1] + piles[i][j];\n }\n }\n\n for (int i = 1; i <= n; i++) {\n for (int j = 1; j <= k; j++) {\n // Let the coins chosen from the current pile be cur\n for (int cur = 0; cur <= piles[i - 1].size(); cur++) {\n // Check for all combinations of coins that sum up to j coins.\n // We can pick w coins from this pile and j-w coins from previous piles (dp[i-1][j-w]).\n // i.e., (j-w) + w = j coins in total.\n if(cur <= j)\n if(cur > 0){\n // if cur > 0 we can consider prefix sum since in-bounds\n dp[i][j] = max(dp[i][j], dp[i - 1][j - cur] + pref[i - 1][cur - 1]);\n }\n else{\n dp[i][j] = max(dp[i][j], dp[i - 1][j - cur]);\n }\n }\n }\n }\n return dp[n][k];\n }\n};\n\n\n```\nPython code for the same:\n```\nclass Solution:\n def maxValueOfCoins(self, piles: List[List[int]], k: int) -> int:\n n = len(piles)\n dp = [[0] * (k + 1) for _ in range(n + 1)]\n pref = [[] for _ in range(n)] \n for i in range(n):\n pref[i] = [0] * len(piles[i]) \n pref[i][0] = piles[i][0] \n for j in range(1, len(piles[i])):\n pref[i][j] = pref[i][j - 1] + piles[i][j]\n\n for i in range(1, n + 1):\n for j in range(1, k + 1):\n for cur in range(len(piles[i - 1]) + 1):\n if cur <= j:\n if cur > 0:\n dp[i][j] = max(dp[i][j], dp[i - 1][j - cur] + pref[i - 1][cur - 1])\n else:\n dp[i][j] = max(dp[i][j], dp[i - 1][j - cur])\n return dp[n][k]\n```
| 5
| 0
|
['Prefix Sum', 'Python', 'C++', 'Python3']
| 2
|
maximum-value-of-k-coins-from-piles
|
[Java] Knapsack variation | Dynammic Programming | Easy to undestand,
|
java-knapsack-variation-dynammic-program-k676
|
TC - O(N*M) \nn=size of piles,\nm=size of piles[i]\n\nclass Solution {\n public int helper(List> piles,int idx,int k,int [][]dp){\n \n if(idx<0
|
Princearya23
|
NORMAL
|
2022-05-21T09:16:49.909698+00:00
|
2022-05-21T09:16:49.909736+00:00
| 475
| false
|
TC - O(N*M) \nn=size of piles,\nm=size of piles[i]\n\nclass Solution {\n public int helper(List<List<Integer>> piles,int idx,int k,int [][]dp){\n \n if(idx<0 || k == 0) return 0;\n if(dp[idx][k] != -1) return dp[idx][k];\n \n \n // exclude case \n int exclude = helper(piles,idx-1,k,dp);\n \n \n // include case\n int sum = 0;\n int include = 0;\n \n List<Integer> curr_pile = piles.get(idx);\n \n for(int i=0;i<Math.min(curr_pile.size(),k);i++){\n sum += curr_pile.get(i);\n include = Math.max(sum + helper(piles,idx-1,k-i-1,dp),include);\n }\n return dp[idx][k] = Math.max(include,exclude);\n }\n public int maxValueOfCoins(List<List<Integer>> piles, int k) {\n \n int n = piles.size();\n int [][]dp = new int[n+1][k+1];\n for(int []d:dp) Arrays.fill(d,-1);\n \n return helper(piles,n-1,k,dp);\n }\n}
| 5
| 0
|
['Array', 'Dynamic Programming', 'Memoization', 'Java']
| 0
|
maximum-value-of-k-coins-from-piles
|
Recursion to Space Optimized DP | Java explained solution | Easy to understand
|
recursion-to-space-optimized-dp-java-exp-tvjm
|
\nThis question is a variation of 0/1 Unbounded Knapsack. Here we are allowed to pick coins any no. of times with 2 included constraints. \n- These picking up o
|
imkashyap
|
NORMAL
|
2022-03-31T19:21:38.717134+00:00
|
2022-03-31T19:25:43.716393+00:00
| 468
| false
|
\nThis question is a variation of 0/1 Unbounded Knapsack. Here we are allowed to pick coins any no. of times with 2 included constraints. \n- These picking up of coins from a particular pile cannot exceed k\n- The coins in a particular pile are of different denomination\n\nIf these two constraints are removed the question is basic 0/1 Unbounded knapsack. So, similarly we have two options to go for.\n- either to not pick any coin from a pile\n- or pick 1 to k coins from a pile\n\nRecursion\n```\n public int maxValueOfCoins(List<List<Integer>> piles, int k) {\n int n=piles.size();\n return solve(piles,n,k);\n }\n \n public int solve(List<List<Integer>> piles,int i,int k){\n if(k==0)return 0;\n if(i==0)return 0;\n int best=solve(piles,i-1,k);\n List<Integer> pile=piles.get(i-1);\n int sum=0;\n for(int x=0;x<Math.min(k,pile.size());x++){\n sum+=pile.get(x);\n best=Math.max(best,+solve(piles,i-1,k-(x+1)));\n }\n return best;\n }\n```\nTC= Exponential (For every pile we have either to pick upto k coins or not pick at all)\nSC= O(nk)\n\nRecursion with Memoization\n```\n public int maxValueOfCoins(List<List<Integer>> piles, int k) {\n int n=piles.size();\n\t\tint[][] dp=new int[n+1][k+1];\n for(int i=0;i<=n;i++)\n\t\t\tArrays.fill(dp[i],-1);\n return solve(piles,n,k,dp);\n }\n \n public int solve(List<List<Integer>> piles,int i,int k,int[][] dp){\n\t\tif(k==0)return 0;\n if(i==0)return 0;\n\t\tif(dp[i][k]!=-1)return dp[i][k];\n int best=solve(piles,i-1,k,dp);\n List<Integer> pile=piles.get(i-1);\n int sum=0;\n for(int x=0;x<Math.min(k,pile.size());x++){\n sum+=pile.get(x);\n best=Math.max(best,+solve(piles,i-1,k-(x+1),dp));\n }\n return dp[i][k]= best;\n }\n```\nTC= O(nk)\nSC= O(nk)+O(nk)\n\nTabulation DP\n```\n \n public int maxValueOfCoins(List<List<Integer>> piles, int k) {\n int n=piles.size();\n int[][] dp=new int[n+1][k+1];\n for(int i=0;i<=n;i++){\n for(int j=0;j<=k;j++){\n if(i==0 || j==0)dp[i][j]=0;\n else{\n int best=dp[i-1][j];\n List<Integer> pile=piles.get(i-1);\n int sum=0;\n for(int x=0;x<Math.min(j,pile.size());x++){\n sum+=pile.get(x);\n best=Math.max(best,sum+dp[i-1][j-(x+1)]);\n }\n dp[i][j]= best;\n }\n }\n }\n return dp[n][k];\n }\n```\nTC= O(nk)\nSC= O(nk)\n\nTabulation DP with Space optimization\n```\n public int maxValueOfCoins(List<List<Integer>> piles, int k) {\n int n=piles.size();\n int[] prev=new int[k+1];\n for(int i=0;i<=n;i++){\n int[] curr=new int[k+1];\n for(int j=0;j<=k;j++){\n if(i==0 || j==0)curr[j]=0;\n else{\n int best=prev[j];\n List<Integer> pile=piles.get(i-1);\n int sum=0;\n for(int x=0;x<Math.min(j,pile.size());x++){\n sum+=pile.get(x);\n best=Math.max(best,sum+prev[j-(x+1)]);\n }\n curr[j]= best;\n }\n }\n prev=curr;\n }\n return prev[k];\n }\n```\nTC= O(nk)\nSC= O(2k)=O(k)\n\nHope you liked the solution. If yes, do upvote. Thanks!
| 5
| 0
|
['Dynamic Programming', 'Recursion', 'Java']
| 0
|
maximum-value-of-k-coins-from-piles
|
[CPP] DP (Recursive Approach) | Easy to Understand
|
cpp-dp-recursive-approach-easy-to-unders-kf4t
|
Explantion: The problem is similar to knapsack\'s dp solution, where everything all boils down to select / not select current value. Similary In this problem we
|
nishit130
|
NORMAL
|
2022-03-27T04:34:58.353581+00:00
|
2022-10-10T14:22:13.072695+00:00
| 395
| false
|
**Explantion**: The problem is similar to knapsack\'s dp solution, where everything all boils down to select / not select current value. Similary In this problem we traverse pile by pile (denoted by `i`) and for every value in pile (`j`) we select (add `pile[i][j]` to our wallet) or we move to next pile (`i+1`). For Memoization, we make use of variables `i` and `k` denoting pile number and coin added in wallet respectively. We store value in DP vector only when our value of `j` is 0 i.e we have moved to new pile.\n\n\n```\nclass Solution {\npublic:\n int solve (vector<vector<int>> &piles, int i, int j, int k, vector<vector<int>> &dp) {\n if (k == 0)\n return 0;\n \n if (i >= piles.size())\n return INT_MIN;\n \n if (j >= piles[i].size())\n return solve (piles, i+1, 0, k, dp); // emptied current pile, move to next pile\n\t\t\t\n if (dp[i][k] != -1 && j == 0)\n return dp[i][k];\n\t\t\t\n int a = 0, b = 0;\n a = solve (piles, i, j+1, k-1, dp) + piles[i][j]; // Pick current pile\'s top\n b = solve (piles, i+1, 0, k, dp); // Don\'t pick and move to next pile\n \n if (j == 0)\n dp[i][k] = max (a, b);\n \n return max (a, b);\n }\n int maxValueOfCoins(vector<vector<int>>& piles, int k) {\n \n int n = piles.size();\n vector<vector<int>> dp (n+1, vector<int> (k+1, -1));\n int ans = solve (piles, 0, 0, k, dp);\n return ans;\n }\n};\n```
| 5
| 0
|
['Dynamic Programming', 'Recursion', 'C', 'C++']
| 2
|
maximum-value-of-k-coins-from-piles
|
[Java] Top Down DP
|
java-top-down-dp-by-crimsonalien17-qc4u
|
Logic\nYou have n piles\nSo you can take from ith pile min = 0 coins and atmost max(sizeOf(pile), k) \nWe can do it with dynamic programming using dp table\n\n\
|
CrimsonAlien17
|
NORMAL
|
2022-03-27T04:04:36.528008+00:00
|
2022-03-27T04:04:36.528037+00:00
| 531
| false
|
**Logic**\nYou have n piles\nSo you can take from `ith` pile min = 0 coins and atmost max(sizeOf(pile), k) \nWe can do it with dynamic programming using dp table\n\n\n```\nclass Solution {\n Integer dp[][]; // store state\n private int solve(List<List<Integer>>piles, int i, int k){\n // if i < 0 there are no piles or \n // k <= 0 you cannnot pick any \n // return 0\n if(i < 0 || k <= 0) return 0; \n // if already stored that state return value\n if(dp[i][k] != null) return dp[i][k];\n // you can take max(size of that pile, k)\n int n = Math.min(piles.get(i).size(), k);\n // you will not choose that pile\n int exclude = solve(piles, i-1, k);\n // you will take 1, 2, ... k from that pile\n // and store the max in \'include\' variable\n int include = 0;\n for(int j=0, sum=0; j<n; j++){\n // store the sum from 0th index to jth index\n sum += piles.get(i).get(j);\n // take max from (sum + remaining k coins) and max value \n include = Math.max(sum + solve(piles, i-1, k-j-1), include);\n }\n // take max of include, exclude\n int res = Math.max(include, exclude);\n // store in dp\n dp[i][k] = res;\n return res;\n }\n \n public int maxValueOfCoins(List<List<Integer>> piles, int k) {\n int n=piles.size();\n dp = new Integer[n+5][k+5];\n return solve(piles, piles.size()-1, k);\n }\n}\n```
| 5
| 0
|
['Dynamic Programming', 'Memoization', 'Java']
| 1
|
maximum-value-of-k-coins-from-piles
|
💥Runtime beats 100.00%, Memory beats 84.38% [EXPLAINED]
|
runtime-beats-10000-memory-beats-8438-ex-vt8y
|
\n# Intuition\nYou have several piles of coins, and you need to select exactly k coins in total from these piles to maximize their combined value. Each pile all
|
r9n
|
NORMAL
|
2024-09-19T19:45:33.367218+00:00
|
2024-09-19T19:45:33.367239+00:00
| 24
| false
|
\n# Intuition\nYou have several piles of coins, and you need to select exactly k coins in total from these piles to maximize their combined value. Each pile allows you to only pick coins from the top.\n\n\n# Approach\nDynamic Programming (DP) Array: Think of it like a big list where each position represents the maximum money you can get if you pick that many coins. We use this list to keep track of the best choices as we process each pile.\n\n\nPrefix Sums: For each pile, calculate the total value of picking the top 1, 2, 3, etc., coins. This helps us quickly find out how much money we get if we decide to take a certain number of coins from the pile.\n\n\nUpdate the DP Array: For each pile, update the DP list to include the new maximum values you can get by adding coins from the current pile.\n\n# Complexity\n- Time complexity:\nO(n * k): Where n is the number of piles, and k is the number of coins you want to pick. We go through each pile and update our list of possible maximum values.\n\n- Space complexity:\nO(k): Because we use a list to keep track of the maximum values for up to k coins.\n\n# Code\n```csharp []\npublic class Solution {\n public int MaxValueOfCoins(IList<IList<int>> piles, int k) {\n int[] dp = new int[k + 1]; // DP array to store the max value for picking x coins\n\n foreach (var pile in piles) {\n int pileSize = pile.Count;\n int[] prefixSum = new int[pileSize + 1]; // Prefix sum to quickly calculate the sum of first x coins in the pile\n\n // Calculate prefix sum for the current pile\n for (int i = 0; i < pileSize; i++) {\n prefixSum[i + 1] = prefixSum[i] + pile[i];\n }\n\n // Update DP array from back to front\n for (int coins = k; coins > 0; coins--) {\n // Try taking 0 to min(coins, pileSize) coins from the current pile\n for (int taken = 1; taken <= Math.Min(coins, pileSize); taken++) {\n dp[coins] = Math.Max(dp[coins], dp[coins - taken] + prefixSum[taken]);\n }\n }\n }\n\n return dp[k]; // The answer is the maximum value we can get by taking exactly k coins\n }\n}\n\n```
| 4
| 0
|
['C#']
| 0
|
maximum-value-of-k-coins-from-piles
|
C++ || MEMOIZATION || DP || EASY TO UNDERSTNAD
|
c-memoization-dp-easy-to-understnad-by-y-j0ji
|
\nclass Solution {\npublic:\n int solve(vector<vector<int>> &v,vector<vector<int>> &dp,int s,int k,int &n){\n if(s>=n)return 0;\n if(k==0)retur
|
yash___sharma_
|
NORMAL
|
2023-04-15T05:20:38.442126+00:00
|
2023-04-15T05:20:38.442154+00:00
| 1,130
| false
|
````\nclass Solution {\npublic:\n int solve(vector<vector<int>> &v,vector<vector<int>> &dp,int s,int k,int &n){\n if(s>=n)return 0;\n if(k==0)return 0;\n if(dp[s][k] != -1)return dp[s][k];\n int mx = solve(v,dp,s+1,k,n);\n int cur = 0;\n for(int i = 0; i < v[s].size(); i++){\n cur += v[s][i];\n if(k-i-1 >= 0){\n mx = max(mx,cur+solve(v,dp,s+1,k-i-1,n));\n }\n }\n return dp[s][k] = mx;\n }\n int maxValueOfCoins(vector<vector<int>>& piles, int k) {\n int n = piles.size();\n vector<vector<int>> dp(n+1,vector<int> (k+1,-1));\n return solve(piles,dp,0,k,n);\n }\n};\n````
| 4
| 1
|
['Dynamic Programming', 'Recursion', 'Memoization', 'C', 'C++']
| 1
|
maximum-value-of-k-coins-from-piles
|
Basic Approach (Java) (DP)
|
basic-approach-java-dp-by-may51936-23oc
|
Code\n\nclass Solution {\n public int maxValueOfCoins(List<List<Integer>> piles, int k) {\n //dp[i][j] means when we just use the first i piles and j
|
may51936
|
NORMAL
|
2023-04-15T03:58:38.599478+00:00
|
2023-04-15T03:58:38.599516+00:00
| 479
| false
|
# Code\n```\nclass Solution {\n public int maxValueOfCoins(List<List<Integer>> piles, int k) {\n //dp[i][j] means when we just use the first i piles and j picks, the maximum coins we can get\n int[][] dp = new int[piles.size()+1][k+1];\n for (int i = 1; i <= piles.size(); i++){\n for (int j = 1; j <= k; j++){\n int sum = 0;\n // At first we don\'t pick anything, so the coins you can get is the same and for i-1 condition\n dp[i][j] = dp[i-1][j];\n //Begin to traverse the ith pile\n //Note here we use min function to prevent index out of bound\n for (int h = 0; h < Math.min(j, piles.get(i-1).size()); h++){\n //We take the current (hth) coin\n sum += piles.get(i-1).get(h);\n //Check if pick it can maximize our score\n //Note that if we pick it, we can only get the coins for j-1-h picks when we are at i-1th coin\n dp[i][j] = Math.max(dp[i][j], sum + dp[i-1][j-1-h]);\n }\n }\n }\n //The result is when we use all of the piles and k picks\n return dp[piles.size()][k]; \n }\n}\n```
| 4
| 0
|
['Dynamic Programming', 'Java']
| 0
|
maximum-value-of-k-coins-from-piles
|
Easy to Understand | Python | Logically Explained | DP
|
easy-to-understand-python-logically-expl-gwci
|
Pre-Requisites - 0/1 Knapsack\n\nSolution -\nLet\'s do some ground work first.\nFor all the piles we can make them into prefix sum arrays\neg:- [2, 7, 3] -> [0,
|
Naman777
|
NORMAL
|
2023-04-15T03:17:21.710713+00:00
|
2023-04-15T03:48:45.191949+00:00
| 434
| false
|
**Pre-Requisites - 0/1 Knapsack**\n\n**Solution -**\nLet\'s do some ground work first.\nFor all the piles we can make them into prefix sum arrays\neg:- [2, 7, 3] -> [0, 2, 9, 12]\nNow the question is not how many of elements of each array to take rather which element of each prefix sum array to take.\nAlso, we can associate weights with each element (basically denoting the number of elements taken from that array).\nTaking the previous array, [[0, 0], [2, 1], [9, 2], [12, 3]] - 0, 1, 2, 3 are the number of elements taken\n\nNow, we have to take one of them from each pile and the sum of weights should be k, seems kinda like knapsack, right?\nThe only difference is we can\'t independently take elements as taking [2, 1] & [9, 2] would just mean we\'re taking the element \'2\' twice.\nSo we have to take one element from each pile (more preceisely one element of prefix sum array)\n\nNow this is easily solvable as in 0/1 knapsack, we used to go to the previous row to check the maximum possible answer with remaining weight (column_number - weight) and in this we\'ll go to the last row which contained weights from the previous pile and not the current one (to avoid picking up any weight twice)\n\n**Code -**\n```\nclass Solution:\n def maxValueOfCoins(self, piles: List[List[int]], k: int) -> int:\n \n n = len(piles)\n \n prefix = []\n \n #prev array represents where the elements from last pile ended\n prev = [0]\n \n for pile in piles:\n curr = [0]\n for ele in pile:\n curr.append(curr[-1]+ele)\n prefix.append(curr)\n \n prev.append(prev[-1]+len(pile))\n \n dp = [[0]*(k+1) for i in range(prev[-1]+1)]\n \n for i in range(n):\n for j in range(1, len(prefix[i])):\n \n profit = prefix[i][j]\n wt = j\n\n # lvl represents row number\n # We\'ve given a different row to every prefix sum array element. \n lvl = prev[i]+j \n \n for w in range(1, k+1): \n if wt > w:\n dp[lvl][w] = dp[lvl-1][w]\n else:\n dp[lvl][w] = max(dp[lvl-1][w], profit+dp[prev[i]][w-wt])\n return dp[-1][-1]
| 4
| 0
|
['Dynamic Programming', 'Python']
| 0
|
maximum-value-of-k-coins-from-piles
|
python3 Solution
|
python3-solution-by-motaharozzaman1996-0hkz
|
\n\nclass Solution:\n def maxValueOfCoins(self, piles: List[List[int]], k: int) -> int:\n \n @functools.lru_cache(None)\n def dp(i,K):\n
|
Motaharozzaman1996
|
NORMAL
|
2023-04-15T02:54:21.753560+00:00
|
2023-04-15T02:54:21.753591+00:00
| 974
| false
|
\n```\nclass Solution:\n def maxValueOfCoins(self, piles: List[List[int]], k: int) -> int:\n \n @functools.lru_cache(None)\n def dp(i,K):\n if k==0 or i==len(piles):\n return 0\n\n res,cur=dp(i+1,K),0\n\n for j in range(min(len(piles[i]),K)):\n cur+=piles[i][j]\n res=max(res,cur+dp(i+1,K-j-1))\n\n return res\n\n\n return dp(0,k) \n```
| 4
| 0
|
['Python', 'Python3']
| 0
|
maximum-value-of-k-coins-from-piles
|
Easy Understanding DP + Memoziation Solution
|
easy-understanding-dp-memoziation-soluti-99rm
|
UPVOTE IF YOU LIKE THE SOLUTION.\n\nclass Solution {\npublic:\n //memoization Solution\n int helper(int i, vector<vector<int>>& piles, int k, vector<vecto
|
singhalPratham
|
NORMAL
|
2022-10-09T19:58:22.575911+00:00
|
2022-10-13T17:07:01.743371+00:00
| 330
| false
|
UPVOTE IF YOU LIKE THE SOLUTION.\n```\nclass Solution {\npublic:\n //memoization Solution\n int helper(int i, vector<vector<int>>& piles, int k, vector<vector<int>>& dp){\n //base condition\n if(i == piles.size() || k <= 0){\n return 0;\n }\n \n //check if this condition is reached before\n if(dp[i][k] != -1){\n return dp[i][k];\n }\n \n long long ans = INT_MIN;\n for(int j = 0; j < piles[i].size(); j++){\n //if j becomes greater than k-1 break\n if(j > k-1)\n break;\n \n //take starting j+1 coins from the ith pile\n long long take = piles[i][j] + helper(i+1, piles, k-j-1, dp);\n \n //store the max value in ans\n ans = max(ans, take);\n }\n \n //donot take any coins from ith piles\n long long ntake = helper(i+1, piles, k, dp);\n ans = max(ans, ntake);\n \n //memoize it\n return dp[i][k] = ans;\n }\n int maxValueOfCoins(vector<vector<int>>& piles, int k) {\n //dp vector\n vector<vector<int>> dp(piles.size(), vector<int>(k+1,-1));\n \n //prefix vector\n vector<vector<int>> prefix;\n for(auto a: piles){\n int n = a.size();\n vector<int> temp(n);\n temp[0] = a[0];\n for(int i = 1; i < n; i++){\n temp[i] = temp[i-1] + a[i];\n }\n prefix.push_back(temp);\n }\n return helper(0, prefix, k, dp);\n }\n};\n```
| 4
| 0
|
['Dynamic Programming', 'Recursion', 'Memoization', 'C']
| 0
|
maximum-value-of-k-coins-from-piles
|
[Python] Explained with diagram, Iterative DP solution, (Beats 98% TC)
|
python-explained-with-diagram-iterative-bllx6
|
Worst Case time complexity = O(nk^2)\n\nIntuition* - Let\'s say we are standing at pile[i] and have already computed piles<i. And we have calculated the maximum
|
captain_vince
|
NORMAL
|
2022-09-02T19:14:07.143943+00:00
|
2022-09-03T06:09:00.505689+00:00
| 371
| false
|
Worst Case time complexity = O(n*k^2)\n\n**Intuition** - Let\'s say we are standing at pile[i] and have already computed piles<i. And we have calculated the maximum possible sum of r (0<r<=k) number of coins uptill pile[i]. Now to calculate maximum possible sum using pile[i] following steps can be followed:-\n1) maximum sum uptill pile[i] is stored in array max_arr for 0<coins<=k\n2) maintain an array cur_arr which stores coin sum including pile[i]. In pile[i], we have to calculate sum one by one using 0<top-coins<=k from pile[i]. cur_arr will hold the maximum value for a particular no. of coins less than using pile[i].\n3) After cur_arr is calculated using k coins of pile[i], max_arr is updated to include greater values from cur_arr.\n4) After all n piles are iterated, return max_arr[k].\n 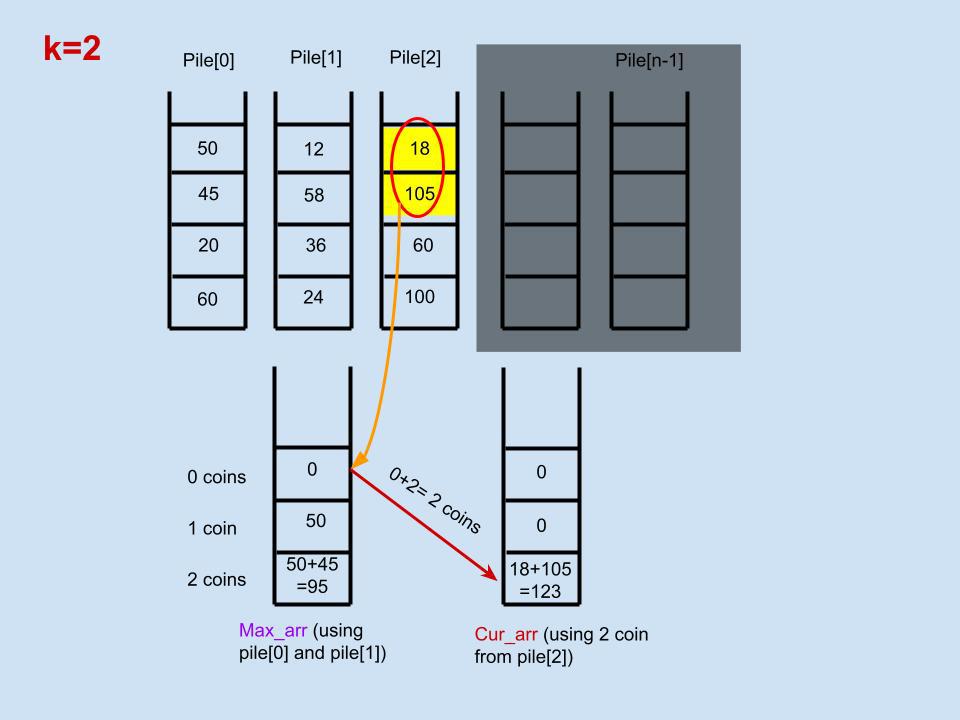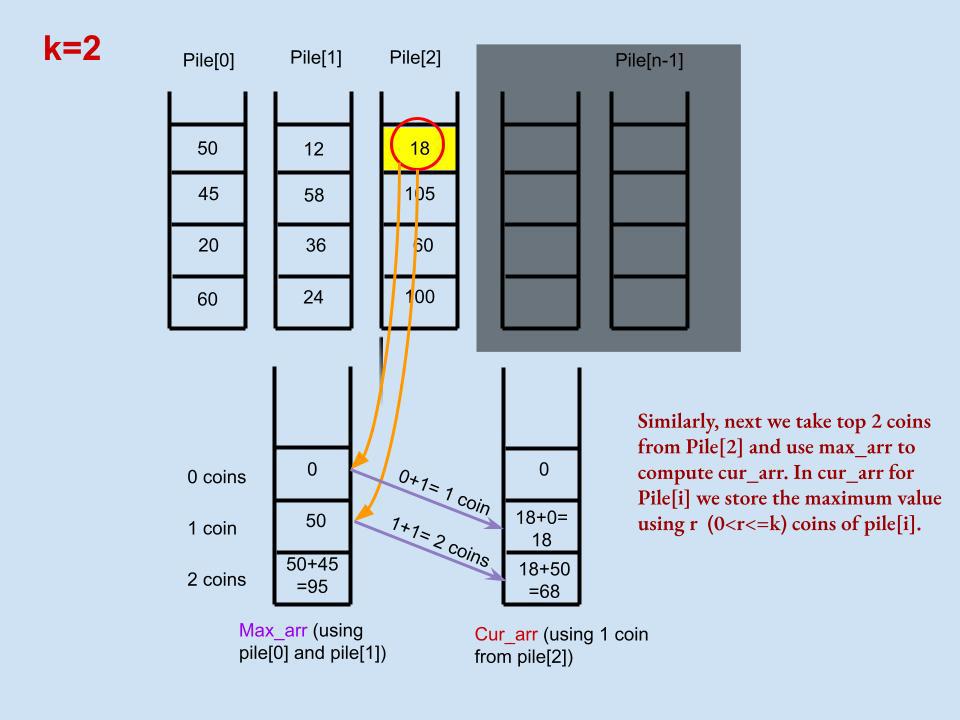\n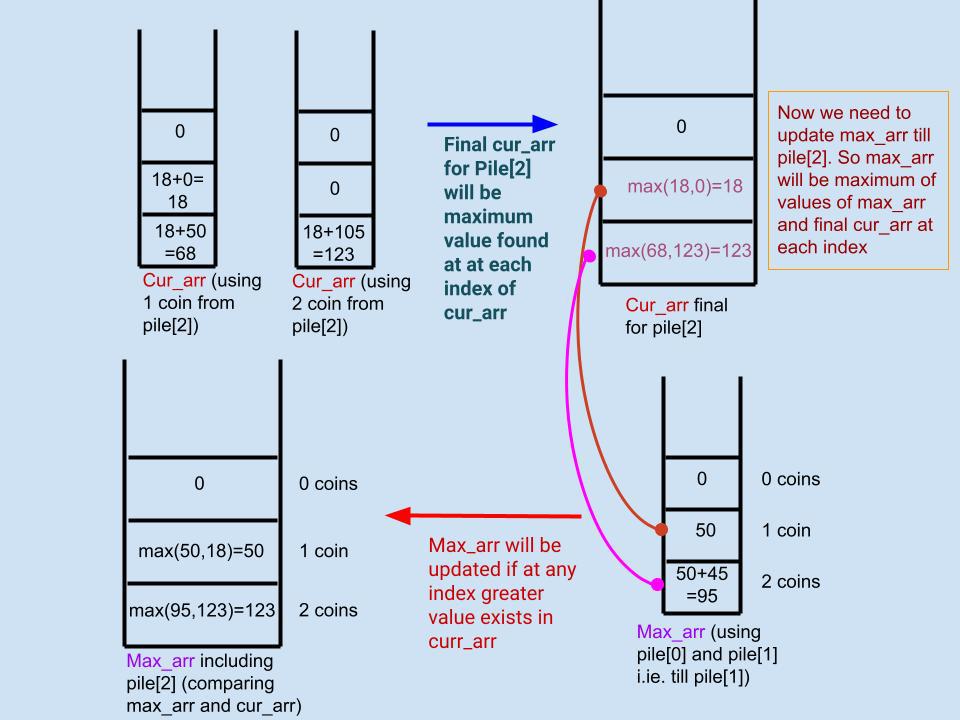\n\n\n\n\n```\nclass Solution:\n def maxValueOfCoins(self, piles: List[List[int]], k: int) -> int:\n \n n=len(piles)\n topk=[]\n \n cur_arr=[0]*(k+1)\n max_arr=[0]*(k+1)\n \n for x in piles:\n i=0\n cursum=0\n while i<k and i<len(x):\n cursum+=x[i]\n j=0\n while i+1+j<=k:\n if j>0 and max_arr[j]==0:\n break\n cur_arr[i+1+j]=max(cur_arr[i+1+j],max_arr[j]+cursum)\n j+=1\n i+=1\n \n for t in range(i+j):\n if cur_arr[t]>max_arr[t]:\n max_arr[t]=cur_arr[t]\n \n return max_arr[k]\n \n \n ```
| 4
| 0
|
['Dynamic Programming', 'Python']
| 0
|
maximum-value-of-k-coins-from-piles
|
DP - Memoization (well explained) C++
|
dp-memoization-well-explained-c-by-gunja-zjwo
|
The main idea here is to use Dynamic programming and I have used prefix sum to get the total sum of the top elements uptil the index where I am standing at any
|
gunjan10
|
NORMAL
|
2022-03-30T06:57:58.179249+00:00
|
2022-04-03T07:23:01.911345+00:00
| 344
| false
|
The main idea here is to use **Dynamic programming** and I have used **prefix sum** to get the total sum of the top elements uptil the index where I am standing at any instance.\n\nDp states are : (index , k) \n* ***index*** defines the stack which we are currently on \n* ***k*** defines the number of elements which we can remove from the top of the stacks\n\nWe have 2 choice sstanding at any index : either take the elements \n\t\t\t\t\t\t\t\t\t\t\t\t\t\t\t\t\t\tor skip the current stack and find for optimal answers in other indexes;\n\t\t\t\t\t\t\t\t\t\t\t\t\t\t\t\t\nIf we take the elements from the stack we have options to take as much elements from the current stack as we want( limitations : until k gets finished or the stack gets finished ) by running a loop we can iterate over all the possibilities and get the optimal option from it.\n\nDo upvote if you like my approach!! \n\n```\nclass Solution {\n \n int help(int ind , int k, vector<vector<int>>&a, vector<vector<int>>&dp){\n\t\t//base cases\n\t\tif(k == 0) return 0;\n if(k < 0) return INT_MIN;\n if(ind < 0) return 0;\n\t\t\n\t\t//memoization step\n int &ans = dp[ind][k];\n if(ans != -1) return ans; \n\t\t//you can either skip the current stack or take from it\n\t\t\n ans = help(ind-1, k , a, dp); // option 1. skip the current stack\n int current_pile_size = a[ind].size();\n\t\t// this is the limit of elements you can take from the current stack\n int limit = min(k, current_pile_size-1); \n \n for(int i=0;i<=limit;i++){ //this loop will give me how many items i can take from the stack\n int take = a[ind][i] ; // since prefix sum is done we get the total elements uptil this index using a[ind][i]\n ans = max(ans, take + help(ind-1, k-i-1, a, dp)); // we take the max of all the available options\n }\n return ans;\n }\npublic:\n int maxValueOfCoins(vector<vector<int>>& piles, int k) {\n int size = piles.size(); \n for(auto &it: piles){\n int n = it.size();\n for(int i=1;i<n;i++)\n it[i] += it[i-1]; // prefix sum ...so we can get cumulative sum upto a point\n }\n vector<vector<int>>dp(size+1, vector<int>(k+1, -1));\n return help(size-1, k, piles, dp);\n }\n};\n```
| 4
| 0
|
['Dynamic Programming', 'Memoization', 'C', 'Prefix Sum']
| 1
|
maximum-value-of-k-coins-from-piles
|
Typescript | DP + Iterative + Beats 100.00% + Time: O(nk^2) - Space: O(k)
|
typescript-dp-iterative-beats-10000-time-p923
|
Time: O(nk^2)\nSpace: O(k)\nLanguage: javascript, typescript\n\nRuntime: 325 ms, faster than 100.00%\nMemory Usage: 45.1 MB, less than 100.00%\n\n\nfunction max
|
queriel
|
NORMAL
|
2022-03-27T06:00:24.124812+00:00
|
2022-03-27T06:18:46.128333+00:00
| 457
| false
|
Time: O(nk^2)\nSpace: O(k)\nLanguage: javascript, typescript\n\nRuntime: 325 ms, faster than 100.00%\nMemory Usage: 45.1 MB, less than 100.00%\n\n```\nfunction maxValueOfCoins(piles: number[][], coins: number): number {\n let dp = new Array(coins + 1).fill(0);\n \n for (let i = 0; i < piles.length; ++i) {\n\t for (let j = coins; j > 0; --j) {\n\t\t\t// "sum" is a count of coins from piles[i]\n let sum = 0;\n\n for (let k = 1; k <= Math.min(j, piles[i].length); k++) {\n sum += piles[i][k - 1];\n\n\t\t\t\t// take "k" coins from piles[i] and the previous best "j-k" coins\n dp[j] = Math.max(dp[j], dp[j-k] + sum);\n }\n }\n }\n \n return dp[coins];\n}\n```
| 4
| 0
|
['Dynamic Programming', 'Iterator', 'TypeScript', 'JavaScript']
| 0
|
maximum-value-of-k-coins-from-piles
|
[C++ Solution] Simple solution using DP
|
c-solution-simple-solution-using-dp-by-p-zl2d
|
\nclass Solution {\npublic:\n long long dp[2005][2005];\n \n int K;\n long long MaxValue(vector<vector<int>>& piles, int taken,int pile)\n {\n
|
pizza_slice
|
NORMAL
|
2022-03-27T04:01:24.189650+00:00
|
2022-03-27T04:04:06.881218+00:00
| 596
| false
|
```\nclass Solution {\npublic:\n long long dp[2005][2005];\n \n int K;\n long long MaxValue(vector<vector<int>>& piles, int taken,int pile)\n {\n if(taken==K) return 0;\n if(pile>=piles.size()||taken>K) return INT_MIN;\n \n if(dp[taken][pile]!=-1) return dp[taken][pile];\n \n long long ans=0;\n\t\t// if we want to pick and try atleast one coin from this pile\n\t\t\n for(int i=0;i<piles[pile].size();i++)\n {\n ans=max(ans,piles[pile][i]+MaxValue(piles,taken+i+1,pile+1));\n }\n \n ans=max(ans,MaxValue(piles,taken,pile+1)); // if we want to skip this pile altogether\n \n return dp[taken][pile]=ans;\n }\n \n int maxValueOfCoins(vector<vector<int>>& piles, int k) {\n memset(dp,-1,sizeof(dp));\n\t\t\n\t\t// storing the prefix sum so as to know if we pick the ith coin out of a pile, what will be the total sum of all the coins above the ith coin \n\t\t\n for(int i=0;i<piles.size();i++)\n {\n for(int j=1;j<piles[i].size();j++) piles[i][j]+=piles[i][j-1];\n }\n \n K=k;\n return MaxValue(piles,0,0);\n }\n};\n```
| 4
| 1
|
['Dynamic Programming', 'Recursion', 'C']
| 0
|
maximum-value-of-k-coins-from-piles
|
prefix sum + 2d DP
|
prefix-sum-2d-dp-by-trpaslik-nbqa
|
Intuition\nUse DP and prefix sum\n\n# Approach\nFirst for each pile, build a prefix sum (aka cummulative sum) up to k elements (we can just trim/ignore if there
|
trpaslik
|
NORMAL
|
2023-04-15T19:37:25.941494+00:00
|
2023-04-15T19:45:52.826651+00:00
| 161
| false
|
# Intuition\nUse DP and prefix sum\n\n# Approach\nFirst for each pile, build a prefix sum (aka cummulative sum) up to k elements (we can just trim/ignore if there is more).\n\nThen focus on the first pile.\nWe can take first coin, or two, or ... k and then deal with smaller problem (one less pile and same or less coins to consider).\n\nSo the base cases are:\n- we have considered all piles\n- we have no more coins to take\n\nIn the meoized helper DP function, we take two parameters:\n`start_pile` - index of the pile we focus on (and later deal only with piles with bigger index)\n`hp` - the helper version of k, that is remaining coins we need to consider\n\nOn the helper function we looking for the maximum,\nconsidering taking from the start_pile 0 up to hk coins and remaining coins from the next piles recursively.\n\nHaving such helper function, the answer will be found by `helper(start_pile=0, hk=k)`\n\nIf you find it helpful please up-vote. Thank you!\n\n# Complexity\n- Time complexity: $$O(n\\times k)$$ I think...\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n\\times k)$$ I think...\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def maxValueOfCoins(self, piles: List[List[int]], k: int) -> int:\n n = len(piles)\n\n # Turn each pile to cummulative sum trimmed to k elements\n for pi in range(n):\n piles[pi] = list(accumulate(piles[pi][:k]))\n \n @cache\n def helper(start_pile: int, hk: int):\n if start_pile >= n or hk == 0:\n return 0\n # Consider we don\'t take anything from start_pile\n ans = helper(start_pile + 1, hk)\n for i, v in enumerate(piles[start_pile], start=1):\n # Consider we take first i coins from start_pile\n ans = max(ans, v + helper(start_pile + 1, hk - i))\n if i == hk:\n break\n return ans\n \n return helper(0, k)```
| 3
| 0
|
['Dynamic Programming', 'Prefix Sum', 'Python3']
| 0
|
maximum-value-of-k-coins-from-piles
|
✔💯Easy JAVA Solution ✔💯|| Dynamic Programming
|
easy-java-solution-dynamic-programming-b-mm7v
|
\n\n\n# Code\n\nclass Solution {\n int dp[][];\n public int maxValueOfCoins(List<List<Integer>> piles, int k) {\n int n = piles.size();\n dp
|
HitenAgarwal
|
NORMAL
|
2023-04-15T10:42:11.307374+00:00
|
2023-04-15T10:42:11.307408+00:00
| 163
| false
|
\n\n\n# Code\n```\nclass Solution {\n int dp[][];\n public int maxValueOfCoins(List<List<Integer>> piles, int k) {\n int n = piles.size();\n dp = new int[n+1][k+1];\n for(int i = 1; i <= n; i++){\n for(int coins = 0; coins <= k; coins++){\n dp[i][coins] = -1;\n }\n }\n return helper(piles,n,k);\n }\n\n private int helper(List<List<Integer>> piles, int i, int coins){\n if(i==0)return 0;\n\n if(dp[i][coins] != -1)return dp[i][coins];\n\n int currSum = 0;\n for(int currCoins = 0; currCoins <= Math.min(piles.get(i-1).size(), coins); currCoins++){\n if(currCoins > 0){\n currSum += piles.get(i-1).get(currCoins-1);\n }\n dp[i][coins] = Math.max(dp[i][coins], helper(piles, i-1, coins-currCoins)+currSum);\n }\n return dp[i][coins];\n }\n}\n```
| 3
| 0
|
['Java']
| 0
|
maximum-value-of-k-coins-from-piles
|
Bottom-up DP explained
|
bottom-up-dp-explained-by-piyush01123-rycq
|
We define dp[i][j] as the the answer considering 1st i piles for at most j coins. Hence final answer is dp[n][k]. In base case we consider i=0 ie considering ze
|
piyush01123
|
NORMAL
|
2023-04-15T09:38:50.191109+00:00
|
2023-04-15T09:42:55.785170+00:00
| 316
| false
|
We define `dp[i][j]` as the the answer considering 1st `i` piles for at most `j` coins. Hence final answer is `dp[n][k]`. In base case we consider `i=0` ie considering zero piles. This row will be just zeroes. Similarly for `j=0` column also, it will be all zeroes. \n\nConsider any general `dp[i][j]`. \n\nWe can take 0 coins from `i`th pile and all the `j` coins from the first `i-1` piles. The value for this situation is `dp[i-1][j] + 0`.\n\nWe can also take 3 coins from `ith pile` (assume valid) and `j-3` coins from the first `i-1` piles. The value for this situation is `dp[i-1][j-3] + piles[i-1][0]+piles[i-1][1]+piles[i-1][2]`. \n\nSimilarly we can have other possiblities as well. `dp[i][j]` is the maximum of all these possibilities.\n\nWe define `cur` as the number of coins we take from the current pile and `curSum` as the sum of values of these `cur` coins.\n\n\n```\nint maxValueOfCoins(vector<vector<int>>& piles, int k) \n{\n int n = piles.size();\n vector<vector<int>> dp(n+1, vector<int>(k+1, 0));\n for (int i=1; i<=n; i++)\n {\n for (int j=0; j<=k; j++)\n {\n dp[i][j] = dp[i-1][j]; // cur=0\n int curSum = 0;\n for (int cur=1; cur<=min((int)piles[i-1].size(),j); cur++)\n {\n curSum += piles[i-1][cur-1];\n dp[i][j] = max(dp[i][j], dp[i-1][j-cur]+curSum);\n }\n }\n }\n return dp[n][k];\n}\n```\n\n$$TC= O(n\\sum_{i=1}^n {P_i})$$ where $P_i$ is the size of ith pile.\n$$SC: O(nk)$$
| 3
| 0
|
['Dynamic Programming', 'C++']
| 0
|
maximum-value-of-k-coins-from-piles
|
C++ | Easiest Solution | Memoization | Top Down DP | Recursive |
|
c-easiest-solution-memoization-top-down-h0mxh
|
APPROACH\nI have two option\nOption 1: I will not anything from the current ith pile\nOption 2: I wiil take some coins the from current ith pile and rest from o
|
rafikulalam2000off
|
NORMAL
|
2023-04-15T09:25:11.225653+00:00
|
2023-04-15T09:25:11.225700+00:00
| 376
| false
|
**APPROACH**\n**I have two option**\n**Option 1: I will not anything from the current ith pile**\n**Option 2: I wiil take some coins the from current ith pile and rest from other piles**\n```\nclass Solution\n{\n public:\n int dp[1001][2001];\n int solver(vector<vector < int>> &arr, int coins, int idx=0)\n {\n\n \t// I have no coin and no piles\n if (idx >= arr.size() || coins == 0) return 0;\n\n if (dp[idx][coins] != -1) return dp[idx][coins];\n\n int ans = INT_MIN;\n\n \t//Option1: I will not take anything from this pile\n ans = solver(arr, coins, idx + 1);\n\n \t//options2: I will try to take some coins from here and other coins from some other pile ..so that I can have maximum amount\n\n\t\t//current pile size\n int sz = arr[idx].size();\n int sum = 0;\n\t\t\n\t //[Need to iterate till min(coins,sz)because we can take only k coins at max ]\n for (int i = 0; i < min(coins, sz); i++)\n {\n sum = sum + arr[idx][i];\n\n \t//trying to take some coins from others also including mine\n ans = max(ans, sum + solver(arr, coins - (i + 1), idx + 1));\n }\n\n return dp[idx][coins] = ans;\n }\n int maxValueOfCoins(vector<vector < int>> &piles, int k)\n {\n memset(dp, -1, sizeof(dp));\n return solver(piles, k);\n }\n};\n```
| 3
| 0
|
['Dynamic Programming', 'Recursion', 'Memoization', 'C']
| 0
|
maximum-value-of-k-coins-from-piles
|
Rust, DP, concise.
|
rust-dp-concise-by-dfomin-132c
|
Intuition\nThis is dynamic programming task. The only tricky part is to find subtask.\nThe subtask is to solve it for smaller number of piles (i left most piles
|
dfomin
|
NORMAL
|
2023-04-15T08:57:27.848592+00:00
|
2023-04-15T09:20:20.132692+00:00
| 217
| false
|
# Intuition\nThis is dynamic programming task. The only tricky part is to find subtask.\nThe subtask is to solve it for smaller number of piles (i left most piles) and for smaller k.\nOn each step we iterate over new pile for all numbers from `0` to `k` and search for best value of `l` coins from new pile and `k - l` from previous subtask.\n\n\n# Code\n```\nuse std::cmp::{min,max};\n\nimpl Solution {\n pub fn max_value_of_coins(piles: Vec<Vec<i32>>, k: i32) -> i32 {\n let k = k as usize;\n let mut dp = vec![vec![0; k + 1]; piles.len() + 1];\n for i in 1..dp.len() {\n for j in 1..k + 1 {\n let mut s = 0;\n for l in 0..min(j + 1, piles[i - 1].len() + 1) {\n dp[i][j] = max(dp[i][j], s + dp[i - 1][j - l]);\n if l < piles[i - 1].len() {\n s += piles[i - 1][l];\n }\n }\n }\n }\n\n return dp[piles.len()][k];\n }\n}\n```
| 3
| 0
|
['Rust']
| 2
|
maximum-value-of-k-coins-from-piles
|
C++ || Dynamic Programming
|
c-dynamic-programming-by-sosuke23-ufft
|
Code\n\nclass Solution {\npublic:\n int maxValueOfCoins(vector<vector<int>>& piles, int k) {\n int n = piles.size();\n \n int dp[n+1][k+
|
Sosuke23
|
NORMAL
|
2023-04-15T02:01:13.967103+00:00
|
2023-04-15T02:01:13.967136+00:00
| 681
| false
|
# Code\n```\nclass Solution {\npublic:\n int maxValueOfCoins(vector<vector<int>>& piles, int k) {\n int n = piles.size();\n \n int dp[n+1][k+1];\n memset(dp,0,sizeof(dp));\n\n for(int i=1; i<=n; i++)\n {\n int sz = piles[i-1].size();\n for(int j=1; j<=k; j++)\n {\n int tmp = dp[i-1][j];\n int curr = 0, s = 0;\n for(int t=1; t<=sz; t++)\n {\n s += piles[i-1][t-1];\n if(j-t >= 0)\n curr = max(curr, dp[i-1][j-t] + s);\n\n dp[i][j] = max(dp[i-1][j], curr);\n }\n }\n }\n\n return dp[n][k];\n }\n};\n```
| 3
| 0
|
['Dynamic Programming', 'C++']
| 2
|
maximum-value-of-k-coins-from-piles
|
🗓️ Daily LeetCoding Challenge April, Day 15
|
daily-leetcoding-challenge-april-day-15-kpwje
|
This problem is the Daily LeetCoding Challenge for April, Day 15. Feel free to share anything related to this problem here! You can ask questions, discuss what
|
leetcode
|
OFFICIAL
|
2023-04-15T00:00:17.614482+00:00
|
2023-04-15T00:00:17.614538+00:00
| 3,060
| false
|
This problem is the Daily LeetCoding Challenge for April, Day 15.
Feel free to share anything related to this problem here!
You can ask questions, discuss what you've learned from this problem, or show off how many days of streak you've made!
---
If you'd like to share a detailed solution to the problem, please create a new post in the discuss section and provide
- **Detailed Explanations**: Describe the algorithm you used to solve this problem. Include any insights you used to solve this problem.
- **Images** that help explain the algorithm.
- **Language and Code** you used to pass the problem.
- **Time and Space complexity analysis**.
---
**📌 Do you want to learn the problem thoroughly?**
Read [**⭐ LeetCode Official Solution⭐**](https://leetcode.com/problems/maximum-value-of-k-coins-from-piles/solution) to learn the 3 approaches to the problem with detailed explanations to the algorithms, codes, and complexity analysis.
<details>
<summary> Spoiler Alert! We'll explain this 0 approach in the official solution</summary>
</details>
If you're new to Daily LeetCoding Challenge, [**check out this post**](https://leetcode.com/discuss/general-discussion/655704/)!
---
<br>
<p align="center">
<a href="https://leetcode.com/subscribe/?ref=ex_dc" target="_blank">
<img src="https://assets.leetcode.com/static_assets/marketing/daily_leetcoding_banner.png" width="560px" />
</a>
</p>
<br>
| 3
| 0
|
[]
| 11
|
maximum-value-of-k-coins-from-piles
|
[Java/C++/Python]O(n)time/BEATS 99.97% MEMORY/SPEED 0ms APRIL 2022
|
javacpythonontimebeats-9997-memoryspeed-c411b
|
Java\n\nclass Solution {\n public int maxValueOfCoins(List<List<Integer>> piles, int k) {\n int n=piles.size();\n int[] dp=new int[k+1];// k st
|
darian-catalin-cucer
|
NORMAL
|
2022-04-24T06:59:23.603686+00:00
|
2022-04-24T08:12:43.868196+00:00
| 478
| false
|
***Java***\n```\nclass Solution {\n public int maxValueOfCoins(List<List<Integer>> piles, int k) {\n int n=piles.size();\n int[] dp=new int[k+1];// k steps dynamic programming;\n // for each pile to do dp.\n for(List<Integer> pile:piles){\n //use prefix sum to record each pile\'s first i elments;\n int m=pile.size();\n int[] cum=new int[m+1];\n for(int i=0;i<m;i++) cum[i+1]=cum[i]+pile.get(i);\n //use current pile to do dp, the dp is\n // we have two pile previous pile\'s dp result and current pile--> reduce to two pile problem.\n // pile 0, 1 ,2 ,3 , 4, ...\n // pile (0,1),2,3,4...\n // (0,1) is dp result for next calculation.\n // pile (0,1,2),3,4...\n // ...\n // pile (0,1,2,3,4... )\n int[] curdp=new int[k+1];\n for(int i=0;i<=k;i++){\n for(int j=0;j<=m&& i+j <=k;j++){\n curdp[i+j]=Math.max(curdp[i+j],dp[i]+cum[j]);\n }\n }\n dp=curdp;\n }\n return dp[k];\n }\n}\n```\n\n***C++***\n```\nclass Solution {\npublic:\n int dp[1001][2001]; //Dp array For Memoization.\n int solve(vector<vector<int>>&v,int index,int coin)\n {\n if(index>=v.size()||coin==0) //Base Condition\n return 0;\n if(dp[index][coin]!=-1) //Check wheather It is Already Calculated Or not.\n return dp[index][coin];\n \n \n /* Our 1st choice :- We not take any Coin from that pile*/\n int ans=solve(v,index+1,coin); //Just Call function for next Pile.\n \n \n /*Otherwise we can take Coins from that Pile.*/\n int loop=v[index].size()-1;\n int sum=0;\n \n for(int j=0;j<=min(coin-1,loop);j++) //\n {\n sum=sum+v[index][j];\n ans=max(ans,sum+solve(v,index+1,coin-(j+1)));\n \n /*Aove we Pass coin-(j+1). Because till j\'th index we have taken j+1 coin from that pile.*/\n }\n \n return dp[index][coin]=ans;\n }\n int maxValueOfCoins(vector<vector<int>>& piles, int k) {\n memset(dp,-1,sizeof(dp));\n return solve(piles,0,k);\n }\n};\n```\n\n***Python***\n```\nimport numpy as np\nclass Solution:\n def maxValueOfCoins(self, piles: List[List[int]], k: int) -> int:\n best = np.zeros(k+1)\n for pile in piles:\n temp = best.copy()\n for used, value in enumerate(accumulate(pile), 1):\n if used > k: break\n temp2 = best+value\n temp2 = np.concatenate((np.zeros(used), temp2[:-used]))\n temp = np.maximum(temp, temp2)\n best = temp\n return int(best[-1])\n```\n\n***Consider upvote if useful!***
| 3
| 0
|
['C', 'Combinatorics', 'Python', 'C++', 'Java']
| 3
|
maximum-value-of-k-coins-from-piles
|
C++ | 2D - DP
|
c-2d-dp-by-archit-bikram-dpim
|
\nclass Solution {\npublic:\n int maxValueOfCoins(vector<vector<int>>& P, int k) {\n int m = P.size();\n for(int i = 0 ; i< m ; i++){\n
|
Archit-Bikram
|
NORMAL
|
2022-03-27T04:59:49.568460+00:00
|
2022-03-27T05:08:10.999955+00:00
| 214
| false
|
```\nclass Solution {\npublic:\n int maxValueOfCoins(vector<vector<int>>& P, int k) {\n int m = P.size();\n for(int i = 0 ; i< m ; i++){\n int n = P[i].size();\n for(int j = 1 ; j<n; ++j){\n P[i][j] += P[i][j-1];\n }\n }// sum of value if we take j elements from top of any pile of coins.\n vector<int> mxc(k+1,0);\n for(int j = min(k,(int)P[0].size()) ; j>0; --j){\n mxc[j] = P[0][j-1];\n }\n for(int i = 1 ; i< m ; i++){\n int n = P[i].size();\n for(int j=k; j>0 ; --j){//Final Sum\n for(int l=min(j,n); l>0; --l){\n mxc[j] = max(mxc[j-l]+P[i][l-1],mxc[j]);\n }\n \n }\n }\n return mxc[k];\n \n }\n};\n```\n\n0-1 Knapsack problem variant.
| 3
| 0
|
[]
| 1
|
maximum-value-of-k-coins-from-piles
|
Greedy Fails||Dynamic Programming (front partition)!!!
|
greedy-failsdynamic-programming-front-pa-bxrp
|
Intuition\nsince we have to take starting few of the elements so can do like take starting 1 or 2 or 3 upto the length number of elements from current pile an
|
ankii09102003
|
NORMAL
|
2024-08-26T05:40:48.734419+00:00
|
2024-08-26T05:40:48.734458+00:00
| 98
| false
|
# Intuition\nsince we have to take starting few of the elements so can do like take starting 1 or 2 or 3 upto the length number of elements from current pile and in each case apply a call of dp with a guide that take the elements from next pile \nalso, prefix sum can be calculated but not beneficial as it would take continuous memory (OS concept : allocating memory in chunks would be very helpful as compare to continuos high block of memory. ) \n\n# Approach\n<!-- Describe your approach to solving the problem. -->the reason why greedy fails is that we have not given a fixed order of elements so that we can apply the priority queue approach like applied in merger k sorted arrays type...\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\nint solve(vector<vector<int>>&piles,int k, int index,vector<vector<int>>&dp){\n if(k==0){\n return 0;\n }\n if(k<0){\n return -1e9;\n }\n if(index>=piles.size()){\n return -1e9;\n }\n if(dp[k][index]!=-1)\n return dp[k][index];\n int sum=0;\n int curr_sum=0;\n for(int i=0;i<piles[index].size();i++){\n curr_sum+=piles[index][i];\n\n sum=max(sum,curr_sum+solve(piles,k-i-1,index+1,dp));\n }\n int nottake=solve(piles,k,index+1,dp);\n return dp[k][index]= max(sum,nottake);\n}\n int maxValueOfCoins(vector<vector<int>>& piles, int k) {\n // int ans=0;\n // priority_queue<pair<int,pair<int,int>>,vector<pair<int,pair<int,int>>>,greater<pair<int,pair<int,int>>>>pq;\n // for(int i=0;i<piles.size();i++){\n // pq.push({piles[i][0],{i,0}});\n // }\n // while(k--){\n // auto top=pq.top();\n // pq.pop();\n // int val=top.first;\n // int row=top.second.first;\n // int col=top.second.second;\n // ans+=val;\n // col++;\n // if(col<piles[row].size()){\n // pq.push({piles[row][col],{row,col}});\n // }\n // }\n // return ans;\n //so this greedy fails \n //as, we are not given a fix order of elements\n //applying dp, like taking any number of elements from one pile and then move to the next pile \n\n\n vector<vector<int>>dp(k+1,vector<int>(piles.size()+1,-1));\n\n return solve(piles,k,0,dp);\n }\n};\n```
| 2
| 0
|
['C++']
| 0
|
maximum-value-of-k-coins-from-piles
|
C++ || Memoization || easy to understand
|
c-memoization-easy-to-understand-by-anki-2tov
|
\n\n# Code\n\nclass Solution {\npublic:\n int helper(vector<vector<int>>& piles, int k, int ind, vector<vector<int>> & dp){\n if(ind<0)return 0;\n
|
ankitkr23
|
NORMAL
|
2023-05-19T23:24:27.487124+00:00
|
2023-05-19T23:24:27.487157+00:00
| 11
| false
|
\n\n# Code\n```\nclass Solution {\npublic:\n int helper(vector<vector<int>>& piles, int k, int ind, vector<vector<int>> & dp){\n if(ind<0)return 0;\n if(k==0)return 0;\n if(dp[ind][k]!=-1)return dp[ind][k];\n int a=helper(piles, k, ind-1, dp);\n \n int ans=a;\n for(int i=0; i<piles[ind].size(); i++){\n int b=0;\n if(i+1<=k){\n b=piles[ind][i]+helper(piles, k-i-1, ind-1, dp);\n ans=max(ans, b);\n }\n }\n return dp[ind][k]=ans;\n }\n int maxValueOfCoins(vector<vector<int>>& piles, int k) {\n int n=piles.size();\n for(int i=0; i<piles.size(); i++){\n for(int j=1; j<piles[i].size(); j++){\n piles[i][j]+=piles[i][j-1];\n }\n }\n vector<vector<int>> dp(n, vector<int>(k+1, -1));\n return helper(piles, k, n-1, dp);\n }\n};\n```
| 2
| 0
|
['C++']
| 0
|
maximum-value-of-k-coins-from-piles
|
Python short and clean. Recursive. DP. Functional programming.
|
python-short-and-clean-recursive-dp-func-fne4
|
Complexity\n- Time complexity: O(m * k)\n\n- Space complexity: O(m)\n\nwhere,\nm is number of total coins from all piles\n\n# Code\npython\nclass Solution:\n
|
darshan-as
|
NORMAL
|
2023-04-15T20:04:34.675564+00:00
|
2023-04-15T20:04:34.675613+00:00
| 65
| false
|
# Complexity\n- Time complexity: $$O(m * k)$$\n\n- Space complexity: $$O(m)$$\n\nwhere,\n`m is number of total coins from all piles`\n\n# Code\n```python\nclass Solution:\n def maxValueOfCoins(self, piles: list[list[int]], k_: int) -> int:\n prefix_piles = [list(accumulate(p, initial=0)) for p in piles]\n\n @cache\n def max_value(n: int, k: int) -> int:\n return max(\n max_value(n - 1, k - i) + x\n for i, x in enumerate(islice(prefix_piles[n - 1], k + 1))\n ) if n and k else 0\n \n return max_value(len(piles), k_)\n\n\n```
| 2
| 0
|
['Array', 'Dynamic Programming', 'Prefix Sum', 'Python', 'Python3']
| 0
|
maximum-value-of-k-coins-from-piles
|
C++ || Recursion + Memoization
|
c-recursion-memoization-by-jillchaudhary-r2c4
|
\n\n# Code\n\nclass Solution {\npublic:\n int dp[1001][2001];\n int fun(int i, int k, vector<vector<int>> &v, int n, vector<vector<int>> &pre){\n i
|
jillchaudhary39
|
NORMAL
|
2023-04-15T15:37:51.782112+00:00
|
2023-04-15T15:37:51.782152+00:00
| 10
| false
|
\n\n# Code\n```\nclass Solution {\npublic:\n int dp[1001][2001];\n int fun(int i, int k, vector<vector<int>> &v, int n, vector<vector<int>> &pre){\n if(i>=n || k==0) return 0;\n if(dp[i][k]!=-1) return dp[i][k];\n int maxi=-1;\n for(int p=0;p<=min(k,(int)v[i].size());p++){\n int ans=0;\n if(p==0){\n if(dp[i+1][k]!=-1)\n ans+=dp[i+1][k];\n else\n ans+=fun(i+1,k,v,n,pre);\n }\n else{\n ans+=pre[i][min({p,k,(int)v[i].size()})-1];\n if(dp[i+1][k-min({p,k,(int)v[i].size()})]!=-1)\n ans+=dp[i+1][k-min({p,k,(int)v[i].size()})];\n else\n ans+=fun(i+1,k-min({p,k,(int)v[i].size()}),v,n,pre);\n }\n maxi=max(maxi,ans);\n }\n return dp[i][k]=maxi;\n }\n int maxValueOfCoins(vector<vector<int>>& piles, int k) {\n memset(dp,-1,sizeof(dp));\n vector<vector<int>> pre;\n for(int i=0;i<piles.size();i++){\n int sum=0;\n vector<int> p;\n for(int j=0;j<piles[i].size();j++){\n sum+=piles[i][j];\n p.push_back(sum);\n }\n pre.push_back(p);\n }\n \n return fun(0,k,piles,piles.size(),pre);\n }\n};\n```
| 2
| 0
|
['C++']
| 0
|
maximum-value-of-k-coins-from-piles
|
C++ | Recursion + DP
|
c-recursion-dp-by-__priyanshu-g6nd
|
Code\n\nclass Solution {\npublic:\n int maxValueOfCoins(vector<vector<int>>& piles, int k) {\n \n vector<vector<int>> dp(piles.size(), vector<i
|
__priyanshu__
|
NORMAL
|
2023-04-15T13:59:18.660107+00:00
|
2023-04-15T13:59:38.799876+00:00
| 83
| false
|
# Code\n```\nclass Solution {\npublic:\n int maxValueOfCoins(vector<vector<int>>& piles, int k) {\n \n vector<vector<int>> dp(piles.size(), vector<int> (k + 1, -1));\n return helper(piles, 0, k, dp);\n }\n\n int helper(vector<vector<int>> &piles, int i, int k, vector<vector<int>> &dp)\n {\n if(i >= piles.size() || k == 0)\n return 0;\n\n if(dp[i][k] != -1)\n return dp[i][k];\n\n int mx = helper(piles, i + 1, k, dp), sum = 0;\n for(int j = 0; j < piles[i].size() && j < k; j++)\n mx = max(mx, (sum += piles[i][j]) + helper(piles, i + 1, k - j - 1, dp));\n\n return dp[i][k] = mx;\n }\n};\n```
| 2
| 0
|
['Dynamic Programming', 'Recursion', 'Memoization', 'C++']
| 0
|
maximum-value-of-k-coins-from-piles
|
Ruby: prefix sum and recursion
|
ruby-prefix-sum-and-recursion-by-lacross-l1ox
|
Code\nruby\nclass Array\n def scan(st) = map { st = yield st, _1 }\n def prefsum = scan(0, &:+).unshift(0)\nend\n\ndef max_value_of_coins(piles, k)\n @pile_p
|
lacrosse
|
NORMAL
|
2023-04-15T11:48:19.082690+00:00
|
2023-04-15T11:48:19.082729+00:00
| 140
| false
|
# Code\n```ruby\nclass Array\n def scan(st) = map { st = yield st, _1 }\n def prefsum = scan(0, &:+).unshift(0)\nend\n\ndef max_value_of_coins(piles, k)\n @pile_prefs = piles.map(&:prefsum)\n @size_prefs = piles.map(&:size).prefsum\n @_dp = Array.new(piles.size) { [] } << -> _ { 0 }\n dp(0, k)\nend\n\ndef dp(i, k)\n @_dp[i][k] ||= begin\n pref = @pile_prefs[i]\n rem = @size_prefs[-1] - @size_prefs[i + 1]\n (max(0, k - rem)..min(k, pref.size - 1)).map { pref[_1] + dp(i + 1, k - _1) }.max\n end\nend\n\ndef min(a, b) = a < b ? a : b\ndef max(a, b) = a > b ? a : b\n```\n\n# Time complexity\n\n$$\\mathcal{O}(\\sum|\\text{piles}_i|)$$\n\n# Space complexity\n\n$$\\mathcal{O}(\\sum|\\text{piles}_i|)$$
| 2
| 0
|
['Recursion', 'Prefix Sum', 'Ruby']
| 0
|
maximum-value-of-k-coins-from-piles
|
[Kotlin] Prefix Sum DP Solution
|
kotlin-prefix-sum-dp-solution-by-devle79-km5y
|
Approach\n Describe your approach to solving the problem. \n\nUse top-down dp to find max value of coin.\n\nSave every optimal value in dp table and use that va
|
devle79
|
NORMAL
|
2023-04-15T10:30:47.576528+00:00
|
2023-04-15T10:30:47.576565+00:00
| 34
| false
|
# Approach\n<!-- Describe your approach to solving the problem. -->\n\nUse top-down dp to find max value of coin.\n\nSave every optimal value in dp table and use that value at next iteration.\n\nFlow goes like this:\n\n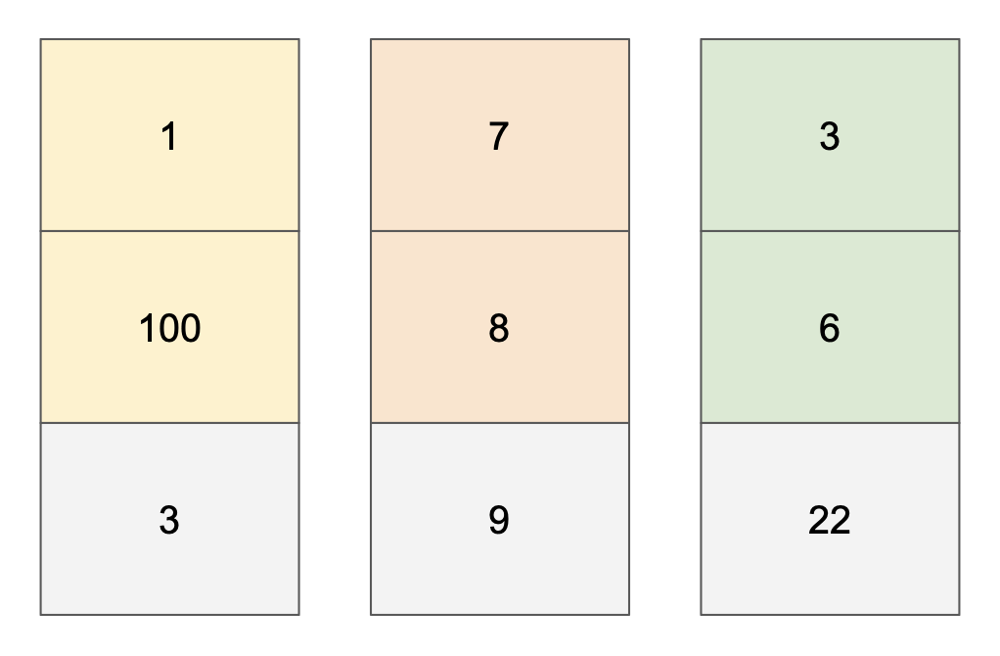\n\n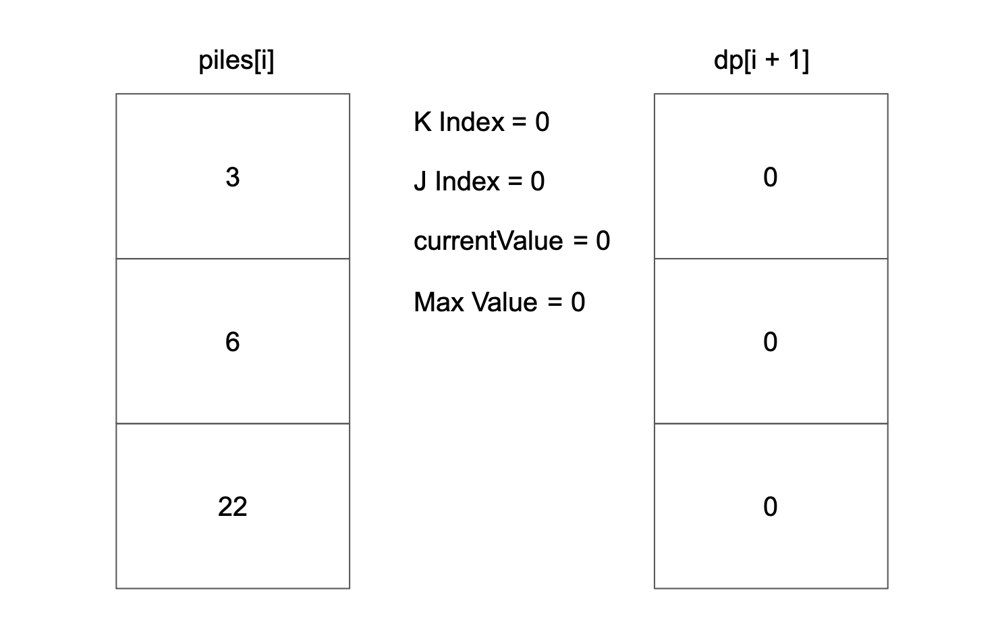\n\n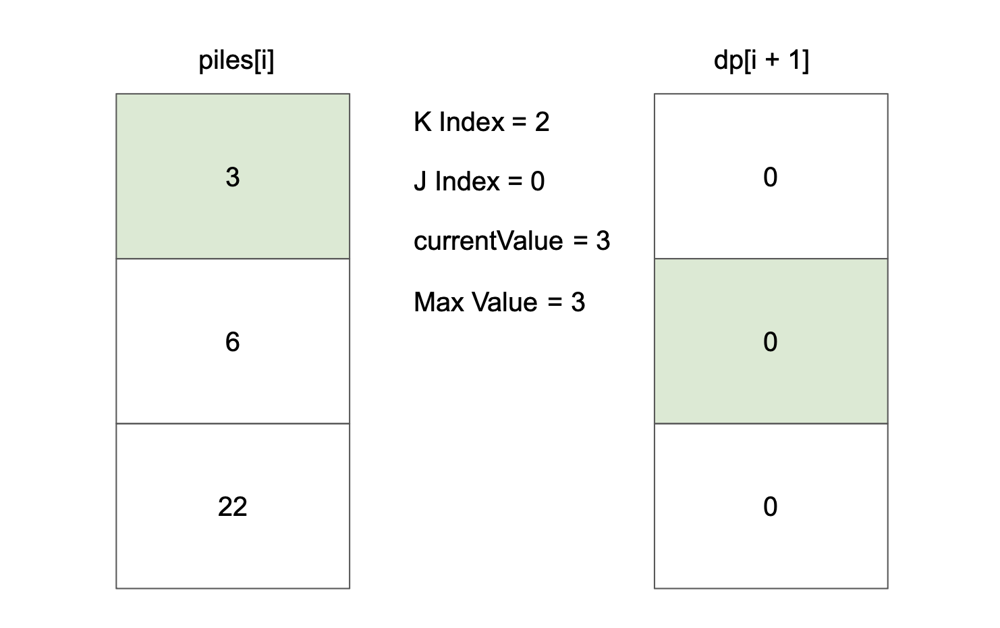\n\n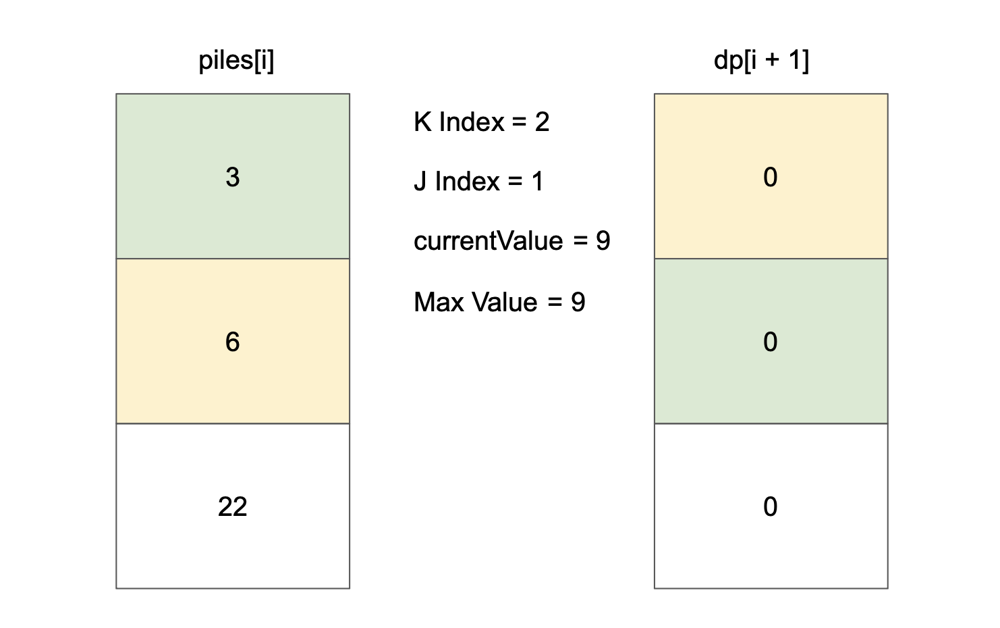\n\n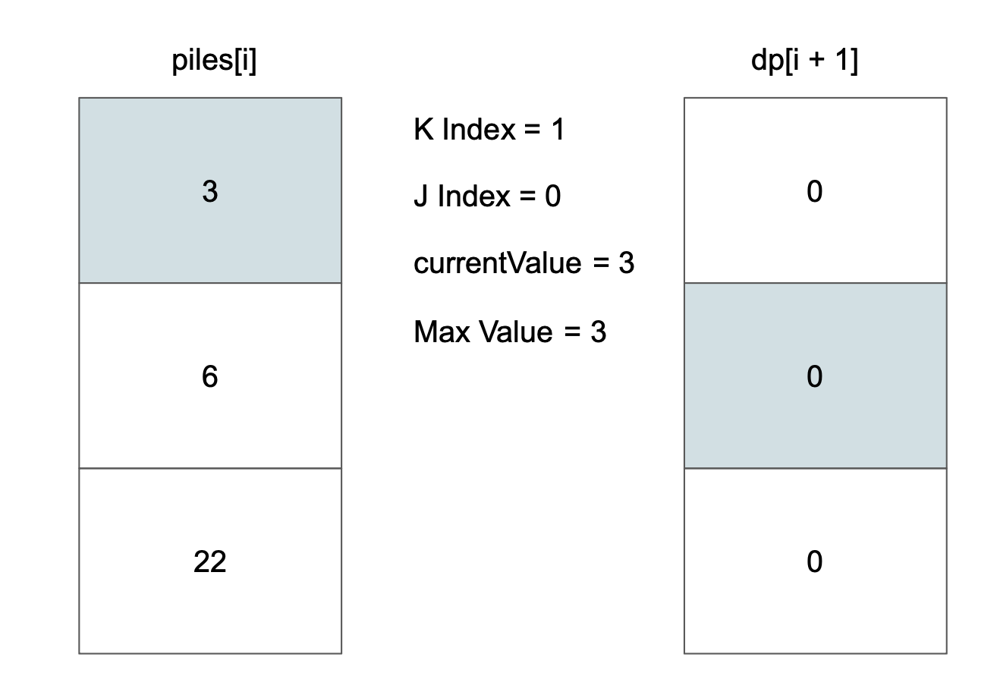\n\n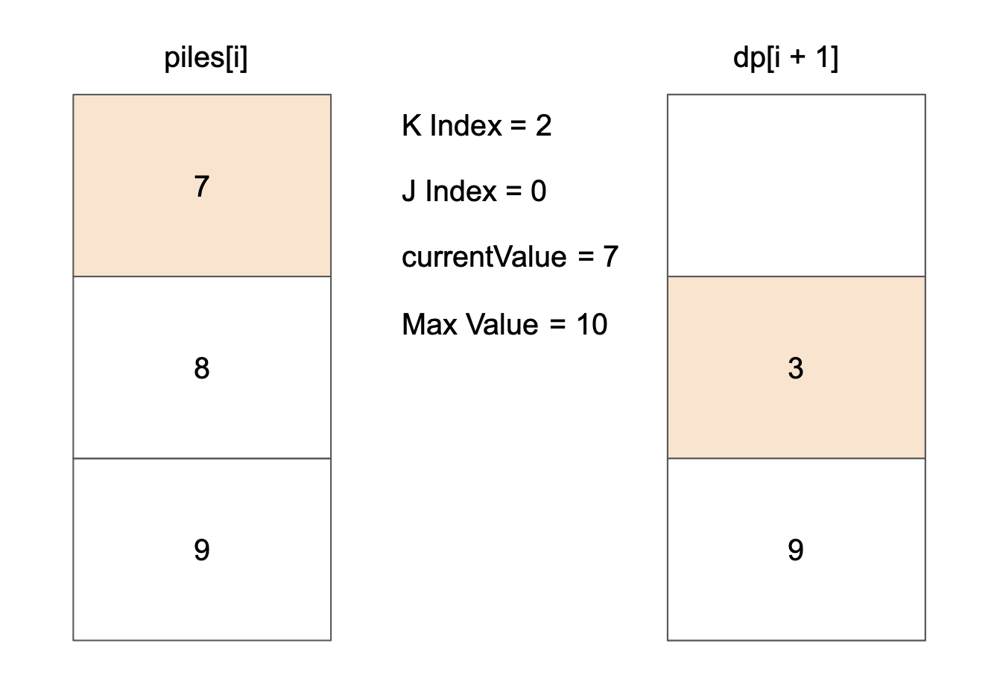\n\n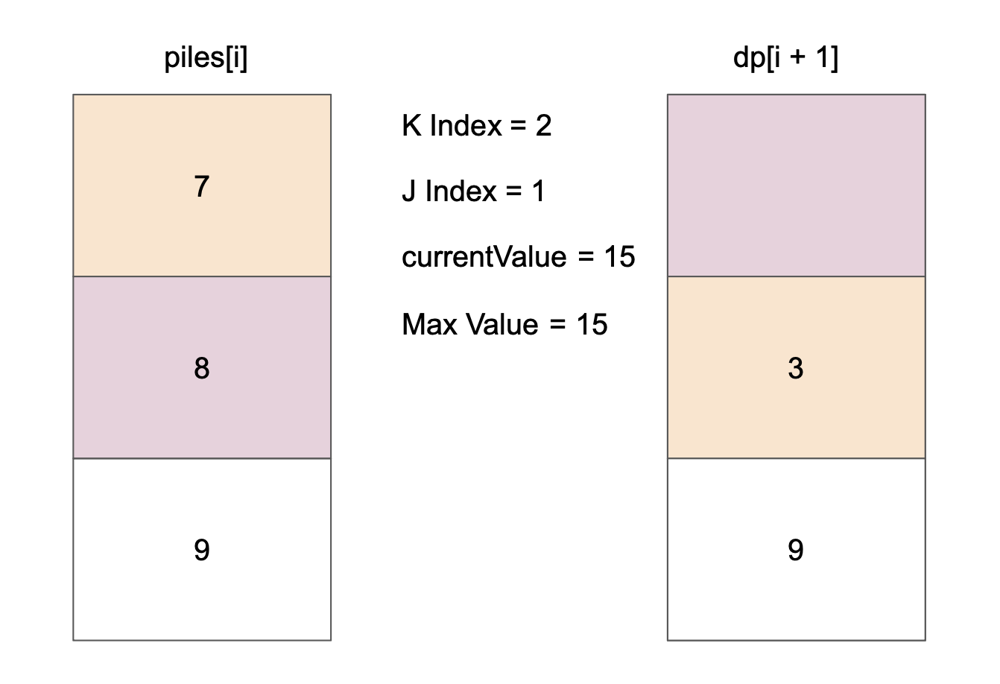\n\n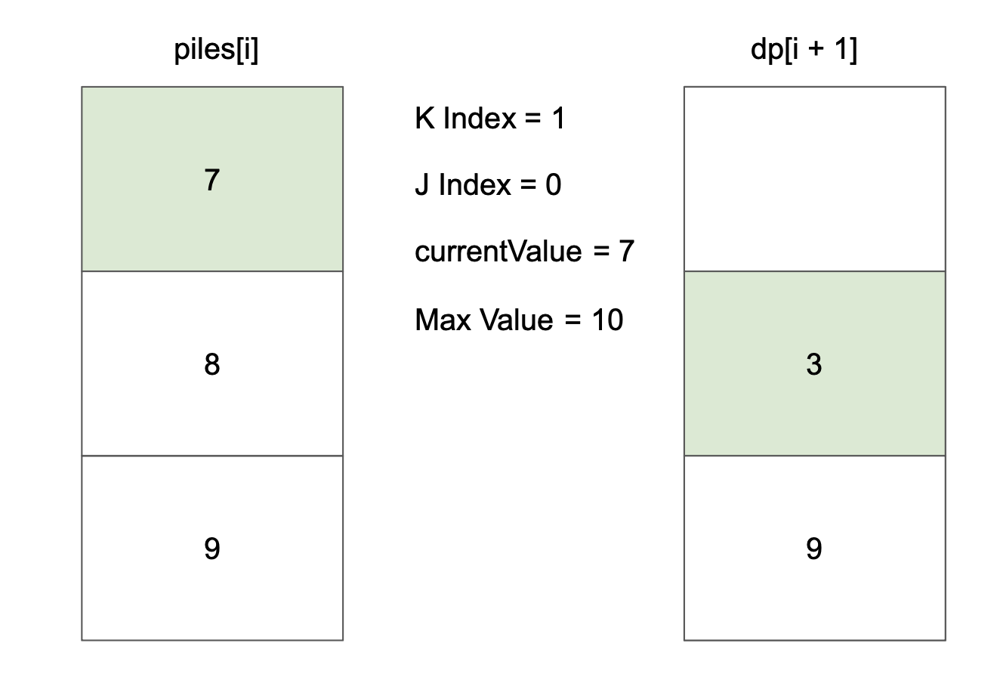\n\n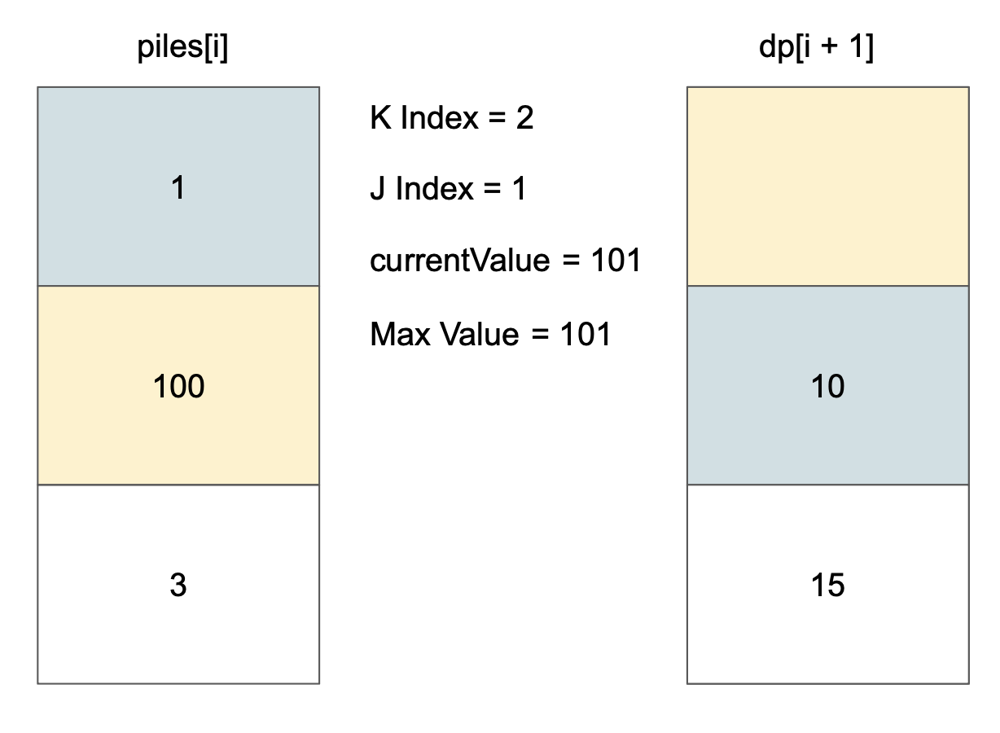\n\n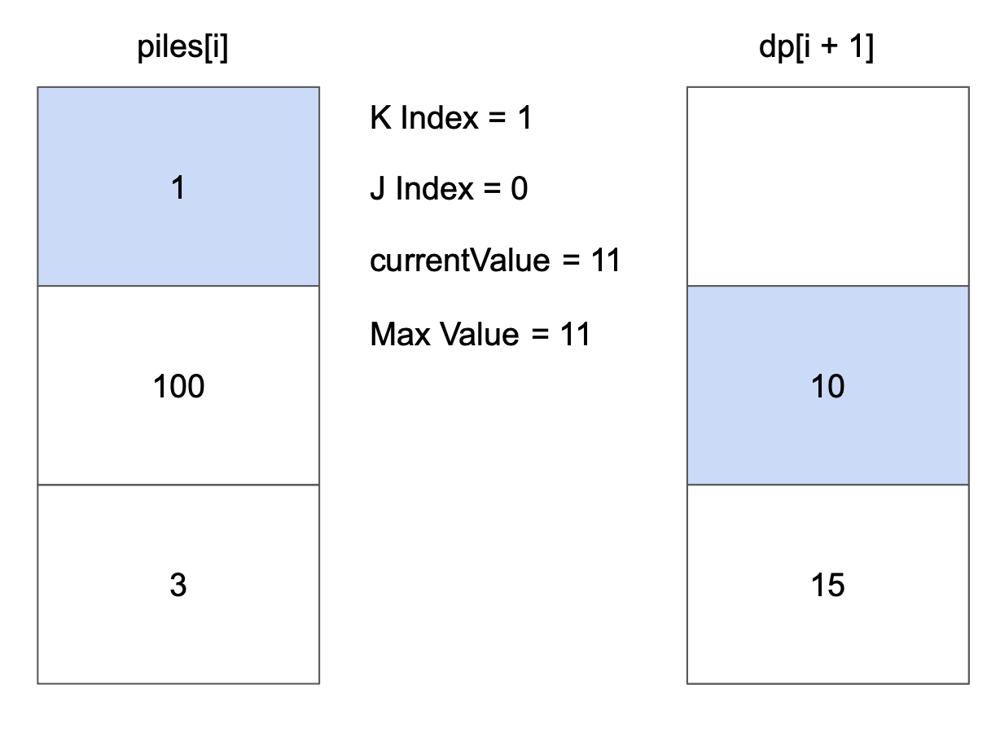\n\n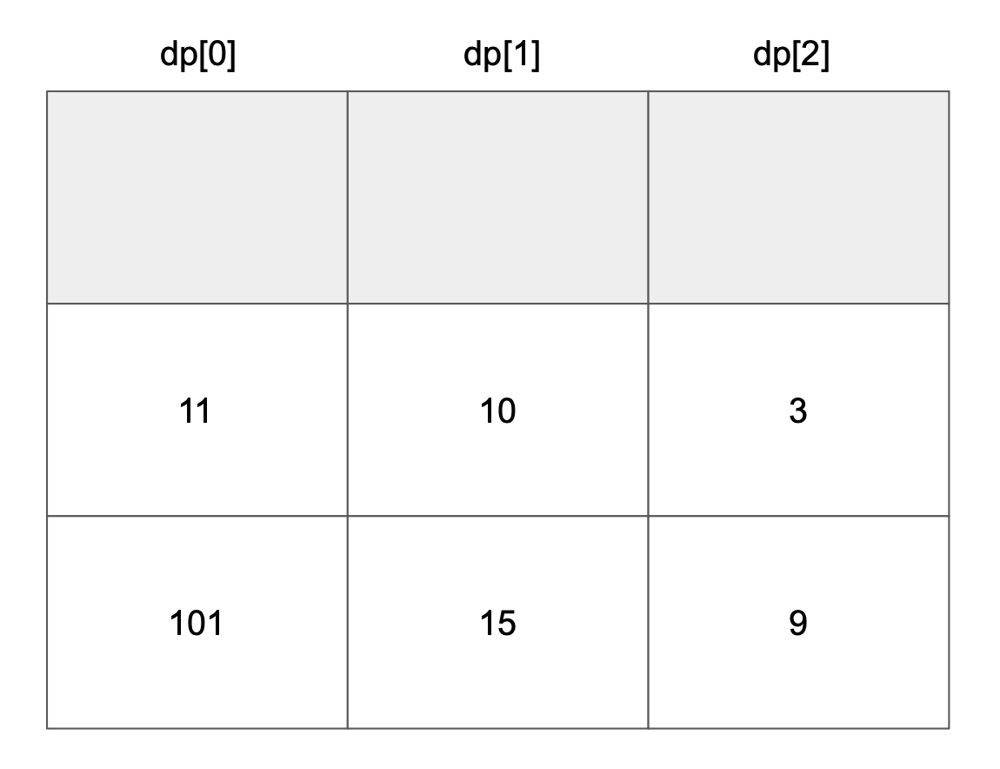\n\n\n# Complexity\n- Time complexity: $$O(n * k)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(n * k)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n\n fun maxValueOfCoins(piles: List<List<Int>>, k: Int): Int {\n val dp = Array(piles.size + 1) { IntArray(k + 1) }\n\n for (i in piles.lastIndex downTo 0) {\n for (kIndex in k downTo 1) {\n var currentValue = 0\n var maxValue = dp[i + 1][kIndex]\n\n for (j in 0 until minOf(kIndex, piles[i].size)) {\n currentValue += piles[i][j]\n maxValue = maxOf(maxValue, currentValue + dp[i + 1][kIndex - (j + 1)])\n }\n\n dp[i][kIndex] = maxValue\n }\n }\n\n return dp[0][k]\n }\n\n}\n```
| 2
| 0
|
['Array', 'Dynamic Programming', 'Prefix Sum', 'Kotlin']
| 0
|
maximum-value-of-k-coins-from-piles
|
Simple solution using recursion and memoization
|
simple-solution-using-recursion-and-memo-pgd2
|
\n\n# Code\n\nclass Solution\n{\npublic:\n int sumi(int index, vector<vector<int>> &piles, int k, int n, vector<vector<int>> &dp)\n {\n if (index == n or k
|
priyanshu11_
|
NORMAL
|
2023-04-15T09:53:19.642415+00:00
|
2023-04-15T09:53:19.642453+00:00
| 90
| false
|
\n\n# Code\n```\nclass Solution\n{\npublic:\n int sumi(int index, vector<vector<int>> &piles, int k, int n, vector<vector<int>> &dp)\n {\n if (index == n or k == 0)\n return 0;\n if (dp[index][k] != -1)\n return dp[index][k];\n int notPick = sumi(index + 1, piles, k, n, dp);\n int pick = 0, coins = k, sum = 0;\n for (int i = 0; i < piles[index].size() and coins > 0; i++)\n {\n sum += piles[index][i];\n coins--;\n int x = sum + sumi(index + 1, piles, coins, n, dp);\n pick = max(pick, x);\n }\n return dp[index][k] = max(pick, notPick);\n }\n int maxValueOfCoins(vector<vector<int>> &piles, int k)\n {\n int n = piles.size();\n int index = 0;\n vector<vector<int>> dp(n, vector<int>(k + 1, -1));\n return sumi(index, piles, k, n, dp);\n }\n};\n```
| 2
| 0
|
['Array', 'Dynamic Programming', 'C++', 'Java']
| 0
|
maximum-value-of-k-coins-from-piles
|
Solution in C++
|
solution-in-c-by-ashish_madhup-1bab
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
ashish_madhup
|
NORMAL
|
2023-04-15T06:07:08.563294+00:00
|
2023-04-15T06:07:08.563332+00:00
| 42
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<vector<int>> dp;\n int func(vector<vector<int>>& p,int i,int k)\n {\n if(i==p.size()) return 0;\n if(dp[i][k]!=-1) return dp[i][k];\n int ans=func(p,i+1,k);\n int a=0;\n for(int j=0;j<p[i].size()&&j<k;j++)\n {\n a+=p[i][j];\n ans=max(ans,a+func(p,i+1,k-j-1));\n }\n return dp[i][k]=ans;\n }\n int maxValueOfCoins(vector<vector<int>>& p, int k) \n {\n dp=vector<vector<int>>(p.size(),vector<int>(k+1,-1));\n return func(p,0,k);\n }\n};\n```
| 2
| 0
|
['C++']
| 0
|
maximum-value-of-k-coins-from-piles
|
PYTHON || easy solution with explanation || recursion with caching
|
python-easy-solution-with-explanation-re-2gli
|
Intuition\n Describe your first thoughts on how to solve this problem. \ndynamic programming problem \n# Approach\n Describe your approach to solving the proble
|
bohaa
|
NORMAL
|
2023-04-15T03:20:18.330965+00:00
|
2023-04-15T03:22:31.393917+00:00
| 430
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\ndynamic programming problem \n# Approach\n<!-- Describe your approach to solving the problem. -->\n- we first skip all nodes to start from last assume i have 4 piles (try last piles , then try 3rd and last pile , etc)\n- with base case if i ==n or k ==0 return 0\n- in for loop i try all possible coins in cur pile to last pile in limit with k\n- cur_val save the value of cur try , ans res save max res of all tries \n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\no(n2)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\no(n)\n# Code\n```\nclass Solution(object):\n def maxValueOfCoins(self, piles, k):\n """\n :type piles: List[List[int]]\n :type k: int\n :rtype: int\n """\n cache ={}\n def dfs(i,k ):\n if (i,k) in cache:\n return cache[(i,k)]\n if k==0 or i == len(piles):\n return 0\n # skip piles until reach end , then try all possible from last to first \n dfs(i+1 , k) \n res , cur_val = dfs(i+1 , k),0\n for j in range(min(k , len(piles[i]))):\n cur_val += piles[i][j]\n # print(cur_val ,res )\n res = max(res , cur_val + dfs(i+1 , k-j-1))\n cache[(i,k)]=res\n return cache[(i,k)]\n return dfs(0,k)\n\n```
| 2
| 0
|
['Dynamic Programming', 'Recursion', 'Memoization', 'Python', 'Python3']
| 1
|
maximum-value-of-k-coins-from-piles
|
C++ Simple (Recursion + Memorization)
|
c-simple-recursion-memorization-by-haris-gwnx
|
Approach\n Describe your approach to solving the problem. \n1. For each pile we add top coins ans so for any dp[i][k] it will store the max coins we can get fro
|
HarishRa9a
|
NORMAL
|
2023-04-15T00:45:04.172375+00:00
|
2023-05-25T17:23:02.528187+00:00
| 26
| false
|
# Approach\n<!-- Describe your approach to solving the problem. -->\n1. For each pile we add top coins ans so for any dp[i][k] it will store the max coins we can get from ith pile using k coins.\n2. For a pile we can either choose 0,1,....k coins and then proceede toward next pile.\n# Complexity\n- Time complexity: O(n*m)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n*k)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n vector<vector<int>> aux;\n int n;\n\n int rec(vector<vector<int>>& piles, int k,int i){\n if(i==n){return 0;}\n if(aux[i][k]==-1){\n aux[i][k]=rec(piles,k,i+1);\n // Loop will run till ith pile is empty OR we can\'t pick any more coins i.e k==0\n for(int j=0,x=0; j<piles[i].size() && k-j-1>=0; j++){\n x+=piles[i][j];\n aux[i][k]=max(aux[i][k],rec(piles,k-j-1,i+1)+x);\n }\n }\n return aux[i][k];\n }\n\n int maxValueOfCoins(vector<vector<int>>& piles, int k) {\n n=piles.size();\n aux.resize(n,vector<int>(k+1,-1)); \n return rec(piles,k,0);\n }\n};\n```
| 2
| 0
|
['Dynamic Programming', 'Recursion', 'Memoization', 'C++']
| 0
|
maximum-value-of-k-coins-from-piles
|
DP isn't scary dude
|
dp-isnt-scary-dude-by-imprayas12-lls0
|
\nclass Solution {\n public int maxValueOfCoins(List<List<Integer>> piles, int k) {\n /*\n -> Pick the first coin from the pile and move to next.\n
|
imprayas12
|
NORMAL
|
2022-09-29T08:38:12.607023+00:00
|
2022-09-29T08:38:12.607065+00:00
| 168
| false
|
```\nclass Solution {\n public int maxValueOfCoins(List<List<Integer>> piles, int k) {\n /*\n -> Pick the first coin from the pile and move to next.\n -> Don\'t pick the first coin from pile and move to next.\n -> Pick first coin and stay on the same pile to pick the next coin.\n */ \n int[][] dp = new int[piles.size()][k + 1];\n for(var i:dp) Arrays.fill(i,-1);\n return move(piles,k,0,dp);\n }\n private int move(List<List<Integer>> piles, int k, int pileInd,int[][] dp) {\n if(k == 0) return 0;\n if(pileInd == piles.size())\n return 0;\n if(dp[pileInd][k] != -1) return dp[pileInd][k];\n int dontPick = move(piles,k,pileInd + 1,dp);\n int s = 0;\n for(int i = 0; i < k && i < piles.get(pileInd).size(); i++) {\n s += piles.get(pileInd).get(i);\n dontPick = Math.max(dontPick,s + move(piles,k - (i + 1), pileInd + 1,dp));\n }\n // int dontPick = move(piles,k,pileInd + 1,sum,dp);\n return dp[pileInd][k] = dontPick;\n }\n}\n```
| 2
| 0
|
[]
| 0
|
maximum-value-of-k-coins-from-piles
|
✔ C++ Solution | DP | O(m * k) Time | O(k) Space
|
c-solution-dp-om-k-time-ok-space-by-saty-4co7
|
Time Complexity : O(m * k)\nSpace Complexity : O(k)\n\nclass Solution {\npublic:\n int maxValueOfCoins(vector<vector<int>>& piles, int k) {\n vector<i
|
satyam2001
|
NORMAL
|
2022-09-03T06:57:34.259500+00:00
|
2022-09-03T06:57:34.259529+00:00
| 214
| false
|
`Time Complexity` : `O(m * k)`\n`Space Complexity` : `O(k)`\n```\nclass Solution {\npublic:\n int maxValueOfCoins(vector<vector<int>>& piles, int k) {\n vector<int> dp(k + 1, 0);\n for(auto& pile: piles) {\n for(size_t i = k; i >= 1; i--) {\n int csum = 0;\n for(int j = 0; j < min(i, pile.size()); j++) {\n csum += pile[j];\n dp[i] = max(dp[i], dp[i - j - 1] + csum);\n }\n }\n }\n return dp[k];\n }\n};\n```
| 2
| 0
|
['Dynamic Programming', 'C']
| 0
|
maximum-value-of-k-coins-from-piles
|
Recursive 3d dP , With 2d->1d mapping reduction using hashing
|
recursive-3d-dp-with-2d-1d-mapping-reduc-2tqn
|
I kept 3 variables for a state ,\nIndex_of_pile --> which pile am i currently standing at --> [i]\nindex_in_current_pile --> which index is at the top at the
|
are_you_in_illusion
|
NORMAL
|
2022-08-18T19:31:23.940514+00:00
|
2022-09-12T11:11:43.274348+00:00
| 88
| false
|
I kept 3 variables for a state ,\nIndex_of_pile --> which pile am i currently standing at --> [i]\nindex_in_current_pile --> which index is at the top at the moment for piles[index], --> [j]\nNo_of_purchaces_remaining ---> how many transactions do I have left with me ---> [k]\n\nDp[i][j][k] = returns me the maximum money i can retreive from here \nat this state i have 2 choices \ntake the jth coin (topmost coin) on pile i and stay on the same pile\ndont take the jth coin and move the next pile\n\ntake : piles[i][j] + func(i , j + 1 , k - 1)\ndont take : func(i + 1 , 0 , k - 1 ) --> 0 because now 0 is the topmost coin of the new pile\n\nTime Complexity : O(piles.size()*K + calculationforhas = Piles.size())\n\n```class Solution {\n \n \n \n \n int dp[3003][2001];\n\t\n\t /*\n state which i can think of is that \n given (index_of_pile , index_in_pile , no_of_transactions_left) \n what is the maximum money i can generate \n index_in_pile---> the index of the coin to be pick from pile(index_of_pile)\n */\n \npublic:\n int maxValueOfCoins(vector<vector<int>>& piles, int k) {\n memset(dp , -1 , sizeof(dp));\n vector<vector<int>> has;\n int cnt = -1;\n \n for(int i = 0 ; i < piles.size() ; i ++ ) {\n vector<int> row;\n for(int j = 0 ; j < piles[i].size() ; j ++) {\n row.push_back(-1);\n }\n row.push_back(-1);\n has.push_back(row);\n }\n \n \n for(int i = 0 ; i < has.size() ; i ++ ) {\n for(int j = 0 ; j < has[i].size() ; j ++ ) {\n has[i][j] = ++cnt;\n // this has function is \n // converting the row and the col of the cell \n // into a single value\n // has{i , j} ---> cnt\n }\n } \n \n \n return func(piles , k , 0 , 0 , has);\n \n }\n \n \n \n int func(vector<vector<int>>& piles, int no_of_transactions , int index , int pileposition , \n vector<vector<int>>& has ) {\n if(index >= piles.size() or no_of_transactions <= 0 ) \n return 0;\n \n // if(pileposition >= piles[index].size()) {\n // return 0;\n // }\n int i = index;\n int j = pileposition;\n int k = no_of_transactions;\n \n if(dp[has[i][j]][k] != -1)\n return dp[has[i][j]][k]; \n \n \n int take = 0;\n int dont_take = 0;\n // two choices , i decide to take the index\n if(pileposition < piles[index].size()) {\n take = +piles[index][pileposition] + func(piles , no_of_transactions - 1 , index , pileposition + 1 , has);\n }\n \n // I stop taking values from pile number index and start taking from the next pile , hence the pile no index will never be \n // considered in the future if i make this move\n // pile position will now become 0 , because am again going to take coins from the top of the new pile \n // we increment the index of the pile to index + 1\n dont_take = func(piles , no_of_transactions , index + 1 , 0 , has);\n \n // if(pileposition >= piles[index].size()) {\n // // i did this just to make the 3rd dp state call pass , \n // // since we dont have entry for pileposition >= piles[index].size\n // // in the has table so we have to query this way \n // // but am proud of the state table that i came up with myself \n // return dont_take;\n // }\n return dp[has[i][j]][k] = max(take , dont_take);\n }\n};
| 2
| 0
|
[]
| 0
|
maximum-value-of-k-coins-from-piles
|
C++ Top-down DP solution with Explaination
|
c-top-down-dp-solution-with-explaination-8996
|
Intuition\nTop down dynamic programming.\n\n\nExplanation\ndp[i,k] means picking k elements from pile[i] to pile[n-1].\nWe can pick 0,1,2,3... elements from the
|
_limitlesspragma
|
NORMAL
|
2022-07-01T15:49:21.928585+00:00
|
2022-07-01T15:49:21.928622+00:00
| 126
| false
|
**Intuition**\nTop down dynamic programming.\n\n\n**Explanation**\ndp[i,k] means picking k elements from pile[i] to pile[n-1].\nWe can pick 0,1,2,3... elements from the current pile[i] one by one.\nIt asks for the maximum total value of coins we can have,\nso we need to return max of all the options.\n\n\n**Complexity**\nTime `O(nm)`\nSpace `O(nk)`\nwhere `m = sum(piles[i].length) <= 2000`\n\n***C++ CODE :***\n```\nclass Solution {\npublic:\n int maxValueOfCoins(vector<vector<int>>& piles, int k) {\n ios::sync_with_stdio(false);\n cin.tie(NULL);\n cout.tie(NULL);\n \n int n=piles.size();\n vector<vector<int>> memo(n+1, vector<int>(k+1,0));\n \n function <int (int,int)> dp = [&](int i,int k){\n if(i==n || k==0)\n return 0;\n if(memo[i][k]) \n return memo[i][k];\n \n int res=dp(i+1,k), curr=0;\n \n for(int j=0;j<piles[i].size() and j<k ;++j){\n curr += piles[i][j];\n res=max(res,dp(i+1,k-j-1)+curr);\n }\n return memo[i][k]=res;\n };\n return dp(0,k);\n }\n};\n```
| 2
| 0
|
['Dynamic Programming']
| 0
|
maximum-value-of-k-coins-from-piles
|
🎨 The ART of Dynamic Programming
|
the-art-of-dynamic-programming-by-clayto-dqwv
|
\uD83C\uDFA8 The ART of Dynamic Programming\n\n1. All possibilities are considered via top-down brute-force depth-first-search\n2. Remember each subproblem\'s
|
claytonjwong
|
NORMAL
|
2022-04-01T00:41:06.021444+00:00
|
2022-04-01T14:10:35.018346+00:00
| 234
| false
|
[\uD83C\uDFA8 The ART of Dynamic Programming](https://leetcode.com/discuss/general-discussion/712010/The-ART-of-Dynamic-Programming-An-Intuitive-Approach%3A-from-Apprentice-to-Master)\n\n1. **A**ll possibilities are considered via top-down brute-force depth-first-search\n2. **R**emember each subproblem\'s optimal solution via a DP memo\n3. **T**urn the top-down solution upside-down to create the bottom-up solution\n4. Memory optimization (ie. we only need the previous row to formulate the current row)\n\nRecursively include each `j`<sup>th</sup> value of each `i`<sup>th</sup> row of the input matrix `A` onto a running total `t` to consider each candidate `cand` in order to find the `best` candidate for each `i`<sup>th</sup> row. Then we have 2 choices for each each `i`<sup>th</sup> row\'s `best` candidate:\n\n1. \u2705 include\n2. \uD83D\uDEAB exclude\n\nOptimally choose the maximum at each `i`<sup>th</sup> sub-problem to formulate the overall optimal solution as the recursive stack unwinds.\n\n**Note:** the problem statement\'s image is misleading, ie. "buckets" are drawn as columns, however, the "buckets" are actually stored in the input matrix `A` as rows.\n\n---\n\n**Kotlin Solutions:**\n\n1. **A**ll possibilities are considered via top-down brute-force depth-first-search\n```\nclass Solution {\n fun maxValueOfCoins(A: List<List<Int>>, K: Int): Int {\n var M = A.size\n fun go(i: Int = 0, k: Int = K): Int {\n if (i == M || k == 0)\n return 0\n var (t, best) = Pair(0, 0)\n for (j in 0 until Math.min(A[i].size, k)) {\n t += A[i][j]\n var cand = t + go(i + 1, k - 1 - j)\n best = Math.max(best, cand)\n }\n return Math.max(best, go(i + 1, k)) // \u2705 include or \uD83D\uDEAB exclude i-th row\'s best candidate\n }\n return go()\n }\n}\n```\n\n2. **R**emember each subproblem\'s optimal solution via a DP memo\n```\nclass Solution {\n fun maxValueOfCoins(A: List<List<Int>>, K: Int): Int {\n var M = A.size\n var m = mutableMapOf<String, Int>()\n fun go(i: Int = 0, k: Int = K): Int {\n if (i == M || k == 0)\n return 0\n var key = "$i,$k"\n if (!m.contains(key)) {\n var (t, best) = Pair(0, 0)\n for (j in 0 until Math.min(A[i].size, k)) {\n t += A[i][j]\n var cand = t + go(i + 1, k - 1 - j)\n best = Math.max(best, cand)\n }\n m[key] = Math.max(best, go(i + 1, k)) // \u2705 include or \uD83D\uDEAB exclude i-th row\'s best candidate\n }\n return m[key]!!\n }\n return go()\n }\n}\n```\n\n3. **T**urn the top-down solution upside-down to create the bottom-up solution\n```\nclass Solution {\n fun maxValueOfCoins(A: List<List<Int>>, K: Int): Int {\n var M = A.size\n var dp = Array(M + 1) { IntArray(K + 1 ) { 0 } }\n for (i in M - 1 downTo 0) {\n for (k in 1..K) {\n var (t, best) = Pair(0, 0)\n for (j in 0 until Math.min(A[i].size, k)) {\n t += A[i][j]\n var cand = t + dp[i + 1][k - 1 - j]\n best = Math.max(best, cand)\n }\n dp[i][k] = Math.max(best, dp[i + 1][k]) // \u2705 include or \uD83D\uDEAB exclude i-th row\'s best candidate\n }\n }\n return dp[0][K]\n }\n}\n```\n\n4. Memory optimization (ie. we only need the previous row to formulate the current row)\n```\nclass Solution {\n fun maxValueOfCoins(A: List<List<Int>>, K: Int): Int {\n var M = A.size\n var pre = IntArray(K + 1) { 0 }\n for (i in M - 1 downTo 0) {\n var cur = IntArray(K + 1) { 0 }\n for (k in 1..K) {\n var (t, best) = Pair(0, 0)\n for (j in 0 until Math.min(A[i].size, k)) {\n t += A[i][j]\n var cand = t + pre[k - 1 - j]\n best = Math.max(best, cand)\n }\n cur[k] = Math.max(best, pre[k]) // \u2705 include or \uD83D\uDEAB exclude i-th row\'s best candidate\n }\n pre = cur\n }\n return pre[K]\n }\n}\n```\n\n---\n\n**Javascript Solutions:**\n1. **A**ll possibilities are considered via top-down brute-force depth-first-search\n```\nlet maxValueOfCoins = (A, K) => {\n let M = A.length;\n let go = (i = 0, k = K) => {\n if (i == M || !k)\n return 0;\n let [t, best] = [0, 0];\n for (let j = 0; j < Math.min(A[i].length, k); ++j) {\n t += A[i][j];\n let cand = t + go(i + 1, k - 1 - j);\n best = Math.max(best, cand);\n }\n return Math.max(best, go(i + 1, k)); // \u2705 include or \uD83D\uDEAB exclude i-th row\'s best candidate\n };\n return go();\n};\n```\n\n2. **R**emember each subproblem\'s optimal solution via a DP memo\n```\nlet maxValueOfCoins = (A, K, m = new Map()) => {\n let M = A.length;\n let go = (i = 0, k = K) => {\n if (i == M || !k)\n return 0;\n let key = `${i},${k}`;\n if (!m.has(key)) {\n let [t, best] = [0, 0];\n for (let j = 0; j < Math.min(A[i].length, k); ++j) {\n t += A[i][j];\n let cand = t + go(i + 1, k - 1 - j);\n best = Math.max(best, cand);\n }\n m.set(key, Math.max(best, go(i + 1, k))); // \u2705 include or \uD83D\uDEAB exclude i-th row\'s best candidate\n }\n return m.get(key);\n };\n return go();\n};\n```\n\n3. **T**urn the top-down solution upside-down to create the bottom-up solution\n```\nlet maxValueOfCoins = (A, K) => {\n let M = A.length;\n let dp = [...Array(M + 1)].map(_ => Array(K + 1).fill(0));\n for (let i = M - 1; 0 <= i; --i) {\n for (let k = 1; k <= K; ++k) {\n let [t, best] = [0, 0];\n for (let j = 0; j < Math.min(A[i].length, k); ++j) {\n t += A[i][j];\n let cand = t + dp[i + 1][k - 1 - j];\n best = Math.max(best, cand);\n }\n dp[i][k] = Math.max(best, dp[i + 1][k]); // \u2705 include or \uD83D\uDEAB exclude i-th row\'s best candidate\n }\n }\n return dp[0][K];\n};\n```\n\n4. Memory optimization (ie. we only need the previous row to formulate the current row)\n```\nlet maxValueOfCoins = (A, K) => {\n let M = A.length;\n let pre = Array(K + 1).fill(0);\n for (let i = M - 1; 0 <= i; --i) {\n let cur = Array(K + 1).fill(0);\n for (let k = 1; k <= K; ++k) {\n let [t, best] = [0, 0];\n for (let j = 0; j < Math.min(A[i].length, k); ++j) {\n t += A[i][j];\n let cand = t + pre[k - 1 - j];\n best = Math.max(best, cand);\n }\n cur[k] = Math.max(best, pre[k]); // \u2705 include or \uD83D\uDEAB exclude i-th row\'s best candidate\n }\n pre = cur;\n }\n return pre[K];\n};\n```\n\n---\n\n**Python3 Solutions:**\n1. **A**ll possibilities are considered via top-down brute-force depth-first-search\n```\nclass Solution:\n def maxValueOfCoins(self, A: List[List[int]], K: int) -> int:\n M = len(A)\n def go(i = 0, k = K):\n if i == M or not k:\n return 0\n t, best = 0, 0\n for j in range(0, min(len(A[i]), k)):\n t += A[i][j]\n cand = t + go(i + 1, k - 1 - j)\n best = max(best, cand)\n return max(best, go(i + 1, k)) # \u2705 include or \uD83D\uDEAB exclude i-th row\'s best candidate\n return go()\n```\n\n2. **R**emember each subproblem\'s optimal solution via a DP memo\n```\nclass Solution:\n def maxValueOfCoins(self, A: List[List[int]], K: int) -> int:\n M = len(A)\n @cache\n def go(i = 0, k = K):\n if i == M or not k:\n return 0\n t, best = 0, 0\n for j in range(0, min(len(A[i]), k)):\n t += A[i][j]\n cand = t + go(i + 1, k - 1 - j)\n best = max(best, cand)\n return max(best, go(i + 1, k)) # \u2705 include or \uD83D\uDEAB exclude i-th row\'s best candidate\n return go()\n```\n\n3. **T**urn the top-down solution upside-down to create the bottom-up solution\n```\nclass Solution:\n def maxValueOfCoins(self, A: List[List[int]], K: int) -> int:\n M = len(A)\n dp = [[0] * (K + 1) for _ in range(M + 1)]\n for i in range(M - 1, -1, -1):\n for k in range(K, -1, -1):\n t, best = 0, 0\n for j in range(0, min(len(A[i]), k)):\n t += A[i][j]\n cand = t + dp[i + 1][k - 1 - j]\n best = max(best, cand)\n dp[i][k] = max(best, dp[i + 1][k]) # \u2705 include or \uD83D\uDEAB exclude i-th row\'s best candidate\n return dp[0][K]\n```\n\n4. Memory optimization (ie. we only need the previous row to formulate the current row)\n```\nclass Solution:\n def maxValueOfCoins(self, A: List[List[int]], K: int) -> int:\n M = len(A)\n pre = [0] * (K + 1)\n for i in range(M - 1, -1, -1):\n cur = [0] * (K + 1)\n for k in range(K, -1, -1):\n t, best = 0, 0\n for j in range(0, min(len(A[i]), k)):\n t += A[i][j]\n cand = t + pre[k - 1 - j]\n best = max(best, cand)\n cur[k] = max(best, pre[k]) # \u2705 include or \uD83D\uDEAB exclude i-th row\'s best candidate\n pre = cur\n return pre[K]\n```\n\n---\n\n**Rust Solutions:**\n\n1. **A**ll possibilities are considered via top-down brute-force depth-first-search\n```\n// TODO: how to write recursive closure in Rust which captures the parent\'s scope?\n```\n\n2. **R**emember each subproblem\'s optimal solution via a DP memo\n```\n// TODO: how to write recursive closure in Rust which captures the parent\'s scope?\n```\n\n3. **T**urn the top-down solution upside-down to create the bottom-up solution\n```\ntype VI = Vec<i32>;\ntype VVI = Vec<VI>;\nuse std::cmp::min;\nuse std::cmp::max;\nimpl Solution {\n pub fn max_value_of_coins(A: VVI, K_: i32) -> i32 {\n let M = A.len();\n let K = K_ as usize;\n let mut dp = vec![vec![0; K + 1]; M + 1];\n for i in (0..M).rev() {\n for k in 1..=K {\n let (mut t, mut best) = (0, 0);\n for j in 0..min(A[i].len(), k) {\n t += A[i][j];\n let cand = t + dp[i + 1][k - 1 - j];\n best = max(best, cand);\n }\n dp[i][k] = max(best, dp[i + 1][k]); // \u2705 include or \uD83D\uDEAB exclude i-th row\'s best candidate\n }\n }\n return dp[0][K];\n }\n}\n```\n\n4. Memory optimization (ie. we only need the previous row to formulate the current row)\n```\ntype VI = Vec<i32>;\ntype VVI = Vec<VI>;\nuse std::cmp::min;\nuse std::cmp::max;\nimpl Solution {\n pub fn max_value_of_coins(A: VVI, K_: i32) -> i32 {\n let M = A.len();\n let K = K_ as usize;\n let mut pre = vec![0; K + 1];\n for i in (0..M).rev() {\n let mut cur = vec![0; K + 1];\n for k in 1..=K {\n let (mut t, mut best) = (0, 0);\n for j in 0..min(A[i].len(), k) {\n t += A[i][j];\n let cand = t + pre[k - 1 - j];\n best = max(best, cand);\n }\n cur[k] = max(best, pre[k]); // \u2705 include or \uD83D\uDEAB exclude i-th row\'s best candidate\n }\n pre = cur;\n }\n return pre[K];\n }\n}\n```\n\n---\n\n**C++ Solutions:**\n\n1. **A**ll possibilities are considered via top-down brute-force depth-first-search\n```\nclass Solution {\npublic:\n using VI = vector<int>;\n using VVI = vector<VI>;\n using fun = function<int(int, int)>;\n int maxValueOfCoins(VVI& A, int K) {\n int M = A.size();\n fun go = [&](auto i, auto k) {\n if (i == M || !k)\n return 0;\n auto [t, best] = make_pair(0, 0);\n for (auto j{ 0 }; j < min((int)A[i].size(), k); ++j) {\n t += A[i][j];\n auto cand = t + go(i + 1, k - 1 - j);\n best = max(best, cand);\n }\n return max(best, go(i + 1, k)); // \u2705 include or \uD83D\uDEAB exclude i-th row\'s best candidate\n };\n return go(0, K);\n }\n};\n```\n\n2. **R**emember each subproblem\'s optimal solution via a DP memo\n```\nclass Solution {\npublic:\n using VI = vector<int>;\n using VVI = vector<VI>;\n using fun = function<int(int, int)>;\n using Map = unordered_map<string, int>;\n int maxValueOfCoins(VVI& A, int K, Map m = {}) {\n int M = A.size();\n auto hash = [](auto i, auto k) {\n stringstream ss; ss << i << "," << k;\n return ss.str();\n };\n fun go = [&](auto i, auto k) {\n if (i == M || !k)\n return 0;\n auto key = hash(i, k);\n if (m.find(key) == m.end()) {\n auto [t, best] = make_pair(0, 0);\n for (auto j{ 0 }; j < min((int)A[i].size(), k); ++j) {\n t += A[i][j];\n auto cand = t + go(i + 1, k - 1 - j);\n best = max(best, cand);\n }\n m[key] = max(best, go(i + 1, k)); // \u2705 include or \uD83D\uDEAB exclude i-th row\'s best candidate\n }\n return m[key];\n };\n return go(0, K);\n }\n};\n```\n\n3. **T**urn the top-down solution upside-down to create the bottom-up solution\n```\nclass Solution {\npublic:\n using VI = vector<int>;\n using VVI = vector<VI>;\n int maxValueOfCoins(VVI& A, int K) {\n int M = A.size();\n VVI dp(M + 1, VI(K + 1));\n for (auto i{ M - 1 }; 0 <= i; --i) {\n for (auto k{ 1 }; k <= K; ++k) {\n auto [t, best] = make_pair(0, 0);\n for (auto j{ 0 }; j < min((int)A[i].size(), k); ++j) {\n t += A[i][j];\n auto cand = t + dp[i + 1][k - 1 - j];\n best = max(best, cand);\n }\n dp[i][k] = max(best, dp[i + 1][k]); // \u2705 include or \uD83D\uDEAB exclude i-th row\'s best candidate\n }\n }\n return dp[0][K];\n }\n};\n```\n\n4. Memory optimization (ie. we only need the previous row to formulate the current row)\n```\nclass Solution {\npublic:\n using VI = vector<int>;\n using VVI = vector<VI>;\n int maxValueOfCoins(VVI& A, int K) {\n int M = A.size();\n VI pre(K + 1);\n for (auto i{ M - 1 }; 0 <= i; --i) {\n VI cur(K + 1);\n for (auto k{ 1 }; k <= K; ++k) {\n auto [t, best] = make_pair(0, 0);\n for (auto j{ 0 }; j < min((int)A[i].size(), k); ++j) {\n t += A[i][j];\n auto cand = t + pre[k - 1 - j];\n best = max(best, cand);\n }\n cur[k] = max(best, pre[k]); // \u2705 include or \uD83D\uDEAB exclude i-th row\'s best candidate\n }\n pre = cur;\n }\n return pre[K];\n }\n};\n```
| 2
| 0
|
[]
| 0
|
maximum-value-of-k-coins-from-piles
|
C++ || 2D DP
|
c-2d-dp-by-pandeyji2023-4ygk
|
\nclass Solution {\npublic:\n \n int dp[2001][2001];\n \n int helper(int idx,vector<vector<int>>& preffix,int k){\n \n if(idx >= preff
|
pandeyji2023
|
NORMAL
|
2022-03-27T11:34:49.088687+00:00
|
2022-03-27T11:34:49.088727+00:00
| 132
| false
|
```\nclass Solution {\npublic:\n \n int dp[2001][2001];\n \n int helper(int idx,vector<vector<int>>& preffix,int k){\n \n if(idx >= preffix.size() || k<=0){\n return 0;\n }\n \n if(dp[idx][k] != -1){\n return dp[idx][k];\n }\n \n int max_score = INT_MIN;\n \n \n for(int i=0;i<=k && i<=preffix[idx].size();i++){\n int sum = 0;\n \n if(i>0){\n sum += preffix[idx][i-1]; \n }\n \n int score = helper(idx+1,preffix,k-i) + sum;\n max_score = max(max_score,score); \n }\n \n return dp[idx][k] = max_score;\n }\n \n int maxValueOfCoins(vector<vector<int>>& piles, int k){\n memset(dp,-1,sizeof(dp));\n \n vector<vector<int>> preffix;\n \n for(int i=0;i<piles.size();i++){\n vector<int> v(piles[i].size());\n v[0] = piles[i][0];\n \n \n for(int j=1;j<piles[i].size();j++){\n v[j] = piles[i][j] + v[j-1];\n }\n \n preffix.push_back(v);\n }\n \n return helper(0,preffix,k);\n }\n};\n```
| 2
| 0
|
['Dynamic Programming']
| 1
|
maximum-value-of-k-coins-from-piles
|
[C++] Simple Bottom-up DP
|
c-simple-bottom-up-dp-by-leetcode07-v9n0
|
Solution:\n\nclass Solution {\npublic:\n int maxValueOfCoins(vector<vector<int>>& piles, int k) {\n int n=piles.size();\n \n // dp[i][j]
|
leetcode07
|
NORMAL
|
2022-03-27T08:47:01.700517+00:00
|
2022-03-27T08:56:59.654831+00:00
| 85
| false
|
Solution:\n```\nclass Solution {\npublic:\n int maxValueOfCoins(vector<vector<int>>& piles, int k) {\n int n=piles.size();\n \n // dp[i][j] = maximum money after taking j coins from first i piles.\n vector<vector<int> > dp(n+1, vector<int>(k+1, -2000000000));\n \n dp[0][0]=0;\n \n for(int i=0; i<n; i++){\n for(int j=0; j<=k; j++){\n \n // do not take any coin from this pile.\n dp[i+1][j]=max(dp[i+1][j], dp[i][j]);\n \n int sum=0, cnt=0;\n for(int p: piles[i]){\n sum+=p;\n cnt++;\n if(j+cnt<=k)\n // take first cnt coins from this pile.\n dp[i+1][j+cnt]=max(dp[i+1][j+cnt], dp[i][j]+sum);\n }\n }\n }\n return dp[n][k];\n }\n};\n```\n\nTime complexity: O(k * sum(piles[i].length))\nProof: In iterative solutions it is much easier to deduce the time complexity.\n```\nfor each pile:\n\tfor each k:\n\t\tfor each prefix of pile:\n```\nis equivalent to\n```\nfor each pile:\n\tfor each prefix of pile:\n\t\tfor each k:\n```\n\nO(piles[0].length * k + piles[1].length * k + ...... + piles[n-1].length * k) = O(k * sum(piles[i].length))
| 2
| 0
|
[]
| 0
|
maximum-value-of-k-coins-from-piles
|
[C++] bottom up DP
|
c-bottom-up-dp-by-praveenchiliveri-2cum
|
```\nclass Solution {\npublic:\n int maxValueOfCoins(vector>& piles, int k) {\n int n=piles.size();\n\t\t//dp[i][j] - > maximum total value of coins u
|
praveenchiliveri
|
NORMAL
|
2022-03-27T05:48:57.952912+00:00
|
2022-03-27T05:51:33.557387+00:00
| 169
| false
|
```\nclass Solution {\npublic:\n int maxValueOfCoins(vector<vector<int>>& piles, int k) {\n int n=piles.size();\n\t\t//dp[i][j] - > maximum total value of coins using i piles and j coins.\n vector<vector<int>> dp(n+1,vector<int>(k+1));\n\t\t// store the prefix sum for each pile.\n for(int i=0;i<n;i++)\n for(int j=1;j<(int)piles[i].size();j++)\n piles[i][j]+=piles[i][j-1];\n \n\t\t\n for(int i=1;i<=n;i++)\n for(int j=1;j<=k;j++) // calculate max total value to pick j coins using i piles.\n for(int w=0;w<=(int)piles[i-1].size() and w<=j;w++) // check for all combinations of coins that sum upto j coins. we can pick w coins from this pile and j-w coins from previous piles(dp[i-1][j-w]) i.e=> (j-w)+w=j coins in total.\n dp[i][j]=max(dp[i][j],dp[i-1][j-w]+((w-1>=0)?piles[i-1][w-1]:0));\n \n return dp[n][k];\n }\n};
| 2
| 0
|
['Dynamic Programming', 'Iterator']
| 1
|
maximum-value-of-k-coins-from-piles
|
Ignore the SC and understand the logic.
|
ignore-the-sc-and-understand-the-logic-b-qnit
|
There are only 2 ways\n1. Take :\n\tif you choose the top element there are again two possibilities \n\t1. take current element and move to next list or \n\t2.
|
yadavharsha50
|
NORMAL
|
2022-03-27T05:31:22.677300+00:00
|
2022-03-27T05:43:43.481698+00:00
| 111
| false
|
There are only 2 ways\n1. Take :\n\tif you choose the top element there are again two possibilities \n\t1. take current element and move to next list or \n\t2. take curr element and stand on the same list and call recursion for the next element in the same list.\n2. Not Take :\n\tjust simply move to next list.\n```\nclass Solution {\n public int maxValueOfCoins(List<List<Integer>> piles, int k) {\n int max=0;\n for(List<Integer> curr: piles){\n max=Math.max(max,curr.size());\n }\n Integer dp[][][]=new Integer[piles.size()][max][k+1];\n return f(piles,piles.size()-1,0,k,dp);\n }\n \n public int f(List<List<Integer>> piles, int n, int i, int k,Integer dp[][][]){\n if(n==-1 || i>=piles.get(n).size() || k<=0){\n return 0;\n }\n \n if(dp[n][i][k]!=null) return dp[n][i][k];\n int take=0;\n if(i<piles.get(n).size()){\n \n take=piles.get(n).get(i)+ Math.max(f(piles,n,i+1,k-1,dp),f(piles,n-1,0,k-1,dp));\n }\n int notTake=f(piles,n-1,0,k,dp);\n return dp[n][i][k]=Math.max(take,notTake);\n }\n}\n```
| 2
| 0
|
['Dynamic Programming', 'Memoization', 'Java']
| 1
|
maximum-value-of-k-coins-from-piles
|
DP | C++
|
dp-c-by-return_404-sed3
|
Let\'s define dp[i][j] = maximum total value with j coins till i-th pile .\n\nif we take x coins from i-th pile then we need (j-x) coins till (i-1)-th pile i.e
|
return_404
|
NORMAL
|
2022-03-27T05:00:41.485729+00:00
|
2022-03-27T05:00:41.485768+00:00
| 87
| false
|
Let\'s define dp[i][j] = maximum total value with j coins till i-th pile .\n\nif we take x coins from i-th pile then we need (j-x) coins till (i-1)-th pile i.e dp[i-1][j-x] . \n\n```\n\nclass Solution {\npublic:\n int maxValueOfCoins(vector<vector<int>>& piles, int k) {\n int n=piles.size();\n int dp[n+1][k+1];\n memset(dp,0,sizeof(dp));\n for(int i=1;i<=n;i++){\n for(int j=1;j<=k;j++){\n dp[i][j]=dp[i-1][j];\n int sum=0;\n for(int x=1;x<=j && x<=piles[i-1].size();x++){\n sum += piles[i-1][x-1];\n dp[i][j]=max(dp[i][j], sum + dp[i-1][j-x]);\n }\n }\n }\n return dp[n][k];\n }\n};\n```
| 2
| 0
|
[]
| 0
|
maximum-value-of-k-coins-from-piles
|
✅ C++ || 2D dp + Memoization || Easy
|
c-2d-dp-memoization-easy-by-yogaboi-59ig
|
\n1. Easy C++\n2. Line by Line Explanation with Comments.\n3. Detailed Explanation \u2705\n4. 2D dp + Memoization.\n5. Please Upvote if it helps\u2B06\uFE0F\n\n
|
Yogaboi
|
NORMAL
|
2022-03-27T04:56:49.723768+00:00
|
2022-03-27T04:56:49.723800+00:00
| 144
| false
|
```\n1. Easy C++\n2. Line by Line Explanation with Comments.\n3. Detailed Explanation \u2705\n4. 2D dp + Memoization.\n5. Please Upvote if it helps\u2B06\uFE0F\n```\n\n**EXPLANATION**\n* Base Case-> if piles completed or k coins taken\n* skip current pile and call recursion\n* check for current pile and call recursion for further piles\n* keep max value\n* update memoizated 2d vector\n\n\n\nTIME COMPLEXITY : O(N^N) , N is size of matrix **Beats 90.02%**\nSPACE COMPLEXITY : O(N^N), **Beats 70.50%**\n\n\n\n\n\n\n\n\n\n```\n int solve(int i,vector<vector<int>>&p, int k,vector<vector<int>> &dp){\n if(i>=p.size() || k<=0) return 0; //Base Case-> if piles completed or k coins taken\n if(dp[i][k]!=-1) return dp[i][k];\n int fur = solve(i+1,p,k,dp), cur=0; // skip current pile\n \n for(int idx=0;idx<p[i].size() && idx<k; idx++){ // check for current pile \n cur += p[i][idx];\n fur = max(fur, cur+solve(i+1,p,k-idx-1,dp)); // recursive call for further piles\n }\n return dp[i][k]=fur; // update dp\n }\n \n int maxValueOfCoins(vector<vector<int>>& p, int k) {\n vector<vector<int>> dp(p.size(), vector<int>(k+1,-1));\n return solve(0,p,k,dp);\n }\n```
| 2
| 0
|
['C++']
| 0
|
maximum-value-of-k-coins-from-piles
|
Java Solution Memoization
|
java-solution-memoization-by-piyushja1n-ivgy
|
\nclass Solution {\n \n Integer [][]dp;\n \n public int maxValueOfCoins(List<List<Integer>> piles, int k) {\n dp = new Integer[piles.size() +
|
piyushja1n
|
NORMAL
|
2022-03-27T04:21:56.810085+00:00
|
2022-03-27T04:46:51.664281+00:00
| 144
| false
|
```\nclass Solution {\n \n Integer [][]dp;\n \n public int maxValueOfCoins(List<List<Integer>> piles, int k) {\n dp = new Integer[piles.size() + 1][k + 1];\n return maxPoints(piles, piles.size() - 1, k);\n }\n \n \n private int maxPoints(List<List<Integer>>piles, int i, int k){\n\n if(i < 0 || k <= 0) \n return 0;\n\n if(dp[i][k] != null) \n return dp[i][k];\n\n int notTake = maxPoints(piles, i-1, k);\n\n int take = 0;\n \n for(int j=0, sum=0; j < Math.min(piles.get(i).size(), k) ; j++){\n\n sum += piles.get(i).get(j);\n\n take = Math.max(sum + maxPoints(piles, i-1, k-j-1), take);\n }\n\n int res = Math.max(take, notTake);\n\n dp[i][k] = res;\n return res;\n }\n}\n```\n\n#### BOTTOM UP\n```\nclass Solution {\n public int maxValueOfCoins(List<List<Integer>> piles, int k) {\n \n int n = piles.size();\n int[][] dp = new int[n+1][k+1];\n\n for(int i = 1; i <= n; i ++) {\n for(int j = 1; j <= k; j ++) {\n \n dp[i][j] = dp[i-1][j];\n int sum = 0;\n \n for(int l = 1 ; l <= Math.min(piles.get(i-1).size() , j) ; l++) {\n\n sum += piles.get(i - 1).get(l - 1);\n dp[i][j] = Math.max(dp[i][j], dp[i-1][j-l]+sum);\n \n }\n }\n }\n return dp[n][k];\n }\n}\n```
| 2
| 0
|
['Dynamic Programming', 'Java']
| 0
|
maximum-value-of-k-coins-from-piles
|
Top down approach | Python3 | Intuitive solution
|
top-down-approach-python3-intuitive-solu-96qt
|
Please UpvoteCode
|
Alpha2404
|
NORMAL
|
2025-03-12T03:09:07.167067+00:00
|
2025-03-12T03:09:07.167067+00:00
| 27
| false
|
# Please Upvote
# Code
```python3 []
from typing import List
from functools import lru_cache
class Solution:
def maxValueOfCoins(self, piles: List[List[int]], k: int) -> int:
n = len(piles)
prefixSums = []
for pile in piles:
cur = [0]
for coin in pile:
cur.append(cur[-1] + coin)
prefixSums.append(cur)
@lru_cache(maxsize=None)
def dp(i, r):
if i == n or r == 0:
return 0
best = dp(i + 1, r)
for j in range(1, min(len(prefixSums[i]), r + 1)):
best = max(best, prefixSums[i][j] + dp(i + 1, r - j))
return best
return dp(0, k)
```
| 1
| 0
|
['Array', 'Dynamic Programming', 'Memoization', 'Prefix Sum', 'Python3']
| 0
|
maximum-value-of-k-coins-from-piles
|
Easy DP approach
|
easy-dp-approach-by-twasim-uz2z
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
twasim
|
NORMAL
|
2024-06-28T08:42:53.064591+00:00
|
2024-06-28T08:42:53.064635+00:00
| 4
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(k*n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\ndepends how you define the dp vector \nIn my case: O(1001*2002);\n# Code\n```\nclass Solution {\nint t[1001][2002];\npublic:\n int solve(int i, int k, vector<vector<int>>& piles, int n){\n if (i==n or k<=0)return 0;\n if (t[i][k]!=-1){return t[i][k];}\n int ans = solve(i+1,k,piles,n);\n int temp = 0;\n for (int kk=0;kk<min((int)piles[i].size(),k);kk++){\n temp+=piles[i][kk];\n ans=max(ans,temp + solve(i+1,k-1-kk,piles,n));\n }\n return t[i][k]=ans;\n }\n int maxValueOfCoins(vector<vector<int>>& piles, int k) {\n int n = piles.size();\n memset(t,-1,sizeof(t));\n return solve(0,k,piles,n);\n }\n};\n```
| 1
| 0
|
['Dynamic Programming', 'Prefix Sum', 'C++']
| 0
|
maximum-value-of-k-coins-from-piles
|
Java Clean Dp Solution
|
java-clean-dp-solution-by-shree_govind_j-v9yv
|
Code\n\nclass Solution {\n private int solveMemo(List<List<Integer>> piles, int idx, int k, int[][] dp) {\n // Base case\n if (idx >= piles.siz
|
Shree_Govind_Jee
|
NORMAL
|
2024-02-10T03:11:34.476164+00:00
|
2024-02-10T03:11:34.476184+00:00
| 125
| false
|
# Code\n```\nclass Solution {\n private int solveMemo(List<List<Integer>> piles, int idx, int k, int[][] dp) {\n // Base case\n if (idx >= piles.size() || k <= 0) {\n return 0;\n }\n\n // step-2 =>if dp[idx][k] is calculated just return it..\n if (dp[idx][k] != -1) {\n return dp[idx][k];\n }\n\n // step-3 =>if dp[idx][k] isn\'t calculated just calculate it...\n int res = solveMemo(piles, idx + 1, k, dp);\n int count = 0;\n for (int i = 0; i < piles.get(idx).size() && i < k; i++) {\n count += piles.get(idx).get(i);\n res = Math.max(res, count + solveMemo(piles, idx + 1, k - i - 1, dp));\n }\n return dp[idx][k] = res;\n }\n\n\n\n public int maxValueOfCoins(List<List<Integer>> piles, int k) {\n // step-1 => dp creation....\n int[][] dp = new int[piles.size() + 1][k + 1];\n for (int[] d : dp) {\n Arrays.fill(d, -1);\n }\n\n return solveMemo(piles, 0, k, dp);\n }\n}\n```
| 1
| 0
|
['Array', 'Dynamic Programming', 'Recursion', 'Memoization', 'Prefix Sum', 'Java']
| 0
|
maximum-value-of-k-coins-from-piles
|
DP
|
dp-by-recursive45-gmbv
|
Code\n\nclass Solution {\npublic:\n int solve(int r, vector<vector<int>> &piles, int k, vector<vector<int>> &dp)\n{\n if (r == piles.size())\n {\n
|
Recursive45
|
NORMAL
|
2023-08-12T02:57:55.814772+00:00
|
2023-08-12T02:57:55.814809+00:00
| 50
| false
|
# Code\n```\nclass Solution {\npublic:\n int solve(int r, vector<vector<int>> &piles, int k, vector<vector<int>> &dp)\n{\n if (r == piles.size())\n {\n if(k == 0)\n {\n return 0;\n }\n return -1e9;\n }\n \n if(dp[r][k] != -1)\n {\n return dp[r][k];\n }\n \n int ans = solve(r + 1, piles, k, dp);\n int temp = 0;\n\n for (int i = 0; i < min((int)piles[r].size(), k); i++)\n {\n temp += piles[r][i];\n ans = max(ans, temp + solve(r + 1, piles, k - i - 1, dp));\n }\n\n return dp[r][k] = ans;\n}\n\nint maxValueOfCoins(vector<vector<int>> &piles, int k)\n{\n int n = piles.size();\n vector<vector<int>> dp(n, vector<int>(k + 1, -1));\n return solve(0, piles, k, dp);\n}\n};\n```
| 1
| 0
|
['C++']
| 0
|
maximum-value-of-k-coins-from-piles
|
Ex-Amazon explains solution with a video, Python, JavaScript, Java and C++
|
ex-amazon-explains-solution-with-a-video-888z
|
My youtube channel - KeetCode(Ex-Amazon)\nI create 154 videos for leetcode questions as of April 21, 2023. I believe my channel helps you prepare for the coming
|
niits
|
NORMAL
|
2023-04-21T05:09:57.990276+00:00
|
2023-04-21T05:09:57.990299+00:00
| 48
| false
|
# My youtube channel - KeetCode(Ex-Amazon)\nI create 154 videos for leetcode questions as of April 21, 2023. I believe my channel helps you prepare for the coming technical interviews. Please subscribe my channel!\n\n### Please subscribe my channel - KeetCode(Ex-Amazon) from here.\n\n**I created a video for this question. I believe you can understand easily with visualization.** \n\n**My youtube channel - KeetCode(Ex-Amazon)**\nLink from LeetCode profile\nhttps://leetcode.com/niits/\n\n\n\n\n---\n\n\n\n# Intuition\nApply Dynamic Programming to this question.\n\n# Approach\n1. Initialize an array prev with k + 1 elements, all set to 0.\n\n2. Iterate over each pile in piles:\n\n - Initialize an array sum_list with a single element 0, representing the prefix sum of coins in the pile.\n - Initialize a variable total to 0, to keep track of the total sum of coins in the pile.\n - Iterate over each coin in the pile:\nAdd the coin to total.\nAppend total to sum_list, representing the cumulative sum of coins in the pile.\n\n3. Initialize an array cur_max with k + 1 elements, all set to 0, to keep track of the maximum value for each number of coins picked.\n\n4. Iterate over each number of coins n from 1 to k:\n\n - Calculate the range of elements to consider in sum_list as calc_range, which is the minimum of n + 1 and the length of sum_list.\n - For each position pos in the range of calc_range:\n - Update cur_max[n] with the maximum value between its current value and the sum of sum_list[pos] and prev[n - pos], which represents the maximum value achievable by picking n coins from the current pile.\n\n5. Update prev with the values of cur_max, representing the maximum value achievable by picking n coins from all previous piles.\n\n6. After iterating over all piles, the final result will be stored in prev[k], which represents the maximum value achievable by picking k coins from all piles.\n\n7. Return prev[k] as the result of the function.\n\n# Complexity\n- Time complexity: O(NK)\nN is the length of the piles list (number of piles) and K is the input integer k. This is because the code iterates over each pile and for each pile, it performs calculations up to k iterations.\n\n- Space complexity: O(K)\nThe code uses two lists (prev and cur_max) of length k + 1 to store intermediate results for each value of k. The sum_list list also has a maximum length of k + 1 for each pile. Therefore, the total space complexity is dominated by the prev and cur_max lists, which have a space complexity of O(K).\n\n# Python\n```\nclass Solution:\n def maxValueOfCoins(self, piles: List[List[int]], k: int) -> int:\n\n prev = [0] * (k + 1)\n\n for pile in piles:\n sum_list = [0]\n total = 0\n for coin in pile:\n total += coin\n sum_list.append(total)\n \n cur_max = [0] * (k + 1)\n\n for n in range(1, k + 1):\n calc_range = min(n + 1, len(sum_list))\n cur_max[n] = max(sum_list[pos] + prev[n - pos] for pos in range(calc_range))\n \n prev = cur_max\n \n return prev[k]\n```\n# JavaScript\n```\n/**\n * @param {number[][]} piles\n * @param {number} k\n * @return {number}\n */\nvar maxValueOfCoins = function(piles, k) {\n let prev = new Array(k + 1).fill(0);\n\n for (let pile of piles) {\n let sumList = [0];\n let total = 0;\n for (let coin of pile) {\n total += coin;\n sumList.push(total);\n }\n\n let curMax = new Array(k + 1).fill(0);\n\n for (let n = 1; n <= k; n++) {\n let calcRange = Math.min(n + 1, sumList.length);\n for (let pos = 0; pos < calcRange; pos++) {\n curMax[n] = Math.max(curMax[n], sumList[pos] + prev[n - pos]);\n }\n }\n\n prev = curMax;\n }\n\n return prev[k];\n};\n```\n# Java\n```\nclass Solution {\n public int maxValueOfCoins(List<List<Integer>> piles, int k) {\n int[] prev = new int[k + 1];\n\n for (List<Integer> pile : piles) {\n List<Integer> sumList = new ArrayList<>();\n sumList.add(0);\n int total = 0;\n for (int coin : pile) {\n total += coin;\n sumList.add(total);\n }\n\n int[] curMax = new int[k + 1];\n\n for (int n = 1; n <= k; n++) {\n int calcRange = Math.min(n + 1, sumList.size());\n for (int pos = 0; pos < calcRange; pos++) {\n curMax[n] = Math.max(curMax[n], sumList.get(pos) + prev[n - pos]);\n }\n }\n\n prev = curMax;\n }\n\n return prev[k]; \n }\n}\n```\n# C++\n```\nclass Solution {\npublic:\n int maxValueOfCoins(vector<vector<int>>& piles, int k) {\n std::vector<int> prev(k + 1, 0);\n\n for (const auto& pile : piles) {\n std::vector<int> sumList(1, 0);\n int total = 0;\n for (int coin : pile) {\n total += coin;\n sumList.push_back(total);\n }\n\n std::vector<int> curMax(k + 1, 0);\n\n for (int n = 1; n <= k; n++) {\n int calcRange = std::min(n + 1, static_cast<int>(sumList.size()));\n for (int pos = 0; pos < calcRange; pos++) {\n curMax[n] = std::max(curMax[n], sumList[pos] + prev[n - pos]);\n }\n }\n\n prev = curMax;\n }\n\n return prev[k]; \n }\n};\n```
| 1
| 0
|
['C++', 'Java', 'Python3', 'JavaScript']
| 0
|
maximum-value-of-k-coins-from-piles
|
[Python] Divid and Conquer without DP, 100%
|
python-divid-and-conquer-without-dp-100-ur7op
|
Idea\nCreate a helper function getValues(s, e) that returns a vector vals. \nvals[i] stores the maximum value that you can get from picking i coins from piles s
|
pongpong99
|
NORMAL
|
2023-04-17T07:38:29.039045+00:00
|
2023-04-17T07:38:29.039079+00:00
| 17
| false
|
#### Idea\nCreate a helper function getValues(s, e) that returns a vector vals. \nvals[i] stores the maximum value that you can get from picking i coins from piles s, s+1, s+2, ..., e.\nWith the helper fucntion, the final result will be geValues(1, n)[k].\n\nThe basic case of getValues is when s equal to t. In this case, there is only one pile. Therefore, for vals[i], we just need to pick the first i coins.\nFor s < e, we split the piles into two parts ( (s, mid), (mid+1, e)) and get the values of both parts. \nWith the vals of left and right piles, we can calculate vals[i] by consider taking different j coins from the left part piles and take i-j coins from the right part piles and select the j that can have the maximum value.\n\n#### Complexity\n\nTime: O(K^2) \nThis method is better than the DP solution when sum(piles[i].length) is larger than 2000, such as sum(piles[i].length) = 20000.\nSpace: O(K)\n\n#### Code\n```\nclass Solution:\n def maxValueOfCoins(self, piles: List[List[int]], k: int) -> int:\n \n def getValues(s, e): # return maximum values of getting different numbers from pile s to plie e\n if s == e: # only one piles\n coin_num = min(len(piles[s]), k)\n vals = [0] * (coin_num+1)\n for i in range(1, coin_num + 1):\n vals[i] = (vals[i-1] + piles[s][i-1])\n return vals\n \n # more than one piles\n mid = (s+e)//2\n left_vals = getValues(s, mid)\n right_vals = getValues(mid+1, e)\n \n coin_num_l = len(left_vals) -1\n coin_num_r = len(right_vals) -1\n coin_num = min(k, coin_num_l+coin_num_r)\n vals = [0] * (coin_num+1)\n for i in range(1, coin_num+1): # calculate max value of picking i coins (vals[i])\n vals[i] = -1\n min_l = max(0, (i - coin_num_r)) # minimum coins that need to take from left in order to take i coins from both sides \n max_l = min(i, coin_num_l) + 1 # maxmum coins that need to take from left in order to take i coins from both sides \n for j in range(min_l, max_l): # consider the case of select j coins from the left side\n tmp = left_vals[j] + right_vals[i-j] \n if vals[i] < tmp:\n vals[i] = tmp\n return vals\n \n vals = getValues(0, len(piles)-1)\n \n return vals[k]\n```
| 1
| 0
|
['Divide and Conquer', 'Python']
| 0
|
maximum-value-of-k-coins-from-piles
|
DP Solution | Easy to Understand | Step by Step Explanation | C++
|
dp-solution-easy-to-understand-step-by-s-tfzk
|
Intuition\n \nIt\'s obvious that there is no greedy solution for this problem since there are multiple combinations and also restriction of picking topmost of p
|
f_in_the_chat
|
NORMAL
|
2023-04-15T20:39:30.495188+00:00
|
2023-04-15T20:39:30.495226+00:00
| 174
| false
|
# Intuition\n<!-- -->\nIt\'s obvious that there is no greedy solution for this problem since there are multiple combinations and also restriction of picking topmost of pile.\n So, we are probably going to explore all combinations and choose the most optimal one. \nThis should give a hint for a recursive complete search solution.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nLet the **state** of our DP be DP[i][k].\n\nHere DP[i][k] is defined as the maximum profit we can get starting from the i-th pile and still having room for k more coins.\n\nNow, the **transition** is going to be simple. There are two choices:\n1. Don\'t pick any coin from this pile. In that case, DP[i][k] = DP[i+1][k]\n2. Pick exactly j coins from this pile (given that j <= k).\nIn this case, DP[i][k] = sum of topmost j coins + DP[i+1][k-j].\n\nNow, coming to the **base cases**:\n1. If we don\'t have space for any more coins, then profit will be 0.\n So, DP[...][0]=0\n2. If we are at the end of our list of piles, we can no longer generate anymore profit. \n So, DP[n][...]=0\n\nOur final answer, is going to be present in DP[0][k]. \nWe can construct a DP table of size (N*K) and use it to store and fill in the DP values. \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n* k * |pile[i]| )$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n*k)$$\n# Code\nHere\'s the Dynamic Programming Solution:\n```\nclass Solution {\npublic:\n int maxValueOfCoins(vector<vector<int>>& piles, int k) {\n int n=(int)piles.size();\n vector<vector<int>>dp;\n dp.resize(n+1, vector<int>(k+1,0));\n // State: dp[i][k]-> Max profit starting from i-th pile and remaining k coins\n // Transition: dp[i][k]=max(dp[i+1][k], (pick first j coins) -> dp[i+1][k-j])\n // Base Case: dp[n][...]=0, dp[...][0]=0\n // Final Answer: dp[0][k]\n for(int i=0;i<n;i++){\n dp[i][0]=0;\n }\n for(int i=n-1;i>=0;i--){\n for(int coins=0;coins<=k;coins++){\n // Don\'t take any coin.\n dp[i][coins]=dp[i+1][coins];\n int cost=0;\n // Take j coins (j<=coins)\n for(int j=0;j<(int)piles[i].size() && j<coins;j++){\n cost+=piles[i][j];\n dp[i][coins]=max(dp[i][coins], cost + dp[i+1][coins - (j+1)]);\n }\n }\n }\n return dp[0][k];\n }\n};\n```
| 1
| 0
|
['Dynamic Programming', 'Recursion', 'Memoization', 'C++']
| 0
|
maximum-value-of-k-coins-from-piles
|
Easy C++ solution: recursion to memoization using prefix sum
|
easy-c-solution-recursion-to-memoization-b9kh
|
Intuition\nWe can iterate through piles and decide if we want to take something from the pile or not take it. \nIf we decide to take coins from a particular pil
|
itIsWhatItIs713
|
NORMAL
|
2023-04-15T19:45:26.522686+00:00
|
2023-04-15T19:45:26.522719+00:00
| 83
| false
|
# Intuition\nWe can iterate through piles and decide if we want to take something from the pile or not take it. \nIf we decide to take coins from a particular pile, then we have the choice of how many coins to take.\n\n# Approach\nLet\'s try to think of a recursive solution. \nWe have two choices, to take coins from a particular pile, or to take nothing. Suppose we start from the last pile, then we have two choices:\n\n**notTake: f(i-1, k)** // *just move to the next pile*\n**take: (sum of x coins) + f(i-1, k-x)** // *if we decide to take x coins from pile[i], then we need the sum of all coins from 0 to x, and my k is reduced accordingly, this can be done using a for loop*\n\nInstead of calculating sum of x coins everytime I decide to take coins from the pile, we can make a prefix sum array so we can access the sum by going the xth index in the ith pile, it piles[i][x];\n\n\n# Code\n**Recursion:**\n```\nclass Solution {\npublic:\n int f(int i, int k, vector<vector<int>>& prefixPiles){\n // if we reach the end of piles, or k becomes 0 we return 0\n if(i<0 || k==0) return 0;\n\n int temp=prefixPiles[i].size();\n //we can only take coins from a pile n times.\n int n=min(temp, k);\n\n //move to the next index and k remains same\n int notTake=f(i-1, k, prefixPiles);\n\n int take=0;\n for(int j=0; j<n; j++){\n //take coins from pile\n take=max(take, prefixPiles[i][j]+f(i-1, k-j-1, prefixPiles));\n }\n //return max\n return max(take, notTake);\n }\n int maxValueOfCoins(vector<vector<int>>& piles, int k) {\n //making a prefix sum array to aviod adding coins everytime.\n vector<vector<int>> prefixPiles;\n for(int i=0; i<piles.size(); i++){\n vector<int> temp;\n temp.push_back(piles[i][0]);\n for(int j=1; j<piles[i].size(); j++){\n temp.push_back(temp[j-1]+piles[i][j]);\n }\n prefixPiles.push_back(temp);\n }\n //calling recursion starting from the last pile\n return f(piles.size()-1, k, prefixPiles);\n }\n};\n```\n\n**Memoization:**\n```\nclass Solution {\npublic:\n int f(int i, int k, vector<vector<int>>& prefixPiles, vector<vector<int>>& dp){\n if(i<0 || k==0) return 0;\n\n //if value is available for a particular index, use it\n if(dp[i][k]!=-1) return dp[i][k];\n int temp=prefixPiles[i].size();\n int n=min(temp, k);\n int notTake=f(i-1, k, prefixPiles, dp);\n\n int take=0;\n for(int j=0; j<n; j++){\n take=max(take, prefixPiles[i][j]+f(i-1, k-j-1, prefixPiles, dp));\n }\n //store max in dp array\n return dp[i][k]=max(take, notTake);\n }\n int maxValueOfCoins(vector<vector<int>>& piles, int k) {\n //making a prefix sum array to aviod adding coins everytime.\n vector<vector<int>> prefixPiles;\n for(int i=0; i<piles.size(); i++){\n vector<int> temp;\n temp.push_back(piles[i][0]);\n for(int j=1; j<piles[i].size(); j++){\n temp.push_back(temp[j-1]+piles[i][j]);\n }\n prefixPiles.push_back(temp);\n }\n //declare dp array\n vector<vector<int>> dp(piles.size()+1, vector<int>(k+1,-1));\n return f(piles.size()-1, k, prefixPiles, dp);\n }\n};\n```\n**Please upvote if you understood the solution.**
| 1
| 0
|
['Array', 'Dynamic Programming', 'Prefix Sum', 'C++']
| 0
|
maximum-value-of-k-coins-from-piles
|
PHP Dynamic Programming
|
php-dynamic-programming-by-punkundead-3cmq
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
punkundead
|
NORMAL
|
2023-04-15T19:39:42.837443+00:00
|
2023-04-15T19:39:42.837485+00:00
| 9
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(k * s)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(k)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution\n{\n\n /**\n * @param Integer[][] $piles\n * @param Integer $k\n * @return Integer\n */\n function maxValueOfCoins($piles, $k)\n {\n $a = array_fill(0, 2, array_fill(1, $k, 0));\n $c = 0;\n foreach ($piles as $pile) {\n for ($i = 1; $i <= $k; $i++) {\n for ($j = 0, $s = 0, $kk = min($i, count($pile)) ; $j < $kk; $j++) {\n $s += $pile[$j];\n $a[$c][$i] = max($a[$c][$i], $a[1 - $c][$i], $s + $a[1 - $c][$i - $j - 1]);\n }\n }\n $c = 1 - $c;\n }\n\n return end($a[1 - $c]);\n }\n}\n\n```
| 1
| 0
|
['Dynamic Programming', 'PHP']
| 0
|
maximum-value-of-k-coins-from-piles
|
C++ | ✅ Top Down DP Linear Space Complexity | ✅ Bottom Up DP
|
c-top-down-dp-linear-space-complexity-bo-0i9y
|
Top Down DP linear space\n\nclass Solution {\n\npublic:\n int maxValueOfCoins(vector<vector<int>>& piles, int k) {\n \n int n = piles.size();\n
|
anxiousLeetcoder
|
NORMAL
|
2023-04-15T17:38:07.950450+00:00
|
2023-04-15T17:38:07.950490+00:00
| 62
| false
|
# Top Down DP linear space\n```\nclass Solution {\n\npublic:\n int maxValueOfCoins(vector<vector<int>>& piles, int k) {\n \n int n = piles.size();\n vector<int> dp(k + 1);\n dp[0] = 0;\n\n for(int j = 1; j <= k; j++)\n dp[j] = dp[j - 1] + (j - 1 < piles[n - 1].size() ? piles[n - 1][j - 1] : 0);\n \n for(int i = n - 2; i >= 0; i--)\n {\n vector<int> _dp(k + 1);\n _dp[0] = 0;\n for(int j = 1; j <= k; j++)\n {\n int preSum = 0;\n int currMax = dp[j];\n for(int x = 1; x <= j && x - 1 < piles[i].size(); x++)\n {\n preSum += piles[i][x - 1];\n currMax = max(currMax, preSum + dp[j - x]);\n }\n _dp[j] = currMax;\n }\n dp.swap(_dp);\n }\n\n return dp[k];\n }\n};\n\n```\n\n\n# Bottom Up DP\n```\n\nclass Solution {\n\n int DFS(int index, int k, vector<vector<int>>& piles, vector<vector<int>> &dp)\n {\n if(index >= piles.size() || k == 0)\n return 0;\n\n if(dp[index][k] != -1)\n return dp[index][k];\n\n int ret = 0;\n int preSum = 0;\n \n // completely ignore the current pile\n ret = DFS(index + 1, k, piles, dp);\n\n // try to add more and more coins from current pile and then move on\n for(int i = 0; i < piles[index].size() && k - i - 1 >= 0; i++)\n {\n preSum += piles[index][i];\n ret = max(ret, preSum + DFS(index + 1, k - i - 1, piles, dp));\n }\n\n return dp[index][k] = ret;\n }\n\npublic:\n int maxValueOfCoins(vector<vector<int>>& piles, int k) {\n \n vector<vector<int>> dp(piles.size(), vector<int>(k + 1, -1));\n return DFS(0, k, piles, dp);\n }\n};\n```
| 1
| 0
|
['C++']
| 0
|
maximum-value-of-k-coins-from-piles
|
Easy python solution
|
easy-python-solution-by-sghorai-rtf3
|
\nclass Solution:\n def maxValueOfCoins(self, piles: List[List[int]], k: int) -> int:\n presum = [list(accumulate(p, initial=0)) for p in piles]\n
|
sghorai
|
NORMAL
|
2023-04-15T17:35:04.573736+00:00
|
2023-04-15T17:35:04.573786+00:00
| 81
| false
|
```\nclass Solution:\n def maxValueOfCoins(self, piles: List[List[int]], k: int) -> int:\n presum = [list(accumulate(p, initial=0)) for p in piles]\n n = len(piles)\n dp = [[0] * (k + 1) for _ in range(n + 1)]\n for i, s in enumerate(presum, 1):\n for j in range(k + 1):\n for idx, v in enumerate(s):\n if j >= idx:\n dp[i][j] = max(dp[i][j], dp[i - 1][j - idx] + v)\n return dp[-1][-1]\n \n```
| 1
| 0
|
['Array', 'Dynamic Programming', 'Python3']
| 0
|
maximum-value-of-k-coins-from-piles
|
Easy C++ Dp --> Memoization Without Prefix Sum
|
easy-c-dp-memoization-without-prefix-sum-fuxh
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Mridul2003
|
NORMAL
|
2023-04-15T15:59:56.226739+00:00
|
2023-04-15T15:59:56.226766+00:00
| 72
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\nMEMOIZATION\n```\nclass Solution {\npublic:\n int solve(int i,int k,vector<vector<int>>& dp,vector<vector<int>>& piles)\n {\n if(k==0)return 0;\n if(i>=piles.size())return 0;\n if(dp[i][k]!=-1)return dp[i][k];\n int np = solve(i+1,k,dp,piles);\n int p=0;\n int sum=0;\n for(int ind=0;ind<piles[i].size() and ind+1<=k;ind++)\n {\n sum+=piles[i][ind];\n p=max(p,sum+solve(i+1,k-ind-1,dp,piles));\n \n }\n return dp[i][k]=max(p,np);\n }\n int maxValueOfCoins(vector<vector<int>>& piles, int k) {\n \n int n=piles.size();\n vector<vector<int>> dp(n+1,vector<int> (k+1,-1));\n return solve(0,k,dp,piles); \n }\n```
| 1
| 0
|
['C++']
| 0
|
maximum-value-of-k-coins-from-piles
|
Easy C++ Dp --> Memoization->Tabulation with Prefix Sum
|
easy-c-dp-memoization-tabulation-with-pr-no4e
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Mridul2003
|
NORMAL
|
2023-04-15T15:42:14.039593+00:00
|
2023-04-15T15:58:23.093578+00:00
| 34
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\nMEMOIZATION\n```\nclass Solution {\npublic:\n int solve(int i,int k,vector<vector<int>>& dp,vector<vector<int>>& piles)\n {\n if(k==0)return 0;\n if(i>=piles.size())return 0;\n if(dp[i][k]!=-1)return dp[i][k];\n int np = solve(i+1,k,dp,piles);\n int p=0;\n for(int ind=0;ind<piles[i].size();ind++)\n {\n if(ind+1<=k)\n {\n p=max(p,piles[i][ind]+solve(i+1,k-ind-1,dp,piles));\n }\n else\n {\n break;\n }\n }\n return dp[i][k]=max(p,np);\n }\n int maxValueOfCoins(vector<vector<int>>& piles, int k) {\n \n int n=piles.size();\n for(int i=0;i<n;i++)\n for(int j=1;j<piles[i].size();j++)\n piles[i][j]=piles[i][j]+piles[i][j-1];\n vector<vector<int>> dp(n+1,vector<int> (k+1,-1));\n return solve(0,k,dp,piles); \n }\n};\n```\nTABULATION\n```\n int maxValueOfCoins(vector<vector<int>>& piles, int k) {\n \n int n=piles.size();\n for(int i=0;i<n;i++)\n for(int j=1;j<piles[i].size();j++)\n piles[i][j]=piles[i][j]+piles[i][j-1];\n vector<vector<int>> dp(n+1,vector<int> (k+1,0));\n for(int i=n-1;i>=0;i--)\n {\n for(int j=1;j<=k;j++)\n {\n int np = dp[i+1][j];\n int p=0;\n for(int ind=0;ind<piles[i].size();ind++)\n {\n if(ind+1<=j)\n {\n p=max(p,piles[i][ind]+dp[i+1][j-ind-1]);\n }\n else\n { \n break;\n }\n }\n dp[i][j]=max(p,np); \n }\n }return dp[0][k];\n\n //return solve(0,k,dp,piles); \n }\n```
| 1
| 0
|
['C++']
| 0
|
maximum-value-of-k-coins-from-piles
|
Java || Runtime 53 ms Beats 95.6% Memory 43.1 MB Beats 82.72%
|
java-runtime-53-ms-beats-956-memory-431-xqmje
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Akash2023
|
NORMAL
|
2023-04-15T15:37:33.564262+00:00
|
2023-04-15T15:37:33.564304+00:00
| 110
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int maxValueOfCoins(List<List<Integer>> piles, int k) {\n int n=piles.size();\n int[] dp=new int[k+1];// k steps dynamic programming;\n for(List<Integer> pile:piles){\n int m=pile.size();\n int[] cum=new int[m+1];\n for(int i=0;i<m;i++) cum[i+1]=cum[i]+pile.get(i);\n int[] curdp=new int[k+1];\n for(int i=0;i<=k;i++){\n for(int j=0;j<=m&& i+j <=k;j++){\n curdp[i+j]=Math.max(curdp[i+j],dp[i]+cum[j]);\n }\n }\n dp=curdp;\n }\n return dp[k];\n }\n}\n```
| 1
| 0
|
['Java']
| 0
|
maximum-value-of-k-coins-from-piles
|
Java Solution
|
java-solution-by-ojus_jaiswal-cbab
|
\n# Code\n\nclass Solution {\n\tpublic static int maxValueOfCoins(List<List<Integer>> piles, int k) {\n\t\tint[] mv = new int[k + 1];\n\t\tint[] pileSum = new i
|
Ojus_Jaiswal
|
NORMAL
|
2023-04-15T13:46:33.375045+00:00
|
2023-04-15T13:46:33.375076+00:00
| 49
| false
|
\n# Code\n```\nclass Solution {\n\tpublic static int maxValueOfCoins(List<List<Integer>> piles, int k) {\n\t\tint[] mv = new int[k + 1];\n\t\tint[] pileSum = new int[k + 1];\n\t\tfor (List<Integer> pile : piles) {\n\t\t\tint n = Math.min(k, pile.size());\n\t\t\tint sum = 0;\n\t\t\tfor (int i = 1; i <= n; i++)\n\t\t\t\tpileSum[i] = sum += pile.get(i - 1);\n\t\t\tfor (int i = k; i > 0; i--) {\n\t\t\t\tint max = 0;\n\t\t\t\tfor (int j = Math.min(i, n); j >= 0; j--)\n\t\t\t\t\tmax = Math.max(max, pileSum[j] + mv[i - j]);\n\t\t\t\tmv[i] = max;\n\t\t\t}\n\t\t}\n\t\treturn mv[k];\n\t}\n}\n```
| 1
| 0
|
['Java']
| 0
|
maximum-value-of-k-coins-from-piles
|
choose or dont choose that pile with how many are you going to choose from that pile: is the idea
|
choose-or-dont-choose-that-pile-with-how-aurm
|
\nclass Solution {\npublic:\n \n int dfs(int npile , int coins, int n,vector<vector<int>>& p,vector<vector<int>> &c)\n {\n if(npile>=n || coins
|
mr_stark
|
NORMAL
|
2023-04-15T13:40:46.443265+00:00
|
2023-04-15T13:40:46.443301+00:00
| 42
| false
|
```\nclass Solution {\npublic:\n \n int dfs(int npile , int coins, int n,vector<vector<int>>& p,vector<vector<int>> &c)\n {\n if(npile>=n || coins <= 0)\n return 0;\n if(c[npile][coins]!=-1)\n return c[npile][coins];\n c[npile][coins] = dfs(npile+1,coins,n,p,c);\n int cpile = 0;\n for(int j=0;j<min(coins,(int)p[npile].size());j++)\n {\n cpile+=p[npile][j];\n c[npile][coins] = max(c[npile][coins],cpile+dfs(npile+1,coins-1-j,n,p,c));\n }\n return c[npile][coins];\n }\n int maxValueOfCoins(vector<vector<int>>& p, int k) {\n \n int n = p.size();\n vector<vector<int>> cache(n+1,vector<int> (k+1,-1));\n return dfs(0,k,n,p,cache);\n }\n};\n```
| 1
| 0
|
['C']
| 1
|
maximum-value-of-k-coins-from-piles
|
2218. Maximum Value of K Coins From Piles || Java
|
2218-maximum-value-of-k-coins-from-piles-si12
|
\nclass Solution {\n public int solve (List<List<Integer>> piles,int i,int k,int [][] dp )\n {\n if(i>=piles.size())\n return 0;\n
|
ArpAry
|
NORMAL
|
2023-04-15T12:06:13.972108+00:00
|
2023-04-15T12:06:13.972157+00:00
| 8
| false
|
```\nclass Solution {\n public int solve (List<List<Integer>> piles,int i,int k,int [][] dp )\n {\n if(i>=piles.size())\n return 0;\n if(dp[i][k]!=-1)\n return dp[i][k];\n int max=0;\n max=Math.max(max,solve(piles,i+1,k,dp));\n for(int j=0;j<piles.get(i).size();j++)\n {\n if(j+1<=k)\n max=Math.max(max,piles.get(i).get(j)+solve(piles,i+1,k-j-1,dp));\n else\n break;\n }\n return dp[i][k]=max;\n }\n public int maxValueOfCoins(List<List<Integer>> piles, int k) {\n for(int i=0;i<piles.size();i++)\n {\n \n for(int j=1;j<piles.get(i).size();j++)\n { \n int removed= piles.get(i).get(j);\n removed+= piles.get(i).get(j-1);\n piles.get(i).set(j,removed); \n } \n }\n int n=piles.size();\n int [][]dp=new int [n+1][k+1];\n for(int x[]:dp)\n Arrays.fill(x,-1);\n return solve(piles,0,k,dp);\n }\n}\n```
| 1
| 0
|
[]
| 0
|
maximum-value-of-k-coins-from-piles
|
c++ | take and notTake dp | memoization | simple and easy to understand
|
c-take-and-nottake-dp-memoization-simple-2ssn
|
Complexity\n- Time complexity:\no(nk)\n\n- Space complexity:\no(nk)\n\n# Code\n\nclass Solution {\nprivate:\n int solve(int ind, vector<vector<int>>& piles,
|
jatinwatts
|
NORMAL
|
2023-04-15T11:59:56.534055+00:00
|
2023-04-15T11:59:56.534095+00:00
| 35
| false
|
# Complexity\n- Time complexity:\no(n*k)\n\n- Space complexity:\no(n*k)\n\n# Code\n```\nclass Solution {\nprivate:\n int solve(int ind, vector<vector<int>>& piles, vector<vector<int>>& dp, int k) {\n if(ind >= piles.size()) return 0;\n\n if(dp[ind][k] != -1) return dp[ind][k];\n\n int sum = 0, take = 0;\n\n //not taking from current pile;\n int notTake = 0 + solve(ind+1,piles,dp,k);\n\n //taking from current pile if we can take according to given k and move towards next ind\n for(int i=0;i<piles[ind].size();i++) {\n sum += piles[ind][i];\n\n if(k - (i+1) >= 0) {\n take = max(take, sum + solve(ind+1, piles, dp, k-(i+1)));\n }\n }\n\n return dp[ind][k] = max(take, notTake);\n }\n\npublic:\n int maxValueOfCoins(vector<vector<int>>& piles, int k) {\n int n = piles.size();\n vector<vector<int>> dp(n+1, vector<int>(k+1, -1));\n return solve(0,piles,dp,k);\n }\n};\n```
| 1
| 0
|
['C++']
| 1
|
maximum-value-of-k-coins-from-piles
|
C#: DP, Recursion
|
c-dp-recursion-by-igor0-sn3s
|
Intuition\nUse DP and recursion.\n\n# Approach\nCreate the method\n\nprivate int MaxValueOfCoins((int index, int k) key, Dictionary<(int index, int k), int> dic
|
igor0
|
NORMAL
|
2023-04-15T10:23:43.232498+00:00
|
2023-04-15T10:23:43.232545+00:00
| 89
| false
|
# Intuition\nUse DP and recursion.\n\n# Approach\nCreate the method\n```\nprivate int MaxValueOfCoins((int index, int k) key, Dictionary<(int index, int k), int> dic, IList<IList<int>> piles)\n```\n, where\n- (int index, int k) key contains the index of a current pile and k - the number of coins\n- Dictionary<(int index, int k), int> dic is a dictionary with a result for a certain key\n- IList<IList<int>> piles is an initial piles\nCall this method recursively.\n# Complexity\n- Time complexity:\n$$O(sum(len(piles[i])))$$\n\n- Space complexity:\n$$O(sum(len(piles[i])))$$\n\n# Code\n```\npublic class Solution {\n public int MaxValueOfCoins(IList<IList<int>> piles, int k) {\n var rs = MaxValueOfCoins((0, k), new Dictionary<(int index, int k), int>(), piles);\n return rs;\n }\n private int MaxValueOfCoins((int index, int k) key, Dictionary<(int index, int k), int> dic, IList<IList<int>> piles)\n {\n if (piles.Count <= key.index || key.k <= 0) return 0;\n if (dic.ContainsKey(key)) return dic[key];\n var rs = MaxValueOfCoins((key.index + 1, key.k), dic, piles);\n var sum = 0;\n for (int i = 0; i < Math.Min(piles[key.index].Count, key.k); i++)\n {\n sum += piles[key.index][i];\n var rs0 = sum + MaxValueOfCoins((key.index + 1, key.k - (i + 1)), dic, piles);\n if (rs < rs0) rs = rs0;\n }\n if (!dic.ContainsKey(key)) dic.Add(key, rs);\n return rs;\n }\n}\n```
| 1
| 0
|
['Dynamic Programming', 'Recursion', 'C#']
| 0
|
maximum-value-of-k-coins-from-piles
|
No-brainer DFS solution with cache
|
no-brainer-dfs-solution-with-cache-by-je-xtp2
|
Intuition\nIntuition 1: for pile i, I can pick l = 0, 1, ..., min(k, len(pile[i])) coins from pile i;\nIntuition 2: when I pick l coins on pile i, I then can pi
|
jennitheric
|
NORMAL
|
2023-04-15T09:58:41.299721+00:00
|
2023-04-15T10:04:19.992794+00:00
| 97
| false
|
# Intuition\nIntuition 1: for pile i, I can pick l = 0, 1, ..., min(k, len(pile[i])) coins from pile i;\nIntuition 2: when I pick l coins on pile i, I then can pick k-l coins from i+1 to N-1 piles.\n \n# Approach\nSolve a subproblem: Find the maximum total value if we are picking from ith pile upto (N-1)th pile for a total of k coins.\n\n# Complexity\n- Time complexity:\n$$O(Nmk)$$ - N is the length of piles, m is the number of coins in each pile.\n\n- Space complexity:\n$$O(Nk)$$ - N is the length of piles.\n\n# Code\n```python\nclass Solution:\n def maxValueOfCoins(self, piles: List[List[int]], k: int) -> int:\n """\n Intuition 1: for pile i, I can pick l = 0, 1, ..., min(k, len(pile[i])) coins from pile i;\n Intuition 2: when I pick l coins on pile i, from i+1 to N-1 piles, I then can k-l coins.\n Subproblem: Find the maximum total value if we pick from i-th pile and up for a total of k coins.\n """\n @cache\n def solve(i: int, k: int) -> int:\n # end of piles or no more room for any coin\n if i == len(piles) or k == 0:\n return 0\n\n # don\'t pick this pile\n res = solve(i+1, k)\n cur_total = 0\n\n # If we pick this pile, try all possible number of coins that we can pick, e.g. 1, 2, ..., or\n # up to k or the total number of coins in piles[i] whenever which one comes first.\n for l in range(min(k, len(piles[i]))):\n cur_total += piles[i][l]\n\n # once I pick l+1 coins in i-th pile, then solve the subproblem\n # for (i+1)th and onward piles, with k-l-1 room left to fill.\n res = max(res, cur_total + solve(i+1, k-l-1))\n\n return res\n\n return solve(0,k)\n```
| 1
| 0
|
['Python3']
| 0
|
maximum-value-of-k-coins-from-piles
|
C++ || Memoization || Tabulation
|
c-memoization-tabulation-by-rounak_25-f1wj
|
Memoization Code\n\nclass Solution {\npublic:\nint dp[1001][2001];\nint solve(vector<vector<int>> &piles, int idx, int k)\n{\n if (k == 0)\n return 0;
|
Rounak_25
|
NORMAL
|
2023-04-15T09:47:21.053275+00:00
|
2023-06-16T14:56:04.743450+00:00
| 128
| false
|
# Memoization Code\n```\nclass Solution {\npublic:\nint dp[1001][2001];\nint solve(vector<vector<int>> &piles, int idx, int k)\n{\n if (k == 0)\n return 0;\n if (idx >= piles.size())\n return 0;\n if (dp[idx][k] != -1)\n return dp[idx][k];\n\n int ans = INT_MIN;\n int s = 0;\n int res = solve(piles, idx + 1, k);// if not choosing idxth pile\n for (int j = 0; j < piles[idx].size() && j<=k-1; j++)\n {\n s = s + piles[idx][j];\n ans = max({ans, s + solve(piles, idx + 1, k - (j + 1)), res});\n }\n if (ans < 0) return dp[idx][k] = 0;\n return dp[idx][k] = ans;\n}\nint maxValueOfCoins(vector<vector<int>> &piles, int k)\n{\n memset(dp, -1, sizeof(dp));\n return solve(piles, 0, k);\n}\n};\n```\n# Tabulation Code\n```\nclass Solution {\npublic:\nint solve_tab(vector<vector<int>> &piles, int k)\n{\n int n = piles.size();\n vector<vector<int>> dp(n + 1, vector<int>(k + 1, 0));\n\n // last row and first column initialized with 0\n // for idx use r and for k use c\n for (int r = n - 1; r >= 0; r--)\n {\n for (int c = 1; c <= k; c++)\n {\n int ans = INT_MIN;\n int s = 0;\n int res = dp[r+1][c];// if not choosing rth pile\n for(int j=0; j<piles[r].size() && j<=c-1; j++)\n {\n s = s+piles[r][j];\n ans = max({ ans, s+dp[r+1][c-(j+1)] , res });\n }\n if(ans<0) dp[r][c] = 0;\n else dp[r][c] = ans;\n }\n }\n return dp[0][k];\n}\nint maxValueOfCoins(vector<vector<int>> &piles, int k)\n{\n return solve_tab(piles, k);\n}\n};\n```
| 1
| 0
|
['Dynamic Programming', 'Recursion', 'Memoization', 'Prefix Sum', 'C++']
| 0
|
maximum-value-of-k-coins-from-piles
|
Maximum Value of K Coins From Piles C#
|
maximum-value-of-k-coins-from-piles-c-by-qf6e
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
MaddiSwetha
|
NORMAL
|
2023-04-15T09:40:16.100165+00:00
|
2023-04-15T09:40:16.100209+00:00
| 48
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\npublic class Solution {\n public int MaxValueOfCoins(IList<IList<int>> piles, int k) {\n int n = piles.Count;\n int[][] dp = new int[n + 1][];\n for (int i = 0; i < dp.Length; i++) {\n dp[i] = new int[k + 1];\n }\n for (int i = 1; i <= n; i++) {\n for (int coins = 0; coins <= k; coins++) {\n int current_sum = 0;\n for (int current_coins = 0; current_coins <= Math.Min(piles[i - 1].Count, coins); current_coins++) {\n if (current_coins > 0) {\n current_sum += piles[i - 1][current_coins - 1];\n }\n dp[i][coins] = Math.Max(dp[i][coins], dp[i - 1][coins - current_coins] + current_sum);\n }\n }\n }\n return dp[n][k]; \n }\n}\n```
| 1
| 0
|
['C#']
| 0
|
maximum-value-of-k-coins-from-piles
|
Ruby || recursion + memoization
|
ruby-recursion-memoization-by-alecn2002-jwcx
|
Intuition\nTry (1..k) from the first pile and calculate max for the rest with new k = k - tried, and so on\n\n# Approach\nReworked translation to Ruby of aryan_
|
alecn2002
|
NORMAL
|
2023-04-15T09:25:32.214576+00:00
|
2023-04-15T09:25:32.214634+00:00
| 46
| false
|
# Intuition\nTry (1..k) from the first pile and calculate max for the rest with new k = k - tried, and so on\n\n# Approach\nReworked translation to Ruby of [aryan_0077 C++ solution](https://leetcode.com/problems/maximum-value-of-k-coins-from-piles/solutions/3417959/image-explanation-top-down-dp-easy-concise-c-java-python/) (same idea, technical details taken from his solution)\n\n# Complexity\n- Time complexity:\n$$O(n*k)$$\n\n- Space complexity:\n$$O(n*k)$$\n\n# Code\n```ruby\n# Reworked translation to Ruby of aryan_0077 C++ solution\n\nclass Solver\n attr_reader :piles, :k, :dp\n\n def initialize(piles, k)\n @piles, @k = piles, k\n @dp = Array.new(piles.size + 1) {|i| Array.new(k + 1) }\n end\n\n def solve(i = 0, kk = k)\n cur = 0 # If cur is included in inject() param below then TLE\n @dp[i][kk] ||= (i >= piles.size || !kk.positive?) ? \n 0 :\n [piles[i].size, kk].min.times.inject(solve(i + 1, kk)) {|res, j|\n cur += piles[i][j]\n [res, cur + solve(i + 1, kk - j - 1)].max\n }\n end\nend\n\ndef max_value_of_coins(piles, k)\n Solver.new(piles, k).solve\nend\n\n```
| 1
| 0
|
['Recursion', 'Memoization', 'Ruby']
| 0
|
maximum-value-of-k-coins-from-piles
|
Prefix Sum + DP | C++
|
prefix-sum-dp-c-by-tusharbhart-96w7
|
\nclass Solution {\n int dfs(int i, int k, int n, vector<vector<int>> &piles, vector<vector<int>> &dp) {\n if(!k || i == n) return 0;\n if(dp[i
|
TusharBhart
|
NORMAL
|
2023-04-15T08:43:19.708378+00:00
|
2023-04-15T08:43:19.708407+00:00
| 20
| false
|
```\nclass Solution {\n int dfs(int i, int k, int n, vector<vector<int>> &piles, vector<vector<int>> &dp) {\n if(!k || i == n) return 0;\n if(dp[i][k] != -1) return dp[i][k];\n\n int ans = 0;\n for(int j=0; j<min((int)piles[i].size(), k); j++) {\n int notpick = dfs(i + 1, k, n, piles, dp), pick = 0;\n if(k - j - 1 >= 0) pick = piles[i][j] + dfs(i + 1, k - j - 1, n, piles, dp);\n ans = max({ans, pick, notpick});\n }\n return dp[i][k] = ans;\n }\npublic:\n int maxValueOfCoins(vector<vector<int>>& piles, int k) {\n int n = piles.size();\n for(auto &p : piles) {\n for(int i=1; i<p.size(); i++) p[i] += p[i - 1];\n }\n vector<vector<int>> dp(n, vector<int>(k + 1, -1));\n return dfs(0, k, n, piles, dp);\n }\n};\n\n\n```
| 1
| 0
|
['Dynamic Programming', 'Memoization', 'Prefix Sum', 'C++']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
Easy - Compare Left and Right Distances
|
easy-compare-left-and-right-distances-by-m4xn
|
Intuition\nSince the task is to return the lexicographically smallest string, so we will try to convert the beginning characters into \'a\', if possible.\n\n# A
|
AdityaRaj_cpp
|
NORMAL
|
2024-04-07T05:18:40.146884+00:00
|
2024-04-07T14:16:01.536865+00:00
| 2,638
| false
|
# Intuition\nSince the task is to return the lexicographically smallest string, so we will try to convert the beginning characters into \'a\', if possible.\n\n# Approach\n1. It iterates through each character`ch`in the input string`s`.\n3. For each character`ch`, it calculates two values:\n\u2022 `left` : The distance between the character and \'a\' on left side.\n\u2022 `right`: The distance between the character and \'a\' on the right side.\n4. It then calculates`mnn`,which is the minimum of`left`and`right`.\n5. If`k`(the remaining operations) is greater than or equal to `mnn`, it reduces`k`by`mnn`and sets the current character`ch`to \'a\'.\n6. Otherwise, it subtracts `k` from the current character `ch` and break the loop.\n7. Finally, it returns the modified string`s`.\n\n# Complexity\n- Time complexity: `O(n)`\n\n# Code\n```\nclass Solution\n{\npublic:\n string getSmallestString(string s, int k)\n {\n string ans = s;\n for (char &ch : s)\n {\n int left = ch - \'a\';\n int right = \'z\' - ch + 1;\n int mnn = min(left, right);\n if (k >= mnn)\n {\n k -= mnn;\n ch = \'a\';\n }\n else\n {\n ch = ch - k;\n break;\n }\n }\n return s;\n }\n};\n```
| 36
| 0
|
['String', 'Greedy', 'C++']
| 7
|
lexicographically-smallest-string-after-operations-with-constraint
|
Short and Sweet
|
short-and-sweet-by-votrubac-t7t6
|
Our strategy is to change characters to a left-to-right, while we can.\n\nWe first calculate how many operations we need to change it to a: \n- dist_a = min(s[i
|
votrubac
|
NORMAL
|
2024-04-07T05:35:43.980996+00:00
|
2024-04-07T17:58:37.621670+00:00
| 692
| false
|
Our strategy is to change characters to `a` left-to-right, while we can.\n\nWe first calculate how many operations we need to change it to `a`: \n- `dist_a = min(s[i] - \'a\', \'z\' - s[i] + 1)`.\n\nIf we have enough operations left (`dist_a <= k`), we change the character to `a`, and subtract `dist_a` from `k`.\n\nIf we cannot make `a`, we decrease the current character using the remaninig operations.\n\n> Note that we consider incrementing the current character only if we can cyclically reach `a`.\n> Otherwise, it only makes sense to decrease the current character.\n\n**C++**\n```cpp\nstring getSmallestString(string s, int k) {\n for (int i = 0; i < s.size() && k > 0; ++i) {\n int dist_a = min(s[i] - \'a\', \'z\' - s[i] + 1);\n s[i] = dist_a <= k ? \'a\' : s[i] - k;\n k -= dist_a;\n }\n return s;\n}\n```
| 29
| 0
|
['C']
| 2
|
lexicographically-smallest-string-after-operations-with-constraint
|
Simple java solution
|
simple-java-solution-by-siddhant_1602-boqt
|
Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(1)\n\n# Code\n\nclass Solution {\n public String getSmallestString(String s, int k) {\n S
|
Siddhant_1602
|
NORMAL
|
2024-04-07T04:04:05.032165+00:00
|
2024-04-07T04:04:05.032198+00:00
| 871
| false
|
# Complexity\n- Time complexity: $$O(n)$$\n\n- Space complexity: $$O(1)$$\n\n# Code\n```\nclass Solution {\n public String getSmallestString(String s, int k) {\n StringBuilder nm=new StringBuilder();\n for(int i=0;i<s.length();i++)\n {\n char c=s.charAt(i);\n int val=Math.min(123-c, c-97);\n if(k>0)\n {\n if(val<=k)\n {\n nm.append("a");\n k-=val;\n }\n else\n {\n c=(char)(c-k);\n nm.append(c);\n k-=val;\n }\n }\n else\n {\n nm.append(c);\n }\n }\n return nm.toString();\n }\n}\n```
| 17
| 0
|
['Java']
| 2
|
lexicographically-smallest-string-after-operations-with-constraint
|
Simple Video Solution with TC: O(26*N)->O(N) 🔥
|
simple-video-solution-with-tc-o26n-on-by-zvly
|
Easy Video Solution\n\nhttps://youtu.be/qr_2aqMARWE\n\n# Code\n\nclass Solution {\npublic:\n string getSmallestString(string s, int k) {\n string ans=
|
ayushnemmaniwar12
|
NORMAL
|
2024-04-07T04:05:08.572979+00:00
|
2024-04-07T07:48:59.201799+00:00
| 950
| false
|
# Easy Video Solution\n\nhttps://youtu.be/qr_2aqMARWE\n\n# Code\n```\nclass Solution {\npublic:\n string getSmallestString(string s, int k) {\n string ans="";\n int n=s.size();\n for(int i=0;i<n;i++) {\n int f=0;\n for(char ch=\'a\';ch<=\'z\';ch++) {\n int d1=abs((s[i]-\'a\')-(ch-\'a\'));\n int d2=26-d1;\n int d=min(d1,d2);\n if(d<=k) {\n f=1;\n ans.push_back(ch);\n k=k-d;\n break;\n }\n }\n if(f==0)\n ans.push_back(s[i]);\n }\n return ans;\n }\n};\n```
| 16
| 0
|
['Math', 'String Matching', 'C++']
| 2
|
lexicographically-smallest-string-after-operations-with-constraint
|
Python 3 || 9 lines, w/ explanation || T/S: 99% / 93%
|
python-3-9-lines-w-explanation-ts-99-93-ioafe
|
Here\'s the plan:\n\n1. We iterate across the ords of the characters in s.\n\n1. If the value of k is sufficient, we move each character of s to a along the sho
|
Spaulding_
|
NORMAL
|
2024-04-07T20:03:07.659093+00:00
|
2024-05-24T18:38:28.532668+00:00
| 219
| false
|
Here\'s the plan:\n\n1. We iterate across the *ords* of the characters in `s`.\n\n1. If the value of `k` is sufficient, we move each character of `s` to *a* along the shortest path for that character and decrement `k` accordingly.\n1. If the value of `k` is not sufficient, we spend all of `k` to move a character as far forward toward *a* as possible.\n1. We append any tail of `s` left after `k` is exhausted.\n\n\n```\nclass Solution:\n def getSmallestString(self, s: str, k: int, ans = \'\' ) -> str:\n\n for i, num in enumerate(map(lambda x: ord(x) - 97, s)):\n # <--1)\n dist = min(num, 26 - num)\n if dist <= k: # <--2)\n k-= dist\n ans+= \'a\'\n else: \n ans+= chr(num + 97 - k) # <--3)\n break\n\n return ans + s[i+1:] # <--4)\n```\n[https://leetcode.com/problems/lexicographically-smallest-string-after-operations-with-constraint/submissions/1266897847/](https://leetcode.com/problems/lexicographically-smallest-string-after-operations-with-constraint/submissions/1266897847/)\n\n\n\nI could be wrong, but I think that time complexity is *O*(*N*) and space complexity is *O*(*N*), in which *N* ~ `len(s)`.
| 14
| 0
|
['Python3']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
Beats 100% of users with c++ || O(26*N)❌O(N)✅
|
beats-100-of-users-with-c-o26non-by-vebz-gmyq
|
Intuition\nThe idea is to check if it\'s possible for result[i] to be \'a\'\n(for each index i)\n\n# Approach\nLet res be the result string (of same length)\n\n
|
vebzb
|
NORMAL
|
2024-04-07T05:56:53.424752+00:00
|
2024-04-07T05:56:53.424771+00:00
| 274
| false
|
# Intuition\nThe idea is to check if it\'s possible for result[i] to be \'a\'\n(for each index *i*)\n\n# Approach\nLet res be the result string (of same length)\n\n For each index i:\n if(distance(s[i],\'a\')<=k): \n res[i]=\'a\'\n k-=distance(s[i],\'a\')<=k\n else\n res[i]=lexicographically least character at distance k\n //s[i]-k\n break\n copy the remaining characters to the remaining integers\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(N) to store the result\n\n\n\n\n\n# Code\n```\nclass Solution {\npublic:\n string getSmallestString(string s, int k) {\n string res;\n int i;\n for(i=0;i<s.length();i++)\n {\n if((s[i]-\'a\')<=k||\'z\'-s[i]+1<=k)\n {\n res.push_back(\'a\');\n k-=min(\'z\'-s[i]+1,s[i]-\'a\');\n }\n else\n {\n res.push_back(s[i]-k);\n break;\n }\n }\n for(int j=i+1;j<s.length();j++)\n res.push_back(s[j]);\n return res;\n }\n};\n```\n\nPLEASE UPVOTE IF YOU FIND IT USEFUL\uD83E\uDD7A\uD83E\uDD7A\uD83E\uDD7A
| 11
| 0
|
['C++']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
Java - Compare left and right distances
|
java-compare-left-and-right-distances-by-3tsv
|
Intuition\n Describe your first thoughts on how to solve this problem. \n- For each character, check if the left side distance or the right side distance is sma
|
makubex74
|
NORMAL
|
2024-04-07T04:15:00.012455+00:00
|
2024-04-08T06:11:45.109288+00:00
| 294
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- For each character, check if the left side distance or the right side distance is smaller and update accordingly.\n- If you\'re able to move to character `\'a\'` in less than `k` steps, then directly set that character to `\'a\'` and decrement `distToA` from `k`.\n- Else, try to move your character left as much as possible.\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(n)\n# Code\n```\nclass Solution {\n public int cyclicDistance(char ch1, char ch2) {\n int dist = Math.abs(ch1 - ch2);\n return Math.min(dist, 26 - dist);\n }\n public String getSmallestString(String s, int k) {\n char[] sArray = s.toCharArray();\n for(int i = 0; i < sArray.length; i++) {\n int distToA = cyclicDistance(sArray[i], \'a\');\n if(distToA <= k) {\n sArray[i] = \'a\';\n k -= distToA;\n } else if(k > 0) {\n sArray[i] = (char) (sArray[i] - k);\n k = 0;\n }\n }\n return new String(sArray);\n }\n}\n```
| 7
| 0
|
['Java']
| 2
|
lexicographically-smallest-string-after-operations-with-constraint
|
Easy 🔥🔥 Python 🐍 // Java // Python3 // C++ 🔥🔥 Explained 💀☠️ Beats 💯
|
easy-python-java-python3-c-explained-bea-6ewj
|
Intuition\n\n\n\n\n\n\n\n Describe your first thoughts on how to solve this problem. \nC++ []\nclass Solution {\npublic:\n string getSmallestString(string s,
|
Edwards310
|
NORMAL
|
2024-04-07T04:02:42.442309+00:00
|
2024-04-11T08:27:40.741872+00:00
| 169
| false
|
# Intuition\n\n\n\n\n\n\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n```C++ []\nclass Solution {\npublic:\n string getSmallestString(string s, int k) {\n int n = s.size();\n string t = s;\n for(int i = 0; i < n; i++){\n int c = s.at(i)- \'a\';\n for(int j = 0; j < 26; j++){\n int d = min(abs(c - j), 26 - abs(c - j));\n if(d <= k){\n t.at(i) = char(j + \'a\');\n k -= d;\n break;\n }\n }\n }\n return t;\n }\n};\n```\n```python3 []\nclass Solution:\n def getSmallestString(self, s: str, k: int) -> str:\n n = len(s)\n result = list(s)\n for i in range(n):\n for j in range(26):\n new_char = chr(ord(\'a\') + j)\n diff = min((ord(new_char) - ord(s[i])) % 26 , (ord(s[i]) - ord(new_char)) % 26)\n if diff <= k:\n result[i] = new_char\n k -= diff\n break\n return "".join(result)\n```\n```Java []\nclass Solution {\n public String getSmallestString(String s, int k) {\n StringBuilder sb = new StringBuilder("");\n int n = s.length();\n for(int i = 0; i < n; i++){\n char c = s.charAt(i);\n if(c == \'a\')\n sb.append(\'a\');\n else{\n int min = Math.min(c - \'a\', (\'z\' - c) + 1);\n if(min <= k){\n k -= min;\n sb.append(\'a\');\n }\n else{\n int y = ((c - \'a\') - k);\n sb.append((char)(y + \'a\'));\n k = 0;\n }\n }\n }\n return sb.toString();\n }\n}\n```\n```Python []\nclass Solution(object):\n def getSmallestString(self, s, k):\n """\n :type s: str\n :type k: int\n :rtype: str\n """\n ts = [ord(x) - ord(\'a\') for x in s]\n pre = 0\n ans = \'\'\n for i, x in enumerate(ts):\n down = x\n up = 26 - x\n cost = min(up, down)\n if cost <= k:\n ans += \'a\'\n k -= cost\n else:\n ans += chr(x - k + ord(\'a\'))\n return ans + s[i + 1 : ]\n return ans\n```\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n O(n)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n O(n)\n# Code\n```\nclass Solution:\n def getSmallestString(self, s: str, k: int) -> str:\n n = len(s)\n result = list(s)\n for i in range(n):\n for j in range(26):\n new_char = chr(ord(\'a\') + j)\n diff = min((ord(new_char) - ord(s[i])) % 26 , (ord(s[i]) - ord(new_char)) % 26)\n if diff <= k:\n result[i] = new_char\n k -= diff\n break\n return "".join(result)\n```\n# Please upvote if it\'s useful ...\n\n
| 7
| 0
|
['Python', 'C++', 'Java', 'Python3']
| 1
|
lexicographically-smallest-string-after-operations-with-constraint
|
C++ 100% Faster | String Matching | Easy Step By Step Solution
|
c-100-faster-string-matching-easy-step-b-2tx3
|
\n\n# Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem asks us to minimize the distance between a string s and another strin
|
VYOM_GOYAL
|
NORMAL
|
2024-04-07T04:00:35.754199+00:00
|
2024-04-07T04:00:35.754230+00:00
| 490
| false
|
\n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem asks us to minimize the distance between a string s and another string t through character changes. We can achieve this by iterating through s and analyzing the distance between each character and its lexicographically smallest neighbor (\'a\').\n\n- Here\'s the key insight:\n - If the distance between a character s[i] and \'a\' is less than or equal to the available operations (k), we can directly change s[i] to \'a\'. This minimizes the distance for that character.\n - If the distance is greater than k, we can still make some changes. We need to find the new character for s[i] that utilizes the remaining operations (k) most effectively. We can either move s[i] closer to \'a\' (if possible) or move it as far away from \'z\' (the character with the maximum distance from \'a\').\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. **Iterate through the string:**\n - For each character s[i], calculate its distance to \'a\':\n - dist = min(s[i] - \'a\', \'z\' - s[i] + 1). This considers both clockwise and counter-clockwise rotations in the cyclic order of characters.\n2. **Change characters based on distance and available operations:**\n - If dist <= k:\n - Change s[i] to \'a\'. This minimizes the distance for this character and consumes dist operations.\n - Decrement k by dist to reflect the used operations.\n - If dist > k and k > 0:\n - If moving s[i] closer to \'a\' is possible (i.e., s[i] - k >= \'a\'), decrement s[i] by k.\n - Otherwise, move s[i] as far away from \'z\' as possible using the remaining operations. Set s[i] to \'z\' - (k - 1).\n - In both cases, set k to 0 as all remaining operations are used.\n3. **Return the modified string:**\n - After iterating through the entire string, return the modified s.\n\n# Complexity\n- Time complexity: **O(n)**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: **O(1)**\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n#pragma GCC optimize("03", "unroll-loops")\nclass Solution {\npublic:\n string getSmallestString(string s, int k) {\n for (int i = 0; i < s.size(); ++i) {\n int dist = min(s[i] - \'a\', \'z\' - s[i] + 1);\n if(k >= dist){\n k -= dist;\n s[i] = \'a\';\n }else{\n if(k > 0){\n if(s[i] - k >= \'a\'){\n s[i]-=k;\n }else{\n s[i] = \'z\' - (k - 1);\n }\n k=0;\n }\n break;\n }\n }\n return s;\n }\n};\nauto init = [](){\n ios::sync_with_stdio(false);\n cin.tie(nullptr);\n cout.tie(nullptr);\n return \'c\';\n}();\n```
| 7
| 1
|
['String', 'C++']
| 1
|
lexicographically-smallest-string-after-operations-with-constraint
|
C++ || O(N)
|
c-on-by-abhay5349singh-4ope
|
Connect with me on LinkedIn: https://www.linkedin.com/in/abhay5349singh/\n\nApproach:\n convert most significant chars within available moves to lowest char poo
|
abhay5349singh
|
NORMAL
|
2024-04-07T04:02:44.695787+00:00
|
2024-04-07T04:02:44.695818+00:00
| 427
| false
|
**Connect with me on LinkedIn**: https://www.linkedin.com/in/abhay5349singh/\n\n**Approach:**\n* convert most significant chars within available moves to lowest char poosible\n* next_idx = (idx+cur_k)%26; => possible char after shifting in forward direction\n* prev_idx = (idx-cur_k+26)%26; => possible char after shifting in backward direction\n\n```\nclass Solution {\npublic:\n string getSmallestString(string s, int k) {\n int n=s.length();\n \n string ans="";\n for(int i=0;i<n;i++){\n int cur_k = min(k,25); // max number of moves required to transform char to [a,z] \n int extra_moves = k-cur_k;\n \n if(k==0){\n ans += s.substr(i);\n break;\n }\n \n char ch = s[i];\n \n // utilizing max moves possible to get minimum char for current position\n int idx = ch-\'a\';\n int next_idx = (idx+cur_k)%26; \n int prev_idx = (idx-cur_k+26)%26;\n \n // check if it was possible to get \'a\' with less number of moves available \n \n int k1=cur_k;\n if(next_idx > 0){\n next_idx = 0;\n k1 = 26-idx;\n }\n \n int k2=cur_k;\n if(prev_idx > idx){\n prev_idx = 0;\n k2 = idx;\n }\n \n // assigning random char with ascii > z\n char ch1=\'|\', ch2=\'|\';\n \n if(k1 <= cur_k) ch1 = (char)(next_idx+\'a\');\n if(k2 <= cur_k) ch2 = (char)(prev_idx+\'a\');\n \n if(ch1 < ch2){\n ans += ch1;\n cur_k -= k1;\n }else if(ch2 < ch1){\n ans += ch2;\n cur_k -= k2;\n }else{\n ans += ch1;\n cur_k -= min(k1,k2);\n }\n \n k = cur_k + extra_moves;\n }\n \n return ans;\n }\n};\n```\n\n**Do upvote if it helps :)**
| 6
| 0
|
[]
| 1
|
lexicographically-smallest-string-after-operations-with-constraint
|
EASY C++ SOLUTION 🚀🔥 || SIMPLE FORCE APPROACHWITH DRY RUN ✅
|
easy-c-solution-simple-force-approachwit-zbiv
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n1. Initialize a string
|
_cupcake
|
NORMAL
|
2024-04-07T04:54:47.710829+00:00
|
2024-04-07T04:54:47.710851+00:00
| 411
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Initialize a string t with the same characters as string s.\n2. Iterate over each character in string s.\n3. For each character, iterate over the lowercase English letters from \'a\' to \'z\'.\n4. Calculate the minimum distance required to change the character in s to the current letter \'ch\'.\n- For each character, we try all possible lowercase English letters from \'a\' to \'z\' to find the lexicographically smallest letter that satisfies the distance constraint.\n\nWe calculate the distance between the current character s[i] and the candidate letter ch in three cases:\n\n- Direct distance: abs(s[i] - ch)\n- Distance when ch is after s[i] in cyclic order: s[i] + 26 - ch\n- Distance when ch is before s[i] in cyclic order: ch + 26 - s[i]\n\nWe choose the candidate letter ch that minimizes the distance and satisfies the distance constraint (i.e., the distance is less than or equal to k)\n5. If the distance is less than or equal to the allowed value k, update the character in the resulting string t.\n6. Subtract the distance from k.\n7. Move to the next character in string s.\n8. Return the resulting string t.\n\n\n**DRY RUN**\nStarting with s = "xaxcd" and k = 4, we\'ll iterate over each character in the string:\n\n1. For the first character \'x\':\n- The minimum distance to change \'x\' to \'a\' is 23.\n- Since 23 > 4, we do not update t.\n\n2. For the second character \'a\':\n- The minimum distance to change \'a\' to \'w\' is 3.\n- Since 3 <= 4, we update t to "waxcd" and decrement k to 1.\n\n3. For the third character \'x\':\n- The minimum distance to change \'x\' to \'a\' is 23.\n- Since 23 > 1, we do not update t.\n\n4. For the fourth character \'c\':\n - The minimum distance to change \'c\' to \'a\' is 2.\n- Since 2 <= 1, we update t to "waacd" and decrement k to 0.\n\n5. For the fifth character \'d\':\n- The minimum distance to change \'d\' to \'a\' is 3.\n- Since 3 > 0, we do not update t.\n\nFinally, we return t, which is "waacd".\n\n# Complexity\n- Time complexity: **O( N )**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: **O( N )**\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n string getSmallestString(string s, int k) {\n int n = s.size(); // Length of the string\n string t = s; // Initialize the resulting string with the original string\n\n // Iterate over each character in the string\n for (int i = 0; i < n; ++i) {\n // Iterate over each lowercase English letter (\'a\' to \'z\')\n for (char ch = \'a\'; ch <= \'z\'; ++ch) {\n // Calculate the minimum distance to change s[i] to ch\n int dist = min(abs(s[i] - ch), min(s[i] + 26 - ch, ch + 26 - s[i]));\n // If the distance is within the allowed value k, update the character in the resulting string\n if (dist <= k) {\n t[i] = ch;\n // Reduce k by the distance changed\n k -= dist;\n // Move to the next character in the original string\n break; \n }\n }\n }\n return t; \n }\n};\n```
| 5
| 0
|
['String', 'Greedy', 'C++']
| 4
|
lexicographically-smallest-string-after-operations-with-constraint
|
Java | C++ | Greedy Approach | Distance of Characters | T(N)= O(N*26)
|
java-c-greedy-approach-distance-of-chara-prip
|
Intuition\nFor each character in string we try all letters from \'a\' to \'z\', selecting the first one as which has less or equal distance to k\n\n# Approach\n
|
niveshpritmani
|
NORMAL
|
2024-04-07T04:40:42.158854+00:00
|
2024-04-07T04:40:42.158875+00:00
| 298
| false
|
# Intuition\nFor each character in string we try all letters from \'a\' to \'z\', selecting the first one as which has less or equal distance to k\n\n# Approach\n### Distance Function (distance(char s1, char s2))\n\nThis function calculates the distance between two characters `s1` and `s2`. It considers the characters as arranged in a circle, where \'a\' and \'z\' are neighbors.\n\nHere\'s how it works:\n\n1. **Absolute Difference:** It calculates the absolute difference between the ASCII codes of the characters using `Math.abs(s1 - s2)`.\n\n2. **Circular Adjustment:** Since the alphabet is circular, it considers the minimum distance. It achieves this by finding the minimum of:\n - The absolute difference (`diff`) calculated in step 1.\n - The difference between 26 (number of letters in the alphabet) and the absolute difference (`26 - diff`).\n\nThis ensures that characters near the beginning and end of the alphabet (like \'a\' and \'z\') have a distance of 1 when considering the circular nature.\n\n**Example:**\n\n- `distance(\'a\', \'z\')`:\n - Absolute difference: `Math.abs(\'a\' - \'z\')` = 25\n - Circular adjustment: `min(25, 26 - 25)` = 1 (distance is 1 considering the circle)\n### getSmallestString(String s, int k) Function\n\nThis function finds the lexicographically smallest string `t` that can be obtained from the input string `s` by changing at most `k` characters. It considers a distance between characters when making these changes.\n\nHere\'s a breakdown of the steps involved:\n\n**1. Conversion to Character Array:**\n - `char[] result = s.toCharArray();`: This line converts the input string `s` into a character array named `result`. This array will hold the modified string.\n\n**2. Iterating Through Characters:**\n - The function uses an outer `for` loop to iterate through each character `i` in the original string `s`.\n\n**3. Finding the Best Replacement Character:**\n - An inner `for` loop iterates through all lowercase letters (`char c = \'a\'; c <= \'z\'; c++`).\n - Inside the inner loop:\n - `distance(s.charAt(i), c)`: This calculates the distance between the current character `s[i]` and the candidate replacement character `c` using a separate `distance` function (assumed to be defined elsewhere).\n - `if (distance(s.charAt(i), c) <= k)`: This checks if changing the current character to `c` is allowed within the `k` limit based on the distance.\n - If the distance is less than or equal to `k`:\n - `result[i] = c;`: The character in the `result` array at position `i` is updated with the new character `c`.\n - `k -= distance(s.charAt(i), c);`: The remaining allowed changes (`k`) are decremented by the distance used for this replacement.\n - `break;`: The inner loop exits as a suitable replacement has been found within the limit.\n\n**4. Returning the Modified String:**\n - `return new String(result);`: This line converts the modified character array `result` back into a String object and returns it.\n\n\n## Example: s = "zbbz", k = 3\n\nLet\'s walk through how the code works for the input string `s = "zbbz"` and `k = 3` allowed changes:\n\n**1. Initialization:**\n\n- The input string `s` is converted to a character array: `result = [\'z\', \'b\', \'b\', \'z\']`.\n- The number of allowed changes `k` is set to 3.\n\n**2. Iterating Through Characters:**\n\n**Iteration 1: i = 0 (Character \'z\')**\n\n- The inner loop iterates through all lowercase letters (`c = \'a\'; c <= \'z\'; c++`).\n- `c = \'a\'`: The distance between \'z\' and \'a\' is 1, which is less than `\'k\'=3`.\n- so `result[i]` is updated to \'a\'.\n- `k` is decremented becomes 2.\n- we exit this loop\n\n\n**Iteration 2: i = 1 (Character \'b\')**\n\n- The inner loop iterates through characters.\n- `distance(\'b\', \'a\')` is 1 (within `k`), so `result[i]` is updated to \'a\'.\n- `k` is decremented becomes `1`.\n- we exit this loop\n\n**Iteration 3: i = 2 (Character \'b\')**\n\n- Similar to iteration 2, `\'b\'` is changed to `\'a\'` (distance 1), and `k` becomes `0`.\n\n**Iteration 4: i = 3 (Character \'z\')**\n\n- no change is made to `\'z\'` as `k` becomes `0`we do not find distance equal to `0`.\n\n**3. Returning the Result:**\n\n- The final modified character array is `[\'a\', \'a\', \'a\', \'z\']`.\n- It\'s converted back to a string: `"aaaz"`.\n\nTherefore, the output for `s = "zbbz", k = 3` is `"aaaz"`.\n## Complexity\n\n### Time Complexity\n\nThe time complexity of the code depends on the nested loops:\n\n* **Outer loop:** Iterates `n` times, once for each character in the input string `s`.\n* **Inner loop:** Iterates through all lowercase letters (26 characters) in the worst case.\n\n## In the worst case, the inner loop runs completely for every character in the outer loop (if all characters need to be replaced). This leads to a total of `n * 26` iterations.\n\nHowever, in some cases, the inner loop might exit early if a suitable replacement is found within the allowed `k` changes. This reduces the total number of iterations.\n\nTherefore, the time complexity is considered **O(n * k)** in the worst case.\n\n### Space Complexity\n\nThe space complexity of the provided code is dominated by the character array `result` used to store the modified string.\n\n* The size of `result` is directly proportional to the input string length `n`.\n* In the worst case, all characters in the string might be changed, so `result` will hold `n` characters.\n\nTherefore, the space complexity is considered **O(n)**.\n\n# Code\n```java []\nclass Solution {\n public int distance(char s1, char s2) {\n int diff = Math.abs(s1 - s2);\n return Math.min(diff, 26 - diff);\n }\n public String getSmallestString(String s, int k) {\n char[] result = s.toCharArray();\n for (int i = 0; i < s.length(); i++) {\n for (char c = \'a\'; c <= \'z\'; c++) {\n if (distance(s.charAt(i), c) <= k) {\n result[i] = c;\n k -= distance(s.charAt(i), c);\n break;\n }\n }\n }\n return new String(result);\n \n }\n}\n```
| 5
| 0
|
['String', 'Greedy', 'C++', 'Java']
| 2
|
lexicographically-smallest-string-after-operations-with-constraint
|
Easy C++ Solution
|
easy-c-solution-by-ishajangir2002-c41b
|
\n# Intuition\nTo find the smallest lexicographically string, we need to start from the beginning of the given string s and convert characters to \'a\' if it re
|
ishajangir2002
|
NORMAL
|
2024-04-07T11:35:18.922577+00:00
|
2024-04-07T11:35:18.922642+00:00
| 42
| false
|
\n# Intuition\nTo find the smallest lexicographically string, we need to start from the beginning of the given string s and convert characters to \'a\' if it reduces the overall lexicographical value. We do this until we exhaust the available operations k.\n\n# Approach\n- We iterate through each character of the string s. For each character, we calculate the distance to \'a\' both forward and backward. \n- - We choose the minimum of these distances as the distance needed to convert the current character to \'a\'. If this distance is less than or equal to the remaining operations k, we update the character to \'a\' and reduce k by the chosen distance. Otherwise, we only perform the operation on this character and break out of the loop.\n\nComplexity\nTime complexity: \n- O(n), where \nn is the length of the string s. We iterate through each character once.\n- Space complexity: \nO(1). We are using only a constant amount of extra space.\n\n# Code\n```\nclass Solution {\npublic:\n string getSmallestString(string s, int k) {\n int n = s.size();\n\n for (int i = 0; i < n; i++) {\n // Calculate the distance to \'a\' from the current character\n int distance_forward = s[i] - \'a\';\n // Calculate the distance to \'a\' from the opposite end\n int distance_backward = (\'z\' - s[i]) + 1;\n // Choose the minimum of the two distances\n int min_distance = min(distance_forward, distance_backward);\n\n // If the minimum distance is less than or equal to remaining k\n if (min_distance <= k) {\n // Reduce k by the chosen distance\n k -= min_distance;\n // Set the current character to \'a\'\n s[i] = \'a\';\n } else {\n // If the minimum distance is greater than remaining k\n // Subtract k from the current character to make it the smallest possible character\n s[i] = s[i] - k;\n // Reset k to 0 as no more changes needed\n k = 0;\n }\n }\n return s;\n }\n};\n```
| 4
| 0
|
['C++']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
✅Easy | Beats 100% | Begineer Friendly | Explained💯
|
easy-beats-100-begineer-friendly-explain-kzxv
|
# Intuition \n\n\n\n\n\n# Complexity\n- Time complexity:O(n)\n\n\n- Space complexity: O(1)\n\n\n# Code\n\npython []\nclass Solution:\n def getSmallestStrin
|
viresh_dev
|
NORMAL
|
2024-04-07T04:27:55.613551+00:00
|
2024-04-07T04:36:52.077649+00:00
| 615
| false
|
<!-- # Intuition -->\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n<!-- # Approach -->\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n\n```python []\nclass Solution:\n def getSmallestString(self, s: str, k: int) -> str:\n res = ""\n for char in s:\n # Calculate the distance to the closest character\n min_d = min(ord(char) - ord(\'a\'), ord(\'z\') - ord(char) + 1)\n # If the total distance exceeds k, prioritize changing characters\n if k >= min_d:\n k -= min_d\n res += \'a\' if min_d <= ord(char) - ord(\'a\') else \'z\'\n else:\n # reduce to minimum possible charecter\n res += chr(ord(char)-k)\n k-=k\n return res\n \n```
| 4
| 0
|
['String', 'Greedy', 'Python3']
| 2
|
lexicographically-smallest-string-after-operations-with-constraint
|
BEAT 100% CPP Code
|
beat-100-cpp-code-by-rtik-eg14
|
Intuition\n1. First take a string of same size of s as "aaaa...n"\n2. Then traverse the string s if s[i]==t[i] continue\n3. Calculate the direct distance and r
|
rtik
|
NORMAL
|
2024-04-09T05:42:41.789305+00:00
|
2024-04-09T05:51:54.420114+00:00
| 205
| false
|
# Intuition\n1. First take a string of same size of s as "aaaa...n"\n2. Then traverse the string s if s[i]==t[i] continue\n3. Calculate the direct distance and reverse distance between "a" or t[i] and s[i] and take minimum of them.\n4. Check if this is smaller than k then we are unable to make "a" so we take character ((s[i]-\'a\'-k))+\'a\'.\n\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\nTime complexity: O(n)\n\n\n Space complexity: O(1) \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n string getSmallestString(string s, int k) {\n int n=s.size();\n // let the smallest string of size n be "aaa....n"\n string t="";\n for(int i=0;i<n;i++){\n t+=\'a\';\n }\n int i=0;\n while(i<n && k>0){\n if(s[i]==t[i]){\n i++;\n continue;\n }\n char ch=s[i];\n char c=t[i];\n int direct_dis=(ch-\'a\')- (c-\'a\');\n int reverse_dis=26-(ch-\'a\')+(c-\'a\');\n int dis=min(direct_dis,reverse_dis);\n // minimum distance is also greater than k than we have to replace the char\n if(k<dis){\n // replacing the char in t[i]\n t[i]=((ch-\'a\')-k)+\'a\';\n // no k left\n k=0;\n }\n else{\n k-=dis;\n }\n i++;\n }\n // for testcase lol we have to again travere the s.\n while(k==0 && i<n ){\n t[i]=s[i];\n i++;\n }\n return t;\n }\n};\n```
| 3
| 0
|
['C++']
| 3
|
lexicographically-smallest-string-after-operations-with-constraint
|
Short 2 Step Greedy approach
|
short-2-step-greedy-approach-by-supermom-y6kt
|
Intuition\n Describe your first thoughts on how to solve this problem. \nGreedy approach will help here as a lexicographically ordered string will ideally start
|
SuperMom
|
NORMAL
|
2024-04-07T21:30:26.211411+00:00
|
2024-04-09T07:04:20.953523+00:00
| 89
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nGreedy approach will help here as a lexicographically ordered string will ideally start with the first character which is a. The key is to find minimum offset distance to character \'a\'.\n\n\n# Approach\n1. since the alphabets are cyclical in order- the character can be closer to a from the first half or second half. Get minimum offset distance through minDiff\n2. A lexicographically ordered string ideally starts with a. take the maximum value of k, if k > minDiff to add \'a\' character to result.\n2. Finally subtract the remaining of whatever k is left. Add the resulting character to the result string\n\n# Complexity\n- Time complexity: O(N)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(N)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getSmallestString(self, s: str, k: int) -> str:\n res = \'\'\n for i in range(len(s)):\n beg = ord(s[i]) - ord(\'a\')\n end = ord(\'z\') - ord(s[i]) + 1\n #find closest distance to \'a\'\n minDiff = min(beg, end)\n #As long as k > 0 add character \'a\' to string else add whatever remaining k is left to bring character closer to a\n if k >= minDiff:\n k -= minDiff\n res += \'a\'\n else:\n offset = ord(s[i]) - k \n res += chr(offset)\n k = 0\n return res\n \n \n \n \n \n \n \n \n \n \n \n \n```
| 3
| 0
|
['Python3']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
✅ Beats 100 % || Time O(n) || Space O(n) || Java - 0 ms || Easy Explained ✅
|
beats-100-time-on-space-on-java-0-ms-eas-w0ic
|
\n# Intuition\nThe problem requires us to create the lexicographically smallest string of length k by using the characters from the given string s. To achieve t
|
0xsonu
|
NORMAL
|
2024-04-07T06:03:18.139459+00:00
|
2024-04-07T06:03:18.139476+00:00
| 117
| false
|
\n# Intuition\nThe problem requires us to create the lexicographically smallest string of length `k` by using the characters from the given string `s`. To achieve this, we need to manipulate the characters in `s` such that the resulting string is the smallest possible.\n\n# Approach\n1. Convert the given string `s` into a character array `t`.\n2. Iterate through each character in the array `t`.\n3. For each character:\n - Calculate the distance to character \'a\' using the `distToA` method. This distance represents the number of steps required to change the character to \'a\' in the alphabet. If the character is \'a\', the distance is 0; otherwise, it is the minimum of the difference between the character and \'a\' and the difference between \'z\' and the character plus 1.\n - If the remaining length `k` is greater than or equal to the current distance, decrement `k` by the current distance and set the character to \'a\'.\n - If `k` is less than the current distance, we need to decrement the character value by `k` steps. If the resulting character is still within the range [\'a\', \'z\'], set the character to the new value. Otherwise, adjust the character to wrap around the alphabet (\'z\' to \'a\') and subtract the remaining steps from \'z\'.\n4. After processing all characters, construct a string from the modified character array and return it as the result.\n\n# Complexity\n- Time complexity: \n - The algorithm iterates through each character in the input string once. Each iteration involves constant-time operations. Thus, the time complexity is O(n), where n is the length of the input string.\n- Space complexity:\n - The algorithm uses extra space to store the character array representation of the input string. Therefore, the space complexity is O(n), where n is the length of the input string.\n\n# Code\n```java\nclass Solution {\n public String getSmallestString(String s, int k) {\n char[] t = s.toCharArray();\n\n for (int i = 0; i < t.length; i++) {\n int currentDist = distToA(t[i]);\n\n if (k >= currentDist) {\n k -= currentDist;\n t[i] = \'a\';\n } else {\n if (k > 0) {\n if (t[i] - k >= \'a\') {\n t[i] = (char) (t[i] - k);\n } else {\n t[i] = (char) (\'z\' - (k - 1));\n }\n k = 0;\n }\n }\n }\n return new String(t);\n }\n\n private int distToA(char c) {\n return Math.min(c - \'a\', 26 - (c - \'a\'));\n }\n}\n```
| 3
| 0
|
['Java']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
✅Very easy & Simple Approach💯||🔥2 Examples✅|| Just rephrase the Problem ||✅Compare distance to 'a'
|
very-easy-simple-approach2-examples-just-oc76
|
Intuition\n Describe your first thoughts on how to solve this problem. \nThe problem at first may look critical. But it is not. We are given an integer \'k\' th
|
priyankarkoley
|
NORMAL
|
2024-04-07T05:25:16.876556+00:00
|
2024-04-07T05:34:26.491812+00:00
| 89
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe problem at first may look critical. But it is not. We are given an integer \'k\' that is the ***"maximum"*** distance between answer and original string \'s\'. You have to return a string that is lexicographically smallest.\n\nIt can also be rephrased to, generating string closest to "aaa..."(length same as \'s\'), with a distance of \'k\' or less.\n\nYou can also think of it as we can transform any character to its immediate neighbour a total of \'k\' or less times to make string \'s\' closest to "aaa..."(length same as \'s\').\n\nThe preference is given to left most char, as it it most significant in determining the lexicographical order.\n\nSo we start operating from left to right. Also dont forget about the cyclic thing. We have a,b,c... after we reach z.\n\n---\n\n# Examples\n\n##### 1. For a string `s= "ybdc"` and `k=7`\n\n- At first we can change `0th char \'y\'` to its next neighbour 2 times to make it \'a\'. We use 2 opeations. And the operations left is (k-2) = (7-2) = 5. (The distance of current string from original string is 2.) Current string is `"abdc"`\n 1. y->z\n 2. z->a\n- Next we change `1st char \'b\'` to its previous neighbour 1 time to make it \'a\'. We use 1 opeation. And the operations left is (k-2-1) = (7-2-1) = 4. (The distance of current string from original string is 3.) Current string is `"aadc"`\n 1. b->a\n\n- Next we change `2nd char \'d\'` to its previous neighbour 3 time to make it \'a\'. We use 3 opeation. And the operations left is (k-2-1-3) = (7-2-1-3) = 1. (The distance of current string from original string is 6.) Current string is `"aaac"`\n 1. d->c\n 2. c->b\n 3. b->a\n- Next we change `3rd char \'c\'` to its previous neighbour 1 time to make it \'b\'. As we are only left with 1 operation. We use 1 opeation. And the operations left is (k-2-1-3-1) = (7-2-1-3-1) = 0. (The distance of current string from original string is 7.) Current string is `"aaab"`\n 1. c->b\n- We have no more oprations left. Or, we have reached the maximum distance. So, we return the answer.\n\n---\n\n##### 2. For a string `s= "ybdc"` and `k=77`\n\n- At first we can change `0th char \'y\'` to its next neighbour 2 times to make it \'a\'. We use 2 opeations. And the operations left is (k-2) = (77-2) = 75. (The distance of current string from original string is 2.) Current string is `"abdc"`\n 1. y->z\n 2. z->a\n- Next we change `1st char \'b\'` to its previous neighbour 1 time to make it \'a\'. We use 1 opeation. And the operations left is (k-2-1) = (77-2-1) = 74. (The distance of current string from original string is 3.) Current string is `"aadc"`\n 1. b->a\n\n- Next we change `2nd char \'d\'` to its previous neighbour 3 time to make it \'a\'. We use 3 opeation. And the operations left is (k-2-1-3) = (77-2-1-3) = 71. (The distance of current string from original string is 6.) Current string is `"aaac"`\n 1. d->c\n 2. c->b\n 3. b->a\n- Next we change `3rd char \'c\'` to its previous neighbour 2 time to make it \'a\'. We use 2 opeation. And the operations left is (k-2-1-3-1) = (77-2-1-3-2) = 69. (The distance of current string from original string is 8.) Current string is `"aaaa"`\n 1. c->b\n 2. b->a\n\n- We have no characters left. This is lexicographically smallest string. So, we return the answer.\n\n\n---\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n- In any iteration, We have to make the ith char closest to a. So, we first calculate to distance of ith char to \'a\' in a cyclic manner. We take the minimum the distance of both by moving forward and by moving backward. \n\n- In any case if \'a\' is not reachable with no of opeations left (`distanceToa>k`). We simply change the character to its previous character k times.\n\n- Otherwise, we make the `s[i]=\'a\'`, use `distanceToa` operations, decreasing the no of operations by distanceToa.\n\n---\n\n# Complexity\n- Time complexity: ***O(n)***\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: ***O(1)***\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n---\n# Code\n```\nclass Solution {\npublic:\n string getSmallestString(string s, int k) {\n for(int i=0; i<s.size(); i++){\n if(k==0)return s;\n int distanceToa = min(s[i]-\'a\', \'z\'+1-s[i]);\n if(distanceToa<=k){\n s[i]=\'a\';\n k-=distanceToa;\n }else{\n s[i]=s[i]-k;\n k=0;\n }\n }\n return s;\n }\n};\n```\n---\n\n## HOPE MY ANSWER HELPS. IF IT HELPED, UPVOTE PLEASE.\n\n\n\n
| 3
| 0
|
['C++']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
Python Easy Greedy Solution!!
|
python-easy-greedy-solution-by-kevinliu0-gh1f
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n\n# Code\n\nclass Solution:\n def getSmallestString(self, s: str, k: int) -> str:\
|
kevinliu0905
|
NORMAL
|
2024-04-07T04:14:56.108639+00:00
|
2024-04-07T04:14:56.108666+00:00
| 254
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n\n# Code\n```\nclass Solution:\n def getSmallestString(self, s: str, k: int) -> str:\n res_list = []\n count = 0\n dic = [\'a\', \'b\', \'c\', \'d\', \'e\', \'f\', \'g\', \'h\', \'i\', \'j\', \'k\', \'l\', \'m\', \'n\', \'o\', \'p\', \'q\', \'r\', \'s\', \'t\', \'u\', \'v\', \'w\', \'x\', \'y\', \'z\']\n\n def findMinDist(c1, c2):\n dis1 = (ord(c1) - ord(c2)) % 26\n dis2 = (ord(c2) - ord(c1)) % 26\n return min(dis1, dis2)\n\n for c in s:\n for dic_c in dic:\n curMinDist = findMinDist(c, dic_c)\n if count + curMinDist <= k:\n count += curMinDist\n res_list.append(dic_c)\n break\n \n return \'\'.join(res_list)\n\n \n \n \n \n \n```
| 3
| 0
|
['Python3']
| 2
|
lexicographically-smallest-string-after-operations-with-constraint
|
100% beats | simple approach
|
100-beats-simple-approach-by-sparker_724-zc5v
|
Approach\nJust check how small the current character can be made.\nIt can be made \'a\' in every step except at the last step where it may or may not be made \'
|
Sparker_7242
|
NORMAL
|
2024-04-07T04:07:20.481979+00:00
|
2024-04-07T04:07:20.482013+00:00
| 24
| false
|
# Approach\nJust check how small the current character can be made.\nIt can be made \'a\' in every step except at the last step where it may or may not be made \'a\' and then you run out of k operations\n\n# Complexity\n- Time complexity: O(n)\n\n# Code\n```\nclass Solution {\npublic:\n string getSmallestString(string s, int k) {\n string ans = s;\n for (int i = 0; i < s.size(); i++){\n if (k == 0) break;\n int z = min(int(s[i]-\'a\'),26-int(s[i]-\'a\'));\n if (k >= z){\n ans[i] = \'a\';\n k -= z;\n } else {\n ans[i] -= k;\n break;\n }\n }\n return ans;\n }\n};\n```
| 3
| 0
|
['C++']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
Short and intuitive greedy method: TC(26n) + SC(1)
|
short-and-intuitive-greedy-method-tc26n-j32it
|
Complexity\n- Time complexity: O(26n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(1)\n Add your space complexity here, e.g. O(n) \n\n#
|
timchen10001
|
NORMAL
|
2024-04-07T04:04:42.018199+00:00
|
2024-04-07T04:30:18.650510+00:00
| 184
| false
|
# Complexity\n- Time complexity: O(26n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n string getSmallestString(string s, int k) {\n int n = s.size();\n for (int i = 0; i < n; i++) {\n char oldCh = s[i];\n s[i] = \'a\';\n while (k - min(26-abs(s[i]-oldCh), abs(s[i]-oldCh)) < 0)\n s[i]++;\n k -= min(26-abs(s[i]-oldCh), abs(s[i]-oldCh));\n }\n return s;\n }\n};\n```
| 3
| 0
|
['Greedy', 'C++']
| 0
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.