question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
lexicographically-smallest-string-after-operations-with-constraint
|
Greedy solution (readable code with explanation)
|
greedy-solution-readable-code-with-expla-krtb
|
Approach\nTo make the lexicographically smallest string, we spend the cost at leftest character.\n\nFor example, if s = \'cb\', k = 1, we must use this cost at
|
a127000555
|
NORMAL
|
2024-04-08T16:42:35.993846+00:00
|
2024-04-08T16:43:33.628481+00:00
| 26
| false
|
# Approach\nTo make the lexicographically smallest string, we spend the cost at leftest character.\n\nFor example, if `s = \'cb\', k = 1`, we must use this cost at the first character, unless it already becomes to `\'a\'`.\n\nThus, we only need to consider two cases:\n* If there\'s enough k, make character become `\'a\'`.\n* If there\'s no enough k, make character minus `k`.\n> You may have question why we minus `k` rather than add `k`? Because if we can achieve to smaller character using this `k`, that means it has enough `k` to make character become `\'a\'`.\n\nHow to calculate the distance between character `c` and `\'a\'`? \n* `c` minus to `\'a\'`: distance is `c - \'a\'`\n* `c` plus to `\'a\'`: distance is `\'a\' + 26 - c = 26 - (c - \'a\')`\n* Choose the smaller one.\n\n# Complexity\n- Time complexity: $O(n)$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(n)$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python\nclass Solution:\n def getSmallestString(self, s: str, k: int) -> str:\n out = []\n for c in s:\n distance = ord(c) - ord(\'a\')\n distance = min(distance, 26 - distance)\n # If there\'s enough k to make c become \'a\'\n if distance <= k:\n out.append(\'a\')\n k -= distance\n else:\n out.append( chr(ord(c) - k) )\n k = 0\n return \'\'.join(out)\n```
| 2
| 0
|
['Python3']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
✅ Java Solution
|
java-solution-by-harsh__005-avq1
|
CODE\nJava []\npublic String getSmallestString(String s, int k) {\n\tStringBuffer res = new StringBuffer("");\n\tchar arr[] = s.toCharArray();\n\tint i=0, n=arr
|
Harsh__005
|
NORMAL
|
2024-04-07T04:01:19.538779+00:00
|
2024-04-07T04:01:19.538803+00:00
| 225
| false
|
## **CODE**\n```Java []\npublic String getSmallestString(String s, int k) {\n\tStringBuffer res = new StringBuffer("");\n\tchar arr[] = s.toCharArray();\n\tint i=0, n=arr.length;\n\n\twhile(k > 0 && i<n){\n\t\tint id = (arr[i++]-\'a\');\n\t\tint min = Math.min(id, 26-id);\n\n\t\tif(min <= k) {\n\t\t\tres.append(\'a\');\n\t\t\tk -= min;\n\t\t} else {\n\t\t\tid -= k;\n\t\t\tres.append((char)(id+\'a\'));\n\t\t\tbreak;\n\t\t}\n\t}\n\n\twhile(i < n){\n\t\tres.append(arr[i++]);\n\t}\n\n\treturn res.toString();\n}\n```
| 2
| 0
|
['Java']
| 1
|
lexicographically-smallest-string-after-operations-with-constraint
|
Best solution | C++ | Smallest string
|
best-solution-c-smallest-string-by-nssva-x0om
|
IntuitionWe need to construct a lexicographically smallest string t such that the cyclic distance between s and t is at most k. This approach ensures that we ob
|
nssvaishnavi
|
NORMAL
|
2025-02-03T13:06:41.010059+00:00
|
2025-02-03T13:06:41.010059+00:00
| 21
| false
|
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
We need to construct a lexicographically smallest string t such that the cyclic distance between s and t is at most k. This approach ensures that we obtain the smallest lexicographical string while keeping the distance constraint satisfied.
# Approach
<!-- Describe your approach to solving the problem. -->
The cyclic distance between two characters s[i] and t[i] is given by:
min(∣s[i]−t[i]∣,26−∣s[i]−t[i]∣)
Since we want t to be lexicographically smallest, we try to change each character in s to 'a' first, as 'a' is the smallest letter.
# Algorithm
Traverse s from left to right.
For each character s[i], check how much it costs to change it to 'a'.
The cost is min(|s[i] - 'a'|, 26 - |s[i] - 'a'|).
If we can afford to change s[i] to 'a' (i.e., cost ≤ k), we do it and subtract the cost from k.
Otherwise, we decrement s[i] lexicographically as much as possible within the remaining k.
Stop when k == 0 or after processing the entire string.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
string getSmallestString(string s, int k) {
int n = s.size();
for (int i = 0; i < n; i++) {
int costToA = min(s[i] - 'a', 26 - (s[i] - 'a'));
if (k >= costToA) {
s[i] = 'a';
k -= costToA;
} else {
s[i] = s[i] - k;
k = 0;
break;
}
}
return s;
}
};
```
| 1
| 0
|
['C++']
| 1
|
lexicographically-smallest-string-after-operations-with-constraint
|
Easy cpp
|
easy-cpp-by-pb_matrix-2eoy
|
\nclass Solution {\npublic:\nstring getSmallestString(string s, int k) {\nint n=s.size();\nfor(int j=0;j<n;j++){\n char p=s[j];\n for(char c=\'a\';c<=\'z\';c++)
|
pb_matrix
|
NORMAL
|
2024-06-10T15:26:07.445035+00:00
|
2024-06-10T15:26:07.445068+00:00
| 1
| false
|
```\nclass Solution {\npublic:\nstring getSmallestString(string s, int k) {\nint n=s.size();\nfor(int j=0;j<n;j++){\n char p=s[j];\n for(char c=\'a\';c<=\'z\';c++){\n int x=s[j]-c;\n int yes=min(x,26-x);\n if(k>=yes) \n {s[j]=min(s[j],c),k-=yes; break;}\n}}\nreturn s; }\n};\n```
| 1
| 0
|
[]
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
Greedyyyy, ⌛: O(N)
|
greedyyyy-on-by-ndr0216-cpwa
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
ndr0216
|
NORMAL
|
2024-05-29T00:58:33.862218+00:00
|
2024-07-20T02:58:57.616822+00:00
| 4
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: $$O(N)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n string getSmallestString(string s, int k) {\n for (int i = 0; i < s.size(); i++) {\n int dist_a = min(s[i] - \'a\', \'z\' + 1 - s[i]); // distance to \'a\'\n if (dist_a <= k) { // can be changed to \'a\'\n s[i] = \'a\';\n k -= dist_a;\n } else {\n s[i] -= k;\n k = 0;\n }\n }\n\n return s;\n }\n};\n```\n\n---\n# If you have any question or advice, welcome to comment below.
| 1
| 0
|
['String', 'Greedy', 'C++']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
Beats 100%🔥|| easy JAVA Solution✅
|
beats-100-easy-java-solution-by-priyansh-gbz2
|
Code\n\nclass Solution {\n public String getSmallestString(String s, int k) {\n char arr[]=s.toCharArray();\n for(int i=0;i<arr.length;i++){\n
|
priyanshu1078
|
NORMAL
|
2024-05-10T18:20:15.017144+00:00
|
2024-05-10T18:20:15.017165+00:00
| 5
| false
|
# Code\n```\nclass Solution {\n public String getSmallestString(String s, int k) {\n char arr[]=s.toCharArray();\n for(int i=0;i<arr.length;i++){\n Pair x=sol(arr[i],k);\n arr[i]=x.ch;\n k-=x.val;\n if(k==0) break;\n }\n return new String(arr);\n }\n public Pair sol(char ch,int k){\n for(char i=\'a\';i<=\'z\';i++){\n int a=Math.abs(ch-i);\n int b=Math.abs(i-ch+26);\n if(a<=k || b<=k){\n return new Pair(Math.min(a,b),i);\n }\n }\n return new Pair(1000000,\'n\');\n }\n}\nclass Pair{\n int val;\n char ch;\n Pair(int val,char ch){\n this.val=val;\n this.ch=ch;\n }\n}\n```
| 1
| 0
|
['Java']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
Cleanest Java Code. Only one if-else. Greedy. Simple Intuition. Please Upvote.
|
cleanest-java-code-only-one-if-else-gree-mr3v
|
Intuition\n Describe your first thoughts on how to solve this problem. \nGreedy is the way to go.\nMain reason for this is that we want the smalles lexicographi
|
kod3r
|
NORMAL
|
2024-05-02T06:22:50.375091+00:00
|
2024-05-02T06:24:06.956619+00:00
| 40
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nGreedy is the way to go.\nMain reason for this is that we want the smalles lexicographical string. Therefore we want to invest as much as we can on the earlier letters. \nAs even bzzzz is smaller than caaaa\n\nTry to make every letter starting from the first in the string to \'a\'. If you can\'t then try to get as close to a.\n\nTo handle the circular nature of the letter, just add a check for which is less. Going to a (0) or going to z+1 (26).\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nChange the string to char array. Then just minimize the chars as the budget allows.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N)\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(N) because String manipulation in Java is jank.\nIf the question provided a char array this could have been done in O(1);\n# Code\n```\nclass Solution {\n public String getSmallestString(String s, int k) {\n char[] chars = s.toCharArray();\n int i = 0;\n while(k>0 && i <s.length()){\n int distance = Math.min(chars[i] - \'a\', \'z\' - chars[i] + 1);\n if(distance > k){\n chars[i] = (char) (chars[i] - k); \n } else {\n chars[i] = \'a\';\n }\n k -= distance;\n i++;\n }\n return new String(chars);\n }\n}\n```
| 1
| 0
|
['Java']
| 1
|
lexicographically-smallest-string-after-operations-with-constraint
|
Simple Greedy Approach with explanation
|
simple-greedy-approach-with-explanation-l1phl
|
\n# Approach\n Describe your approach to solving the problem. \nGreedy\n# Complexity\n- Time complexity:O(n)\n Add your time complexity here, e.g. O(n) \n\n- Sp
|
kmuhammadjon
|
NORMAL
|
2024-04-19T12:12:23.218983+00:00
|
2024-04-19T12:12:23.219005+00:00
| 10
| false
|
\n# Approach\n<!-- Describe your approach to solving the problem. -->\nGreedy\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfunc getSmallestString(s string, k int) string {\n newStringWithKDiff := ""\n for i := 0; i < len(s); i++{\n if s[i] == \'a\'{\n newStringWithKDiff += string(s[i])\n continue\n }\n // first we need know distances between current char and\n // \'a\' why? to make smallest string it should move\n // to \'a\' or to up in aphabetically\n // so if possible replace it with \'a\' not replace it \n // with one that is aphabetically small like \n // \'a\' not possible next best char is \'b\' then \'c\'\n // logic of problem is like that i hope you understood\n // any question feel free to comment\n distanceToZ := 123 - int(s[i])\n distanceToA := int(s[i]) - 97\n if distanceToZ > distanceToA && k >= distanceToA{\n k -= distanceToA\n newStringWithKDiff += "a"\n }else if distanceToZ < distanceToA && k >= distanceToZ{\n k -= distanceToZ\n newStringWithKDiff += "a"\n }else if distanceToZ == distanceToA && k >= distanceToZ{\n k -= distanceToZ\n newStringWithKDiff += "a"\n }else if k > 0{\n newStringWithKDiff += string(int(s[i]) - k)\n k = 0\n }else{\n newStringWithKDiff += string(s[i])\n }\n }\n return newStringWithKDiff\n}\n```
| 1
| 0
|
['String', 'Greedy', 'Go']
| 1
|
lexicographically-smallest-string-after-operations-with-constraint
|
Beats 96% users... #Quality Code
|
beats-96-users-quality-code-by-aim_high_-q4us
|
\n# Code\n\nclass Solution:\n def getSmallestString(self, s: str, k: int) -> str:\n n = len(s)\n t = list(s) # Start with t as a copy of s, we
|
Aim_High_212
|
NORMAL
|
2024-04-11T11:38:31.111762+00:00
|
2024-04-11T11:38:31.111780+00:00
| 12
| false
|
\n# Code\n```\nclass Solution:\n def getSmallestString(self, s: str, k: int) -> str:\n n = len(s)\n t = list(s) # Start with t as a copy of s, we will modify this list in place\n for i in range(n):\n original_char = s[i]\n cost_to_a = min((ord(original_char) - ord(\'a\')) % 26, (ord(\'a\') - ord(original_char)) % 26)\n if cost_to_a <= k:\n t[i] = \'a\'\n k -= cost_to_a\n else:\n t[i] = chr(ord(original_char) - k)\n \n break\n\n return \'\'.join(t)\n```
| 1
| 0
|
['Python', 'Python3']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
C++ || Easy Strings || ✔✔
|
c-easy-strings-by-akanksha984-kuce
|
Complexity\n- Time complexity: O(n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(1)\n Add your space complexity here, e.g. O(n) \n\n# Co
|
akanksha984
|
NORMAL
|
2024-04-09T07:18:52.982744+00:00
|
2024-04-09T07:18:52.982778+00:00
| 11
| false
|
# Complexity\n- Time complexity: $$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n string getSmallestString(string s, int k) {\n for (int i=0; i<s.size(); i++){\n int dis= min(s[i]-\'a\',\'z\'-s[i]+1);\n if (dis<=k){\n s[i]=\'a\';\n k-= dis;\n }else{\n s[i]= min(s[i],char(s[i]-k));\n k=0;\n break;\n }\n }\n return s;\n }\n};\n```
| 1
| 0
|
['String', 'Greedy', 'C++']
| 1
|
lexicographically-smallest-string-after-operations-with-constraint
|
scala
|
scala-by-len_master-brjo
|
scala \n def getSmallestString(s: String, k: Int): String = {\n @scala.annotation.tailrec\n def f(ch: List[Char], remaining: Int, acc: List[Char]): List[
|
len_master
|
NORMAL
|
2024-04-09T05:14:50.934535+00:00
|
2024-04-09T05:14:50.934565+00:00
| 2
| false
|
```scala \n def getSmallestString(s: String, k: Int): String = {\n @scala.annotation.tailrec\n def f(ch: List[Char], remaining: Int, acc: List[Char]): List[Char] = ch match {\n case Nil => acc.reverse\n case head :: tail =>\n val dis = (head - \'a\').min(\'z\' - head + 1)\n if (dis > remaining) ((head - remaining).toChar :: acc).reverse ::: tail\n else f(tail, remaining - dis, \'a\' :: acc)\n }\n\n f(s.toList, k, Nil).mkString\n }\n```
| 1
| 0
|
['Scala']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
*Iterate and consider 3 cases.. Simple Python solution
|
iterate-and-consider-3-cases-simple-pyth-myiv
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
yashaswisingh47
|
NORMAL
|
2024-04-07T13:50:18.176228+00:00
|
2024-04-07T13:50:18.176262+00:00
| 33
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getSmallestString(self, s: str, k: int) -> str:\n \n def a_dist(string):\n if ord(string) - ord(\'a\') <= 13:\n return True\n return False \n\n res = []\n for i in range(len(s)):\n idx = ord(s[i]) - ord(\'a\') + 1 \n print(\'idx: \',idx)\n # can be made \'a\' #case 1 : when char is close to a :: \n if idx - k <= 0 and a_dist(s[i]):\n res.append(\'a\')\n diff = ord(s[i]) - ord(\'a\') \n k -= diff\n # can be made \'a\' #case 2 : when char is close to z :: \n elif idx + k > 26 and not a_dist(s[i]):\n res.append(\'a\')\n diff = ord(\'z\') - ord(s[i]) + 1\n k -= diff\n #when char cannot be made \'a\' .. exhaust k and append rest of the list \n else:\n new_char = chr(ord(s[i]) - k)\n res.append(new_char) \n res.append(s[i+1:])\n break\n # print(res)\n return \'\'.join(res)\n```
| 1
| 0
|
['Python3']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
Simple C++ Solution | Linear Time Complexity with constant space
|
simple-c-solution-linear-time-complexity-7o7v
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
AK200199
|
NORMAL
|
2024-04-07T12:50:52.492298+00:00
|
2024-04-07T12:50:52.492320+00:00
| 8
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n string getSmallestString(string s, int k) {\n int i=0;\n while(k>0&&i<s.length()){\n int t=\'z\'-s[i]+1,p=s[i]-\'a\';\n int take=min(t,p);\n if(take<=k){\n s[i]=\'a\';\n k=k-take;\n }\n else{\n s[i]=s[i]-k;\n k=0;\n }\n i++;\n }\n return s;\n}\n};\n```
| 1
| 0
|
['C++']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
JAVA MOST OPTIMAL SOLUTION || BEATS 100 % Users || Do UpVote
|
java-most-optimal-solution-beats-100-use-zlzw
|
Let\'s first Understand the Problem Statement first : \n\nSince the problem states that find the samllest possible String. \n\n1.Let\'s Understand By an Example
|
Gourav__5442
|
NORMAL
|
2024-04-07T12:38:08.073676+00:00
|
2024-04-07T12:38:08.073705+00:00
| 7
| false
|
# Let\'s first Understand the Problem Statement first : \n\n**Since the problem states that find the samllest possible String.** \n\n**1.Let\'s Understand By an Example what is the smallest String :** \nSuppose we have Two Strings s1 and s2\ns1 = "xawb"\ns2 = "yawb" \n\nsmallest = s1\nHere Both the Strings are similar but s1 has the differentiator character(x) and s2 has(y) and accoring to the alphabets x appears before y hence the s1 string is smaller. \n\n2.In this problem we are given a String and a k Integer which states that : We are at most allowed to flip a character by the most k value\nonce we fliped a character reduce the value of k.\n\n# NOTE: The Distance between the two characters can be in cyclic direction for example the distance between (a , c) = 2 , (a , d) = 3 , (z , a) = 1 because of cycle a will appear after z . (x , a) = 3\n\n\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n**The Intuition is explained in 4 steps : **\n1. My Most priority character will be \'a\' because as it is the most smallest characters\n\n2. If I am standing on a character char(i) then look in both the directions left and right calculate the distance between the char(i) to char \'a\' and choose the minimum distance.\n\n3. If the minimum distance is lesser or Equal to K then make that character as \'a\' and reduce the k value by k - minDistanceToCharacterA\n\n4. If the minimumDistance is > k then we cannot replace the current character to \'a\'. In this case choose the most smallest character which is in range of k for eg: String : "upvote" and k = 2 in this case we cannot change the char(0) to \'a\' hence the smallest character of the u are (a-t) and k = 2 hence u will become as (\'u\' - k) = (\'u\' - 2) == s . Final String = \'spvote\' \n# Approach\n<!-- Describe your approach to solving the problem. -->\nIterate on the String and do all the checks written in Intuition Steps . If didn\'t understand then please read the 4 steps again.\n\n# Complexity\n- Time complexity:\n- O(N) since atmost we will iterate on the entire given String.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n.\n\n- Space complexity:\n- O(1) because we are not using any extra space for solving the answer . Since Function is expected to return a String . O(N) ans String is used to store the final Answer.\n- Overall Space Complexity : O(1);\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```\nclass Solution {\n public String getSmallestString(String s, int k) {\n \n StringBuilder ans = new StringBuilder();\n int n = s.length();\n\n for(int i = 0 ; i < n ; i++){\n //Check smallest Distance to reach \'a\'\n int leftDist = (\'z\' - s.charAt(i)) + 1; //LeftDirection\n int rightDist = (s.charAt(i) - \'a\'); //RightDirection Formula\n\n int finalDist = Math.min(leftDist , rightDist);\n\n //Check whether distance to reach a is <= k \n if(k >= finalDist){ //Possible\n ans.append(\'a\');\n k -= finalDist;\n }else{ //Not Possible to reach \'a\'\n char ch = (char) (s.charAt(i) - k);\n ans.append(ch);\n //add the remaining Substring to answer and break\n if(i+1 < n){\n ans.append(s.substring(i+1));\n }\n break;\n }\n }\n return ans.toString();\n }\n}\n```
| 1
| 0
|
['Java']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
6 Liner Solution || Very Easy || Python3
|
6-liner-solution-very-easy-python3-by-ya-4fee
|
Time Complexity:- O(n)\n\nSpace Complexity:- O(n)\n\nExplanation of my code:\n\n=> Initialize an empty string \'res\' to store the result.\n\n=> Iterate through
|
YangZen09
|
NORMAL
|
2024-04-07T08:16:00.195733+00:00
|
2024-04-07T08:16:00.195767+00:00
| 94
| false
|
**Time Complexity:-** *O(n)*\n\n**Space Complexity:-** *O(n)*\n\n**Explanation of my code:**\n\n**=>** *Initialize an empty string \'res\' to store the result.*\n\n**=>** *Iterate through each character in the input string \'s\'.*\n\n**=>** *For each character, calculate the minimum distance to reach \'a\' or \'z\' from the current character.*\n\n**=>** *Append \'a\' to the result string if the remaining steps are greater than or equal to the minimum distance, else decrement the character value by the remaining steps.*\n\n**=>** *Update the remaining steps based on the minimum distance taken.*\n\n**=>** *Return the resulting smallest string.*\n\n**CODE:-**\n```\nclass Solution:\n def getSmallestString(self, s: str, k: int) -> str:\n res = "" # Initialize an empty string to store the result\n for char in s:\n # Calculate the minimum distance to reach \'a\' or \'z\' from the current character\n min_d = min(ord(char) - ord(\'a\'), ord(\'z\') - ord(char) + 1)\n # Append \'a\' if remaining steps are greater than or equal to the minimum distance, else decrement the character value\n res += \'a\' if k >= min_d else chr(ord(char) - k)\n # Update remaining steps based on the minimum distance taken\n k -= min_d if k >= min_d else k\n return res # Return the smallest string\n```\n\n**If this is helpful please upvote it**
| 1
| 0
|
['String', 'Python3']
| 3
|
lexicographically-smallest-string-after-operations-with-constraint
|
Python Solution
|
python-solution-by-shoo-lin-6s31
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Shoo-lin
|
NORMAL
|
2024-04-07T06:49:22.244799+00:00
|
2024-04-07T06:49:22.244826+00:00
| 11
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\n```\nclass Solution:\n def getSmallestString(self, s: str, k: int) -> str:\n\n ans = ""\n\n for i in range(len(s)):\n\n newOrder = ord(s[i])-96\n \n if k <=0:\n\n ans+=s[i]\n\n elif 27 - newOrder <= k or newOrder-1 <=k:\n\n ans+="a"\n\n k-=min((27-newOrder),newOrder-1)\n\n else:\n\n ans+=chr(96+(newOrder-k))\n \n k=0\n\n return ans\n\n\n\n\n\n\n\n\n\n\n\n\n\n\n \n\n\n \n```
| 1
| 0
|
['Python3']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
easy python solution
|
easy-python-solution-by-prashasst-gh88
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
prashasst
|
NORMAL
|
2024-04-07T06:00:25.384233+00:00
|
2024-04-07T06:00:25.384263+00:00
| 6
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getSmallestString(self, s: str, k: int) -> str:\n ans=""\n for st in s:\n if k<=0 or st=="a":\n ans+=st\n continue\n val=ord(st)-96 #making in 26 indexed \n dis=0\n\n if val<=13: # if before half\n dis=val-1\n if dis<=k: \n ans+="a" # if possible making it a \n else: \n ans+= chr(ord(st)-k) # else reducing it as much possible\n\n else: #second half\n dis=((26-val)+1)%26\n if dis<=k:\n ans+="a" # if possible making it a \n else:\n ans+= chr(ord(st)-k) # else reducing it as much possible\n k-=dis\n return ans\n\n\n\n \n```
| 1
| 0
|
['Python3']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
Easy python
|
easy-python-by-ekambareswar1729-s86w
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
ekambareswar1729
|
NORMAL
|
2024-04-07T05:48:34.955037+00:00
|
2024-04-07T05:48:34.955063+00:00
| 8
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def getSmallestString(self, s: str, k: int) -> str:\n arr = list(s)\n \n for i in range(len(arr)):\n if k==0:\n break \n\n l=ord(s[i]) - ord(\'a\')\n r=26 - (ord(s[i]) - ord(\'a\'))\n \n if k>=min(l,r) :\n if l<r: \n arr[i]=\'a\'\n k-=l\n else:\n arr[i]=\'a\'\n k-=r\n\n elif k>0:\n arr[i] = chr(ord(arr[i]) - k) \n k = 0\n break\n\n return \'\'.join(arr)\n \n```
| 1
| 0
|
['Python3']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
JS - Simple O(n) Solution
|
js-simple-on-solution-by-e4truong-ell9
|
Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(1)\n\n# Code\n\n/**\n * @param {string} s\n * @param {number} k\n * @return {string}\n */\nvar getS
|
e4truong
|
NORMAL
|
2024-04-07T04:50:05.556141+00:00
|
2024-04-07T04:50:05.556159+00:00
| 45
| false
|
# Complexity\n- Time complexity: O(n)\n\n- Space complexity: O(1)\n\n# Code\n```\n/**\n * @param {string} s\n * @param {number} k\n * @return {string}\n */\nvar getSmallestString = function (s, k) {\n const str = s.split("");\n\n for (let i = 0; i < str.length && k >= 0; i++) {\n const distanceFromA = str[i].charCodeAt(0) - \'a\'.charCodeAt(0);\n const cyclicDistanceFromA = Math.min(distanceFromA, 26 - distanceFromA);\n \n // Try to set the current character to \'a\' if possible\n if (cyclicDistanceFromA <= k) {\n str[i] = \'a\';\n k -= cyclicDistanceFromA;\n // Otherwise, move it as close to \'a\' as possible\n } else {\n str[i] = String.fromCharCode(str[i].charCodeAt(0) - k);\n k = 0;\n }\n }\n\n return str.join("");\n};\n```
| 1
| 0
|
['Greedy', 'JavaScript']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
✅ My Well Commented C++ Solution || Beats 100% C++ of users || Easy to Understand
|
my-well-commented-c-solution-beats-100-c-hyrz
|
Intuition\nWhen I first encountered this problem, I thought of weather to go to the right side of the current character or left side. and then to know weather t
|
NachiketGavad
|
NORMAL
|
2024-04-07T04:47:40.473690+00:00
|
2024-04-07T05:07:33.365258+00:00
| 97
| false
|
# Intuition\nWhen I first encountered this problem, I thought of weather to go to the right side of the current character or left side. and then to know weather to perform which operation for each character, based on the low cost to perform that operation on every character.\n\n# Approach \nI iterated through each character of the string from left to right. For each character, I calculated the cost of adding \'a\' (`add`) and the cost of subtracting from the current character (`subtract`). Then, I chose the operation with the lowest cost that didn\'t exceed the remaining cost `k`. I applied the operation if it was necessary. Finally, I returned the modified string.\n\n1. **Iterating through each character**: The algorithm starts by iterating through each character of the input string `s` from left to right. This allows us to process each character individually and make decisions based on its properties.\n\n2. **Calculating costs**: For each character, we calculate two costs:\n - **add**: The cost of shifting the current character to the right in the alphabet to make it lexicographically smaller. This is calculated as the absolute difference between the ASCII value of \'z\' and the ASCII value of the current character plus 1. For example, if the current character is \'c\', then the cost of making it to \'a\' would be 23, because we need to go from \'c\' to \'z\' and then to \'a\'.\n - **subtract**: The cost of shifting the current character to the left in the alphabet to make it lexicographically smaller. This is calculated as the minimum of the absolute difference between the ASCII value of the current character and the ASCII value of \'a\', and the remaining available cost `k`. This ensures that we don\'t exceed the available cost. For example, if the current character is \'c\' and the remaining cost `k` is 10, but it only takes a cost of 2 to go from \'c\' to \'a\', then we would choose 2 as the cost of subtraction.\n\n\n3. **Choosing the lowest cost operation**: Once we have calculated the costs, we choose the operation with the lowest cost that doesn\'t exceed the remaining cost `k`. We prioritize adding \'a\' if it has a lower cost, or subtracting from the current character if it has a lower cost and doesn\'t exceed `k`.\n\n4. **Applying the chosen operation**: After choosing the operation, we apply it if necessary. If we chose to add \'a\', we subtract the corresponding cost from `k` and modify the current character accordingly. If we chose to subtract from the current character, we also modify the character and subtract the corresponding cost from `k`.\n\n5. **Returning the modified string**: Finally, after processing all characters, we return the modified string `s`.\n\nThis approach ensures that we minimize the overall cost while transforming the input string into the smallest lexicographically string under the given constraints.\n\n\n# Complexity \n- Time complexity: $$O(n)$$, where $$n$$ is the length of the input string.\n- Space complexity: $$O(1)$$, as I used only a constant amount of extra space.\n\n# Code\n```\nclass Solution {\npublic:\n string getSmallestString(string s, int k) {\n int n = s.size();\n\n // Start from left and replace characters based on the lowest cost\n for (int i = 0; i < n; ++i) {\n // If the current character is \'a\', no need to change\n if(s[i]==\'a\'){\n continue;\n }\n int add = abs(\'z\' - s[i] + 1); // Cost of addition\n int subtract = min(abs(s[i] - \'a\'),k); // Cost of subtraction\n\n // Choose the lowest cost operation\n if ((add < subtract || add == subtract && add <= k) && add <= k) {\n s[i] = char(s[i]-26+add); // Change the character\n k -= add;\n } \n else if (subtract < add && subtract <= k) {\n s[i] = char(s[i]-subtract); // Change the character\n k -= subtract;\n }\n }\n return s;\n }\n};\n\n```
| 1
| 0
|
['C++']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
[ Swift ] O(n) solution
|
swift-on-solution-by-icedcappuccino-nde0
|
Intuition\nLexicographical order of s string is determined by the letters from left to right.\n\nTherefore, we should prioritize making each letter in the strin
|
icedcappuccino
|
NORMAL
|
2024-04-07T04:46:10.960467+00:00
|
2024-04-07T04:50:09.551855+00:00
| 11
| false
|
# Intuition\nLexicographical order of s string is determined by the letters from left to right.\n\nTherefore, we should prioritize making each letter in the string as lexographically small as possible, starting from the left.\n\n# Complexity\n- Time complexity: $$O(n)$$\n- Space complexity: $$O(1)$$, excluding the space used for the answer\n\n# Code\n```\nclass Solution {\n func getSmallestString(_ s: String, _ k: Int) -> String {\n guard k > 0 else {\n return s\n }\n var ans: String = ""\n var remK: Int = k\n for c in s {\n if remK > 0 {\n let newC = lowestCharWithinK(c, remK)\n remK -= distanceBetween(newC, c)\n ans.append(newC)\n } else {\n ans.append(c)\n }\n }\n return ans\n }\n \n func charToInt(_ c: Character) -> Int {\n return Int(exactly: c.asciiValue!)! - 97\n }\n \n func intToChar(_ n: Int) -> Character {\n return Character(UnicodeScalar(n + 97)!) \n }\n \n // Calculate cyclic distance between 2 chars\n func distanceBetween(_ a: Character, _ b: Character) -> Int {\n if a == b {\n return 0\n } else {\n var diff: Int = abs(charToInt(a) - charToInt(b))\n return min(diff, 26 - diff)\n }\n }\n \n // Find the lexographically smallest char within k distance of c\n // Either "a" or k letters before c\n func lowestCharWithinK(_ c: Character, _ k: Int) -> Character {\n let c: Int = charToInt(c)\n if c - k > 0 && c + k < 26 {\n return intToChar(c - k)\n }\n return intToChar(0)\n }\n}\n```
| 1
| 0
|
['Greedy', 'Swift']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
🔥Beats 100% - O(n) - Easiest Approach | Clean Code | C++ |
|
beats-100-on-easiest-approach-clean-code-d27e
|
Code\n\nclass Solution {\npublic:\n string getSmallestString(string s, int k) {\n for (int i = 0; i < s.size(); i++) \n {\n \n
|
Antim_Sankalp
|
NORMAL
|
2024-04-07T04:20:08.786939+00:00
|
2024-04-07T04:20:08.786958+00:00
| 58
| false
|
# Code\n```\nclass Solution {\npublic:\n string getSmallestString(string s, int k) {\n for (int i = 0; i < s.size(); i++) \n {\n \n if (s[i] == \'a\')\n continue;\n\n int distanceToA = s[i] - \'a\';\n int cyclicDistanceToA = min(distanceToA, 26 - distanceToA);\n\n if (k >= cyclicDistanceToA) \n {\n s[i] = \'a\';\n k -= cyclicDistanceToA;\n } \n else \n {\n s[i] -= k;\n k = 0;\n }\n \n if (k == 0)\n break;\n }\n \n return s;\n }\n};\n\n```
| 1
| 0
|
['C++']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
Easy To Understand
|
easy-to-understand-by-ad18-06rm
|
Approach\n- Create a string of size N contanining only \'a\', Because we need Lexicographical String.\n- calculate the cyclic distance, check :- \n1. If less th
|
AD18
|
NORMAL
|
2024-04-07T04:11:16.744751+00:00
|
2024-04-07T04:11:16.744769+00:00
| 23
| false
|
# Approach\n- Create a string of size N contanining only \'a\', Because we need Lexicographical String.\n- calculate the cyclic distance, check :- \n1. If less than k, may that character remain same (i.e,\'a\').\n2. else if(k>0) then choose the character, which has distance equal to k.\n3. else make remaining characters as answer, Because we cannot change those character.\n\n# Complexity\n- Time complexity:\n $$O(n)$$\n\n- Space complexity:\n $$O(1)$$\n\n# Code\n```\nclass Solution {\npublic:\n int dist(char a,char b)\n {\n int d = abs(b-a);\n return min(d,26-d);\n \n }\n char sm(char g,int k)\n {\n return ((g-\'a\'-k+26)%26 + \'a\');\n }\n string getSmallestString(string s, int k) {\n int n = s.length();\n string ans = string(n,\'a\');\n \n for(int i= 0;i < n ;i++)\n if(dist(s[i],ans[i]) <= k)\n k-=dist(s[i],ans[i]);\n else if(k>0)\n {\n ans[i] = sm(s[i],k);\n k = 0;\n }\n else\n ans[i] = s[i];\n \n\n \n return ans;\n }\n};\n```
| 1
| 0
|
['C++']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
Cpp
|
cpp-by-laxsingh9659-in09
|
Complexity\n- Time complexity: O(n*26)\n Add your time complexity here, e.g. O(n) \n\n\n# Code\n\nclass Solution {\npublic:\n string getSmallestString(string
|
LaxmanSinghBisht
|
NORMAL
|
2024-04-07T04:10:32.095584+00:00
|
2024-04-07T04:11:20.706772+00:00
| 30
| false
|
# Complexity\n- Time complexity: O(n*26)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n# Code\n```\nclass Solution {\npublic:\n string getSmallestString(string s, int ki) {\n string ans="";\n for(int i=0;i<s.length();i++){\n bool flag=true;\n for(int k=0;k<26;k++){\n int left=(26-(s[i]-\'a\')+k);\n int right=(s[i]-\'a\')-k; \n if(left<=right && ki>=left){\n ki-=left;\n ans+=\'a\'+k;\n flag=false;\n break;\n }\n else if(left>right && ki>=right ){ \n ki-=right;\n ans+=\'a\'+k;\n flag=false;\n break;\n }\n\n }\n if(flag==true){\n ans+=s[i];\n }\n } \n \n return ans;\n }\n};\n```
| 1
| 0
|
['C++']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
O(n) Time O(1) Space, Simplest
|
on-time-o1-space-simplest-by-ayunick-k6xr
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
ayunick
|
NORMAL
|
2024-04-07T04:07:42.724389+00:00
|
2024-04-07T04:08:52.547809+00:00
| 34
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\n#include <bits/stdc++.h>\nusing namespace std;\n\nclass Solution\n{\npublic:\n string getSmallestString(string s, int k)\n {\n int n = s.size();\n for (int i = 0; i < n; i++)\n {\n int minDist = min(s[i] - \'a\', \'z\' - s[i] + 1); \n if (minDist <= k)\n {\n k -= minDist; \n s[i] = \'a\'; \n }\n else\n {\n s[i] = char(s[i] - k);\n k = 0; \n }\n }\n return s;\n }\n};\n\n```
| 1
| 0
|
['Greedy', 'C++']
| 1
|
lexicographically-smallest-string-after-operations-with-constraint
|
Straightforward simple one pass Java solution | O(n)
|
straightforward-simple-one-pass-java-sol-pphc
|
Intuition\nOur goal is to 1st make each character \'a\', else decrement to whatever is the least possible character.\n\n Describe your first thoughts on how to
|
shashankbhat
|
NORMAL
|
2024-04-07T04:06:21.294039+00:00
|
2024-04-07T04:06:21.294070+00:00
| 50
| false
|
# Intuition\nOur goal is to 1st make each character \'a\', else decrement to whatever is the least possible character.\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\nWe have 2 conditions to check:\n1. If incrementing characters upto k times can get us \'a\'.\n2. If decrementing characters upto k times can get us \'a\'.\n\nIf <b>1st</b> conditions is satisfied then we can be sure that current character can be replaced by \'a\'. The only condition to check would be if decrementing leads to lesser operations.\n\nIf <b>2nd</b> condition is true, then decrement k by the difference of current character and \'a\'. <br> If none of the conditions is true, just decrement the character by k.\n\nEach iteration, we need to reduce the value of k by appropriate difference.\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public String getSmallestString(String s, int k) {\n char[] arr = s.toCharArray();\n \n for(int i=0; i<s.length() && k > 0; i++) {\n if(arr[i] == \'a\')\n continue;\n int curr = arr[i] - \'a\';\n \n boolean canBeA = curr + k >= 26;\n if(canBeA) {\n arr[i] = \'a\';\n int leftDist = Math.min(curr, k);\n int rightDist = 26 - curr;\n \n int minDist = Math.min(leftDist, rightDist);\n k -= minDist;\n } else {\n if(curr <= k) {\n arr[i] = \'a\';\n k -= curr;\n } else {\n arr[i] = (char)(curr - k + \'a\');\n k = 0;\n }\n }\n }\n \n return new String(arr);\n }\n}\n```
| 1
| 0
|
['String', 'Java']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
Java/Python Clean Solution
|
javapython-clean-solution-by-shree_govin-pirj
|
Complexity\n- Time complexity:O(n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity:O(n)\n Add your space complexity here, e.g. O(n) \n\n# Code
|
Shree_Govind_Jee
|
NORMAL
|
2024-04-07T04:04:02.966372+00:00
|
2024-04-07T04:04:02.966395+00:00
| 133
| false
|
# Complexity\n- Time complexity:$$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n**Java**\n```\nclass Solution {\n \n private int helper(char ch){\n return Math.min(ch-\'a\', 26-(ch-\'a\'));\n }\n \n public String getSmallestString(String s, int k) {\n char[] ch = s.toCharArray();\n \n for(int i=0; i<ch.length; i++){\n int curr = helper(ch[i]);\n \n if(k >= curr){\n k-=curr;\n ch[i] = \'a\';\n } else{\n if(k>0){\n if(ch[i]-k >= \'a\'){\n ch[i] = (char)(ch[i]-k);\n } else{\n ch[i] = (char)(\'z\'-(k-1));\n }\n k=0;\n }\n break;\n }\n }\n return new String(ch);\n }\n}\n```\n**Python**\n```\nclass Solution:\n def getSmallestString(self, s: str, k: int) -> str:\n t = list(s)\n def dist_to_a(c):\n return min(ord(c)-ord(\'a\'), 26-(ord(c)-ord(\'a\')))\n \n \n for i in range(len(t)):\n curr_dist = dist_to_a(t[i])\n \n if k>= curr_dist:\n k -= curr_dist\n t[i] = \'a\'\n else:\n if k>0:\n if ord(t[i])-k>=ord(\'a\'):\n t[i] = chr(ord(t[i])-k)\n else:\n t[i] = chr(ord(\'z\')-(k-1))\n k=0\n break\n return \'\'.join(t)\n```
| 1
| 0
|
['Array', 'String', 'String Matching', 'Java', 'Python3']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
✅C++ Accepted | Greedy | O(26*n)⛳
|
c-accepted-greedy-o26n-by-manii15-ntpt
|
\n# Code\n\nclass Solution {\npublic:\n string getSmallestString(string s, int k) {\n string res = "";\n \n map<char,pair<int,int>> mp;\
|
manii15
|
NORMAL
|
2024-04-07T04:03:54.883998+00:00
|
2024-04-07T04:03:54.884020+00:00
| 13
| false
|
\n# Code\n```\nclass Solution {\npublic:\n string getSmallestString(string s, int k) {\n string res = "";\n \n map<char,pair<int,int>> mp;\n for(int i=1;i<=26;i++){\n mp[\'a\'+i-1] = {i,i+26};\n }\n \n for(int i=0;i<s.size();i++){\n for(char c = \'a\'; c<=\'z\' ; c++){\n pair<int,int> p1 = mp[c];\n pair<int,int> p2 = mp[s[i]];\n int mini = 1e9;\n mini = min(mini,abs(p1.first-p2.first));\n mini = min(mini,abs(p1.second-p2.first));\n mini = min(mini,abs(p1.first-p2.second));\n mini = min(mini,abs(p1.second-p2.second));\n if( mini <= k){\n res += c;\n k -= mini;\n break;\n }\n } \n }\n return res;\n }\n};\n```
| 1
| 0
|
['C++']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
My Contest Solution
|
my-contest-solution-by-spravinkumar9952-07xc
|
\n# Code\n\nclass Solution {\npublic:\n \n int dist(char a, char b){\n int may1 = abs(b-a);\n int may2 = 26 - may1;\n return min(may1
|
spravinkumar9952
|
NORMAL
|
2024-04-07T04:03:48.755877+00:00
|
2024-04-07T04:03:48.755897+00:00
| 40
| false
|
\n# Code\n```\nclass Solution {\npublic:\n \n int dist(char a, char b){\n int may1 = abs(b-a);\n int may2 = 26 - may1;\n return min(may1, may2);\n }\n \n \n string getSmallestString(string s, int k) {\n \n for(char &c : s){\n int d = dist(c, \'a\');\n if(d <= k){\n c = \'a\';\n k -= d;\n }else{\n for(char i = \'a\'; i <= \'z\'; i++){\n if(dist(c, i) <= k){\n k -= dist(c, i);\n c = i;\n return s;\n }\n }\n }\n }\n \n return s;\n }\n};\n```
| 1
| 0
|
['C++']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
Easy solution in C++
|
easy-solution-in-c-by-bug-setter-cy8s
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
bug-setter
|
NORMAL
|
2024-04-07T04:02:57.184169+00:00
|
2024-04-07T04:02:57.184193+00:00
| 12
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\nint getMinDiff(char one, char two)\n{\n int diff1 = abs(two - one);\n int diff2 = abs((\'z\' - two) + (one - \'a\') + 1);\n int diff3 = abs(one - two);\n int diff4 = abs((\'z\' - one) + (two - \'a\') + 1);\n int ans = min({diff1, diff2, diff3, diff4});\n return ans;\n}\n\nchar getMinChar(char ch, int k)\n{\n char ans1 = \'a\';\n char ans2 = \'a\';\n for (int i = 0; i < 26; i++)\n {\n char one = \'a\' + i;\n if (getMinDiff(ch, one) == k)\n {\n ans1 = one;\n break;\n }\n }\n for (int i = 26; i >= 0; i--)\n {\n char one = \'a\' + i;\n if (getMinDiff(ch, one) == k)\n {\n ans2 = one;\n break;\n }\n }\n char ans = min(ans1, ans2);\n return ans;\n}\n\nstring getSmallestString(string s, int k)\n{\n for (int i = 0; i < s.size() && k > 0; i++)\n {\n int diff = getMinDiff(s[i], \'a\');\n if (diff <= k)\n {\n k -= diff;\n s[i] = \'a\';\n }\n else\n {\n char ch = getMinChar(s[i], k);\n s[i] = ch;\n k = 0;\n break;\n }\n }\n\n return s;\n}\n};\n```
| 1
| 0
|
['C++']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
Simple Recursion 🔥🔥
|
simple-recursion-by-vritant-goyal-np9d
|
Code\n\nclass Solution {\n public int findans(char first,char last){\n int diff1 = first-last;\n int diff2=last-first;\n if (diff1 < 0)d
|
vritant-goyal
|
NORMAL
|
2024-04-07T04:02:17.705529+00:00
|
2024-04-07T04:05:57.029452+00:00
| 13
| false
|
# Code\n```\nclass Solution {\n public int findans(char first,char last){\n int diff1 = first-last;\n int diff2=last-first;\n if (diff1 < 0)diff1 += 26;\n if(diff2<0)diff2+=26;\n return Math.min(diff1,diff2);\n }\n public String helper(String s,int k,int ind){\n if(ind==s.length())return "";\n if(s.charAt(ind)==\'a\')return \'a\'+helper(s,k,ind+1);\n for(char i=\'a\';i<=\'z\';i++){\n char first=i;\n char last =s.charAt(ind);\n int diff = findans(first,last);\n if(k-diff<0)continue;\n return i+helper(s,k-diff,ind+1);\n }\n return "";\n }\n public String getSmallestString(String s, int k) {\n if(k==0)return s;\n return helper(s,k,0);\n }\n}\n```
| 1
| 0
|
['Java']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
3106. Lexicographically Smallest String After Operations With Constraint | Adhoc | Strings
|
3106-lexicographically-smallest-string-a-myk8
|
🧠 # IntuitionOkay, so you’re handed a string s, and you’re allowed to reduce the characters in it to make it lexicographically smaller. But—there’s a catch—you
|
Shingini
|
NORMAL
|
2025-04-11T10:41:05.766717+00:00
|
2025-04-11T10:41:05.766717+00:00
| 1
| false
|
### 🧠 # Intuition
Okay, so you’re handed a string `s`, and you’re allowed to **reduce the characters** in it to make it lexicographically smaller. But—there’s a catch—you can only **spend `k` units total**.
Each character can only be reduced *towards* `'a'` by using your `k` points. For example:
- `'d' -> 'a'` costs 3
- `'c' -> 'a'` costs 2
- `'b' -> 'a'` costs 1
Your goal is to make the string as small (lexicographically) as possible by using those k points wisely. Like playing a game where you downgrade letters, but you don’t want to overspend.
---
### ⚙️ # Approach
Let’s think of it step-by-step, like we’re solving a puzzle:
1. **Loop through each character** of the string.
2. For each character, ask yourself:
> “How much would it cost to turn this guy into an `'a'`?”
There are two options:
- Go **forward** from `s[i]` to `'z'` and then wrap around to `'a'`
- OR just go **backward** directly to `'a'`
But here’s the twist in the logic:
Since we’re only allowed to **decrease** letters (not cycle), we don’t need to think about wrapping around. So the actual cost is:
```cpp
min('z' - s[i] + 1, s[i] - 'a')
```
Actually... wait — this line looks like it allows **wrapping around**, which isn’t required in this problem unless explicitly stated. Usually, it’s just:
```cpp
cost = s[i] - 'a';
```
Because we can only move **towards `'a'`**, not past it.
Assuming that’s clarified...
3. If `cost <= k`, spend it and change the character to `'a'`.
4. If `cost > k`, we can’t afford a full downgrade. So we just reduce as much as we can by subtracting `k` from the character and setting `k = 0`.
---
### 📊 # Complexity
- **Time Complexity:**
We’re visiting each character exactly once and doing constant-time operations — so:
$$O(n)$$ where *n* is the length of the string.
- **Space Complexity:**
We're building a new string, same length as input →
$$O(n)$$ space for the answer.
---
### 💻 # Code Cleanup & Comments
Let’s rewrite it with super-clear comments for logic clarity:
```cpp
class Solution {
public:
string getSmallestString(string s, int k) {
string ans = "";
for (int i = 0; i < s.size(); i++) {
// How far is this char from 'a'?
int cost = s[i] - 'a';
// If we can afford to make it 'a', do it
if (cost <= k) {
k -= cost;
ans += 'a';
} else {
// Reduce it as much as possible
ans += s[i] - k;
k = 0; // all used up
}
}
return ans;
}
};
```
---
### 🧩 Deep Logic Vibes
This is basically a **greedy approach**—you’re trying to make **every character as small as possible**, starting from the front. Why? Because the front characters matter *more* in lexicographical order.
| 0
| 0
|
['C++']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
C++ greedy string
|
c-greedy-string-by-czxoxo-95c1
|
Make this faster by doing it in place. Greedily increment with a budget (in this case the "distance").Code
|
czxoxo
|
NORMAL
|
2025-03-27T20:06:10.309976+00:00
|
2025-03-27T20:06:10.309976+00:00
| 2
| false
|
Make this faster by doing it in place. Greedily increment with a budget (in this case the "distance").
# Code
```cpp []
class Solution {
public:
string getSmallestString(string s, int k) {
// this means, throughout this string we need to find the letter that can substitute the letter in the original string, and still keep the distance below k. greedy?
for (int i = 0; i < s.size() && k > 0; i += 1) {
// greedily try to change this letter to "a" via moving forward or backwards
int min_moves_to_a = min('z' - s[i] + 1, s[i] - 'a');
if (min_moves_to_a <= k) {
s[i] = 'a';
k -= min_moves_to_a;
}
// not enough to, just sink this letter straight down
else {
s[i] -= k;
return s;
}
}
return s;
}
};
```
| 0
| 0
|
['C++']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
Python3 - simple O(n) solution
|
python3-simple-on-solution-by-saitama1v1-e7xl
|
Complexity
Time complexity:
O(n)
Space complexity:
O(n)
Code
|
saitama1v1
|
NORMAL
|
2025-02-16T16:11:47.255606+00:00
|
2025-02-16T16:16:12.255388+00:00
| 4
| false
|
# Complexity
- Time complexity:
O(n)
- Space complexity:
O(n)
# Code
```python3 []
class Solution:
def getSmallestString(self, s: str, k: int) -> str:
if k == 0:
return s
a = "abcdefghijklmnopqrstuvwxyz"
res = ""
for l in s:
if k <= 0 or l == 'a':
res += l
continue
moves_back = ord(l) - ord('a')
moves_forward = ord('z') - ord(l) + 1
moves = min(moves_back, moves_forward)
if k >= moves:
res += 'a'
else:
res += a[moves_back - k]
k -= moves
return res
```
| 0
| 0
|
['Python3']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
Easy Solution Using Greedy.
|
easy-solution-using-greedy-by-akshatuke-0ct2
|
Code
|
AkshatUke
|
NORMAL
|
2025-02-08T18:15:14.739177+00:00
|
2025-02-08T18:15:14.739177+00:00
| 3
| false
|
# Code
```java []
class Solution {
public String getSmallestString(String s, int k) {
String ans = "";
int i = 0;
for(i = 0;i < s.length();i++) {
int x = s.charAt(i)-'a';
if(26 - x < x) {
x = 26-x;
}
if(k >= x) {
ans += 'a';
k -= x;
}
else {
break;
}
}
if(i < s.length() && k > 0) {
int x = s.charAt(i)-'a';
x = x - k;
x = Math.min(x, (x+k)%26);
ans += (char)(x+'a');
}
ans += s.substring(ans.length());
return ans;
}
}
```
| 0
| 0
|
['String', 'Greedy', 'Java']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
(Beats 100% python) Why do you ask me to do unnecessary things?
|
why-do-you-ask-me-to-do-unnecessary-thin-m15o
|
IntuitionDefinitely a medium problem. Had to rack my brain for how to represent the cyclic distance efficiently, without using something like a circular buffer
|
Alex_Tilson
|
NORMAL
|
2025-02-04T01:28:15.543856+00:00
|
2025-02-04T01:32:34.248540+00:00
| 2
| false
|
# Intuition
Definitely a medium problem. Had to rack my brain for how to represent the cyclic distance efficiently, without using something like a circular buffer of length 26.
Most importantly, there is always a '$$center$$' character that actually changes to anything other than an 'a'. If I could figure out what and where this character went, I thought could pay off in elegance and compute speed.
# Approach
Again, I was looking for elegance, not speed, and spend more time to drive down complexity on this problem.
And this approach paid off, as this apparently is the best performing solution according to the meter at the top of the page? ("beats 100%", I presume thats what this means).
That being said, the most interesting part about this problem was the cyclic distance function it asks you to make.
I ended up making a really elegant pair of functions to solve this, but it ended up being almost completely irellevant to the actual problem's solution through the approach I used. Regardless, I've included these in this post.
The solution simply requires you to loop through the string of characters, and only continue while 'k' is high enough to pay the distance cost. You can assume that for every iteration, there should be an 'a' at the beginning the the return string.
Most difficult was figuring out the precise logic for the 'middle' character. But its as simple as subtracting the remaining 'k'.
The edge cases were annoying too, but these were easily resolved using the "for... else" and returning all "a"'s under certain conditions.
# Complexity
- Time complexity: $$O(N)$$
- Space complexity: $$O(N)$$ (? unless you count the output string)
# Code
```python []
def chdist((c1,c2)):
distance = ord(c1) - ord(c2)
if distance > 13:
distance = 26-distance
return distance
def distance(s1, s2):
return map(chdist, zip(s1,s2))
class Solution(object):
def getSmallestString(self, s, k):
i = 0
dist = 0
sign = None
for i in range(len(s)):
dist = ord(s[i]) - 97
if dist > 13:
dist = 26 - dist
if k - dist <= 0:
break
else:
k -= dist
else:
return "a" * len(s)
if k >= dist:
char = "a"
else:
char = chr(ord(s[i]) - k)
return ("a" * i) + char + s[i+1:]
```
| 0
| 0
|
['Python']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
Easy Solution
|
easy-solution-by-muskan_kutiyal-oxdj
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
Muskan_Kutiyal
|
NORMAL
|
2025-02-03T13:14:24.351706+00:00
|
2025-02-03T13:14:24.351706+00:00
| 2
| false
|
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```javascript []
/**
* @param {string} s
* @param {number} k
* @return {string}
*/
var getSmallestString = function(s, k) {
let res = "";
let ach = "a".charCodeAt(0);
let zch = "z".charCodeAt(0);
for (let i = 0; i < s.length; ++i) {
let ch = s.charCodeAt(i);
if (ch == ach || k <= 0) {
res += s[i];
continue;
}
const d = Math.min(Math.abs(ch-ach), zch + 1 - ch);
if (d <= k) {
k -= d;
res += "a";
} else {
res += String.fromCharCode(ch - k);
k = 0;
}
}
return res;
};
```
| 0
| 0
|
['JavaScript']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
StringBuilder to track return string, loop chars to check if it can be changed lower
|
stringbuilder-to-track-return-string-loo-jw4i
|
IntuitionApproachComplexity
Time complexity:
O(N)
Space complexity:
O(N)Code
|
linda2024
|
NORMAL
|
2025-01-29T22:52:01.502610+00:00
|
2025-01-29T22:52:01.502610+00:00
| 5
| false
|
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(N)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(N)
# Code
```csharp []
public class Solution {
public string GetSmallestString(string s, int k) {
int len = s.Length;
StringBuilder sb = new StringBuilder(s);
int start = 0;
while(start < len && k > 0)
{
char c = s[start];
// Console.WriteLine($"before cal k is {k}");
if(c != 'a')
{
int idx = c - 'a';
int minDiff = Math.Min(idx, 26-idx);
// Console.WriteLine($"k: {k}, minDiff: {minDiff}");
if(k >= minDiff)
{
sb[start] = 'a';
k -= minDiff;
}
else
{
sb[start] = ((char)((idx-k) + 'a'));
k = 0;
}
}
start++;
// Console.WriteLine($"after cal k is {k}");
}
return sb.ToString();
}
}
```
| 0
| 0
|
['C#']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
[JavaScript] Easy solution
|
javascript-easy-solution-by-liew-li-mgb4
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
liew-li
|
NORMAL
|
2025-01-28T04:28:39.067075+00:00
|
2025-01-28T04:28:39.067075+00:00
| 2
| false
|
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```javascript []
/**
* @param {string} s
* @param {number} k
* @return {string}
*/
var getSmallestString = function(s, k) {
let res = "";
let ach = "a".charCodeAt(0);
let zch = "z".charCodeAt(0);
for (let i = 0; i < s.length; ++i) {
let ch = s.charCodeAt(i);
if (ch == ach || k <= 0) {
res += s[i];
continue;
}
const d = Math.min(Math.abs(ch-ach), zch + 1 - ch);
if (d <= k) {
k -= d;
res += "a";
} else {
res += String.fromCharCode(ch - k);
k = 0;
}
}
return res;
};
```
| 0
| 0
|
['JavaScript']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
3106. Lexicographically Smallest String After Operations With Constraint
|
3106-lexicographically-smallest-string-a-jfgd
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
G8xd0QPqTy
|
NORMAL
|
2025-01-22T08:01:38.107673+00:00
|
2025-01-22T08:01:38.107673+00:00
| 1
| false
|
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```dart []
class Solution {
String getSmallestString(String s, int k) {
String finalResult = '';
for (int i = 0; i < s.length; i++) {
int value = s.codeUnitAt(i) - 'a'.codeUnitAt(0);
int minChange = value < (26 - value) ? value : (26 - value);
if (minChange <= k) {
k -= minChange;
finalResult += 'a';
} else {
finalResult += String.fromCharCode(value + 'a'.codeUnitAt(0) - k);
break;
}
}
return finalResult + s.substring(finalResult.length);
}
}
```
| 0
| 0
|
['Dart']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
Python O(n) Solution with Code Comments
|
python-on-solution-with-code-comments-by-ki9q
|
Complexity
Time complexity: O(n)
Space complexity: O(n) - returning string.
Code
|
William_Pattison
|
NORMAL
|
2025-01-11T19:56:30.254844+00:00
|
2025-01-11T19:56:30.254844+00:00
| 3
| false
|
# Complexity
- Time complexity: O(n)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(n) - returning string.
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def getSmallestString(self, s: str, k: int) -> str:
answer = ""
for i in range(len(s)):
if s[i] == 'a' or k == 0:
answer += s[i]
else:
# distance from 'a' to the right
r_dist = ( (26 + ord('a')) - ord(s[i]))
# initialize to 'z' so that we don't use it
right_char = 'z'
# closest achievable distance from s[i] such that char is minimized from left
l = min(ord(s[i]) - ord('a'), k)
# If we can reach 'a' by wrapping around, set right char to 'a'
if r_dist <= k:
right_char = 'a'
# smallest lexigraphic string from the left side.
left_char = chr( ord(s[i]) - l)
# Always take the smaller distance to optimal char if they're equal
if right_char == left_char:
answer += left_char
k -= min(r_dist, l)
# Otherwise, take the optimal char and subtract, since we want smallest string.
elif right_char < left_char:
answer += right_char
k -= r_dist
else:
answer += left_char
k -= l
return answer
```
| 0
| 0
|
['Python3']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
SIMPLE ONE PASS SOLUTION
|
simple-one-pass-solution-by-mohit_kukrej-keo1
|
Complexity
Time complexity: O(n)
Code
|
Mohit_kukreja
|
NORMAL
|
2025-01-08T06:37:13.415335+00:00
|
2025-01-08T06:37:13.415335+00:00
| 4
| false
|
# Complexity
- Time complexity: O(n)
# Code
```cpp []
class Solution {
public:
string getSmallestString(string s, int k) {
int n = s.size();
for(auto &i: s){
int back = i - 'a';
int front = ('a' - i + 26) % 26;
if(front <= back && front <= k){
k -= front;
i = 'a';
}
else{
int maxBack = min(back, k);
i = (i - 'a' - maxBack) + 'a';
k -= maxBack;
}
}
return s;
}
};
```
| 0
| 0
|
['C++']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
[Java] ✅ 1MS ✅ 100% ✅ FASTEST ✅ BEST ✅ CLEAN CODE
|
java-1ms-100-fastest-best-clean-code-by-ud0fw
|
Approach\n1. The smallest lexic string starts with lowest chars (a) first\n2. Apply a greedy algorithm, trying to lower the first chars while k allows it.\n3. T
|
StefanelStan
|
NORMAL
|
2024-12-01T00:44:43.211777+00:00
|
2024-12-01T00:44:43.211804+00:00
| 2
| false
|
# Approach\n1. The smallest lexic string starts with lowest chars (a) first\n2. Apply a greedy algorithm, trying to lower the first chars while k allows it.\n3. Traverse from first :\n - if k == 0, then you cannot do any modification; append the current letter as it is\n - else, figure out the min distance from current letter to a : current - \'a\' or 123 - current. \n - if this distance <= k, reduce k by it and append \'a\'\n - else if cannot reach a, but a char to the left of current char by k. Append that and reduce k\n\n# Complexity\n- Time complexity:$$O(n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(n)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```java []\nclass Solution {\n public String getSmallestString(String s, int k) {\n StringBuilder stb = new StringBuilder(s.length());\n char currentChar;\n for (int i = 0; i < s.length(); i++) {\n currentChar = s.charAt(i);\n if (k > 0) {\n k -= appendAndReduce(stb, currentChar, k);\n } else {\n stb.append(currentChar);\n }\n }\n return stb.toString();\n }\n\n private int appendAndReduce(StringBuilder stb, char currentChar, int k) {\n int minDistance = Math.min(123 - currentChar, currentChar - \'a\');\n if (k >= minDistance) {\n stb.append(\'a\');\n return minDistance;\n } else {\n stb.append((char)(currentChar - k));\n return k;\n }\n }\n}\n```
| 0
| 0
|
['Java']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
C++ Seriously faster and simpler than all other solutions
|
c-seriously-faster-and-simpler-than-all-2uk4i
|
Thoughts\n\nWhile writing the code I was thinking about what makes fast code:\n- Solve as much as you can at compile time (not runtime)\n- Minimize branching\n
|
atspam
|
NORMAL
|
2024-11-17T06:26:50.211075+00:00
|
2024-11-17T06:26:50.211097+00:00
| 6
| false
|
# Thoughts\n\nWhile writing the code I was thinking about what makes fast code:\n- Solve as much as you can at compile time (not runtime)\n- Minimize branching\n - maximize predictive branching\n- Minimize expensive computations\n\nThese points helped me craft the answer and I think it led to more intuitive code. The comments explain more below.\n\n# Code\n```cpp []\n#include<string>\n\nclass Solution {\npublic:\n std::string getSmallestString(std::string s, int k) {\n //No need to create a new string. s is already a copy we can return.\n //No need to do lots of calculations at runtime. Just find the difference between\n //s[i] and \'a\' and use that difference as an index into the shift_amount array\n int shift_amount[] = {0,1,2,3,4,5,6,7,8,9,10,11,12,13,12,11,10,9,8,7,6,5,4,3,2,1};\n for (size_t i = 0; i < s.size(); i++) {\n //int shift is the smallest number of characters we need to shift if we want to get to \'a\'\n int shift = shift_amount[s[i] - \'a\'];\n //Notice only one runtime conditional branch statement.\n if (k >= shift) {\n s[i] = \'a\';\n k -= shift;\n }\n //if we do not have enough k left to shift to an \'a\',\n //we can only walk back k amount (we no longer have enough k to wrap back to a)\n else {\n s[i] = s[i] - k;\n //leave early since we ran out of k\n return s;\n }\n }\n return s;\n }\n};\n```
| 0
| 0
|
['C++']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
C# Solution || Easy Solution
|
c-solution-easy-solution-by-mohamedabdel-jviv
|
csharp []\npublic class Solution {\n public string GetSmallestString(string s, int k) {\n var arr = s.ToCharArray();\n for(int i = 0;i < arr.Le
|
mohamedAbdelety
|
NORMAL
|
2024-11-11T17:45:54.221627+00:00
|
2024-11-11T17:45:54.221660+00:00
| 3
| false
|
```csharp []\npublic class Solution {\n public string GetSmallestString(string s, int k) {\n var arr = s.ToCharArray();\n for(int i = 0;i < arr.Length && k > 0;i++){\n int diff = arr[i] - \'a\';\n int opDiff = 26 - diff;\n if(opDiff < diff && opDiff <= k){\n arr[i] = \'a\';\n k-= Math.Min(k,opDiff);\n }else{\n arr[i] = (char)(arr[i] - Math.Min(k,diff));\n k-= Math.Min(k,diff);\n }\n }\n return new string(arr);\n }\n}\n```
| 0
| 0
|
['C#']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
Simple C++ | Easy to understand | Beats 100%
|
simple-c-easy-to-understand-beats-100-by-q9ca
|
Approach\nSince, we want to get the lexicograpically sorted, we can think of greedy approach of trying to keep the initial characters smaller. \n\n# Complexity\
|
kapiswayatul
|
NORMAL
|
2024-11-07T20:35:44.952142+00:00
|
2024-11-07T20:35:44.952176+00:00
| 3
| false
|
# Approach\nSince, we want to get the lexicograpically sorted, we can think of greedy approach of trying to keep the initial characters smaller. \n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```cpp []\nclass Solution {\npublic:\n string getSmallestString(string s, int k) {\n for(int i = 0; i < s.size(); i++) {\n if (k > 0) {\n s[i] = getSmallestCharacter(s[i], k);\n }\n }\n return s;\n }\n\n char getSmallestCharacter(char c, int &k) {\n int leftDist = c - \'a\', rightDist = (\'z\' - c) + 1;\n int mn = min(leftDist, rightDist);\n if (k >= mn) {\n k -= mn;\n return \'a\';\n }\n char res = c - k;\n k = 0;\n return res;\n }\n};\n```
| 0
| 0
|
['C++']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
C++ greedy
|
c-greedy-by-the_ghuly-81rs
|
Code\ncpp []\nclass Solution {\npublic:\n string getSmallestString(string s, int k) {\n for(int i = 0;k && i<s.size();++i)\n {\n int
|
the_ghuly
|
NORMAL
|
2024-10-29T07:39:02.668847+00:00
|
2024-10-29T07:39:02.668876+00:00
| 1
| false
|
# Code\n```cpp []\nclass Solution {\npublic:\n string getSmallestString(string s, int k) {\n for(int i = 0;k && i<s.size();++i)\n {\n int dist = min(s[i]-\'a\',26-s[i]+\'a\');\n if(dist>k)\n {\n s[i]-=k;\n return s;\n }\n s[i]=\'a\';\n k-=dist;\n }\n return s;\n }\n};\n```
| 0
| 0
|
['C++']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
Python3 || O(n) || 3ms beats 100%
|
python3-on-3ms-beats-100-by-stygian84-a69j
|
Intuition\n- Check the steps needed to get each letter to a starting from left\n- At each iteration, reduce k by no. of steps\n- If no. of steps>=k, then we red
|
stygian84
|
NORMAL
|
2024-10-24T08:54:12.857179+00:00
|
2024-10-24T08:54:12.857214+00:00
| 1
| false
|
# Intuition\n- Check the steps needed to get each letter to ```a``` starting from left\n- At each iteration, reduce ```k``` by no. of steps\n- If no. of steps>=k, then we reduce the letter by ```k``` steps and terminate the loop. \n\n# Complexity\n- Time complexity: O(n)\n\n# Code\n```python3 []\nclass Solution:\n def getSmallestString(self, s: str, k: int) -> str:\n # make each letter as small as possible starting from left\n\n ls = list(s)\n\n for i in range(len(ls)):\n letter = ls[i]\n\n #check if getting to a is faster from front or back\n \n diff = min(ord(letter)-ord(\'a\'), ord(\'z\')-ord(letter)+1) \n if k-diff<0:\n ls[i] = chr(ord(letter) - k)\n else:\n ls[i] = \'a\'\n\n k-=diff\n if k <= 0:\n break\n\n return "".join(ls)\n```\n\n\n
| 0
| 0
|
['Python3']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
Beats 100% Solutions. Python Greedy Solution.
|
beats-100-solutions-python-greedy-soluti-t3hx
|
idea: if k > len(s) * 26, means we got more than enough k, so return "a" * len(s)\n # if not, make a res string first\n # now iterate the string,
|
wasiflatifhussain
|
NORMAL
|
2024-09-16T15:11:16.097993+00:00
|
2024-09-16T15:11:16.098024+00:00
| 0
| false
|
# idea: if k > len(s) * 26, means we got more than enough k, so return "a" * len(s)\n # if not, make a res string first\n # now iterate the string, and for each char, check distance to get to "a" in both forward and backward \n # direction, as it is CYCLIC\n # now if distForward <= distBackward and distForward <= k, means we can go forwards, so go that way and decrement k and also add "a" to res\n # if distForward > distBackward and distBackward <= k, means we go backwards and reach "a"\n # else, we simply go backwards as much as possible while k lasts\n # because the idea is we try to be GREEDY and make the first letters as close to "a" as possible\n # then the result will always be lexicographically smallest possible\n\n# Code\n```python3 []\nclass Solution:\n def getSmallestString(self, s: str, k: int) -> str:\n if k >= len(s) * 26:\n return "a" * len(s)\n\n res = ""\n i = 0\n while k and i < len(s):\n distForward = (25 + 1) - (ord(s[i]) - ord(\'a\'))\n distBackward = ord(s[i]) - ord(\'a\') \n if distForward <= distBackward and distForward <= k:\n k -= distForward\n res += "a"\n elif distForward > distBackward and distBackward <= k:\n k -= distBackward\n res += "a"\n else:\n res += chr(ord(s[i]) - k)\n k = 0\n\n i += 1\n \n if len(res) == len(s): return res\n else:\n res += s[len(res)::]\n return res\n```
| 0
| 0
|
['Python3']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
Python 3, Beats 98%, One pass, Greedy
|
python-3-beats-98-one-pass-greedy-by-roh-n25c
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
rohanchoudhary2000
|
NORMAL
|
2024-09-09T19:31:25.728094+00:00
|
2024-09-09T19:31:25.728111+00:00
| 1
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def getSmallestString(self, s: str, k: int) -> str:\n N = len(s)\n ans = ""\n\n for ch in s:\n if k == 0: break\n\n dst_left_a = ord(ch) - ord(\'a\')\n dst_right_a = 26 - dst_left_a\n dst = min(dst_left_a, dst_right_a)\n \n if dst <= k:\n k -= dst\n ans += \'a\'\n else:\n ans += chr(ord(ch) - k)\n k = 0\n\n ln_ans = len(ans) \n return ans + s[ln_ans:]\n \n \n```
| 0
| 0
|
['String', 'Greedy', 'Python3']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
Easy to understand, explained solution || Python
|
easy-to-understand-explained-solution-py-2iui
|
Complexity\n- Time complexity: O(n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity: O(n)\n Add your space complexity here, e.g. O(n) \n\n# Co
|
georges_dib
|
NORMAL
|
2024-08-31T16:21:57.957228+00:00
|
2024-08-31T16:21:57.957258+00:00
| 0
| false
|
# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python3 []\nclass Solution:\n def getSmallestString(self, s: str, k: int) -> str: \n s = list(s)\n for i in range(len(s)):\n char = s[i]\n\n # get the distance between this char, and \'a\'\n dist = self.distance(char, \'a\')\n if dist <= k:\n # if that distance is <= k, then immediately assign \'a\' to\n # the char, because it is the smallest letter lexicographically\n s[i] = \'a\'\n k -= dist\n else:\n # otherwise, get the smallest letter that k allows, and break\n # from the loop as no further changes are allowed for next chars\n s[i] = chr(ord(char) - k)\n break\n\n return "".join(s)\n\n def distance(self, c1, c2):\n ord1, ord2 = None, None\n\n # this part is just to make it easier to know that ord1 < ord2\n if c1 < c2:\n ord1, ord2 = ord(c1), ord(c2)\n else:\n ord1, ord2 = ord(c2), ord(c1)\n\n # return the min distance between the two chars, whether that\n # is by looping over the edge of \'a\' or \'z\', or not\n return min(ord2 - ord1, ord1 - ord(\'a\') + ord(\'z\') - ord2 + 1)\n```
| 0
| 0
|
['Python3']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
Greedily try all possible differences
|
greedily-try-all-possible-differences-by-dk4g
|
Approach\n Greedy Approach\n\n# Intuition \nSee, we need to make the smallest lexicographical string right? which means the characters from beginning must be a
|
hokteyash
|
NORMAL
|
2024-08-19T09:02:57.427787+00:00
|
2024-08-19T10:28:11.155163+00:00
| 4
| false
|
# Approach\n Greedy Approach\n\n# Intuition \nSee, we need to make the smallest lexicographical string right? which means the characters from beginning must be as minimal or smaller as possible by taking care of k value as well.\n\nRight? It means the character from beginning must be starts with something similar to this pattern -> \n\n\'a\',\n\'b\',\n\'c\',\n\'d\',\n..\n..\n..\n\'z\'\n\nI hope till now you are able to follow me!\n\nSo by observing this pattern, now I\'m sure that okay i can try taking the difference of current character with all the characters from \'a\' to \'z\' why? \n\nBecause it is in a sorted manner, which means if we follow this sequence then we will be able to generate lexicographically smallest sequence, isn\'t it?\n\nSo, our job is done now! Compare current character with all the alphabets and check the difference if the difference is less than 14 then we dont need to do anything, but if the difference in greater than 13 then we need to cyclically calculate then only we can get the minimum character so for that we need to subtract 26 - difff.\n\nLet me explain you practically:\nchar -> \'b\' , k = 4\n\'b\' - \'a\' -> 1\n\nbut :\nchar -> \'z\' , k = 4\n\'z\' - \'a\' -> 25 but cyclically it should give 1 so for that we need to subtract 26-25 if the difference is greater than 13.\n\nAnd in the end we need to return modified string.\n\nHope you got the clarity about this greedy approach :)\n\n\n# Code\n```java []\nclass Solution {\n public int reducerFunction(char[]str,char ch,int index,int k){\n for(char chr=\'a\';chr<=\'z\';chr++){\n int diff = ch-chr;\n if(diff>13) diff = 26-diff;\n if(diff<=k){\n str[index]=chr;\n return diff;\n }\n }\n return 0;\n }\n public String getSmallestString(String s,int k){\n char []str = s.toCharArray();\n for(int i=0;i<str.length;i++){\n if(k<=0) break;\n int reduced = reducerFunction(str,str[i],i,k);\n k-=reduced;\n }\n return new String(str);\n }\n\n }\n\n```
| 0
| 0
|
['String', 'Greedy', 'Java']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
Easy CPP Solution
|
easy-cpp-solution-by-clary_shadowhunters-2fna
|
\n# Code\n\nclass Solution {\npublic:\n string getSmallestString(string s, int k) {\n string ans="";\n int cur=0;\n int i=0;\n fo
|
Clary_ShadowHunters
|
NORMAL
|
2024-08-15T10:22:29.275407+00:00
|
2024-08-15T10:22:29.275434+00:00
| 4
| false
|
\n# Code\n```\nclass Solution {\npublic:\n string getSmallestString(string s, int k) {\n string ans="";\n int cur=0;\n int i=0;\n for (i=0;i<s.size();i++)\n {\n for (int ch=\'a\';ch<=s[i];ch++)\n {\n int diff=abs(s[i]-ch);\n diff=min(diff,26-diff);\n if (diff<=k) \n {\n ans.push_back(ch);\n k-=diff;\n break;\n }\n }\n }\n return ans;\n }\n};\n```
| 0
| 0
|
['C++']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
Java - Circular arrangement of letters
|
java-circular-arrangement-of-letters-by-p59ej
|
Intuition\n Describe your first thoughts on how to solve this problem. \nIt is clear as soon as the problem is seen that each character has to be calculated unt
|
sm_19
|
NORMAL
|
2024-08-05T02:44:39.868692+00:00
|
2024-08-05T02:44:39.868722+00:00
| 1
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nIt is clear as soon as the problem is seen that each character has to be calculated until the \'k\' is totally used up. So, for each character the smallest possible character within \'k\' distance has to be found.\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe approach is for each character compute the smallest character in k reach. \n\nIt is important to identify the condition that each letter could find its next smallest character not just in the forward direction but in backward direction as well. \nEx. for character \'z\', the smallest character in reach with distance greater than 0 is \'a\' (considering the characters are in a circular form)\n\n........ - \'y\' - \'z\' - \'a\' - \'b\' - \'c\' - \'d\' - ...... - \'x\' - \'y\' - \'z\' - \'a\' - \'b\' - ......\n\nSo, we compute both the forward smallest character and backward smallest character and their respective distances. \n\nThen we have 3 conditions:\n1. Smallest Character is the character found in forward direction, return it.\n2. Smallest Character is the character found in backward direction, return it.\n3. Smallest Character is the same in both directions, compare their forward and backward distances and use the smallest distance.\n\nHave a globalK to keep track of the remaining k that can be used up.\n# Complexity\n- Time complexity: O(n) \n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n) \n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n# Code\n```\nclass Solution {\n int globalK = 0;\n int distf = 0;\n int distb = 0;\n public String getSmallestString(String s, int k) {\n globalK = k;\n StringBuilder strb = new StringBuilder();\n for(char c: s.toCharArray()){\n if(globalK==0){\n strb.append(c);\n continue;\n }\n char x = smallestChar(c, globalK);\n strb.append(x);\n }\n return strb.toString();\n }\n\n char smallestChar(char c, int k){\n char fwd = smallestCharInFwd(c, k);\n char bwd = smallestCharInBwd(c, k);\n if(fwd < bwd){\n globalK -= distf;\n // System.out.println("1"+fwd+" "+distf);\n return fwd;\n }else if(bwd < fwd){\n globalK -= distb;\n // System.out.println("2"+bwd+" "+distb);\n return bwd;\n }else if(distf < distb){\n globalK -= distf;\n // System.out.println("1"+fwd+" "+distf);\n return fwd;\n }else{\n globalK -= distb;\n // System.out.println("2"+bwd+" "+distb);\n return bwd;\n }\n }\n\n char smallestCharInFwd(char c, int k){\n if((c-\'a\')<=k){ \n distf = c-\'a\';\n return \'a\';\n }\n else{ \n distf = k;\n return (char)(c-k);\n }\n }\n\n char smallestCharInBwd(char c, int k){\n if((\'z\'-c)<k){ \n distb = (int)(\'z\'-c)+1;\n return \'a\';\n }\n else{\n distb = k;\n return (char)(c+k);\n }\n }\n}\n```
| 0
| 0
|
['Java']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
Java Greedy soln
|
java-greedy-soln-by-vharshal1994-rmor
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
vharshal1994
|
NORMAL
|
2024-08-04T13:17:54.280795+00:00
|
2024-08-04T13:17:54.280824+00:00
| 0
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n /**\n We greedily make every character as \'a\' if possible.\n This can be done in 2 ways, current character could be close to \'a\'\n like \'b\' or \'z\' as its circular. So we can check left and right diffs from \'a\'\n If not, we just make current character small by remaining k.\n */\n public String getSmallestString(String s, int k) {\n char[] arr = s.toCharArray();\n \n for (int i = 0; i < s.length(); i++) {\n char ch = arr[i];\n int leftDiff = ch - \'a\';\n int rightDiff = \'z\' - ch + 1;\n int minDiff = Math.min(leftDiff, rightDiff);\n\n if (k - minDiff >= 0) {\n k -= minDiff;\n arr[i] = \'a\';\n } else {\n arr[i] = (char) (ch - k);\n k = 0;\n }\n }\n\n return new String(arr);\n }\n}\n```
| 0
| 0
|
['Java']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
EASY beat 100% JAVA C++
|
easy-beat-100-java-c-by-vivek__kumar__09-wfek
|
Intuition\nput a as times as possible.\n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space comp
|
vivek4565
|
NORMAL
|
2024-08-03T18:17:20.089015+00:00
|
2024-08-03T18:17:20.089042+00:00
| 3
| false
|
# Intuition\nput a as times as possible.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution {\n public int dist(char ch){\n return Math.min(26-Math.abs(ch-\'a\'),Math.abs(\'a\'-ch));\n }\n public String getSmallestString(String s, int k) {\n StringBuilder sb=new StringBuilder();\n for(int i=0;i<s.length();i++){\n if(dist(s.charAt(i))<=k){\n sb.append(\'a\');\n k-=dist(s.charAt(i));\n }\n else if(k>0){\n sb.append(((char)(s.charAt(i)-k)));\n k=0;\n }\n else{\n sb.append(s.charAt(i));\n }\n }\n return sb.toString();\n }\n}\n```
| 0
| 0
|
['Greedy', 'C++', 'Java', 'Python3']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
C++ solution
|
c-solution-by-oleksam-hufx
|
\n// Please, upvote if you like it. Thanks :-)\nstring getSmallestString(string s, int k) {\n\tint n = s.size();\n\tfor (int i = 0; i < n & k > 0; i++) {\n\t\ti
|
oleksam
|
NORMAL
|
2024-08-01T18:46:08.246118+00:00
|
2024-08-01T18:46:08.246145+00:00
| 0
| false
|
```\n// Please, upvote if you like it. Thanks :-)\nstring getSmallestString(string s, int k) {\n\tint n = s.size();\n\tfor (int i = 0; i < n & k > 0; i++) {\n\t\tint dist = min(s[i] - \'a\', \'z\' - s[i] + 1);\n\t\ts[i] = (dist <= k ? \'a\' : s[i] - k);\n\t\tk -= dist;\n\t}\n\treturn s;\n}\n```
| 0
| 0
|
['Greedy', 'C', 'C++']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
✅Easy and Simple ✅Clean Code
|
easy-and-simple-clean-code-by-ayushluthr-7wz9
|
Guy\'s if you find this solution helpful \uD83D\uDE0A, PLEASE do UPVOTE. By doing that it motivate\'s me to create more better post like this \u270D\uFE0F\nFoll
|
ayushluthra62
|
NORMAL
|
2024-07-26T20:03:29.188807+00:00
|
2024-07-26T20:03:29.188833+00:00
| 2
| false
|
***Guy\'s if you find this solution helpful \uD83D\uDE0A, PLEASE do UPVOTE. By doing that it motivate\'s me to create more better post like this \u270D\uFE0F***<br>\n**Follow me on LinkeDin [[click Here](https://www.linkedin.com/in/ayushluthra62/)]**\n\n# Complexity\n- Time complexity:\nO(N)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution {\npublic:\n string getSmallestString(string s, int k) {\n if(k == 0) return s;\n int curr =0;\n for(int i=0;i<s.length();i++){\n int right = (\'z\'-s[i])+1;\n int left = s[i]-\'a\';\n int mini = min(left,right);\n if(k>=mini){\n s[i]=\'a\';\n k-=mini;\n }else{\n char ch =s[i]-k;\n s[i]=ch;\n k=0;\n }\n }\n return s;\n }\n};\n```\n***Guy\'s if you find this solution helpful \uD83D\uDE0A, PLEASE do UPVOTE. By doing that it motivate\'s me to create more better post like this \u270D\uFE0F***<br>\n**Follow me on LinkeDin [[click Here](https://www.linkedin.com/in/ayushluthra62/)]**
| 0
| 0
|
['String', 'Greedy', 'C++']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
Golang simple O(n) solution
|
golang-simple-on-solution-by-tjucoder-46ep
|
Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(n)\n\n# Code\ngo\nfunc getSmallestString(s string, k int) string {\n\t// abcdefghijklm\n\t// nopq
|
tjucoder
|
NORMAL
|
2024-07-22T13:11:15.815854+00:00
|
2024-07-22T13:11:15.815874+00:00
| 0
| false
|
# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```go\nfunc getSmallestString(s string, k int) string {\n\t// abcdefghijklm\n\t// nopqrstuvwxyz\n\tsb := strings.Builder{}\n\tfor _, v := range s {\n\t\tif k == 0 {\n\t\t\tsb.WriteRune(v)\n continue\n\t\t}\n\t\tstep2a := 0\n\t\tif v <= \'m\' {\n\t\t\tstep2a = int(v - \'a\')\n\t\t} else {\n\t\t\tstep2a = int(\'z\' - v + 1)\n\t\t}\n\t\tif k >= step2a {\n\t\t\tsb.WriteRune(\'a\')\n\t\t\tk -= step2a\n\t\t\tcontinue\n\t\t}\n\t\tsb.WriteRune(v - rune(k))\n k = 0\n\t}\n\treturn sb.String()\n}\n```
| 0
| 0
|
['Go']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
EASY C++ || GREEDY || STRING
|
easy-c-greedy-string-by-sanskarkumar028-hslj
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
sanskarkumar028
|
NORMAL
|
2024-07-19T17:33:52.804502+00:00
|
2024-07-19T17:33:52.804536+00:00
| 0
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n string getSmallestString(string s, int k) {\n string ans = "";\n for(int i = 0; i < s.size(); i++)\n {\n int d1 = s[i] - \'a\';\n int d2 = \'z\' - s[i];\n\n if(d1 < d2 + 1)\n {\n if(d1 <= k)\n {\n ans += \'a\';\n k = k - d1;\n }\n else{\n ans += s[i] - k;\n k = 0;\n }\n \n }\n else\n {\n if(d2 + 1 <= k)\n {\n ans += \'a\';\n k = k - d2 - 1;\n }\n else{\n ans += s[i] - k;\n k = 0;\n }\n\n }\n }\n return ans;\n }\n};\n```
| 0
| 0
|
['String', 'Greedy', 'C++']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
Java | O(n) | Greedy check both direction | Easy with comments
|
java-on-greedy-check-both-direction-easy-29cz
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
meltawab
|
NORMAL
|
2024-07-10T20:04:21.365782+00:00
|
2024-07-10T20:04:21.365813+00:00
| 0
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public String getSmallestString(String s, int k) {\n StringBuilder sb = new StringBuilder(s);\n for(int i = 0; i < s.length() && k != 0; i++){\n int c = (int) s.charAt(i) - \'a\';\n int distanceToA = Math.min(c, 26 - c); // Check both directions\n if(distanceToA <= k){\n sb.setCharAt(i, \'a\');\n k = k - distanceToA;\n } else {\n char next = (char) ((c - k) + \'a\'); // Minimize c to closest to a "Lexicographically Small"\n sb.setCharAt(i, next);\n k = 0;\n }\n }\n return sb.toString();\n }\n}\n```
| 0
| 0
|
['Java']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
Simple O(N) TC and SC solution
|
simple-on-tc-and-sc-solution-by-batmansa-0mox
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
batmansachin
|
NORMAL
|
2024-06-23T13:51:56.432652+00:00
|
2024-06-23T13:51:56.432678+00:00
| 0
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public String getSmallestString(String s, int k) {\n StringBuilder sb = new StringBuilder();\n if(k == 0) return s;\n int i;\n for(i = 0; i < s.length() && k > 0; i++) {\n if(s.charAt(i) == \'a\') {\n sb.append(s.charAt(i));\n continue;\n }\n char c = s.charAt(i);\n int minDist = Math.min((int) c - \'a\' , \'z\' - (int)c + 1);\n if(k >= minDist) {\n k -= minDist;\n sb.append(\'a\');\n }\n else { \n sb.append((char)((int) c - k));\n k -= (int) c - \'a\';\n }\n \n }\n for(; i < s.length(); i++) {\n sb.append(s.charAt(i));\n }\n return sb.toString();\n }\n\n // private Character getCharatcer(Character c, int k) {\n // int minDist = Math.min((int) c - \'a\' , \'z\' - (int)c + 1);\n \n // }\n}\n```
| 0
| 0
|
['Java']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
Beats 100% simple iteration through string
|
beats-100-simple-iteration-through-strin-7grl
|
Intuition\n Describe your first thoughts on how to solve this problem. \n1. Initialization:\nDetermine the length n of the string s.\nIf k is zero, return the o
|
saurabh0047
|
NORMAL
|
2024-06-15T10:42:49.247857+00:00
|
2024-06-15T10:42:49.247894+00:00
| 2
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n1. Initialization:\nDetermine the length n of the string s.\nIf k is zero, return the original string as no operations are allowed.\n\n2. Iterate Over the String:\nLoop through each character in the string from left to right. The earlier in the string a change is made, the more it can affect the lexicographical order, so prioritize changes starting from the beginning.\n3. Determine Minimum Change:\nFor each character s[i], calculate the minimum of either reducing s[i] to \'a\' directly (s[i] - \'a\') or wrapping around the alphabet to \'a\' (26 - (s[i] - \'a\')).\n\n4. Perform the Change:\nIf changing the current character to \'a\' uses fewer or equal operations than k, make the change, reduce k by the number of operations used, and set s[i] to \'a\'.\nIf changing the character to \'a\' would exceed the remaining operations k, just decrease the character by k positions in the alphabet and set k to 0.\n5. Handle Early Termination:\nIf k reaches zero during the iteration, break out of the loop early since no further changes can be made.\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n string getSmallestString(string s, int k) {\n int n=s.size();\n if(k==0)return s;\n // return "";\n for(int i=0;i<n;i++){\n if(k==0){\n break;\n }\n int x=min((s[i]-\'a\'),(26-(s[i]-\'a\')));\n if(s[i]==\'a\'){\n continue;\n }\n else if(x<=k){\n k-=x;\n s[i]=\'a\';\n }\n // else if(26-((s[i]-\'a\')+k)<=0){\n // k=k-(26-(s[i]-\'a\'));\n // s[i]=\'a\';\n // }\n else{\n s[i]=s[i]-k;\n k=0;\n }\n }\n return s;\n }\n};\n```
| 0
| 0
|
['C++']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
[C++] Greedy
|
c-greedy-by-ericyxing-ttdq
|
Code\n\nclass Solution {\npublic:\n string getSmallestString(string s, int k) {\n string ans = s;\n int n = s.size(), i = 0;\n while (k
|
EricYXing
|
NORMAL
|
2024-06-11T05:33:03.936867+00:00
|
2024-06-11T05:33:03.936902+00:00
| 2
| false
|
# Code\n```\nclass Solution {\npublic:\n string getSmallestString(string s, int k) {\n string ans = s;\n int n = s.size(), i = 0;\n while (k > 0 && i < n)\n {\n int d = min(s[i] - \'a\', \'z\' - s[i] + 1);\n if (k > d)\n {\n ans[i] = \'a\';\n k -= d;\n }\n else\n {\n int c = min(s[i] - \'a\' - k, (s[i] - \'a\' + k) % 26);\n ans[i] = \'a\' + c;\n k = 0;\n }\n i++;\n }\n return ans;\n }\n};\n```
| 0
| 0
|
['Greedy', 'C++']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
simple if else
|
simple-if-else-by-sumit1906-04wu
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
sumit1906
|
NORMAL
|
2024-06-07T04:22:20.943647+00:00
|
2024-06-07T04:22:20.943686+00:00
| 0
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(N)\n\n- Space complexity: O(1)\n\n# Code\n```\nclass Solution {\npublic:\n string getSmallestString(string s, int k) \n {\n string ans="";\n\n if(k==0)\n return s;\n\n for(int i=0;i<s.length();i++)\n { \n int x=s[i]-\'a\';\n int y=\'z\'-s[i]+1;\n if(k==0)\n {\n ans.push_back(s[i]);\n }\n\n else if(x<y)\n {\n if(x>=k)\n {\n ans.push_back(char((int)s[i]-k));\n k=0;\n\n }else\n {\n ans.push_back(\'a\');\n k=k-x;\n }\n } \n else\n {\n if(y>k)\n {\n ans.push_back(char((int)s[i]-k));\n k=0;\n }\n else\n {\n ans.push_back(\'a\');\n k=k-y;\n }\n } \n }\n return ans;\n }\n};\n```
| 0
| 0
|
['C++']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
Simple Java Solution
|
simple-java-solution-by-vansh_goel-e894
|
Beats 100%\n\n# Code\n\nclass Solution {\n public String getSmallestString(String s, int k) {\n if(k==0) return s;\n StringBuilder sb=new Strin
|
vg_85
|
NORMAL
|
2024-06-04T18:16:32.063828+00:00
|
2024-06-04T18:16:32.063856+00:00
| 5
| false
|
Beats 100%\n\n# Code\n```\nclass Solution {\n public String getSmallestString(String s, int k) {\n if(k==0) return s;\n StringBuilder sb=new StringBuilder();\n int i=0;\n for(i=0;i<s.length();i++){\n if(k==0) break;\n int c=s.charAt(i)-\'a\';\n if(c>13) c=26-c;\n if(c<=k){\n sb.append(\'a\');\n k-=c;\n }\n else{\n sb.append((char)(s.charAt(i)-k));\n k=0;\n }\n }\n while(i<s.length()){\n sb.append(s.charAt(i++));\n }\n return sb.toString();\n }\n}\n```
| 0
| 0
|
['String', 'Java']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
C++ || EASY CLEAN || SHORT CODE
|
c-easy-clean-short-code-by-gauravgeekp-8dre
|
\n\n# Code\n\nclass Solution {\npublic:\n string getSmallestString(string s, int k) {\n int n=s.size(),c=0;\n string f=s;\n for(int i=0;
|
Gauravgeekp
|
NORMAL
|
2024-06-03T23:04:41.709336+00:00
|
2024-06-03T23:04:41.709359+00:00
| 2
| false
|
\n\n# Code\n```\nclass Solution {\npublic:\n string getSmallestString(string s, int k) {\n int n=s.size(),c=0;\n string f=s;\n for(int i=0;i<n;i++)\n {\n for(char g=\'a\';g<=\'z\';g++)\n {\n int m=min(abs(g-s[i]),26-abs(g-s[i]));\n if(m+c<=k)\n {\n c+=m;\n f[i]=g;\n break;\n }\n }\n }\n return f;\n }\n};\n```
| 0
| 0
|
['C++']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
Simple Solution
|
simple-solution-by-chris1337-u1z9
|
\n# Code\n\n# @param {String} s\n# @param {Integer} k\n# @return {String}\ndef get_smallest_string(s, k)\n hash = {}\n # Dump the alphabet into an array.\
|
Chris1337
|
NORMAL
|
2024-06-03T22:33:16.808707+00:00
|
2024-06-03T22:33:16.808732+00:00
| 1
| false
|
\n# Code\n```\n# @param {String} s\n# @param {Integer} k\n# @return {String}\ndef get_smallest_string(s, k)\n hash = {}\n # Dump the alphabet into an array.\n alphabet = ("a".."z").to_a\n\n # Create a hash mapping all \n # letters of the alphabet to the\n # shortest distance to "a"\n dist = 0\n ("a".."n").each do |char|\n hash[char] = dist\n dist += 1 \n end\n dist = 12\n ("o".."z").each do | char|\n hash[char] = dist\n dist -= 1\n end\n \n # loop until we get k to 0 or\n # we run out of chars to reduce\n # to a lower lexicographical\n # order.\n chars = s.chars\n i = 0\n while k > 0 and i < chars.size\n # Skip as it\'s minimized.\n if chars[i] == "a"\n i += 1\n # If we have enough k to get our current\n # char down to 0, reduce k and our char to "a"\n elsif hash[chars[i]] <= k\n k -= hash[chars[i]]\n chars[i] = "a"\n i += 1\n # Otherwise reduce char as low as possible.\n else\n chars[i] = alphabet[alphabet.index(chars[i]) - k]\n k = 0\n end\n\n end\n\n chars.join\nend\n\n```
| 0
| 0
|
['Ruby']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
Easy solution with php
|
easy-solution-with-php-by-husniddinuz-ij6m
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Husniddinuz
|
NORMAL
|
2024-05-29T09:43:52.544694+00:00
|
2024-05-29T09:43:52.544723+00:00
| 1
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public function getSmallestString($s, $k) {\n $res = "";\n $len = strlen($s);\n\n for ($i = 0; $i < $len; $i++) {\n $char = $s[$i];\n $min_d = min(ord($char) - ord(\'a\'), ord(\'z\') - ord($char) + 1);\n\n if ($k >= $min_d) {\n $k -= $min_d;\n $res .= ($min_d <= ord($char) - ord(\'a\')) ? \'a\' : \'z\';\n } else {\n $res .= chr(ord($char) - $k);\n $k -= $k;\n }\n }\n\n return $res;\n }\n}\n\n```
| 0
| 0
|
['PHP']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
Python3. Greedily force "a" at start
|
python3-greedily-force-a-at-start-by-nik-vf5x
|
Intuition\nSeems like need to greedily set the first letter to "a" or the lowest possible, then the second letter etc.\n\n# Approach\nGo letter by letter, pick
|
nikamir
|
NORMAL
|
2024-05-27T23:20:56.129080+00:00
|
2024-05-27T23:20:56.129098+00:00
| 1
| false
|
# Intuition\nSeems like need to greedily set the first letter to "a" or the lowest possible, then the second letter etc.\n\n# Approach\nGo letter by letter, pick the minimal cost of changing to "a" or the lowest possible letter.\n\n# Complexity\n- Time complexity:\n$$O(n)$$, scan the string\n\n- Space complexity:\n$$O(n)$$, additional space to allocate the result $$t$$\n\n# Code\n```\nclass Solution:\n def getSmallestString(self, s: str, k: int) -> str:\n # to get lexicographically smallest, need to try to place the lowest letters first\n # k is the budget, just greedily spend it trying to make the first letter as close to a as possitble\n\n # trivial case\n if k == 0:\n return s\n\n t = []\n it = iter(s)\n for c in it:\n # convert ASCII to 0-25 range\n c = ord(c) - 97\n # cost to "a" through "z"\n upCost = 26 - c\n # cost to "a" by decreasing\n downCost = c\n\n # if there is no path to "a", do as much as possible\n if upCost > k and downCost > k:\n # no budget is left, append the rest of s and break\n t.append(chr(97 + c - k))\n t.extend(it)\n break\n\n # take "a" with the minimal cost\n t.append(\'a\')\n k -= min(upCost, downCost)\n\n return "".join(t)\n```
| 0
| 0
|
['Python3']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
lexicographically-smallest-string-after-operations-with-constraint
|
lexicographically-smallest-string-after-6eh2f
|
Intuition\nIt is brute force approach to check\nif it is possible to get \'a\' from either left or right side\nChoose the min side\n# Approach\nAlways try to ge
|
sai_teja13
|
NORMAL
|
2024-05-26T00:04:46.566091+00:00
|
2024-05-26T00:06:33.913443+00:00
| 1
| false
|
# Intuition\nIt is brute force approach to check\nif it is possible to get \'a\' from either left or right side\nChoose the min side\n# Approach\nAlways try to get \'a\' because we need lexicographically-smallest-string\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n# Code\n```\nclass Solution:\n def getSmallestString(self, s: str, k: int) -> str:\n s = list(s)\n n = len(s)\n for i in range(n):\n \n asc = ord(s[i]) - 97\n m1 = 1<<31\n m2 = 1<<31\n if(asc - k <= 0):\n m1 = asc\n if(asc + k >= 26):\n m2 = 26-asc\n if(m1 == 1<<31 and m2 == 1<<31):\n s[i] = chr(asc - k + 97)\n break\n if(m1 < m2):\n k -= asc\n else:\n k -= (26-asc)\n s[i] = \'a\'\n \n \n #print(k)\n return "".join(s)\n\n \n\n \n```
| 0
| 0
|
['Python3']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
[C++] Greedy Solution
|
c-greedy-solution-by-quater_nion-h844
|
Intuition\nCyclic distance between two characters = min((b-a+26)%26, (a-b+26)%26)\nIterate through all the characters from left to right. If we have enough K le
|
quater_nion
|
NORMAL
|
2024-05-22T17:16:15.825181+00:00
|
2024-05-22T17:50:30.793958+00:00
| 0
| false
|
# Intuition\nCyclic distance between two characters = `min((b-a+26)%26, (a-b+26)%26)`\nIterate through all the characters from left to right. If we have enough K left to make the character to make the character \'a\', then make it while decreasing k accordingly. Else decrease the character as much as possible with the available K. Than break out of the loop. The resulting string is the answer. \n\n# Complexity\n- Time complexity:\n$$O(n)$$\n\n- Space complexity:\n$$O(1)$$\n\n# Code\n```\nclass Solution {\n int dist(char a, char b){\n return min((a-b+26)%26, (b-a+26)%26);\n }\npublic:\n string getSmallestString(string s, int k) {\n int n=s.length(), i=0;\n while(k && i<n){\n if(dist(s[i], \'a\')<=k){\n k-=dist(s[i], \'a\');\n s[i]=\'a\';\n }else{\n s[i]-=k;\n break;\n }\n i++;}\n return s;\n }\n};\n```
| 0
| 0
|
['Greedy', 'C++']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
Easily understandable O(n) solution
|
easily-understandable-on-solution-by-vis-w3ms
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
vishwasrajbatham151
|
NORMAL
|
2024-05-22T02:53:48.430596+00:00
|
2024-05-22T02:53:48.430623+00:00
| 0
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n string getSmallestString(string s, int k) {\n int n=s.size();\n for(int i=0; i<n; i++){\n \n int x=(s[i]-\'a\');\n int mindis=x<13?x:(26-x);\n if(k>=mindis){\n k-=mindis;\n s[i]=\'a\';\n }\n else{\n s[i]=char(s[i]-k);\n k=0;\n }\n if(k==0) break;\n }\n return s;\n }\n};\n```
| 0
| 0
|
['C++']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
simple if else statements || Beats 97 || o(n) ||
|
simple-if-else-statements-beats-97-on-by-4160
|
\n\n# Code\n\nclass Solution:\n def getSmallestString(self, s: str, k: int) -> str:\n res=""\n for i in s:\n minimumDistance=min(ord
|
sumanth2328
|
NORMAL
|
2024-05-19T21:19:18.799656+00:00
|
2024-05-19T21:19:18.799673+00:00
| 1
| false
|
\n\n# Code\n```\nclass Solution:\n def getSmallestString(self, s: str, k: int) -> str:\n res=""\n for i in s:\n minimumDistance=min(ord("z")-ord(i)+1,ord(i)-ord("a"))\n if i=="a":\n res+="a"\n elif minimumDistance<k+1:\n res+="a"\n k=k-minimumDistance\n elif k>0:\n res+=chr(ord(i)-k)\n k=0\n else:\n res+=i\n return res\n```
| 0
| 0
|
['String', 'Greedy', 'Python3']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
Best Most Optimal Clean Code
|
best-most-optimal-clean-code-by-f2017164-zsjt
|
Intuition\n Describe your first thoughts on how to solve this problem. \nThink Greedy\n# Approach\n Describe your approach to solving the problem. \nStarting fr
|
f20171647
|
NORMAL
|
2024-05-18T20:01:09.381441+00:00
|
2024-05-18T20:01:09.381476+00:00
| 0
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThink Greedy\n# Approach\n<!-- Describe your approach to solving the problem. -->\nStarting from the left, try all 26 characters within the distance k, return t when k is exhausted\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(n) - one pass\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1) - extra space\n\n# Code\n```\nclass Solution {\npublic:\n int dist(char c, char d) {\n return min(c - d + 26, d - c);\n }\n\n string getSmallestString(string s, int k) {\n int d;\n for (int i = 0; i < s.size() and k; i++) {\n for (char c = \'a\'; c <= \'z\'; c++) {\n d = dist(c, s[i]);\n if (d <= k) {\n k -= d;\n s[i] = c;\n break;\n }\n }\n }\n return s;\n }\n};\n```
| 0
| 0
|
['C++']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
Intuitive Java Solution
|
intuitive-java-solution-by-bapatanuparth-k6q1
|
Intuition\n Describe your first thoughts on how to solve this problem. \n- To get lexicographically smallest, firstly make as many characters == \'a\' as possib
|
bapatanuparth
|
NORMAL
|
2024-05-16T18:41:34.368811+00:00
|
2024-05-16T18:41:34.368835+00:00
| 5
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n- To get lexicographically smallest, firstly make as many characters == \'a\' as possible from left of the string. Then if we dont have enough \'k\' to reach \'a\', then reach the lowest possible character by utilizing all the \'k\' on that character\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity: O(n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(n)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public String getSmallestString(String s, int k) {\n // System.out.println(distance(\'a\', \'z\'));\n int i=0, sum=0;\n StringBuilder sb= new StringBuilder(s);\n while(i<s.length() && sum + distance(\'a\', s.charAt(i)) <= k){\n sb.setCharAt(i, \'a\');\n k-=distance(\'a\', s.charAt(i));\n i++;\n }\n if(i<s.length()){\n char ch= s.charAt(i);\n int n= Math.min((ch-\'a\' + k)%26 ,(ch-\'a\' - k +26)%26);\n sb.setCharAt(i, (char)(n+\'a\'));\n }\n\n return sb.toString();\n }\n\n\n int distance(char a, char b){\n return Math.min(Math.abs((a-\'a\')- (b-\'a\')), Math.abs((26 + (a-\'a\'))-(b-\'a\')));\n }\n}\n```
| 0
| 0
|
['Java']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
Java | String builder Simple solution
|
java-string-builder-simple-solution-by-s-qhwh
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
sheerapthinath
|
NORMAL
|
2024-05-14T02:32:50.473505+00:00
|
2024-05-14T02:32:50.473536+00:00
| 6
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public String getSmallestString(String s, int k) {\n StringBuilder sb = new StringBuilder();\n for(int i=0; i<s.length(); i++) {\n int adist = s.charAt(i)-\'a\';\n int zdist = \'z\' - s.charAt(i) + 1;\n int mindist = Math.min(adist,zdist);\n if(k>=mindist) {\n k-=mindist;\n sb.append(\'a\');\n } else {\n if(k>0) {\n sb.append((char)(s.charAt(i)-k));\n k=0;\n } else {\n sb.append(s.charAt(i));\n }\n \n }\n\n }\n return sb.toString();\n }\n}\n```
| 0
| 0
|
['Java']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
greedy move from index 0 to n-1 || easy to understand || must see
|
greedy-move-from-index-0-to-n-1-easy-to-f1n00
|
Code\n\nclass Solution {\npublic:\n string getSmallestString(string s, int k) {\n \n int dis = 0;\n if(k == 0) return s;\n
|
akshat0610
|
NORMAL
|
2024-05-12T17:34:37.038989+00:00
|
2024-05-12T17:34:37.039020+00:00
| 1
| false
|
# Code\n```\nclass Solution {\npublic:\n string getSmallestString(string s, int k) {\n \n int dis = 0;\n if(k == 0) return s;\n string ans = s;\n for(int i = 0 ; i < s.length() ; i++){\n if(dis == k) return ans;\n if(s[i] == \'a\') continue;\n \n //the leeter must have been a bigger letter and \n //can be changed to a smaller letter with respect to k\n\n char ch = fun(s,i,k);\n ans[i] = ch;\n }\n return ans;\n }\n char fun(string &str , int &idx , int &k){\n \n //we will move the left side \n char ch = str[idx];\n\n \n int k1 = k;\n char ch1 = ch;\n while(true){ //moving towards left or a\n if(k1 == 0 or ch1 == \'a\') break;\n ch1 = char(ch1 - 1);\n k1 = k1 - 1;\n }\n\n //we will move the right side\n int k2 = k;\n char ch2 = ch;\n while(true){ //moving towards right or z\n if(k2 == 0 or ch2 == \'a\') break;\n ch2 = char(ch2 + 1);\n if(ch2 > \'z\') ch2 = \'a\';\n k2 = k2 - 1;\n }\n \n // cout<<"idx = "<<idx<<" "<<"ch1 = "<<ch1<<" "<<"ch2 = "<<ch2<<endl;\n // cout<<"idx ="<<idx<<"k1 = "<<k1<<" "<<"k2 = "<<k2<<endl;\n\n if(ch1 == ch2){\n k = max(k1,k2);\n return ch1;\n }\n else if(ch1 < ch2){\n k = k1;\n return ch1;\n }\n else {\n k = k2;\n return ch2;\n }\n return \'*\';\n }\n};\n```
| 0
| 0
|
['String', 'Greedy', 'C++']
| 0
|
lexicographically-smallest-string-after-operations-with-constraint
|
Beats100%,O(n)
|
beats100on-by-amanbaghel-yw5n
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
AmanBaghel
|
NORMAL
|
2024-05-09T21:09:00.691291+00:00
|
2024-05-09T21:09:00.691321+00:00
| 2
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\nO(n)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution {\npublic:\n string getSmallestString(string s, int k) {\n int cnt=0;\n for(int i=0;i<s.size();i++){\n int s1=s[i]-\'a\';\n int s2=26-s1;\n int num=min(s1,s2);\n if(num<=k){\n s[i]=\'a\';\n k=k-num;\n }\n else{\n s[i]=s[i]-k;\n k=0;\n }\n }\n return s;\n }\n};\n```
| 0
| 0
|
['C++']
| 0
|
find-products-of-elements-of-big-array
|
C++ Bit count and binary search, Clean code with a lot explanitions.
|
c-bit-count-and-binary-search-clean-code-53jm
|
Intuition\n\nLet\'s think top-down and conquer each individual tasks one by one.\n\n Describe your first thoughts on how to solve this problem. \n1. The big_num
|
cowtony
|
NORMAL
|
2024-05-12T00:26:31.501749+00:00
|
2024-05-12T23:52:17.618623+00:00
| 1,349
| false
|
# Intuition\n\nLet\'s think top-down and conquer each individual tasks one by one.\n\n<!-- Describe your first thoughts on how to solve this problem. -->\n1. The `big_nums` array is all power of 2. So we can represent it with the power only.\n ```\n [1, 2, 1, 2, 4, 1, 4, 2, 4, 1, 2, 4, 8, 1, 8, ...] (2 ^ bit)\n - - ---- - ---- ---- ------- - ----\n [0, 1, 0, 1, 2, 0, 2, 1, 2, 0, 1, 2, 3, 0, 3, ...] (bit)\n - - ---- - ---- ---- ------- - ----\n2. Once converted, the **multiplication** will become **addition**. We will then need to sum the value from `from = query[0]` to `to = query[1]`.\n `2^i * 2^j = 2^(i + j)`\n3. The above summation can also be converted as prefix sum, so that we can easily get `prefix_sum[to] - prefix_sum[from - 1]`.\n4. Assuming we have a function `LL prefixSumTillIndex(index)` which can sum the value of each bit for the first `index` elements in the converted `big_nums` (took `log_2` of it).\n Then we can simplly calculate the result with some `mod` helper function:\n ```C++\n for (const auto& query : queries) {\n LL prefix_sum_1 = prefixSumTillIndex(query[0]);\n LL prefix_sum_2 = prefixSumTillIndex(query[1] + 1);\n \n // This is `2^sum % mod`\n result.push_back(pow(2, prefix_sum_2 - prefix_sum_1, query[2]));\n } \n ```\n Where the helper `pow` function calculates `(x ^ y % mod)`:\n ```C++\n // Calculate `(x ^ y) % mod` by converting the y into binary bits.\n int pow(LL x, LL y, int mod) {\n if (y <= 0) {\n return 1 % mod;\n }\n x %= mod;\n LL result = 1;\n while (y) {\n if (y & 1) {\n result = multiply(result, x, mod);\n }\n x = multiply(x, x, mod);\n y >>= 1;\n }\n return result;\n }\n\n int multiply(LL x, LL y, int mod) {\n return ((x % mod) * (y % mod)) % mod;\n }\n ```\n5. However now the problem is **how to implement function `prefixSumTillIndex`**, it seems simpler to sum bits from 1 to a **`value`**, instead of all bits which is **`index`** because it\'a hard to control how many bits 1 (indexes occupied) per value. So we will need another helper function to find the value for a given index: `LL getValueFromIndex(LL index)`. But let\'s implement prefixSum first assuming that function is already done:\n ```C++\n LL prefixSumTillIndex(LL index) {\n LL value = getValueFromIndex(index);\n auto [bit_sum, bit_count] = sumAndCountBitsBeforeValue(value);\n // Also include the last value\'s partial bits.\n if (bit_count < index) {\n for (int bit = 0; bit_count < index; bit++, value >>= 1) {\n bit_sum += bit * (value % 2);\n bit_count += value % 2;\n }\n }\n return bit_sum;\n }\n\n // Count the bits for all numbers from 1 to `value - 1`.\n // Return the bit value sum and total count.\n pair<LL, LL> sumAndCountBitsBeforeValue(LL value) {\n LL bit_sum = 0;\n LL bit_count = 0;\n for (LL bit = 0, power = 1; power < value; bit++, power <<= 1) {\n LL cur = (value >> (bit + 1)) << bit;\n cur += max(0LL, (value % (power << 1)) - power);\n bit_count += cur;\n bit_sum += bit * cur;\n }\n return {bit_sum, bit_count};\n }\n ```\n6. Now for `LL getValueFromIndex(LL index)`, this would lead me to think about binary serach, by reusing the function `sumAndCountBitsBeforeValue` above:\n ```C++\n LL getValueFromIndex(LL index) {\n index++;\n LL low = 1, high = 1LL << 50;\n\n while (low < high) {\n LL mid = low + (high - low) / 2;\n if (sumAndCountBitsBeforeValue(mid + 1).second < index) {\n low = mid + 1;\n } else {\n high = mid;\n }\n }\n return low;\n }\n ```\n7. Finally we get every component ready, the finally solution is as follows.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```C++\nusing LL = long long;\n\nclass Solution {\npublic:\n vector<int> findProductsOfElements(vector<vector<LL>>& queries) {\n vector<int> result;\n result.reserve(queries.size());\n for (const auto& query : queries) {\n LL prefix_sum_1 = prefixSumTillIndex(query[0]);\n LL prefix_sum_2 = prefixSumTillIndex(query[1] + 1);\n\n result.push_back(pow(2, prefix_sum_2 - prefix_sum_1, query[2]));\n }\n\n return result;\n }\n\nprivate:\n // Count the bits for all numbers from 1 to `value - 1`.\n // Return the bit value sum and total count.\n pair<LL, LL> sumAndCountBitsBeforeValue(LL value) {\n LL bit_sum = 0;\n LL bit_count = 0;\n for (LL bit = 0, power = 1; power < value; bit++, power <<= 1) {\n LL cur = (value >> (bit + 1)) << bit;\n cur += max(0LL, (value % (power << 1)) - power);\n bit_count += cur;\n bit_sum += bit * cur;\n }\n return {bit_sum, bit_count};\n }\n\n LL getValueFromIndex(LL index) {\n index++;\n LL low = 1, high = 1LL << 50;\n\n while (low < high) {\n LL mid = low + (high - low) / 2;\n if (sumAndCountBitsBeforeValue(mid + 1).second < index) {\n low = mid + 1;\n } else {\n high = mid;\n }\n }\n return low;\n }\n\n LL prefixSumTillIndex(LL index) {\n LL value = getValueFromIndex(index);\n auto [bit_sum, bit_count] = sumAndCountBitsBeforeValue(value);\n // Also include the last value\'s partial bits.\n if (bit_count < index) {\n for (int bit = 0; bit_count < index; bit++, value >>= 1) {\n bit_sum += bit * (value % 2);\n bit_count += value % 2;\n }\n }\n return bit_sum;\n }\n\n // Calculate `(x ^ y) % mod` by converting the y into binary bits.\n int pow(LL x, LL y, int mod) {\n if (y <= 0) {\n return 1 % mod;\n }\n x %= mod;\n LL result = 1;\n while (y) {\n if (y & 1) {\n result = multiply(result, x, mod);\n }\n x = multiply(x, x, mod);\n y >>= 1;\n }\n return result;\n }\n\n int multiply(LL x, LL y, int mod) {\n return ((x % mod) * (y % mod)) % mod;\n }\n};\n```
| 33
| 0
|
['Binary Search', 'Bit Manipulation', 'C++']
| 7
|
find-products-of-elements-of-big-array
|
[Python] Binary Search
|
python-binary-search-by-lee215-ez0d
|
Explanation\ncount(x) returns the sum of bits from 1 to x.\nmul(x) returns the pow of product of powerful arrays from 1 to x.\nquery(k) returns the pow of produ
|
lee215
|
NORMAL
|
2024-05-11T16:18:40.229069+00:00
|
2024-05-11T16:18:40.229097+00:00
| 1,218
| false
|
# **Explanation**\n`count(x)` returns the sum of bits from `1` to `x`.\n`mul(x)` returns the pow of product of powerful arrays from `1` to `x`.\n`query(k)` returns the pow of product of `k` first integers in `big_nums`.\n<br>\n\n# **Complexity**\nTime `O(Q * logR * logR)`\nSpace `O(Q + logR)`\n<br>\n\n\n**Python**\n```py\n def findProductsOfElements(self, queries: List[List[int]]) -> List[int]:\n def count(x):\n if x == 0:\n return 0\n b = x.bit_length() - 1\n v = 1 << b\n res = b * (v >> 1)\n return res + count(x - v) + x - v\n\n def mul(x):\n if x == 0:\n return 0\n b = x.bit_length() - 1\n v = 1 << b\n res = (b - 1) * b * v >> 2\n return res + mul(x - v) + b * (x - v)\n\n def query(k):\n if k == 0:\n return 0\n k += 1\n x = bisect_left(range(1, 10 ** 15), k, key=count)\n res = mul(x)\n k -= count(x)\n for _ in range(k):\n b = x & -x\n res += b.bit_length() - 1\n x -= b\n return res\n\n return [pow(2, query(j) - query(i - 1), mod) for i, j, mod in queries]\n```\n
| 12
| 2
|
[]
| 3
|
find-products-of-elements-of-big-array
|
Video Explanation (With ALL proofs)
|
video-explanation-with-all-proofs-by-cod-9t15
|
Explanation\n\nClick here for the video\n\n# Code\n\ntypedef long long int ll;\n\nclass Solution {\n \n ll CountOf2TillX (ll x) {\n if (x <= 1) ret
|
codingmohan
|
NORMAL
|
2024-05-12T17:42:41.287204+00:00
|
2024-05-12T17:42:41.287221+00:00
| 282
| false
|
# Explanation\n\n[Click here for the video](https://youtu.be/ku2RBhkBBIw)\n\n# Code\n```\ntypedef long long int ll;\n\nclass Solution {\n \n ll CountOf2TillX (ll x) {\n if (x <= 1) return 0;\n if (x == 2) return 1;\n if (x == 3) return 2;\n \n ll largest_i = 0;\n for (ll i = 2; i < 61; i ++) {\n if ((1LL << i) <= x) continue;\n largest_i = i;\n break;\n }\n largest_i --;\n \n ll ans = (1LL << (largest_i-2))*largest_i*(largest_i-1);\n ll lft = x - ((1LL << largest_i) - 1);\n return (ans + lft*largest_i + CountOf2TillX(lft-1));\n }\n \n ll TermsTillX (ll x) {\n if (x == 0) return 0;\n if (x == 1) return 1;\n \n ll largest_i = 0;\n for (ll i = 0; i < 61; i ++) {\n if ((1LL << i) <= x) continue;\n largest_i = i;\n break;\n }\n largest_i --;\n \n ll ans = (1LL << (largest_i-1))*largest_i;\n ll lft = x - ((1LL << largest_i) - 1);\n return (ans + lft + TermsTillX(lft-1));\n }\n \n ll CountOf2TillIndex (ll ind) {\n if (ind == 1) return 0;\n \n ll l = 0, r = 1e15;\n while (l < r) {\n ll m = (l+r) >> 1;\n if (TermsTillX(m) >= ind) r = m;\n else l = m+1;\n }\n if (TermsTillX(l) > ind) l --;\n \n ll ans = CountOf2TillX(l);\n \n ind -= TermsTillX(l);\n for (int i = 0; ind > 0 && i < 61; i ++) {\n if (((1LL << i) & (l+1)) == 0) continue;\n ind --;\n ans += i;\n }\n \n return ans;\n }\n \n ll FastPower (ll a, ll b, ll M) {\n ll ans = 1;\n while (b) {\n if (b&1) ans = (ans * a) % M;\n a = (a * a) % M;\n b /= 2;\n }\n return ans % M;\n }\n \npublic:\n vector<int> findProductsOfElements(vector<vector<long long>>& queries) {\n vector<int> ans;\n \n for (auto q: queries) {\n ll cnt_2 = CountOf2TillIndex(q[1]+1) - CountOf2TillIndex(q[0]);\n ans.push_back(FastPower(2, cnt_2, q[2])); \n }\n return ans;\n }\n};\n```
| 9
| 0
|
['C++']
| 0
|
find-products-of-elements-of-big-array
|
Binary Search + Count contribution of each bit till given index
|
binary-search-count-contribution-of-each-5t33
|
Intuition\nWe\'ll count frequency of each bit till index i\n\n# Approach\nmaintain two vectors vector<int> cnt1(60,0), cnt2(60, 0) where cnt1[i] = freq of ith b
|
artAbhi
|
NORMAL
|
2024-05-11T16:13:17.055367+00:00
|
2024-05-11T16:25:00.057101+00:00
| 1,139
| false
|
# Intuition\nWe\'ll count frequency of each bit till index i\n\n# Approach\nmaintain two vectors `vector<int> cnt1(60,0), cnt2(60, 0)` where `cnt1[i] = freq of ith bit till queries[x][1] index` and `cnt2[i] = freq of ith bit till queries[x][0]-1` index\n\nThen doing `cnt1[i] - cnt2[i]` for every ith bit will tell us how many times `ith` bit appears in index range `[queries[x][0], queries[x][1]]`.\n\nSince, we know the freq of each bit in given range, just do `mod_pow(1<<i, freq[i], mod)` to find contribution of `ith` bit in final ans.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nT.C = `O(len(queries) * log(MX) * LIM)`, where `MX = 1e15` and `LIM = 60`\n\n# Code\n```\nusing ll = long long;\nconst ll MX = 1e15 + 6, LIM = 60;\nclass Solution {\npublic:\n \n ll add(ll x, ll y, ll mod) { ll res = 0ll + x + y; return (res >= mod ? res - mod : res); }\n ll sub(ll x, ll y, ll mod) { ll res = x - y; return (res < 0 ? res + mod : res); }\n ll mul(ll x, ll y, ll mod) { x %= mod, y %= mod; ll res = 1ll * x * y; return (res >= mod ? res % mod : res); }\n ll mod_pow(ll x, ll y, ll mod) { if (y <= 0) return 1; ll ans = 1; x %= mod; while (y) { if (y & 1) ans = mul(ans, x, mod); x = mul(x, x, mod); y >>= 1; } return ans; }\n ll mod_inverse(ll x, ll mod) {return mod_pow(x, mod - 2, mod);}\n \n vector<int> findProductsOfElements(vector<vector<long long>>& queries) {\n int m = queries.size();\n vector<int> ret;\n \n // find the integer x such that integers [1,2,3 .... x]\'s\n // powers of 2 makes up till any index i\n // [1,2 ... x-1]\'s power of 2 representation and some or all \n // power of 2 of x\'s total count equals index i\n auto calc = [&] (ll n)\n {\n if (n <= 0) return n;\n ll lo = 1, hi = MX;\n while (lo <= hi)\n {\n ll mid = (lo+hi)/2, sum = 0;\n for (int i=0; i<LIM; i++)\n {\n ll p = (1ll<<(i+1));\n ll cur = ((mid+1)/p) * (1ll<<i);\n cur += max(0ll, ((mid+1)%p) - (1ll<<i));\n sum += cur;\n }\n if (sum >= n) hi = mid-1;\n else lo = mid+1;\n }\n return hi+1;\n };\n \n // finds freq of each bit till index tot-1\n auto calc2 = [&] (ll n, ll tot)\n {\n vector<ll> cnt(LIM, 0);\n if (n <= 0) return cnt;\n ll sum = 0;\n for (int i=0; i<LIM; i++)\n {\n ll p = (1ll<<(i+1));\n ll cur = (n/p) * (1ll<<i);\n cur += max(0ll, (n%p) - (1ll<<i));\n sum += cur;\n cnt[i] = cur;\n }\n if (sum < tot)\n {\n for (int i=0; i<LIM; i++)\n {\n if (sum >= tot) break;\n if ((n>>i)&1)\n {\n cnt[i]++;\n sum++;\n }\n }\n }\n return cnt;\n };\n \n for (auto q:queries)\n {\n vector<ll> v1 = calc2(calc(q[1]+1), q[1]+1), v2 = calc2(calc(q[0]), q[0]);\n \n ll val = 1;\n for (int i=0; i<LIM; i++)\n {\n ll p = (1ll<<i);\n ll temp = mod_pow(p, v1[i]-v2[i], q[2]);\n val = (val*temp) % q[2];\n }\n ret.push_back((int)val);\n }\n return ret;\n }\n};\n```
| 8
| 0
|
['Binary Search', 'Bit Manipulation', 'C++']
| 1
|
find-products-of-elements-of-big-array
|
Python Solution
|
python-solution-by-kg-profile-dwkj
|
\n# Code\n\nclass Solution:\n def findProductsOfElements(self, queries: List[List[int]]) -> List[int]:\n def countOnes(max_val):\n total_se
|
KG-Profile
|
NORMAL
|
2024-05-11T16:15:03.943532+00:00
|
2024-05-11T16:15:03.943559+00:00
| 233
| false
|
\n# Code\n```\nclass Solution:\n def findProductsOfElements(self, queries: List[List[int]]) -> List[int]:\n def countOnes(max_val):\n total_set_bits = 0\n n = max_val + 1\n p = 0\n while (1 << p) <= max_val:\n total_pairs = n // (1 << (p + 1))\n total_set_bits += total_pairs * (1 << p)\n total_set_bits += max(0, n % (1 << (p + 1)) - (1 << p))\n p += 1\n return total_set_bits\n\n def grab(n):\n res = [0] * 64\n for p in range(64):\n total_pairs = (n + 1) // (1 << (p + 1))\n res[p] += total_pairs * (1 << p)\n remainder = (n + 1) % (1 << (p + 1))\n if remainder > (1 << p):\n res[p] += remainder - (1 << p)\n return res\n\n def upTo(max_index):\n min_val, max_val = 0, max_index + 5\n highest, excess = 0, max_index + 1\n while min_val <= max_val:\n mid_val = min_val + (max_val - min_val) // 2\n amt_of_ones = countOnes(mid_val)\n if amt_of_ones < max_index + 1:\n highest = mid_val\n excess = max_index + 1 - amt_of_ones\n min_val = mid_val + 1\n elif amt_of_ones > max_index + 1:\n max_val = mid_val - 1\n else:\n highest = mid_val\n excess = 0\n break\n bit_counts = grab(highest)\n if excess == 0:\n return bit_counts\n higher = max_val + 1\n for p in range(64):\n if (higher & (1 << p)) != 0:\n bit_counts[p] += 1\n excess -= 1\n if excess == 0:\n return bit_counts\n return bit_counts\n\n def modPow(base, pow, mod):\n if pow == 0:\n return 1\n lesser = modPow(base, pow // 2, mod)\n lesser = (lesser * lesser) % mod\n if pow % 2 == 1:\n lesser = (lesser * base) % mod\n return lesser\n\n def fulfil(query):\n from_val, to_val, mod = query\n up_to = upTo(to_val)\n littler = upTo(from_val - 1)\n res = 1\n pow_val = 1\n for i in range(63):\n amt = up_to[i] - littler[i]\n if amt == 0:\n pow_val = (pow_val * 2) % mod\n continue\n mult = modPow(1 << i, amt, mod)\n res = (res * mult) % mod\n pow_val = (pow_val * 2) % mod\n if res == 0:\n return 0\n return res\n\n res = []\n for query in queries:\n res.append(fulfil(query))\n return res\n\n```
| 6
| 0
|
['Python3']
| 1
|
find-products-of-elements-of-big-array
|
[Python3][Binary Search] + Bit ordering || Illustration || 800ms
|
python3binary-search-bit-ordering-illust-lvw2
|
Intuition\n Describe your first thoughts on how to solve this problem. \nLet\'s break down the problem.\nFor each query, we have start, end, and modulus.\n- If
|
andrei_bis
|
NORMAL
|
2024-05-11T21:41:12.250067+00:00
|
2024-05-11T21:41:12.250089+00:00
| 125
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nLet\'s break down the problem.\nFor each query, we have start, end, and modulus.\n- If we had a function that for a given number would give us the frequencies of the the power of 2 in the big nums array from index 0 to the queried index, we could answer each query\n- Indeed, given this function, we would query (start-1) and end, take the difference of the 2 dictionaries, and then compute each result\n- So how to compute the frequency dictionary given a position ; i.e. return the frequency of each power of 2 in big nums from 0 up to n ; this is what the problem is all about\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nHow to compute this frequency dictionary ?\nFor this, the main intuition is to notice a pattern in the distribution of power of 2s when you list all integers consecutively.\nBelow are listed the binary representation of numbers from 0 to 20:\n\n| Integer | Bit 4 | Bit 3 | Bit 2 | Bit 1 | Bit 0 |\n| ------- | ----- | ----- | ----- | ----- | ----- |\n| 0 | 0 | 0 | 0 | 0 | 0 |\n| 1 | 0 | 0 | 0 | 0 | 1 |\n| 2 | 0 | 0 | 0 | 1 | 0 |\n| 3 | 0 | 0 | 0 | 1 | 1 |\n| 4 | 0 | 0 | 1 | 0 | 0 |\n| 5 | 0 | 0 | 1 | 0 | 1 |\n| 6 | 0 | 0 | 1 | 1 | 0 |\n| 7 | 0 | 0 | 1 | 1 | 1 |\n| 8 | 0 | 1 | 0 | 0 | 0 |\n| 9 | 0 | 1 | 0 | 0 | 1 |\n| 10 | 0 | 1 | 0 | 1 | 0 |\n| 11 | 0 | 1 | 0 | 1 | 1 |\n| 12 | 0 | 1 | 1 | 0 | 0 |\n| 13 | 0 | 1 | 1 | 0 | 1 |\n| 14 | 0 | 1 | 1 | 1 | 0 |\n| 15 | 0 | 1 | 1 | 1 | 1 |\n| 16 | 1 | 0 | 0 | 0 | 0 |\n| 17 | 1 | 0 | 0 | 0 | 1 |\n| 18 | 1 | 0 | 0 | 1 | 0 |\n| 19 | 1 | 0 | 0 | 1 | 1 |\n| 20 | 1 | 0 | 1 | 0 | 0 |\n\nBit 0 alternates with a periodicity of 2 (0 then 1) etc\nBit 1 alternates with a periodicity of 4 (0 0 1 1 ) etc\nBit 2 alternates with a periodicity of 8 (0 0 0 0 1 1 1 1 ) etc\netc\n\nso for a given integer n, to compute the number of entries in the big nums array than come before it you can apply the following formula:\nfor each bit in binary representation of the integer:\n- compute how many period fit before the integer, and multiply the number of period by the size of the period // 2\n- for the last part if any (truncated period), if the truncated part is more than half the period, and the difference, i.e. truncated_part - (period // 2)\nThis gives you the frequency dictionary for big nums for all integers between 0 and n\nPlease note : you need to adapt the integer and add 1, since we start at 0\n\n**Example with 18 (need to increase by 1 so 19)**\nBinary representation : 10010\nBit 0 : period length 2; 1s per period : 1 ; nb full periods : 19 // 2 = 9 ; truncated_period : 19 % 2 == 1 ; frequency : 9 * 1 + 0\nBit 1 : period length 4, 1s per period : 2 ; nb full periods : 19 // 4 = 4 ; truncated_period : 3 ; frequency : 4 * 2 + 3 - (4//2) = 9\netc.\n\n\nBut we want something slightly different, we want the frequency dictionary for entries between 0 and and index i, not the number of entries of big nums for all integers from 0 to n\nWe need to introduce binary search here:\nBinary search from 1 to index (this is a reasonable upper limit), each time querying the number of entries the candidate integer yields, this allows you to find the integer which is at the limit of the index you are interested in (that yields just below the number of entries that you are interested in).\n\nIf this integer yields too few values, add to the frequency dictionary entries from the next integer until you have enough entries in bignums array.\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(q * (log n)^2) \nFor each query:\nwe need to binary search of start and end\neach binary search is takes O(log n) computation to determine number of previous entries in the big nums array\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n0(q log (n))\nwe need to store the frequency dictionary\n\n\n# Code\n```\nclass Solution:\n \n def findProductsOfElements(self, queries: List[List[int]]) -> List[int]:\n \n #helper function 1 : to compute freq dictionary given integer\n def compute_integer(n):\n res = dict()\n n += 1\n f = format(n, \'b\')\n\n for i in range(len(f)):\n period = pow(2,i+1)\n full_periods = n // period\n res[i] = full_periods * (period//2)\n rest = n % period\n to_add = rest - (period // 2)\n if to_add > 0:\n res[i] += to_add\n \n return res\n \n #helper function 2 : binary search to find correct integer given position requested\n def binary_search_integers(index):\n\n lower = 1\n upper = index\n\n while lower <= upper:\n\n x = (lower + upper) // 2\n tmp = compute_integer(x)\n total_freq = sum((v for v in tmp.values()))\n\n if total_freq == index:\n upper = x\n break\n\n if total_freq < index:\n lower = x +1\n else:\n upper = x-1\n \n res = compute_integer(upper)\n total_freq = sum((v for v in res.values()))\n if total_freq == index:\n return res\n \n extra = format(upper+1, \'b\')[::-1]\n for i in range(len(extra)):\n if extra[i] == \'1\':\n res[i] += 1\n total_freq += 1\n if total_freq == index:\n return res\n \n res = []\n for si,ei,modi in queries:\n tmp = 1\n d_start = binary_search_integers(si)\n d_end = binary_search_integers(ei+1)\n\n for k,v in d_start.items():\n d_end[k] -= v\n\n for k,v in d_end.items():\n tmp *= pow(pow(2,k,modi),v, modi)\n \n res.append(tmp % modi)\n \n return res\n \n\n\n```
| 4
| 0
|
['Python3']
| 3
|
find-products-of-elements-of-big-array
|
Python 3 || Bisearch, count 1's and accumulate 0's
|
python-3-bisearch-count-1s-and-accumulat-8p1r
|
Intuition\n Describe your first thoughts on how to solve this problem. \nFirst, bi-search the number target in the big_nums before decomposition (i.e. [1,2,3,..
|
zsq007
|
NORMAL
|
2024-05-11T16:12:38.807902+00:00
|
2024-05-11T17:29:10.888733+00:00
| 449
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFirst, bi-search the number `target` in the `big_nums` before decomposition (i.e. `[1,2,3,...]`) such that the index `bound` falls in its decmoposition.\n\nThen, count the accumulative number of 0\'s from `1` to `target-1`, plus the residual 0\'s in `target` (before `bound`).\n\nWith the number of 0\'s in `[low,high+1)`, answers to the queries are `pow(2,cnt,mod)`.\n\n# Approach\n\n`cnt1()`: Given a bound `num`, it returns the number of 1\'s from `1` to `num`. At each level `i`, there are `num // (1<<(i+1))` groups of 1\'s, each containing `1<<i` of 1\'s. Besides, for the last group, if ` cur >= 1<<i`, it contains `cur+1 - (1<<i)` 1\'s.\n\n`acc0()`: Similar to `cnt1()`, we also count the 1\'s, but this time, each 1 at level `i` brings `i` of 0\'s into the accumulative count.\n\n**One little trick:** `target < bound`.We don\'t need to bisect from `10**15` each time, just bisect in `range(bound)`.\n\n# Complexity\n- Time complexity: $O(Q \\cdot \\log^2 M)$, where $Q$ is the length of `queries`, $M$ is the maximum bound in `queries`.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: $O(Q)$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```python\nclass Solution:\n def findProductsOfElements(self, queries: List[List[int]]) -> List[int]:\n \n def cnt1(num: int) -> int:\n res = 0\n for i in range(num.bit_length()):\n cur = num % (1<<i+1)\n res += (num-cur) // 2 \n if cur >= 1<<i:\n res += cur+1 - (1<<i)\n return res\n \n def acc0(num: int) -> int:\n res = 0\n for i in range(num.bit_length()):\n cur = num % (1<<i+1)\n res += (num-cur) // 2 * i\n if cur >= 1<<i:\n res += (cur+1 - (1<<i)) * i\n return res\n \n def count(bound: int) -> int:\n # target is the number in the big_nums before decomposition that bound locates in\n target = bisect_left(range(bound), bound, key=cnt1)\n\n rest = bound - cnt1(target-1)\n cnt = acc0(target-1)\n \n for i in range(target.bit_length()):\n if target & (1<<i):\n cnt += i\n rest -= 1\n if not rest: break\n\n return cnt\n \n return [pow(2,count(high+1)-count(low),mod) for low,high,mod in queries]\n```
| 3
| 0
|
['Binary Search', 'Bit Manipulation', 'Python3']
| 0
|
find-products-of-elements-of-big-array
|
Java solution - 80ms
|
java-solution-80ms-by-darshit901-zl63
|
Intuition\n Describe your first thoughts on how to solve this problem. \nFor integers in ascending order, each power of 2 is present in a pattern. Let us consid
|
darshit901
|
NORMAL
|
2024-05-11T18:29:06.831947+00:00
|
2024-05-11T18:30:26.100353+00:00
| 253
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nFor integers in ascending order, each power of 2 is present in a pattern. Let us consider the numbers up to 8 for reference and list their binary representations, up to 4 digits:\n\n0 --> 0000\n1 --> 0001\n2 --> 0010\n3 --> 0011\n4 --> 0100\n5 --> 0101\n6 --> 0110\n7 --> 0111\n8 --> 1000\n\nNow look at the pattern for each power of 2(column). Then each power of 2 has this pattern:\n1 --> $$01$$0101010\n2 --> $$0011$$00110\n4 --> $$00001111$$0\n\n1. We can use this to know the counts of each power of 2 in the *big_num* array before the representation starts for any given number x. \n\n2. Using 1, we can find the counts for each power of 2 in the desired index range.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Process each query individually.\n2. For each query [s, t, mod], binary search to find the numbers whose representation will contain the (s+1)th index and (t+1)th index, say m and n.\n3. Calculate the counts of each power of 2 less than m and less than n, to get the counts of each powers of 2 in the desired range.\n4. For a given ith power of 2 with count c, its contribution in the desired product will be $$2^{i*c}$$. Transfer over as much of the expoenent as you can to the next highest power of 2, by representing this exponent as: \n$$i*c = (i+1) * \\lfloor((c*i)/(i+1))\\rfloor + ((c*i) mod (i+1)))$$\n\n Now, the floor part of the previous formula is added to the count of the next power, while the remainder(which will be a lower power of 2 than i+1), is used in the product.\n5. For the highest power of 2, reduce the count until it is zero, by doubling the base of the exponent iteratively.\n\n\n\n# Complexity\n- Time complexity:\n\n 1. Binary search in the given range [1, n] will take $$O(log(n))$$ iterations.\n 2. For each number n, counting the sum of freq of powers of 2 will take $$O(log(n))$$ time.\n 3. Reducing the counts of each power of 2 to 0 will take a further $$O(log(n))$$ time.\n \n Hence for Q queries, the total time taken will be $$O(Q*(log^{2}(n))$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n $$O(Q + log(n))$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\n public int[] findProductsOfElements(long[][] queries) {\n \n int[] response = new int[queries.length];\n \n for(int i=0; i<response.length; i++) {\n response[i] = solve(queries[i][0], queries[i][1]+1, queries[i][2]);\n }\n \n return response;\n }\n \n public int solve(long s, long t, long mod) {\n // Get the highest number x s.t. the sum of count of \n // powers of 2 in integers in the range [0, x-1] is <= s\n long n1 = s > 0 ? getNextHigher(1L, 100000_00000_00000L, s) : 0L;\n // Get the sum of counts of each power for 2 in all \n // integers less than x\n long[] c1 = s > 0 ? getLowerCounts(n1) : new long[51];\n // When the total count is less than target, use powers of \n // 2 present in the binary rep. of x until total matches target\n adjust(c1, n1, s);\n\n // Do the same process for the higher target(t)\n long n2 = getNextHigher(1L, 100000_00000_00000L, t);\n long[] c2 = getLowerCounts(n2);\n adjust(c2, n2, t);\n\n // Calculate diff of counts to find counts of each \n // powers in the desired range\n for(int i=0; i<50; i++) {\n c2[i] -= c1[i];\n }\n \n // Calculate mod of each power of 2 for the current query\n long[] pow = new long[50];\n pow[0] = 1L;\n for(int i=1; i<50; i++) {\n pow[i] = pow[i-1] << 1;\n pow[i] %= mod;\n }\n \n // Calculate desired product here\n long prod = 1L;\n long next = 2L;\n // Using the last element as sum of counts, no longer required\n c2[50] = 0;\n\n // For each power of 2, use the minimum count necessary \n // to use, and roll over as much as possible into the next higher power\n for(int i=1; i<50; i++) {\n int rem = (int)((c2[i]*(i)) % (i+1));\n long div = (c2[i]*i) / (i+1);\n prod *= pow[rem];\n prod %= mod;\n \n c2[i+1] += div;\n next <<= 1;\n }\n \n // For the highest power of 2, continually reduce the \n // base of the exponent until the count is reduced to 0\n long base = next % mod;\n while(c2[50] > 0) {\n prod *= (c2[50] % 2 == 1) ? base : 1L;\n prod %= mod;\n \n base *= base;\n base %= mod;\n c2[50] >>= 1;\n }\n \n return (int)(prod % mod);\n }\n \n public void adjust(long[] c, long x, long target) {\n int i=0;\n // Start from the lowest bit, and increment until the \n // total matches the target for each set bit\n while(c[50] != target) {\n if(x == 0) {\n System.out.println("Error");\n break;\n }\n if(x % 2 != 0) {\n c[i]++;\n c[50]++;\n }\n \n x >>= 1;\n i++;\n }\n }\n \n public long getNextHigher(long from, long to, long target) {\n // Binary search for the highest number for which total \n // count of powers of 2 for numbers <= target\n if(from == to) {\n return from;\n }\n long mid = from + (to+1-from)/2;\n long[] counts = getLowerCounts(mid);\n if(counts[50] > target) {\n return getNextHigher(from, mid-1, target);\n } else {\n return getNextHigher(mid, to, target);\n }\n }\n \n public long[] getLowerCounts(long x) {\n long[] response = new long[51];\n long total = 0;\n int i = 0;\n long next = 1L;\n // For a given power of 2(i), it is unset in the first 2^i nums, \n // then set for the next 2^i nums and the pattern repeats. \n while(next < x) {\n response[i] = (x/(2*next))*next + Math.max((x % (2*next))-next, 0);\n total += response[i];\n i++;\n next <<= 1;\n }\n // Using the last element as a special num to represent total\n response[50] = total;\n return response;\n }\n}\n```
| 2
| 0
|
['Java']
| 0
|
find-products-of-elements-of-big-array
|
Java Clean Solution | BiWeekly Contest
|
java-clean-solution-biweekly-contest-by-44zou
|
Code\n\n// class Solution {\n\n// private long getProduct(int[] arr) {\n// long prod = 1;\n// for (int i = 0; i < arr.length; i++) {\n//
|
Shree_Govind_Jee
|
NORMAL
|
2024-05-11T16:10:45.449281+00:00
|
2024-05-11T16:10:45.449300+00:00
| 142
| false
|
# Code\n```\n// class Solution {\n\n// private long getProduct(int[] arr) {\n// long prod = 1;\n// for (int i = 0; i < arr.length; i++) {\n// prod *= arr[i];\n// }\n// return prod;\n// }\n\n// public int[] findProductsOfElements(long[][] queries) {\n// int lmt = 1015;\n// int[][] pow2 = new int[lmt + 1][];\n// for (int i = 1; i <= lmt; i++) {\n// PriorityQueue<Integer> pq = new PriorityQueue<>(Comparator.reverseOrder());\n// long sum = 0;\n// for (int p = 1; p <= 30; p++) {\n// if ((1 << p) > i) {\n// break;\n// }\n// pq.add(1 << p);\n// sum += (1 << p);\n// }\n\n// int size = pq.size();\n// int[] arr = new int[size];\n// for (int j = 0; j < size; j++) {\n// arr[j] = pq.poll();\n// }\n// pow2[i] = arr;\n// }\n\n// int[] res = new int[queries.length];\n// for (int i = 0; i < queries.length; i++) {\n// long[] query = queries[i];\n// long fi = query[0];\n// long toi = query[1];\n// long prod = 1;\n// for (long k = fi; k <= toi; k++) {\n// prod *= getProduct(pow2[(int) k]);\n// prod %= (int) query[2];\n// }\n// res[i] = (int) prod;\n// }\n// return res;\n// }\n// }\n\n\nclass Solution {\n public int[] findProductsOfElements(long[][] queries) {\n // for (int val = 0; val < 10; val++) System.out.println(val+" has "+countOnes(val)+" ones filled.");\n int[] res = new int[queries.length];\n for (int i = 0; i < res.length; i++) res[i] = fulfil(queries[i]);\n return res;\n }\n private int fulfil(long[] query) {\n long from = query[0]; long to = query[1]; long mod = query[2];\n long[] upTo = upTo(to);\n long[] littler = upTo(from - 1);\n // System.out.println(to+": "+Arrays.toString(upTo));\n // System.out.println((from - 1)+": "+Arrays.toString(littler));\n long res = 1;\n long pow = 1;\n for (int i = 0; i < 63; i++) {\n long amt = upTo[i] - littler[i];\n if (amt == 0) {\n pow = (pow * 2) % mod;\n continue;\n }\n long mult = modPow(1l << i, amt, mod);\n res = (res * mult) % mod;\n pow = (pow * 2) % mod;\n if (res == 0) return 0;\n }\n return (int) res;\n }\n private long modPow(long base, long pow, long mod) {\n if (pow == 0) return 1;\n long lesser = modPow(base, pow / 2, mod);\n lesser = (lesser * lesser) % mod;\n if (pow % 2 == 1) lesser = (lesser * base) % mod;\n return lesser;\n }\n private long[] upTo(long maxIndex) {\n long minVal = 0, maxVal = maxIndex + 5;\n long highest = 0, excess = maxIndex + 1;\n while (minVal <= maxVal) {\n long midVal = minVal + (maxVal - minVal) / 2;\n long amtOfOnes = countOnes(midVal);\n // System.out.println(midVal+": "+amtOfOnes);\n if (amtOfOnes < maxIndex + 1) {\n highest = midVal;\n excess = maxIndex + 1 - amtOfOnes;\n minVal = midVal + 1;\n } else if (amtOfOnes > maxIndex + 1) {\n maxVal = midVal - 1;\n } else {\n highest = midVal;\n excess = 0;\n break;\n }\n }\n // System.out.println("For "+maxIndex+" index, I pick value: "+highest+" with "+excess+" extra ones.\\n");\n long[] bitCounts = grab(highest);\n if (excess == 0) return bitCounts;\n long higher = maxVal + 1;\n for (int p = 0; p < 64; p++) {\n if ((higher & (1l << p)) != 0) {\n bitCounts[p]++;\n if (--excess == 0) return bitCounts;\n }\n }\n return bitCounts;\n }\n public long[] grab(long n) {\n long[] res = new long[64];\n for (int p = 0; p < 64; p++) {\n long totalPairs = (n + 1) / (1l << (p + 1));\n res[p] += totalPairs * (1l << p);\n long remainder = (n + 1) % (1l << (p + 1));\n if (remainder > (1l << p)) res[p] += remainder - (1l << p);\n }\n return res;\n }\n public long countOnes(long max) {\n long totalSetBits = 0;\n long n = max + 1;\n for (long p = 0; (1l << p) <= max; p++) {\n long totalPairs = n / (1l << (p + 1));\n totalSetBits += totalPairs * (1l << p);\n totalSetBits += (long) Math.max(0, n % (1l<< (p + 1)) - (1l << p));\n }\n\n return totalSetBits;\n }\n}\n```\n\n---\n\n**C++**\n\n```\nclass Solution {\n\n const int MOD = 1000000009;\n\npublic:\n int cal(vector<int> big, int fi, int ti, int mi) {\n int p = 1;\n for (int i = fi; i <= ti; i++) {\n p = (1ll * p * big[i]) % mi;\n }\n return p;\n }\n\npublic:\n vector<int> gen(int x) {\n vector<int> pow;\n int powe = 1;\n while (x > 0) {\n if (x & 1) {\n pow.push_back(powe);\n }\n x >>= 1;\n powe <<= 1;\n }\n return pow;\n }\n\npublic:\n vector<int> findProductsOfElements(vector<vector<long long>>& queries) {\n vector<int> big;\n for (int i = 1; i <= 100; i++) {\n vector<int> pow = gen(i);\n big.insert(big.end(), pow.begin(), pow.end());\n }\n\n vector<int> ans;\n for (const auto& q : queries) {\n int fi = q[0];\n int ti = q[1];\n int mi = q[2];\n int res = cal(big, fi, ti, mi);\n ans.push_back(res);\n }\n return ans;\n }\n};\n```
| 2
| 2
|
['Array', 'Bit Manipulation', 'Bitmask', 'Java']
| 1
|
find-products-of-elements-of-big-array
|
💥💥 Beats 100% on runtime and memory [EXPLAINED]
|
beats-100-on-runtime-and-memory-explaine-kaha
|
IntuitionWe have to count the number of set bits (1s) in a number efficiently. A direct approach would be too slow, so I used dynamic programming (via memoizati
|
r9n
|
NORMAL
|
2025-01-30T16:18:52.896981+00:00
|
2025-01-30T16:18:52.896981+00:00
| 4
| false
|
# Intuition
We have to count the number of set bits (1s) in a number efficiently. A direct approach would be too slow, so I used dynamic programming (via memoization) to store and reuse results for previously calculated numbers. This way, I didn’t have to recompute the same values multiple times, which greatly improves performance.
# Approach
I calculated the number of set bits using a helper function with memoization to store previous results, combined binary search for efficiency in determining the maximum number, and used a simple loop to calculate the total sum of bits.
# Complexity
- Time complexity:
O(log n) for most operations, as we work with bits, and each step involves halving the problem size using binary search.
- Space complexity:
O(n) due to the memoization storage for the number of set bits for numbers up to n.
# Code
```kotlin []
class Solution {
private val dp = mutableMapOf<Long, Long>()
private fun power(n: Long, expo: Long, mod: Long): Long {
var ans = 1L
var base = n
var exp = expo
while (exp > 0) {
if (exp % 2 != 0L) {
ans = (ans * base) % mod
}
base = (base * base) % mod
exp /= 2
}
return ans
}
private fun getNumBits(n: Long): Long {
if (n == 0L) return 0L
dp[n]?.let { return it }
var ans = 0L
var num = n + 1
for (i in 60 downTo 0) {
if ((1L shl i) < num) {
ans = getNumBits((1L shl i) - 1)
val rem = num - (1L shl i)
ans += getNumBits(rem - 1) + rem
break
}
}
dp[n] = ans
return ans
}
private fun getMaxNum(n: Long): Long {
var left = 1L
var right = 1e15.toLong()
var ans = 0L
while (left <= right) {
val mid = (left + right) / 2
val placesOccupied = getNumBits(mid)
if (placesOccupied <= n) {
ans = mid
left = mid + 1
} else {
right = mid - 1
}
}
return ans
}
private fun getSum(n: Long): Long {
var res = 0L
for (i in 1 until 50) {
val blockSize = 1L shl (i + 1)
val onesInBlock = blockSize / 2
val completeBlocks = n / blockSize
res += completeBlocks * onesInBlock * i
val rem = n % blockSize
res += maxOf(0L, rem + 1 - onesInBlock) * i
}
return res
}
private fun func(n: Long): Long {
if (n == 0L) return 0L
val maxNum = getMaxNum(n)
val placesOccupied = getNumBits(maxNum)
var ans = getSum(maxNum)
var remaining = n - placesOccupied
var maxNumPlusOne = maxNum + 1
for (i in 0 until 64) {
if (maxNumPlusOne and (1L shl i) != 0L) {
remaining--
ans += i
}
if (remaining <= 0) break
}
return ans
}
fun solve(query: LongArray): Int {
val (L, R, mod) = query
return (power(2, func(R + 1) - func(L), mod) % mod).toInt()
}
fun findProductsOfElements(queries: Array<LongArray>): IntArray {
return queries.map { solve(it) }.toIntArray()
}
}
```
| 1
| 0
|
['Array', 'Math', 'Binary Search', 'Dynamic Programming', 'Bit Manipulation', 'Simulation', 'Binary Tree', 'Bitmask', 'Kotlin']
| 0
|
find-products-of-elements-of-big-array
|
most overcomplicated python solution???
|
most-overcomplicated-python-solution-by-cbx5i
|
Approach\nCounted the total number of set bits within a range of numbers [1, n] to find the index of a certain number in the large array. Used binary search to
|
bool3
|
NORMAL
|
2024-05-12T17:47:51.767460+00:00
|
2024-05-12T17:47:51.767496+00:00
| 52
| false
|
# Approach\nCounted the total number of set bits within a range of numbers [1, n] to find the index of a certain number in the large array. Used binary search to get from an index to a number. Counted the frequency of certain bits within a range and multiplied each bit\'s frequency into a cumulative variable by using binary exponentiation under mod. The edge cases were the end points of the query\'s interval and I did those manually.\n\nI was so close to solving this in contest :_(\n\n# Complexity\n- Time complexity: O(log^2(n))\n\n- Space complexity: O(q) where q is number of queries\n\n# Code\n```py\nclass Solution:\n def findProductsOfElements(self, queries: List[List[int]]) -> List[int]:\n def fastpow(b, e, m):\n if e == 0: return 1\n t = fastpow(b, e >> 1, m)\n if e & 1: return (b * (t * t) % m) % m\n return (t * t) % m\n \n def countSetBits(n):\n if n == 0: return 0\n m = int(math.log2(n))\n if n == ((1 << (m+1))-1):\n return ((m+1) * (1 << m))\n n -= (1 << m)\n return (n + 1) + countSetBits(n) + (m * (1 << (m-1)))\n \n def getIndex(n):\n return countSetBits(n-1)\n\n def getNumber(idx):\n lo, hi = 1, int(1e15)\n while lo < hi:\n mid = lo + ((hi - lo + 1) >> 1)\n sidx = getIndex(mid)\n if sidx > idx: hi = mid - 1\n else: lo = mid\n return lo\n \n def getBitCountN(n, b):\n if b == 0: return n >> 1\n tp = n >> b\n cnt = (tp >> 1) << b\n if tp & 1: cnt += n & ((1 << b) - 1)\n return cnt\n \n def getBitCount(f, t, b):\n return getBitCountN(t+1, b) - getBitCountN(f, b)\n \n def getPowerfulArr(n):\n s = bin(n)[2:][::-1]\n return [(1 << i) for i in range(len(s)) if int(s[i])]\n \n ans = []\n for f, t, m in queries:\n a, b = getNumber(f), getNumber(t)\n if a == b:\n c = getIndex(a)\n t -= c; f -= c; cur = 1\n pa = getPowerfulArr(a)\n for i in range(f, t+1):\n cur *= pa[i]\n cur %= m\n ans.append(cur)\n continue\n s, e, cur = a + 1, b - 1, 1\n if e >= s:\n for i in range(64):\n p = 1 << i\n cur *= fastpow(p, getBitCount(s, e, i), m)\n cur %= m\n pa, pb = getPowerfulArr(a)[::-1], getPowerfulArr(b)\n for i in range(t+1-getIndex(b)):\n cur *= pb[i]\n cur %= m\n for i in range(getIndex(a+1)-f):\n cur *= pa[i]\n cur %= m\n ans.append(cur)\n return ans\n```
| 1
| 0
|
['Python3']
| 0
|
find-products-of-elements-of-big-array
|
Easy to understand || Beats 100% || Bit Manipulation + Binary Search || C++
|
easy-to-understand-beats-100-bit-manipul-8g5j
|
Complexity\n- Time complexity:O(q.log^2n)\n Add your time complexity here, e.g. O(n) \n\n- Space complexity:O(logn)\n Add your space complexity here, e.g. O(n)
|
dubeyad2003
|
NORMAL
|
2024-05-11T19:29:22.216030+00:00
|
2024-05-12T04:52:19.834799+00:00
| 118
| false
|
# Complexity\n- Time complexity:$$O(q.log^2n)$$\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:$$O(logn)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n using ll = long long;\n // binary exponentiation for computing the power of the number\n ll binpow(ll a, ll b, ll m) {\n a %= m;\n ll res = 1;\n while (b > 0) {\n if (b & 1)\n res = res * a % m;\n a = a * a % m;\n b >>= 1;\n }\n return res;\n }\n // function to find the setBitsCount at the bit position for the numbers from 0...n\n vector<ll> setBitsCount(ll num){\n vector<ll> cnt(61);\n for(ll i=60; i>=0; i--){\n ll d = 1LL << i;\n ll q = num / d;\n if(q & 1){\n cnt[i] += num - d * q;\n }\n cnt[i] += q/2 * d;\n }\n return cnt;\n }\n // function to find the total count of the set bits for the numbers from 0...n\n ll totalBits(ll num){\n vector<ll> cnt = setBitsCount(num + 1);\n ll sum = 0;\n for(ll i=0; i<61; i++) sum += cnt[i];\n return sum;\n }\n // function to find the number which is at the query index\n ll findLimit(ll num){\n ll s = 1, e = 1e15;\n ll ans = 1e15;\n while(s <= e){\n ll mid = s + (e - s) / 2;\n if(totalBits(mid) >= num){\n ans = mid;\n e = mid - 1;\n }else s = mid + 1;\n }\n return ans;\n }\n vector<int> findProductsOfElements(vector<vector<long long>>& queries) {\n /* \n Steps to solve this problem:\n 1. First find the lower and upper limit of the range using binary search.\n 2. Find the bit frequency within the range of the limits\n 3. Just do binary exponentiation and find out the result\n */\n vector<int> ans;\n for(auto it: queries){\n ll cl = it[0], ch = it[1] + 1, mod = it[2];\n ll l = findLimit(cl) - 1;\n ll h = findLimit(ch);\n vector<ll> cntL = setBitsCount(l + 1);\n vector<ll> cntH = setBitsCount(h + 1);\n ll sumH = totalBits(h);\n ll sumL = totalBits(l);\n // handling the excess case, when the total set bit count is greater than the required.\n for(ll i=60; i>=0; i--){\n if((h >> i) & 1){\n if(ch < sumH){\n sumH--;\n cntH[i]--;\n }\n }\n }\n l += 1;\n // handling the limit, when the total set bit count is lesser than the required.\n for(ll i=0; i<61; i++){\n if((l >> i) & 1){\n if(cl > sumL){\n sumL++;\n cntL[i]++;\n }\n }\n }\n // now finding the set bit count of each bit position for the numbers within the range\n for(ll i=0; i<61; i++) cntH[i] -= cntL[i];\n ll pd = 1;\n // now computing the required result\n for(ll i=0; i<61; i++){\n pd = (pd * binpow(1LL << i, cntH[i], mod)) % mod;\n }\n ans.push_back(pd);\n }\n return ans;\n }\n};\n```
| 1
| 2
|
['C++']
| 0
|
find-products-of-elements-of-big-array
|
Complicated recurrence, faster than 100%
|
complicated-recurrence-faster-than-100-b-b6hq
|
Intuition\n Describe your first thoughts on how to solve this problem. \nThe answer is a power of 2 modulo the given mod. It suffices to keep track of the power
|
mbeceanu
|
NORMAL
|
2024-05-11T18:22:46.560458+00:00
|
2024-05-16T03:09:43.609749+00:00
| 113
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nThe answer is a power of 2 modulo the given mod. It suffices to keep track of the power of 2 and further it suffices to compute the total power of 2 from the start of the array up to each given index, then subtract the lower bound from the upper bound.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nHere is the derivation of the recurrence relation.\nSuppose we have an array with the representation of a consecutive sequence of numbers. Each representation ends with a fixed suffix $prd\\_lst$ of length $x$, where $x$ can be $0$.\nFor example, such a list can be\n$$\n4, 1, 4, 2, 4, 1, 2, 4\n$$\nas given in the problem. Here $x=1$ and the suffix is $4$. The list starts with the suffix itself, then (1, 4), (2, 4), (1, 2, 4), $\\ldots$, each term being the binary representation of some number ending in the suffix.\n\nThis is a slight generalization of the initial problem, but is easier to solve because we can use recursion. In the initial problem, $x=0$ and there is no suffix.\n\nThe problem is determining the product of all numbers up to the $a$-th position in this list.\nIf $a \\leq x$, then we take the product of some subsequence of $prd\\_lst$.\nOtherwise, we consider sublists of this list, of length\n$$\n\\ell_0=x,\\ \\ell_{k+1}=2\\ell_k+2^k.\n$$\nIn the example above, the sublists are\n$$\n\\{4\\},\\ \\{4, 1, 4\\}, \\{4, 1, 4, 2, 4, 1, 2, 4\\},\n$$\nof length $\\ell_0=1$, $\\ell_1=2\\cdot 1+2^0=3$, $\\ell_3=2\\cdot 3+2^1=8$.\nEach sublist contains all the numbers up to a certain last binary digit: the first one is going up to $0$, the second one is going up to $1$, the third one is going up to $2$.\n\nEach new sublist contains two copies of the previous sublist, namely one identical copy in the beginning followed by one modified copy in which each listing has an extra suffix. For example, the sublist corresponding to $k=2$\n$$\n4, 1, 4, 2, 4, 1, 2, 4\n$$\ncontains one identical copy of the previous sublist $4,(1,4)$, followed by a modified copy in which the suffix $4$ is replaced by $2,4$. The second half has $2^{k-1}$ extra values of $2^{k-1}=2$.\nIn the same way, we can count the total power of $2$ in each sublist, which is given by the recurrence relation\n$$\np_0=prod,\\ p_{k+1}=2*p_0+k \\cdot 2^k.\n$$\nHere $prod$ is the power of $2$ in the product of the elements in the suffix $prod\\_lst$. The $k+1$-th sublist always contains two copies of the $k$-th sublist and has $2^k$ extra elements equal to $2^k$.\n\nWhen computing the product of all elements up to $a$, we look for the longest sublist such that $\\ell_k<a$. The answer contains the computed value of $p_k$ and we then use recursion for the next segment from $\\ell_k+1$ to $a$.\nThis second computation uses exactly the same method, but $a$ is replaced by $a-\\ell_k$, we increase $x$ by $1$, and we include $2^k$ in the suffix.\n\nThis algorithm is used in the program below.\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nOn the latest run, this solution ran in 119ms.\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def findProductsOfElements(self, queries: List[List[int]]) -> List[int]:\n @cache\n def pr(a):\n return pro(a, 0, 0, ())\n def pro(a, x, prd, prd_lst):\n if a<=x:\n return sum(prd_lst[:a])\n k=0\n ans=prd\n l=x\n nxt=(l<<1)+(1<<k)\n while nxt<a:\n l=nxt\n ans=(ans<<1)+(k<<k)\n k+=1\n nxt=(l<<1)+(1<<k)\n return ans+pro(a-l, x+1, prd+k, (k,)+prd_lst)\n return [pow(2, pr(b+1)-pr(a), p) for a, b, p in queries] \n```
| 1
| 1
|
['Python3']
| 0
|
find-products-of-elements-of-big-array
|
Dynamic Programming and Binary Search for Powerful Array Queries
|
dynamic-programming-and-binary-search-fo-e8v4
|
Intuition\nThe problem requires finding products of elements within a certain range modulo a given number. To efficiently solve this problem, we can use dynamic
|
pavan_riser
|
NORMAL
|
2024-05-11T16:40:35.634112+00:00
|
2024-05-11T16:40:35.634131+00:00
| 348
| false
|
# Intuition\n**The problem requires finding products of elements within a certain range modulo a given number. To efficiently solve this problem, we can use dynamic programming to calculate the number of bits required to represent a number, perform binary search to find the maximum number within a given range, and calculate the summation of bits within the range.**\n\n# Approach\n***Dynamic Programming for Number of Bits:***\n\nUtilize dynamic programming to calculate the number of bits required to represent a number.\nStore the calculated number of bits for each number in a map to avoid redundant computations.\n\n***Binary Search for Maximum Number:***\n\nPerform a binary search to find the maximum number within a given range.\nUtilize the previously calculated number of bits to determine if a number falls within the range.\n\n***Summation of Bits:***\n\nCalculate the summation of bits within a given range.\nIterate through each bit position, calculating the contribution of ones in complete blocks and any remaining bits.\n\n***Main Function to Compute Result:***\n\nCombine the above calculations to compute the final result for a given range.\nCalculate the sum of bits within the range and adjust for any remaining bits.\n\n***Power Function and Modular Arithmetic:***\n\nCompute the result for each query using the previously defined functions.\nUtilize a power function to efficiently compute powers modulo the given number.\n\n# Complexity\n- Time complexity:\n**O(QlogN), where Q is the number of queries and N is the maximum number in the queries.**\n\n- Space complexity:\n**O(logN), due to dynamic programming and additional space for storing intermediate results.**\n\n# Code\n```\nclass Solution {\nprivate:\n unordered_map<long long, long long> dp;\n \n long long power(long long n, long long expo, long long mod)\n {\n long long ans = 1;\n \n while (expo)\n {\n if (expo % 2)\n ans = ans * n % mod;\n \n n = n * n % mod;\n expo /= 2;\n }\n \n return ans;\n }\n \n long long getNumBits(long long n)\n {\n if (n == 0)\n return 0;\n \n if (dp.count(n))\n return dp[n];\n \n long long ans = 0, num = n + 1;\n \n for (int i = 60; i >= 0; i--)\n if ((1LL << i) < num)\n {\n ans = getNumBits((1LL << i) - 1);\n \n long long rem = num - (1LL << i);\n \n ans += getNumBits(rem - 1) + rem;\n break;\n }\n \n return dp[n] = ans;\n }\n \n long long getMaxNum(long long n)\n {\n long long left = 1, right = 1e15, ans = 0;\n \n while (left <= right)\n {\n long long mid = (left + right) / 2;\n \n long long placesOccupied = getNumBits(mid);\n \n if (placesOccupied <= n)\n ans = mid, left = mid + 1;\n else\n right = mid - 1;\n }\n \n return ans;\n }\n \n long long getSum(long long n)\n {\n long long res = 0;\n \n for (int i = 1; i < 50; i++)\n {\n long long blockSize = (1LL << (i + 1));\n long long onesInBlock = blockSize / 2;\n \n long long completeBlocks = n / blockSize;\n \n res += completeBlocks * onesInBlock * i;\n \n long long rem = n % blockSize;\n res += max(0LL, rem + 1 - onesInBlock) * i;\n }\n \n return res;\n }\n \n long long func(long long n)\n {\n if (n == 0)\n return 0;\n \n long long maxNum = getMaxNum(n);\n long long placesOccupied = getNumBits(maxNum);\n \n long long ans = getSum(maxNum);\n \n maxNum++;\n long long rem = n - placesOccupied;\n \n for (int i = 0; rem > 0; i++)\n if (maxNum & (1LL << i))\n {\n rem--;\n ans += i;\n }\n \n return ans;\n }\n \n int solve(vector<long long> &query) {\n long long L = query[0], R = query[1], mod = query[2];\n \n return power(2, func(R + 1) - func(L), mod) % mod;\n }\npublic:\n vector<int> findProductsOfElements(vector<vector<long long>>& queries) {\n vector<int> res;\n \n for (auto q: queries)\n res.push_back(solve(q));\n \n return res;\n }\n};\n\n```
| 1
| 0
|
['Binary Search', 'Dynamic Programming', 'C++']
| 0
|
find-products-of-elements-of-big-array
|
🔥🔥 Beats 100.00% || 3772ms || Hard 🔥🔥
|
beats-10000-3772ms-hard-by-umair__saad-ch56
|
\n\n# Code\nPython []\ndef getcount(n, k):\n n += 1\n res = (n >> (k + 1)) << k\n if (n >> k) & 1:\n res += n & ((1 << k) - 1)\n return res\n
|
Umair__Saad
|
NORMAL
|
2024-05-11T16:05:19.644646+00:00
|
2024-05-11T16:05:19.644664+00:00
| 210
| false
|
\n\n# Code\n```Python []\ndef getcount(n, k):\n n += 1\n res = (n >> (k + 1)) << k\n if (n >> k) & 1:\n res += n & ((1 << k) - 1)\n return res\n\ndef gettotal(n):\n res = 0\n for b in range(60):\n res += getcount(n, b)\n return res\n\nclass Solution:\n def findProductsOfElements(self, queries: List[List[int]]) -> List[int]:\n res = []\n for f, t, mod in queries:\n beg = 1\n end = 10 ** 15\n l = r = 0\n while beg <= end:\n mid = (beg + end) // 2\n if gettotal(mid - 1) >= f:\n l = mid\n end = mid - 1\n else:\n beg = mid + 1\n beg = 1\n end = 10 ** 15\n while beg <= end:\n mid = (beg + end) // 2\n if gettotal(mid) - 1 <= t:\n r = mid\n beg = mid + 1\n else:\n end = mid - 1\n s = 0\n for b in range(60):\n if l > r:\n continue\n s += b * (getcount(r, b) - getcount(l - 1, b))\n curr = pow(2, s, mod)\n val = l - 1\n pos = gettotal(val - 1)\n pw = 1\n while val:\n if val & 1:\n if f <= pos <= t:\n curr *= pw\n curr %= mod\n pos += 1\n pw *= 2\n val //= 2\n if r + 1 != l - 1:\n val = r + 1\n pos = gettotal(val - 1)\n pw = 1\n while val:\n if val & 1:\n if f <= pos <= t:\n curr *= pw\n curr %= mod\n pos += 1\n pw *= 2\n val //= 2\n res.append(curr)\n return res\n```
| 1
| 2
|
['Python3']
| 0
|
find-products-of-elements-of-big-array
|
Count bits in range using BS
|
count-bits-in-range-using-bs-by-theabbie-bc3n
|
\ndef getcount(n, k):\n n += 1\n res = (n >> (k + 1)) << k\n if (n >> k) & 1:\n res += n & ((1 << k) - 1)\n return res\n\ndef gettotal(n):\n
|
theabbie
|
NORMAL
|
2024-05-11T16:01:02.534971+00:00
|
2024-05-11T16:01:02.535014+00:00
| 203
| false
|
```\ndef getcount(n, k):\n n += 1\n res = (n >> (k + 1)) << k\n if (n >> k) & 1:\n res += n & ((1 << k) - 1)\n return res\n\ndef gettotal(n):\n res = 0\n for b in range(60):\n res += getcount(n, b)\n return res\n\nclass Solution:\n def findProductsOfElements(self, queries: List[List[int]]) -> List[int]:\n res = []\n for f, t, mod in queries:\n beg = 1\n end = 10 ** 15\n l = r = 0\n while beg <= end:\n mid = (beg + end) // 2\n if gettotal(mid - 1) >= f:\n l = mid\n end = mid - 1\n else:\n beg = mid + 1\n beg = 1\n end = 10 ** 15\n while beg <= end:\n mid = (beg + end) // 2\n if gettotal(mid) - 1 <= t:\n r = mid\n beg = mid + 1\n else:\n end = mid - 1\n s = 0\n for b in range(60):\n if l > r:\n continue\n s += b * (getcount(r, b) - getcount(l - 1, b))\n curr = pow(2, s, mod)\n val = l - 1\n pos = gettotal(val - 1)\n pw = 1\n while val:\n if val & 1:\n if f <= pos <= t:\n curr *= pw\n curr %= mod\n pos += 1\n pw *= 2\n val //= 2\n if r + 1 != l - 1:\n val = r + 1\n pos = gettotal(val - 1)\n pw = 1\n while val:\n if val & 1:\n if f <= pos <= t:\n curr *= pw\n curr %= mod\n pos += 1\n pw *= 2\n val //= 2\n res.append(curr)\n return res\n```
| 1
| 1
|
['Python']
| 0
|
find-products-of-elements-of-big-array
|
Modular Code | Observations | Visualisation
|
modular-code-observations-visualisation-sl0zh
|
Here's how i visualised the solution :Calculation of no. of setbits at a position i for numbers from 0 to x
consider (0 based), cycle starts at 0
f(i,x) = 2^i *
|
lokeshwar777
|
NORMAL
|
2025-02-07T07:08:58.686403+00:00
|
2025-02-07T07:20:33.995811+00:00
| 9
| false
|
Here's how i visualised the solution :
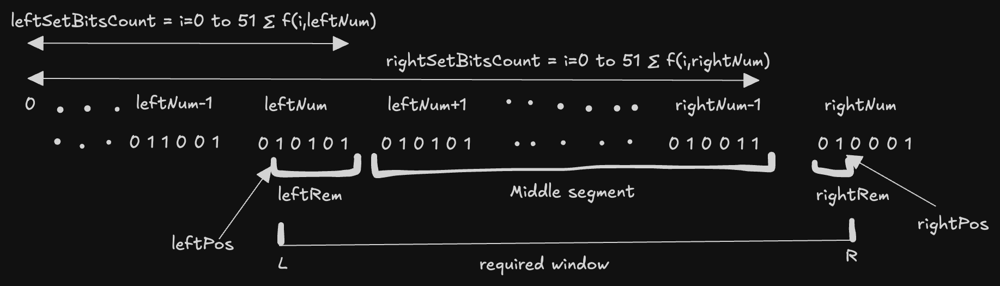
### Calculation of no. of setbits at a position i for numbers from 0 to x
- consider (0 based), cycle starts at 0
- `f(i,x) = 2^i * (x+1)/(2^(i+1)) + max(0,(x+1)%(2^(i+1)) - 2^i)`
- `f(i,x)= set bits in each cycle * no. of cycles + remaining`
- remaining =`max(0,(x % no. of cycles)` - unset bits in each cycle
- set bits = unset bits = `2^i` in each cycle
# Code
```python3 []
'''
1. big_nums is formed from 1's
2. f(i,x) - no of setbits at ith position in all numbers from 0->x
3. binary search on ∑f(i,x) to get the num contains the position of 'from' and 'to'
4. consider 3 segments - partia(leftNum) + [leftNum+1 + ... + rightNum-1] + partial(rightNum)
5. carefully preform bit manipulations if you are doing << or >> to check for 0th bit
((num>>i)&1) - this is correct
(num&(1<<i)) - this is wrong
6. the answer is some power of 2 with mod as all the elements of big_nums are powers of 2
7. we just need to find the power of 2 which is the sum of set bits in the range(from,to)
'''
class Solution:
maxBits=50
# returns no. of set bits i->[0,..),x->[0,...)
def getSetBitsAtPos(self,i,x): return (1<<i)*((x+1)//(1<<(i+1))) + max(0,(x+1)%(1<<(i+1))-(1<<i))
def getNum(self,low,high,k,ans):
while low<=high:
mid=low+((high-low)>>1)
cnt=sum(self.getSetBitsAtPos(i,mid) for i in range(self.maxBits))
if cnt>=k:
ans=mid
high=mid-1
else:
low=mid+1
return ans
def getPos(self,reqBits,currNum):
currBits=sum(self.getSetBitsAtPos(i,currNum) for i in range(self.maxBits))
diff=reqBits-currBits
currNum+=1
for pos in range(self.maxBits):
diff-=(currNum>>pos)&1
if diff==0:return pos
return 0
def findProductsOfElements(self, queries):
res=[]
for left,right,mod in queries:
left+=1
right+=1
leftNum=self.getNum(0,int(1e15),left,0)
leftPos=self.getPos(left,leftNum-1)
leftRem=(leftNum>>leftPos)<<leftPos
# print(leftNum,leftPos,leftRem)
rightNum=self.getNum(0,int(1e15),right,0)
rightPos=self.getPos(right,rightNum-1)
rightRem=0
for i in range(rightPos+1):rightRem|=(1<<i)&rightNum
# print(rightNum,rightPos,rightRem)
bitsCount=sum(i*(
self.getSetBitsAtPos(i,rightNum-1) - self.getSetBitsAtPos(i,leftNum) # middleSetBits
+ ((leftRem>>i)&1) + ((rightRem>>i)&1)
) for i in range(self.maxBits))
# print(bitsCount)
res.append(pow(2,bitsCount,mod))
return res
```
Thank You @vivgupta98
| 0
| 0
|
['Binary Search', 'Bit Manipulation', 'Counting', 'Prefix Sum', 'Python3']
| 0
|
find-products-of-elements-of-big-array
|
Explained bit manipulation, clean code
|
explained-bit-manipulation-clean-code-by-ct93
|
Approach
For each query [L, R, MOD], we:
Calculate counts of powers of 2 up to L and R+1
Use difference array technique to get counts in range [L, R]
Compute
|
ivangnilomedov
|
NORMAL
|
2025-01-05T14:30:37.863562+00:00
|
2025-01-05T14:30:37.863562+00:00
| 9
| false
|
# Approach
1. For each query [L, R, MOD], we:
- Calculate counts of powers of 2 up to L and R+1
- Use difference array technique to get counts in range [L, R]
- Compute product using modular exponentiation
2. The core bit manipulation magic happens in `calculate_pow2_counts_till_value`:
- Visualize numbers as rows in binary matrix
- For each column k (power of 2):
```
Row Binary k=0 k=1 k=2
0 000 0 0 0
1 001 1 0 0
2 010 0 1 0
3 011 1 1 0
4 100 0 0 1
```
- Observe that 1s appear in periods of size 2^(k+1)
- Count complete periods with `(M >> (k + 1)) << k`
- Handle incomplete period by checking k-th bit and remainder
# Complexity
- Time complexity: $$O(Q \cdot \log^2 M)$$ where Q is number of queries and M is maximum value
- Each query requires binary search and bit counting operations
- Space complexity: $$O(\log M)$$ to store counts of powers of 2
# Code
```cpp []
class Solution {
public:
vector<int> findProductsOfElements(vector<vector<long long>>& queries) {
vector<int> res(queries.size());
transform(queries.begin(), queries.end(), res.begin(),
[](const auto& q) { return calculate_product(q[0], q[1], q[2]); });
return res;
}
private:
static int calculate_product(long long q_beg, long long q_end, long long q_mod) {
vector<long long> pow_count_beg = calculate_pow2_counts(q_beg);
vector<long long> pow_count_end = calculate_pow2_counts(q_end + 1);
for (int i = 0; i < pow_count_beg.size(); ++i)
pow_count_end[i] -= pow_count_beg[i];
long long res = 1;
for (int i = 1; i < pow_count_end.size(); ++i)
res = res * qpow(1LL << i, pow_count_end[i], q_mod) % q_mod;
return res % q_mod;
}
/** Calculates the count of each power of 2 in powerful arrays up to given size.
* 1. Binary search to find largest complete powerful array that fits
* 2. Calculate counts for complete arrays
* 3. Add remaining powers from the last incomplete array */
static vector<long long> calculate_pow2_counts(long long big_nums_prefix_size) {
long long beg = 0, end = big_nums_prefix_size + 1;
while (beg < end) {
long long mid = (beg + end) / 2;
if (calculate_pow2_counts_till_value(mid) > big_nums_prefix_size)
end = mid;
else
beg = mid + 1;
}
vector<long long> pow2_counts;
calculate_pow2_counts_till_value(beg - 1, &pow2_counts);
// Add remaining value i.e. beg to complete size to big_nums_prefix_size
long long size = accumulate(pow2_counts.begin(), pow2_counts.end(), 0LL);
for (int i = 0; beg > 0 && size < big_nums_prefix_size; ++i, beg >>= 1) {
if (beg & 1) {
if (pow2_counts.size() < i + 1)
pow2_counts.resize(i + 1);
++pow2_counts[i];
++size;
}
}
return pow2_counts;
}
/** Calculates the count of each power of 2 in powerful arrays up to a value.
* NOTE: value is the encoded positive number i.e. value=5 encoded as fragment: [.., 1, 4, ..]
* i.e. every value would be encoded into one or many elements; thus idx-es of value are > value
* @param out Optional vector to store the counts
* @return Total count of all powers of 2
* Uses bit manipulation. */
static long long calculate_pow2_counts_till_value(long long last_present_value, vector<long long>* out = nullptr) {
long long M = last_present_value + 1;
long long res = 0;
/** Calculate count of set bits (1s) in k-th column up to row M-1 in binary matrix:
* Row Binary k=0 k=1 k=2
* 0 000 0 0 0
* 1 001 1 0 0
* 2 010 0 1 0
* 3 011 1 1 0
* 4 100 0 0 1
* 5 101 1 0 1
* etc... */
for (long long k = 0; 1LL << k < M; ++k) {
// For k-th column, pattern of 1s and 0s has period of 2^(k+1)
// Each period contains 2^k ones
// ⌊M/(2^(k+1))⌋ gives number of complete periods
// Multiply by 2^k to get total ones in complete periods
long long count = (M >> (k + 1)) << k;
// Now handle the incomplete period at the end:
// Check if M has 1 in k-th position ((M >> k) & 1)
if ((M >> k) & 1)
// If yes, we need to count ones in remainder:
// M & (2^k - 1) gives remainder after last complete period
count += M & ((1LL << k) - 1);
res += count;
if (out)
out->push_back(count);
}
return res;
}
static long long qpow(long long b, long long p, long long mod) {
b %= mod;
long long res = 1;
for (; p > 0; p >>= 1, b = b * b % mod)
if (p & 1)
res = res * b % mod;
return res;
}
};
```
| 0
| 0
|
['C++']
| 0
|
find-products-of-elements-of-big-array
|
using binary search
|
using-binary-search-by-prazz_18-pb3e
| null |
prazz_18
|
NORMAL
|
2024-12-10T11:26:40.567256+00:00
|
2024-12-10T11:26:40.567256+00:00
| 6
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\nclass Solution {\npublic:\n #define ll long long \n ll binpow(ll a, ll n, ll m) {\n a = a%m;\n ll res = 1;\n while (n) {\n if (n & 1) {\n res = (res * a) % m;\n n--;\n }\n else {\n n /= 2;\n a = (a * a) % m;\n }\n }\n return res;\n }\n void build(ll x, vector<ll>&cb) {\n ll i = 1;\n x++;\n ll tot = 0;\n ll f = 1;\n while (f) {\n ll cnt = x / (1ll << i);\n ll rem = x % (1ll << i);\n cnt = cnt * (1ll << (i - 1));\n cnt += max(0ll, rem - (1ll << (i - 1)));\n cb[i - 1] = cnt;\n i++;\n if (cnt == 0)f = 0;\n }\n }\n ll cnt(ll x) {\n x++;\n ll i = 1;\n ll tot = 0;\n ll f = 1;\n while (f) {\n ll cnt = x / (1ll << i);\n ll rem = x % (1ll << i);\n cnt = cnt * (1ll << (i - 1));\n cnt += max(0ll, rem - (1ll << (i - 1)));\n tot += cnt;\n i++;\n if (cnt == 0)f = 0;\n }\n return tot;\n }\n ll f(ll r) {\n ll lo = 0; ll hi = 1e15;\n ll ans = 0;\n auto chk = [&](ll x) -> bool {\n ll tot = cnt(x);\n // db(x, cnt(x));\n return (tot - 1 <= r);\n };\n while (lo <= hi) {\n ll mid = (lo + hi) >> 1;\n if (chk(mid)) {\n lo = mid + 1;\n ans = mid;\n }\n else hi = mid - 1;\n }\n return ans;\n }\n\n vector<int> findProductsOfElements(vector<vector<long long>>& qry) {\n ll q = size(qry);\n vector<int>res(q);\n for(int i=0;i<q;++i){\n ll l,r,m;\n l = qry[i][0];\n r = qry[i][1];\n m = qry[i][2];\n // to find a y such that total number of set bits <= r-1\n ll y = f(r);\n // db(y);\n vector<ll>cb1(63, 0), cb2(63, 0);\n build(y, cb2);\n if (cnt(y) - 1 <= r) {\n ll left = r + 1 - cnt(y);\n y++;\n for (ll i = 0; i < 63; ++i) {\n if (((1ll << i) & y) && left) {\n cb2[i]++;\n left--;\n }\n }\n }\n ll x = f(l - 1);\n build(x, cb1);\n if (cnt(x) <= l - 1) {\n ll left = l - cnt(x);\n x++;\n // db(left, x);\n for (ll i = 0; i < 63; ++i) {\n if (((1ll << i) & x) && left) {\n cb1[i]++;\n left--;\n }\n }\n }\n for (ll i = 0; i < 63; ++i) {\n cb2[i] = (cb2[i] - cb1[i]);\n }\n \n ll ans = 1;\n for (ll i = 0; i < 63; ++i) {\n ll x = binpow((1ll << i), cb2[i], m);\n ans = (ans * x) % m;\n }\n res[i] = ans;\n }\n return res;\n }\n};\n```
| 0
| 0
|
['C++']
| 0
|
find-products-of-elements-of-big-array
|
Multiple Ques in a single ques. || Binomial Modularity || Binary search || O(logn) || Math
|
multiple-ques-in-a-single-ques-binomial-9ea8h
|
\n# Complexity\n- Time complexity:\n Add your time complexity here, e.g. O(n) \nO(logn)\n- Space complexity:\n Add your space complexity here, e.g. O(n) \nO(n)\
|
Priyanshu_pandey15
|
NORMAL
|
2024-08-29T19:13:34.358446+00:00
|
2024-08-29T19:15:36.685855+00:00
| 9
| false
|
\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(logn)$$\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(n)$$\n# Code\n```java []\nclass Solution {\n \n public int[] findProductsOfElements(long[][] queries) {\n int n = queries.length;\n int[] res = new int[n];\n for (int i = 0; i < n; i++) {\n long from = queries[i][0] + 1;\n long to = queries[i][1] + 1;\n long mod = queries[i][2];\n \n long lbb = lb(from);\n long ubb = ub(to);\n long[] a1 = make(lbb);\n long[] a2 = make(ubb);\n \n increase(a1, from, lbb);\n decrease(a2, to, ubb);\n improve(a2, a1);\n \n long sum = set(a2);\n res[i] = (int) me(sum, mod);\n }\n return res;\n }\n\n public static long me( long ex, long mod) {\n long result = 1 , x = 1 , y = 2;\n if(mod == 1) return 0;\n while(x <= ex){\n if( (ex & x) == x ){\n result *= y;\n result %= mod;\n }\n x <<= 1l;\n y *= y;\n y %= mod;\n }\n return result;\n }\n\n static long set(long[] a2) {\n long sum = 0;\n for (int i = 1; i < a2.length; i++) {\n sum += (i * a2[i]);\n }\n return sum;\n }\n\n static void improve(long[] a2, long[] a1) {\n int n = a2.length;\n for (int i = 1; i < n; i++) {\n a2[i] -= a1[i];\n }\n }\n\n static void decrease(long[] ub, long to, long ubb) {\n long x = bits(ubb) - to;\n int i = ub.length - 1;\n while (i >= 0 && x > 0) {\n if (((ubb >> i) & 1) == 1) {\n x--;\n ub[i]--;\n }\n i--;\n }\n }\n\n static void increase(long[] lb, long from, long lbb) {\n long x = from - bits(lbb) - 1;\n int i = 0,n = lb.length;\n while (i < n && x > 0) {\n if (((lbb + 1 >> i) & 1) == 1) {\n x--;\n lb[i]++;\n }\n i++;\n }\n }\n\n static long[] make(long n) {\n long[] arr = new long[47];\n long x = 1 , kk = arr.length;\n for (int i = 0; i < kk; i++) {\n arr[i] = ((n / x) / 2) * x + ((n % x + 1) * ((n / x) % 2));\n x *= 2;\n }\n return arr;\n }\n\n static long ub(long to) {\n long s = 0, e = to, m, ans = -1;\n while (s <= e) {\n m = s + (e - s) / 2;\n if (bits(m) >= to) {\n ans = m;\n e = m - 1;\n } else {\n s = m + 1;\n }\n }\n return ans;\n }\n\n static long lb(long from) {\n long s = 0, e = from, m, ans = -1;\n while (s <= e) {\n m = s + (e - s) / 2;\n if (bits(m) < from) {\n ans = m;\n s = m + 1;\n } else {\n e = m - 1;\n }\n }\n return ans;\n }\n\n static long bits(long n) {\n long x = 1, s = 0;\n for (int i = 0; i < 47; i++) {\n s += ((n / x) / 2) * x + (n % x + 1) * ((n / x) % 2);\n x *= 2;\n }\n return s;\n }\n}\n\n```
| 0
| 0
|
['Array', 'Math', 'Binary Search', 'Bit Manipulation', 'Java']
| 0
|
find-products-of-elements-of-big-array
|
520 ms
|
520-ms-by-0x81-xva5
|
ruby\ndef pref t\n rc = 0\n x = (0..[t, 45 * 10 ** 12].min).bsearch do | x |\n c = 0\n d = 1\n y = d << 1\n while d <= x\n
|
0x81
|
NORMAL
|
2024-08-04T11:03:21.013655+00:00
|
2024-08-04T11:18:51.421043+00:00
| 3
| false
|
```ruby\ndef pref t\n rc = 0\n x = (0..[t, 45 * 10 ** 12].min).bsearch do | x |\n c = 0\n d = 1\n y = d << 1\n while d <= x\n a, b = x .divmod y\n c += a * d + (b - d.pred).clamp(0, d)\n d <<= 1\n y <<= 1\n end\n c >= t && !!(rc = c)\n end\n s = 0\n p = 1\n d = 2\n y = d << 1\n while d <= x\n a, b = x .divmod y\n s += (a * d + (b - d.pred).clamp(0, d)) * p\n d <<= 1\n y <<= 1\n p += 1\n end\n s -\n 50.times\n .select { x[_1] == 1 }\n .reverse!\n .take(rc - t)\n .sum\nend\n\ndef find_products_of_elements(q) =\n q.map! { 2.pow pref(_2.next) - pref(_1), _3 }\n```
| 0
| 0
|
['Ruby']
| 0
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.