question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
find-maximum-number-of-string-pairs
|
[ Python ] ✅✅ Simple Python Solution Using HashMap | 95 % Faster🥳✌👍
|
python-simple-python-solution-using-hash-wr0i
|
If You like the Solution, Don\'t Forget To UpVote Me, Please UpVote! \uD83D\uDD3C\uD83D\uDE4F\n# Runtime: 52 ms, faster than 95.84% of Python3 online submission
|
ashok_kumar_meghvanshi
|
NORMAL
|
2023-06-28T10:46:16.813176+00:00
|
2023-06-28T10:46:16.813208+00:00
| 189
| false
|
# If You like the Solution, Don\'t Forget To UpVote Me, Please UpVote! \uD83D\uDD3C\uD83D\uDE4F\n# Runtime: 52 ms, faster than 95.84% of Python3 online submissions for Find Maximum Number of String Pairs.\n# Memory Usage: 16.3 MB, less than 77.61% of Python3 online submissions for Find Maximum Number of String Pairs.\n\n\n\n\tclass Solution:\n\t\tdef maximumNumberOfStringPairs(self, words: List[str]) -> int:\n\n\t\t\tresult = 0\n\t\t\thash_map = {}\n\n\t\t\tfor word in words:\n\n\t\t\t\treverse_word = word[::-1]\n\n\t\t\t\tif reverse_word in hash_map:\n\t\t\t\t\thash_map[reverse_word] = hash_map[reverse_word] + 1\n\n\t\t\t\telif word not in hash_map:\n\t\t\t\t\thash_map[word] = 1\n\n\t\t\tfor key in hash_map:\n\n\t\t\t\tif hash_map[key] > 1:\n\t\t\t\t\tresult = result + 1\n\n\t\t\treturn result\n\t\t\t\n# Thank You \uD83E\uDD73\u270C\uD83D\uDC4D
| 1
| 0
|
['Hash Table', 'String', 'Python', 'Python3']
| 1
|
find-maximum-number-of-string-pairs
|
Easy and Understandable Code || Accepted✅✅
|
easy-and-understandable-code-accepted-by-a1us
|
Intuition\n Describe your first thoughts on how to solve this problem. \nReverse can help\n\n# Approach\n Describe your approach to solving the problem. \n1. It
|
Sanjeev_PU
|
NORMAL
|
2023-06-26T17:39:25.846528+00:00
|
2023-06-26T17:39:25.846545+00:00
| 92
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nReverse can help\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Iterate the loop\n2. each and every word reverse\n3. and check weather they are equal or not\n4. print result \n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n$$O(n2)$$\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n$$O(1)$$\n\n# Code\n```\nclass Solution {\npublic:\n int maximumNumberOfStringPairs(vector<string>& words) {\n int n = words.size();\n int ans = 0;\n for(int i=0;i<n;i++){\n for(int j = i+ 1;j<n;j++){\n string s1 = words[i];\n string s2 = words[j];\n reverse(s2.begin(), s2.end());\n // cout<<s1<<" "<<s2<<endl;\n if(s1 == s2){\n ans++;\n // cout<<ans;\n }\n \n }\n }\n return ans;\n \n }\n};\n```
| 1
| 0
|
['C++']
| 0
|
find-maximum-number-of-string-pairs
|
easy one xd
|
easy-one-xd-by-shellpy03-2gox
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
shellpy03
|
NORMAL
|
2023-06-26T16:48:50.193833+00:00
|
2023-06-26T16:48:50.193915+00:00
| 90
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\nfunc maximumNumberOfStringPairs(words []string) int {\n\tst := make(map[string]bool)\n\tres := 0\n\tfor _, i := range words {\n\t\ts := i\n\t\ti = reverseString(i)\n\t\tif !st[i] {\n\t\t\tst[s] = true\n\t\t} else {\n\t\t\tres++\n\t\t}\n\t}\n\treturn res\n}\n\nfunc reverseString(s string) string {\n\trunes := []rune(s)\n\tfor i, j := 0, len(runes)-1; i < j; i, j = i+1, j-1 {\n\t\trunes[i], runes[j] = runes[j], runes[i]\n\t}\n\treturn string(runes)\n}\n```
| 1
| 0
|
['Go']
| 0
|
find-maximum-number-of-string-pairs
|
easy one xd
|
easy-one-xd-by-shellpy03-sqb1
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
shellpy03
|
NORMAL
|
2023-06-26T16:48:48.512980+00:00
|
2023-06-26T16:48:48.513015+00:00
| 18
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\nO(N)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nO(1)\n# Code\n```\nfunc maximumNumberOfStringPairs(words []string) int {\n\tst := make(map[string]bool)\n\tres := 0\n\tfor _, i := range words {\n\t\ts := i\n\t\ti = reverseString(i)\n\t\tif !st[i] {\n\t\t\tst[s] = true\n\t\t} else {\n\t\t\tres++\n\t\t}\n\t}\n\treturn res\n}\n\nfunc reverseString(s string) string {\n\trunes := []rune(s)\n\tfor i, j := 0, len(runes)-1; i < j; i, j = i+1, j-1 {\n\t\trunes[i], runes[j] = runes[j], runes[i]\n\t}\n\treturn string(runes)\n}\n```
| 1
| 0
|
['Go']
| 0
|
find-maximum-number-of-string-pairs
|
Easy Java using Map
|
easy-java-using-map-by-pushprajdubey-tdvl
|
\n\n# Code\n\nclass Solution {\n public int maximumNumberOfStringPairs(String[] words) {\n int ans = 0;\n Map<String, Integer> wordss= new Hash
|
pushprajdubey
|
NORMAL
|
2023-06-26T14:38:27.058196+00:00
|
2023-06-26T14:38:27.058220+00:00
| 26
| false
|
\n\n# Code\n```\nclass Solution {\n public int maximumNumberOfStringPairs(String[] words) {\n int ans = 0;\n Map<String, Integer> wordss= new HashMap<>();\n\n for (String a : words) {\n String rWord = new StringBuilder(a).reverse().toString();\n int cnt = wordss.getOrDefault(rWord, 0);\n ans += cnt; \n wordss.put(a, cnt + 1); \n }\n\n return ans;\n }\n}\n```
| 1
| 0
|
['Hash Table', 'Ordered Map', 'Java']
| 0
|
find-maximum-number-of-string-pairs
|
Python || Beginner Friendly
|
python-beginner-friendly-by-sumedh0706-7zs3
|
Complexity\n- Time complexity:\nO(n^2)\n\n- Space complexity:\nO(1)\n\n# Code\n\nclass Solution:\n def maximumNumberOfStringPairs(self, words: List[str]) ->
|
Sumedh0706
|
NORMAL
|
2023-06-25T12:02:47.543997+00:00
|
2023-06-25T12:02:47.544019+00:00
| 259
| false
|
# Complexity\n- Time complexity:\nO(n^2)\n\n- Space complexity:\nO(1)\n\n# Code\n```\nclass Solution:\n def maximumNumberOfStringPairs(self, words: List[str]) -> int:\n cnt=0\n for i in range(len(words)):\n for j in range(i+1,len(words)):\n if words[i]==words[j][::-1]:\n cnt+=1\n break\n return cnt\n \n```
| 1
| 1
|
['Python3']
| 0
|
find-maximum-number-of-string-pairs
|
Go | Straightforward
|
go-straightforward-by-tucux-ucqo
|
\nfunc maximumNumberOfStringPairs(words []string) int {\n res := 0\n h := make(map[string]bool)\n for _, w := range words {\n if r := fmt.Sprint
|
tucux
|
NORMAL
|
2023-06-25T11:55:11.052338+00:00
|
2023-06-25T11:55:11.052366+00:00
| 61
| false
|
```\nfunc maximumNumberOfStringPairs(words []string) int {\n res := 0\n h := make(map[string]bool)\n for _, w := range words {\n if r := fmt.Sprintf("%c%c", w[1], w[0]); h[r] {\n res++\n } else {\n h[w] = true\n }\n }\n return res\n}\n```
| 1
| 0
|
['Go']
| 0
|
find-maximum-number-of-string-pairs
|
💀NO MAP , NO SET || Using Find( ) ||🔥 Easy C++
|
no-map-no-set-using-find-easy-c-by-nisha-3ja4
|
Intuition\nSimply Pick each words Reverse it and check by using find().\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n- Dry run t
|
Nishant_405
|
NORMAL
|
2023-06-25T07:32:46.756287+00:00
|
2023-06-28T08:23:33.612709+00:00
| 48
| false
|
# Intuition\nSimply Pick each words Reverse it and check by using find().\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n- Dry run the 1st Test Case.\n- pick the 1st string of the words and reverse it .\n- Befor finding the reversed string first check either 1st and 2nd letter are same or not (since there is only 2 char) \n- NOW using find().. we search for str(ie reversed string) in words[]\n- if found then increase the count \n- AND Here the important stepwe have to make words[i]=str ?? think u will get if not then....\n\n---> because if we futher check we will again reach to element whose reversed is present before ie increase the count 2 times .\n\n---> Eg ; 1St TC : ["cd","ac","dc",...] for "cd" we get "dc" in words[] and again for "dc" we get "cd" means extra count so replace with reversed(ie str itself) simpply...\n\ndry run more .... :)\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:O(N^2)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int maximumNumberOfStringPairs(vector<string>& words) {\n int cnt=0;\n for(int i=0;i<words.size();i++)\n {\n string str=words[i];\n reverse(str.begin(),str.end());\n if(str[0]==str[1]) continue; \n\n auto it = find(words.begin(),words.end(),str);\n if(it!=words.end())\n {\n cnt++;\n }\n words[i]=str;\n }\n return cnt;\n }\n};\n```
| 1
| 0
|
['String', 'String Matching', 'C++']
| 2
|
find-maximum-number-of-string-pairs
|
Swift | Simple Set && Self-made hash solutions
|
swift-simple-set-self-made-hash-solution-0lgs
|
Simple Set\n## Complexity\n- Time complexity: $O(n)$\n- Space complexity: $O(n)$\n$n$ is words count\n\n\nclass Solution {\n func maximumNumberOfStringPairs(
|
VladimirTheLeet
|
NORMAL
|
2023-06-25T07:18:04.841768+00:00
|
2023-06-25T10:49:28.499603+00:00
| 56
| false
|
# Simple Set\n## Complexity\n- Time complexity: $O(n)$\n- Space complexity: $O(n)$\n$n$ is words count\n\n```\nclass Solution {\n func maximumNumberOfStringPairs(_ words: [String]) -> Int\n {\n var wordSet: Set<String> = [], count = 0\n for word in words\n {\n if wordSet.contains(String(word.reversed())) { count += 1 }\n else { wordSet.insert(word) }\n }\n return count\n }\n}\n```\n\n# Custom hash\n\nAs the words are constained to have just 2 letters, we can do without the Set with its costly hash calculation. Just use ascii values of two letters, which can produce 26 * 26 = 676 combinations and map these combinations to a bit array.\nAlso when calculating hash we first bring the word\'s letters to ascending order. This conveniently ensures that reversals, i.e. pair words that we need to count will have the same hash value.\n\n## Complexity\n- Time complexity: $O(n)$\n- Space complexity: $O(26^m)$\n$n$ is words count, m is words letter count (currently 2)\n\n```\nclass Solution {\n func maximumNumberOfStringPairs(_ words: [String]) -> Int\n {\n var wordSet: [UInt8] = Array(repeating: 0, count: 26*26/8 + 1)\n let a: UInt8 = 97 //asciiValue\n\n func hash(_ word: String) -> Int\n {\n var chars = Array(word)\n if chars[0] > chars[1] { chars.swapAt(0, 1) }\n return Int(chars[0].asciiValue! - a) * 26 + Int(chars[1].asciiValue! - a)\n }\n func contains(_ word: String) -> Bool {\n let hashValue = hash(word)\n return wordSet[hashValue / 8] & (1 << (hashValue % 8)) != 0\n }\n func insert(_ word: String) {\n let hashValue = hash(word)\n wordSet[hashValue / 8] |= (1 << (hashValue % 8))\n }\n \n var count = 0\n for word in words\n {\n if contains(word) { count += 1 }\n else { insert(word) }\n }\n return count\n }\n}\n```
| 1
| 0
|
['Hash Table', 'Bit Manipulation', 'Swift', 'Hash Function']
| 0
|
find-maximum-number-of-string-pairs
|
Easy C++ Solution | Map
|
easy-c-solution-map-by-_white_rabbit-y3bs
|
Code\n\nclass Solution {\npublic:\n int maximumNumberOfStringPairs(vector<string>& words) {\n unordered_map<string, int> mp;\n int cnt = 0;\n
|
_White_Rabbit_
|
NORMAL
|
2023-06-24T17:38:13.366820+00:00
|
2023-06-24T17:38:13.366847+00:00
| 76
| false
|
# Code\n```\nclass Solution {\npublic:\n int maximumNumberOfStringPairs(vector<string>& words) {\n unordered_map<string, int> mp;\n int cnt = 0;\n for(int i=0;i<words.size();i++) {\n if(mp.find(words[i]) != mp.end()) {\n cnt++;\n mp.erase(words[i]);\n } else {\n swap(words[i][0], words[i][1]);\n mp[words[i]]++;\n }\n }\n return cnt;\n }\n};\n```
| 1
| 0
|
['C++']
| 0
|
find-maximum-number-of-string-pairs
|
🔥🔥 SIMPLE C++ SOLTION 🔥WITHOUT MAP🔥🔥
|
simple-c-soltion-without-map-by-aman91k-c1mv
|
\'\'\'\nclass Solution {\npublic:\n\n int maximumNumberOfStringPairs(vector& words) {\n int n=words.size();\n int cnt=0;\n \n for
|
aman91k
|
NORMAL
|
2023-06-24T16:39:32.257456+00:00
|
2023-06-24T16:39:32.257475+00:00
| 307
| false
|
\'\'\'\nclass Solution {\npublic:\n\n int maximumNumberOfStringPairs(vector<string>& words) {\n int n=words.size();\n int cnt=0;\n \n for(int i=0; i<n-1; i++){\n string s=words[i];\n for(int j=i+1; j<n; j++){\n string t=words[j];\n reverse(t.begin(), t.end());\n if(t==s && s[0]!=s[1]) cnt++;\n \n }\n }\n \n return cnt;\n }\n};\n\n\'\'\'\n\n-----------------UPVOTE--------------------
| 1
| 0
|
[]
| 0
|
find-maximum-number-of-string-pairs
|
c++ hash table
|
c-hash-table-by-lovelydays95-b9cx
|
c++\nclass Solution {\npublic:\n int maximumNumberOfStringPairs(vector<string>& words) {\n unordered_set<string> us;\n int res = 0;\n fo
|
lovelydays95
|
NORMAL
|
2023-06-24T16:17:18.209374+00:00
|
2023-06-24T16:17:18.209414+00:00
| 23
| false
|
```c++\nclass Solution {\npublic:\n int maximumNumberOfStringPairs(vector<string>& words) {\n unordered_set<string> us;\n int res = 0;\n for(auto w : words) {\n if(us.count(w)) res += 1;\n reverse(begin(w), end(w));\n us.insert(w);\n }\n return res;\n }\n};\n\n```
| 1
| 0
|
[]
| 0
|
find-maximum-number-of-string-pairs
|
a few solutions
|
a-few-solutions-by-claytonjwong-96tm
|
Peform a linear scan of each string s in the input array A and count cnt reductions performed when target t is previously seen.\n\n---\n\nKotlin\n\nclass Soluti
|
claytonjwong
|
NORMAL
|
2023-06-24T16:08:24.554089+00:00
|
2023-06-24T16:17:58.164680+00:00
| 6
| false
|
Peform a linear scan of each string `s` in the input array `A` and count `cnt` reductions performed when target `t` is previously `seen`.\n\n---\n\n*Kotlin*\n```\nclass Solution {\n fun maximumNumberOfStringPairs(A: Array<String>): Int {\n var cnt = 0\n var seen = mutableSetOf<String>()\n for (s in A) {\n var t = s.toCharArray().reversed().joinToString("")\n if (seen.contains(t)) {\n ++cnt; seen.remove(t)\n } else {\n seen.add(s)\n }\n }\n return cnt\n }\n}\n```\n\n*Javascript*\n```\nlet maximumNumberOfStringPairs = (A, seen = new Set(), cnt = 0) => {\n for (let s of A) {\n let t = s.split(\'\').reverse().join(\'\');\n if (seen.has(t))\n ++cnt, seen.delete(t);\n else\n seen.add(s);\n }\n return cnt;\n};\n```\n\n*Python3*\n```\nclass Solution:\n def maximumNumberOfStringPairs(self, A: List[str], cnt = 0) -> int:\n seen = set()\n for s in A:\n t = \'\'.join(reversed(list(s)))\n if t in seen:\n cnt += 1; seen.remove(t)\n else:\n seen.add(s)\n return cnt\n```\n\n*Rust*\n```\ntype VS = Vec<String>;\nuse std::collections::HashSet;\nimpl Solution {\n pub fn maximum_number_of_string_pairs(A: VS) -> i32 {\n let mut cnt = 0;\n let mut seen = HashSet::new();\n for s in A {\n let t = s.clone().chars().rev().collect::<String>();\n if seen.contains(&t) {\n cnt += 1; seen.remove(&t);\n } else {\n seen.insert(s);\n }\n }\n cnt\n }\n}\n```\n\n*C++*\n```\nclass Solution {\npublic:\n using VS = vector<string>;\n using Set = unordered_set<string>;\n int maximumNumberOfStringPairs(VS& A, Set seen = {}, int cnt = 0) {\n for (auto& s: A) {\n auto t = string{s.rbegin(), s.rend()};\n if (seen.find(t) != seen.end())\n ++cnt, seen.erase(t);\n else\n seen.insert(s);\n }\n return cnt;\n }\n};\n```
| 1
| 0
|
[]
| 0
|
find-maximum-number-of-string-pairs
|
Using Hashing || Easy-Commented Code ✅✅
|
using-hashing-easy-commented-code-by-nee-sef6
|
Guys consider upvoting! Thanks!\n# Code\n\nclass Solution {\npublic:\n int maximumNumberOfStringPairs(vector<string>& words) {\n int n = words.size()
|
neergx
|
NORMAL
|
2023-06-24T16:07:51.461425+00:00
|
2023-06-24T16:17:33.458227+00:00
| 40
| false
|
# Guys consider upvoting! Thanks!\n# Code\n```\nclass Solution {\npublic:\n int maximumNumberOfStringPairs(vector<string>& words) {\n int n = words.size();\n unordered_map<string, int> mp;\n //add words to the map\n for(int i = 0; i < n; i++){\n mp[words[i]]++;\n }\n \n int ans = 0;\n for(int i = 0; i < n; i++){\n string temp = words[i];\n reverse(temp.begin(), temp.end());\n // if reverse is present and is not equal (eg "zz")\n if(words[i] != temp){\n if(mp.count(temp) > 0){\n ans++;\n // reducing the count to remove duplicates\n mp[temp]--;\n mp[words[i]]--;\n // if count is zero we remove it\n if(mp[temp] == 0)\n mp.erase(temp);\n if(mp[words[i]] == 0)\n mp.erase(words[i]);\n }\n }\n }\n return ans;\n }\n};\n```
| 1
| 0
|
['Hash Table', 'C++']
| 0
|
maximum-candies-allocated-to-k-children
|
[Java/C++/Python] Binary Search with Explanation
|
javacpython-binary-search-with-explanati-9rcq
|
Intuition\nBinary search\n\n\n# Explanation\nAssume we want give each child m candies, for each pile of candies[i],\nwe can divide out at most candies[i] / m su
|
lee215
|
NORMAL
|
2022-04-03T04:04:28.275674+00:00
|
2022-04-03T06:27:51.592601+00:00
| 20,204
| false
|
# **Intuition**\nBinary search\n<br>\n\n# **Explanation**\nAssume we want give each child `m` candies, for each pile of `candies[i]`,\nwe can divide out at most `candies[i] / m` sub piles with each pile `m` candies.\n\nWe can sum up all the sub piles we can divide out, then compare with the `k` children.\n\nIf `k > sum`, \nwe don\'t allocate to every child, \nsince the pile of `m` candidies it too big,\nso we assign `right = m - 1`.\n\nIf `k <= sum`, \nwe are able to allocate to every child, \nsince the pile of `m` candidies is small enough\nso we assign `left = m`.\n\nWe repeatly do this until `left == right`, and that\'s the maximum number of candies each child can get.\n<br>\n\n# **Tips**\nTip1. `left < right` Vs `left <= right`\n\nCheck all my solution, I keep using `left < right`.\nThe easy but important approach: \nfollow and upvote my codes,\ntry to do the same.\nyou\'ll find all binary search is similar,\nnever bother thinking it anymore.\n\nTip2. `mid = (left + right + 1) / 2` Vs `mid = (left + right) / 2`\n\n`mid = (left + right) / 2` to find **first** element valid\n`mid = (left + right + 1) / 2 `to find **last** element valid\n<br>\n\n# **Complexity**\nTime `O(nlog10000000)`\nSpace `O(1)`\n<br>\n\n**Java**\n```java\n public int maximumCandies(int[] A, long k) {\n int left = 0, right = 10_000_000;\n while (left < right) {\n long sum = 0;\n int mid = (left + right + 1) / 2;\n for (int a : A) {\n sum += a / mid;\n }\n if (k > sum)\n right = mid - 1;\n else\n left = mid;\n }\n return left;\n }\n```\n\n**C++**\n```cpp\n int maximumCandies(vector<int>& A, long long k) {\n int left = 0, right = 1e7;\n while (left < right) {\n long sum = 0, mid = (left + right + 1) / 2;\n for (int& a : A) {\n sum += a / mid;\n }\n if (k > sum)\n right = mid - 1;\n else\n left = mid;\n }\n return left;\n }\n```\n\n**Python**\n```py\n def maximumCandies(self, A, k):\n left, right = 0, sum(A) / k\n while left < right:\n mid = (left + right + 1) / 2\n if k > sum(a / mid for a in A):\n right = mid - 1\n else:\n left = mid\n return left\n```\n<br>\n\n# More Good Binary Search Problems\nHere are some similar binary search problems.\nAlso find more explanations.\nGood luck and have fun.\n\n- 2226. [Maximum Candies Allocated to K Children](https://leetcode.com/problems/maximum-candies-allocated-to-k-children/discuss/1908888/JavaC%2B%2BPython-Binary-Search-with-Explanation)\n- 1802. [Maximum Value at a Given Index in a Bounded Array](https://leetcode.com/problems/maximum-value-at-a-given-index-in-a-bounded-array/discuss/1119801/Python-Binary-Search)\n- 1539. [Kth Missing Positive Number](https://leetcode.com/problems/kth-missing-positive-number/discuss/779999/JavaC++Python-O(logN))\n- 1482. [Minimum Number of Days to Make m Bouquets](https://leetcode.com/problems/minimum-number-of-days-to-make-m-bouquets/discuss/686316/javacpython-binary-search)\n- 1283. [Find the Smallest Divisor Given a Threshold](https://leetcode.com/problems/find-the-smallest-divisor-given-a-threshold/discuss/446376/javacpython-bianry-search)\n- 1231. [Divide Chocolate](https://leetcode.com/problems/divide-chocolate/discuss/408503/Python-Binary-Search)\n- 1011. [Capacity To Ship Packages In N Days](https://leetcode.com/problems/capacity-to-ship-packages-within-d-days/discuss/256729/javacpython-binary-search/)\n- 875. [Koko Eating Bananas](https://leetcode.com/problems/koko-eating-bananas/discuss/152324/C++JavaPython-Binary-Search)\n- 774. [Minimize Max Distance to Gas Station](https://leetcode.com/problems/minimize-max-distance-to-gas-station/discuss/113633/Easy-and-Concise-Solution-using-Binary-Search-C++JavaPython)\n- 410. [Split Array Largest Sum](https://leetcode.com/problems/split-array-largest-sum/)\n<br>\n
| 334
| 2
|
['C', 'Python', 'Java']
| 44
|
maximum-candies-allocated-to-k-children
|
✔️ Binary Search | Python | C++ | Java | JS | Go | C# | Swift
|
binary-search-python-c-java-by-otabek_kh-fuhi
|
IntuitionThis problem asks us to find the maximum number of candies we can give to each of k children. Since we can divide piles but can't merge them, and we're
|
otabek_kholmirzaev
|
NORMAL
|
2025-03-14T00:45:06.037586+00:00
|
2025-03-14T02:35:29.557697+00:00
| 22,228
| false
|
# Intuition
This problem asks us to find the **maximum number of candies** we can give to each of k children. Since we can divide piles but can't merge them, and we're looking for a maximum value, this is a perfect candidate for **binary search**.
# Approach
## Binary Search Setup:
- `left = 1`: Minimum possible candies per child (if possible)
- `right = max(candies)`: Maximum possible candies per child (limited by the largest pile)
- `result = 0`: Variable to store our current best answer
## Binary Search Process:
- For each middle value `mid`, calculate how many children can receive `mid` candies
- This is done by summing up `pile / mid` for each pile
- If we can satisfy at least `k` children, update our `result` to `mid` and search for larger values
- Otherwise, search for smaller values
# Complexity
- Time complexity: `O(n * log(m))`
- `n` is the length of the candies array
- `m` is the maximum value in the candies array
- Space complexity: `O(1)`
# Code
```python3 []
class Solution:
def maximumCandies(self, candies: List[int], k: int) -> int:
left, right = 1, max(candies)
result = 0
while left <= right:
mid = (left + right) // 2
children_count = sum(pile // mid for pile in candies)
if children_count >= k:
result = mid
left = mid + 1
else:
right = mid - 1
return result
```
```cpp []
class Solution {
public:
int maximumCandies(vector<int>& candies, long long k) {
long long left = 1, right = *max_element(candies.begin(), candies.end());
int result = 0;
while (left <= right) {
long long mid = left + (right - left) / 2;
long long children_count = 0;
for (int pile : candies) {
children_count += pile / mid;
}
if (children_count >= k) {
result = mid;
left = mid + 1;
} else {
right = mid - 1;
}
}
return result;
}
};
```
```java []
class Solution {
public int maximumCandies(int[] candies, long k) {
int left = 1, right = 10_000_000;
int result = 0;
while (left <= right) {
int mid = left + (right - left) / 2;
long childrenCount = 0;
for (int candy : candies) {
childrenCount += candy / mid;
}
if (childrenCount >= k) {
result = mid;
left = mid + 1;
} else {
right = mid - 1;
}
}
return result;
}
}
```
```javascript []
var maximumCandies = function(candies, k) {
let left = 1, right = Math.max(...candies);
let result = 0;
while (left <= right) {
let mid = Math.floor((left + right) / 2);
let childrenCount = candies.reduce((sum, pile) => sum + Math.floor(pile / mid), 0);
if (childrenCount >= k) {
result = mid;
left = mid + 1;
} else {
right = mid - 1;
}
}
return result;
};
```
```go []
func maximumCandies(candies []int, k int64) int {
left, right := 1, 10_000_000
result := 0
for left <= right {
mid := left + (right-left)/2
var childrenCount int64 = 0
for _, candy := range candies {
childrenCount += int64(candy / mid)
}
if childrenCount >= k {
result = mid
left = mid + 1
} else {
right = mid - 1
}
}
return result
}
```
```csharp []
public class Solution {
public int MaximumCandies(int[] candies, long k) {
int left = 1, right = candies.Max();
int result = 0;
while (left <= right) {
int mid = (left + right) / 2;
long childrenCount = 0;
foreach (int candy in candies) {
childrenCount += candy / mid;
}
if (childrenCount >= k) {
result = mid;
left = mid + 1;
} else {
right = mid - 1;
}
}
return result;
}
}
```
```swift []
class Solution {
func maximumCandies(_ candies: [Int], _ k: Int) -> Int {
var left = 1
var right = candies.max() ?? 0
var result = 0
while left <= right {
let mid = (left + right) / 2
let childrenCount = candies.reduce(0) { $0 + $1 / mid }
if childrenCount >= k {
result = mid
left = mid + 1
} else {
right = mid - 1
}
}
return result
}
}
```
---

| 106
| 5
|
['Binary Search', 'Swift', 'C++', 'Java', 'Go', 'Python3', 'JavaScript', 'C#']
| 10
|
maximum-candies-allocated-to-k-children
|
Binary Search
|
binary-search-by-votrubac-myn3
|
Say we decide to allocate m candies. We can check if all k kids can get m candies in O(n).\n\nTherefore, we can binary-search for the maximum value m. The overa
|
votrubac
|
NORMAL
|
2022-04-03T04:00:27.458747+00:00
|
2022-04-03T04:15:34.656398+00:00
| 5,486
| false
|
Say we decide to allocate `m` candies. We can check if all `k` kids can get `m` candies in O(n).\n\nTherefore, we can binary-search for the maximum value `m`. The overall runtime complexity will be O(n * log m), where `m` is maximum number of candies in a single pile (10000000).\n\nThe fact that we can split piles could be confusing. But it simply means that we can distribute `m` candies to ` candies[i] / m` children from pile `i`.\n\n**C++**\n```cpp \nint maximumCandies(vector<int>& candies, long long k) {\n int l = 0, r = 10000000;\n while(l < r) {\n long long m = (l + r + 1) / 2, cnt = 0;\n for (int i = 0; i < candies.size() && cnt < k; ++i)\n cnt += candies[i] / m;\n if (cnt >= k)\n l = m;\n else\n r = m - 1;\n }\n return l;\n}\n```
| 44
| 1
|
[]
| 11
|
maximum-candies-allocated-to-k-children
|
C++ Easy solution, with Explanation
|
c-easy-solution-with-explanation-by-rohi-21ek
|
Lets see about the brute force solution.\n\nWe can check for candies=1,2 and so,on until we find an answer.\n\nCan\'t we do something better,instead of linear s
|
Rohithch7102
|
NORMAL
|
2022-04-03T04:01:12.810796+00:00
|
2022-04-03T05:12:25.165288+00:00
| 3,622
| false
|
Lets see about the brute force solution.\n\nWe can check for candies=1,2 and so,on until we find an answer.\n\nCan\'t we do something better,instead of linear search ?.\n\nYes, we can do **binary search.**\n \nIf we can divide the candies into piles containing x number of candies all the numbers below x,\nwill also be satisfied.\n\nIn this question we have to find the maximum number of candies.\n\nLets see the lowest value is 1 and highest value as the maximum element in candies.\n\nNow we will find the mid, and we will check weather we can divide mid amount of candies into piles \nsuch that they will be sufficient for k children.\n\nFinally we return the ans.\n\n```\nclass Solution {\npublic:\n typedef long long ll;\n \n bool solve(vector<int>& v, ll mid, ll k){\n int n = v.size();\n ll cnt = 0;\n for(int i=0;i<n;i++){\n cnt += (v[i]/mid);\n if(cnt>=k) return true;\n }\n return false;\n }\n \n // v is the candies vector.\n int maximumCandies(vector<int>& v, long long k) {\n int n = v.size();\n\t\tint mx = 0;\n for(int i=0;i<n;i++){\n\t\t\tmx = max(mx,v[i]);\n }\n \n ll low = 1, high = mx;\n ll ans = 0;\n while(low<=high){\n ll mid = low + (high-low)/2;\n if(solve(v,mid,k)){\n ans = mid;\n low = mid+1;\n }\n else{\n high = mid-1;\n }\n }\n return ans;\n }\n};\n```\n\n**Time Complexity= O(nlogp) // p is the maximum candy.\nSpace Complexity- O(1);**\n\n\nUpvote if it helps!!\nThank you!!\n\nMore binary search problems:\n\nhttps://leetcode.com/problems/capacity-to-ship-packages-within-d-days/\nhttps://leetcode.com/problems/kth-smallest-element-in-a-sorted-matrix/\nhttps://leetcode.com/problems/find-the-duplicate-number/\nhttps://leetcode.com/problems/minimum-size-subarray-sum/\nhttps://leetcode.com/problems/minimum-limit-of-balls-in-a-bag/\nhttps://leetcode.com/problems/most-beautiful-item-for-each-query/\nhttps://leetcode.com/problems/find-the-smallest-divisor-given-a-threshold/\nhttps://leetcode.com/problems/minimized-maximum-of-products-distributed-to-any-store/\nhttps://leetcode.com/problems/heaters/\nhttps://leetcode.com/problems/minimum-absolute-sum-difference/\nhttps://leetcode.com/problems/frequency-of-the-most-frequent-element/
| 36
| 0
|
['Binary Search', 'C']
| 4
|
maximum-candies-allocated-to-k-children
|
Binary Search Solution with Explanation | Java | O(n log(max(candies)))
|
binary-search-solution-with-explanation-e8su8
|
Simple Binary Search Solution | Java | O(n log(max(candies)))\n\nIdea:\nBrute force :Start with 1 candy and see if we can allocate. If yes, then check for 2 can
|
shaishavjogani
|
NORMAL
|
2022-04-03T04:02:17.004643+00:00
|
2022-04-03T04:19:44.555564+00:00
| 2,728
| false
|
Simple Binary Search Solution | Java | O(n log(max(candies)))\n\n**Idea**:\nBrute force :Start with 1 candy and see if we can allocate. If yes, then check for 2 candy. \nOptimization: Instead of checking every candy at a time, why can\'t we directly check for a number to see if we can allocate that many candy. This way we reduce our search space. Best way to do it is binary search.\n\n**Approach**:\nFirst go through each pile and store the maximum of candy of that pile.\nNow your seach space will be `[0 - max]`. Now, we will pick `mid` from that and check if we can allocate that many candies to k children. If yes, update `lo`, if not update `hi`.\n0 is trickey number because you can always allocate that many candies. So, at the end I do a check one more time on lo to see if I can allocate that candies. otherwise return lo-1.\n\n**TimeComplexity**:\n`O(n)` to check if you can allocate x candies to k people\ncalling above function `log(max(candies))`.\nSo, overall time complexity `O(n log(max(candies)))`\n\n**Upvote if it helps. Thanks :)**\n\n```\nclass Solution {\n public int maximumCandies(int[] candies, long k) {\n \n int max = 0;\n for(int candy : candies)\n max = Math.max(max, candy);\n int lo = 0, hi = max;\n \n while(lo < hi) { \n int mid = lo + (hi-lo)/2;\n if(canAllocate(candies, k, mid)) {\n lo = mid+1;\n } else {\n hi = mid ;\n }\n } \n return canAllocate(candies, k, lo) ? lo : lo-1;\n }\n \n public boolean canAllocate(int[] candies, long k, int allow) {\n if(allow == 0)\n return true;\n long total = 0;\n for(int candy : candies) {\n total += candy / allow;\n if(total >= k)\n return true;\n }\n return false;\n }\n}\n```
| 32
| 1
|
['Binary Tree', 'Java']
| 2
|
maximum-candies-allocated-to-k-children
|
🔥BEATS 💯 % 🎯 |✨SUPER EASY BEGINNERS 👏| JAVA | C | C++ | PYTHON| JAVASCRIPT | DART
|
beats-super-easy-beginners-java-c-c-pyth-1pax
|
IntuitionThe problem requires us to distribute candies among k children such that each child gets the same number of candies, and we want to maximize this numbe
|
CodeWithSparsh
|
NORMAL
|
2025-03-14T04:05:55.593710+00:00
|
2025-03-14T11:38:08.475856+00:00
| 3,380
| false
|
---
# Intuition
The problem requires us to distribute candies among `k` children such that each child gets the same number of candies, and we want to maximize this number.
To solve this efficiently, we can use **binary search** on the number of candies each child receives. The minimum possible candies per child is `1`, and the maximum is determined by the **largest pile**.
---
# Approach
1. **Binary Search Setup**:
- The **search range** is `[1, max(candies)]`.
- If the total number of candies is **less than `k`**, we immediately return `0`, as it's impossible to distribute at least one candy per child.
2. **Binary Search Execution**:
- We pick a middle value `mid` and check whether it's possible to distribute **at least `k`** candies per child (`canDistribute` function).
- If possible, move the **left boundary (`left = mid + 1`)** to search for a higher possible value.
- Otherwise, move the **right boundary (`right = mid - 1`)**.
3. **Checking Distribution** (`canDistribute` function):
- We iterate over all candy piles and count how many children can be served if each child gets `mid` candies.
- If we can serve `k` children or more, return `true`, otherwise return `false`.
---
# Complexity
- **Time Complexity**:
- The **binary search** runs in **O(log M)**, where `M` is the max pile size.
- Checking distribution takes **O(N)**, where `N` is the number of candy piles.
- **Total Complexity**: **O(N log M)**.
- **Space Complexity**: **O(1)** (No extra space used apart from variables).
---
```dart []
import 'dart:math';
class Solution {
int maximumCandies(List<int> candies, int k) {
int left = 1, right = candies.reduce(max); // Maximum pile size
if (candies.reduce((a, b) => a + b) < k) return 0; // Not enough candies
int result = 0;
while (left <= right) {
int mid = (left + right) ~/ 2;
if (canDistribute(candies, k, mid)) {
result = mid;
left = mid + 1; // Try a larger value
} else {
right = mid - 1; // Try a smaller value
}
}
return result;
}
bool canDistribute(List<int> candies, int k, int val) {
int count = 0;
for (int c in candies) {
count += c ~/ val;
}
return count >= k;
}
}
```
```java []
class Solution {
public int maximumCandies(int[] candies, long k) {
int left = 1, right = 0;
for (int c : candies) right = Math.max(right, c); // Find max candy pile
long total = 0;
for (int c : candies) total += c;
if (total < k) return 0; // Not enough candies
int result = 0;
while (left <= right) {
int mid = left + (right - left) / 2;
if (canDistribute(candies, k, mid)) {
result = mid;
left = mid + 1; // Try larger value
} else {
right = mid - 1; // Reduce value
}
}
return result;
}
private boolean canDistribute(int[] candies, long k, int val) {
long count = 0;
for (int c : candies) {
count += c / val;
if (count >= k) return true;
}
return false;
}
}
```
```cpp []
#include <vector>
#include <algorithm>
using namespace std;
class Solution {
public:
int maximumCandies(vector<int>& candies, int k) {
int left = 1, right = *max_element(candies.begin(), candies.end());
long long total = 0;
for (int c : candies) total += c;
if (total < k) return 0; // Not enough candies
int result = 0;
while (left <= right) {
int mid = left + (right - left) / 2;
if (canDistribute(candies, k, mid)) {
result = mid;
left = mid + 1;
} else {
right = mid - 1;
}
}
return result;
}
private:
bool canDistribute(vector<int>& candies, int k, int val) {
int count = 0;
for (int c : candies) count += c / val;
return count >= k;
}
};
```
```python []
from typing import List
class Solution:
def maximumCandies(self, candies: List[int], k: int) -> int:
if sum(candies) < k: return 0 # Not enough candies
left, right = 1, max(candies)
result = 0
while left <= right:
mid = (left + right) // 2
if self.canDistribute(candies, k, mid):
result = mid
left = mid + 1 # Try larger `mid`
else:
right = mid - 1 # Try smaller `mid`
return result
def canDistribute(self, candies: List[int], k: int, val: int) -> bool:
return sum(c // val for c in candies) >= k
```
```javascript []
var maximumCandies = function(candies, k) {
let left = 1, right = Math.max(...candies);
let total = candies.reduce((sum, c) => sum + c, 0);
if (total < k) return 0; // Not enough candies
let result = 0;
while (left <= right) {
let mid = Math.floor((left + right) / 2);
if (canDistribute(candies, k, mid)) {
result = mid;
left = mid + 1;
} else {
right = mid - 1;
}
}
return result;
};
function canDistribute(candies, k, val) {
let count = 0;
for (let c of candies) count += Math.floor(c / val);
return count >= k;
}
```
---
------
 {:style='width:250px'}
| 23
| 0
|
['Array', 'Binary Search', 'C', 'Python', 'C++', 'Java', 'Python3', 'JavaScript', 'Dart', 'Python ML']
| 7
|
maximum-candies-allocated-to-k-children
|
✅Range Based Binary Search 🔥| Visualization ✨| Math | Python | C++ | Java ✨
|
range-based-binary-search-visualization-317o1
|
Approach
Complexity
Time complexity: O(nlog(m))
Space complexity: O(1)
Code
|
Raw_Ice
|
NORMAL
|
2025-03-14T02:19:17.183128+00:00
|
2025-03-14T02:19:17.183128+00:00
| 4,198
| false
|
# Approach
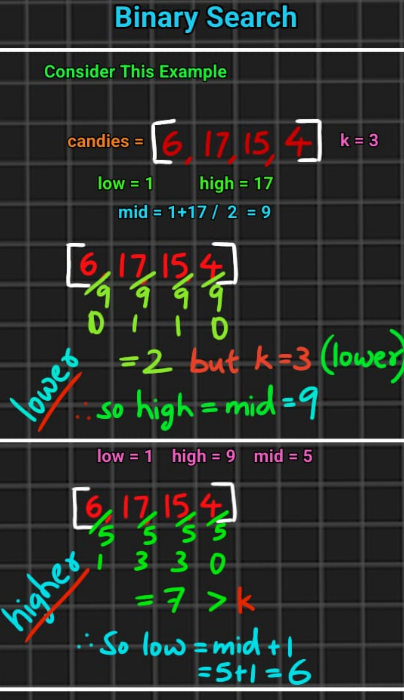
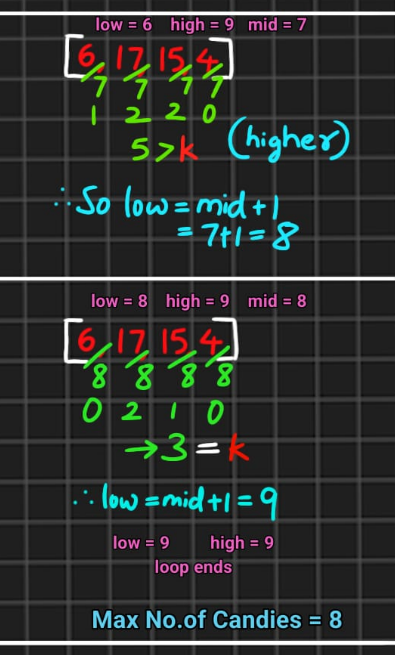
# Complexity
- Time complexity: $$O(nlog(m))$$
- Space complexity: $$O(1)$$
# Code
```python []
class Solution(object):
def maximumCandies(self, candies, k):
def can_allocate(candies, k, pile_size):
if pile_size == 0:
return True
total_piles = 0
for candy in candies:
total_piles += candy // pile_size
if total_piles >= k:
return True
return False
if sum(candies) < k:
return 0
low, high = 1, max(candies)
while low < high:
mid = (low + high + 1) // 2
if can_allocate(candies, k, mid):
low = mid
else:
high = mid - 1
return low
```
```C++ []
class Solution {
public:
int maximumCandies(vector<int>& candies, long long k) {
auto canAllocate = [&](vector<int>& candies, long long k, int pileSize) {
if (pileSize == 0) return true;
long long totalPiles = 0;
for (int candy : candies) {
totalPiles += candy / pileSize;
if (totalPiles >= k) return true;
}
return false;
};
long long sum = 0;
for (int candy : candies) sum += candy;
if (sum < k) return 0;
int low = 1, high = *max_element(candies.begin(), candies.end());
while (low < high) {
int mid = (low + high + 1) / 2;
if (canAllocate(candies, k, mid)) {
low = mid;
} else {
high = mid - 1;
}
}
return low;
}
};
```
```Java []
class Solution {
public int maximumCandies(int[] candies, long k) {
if (sum(candies) < k) {
return 0;
}
int low = 1, high = getMax(candies);
while (low < high) {
int mid = (low + high + 1) / 2;
if (canAllocate(candies, k, mid)) {
low = mid;
} else {
high = mid - 1;
}
}
return low;
}
private boolean canAllocate(int[] candies, long k, int pileSize) {
if (pileSize == 0) return true;
long totalPiles = 0;
for (int candy : candies) {
totalPiles += candy / pileSize;
if (totalPiles >= k) return true;
}
return false;
}
private long sum(int[] candies) {
long sum = 0;
for (int candy : candies) {
sum += candy;
}
return sum;
}
private int getMax(int[] candies) {
int max = 0;
for (int candy : candies) {
max = Math.max(max, candy);
}
return max;
}
}
```

| 22
| 0
|
['Array', 'Math', 'Binary Search', 'Python', 'C++', 'Java']
| 3
|
maximum-candies-allocated-to-k-children
|
binary search of Koko's type||3ms Beats 99.82%
|
binary-search-of-kokos-type3ms-beats-998-o20y
|
IntuitionUse binary search.
C++ & Python are doneApproachbool get_c(vector<int>& candies, long long k, int c) is defined to judge whether every child can get c
|
anwendeng
|
NORMAL
|
2025-03-14T02:16:15.073863+00:00
|
2025-03-14T05:55:46.409439+00:00
| 2,210
| false
|
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Use binary search.
C++ & Python are done
# Approach
<!-- Describe your approach to solving the problem. -->
`bool get_c(vector<int>& candies, long long k, int c)` is defined to judge whether every child can get c candies for k children.
It's to note during the loop `while(l<r){...}`, when `l=m, r=m-1` is used **the upper mid should be taken**, whereas the lower mid is used if `l=m+1, r=m` is used.
Otherwise it is very similar to solve [875. Koko Eating Bananas](https://leetcode.com/problems/koko-eating-bananas/solutions/3685871/w-explanation-easy-binary-search-c-solution/)
[Please turn on the English subtitles]
[https://youtu.be/KtZOZ4E1zww?si=o3rhF07qrvaTJn1z](https://youtu.be/KtZOZ4E1zww?si=o3rhF07qrvaTJn1z)
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
$O(\log (sum/k+n) n)$ where n=|candies|, sum=sum(candies)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
$O(1)$
# Code||C+++ 3ms Beats 99.82%
```cpp []
class Solution {
public:
bool get_c(vector<int>& candies, long long k, int c) {
[[unroll]]
for (int x : candies) {
k-=x/c;
if (k<=0) return 1;
}
return 0;
}
int maximumCandies(vector<int>& candies, long long k) {
const long long sum=accumulate(candies.begin(), candies.end(), 0LL);
if (sum<k) return 0;
int l=1, r=sum/k, m; // sum/k as the upper bound
while (l<r) {
m=l+(r-l+1)/2; // upper mid to avoid infinite loop
if (get_c(candies, k, m)) l=m;
else r=m-1;
}
return l;
}
};
```
```Python []
class Solution:
def maximumCandies(self, candies: List[int], k: int) -> int:
def get_c(c, k):
for x in candies:
k-=x//c
if k<=0:
return True
return False
Sum=sum(candies)
if Sum<k:
return 0
l, r=1, Sum//k
while l<r:
m=(l+r+1)//2
if get_c(m, k):
l=m
else:
r=m-1
return l
```
| 21
| 0
|
['Binary Search', 'C++', 'Python3']
| 5
|
maximum-candies-allocated-to-k-children
|
Binary_Search || Intutive || Intution-Explanation
|
binary_search-intutive-intution-explanat-b9n3
|
Intution : We Know we had to distribute maximum candies , whenever face Problem in which we have to distribute and finding the maximum or minium, See the
|
crazy_zoker
|
NORMAL
|
2022-04-03T04:03:40.902705+00:00
|
2022-04-03T19:15:51.491027+00:00
| 1,367
| false
|
Intution : We Know we had to distribute maximum candies , whenever face Problem in which we have to distribute and finding the maximum or minium, See the Time Complexity if Time Complexity isaround 10^4, and your answer require optimal ways then think of dp solution, if Time Complexity is around 10^5 either it can be done by sorting with greedy or binary search on ans. Now with this it was clear it is binary search on ans problem. So Just checked how can I distribute \n1. Search space can be 1 to sum(candies), Why\n Becuase you have to give them at least one so low = 1.\n 2. Just find the mid and check, if distributing mid candies it is possible to distribute if yes, then reduce your search space so that more optimal ans can be find.\n\n**Please UPVOTE Guys , If it helps, That motivates**\n```\nclass Solution {\npublic:\n bool check(vector<int>& candies, long long k, long long mid) {\n long long split = 0;\n for(int i = 0; i < candies.size(); ++i) {\n split += candies[i]/mid;\n } \n return split>=k;\n }\n \n int maximumCandies(vector<int>& candies, long long k) {\n long long sum = 0;\n for(int i = 0; i < candies.size(); ++i) {\n sum += candies[i];\n }\n \n long long start = 1, end = sum;\n long long ans = 0;\n \n while(start <= end) {\n long long mid = (start + end)/2;\n if(check(candies, k, mid)) {\n ans = mid;\n start = mid + 1;\n } else {\n end = mid-1;\n }\n }\n return ans;\n }\n};\n\nTime Complexity : nlog(m}\nSpace Complexity: O(1)
| 19
| 1
|
[]
| 5
|
maximum-candies-allocated-to-k-children
|
100% faster | C++ | Python | Java | Binary Search with Logic
|
100-faster-c-python-java-binary-search-w-ebwe
|
\n\nIdea\n\n start can be taken as 1 , highest we can distribute equally is average.\n\n Use Binary Search and try to distribute the candies equal to mid, if po
|
TejPratap1
|
NORMAL
|
2022-04-03T04:01:54.923815+00:00
|
2022-04-05T15:09:56.362971+00:00
| 2,324
| false
|
\n\n**Idea**\n\n* start can be taken as 1 , highest we can distribute equally is average.\n\n* Use Binary Search and try to distribute the candies equal to mid, if possible try to maximize it by moving on right, else if not possible try it by decreasing the value by moving on left\n* **TC: O(NlogN) SC: O(1)**\n\n```\ndef canSplit(candies, mid, k):\n split = 0\n for i in candies:\n split += i//mid\n if split >= k:\n return True\n else:\n return False\n \nclass Solution:\n def maximumCandies(self, candies: List[int], k: int) -> int:\n end = sum(candies)//k\n start = 1\n ans = 0\n while start <= end:\n mid = (start + end)//2\n if canSplit(candies, mid, k):\n start = mid + 1\n ans = mid\n else:\n end = mid - 1\n return ans\n \n```\n\n**C++**\n\n```\nclass Solution {\npublic:\n bool canSplit(vector<int>& candies, long long k, long long mid) {\n long long split = 0;\n for(int i = 0; i < candies.size(); ++i) {\n split += candies[i]/mid;\n } \n if(split >= k)\n return true;\n else\n return false;\n }\n \n int maximumCandies(vector<int>& candies, long long k) {\n long long sum = 0;\n for(int i = 0; i < candies.size(); ++i) {\n sum += candies[i];\n }\n long long start = 1, end = sum/k;\n long long ans = 0;\n while(start <= end) {\n long long mid = (start + end)/2;\n if(canSplit(candies, k, mid)) {\n ans = mid;\n start = mid + 1;\n } else {\n end = mid-1;\n }\n }\n return ans;\n }\n};\n```\n\n**Java**\n```\nclass Solution {\n public boolean canSplit(int[] candies, long k, long mid) {\n long split = 0;\n for(int i = 0; i < candies.length; ++i) {\n split += candies[i]/mid;\n } \n if(split >= k)\n return true;\n else\n return false;\n }\n \n public int maximumCandies(int[] candies, long k) {\n long sum = 0;\n for(int i = 0; i < candies.length; ++i) {\n sum += candies[i];\n }\n long start = 1, end = sum;\n long ans = 0;\n while(start <= end) {\n long mid = (start + end)/2;\n if(canSplit(candies, k, mid)) {\n ans = mid;\n start = mid + 1;\n } else {\n end = mid-1;\n }\n }\n return (int)ans;\n }\n}\n```
| 14
| 0
|
['Binary Search', 'C', 'Python', 'C++', 'Java']
| 1
|
maximum-candies-allocated-to-k-children
|
Binary Search || Explained
|
binary-search-explained-by-kamisamaaaa-0wgy
|
Explanation :\nBinary search between [1, max(candies)] to find the result.\nif we can allocate currCandy candies to k children. then update start, if not update
|
kamisamaaaa
|
NORMAL
|
2022-04-03T04:00:45.326176+00:00
|
2022-04-03T04:39:03.739191+00:00
| 1,051
| false
|
**Explanation :**\nBinary search between **[1, max(candies)]** to find the result.\n**if we can allocate currCandy candies to k children. then update start, if not update end.**\nSimilar Question : [https://leetcode.com/problems/koko-eating-bananas/]\n**Time O(Nlog(MaxC))\nSpace O(1)**\n \n \n```\nclass Solution {\npublic:\n \n bool doit(int currCandy, vector<int>& candies, long long k) {\n \n\t\t// c candies can be divided into (c/currCandy) number of piles of size currCandy.\n for (auto& c : candies) k -= (c/currCandy);\n return k <= 0;\n }\n \n \n int maximumCandies(vector<int>& candies, long long k) {\n \n int start(1), end(INT_MIN);\n for (auto& candy : candies) end = max(end, candy);\n \n while (start <= end) {\n int currCandy = start+(end-start)/2;\n\t\t\t// If we can divide the candies into piles containing currCandy number of candies all the numbers below currCandy can be distributed too.\n if (doit(currCandy, candies, k)) start = currCandy+1;\n else end = currCandy-1;\n }\n return end;\n }\n};\n```
| 10
| 2
|
['C', 'Binary Tree']
| 2
|
maximum-candies-allocated-to-k-children
|
Simple and Beginner-Friendly Approach to Maximum Candies Problem
|
simple-and-beginner-friendly-approach-to-jwxe
|
IntuitionThe problem requires us to distribute candies among k children such that each child gets the maximum possible equal number of candies. Since distributi
|
navaneeth02
|
NORMAL
|
2025-03-14T03:41:45.088883+00:00
|
2025-03-14T03:43:40.453415+00:00
| 1,177
| false
|
---
## **Intuition**
The problem requires us to distribute candies among `k` children such that each child gets the maximum possible equal number of candies. Since distributing `x` candies per child means checking whether we can form at least `k` groups, we need to find the **maximum possible `x`** that satisfies this condition.
A naive approach would be to iterate from 1 to the maximum number of candies and check if it's possible to distribute them, but this is inefficient. Instead, we can use **binary search** to efficiently find the maximum value of `x`.
---
## **Approach**
1. **Determine the Search Space:**
- The minimum possible candies a child can get is `1`.
- The maximum is `max(candies)`, as we cannot give more than what we have in the largest pile.
2. **Binary Search on the Answer:**
- Use binary search between `low = 1` and `high = max(candies)`.
- Calculate `mid = (low + high) / 2`, which represents a possible number of candies each child can get.
- Check if it's possible to distribute at least `k` groups of `mid` candies using the `valid()` function:
- Iterate through `candies`, summing up `candies[i] / mid` (i.e., how many full groups of `mid` can be formed).
- If the total count is `>= k`, it's a valid distribution.
- If `valid(mid) == true`, update `ans = mid` and move `low` to `mid + 1` (search for a larger possible value).
- Otherwise, move `high` to `mid - 1` (reduce the number of candies per child).
3. **Return `ans` as the maximum valid `mid`.**
---
## **Complexity Analysis**
- **Time Complexity:**
- We perform a binary search on values from `1` to `max(candies)`, which takes **\( O( log M) \)** iterations, where \( M \) is the maximum number of candies in any pile.
- Each binary search step requires checking all elements in `candies`, which is **\( O(N) \)**.
- **Total time complexity:** \( O(N log M) \).
- **Space Complexity:**
- We use only a few extra variables (`low`, `high`, `mid`, etc.), so the space complexity is **\( O(1) \)**.
---
# Code
```java []
class Solution {
public int maximumCandies(int[] candies, long k) {
int max=candies[0];
for(int i=1;i<candies.length;i++)
{
max=Math.max(candies[i],max);
}
int low=1,high=max;
int ans=0;
while(low<=high)
{
int mid=(low+high)/2;
if(valid(mid,candies,k))
{
ans=mid;
low=mid+1;
}
else
{
high=mid-1;
}
}
return ans;
}
public boolean valid(int mid,int candies[],long k)
{
long c=0;
for(int i=0;i<candies.length;i++)
{
if(candies[i]>=mid)
{
c+=candies[i]/mid;
}
}
if(c>=k)
return true;
return false;
}
}
```
---
| 9
| 0
|
['Array', 'Binary Search', 'Java']
| 0
|
maximum-candies-allocated-to-k-children
|
Easy to understand, optimized binary search approach, beginner friendly, detail explained.
|
easy-to-understand-optimized-binary-sear-9zxg
|
\n# Approach\n1. minimum size of candy can be 1,less than 1 can not be possible.\n2. maximum size of candy can be maximum element of given candies array,greater
|
ysr_code
|
NORMAL
|
2023-03-07T00:54:37.801432+00:00
|
2023-03-07T01:12:37.742107+00:00
| 901
| false
|
\n# Approach\n1. minimum size of candy can be 1,less than 1 can not be possible.\n2. maximum size of candy can be maximum element of given candies array,greater than max element can not be possible.\n3. we chose candy size by bianry search, so that we can choose in optimised time.\n4. function func give information about that, candies array\'s element can be divided into mid size.\n5. In function func,\'cnt\' count the nummber of \'mid\' size candy can be divided from candies array elements.\n6. when count of mid size candy greater than our need(k), then we return true, *i.e.* our answer should be mid but greater than mid can be possible.\n# Complexity\n- Time complexity:$$O(N*logN)$$\n\n- Space complexity:$$O(1)$$\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n bool func(vector<int>&pile,long long h,int mid)\n {\n long long cnt=0;\n for(int i=0;i<pile.size();i++)\n {\n cnt += pile[i]/mid ;\n if(cnt>h)\n return true;\n }\n return cnt>=h;\n }\n int maximumCandies(vector<int>& candies, long long k) \n {\n int s = 1,e = *max_element(candies.begin(),candies.end());\n int ans=0;\n while(s<=e)\n {\n int mid = s+ (e-s)/2;\n if(func(candies,k,mid))\n {\n ans = mid;\n s = mid+1;\n }\n else\n e = mid-1;\n }\n return ans;\n }\n};\n```\n**If you feel this helpful then plz like and upvote this solution \uD83D\uDE0A\nKEEP LEETCODING.............**\n\n
| 9
| 0
|
['Binary Search', 'C++']
| 2
|
maximum-candies-allocated-to-k-children
|
Easy to Understand & Simplified Solution using Binary Search
|
easy-to-understand-simplified-solution-u-l4qp
|
\n# Please upvote my solution I am crying :-(\n# Intuition\n Describe your first thoughts on how to solve this problem. \nEasy to understand problem by using Bi
|
ShivaanjayNarula
|
NORMAL
|
2024-06-14T15:55:17.983460+00:00
|
2024-06-14T15:55:17.983493+00:00
| 303
| false
|
\n# Please upvote my solution I am crying :-(\n# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nEasy to understand problem by using Binary Search in an effective way:))\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n1) Problem Breakdown:\n\nYou have a list of integers candies, where each integer represents the number of candies in a pile.\n\nYou need to distribute these candies to k children such that each child receives the maximum possible equal number of candies.\n\nThe goal is to determine this maximum number.\n\n\n2) Binary Search Approach:\n\nThe problem can be approached using binary search because we are looking for the maximum number of candies each child can get, which can be treated as a search for a maximum value in a sorted range.\n\n\n3) Range of Binary Search:\n\nThe minimum possible value (left) for the candies each child can receive is 1 (each child gets at least one candy if possible).\n\nThe maximum possible value (right) is the size of the largest pile of candies (*max_element(candies.begin(), candies.end())), because no child can receive more candies than the largest pile.\n\n\n4) Binary Search Execution:\n\nThe code iteratively narrows down the possible values for the maximum number of candies each child can receive (mid).\n\nFor each midpoint value (mid), the code calculates the total number of children that can be satisfied if each child gets mid candies using the formula sum += i / mid for each pile i.\n\nIf the number of children that can be satisfied (sum) is less than k, it means mid is too large, so the search space is reduced to the left half (right = mid).\n\nIf the number of children that can be satisfied is at least k, it means mid is feasible, so the search space is shifted to the right half (left = mid + 1).\n\n\n5) Result:\n\nThe loop continues until left is no longer less than right.\n\nThe result is left - 1, which is the maximum number of candies each child can receive.\n# Complexity\n- Time complexity: O(n log n)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int maximumCandies(vector<int>& candies, long long k) {\n int left = 1;\n int right = *max_element(candies.begin(), candies.end()) + 1; // Binary search range\n while (left < right) {\n long long sum = 0;\n int mid = (left + right) / 2; // Midpoint\n for (auto i : candies) {\n sum += i / mid; // Calculate total children satisfied with mid candies each\n }\n if (k > sum) { // If fewer children are satisfied\n right = mid; // Move left\n } else {\n left = mid + 1; // Move right\n }\n }\n return left - 1; // Result is left - 1\n }\n};\n\n```
| 8
| 0
|
['Array', 'Binary Search', 'C++']
| 1
|
maximum-candies-allocated-to-k-children
|
C++ Solution 100% Faster 💫💫💫
|
c-solution-100-faster-by-himanshu_52-aiv3
|
"""\n#define ll long long\nclass Solution {\npublic:\n int maximumCandies(vector& candies, long long k) {\n ll left=1,right=*max_element(candies.begin
|
himanshu_52
|
NORMAL
|
2022-04-03T04:43:32.480004+00:00
|
2022-04-03T05:22:41.979850+00:00
| 538
| false
|
"""\n#define ll long long\nclass Solution {\npublic:\n int maximumCandies(vector<int>& candies, long long k) {\n ll left=1,right=*max_element(candies.begin(),candies.end());\n ll size=candies.size();\n ll maxi=0;\n while(left<=right){\n ll mid=left+(right-left)/2;\n ll temp=0;\n for(int i=0;i<size;i++){\n temp+=candies[i]/mid;\n }\n if(temp>=k){\n maxi=mid;\n left=mid+1;\n }else{\n right=mid-1;\n }\n }\n return maxi;\n }\n};\n"""\n\nPlease Upvote if you find it Helpful \uD83D\uDE42.
| 8
| 0
|
['Binary Search', 'C']
| 1
|
maximum-candies-allocated-to-k-children
|
C++ || Binary Search On Answer || Explained || O(NlogN)
|
c-binary-search-on-answer-explained-onlo-8h71
|
CONCEPT\n In these type of question first we have to find search space which is the possible set of answers which this question can have. Like in this case mini
|
niks07
|
NORMAL
|
2022-04-03T04:12:34.122160+00:00
|
2022-04-03T06:44:14.263984+00:00
| 639
| false
|
**CONCEPT**\n* In these type of question first we have to find search space which is the possible set of answers which this question can have. Like in this case minimum answer can be zero and maximum can be maximum of the candies not more than that. \n* Simply apply binary search on this range [0,max] and if mid is possible answer than we will try to increase this answer by reducing our search space to [mid+1,max] else we will try to find answer in [0,mid].\n* isPossible function tells whether is it possible to divide the candies or not. So it is implemented greedily. So i have count the maximum number of children i can distribute candies to and if it is greater than equal to k than it is possible to divide else not.\n* Time:O(NlogN) and Space:O(1\n```\nclass Solution {\npublic:\n bool isPossible(vector<int>& nums, long long k, long long mid){\n long long cnt=0;\n for(int i=0;i<nums.size();i++){\n if(nums[i]>=mid){\n cnt+=(nums[i]/mid);\n }\n }\n return cnt>=k;\n }\n \n \n \n int maximumCandies(vector<int>& candies, long long k) {\n sort(candies.begin(),candies.end());\n int n=candies.size();\n long long sum=0;\n int mx=INT_MIN;\n for(int i=0;i<n;i++){\n sum+=candies[i];\n mx=max(mx,candies[i]);\n \n }\n \n long long l=1,r=mx;\n int res=0;\n while(l<=r){\n long long mid=l+(r-l)/2;\n if(isPossible(candies,k,mid)){\n l=mid+1;\n }else{\n r=mid-1;\n }\n }\n \n return r;\n }\n};\n```
| 8
| 1
|
['Binary Search', 'C']
| 0
|
maximum-candies-allocated-to-k-children
|
C++ Binary Search
|
c-binary-search-by-lzl124631x-x0or
|
\nSee my latest update in repo LeetCode\n\n## Solution 1. Binary Answer\n\nBinary search in range L = 1, R = max(A).\n\nFor a given M = (L + R) / 2, we test if
|
lzl124631x
|
NORMAL
|
2022-04-03T04:02:43.437548+00:00
|
2022-04-03T04:02:43.437576+00:00
| 856
| false
|
\nSee my latest update in repo [LeetCode](https://github.com/lzl124631x/LeetCode)\n\n## Solution 1. Binary Answer\n\nBinary search in range `L = 1, R = max(A)`.\n\nFor a given `M = (L + R) / 2`, we test if we can give `M` candies to each child, which can be done by traversing the array once, taking `O(N)` time. \n\nIf possible/valid, we make `L = M + 1`; otherwise, we make `R = M - 1`.\n\nIn the end, since we are looking for the greatest valid number, we return `R`.\n\n```cpp\n// OJ: https://leetcode.com/contest/weekly-contest-287/problems/maximum-candies-allocated-to-k-children/\n// Author: github.com/lzl124631x\n// Time: O(Nlog(sum(A)))\n// Space: O(1)\nclass Solution {\npublic:\n int maximumCandies(vector<int>& A, long long k) {\n long L = 1, R = *max_element(begin(A), end(A)), N = A.size();\n auto valid = [&](long m) {\n long cnt = 0;\n for (int n : A) {\n cnt += n / m;\n if (cnt >= k) return true;\n }\n return false;\n };\n while (L <= R) {\n long M = L + (R - L) / 2;\n if (valid(M)) L = M + 1;\n else R = M - 1;\n }\n return R;\n }\n};\n```
| 8
| 1
|
[]
| 2
|
maximum-candies-allocated-to-k-children
|
✅ One Line Solution
|
one-line-solution-by-mikposp-juxr
|
(Disclaimer: this is not an example to follow in a real project - it is written for fun and training mostly)Code #1.1Time complexity: O(n∗log(m)). Space complex
|
MikPosp
|
NORMAL
|
2025-03-14T08:54:53.403069+00:00
|
2025-03-14T08:54:53.403069+00:00
| 814
| false
|
(Disclaimer: this is not an example to follow in a real project - it is written for fun and training mostly)
# Code #1.1
Time complexity: $$O(n*log(m))$$. Space complexity: $$O(1)$$.
```python3
class Solution:
def maximumCandies(self, a: List[int], k: int) -> int:
return bisect_left(range(max(a)+1),1,1,key=lambda q:sum(v//q for v in a)<k)-1
```
# Code #1.2
Time complexity: $$O(n*log(m))$$. Space complexity: $$O(1)$$.
```python3
class Solution:
def maximumCandies(self, a: List[int], k: int) -> int:
return bisect_left(range(max(a)),1,key=lambda q:sum(v//-~q for v in a)<k)
```
(Disclaimer 2: code above is just a product of fantasy packed into one line, it is not considered as 'true' oneliners - please, remind about drawbacks only if you know how to make it better)
| 7
| 0
|
['Array', 'Binary Search', 'Python', 'Python3']
| 2
|
maximum-candies-allocated-to-k-children
|
Maximum Candies Allocated to K Children [C++]
|
maximum-candies-allocated-to-k-children-ahrmp
|
IntuitionWe need to determine the maximum number of candies each child can receive when distributing candies among k children. The key observation is that binar
|
moveeeax
|
NORMAL
|
2025-03-14T07:19:19.058477+00:00
|
2025-03-14T07:19:19.058477+00:00
| 41
| false
|
## **Intuition**
We need to determine the maximum number of candies each child can receive when distributing `candies` among `k` children. The key observation is that **binary search** can be applied to find the optimal maximum number of candies each child can receive.
---
## **Approach**
1. **Check Feasibility Function**:
- We define a helper function `canAllocate(candies, k, mid)`, which checks if we can distribute `mid` candies to each child and satisfy `k` children.
- This is done by counting how many children can receive `mid` candies using `count += c / mid` for each `c` in `candies`.
2. **Binary Search on the Maximum Possible Candies Per Child**:
- The search range is between `1` (minimum valid distribution) and `max(candies)` (maximum a child can receive if only one child is considered).
- Use binary search to check if a given `mid` can be a valid maximum distribution.
- If `canAllocate(mid) == true`, move `left` to `mid + 1` to try a larger number.
- Otherwise, move `right` to `mid - 1` to try a smaller number.
---
## **Complexity Analysis**
- **Time Complexity**: \(O(n \log M)\)
- **Binary search** runs in \(O(\log M)\), where \(M\) is `max(candies)`.
- **Checking feasibility** takes \(O(n)\) for each binary search iteration.
- Overall, this results in \(O(n \log M)\).
- **Space Complexity**: \(O(1)\)
- We use only a few integer variables, so space usage is constant.
---
## **Optimized C++ Solution**
```cpp
class Solution {
public:
bool canAllocate(vector<int>& candies, long long k, int mid) {
long long count = 0;
for (int c : candies) {
count += c / mid;
if (count >= k) return true;
}
return false;
}
int maximumCandies(vector<int>& candies, long long k) {
long long total_candies = accumulate(candies.begin(), candies.end(), 0LL);
if (total_candies < k) return 0;
int left = 1, right = *max_element(candies.begin(), candies.end()), res = 0;
while (left <= right) {
int mid = left + (right - left) / 2;
if (canAllocate(candies, k, mid)) {
res = mid;
left = mid + 1;
} else {
right = mid - 1;
}
}
return res;
}
};
```
---
## **Key Takeaways**
- **Binary search** is a powerful tool when looking for an optimal maximum/minimum value.
- Using **greedy checking** inside the binary search allows us to quickly determine feasibility.
- The solution efficiently distributes the candies while minimizing unnecessary computations. 🚀
| 7
| 0
|
['C++']
| 0
|
maximum-candies-allocated-to-k-children
|
Beginner Friendly | 🔍 Binary Search | 🔥 Optimized Solution | ⏳ O(n log m) | 💻 Java
|
beginner-friendly-binary-search-optimize-fw2m
|
🍬 Distributing Candies Optimally using Binary SearchImagine you have different piles of candies 🍭🍬 and k children 🧑🤝🧑. Each child should get equal candies fro
|
himanshu7437
|
NORMAL
|
2025-03-14T01:46:14.838680+00:00
|
2025-03-14T20:38:15.555746+00:00
| 559
| false
|
### **🍬 Distributing Candies Optimally using Binary Search**
Imagine you have **different piles of candies** 🍭🍬 and **k children** 🧑🤝🧑. Each child should get **equal candies** from a **single pile**, and you can only **split piles** (not merge them). Our goal is to find **the maximum number of candies** each child can get.
---
## **💡 Intuition (Step-by-Step Understanding)**
### **🔹 Step 1: Understanding the Problem**
1. Each pile has a certain number of candies 🍬.
2. We must **distribute candies fairly**, meaning each child should get the **same number** of candies.
3. We can **split piles into smaller ones**, but **not merge** them.
4. The objective is to **maximize the candies each child gets** while ensuring we can satisfy at least `k` children.
### **🔹 Step 2: Constraints and Observations**
- The **maximum number of candies a child can get** is limited by the **largest pile**.
- The **minimum** candies each child can get is `1`.
- If `k` is **larger than the total number of possible candy distributions**, return `0`.
### **🔹 Step 3: Using Binary Search for Efficiency**
Instead of checking every possible amount of candies (`1` to `max(candies)`) one by one (**brute force**), we use **binary search** to quickly find the largest possible valid value.
---
## **🚀 Approach (Step-by-Step with Emojis)**
1️⃣ **Define the Range of Candies** 🎯
- The **minimum** candies per child = `1`.
- The **maximum** candies per child = `max(candies)`.
- We will **search in this range** using **binary search**.
2️⃣ **Binary Search to Find the Maximum Candies per Child** 🔍
- Pick a **mid value** = `(left + right) / 2` (possible candies per child).
- Check **how many children we can satisfy** by dividing each pile by `mid`.
- If we can **satisfy at least `k` children**, we **increase** `mid` (search for a larger number of candies per child).
- Otherwise, we **decrease** `mid` (search for a smaller number of candies per child).
3️⃣ **Stopping Condition** ⛔
- The search stops when **left > right**.
- The **highest valid `mid`** found is the answer.
---
## **🔢 Example Walkthrough**
### **Example 1**
```plaintext
Input: candies = [5, 8, 6], k = 3
```
### **Step-by-Step Execution**
#### **1️⃣ Initial Range**
- **Left** = `1`, **Right** = `8` (max of array)
#### **2️⃣ Binary Search Steps**
| Left | Right | Mid (Candies per Child) | Children We Can Satisfy | Action |
|------|------|-------------------|----------------------|--------|
| 1 | 8 | 4 | `(5/4) + (8/4) + (6/4) = 1 + 2 + 1 = 4` ✅ | Increase `mid` (`left = 5`) |
| 5 | 8 | 6 | `(5/6) + (8/6) + (6/6) = 0 + 1 + 1 = 2` ❌ | Decrease `mid` (`right = 5`) |
| 5 | 5 | 5 | `(5/5) + (8/5) + (6/5) = 1 + 1 + 1 = 3` ✅ | Increase `mid` (`left = 6`) |
#### **3️⃣ Final Answer**
```plaintext
Output: 5 (Max candies per child)
```
Each child gets **5 candies**, which is the maximum possible.
---
## **⏳ Time Complexity Analysis**
| **Operation** | **Time Complexity** | **Explanation** |
|----------------------|--------------------|-----------------|
| **Binary Search** 🔍 | `O(log m)` | Searching in the range `[1, max(candies)]`. |
| **Checking Feasibility** 🏗️ | `O(n)` | Looping through `candies` to count children. |
| **Total Complexity** ⏳ | `O(n log m)` | Much better than brute force `O(n * max(candies))`. |
---
## **🔥 Why is Binary Search Better?**
**Brute Force** (Checking all `candiesPerChild` values) ⏳
- Tries every value from `1` to `max(candies)`.
- **Worst Case Complexity**: `O(n * max(candies))` (Too slow 😵).
**Binary Search** (Efficiently finding the best value) 🚀
- Eliminates **half** of the search space each time.
- **Complexity**: `O(n log m)` (Fast ✅).
---
## **💻 Optimized Java Code**
```java
class Solution {
public int maximumCandies(int[] candies, long k) {
if (k == 0) return 0; // Edge case: No children
int left = 1, right = 0;
for (int candy : candies) {
right = Math.max(right, candy); // Get max candy in a pile
}
int result = 0;
while (left <= right) {
int mid = left + (right - left) / 2;
// Count children we can satisfy
long childrenCount = 0;
for (int candy : candies) {
childrenCount += candy / mid;
}
if (childrenCount >= k) { // We can distribute at least k children
result = mid;
left = mid + 1; // Try for a larger candy per child
} else {
right = mid - 1; // Try for a smaller value
}
}
return result;
}
}
```
---

| 7
| 0
|
['Array', 'Two Pointers', 'Binary Search', 'Java']
| 2
|
maximum-candies-allocated-to-k-children
|
Beats 100% 🚀🔥| Optimized Binary Search Solution for Maximum Candies 🍬
|
beats-100-optimized-binary-search-soluti-yiee
|
Intuition 💡🤔The goal is to distribute candies 🍬 among k children 👦👧 such that each child gets the maximum possible number of candies.Instead of checking all pos
|
Omkrishna123
|
NORMAL
|
2025-03-14T03:55:17.798626+00:00
|
2025-03-14T03:57:56.981036+00:00
| 478
| false
|
# Intuition 💡🤔
The goal is to distribute candies 🍬 among `k` children 👦👧 such that each child gets the **maximum possible number of candies**.
Instead of checking all possible values (which is slow ❌), we recognize that the **maximum possible candies per child** lie between `1` and `sum(candies) / k`. Using **binary search 🔍**, we efficiently find this maximum value without unnecessary calculations.
---
# Approach 🚀⚡
We use **binary search** 🏹 to determine the **largest possible** number of candies 🍬 that can be evenly distributed among `k` children.
---
### **Steps 📝**
1️⃣ **Compute the total number of candies (`sum`)** and **find the smallest candy pile (`mini`)**.
2️⃣ **Edge Case Check 🔴:**
- If `sum < k`, it's impossible to give at least one candy 🍬 to each child 👦 → return `0`.
3️⃣ **Binary Search Setup 📏:**
- `low = 1` (minimum possible candies per child)
- `high = sum / k` (maximum possible candies per child)
4️⃣ **Binary Search Execution 🔍:**
- Pick `mid` as the potential max candies per child.
- Use `isit()` function ✅ to check if it's possible to distribute at least `mid` candies per child.
- If **yes** 🎉 → Try increasing `mid` by moving `low` up ⬆️.
- If **no** ❌ → Decrease `mid` by moving `high` down ⬇️.
5️⃣ **Return `ans` 🎯**, which stores the max candies per child.
---
# Complexity ⏳⚙️
| Complexity Type | Value | Explanation 📖 |
|------------------|------------|----------------|
| **Time Complexity ⏱️** | `O( log (sum/k) )` | Binary search runs in `O( log (sum/k) )`, and each check runs in `O(n)`. |
| **Space Complexity 📦** | `O(1)` | Only a few extra variables are used. ✅ |
---
# Code 💻🔢
```cpp
class Solution {
public:
bool isit(vector<int>& candies, long long k, long long part) {
long long count = 0;
for (int &i : candies) {
count = count + (i / part);
}
return count >= k;
}
long long maximumCandies(vector<int>& candies, long long k) {
long long sum = 0;
int mini = INT_MAX;
for (int &i : candies) {
sum += i;
mini = min(mini, i);
}
if (sum < k) return 0;
long long low = 1, high = sum / k, ans = 0;
while (low <= high) {
long long mid = low + (high - low) / 2;
if (isit(candies, k, mid)) {
ans = mid;
low = mid + 1;
}
else {
high = mid - 1;
}
}
return ans;
}
};
```
| 6
| 0
|
['Array', 'Binary Search', 'C++']
| 4
|
maximum-candies-allocated-to-k-children
|
[C++] accepted solution || Binary Search || faster than 100%
|
c-accepted-solution-binary-search-faster-eayl
|
\nclass Solution {\npublic:\n int maximumCandies(vector<int>& candies, long long k) {\n \n long long sum=0;\n \n int n=candies.si
|
soujash_mandal
|
NORMAL
|
2022-04-03T05:26:43.873500+00:00
|
2022-04-03T05:38:53.422596+00:00
| 477
| false
|
```\nclass Solution {\npublic:\n int maximumCandies(vector<int>& candies, long long k) {\n \n long long sum=0;\n \n int n=candies.size();\n \n //calculate sum\n for(int i=0;i<n;i++)\n {\n sum+=(long long)candies[i];\n }\n \n \n // if sum<k then we are not able to give a single one candy\n if(sum<k) return 0;\n \n \n long long h=sum/k; // max possible ans cant exceed sum/k\n long long l=1; // min possible ans will be 1\n long long res=1;\n \n \n //next part is just binary search\n while(h>=l)\n {\n long long m=(h+l)/2;\n long long count=0;\n for(int i=0;i<n;i++)\n {\n count+=candies[i]/m;\n }\n \n if(count>=k)\n {\n res=max(res,m);\n l=m+1;\n }\n else\n {\n h=m-1;\n }\n }\n return res;\n \n \n }\n};\n```\n**upvote**
| 6
| 0
|
['C', 'Binary Tree']
| 1
|
maximum-candies-allocated-to-k-children
|
Easy & Detailed Approch ✅🚀 | Binary Search 🔎 | C++ | Java | Python | Js 🔥
|
easy-detailed-approch-binary-search-c-ja-4322
|
Intuition🧠 The key idea is to use Binary Search to efficiently find the maximum number of candies that can be distributed per child. Since the number of candies
|
himanshu_dhage
|
NORMAL
|
2025-03-14T09:33:47.962804+00:00
|
2025-03-14T09:33:47.962804+00:00
| 635
| false
|
# Intuition
🧠 The key idea is to use **Binary Search** to efficiently find the maximum number of candies that can be distributed per child. Since the number of candies per child can range between 1 and the maximum candy count, Binary Search optimizes the search space.
# Approach
🚀 Steps to solve the problem:
1. **Sort** the `candies` array to simplify the Binary Search process.
2. Use **Binary Search** with `start = 1` and `end = max(candies)`.
3. In each iteration, calculate `mid` as the potential maximum candies per child.
4. Use the `solve` function to check if distributing `mid` candies per child is possible.
- In `solve`, iterate through the array and calculate the total number of pieces each element can contribute.
5. If `solve` returns `true`, update `answer` and move the `start` pointer to `mid + 1`.
6. Otherwise, move the `end` pointer to `mid - 1`.
7. Return the maximum valid answer.
# Complexity
⏳ **Time Complexity:** $$O(n \log m)$$
- `n` is the size of the `candies` array.
- `m` is the maximum number of candies in the array (range of binary search).
🧱 **Space Complexity:** $$O(1)$$
- Only a few extra variables are used for calculation.
# Code
```cpp []
class Solution {
public:
// Function to check if 'val' candies can be given to at least 'k' children
bool solve(vector<int>& candies, long long k, int val) {
long long total_pieces = 0; // Total pieces we can create
for (int i = 0; i < candies.size(); i++) {
if (val > candies[i]) {
continue; // Skip if current candy count is less than 'val'
} else {
total_pieces += candies[i] / val; // Count how many pieces we can create
}
}
return total_pieces >= k; // Return true if we can distribute enough pieces
}
int maximumCandies(vector<int>& candies, long long k) {
sort(candies.begin(), candies.end()); // Sort candies array
int start = 1; // Minimum possible candy count per child
int end = candies[candies.size() - 1]; // Maximum possible candy count per child
int answer = 0; // Store the maximum valid answer
// Binary Search to find the maximum valid number of candies per child
while (start <= end) {
int mid = (start + end) / 2; // Midpoint for binary search
if (solve(candies, k, mid)) {
answer = mid; // Store the valid value
start = mid + 1; // Try for a bigger value
} else {
end = mid - 1; // Try for a smaller value
}
}
return answer; // Return the maximum valid answer
}
};
```
```javascript []
var maximumCandies = function(candies, k) {
// Function to check if 'val' candies can be distributed to at least 'k' children
const solve = (candies, k, val) => {
let totalPieces = 0; // Track total number of candy pieces
// Iterate through each candy count
for (let candy of candies) {
if (val <= candy) { // Only count valid pieces
totalPieces += Math.floor(candy / val);
}
}
return totalPieces >= k; // Return true if enough pieces are possible
};
// Sort the candies array for efficient binary search
candies.sort((a, b) => a - b);
let start = 1, end = candies[candies.length - 1], answer = 0;
// Binary search to find the maximum number of candies per child
while (start <= end) {
let mid = Math.floor((start + end) / 2); // Calculate mid value
if (solve(candies, k, mid)) {
answer = mid; // Update valid answer
start = mid + 1; // Try for larger values
} else {
end = mid - 1; // Reduce search range
}
}
return answer; // Return the maximum valid answer
};
```
```python []
def maximumCandies(candies, k):
# Function to check if 'val' candies can be distributed to at least 'k' children
def solve(candies, k, val):
total_pieces = sum(candy // val for candy in candies if val <= candy)
return total_pieces >= k
# Sort the candies array for efficient binary search
candies.sort()
start, end, answer = 1, candies[-1], 0
# Binary search to find the maximum number of candies per child
while start <= end:
mid = (start + end) // 2 # Calculate mid value
if solve(candies, k, mid):
answer = mid # Update valid answer
start = mid + 1 # Try for larger values
else:
end = mid - 1 # Reduce search range
return answer # Return the maximum valid answer
```
```java []
import java.util.*;
class Solution {
// Function to check if 'val' candies can be distributed to at least 'k' children
public boolean solve(int[] candies, long k, int val) {
long totalPieces = 0; // Track total number of candy pieces
for (int candy : candies) {
if (val <= candy) {
totalPieces += candy / val; // Add possible pieces
}
}
return totalPieces >= k; // Return true if enough pieces are possible
}
public int maximumCandies(int[] candies, long k) {
Arrays.sort(candies); // Sort the array for efficient binary search
int start = 1, end = candies[candies.length - 1], answer = 0;
// Binary search to find the maximum number of candies per child
while (start <= end) {
int mid = (start + end) / 2; // Calculate mid value
if (solve(candies, k, mid)) {
answer = mid; // Update valid answer
start = mid + 1; // Try for larger values
} else {
end = mid - 1; // Reduce search range
}
}
return answer; // Return the maximum valid answer
}
}
```
| 5
| 0
|
['Array', 'Binary Search', 'C++', 'Java', 'Python3', 'JavaScript']
| 1
|
maximum-candies-allocated-to-k-children
|
Python | Simple Binary Search | O(n log m), O(1) | Beats 100%
|
python-simple-binary-search-olog-m-n-o1-n6yo7
|
CodeComplexity
Time complexity: O(log(m)∗n). The binary search has initial range from 0 to m where m is average of total candies, time is log(m). isValidSize()
|
2pillows
|
NORMAL
|
2025-03-14T01:39:08.711288+00:00
|
2025-03-14T01:44:57.104666+00:00
| 410
| false
|
# Code
```python3 []
class Solution:
def maximumCandies(self, candies: List[int], k: int) -> int:
def isValidSize(group_candies):
groups = 0
for candy in candies:
groups += candy // group_candies # add groups that can be made from candy
return groups >= k
left, right = 0, sum(candies) // k # min is 0 candy per group, max is split all candies evenly
while left < right: # binary search to find max number of candies per group
mid = 1 + (left + right) // 2 # 1 + or ceil( / 2) to avoid looping with left = mid
if isValidSize(mid): # true if can make k groups of mid size
left = mid # valid group, move left up and check higher group sizes
else:
right = mid - 1 # invalid group, move right down and check lower group sizes
return left # left = right = max valid size. right + 1 is first invalid size
```
# Complexity
- Time complexity: $$O(log(m)*n)$$. The binary search has initial range from 0 to m where m is average of total candies, time is log(m). isValidSize() checks n candies and performs constant operations to find how many groups can be made for a given size, time is n. Each iteration of the binary search calls isValidSize(), so overall time is log(m) * n.
- Space complexity: $$O(1)$$. Only uses constant space variables.
# Performance
| 5
| 0
|
['Binary Search', 'Python3']
| 1
|
maximum-candies-allocated-to-k-children
|
4 Lines | Concise | Binary Search | C++ | Python | Java | Go | JS
|
4-linesconcisebinary-searchc-by-sapilol-d1o1
|
Implementation
|
LeadingTheAbyss
|
NORMAL
|
2025-03-14T00:56:37.464254+00:00
|
2025-03-14T01:19:46.221328+00:00
| 923
| false
|
# Implementation
```cpp []
class Solution {
public:
int maximumCandies(vector<int>& A, long long k , int l = 0 , int r = 1e7) {
while(l < r){
int m = (l + r + 1)/2; long s = 0;
for(auto p : A) s += p/m;
if(s < k) r = m - 1; else l = m;
}
return l;
}
};
```
```Java []
class Solution {
public int maximumCandies(int[] candies, long k) {
int l = 0, r = (int)1e7;
while (l < r) {
int m = (l + r + 1) / 2;
long s = 0;
for (int p : candies) s += p / m;
if (s < k) r = m - 1;
else l = m;
}
return l;
}
}
```
```Python []
class Solution:
def maximumCandies(self, A, k):
l, r = 0, int(1e7)
while l < r:
m = (l + r + 1) // 2
s = sum(p // m for p in A)
if s < k:
r = m - 1
else:
l = m
return l
```
```Go []
func maximumCandies(A []int, k int64) int {
l, r := 0, int(1e7)
for l < r {
m := (l + r + 1) / 2
var s int64
for _, p := range A {
s += int64(p / m)
}
if s < k {
r = m - 1
} else {
l = m
}
}
return l
}
```
```Javascript []
var maximumCandies = function(A, k) {
let l = 0, r = 1e7;
while (l < r) {
let m = Math.floor((l + r + 1) / 2);
let s = A.reduce((sum, p) => sum + Math.floor(p / m), 0);
if (s < k) r = m - 1;
else l = m;
}
return l;
};
```
| 5
| 0
|
['Array', 'Binary Search', 'Python', 'C++', 'Java', 'Go', 'JavaScript']
| 0
|
maximum-candies-allocated-to-k-children
|
Easy Tricky Binary Search Approach Explained Along with Code.
|
easy-tricky-binary-search-approach-expla-hy5v
|
This problem is a kind of Upper Bond problem of Binary search.\nHere we just simply have to make an binary search call by setting the min and max variables whic
|
adityasada
|
NORMAL
|
2022-04-03T06:11:54.861635+00:00
|
2022-06-29T13:35:07.461063+00:00
| 581
| false
|
# This problem is a kind of Upper Bond problem of Binary search.\nHere we just simply have to make an binary search call by setting the min and max variables which is the range in which we have to be get the correct answer. Since we can give as minimum as 0 candies to k children because there are not many candies for everyone so our min = 0. and the maximum candies which we can give is the maximum pile of candie which is available with us because there is no way we can distribute more candies than what we have available.\nTo Calculate mid we will use this formula **mid = min + (max-min)/2** this will give us the exact possible value of mid everytime.\nAnd then we need a condtion to verify if the current **mid** is a right input so for that we have a condition that the number of candie pile can be divided such that all the **k** childeren should get same number of candy so we will make a boolean function to check the exact same thing which we discussed.\n\n\n```\nclass Solution {\n public int maximumCandies(int[] candies, long k) {\n int min = 1;\n int max = Integer.MIN_VALUE;\n for(int candie : candies){\n max = Math.max(candie,max);\n }\n \n int answer = 0;\n while(min <= max){\n int mid = min + (max - min)/2;\n if(checkIfTrue(candies,k,mid)){\n answer = mid;\n min = mid+1;\n }else{\n max = mid-1;\n }\n }\n return answer;\n }\n \n public boolean checkIfTrue(int[] candies,long k,int divid){\n long cnt = 0;\n for(int candie : candies){\n cnt += (long) Math.floor(candie/divid);\n }\n if(cnt >= k) return true;\n return false;\n }\n}\n```\n
| 5
| 0
|
['Binary Tree', 'Java']
| 0
|
maximum-candies-allocated-to-k-children
|
JAVA
|
java-by-ayeshakhan7-l3pn
|
ApproachBinary Search on answerComplexity
Time complexity: O(n * log(maxC))
Space complexity: O(1)
Code
|
ayeshakhan7
|
NORMAL
|
2025-03-14T17:13:55.001202+00:00
|
2025-03-14T17:13:55.001202+00:00
| 93
| false
|
# Approach
<!-- Describe your approach to solving the problem. -->
Binary Search on answer
# Complexity
- Time complexity: O(n * log(maxC))
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
private boolean canDistr(int[] candies, int mid, long k) {
int n = candies.length;
for (int i = 0; i < n; i++) {
k -= candies[i] / mid;
if (k <= 0) { // all children got mid candies
return true; // Early return
}
}
return k <= 0; // all children got the mid candies
}
public int maximumCandies(int[] candies, long k) {
int n = candies.length;
int maxC = 0;
long total = 0;
for (int i = 0; i < n; i++) {
total += candies[i];
maxC = Math.max(maxC, candies[i]);
}
if (total < k) {
return 0;
}
int l = 1;
int r = maxC;
int result = 0;
while (l <= r) {
int mid = l + (r - l) / 2;
if (canDistr(candies, mid, k)) {
result = mid;
l = mid + 1;
} else {
r = mid - 1;
}
}
return result;
}
}
```
| 4
| 0
|
['Java']
| 0
|
maximum-candies-allocated-to-k-children
|
3 ms/8 ms C++/JS. Binary Search. Beats 100.00%
|
3-ms8-ms-cjs-binary-search-beats-10000-b-7ct0
|
ApproachBinary search for the appropriate number of candies. Check if the number of candies is appropriate using the test function.Complexity
Time complexity: O
|
nodeforce
|
NORMAL
|
2025-03-14T11:22:55.622272+00:00
|
2025-03-14T11:22:55.622272+00:00
| 159
| false
|
# Approach
Binary search for the appropriate number of candies. Check if the number of candies is appropriate using the `test` function.
# Complexity
- Time complexity: $$O(nlogn)$$
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: $$O(1)$$
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
int maximumCandies(vector<int>& a, long long k) {
const int n = a.size();
const auto test = [&a, &n, &k](int x) {
long p = 0;
for (int i = 0; i < n; ++i) p += a[i] / x;
return p >= k;
};
long s = 0;
for (int i = 0; i < n; ++i) s += a[i];
int i = 1;
int j = s / k;
if (j <= 1) return j;
while (i <= j) {
const int m = (i + j) / 2;
if (test(m)) i = m + 1;
else j = m - 1;
}
return j;
}
};
```
```javascript []
const maximumCandies = (a, k) => {
const n = a.length;
const test = (x) => {
let p = 0;
for (let i = 0; i < n; ++i) p += (a[i] / x) >> 0;
return p >= k;
};
let s = 0;
for (let i = 0; i < n; ++i) s += a[i];
let i = 1;
let j = (s / k) >> 0;
if (j <= 1) return j;
while (i <= j) {
const m = (i + j) >> 1;
if (test(m)) i = m + 1;
else j = m - 1;
}
return j;
};
```
| 4
| 0
|
['Array', 'Binary Search', 'C', 'C++', 'TypeScript', 'JavaScript']
| 0
|
maximum-candies-allocated-to-k-children
|
✅ 🔥 Python3 | Binary search | Faster 100% ✅ 🔥
|
python3-binary-search-faster-100-by-sure-v189
|
IntuitionSince each student needs to have an equal number of candies, we divide the array into different groups, ensuring the total is divisible by the number o
|
Surendaar
|
NORMAL
|
2025-03-14T10:21:42.235838+00:00
|
2025-03-14T10:21:42.235838+00:00
| 148
| false
|
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
Since each student needs to have an equal number of candies, we divide the array into different groups, ensuring the total is divisible by the number of students. Then, we check whether it is possible to distribute the candies accordingly.
# Approach
<!-- Describe your approach to solving the problem. -->
Use binary search to determine if it is possible to distribute the given number of candies among the students. If possible, adjust the left boundary; otherwise, reduce the right boundary to mid - 1.
# Complexity
- Time complexity:O(N Log(k))
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def maximumCandies(self, candies: List[int], k: int) -> int:
sum = 0
for i in range(len(candies)):
sum += candies[i]
if sum < k:
return 0
def isPossible(mid):
count = 0
for i in range(len(candies)):
if candies[i] >= mid:
count += candies[i] // mid
if count >= k:
return True
return False
left, right = 0, sum // k
#print(f"{left} {right} {sum}")
while left < right:
mid = left + (right - left+1) // 2
#print(f"{left} {right} mid : {mid}")
if isPossible(mid):
left = mid
else:
right = mid - 1
return left
```
| 4
| 0
|
['Python3']
| 0
|
maximum-candies-allocated-to-k-children
|
## 🔥 C++ | 🚀 Fast & Optimized | 🔍 binary-search - 🍭 greedy - 📊 array - 🎯 two-pointer
|
c-fast-optimized-binary-search-greedy-ar-e6wq
|
IntuitionThe goal is to distribute candies fairly among k children.We need to find the maximum possible number of candies per childsuch that at least k children
|
El_shamy
|
NORMAL
|
2025-03-14T06:44:57.246891+00:00
|
2025-03-14T06:44:57.246891+00:00
| 9
| false
|
## Intuition
## The goal is to distribute candies fairly among `k` children.
## We need to find the **maximum possible number of candies per child**
## such that at least `k` children get that amount.
## We can use **Binary Search** 🧐 to efficiently find this maximum value.
## Approach
## 1️⃣ **Define the search space:**
## - Minimum possible candies per child = `1` 🍬
## - Maximum possible = `sum(candies)`, if one child takes everything.
## 2️⃣ **Use Binary Search to find the best value:**
## - Pick a mid-value `mid = (left + right) / 2`.
## - Check how many children can get `mid` candies.
## - If at least `k` children can get `mid`, try a larger value.
## - Otherwise, try a smaller value.
## 3️⃣ **Continue until the best valid value is found.**
## Complexity
## - **Time Complexity:** `O(N log M)` 🕒
## - `N` = number of candy piles.
## - `M` = total number of candies.
## - We do a binary search (`log M` steps), and each step checks all candies (`O(N)`).
## - **Space Complexity:** `O(1)` 💾
## - We use only a few extra variables, no extra space needed.
# Code
```cpp []
// بسم الله الرحمن الرحيم
// والصلاة والسلام على رسول الله ﷺ
// Author: Ahmed Elshamy
// In the name of Allah, the Most Gracious, the Most Merciful.
// May peace and blessings be upon the Prophet Muhammad ﷺ.
// Welcome to my solution! I hope you find it useful 🚀
// مرحبًا بكم في كودي! أتمنى لكم تجربة ممتعة في البرمجة التنافسية 💡🔥
#include <bits/stdc++.h>
using namespace std;
#define ll long long
class Solution
{
public:
int maximumCandies(vector<int> &candies, ll k)
{
ll total_candies = accumulate(candies.begin(), candies.end(), 0LL);
// If total candies are less than k, it's impossible to distribute
if (total_candies < k)
return 0;
ll left = 1, right = total_candies, max_size = 0;
while (left <= right)
{
ll mid = left + (right - left) / 2; // Prevent overflow
ll child_count = 0; // Tracks how many children can receive candies
// Count how many children can get at least `mid` candies
for (const auto &candy : candies)
{
child_count += candy / mid;
if (child_count >= k)
break; // No need to check further
}
if (child_count >= k)
{ // Valid distribution, try larger size
max_size = mid;
left = mid + 1;
}
else
{ // Not enough children can get `mid` candies
right = mid - 1;
}
}
return max_size;
}
};
```
| 4
| 0
|
['Array', 'Binary Search', 'C++']
| 0
|
maximum-candies-allocated-to-k-children
|
100% Best solution using C# (easy beginner friendly)
|
100-best-solution-using-c-easy-beginner-o7mju
|
ExplanationWe need to find the maximum number of candies that can be evenly distributed among k children. The goal is to determine the largest possible pile siz
|
rickeyrohit7
|
NORMAL
|
2025-03-14T05:42:29.268197+00:00
|
2025-03-14T05:42:29.268197+00:00
| 363
| false
|
### **Explanation**
We need to find the **maximum** number of candies that can be evenly distributed among **k** children. The goal is to determine the largest possible **pile size** each child can receive.
#### **Intuition**
- If we fix a pile size **m**, we can check how many children can get at least **m** candies by dividing each candy pile by **m** and summing up the results.
- Since increasing **m** will reduce the number of children that can be served, we can apply **binary search** on **m** to efficiently determine the optimal pile size.
#### **Approach**
1. **Binary Search on Answer:**
- The **minimum pile size** (`l`) is `1` (each child gets at least one candy).
- The **maximum pile size** (`r`) is `max(candies)`, since we can’t have a pile size greater than the largest candy pile.
- We perform binary search in this range `[1, max(candies)]` to find the **largest valid pile size**.
2. **Counting Children Served:**
- For a given pile size **m**, compute the total number of children that can be served:
\[
\sum \frac{\text{candies[i]}}{m}
\]
- If this count is **greater than or equal to k**, then **m** is valid, so we try a larger **m**.
- Otherwise, we try a smaller **m**.
3. **Binary Search Termination:**
- When `l > r`, the optimal pile size is `r`.
---
### **C# Code Implementation**
```csharp
using System;
using System.Linq;
public class Solution {
public int MaximumCandies(int[] candies, long k) {
int l = 1;
int r = candies.Max(); // Maximum candy pile size
while (l <= r) {
int m = (l + r) / 2; // Mid value for binary search
long count = 0;
// Calculate how many children can receive at least `m` candies
foreach (int candy in candies) {
count += candy / m;
}
// If we can serve at least `k` children, try a larger pile size
if (count >= k) {
l = m + 1;
}
// Otherwise, reduce the pile size
else {
r = m - 1;
}
}
return r; // Maximum valid pile size
}
}
```
---
### **Complexity Analysis**
- **Time Complexity:**
- **Binary search range:** `O(log(max(candies)))`
- **Iteration through `candies` per binary search step:** `O(n)`
- **Total complexity:** `O(n log(max(candies)))`
- **Space Complexity:**
- `O(1)`, since we only use a few integer variables.
---
### **Example Walkthrough**
#### **Example 1**
```csharp
int[] candies = {5, 8, 6};
long k = 3;
Solution sol = new Solution();
Console.WriteLine(sol.MaximumCandies(candies, k)); // Output: 5
```
##### **Explanation**
- Maximum candy pile size **5** is possible:
- `{5, 8, 6} → {1, 1, 1}` (each child gets **5** candies, total `3` children served)
- Trying **6** fails since only `2` children can be served (`{5,8,6} → {0,1,1}`)
- Hence, the answer is **5**.
---
### **Edge Cases Considered**
✔ **Single pile of candies**: `{10}, k = 5`
✔ **All elements are equal**: `{4, 4, 4, 4}, k = 3`
✔ **Large `k` where no valid split exists**
✔ **Largest possible candy pile is less than `k`**
# Please upvote for 5 years of good luck
| 4
| 1
|
['C++']
| 4
|
maximum-candies-allocated-to-k-children
|
Easy to understand || simple code || Binary Search || c++ || python || java
|
easy-to-understand-simple-code-binary-se-s2qt
|
Intuition
We need to maximize the number of candies that each person can receive. By checking if a candidate number of candies per person is feasible, we can us
|
jayanthmarupaka29
|
NORMAL
|
2025-03-14T00:51:41.287457+00:00
|
2025-03-14T01:08:06.755212+00:00
| 489
| false
|
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
- We need to maximize the number of candies that each person can receive. By checking if a candidate number of candies per person is feasible, we can use binary search to efficiently find the maximum possible value.
# Approach
<!-- Describe your approach to solving the problem. -->
1. Create a helper function 'solve' that, given a candidate value `res`, calculates how many people can be served by summing up `candies[i] / res` for each candy pile.
2. In the main function, first check if the total number of candies is less than `k` (which means it's impossible to give even one candy per person).
3. Use binary search over the range [1, maximum candies in a single pile] to find the highest value of candies per person that can serve `k` people.
4. For each mid value in the binary search, use the helper function to determine if the candidate distribution is possible, then adjust the search range accordingly.
# Complexity
- Time complexity:O(n * log(max_candies))
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
bool solve(int res,vector<int>& candies, long long k){
long long cnt=0;
for(auto it:candies){
cnt+=it/res;
}
return cnt>=k;
}
int maximumCandies(vector<int>& candies, long long k) {
int n=candies.size();
long long sum=0;
for(auto it:candies){
sum+=it;
}
if(sum<k){
return 0;
}
int low=1;
int high=*max_element(candies.begin(),candies.end());
int ans=low;
while(low<=high){
int mid=(low+high)/2;
if(solve(mid,candies,k)){
ans=mid;
low=mid+1;
}else{
high=mid-1;
}
}
return ans;
}
};
```
```python []
from typing import List
class Solution:
def solve(self, res: int, candies: List[int], k: int) -> bool:
cnt = 0
for candy in candies:
cnt += candy // res
return cnt >= k
def maximumCandies(self, candies: List[int], k: int) -> int:
if sum(candies) < k:
return 0
low = 1
high = max(candies)
ans = low
while low <= high:
mid = (low + high) // 2
if self.solve(mid, candies, k):
ans = mid
low = mid + 1
else:
high = mid - 1
return ans
```
```java []
class Solution {
private boolean solve(int res, int[] candies, long k) {
long cnt = 0;
for (int candy : candies) {
cnt += candy / res;
}
return cnt >= k;
}
public int maximumCandies(int[] candies, long k) {
long sum = 0;
for (int candy : candies) {
sum += candy;
}
if (sum < k) {
return 0;
}
int low = 1;
int high = 0;
for (int candy : candies) {
high = Math.max(high, candy);
}
int ans = low;
while (low <= high) {
int mid = low + (high - low) / 2;
if (solve(mid, candies, k)) {
ans = mid;
low = mid + 1;
} else {
high = mid - 1;
}
}
return ans;
}
}
```
| 4
| 0
|
['Array', 'Binary Search', 'C++', 'Java', 'Python3']
| 2
|
maximum-candies-allocated-to-k-children
|
C++ || Binary Search || Simple Explanation
|
c-binary-search-simple-explanation-by-dh-qgfb
|
Approach\n Describe your approach to solving the problem. \nWhat comes to my mind is to check what number of candies(search space) is satisfying children.\nSo b
|
dhruvil2511
|
NORMAL
|
2023-03-31T07:07:34.586636+00:00
|
2023-04-15T08:15:42.942633+00:00
| 420
| false
|
# Approach\n<!-- Describe your approach to solving the problem. -->\nWhat comes to my mind is to check what number of candies(search space) is satisfying children.\nSo by this intuition we can find the search space. \n\nMinimum candy child can get will be 1:\nExample: [1,2,3,4] and k=5\nTotal 5 children and all of them should have same amount of candies\nso for example let candy=2 now check whether we can get 2 candies from all the piles or not\n1st pile:- candies[0]=1 and we can\'t get 2 candies -> count=0\n2nd pile:- candies[1]=2 we can get 2 candies -> count=1\n3rd pile:- candies[2]=3 we can get 2 candies -> count=2\n4th pile:- candies[3]=4 we can get total pair of 2 candy -> count=4\n\nAt end we can only satisfy 4 children but we need to satisfy 5 children(k=5)\nso minimum value child can get will be 1 candy.\n\nMaximum candy child can get will be maximum element in candies:\nExample candies=[1,2,3,4] and k=1\nHere we need to satisy 1 children and it should have maximum candy we can just allocate all candy to single children \nso maximum value of candy child can get will be 4.\n\nWe got our search space here\nstart=1 and end=max_element\n\nNow approach is to apply binary search and check whether particular number of candies satisfies all the children or not\nExample: candies=[5,8,6], k = 3\nsuppose we reached mid=5 now count the number of 5 candies from each pile:\n```\n bool isSatisfying(vector<int> candies,long long mid ,long long k){\n long long count=0;\n\n for(auto x: candies){\n count=count+(x/mid);\n }\n if(count>=k) return true;\n return false;\n }\n```\nWe are dividing each piles with mid value and checking how many number of 5 candies we can get.\nFor [5,8,6]->\n Each child gets 1 pile of total 5 candies\n 5/5=1 -> For first child\n 8/5=1 -> For second child\n 6/5=1 -> For third child\n\nWe can distribute max 5 candies to 3 children\nIf count is greater or equal to children then we can distribute equal candies to all children .\n\n# Complexity\n- Time complexity:\n $$O(n(log(end)))$$ where n=candies.size() and end=max_element\n\n- Space complexity\n $$O(1)$$\n\n# Code\n```\nclass Solution {\npublic:\n bool isSatisfying(vector<int> candies,long long mid ,long long k){\n long long count=0;\n\n for(auto x: candies){\n count=count+(x/mid);\n }\n\n if(count>=k) return true;\n return false;\n }\n int maximumCandies(vector<int>& candies, long long k) {\n int start=1;\n int end=*max_element(candies.begin(),candies.end());\n int ans=0;\n\n while(start<=end){\n int mid=start+(end-start)/2;\n if(isSatisfying(candies,mid,k)){\n //we need to maximize search space so storing answer and finding anther maxi\n ans=mid;\n start=mid+1;\n }\n else{\n end=mid-1;\n }\n }\n\n return ans;\n }\n};\n```
| 4
| 0
|
['Array', 'Math', 'Binary Search', 'C++']
| 0
|
maximum-candies-allocated-to-k-children
|
Easy To Understand Python Solution (Binary Search)
|
easy-to-understand-python-solution-binar-ft1g
|
\nclass Solution:\n def maximumCandies(self, candies, k):\n n = len(candies)\n left = 1 # the least number of candy in each stack we can give
|
danielkua
|
NORMAL
|
2022-04-04T03:00:06.876607+00:00
|
2022-04-04T03:00:54.858099+00:00
| 918
| false
|
```\nclass Solution:\n def maximumCandies(self, candies, k):\n n = len(candies)\n left = 1 # the least number of candy in each stack we can give to each student is one\n right = max(candies) # the max number of candy in each stack that we can give to each student is the maximum number in the candies array\n ans = 0 # ans here is used to store the maximum amount in each stack that we can give to each children. \n # If we don\'t have enough to distribute, we will return 0 at the end so we initialize it to be 0 now.\n\n while left <= right: # binary search\n numberOfPiles = 0\n mid = (left) + (right - left) // 2 # the number of candies we require to form a stack\n\n for i in range(n): # loop through the array to find the numbers of stack we can form\n numberOfPiles += candies[i] // mid # we add to the numberOfPiles whenever we find that this current stack (candies[i]) can be split into mid (the number of candies we require to form a stack)\n\n if numberOfPiles >= k: # if our number of piles is greater or equal than the students we have, so we have enough to distribute\n ans = max(ans, mid) # we first store the max no. of candies in each stack that we can give to each student \n left = mid + 1 # we will try to increase the number of candies in each stack that we can give to each student\n else: \n right = mid - 1 # we will try to reduce the number of candies in each stack that we can give to each student\n return ans\n```\n
| 4
| 0
|
['Binary Search', 'Binary Tree', 'Python', 'Python3']
| 0
|
maximum-candies-allocated-to-k-children
|
1-liner Python / Ruby
|
1-liner-python-ruby-by-stefanpochmann-g8h6
|
Binary-search the smallest allocation a that\'s too large, the answer is 1 lower. Ruby still excels at this, though Python improved now that it supports a key.\
|
stefanpochmann
|
NORMAL
|
2022-04-03T20:20:50.914196+00:00
|
2022-04-03T20:22:09.211581+00:00
| 303
| false
|
Binary-search the smallest allocation `a` that\'s too large, the answer is 1 lower. Ruby still excels at this, though Python improved now that it supports a `key`.\n\nRuby:\n```\ndef maximum_candies(candies, k)\n (1..10**8).bsearch { |a| candies.sum { |c| c / a } < k } - 1\nend\n```\nPython:\n\n def maximumCandies(self, candies: List[int], k: int) -> int:\n return bisect_left(range(1, 10**8), True, key=lambda a: sum(c // a for c in candies) < k)\n
| 4
| 1
|
['Binary Tree', 'Python', 'Ruby']
| 1
|
maximum-candies-allocated-to-k-children
|
[JavaScript] 2226. Maximum Candies Allocated to K Children
|
javascript-2226-maximum-candies-allocate-sxpd
|
\nWeekly Contest 287\n\n- Q1 answer\n - https://leetcode.com/problems/minimum-number-of-operations-to-convert-time/discuss/1908839/JavaScript-2224.-Minimum-Num
|
pgmreddy
|
NORMAL
|
2022-04-03T04:04:29.446572+00:00
|
2023-02-15T12:28:20.325552+00:00
| 441
| false
|
\n**Weekly Contest 287**\n\n- Q1 answer\n - https://leetcode.com/problems/minimum-number-of-operations-to-convert-time/discuss/1908839/JavaScript-2224.-Minimum-Number-of-Operations-to-Convert-Time\n- Q2 answer\n - https://leetcode.com/problems/find-players-with-zero-or-one-losses/discuss/1908871/JavaScript-2225.-Find-Players-With-Zero-or-One-Losses\n- Q3 answer\n - https://leetcode.com/problems/maximum-candies-allocated-to-k-children/discuss/1908890/JavaScript-2226.-Maximum-Candies-Allocated-to-K-Children\n - **below**\n - Similar to some other DP problems, but this is greedy\n - **Less code** solution\n - **More code - with comments** solution\n\n---\n\nHope it is simple to understand.\n\n---\n\n**Less code** solution\n\n```\nvar maximumCandies = function (candies, k) {\n function ok(min_candy) {\n let count = 0;\n for (let candy of candies) count += Math.floor(candy / min_candy);\n return count >= k;\n }\n\n let l = 0,\n h = Math.max(...candies);\n\n while (l <= h) {\n let m = l + Math.trunc((h - l) / 2);\n if (ok(m)) l = m + 1;\n else h = m - 1;\n }\n return h;\n};\n```\n\n---\n\n**More code - with comments** solution\n\n```\nvar maximumCandies = function (cand, k) {\n function is_good_number_of_candies(cmin) {\n let count = 0;\n for (let c of cand) {\n count += Math.trunc(c / cmin); // how many mins (cmin) can we give from this pile (c)\n }\n return count >= k;\n }\n\n let sum = cand.reduce((sum, x) => sum + x, 0);\n if (sum < k) return 0; // not enough, to give at least 1 candy\n\n let lo = 1; // 1 is possible\n let hi = cand.reduce((max, x) => Math.max(max, x), -Infinity); // max possible\n\n // since # of candies are too large, try binary search\n while (lo <= hi) {\n let mid = lo + Math.trunc((hi - lo) / 2);\n if (is_good_number_of_candies(mid)) {\n lo = mid + 1; // mid is good (##), try next one\n } else {\n hi = mid - 1;\n }\n }\n return lo - 1; // last good was mid, 1 below lo (## above)\n};\n```\n\n---\n
| 4
| 0
|
['JavaScript']
| 0
|
maximum-candies-allocated-to-k-children
|
[Binary Search🔥] | Beginner Friendly Explanation🚀 | Java, Python, C++, JavaScript
|
binary-search-beginner-friendly-explanat-ia0z
|
IntuitionWe need to distribute candies among k children such that each child gets the same number of candies. Our goal is to maximize the number of candies each
|
PradhumanGupta
|
NORMAL
|
2025-03-16T07:57:50.055867+00:00
|
2025-03-16T07:57:50.055867+00:00
| 17
| false
|
# Intuition
We need to **distribute candies** among `k` children such that each child gets the **same number of candies**. Our goal is to **maximize** the number of candies each child receives.
Since a child can only receive **whole** candies, we can use **binary search** on the maximum possible number of candies per child.
- If `mid` candies per child is **possible**, we try a **larger** value (`l = mid + 1`).
- Otherwise, we reduce the value (`r = mid - 1`).
- The highest valid `mid` is our answer.
# Approach
1. **Sort the candies array** to efficiently pick maximum candy values.
2. **Use binary search** to find the largest possible `mid` (candies per child).
- `l = 1` (minimum possible candies per child).
- `r = max(candies)` (maximum possible candies per child).
3. **Check feasibility (`isPossible` function)**:
- For each pile, count how many children can get `mid` candies.
- If `k` children can be satisfied, return `true`.
4. **Update search range** based on feasibility and return the best result.
# Complexity
- **Time Complexity:** $$O(n \log m)$$, where `n` is the number of candy piles and `m` is the maximum candy count.
- **Space Complexity:** $$O(1)$$ (only a few extra variables).
# Code
```java []
import java.util.Arrays;
class Solution {
public int maximumCandies(int[] candies, long k) {
Arrays.sort(candies); // Sort candies for efficient searching
int length = candies.length;
int l = 1, r = candies[length - 1]; // Binary search range
int result = 0;
while (l <= r) {
int mid = l + (r - l) / 2; // Mid candies per child
if (mid == 0) break; // Prevent division by zero
if (isPossible(candies, k, mid)) {
result = mid; // Store the valid maximum
l = mid + 1; // Try for a larger value
} else {
r = mid - 1; // Reduce the value
}
}
return result;
}
// Checks if it's possible to give 'mid' candies per child
public boolean isPossible(int[] candies, long k, int mid) {
for (int pile : candies) {
k -= pile / mid; // Count how many children can get mid candies
if (k <= 0) return true; // Enough children satisfied
}
return false;
}
}
```
```python3 []
class Solution:
def maximumCandies(self, candies: list[int], k: int) -> int:
candies.sort() # Sort for efficiency
l, r, result = 1, candies[-1], 0
while l <= r:
mid = (l + r) // 2 # Mid candies per child
if mid == 0: break # Avoid division by zero
if self.isPossible(candies, k, mid):
result = mid # Store valid max
l = mid + 1 # Try for more
else:
r = mid - 1 # Reduce value
return result
def isPossible(self, candies: list[int], k: int, mid: int) -> bool:
for pile in candies:
k -= pile // mid # Count children that can get 'mid' candies
if k <= 0:
return True
return False
```
```cpp []
#include <vector>
#include <algorithm>
using namespace std;
class Solution {
public:
int maximumCandies(vector<int>& candies, long long k) {
sort(candies.begin(), candies.end()); // Sort for efficiency
int l = 1, r = candies.back(), result = 0;
while (l <= r) {
int mid = l + (r - l) / 2; // Mid candies per child
if (mid == 0) break; // Prevent division by zero
if (isPossible(candies, k, mid)) {
result = mid; // Store valid max
l = mid + 1; // Try for more
} else {
r = mid - 1; // Reduce value
}
}
return result;
}
private:
bool isPossible(vector<int>& candies, long long k, int mid) {
for (int pile : candies) {
k -= pile / mid; // Count children that can get 'mid' candies
if (k <= 0) return true;
}
return false;
}
};
```
```javascript []
var maximumCandies = function(candies, k) {
candies.sort((a, b) => a - b); // Sort for efficiency
let l = 1, r = candies[candies.length - 1], result = 0;
while (l <= r) {
let mid = Math.floor((l + r) / 2); // Mid candies per child
if (mid === 0) break; // Prevent division by zero
if (isPossible(candies, k, mid)) {
result = mid; // Store valid max
l = mid + 1; // Try for more
} else {
r = mid - 1; // Reduce value
}
}
return result;
};
// Checks if it's possible to give 'mid' candies per child
function isPossible(candies, k, mid) {
for (let pile of candies) {
k -= Math.floor(pile / mid); // Count children that can get 'mid' candies
if (k <= 0) return true;
}
return false;
}
```
**Please Upvote⬆️** 🚀

| 3
| 0
|
['Array', 'Binary Search', 'C++', 'Java', 'Python3', 'JavaScript']
| 1
|
maximum-candies-allocated-to-k-children
|
Easy BS on ANS (BEATS 100%)
|
easy-bs-on-ans-beats-100-by-pranavb16-vdyk
|
IntuitionSo , we have to find the maximum number of candies a child can get and keep in mind that he gets it from a single pile.We have to maximize the number o
|
pranavb16
|
NORMAL
|
2025-03-14T16:55:13.594050+00:00
|
2025-03-14T16:55:13.594050+00:00
| 55
| false
|
# Intuition
So , we have to find the maximum number of candies a child can get and keep in mind that he gets it from a single pile.We have to maximize the number of candies , so we can think of binary search on ans and the constraints also point towards the same.
# Approach
- Calculating the sum and dividing it by k , gives us the best ans that may or may not be possible.
- This gives us the ending point for applying bs.
- So s=0 and e=sum/k;
- Now for each mid, we are trying to check if it is valid or not using the check function.
- If it is possible we are storing the ans and then searching for a better ans.
# Complexity
- Time complexity:
O(nlogn)
- Space complexity:
O(1)
# Code
```cpp []
class Solution {
public:
bool check(long long mid,vector<int>& candies, long long k)
{
if(mid==0)
return true;
for(auto it:candies)
{
long long poss=it/mid;
k-=poss;
if(k<=0)
return true;
}
return false;
}
int maximumCandies(vector<int>& candies, long long k)
{
long long sum=accumulate(candies.begin(),candies.end(),0LL);
sum=sum/k;
long long s=0;
long long e=sum;
long long mid=s+(e-s)/2;
long long ans=0;
while(s<=e)
{
if(check(mid,candies,k))
{
ans=mid;
s=mid+1;
}
else
e=mid-1;
mid=s+(e-s)/2;
}
return ans;
}
};
```
| 3
| 0
|
['Binary Search', 'C++']
| 1
|
maximum-candies-allocated-to-k-children
|
Binary Search, O(nlogm), Easy to understand (:
|
binary-search-onlogm-easy-to-understand-1v9q8
|
Complexity
Time complexity: O(nlogm)
Space complexity: O(1)
Code
|
mak2rae
|
NORMAL
|
2025-03-14T11:34:33.643360+00:00
|
2025-03-14T11:34:33.643360+00:00
| 58
| false
|
# Complexity
- Time complexity: O(nlogm)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def maximumCandies(self, candies: List[int], k: int) -> int:
def can_divided(c):
cnt = 0
for candy in candies:
cnt += candy // c
if cnt >= k:
return True
return False
l, r = 0, max(candies)
if sum(candies) < k: return 0
while l <= r:
m = (l + r) // 2
if m == 0 or can_divided(m):
l = m + 1
else:
r = m - 1
return r
```
| 3
| 0
|
['Binary Search', 'Python3']
| 0
|
maximum-candies-allocated-to-k-children
|
Binary Search Approach for Maximum Candies Allocation
|
binary-search-approach-for-maximum-candi-45t4
|
IntuitionWhen distributing candies among k children, each child must receive the same amount, and the candies from a single pile cannot be merged with others. T
|
Samandardev02
|
NORMAL
|
2025-03-14T05:42:31.801915+00:00
|
2025-03-14T05:42:31.801915+00:00
| 68
| false
|
## Intuition
When distributing candies among `k` children, each child must receive the same amount, and the candies from a single pile cannot be merged with others. The key observation is that the maximum number of candies each child can receive must be some integer `x` such that there are at least `k` piles of size `x`.
Since we can split the piles but not merge them, our goal is to determine the largest possible value of `x` for which there exist at least `k` piles.
## Approach
We use **binary search** on the possible values of `x`. The lowest possible value is `1` (each child gets at least one candy), and the highest possible value is `max(candies)`, since no child can receive more candies than what exists in the largest pile.
1. **Define a helper function:** This function checks whether it is possible to distribute at least `k` piles of size `x` by counting how many full piles of size `x` can be made from the given candy piles.
2. **Binary Search:** We perform binary search between `1` and `max(candies)`. For each middle value (`midValue`):
- If it's possible to form `k` piles of at least `midValue` candies, we try increasing `midValue` (search in the upper half).
- Otherwise, we search in the lower half.
3. **Return the largest valid `midValue` found.**
## Complexity
- **Time Complexity:** $$O(n \log m)$$, where:
- $$n$$ is the number of elements in `candies`.
- $$m$$ is the maximum value in `candies`.
- The binary search runs in $$O(\log m)$$, and for each search step, we iterate through `candies` in $$O(n)$$.
- **Space Complexity:** $$O(1)$$, since we use only a few extra variables for computation.
## Code
```typescript
function maximumCandies(candies: number[], k: number): number {
let minValue = 1;
let maxValue = Math.max(...candies);
const helper = (num: number): boolean => {
let sum = 0;
for (const candie of candies) {
sum += Math.floor(candie / num);
}
return sum >= k;
};
while (minValue <= maxValue) {
const midValue = Math.floor((minValue + maxValue) / 2);
if (helper(midValue)) {
minValue = midValue + 1;
} else {
maxValue = midValue - 1;
}
}
return minValue - 1;
}
```
| 3
| 0
|
['TypeScript']
| 0
|
maximum-candies-allocated-to-k-children
|
Well explained solution-beats 91%
|
well-explained-solution-beats-91-by-mala-caml
|
IntuitionWe need to distribute candies such that each child gets the same maximum number of candies. The challenge is that we can split a pile but cannot merge
|
malayp2820
|
NORMAL
|
2025-03-14T05:30:31.929727+00:00
|
2025-03-14T05:30:31.929727+00:00
| 175
| false
|
# Intuition
We need to distribute candies such that each child gets the same maximum number of candies. The challenge is that we can split a pile but cannot merge piles together. This means the maximum number of candies a child can receive must be within the range [1, maxPileSize] (where maxPileSize is the largest pile).
To find the maximum valid number, we can use Binary Search because:
- The answer lies between 1 and maxPileSize.
- If a given number of candies per child X is possible, then all values less than X are also possible.
- If X is not possible, all values greater than X are also not possible.
Using binary search helps efficiently check for the largest possible value.
# Why Binary Search?
- We need to find the maximum number of candies per child (X). Checking all possible values from 1 to maxPileSize would be inefficient (O(n * maxPileSize) in brute force). Binary Search efficiently narrows down the range in O(log maxPileSize) steps.
- Since the answer space is monotonic (if X is possible, all values ≤ X are possible), binary search is the best approach.
# Approach
1. Find the largest pile (maxPileSize) in candies[] since the maximum possible candies per child cannot exceed this value.
2. Use Binary Search within the range [1, maxPileSize]:
- Mid = (l + r) / 2, representing the number of candies per child we are currently checking.
3. Use a helper function isPossibleToDistribute(candies, k, mid):
- For each pile, calculate how many children can receive `mid` candies from that pile.
- Sum up the total number of children that can be satisfied.
- If at least `k` children are satisfied, `mid` is a valid candidate → move right (`l = mid + 1`) to try a higher number.
- Otherwise, move left (`r = mid - 1`).
4. The final answer is the largest valid `mid` found.
# Complexity
- Time Complexity:
- Finding the maxPileSize: $$O(n)$$
- Binary Search range: $$O(\log \text{maxPileSize})$$
- Checking each mid value (`isPossibleToDistribute` function): $$O(n)$$
- Overall: $$O(n \log \text{maxPileSize})$$
- Space Complexity: $$O(1)$$
<!-- (Using only variables, no extra data structures) -->
# Code
```java []
class Solution {
public int maximumCandies(int[] candies, long k) {
int maxPileSize = 0;
for(int candy:candies){
maxPileSize = Math.max(candy, maxPileSize);
}
int l=1,r=maxPileSize,mid,ans=0;
while(l<=r){
mid = (l+r)/2;
if(isPossibleToDistribute(candies, k, mid)){
ans=mid;
l=mid+1;
}
else{
r=mid-1;
}
}
return ans;
}
public boolean isPossibleToDistribute(int[] candies, long k, int distributeCandies){
int numberOfChildren;
for(int candiesInPile:candies){
numberOfChildren = candiesInPile/distributeCandies;
k -= numberOfChildren;
if(k<=0){
return true;
}
}
return false;
}
}
```
| 3
| 0
|
['Binary Search', 'Java']
| 0
|
maximum-candies-allocated-to-k-children
|
Easy BinarySearch solution
|
easy-binarysearch-solution-by-allaboinad-cjck
|
Intuition
We want to maximize the number of candies each child gets while ensuring that at least k children receive them.
Since giving more candies means ser
|
allaboinadivakar
|
NORMAL
|
2025-03-14T04:37:00.353899+00:00
|
2025-03-14T04:37:00.353899+00:00
| 142
| false
|
# Intuition
1. We want to maximize the number of candies each child gets while ensuring that at least `k` children receive them.
2. Since giving more candies means serving fewer children, we use **binary search** to efficiently find the largest valid number of candies per child.
3. For each `mid` (possible candies per child), we check if distributing them to at least `k` children is possible, adjusting our search range accordingly.
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
1. Use **binary search** on the possible candy distribution range (`1` to `maxElement`) to find the maximum candies each child can get.
2. For each mid-value, use the `check` function to count how many children can receive at least `mid` candies and verify if it's at least `k`.
3. If possible, move `low` up to find a larger valid `mid`, otherwise move `high` down, and return the best found `mid` as the answer.
# Complexity
- Time complexity:O(n*log(maxelement in candies))
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
bool check(vector<int>&c,int mid,long long k)
{
for(int i=0;i<c.size();i++)
{
k-=(c[i]/mid);
if(k<=0)
{
return true;
}
}
return false;
}
int maximumCandies(vector<int>& c, long long k) {
int n=c.size();
int low=1;
int high=*max_element(c.begin(),c.end());
int ans=0;
while(low<=high)
{
int mid=(low+high)>>1;
if(check(c,mid,k))
{
ans=mid;
low=mid+1;
}
else
{
high=mid-1;
}
}
return ans;
}
};
```
| 3
| 0
|
['Binary Search', 'C++']
| 2
|
maximum-candies-allocated-to-k-children
|
Learn this kind of Binary Search.
|
learn-this-kind-of-binary-search-by-josh-ou72
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
Joshi_Y
|
NORMAL
|
2025-03-14T01:49:58.052005+00:00
|
2025-03-14T01:49:58.052005+00:00
| 183
| false
|
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
search for each number of candies that k children can get equally
until we get the maximum answer.
# Approach
<!-- Describe your approach to solving the problem. -->
Use Binary Search to get the maximum number of candies that k
children could divide equally.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(n log(sum))
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(1)
# Code
```cpp []
#define INCL() \
ios_base::sync_with_stdio(0); \
cin.tie(0); \
cout.tie(0)
class Solution {
public:
long long canFeed(long long candy, vector<int>& candies) {
long long child = 0;
for (int& currCandy : candies) {
child += (currCandy / candy);
}
return child;
}
int maximumCandies(vector<int>& candies, long long k) {
INCL();
long long sum = accumulate(candies.begin(), candies.end(), 0LL);
long long left = 1, right = sum;
long long result = 0;
while (left <= right) {
long long mid = left + (right - left) / 2;
if (canFeed(mid, candies) >= k) { //can feed at least these many candies equally
result = mid;
left = mid + 1;
} else { //if we cannot feed these candies equally, check for less candies
right = mid - 1;
}
}
return result;
}
};
```
| 3
| 0
|
['Array', 'Binary Search', 'C++']
| 0
|
maximum-candies-allocated-to-k-children
|
Binary Search. Java | Kotlin | Python | Javascript. 100% runtime
|
binary-search-java-kotlin-python-javascr-w0vw
|
IntuitionThe task is to find the number of candies that can be taken with the same amount among k childrenApproachThis problem can be solved with brute force so
|
zohidjonakbarov
|
NORMAL
|
2025-03-14T01:46:23.174171+00:00
|
2025-03-14T01:46:23.174171+00:00
| 154
| false
|
# Intuition
The task is to find the number of candies that can be taken with the same amount among k children
# Approach
This problem can be solved with brute force solution easily by checking can k children take 1, 2, 3, 4 and so and until they cann't take it.
but this is not good in Time complexity which takes $$O(n^2)$$
**Optimal way using binary search**
- starting point 0
- end point the biggest item
- every time we check the middle number if it statisfy we continue checking on the right else we check the left.
# Complexity
- Time complexity:
O(n*Log(m)) m is the biggest item in the candies[i]
- Space complexity:
O(1)
# Code
```kotlin []
class Solution {
fun maximumCandies(candies: IntArray, k: Long): Int {
var sum = 0L
var right = 0
for(item in candies){
sum+=item
right = max(right,item)
}
if(sum<k)return 0
var left = 0
var result = 0
while(left<=right){
val mid = (left+right)/2
if(helper(candies,mid,k)){
result = mid
left = mid+1
}else{
right = mid-1
}
}
return result
}
fun helper(candies:IntArray,n:Int,k:Long):Boolean{
var sum = 0L
if(n==0)return true
for(item in candies){
sum+=(item/n)
}
return sum>=k
}
}
```
```javascript []
class Solution {
maximumCandies(candies, k) {
let total = candies.reduce((sum, item) => sum + item, 0);
let right = Math.max(...candies);
if (total < k) return 0;
let left = 0, result = 0;
while (left <= right) {
let mid = Math.floor((left + right) / 2);
if (this.helper(candies, mid, k)) {
result = mid;
left = mid + 1;
} else {
right = mid - 1;
}
}
return result;
}
helper(candies, n, k) {
if (n === 0) return true;
let total = candies.reduce((sum, item) => sum + Math.floor(item / n), 0);
return total >= k;
}
}
```
```python []
class Solution:
def maximumCandies(self, candies: list[int], k: int) -> int:
total = sum(candies)
right = max(candies)
if total < k:
return 0
left, result = 0, 0
while left <= right:
mid = (left + right) // 2
if self.helper(candies, mid, k):
result = mid
left = mid + 1
else:
right = mid - 1
return result
def helper(self, candies: list[int], n: int, k: int) -> bool:
if n == 0:
return True
total = sum(item // n for item in candies)
return total >= k
```
```Java []
import java.util.*;
class Solution {
public int maximumCandies(int[] candies, long k) {
long total = Arrays.stream(candies).sum();
int right = Arrays.stream(candies).max().getAsInt();
if (total < k) return 0;
int left = 0, result = 0;
while (left <= right) {
int mid = (left + right) / 2;
if (helper(candies, mid, k)) {
result = mid;
left = mid + 1;
} else {
right = mid - 1;
}
}
return result;
}
private boolean helper(int[] candies, int n, long k) {
if (n == 0) return true;
long total = 0;
for (int item : candies) {
total += item / n;
}
return total >= k;
}
}
```
| 3
| 0
|
['Python', 'Java', 'Kotlin', 'JavaScript']
| 0
|
maximum-candies-allocated-to-k-children
|
Functional JavaScript 1-liner binary search by value
|
functional-javascript-1-liner-binary-sea-0mzf
|
IntuitionUse binary search up to maximum number of candies per pile, which is 107<224.Time: O(n∗log(m))
Space: O(1)
|
Serhii_Hrynko
|
NORMAL
|
2025-03-14T01:08:52.167912+00:00
|
2025-03-14T23:14:18.977069+00:00
| 136
| false
|
# Intuition
Use binary search up to maximum number of candies per pile, which is $$10^7 < 2^{24}$$.
``` reduce []
maximumCandies = (candies, k) => [...Array(24).keys()]
.reduce((s, x) => _.sumBy(candies, y => ~~(y / x), x = s + (1 << 23 - x)) < k ? s : x, 0)
```
``` recursion []
maximumCandies = (candies, k,
$ = (l, r, m = l + r + 2 >> 1) => r > l
? _.sumBy(candies, y => ~~(y / m)) < k
? $(l, m - 1)
: $(m, r)
: l
) => $(0, ~~(_.sum(candies) / k))
```
``` minified []
// reduce
maximumCandies=(c,k)=>[...Array(25).keys()].reduce((s,x)=>_.sumBy(c,y=>~~(y/x),x=s+(1<<24-x))<k?s:x)
// recursion
maximumCandies=(c,k,$=(l,r,m=l+r+2>>1)=>r>l?_.sumBy(c,y=>~~(y/m))<k?$(l,m-1):$(m,r):l)=>$(0,1e7)
```
Time: $$O(n*log(m))$$
Space: $$O(1)$$
| 3
| 0
|
['Array', 'Binary Search', 'JavaScript']
| 1
|
maximum-candies-allocated-to-k-children
|
Simple Binary search | C++ | Well explained | Happy Holi !!!
|
binary-search-c-by-iitian_010u-67td
|
IntuitionWe have to find that maximum number, candies should be equally distributed among k children.ApproachExample :
candies = {12, 34, 23, 56, 78, 45, 67, 89
|
iitian_010u
|
NORMAL
|
2025-03-14T00:43:04.143620+00:00
|
2025-03-14T01:18:15.532731+00:00
| 557
| false
|
# Intuition
We have to find that maximum number, candies should be equally distributed among k children.
# Approach
Example :
candies = {12, 34, 23, 56, 78, 45, 67, 89, 90, 100}
k = 15
**Step 1**: Our final answer lies in 1 to maximum element(here 100).
**step 2**: check on binary search over 1 to 100 ( for this ex.)
See below table for this ex. how its work (image: ai generated but not solution)
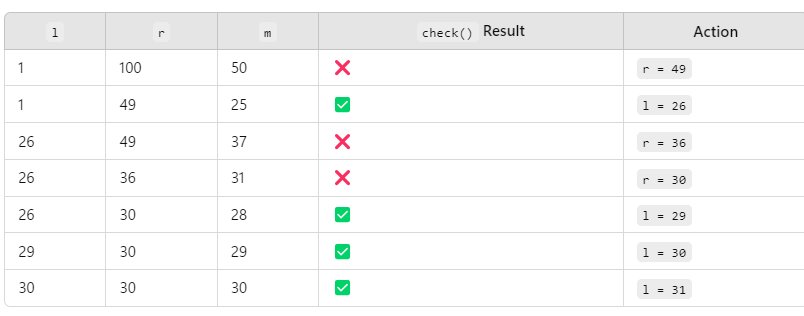
# Complexity
- Time complexity: O(nlog(r)))
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
public:
bool check(vector<int>&candies, int &m, long long &k){
long long ans = 0;
for(int i=0;i<candies.size();++i){
ans+=candies[i]/m;
}
return ans>=k;
}
int maximumCandies(vector<int>& candies, long long k) {
int l = 1, r = *max_element(candies.begin(),candies.end());
while(l<=r){
int m = l + (r-l)/2;
if(check(candies,m,k)) l =m+1;
else r = m-1;
}
return r;
}
};
```
Yes, above code can be reduced into 4-5 lines but that is not our aim, understanding matters.
| 3
| 0
|
['Array', 'Binary Search', 'C++']
| 1
|
maximum-candies-allocated-to-k-children
|
🌟🔥Best Solution in C++ || BinarySearch on Answer🔥💯
|
best-solution-in-c-binarysearch-on-answe-w6ir
|
Complexity\n- Time complexity:\nO(nlogn)\n\n- Space complexity:\nO(1)\n\n# Code\nPlease Upvote if u liked my Solution\uD83E\uDD17\n\nclass Solution {\npublic:\n
|
aDish_21
|
NORMAL
|
2023-02-13T18:32:56.765456+00:00
|
2023-02-13T18:32:56.765496+00:00
| 324
| false
|
# Complexity\n- Time complexity:\nO(nlogn)\n\n- Space complexity:\nO(1)\n\n# Code\n**Please Upvote if u liked my Solution**\uD83E\uDD17\n```\nclass Solution {\npublic:\n bool occurrences(int x,vector<int>& candies,long k){\n long ans=0;\n for(auto it:candies){\n ans+=it/x;\n if(ans>=k)\n return true;\n }\n return false;\n }\n int maximumCandies(vector<int>& candies, long long k) {\n int size=candies.size(),ans=-1;\n long sum=0;\n for(auto it:candies)\n sum+=it;\n if(sum<k)\n return 0;\n int ll=1,ul=sum/k,mid;\n while(ll<=ul){\n mid= (ll+ul) >> 1;\n if(occurrences(mid,candies,k)){\n ans=mid;\n ll=mid+1;\n }\n else\n ul=mid-1;\n }\n return ans;\n }\n};\n```
| 3
| 0
|
['Array', 'Binary Search', 'C++']
| 0
|
maximum-candies-allocated-to-k-children
|
Concise Binary Search | C++
|
concise-binary-search-c-by-tusharbhart-pj53
|
\nclass Solution {\n bool good(int x, vector<int> &c, long long k) {\n long long cnt = 0;\n for(int i : c) cnt += i / x;\n return cnt <
|
TusharBhart
|
NORMAL
|
2022-12-27T15:56:44.990616+00:00
|
2022-12-27T15:56:44.990661+00:00
| 800
| false
|
```\nclass Solution {\n bool good(int x, vector<int> &c, long long k) {\n long long cnt = 0;\n for(int i : c) cnt += i / x;\n return cnt < k ? false : true;\n }\npublic:\n int maximumCandies(vector<int>& candies, long long k) {\n int s = 1, e = 1e9, ans = INT_MIN;\n while(s <= e) {\n int m = (s + e) / 2;\n if(good(m, candies, k)) ans = max(ans, m), s = m + 1;\n else e = m - 1;\n }\n return ans == INT_MIN ? 0 : ans;\n }\n};\n```
| 3
| 0
|
['Binary Search', 'C++']
| 1
|
maximum-candies-allocated-to-k-children
|
Java solution | using binary search
|
java-solution-using-binary-search-by-kav-e0gr
|
\nprivate boolean isPossible(int[] candies,int max,long k){\n long sum = 0;\n for(int i = 0; i<candies.length;i++){\n sum += (candies[i
|
Kavya_Yadav
|
NORMAL
|
2022-08-16T15:01:31.313106+00:00
|
2022-08-16T15:01:31.313138+00:00
| 341
| false
|
```\nprivate boolean isPossible(int[] candies,int max,long k){\n long sum = 0;\n for(int i = 0; i<candies.length;i++){\n sum += (candies[i]/max);\n }\n if(sum>=k){\n return true;\n }\n return false;\n }\n public int maximumCandies(int[] candies, long k) {\n int s = 1;\n int e = 0;\n for(int i = 0; i< candies.length;i++){\n e = Math.max(e,candies[i]); // ans can\'t be more than the height number in the array so take end, the max candie from array.\n }\n int ans = 0;\n while(s<=e){\n int mid = s+(e-s)/2;\n if(isPossible(candies,mid,k)){ // if posible to distribute candies with mid then store ans and increase start to mid + 1, Becoz we need maximum possible ans according to question.\n ans = mid;\n s = mid+1;\n }\n else{\n e = mid-1;\n }\n }\n return ans;\n }\n```
| 3
| 0
|
['Binary Tree', 'Java']
| 0
|
maximum-candies-allocated-to-k-children
|
python | easy to understand | 50% faster
|
python-easy-to-understand-50-faster-by-r-4bxr
|
\nclass Solution:\n """\n approach: \n the problem can be tackled using binary search \n max_candies that can be allocated to children = max(candies
|
rktayal
|
NORMAL
|
2022-04-23T18:06:43.646888+00:00
|
2022-04-23T18:06:43.646935+00:00
| 337
| false
|
```\nclass Solution:\n """\n approach: \n the problem can be tackled using binary search \n max_candies that can be allocated to children = max(candies)\n min_candies that can be allocated to children = 1\n \n we will apply binary search on finding the optimal values of candies that can be\n distributed to children. \n """\n def check_fulfilment(self, candies, elem, k):\n count = 0\n for candy in candies:\n count+= candy // elem\n if count >= k:\n return True\n return False\n def maximumCandies(self, candies: List[int], k: int) -> int:\n low = 1\n high = max(candies)\n if sum(candies) < k:\n return 0\n while low <= high:\n mid = (low+high) // 2\n # check if I can fulfil that order\n status = self.check_fulfilment(candies, mid, k)\n if status:\n low = mid+1\n else: \n high = mid-1\n # low is the maximum number of candies that can be distributed\n return high\n```
| 3
| 0
|
['Binary Tree', 'Python']
| 0
|
maximum-candies-allocated-to-k-children
|
C++|Discrete Binary search
|
cdiscrete-binary-search-by-ajai_cr_7-8jaj
|
\nclass Solution {\npublic:\n bool check(long val,vector<int>&candies,long k){\n long sum = 0;\n for(auto it : candies){\n sum += (i
|
ajai_cr_7
|
NORMAL
|
2022-04-18T09:11:30.022315+00:00
|
2022-04-18T09:11:30.022371+00:00
| 210
| false
|
```\nclass Solution {\npublic:\n bool check(long val,vector<int>&candies,long k){\n long sum = 0;\n for(auto it : candies){\n sum += (it/val);\n }\n return sum >= k;\n }\n int maximumCandies(vector<int>& candies, long long k) {\n long start = 1, end = 1e9;\n while(start < end){\n long mid = (start + end) / 2;\n if(!check(mid,candies,k)){\n end = mid;\n }\n else start = mid+1;\n }\n return start-1;\n }\n};\n```
| 3
| 0
|
['C', 'Binary Tree']
| 1
|
maximum-candies-allocated-to-k-children
|
C++ | O(N) solution with explanation | Binary Search
|
c-on-solution-with-explanation-binary-se-ldrq
|
Code:\nTC: O(N), SC: O(1)\n\nclass Solution {\npublic:\n \n bool isPossible(vector<int>& candies, int mid, long long k)\n {\n //it contains pile
|
Yash2arma
|
NORMAL
|
2022-04-03T08:34:16.329972+00:00
|
2022-04-03T08:34:16.330008+00:00
| 345
| false
|
**Code:**\n**TC: O(N), SC: O(1)**\n```\nclass Solution {\npublic:\n \n bool isPossible(vector<int>& candies, int mid, long long k)\n {\n //it contains piles of candies that tells whether we can distribute or not assign to children equally \n long count=0;\n for(auto it:candies)\n {\n count += it/mid;\n \n //whenever count is greater than or equal to k it tells we can distribute mid to k children and return true;\n if(count>=k) return true;\n }\n //when we can\'t distribute mid piles to k children, we return false;\n return false;\n }\n \n int maximumCandies(vector<int>& candies, long long k) \n {\n //initialize two pointers, 1 for minimum no. of candy, 1 for maximum no. of candy\n int min_candy = 1;\n int max_candy = *max_element(begin(candies), end(candies)); //we can also use for(auto it:candies) max_candy = max(max_candy, it)\n \n //use binary search for finding candies that can get by each child\n while(min_candy<=max_candy)\n {\n //find mid value\n long mid = (min_candy+max_candy)>>1;\n \n //if we can distribute mid piles of candies to k children successfully\n //we check for next greater candies\n if(isPossible(candies, mid, k))\n {\n min_candy = mid+1;\n }\n \n //if we can\'t distribute mid piles of candies to k children\n //we check for lesser candies\n else\n {\n max_candy = mid-1;\n \n }\n }\n \n //return maxi_candies that can assign to each child\n return max_candy;\n \n \n }\n};\n```
| 3
| 0
|
['C', 'Binary Tree', 'C++']
| 2
|
maximum-candies-allocated-to-k-children
|
Easy Understandable JAVA ACCEPTED
|
easy-understandable-java-accepted-by-adi-yy0r
|
\nclass Solution {\n public static int maximumCandies(int[] arr, long k) {\n\t\tArrays.sort(arr);\n\t\tint low = 1;\n\t\tint right = arr[arr.length - 1];\n\t
|
Aditya_jain_2584550188
|
NORMAL
|
2022-04-03T06:06:48.242917+00:00
|
2022-04-03T06:08:20.007179+00:00
| 254
| false
|
```\nclass Solution {\n public static int maximumCandies(int[] arr, long k) {\n\t\tArrays.sort(arr);\n\t\tint low = 1;\n\t\tint right = arr[arr.length - 1];\n\t\twhile (low <= right) {\n\t\t\tint mid = (right - low) / 2 + low;\n\t\t\tif (helper(arr, k, mid)) {\n\t\t\t\tlow = mid + 1;\n\t\t\t} else {\n\t\t\t\tright = mid - 1;\n\t\t\t}\n\t\t}\n\t\treturn right;\n\t}\n\n\tpublic static boolean helper(int[] arr, long k, int mid) {\n\t\tlong curr = 0;\n\t\tfor (int i = arr.length - 1; i >= 0 && curr < k; i--) {\n\t\t\tcurr += arr[i] / mid;\n\t\t}\n\t\treturn curr >= k;\n\t}\n}\n```
| 3
| 0
|
['Binary Search', 'Java']
| 0
|
maximum-candies-allocated-to-k-children
|
Intuition behind Binary Search on Answers
|
intuition-behind-binary-search-on-answer-in8m
|
\n\nWhen there are multiple answers that are valid but we need to find the maximum possible valid answer or minimum possible valid answer then we can use binary
|
bitmasker
|
NORMAL
|
2022-04-03T04:32:16.641424+00:00
|
2022-04-03T04:36:06.830181+00:00
| 168
| false
|
<br>\n\n`When there are multiple answers that are valid but we need to find the maximum possible valid answer or minimum possible valid answer then we can use binary search on answers.`\n\n**How does it work ?**\n\nin this problem we know that minimum number of candies that we can allocate is 0 and maximum is max(candies), so in all such problems we need to find the **minimum possible answer** and **maximum possible answer** and binary search between them to find **maximum / minimum valid answer** in logarithmic time.\n\nAnd binary search on answers can be used only in those problems in which **we can validate whether the current answer in valid or not**. In this problem we can do that by checking if we can allocate x number of candies among k children by dividing some piles, so we can do binary search here.\n\n<br>\n\n```\nclass Solution {\npublic:\n int maximumCandies(vector<int>& candies, long long k) {\n \n int left = 1, ans = 0;\n int right = *max_element(candies.begin(), candies.end());\n \n while(left <= right) {\n int mid = left + (right - left) / 2;\n if(canAllocate(candies, k, mid)) {\n left = mid + 1;\n ans = mid;\n }\n else {\n right = mid - 1;\n }\n }\n \n return ans;\n }\n\nprivate:\n bool canAllocate(vector<int>& candies, long long k, int candy) {\n \n long long total = 0;\n \n for(int c: candies) {\n total += c / candy;\n if(total >= k) return true;\n }\n \n return false;\n }\n};\n```\n<br>\n\n**Time complexity: O(n) * log(max(candies))\nSpace complexity: O(1)**\n\n<br>
| 3
| 0
|
['Binary Search', 'C', 'Binary Tree']
| 1
|
maximum-candies-allocated-to-k-children
|
C++ || BINARY SEARCH
|
c-binary-search-by-vineet_raosahab-4jxv
|
\nclass Solution {\npublic:\n \n int maximumCandies(vector<int>& candies, long long k) {\n long long l=1,h=0;\n for(int& t:candies)\n
|
VineetKumar2023
|
NORMAL
|
2022-04-03T04:16:47.337631+00:00
|
2022-04-03T04:16:47.337677+00:00
| 190
| false
|
```\nclass Solution {\npublic:\n \n int maximumCandies(vector<int>& candies, long long k) {\n long long l=1,h=0;\n for(int& t:candies)\n h+=t;\n int ans=0;\n while(l<=h)\n {\n long long mid=l+(h-l)/2;\n long long val=0;\n for(auto t:candies)\n val+=(t/mid);\n if(val>=k)\n {\n ans=mid;\n l=mid+1;\n }\n else h=mid-1;\n }\n return ans;\n }\n};\n```
| 3
| 0
|
['Binary Search', 'C', 'C++']
| 0
|
maximum-candies-allocated-to-k-children
|
[C++] || Binary search || fastest
|
c-binary-search-fastest-by-4byx-zzw0
|
\nclass Solution {\npublic:\n long long solve(vector<int>& c , long long mid){\n int n = c.size();\n long long cnt = 0;\n for(int i = n-
|
4byx
|
NORMAL
|
2022-04-03T04:01:33.339234+00:00
|
2022-04-03T04:52:23.843008+00:00
| 235
| false
|
```\nclass Solution {\npublic:\n long long solve(vector<int>& c , long long mid){\n int n = c.size();\n long long cnt = 0;\n for(int i = n-1 ; i >= 0 ; i--){\n cnt += (c[i]/mid);\n }\n return cnt;\n }\n int maximumCandies(vector<int>& c, long long k) {\n long long sol = 0;\n int n = c.size();\n int low = 1;\n int high = *max_element(c.begin(),c.end());\n while(low <= high){\n long long mid = (high+low)/2;\n cout<<mid<<" ";\n if(solve(c,mid) >= k){\n sol = mid;\n low = mid+1;\n }\n else{\n high = mid-1;\n }\n }\n \n return sol;\n\n }\n};\n```
| 3
| 0
|
['C']
| 1
|
maximum-candies-allocated-to-k-children
|
⭐Python Solution with Binary Search Explained
|
python-solution-with-binary-search-expla-itm0
|
\nclass Solution:\n def maximumCandies(self, candies: List[int], k: int) -> int:\n # The lower bound is 1 and higher bound is maximum value from candi
|
ancoderr
|
NORMAL
|
2022-04-03T04:01:03.076763+00:00
|
2022-04-03T04:04:47.792495+00:00
| 370
| false
|
```\nclass Solution:\n def maximumCandies(self, candies: List[int], k: int) -> int:\n # The lower bound is 1 and higher bound is maximum value from candies. \n lo, hi = 1, max(candies)\n # This higher bound is not generally possible except for cases like candies = [5,5,5,5] & k = 4\n res = 0 # Current maximum result\n if sum(candies) < k: # If true then we cannot give even 1 candy to each child thus return 0\n return 0\n \n def cal_num_of_piles(pile_size): # Criterion function\n count = 0\n for c in candies:\n count += c // pile_size\n return count >= k\n \n while lo <= hi: # Binary Search Algorithm \n mid = (lo + hi + 1) // 2 # Expected answer\n if cal_num_of_piles(mid): # Check if mid is a possible answer.\n res = mid # Update the current maximum answer\n lo = mid + 1 # Check ahead of mid\n else:\n hi = mid - 1 # Check below mid\n return res\n```\n\n**Concept of Binary Search on Answer:**\nThe best way to explain Binary Search the Answer is that we use binary search to guess the answer to the problem. By guessing we mean that we will get several \u201CYES\u201D or \u201CNO\u201D feedback or maybe \u201Ctoo high\u201D, \u201Ctoo low\u201D, or \u201Cexactly\u201D responses. Since we need the maximum answer Binary Search tries to converge on the largest possible answer till the possibility exists.\n\n**Binary Search on Answer has 3 basic requirements:**\n1. The problem must have multiple possible answers. **[Range of possible solutions]**\n2. The problem must be an optimization problem. **[Minimizing/Maximizing the result]**\n3. We must develope a function/criterion to determine when to update left and right pointers. **[Criterion to update pointers]**\n\n**Observations:**\n`For candies = [5,8,6] & k = 3` we have many possible answers: 1, 2, 3, 4, 5 all seem to work fine but we return 5 as it is the largest.\n1. Thus we have a range of solutions and we are asked to maximize the final result. **Requirement 1 and 2 are fulfilled**.\n2. One might feel that the possible answers must be smaller than the smallest value of an array. Eg: `for candies = [5,6,8] & k = 3` then the answer is 5. For say `candies = [7,9,13] & k = 4` the possible answers are 6, 5...2, 1. However this is not always correct. For Eg: `candies = [1,2,3,4,10] & k = 5` the possible answers are 1, 2, 3. Here we can neglect the 0th and 1st piles to get a better answer. This is because we are told that we may let some piles of candies go unused.\n3. **Developing the criterion:** Since we only need to check if a given value can be possibly divided k times with the given candies array. Hence we get an easy update function. \n\t```\n\tdef cal_num_of_piles(pile_size):\n\t\tcount = 0 # Number of divisions with current pile_size\n\t\tfor c in candies:\n\t\t\tcount += c // pile_size # Add how many piles can be generated with ith candies with given pile_size\n\t\treturn count >= k\n\t```\n***So all three requirements are now fulfilled.***\n
| 3
| 1
|
['Binary Tree', 'Python', 'Python3']
| 1
|
maximum-candies-allocated-to-k-children
|
✅✅ Binary Search || Beginner Friendly || Easy Solution
|
binary-search-beginner-friendly-easy-sol-d0c4
|
Intuition
We need to distribute candies among k children such that each child gets the same maximum number of candies.
The goal is to maximize this number.
Inst
|
Karan_Aggarwal
|
NORMAL
|
2025-03-16T12:51:07.463223+00:00
|
2025-03-16T12:51:07.463223+00:00
| 6
| false
|
# **Intuition**
- We need to distribute `candies` among `k` children such that **each child gets the same maximum number of candies**.
- The goal is to **maximize** this number.
- Instead of distributing candies one by one, we **binary search** for the maximum number of candies each child can receive.
# **Approach**
### **1. Binary Search on Possible Candy Distribution**
- The possible range of answers is `[1, max(candies)]` (1 means each child gets at least one, `max(candies)` means one child gets all candies).
- We perform **binary search** to determine the maximum candies (`mid`) each child can get.
### **2. Checking Feasibility (`canDistr` function)**
- Given a `mid` value (candies per child), check if we can distribute them among `k` children:
- Count how many children we can satisfy by doing `candies[i] / mid`.
- If the count ≥ `k`, it's possible.
- If `k` children can get `mid` candies each, move **right** to check for a larger `mid`.
- Otherwise, move **left** to decrease `mid`.
### **3. Binary Search Execution**
- **If `mid` candies per child is possible** → move **right** (`l = mid + 1`).
- **Otherwise** → move **left** (`r = mid - 1`).
- The final answer is stored in `ans`.
# **Time Complexity Analysis**
1. **Binary Search:**
- The search space is `[1, max(candies)]`, which takes **O(log maxC)**.
2. **Checking Feasibility (`canDistr`)**
- **O(N)** for iterating over `candies`.
3. **Total Complexity:**
- **O(N log maxC)**.
# **Space Complexity**
- **O(1)** (only variables used).
# Code
```cpp []
class Solution {
public:
int N;
bool canDistr(vector<int>&candies,long long k,int mid){
for(int i=0;i<N;i++){
k-=candies[i]/mid;
// Early return - All children got mid candies
if(k<=0) return true;
}
// All children got the mid candies
return k<=0;
}
int maximumCandies(vector<int>& candies, long long k) {
N=candies.size();
int maxC=0;
long long total=0;
for(int i=0;i<N;i++){
total+=candies[i];
maxC=max(maxC,candies[i]);
}
if(total<k) return 0;
int l=1;
int r=maxC;
int ans=0;
while(l<=r){
int mid=l+(r-l)/2;
if(canDistr(candies,k,mid)){
ans=mid;
l=mid+1;
} else{
r=mid-1;
}
}
return ans;
}
};
```
# Have a Good Day 😊 UpVote?
| 2
| 0
|
['Array', 'Binary Search', 'C++']
| 0
|
maximum-candies-allocated-to-k-children
|
Easy Solution 👍 | Beginner Friendly 😊| Binary Search 🔥| 100% beats ✅ | 0(1) SC🔥
|
easy-solution-beginner-friendly-binary-s-rkts
|
IntuitionThis question is almost similar to the famous "Aggressive Cow" problem where we pick up random numbers from the range and check how many cows can be di
|
SayanX
|
NORMAL
|
2025-03-14T19:08:07.791369+00:00
|
2025-03-14T19:13:23.931120+00:00
| 26
| false
|
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
This question is almost similar to the famous "Aggressive Cow" problem where we pick up random numbers from the range and check how many cows can be distributed.
# Approach
<!-- Describe your approach to solving the problem. -->
see the maximum possible number of candies we can distribute is the maximum size of piles as we can't merge any two piles. And minimum possibility will be 1. Now we will be using binary search algo to pick up a random number from the range defined and will check whether it can be valid answer or not.
So in the checking function we will be checking the possiblity. A number of candies n(say) can be a valid answer if sum of all the quotient of (Candies[i]/n) is greater than or equal to total numbers of children. In this case we'll be returning true otherwise false.
If it's true then we'll be upgrading the low to mid+1 and otherwise changing high to mid-1.
As we need the max possible answer so we'll be returning high value.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ --> O(N∗Log(Max(C))
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ --> 0(1)
# Code
```cpp []
class Solution
{
public:
bool Check(vector<int> c, int candy, long long k)
{
long long total = 0;
for (int i : c)
{
total += (i / candy);
}
if (total >= k)
return true;
return false;
}
int maximumCandies(vector<int> &candies, long long k)
{
int n = candies.size();
int high = *max_element(candies.begin(), candies.end());
int low = 1;
if (k == 0)
return 0;
while (low <= high)
{
int mid = low + (high - low) / 2;
if (Check(candies, mid, k))
low = mid + 1;
else
high = mid - 1;
}
return high;
}
};
```
| 2
| 0
|
['C++']
| 2
|
maximum-candies-allocated-to-k-children
|
Sol
|
sol-by-ansh1707-2yb1
|
Code
|
Ansh1707
|
NORMAL
|
2025-03-14T18:08:19.843610+00:00
|
2025-03-14T18:08:19.843610+00:00
| 6
| false
|
# Code
```python []
class Solution(object):
def maximumCandies(self, candies, k):
"""
:type candies: List[int]
:type k: int
:rtype: int
"""
if sum(candies) < k:
return 0
low, high = 1, max(candies)
res = 0
while low <= high:
mid = (low + high) // 2
total_children = sum(c // mid for c in candies)
if total_children >= k:
res = mid
low = mid + 1
else:
high = mid - 1
return res
```
| 2
| 0
|
['Python']
| 0
|
maximum-candies-allocated-to-k-children
|
🔍 Binary Search on probable answer space || Easy solution
|
binary-search-on-probable-answer-space-e-o6sd
|
IntuitionThe minimum candy a child can get is 1, and the maximum is the largest pile size. We can use binary search on the answer to find the maximum number of
|
AlgoZen01
|
NORMAL
|
2025-03-14T15:18:35.515862+00:00
|
2025-03-14T15:18:35.515862+00:00
| 10
| false
|
# Intuition
The minimum candy a child can get is 1, and the maximum is the largest pile size. We can use binary search on the answer to find the maximum number of candies that can be allocated to k children.
# Approach
- Binary Search between 1 and max(candies).
- Helper Function counts how many children can get mid candies.
- If childCount >= k, update ans and search right (mid + 1); else, search left (mid - 1).
- Return the maximum feasible candies per child.
# Complexity
- Time complexity:
The binary search runs in O(logM), where M is the maximum candy count.
The helper function $$findChildCount$$ iterates through candies, taking O(N).
Hence, the total complexity is O(NlogM).
- Space complexity: O(1)
# Code
```cpp []
class Solution {
public:
long long findChildCount(vector<int>& candies,int candy){
long long child=0;
for(int i=0;i<candies.size();i++){
child+=(candies[i]/candy);
}
return child;
}
int maximumCandies(vector<int>& candies, long long k) {
int start=1;
int end=*(max_element(candies.begin(),candies.end()));
int ans=0;
while(start<=end){
int mid=(start+end)/2;
//find mid number of candies kitne child ko de sakte h
long long childCount=findChildCount(candies,mid);
if(childCount>=k){
//matlab itna candy to de sakte h ab max nikalna h to right me jao
ans=mid;
start=mid+1;
}
else{
end=mid-1;
}
}
return ans;
}
};
```
| 2
| 0
|
['Array', 'Binary Search', 'C++']
| 0
|
maximum-candies-allocated-to-k-children
|
Simple Solution using binary search 92% beats 🔥🔥| java
|
simple-solution-using-binary-search-92-b-3a7g
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
harshit_4149
|
NORMAL
|
2025-03-14T13:40:32.520085+00:00
|
2025-03-14T13:40:32.520085+00:00
| 15
| false
|
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public boolean canDist(int candies[],int mid , long k){
for(int i=0;i<candies.length;i++){
k -= candies[i]/mid;
if(k<=0) return true;
}
return k<=0;
}
public int maximumCandies(int[] candies, long k) {
long sum = 0;
int n = candies.length;
int maxCand = 0;
for(int i=0;i<n;i++){
sum += candies[i];
maxCand = Math.max(maxCand,candies[i]);
}
// 8 7 6 5 4 3 2 1 (range from 1 to maxElement in candies arr)
// Apply binary search on this
int l = 1;
int r = maxCand;
int res = 0;
while(l<=r){
int mid = l + (r-l)/2;
if(canDist(candies,mid,k)){
res = mid;
l = mid +1 ;
}
else{
r = mid -1;
}
}
return res;
}
}
```
| 2
| 0
|
['Binary Search', 'Java']
| 0
|
maximum-candies-allocated-to-k-children
|
Python✅✅ | Simplest approach🚀🚀
|
python-simplest-approach-by-aayu_t-r8v2
|
Code
|
aayu_t
|
NORMAL
|
2025-03-14T13:25:38.993191+00:00
|
2025-03-14T13:25:38.993191+00:00
| 12
| false
|
# Code
```python3 []
class Solution:
def maximumCandies(self, candies: List[int], k: int) -> int:
n = len(candies)
def check(mid):
cnt = sum(candy // mid for candy in candies)
return cnt >= k
l, h = 1, sum(candies)
ans = 0
while l <= h:
mid = (l + h) // 2
if check(mid):
ans = mid
l = mid + 1
else:
h = mid - 1
return ans
```
| 2
| 0
|
['Array', 'Binary Search', 'Python3']
| 0
|
maximum-candies-allocated-to-k-children
|
✅ 100% 🧊 10 ms | Binary Search & optimizations
|
100-10-ms-binary-search-optimizations-by-3cmv
|
Please Upvote 🔝 Appreciations!CodeComplexity
Time complexity: O( n log n )
Space complexity: O( 1 )
|
sunnoca
|
NORMAL
|
2025-03-14T09:56:48.205040+00:00
|
2025-03-14T10:00:16.465454+00:00
| 83
| false
|
# Please Upvote 🔝 Appreciations!
# Code
``` kotlin []
class Solution {
fun maximumCandies(candies: IntArray, k: Long): Int {
var right = (candies.sumOf { it.toLong() } / k).toInt()
var left = 0
while (left < right) {
val curr: Int = (left + right + 1) / 2
var count: Long = 0L
for (pile in candies) {
count += pile / curr
if (count >= k) break
}
if (count >= k) left = curr
else right = curr - 1
}
return left
}
}
```
``` kotlin []
class Solution {
fun maximumCandies(candies: IntArray, k: Long): Int {
var right: Int = (candies.sumOf { it.toLong() } / k).toInt()
var left = 0
while (right > 0) {
val curr = (left + right + 1) / 2
var count: Long = 0
for (pile: Int in candies) {
if (pile >= curr) count += pile / curr
if (count >= k) { left = curr; break }
}
if (count < k) right = curr - 1
if (left == right) break
}
return right
}
}
```
# Complexity
- Time complexity: **O(** n log n **)**
- Space complexity: **O(** 1 **)**
| 2
| 0
|
['Array', 'Math', 'Binary Search', 'Java', 'Kotlin']
| 1
|
maximum-candies-allocated-to-k-children
|
Simple and Beginner-Friendly Binary Search | Python | java | cpp || LC : 2226 || (❁´◡`❁)✨
|
simple-and-beginner-friendly-binary-sear-cgod
|
Intuition : We need to maximize the candy piece size that can be distributed equally among k children. Using binary search, we find the largest possible size mi
|
__aj__17
|
NORMAL
|
2025-03-14T08:23:08.111274+00:00
|
2025-03-14T08:23:08.111274+00:00
| 119
| false
|
# Intuition : We need to maximize the candy piece size that can be distributed equally among k children. Using binary search, we find the largest possible size mid such that the total number of pieces (sum(candies[i] / mid)) is at least k.
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach : Binary Search
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity: O(n log max(candies))
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```cpp []
class Solution {
long long func(vector<int>& arr, int mid, long long k) {
long long ans = 0;
for (int i = 0; i < arr.size(); i++)
if (mid > 0) ans += (arr[i] / mid);
return ans >= k;
}
public:
long long maximumCandies(vector<int>& candies, long long k) {
long long l = 1;
long long h = *max_element(candies.begin(), candies.end());
while (l <= h) {
long long mid = (h + l) / 2;
if (func(candies, mid, k)) {
l = mid + 1;
} else {
h = mid - 1;
}
}
return h;
}
};
```
```python []
class Solution:
def canDistribute(self, candies: List[int], mid: int, k: int) -> bool:
return sum(c // mid for c in candies) >= k
def maximumCandies(self, candies: List[int], k: int) -> int:
l, h = 1, max(candies)
ans = 0
while l <= h:
mid = (l + h) // 2
if self.canDistribute(candies, mid, k):
ans = mid
l = mid + 1 # Try larger piece size
else:
h = mid - 1 # Reduce piece size
return ans
```
```Java []
class Solution {
private boolean canDistribute(int[] candies, int mid, long k) {
long count = 0;
for (int c : candies) {
count += c / mid;
}
return count >= k;
}
public int maximumCandies(int[] candies, long k) {
int l = 1, h = Arrays.stream(candies).max().getAsInt();
int ans = 0;
while (l <= h) {
int mid = l + (h - l) / 2;
if (canDistribute(candies, mid, k)) {
ans = mid;
l = mid + 1;
} else {
h = mid - 1;
}
}
return ans;
}
}
```
```
| 2
| 0
|
['Array', 'Binary Search', 'C++', 'Java', 'Python3']
| 0
|
maximum-candies-allocated-to-k-children
|
[ Kotlin | Java | C++ | Python ] Simple Binary Search solution, detailed explanation
|
kotlin-java-c-python-simple-binary-searc-h8h6
|
IntuitionThis is a classic application of binary search on the answer space. The problem asks us to find the maximum number of candies that can be allocated to
|
DmitryNekrasov
|
NORMAL
|
2025-03-14T07:13:36.464925+00:00
|
2025-03-14T07:13:36.464925+00:00
| 82
| false
|
# Intuition
This is a classic application of binary search on the answer space. The problem asks us to find the maximum number of candies that can be allocated to each child, where:
1. Each child must get the same number of candies
2. Candies can only be taken from a single pile per child
3. Piles can be divided but not merged
4. Some piles may remain unused
Since we want to maximize the number of candies per child, we can try different possible answers and check their feasibility. The key insight is that if we can allocate x candies to each child, we can also allocate any number less than x. This monotonic property makes binary search an ideal approach.
# Approach
1. Define a search space for the possible number of candies per child:
- Minimum: 1 (since we can't give 0 candies if a valid solution exists)
- Maximum: The maximum value in the candies array (since we can't give more than the largest pile)
2. Implement a `check(value)` function that determines if it's possible to give `value` candies to each of the `k` children:
- For each pile of size `candies[i]`, we can create `candies[i] / value` sub-piles of size `value`
- Sum up the total number of sub-piles we can create across all piles
- If this sum is at least `k`, then we can give `value` candies to each child
3. Use binary search to find the maximum valid value:
- If `check(mid)` is true, search in the right half (mid+1, right)
- Otherwise, search in the left half (left, mid)
4. When the binary search terminates, we need to subtract 1 from the result since our algorithm finds the smallest value that does NOT work, so we need to return the previous value.
5. Special case: If the total number of candies is less than `k`, return 0 as it's impossible to give each child at least 1 candy. This is handled implicitly by our binary search, which will return 1-1=0.
# Complexity Analysis
## Time Complexity: $$O(N log M)$$
- `N` is the number of piles (length of the candies array)
- `M` is the maximum value in the candies array
- The binary search performs `log M` iterations
- For each iteration, we check all `N` piles in the worst case
## Space Complexity: $$O(1)$$
- We only use a constant amount of extra space regardless of the input size
- The recursive calls in the binary search use $$O(log M)$$ stack space, but this can be converted to an iterative solution with $$O(1)$$ space
# Code
```kotlin []
class Solution {
fun maximumCandies(candies: IntArray, k: Long): Int {
fun check(value: Int) = candies.sumOf { it.toLong() / value } >= k
fun binSearch(left: Int = 1, right: Int = candies.max() + 1): Int {
if (left >= right) return right
val mid = left + (right - left) / 2
return if (check(mid)) binSearch(mid + 1, right) else binSearch(left, mid)
}
return binSearch() - 1
}
}
```
```java []
class Solution {
private static final int MAX = 10_000_001;
public int maximumCandies(int[] candies, long k) {
return binSearch(candies, k, 1, MAX) - 1;
}
private boolean check(int[] candies, long k, int value) {
long sum = 0;
for (int candy : candies) {
sum += (long) candy / value;
}
return sum >= k;
}
private int binSearch(int[] candies, long k, int left, int right) {
if (left >= right) return right;
int mid = left + (right - left) / 2;
return check(candies, k, mid)
? binSearch(candies, k, mid + 1, right)
: binSearch(candies, k, left, mid);
}
}
```
```cpp []
class Solution {
private:
static const int MAX = 10000001;
bool check(vector<int>& candies, long long k, int value) {
long long sum = 0;
for (int candy : candies) {
sum += (long long)candy / value;
}
return sum >= k;
}
int binSearch(vector<int>& candies, long long k, int left, int right) {
if (left >= right) return right;
int mid = left + (right - left) / 2;
return check(candies, k, mid)
? binSearch(candies, k, mid + 1, right)
: binSearch(candies, k, left, mid);
}
public:
int maximumCandies(vector<int>& candies, long long k) {
return binSearch(candies, k, 1, MAX) - 1;
}
};
```
```python3 []
class Solution:
def maximumCandies(self, candies: list[int], k: int) -> int:
MAX = 10_000_001
def check(value: int) -> bool:
return sum(candy // value for candy in candies) >= k
def binSearch(left: int, right: int) -> int:
if left >= right:
return right
mid = left + (right - left) // 2
return binSearch(mid + 1, right) if check(mid) else binSearch(left, mid)
return binSearch(1, MAX) - 1
```
| 2
| 0
|
['Array', 'Binary Search', 'Python', 'C++', 'Java', 'Python3', 'Kotlin']
| 0
|
maximum-candies-allocated-to-k-children
|
🔥Beats 100%🔥Easy & Visual Explaination | 18ms | Beginner Level | Binary Search Approach
|
beats-100easy-visual-explaination-18ms-b-u6mx
|
:) Problem UnderstandingYou have an array candies, where each element represents a pile of candies. You need to distribute these candies among k children equall
|
AryanDarji07
|
NORMAL
|
2025-03-14T06:58:12.953776+00:00
|
2025-03-14T06:58:12.953776+00:00
| 233
| false
|
# :) Problem Understanding
You have an array `candies`, where each element represents a pile of candies. You need to distribute these candies among `k` children equally, ensuring that each child gets the same number of candies. You can split the piles but cannot merge them together.
---
# :) Binary Search Solution (Efficient Approach)
We binary search on the possible values of `x` (candies per child), where `x` can be between `1` and `max(candies)`.
### Step-by-Step Approach :
**1️⃣ Define the search range :**
- `left = 0` (minimum candies per child)
- `right = max(candies)` (maximum possible candies per child)
**2️⃣ Binary Search to find the largest possible x (candies per child) :**
- Midpoint (`mid`) represents a possible number of candies per child.
- Check feasibility: Can we distribute `mid` candies per child among `k` children?
- For each pile `y`, count how many children can get `y/mid` full shares.
- If the total number of children we can satisfy (`sum`) is greater than or equal to `k`, increase `mid` (search right).
- Otherwise, decrease `mid` (search left).
**3️⃣ Return the largest possible x that satisfies the condition.**
---
# :) Visual Intuition
Imagine you have `candies = [5,8,6]` and `k = 3`.
We binary search for `x` :
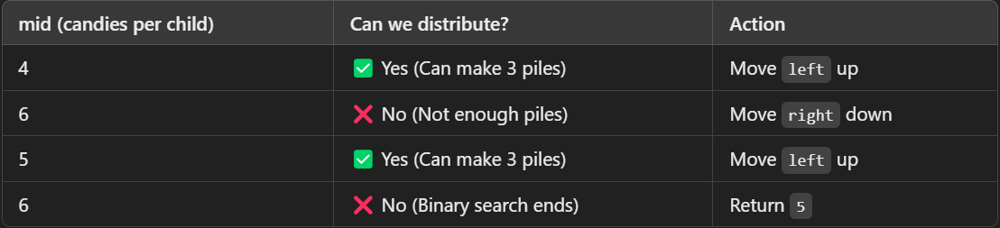
Thus, the answer is **5 candies per child**. 🎯
---

---
# :) Complexity
- Time complexity : O(N log M)
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity : O(1)
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
---
# :) Bro'Code
```javascript []
var maximumCandies = function(candies, k) {
let left =0,right = Math.max(...candies);
const check = (x)=>{
let sum =0;
for(const y of candies){
sum+=Math.floor(y/x);
}
return sum>=k;
}
while(left<=right){
let mid = Math.floor((left+right)/2);
if(!check(mid)){
right = mid-1;
}else{
left = mid+1;
}
}
return right;
};
```
```typescript []
function maximumCandies(candies: number[], k: number): number {
let left = 0, right = Math.max(...candies);
const canDistribute = (x: number): boolean => {
let count = 0;
for (const c of candies) {
count += Math.floor(c / x);
}
return count >= k;
};
while (left <= right) {
let mid = Math.floor((left + right) / 2);
if (!canDistribute(mid)) {
right = mid - 1;
} else {
left = mid + 1;
}
}
return right;
}
```
```C []
bool canDistribute(int* candies, int candiesSize, long long k, int x) {
long long count = 0;
for (int i = 0; i < candiesSize; i++) {
count += candies[i] / x;
}
return count >= k;
}
int maximumCandies(int* candies, int candiesSize, long long k) {
int left = 0, right = 0;
// Find the maximum value in the candies array
for (int i = 0; i < candiesSize; i++) {
if (candies[i] > right) {
right = candies[i];
}
}
while (left <= right) {
int mid = left + (right - left) / 2;
if (!canDistribute(candies, candiesSize, k, mid)) {
right = mid - 1;
} else {
left = mid + 1;
}
}
return right;
}
```
```C++ []
class Solution {
public:
bool canDistribute(vector<int>& candies, long long k, int x) {
long long count = 0;
for (int c : candies) {
count += c / x;
}
return count >= k;
}
int maximumCandies(vector<int>& candies, long long k) {
int left = 0, right = *max_element(candies.begin(), candies.end());
while (left <= right) {
int mid = left + (right - left) / 2;
if (!canDistribute(candies, k, mid)) {
right = mid - 1;
} else {
left = mid + 1;
}
}
return right;
}
};
```
```C# []
public class Solution {
public int MaximumCandies(int[] candies, long k) {
int left = 0, right = candies.Max();
bool CanDistribute(int x) {
long count = 0;
foreach (int c in candies) {
count += c / x;
}
return count >= k;
}
while (left <= right) {
int mid = left + (right - left) / 2;
if (!CanDistribute(mid)) {
right = mid - 1;
} else {
left = mid + 1;
}
}
return right;
}
}
```
```java []
class Solution {
public int maximumCandies(int[] candies, long k) {
int left = 0, right = 0;
// Find the maximum candy pile
for (int candy : candies) {
right = Math.max(right, candy);
}
// Binary search for the maximum candies per child
while (left <= right) {
int mid = left + (right - left) / 2;
if (!canDistribute(candies, k, mid)) {
right = mid - 1;
} else {
left = mid + 1;
}
}
return right;
}
private boolean canDistribute(int[] candies, long k, int x) {
if (x == 0) return false;
long count = 0;
for (int candy : candies) {
count += candy / x;
}
return count >= k;
}
}
```
```python []
class Solution(object):
def maximumCandies(self, candies, k):
"""
:type candies: List[int]
:type k: int
:rtype: int
"""
left, right = 0, max(candies)
def canDistribute(x):
return sum(c // x for c in candies) >= k
while left <= right:
mid = (left + right) // 2
if not canDistribute(mid):
right = mid - 1
else:
left = mid + 1
return right
```
```Go []
func maximumCandies(candies []int, k int64) int {
left, right := 0, 0
// Find the maximum value in candies array
for _, c := range candies {
if c > right {
right = c
}
}
// Binary search for the maximum candies per child
for left <= right {
mid := left + (right-left)/2
if !canDistribute(candies, k, mid) {
right = mid - 1
} else {
left = mid + 1
}
}
return right
}
// Helper function to check if we can distribute 'x' candies per child
func canDistribute(candies []int, k int64, x int) bool {
if x == 0 {
return false
}
var count int64 = 0
for _, c := range candies {
count += int64(c / x)
}
return count >= k
}
```
```ruby []
def maximum_candies(candies, k)
left, right = 0, candies.max
# Helper function to check if we can distribute 'x' candies per child
def can_distribute?(candies, k, x)
candies.sum { |c| c / x } >= k
end
while left <= right
mid = (left + right) / 2
if !can_distribute?(candies, k, mid)
right = mid - 1
else
left = mid + 1
end
end
right
end
```
| 2
| 0
|
['Binary Search', 'C', 'Python', 'C++', 'Java', 'Go', 'TypeScript', 'Ruby', 'JavaScript', 'C#']
| 1
|
maximum-candies-allocated-to-k-children
|
Maximum Candies Distribution - Binary Search (Easiest and Optimal approach)
|
maximum-candies-distribution-binary-sear-e4c8
|
IntuitionThe problem boils down to distributing candies into k piles as evenly as possible, ensuring each child gets the maximum number of candies. The intuitio
|
Sharvesh_Kanagaraj
|
NORMAL
|
2025-03-14T06:27:38.472553+00:00
|
2025-03-14T06:36:19.231017+00:00
| 10
| false
|
# Intuition
The problem boils down to distributing candies into k piles as evenly as possible, ensuring each child gets the maximum number of candies. The intuition here is to treat the problem like a "binary search on answers" — where the answer is the maximum number of candies a child can get. We guess a possible solution (mid candies per child) and check if it's feasible.
If we can distribute candies to satisfy all k children with this amount (mid), we try for a higher number (mid + 1), aiming for a better result. Otherwise, we reduce our guess (mid - 1).
This search strategy ensures we efficiently hone in on the maximum possible candies per child.
# Approach
Define the Search Space:
The minimum number of candies per child is 1 (smallest possible split), and the maximum is the largest pile (max(candies)).
**Binary Search Setup:**
Set start = 1 and end = max(candies).
For each mid = (start + end) / 2, check if it's feasible to give each child mid candies.
Feasibility Check (can_assign function):
Count how many children can get mid candies using each pile (count += candies[i] / mid).
If count >= k, the current mid is feasible, and we try for a larger value (start = mid + 1).
Otherwise, reduce the search space (end = mid - 1).
Result:
Track the largest feasible mid in res and return it at the end.
# Complexity
- Time complexity:
Each binary search iteration halves the search space, giving ***O(log(max(candies)))*** iterations.
For each guess, we loop through the candies array to count feasible splits, which takes ***O(n)*** times, hence total time is ***O(n * log(max(candies)))***.
- Space complexity:
We use extra variables (count, start, end, mid) so it results in **O(1)** extra space. The candies array is given as input, so it doesn't count towards extra space.
Hope you'll find this solution useful!
# Code
```cpp []
class Solution {
public:
#define ll long long
bool can_assign(long long& mid, vector<int>& candies, long long& k){
ll count = 0;
for (ll i : candies){
if (i >= mid){
count += i/mid;
}
}
return count >= k;
}
int maximumCandies(vector<int>& candies, long long k) {
ll start = 1;
ll end = *max_element(candies.begin(), candies.end());
ll mid;
ll res = 0;
while(start <= end){
mid = start + (end - start)/2;
if(can_assign(mid,candies,k)){
res = mid;
start = mid + 1;
}
else{
end = mid - 1 ;
}
}
return res;
}
};
```
| 2
| 0
|
['Array', 'Binary Search', 'C++']
| 0
|
maximum-candies-allocated-to-k-children
|
Have some candies :) 🍭🍭
|
have-some-candies-by-yojitkataria-oj9h
|
THINKcandies = [5, 8, 6], k = 3TC:
Binary search range: O(log(max(candies)))
Each iteration: O(n) to compute count
Total complexity: O(n log m), where m = max(c
|
YOJITKATARIA
|
NORMAL
|
2025-03-14T06:16:57.657370+00:00
|
2025-03-14T06:16:57.657370+00:00
| 131
| false
|
# THINK
candies = [5, 8, 6], k = 3
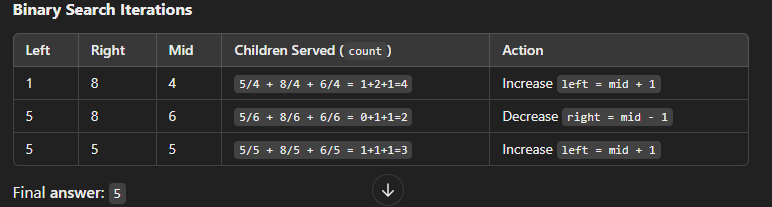
# TC:
- Binary search range: O(log(max(candies)))
- Each iteration: O(n) to compute count
- Total complexity: O(n log m), where m = max(candies)
- This is an efficient solution compared to brute force.
# Code
```cpp []
class Solution {
public:
// Why kids only have all the fun
// Your candies 🍭🍭
int maximumCandies(vector<int>& candies, long long k) {
int left = 1; // This is the min candies in the pile
int right = *max_element(candies.begin(),candies.end());
// max_element returns the max element in the arr
int result = 0;
//Using the binary search
while(left<=right){
long long mid = left + (right - left)/2;
long long count = 0;
for(int c : candies){
count += c/mid;
}
if(count>=k){
result = mid;
left = mid+1;
}
else{
right= mid-1;
}
}
return result;
}
};
```
| 2
| 0
|
['Array', 'Binary Search', 'C++']
| 0
|
maximum-candies-allocated-to-k-children
|
C# Solution for Maximum Candies Allocated To K Children Problem
|
c-solution-for-maximum-candies-allocated-l0ao
|
IntuitionWe need to distribute candies among k children such that:
Each child gets the same number of candies.
A child can receive candies only from one pile.
S
|
Aman_Raj_Sinha
|
NORMAL
|
2025-03-14T06:01:39.863595+00:00
|
2025-03-14T06:01:39.863595+00:00
| 79
| false
|
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
We need to distribute candies among k children such that:
1. Each child gets the same number of candies.
2. A child can receive candies only from one pile.
3. Some piles may go unused.
4. The goal is to maximize the number of candies each child gets.
Since we can divide but not merge piles, we need to determine the largest possible number of candies per child that allows at least k children to receive candies.
This naturally suggests a binary search approach
# Approach
<!-- Describe your approach to solving the problem. -->
1. Define the Search Space:
• Minimum candies per child = 1 (if distribution is possible).
• Maximum candies per child = max(candies), since no child can get more than the largest pile.
2. Binary Search Execution:
• Pick mid = (left + right) / 2 as the potential candies per child.
• Count how many children can be served if each gets exactly mid candies.
• If we can serve at least k children, it means we might be able to give more, so we search in the upper half (left = mid + 1).
• Otherwise, we reduce mid and search in the lower half (right = mid - 1).
3. Checking Feasibility:
• Given mid candies per child, we iterate through candies[] and compute: total children served = sum frac{candies[i]}{mid}
• If total children served >= k, mid is a valid candidate.
4. Return the best valid mid found.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
• Binary Search: The search space is from 1 to max(candies), which means O(log max(candies)) ≈ O(24).
• Feasibility Check: For each mid, we iterate through candies, which takes O(n).
• Total Complexity: O(n log max(candies)) = O(10^5 x 24) = O(2.4 x 10^6)
This is efficient.
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
• Binary search variables (left, right, mid, result): O(1)
• Feasibility check (count): O(1)
• Total Space Complexity: O(1) (constant extra space used).
# Code
```csharp []
public class Solution {
public int MaximumCandies(int[] candies, long k) {
if (candies.Sum(c => (long)c) < k) return 0;
int left = 1, right = candies.Max();
int result = 0;
while (left <= right) {
int mid = left + (right - left) / 2;
if (CanDistribute(candies, k, mid)) {
result = mid;
left = mid + 1;
} else {
right = mid - 1;
}
}
return result;
}
private bool CanDistribute(int[] candies, long k, int mid) {
long count = 0;
foreach (int candy in candies) {
count += candy / mid;
if (count >= k) return true;
}
return count >= k;
}
}
```
| 2
| 0
|
['C#']
| 0
|
maximum-candies-allocated-to-k-children
|
🚀Simple Python Solution | Binary Search Approach 💡
|
simple-python-solution-binary-search-app-edsr
|
IntuitionWe need to distribute candies as evenly as possible among k children while maximizing the number of candies each child gets. Since we are dividing cand
|
smit-panchal
|
NORMAL
|
2025-03-14T05:55:08.049778+00:00
|
2025-03-14T06:02:04.277161+00:00
| 43
| false
|
# Intuition
We need to distribute candies as evenly as possible among k children while maximizing the number of candies each child gets. Since we are dividing candies from different piles, we can use binary search to efficiently find the maximum number of candies each child can receive.
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
1. Binary Search on Maximum Candies Per Child:
- Initialize l = 1 and r = max_value (largest pile).
- Use binary search to find the highest possible needed_piles that allows at least k children to get candies.
2. Check Feasibility (candies_distribution_possible):
- Compute total_piles = sum(candie // needed_piles for candie in candies).
- If total_piles >= k, update max_candies and increase l. Otherwise, decrease r.
3. Return max_candies.
# Complexity
- Time complexity: O(nlogm)
- n is the number of piles, and m is the maximum candies in any pile.
- Binary search runs in 𝑂(log 𝑚), and for each mid, we check O(n).
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity: O(1)
- We use only a few extra variables, so space usage is constant.
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
class Solution:
def maximumCandies(self, candies: List[int], k: int) -> int:
max_value=max(candies)
def candies_distribution_possible(needed_piles):
total_piles=0
for candie in candies:
total_piles+=(candie//needed_piles)
return True if total_piles>=k else False
def binary_search(max_value):
l=1
r=max_value
max_candies=0
while l<=r:
mid=(r-l)//2+l
if mid>0 and candies_distribution_possible(mid):
max_candies=mid
l=mid+1
else:
r=mid-1
return max_candies
return binary_search(max_value)
```
| 2
| 0
|
['Binary Search', 'Python3']
| 0
|
maximum-candies-allocated-to-k-children
|
✅🚀 easy binary search code with explanation in all language
|
easy-understandable-code-with-explanatio-b1h1
|
exampleComplexityCode
|
thakur_saheb
|
NORMAL
|
2025-03-14T05:47:03.736900+00:00
|
2025-03-14T05:50:01.499371+00:00
| 68
| false
|
# example
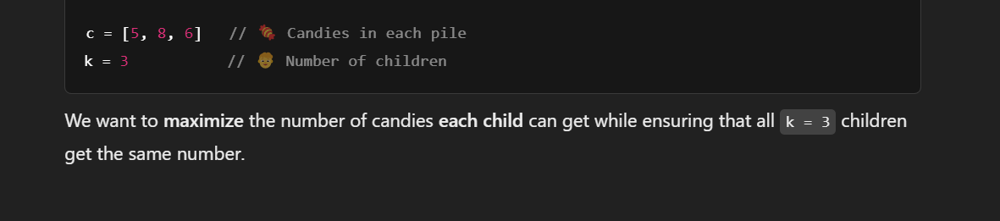
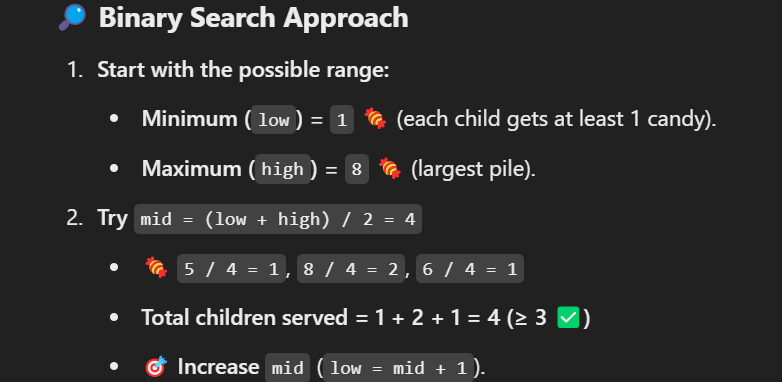
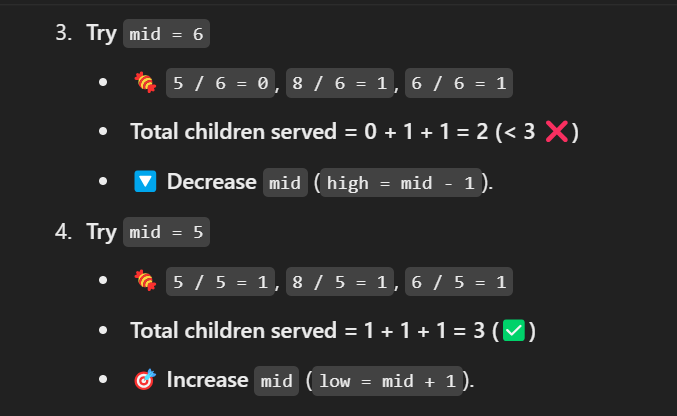
# Complexity

# Code
```cpp []
class Solution {
public:
int maximumCandies(vector<int>& c, long long k) {
long long sum=accumulate(c.begin(),c.end(),0LL);
if(sum<k)return 0;
int low = 1, high = *max_element(c.begin(), c.end()), ans = 0;
while (low <= high) {
int mid = low + (high - low) / 2;
long long count = 0;
for (int candies : c) count += candies / mid;
if (count >= k) {
ans = mid;
low = mid + 1;
} else {
high = mid - 1;
}
}
return ans;
}
};
```
```java []
import java.util.*;
class Solution {
public static int maximumCandies(int[] c, long k) {
long sum = 0;
for (int num : c) sum += num;
if (sum < k) return 0;
int low = 1, high = Arrays.stream(c).max().getAsInt(), ans = 0;
while (low <= high) {
int mid = low + (high - low) / 2;
long count = 0;
for (int candies : c) {
count += candies / mid;
if (count >= k) break;
}
if (count >= k) {
ans = mid;
low = mid + 1;
} else {
high = mid - 1;
}
}
return ans;
}
public static void main(String[] args) {
int[] c = {5, 8, 6};
long k = 3;
System.out.println(maximumCandies(c, k)); // Output: 5
}
}
```
``` python []
def maximumCandies(c, k):
if sum(c) < k:
return 0
low, high, ans = 1, max(c), 0
while low <= high:
mid = (low + high) // 2
count = sum(candies // mid for candies in c)
if count >= k:
ans = mid
low = mid + 1
else:
high = mid - 1
return ans
print(maximumCandies([5, 8, 6], 3)) # Output: 5
```
```rust []
fn maximum_candies(c: Vec<i32>, k: i64) -> i32 {
let sum: i64 = c.iter().map(|&x| x as i64).sum();
if sum < k {
return 0;
}
let (mut low, mut high, mut ans) = (1, *c.iter().max().unwrap(), 0);
while low <= high {
let mid = (low + high) / 2;
let count: i64 = c.iter().map(|&candies| (candies as i64) / (mid as i64)).sum();
if count >= k {
ans = mid;
low = mid + 1;
} else {
high = mid - 1;
}
}
ans
}
fn main() {
let c = vec![5, 8, 6];
let k = 3;
println!("{}", maximum_candies(c, k)); // Output: 5
}
```
``` ruby []
def maximum_candies(c, k)
return 0 if c.sum < k
low, high, ans = 1, c.max, 0
while low <= high
mid = (low + high) / 2
count = c.sum { |candies| candies / mid }
if count >= k
ans = mid
low = mid + 1
else
high = mid - 1
end
end
ans
end
puts maximum_candies([5, 8, 6], 3) # Output: 5
```
``` go []
package main
import (
"fmt"
"sort"
)
func maximumCandies(c []int, k int64) int {
sum := int64(0)
for _, num := range c {
sum += int64(num)
}
if sum < k {
return 0
}
low, high, ans := 1, c[len(c)-1], 0
for low <= high {
mid := (low + high) / 2
count := int64(0)
for _, candies := range c {
count += int64(candies) / int64(mid)
if count >= k {
break
}
}
if count >= k {
ans = mid
low = mid + 1
} else {
high = mid - 1
}
}
return ans
}
func main() {
fmt.Println(maximumCandies([]int{5, 8, 6}, 3)) // Output: 5
}
```
``` javascript []
function maximumCandies(c, k) {
let sum = c.reduce((a, b) => a + b, 0);
if (sum < k) return 0;
let low = 1, high = Math.max(...c), ans = 0;
while (low <= high) {
let mid = Math.floor((low + high) / 2);
let count = c.reduce((acc, candies) => acc + Math.floor(candies / mid), 0);
if (count >= k) {
ans = mid;
low = mid + 1;
} else {
high = mid - 1;
}
}
return ans;
}
console.log(maximumCandies([5, 8, 6], 3)); // Output: 5
```
| 2
| 0
|
['C', 'Python', 'C++', 'Java', 'Go', 'TypeScript', 'Rust', 'Ruby', 'JavaScript', 'C#']
| 0
|
maximum-candies-allocated-to-k-children
|
Easy Python Code
|
easy-python-code-by-akshaya0108-xvyp
|
Code
|
Akshaya0108
|
NORMAL
|
2025-03-14T05:32:37.786904+00:00
|
2025-03-14T05:32:37.786904+00:00
| 88
| false
|
# Code
```python3 []
class Solution:
def maximumCandies(self, candies: List[int], k: int) -> int:
if sum(candies) < k:
return 0
left, right = 1, max(candies)
result = 0
while left <= right:
mid = (left + right) // 2
count = sum(c // mid for c in candies)
if count >= k:
result = mid
left = mid + 1
else:
right = mid - 1
return result
```
| 2
| 0
|
['Python3']
| 0
|
maximum-candies-allocated-to-k-children
|
Maximum Candies Distribution Using Binary Search 🚀
|
maximum-candies-distribution-using-binar-fw1i
|
IntuitionWe need to determine the maximum number of candies each child can receive, given that we have k children and an array of candies distributed in differe
|
2u2CuogQQc
|
NORMAL
|
2025-03-14T04:28:56.178319+00:00
|
2025-03-14T04:28:56.178319+00:00
| 5
| false
|
# Intuition
We need to determine the maximum number of candies each child can receive, given that we have k children and an array of candies distributed in different piles. The key observation is that if x candies per child is possible, then any value less than x is also possible. This suggests a binary search approach.
# Approach
Calculate Total Candies and Maximum Candy Pile
Compute the total number of candies available.
Find the maximum number of candies in a single pile.
Edge Case
If the total number of candies is less than k, it is impossible to distribute at least one candy to each child, so return 0.
Binary Search for Maximum Candy per Child
The search space is from 1 to min(maxCandy, total/k), as no child can receive more than the largest pile, and distributing more than total/k per child is impossible.
Use binary search to find the largest possible x such that k children can be given x candies each.
Check Feasibility with Helper Function
Iterate through the candies array and check if dividing candies into groups of size mid can satisfy k children.
# Complexity
- Time complexity:
The binary search runs in O(log maxCandy).
The canAllocate function iterates through the array O(n) in the worst case.
- Space complexity:
We use only a few extra variables, so the space complexity is O(1).
# Code
```java []
class Solution {
public int maximumCandies(int[] candies, long k) {
long total = 0;
int maxCandy = 0;
for (int c : candies) {
total += c;
maxCandy = Math.max(maxCandy, c);
}
if (total < k) return 0;
int left = 1, right = (int) Math.min(maxCandy, total / k), result = 0;
while (left <= right) {
int mid = left + (right - left) / 2;
if (canAllocate(candies, k, mid)) {
result = mid;
left = mid + 1;
} else {
right = mid - 1;
}
}
return result;
}
private boolean canAllocate(int[] candies, long k, int mid) {
long count = 0;
for (int c : candies) {
count += c / mid;
if (count >= k) return true;
}
return false;
}
}
```
| 2
| 0
|
['Java']
| 0
|
maximum-candies-allocated-to-k-children
|
Easy code | Must try | code in java
|
easy-code-must-try-code-in-java-by-notad-o7sx
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
NotAditya09
|
NORMAL
|
2025-03-14T03:59:11.595703+00:00
|
2025-03-14T03:59:11.595703+00:00
| 135
| false
|
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```java []
class Solution {
public int maximumCandies(int[] candies, long k) {
int l = 1;
int r = (int) (Arrays.stream(candies).asLongStream().sum() / k);
while (l < r) {
final int m = (l + r) / 2;
if (numChildren(candies, m) < k)
r = m;
else
l = m + 1;
}
return numChildren(candies, l) >= k ? l : l - 1;
}
private long numChildren(int[] candies, int m) {
return Arrays.stream(candies).asLongStream().reduce(0L, (subtotal, c) -> subtotal + c / m);
}
}
```
| 2
| 0
|
['Java']
| 0
|
maximum-candies-allocated-to-k-children
|
Simple Binary Search Solution
|
simple-binary-search-solution-by-aadithy-prtx
|
CodeThank you,
aadithya18.
|
aadithya18
|
NORMAL
|
2025-03-14T02:34:27.228806+00:00
|
2025-03-14T02:34:27.228806+00:00
| 78
| false
|
# Code
```cpp []
class Solution {
public:
bool fun(vector<int>& candies, int mi, long long &k){
long long r = 0;
for(int i = 0; i<candies.size();i++){
r += (candies[i]/mi);
}
return r >= k;
}
int maximumCandies(vector<int>& candies, long long k) {
int mx = 0;
for(int i: candies){
mx = max(mx, i);
}
int l = 1, r = mx;
while(l <= r){
int m = l + (r - l) / 2;
if(fun(candies, m, k)){
l = m+1;
}
else r = m-1;
}
if(l-1 > mx) return 0;
return l-1;
}
};
```
Thank you,
aadithya18.
| 2
| 0
|
['Array', 'Binary Search', 'C++']
| 0
|
maximum-candies-allocated-to-k-children
|
The Simplest Approach Towards Better Solution
|
the-simplest-approach-towards-better-sol-2rqj
|
🍬 Problem Statement: Maximum Candies Allocation
You have an array of candies 🏗️, where each pile has some number of candies.
You need to distribute the candies
|
DS_Sijwali
|
NORMAL
|
2025-03-14T01:51:53.508813+00:00
|
2025-03-14T01:51:53.508813+00:00
| 111
| false
|
## **🍬 Problem Statement: Maximum Candies Allocation**
- You have an array of **candies** 🏗️, where each pile has some number of candies.
- You need to distribute the candies among **k children** 👶 such that:
- Each child gets the **same** number of candies 🍫.
- All candies taken by a child must come from a single pile.
- Find the **maximum** candies each child can get! 🎯
---
## **🔍 Approach: Binary Search on Answer**
### **Why Binary Search? 🤔**
Instead of checking all possible values manually **(brute force = slow 🚶♂️💨)**,
using **Binary Search** helps find the answer efficiently **(fast 🚀)**.
### **🔢 Steps**
1️⃣ **Find the search space**:
- `start = 1` (each child gets at least 1 candy) 🍬
- `end = max(candies[])` (no child can get more than the largest pile) 🎯
2️⃣ **Apply Binary Search** 🧐
- Pick `mid = (start + end) / 2` (this is our current "guess" for max candies per child).
- Check if we can **distribute** at least `k` children with `mid` candies each ✅.
- If possible → **Increase `mid`** (move right ➡️)
- If not possible → **Decrease `mid`** (move left ⬅️)
3️⃣ **Return the maximum valid `mid`** 🎉
---
## **💻 Code Walkthrough**
```java []
public int maximumCandies(int[] candies, long k) {
int start = 1, end = Integer.MIN_VALUE;
// 🎯 Step 1: Find the maximum number of candies in a pile
for (int val : candies) {
end = Math.max(val, end);
}
int ans = 0;
while (start <= end) {
int mid = start + (end - start) / 2; // 🔍 Mid-point (candidate answer)
// 🛠️ Check if we can distribute 'mid' candies per child to at least 'k' children
if (check(candies, k, mid)) {
ans = mid; // ✅ Valid answer found
start = mid + 1; // 🔼 Try for a larger answer
} else {
end = mid - 1; // 🔽 Reduce search space
}
}
return ans; // 🎯 Maximum candies per child
}
// 🛠️ Helper function to check if 'mid' candies per child is possible
private boolean check(int[] candies, long k, int mid) {
long count = 0;
// 🍬 Count how many children can be satisfied with 'mid' candies per child
for (int val : candies) {
count += val / mid; // Each pile contributes 'val / mid' children
if (count >= k) return true; // ✅ At least 'k' children satisfied
}
return false;
}
```
---
## **📌 Example Walkthrough**
### **Example 1**
**Input**:
```java
candies = [5, 8, 6]
k = 3
```
**Process**:
- `max(candies[]) = 8`, so `start = 1`, `end = 8`
- **Binary Search Iterations**:
| 🔢 `mid` | 🍬 Candies Distributed | ✅ Possible? | 🔄 Action |
|----------|----------------------|------------|----------|
| 4 | `5/4 + 8/4 + 6/4 = 1+2+1 = 4` ✅ | Move `start = mid + 1` | (search right) |
| 6 | `5/6 + 8/6 + 6/6 = 0+1+1 = 2` ❌ | Move `end = mid - 1`| (search left) |
| 5 | `5/5 + 8/5 + 6/5 = 1+1+1 = 3` ✅ | Move `start = mid + 1` |(search right) |
**🎯 Final Answer**: `5`
---
## **⏳ Time and Space Complexity**
### **⌛ Time Complexity**:
1️⃣ **Binary Search Complexity**:
- Searching in `[1, max(candies[])]` takes **O(log max(candies[]))** ⏳.
2️⃣ **Checking Function Complexity** (`check()` runs in O(n)):
- Iterating through `candies[]` in each step takes **O(n)**.
3️⃣ **Total Complexity**:
- **O(n log max(candies[]))** 🚀 (Efficient for large inputs).
### **📦 Space Complexity**:
- **O(1)** (Only a few integer variables used) ✅.
---
## **🌟 Key Takeaways**
✔ **Binary Search makes the problem efficient** 🏎️.
✔ **Handles large values of `k` using `long` to prevent overflow** 📏.
✔ **Optimal solution with `O(n log max(candies[]))` complexity** 🔥.
| 2
| 0
|
['Binary Search', 'Java']
| 0
|
maximum-candies-allocated-to-k-children
|
Beat 100% ✅ - Maximum Candies with Binary Search
|
beat-100-maximum-candies-with-binary-sea-ldkv
|
CodePlease Up Vote ⬆️⬆️ If it is helpfulApproachThis approach uses binary search to efficiently determine the maximum number of candies that can be distributed
|
lehieu99666
|
NORMAL
|
2025-03-14T00:37:39.260135+00:00
|
2025-03-14T00:37:39.260135+00:00
| 226
| false
|
# Code
```python3 []
class Solution:
def maximumCandies(self, candies: List[int], k: int) -> int:
# Early check: if total candies is less than k, return 0
total = sum(candies)
if total < k:
return 0
# Binary search for the maximum possible allocation
left, right = 1, total // k
while left < right:
mid = (left + right + 1) // 2 # Ceiling division to avoid infinite loop
# Count how many children can get 'mid' candies
count = sum(candy // mid for candy in candies)
if count >= k:
left = mid # We can allocate at least 'mid' candies to each child
else:
right = mid - 1 # We need to allocate fewer candies
return left
```
## Please Up Vote ⬆️⬆️ If it is helpful
# Approach
<!-- Describe your approach to solving the problem. -->
This approach uses **binary search** to efficiently determine the maximum number of candies that can be distributed to `k` children while ensuring each child gets the same number of candies.
### Steps:
1. **Check if distribution is possible**: If the total number of candies is less than `k`, return `0` immediately.
2. **Use binary search** to determine the maximum possible number of candies each child can receive:
- Set `left = 1` (minimum possible allocation).
- Set `right = total // k` (maximum possible allocation).
- Use a **midpoint (`mid`)** to check how many children can receive at least `mid` candies.
- If we can distribute at least `k` portions, move `left` to `mid` to search for a higher possible value.
- Otherwise, reduce `right` to `mid - 1` to try smaller allocations.
3. **Return `left`**, which holds the maximum number of candies each child can get.
# Complexity
- **Time complexity**: $$O(n \log M)$$, where `n` is the number of candy piles and `M` is the total number of candies.
- Binary search runs in $$O(\log M)$$.
- Each binary search iteration calculates `sum(candy // mid)`, which takes $$O(n)$$.
- Thus, the total complexity is $$O(n \log M)$$.
- **Space complexity**: $$O(1)$$, as only a few extra variables are used.
| 2
| 0
|
['Array', 'Binary Search', 'Python3']
| 0
|
maximum-candies-allocated-to-k-children
|
🍬 Maximum Candies Allocated to K Children 🍬 | 🎯 Easy Binary Search Explaination! 🚀
|
maximum-candies-allocated-to-k-children-7n5ml
|
IntuitionThe problem requires us to distribute candies among k children such that each child receives the maximum possible equal number of candies. The challeng
|
akshatksingh25
|
NORMAL
|
2025-03-01T10:15:21.911912+00:00
|
2025-03-01T10:15:21.911912+00:00
| 94
| false
|
# Intuition
The problem requires us to distribute candies among `k` children such that each child receives the maximum possible **equal** number of candies. The challenge is to determine this maximum number efficiently.
To solve this, consider the following observations:
- If we know the number of candies each child should receive, we can easily check whether it's possible to distribute the candies among `k` children.
- The problem can be reframed as **a search for the maximum valid number of candies per child**.
- Since the number of candies per child ranges from `1` to `max(candies)`, we can use **binary search** to efficiently find the optimal value.
Using these insights, binary search becomes a natural choice for solving this problem in an optimized manner.
---
# Approach
### **Step 1: Define the Search Space**
We need to determine the maximum number of candies each child can get. The possible values range from `1` to `max(candies)`, so we define:
- `low = 1` (minimum possible candies per child)
- `high = max(candies)` (maximum possible candies per child from any pile)
### **Step 2: Implement Binary Search**
- **Compute the middle value `mid`**: This represents the candidate number of candies each child could receive.
- **Check if `mid` is feasible**:
- Iterate over all candy piles and determine the number of children that can receive `mid` candies.
- If the number of children `>= k`, increase `mid` (move right).
- Otherwise, decrease `mid` (move left).
### **Step 3: Define the Check Function**
The function `check(candies, k, mid)` determines if it is possible to distribute `mid` candies per child to at least `k` children:
- Iterate through all candy piles.
- Compute how many full portions of `mid` can be made from each pile.
- Sum up these values to get the total number of children that can be served.
- If this total is `>= k`, return `true`; otherwise, return `false`.
### **Step 4: Binary Search Execution**
- Start with `low = 1`, `high = max(candies)`, and apply binary search.
- Continue adjusting the search range until `low > high`.
- The final answer is stored in `high`, representing the largest possible number of candies each child can receive.
---
# Complexity
[]()
- **Time complexity:**
- **Binary search range:** The search range for `mid` is from `1` to `max(candies)`, which takes **`O(log max(candies))`** iterations.
- **Checking feasibility (`check` function)**: Each check iteration requires a pass over `candies`, taking **`O(n)`**.
- **Total complexity**: Since we perform **`O(log max(candies))`** binary search iterations, and each iteration runs in **`O(n)`**, the total complexity is:
[]()
- **Space complexity:**
- We use a few extra variables (`low`, `high`, `mid`, `sum`) and do not use additional data structures.
- The space complexity is **`O(1)`** (constant extra space).
---
# Code
```cpp []
class Solution {
private:
long long check(vector<int>& candies, long long k, long long mid){
long long cntStud=0;
for(int i=0;i<candies.size();i++){
cntStud+=candies[i]/mid;
}
return cntStud;
}
public:
int maximumCandies(vector<int>& candies, long long k) {
long long low = 1;
long long high=*max_element(candies.begin(),candies.end());
long long sum = accumulate(candies.begin(), candies.end(), 0LL);
if(sum<k) return 0;
while (low <= high) {
long long mid = low + (high - low) / 2;
long long stud = check(candies, k, mid);
if(stud>=k) low=mid+1;
else high=mid-1;
}
return (int)high;
}
};
```
| 1
| 0
|
['Binary Search', 'C++']
| 0
|
maximum-candies-allocated-to-k-children
|
One line | Python | Binary Search
|
one-line-python-binary-search-by-popzkk-h9i8
|
Approach\nNothing special. Posting here to share a simple one-liner using bisect.\n\n# Code\npython3\nclass Solution:\n def maximumCandies(self, candies: Lis
|
popzkk
|
NORMAL
|
2024-03-29T00:53:58.847846+00:00
|
2024-03-29T00:53:58.847870+00:00
| 295
| false
|
# Approach\nNothing special. Posting here to share a simple one-liner using `bisect`.\n\n# Code\n```python3\nclass Solution:\n def maximumCandies(self, candies: List[int], k: int) -> int:\n return bisect_left(range(1, sum(candies) // k + 1), True, key=lambda c: sum(x // c for x in candies) < k)\n```
| 2
| 0
|
['Binary Search', 'Python3']
| 0
|
maximum-candies-allocated-to-k-children
|
Easy C++ Solution | Step-wise Approach | Beats 97.73% | Binary Search
|
easy-c-solution-step-wise-approach-beats-rhwk
|
Intuition and Approach\n\nThe problem involves distributing candies into piles such that each pile contains a certain number of candies. The goal is to maximize
|
darkaadityaa
|
NORMAL
|
2024-02-08T20:34:34.034151+00:00
|
2024-02-08T20:34:34.034181+00:00
| 31
| false
|
# Intuition and Approach\n\nThe problem involves distributing candies into piles such that each pile contains a certain number of candies. The goal is to maximize the number of candies in each pile while ensuring that at least k piles are formed.\n\n-- The maximum candies a person can get would be the maximum element present in the candies array. \n\n1) **Initial Bounds**: \n-- Initially, we set our lower bound ($$low$$) to 1, as we can\'t have a pile with zero candies, and our upper bound (high) to the maximum number of candies in the given candies array.\n\n2) **Binary Search:** \n-- Since we want to maximize the number of candies in each pile, we can use binary search to efficiently find the optimal number. \n-- We\'ll iteratively narrow down our search space until we find the maximum number of candies that satisfies the condition of having at least k piles.\n\n3) **Checking Validity:** \n-- The $$isValid()$$ function checks whether it\'s possible to form at least k piles with a given number of candies (mid) per pile. It iterates through the candies vector, calculates how many piles can be formed with the current number of candies per pile ($$mid$$), and checks if this count is greater than or equal to k.\n\n4) **Updating Bounds:** \n-- Based on the result of the validity check, we update our search bounds accordingly. \n-- If it\'s possible to form at least k piles with $$mid$$ candies per pile, we update the result and adjust our lower bound to mid + 1, indicating that we can potentially increase the number of candies per pile. \n-- Otherwise, we adjust our upper bound to mid - 1, indicating that we need to decrease the number of candies per pile.\n\n-------\n\n# Complexity\n- Time complexity: O(N*log(max_candies))\n \n-- where N is the number of candies in the input vector and max_candies is the maximum number of candies in the input vector.\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n-----\n\n### If you find this solution helpful, consider giving it an upvote!\n\n#### Do check out all other solutions posted by me here: https://github.com/adityajamwal02/Leetcode-Community-Solutions\n---\n\n# Code\n```\nclass Solution {\npublic:\n bool isValid(vector<int> &candies, long long k, long long mid){\n long long counter=0; // No. of piles\n for(auto it : candies){\n counter+=(it/mid);\n }\n return counter>=k;\n }\n \n int maximumCandies(vector<int>& candies, long long k) {\n long long n=candies.size(), low=1, high=*max_element(candies.begin(),candies.end()), result=0;\n while(low<=high){\n long long mid=low+(high-low)/2;\n if(isValid(candies,k,mid)){\n result=mid;\n low=mid+1;\n }else{\n high=mid-1;\n }\n }\n return (int)result;\n }\n};\n```
| 2
| 0
|
['Array', 'Binary Search', 'C++']
| 0
|
maximum-candies-allocated-to-k-children
|
Easy understandable C++ solution || Binary search on answers approach
|
easy-understandable-c-solution-binary-se-096g
|
\n\nclass Solution {\npublic:\n bool isPossible(vector<int>& candies, int mid, long long k){\n long long count = 0;\n int n = candies.size();\n
|
bharathgowda29
|
NORMAL
|
2023-12-30T19:55:32.849401+00:00
|
2023-12-30T19:55:32.849433+00:00
| 419
| false
|
\n```\nclass Solution {\npublic:\n bool isPossible(vector<int>& candies, int mid, long long k){\n long long count = 0;\n int n = candies.size();\n for(int i=0; i<n; i++){\n count += candies[i]/mid;\n }\n\n if(count < k){\n return false;\n }\n\n return true;\n }\n\n\n int maximumCandies(vector<int>& candies, long long k) {\n int start = 1, end = *max_element(candies.begin(), candies.end());\n int ans = 0;\n while(start <= end){\n int mid = start + (end-start)/2;\n if(isPossible(candies, mid, k)){\n ans = mid;\n start = mid+1;\n }\n else{\n end = mid-1;\n }\n }\n\n return ans;\n }\n};\n```
| 2
| 0
|
['Array', 'Binary Search', 'C++']
| 0
|
maximum-candies-allocated-to-k-children
|
Binary Search | C++ Easy | O(N log K) | Detailed Explanation of each step
|
binary-search-c-easy-on-log-k-detailed-e-d4qv
|
Intuition\n Describe your first thoughts on how to solve this problem. \nTo solve this problem, you can use binary search to efficiently find the maximum number
|
leftrecursion
|
NORMAL
|
2023-12-17T12:52:14.266012+00:00
|
2023-12-17T12:52:14.266040+00:00
| 203
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nTo solve this problem, you can use binary search to efficiently find the maximum number of candies that can be allocated to each child. The key observation is that if it\'s possible to allocate mid candies to each child, then it\'s also possible to allocate any number less than mid. Conversely, if it\'s not possible to allocate mid candies to each child, then it\'s also not possible to allocate any number greater than mid. This binary search approach helps narrow down the search space quickly.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n1. Calculate the sum of all candies in the candies array, denoted by sum.\n2. Set the initial search space boundaries: s = 1 (minimum candies per child) and e = sum (maximum candies per child).\n3. Perform a binary search on the search space (s to e).\n4. In each iteration of the binary search, calculate the mid-point (mid) and check if it\'s possible to allocate mid candies to each child using the isPossible function.\n5. If it\'s possible, update the answer (ans) to mid and adjust the search space to the right (s = mid + 1).\n6. If it\'s not possible, adjust the search space to the left (e = mid - 1).\n7. Continue the binary search until the search space is exhausted (s > e).\n8. Return the maximum number of candies (ans) found during the search.\n\nThe isPossible() function checks if it\'s possible to allocate a certain number of candies (mid) to each child by iterating through the piles and counting how many candies each child would get. If the total count is greater than or equal to k, it\'s possible.\n\nThis approach efficiently finds the maximum number of candies that can be allocated to each child while adhering to the given constraints. The use of binary search ensures a logarithmic time complexity.\n\n\n# Complexity\n- Time complexity: O(N log K), where N is the number of elements in the candies array, and K is the sum of all candies in the array.\n\n- Space complexity: O(1)\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n bool isPossible(vector<int>& candies, long long mid, long long k){\n long long count=0;\n for(int i=0; i<candies.size(); i++){\n int x=candies[i];\n count+=(x/mid);\n }\n if(count>=k){\n return true;\n }\n else{ \n return false;\n }\n }\n int maximumCandies(vector<int>& candies, long long k) {\n int s=1;\n long long e, sum=0;\n long long ans=0;\n\n for(int i=0; i<candies.size();i++){\n sum+=candies[i];\n }\n e=sum;\n if(sum==k){\n return 1;\n }\n else if(sum<k){\n return 0;\n }\n else{\n long long mid=s+(e-s)/2;\n\n while(s<=e){\n if(isPossible(candies,mid,k)){\n ans = max(ans,mid);\n s=mid+1;\n }\n else{\n e=mid-1;\n }\n mid=s+(e-s)/2;\n }\n return ans;\n }\n }\n};\n```\n
| 2
| 0
|
['Binary Search', 'C++']
| 0
|
maximum-candies-allocated-to-k-children
|
Simple Binary Search
|
simple-binary-search-by-juwnl-usak
|
Intuition\nBinary Search and check condition every search\n\n# Approach\nBinary Search\n\n# Complexity\n- Time complexity:\nO(n*logn)\n\n- Space complexity:\nO(
|
JuWnL
|
NORMAL
|
2023-10-24T05:50:40.807585+00:00
|
2023-10-24T05:50:40.807603+00:00
| 257
| false
|
# Intuition\nBinary Search and check condition every search\n\n# Approach\nBinary Search\n\n# Complexity\n- Time complexity:\n$$O(n*logn)$$\n\n- Space complexity:\n$$O(1)$$\n\n# Code\n``` python\nclass Solution:\n def maximumCandies(self, candies: List[int], k: int) -> int:\n def check(candyPerPile):\n pile = 0\n for candy in candies:\n pile += candy // candyPerPile\n \n return pile >= k\n\n left = 1\n right = sum(candies) // k\n\n while left <= right:\n mid = (left + right) // 2\n\n if check(mid):\n left = mid + 1 \n else:\n right = mid - 1\n return right\n\n```
| 2
| 0
|
['Binary Search', 'Python3']
| 0
|
maximum-candies-allocated-to-k-children
|
C++ solution using Binary Search
|
c-solution-using-binary-search-by-vasant-x4tg
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n\n# Approach\n Describe your approach to solving the problem. \nbinary search approac
|
vasanthkokkiligadda
|
NORMAL
|
2023-09-16T18:00:15.885000+00:00
|
2023-09-16T18:00:15.885018+00:00
| 12
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nbinary search approach similar to koko eating bananas\n\n# Complexity\n- Time complexity:\n- O(nlogn)\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n- O(1)\n\n\n# Code\n```\nclass Solution {\npublic:\n bool noOfCandies(vector<int> candies,int n,long long candiesPerChild,long long totalNoOfKids){\n long long noOfKidsWithCandies=0;\n for(int i=0;i<n;i++){\n noOfKidsWithCandies+=candies[i]/candiesPerChild;\n if(noOfKidsWithCandies>=totalNoOfKids){\n return true;\n }\n }\n return false;\n } \n int maximumCandies(vector<int>& candies, long long k) {\n int n=candies.size();\n long long low=1;\n long long high=0;\n for(int i=0;i<n;i++){\n high+=candies[i];\n }\n if(k>high){\n return 0;\n }\n while(low<=high){\n long long mid=low+(high-low)/2;\n if(noOfCandies(candies,n,mid,k)){\n low=mid+1;\n }\n else{\n high=mid-1;\n }\n }\n return high;\n }\n};\n```
| 2
| 0
|
['C++']
| 0
|
maximum-candies-allocated-to-k-children
|
C++ || [Binary Search]
|
c-binary-search-by-shivamr066-tp82
|
Code\n\nclass Solution {\npublic:\n int maximumCandies(vector<int>& arr, long long k) {\n long long int result = 0 ;\n long long int low =
|
shivamR066
|
NORMAL
|
2023-08-18T06:38:35.501049+00:00
|
2023-08-18T06:38:35.501077+00:00
| 320
| false
|
# Code\n```\nclass Solution {\npublic:\n int maximumCandies(vector<int>& arr, long long k) {\n long long int result = 0 ;\n long long int low = 1;\n auto it = max_element(arr.begin() , arr.end());\n long long int high = (long long int)(*it);\n int n = arr.size();\n while(low <= high){\n long long int mid = low + (high - low)/2;\n long long int count = 0;\n for(int i = 0 ; i < n ; i++){\n count += ((long long int)arr[i] / mid);\n if(count >= k)break;\n }\n if(count >= k){\n result = mid;\n low = mid + 1;\n }else{\n high = mid - 1;\n }\n }\n return result;\n }\n};\n```
| 2
| 0
|
['C++']
| 0
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.