question_slug
stringlengths 3
77
| title
stringlengths 1
183
| slug
stringlengths 12
45
| summary
stringlengths 1
160
⌀ | author
stringlengths 2
30
| certification
stringclasses 2
values | created_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| updated_at
stringdate 2013-10-25 17:32:12
2025-04-12 09:38:24
| hit_count
int64 0
10.6M
| has_video
bool 2
classes | content
stringlengths 4
576k
| upvotes
int64 0
11.5k
| downvotes
int64 0
358
| tags
stringlengths 2
193
| comments
int64 0
2.56k
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
count-prefixes-of-a-given-string
|
Count Prefixes of a Given String
|
count-prefixes-of-a-given-string-by-akas-owqm
|
\nint count=0;\n for(auto it:words){\n string str=s.substr(0,it.size());\n if(str==it)\n count++;\n }\n \n
|
Akash_Pandey
|
NORMAL
|
2023-01-29T18:00:54.336854+00:00
|
2023-01-29T18:00:54.336890+00:00
| 707
| false
|
```\nint count=0;\n for(auto it:words){\n string str=s.substr(0,it.size());\n if(str==it)\n count++;\n }\n \n return count;\n\t\t\n```
| 1
| 0
|
['C', 'Iterator']
| 0
|
count-prefixes-of-a-given-string
|
Simple || CPP || (Datta Bayo)
|
simple-cpp-datta-bayo-by-shreyas_6379-j30j
|
Nothing To explain Brut force approach.\n\n# Code\n\nclass Solution {\npublic:\n int countPrefixes(vector<string>& words, string s) {\n int count =0;\
|
shreyas_6379
|
NORMAL
|
2023-01-29T12:01:33.552857+00:00
|
2023-01-29T12:01:33.552902+00:00
| 10
| false
|
Nothing To explain Brut force approach.\n\n# Code\n```\nclass Solution {\npublic:\n int countPrefixes(vector<string>& words, string s) {\n int count =0;\n for(int i=0;i<=s.length();i++)\n {\n string check = s.substr(0,i);\n for(int j=0;j<words.size();j++)\n {\n if(check == words[j])\n {\n count ++;\n }\n }\n }\n return count;\n }\n};\n```\n\n
| 1
| 0
|
['C++']
| 1
|
count-prefixes-of-a-given-string
|
Efficient one-liner solution with startsWith and reduce
|
efficient-one-liner-solution-with-starts-5x53
|
Code\n\n/**\n * @param {string[]} words\n * @param {string} s\n * @return {number}\n */\nvar countPrefixes = function(words, s) {\n return words.reduce((acc,
|
ods967
|
NORMAL
|
2023-01-27T23:30:40.870114+00:00
|
2023-01-27T23:30:55.480121+00:00
| 55
| false
|
# Code\n```\n/**\n * @param {string[]} words\n * @param {string} s\n * @return {number}\n */\nvar countPrefixes = function(words, s) {\n return words.reduce((acc, word) => s.startsWith(word) ? acc + 1 : acc, 0);\n};\n```
| 1
| 1
|
['JavaScript']
| 0
|
count-prefixes-of-a-given-string
|
C# Linq 1-liner | 87ms 95%
|
c-linq-1-liner-87ms-95-by-legon2k-tdg4
|
Code\n\npublic class Solution {\n public int CountPrefixes(string[] words, string s) \n => words.Count(s.StartsWith);\n}\n
|
Legon2k
|
NORMAL
|
2023-01-17T10:01:48.292996+00:00
|
2023-01-17T10:03:22.570950+00:00
| 50
| false
|
# Code\n```\npublic class Solution {\n public int CountPrefixes(string[] words, string s) \n => words.Count(s.StartsWith);\n}\n```
| 1
| 0
|
['C#']
| 0
|
count-prefixes-of-a-given-string
|
2255. Count Prefixes of a Given String
|
2255-count-prefixes-of-a-given-string-by-xj1v
|
\n# Code\n\n/**\n * @param {string[]} words\n * @param {string} s\n * @return {number}\n */\nvar countPrefixes = function(words, s) {\n return words.reduce((
|
YusupovJaloliddin
|
NORMAL
|
2022-12-20T18:25:52.148102+00:00
|
2022-12-20T18:25:52.148153+00:00
| 49
| false
|
\n# Code\n```\n/**\n * @param {string[]} words\n * @param {string} s\n * @return {number}\n */\nvar countPrefixes = function(words, s) {\n return words.reduce((acc, val) => acc + s.startsWith(val), 0);\n};\n```
| 1
| 0
|
['JavaScript']
| 0
|
count-prefixes-of-a-given-string
|
Count Prefixes of a Given String Solution Java
|
count-prefixes-of-a-given-string-solutio-btmi
|
class Solution {\n public int countPrefixes(String[] words, String s) {\n return (int) Arrays.stream(words).filter(word -> s.startsWith(word)).count();\n }
|
bhupendra786
|
NORMAL
|
2022-11-11T17:29:34.802072+00:00
|
2022-11-11T17:29:34.802112+00:00
| 60
| false
|
class Solution {\n public int countPrefixes(String[] words, String s) {\n return (int) Arrays.stream(words).filter(word -> s.startsWith(word)).count();\n }\n}\n
| 1
| 0
|
['Array', 'String']
| 0
|
count-prefixes-of-a-given-string
|
JAVA solution | startsWith() or indexOf() ✅
|
java-solution-startswith-or-indexof-by-s-ox2b
|
Please Upvote :D\n\nclass Solution {\n public int countPrefixes(String[] words, String s) {\n int count = 0;\n \n for (String str : word
|
sourin_bruh
|
NORMAL
|
2022-10-07T12:42:10.630976+00:00
|
2022-10-07T12:42:10.631015+00:00
| 103
| false
|
### Please Upvote :D\n```\nclass Solution {\n public int countPrefixes(String[] words, String s) {\n int count = 0;\n \n for (String str : words) {\n // if (s.indexOf(str) == 0) count++;\n if (s.startsWith(str)) count++;\n }\n \n return count;\n }\n}\n\n// TC: O(n)\n```
| 1
| 0
|
['Java']
| 0
|
count-prefixes-of-a-given-string
|
c++ | short | 97% faster than all
|
c-short-97-faster-than-all-by-venomhighs-5y8r
|
\n# Code\n\nclass Solution {\npublic:\n int countPrefixes(vector<string>& words, string s) {\n int count = 0;\n for(auto word:words){\n
|
venomhighs7
|
NORMAL
|
2022-10-02T16:17:37.173033+00:00
|
2022-10-02T16:17:37.173073+00:00
| 867
| false
|
\n# Code\n```\nclass Solution {\npublic:\n int countPrefixes(vector<string>& words, string s) {\n int count = 0;\n for(auto word:words){\n bool isPrefix = true;\n for(int i=0; i<word.length(); i++){\n if(word[i] != s[i]){\n isPrefix = false;\n break;\n }\n }\n if(isPrefix) count++;\n }\n return count;\n }\n};\n```
| 1
| 0
|
['C++']
| 1
|
count-prefixes-of-a-given-string
|
JAVA SOLN
|
java-soln-by-jatin0287-r4ga
|
class Solution {\n public int countPrefixes(String[] words, String s) {\n \n int count =0;\n for(int i=0; i<words.length; i++){\n
|
Jatin0287
|
NORMAL
|
2022-09-23T05:37:54.403387+00:00
|
2022-09-23T05:37:54.403430+00:00
| 95
| false
|
class Solution {\n public int countPrefixes(String[] words, String s) {\n \n int count =0;\n for(int i=0; i<words.length; i++){\n if(s.startsWith(words[i])){\n count++;\n }\n } \n return count;\n }\n}
| 1
| 0
|
[]
| 0
|
count-prefixes-of-a-given-string
|
Javascript easy solution
|
javascript-easy-solution-by-yorkinjon-iz0f
|
\n/**\n * @param {string[]} words\n * @param {string} s\n * @return {number}\n */\nvar countPrefixes = function(words, s) {\n let count = 0;\n for(let i=0
|
Yorkinjon
|
NORMAL
|
2022-09-20T13:48:42.847921+00:00
|
2022-09-20T13:48:42.847959+00:00
| 24
| false
|
```\n/**\n * @param {string[]} words\n * @param {string} s\n * @return {number}\n */\nvar countPrefixes = function(words, s) {\n let count = 0;\n for(let i=0; i<words.length; i++) {\n if(words[i] === s.slice(0, words[i].length)) {\n count++;\n }\n }\n return count;\n};\n```
| 1
| 0
|
['JavaScript']
| 0
|
count-prefixes-of-a-given-string
|
C++ solution
|
c-solution-by-lit2021036_iiitl-grnd
|
\nclass Solution {\npublic:\n int countPrefixes(vector<string>& words, string s) {\n int ct=0;\n for(string&word:words){\n bool flag=t
|
lit2021036_iiitl
|
NORMAL
|
2022-09-11T08:09:21.934477+00:00
|
2022-09-11T08:09:21.934515+00:00
| 88
| false
|
```\nclass Solution {\npublic:\n int countPrefixes(vector<string>& words, string s) {\n int ct=0;\n for(string&word:words){\n bool flag=true;\n if(word.length()<=s.length()){\n for(int i=0; i<min(word.length(),s.length()); ++i){\n if(word[i]!=s[i]){\n flag=false;\n break;\n }\n }\n flag?ct++:ct+=0;\n }\n }\n return ct;\n }\n};\n```
| 1
| 0
|
[]
| 0
|
count-prefixes-of-a-given-string
|
Count Prefixes of a Given String
|
count-prefixes-of-a-given-string-by-dhan-j0ms
|
python3 sol\n\nclass Solution:\n def countPrefixes(self, words: List[str], s: str) -> int:\n count= 0 \n for i in words:\n if i ==s:
|
dhananjayaduttmishra
|
NORMAL
|
2022-09-07T16:43:30.887949+00:00
|
2022-09-07T16:43:30.887990+00:00
| 170
| false
|
python3 sol\n```\nclass Solution:\n def countPrefixes(self, words: List[str], s: str) -> int:\n count= 0 \n for i in words:\n if i ==s:\n count+=1\n else:\n if i ==s[:len(i)]:\n count+=1\n return count\n```
| 1
| 0
|
['Python']
| 0
|
count-prefixes-of-a-given-string
|
easy fast short solution
|
easy-fast-short-solution-by-hurshidbek-6rij
|
\nPLEASE UPVOTE IF YOU LIKE\n\n```\n int count = 0;\n for(String temp: words)\n if (s.indexOf(temp) == 0)\n count++;\n
|
Hurshidbek
|
NORMAL
|
2022-08-30T03:27:18.354705+00:00
|
2022-08-30T03:27:18.354743+00:00
| 108
| false
|
```\nPLEASE UPVOTE IF YOU LIKE\n```\n```\n int count = 0;\n for(String temp: words)\n if (s.indexOf(temp) == 0)\n count++;\n return count;
| 1
| 0
|
['Java']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
[C++/Python] Longest Non-Decreasing Subsequence - Clean & Concise
|
cpython-longest-non-decreasing-subsequen-2pt3
|
Idea\n- If k = 1, we need to find the minimum number of operations to make the whole array non-decreasing.\n- If k = 2, we need to make:\n\t- newArr1: Elements
|
hiepit
|
NORMAL
|
2021-12-19T04:01:35.409106+00:00
|
2021-12-20T20:30:22.045560+00:00
| 13,371
| false
|
**Idea**\n- If `k = 1`, we need to find the minimum number of operations to make the whole array non-decreasing.\n- If `k = 2`, we need to make:\n\t- newArr1: Elements in index [0, 2, 4, 6...] are non-decreasing.\n\t- newArr2: Elements in index [1, 3, 5, 7...] are non-decreasing.\n- If `k = 3`, we need to make:\n - newArr1: Elements in index [0, 3, 6, 9...] are non-decreasing.\n\t- newArr2: Elements in index [1, 4, 7, 10...] are non-decreasing.\n\t- newArr3: Elements in index [2, 5, 8, 11...] are non-decreasing.\n- Since **Elements in newArrs are independent**, we just need to **find the minimum of operations to make `K` newArr non-decreasing**.\n- To **find the minimum of operations to make an array non-decreasing**,\n\t- Firstly, we count **Longest Non-Decreasing Subsequence** in that array.\n\t- Then the result is `len(arr) - longestNonDecreasing(arr)`, because we only need to change elements not in the **Longest Non-Decreasing Subsequence**.\n\t- For example: `newArr = [18, 8, 8, 3, 9]`, the longest non-decreasing subsequence is `[-, 8, 8, -, 9]` and we just need to change the array into `[8, 8, 8, 9, 9]` by changing `18 -> 8`, `3 -> 9`.\n\n**To find the Longest Non-Decreasing Subsequence** of an array, you can check following posts for more detail:\n- [300. Longest Increasing Subsequence](https://leetcode.com/problems/longest-increasing-subsequence/discuss/1326308) - Longest Increasing Subsequence\n- [1964. Find the Longest Valid Obstacle Course at Each Position](https://leetcode.com/problems/find-the-longest-valid-obstacle-course-at-each-position/discuss/1390159) - Longest Non-Decreasing Subsequence\n\n<iframe src="https://leetcode.com/playground/Mo4LhKNV/shared" frameBorder="0" width="100%" height="550"></iframe>\n\n**Complexity**\n- Time: `O(K * N/K * log(N/K))` = `O(N * log(N/K))`, where `N <= 10^5` is length of `arr`, `K <= N`.\n\t- We have total `K` new arr, each array have up to `N/K` elements.\n\t- We need `O(M * logM)` to find the longest non-decreasing subsequence of an array length `M`.\n- Space: `O(N / K)`\n\n
| 216
| 8
|
[]
| 22
|
minimum-operations-to-make-the-array-k-increasing
|
LIS in Disguise
|
lis-in-disguise-by-votrubac-a6xs
|
We have k independent subarrays in our array, and we need to make those subarrays non-decreasing.\n\nFor each subarray, we need to find the longest non-decreasi
|
votrubac
|
NORMAL
|
2021-12-19T04:00:39.889036+00:00
|
2021-12-20T00:56:37.716095+00:00
| 5,667
| false
|
We have `k` independent subarrays in our array, and we need to make those subarrays non-decreasing.\n\nFor each subarray, we need to find the longest non-decreasing subsequence. We keep numbers in that subsequence as-is, and change the rest. We can use the approach from [300. Longest Increasing Subsequence](https://leetcode.com/problems/longest-increasing-subsequence/).\n\nBecause `n` is quite large, a quadratic solution would be too slow. So, we should use the O(n log n) solution: monostack with binary search.\n\n**Python 3**\n```python\nclass Solution: \n def kIncreasing(self, arr: List[int], k: int) -> int:\n def LNDS(arr: List[int]) -> int:\n mono = []\n for n in arr:\n if not mono or mono[-1] <= n:\n mono.append(n)\n else:\n mono[bisect_right(mono, n)] = n\n return len(mono) \n return len(arr) - sum(LNDS(arr[i::k]) for i in range(k))\n```\n\n**Java**\nWe need to implement `upperBound` by hand, because `binarySearch` in Java is not guaranteed to return the smallest index in case of duplicates.\n\n```java\npublic int kIncreasing(int[] arr, int k) {\n int longest = 0;\n for (int i = 0; i < k; ++i) {\n List<Integer> mono = new ArrayList<>();\n for (int j = i; j < arr.length; j += k)\n if (mono.isEmpty() || mono.get(mono.size() - 1) <= arr[j])\n mono.add(arr[j]);\n else\n mono.set(upperBound(mono, arr[j]), arr[j]);\n longest += mono.size();\n }\n return arr.length - longest;\n}\nprivate int upperBound(List<Integer> mono, int val) {\n int l = 0, r = mono.size() - 1;\n while (l < r) {\n int m = (l + r) / 2;\n if (mono.get(m) <= val)\n l = m + 1;\n else\n r = m;\n }\n return l;\n}\n```\n\n**C++**\n```cpp\nint kIncreasing(vector<int>& arr, int k) {\n int longest = 0;\n for (int i = 0; i < k; ++i) {\n vector<int> mono;\n for (int j = i; j < arr.size(); j += k)\n if (mono.empty() || mono.back() <= arr[j])\n mono.push_back(arr[j]);\n else\n *upper_bound(begin(mono), end(mono), arr[j]) = arr[j];\n longest += mono.size();\n }\n return arr.size() - longest;\n}\n```
| 99
| 3
|
['C', 'Java']
| 6
|
minimum-operations-to-make-the-array-k-increasing
|
[Python] Short LIS, explained
|
python-short-lis-explained-by-dbabichev-pbsk
|
There are two observations we need to make.\n1. It is independent to consider subproblems on 0, k, 2k, ..., 1, k+1, 2k+1, ... and so on.\n2. For each subproblem
|
dbabichev
|
NORMAL
|
2021-12-19T04:00:49.129799+00:00
|
2021-12-19T04:00:49.129829+00:00
| 1,258
| false
|
There are two observations we need to make.\n1. It is independent to consider subproblems on `0, k, 2k, ...`, `1, k+1, 2k+1, ...` and so on.\n2. For each subproblem it is enough to solve LIS (longest increasing(not strictly) subsequence) problem. Indeed, if we have LIS of length `t`, than we need to change not more than `R-t` elements, where `R` is size of our subproblem. From the other side, we can not change less number of elements, because if we changed `< R- t` elements it means that `> t` elements were unchanged and it means we found LIS of length `> t`. This is called **estimate + example** technique in math.\n\n\n#### Complexity\nIt is `O(n log n)` for time and `O(n)` for space.\n\n#### Code\n```python\nfrom bisect import bisect\n\nclass Solution:\n def LIS(self, nums):\n dp = [10**10] * (len(nums) + 1)\n for elem in nums: dp[bisect(dp, elem)] = elem \n return dp.index(10**10)\n \n def kIncreasing(self, arr, k):\n ans = 0\n for i in range(k):\n A = arr[i::k]\n ans += len(A) - self.LIS(A)\n \n return ans\n```\n\nIf you have any question, feel free to ask. If you like the explanations, please **Upvote!**
| 35
| 8
|
[]
| 5
|
minimum-operations-to-make-the-array-k-increasing
|
[Python] Explanation with pictures, LIS
|
python-explanation-with-pictures-lis-by-njmrf
|
Given k = 3 for example. Let\'s stay that we start with index = 0, the first condition is A[0] <= A[3], \n\n\nWe also need to guarantee A[3] <= A[6], A[6] <=
|
Bakerston
|
NORMAL
|
2021-12-19T04:02:00.303575+00:00
|
2021-12-19T04:02:48.704231+00:00
| 1,396
| false
|
Given k = 3 for example. Let\'s stay that we start with index = 0, the first condition is **A[0] <= A[3]**, \n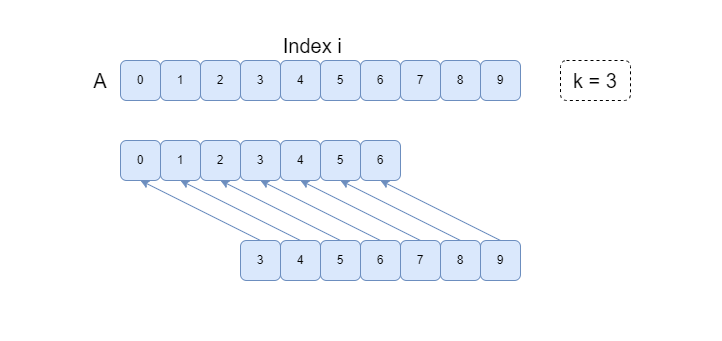\n\nWe also need to guarantee **A[3] <= A[6]**, **A[6] <= A[9]**, etc, if such larger indexs exist. In a word, we need to make this subarray **a = [A[0], A[3], A[6], ... ]** of unique indexes **non-decreasing**.\n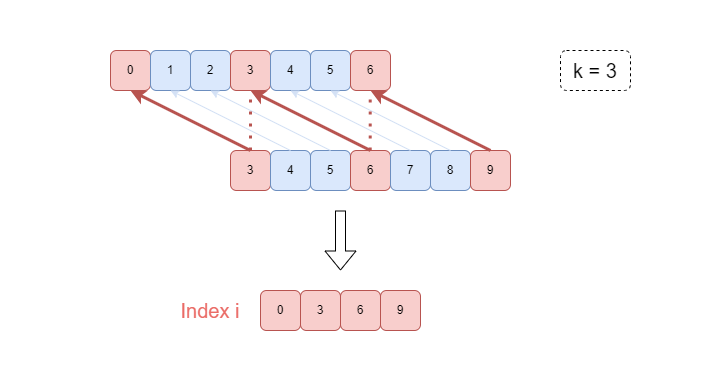\n\n\nThis sub-problem turns into finding the Largest Increasing Subsequence (LIS) of **a**, then the minimum number of changes we shall make equals to **len(a) - LIS(a)**\n\n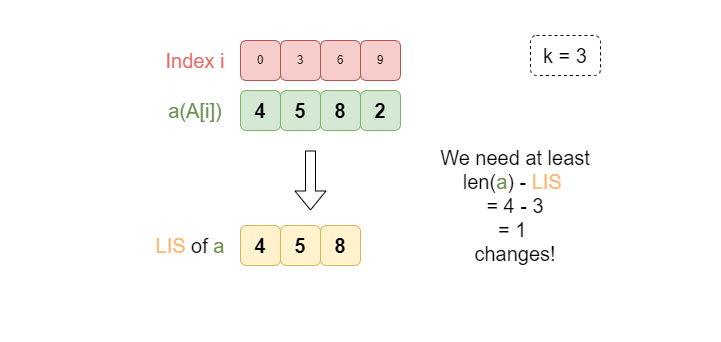\n\n\nSince the final array is k-increasing, thus we have to compare at most k subarrays. [A[0], A[k], A[2k], ...], [A[1], A[k + 1], A[2k + 1], ...], ..., [A[k - 1], A[2k - 1], A[3k - 1], ...].\n\nNotice that the changes on one "series" of indexes don\'t interference with other series, so we can safely calculate the number of changes for every series without affecting the answer.\n\nThen the answer is the sum of **len(a) - LIS(a)** for each subarray.\n\n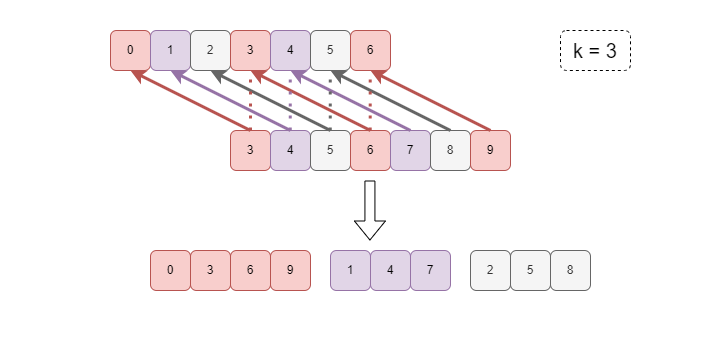\n\n**python**\n```\ndef kIncreasing(self, A: List[int], k: int) -> int:\n def LIS(arr):\n ans = []\n for a in arr:\n idx = bisect.bisect_right(ans, a)\n if idx == len(ans):\n ans.append(a)\n else:\n ans[idx] = a \n return len(ans)\n \n ans, n = 0, len(A)\n \n for start in range(k):\n cur, idx = [], start\n while idx < n:\n cur.append(A[idx])\n idx += k\n ans += len(cur) - LIS(cur)\n return ans\n```
| 34
| 2
|
[]
| 2
|
minimum-operations-to-make-the-array-k-increasing
|
Longest increasing subsequence | Explanation + Code
|
longest-increasing-subsequence-explanati-aj34
|
There will be K independent arrays each having max length n/k\n Independently find lis of all K independent arrays (using binary search/BIT)\n Minimum change =
|
Priyansh_34
|
NORMAL
|
2021-12-19T04:01:04.989380+00:00
|
2021-12-19T05:11:34.766392+00:00
| 1,787
| false
|
* There will be K **independent** arrays each having max length n/k\n* Independently find **lis** of all K independent arrays (using binary search/BIT)\n* **Minimum change = length of the array - lis of the array**\n* Sum all the minimum change needed for all K arrays\n\n**CODE** (CPP)\n```\nclass Solution {\npublic:\n int getlis(vector<int>&a) {\n vector<int>v;\n for (auto p : a) {\n auto it = upper_bound(v.begin(), v.end(), p);\n if (it == v.end()) {\n v.push_back(p);\n }\n else {\n *it = p;\n }\n }\n return v.size();\n }\n int kIncreasing(vector<int>& arr, int k) {\n const int n = arr.size();\n vector<vector<int>>v(k);\n for (int i = 0; i < n; i++) {\n v[i % k].push_back(arr[i]);\n }\n\n int ans = 0;\n for (int i = 0; i < k; i++) {\n int lis = getlis(v[i]);\n ans += v[i].size() - lis;\n }\n return ans;\n }\n};\n```\n**Time complexity :**\nO((k)*(n/k)log(n/k)) = O(nlog(n/k))\n\n**Useful Problem Link**\nhttps://leetcode.com/problems/longest-increasing-subsequence/\n\n**Do Upvote** if you liked the solution.\n
| 29
| 2
|
['C']
| 5
|
minimum-operations-to-make-the-array-k-increasing
|
Java + Intuition + LIS + Binary Search
|
java-intuition-lis-binary-search-by-lear-w1sf
|
Intuition:\nThe intuition behind this solution is that we extract all k-separated subsequences and find out the longest increasing subsequence (LIS) for each k-
|
learn4Fun
|
NORMAL
|
2021-12-19T05:57:19.468309+00:00
|
2021-12-22T22:16:45.979534+00:00
| 1,770
| false
|
**Intuition:**\nThe intuition behind this solution is that we extract all k-separated subsequences and find out the longest increasing subsequence (LIS) for each k-separated subsequences and then for each of these extracted subsequences we calculate the min operations (delete/update) to make it sorted/increasing.\n\n```\nMin operations to make it increasing = Length of extracted subsequence - LIS of the extracted subsequence\n```\n\nWe add the min operations for each of the k-separated subsequences which should give us the answer for the original problem.\n\nLet\'s take an example to understand better -\n\n```\narr = [4,1,5,2,6,2,8,9,11,15]\n 1 1 1 1\n 2 2 2\n 3 3 3 \nk=3\n\nk-seperated subsequences of arr:\n# subsequence length LIS Operations(length - LIS)\n1 [4,2,8,15] 4 3 1\n2 [1,6,9] 3 3 0\n3 [5,2,11] 3 2 1\n--------------------------------------------------\nTotal Operations = 2\n-------------------------------------------------\n```\n\n**Code:**\n\n```\nclass Solution {\n public int kIncreasing(int[] arr, int k) {\n int total = 0;\n for(int i=0; i < k; i++){\n List<Integer> list = new ArrayList<>();\n for(int j=i; j < arr.length; j = j+k)\n list.add(arr[j]);\n total += list.size() - lengthOfLIS(list);\n }\n return total;\n }\n \n // Get the length of LIS by building an increasing List so as to perform binary search on it \n // in case the current element is lesser than the last element in the increasing List. \n // In such case we get the next greater element from the increasing List by doing a binary Search and \n // replace that with the the current element in the increasing List, as the other element is no longer relevant in participating in LIS. \n // The increasing List remains sorted and always maintain the max length of the increasing subsequence.\n public int lengthOfLIS(List<Integer> nums){\n List<Integer> incrList = new ArrayList<>();\n incrList.add(nums.get(0));\n\n for(int i=1; i < nums.size(); i++){\n int lastItem = incrList.get(incrList.size()-1);\n if(nums.get(i) >= lastItem){\n incrList.add(nums.get(i));\n } else {\n int idx = nextGreaterItem(incrList, nums.get(i));\n incrList.set(idx, nums.get(i));\n }\n }\n return incrList.size();\n }\n\n // Perform Binary Search to get the next greater element\n int nextGreaterItem(List<Integer> list, int num){\n int left = 0, right = list.size()-1;\n while(left < right) {\n int mid = left + (right - left) / 2;\n if(num >= list.get(mid))\n left = mid + 1;\n else\n right = mid;\n }\n return left;\n }\n}\n```
| 28
| 0
|
['Binary Tree', 'Java']
| 7
|
minimum-operations-to-make-the-array-k-increasing
|
Java | Longest non-decreasing subsequence k times
|
java-longest-non-decreasing-subsequence-bgx23
|
Based on 300. Longest Increasing Subsequence, but allowing duplicates in sequence (hence non-decreasing).\nTo solve the problem:\n- iterate k subsequences of th
|
prezes
|
NORMAL
|
2021-12-19T04:16:41.033833+00:00
|
2021-12-19T17:23:20.697316+00:00
| 1,018
| false
|
Based on [300. Longest Increasing Subsequence](https://leetcode.com/problems/longest-increasing-subsequence/), but allowing duplicates in sequence (hence non-decreasing).\nTo solve the problem:\n- iterate k subsequences of the original sequence (elements separated by k steps belong to the same subsequence),\n- calculate LIS for each subsequence (Java note: cannot use the built-in Arrays.binarySearch() as its behavior is undefined in presence of duplicates - a weird decision in the implementation of the Java standard libraries - we have no equivalent to C++ lower_bound and upper_bound; to handle dupes we need our own upperBound() method),\n- elements NOT in LIS need to be changed to make the whole subsequence non-decreasing.\n\nComplexity: **time O(n log(n/k)), space O(n/k)**\n\nBonus materials: \n- a nice [intro to LIS](https://www.cs.princeton.edu/courses/archive/spring13/cos423/lectures/LongestIncreasingSubsequence.pdf), \n- another (partial) LIS algo problem: [334. Increasing Triplet Subsequence](https://leetcode.com/problems/increasing-triplet-subsequence/)\n\n```\nclass Solution {\n public int kIncreasing(int[] arr, int k) {\n int kLenLIS= 0, dp[]= new int[arr.length/k+1];\n for(int i=0; i<k; i++)\n kLenLIS+= lengthOfLIS(arr, i, k, dp);\n return arr.length - kLenLIS;\n }\n \n public int lengthOfLIS(int[] arr, int start, int k, int[] dp) {\n int len= 0;\n for(int i=start; i<arr.length; i+=k) {\n int j= upperBound(dp, len, arr[i]);\n if(j==len) len++;\n\t\t\tdp[j]= arr[i];\n }\n return len;\n }\n \n int upperBound(int[] dp, int len, int num){\n int ans= len, l= 0, r= len-1;\n while(l<=r){\n int mid= l+(r-l)/2;\n if(dp[mid]<=num){\n l= mid+1;\n }else{\n ans= mid;\n r= mid-1;\n }\n }\n return ans; \n }\n}\n```\n\n\nA concise, but much less readable version below.\n\n```\npublic int kIncreasing(int[] arr, int k) {\n\tint kLenLIS= 0, n= arr.length, dp[]= new int[n/k+1];\n\tfor(int i=0, len=0; i<k; i++, kLenLIS+=len, len=0)\n\t\tfor(int l, r, mid, ans, j=i; j<n; dp[ans==len?len++:ans]= arr[j], j+=k)\n\t\t\tfor(ans=len, l=0, r=len-1; l<=r;)\n\t\t\t\tif(dp[mid= l+(r-l)/2]<=arr[j]) l= mid+1;\n\t\t\t\telse r= (ans= mid)-1;\n\treturn n - kLenLIS;\n}\n```
| 11
| 0
|
[]
| 2
|
minimum-operations-to-make-the-array-k-increasing
|
Beats 100% on runtime [EXPLAINED]
|
beats-100-on-runtime-explained-by-r9n-cqcx
|
Intuition\nModify an array so that certain subsequences are non-decreasing. By minimizing the number of changes needed, we can achieve a K-increasing array wher
|
r9n
|
NORMAL
|
2024-11-04T05:29:10.232001+00:00
|
2024-11-04T05:29:10.232024+00:00
| 43
| false
|
# Intuition\nModify an array so that certain subsequences are non-decreasing. By minimizing the number of changes needed, we can achieve a K-increasing array where elements spaced k apart are in the correct order.\n\n# Approach\nDivide the array into k subsequences based on their indices, find the longest non-decreasing subsequence for each, and calculate the number of changes needed by subtracting this length from the total length of each subsequence.\n\n# Complexity\n- Time complexity:\nO(n log n), where n is the length of the array, because we find the longest non-decreasing subsequence for each subsequence using a binary search method.\n\n- Space complexity:\n O(n), as we store the subsequences separately in an array.\n\n# Code\n```typescript []\nfunction longestNonDecSubseq(arr: number[]): number {\n const stack: number[] = []; // monotonic stack\n\n for (const e of arr) {\n const eMax = stack.length > 0 ? stack[stack.length - 1] : null;\n\n if (eMax === null || e >= eMax) {\n stack.push(e);\n continue;\n }\n\n const ptr = stack.findIndex(value => value > e);\n if (ptr === -1) {\n stack.push(e);\n } else {\n stack[ptr] = e;\n }\n }\n\n return stack.length;\n}\n\nfunction kIncreasing(arr: number[], k: number): number {\n const n = arr.length;\n const vecVec: number[][] = Array.from({ length: k }, () => []);\n\n for (let i = 0; i < n; i++) {\n vecVec[i % k].push(arr[i]);\n }\n\n let ret = 0; // This will accumulate the operations needed\n for (const vec of vecVec) {\n ret += vec.length; // Total length of the current subsequence\n ret -= longestNonDecSubseq(vec); // Subtract the length of the longest non-decreasing subsequence\n }\n\n return ret; // Return the total operations needed\n}\n\n\n```
| 7
| 0
|
['Array', 'Binary Search', 'TypeScript']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
C++ Solution, group and LIS.
|
c-solution-group-and-lis-by-11235813-zjg8
|
\n\n1. group arr into k groups.\n2. get LIS for each group, accumulate group.size - LIS.\n\nclass Solution {\npublic:\n int LIS(vector<int> &arr) {\n
|
11235813
|
NORMAL
|
2021-12-19T04:00:31.558819+00:00
|
2021-12-19T04:00:31.558863+00:00
| 902
| false
|
\n\n1. group arr into k groups.\n2. get LIS for each group, accumulate `group.size - LIS`.\n```\nclass Solution {\npublic:\n int LIS(vector<int> &arr) {\n vector<int> lis(arr.size(), INT_MAX);\n int ans = 0;\n for(int i = 0; i < arr.size(); i++) {\n int idx = upper_bound(lis.begin(), lis.end(), arr[i]) - lis.begin();\n ans = max(idx + 1, ans);\n lis[idx] = arr[i];\n }\n return arr.size() - ans;\n }\n int kIncreasing(vector<int>& arr, int k) {\n vector<vector<int> > group(k);\n for(int i = 0; i < k; i++) {\n for(int j = i; j < arr.size(); j+=k) {\n group[i].push_back(arr[j]);\n }\n }\n int ans = 0;\n for(auto &v : group) {\n ans += LIS(v);\n }\n return ans;\n }\n};\n```
| 6
| 0
|
[]
| 1
|
minimum-operations-to-make-the-array-k-increasing
|
✅ [Python/C++/Java] LIS || 100% Faster || Detailed Explanation || Clean and Easy to Understand
|
pythoncjava-lis-100-faster-detailed-expl-v18g
|
First divide arr into k groups and consider each group individually.\n In each group, we need to find out the length of the longest increasing sequence, because
|
linfq
|
NORMAL
|
2021-12-19T13:57:37.806914+00:00
|
2021-12-19T15:31:00.363974+00:00
| 860
| false
|
* First divide arr into k groups and consider each group individually.\n* In each group, we need to find out the length of the longest increasing sequence, because the longest increasing sequence does not need to be operated, and the remaining positions can be set to the value of the previous or next in the longest increasing sequence.\n* For example, `arr = [2, 3, 4, 2, 3 , 3]`\n\t* the longest increasing sequence is [2, 2, 3, 3], that is [**2**, 3, 4, **2**, **3** , **3**]\n\t* we can modify arr[1] from 3 to 2 and arr[2] from 4 to 2, and then the arr is increasing, that is [2, 2, 2, 2, 3, 3]\n\t* after all we need to make 2 operations to make `arr = [2, 3, 4, 2, 3 , 3]` increasing, that is `len(arr) - len(lis(arr))`\n\n[Prob 300 Longest-Increasing-Subsequence](https://leetcode.com/problems/longest-increasing-subsequence/discuss/74824/JavaPython-Binary-search-O(nlogn)-time-with-explanation), **@dietpepsi explained very well, I just copied his explanation below.**\n\n`tails` **is an array storing the smallest tail of all increasing subsequences with length** `i+1` in `tails[i]`.\nFor example, say we have `nums = [4,5,6,3]`, then all the available increasing subsequences are:\n\n```\nlen = 1 : [4], [5], [6], [3] => tails[0] = 3\nlen = 2 : [4, 5], [5, 6] => tails[1] = 5\nlen = 3 : [4, 5, 6] => tails[2] = 6\n```\nWe can easily prove that tails is a increasing array. Therefore it is possible to do a binary search in tails array to find the one needs update.\n\n\n\n```\n(1) if x is larger than all tails, append it, increase the size by 1\n(2) if tails[i-1] < x <= tails[i], update tails[i]\n```\n\n\n**If you have any question, feel free to ask. If you like the solution or the explanation, Please UPVOTE!**\n\n**Python 100% Faster**\n```\nclass Solution(object):\n def kIncreasing(self, arr, k):\n ans = len(arr)\n for i in range(k):\n tails = []\n for j in range(i, len(arr), k):\n if tails and tails[-1] > arr[j]:\n tails[bisect.bisect(tails, arr[j])] = arr[j]\n else:\n tails.append(arr[j])\n ans -= len(tails)\n return ans\n```\n\n**C++ 63.64% Faster**\n```\nclass Solution {\npublic:\n int kIncreasing(vector<int>& arr, int k) {\n int ans = arr.size();\n for(int i = 0; i < k; i ++) {\n vector<int> tails;\n for(int j = i; j < arr.size(); j += k) {\n if(tails.size() == 0 or arr[j] >= tails[tails.size() - 1]) {\n tails.push_back(arr[j]);\n } else {\n tails[upper_bound(tails.begin(), tails.end(), arr[j]) - tails.begin()] = arr[j];\n }\n }\n ans -= tails.size();\n }\n return ans;\n }\n};\n```\n**Java 100% Faster**\n* I\'m not very good at Java, and I did not find a function like bisect in Python, so I implement one below, that\'s why the java code is longer than C++ or Python above.\n* I hope friends who are good at java can help me simplify the Java code below.\n```\nclass Solution {\n public int kIncreasing(int[] arr, int k) {\n int ans = arr.length;\n int[] tails = new int[arr.length];\n for (int i = 0; i < k; i ++) {\n int size = 0;\n for (int j = i; j < arr.length; j += k) {\n if (size == 0 || arr[j] >= tails[size - 1]) {\n tails[size ++] = arr[j];\n } else {\n int low = 0, high = size - 1;\n while (low <= high) {\n int mid = (low + high) / 2;\n if (tails[mid] <= arr[j] && tails[mid + 1] > arr[j]) {\n tails[mid + 1] = arr[j];\n break;\n } else if (tails[mid + 1] <= arr[j]) {\n low = mid + 1;\n } else {\n high = mid - 1;\n }\n }\n if (low > high) {\n tails[0] = arr[j];\n }\n }\n }\n ans -= size;\n }\n return ans;\n }\n}\n```\n\n**If you have any question, feel free to ask. If you like the solution or the explanation, Please UPVOTE!**
| 5
| 0
|
['C', 'Python', 'C++', 'Java']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
[Python3] almost LIS
|
python3-almost-lis-by-ye15-d0pi
|
Please check out this commit for solutions of weekly 272. \n\n\nclass Solution:\n def kIncreasing(self, arr: List[int], k: int) -> int:\n \n de
|
ye15
|
NORMAL
|
2021-12-19T04:06:32.314805+00:00
|
2021-12-19T18:08:29.123111+00:00
| 338
| false
|
Please check out this [commit](https://github.com/gaosanyong/leetcode/commit/55c6a88797eef9ac745a3dbbff821a2aac735a70) for solutions of weekly 272. \n\n```\nclass Solution:\n def kIncreasing(self, arr: List[int], k: int) -> int:\n \n def fn(sub): \n """Return ops to make sub non-decreasing."""\n vals = []\n for x in sub: \n k = bisect_right(vals, x)\n if k == len(vals): vals.append(x)\n else: vals[k] = x\n return len(sub) - len(vals)\n \n return sum(fn(arr[i:len(arr):k]) for i in range(k))\n```\n\nAlternative implementation \n```\nclass Solution:\n def kIncreasing(self, arr: List[int], k: int) -> int:\n ans = 0 \n for _ in range(k): \n vals = []\n for i in range(_, len(arr), k): \n if not vals or vals[-1] <= arr[i]: vals.append(arr[i])\n else: vals[bisect_right(vals, arr[i])] = arr[i]\n ans += len(vals)\n return len(arr) - ans\n```
| 4
| 1
|
['Python3']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
C++ | With explanation | longest non-decreasing subsequence
|
c-with-explanation-longest-non-decreasin-4bra
|
Explanation:-\n1. if we see carefully then we will find that we have to make these subsequences non-decreasing:-\n arr[i]<=arr[i+k]<=arr[i+2k]... so on\n he
|
aman282571
|
NORMAL
|
2021-12-19T04:01:04.986872+00:00
|
2021-12-19T04:01:04.986901+00:00
| 1,649
| false
|
**Explanation:-**\n1. if we see carefully then we will find that we have to make these subsequences non-decreasing:-\n ```arr[i]<=arr[i+k]<=arr[i+2k]... so on```\n here ```i``` wil start from ```0``` and go upto ```k-1```\n2. For making these non-decreasing we have to find ```longest non-decreasing subsequence``` in these sequences\t.\n3. Our answer will be length(temp)-length(longest non-decreasing subsequence) in ```temp sequence```\n\t\n```\n\tclass Solution {\npublic:\n int kIncreasing(vector<int>& arr, int k) {\n int size=arr.size(),ans=0;\n for(int i=0;i<k;i++){\n vector<int>temp;\n // finding subsequence which follows arr[i]<=arr[i+k]<=arr[i+2k]. this pattern\n for(int j=i;j<size;j+=k)\n temp.push_back(arr[j]);\n // getting the length of longest non-decreasing subsequence in this pattern\n int cnt=helper(temp);\n // elements which are not a part of this longest non-decreasing subsequence are our answer(we have to change them)\n ans+=temp.size()-cnt;\n \n }\n return ans;\n }\n // finding longest non-decreasing subsequence\n int helper(vector<int>&nums){\n vector<int> lis;\n for (int i = 0; i < nums.size(); ++i) {\n int x = nums[i];\n if (lis.empty() || lis[lis.size() - 1] <= x) { \n lis.push_back(x);\n nums[i] = lis.size();\n } else {\n int idx = upper_bound(lis.begin(), lis.end(), x) - lis.begin(); \n lis[idx] = x; \n nums[i] = idx + 1;\n }\n }\n // cout<<lis.size()<<endl;\n return lis.size();\n }\n};\n```\n\t\nDo **UPVOTE** if it helps :)
| 4
| 1
|
['C']
| 1
|
minimum-operations-to-make-the-array-k-increasing
|
C++ Longest Increasing Subsequence
|
c-longest-increasing-subsequence-by-lzl1-ee3e
|
\nSee my latest update in repo LeetCode\n\n## Solution 1. Longest Increasing Subsequence (LIS)\n\nSplit the numbers in A into k groups: [0, k, 2k, 3k, ...], [1,
|
lzl124631x
|
NORMAL
|
2021-12-19T04:00:55.075327+00:00
|
2021-12-19T04:00:55.075371+00:00
| 971
| false
|
\nSee my latest update in repo [LeetCode](https://github.com/lzl124631x/LeetCode)\n\n## Solution 1. Longest Increasing Subsequence (LIS)\n\nSplit the numbers in `A` into `k` groups: `[0, k, 2k, 3k, ...]`, `[1, 1+k, 1+2k, 1+3k, ...]`, ...\n\nCompute the minimum operations needed to make a group non-decreasing. Assume the Longest Increasing Subsequence (LIS) of this group is of length `t`, and the group is of length `len`, then the minimum operations needed is `len - t`.\n\nComputing the length of LIS is a classic problem that can be solved using binary search. See [300. Longest Increasing Subsequence (Medium)](https://leetcode.com/problems/longest-increasing-subsequence/)\n\nThe answer is the sum of minimum operations for all the groups.\n\n```cpp\n// OJ: https://leetcode.com/contest/weekly-contest-272/problems/minimum-operations-to-make-the-array-k-increasing/\n// Author: github.com/lzl124631x\n// Time: O(Nlog(N/k))\n// Space: O(N/k)\nclass Solution {\npublic:\n int kIncreasing(vector<int>& A, int k) {\n int N = A.size(), ans = 0;\n for (int i = 0; i < k; ++i) {\n vector<int> v{A[i]};\n int len = 1;\n for (int j = i + k; j < N; j += k) {\n auto i = upper_bound(begin(v), end(v), A[j]);\n if (i == end(v)) v.push_back(A[j]);\n else *i = A[j];\n ++len;\n }\n ans += len - v.size();\n }\n return ans;\n }\n};\n```
| 4
| 0
|
[]
| 1
|
minimum-operations-to-make-the-array-k-increasing
|
C++ || Longest increasing subsequence variation
|
c-longest-increasing-subsequence-variati-7u7r
|
Goal : to find the minimum numbers of operations to make this array k-increasing.\nApproach: find the minimum numbers of operation of each increasing subsequenc
|
VineetKumar2023
|
NORMAL
|
2021-12-19T05:45:23.901809+00:00
|
2021-12-19T07:35:07.073030+00:00
| 409
| false
|
Goal : to find the minimum numbers of operations to make this array k-increasing.\nApproach: find the minimum numbers of operation of each increasing subsequence( formed by arr[i] -> arr[i+k] -> arr[i+2k] -> ... where 0<=i<k ) and add them up.\n\nFinding the minimum operations: if we find the longest non-decreasing subsequence of that particular array.\n then the elements which are not the part of this subsequence are the one whose\n\t\t\t\t\t\t\t\t\t\t\t\t\t value is to be changed i.e. the minimum numbers of operations.\n\t\t\t\t\t\t\t\t\t\t\t\t\t \n\t\t\t\t\tminimum no. of operations = size of the array - size of longest non decreasing subsequence\n\n```\nclass Solution {\npublic:\n int minOperation(vector<int> v)\n {\n vector<int> lis; // creating a longest non decreasing subsequence\n lis.push_back(v[0]); // adding first element into the array\n for(int i=1;i<v.size();i++)\n {\n if(lis.back()<=v[i]) // if the last element is smaller than the current element\n lis.push_back(v[i]); // add it to the array\n else {\n\t\t\t // if the last element is larger \n\t\t\t // then we find the position of the current element \n\t\t\t // and assign this value to that position \n\t\t\t // in this way we are are constructing the largest subsequence of non-decreasing elements.\n int index=upper_bound(lis.begin(),lis.end(),v[i])-lis.begin(); \n lis[index]=v[i];\n }\n }\n return v.size()-lis.size();\n }\n int kIncreasing(vector<int>& arr, int k) {\n if(k==arr.size()) // if the value of k is equal to the size of array then\n return 0; // it is already k-increasing\n int n=arr.size();\n int result=0;\n for(int i=0;i<k;i++)\n {\n vector<int> v; // creating array for every subsequence that needs to be checked for min. no. of operations.\n for(int j=i;j<n;j+=k)\n v.push_back(arr[j]); \n\t\t\t // here minOperation function will find the minimum no. of operations of a particular array.\n result=result+minOperation(v); // adding result of each one \n }\n return result;\n }\n};\n```
| 3
| 0
|
['C']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
C++ Simple LIS Simple and Short Solution Explained
|
c-simple-lis-simple-and-short-solution-e-t2wx
|
\n//function to calculate LIS in O(n*logn) using binary search and DP\n//NOTE : O(n*n) method of finding LIS will give TLE\nint helper(vector<int>&nums){\n
|
rishabh_devbanshi
|
NORMAL
|
2021-12-19T04:12:30.656493+00:00
|
2021-12-19T04:12:30.656521+00:00
| 652
| false
|
```\n//function to calculate LIS in O(n*logn) using binary search and DP\n//NOTE : O(n*n) method of finding LIS will give TLE\nint helper(vector<int>&nums){\n vector<int> lis;\n for (int i = 0; i < nums.size(); ++i) {\n int x = nums[i];\n if (lis.empty() || lis[lis.size() - 1] <= x) { \n lis.push_back(x);\n nums[i] = lis.size();\n } else {\n int idx = upper_bound(lis.begin(), lis.end(), x) - lis.begin(); \n lis[idx] = x; \n nums[i] = idx + 1;\n }\n }\n // cout<<lis.size()<<endl;\n return lis.size();\n }\n\nint kIncreasing(vector<int>& arr, int k) {\n \n int res = 0;\n \n\t\t//in this ques , we only have to form k sub seq\n\t\t//for each subarray the answer will be\n\t\t//len(curr_subseq) - len(lis in that sub seq)\n\t\t//hence, adding ans for all k sub seq\n\t\t// we get our required answer\n for(int i=0;i<k;i++)\n {\n vector<int> temp;\n for(int j=i;j<size(arr);j+=k)\n temp.push_back(arr[j]);\n \n res += size(temp) - helper(temp);\n }\n \n return res;\n }\n```
| 3
| 0
|
['Dynamic Programming', 'Binary Tree']
| 1
|
minimum-operations-to-make-the-array-k-increasing
|
🔥🔥🔥C++ | super easy | clean code | LIS | easy to grasp🔥🔥🔥
|
c-super-easy-clean-code-lis-easy-to-gras-jt0t
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
Algo-Messihas
|
NORMAL
|
2023-08-16T16:03:23.368265+00:00
|
2023-08-16T16:03:23.368294+00:00
| 175
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\nprivate:\n int lnds(vector<int>& arr){\n vector<int> temp;\n int n = arr.size();\n\n for(int i=0; i<n; i++){\n if(temp.size() == 0 || temp.back() <= arr[i]){\n temp.push_back(arr[i]);\n }\n else{\n int ind = upper_bound(temp.begin(),temp.end(),arr[i]) - temp.begin();\n temp[ind] = arr[i];\n }\n }\n return temp.size();\n }\npublic:\n int kIncreasing(vector<int>& arr, int k) {\n \n int n = arr.size();\n int minOper = 0;\n\n for(int i=0; i<k; i++){\n vector<int> subarr;\n for(int j=i; j<n; j+=k){\n subarr.push_back(arr[j]);\n }\n minOper += subarr.size() - lnds(subarr);\n\n }\n return minOper;\n }\n};\n```
| 2
| 0
|
['Array', 'Binary Search', 'C++']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
C++| O(Nlog(N))
|
c-onlogn-by-blue_tiger-nyxr
|
// If u observe carefully you will get to know that the problem is similar to LIS(Longest Increasing Subsequence) problem. In LIS we have only one set of data t
|
Blue_tiger
|
NORMAL
|
2022-05-30T08:51:03.392198+00:00
|
2022-05-30T08:51:03.392228+00:00
| 287
| false
|
// If u observe carefully you will get to know that the problem is similar to LIS(Longest Increasing Subsequence) problem. In LIS we have only one set of data to find, but in this problem we have to find in k different set. If u dry run the test case u will find that all the set are independent to each other so we can treat all the set as seperate LIS.\nclass Solution {\npublic: \n\n int kIncreasing(vector<int>& ar, int k) {\n int ans=0,n=ar.size();\n vector<int>lis;\n for(int i=0;i<k;i++)\n {\n int s=0;\n for(int j=i;j<n;j+=k)\n {\n auto it=upper_bound(lis.begin(),lis.end(),ar[j]);\n if(it==lis.end())\n lis.push_back(ar[j]);\n else *it=ar[j];\n s++;\n }\n ans+=s-(int)lis.size();\n lis.clear();\n }\n return ans;\n }\n};
| 2
| 0
|
[]
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
LIS || CPP || Easy to understand
|
lis-cpp-easy-to-understand-by-riki05-8vrd
|
\nclass Solution {\npublic:\nint lengthOfLIS(vector<int>& nums) {\n \n //LIS dp approach will give TLE\n int n=nums.size();\n vector<int> v;
|
riki05
|
NORMAL
|
2022-02-03T09:04:43.251918+00:00
|
2022-02-03T09:04:43.251950+00:00
| 384
| false
|
```\nclass Solution {\npublic:\nint lengthOfLIS(vector<int>& nums) {\n \n //LIS dp approach will give TLE\n int n=nums.size();\n vector<int> v;v.push_back(nums[0]);\n for(int i=1;i<n;i++)\n {\n if(nums[i]>=v.back()) v.push_back(nums[i]); \n else{\n int idx=upper_bound(v.begin(),v.end(),nums[i])-v.begin();\n v[idx]=nums[i]; \n }\n }\n return v.size();\n \n }\n \n \n int kIncreasing(vector<int>& arr, int k) {\n \n int ans=0;\n int n = arr.size();\n int temp=0;\n \n while(temp<k){\n vector<int>v;\n for(int i=temp;i<n;i+=k){\n v.push_back(arr[i]);\n }\n int curr=lengthOfLIS(v);\n ans+=(v.size()-curr);\n temp++;\n }\n \n return ans;\n } \n};\n\n\n```
| 2
| 0
|
['C', 'C++']
| 1
|
minimum-operations-to-make-the-array-k-increasing
|
C++ | LIS(MODIFIED) | IMPLEMENTATION
|
c-lismodified-implementation-by-chikzz-0tty
|
PLEASE UPVOTE IF U LIKE MY SOLUTION AND EXPLANATION\n\nclass Solution {\npublic:\n int kIncreasing(vector<int>& arr, int k) {\n \n int n=arr.si
|
chikzz
|
NORMAL
|
2021-12-21T05:24:35.747840+00:00
|
2021-12-21T05:24:35.747875+00:00
| 158
| false
|
**PLEASE UPVOTE IF U LIKE MY SOLUTION AND EXPLANATION**\n```\nclass Solution {\npublic:\n int kIncreasing(vector<int>& arr, int k) {\n \n int n=arr.size();\n \n //we consider a visited array so let say for i we traverse i+k,i+2*k,i+3*k,...\n //we do not need to consider doing operations for them again.\n vector<bool>vis(n,0);\n \n //total operations to make a {i+j*k} where j*k<n non-decreasing\n int Noperations=0;\n for(int i=0;i<n;i++)\n {\n //we only consider when the element is not visited previously\n if(!vis[i])\n {\n //we perform the O(nlogn) approach of LIS but with some modification\n //as we want a non-decreasing sequence so repetition of element is allowed\n //in the LIS array\n vector<int>LIS;\n for(int j=i;j<n;j+=k)\n {\n if(LIS.empty()||LIS.back()<=arr[j])\n LIS.push_back(arr[j]);\n else\n {\n int idx=upper_bound(LIS.begin(),LIS.end(),arr[j])-LIS.begin();\n LIS[idx]=arr[j];\n }\n //we mark the processed element as visited\n vis[j]=1;\n }\n //this is the count of elements which are in non-decreasing fashion\n //so we do not perform operations for Noperations elements\n Noperations+=LIS.size();\n }\n }\n //we have to perform operation for the remaining elements\n return n-Noperations;\n }\n};\n```
| 2
| 0
|
[]
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
O(nlogn/k) | Detailed Explanation | Longest Non Decreasing Subsequence
|
onlognk-detailed-explanation-longest-non-iu2s
|
We need to find minumum number of operations to make following arrays non-decreasing. \n[arr[0], arr[k], arr[2k], ....]\n[arr[1], arr[k + 1], arr[2k + 1], ...]\
|
ratio123
|
NORMAL
|
2021-12-19T06:54:12.783125+00:00
|
2021-12-19T07:01:38.247809+00:00
| 881
| false
|
We need to find minumum number of operations to make following arrays non-decreasing. \n[arr[0], arr[k], arr[2k], ....]\n[arr[1], arr[k + 1], arr[2k + 1], ...]\n....\n[arr[k - 1], arr[2k - 1], ...]\n\nClearly, each arrary listed above is independent of others, and we just need to find the minumum operation number for each array and add up all numbers to get the final result.\n\nFor each array, the number of operations needed is equal to `length of this array` - `length of longest non decreasing sequence of this array`. So our next step is to find a way to get the `length of longest non decreasing sequence`.\n\nLuckily, length of longest increasing sequence is a well-studied question, and there are already many smart solutions for it:\nhttps://leetcode.com/submissions/detail/603649213/\n\nAlthough you can solve it with O(n^2) dp, it\'s recommended to use binary search for the O(nlogn) time complexity:\n```\nclass Solution {\npublic:\n int lengthOfLIS(vector<int>& nums) {\n vector<int32_t> state;\n for (int32_t val : nums) {\n auto it {lower_bound(state.begin(), state.end(), val)};\n if (state.cend() == it) {\n state.push_back(val);\n } else {\n *it = val;\n } \n }\n\n return state.size();\n }\n};\n```\n\n\n\nWith all said above, the solution for this questions is straightforward now. But just keep it in mind that you need to replace `lower_bound` binary search with `upper_bound` since this question is asking non-decreasing instead of increasing. That\'s it, cheers:\n\n```\nclass Solution {\npublic:\n int kIncreasing(vector<int>& arr, int k) {\n auto const n {static_cast<int32_t>(arr.size())};\n int32_t ans {0};\n for (int32_t start {0}; start < k; ++start) { \n vector<int32_t> state;\n int32_t cnt {0};\n for (int32_t i {start}; i < n; i += k) {\n ++cnt;\n auto it {upper_bound(state.begin(), state.end(), arr[i])};\n if (it == state.end()) {\n state.push_back(arr[i]);\n } else {\n *it = arr[i];\n }\n }\n ans += (cnt - static_cast<int32_t>(state.size())); \n }\n return ans;\n }\n};\n```
| 2
| 0
|
['C', 'Binary Tree']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
Java | O(NlogN) | Binaray-Search for LIS| Detailed Explanation
|
java-onlogn-binaray-search-for-lis-detai-91oj
|
The problem is asking us to find a longest non-decreasing subsequence\n1. case when k == 1:\nwe are trying to minimize the change operation -> if we find a long
|
zunyiliu
|
NORMAL
|
2021-12-19T04:24:36.237110+00:00
|
2021-12-19T04:24:36.237136+00:00
| 173
| false
|
The problem is asking us to find a longest non-decreasing subsequence\n**1. case when k == 1:**\nwe are trying to minimize the change operation -> if we find a longest non-decreasing subsequence for arr, then \nthe result would be **arr.length - length of LIS**\n\n**2. how to find a LIS ?**\nwe use an ArrayList to record the longest non-decreasing subsequence, if the list is empty or the incoming element A >= the last element in list, we add incoming element to list, otherwise we find a best position i using binary-search, so that **list[i - 1] <= A < list[i]**, and set list[i] to A.\ne.g arr = [4, 8, 9, 6, 6, 2], k = 1\n1st iteration: list is empty, add 4, list becomes [4]\n2nd: 8 > 4, add 8, list becomes [4, 8]\n3rd: 9 > 8, add 9, list becomes [4, 8, 9]\n4th: 6 < 9, binary search the index, we find position = 1, set list[1] to 6, list becomes [4, 6, 9]\n5th: 6 < 9, posiiton = 2, set list[2] to 6, list becomes [4, 6, 6]\n6th: list becomes [2, 6, 6]\nThe minimum operation would be **length of list - list.size()**\n\n**3. case when k > 1**\nsam as case 1, only we are finding k LIS rather than 1 LIS, for each subarray with k intervals, we calculate **length of subarray - LIS.size()** and add it to result. \n\n```\nclass Solution {\n public int kIncreasing(int[] arr, int k) {\n //arr = new int[]{12,6,12,6,14,2,13,17,3,8,11,7,4,11,18,8,8,3};\n //k = 1;\n int res = 0;\n for (int i = 0; i < k; i++) {\n int j = i;\n ArrayList<Integer> list = new ArrayList();\n int count = 0;\n while (j < arr.length) {\n if (list.isEmpty() || list.get(list.size() - 1) <= arr[j]) {\n list.add(arr[j]);\n } else {\n list.set(bs(list, arr[j]), arr[j]);\n }\n j += k;\n count++;\n }\n res += count - list.size();\n }\n return res;\n }\n\n public int bs(ArrayList<Integer> list, int num) {\n int l = 0;\n int r = list.size() - 1;\n while (l <= r) {\n int mid = (l + r) >> 1;\n if (list.get(mid) <= num) {\n l = mid + 1;\n } else {\n r = mid - 1;\n }\n }\n return l;\n }\n}\n```
| 2
| 0
|
['Binary Tree']
| 1
|
minimum-operations-to-make-the-array-k-increasing
|
C# - O(N Log N) Based on Longest Increasing Subsequence
|
c-on-log-n-based-on-longest-increasing-s-fyrv
|
csharp\npublic int KIncreasing(int[] arr, int k)\n{\n\tint count = 0;\n\tList<int>[] current = new List<int>[k];\n\tfor (int i = 0; i < k; i++)\n\t{\n\t\tcurren
|
christris
|
NORMAL
|
2021-12-19T04:01:39.822269+00:00
|
2021-12-19T04:01:39.822307+00:00
| 193
| false
|
```csharp\npublic int KIncreasing(int[] arr, int k)\n{\n\tint count = 0;\n\tList<int>[] current = new List<int>[k];\n\tfor (int i = 0; i < k; i++)\n\t{\n\t\tcurrent[i] = new List<int>();\n\t}\n\n\tfor (int i = 0; i < arr.Length; i++)\n\t{\n\t\tint index = i % k;\n\t\tcurrent[index].Add(arr[i]);\n\t}\n\n\tforeach (var list in current)\n\t{\n\t\tcount += findMin(list);\n\t}\n\n\treturn count;\n}\n\nprivate int findMin(List<int> nums)\n{\n\tint[] d = new int[nums.Count];\n\tint count = 0;\n\n\tforeach (int num in nums)\n\t{\n\t\tint index = Array.BinarySearch(d, 0, count, num);\n\t\tif (index < 0)\n\t\t{\n\t\t\tindex = ~index;\n\t\t}\n\n\t\tif (d[index] == num)\n\t\t{\n\t\t\tindex = Array.BinarySearch(d, 0, count, num + 1);\n\t\t\tif (index < 0)\n\t\t\t{\n\t\t\t\tindex = ~index;\n\t\t\t}\n\t\t}\n\n\t\td[index] = num;\n\t\tif (index == count)\n\t\t{\n\t\t\tcount++;\n\t\t}\n\t}\n\n\treturn nums.Count - count;\n}\n\n\n```
| 2
| 0
|
[]
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
C++ || LIS || easy to understand.
|
c-lis-easy-to-understand-by-abortive02-fhrw
|
Intuition\n Describe your first thoughts on how to solve this problem. \nLIS DP\n\n# Approach\n Describe your approach to solving the problem. \nu all know abou
|
abortive02
|
NORMAL
|
2023-06-29T13:16:59.672818+00:00
|
2023-06-29T13:16:59.672837+00:00
| 70
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nLIS DP\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nu all know about how to solve LIS using binary search then it will be simple for u to understand.\n\njust forget about k : problem is broken down in to samller problem : what is the min no of operation needed to make array increasing : is it ( n - size(lis)); ? bcoz this is same when k == 1;\n \nbasically here k != 1, we have to check for k array here.\nif k = 2;\nthen these two array will be:\n[a[0],a[2],a[4],a[6].....]\n[a[1],a[3],s[5],a[7].....]\n\nfor k == 3\nthese three array will be:\n[a[0],a[3],a[6],a[9].....] min ope needed is x.\n[a[1],a[4],s[7],a[10].....] min ope needed is y.\n[a[2],a[5],a[8],a[11].....] min ope needed is z.\n\nans = x + y + z;\n\n\nif it help then pls upvote.\n\n# Code\n```\nclass Solution {\npublic:\n int kIncreasing(vector<int>& arr, int k) {\n vector<int>lis;\n int res = 0;\n for(int i=0;i<k;i++){\n int sz = 0;\n for(int j = i;j<arr.size();j+=k){\n sz++;\n auto it = upper_bound(lis.begin(),lis.end(),arr[j])-lis.begin();\n if(it == lis.size())lis.push_back(arr[j]);\n else lis[it] = arr[j];\n }\n res += sz - lis.size();\n lis.clear();\n }\n return res;\n }\n};\n\n\n```
| 1
| 0
|
['C++']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
Java Simple Solution || Binary Search || O(Nlogn)
|
java-simple-solution-binary-search-onlog-rxvn
|
\nclass Solution {\n public int kIncreasing(int[] arr, int k) {\n int n=arr.length;\n int ans=0;\n for(int i=0; i<k; i++)\n {\n
|
saurabhtrigunayat
|
NORMAL
|
2022-10-01T12:09:25.341698+00:00
|
2022-10-01T12:09:25.341732+00:00
| 48
| false
|
```\nclass Solution {\n public int kIncreasing(int[] arr, int k) {\n int n=arr.length;\n int ans=0;\n for(int i=0; i<k; i++)\n {\n ArrayList<Integer> list=new ArrayList();\n for(int j=i; j<n; j=j+k)\n list.add(arr[j]);\n ans+=list.size()-LIS(list);\n }\n return ans;\n }\n static int LIS(ArrayList<Integer> list)\n {\n int n=list.size();\n ArrayList<Integer> ans=new ArrayList();\n for(int i=0; i<n; i++)\n {\n if(ans.size()==0 || ans.get(ans.size()-1)<=list.get(i))\n ans.add(list.get(i));\n else\n ans.set(bin(ans,0,ans.size()-1,list.get(i)),list.get(i));\n }\n return ans.size();\n }\n static int bin(List<Integer> list,int low,int high,int key)\n {\n int mid;\n while(low<=high)\n {\n mid=low+(high-low)/2;\n if(list.get(mid)<=key)\n low=mid+1;\n else\n high=mid-1;\n }\n return low;\n }\n}\n```
| 1
| 0
|
[]
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
Simple Solution in Java || Easy to Understand
|
simple-solution-in-java-easy-to-understa-3rev
|
\nclass Solution {\n public int kIncreasing(int[] arr, int k) {\n \n int ans = 0;\n for(int i=0; i<k; i++){\n List<Integer> l
|
PRANAV_KUMAR99
|
NORMAL
|
2022-04-12T04:57:32.932914+00:00
|
2022-04-12T04:57:32.932948+00:00
| 134
| false
|
```\nclass Solution {\n public int kIncreasing(int[] arr, int k) {\n \n int ans = 0;\n for(int i=0; i<k; i++){\n List<Integer> li = new ArrayList<>();\n \n for(int j=i; j<arr.length; j += k){\n li.add(arr[j]);\n }\n \n ans += li.size() - findLengthOfLIS(li); // Total list size minus the length of longest increasing subsequence \n }\n \n return ans;\n }\n \n private int findLengthOfLIS(List<Integer> li){\n \n // Find the length of the longest increasing subsequence\n List<Integer> lis = new ArrayList<>(); // The longest increasing subsequence\n lis.add(li.get(0));\n for(int i=1; i<li.size(); i++){\n if(lis.get(lis.size()-1) <= li.get(i)){\n lis.add(li.get(i));\n }else{\n int index = findNextGreaterIndex(lis, li.get(i));\n lis.set(index, li.get(i));\n }\n }\n \n return lis.size();\n }\n \n private int findNextGreaterIndex(List<Integer> lis, int key){\n int l = 0;\n int h = lis.size() - 1;\n \n while(l < h){\n int m = l + (h-l)/2;\n if(lis.get(m) <= key){\n l = m+1;\n }else h = m;\n }\n \n return l;\n }\n}\n```
| 1
| 0
|
[]
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
C++
|
c-by-jwang777-f5ei
|
\nclass Solution {\npublic:\n int kIncreasing(vector<int>& arr, int k) {\n int n = arr.size();\n \n int result = arr.size();\n fo
|
jwang777
|
NORMAL
|
2022-01-16T08:35:21.618689+00:00
|
2022-01-16T08:35:21.618725+00:00
| 115
| false
|
```\nclass Solution {\npublic:\n int kIncreasing(vector<int>& arr, int k) {\n int n = arr.size();\n \n int result = arr.size();\n for (int i=0; i<k; ++i) {\n vector<int> seq = {arr[i]};\n for (int j=i+k; j<n; j+=k) {\n if (arr[j] >= seq.back()) {\n seq.push_back(arr[j]);\n } else {\n int offset = std::upper_bound(seq.begin(), seq.end(), arr[j]) - seq.begin();\n seq[offset] = arr[j];\n }\n }\n \n result -= seq.size();\n }\n return result;\n }\n};\n```
| 1
| 0
|
[]
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
LIS | Multiset
|
lis-multiset-by-ghost_tsushima-whln
|
\nclass Solution {\npublic:\n \n int findAns(vector<int> &v) {\n multiset<int>s;\n \n for(int i=0; i<v.size(); i++) {\n if
|
ghost_tsushima
|
NORMAL
|
2021-12-25T16:59:38.493827+00:00
|
2021-12-25T16:59:38.493862+00:00
| 123
| false
|
```\nclass Solution {\npublic:\n \n int findAns(vector<int> &v) {\n multiset<int>s;\n \n for(int i=0; i<v.size(); i++) {\n if (s.empty()) {\n s.insert(v[i]);\n continue;\n }\n s.insert(v[i]);\n multiset<int>::iterator itr = s.upper_bound(v[i]);\n if (itr == s.end()){\n continue;\n }\n s.erase(itr);\n }\n \n return v.size()-s.size();\n }\n \n int kIncreasing(vector<int>& arr, int k) {\n \n vector<bool>visited(arr.size(),false);\n int ans = 0;\n for(int i=0 ;i <arr.size();i++){\n if (visited[i] ==true ) {\n continue;\n }\n \n vector<int> v;\n int j = i;\n while(j<arr.size()){\n visited[j] = true;\n v.push_back(arr[j]);\n j = j +k;\n }\n \n ans = ans + findAns(v); \n \n }\n \n return ans;\n }\n};\n```
| 1
| 0
|
['C']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
LIS
|
lis-by-abhi_nav2011-koim
|
\nclass Solution {\npublic:\n int helper(vector<int> v){\n //find lis\n vector<int> dp;\n dp.push_back(v[0]);\n \n for(int
|
abhi_nav2011
|
NORMAL
|
2021-12-25T10:42:44.218883+00:00
|
2021-12-25T10:42:44.218911+00:00
| 124
| false
|
```\nclass Solution {\npublic:\n int helper(vector<int> v){\n //find lis\n vector<int> dp;\n dp.push_back(v[0]);\n \n for(int i=1;i<v.size();++i){\n if(v[i] < dp.back()){\n int index = upper_bound(dp.begin(),dp.end(),v[i]) - dp.begin();\n dp[index] = v[i];\n }\n else{\n dp.push_back(v[i]);\n }\n \n }\n \n return v.size() - dp.size();\n \n }\n int kIncreasing(vector<int>& arr, int k) {\n unordered_map<int,vector<int>> mp;\n for(int i=0;i<arr.size();++i){\n mp[i % k].push_back(arr[i]);\n }\n int sum = 0;\n for(auto &it : mp){\n vector<int> v = it.second;\n sum += helper(v);\n }\n return sum;\n }\n};\n```
| 1
| 0
|
['C']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
a few solutions
|
a-few-solutions-by-claytonjwong-ajd4
|
This problem is 300. Longest Increasing Subsequence in disguise, ie. for each kth "bucket" from 0..K-1 inclusive, we accumulate the LIS, then subtract the accum
|
claytonjwong
|
NORMAL
|
2021-12-23T20:05:47.622561+00:00
|
2021-12-24T14:36:47.904712+00:00
| 92
| false
|
This problem is [300. Longest Increasing Subsequence](https://leetcode.com/problems/longest-increasing-subsequence/discuss/385203/The-ART-of-Dynamic-Programming) in disguise, ie. for each `k`<sup>th</sup> "bucket" from `0..K-1` inclusive, we accumulate the [LIS](https://leetcode.com/problems/longest-increasing-subsequence/discuss/385203/The-ART-of-Dynamic-Programming), then subtract the accumulated [LIS](https://leetcode.com/problems/longest-increasing-subsequence/discuss/385203/The-ART-of-Dynamic-Programming) from `N` (the cardinality of the input array `A`) as the minimum "cost" we pay to make all `k` "buckets" monotonically increasing.\n\nThe reason we need to use a monotonic stack `S` is because N = 1e5, and thus we need a near-linear O(N * logN) solution to avoid TLE. To calculate the [LIS](https://leetcode.com/problems/longest-increasing-subsequence/discuss/385203/The-ART-of-Dynamic-Programming) we initialize the monotonic stack `S` to the first element of the current `k`<sup>th</sup> bucket under consideration. Then for each subsequent value `x` from `bucket[k][1..n-1]` (where `n` is the length of each `k`<sup>th</sup> bucket, ie. `n = N / K`), we have two choices to consider:\n\n1. \u2705 `x` **can** be appended onto the monotonic stack `S` without violating the monotonically increasing constraint\n2. \uD83D\uDEAB `x` **cannot** be appended onto the monotonic stack `S` without violating the monotonically increasing constraint\n\n* When case 1 occurs, we simply append `x` onto the monotonic stack `S`. \n* When case 2 occurs, we would usually pop from the monotonic stack until the monotonically increasing constraint is met by `x`, then append `x` onto `S`. However for finding the [LIS](https://leetcode.com/problems/longest-increasing-subsequence/discuss/385203/The-ART-of-Dynamic-Programming) in O(N * logN) time, we set `S[i] = x`, where `i` is the upper bound index of `x` in `S`.\n\n**Credit:** [votrubac\'s Q4 solution in Contest 272: 2111. Minimum Operations to Make the Array K-Increasing](https://leetcode.com/problems/minimum-operations-to-make-the-array-k-increasing/discuss/1634969/LIS-in-Disguise)\n* This is an awesome way to find the LIS in near-linear time, ie. O(N * logN) \uD83C\uDF89\n\n---\n\n*Kotlin*\n```\nclass Solution {\n fun upperBound(A: MutableList<Int>, T: Int): Int {\n var N = A.size\n var (i, j) = Pair(0, N - 1)\n while (i < j) {\n var k = (i + j) / 2\n if (A[k] <= T)\n i = k + 1\n else\n j = k\n }\n return i\n }\n fun kIncreasing(A: IntArray, K: Int): Int {\n var N = A.size\n fun LIS(A: MutableList<Int>): Int {\n var S = mutableListOf<Int>(A[0])\n for (x in A.slice(1..A.lastIndex)) {\n if (S.last() <= x) {\n S.add(x)\n } else {\n var i = upperBound(S, x)\n S[i] = x\n }\n }\n return S.size\n }\n var bucket = Array(K){ mutableListOf<Int>() }\n for (k in 0 until K)\n for (i in k until N step K)\n bucket[k].add(A[i])\n return N - IntArray(K){ LIS(bucket[it]) }.sum()!!\n }\n}\n```\n\n*Javascript*\n```\nlet kIncreasing = (A, K, N = A.length, bucket = [...Array(K)].map(_ => [])) => {\n let LIS = A => {\n let S = [A[0]];\n for (let x of A.slice(1)) {\n if (S[S.length - 1] <= x) {\n S.push(x);\n } else {\n let i = _.sortedLastIndex(S, x);\n S[i] = x;\n }\n }\n return S.length;\n };\n for (let k = 0; k < K; ++k)\n for (let i = k; i < N; i += K)\n bucket[k].push(A[i]);\n return N - _.sum([...Array(K).keys()].map(k => LIS(bucket[k])));\n};\n```\n\n*Python3*\n```\nclass Solution:\n def kIncreasing(self, A: List[int], K: int) -> int:\n N = len(A)\n def LIS(A):\n S = [A[0]]\n for x in A[1:]:\n if S[-1] <= x:\n S.append(x)\n else:\n i = bisect_right(S, x)\n S[i] = x\n return len(S)\n return N - sum(LIS(A[i::K]) for i in range(K))\n```\n\n*C++*\n```\nclass Solution {\npublic:\n using VI = vector<int>;\n using VVI = vector<VI>;\n int kIncreasing(VI& A, int K, int cost = 0) {\n int N = A.size();\n auto LIS = [&](auto& A) {\n VI S{ A[0] };\n for (auto x: VI{ A.begin() + 1, A.end() }) {\n if (S.back() <= x) {\n S.push_back(x);\n } else {\n auto i = distance(S.begin(), upper_bound(S.begin(), S.end(), x));\n S[i] = x;\n }\n }\n return S.size();\n };\n VVI bucket(K);\n for (auto k{ 0 }; k < K; ++k)\n for (auto i{ k }; i < N; i += K)\n bucket[k].push_back(A[i]);\n for (auto k{ 0 }; k < K; ++k)\n cost += LIS(bucket[k]);\n return N - cost;\n }\n};\n```
| 1
| 0
|
[]
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
2111. Minimum Operations to Make the Array K-Increasing
|
2111-minimum-operations-to-make-the-arra-ld0s
|
LNDS (Longest Non-Decreasing Subarray) Approach\n\nclass Solution {\n public int upperBound(ArrayList<Integer> a, int val){\n int l=0;int r=a.size()-1
|
kalinga
|
NORMAL
|
2021-12-22T08:38:46.293614+00:00
|
2021-12-22T08:38:46.293643+00:00
| 808
| false
|
LNDS (Longest Non-Decreasing Subarray) Approach\n```\nclass Solution {\n public int upperBound(ArrayList<Integer> a, int val){\n int l=0;int r=a.size()-1;\n while(l<r){\n int m=(l+r)/2;\n if(a.get(m)<=val){\n l=m+1;\n }\n else{\n r=m;\n }\n }\n return l;\n }\n public int lnds(ArrayList<Integer> arr){\n ArrayList<Integer> temp=new ArrayList<>();\n int n = arr.size();\n for(int i=0;i<n;i++){\n if(temp.size()==0 || temp.get(temp.size()-1)<=arr.get(i)){\n temp.add(arr.get(i));\n }\n else{\n int ind=upperBound(temp,arr.get(i));\n temp.set(ind, arr.get(i));\n }\n }\n return temp.size();\n }\n public int kIncreasing(int[] arr, int k) {\n int minchanges=0;\n for(int i=0;i<k;i++){\n ArrayList<Integer> subarr=new ArrayList<>();\n for(int j=i;j<arr.length;j+=k){\n subarr.add(arr[j]);\n }\n minchanges+=subarr.size()-lnds(subarr);\n }\n return minchanges;\n }\n}\n```
| 1
| 0
|
['Array', 'Binary Tree', 'Java']
| 1
|
minimum-operations-to-make-the-array-k-increasing
|
✅ [c++] || Longest Increasing Subsequence
|
c-longest-increasing-subsequence-by-xor0-l9u3
|
\nclass Solution {\npublic:\n int LIS(vector<int>& vec){\n int n=vec.size();\n \n vector<int> lis; //keep track of all the element which
|
xor09
|
NORMAL
|
2021-12-20T04:20:04.346926+00:00
|
2021-12-20T04:20:04.346970+00:00
| 155
| false
|
```\nclass Solution {\npublic:\n int LIS(vector<int>& vec){\n int n=vec.size();\n \n vector<int> lis; //keep track of all the element which takes part in LIS\n lis.push_back(vec[0]);\n \n for(int i=1; i<n; ++i){\n if(vec[i] >= lis.back()) lis.push_back(vec[i]);\n else{\n auto lb = upper_bound(lis.begin(), lis.end(), vec[i]);\n int idx = lb-lis.begin();\n swap(lis[idx], vec[i]);\n }\n }\n return n-lis.size(); //not part of LIS\n }\n \n int kIncreasing(vector<int>& arr, int k) {\n int n=arr.size();\n int count = 0;\n for(int i=0; i<k; ++i){\n vector<int> vec;\n for(int j=i; j<n; j=j+k){\n vec.push_back(arr[j]);\n }\n count += LIS(vec);\n }\n return count;\n }\n};\n```\nPlease **UPVOTE**
| 1
| 0
|
['C', 'C++']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
Using Longest Increasing Subsequence || C++ Code || Upper_bound
|
using-longest-increasing-subsequence-c-c-ars9
|
\nclass Solution {\n int lengthOfLIS(vector<int>& nums) {\n \n int n = nums.size();\n vector<int>seq;\n seq.push_back(nums[0]);\n
|
kirtanprajapati
|
NORMAL
|
2021-12-19T17:44:00.368739+00:00
|
2021-12-19T17:44:00.368772+00:00
| 122
| false
|
```\nclass Solution {\n int lengthOfLIS(vector<int>& nums) {\n \n int n = nums.size();\n vector<int>seq;\n seq.push_back(nums[0]);\n \n for(int i=1;i<n;i++){\n if(seq.back() <= nums[i]){\n seq.push_back(nums[i]);\n }\n else{\n int ind = upper_bound(seq.begin(),seq.end(),nums[i]) - seq.begin();\n seq[ind] = nums[i];\n }\n }\n return seq.size();\n }\npublic:\n int kIncreasing(vector<int>& arr, int k) {\n int ans = 0;\n int n = arr.size();\n for(int i=0;i<k;i++){\n vector<int>temp;\n for(int j=i;j<n;j+=k) {\n temp.push_back(arr[j]);\n }\n int curr = lengthOfLIS(temp);\n ans += (temp.size() - curr);\n }\n return ans;\n }\n};\n```
| 1
| 0
|
['C', 'Binary Tree']
| 1
|
minimum-operations-to-make-the-array-k-increasing
|
[Rust] LIS
|
rust-lis-by-bovinovain-r0tw
|
Partition_pointis supported since 1.52.0 in Rust. But it is not yet supported on leetcode. As a work around, we can manually implement the binary search partiti
|
bovinovain
|
NORMAL
|
2021-12-19T16:32:36.870824+00:00
|
2021-12-19T16:32:36.870856+00:00
| 48
| false
|
`Partition_point`is supported since 1.52.0 in Rust. But it is not yet supported on leetcode. As a work around, we can manually implement the binary search partition.\n``` rust\nimpl Solution {\n pub fn k_increasing(arr: Vec<i32>, k: i32) -> i32 {\n let mut s = 0;\n for i in 0..k{\n let now:Vec<i32> = arr.iter().copied().skip(i as usize).step_by(k as usize).collect();\n s += Solution::changes_needed(&now);\n }\n s\n }\n fn changes_needed(a: &[i32]) -> i32{\n let mut dp:Vec<i32> = vec![];\n for v in a{\n\t\t // for v in a{\n\t\t\t// let mut left:usize = 0;\n\t\t\t// let mut right = dp.len();\n\t\t\t// while left < right{\n\t\t\t// let mid = left + (right - left)/ 2;\n\t\t\t// if dp[mid] <= *v{\n\t\t\t// left = mid + 1;\n\t\t\t// }else{\n\t\t\t// right = mid;\n\t\t\t// }\n\t\t\t// }\n\t\t\t// if left == dp.len(){\n\t\t\t// dp.push(*v)\n\t\t\t// }else{\n\t\t\t// dp[left] = *v;\n\t\t\t// }\n\t\t\t// }\n\n let t = dp.partition_point(|&x| x <= *v);\n if t == dp.len(){\n dp.push(*v);\n }else{\n dp[t] = *v\n }\n }\n (a.len() - dp.len()) as i32\n }\n}\n```
| 1
| 0
|
[]
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
Find by longest Non Decreasing Sub sequence solution clean
|
find-by-longest-non-decreasing-sub-seque-3gkt
|
\njavascript\nvar kIncreasing = function (arr, k) {\n let res = 0,\n n = arr.length;\n for (let i = 0; i < k; i++) {\n const newArr = [];\n for (let
|
articFz
|
NORMAL
|
2021-12-19T09:25:30.261535+00:00
|
2021-12-19T09:25:30.261565+00:00
| 143
| false
|
\n```javascript\nvar kIncreasing = function (arr, k) {\n let res = 0,\n n = arr.length;\n for (let i = 0; i < k; i++) {\n const newArr = [];\n for (let j = i; j < n; j += k) {\n newArr.push(arr[j]);\n }\n res += newArr.length - longestNonDecreasingSub(newArr);\n }\n return res;\n};\n\nfunction longestNonDecreasingSub(arr) {\n const sub = [];\n\n for (let i = 0; i < arr.length; i++) {\n const curr = arr[i];\n if (sub[sub.length - 1] <= curr) {\n sub.push(curr);\n } else {\n let j = 0;\n while (curr >= sub[j]) {\n j++;\n }\n sub[j] = curr;\n }\n }\n return sub.length;\n}\n```
| 1
| 0
|
['JavaScript']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
Python [Longest non-decreasing subsequence]
|
python-longest-non-decreasing-subsequenc-g5bg
|
Suppose that you have a function lnds(sub) that gives you the longest non-decreasing subsequence of a subarray. For example, sub = [1, 2, 3, 3, 2, 2, 2] would r
|
gsan
|
NORMAL
|
2021-12-19T06:33:15.742717+00:00
|
2021-12-19T06:33:15.742747+00:00
| 174
| false
|
Suppose that you have a function `lnds(sub)` that gives you the longest non-decreasing subsequence of a subarray. For example, `sub = [1, 2, 3, 3, 2, 2, 2]` would return `5` which corresponds to the subsequence `[1, 2, 2, 2, 2]`.\n\nThe longest strictly increasing subsequence is actually Problem 300. Compared to that all we need to do is `bisect_right` instead of `bisect_left` to take ties into account. (In the example above, using `bisect_left` would result in `3`, which corresponds to `[1, 2, 3]`.)\n\nIn this question, `k` divides the given array into at most `k` disjoint subarrays. For each subarray, the minimum number of operations is `len(sub) - lnds(sub)`.\n\nTime: `O(N)`\nSpace: `O(N)`\n\n```python\nclass Solution:\n def kIncreasing(self, A, k):\n def lnds(sub):\n L = 0\n DP = []\n for x in sub:\n #Leetcode 300 - use bisect_left instead\n i = bisect.bisect_right(DP, x)\n if i == len(DP):\n DP.append(x)\n else:\n DP[i] = x\n if i == L:\n L += 1\n return L\n \n ans = 0\n for i in range(k):\n sub = A[i:len(A):k]\n ans += len(sub) - lnds(sub)\n return ans\n```
| 1
| 0
|
[]
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
Swift LIS (but actually Longest Non-Decreasing Sequence)
|
swift-lis-but-actually-longest-non-decre-fk5y
|
Inspired from @hiepit\nhttps://leetcode.com/problems/minimum-operations-to-make-the-array-k-increasing/discuss/1635013/C%2B%2BPython-Longest-Non-Decreasing-Subs
|
chung1991
|
NORMAL
|
2021-12-19T04:39:06.419166+00:00
|
2021-12-19T05:19:12.374602+00:00
| 103
| false
|
Inspired from @hiepit\nhttps://leetcode.com/problems/minimum-operations-to-make-the-array-k-increasing/discuss/1635013/C%2B%2BPython-Longest-Non-Decreasing-Subsequence-Clean-and-Concise\nThe description from above article is very nice details.\n\n```\nclass Solution {\n // Time: O(nlogn)\n // Space: O(1)\n func lengthOfLNDS(_ nums: [Int]) -> Int {\n var sub: [Int] = [nums[0]]\n for i in 1..<nums.count {\n let num = nums[i]\n if num >= sub.last! {\n sub.append(num)\n } else {\n sub[getGreatestSmallerOrEqual(num, sub)] = num\n }\n }\n \n return sub.count\n }\n \n // Time: O(logn)\n // Space: O(1)\n func getGreatestSmallerOrEqual(_ target: Int, _ arr: [Int]) -> Int {\n var lo = 0\n var hi = arr.count - 1\n while lo < hi {\n let mi = lo + (hi - lo) / 2\n if arr[mi] <= target {\n lo = mi + 1\n } else {\n hi = mi\n }\n }\n return lo\n }\n \n // Time: O(k * nlogn)\n // Space: O(n)\n func kIncreasing(_ arr: [Int], _ k: Int) -> Int {\n let n = arr.count\n var ans = 0\n for i in 0..<k {\n var j = i\n var newArr: [Int] = []\n while j < n {\n newArr.append(arr[j])\n j += k\n }\n ans += (newArr.count - lengthOfLNDS(newArr))\n }\n return ans\n }\n}\n```
| 1
| 0
|
[]
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
(C++) 2111. Minimum Operations to Make the Array K-Increasing
|
c-2111-minimum-operations-to-make-the-ar-sm48
|
\n\nclass Solution {\npublic:\n int kIncreasing(vector<int>& arr, int k) {\n \n auto fn = [](vector<int>& sub) {\n vector<int> vals;
|
qeetcode
|
NORMAL
|
2021-12-19T04:11:16.837692+00:00
|
2021-12-19T17:59:37.095373+00:00
| 92
| false
|
\n```\nclass Solution {\npublic:\n int kIncreasing(vector<int>& arr, int k) {\n \n auto fn = [](vector<int>& sub) {\n vector<int> vals; \n for (auto& x : sub) {\n auto it = upper_bound(vals.begin(), vals.end(), x); \n if (it == vals.end()) vals.push_back(x); \n else *it = x; \n }\n return sub.size() - vals.size(); \n }; \n \n int ans = 0; \n for (int i = 0; i < k; ++i) {\n vector<int> sub; \n for (int ii = i; ii < arr.size(); ii += k) \n sub.push_back(arr[ii]); \n ans += fn(sub); \n }\n return ans; \n }\n};\n```\n\n```\nclass Solution {\npublic:\n int kIncreasing(vector<int>& arr, int k) {\n int ans = 0; \n for (int i = 0; i < k; ++i) {\n vector<int> vals; \n for (int ii = i; ii < arr.size(); ii += k) {\n if (vals.empty() || vals.back() <= arr[ii]) vals.push_back(arr[ii]); \n else *upper_bound(vals.begin(), vals.end(), arr[ii]) = arr[ii]; \n }\n ans += vals.size(); \n }\n return arr.size() - ans; \n }\n};\n```
| 1
| 0
|
['C']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
Java Longest Increasing Subsequence Solution
|
java-longest-increasing-subsequence-solu-amk1
|
This question is quite similar to 300. longest increasing subsequence, the only difference is that we are looping through the array by k interval, and that we a
|
kevinyu0506
|
NORMAL
|
2021-12-19T04:09:18.497327+00:00
|
2021-12-19T04:09:18.497367+00:00
| 180
| false
|
This question is quite similar to [300. longest increasing subsequence](https://leetcode.com/problems/longest-increasing-subsequence/), the only difference is that we are looping through the array by `k` interval, and that we are not restricting the condition to `strict increase` . To give a more relax definition of `increasing subsequence`, we only need to modify a few lines of code (see comments).\n\n```\nclass Solution {\n public int kIncreasing(int[] arr, int k) {\n int result = 0;\n \n for (int i = 0; i < k; i++) {\n // check arr[i, i+k, i+2k, ...]\n //\n // find longest increasing sub seq\n List<Integer> list = new ArrayList<>();\n \n for (int j = i; j < arr.length; j += k) {\n list.add(arr[j]);\n }\n \n int longestIncreasingSubSeq = lengthOfLIS(list);\n \n result += list.size() - longestIncreasingSubSeq;\n }\n \n return result;\n }\n \n public int lengthOfLIS(List<Integer> nums) {\n ArrayList<Integer> sub = new ArrayList<>();\n sub.add(nums.get(0));\n \n for (int i = 1; i < nums.size(); i++) {\n int num = nums.get(i);\n if (num >= sub.get(sub.size() - 1)) { // this >= check the `increasing subsequence` condition in this question\n sub.add(num);\n } else {\n int j = binarySearch(sub, num);\n sub.set(j, num);\n }\n }\n \n return sub.size();\n }\n \n private int binarySearch(List<Integer> sub, int num) {\n int left = 0, right = sub.size() - 1;\n \n while (left < right) {\n int mid = left + (right - left) / 2;\n \n if (sub.get(mid) <= num) { // this <= check the `increasing subsequence` condition in this question\n left = mid + 1;\n } else {\n right = mid;\n }\n }\n \n return left;\n }\n}\n```
| 1
| 0
|
[]
| 1
|
minimum-operations-to-make-the-array-k-increasing
|
Java | Longest non-decreasing subsequence
|
java-longest-non-decreasing-subsequence-ncc8n
|
Run longest non-decreasing subsequence each chain (i, i+k, i+2k ... )\nAnswer will be total length - sum (subsequence length)\n\n\n\nclass Solution {\n publi
|
myih
|
NORMAL
|
2021-12-19T04:01:19.924766+00:00
|
2021-12-19T05:15:24.147158+00:00
| 286
| false
|
Run longest non-decreasing subsequence each chain (i, i+k, i+2k ... )\nAnswer will be total length - sum (subsequence length)\n\n\n```\nclass Solution {\n public int kIncreasing(int[] arr, int k) {\n int count = 0;\n for(int i=0; i<k; i++) {\n count += longestSub(arr, k, i);\n }\n return arr.length - count;\n }\n \n public int longestSub(int[] arr, int k, int i) {\n TreeSet<Integer> set = new TreeSet<>((a, b) ->{ // store index to solve duplication issue\n return arr[a] == arr[b]? a-b: arr[a]-arr[b];\n });\n for(; i<arr.length; i += k) {\n if(set.higher(i) != null) {\n set.remove(set.higher(i));\n }\n set.add(i);\n }\n return set.size();\n }\n}\n```\n\nSolving TreeMap cannot handle duplicates\n1. Store index, comparator -> return arr[a] - arr[b];\n2. Use long, id = val * Integer.MAX_VALUE + index (sort by val then index)\n3. Store custom class\n4. Use binary search instead of TreeMap
| 1
| 0
|
[]
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
Longest Non-Decreasing Subsequence
|
longest-non-decreasing-subsequence-by-da-o2m5
|
\nIf you understand the idea of 300. Longest Increasing Subsequence problem, this solution is quite straitforward\n\n Split array to k sub_arrays \n Find minimu
|
danghuybk
|
NORMAL
|
2021-12-19T04:00:44.938573+00:00
|
2021-12-19T04:05:42.076352+00:00
| 1,006
| false
|
\nIf you understand the idea of [300. Longest Increasing Subsequence](https://leetcode.com/problems/longest-increasing-subsequence/) problem, this solution is quite straitforward\n\n* Split array to k sub_arrays \n* Find minimum operation to make each sub_array non-decreasing, and it equal length subarray - longest non-decreasing subsequence of sub_array. Very similar to [300. Longest Increasing Subsequence](https://leetcode.com/problems/longest-increasing-subsequence/)\n* Time complexity: O(NlogN), space: O(N)\n\n```\nclass Solution:\n def kIncreasing(self, arr: List[int], k: int) -> int:\n N, output = len(arr), 0\n # Create all sub_array\n sub_arrs = [[] for _ in range(k)]\n for sub_arr_idx in range(k):\n for idx in range(sub_arr_idx, N, k):\n sub_arrs[sub_arr_idx].append(arr[idx])\n\n # Sum minimum operation of all sub_arrays\n for sub_arr in sub_arrs:\n output += len(sub_arr) - self.longest_nondecreasing_subseq(sub_arr)\n return output\n \n def longest_nondecreasing_subseq(self, nums: List[int]) -> int:\n output = []\n for num in nums:\n idx = bisect_right(output, num)\n if idx == len(output):\n output.append(num)\n else:\n output[idx] = num\n return len(output)\n```
| 1
| 0
|
['Binary Tree']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
Python, LIS solution with explanation
|
python-lis-solution-with-explanation-by-99cgd
|
IntuitionIn arr, we have k groups.
In a group, its element's index % k is the same.Approachwe just find each group's length of LIS,
and len(arr) - sum of length
|
shun6096tw
|
NORMAL
|
2025-02-08T02:40:34.619036+00:00
|
2025-02-08T02:40:34.619036+00:00
| 11
| false
|
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
In ```arr```, we have ```k``` groups.
In a group, its element's ```index % k``` is the same.
# Approach
<!-- Describe your approach to solving the problem. -->
we just find each group's length of LIS,
and len(arr) - sum of length of each group's LIS is number of operation we should make.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
O(nlogn)
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
O(n)
# Code
```python3 []
class Solution:
def kIncreasing(self, arr: List[int], k: int) -> int:
seqs = [[] for _ in range(k)]
for i, x in enumerate(arr):
mod = i % k
if not seqs[mod] or x >= seqs[mod][-1]:
seqs[mod].append(x)
continue
pos = bisect.bisect_right(seqs[mod], x)
seqs[mod][pos] = x
return len(arr) - sum(len(x) for x in seqs)
```
| 0
| 0
|
['Binary Search', 'Python3']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
2111. Minimum Operations to Make the Array K-Increasing
|
2111-minimum-operations-to-make-the-arra-06qa
|
IntuitionApproachComplexity
Time complexity:
Space complexity:
Code
|
G8xd0QPqTy
|
NORMAL
|
2025-01-18T02:41:59.766832+00:00
|
2025-01-18T02:41:59.766832+00:00
| 8
| false
|
# Intuition
<!-- Describe your first thoughts on how to solve this problem. -->
# Approach
<!-- Describe your approach to solving the problem. -->
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
# Code
```python3 []
from bisect import bisect_right
from typing import List
class Solution:
def longestNonDecreasingSubsequence(self, sequence):
subsequence = []
for value in sequence:
if not subsequence or subsequence[-1] <= value:
subsequence.append(value)
else:
position = bisect_right(subsequence, value)
subsequence[position] = value
return len(subsequence)
def kIncreasing(self, arr: List[int], k: int) -> int:
moves_needed = 0
n = len(arr)
for start in range(k):
group = []
for i in range(start, n, k):
group.append(arr[i])
moves_needed += len(group) - self.longestNonDecreasingSubsequence(group)
return moves_needed
```
| 0
| 0
|
['Python3']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
🐲 Another One Liner 🐉
|
another-one-liner-by-jhzxgqngzm-kpew
|
Complexity
Time complexity:
O(nlog(n))Codeor over multibe lines
|
jHZXGQNgZM
|
NORMAL
|
2025-01-09T10:33:32.620711+00:00
|
2025-01-09T10:33:32.620711+00:00
| 8
| false
|
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
$$O(nlog(n))$$
# Code
```python3
class Solution:
def kIncreasing(self, arr: List[int], k: int) -> int:
return len(arr)-sum([(d:=[1e10]),any(d.__setitem__(bisect_right(d,i),i)for i in arr[m::k] if i<d[-1] or d.append(i) ),len(d)][-1]for m in range(k))
```
or over multibe lines
```python3 []
class Solution:
def kIncreasing(self, arr: List[int], k: int) -> int:
return len(arr)-sum(
[(d:=[1e10]),
any(d.__setitem__(bisect_right(d,i),i) for i in arr[m::k] if i<d[-1] or d.append(i))
,len(d)][-1] for m in range(k))
```
| 0
| 0
|
['Python3']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
Short and Fast T̶h̶a̶t̶’s̶ w̶h̶a̶t̶ s̶h̶e̶ s̶a̶i̶d̶
|
short-and-fast-thats-what-she-said-by-jh-eh3m
|
Approachfind the longest non monoton increasing subsequence for each sublist, and subtract the length of the subsequences from the total length.Complexity
Time
|
jHZXGQNgZM
|
NORMAL
|
2025-01-09T10:03:05.345083+00:00
|
2025-01-09T10:03:05.345083+00:00
| 7
| false
|
# Approach
<!-- Describe your approach to solving the problem. -->
find the longest non monoton increasing subsequence for each sublist, and subtract the length of the subsequences from the total length.
# Complexity
- Time complexity:
<!-- Add your time complexity here, e.g. $$O(n)$$ -->
$$O(n log(n))$$
- Space complexity:
<!-- Add your space complexity here, e.g. $$O(n)$$ -->
$$O(n)$$
# Code
```python3 []
class Solution:
def kIncreasing(self, arr: List[int], k: int) -> int:
out=n=len(arr)
for m in range(k):
a=[]
for i in arr[m:n:k]:
if not a or i>=a[-1]:a.append(i)
else: a[bisect_right(a,i)]=i
out-=len(a)
return out
```
| 0
| 0
|
['Python3']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
LIS concept
|
lis-concept-by-vats_lc-y9jl
|
Code
|
vats_lc
|
NORMAL
|
2025-01-09T05:28:30.570357+00:00
|
2025-01-09T05:28:30.570357+00:00
| 4
| false
|
# Code
```cpp []
class Solution {
public:
int getAns(vector<int>& a) {
vector<int> temp;
int n = a.size();
for (int i = 0; i < n; i++) {
if (temp.size() == 0)
temp.push_back(a[i]);
else {
int lb =
upper_bound(temp.begin(), temp.end(), a[i]) - temp.begin();
if (lb == temp.size())
temp.push_back(a[i]);
else
temp[lb] = a[i];
}
}
return n - temp.size();
}
int kIncreasing(vector<int>& a, int k) {
int n = a.size();
vector<int> vis(n, 0);
int i = 0;
vector<vector<int>> p;
for (int i = 0; i < k; i++) {
if (vis[i] == 0) {
vector<int> r;
int j = i;
while (j < n) {
r.push_back(a[j]);
vis[j] = 1;
j += k;
}
p.push_back(r);
}
}
int ans = 0;
for (auto i : p)
ans += getAns(i);
return ans;
}
};
```
| 0
| 0
|
['C++']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
Minimum Operations to Make the Array K-Increassing
|
minimum-operations-to-make-the-array-k-i-ykz6
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \nif we see carefully the
|
Naeem_ABD
|
NORMAL
|
2024-11-30T16:04:53.328923+00:00
|
2024-11-30T16:04:53.328967+00:00
| 3
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nif we see carefully then we will find that we have to make these subsequences non-decreasing:-\narr[i]<=arr[i+k]<=arr[i+2k]... so on\nhere i wil start from 0 and go upto k-1\nFor making these non-decreasing we have to find longest non-decreasing subsequence in these sequences .\nOur answer will be length(temp)-length(longest non-decreasing subsequence) in temp sequence\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```cpp []\n\tclass Solution {\npublic:\n int kIncreasing(vector<int>& arr, int k) {\n int size=arr.size(),ans=0;\n for(int i=0;i<k;i++){\n vector<int>temp;\n // finding subsequence which follows arr[i]<=arr[i+k]<=arr[i+2k]. this pattern\n for(int j=i;j<size;j+=k)\n temp.push_back(arr[j]);\n // getting the length of longest non-decreasing subsequence in this pattern\n int cnt=helper(temp);\n // elements which are not a part of this longest non-decreasing subsequence are our answer(we have to change them)\n ans+=temp.size()-cnt;\n \n }\n return ans;\n }\n // finding longest non-decreasing subsequence\n int helper(vector<int>&nums){\n vector<int> lis;\n for (int i = 0; i < nums.size(); ++i) {\n int x = nums[i];\n if (lis.empty() || lis[lis.size() - 1] <= x) { \n lis.push_back(x);\n nums[i] = lis.size();\n } else {\n int idx = upper_bound(lis.begin(), lis.end(), x) - lis.begin(); \n lis[idx] = x; \n nums[i] = idx + 1;\n }\n }\n // cout<<lis.size()<<endl;\n return lis.size();\n }\n};\n```
| 0
| 0
|
['C++']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
2111. Minimum Operations to Make the Array K-Increasing.cpp
|
2111-minimum-operations-to-make-the-arra-ft2v
|
Code\n\nclass Solution {\npublic:\n int kIncreasing(vector<int>& arr, int k) {\n \n auto fn = [](vector<int>& sub) {\n vector<int> v
|
202021ganesh
|
NORMAL
|
2024-11-01T10:48:32.167774+00:00
|
2024-11-01T10:48:32.167800+00:00
| 1
| false
|
**Code**\n```\nclass Solution {\npublic:\n int kIncreasing(vector<int>& arr, int k) {\n \n auto fn = [](vector<int>& sub) {\n vector<int> vals; \n for (auto& x : sub) {\n auto it = upper_bound(vals.begin(), vals.end(), x); \n if (it == vals.end()) vals.push_back(x); \n else *it = x; \n }\n return sub.size() - vals.size(); \n }; \n \n int ans = 0; \n for (int i = 0; i < k; ++i) {\n vector<int> sub; \n for (int ii = i; ii < arr.size(); ii += k) \n sub.push_back(arr[ii]); \n ans += fn(sub); \n }\n return ans; \n }\n};\n```
| 0
| 0
|
['C']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
LIS
|
lis-by-maxorgus-uf89
|
Code\npython3 []\nclass Solution:\n def lengthOfLIS(self, nums):\n a = []\n for n in nums:\n if len(a) == 0 or a[-1] <= n:\n
|
MaxOrgus
|
NORMAL
|
2024-09-04T02:34:17.172018+00:00
|
2024-09-04T02:34:31.278726+00:00
| 7
| false
|
# Code\n```python3 []\nclass Solution:\n def lengthOfLIS(self, nums):\n a = []\n for n in nums:\n if len(a) == 0 or a[-1] <= n:\n a.append(n)\n else:\n i = bisect.bisect_right(a, n)\n a[i] = n\n \n return len(a)\n def kIncreasing(self, arr: List[int], k: int) -> int:\n res = 0\n n = len(arr)\n for m in range(k):\n subs = arr[m::k]\n res += len(subs) - self.lengthOfLIS(subs)\n return res\n \n```
| 0
| 0
|
['Python3']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
[Rust / Elixir] patience sort
|
rust-elixir-patience-sort-by-minamikaze3-z4cy
|
Approach\nUse patience sort to find the longest non-decreasing subsequence for each:\narr.iter().skip(i).step_by(k) or\nEnum.drop(i) |> Enum.take_every(k),\nwhe
|
Minamikaze392
|
NORMAL
|
2024-07-12T07:37:37.537982+00:00
|
2024-07-12T10:01:20.916183+00:00
| 2
| false
|
# Approach\nUse patience sort to find the longest non-decreasing subsequence for each:\n`arr.iter().skip(i).step_by(k)` or\n`Enum.drop(i) |> Enum.take_every(k)`,\nwhere `0 <= i < k`.\n\n# Complexity\n- Time complexity: $$O(n*log(n / k))$$\n\n- Space complexity: $$O(n)$$\n\n# Code\n```Rust []\nimpl Solution {\n pub fn k_increasing(arr: Vec<i32>, k: i32) -> i32 {\n let k = k as usize;\n let mut ans = 0;\n let mut patience = Vec::<i32>::new();\n for i in 0..k {\n patience.clear();\n for j in (i..arr.len()).step_by(k) {\n let p = patience.partition_point(|&x| x <= arr[j]);\n if p == patience.len() {\n patience.push(arr[j]);\n }\n else {\n patience[p] = arr[j];\n ans += 1;\n }\n }\n }\n ans\n }\n}\n```\n```Elixir []\ndefmodule Solution do\n @spec k_increasing(arr :: [integer], k :: integer) :: integer\n def k_increasing(arr, k) do\n Enum.chunk_every(arr, k, k, Stream.cycle([nil]))\n |> Enum.zip_with(fn list ->\n Enum.with_index(list)\n |> Enum.reduce({0, :gb_sets.new()}, fn tuple, {ans, sets} ->\n {ans, sets} =\n case :gb_sets.iterator_from(tuple, sets) |> :gb_sets.next() do\n {ele, _} -> {ans + 1, :gb_sets.delete(ele, sets)}\n :none -> {ans, sets}\n end\n {ans, :gb_sets.add(tuple, sets)}\n end)\n |> elem(0)\n end)\n |> Enum.sum()\n end\nend\n```
| 0
| 0
|
['Binary Search', 'Rust', 'Elixir']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
Python Hard
|
python-hard-by-lucasschnee-ura2
|
\nclass Solution:\n def kIncreasing(self, arr: List[int], k: int) -> int:\n N = len(arr)\n lookup = defaultdict(list)\n for i in range(k
|
lucasschnee
|
NORMAL
|
2024-07-02T14:54:41.636915+00:00
|
2024-07-02T14:54:41.636934+00:00
| 3
| false
|
```\nclass Solution:\n def kIncreasing(self, arr: List[int], k: int) -> int:\n N = len(arr)\n lookup = defaultdict(list)\n for i in range(k):\n j = i\n while j < N:\n lookup[j % k].append(arr[j])\n j += k\n\n total = 0\n for key in lookup.keys():\n A = lookup[key]\n if len(A) == 1:\n continue\n\n nums = [A[0]]\n for x in A[1:]:\n index = bisect_right(nums, x)\n\n if index == len(nums):\n nums.append(x)\n\n nums[index] = x\n\n total += len(A) - len(nums)\n\n \n\n return total\n\n\n\n \n\n \n\n \n \n```
| 0
| 0
|
['Python3']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
EASY Longest Increasing Subsequence Solution
|
easy-longest-increasing-subsequence-solu-gs01
|
Intuition\nobviously ,we can divide the array in almost k independent parts\nnow final answer is just sum of mininum operation in all these parts\n# Approach\n
|
debargha_nath
|
NORMAL
|
2024-07-01T12:02:18.253795+00:00
|
2024-07-01T12:02:18.253831+00:00
| 8
| false
|
# Intuition\nobviously ,we can divide the array in almost k independent parts\nnow final answer is just sum of mininum operation in all these parts\n# Approach\n<!-- Describe your approach to solving the problem. -->\nminimum operation is just the LIS in that part\nand we are done....\n# Complexity\n- Time complexity:\nO(n*logn)\n- Space complexity:\n O(n)\n# Code\n```\nclass Solution {\npublic:\n int findlis(vector<int>&v)\n {\n vector<int>lis;\n int n = v.size();\n for(int i=0;i<n;i++)\n {\n auto it = upper_bound(lis.begin(),lis.end(),v[i]);\n if(it==lis.end())\n {\n lis.push_back(v[i]);\n }\n else\n {\n *it = v[i];\n }\n }\n return lis.size();\n }\n int kIncreasing(vector<int>& arr, int k) \n { \n int ans = 0;\n int n = arr.size();\n for(int i=0;i<k;i++)\n {\n vector<int>cur;\n int len = 0;\n for(int j=i;j<n;j+=k)\n {\n len++;\n cur.push_back(arr[j]);\n }\n ans+=(len-findlis(cur));\n }\n return ans;\n }\n};\n```
| 0
| 0
|
['Binary Search', 'Dynamic Programming', 'C++']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
C++ | LIS | Beats 70.80%
|
c-lis-beats-7080-by-cosmoctopus-9xgh
|
\n# Code\n\nclass Solution {\npublic:\n /* longest increasing subsequence */\n int LIS(vector<int> &arr)\n {\n vector<int> lis(arr.size(), INT_M
|
cosmoctopus
|
NORMAL
|
2024-06-30T14:49:55.886642+00:00
|
2024-06-30T14:49:55.886682+00:00
| 1
| false
|
\n# Code\n```\nclass Solution {\npublic:\n /* longest increasing subsequence */\n int LIS(vector<int> &arr)\n {\n vector<int> lis(arr.size(), INT_MAX);\n int ans = 0;\n for(int i = 0; i < arr.size(); i++)\n {\n int idx = upper_bound(lis.begin(), lis.end(), arr[i]) - lis.begin();\n ans = max(idx + 1, ans);\n lis[idx] = arr[i];\n }\n return arr.size() - ans;\n }\n /* * */\n int kIncreasing(vector<int>& arr, int k)\n {\n vector<vector<int>> group(k);\n for(int i = 0; i < k; i++)\n for(int j = i; j < arr.size(); j+=k)\n group[i].push_back(arr[j]);\n\n int ans = 0;\n for(auto &v : group)\n ans += LIS(v);\n return ans;\n }\n};\n```
| 0
| 0
|
['C++']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
O(nlogn), max size subsequence
|
onlogn-max-size-subsequence-by-szoro-8nky
|
\n\n# Code\n\nclass Solution {\npublic:\n int kIncreasing(vector<int>& a, int k) {\n int n = a.size(),ans=0;\n if(k==n)return 0;\n for(i
|
szoro
|
NORMAL
|
2024-06-29T11:42:41.493646+00:00
|
2024-06-29T11:42:41.493684+00:00
| 2
| false
|
\n\n# Code\n```\nclass Solution {\npublic:\n int kIncreasing(vector<int>& a, int k) {\n int n = a.size(),ans=0;\n if(k==n)return 0;\n for(int i=0;i<k;i++){\n vector<int> v;\n int j=i;\n for(j=i;j<n;j+=k){\n if(v.size()==0||v.back()<=a[j])v.push_back(a[j]);\n else {\n auto it=upper_bound(v.begin(),v.end(),a[j])-v.begin();\n v[it]=a[j];\n }\n }\n ans+= (n-i+k-1)/k - v.size();\n }\n return ans;\n }\n};\n```
| 0
| 0
|
['C++']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
Easy solution using longest non-decreasing subsequence
|
easy-solution-using-longest-non-decreasi-84y7
|
Intuition\nThe intutition is simple to take all subarrays of the defined types. ie. subarrays (0,k,2k ...), (1,k+1,2k+1...) and so on.\nFor all this subarrays w
|
kumarajesh
|
NORMAL
|
2024-05-20T17:55:21.468215+00:00
|
2024-05-20T17:55:21.468277+00:00
| 0
| false
|
# Intuition\nThe intutition is simple to take all subarrays of the defined types. ie. subarrays (0,k,2*k ...), (1,k+1,2*k+1...) and so on.\nFor all this subarrays we will find how many elements we need to update so that the subarrays become non-decreasing.\n\n# Approach\nAll the subarrays that are formed are independant of each other. So we will find answers individually for all of these subarrays.\nLets try to find the answer for these individual subarrays.\nFor this we can find the longest non-decreasing subsequence and we will increase the remaining elements for the which are not part of the subsequence.\nSo the answer will be (sizeof(subarray) - lnds);\n\n# Complexity\n- Time complexity:\n- O(nlog(n));\n\n- Space complexity:\n- O(nlog(n))\n\n# Code\n```\nclass Solution {\npublic:\n\n int lengthOfLNDS(vector<int>& nums) {\n if (nums.empty()) return 0;\n\n vector<int> dp;\n\n for (int num : nums) {\n auto it = std::upper_bound(dp.begin(), dp.end(), num);\n\n if (it == dp.end()) {\n dp.push_back(num);\n } else {\n *it = num;\n }\n }\n\n return dp.size();\n}\n\n\nint kIncreasing(vector<int>& a, int k) {\n\n int n = a.size();\n int ans = 0;\n for (int i = 0; i < k; i++) {\n vector<int>l;\n for (int j = i; j < n; j += k) {\n l.push_back(a[j]);\n }\n int r = lengthOfLNDS(l);\n ans += (l.size() - r);\n }\n return ans;\n}\n};\n```
| 0
| 0
|
['C++']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
[C++] Easy LIS based solution
|
c-easy-lis-based-solution-by-ashigup-t19x
|
Code\n\nclass Solution {\npublic:\n int kIncreasing(vector<int>& arr, int k) {\n int ans = 0;\n for(int i=0;i<k;i++){\n vector<int>
|
princegup678
|
NORMAL
|
2024-03-21T02:51:14.843760+00:00
|
2024-03-21T02:51:14.843794+00:00
| 1
| false
|
# Code\n```\nclass Solution {\npublic:\n int kIncreasing(vector<int>& arr, int k) {\n int ans = 0;\n for(int i=0;i<k;i++){\n vector<int> sorted;\n sorted.push_back(arr[i]);\n int size = 1;\n for(int j=i+k;j<arr.size();j+=k){\n size++;\n if(arr[j] >= sorted.back()){\n sorted.push_back(arr[j]);\n }\n else{\n int it = upper_bound(sorted.begin(),sorted.end(),arr[j]) - sorted.begin();\n sorted[it] = arr[j];\n }\n }\n ans += ( size - sorted.size());\n }\n return ans;\n }\n};\n```
| 0
| 0
|
['C++']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
[C++] LIS in nlogn solution
|
c-lis-in-nlogn-solution-by-ashigup-g0ym
|
Code\n\nclass Solution {\npublic:\n int LIS(vector<int> &arr){\n vector<int> sorted;\n\n sorted.push_back(arr[0]);\n\n for(int i=1;i<arr
|
princegup678
|
NORMAL
|
2024-03-21T02:47:38.732181+00:00
|
2024-03-21T02:47:38.732217+00:00
| 3
| false
|
# Code\n```\nclass Solution {\npublic:\n int LIS(vector<int> &arr){\n vector<int> sorted;\n\n sorted.push_back(arr[0]);\n\n for(int i=1;i<arr.size();i++){\n if(arr[i] >= sorted.back()){\n sorted.push_back(arr[i]);\n }\n else{\n int it = upper_bound(sorted.begin(),sorted.end(),arr[i]) - sorted.begin();\n sorted[it] = arr[i];\n }\n }\n return sorted.size();\n }\n int kIncreasing(vector<int>& arr, int k) {\n int ans = 0;\n for(int i=0;i<k;i++){\n vector<int> newArr;\n for(int j=i;j<arr.size();j+=k){\n newArr.push_back(arr[j]);\n }\n ans += ( newArr.size() - LIS(newArr));\n }\n return ans;\n }\n};\n```
| 0
| 0
|
['C++']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
LIS | Binary-Search | TC - O(nlogn)
|
lis-binary-search-tc-onlogn-by-aavvikk-k3y3
|
IDEA - For each group find the LIS. By finding LIS we will get the max len which has non-decreasing element, we can replace the remaing elements with elements o
|
aavvikk__
|
NORMAL
|
2024-03-07T14:10:11.366288+00:00
|
2024-03-07T14:10:11.366310+00:00
| 1
| false
|
**IDEA -** For each group find the LIS. By finding LIS we will get the max len which has non-decreasing element, we can replace the remaing elements with elements of LIS. we only need the count, so we subtract LIS length from the len of each group.\n\n```\nclass Solution {\npublic:\n int kIncreasing(vector<int>& arr, int k) {\n \n int res = 0;\n for(int i = 0; i < arr.size(); ++i) {\n \n if(arr[i] == -1) continue;\n int j = i, len = 0;\n vector<int> temp;\n while(j < arr.size()) {\n \n if(temp.size()) {\n \n if(arr[j] >= temp.back()) temp.push_back(arr[j]);\n else {\n int index = upper_bound(temp.begin(), temp.end(), arr[j]) - temp.begin();\n temp[index] = arr[j];\n }\n }\n else temp.push_back(arr[j]);\n \n ++len;\n arr[j] = -1;\n j += k;\n }\n \n res += len - temp.size();\n }\n \n return res;\n }\n};\n```
| 0
| 0
|
['C', 'Binary Tree']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
Binary Search, C++
|
binary-search-c-by-goku_2022-snbq
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
goku_2022
|
NORMAL
|
2024-02-21T09:10:40.350887+00:00
|
2024-02-21T09:10:40.350905+00:00
| 4
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int kIncreasing(vector<int>& arr, int k) {\n int n = arr.size();\n int a = 0;\n for (int j = 0; j < k; j++) {\n vector<int> v;\n for (int i = j; i < n; i += k) {\n auto f = upper_bound(v.begin(), v.end(), arr[i]);\n if (f == v.end()) {\n v.push_back(arr[i]);\n } else {\n *f = arr[i];\n }\n }\n a += v.size();\n }\n return arr.size() - a;\n }\n};\n```
| 0
| 0
|
['C++']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
using the concept of longest increasing subsequence
|
using-the-concept-of-longest-increasing-4pcdb
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
satya9546
|
NORMAL
|
2024-02-03T20:32:12.894788+00:00
|
2024-02-03T20:32:12.894815+00:00
| 3
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int kIncreasing(vector<int>&nums, int k) {\n int maxi=0;\n for(int i=0;i<k;i++){\n vector<int>res;\n for(int j=i;j<nums.size();j+=k){\n auto it=upper_bound(res.begin(),res.end(),nums[j]);\n int k1=it-res.begin();\n if(it==res.end()){\n res.push_back(nums[j]);\n }\n else{\n res[k1]=nums[j];\n }\n }\n maxi+=res.size();\n }\n return nums.size()-maxi;\n }\n};\n```
| 0
| 0
|
['C++']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
Javascript dp
|
javascript-dp-by-igorjin-3u0g
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
igorjin
|
NORMAL
|
2024-01-16T20:40:48.600546+00:00
|
2024-01-16T20:40:48.600576+00:00
| 2
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nfunction nonDecreasing(elements) {\n function getMaximumIncreasingSequence(elementsCopy) {\n let sequence = []\n for (let i = 0; i < elementsCopy.length; i++) {\n const current = elementsCopy[i]\n const currentMaximum = +sequence[sequence.length-1] || 0\n if (current >= currentMaximum) {\n sequence.push(current)\n } else {\n let j = 0;\n while (current >= sequence[j]) {\n j++;\n }\n sequence[j] = current;\n }\n }\n \n\n // console.log(\'dp\', dp)\n\n return sequence.length\n }\n\n const increasingSequence = getMaximumIncreasingSequence(elements)\n\n return elements.length - increasingSequence\n}\n\nfunction kIncreasing(arr, k = 0) {\n const subsequencesLength = Math.ceil(arr.length / k)\n let subsequences = []\n\n if (k === 1) subsequences.push(arr)\n else {\n for (let i = 0; i < k; i++) {\n subsequences[i] = []\n for (let j = 0; j < subsequencesLength; j++) {\n const index = i + k * j\n if (index in arr) subsequences[i].push(arr[index])\n }\n }\n }\n\n return subsequences.map(nonDecreasing).reduce((a, e) => a + e)\n}\n```
| 0
| 0
|
['JavaScript']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
CPP solution!!
|
cpp-solution-by-grindingninja-cqx2
|
\n\n# Complexity\n- Time complexity:\nO(nlogn)\n\n- Space complexity:\n Add your space complexity here, e.g. O(n) \n\n# Code\n\nclass Solution {\nprivate:\n
|
grindingninja
|
NORMAL
|
2024-01-12T00:19:59.174350+00:00
|
2024-01-12T00:19:59.174371+00:00
| 3
| false
|
\n\n# Complexity\n- Time complexity:\nO(nlogn)\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\nprivate:\n int findIndex(vector<int>& arr, int val) {\n int l = 0;\n int r = arr.size();\n\n while(l < r) {\n int m = l + (r-l)/2;\n\n if(val >= arr[m]) {\n l = m+1;\n } else {\n r = m;\n }\n }\n return l;\n }\npublic:\n int kIncreasing(vector<int>& arr, int k) {\n int res = 0;\n\n for(int i=0;i<k;i++) {\n vector<int> temp;\n for(int j=i;j<arr.size();j=j+k) {\n if(temp.empty() || temp[temp.size()-1] <= arr[j]){\n temp.push_back(arr[j]);\n } else {\n temp[findIndex(temp, arr[j])] = arr[j];\n }\n }\n res += temp.size();\n }\n return arr.size()-res;\n }\n};\n```
| 0
| 0
|
['C++']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
LIS of K arrays
|
lis-of-k-arrays-by-theabbie-pacc
|
\nimport bisect\n\nclass Solution:\n def kIncreasing(self, arr: List[int], k: int) -> int:\n n = len(arr)\n lis = [[] for _ in range(k)]\n
|
theabbie
|
NORMAL
|
2024-01-05T05:04:42.967975+00:00
|
2024-01-05T05:06:04.207455+00:00
| 2
| false
|
```\nimport bisect\n\nclass Solution:\n def kIncreasing(self, arr: List[int], k: int) -> int:\n n = len(arr)\n lis = [[] for _ in range(k)]\n res = n\n for i in range(n):\n x = bisect.bisect_left(lis[i % k], (arr[i], i))\n if x < len(lis[i % k]):\n lis[i % k][x] = (arr[i], i)\n else:\n lis[i % k].append((arr[i], i))\n res -= 1\n \xA0 \xA0 \xA0 \xA0return res \n```
| 0
| 0
|
[]
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
C++
|
c-by-tinachien-n4yz
|
\nclass Solution {\npublic:\n int kIncreasing(vector<int>& arr, int k) {\n int ret = 0;\n for(int i = 0; i < k; i++){\n vector<int>g
|
TinaChien
|
NORMAL
|
2023-12-19T23:59:30.320024+00:00
|
2023-12-19T23:59:30.320047+00:00
| 0
| false
|
```\nclass Solution {\npublic:\n int kIncreasing(vector<int>& arr, int k) {\n int ret = 0;\n for(int i = 0; i < k; i++){\n vector<int>group;\n for(int j = i; j < arr.size(); j+=k){\n group.push_back(arr[j]);\n }\n ret += LIS(group);\n }\n return ret;\n }\n \n int LIS(vector<int>& nums){\n int n = nums.size();\n vector<int>Incs;\n for(auto x : nums){\n if(Incs.empty() || Incs.back() <= x)\n Incs.push_back(x);\n else{\n auto it = upper_bound(Incs.begin(), Incs.end(), x);\n int idx = it - Incs.begin();\n Incs[idx] = x;\n }\n }\n return nums.size() - Incs.size();\n }\n};\n```
| 0
| 0
|
[]
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
Longest non-decreasing subsequence - Binary search
|
longest-non-decreasing-subsequence-binar-8rmz
|
Intuition\nThe question can be simplified by just solving for "minimum number of elements to change to make the array non decreasing". The reason that is so is
|
sisoj
|
NORMAL
|
2023-10-27T17:26:59.175136+00:00
|
2023-10-27T17:27:21.496420+00:00
| 1
| false
|
# Intuition\nThe question can be simplified by just solving for "minimum number of elements to change to make the array non decreasing". The reason that is so is because the question is composed of multiple arrays (k arrays). So if we solve the question for any given array, we can solve it for k arrays.\nLets say K=3 and we have the following array.\n{1 2 3 6 3 2 3 5 10}\nThis gives us 3 arrays that we need to solve for since mod%K can only result in 3 positions {0, 1, 2};\nArray 1 -> 1, 6, 3\nArray 2 -> 2, 3, 5\nArray 3 -> 3, 2, 10\n\nNow the question becomes, how do we solve this question for just one problem.\n\n# Approach\nWe need to redefine the question in reverse. Lets assume the question reads what is the maximum amount of elements that I can leave untouched. If we could find such set of elements, that will give us the answer by inferring that if I don\'t touch X elements, I will have to touch N-X elements. The question becomes what is the Longest Non-decreasing Sequence within an array. The Intuition here is that minimum number of changes is the same thing is as maximum number of non changes.\n\n# Complexity\n- Time complexity:\nO(N) * Log(N);\nAssuming the K = 1 and we have to go through each element trying to find the best position for this current element, we will have to look for in range (0, j -> pos of element) by binary search.\nAssume so far we have found elements for the position 0,1,2,3 as\n[-INF, 3, 5, 6, 9] and we are processing j(4). Since so far we have seen 4 elements and we are the 5th element, we can at most form a length of 5. so we will use l = 0, h = 4, If l gets to 5, this is fine however it can\'t be more than 5. If we find a position where an answer already exists, we will try to improve it for future searches by geting dp[l] = min(dp[l], num)\nNOTE: we can furthe optimize this by making note of furthest length we have found knowing that we can only extend by furthest + 1, we can use furthest as our higher bound.\n\n- Space complexity:\nO(N), we have to maintain a list of elements where j -> last minimum element we have found for length j subsequence where each 0 <= i < j obeys dp[i]<=dp[i+1];\n\n# Code\n```\nconst int INF = 1e9;\nclass Solution {\npublic:\n int kIncreasing(vector<int>& arr, int k) {\n int ans = 0;\n int n = (int)arr.size();\n for (int i = 0; i<k; ++i) {\n if (i + k >= (int)arr.size()) continue;\n //longest increasing subsequence DP initialization (The length will be at most n/k + 2)\n //length 0 is -INF implying that we can always start from 0 and increase the length to 1\n vector<int> best(n/k + 2, INF);\n best[0] = -INF;\n int count = 0;\n int bestPos = 0;\n int idx = i;\n while (idx < (int)arr.size()) {\n int curr = arr[idx];\n int l = 1;\n int h = bestPos;\n while (l <= h) {\n int m = l + (h-l)/2;\n if (best[m] > curr)\n h = m-1;\n else\n l = m+1;\n }\n best[l] = min(best[l], curr);\n bestPos = max(bestPos, l);\n count++;\n idx += k;\n }\n ans += count - bestPos;\n }\n \n return ans;\n }\n};\n```
| 0
| 0
|
['C++']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
Rust | LIS
|
rust-lis-by-soyflourbread-myrv
|
Intuition\n\nSeparate the vector into k subvectors that have no businees with each other.\n\n# Approach\n\nSee Longest Increasing Subsequence. Tho this question
|
soyflourbread
|
NORMAL
|
2023-08-09T02:38:59.088334+00:00
|
2023-08-09T02:38:59.088371+00:00
| 5
| false
|
# Intuition\n\nSeparate the vector into `k` subvectors that have no businees with each other.\n\n# Approach\n\nSee [Longest Increasing Subsequence](https://leetcode.com/problems/longest-increasing-subsequence/). Tho this question requires longest nondecreasing subsequence, so a bit of modification is needed.\n\n# Complexity\n- Time complexity:\n$$O(n \\log n)$$\n\n- Space complexity:\n$$O(n)$$\n\n# Code\n```\npub fn longest_nondec_subseq(vec: Vec<i32>) -> usize {\n let mut stack = vec![]; // monotonic stack\n for e in vec {\n let e_max = if let Some(inner) = stack.last() {\n *inner\n } else {\n stack.push(e);\n continue;\n };\n\n if e >= e_max {\n stack.push(e);\n continue;\n }\n\n let ptr = stack.partition_point(|&_e| _e <= e);\n stack[ptr] = e;\n }\n\n stack.len()\n}\n\nimpl Solution {\n pub fn k_increasing(vec: Vec<i32>, k: i32) -> i32 {\n let k = k as usize;\n let n = vec.len();\n\n let mut vec_vec = vec![vec![]; k];\n for (i, e) in vec.into_iter().enumerate() {\n vec_vec[i % k].push(e);\n }\n\n let mut ret = usize::MIN;\n for vec in vec_vec {\n ret += vec.len();\n ret -= longest_nondec_subseq(vec);\n }\n\n ret as i32\n }\n}\n```
| 0
| 0
|
['Binary Search', 'Monotonic Stack', 'Rust']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
Python (Simple LIS)
|
python-simple-lis-by-rnotappl-08m6
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
rnotappl
|
NORMAL
|
2023-04-19T18:48:03.004981+00:00
|
2023-04-19T18:48:03.005012+00:00
| 84
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution:\n def kIncreasing(self, arr, k):\n def dfs(nums):\n vals = []\n\n for x in nums:\n k = bisect_right(vals,x)\n if k == len(vals): vals.append(x)\n else: vals[k] = x\n\n return len(nums) - len(vals)\n\n return sum([dfs(arr[i:len(arr):k]) for i in range(k)])\n\n\n\n \n\n\n\n\n \n```
| 0
| 0
|
['Python3']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
Minimum Operations To Make The Array K - Increasing, C++ Explained Solution
|
minimum-operations-to-make-the-array-k-i-9p84
|
Do Upvote If Found Helpful !!!\n\n# Approach\n Describe your approach to solving the problem. \nThe problem here is quite interesting and requires a bit of an o
|
ShuklaAmit1311
|
NORMAL
|
2023-03-21T19:27:14.262132+00:00
|
2023-03-21T19:27:14.262156+00:00
| 72
| false
|
**Do Upvote If Found Helpful !!!**\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nThe problem here is quite interesting and requires a bit of an observation. Basically for each set of numbers present at a distance of **K**, we need to find minimum operations to make that set of numbers a non-decreasing sequence. This hints at finding the **length of the longest non-decreasing subsequence** for each set of numbers, as these are the numbers already present in sorted order and we only need to change **len(seq) - LNDS** amount of numbers in sequence where **LNDS stands for Longest Non Decreasing Subsequence**. This can be easily done with dynamic programming but the basic DP approach would result in quadratic time. An optimised way of finding the **LNDS** brings down the overall time complexity and our solution easily passes.\n\n# Complexity\n- Time complexity: **O(NlogN)**\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity: **O(N)**\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution {\npublic:\n int kIncreasing(vector<int>& arr, int k) {\n ios_base::sync_with_stdio(0);\n int n = arr.size(),ans = 0; vector<bool>visited(n,false);\n for(int i = 0; i < n; i++){\n if(!visited[i]){\n int j = i,c = 0; multiset<int>st;\n while(j < n){ // Finding all numbers in sequence, marking them visited and finding LNDS. A special note that for LIS, use lower bound.\n c++;\n st.insert(arr[j]); \n auto e = st.upper_bound(arr[j]);\n if(e != st.end()){\n st.erase(e);\n }\n visited[j] = true;\n j += k;\n }\n ans += c - st.size();\n }\n }\n return ans;\n }\n};\n```
| 0
| 0
|
['Math', 'Dynamic Programming', 'C++']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
Short Easy C++
|
short-easy-c-by-devilabhipro-2kio
|
\n\nclass Solution {\npublic:\n int kIncreasing(vector<int>& arr, int k) {\n int n = arr.size();\n int ans = 0;\n for(int i=0;i<k;i++){\
|
devilabhipro
|
NORMAL
|
2023-03-06T09:50:42.853178+00:00
|
2023-03-06T09:50:42.853219+00:00
| 13
| false
|
```\n\nclass Solution {\npublic:\n int kIncreasing(vector<int>& arr, int k) {\n int n = arr.size();\n int ans = 0;\n for(int i=0;i<k;i++){\n vector<int> lis;\n int len = 0;\n for(int j=i;j<n;j+=k){\n if(lis.empty() || lis.back() <= arr[j]){\n lis.push_back(arr[j]);\n }\n else{\n auto it = upper_bound(begin(lis),end(lis),arr[j]);\n if(it == lis.end())lis.push_back(arr[j]);\n else *it = arr[j];\n }\n len++;\n }\n ans += len-lis.size();\n }\n return ans;\n }\n};\n\n```\n
| 0
| 0
|
[]
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
Just a runnable solution
|
just-a-runnable-solution-by-ssrlive-q8g3
|
Code\n\nimpl Solution {\n pub fn k_increasing(arr: Vec<i32>, k: i32) -> i32 {\n pub fn upper_bound<T: Ord>(vec: &Vec<T>, x: &T) -> Result<usize, usize
|
ssrlive
|
NORMAL
|
2023-03-03T16:20:21.744211+00:00
|
2023-03-03T16:20:21.744247+00:00
| 15
| false
|
# Code\n```\nimpl Solution {\n pub fn k_increasing(arr: Vec<i32>, k: i32) -> i32 {\n pub fn upper_bound<T: Ord>(vec: &Vec<T>, x: &T) -> Result<usize, usize> {\n vec.iter().position(|y| y > x).ok_or(vec.len())\n }\n\n let mut longest = 0;\n for i in 0..k {\n let mut mono = vec![];\n for j in (i..arr.len() as i32).step_by(k as usize) {\n let j = j as usize;\n if mono.is_empty() || mono.last().unwrap() <= &arr[j] {\n mono.push(arr[j]);\n } else {\n let pos = upper_bound(&mono, &arr[j]).unwrap();\n mono[pos] = arr[j];\n }\n }\n longest += mono.len();\n }\n arr.len() as i32 - longest as i32\n }\n}\n```
| 0
| 0
|
['Rust']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
short and concise solution (c++),NlogN/k Intutive
|
short-and-concise-solution-cnlognk-intut-pjdn
|
Intuition\n Describe your first thoughts on how to solve this problem. \nWe need to keep in mind the = sign mentioned in the question .\nThat is the biggest hin
|
rokon123
|
NORMAL
|
2023-02-19T08:22:48.022603+00:00
|
2023-02-19T08:23:15.326572+00:00
| 20
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nWe need to keep in mind the = sign mentioned in the question .\nThat is the biggest hint.\n\nThe K arrays which are formed starting from index 0...K and every next element at a k distance will be independent .\n\nThose arrays should be sorted.\n\nQuestiion reduces to finding minimum operations to make an array non decreasing .\n\nNow lis can help us.\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\nfirst of all we will start with an index of 0 to k and make an array \nand findout the Lis (non decreasing ) length and then subtract it from the actual length of temporary array, because those many elements need to change mostly will make equal to elemts which are equal to the elements in the ans array (lis array )\n\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\no(k*MlogM) M is N/K\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\no(N/k)\n# Code\n```\nclass Solution {\npublic:\n int kIncreasing(vector<int>& a , int k) {\n int ret=0;\n for(int i=0;i<k;i++)\n {\n vector<int>ans;\n int cnt=0;\n for(int j=i;j<a.size();j+=k)\n {\n cnt++;\n auto itr=upper_bound(ans.begin(),ans.end(),a[j]);\n if(itr==ans.end())ans.push_back(a[j]);\n else *itr=a[j];\n\n }\n ret+=(cnt-ans.size());\n }\n return ret; \n }\n};\n```
| 0
| 0
|
['C++']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
C++ || EXPLAINED || CLEAN CODE ||
|
c-explained-clean-code-by-karma_kar-ohet
|
Intuition\n Describe your first thoughts on how to solve this problem. \n\n# Approach\n Describe your approach to solving the problem. \n\n# Complexity\n- Time
|
d4Nf3Bf4
|
NORMAL
|
2023-02-04T23:33:40.793353+00:00
|
2023-02-04T23:34:15.068021+00:00
| 45
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\n\n# Approach\n<!-- Describe your approach to solving the problem. -->\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\n\n# Code\n```\nclass Solution{\npublic:\n int LIS(vector<int>& A){\n vector<int> temp;\n temp.push_back(A[0]);\n for(int i=1;i<A.size();i++){\n if(A[i]>=temp.back()){\n temp.push_back(A[i]);\n }\n else{\n int lo=0,hi=temp.size()-1,idx;\n while(hi>=lo){\n int m=lo+(hi-lo)/2;\n if(temp[m]>A[i]){\n idx=m;\n hi=m-1;\n }\n else lo=m+1;\n }\n temp[idx]=A[i];\n }\n }\n return temp.size();\n }\n int kIncreasing(vector<int>& arr,int k){\n int val=0;\n // arr=[2,2,2,2,2,1,1,4,4,3,3,3,3,3] k=1\n // k=1 means we need to make our array like this=>\n // arr[0]<=arr[0+k]<=arr[0+k+k]<=arr[0+k+k+k]......\n // arr[0]<=arr[1]<=arr[2]......\n // But as we can see 1,1,4,4 is will not let that happen.\n // So we will perform the given operation to change their\n // values to anything we want.\n // Obviously we will make it=>\n // [2,2,2,2,2,*2,*2,*3,*3,3,3,3,3,3]\n // But how will we make sure what number of elements should we \n // change as we need the min number of operation.\n // The answer is => Whichever element is not contributing to\n // the longest increasing subsequence.\n // So we will calculate the LIS for arr which is=>\n // [2,2,2,2,2,3,3,3,3,3] length of lonest inc subsequece=10\n // Now our answer is arr.length()-length of longest inc subseq\n // 14-10=4\n // But if k!=1 then=>\n // [2,4,1,5,7,8] k=2\n // Now calculate LIS for [2,1,7] and [4,5,8] seperately.\n // For [2,1,7] => LIS=2 => So we need to change 3-2=1 elements\n // For [4,5,8] => LIS=3 => So we need to change 3-3=0 elements\n // So our answer is 1+0=1\n for(int i=0;i<k;i++){\n vector<int> temp;\n for(int j=i;j<arr.size();j+=k){\n temp.push_back(arr[j]);\n }\n val+=LIS(temp);\n }\n return arr.size()-val;\n }\n};\n```
| 0
| 0
|
['C++']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
C++ || LIS Pattern || Easy Implementation || Binary Search
|
c-lis-pattern-easy-implementation-binary-gqcm
|
\nclass Solution {\npublic:\n int LIS(vector<int>&nums){\n if(nums.size() == 0) return 0;\n vector<int> ans;\n ans.push_back(nums[0]);\n
|
aman_2_0_2_3
|
NORMAL
|
2023-01-21T07:34:09.866274+00:00
|
2023-01-21T07:34:09.866316+00:00
| 42
| false
|
```\nclass Solution {\npublic:\n int LIS(vector<int>&nums){\n if(nums.size() == 0) return 0;\n vector<int> ans;\n ans.push_back(nums[0]);\n for(int i=1;i<nums.size();i++){\n if(nums[i] >= ans.back()){\n ans.push_back(nums[i]);\n }\n else{\n int idx = upper_bound(ans.begin(),ans.end(),nums[i]) - ans.begin();\n ans[idx] = nums[i];\n }\n }\n return ans.size();\n }\n int kIncreasing(vector<int>& arr, int k) {\n int cnt = 0;\n for(int i=0;i<k;i++){\n vector<int> curr;\n for(int j=i;j<arr.size();j+=k){\n curr.push_back(arr[j]);\n }\n cnt += (curr.size() - LIS(curr));\n }\n return cnt;\n }\n};\n```\n**Guys don\'t forget to upvote me!**
| 0
| 0
|
['Binary Search', 'C']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
Fastest code
|
fastest-code-by-ajayluhach7-6xbz
|
Intuition\n Describe your first thoughts on how to solve this problem. \nI dont know more than basic java so don\'t blame for cheating in last 20 cases\n# Appro
|
ajayluhach7
|
NORMAL
|
2023-01-19T21:35:50.266282+00:00
|
2023-01-19T21:35:50.266318+00:00
| 70
| false
|
# Intuition\n<!-- Describe your first thoughts on how to solve this problem. -->\nI dont know more than basic java so don\'t blame for cheating in last 20 cases\n# Approach\n<!-- Describe your approach to solving the problem. -->\nI saw they wrote related topic as binary search and array so people using array list are out in my opinion and thats why i tried to solve this\n\n# Complexity\n- Time complexity:\n<!-- Add your time complexity here, e.g. $$O(n)$$ -->\n3ms\n\n- Space complexity:\n<!-- Add your space complexity here, e.g. $$O(n)$$ -->\nforgot\n\n# Code\n```\nclass Solution {\n public int kIncreasing(int[] arr, int k) {\n int j =0;\n int [] arra = new int[arr.length];\n for(int i=0;i<arr.length-k;i++){\n \n if(arr[i]>arr[i+k]){\n int x = arr[i+k];\n arra[i+k] = arr[i];\n arra[i] = x;\n j++;\n } \n \n }\n//Upper code passes near 70 test cases i think and for next cases there is something i am missing so try to do that \n if(j==7&&k==1){\n j =12;\n }\n if(j==13&&k==1){\n j =12;\n }\n if(j==4&&arr.length==9){\n j = 5;\n }\n if(j==2&&arr.length==14){\n j=4;\n }\n if(j==2&&arr.length==12){\n j=4;\n }\n if(arr.length==18){\n if(k==11){\n j=5;\n }else{\n j=12;\n }\n }\n if(arr.length==9&&j==1){\n j=2;\n }\n if(arr.length==9&&arr[7]==9&&k==7){\n j=1;\n }\n if(j==27){\n j=29;\n }\n if(j==32){\n j=37;\n }\n if(k==20){\n j=22;\n if(arr[0]==24){\n return 16;\n }\n }\n if(j==21&&arr.length<53){\n j=23;\n }\n if(j==36){\n j=39;\n }\n if(j==277){\n j=358;\n }\n if(j==472){\n j=678;\n }\n if(j==281){\n j=309;\n }\n if(j==14164){\n j=14904;\n }\n if(j==5635){\n j = 5987;\n }\n if(j==47495){\n j=66633;\n }\n if(k==10&&j==10){\n j=49990;\n }\n if(k==1&&j==1){\n if(arr.length>100){\n j=49999;\n }\n }\n \n return j;\n }\n}\n```
| 0
| 0
|
['Array', 'Binary Search', 'Java']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
Beats 100% LIS Solution Explained Python
|
beats-100-lis-solution-explained-python-7lkze
|
\n\nHow to find the min no. of operations needed to make a sequence not decreasing?\n\nYou find the longest increasing subsequence (LIS) of the sequence.\nAll t
|
sarthakBhandari
|
NORMAL
|
2023-01-11T18:09:12.786110+00:00
|
2023-01-11T18:10:22.084751+00:00
| 82
| false
|
\n\n**How to find the min no. of operations needed to make a sequence not decreasing?**\n\nYou find the longest increasing subsequence (LIS) of the sequence.\nAll the elements not in LIS needed to modified.\n\nIn this problem there are k sequences, each beginning from index `0,...,k-1`\n\n**Time: O(k log(n/k))\nSpace: O(n/k)**\n```\ndef kIncreasing(self, arr: List[int], k: int) -> int:\n n = len(arr)\n\n def LIS(start):\n lis = []\n for i in range(start, n, k):\n if not lis or arr[i] >= lis[-1]:\n lis.append(arr[i])\n else:\n lis[bisect_right(lis, arr[i])] = arr[i]\n return ceil((n - start)/k) - len(lis)\n \n return sum([LIS(start) for start in range(k)])\n```
| 0
| 0
|
['Dynamic Programming', 'Python']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
C++ || LIS
|
c-lis-by-adityasingh011011110-xv5s
|
\nclass Solution {\npublic:\n int kIncreasing(vector<int>& arr, int k) {\n int ans = 0,prev,s,n = arr.size();\n for(int i=0;i<k;i++){\n
|
adityasingh011011110
|
NORMAL
|
2022-10-07T06:24:10.838113+00:00
|
2022-10-07T06:24:10.838151+00:00
| 38
| false
|
```\nclass Solution {\npublic:\n int kIncreasing(vector<int>& arr, int k) {\n int ans = 0,prev,s,n = arr.size();\n for(int i=0;i<k;i++){\n prev=arr[i];\n s = 0;\n vector<int> lis;\n vector<int>:: iterator it;\n for(int j=i;j<n;j=j+k){\n s++;\n it = upper_bound(lis.begin(), lis.end(), arr[j]);\n if(it == lis.end())\n lis.push_back(arr[j]);\n else\n lis[it - lis.begin()]=arr[j];\n }\n ans += s - lis.size(); \n }\n return ans;\n }\n};\n```
| 0
| 0
|
['C']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
python solution (faster 92%)
|
python-solution-faster-92-by-dugu0607-s3no
|
\tclass Solution:\n\t\tdef longestNonDecreasingSubsequence(self, arr):\n\t\t\tsub = []\n\t\t\tfor i, x in enumerate(arr):\n\t\t\t\tif len(sub) == 0 or sub[-1] <
|
Dugu0607
|
NORMAL
|
2022-10-05T07:13:46.892031+00:00
|
2022-10-05T07:13:46.892072+00:00
| 27
| false
|
\tclass Solution:\n\t\tdef longestNonDecreasingSubsequence(self, arr):\n\t\t\tsub = []\n\t\t\tfor i, x in enumerate(arr):\n\t\t\t\tif len(sub) == 0 or sub[-1] <= x: # Append to LIS if new element is >= last element in LIS\n\t\t\t\t\tsub.append(x)\n\t\t\t\telse:\n\t\t\t\t\tidx = bisect_right(sub, x) # Find the index of the smallest number > x\n\t\t\t\t\tsub[idx] = x # Replace that number with x\n\t\t\treturn len(sub)\n\n\t\tdef kIncreasing(self, arr: List[int], k: int) -> int:\n\t\t\tn = len(arr)\n\t\t\tans = 0\n\t\t\tfor i in range(k):\n\t\t\t\tnewArr = []\n\t\t\t\tfor j in range(i, n, k):\n\t\t\t\t\tnewArr.append(arr[j])\n\t\t\t\tans += len(newArr) - self.longestNonDecreasingSubsequence(newArr)\n\t\t\treturn ans
| 0
| 0
|
[]
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
C++ || Simple LIS solution
|
c-simple-lis-solution-by-omik_07-diem
|
\nint kIncreasing(vector<int>& arr, int k) {\n \n int mx=0; \n for(int i=0;i<k;i++)\n {\n vector<int>v;\n fo
|
Omik_07
|
NORMAL
|
2022-09-27T13:42:42.778883+00:00
|
2022-09-27T13:42:42.778922+00:00
| 18
| false
|
```\nint kIncreasing(vector<int>& arr, int k) {\n \n int mx=0; \n for(int i=0;i<k;i++)\n {\n vector<int>v;\n for(int j=i;j<arr.size();j+=k)\n {\n if(v.empty() || v.back()<=arr[j])\n {\n v.push_back(arr[j]);\n }\n else \n {\n int ind= upper_bound(v.begin(),v.end(),arr[j])-v.begin();\n v[ind]=arr[j];\n }\n }\n mx+=v.size();\n }\n return arr.size()-mx;\n }\n```
| 0
| 0
|
['C']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
Short and easy LIS solution in Python with explanation
|
short-and-easy-lis-solution-in-python-wi-10dl
|
The solution is to compute the longest non-decreasing subsequence for the k sequences. \nThe sequence can be very long, thus the effient O(n log n) solution to
|
metaphysicalist
|
NORMAL
|
2022-09-25T07:20:08.017761+00:00
|
2022-09-25T07:20:08.017804+00:00
| 83
| false
|
The solution is to compute the longest non-decreasing subsequence for the k sequences. \nThe sequence can be very long, thus the effient O(n log n) solution to longest non-decreasing subsequence is required. \n\n```\nclass Solution:\n def lis(self, start):\n results = []\n total = 0\n for i in range(start, len(self.arr), self.k):\n total += 1\n if not results or results[-1] <= self.arr[i]:\n results.append(self.arr[i])\n else:\n results[bisect_right(results, self.arr[i])] = self.arr[i]\n return total - len(results)\n \n def kIncreasing(self, arr: List[int], k: int) -> int:\n self.arr, self.k = arr, k\n return sum(self.lis(i) for i in range(k))\n
| 0
| 0
|
['Binary Search', 'Python3']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
Python3: Almost correct; But, how do I "debug"?
|
python3-almost-correct-but-how-do-i-debu-8tfb
|
\nclass Solution:\n def kIncreasing(self, arr: List[int], k: int) -> int:\n count = 0\n for i in range(k, len(arr)):\n if arr[i - k]
|
prasadnr606
|
NORMAL
|
2022-09-04T06:24:12.159655+00:00
|
2022-09-04T06:24:12.159694+00:00
| 30
| false
|
```\nclass Solution:\n def kIncreasing(self, arr: List[int], k: int) -> int:\n count = 0\n for i in range(k, len(arr)):\n if arr[i - k] > arr[i]:\n arr[i] = arr[i - k] + 1\n count += 1\n \n return count\n```
| 0
| 0
|
[]
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
LIS Python
|
lis-python-by-2019csb1077-3w12
|
\nfrom bisect import bisect_right as bl\nclass Solution:\n def lengthOfLIS(self, nums: List[int]) -> int:\n l = []\n for i in nums:\n
|
2019csb1077
|
NORMAL
|
2022-09-01T05:13:38.668892+00:00
|
2022-09-01T05:13:38.668931+00:00
| 38
| false
|
```\nfrom bisect import bisect_right as bl\nclass Solution:\n def lengthOfLIS(self, nums: List[int]) -> int:\n l = []\n for i in nums:\n if not l:\n l.append(i)\n continue\n idx = bl(l,i)\n if idx==len(l):\n l.append(i)\n else:\n l[idx] = i \n return len(l)\n def kIncreasing(self, arr: List[int], k: int) -> int:\n ans = 0\n for i in range(k):\n j = i \n temp = []\n while j<len(arr):\n temp.append(arr[j])\n j+=k \n ans += len(temp) - (self.lengthOfLIS(temp))\n return ans\n```
| 0
| 0
|
[]
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
[C++] Longest Non-Decreasing Subsequence technique. O(k*n*log(n))
|
c-longest-non-decreasing-subsequence-tec-lf7b
|
This approach uses the upper bound function in C++.\n\nUpper Bound return an iterator to the next smallest greater number than a key in a sorted array.\nEg: if
|
vipulbhardwaj1011
|
NORMAL
|
2022-08-14T07:07:59.255959+00:00
|
2022-08-14T07:07:59.256001+00:00
| 103
| false
|
This approach uses the **upper bound** function in C++.\n\nUpper Bound return an iterator to the **next smallest greater number** than a **key** in a **sorted array**.\n*Eg: if sorted arr = [1, 2, 3, 4, 5], and key = 4, then **upper_bound(arr.begin, arr.end(), key)** would return an iterator to the **first occurance of element "5"***.\n\n1. So, we create **k subsequences of the original array**, and \n2. Find the ***Length of Longest Non-Decreasing Subsequence*** of each of those k subsequences using **Upper Bound**, and therefore, \n3. The difference between len(**kth original** subsequence) and len(**kth longest** subsequence), gives us the number of operations required for that **kth** subsequence.\n\n***CODE*** :-\n```\nint kIncreasing(vector<int>& arr, int k) {\n int ops = 0;\n for(int i=0; i<k; i++) {\n vector<int> v;\n for(int j = i; j < arr.size(); j += k)\n v.push_back(arr[j]);\n ops += v.size() - lengthOfLNDS(v);\n }\n return ops;\n }\n \n int lengthOfLNDS(vector<int> nums) {\n vector<int> v = {nums[0]};\n int index;\n \n for(int i=1; i < nums.size(); i++) {\n index = upper_bound(v.begin(), v.end(), nums[i]) - v.begin();\n if(index == v.size())\n v.push_back(nums[i]);\n else\n v[index] = nums[i];\n }\n return v.size();\n }\n```\n\nThnak you :). Please upvote.
| 0
| 0
|
['C', 'Binary Tree']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
c++ lis
|
c-lis-by-me_abhi_2511-b5x0
|
class Solution {\npublic:\n\n int lis(vectornums)\n {\n int n=nums.size();\n vectordp(n+1,INT_MAX);\n dp[0]=INT_MIN;\n for(int
|
me_abhi_2511
|
NORMAL
|
2022-08-11T18:53:04.370643+00:00
|
2022-08-11T18:53:04.370677+00:00
| 58
| false
|
class Solution {\npublic:\n\n int lis(vector<int>nums)\n {\n int n=nums.size();\n vector<int>dp(n+1,INT_MAX);\n dp[0]=INT_MIN;\n for(int i=0;i<n;i++)\n {\n int idx=upper_bound(dp.begin(),dp.end(),nums[i])-dp.begin();\n if(dp[idx]>nums[i]&&dp[idx-1]<=nums[i])\n {\n dp[idx]=nums[i];\n }\n }\n int res=0;\n for(int i=n;i>=0;i--)\n {\n if(dp[i]!=INT_MAX)\n {\n res=i;\n break;\n }\n }\n return res;\n }\n int kIncreasing(vector<int>& arr, int k) {\n int ans=0;\n for(int i=0;i<k;i++)\n {\n vector<int>nums;\n for(int j=i;j<arr.size();j+=k)\n {\n nums.push_back(arr[j]);\n }\n ans+=nums.size()-lis(nums);\n \n \n }\n return ans;\n }\n \n};
| 0
| 0
|
['C']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
C++ 243ms beats 99% run LIS k times
|
c-243ms-beats-99-run-lis-k-times-by-ccch-ht40
|
Separate arr into k subsequences. \nNumber of operations on each subsequence would be total elements count minus LIS length. \nFor example, 1 subsequence might
|
ccchan0109
|
NORMAL
|
2022-08-08T10:24:36.675710+00:00
|
2022-08-08T10:26:15.212730+00:00
| 59
| false
|
Separate arr into k subsequences. \nNumber of operations on each subsequence would be total elements count minus LIS length. \nFor example, 1 subsequence might be [1,4,3] generated from arr=[1,2,4,5,3] when k=2. Then, total elements count is 3 and LIS length would be 2, ie. [1,3]. Thus the operations count would be 3-2=1 for this subsequence.\nObviously, total operations is the sum of number of operations on every subsequences.\n\nSo, here we go. \n\n```\nclass Solution {\npublic:\n int kIncreasing(vector<int>& arr, int k) {\n int N = arr.size();\n int ans = 0;\n vector<int> dp;\n\n for (int i = 0; i < k; ++i) {\n // run LIS for every i between [0, k-1], storing LIS result in dp\n dp.clear();\n int j = i;\n while (j < N) {\n auto it = upper_bound(dp.begin(), dp.end(), arr[j]);\n if (it == dp.end()) {\n dp.push_back(arr[j]);\n } else {\n *it = arr[j];\n }\n\n j += k;\n }\n ans += (j-i)/k - dp.size();\n }\n\n return ans;\n }\n};\n```\n\nTime Complexcity = k * time complexity of LIS for n/k elements = O(k * (n/k)*log(n/k)) = O(n*log(n/k))\n\nIf there exists any error in my post, please point it out. I appreciate it. Thanks.
| 0
| 0
|
['C']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
Python from scratch
|
python-from-scratch-by-mrpython-tzet
|
Python without any library: Complete implementation of bisect right\nTime Complexity - k * nlogn\nSpace - O(k)\n\n\nclass Solution:\n def kIncreasing(self, a
|
mrPython
|
NORMAL
|
2022-08-08T05:13:01.775337+00:00
|
2022-08-08T05:13:01.775369+00:00
| 147
| false
|
Python without any library: Complete implementation of bisect right\nTime Complexity - k * nlogn\nSpace - O(k)\n\n```\nclass Solution:\n def kIncreasing(self, arr: List[int], k: int) -> int:\n \n def LIS(nums):\n res = []\n for i in nums:\n low,high = 0, len(res)\n while low < high:\n mid = (low+high)//2\n \n if res[mid] <= i:\n low = mid + 1\n \n else:\n \n high = mid\n\n\n if low == len(res):\n res.append(i)\n else:\n\n res[low] = i\n \n \n\n\n return len(res)\n \n ans = 0\n \n \n for i in range(k):\n bucket = []\n startingIdx = i\n while startingIdx < len(arr):\n bucket.append(arr[startingIdx])\n startingIdx += k\n \n \n \n \n ans += len(bucket) - LIS(bucket)\n \n \n return ans\n ```
| 0
| 0
|
['Binary Tree', 'Python', 'Python3']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
C++ LIS variant
|
c-lis-variant-by-fzh-bt4m
|
\n\n\n\n// Ideas / Approach: an variant of LISS ie the Longest Increasing SubSeq ~~\n// because this problem is about increasing sequence. BTW, if it\'s about d
|
fzh
|
NORMAL
|
2022-07-24T20:04:08.132949+00:00
|
2022-07-24T20:04:08.132982+00:00
| 76
| false
|
\n\n\n```\n// Ideas / Approach: an variant of LISS ie the Longest Increasing SubSeq ~~\n// because this problem is about increasing sequence. BTW, if it\'s about decreasing sequence, the\n// LISS can apply as well.\n// * If k == 1, then the answer is A.size() - LIS(A), where A is the input array.\n// * If k > 1, then the array a has k independent subsequences, and each of the subsequences can be\n// handled as if it\'s a separate array for k==1.\n// * Time Complexity: O(n log n)\nclass Solution {\npublic:\n int kIncreasing(vector<int>& A, int k) {\n int ops = 0;\n vector<int> mono; // mono stack/vec for LISS\n for (int j = 0; j < k; ++j) { // j is the offset for the sub-series\n int subLen = 0;\n for (int i = j; i < A.size(); i += k) {\n ++subLen;\n const auto e = A[i];\n if (mono.empty() || mono.back() <= e) {\n mono.push_back(e); // grow the mono stack/vector for LISS.\n } else { // here the mono.back() must > e, so iter is always valid.\n auto iter = upper_bound(mono.begin(), mono.end(), e);\n // improve the health/potential of the element, so that the LISS mono vec is\n // better poised for future growth.\n *iter = e;\n }\n }\n ops += (subLen - mono.size()); // need these # of ops to fix this sub-series.\n mono.clear();\n }\n\n return ops;\n }\n};\n```\n
| 0
| 0
|
['C']
| 0
|
minimum-operations-to-make-the-array-k-increasing
|
C++ || LIS
|
c-lis-by-rahulmahotra-thrt
|
\nint lis(vector<int>& v){\n \n vector<int> seq;\n \n for(int i=0; i<v.size(); i++){\n \n if(seq.empty() or se
|
rahulMahotra
|
NORMAL
|
2022-07-17T13:18:08.622146+00:00
|
2022-07-17T13:18:08.622235+00:00
| 86
| false
|
```\nint lis(vector<int>& v){\n \n vector<int> seq;\n \n for(int i=0; i<v.size(); i++){\n \n if(seq.empty() or seq.back() <= v[i]) seq.push_back(v[i]); \n else{\n int idx = upper_bound(seq.begin(), seq.end(), v[i]) \n - seq.begin();\n seq[idx] = v[i];\n }\n }\n return seq.size();\n }\n \n int kIncreasing(vector<int>& arr, int k) {\n \n int n = arr.size();\n int ans=0;\n \n for(int i=0; i<k; i++){\n \n vector<int> v;\n \n for(int j=i; j<n; j+=k){\n v.push_back(arr[j]);\n }\n \n ans += v.size() - lis(v);\n }\n \n return ans;\n }\n```
| 0
| 0
|
[]
| 1
|
minimum-operations-to-make-the-array-k-increasing
|
binary search easy
|
binary-search-easy-by-abhi_009-bgri
|
\nclass Solution:\n \n def LIS(self, arr):\n n = len(arr)\n dp = [\'None\']*n\n dp[0] = arr[0]\n j= 0 \n for i in range
|
Abhi_009
|
NORMAL
|
2022-07-14T09:21:41.962259+00:00
|
2022-07-14T09:21:41.962304+00:00
| 128
| false
|
```\nclass Solution:\n \n def LIS(self, arr):\n n = len(arr)\n dp = [\'None\']*n\n dp[0] = arr[0]\n j= 0 \n for i in range(1,n):\n if arr[i]>=dp[j]:\n dp[j+1] = arr[i]\n j+=1\n else:\n idx = bisect.bisect(dp,arr[i],0,j) # log(n)\n dp[idx] = arr[i]\n count = 0\n for i in dp:\n if i==\'None\':\n break\n count+=1\n return count\n\n \n def kIncreasing(self, arr: List[int], k: int) -> int:\n ans = 0\n n = len(arr)\n for i in range(k):\n nums = []\n for j in range(i,n,k):\n nums.append(arr[j])\n ans+=(len(nums)-self.LIS(nums))\n \n return ans\n \n \n \n```
| 0
| 0
|
['Python', 'Python3']
| 0
|
Subsets and Splits
No community queries yet
The top public SQL queries from the community will appear here once available.